Дифференциальное и интегральное исчисления. В 2 томах. Том 2 - Пискунов Н.С

Автор: Пискунов Н.С
Теги: анализ дифференциальное исчисление высшая математика интегральное исчисление
Год: 1985
Похожие
Дифференциальное и интегральное исчисления. В 2 томах. Том 1
Курс дифференциального и интегрально-интегрального исчисления. В 3 томах. Том II
Курс дифференциального и интегрального исчисления. Том 2
Дифференциальное и интегральное исчисления. Том 1
Текст
                    Н. С. ПИСКУНОВ
ДИФФЕРЕНЦИАЛЬНОЕ
И ИНТЕГРАЛЬНОЕ
ИСЧИСЛЕНИЯ
ДЛЯ ВТУЗОВ
том второй
ИЗДАНИЕ ТРИНАДЦАТОЕ
Допущено Министерством
высшего и среднего специального образования СССР
е качестве учебного пособия
?ля алсших технических учебных заведений
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1985

22.161.1
П34
УДК 517
Пискунов Н. С. Дифференциальное и
интегральное исчисления для втузов, т. 2?
Учебное пособие для втузов.—13-е изд.— М.:
Наука, Главная редакция физико-математиче-
скёй литературы, 1985.—560 с.
Хорошо известное учебное пособие по мате-
математике для втузов с достаточно широкой мате-
математической подготовкой.
Второй том включает разделы: дифферен-
дифференциальные уравнения, кратные и криволинейные
интегралы, интегралы по поверхности, ряды,
уравнения математической физики, операцион-
операционное исчисление, элементы теории вероятностей
и математической статистики, .матрицы.
Для студентов высших технических учебных
заведений.
Николщй Семенович Пискунов
ДИФФЕРЕНЦИАЛЬНОЕ И ИВДЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
для втузов
том 2
Редактор В. В. Донченко
Техн. редактор И. Ш. Аксельрод Корректор Л. С. Сомова
ИБ № 12688
Сдано в набор 06.08.84 Подписано в печать 31 01 85. Формат 60x90Vie- Бумага тип.
№ 2. Гарнитура литературная. Высокая печать. Усл. печ. л. 35 Уел кр.-отт. 35,2 5.
Уч.-изд. л. 33,67. Тираж 2 50 000 экз. A-й завод 1—-150 000 экз ) Заказ №3531.
Цена 1 р. 30 к
Ордена Трудового Красного Знамени издательство «Наука»
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
МПО «Первая Образцовая типография» Союзполиграфпрома при Государственном коми-
комитете СССР по делам издательств, полиграфии и книжной торговли. 113054, Москва, Ва-
Валовая, 28
п 1702050000-042
П 053@2)^85

ОГЛАВЛЕНИЕ
Предисловие к девятому изданию ¦ .».,»¦#•»• 9
Предисловие к пятому изданию , , .*•*.»*•• 11
ГЛАВА XIII
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§ 1. Постановка задачи. Уравнение движения тела при сопротивлении
среды, пропорциональном скорости. Уравнение цепной линии ... 13
§ 2. Определения 16
§ 3. Дифференциальные уравнения первого порядка (общие понятия) 17
§ 4. Уравнения с разделенными и разделяющимися переменными.
Задача о распаде радия ,,..*.., 22
§ 5. Однородные уравнения первого порядка t * 25
§ 6. Уравнения, приводящиеся к однородным * 27
§ 7. Линейные уравнения первого порядка • 30
§ 8. Уравнение Бернулли * 33
§ 9. Уравнение в полных дифференциалах « 35
§ 10. Интегрирующий множитель * 38
§ 11. Огибающая семейства кривых • 39
§ 12. Особые решения дифференциального уравнения первого порядка. • 45
§ 13. Уравнение Клеро «»*»*******.* 47
§ 14. Уравнение Лагранжа « 49
§ 15. Ортогональные и изогональные траектории 50
§ 16. Дифференциальные уравнения высших порядков (общие понятия) 55
§ 17. Уравнение вида yW = f(x) 56
§ 18. Некоторые типы дифференциальных уравнений второго порядка,
приводимых к уравнениям первого порядка. Задача о второй кос-
космической скорости 59
§ 19. Графический метод интегрирования дифференциального уравнения
второго порядка 66
§ 20. Линейные однородные уравнения. Определения и общие свойства 68
§ 21. Линейные однородные уравнения второго порядка с постоянными
коэффициентами 74
§ 22. Линейные однородные уравнения n-го порядка с постоянными
коэффициентами 79
§ 23. Неоднородные линейные уравнения второго порядка 81
§ 24. Неоднородные линейные уравнения второго порядка с постоянными
коэффициентами 84
§ 25. Неоднородные линейные уравнения высших порядков « 90
§ 26. Дифференциальное уравнение механических колебаний . . . . , 94
§ 27. Свободные колебания. Векторное и комплексное изображение гар-
гармонических колебаний ,..,.< , # ¦ 96
§ 28. Вынужденные колебания , . t . , , 99
§ 29. Системы обыкновенных дифференциальных уравнений «,..,, 103

4 ОГЛАВЛЕНИЕ
§ 30. Системы линейных дифференциальных уравнений с постоянными
коэффициентами р 108
§ 31. Понятие о теории устойчивости Ляпунова. Поведение траектории
дифФеРенДиального уравнения в окрестности особой точки .... 113
§ 32. Приближенное решение дифференциальных уравнений первого по-
порядка методом Эйлера 127
§ 33. Разностный метод приближенного решения дифференциальных
уравнений, основанный на применении формулы Тейлора. Метод
Адамса 130
§ 34. Приближенный метод интегрирования систем дифференциальных
уравнений первого порядка ,...».,.»... 136
Упражнения к главе XIII , , . в »••«•••••••• *4*
ГЛАВА XIV
КРАТНЫЕ ИНТЕГРАЛЫ
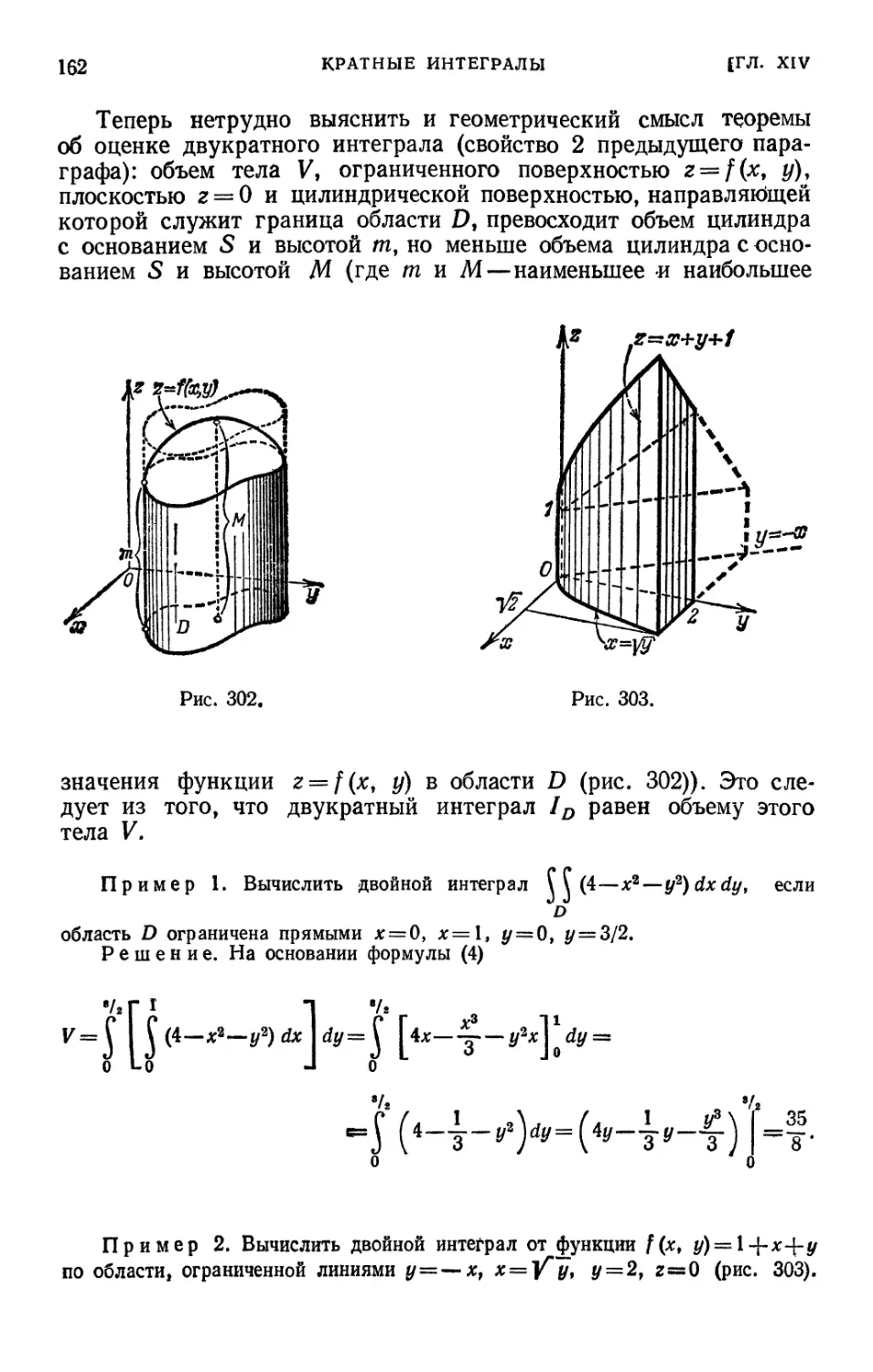
§ 1. Двойной интеграл •»#•».».» 152
§ 2. Вычисление двойного интеграла 151
§ 3. Вычисление двойного интеграла (продолжение) 160
§ 4. Вычисление площадей и объемов с помощью двойных интегралов 168
§ 5. Двойной интеграл в полярных координатах 168
§ 6. Замена переменных в двойном интеграле (общий случай) , . . . 174
§ 7. Вычисление площади поверхности 179
§ 8. Плотность распределения вещества и двойной интеграл ¦ . . . . 182
§ 9. Момент инерции площади плоской фигуры 184
§ 10. Координаты центра масс площади плоской фигуры 188
§ П. Тройной интеграл 190
§ 12. Вычисление тройного интеграла , . . . 191
§ 13. Замена переменных в тройном интеграле , 196
§ 14. Момент ^инерции и координаты центра масс тела 199
§ 15. Вычисление интегралов, зависящих от параметра 201
Упражнения к главе XIV , *•»#.» 202
ГЛАВА XV
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ
§ 1. Криволинейный интеграл ..,».,... 208
§ 2. Вычисление криволинейного интеграла 211
§ 3. Формула Грина 217
§ 4. Условия независимости криволинейного интеграла от пути интег-
интегрирования 219
§ 5. Поверхностный интеграл ¦ 224
§ 6. Вычисление поверхностного интеграла 225
§ 7. Формула Стокса 229
§ 8 Формула Остроградского 233
§ 9. Оператор Гамильтона. Некоторые его применения 236
Упражнения к главе XV , 239
ГЛАВА XVI
ряды
§ 1. Ряд. Сумма ряда 245
§ 2. Необходимый признак сходимости ряда 248
§ 3. Сравнение рядов с положительными членами 250
§ 4. Признак Даламбера 252
§ 5. Признак Коши 256
§ 6. Интегральный признак сходимрсти ряда 257
§ 7. Знакочередующиеся ряды. Теорема Лейбница 260

ОГЛАВЛЕНИЕ 5
§ 8. Знакопеременные ряды. Абсолютная и условная сходимость . . , 263
§ 9. Функциональные ряды 266
§ 10. Мажорируемые ряды 267
§ 11. Непрерывность суммы ряда 269
§ 12. Интегрирование и дифференцирование рядов 272
§ 13. Степенные ряды. Интервал сходимости 275
§ 14. Дифференцирование степенных рядов 279
§ 15. Ряды по степеням х—а 280
§ 16. Ряды Тейлора и Маклорена 282
§ 17. Примеры разложения функций в ряды « 283
§ 18. Формула Эйлера 285
§ 19. Биномиальный ряд 286
§ 20. Разложение функции ln(l+*) в степенной ряд. Вычисление лога-
логарифмов . 288
§ 21. Вычисление определенных интегралов с помощью рядов 290
§ 22. Интегрирование дифференциальных уравнений с помощью рядов 292
§ 23. Уравнение Бесселя 295
§ 24. Ряды с комплексными членами 299
§ 25. Степенные ряды с комплексной переменной 300
§ 26. Решение дифференциального уравнения первого порядка методом
последовательных приближений (метод итераций) 302
§ 27. Доказательство существования решения дифференциального урав-
уравнения. Оценка погрешности при приближенном решении .... 304
§ 28. Теорема единственности решения дифференциального уравнения 308
Упражнения к главе XVI ' 310
ГЛАВА XVII
РЯДЫ ФУРЬЕ
§ 1. Определение. Постановка задачи 318
§ 2. Примеры разложения функций в ряды Фурье 322
§ 3. Одно замечание о разложении периодической функции в ряд
Фурье 327
§ 4. Ряды Фурье для четных и нечетных функций 329
§ 5. Ряд Фурье для функции с периодом 2/ 331
§ 6. О разложении непериодической функции в ряд Фурье 332
§ 7. Приближение в среднем заданной функции с помощью тригоно-
тригонометрического многочлена 334
§ 8. Интеграл Дирихле 339
§ 9. Сходимость ряда Фурье в данной точке 341
§ 10. Некоторые достаточные условия сходимости ряда Фурье .... 343
§ 11. Практический гармонический анализ 345
§ 12. Ряд Фурье в комплексной форме 346
§ 13. Интеграл Фурье 349
§ 14. Интеграл Фурье в комплексной форме 352
§ 15. Ряд Фурье по ортогональной системе функций 355
§ 16. Понятие о линейном функциональном пространстве. Аналогия
между разложением функций в ряд Фурье и разложением век-
векторов 357
Упражнения к главе XVII 362
ГЛАВА XVIII
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
§ 1. Основные типы уравнений математической физики 364
§ 2. Вывод уравнения колебаний струны. Формулировка краевой за-
задачи. Вывод уравнений электрических колебаний в проводах . . 365
§ 3. Решение уравнения колебаний струны методом разделения пере-
переменных (методом Фурье) # . . , , 368

6 ОГЛАВЛЕНИЕ
§ 4. Уравнение распространения тепла в стержне. Формулировка крае-
краевой задачи 372
§ 5. Распространение тепла в пространстве 374
§ 6. Решение первой краевой задачи для уравнения теплопроводности
методом конечных разностей 377
§ 7. Распространение тепла в неограниченном стержне 379
§ 8. Задачи, приводящие к исследованию решений уравнений Лапласа.
Формулировка краевых задач 384
§ 9. Уравнение Лапласа в цилиндрических координатах. Решение за-
задачи Дирихле для кольца с постоянными значениями искомой
функции на внутренней и внешней окружностях 389
§ 10. Решение задачи Дирихле для круга 390
§ 11. Решение задачи Дирихле методом конечных разностей 394
Упражнения к главе XVIII ,,,,.,..,,.,.., 396
ГЛАВА XIX
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ И НЕКОТОРЫЕ ЕГО ПРИЛОЖЕНИЯ
§ 1. Начальная функция и ее изображение 400
§ 2. Изображение функций oQ (t), sin ty cos t 402
§ 3. Изображение функции с измененным масштабом независимой пе-
переменной. Изображение функций sin at, cos at 403
§ 4. Свойство линейности изображения 405
§ 5. Теорема смещения 405
§ 6. Изображение функций е~а^ shat, cha/, е-*** sin at, е~а* cos at 405
§ 7. Дифференцирование изображения 407
§ 8. Изображение производных 409
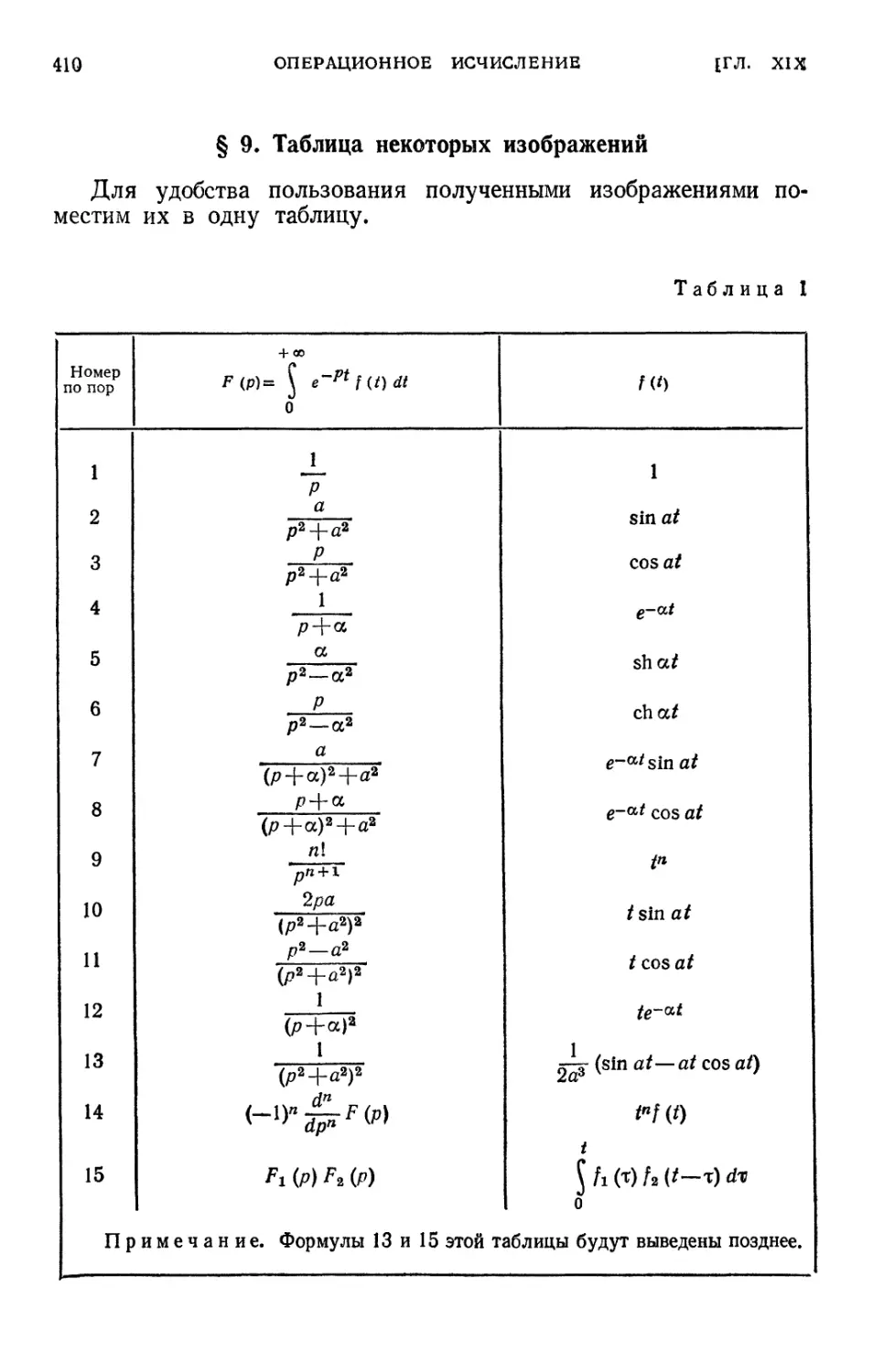
§ 9. Таблица некоторых изображений 410
§ 10. Вспомогательное уравнение для данного дифференциального урав-
уравнения 411
§ 11. Теорема разложения 415
§ 12. Примеры решения дифференциальных уравнений и систем диффе-
дифференциальных уравнений операционным методом 417
§ 13. Теорема свертывания 418
§ 14. Дифференциальные уравнения механических колебаний. Дифферен-
Дифференциальные уравнения теории электрических цепей 420
§ 15. Решение дифференциального уравнения колебаний * . . 421
§ 16. Исследование свободных колебаний 423
§ 17. Исследование механических и электрических колебаний в случае
периодической внешней силы 424
§ 18. Решение уравнения колебаний в случае резонанса 426
§ 19. Теорема запаздывания 427
§ 20. Дельта-функция и ее изображение , . . . . 428
Упражнения к главе XIX 9 431
ГЛАВА XX
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
§ 1. Случайное событие. Относительная частота случайного события.
Вероятность события. Предмет теории вероятностей 434
§ 2. Классическое определение вероятности и непосредственный подсчет
вероятностей 436
§ 3. Сложение вероятностей. Противоположные случайные события . . 438^
§ 4. Умножение вероятностей независимых событий 441
§ 5. Зависимые события. Условная вероятность. Полная вероятность 443
§ 6. Вероятность гипотез. Формула Байеса 446
§ 7. Дискретная случайная величина. Закон распределения дискретной
случайной величины ,,,,,.., 449

ОГЛАВЛЕНИЕ 7
§ 8. Относительная частота и вероятность относительной частоты при
повторных испытаниях 451
§ 9. Математическое ожидание дискретной случайной величины . . . 455
§ 10. Дисперсия. Среднеквадратичное отклонение. Понятие о моментах 460
§ 11. Функции от случайных величин 463
§ 12. Непрерывная случайная величина. Плотность распределения не-
непрерывной случайной величины. Вероятность попадания случайной
величины в заданный интервал 464
§ 13. Функция распределения, или интегральный закон распределения.
Закон равномерного распределения вероятностей 468
§ 14. Числовые характеристики непрерывной случайной величины . . . 471
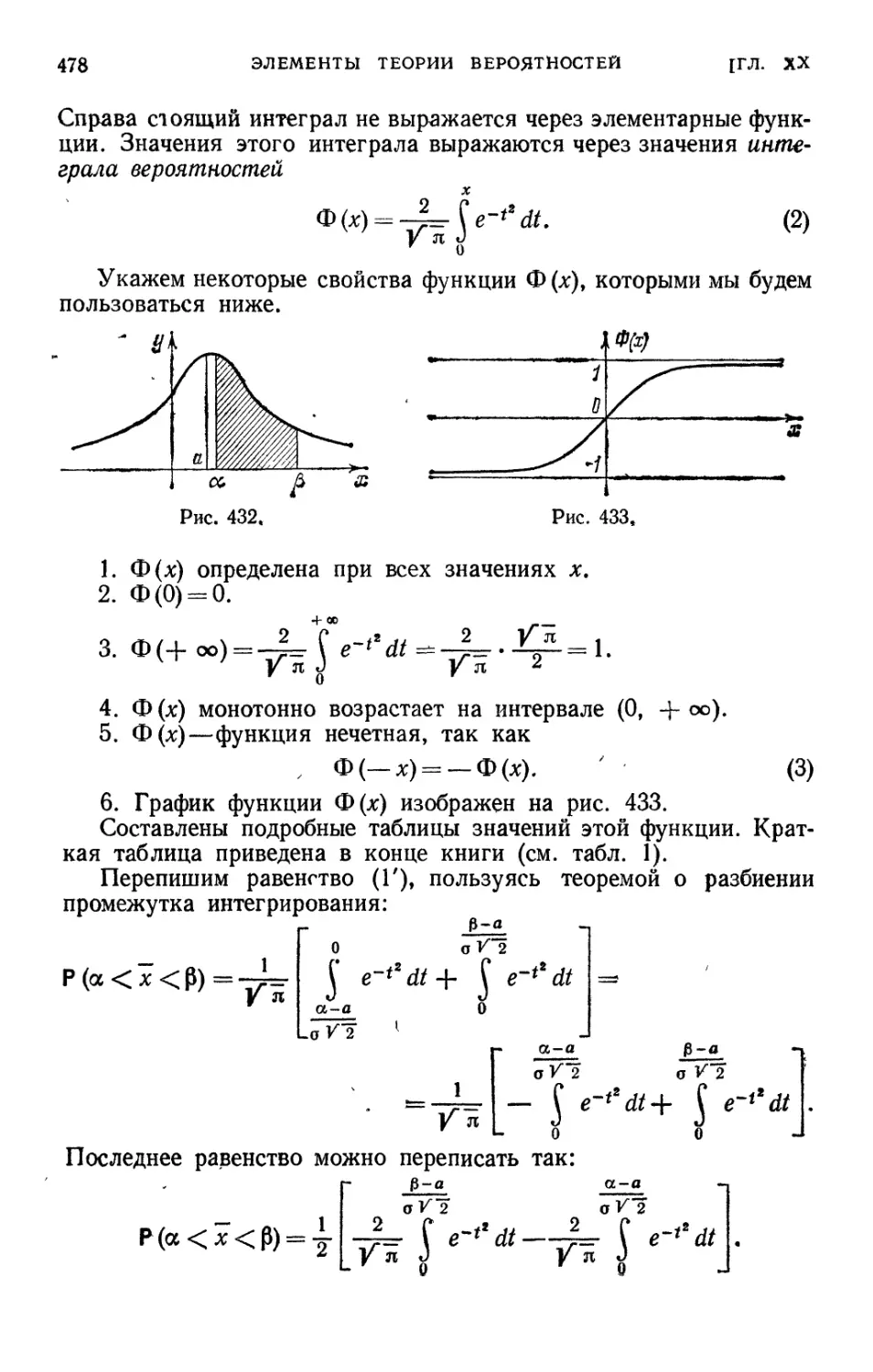
§ 15. Нормальный закон распределения. Математическое ожидание нор-
нормального распределения 474
§ 16. Дисперсия и среднеквадратичное отклонение случайной величины,
подчиненной нормальному закону распределения 476
§ 17. Вероятность попадания значения случайной величины в заданный
интервал. Функция Лапласа. Интегральная функция распреде-
распределения для нормального закона , 477
§ 18. Вероятное (срединное) отклонение или срединная ошибка .... 481
§ 19. Выражение нормального закона распределения через срединное
отклонение. Приведенная функция Лапласа 483
§ 20. Правило трех сигм. Шкала вероятностей распределения ошибок 484
§ 21. Среднеарифметическая ошибка 486
§ 22. Мера точности. Соотношение между характеристиками распреде-
распределения ошибок 486
§ 23. Двумерная случайная величина 487
§ 24. Нормальный закон распределения на плоскости 491
§ 25. Вероятность попадания двумерной случайной величины в прямо-
прямоугольник со сторонами, параллельными главным осям рассеива-
рассеивания, при нормальном законе распределения 492
§ 26. Вероятность попадания двумерной случайной величины в зллипс
рассеивания 494
§ 27. Задачи математической статистики. Статистический материал . . 495
§ 28. Статистический ряд. Гистограмма 496
§ 29. Определение подходящего значения измеряемой величины .... 499
§ 30. Определение параметров закона распределения. Теорема Ляпу-
Ляпунова. Теорема Лапласа 500
Упражнения к главе XX 504
ГЛАВА XXI
МАТРИЦЫ. МАТРИЧНАЯ ЗАПИСЬ СИСТЕМ И РЕШЕНИЙ СИСТЕМ
ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 1. Линейные преобразования. Матрица 508
§ 2. Общие определения, связанные с понятием матрицы 511
§ 3. Обратное преобразование 513
§ 4. Действия над матрицами. Сложение матриц 515
§ 5. Преобразование вектора в другой вектор с помощью матрицы . . 518
§ 6. Обратная матрица 519
§ 7. Нахождение матрицы, обратной данной 520
§ 8. Матричная запись системы линейных уравнений 522
§ 9. Решение системы линейных уравнений матричным методом . . . 523
§ 10. Ортогональные отображения. Ортогональные матрицы 525
§ 11. Собственный вектор линейного преобразования 528
§ 12. Матрица линейного преобразования, при котором базиСхиые век-
векторы являются собственными векторами 531
§ 13. Преобразование матрицы линейного преобразования при переходе
от одного базиса к другому 532

8 ОГЛАВЛЕНИЕ
§ 14. Квадратичные формы и их преобразования 534
§ 15. Рангоматрицы. Существование решений системы' Линейных 'урав-
'уравнении Jr 536
§ 16. Дифференцирование и интегрирование матриц 537
§ 17. Матричная запись системы дифференциальных уравнений и. реше-
решений системы дифференциальных уравнений с постоянными коэф-
коэффициентами в 539
§ 18. Матричная запись линейного уравнения п-го порядка 543
§ 19. Решение систем линейных дифференциальных уравнений' с пере-
переменными коэффициентами методом последовательных' приближений
с использованием аматричной записи 544
Упражнения к главе XXI . . . 548
Приложения 550
Предметный указатель 553

ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ
Девятое издание данного учебника отличается от его восьмого
издания. Это издание полностью соответствует программе по ма-
математике для втузов, рассчитанной на 400 — 450 часов.
В учебник включены две новые главы XX и XXI.
Глава XX «Элементы теории вероятностей и математической
статистики» содержит материал, предусмотренный соответствующим
разделом обязательной программы по математике МВССО СССР.
Глава XXI «Матрицы. Матричная запись систем и решений
систем линейных дифференциальных уравнений» также содержит
материал, предусмотренный обязательной программой. Но, кроме
того, в этой главе обращено большое внимание на матричную
запись систем линейных дифференциальных уравнений и решений
систем линейных дифференциальных уравнений.
Использована матричная запись последовательных приближен-
приближенных решений системы линейных дифференциальных уравнений
с переменными коэффициентами. Этот материал необходимо поме-
поместить в курсе дифференциального и интегрального исчисления
для втузов потому, что в настоящее время во многих книгах по
электротехнике, радиотехнике, автоматике исследование решений
систем дифференциальных уравнений производится с использова-
использованием аппарата теории матриц.
Написаны новые §§ 26, 27, 28 гл. XVI. Здесь рассмотрен метод
последовательных приближений решения дифференциальных урав-
уравнений, доказывается теорема о существовании решения дифферен-
дифференциального уравнения и теорема единственности. Обращено вни-
внимание на строгость изложения всей главы о дифференциальных
уравнениях.
Параграф 31 гл. XIII «Понятие о теории устойчивости Ляпу-
Ляпунова» значительно расширен. В этом издании он называется так:
«Понятие о теории устойчивости Ляпунова. Поведение траекторий
дифференциального уравнения в окрестности особой точки». Здесь
параллельно с рассмотрением устойчивости решений, систем диф-
дифференциальных уравнений рассмотрено поведение траекторий
вблизи особой точки на фазовой плоскости. Это необходимо было
сделать потому, что при изучении соответствующих вопросов
в курсах электротехники, радиотехники, автоматики этими поня-
понятиями необходимо свободно пользоваться. Заново написаны неко-

10 ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ
торые параграфы с изложением теории комплексных чисел. Суще-
Существенно расширен § 2 гл. XI, где дано доказательство существо-
существования определенного интеграла от непрерывной функции. Написан
дополнительный § 11 гл. XI «Интегрирование комплексной функ-
функции действительной переменной». Написаны новые §§ 24 и 25
гл. XVI, посвященные рядам с комплексными членами и степен-
степенным рядам с комплексной переменной. Написан новый § 12 гл. XVII,
посвященный рядам Фурье в комплексной форме. Расширено из-
изложение вопроса об интеграле Фурье. Освещены понятия, исполь-
используемые в специальной прикладной литературе (спектр, спектраль-
спектральная функция). Написаны новые § 15 «Ряд Фурье по ортогональной
системе функций» и § 16 «Понятие о линейном функциональном
пространстве. Аналогия между разложением функций в ряд Фурье
и разложением векторов» в гл. XVIL Этот материал изложен
таким образом, чтобы студенты и инженеры могли понимать ма-
материал других дисциплин, опирающийся на этот математический
аппарат.
В главе XIX написан новый § 20 «Дельта-функция и ее
изображение».
В главе VIII помещен § 19 «Получение функции на основа-
кии экспериментальных данных по методу наименьших квадратов».
Содержанием этого параграфа ранее являлось Приложение I, по-
помещавшееся в конце первого тома этого учебника.
В главе VII даны § 10 «Интерполяционная формула Ньютона»
и § 11 «Численное дифференцирование». Содержанием этих пара-
параграфов ранее являлось Приложение II.
Произведены некоторые дополнения в главах V, VII, IX,
XII, XIII.
Глава XIII «Дифференциальные уравнения» целиком перене-
перенесена во второй том.
Автор
Настоящее A3-е) издание не отличается от предыдущего
A978 г.).

ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
В пятом издании полностью сохранен без изменений весь текст
четвертого издания, но этот материал разделен на два тома (для
удобства использования настоящего и предыдущих изданий учеб-
учебника нумерация глав тоже оставлена без изменения).
Содержание всего учебника определяется программами курса
математики для втузов, рассчитанными на 300 — 450 часов. Учеб-
Учебник предназначается для изучения курса математики как в ста-
стационарных, так и в заочных втузах. Это учитывалось при изло-
изложении материала; в частности, с этой целью в учебнике разобрано
много примеров, иллюстрирующих изложенный теоретический
материал и дающих образцы решения задач.
Первый том содержит материал, соответствующий программе
1-го курса втуза, за исключением главы XIII «Дифференциаль-
«Дифференциальные уравнения», которая, как правило, проходится на 2-м курсе.
Но так как в некоторых втузах предварительные сведения о диф-
дифференциальных уравнениях, необходимые для последующих дис-
дисциплин, даются на 1-м курсе, то часть этой главы (§§ 1 —28) и
помещена в первом томе.
Отметим, что материал, содержащийся в программе втузов,
рассчитанный на число часов порядка 300, почти полностью со-
содержится в первом томе (но в нем содержится и материал, выхо-
выходящий за рамки этой программы).
Второй том —конец главы XIII (§§ 29 — 34), главы XIV —
XIX —содержит материал, соответствующий программе 2-го курса
втуза.
Первые две главы первого тома —«Число. Переменная. Функ-
Функция» и «Предел. Непрерывность функций» написаны в пределах
возможного кратко. Некоторые вопросы, обычно излагаемые в этих
главах, без ущерба для дела перенесены в третью и последую-
последующие главы. Это дало возможность раньше перейти к основному
понятию дифференциального исчисления —производной, чего тре-
требуют другие дисциплины втузовского курса (целесообразность
такого расположения материала подтверждается опытом работы).
В связи с включением во втузовскую программу по высшей
математике вопросов, необходимых для обеспечения курсом мате-
математики втузовских дисциплин, связанных с автоматикой и вычис-

12 ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
лительной техникой, в учебнике подробно изложены соответст-
соответствующие разделы:
«Численное интегрирование дифференциальных уравнений и
систем дифференциальных уравнений»*), «Интегрирование систем
линейных дифференциальных уравнений», «Понятие о теории устой-
устойчивости Ляпунова», «Оператор Гамильтона», «Интеграл Фурье»
и т. д.
В главе XVIII рассмотрены основные уравнения математиче-
математической физики.
Обращено большое внимание на выяснение характера физи-
физических явлений, приводящих к уравнениям различных типов и
соответствуьощим краевым задачам. Большое внимание уделено
численным методам решения дифференциальных уравнений в част-
частных производных.
В главе XIX излагаются основные понятия операционного
исчисления и операционный метод решения дифференциальных
уравнений. Это требуется для многих последующих дисциплин,
и особенно электротехнических.
В учебник включено большое количество задач и примеров
для упражнений, многие из которых иллюстрируют связь мате-
математики с другими дисциплинами.
Задачи и примеры специально подобраны по каждому разделу
курса, что способствует усвоению излагаемого материала. Это
обстоятельство также делает книгу удобной для самостоятельного
изучения курса математики, в частности для студентов-заочников.
Автор
Шестое издание отличается от пятого только тем, что в конце
1-го тома дано приложение, где изложен важный для инженеров
вопрос «Получение функции на основании экспериментальных
данных по методу наименьших квадратов».
Седьмое издание отличается от шестого только тем, что в
конце 1-го тома дано приложение «Интерполяционная формула
Ньютона. Численное дифференцирование».
*) Обычно излагаемые численные методы анализа также изложены в дан-
данном учебнике.

ГЛАВА XIII
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§ 1. Постановка задачи. Уравнение движения тела
при сопротивлении среды, пропорциональном скорости.
Уравнение цепной линии
Пусть функция y = f(x) отражает количественную сторону
некоторого явления. Часто, рассматривая это явление, мы не
можем непосредственно установить характер зависимости у от х,
а можем установить зависимость между величинами х и у и про-
производными от у по х: у\ у", .•., у{п), т. е. написать дифферен-
дифференциальное уравнение.
Из полученной зависимости между переменными х, у и про-
производными^ требуется установить непосредственную зависимость у
от х, т. е. найти y = f{x) или, как говорят, проинтегриро-
проинтегрировать дифференциальное уравнение.
Рассмотрим два примера.
Пример 1. С некоторой высоты сброшено тело, масса которого т. Тре-
Требуется установить, по какому закону будет изменяться скорость v падения
этого тела, если на него, кроме силы тяжести, действует тормозящая сила
сопротивления воздуха, пропорциональная скорости (с коэффициентом пропор-
пропорциональности k), т. е требуется найти v = f(t).
Решение. По второму закону Ньютона
du _
F
dv ,
где —rr есть ускорение движущегося тела (производная от скорости по вре-
времени), a F—сила, действующая на тело в направлении движения. Эта сила
складывается из двух: силы тяжести mg и силы сопротивления воздуха—ко
(мы берем ее с минусом, так как она направлена в сторону, противоположную
направлению скорости). Итак,
m-jj-—tng~kv. (i)
Мы получили соотношение, связывающее неизвестную функцию о и ее произ-
dv
водную -^тт-» т. е. дифференциальное уравнение относитель-

14
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ. ХШ
но неизвестной функции v. (Это уравнение движения некоторых типов
парашютов.) Решить дифференциальное уравнение—это значит найти такую
функцию v = f(t), которая тождественно удовлетворяет данному дифференци-
дифференциальному уравнению. Таких функций имеется бесконечное множество.
Читатель легко проверит, что всякая функция вида
v = Ce~f+?!? B)
к
удовлетворяет уравнению A), каково бы ни было постоянное число С. Какая
же из этих функций даст искомую зависимость v от t? Для того чтобы ее
найти, используем дополнительное условие: при
сбрасывании тела ему была придана началь-
начальная скорость v0 (которая, в частности, может
быть равной нулю); мы предполагаем эту на-
начальную скорость известной. Но тогда искомая
функция v—-f(t) должна быть такова, чтобы
при ? = 0 (в начале движения) выполнялось
условие v = vQr Подставляя 2 = 0, v = vQ в фор-
формулу B), найдем
vo = C+-? , откуда C = i'o — ^f.
Таким образом, постоянная С найдена.
Следовательно, искомая зависимость v от t
такова:
I ~. О \ р
kt
k •
B0
Из этой формулы следует, что при достаточно больших / скорость v мало за-
зависит от v0.
Заметим, что если & = 0 (т.е. сопротивление воздуха отсутствует или оно
столь мало, что мы можем им пренебречь), то мы получаем известный из
физики результат *):
v = vo+gt. (Г)
Эта функция удовлетворяет дифференциальному уравнению A) и начальному
условию v — v0 при 2 = 0.
Пример 2. Гибкая однородная нить подвешена за два конца. Найти
уравнение кривой, по которой расположится нить под действием собственного
веса (так располагаются подвешенные канаты, провода, цепи).
Решение. Пусть Мо @, Ь) — наиболее низкая точка нити, М — ее про-
произвольная точка (рис. 250). Рассмотрим часть нити М0М. Эта часть нахо-
находится в равновесии под действием трех сил:
1) нзтяжение 71, действующее по касательной в точке М и составляющее
с осью Ох угол ф;
2) натяжение Н в точке Мо, действующее горизонтально;
3) вес нити ys, направленный вертикально вниз, где s—длина дуги M0Mt
у—линейный удельный вес нити.
*) Формула B) может быть получена из B') с помощью предельного
перехода:
?.[(*-?)
lira
k
= vo+gt.

§ 1] ПОСТАНОВКА ЗАДАЧИ 15
Разлагая натяжение Т на горизонтальную и вертикальную составляющие,
получим уравнение равновесия:
Т cos ф = Я, Т sin ф == ys.
Деля члены второго равенства на составляющие члены первого, получим
-J-s. C)
Положим теперь, что уравнение искомой кривой можно записать в виде
g = f(x). Здесь к/(л;) — неизвестная функция, которую надлежит найти. Заме-
Заметим, что
Следовательно *
я
где через а обозначено отношение —.
Продифференцируем обе части равенства D) по
d2y 1 ds
Но, как известно (см. § I гл. VI),
ds
Подставляя значение -тг в уравнение E), получим дифференциальное урав-
уравнение искомой кривой:
' """. (б)
Оно выражает связь между первой и второй производными от неизвестной
функции у.
Не останавливаясь на методах решения уравнений, укажем, что всякая
функция вида
{^^ G)
удовлетворяет уравнению F) при любых значениях постоянных Ci и С2, в чем
можно легко убедиться, подставив первую и вторую производные указанной
функции в уравнение F). Укажем далее без доказательства, что этими функ-
функциями (при различных С2 и С2) исчерпываются все возможные решения урав-
уравнения F). Это будет показано в § 18.
Графики всех полученных таким образом функций называются цепными
линиями.
Выясним теперь, как надо подобрать постоянные Сг и С2, чтобы получить
именно ту цепную линию, низшая точка М которой имеет координаты (О, Ь).
Так как при л: = 0 точка цепной линии занимает наинизшее положение, то
в этой точке касательная горизонтальна, т. е. -р = 0. Кроме того, по условию,
в этой точке ордината равна 6, т. е. у = Ь.
Из уравнения G) находим

16 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
Подставляя сюда * = 0, получим O^shCf. Следовательно, Ci = 0.
Если ордината точки Мо есть Ьу то у — Ь при х = 0.
Из уравнения G), полагая * = 0 и С1 = 01 получаем Ь = ~ A + 1) +С2,
откуда С2 = Ь—а. Окончательно находим
y — ach (x/a)-{-b—a.
Уравнение G) принимает особенно простой вид, если ординату точки Мо
взять равной числу а. Тогда уравнение цепной линии будет
y — ach (х/а).
§ 2. Определения
Определение 1. Дифференциальным уравнением называется
уравнение, связывающее независимую переменную х, искомую
функцию y = f(x) и ее производные у', у", ..., у(п\
Символически дифференциальное уравнение можно написать
так:
F(x% у, у\ у\ ..., у(л>) = 0
или
г ( аУ
t \Х> У> dbc>
Если искомая функция y=f(x) есть функция одной неза-
независимой переменной, то дифференциальное уравнение называется
обыкновенным. В настоящей главе мы будем заниматься только
обыкновенными дифференциальными уравнениями *).
Определение 2. Порядком дифференциального уравнения
называется порядок наивысшей производной, входящей в урав-
уравнение.
Так, например, уравнение
есть уравнение первого порядка.
*) Наряду с обыкновенными дифференциальными уравнениями в матема-
математическом анализе изучаются также уравнения в частных производных. Диф-
Дифференциальным уравнением в частных производных называется соотношение
между неизвестной функцией z, зависящей от двух или нескольких перемен-
переменных х, у, ..., этими переменными х, у, ... и частными производными от z:
dz dz d2z
Тх* ду% 1х^ И Т' Д'
Дифференциальным уравнением в частных производных с неизвестной
функцией z (х, у) является, например, уравнение х^- = у j- .
Легко проверить, что этому уравнению удовлетворяет функция z = x2y2
(и еще множество других функций).
В настоящем курсе уравнениям в частных производных посвящена
гл. XVIII.

§3] УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 17
Уравнение
есть уравнение второго порядка и т. д.
Уравнение, рассмотренное в предыдущем параграфе в примере 1,
является уравнением первого порядка, а в примере 2 —уравнением
второго порядка.
Определение 3. Решением или интегралом дифференциаль-
дифференциального уравнения называется всякая функция y=f(x), которая,
будучи подставлена в уравнение, превращает его в тождество.
d2u
Пример 1. Пусть мы имеем уравнение -т-|
Функция y = sinXi t/ = 2cos#, y = 3sinx—cos* и вообще функции вида
0 = CiSin#, y = C2cosx или у = Ci sin * + C2 cos x являются решениями дан-
данного уравнения при любом выборе постоянных Сг и С2; в этом легко убедиться,
подставив указанные функции в уравнение.
Пример 2. Рассмотрим уравнение у'х—х2—у — О.
Его решениями будут все функции вида у — х2-\-Сх, где С—любая постоян-
постоянная. Действительно, дифференцируя функцию у — х2-{-Сх, находим #' = 2дг+С.
Подставляя выражения у и у' в исходное уравнение, получаем тождество
Bх+С) х—х2 —х2—Сх=0.
Каждое из уравнений, рассмотренных в примерах 1 и 2, имеет бесчислен-
бесчисленное множество решений.
§ 3. Дифференциальные уравнения первого порядка
(общие понятия)
1. Дифференциальное уравнение первого порядка имеет вид
F(x, у, 0') = О. (!)
Если это уравнение можно разрешить относительно у\ та его
можно записать в виде
#' = /(*, у). (П
В этом случае мы говорим, что дифференциальное уравнение
разрешено относительно производной. Для такого уравнения спра-
справедлива следующая теорема, которая называется теоремой о суще-
существовании и единственности решения дифференциального уравнения.
Теорема. Если в уравнении
»' = /<*. У)
функция f (x, у) и ее частная производная ~ по у непрерывны
в некоторой области D на плоскости Оху, содержащей некоторую
точку (х0; #0), то существует единственное решение этого урав-
уравнения
удовлетворяющее условию у=у0 при х = х0.
Эта теорема будет доказана в § 27 гл. XVI.

18 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ- ХШ
Геометрический смысл теоремы заключается в том, что суще-
существует и притом единственная функция у = ц>(х)> график которой
проходит через точку (лу, у0).
Из только что высказанной теоремы вытекает, что уравне-
уравнение (Г) имеет бесконечное число различных решений (например,
решение, график которого проходит через точку (xQ; у0); другое
решение, график которого проходит через точку (л;0; у±) и т. д.,
если только эти точки лежат в области D).
Условие, что при х = х0 функция у должна равняться задан-
заданному числу у0, называется начальным условием. Оно часто запи-
записывается в виде
Определение 1. Общим решением дифференциального урав-
уравнения первого порядка называется функция
У = Ф(*, С), B)
которая зависит от одной произвольной постоянной С и удовле-
удовлетворяет следующим условиям:
а) она удовлетворяет дифференциальному уравнению при любом
конкретном значении постоянной С;
б) каково бы ни было начальное условие у=у0 при х=х0,
т. е. у\х=Хо=у09 можно найти такое значение С = С0, что функция
У = Ч(х, Со) удовлетворяет данному начальному условию. При
этом предполагается, что значения х0 и у0 принадлежат к той
области изменения переменных х и у, в которой выполняются
условия теоремы существования и единственности решения.
2. В процессе разыскания общего решения дифференциального
уравнения мы нередко приходим к соотношению вида
Ф(*, J/, С) = 0, B')
не разрешенному относительно t/. Разрешив это соотношение отно-
относительно у, получаем общее решение. Однако выразить у из соот-
соотношения B') в элементарных функциях не всегда оказывается
возможным; в таких случаях общее решение оставляется в неяв-
неявном виде. Равенство вида Ф(х, у, С) = 0, неявно задающее общее
решение, называется общим интегралом дифференциального урав-
уравнения.
Определение 2. Частным решением называется любая
функция y = (f(x, Co), которая получается из общего решения
у = у(х, С), если в последнем произвольной постоянной С при-
придать определенное значение C = CQ. Соотношение Ф(х, уу С0) = 0
называется в этом случае частным интегралом уравнения.
Пример 1. Для уравнения первого порядка
^= — JL
dx х

§31
УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
19
общим решением будет семейство функций у——\ это можно проверить про-
простой подстановкой в уравнение.
Найдем частное решение, удовлетворяющее следующему начальному усло-
условию: уо = 1 при хо = 2. Подставляя эти значения х0 и у0 в формулу у = С;'х,
получим 1 = С/2, или С = 2. Следовательно, искомым частным решением будет
функция у = 2/х.
С точки зрения геометрической общий интеграл пред-
представляет собой семейство кривых на координатной плоско-
плоскости, зависящее от одной произвольной постоянной С (или, как
говорят, от одного параметра С). Эти кривые называются инте-
интегральными кривыми данного дифференциального уравнения. Част-
Частному интегралу соответствует одна кривая этого семейства,
проходящая через некоторую заданную точку плоскости.
Так, в последнем примере общий интеграл геометрически изо-
изображается семейством гипербол у = С/х, а частный интеграл, опре-
определенный указанным начальным условием, изображается 'одной
из этих гипербол, проходящей через точку MQB; 1). На рис. 251
изображены кривые семейства, соответствующие некоторым зна-
значениям параметра: С =1/2, С=1, С = 2, С = —1 и т. д.
Чтобы сделать рассуждения более наглядными, мы будем
в дальнейшем называть решением уравнения не только
функцию y = y(xi Co), удовлетворяющую уравнению, но и соот-
соответствующую интегральную кривую. В связи с этим мы
будем говорить, например, о решении, проходящем через
точку (*0; г/0).

20
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ XIII
Замечание. Уравнение ¦?c=z—~ не имеет решения, прохо-
проходящего через точку, лежащую на оси Оу (см. рис. 251), так как
правая часть уравнения при х = 0 не определена и, следовательно,
не является непрерывной.
Решить или, как часто говорят, проинтегрировать
дифференциальное уравнение — значит:
а) найти его общее решение или общий интеграл (если началь-
начальные условия не заданы) или
б) найти то частное решение уравнения, которое удовлетворяет
заданным начальным условиям (если таковые имеются).
k^A
Рис. 252.
3. Дадим геометрическую интерпретацию дифференциального
уравнения первого порядка.
Пусть дано дифференциальное уравнение, разрешенное относи-
относительно производной:
аИ <*.*). (П
и пусть у — у(х, С) есть общее решение данного уравнения. Это
общее решение определяет семейство интегральных кривых на
плоскости Оху.
Уравнение (Г) для каждой точки М с координатами хну
определяет значение производной j-, т. е. угловой коэффициент
касательной к интегральной кривой, проходящей через эту точку.
Таким образом, дифференциальное уравнение (Г) дает совокуп-
совокупность направлений или, как говорят, определяет поле направле-
направлений на плоскости Оху.

§3]
УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
21
Следовательно, с геометрической точки зрения задача интегри-
интегрирования дифференциального уравнения заключается в нахожде-
нахождении кривых, направление касательных к которым совпадает с
направлением поля в соответствующих точках.
Для дифференциального уравнения A) геометрическое место
точек, в которых выполняется соотношение -7~ = & = const, назы-
называется изоклиной данного дифференциального уравнения.
При различных значениях k получаем различные изоклины.
Уравнение изоклины, соответствующей значению &, будет, оче-
очевидно, /(х, y) = k. Построив
семейство изоклин, можно при-
приближенно построить семейство
интегральных кривых. Говорят,
что, зная изоклины, можно
качественно определить распо-
расположение интегральных кривых С-%
на плоскости.
На рис. 252 изображено по-
поле направлений, определяемое
дифференциальным уравнением
dx
Рис. 253.
Изоклинами данного диффе-
ренциального уравнения явля-
являются — y/x = k, или у = — kx. Это семейство прямых. Они по-
построены на рис. 252.
4. Рассмотрим такую задачу.
Пусть дано семейство функции, зависящее от одного пара-
параметра С:
У = Ф(*. Q, B)
причем через каждую точку плоскости (или некоторой области
на плоскости) проходит только одна кривая из этого семейства.
Для какого дифференциального уравнения это семейство функ-
функций является общим интегралом?
Из соотношения B), дифференцируя по х, найдем
?-*(*. о-
C)
Так как через каждую точку плоскости проходит только одна
кривая семейства, то для каждой пары чисел х и у определяется
единственное значение С из уравнения B). Подставляя это зра-
чение С в соотношение C), найдем ~ как функцию от х и у.
Это и дает нам дифференциальное уравнение, которому удовлет-
удовлетворяет Есякая функция из семейства B).

22 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [гл- хш
Следовательно, чтобы установить связь между х, у и ^, т. е.
чтобы написать дифференциальное уравнение, общий интеграл
которого определяется формулой B), нужно исключить С из соот-
соотношений B) и C).
Пример 2. Найти дифференциальное уравнение семейства парабол
д = Сх2 (рис. 253).
Дифференцируя по х уравнение семейства, найдем
dx
Подставляя сюда значение
С = у/х*
из уравнения семейства, получаем дифференциальное уравнение данного се-
семейства:
dy = 2y
dx x *
Это дифференциальное уравнение имеет смысл при х ф. О, т. е. в любой
области, не содержащей точек на оси Оу.
§ 4. Уравнения с разделенными и разделяющимися переменными.
Задача о распаде радия
Рассмотрим дифференциальное уравнение вида
где правая часть есть произведение функции, зависящей только
от х, на функцию, зависящую только от у. Преобразуем его сле-
следующим образом (предполагая, что }2(у)ф0):
^ (Г)
Считая у известной функцией от х, равенство (Г) можно рас-
рассматривать как равенство двух дифференциалов, а неопределен-
неопределенные интегралы от них будут отличаться постоянным слагаемым.
Интегрируя левую часть по у, а правую по х, найдем
Мы получили соотношение, связывающее решение у, независимую
переменную х и произвольную постоянную С, т. е. получили
общий интеграл уравнения A).
1. Дифференциальное уравнение типа (Г)
M{x)dx + N(y)dy = O B)
называют уравнением с разделенными переменными. Общий

§4J УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
интеграл его по доказанному есть
23
Пример 1. Дано уравнение с разделенными переменными xdx-{-y dy = Q,
Интегрируя, получим общи^ интеграл:
х2 и2 >w
-?—\-~=zClt Так как левая часть послед-
последнего равенства неотрицательна, то и правая
часть тоже неотрицательна. Обозначив 2Ci
через С2, будем иметь х2-\-у2 — С2. Это —
уравнение семейства концентрических окруж-
окружностей (рис. 254) с центром в начале коор-
координат и радиусом С.
2. Уравнение вида
Мг {х) #! (у) dx + М2 (х) N2 (у) dy = O
C)
называется уравнением с разделяющи-
разделяющимися переменными. Оно может быть
приведено*) к уравнению с разде-
разделенными переменными путем деления обеих его частей на вы-
выражение N1{y)M2(x):
M1(x)N1(y)^ M2(x)N2(y) п
Рис. 254,
N1(y)M2(x)
ИЛИ
т. е. к уравнению вида B).
Пример 2. Дано уравнение -^=——, Разделяем переменные: — =
ах х у
. Интегрируя, находим \ — =— \ \-Cf т. е. In | у | = — In | x \
% J У J %
I | С | **) I | | I | С/ | б С/
J У J
In | С | **) или In | у | = In | С/х |; отсюда получаем общее решение: у = С/х.
Пример 3. Дано уравнение (\-\-х)уdx-\-(\—y)xdy = 0. Разделяя не-
не<dx-\ ?-dy = O, ( p-ljcU+f 1 J dy — Q. Ин-
}^{C
ременные, находим
(\)у\(
?-dy = O, ( p-ljc
тегрируя, получаем In | д:|+^ + 1п | у \ — t/ = C, или In | xy }^{-x—y = C; послед-
последнее соотношение есть общий интеграл данного уравнения.
Пример 4. Установлено, что скорость распада радия прямо пропор-
пропорциональна его количеству в каждый данный момент. Определить закон изме-
изменения массы радня в зависимости от времени, если при / = 0 масса радия
была т0.
*) Эти преобразования законно производить только в той области, где ни
Ni (у), ни М2 (х) не обращаются в нуль.
**) Имея в виду дальнейшие преобразования, мы обозначили произвольную
постоянную через 1п|С|, что допустимо, так как 1п[С| (при С Ф 0) может
принимать любое значение от —оо до +00»

24 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
Скорость распада определяется следующим образом. Пусть в момент t была
масса т, в момент t-\-At— масса m-f-Дт. За время At распалась масса Am.
Отношение —гт- есть средняя скорость распада. Предел этого отношения при
lim ^L=i™
At -+ о Д* dt
есть скорость распада радия в момент t.. По
условию задачи
Рис.255. W=-km> D)
где &—коэффициент пропорциональности (k > 0). Мы ставим знак минус по-
потому, что при увеличении времени масса радия убывает и, следовательно,
Уравнение D) есть уравнение с разделяющимися переменными. Разделяем
переменные:
dm .
kdi
Решая уравнение, получим \пт — —kt-{~lnCt откуда ln-^- = —ktt
т = Се~М. E)
Так как при / = 0 масса радия была т0, то С должно удовлетворять соотно-
соотношению mo = Ce~k °— О. Подставляя это значение С в равенство E), получим
искомую зависимость (рис. 255) массы радия как функцию времени:
m = moe-kt. (б)
Коэффициент k определяется из наблюдений следующим образом. Пусть за
время tQ распадается а% первоначальной массы радия. Следовательно, выпол-
выполняется соотношение
откуда
ила
Таким образом было определено, что для радия & = 0,000436 (единица изме-
измерения времени—год). Подставляя это значение k в формулу F), получим
Найдем период полураспада радия, т. е. промежуток времени, за который
распадается половина первоначальной -массы радия. Подставляя в последнюю
формулу вместо т значение -~, получим ~^-=т0е~0>00043бГ, откуда

§5J ОДНОРОДНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 25
—0,000436Г=*—in 2, или
г
Заметим, что к уравнению вида D) приводят и другие задачи физики и
химии.
Замечание 1. Пусть функция /2(#)> входящая в уравне-
уравнение A), имеет корень у = Ь, т.е. f2(b) = 0. Тогда, очевидно,
функция у = Ь есть решение уравнения A), в чем легко убе-
убедится непосредственной подстановкой. Решение у — b может и не
получиться из формулы (Г'). Мы будел! проводить анализ этого
случая, но отметим, что на прямой у = 6 может нарушиться
условие единственности.
Приведем пример. Уравнение у' = 2Угу имеет общее решение
у = (х-\-сJ и решение у = 0, которое не получается из общего
решения. На прямой у = 0 нарушается условие единственности.
Замечание 2. Простейшим дифференциальным уравнением
с разделенными переменными является уравнение вида ^ = /(*)>
или dy = f (х) dx. Его общий интеграл имеет вид*/ = } f(x)dx + С,
Решением уравнений этого вида мы занимались в главе X.
§ 5. Однородные уравнения первого порядка
Определение 1. Функция /(х, у) называется однородной
функцией п-го измерения относительно переменных х и у, если
при любом К справедливо тождество
Пример 1. Функция / (х, у) = ^/хъ-\-уъ—однородная функция первого
измерения, так как f (Xx, hj) = ?/(.UK + (Xyf = X \/х*+у* = Xf (x, у).
Пример 2. /{ху)~ху—у2 есть однородная функция второго измерения,
так как (JU) (%у)-(ХуJ = Х2 (ху-у2).
Х2 у2
Пример 3. f (х, у) = ^— есть однородная функция нулевого изме-
пх\ 2 (\уJ х2 ф
рения, так как ' ? * ==—^~, т. е. f (kx, ky) = f(x, у), или
)
, у).
Определение 2. Уравнение первого порядка
называется однородным относительно х и у, если функция f(xy у)
есть однородная функция нулевого измерения относительно х и у.

26 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
Решение однородного уравнения. По условию
f(kx>Xy) = f(x>y). Положив в этом тождестве К=1/х, получим
т. е. однородная функция нулевого измерения зависит только
от отношения аргументов.
Уравнение A) в этом случае примет вид
Сделаем подстановку
Тогда будем иметь
и = —, т. е. у = их.
X
Подставляя это выражение производной в уравнение (Г), получим
Это — уравнение с разделяющимися переменными:
du г /
x-^ = f(
Интегрируя, найдем
du г /л ч du dx
^ = f(l,u)-u, или f(hu)_u=—
Г du Г dx | г
J /A. а) —а — J * ^Ь'
Подставляя после интегрирования вместо м отношение у/х9
получим интеграл уравнения (I').
Пример 4. Дано уравнение
dy _ ху
dx x2—y2 '
Справа стоит однородная функция нулевого измерения; следовательно^
имеем однородное уравнение. Делаем замену у/х = и; тогда
dy . du
у —их, -— = и 4- л: -г-.
. du и du и3
1J I у у ¦ ,
^л: I — и2 dx l — u2
Разделяя переменные, будем иметь
i — u2) du _ dx
u3

§61 УРАВНЕНИЯ, ПРИВОДЯЩИЕСЯ К ОДНОРОДНЫМ 27
отсюда, интегрируя, находим
— -gjjr —1п|и| = 1п|дс| + 1п|С|, или — —-.-~\п\ихС\.
Подставляя и = у!х, получим общий интеграл исходного уравнения:
--*L = ln\Cy\.
Получить д как явную функцию от х, записанную с помощью элементарных
функций, в данном случае невозможно. Впрочем, здесь легко выразить х
через у:
х=уУт—2\п\Су\.
Замечание. Уравнение вида
М{х9
будет однородным в том и только в том случае, когда М (х, у) и
N (#, у) являются однородными функциями одного и того же
измерения. Это вытекает из того, что отношение двух однород-
однородных функций одного и того же измерения является однородной
функцией нулевого измерения.
Пример 5. Уравнения
Bх+3у) dx+(x—2y)dy = 0, (х2+у2) dx—2xgdy=0
являются однородными.
§ 6. Уравнения, приводящиеся к однородным
К однородным уравнениям приводятся уравнения вида
dy __ ax+bg+c m
dx I1'
Если ^ = ? = 0, то уравнение A) есть, очевидно, однородное.
Пусть теперь с и ct (или одно из них) отличны от нуля. Сде-
Сделаем замену переменных
x = x± + h, y = yx + k. B)
Тогда
dy == dy± ^
dx dxi *
Подставляя в уравнение A) выражения х9 у и —-, будем иметь
dyt _
d

28 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
Подберем h и k так, чтобы выполнялись равенства
'-о' I <4>
т. е. определим h и k как решения системы уравнений D). При
этом условии уравнение C) становится однородным:
dyx
dx1
Решив это уравнение и перейдя снова к а: и у по формулам B),
получим решение уравнения A).
Система D) не имеет решения, если
а I =<>.
at Ъг
т. е. ab1 = a1b. Но в этом случае —^-y"^» т- е- ^ — Ха,
Ьг = ХЬ и, следовательно, уравнение A) можно преобразовать
к виду
dy __ (ax + by)+c -
dx ~~ X(ax + by)+Cl * К '
Тогда подстановкой
F)
уравнение приводится к уравнению с разделяющимися перемен-
переменными.
Действительно,
dz
откуда
dx~~ b dx b%
Подставляя в уравнение E) выражения F) и G), получим
1 dz a z-\-c
а это есть уравнение с разделяющимися переменными.
Прием, примененный к интегрированию уравнения A), приме-
применяется и к интегрированию уравнения
dy г/ ax+by+c \
dx ' \aix+b1y+c1)t
где /—какая угодно непрерывная функция.

6] УРАВНЕНИЯ, ПРИВОДЯЩИЕСЯ К ОДНОРОДНЫМ 29
Пример 1. Дано уравнение
—3
dx x—y—1
Чтобы преобразовать его в однородное уравнение, делаем замену х~хх-\-к%
\k. Тогда
гy±\ — k—1
Решая систему двух уравнений
Л + Л—3 = 0, Я—^ — 1 =0,
находим
Л = 2, *=1.
В результате получаем однородное уравнение
dx! x1—y1i
которое решаем подстановкой
xi
тогда
dyx . du
du \-\-u
и мы получаем уравнение с разделяющимися переменными
du \-\-u2
Разделяем переменные:
1 + и2
Интегрируя, находим
arctg и —g. In (I + и2) = In f Xi | + In | С |,
arctg и = In| С*! ]/+м21,
ИЛИ
Подставляя сюда — вместо «, получим
Xi
Наконец, переходя к переменным х и у, окончательно получаем

30 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
Пример 2. Уравнение
уже нельзя решить подстановкой x = xx+ht у^у^ + к, так как в этом случае
система уравнений, служащая для определения h и k, неразрешима ("здесь
определитель
2 1
из коэффициентов при переменных равен нулю ).
можно свети
(
)
Это уравнение можно свести к уравнению с разделяющимися переменными
заменой
2х+у = г<
Тогда у' = г'—2, и уравнение приводится к виду
или
5Н-9
Решая его, найдем
Так как z — 2x-\-y, то мы получим окончательно решение исходного уравне-
уравнения в виде
или
Hty—5* +7 In) 10*+5#+9 \ = Си
т. е. в виде неявной функции у от х,
§ 7. Линейные уравнения первого порядка
Определение. Линейным уравнением первого порядка на-
называется уравнение, линейное относительно неизвестной функции
и ее производной. Оно имеет вид
d? + P(x)y=Q(x), A)
где Р (х) и Q(x)—заданные непрерывные функции от х (или
постоянные).
Решение линейного уравнения A). Будем искать
решение уравнения A) в виде произведения двух функций от х:
y = u(x)v{x). B)
Одну из этих функций можно взять произвольной, другая
определится на основании уравнения A).

§7] ЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 31
Дифференцируя обе части равенства B), находим
dx-^dx^^Tx
Подставляя полученное выражение производной ^ в уравне-
уравнение A), будем иметь
dv . du
ИЛИ
Выберем функцию v такой, чтобы
| = 0. D)
Разделяя переменные в этом дифференциальном уравнении отно-
относительно функции v, находим
Интегрируя, получаем
-inlCil + lnlvl^-^ Pdxt
или
Так как нам достаточно какого-нибудь отличного от нуля реше-
решения уравнения D), то за функцию v (х) возьмем
t ч - Г Р dx 71-ч
v(x) = e J , E)
где }Pdx—какая-нибудь первообразная. Очевидно, что v
П )
Подставляя найденное значение v (x) в уравнение C), полу-
получим (учитывая, что )
или
du _ Q (х)
dx~~v (x) '
откуда
Подставляя и и v в формулу B), окончательно получаем

32 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ XIII
ИЛИ
^ x). F)
Замечание. Очевидно, что выражение F) не изменится,
если вместо функции v(x), определенной равенством E), мы
возьмем какую-нибудь функцию v1(x) = Cv(x). Действительно,
подставляя в F) ^(л:) вместо v(x), получим
В первом слагаемом С сокращаются; во втором слагаемом про-
произведение СС есть произвольная постоянная, которую обозначаем
одной буквой С, и снова приходим к выражению F). Если обо-
Г О (х)
значим \ -^—у dx = q>(x), то выражение F) примет вид
x). F')
Очевидно, что это—общий интеграл, так как С можно подобрать
так, что будет удовлетворяться начальное условие у = у0 при
х = х9.
Значение С определяется из уравнения
y<> = v(x
Пример. Решить уравнение
dy 2
Решение. Полагаем y = uv, тогда
dy du | du
dx dx ' dx
du
Подставляя выражение -j- в исходное уравнение, будем иметь
dv , du
d ' d
dx ' dx x-{~\ vi/'
[dv 2 "\ t <*и / , is* ,r,\
и j rrv \-\-v — = (л:+1K. G)
\dx x~\-\ J ' dx v ' ' x '
dv 2 л dv 2dx
Для определения v получим уравнение -z ХТУ=:"» т# е# "~~а Г»
а х х —р" 1 v х ~~у~ 1
откуда ln| v |=2 In) x+\ |, или v = (x-\-\J. Подставляя выражение функции
v в уравнение G), получаем для определения и уравнение (х-\-\)* -р =
или г? = х+1> откуда M = (l±i
Следовательно, общий интеграл заданного уравнения будет иметь вид

§ 8] УРАВНЕНИЕ БЕРНУЛЛИ 33
Полученное семейство является общим решением. Каково бы ни было
начальное условие (х0; у0), где х0 Ф —1, всегда можно так подобрать С, чтобы
соответствующее частное решение удовлетворяло заданному начальному усло-
условию. Например, частное решение, удовлетворяющее условию уо — 3прп лго = О,
найдется следующим образом: 3= "L + С@+02> С = 5/2. Следовательно,
искомое частное решение таково: у~ ' Ч—тН^-НJ* Однако, если на-
начальное условие (х0; у0) выбрать так, что х0 ——1, то мы не найдем частного
решения, удовлетворяющего этому условию. Это объясняется тем, что при
Л'о =—1 функция Р(х)= -j—r разрывна и, следовательно, условия теоремы
существования решения не соблюдены.
Замечание. В приложениях часто встречаются линейные
уравнения с постоянными коэффициентами
di+«y = b, (8)
где а и Ь—постоянные.
Его можно решить и с помощью подстановки B) или путехМ
разделения переменных:
dy = {-ay+b)dxt zz^-dx, -Un\-
\ = — (ax + C*), где C* =
или окончательно
/где обозначено —— е~с* — С) . Это и есть общее решение урав-
уравнения (8).
§ 8. Уравнение Бернулли
Рассмотрим уравнение вида*)
А..
y=Q(x) yny A)
где Р(х) и Q (х)—непрерывные функции от х (или постоянные),
а пфО и пф1 (в противном случае получилось бы линейное
уравнение). Это уравнение, называемое уравнением Бернулли,
приводится к линейному следующим преобразованием.
*) К этому уравнению приводит задача о движении тела, если сопротив-
сопротивление среды F зависит^от скорости так: /7 = XiU+^2yW- Уравнение движения
будет тогда m-^ = —-fatr—A^V*, или ~-j—±v = -vn.
at at m m
* H, С. Пискунов, т. 2

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ I™. ХШ
Разделив все члены уравнения на у*, получим
г+г =Q. B)
Сделаем, далее, замену
Тогда
Подставляя эти значения в уравнение B), будем иметь линей-
линейное уравнение
Найдя его общий интеграл и подставив вместо z выражение
y-n+iy получим общий интеграл уравнения Бернулли.
Пример. Решить уравнение
~~f + ху = #3 У^. C)
Решение. Разделив все члены на t/3, получим
У~*у' + ху-2=*х*, D)
Введем новую функцию z = y-2; тогда -т- =—2у~ъ-~-. Подставляя эти значе-
значения в уравнение D), получим линейное уравнение
J:—2xz=;-2x*. E)
Найдем его общий интеграл:
_ dz __ dv .du
Z~UV* dx~~Udx+dx~V*
Подставляем в уравнение E) выражения ги г:
dv . du
или
\55 у ' дх~~
Приравниваем нулю выражение, стоящее в скобках:
dx ~~ ' 1Г~~ '
Для определения ^ получаем уравнение
Разделяем переменные:
du = — 26-*2*3 <iA:, «i = — 2 С е-*V ^+С.

$3] УРАВНЕНИЕ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ 35
Интегрируя по частям* найдем
, z = «у = *2 +1 + Се*2.
Следовательно, общий интеграл данного уравнения есть
', или #=-
Замечание. Аналогично тому, как это делалось для ли-
линейных уравнений, можно показать, что решение уравнения Бер-
нулли можно искать в виде произведения двух функций:
y = u(x)v(x),
где v(x)—какая-либо функция, отличная от нуля и удовлетво-
удовлетворяющая уравнению v'+Pv = 0.
§ 9. Уравнение в полных дифференциалах
Определение. Уравнение
0 (I)
называется уравнением в полных дифференциалах, если М(х, у)
и N (х, у)—непрерывные, дифференцируемые функции, для кото-
которых выполняется соотношение
дМ__дМ
причем у- и -^ непрерывны в некоторой области.
Интегрирование уравнений в полных дифферен-
дифференциалах. Докажем, что если левая часть уравнения A) есть
полный дифференциал, то выполняется условие B), и обратно —
при выполнении условия B) левая часть уравнения A) есть пол-
полный дифференциал некоторой функции и(х, у), т. е. уравнение A)
имеет вид
du(x9y) = 09 C)
и, следовательно, его общий интеграл есть и (х, у) = С.
Предположим сначала, что левая часть уравнения A) есть
полный дифференциал некоторой функции и(х9 у), т. е.
тогда
2»

3G ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Сгл ХПГ
Дифференцируя первое соотношение по у, а второе—по х,
получим
дМ __ д2и ayv д2и
ду дх ду' дх ду дх'
Предполагая непрерывность вторых производных, будем иметь
дМ __dN
~ду~~дх>
т. е. равенство B) является необходимым условием для того,
чтобы левая часть уравнения A) была полным дифференциалом
некоторой функции и(х, у). Покажем, что это условие является
и достаточным, т. е. что при выполнении равенства B) левая
часть уравнения A) есть полный дифференциал некоторой функ-
функции и(х, у).
х
Из соотношения ^ = М (л:, у) находим и=}М(х, у)dx + Ф (у)у
где Хь—абсцисса любой точки из области существования решения.
При интегрировании по х мы считаем у постоянным и поэтому
произвольная постоянная интегрирования может зависеть от у.
Подберем функцию <р(у) так, чтобы выполнялось второе из соот-
соотношений D). Для этого продифференцируем*) обе части послед-
последнего равенства по у и результат приравняем N (х, у):
х0
X
но так как •^-" — "тг" > то можем написать \ -jn-djH-cp' (y)=N, т. е.
) N{)
N (х, y)-N (х„ у)+у' (у) = N (х, у).
Следовательно,
или
Уо
*) Интеграл V М (х, у) dx зависит ог у. Для того чтобы найти производ-
А'о
ную от этого интеграла по у, нужно продифференцировать по у подынтеграль-
* X
ную функцию: — \ М (х, у) dx = \ -^— dx. Это вытекает из теоремы Лейб-
х0 х0
ница о дифференцировании определенного интеграла по параметру (см. § 10
гл. XI).

§ 9] УРАВНЕНИЕ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ 37
Таким образом, функция и (х, у) будет иметь вид
х у
u=\M(x,y)dx+\N(x0, у)dg + C,.
Здесь Р(х0; у0)—точка, в окрестности которой существует реше-
решение дифференциального уравнения A).
Приравнивая это выражение произвольной постоянной С, по-
получим общий интеграл уравнения A):
х у
5 М (х, y)dx+<\N {xQ, у) dy = С. E)
Х0 Уо
Пример. Дано уравнение
Проверяем, не есть ли это уравнение в полных дифференциалах.
Обозначим
А1?? jy
У3 У*
тогда
дм__ вх <т___ вх
~ду у* ' дх ijv
Условие B) при у Ф 0 выполняется. Значит, левая часть данного уравнения
есть полный дифференциал некоторой неизвестной функции и (х, у). Найдем
эту функцию
эту функцию.
Так как ^=~з » то» следовательно,
где ф (у)—не определенная пока функция от у.
Дифференцируя это соотношение по у и учитывая, что
ди дт у2—Зх2
? ?~'
находим
следовательно,
|
Таким образом, общий интеграл исходного уравнения есть
? 1-е
У3 У

38 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ ХШ
§ 10. Интегрирующий множитель
Пусть левая часть уравнения
М(х9 y)dx + N(x,y)dy = O A)
не есть полный дифференциал. Иногда удается подобрать такую
функцию \i(xy у), после умножения на которую всех членов урав-
уравнения левая часть уравнения становится полным дифференциалом.
Общее решение полученного таким образом уравнения совпадает
с общим решением первоначального уравнения; функция \к{х> у)
называется интегрирующим множителем уравнения A).
Для того чтобы найти интегрирующий множитель jx, посту-
поступаем следующим образом-: умножим обе части данного уравнения
на неизвестный пока интегрирующий множитель |х:
Для того чтобы последнее уравнение было уравнением в полных
дифференциалах, необходимо и достаточно, чтобы выполнялось
соотношение
ду дх
т. е.
дМ
ИЛИ
После деления обеих частей последнего уравнения на jx, получим
м дХпУ Nд]п^ —дМ дМ (9\
Очевидно, что всякая функция [i(x> у), удовлетворяющая по-
последнему уравнению, является интегрирующим множителем урав-
уравнения A). Уравнение B) является уравнением в частных произ-
производных с неизвестной функцией f,i, зависящей от двух переменных
хну. Можно доказать, что при определенных условиях оно
имеет бесчисленное множество решений и, следовательно, уравне-
уравнение A) имеет интегрирующий множитель. Но в общем случае
задача нахождения \х(х, у) из уравнения B) еще труднее, чем
первоначальная задача интегрирования уравнения A). Только
в некоторых частных случаях удается найти функцию \l(x, у).
Пусть, например, уравнение A) допускает интегрирующий
множитель, зависящий только от у. Тогда

§11] ОГИБАЮЩАЯ СЕМЕЙСТВА КРИВЫХ 39
и для отыскания fx мы получаем обыкновенное дифферен-
дифференциальное уравнение
dN dM
d\n\i дх ду
из которого определяется (одной квадратурой) 1пц,, а следова-
следовательно, и \i. Ясно, что так можно поступать только в том слу-
случае, если выражение ох м у не зависит от х.
dN дм
Аналогично, если выражение ¦ * N y не зависит от у, а за-
зависит только от ху то легко находится интегрирующий множи-
множитель, зависящий только от х.
Пример. Решить уравнение
iy+xy2) dx—xdy = 0.
Решение. Здесь М=у-\-ху2> N = — x,
дМ__ 2 dN__ дМ dN
~ду~~ ХУ' дх~~~~ ' ~ду ~дх'
Следовательно, левая часть уравнения не есть полный дифференциал.
Посмотрим, не допускает ли это уравнение интегрирующего множителя, зави-
зависящего только от у. Заметив, что
dN дМ
~дх~~"ду__—\ — \—2ху_ 2
М У-\~ХУ2 У '
заключаем, что уравнение допускает интегрирующий множитель, зависящий
только от у. Находим его: , г = ; отсюда lnu==—2 In r/, т.е. u=l/w2.
йУ У
После умножения всех членов данного уравнения на найденный интегрирую-
/1 , \, х .
щии множитель \х получаем уравнение ( —\-х ) dx ^dy — О в полных диф-
(дМ dN 1 \ _ У У л т
ференциалах ("Т~;==;~== г)* Решая это уравнение, найдем его общий
§ И. Огибающая семейства кривых
Пусть дано уравнение вида
Ф(*. У, Q = 0# A)
где х и у—переменные декартовы координаты, а С—параметр,
могущий принимать различные фиксированные значения.

40
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ. ХЦ1
При каждом данном значении параметра С уравнение A) опре-
определяет некоторую кривую на плоскости Оху. Придавая С все-
всевозможные значения, мы получаем семейство кривых, зави-
зависящих от одного параметра, или — как часто говорят—одно-
параметрическое семейство кривых. Таким образом,
Уравнение A) есть уравнение одно-
параметрического семейства кривых
(так как оно содержит только од-
одну произвольную постоянную).
Рис. 256.
Рис. 257.
Определение. Линия L называется огибающей однопара-
метрического семейства линий, если она в каждой своей точке
касается той или иной линии семейства, причем в различных
точках линии L ее касаются различные линии данного семейства
(рис. 256).
Пример 1. Рассмотрим семейство линий (а:—СJ+#2 = #2, где R—
постоянная, С—параметр. Это—семейство окружностей радиуса/? с центрами
на оси Ох. Очевидно, что это семейство будет иметь огибающими прямые y—R,
tj = — R (рис. 257)."
Нахождение уравнения огибающей данного се-
семейства. Пусть дано семейство кривых
Ф(*, у, С)-0, A)
зависящих от параметра С.
Предположим, что это семейство имеет огибающую, уравнение
которой можно записать в виде у = ц>(х)у где ф(х)—непрерывная
и дифференцируемая функция от х. Рассмотрим некоторую точку
М(х\ у)у лежащую на огибающей. Эта точка также лежит на не-
некоторой кривой семейства A). Этой кривой соответствует опреде-
определенное значение параметра С, которое при данных хну опре-
определяется из уравнения A): С = С(ху у). Следовательно, для всех
точек огибающей удовлетворяется равенство
Ф(*. У, С(ху у)) = 0. B)
Допустим, что С (л:, у)—дифференцируемая функция, не постоян-
постоянная ни на каком интервале рассматриваемых значений х, у. Из
уравнения B) огибающей найдем угловой коэффициент каса-
касательной к огибающей в точке М(х\ у). Продифференцируем

§Uj ОГИБАЮЩАЯ СЕМЕЙСТВА КРИВЫХ 41
равенство B) по дг, считая, что у есть функция от х:
дФ , дФ^д? , /дФ , дФ_дС_\ ,_0
ал: "•" ОС дх "*" V &/ ¦*" дС ду ) У ~~ '
ИЛИ
{|| )о. C)
Далее, угловой коэффициент касательной к кривой семейст-
семейства A) в точке М(х\ у) найдется из равенства
= 0 D)
(С на данной кривой постоянно).
Мы предполагаем, что Ф^=^0, в противном случае мы счи-
считали бы х функцией, а у аргументом. Так как угловой коэффи-
коэффициент k огибающей равен угловому коэффициенту k кривой се-
семейства, то из C) и D) получаем
Но так как на огибающей С(ху у) Ф const, то
дх ^ ду
и потому для ее точек справедливо равенство
&с(х> у,С) = 0. E)
Таким образом, для определения огибающей служат следующие
два уравнения:
ф(*. у, О=о, л
Ф'с(х, у, 0 = 0. ) (Ь)
Обратно, если, исключая С из этих уравнений, получим уравне-
уравнение у^у(х), где ф(х)—дифференцируемая функция, при этом
значение С =# const на этой кривой, то у = ц>(х) есть уравнение
огибающей.
Замечание 1. Если для семейства A) некоторая функция
у = ф (х) является уравнением геометрического места особых точек,
т. е. точек, где Ф^ = 0 и Ф^ = 0, то координаты этих точек так-
также удовлетворяют уравнениям F).
Действительно, координаты особых точек можно выразить через
параметр С, входящий в уравнение A):
G)
Если эти выражения подставим в уравнение A), то получим
тождество относительно С:
Ф(ЦС),

42 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Дифференцируя это тождество по С, получим:
[ГЛ. ХШ
так как для любых точек выполняются равенства Ф* = 0, Ф^ = 0,
то, следовательно, для них также выполняется равенство Фс — 0.
Этим мы и доказали, что координаты особых точек удовлет-
удовлетворяют уравнениям F).
Итак, уравнения F) определяют либо огибающую, либо гео-
геометрическое место особых точек кривых семейства A), либо соче-
сочетание того и другого. Таким образом, получив кривую, удовлет-
удовлетворяющую уравнениям F), необходимо
дополнительно исследовать, является ли
она огибающей или геометрическим ме-
местом особых точек.
Рис. 258.
Рис. 259.
Пример 2. Найти огибающую семейства окружностей
зависящих от одного параметра С.
Решение. Дифференцируя уравнение семейства по С, получаем 2 (х—С)=
= 0. Исключая С из этих двух уравнений, получим уравнения у%—R2 — Q или
y=±R-
Из геометрических соображений ясно, что полученная пара прямых
является огибающей (а не геометрическим местом особых точек, так как
окружности, входящие в семейство, не имеют особых точек).
Пример 3. Найти огибающую семейства прямых:
*cosa+#sina—p = 0, (а)
где a—параметр.
Решение. Дифференцируя по а данное уравнение семейства, будем
иметь:
—*sina+#cosa = 0. (b)
Для исключения параметра а из уравнений (а) и (Ь) умножим члены пер-
первого на cos a, а второго—на sin^fc- и вычтем из первого второе; тогда будем
иметь *=pcosa. Подставляя это выражение в равенство (Ь), найдем у =
= р sin а. Возводя члены двух последних уравнений в квадрат и складывая
почленно, получим #2 + */2 = /?2. Это—окружность. Она является огибаю-
огибающей семейства (а не геометрическим местом особых точек, так как прямые
линии не имеют особых точек) (рис. 258).
П р и м е р 4. Найти огибающую траекторий снарядов, выпущенных из пушки
со скоростью vQ под различными углами наклона ствола орудия к горизонту.
При этом будем считать, что орудие находится в начале координат, а траек-
траектории снарядов лежат в плоскости Qxij (сопротивлеаием воздуха пренебрегаем).

5 ИЗ
ОГИБАЮЩАЯ СЕМЕЙСТВА КРИВЫХ
43.
Решение. Найдем сначала уравнение траектории снаряда в том случае,
когда ствол орудия составляет с положительным направлением оси Ох угол а.
Во время полета снаряд участвует одновременно в двух движениях: равномер-
равномерное движение со скоростью v0 в направлении ствола орудия и падение вниз
под действием силы тяжести. Поэтому в каждый момент времени t положение
снаряда М (рис. 259) будет определяться равенствами
x=vot cos a, y — Votsin<x—~г-.
z
Это—параметрические уравнения траектории (параметром является время t).
Исключив t, найдем уравнение траектории в виде
наконец, введя обозначения tga = k,
2vq cos2 a
=я, получим
(8)
Это уравнение определяет параболу с вертикальной осью, проходящую через
начало координат и обращенную ветвями вниз. Для различных значений k
мы получим различные траектории. Следовательно, уравнение (8) является
уравнением однопараметрического семейства парабол, являющихся траекто-
траекториями снаряда при различных углах а и данной начальной скорости vQ
(рис. 260).
Найдем огибающую этого семейства парабол.
Дифференцируя по к обе части уравнения (8), имеем
х—2akx2=0. (9)
Исключая к из уравнений (8) и (9), получим
у==*ах2.
* 4а
Это—уравнение параболы с вершиной в точке (О; т~), ось которой
совпадает с осью Оу. Она не является геометрическим местом особых точек
(так как параболы (8) не имеют особых точек). Итак, парабола
»«2
является огибающей семейства траекторий. Она называется параболой
б^е з о п а с н о с т и, так как ни одна точка за ее пределами не достижима для
снаряда, выпущенного из данного орудия -с данной начальной скоростью v0.

44
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ ХШ
Пример 5. Найти огибающую семейства полукубических парабол
if—(x—CJ = 0.
Решение. Дифференцируем по параметру С данное уравнение семейства:
2(*—О = 0.
Исключая параметр С из двух уравнений, получим
У=-0.
Ось Ох является геометрическим местом особых точек—точек возврата
первого рода (рис. 261). Действитель-
У но, найдем особые точки кривой
при фиксировании значения С. Диф-
Дифференцируя по х и у, находим
Геометрическое
Рис. 261.
Решая совместно три предыдущих уравнения, найдем координаты особой
точки: #—С, */ = 0; таким образом, каждая кривая данного семейства имеет
особую точку на оси Ох.
При непрерывном изменении параметра С особые точки заполнят всю
ось Ох.
Пример 6. Найти огибающую и геометрическое место особых точек
семейства
(у-О3—j (*-Q3=o. (Ю)
Решение. Дифференцируя по С обе части равенства A0), найдем
или
?_С-(л:-О2 = 0. A1)
Исключим теперь параметр С из полученного равенства A1) и из уравне-
уравнения A0) семейства. Подставив выражение у—С = (х — О2 в уравнение семей-
семейства, получим
(x_CL-|-(*--O3 = (), пли (x-Cf Г(Л—Q—11=0;
отсюда получаем два возможных значения С и два соответствующих им реше-
решения задачи.
Первое решение:
С=х;
поэтому из равенства A1) находим
или
У=х.
Второе решение:
поэтому из равенства A1) находим
2 Г 2 12
*+ |+]
или

§12]
ОСОБЫЕ РЕШЕНИЯ
45
Мы получили две прямые у=х и у=х—-^-. Первая из них является гео-
геометрическим местом особых точек, а вторая—огибающей (рис. 262)»
Замечание 2. В §7 гл. VI было доказано, что нормаль
к кривой служит касательной к ее эволюте. Следовательно, семей-
семейство нормалей к данной кривой является в то же время семей-
семейством касательных к ее эволюте. Таким образом, эволюта
кривой является огибающей семейства нормалей
этой кривой (рис. 263).
Рис. 262.
Рис, 263.
Это замечание позволяет указать еще один метод для нахож-
нахождения эволюты: чтобы получить уравнение эволюты, надо сначала
найти семейство всех нормалей данной кривой, а затем найти
огибающую этого семейства.
§ 12. Особые решения дифференциального уравнения
первого порядка
Пусть дифференциальное уравнение
имеет общий интеграл
Ф(*. у, С) = 0.
A)
B)
Предположим, что семейство интегральных кривых, соответ-
соответствующее уравнению B), имеет огибающую. Докажем, что эта
огибающая также является интегральной кривой дифференциаль-
дифференциального уравнения A).

46 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
Действительно, в каждой своей точке огибающая касается
некоторой кривой семейства, т. е. имеет с ней общую касательную.
Следовательно, в каждой общей точке огибающая и кривая се-
семейства имеют одинаковые значения величин х, у, у'.
Но для кривой из семейства числа х, уу у' удовлетворяют
уравнению A). Следовательно, тому же уравнению удовлетворяют
абсцисса, ордината и угловой коэффициент каждой точки огибаю-
огибающей. Но это и означает, что огибающая является интеграль-
интегральной кривой, а ее уравнение является решением данного диффе-
дифференциального уравнения.
Так как огибающая не является, вообще говоря, кривой семей-
семейства, то ее уравнение не может быть получено из общего инте-
интеграла B) ни при каком частном значении С. Решение дифферен-
дифференциального уравнения, не получающееся из общего интеграла ни
при каком значении С и имеющее своим графиком огибающую
семейства интегральных кривых, входящих в общее решение,
называется особым решением дифференциального уравнения.
Пусть известен общий интеграл
Ф(х, у, С) = 0;
исключая С из этого уравнения и уравнения Ф^ (ху у, С) = О,
получим уравнение я|э (#, у) = 0. Если эта функция удовлетворяет
дифференциальному уравнению (и не принадлежит семейству B)),
то это и есть особый интеграл.
Отметим, что через каждую точку кривой, изображающей особое
решение, проходит по крайней мере по две интегральные кривые,
т. е. в каждой точке особого решения нарушается
единственность решения.
Заметим, что точка, в которой нарушается единственность
решения дифференциального уравнения., т. е. точка, через кото-
которую проходит по крайней мере две интегральные кривые, назы-
называется особой точкой *). Таким образом, особое решение состоит
из особых точек.
Пример. Найти особое решение уравнения
Решение. Найдем его общий интеграл. Разрешим уравнение относи-
относительно у'\
dx=±
Разделяя переменные, получим
•) Граничные точки области существования решения также называют
особыми. Внутренняя точка области, через которую проходит единственная
интегральная кривая дифференциального уравнения, называется обыкновенной
точкой.

§13] УРАВНЕНИЕ КЛЕРО 47
Отсюда, интегрируя, находим общий интеграл
(x-C)*+y*=R2.
Легко видеть, что семейство интегральных линий представляет собой семей-
семейство окружностей радиуса R с центрами на оси абсцисс. Огибающей семейства
кривых будет пара прямых у= ± R.
Функции y=±R удовлетворяют дифференциальному уравнению (*). Сле-
Следовательно, это есть особый интеграл.
§ 13. Уравнение Клеро
Рассмотрим так называемое уравнение Клеро
Оно интегрируется с помощью введения вспомогательного пара-
параметра. Именно, положим -?с = р\ тогда уравнение A) примет вид
у = хр+$(р). (Г)
Продифференцируем по х все члены последнего уравнения,
имея в виду, что р = -г является функцией от х:
или
Приравнивая каждый множитель нулю, получим
И
C)
1) Интегрируя равенство B), получаем р = С (С=const). Под-
Подставляя это значение р в уравнение (Г), найдем его общий
интеграл
D)
который с геометрической точки зрения представляет собой се-
семейство прямых линий.
2) Если из уравнения C) найдем р как функцию от л: и под-
подставим ее в уравнение (Г), то получим функцию
У = хр(х)+Ц[р(хI (Г)
которая, как легко показать, представляет собой решение урав-
уравнения A).

48
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ. XIII
В самом деле, в силу равенства C)
находим -^ =
~& » т- е- Тх = р' Поэтому, подставляя функцию (Г')
в уравнение A), получаем тождество xp-\-ty(p) = p\ty(p)
Решение (Г') не получается из общего интеграла D) ни при
каком значении С. Это есть особое решение; оно получается
в результате исключения параметра р из уравнений
/>) = О,
или, что все равно, исключением С из уравнений
Следовательно,
особое решение уравнения Клеро
определяет огибающую семей-
семейства прямых, заданных общим
интегралом D).
Пример. Найти общий и особый интегралы
уравнения
dy
dx
4
dx
Яастпныа
шения
X
Решение. Общий интеграл получаем, заме-
dy
dx
аС
du
няя -г на С:
Рис. 264.
Для получения особого решения дифференцируем последнее уравнение по С:
¦ а =о.
Особое решение ^уравнение огибающей) получается в параметрическом виде
(где параметром служит С)
*=— - а аС*
Исключив параметр С, можем получить непосредственную зависимость между
х я у. Возводя обе части каждого уравнения в степень — и складывая
о
почленно полученные уравнения, найдем особое решение в следующем виде:
Это — астроида. Однако огибающей семейства (а следовательно, и особым ре-
решением) является не вся астроида, а только ее левая половина (так как из
параметрических уравнений огибающей видно, что х^О) (рис. 264).

§14] УРАВНЕНИЕ ЛАГРАНЖА 49
§ 14. Уравнение Лагранжа
Уравнением Лагранжа называется уравнение вида
где ф и г|э — известные функции от ~.
Это уравнение линейно относительно у к х. Рассмотренное
в предыдущем параграфе уравнение Клеро является частным
случаем уравнения Лагранжа при ф(у') = */'. Интегрирование
уравнения Лагранжа, так же как и интегрирование уравнения
Клеро, производится с помощью введения вспомогательного па-
параметра р. Положим
</' = />;
тогда исходное уравнение запишется в виде
У = хч{р)+Ц(р). (Г)
Дифференцируя пол:, получим
ИЛИ
р-ф(р) = [*ф'(р)+*'(р)]-?. О")
Из этого уравнения сразу можно найти некоторые решения:
именно, оно обращается в тождество при всяком постоянном
значении р = р0, удовлетворяющем условию
Действительно, при постоянном значении р производная -р = 0,
и обе части уравнения (Г) обращаются в нуль.
Решение, соответствующее каждому значению р = р0, т. е.
~^ = р0, является линейной функцией от х(так как производ-
производная ~ постоянна только у линейных функций). Для того чтобы
найти эту функцию, достаточно подставить в равенство (Г) зна-
значение р = р0:
Если окажется, что это решение не получается из общего ни
при каком значении произвольной постоянной, то оно будет
особым решением.
Найдем теперь общее решение. Для этого запишем урав-
уравнение (Г') в виде
dx х <?'(р) = У(р)
dp р — ф(р) р~~ ф(р)

50 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [гл- ХШ
и будем рассматривать х как функцию- от р~ Тогда полученное
уравнение будет линейным дифференциальным уравнением отно-
относительно функции х от р.
Решая его, найдем
* = ©(/>, Q. B)
Исключая параметр р из уравнений (Г) и B), получим общий
интеграл уравнения A) в виде
Пример- Дано уравнение
У = ху'*+у'*. (I)
Положив у' — р, будем иметь
у = хр* + р*. (Г)
Дифференцируя по х, получим
р = р* + [2хр + 2р]^9 (Г)
Найдем особые решения. Так как р — р2 при /;0=0 и рх = 1, то
решениями будут линейные функции [см. (Г)] [# = л;-02-{-02, т. е. у=0, и
У = х+\.
Будут ли эти функции частными или особыми решениями, мы увидим,
когда найдем общий интеграл., Для его разыскивания запишем уравнение (I")
dx 2 2
в виде -т х-. ==ТИ— и ^Удем Рассматривать х как функцию незави-
независимой переменной р. Интегрируя полученное линейное (относительно #) урав-
уравнение, находим
Исключая р иа уравнения: (Г) и (II), получим общий интеграл
Особым интегралом исходного уравнения будет
* = 0,
поскольку это решение не получается из общего ни при каком значении С.
Функция же у — х-\-\ является не особым, а частным решением; она
получается из общего решения при С=0.
§ 15. Ортогональные и изогональные траектории
Пусть им^ем одаопараметрическое семейство кривых
ф(*, у, О-о, A)
Линииг пересекающие все кривые данного семейства A) под
постоянным углом, называются изогональными траекториями.
Если этот угол прямой, то траектории называются ортогональ-
ортогональными траекториями.,

$15]
ОРТОГОНАЛЬНЫЕ И ИЗОГОНАЛЬНЫЕ ТРАЕКТОРИИ
51
Ортогональные траектории. Найдем уравнение орто-
ортогональных траекторий. Напишем дифференциальное уравнение
данного семейства кривых, исключая параметр С из уравнений
и
дФ . дФ cly п
Пусть это дифференциальное уравнение будет
= 0. (Г)
Здесь ~ есть угловой коэффициент касательной к кривой семей-
семейства в точке М(х\ у). Так как орто-
ортогональная траектория, проходящая че-
через точку М(х; у), перпендикулярна
к соответствующей кривой семейства,
то угловой коэффициент касательной
к ней -р связан с -г соотношением
(рис. 265)
dx
dy-p
Чх
Подставляя это выражение в уравне-
уравнение (Г) и опуская индекс Т, получим Рис 2б5.
соотношение между координатами про-
произвольной точки (х; у) и угловым коэффициентом ортогональной
траектории в этой точке, т. е. дифференциальное урав-
уравнение ортогональных траекторий
F(x* y~wY°- ©
\ dx J
Общий интеграл этого уравнения
Ф±(х, У, С) = 0
дает семейство ортогональных траекторий.
С ортогональными траекториями приходится иметь дело, на-
например, при рассмотрении плоского течения жидкости.
Положим, что течение жидкости на плоскости происходит так,
что в каждой точке плоскости Оху определен вектор v (x, у)
скорости движения. Если этот вектор зависит только от поло-
положения точки на плоскости, но не зависит от времени, то движе-
движение называется стационарным, или установившимся. Такое дви-

52
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ. XIII
жение мы и будем рассматривать. Кроме того, мы допустим, что
существует потенциал скоростей, т. е. такая функция и(х, у),
что проекции вектора v (х, у) на оси координат vx (x, у) и vy (х, у)
являются ее частными производными по х и у:
ди
Линии семейства
ди
и(х, у)-=
D)
E)
называются эквипотенциальными линиями (т. е. линиями равного
потенциала).
Линии, касательные к которым во всех точках совпадают по
направлению с вектором v(x> у), называются линиями тока и
дают траектории движущихся точек.
Покажем, что линии тока суть ортогональные траектории
семейства эквипотенциальных линий (рис. 266).
Пусть ф —угол, образованный вектором скорости v с осью
Ох. Тогда на основании соотношения D)
L
дм(*, у)
~дГ~
= | v\ sinq>;
отсюда находим угловой коэффициент ка-
касательной к линии тока
F)
Рис. 266.
Угловой коэффициент касательной к эквипотенциальной линии
получим, дифференцируя по х соотношение E):
откуда
dx
дх
ди
ду
G)
Таким образом, угловой коэффициент касательной к эквипотен-
эквипотенциальной линии обратен по величине и противоположен по знаку
угловому коэффициенту касательной к линии тока. Отсюда и сле-
следует, что эквипотенциальные линии и линии тока взаимно орто-
ортогональны.

§15]
ОРТОГОНАЛЬНЫЕ И ИЗОГОНАЛЬНЫЕ ТРАЕКТОРИИ
53
В случае электрического или магнитного поля ортогональными
траекториями семейства эквипотенциальных линий служат сило-
силовые линии этого поля.
Пример 1. Найти ортогональные траектории семейства парабол
у = Сх\
Решение. Напишем дифференциальное уравнение семейства
t/ 2 1
Исключая С, получим -^— = — . Заменяя здесь у' на г , получим диф-
У х У
ференциальное уравнение семейства ортогональных траекторий -=—,
xdx
или уау— 2~.
Его общий интеграл
Следовательно, ортогональными траекториями данного семейства парабол будет
некоторое семейство эллипсов с полуосями а=-2С, Ь = СУ~2 (рис. 267).
Рис. 267.
Изогональные траектории. Пусть траектории пере-
пересекают кривые данного семейства под углом а, причем tga^=k
Угловой коэффициент ^=tgq) (рис. 268) касательной к кри-
кривой семейства и угловой коэффициент -р = tg -ф к изогональной
траектории связаны соотношением
tg ф = tg (ф — ос) = •

54
т. е.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ. XIII
dy
dx
B')
dx
Подставляя это выражение в уравнение (Г) и опуская ин-
индекс 7\ получим дифференциальное уравнение изогональных тра-
траекторий.
Пример 2. Найти изогональные траектории семейства прямых
У = Сх, (8)
пересекающие линии данного семейства под углом а, тангенс которого
Решение. Напишем дифференциальное уравнение данного семейства.
Дифференцируя по х уравнение (8), находим ~ = С. С другой стороны, из
того же уравнения С=у/х. Следователь-
Следовательно, дифференциальное уравнение дан-
du и
ного семейства имеет вид -~ = —.
dx х
Рис. 268.
Рис. 269.
Пользуясь соотношением B'), получим дифференциальное уравнение изо-
изогональных траекторий
dM_k
dx
y
х
"dx^1
Отсюда, опуская индекс Т, находим
dy__ ~x
dx
1-fti
Интегрируя это однородное уравнение, получаем общий интеграл
In l/"**+ya=-r- arctg -^-4-In Ct (9)
ft V ' ^ '

§ 16] УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ 55
который и определяет семейство изогональных траекторий. Чтобы выяснить,
какие именно кривые входят в это семейство, перейдем к полярным коорди-
координатам:
натам:
Подставляя эти выражения в равенство (9), получим 1пр=— Ф + lnC, или
p=<p/Cg*. Следовательно, семейство изогональных траекторий является семей-
семейством логарифмических спиралей (рис. 269).
§ 16. Дифференциальные уравнения высших порядков
(общие понятия)
Как уже указывалось выше (см. § 2), дифференциальное урав-
уравнение n-го порядка символически можно записать в виде
F(x,y,y',y", ..., */<«>) = 0, A)
или, если его можно разрешить относительно n-й производной,
yln) = f(x, у, у', у", ..., у<»-»). (Г)
В настоящей главе мы будем рассматривать только такие
уравнения высших порядков, которые можно разрешить относи-
относительно высшей производной. Для этих уравнений имеет место
теорема о существовании и единственности решения, аналогичная
соответствующей теореме о решении уравнения первого порядка.
Теорема. Если в уравнении
y{n) = f(x, у, у\ ..., у'п~г))
функция f(x> у, у\ ..., у{п~1]) и ее частные производные по
аргументам у, у'> ..., у{п) непрерывны в некоторой области,
содержащей значения
х = х0, у=у0, y' = yi, ..., У{п'1] = Уоп},
то существует и притом единственное решение у = у (х) уравне-
уравнения, удовлетворяющее условиям
У]х=х0— Уоу У \x-Xq — Уоу •••» У 1*=*0— Уо • W
Эти условия называются начальными условиями. Доказатель-
Доказательство этой теоремы выходит за рамки данной книги.
Если рассматривать уравнение второго порядка
/ = /(*, У> У*)>
то начальными условиями при х^=х0 для решения будут условия
где х0У у0У у о—заданные числа. Геометрический смысл этих усло-
условий следующий: через заданную точку плоскости (*0;#0)с задан-

56 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. ХШ
ным тангенсом угла наклона касательной у'о проходит единствен-
единственная кривая. Из этого, далее, следует, что если мы будем задавать
различные значения у'о при постоянных х0 и у0, то получим бес-
бесчисленное множество интегральных кривых с различными углами
наклона, проходящих через заданную точку.
Введем теперь понятие общего решения уравнения п-го порядка.
Определение. Общим решением дифференциального урав-
уравнения п-го порядка называется функция
С19 С
2,
зависящая от п произвольных постоянных Си С2, ..., Сп и такая,
что:
а) она удовлетворяет уравнению при любых значениях посто-
постоянных Си С2, ..., Сп\
б) при заданных начальных условиях
У\хшх> = Уо> У' \х=х0 = У*, • •, У{п~1] |л-= v0 = y{Qn'l)
постоянные С19 С2, ..., Сп можно подобрать так, что функция
у = у(х, С1У С2, ..., Сп) будет удовлетворять этим условиям (пред-
(предполагая, что начальные значения х09 у0, yQy ..., у^} принад-
принадлежат области, где выполняются условия существования ре-
решения).
Соотношение вида Ф (х, у, Си С2, ..., Сп) = 0, неявно опре-
определяющее общее решение, называется общим интегралом диффе-
дифференциального уравнения.
Всякая функция, получающаяся из общего решения при кон-
конкретных значениях постоянных Ciy C2, ..., Сп, называется част-
частным решением. График частного решения называется интеграль-
интегральной кривой данного дифференциального уравнения.
Решить (проинтегрировать) дифференциальное уравнение п-го
порядка—значит:
1) найти его общее решение (если начальные условия не
заданы) или
2) найти то частное решение уравнения, которое удовлетво-
удовлетворяет заданным начальным условиям (если таковые имеются).
В следующих параграфах будут изложены методы решения
различных уравнений п-го порядка.
§ 17. Уравнение вида y(n)=f(x)
Простейшим уравнением п-го порядка является уравнение вида
#(п) = /(*)• A)
Найдем общий интеграл этого уравнения.

§ 17J УРАВНЕНИЕ ВИДА yin)=f (x) 57
Интегрируя по х левую и правую части и принимая во вни-
внимание, что у{п) = (у{п^1)УУ получим
х0
где x{i—любое фиксированное значение х, а Сх — постоянная инте-
интегрирования.
Интегрируя еще раз, получим
Продолжая далее, получим, наконец (после п интегрирований),
выражение общего интеграла
(я —2I
Чтобы найти частное решение, удовлетворяющее начальным усло-
условиям
Уи=лгэ — Уо» У |дг=^0 — Уо> •••,[/ 1а = а'о— ?/о г
достаточно положить
Пример 1. Найти общий интеграл уравнения
#" = sin (&*)
и частное решение, удовлетворяющее начальным условиям
р|*-о = О, У' U—о = 1 •
Решение.
X
cos kx—1
'= \ sinkxdx+C1 =
О
г—
или
Это есть общий интеграл. Чтобы найти частное решение, удовлетворяю-
удовлетворяющее данным начальным условиям, достаточно определить соответствующие
значения Сг и С2.
Из условия у \х=*о находим С2 = 0.
Из условия у' 1^=0 = 1 находим Сх = 1.

5g ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. ХШ
Таким образом, искомое частное решение имеет вид
__ sin kx .
у~~~ k* ""*"
Дифференциальные уравнения рассмотренного вида встречаются в теории
изгибания балок.
Пример 2. Рассмотрим упругую призматическую балку, изгибающуюся
под действием внешних сил, как непрерывно распределенных (вес, нагрузка),
так и сосредоточенных. Направим ось Ох горизонтально, по оси балки в ее
недеформированном состоянии, ось Оу—верти-
Оу—вертикально вниз (рис. 270).
Каждая сила, действующая на балку (на-
(например, нагрузка балки, реакция опор), имеет
момент относительно какого-нибудь поперечно-
поперечного сечения балки, равный произведению силы
на расстояние точки приложения силы от дан-
данного сечения. Сумма М (х) моментов всех сил,
приложенных к части балки, расположенной
по одну сторону от „данного сечения, с абс-
Рис. 270. циссой х, называется изгибающим моментом
балки относительно данного сечения. В курсе
сопротивления материалов доказывается, что изгибающий момент балки ра-
равен EJ/R, где Е—так называемый модуль упругости, зависящий от мате-
материала балки; J—момент инерции площади поперечного сечения балки от-
относительно горизонтальной линии', проходящей через центр тяжести пло-
площади поперечного сечения; R—радиус кривизны оси изогнутой балки, кото-
который выражается формулой (§ 6 гл. VI)
0
* а?
—**;
4t
л1* . .. Л
и
Р
at
ч~ \у"\ '
Таким образом, дифференциальное уравнение изогнутой оси балки имеет
вид
у" ^Л1*1. B)
,3/2 EJ ' {Z)
Если считать, что деформации малы и что касательные к оси балки при
изгибе [образуют малый угол с осью Ох, то мы можем пренебречь квадратом
малой величины у'2 и считать R = \/y".
Тогда дифференциальное уравнение изогнутой балки примет вид
*"=4г-« <2'>
а это уравнение есть уравнение вида A).
Пример 3. Балка наглухо заделана в конце О и подвергается действию
сосредоточенной вертикальной силы Р, приложенной к концу балки L на рас-
расстоянии / от места закрепления (рис. 270). Весом балки пренебрегаем.
Рассмотрим сечение в точке N (х). Изгибающий момент относительно сече-
сечения N в данном случае будет равен М (#) = (/—х)Р. Дифференциальное урав-
уравнение B') примет вид
Начальные условия: при я = 0 прогиб у равен нулю и касательная к изогну-
изогнутой оси балки совпадает с осью Ох, т, е, #)*=<> = 0, ^/' |АГв0 = 0. Интегрируя

§ 18] НЕКОТОРЫЕ ТИПЫ УРАВНЕНИЙ
уравнение, найдем
В частности, из_ формулы C) определяется прогиб h на конце балки L:
Plz
hy\
§18. Некоторые типы дифференциальных уравнений
второго порядка, приводимых к уравнениям первого порядка.
Задача о второй космической скорости
I. Уравнение вида
dx2 ' [Ху dx) W
не содержит явным образом искомой функции у.
Решение. Обозначим производную ~ через р, т. е. положим
dy гг. Л d2y dp
-2т = d. i огда —г-z =* -%—.
dx ^ dx2 dx
Подставляя эти выражения производных в уравнение A), полу-
получим уравнение первого порядка
относительно неизвестной функции р от х. Проинтегрировав это
уравнение, находим его общее решение
а затем из соотношения -г- = Р получаем общий интеграл уравне-
уравнения A)
Пример 1. Рассмотрим дифференциальное уравнение цепной линии
(см. § 1)
Положим

60 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [гл- хш
тогда
<Ру_ dp
dx1 ~~ dx '
и мы получаем дифференциальное уравнение первого порядка относительно
вспомогательной функции р от х
Разделяя переменные, будем иметь
dp _dx
откуда
In (р
Но так как р = —¦ , то последнее соотношение представляет собой дифферен-
дифференциальное уравнение относительно искомой функции */. Интегрируя его, полу-
получим уравнение цепной линии (см. § 1)
Найдем частное решение, удовлетворяющее следующим начальным условиям:
#U=o = a, у' U=o = O.
Второе условие дает ^ = 0, первое С2—0*
Окончательно получаем
y — ach (х/а).
Замечание. Аналогичным способом можно проинтегриро-
проинтегрировать уравнение
Полагая у{п)~ру получим для определения р уравнение
первого порядка
Узнав отсюда р как функцию от х, из соотношения у{п~1] = р
на эдем у (см. § 17).
II. Уравнение вида
> dx
B)
не содержит явным образом независимой пере-
переменной х.

§18] НЕКОТОРЫЕ ТИПЫ УРАВНЕНИЙ 61
Для его решения снова положим
но теперь мы будем считать р функцией от у (а не
от х, как прежде). Тогда
d2y dp dp dy dp
dx2 dx dy dx dy P'
Подставляя в уравнение B) выражения ^ и ^f, получим урав-
уравнение первого порядка относительно вспомогательной функции р
% Р). D)
Интегрируя его, найдем р как функцию от у и произвольной
постоянной Сг\
Подставляя это значение в соотношение C), получим дифферен-
дифференциальное уравнение первого порядка для функции у от х
Разделяя переменные, находим
Интегрируя это уравнение, получим общий интеграл исходного
уравнения
Ф(х, у, Clt C,) = 0.
Прим е,р 2. Найти общий интеграл уравнения
Решение. Положим з^ = Р» рассматривая р как функцию от у. Тогда
У" — Р~т~* и МЬ1 получаем уравнение первого порядка для вспомогательной
функции р
Интегрируя это уравнение, находим/?2 = СХ—у"^3 илпр=± \ С±—#~2/з.
и dy
Но Р — -Т- ; следовательно, для определения у получаем уравнение
dy . vxUdu
= dx. или У иУ . = dx, откуда дг+С2 =
\ —У аУ .. Для вычисления последнего интеграла сделаем подста-

62 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XII
новку C%yl* — I =t2. Тогда
1)'/. » , ^=3* (<*+ i)V. -i-Л.
Следовательно,
Г y''dy __ 1 C3t(t*+\
Окончательно получаем
*+C2 = ±
3 / ** х
Пример 3. Пусть точка движется по оси Ох под действием силы,
зависящей только от положения точки. Дифференциальное уравнение движе-
движения будет
— ~F(
j. л * dx
Пусть при / = 0 будет x~xQ, — = v0.
Умножив обе части уравнения на -тт- dt и проинтегрировав в пределах
от 0 до /, получим
X
или
|=~/П1/о = const.
Первое слагаемое последнего равенства представляет собой кинетическую
энергию, второе—потенциальную энергию движущейся точки. Из полученного
равенства следует, что сумма кинетической и потенциальной энергии остается
постоянной во все время движения.
Задача о математическом маятнике. Пусть материальная
точка массы m под действием силы тяжести движется по окружности L, лежа-
лежащей в вертикальной плоскости. Найдем уравнение движения точки, пренебре-
пренебрегая силами сопротивления (т. е. силой трения, силой сопротивления воздуха
и т. п.).
Поместим начало координат в низшей точке окружности, ось Ох направим
по касательной к окружности (рис. 271).
Обозначим через / радиус окружности, через s—длину дуги от начала О
до переменной точки М, где находится масса т, причем эту длину берем с соот-
соответствующим знаком (s > 0, если точка М правее точки О; s < 0, если М
левее О).
Наша задача заключается в установлении зависимости s от времени t.
Разложим силу тяжести mg на тангенциальную и нормальную составляю-
составляющие. Первая, равная—mgsinq), вызывает движение! вторая уничтожается
реакцией кривой, по которой движется масса т.

§18]
НЕКОТОРЫЕ ТИПЫ УРАВНЕНИЙ
63
Таким образом, уравнение движения имеет вид
d2s
т
dt*
•= — mgstacp.
Так как для окружности угол ср = $//, то мы получаем уравнение
Это дифференциальное уравнение II типа (так
как оно не содержит явным образом независимой
переменной t).
Интегрируем его соответствующим образом:
ds d2s dp
Следовательно, р —р- = — g sin у-, или р dp =
=— g sin у ds, откуда
= 2gt cos j
Обозначим через s0 наибольшую длину ду-
дуги, на которую отклоняется точка М. При s = sQ
скорость точки равна нулю:
ds | Л
Рис. 27U
Это дает возможность определить Сг\ О = 2gl cos-j-+ Ci, откуда Сг ==
=—2 gl cos -у-. Поэтому р2 = f -~- J = 2g/ f cos -т—cos -j-) , или, приме-
применяя к последнему выражению формулу для разности косинусов,
откуда *)
E)
F)
Это—уравнение с разделяющимися переменными. Разделяя переменные,
получим
sin
2/
sin
s0— s
2/
G)
*) Перед корнем мы берем знак плюс. Из замечания в конце решения
задачи следует, что рассматривать случай, когда берется знак минус, нет
надобности,

64 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ XIII
Будем пока предполагать, что s Ф s0, тогда знаменатель дроби отличен от
нуля. Если считать, что s = 0 при ? = 0, то из равенства G) получаем
s
f
J
О
j/ s
o — S
(8)
Это равенство и дает зависимосгь s от t. Интеграл, стоящий слева, не выра-
выражается через элементарные функции, не выражается через элементарные функ-
функции и функция s от t. Рассмотрим поставленную задачу приближенно. Будем
предполагать, что углы so/l и s/l малы. Углы (s+so)/2/ и (s0—s)/2/ не будут
превосходить s0//. В уравнении F) синусы углов заменим приближенно углами:
ds
dt — r б* V 2/ 2/
или
Разделяя переменные, получим (предполагаем пока, что s Ф s0)
Снова будем считать, что s=t) при ^ = 0. Интегрируя последнее уравнение,
получим
==/!•
ИЛИ
arcsin—= J/ -y-f,
откуда
s = sosin у -S-1. (9)
Замечание. При решении мы предполагали, что s Ф s0. Но путем
непосредственной подстановки убеждаемся, что функция (9) есть решение
уравнения F') при любом значении t.
Напомним, что решение (9) является приближенным решением уравнения
E), так как уравнение F) мы заменили приближенным уравнением F').
Равенство (9) показывает, что точка М (которую можно рассматривать
как конец маятника) совершает гармонические колебания с периодом колеба-
колебания Т = 2л у —• Этот период не зависит от амплитуды колебания s0.
Пример 4. Задача о второй космической скорости.
Определить наименьшую скорость, с какой нужно бросить тело верти-
вертикально вверх, чтобы оно не вернулось на Землю. Сопротивлением воздуха
пренебречь.
Решение. Обозначим массу Земли и массу брошенного тела соответст-
соответственно через М и т. По закону тяготения Ньютона сила / притяжения,
действующая на тело т, будет
, .Mm

§18] НЕКОТОРЫЕ ТИПЫ УРАВНЕНИЙ 65
где г—расстояние между центром Земли и центром масс брошенного тела,
k—гравитационная постоянная.
Дифференциальное уравнение движения указанного тела с массой т будет
или
d2r M tm
Мы взяли знак минус потому, что в задаче ускорение отрицательно.
Дифференциальное уравнение A0) есть уравнение вида B). Будем решать это
уравнение при следующих начальных условиях: r=/?, ~Jf~vo ПРИ *==0«
Здесь/?—радиус Земли, v0—скорость бросания. Обозначим —тг-^и, -щ- —
dv dv dr dv _.
= -—=~—-—-=^-7-, где v—скорость движения. Подставляя в уравне-
dt dr dt dr
ние A0), получим v-r^—^~i~- Разделяя переменные, получаем vdv =
=—kM—? . Интегрируя это уравнение, находим
Из условия, что v = v0 на поверхности Земли (при r = R), определим С\.
или
С -__^4-—
Подставим найденное значение Сг в равенство A1):
ИЛИ
По условию тело должно двигаться так, чтобы скорость всегда была положи-
положительной, следовательно, v2/2 > 0. Так как/величина kM/r при неограниченном
возрастании г делается как угодно малой, то условие v2j2 > 0 будет выпол-
выполняться при любом г только в случае '
vl kM л
-2~ Х^0, A3)
или
— •
Следовательно, наименьшая скорость будет определяться равенством
Н. С. Пискунов, т. 2

gg ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
где
fc = 6,66.Ю-8 -^V, Я =63-107 см.
г-с2
На поверхности Земли при r = R ускорение силы тяжести равно
g(g=981 см/с2). На основании этого из равенства A0) получаем g~k-^-f
или M^zS—. Подставляя это значение М в формулу A4), получаем
= У%-981-63-107 » 11,2-105 см/с=11,2 км/с,
§ 19. Графический метод интегрирования
дифференциального уравнения второго порядка
Выясним геометрический смысл дифференциального уравнения
второго порядка. Пусть имеем уравнение
/ = /(*, У, У')- A)
Обозначим через ср угол, который касательная к кривой образует
с положительным направлением оси Ох; тогда
|=tgq>. B)
Чтобы выяснить геометрический смысл второй производной,
вспомним формулу, определяющую радиус кривизны кривой
в данной точке *),
Отсюда
у. R
Но
у'3 = 1 -htg^ф = sec2Ф, A + у^/^i5есф{=?_2_^
поэтому
Подставляя теперь в уравнение A) полученные выражения для
у и у", будем иметь
*) До сих пор мы всегда считали радиус кривизны положительным
числом, однако в настоящем параграфе мы будем считать радиус кривизны
числом, которое может принимать как положительные, так и отрицательные
значения: если кривая выпукла (у" < 0), мы считаем радиус кривизны отри-
отрицательным (R < 0); если кривая вогнута (у" > 0),— положительным (R > 0).

i 19]
ГРАФИЧЕСКИЙ МЕТОД ИНТЕГРИРОВАНИЯ
67
ИЛИ
П __.
1
cos3ф |./(*> у, tg<p)
D)
Уо
0
Mo
с
ё
ч
/яр*
k у
Отсюда видно, что дифференциальное уравнение второго порядка
определяет величину радиуса кривизны интегральной линии, если
заданы координаты точки и направле-
направление касательной в этой точке.
Из предыдущего вытекает способ
приближенного построения интеграль-
интегральной кривой при помощи гладкой
кривой, составленной из дуг окруж-
окружностей*). Пусть, например, требу-
требуется найти решение уравнения A),
удовлетворяющее следующим началь-
начальным условиям:
У \х=хо = Уо, У' \х=х0 = У1 Рис. 272,
Через точку М0(х0; у0) проведем луч М0Т0 с угловым коэф-
коэффициентом у' = tg ф0 = у'о (рис. 272). Из уравнения D) найдем
величину R = R0. Отложим отрезок М0С0, равный R0J на перпен-
перпендикуляре к направлению М0Т0, и из точки Со, как из центра,
опишем небольшую дугу М0М± радиусом 7?0. Заметим при этом,
что если Ro < 0, то отрезок М0С0 нужно направлять в ту сто-
сторону, чтобы дуга окружности была обращена выпуклостью вверх,
а при R0 > 0 — выпуклостью вниз (см. сноску на предыдущей
странице).
Пусть, далее, х1У yi — координаты точки Miy лежащей на
построенной дуге и достаточно близкой к точке Мо, a tgq^ —
угловой коэффициент касательной MtTt к проведенной окруж-
окружности в точке М±. Из уравнения D) найдем соответствующее
точке Mi значение R=Rt. Проведем отрезок №гС1у перпендику-
перпендикулярный к M±Tiy равный Rly и из точки Q, как из центра, .опишем
дугу МХМ2 радиусом Rt. Затем на этой дуге возьмем близкую
к Mt точку М2(х2У у2) и продолжаем таким образом построение,
пока не получим достаточно большой кусок кривой, состоящей
из дуг окружностей. Из предыдущего ясно, что эта кривая при-
приближенно является интегральной линией, проходящей через
точку Мо. Очевидно, что построенная кривая будет тем ближе
к интегральной кривой, чем меньше будут дуги MQMiy MtM2y .. ¦
*) Кривая называется гладкой, «ели она имеет касательную во всех точ-
точках, причем угол наклона этой касательной есть непрерывная функция
от длины дуги s.
3*

68 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
§ 20. Линейные однородные уравнения. Определения
и общие свойства
Определение 1. Дифференциальное уравнение п-го порядка
называется линейным, если оно первой степени относительно сово-
совокупности искомой функции у и ее производных у\ ..., уКп""г\ уКп\
т. е. имеет вид
aoy{») + a1y^)+...+any = f(x)y A)
где а0, aiy а2, ..., ап и f(x) — заданные функции от х или постоян-
постоянные, причем а0ф0 для всех значений х из той области, в кото-
которой мы рассматриваем уравнение A). В дальнейшем мы будем
предполагать, что функции а0, aiy ..., ап и f(x) непрерывны при
всех значениях х, причем коэффициент ао= 1 (если он не равен 1,
мы можем все члены уравнения поделить на него). Функция f{x),
стоящая в правой части уравнения, называется правой частью
уравнения.
Если }(х)фО, то уравнение называется линейным неоднород-
неоднородным или уравнением с правой частью. Если же / (л;)==0, то урав-
уравнение имеет вид
и называется линейным однородным или уравнением без правой
части (левая часть этого уравнения является однородной функ-
функцией первой степени относительно у, у\ у\ ..., у{п)).
Установим некоторые основные свойства линейных однородных
уравнений, ограничиваясь в доказательствах уравнениями второго
порядка.
Теорема 1. Если уг и у2—два частных решения линейного
однородного уравнения второго порядка
у" + а1у'+а2у = 0, C)
то yiJry2 есть также решение этого уравнения.
Доказательство. Так как ух и у2 — решения уравнения,то
У1 + агУ[ + а2у± = 0, yl + агу2 + а2у2 = 0. D)
Подставляя в уравнение C) сумму у± + у2 и принимая во внима-
внимание тождества D), будем иметь
(Ух + У%У + аг {уг + У2У + а2 {уг + у2) =
= (Ух + агУг + я 2#i) + (У1 + йхУг + ад) = 0+0 = 0,
т.е. Уг + у2 есть решение уравнения.
Теорема 2. Если ух есть решение уравнения C) и С — по-
постоянная , то Суг есть также решение уравнения C).

ЛИНЕЙНЫЕ ОДНОРОДНЫЕ УРАВНЕНИЯ
69
Доказательство. Подставляя в уравнение C) выраже-
выражение Суъ получим
(СУгУ + а± (Суху + а2 (Сух) = С(у'[ + а±у[ + а2 уг) = С ¦ 0 = 0;
тем самым теорема доказана.
Определение 2. Два решения уравнения C) у± и у2 назы-
называются линейно независимыми на отрезке [а, 6], если их отноше-
отношение на этом отрезке не является постоянным, т. е. если
f#const.
В противном случае решения называются линейно зависимыми.
Иными словами, два решения у± и у2 называются линейно зави-
зависимыми на отрезке [а, 6], если существует такое постоянное
число л, что — = Я при а^х^Ь. В этом случае yt = ky2.
Пример 1. Пусть имеем уравнение у"—у~0. Легко проверить, что
функции ех, е~х, Зех, 5е~х являются решениями этого уравнения. При этом
функции ех и е~х линейно независимы на любом отрезке, так как отношение
__-=е2* не остается постоянным при изменении х. Функции же ех и Зех
Зех о
линейно зависимы, так как —?-s=3 = const.
Определение 3. Если yt и у2 суть функции от х, то опре-
определитель
TV7/4. и \ #1
У'г У г
= УгУ* - У1У2
называется определением Вронского, или вронскианом данных
функций.
Теорема 3. Если функции yt и у2 линейно зависимы на
отрезке [а, Ь\ то определитель Вронского на этом отрезке
тождественно равен нулю.
Действительно, если y2 = hyb где к = const, то #2 = ^i и
ь У 2) =
yi Уг
У± tyi
у[ К
У1 У1
= 0.
Теорема 4. Если определитель Вронского W(y±, t/2), состав-
составленный для решений ух и у2 линейного однородного уравнения C),
не равен нулю при каком-нибудь значении х = хона отрезке \ау Ь\
где коэффициенты уравнения непрерывны, то он не обращается
в нуль ни при каком значении х на этом отрезке.
Доказательство. Так как yt и у2 — два решения урав-
уравнения C), то
У % + ащ\ + а2у2 = 0,
г - 0.

70 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 1ГЛ. XIII
Умножая члены первого равенства на у1У члены второго ра-
равенства на у2 и вычитая из первых вторые, получим
(УгУ1 - yiy2) + <Н (У1У2 - У [у 2) = 0. E)
Разность, стоящая во второй скобке, есть определитель Врон-
Вронского W(yi9 у2)9 а именно, W (yi9 у2) = у1у2-у'1Уъ. Разность, стоя-
стоящая в первой скобке,-есть производная от определителя Вронского
W'x (Уи У%) = (УгУ* - У1У2У = УлУ\ - У\У*
Следовательно, равенство E) принимает вид
= 0. F)
Найдем решение последнего уравнения, удовлетворяющего
начальному условию W \х=Хо = WQ. Найдем сначала общее решение
уравнения F) в предположении, что W Ф 0. Разделяя переменные
в уравнении F), получаем -^ = — агйх.
Интегрируя, находим
ИЛИ
t W С ,
1п-^- = —j axdx%
х0
откуда
х
-J atdx
W C
G)
Заметим, что можно было написать функцию G) и сказать,
что эта функция удовлетворяет уравнению F), в чем можно легко
убедиться непосредственной подстановкой этой функции в урав-
уравнение F). Предположение №ф0 пе требуется.
Формула G) называется формулой Лиувилля.
Определим С так, чтобы удовлетворялось начальное условие.
Подставляя х = х0 в левую и правую часть равенства G), получаем
Следовательно, решение, удовлетворяющее начальным усло-
условиям, примет вид
х
-J axdx
W = Woe *<> . G')
По условию W0=?0. Но тогда из равенства G') следует, что
W Ф 0 ни при каком значении х, потому что показательная функ-

§ 203 ЛИНЕЙНЫЕ ОДНОРОДНЫЕ УРАВНЕНИЯ 71
ция не обращается в нуль ни при каком конечном значении
аргумента. Теорема доказана.
Замечание 1. Если определитель Вронского равен нулю
при каком-нибудь значении х = х0У то он равен также нулю при
любом значении х из рассматриваемого отрезка. Это непосредст-
непосредственно следует из формулы G): если W = Q при х = х0, то
следовательно, W = 0, каково бы ни было значение верхнего
предела х в формуле G).
Теорема 5. Если решения уг и у2 уравнения C) линейно
независимы на отрезке [а, 6], то определитель Вронского W>
составленный для этих решений, не обращается в нуль ни в одной
точке указанного отрезка.
Доказательство. Предварительно заметим следующее.
Функция у==0 есть решение уравнения C) на отрезке [а, 6],
удовлетворяющее начальным условиям
У \x=xQ = 0, у' \х=Хо = 0,
где х0 — любая точка отрезка [а, Ь]. Из теоремы существования
и единственности (см. § 16), которая применима к уравнению C),
следует, что не существует другого решения уравнения C), удов-
удовлетворяющего начальным условиям
Из этой теоремы так же следует, что если решение уравне-
уравнения C) тождественно равно нулю на некотором отрезке или интер-
интервале (а, р), принадлежащем отрезку [а, 6], то это решение тожде-
тождественно равно нулю на всем отрезке [а, Ь]. Действительно, в точке
х = $ (и в точке х — а) решение удовлетворяет начальным условиям
у|*=р = О, у' U=p = 0.
Следовательно, по теореме единственности оно равно нулю в неко-
некотором интервале |3 — d<#<p + d, где d определяется величиной
коэффициентов уравнения C). Таким образом, расширяя интервал
каждый раз на величину d, где у = 0, мы докажем, что у = 0
на всем отрезке [а, Ь].
Теперь приступим к доказательству теоремы 5. Допустим, что
^ (#it У2) = 0 в некоторой точке отрезка [а, Ь]. Тогда по теореме 3
определитель Вронского W (у19 у2) будет равен нулю во всех точ-
точках отрезка [а, Ь\\ W = 0 или у1у'2—у'1у2 = Ъ.
Допустим, что угф0 на отрезке [а, Ь]. Тогда на основании
последнего равенство можно написать —2 , * 2 =0 или (—\ —0.
Отюда следует
Jj-=X = const,

72 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ?гл- хш
т. е. решения уг и у2 линейно зависимы, что противоречит пред-
предположению о их линейной независимости.
Допустим далее, что r/f = 0 в точках xiy х2, ..., хкУ принад-
принадлежащих отрезку [а, Ь]. Рассмотрим интервал (а, хг). На этом
интервале у± Ф 0. Следовательно, на основании только что дока-
доказанного следует, что на интервале (а, л^)
-^- = Х = const, или y2==hyi>
Рассмотрим функцию у = у2 — ^у^ Так как у2 и у± суть решения
уравнения C), то у = у2 — куг — решение уравнения C) и у = 0
на интервале (а, хг). Следовательно, на основании замечания
в начале доказательства следует, что у = Уъ — 'Ьу±==0 на отрезке
[а, 6], или
на отрезке [а, Ь], т. е. у2 и у± линейно зависимы.
Но это противоречит предположению о линейной независимости
решений у2 и у±и Таким образом, мы доказали, что определитель
Вронского не обращается в нуль ни в одной из точек отрезка [а, Ь].
Теорема 6. Если у± и у2 — два линейно независимых реше-
решения уравнения,C), то
(8)
где Сг и С2—произвольные постоянные^ есть его общее решение.
Доказательство. Из теорем 1 и 2 следует, что функция
С1у1-\-С2у2 есть решение уравнения C) при любых значениях
Сг и С2.
Докажем теперь, что каковы бы ни были начальные условия
у |л-=а'о = Уоу у'\х=х0 = У'о> можно так подобрать значения произволь-
произвольных постоянных С± и С2, чтобы соответствующее частное решение
СхУ1 + С2у2 удовлетворяло заданным начальным условиям.
Подставляя начальные условия в равенство (8), будем иметь
У о = Сгу10 + С2у20У у о = Сгу[0 + С2у'20> (9)
где обозначено
У1\х=х0 = Ум* У2 U=^o== #20> Уг \х=хо — У10) Уч |^=лг0=:У20.
Из системы (9) можно определить Ct и С2, так как определитель
этой системы
Ю У20
0 «/20
есть определитель Вронского при х = х0 и, следовательно, не
равен 0 (в силу линейной независимости решений yt и у2). Част-
Частное решение, которое получится из семейства (8) при найденных
значениях Cf и С2, удовлетворяет заданным начальным условиям.
Таким образом, теорема доказана.

§20J ЛИНЕЙНЫЕ ОДНОРОДНЫЕ УРАВНЕНИЯ 73
Пример 2. Уравнение у"-\ у' -у=0, коэффициенты которого
«1=1/л: и а2 = —1/jc2 непрерывны на любом отрезке, не содержащем точки
х = 0у допускает частные решения у\ — х, у2 = 1/х (это легко проверить под-
подстановкой в уравнение). Следовательно, его общее решение имеет вид
Замечание 2. Не существует общих методов для нахожде-
нахождения в конечном виде общего решения линейного уравнения
с переменными коэффициентами. Однако для уравнения с посто-
постоянными коэффициентами такой метод существует. Он будет изло-
изложен в следующем параграфе. Для случая же уравнений с пере-
переменными коэффициентами в главе XVI «Ряды» будут указаны
некоторые приемы, которые дадут возможность находить прибли-
приближенные решения, удовлетворяющие определенным начальным
условиям.
Здесь мы докажем теорему, которая позволяет находить общее
решение дифференциального уравнения второго порядка с пере-
переменными коэффициентами, если известно одно его частное реше-
решение. Так как иногда удается найти или угадать одно частное
решение непосредственно, то эта теорема во многих случаях
может оказаться полезной.
Теорема 7. Если известно одно частное решение линейного
однородного уравнения второго порядка, то нахождение общего
решения сводится к интегрированию функций.
Доказательство. Пусть ух есть известное частное реше-
решение уравнения у"-|-а1уЧ-а2у = 0. Найдем другое частное решение
данного уравнения так, чтобы ух и у2 были линейно независимы.
Тогда общее решение выразится формулой у = 0^ + 0^2, где Си
С2—произвольные постоянные. На основании формулы G) (см. до-
доказательство теоремы 4) можно написать у'2у±—y2y'x = Ce~*atdx. Та-
Таким образом, для определения у2 мы получаем линейное урав-
уравнение первого порядка. Проинтегрируем его следующим образом.
Разделим все члены на у\: ^/^ ^\Ce'^d\ или ±(Щ =
У у ах\ Уг /
"¦dx + C.
1 Г н
г- Се' Jai * ; отсюда
Уг
у\
Так как мы ищем частное решение, то, положив С'=0, С=1,
получаем
-=з—dx. A0)

74 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [гл ХШ
Очевидно, что ух и у2—линейно независимые решения, так как
i!l=^=const.
Ух
Таким образом, общее решение исходного уравнения имеет вид
^-dx. (И)
Пример 3. Найти общее решение уравнения
A— х*)у" —2х
Решение. Непосредственной проверкой убеждаемся, что это уравнение
имеет частное решение у! = х. Найдем второе частное решение у2 так, чтобы
Ух и у2 были линейно независимы.
—— 2х
Заметим, что в нашем случае %=^ 2~» жа основании формулы (Щ
получаем
S2x dx
»=*J —-W-dx=x] Р dx^x) #\\-*\~
Следовательно, общее решение имеет вид
1+*
1-х
о-
§ 21. Линейные однородные уравнения второго порядка
с постоянными коэффициентами
Имеем линейное однородное уравнение второго порядка
O, A)
где р и q—постоянные действительные числа. Чтобы найти об-
общий интеграл этого уравнения, достаточно, как было доказано
выше, найти два линейно независимых частных решения.
Будем искать частные решения в виде
# = е**, где k = const; B)
тогда
Подставляя полученные выражения производных в уравнение
A), находим
Так как е^фО, то, значит,
O. C)

§21] ОДНОРОДНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 75
Следовательно, если k будет удовлетворять уравнению C), то
ekx будет решением уравнения A). Уравнение C) называется
характеристическим уравнением по отношению к уравнению A).
Характеристическое уравнение есть квадратное уравнение,
имеющее два корня; обозначим их через kt и k2. При этом
Возможны следующие случаи:
I. kx и k2—действительные и притом не равные между собой
числа (&1=^&2);
II. kf и k2—комплексные числа;
III. &! и k2—действительные равные числа {ki = k2).
Рассмотрим каждый случай отдельно.
I.Корни характеристическогоуравнения дейст-
действительны и различны: кхфк2. В этом случае частными
решениями будут функции
Эти решения линейно независимы,, так как
К* = J^l = e^ ~ы*ф const.
Уг eRiX
Следовательно, общий интеграл имеет вид
Пример 1. Дано уравнение
?+
Характеристическое уравнение имеет вид
Находим корни характеристического уравнения:
Общий интеграл есть
II. Корни характеристического у равнения ком-
комплексные. Так как комплексные корни входят попарно сопря-
сопряженными, то обозначим
где
« = _?. ft =

76 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ XIII
Частные решения можно записать в форме
y^ete+W*, j/a = e«*-'3>*. D)
Это—комплексные функции действительного аргумента, удовлет-
удовлетворяющие дифференциальному уравнению A) (см. § 4 гл. VII).
Очевидно, что если какая-либо комплексная функция действи-
действительного аргумента
y = u(x) + iv(x) E)
удовлетворяет уравнению A), то этому уравнению удовлетворяют
функции и (х) и v(x).
Действительно, подставляя выражение E) в уравнение A),
будем иметь
или
(и* + ри> + qu) + i (v" + pv' + qv) = 0.
Но комплексная функция равняется нулю тогда и только тогда,
когда равны нулю действительная часть и мнимая часть, т. е.
Мы и доказали, что и (х) и v (x) являются решениями уравнения.
Перепишем комплексные решения D) в виде суммы действи-
действительной и мнимой части:
уг = еах cos р# + ieax sin fix, y2 = еах cos fix—ieax sin fix.
По доказанному частными решениями уравнения A) будут дей-
действительные функции
S^^'cosP*, F')
у2 = еах sin fix. F")
Функции ~ух и у2 линейно независимы, так как
n p*
у2 еах sin
Следовательно, общее решение уравнения A) в случае комплекс-
комплексных корней характеристического уравнения имеет вид
У = Сгух + С2у2 = Cte<** cos fix + C2e«x sin fix,
или
у = еР* (Ct cos fix + C2 sin fix), G)
где Ct и C2—произвольные постоянные.

§21] ОДНОРОДНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 77
Важным частным случаем решения G) является случай, когда
корни характеристического уравнения чисто мнимые.
Это имеет место тогда, когда в уравнении A) /? = 0, и оно
имеет вид
Характеристическое уравнение C) принимает вид
k* + q = Oy <7>0.
Корни характеристического уравнения
Решение G) принимает вид
у = Сг cos fk -f С2 sin рл\
Пример 2. Дано уравнение
Найти общий интеграл и частное решение, удовлетворяющее начальным усло-
условиям
Построить график.
Решение. 1) Напишем харак-
характеристическое уравнение
и найдем его корни 71
\
Следовательно, общий интеграл есть
у = е~х (C1cos2x+C2sin2x).
2) Найдем частное решение, удов-
удовлетворяющее данным начальным ус- Рис. 273.
ловиям, и определим соответствующие
значения Сх и С2. На основании первого условия находим: 0 = е~° (С* cos B-0) +
+ C2sinB-0)), откуда Сх = 0. Заметив, что у'=^е~х-2С2 cos2x—e~xC2 sin 2xt
из второго условия получаем 1=2С2, т. е. С2 = 1/2. Таким образом, искомое
частное решение есгь у = -~.е~хsin 2x. График его показан на рис. 273.
Пример 3. Дано уравнение
Найти общий интеграл и частное решение, удовлетворяющее начальным
условиям
у|*=о = О, У'1**0 = 3.
Решение. Напишем характеристическое уравнение
?2 + 9 = 0.
Находим его корни:
^ = 3/, fca = —3/.
Общий интеграл есть
у = Сг cos За: + С2 sin 3*.

78 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [гл- хш
Найдем частное решение. Предварительно найдем
у' = — ЗСг sin 3*+ЗС2 cos Зх.
Постоянные С± и С2 определяются из начальных условий:
0 = d cos Q + C2 sin 0, 3 = — 3Cj sin 0 + 3C2<:os 0.
Они равны
C\ = 0, C2 = 1 *
Частное решение:
y = sin Зх,
III. Корни ха рактеристического у равней и я дей-
действительные и равные. В этом случае kt = k2.
Одно частное решение yt = ek^x получается на основании пре-
предыдущих рассуждений. Нужно найти второе частное решение,
линейно независимое с первым (функция ekzX тождественно равна
ektx и поэтому не может рассматриваться в качестве второго част-
частного решения).
Будем искать второе частное решение в виде
у2 = и (х) ek>\
где и(х)—неизвестная функция, подлежащая определению.
Дифференцируя, находим
= ek^x (и! + ktu)9
ek^x = ek>x (и" + 2kxuf + k\u).
Подставляя выражения производных в уравнение A), получаем
ebx {и» + {2кг + р)и' + (k\ + рК + Я)и\ = 0.
Так как ^х —кратный корень характеристического уравнения, то
Кроме того, k1 = k2 = — р/2 или 2АХ = — р, 21 p
Следовательно, для того этобы найти и (х)> надо решить урав-
уравнение е^хи" = 0, или ц" = 0. Интегрируя, получаем и—Ах-\-В.
В частности, можно положить Л = 1, В = 0\ тогда и = х. Таким
образом, в качестве второго частного решения можно взять
Это решение линейно независимо с первым, так как
^ = хф const.
У1
Поэтому общим интегралом будет функция
у = С^х + C2xek>x = ek*x {Сг + С2х).
Пример 4. Дано уравнение

§22] ОДНОРОДНЫЕ УРАВНЕНИЯ п-ТО ПОРЯДКА 79
Пишем характеристическое уравнение № — 4& + 4 = 0. Находим его корни:
k1 = k2 — 2. Общим интегралом будет
§ 22. Линейные однородные уравнения п-го порядка
с постоянными коэффициентами
Рассмотрим линейное однородное уравнение n-го порядка
= 0. A)
Будем предполагать, что а1У а2, ..., ап—постоянные. Прежде
чем указывать метод решения уравнения A), введем определение,
нужное нам для дальнейшего.
Определение 1. Если для всехх отрезка [а, Ь] имеет место
равенство
где Аъ Л2, ..., Ап_г—постоянные числа, не все равные нулю,
то говорят, что Ф„(лг) выражается линейно через функции ()
Ф2(>> > Ф^-iW
Определение 2. п функций q^ (*), ф2 (л:), ..., чп„±(х), ф„ (л:)
называются линейно независимыми, если никакая из этих функ-
функций линейно не выражается через остальные.
Замечание 1. Из определений следует, что если функции
Фх(л:), Ф2(#), ..., ф„(#) линейно зависимы, то найдутся постоян-
постоянные С1У С2, ..., Сп, не все равные нулю, такие, что для всех х
отрезка [а, Ь] будет выполняться тождество
С1ф1 (х) + С2ср2 (х)+...+ Спуп (х) = 0.
Пример 1. Функции Ух = ех, у2 = е2х, у3 — 3ех линейно зависимы, так
как при Ci = l, С2 = 0, С3 = —5" имеет место тождество
о
С2е2х + С3 • Зех = 0.
Пример 2. Функции #i = l, Уъ — х, у3 — х2 линейно независимы, так как
ни при каких Clt C2, С3, одновременно не равных нулю, выражение С1-\-\-
+ С2д;+Сзл:2 не будет тождественно равно нулю.
Пример 3. Функции yi — ekiX, y^ ~ek*x, ..., yn—eknX, ..., где k&
&2> •••» ^«» •••—различные числа, линейно независимы. (Это утверждение мы
приводим без доказательства.)
Перейдем теперь к решению уравнения A). Для этого урав-
уравнения справедлива следующая теорема.
Теорема. Если функции уи у21 ..., уп являются линейно
независимыми решениями уравнения A), то его общее решение
есть
У = С1у1 + С2у2+...+СпУпУ B)
где Clf ..., Сп—произвольные постоянные.

80 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
Если коэффициенты уравнения A) постоянны, то общее реше-
решение находится так же, как и в случае уравнения второго по-
порядка.
1) Составляем характеристическое уравнение
2) Находим корни характеристического уравнения kly k2i ..., kn.
3) По характеру корней выписываем частные линейно неза-
независимые решения, руководствуясь тем, что:
а) каждому действительному однократному корню k соответ-
соответствует частное решение е**;
б) каждой паре комплексных сопряженных однократных кор-
корней ?ш = а-НР и йB) = а—*р соответствуют два частных реше-
решения еахсо$>$х и e^smfbr,
в) каждому действительному корню k кратности г соответствует
г линейно независимых частных решений екху xekxy ..., xr~lekx\
г) каждой паре комплексных сопряженных корней
кратности \i соответствуют 2\х частных решений
еах cos fix, xeax cos |5х, ..., х^~1еах cos fk,
Этих частных решений будет ровно столько, какова степень
характеристического уравнения (т. е. столько, каков порядок
данного линейного дифференциального уравнения). Можно дока-
доказать, что эти решения линейно независимы.
4) Найдя п линейно независимых частных решений yiy y2, ...
..., уп, строим общее решение данного линейного уравнения
У=С1у1 + С2у2+ ... +Спуаг
где Си С2, ..., Сп — произвольные постоянные.
Пример 4. Найти общее решение уравнения
ylV-y = 0.
Решение. Составляем характеристическое уравнение
А:4—1=0.
Находим корни характеристического уравнения:
ki = 1, k2 = — 1, &з = *> &4 = — *•
Пишем общий интеграл
у = С1ех+С2е~х + С3 cos x+C4sin x,
где Cf, C2, С3, С4—произвольные постоянные.
Замечание 2. Из изложенного следует, что вся трудность
решения линейных однородных дифференциальных уравнений с по-
постоянными коэффициентами заключается р решении характери-
характеристического уравнения.

§23] НЕОДНОРОДНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 81
§ 23. Неоднородные линейные уравнения второго порядка
Пусть имеем неоднородное линейное уравнение второго по-
порядка
" ' f(x). A)
Структура общего решения такого уравнения A) определяется
следующей теоремой:
Теорема 1. Общее решение неоднородного уравнения A) пред-
представляется как сумма какого-нибудь частного решения этого
уравнения у* и общего решения if соответствующего однородного
уравнения
У" + а1У'+а2у = 0. B)
Доказательство. Нужно доказать, что сумма
У=У+У* C)
есть общее решение уравнения A). Докажем сначала, что
функция C) есть решение уравнения A).
Подставляя сумму ~у + У* в уравнение A) вместо у, будем
иметь (]}+ tfl" + a^Q+tft' +аЛ(у+ tf)== f (х), или
{? + аху1 + а2у) + (у*" + агу*' + а2у*) = /(*). D)
Так как у есть решение уравнения B), то выражение, стоя-
стоящее в первых скобках, тождественно равно нулю. Так как у*
есть решение уравнения A), то выражение, стоящее во вторых
скобках, равно /(#). Следовательно, равенство D) является тож-
тождеством. Таким образом, первая часть теоремы доказана.
Докажем теперь, что выражение C) есть общее решение
уравнения (J), т. е. докажем, что входящие в него произвольные
постоянные можно подобрать так, чтобы удовлетворялись началь-
начальные условия:
»[*«*•= Уо. У'\х = х0=Уо, E)
каковы бы ни были числа лг0, у0 и у'о (лишь бы лг0 было взято из
той области, где функции aiy а2 и f(x) непрерывны).
Заметив, что у можно представить в форме y = C1yi + C2y2i
где yt и у2—линейно независимые решения уравнения B), a Ct
и С2—произвольные постоянные, можем переписать равенство C)
в виде
У = С1У1 + С2у2 + у\ C')
Тогда на основании условий E) будем иметь *)
*) Здесь Шо»/1/2о»/ Уо9 ?'1<ь #20, */о' обозначают числовые значения функ-
функций УЬ у29 У*, Уь #2, У*' При Х = Х0.

32 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
Из этой системы уравнений нужно определить Сг и С2. Перепи-
Переписав систему в виде
20 = yQ—yt, C^io + C2y'2Q = у'о—Уо', F)
замечаем, что определитель этой системы есть определитель Врон-
Вронского для функций yt и у2 в точке х = х0. Так как эти функции
по условию линейно независимы, то определитель Вронского не
равен нулю; следовательно, система F) имеет определенное реше-
решение С± и С2, т. е. существуют такие значения Ct и С2, при кото-
которых формула C) определяет решение уравнения A), удовлетво-
удовлетворяющее данным начальным условиям. Теорема полностью доказана.
Таким образом, если известно общее решение 1} однородного
уравнения B), то основная задача при интегрировании неоднород-
неоднородного уравнения A) состоит в нахождении какого-либо его част-
частного решения у*.
Укажем общий метод нахождения частных решений неодно-
неоднородного уравнения.
Метод вариации произвольных постоянных.
Напишем общее решение однородного уравнения B)
2. G)
Будем искать частное решение неоднородного уравнения A)
в форме G), рассматривая Ct и С2 как некоторые пока неизвест-
неизвестные функции от х.
Продифференцируем равенство G):
У' = СгУ'г + С2у'2 + С[уг + С2у2.
Подберём искомые функции Ct и С2 так, чтобы выполнялось
равенство
Qy. + Qy^O. (8)
Если учесть это дополнительное условие, то первая производная
у' примет вид
Дифференцируя теперь это выражение, найдем уп\
У° = СгУг + С2у1 + С[у[ + С2у2.
Подставляя уу у' и у" в уравнение A), получим
СгУ1 + С2у1 + С[у[ + Сгуг + at {Сху[ + Сф) + а2 (Сгуг + С2у2) = / (д),
или
Сг (yl + агу[ + а2ух) + С2 (У; + агу, + а2у2) + С[у[ + С2у2 = f(x).
Выражения, стоящие в первых двух скобках, обращаются в нуль,

§23] НЕОДНОРОДНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 83
так как ух и у2 —- решения однородного уравнения. Следовательно,
последнее равенство принимает вид
С& + С;й = /(*). (9)
Таким образом, функция G) будет решением неоднородного
уравнения A) в том случае, если функции Сг и С2 удовлетво-
удовлетворяют системе уравнений (8) и (9), т. е. если
С'гУг + С2у2 = О, С[у[ + С2уг = /(*).
Так как определителем этой системы является определитель
Вронского для линейно независимых решений yt и у2 уравнения B),
то он не равен нулю; следовательно, решая систему, мы найдем
С[ и С2 как определенные функции от х:
С! = чг(х), с;=<р,(*).
Интегрируя, получим
где Сх и С2 — постоянные интегрирования.
Подставляя полученные выражения Q и С2 в равенство G),
найдем интеграл, зависящий от двух произвольных постоянных
Сг и С2, т. е. общее решение неоднородного уравнения*).
Пример. Найти общее решение уравнения
Решение. Найдем общее решение однородного уравнения
Так как -^г=—, то 1п^/ = 1пд:+1пс; t/' = cx; итак, */ = Ci +
Чтобы последнее выражение было решением данного уравнения, надо оп-
определить Сх и С2 как функции от х из системы
Решая эту систему, найдем
C1-V2, С2
откуда в результате интегрирования получаем
\С
Подставляя найденные функции в формулу у = С1х2-\-С2, получаем общее
решение неоднородного уравнения
— — Xs ~ —
или г/==С1^2 + С2+-^-, где Сг и С2—произвольные постоянные.
*) Если положить Ci = C2=0, то получим частное решение уравнения A).

84 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ?ГЛ. XIII
При отыскании частных решений полезно пользоваться ре-
результатами следующей теоремы.
Теорема 2. Решение у* уравнения
x)t A0)
где правая часть есть сумма двух функций /х (л:) и f2 (x) *),
можно представить в виде суммы у* = yl + yl, где у\ и yl —со-
—соответственно решения уравнений
Г^Щх), A1)
у1 = f2 (x). A2)
Доказательство. Складывая правые и левые части ра-
равенств A1) и A2), получим
x). A3)
Из последнего равенства и следует, что сумма
есть решение уравнения A0).
Пример. Найти частное решение у* уравнения
Решение. Частное решение уравнения
У
будет
> 1
Частное решение уравнения
1/2
будет
Частное решение у* данного уравнения будет
§ 24. Неоднородные линейные уравнения второго порядка
с постоянными коэффициентами
Пусть имеем уравнение
tf + py' + qy = f(x), A)
где р и # — действительные числа.
*) Очевидно, что соответствующая теорема остается справедливой при
любом числе слагаемых правой части.

§24] НЕОДНОРОДНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 85
В предыдущем параграфе был указан общий метод нахожде-
нахождения решения неоднородного уравнения. В случае уравнения с по-
постоянными коэффициентами частное решение иногда бывает воз-
возможно найти проще, не прибегая к интегрированию. Рассмотрим
несколько таких возможностей для уравнения A).
I. Пусть правая часть уравнения A) представляет собой про-
произведение показательной функции на многочлен, т. е. имеет вид
f(x) = Pn(x)e™, B)
где Рп (х) — многочлен n-й степени. Тогда возможны следующие
частные случаи:
а) Число а не является корнем характеристического
уравнения
В этом случае частное решение нужно искать в виде
у* = (Аох«+А1х»~1+ ...+Ап) #**=Qn (х) (Р*. C)
Действительно, подставляя #* в уравнение A) и сокращая все
члены на множитель еах, будем иметь:
(x) = Pn(x). D)
Qп(х) — многочлен степени n, Q'n(х) — многочлен степени п — 1,
Q'n Iх) ~ многочлен степени п — 2. Таким образом, слева и справа
от знака равенства стоят многочлены n-й степени. Приравнивая
коэффициенты при одинаковых степенях х (число неизвестных
коэффициентов равно я+1), получим систему я+1 уравнений
для определения неизвестных коэффициентов Ло, Л1Э Л2, ..., Ап.
б) Число а есть простой (однократный) корень ха-
характеристического уравнения.
Если бы в этом случае частное решение мы стали искать
в форме C), то в равенстве D) слева получился бы многочлен
(/г— 1)-й степени, так как коэффициент при Qn (х), т. е. a2+pa+q,
равен нулю, а многочлены Q'n(x) и Q"n(x) имеют степень, мень-
меньшую п. Следовательно, ни при каких Ло, Af, ..., Ап равенство D)
не было бы тождеством. Поэтому в рассматриваемом случае част-
частное решение нужно брать в виде многочлена (п+1)-й степени,
но без свободного члена (так как свободный член этого много-
многочлена исчезнет при дифференцировании) *):
в) Число а есть двукратный корень характеристиче-
характеристического уравнения. Тогда в результате подстановки в дифферен-
дифференциальное уравнение функции Qn(x)eax степень многочлена пони-
*) Заметим, что все приведенные выше результаты остаются в силе и в
том случае, когда а—комплексное число (это следует из правил дифферен-
дифференцирования функции етх% где т—любое комплексное число; см. § 4 гл. VII).

g5 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ {ГЛ. XIII
жается на две единицы. Действительно, если а —корень харак-
характеристического уравнения, то а2 -\-ра -{- q — 0; кроме того, так как а
является двукратным корнем, то 2а = —р (так как по .известной
теореме элементарной алгебры сумма корней приведенного квад-
квадратного уравнения равна коэффициенту при неизвестном в первой
степени, взятому с обратным знаком). Итак, 2а + р = 0.
Следовательно, в левой части равенства D) останется Qn(*)»
т.е. многочлен (п — 2)-й степени. Для того чтобы в результате
подстановки получить многочлен степени я, следует частное ре-
решение искать в виде произведения еах на многочлен (я + 2)-й
степени. При этом свободный член этого многочлена и член в пер-
первой степени исчезнут при дифференцировании; поэтому их можно
не включать в частное решение.
Итак, в случае, когда а является двукратным корнем харак-
характеристического уравнения, частное решение можно брать в форме
Пример 1. Найти общее решение уравнения
у"+4у'+3у = х.
Решение. Общее решение соответствующего однородного уравнения есть
Так как правая часть данного неоднородного уравнения имеет вид хеох (т. е.
вид Pi(x)eox)y причем 0 не является корнем характеристического уравнения
k24-4?+3=0, то частное решение будем искать в форме y*=Qi (х) еох, т.е.
положим
Подставляя это выражение в заданное уравнение, будем иметь
4Л0+3(Л0*+Л1)=*.
Приравнивая коэффициенты при одинаковых степенях х, получим
ЗЛ0 = 1', 4Ло + ЗЛх=:О,
откуда
40=1/3, Лх=-—4/9.
Следовательно,
* 1 4
Общее решенае # = */+#* будет
у = Сге-* + С*-**+±х—±.
Пример 2. Найти общее решение уравнения
2\9
Решение. Общее решение однородного уравнения найдем легко:
~у = Сг cos Зх+С2 sin Зх.
Правая часть заданнога уравнения (х2-\-1)е3х имеет вид Р2(х)е?х. Так кяк
коэффициент 3 в показателе степени не является корнем характеристического

§24] НЕОДНОРОДНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 87
уравнения, то частное решение ищем в виде*/*=ф2(.х:) е3*, или у*~(Ах2-\-Вх-\-С)еЬх.
Подставляя это выражение в дифференциальное уравнение, будем иметь
Сокращая на еВх и приравнивая коаффициенты при одинаковых степенях х,
получим
18Л = 1, 12Л + Ш = 0, 2А + 6В+\8С=\,
откуда А = 1/18, В =—1/27, С = 5/81. Следовательно, частное решение будет
и общее решение
у = С1 cos Зх+С2 sin Зх+ (jz*2-%*-f gj) в**.
Пример 3. Решить уравнение
Решение. Здесь правам часть имеет вид Р1(х)е1'ху причем коэффици-
коэффициент 1 в показателе степени является простым корнем характеристического
многочлена. Следовательно, частное решение ищем в виде y* = xQi(x)ex, или
у* = х(Ах+В)ех;
подставляя это выражение в уравнение, будем иметь
ЦАх2+Вх) + DАх + 2В) + 2А — 7 (Ах* + Вх) — 7 BАх+В) + б (Ах2 + Вх)] е* =
или
(—• Шх—
Приравнивая коэффициенты при одинаковых степенях х, получим
—ЮЛ = 1, —5В+2Л=—2,
откуда А= —1/10, 5 = 9/25. Следовательно, частным решением является
а общим
II. Пусть правая частъ имеет вид
f{x) = P (x) e«x cos |3х + Q (x) e™ sin Pjc, E)
где Р (х) и Q (х) — многочлены.
Этот случай может быть рассмотрен приемом, примененным
в предыдущем случае, если перейти от тригонометрических функ-
функций к показательным. Заменяя cosfbt и sinpjc через показатель-
показательные функции по формулам Эйлера {см. § 5 гл. VII), получим
или
. F)

88 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
Здесь в квадратных скобках стоят многочлены, степени которых
равняются высшей из степеней многочленов Р(х) и Q(x). Таким
образом, получили правую часть вида, рассмотренного в случае 1.
Доказывается (приводить доказательство мы не будем), что
можно найти частные решения, не содержащие комплексные числа.
Итак, если правая часть уравнения A) имеет вид
f(x) = P (x) еах cos Р* + Q (x) e*x sin р*, G)
где Р (х) и Q (х) —• многочлены от х, то форма частного решения
определяется так:
а) если число a + ifi не является корнем характеристического
уравнения, то частное решение уравнения A) следует искать
в виде
у* = U(x) еах cos fix + V (х) еах sin fix, (8)
где U(x) и V (х) — многочлены, степень которых равна наивыс-
наивысшей степени многочленов Р (х) и Q(x);
б) если число a + ifi есть корень характеристического урав-
уравнения, то частное решение ищем в виде
у* = х [U(x) е*х cos Р*+V (х) е™ sin p*]. (9)
При этом во избежание возможных ошибок надо отметить,
что указанные формы частных решений (8) и (9), очевидно, со-
сохраняются и в том случае, когда в правой части уравнения A)
один из многочленов Р (х) и Q (х) тождественно равен нулю, т. е.
когда правая часть имеет вид Р (х) еах cos Рл; или Q (л:) еах sin Рл;.
Рассмотрим, далее, важный частный случай. Пусть правая
часть линейного уравнения второго порядка имеет вид
f(x) = M cos fix + N sin p*, G')
где М и N—-постоянные числа.
а) Если pi не является корнем характеристического уравне-
уравнения, то частное решение следует искать в виде
у* = A cos fix + В sin px. (8')
б) Рхли р; является корнем характеристического уравнения,
то частное решение следует искать в виде
у* = х (A cos fix + B sin fix). (9')
Отметим, что функция G') является частным случаем функ-
функции G) (Р(х) = М, Q(*) = tf, а = 0); функции (8') и (9') явля-
являются частными случаями функций (8) и (9).
Пример 4. Найти общий интеграл линейного неоднородного уравнения
Решение. Характеристическое уравнение &2+2& + 5 = 0 имеет кор-
корни Я?! = —1+2**; &2 — —1— 2*. Поэтому общий интеграл соответствующего

§24] НЕОДНОРОДНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 89
однородного уравнения есть
Jf=e-X (Cx cos 2х+С2 sin 2л;).
Частное решение неоднородного уравнения ищем в виде
у* = А cos x-\-B sinx,
где Л и В—постоянные коэффициенты, подлежащие определению.
Подставляя у* в заданное уравнение, будем иметь
—Л cos х— В sin х+2 (—Л sin х+В cos *) + 5 (A cos х+В sin *) = 2 cos х.
Приравнивая коэффициенты при cos x и sin x, получим два уравнения для
определения А и В.
откуда А = 2/5, В =1/5. Общее решение данного уравнения: #==#+#*, т.е.
Пример 5. Решить уравнение y"-{-4y = cos2x.
Решение. Характеристическое уравнение имеет корни ki = 2it k2 =—2i;
поэтому общее решение однородного уравнения имеет вид
у = Сг cos 2х + С2 sin 2лт.
Частное решение неоднородного уравнения ищем в форме
у* = х (A cos 2x+В sin 2x).
Тогда
#*' = 2х {—A sin 2л:+5 cos 2х) + (Л cos 2л:+В sin 2лг),
у*'' = 4х (—A cos 2* — В sin 2*) -f 4 (—A sin 2* + 5 cos 2x).
Подставляя эти выражения производных в данное уравнение и приравни-
приравнивая коэффициенты при cos 2x и sin2Ar, получаем систему уравнений для опре-
определения А и В: 4#=1, —4Л=0, откуда Л = 0, В = 1/4. Таким образом, об-
общий интеграл данного уравнения
у = Сг cos 2x+C2 sin 2ЛГ+-Т- х sin 2л\
Пример 6. Решить уравнение у"—у = Зе2х cos x.
Решение. Правая часть уравнения имеет вид
/ (х) = е2* (М cosx + Nsin x),
причем Л1 = 3, iV=0. Характеристическое уравнение &2—1=0 имеет корни
/гх=1, k2 = —1. Общее решение однородного уравнения есть
Так как число а+Ф=2 + М не является корнем характеристического урав-
уравнения, то частное решение ищем в виде
у* = е2Х (д Cos х + В sin х).
Подставляя это выражение в уравнение, получим после приведения подобных
членов
Bл + 4Я) е2х cos х + (—4Л +2Б) е2х sin л: = Зе2х cos л:.
Приравнивая коэффициенты при cos* и sin*, получим

90 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. ХШ
Отсюда А = 3/10, ? = 3/5. Следовательно, частное решение
а / 3 ,3
а общее
Замечание. Отметим, что все рассуждения этого параграфа
справедливы и для линейного уравнения первого порядка. Рас-
Рассмотрим, например, уравнение первого порядка с постоянными
коэффициентами (это уравнение часто встречается в технических
приложениях)
% Ь, A0)
где а и Ь— постоянные. Находим общее решение однородного
уравнения
Составляем характеристическое уравнение
&4-а = 0, k = —а.
Общее решение однородного уравнения будет
"$=Се-"х.
Ищем частное решение у* неоднородного уравнения в форме
У* = В.
Подставляя в уравнение A0), получаем аВ = Ь, В = Ь/а. Итак,
у*-6/а.
Общее решение уравнения A0) будет
или y = Ce'aK + bla. A1)
§ 25. Неоднородные линейные уравнения высших порядков
Рассмотрим уравнение
-1)+...+апу = 1(х)у A)
где аъ а2, ..., аи, /(х) — непрерывные функции от х (или посто-
постоянные числа). Пусть нам известно общее решение
а B)
соответствующего однородного уравнения
уш + uifn-i) + a2yin^ +...+аау = 0. C)

§25] НЕОДНОРОДНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ 91
Как и в случае уравнения второго порядка, для уравнения A)
справедливо следующее утверждение.
Теорема. Если у—общее решение однородного уравнения C),
а у*—частное решение неоднородного уравнения A), то
есть общее решение неоднородного уравнения.
Таким образом, задача интегрирования уравнения A), как
и в случае уравнения второго порядка, сводится к нахождению
частного решения неоднородного уравнения.
Как и в случае уравнения второго порядка, частное решение
уравнения A) можно находить способом вариации произвольных
постоянных, считая в выражении B) Си Са, ..., Сп функциями
от х.
Составим систему уравнений (ср. § 23)
'гУг + Q/2 + • • • + С'пУп = °>
... +• С'пу'п = О,
D)
О/Г2) + ад-* +... + с;гУг2у = о,
Эта система уравнений с неизвестными функциями С'1У С'2у ..., С'п
имеет вполне определенные решения. (Определитель из коэффици-
коэффициентов при Q, Сг, ..., С'п представляет собой определитель Врон-
Вронского, составленный для частных решений у19 у2У ..., уп однород-
однородного уравнения, а так как эти частные решения по условию
линейно независимы, то определитель Вронского отличен от нуля.)
Итак, система D) может быть решена относительно функций
Ci, Q, ..., С'п. Найдя их и интегрируя, получим
где Cl9 C2, ..., Сп—постоянные интегрирования.
Докажем, что в таком случае выражение
п E)
есть общее решение неоднородного уравнения A).
Дифференцируем выражение E) п раз, принимая каждый раз
во внимание равенства D); тогда будем иметь
+С2у2 +.
+С2у2 +..

92 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
Умножая члены первого, второго, ... и, наконец, последнего
уравнения соответственно на ап, ап_и ..., аг и 1 и складывая,
получим
так как yi9 у2, ..., уп—частные решения однородного уравнения,
и поэтому суммы членов, полученные при сложении по вертикаль-
вертикальным столбцам, равны нулю.
Следовательно, функция
(где Сь ..., Сп—функции от ху определенные из уравнений D))
является решением неоднородного уравнения A). Это__решение
зависит от п произвольных постоянных С1У С2, ..., Сп. Как и
в случае уравнения второго порядка, доказывается, что это есть
общее решение.
Таким образом, утверждение доказано.
В случае неоднородного уравнения высшего порядка с постоян-
постоянными коэффициентами (ср. § 24) частные решения иногда находятся
проще, а именно:
I. Пусть в правой части дифференциального уравнения стоит
функция f(x) = P(x)eaxJ где Р (х)—многочлен от х\ тогда надо
различать два случая:
а) если а не является корнем характеристического уравнения,
то частное решение можно искать в виде
y*=Q(x)e™,
где Q (л:)—многочлен той же степени, что и Р(х), но с неопреде-
неопределенными коэффициентами;
б) если а есть корень кратности \х характеристического урав-
уравнения, то частное решение неоднородного уравнения можно искать
в форме
где Q(x)—многочлен той же степени, что и Р(х).
II. Пусть правая часть уравнения имеет вид
f (х) = М cos P# + N sin fk,
где М и N — постоянные числа. Тогда вид частного решения опре-
определяется следующим образом:
а) если число C/ не есть корень характеристического уравне-
уравнения, то частное решение имеет вид
у* = A cos fk + В sin fk,
где А и В—постоянные неопределенные коэффициенты;

§ 25] НЕОДНОРОДНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ 93
б) если число р* есть корень характеристического уравнения
кратности (I, то
#* = х» (A cos Р* + В sin p*).
III. Пусть
f(x) = P (x) еах cos р* + Q (*) еа* sin рл:,
где Р(л:) и Q(x)—многочлены от х. Тогда:
а) если число a + $i не является корнем характеристического
многочлена, то частное решение ищем в виде
y* = U (х) еах cos р* + V (х) е«х sin P*,
где U (х) и V (х)—многочлены, степень которых равна наивысшей
степени многочленов Р(х) и Q(x)\
б) если число a -f р/ является корнем кратности (ш характери-
характеристического многочлена, то частное решение ищем в виде
у* = х» [U (х) е«х cos Рх + V (х) еах sin P*],
где U (х) и V(x) имеют тот же смысл, что и в случае а).
Общее замечание к случаям II и III. Даже тогда,
когда в правой части уравнения стоит выражение, содержащее
только cos Ра; или только sin Ра;, мы должны искать решение
в том виде, как было указано, т. е. с синусом и косинусом. Иными
словами, из того, что правая часть не содержит cosPa: или sin Ра;,
отнюдь не следует, что частное решение уравнения не содержит
этих функций. В этом мы могли убедиться, рассматривая примеры
4, 5, 6 предыдущего параграфа, а также пример 2, приведенный
в этом параграфе.
Пример 1. Найти общее решение уравнения yiv—у = хв-{-1.
Решение. Характеристическое уравнение №—1=0 имеет корни
k± = 1, k2 = — 1, ks=i, k± — — i.
Находим общее решение однородного уравнения (см. пример 4 § 22)
7= Схех + С2е~х + С3 cos x+C4 sin x.
Частное решение неоднородного уравнения ищем в форме
Дифференцируя у* четыре раза и подставляя полученные выражения
в заданное уравнение, получим
+
Приравняем коэффициенты при одинаковых степенях х:
— Ло = 1, —^ = 0, — Л2 = 0, —Л3=1.
Следовательно,
у* = -.Х3 — \.
Общий интеграл неоднородного уравнения находится по формуле у = у"+у*, т. е<
у = Схех + С2е~* + С3 cos *+C4 sin Jt—*3— 1.

94 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. ХШ
Пример 2. Решить уравнение i/IV—у — $соьх.
Решение. Характеристическое уравнение k*—1=0 имеет корни kx = 1,
k2——1, &з —*\ ^4 = —*• Следовательно, общим решением соответствующего
однородного уравнения является:
С cos x+C4 sin x.
Далее, правая часть данного неоднородного уравнения имеет вид
/ (х)=М cosAr+iVsinA;,
где М = 5, N = 0.
Так как * является простым корнем характеристического уравнения, то
частное решение ищем в виде
у* = х(Л cos х~\-В sin a:).
Подставляя это выражение в уравнение, найдем
4A sin х— 4В cos х = 5 cos л:,
откуда
4Л=0, — 4В = 5,
или Л = 0, В — —5/4. Следовательно, частным решением дифференциального
уравнения является
*
а общим решением
'5
у = С1ех + С2е~х-{-С3 cos a:+C4 sin x—-j x sin a:.
§ 26. Дифференциальное уравнение механических колебаний
В настоящем и следующих параграфах мы рассмотрим одну
задачу прикладной механики, исследовав и разрешив ее с помощью
линейных дифференциальных уравнений.
Пусть груз массы Q покоится на упругой рессоре (рис. 274).
Отклонение груза от положения равновесия обозначим через у.
Отклонение вниз будем считать положительным, вверх—отри-
вверх—отрицательным. В положении равновесия вес уравновешивается уп-
упругостью пружины. Предположим, что сила, стремящаяся вер-
вернуть груз в положение равновесия,— так называемая восстанав-
восстанавливающая сила—пропорциональна отклонению, т. е. равна —ky,
где k—некоторая постоянная для данной рессоры величина (так
называемая «жесткость рессоры») *).
Предположим, что движению груза Q препятствует сила сопро-
сопротивления, направленная в сторону, противоположную направле-
направлению движения, и пропорциональная скорости движения груза
относительно нижней точки рессоры, т. е. сила — fa> = — Я -^-, где
К = const ^ 0 (амортизатор). Напишем дифференциальное уравне-
*) Рессоры, у которых восстанавливающая сила пропорциональна откло-
отклонению, называются рессорами с «линейной характеристикой».

$26]
УРАВНЕНИЕ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ
95
ние движения груза на рессоре. На основании второго закона
Ньютона будем иметь
О d2y _ ku * *У.
Ч dt2 - *У N dt
A)
(здесь k и %—положительные числа). Мы получили линейное
однородное дифференциальное уравнение второго порядка с посто-
постоянными коэффициентами.
Это уравнение можно переписать так:
(Г)
где обозначено
Предположим, далее, что нижняя точка рессоры совершает
вертикальные движения по закону z = q>(t). Это, например, будет
• Положение рвЗноВесия
Рис. 275,
иметь место, если нижний конец рессоры прикреплен к катку,
который вместе с рессорой и грузом движется по неровности
(рис. 275).
В этом случае восстанавливающая сила будет равна не — ky,
а — &[# + ф@]»сила сопротивления будет —Цу' + <р' (/)], и вместо
уравнения A) мы получим уравнение
ИЛИ
где обозначено
dt
B)
B')
Мы получили неоднородное дифференциальное уравнение вто-
второго порядка.
Уравнение (Г) называют уравнением свободных колебаний,
уравнение B')—уравнением вынужденных колебаний.

96 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
§ 27. Свободные колебания. Векторное и комплексное
изображение гармонических колебаний
Рассмотрим сначала уравнение свободных колебаний
!?+РУ' + ЯУ = О (Р>О, <7>0, см. § 26). A)
Напишем соответствующее характеристическое уравнение
и найдем его корни:
1) Пусть р2/4 > </. Тогда корни k^ и k2—действительные отри-
отрицательные числа. Общее решение выражается через показатель-
показательные функции:
у = CleV + c,eV {К < 0, k2 < 0). B)
Из этой формулы следует, что отклонение у при любых началь-
начальных условиях асимптотически стремится к нулю, если t—*оо.
В данном случае колебаний не будет, так как силы сопротивле-
сопротивления велики по сравнению с коэффициентом жесткости рессоры k.
2) Пусть /?2/4 = q\ тогда корни kx и k2 равны между собой (и равны
отрицательному числу — р/2). Поэтому общее решение будет
"t ~Tt e~~. C)
Здесь отклонение также стремится к нулю при t—>oo, однако
не так быстро, как в предыдущем случае (благодаря наличию
сомножителя Сг + С^).
3) Пусть р = 0, т. е. отсутствует сила сопротивления. Уравне-
Уравнение A) примет вид
0. D)
Характеристическое уравнение имеет вид k2 + q = 0, а его корни
равны &i = pi, k2 = — $i9 где $^Vq. Общее решение:
y = Ci cos fit + С2 sin fit. E)
В последней формуле произвольные постоянные Сх и С2 заме-
заменим другими. Именно, введем постоянные А и ф0, связанные с С±
и С2 соотношениями
Ct = A sin ср0, С2 = А cos ф0.
А и ф0 через Q и С2 определяются так:

§27]
СВОБОДНЫЕ КОЛЕБАНИЯ
97
Подставляя значения Сг и С2 в формулу E), будем иметь
у = A sin ф0 cos p/ + A cos cp0 sin р/,
или
F)
Колебания в этом случае называются гармоническими. Интег-
Интегральными кривыми являются синусоиды. Промежуток времени Т,
за который аргумент синуса изменяется на 2я, называется перио-
периодом колебаний; в данном случае T = 2n/fi. Частотой колебания
называется число колебаний за время 2я; в данном случае частота
равна Р; А—величина наибольшего
отклонения от положения равнове- yt
сия—называется амплитудой колеба-
колебания; ф0 называется начальной фазой.
График функции F) изображен на
рис. 276.
К Zr
Рис. 276.
Рис. 277.
В электротехнических и других дисциплинах широко исполь-
используют комплексное и векторное изображения гармонических коле-
колебаний.
Рассмотрим в комплексной плоскости хОу радиус-вектор А = A (t)
постоянной длины | А | = А = const.
Конец вектора А при изменении параметра t (в данном случае
t—время) описывает окружность радиуса А с центром в начале
координат (рис. 277). Пусть угол г|), образованный вектором А
и осью 0ху выражается так: *ф = Р^ + Ф0. Величина Р называется
угловой скоростью вращения вектора А. Проекции вектора А на
оси Оу и Ох будут
G)
Выражения G) суть решения уравнения D).
Рассмотрим комплексную величину
г = х + iу = A cos (р/ + ср0) + iA sin (р/ + <р0),
или
z = A [cos (fit + Фо) + i sin (fit + %)]. (8)
Комплексная величина г, как это было указано в § 1 гл. VII,
изображается вектором А.
4 Н. С, Пискунов, т# 2

98
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ. XIII
Таким образом, решения уравнения гармонических колебаний
D) можно рассматривать как проекции вектора А на оси О у и Ох,
вращающегося с угловой скоростью |3 при начальной фазе ср0.
Пользуясь формулой Эйлера (см. D) § 5 гл. VII), выражение
(8) можно переписать так:
г = Ле*0'+Фо). (9)
Мнимая и действительная части выражения (9) являются реше-
решениями уравнения D). Выражение (9) называется комплексным
ДО
Рис. 278.
решением уравнения D). Перепишем выражение (9) так:
m. A0)
Выражение Ае1®* называют комплексной амплитудой. Обозна-
Обозначим ее через Л*. Тогда комплексное решение A0) перепишется так:
г = А*е'&. A1)
4) Пусть р Ф 0 и —- < q.
В этом случае корни характеристического уравнения—комп-
уравнения—комплексные числа
где
Общий интеграл имеет вид
у = eat (Ct cos p* + С2 sin fit),
или
A2)
A3)
Здесь в качестве амплитуды приходится рассматривать вели-
величину Ле"', зависящую от времени. Так как а < 0, то она стре-

§28] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ 99
мится к нулю при t—>oo, т. е. здесь мы имеем дело с затухаю-
затухающими колебаниями. График затухающих колебаний изображен на
рис. 278.
§ 28. Вынужденные колебания
Уравнение вынужденных колебаний имеет вид
(р>0, <7>0, см. § 26). A)
Рассмотрим практически важный случай, когда возмущающая
внешняя сила является периодической и изменяется по закону
тогда уравнение A) примет вид
(Г)
1) Предположим сначала, что рфО и ^~<<7> т» е. корни
характеристического уравнения—комплексные числа а± j(J. В^том
случае (см. формулы A2) и A3) § 27) общее решение однородного
уравнения имеет вид
y = Ae^sm(^t + %). B)
Частное решение неоднородного уравнения ищем в форме
у* = М cos tot + N sin cat. C)
Подставляя это выражение у* в исходное дифференциальное
уравнение, находим значения М и N:
м - — Р™ 1, (д—а>*)а
IYl (q—co2J + /?2co2 » й—(О2J+Р2со2*
Прежде чем подставить найденные значения М и N в равенство
C), введем новые постоянные А* и ср*, положив
М = Л* sin ф*, JV = A* cos ф*,
т. е.
Тогда частное решение неоднородного уравнения можно записать
в форме
у* = Л* sin ф* cos со^ + Л* cos ф* sin со/ = Л* sin (со^ + Ф*)»
или окончательно
у* = r sin (at + Ф*).

100 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ . [ГЛ. XIII
Общий интеграл уравнения A) равен */=*/+#*, т. е.
Первый член суммы, стоящей в правой части (решение одно-
однородного уравнения), представляет затухающие колебания; при
увеличении t он убывает, и, следовательно, через некоторый про-
промежуток времени главное значение будет иметь второй член, опре-
определяющий вынужденные колебания. Частота со этих колебаний
равна частоте внешней силы f(t); амплитуда вынужденных коле-
колебаний тем больше, чем меньше р и чем ближе со2 к q.
Исследуем подробнее зависимость амплитуды вынужденных
колебаний от частоты со при различных значениях /?. Для этого
обозначим амплитуду вынужденных колебаний через D(co):
D(©) =
Положим G = PI (Pi ПРИ р — 0 равнялась бы частоте собственных
колебаний). Тогда
Введем обозначения
co/Pi = b,
где X —отношение частоты возмущающей силы к частоте свобод-
свободных колебаний системы, а постоянная у не зависит от возму-
возмущающей силы.. Тогда величина амплитуды будет выражаться
формулой
Найдем максимум этой функции. Он, очевидно, будет при том
значении X, при котором квадрат знаменателя имеет минимум.
Но минимум функции
V(l-V)* + y4.* E)
достигается при
и равен

Т
Следовательно, максимальная величина амплитуды равна
Дпак

§28]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
101
Графики функции D(k) при различных значениях у показаны
на рис. 279 (для определенности при построении графиков поло-
положено а=1, Pi=l). Эти кривые называются кривыми резонанса.
0,15 0,5 0,75
1,0 1,15 %5 1,75 Zfl 2,15 Л
Рис. 279.
Из формулы E) следует, что при малых у максимальное
значение амплитуды достигается при значениях X, близких к еди-
единице, т. е. когда частота внешней силы близка к частоте свобод-
свободных колебаний. Если y = 0 (следовательно, /7 = 0), т. е. если
отсутствует сопротивление движению, амплитуда вынужденных
колебаний^неограниченно возрастает при X—>1, т. е. при <о—*
\imD(X) = oo.
G=0)
При со2 = G имеет место явление резонанса.
2) Предположим теперь, что /? = 0, т. е. рассмотрим уравнение
упругих колебаний без сопротивления при наличии периодичес-
периодической внешней силы
У"
= а sin со/.
F)

102 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Общее решение однородного уравнения
[ГЛ. XIII
Если Р=^=со, т. е. если частота внешней силы не равна час*
тоте собственных колебаний, то частное решение неоднородного
уравнения имеет вид
у* = М cos (ot + N sin со?.
Подставляя это выражение в
исходное уравнение, найдем
> q—со2 '
Общее решение есть
у = A sin (Р^ + ф0) + _^ а sinco^.
Таким образом, движение полу-
получается в результате наложения
собственного колебания с часто-
частотой Р и вынужденного колебания
с частотой о.
Если (о = р, т. е. частота соб-
собственных колебаний совпадает с
частотой внешней силы, то функ-
функция C) не является решением
уравнения F). В этом случае в
соответствии с результатами § 24 частное решение надо искать
в форме
y* = t(M cos fit + N sin fit). G)
Подставляя это выражение в уравнение, найдем М п N:
Рис. 280.
Следовательно,
Общее решение будет иметь вид
у = A sin (р/ + ф0) — -|g t cos p?.
Второй член, стоящий в правой части, показывает, что в этом
случае амплитуда колебания неограниченно возрастает при не-
неограниченном возрастании времени t. Это явление, имеющее место

§29] СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ЮЗ
при совпадении частоты собственных колебаний системы с часто-
частотой внешней силы, называется резонансом.
График функции у* изображен на рис. 280.
§ 29. Системы обыкновенных дифференциальных уравнений
При решении многих задач требуется найти функции Уг—у±(х),
у2 = у2 (х)у ..., уп = уп (х)у которые удовлетворяют системе диф-
дифференциальных уравнений, содержащих аргумент х, искомые
функции у1У у2, ..., {/„ и их производные.
Рассмотрим систему уравнений первого порядка
igL_/ (х и и и)
dx
г> У** ••-. Уп)>
где уь у„ ..., уп — искомые функции, х —аргумент.
Такая система, когда в левой части уравнений стоят произ-
производные первого порядка, а правые части не содержат производ-
производных, называется нормальной.
Проинтегрировать систему — значит определить функции yif
#2» •••» Уп» удовлетворяющие системе уравнений A) и данным
начальным условиям
У\ | *=*о — Ую> У* \ Х-Хо ^ ^20» • • • > Уп I * = *о ~ J/nO* B)
Интегрирование системы вида A) можно произвести следую-
следующим образом.
Дифференцируем по х первое из уравнений A):
dx2 ~~ дх ^дуг dx ^ '# * ^ дуп dx '
Заменяя производные ~~, -^, ..., -^ их выражениями
fi> /2» •••! fn из Уравнений A), будем иметь уравнение
Дифференцируя полученное ураввейие и поступая аналогично
предыдущему, найдем
^sfr. Уи Уъ> ..-, У„).

Ю4
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ. XIII
Продолжая далее, таким же образом получим, наконец, урав-
уравнение
Итак, мы получаем следующую систему:
^ = М*. у* •••• *»>•
^ = F (x и и)
Из первых /г — 1 уравнений определим i
зив их через х, у± и производные —•, -—
лагается, что эти операции выполнимы):
C)
$, ...» #rt, выра-
., dxn-i (предпо-
(предпоПодставляя эти выражения в последнее из уравнений C)t
получим уравнение /г-го порядка для определения yi
, уи у{, .... «/Г»).
E)
Решая это уравнение, определим yt:
У^Ы*> Ci9 Ca, .•., Сп). F)
Дифференцируя последнее выражение п — 1 раз, найдем про-<
dm d?in dn~~ittt * л л л
изводные -J^ t -^t, •.., -j^ как функции от х, Си С2, ..., Сл^
Подставляя эти функции в уравнение D), определяем у%, у8,..., уй:
У2 = ^2 (^i Q» Q> • • • » ^п)?
G)
Для того чтобы полученное решение удовлетворяло заданным
начальным условиям B), остается лишь найти из уравнений F)
и G) соответствующие значения постоянных С|, Са, ..., Сп (по-
(подобно тому, как мы это делали в случае одного дифференци-
дифференциального уравнения).
Замечание 1. Если система A) линейна относительно иско-
искомых функций, то и уравнение E) будет линейным.

§29] СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ Ю5
Пример 1. Проинтегрировать систему
^ g (a)
при начальных условиях
у\Хтя0=\, 2|л-.0=0. (б)
Решение. 1) Дифференцируя по х первое уравнение, будем иметь
*y_dy >dz
dx^^dx^dx^'
Подставляя сюда выражения -У- и j- из уравнений (а), получим
или
g=-3i/-22+3*+l. (в)
2) Из первого уравнения системы (а) находим
и подставляем в только что полученное уравнение; получаем
ИЛИ
0+2|+,=5*+1. (д)
Общее решение последнего уравнения есть
y = (CH-Ct*)e-*+5*-9 (e)
и на основании (г)
z = (C2—2Ct—2С2*)е-*--6а:+14. (ж)
Подберем постоянные С| и С2 так, чтобы удовлетворялись начальные
условия (б): ylx=o=^\, z |лг=о=0. Тогда из равенств (е) и (ж) получаем
1=Cj:—9, 0=С2—2Ci+14,
откуда Cf=10, C2=6. Таким образом, решение, удовлетворяющее заданным
начальным условиям (б), имеет вид
e-*+5*—9, г = (— 14— \2х)е~х—6*+14.
Замечание 2. В приведенных рассуждениях мы предпо-
предполагали, что из первых п — 1 уравнений системы C) можно опре-
определить функции t/2, */g, ..., уп. Может случиться, что перемен-
переменные у2, ..., уп исключаются не из п> а из меньшего числа
уравнений. Тогда для определения у мы получим уравнение,
порядок которого ниже п.
Пример 2. Проинтегрировать систему
dx , dy , dz ,
Щ^У+г f=x+z Ш=*+У

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
Решение. Дифференцируя по t первое уравнение, находим
Исключая переменные у и z из уравнений
dx
будем иметь уравнение второго порядка относительно х
dt* dt ZX~U'
Интегрируя это уравнение, получим его общее решение
(а)
Отсюда находим
p и y = ^-z = -Cie-t+2C,e*t-z. ф)
Подставляя в третье из заданных уравнений найденные выражения для х и у%
получим уравнение для определения г
Интегрируя это уравнение, найдем
Но тогда на основании уравнений ф) получаем
(б)
Уравнения (а), (б) и (у) дают общее решение заданной системы.
В дифференциальные уравнения системы могут входить про-
производные высших порядков. В этом случае получается система
дифференциальных уравнений высших порядков.
Так, например, задача о движении материальной точки под действием
силы F сводится к системе трех дифференциальных уравнений второго порядка.
Пусть Fxt Fyi Fz—проекции силы F на оси координат. Положение точки
в любой момент времени t определяется ее координатами я, (/, z. Следова-
Следовательно, х, у, z являются функциями от /. Проекции вектора скорости точки
^ dx dy dz
на оси координат будут ^, -^, ^.
Предположим, что сила F, а следовательно, и ее проекции FX1 Fyi Fz
зависят от времени t, положения #, уг г точки и от скорости движения точки,
dx dy dz
т-е'от TfdfTf
Искомыми функциями в этой задаче являются три функции

$29] СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ Ю7
Эти функции определяются из уравнений динамики (закон Ньютона)
d2x—F (+ dx dy dz\
т~Ш * V ' *' У' *' di ' Ш ' Tt)>
d2y r 11 dx dy dz
&Ч _ /, dx dy dz
тШ*~р{(хугпТ
Получили систему трех дифференциальных уравнений второго порядка. В слу-
случае плоского движения, т. е. движения, когда траекторией является плоская
кривая (лежащая, например* в плоскости Оху), получаем систему двух урав-
уравнений для определения функций x(t) и у (t):
d*x г Л dx dy\
Решать систему дифференциальных уравнений высших порядков можно
путем сведения ее к системе уравнений первого порядка. На примере уравне-
уравнений (9) и A0) покажем, как это делается. Введем обозначения
dx __ dy _
Тогда
d2x du d2y _ dv
Система двух уравнений второго порядка (9), A0) с двумя искомыми функ-
функциями х (t) и у (t) заменяется системой четырех уравнений первого порядка
с четырьмя искомыми функциями х, у, и, v
dx __ dy _
— — F (t \ —~F(t \
Заметим в заключение, что рассмотренный нами общий прием решения си-
системы может быть в некоторых конкретных случаях заменен тем или иным
искусственным приемом, быстрее приводящим к цели.
Пример 3. Найти общее решение системы дифференциальных уравнений
d2y _ d2z _
dx2 * dx2
Решение. Дифференцируем по х два раза обе части первого уравнения:
d*y = d2z
dx* ~~ dx2 '
Но -j-?=:0, поэтому получаем уравнение четвертого порядка ~т-х=0. Инте-
Интегрируя это уравнение, получим его общее решение (см. § 22, пример 4)
у = de*+С2е~х + С3 cos х+С4 sin x.
d2u
Находя отсюда --~ и подставляя в первое уравнение, найдем гз

108 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
§ 30. Системы линейных дифференциальных уравнений
с постоянными коэффициентами
Пусть №ы имеем систему дифференциальных уравнений
j/ и11Л1 Г а12Л2 I * * • I UlnXtl>
J?l.-a x 4-a x 4- 4-a x
Л — и21Л1 • и22Л2 I * * • I U2nA«»
где коэффициенты aif суть постоянные. Здесь t — аргумент, i()
x2(t), ..., хп(t) — искомые функции. Система A) называется
системой линейных однородных дифференциаль-
дифференциальных уравнений с постоянными коэффициентами.
Как уже указывалось в предыдущем параграфе, эту систему
можно решить путем сведения к одному уравнению я-го порядка,
которое в данном случае будет линейным (это было указано
в замечании 1 предыдущего параграфа). Но можно решать си-
систему A) и другим методом, не сводя к уравнению я-го порядка.
Этот метод дает возможность более наглядно анализировать харак-
характер решений.
Будем искать частное решение системы в следующем виде:
x1 = a1ektf x2 = a2eht, .... хя = аяе". B)
Требуется определить постоянные аъ а2, ..., ап и k так, чтобы
функции агем, a2ekt, ..., anekt удовлетворяли системе уравне-
уравнений A). Подставляя их в систему A), получим
kaxeht = (aua! + a12a2 + ... + ainan) ek\
ka2ekt = (а21аг + а22а2 + ... + a2nan) ek\
kaneht - (anlax + an2a2 + ... + annan) ekt.
Сократим на ekt. Перенося все члены в одну сторону и собирая
коэффициенты при alf a2, ..., ап, получим систему уравнений
Выберем ai9 a2, ..., an и k такими, чтобы удовлетворялась
система C). Эта система есть система линейных однородных ал-
алгебраических уравнений относительно att a2, •..,<*„. Составим

§30]
СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
109
определитель системы C):
п—-k
a22—k ...
D,
Если k таково, что определитель А отличен от нуля, то система C)
имеет только нулевые решения а1 = а2= ... =an = 0, а следова-
следовательно, формулы B) дают только тривиальные решения
Таким образом, нетривиальные решения B) мы получим только
при таких ky при которых определитель D) обращается в нуль.
Мы приходим к уравнению n-го порядка для определения k:
яг*
Clnn — k
-0.
E)
Это уравнение называется характеристическим уравне-
уравнением для системы A), его корни называются корнями ха-
характеристического уравнения.
Рассмотрим несколько случаев.
I. Корни характеристического уравнения дей-
действительные и различные. Обозначим через kly k2J ...,йЛ
корни характеристического уравнения. Для каждого корня kt на-
напишем систему C) и определим коэффициенты о#\ а$\ ...,a{f}.
Можно показать, что один из них произвольный, его можно счи-
считать равным единице. Таким образом, получаем:
для корня kt решение системы A)
для корня k2 решение системы A)
для корня kn решение системы A)
Xi — otj e n , Л2 — ota ^ t • • • 9 Xn = 06/i e n •
Путем непосредственной подстановки в уравнения можно убе-
убедиться, что система функций
xt =
+ C2af >Л* + ... 4- Cnaf
F)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ. XIII
где С1э С2, ..., Сп — произвольные постоянные, тоже является
решением системы дифференциальных уравнений A). Это есть
общее решение системы A). Легко показать, что можно
найти такие значения постоянных, при которых решение будет
удовлетворять заданным начальным условиям.
Пример 1, Найти общее решение системы уравнений
Решение. Составляем характеристическое уравнение
2-fc 2
1 8-*
или k2—5& + 4=0. Каходим его корни &i = l, &2 = 4. Решение системы ищем
в виде
Составляем систему C) для корня ^=1 и определяем ai1} и
или
откуда а21}?=—о6!1*» Полагая ai1^!, получаем а}р=—g-. Таким обра-
образом, мы получили решение системы
Составляем далее систему C) для корня k2 — 4 и определяем ai2) и ai2)'
откуда
ci2>
= a22) и cci2> = 1, a22) = l. Получаем второе решение системы
Общее решение системы будет (см. F))
И. Корни характеристического уравнения раз-
различные, но среди них есть комплексные. Пусть
среди корней характеристического уравнения имеется два комп-
комплексных сопряженных корня:
Этим корням будут соответствовать решения
*</> - a}1 Va+'P>' (/=1,2 л), G)
х}Я) = а?>в<а-^' (/=1,2, ...,п). (8)
Коэффициенты а}1} и ар определяются из системы уравнений C).

§30] СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ \\\
Так же как ив § 21, можно показать, что действительные
и мнимые части комплексного решения тоже являются решениями.
Таким образом, мы получаем два частных решения
^-^(M^cospx + Xf ship*),
хJ) = eat (Kf> sin px + fya> cos px), U
где М1}, Ц2\ Цг\ №} — действительные числа, определяемые через
а^и af.
Соответствующие комбинации функций (9) войдут в общее
решение системы.
Пример 2. Найти общее решение системы
dx-t dx%
dt dt
Решение. Составляем характеристическое уравнение
~7s2k _5_*И
или ?2 + 12&+37 = 0 и находим его корни
Подставляя k± ——6 +г в систему C), находим
Пишем решение G):
Подставляя ?2 = — 6— i в систему C), находим
Получим вторую систему решений (8):
Перепишем решение G'):
jcx1> =e~6* (cos t-\-i sin t), xi } = A + 0 e~6* (cos t-\-i sin t)t
или
x?) = e-(it (cos t—sin t)-\-ie-6t (cos /+sin t).
Перепишем решение (8'):
A'22) =е~6* (cos t—sin t) — ie~^ (cos ?+sin t).
За системы частных решений можно взять отдельно действительные части и
отдельно мнимые части:
= e-6*cos?, хъ^^е-ы (cos t—sin 0» \
Общим решением системы будет
JCl = C1e-6t cos
jc2 = Ci^-6t (cos /—sin 0 +C2e-e* (cos *+sin t).

112 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
Аналогичным методом можно находить решение системы линей-
линейных дифференциальных уравнений высших порядков с постоян-
постоянными коэффициентами.
В механике и теории электрических цепей исследуется, на-
например, решение системы дифференциальных, уравнений второго
порядка
= а1гх + а12у, ^ = a2ix + a22y. A0)
Снова ищем решение в форме
Подставляя эти выражения в систему A0) и сокращая на ekt,
получаем систему уравнений для определения а, р и k
0f а21а + (а22-?2)|3 = 0. A1)
Отличные от нуля а и (J определяются только в том случае,
когда определитель системы будет равен нулю:
Это есть характеристическое уравнение для системы A0); оно
является уравнением 4-го порядка относительно k. Пусть kit k2,
k3 и &4 —его корни (предполагаем, что корни различны). Для
каждого корня kt из системы A1) находим значения аир. Общее
решение, аналогично F), будет иметь вид
х = Сга™ё* + CjxW + С&™е№ + С4аше№9
у = С$™е*** + CJPW + C?we№ + Сф™**.
Если среди корней будут комплексные, то каждой паре ком-
комплексных корней в общем решении будут соответствовать выра-
выражения вида (9).
Пример 3. Найти общее решение системы дифференциальных уравнений
dH . d2y
Решение. Пишем характеристическое уравнение A2) и находим его
корни:
М&2
I —1 1— к*
Решение будем искать в форме
= 0,
) = а<3> еУТ t,

§311 ПОНЯТИЕ О ТЕОРИИ УСТОЙЧИВОСТИ ЛЯПУНОВА ЦЗ
Из системы A1) находим а^> и pw>:
а<« = 1, ра> = 1/2,
а<2> = 1, р<2) = 1/2,
aC) = if pw = _l/2,
сс<4> = 1, р<4> =—1/2.
Выпишем комплексные решения:
**> = e-tt=: cos *¦— t sin *, ^2) = о,5 (cos *—- i sin 0-
Решением будут действительные и мнимые части:
Теперь можем написать общее решение
x=Ct cos t + C2 sin
0=y Ci cos *+y C* sin t~ C/Zt ~~ C4e"K?/.
Замечание. Мы не рассматривали в этом параграфе случай кратных
корней характеристического уравнения. Этот вопрос подробно изложен, напри-
например, в книге: Петровский И. Г. Лекции по теории обыкновенных диф-
дифференциальных уравнений.— М.: Наука, 1970.
§ 31. Понятие о теории устойчивости Ляпунова.
Поведение траектории дифференциального уравнения
в окрестности особой точки
Так как решения большинства дифференциальных уравнений
и систем уравнений не выражаются через элементарные функции
или квадратуры, то в этих случаях при решении конкретных
дифференциальных уравнений применяются приближенные методы
интегрирования. Понятие об этих методах было дано в § 3; кроме
того, некоторые из этих методов будут рассмотрены в §§ 32—34,
а также в главе XVI.
Недостаток этих методов заключается в том, что они дают
только одно частное решение; чтобы получить другие частные
решения, нужно все вычисления проводить снова. Зная одно
частное решение, нельзя сделать заключение о характере других
решений.
Во многих задачах механики и техники бывает важно знать
не конкретные значения решения при данном конкретном значе-
значении аргумента, а характер поведения решения при изменении аргу-
аргумента и, в частности, при неограниченном возрастании аргумента.
Например, бывает важно знать, являются ли решения, удовлет-
удовлетворяющие данным начальным условиям, периодическими, прибли-
приближаются ли они асимптотически к какой-либо известной функции
и т. д. Этими вопросами занимается качественная теория диффе-
дифференциальных уравнений.

114 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
Одним из основных вопросов качественной теории является
вопрос об устойчивости решения или об устойчивости движения;
этот вопрос был подробно исследован знаменитым русским мате-
математиком А. М. Ляпуновым A857—1918).
Пусть дана система дифференциальных уравнений
TT = ft(t,x9y), % = f.(t,x9y). A)
Пусть x = x(t) и y=y(t) — решения этой системы, удовлетворяю-
удовлетворяющие начальным условиям
*|*=о = *о> У\г=о = Уо- (Г)
Пусть далее, ~x = x(t) и у = у (t) — решения уравнения A), удов-
удовлетворяющие начальным условиям
*|*=о = *о, У\ыо = ~Уо- (Г)
Определение. Решения х = х(t) и у = у(t), удовлетворяю-
удовлетворяющие уравнениям A) и начальным условиям A'), называются
устойчивыми по Ляпунову при t—*оо, если для каждого как
угодно малого е > О можно указать S > 0 такое, что при всех
значениях t > 0 будут выполняться неравенства
s, \y(t)-y(t)\<e, B)
если начальные данные удовлетворяют неравенствам
K~*o|<S, 1*Го-Уо|<а. C)
Выясним смысл этого определения. Из неравенств B) и C)
следует, что при малых изменениях начальных условий мало
отличаются соответствующие решения при всех положительных
значениях t. Если система дифференциальных уравнений является
системой, описывающей некоторое движение, то в случае устойчи-
устойчивости решений характер движений мало изменяется при малом
изменении начальных данных.
Разберем это на примере одного уравнения первого порядка.
Пусть дано дифференциальное уравнение
dy , .
1Г=-^ + 1- (а)
Общим решением этого уравнения является функция
у = Св-* + 1. (б)
Найдем частное решение, удовлетворяющее начальному условию
#!*=о=1. (в)
Очевидно, что это решение у=\ получится при С = 0 (рис. 281). Найдем,
далее, частное решение, удовлетворяющее начальному условию
l/lt=o=]/o-

§311 ПОНЯТИЕ О ТЕОРИИ УСТОЙЧИВОСТИ ЛЯПУНОВА
Найдем значение С из уравнения (б):
откуда
Подставляя это значение С в равенство (б), получаем
Очевидно, решение у—\ является устойчивым. Действительно,
Ц5
при t —> оо.
Следовательно, при произвольном е будет выполняться неравенст-
неравенство C), если будет выполняться нера-
неравенство
~
(УО— 1) = 6 < 8.
Если уравнения A) описы- $
вают движение, где аргумент t
есть время, и при этом уравне-
уравнения не содержат явно времени
t, т. е. имеют вид
Рис-281'
то эта система называется автономной.
Рассмотрим, далее, систему линейных дифференциальных
уравнений
--jj — cx + gy, -yf =ax~\-by. D)
Будем предполагать, что коэффициенты a, b, cy g постоянные,
при этом очевидно, что х = 0, у = 0 есть решение системы D),
в чем убеждаемся непосредственной подстановкой. Исследуем
вопрос о том, каким условиям должны удовлетворять коэффи-
коэффициенты системы, чтобы решение х = О, у = 0 было устойчиво. Эта
исследование проводится так.
Дифференцируем первое уравнение и исключаем у и -?-- на
основании уравнений системы:
d*x _ d,
dt2~~c d
или
E)

Цб ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ?ГЛ. XIII
Характеристическое уравнение дифференциального уравнения E)
имеет вид
%2—(b + c) I—(ag—be) = 0. F)
Это уравнение принято записывать в виде определителя
С-Ь ? [-о G)
(см. уравнение D) § 30).
Обозначим корни характеристического уравнения G) через Kt
и Я2. Как мы увидим ниже, устойчивость или неустойчивость
решений системы D) определяется характером корней %t и %г.
Рассмотрим все возможные случаи,
I. Корни характеристического уравнения дей-
действительные, отрицательные и различные: ^ <0,
>v2<0, %1фк2. Из уравнения E) находим
Зная х, из первого уравнения D) находим у. Таким образом,
решение системы D) имеет вид
L (8>
Замечание. Если g = 0 и афО, то уравнение E) мы со-
составим для функции у. Найдя у, из второго уравнения системы D)
находим х. Структура решений (8) сохранится. Если же g = 0,
а = 0, то решение системы уравнений принимает вид:
Анализ характера решений в этом случае производится проще.
Подберем Сг и С2 так, чтобы решения (8) удовлетворяли
начальным условиям
Решение, удовлетворяющее начальным условиям, будет
& | Я A CJ у
Из последних равенств следует, что при любом е > 0 можно вы-
выбирать |л;01 и \уо\ столь малыми, что для всех f>0 будет
1*@|<е. \y{t)\<e, так как е.**<\; в^<1.
Отметим, что в данном случае
lim х @ = 0, Ит y(t) = Q. A0)
t -»¦ + » t -» + »

§31J ПОНЯТИЕ О ТЕОРИИ УСТОЙЧИВОСТИ ЛЯПУНОВА Ц7
Рассмотрим плоскость хОу. Для системы дифференциальных
уравнений D) и дифференциального уравнения E) эта плоскость
называется фазовой плоскостью. Решения (8) и (9) системы D)
будем рассматривать как параметрические уравнения некоторой
кривой на фазовой плоскости хОу:
* = Ф(*. Съ С2), y = y(U Си С2), A1)
xot Уо). A2)
Эти кривые являются интегральными кривыми, или траекториями
дифференциального уравнения
dy_ax+by
которое получается из системы D) путем деления друг на друга
правых и левых частей.
Начало координат О@; 0) является особой точкой для диф-
дифференциального уравнения A3), так как эта точка не принад-
принадлежит к области существования и единственности решения.
Характер решений (9) и вообще решений системы D) наглядно
иллюстрируется расположением интегральных кривых
F(x, y% Q = 0,
образующих общий интеграл дифференциального уравнения A3).
Постоянная С определяется из начального условия у \х=Хо = у0.
После подстановки значения С получаем уравнение семейства
в форме
Fix, у, *0, Уо). A4)
В случае решений (9) особая точка называется устойчивым узлом.
Говорят, что точка, двигаясь по траектории, неограниченно при-
приближается к особой точке при t—* + оо.
Очевидно, что соотношение A4) может быть получено путем
исключения параметра t из системы A2). Не производя в дальней-
дальнейшем полного анализа характера расположения интегральных кри-
кривых вблизи особой точки на фазовой плоскости при всех возмож-
возможных случаях корней характеристического уравнения, ограничимся
иллюстрацией этого на простейших примерах, не требующих про-
проведения громоздких вычислений. Отметим, что характер поведения
траекторий уравнения A3) вблизи начала координат при произ-
произвольных коэффициентах качественно такой же, какой будет рас-
рассмотрен в примерах.
Пример 1. Исследовать устойчивость решения # = 0, у = 0 системы
уравнений
dx dy n

118
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ. XIII
Решение. Характеристическое уравнение будет
I— 1—Л- 0 1^
О —2-Я
Корни характеристического уравнения
^1==— 1, Я,2 = —2.
Решения (8') в данном случае будут
* = de-*f у = Сф~*.
Решения (9) будут
х = хое-*, У = Уое~*К (а)
Очевидно, что х (t)—у О и у (t) —> 0 при ? —Н-°° • Решение л:=0, у=0 устойчиво.
Обратимся теперь к фазовой плоскости. Исключая параметр t из уравнений (а),
получаем уравнение вида A4)
*о
У о
(б)
Это семейство парабол (рис. 282).
Уравнение вида A3) для данного
примера будет
3i dx х
Интегрируя, получаем
= Сх\ (в)
Определим С из условия
Рис. 282.
Подставляя найденное значение С в (в), получаем решение (б). Особая точка
О @; 0) есть устойчивый узел.
II.Корни характеристического у равнения дей-
действительные, положительные, различные: A,j>0,
^2>0, ^\Ф\- В этом случае решения выражаются также форму-
формулами (8) и соответственно (9). Но в данном случае при как угодно
малых |лго( и |#0| будет |*(/)|—>оо, \y(t)\—+oo при t—>-f°o,
так как е**' —> оо и ек** —у оо при t —> 4" °° • На фазовой плоскости
особая точка—неустойчивый узел: при ?—>-foo точка на траекто-
траектории удаляется от точки покоя х = 0у у = 0.
Пример 2. Исследовать устойчивость решений системы
dx dy n
Ж=х' Ж=2«-
Решение. Характеристическое уравнение будет
1—1 0
0 2-Я,
=0;
его решения

§31J ПОНЯТИЕ О ТЕОРИИ УСТОЙЧИВОСТИ ЛЯПУНОВА Ц9
Решение будет
Решение неустойчиво, так как |*@1—><*>* 1#@1—> °° ПРИ *—>-+оо.
Исключая t, получаем
\х0) у о
(рис. 283). Особая точка 0@; 0) есть неустойчивый узел.
Рис. 283,
Рис. 284,
III. Корни характеристического ураанения
действительные, разных знаков, например, ^i>0,
Х2<0. Из формул (9) следует, что при как угодно малых |*0{
и | у01, если cx0+gy0—xol2 Ф О, будет | x{t) \ —* оо, j у (t) | -+ со при
г—^^оо. Решение неустойчиво. На фазовой плоскости особая
точка называется седлом.
Пример 3. Исследовать устойчивость решения системы
dx dy
Ж~~х* ~dt"~"~~ У'
Решение. Характеристическое уравнение будет
О —2-Х
следовательно, Аа = 1, Я2 = —2. Решение будет
==0,
Решение неустойчиво. Исключая параметр /, получаем семейство кривых на
фазовой плоскости
Особая точка О @; 0) есть седло (рис. 284).
IV. Корни характеристического уравнения
комплексные с отрицательной действительной
частью: ?^ = а4-*'Р, К^1**—*'Р(<* <0)- Решение системы D)

120 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. ХШ
будет
у=± e«f [(aCt+PC2 -cCt) cos p/ -f («C2-pCf -cC2) si
о
Если ввести обозначение
iS = ?, cos 6 = ^,
то уравнения A5) можно переписать в виде
где Ct и С2—произвольные постоянные, которые определяются
из начальных условий х = х0, у~у0 при ? = 0, причем
хо = С sin б, у0 = -~ [(а—с) sin б -fP cos6],
о
откуда находим
С1в^, Сг = ^-у~С) . A7)
Снова заметим, что если g = 0, то вид решения будет несколько
иной, но характер анализа не изменится.
Очевидно, что при любом е>0 при достаточно малых \хо\
и \Уо\ будут выполняться соотношения
ИОК*. \y(t)\<*-
Решение устойчиво. В данном случае при t—>^oo
х@-*0 и 1/@ — 0,
неограниченное число раз меняя знаки. На фазовой плоскости
особая точка называется устойчивым фокусом.
Пример 4. Исследовать устойчивость решения системы уравнений
dx , dy
ж=-х+у' чг=-х-у-
Решение, Составляем характеристическое уравнение и находим его
корни:
Находим Ct и С2 по формулам A7): Ci=xOi C2=y0. Подставляя в A5), по-
получаем
x = e~i(x0cost-{-y0sintI y = e-f (y0 cos t—xosin t). (A)
Очевидно, что при любых значениях t
При /—^+оо имеем x(t)—>0, е/@-*>0. Решение устойчиво.

§31j ПОНЯТИЕ О ТЕОРИИ УСТОЙЧИВОСТИ ЛЯПУНОВА 121
Выясним характер расположения кривых на фазовой плоскости в этом
случае. Преобразуем выражения (А). Пусть
Тогда равенства (А) примут вид
x^Me-tcos (t—Ь), y = Me~f sin (*—6). (В)
На фазовой плоскости перейдем к полярным координатам р и Э и установим
зависимость р = /@). Уравнения (В) принимают вид
р cos Э = Me-'cos (*—6), psln8 = Me-*sin(*—6). (С)
Возведя в квадрат правые и левые части и складывая, получим
или
Установим зависимость t от 9. Деля члены нижнего из равенств (С) на соот-
соответствующие члены верхнего равенства, получим
откуда
f-9+б.
Подставляя в (D), получаем
или
Р = Ме~6-д.
Обозначая Me~6 = Mi, окончательно получаем
р^Мхе-в. (Е)
Это семейство логарифмических спиралей. В этом случае при t —»- оо точка
по траектории приближается к началу координат. Особая точка 0@; 0) есть
устойчивый фокус.
V. Корни характеристического уравнения ком-
комплексные с положительной действительной ча-
частью: ^ = а + Ф, %2 = а—ф (а>0). В этом случае решение
также выразится формулами A5), где а > 0. При любых началь-
начальных условиях х0 и уо{Ух1 + у*офО) и при t-+ + oo величины
1*@1 и 11/@1 могут принимать как угодно большие значения.
Чтение неустойчиво. На фазовой плоскости особая точка назы-
называется неустойчивым фокусом. Точка по траектории неограни-
неограниченно удаляется от начала координат.
Пример 5. Исследовать устойчивость решения системы уравнений
dx , dy
ж=х+у ж=
Решение. Составим характеристическое уравнение:

122
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ. XIII
Решение A5) с учетом A7) в данном случае будет
х = е*(х0 cost-\-y0sin t),
у — ё*(у0 cos t—#о sin t).
На фазовой плоскости получим кривую в полярных координатах
Особая точка — неустойчивый фокус (рис. 285).
«2?
Рис. 285.
Рис. 286.
VI. Корни характеристического уравнения
чисто мнимые: %± = ф9 Х2 = — ф. Решения A5) в этом случае
примут вид
y=J
j pCi— cC2) sin Щ.
Постоянные С± и С2 определяются по формулам A7):
г —y Г 8У+сх
A8)
A9)
Очевидно, что при любом е > 0 и при всех достаточно малых | х0 \
и | j/o I будет | х (t) | < е, | у (t) | < е при любом t. Решение устойчиво.
Здесь х и у—периодические функции от t.
Чтобы произвести анализ интегральных кривых на фазовой
плоскости, целесообразно первое из решений A-8) записать в сле-
следующем виде (см. A6)):
B0)
где С, б—произвольные постоянные. Из выражений B0) следует,
что х и у—периодические функции от t. Исключаем параметр t
из уравнений B0):

§31] ПОНЯТИЕ О ТЕОРИИ УСТОЙЧИВОСТИ ЛЯПУНОВА 123
Освобождаясь от радикала, получим
Это семейство кривых 2-го порядка (кривые действительные),
зависящих от произвольной постоянной С. Каждая из них не
имеет неограниченно удаленных точек. Следовательно, это семей-
семейство эллипсов, окружающих начало координат (при с = 0 оси
эллипсов параллельны осям координат). Особая точка называется
центром (рис. 286).
Пример 6. Исследовать устойчивость решения системы уравнений
dx dy .
Решение. Составим характеристическое уравнение и найдем его корни:
— А, 1
— 4 — X
= 0,
Решения B0) будут
Уравнение B1) будет иметь вид
На фазовой плоскости имеем систему эллипсов. Особая точка — центр.
VII. Пусть A,i = 0, ?v2 < 0. Решение (8) в этом случае при-
принимает вид
y — i-C.c + C^-c)^]. B2)
Очевидно, что при любом е>0 и при достаточно малых |а:0| и
| у01 будет |х(t)\ < е, \y(t)\<& при t > 0. Следовательно, ре-
решение устойчиво.
Пример 7. Исследовать устойчивость решения системы
dx r, dy . .
HF=0' Ж — »' <«>
Решение. Находим корни характеристического уравнения;
Здесь g — 0. Решения находим непосредственно, решая систему, не пользуясь
формулами B2):
x = Ci9 y = C2e~t. (P)
Решение, удовлетворяющее начальным условиям x=xQy у = Уо при ^ = 0, будет
х = х0, y = yoe-f. (у)
Очевидно, что решение устойчиво. Дифференциальное уравнение на фазовой
плоскости будет -т-=0. Общий интеграл будет дс = С. Траектории—прямые,

124
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ. XIII
параллельные оси Оу, Из уравнений G) следует, что точки по траекториям
приближаются к прямой у = 0 (рис. 287).
VIII. Пусть ^? = 0, >i2>0. Из формул B2) или (8') следует,
что решение неустойчиво, так как | х (t) \+\ у (t) \ —+ оо при t —>+оо.
IX. Пусть 911 = Я2<0. Решение будет
B3)
Так как е***—>0 и teK>*—+0 при
0
, то для любого е>0
Рис. 287.
Рис. 288.
можно подобрать Ct и С2 такие (путем выбора xQ и у0), что будет
1*@1<8> |у@1<8 ПРИ любом t > 0. Следовательно, решение
устойчиво. При этом x{t)—>0 и y(t)—+O при /—> + оо.
Пример 8. Исследовать устойчивость решения системы
dA: dy
It х' Ж~"~у'
Решение. Находим корни характеристического уравнения*
I —1 —А, 0
I о — 1 —;
Здесь g = 0. Решение системы будет иметь форму (8'):
причем х—>0, у—^0 при /—>+<*>• Решение устойчиво. Семейство кривых
на фазовой плоскости будет
— ssss~^—=г^} Т. е. у = кХ.
X ^**1
Это семейство прямых, проходящих через начало координат. Точки по тра-
траекториям приближаются к началу координат. Особая точка О@; 0) есть узел
(рис. 288).

§31]
ПОНЯТИЕ О ТЕОРИИ УСТОЙЧИВОСТИ ЛЯПУНОВА
125
Заметим, что в случае ^f = Я2 > 0 форма решения B2) со-
сохраняется, но при t—++00
I * (О I "—"УО° и If/COl""^00-
Решение неустойчиво.
X. Пусть Х1 = %2 = 0. Тогда
1 г -^ ' ^ -cC2f]. B4)
Откуда видно, что х -> оо и */->оо при ?->-f-oo. Решение
успгойчиео.
Пример 9. Исследовать устойчивость решения системы уравнений
dx dij л
Решение. Находим корни характеристического уравнения:
Находим решения
Очевидно, что х —*оопри /—^+ °°« Решение неустойчиво. Уравнение на фазовой
Облает
неустойчивых
0
W ._
Я А*
решений
Рис. 289.
Рис. 290.
плоскости будет ;/=0. Траектории ^=С—-прямые, параллельные оси (рис. 289).
Особая точка называется вырожденным седлом.
Чтобы дать общий критерий устойчивости решения системы
D), поступим следующим образом.
Запишем корни характеристического уравнения в форме ком-
комплексных чисел:
(в случае действительных корней A,i* = 0 и hi* =0).

126 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 1ГЛ. ХШ
Возьмем плоскость к*к** комплексной переменной и будем
изображать корни характеристического уравнения точками на
этой плоскости. Тогда на основании рассмотренных случаев ус-
условие устойчивости решения системы D) можно сформулировать
следующим образом.
Если ни один из корней 9^, к2 характеристического уравне-
уравнения F) не лежит справа от мнимой оси, причем хотя бы один
корень отличен от нуля, то решение устойчиво; если же хотя
бы один корень лежит справа от мнимой оси или оба корня равны
нулю, то решение неустойчиво (рис. 290).
Рассмотрим теперь более общую систему уравнений
B5)
Решение такой системы, кроме исключительных случаев, не вы-
выражается через элементарные функции и квадратуры.
Для того чтобы установить, устойчивы или неустойчивы реше-
решения этой системы, ее сравнивают с решениями линейной систе-
системы. Предположим, что при х -* 0 и у -*¦ О функции Р (х, у) и
Q (*> У) также стремятся к нулю и притом быстрее, чем р, где
иными словами,
^ = 0, lim Q (*>y)=0.
Тогда можно доказать, что, кроме исключительного случая, ре-
решение системы B5) будет устойчиво тогда, когда устойчиво ре-
решение системы
% = cx + gy, % = ax + by, D)
и неустойчиво, когда решение системы D) неустойчиво. Исклю-
Исключение составляет тот случай, когда оба корня характеристичес-
характеристического уравнения лежат на мнимой оси; в этом случае вопрос об
устойчивости или неустойчивости решения системы B5) решается
значительно сложнее.
А. М. Ляпунов *) исследовал вопрос об устойчивости решений
систем уравнений при довольно общих предположениях относи-
относительно вида этих уравнений.
В теории колебаний часто рассматривают уравнение
d2x р / dx\ /о«ч
?[x) <26>
*) Ляпунов А. М. Общая задача об устойчивости движения.— М.; Лл
ОНТИ, 1935.

§32] МЕТОД ЭЙЛЕРА 127
Обозначим
<27>
Тогда получаем систему уравнений
ah". 2=/<*•">¦ <28>
Фазовой плоскостью для этой системы будет плоскость (х, v).
Траектории на фазовой плоскости дают геометрическое изобра-
изображение зависимости скорости v от координаты х и наглядно ка-
качественно характеризуют изменение х и v. Если точка # = 0,
и = 0 является особой точкой, то она определяет положение рав-
равновесия.
Так, например, если особая точка системы уравнений есть
центр, т. е. траектории на фазовой плоскости представляют собой
замкнутые линии, окружающие начало координат, то движения,
определяемые уравнением B6),— незатухающие колебательные
движения. Если особая точка фазовой плоскости есть фокус (при
этом \х\ -*•(), \v\ ->0 при t-+oo), то движения, определяемые
уравнением B6),— затухающие колебания. Если особая точка
есть узел или седло (и это единственная особая точка), то х ->-
->±оо при t -*oo. В этом случае движущаяся материальная
точка уходит в бесконечность.
Если уравнение B6) линейное вида j^r^^x-t-b—, то система
B8) имеет вид
dx dv
v a
Это система вида D). Точка # = 0, v = 0 есть особая точка, она
определяет положение равновесия. Отметим, что переменная х—
не обязательно механическое перемещение точки. Она может
иметь различный физический смысл, например, обозначать вели-
величину, характеризующую электрические колебания,
§ 32.: Приближенное решение дифференциальных уравнений
первого порядка методом Эйлера
Мы рассмотрим два метода численного решения дифференци-
дифференциального уравнения первого порядка. В этом параграфе рассмот-
рассмотрим метод Эйлера. Найдем приближенно решение уравнения
на отрезке [х09Ь]9 удовлетворяющее начальному условию y=yQ
при х = х0. Разделим отрезок [xQj b] точками д:0, xi9 x2, ..., хп = Ь
на п равных частей (здесь xQ < х± < х2 <.,. < хп). Обозначим

128 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 1ГЛ. XIII
х±—х0 = х2 — хг = .., = Ь — xn_t = kx = h, следовательно,
h b~~x°
Пусть y = q>(x) есть некоторое приближенное решение урав-
уравнения A) и
Обозначим
В каждой из точек х0, Xf, •,., х„ в уравнении A) производную
заменим отношением конечных разностей:
При дс = дсв будем иметь
^ = / (*о> Уо), АУо = f (^о.
или
В этом равенстве #0, у0, ft известны, следовательно, находим
При * = *f уравнение B') примет вид
или
уг) ft.
Здесь известными являются я*, уъ ft, а г/2 определяется.
Аналогично находим
2, У.) А,
Таким образом, приближенные значения решения в точках х0,
Xf,..., хп найдены. Соединяя на координатной плоскости точки
(*0; Уо)> (Xi\ Ух), • • •, (хп; уп) отрезками прямой, получим лома-
ломаную—приближенное изображение интегральной кривой (рис. 291).
Эта ломаная называется ломаной Эйлера.

г 321
МЕТОД ЭЙЛЕРА
129
Замечание. Обозначим через y = (fh(x) приближенное ре-
решение уравнения A), соответствующее ломаной Эйлера при &x=h.
Можно доказать*), что если сущест-
существует единственное решение у = у*(х)
уравнения A), удовлетворяющее на-
начальным условиям и определенное на
отрезке [л:0, 6], то ,iim | фл (х)—ф* (х) |=
=0 при любом х из отрезка [х0У 6].
Пример. При л:—1 найти прибли-
приближенное значение решения уравнения
удовлетворяющего начальному условию
yQ=\ при хо=О.
Рис, 291.
*%
Решение* Разделим отрезок [0, 1] на 10 частей точками
С ft = 0,l. З
р
0,1; 0,2; ..., 1,0. Следовательно,
кать по формуле B'):
или
Таким образом, получаем
г/2=1,1 + A,1+0,1).0,1 = 1,22,
В процессе решения составляем таблицу:
]
Значения ylt y2i ,,., уп будем
хк
Xq =0
х± =0,1
х2 =0,2
х3 =0,3
*4 =0,4
хь =0,5
*в =0,6
х7 =0,7
хв =0,8
х9 =0,9
,000
,100
,220
1,362
1,524
1,7164
1,9380
2,1918
2,4810
2,8091
3,1800
Ук+Хк
1,000
1,200
1,420
1,620
1,924
2,2164
2,5380
2,8918
3,2810
3,7091
0,100
0,120
0,142
0,162
0,1924
0,2216
0,2538
0,2892
0,3281
0,3709
Мы нашли приближенное значение у |x=i = 3,1800. Точное решение дан-
данного уравнения, удовлетворяющее указанным начальным условиям, будет
*) Доказательство см., например, в книге: Петровский И. Г. Лекции
по теории обыкновенных дифференциальных уравнений.— М.: Наука, 1970,
Н. С. Пискунов, т, 2

|30 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ XIII
Следовательно,
Абсолютная погрешность: 0,2566; относительная погрешность: ~^gg=O,075«
= 2(*—l)= 3,4366.
тная погрешность: 0,256
«8%.
§ 33, Разностный метод приближенного решения
дифференциальных уравнений, основанный на применении
формулы Тейлора* Метод Адамса
Снова будем искать решение уравнения
y' = f(*,y) A)
на отрезке [л;0, 6], удовлетворяющее начальному условию у = у0
при х = х0. Введем нужные для дальнейшего обозначения. При-
Приближенные значения решения в точках х0, xi9 х2, . •., хп будут
Уоу Ун У%у •••> Уп* Первые разности, или разности первого по-
порядка:
ЬУо = У1-Уо, Ьу1 = уъ-уи ,.., куп-1 = Уп-Уп-ь
Вторые разности, или разности второго порядка:
Д2г/0 = Ayt - А */0 = уш - 2ft +1/0,
Д2^1 = д#2 - д Уг == Уз -
№Уп-2 = ДУ«-1 - Д^-2 = Уп - 2У«
Разности вторых разностей называются разностями третьего по-
порядка и т. д. Через y'Qi y'u ...,#„ обозначим приближенные зна-
значения производных, через yl, ft, ..., i/^ — приближенные значе-
значения вторых производных и т. д. Аналогично определяются пер-
первые разности производных
вторые разности производных
и т. д.
Напишем далее формулу Тейлора для решения уравнения в
окрестности точки х = х0 (т. I, гл. IV, § 6, формула F));
m. B)
В этой формуле у0 известно, а значения y'Of y"Q, ... производных

§33] РАЗНОСТНЫЙ МЕТОД 131
находятся из уравнения A) следующим образом. Подставляя в
правую часть уравнения A) начальные значения х0 и yOf найдем yi:
Дифференцируя члены уравнения A) по х, получим
*¦-%,+%«¦¦ <3>
Подставляя в правую часть значения х0, у0, y9 найдем
^= \Тх+ТуУ) |,„„ ушу., ушу?
Дифференцируя еще раз равенство C) по х и подставляя значе-
значения х09 у0, Уоу у'о, найдем у'о". Продолжая*) так, можем найти
значения производных любого порядка при х = х0. Все члены,
кроме остаточного члена Rm, в правой части формулы B) из-
известны. Таким образом, пренебрегая остаточным членом, мы можем
получить приближенные значения решения при любом значении х;
их точность будет зависеть от величины \х — хо\ и числа членов
в разложении.
В рассмотренном ниже методе по формуле B) определяют
только несколько первых значений у, когда \х — хд\ мало. Мы
определим значения yf и у2 при x1 = xQ + h и при x2 = x0 + 2hf
беря четыре члена разложения (у0 известно на основании на-
начальных данных):
^ + ТТг^ + зГ^0 » W
1у'.+^у; + ^У»'. D')
Таким образом, будем считать, что известны три значения **)
функции yQJ yly у2. На основании этих значений, пользуясь
уравнением A), определяем
Уо = / (ХО9 у0), y[ = f (Xit Ух), у'% = f(x2, y2).
Зная уо» Уи У*2, можно определить Дуо, Ayi, А2у0. Результаты
вычисления заносим в таблицу:
*) Мы в дальнейшем будем предполагать, что функция f (х, у) столько
раз дифференцируема по х и по у, сколько требуется по ходу рассуждений.
**) Если бы мы стали находить решение с большей точностью, то потре-
потребовалось бы вычислять больше трех первых значений у. Подробно об этом
см., например: Безикович Я. С, Приближенные вычисления»—М.; Гос-
техиздат, 1949,
5*

132
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
|ГЛ. ХШ
X
х0
xt == Xq + h
x2 = x0 + 2h
...
**-i = *e + №— 0*
** = *о + *А
Уо
Уг
...
у!
...
Ai/'
...
...
Допустим теперь, что нам известны значения решения у9, у19
у2У ..., yk. На основании этих значений, пользуясь уравнением A),
мы можем вычислить значения производных у'О9 y'lf уг, ..., j4,
а следовательно, Д^, Ly'u ..., Аг/Li и Д2#;, Д2у;, ..., Д2у^2.
Определим значение yk+i по формуле Тейлора, полагая а = хк9
+ h
— 4- '4- "J- '"Л- jl.<i
Ограничимся в нашем случае четырьмя членами разложения:
ЖчУь • E)
В этой формуле неизвестными являются yl и у^\ которые мы
попытаемся определить через известные разности первого и вто-
второго порядков.

§33] РАЗНОСТНЫЙ МЕТОД ]33
Предварительно представим по формуле Тейлора у'к_и пола-
полагая a = xk, х — а =— ft:
У'ь-г = Й + Ц** # + (-=# Ун% F)
и tjk-г, полагая а = хкУ х — а =—2ft:
Из равенства F) находим
Ук ~ y'k-i=&yLi = т ifi—П2 #*"• (8)
Вычитая из членов равенства F) члены равенства G), получим
y'k-t - y'k-ъ = Д^-2 = у У* y y'k"- (9)
Из (8) и (9) находим
или
^' = 1Д^_2. A0)
Подставляя выражение y'k" в равенство (8), получим
йв*?=!+?й=2. A1)
Итак, у? и ^" найдены. Подставляя выражения A0) и (И)
в разложение E), получим
Это и есть так называемая формула Адамса с четырьмя членами,
Формула A2) дает возможность, зная yk, ук_г, ук_2У определить
ук+1. Таким образом, зная у0, ух и */2, мы можем найти уъ и далее
У*, Уъ, •••
Замечание 1. Укажем без доказательства, что если суще-
существует единственное решение уравнения A) на отрезке [х0, Ь\
удовлетворяющее начальным условиям, то погрешность прибли-
приближенных значений, определенных по формуле A2), по абсолютной
величине не превосходит yVf/i4, где М — постоянная, зависящая от
длины интервала и вида функции / (г, у) и не зависящая от ве-
величины ft.
Замечание 2. Если мы хотим получить большую точность
вычисления, то следует брать больше, чем в разложении E),
членов, и формула A2) соответствующим образом изменится. Так,

134 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
если вместо формулы E) мы возьмем формулу, содержащую справа
пять членов, т. е. дополним членом порядка fi4, то вместо фор-
формулы A2) аналогичным путем получим формулу
h f , h A , . Ых к в* г .
Здесь f/^+i определяется через значения yk, yk_it yk_2 и yk^^.
Таким образом, чтобы начать вычисления по этой формуле, нужно
знать четыре первых значения решения у0, yi9 y2, t/3- При вычис-
вычислении этих значений по формулам типа D) следует брать пять
членов разложения.
Пример 1. Найти приближенные значения решения уравнения у' = у-{-х,
удовлетворяющего начальному условию Уо—1 при #0 = 0. Значения "решения
определить при #=0,1; 0,2; 0,3; 0,4.
Решение. Найдем сначала у$ и у2 по формулам D) и D'), Из уравне-
уравнения и начальных данных получаем
Дифференцируя данное уравнение, получим
/ = */'+!.
Следовательно,
y; = fo' + l)L=o==l + l=2.
Дифференцируем еще раз:
Следовательно,
Подставляя в равенство D) значения yOi y'o, yl и h = 0,1» получим
Аналогично при h = 0,2 получим
0 2 0 22 0 2
Зная i/q, yi, у2, на основании уравнения находим
i= 1,1103+0,1 = 1,2103,
2= 1,2427+0,2 = 1,4427,
Д^= 0,2324, A2i/i = 0
Полученные значения заносим в таблицу:

§33]
РАЗНОСТНЫЙ МЕТОД
135
X
*i = 0,l
*2 = 0,2
*з = 0,3
*4 = 0,4
У
уо = 1,0000
#1 = 1,1103
у2=^ 1,2427
1/з=1,3995
t/4 = l,5833
0*
00=1
у[= 1,2103
й = 1,4427
0з=1,6995
А0'
Д0о' = 0,2103
A0i = 0,2324
Д02 =0,2568
ду
Д20о = 0,0221
A2^ = 0,0244
По формуле A2) находим 03:
03 = 1,2427+^ • 1,4427+^ • 0,2324+^i . 0,0221 =1,3995.
Далее находим значения 03, Д02, Д20ь Снова по формуле A2) находим 04Т
Точное выражение решения данного уравнения:
у = 2е*—х— 1.
Следовательно, у\х-^л — 2е0'4—0»4—1 = 1,58364. Абсолютная погрешность:
0 0003
0,0003; относительная погрешность: -г~Еооа ^ 0,0002 = 0,02%. (Абсолютная по-
1,ООО0
грешность значения 04, вычисленного по методу Эйлера: 0,06; относительная
погрешность: 0,038 = 3,8%.)
Пример 2. Найти приближенные значения решения уравнения
удовлетворяющего начальному условию 0О=О при дго = О. Значения решения
определить при # = 0,1; 0,2; 0,3; 0,4.
Решение. Находим

136 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
По формулам D) и D') получаем
[ГЛ ХШ
Из уравнения находим
= 0,0400.
На основании этих данных составляем первые строки таблицы, а затем
значения ув и уА определяем по формуле A2).
X
*x = 0,i
*2 = 0,2
*3 = 0,3
*4=0,4
У
уо=0
«/! = 0,0003
у2 =0,0027
#3=0,0090
^=0,0213
у'
Уо = 0
(/1=0,0100
1/2 = 0,0400
уз =0,0901
Д#о = 0,0100
Ду1 = 0,0300
Д(/2 = 0,0501
Д2у;=0,0200
А2у1 = 0,0201
Итак,
^3 = 0,0027+^-0,0400+^.0,0300+1.0,1.0,0200 =
^ = 0,0090+^-0,0901 +^1.0,0501 +--0,1.0,0201=0,02133.
Отметим, что первые верные четыре знака в у± таковы: */4 = 0,0213. (Это
можно получить другими, более точными методами, с оценкой погрешности.)
§ 34. Приближенный метод интегрирования систем
дифференциальных уравнений первого порядка
Рассмотренные в §§ 32 и 33 методы приближенного интегри-
интегрирования дифференциальных уравнений применимы и для решения
систем дифференциальных уравнений первого порядка. Рассмотрим

§341 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ СИСТЕМ 137
здесь разностный метод для решения систем уравнений. Рассуж-
Рассуждения будем проводить для системы двух уравнений с двумя
искомыми функциями.
Требуется найти решения системы уравнений
dy ? / v /л\
d? = h(x,y,*), B)
удовлетворяющие начальным условиям у = у0, z = zQ при х = х0.
Будем определять значения функции у и г при значениях
аргумента #0, xiy x2> ..., хкУ хк+ь ..., хп. Пусть снова
Приближенные значения функции обозначим
и соответственно
Напишем рекуррентные формулы типа A2) § 33j
А ' jl.1Lд ' -|_—/iA2 ' D}
Чтобы начать вычисления по этим формулам, нужно знать кроме
заданных у0 и г0 еще у^ у2\ ziy г2; эти значения находим по
формулам типа D) и D') § 33:
h , , Л2 „ . Л8 ,„
^1 == ^о 4" "f го "Ь ~ го Ч* "зГ 2° '
^2 == ^о г "у ^о Н 2—^oi—3J—^° '
Для применения этих формул нужно знать y'Oi yly у'ъ\ z'Of 2j,
2j", к определению которых мы сейчас и приступим. Из уравне-
уравнений A) и B) находим
y'o = fi(*o> У*, г0), z'9 = f2(x0t у0У г0).

138
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ. ХШ
Дифференцируя уравнения A) и B) и подставляя значения х0, yQ9
*о» Уо и z'o, найдем
Дифференцируя еще раз, найдем у'о" и г'0'\ Зная уь y2, гъ z2,
находим из данных уравнений A) и B) у[9 у'2, г'и г'2, Ау09 А#;,
А2(/0, AzJ, Az'u A2zJ, после чего мы можем заполнить первые пять
строк таблицы:
X
Xq
Ч
х3
У
Уо
У±
Уч
Уз
У'
Уо
я
У1
У*
Уъ
&у'о
&У1
At/2
А2 у'
А2Уо
A2yi
г
20
Zi
22
23
г'
л
20
к
22
г'з
Az'
Аз'
Az[
А22
АН
А2го
A>z[
По формулам D) и E) найдем у3 и г3, а из уравнений A) и
B) найдем у3 и г3. Вычислив Ау^ &2Уи Агг, А2г^, снова по фор-
формулам D) и E) найдем у4 и г4 и т. д.
Пример 1. Найти приближенные значения решений системы
с начальными условиями #о = О, zo=l при дго = 0. Вычислить значения реше-
решений при *=0,1; 0,2; 0,3; 0,4.
Решение. Из данных уравнений находим
* \ 1 * I /\

§341 ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ СИСТЕМ 139
Дифференцируя данные уравнения, найдем
По формулам типа D) и E) находим
w=o+5fi. i+^.o+^-1=0,1002,
0 9 0 92 0 2
</=0+^ • 1+М • 0+^
^ М- • 0+^- . 1=0,2013,
= 1 +^ • 0+°^ • 1 +°-? • 0= 1,0050.
*=1+М. 0+^.1+^.0=1,0200.
На основании данных уравнений находим
^=1,0050, 21 = 0,1002,
t/2 = 1,0200, 22=0,2013,
Ау[ = 0,0150, Azi =
А2«/о = 0,0100, А2*; = 0,0009
и заполняем первые пять строк таблицы (см. с. 140),
Далее по формулам D) и E) находим
?±1.0,1011+—• 0,1-0,0009=1,0452
и аналогично
^! • 1,0452+^1.0,0252 +~0,1-0,0102 = 0,4107,
^1. 0,3045+^-.0,1032 + ~.0,Ь0,0021 = 1,0809.
Очевидно, что точные решения данной системы уравнений, удовлетворяю-
удовлетворяющие указанным начальным условиям, будут
у — sh дс, z — ch х.
Поэтому пять верных после запятой знаков решений будут
#4 = sh 0,4 = 0,41075, z4=ch 0,4= 1,08107.
Замечание. Так как уравнения высших порядков и си-
системы уравнений высших порядков во многих случаях сводятся
к системе уравнений первого порядка, то изложенные методы
применимы к решению этих задач.

140
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ XIII
о
о
о
о
см
я
сГ
S
о
о
ю
о
§
8
о"
2
о
о
050
S
о"
о*
со
о
о
и
со
о*
сГ

УПРАЖНЕНИЯ К ГЛАВЕ ХШ 141
Упражнения к главе XIII
Показать, что указанные функции, зависящие от произвольных постоян-
постоянных, удовлетворяют соответствующим дифференциальным уравнениям:
Функции Дифференциальные уравнения
2. у =
п d?y 3 d2y
dx3 x rfjc2
6. y =
8. u = -
dx* ^ x dx
Проинтегрировать дифференциальные уравнения с разделяющимися пере-
переменными.
9. ydx—xdy = 0. Отв. у = Сх. 10. (l+a) vdu+(\— v) и dv=0.
Отв. inuv + u-*v = C. 11. (\+y)dx—(\—x)dy = 0. Отв. (\+y) (I— x) = C.
14. zdt — (t*—a2)dz = 0. Отв. г2а = С^~. 15. ~
^-- !6- (l+s)^— ^Frfs^O. Отв. 21^*?—arctgs=C.
— ьу
17. dp-}-ptg9d9=0. Отв. p = Ccos9.
18. sin9cosq>d0—cos Ввтф dcp—O. Отв.
19. sec29tg9d9+sec29tg9rf<p = 0. Ome.
20. sec29tg^^4-sec29tg9d9=0. Ome. sin2 9+sin2<p=-C.
21. (l+л:2) dy— V\—y2dx=0. Ome. arosiny—a
22. Y"U^dy—VT^dx = 0. Отв. у УТ^с2—
23. 3e*tgt/d*+(l— e^) sQczydy = O. Ome. tg>=
24. (л:—</2л)д(а:+(^—x*y)dy = 0. Ome.
Задачи на составление дифференциальных
ур авнен ий
25. Доказать, что кривая, у которой угловой коэффициент касательной
в любой точке пропорционален абсциссе точки касания, есть парабола.
Отв. у==ах2-\-С.
26. Найти такую кривую, проходящую через точку @; —2), чтобы угло-
угловой коэффициент касательной в любой ее точке равнялся ординате этой точки,
увеличенной на три единицы, Отеш у — ех—3,

142 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
27. Найти такую кривую, проходящую через точку A; 1), чтобы угловой
коэффициент касательной к кривой в любой точке был пропорционален квад-
квадрату ординаты этой точки. Отв. k(x—\)у—*/-}-1=0.
28. Найти такую кривую, для которой угловой коэффициент касательной
в любой точке в п раз более углового коэффициента прямой, соединяющей ту
же точку с началом координат. Отв. у = Схп.
29. Через точку B; 1) провести кривую, для которой касательная в любой
точке совпадает с направлением радиус-вектора, проведенного из начала коор-
координат в ту же точку. Отв. у — х/2.
30. Найти в полярных координатах уравнение такой кривой, в каждой
точке которой тангенс угла между радиус-вектором и касательной равен обрат-
обратной величине радиус-вектора, взятой с обратным знаком. Отв. гF+С) = 1-
31. Найти в полярных координатах уравнение такой кривой, в каждой
точке которой тангенс угла, образуемого радиус-вектором с касательной, равен
квадрату радиус-вектора. Отв. г2 = 2(8+С).
32. Доказать, что кривая, обладающая тем свойством, что все ее нормали
проходят через постоянную точку, есть окружность.
33. Найти такую кривую, чтобы в каждо? ее точке длина подкасательной
равнялась удвоенной абсциссе. Отв. у = С^ х.
34. Найти кривую, для которой радиус-вектор равен длине касательной
между точкой касания и осью х.
Решение. По условиям задачи -^-1 V"l +J/'2 = У^ + У2* откуда — =
= ± — . Интегрируя, получаем два семейства кривых у = Сх и у — —,
X X *
35. По закону Ньютона скорость охлаждения какого-либо тела в воздухе
пропорциональна разности между температурой тела и температурой воздуха.
Если температура воздуха равна 20° С и тело в течение 20 мин охлаждается
со 100° до 60° С, то через сколько времени его температура понизится до 30° С?
Решение, Дифференциальное уравнение задачи ^-jr—kiT—20). Инте-
Интегрируя, находим Т—20 = Се**; Т=100 при t = 0, Г = 60 при *=20, поэтому
С = 80, 40 = Се2<>*, **=(уI/2°> следовательно, 7 = 20+80 (~V/2°. Пола-
Полагая Т = 30, найдем / = 60 мин.
36. В какое время Т вода вытечет через отверстие 0,5 см2 на дне кониче-
конической воронки высотой 10 см с углом при вершине d = 60°?
Решение. Подсчитаем двумя способами объем воды, вытекшей за время
между моментами t и t-\-At. При постоянной скорости у за 1 с через отвер-
отверстие вытекает цилиндр воды с основанием 0,5 см2 и высотой у, а за время А?
вытекает объем воды dv, равный—dv = — 0,5vdt =—0,3 V2gh at *).
С другой стороны, вследствие утечки высота воды получает отрицательное
* приращение» dh, и дифференциал объема вытекшей воды равен
—dv = яг2 dh = -jr(h+ 0,7J dh.
Таким образом,
^(h + 0,7Jdh = — 0,3
*) Скорость v истечения воды из отверстия, находящегося на расстоянии h
от свободной поверхности, дается формулой v = 0,6^2^ где g—ускорение
силы тяжести,

УПРАЖНЕНИЯ К ГЛАВЕ Х1Ц 143
отсюда
t = 0,0315 (lO5/2-/i5/2) + 0,0732
Полагая h = 0, получаем время истечения Т— 12,5с.
37. Замедляющее действие трения на диск, вращающийся в жидкости,
пропорционально угловой скорости вращения со. Найти зависимость этой
угловой скорости от времени, если известно, что диск, начав вращаться со
скоростью 100 об/мин, по истечении I мин вращается со скоростью 60 об/мин»
Отв. @=100 C/5)* об/мин.
38. Допустим, что в вертикальном воздушном столбе давление на каждом
уровне обусловлено давлением вышележащих слоев. Найти зависимость дав-
давления от высоты, если известно, что на уровне моря это давление равно 10 Н
на 1 см2, а на высоте 500 м оно равно 9,2 Н на 1 см2.
Указание. Воспользоваться законом Бойля—Мариотта, в силу кото-
которого плотность газа пропорциональна давлению. Дифференциальное уравнение
задачи dp = —kpdh, откуда р= 10е-°»00017^. Отв. р = 10е-°>00017>*.
Проинтегрировать следующие однородные дифференциальные уравнения:
39. (у—х) dx+(y+x) dy = O. Отв. y2 + 2xy—x2=Ct 40. (х+у) dx+x dy = O.
Отв. x2 + 2xy = Ct 41. (х+у) dx+(y—x) dy = 0. Отв. ln(*2 + */2)V2 —
_arctg-^-=:C. 42. xdy—y dx=}fx2+y2 dx. Отв. l+2Cy—C2x2 = 0.
43. (8ij+10*) dx+Ey+7x) dy = 0. Отв. (x+yJ Bx+yK=C. 44. B VTt — s)dt+
+ tds = O. Отв. teVs/t = Ct или s = Hn2y. 45. (t—s) dt+tds=O.
Отв. tesft^C, или s = t\x\ — % 46. xy2 dy = (xb + t^) dx. Отв. у =
47. x cos ~ {y dx-\-xdy) =ysin~(x dy—у dx)t Отв. xy cos — = C«
XX X
Проинтегрировать дифференциальные уравнения, приводящиеся к одно-
однородным
48. (Zy—7x+7)dx—Cx—7y—3)dy = 0. Отв. (х+у—If (*—у— 1J = С
49. (x+2y+l)dx—Bx + 4y+3)dy = 04 Отв. 1D+8+Ь)+84
50. (x+2y+l)dx—Bx—3)dy = 0. Отв. InBл:—3)—
51. Определить кривую, поднормаль которой есть среднее арифметическое
между абсциссой и ординатой. Отв. (х—уJ(х+2у) = С.
52. Определить кривую, у которой отношение отрезка, отсекаемого каса-
касательной на оси Оу, к радиус-вектору равно постоянной величине»
dy
it у ^
dx ( х \т
Решение» По условиям задачи =т, откуда (-7т-) —
V х2+у2 Vе/
/ С \т_2у
~\~) -7f
53. Определить кривую, у которой отношение отрезка, отсекаемого нор-
нормалью на оси Ох, к радиус-вектору равно постоянной величине,
?
Решение. По условию задачи ¦¦ =/п, откуда х2+у2=/п2 (лг—СJ.
Ух2+у*
54. Определить кривую, у которой отрезок, отсекаемый касательной на
оси Оу, равен asec0, где 0—угол между радиус-вектором и осью х%

144 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ XIII
Решение. Так как tg 6 = — и по условию задачи t/—л: ~=л sec 0, то
dy V*2 + y2 Л -~+ь -(±+ь)\
получаем y—xj- = a- -*-, откуда у = — L е х —е ^х 'J •
55. Определить кривую, для которой отрезок, отсекаемый на оси ординат
нормалью, проведенной в какой-нибудь точке кривой, равен расстоянию этой
точки от начала координат.
х
Решение. Отрезок, отсекаемый нормалью на оси Оу, равен у-\—- ;
поэтому по условию задачи имеем у-\—г= Ух2-\-у2 , откуда х2 = С Bу-\-С).
56. Найти форму зеркала, которое все лучи, выходящие из одной и той
же точки О, отражало бы параллельно данному направлению.
Решение. За ось х принимаем данное направление, точку О—за начало
координат. Пусть ОМ — падающий луч, МР— отраженный, MQ — нормаль
к искомой кривой: а=Р, ОМ = OQt NM=y, NQ = Y~
= S/ctg § = y~ji , откуда ydy~(—x-\- Vx2 + y2) dx; интегрируя, имеем у2
Проинтегрировать следующие линейные дифференциальные уравнения:
5 ±1
Отв. У^Сха+\^Г-\* 59- (х
Отв. у=ах+СхУ\—х2, 60. -^г cos t+ssin t = ].Ome. s = sin /+Ceosf.
61. ^-+sQ0st = ^-s\n2t. Отв. s^slnt— 1+Ce~sln^. 62. y'*- — y=e*xn.
tit ? x
Отв. у = хп(е* + С). 63. ^ + ~^ = ^-. Отв. хпу = ах+С. 64. y' + y = e~*.
Отв. e*y=-x+C. 65. y'+iz^^—1=0. Отв. у = х2 (\ + CeVx).
x
Проинтегрировать уравнения Бернулли:
66. у'+ху = х3у*. Отв. у2(х2+1+Се*2)=1. 67. (\—у2)у'—Ху—аху2 = 0.
Отв. {CV~\—x2—a)y=\. 68. Зу2у'~ау*—х—\=0. Отв. а2у3 = Сеа* —
[2/ ] 2/
{V)y уу у
— а(х+\)— 1. 69. у'(*У+*у)-=1. Отв. х [B—у2) е^2/2+ С]= еу2/2 .
70. (у\пх—2)ydx=xdy. Отв. у (Сх2 + Ых2+\) = 4. 71. y—y'fiosx =
l— ътх). Отв. ^ =
—1—-.,
Проинтегрировать следующие уравнения в полных дифференциалах:
72. (x2+y)dx + (x—2y)dy = 0. Отв. -^- + */*—У2 = С. 73. (t/—Зд:2)^—
y—x)dy = 0. Отв. 2у2—ху+х3 = С. 74. (у*—х)у' = у. Отв. у* =
Е
76. 2C^2+2д:3)^а:+3Bл:2^+1/2)^ = 0. Отв. *+З22+*
.c. 7, (^
о™. ,•+„'=&«. 79.
V^ — Ю- ^—У
80. xdx+ydy= У ^~\У . Опт. Jt2+^_2arctg- = C.
* т1/ У

УПРАЖНЕНИЯ К ГЛАВЕ XIII 145
81. Определить кривую, обладающую тем свойством, что произведение
квадрата расстояния любой ее точки от начала координат на отрезок, отсе-
отсекаемый на оси абсцисс нормалью в этой точке, равно кубу абсциссы этой
точки. Отв. у2Bх2+у2) = С.
82. Найти огибающую следующих семейств линий: а) у = Сх-\-С2.
Отв. *2+4*/ = 0. b) у = ^-+С2. Отв. 27х2 = 4у3. с) ~ Ijk^2-
Отв. 27у = х*. d) С2х + Су— 1 =0. Отв. у* + 4х = 0. е) (*—СK +
+ (у-СJ = С2. Отв. х = 0; у = 0. f) (х-СJ+у2 = 4С. Отв. у2 = 4х+4.
g) (х-СJ + (у-СJ = 4. Отв. (х-у)ъ = ъ. h) Cx* + C*y = l.
Отв. х*~\-4у = 0.
83. Прямая перемещается так, что сумма отрезков, отсекаемых ею на
осях координат, сохраняет постоянную величину а. Составить уравнение оги-
огибающей всех положений прямой. Отв. х1^2 + г/1/2 = а1/2 (парабола).
84. Найти огибающую семейства прямых, на которых оси координат отсе-
отсекают отрезок постоянной длины а. Отв. я2/3 -\-y2l* = а2/3.
85. Найти огибающую семейства окружностей, диаметрами которых слу-
служат удвоенные ординаты параболы у2 = 2рх. Отв. у2 — 2р (*+*к-) •
86. Найти огибающую семейства окружностей, центры которых лежат на
параболе у2 = 2рх, причем все окружности семейства проходят через вершину
этой параболы. Отв. Циссоида хв-\-у2 (х-{-р) = 0.
87. Найти огибающую семейства окружностей, диаметрами которых слу-
служат перпендикулярные к оси х хорды эллипса ЬЧ2 + а2*/2 = a2b2.
88. Найти эволюту эллипса x2b2-\-a2y2 = a2b2 как огибающую его норма-
нормалей. Отв. (ахJ/з+(Ьу)Уз = (а2 — Ь2J/з.
Проинтегрировать следующие уравнения (уравнения Лагранжа):
89. у = 2ху' + у'*. Отв. х = ^~р9 у=??=-?. 90. у=ху'*+у'*.
Отв. у = (Ух+\ + СJ. Особое решение: у = 0. 91. у = хA +*/') + (уУ-
Отв. х = Се-Р—2р+2, у = С (р + \)е-Р—р*+2. 92. у = уу'2+2ху'.
Отв. 4Сх — 4С2—у2. 93. Найти кривую, имеющую постоянную нормаль.
Отв. (х—СJ-\-у2 = а2. Особое решение: у=±а.
Проинтегрировать данные уравнения Клеро:
94. у = ху'+у'—у'2. Отв. у = Сх+С—С2. Особое решение: 4у = (х + \J.
rl— у'2. Отв. у = Сх+У\—С2. Особое решение: #2—х2 = 1.
Отв. у = Сх+С. 97. у=ху' + -±г. Отв. у = ^
У с
Особое решение: у2 = 4х. 98. у~ху' 71.0тв.у = Сх—~г2. Особое решение:
99. Площадь треугольника, образованного касательной к искомой кривой
и осями координат, есть величина постоянная. Найти кривую. Отв. Равнобо-
кая гипербола 4ху— ± а2. Кроме того, любая прямая семейства у — Сх ± аУ^С.
100. Найти такую кривую, чтобы отрезок ее касательной между коорди-
координатными осями имел постоянную длину а. Отв. у = Сх ± . Особое
решение: *2/з+//з=а2/3.
101. Найти кривую, касательные к которой образуют на осях отрезки,
сумма которых равна 2а. Отв. у — Сх—-—^. Особое решение: (у—х—2аJ=8ах.

146 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ?гл хш
102. Найти кривые, для которых произведение расстояния любой каса-
касательной до двух данных точек постоянно. Отв. Эллипсы и гиперболы» (Орто-
(Ортогональные и изогональные траектории.)
103. Найти ортогональные траектории семейства кривых у = ахп.
Отв. х2 + пу2 = С.
104. Найти ортогональные траектории семейства парабол у2—2р{х—а)
(ее — параметр семейства). Отв. у = Се~х^р.
105. Найти ортогональные траектории семейства кривых х2—*/2 = а
(а—параметр). Отв. у = С/х.
106. Найти ортогональные траектории семейства окружностей х2-{-у2 =
= 2ах Отв. Окружности: у = С (х2 -{- у2).
107. Найти ортогональные траектории равных парабол, касающихся в вер-
вершине данной прямой* Отв. Если 2р—параметр парабол и данная прямая
взята за ось Оу, то уравнение траектории будет y-\-C — -g у — ж3 .
х3
108. Найти ортогональные траектории циссоид #2==о *
Отв. (х2+у2J = С(у2 + 2х2).
109. Найти ортогональные траектории лемнискат (х2-{-у2J = (х2—у2) а2.
Отв. (х2+у2J = Сху. _
110. Найти изогональные траектории семейства кривых х2 — 2а (у—лг|^*3),
где а—переменный параметр, если постоянный угол, который образуют траек-
траектории с линиями семейства, равен со = 60°.
Решение. Находим дифференциальное уравнение семейства у' =—— f 3
и заменяем у' выражением <7 = -Д—тт-—• Если со=60°, то а—— ~=—,и
мы получаем дифференциальное уравнение -^ ~=i=~—У 3 . Общий ин-
+ у}
теграл у2 = С\х—у КЗ) дает искомое семейство траекторий.
111. Найти изогональные траектории семейства парабол у2 = 4Сх, когда
о> = 45°. Отв. у2—ху+2х2 = СеГ 7 xY 7,
112. Найти изогональные траектории семейства прямых у = Сх для случая
2 КТ arctg -^
со=ЗО°, 45°. Отв. Логарифмические спирали х2+у2=е х ;
х
113. у = С1ех-\-С%е~х, Исключить Ct и С2. Отв. у"—у = 0.
114. Написать дифференциальное уравнение всех окружностей, лежащих
в одной плоскости. Отв. (l+y'2)y"f—Зу'у — 0.
115. Написать дифференциальное уравнение всех центральных кривых вто-
второго порядка, главные оси которых совпадают с осями Ох, Оу. Отв.
2
116. Даны дифференциальное уравнение у'"—2уп—у'-\-2у=0 и его общее
решение у = С1ех + С2е"х + Сде2х.
Требуется: 1) проверить, что данное семейство кривых действительно яв-
является общим решением; 2) найти частное решение, если при # = 0 имеем
#=i, #'=(), /=—1. Отв. */=*-?-

УПРАЖНЕНИЯ К ГЛАВЕ XIII 147
117. Даны дифференциальное уравнение у"**^ и его общее решение
Требуется: 1) проверить, что данное семейство кривых действительно яв-
является общим решением; 2) найти интегральную кривую, проходящую через
точку A; 2), если касательная в этой точке составляет с положительным
направлением оси Ох угол 45°. Отв. t/=-o-V"*3+-j.
Проинтегрировать некоторые простейшие типы дифференциальных уравне-
уравнений второго порядка, приводящиеся к уравнениям первого порядка.
118. ху"' = 2. Отв. у — х2 In х+Сгх2+С2х+С3; выделить частное решение,
удовлетворяющее следующим начальным условиям: х=1, у=\, #'=1, #" = 3.
120. уп = а2у. Отв. ах = In (ay + Va2y2 + Сх) + С2 или y^
121. y" = aly*. Отв. (С1х+С2J = С1у2-а.
В примерах 122—125 выделить частное решение, удовлетворяющее сле-
следующим начальным условиям: # = 0, t/ =—1, у'~0.
122. ху"—у'=х2ех. Отв. у = ех (х— 1)+Ci*2+C2. Частное решение:
y = e* (*__!). 123. ##"—(i/'J + (^'K = 0. Ome. y+Ct \ny=x-\-C2. Частное ре-
решение: # = — 1. 124. i/"+|/' tgA: = sin2A:. Отв. y = C+Csinxx
Частное решение: у = 2 sin х—sin x cos х—х—1. 125. (у"J + (у'J = а2. Отв.
у = С2—a cos (#+Cx). Частные решения: # = а—1—acosx, y=acosx—(#+1).
(Указание. Параметрическая форма у" = a cost, y' = asint.) 126. у"^^*
Отв. у= ± -| (*+CiK/2 + C;2. 127. у"' = уГ*. Отв.у = (С1-х) [In (Ci-*)-l
2+з. 128. у'у"'—ЗуГ2 = 0. Отв. х = С1У2+С2у+С3.
Проинтегрировать следующие линейные дифференциальные уравнения
с постоянными коэффициентами:
\29. у" = 9у. Отв. у^Сгё*х-\-С2е~*х. 130. /+г/ = 0. Отв. у = Л cos * +
131. #"—1/' = 0. Ome. у = Сг-\-С2ех. Ш. у"-\-\2у = 7у\ Отв. у =
+Cae4*. 133. г/"—.4^ + 4г/ = 0. Отв. у = (Сг+С2х) е2х. 134. ^'+2г/' +
= 0. Отв. ^ = e-^f^_cos3^+5sin3A:). 135. у"+3у'—2y = Q. Отв. у =
^ -3-V17
2 *. 136. 4у"— \2у'+9у=0. Отв. y =
137. у"+У' + У = О- Отв. ^ = e-
t38. Два одинаковых груза подвешены к концу пружины. Найти движение,
которое получит один груз, если другой оборвется. Отв. х — a cos f l/ — t j,
где а есть увеличение длины пружины под действием одного груза в состоя-
состоянии покоя.
139. Материальная точка массы т притягивается каждым из двух центров
с силой, пропорциональной расстоянию. Множитель пропорциональности
равен k. Расстояние между центрами равно 2с. В начальный момент точка
находится на линии соединения центров на расстоянии а от ее середины.
Начальная скорость равна нулю. Найти закон движения точки. Отв. х~
i a cos

148 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. XIII
140. t/V — Ьуп+ 4«/ = 0. Отв. у = С1ех + С2е"х + С3е2х + С4ех. 141. у'" —
— 2у" — у'-\-2у=0.Отв. у=С1е2х4-С2ех+С3е~х. 142. у'" — Зау"+3а2у — а?у=0.
+ C^x+Cbej2x. 144. ^1уЧ-2/+9г/=0. Ome. y=(C1cosVr2i+C,
+(С3 cos уг2лг + С4 зш^гл:) ел'. 145. i/lv—8/+16^/ = 0. Отв. ^=С
g-2;f. 146. t/iv.L^^o. Отв. y = eV 2
+е
147. yiv — aAy — O. Найти общее решение и выделить частное решение,
удовлетворяющее начальным условиям у=\, t/'=0, у" = —а2, у'" = 0 при
л:0=0. Отв. Общее решение: y = Cieax + C2e-ax+C3cos ax-\-C4sin ax. Частное
решение: t/0 — cos ax,
Проинтегрировать следующие неоднородные линейные дифференциальные
уравнения (найти общее решение):
148. у"—7у' + 12у = х. Отв. у = С1^х+С2е^ + 12^7 . 149. s"—a*s=
Отв. s^C^ + Cae-^ —-^ti-. 150. у" + у'—2у = 8sin 2л:. Отв. у = С1ех +
4- Fsin2*-l-2cos2;t). 151. ^—у=5^+2. Отв. ^=^^+025-^—5*—2.
о
152. s"—2as'+«2s = e* (аф\). Отв. s = C1eat+C2tea^+/ е П2 . 153. у* +
(а— l)*
==в2^. Отв. у = С1е-х + С2е-5х+^е2х. 154. #" + 9# = &>3*. Отв.
je3^. 155. ^—3/ = 2—6ж. Отв. y =
. Отв. у=ех(С
157. ^+4^ = 2sin2^. Отв. y = C1sin2x+C2cos2x—~
158. e//ff—4y"+5y'—2y = 2x+3. Отв. y^(Ci+C2x)ex+C^x—x^^
159. ^v—a*y = 5a*eaxsinax. Отв. y = (Ci—sin ax) eax+C2e~ax+C3 cos ax+
+ Ctslnax. 160. yW+2a2y"+a*y = 8cosax. Отв. у = (Cx + C2*) cos^jc +
+ (^з+Q*) sin ax g cos ax.
161. Найти интегральную кривую уравнения y"+#ty = 0, проходящую
через точку М (х0; у0) и касающуюся в точке М прямой у = ах. Отв. у =
= у0 cos А; (*— ^о) + у sin ^ (дс—д:0).
162. Найти решение уравнения ^/+2%' + rt2y = 0, удовлетворяющее усло-
условиям у = а> у' = С при * = 0. Отв. y = e-hx (acosyOi2—h?x-\—^а1г у
\ У л2—/*2
^ при Л< п; y = e~hx [(C+ah)x+a] при & = л; у =
при /г > /г.

УПРАЖНЕНИЯ К ГЛАВЕ XIII 149
163. Найти решение уравнения у"-{-п2у = ks\n px (p ф я), удовлетворяющее
условиям */ = я, у' = С при * = 0. Отв. y = acosnx-\ ^П ~Р Т sinn* +
+ 1 2 sin Рх'
164. Груз массой 4 кг привешен к пружине и увеличивает ее длину на 1 см.
Найти закон движения этого груза, полагая, что верхний конец пружины
совершает гармоническое колебание, закон которого # = sin]/*100g/, где у из-
измеряется по вертикали.
Решение. Обозначая через х вертикальную координату груза, считае-
считаемую от положения покоя, имеем
4 п*х
где /—длина пружины в свободном состоянии и & —400, как легко видеть из
начальных условий. Отсюда -—|-+100g# = 100gsinVlQOgt +100/g. Частный
интеграл этого уравнения мы должны искать в виде
t (Cx cosj/ToO^ + Ca sinV \OOgt) + /,
так как первый член правой части уравнения входит в решение однородного
уравнения.
165. В условиях задачи 139 начальная скорость равна v0 и направление
перпендикулярно к прямой, соединяющей центры. Найти траектории.
Решение. Если начало координат взять в середине расстояния между
центрами, то дифференциальные уравнения движения будут иметь следующий
d^x d^ii
вид: т--77т = ? (С—х)—k(C4-x) = —2kx, m-?%>~—2ky. Начальные данные
at* ut'j
при / = 0:
Интегрируя, находим
л х . уЧк t .
Отсюда ^-+?—г—* (эллипс).
а tnvo
166. Горизонтальная трубка вращается около вертикальной оси с постоян-
постоянной угловой скоростью со. Шар, помещенный внутри трубки, скользит по ней
без трения. Найти закон движения шара, если в начальный момент он нахо-
находится на оси вращения и имеет скорость vQ (вдоль трубки).
Указание. Дифференциальное уравнение движения есть -тр- = 0Jг. На-
Начальные данные: г=0, -зт=уо при г=0. Интегрируя, находим г^=~ [е®*— е~®{].
Применяя метод вариации произвольных постоянных, проинтегрировать
следующие дифференциальные уравнения:
167. 2f--70' + 6y==sin*. Отв. y = Cle*+C2e**+ 5sin* + 7 cos*
168. y"-\-y = secx. Отв. y = Ci cos# + C2sin#4-*sinje +
169. y"+y— # Отв. y = Ci cos x+C2 sin x— У cos 2x.
cos 2x у cos 2x
Проинтегрировать следующие уравнения различных типовз

150
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[ГЛ XIII
Опгв. -^—=С. 172. у = ху'2-\-у'2. Отв. у = (У~х+\+СJ. Особые решения:
у = 0, *+1=0. 173. y"+y = secx. Отв. у = Сг cosx + C2 sinx+x sin х +
+ cos х In cos x. 174. (\+х2)у'—ху~а = 0. Отв. у = ах+С}Г\ -\-х2.
175.
— -?=zycos——x. Отв.
=С. 176. #" — 4у = е2х sin ?*.
177.
Отв.
(\пх+\+Сх)у = \. 178. Bx + 2y—\)dx+(x+y—2)dy = 0. +
—3 In (х+(/ + 1)=С. 179. Зв^ tg у Лс + A —бх) sec2 г/ d«/ = 0. Отв. tgy = C(i —
Проинтегрировать следующие системы уравнений:
180. -п=у+1, -^=д:+1. Выделить частные решения, удовлетворяющие
начальным условиям #=—2, (/ = 0 при * = 0. Отв. y = C1et-\-C2e'-i—I,
x = Ci€t—Сф~*—1. Частное решение: х* =—е~* — 1, у* = е~*—1.
181. —=х—2yt -~-=ix—у. Выделить частные решения, удовлетворяю-
удовлетворяющие начальным условиям х=\, у = \ при ? = 0. Отв. y = CfCOS * + C2sin t,
(С + С) cos t-\-(C2—Ci) sin t. Частное решение: #*^=cos t—sin t, t/* = cos t.
t.
184.
185.
186.
Ш- < %+Ъ+м-тп*.
Отв. x = C1et + C2e~i+C3cost + C4smtt
-t—c3 cos t—C4 sin t.
Отв. х = Сг
|—„-3,
Отв. y =
Отв. у=Cf+C2a:+2 sin *,
2 = — 2Cj—C2B*+l)
—3sin#

188.
189.
190.
dx
ж
dy
dz
dz
~dx"
dx yz *
dzx
УПРАЖНЕНИЯ К ГЛАВЕ XIII
0тв9 х=Сге-
151
Отв9 z=
Отв. —~
Исследовать, является ли решение * = 0, у =0 устойчивым для следующих
систем дифференциальных уравнений;
191. ( dx о Q Отв, Неустойчиво.
192.
193.
dx _
dt
2у.
0тв9 Устойчиво,
Отв. Неустойчиво.
194. Найти приближенные значения решения уравнения у'=у2+х, удов-
удовлетворяющего начальному условию у=\ при * = 0. Значения решения найти
при значениях *=0,1; 0,2; 0,3; 0,4; 0,5. Отв. у @,5) =2,235.
195. Найти приближенное значение y\x-i^ решения уравнения
удовлетворяющего начальному условию #=1 при х—1. Сравнить полученный
результат с точным решением.
196. Найти приближенные значения #|f=i,4 и у lf-1,4 решений системы
уравнений ' ~
dx dy o
удовлетворяющих начальным условиям jc=O, y=l при t—\. Сравнить полу-
полученные значения с точными.

ГЛАВА XIV
КРАТНЫЕ ИНТЕГРАЛЫ
§ 1. Двойной интеграл
Рассмотрим в плоскости Оху замкнутую *) область Z), ограни-
ограниченную линией L.
Пусть в области D задана непрерывная функция
* = /(*. {/)•
Разобьем область D какими-нибудь линиями на п частей
AS tS ( 292) б
AS2, AS3,
у X
tsSn (рис. 292), которые будем называть площад-
площадками. Чтобы не вводить новых символов,
будем обозначать через ASX, ..., ASn не
только названия соответствующих пло-
площадок, но и их площади. В каждой из
площадок ASf. (внутри или на грани-
границе—безразлично) возьмем точку Pt\ тог-
тогда будем иметь п точек Pi9 Р2, ..., Рп.
Обозначим через f(PJt /(Р2), ..., f(Pn)
значения функции в выбранных точ-
точках и составим сумму произведений
вида f(P)bS
292.
= | f(P§)bSt. A)
Эта сумма называется интегральной суммой для функции f(xyy)
в области D.
Если />0 в области D, то каждое слагаемое f(Pi)ASi можно
представить геометрически как объем малого цилиндра, основание
которого есть AS,., а высота f(Pi).
Сумма Vn есть сумма объемов указанных элементарных цилинд-
цилиндров, т. е. объем некоторого «ступенчатого» тела (рис. 293).
*) Область D называется замкнутой, если она ограничена замкнутой ли-
линией, и точки, лежащие на границе, считаются принадлежащими области D.

§1]
ДВОЙНОЙ ИНТЕГРАЛ
153
Рассмотрим произвольную последовательность интегральных
сумм, составленных с помощью функции f(xt у) для данной
области D:
у пхч угс2» • • • ¦
B)
при различных способах разбиения области D на части AS{.
Будем предполагать, что максимальный диаметр площадок AS^
стремится к нулю при nk—+oo. При этом оказывается справедливым
следующее утверждение, которое мы приводим без доказательства.
л
Рис. 293.
Рис. 294,
Теорема 1. Если функция f(x> у) непрерывна в замкнутой
области D, то существует предел последовательности B) инте-
интегральных сумм A), если максимальный диаметр площадок ASt
стремится к нулю, an—»-оо. Этот предел один и тот же для
любой последовательности вида B), т. е. он не зависит ни от
способов разбиения области D на площадки ASh ни от вырора
точки Pi внутри площадки AS(.
Этот предел называется двойным интегралом от функции f (к, у)
по области D и обозначается так: §j[/4P)dS или $$/(#, y)dxdy,
D D
т. е.
lira
< ^ И f (*> У)dx аУ-
Здесь область D называется областью интегрирования.
Если f (ху у) ^ 0, то двойной интеграл от функции / (х, у) по
области D равен объему тела Q, ограниченного поверхностью,
образующие которой параллельны оси Ог, а направляющей слу-
служит граница области D (рис. 294).
Рассмотрим, далее, следующие теоремы о двойном интеграле.
Теорема 2. Двойной интеграл от суммы двух функций
)+$(> У) по области D равен сумме двух двойных интег-

154 КРАТНЫЕ ИНТЕГРАЛЫ [ГЛ. XIV
ралов по области D от каждой из функций в отдельности:
Теорема З. Постоянный множитель можно вынести за знак
двойного интеграла: если а = const, то
Доказательство обеих этих теорем приводится совершенно так
же, как доказательство соответствующих теорем для определен-
определенного интеграла (см. т. I, гл. XI,
!у §з).
Теорема 4. Если область D раз-
разбита на две области Dx и D2 без- об-
общих внутренних точек и функция
f (Ху у) непрерывна во всех точках обла-
области D, то
Рис.295, + \\f{xyy)dxdy. C)
Доказательство. Интегральную сумму по области D
можно представить в виде (рис. 295)
2 / (Р() AS, = 2 / {Рд AS, + S / (Рд AS/, D)
D Dt D2
где первая сумма содержит слагаемые, соответствующие площад-
площадкам области Diy вторая— слагаемые, соответствующие площадкам
области D2. В самом деле, так как двойной интеграл не зависит
от способа разбиения, то мы производим разбиение области D так,
что общая граница областей D± и D2 является границей площа-
площадок AS,-. Переходя в равенстве D) к пределу при ASt-—^0, получим
равенство C). Очевидно, что эта теорема справедлива для любого
числа слагаемых.
§ 2. Вычисление двойного интеграла
Пусть область D> лежащая в плоскости Оху, такова, что
всякая прямая, параллельная одной из координатных осей, на-
например оси Оу, и проходящая через внутреннюю*) точку
*) Под внутренней точкой области мы подразумеваем точку, не лежащую
яа границе области.

§ 21
ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
155
области, пересекает границу области в двух точках Nt и ЛГ3
(рис. 296).
Мы предположим, что в рассматриваемом случае область D
ограничена линиями f/ = <Pi(#), У = ф2(#), х = а9 х = Ь, причем
4i(x) ^Ф2(*)> a<by a функции щ(х) и Ф2(#) непрерывны на от-
отрезке [а, Ь]. Такую область мы будем называть правильной
в направлении оси Оу. Аналогично определяется область, пра-
правильная в направлении оси Ох.
Область, правильную как в направлении оси Ох, так и в нап-
направлении оси Оу, мы будем называть просто правильной областью.
На рис. 296 показана именно правиль-
правильная область D.
Пусть функция f(x, у) непрерывна
в области D.
Рассмотрим выражение
а \ф, (х)
которое мы будем называть двукрат-
двукратным интегралом от функции /(#, у)
по области D. В этом выражении сначала вычисляется интег-
интеграл, стоящий в скобках, причем интегрирование производится
по у, а х считается постоянным. В результате интегрирования
получится непрерывная *) функция от х:
ф2(*)
(*)= J f(x,y)dy.
Эту функцию мы интегрируем по х в пределах от а до Ь:
ь
В результате получается некоторое постоянное число.
Пример. Требуется вычислить двукратный интеграл
Решение. Вычисляем сначала внутренний интеграл (стоящий в скобках):
*) Мы здесь не доказываем того, что функция Ф (х) непрерывна,

156
КРАТНЫЕ ИНТЕГРАЛЫ
[ГЛ. XIV
Интегрируя полученную функцию в пределах от 0 до 1, находим
о
= 105 *
Определим область D. В данном случае в качестве D рассматривается область,
ограниченная линиями (рис. 297) у = 0, у = х2, х = 0, х—\.
Может случиться, что область D такова, что одна из функций
y=(fi(x)J y = q>2(x) не может быть задана одним аналитическим
выражением на всем участке изменения х (от * = а до х = Ь).
i
0
У
1
rfffffl
к
ш
а
Рис. 297,
Пусть, например, а
Рис. 298#
р <6, причем фх(х) = \р(х) на отрезке [а, с],
на отрезке [с, ft], где г|?(л:) и % (*) — функции, задан-
заданные аналитически (рис. 298). Тогда двукратный интеграл запи-
запишется следующим образом:
а \ф, (дг)
ф4
КФ2(л;
y)dy)dx+
f(x,y)dy)dx.
Первое из этих равенств написано на основании известного свой-
свойства определенного интеграла, а второе —в силу того, что на
участке [а, с] имеем <Pi(x) = t|)(x:), a на участке [с, ft] имеем
Vi()%{)
Аналогичная запись для двукратного интеграла имела бы место
и в том случае, если бы функция <р2 (х) задавалась различными
аналитическими выражениями на различных участках отрезка
[*, Ь].
Установим некоторые свойства двукратного интеграла.
Свойство 1. Если правильную в направлении оси Оу область
D разбить на две области Dt и Ь2 прямой, параллельной оси Оу
или оси Ох, то двукратный интеграл ID no области D будет равен

§21 ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
сумме таких же интегралов по областям D* и Dz> m. e.
157
Доказательство, а) Пусть прямая х = с(а<Сс<Ь) раз-
разбивает область D на две правильные в направлении оси О у
области *) Di и D2. Тогда
Ь/ф2(х) v Ь с Ь
! S f(x9 y)dy)dx=\ O(x)dx=[<b(x)dx+) Ф(х)йх =
\фг (л:) /а а с
J /(х, jr)dHde+$( J f(x,y)dy\dx = IDl + IDt.
а \ ф! (л) / с \ф! (*) '
б) Пусть прямая у = h разбивает область D на две правильные
в направлении оси О у области D1 и D2 так, как изображено на
рис. 299. Обозначим через Mi и М2
точки пересечения прямой y = h с гра-
границей L области D. Абсциссы этих то- h
чек обозначим через а^ и &1в
Область D? ограничена непрерыв-
непрерывными линиями:
D У = Ч?Лх);
2) кривой AtMiMzB, уравнение ко-
которой условно запишем в форме
имея при этом в виду, что ср! (#) = ф2 (х) при
b^^b и что
и при
(pj(#)=ft при
3) прямыми х — а, х = Ь.
Область Dz ограничена лини ями у = (fl (x)> у == ф2 (х) f где
Напишем тождество, применяя к внутреннему интегралу тео-
теорему о разбиении промежутка интегрирования:
J
<Pl<*)
^Ф8() \ ф2(>
J f(*,y)dy)dx=U J f(x9y)dy+ J f(x>y)dy)dx=
<) ^ \<) *
*) Тот факт, что часть границы области Dt (и области D2) является
куском вертикальной прямой, не мешает этой области быть правильной в на-
направлении оси Оу: ведь для того, чтобы область была правильной, необхо-
необходимо только, чтобы всякая вертикальная прямая, проходящая через внутрен-
внутреннюю точку области, имела с границей не более двух общих точек.

158
КРАТНЫЕ ИНТЕГРАЛЫ
[ГЛ XIV
Последний интеграл разобьем на три интеграла, применяя
к внешнему интегралу теорему о разбиении промежутка интегри-
интегрирования:
5( J f(x,y)dy)dx=U J f{x,y)dy)dx+
а \q>; <*) J a \q>; (x) J
Ьх ,ф.(ДС) v 6 ф2(*) v
+ S( J /(*,*)<**) <М-$( J f(x%y)dy)dx\
а>\1(х) У bt\q>l(x) J
так как ч\(х) = Чъ{х) на отрезке [а, ах] и на отрезке [Ьи Ь], то
первый и третий интегралы тождественно равны нулю. Поэтому
Ь/Ч>1{х) ч &, ФИ*)
'd=51 S /(^Й^)л+$( J f(x,y)dy)dx.
a V(*) У «Aq>J<*) /
Здесь первый интеграл есть двукратный интеграл по области Di%
второй —по области D2. Следовательно,
Доказательство будет аналогично при любом положении секу-
секущей прямой МгМ2. Если прямая МгМ2 разобьет область D на
три или большее число областей, то
получим соотношение, аналогичное со-
соотношению A), в правой части которо-
которого будет стоять соответствующее число
слагаемых.
Следствие. Каждую из полу-
полученных областей мы можем прямой,
параллельной оси Оу или оси Ох, сно-
снова разбить на правильные в направле-
направлении оси О у области и к ним приме-
применить равенство A). Таким образом,
область D можно разбить прямыми,
параллельными осям координат, на любое число правильных
областей Dl9 D2, Ц,, ..., Db и при этом будет справедливо
утверждение, что двукратный интеграл по области D равен сумме
двукратных интегралов по частичным областям, т. е. (рис. 300)
i
0
v
\
a
ч
^*-
•*•
Ш
•a*
>
b as
Рис, 300#
(о
Свойство 2 (оценка двукратного интеграла).
Пусть т и М—наименьшее и наибольшее значения функции
f (x, у) в области D. Обозначим через S площадь области D. Тогда
имеет место соотношение
J /(*, y)dy)dx^MS. C)

§2] ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА 159
Доказательство. Произведем оценку внутреннего интег-
интеграла, обозначив его через Ф(л;):
<р2 (*) ф2 (*)
Ф(*) = S f(*> У)ЛУ< S Mdy = M[<ft{x)
<Pl (X) ^ (X)
Тогда
$ J fix,
a \(pi(x)
т. e.
ID^MS. C')
Аналогично,
Ф1 (л:) Ф1 (х)
Ь Ь
lD = J ф (х) dx^\ т [ф2 (дс)—Фх (a:)] dx = mS,
/D>mS. C")
Из неравенств C') и C") и следует соотношение C):
mS < ID < MS.
В следующем параграфе мы выясним геометрический смысл этой
теоремы.
Свойство 3 (теорема о среднем). Двукратный ин-
интеграл ID от непрерывной функции f (л:, у) по области D с пло-
площадью S равен произведению площади S на значение функции
в некоторой точке Р области D, т. е.
S f(x,y)dy)dx = f(P)S. D)
- -<PiK*> J
Доказательство. Из соотношения C) получаем
Число ~^-ID заключено между наибольшим и наименьшим значе-
значениями функции f(x, у) в области D. В силу непрерывности функ-
функции f(x, у) она принимает в некоторой точке Р области D зна-
значение, равное числу -о-//>, т. е.
откуда
f(PS E)

160 КРАТНЫЕ ИНТЕГРАЛЫ [ГЛ. XIV
§ 3. Вычисление двойного интеграла (продолжение)
Теорема. Двойной интеграл от непрерывной функции f (х, у)
по правильной области D равен двукратному интегралу от этой
функции по области D> т. е.*)
S$(*f y)dxdy=U S /(*, y)dy)dx.
D а \ф!(х) /
Доказательство. Разобьем область Dпрямыми, параллель-
параллельными осями координат, на п правильных (прямоугольных) обла-
областей AS±, AS2, ..., ASn.
На основании свойства 1 (формула B)) предыдущего параграфа
имеем
п
//> = /as1 + /as1+ • •• +/ASn= 2 hsr A)
Каждое из слагаемых, стоящих справа, преобразуем по тео-
теореме о среднем для двукратного интеграла:
/as, = /(/>,) AS,.
Тогда равенство A) примет вид
1 + f(P2)AS2+...+f(Pn)ASn= S /(Л)AS,, B)
где Рг—некоторая точка области AS,-. Справа стоит интеграль-
интегральная сумма для функции f(xy у) по области D. По теореме о су-
существовании двойного интеграла следует, что предел этой суммы
при п—>>оо и стремлении наибольшего диаметра площадок AS;
к нулю существует и равен двойному интегралу от функции / (л:, у)
по области D. Величина двукратного интеграла ID, стоящего
в левой части равенства B), не зависит от п. Таким образом,
переходя к пределу в равенстве B), получим
ID= Hm
diam AS
или
$$/(*. y)dxdy^ID. C)
D
Выписывая подробно выражение двукратного интеграла ID,
окончательно получим
Кф2<*) \
J f(x, y)dy)dx. D)
*) При этом мы снова полагаем, что область D правильная в направле-
направлении оси Оу и ограничена линиями у~уг(х)} # = <р2(*), х = а, х = Ь.

S3]
ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА (ПРОДОЛЖЕНИЕ)
161
Замечание 1. Для случая, когда /(ху у)^О, формула D)
имеет наглядное геометрическое толкование. Рассмотрим тело,
ограниченное поверхностью z = f(x, y)y плоскостью г = 0 и ци-
цилиндрической поверхностью, образующие которой параллельны
оси Ог, а направляющей служит граница области D (рис. 301).
Вычислим объем этого тела V. Выше было показано, что объем
этого тела равняется двой-
двойному интегралу от функции
}(ху у) по области D: z
(ху y)dxdy. E)
Вычислим теперь объем
этого тела, пользуясь ре-
результатами § 4 гл. XII
т. 1 о вычислении объема
тела по площадям парал-
параллельных сечений. Прове-
Проведем плоскость х = const (a <
< х < Ь)у рассекающую рас-
рассматриваемое тело. Вычи-
Вычислим площадь S(x) фигуры,
получающейся в сечении х = const. Эта фигура есть криволи-
криволинейная трапеция, ограниченная линиями z = f(xy у) (х = const),
2 = 0, y = q>i(x), y = (<p2)x. Следовательно, эта площадь выразится
интегралом
F)
О
а
Рис. 301 „
= S f(x, y)dy.
Зная площади параллельных сечений, легко найти объем тела
ъ
или, подставляя выражение F) для площади 5(х), получаем
К
f(x, y)dy)dx.
G)
В формулах E) и G) левые части равны, следовательно, равны
и правые:
J /(*, y)dy)dx.
- Ф1М /
Н, С, Пискунов, т. 2

162
КРАТНЫЕ ИНТЕГРАЛЫ
|ГЛ. XIV
Теперь нетрудно выяснить и геометрический смысл теоремы
об оценке двукратного интеграла (свойство 2 предыдущего пара-
параграфа): объем тела V, ограниченного поверхностью г = /(л:, у)у
плоскостью г = 0 и цилиндрической поверхностью, направляющей
которой служит граница области D, превосходит объем цилиндра
с основанием S и высотой т, но меньше объема цилиндра с осно-
основанием S и высотой М (где т и М—наименьшее и наибольшее
Рис. 302,
'X
z
J
к
о ,.
с?
J \
*
:;
Рис. 303.
I \
\
\
\
\
Л
i
i
s
Is
значения функции z = f(x9 у) в области D (рис. 302)). Это сле-
следует из того, что двукратный интеграл lD равен объему этого
тела V.
Пример 1. Вычислить двойной интеграл С \ D—х2—у2) dx dyt если
D
область D ограничена прямыми # = 0, х=\, у = 0, у — 3/2.
Решение. На основании формулы D)
Пример 2. Вычислить двойной интеграл от функции f(xf y) — \+x-\-y
по области, ограниченной линиями у=—х, х = Уу, у = 2, г=0 (рис. 303).

§3J ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА (ПРОДОЛЖЕНИЕ)
Решение,
163
с\ с I
у=\| \ (\+x-\-y)dx \dy =
0J Ц J
15
Замечание 2. Пусть правильная в направлении оси Ох
область D ограничена линиями * = %(#),
х = ty2 (У), У = с, y = d, причем ^ (г/) < % (у)
(рис. 304).
Очевидно, что в этом случае
(8)
Для вычисления двойного интеграла
его надо представить в виде двукратного.
Как мы видели выше, это можно сделать
двумя различными способами: или по фор-
формуле D) или по формуле (8). В каждом
конкретном случае в зависимости от вида
области D или подынтегральной функции мы выбираем ту или
иную формулу для вычисления двойного интеграла.
Пример 3. Изменить порядок интегрирования в интеграле
1 \
f(x,y)dy)dx.
6\х /
Решение. Область интегрирования ограничена прямой #=# и парабо-
параболой y=Yх (рис. 305).
х
Рис, 304,
SS
Рис. 305.
Рис. 306.
Всякая прямая, параллельная оси Ох, пересекает границу области не
более чем » двух точках; следовательно, можно вычислять интеграл по
6*

164
формуле (8), полагая
тогда
КРАТНЫЕ ИНТЕГРАЛЫ
1ГЛ. XIV
5
\
^ y)dx)dg.
У
Пример 4. Вычислить \\e^*<iS, если область D представляет тре-
D
угольник, ограниченный прямыми у=х, #=0, #=1 (рис. 306).
Решение. Заменим данный двойной интеграл двукратным. При этом
воспользуемся формулой D). (Если бы мы применили формулу (8), то нам
пришлось бы интегрировать функцию еУ1* по х\ но этот интеграл не берется
в элементарных функциях.)
t , Я \ I X
С С еУ1* dS = W f еУ'х dy j dx= f (хе&*) j
о о \o /о о
dx--
Замечание З. Если область D не является правильной
ни в направлении оси Оху ни в направлении оси Оу (т. е. су-
существуют вертикальные и горизонтальные прямые, которые, про-
проходя через внутренние точки области, пересекают границу области
более чем в двух точках), то двойной интеграл по этой области
мы не можем представить в виде двукратного. Если удается раз-
разбить неправильную область D на конечное число правильных
или в направлении оси Ох, или в направлении оси Оу областей
Dlt D2, .. ¦, Dn, то, вычисляя двойной интеграл по каждой из
этих областей с помощью двукратного и складывая получившиеся
результаты, мы получим искомый интеграл по области D.
Рис. 307#
t о
Рис, 308.
На рис. 307 показан пример того, как неправильную область
D можно разбить на три правильные области Dt, D2 и Du.

§3] ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА (ПРОДОЛЖЕНИЕ) 165
Пример 5. Вычислить двойной интеграл
[ С ex+ydS
D
по области D, заключенной между двумя квадратами с центром в начале коор-
координат и сторонами, параллельными осям координат, если каждая сторона
внутреннего квадрата равна 2, а внешнего 4 (рис. 308).
Решение. Область D является неправильной. Однако прямые х = —I
и *=1 разбивают ее на четыре правильные области Dlt D2, D3, D4. Поэтому
\] H eX+y dS + $ I eX+y ds+ § \ eX+y dS-
D Dt Dz ?>3 D4
-1,2
= [ I J
Представляя каждый из этих интегралов в виде двукратного, найдем;
-1/2 v 1/2 ч
e*+ydy)dx+ U [ e*+ydy )dx+
,-1 ч 2
ex+ydy )dx+\
-e~2) (e2—e) = (e3—e"~3) (e—e-x) = 4 sh 3shl.
1 /-1
-i\-2
Замечание 4. В дальнейшем, записывая двукратный ин-
интеграл
$ /(*, y)dy)dx,
Кф2
мы будем опускать скобки, в которые заключен внутренний ин-
интеграл, т. е. будем писать
Ь ф« <лг)
а ф! (х)
При этом, так же как и при наличии скобок, мы буде^ считать,
что первое интегрирование совершается по той перемейной, диф-
дифференциал которой написан первым, а затем по той переменной,
дифференциал которой написан вторым. (Заметим, одйако, что
это не является общепринятым; в некоторых книгах принято про-
противоположное условие: интегрировать сначала по той переменной,
дифференциал которой занимает последнее место*).)
*) Очень часто употребляется также такой вид записи:
/Фа
К Фа \ о ц>2
Фи ' в ф^

166
КРАТНЫЕ ИНТЕГРАЛЫ
|ГЛ. XIV
§ 4. Вычисление площадей и объемов
с помощью двойных интегралов
1. Объем. Как мы видели в § 1, объем V тела, ограничен-
ограниченного поверхностью z = f(x, у), где f(x, у)—неотрицательная функ-
функция, плоскостью z = 0 и цилиндрической поверхностью, направ-
направляющей для которой служит граница области D, а образующие
параллельны оси Ог, равен двойному интегралу от функции
/(#, у) по области D:
Пример 1. Вычислить объем тела, ограниченного поверхностями
*=0, у=0, х+у+г=\, z=0 (рис. 309).
Рис. 309.
Рис. 310,
Решение. У=\ \ (\—x—y)dydx, где D—заштрихованная на рис. 309
D
треугольная область в плоскости Оху, ограниченная прямыми *=0, y=0f
\ = \. Расставляя пределы в двойном интеграле, вычислим объем:
1 1-* 1 l
Итак, V=-?-Ky6. единиц.
Замечание 1. Если тело, объем которого ищется, ограни-
ограничено сверху поверхностью г = Ф2(#, #)^0, а снизу—поверхостью
г = Ф1(х9 у)^0, причем проекцией обеих поверхностей на пло-
плоскость Оху является область Z), то объем V этого тела равен
разности объемов двух «цилиндрических» тел; первое из этих
цилиндрических тел имеет нижним основанием область D, а верх-
верхним—поверхность г = Ф2(*, у); второе тело имеет нижним осно-
основанием также область D, а верхним—поверхность г^Ф^я, у)
(рис. 310).

§41
ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
167
Поэтому объем V равен разности двух двойных интегралов:
-llox(x9 y)dS9
или
. у)-Фг(х9 y)]dS.
A)
Легко, далее, доказать, что формула A) верна не только
в том случае, когда Фх(ху у) и Ф2(л;, у) неотрицательны, но и
тогда, когда Фг(ху у) и Ф2(л:, у)—любые непрерывные функции,
удовлетворяющие соотношению
Замечание 2. Если в области D функция f(x, у) меняет
знак, то разбиваем область на две части: 1) область Di9 где
/(*> #)^°; 2) область D2, где }(х, */)<0. Предположим, что
области Df и D2 таковы, что двойные интегралы по этим обла-
областям существуют. Тогда интеграл по области Dx будет положи-
положителен и будет равен объему тела, лежащего выше плоскости Ох у.
Интеграл по D2 будет отрицателен и по абсолютной величине
равен объему тела, лежащего ниже плоскости Оху. Следовательно,
интеграл по D будет выражать раз-
разность соответствующих объемов.
2. Вычисление площади
плоской области. Если мы со-
составим интегральную сумму для
функции / (х, у) = 1 по области D,
то эта сумма будет равна площа-
площади S,
S=2 l.AS|f
при любом способе разбиения. Пере-
Переходя к пределу в правой части равен-
равенства, получим
г с
Рис. 311.
Если область D правильная (см., например, рис. 296), то площадь
выразится двукратным интегралом
dy)dx.

168
КРАТНЫЕ ИНТЕГРАЛЫ
[ГЛ XIV
Производя интегрирование в скобках, имеем, очевидно,
ь
(ср. § 1 гл. XII т. I).
Пример 2. Вычислить площадь области, ограниченной кривыми
Решение. Определим точки пересечения данных кривых (рис. 311).
В точке пересечения ординаты равны, т. е. *=2—jc2, отсюда х*-\~х—2 = 0,
кг=—2, *2=1. Мы получили две точки пересечения
Mi (-2; -2), М2(\; 1).
Следовательно, искомая площадь
С] )
$
-2
]
-2
§ 5. Двойной интеграл в полярных координатах
Пусть в полярной системе координат 9, р задана такая область Д
что каждый луч*), проходящий через внутреннюю точку области,
пересекает границу области D не более чем в двух точках. Предпо-
Предположим, что область D ограничена
кривыми
р-ФМ
и лучами
= а и 0 = р,
причем
(рис. 312). Такую область снова
будем называть правильной.
Пусть в области D задана не-
непрерывная функция от коорди-
координат 0 и р:
Рис. 312, *
Разобьем область D каким-нибудь способом на площадки
AS2, ..., ASn.
*) Лучом мы будем называть каждую полупрямую, исходящую из начала
координат, т. е. из полюса Р.

§51 ДВОЙНОЙ ИНТЕГРАЛ В ПОЛЯРНЫХ КООРДИНАТАХ 169
Составим интегральную сумму:
itbSk9 A)
где Pk—некоторая точка площадки ASk.
Из теоремы существования двойного интеграла следует, что при
стремлении наибольшего диаметра площадки ASk к нулю сущест-
существует предел V интегральной суммы A). Этот предел V есть, по
определению, двойной интеграл от функции F (О, р) по области D:
B)
Займемся вычислением двойного интеграла в этом случае.
Так как предел интегральной суммы не зависит от способа
разбиения области D на площадки ASk, то мы можем разбить
область наиболее удобным способом. Таким наиболее удобным для
вычисления способом будет разбиение области с помощью лучей
6 = 00,6=6*6 = 9,, ...,е = е„(гдеео=а,е„=р,ео<е<<02<...
... < GJ и концентрических окружностей р = р0, р = р* ..., р = рт
(где р0 равно наименьшему значению функции ФхF), а рт—наи-
рт—наибольшему значению функции Ф2@) в промежутке ^б^Р
Ро < Pi < • • • < Р*)- о
Обозначим через ASik площадку, ограниченную линиями
Площадки &Sik будут трех видов: 1) не пересекаемые границей,
лежащие в области Ь; 2) не пересекаемые границей, лежащие вне
области D\ 3) пересекаемые границей области D.
Сумма слагаемых, соответствующих пересекаемым границей пло-
площадкам, имеет пределом нуль при Д0*—*0 и Ар,—¦>(), и потому
эти слагаемые мы не будем принимать в расчет. Площадки AS?fc,
которые лежат вне области Df вообще не входят в интегральную
сумму и поэтому нас не интересуют. Следовательно, интегральную
сумму можно записать следующим образом:
где Pik—произвольная точка площадки AS;*.
Двойной знак суммирования здесь следует понимать в том
смысле, что мы сначала производим суммирование по индексу t,
считая k постоянным (т. е. отбираем все слагаемые, соответствую-
соответствующие площадкам, заключенным между двумя соседними лучами *)).
*) Заметим, что при суммировании по индексу i этот индекс будет про-
пробегать не все значения от i до т, так как не все площадки, лежащие между
лучами 9 = 0/5 и 0 = 0ft+i, принадлежат области D,

170 КРАТНЫЕ ИНТЕГРАЛЫ [ГЛ. XIV
Внешний знак суммирования означает, что мы собираем вместе
все суммы, получившиеся при первом суммировании (т. е. суммируем
по индексу k).
Найдем выражение площади площадки ASik> не пересекаемой
границей области. Она будет равна разности площадей двух
секторов:
или ASik = р* Др? Д8*, где р, < pj < р, + Ар,.
Таким образом, интегральная сумма будет иметь вид*)
гдеР (б?; pj)—точка площадки ASik. Вынесем теперь множитель Авк
за знак внутренней суммы (это можно сделать, так как он яв-
является общим множителем для всех слагаемых этой суммы):
Предположим, что Др^ —->• 0, а Авк остается постоянным. Тогда
выражение, стоящее в скобках, будет стремиться к интегралу
)
J F<e;f Р)рф.
Теперь, полагая, что Д9Й-—>(), окончательно получим**)
Кф« (в) \
J F@, p)pdjpW. C)
„ Ф4 @) /
Формула C) служит для вычисления двойного интеграла в поляр-
полярных координатах.
*) Рассматривать интегральную сумму в таком виде мы можем потому,
что предел суммы не зависит от положения точки внутри площадки*
¦*) Наш вывод формулы C) не является строгим; при выводе этой фор-
формулы мы стремили к нулю сначала Ар/, оставляя Д6& неизменным, и только
затем стремили Д0^ к нулю. Это не вполне соответствует определению двой-
двойного интеграла, который мы рассматриваем как предел интегральной суммы
при стремлении диаметров площадок к нулю (т. е. при одновременном стрем-
стремлении к нулю А9д и Ар{). Однако, несмотря на допущенную нестрогость
доказательства, результат верен (т. е. формула C) справедлива). Строгий
вывод этой формулы можно было бы получить тем же методом, который был
применен при рассмотрении двойного интеграла в прямоугольных координатах.
Заметим также, что эта формула будет выведена еще раз в § 6 из других
соображений (как частный случай более общей формулы преобразования коор-
координат в данном интеграле).

ДВОЙНОЙ ИНТЕГРАЛ В ПОЛЯРНЫХ КООРДИНАТАХ
171
Если первое интегрирование производить по в, а второе по р,
то получим формулу (рис. 313)
C')
Ps/MP)
=S( J F<?> P)
Pi ^COj (p)
Пусть требуется вычислить двойной интеграл от функции/ (л:, у)
по области D, заданной в прямоугольных координатах:
Hf{x,y)dxdy.
D
Если область D является правильной в полярных координатах G, р,
У
Рис. 313.
Рис. 314.
то вычисление данного интеграла можно свести к вычислению
двукратного интеграла в полярных координатах.
Действительно, так как
= F(e, p),
то, следовательно,
Кф* (в) \
J /(pcosG, psin0)pdpW D)
_ „ ФИЭ) /
Пример 1. Вычислить объем V тела, ограниченного сферической по-
поверхностью
и цилиндром
Решение. За область интегрирования здесь можно взять основание
цилиндра х2+#2—2ш/ = 0, т. е. круг с центром в точке @, а) и радиусом а.
Уравнение границы этого круга можно записать в виде х2+(у—аJ=аа
(рис. 314). Вычислим 1/4 искомого объема V, а именно ту его часть, которая
расположена в первом октанте. Тогда в качестве интегрирования придется взять

172
КРАТНЫЕ ИНТЕГРАЛЫ
[ГЛ. XIV
полукруг, границе которого определяются уравнениями
*=<Pi(#) = 0, х=-у2(у)=У2ау—У2> У = 0
Подынтегральная функция
Следовательно,
2 а /V2ay-y2
1 Г* / f* —¦^
— у= \ ( \ У4а2—х2—у2dx )dy.
4 J \ J у
0 0
Преобразуем полученный интеграл к полярным координатам 8, р:
;t=pcos9, # psin8.
Определим границы интегрирования. Для этого нгпишем уравнение дан-
данной окружности в полярных координатах: так как
2+2 2 i9
j/==psin 9,
то р2—2<2psin9 = 0, или p = 2csin0. Следовательно, в полярных координатах
Рис. 315,
Рис. 316,
(рис. 315) границы области определяются уравнениями
Р = Ф*@) = О, p = CP2F):=2asine, a = 0, Р =
а подынтегральная функция имеет вид
Таким образом, получаем
31/2
л/2
Dа2 р2K/2"!2а sin 0
3 |о
я/2
=^. f (l-cos3e)dG=
о
Пример 2. Вычислим интеграл Пуассона
+ 00
J в-**Дь

§5]
ДВОЙНОЙ ИНТЕГРАЛ В ПОЛЯРНЫХ КООРДИНАТАХ
173
Решение. Вычислим сначала интеграл /д= \ \ e~x% yt dxdy, где
о
область интегрирования D есть круг x2-{-y2 = R2 (рис. 316).
Перейдя в приведенном интеграле к полярным координатам 9, р, получаема
О ^0
Если теперь мы будем неограниченно увеличивать радиус R, т. е. неогра-
неограниченно расширять область интегрирования, то получим так называемый
несобственный кратный интеграл:
ч 2зТ /R \
И9= Um U^-p2pdp]rf0= lira яA—в-«")=
о \o
Покажем, что интеграл \ С e~x*~yt dxdy стремится к пределу я, если
область D' произвольной формы расширяется так, что в конце концов любая
точка плоскости попадает в область D' и остается в ней (такое расширение
области D' мы будем условно записывать соот-
соотношением D'—>-j-00)-
Пусть /?х и R2—наименьшее и наибольшее
расстояния границы области ?>' от начала коор-
координат (рис. 317).
Так как функция e~K*~yt > 0 всюду, то
справедливы неравенства
или
я A—е
Рис. 317.
Так как при D'—>+оо, очевидно, Ri—++oo и /?2•—>+«>, то крайние
части неравенства стремятся к одному и тому же пределу я. Следовательно,
к этому пределу стремится и средний член, т. е.
lint
E)
Пусть, в частности, область ?)'—квадрат со стороной 2а с центром в начале
координат; тогда

174 КРАТНЫЕ ИНТЕГРАЛЫ [ГЛ. XIV
Вынесем теперь за знак внутреннего интеграла сомножитель е~у2 (эю можно
сделать, так как е~У* не зависит от переменной интегрирования х). Тогда
JJ I -У'( J e-**dx)dy.
D* -а \-а У
а
Положим V е~*2 dx=Ba. Это—постоянное число (зависящее только от а);
-а
поэтому
(a a v
потому что С e-**dx= [ e~y*dy\
следовательно,
Перейдем в этом равенстве к пределу, заставляя стремиться а к бесконечности
(при этом D' безгранично расширяется):
[О -12 Г +оо П2
[e~*2dx = [ e~**dx \.
-a J L-» J
Но, как было доказано (см. E)),
Следовательно,
"•]-
или
+ 00
Этот интеграл часто встречается в теории вероятностей и в статистике. Заме-
Заметим, что непосредственно вычислить этот интеграл (с помощью неопределен-
неопределенного интеграла) мы бы не смогли, так как первообразная от е~х2 не выра-
выражается в элементарных функциях.
§ 6. Замена переменных в двойном интеграле (общий случай)
Пусть в плоскости Оху дана область D, ограниченная линией L.
Предположим, что координаты хну являются функциями новых
переменных и и v:
х = у(и, v), y = ip(uf v), A)

§6]
ЗАМЕНА ПЕРЕМЕННЫХ
175
причем функции ф(«, v) и г|)(м, v) однозначны, непрерывны и имеют
непрерывные производные в некоторой области D\ которая будет
определена ниже. Тогда по формулам A) каждой паре значений
и и v соответствует единственная пара значений х и у. Предпо-
Предположим далее, что функции <р и г|) таковы, что если мы дадим х и у
определенные значения из области D, то по формулам A) найдем
определенные значения и и v.
Рассмотрим прямоугольную систему координат Ouv (рис. 318).
На основании сказанного следует, что каждой точке Р(х\ у) на
плоскости Оху (рис. 319) однозначно соответствует точка Р' (и; v)
и и-гАи, и.
Рис. 318.
ш
Рис. 319.
на плоскости Ouv с координатами и> v> которые определяются
по формулам A). Числа и и v называются криволинейными коор-
координатами точки Р.
Если в плоскости Оху точка опишет замкнутую линию L,
ограничивающую область D, то в плоскости Ouv соответствующая
точка опишет замкнутую линию Z/, ограничивающую некоторую
область D'\ при этом каждой точке области D* соответствует точка
области Z).
Таким образом, формулы A) устанавливают взаимно одно-
однозначное соответствие между точками областей D
и U или, как говорят, взаимно однозначно отображают
область D на область D'.
Рассмотрим в области D' линию и = const. По формулам A)
найдем, что в плоскости Оху ей будет соответствовать, вообще
говоря, некоторая кривая. Точно так же каждой прямой v = const
плоскости Ouv будет соответствовать некоторая линия в плоско-
плоскости Оху.
Разобьем область D' прямыми и = const и v = const на прямо-
прямоугольные площадки (при этом площадки, задевающие границу
области D', мы не будем принимать в расчет). Соответствующими
кривыми линиями область D разобьется на некоторые криволи-
криволинейные четырехугольники (рис. 319).
Рассмотрим в плоскости Ouv прямоугольную площадку AS\
ограниченную прямыми и = const, u + Au = const, v = const, v +

|76 КРАТНЫЕ ИНТЕГРАЛЫ [ГЛ. XIV
+ Аи = const, и соответствующую ей криволинейную площадку AS
в плоскости Ох у. Площади этих площадок тоже обозначим соот-
соответственно через AS' и AS. Тогда, очевидно,
AS' = Аи Av.
Вообще говоря, площади AS и AS' различны.
Пусть в области D задана непрерывная функция
* = /(*. У)-
Каждому значению функции z = f(x9 у) в области D соответ-
соответствует то же самое значение функции z = F (и, v) в области D', где
F(u, ») = /[<p(a, v), 4>(и, v)].
Рассмотрим интегральные суммы от функции z по области D.
Очевидно, имеет место следующее равенство:
2/(*. y)AS = %F(u, v)AS. B)
Вычислим AS, т. е. площадь криволинейного четырехугольника
РгР2РъР* в плоскости Оху (см. рис. 319).
Определим координаты его вершин:
Ф )
2 У*) 2 ( , v), у2 = Ц(и + &и, v),
з'> Уз), хя = у(и + Аи, v + Av), y3 = ty(u + Au, v + Av),
) ( + Д) У4 = ^(^, v + Av).
При вычислении площади криволинейного четырехугольника
PiPzPsP* будем считать линии РХР19 Р2Р3, Р3Р±, P^Pt попарно
параллельными прямыми; кроме того, приращения функций будем
заменять соответствующими дифференциалами. Таким образом, мы
будем пренебрегать бесконечно малыми высшего порядка по срав-
сравнению с бесконечно малыми Аи, Av. Тогда формулы C) будут
иметь вид
** = ф(и, v), У± = Ъ(и, v),
При сделанных допущениях криволинейный четырехугольник
P\PJ*bPi можно рассматривать как параллелограмм. Его площадь
AS приближенно равна удвоенной площади треугольника PiP2PB

ЗАМЕНА ПЕРЕМЕННЫХ
177
и находится no формуле аналитической геометрии:
AS « | (х9—хг) (Уз—у2)—(х3—х2) (Уз—Уг) I =*
ди dv dv ди
ди
д\р
~ди~
-w
dty
здесь вторые (внешние) вертикальные линейки означают, что этот
определитель берется по абсолютной величине. Введем обозна-
обозначение
дф
ди
д\$
ди
up
ди
dip
dv
Таким образом,
AS«|/|AS'.
D)
Определитель / называется функциональным определителем
функций <р(н, v) и i|)(a, v). Его называют также якобианом по
имени немецкого математика Якоби.
Равенство D) является только приближенным, так как в про-
процессе вычисления площади AS мы пренебрегли бесконечно малыми
высшего порядка. Однако чем меньшими будут размеры площа-
площадок AS и AS', тем это равенство будет точнее. Оно становится
совершенно точным в пределе, когда диаметры площадок AS и AS'
стремятся к нулю:
|/|= lim ^.
diam AS' -* 0 ао
Применим теперь полученное равенство к вычислению двой-
двойного интеграла. На основании равенства B) можем написать
(интегральная сумма справа распространена на область D'). Пере-
Переходя к пределу при diam AS' —+ 0, получим точное равенство:
$$/(*,
v)\I\dudv.
E)
Это и есть формула преобразования координат
в двойном интеграле. Она дает возможность свести вы-
вычисление двойного интеграла по области D к вычислению двои-

178
КРАТНЫЕ ИНТЕГРАЛЫ
[ГЛ. XIV
ного интеграла по области D', что может упростить задачу.
Впервые строгое доказательство этой формулы было дано выдаю-
выдающимся русским математиком М. В. Остроградским.
Замечание. Переход от прямоугольных координат к поляр-
полярным, рассмотренный в предыдущем параграфе, является частным
4
м'\
0
А'
ш
\
M'
Рис. 321,
fi *
Рис. 320.
случаем замены переменных в двойном интеграле. В этом случае
Кривая ЛВ(р = р1) на плоскости Оху (рис. 320) переходит
в прямую А'В' на плоскости О0р (рис. 321). Кривая 1>С(р = р2)
на плоскости Оху переходит в прямую DC на плоскости 00р.
Прямые AD и ВС плоскости Оху переходят в прямые A'D'
и В'С плоскости ОЭр. Кривые Lt и L2 переходят в кривые Ц и L'2.
Вычислим якобиан преобразования декартовых координат х и у
в полярные 6 и р:
| — р sin 9 cos 91
дх
дв
ду
дд
дх
Ф
ду
др
Следовательно, | /1 = р, и поэтому
H J , P)pdp)d9.
D a \Ot @) /
Эта формула и была установлена в предыдущем параграфе.
Пример. Пусть требуется вычислить двойной интеграл
Of—др) дх dy
по области D в плоскости Оху, ограниченной прямыми
у=х—3, У=-—~х-\'—, у=—-

§7]
ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ
179
Непосредственное вычисление этого двойного интеграла было бы затрудни-
затруднительным; однако простая замена переменных позволяет свести этот интеграл
к интегралу по прямоугольнику, стороны которого параллельны осям координат.
Положим
и=у—х, v = y-\~Tx. F)
Тогда прямые у—х-\-\, у — х—3 перейдут соответственно в прямыеи=1,
и — — 3 на плоскости Ouv; прямые же у=—^-х-\—~-, #=—"о~х-\-Ъ перей-
о о о
дут в прямые v = 7/3, v = 5.
Следовательно, заданная область D преобразуется в прямоугольную об-
область D', изображенную на рис. 322. Остается вычислить якобиан преобразо-
преобразования. Для этого выразим хну через и и v.
Решая систему уравнений F), получим
3,3 1,3
Следовательно,
дх
ду
ду
ди
дх
dv
ду
dv
3
4
1
4
3
4
3
4
16
3_
16=
и абсолютная величина якобиана равна |/| = 3/4. Поэтому
-ududv=—8.
-з
§ 7. Вычисление площади поверхности
Пусть требуется вычислить площадь поверхности, ограничен-
ограниченной линией Г (рис. 323); поверхность задана уравнением z ==f (x> у),
где функция /(*, у) непрерывна и имеет непрерывные частные
производные. Обозначим проекцию линии Г на плоскость Оху
через L. Область на плоскости Оху, ограниченную линией L, обо-
обозначим через ?>,
Разобьем произвольным образом область D на п элементарных
площадок ASU AS2,
ASn. В каждой площадке AS.- возьмем
точку Pi (ii\ i\i). Точке Pt будет соответствовать на поверхности
точка Mi [|z-; i\{\ f(lh T)f)]. Через точку М( проведем касатель-
касательную плоскость к поверхности. Уравнение ее имеет вид
A)

180
КРАТНЫЕ ИНТЕГРАЛЫ
[ГЛ. XIV
(см. § 6, гл. IX, т. 1). На этой плоскости выделим такую пло-
площадку Да?> которая проектируется на плоскость Оху в виде пло-
п
щадки &St. Рассмотрим сумму всех площадок Да,-: 2 Д^-
Предел а этой суммы, когда наибольший из диаметров пло-
площадок Д(Т; стремится к нулю, мы будем называть площадью по-
поверхности, т. е. по определению положим
в= lim
diam Aof
2
0 i = 1
B)
Займемся теперь вычислением площади поверхности. Обозна-
Обозначим через Yi угол между касательной плоскостью и плоскостью Оху.
Рис. 324.
На основании известной формулы аналитической геометрии можно
написать (рис. 324)
AS,- =
или
» cos vi
C)
Угол y« есть в то же время угол между осью Ог и перпен-
перпендикуляром к плоскости A). Поэтому на основании уравнения A)
и формулы аналитической геометрии имеем
cos Y/ =
Следовательно,
?, a,)

§7] ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ J81
Подставляя это выражение в формулу B), получим
с = Игл 2 ^1+/;2(?/, rid + ffdt, Я/
diam AS;-* 0 t-~Q
Так как предел интегральной суммы, стоящей в правой части
последнего равенства, по определению представляет собой двой-
двойной интеграл JJ г*^~(ж) ~^{ж) dxdH, то окончательно
получаем
-JJ У'+№)¦+№)"
Это и есть формула, по которой вычисляется площадь поверх-
поверхности z = f(x, у).
Если уравнение поверхности дано в виде x = \i(y, %) или
в виде у = х(х, г), то соответствующие формулы для вычисления
поверхности имеют вид
где D' и D;/—области на плоскостях Oyz и О*г, в которые проек-
проектируется данная поверхность.
Пример 1. Вычислить поверхность а сферы
x2+y2+z2 = R2.
Решение. Вычислим поверхность верхней половины сферы z =
х2_^2 (рис# 325). В этом случае
дг__ х дг___ у
Следовательно, подынтегральная функция примет вид
Область интегрирования определяется условием x2-\-y2*s^R2. Таким образом,
на основании формулы D) будем иметь
Для вычисления полученного двойного интеграла перейдем к поляр-
полярным координатам. В полярных координатах граница области интегрирования

182
КРАТНЫЕ ИНТЕГРАЛЫ
[ГЛ. XIV
определяется уравнением р = #. Следовательно,
сг=2\ | V р dp )dQ = 2R \ [—К /?2—Р2]о </9=2#
J \ J К/?2—-р2 У J
О \0 г / 0 и
Пример 2. Найти площадь той части поверхности цилиндра #2+#2 =а2,
которая вырезается цилиндром л:2+г'2 = а2.
Рис. 325,
Рис. 326.
Решение. На рис. 326 изображена 1/8 часть искомой поверхности.
Уравнение поверхности имеет вид у=Уа2—х2; поэтому
*—Xй у а2 Х2
Область интегрирования представляет собой четверть круга, т. е. опреде-
определяется условиями
Следовательно,
a /Va2-x*
W( I 7*=**)—'177=1
и
dx=a\ dx = a*f
§ 8. Плотность распределения вещества и двойной интеграл
Пусть в области D распределено некоторое вещество, так что
на каждую единицу площади области D приходится определенное
количество этого вещества. Мы будем говорить в дальнейшем
о распределении массы, хотя наши рассуждения сохранятся
и в том случае, когда идет речь о распределении электрического
заряда, количества тепла и т. п.
Рассмотрим произвольную площадку AS области D. Пусть
масса вещества, приходящаяся на данную площадку, есть Am.

§8] ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕЩЕСТВА J83
Тогда отношение -^ называется средней поверхностной плотно-
плотностью вещества в области AS.
Пусть теперь площадка AS уменьшается, стягиваясь к точке
Р(х\ у). Рассмотрим предел lim -д^-. Если этот предел суще-
AS -> О АС>
ствует, то, вообще говоря, он будет зависеть от положения точ-
точки Р, т. е. от ее координат х и у, и будет представлять собой
некоторую функцию f(P) точки Р. Будем называть этот предел
поверхностной плотностью вещества в точке Р:
Таким образом, поверхностная плотность есть функция / (х, у)
координат точки области.
Пусть теперь, обратно, в области D задана поверхностная
плотность некоторого вещества как некоторая непрерывная функ-
функция f(P):=f(Xy у) и требуется определить общее количество ве-
вещества М, содержащегося в области D. Разобьем область D на
площадки ASi (i = l, 2, ..., п) и в каждой площадке возьмем
точку Рг\ тогда /(Р/) есть поверхностная плотность в точке Р{.
Произведение /(Pi)AS/ с точностью до бесконечно малых выс-
высшего порядка, дает нам количество вещества, содержащегося на
п
площадке AS,-, а сумма 2 /(Л*)^? приближенно выражает
общее количество вещества, распределенного в области D. Но
это—интегральная сумма для функции f(P) в области D. Точное
значение мы получим в пределе при ASj —*0.
Таким образом*),
Af= Hm % f(Pt)bSi=llf(P)dS=l$f(x9 y)dxdy9 B)
т. е. общее количество вещества в области D равно двойному
интегралу по области D от плотности f(P) = f(x> у) этого вещества.
Пример. Определить массу круглой пластинки радиуса/?, если поверх-
поверхностная плотность / (*, у) материала пластинки в каждой точке Р (х; у) про-
пропорциональна расстоянию точки (х; у) от центра круга, т. е. если
fix, y) =
Решение. По формуле B) имеем
где область интегрирования D есть круг
¦) Соотношение AS* —у 0 мы понимаем в том смысле, что диаметр области
AS/ стремится к нулю.

134 КРАТНЫЕ ИНТЕГРАЛЫ ?ГЛ XIV
Переходя к полярным координатам, получаем
R
о \о / о
§ 9. Момент инерции площади плоской фигуры
Моментом инерции I материальной точки М с массой т
относительно некоторой точки О называется произведение массы т
на квадрат ее расстояния г от точки О:
Момент инерции системы материальных точек ти т2, ..., тп
относительно точки О есть сумма моментов инерции отдельных
точек системы:
Определим теперь момент инерции
материальной плоской фигуры D.
Пусть фигура D расположена в коор-
5" динатной плоскости Оху. Определим мо-
момент инерции этой фигуры относитель-
относительно начала координат, предполагая, что
поверхностная плотность всюду равна единице.
Разобьем область D на элементарные площадки AS( (i = 1,
2, ..., п) (рис. 327). На каждой площадке возьмем точку Р{
с координатами ?;, г\{. Назовем элементарным моментом инер-
инерции A/t- площадки AS{ произведение массы площадки ASl на
квадрат расстояния г) = Ц + }
и составим сумму таких моментов
Она представляет собой интегральную сумму для функции f (х, #)=а
=зх24~У2 по области D.
Момент инерции фигуры D определим как предел этой интег-
интегральной суммы, когда диаметр каждой элементарной площадки ASt
стремится к нулю:
2!
diam ASt--*0 is 0
Пределом этой суммы является двойной интеграл )^(x2+y*)dxdy.

§9] МОМЕНТ ИНЕРЦИИ ПЛОЩАДИ ПЛОСКОЙ ФИГУРЫ 185
Следовательно, момент инерции фигуры D относительно начала
координат равен
D
где D — область, совпадающая с данной плоской фигурой.
Интегралы
B)
<3>
называются соответственно моментами инерции фигуры D отно-
относительно осей Ох и Оу.
Пример I. Вычислить момент инерции площади круга D радиуса R
относительно центра О.
Решение. По формуле A) имеем /0= \ \ (*2+#2)dxdy. Длявычисле-
D
ния этого интеграла перейдем к полярным координатам в, р. Уравнение окруж-
окружности в полярных координатах есть p = R. Поэтому
2я .R .
о /
Замечание. Если поверхностная плотность 7 не равна
единице, а является некоторой функцией от х и у, т. е. у —
= У(Х9 У)» т0 масса площадки AS( будет с точностью до беско-
бесконечно малых высшего порядка равна Y(?t> Л*)Д^*» и поэтому
момент инерции плоской фигуры относительно начала координат
будет
Пример 2. Вычислить момент инерции плоской материальной фигуры D,
ограниченной линиями у2~\—х, дс = О, у=0, относительно оси Оу, если
поверхностная плотность в каждой точке равна у (рис. 328).
Решение.
Эллипс инерции. Определим момент инерции площади
плоской фигуры D относительно некоторой оси OL, проходящей
через точку О, которую мы примем за начало координат. Обо-
Обозначим через ф угол, образованный прямой OL с положительным
направлением оси Ох (рис. 329).

186
КРАТНЫЕ ИНТЕГРАЛЫ
Нормальное уравнение прямой OL есть
х sin ф — у cos ф = 0.
Расстояние г какой-либо точки М (х\ у) от этой прямой равно
Момент инерции / площади области D относительно прямой OL
Рис. 328#
по определению выражается интегралом
/ =
Рис. 329.
= JJ (xsinq—у cosyJ dxdy = sin2 у ^
D D
—2 sin ф cos ф J ) xy dx dy + cos2 ф J J y2 dx dy.
D D
Следовательно,
=s Jyy sin2 ф — 21 Xy sin ф cos ф + Ixx cos2 ф,
D)
Jyy sin ф 21 Xy
здесь 1уУ~\\х2dxdy — момент инерции фигуры относительно
D
оси у; /хх= j jt/adxdy — момент инерции относительно оси xf a
D
lxy = \\xydxdy. Разделив все члены последнего равенства на/,
D
получим
Возьмем на прямой OL точку А (X; У) так, чтобы ОЛ=1/|/7.
Различным направлениям оси OL, т. е. различным значениям
угла ф, соответствуют различные значения / и различные точки Л.
Найдем геометрическое место точек А. Очевидно,
X==
F7
C0S(p'

§91
МОМЕНТ ИНЕРЦИИ ПЛОЩАДИ ПЛОСКОЙ ФИГУРЫ
187
В силу равенства E) величины X и У связаны между собой
соотношением
\ = IxxX*-2IxyXY + IyvY\ F)
Таким образом, геометрическое место точек А(Х\ Y) есть кри-
кривая второго порядка F). Докажем, что
эта кривая есть эллипс.
Справедливо следующее очень важное
в приложениях неравенство, установлен-
установленное русским математиком В. Я. Буняков-
ским*):
(\\xydxdyY
или
Таким образом, дискриминант кривой F) положителен и, сле-
следовательно, эта кривая есть эллипс (рис. 330). Этот эллипс назы-
*) Для доказательства неравенства Буняковского рассмотрим следующее
очевидное неравенство:
где к — постоянная. Знак равенства возможен только тогда, когда f(x, у)—
— taf(#, у)^0> т- е- если f (х, у) = Ху(х9 у). Если предположим, что
f (*> */)/ф (*¦ У) ^ const = Я, то всегда будет иметь место знак неравенства.
Таким образом, раскрывая скобки под знаком интеграла, получим
$$Р(*. y)dxdy—2k^f(x9 y)q>(xt y)dxdy+№ J J q>*(x, y)dxdg>0.
D D D
Рассмотрим выражение, стоящее слева, как функцию от К. Это—много-
Это—многочлен второй степени, никогда не обращающийся в нуль; следовательно, его
корни комплексны, а это будет тогда, когда дискриминант, составленный из
коэффициентов квадратного многочлена, отрицателен, т. е.
/ J J f<pdxdy\2- J
\ D / D
dx
dx dy < 0,
ИЛИ
fydxdyV < J J /2 dxdy J J ер* dxdg.
/ D D
Это и есть неравенство Буняковского.
В нашем случае f (х, у) = х, <р(*, у) = у% х/у ф const.
Замечательное неравенство Буняковского постоянно применяется в различ-
различных областях математики. Это неравенство во многих учебниках неправильно
называют неравенством Шварца. В. Я. Буняковский опубликовал его (среди
других важных неравенств) в 1859 г., а Шварц лишь в 1875 г.

188 КРАТНЫЕ ИНТЕГРАЛЫ [ГЛ XIV
вается эллипсом инерции. Понятие эллипса инерции имеет
существенное значение в механике.
Заметим, что длины осей эллипса инерции и его положение
на плоскости зависят от формы данной плоской фигуры. Так как
расстояние от начала координат до какой-либо точки А эллипса
равно \/У/, где /—момент инерции фигуры относительно оси О А,
то, построив эллипс, можно легко подсчитать момент инерции
фигуры D относительно какой-либо прямой, проходящей через
начало координат. В частности, легко видеть, что момент инер-
инерции фигуры будет наименьшим относительно большой оси эллипса
инерции и наибольшим относительно малой оси этого эллипса.
§ 10. Координаты центра масс площади плоской фигуры
В § 8 гл. XII (т. I) указывалось, что координаты центра масс
системы материальных точек Piy Р2, ..., Рп с массами ти т2, .. •
..., тп определяются по формулам
Определим теперь координаты центра масс плоской фигуры D.
Разобьем эту фигуру на очень малые элементарные площадки Д5{.
Если поверхностную плотность принять равной единице, то масса
площадки будет равна ее площади. Если приближенно считать,
что вся масса элементарной площадки AS t сосредоточена в какой-
либо ее точке Р*(?,-; rjj), то можно рассматривать фигуру D как
систему материальных точек. Тогда по формулам A)
координаты центра масс этой фигуры будут приближенно
определяться равенствами
У^~Ч
5 A5i S Д51
В пределе при diam ASf —> 0 интегральные суммы, стоящие
в числителях и знаменателях дробей, перейдут в двойные инте-
интегралы, и мы получим точные формулы для вычисления координат
центра масс плоской фигуры:
xdx dy V V у dx dy
yc = -h • B)
\\dxdy \\dxdy
D D
Эти формулы, выведенные для плоской фигуры с поверхностной

КООРДИНАТЫ ЦЕНТРА МАСС
189
плотностью 1, остаются, очевидно, в силе и для фигуры, имею-
имеющей любую другую постоянную во всех точках плотность у.
Если же поверхностная плотность переменна:
то соответствующие формулы будут иметь вид
55 Y(*. y)xdxdy
у(х, у) ydxdy
5 5 у (*> у)dx dy
Выражения
M «r = S J V ^» У)хахс1У и
^ y)ydxdy
называются статическими моментами плоской фигуры D отно-
относительно осей Оу и Ох.
Интеграл 5 \ У (*» У) dx dy выражает j
ф
величину массы рассматриваемой фи-
фигуры.
Пример. Определить координаты центра
масс четверти эллипса (рис. 331)
и2
У 1
полагая, что поверхностная плотность во всех
точках равна 1.
Решение. По формулам B) получаем
./f ^
a f a \ 4
4- nab
4
-;- nab
4
ydy jdx
ib
— nab
4
а
О __4я

190 КРАТНЫЕ ИНТЕГРАЛЫ [ГЛ XIV
§ 11. Тройной интеграл
Пусть в пространстве задана некоторая область V, ограни-
ограниченная замкнутой поверхностью S. Пусть в области У и на ее
границе определена некоторая непрерывная функция /(*, у, г),
где х, у, г—прямоугольные координаты точки области. Для
ясности в случае, если /(#, у, z)^0, мы можем считать эту
функцию плотностью распределения некоторого вещества в об-
области V.
Разобьем область V произвольным образом на области Avi9
обозначая символом Avt не только саму область, но и ее объем.
В пределах каждой частичной области Avt выберем произвольную
точку Р{ и обозначим через f(Pt) значение функции / в этой
точке. Составим интегральную сумму вида
и будем неограниченно увеличивать число малых областей Avt
так, чтобы наибольший диаметр Av( стремился к нулю *). Если
функция /(#, у, z) непрерывна, то при этом будет существовать
предел интегральных сумм вида A), где предел интегральных
сумм понимается в таком же смысле, как это было указано при
определении двойного интеграла**). Этот предел, не зависящий
ни от способа разбиения области У, ни от выбора точек Ph обо-
обозначается символом \ \ \ / (Р) do и называется тройным интегра-
v
лом. Таким образом, по определению
Нт ]
diam Av> -> О
ИЛИ
/•/*/• fr f» Г*
(х, у, z)dxdydz. B)
Если f(x, у, z) считать объемной плотностью распределения
вещества в области У, то интеграл B) даст массу всего вещества,
заключенного в объеме V.
*) Диаметром области Аи/ называется максимальное расстояние между
точками, лежащими на границе области.
**) Эта теорема о существовании предела интегральных сумм (т. е. о су-
существовании тройного интеграла) для всякой функции, непрерывной в замкну-
замкнутой области V (включая границу), принимается нами без доказательства.

fi2]
ВЫЧИСЛЕНИЕ ТРОЙНОГО ИНТЕГРАЛА
191
§ 12. Вычисление тройного интеграла
Предположим, что пространственная (трехмерная) область V,
ограниченная замкнутой поверхностью S, обладает следующими
свойствами:
1) всякая прямая, параллельная оси Ог, проведенная через
внутреннюю (т. е. не лежащую на границе S) точку облгсти V,
пересекает поверхность S в двух точ-
точках;
2) вся область V проектируется на
плоскость Оху в правильную (двумер-
(двумерную) область D;
fay)
Рис. 332.
3) всякая часть области V, отсеченная плоскостью, параллель-
параллельной любой из координатных плоскостей (Охуу Oxz, Oyz), также
обладает свойствами 1) и 2).
Область F, обладающую указанными свойствами, мы будем
называть провальной трехмерной областью.
Правильными трехмерными областями являются, например,
эллипсоид, прямоугольный параллелепипед, тетраэдр и т. д.
Пример неправильной трехмерной области дан на рис. 332. В на-
настоящем параграфе мы будем рассматривать только правильные
области.
Пусть поверхность, ограничивающая область V снизу, имеет
уравнение z — %(x, у), а поверхность, ограничивающая эту область
сверху, имеет уравнение z = ty(x, у) (рис. 333).
Введем понятие трехкратного интеграла Iv по области V
от функции трех переменных f(x, у, г), определенной и непре-
непрерывной в области V. Предположим, что область D—проекция
области V на плоскость Оху—ограничена линиями
Тогда трехкратный интеграл от функции f (х, у, г) по области V

192
КРАТНЫЕ ИНТЕГРАЛЫ
[ГЛ. XIV
определяется так:
= S М J Г(*'У' z)dz\dy\dx.
а {Фа (х) LX (х, у) J )
A)
Заметим, что в результате интегрирования по г и подстановки
пределов в фигурных скобках получится функция от х и у.
Далее, вычисляется двойной интеграл от этой функции по обла-
области D, как это было рассмотрено выше.
Приведем пример вычисления трехкратного интеграла по области У.
Пример 1. Вычислить трехкратный интеграл от функции / (х, у> г) =
s=xyz по области V, ограниченной плоскостями
Решение. Эта область правильная, она
ограничена сверху и снизу плоскостями 2 = 0 и
2=1—х—у и проектируется на плоскость Оху
в правильную плоскую область D, представляю-
представляющую собой треугольник, ограниченный прямыми
л;с=0, у = 0, у—\—х (рис. 334). Поэтому трех-
трехкратный интеграл /у вычислится следующим об-
образом:
о у^о /\
Рис. 334.
xyzdzUo.
J
Расставляя пределы в этом двукратном интеграле по области D, получим
dx =
Рассмотрим теперь некоторые свойства трехкратного интеграла.
Свойство 1. Если область V разбить на две области Vt
и V2 плоскостью, параллельной какой-либо из плоскостей коорди-
координат, то трехкратный интеграл по области V равен сумме трех-
трехкратных интегралов по областям Vt и V2.
Доказательство этого свойства проводится совершенно так
же, как и доказательство соответствующего свойства для дву-
двукратных интегралов. Поэтому нет необходимости повторять его
снова.
Следствие. При любом разбиении области V на конечное
число областей VIf •.., Vn плоскостями, параллельными коорди-
координатным плоскостям, имеет место равенство

§12] ВЫЧИСЛЕНИЕ ТРОЙНОГО ИНТЕГРАЛА 193
Свойство 2 (теорема об оценке трехкратного
интеграла). Если т и М—соответственно наименьшее и
наибольшее значения функции f(x, у, г) в области У, то имеет-
место неравенство
где V есть объем данной области, a Iv—трехкратный интеграл
от функции f(x, у у г) по области V.
Доказательство. Оценим сначала -внутренний интеграл
[Ъ(х> У) 1
j / (*, У> z) dz do:
%(х, у) J
у)
У)
% (AT, У)
v 1 i\ л/ i v //if
Итак, внутренний интеграл не превосходит выражения М [ty{x, у)—
— %{х> У)]- Поэтому в силу теоремы § 1 о двойных интегралах
получим (обозначая через D проекцию области V на плоскость Оху)
ГЪ(х, у) 1
'v = SS J f(*> y>*)d2\do^llMto(x9 y)-%(xty)]do=*
D L%(x,y) J D
\\д)-1(х> У)]do.
Но последний двукратный интеграл равен двойному интегралу
от функции if(x, у)—х(#» У) и» следовательно, равен объему
той области, которая Заключена между поверхностями z=*%(x9 у)
и г = -ф(х, у)у т. е. объему области V. Поэтому
Аналогично доказывается, что Iv^mV. Таким образом, свой-
свойство 2 доказано.
Свойство 3 (теорема о среднем). Трехкратный инте-
интеграл Iv от непрерывной функции f(x> у, z) no области V равен
произведению его объема V *на значение функции в некоторой
точке Р области У, т. *.
=S И J f(x.y.*)dz\dy\dx = f(P)V. B)
a VPt(*) LX(x.y) J J
Доказательство этого свойства проводится так же, как и до-
доказательство аналогичного свойства для двукратного интеграла
(см. § 2, свойство 3, формула D)). Теперь мы можем доказать
теорему о вычислении тройного интеграла.
Н. С. Пи ежу нов, т. 2

|94 КРАТНЫЕ ИНТЕГРАЛЫ [ГЛ, XIV
Теорема. Тройной интеграл от функции f(x, у, г) по
правильной области V равен трехкратному интегралу по той
же области, т. е.
=l\ J S f(x,y,z)dz\dy\dx.
a V<PtU) LXU, У) J J
Доказательство. Разобьем область V плоскостями, па-
параллельными координатным плоскостям, на п правильных облас-
областей: А^, Ду2, . •., До„. Как и выше, обозначим через lv трех-
трехкратный интеграл от функции f(x9 у, z) по области V, а через
/до. трехкратный интеграл от этой функции по области Avt.
Тогда на основании следствия из свойства 1 можем написать
равенство
1у — ^Afi ~Ь ^Аг>2 4" • • • + /д&л. C)
Каждое из слагаемых, стоящих в правой части этого равенства,
преобразуем по формуле B):
», + ... + f (Pn) Аул, D)
где Р(—некоторая точка области Avt.
В правой части этого равенства стоит интегральная сумма.
По предположению функция / (х, у, z) непрерывна в области V и
потому предел этой суммы при стремлении к нулю наибольшего
диаметра Avi существует и равняется тройному интегралу от функ-
функции f(xy y,sz) по области V. Таким образом, переходя к пределу
в равенстве D) при diamAyt-—>0, получим
или окончательно, меняя местами стоящие справа и слева выра-
выражения,
1 Л
*\dy\
J )
f(x>V.*)d*\dy\dx.
Y.(x, у) J )
Теорема доказана.
Здесь z = %(x, у) и z = ip(*, у) — уравнения поверхностей,
ограничивающих правильную область V снизу и сверху. Линии
y = <Pi(*)> У = ФЯ(^)» ^ = ^» х = Ь ограничивают область D, являю-
являющуюся проекцией области V на плоскость Оху.
Замечание. Аналогично тому, как это было в случае дву-
двукратного интеграла, можно составить трехкратный интеграл с дру-
другим порядком интегрирования по переменным и другими преде-
пределами, если, конечно, это позволяет форма области V.
Вычисление объема тела с помощьй трехкрат-
трехкратного интеграла. Если подынтегральная функция f (я, у,г)=1,

§12]
ВЫЧИСЛЕНИЕ ТРОЙНОГО ИНТЕГРАЛА
195
то тройной интеграл по области V вы-
выражает объем области V:
V=[\\dxdydz. E)
Пример 2. Вычислить объем эллип-
2 2 2
Решение. Эллипсоид (рис. 335) ог-
ограничен снизу поверхностью z =
a сверху—поверх-
сверху—поверхностью z — c у 1 ?—-~, Проекцией этого эллипсоида на плоскость Оху
х2 ф
(область D) является эллипс —2^ГТ2~^1 Следовательно, сводя вычисление
объема к вычислению трехкратного интеграла, получим
Г
v =
dz ]dy
и
J
При вычислении внутреннего интеграла ^ считается постоянным. Сделаем под*
становку
у = Ь у l—^
sin ?, dy =
Переменная у изменяется рт
—-Ь у 1—"^ до Ь у 1— ^,
поэтому ^ ме-
няется от —л/2 до я/2. Подставляя в интеграл новые пределы, получим
я/2
' " ~ X*
а Г Я/2
-а Ь-я/
•ь
я/2
-Я/2
Итак,
V = 4nabc/3.
Если а = Ь=сг то получаем объем шара:
4atabo

196
КРАТНЫЕ ИНТЕГРАЛЫ
[ГЛ. XIV
§ 13. Замена переменных в тройном интеграле
1. Тройной интеграл в цилиндрических коор-
координатах. В случае так называемых цилиндрических координат
положение точки Р в пространстве определяется тремя числами
б, р, г, где 6 и р—полярные координаты проекции точки Р на
плоскость Ох у и z—аппликата точки Р, т, е. расстояние точки
до плоскости Оху, взятое со знаком плюс, если точка лежит выше
плоскости Ох у, и со знаком минус—если ниже (рис. 336).
В этом случае данную, пространственную область V разбиваем
на элементарные объемы координатными поверхностями 6 = в?,
р = Ру, г = гк (полуплоскости, примыкающие к оси Ог, круговые
цилиндры, ось которых совпадает с осью Ог, плоскости, перпен-
перпендикулярные к оси О г). Элементарным объемом будет криволиней-
криволинейная «призма» (изображенная на рис. 337). Площадь основания
этой призмы с точностью до бесконечно малых высшего порядка рав-
равна р Д9 Др, высота равна Дг (индексы i, /, к для простоты записи
опускаем). Следовательно, До = рД0ДрДг. Поэтому тройной инте-
интеграл от функции ^(8, р, г) по области V имеет вид
= $S$
A)
Пределы интегрирования определяются формой области V.
Если дан тройной интеграл от функции /(#, у, г) в прямо-
прямоугольных координатах, то его легко преобразовать в тройной
интеграл в цилиндрических координатах. В самом деле, заме-
заметив, что
получим
JJS К*> У>
z = z,
= JJJ F@, p, z)pdQdpdzf

§13] ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНОМ ИНТЕГРАЛЕ 197
ТЖ
/(pcosG, psinO, z) = F@, p, г).
Пример. Определить массу М полушара радиуса R "с центром в на-
начале координат, если плотность F его вещества в каждой точке (х; у; г) про-
пропорциональна расстоянию этой точки от основания, т. е. F = kz.
Решение. Уравнение верхней части полусферы
в цилиндрических координатах имеет вид
Следовательно,
2ЯГУ? /VRp \ И
M=[[[kzpdQdpdz=[ \[( [ kzdz)pdp\dQ =
*v о Lo \ о / J
2л,
i п и \
" 4^#
2. Тройной интеграл в сферических координа-
координатах, В сферических координатах положение точки Р в простран-
пространстве определяется тремя числами 0, г, ф, где г—расстояние точки
от начала координат, так называемый радиус вектор точки, ф —
угол между радиус-вектором и осью Ог, 0—угол между проек-
проекцией радиус-вектора на плоскость Оху и осью 0xt отсчитываемый
от этой оси в положительном направлении (т. е. против часовой
стрелки) (рис. 338). Для любой точки пространства имеем
О < 0 < 2л.
Разобьем данную область V на элементарные части Ai> коор-
координатными поверхностями г = const (сферы), ф = const (конические
поверхности с вершинами в начале координат), 8 = const (полу-
(полуплоскости, проходящие через ось Oz). С точностью до бесконечно
малых высшего порядка элементарный объем Ду можно считать
параллелепипедом с ребрами длиньГ Аг, г Дер, г sin ф ДО. Тогда
элементарный объем равен (рис. 339)
Av = r% sin ф Дг Д0 Дф.
Тройной интеграл от функции F @, г, ф) по области V имеет вид
/ = J f J F @, г, ф) г2 sin <pdr dQ d(f. (Г)
v
Границы интегрирования определяются формой области V.
Из рис. 338 легко устанавливаются выражения декартовых

198
КРАТНЫЕ ИНТЕГРАЛЫ
[ГЛ. XIV
координат через сферические:
x=r sin ф cos 0, у — г sin ф sin 9, z = r cos ср.
Поэтому формула преобразования тройного интеграла от декар-
декартовых координат к сферическим имеет вид
/(*, у, z)dxdydz =
ш,
s= \ \ \ / (г sin ф cos 9, г sin ф sin 9, г cosy) r2 sin q> drdQdq.
v
3. Общая замена переменных в тройном инте-
интеграле. Переходы от декартовых координат к цилиндрическим
и сферическим в тройном интеграле—это частные случаи общего
преобразования координат в пространстве.
Рис. 338.
Рис. 339,
Пусть функции
* = Ф(и, t, w), y = ty(u,t,w), z = %(u,t,w)
взаимно однозначно отображают область V в декартовых коор-
координатах х, уу z на область V в криволинейных координатах и>
ty w. Пусть элемент объема Av области V переходит в элемент
Дс/' области У и пусть
hm т-, = \1 .
дУ'->оАу j 1
Тогда
f(x, у, z)dxdydz=*
*> w)> *("»'» w)> %(u,t9w)]\I\dudtdw.
v
Аналогично тому, как это имело место в двойном интеграле,
/ называется якобианом; подобно тому как это делалось для

§14]
МОМЕНТ ИНЕРЦИИ И КООРДИНАТЫ ЦЕНТРА МАСС ТЕЛА
199
двойных интегралов, можно доказать, что якобиан численно равен
определителю третьего порядка:
dx dxdx
du dt dw
, __ ду ду ду
ди dt dw
dz dz dz
du dt dw
Так, в случае цилиндрических координат имеем
f = psin0, z = z (p = u, Q = t,
cos 9 —psin6 0
sin в р cos 9 О
О 0 1
В случае сферических координат
л; = г sin cp cos 9, */ = rsinq>sin9, z = rcoscp (r = u,
sin ф cos 6 r cos ф cos 9 — r sin ф sin 9
/ = sin ф sin 9 r cos ф sin 9 r sin ф cos 9 = r2
I cos ф — r sin ф О
§ 14. Момент инерции и координаты центра масс тела
1. Момент инерции тела. Моменты инерции точки
М(х; у\ z) массы т относительно координатных осей Ox, Oy> Oz
(рис. 340) выражаются соответственно фор-
формулами
Моменты инерции тела выражаются
соответствующими интегралами. Так, на-
например, момент инерции тела относитель-
относительно оси Oz выражается интегралом 1гг =
— JSS^'+^M*. y,*)dxdydzy где у(х9
V Рис. 340,
у, z)—ллотность вещества.
Пример 1. Вычислить момент инерции прямого кругового цилиндра
высоты 2h и радиуса R относительно диаметра его среднего сечения, считая
плотность постоянной и равной у0.
Решение. Выберем систему координат следующим образом: направим
ось Oz вдоль оси цилиндра, а начало координат поместим в его центре сим-
симметрии (рис. 341).
Тогда задача сведется к вычислению момента инерции цилиндра относи-
относительно оси Ох: 1ХХ— \ \ \ (y2 + z2) yodxdydz. Переходя в этом интеграле к
v

200
КРАТНЫЕ ИНТЕГРАЛЫ
1ГЛ. XIV
цилиндрическим координатам, получим
2Я , R Г h -1 ,
(г2 + р2 sin2 Q)dz p dp > d9 =
2я f # Л 2jt
—«J =
2. Координаты центра масс тела. Аналогично тому,
что мы имели в § 8 гл. XII (т. I) для плоских фигур, коорди-
координаты центра масс тела выражаются форму-
формулами
y(x,ytz)dxdydz
УУ (х, у, г) dxdy dz
Рис. 34L
где
— плотность.
Пример 2. Определить координаты центра масс верхней половины шара
радиуса /? с центром в начале координат, считая плотность у0 постоянной.
Решение. Полушар ограничен поверхностями z = Y~R2 —х2—у2, г = 0.
Аппликата его центра масс определяется формулой
г^°dx dy dz
Переходя к сферическим координатам, получаем
2Я/ ТС/2 Г R  ч
То \ \ [ \ \ rcosфг2sinфdr \d<p\
9 _ о I о [о J I
Yo
J {J J
о ч Lo
dO , „/?* 1
2яХ*Т я
dQ
Очевидно, что в силу симметрии полушара хс = ус=^0.

§ 15J ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ, ЗАВИСЯЩИХ ОТ ПАРАМЕТРА 201
§ 15. Вычисление интеграловг зависящих от параметра
Рассмотрим интеграл, зависящий от параметра а:
(Такие интегралы мы рассматривали в § 10 гл. XI т. I.) Укажем
без доказательства^ что если функция / (лс, а) непрерывна по х
на отрезке [а, 6] и по а на отрезке [alt a2], то функция
является непрерывной функцией на отрезке [а?, а2]. Следовательно,
функцию / (а) можно интегрировать по а на отрезке [alf a2]:
/ (лс, a) dx ) d<x.
Выражение, стоящее справа, есть двукратный интеграл от функ-
функции f (дс, а) по прямоугольнику, расположенному в плоскости
Олса. Можно изменить порядок интегрирования в этом интеграл^:
Ь ,QLt
at\a
Эта формула показывает, что для интегрирования интеграла,
зависящего от параметра а, достаточно проинтегрировать* по па-
параметру а подынтегральное выражение. Эта формула также бы-
бывает полезна при вычислении определенных интегралов.
Пример. Вычислить интеграл \ dx (a > 0, Ь > 0).
о
Неопределенный интеграл от подынтегральной функции не берется в эле-
элементарных функциях. Для его вычисления рассмотрим другой интеграл, кото-
который можно легко вычислить:
+ 00
\
(X
Интегрируя это равенство в пределах от a = a до а~6, получим
Ь / + (*з \ Ь

202 КРАТНЫЕ ИНТЕГРАЛЫ 1ГЛ. XIV
Меняя порядок интегрирования в первом интеграле, перепишем это равенство
в следующем виде:
+ оо Г Ъ П
откуда, вычисляя внутренний интеграл, получаем
1 Ь
;=1п—•.
а
Упражнения к г лаве XIV
Вычислить интегралы *):
0ms. f 2. |||^L. Оте. tag.
2 *Уз 2я а
3. J J xydxdy. Отв. ~. 4. Г [
I х 0 а sin
3. J J xydxdy. Отв. ~. 4. Г [ rdtdQ. Отв. \па\
sin в
-Отв- f
ос/а 0 у-а
ft л/2
С С 3
7» \ \ р dQ dp. Отв. -r-z tib*.
i2 i 16
Определить пределы интегрирования для интеграла \ \ / (#, у) dx dyt где
область интегрирования ограничена линиями:
3 5
8. * = 2, х = 3, у = — 1, у = 5. Отв. \ [
2 -1
1 1-х2
-1 о
10. х2+у2 = а2. Отв. [ [ f(xty)dydx.
N L
*) Если интеграл написан так: \ \f(xiy)dxdy1 то, как было указано
м к
выше, мы будем считать, что первое интегрирование совершается по той пе«
ременной, дифференциал которой занимает первое место, т. е.
N L N /L \
J \
мк

УПРАЖНЕНИЯ К ГЛАВЕ XIV 203
2
I \+х*
11- У==Т+72* У==Л 0Ш' I I f(x,y)dydx.
-1 х*
а у+ 2а
12. # = 0, у=а, у=х, у=х—2а. Отв. $$/(*» y)dxdy.
0 у
Изменить порядок интегрирования в интегралах:
2 4 4 2
13. 5 5 /(*> y)dydx. Отв. Hf(x, y)dxdy.
13 3 1
14. J J /(*, y)dy^. Ome. J
0 jc» 0 i
a V2ax-y2 a a*
15. J ? / (*, y) rfA: dy. Ome. J J / (*,
0 0 0 д_КЯП^5
1
16. J J f(x,y)dydx. Отв. J J f(Xiy)dxdy.
-io о -vrrp
11-^ 0 VT^x* 1 1 —л?
17. J J f(Xiy)dxdy. Отв. [ J /(*,*)<tyd*+$ $ f(x,y)dydx.
о -VT^p -^io oo
Вычислить следующие интегралы путем перехода к полярным координатам:
18. Г С Va*—x*—y*dydx. Отв. J J yV—
а Уа2-^2 я/2 а
19,
r-~
i. С f (x2+f/2)^^. Отв. Г Ср3ф^9=^-.
00 + QO я/2 + со
С С e-^+J^dyd*. Отв. J J rp2prfprf9=i.
я/2 2fl cos 0
У2ДЛГА: я/2 2fl co
21. \ f dy(te. Отв. f f
Преобразовать двойные интегралы, введя новые переменные и и у, свя-
связанные, с # и # формулами # = w—uv, y = uv:
J в_
е fix 1 +j3 1 - v
22. \ [ f (jc, I/) dy dx. Отв. \ \ f(u—uv, uv) и du dv.
0 ax a 0
1+06

204 КРАТНЫЕ ИНТЕГРАЛЫ [ГЛ. XIV
с Ъ
23. J lf(x,y)dydx.
о о
о о
b с Ъ_
Ь+с 1 - v b v
Отв. \ \ f (и—uv, uv)ududv-\- \ \ f(u—uv,
О о __ь_ о
Ь+с
Вычисление площадей посредством
двойного интеграла
24. Вычислить площадь фигуры, ограниченной параболой у2 = 2х и пря-
прямой у = х. Отв. 2/3.
25. Вычислить площадь фигуры, ограниченной линиями у2 = 4ах, *-+*/==
= 3а, # = 0. Отв. 10а2/3.
26. Вычислить площадь фигуры, ограниченной линиями x1I2-}-y1t2 = a1J2,
j = a. Отв. я2/3.
27. Вычислить площадь фигуры, ограниченной линиями # = sinx, y = cosxt
х = 0. Отв. У—\.
28. Вычислить площадь петли кривой p = asin29. Отв. па2/8.
29. Вычислить всю площадь, ограниченную лемнискатой p2 = c2cos2cp.
Отв. а2.
30. Вычислить шющадь петли кривой f^-a+p") =—y*
Указание. Перейти к новым переменным ^=pacos0 и y~pbsin9.
Отв. a2b2/c2.
Вычисление объемов
Вычислить объемы тел, ограниченных поверхностямиз
х у z пЬс
CL Ъ С 6
32. 2 = 0, х2+у2=\, *-j-i/+z = 3. Отв. Зя.
33. (*—1J+(г/—1J=1, ху = г, 2 = 0. Отв. я,
35. г/=д:2, a:=z/2, 2 = 0, 2 = 12+^/—х2. Отв. 549/144.
36. Вычислить объем тела, ограниченного координатными плоскостями,
плоскостью 2х+3у—12 = 0 и цилиндром z = y2/2. -Отв. 16.
37. Вычислить объем тела, ограниченного круговым цилиндром радиуса а,
ось которого совпадает с осью Oz, плоскостями координат и плоскостью
—I—=?1. Отв.
38. Вычислить объем тела, ограниченного цилиндрами х2-\-у2 — а29 х2-\-г2—сР.
Отв. -q-я3.
Вычислить объемы тел, ограниченных поверхностями:

упражнения К главе xiv 205
42. p2 = a2cos29, *2+#2 + z2 = a2, г = 0. (Вычислить объем, внутренний
по отношению к цилиндру.) Отв. тг-а3(Зя+20
у
Вычисление площади поверхности
43. Вычислить площадь той части поверхности конуса x2-\-y2 = z2, которая
высекается цилиндром х2+у2 = 2ах. Отв. 2яа2 ]/~.
44. Вычислить площадь той части плоскости я+#+г = 2а, которая лежит
в первом октанте1 и ограничена цилиндром х2-\-у2=а2. Отв. -т-^З.
45. Вычислить площадь поверхности сферического сегмента (меньшего),
если радиус сферы а, а радиус основания сегмента Ь. Отв. 2п(аг—и^а2—б2).
46. Найти площадь той части поверхности сферы *2+#2+z2 = a2, которая
Х и
вырезана поверхностью цилиндра -а+гг^1 (<* > Ь). Отв. 4яа2 —
гГа2 ?2
— 8а2 arcsin -^ .
а
47. Найти площадь поверхности тела, являющегося общей частью двуя
цилиндров х2+у2 = а2, у2+г2 = а2. Отв. 16а2.
48. Вычислить площадь той части поверхности цилиндра х2+у2 = 2ах,
которая содержится между плоскостью г=0и конусом x2-{-y2 = z2. Отв. 8аа.
49. Вычислить площадь той части поверхности цилиндра х2-\-у2 = сР, ко-
которая содержится между плоскостью г = тх и плоскостью z=0. Отв. 2та2.
50. Вычислить площадь той части поверхности параболоида у2+г%=2ах,
которая содержится между параболическим цилиндром у2=ах и плоскостью
*=а. Отв. i-яа2
о
Вычисление массы, координат центра масс,
момента инерции плоских фигур
(Всюду в задачах 51—62 и 64 считаем поверхностную плотность постоян-
постоянной и равной единице.)
51. Определить массу пластинки, имеющей форму круга с радиусом а,
если плотность в любой точке Р обратно пропорциональна расстоянию точки Р
от оси цилиндра (множитель пропорциональности равняется /(). Отв. 2паК.
52. Вычислить координаты центра масс равностороннего треугольника,
принимая его_высоту за ось Ох, а вершину треугольника за начало координат.
Отв. х=аУ^3/3, у=0.
53. Найти координаты центра масс кругового сектора радиуса а, прини-
принимая биссектрису его угла за ось Ох. Угол раствора сектора «равен 2а.
л 2а sin а л
Отв. хс=—^—, ус = 0.
54. Найти координаты центра масс верхней половины круга #2+#2=а2.
Отв. хс = 0у ус = 4а/3я.
55. Найти координаты центра масс площади одной арки циклоиды
x = a(t—sin 0, y = a(\—co$t). Отв. дсс = ая, ус = 5а/6.
56. Найти координаты центра масс площади, ограниченной петлей кривой
2 = а2cos29. Отв. хс =
57. Найти координаты центра масс площади кардиоиды p=a(l-{-cos9).
Отв. дгс 5/6 0

206 КРАТНЫЕ ИНТЕГРАЛЫ [ГЛ. XIV
58. Вычислить момент инерции площади прямоугольника, ограниченного
прямыми * = 0, х = а, # = 0, у = Ь, относительно начала координат. Отв.
аЪ (* + Ь2)
3
х2 и2
59. Вычислить момент инерции эллипса —+4г2-=1- а) относительно
оси Оу; б) относительно начала координат. Отв. a) na3b/4; б) nab (a2+62)/4.
60. Вычислить момент инерции площади круга р = 2а cos 9 относительно
полюса. Отв. Зяа4/2.
61. Вычислить момент инерции площади кардиоиды р = яA—cos 6) отно-
относительно полюса. Отв. 35яа4/16.
62. Вычислить момент инерции площади круга (я—яJ+(#—bJ = 2az
относительно оси Оу. Отв. Зяа4.
63. Плотность в любой точке квадратной пластинки со стороной а про-
пропорциональна расстоянию этой точки от одной из вершин квадрата. Вычислить
момент инерции пластинки относительно стороны, проходящей через эту вер-
вершину. Отв. 7^&a5[7j/" + 31n(]/"i2+1}]> где &—множитель пропорциональ-
пропорциональности.
64. Вычислить момент инерции площади фигуры, ограниченной параболой
у2 = ах и прямой х~а, относительно прямой г/=— а. Отв. 8а4/5.
Тройные интегралы
65. Вычислить \ \ \ •:—;—%—гттч $ если область интегрирования огра-
JJJ (х+У+г+\K' 12 5
ничена координатными плоскостями и плоскостью x-{-y + z=\. Отв. —^ т^.
а ( хГ д -1 \
С I ГI С II aQ
66. Вычислить \ 1 \ I \ хуг dz \dy I dx. Отв. -j^.
о ч Lo J J
67. Вычислить объем тела, ограниченного сферой #2 + */2 + z2 = 4 и поверх-
19
ностью параболоида x2-\-y2 = 3z. Отв. —я.
6
68*). Вычислить координаты центра масс и моменты инерции пирамиды, огра-
ограниченной плоскостями *=0, у = 0, 2 = 0, — -|—^--}-—= 1. Отв. хс = а/4, ус=з
= 6/4, гс = с/4; Ix=a*bc/60, Iy = b*ac/60t Iz = c3ab/60, /o=-^ (a2 + b2+c2).
69. Вычислить момент инерции кругового прямого конуса относительно
его оси. Отв. удя/гг4, где h—высота, г—радиус основания конуса.
70. Вычислить объем тела, ограниченного поверхностью с уравнением
(х2+у2+г2J = а*х. Отв. яа3/3.
71. Вычислить момент инерции круглого конуса относительно диаметра
основания. Отв. ^
72. Вычислить координаты центра масс тела, содержащегося между сферой
радиуса а и конической поверхностью с углом при вершине 2а, если вершина
о
конуса, совпадает с центром сферы. Отв. хс = 0, ус = 0, zc=-?-a(l+cosa)
(ось конуса принята за ось 02, вершина помещена в начале координат).
*) В задачах 68—69, 71—73 считаем плотность постоянной и равной еди«
нице.

УПРАЖНЕНИЯ К ГЛАВЕ XIV 207
73. Вычислить координаты центра масс тела, ограниченного сферой ра-
радиуса а и двумя плоскостями, проходящими через центр сферы и образую-
образующими угол 60Q. Отв. р?=у?а, 9 = 0, ф=-гг (линия пересечения плоскостей
принята за ось Oz} центр сферы—за начало координат; р, 0, ф—сферические
координаты).
+ 00
1 2 Г* 2
74. Пользуясь равенством • -_ = \ е~а xda(a >0), вычислить
Ух Уп 0
Г* cos х dx С sin х dx л п /~~гГ -, f~zC
интегралы \ —^=г~ и \ —Т=г-. Отв. Л/ -к-\ Л/ тт •
J У х J Ух Г 2 Г 2

ГЛАВА XV
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ
ПО ПОВЕРХНОСТИ
§ 1. Криволинейный интеграл
Пусть точка Р(х\ у) движется вдоль некоторой плоской ли-
линии L от точки М к точке N. К точке Р приложена сила /% ко-
которая меняется по величине и
направлению* при перемещений
точки Р, т. е. представляет собой
некоторую функцию координат
точки Р:
Вычислим работу А силы
F при перемещении точки~~Р из
положения М в положение N
(рис. 342). Для этого разобьем
*- кривую MN на п произвольных
* частей точками М=М0У Мь М2,...
..., Мп =N в направлении от
М к N и обозначим через Ди-
Дивектор ~MiMi+1. Величину силы F в точке М( обозначим через F(.
Тогда скалярное произведение FfiSi можно рассматривать как
приближенное выражение работы силы F вдоль дуги MtMi+1:
Пусть
x, y)J9
где Х(х, у) и Y(x9 у)—проекции вектора F на. оси Ох и Оу.
Обозначив через Axt и Hyt приращения координат X; и у( при
переходе от точки Mi к точке Af/+1, получаем

§11 КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 209
Следовательно,
Приближенное значение работы А силы F на всей кривой MN
будет
А ж Д F, Д^ ^ Д [X (л:,., I/,) А*, + Y (xl9 yd Ау(]. A)
Не делая точных формулировок, укажем пока, что если су-
существует предел выражения, стоящего в правой части равенства
при AS;—*0 (при этом, очевидно, Дд:,- —>0 и Ду,—>-0), то этот
предел выражает работу силы F по кривой L от точки М до
точки N:
А « Urn 2 [Х(*„ у,)Д*1 + У(*„ j^Ajf,]. B)
Справа стоящий предел*) называют криволинейным интегралом
от X (х, у) и F(x, у) по кривой L и обозначают так:
Л=5Х(*. ^)dx+F(x, t/)^ C)
ИЛИ
(N)
Л= J X(*f у)^ + У(^, y)dy. C')
Пределы сумм вида B) часто встречаются в математике и ме-
механике, при этом Х(х, у) и Y(x, у) рассматриваются как функ-
функции двух переменных в некоторой области D.
Буквы М и JV, стоящие вместо пределов интегрирования,
заключены в скобки в знак того, что это не числа, а обозначе-
обозначения концов линии, по которой берется криволинейный интеграл.
Направление по кривой L от точки М к точке N называется
направлением интегрирования.
Если кривая L пространственная, то криволинейный интеграл
от трех функций Х(х, у, г), У (х, уу z), Z(x, у, г) определяется
аналогично:
х, у, z)dx+Y(x, у, z)dy+Z(x, у,
)Ь+2( ykt
0 Л=
*) Здесь предел интегральной суммы понимается в том же смысле, как
wo было в случае определенного интеграла, см. § 2 гл. XI т. I.

210 КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ [ГЛ. XV
Буква L, стоящая под знаком интеграла, указывает на то, что
интегрирование совершается вдоль кривой L.
Отметим два свойства криволинейного интеграла.
Свойство 1. Криволинейный интеграл.определяется подын-
подынтегральным выражением, формой кривой интегрирования и ука-
указанием направления интегрирования.
При изменении направления интегрирования криволинейный
интеграл меняет знак, так как при этом вектор As, а следова-
следовательно, и его проекции А* и А у меняют знаки.
Свойство 2. Разобьем кривую L точкой К на части Ьг и
L2 так, что MN = MK + KN (рис. 343). Тогда из формулы A)
непосредственно следует
(АО (К) (N)
5 Xdx + Ydy= J Xdx + Ydy+ J Xdx + Ydy.
(Af) (M) (K)
Это соотношение справедливо для любого числа слагаемых.
Отметим еще, что определение криволинейного интеграла
остается в силе и в-том случае, когда кривая
L замкнута.
В этом случае начальная и конечная точ-
точки на кривой совпадают. Поэтому в случае
замкнутой кривой мы не можем писать
(АО
^ Xdx + Y dy, а только ^ Xdx-\-Y dy> ука-
Рис. 343, <М) L
зывая при этом обязательно направление
обхода по замкнутой кривой L. Для обозначения криволи-
криволинейного интеграла по замкнутому контуру L очень ча-
часто употребляется также символ
§¦
Xdx + Ydy.
'L
Замечание. Мы пришли к понятию криволинейного интег-
интеграла, рассматривая задачу о работе силы F на криволинейном
пути L.
В этом случае во всех точках кривой L была задана сила F
как векторная функция F от координат точки приложения (х; у);
проекции переменного вектора F на оси координат равны скаляр-
скалярным (т. е. числовым) функциям Х(х, у) и Y(x> у). Поэтому кри-
криволинейный интеграл вида ^Xdx + Ydy можно рассматривать
как интеграл от векторной функции F, заданной проек-
проекциями X и Y. Интеграл от векторной функции F го кривой L
обозначается символом

§2]
ВЫЧИСЛЕНИЕ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА
211
Если вектор F определяется своими проекциями X, F, Z, то
этот интеграл равен криволинейному интегралу \^ Xdx + Y dy +
L
+ Zdz. В частности, если вектор F лежит на плоскости Оху, то инте-
интеграл от этого вектора равен \ X dx + Ydy.
L
В тех случаях, когда криволинейный интеграл от векторной
функции F берется по замкнутой кривой L, этот криволинейный
интеграл называют также циркуляцией вектора F по замкнутому
контуру L.
§ 2. Вычисление криволинейного интеграла
В этом параграфе мы уточним понятие предела суммы A) § 1
и в связи с этим уточним понятие криволинейного интеграла и
укажем способ его вычисления,
Пусть кривая L задана уравнениями в. параметрической форме
Рассмотрим дугу MN этой кривой (рцс. 344). Пусть точкам М
и N соответствуют значения параметра аир. Разделим дугу MN
на части As^ точками М±(хг\ уг),
Mt(xt;y%), ...,Mn(xn\ уп), при этом
положим л:1- = ф(/{), #f = i|)(f/).
Рассмотрим криволинейный ин-
интеграл
X(*f y)dx + Y(x9 y)dy9 A)
определенный в предыдущем пара-
графе. Приведем без доказатель-
доказательства теорему существова-
существования криволинейного интеграла. Если функции ф(г) и
<ф (t) непрерывны и имеют непрерывные производные q>' (t) и
ij)'(O, а также непрерывны функции Х[ср(^), t|)(/)] и К[ф(/),
^(OJ как функции t на отрезке [а, Р], то существуют пре-
пределы
lim
О I
lim
0 i
^В, B)
где Jct и ~у{—координаты некоторой точки, лежащей на дуге Ast.
Эти пределы не зависят от способа деления дуги L на частич-
частичные дуги^ А^ при условии, что Asj—>0, не зависят от выбора
точки М( (xh yt) на дуге Ast; они называются криволинейными

212 КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ 1ГЛ. XV
интегралами и обозначаются так:
А - J Х(х, y)?tef B= J Г(
Замечание. Из теоремы следует, что к тому же пределу —
криволинейному интегралу—стремятся суммы, определенные в пре-
предыдущем параграфе, где точки Mt(xh yt) являются концами
дуги Asj, а система разбиения дуги L на части Ast любая.
Сформулированная теорема дает возможность получить способ
вычисления криволинейного интеграла.
Итак, по определению имеем
J X{x, y)dx = lim S Х(д^ yt)bxl9 C)
(М) Ax^Ofal
где
Преобразуем последнюю разнбсть по формуле Лагранжа:
где т?—некоторое значение_^, заключенное между значениями timmt
и tt. Т^к как точку xh yt на дуге Ast- можно выбирать произ-
произвольно, то выберем ее так, чтобы ее координаты соответствовали
значению параметра т?:
Подставляя найденные значения */f t/e- и Дл:^ в формулу C), по-
получим
I X(x, y)dx= lim S
(М) Л^.-^Ot = 1
Справа стоит предел интегральной суммы для непрерывной функ-
функции одной переменной X[<p(t), ф(О]ф'A) на отрезке [a, |JJ.
Следовательно, этот предел равняется определенному интегралу
от этой функции;
J X(x, y)dx=[X[<p{t), ¦@]ф'@Л.
(М) а
Аналогично получается формула
(ЛГ) 0
J Y(x, y)dy^lY[<f(t), ¦ (*)]¦'(ОЛ.
(Л1) а

§.2] ВЫЧИСЛЕНИЕ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА
Складывая почленно эти равенства, получим
213
Х(х% y)dx+Y(x9
(М)
{X [Ф (о, * @] ф' @+у [ф @. Ч> @] ¦' @) л.
Это и есть искомая формула для вычисления криволинейного
интеграла.
Аналогичным образом вычисляется кри- „
волинейный интеграл *
Xdx + Ydy + Zdz
по пространственной
уравнениями х = <р(/),
кривой,
(t)
заданной
= %(t).
Пример 1. Вычислить криволинейный ин-
интеграл от тройки функций я3; Згу2; —4с2у (или,
что то же, от векторной функции xzi-\-3zy2j—х2ук)
вдоль отрезка прямой, идущего от точки М C; 2;
1) до точки N @; 0; 0) (рис. 345).
Решение. Для того чтобы найти параметри-
параметрические уравнения линии MN, вдоль которой надле-
Рис. 345,
Рис. 346,
зкит интегрировать, напишем уравнение прямой, проходящей че^ез две точ-
точки:
з~~2~- 1 5
обозначив все эти отношения одной буквой t, получим уравнения прямой
в параметрическом виде:
При этом началу отрезка MN^ соответствует, очевидно, значение параметра
* = 1, а концу отрезка—значение * = 0. Производные от х, уу г по параметру t
(которые понадобятся при вычислении криволинейного интеграла) находятся
легко;
*/ = 3, у/= 2, 2t = \.

214 КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ |ГЛ. XV
Теперь искомый криволинейный интеграл можно вычислить с помощью
формулы D):
(N) о о
J x*d*+3zy*dy —x2ydz = J [C03-3 + 3*-B02-2 — CQ2.2M] dt = J Шъdt=*
Ш) l l
87
Пример 2. Вычислить криволинейный интеграл от пары функций Ъх*д%
10л#2 вдоль плоской кривой у = х3 от точки М A; 1) до точки W B; 8) (рис. 346).
Решение, Для вычисления искомого интеграла
6x2ydx+\0xy*dg
(М)
надо иметь параметрические уравнения данной кривой. Однако заданное явно
уравнение кривой у=х* является частным случаем параметрического: здесь
параметром служит абсцисса х точки кривой, и параметрические уравнения
кривой таковы:
х=х, у=х3.
Параметр х меняется от #i = l до х2=2. Производные по параметру легко
вычислить:
Следовательно,
2 2
е= J Fа:2а:3.1 + 1Ол:^.За:2) ^л: = J Fл:5+30л:9) ^дг = [л:6+Зл:1»]? = 3132.
1 1
Укажем теперь на некоторые приложения криволинейного ин-
интеграла.
1. Выражение площади области, ограниченной
кривой, через криволинейный интеграл. Пусть
в плоскости Оху дана такая ограниченная контуром L область D,
что всякая прямая, параллельная той или иной из координатных
осей и проходящая через внутреннюю точку области, пересекает
границу L области не более чем в двух точках (т. е. область D
правильная) (рис. 347).
Предположим, что на ось Ох область D проектируется в отре-
отрезок [а, 6], причем снизу она ограничивается кривой (/х):
а сверху—кривой (/2):
(Ух (*

§2]
ВЫЧИСЛЕНИЕ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА
215
Тогда площадь области D равна
ь ь
S=ly2(x)dx—\y1(x)dx.
Но первый интеграл есть криволинейный интеграл по кривой
12(MPN), так как у—у2{^) есть, уравнение этой кривой; следо-
следовательно,
ь
y2(x)dx=^ \ ydx.
MPN
Второй интеграл есть криволинейный интеграл по кривой
li(MQN), т. е.
ь
lyt(x)dx=* S ydx.
a MQN
На основании свойства 1 криволинейного интеграла имеем
Следовательно,
MPN
; = — ) ydx.
NPM
E)
NPM MQN L
При этом кривая L обходится в направлении против часовой
стрелки.
м
а
Рис. 347,
Если часть границы L составляет отрезок М±М, параллель-
(М)
ный оси О у, то ^ ydx = 0, и равенство E) остается справедли-
справедливо
вым и в этом случае (рис. 348).
Аналогично можно показать, что
F)

КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ 1ГЛ. XV
Складывая почленно равенства E) и F) и деля на 2, полу-
получим еще одну формулу для вычисления площади S:
dy—ydx. G)
Пример 3. Вычислить площадь эллипса х~а cos t, y = bsint.
Решение. По формуле G) нзходим:
1 Г
S = -^ \ [a cos t ф cos t) —b sin t (— a sin /)] dt = nab»
о
Отметим, что формула G), а также формулы E) и F) спра-
справедливы и для площадей, границы которых пересекаются линиями,
Рис. 349.
Рис. 350.
параллельными координатным осям, более чем в двух точках
(рис. 349). Для доказательства этого разобьем данную область
(рис. 349) с помощью линии /• на две правильные области. Для
каждой из них справедлива формула G). Складывая левые и пра-
правые части, получим слева площадь данной области, справа — кри-
криволинейный интеграл F коэффициентом 1/2)> взятый по всей гра-
границе, так как криволинейный интеграл по линии раздела /*
берется дважды— в прямом и обратном направлениях и, следо-
следовательно, равен нулю.
2. Задача о вычислении работы переменной
силы F на некотором криволинейном пути L. Как
было показано в начале § 1, работа, совершенная силой F=
= Х(х, у, z)i + Y(x, у9 z)J-{-Z(x, уу z)k вдоль линии L = M'N,
равна криволинейному интегралу:
(N)
xt у, z)dz.
А= S X(x,y9 z)d
(М)
Рассмотрим пример, показывающий, как производится вычис-
вычисление работы силы в конкретных случаях.

§ 31 ФОРМУЛА ГРИНА 217
Пример 4. Определить работу А силы тяжести F при перемещении
массы т из точки Мх (аь blt cx) в точку М2 (а2, &2> с2) по произвольному
пути L (рис. 350).
Решение. Проекции силы тяжести F на оси координат равны
Следовательно, искомая работа
(М2) сг
Л== \
А)
Следовательно, в этом случае криволинейный интеграл не зависит от пути
интегрирования, а зависит только от начальной и конечной точек. Точнее,
работа 1Силы тяжести зависит только от разности высот конечной и начальной
точек пути.
§ 3. Формула Грина
Установим связь между двойным интегралом по некоторой
плоской области D и криволинейным интегралом по границе L
этой области.
Пусть в плоскости Oxfy дана ограниченная замкнутым конту-
контуром L область D, правильная как в направлении оси Ок9 так и
в направлении оси Оу. Нусть эта область ограничена снизу кри-
кривой у =#х(х), а сверху кривой у = у2(лг), ух(х)^yz{x)(a^x^b)
(рис. 347).
В совокупности обе эти кривые составляют замкнутый контур L.
Пусть в области D заданы непрерывные функции X (х, у) и
Y(x, У), имеющие непрерывные частные производные. Рассмотрим
интеграл
Представляя его в виде двукратного, получим:
Ъ
l A)
а
Заметим, что интеграл
ъ
численно равен криволинейному интегралу
X (х, у) dx,
MPN*

218 КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ [ГЛ. XV
взятому по кривой MPN, уравнения которой в параметрической
форме суть
х = х, у=у2(х),
где я —параметр.
Таким образом,
ь
[X(x,y2{x))dx = \ X(x,y)dx. B)
a MPN
Аналогично интеграл
ь
а
численно равен криволинейному интегралу по дуге MQNi
ъ
lX(x,yi(x))dx= $ X(x,y)dx. C)
Подставляя выражения B) и C) в формулу A), получим:
W™dxdy= f X(x,y)dx- f X(x,y)dx. D)
D MPN MQN
Ho
J X(x,y)dx = - J X(x,y)dx
MQN NQM
(cm. § 1, свойство 1). Следовательно, формулу D) можно напи-
написать так:
H%dxdy^ Г X(x,y)dx+ J X(x,y)dx.
D MPN NQM
Но сумма криволинейных интегралов, стоящих в правой части,
равна криволинейному интегралу, взятому по всей замкнутой
кривой L в направлении по часовой стрелке. Следовательно,
последнее равенство можно привести к такому виду:
^§ E)
Если часть границы составляет отрезок /3, параллельный оси
Оу, то
и
и равенство E) остается справедливым и в этом случае.
Аналогично найдем
^ F)
ь

§4J УСЛОВИЯ НЕЗАВИСИМОСТИ 219
Вычитая E) из F), получим
D L
Если обход контура L совершается против часовой стрелки, то *)
С С ! dY дХ \ с
ЖаГ ду) х У-f х У-
Это и есть формула Грина, названная так по имени английского
физика и математика Д. Грина A793—1841)**).
Мы предполагали, что область D правильная. Но, как и
в задаче о площади (см. § 2), можно показать, что эта формула
справедлива для любой области, которую можно разбить на пра-
правильные области.
§ 4. Условия независимости криволинейного интеграла
от пути интегрирования
Рассмотрим криволинейный интеграл
(N)
J Xdx + Xdy,
(М)
взятый по некоторой плоской кривой L, соединяющей точки М и N.
Будем предполагать, что функции X (я, у) и
У (х, у) имеют непрерывные частные произ-
производные в рассматриваемой области D. Вы-
Выясним, при каких условиях написанный ^^s^^00 пщ
криволинейный интеграл не зависит от фор-
формы кривой L, а зависит только от поло- Рис, 351.
жения начальной и конечной точек М и N.
Рассмотрим две произвольные кривые MPN и MQN, лежащие
в рассматриваемой области D и соединяющие точки М и N
(рис. 351). Пусть
J Xdx + Ydy = J Xdx + Ydy, A)
MPN MQN
т. е.
5 Xdx + Ydy- J
MPN MQN
*) Если в криволинейном интеграле по замкнутому контуру не указано
направление обхода контура, то предполагается, что этот обход производится
против часовой стрелки. Если же обход производится по часовой стрелке, то
это должно быть специально оговорено.
**) Эта формула является частным случаем более общей формулы, откры-
открытой русским математиком М, В. Остроградским.

220 КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ [ГЛ. XV
Тогда на оснбвании свойств 1 и 2 криволинейных интегралов
(§ 1) имеем
$" Xdx + Ydy+ J Xdx + Ydy=0,
MPN NQM
т. е. криволинейный интеграл по замкнутому контуру L
j)Xdx + Ydy = 0. B)
L
В последней формуле криволинейный интеграл взят по замкну-
замкнутому контуру L, составленному из кривых MPN и NQM. Этот
контур L можно, очевидно, считать произвольным.
Таким образом, из условия, что для любых двух точек М и N
криволинейный интеграл не зависит от формы соединяющей их
кривой, а зависит только от положения этих точек, следует, что
криволинейный интеграл по любому замкнутому
контуру равен нулю.
Справедливо и обратное заключение: если криволинейный
интеграл по любому замкнутому контуру равен нулю, то этот
криволинейный интеграл не зависит от формы кривой, соединяю-
соединяющей две любые точки, а зависит только от положений
этих точек, Действительно, из равенства B) следует равен-
равенство A).
В примере 4 § 2 криволинейный интеграл не зависит от пути
интегрирования, в примере 3 криволинейный интеграл зависит
от пути интегрирования, так как в этом примере интеграл по
замкнутому контуру не равняется нулю, а дает площадь, огра-
ограниченную рассматриваемым контуром; в примерах 1 и 2 криво-
криволинейные интегралы также зависят от пути интегрирования.
Естественно возникает вопрос: каким условиям должны удов-
удовлетворять функции Х(х, у) и Y(x, у) для того, чтобы криволи-
криволинейный интеграл ^Xdx + Ydy по любому замкнутому контуру
был равен нулю. Ответ на этот вопрос дает следующая теорема:
Теорема. Пусть во всех точках некоторой области D функ-
функции Х(х, у), Y(xy у) вместе со своими частными производными
—д У) и —дх непрерывны. Тогда, для того чтобы криво-
криволинейный интеграл по любому замкнутому контуру L, лежа-
лежащему в области D, был равен нулю, т. е. чтобы
:0, B')
необходимо и достаточно выполнение равенства
ду ~~ дх \ '
во всех течках области D.

§ 41 УСЛОВИЯ НЕЗАВИСИМОСТИ 221
Доказательство. Рассмотрим произвольный замкнутый
контур L в области D и для него напишем формулу Грина:
L
Если выполняется условие C), то двойной интеграл, стоящий
слева, тождественно равен нулю и, следовательно,
Таким образом, достаточность условия C) доказана.
Докажем теперь необходимость этого условия, т. е.
докажем, что если равенство B) выполняется для любой замкну-
замкнутой кривой L в области Z), та в каждой точке этой области
выполняется и условие C).
Допустим, напротив, что равенство B) выполняется, т. е.
(pXdx + Ydy^O,
L
а условие C) не выполняется, т. е.
дх ду
хотя бы в одной точке. Пусть, например, в некоторой точке
Р(х0; у0) имеем неравенство
дх ду ^
Так как в левой части неравенства стоит непрерывная функ-
функция, то она будет положительна и больше некоторого числа
6>0 во всех точках некоторой достаточно малой области D',
содержащей точку Р(х0; у0). Возьмем двойной интеграл по этой
области от разности -^ g—. Он будет иметь положительное
значение. Действительно,
Но по формуле Грина левая часть последнего неравенства
равна криволинейному интегралу по границе U области D',
который равен нулю. Следовательно, последнее неравенство
противоречит условию B) и, значит, предположение, что g у-
отлично от нуля хотя бы в одной точке, неверно. Отсюда

222 КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ [ГЛ. XV
вытекает, что
дх ду ~U
во всех точках данной области D.
Таким образом, теорема полностью доказана.
В § 9 гл. XIII было доказано, что выполнение условия
дУ(х,у) ^дХ(х,у)
дх ду
равносильно тому, что выражение Xdx + Ydy есть полный
дифференциал некоторой функции и(х> у), т. е.
= du (х, у),
причем
Х(х,у) = ж, Y(x,y) = Ty
Но в этом случае вектор
есть градиент функции и(х, у)\ функция и (л:, у), градиент которой
равен вектору Xi + YJ, называется потенциалом этого вектора.
Докажем, что в этом случае криволинейный интеграл
(N)
/== ^ Xdx + Ydy no любой кривой L, соединяющей точки М и N,
Ш)
равняется разности значений функции* и в этих точках:
(N) (N)
J Xdx + Ydy= J du(x,y) = u(N)-u(M).
(М) (М)
Доказательство. Если Xdx + Y dy является полным диф-
дифференциалом функции и(х, у), то Х = ~, Y = -jf и криволиней-
криволинейный интеграл примет вид
(M)
Для вычисления этого интеграла напишем параметрические урав-
уравнения кривой L, соединяющей точки М и N:
Будем считать, что значению параметра t = 't0 соответствует
точка М, а значению t — T — точка N. Тогда криволинейный

§ 41 УСЛОВИЯ НЕЗАВИСИМОСТИ 223
интеграл, сведется к следующему определенному интегралу:
т
ди dx ,ди d
Выражение, стоящее в скобках, есть функция от if являющаяся
полной производной от функции и[ср(О> *Ф@] по '• Поэтому
Как мы видим, криволинейный интеграл от полного
дифференциала не зависит от формы кривой, по
которой производится интегрирование.
Аналогичное утверждение имеет место и для криволинейного
интеграла по пространственной кривой (см. ниже § 7).
Замечание. Иногда приходится рассматривать криволиней-
криволинейные интегралы по длине дуги L от некоторой функции X (х, у):
S X (ху у) ds = hm S X (*/f y,) As/f D)
где ds — дифференциал дуги. Вычисляются такие интегралы ана-
аналогично вычислению рассмотренных выше криволинейных инте-
интегралов. Пусть кривая L задана параметрическими уравнениями
где ф@> Ф@» ф'@> Ф' @"" непрерывные функции от ?.
Пусть а и Р — значения параметра ^, соответствующие началу
и концу дуги L.
Так как
то мы получаем формулу для вычисления интеграла D):
J
Можно рассматривать криволинейный интеграл по дуге простран-
пространственной кривой x = <p(t)> y = ty(t)y z = x(ty.
y X@1

224 КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ [ГЛ. XV
С помощью криволинейных интегралов по дуге определяются,
например, координаты центра масс линий.
Рассуждая так же, как в§8 гл. XII (т. I), получим формулу
для вычисления координат центра масс пространственной
кривой:
\xds [yds $zds
Хс ~ ~~л э Ус== ~"р > zc=z ~7 * У )
\ds ^ds \ds
L L L
Пример. Найти координаты центра масс одного витка винтовой линии
если ее линейная плотность постоянна.
Решение. Применяя формулу E), найдем
x _ 0
2я 2я
С a cos t У a2 sin21+a2 cos2 t + b2 dt \a cos tY^
0
x
Va2 sin2 t+a2 cos2 t + b2 dt С Ya*+b2dt
о о
Аналогично #c = 0,
2Л
f ft/ )/*a2
о
Z°~~ 2яVra2^-ft2 ~" 2л'2 ~Л '
Итак, координаты центра масс одного витка винтовой линии равны
*<? = 0, ус = 0, zc — nb.
§ 5. Поверхностный интеграл
Пусть в прямоугольной системе координат Охуг задана неко-
некоторая область V. Пусть в области V задана поверхность а, огра-
ограниченная некоторой пространственной линией %.
Относительно поверхности а мы будем предполагать, что в каж-
каждой ее точке Р определяется положительное направление нормали
единичным вектором п (Р), направляющие косинусы которого явля-
являются непрерывными функциями координат точек поверхности.
Пусть в каждой точке поверхности определен вектор
F=X(x, у, z)i + Y(x9 у, z)J+Z(x, у, г)к,
где X, У, Z—непрерывные функции координат.
Разобьем поверхность каким-либо способом на элементарные
площадки АсГ|. На каждой площадке возьмем произвольную точку

§ 5. ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ
225
Р( и рассмотрим сумму
A)
где F(Pi)—значение вектора F в точке Рг площадки Acr,, n (PJ) —
единичный вектор нормали в этой точке, Fn—скалярное произве-
произведение этих векторов.
Предел суммы A), распространенный на все площадки аа{ при
стремлении к нулю диаметров всех таких площадок, называется
поверхностным интегралом и обозначается символом
Таким образом, по определению *)
lim
diam Да
= \\ Fnda.
G
Каждое слагаемое суммы A)
icos(nh
B)
C)
может быть истолкоБ-ано механически следующим образом: этЬ
произведение равно объему цилиндрах основанием Аа( и высо-
высотой F;cos(ii/, Ft). Если вектор F есть
скорость жидкости, протекающей че-
через поверхность а, то произведение C)
равно количеству жидкости, протекаю-
протекающей через площадку Aaf. за единицу
времени в направлении вектора щ
(рис. 352).
Выражение ^ $ Fn do представляет
а
собой общее количество жидкости, про-
протекающей в единицу времени через по-
поверхность а в положительном направ-
направлении, если под вектором F подразуме-
подразумевать вектор скорости течения Жидкости
в данной точке. Поэтому поверхностный интеграл B) называется
потоком векторного поля F через поверхность а.
Рис. 352.
*) Если поверхность а такова, что в каждой ее точке существует каса-
касательная плоскость, которая непрерывно меняется с перемещением точки Р
по поверхности, и если векторная функция F непрерывна на этой поверхности,
то этот предел существует (эту теорему существования интеграла по поверх-
поверхности мы принимаем без доказательства).
Н. С. Пискунов, т. 2

225
КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ 1ГЛ. XV
Из определения поверхностного интеграла следует, что если
поверхность а разбить на части ои аа, ••., ок, то
= \ J Fnda + J $
... 4- $$ fiidcr.
Выразим единичный вектор п через его проекции на оси коор-
координат: n = cos(n, x)i+cos(n, y)j+cos(n, z)k*).
Подставляя в интеграл B) выражения векторов Fun через
их проекции, получим
=* Ц [Xcos(п, x) + Ycos(n, y) + Zcos(n, г)]da. B')
Произведение Дасо^(я, г) есть проекция площадки Да на пло-
плоскость Ох у (рис. 353); аналогичное утверждение справедливо и
для произведений Да cos (n, х) и
Да cos (/I, у):
Да cos (я, x) =
Да cos (л, у) =
Да cos (л, г) =
D)
Рис, 353,
где Дауг, Дах<г, Да^—проекции пло-
площадки Да на соответствующие коор-
координатные плоскости.
На основании этого интеграл
B') записывают также" в другой
форме:
cos
t y)-\-Zcos(n,
. B")
§ 6$ Вычисление поверхностного интеграла
Вычисление интеграла по кривой поверхности сводится к вычис-
вычислению двойного интеграла по плоской области.
Укажем, например, способ вычисления интеграла
$$Zcos(/&, г)da.
Пусть поверхность а такова, что всякая прямая, параллель-
параллельная оси 0г% пересекает ее в одной точке. Тогда уравнение поверх-
*) В упражнениях встречаются обозначения
cos (л, х) = cos о&| cos (л, у) = cos f&j cos (я, г)=cos у.

§61 ВЫЧИСЛЕНИЕ ПОВЕРХНОСТНОГО ИНТЕГРАЛА 227
ности можно написать в виде
* = /(*, */)•
Обозначая через D проекцию поверхности а на плоскость Оху,
получим (на основании определения поверхностного интеграла)
\[ Z (х, у, z) cos (n, z) do = lim JJ Z (xh yh zt) cos (nh z) Aot.
a diam Aaf- -*0i=l
Учитывая, далее, последнюю из формул D) § 5, получим
z)do= lim j}Z(xi9 yh f{xiy &))(Aa ),=*
0 diam До -* Of = 1
«=± lim 2 z(xi> У и f(*i, yt))\b0xv\t$
а последнее выражение есть интегральная сумма для двойного
интеграла от функции Z(x, у, f(x, у)) по области D. Поэтому
$$Zcos(/i, z)do=±[^Z(xy у, /(*, y))dxdy.
a D
При этом перед двойным интегралом берется знак плюс, если
cos (л, г)^0, и знак минус, если cos (я, г)^0.
Если поверхность а не удовлетворяет условию, указанному
в начале этого параграфа, то ее разбивают на части, удовлетво-
удовлетворяющие этому условию, и вычисляют интеграл по каждой части
отдельно.
Аналогично вычисляются интегралы
X cos (я, х) da, ^Y cos (n, у) do.
а
Доказанное оправдывает запись поверхностного интеграла
в форме B") из § 5.
При этом правую часть равенства B") можно рассматривать
как сумму двойных интегралов по соответствующим проекциям
области а, причем знаки этих двойных интегралов (или, как
говорят иначе, знаки произведений dydz, dx dz% dx dy) берутся в соот-
соответствии с указанным выше правилом.
Пример 1. Пусть замкнутая поверхность о такова, что всякая прямая,
параллельная оси Ог, пересекает ее не более чем в двух точках.
Рассмотрим интеграл
С f г cos (n, z) do.V[
Положительнь/м направлением нормали будем считать внешнюю нормаль,
В данном случае поверхность можно разбить на две части: нижнюю и
верхнюю; их уравнения будут соответственно г~к(хг у) и г = /2(** У)*
8*

228
КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ [ГЛ. XV
Обозначим через D проекцию а на плоскость Оху (рис. 354); тогда
(xt у) dx dy— J J ft (xt y)dxdy.
Знак минус у второго интеграла взят потому, что в поверхностном инте-
интеграле знак dxdy на поверхности z — f1(xt у) нужно взять отрицательным, так
как для нее cos (л, г) отрицателен.
Рис. 354.
Рис. 355.
Но разность интегралов, стоящих справа в последней формуле, дает объем,
ограниченный поверхностью а. Значит, объем тела, ограниченного замкнутой
поверхностью а, равен следующему интегралу по поверхности:
= '\ С z cos (л, г) da.
Пример 2. Положительный электрический заряд е, помещенный в на-
начале координат, создает векторное поле, так что в каждой точке пространства
определяется вектор F по закону Кулона:
где г — расстояние рассматриваемой точки от начала координат; г—единичный
вектор, направленный по радиус-вектору данной точки (рис. 355); &—постоян-
&—постоянный коэффициент. Определить поток векторного поля через сферу радиуса R
с центром в начале координат.
Решение. Принимая во внимание, что r=/?=c.onst, будем иметь
Но последний интеграл равен площади поверхности а. Действительно, по оп-
определению интеграла (учитывая, что гл— 1) получим
JJ
= lim
к= lim
ke ke
Следовательно, поток равняется -щ- a =
= 4nke.

§71
ФОРМУЛА СТОКСА
229
§ 7. Формула Стокса
Пусть имеем поверхность а такую, что всякая прямая, парал-
параллельная оси Ог, пересекает ее в одной точке. Границу поверх-
поверхности а обозначим через Я. Положительное направление норма-
нормали п возьмем так, чтобы она образовывала с положительным
направлением оси Ог острый угол (рис. 356).
Пусть уравнение поверхности есть z-=f(x,_ у). Направляющие
косинусы нормали выражаются формулами (см. § 6 гл. IX т. I):
cos(n, *) =
дх
?J+(f )¦'
cos (я, у) = -
cos (я, z) =
УЩТШ'
A)
Будеэд предполагать, что поверхность а всеми своими точками
лежит в некоторой области V. Пусть в области V задана функ-
функция Х(х, у, г)9 непрерывная вместе с
частными производными первого порядка.
Рассмотрим криволинейный интеграл по
кривой X
§Х(х, у, z)dx.
А*
На линии % имеем 2 = /(*;, у), где*, #—
координаты точек линии L, являющейся
проекцией линии X на плоскость Оху
(рис. 356). Следовательно, мы можем на-
написать равенство
§Х(х, у, z)dx = §X(x, у, f(x, y))dx. *
B)
Рис. 356.
Последний интеграл есть криволинейный интеграл по линии L.
Преобразуем этот интеграл по формуле Грина, положи*
Х{х, у, /(*, у)) = Х(*, у), 0 = Y(x, у).
Подставляя в формулу Грина вместо X и Y их выражения,
получим
ff ""%"" »f (х, у, Ш, УМ*. C,

230 КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЦ [ГЛ. XV
где область D ограничена линией L. На основании производной
сложной функции Х(х, у, f(x, y)\ где у входит и непосредст-
непосредственно, и через функцию z = f(x, у), найдем
дХ(х, у, f (х, у)) _ дХ(х, у, г) |ч дХ(х, у, г) df (х, у) ^
ду ~ ду ~*~ дх ду ш к }
Подставляя выражение D) в левую часть равенства C), получим
-^[Щ^+дХ V г)д!%У)] dxdy=§X(x,y,f(x,y))dx.
D L
Последнее равенство с учетом равенства B) можно переписать так:
E)
Последние два интеграла преобразуются в интегралы по. поверх-
поверхности. Действительно, на основании формулы B") из § 5 следует,
что если имеем некоторую функцию А(х, у, г), то справедливо
равейство
Ц*> У, z) cos (#, z)da= }} A dxdy.
a
На основании этого равенства интегралы, стоящие в правой части
равенства E), преобразуются следующим образом:
¦wdxdy={№cos{n> z)da>
' z)da'
Последний интеграл преобразуем с помощью формул A) настоящего
параграфа: деля почленно второе из этих равенств на третье,
находим
cos (п, у)_ df
cos (л, z)~~" ду *
ИЛИ
-§jcos(n, г) = — cos (я, у).
Следовательно,
П^ИТГ^ У)йо. G)
D а
Подставляя выражения F) и G) в равенство E), получаем
х9 у, z)dx = -^-^-cos(n, z)de+^2X_cos(n, у)А*. (8)

§7] ФОРМУЛА СТОКСА 231
Направление обхода контура к должно быть согласно с выбран-
выбранным направлением положительной нормали п. Именно, если
наблюдатель смотрит с конца нормали, то он видит обход вдоль
кривой к против часовой стрелки*
Формула (8) справедлива для любой поверхности, если эту
поверхность можно разбить на части, уравнения которых имеют
вид z = /(x, у).
Аналогично можно написать формулы
Y (*, у, z) dy = J J [- -§- cos (л, х) + ~ cos (л, г)] da, (8')
Z (х, у, z) dz = J J Г- -g- cos (я, *)+-§¦ cos (я, *)] dor. (8")
а
Складывая левые и правые части равенств (8), (8') и (8"), полу-
получим формулу
Эта формула называется формулой Стокда по имени английского
физика и математика Д. Стокса.A819—1903). Она устанавливает
зависимость между интегралом по поверхности а и криволиней-
криволинейным интегралом по границе X этой поверхности, причем обход
по кривой К совершается по тому же правилу, которое было ука-
указано выше.
Вектор Ву определяемый проекциями
***-~ ду dz ' у~ dz дх ' **z~ дх ду '
называется вихрем или ротором векторной функции F=Xi +
+ Yj+Zk и обозначается*) символом rotF.
Следовательно, в векторной форме формула (9) будет иметь
вид
§^ (9')
и теорема Стокса формулируется так:
Циркуляция вектора вдоль контура некоторой поверхности
равна потоку вихрятчерез эту поверхность.
Замечание. Если поверхность а есть кусок плоскости,
параллельной плоскости Оху, то Дг = 0, и мы получаем формулу
Грина как частный случай формулы Стокса.
*) rot—три буквы французского слова rotation, что значит звращениеа.

232 КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ?ГЛ. XV
Из формулы (9) следует, что если
дУ дх п ы дУ 0 ах az0
0 0 0
то криволинейный интеграл по любой пространственной замкну-
замкнутой кривой К равен нулю:
= O. A1)
Отсюда следует, что в этом случае криволинейный интеграл не
зависит от формы кривой'интегрирования.
Как и в случае плоской кривой, можно показать, что для
выполнения равенства A1) условия A0) являются не только
достаточными, но и необходимыми.
При выполнении этих условий подынтегральное выражение
есть полный дифференциал некоторой функции и(х, у, г):
Xdx + Ydy + Zdz = du(x, у, z)
и, следовательно,
(М)
{М)
Это доказывается так же, как соответствующая формула для
функции двух переменных (см. § 4).
Пример 1. Напишем основные уравнения динамики материальной точки
mdv*-~Y trdVy-V mdV*-~7
m~dt~x' mW-Y' m!f-z'
Здесь m—масса точки; X, У, Z—проекции на оси координат силы, действую-
„ dx du dz
щей на точку; vx~r* vv~~3T^ Vz~~~di—пРоекЦии скорости v на оси
координат. Умножим левые и правые части написанных уравнений на выра-
выражения
vxdt = dx, vydt = dy, vzdt = dz.
Сложив почленно данные равенства, получим
m\vx dvx + vy dvy\-vz dvz)
Так как ^+^+t'l=c2; то мы можем написать
~ mxA =X dx-\-y dy+Z dz.
Возьмем интеграл вдоль траектории, соединяющей точки Mt и М2:
(Mt)
— mvl-Y^ I
*где vt и t>2—скорости в точках Mi и М

§81 , ФОРМУЛА ОСТРОГРАДСКОГО 233
Последнее равенство выражает теорему живых сил: приращение кинети-
кинетической энергии при переходе из одной точки в другую равно работе силы,
действующей на массу т.
Пример 2. Определить работу силы ньютонова притяжения к непод-
неподвижному центру массы т при перемещении единичной массы из положения
Mi(ai; bx\ Ci) в положение М2 (я2; ^; сё-
Ре ше н_и_е_._ Пусть начало координат помещено в неподвижный центр при-„
тяжения. Обозначим через г радиус-вектор точки М (рис. 357), соответствую-
соответствующий произвольному положению единичной мас-
массы, а через г°—единичный вектор, направлен-
направленный по вектору г. Тогда F = ^r°, где
k—гравитационная постоянная. Проекции си-
силы F на оси координат будут
/ Г* Г ' ~~ Г% Г*
1 2
Тогда работа силы F на пути-Л^Мз равна Рис. 357.
(М2) (Ms) .
и С txdx+ydy+zdz ' С г dr .
—km J -™/-t- —km \ -r-
(Mi) (Mt)
(так как t2=a:2+^+z2, rdr=xdx-{-ydy+zdz). Если обозначить через
и г2 длины' радиус-векторов точек Мг и М2, то
Таким образом, здесь криволинейный интеграл также не зависит от4>ормы
кривой интегрирования, а зависит только от положения начальной и конечной
_ km
точек. Функция « = ~ называется потенциалом поля тяготения, создаваемого
массой т. В данном случае
v ди >_ ди „ ди Л
X Г Z Л
т. е. работа при перенесении единичной массы равняется разности значений
потенциала в конечной и начальной точках.
§ 8. Формула Остроградского
Пусть в пространстве задана правильная трехмерная область V,
ограниченная замкнутой поверхностью а и проектирующаяся на
плоскость Ох у в правильную двухмерную область D. Мы пред-
предположим, что поверхность а можно разбить на три части alt ot
и ай так, что уравнения первых двух имеют вид z = f1(x, у) и
z^hix* У), где ft(xf у) и f2(x, у)—функции, непрерывные в об-
области D, а третья часть а3 есть цилиндрическая поверхность
с образующей, параллельной оси Ог.

234 КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ |ГЛ. XV
Рассмотрим интеграл
Произведем сначала интегрирование по г:
мКТ)
D Ч<*. д) '
~l]Z(x, у, /,(*, y))dxdy-HZ(x, у, U(x, y))dxdy. A)
D D
Выберем на нормали к поверхности определенное направление,
а именно то, которое совпадает с направлением внешней нормали
к поверхности а. Тогда cos (я, г) будет на поверхности а2 поло-
положительным, а на поверхности"" о^ отрицательным; на поверхности
ст3 он равен нулю.
Двойные интегралы, стоящие в правой части равенства A),
равны соответствующим интегралам по поверхности:
$$ V* М*. y))dxdy=[]z(x, у, z)cos(n, z)da;
Ц2(х, у, h(х9 у))&х&у= \\Z(x, у, г)(-cos(n, г))da.
D 0i
В последнем интеграле мы написали (—cos (я, г)) потому, что
элемент поверхности at и элемент площади As области D связаны
соотношением As = Aa[—cos (я, г)], так как угол (я, г) тупой.
Итак,
SJ2(*, У, /*(*, y))dxdy = —\\Z(x,y, h(x, y)}c6s(n, г)da. B")
Подставляя B') и B") в равенство A), получим
{*, y9 z)cos(n, z)de+ JJ Z(x9 у, z)cos(n, г)da.
Для удобства дальнейших формул последнее равенство перепишем
так (прибавив $$Z(#, уу г) cos (я, г) da = 0, так как на поверхно-
ста <г3 выполняется равенство cos (я, г) = 0):
, г) da.
о,

$ 8] ФОРМУЛА ОСТРОГРАДСКОГО 235
Но сумма интегралов, стоящих в правой части последнего равен-
равенства, есть интеграл по всей замкнутой поверхности а; поэтому
Ш ъ**dy dz=Иz {х* у>z) cos {п*г) da'
Аналогично можно получить соотношения
Складывая почленно три последних равенства, получим фор-
формулу Остроградского*)
= J J (X.cos (», x) + Y cos (я, у)+Z cos (я, г)) da. B)
Выражение -^- + —V~fa называется дивергенцией вектора
(или дивергенцией векторной функции)
и обозначается**) символом divF:
ах . 0
Отметим, что эта формула справедлива для любой области,
которая может быть разбита на области, удовлетворяющие усло-
условиям,, указанным в начале этого параграфа.
Дадим гидромеханическую интерпретацию полученной формулы.
Пусть вектор F=Xi-{-Yj+Zk есть вектор скорости жидкости,
протекающей через область V. Тогда интеграл по поверхности,
стоящей в формуле B), есть интеграл от проекции вектора F на
внешнюю нормаль п\ он дает количество жидкости, вытекающей
из области V через поверхность а в единицу времени (или вте-
втекающей в область F, если этот интеграл отрицателен). Это коли-
количество выражается через тройной интеграл от divF.
*) Эта формула (называемая иногда формулой Остроградского—Гаусса)
была открыта знаменитым русским математиком М. В. Остроградским
A801 — 1861) и опубликована им в 1828 г. в статье «Заметка по теории теплоты».
**) div—три первые буквы французского слова divergence, что значит,
(расходимость».

236 КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ {ГЛ. XV
Если divF^O, то двойной интеграл но любой замкнутой
поверхности равен нулю, т. е. количество вытекающей (или вте-
втекающей) через любую замкнутую поверхность а жидкости будет
равно нулю (отсутствуют источники). Точнее говоря, количество
жидкости, втекающей внутрь области, равно количеству жидкости,
вытекающей из этой области.
В векторной форме формула Остроградского имеет вид
(У)
и читается так: интеграл от дивергенции векторного поля F,
распространенный по некоторому объему, равен потоку вектора
через поверхность, ограничивающую данный объем.
§ 9. Оператор Гамильтона. Некоторые его применения
Пусть мы имеем функцию и = и(х, у, г). В каждой точке об-
области, где определена и дифференцируема функция и{х, у, г),
определяется градиент
Градиент функции и(х, у, г) иногда обозначают так:
знак V читается «набла».
1) Равенство B)" удобно символически записать так:
4
и рассматривать символ
'?|- C)
как «символический вектор». Этот символический вектор назы-
называется оператором Гамильтона или набла-оператором (^-опера-
(^-оператором). Из формул B) и B7) следует, что при «умножении» сим-
символического вектора V на скалярную функцию и получается
градиент этой функции: .
V« = gradw. D)
2) Можно составить скалярное произведение символического
вектора V на вектор JF= iX <+JY + fcZ:

§9]
(см. § 8). Итак,
ОПЕРАТОР ГАМИЛЬТОНА
VF-divF.
237
E)
3) Составим векторное произведение символического вектора V
на вектор F=iX+jY + kZ:
d
Ту
Y
д
dz
Z
J
-/1
d
dx
X
d
dz
Z
d
dx
X
d
ду
Y
t J k
d d d
dx dy dz
X Y Z
dZ__dY\ _ jfdZL_d2^\ , d dY dX
dZ dY\ , JdX dZ\ , Л dY dX:
(cm. § 7). Итак,
VxF=rotF.
Из сказанного следует, что употребление символического век-
вектора V позволяет очень коротко выражать векторные операции.
Рассмотрим еще несколько формул.
4) Векторное mMeF(#, r/, г) = iX+JY+kZ называется потен-
потенциальным векторным полем, если вектор F есть градиент некото-
некоторой скалярной функции и(х, у, z): F=grada, или
В этом случае проекции вектора F будут
ди
:S1
ди
ди
Из этих равенств следует (см. т. 1, гл. VIII, § 12)
ду дх ' dz ду * dz ~дх*
дХ dY Л дХ dZ. Л дХ dZ л
ИЛИ
Следовательно, для рассматриваемого вектора F
rotF=0.
Таким образом, получаем
rot (grad и) = 0.
G)

238 КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ?ГЛ. XV
Применяя оператор V, равенство G) на основании формул D) и
F) можно записать так:
Пользуясь тем свойством, что для умножения векторного произ-
произведения на скаляр достаточно умножить на этот скаляр один из
сомножителей, запишем:
= 0. G")
Здесь оператор V снова обладает свойствами обыкновенного век-
вектора: векторное произведение вектора на себя равно нулю.
Векторное поле F(x, у, г), для которого rotF=0, называется
безвихревым. Из равенства G) следует, что всякое потенциальное
поле является безвихревым.
Справедливо и обратное заключение, т. е. если некоторое век-
векторное поле F является безвихревым, то оно потенциально. Спра-
Справедливость етого утверждения следует из рассуждений, проведен-
проведенных в конце § 7.
5) Векторное поле F(x, у, г), для которого divF=0, т. е.
векторное поле, в котором отсутствуют источники (см. § 8), на-
называется соЛеноидальным или трубчатым. Докажем, что
div(rotF) = 0, (8)
т. е. что поле вихрей свободно от источников.
Действительно, если F=iX-\-jY+kZ, то
и поэтому
д fdZ dY\ ,д[дХ dZ\,dfdY дХ \
С помощью оператора V равенство (8) запишется так:
0. (8')
Левую часть этого равенства можно рассматривать как векторно-
скалярное (смешанное) произведение, трех векторов: V, V, F, из
которых два одинаковых. Это произведение, очевидно, равно нулю.
6) Пусть имеем скалярное поле и = и(ху уу г). Определим поле
градиентов:
Найдем далее divfe,adl0 = |(*) + 4(*)+ ?(*). „ли
^^5-. (9,

УПРАЖНЕНИЯ К ГЛАВЕ XV 239
Правая часть этого выражения обозначается
д„ д2и д2и
или символически
Символ
называется оператором Лапласа.
Следовательно, равенство (9) можно записать так:
div (grad и) = Аи. A1)
С помощью оператора V равенство A1) записываем в виде
(W«) = Aa, т. е. A==V2. AГ)
Заметим, что уравнение
+ + 0
или
Аи^О A2')
называется уравнением Лапласа. Функция, удовлетворяющая урав-
уравнению Лапласа, называется гармонической функцией.
Упражнения к главе XV
Вычислить следующие криволинейные интегралы:
1. \ у2dx-\-2xy dy по окружности # = асо5*, y—asint. Отв. 0.
2. \ydx-xdy по дуге эллипса x~acost, y = bslnt. Отв. —27tab.
Г* х v
3# \ х2 4-ц2 dx 2 f 2 dy по окружности с центром в начале координат.
Отв. 0.
4. \ ^—2^" 2 ¦ по отрезку прямой у = х от ^=1 до х=2. Отв. In 2.
5. V yzdx+xzdy+xydz по дуге винтовой линии #=acosf, y =
z=kt при изменении t от 0 до 2тс. Отв. 0.
С f 3
6. \xdy-ydx по дуге астроиды #=acos3*, y=asis?t. Отв. -^
(удвоенная площадь астроиды).
7. \xdy-ydx по петле декартова листа ^^yq^
(удвоенная площадь области j ограниченной указанной петляй).
—ухр- 0/п*- За1

240 КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ [ГЛ. XV
8. {xdy—ydx по кривой x=a(t—sin t), у —а A — cos /) (<Х*^2я).
Отв. — бзха2 (удвоенная площадь области, ограниченной одной аркой циклоиды
и осью Ох).
Доказать, что:
9. grad(<xp) = cgrad<p, где с—постоянная.
10. grad(c1q)+c2t[?)=c1grad9+c2gradi|?, где с* и с2—постоянные.
И. gradfcpiJ^cpgradilJ+^gradcp.
12. Найти gradr, gradr2, grad 1/г5 grad/(r), где r=Vx2+y2 + z2.
Отв. г In 2r; -rlr*;J'(r)r/r.
13. Доказать, что div(A+B) = div A + div В.
14. Вычислить diyr, где r = xi+yj+zk. Отв. 3.
15. Вычислить div (Лф), где А—векторная функция, а <р—скалярная
функция. Отв. cpdiv ;4 + (gradq>, Л).
16. Вычислить div (re), где с—постоянный вектор. Отв. сг/г.
17. Вычислить div В (гА). Отв. АВ.
Доказать, что:
18. rot (CiAi+c2A2)=CiYoi Л1+с2rot Л2? где с± и с2—постоянные.
19. rot-B4c) = gi;ad Axe, где <?—постоянный вектор.
- 20. rot rot Л = grad div Л — ДЛ.
21. ЛXgradф = гot (фЛ).
Интегралы по поверхности
22. Доказать, что С \ cos (я, 2)da=0, если а—замкнутая поверхность*
п—нормаль к ней.
23. Найти момент инерции поверхности сегмента сферы с уравнением
а+2+2Я* отсекаемого плоскостью z = Ht относительно оси Ог.
Отв. ^
24. Найти момент инерции поверхности параболоида вращения х2+у2 = 2сг,
отсеченной плоскостью z = cf относительно оси Ог. Отв. 4яс4— S* .
1о
25. Вычислить координаты центра масс части поверхности конуса
x2-\-y2=R2z2/H2, отсеченной плоскостью г = Я. Отв. @; 0; 2Я/3). -
^26* Вычислить координаты центра масс сегмента поверхности сферы
*2+y2+z2=R2, отсекаемого плоскостью г = Н. Отв. @; 0; (R + H)/2)^
27. Найти \ V [*cos (я, x)-\-ycos (я, ^) + 2cos (я, 2)] do, где а—замкну-
тая поверхность. Отв. 3V, где V—объем тела, ограниченного поверхностью а.
28. Найти \ \zdxdy, где о—внешняя сторона сферы Jt2+#2+z2=#2,
a
Отв. 4-яЯ3.
о
29. Найти \\x2dy4z-\-y2dzdx-\'Z2dxdy9 где а—внешняя сторона по-
пост
верхности сферы x2+y2+z2=>R2. Отв. 0.
И
V\x2-\-y2do, где а—боковая поверхность конуса

УПРАЖНЕНИЯ К ГЛАВЕ XV 241
31. По формуле Стокса преобразовать интеграл ф ydx-\-zdy-\-x dz.
i
Отв. —¦ \ \ (cos a+cos P+cos у) da.
о
Найти криволинейные интегралы, применяя формулу Стокса и непосред-
непосредственно: —
32. ф (y+z)dx-\-(z + x)dy+(x+y)dztгде!—окружностьx2+y2 + z2 = a29
x+y+z = 0. Отв. О*
33. (hx2tpdx-{-dy-{-zdz, где 'L —окружность x2+y2 = R2i 2 = 0. Отв.
Щ1
Применяя формулу Остроградского, преобразовать поверхностные инте-
интегралы в интегралы по объему:
34. С f
a v
35. J \(х2+У2+г2) (dy dz+dx dz+dxdy). Отв. 2
a -^
36. \ V xy dx dy-\-yz dy dz-\-zx dz dx. Отв. О.
dd2+Tzdxdy- Ome-
С помощью формулы Остроградского вычислить следующие интегралы:
38. \ \ (х cos a+^ cos Р + г cos у) da, где a—поверхность эллипсоида
a
у2 t/2 22
* +|5.+±.==1. Отв. 4nabc.
a2 l b2 l с2
39. у \ (х? cos a-j^t/3 cos P + 23 cos y) ^cr» где a—поверхность сферы х2 -f-
+ «•+2*1/?». Ome. 12я/?5/5.
40. \ \ х2 dy dz-\-y2 dz dx + z2 dx dy, где a—поверхность конуса —^+-^—
a
0 @<2^6). Ome.
41. \ \ xdydz+ydxdz-\-zdxdy, где а—поверхность цилиндра х2-\-у2 = а2,
— #<*<#. Отв. Zna2H.
С С ( д2и д2и \ р ди
42. Доказать тождество \ \ ( •jt+-tt ) «*"#=(!>~3br"s» гДе ^—кон*
J J \ ОХ Оуй / ' "
D
тур, ограничивающий область 1>, а -^ производная по направлению внеш-
внешней нормали.
Решение.
(s, *L-^sin(s, x)] ds,

242 КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ?ГЛ. XV
где (s, дс)—угол между касательной к контуру С и осью Ох. Если через
(пу х) обозначим угол между нормалью-и осью Ох, то sin(s, *) = cos (w, x)9
cos (s, #) = ¦— sin (л, х). Следовательно,
„ -, ди -. ди
Полагая X = ^, Y =. -^ , получим
и v ^ C0S ^Л> ^^"%"Sin ^ ^V Sj
или
а«
43. Доказать тождество (так называемую формулу Грина)
где и и t;—функции, непрерывные и имеющие непрерывные производные до
второго порядка в области и.
Символы Аи и Ду обозначают следующее:
д2и . д2и . д2и . d2v . дЪ . ,d2v
ду2 * ^22
Решение.* В формуле
Ш' ах . аг . dz
-авг+а^+"яг
= JJ [X cos (и, x)+Y cos (л, y)+Z cos (л, г)] Жт
а
положим X =5= ш^—«y^j Y~vuy—uv'yi Z = vuz—uvz. Тогда
дХ , dY . dZ
Xcos(/t, jc) + Kcos(/i, y)+Z cos (n, z) =
= d («/cos (л, ^)+«^ cos (n,
—«(^cos(w, *)+^cos(/*, y)+v'zcos(n, г))^г?—и~^.
Следовательно,
44. Доказать тождество

УПРАЖНЕНИЯ К ГЛАВЕ XV ' 243
Решение. Положим в формуле Грина, выведенной в предыдущем при-
примере, 0=1. Тогда Дс/=О, и мы получаем указанное .тождество.
45. Если и (х, у, г)—гармоническая функция в некоторой области * т. е,
такая функция, которая в любой точке этой области удовлетворяет уравне-
уравнению Лапласа
д2и . д2и . д2ы
то
Иди ,
где а—замкнутая поверхность.
Решение. Это непосредственно следует из формулы задачи 44.
46. Пусть и(х, у, 2)—гармоническая функция в некоторой области V и
пусть в области V находится сфера а с центром в точке М (хх; ух; zx) и ра-
радиусом R. Доказать, что
Решение. Рассмотрим область Q, ограниченную двумя сферами a, a
радиусов R и р (р < R) с центрами в точке М (jcx; y±; Zi). Применим к этой
области формулу Грина, установленную в задаче 43, приняв за и указанную
выше функцию, а за функцию v
Г
Непосредственным дифференцированием и подстановкой убеждаемся, что
dh) , d2v . d2v л ^
№+W+~д? % Следовательно,
Jl\TTn-u-dir)da={
На поверхностях а и_а величина 1/г постоянна A/i? и 1/р) и потому может
быть вынесена за знак интеграла, В силу результатаг установленного в за-
задаче 45, имеем
i? JJ дп P JO дп
Следовательно|
»=о,

244 ' КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ [ГЛ. XV
НО
дп dr
Поэтому
или
Применим к интегралу, стоящему слева, теорему о среднем:
2 о
9 *
где a(g, rj, С)—точка на поверхности сферы радиуса р с центром в точке
Заставим р стремиться к нулю; тогда и (|, rj, Q —> и (xi, уь Zi):
" - l'??j 4лР2 л
Р2 J_J Р2
a
Следовательно, при р—*0 получаем
pi" JJada—*"(**• W» «i)'4«-
Далее, так как правая часть равенства A) не зависит от р, то при р—*0
окончательно получим
-?-2 У V и da^lnu (дгь уь г{),
или
и{хи у и Zi) =

ГЛАВА XVI
РЯДЫ
I
§ 1. Ряд. Сумма ряда
Определение 1. Пусть задана бесконечная последователь-
последовательность чисел*)
Выражение
и1 + и2 + ив+...+ип+... . A)
называется числовым рядом, При этом числа %, u2i ..., ип, ...
называются членами ряда.
Определение 2. Сумма конечного числа п первых членов
ряда называется п-й частичной суммой ряда:
Рассмотрим частичные суммы
uz+. „ +иа.
Если существует конечный предел
?= Urn sn9 -
П-> CD
то его называют суммой ряда A) и говорят, что ряд сходится.
Если lim sn не существует (например, sft—>оо при п—>оо),
Л->00
то ггоорят, что ряЗ A) расходится и суммы- не имеет.
Пример. Рассмотрим ряд
' a+aq+af+..:+aqn-i+... B)
*) Последовательность считается заданной, если известен закон, по кото-
которому можно вычислить любой ее^член ип при данном п.

246 рЯДЫ |ГЛ. XVI
Это—геометрическая прогрессия с первым членом а и знаменателем? (а
Сумма п первых членов геометрической прогрессии равна (при q Ф 1)
или
1) Если \q\< li то qn~+0 при /г-*оо и, следовательно,
Значит, в случае | q | < 1 ряд B) сходится и его сумма
_ а
2) Если | <71 > 1, то f qn | -> оо при п -> оо и тогда a~~a(f > ± оо при
/t-»-oo, т. е. lim s^ не существует. Таким образом, в случае |<7| > 1 ряд B)
расходится.
3) Если 0=1, то ряд B) имеет вид
В этом случав „
т. е. ряд расходится.
4) Если <7=— 1, то ряд B) имеет вид
а—а-\-а—#-[-..•
В этом случав
~~_ ( 0 при п четном,
"~~ \ а при п нечетном.
Следовательно, sn предела не имеет—ряд расходится.
Таким образом, геометрическая прогрессия (с первым членом, отличным
от нуля) сходится только тогда, когда знаменатель прогрессии по абсолютной
величине меньше единицы.
Теорема 1. Если сходится ряд, получившийся из данного
ряда A) отбрасыванием нескольких его членов, то сходится и
сам данный ряд. Обратно, если сходится данный ряд, то схо-
сходится и ряд, получившийся из данного отбрасыванием нескольких
членов.
Иными словами, на сходимость ряда не влияет отбрасывание
конечного числа его членов.
Доказательство. Пусть sn — сумма п первых" членов
ряда A), ck—сумма k отброшенных членов (заметим, что при
достаточно большом п все отброшенные члены содержатся в сум-
сумме sn)f on-k—сумма членов ряда, входящих в сумму sn и не

§1] РЯД. СУММА РЯДА 247
входящих в ск. Тогда имеем:
где ск—постоянное число, не зависящее от п.
Из последнего соотношения следует, что если существует
\\тап^кУ то существует и limsre; если существует lim sw, то суще-
ствует и limaw_ft, a это и доказывает справедливость теоремы.
Я->оо
В заключение параграфа укажем два простых свойства рядов.
Теорема 2. Если ряд
... C)
сходится и его сумма равна s, то ряд
+...1 D)
где с — какое-либо фиксированное число, также сходится и его
сумма равна cs.
Доказательство. Обозначим n-ю частичную сумму ряда C)
через sn, а ряда D) —через ап. Тогда
Отсюда ясно, что предел n-й частичной суммы ряда D) сущест-
существует, так как
lim ап = lim (csn) = с lim sn = cs.
Итак, ряд D) сходится и его сумма равна cs.
Теорема 3. Если ряды
+..; E)
и
Ьг + Ь%+... 'F)
сходятся и их суммы соответственно равны s и !, то ряды
(а1 + Ь1) + (а2 + Ь2)+... G)
и
te-*i) + (*.-&,)+... (8)
также сходятся и их суммы соответственно равны s+~s и s—1.
Доказательство. Докажем сходимость ряда G). Обозна-
Обозначая его л-ю частичную сумму через сгЛ, а_п-е частичные суммы
рядов E) и F) соответственно через sn n~sny получим

248 * рЯДЫ ?ГЛ. xvi
Переходя в этом равенстве к пределу при п—>оо, получим
lim ап = lira (sn + sn) = linr sn + lim Jn — s.+7.
Таким образом, ряд G) сходится "и его сумма равйа s-J-lr.
Аналогично доказывается, .что ряд (8) также сходится и его
сумма равна s—F.
Про ряды G) и (8) говорят, что они получены в результате
почленного сложения или соответственно почленного
вычитания рядов E) и F)/
§ 2. Необходимый признак «сходимости ряда
При исследовании рядов одним из основных вопросов явля-
является вопрос о том, сходится ли. данный ряд или расходится.
Ниже будут установлены достаточные признаки, на основании
которых можно решить этот вопрос. Здесь же мы рассмотрим
необходимый признак сходимости ряда, т. е. установим условие,
при невыполнении которого ряд расходится. - ~
Теорема. Если ряд сходится, то его п-й член стремится
к нулю при неограниченном возрастании п.
Доказательство,* Пусть ряд
сходится, т. е. имеет место равенство
lim sn = s,
где s—-сумма ряда (т. е. конечное фиксированное число); но тогда
имеет место также равенство
так как при п—>оо и л — 1—*оо. Вычитая почленно из первого
равенства второе, получаем
lim s4- lim snmml= 0,
ИЛИ
lim (sn-sn_i) = O.
Но
Sn-Sn_i = Un.
Следовательно,
litti un = 0,
что и требовалось доказать.

§ 2] НЕОБХОДИМЫЙ ПРИЗНАК СХОДИМОСТИ РЯДА 249
Следствие. Если п-й член ряда не стремится к нулю при
п—^оо,-~7по ряд расходится.
Пример. Ряд
3 ^,5^7^- •' » 2л+1
расходится, так как
Подчеркнем, что рассмотренный признак является только необ-
необходимым, но не является достаточным, т. е. из того, что п-й
член стремится к нулю, еще не следует, что ряд сходится, —
ряд может и расходиться.
Например, так называемый гармонический ряд
4|1|1.|Х| | 1. |
расходится, хотя
lim ua— lim — = 0.
"Чтобы доказать это, напишем подробнее гармонический ряд
,1,1,1. lflf
+ "9"+l0 + TT + T2 + l3+T4 + T5 + T6
Напишем, далее, вспомогательный ряд
16 слагаемых
,1,1,1,1,1,1,1,1,1, Г.1! - ,С>\
Ряд B) строится следующим образом: его первый член ра-
равен 1, второй равен 1/2, третий и четвертый равны 1/4, члены
с пятого по восьмой равны 1/$, члены с девятого по 16-й рав-
равны 1/16, члены с 17-го по 32-й равны 1/32 и т. д.
Обозначим через s™ сумму п первых членов гармонического
ряда A) и чер'ез 42) сумму п первых членов ряда B).
Так как каждый член ряда A) больше соответствующего
члена ряда B) или равен ему, то для п > 2 -
# > #>. - C)

250 РЯДЫ |гл. xvi
Подсчитаем частичные суммы ряда B) для значений п, равных
21, 22, 23, 2*. 25:
1+ +
4 слагаемых * 8 слагаемых
1
-1+4.1
4 слагаемых 8 слагаемых
16 слагаемых
точно так же подсчитывается, что s2« = 1 + 6• -g-> S27 = l + 7-j
и, вообще, s2b = 1 -f k • у.
Таким образом, частичные суммы ряда B) при достаточно
большом k могут быть сделаны больше любого положительного
числа, т. е.
lim s?2) = oo,
но тогда из соотношения C) следует, что и
lim 5^ = 00,
т. е. гармонический ряд A) расходится.
§ 3. Сравнение рядов с положительными членами
Пусть имеем два ряда с положительными членами ,
+...f A)
+ ... B)
Для них справедливы следующие утверждения.
Теорема 1. Если члены ряда (I) не больше соответствую-
соответствующих членов ряда B), т. е.
un<vn (п=19% ...), ' C)
и ряд B) сходится, то сходится и ряд A).

§3J СРАВНЕНИЕ РЯДОВ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ 251
Доказательство. Обозначим через sn иапсоответственно
частичную сумму первого и второго рядов:
i« I ?= 1
Из условия C) следует, что.
*»<<V • D)
Так как ряд B) сходится, то существует предел а его час-
частичной суммы
lim в„ = о.
П-+СО
Из того, что члены рядов A) и B) положительны, следует,
что crrt < а, и тогда в силу неравенства D)
sn<a. '
Итак, мы доказали, что частичные суммы sn ограничены. Заме-
Заметим, что при увеличении п частичная сумма sn возрастает, а из
того, что последовательность Частичных сумм возрастает и огра-
ограничена, следует, что она имеет предел *)
lim sn — s,
П->-а>
причем очевидно, что
На основании теоремы 1 можно судить о сходимости некото-
некоторых рядов.
Пример I. Ряд
сходится» так как его члены не больше соответствующих членов ряда
1 +22 +2? +2**+'" +2^+ '• *
Но последний ряд сходится, так как его члены, начиная со второго, образуют
геометрическую прогрессию со знаменателем 1/2. Сумма этого ряда равна 3/2.
Следовательно, в силу теоремы 1 данный ряд тоже сходится, причем его сумма
не превосходит 3/2.
*) Для того чтобы убедиться, что переменная sn имеет предел, вспомним
один признак существования предела последовательности (см. теорему 7 § Б
гл. II т. I): если переменная возрастает и ограничена, то она имеет предел.
В данном случае последовательность сумм $п возрастает и ограничена, следо-
следовательно, имеет предел, т. е. ряд сходится.

252 РЯДЫ - |гл. xvi
Теорема 2. Если члены ряда A) не меньше соответствую-
соответствующих членов ряда B), т. е.
un>vn, E)
и ряд B) расходится, то и ряд A) расходится.
Доказательство. Из условия E) следует, что
*»>*»¦ F)
Так как члены ряда B) положительны, то его частичная
сумма ап возрастает при возрастании п, а так как он расхо-
расходится, то
Но тогда в силу неравенства F)
lim sn = со,
т. е. ряд A) расходится.
Пример 2. Ряд
расходится, так как его члены (начиная со второго) больше соответствующих
членов гармонического ряда
который, как известно, расходится.
Замечание 1. Оба доказанных признака (теоремы 1 и 2)
справедливы только для рядов с положительными членами. Они
остаются в силе и для того случая, если некоторые члены 1-го
или 2-го ряда —нули. Однако эти признаки, перестают быть вер-
верными, если среди членов ряда имеются отрицательные числа.
Замечание 2. Теоремы 1 и, 2 справедливы и в случае,
если неравенства C) или F) начинают выполняться лишь для
n^N, а не для всех п=1, 2, 3, ...
§ 4, Признак Даламбера
Теорема (признак Даламбера). Если в ряде с поло-
положительными членами
«i + «2 + «a-f •••+«»+••• (О
отношение (п+1)-го члена к п-му при я-too имеет (конечный)
предел I, т. е.

§4] ПРИЗНАК ДАЛАМБЕРА ' 253
то:
1) ряд сходится в случае /< 1,
2) ряд расходится в случае I > 1.
(В случае / = 1 ответа на вопрос о сходимости или расходи-
расходимости рада теорема не дает.)
Доказательство. 1) Пусть /<1. Рассмотрим число q,
удовлетворяющее соотношению / < ? < 1 (рис. 358).
Из определения предела и соотношения B) следует, что для
всех значений л, начиная с некоторого номера N, т.* е. для
n^zN, будет иметь место неравенство
Я- B')
Действительно, так как величина t^1 стремится к пределу /,
то разность между величиной -??± и числом / может быть сде-
сделана (начиная с некоторого номера N) по абсолютному значению
меньше любого положительного числа, в
частности, меньше q—/, т. е. '^ tJ^J^,J^f
Из последнего неравенства и следует не- ~ Рис' 358t
равенство B'). Записывая неравенство B')
для различных значений /г, начиная с номера ЛГ, получим
«лг+1< quNf
Рассмотрим теперь два ряда
-[r . . ., ^ A)
(V)
Ряд (Г) есть геометрическая прогрессия с положительным
Знаменателем q<\. Следовательно, этот ряд сходится. Члены
ряда A), начиная с uN+if меньше членов ряда (Г). На основа-
основании теоремы 1 § 3 и теоремы 1 § 1 следует, что ряд A) сходится.
2) Пусть />1\ Тогда из равенства lim^^^l (где / > 1)
м-*-» tin
следует, что, начиная с некоторого номера N, т. е. для
будет имет$> место неравенство

254 РЯДЫ [гл. xvi
(рис. 359), или un+i>un для всех n^N. Но это означает, что
члены ряда возрастают, начиная с номера N + 1, и поэтому
общий член ряда не стремится к нулю. Следовательно, ряд рас-
ХОДИТСЯ.
Замечание 1. Ряд будет расходить-
ся и в том случае, когда lim ^±1= оо.Это
и
и
п
Рис. 359, следует из того, что если lim ^^ = оо, то,
начиная с некоторого номера n = N', будет иметь место неравенство
1, или un+i>un.
Пример 1. Исследовать сходимость ряда
1 + Ь2+Г2Тз+ • •' +-1.2.3-...-Л+#' *
Решение. Здесь
.11 11
u
"п, ""(л
Следовательно,
lim lm
1 Я->оо Un П^оо
Ряд сходится. _
Пример 2. Исследовать сходимость ряда
Решение. Здесь
==0<1.
«.-?, «.-м-ет» ^в2гтт» пт^-и-.* a>i.
Ряд расходится, причем его общий член ип стремится к бесконечности.
Замечание 2. Признак Даламбера дает ответ на вопрос
о том, сходится ли данный положительный ряд, только в том
случае, когда lim ^^ существует и отличен от 1. Если же этот
предел не существует или ^существует, но lim ^±1—^ то при-
знак Даламбера не дает возможности установить, сходится ряд
или расходится, так как в этом случае ряд может оказаться и
сходящимся и расходящимся. Для решения вопроса о сходимости
таких рядов надо применить какой-либо другой признак.
Замечание 3. Если lim^^^l, но отношение ^^ для
всех номеров /г, начиная с некоторого, больше единицы, то ряд

§41 ПРИЗНАК ДАЛАМБЕРА 255
расходится. Это следует из того, что если ^~±J> 1, то un+i> ип
и общий член не^стремится к нулю при /г—*оо.
Рассмотрим примеры, иллюстрирующие сказанное.
Пример 3. Исследовать сходимость ряда
Решение. Здесь
п+1
Ura «±I
Un
В данном случае ряд расходится,- -так как ~?±2 > i для всех м
Un
'
Пример 4. Применяя признак Даламбера к гармоническому ряду
1 , 1 . . 1 . 1 1
++'"+7Г^"""' замечаем» что UnZ==z~j;* "л+^^^ХТ и> следова-
следовательно, lim -S±I= lim 1 = 1. Значит, на основании признака Даламбера
нельзя установить сходимость или расходимость данного ряда. Но ранее мы
установили другим путем, что гармонический ряд расходится.
Пример 5. Исследовать сходимость ряда
1 4- 1 4- 1 Л- Д!4
Решение. Здесь
lim 22±!=и
На основании признака Даламбера сделать заключения о сходимости
ряда нельзя, однако, исходя из других соображений, можно установить, что
этот ряд сходится. Заметив, что —-—г-г^ —гт * мы можем записать
П(П-\-1) П Al-f-1
данный ряд в виде
Частичная сумма п первых членов после раскрытия скобок и сокращения
будет равна *
вя==1~д+Т'
Следовательно,
lim sn=lim
t. e. ряд сходится и его сумма равна 1.

256 РЯДЫ . . [ГЛ. XVI
§ 5. Признак Коши
Теорема (признак Коши). Если для ряда с положи-
положительными членами
3+ • • • +ип+ .„ A)
величина 1/ип имеет конечный предел I при п—*оо, т. е.
то:
1) в случае I < 1 ряд сходится;
2) в случае J> 1 ряд расходится.
Доказательство. 1) Пусть /<1. Рассмотрим числом»
удовлетворяющее соотношению / < q < 1.
Начиная с некоторого номера n = Nt будет иметь место соот-
соотношение
\yiTn-l\<q-l;
отсюда следует, что
ИЛИ
для всех
Рассмотрим теперь два ряда:
.., A)
(Г)
Ряд (Г) сходится, так как его члены образуют убывающую
геометрическую прогрессию. Члены ряда A), начиная с uN, меньше
членов ряда (V). Следовательно, ряд A) сходится.
2) Пусть 1>А. Тогда, начиная с некоторого номера n = Nt
будем иметь
или
ип>\.
Но если все члены рассматриваемого' ряда, начиная с uN> больше 1,
то ряд расходится, так как его общий член не стремится к нулю.
П р и-м е р. Исследовать сходимость ряда
Решение. Применим признак Коши:
lim V»n= lim Y(?-r)n= lim
Ряд сходится.

» » ИНТЕГРАЛЬНЫЙ ПРИЗНАК: СХОДИМОСТИ РЯДА
Замечание. Как и в признаке Даламбера, случай
требует дополнительного исследования. Среди рядов, удовлетво-
удовлетворяющих этому условию, могут встретиться как сходящиеся, так и
расходящиеся ряды. Так, для гармонического ряда (который, как
известно, расходится)
Я-> СО й-> 00
Для того чтобы убедиться в этом, докажем, что lim lnj/l/n = 0.
. Действительно,
Здесь числитель и знаменатель дроби стремятся ^бесконечности.
Применяя правило Лопиталя, найдем:
— * —J_
. lim In |/"ii— lim =±L1^ lim ^- = 0.
/1-х»
Итак^ 1П|/1/я—>0, но тогда ^/.l/n—*l, т.
lim YTjn = \.
Для ряда .
+ + + ++
также имеет место равенство
lim У7?= lim уТ]п*= lim
П-> оо «-> оо
но этот ряд сходится, так как если отбросим первый член, то
члены оставшегося ряда будут меньше соответствующих членов-
сходящегося ряда
(см. пример 5 § 4).
§ 6. Интегральный признак сходимости ряда
Т е о р е м а. Пусть члены, ряда
ui + u2 + u3+...+un+...}i A)
положительны и не возрадтают% т. е.
%>"*>",>..., . (У)
S Н. С, Пиекунов, ». 2

2S&
РЯДЫ
|ГЛ. ХУГ
и пусть f (x) — такая непрерывная невозрастающт функция, что
Тогда справедливы следующие утверждениям
1) если несобственный интеграл С f(x)dx сходится (см. § 7
гл. XI т. 1), то сходится и ряд A);
2) если указанный интеграл расходится, то расходится и ряд A).
Доказательство. Изобразим члены ряда геометрически,от-
геометрически,откладывая по оси абсцисс4 номера 1, 2, 3, ..M'n,7i+lf ••• членов
ряда, а по оси ординат — соответствующие значения членов ряда
ui9 и29 *..,-«„, ••• (рис. 360).
if
12 2 л Л+1
Рис, 361.
Построим на том же чертеже график непрерывной невозра*
стающей функции
удовлетворяющей условию B)„
Рассматривая рис. 360, замечаем, что первый из построенных
прямоугольников имеет основание, равное 1, и высоту f(l) = ui.
Следовательно, площадь этого прямоугольника равна щ. Площадь
второго прямоугольника равна щ и т. д.; наконец, площадь по-
последнего (я-го) из построенных прямоугольников равна ип. Сумма
площадей построенных прямоугольников равна сумме sn первых п
членов ряда. С другой стороны, ступенчатая фигура, образован-
образованная этими прямоугольниками, заключает область, ограниченную
кривой y = f(x) и .прямыми *=1, я=я+1, у = 0; площадь этой
области равна \ f(x)dx. Следовательно,
л+1
Л
f(x)dx.

§ ei интегральный признак сходимбсти ряда 559
Рассмотрим теперь рис. 361. Здесь первый (слева) из построен-
построенных прямоугольников имеет высоту^ и2; следовательно, его пло-
площадь также равна щ. Площадь второго прямоугольника
равна и3 и т. д. Площадь последнего из построенных пря-
прямоугольников равна un+i. Следовательно, сумма площадей
всех построенных прямоугольников равна сумме всех чле-
членов J ряда, начиная от второго до (п+1)-го, т. е. равна
Sn+i'—iij. С другой стороны, как легко видеть, ступенчатая фи-
фигура, образованная этими прямоугольниками, содержится внутри
криволинейной фигуры, ограниченной кривой у = f (х) и прямыми
х=19 jc = n +1, # = 0. Площадь этой криволинейной фигуры равна
л+1
/ (х) dx. Следовательно,
\
л+1
откуда
п+1
5й+1< ^ f(x)dx+tH. D)
Рассмотрим теперь оба случая.
+ 00
*1) Предположим, что интеграл \ / (х) dx сходится, т. е. имеет
конечное значение.
Так как
П+ 1 +00
f f(x)dx< f f{x)dxt
i Г
то в силу неравенства D)
4 +оо
'f(x)dx + ul9
т. е. частичная сумма sn остается ограниченной при всех значе-
значениях п. Но при увеличении п она возрастает, так как все члены
ип положительны. Следовательно, sn при /г—*оо имеет конечный
предел lim sn = s, т, е. ряд сходится.
л-> оо
+ 00
2) Предположим далее, что Г/(*)Жс=*оа. Это значит,
п+
/ (x) dx неограниченно возрастает при возрастании п. Но тогда
9*

j , . 1ГЛ.
в силу неравенства C) sn также неограниченно возрастает* при
возрастании п, т. е. ряд расходится.
Таким образом, теорема полностью доказана.
Замечание. Доказанная теорема остается справедливой,
если неравенства (Г) выполняются, лишь начиная с некоторого N.
Пример. Исследовать сходимость ряда
1 ¦ 1
Решейие, Применим интегральный признак, положив ft*) = l/jeJ\ Эта
функция удовлетворяет всем условиям теоремы. Рассмотрим интеграл
при р = 1.
Устремляя N к бесконечности, выясним, сходится ли несобственный инте-
интеграл в различных случаях.
На основе этого можно будет судить о сходимости или расходимости ряда
при различных значениях /?.
00
* » /* ft V \ ->
В случае р > 1 'будет \ -^= ri т. е. интеграл конечен и, следова-
х р
тельно, ряд сходится;
00
Cdx
\ — = 00 ——
J хр
в случае р< 1 будет \ ~ = оо — интеграл бесконечен, ряд расходится;
в случае p=ii будет V—=оо—интеграл бесконечен, ряд расходится.
г х
Заметим, что ни признак Даламбера, ни признак Коши, рассмотренные
ранее, не решают вопроса о сходимости этого ряда, так как
Гр=Иш ( 1/ — J =1я = Ь
§ 7. Знакочередующиеся ряды. Теорема Лейбница
До сих йбр мы рассматривали ряды, члены которых положи-
положительны. В этом параграфе будем рассматривать ряды, члены ко-
которых имеют чередующиеся знаки, т. е. ряды вида
где иь «2, ..., unt ¦.. положительны.

-5 71 : ЗНАКОЧЕРЕДУЮЩИЕСЯ РЯДЫ. ТЕОРЕМА ЛЕЙБНИЦА 261
;¦ Теорема Лейбница. Если в знакочередующемся ряде '"
«i- + «3—«*+•-. ("п>0) , A)
члены таковы, что
щ>и2>и3>..; B)
Hm и„=0, ' - C)
то ряд A) сходится, его сумма положительна и не превосходит
первого члена.
Доказательство. Рассмотрим сумму л = 2т первых чле-
членов ряда A):
Из условия B) следует, что выражение в каждой скобке поло-
положительно. Следовательно, сумма s2m положительна,
и возрастает с возрастанием т. Запишем теперь эту же сумму так:
s2m^ut— (и2—и9) - (и,—иъ)—... — {и2тгъ—и2т_±)—и2т.
В силу условия B) каждая из скобок положительна. Поэтому
в результате вычитания этих скобок из щ мы получим число,
меньшее а?, т. е. v
, Таким образом, мы установили, что s2m при возрастании т воз-
возрастает и ограничена сверху. Отсюда следует, что s2m имеет предел s:
и .. Urn s2m = s,
причем
О < s < ttf.
Однако сходимость ряда еще не "доказана; мы доказали только,
что последовательность «четных» частичных сумм имеет пределом
число s. Докажем теперь, что «нечетные» частичные суммы также
стремятся к пределу s. .
Рассмотрим для этого сумму п — 2т+\ первых членов ряда A):
Так как по условию C) Hm . u2m+i = 0, то, следовательно
Hm s2fll+1= lim s2ta+ Iimu2m+i= Hm s2m^'s.
Тем самым мы доказали, что lim sn — s как при четном п} так
и при нечетном п. Следовательно, ряд A) сходится.

262
РЯДЫ
)[ГЛ. XVI
Замечание 1. Теорема Лейбница справедлива, если нера-
неравенства B) выполняются, начиная с некоторого N.
, Замечание 2. Теорема Лейбница иллюстрируется геомет-
геометрически следующим образом. Будем на числовой прямой откла-
откладывать частичные суммы (рис. 362)
И т. д.
Точки, соответствующие частичным суммам, будут прибли-
приближаться к некоторой точке s, которая изображает сумму ряда.
При этом точки, соответствующие четным частичным суммам, рас-
располагаются слева от s, a
точки, * соответствующие
нечетным частичным сум-
суммам,— справа от s.
Замечание 3. Если
знакочередующийся ряд
удовлетворяет условию тео-
теоремы Лейбница, то нетруд-
нетрудно оценить погрешность, ко-
которая получится, если заме-
заменить его сумму s частичной суммой sn. При такой замене мы от-
отбрасываем все члены ряда, начиная с ип+ь Но эти числа сами об-
образуют знакочередующийся ряд, сумма которого по абсолютной
величине меньше первого «тлена этого ряда (т. е. меньше un+i).
Значит, погрешность, получающаяся при замене s на sn, не
превосходит по абсолютной величине первого из отброшенных
членов.
Пример 1, Ряд
сходится, так как
1) 1 > 1/2 > 1/3 >...;
2) lim «„= lim 1/я = 0.
Сумма п первых членов этого ряда
отличается от суммы ряда s на величину, меньшую
П р и м е р. 2., Ряд
сходится в силу теоремы Лейбница.

<§8J ЗНАКОПЕРЕМЕННЫЕ РЯДЫ ,263
§ 8. Знакопеременные ряды. Абсолютная
и условная сходимость
Ряд называется знакопеременным, если среди его членов
имеются как положительные, так и отрицательные.
Рассмотренные в предыдущем параграфе знакочередую-
знакочередующиеся ряды являются, очевидно, частным случаем знако-
знакопеременных рядов.
Мы рассмотрим здесь некоторые свойства знакопеременных
рядов. При этом в отличие от соглашения, принятого в предыдущем
параграфе, мы будем теперь полагать, что числа uiy и2У
..., и&% ... могут быть как положительными, так и отрицатель-
отрицательными.
Прежде всего, дадим один важный достаточный признак схо-
сходимости знакопеременного ряда.
Теорема 1. Если знакопеременный ряд
+..л, A)
таков, что ряд, составленный из абсолютных величин его членов,
,| + ...+|ив|+:.., B)
сходится, то и данный знакопеременный ряд также сходится.
Доказательство* Пусть sn и ап—суммы п первых,чле-
первых,членов рядов A) и B).
Пусть далее s'n—сумма всех положительных, a s"n—сумма
абсолютных величин всех отрицательных членов среди первых п
членов данного ряда; тогда
По условию, ап имеет предел сг; s'n и s^—положительные воз-
возрастающие величины, меньшие ст. Следовательно, они имеют пре-
пределы s' и s". Из соотношения sn — s'n—s"n следует, что и sn имеет
предел и этот предел равен s'—s", т. е. знакопеременный ряд A)
сходится.
Доказанная теорема дает возможность судить о сходимости
некоторых знакопеременных рядов. Исследование вопроса о схо-
сходимости знакопеременного ряда сводится в этом случае к иссле-
исследованию ряда с положительными членами.
Рассмотрим два примера.
Пример 1. Исследовать сходимость ряда
sinos , sin 2а , sin За , , sin па , ~
^Г-т р 1 з^ г"'" "• ^ г • • i W
где а—любое число.
Решение. Наряду с данным рядом, рассмотрим ряды
Isinot , sin2g[
b

РЯДЫ - ?ГЛ. 'XVI
+
Ряд E) сходится (см. § 6). Члены ряда D) не больше соответственных
членов ряда E); следовательно, ряд D) тоже сходится. Но тогда в силу
"Доказанной теоремы данный знакопеременный ряд C) тоже сходится.
Пример 2. 'Исследовать сходимость ряда
cos(jt/4) , cosCtt/4) , cosEft/4) , cos (Bл--1) я/4)
з h 32 t 35 f"**;*1 3^
Решение. Наряду с данным рядом, рассмотрим ряд
Этот ряд сходится, так как он является убывающей геометрической про-
прогрессией со знаменателем 1/3. Но тогда сходится и заданный ряд F), так как
абсолютные величины его членов меньше соответствующих- членов ряда G).
Заметим, что признак сходимости, доказанной выше, является
только достаточным признаком сходимости знакочередующе^
гося ряда, но не необходимым: существуют такие знакоперемен-
знакопеременные ряды, которые сами сходятся, но ряды, составленные из
абсолютных величин их членов, расходятся. В связи с этим
полезно ввести понятия об абсолютной и условной сходимости-
знакопеременного ряда и на основе этих понятий классифици-
классифицировать знакопеременные ряды.
Определение. Знакопеременный ряд
Wi4-«2 + tt3+--+^+ ... ^ A)
называется абсолютно сходящимся^ если сходится ряд, составлен-
составленный из абсолютных величин его членов:
\Ui\ + \uz\ + \u3\+...+\un\+.r. , _ B)
Если же знакопеременный ряд A) сходится, а ряд B), состав-
составленный из абсолютных величин его членов, расходится, то дан-
данный знакопеременный ряд A) называется условно или неабсо-
лютно сходящимся рядом.
Пример 3. Знакопеременный ряд 1 —-«Г+-О-—x~t~ • • • является У с-
ловно сходящимся, так как ряд, составленный из абсолютных величин его
членовi есть гармонический ряд ^+^""Ь"з"+"^~*# *» который расходится.
Сам же ряд сходится, что легко проверить с помощью признака Лейбница.
Пример 4. Знакопеременный ряд 1—оГ+оГ—4Г~Ь*** есть Ряд абсо-
лютно сходящийся, так как ряд, составленный из абсолютных величин его
членов 1+ог+"о7+Г+"*' сходится, как это было установлено в § 4.
?\ о\ 4! *

S в] " ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
С помощью понятия абсолютной сходимости теорему 1 часто
формулируют следующим образом: всякий абсолютно сходящийся
ряд есть ряд сходящийся.
В заключение отметим (без доказательства) следующие свой-
свойства абсолютно сходящихся и условно сходящихся рядов.
Теорема 2. Если ряд сходится абсолютно, то он остается
абсолютно сходящимся при любой перестановке его членов. При
атом сумма ряда не зависит от порядка его членов.
Это свойство не сохраняется для условно сходящихся рядов.
Теорема 3. Если ряд сходится условно, то, какое бы мы
ни задали число А, можно так переставить члены этого ряда,
чтобы его сумма оказалась в точности равной А. Более того,*
можно так переставить члены условно сходящегося ряда, чтобы
ряд, полученный после перестановки, оказался расходящимся.
Доказательство этих теорем выходит за рамки данного курса.
Его можно найти в более подробных учебниках (см., например,
Фихтенгольц Г. М. Курс дифференциального и интегрального
исчисления, т. П.— М.: Физматгиз, 1962, с. 319—320).
Для иллюстрации того, что сумма условно сходящегося ряда
может меняться при перестановке его членов, рассмотрим сле-
следующий пример.
Пример 5. Знакопеременный ряд
сходится неабсолютно. .Обозначим его сумму через s. Очевидно, что s > 0.
Сделаем перестановку членов ряда (8) так, чтобы кза одним положительным
членом следовали два отрицательных;
Та о "Б 5 Г*в '
2fc—i 46—2
ы i у ^ ¦ i >/m, ^ ¦ ^———v— t •«
Докажем,- что полученный ряд сходится, но что его сумма s' в два раза
меньше суммы ряда (8), т. е. равна -^-s. Обозначим через sn и s^ частичные
суммы рядов (8) и (9). Рассмотрим сумму Zk члейов ряда (9);
1
Следовательно,
lim slk = lim т s2k = т s.

266 ряды *гл. xvi
Далее,
Iims3fe+i
3fe+i~lim ( s'zk + кгта )—Тs
fe-*o
Таким образом, получаем
1. V , I r
hm sn = s =-о" s.
Итак, в данном случае сумма ряда изменилась после перестановки его
членов (уменьшилась вдвое).
§ 9. Функциональные ряды
Ряд
называется функциональным, если его члены являются функция-
функциями от х.
Рассмотрим функциональный ряд
ut (х) + и2 (х) + и3 (х) + . •. + ип (х) + ¦;. A)
Давая х определенные числовые значения, мы получаем раз-
различные числовые ряды, которые могут оказаться сходящимися
или расходящимися.
Совокупность тех значеций л:, при которых функциональный
ряд сходится, называют областью сходимости этого ряда.
Очевидно, что в области сходимости ряда его сумма является
некоторой функцией от х. Поэтому сумму функционального ряда
обозначают через s(x).
Пример. Рассмотрим функциональный ряд
Этот ряд сходится при всех значениях х в интервале (—I, 1), т. е. при
всех х, удовлетворяющих условию \х\ < 1, Для каждого значения х в интер-
интервале (—1, 1) сумма ряда равна -. (сумма убывающей геометрической про-
1 ™~— X
грессии со знаменателем х). Таким образом, в-интервале (—lt 1) данный ряд
определяет функцию
которая является суммой ряда, т. е»
Обозначим через sn(x) сумму первых п членов ряда A). Если
Этот ряд сходится и сумма его равна s(x), то

S lOJ . МАЖОРИРУЕМЫЕ РЯДЫ 267
где гп(х) есть сумма ряда un+i(x) + un+2(x)+...9 т. е.
В этом случае величина гп (х). называется остатком ряда A).
Для всех значений х в области сходимости ряда имеет место
соотношение limsn(x) = s(x), поэтому
lim rn (x) = lim [s (х) — sn (x)] = 0,
П->0О tt->0O
т. е. остаток гп(х) сходящегося ряда стремится к
нулю при п—>оо.
§ 10. Мажорируемые ряды
Определение. Функциональный ряд
ui(x) + u2(x) + uz[(x)+...+un(x)+..? A)
называется мажорируемым в некоторой области изменения х,
если существует такой сходящийся числовой ряд
с положительными членами, что для всех значений х и& данной
области выполняются соотношения г ,
Иначе говоря, ряд называется мажорируемым, если каждый его
член по абсолютной величине не больше соответствующего члена
некоторого сходящегося числового ряда с положительными чле-
членами.
Например, ряд
cos х , cos 2х , cos Зх * . , cos пх ,
—I • ""IP ' з^"""""^ ' * * ' д2 •" • • •
есть ряд, мажорируемый на всей оси Ох. Действительно, для
всех значений х выполняется соотношение
1 COS ПХ 1 < 1 /ni о ч
а ряд
1 д. 4 л. ! л.
Т "*"3" ' З5" ' #' '*
как известно, сходится.
Непосредственно из определения следует, что ряд, мажори-
мажорируемый в некоторой области, абсолютно сходится во всех точках
этой области (см, § 8). Кроме того, мажорируемый ряд обладает
еще следующим важным свойством.

268 ^ ряды |гл. *
Теорема,. Пусть функциональный ряд
их (х)+и%(х\+ ...+ип (х)+ .. ¦
мажорируем на отрезке [а, ft]. Пусть s(x)—сумма этого ряда,
sn(x)—сумма п первых членов этого ряда. Тогда для каждого» как
угодно малого числа ё > О найдется положительное число N такое,
что при всех n^N будет выполняться неравенство
\s(x)—sn(x)[<e9 .
каково бы ни, было х из отрезка \[а, ft].
Доказательство. Обозначим через а сумму ряда <2): .'
тогда
где ап—сумма п первых членов ряда B), а гп—сумма всех
остальных членов этого ряда, т. е.
Так как этот ряд сходится, то
lim ап = а
и, следовательно,
lira гп = О*
Представим теперь сумму функционального ряда A) в виде
где
sn(x)=Ut(x)+...+un(x)9
Из условия C) следует, что
и поэтому
для всех-л: из рассматриваемой области.
Таким образом, »
\$(x)—sn(x)\<en
для всех л: из отрезка [a, ft], причем гп—>0 при п—*-оо.
Замечание 1. Полученный результат можно геометрически
иллюстрировать следующим образом.
Рассмотрим график функции y = s(x). Построим около этой
кривой полосу шириной 2е„, т. е. построим кривые yz=s(x)-\-en

НЕПРЕРЫВНОСТЬ СУММЫ РЯДА
и y=zs(x)—гп (рис. 363). Тогда при любом е„ график функции
sn (x) будет лежать целиком в рассматриваемой полосе. В этой же
полосе будут лежать графики всех последующих частичных сумм.
Замечание 2. Не вся-
всякий функциональный ряд, ^
сходящийся на отрезке [а,
6], обладает свойством, ука-
указанным в доказанной теоре-
теореме. Но существуют и нема-
жорируемые ряды, которые
обладают указанным свойст-
свойством. Всякий ряд, обладающий
указанным свойством, назы-
называется равномерно сходящим-
ся рядом на отрезке [а, 6].
Итак, функциональный
ряд . и± (х) + щ (х) + ...
• • • + ип(х) + • • • называется равномерно сходящимся на отрезке
V
->-&
Рис. 363.
+ n() + рр щ р
[а, Ь], если для любого как ^угодно малого е > 0 найдется такой
номер N, что при всех n^N будет выполняться неравенство
\s(x)-sn(x)\<B
для любого х из отрезка [а, 6].
На основании доказанной теоремы следует, что мажорируемый
ряд является рядом, равномерно сходящимся.
§ П. Непрерывность суммы ряда
Пусть имеем ряд из непрерывных функций
сходящийся на некотором отрезке [а, 6].
В главе 1Мт. I) мы доказали теорему о том, что сумма ко-
конечного числа непрерывных функций есть функция непрерывная.
Для суммы ряда (состоящего из бесконечного числа слагаемых)
это свойство не сохраняется. Некоторые функциональные ряды
с непрерывными членами имеют в качестве суммы непрерывную
функцию, у других функциональных рядов с непрерывными чле-
членами сумма является разрывной функцией.
Пример. Рассмотрим ряд
Члены это.го ряда (каждый из них заключен в скобки) суть непрерывные
функции при всех значениях х. Докажем, что этот ряд сходится и его сумма
есть»разрывная функция.
Найдем сумму п первых членов этого ряда: $п==хг^2п+1^—х. Найдем
сумму ряда:

270
вяды
€СЛИ X > О, ТО
s= Iimsn(A:)= lim
если д: < 0, то
s= limsrt(x) = lim (-J)
n-*co /г->оо
если *=0, то sn = 0, и поэтому s= limsrt = 0.
П->оо
Таким образом^ имеем
s (^) =—1 —л: при х < О*
s(*) = 0 при л;=0,
s (д:) = 1 —д? при х > О*
Итак, сумма приведенного ряда есть функция разрывная. Ее трафик изображен
на рис. 364, где показаны также графики частичных гумм s*(#), s2>(x) иD
-/-а? для х<0
О для (в—О
1-х для з}>0
Рис. 364,
Для мажорируемых рядов спрредлива следующая теорема.
Теорема. Сумма ряда непрерывных функций, мажорируе-
мажорируемого на некотором отрезке [а, 6], есть функция, непрерывная
на этом отрезке.
Доказательство. Пусть имеем мажорируемый .на отрезке
[а, о\ ряд непрерывных функций
Иг(х) + и2(х)+и3(х)+.,. A)
Представим его сумму в виде
где
+ип(х),

НЕПРЕРЫВНОСТЬ СУММЫ РЯДА 2TV
Возьмем на отрезке [а, Ь\ произвольное значение аргумента х
и придадим ему такое приращение Ах, чтобы точка #+Ах лежала
тоже на отрезке [а, Ь].
Введем обозначения
As = s (x+Ax)—s (х)г Asn = sn (x+Ax)—sn (x)t
тогда
откуда
\A\\A\\(+A)\ + \n{xy\. B)
Это неравенство справедливо для любого номера п.
Чтобы доказать непрерывность s(x), нужно показать, что при
любом наперед заданном и как угодно малом 8 > 0 найдется число
б > 0 такое, что при всех | Дл; | < б будет | As | < в.
Так' как данный ряд A) мажорируемый, то при любом наперед
заданном е>0 найдется такой но^ер N, что при всех n^Nf
и в частности при n=^Nt будет выполняться неравенство
I/>(*)|< в/3- C)
при любом х из отрезка [а, Ь]. Значение х-\-Ах лежит на отрезке
[а, 6] и потому выполняется неравенство
\rN(x+Ax)\<e/3. C')
Далее, при выбранном N частичная сумма s'N (x) есть функция
непрерывная (сумма конечного числа непрерывных функций)
и, следовательно, можно подобрать такое положительное число*8$
что для всякого Ал:, удовлетворяющего условию [ Д# | < б, выпол-
выполняется неравенство
На основании, неравенств B), C), C') и D) получаем-
т. е,
| As\ < е при | Д# | < б,N
а это и означает, что s(x) является непрерывной функцией в точке ж
(и, следовательно, в любой точке отрезка [а, Ь]).
Замечание. Из доказанной теоремы следует, что если сумма
ряда на каком-либо отрезке [а, Ь] разрывна, то ряд не мажорируем
на этом отрезке. В частности, не мажорируемым (на любом отрезке,,
содержащем тючку л; = 0, т. е. точку разрыва суммы ряда) является
ряд, приведенный в примере.

272. РЯДЫ : [ГЛ. XV?
Отметим, наконец, что обратное предложение неверно: сущест-
существуют ряды, не .мажорируемые на отрезке и, однако, сходящиеся
на этом отрезке к" "нейрерывной функции. В частности, всякий
равномерно сходящийся на отрезке [а, Ь] ряд (даже если он не
мажорируем) имеет в качестве, суммы непрерывную функцию
(конечно, если все члены ряда непрерывны).
§ 12. Интегрирование и дифференцирование рядов
Теорема 1. Пусть имеем ряд непрерывных функций
2(х) + . •. +ип(х)+ ..., A)
мажорируемый на отрезке [а, Ь\ и пусть s (x) есть сумма этого
ряда. Тогда интеграл от s(x) в пределах от а до х, принадле-
принадлежащих отрезку [а, Ь\ равняется сумме таких же интегралов
от членов данного ряда, т. е.
= S u±(t)dt+ $ u,(t)dt + ... + J utt(t)dt + ...
а а а
Доказательство. Функцию s(x) можно представить в виде
six) = sn(x) + rn(x),
или
s(x)^ui(x) + u2(x)+...+un(x) + rn(x).
Тогда
XX X X X -
J s(t)dt= $Ul(t)dt+ $ u2(t)dt+... + J utt(t)dt)+ $ ra(t)dt B)
a a a a a
(интеграл от суммы конечного числа слагаемых равен сумме
интегралов от этих слагаемых).
Так как исходный ряд A) мажорируем, то при любом* имеем
| тп (х) | < в„, где гп —*0 при п —^ оо. Поэтому *)
X
\rh{t)dt
a
a
Так как гп—*0, то
х
lim
Но из равенства B) получаем:
х х
*) В приводимых ниже оценках при a < х берется знак +, а при х < се —
знак —•

$ I2J< ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ РЯДОВ 273:
Следовательно,
lira
ИЛИ
Hm \it4(t)dt+... + {uu(t)dt\=ls(t)dt. C)
Сумма, стоящая в квадратных скобках, есть частичная сумма ряда
n(t)dt+... D)
a a
Поскольку частичные* суммы этого ряда имеют предел, этот ряд
х
сходится и^егр сумма в силу равенства C) равна }s(t)dt, т. е.
a
ххх х
а это и есть равенство, которое требовалось доказать.
Замечание 1. Если ряд не мажорируем, * то почленное
интегрирование ряда не всегда возможно. Это надо понимать в том
X ^
смысле, что интеграл j s (t) dt от суммы ряда A) не всегда рав^н
a
сумме интегралов от его членов (т. е. сумме ряда D)).
Теорема 2. Если ряд
-составленный из функций, имеющих непрерывные производные на
отрезке [а, 6], сходится на этом отрезке к сумме s(x) и ряд
..9 . F)
составленный из производных его членов^ мажорируем на том же
отрезке, то сумма ряда производных равна производной от суммы
первоначального ряда, яг. е.
Доказательство. Обозначим через F(x) сумму ряда F):
F(x) = dl
и докажем, что

РЯДЫ. 1гл. X.VI
• Так как ряд F) мажорируем, то на основании предыдущей
теоремы
х хх х
lF(t)dt=l «ИО dt+ S* u',{t)dt + ...
Производя интегрирование, будем иметь
= [ (*)—"i («)]+[w2 (*)—"г («)] + •••+[«. (*)—"»(«
/
Hq/jio условию
s(а) = uf (а) + u2 (а) + . • • +ип (а) +
каковы бы ни были числа х и а на отреаке [а, 6]. Поэтому
(O^ = s(x) — s(a).
Дифференцируя по а; обе части последнего равенства, получим
Таким образом, мы доказали, что при выполнения условий
теоремы производная от суммы ряда равна сумме производных
от членов ряда.
Замечание 2. Требование мажорируемости ряда производ-
производных является- весьма существенным, и его невыполнение может
привести к невозможности почленного дифференцирования ряда.
В подтверждение этого приведем, пример, мажорируемого ряда, не
допускающего почленного дифференцирования.
Рассмотрим ряд
sin 14х , sin 24х , sin 34х , < , sinn4x ,
Этот ряд сходится к непрерывной функции, так как он мажорируем
Действительно^ при любом х его члены по абсолютной величине
меньше членов числового сходящегося ряда с положительным»
членами ,
I > 1 I 1
Ь НЧ +
Напишем ряд, составленный из производных членов исходного
ряда:
cos х 4- 22 pos 2i%-f.., + л' cos п4

СТЕПЕННБ1Е РЯДЫ. ИНТЕРВАЛ СХОДИМОСТИ Жб
Этот ряд^расходится. Так, например, при х=*0 он превращается
в ряд
(Можно показать, что он расходится не только при ,#=,0.)
§ 13, Степенные ряды. Интервал сходимости
Определение 1. Степенным рядом называется функцио-
функциональный ряд вида
п + ..., A)
где а0, af, а2, .^., апУ ,..—постоянные числа, называемые коэф-
коэффициентами .ряда.
Областью сходимости степенного ряда всегда является некоторый
интервал, который, в частности, может вырождаться в точку. Для
того, чтобы убедиться в этом, докажем сначала следующую ?ео-
рему, очень важную для ясен теории степенных рядов.
- Теорема 1 (теорема Абеля). 1) Если степенной ряд
сходится при некотором значении х0, не равном нулю, то он
абсолютно сходится при всяком значении х9для которого \х | < | х01;
2) если ряд расходится при некотором значении х'о, то 'он
расходится при всяком х, для которого \х\>\х'0\.
Доказательство. 1) Так как по предположению1 числовой
ряд
а0+аг
сходится, то его общий член апХо—*0 при п—>оо,а это значит,
что существует такое положительное число М, что все члены ряда
по абсолютной величине меньше М.
Перепишем ряд A) в виде
+•.- C)
и рассмотрим ряд из абсолютных величин его членов:
К1+|вЛ||^| + |^||^|Ч...+|ая«||^Ч-- D)
Члены этого ряда меньше соответствующих членов ряда
При | х\ < | х0 [ последний ряд представляет собой геометрическую
прогрессию со знаменателем.
- < 1 и, следовательно, сходится.
хо I
как члены ряда D) меньше соответствующих членов ряда E),
то ряд D) тоже сходится, а это и^ значит, что ряд C) или A) схо-
^дится абсолютно. ,

276 РЯДЫ ?ГЛ. XVI
2) Теперь нетрудно доказать и вторую часть теоремы: пусть
в некоторой точке х'й ряд A) расходится. Тогда он будет расхо-
расходиться в любой точке х, удовлетворяющей условию |х|>|хо|.
Действительно, если бы в какой-либо точке х% удовлетворяющей
этому условию, ряд сходился, то в силу только что доказанной
первой части теоремы он должен был бы сходиться и в точке х'о,
так как |*il<|Jt|. Но это противоречит условию, что в точке
х'ь ряд расходится. Следовательно, ряд расходится и в точке х.
Таким образом, теорема полностью доказана.
Ряд сходится
Ряд расходится ' Ряд расходится
Рис. 365,
Теорема Абеля позволяет судить о расположении точек схо-
сходимости и расходимости степенного ряда. Действительно* если ~х0
есть точка сходимости, то весь интервал (—|л:0|, |л:0[) заполнен
точками абсолютной сходимости. Если х'ь—точка расходимости,
то вся бесконечная полупрямая вправо от точки | x'Q | и вся полу-
полупрямая влево от точки — \х'0\ состоят из точек расходимости.
Из этого можно заключить, что существует такое число /?,
что при \x\<R мы имеем точки абсолютной сходимости и при
|л:| > /?—точкиг расходимости. Таким образом, имеет место сле-
следующая теорема о строении области сходимости степенного ряда:
Теорема 2. Областью сходимости степенного ряда является
интервал с центром в начале координат.
Определение 2. Интервалом сходимости степенного ряда
называется такой интервал от —R до -\-R, что для всякой точки ху
лежащей йнутрй этого интервала, рйд сходится и притом^бсолютно,
а для точек ху лежащих вне его, ряд расходится (рис. 365). Число R
называют, радиусом сходимости степенного ряда.
На концах интервала (т. е. при x = R и при х = — R) вопрос
о сходимости или расходимости данного ряда решается индивиду-
индивидуально для каждого конкретного ряда.
Отметим, что у некоторых рядов интервал сходимости вырож-
вырождается в точку (/?=0);у других охватывает всю ось Ox(R = <x>)..
Укажем, -способ определения радиуса сходимости степенного
ряда.
Пусть имеем ряд
ао + а1х+,а2&+ ... +art#n-f-.. • A)
Рассмотрим ряд, составленный из абсолютных величин его
членов:

- СТЕПЕННЙЕ РЯДЫ. ИНТЕРВАЛ СХОДИМОСТИ ?77
Для определения сходимбсти последнего ряда к (с -положитель-
-положительными членами!) применим признак Даламбера.
- Допустим, что .существует предел
Тогда по признаку Даламбера ряд F) сходится, если L\x\<\%
т! е. если )#|<1/L, и расходится, если L"|jd>h т. е. если
\x\>\/L.
Следовательно, ряд A) сходится абсолютно при |л;|<1/?.
Если же | х | > 1/L, то lim ff?±i= | x | L > 1, и ряд F) расходится;
* п -> со л
причем его общий член не стремится к нулю *). Но_тогда и общий
член дайного степенного ряда A) не стремитей к нулю, а это
значит на основании необходимого признака сходимости, что этот
степенной ряд расходится (при |x|>l/L).
i Из предыдущего следует, что интервал (— l/L, 1/L) есть интер-
интервал сходимости степенного ряда A), т. е.
R = 4- = Нт
L П^ОО
Аналогичным образом для определения интервала сходимости
можно пользоваться признаком Коши, и тогда
Hm У|а„Г
П-> со г
Пример I. Определить интервал сходимости ряда
1 _|_*4-*2+*3+... +хп+...
Решение. Применяя непосредственно признак Даламбера, получаем
lim
Следовательно, ряд сходится при |^| < I и расходится при |*| > I. На
границах же интервала (— 1, 1) исследование ряда с помощью признака Далам-
Даламбера невозможно* Однако непосредственно видно, что при х^тг * и при #=1
ряд расходится.
Пример 2, Определить интервал сходимости ряда
2х B*)а,B*)8*
*) Напомним, что при доказательстве признака Даламбера (см. § 4) мы
аружили, что если lim n + 1 >
довательно/ не стремится к нулю.
обнаружили, что если lim-^^ > 1, то общий член ряда возрастает и, слег
Ы ft -

278 РЯДЫ 1ГЛ. XVE
Решение. Применяем признак Даламбераз
Bх)п+1
lim
П-+
1 = lim
Bx)n
п
п
Ряд сходится, если \2х\ < 1, т. е. если \х\ < 1/2; при #=1/2 ряд сходится;
цри х — — 1/2 ряд расходится.
Пример 3. Определить интервал сходимости ряда
х% .хъ , , хп ,
Решение. Применяя признак Даламбера, получим
1= lim I-JL- 1 = 0 <!.
, lim 2»±? U lim
П -> оо I Ил I" я ->• оо
Так как предел не зависит от х и меньше единицы, то, значит, ряд сходится
при всех значениях х.
Примеру. Ряд
расходится при всех значениях х, кроме х=0, так как {пх)п —* оо при п —>- оо,
каково бы ни было х, отличное от нуля.
Теорема 3. Степенной ряд
.. < +апхп+.. s A)
мажорируем-кна любом отрезке [—р, р], целиком лежащем внутри
интервала сходимости.
Интервал сходамосты
¦+-
мажорирувтшП
Рис. 366.
Доказательство. По условию р < R (рис. 366), а потому
числовой ряд (с положительными членами)
2|р2+...+|ал|р»4-^.; % G)
сходится. Но при |#|<р члены ряда A) по абсолютной величине
не больше соответствующих членов ряда G). Следовательно, ряд
A) мажорируем на отрезке [—р, р].
Следствие 1. На всяком отрезке, целиком лежащем внутри
интервала сходимости^ сумма степенного ряда есть непрерывная
функция.
Действительно, на этом отрезке ряд мажорируем, а члены его
являются непрерывными функциями от х. Следовательно, на осно-
основании теоремы 1 § 11 сумма этого ряда есть непрерывная функция.

§14] ДИФФЕРЕНЦИРОВАНИЕ СТЕПЕННБ1Х РЯДОВ ,279
Следствие 2. Если пределы интегрирования а, Р лежат
внутри интервала сходимости степенного ряда, то интеграл от
суммы ряда равен сумме интегралов от членов ряда} так как
Рис, 367,
область интегрирование можно заключить в отрезок [— р, р], где
ряд мажорируем (рйс. 367) (см. теорему 1 § 12 о возможности
почленного интегрирования мажорируемого ряда).
§ 14. Дифференцирование степенных рядов
Теорема Г. Если степенной ряд
s(x) = aQ + a1x + a2x2 + a3xz + a±x*-{~... +апхп+ ¦.." A)
имеет интервал сходимости (—R, R), то ряд
Ф (х) ^а± + 2а2х+За3х2 +... + папхп~г + •.., B)
полученный почленным дифференцированием ряда A), имеет тот
же интервал сходимости (—R, R); при этом
y(x)~s' (x), если |*|</?f
m. e. внутри интервала сходимости производная от суммы сте-
степенного ряда A) равна сумме ряда, полученного почленным диф-
дифференцированием ряда A).
. \ }., 1 „ j ?—М 1 1Ч-" ¦>¦
Рис. 368
Доказательство. гДокажем, что ряд B) мажорируем на
любом отрезке [—р, р]„ целиком лежащем внутри интервала
сходимости.
Возьмем точку % такую, что р < ? < R (рис. 368). В этой точке
ряд A) сходится, следовательно, lim anln = Q, поэтому можно
п -> се
указать такое постоянное число М, что
К5Я|<Л! (п=1, 2, ...)•
Если |х|<р, то

280, рЯДЫ [ГЛ. XVf
где
Таким образом, члены ряда [B) при |л;|^р по абсолютной
величине меньше членов числового положительного ряда с посто-
постоянными членами
Но последний ряд сходится, в чем можно убедиться, применяя
признак Даламбера:
-1
Следовательно, ряд B) мажорируем на отрезке [—р, р], и на
"основании теоремы 2 § 12 его сумма есть производная от суммы
данного ряда на отрезке [—р, pj, т. е.
Г" <р (*) = «'(*).
Так как всякую внутреннюю точку интервала^—R, R)можно
заключить Ъ некоторый отрезок [—р, р], то отсюда следует, что
ряд B) сходится в любой внутренней точке интервала (—Rf R).
Докажем, что вне интервала (—R, R) ряд B) расходится.
Допустим, что ряд B) сходится при- xt> R. Интегрируя его
почленно в интервале @, х2), где R < хй < Xi, мы получили бы,
что ряд A) сходится в точке х^, а это' противоречит условиям
теоремы. Таким образом, интервал (—R, R) есть интервал схо-
сходимости ряда B). Теорема полностью доказана.
Ряд B) снова можно почленно дифференцировать и продол-
продолжать так сколь угодно раз. Таким образом, получаем вывод:
Теорема 2. Если степенной ряд сходится в интервале
(—Rf R)i то его сумма представляет собой фщщщо, имеющую
внутри интервала сходимости производные любого порядка, каж-
каждая из которых есть сумма ряда, получающегося в результате
почленного дифференцирования данного ряда соответствующее
число раз; при этом интервал сходимости каждого ряда, полу-
получившегося в результате дифференцирования, есть тот же интер-
интервал (-R, R).
§ 15. Ряды по степеням х — а
Степенньш рядом также называется функциональный ряд вида
а9+а1{х—аУ+аЛ(х—ау+...+ап(х^а)^+^.9 A)
где постоянные а0У at, ..., ап, ... также называются коэффициен-
коэффициентами ряда. Это—степенной ряд, расположенный по степеням
двучлена х—а.

$151 РЯДЫ ПО СТЕПЕНЯМ х-а 2Ш
При а = 0 получаем степенной ряд, расположенный по степе-
степеням ху который, следовательно, является частным случаем рядаA).
Для определений области сходимости ряда A) произведем
в,нем замену переменной'
' х—а = Х.
После этой замены ряд A) примет вид
"+.. -, B)
т. е. получили степенной ряд, расположенный по степеням X.
Пусть интервал—/? <X<R есть интервал сходимости ряда B)
(рис. 3695 а). Отсюда следует, что ряд A) будет сходиться при
Рис. 370.
значениях х, удовлетворяющих неравенству —R< х—а < R или
a—R<x<a+ R. Так как ряд B) расходится при |Х|>/?, то
ряд A) будет расходиться при |jc—а\ > R> т. е. будет расходиться
вне интервала a—R <^x<a+R (рис. 369, р).
Следовательно, интервалом сходимости ряда A) будет интервал
(а—Ry a~\-R) с центром в точке а. Все свойства степенного ряда,
расположенного по степеням х, внутри интервала сходимости
{—Ri -\-R) полностью сохраняются для степенного ряда, рас-
расположенного по степеням х—а, внутри интервала сходимости
(а—/?, a-{-R). Так, например, после почленного интегрирования
степенного ряда A), если пределы интегрирования лежат внутри
интервала сходимости (a — /?, a + R)y получается ряд, сумма кото-
которого равняется соответствующему интегралу от суммы данного
ряда A). При почленном дифференцировании степенного рядаA)
при всех л;, лежащих внутри интервала сходимости (a—R, a + R)t
получается ряд, сумма которого равняется производной от суммы
данного ряда A).
Пример. .Найти область сходимости ряда
(х-2) + (х-2)« + (*-2)»+.., + (др-2)» + ...
Решение. Положив х—2 = Х, получим ряд
ряд сходится при -г-1 < X < +1. Следовательно, данный ряд сходится
при всех jc, для которых —-Л < х—2 < 1, т. е. при 1 < jc <'3 (рис. 370).

282 РЯДЫ {ГЛ. XVI
§ 16. Ряды Тейлора и Маклорена
В § 6 главы IV (т. 1) было показано, что для функции f(x)t
имеющей все производные до (я + 1)-го порядка включительно,
в окрестности точки х = а (т. е. на'некотором интервале, содер-
содержащем точку х = а) справедлива формула Тейлора:
/(*) = /(а)
где так называемый остаточный член Rn (x) вычисляется по формуле
Если функция / (л;) имеет производные всех порядков в окрест-
окрестности точки х = а, то в формуле Тейлора число п можно брать
сколь угодно большим. Допустим, что в рассматриваемой окрест-
окрестности остаточный член Rn стремится к нулю при п—>ооа
lim ?„(*) = 0.
Тогда, переходя в'формуле A) к пределу при тг—><х>, получим
справа бесконечный ряд, который называется рядом Тейлора:
Последнее равенство справедливо лишь в том случае, если Rn (x) —> О
при п—>оо. В этом случае написанный справа ряд сходится и
его сумма равна данной функции f(x). Докажем, что это дейст-
действительно так 5
f(x)=Pn
где
Так как по условию lini Rn(x) = 0, то
f(x)= lim Р„(х).
П -> 00
Но .Рл(л;) есть п-я частичная сумма ряда B); ее предел равен
сумме ряда, стоящего в правой части равенства B). Следовательно,
-равенство B) справедливо:
/(*И/(а)+^
Из предыдущего следует, что ряд Тейлора представ-
представляет данную функцию /(л:) только тогдаг когда

$ 173 ПРИМЕРЫ РАЗЛОЖЕНИЯ ФУНКЦИЙ В РЯДЫ 883
Шп Rn (х) = 0. Если lim Rn (х) Ф 0, то ряд не представляет данной
функции, хотя может и сходиться (к другой функции).
Если в ряде Тейлора положим а = 0, то получим частный слу-
случай ряда Тейлора, который называют рядом Маклорена:
/(*)=/@)+тГ@)+4Г@)+...Ч"^Г->@) + ... C)
Если для какой-нибудь функции формально написан ряд Тей-
Тейлора, то чтобы доказать, что написанный ряд представляет дан-
данную функцию, нужню либо доказать, что остаточный член стре-
стремится к нулю, либо каким-нибудь иным способом убедиться, что
написанный ряд сходится к данной функции.
Отметим, что для каждой из элементарных функций, опреде-
определенных в §-8 главы 1 (т. I) существует такое а и такое R, что
в интервале (а—R, a + R) она разлагается в ряд Тейлора или
(если а = 0) в ряд Маклорена.
§ 17, Примеры разложения функций в ряды
1. Разложение функции f(x) = smx в ряд Макло-
Маклорена.
В § 7 главы IV (т. 1) мы получили формулу
Так как было доказано, что lim R2n (x) = 0, то на основании ска-
занного в предыдущем параграфе получаем разложение sin x в ряд
Маклорена:
Так как остаточный член стремится к нулю при любом х9
то данный ряд сходится и имеет в качестве суммы функцию sin x
при любом х.
На рис. 371 показаны графики функции sin л; и первых трех
частичных сумм ряда A).
Этим рядом пользуются для вычисления значений sin л: при
различных значениях х.
Вычислим, например, sin 10° с точностью до 10~"§. Так как 10°
или, в радианах, -^^ 0,174533, то
— ^ зГ (т§) +г(т8у'
sin
Ограничиваясь первыми двумя членами, получим следующее при-
приближенное равенство:

ряды
[ГЛ. XVI
при этом возникает погрешность 8, которая по'абсолютной вели-
величине меньше первого из отброшенных членов, т. е.
Если каждое слагаемое в выражении для sin щ будем вычис-
вычислять с шестью знаками, то получим:
sin (я/18) = 0,173647. -
За первые четыре знака- можно ручаться.
N
/
/
/
i
i .
\
\
\
\
\
\
\
\\
/
/
S
/
/
a
/
N >
\ у
\
V.
\2
\
\
\
\
\
1
J
1
6
r
\
9
Рис. 371,
• 2. Разложение функции /(х) = е*врядМаклорена.
На основании § 7 главы IV (т. I) имеем
так как было доказано, что lim Rn (x) = 0 для любого х. Следо-
п -> со
вательно, для всех значений х ряд сходится и представляет функ-
функцию е*.
Если в разложении B) заменить х на (—х), то получаем
е~* ;=.!_;
—
2!
—
31
C)

|UJ ФОРМУЛА ЭЙЛЕРА 285
3, Разложение функции /(#) = cos* в .ряд Макло-
рена. v
На основании § 7 главы IV (т. I) имеем
15 + S+! W
при всех значениях х ряд сходится и представляет функцию cos к.
4. Разложение функций
в ряд Маклорена.
Разложение этих функций ле^ко получается путем вычитания
и сложения рядов B) и C) и деления на два.
Итак,
il
§18, Формула Эйлера
До сих Пор вдк рассматривали только ряды с действительными
членами/не затрагивая рядов с комплексными членами. Не при-
приводя полной теории рядов с комплексными членами, которая
выходит за райки данного учебника, рассмотрим" только один
важный пример из этой юбласти.'
В главе VII (т. I) была определена функция ex+if равенством
ех + iy _- ех
При л: = 0 прлучаем формулу ЭйЛера:
Если определить показательную функцию № с мнимым пока-
показателей с помощью формулы B) § ,17, дающей представление
функции & в виде степенного ряда, то мы получим то же равен-
равенство Эйлера. Действительно, определим eiy, положив в равенстве
B) § 17 вместо х выражение iy:
Принимая • во внимание, что ta = —1, i% — — i, l*=l, Vi — lf
?6 = — 1 и т. д., преобразуем формулу A) к виду
* ~1^ 1! 2! 3! +4! ^ 5!

.РЯДЫ ЕГЛ. XVT
Отделяя в этом ряде действительную и мнимую части, найдем
е*в = [ 1 _i- + - „.. J + i [-JJ-—3f +-gj • • • J •
В скобках стоят степенные .ряды, суммы которых равны соответ-
соответственно cost/ и sin у (см. формулы C)-и A) предыдущего параг-
параграфа). Следовательно,
№ = cos y+i sin у. B)
Таким образом, мы пришли снова к формуле Эйлера.
§ 19. Биномиальный ряд
§ р
, Разложим в ряд Мак лорена'функцию
/ММ1+)-
1
где m—произвольное постоянное число.
Здесь оценка остаточного члена представляет некоторые труд-
трудности и потому к разложению данной функции мы подойдем не-
несколько иначе.
Заметив, что функция f(x) = (l+x)m удовлетворяет дифферен-
дифференциальному уравнению -
Ц+х)Г(х)=тНх) A)
и условию
найдем степенной ряд, сумма которого s(x) удовлетворяет урав-
уравнению (J) и условию s @) = 1:
s(x)=l+a1x + a2x*+...+anx»+...*). B)
Подставляя его в уравнение A), получим " -
х)
Приравнивая коэффициенты при одинаковых степенях х в разных
частях равенства, находим
Отсюда для коэффициентов ряда получаем выражения:
_ а2(т—2) __ /n(m~-l)(m~-2)
2-3
... [m—(л—1)]
1-2. „../г
*) Мы приляли свободный чйен ра&ньш единиц в силу начального уело-
вия s@) = l.

БИНОМИАЛЬНЫЙ РЯД ' Щ
Это—биномиальные коэффициенты.
Подставляя их в формулу B), получим
C)
Если m—целое положительное число, то, начиная с члена,
содержащего хт+*, все коэффициенты равны нулю, и ряд превра-
превращается в многочлен. При т дробном или при т целом отрица-
отрицательном имеем бесконечный ряд. Определим радцус сходимости
ряда C):
_ m(m—l)...(m—/t+lX _ rm(m—i)...(m—n+2)
Таким образом, ряд C) сходится при |#|<1.
В интервале (—1, 1) ряд C) представляет функцию s (pc)f удо-
удовлетворяющую дифференциальному уравнению A) и условию
в@)=1.
Так как дифференциальному уравнению A) и условию s@)=l
удовлетворяет единственная функция, то, следовательно, сумма
ряда C) тождественно равна функции A+х)т»н мы получаем
разложение
^^ от(т1^2).. C')
Б частнорти, при' /л = —1 получаем
Ь^=1-*+*2-*3+-- D)
При tn = -x будет
При т = — -к- имеем
2. Применим разложение бинома к разложейию^ других функ-
функций. Разложим & ряд МаКлорена функцию ~ '

(гл.
Подставляя в равенство F) вместо х выражение — х2, • получим
1 -1 1 !хМ ьз^ 1 b3'Vl 1 *-3.5.....B»-1)хз„ ,
2.4.6" -Т-----Г 2.4-6. ....2л
На основании теоремы об интегрировании степенных рядов
получаем при |л:| < 1:
l-3.5-...-Bn —
2-4-6.,.2
Этот ряд сходится в интервале (—1, 1). Можно было бы дока-
доказать, что ряд сходится и для л=±1 и что для этих значений
сумма ряда также равна arcsinx. Тогда, полагая jc=1, мы полу-
получим формулу для вычисления я:
$ 20, Разложение функции 1пA+д:) в степенной ряд*
Вычисление логарифмов
Интегрируя равенство D) § 19 в пределах от 0 до л (при
| < 1), получим
или
Это равенство справедливо в интервале (—1, 1).
Если в этой формуле заменить х на —х, то получается ряд
который сходится в интервале (—1, 1).
С помощью рядов A) и B) можно вычислять логарифмы чисел,
заключенных между нулем и двумя. Отметим, без доказательства,
что при %=1 разложение A) также справедливо.
Выведем формулу для вычисления натуральных логарифмов
любых целых чисел. . >
Так как при почленном вычитании»* двух сходящихся рядов
получается ряд сходящийся (см. § 1, теорему 3), то, вычитая

РАЗЛОЖЕНИЕ ФУНКЦИИ In A+х)
почленно равенство B) из равенства A), находим ,
Положим далее, j—= ^^; тогда х^^р^. При любом
п > 0 имеем 0 < х < 1, поэтому
1п1+*-1пп+1-2Г * 1 * 1 * 1
откуда
При п=*1 отсюда получаем
Для вычисления In 2 о заданной степенью точности б надо
подсчитать частичную сумму sp, выбрав число р ее членов так,
чтобы сумма отброшенных членов (т. е. погрешность Rpf совер-
совершаемая при замене $ на sp) была меньше допустимой погреш-
погрешности б. Для этого оценим погрешность Rp:
В 2 Г * 1- 1 1 ! Л 1
Так как числа 2/Н-З, 2р + 5, ... больше 2р+1, то, заменяя
их на 2р+1> мы Увеличим каждую дробь. Поэтому
или
Ряд, стоящий в квадратных скобках, есть геометрическая про-
прогрессия со знаменателем -^. Подсчитывая сумму этой прогрес-
сии, найдем
Если мы хотим теперь подсчитать In 2, например, с точностью
до 0,000000001, то надо выбрать р так, чтобы было Rp <
< 0,000000001. Этого можно добиться, подобрав р так, чтобы
правая часть неравенства была меньше 0,000000001. Непосред-
Непосредственным подбором находим, что достаточно взять /? = 8. Итак,
10 Н. G. Пискунов, v. 2

29Q РЯДЫ. 1ГЛ. KV»
с точностью до 0,000000001 инеемг
ln2«b = 2|TV.
+TF3ir+-T^r I -0,693147180.
Итак, In 2 = 0,693147180. При этом эти девять знаков верные.
Полагая в формуле C) п = 2, получаем
1,098612288 и т. д.
Таким- ©бравом, мы можем получить н&туралыгеке
любых целых чисел.
Чтобы получить десятичные дагарйфмк. чисел, нужна
воспользоваться (см. § 8 гл. И т. 1) еоотношением
где М = 0,434294. Тогда, например^ псшучим
= 0,434294.0,69$147== 0,30105ft.
§ 21. Вычисление определенных интегралов е помощью рядов
В главах X и XI (т. I) было указано, чта существуют- опре-
определенные интегралы, которые как" функции верхнего предела не
выражаются в конечном виде через элементарные функции. Такие
штегралы иногда бывает удобно вычислять а помощью рядов*
Рассмотрим здесь несколько примеров.
1. Пусть требуется, вычислить интеграл
Здесь первообразная от e~* не является элементарной функцией*
Для вычисления этого интеграла, разложим педынтегральн^ро
функцию в ряд, заменяя в разложении е* (см. формулу B) § 17)
эс на —х2}
e-*zl Ф 4
Интегрируя обе части этога равенства & пределах от 0 до
получим

ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ у§\
С помощью этого равенства мы можем при любом а вычислить
данный интеграл с любой степенью точности.
2. Требуется1 вычислить интеграл
^dx.
Разложим подынтегральную функцию в ряд: из равенства
#3 X? X7
х+
цолучаем
sin х __ « х2 ,х* Xs .
причем последний ряд сходится при всех значениях jp. Интегрируя
почленно, получим
а
fsinx Л*, — » * Ъ Г
Сумма ряда легко вычисляется с любой степенью точности при
любом а.
3. Вычислить эллиптический интеграл
2
Разложим подынтегральную функцию в ^биномиальный ряд,
положив т == ^, x — — k* sin2 q> (см. формулу E) § 19):
*
Этот ряд сходится при всех значениях *<р я допускает почленное
интегрирование, так как он мажорируем на любом интервале.
Поэтому
to*

292 РЯДЫ ?ГЛ. XVI
Интегралы, стоящие справа, вычисляются элементарно. При
Ф = ~ имеем
Я/2
(см. § 6 гл. XI т. I) и, следовательно,
т- ¦¦]
§ 22. Интегрирование дифференциальных уравнений
с помощью рядов
Если интегрирование дифференциального уравнения не сво-
сводится к квадратурам, то прибегают к приближенным методам:
интегрированця уравнения. Одним из таких методов является
представление решения уравнения в виде ряда Тейлора; сумма
конечного числа членов этого "ряда будет приближенно равняться
искЬкЬму частному решению.
Пусть, например, требуется найти решение дифференциального
уравнения второго порядка
iT = F(*f у, у% A)
удовлетворяющее начальным условиям
yQ[ у'\х=Х9 = у1 B)
Допустим, что решение y — f(x) существует и представимо
в виде ряда Тейлора (мы не будем останавливаться #а вопросе,
при каких условиях это имеет место):
^^ C)
Нам нужно найти f(xb), f (x0), f(*0), •••> т, е. значения
производных от частного решения при х = х0. Но это можно сде-
сделать при помощи уравнения A) и условий B).
Действительно, из условий B) следует
из уравнения A) получаем
f'W = /U = /7fe у» yl).
Дифференцируя обе части уравнения (I) по х:
x, yf yr)y'^Fyt(x} у. /)/ D)

§22] ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
и, подставляя значение х—'х0 в правую часть, найдем
Дифференцируя соотношение D) еще раз, найдем
и т. д.
Найденные значения прризводных подставляем в равенство C),
Для тех значений х, для которых этот ряд сходится, он пред-
ставляет решение уравнения.
Пример 1. Найти решение уравнения
удовлетворяющее начальным условиям
Решение. Имеем
Из данного уравнения находим #"U=o = /"(O) = Q; далее,
и, вообще, дифференцируя k раз обе части уравнения по формуле Лейбница,
находим (§ 22 гл. III т. I)
Положив х = 0, будем иметь
или, полагая + ,
j,<"> =- (»-3) («-2) yin-*\
Отсюда
^12>«=— 9.10^8)=(— 1KA -2) E-6) (9-10),
;.; *
|A4fc> = (—1)*ЧЬ2).E.6).(Э.10)....-[DЛ—3)DЛ—2>Ь
.«...,,»** , . . •
Кроме того,
Таким образом, в нуль не обращаются только те производные, порядок
которых кратен четырем.
Подставляя найденные значения производных в ряд Маклорена., получаем*
решение уравнения

294 РЯДО [ГЛ. КШ
С помощью признака Дзламберя можно проверить, что этот ряд сходится
при всех значениях х\ следовательно, он является решением уравнения.
Если уравнение линейное, то удобнее искать коэффициенты
разложения частного решения по методу неопределенных коэф-
коэффициентов. Для этого непосредственно «подставляем» ряд
в> дифференциальное, уравнение и приравниваем коэффициенты,
стоящие при одинаковых степенях х в раакьиг частях уравнешш*
Пример 2. Найти решение уравнения
удовлетворяющее начальным условиям
Решение. Полагаем
На основании начальных условий находим %=0, %
Следовательно,
Подставляя написанные выражения в заданное уравнение и приравнивая
коэффициенты при одинаковых степенях х, получаем
2а2==0, откуда а2==0,
откуда а8— lf
откуда а4=0,
п (я— 1) an=(n~2)>2а„_2+4&/Г.2> откудаап^ ^"р
Следовательно^
Подставляя найденные коэффициенты, получаем искомое решение
Полученный ряд сходится при всех значениях х.
Заметим, что найденное частное, решениег можно * выразить через, элементар-
элементарные функции: вынося х за скобку, получим в скобках разложение функ-
функции е*2. СледовательнО|

УРАВНЕНИЕ БЕССЕЛЯ
§ 23. Уравнение Бесселя
Уравнением Бесселя называется дифференциальное уравнение
вида
. A)
Решение этою уравнения, как и некоторых других уравнений
с переменными коэффициентами, следует искать не в форме сте-
пеннбго ряда, а в виде произведения некоторой степени х на
степенной рйд:
Коэффициент ай мы можем считать отличным от нуля ввиду
неопределенности ^показателя г*
Перепишем выражение B) в виде
tea
и найдем его производные:
у' = 2 (г + к) щ?**-\ у" - 2 (г + к) (г + к -
Подегашпя зхй выражшля ^ ураюение <1):
-/?2) 2
Приравнивая лулю коэффициенты лри х в стегшни г, г
2 Ц* получаем систему уравнений
[Г(Г—1) + Г—^JiZo=X), ИЛИ (Г2_р2)ао==
~р2]а? = 0, или
^0, или [
Рассмотрим равенство
[(г+А)«-/»«За,+в»., = О. C')
Его можно переписать так:

РЯДЫ 1Щ. XV?
По условию а^ФО; следовательно,
поэтому Г|==р или г2 = — Pi
Рассмотрим сначала решение в случае г* = р>0/4
Из системы уравнений C) последовательно определяются все
коэффициенты аь а2, ...; а0 остается произвольным.; (Положим,
например, а0 = 1. Тогда
а
а*~ kBp+k)*
Придавая различные значения k, найдем
0i = O, л8 = 0 и вообще
a2v = (— l)v+ l 2.4.б.... -2v Bp+2) Bp+4).. .Bp+ 2v) » *##
Подставляя найденные коэффициенты в формулу B), получим
Все коэффициенты ^2v oпpeдeлятcяt так как при всяком k
коэффициент при ак в уравнении C)
будет отличен от нуля.
Таким образом, yt является частным решением уравнения A).
Установим далее условия, при которых и при втором корне
г8 = — р определятся все коэффициенты ак. Это будет,, если при
любом целом четном положительном к выполняются неравенства
{гг + Щ*-р*ф0, F)
или
Но p = rif следовательно,
Таким образом, условие F) в этом случае, эквивалентно сле-
следующему:
П—г%Фк,
где k—целое четное положительное число. Но

^ 23j УРАВНЕНИЕ БЕССЕЛЯ Щ7
следовательно,
Таким образом, если р не равно целому числу, то можно напи-
написать второе частное решение, которое получается из выражения E)
заменой р на—р:
' • • J •
Степенные ряды E) и E') сходятся при всех значениях ху что
легко обнаружить на основании признака Даламбера. Также оче-
очевидно, что yt й у2 линейно независимы*).
Решение уи умноженное на некоторую постоянную, называется
функцией Бесселя первого рода р-го порядка и обозначается сим-
символом Jp. Решение у2 обозначают символом J_p.
Таким образом, при /?, не равном целому числу, общее реше-
решение уравнения A) имеет вид
Так, например, при р=1/2 ряд E) будет иметь ввд
у/, [~1 —4 ^ *6 I 1 _
х I1 2.3^2*4-3-5 2.46*35.7^^ .. # j ™
1 Г. ^J-fl ^
Т1 ^ + 5!~7Г
Это решение, умноженное на постоянный множитель У1^, назы-
называется бесселевой функцией /i/2; заметим, что в скобках стоит
ряд, сумма которого равна sin*. Следовательно,
Точно так же, пользуясь формулой E'), получим
Общий интеграл уравнения A) при р=1/2 будет
У = Ci/l/t (д:) + С2/.1/2 (х).
*) Линейная независимость функций проверяется следующим образом.
Рассмотрим отношение
2Т4 (-
У* ^-з
' * * '
Это соотношение не является постоянным, так как при х—*0 оно стремится
к бесконечности. Следовательно, функции у\ и у2 линейно независимы.

298 РЯДЫ • ?гл.
Пусть, далее, р есть целое число, которое оббэштш через
п(/г^0). Решение E) в этом случае будет иметь смысл и яв-
является первым частным решением уравнения A).
• Но решение E') не будет иметь смысла, так как один из мно-
множителей знаменателя в разложении обратится в нуль.
При целом положительном р = п бесселева функция Jn опре-
определяется рядом E), умноженным на постоянный множитель -^f
(а при /г = 0 умноженным на 1):
2«nl I 2{2/г+2) ^2-(+)(+)
# # * J *
2.4-6 {2п+2) B/1+4) B/i+Q
Можно показать, что второе частаое решение в тш
нужно искать в форме
Подставляя это выражение в уравнениеД1), мы определим коэф-
коэффициенты Ьк.
Функция Кп(х) g определенными таким образом коэффициен-
коэффициентами, умноженная на некоторую постоянную, называется функцией
Бесселя второго рода п-го порядка.
Это теть второе решение уравнения A), образующее с первым
линейно независимую систему.
Общий интеграл будет иметь вид
ytn() + Ju(x). (8)
1 Отметим, что
lira Кп(х)=оо.
#-> о
Следовательно, если мы хотим рассматривать конечные реше-
решения при х — 0, то в формуле (8) мы должны положить СЮ
Пример. Найти решение уравнения Бесселя при р=0
удовлетворяющее начальным условиям: при х=0
9=2, 4>' = 0.
Решение. На основании формулы G) иаходии одно частнве решение:
х\шм l (XY 1

РЯДЫ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ
Пользуясь этим решением, можно написать решение, удовлетворяющее
данным начальным условиям, а именно:
y = 2J0(x).
Замечаниие. Если бы нам нужно было найти общий интеграл данного
уравнения, то мы стали бы искать второе частное решение в форме
/to M = 'о (*)!**+2 ****•
Не приводя* веех вычислений, укажем, что. второе частное решение,, кото-
которое мы обозначим Ко (х), имеет вид
Эта функция, умноженная на некоторый постоянный множитель, называется
функцией Шесселя второго рода нулевого порядка*
§ 24. Ряды с комплексными членами
Рассмотрим последовательность комплексных чисел гь г&< ,92
*.., гпУ ..., rjfrzn = aH + ibn (n=l, 2, ...).
Определение Г. Комплексное число zQ = а + fS" называется
пределом последовательности комплексных чисел гп = а1Г-{* ibn^ если
Urn |г„— *в| = 0. A)
Л-* со
Напишем условие A) в развернутом виде:
гп-г^ {а^ iba)-{a+ib) = (ап-а) +1 Фп-Ь)>
lira 12,,-г.|= Ига V(an-af^{bn-bf »0. B)
На^ основании равенства B) следует, что условие A) будет выпол-
выполняться только тогда, когда будут выполняться* условия*
lim ял = а, lira &ft = 6. C)
Составим ряд из комплексных чисел
a>i-fa>2+ ...+wn+..., D)
рде
Рассмотрим сумму ^ членов ряда D), которую обозначим через sn:
$а есть комплеженое числа:
<! 4

300 РЯД!* 1ГЛ.
Определение 2. Если существует предел
lim sn = s =
то ряд D) называется сходящимся рядом и s называется его суммой:
s = ?wk = A + iB. . k G)
На основании равенств C) из условия F) следуют равенства
п п
А= lira S uk, B= lim 2»*. (8)
Если не существует lim snr то ряд D) называется расходящимся.
Для исследования сходимости ряда D) эффективной является
следующая теорема.
Теорема 1. Если сходится ряд, составленный из модулей
членов ряда D), , ..*
/по сходится ряд D).
Доказательство. Из сходимости ряда (9) и условий
следуют равенства (8) (на основании соответствук>щей теоремы об
абсолютной сходимости рядов с действительными членами), а еле-
довательна, равенство G).
Доказанная теорема позволяет применять для исследования
сходимости рядов с комплексными членами,все достаточные при-
признаки сходимости рядов с положительными членами,
§ 25. Степенные ряды с комплексной переменной
Перейдем теперь к рассмотрению степенных рядов с комплекс-
комплексными членами.
Определение 1. Ряд
с9+схг + с,?*+...+сяг»+Л.„ A)
где z — x + iy—комплексная переменная, х и у—действительные
числа, сп — постоянные комплексные или действительные числа,
называется степенным рядом, с комплексной переменной.
Для таких степенных рядов существует теория, аналогичная
теории степенных рядов с действительными членами.
Определение 2. Совокупность значений .г на плоскости
комплексной переменной, при которых ряд A) сходится, назы-
называется областью сходимости степенного ряда' A) (при каждом

СТЕПЕННЫЕ РЯДЫ С КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 301
конкретном значений г ряд A) превращается в числовой ряд
с комплексными членами типа D) § 24).
Определение 3. Ряд A) называется абсолютно сходящимся,
если сходится, ряд, составленный из модулей его членов,
^\+...+\cnz-\+... B)
Приведем без доказательства следующую теорему.
Теорема 1. Область сходимости степенного ряда с комплекс-
ными членами A) есть круг на плоскости комплексной перемен-
переменной г с центром в начале координат. Его называют кругом схо-
сходимости. В точках, лежащих внутри круга сходимости, ряд A)
сходится абсолютно.
Радиус круга сходимости R называют радиусом сходимости
степенного ряда. Если R—радиус сходимости степенного ряда A),
то пишут, что ряд сходится в области
\z\<R.
(Аналогично вопросу о сходимости степенного ряда с действитель-
действительной переменной, на концах интервала вопрос о сходимости ряда
в точках границы |г|=/? решается дополнительным исследованием.)
Заметим, что в зависимости от характера коэффициентов сп радиус
сходимости R может иметь любое значение от R = 0 до R = oo.
В первом случае ряд сходится только в точке г = 0, в последнем
случае ряд сходится при любом значении z.
Напишем равенство
f(z) = cQ + c1z+c2z^... +спг» +... C)
Если z будет принимать различные значения внутри круга схо-
сходимости, то функция f(z) будет принимать различные значения.
Таким образом, каждый степенной ряд с комплексной перемен-
переменной определяет внутри круга сходимости соответствующую функ-
функцию комплексной переменной. Это аналитическая функция ком-
комплексной переменной. Приведем примеры функций комплексной
переменной, определенных степенными рядами
с комплексной переменной.
Это показательная функция комплексной переменной. Если у = 0,
то формула D) превращается в формулу B) § 17. Если # = 0, то
получаем равенство A) § 18.
2) sin z — z fl-j^-51 il-L ## /5)
Это синус комплексной переменной. При t/ = 0 формула E) пре-
превращается в формулу A) § 17.
3) cosz=l— 4г+тг—!!¦ + ••• F)

ряды . {гл.
Это косище комплексной переменной. Если в формуле Щ справа
и слева вместо z подставить iz, то аналогично тому, «как это
делалось в § 18, получхш
G)
()
Это формула Эйлера для комплексного z. Если z—действительное
число, то эта формула совпадает с формулой B) § 18.
4)
Последние две фррмулы аналогичны формулам E) и<(§) § It и
с ними совпадают, если г ^=х<—действительное число.
На основании D), E), F), (8) и (9) путем сложения, вычита-
вычитания рядов, замены z на iz получаются следующие равенства:
* A0)
A2)
Отметим, что ряды D), E), F), (8), (9) сходятся при зсех Значе-
Значениях г, в чем легко убедиться на основании теоремы J данного
Параграфа и теоремы 1 § 24. Аналогично тому, как это делалось
в случае степенных рядов с действительной переменной, рассмат-
рассматриваются ряды х комплексной переменной по степеням 0—-г0, где
г0—некоторое комплексное число:
(z—zoJ+. • • +cn(z—zo)n+.. •, A4)
^—комплексные или действительные.постоянные. Ряд A4) при-
приводится к виду A) подстановкой z—20=tz*. Все свойства и тео-
теоремы, справедливые для ряда вида A), переносятся на ряд вида A4),
только центр круга сходимости ряда A4) находится*не вначале
координат, а в точке z0.
Если R—радиус сходимости ряда A4), то пишут: ряд схо-
сходится в области
\z—zo\<R.
§ 26. Решение дифференциального уравнения первого порядка
методом последовательных приближений (метод итераций)
В §§ 32—34 гл. ХШ были рассмотрены приближенное интег-
интегрирование дифференциальных уравнений и систем дифференциаль-
дифференциальных уравнений разностными методами. Здесь мы изложим другой
метод приближенного интегрирования дифференциального 7Рав

МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ 308
неиия» Отметши, что данное рассмотрение одновременно явится
доказательством теоремы о существований решения дифференциаль-
дифференциального уравнения (см. § 2 гл. XIII). Нам потребуется использовать
теорию рядов.
Пусть требуется найти решение дифференциального уравнения
!=/(*,*/), о)
удовлетворяющее начальному условию
У=Уо при х=х0. B)
Интегрируя члены уравнения A) в пределах от xQ до х и учиты-
учитывая, что #U=*<, = 4fo> получаем м
C)
3 последнем уравнении искомая функция у находится под знаком
интеграла, и потому это уравнение называется интегральным
уравнением.
Функция у^у(я), удовлетворяющая уравнению A) и началь-
начальным условиям B), удовлетворяет уравнению C). Очевидно, что
функция у=у(х), удовлетворяющая уравнению C), удовлетворяет
уравнению A) и начальным условиям {2).
Рассмотрим сначала метод получения приближенных- рещедий
уравнения A) при начальных условиях B).
Будем считать у0 нулевым приближением решения. Подставляя
в подынтегральную функцию в правой части равенства C) вместо
у значение #0, получим
х
Уг (*) = J / (*i Уо) d* + У о* D)
Эго есть первое приближенное решение дифференциального урав-
уравнения A), удовлетворяющее начальным условиям B).
Подставляя первое приближение у±(х) а подынтегральную
функцию в равенства ,C), получаем
х ,
х0
3ta второе приближение. Продолжаем этот процесс!
X
Уъ vv*^ \ I L**t Ь'г \х)\ U'*' * Уъ*
хь
** • ', г F)
yn{x)=lf[x,yn-i(x)

304- РЯДЫ * 1гл. xvi:
О том, какое приближение нужно взять, чтобы оно удовлетво-
удовлетворяло требованиям нужной нам точности, будет указано ниже.
Пример. Найти приближенное решение уравнения у'=х-{-у29 удовлет-
удовлетворяющее начальному условию Уо = 1 при я = 0.
Решение. По формуле D) получаем
и т; д.
§ 27. Доказательство существования решения
дифференциального уравнения. Оценка погрешности
при приближенном решении
Докажем далее следующую теорему.
Теорема. Пусть дано дифференциальное уравнение
и йачальное условие
У=Уо при х = х0. B)
Пусть f(xy у) и fy(x, у) непрерывны в замкнутой области Z),
D{xQ—a^x^xQ+a, уо—Ь^у^у0 + Ь} (рис. 372). C)
Toadh в некотором интервале
хо—1<х<хо + 1 D)
существует решение уравнения A), удовлетворяющее начальному
условию B); при этом решение единственно. Число I будет опре-
определено ниже.
Доказательство. Заме-
Заметим, что из того, что f(x, у)
и [у(х, у) непрерывна в замкну- *
той области D, следует, что су-
существуют такие постоянные
М > О и N > 0, что для всех
точек области выполняются со-
соотношения
1/(*. У)\<М, E)
Рис. 372. | f'y (x, у) | < N. F)

$27j СУЩЕСТВОВАНИЕ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 305^
(Это свойство аналогично свойству, указанному в § 10 гл. II.)
Число / в равенстве D)—наименьшее из чисел аи д|» т. е.
G)
Применим теорему Лагранжа к функции f(x,y} для двух произ-
произвольных точек Аг (х\ t/j) и Л2 (#; t/2), принадлежащих области D:
где yi < У] < у2, следовательно, | f'y (х, r\) | < N. Поэтому для любых
двух точек справедливо неравенство
\f(x, yj-f(x, yO\<N\y%-yi\*). (8)
Вернемся к равенству D) § 26. Из него получаем с учетом ра-
равенств E), D), G)
*' х
Н| \ (9)
Итак, функция t/=#i(x:), определенная равенством D) § 26 на
отрезке D), не выходит из области D.
Перейдем теперь к равенству E) § 26. Аргументы функции
f[x> УЛХ)\ не выходят из области D. Следовательно, можем на-
написать
X
Методом полной индукции можно доказать, что для любого п
\Уп-УА<Ьу A1)
если х принадлежит интервалу D).
Докажем теперь, что существует предел
lim yn(x)=y(x), A2)
Л->00
и функция у(х) удовлетворяет дифференциальному уравнению A)
и начальному условию B). Для доказательства рассмотрим ряд
*) Заметим, что если для некоторой функции F (у) удовлетворяется
условие
где у2 и yi—любые точки некоторой области, /(—постоянное число, то это
условие называется условием Липшица. Таким образом, установив соотноше-
соотношение (8), мы показали, что если функция f (х> у) имеет производную —, огра-
ограниченную в некоторой области, то она в этой области удовлетворяет условию
Липшица. Обратное утверждение может оказаться неверным.

30& РЯДЫ |гл; xvi
с общим членом ип^уп — уп_ъ при этом щ—уй* Очевидно* что
сумма п+1 членов этого ряда равна
Оценим члены ряда A3) по абсолютной величине:
-x4. A5)
На основании D), E) § 26 и F) находим
(берется знак +, если х0 < х9 и знак —, если х0 > *). Итак,
\Уш-i/i
Аналогично с учетом A6)t
X
= IS/И*.
Продолжая так и далее, найдем
Таким образом, для интервала | х — ^а | < / функциональный ряд A3)
мажорируем. Соответствующий числовой ряд с положительными
членами, которые больше абсолютных величин соответствующих
членов ряда A3), будет
!!?!™ + ... A9)
с общим членом vn==M—~-9 Этот ряд сходится, что. легко
обнаруживается по признаку Даламбера;
lim -ju-- lim
%,_x = lira -fi = 0< 1.

§-273 СУЩЕСТВОВАНИЕ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 307
Итак, ряд A3) мажорируем, следовательно, он сходится, Так как
члены его являются непрерывными. функциями, то он сходится
к непрерывной функции у(х). Итак,
Km v.i= lim уп = у(х), B0)
где у (х) — непрерывная функция. Эта функция удовлетворяем
начальному условию, так как для всех п
Докажем, что полученная функция у (х) удовлетворяет уравне-
уравнению A). Снова напишем последнее из равенств F) § 26:
4 BV)
Докажем, чтб
я я
J $ B2)
где у(х) определена равенством B0).
Предварительно заметим следующее. Так как ряд A3) мажо*
рируем, то из B0) следует, что для всякого е > 0 найдется та-
такое п, что будет |
1у-*ш\<*- B3)
С учетом B3) на всем интервале D) можем написать
х, y)dx-lf(x9 yn
Ho lim 8 = 0. Следовательно,
X X
lira | J f(Xf y)dx-\f{x, yn)dx\ **Ъ.
n->fl0 XQ X0
Из последнего равенства следует равенство B2).
Теперь, переходя в обоих частях равенства B1) 8 преде&у
при п-~>оо, получим, что ~у(х), определенная равенством B0),
удовлетворяет уравнению
х
B4)

ЗвГ РЯДЫ ?ГЛ. ХУ1
Как указывалось выше, отсюда следует, что найденная функ-.
ция у(х) удовлетворяет дифференциальному уравнению A) и на-\
чальному условию B).
Замечание 1. Пользуясь другими методами доказательства,
можно утверждать, что существует решение уравнения A), удов-,
летворяющее условиям B), если функция fix, #) непрерывная
в области D (теорема Пеано) *).
Замечание 2. Приемом, аналогичным тому, которым было
получено соотношение A8), можно показать, что погрешность при
замене решения у (х) его n-м приближением уп дается формулой
Пример. Применим эту оценку для пятого приближения^ решения
уравнения
при начальном условии у0 = 1 при х=0.
Пусть область D такова:
т. е. а =1/2, 6 = 1. Тогда М=3/2, ЛГ=2. Определяем, далее»
По формуле B5) получаем
У—Уь I
Заметим, что оценка <25) довольно грубая. В рассмотренном примере другими-
методами можно показать, что погрешность в десятки раз меньше.
§ 28. Теорема единственности решения :
дифференциального уравнения
Докажем далее следующую теорему.
Теорема. Если функция f(x, у) непрерывна и имеет непре-
непрерывную производную -J- в области D, определенную в § 27, то ре-
решение дифференциального уравнения,
1Ы = НХ>У) 0)
при начальном условии
У=Уо при x = xQ B)
*) См., например, книгу: Петровский И. Г. Лекции по теории
обыкновенных дифференциальных уравнений.—М.: Наука, 1970.

§ &8] г ' ТЕОРЕМА ЕДИНСТВЕННОСТИ
единственно, т. е. через точку (х0; у0) проходит единственная
интегральная кривая уравнения A). • •
Доказательство. Допустим, что существует два решения
уравнения A), удовлетворяющие условию B), т. е. две кривые,
выходящие из точки А(х0; у0): у(х) и z(x). Следовательно, обе
эти функции удовлетворяют уравнению B4) § 27:
(*, z)dx.
Рассмотрим разность
'' - х
, у(х)-г (*) = J [/(*, */)-/(*, *)]dx. ^ C)
Преобразуем подынтегральную разность по формуле Лагранжа
с учетом неравенства (б) § 27:
Из этого равенства получаем * -
На основании C) с учетом E) можем написать неравенство ,
Рассмотрим такое значение х, чтобы \х—#0|<~j\f * Для опреде-
определенности будем считать, что хо<х, для случая х <^0 доказа-
доказательство аналогично.
Пусть наибольшее значение |#—z\ на интервале х—#0< -тт-
принимается при х = х* и равно X. Тогда неравенство F) для
точки х* принимает вид ' " 4 * ,1
J
х*
пли
При допущении существования двух различных решений пришли
к противоречию. Следовательно, решение единственно.
Замечание 1. Можно показать, что решение будет един-
единственным при меньших требованиях на функцию /(#, у). См.,
Например, книгу: Петровский И. Г. Лекции ш теории
обыкновенный дифференциальных уравнений.— Мл.- Наука, 1970..

ряды 1гл. xvi
Замечание 2. Если функция /(х, у) имеет неограниченную
частную производную -—в области, то могут существовать не-
несколько решений, удовлетворяющих уравнению» A) и начальным
условиям B).
Действительно, рассмотрим уравнение
G)
с начальным условием
у = 0 при # = 0. (8)
Здесь -J- = xy-*te—+oo при г/~*0.
3 этом случае существуют два решения уравнения G), удов-
удовлетворяющие начальному условию (8):
В том,, что эти функции суть решения уравне-
уравнения G); убеждаемся; непосредственной подста-
подстановкой их в уравнение. Через начало коор-
координат проходят две интегральнне крийш fp
Упражнения к главе XVI
D jf^O *& Написать несколько первых членов ряда по данному
общему членуг
Рис, 37$
Исследовать сходимость следующих рядов:
+...+ . +».. Отв. Расходится.
п. у+т+Й+1Г1">--
* Расходится.
> Расходится"
- От-Сходится-
Нсследоаать сходимость рядов с заданными общими членами}

УПРАЖНЕНИЯ % ГЛАВЕ XVI
&^л=^з-. Отв. Сходится, 14. ип= 3/—' Отв- Расходится, 15. ил
Cte. Расходится. 16. ил==д~^2. Отв. Расходится. 17. ^л
SSln«+2/t+3 ' °тв# Сх0^ится- 18- ц»-1= п1п/г- Отв. Расходится. 19. Дока*
зать неравенство 14~-+~+ '••+Т > Inin+l) > Т+У+'-'+
20. Применима ли теорема Лейбница к ряду
J1 , 1L4 * !
б. -Неприменима, так как члены ряда не убывают монотонно по абсо-
абсолютной величине. Ряд расходится.
" • Сколько первых членов надо взять в рядах, чтобы сумма их отличалась
не более чем на -г^- от суммы соответствующего ряда:
23. -Ja"—-да-+-^—
Выяснить» какие из нижеследующих рядов сходятся абсолютно?
25. l — ^+^—JZ+-g2 + ---+(-'1)n+l @а{)* + -•- Отв-
абсолютно.
лютно.
27- ш~ш+ш~ш+ • • •+(-1)п ш+• • •Отв- Сх°дится у^ов.
111 / пв
28. — l+T7=— T7^+T7r= — ---+V7="+--- 0/W6- Сходится
Найти сумму ряда
29# ГГз+2^++
С1ри каких значениях ^ сходятся ряды:
30. 1+|+^-+...+g+... Отв. -2<*<2.
От*. ]х\< 1/3.
0/Ш- -оо<*<со.
Отв, — оо < х < оо.

312 РЯДЫ 1ГЛ. XVI
Отв.
39. Найти сумму ряда *+2*2+ ... + пхп +... (| дг| < 1). Отв. */A—*)?.
Определить, какие из нижеследующих рядов мажорируемы на указанных
отрезках: « s
40. i+p+^+.--+5+--- @<*<1). Он». Мажорируем.
41. 1+у+у+у+-••+—+-• @<х<1). Отв. Не мажорируем.
лл sin # . sin 2х . sin 3* , . sin nx . гл о - п »* ' '
42. -jj-H—g2—1—32—•" * * * —«2—Ь • • • 1°» 2я1- Отб- Мажорируем.
Разложение функций в ряды
|Q , ¦ по степен
Сходится при —10 < х< 10.
43. Разложить |Q , ¦ по степеням х и определит^' интервал сходимости.
10
44. Разложить cos* по степеням х—%-. Отв.
п
^2. О V 2У
45. Разложить е~^ па степеням #. Отв. 1—*-f~oj—огН"*г#
46. Разложить е* по степеням х—2. Отв. е2+е2(х—2)-\-^- (*— 2J-f-
47. Разложить я3—2jc2+5jc—7 по степеням х — 1. От«. —3-4-4 (а:— 1) -f-
iJH1>3
H
48. Разложить многочлен хг»+2х*—Зх7—6^+Зл^ + бл3—^—2 в ряд
Тейлора по степеням х—1; убедиться, что этот многочлен имеет число 1 трех-
трехкратным корнем. Om*.7(*) = 8t (л:—1K+270 (д:—1L+405 (jc— 1>*4-351(л:—lN-f-
+ 189.(jc—iO+63<jc_ 1)в+12 (л:— 1)»+(лг— l)ib. - " ' . ' '
49. Разложить cos(#-fa) по степеням х. Отв. со& ЦттХ sin a—%rcos a
X* X*
sina+
T3r
60s Разложить In д: по степеням ^—1. Отв. (дг— 1)—о"(^—
5t. Разложить ех в ряд по степеням я+2. Отв. е\ Д+У. ¦ Ь
L «=i w J

УПРАЖНЕНИЯ К ГЛАВЕ XVI 313
52. Разложить cos2* в ряд по степеням #—--г-. О те,
И<С0)-
I
S3. Разложить -^ в ряд по степеням лг+1. Отв.
X
54. Разложить tgx в ряд по степеням х—~. От*, 1+2 ^л;—— ) +
()'
первые четыре члена разложения в ряд по степеням х функций:
55. Щх. О»». *+iJ-+T5"+-5|5+--- W-
Отв..In2+4-+V—?+••• 59- e3i". ""- • ¦ ¦ ** *4
Oma. l+*2~+^*4----- 61. sec л:. Ome.
63. Разложить sinfot по степеням х. Отв. kx—ЦА+Цг—Цг-4-««-
\ч «51 Ol /I -
64. Разложить sin** по степеням я и определить интервал сходимости.
2jc2 23jc4 '25яв 22/|~**2/|
Отв. -^—4Г+1П—--•+(—1)п~1 BпI +'" Ряд СХ°ДИТСЯ пРи всех
значениях х.1 . . -
65. Разложить j . а в Ряд по степеням дс. Отв. 1— *2+je4—л:6+...
. , 66^ Разложить arctgx в ряд по степеням дсг Указание. Воспользовать-
Воспользовать* . Q К *
CuJC JC JC JC
• ' о
r 67. Разложить 71Ч7Т2 в ряд по степеням х. Отв. 1— 2*-J-3*2~-
I).
1 Пользуясь формулами разложения в степенной ряд, функций exf sin a:,
соэдг, ln(l-|-#)» (^+x)m и применяя различные приемы, разложить в степен-
степенные ряды функции и определить интервалы сходимости:
68. sh*. Отв. л;+|г+ЕГ+--- (-00 <*<<*)• 69. chjc. Отв. 1+^ +
• / ! 31
). 70. cos2 х. Отв. 1+4-
). От». х-{
П = 2

314 РЯДЫ** [ГЛ. XVI
От. 1 + ? (-ly-i
/1=2
*»• Г~Л.0ив.
/1=1
82. Доказать равенства
sin (a-\-x)=$ki acos^+cos astaJTi
cos (л+jf)^ cos a cosjc—sin a sia**
разложив левые части по степеням х.
Пользуясь соответствующими рядами, вычислить!
83. cos 10° с точностью до 0,0001. Отв. 0,9848. 84. sin 1Q с точностью до
0,0001. Юте, 0,Ш75в 85. sin 18е с точностью до 0,0001. Отв. 0,3090. 86. «in —
с точностью до 0,000L Отв. 0,7071. 87. arctg-^- о точностью до 0,0001.
о
Отв. 0,1973. 88. in 5 с точностью до 0,001. Отв. 1*609. 89. Ig5 с точностью
до 0,001. Отв. 0,699. 90. arcsin 1 с точностью до 0,00Ш. Отв. 1,5708. 91. У"ё
с точностью до OfiOOl.Ome. 1,6487.92. lg e с точностью до 0,00001. Отв.0,43429.
93. cos 1 с точностью до 0,00001. Отв. 0,54030,
Пользуясь разложением в ряд Маклорена функции f(x)=yaft+x, вы-
вычислить с точностью до 0,001:
94.J/30. Отв. 3,107. 95. У70. Отв. 4,121. 9В. ^500. Отв. 8,367.
97. У250, Юте. 3,017. т. УЫ+ Отв. 9,165. 99. 1/4. Отв. 1,2598.
Разлагая подынтегральную функцию в ряд, вычислить интегралы:
1ТЮ. f — dx с точностью до 10-*. Отв. Я,946О8. tet. {<r~**dx s точ-
oJ * i
я/4
ностью до 0,0001. Отв. 0,7468. 102, \s\n(^)dx о точностью до 0,0001;

ч , УПРАЖНЕНИЯ К ГЛАВЕ XVI " 315
Onto. 0,1571. 103. ?eVxdx с точностью до 0,01. Qm*, 0,ai, 104. Г —^ dx
о
С точностью до 0,001. Отв. 0,487. 105. \cosV xdx с точностью до 0,001.
о
0,25
Отв. 0,764. 106. С ln(l + |TI)cfc<: с точностью до 0,001. Отв. 0,071.
о
I _#*_ (Г,2
107. Ге~ 4 d* с точностью до 0,0001. От». 0,9226. 108. С fta- л* е точ-
о о
05
0,5
гёс&тыо до 0,0001. О/ш, 0,6214. 109. f -гтгтс точностью до 0,001. Otmi 0^494.
„о. |
а
Указание. При, р«ЩенйИ ^>ro примера и двух следующих полезно
иметь в виду равенства:
Z* \ я», у* (—1)я-г_яж
П2г— q> jL* n% —12» ^( )\
/1=1 П=Г П=1Х ' *
которые будут установлены в § 2 гл. XVII.
111. У —* dx. Отв. -^-. 112. \ In г-1 . Отв. -?.
J * 6 J 1— * * 4
о о
Интегрирование дифференциальных уравнений
с помощью рядов
113. Найти решение уравнения #"=##, удовлетворяющее начальным усло-
условиям1 у=1> у' = 0 при х=±0.
Указание. Искать решение в виде ряда, Ош. I +o~q"H>'q н ^+ • • *
()
114, Найти решение уравнения у"+ху'+у=0, удовлетворяющее начальным
v3 ХЪ (\) + 1%1
условиям ,=0.^1 при *=0. Ота. ж--+7-^— ¦¦+ь^
115. Найти общее решение уравнения
Указание. Искать решение в форме у~
cos л:

ЗЬ6. • РЯДЫ . 1ГЛ.ХУ1
|HL.4 Найти решение уравнения ##"+*/' + ху — О, удовлетворяющее началь-
X2 * *
ным условиям у=\, #' = Опрй *=0. Отв. !~^
Замечание. Два последних дифференциальных уравнения являются
частными случаями уравнения Бесселя
Х2у''+ху' + (х2-р2)у=0
при Р—у и Р = °-
117. Найти общее решение уравнения 4xjf+2y'+y = (yi.> .
Указание. Искать^ решение в виде ряда xr (яо+Я1#+Я2*2+.. .)•
Отв. Ci cosjf ~x+C2sinV х.
118. Найти решение уравнения A— х2)у"-~ху' = 0, удовлетворяющее на-
\ х3 1 3 хъ
чальным условиям; у — 0> у' = \ при *=()¦ От, х~\"ъ-"ъ-\~к ¦"Т"с"+
119. Найти решение уравнения A+*2) у"+2ху' = 0, удовлетворяющее
начальным условиям у=0, у'= \ при * = 0. Отв. х—^-\~-~^-„.
120. Найти решение уравнения у"=хуу'9 удовлетворяющее начальным
я3 2jc4 3#6
условиям у=\9 у'=1 при ^=0. Отв. 1 +*+_j-_--j-_-f+ -.¦
121. Найти решение уравнения A— х)у' = \+х—у, удовлетворяющее
начальному условию: у~0 при д: = 0, и указать интервал сходимости лолу-
X2 X3 X*
ченного ряда. Отв. *+у72~1"^3+з^4~Ь"" ("
122. Найти решения уравнения ху"+у = 0, удовлетворяющее начальному
условию: у = 0, у' = 1 при д:=0, и указать интервал сходимости. Отв.
Хп
Щ^Щ^ЩА [(л1)!]л
123. Найти решение уравнения у"-\—#'+0 = 0* удовлетворяющее на-
чальному условию: #=1, у =0 при х = 0. Отв..
124. Найти решение уравнения у"-\—y'-\-y = Q, удовлетворяющее на-?
чальным условиям у= 1, #'=0 при х = 0, и указать интервал сходимости
X2 Х^ Х^ X2**
полученного ряда. Отв. 1— ga+ + + ( 1^
Найти первые три члена разложения в степенной ряд решений нижесле-
нижеследующих дифференциальных уравнений при указанных начальных условиях;
125. у' = х2+у2, у=\ при х=0. Отв. 1+л:+^2 + ~-+...
о
126. уГ = еУ+х, у=\, г/'=0 при х=0. Отв. l+*L+iL+--
X2 X3
127. r/r = sin f/—sin дг, у — 0 при ^ = 0. Отв. — --—~—t.t
2 о

УПРАЖНЕНИЯ К ГЛАВЕ XVI 317
Найти несколько членов разложения в степенной ряд решений дифферен-
дифференциальных уравнений при указанных начальных условиях:
128. tf-rf-*, У=1> *'-1 при *=0. От. |
+-5Г+
129. f'«|f»+*, y = y при *=0. Ойи. Y + TJtr+?*S+'R"
32
130. ^»х9—йг>; у*=0 при *=0. Отв. -|-^-^7.^
131. ^'=дс2у2—1» У = 1 при *=0
132. у' = еУ+ху, у = 0 при *=0. Отв.

ГЛАВА XVII
РЯДЫ ФУРЬЕ
§ 1. Определение. Постановка задачи
, , Функциональный ряд вида
или, более сжато, ряд вида
со
называется тригонометрическим рядом. Постоянные числа я0, ап
и Ьп (я=1, 2, ...) называются коэффициентами тригонометри-
тригонометрического ряда.
Если ряд A) сходится, то его сумма есть периодическая функ-
функция f(x) с периодом 2я, так как sinn* и cos пх являются перио-
периодическими функциями с периодом 2я.
Таким образом,
/() /
Поставим следующую задачу.
Дана функция f(x)f периодическая с периодом 2л. При ка-
каких условиях для f(x) можно найти тригонометри-
тригонометрический ряд, сходящийся к данной функции? i
Эта задача и будет решаться в настоящей главе.
Определение коэффициентов ряда по формулам
Фурье. Пусть периодическая с периодом 2я функция / (х) та-
такова, что она представляется тригонометрическим рядом, сходя-
сходящимся к данной функции в интервале (—л, я), т. е. является
суммой этого ряда:
со
/(aO^TT+S (aaco&nx+bnsln nx). B)
Предположим, что интеграл от функции, стоящей в левой
части этого равенства, равняется сумме интегралов от членов
ряда B). Это, например, будет выполняться, если предположить,

§1| ОПРЕДЕЛЕНИЕ. ПОСТАНОВКА ЗАДАЧИ
что числовой ряд, составленный из коэффициентов данного три-
тригонометрического ряда, абсолютно сходится, т. е. сходится поло-
положительный числовой ряд
|-?| + |flil + l&il + |fl,l + |b.l+...+|aJ + [ftllf+... C)
Тогда ряд A) мажорируем и, следовательно, его можно по-
почленно интегрировать в промежутке от —я до я. Используем
это для вычисления коэффициенФа а0.
Проинтегрируем обе части равенства B) в пределах от —я до я:
-Я л=
Вычислим отдельно каждый интеграл, встречающийся в йрквой
части:
я
ft
-str
cos nxdx —
Я
-Я
J basmnxdx=$n
-я
Следовательно,
откуда
— Я
Для вычисления остальных коэффициентов ряда нам потре-
потребуются некоторые определенные интегралы, которые мы и рас-
рассмотрели предварительно.
Если п и k—целые числа, то имеют место следующие равен-
равенства; если пфк, то
я
cos пх cos kx dx=0$
—я
я
cos пх sin kx dx = О, (I)
sin ш: sin fot йл?= 0.^

320
если
же
Л = Л, ТО
РЯДЫ ФУРЬЕ
я
5 cos* kxdx = nt
-я
я
\ sin kx cos kx dx = 0,
?I7L'XVH
(II)
Вычислим, например, первый интеграл из группы (I). Так как
cos пх cos kx г= у [cos (n+*) *+cos (Л—k)x\t
TO
91 Я Я
cos nx cos Ллс dx = у 5 cos(n + A)#dx-H-j $ cos(n—
—я -я
Подобным образом можно получить и остальные формулы (I)*).
Интегралы группы (II) вычисляются непосредственно (см. гл. X т. I).
Теперь мы можем вычислить коэффициенты ак и Ъ^ ряда B).
Для разыскания коэффициента ak при каком-либо определен-
определенном значении кфО умножим обе части равенства B) на cos Ад::
/(х) coskx^^jcos fo+X (an cosnxcoskx+К sinnx c°^kx). , B')
Ряд, получившийся в' правой части равенства, мажорируем, так
как его члены не превосходят по абсолютной величине членов
сходящегося положительного ряда C). Поэтому его можно по-
почленно интегрировать на любом отрезке.
Проинтегрируем равенство B') в пределах от —л до я:
Г f{x)cos kxdx = -Y
я -я
/ Л
( \ cosnxQ,Q$kxdx~\-bn
*) С помощью формул
—sin (л—k)x]t
sin яя sin ^=-2" [-—cos (n-\-k) x+cos (/г—/г>дс]*

§ 1 ] * ОПРЕДЕЛЕНИЕ. ПОСТАНОВКА ЗАДАЧИ ' Щ\
Принимая во внимание формулы (II) и (I), видим, что все
интегралы в правой части равны нулю, кроме интеграла с коэф-
коэффициентом akl
Следовательно,
л _ я
/(х)coskxdx^ah ^ cos2kxdx =
откуда
Яь = — С f(x)coskxdx. ~~~ E)
я j
Умножая обе части равенства B) на sin А*»и снова интегрируя
от —я до л;, найдём
л п
§ f(x)sinkxdx^bk ^ sin2tedx = ЬАяг F)
откуда
л
* Ьл=г=? J /(*)stated*. G)
Коэффициенты j определенные по формула^ D)—F), назы-
называются коэффициентами Фурье функции /(*), а тригонометри-
тригонометрический ряд A) с такими коэффициентами называется рядом Фурье
функции f(x).
Возвратимся теперь к вопросу, поставленному нами в начале
параграфа: какими свойствами должна обладать функция, чтббы
построенный для нее ряд Фурье сходился и чтобы сумма построен-
построенного ряда Фурье равнялась значениям данной функции в соот-
соответствующих точках?
Мы сформулируем здесь теорему, которая даст-достаточные
условия представимости функции f(x) рядом Фурье.
Определение. Функция f(x) называется кусочно монотон-
монотонной, на отрезке [а, &], если этот отрезок можно разбить конечным
числом точек xiy x29 ..., xn_t на интервалы (a, jq), (*if x2), ...
•••» (xn-i> Щ так» что на каждом из интервалов функция моно-
монотонна, т. е. либо невозрастающая, либо неубывающая.
Из определения* следует, что если функция f(x) кусочно
монотонная и ограниченная на отрезке Га, 6], то она может иметь
только точки разрыва первого рода. Действительно, если х='с
есть точка разрыва функции /(#), то в силу монотонности функ-
функции существуют пределы
.Hm f(x) = f(c-O)9 lim /(*) = /(*+<>),
т. е. точка с есть точка разрыва первого рода (рис. 374).
11 Л. С. Пискунов, т. 2

f(c»O)
322 ' РЯДЫ ФУРЬЕ [ГЛ. XVII
Сформулируем теперь следующую теорему.
Теорема, Если периодическая функция f(x) с периодом 2я
кусочно монотонная и * ограниченная на отрезке [—п, я], то ряд
Фурье, построенный для этой функции, сходится во всех точках.
Сумма полученного ряда s(x) равна значению функции f(x) в- точ-
точках непрерывности функции. В точках раз-
разрыва функции f(x) сумма ряда равняется
среднему арифметическому пределов функ-
функции f(x) справа и слева, т. е. если х = с
—точка разрыва функции f(x), то
сМ, _J(c-~0)+f(c+0)
ь \Х) I х=с — 2 •
Из этой теоремы следует, что класс
функций, представимых рядами' Фурье,
довольно широк. Поэтому ряды Фурье
Рис, 374, нашли широкое применение в различных
отделах математики. Особенно успешно
ряды Фурье применяются в математической физике и ее прило-
приложениях к конкретным задачам механики и физики (см.
гл. XVIII).
Данную теорему мы приводим без доказательства. В § 8—10
будет дано доказательство другого достаточного признака разло-
разложимости функции в ряд Фурье, который относится в некотором
смысле к более узкому классу функций.
§ 2. Примеры разложения функций а ряды Фурье
Приведем примеры разложения функций в ряды Фурье.
Пример 1. Периодическая функция f(х) с периодом 2л определена
следующим образом: f(x)=xf —я < х^я.
Эта функция кусочно монотонная и ограниченная (рис'. 375). Следова-
Следовательно, она допускает разложение в ряд Фурье.
По формуле D) § I находим
-я
Применяя формулу E) § 1 и интегрируя по частям, найдем
—я» f J
По формуле F) § I находим
К
-Я U -л J

$21 ПРИМЕРЫ РАЗЛОЖЕНИЯ ФУНКЦИЙ В РЯДЫ ФУРЬЕ
Таким образом, получаем ряд
323
Это равенство имеет место во всех точкагх, кроме точек разрыва.* В каждой
точке разрыва сумма ряда равна среднему арифметическому ее пределов справа
и слева, т. е. нулю.
у-
7Г
л
п УЗк
/2ъ
Рис. 375.
-4п ~-Зъ ~-?п —к Q я?
^
Рис. 376.
Пример 2. ^Периодическая функция / (я) с периодом 2п определена сле-
следующим образом:
f(x)= — х при —^
f(x)=x при
(т. е. f(x) = \x\) (рис. 376). Эта функция тоже кусочно монотонна и ограни-
ограничена на отрезке —п,<^х*^п.
Определим ее коэффициенты Фурье:
-х) cos kx dx-\- \ x cos kx dx I =
о J
0
О при k четном,
~г2 %ри k, нечетном,
= _ \ (—x)sinkxdx+\ xsinkxdx U=0.
n LA j J
11*

324
РЯДЫ ФУРЬЕ
{ГЛ. XVII
Таким образом, получаем ряд
—n 4 Г cos * . cos Зх . cos 5x . cosBp + \)
-y—jrin^""*" З2 "*" 52 "*"•••"*"
Этот ряд сходится во всех точках, и.его сумма равна данной функции..
• -bit
7
-/
Рис
. 377.
1 ,
Пример 3. Периодическая с периодом 2я функция f (х) определена сле-
следующим образом;
— / (дет) == — i при —я < х < О,
= 1 при
Эта функция (рис; 377) кусочно монотонна и ограничена на отрезке —я ^ х <% к.
Вычислим ее коэффициенты Фурье:
Я Г О Я 1
\ U
[ J v ;
го
If,
о
f
¦~2 Г 0 при fc четном,
s—t-A—cos я^)=-| 4 '
Jt« J —g- при к нечетном.
Следовательно, для рассматриваемой функции, ряд Фурье имеет вид
f(x)^ 4fsmx | sin3x | shl5x [ ... | sin Bp + \)x | 1
Это равенство справедливо во всех точках^ кроме точек разрыва.
- - На рис. 378 наглядно показано, как частичные суммы sn ряда все точнее
и точнее представляют функцию f (x) с увеличением п.
Пример 4. Периодическая с периодом 2я функция f [x) определена
следующим образом;
=*2, — я<*<я (рис. 379).

§,2] . ПРИМЕРЫ РАЗЛОЖЕНИЯ ФУНКЦИЙ В РЯДЫ ФУРЬЕ 325
1
V °
'\ /
^—^^ ¦ ¦ -
/ \
Рис. 378,
Определим ее коэффициенты Фурье:
я
=-1 f
1-я * J
-я 3 '
я
—if-
[я cos ?я] =
-p- при k четном,
--ту при fe нечетном;
п Г я
If,'.. 1 х2 cos fc* я , 2 f
-я L .,
S5S-L Х Sl11 kX.
nk[ k
x cos kx dx
-я J

326
РЯДЫ ФУРЬЕ
[ГЛ. XVII
Значит, ряд Фурье данной функции имеет вид
'2__яа . I cos х cos 2x , cos Зх
Так как функция кусочно монотонна, ограничена и непрерывна, то это ра-
равенство выполняется во всех точках.
—Зп -2п -л О
Рис. 379,
Полагая в полученном равенстве х — я, получим -
fix 1
Пример 5. Периодическая с периодом 2я функция / (х) определена
следующим образом: • N
f(x)=x при 0 < *<я (рис. 380).
Определим коэффициенты Фурье:
п
— -7Г Vsin
i
1 cos kx |я
nk k jo
I я2 я
р при fc нечетном,
О при к четном;
-Ч
bk=~ V^sln*xd«=— -
1 I X COS &*
+-r- \ coskxdx 1 =
» J
= _ JL cos /Ы=
— l/k при & четном.
Таким образом, ряд Фурье будет иметь вид
/(*) =
•.я 2
cos Зле , cos 5*
sinx sin 2л: , sin 3^;
~ 2 ' з^

$31 " ОДНО ЗАМЕЧАНИЕ 327
В точках разрыва функции / (х) сумма ряда равна среднему арифметическому
ее пределов справа и слева (т. е. в данном случае числу я/2).'
л л
Л /1-/1
Рис. 380,
Полагая в полученном, равенстве # = 0, получаем
§ 3. Одно замечание о разложении периодической функции
в ряд Фурье
Отметим следующее свойство периодической функции ф
с периодом 2л:
я
каково бы ни было число К.
Действительно, так как
то, полагая х = 1—2я, можем написать при любых с и d
' d+2jt ?/+2я
' 2Я +2Л
с с+2Л ' с+ 2Я
В частности, принимая с=—л, d = h, получим
-я
поэтому
-Я Я Я+2я
я1

'328
РЯДЫ ФУРЬЕ
[ГЛ. XVII
•• Указанное свойство означает, что интеграл от периодической
функции ty(x) no любому отрезку, длина когйодогд равна,периоду,
имеет всегда одно и то же значение. Этот факт легко иллюстри-
иллюстрируется и геометрически: площади, заштрихованные на рис; 381,
равны между собой. .
Рис. 381.
Из доказанного свойства вытекает, что при вычислении коэф-
коэффициентов Фурье мы можем заменить промежуток интегрирова-
интегрирования ( — я, я) промежутком _ интегрирования (X, Ь + 2ц), т. е.
можем положить
I
an = ^ J f(x)cosnxdx,
Ьп =* — \ f(x) sin nxdxt - 0)
где к — любое число.
Это следует из того, что по условию функция f (x) является
периодической с периодом 2я; следовательно, и функции / (х) cos nx
и f (x) sin nx являются периодическими функциями с периодом 2я.
Покажем на примере, как Доказанное свойство упрощает процесс
нахождения коэффициентов в некоторых случаях.
Пример. Пустьчтребуется разложить в ряд Фурье функцию f (x) с пе-
периодом 2я, которая на отрезке 4> < х^2п задана равенством
if(x)=x.
График функции f(x) изображен на рис. 382. Эта функция на отрезке
[—я, я] задается двумя формулами: /(#) = *-{-2л; на отрезке [—я, 0] и

*4| РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ 329
f(x) = x на отреаке [0, л]. В то же время на отрезке [0, 2я] гораздо проще
она задается одной формулой f (x) — х. Поэтому для разложения этой фущс-
.дни в ряд Фурье выгоднее воспользоваться формулами (I), приняв к—О:
2Я 2Я
ло=— \ fMd*=—\ xdx=2n;
о о
2я 2я
д„=— \ / (х) cos мл: ах=— V х cos шс ах =— I 5— I
И Я J 'U Я J Я I ft Т П1 JO
О - 8
2Я 2я
f 1 f
2Я 2я
n~— \ f(x)$innx dx~— \ xsinnxdx=z— I з— = .
Следовательно,
2 2 2 2
—о" sin2л:—g-sin3x—-j-sin4A; — —
Этот ряд дает заданную функцию во всех точках, кроме точек разрыва (т. е.
кроме точек #=G, 2я, 4л, .. .)• В этих точках сумма ряда равна полусумме
предельных Значений функции^ / (х) справа и слева (т. е. в данном случае
числу зт).
§ 4. Ряды Фурье для четных и нечетных функций
Из определения четной и нечетной функции следует, что если
<ф(#)— четная функция, то
-я О,
Действительно,
О
С -ф {х) dx = С \|> (л:) dAr-f J ф (лг) ^л: = f ф (—J
-я - -л а - о о
*= J-ф (л:)dx + J\j? (л:) d# =
так как по определению четной функции i|>(— x) = ty()
Аналогично можно доказать, чтя если ф(#)—нечетная
функция, то
я ' я я я я
-Я
(л:) йд; = J ф (—лг) Йл: + J ф (л:) dx = — f ф (х) dx + f ф (л:) dx = 0,
0 0 0 0
Если в ряд Фурье разлагается нечетная функцця /(#), то
произведение f (х) соэ*?л; есть функция также нечетная, а

330 РЯДЫ ФУРЬЕ |ГЛ. XVII
/ (х) sin kx — четная; следовательно,
я
~ Г / (jt) cos Ля: Лс = 0t A)
— я
я
-я
т. е. ряд Фурье нечетной функции содержит «только си-
синусы» (см. пример 1 § 2). ^
Если в ряд Фурье разлагается четная функция, то произ-
произведение f(x)sinkx есть функция нечетная, а »/ (х) cos kx-*-четная
и, следовательно,
я
2
B)
•it
г = —. Г f (x) sin Ллг^л: = О,
я J
т. е. ряд Фурье четной функции содержит «только коси-
косинусы» (см. пример 2 § 2).
Полученные формулы позволяют упрощать вычисления при
разыскании коэффициентов Фурье в тех случаях, когда заданная
функция является четной или нечетной. Очевидно, что не всякая
периодическая функция является четной или нечетной (см. при-
пример 5 § 2).
Пример. Пусть требуется разложить вряд Фурье четную функцию
/ (#), которая имеет период 2п и на отрезке [0, п] задана равенством
у = х.
Эту функцию мы уже разлагали в ряд Фурье в примере 2 § 2 (см.
рйс. 376), Вычислим снова коэффициенты Фурье этой функции, используя
тот факт, что заданная функция является чётной.
В силу формул B) 6^ = 0 при любом k\
я . я ¦
2 С 2 С
ае = — \ xdx=nt cik=— \ xcoskxdx=
я J я J
о
0 при k четном,
при ^ счетном.
Мы получили те же коэффициенты, что и в примере 2 § 2, но более корот-
коротким путем.
б о .
__2 fxsinkx coskx~)n_ 2 Г/п* i-i '
Jo | --

§5] РЯД ФУРЬЕ ДЛЯ ФУНКЦИИ С ПЕРИОДОМ 2/ ЗЭ4
§ 5. Ряд Фурье для функции с периодом 21
Пусть / (х) есть периодическая функция с периодом 21, вообще
говоря, отличным от 2л. Разложим ее в ряд Фурье.
Сделаем замену переменной по формуле ,
х = It In.
Тогда функция f{ltjn) будет периодической функцией от t с пе-
периодом 2я. Ее можно разложить в ряд Фурье на отрезке — !
где
я
-к
Возвратимся теперь к старой переменной х:
x~ — t, t = x-j-* at =-г ах.
Тогда будем иметь
x. B)
-t
Формула A) примет вид
(^f) C)
где "коэффициенты a0, ak, bk вычисляются по формулам B). Это
и есть ряд Фурье для периодической функции с периодом 21.
Заметим, что все теоремы, которые имели место для рядов
Фурье от периодических функций с периодом 2я, сохраняются и
для рядов Фурье от периодических функций с каким-либо другим
периодом 21. В частности, сохраняет свою силу достаточный при-
признак разложимости функции в ряд Фурье (см. конец § 1), заме-
замечание о возможности вычислять коэффициенты ряда, интегрируя
по любому отрезку, длина которого равна периоду (см. § 3),

?32
РЯДЫ ФУРБЕ
[ГЛ. XVH
& также замечание о возможности упростить вычисление коэф-
коэффициентов ряда, если функция является четнойиили нечетной (§4).
Пример. Разложить в ряд Фурье периодическую функцию / (х) с пери-
периодом 2/, которая на отрезке [ — /, /] задается равенством }(х) = [х\ (рис'383).
—п -л -я -ь
О 1 21
Рис. 383. *
31
41 . Л
Решение. Так как рассматриваемая функция четная, то
2 Г
а.-ту*х-,_
О при ? четном,
при /
cos
Следовательно, разложение имеет вид
Зя .
cos -у- х
-Ь—з^—ь'-~
§ 6« О разложении непериодической функции в ряд Фурье
Пусть на некотором отрезке [я, Ь] задана кусочно монотонная
функция f(x) (рис. 384). Покажем, что данную функцию f (х)
в точках ее непрерывности можно представить в виде суммы ряда
А
Я а 2?
Рис.384.
Фурье. Для этого рассмотрим произвольную периодическую ку-
кусочно монотонную функцию ft(x) с периодом 2fi^b —а, совпа-
совпадающую с функцией / {х) на9 отрезке [а, Ь]. (Мы дополнили
определение функции /(л:).)

О РАЗЛОЖЕНИИ НЕПЕРИОДИЧЕСКОЙ ФУНКЦИИ В РЯД ФУРЬЕ 333
Разложим функцию ft (х) в ряд Фурье. Сумма этого ряда во
всех точках "отрезка [а, Ь] (кроме точек разрыва) совпадает ъ
заданной функцией f(x), т. е. мы разложили функцию / (х) вряд
Фурье на отрезке [a, b]. ^ -
Рассмотрим, далее, следующий важный случай. Пусть функ-
функция f(x) задана на отрезке [0, /]. Дополняя определение этой
функции произвольным образом на отрезке [ — /, 0] (сохраняя
кусочную монотонность), мы можем разложить эту функцию в ряд
Фурье. В частности, ерли цы дополним определение данной функ-
функции так, чтобы при —/^#<0 было /(*) = /(—л:), в результате
получится четная функций (рис. 385). (В этом случае говорят, что
функция / (х) «продолжена четным образом».) Эту функцию разла-
разлагают в ряд Фурье, который содержит только косинусы. Таким
образом, заданную на отрезке [0, /] функцию f(x) мы разложили
по косинусам.
Если же мы продолжим определение функции f(x) при —/^
^#<0 так: /(*) = —f(—х), то получим нечетную функцию,
которая раздагается по синусам (рис. 386). (Функция f (х) «продол-
«продолжена нечётным образом».) Таким образом, если на отрезке [0, I]
задана некоторая кусочно монотонная функция /•(#), то ее можно
разложить в ряд Фурье как по косинусам; так и по синусам.
Рлс. 385.
Рис. 386.
Пример I. Пусть требуется разложить функцию f(x)=x на отрезке
[0, Jt] в ряд по синусам.
Решение. Продолжая эту функцию нечетным] образом (рис. 375), полу-
получим ряд
— 2 \sinx sln2jc | $*пЗх I
(см. пример 1 § 2).
Пример 2. Разложить функцию f(x)=x на отрезке [0, п] в ряд по
косинусам.
Решение. Продолжая эту функцию четным, образом, мы получимг
(рис. 376). Разлагая ее в ряд, найдем у
я 4 Гссэд: .cos Зле . cos 5* , ;Л

334
РЯДЫ ФУРЬЕ
[ГЛ. XVII
(см. пример 2 § 2). Итак, на отрезке [0, я] имеет место равенство
__ п 4 [cosx , cos3jc 1 cos Ъх t_
§ 7. Приближение в среднем заданной функции
с помощью тригонометрического многочлена
Представление функции бесконечным рядом (Фурье, Тейлора
и т. д!) имеет на практике тот смысл, что конечная сумма,
получающаяся при обрывании ряда на п-м члене, является при-
приближенным выражением
разлагаемой функции; это при-
приближенное выражение можно
довести до какой угодно степени
точности путем выбЬра достаточ-
достаточно большого значения я. Однако
характер приближенного пред-
представления может быть различ-
различным.
Ряс. 387, ^ Так, например, сумма п пер-
первых членов ряда Тейлора sn сов-
совпадает с рассматриваемой функцией в одной точке и в этой точке
имеет производные до n-го порядка, совпадающие с производными
рассматриваемой функции. Многочлен Лагранжа n-й степени
(см. § 9 гл. VII, т. I) совпадает с рассматриваемой функцией
в п+1 точках.
Посмотрим, какой характер имеет приближенное представле-
представление периодической функции f(x) тригонометрическими многочле-
многочленами вида
п
sn (х) = ~
ak cos
ы
где я0, aif Ъъ а2, Ь2, ..., ап, Ьп — коэффициенты Фурье, т. е.
суммой п первых членов ряда Фурье. Сделаем сначала несколько
замечаний.
Допустим, что мы рассматриваем некоторую функцию у = / (х)
на отрезке [а, Ь] и хотим оценить погрешность при замене этой
функции другой функцией ф (х). Можно за меру погрешности
взять тах|/(*)—ц>(х)\ на отрезке [а, Ь\ т. е. так называемое
наибольшее уклонение функции ф(*) от f(x). Но иногда естест-
естественнее за меру погрешности брать так называемое среднеквадра-
среднеквадратичное уклонение^ б, которое определяется равенством
ь
Поясним на рис. 387 различие между среднеквадратичным
уклонением и наибольшим уклонением.

§7] ПРИБЛИЖЕНИЕ В СРЕДНЕМ 335
Пусть сплошная линия изображает функцию у — f (Я), пунктир-
пунктирные линии изображают приближения* (рг (х) и ф2(лс). Наибольшее
уклонение кривой у = уг (х) меньше, чем кривой у = ч>2(х)> но
среднеквадратичное уклонение первой кривой больше, чем вто-
второй, так как кривая у — Ф2(*) значительно отличается от кривой
у == f (x) только на узком участке и поэтому лучше характеризует
кривую y=f(x),<чем первая.
Вернемся теперь к нашей задаче.
Пусть дана периодическая с периодом 2л функция f(x). Среди
всех тригонометрических многочленов п-го порядка
п
требуется найти путем выбора коэффициентов ak и §к тот
многочлен, для которого среднеквадратичное уклонение, опреде-
определяемое равенством
Ь« = Ш I [к*>-ТГ-? (а*соз&с+рлзШЛд:I dx%
имеет наименьшее значение.
Задача сводится к Нахождению минимума функции 2п -{-1
переменных а0, al9 ...r an9 Plt P2, ..., Р„.
Развернув квадрат, стоящий под знаком интеграла, и инте-
интегрируя почленно, получим

336 РЯДЫ ФУРЬЕ [ГЛ. XVU
Заметим, что ;
' Я Я
-^ J f(x)dx'=a0, . ± J f(x) cos kxdx=ak,
Л
1 г
" "я }
коэффициенты Фурье функции /(х). ^
Далее, на основании формул (I) и (II) § 1 имеем: при & = /
f cos2
-п
при любых k и j
и при кф\
я л
у cos йх cos jx dx = Of J sin fee sin jx dx = 0.
Таким образом, получаем
я
1
1
-Л fcs=l .
Прибавляя^и вычитая „сумму
будем иметь
Первые три слагаемых этой суммы не зависят от выбора коэф-
коэффициентов а0, а1э ..., алэ р1э .••, Рп. Остальные слагаемые

§7J , ПРИБЛИЖЕНИЕ Э СРЕДНЕМ §37
неотрицательны. Их сумма достигает наименьшего значения (рав-
(равного нулю), если положить а0 = а0, аг = ах, ..., а„ = а„, fJ2 = blt...
..., Ря = 6Л. При таком выборе коэффициентов а0, а^, . •., aw, Pi, ...
..., Рп тригонометрический многочлен
будет меньше всего отличаться от функции f(x) в том смысле,
что среднеквадратичное уклонение 6? будет наименьшим.
Таким образом, мы доказали теорему:
Среди всех тригонометрических многочленов порядка п наимень-
наименьшее среднеквадратичное уклонение от функции f(x) имеет тот
многочлен, коэффициенты которого суть коэффициенты Фурье
функции f(x).
Величина наименьшего среднеквадратичного уклонения равйа
-Л fe«l
Так, как $%^0, то при любо^ п имеем
-Я Ьв
Следовательно, ряд, стоящий справа, при п—>оо сходится,
и мы можем написать
Это соотношение называется неравенством Бесселя.
Отметим без доказательства, .что для всякой ограниченной
и кусочно монотонной функции среднеквадратичное уклонение-,
получающееся при замене данной функции n-й частичной суммой
ряда Фурье, стремится к нулю при п —> оо t т. е. 6? —> 0 при п —+ оо,.
Но тогда из формулы B) вытекает равенство
C')
которое называется равенством Ляпунова—Парсеваля. Заметим,
что равенство Ляпунова—Парсеваля доказано для более широ-
широкого класса функций, чем тот, который мы здесь рассматриваем.
Из доказанного следует, что для функции, удовлетворяющей
равенству Ляпунова (в частности, для всякой ограниченной

338 ' РЯДЫ ФУРЬЕ [ГЛ. XVH
кусочно монотонной функции), соответствующий ряд Фурье дает
среднеквадратичное уклонение, равное нулю.
Замечание. Установим одно свойство коэффициентов Фурье,
нужное для дальнейшего. Введем сначала определение.
Функция f(x) называется кусочно непрерывной на отрезке [а, &],
если она имеет конечное число точек разрыва первого рода на
этом отрезке (или всюду непрерывна).
Докажем следующее утверждение.
Если функция f{x) кусочно непрерывна на отрезке [—я, я],
то ее коэффициенты Фурье стремятся к нулю при п—* оо, т. е.
Пта„=Ч), Нт&я-О. D)
Доказательство. Если функция /(х) кусочно непрерывна
на отрезке [—я, я], то и функция f2 (x) также является: кусочно
я
непрерывной на этом отрезке. Тогда j f2 (л:) dx существует и яв-
— я
ляется конечным числом *). В этом случае из неравенства Бес-
оо
селя C) следует, что ряд 2 (#«+&«) сходится. Но если ряд схо-
дится, то его общий член стремится к нулю, т. е> в 'данном
случае lim (а%-\-Ь2п) = О. Отсюда непосредственно получаются ра-
венства D). Итак, для кусочно непрерывной и ограниченной
функции справедливы равенства
lim [ f(x)cosnxdx = 0, lim \ f (x) sinnxdx^d.
Если функция f (x) периодична с периодом 2я, то последние
равенства можно переписать следующим образом (для любого а):
lira у f(x)cosnxdx = Of lim \
Заметим, что эти равенства остаются в силе, если в интегралах
взять какой угодно промежуток интегрирования [a, b], т. е.
ь ь
интегралы J / (л:) cos nx dx и j / (я) sin nx dx стремятся к нулю
а а
при неограниченном возрастании п, если f(x)—ограниченная и
кусочно непрерывная функция.
Действительно, считая для определенности Ь—а<2я, рас-
рассмотрим вспомогательную функцию <р (х) х периодом 2я, опреде-
*) Этот интеграл можно представить как сумму определенных интегралов
от непрерывных функций «о отрезкам, на которые разбивается отрезок [—л, п].

ИНТЕГРАЛ ДИРИХЛЕ 539
ленную следующим образом:
Ф (х) — f (х) при а <! х ^ Ь,
ф(х) = 0 при &2
Тогда
f (x) cos nxdx — j ф (х) cos nx dxf
ч a
а+2л
/ (л:) sin nx dx = J ф (л:) sin /u d#.
Так как ф(х) есть ограниченная и кусочно непрерывная функ-
функция, то интегралы, стоящие справа, стремятся к нулю,при я—*оо.
Следовательно, стремятся к нулю, и интегралы, стоящие слева.
Таким образом, утверждение доказано, т. е.
ь ' ь
lim \ f (x) cos nxdx = 0, lim [ f(x) sin nxdx = 0 E)
для любых чисел а и b и "любой кусочно непрерывной и огра-
ограниченной на [а, &] функции f(x).
§ 8. Интеграл Дирихле
В этом параграфе мы выведем формулу, выражающую п-ю
частичную сумму ряда Фурье через некоторый интеграл. Эта
формула будет нам нужна в следующих параграфах.
Рассмотрим п-ю частичную сумму ряда- Фурье для периоди-
периодической функции f(x) с периодом 2п:
п
sn (х) = if + 21 (ak cos kx + h sin kx)t
где
я я
a* =4 J / @ cos *^ *. feft = it J / @ sin *' *.
-Я - Я
Подставляя эти выражения в формулу для sn(x), получим
1 [^ f f(t)cosktdt+^l f(t)smktdt\
-я Л=1 L -я -я J
или, подводя cosfoc и sinfet под знак интеграла (что возможно,
так как cos kx и sin kx не зависят от переменной интегрирования

340 - РЯДЫ ФУРЬЕ . [ГЛ. XVII
и, следовательно, могут рассматриваться как постоянные), получим
1
Я -I
f(t)co$kxco$ktdt+ С f(/)sinfecsinfef(tf I
-я J
Вынося теперь 1/jt за скобки и заменяя сумму интегралов инте-*
гралом от суммы, получим
sn(x) = ± \ {^ + Y[f(t)coskxcoskt + f(t)smkxsmkt]\dt,
ИЛИ
я Г П Т
sn(x) = -i f f(t)\ 4 + У (cos«cosfecH-sinWsmfec)|d« =
— Я L B—l J
l г Г i ,Д T
i L *-i J
Преобразуем выражение, стоящее в квадратных скобках. Пусть
1 ' ' ---"-• ...-{-cosrtz;
тогда
2вп (г) cos 2=cos г4-2 cos г cos z+2 cos^z cos 2г+... +2 cos г cos /12=
== cos г -f- A -f-cos 2г) + (cos 2 + cos Зг) +
... -|-[cos(n—
cos(n
или
2<sn (г) cos z = 2o?n (г) —cos nz + cos (n +1) zf
rt / \cos яг—cos (n+1) г
a* ^Z^ "^ 2A -cos z) •
Ho .
fcos nz— cos (n+1) z = 2 sinBn + 1) у sin у,
1—cos z = 2sin2-|-.
Следовательно,
*in

ИНТЕГРАЛ ДИРИХЛЕ 341
Такйк тбра'зом, равенство A) можно перевисать так:
4 _ «,
1 Р
Так как подынтегральная функция является периодической
(с-периодом 2л), то интеграл сохраняет свое значение" на любом
отрезке интегрирования длины 2я. Поэтому мы можем написать:
* S
=i f fdh
Введем новую переменную а, положив t—x = ct, t = x-\-a.
Тогда мы получим формулу
1*6 B)
2sinT
Интеграл, стоящий в правой части формулы, называется инте-
интегралом Дирихле.
Положим в этой формуле /(x)al; тогда ao=^2r. aft = 0, feft— .0
при fe > 0; следовательно, sn (x) = 1 при любом п, и }ды получаем
тождество
которое потребуется нам в дальнейшем.
§ 9. Сходимость ряда Фурье в данной точке
Предположим, что функция f(x) кусочно непрерывна на от-
отрезке [—я, я].
Умножая обе части тождества C) предыдущего § 8 на f(x)
и подводя f(x) под знак интеграла, получим равенство
Вычтем члены последнего равенства из соответствующих членов
равенства B) § 8, получим
sinBn+l)|-

342 РЯДЫ ФУРЬЕ [ГЛ. КУП
Таким образом, сходимость ряда Фурье к значению функции / (х)
в данной точке зависит от того, будет ли интеграл, стоящий справа,
стремиться к нулю при n—>оо. *
Разобьем последний интеграл на два интеграла:
Я
—f (л:)]-у cosnada,
воспользовавшись тем, что sin Bn •+• l)-^-=sin na cos-^-t-cosnasin ^-.
Zt & 2i
Разобьем первый из интегралов, стоящих в правой части послед-
последнего равенства, на три интеграла:
i ?
Положим Ф1(а)—^^Ц——. Так как f(x)—ограниченная ку-
кусочно непрерывная функция, то Фх(а)—также ограниченная и
кусочно непрерывная периодическая функция от а. Следовательно,
последний интеграл стремится к нулю при п—*оо, так как он
является коэффициентом Фурье от этой функции. Функция
" ограничена при —я<1а<—8 и при

§101 ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ РЯДА ФУРЬЕ 343
где М—верхняя граница величины |/(я)|. Кроме того, функция
Ф2(а) является также кусочно непрерывной. Следовательно, на
основании формул E), из § 7 второй и третий интегралы стре-
стремятся к нулю при п —+ сю.
. Таким образом, можно написать
1 С C0Sf
\im[sn(x)-f(x)] = Hm ? [/(* + «)-/<*)] 2-sinn*da. A)
В выражении, стоящем справа, интегрирование производится
по промежутку —б^а^б; следовательно, интеграл зависит от
значений функции f (х) только на промежутке от х—б до х-\-8.
Таким образом, из последнего равенства следует важное предло-
предложение: сходимость рядов, Фурье в данной точке х зависит лишь
от поведения функции f (x) в как угодно малой окрестности этой
точки. ш •
В ^ этом заключается так называемый принцип локализации
при исследовании рядов Фурье. Если две функции fi(x) и f2(x)
совпадают в окрестности некоторой точки х, то их ряды Фурье
одновременно либо сходятся, либо расходятся в данной точке.
§ 10. Некоторые достаточные условия сходимости
ряда Фурье
В предыдущем параграфе было показано, что если функция
f (х) кусочно непрерывна на отрезке [—я, я], то сходимость ряда
Фурье в данной точке х0 к зна-
значению функции f(x0) зависит от
поведения функции в некоторой
произвольно малой окрестности
[л:0—6, #0 + б] с центром в точ-
точке х0.
Докажем, далее, что если в ок-
окрестности х0 функция f(x) тако-
такова, что существуют конечные Рис. 388,
пределы
fr ^ ()
а в самой точке х0 функция непрерывна (рис. 388), то *) в этой
точке ряд Фурье сходится к соответствующему значению ф
f{x).
*) Если выполняются условия A) и B), то говорят, что функция f(x)
имеет в точке х производную справа и производную слева. На рис. 388 изо-
изображена функция, где ^i = tg9!, k2 = tg(p2, kx фкг. Если kl = k2t т. е. если
производные справа и слева равны, то функция будет дифференцируемой
в данной точке.

344 РЯДЫ ФУРЬЕ ^ . * [ГЛ. XVII
Доказательство. Рассмотрим функцию Ф2 (а), определен-
определенную в предыдущем параграфе:
а
cos т
так как функция f(x) кусочно непрерывна на отрезке [—я, п]
и непрерывна в точке лг0, то, следовательно, она непрерывна
в некоторой окрестности [х0—б, #0 + 8] точки х0. Поэтому функ-
функция Ф2(а) непрерывна во всех точках, где а ФО и |а|<!б. При
а = 0 функция Ф2(а) не определена.
Найдем пределы lim Ф2(<х) и Шп Ф2(а), используя условия
а-*-0 - а->+0
A) и B):
а
COS-s-
lim Ф8(а)= lira 1
в о
[f(^+)f@)]1
«ч--о 2 stay
SIn|
Um f(^+a)fM
а-^-0 а а->-0 sin^L a->-0 *
Таким образом, если мы доопределим функцию Ф2(а), поло-
положив ©2@)=:^, то она будет непрерывной# на отрезке [—б, 0], а
следовательно, и ограниченной. Аналогичным образом докажем,
что
lim Ф2(а) = ?2.
Следовательно, функция Ф2 (а) ограничена и непрерывна в про-
промежутке (О, 6]. Таким образом, на отрезке [—6, б] функция
Ф2 (а) ограничена и кусочно непрерывна. Вернемся теперь к ра-
равенству A) § 9 (обозначив х через л:0):
\ с ^ C0SY
lim [srt(*o)— /(*<>)]= Иш.-г- \ U(x+a) f(x)]
или
о
lim [sn{xQ)—f{x<$]= lim — V Фа(a)sinnada.

§И| ПРАКТИЧЕСКИЙ ГАРМОНИЧЕСКИЙ АНАЛИЗ „ 345
На основании-фврмуя E)*из §7 заключаем, что стоящий справа
предел равен нулю, а поэтому
(*•)-/(*<>)] = О,
"или
lim sn{x0) = f(xQ).
Теорема доказана.
Доказанная теорема отличается от теоремы, сформулирован-
сформулированной в § 1, тем, что если там для сходимости ряда Фурье в точке х0
к значению функции / (л:в) требовалось, чтобы точка х0 была точкой
непрерывности на отрезке [—я, я], а функция была кусочно
монотонной, то здесь требуется, чтобы точка х0 была точкой
непрерывности функции и чтобы выполнялись условия A) и B),
а на всем интервале [—я, я] функция была кусочно непре-
непрерывной и ограниченной. Очевидно, что- эти условия различны.
Замечание 1. Если кусочно непрерывная функции диффе-
дифференцируема в точке х09 то очевидно, что условия A) и B) выпол-
выполняются. При этом kx = k2. Следовательно, в точках, где функция
f(x) дифференцируема, ряд Фурье сходится к значению функции
в соответствующей точке.
Замечание 2. 1°. функция, рассмотренная в примере 2 § 2
(рис. 376), в точках 0, ± 2я, ± 4я, ... удовлетворяет условиям
A) и B). Во всех остальных точках она дифференцируема. Сле-
Следовательно, построенный для нее ряд Фурье сходится в каждой
точке к значению этой функции.
2°. Функция, рассмотренная в примере 4 § 2 (рис. 379), в точ-
точках ±я, ±3я, ±5я, ... удовлетворяет условиям A) и B). Во
всех остальных точках она дифференцируема. Она представляется
рядом Фурье в каждой точке.
3°. Функция, рассмотренная в примере 1 § 2 (рис. 375), в точ-
точках ± я, ±_3я, ± 5я, ... разрывна. Зо всех остальных точках
она дифференцируема. Следовательно, во всех точках, кроме точек
разрыва, соответствующий ей ряд Фурье сходится к значению
функции в соответствующих точках. В точках разрыва сумма ряда
Фурье равняется среднему арифметическому пределов функции
справа и слева, в данном случае она равна нулю.
§ 11. Практический гармонический анализ
Теория разложения функций в ряды Фурье_ называется гар-
гармоническим анализом. Мы сейчас сделаем несколько замечаний
о приближенном вычислении коэффициентов ряда Фурье, т. е.
о практическом гармоническом анализе.

346 РДОЫ ФУРЬЕ [ГЛ. XVI*
Как известно, коэффициенты Фурье для функции /(^/имею-
/(^/имеющей период 2я, определяются по формулам
п
л я
, Я/г = — [f(x)coskxdx, 6*=.— \f(x)smkxdx.
-я -я
Во многих случаях, встречающихся на практике, функция f(x)
задается или в виде таблицы (когда функциональная зависимость
получается в результате эксперимента) или в виде кривой, кото-
которая вычерчивается каким-либо прибором. В этих случаях коэф-
коэффициенты Фурье вычисляются при помощи приближенных методов
интегрирования (см. § 8 гл. XI т. I).
Будем рассматривать промежуток — я ^ х ^ я длины 2я. Этого
можно всегда добиться соответствующим выбором масштаба по
оси Ох.
Разделим промежуток [—я, я] на п равных частей точками
— Я = #0, Хц Х2, . . ., Хп = Я.
Тогда шаг деления будет равен
Значения функции f{x) в точках х0, xi9 x2, . .„, хп обозначим
соответственно через
У* Уь У» •••» У».
Эти значения мы определяем или по таблице или графику данной
функции—измерением соответствующих ординат.
Тогда, пользуясь, например, формулой прямоугольников (см.
формулу (Г) § 8 гл. XI т. 1), определяем .коэффициенты Фурье
Разработаны схемы, упрощающие вычисление коэффициентов Фурье
(см., например, Смирнов В. И. Курс высшей математики,
т. П,*г-М.: Наука, 1974; Лопшиц A.M. Шаблоны для гармо-
гармонического анализа и синтеза.— М.: Гостехиздат, 1948). Мы не
можем здесь останавливаться на подробностях, но отметим, что
существуют приборы (так называемые гармонические анализаторы),
которые по графику данной функции позволяют вычислить при-
приближенные значения коэффициентов Фурье.
§ 12. Ряд Фурье в комплексной форме
Пусть имеем ряд Фурье для периодической функции / (х) с пе-
периодом 2я:
00
Нх) = if + S К cos nx+bn sin nx). A)
/1=1

§ 12] . РЯД ФУРЬЕ В КОМПЛЕКСНОЙ ФОРМЕ 347
Выразим cos ял; и sinm; через показательные функции. Для
этого воспользуемся известными формулами (см. формулы C) § 5
гл. VII т. I):
eiy -\-e~iy eiy е ~iy
cosy = —-^ , siny = ,
Итак,
pinx Л-о—inx pinx p—inx pinx g—inx
-•—^ , sin nx = ——pn ==— f к ¦
Подставляем эти значения cosrt# и sinnx в формулу A) и про-
производим соответствующие преобразования:
- f+II (а^ ^+
Введем обозначения
При, этих обозначениях формула B) примет вид
/1=1
Последнее равенство записывают более компактно:
(*)= 2 спе<»\ D)
«=-<»
Это и есть комплексная форма ряда Фурье.
Выразим коэффициенты сп и с_п через интегралы. Пользуясь
формулами D), E) и F) § 1, можем формулы C) переписать так:
f f(x)co$nxdx—i ~[ f(x)sinnxdx =
'« Л J
Итак,

348 РЯДЫ ФУРЬЕ , [ГЛ. XVII
Аналогично
-я
Формулы E') и E") и выражение с0 можно объединить в одну
формулу
я
«« = Г J / (*) e~inxdx (л = 0, ± 1,' ±2, ±3, ...). F)
— Я
сп и с_„ называются комплексными коэффициентами Фурье для
функции f(x). л
Е<;ли фуйкция f(x) периодическая с периодом 21, то ряд Фурье
для f(x) будет
ее
(см. формулу C) § 5).
Очевидно, что. в этом случае ряд Фурье в комплексной форме
вместо формулы D) выразится формулой
00 .ПП
/(*)= 2 спе '\ (8)
/Jss — 00
Коэффициенты ряда сп выразятся формулами
. пп
(x)e~tl~*dx (n = 0, ±1, ±2, ...)• (9)
Принята, особенно в электротехнике и радиотехнике, следую-
. пп
щая терминология. Выражения е / называются гармониками,
числа ап = -у5. (д = 0, ±1, ±2, ...) называются волновыми чис-
числами функций
Совокупность волновых чисел называется спектром. Если откла-
откладывать эти числа на числовой оси, то получим совокупность от-
отдельных точек. Такую совокупность точек называют дискретной,
а соответствующий спектр—дискретным. Коэффициенты еп> опре-
определяемые формулами (9), называют комплексной амплитудой. От-
Отметим, что.в некоторых трудах по электротехнике и радиотехнике
совокупность модулей амплитуд \сп\ также называют спектром
функции f(x). ' щ

ИНТЕГРАЛ ФУРЬЕ 349
§13. Интеграл Фурье
Пусть функция f(x) определена на бесконечном интервале
(—оо, оо) и абсолютно интегрируема на нем, т. е. существует
интеграл
1- 00
J \f(x)\dx = Q. ' A)
Пусть, далее, функция f(x) такова, что она разлагается в лю-
любом-интервале (—/, +/) в ряд Фурье:
B)
где
"¦Л. C)
-t
Подбавляя в ряд B) выражения коэффициентов ak и Ьк из фор-
формул C), можно написать
^ ^^
00 I
ИЛИ
y?j^*-dt. ¦ D)
Исследуем вопрос о том, какой вид примет разложение D) при
переходе к пределу при /—>оо.-
-Введем следующие обозначения:
, Подставляя"в D), получаем
I
F)

350 РЯДЫ ФУРЬЕ ! 1ТГЛ. XVH
При / —> оо первый член б дравой части стремится к нулю. Дей-
Действительно,
-I
При любом фиксированном / выражение, стоящее в скобках,
есть функция от ak (см. формулы E)), принимающего значения
от я/1 до сю. Б?з доказательства укажем, что если функция f{x)
кусочно монотонна на ^каждом конечном интервале, ограничена
на бесконечном интервале и удовлетворяет условию A), 'то при
/—^.f-oo формула F) примет вид
+ 06 * + 00 ' "\
/(*)=4 \\ \ f(t)cosa(t-x)dt)da: G)
О ^-оо '
Стоящее справа выражение Называется интегралом Фурье для
функции f(x). Равенство G) имеет место для всех точек, где
функция непрерывна. В точках разрыва выполняется равенство
+ 00 / + 00 \ -
4 Д J f(t)Cosa(t-x)dt)dx=, ^+°W(*-°> . . G')
Преобразуем интеграл, стоящий в правой части равенства G),
раскрывая cosa(^—х):
cos a (t—х) = cos at cos ax + sin at sin ax.
Подставляя это выражение в формулу G) и вынося cos ax и sin ax
за знаки интегралов, где интегрирование совершается по перемен-
переменной /, получим
+ 00 / + 00
+ 00 / + 00 \
(*) = -!- J ( j f(t)cosatdt)cosaxda +
О ^-00 '
+ 00 / + 00 - Л
+ 1 П С f(t)smatdt)sinaxda. (8)
О N-oo '
Каждой из интегралов по /, стоящих в скобках, существует, так
как функция / (t) абсолютно интегрируема в интервале (—о©, + оо),
а следовательно, абсолютно интегрируемы и функции f(t) cos at
и f(t)smat.
Рассмотрим частные случаи формулы (8).
1. Пусть f(x)—четная^ функция. В этом случае f(t) cos at —
функция четная, а '/(/) sin at—нечетная и мы получаем
+ 00 + 00 +00
I f\t)cosatdt = 2 J f(t)cosat,dt, "J
- ев 0 -а>

ИНТЕГРАЛ ФУРЬЕ ' 361
Формула (8). в- этом случае примет вид
+ оо / + ао \ -
= |- J M f (t) cos at dt) cos ax da. (9)
Q \ П /
2. Пусть /(#)—нечетная функция. Анализируя характер ин-
интегралов в формуле (8) в этом случае, получим
+ 00 / +00
0^0 '
A0)
Если функция /(л:) определена только в интервале @, +°°)>
то ее можно представить при х > 0 как формулой (9), так и фор-
формулой A0). В первом случае мы ее доопределяем в интервале
(—оо, 0) четным образом, а во втором—:нечетным.
Отметим еще раз, что в точках разрыва вместо выражения / (х)
в левых частях равенств (9) и A0) следует писать выражение
Вернемся к формуле (8). Интегралы, стоящие в скобках,
являются функциями от а. Введем обозначения
/ 4-Q0 + ОО
А(а)=± J f(t)cosatdt, ?(a)=-i J f(t)sinatdt.
— Ofr —09
Тогда формулу (8) можно переписать так:
/(#)= | [Л (a) cos ax + B (a) sin ax] doe. A1)
0 '
Говорят, что формула A1) дает разложение функции /(#) на гар-
гармоники с непрерывно меняющейся от 0 до оо частотой а. Закон
распределения амплитуд и начальных фаз в зависимости от ча-
частоты а выражается чере;з функции А (а) и В {а).
Вернемся к фЪрмуле (9). Положим
+00
f(a)=V^| J /(/) сое о/Л. A2)
О
тогда формула (9) примет вид
+00
/ (х) = j/- Je F (a) cos ax da. (Щ
о
Функция F(a) называется косинус-преобразованием Фурье для
функции /(#).

352 РЯДЫ ФУРЬВ . 1ГЛ. XVII
Если в, равенстве A2) считать F(a) заданной, .a f(t) искомой
.функцией, то оно является интегральным уравнением для функ-
функции f(t). Формула A3) дает решение этого уравнения.
На основании формулы A0) можем написать следующие ра-
равенства:
Y J ^ (М)
" •- • /(*) = ]/~- J <D(a)sinoA;*ta. A5)
о
Функция Ф*(а) называется синус-преобразованием Фурье.
Пример. Пусть
По формуле A2) определяем косинус-преобразование Фурье:
По формуле A4) определяем синус-преобразование Фурье:.
^+00
л J
о
По формулам A3) и A5) находим взаимные соотношения;
Г +оо -
§ 14. Интеграл Фурье в комплексной форме
- В интеграле Фурье (формула G) § 13) в скобках стоит четная
функция от а, следовательно, она -определена и при отрицатель-
отрицательных значениях а. На основании сказанного формулу G) можно
переписать так:
=i И J f Мcosa v~x>>dt)
'

$ 14] ИНТЕГРАЛ ФУРЬЕ В КОМПЛЕКСНОЙ .ФОРМЕ 353
Рассмотрим, далее, следующее выражение, тождественно раэное
нулю:
М / + 00 N
f(t)sina(t—x)dt)da = O.
/
Выражение, стоящее слева, тождественно равно нулю потому,
что функция от а, стоящая в скобках, есть нечетная функция,
а интеграл от нечетной функции в пределах от —М до +М
равен нулю. Очевидно, что
М / + 00 \
lim \ ( [ f(t)sina(t—x)dt)da = O,
или
/+00 Ч
( 5 f(t)sma(t—x)dtjda = O. B)
\ —00 /
— СО \ —00
Замечание. Здесь необходимо указать на следующее обсто-
обстоятельство. Сходящийся интеграл с бесконечными пределами опре-
определяется так:
М
s= lim \ <p(a)da + lim
M -*• + oo _ д| M -> + oo
при условии, что каждый из стоящих справа пределов существует
(см. § 7 гл. XI т. 1). Мы же в равенстве B) написали так:
+ оо М
\ cp(a)da= lim \ ф(а)^ов. (**)
M->+<»M
Очевидно, может случиться, что предел (**) существует, а пре-
пределы, стоящие в правой части равенства (*), не существуют. Вы-
Выражение, стоящее справа в равенстве (**), называется главным
значением интеграла. Итак, в равенстве B) рассматривается глав-
главное значение несобственного (внешнего) интеграла. В этом же
смысле будут писаться и последующие интегралы этого параграфа.
Умножим члены равенства B) на —у- и сложим с соответ-
соответствующими частями равенства A), тогда получим:
+ оо Г + оо Т
/(х)--^ J J /(O(cosa(<—x)—jsinatf—x))<tf da,
— со L — со J
12 H. С. Шоку нов, т. 2

354 . . |гл.
или
C)
Правая часть в формуле C) называется интегралом Фурье
в комплексной форме для функции ftyc).
Перепишем формулу C) так:
или коротко
+ 00
/(*)= J C(a)eta*rfa, E)
— 00
где
С(а)^^ j f(f)e-**dt. , F)
Формула E) аналогична формуле A0) § 12; а также назы-
называется волновым числом, но здесь оно принимает все значения от
— оо до +оо, и спектр волновых чисел называется непрерывным
спектром. Аналогию формулы E) и формулы A0) § 12 можно
проводить и дальше. Если в формуле A0) § 12 волновому числу
ап соответствует комплексная амплитуда сп> то говорят, что в фор-
»*уле E) вшновым числам, заключенным в интеграле (af, ax + Да),
соответствует комплексная амплитуда С(а±). Функцию С (а) назы-
называют спектральной плотностью или спектральной функцией. (Здесь
терюш плотность употребляется в том же смысле, как п в § 8
гл. XIV, где говорилось о плотности распределения по двумер-
двумерней области.)
Равенство D) переписывают в виде двух равенств:
Функция Р*'(а), определенная формулой G), называется пре-
оёраэованием Фурье для функции f(x). Функция /(х),,оцределенная
формулой (8), называется обратным преобразованием Фурье для
функции F*(a) (преобразования отличаются знаком при i). Функ-
Функция F*(a) отличается от функции С (а) постоянным множителем

§ 16] РЯД ФУРЬЕ ПО ОРТОГОНАЛЬНОЙ СИСТЕМЕ ФУНКЦИЙ 355
Из преобразований G) и (8) следуют преобразования A2), A4),
A3) и A5)- § 13 (с точностью до постоянного множителя 1/2),
Преобразования A2) и A4) получатся, если подставить в G)
е- ш = cos af _ i s\n af9 p* (a) = p (a) _ /ф (a)
и приравнять действительные и мнимые части. Аналогичным обра*
зом получаются преобразования A3) и A5) из преобразования (8).
Отметим, что преобразованиями, аналогичными преобразова-
преобразованиям Фурье-, мы будем пользоваться в гл. XIX «Операционное
исчисление и некоторые его приложения».
§ 15. Ряд Фурье по ортогональной системе функций
Определение 1. Бесконечная система функций
ti(x), Ф»(*). •••> <9п(х), •-. A)
называется ортогональной на отрезке [а, Ь], если при любых
выполняется равенство
ь
" B)
При этом предполагается, что
ь
Пример 1. Система функций
1, cosjc, sin*, cos 2x, sin 2x, ..., cos nx, slnnx, ••• rC)
ортогональна на отрезке f— я, я]. Это следует из равенств (I)'и (II) § 1„
Пример 2. Система функций
1, cos-у-*, sin у л:, cos2y-AT, sin2~-A:,T ..., cos^y^-, sin-—^-, ... C;)
ортогональна на отрезке [—/, /], в чем легко убедиться непосредственной
проверкой.
Пример 3. Система функции
1, cosx, cos2*, cos3#, ...f cosnxt »«• D)
ортогональна на отрезке [0, я].
Пример 4; Система функций . • , *
sin л:, sin 2л;, ..., sin nxt .»• : E)
ортогональна на отрезке [0, я], , ,.r ^
Ниже будут указаны другие системы ортогональных*функций.
Пусть функция f(x)y определенная на отрезке [а, 6], такева,
что она представляется рядом по функциям ортогональибй
12*

356 РЯДЫ ФУРЬЕ [ГЛ. XVII
системы 'A), который сходится к данной функции на [а, &]:
/Ю2уЫ> ()
Определим коэффициенты сп. Допустим, что ряд, полученный
после умножения ряда F) на любую q>k (x), допускает почленное
интегрирование.
Умножим обе части равенства F) на q>&(#) и проинтегрируем
в пределах от а до Ь. Учитывая равенства B), получим
ь ь
откуда
G)
Коэффициенты ck> вычисленные по формулам G), называются' ко-
коэффициентами Фурье функции f(x) по системе ортогональных
функций A). Ряд F) называется рядом Фурье по системе функ-
функций A).
Определение 2. Ортогональная система функций
называется полной, если для любой функции f(x) с интегрируемым
квадратом, т. е. такой, что
выполняется равенство
lim J \f (л:)-2 с№
(8)
Равенство (8) в силу определений § 7 можно истолковать и так.
п
Среднеквадратичное уклонение суммы 2 ^Ф* (#) от функции / (х)
*=о
стремится к нулю при п—^оо. *
Если выполняется равенство (8), то говорят, что ряд Фурье
F) сходится к функции f(x) в среднем.

$ J6] ЛИНЕЙНОЕ ФУНКЦИОНАЛЬНОЕ ПРОСТРАНСТВО 357
Очевидно, что из сходимости в среднем не следует сходимость
в каждой точке отрезка [а, Ь].
Отметим без доказательства, что тригонометрические системы,
указанные в примерах 1—4, полны на соответствующих отрезках.
Очень широко используется в приложениях система функций
Бесселя
которые были рассмотрены в § 23 гл. XVI. Здесь %i} Я2, ...
..., %h ...—корни функции Бесселя, т. е. числа, удовлетворяю-
удовлетворяющие соотношению
/я(Х,) = 0 (/ = 1, 2, ...).
Без доказательства укажем, что система функций
VxJn <М. VxJn (Kxh ..., VxJn (Я,х), ... A0)
ортогональна на отрезке [0, 1]:
i
O*) <*#/). A1)
Так же з приложениях используются системы ортогональных
многочленов Лежандра^ которые определяются так:
(л=1, 2,...).
Они удовлетворяют уравнениям
(х*-1)у" + 2ху'-п(п+\)у = 0.
Используются и другие системы ортогональных многочленов.
§ 16. Понятие о линейном функциональном пространстве.
Аналогия между разложением функций в ряд Фурье
и разложением векторов
В аналитической геометрии был определен вектор в .трехмер-
.трехмерном пространстве
*) Если для функций <рд (х), фу (х) выполняется соотношение
ь
то говорят, что функции ф/ (х) ортогональны с весом р (х). Следовательно,
функции Jn(Xix) (при k Ф /) ортогональны с весом х. , ..

' - ?гл.
где,?, /, &—единична .вз^тшо ш^евдшсуляршяе ©ектары, на-
направленные по осям координат. Векторы if /, * будем « даль-
дальнейшем обозначать elt е,, е,.
Аналогичным образом молено определить вектор в /1-мерном
Совеикупяость векторов вида А будем называть п-мерным еекли-
довым пространством и обозначать ?„. Векторы А будем назы-
называть элементами или точками n-мерного евклидова простран-
пространства *). Укажем свойства пространства Еп.
Пусть даны два вектора пространства Д„:
А =
Если Ci и С2—действительные числа, то по аналогии с трехмер-
трехмерным пространством
A)
есть вектор пространства Еп.
Скалярным произведением векторов Ли S называется
S
Векторы е*, е^, ..., ен цpиндjgLJleжaт пространству Еп, к ним
также «рйменима формула B).
С получаем при г
При 1=
^ скалярное произведение которых равно нулю, назы-
называются ортегтпльными. Стедовательно, векторы elt e2t ..., еп
ортогональны.
Как и в трехмерявм л^страйстве, легко устанавливаются
следующие свойства скалярного произведения:
(А, В) = (В, А),
(А+В, С) = (АС)+{ВС% C)
) ^а jr векторы в бесконечномерном
¦*) Вместо (А, ^) и«орда %дем 'Писать ^Л©

$16]
ЛИНЕЙНОЕ ФУНКЦИОНАЛЬНОЕ ПРОСТРАНСТВО
. Длина или модуль вектора А определяется, как и ъ трех-
мерном пространстве:
S/J. , D)
Длину разности двух векторов естественно определяют так:
\А-В\=У ±(А^В{)К E)
В частности, м
| А-А\~ у Jj (Л,-*,)¦•=<>.
Угол f между двумя? векторами определяется такг
=TTiW
Рассмотрим совокупность всех кусочно монотонных ограничен-
ограниченных на отрезке [а, 6] функций *). Обозначим эту совокупность
через Ф и будем называть пространством функций Ф. Функции,
принадлежащие этому пространству, будем называть элементами
или точками пространства Ф. Можно установить операции над
функциями пространства Ф, аналогичные операциям, которые мы
производили над векторами пространства Еп.
Если Cf и С2—любые действительные числа и fi(*J, /2(#) —
элементы пространства! Ф, то '
есть элемент пространства Ф.
Если f(x) и ф(^)—две функции пространства Ф, то скаляр-
скалярным произведением функций f(x} и ц(х} называется выражение
Это выражение аналогично выражению B). Легко проверить^
что -скалярное- произведение (8) обладает свойствами* аналогич-
аналогичными свойствам C) для векторов: • »•. . -
(/, Ф) = (Ф, /),
9) = (/i, Ф)-К/,гФ), (9)
*) Такой класс функций рассматривался в теореме § 1. Можно было бы
рассмотреть * более ш#ро#ий класс функций* для которого все утверждения
§ 1 сохраняется:* * . v •••:.» -*п - -

3G0 РЯДЫ ФУРЬЕ [ГЛ. XVH
Аналогично определению модуля вектора по формуле D) опре-
определяется так называемая норма элемента f(x) пространства Ф:
K(/. /)=K $
)fdx. A0)
Расстояние между элементами f(x) и ф(лг) пространства Ф
аналогично формуле E) будем называть выражение
;)]Чх. A1)
Выражение A1) расстояния между элементами пространства
называется метрикой пространства. Оно с точностью до множи-
множителя \rb—а совпадает со среднеквадратичным уклонением б,
определенным в § 7.
Очевидно, что если f(je) =ф(лс), т. е. f{x) и ф(лс) совпадают
во всех точках отрезка [а, Ь], то |/—ф|| = 0. Но если J/—ф|| = 0,
то / (х) = ф (х) во всех точках отрезка [а, &], кроме конечного числа
точек *). Но в этом случае также говорят, что элементы про-
пространства Ф тождественны.
Пространство кусочно монотонных ограниченных функций,
в котором определены операции G), (8) и метрика определяется
равенством A1), называется линейным функциональным [простран-
[пространством с квадратичной метрикой. Элементы пространства Ф на-
называются точками пространства или векторами.
Рассмотрим, далее, последовательность функций
A2)
принадлежащих пространству Ф.
Последовательность функций A2) называется ортогональной
на отрезке [а, 6], если при любых i, j {1ф}) выполняются
равенства
(Ф* Ф/) = S Ф< (*) Ф/ (*)dx = °- A3)
а
На основании равенств (I) § 1 следует, что, например, система
функций
1, cosjc, sin л:, cos 2л:, sin 2л:, cos Зле, sin Зле, ...
ортогональна на отрезке [—я, я].
Покажем, далее, что разложение функции в ряд Фурье по
ортогональным функциям аналогично разложению вектора по
*) Может быть и бесконечное число точек, где f (х) Ф <р (х).

§ 16] ЛИНЕЙНОЕ ФУНКЦИОНАЛЬНОЕ ПРОСТРАНСТВО 361
ортогональным векторам. Пусть дан вектор
t+ ... + Акек + ... +Апеп. A4)
Мы предполагаем, что векторы elf e2, ..., еп ортогональны, т. е.
если i Ф\у то
(eh ey) = 0. A5)
Чтобы определить проекцию АкУ умножаем скалярно правую
и левую части равенства A4) на вектор ек. На основании свойств
B), C) получаем:
(А, ек) = Аг(е19 ек) + К(в2, ек)+... +Ак(ек9 ек)+... +Ап(еп,ек).
Учитывая A5), получаем
(Л, ек) = Ак(ек, ек),
откуда
Допустим, далее, что функция f(x) разложена по ^системе
ортогональных функций:
/(*)=2ад>*(*). A7)
Умножая скалярно обе части равенства A7) на (рк(х) и учи-
учитывая равенства (9) и A3), получим*)
(/, Ф*)=а*(Ф*. Vh)f
откуда
а
Формула A8) аналогична формуле A6).
Обозначим, далее,
j). A9)
= |/-Ч|(п = 1, 2, ...).¦ B0)
Если
Нгаб„ = О,
то система ортогональных функций A2) является полной на
отрезке Га, 6].
Ряд Фурье A7) сходится к функции f(x) в среднем*
*) Мы предполагаем, что получающиеся в^ процессе рассмотрения ряды
сходятся и почлецное интегрирование законно.

362 РЯДЫ ФУРЬЕ , . [ГЛ XVII
У п р а ж нения к главе XVII
1. Разложить в ряд Фурье в интервале (— щ я) функцию
/ (х) =х при —я < х < О,
f(x) = 2x при
2 /cos* . cos 3* . cosЪх , ,
sin2*. sin Здг
2~+~з
2. Пользуясь разложением функции f(x) = l в интервале (О, я) по сину-
1,1 1 . л я
сам кратных дуг, вычислить сумму ряда 1—о*+"—7" •*• /ш' Т*
3. Пользуясь разложением в ряд Фурье функций f(x)=x2\ вычислить
1 1,1 1 , л я2
сумму ряда -р—22+-32—jr+... Отв. ^
я2 а:2
4. Разложить в ряд Фурье в интервале (—я, я) функцию f(*) = y^—j .
cos 2x , cos Зх cos 4x .
cos* р—|—^^ 15—1-...
5. Разложить в ряд Фурье в интервале, (^- я, я) функцию
f(x)=-^r при -°
/М = ~:5:^ ПРИ
sin2*+
6. Разложить в ряд Фурье в интервале (—я, я) функцию
f(x) = — х при —я
/(х) = 0 при 0
?! cosBm+1)^
"• 4 я Zu Bm-ИJ
7. Разложить в ряд Фурье в интервале (—я, я) функцию
/(*) = 1 при — j
f (*) = —2 при 0 <
Отв. —-тт.
2 я
8. Разложить функцию f(x)=x2 в интервале @, я) в ряд только синусов.
Отв. 4 V (-l)»+i/^+4 [(-!)"-1]\ sin nx.
9. Разложить функцию t/=cos2* в интервале @, я) в ряд только синусов.
п 4 Г sin* , 3sin3* , 5stoSy , 1
итв. —jj j^2_ |+22—За "*" 22—52 "*"''' J '
10. Разложить функцию t/=sin* в интервале- @ $ я)нв~ряд только коси-
л 4 Г 1 . cos2л:,. cos 4* ,
нусов. От. ^l^+TZ^i+rzrp+'

УПРАЖНЕНИЯ К ГЛАВЕ XVII 363
11. Разложить в ряд Фурье функцию у=ех в интервале (—I, /)•
(l^COS (l)
От. e-^+(
/1=1
12. Разложить функцию f(x) = 2x в интервале @, 1) в ряд только ^синусов.
13, Разложить функцию / (лр) =* в интервале @, /) в ряд только синусов.
пах
о/ • sin ^Г
14, Разложить функцию
2—л; при i <x < 2
в интервале @, 2): а) в ряд только синусов; б) в ряд только
о «> sini J-+— t

ГЛАВА XVIII
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
§ 1. Основные типы уравнений математической физики
Основными уравнениями математической физики называют (для
случая функций двух независимых переменных) следующие диф-
дифференциальные уравнения с частными производными второго
порядка.
I. Волновое уравнение:
QpL дх** '
К исследованию этого уравнения приводит рассмотрение про-
процессов поперечных колебаний струны, продольных колебаний
стержня, электрических колебаний в проводе, крутильных колеба-
колебаний вала, колебаний газа и т. д. Это уравнение является прос-
простейшим уравнением гиперболического типа.
II. Уравнение теплопроводности, или уравне-
уравнение Фурье:
К исследованию этого уравнения приводит рассмотрение про-
процессов распространения тепла, фильтрации жидкости и газа в по-
пористой среде (например, фильтрации нефти и газа в подземных
песчаниках), некоторые вопросы теории вероятностей и т. д. Это
уравнение является простейшим уравнением параболического типа,
III. Уравнение Лапласа:
К исследованию этого уравнения приводит рассмотрение задач
об электрических и магнитных полях, о стационарном тепловом
состоянии, задач гидродинамики, диффузии и т. д.. Это уравнение
является простейшим уравнением эллиптического типа.
В уравнениях A), B) и C) искомая функция и зависит от
двух переменных. Рассматриваются также соответствующие урав-

§2] ВЫВОД УРАВНЕНИЯ КОЛЕБАНИЙ СТРУНЫ 365
нения и для функций "с большим числом переменных. Так, вол-
волновое уравнение с тремя независимыми переменными имеет вид
уравнение теплопроводности с тремя независимыми переменными
имеет вид
L
уравнение Лапласа с тремя независимыми переменными имеет вид
§ 2. Вывод уравнения колебаний струны.
Формулировка краевой задачи. Вывод уравнений
электрических колебаний в проводах
В математической, физике под струной понимают гибкую упру-
упругую нить. Напряжения, возникающие в струне в любой момент
врехмени, направлены по касательной к ее профилю. Пусть струна
длины I в начальный момент направлена по отрезку оси Ох от О
до /. Предположим, что концы .
струны закреплены в точках х~ О
и #==/. Если струну отклонить
от ее первоначального положе-
положения, а потом предоставить самой
себе, или, не отклоняя струны, Q ' я Щ
придать в начальный момент ее Рис. 389.
точкам некоторую скорость, или
отклонить струну и придать ее точкам некоторую скорость, то
точки струны будут совершать движения—говорят, что струна
начнет колебаться. Задача заключается в определении формы
струны в любой момент времени и в определении закона движе-
движения каждой точки струны в зависимости от времени.
Будем рассматривать малые отклонения точек струны от на-
начального положения. В силу этого можно предполагать, что
движение точек струны происходит перпендикулярно оси Ох и
в одной плоскости. При этом предположении процесс колебания
струны описывается одной функцией и(х, t)9 которая дает вели-
величину перемещения точки струны с абсциссой х в момент t
(рис. 389).
Так как мы рассматриваем малые отклонения струны в пло-
плоскости (х, и)} то будем предполагать, что длина элемента струны

366 УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ [ГЛ. XVIII
МгМъ равняется ее проекции на ось Охг т. е. *)
Также будем предполагать, что натяжение во всех точках струны
одинаковое; обозначим его че-
через Т.
Рассмотрим элемент струны
ММ' (рис. 390). На концах это-
этого элемента по касательным к
. . ^ струне действуют силы Т. Пусть
касательные образуют с осью Ох
Рис. 390, углы ф и ф + Аф. Тогда проек-
проекция на ось Ои сил, действую-
действующих на элемент ММ', будет равна Т sin (ф +Аф)—Т этф. Так как
угол ф мал, то можно положить tg ф « sin ф, и мы будем иметь
Т$т(ф + Аф)—Гзтф^
t)
о<е<1
(здесь мы применили теорему Лагранжа к выражению, стоящему
в квадратных скобках).
Чтобы получить уравнение движения, нужно внешние силы,
приложенные к элементу, приравнять силе инерции. Пусть р —
линейная плотность струны. Тогда масса элемента струны будет
рД#. Ускорение элемента равно ~?. Следовательно, по прин-
принципу Даламбера будем иметь
Сокращая на Ал: и обозначая Т/р = а2, получаем уравнение дви-
движения
Это и есть волновое уравнение—уравнение колебаний струны. Для
полного определения движения струны одного уравнения A)
недостаточно. Искомая функция и{х> t) должна удовлетворять
еще граничньш условиям, указывающим, что делается на концах
струны (х = 0 и х= /), и начальным условиям, описывающим состоя-
*) Это предположение эквивалентно тому, что мы пренебрегаем величи-
величиной их по срарнению с 1. Действительно, i ,. • •

$2] ВЫВОД УРАВНЕНИЯ КОЛЕБАНИЙ СТРУНЫ Зв7
ние струны в начальный момент (? = 0). Совокупность граничных
и начальных условий называется краевыми условиями.
Пусть, например, как мы предполагали, концы струны при
х = 0 и х = / неподвижны. Тогда при любом t должны выполняться
равенства
и@, 0 = 0, B')
и(/, 0 = 0. B")
Эти равенства являются граничными условиями для нашей задачи.
В начальный момент t = 0 струна имеет определенную форму,
которую мы ей придали. Пусть эта форма определяется функцией
f(x). Таким образом, должно быть
u(xf 0) = а |,яв = /(*). C')
Далее, в начальный момент должна быть задана скорость в каждой
точке струны, которая определяется функцией ф(лг). Таким обра-
образом, должно быть
SLr'W- <3">
Условия C') и C") являются начальными условиями.
Замечание. В частности, может быть / (я) гз 0 или ф (я) =з 0.
Если же /(#)=0 и ф{#) = 0, то струна будет находиться в покое,
следовательно, и(х, 0 — 0.
Как указывалось выше, к уравнению A) приводит и задача
об электрических колебаниях в проводах. Покажем это. Электри-
Электрический ток в проводе характеризуется величиной i (x, t) и напря-
напряжением v(xf 0» которые зависят от координаты х точки провода
и от времени t. Рассматривая элемент провода Да:, можем напи-
написать, что падение напряжения на элементе Ах равно v(x, t) —
— v(x-\-Ax, t)&—л-А*- Это падение напряжения складывается
«з омического, равного iRAx, и индуктивного, равного -g^-
Итак,
-|A* = *A*+-g-LA*, D)
где R и L—сопротивление и коэффициент индуктивности, рас-
рассчитанные на единицу длины провода. Знак минус взят потому,
что ток течет в направлении, обратном возрастанию v. Сокращая
на Дл:, получаем уравнение
Далее, разность тока, выходящего из элемента Длс, и тока, вхо-
входящего в него за время Д?, будет

368 УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ [ГЛ. XVIII
Она расходуется на зарядку элемента, равную С Ах •—• А/, и на
утечку через боковую поверхность провода вследствие несовер-
несовершенства изоляции, равную Av Ах At (здесь А — коэффициент утечки).
Приравнивая эти выражения и сокращая на Ах At, получим урав-
уравнение
L
F)
Уравнения E) и F) принято называть телеграфными уравнениями.
Из системы уравнений E) и F) можно получить уравнение,
содержащее только искомую функцию i (x, /), и уравнение, содер-
содержащее только искомую функцию v(x, /). Продифференцируем
члены уравнения F) по х\ члены уравнения E) продифференци-
продифференцируем по / и умножим их на С. Производя вычитание, получим
Подставляя в последнее уравнение выражение ~ из уравнения E),
получим
или
^^CL^ + (CR + AL)§ + ARi: G)
Аналогичным образом' получается уравнение для «определения
v(x, t):
^ = CL^ + (CR + AL)^+ARv. (8)
Если можно пренебречь утечкой через изоляцию (Л = 0) и
сопротивлением (R = 0), то уравнения G) и (8) переходят в еол-
новые уравнения
2 d2i _ d2i 2 d2v _ д2?
й дх2 "" ~dW ' й ~дхГ ~~ ~dF '
где обозначено а2-= 1/CL. Исходя из физических условий, форму-
формулируются граничные и начальные условия задачи.
§ 3. Решение уравнения колебаний струны методом
разделения переменных (методом Фурье)
Метод разделения переменных (или метод Фурье), который
мы сейчас рассмотрим, является типичным для решения многих
задач математической физики. Пусть требуется найти решение

$3] РЕШЕНИЕ УРАВНЕНИЯ КОЛЕБАНИЙ СТРУНЫ
уравнения
удовлетворяющее краевым условиям
и @, 0 = 0, B)
и (К t) = 0, C)
и(х9 0) = /(*), D)
•зг = *(*>• E)
Будем искать (не равное тождественно нулю) частное решение
уравнения A), удовлетворяющее граничным условиям B) и C),
в виде произведения двух функций Х(х) и Т(/), из которых
первая зависит только от х, а вторая только от t:
Подставляя в уравнение A), получаем X (х) Т" (t) = а*Х" (х) Т (t)
и, разделив члены равенства на агХТу
Г X"
В левой части этого равенства стоит функция, которая не
зависит от ху а в правой—функция, не зависящая от t. Равен-
Равенство G) возможно только. в том случае, когда левая и правая
части не зависят ни от х, ни от t, т. е. равны постоянному числу.
Обозцачрм, его через —Я, где Я>0 (позднее будет рассмотрен
и случай к < 0). Итак,
т" _ х" __ \
Из этих равенств получаем два уравнения
Х" + ХХ = 0, (8)
Т" + а2ХТ = 0. (&)
Общие решения этих уравнений будут (см. гл. XIII, § 21)
Х{х)= A cos J/T х + В sin VIх, A0)
T(t) = CcosaVIt + DsinaVIt, A1)
где Л, 5, С, D—произвольные постоянные.
Подставляя выражения Х(х) и Т (t) в равенство F), получим
Подберем теперь постоянные А и В так, чтобы удовлетворялись
условия B) и C). Так как Т(/)=?0 (в противном случае будет

37Ф УРАЪШЫШ МАТЕМАТИЧЕСКОЙ ФИЗИКИ . [ГЛ. XVIII
u(x, t)=0, что противоречит поставленному условию), то функ-
функция X (х) должна удовлетворять условиям B) и C), т. е. должно
быть X @) = 0, X (/) = 0. Подставляя значения х = 0 и х = /
в равенство A0), на основании B) и C) получаем
Из первого уравнения находим А = 0. Из второго уравнения сле-
следует
ф, так как в противном случае было бы Х = 0 и йе=0, что
противоречит условию. Следовательно, должно быть
откуда
Vl = ~ (я=1, 2, ...) A2)
(мы не берем значение п = 0, так как в этом случае было бы
Х = 0 и а = 0). Итак, мы .получили
X = Bsm™x. A3)
Найденные значения X называются собственными значениями для
данной краевой задачи. Соответствующие им функции X (#) назы-
называются собственными функциями.
Замечание. Если бы] мы взяли вместо —% выражение
k = k\ то уравнение (8) приняло бы вид
X"—**Х = 0.
Общее решение этого уравнения:
Отличное от нуля решение в такой форме не может удовлетво-
удовлетворять граничным условиям B) и C).
Зная VK мы, пользуясь равенством A1), можем написать
^2* + Dsin^* (я = 1, 2, ...). A4)
Для каждого значения п, следовательно, для каждого к, выра-
выражения A3) и A4) подставляем в равенство F) и получаем реше-
решение уравнения A), удовлетворяющее граничным условиям B) и
C). Это решение обозначим un(xf t):
ия(х9 t)=sin^x(cncos^t+Dnsm^t). A5)
Для каждого значения п мы можем брать свои постоянные С и
D и потому тшт Gn и ?>„ (постоянная В включена в Сп и Цп).

§ 3} РЕШЕНИЕ .УРАВНЕНИЯ КОЛЕБАНИЙ СТРУНЫ 371
Так как уравнение A) линейное и однороднее, то сумма решений
также является решением, и потому функция, представленная
рядом
ИЛИ
и(х, 0 = ? fcncos^t+Dnsm^t)sm^-x, A6)
71=1 Ч '
также будет решением дифференциального уравнения A), которое
будет удовлетворять граничным условиям B) и C). Очевидно,
ряд A6) будет решением уравнения A) только в том случае,
если коэффициенты Сп и Dn таковы, что этот ряд сходится и
сходятся ряды, получающиеся после двукратного почленного
дифференцирования по х и по /.
Решение A6) должно еще удовлетворять начальным условиям D)
и E). Этого мы будем добиваться путем подбора постоянных Сп
и Dn. Подставляя в равенство A6) / = 0, получим (см. условие D))
^ A7)
Если функция f(x) такова, что в интервале @, /) ее можно раз-
ложить в ряд Фурье (см. § 1 гл. XVII), то условие A7) ^удет
выполняться, если положить
^ A8)
Далее, дифференцируем члены равенства,A6) по t и подставляем
? = 0. Из условия E) получается равенство
ф(*) = 2- Dn —7-ЫЪ-гХ.
Определяем, коэффициенты Фурье этого ряда:
ИЛИ
Итак, кы доказали, что ряд A6), где коэффициенты Сп и Dn
определены по формулам A8) и A9), если он допускает двукратное

372 УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ [ГЛ. XVIII
почленное дифференцирование, представляет функцию и (х, t)t кото-
которая является решением уравнения A) и удовлетворяет граничным
и начальным условиям B)—E).
Замечание. Решая рассмотренную задачу для волнового
уравнения другим методом, можно доказать, что ряд A6) пред-
представляет решение и в том случае, когда он не допускает почлен-
почленного дифференцирования. При этом функция f(x) должна быть
дважды дифференцируемой, а <р (л:)—один раз дифференцируемой *).
§ 4. Уравнение распространения тепла в стержне*.
Формулировка краевой задачи
Рассмотрим однородный стержень длины /. Будем предполагать,
что боковая поверхность стержня теплонепроницаема и что во
всех точках поперечного сечения стержня температура одинакова.
^ Изучим процесс распростра-
\ 1_1 I I ""' I нения тепла в стержне.
$ $1 $2 I Расположим ось Ох так,
что один конец стержня будет
Рис. 391, совпадать сточкой х = 0, а
другой—с точкой х = 1 (рис.
391). Пусть и (ху t)—температура в сечении стержня с абсциссой
х в момент t. Опытным путем установлено, что скорость распрост-
распространения тепла, т. е. количество тепла, протекающего через сече-
сечение с абсциссой х за единицу времени, определяется формулой
я—ф, • СО
где S—площадь сечения рассматриваемого стержня, k—коэффи-
k—коэффициент теплопроводности **).
Рассмотрим > элемент стержня, заключенный между сечениями
с абсциссами хх и х2(х2—хг = Ах). Количество тепла, прошедшего
через сечение с абсциссой хг за время Д?, будет равно
то же самое для сечения с абсциссой лу.
C)
*) Подробно об этих условиях см., например, в книге: Тихонов А. Н.,
Самарский А. А. Уравнения математической физики.— М.: Наука,
1977.
**) Скорость распространения тепла, или скорость теплового потока, опре-
определяется так;
где AQ—количество тепла-, прошедшего через сечение S за время Д?.

§4] УРАВНЕНИЕ РАСПРОСТРАНЕНИЯ ТЕПЛА В СТЕРЖНЕ 373
Приток тепла AQt—AQ2 в элемент стержня за время Ai будет
равняться
(мы применили теорему Лагранжа к разности ~ —^ ) .
\ ох х=х2 Ох \х=хх/
Этот приток тепла за время At затратился на повышение темпера-
температуры элемента стержня на величину Аи:
или
AQi—AQ2ttcpAxS^At, E)
где с—теплоемкость вещества стержня, р—плотность вещества
стержня (pAxS—масса элемента стержня).
' Приравнивая выражения D) и E) одного и того же количества
тепла AQi—AQ2, получим
ИЛИ
Обозначая
kjcp — а2,
ди
dt ~
k
' Ф
окончательно
ди
о
'дЧ
дх* *
получаем
дЧ
= а'^. F)
Это и есть уравнение распространения тепла (уравнение тепло-
проводности) в однородном стержне.
Чтобы решение уравнения F) было вполне определенно, функ-
функция u(xf t) должна удовлетворять краевым условиям, соответст-
соответствующим физическим условиям задачи. Краевые условия для реше-
решения уравнения F) могут быть различные. Условия, которые
соответствуют так называемой первой краевой задаче для 0<! t ^T,
следующие:
и (х, 0) = cp(x), " G)
и @, t) = tyi(t), . (8)
u(U t) = ty2(t). (9)
Физически условие G) (начальное условие) соответствует тому,
что при ( = 0 в различных сечениях стержня задана температура,
равная <р(я). Условия (8) и (9) (граничные условия) соответствуют
тому, что на концах стержня при х = 0 и при х = 1 поддержи-
поддерживается температура, равная %(t) и "ф2@ соответственно.

374 WTABHBHMfl МАТЕМАТИЧЕСКИЙ -ФИЗИКИ ?ГЛ. ХУШ
В § 6 доказывается, что уравнение F) имеет еденсттешше
решение в области 0<a;</, 0<?<Г, удовлетворяющее усло-
условиям G) —(9).
§ 5. Распространение тепла в пространстве
Рассмотрим процесс распространения тепла в трехмерном про-
пространстве. Пусть и(х, уt г, t)— температура в точке с координа-
координатами (х\ у; г) в момент t. Опытным путем установлено, -что ско-
скорость прохождения тепла через площадку AS, т. е. ^количество
тепла, протекающего за единицу времени, определяется формулой
(аналогичной формуле A) предыдущего параграфа)
AQ = -kd?AS, A)
где k—коэффициент теплопроводности рассматриваемой среды, ко-
которую мы считаем однородной и изотропной, п—единичный век-
вектор, направленный по нормали к площадке AS в направлении
движения тепла. На основании § 14 гл. VIII т. I можем написать
где cos a, cosfJ, cosy—направляющие косинусы вектора я, шш
Подставляя выражение ^ в формулу A), получаем
Д Q = _ kn grad и AS.
Количеств® тепш, дотекающего за враля Ы через площадку US,
будет равно
AQ Д/ = — kn grad и tU AS.
Пишемся к .поставленной в начале параграфа задаче. ® рас-
рассматриваемой среде вщделим малый объем К, ограниченв^ шл^х-
ностью S. количество тепла, протекающего через парерддаасть S,
будет равно
Q= — A*$$fo*grad«dS, B)
где я—еданичный вектор, направленный по внешней нормали
к поверхности S. Очешщно^ что формула (Z) дает количеств
тшт^ поступающего в ©бьем V (или уходящего из о&ьема Щ за
цршя At. Количество тепла, лостувившего в объщ V% идет на
повышение температуры вещества этого объема.

$&] РАСПРОСТРАНЕНИЕ ТЕПЛА В ПРФСТРАШТВЕ 375
. Рассмозгрим элементарный объем Av. Пусть за время At его
температура поднялась на Аи. Очевидно, что количество тепла*
затраченное на это повышение температуры элемента Аи, будет равно
сА vp Аи « сА vp -~ At,
где с—теплоемкость вещества, р—плотность. Общее количество
тепла, затраченное на повышение температуры в объеме V за
время А/, будет
Но это есть тепло, поступившее в объем^ F за время At; оно
определено формулой B). Таким образом, имеет место равенство
—At J j kn grad udS = At Щ cp j? do.
' О v
Сокращай на Af, получаем
^Jp^dv. C)
Поверхностный интеграл, стоящий в левой части этого равен-
равенства, преобразуем по формуле Остроградского (см. § 8 гл. XV),
полагая F=kgvadu:
Заменяя двойной интеграл, стоящий в левой части равенства C),
тройным интегралом, получим
или
D)
Ш [^
Применив теорему о среднем к тройному интегралу, стоящему'
слева (см. § 12 гл. XIV), получим
=0, E)
где Р{хг\ у.г\ ZiX— некоторая точка объема V.
Так как мы можем выделить произвольный объем V в трехмер-
трехмерном пространстве, где происходит распространение тепла, и так-
как мы предполагаем, что подынтегральная, функция в равенстве

37в УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ [ГЛ. XVIH
D) непрерывна, то равенство E) будет выполняться в каждой
точке пространства. Итак,
). F)
Но
ди ш . * ди -
j+kk
(см. § 8 гл. XV). Подставляя в уравнение F), получаем
ди д /, ди \ . д (и ди \ , д (и ди
Если k — постоянная, то
и уравнение F) в этом случае дает
СР dt -**[ дх* + ду* "+"
или, положив — — = а2,
ди 2fd*u , д*и , д2и
Коротко уравнение (8) записывается так:
_а«_ 2д
где д===-§^г+7^2"+-5р—оператор Лапласа, Уравнение (8) и есть
уравнение теплопроводности в пространстве. Для того чтобы
найти его единственное решение, отвечающее поставленной задаче,
нужно задать краевые условия.
Пусть имеем тело Q, поверхность которого or. В этом теле
рассматривается процесс распространения тепла. В начальный
момент температура тела задана. Это соответствует тому, что
известно значение решения при t~ Q —начальное условие:
и(х, у у z, О) = ф(д:, у, г). (9)
Кроме того, должна быть известна температура в любой точке М
поверхности а тела в любой момент времени t—граничное условие:
и(М, t)=zty(M, t). A0)
(Возможны и другие граничные условия.)

§ GJ РЕШЕНИЕ ПЕРВОЙ КРАЕВОЙ ЗАДАЧИ 377
Если искомая функция и (х9 у у г, /) не зависит от z9 что соот-
соответствует тому, что температура не зависит от г, то получаем
уравнение
ди „г(&
а
— уравнение распространения тепла на плоскости. Если рассмат-
рассматривается распространение тепла в плоской области D с границей С,
то краевые условия, аналогично (9) и A0), формулируются так:
и(х, У, 0) = ф(*, у)9 и (М7 /)
где ф и -ф —заданные функции, М — точка границы С.
Если же функция и не зависит ни от г, ни от у% то получаем^
уравнение
ди __ 2 дЧ
dt ~~а дх*
— уравнение распространения тепла в стержне.
§ 6. Решение первой краевой задачи для уравнения
теплопроводности методом конечных разностей
Как и в случае обыкновенных дифференциальных уравнений,
при решении уравнений с частными производными методом конеч-
конечных разностей производные заменяются соответствующими разнос-
разностями (рис. 392):
ди (*, t) u(x + hf t)—u(xt t) n
Щ; ^ h ' W
дЧ (xt t) ^ l_ Г u(x+h, t) — u(xy t) u(xy t)—u(x—ht t)
dj? />*/ h I h h
ИЛИ
дЧ (xt t) _ u(x+h, t)-2u(x, t)+u(x-h, t) . /9
дх* ~ h* 9 KZ)
аналогично
ди(х, t) ^ u(xy t-\-l) — u(xt t) ,~
Первая краевая задача для уравнения теплопроводности фор-
формулируется (гм. § 4) следующим образом. Требуется найти реше-
решение уравнения
удовлетворяющее краевым условиям
и(х9 0) = ф(#), O^jc^L, E)
и@, 0 = ^@, 0<^<Т, F)
u(lt t)=ztyt(t)f 0<^<Г, . G)

Э78
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЕ ФИЗИШ
[ГЛ. XVIII
т. е. требуется найти решение и (ху t) в прямоугольнике, ограни-
ограниченном прямыми * = 0, # = 0, я=Х, * = T, если заданы значения
искомой функции на трех его сторонах ? — 0, * = 0, x = L (рис.
393), Покроем нашу область сеткой, образованной прямыми
x = ih, i= 1, 2, ,..,
t = kl, ft=l, 2, ...,
№ будем определять приближенные значения решения в узлах
сетки, т. е. в точках пересечения этих прямых. Введем обозначе-
обозначения: u,(ih,ki) — uLk. Напишем вместо уравнения D) соответствую-
соответствующее ему уравнение в конечных разностях, для точки (ih; hi).
ft
г\
№
т
)
!..
Нк)
(Ш)
Ы
¦'о
ш
m
Рис. 392#
Рис, 393*
В соответствии с формулами C) и B) получим
i '
Определим
ч k+%:
—^г) Щ
(8)
(9)
Из формулы (9) следует, что если известны три значения в k-u
р(яду: ии л, ui+i k, u^u k, то определяется значение ии k+t в
(^-J-1)-m ряду. Нам известны все значения на прямой г = 0 (см.
формулу E)). По формуле (9) мы определим значения во всех
внутренних точках отрезка, t = l. Значения в крайних точках
этого отрезка нам известны в силу формул F) и G). Так ряд
за рядом мы определим значения искомого решения во всех узлах
сетки.
Можно доказать, что по формуле (9) можно получить прибли-
приближенное значение решения не при произвольном соотношении ша-
шагов h и /, а только в том случае, если /<йг/2аа. Формула (9)
особенно упрощается», если шаг / по оси t выбрать* так, чтобы было
Ittt-P» или /г^ ;

§7] ЛРАСПРОСТ*НШ©§ШЕ ФЕГМА В :ЙЕФГРА4Ш*Ш*Ш©М СТЕРЖНЕ
В этем сдунае у-равяение (§) принимает тщ
!
1
Эта формула особенно удобна для вычислений (рис. 394). Указан-
Указанным методом определяется решение в узлах сетки. Значение ^реше-
^решения между узлами сетки можно полунить, например, экстраполи-
экстраполированием, проводя плоскость через каждые
три точки в пространстве (xt t, w). Обозна-
Обозначим полученное по формуле A0) и экстра-
экстраполированное таким образом решение-через
uh(xy t). Можно доказать, что
Ъти><?. *) = «<*. t), pmm
где u(xf t)-~ решение нашей задачи. М&жно доказать *) также,
что
где М — гшсшяийай, ^е зависящая ^>т ft,
§ 7. Распространение тепла в неограниченном стерж«е
Пусть в начальный момент задана темоература в различных
сечениях неограниченного стержня. Требуехся определить распре-
распределение температуры в стержне в .последующие моменты временя.
(К задаче расцространения тепла в неограниченном стержне сво-
сводятся физмчеекде.задачи в темсйуаде, ж©гда ет€^шв№ ci®^ дадай-
ный, что температура во внутренних точках стержня з рассмат-
рассматриваемые моменты времени мало зависит ох условий на концах
стержня.)
Если стержень совпадает с осью Фх, то щггематически задача
формулируется следующим образом. Найти решение уравнения
в области —
условию
и{х, O) =
Применим для нахождения решеш!я метод ^ааделенш? перемен-
переменных (см. § 3), т.е. будем искать часттое решение уравнения A)
в виде произведения двух функций:
*) Более подробное изложение этого вопроса см., например, в книгах:
П а ж о в Щ. Ш. Сщ>аа(тшк .по численному реагенню. дифференциальных урав-
неяшс s частньис щьшзвщшх.—М.: ;Гостехнздат, 19Ш; *Колла:т.ц ill. 'де-
'деленные методы решения дифференциальных уравнений.—М.: ИЛ, 495§

380 УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ {TJI. XVIII
Подставляя в уравнение A), будем иметь X (х) V (t) = u2X"(x) T (*),
или
Каждое из этих отношений не может зависеть ни от х, ни
от ty и потому их приравниваем постоянной *)— X2. Из D) полу-
получаем два уравнения
09 , E)
0. F)
Решая их, найдем
Т = Се~**\ X = Л cos Хх + В sin to.
Подставляя в C), получаем
«я (л, Ч) = *"Л1/[Л (X) cos Я* + В (Я) sin Хх] G)
(постоянная С включена в А(Х) и ())
Для каждого значения К мы получаем решение вида G). Про-
Произвольные постоянные А и В для каждого значения Я имеют
определенные значения. Поэтому можно считать А и В функция-
функциями от Я. В силу линейности уравнения A) решением является
также сумма решений вида G):
2 г"*** [А (X) cos кх + В (%) sin
Интегрируя выражение G) по параметру X в пределах от 0 до
4- оо, также получим решение
u(x9 t)=* S e-a2vt[A(X)cosXx + B(X)smXx]dX, (8)
если А(Х) и В(Х) таковы, что этот интеграл, его производная
по t и вторая производная по х существуют и получаются путем
дифференцирования интеграла по t и х. Подберем А (X) и В (X)
так, чтобы решение u (x, t) удовлетворяло условию B). Полагая
в равенстве (8) / = 0, на основании условия B) получаем
и(х9 О) = ф(д:)=^ J [А (X) cos Xx + В (X) sin he] dX. (9)
о
Предположим, что функция <р(#) такова, что она представима
*) Так как по смыслу задачи Т (t) должно быть ограниченным при любом
tf если ф (х) ограничена, то T'JT должно быть Отрицательным. Поэтому мы
и пишем —Я2. 1

§ 7J * РАСПРОСТРАНЕНИЕ ГЕПЛА В НЕОГРАНИЧЕННОМ СТЕРЖНЕ 381
интегралом Фурье (см. § 13 гл. XVII):
+ 0О +00
<p(x) = -L f(C <р (ос) cos h (ос — x)d<x }dk,
п J у J I
О \-оо /
ИЛИ
+ <ю Г / + « ч / + оо , ч П
— —С ( J (fb(a)cosXadoc jcosA^ + f J ф(а)эт?1айа)зт)и: \dk.
A0)
Сравнивая правые части (9) и A0), получаем
+ а>
А (к) = — С ср (a) cos tax doc,
Л (И)
— 00
Подставляя найденные выражения А (К) а В (к) в формулу (8),
получим
+ » Г / + оо
и(х9 0=^4" J 2;(
\ 1
ф (a) sin tax da J sin kx \dk =s
/ J
+ « Г +00 
1 f e-e*v4 $ у (a) (cos Ы cos kx +sin kasinkx) da \dk==
о L -^ J
+ 0O
J ф(а)совХ,(а-х)
+ <ю Г у + оо ч "I
a(jcf 0 = 4" I ГР(а)( S ^a^cos^(a~x)d^J da.
или, переставляя порядок интегрирования, окончательно получим
J A2)
Это и есть решение поставленной задачи.
Преобразуем формулу A2). Вычислим интеграл, стоящий в
круглых скобках:
+ 00 +00
cos %. (a - ж) dk = —-Ц- С е -г' cos рг <te. A3)

3&2 УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИК** ' ' [ГЛ. XVIII
Это преобразование интеграла сделано путем подстановок
Обозначим
+ 00
/С(Р)= J е-*см$гAг. A5)
о
Дифференцируя *), получаем
+ 00
о
Интегрируя по частям, найдем
^(P) = y[^2SinP2]^-4
или
К' ф)= 2"^(Р).
Интегрируя это дифференциальное уравнение, получим
э2
Определим постоянную С. Из A5) следует
(см. § 5 гл. XIV); Следовательно, в равенств A6) должно быть
С = —2~- •
Значение A7) интеграла A5) подставляем в A3):
cos X(a-x)dk = —L=-
ay t
Подставляя вместо р его выражение A4), окончательно прлучаем
*) Возможность дифференцирования легко обосновывается.

$71 РАСПРОСТРАНЕНИЕ ТЕШ1А В НЕОГРАНИЧЕННОМ СТЕРЖНЕ 383
значение интеграла A3):
+ оо
\
/^~ ""Г
-*™ cos К (а - х) dk =* — |/^е~ ""Г. A8)
Подставив это выражение интеграла в решение A2), окончательно
получим:
и(х, t) = -?-р=- j ф(а)в" "^ da. A9)
Эта формула, называемая интегралом Пуассона, представляет
собой решение доставленной задачи о распространении тепла в
неограниченном стержне.
Замечание. Можно доказать, что функция и(х, t), опреде-
определенная интегралом A9), является решением уравнения A) и удов-
удовлетворяет условию B), если функция <p(#) ограничена на беско-
бесконечном интервале ( — оо, +оо).
Установим физический смысл формулы^ 19). Рассмотрим функцию
( 0 при — оо < х < х09
<р*(х)=\ <р(х) при *«<*<*. +А*. B0)
4 10 при jco-4-Aa:< x < + сх>.
Тогда функция
есть решение уравнения A), принимающее при ?=0 значешш
Ф*(х). Принимая во внимание B0), можем написать
Применив теорему а среднем к последнему интегралу, получим
2m^^f B2)
Формула B2) дает значение температуры в точке стержня в любой
момент времени, если при * = 0 всюду в стержне температура
ы* = 0, кроме отрезка [хЛ, яо-ЬА*], где она равна ф(дс). Сумма
температур вида B2) и дает решение A9). Заметим, что если р —
линейная плотность стержня, с — теплоемкость материала, то ко-
количество тейла & элементе j>a, х^ + Ах} при ? = 0 будет
B3т)

384 УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 1ГЛ. XVIII
Рассмотрим далее функцию * .
—\=е~ 4*2' • B4)
Сравнивая ее с правой частью формулы B2) с учетом B3),
говорят, что она дает значение температуры в любой точке стерж-
стержня в любой момент времени t, если при / = 0 в сечении g (пре-
(предельный случай при Ая->0) был мгновенный источник тепла с
количеством тепла Q = ф.
§ 8. Задачи, приводящие к исследованию решений
уравнения Лапласа. Формулировка краевых задач
В этом параграфе будут рассмотрены некоторые задачи, при-
приводящие к решению уравнения Лапласа
д2и , д2и д2и 0 m
++0 W
Как уже указывалось, левая часть уравнения A) обозначается
так:
дх2 "Г ду2 "Г дг2 —&U,
где А называется оператором Лапласа. Функции и\ удовлетворя-
удовлетворяющие уравнению Лапласа, называются гармоническими функциями.
I. Стационарное (установившееся) распределе-
распределение температуры в однородном теле. Пусть имеется
однородное, тело Q, ограниченное поверхностью а. В § 5 было
показано, что температура в различных точках тела удовлетво-
удовлетворяет уравнению:
ди__ 2 / д2и д2и . ЬЧ \
dt ~~а [ дх* + ду* + дг* )т
Если процесс установившийся, т.е. если температура не зависит
от времени, а зависит только от координат точек тела, то -— = О
и, следовательно, температура удовлетворяет уравнению Лапласа
л + а* л 0 A)
дх2 i ду2 ' дг2 ч '
Чтобы температура в теле определялась однозначно из этого
уравнения, нужно знать температуру на поверхности а. Таким
образом, для уравнения A) краевая задача формулируется сле-
следующим образом.
Найти функцию и(х, у, г), удовлетворяющую уравнению A)
внутри объема Й и принимающую в каждой точке М поверхно-

§8] ЗАДАЧИ, ПРИВОДЯЩИЕ К ИССЛЕДОВАНИЮ РЕШЕНИЙ 385
сти а заданные значения:
и|о-Ф(А*). B)
Эта задача называется задачей Дирихле или первой краевой за-
задачей для уравнения A).
Если на поверхности тела температура неизвестна, а известен
тепловой поток в каждой точке' поверхности, который пропорцио-
пропорционален ~ (см. § 5), то на поверхности а вместо краевого условия
B) будем иметь условие
д?\ C)
Задача нахождения решения уравнения A), удовлетворяющего
краевому условию C), называется задачей Неймана или второй
краевой задачей.
Если рассматривается распределение температур в плоской
области D, ограниченной контуром С, то функция и будет зави-
зависеть от двух переменных х и у и удовлетворять уравнению
которое называется уравнением Лапласа на плоскости. Краевые
условия B) или C) должны выполняться на контуре С.
II. Потенциальное течение жидкости или газа.
Уравнение неразрывности. Пусть внутри объема Q, огра-
ограниченного поверхностью а (в частности, Q может быть и неогра-
неограниченным), происходит течение жидкости. Пусть р—плотность
жидкости. Скорость жидкости обозначим
v = vxi + vj+v2k9 E)
где vx9 vy, vz—проекции вектора v на оси координат. Выделим
в теле Q малый объем со, ограниченный поверхностью 5. Через
каждый элемент As поверхности S за время At пройдет количе-
количество жидкости
= pvnASAt,
где п—единичный вектор, направленный по внешней нормали
к поверхности 5. Общее количество жидкости Q, поступившее
в объем со (или вытекшее из объема со), выразится интегралом
F)
(см. §§ 5 и 6 гл. XV). Количество жидкости в объеме со в момент t
было
13 Н. С. Пискунов, т. 2

386 УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ [ГЛ. XVIII
За время At количество жидкости в силу изменения плотности
изменится на величину
Предполагая, что в объеме со нет источников, заключаем, что
это изменение вызвано притоком жидкости, количество которой
определено равенством F). Приравнивая правые части равенств
F) и G) и сокращая на At> получим
Преобразуем поверхностный интеграл, стоящий слева, по формуле
Остроградского (§ 8 гл. XV). Тогда равенство (8) примет вид
или
В силу произвольности объема со и непрерывности подынтеграль-
подынтегральной функции получаем
.&_div(pi>) = 0, (9)
или
Это и есть уравнение неразрывности течения сжимаемой жидкости.
Замечание. В некоторых задачах, например при рассмо^
трении процесса движения нефти или газа в подземной пористой
среде к скважине, можно принять
v = — --gradp,
где р—давление, k—коэффициент проницаемости, и
ft, = const. Подставляя в уравнение неразрывности (9), получим
или

§ 8] ЗАДАЧИ, ПРИВОДЯЩИЕ К ИССЛЕДОВАНИЮ РЕШЕНИЙ 387
Если k—постоянная, то это уравнение принимает вид
dt~~ Х\дх^^ dif "*" dz2 J >
и мы приходим к уравнению теплопроводности.
Вернемся к уравнению (9). Если жидкость несжимаемая, то
р = const, -~ = 0 и уравнение (9) принимает вид
div*> = 0. A2)
Если движение потенциальное, т. е. вектор v есть градиент не-
некоторой функции ср:
v = grad ф,
то уравнение A2) принимает вид
div (grad cp) = О,
или
дх2 г ду2 ' dz2 '
т. е. потенциальная функция скорости <р должна удовлетворять
уравнению Лапласа. Во многих задачах, как, например, в задачах
фильтрации, можно принять
*о = — k± grad /?,
где р—давление, &i—постоянная; тогда получаем уравнение Лап-
Лапласа для определения давления
Краевые условия для уравнения A3) или A3') могут быть
следующими:
1. На поверхности а задаются значения искомой функции р —
давления (условие B)). Это задача Дирихле.
2. На поверхности а задаются значения нормальной производ-
производной ~—задается поток через поверхность (условие C)). Это за-
задача Неймана.
3. На части поверхности а задаются значения искомой функ-
функции р—давления, а на части поверхности задаются значения
нормальной производной ~ — потока через поверхность. Это за-
задача Дирихле—Неймана.
Если движение плоско-параллельное, т. е. функция ср (или р)
не зависит от г, то получается уравнение Лапласа в двумерной
области D с границей С:
13*

383 УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ [ГЛ. XVIII
Краевые условия типа B)—задача Дирихле,— или типа C)—задача
Неймана,— задаются на контуре С.
III. Потенциал стационарного электрического
тока. Пусть в однородной среде, заполняющей некоторый объем F,
проходит электрический ток, плотность которого в каждой точке
дается вектором J(x, у, z) = Jxi-\-Jyj-\-Jzk. Предположим, что
плотность тока не зависит от времени t. Предположим далее, что
в рассматриваемом объеме нет источников тока. Следовательно,
поток вектора / через любую замкнутую поверхность S, лежащую
внутри объема V, будет равен нулю:
J i •
s
где п—единичный вектор, направленный по внешней нормали
к поверхности. Из формулы Остроградского заключаем, что
div/=0. A5)
На основании обобщенного закона Ома определяются в рас-
рассматриваемой проводящей среде электрическая сила Е:
Jb = Jfh (lb)
или
где ^ — проводимость среды, которую мы будем считать постоянной.
Из общих уравнений электромагнитного поля следует, что
если процесс стационарный, то векторное поле Е безвихревое, т. е.
rot? = 0. Тогда аналогично тому, что мы имели при рассмотре-
рассмотрении поля скоростей жидкости, векторное поле является потен-
потенциальным (см. § 9 гл. XV). Существует функция ср такая, что
A7)
На основании A6) получаем:
J-Ttgradq). A8)
Из A5) и A8) следует:
к div (grad q>) = О
или
Получили уравнение Лапласа.
Решая это уравнение при соответствующих краевых условиях,
найдем функцию <р, а по формулам A8) и A7) найдем ток J и
электрическую силу Е.

§ 0J УРАВНЕНИЕ ЛАПЛАСА 389
§ 9. Уравнение Лапласа в цилиндрических координатах.
Решение задачи Дирихле для кольца с постоянными значениями
искомой функции на внутренней и внешней окружностях
Пусть и(х, у, г)—гармоническая функция трех переменных.
Тогда >
дх2 ^ ду2 ^ дг2 ~~U- A)
Введем в рассмотрение цилиндрические координаты (г, <р, г):
# = rcoscp, y = r sin ф, 2 —г,
откуда
V |., z = z. , B)
Заменяя независимые переменные я, у и z на г, ф и 2, придем
к функции и*:
и(х, у, г) = и*(г, ф, г).
Найдем уравнение, которому будет удовлетворять и* (г, ф, z) как
функция аргументов г, ф и г.
Имеем
аналогично
д2и д2и* / дг \2
ду2 дг2 [ ду )
кроме того,
ди
дх
' дг дх2
ди* дН
' дг ду2
ди*
~~ дг
j О*'
, о*2
' *" дг
д2и
дг .ди*
дх д(р
и* дг дц> ,
дудх дх '
и* дг д(р
д(р ду ду
\ с*и*
д2и* / дц>\2 ,
дц>2 \ дх J '
, д2и* ( дц> \ 2 ,
^Ф2 \ду )
ди* д\
дф дх2
ди* д2^
дг дг v;
„ дг дг 62r dh dw dw d2q> д2ф
Выражения для^,^, ^, ^, -^, -^, ^^-, -^ находим из
равенств B). Складывая правые части равенств C)—E) и при-
приравнивая сумму нулю (так как сумма левых частей этих равенств
равна нулю в силу A)), получаем
д2и* 1 ди* 1 д2и* д2и* _п (~,
дг2 "г" г дг + гг дфа + дг1 "" \ ^
Это и есть уравнение Лапласа в цилиндрических координатах.
Если функция м не зависит от г и зависит от х и у, то функ-
функция и*у зависящая только от г и ф, удовлетворяет уравнению
Л* ^ г дг ^7* d<f2 ^~U'
где г и ф—полярные координаты на плоскости.

390 УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ [ГЛ. XVIII
Найдем теперь решение уравнения Лапласа в области D (кольце),
ограниченной окружностями Кг: x2 + y2 = Rl и /С2: x24-y2 = Rh
принимающее следующие граничные значения:
u\Kl = ui} (8)
"k=",. (9)
где ^ и и2—постоянные.
Будем решать задачу в полярных координатах. Очевидно, что
целесообразно искать решение, не зависящее от ф. Уравнение G)
в этом случае примет вид
д2и . 1 ди_~
дг* ~* г дг '
Интегрируя это уравнение, найдем
и = Сг]пг + С%. A0)
Определим С* и С2 из условий (8) и (9):
Отсюда находим
In /?i Mi In R2 — u2 In
— ui \U2 ui)
5Б
Подставляя найденные значения Сг и С2 в формулу A0), окон-
окончательно получаем
ln ln«In
(И)
Замечание. Фактически мы решили следующую задачу:
найти функцию и, удовлетворяющую уравнению Лапласа в области,
ограниченной поверхностями (в цилиндрических координатах):
r = Rlf r = R2, z = 0, z = H, и следующим граничным условиям:
Ла\ —о Ла\ —о
дг |2=о ' аг|2=я^и
(задача Дирихле—Неймана). Очевидно, что искомое решение не
зависит ни от г, ни от ф и дается формулой A1).
§ 10. Решение задачи Дирихле для круга
Пусть в плоскости Оху имеется круг радиуса R с центром
в начале координат и на его окружности задана некоторая функ-
функция / (ср), где ф—полярный угол. Требуется найти функцию и (г, ф),

§ 10] РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ КРУГА 391
непрерывную в круге, включая границу, удовлетворяющую внутри
круга уравнению Лапласа
и на окружности круга принимающую заданные значения
и|гв* = /(ф). B)
Будем решать задачу в полярных координатах. Перепишем урав-
уравнение A) в этих координатах:
д*и , _1_ да , 1 дЧ _f
дг2 "Г г дг -Г Г2 дц2 — U>
или
г дг* ^Г дг ^дФ2 и' ^ '
Будем искать решение методом разделения переменных, полагая
и = Ф(Ф)/?(г). C)
Подставляя в уравнение (Г), получим
г2Ф (Ф) R" (г) + гФ(Ф) /?' (г) + Ф" (Ф) R (г) = 0,
или
Ф (ф) "* R (г) К * D)
Левая часть этого равенства не зависит от г, а правая от ф,
следовательно, они равны постоянному числу, которое мы обоз-
обозначаем через —k2. Таким образом, равенство D) дает два урав-
уравнения
Ф"(Ф) + *2Ф(Ф) = О, E)
r*R" (r) + rR' (r) -k*R (г) = 0. E')
Общее решение уравнения E) будет
Ф = A cos fop + В sin fop. F)
Решение уравнения E') будем искать в форме R (г) = гт. Под-
Подставляя R(r) = rm в E*), получим
r2m (m—l) rm + rmrm-l—k2rm = 0,
или
m2—k* = 0.
Итак, имеются два частных линейно независимых решения гк и /""*.
Общее решение уравнения E') будет
*. G)

ЗЭ2 " УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ [ГЛ. XVIII
Выражения F) и G) подставляем в C):
ик = (Ак cos top + Bk sin top) {Ckrk + Dkr~k). (8)
Функция (8) будет решением уравнения (Г) при любом значении к,
отличном от нуля. Если к = 0, то уравнения E) и E') принимают вид
Ф"(ф) = 0, rR"(r) + R'(r) = 0
и, следовательно,
nr). (8')
Решение должно быть периодической функцией от ф, так как при
одном и том же значении г при q> и ф + 2л мы должны иметь
одно и то же значение решения, потому что рассматривается одна
и та же точка круга. Поэтому очевидно, что в формуле (8') должно
быть jB0 = 0. Далее, мы ищем решение, непрерывное и конечное
в круге. Следовательно, в центре круга при г^О решение должно
быть конечным, и потому в формуле (8') должно быть Ь0 = 0,
а в формуле (8) D^O.
Таким, образом, правая часть (8') обращается в произведение
Л^С0, которое мы обозначим через Л0/2. Итак,
Мы будем составлять решение нашей задачи в виде суммы ре-
решений вида (8), так как сумма решений есть решение. Сумма
должна быть периодической функцией от ф. Это будет так, если
каждое слагаемое будет периодической функцией от ф. Для этого
к должно принимать целые значения. (Заметим, что если бы мы
приравняли части равенства D) числу +&2, то не получили бы
периодического решения.) Мы можем ограничиться только поло-
положительными значениями
*=1, 2, ..., л, ...,
так как в силу произвольности постоянных Л, i?, С, D отрица-
отрицательные значения к новых частных решений не дают. Итак,
да
и (г., Ф) = "г + 2 (Ап cos mp + В„ sin жр) г" (9)
(постоянная Сп включена в Ап и Вп). Подберем теперь произ-
произвольные постоянные Ап и Вп так, чтобы удовлетворялось крае-
краевое условие B). Подставляя в равенство (9) г = R, на основании ус-
условия B) получаем
оо
/ (ф)=тг+S(Ап cos щ+5»sin щ)Rn-

§10] РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛ# КРУГА 393
Чтобы имело место равенство A0), нужно, чтобы функция'/(ф)
разлагалась в ряд Фурье в интервале (—я, я) и чтобы AnRn и
BnRn были ее коэффициентами Фурье. Следовательно, Ап и Вп
должны определяться по формулам
я я
Аа = ~ I f (t) cos nt dt, Bn = -jjL. J / @ sin n/ #. A1)
-Я
Итак, ряд (9) с коэффициентами, определенными по формулам
A1), будет решением нашей задачи, если он допускает почленное
двукратное дифференцирование по г и по ф (но это нами не
доказано). Преобразуем формулу (9). Подставляя вместо Ап и Вп
их выражения A1) и производя тригонометрические преобразова-
преобразования, получим
-^*- A2)
J
Преобразуем выражение, стоящее в квадратных скобках *):
г>2 r2
н A3)
1 —2 — cos (^ —ф) +1 "d" )
Заменяя выражение, стоящее в квадратных скобках в формуле A2),
выражением A3), получим
я
V » Н7 —- 2я J '' 'i?2—2ri?cos(^—ф)^-7 *
*) В процессе вывода мы определяем сумму бесконечной геометрической
прогрессни, знаменатель которой есть комплексное число, модуль которого
меньше единицы. Эта формула суммы геометрической прогрессии выводится
так же, как и в случае действительных чисел При этом следует учесть опре-
определение предела комплексной функции действительного аргумента. Здесь
аргументом является п (см. § 4 гл. VII т. I).

394
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
|ГЛ. XVIII
Формула A4) называется интегралом Пуассона. Путем анализа
этой формулы доказывается, что если функция /(ф) непрерывная,
то функция и (г, ф), определенная интегралом A4), удовлетворяет
уравнению (Г) и при r—+R будет и (г, ф) —>/(ф), т. е. и (г, ф)
является решением поставленной задачи Дирихле для круга.
§11. Решение задачи Дирихле методом конечных разностей
Пусть в плоскости Оху дана область D, ограниченная конту-
контуром С. Пусть на контуре С задана непрерывная функция /. Тре-
Требуется найти приближенное решение
уравнения Лапласа
с*-е
а
удовлетворяющее граничному усло-
условию
u\c = f. B)
Проведем два семейства прямых
x=ih и y=khy C)
Рис. 395.
где h—заданное число, i и k прини-
принимают последовательные целочислен-
целочисленные значения. Будем говорить, что область D покрыта сеткой.
Точки пересечения прямых будем называть узлами сетки.
Приближенное значение искомой функции в точке
x=ih, y=kh
будем обозначать иик, т. е. u(ih, kh) = uUk. Аппроксимируем
область D сетчатой областью ?>*, состоящей из всех квадратов,
целиком лежащих в области D, и некоторых пересекаемых гра-
границей С (последние можно и не учитывать). При этом контур С
аппроксимируется контуром С*, состоящим из отрезков прямых
типа C). В каждом узле, лежащем на контуре С*, зададим зна-
значение /*, равное значению функции / в ближайшей точке кон-
контура С (рис. 395).
Значения искомой функции будем рассматривать только в узлах
сетки. Как уже было сказано в § 6, в рассматриваемом прибли-
приближенном методе производные заменяются конечными разностями:
д2и I _ ut+j% k—2tij, k+Щ-и k
дх* \хы
y~kh
/I2
, ft-i
Дифференциальное уравнение A) заменяется разностным уровне*
нием или уравнением в конечных разностях (после сокращения

МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
395
на h2):
или (рис. 396)
D)
AM)
Ш
ш
Для каждого узла сетки, лежащего внутри области D* (и не
лежащего на границе С*), составляем уравнение D). Если точка
(x^ih, y — kh) соседняя с точкой контура С*, то в правой части
равенства D) некоторые слагае-
слагаемые суть известные значения /*.
Таким образом, получаем неод-
неоднородную систему N уравне-
уравнений с N неизвестными (N—
число узлов сетки, лежащих
внутри области D*).
Докажем, что система D)
имеет решение, и притом един-
единственное. Это есть система N
линейных уравнений с N неиз-
неизвестными. Она имеет единствен-
единственное решение в том случае, если
определитель системы отличен от нуля. Определитель системы
отличен от нуля, если однородная система имеет только тривиаль-
тривиальное (нулевое) решение. Система будет однородной, если /* = 0 в уз-
узлах сетки на границе контура С*. Мы докажем, что в этом слу-
случае все значения щч к во всех внутренних узлах сетки равны нулю.
Пусть внутри области есть ul%k, отличные от нуля. Для опреде-
определенности предположим, что наибольшее из них положительно. Обо-
Обозначим его через иик > 0.
На основании формулы D) напишем
- 1 / , , ч /"v
Рис. 396.
Это равенство может иметь место только в том случае, если
все значения а, стоящие справа, равны наибольшему uitk. Теперь
имеем пять точек, в которых значения искомой функции суть и^ к.
Если ни одна из этих точек не есть граничная, то, беря одну
из них и написав для нее равенство D), докажем, что в несколь-
нескольких других точках значение искомой функции будет равно uiik.
Продолжая так, дойдем до границы и докажем, что в граничной
точке значение функции будет равно и*ик. Это противоречит тому,
что в граничных точках /* = 0.
Предполагая, что внутри области имеется отрицательное наи-
наименьшее значение, мы докажем, что на границе значение функции
отрицательно. Это противоречит данному условию.

3% УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ {ТЛ. XV1H
Итак, система D) имеет решение, и притом единственное.
Определенные из системы D) значения uiik
и являются приближенными значениями решения
сформулированной выше задачи Дирихле. Доказано,
что если решение задачи Дирихле для данной области D и данной
функции / существует (обозначим его через и(ху у)) и если ui%h
есть решение системы D), то имеет место соотношение
1"(*> У)-Щ,и\<АН\ E)
где А — постоянная, не зависящая от h.
Замечание. Бывает оправдан, хотя строго и не доказан,
следующий прием для оценки погрешности приближенного реше-
решения. Пусть uf^l — приближенное решение при шаге 2Л, uf;yk —
приближенное решение при шаге Л, Eh(x, у) — погрешность реше-
решения и?\. Тогда имеет место приближенное равенство
F (г
11 h Vх»
i, k — ui, k)
в общих узлах сеток. Итак, для того чтобы определить погреш-
погрешность приближенного решения при шаге А, нужно найти решение
при шаге 2А. Одна треть разности этих приближенных решений
и является оценкой погрешности решения при шаге A. Shrc> заме-
замечание можно отнести и к решению уравнения теплопроводности
методом конечных разностей.
Упражнения к главе XVIII
1. Вывести уравнение крутильных колебаний однородного цилиндриче-
цилиндрического стержня.
Указание. Закручивающий момент в сечении стержня с абсциссой х
определяется формулой M = G7 —, где G (x9 t) — угол закручивания сечения
с абсциссой х в момент t, G—модуль сдвига, /—полярный момент инерции
поперечного сечения стержня.
Отв. -^g- = а*-^-? » где а"—~1Г » ^—момент инерции единицы длины
01 ОХ /с
стержня.
2. Найти решение уравнения -^ = a2 -t-j- » удовлетворяющее условиям
6@, 0-0, в(/, 0 = 0, в(х, 0) = ф(х), de(*'t Q)^0, где
фМ = —р при О^^^
7 при ~
Дать механическую интерпретацию задачи.
,2^Bfe + i)»sin V cos

УПРАЖНЕНИЯ К ГЛАВЕ XVIII 397
3. Вывести уравнение продольных колебаний однородного цилиндриче-
цилиндрического стержня.
Указание. Если ц(х, t)—перемещение сечения стержня с абсциссой х
в момент t, то растягивающее напряжение Т в сечении х определяется фор-
формулой Г~?5-т-,где Е—модуль упругости материала, S—площадь попе-
поперечного сечения стержня.
д*и 9 д2и а Е
Отв. -^y=o*-j-? , где а2 — —, р—плотность материала стержня.
4. Однородный стержень длины 2/ под действием сил, приложенных к его
концам, укоротился на величину 2к. При t — О он освобожден от действующих
внешних сил. Определить смещение и (х, t) сечения стержня с абсциссой х
в момент t (средняя точка оси стержня имеет абсциссу *—0).
One и(х О т У (~')fe+1 сШB*+1)Я*еосB*+1)гШ*
5. Один конец стержня длины I закреплен, а на другой действует растя-
растягивающая сила Р. Найти продольные колебания стержня, если при f =0 сила Р
не действует.
л SPI V4 (—0й Bп+\)пх B/1+1) та/, с с
От- Tw^w+w*5'1* 2i cos—V— (смысл ? и 5 см-
в задаче 3).
6. Найти решение уравнения "л7Г==а "^т» удовлетворяющее условиям
и@, 0 = 0, «(/, 0 = Л sin о/, w(jc, 0)=0, ^
Дать механическое истолкование задачи.
со
Л sin — х sin <$t пл « / i,M i ,
Отв. и(х, t)~ ;— > —v . г-sin—г-sin—г-.
sin—/ n = iOJ—{ —— 1
Указание Решение искать в виде суммы двух ренений:
со
A sin — xsin со/
а
где а> =
sin — /
а
— решение, удовлетворяющее условиям:
о@, 0=0, с(/, /)=0,
I Предполагается, что sin — / Ф 0. j
7. Найти решение урэвнения -^-=а2 -^-g-, удовлетворяющее условиям:
и@, 0=0, //(/, 0=0, Г > 0,
«а- о>-<! х при °<

393 УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ [ГЛ XVIII
Bп+1J n2a2t
О" Т B
Отв. и(х, t)^—^^-^e < 8in^?
Указание. Решить задачу методом разделения переменных.
8. Найти решение уравнения -—= а2-т-^-, удовлетворяющее условиям
и @, t) = u(t, 0 = 0, и(х, 0) =
л тт „ да 9 д2и
9. Найти решение уравнения -^т=^^ д^' Удовлетворяющее условиям:
= 0, иA, О = «о» «(*> 0) = ф(х).
Указать физический смысл задачи.
Отв. и(х, О = ^о+ 2тА^пв соъ —91 х> где
п=о
2
о
Указание. Искать решение в форме u~uo-\-v(x, t).
10. Найти решение уравнения —^а2-—-, удовлетворяющее условиям:
«@, 0 = 0, 4^-
= — Ни ]x=i, и (х, 0) =ф (х).
Указать физический смысл задачи.
Ап— ' ае * sin"/^' где Л« =
/
2 Г* ц jt
= т\ ф (х)sin —у- <±v, p = Hl, fXf, fi2» •••> ^n—положительные корни урав-
0
нения tg fx = — \х/р.
Указание. На конце стержня при х — I происходит теплообмен с окру-
окружающей средой, температура которой равна нулю.
11. Найти (по формуле A0) § 6, полагая h = 0,2) приближенное решение
ди п д2и
уравнения -^г-=2-—-, удовлетворяющее условиям
и (к, 0)==*(-|—*J , и@, 0 = 0, «A, 0 = у

УПРАЖНЕНИЯ К ГЛАВЕ XVIII 399
д2и д2и
12. Найти решение уравнения Лапласа -^-\—^y~^ в п°лосе
У < + °°, удовлетворяющее условиям
и @, у) = 0, и (а, у) = 0, и(х, 0) = Л (l-~) t "(*» + «>
Оли. и(*. 0 = -^-Ще%^
Указание. Искать решение методом разделения переменных.
13. Найти решение уравнения Лапласа -^т+^-г'^О в прямоугольнике
удовлетворяющее условиям
и (л:, 0) = 0, и(х, b)=0, «(О, y) = Ay(b—y), и (а, у) = (
Отв. и(х, 0=
2 Bп+1) .
n=0 SH
b
14. Найти решение уравнения -г-^Н—^т = ^ внутри кольца, ограничен-
2 2
ного окружностями x2-\-y2 = Ri, x2-{-y2—R2, удовлетворяющее условиям
э«| _ Q .., __„
Дать гидродинамическое истолкование задачи.
Указание. Решить задачу в полярных координатах.
Отв. в = «,_^-1п^2..
15. Доказать, что функция и.(х^ у) — е~У$\пх есть решение уравнения
д2и д2и
_-|-_ = 0 в квадрате O^x^l, 0^г/<1, удовлетворяющее условиям
и @, у) = 0, иA, y) = e-^sinl, и(лс, 0) = sin^, и (*, l) = e-isinA:.
16. В задачах 12—15 решить уравнения Лапласа при данных граничных
условиях методом конечных разностей лрл & = 0?25.. Сравнить приближенное
решение с точным.

ГЛАВА XIX
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
И НЕКОТОРЫЕ ЕГО ПРИЛОЖЕНИЯ
Операционное исчисление в настоящее время является одной
из важных областей математического анализа. В физике, меха-
механике, электротехнике и других науках при решении различных
вопросов используются методы операционного исчисления. Осо-
Особенно широкое применение операционное исчисление находит
в современной автоматике и телемеханике. В этой главе (на базе
материала предыдущих глав учебника) будут даны основные поня-
понятия операционного исчисления *) и изложены операционные методы
решения обыкновенных дифференциальных уравнений.
§ 1. Начальная функция и ее изображение
Пусть задана функция действительной переменной /, опреде-
определенная при t^O (иногда мы будем считать, что функция /(/)
определена на бесконечном интервале — оо < ? < -J- оо, но /(/)==- О
при t< 0). Будем предполагать, что функция /(/) кусочно непре-
непрерывная, т. е. такая, что в любом конечном интервале она имеет
конечное число точек разрыва 1-го рода (см. § 9 гл. II т. I).
Для обеспечения существования некоторых интегралоз в беско-
бесконечном интервале 0 ^ / < + оо мы наложим на функцию / (t) допол-
дополнительное ограничение. Именно, будем предполагать, что сущест-
существуют постоянные положительные числа М и sQ такие, что
\f(t)\<Me* A)
при любом значении t из интервала
*) Для дальнейшего изучения операционного исчисления и его приложений
можно указать следующие книги: Лурье А. И. Операционное исчислен!е
и его приложения к задачам механики. — М.; Л.: Гостехиздат, 1950; Дит-
кин В. А. и Кузнецов П. И. Справочник по операционному исчислению.—
М.; Л.: Гостехиздат, 1951; Диткин В. А. и Прудников А. П. Интег-
Интегральные преобразования и операционное исчисление. — М.: Физматгиз, 1901;
Минусинский Я. Операционное исчисление.—М.: ИЛ, 1956.

§ 1] НАЧАЛЬНАЯ ФУНКЦИЯ И ЕЕ ИЗОБРАЖЕНИЕ 401
Рассмотрим произведение функции / (t) на комплексную функ-
функцию е~Р* действительной переменной*) t> где p~a-\-ib(a > 0) —
некоторое комплексное число:
B)
Функция B) — тоже комплексная функция действительной пере-
переменной /:
Рассмотрим, далее, несобственный интеграл
4-со t- <x -f оо 1
= J e~atf (t) cos bidt — i J e-**f(t)svibtdt. C)
Покажем, что если функция f(t) удовлетворяет условию A) й
а > s0, то интегралы, стоящие в правой части равенства C),
существуют и сходимость интегралов абсолютная. Оценим сначала
первый из этих интегралов:
e~atf(t) cosbtdt < \ \e~ai f (t) cos bt\dt <
о
+ 00 ч
о
+ 00 v +00
м
<M
J
о
Аналогичным образом оценивается и второй интеграл. Итак,.инте-
+ 00
грал ^ e"Pif{t)dt существует. Он определяет некоторую функ-
о
цию от р, которую мы обозначим **) F(p):
+ 00
F(P)=[ e-p*f(t)dt. И)
О
Функция F (р) называется лапласовым изображением, или L-
изображением, или просто изображением функции f(t). Функцию
}(t) называют начальной функцией, или оригиналом. Если F(p)
есть изображение функции /(/), то пишут так:
F(p)+>f(t), E)
или
F)
*) О комплексных функциях действительной переменной*см. § 4 гл. VIL
**) Функция F (р) при р Ф 0 есть функция комплексной переменной (см.,
например, книгу: Смирнов В. И. Курс высшей математики, т. HI, q. II.—
М.: Наука, 1974). Преобразование D) аналогично преобразованию Фурье/
рассмотренному в § 14 гл. XVII.

402 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ &ГЛ. XIX
ИЛИ
L{f(t)\ = F(p). G)
Как мы увидим в дальнейшем, смысл введений изображений
заключается в том, что с их помощью удастся упростить решение
многих задач, в частности, свести решение дифференциальных
уравнений к проведению простейших алгебраических операций
для нахождения изображения. Зная изображение, можно найти
оригинал или по заранее составленным таблицам «оригинал—изо-
«оригинал—изображение», или методами, которые изложены ниже. Возникают
следующие естественные вопросы.
Пусть дана некоторая функция F(p). Существует ли функция
/@, для которой F (р) является изображением? Если существует,
то единственна ли такая функция? На оба вопроса при опреде-
определенных предположениях относительно F (р) и /(/) дается положи-
положительный ответ. В частности, единственность изображения уста-
устанавливается следующей теоремой, которую мы приведем без дока-
доказательства:
Теорема единственности. Если две непрерывные функ-
функции ф@ и ty(t) имеют одно и то же L-изображение F (р), то
эти функции тождественно равны.
Эта теорема во всем дальнейшем играет очень важную роль.
Действительно, если при решении практической задачи мы ка-
каким-то образом определили изображение искомой функции, а потом
по изображению нашли начальную функцию, то на основании
сформулированной теоремы мы заключаем, что найденная функция
есть решение поставленной задачи, и других решений не существует.
§ 2. Изображение функций <тоA), sin*, cost
I. Функция f(t)> определенная так:
/@=1 при *>0,
0 при *<0,
называется единичной функцией Хевисайда и обозначается через
ао(О. График этой функции изображен на рис. 397. Найдем
L-изображение функции Хевисайда:
*) При вычислении интеграла \ е~Р* dt можно было бы его представить
о
как сумму интегралов от действительных функций; мы получили бы тот же
результат. Это замечание относится и к последующим двум интегралам.

§3]
Итак
или, точнее,
ИЗМЕНЕННЫЙ МАСШТАБ
403
(8)
В некоторых руководствах по операционному исчислению изо-
изображением функции f(t) называют выражение
F*(p) = p ) e~p*f(f)dt.
о
При таком определении будем иметь сг0 Ц)+-т19
а следовательно, С^-г-С, точнее, Ссг0 (t) «-7- С.
II. Пусть /(/) = sin?; тогда
о
Рис. 397.
» , . ,ъ С -г,* • 4. лг е-Р* (—it?sin ^ — cos Л
L{sin/}= \ е р* sin tdt = —тзп
Итак,
sin
III. Пусть f(t) = cost; тогда
L {cos t\ = i e"^* cos ? cW =
е-Р^ (sin t—p cos 0
+ 00
Итак,
(9)
A0)
§ 3. Изображение функции с измененным масштабом
независимой переменной. Изображение функций sin at, cos at
Рассмотрим изображение функции f(at), где а>0:
L{f(at)}= J e-p{f(at)dt.
о
Сделаем замену переменной в последнем интеграле, полагая
z = at; следовательно, dz = adt; тогда получаем
L{f(at)}=±[e~a f(z)dz,

404 .. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XIX
ИЛИ
L
Таким образом, если
то
l-F(?-)++f(af). (И)
а \ а / ' х ' v
Пример 1. Из формулы (9) на основании A1) непосредственно полу-
получаем
sin at *-!
или
elnct^-p^. A2)
Пример 2. Из формулы A0) на основании формулы (II) получаем
cos at +-1 ;—-
* a ' "
или
§ 4, Свойство линейности изображения
Теорема. Изображение суммы нескольких функций, умно-
умноженных на постоянные, равняется сумме изображений этих функ-
функций, умноженных на соответствующие постоянные, т. е. если
JlQMO (И)
(С;—постоянные) и
то
i - I
Доказательство. Умножая все члены равенства A4) на
e~pf' и интегрируя по t в пределах от 0 до -f oo (вынося множи-
множители Q*3a знак интеграла), получаем равенство A4').
Пример 1. Найти изображение функции
/@=3 sin 4*—2 cos St.

§6] ИЗОБРАЖЕНИЕ ФУНКЦИЙ e~at, she/, ch at 405
Решение. На основании формул A2), A3) и A4') получаем
3 4 о Р 12
/?2+16
Пример 2. Найти начальную функцию, изображение которой выра-
выражается фор2мулой
Решение. Представим F (р) так:
F ^^Т
Следовательно, на основании формул A2), A3) и A4') получаем
/ @=4 sin 2t + 20 cos 3L
Из теоремы единственности в § 1 следует, что это единственная начальная
функция, соответствующая данной F (/?).
§ 5. Теорема смещения
Теорема. Если F(р) есть изображение функции /(/), то
F(p-\-a) есть изображение функции e~aif(t)y т. е.
если F(p)^f(t), то F(p+a)-^e~atf(t). A5)
(Здесь предполагается, что Re (/7 +а) > s0.)
Доказательство. Найдем изображение функции e~atf(t):
СО 00
L \е~«Ч (*)} = $ e'Pi~atf Ю dt = S ^(р+а)'/ @ dt.
о о
Таким образом,
L{e-«'f(t)\ = F(p + a).
Доказанная теорема позволяет значительно расширить класс
изображений, для которых легко находятся начальные функции.
§6. Изображение функций е~а\ sh#/, chat, e~at$inat> e~atcosat
Из формулы (8) на основании формул A5)' непосредственно
следует
^
Аналогично
Вычитая из членов соотношения A6') соответствующие члены
соотношения A6) и деля результаты вычитания на два, получаем

406 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ {ГЛ. XIX
или (записывая а вместо а)
^ A7)
Аналогично, путем сложения A6) и A6') получаем
Ь A8)
Из формулы A2) на основании формул A5) следует
Из формулы A3) на основании формул A5) следует
B0)
Пример 1. Найти начальную функцию, изображение которой задается
формулой
7
Решение. Преобразуем Т7 (р) к виду выражения, стоящего в левой
части соотношения A9):
7 7 _7 4
/?2+10р+41~~(р + 5J+16— 4'
Итак,
Следовательно, на основании формулы A9) будем иметь
4
Пример 2. Найти начальную функцию, изображение которой задается
формулой
Решение. Произведем преобразование функции F (р):
р+3 (Р + 1)+2 Р + 1 2
на основании формул A9) и B0) находим начальную функцию;
F (P) -i-»-e-<cos 3t+ye"* sin 3f.

§7] ДИФФЕРЕНЦИРОВАНИЕ ИЗОБРАЖЕНИЯ 407
§ 7. Дифференцирование изображения
Теорема. Если F(p)-r^f(t), то
$>t*f(t). ' B1)
Доказательство. Докажем сначала, что если /(/) удовле-
удовлетворяет условию A), то интеграл
5 e-pt(-t)»f(t)dt B2)
о
существует.
По условию | / (/) | < Л!е5о*, p = a + ib, a> sQ; при этом а>0,
s0 > 0. Очевидно, что найдется такое 8 > 0, что будет выполняться
неравенство a>so-|-e. Так же, как и в § 1, доказывается, что
существует интеграл
о
Оценим, далее, интеграл B2):
+ 00 +00
J \e-p*t»f(t)\dt= J
о о
Так как функция е~гНп ограничена и по абсолютной величине
меньше некоторого числа N при любом значении t > 0, то можно
написать
+ СО +00 +00
5 \e-p4nf{t)\dt<N J \e-{*-*uf(t)\dt = N ] e-(a~z)t\f{t)\dt < +оо.
0 0 О
Таким образом, доказано, что интеграл B2) существует. Но этот
интеграл можно рассматривать как производную я-го порядка по
параметру *) р от интеграла
+ 00
5 e~P*f(t)dt.
Итак, из формулы
+ 00
=l e-*f(t)dt
*) Мы ранее установили формулу дифференцирования определенного инте-
интеграла по действительному параметру (см. § 10 гл. XI т. I). Здесь параметр
р—комплексное число, но формула дифференцирования остается справедливой.

408 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ ?ГЛ. XIX
получаем формулу
Г e-pH_t)nf(t)dt = 4i; \ e-pff{t)dt.
J dpn J
о о
Из этих двух неравенств получаем
+ 00
т. е. формулу B1).
Используем формулу B2) для нахождения изображения сте-
степенной функции. Напишем формулу (8):
Из этой формулы на основании формулы B1) получаем
или
Аналогично
р3 "^
При любом п получаем
я» .
+ 00
Пример I. Из формулы (см. A2)) ¦ 2 2= \ e-Ptslnatdt путем диф-
о
ференцирования левой и правой частей по параметру р получаем
Пример 2. Из формулы A3) на основании формулы B1) получаем
Пример 3. Из формулы A6) на основании формулы B1) получаем

§8] ИЗОБРАЖЕНИЕ ПРОИЗВОДНЫХ 409
§ 8. Изображение производных
Теорема. Если F(p)-r^f(t)y то
f'(f\- B7)
Доказательство. На основании определения изображения
можем написать
+ 00
L{f'(t)\= I e-#f'(t)dt. B8)
о
Будем предполагать, что все производные /'(/), f"(/), ..., fin)(t)y
которые нам встретятся, удовлетворяют условию A)и, следова-
следовательно, интеграл B8) и аналогичные интегралы для последующих
производных существуют. Вычисляя по частям интеграл, стоящий
в правой части равенства B8), найдем
о
Но по условию A)
lim е~Рга) = 1
$•-¦
о
Поэтому
Теорема доказана. Рассмотрим далее изображение производных
любого порядка. Подставляя в формулу B7) вместо F (р) выра-
выражение pF (/>)—/@), а вместо /(/)—выражение /'(/), получим
или, раскрывая скобки,
p*F (p)-pf @)-Г @) -^Г(О- B9)
Изображение для производной и-го порядка будет
P"F {р)-{р"-Н (Щ+Р"~Т @)+... +р/<«-2> (OJ+f"' @)] ^ /<«> (/).
C0)
Замечание. Формулы B7), B9), C0) упрощаются, если
= Г @) = • • • = /1""х) @) = 0. В этом случае получаем

410
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
ЕГЛ. XIX
§ 9. Таблица некоторых изображений
Для удобства пользования полученными изображениями по-
поместим их в одну таблицу.
Таблица 1
Номер
по пор
1
2
3
4
5
6
7
8
9
10
П
12
13
14
15
(/
if
<-
F
Примечание.
+ 00
0
т
а
Р
1
р+а
а
Р
/?2—а2
а
? + аJ + а2
>+аJ + а2
л!
p« + i
2ра
р*—а*
1
1
(р2+а2J
Формулы 13 и
fit)
1
sinal
cos a*
e-at
shat
chat
0—Cbt oin fit
t * OilJ Ufr
л-— СЬГ ЛГ1С />/
/ otn nt
t bill u»
/ ITIQ /t/
q g \OlIl Wt" Ut K,\JO UlJ
t»f(t)
\h(t)h(t-v)di
0
15 этой таблицы будут выведены позднее.

§103 ВСПОМОГАТЕЛЬНОЕ УРАВНЕНИЕ 411
Замечание. Если за изображение функции f(t) мы возьмем
+ 00
F*(P) = P
то в формулах 1—13 таблицы выражения, стоящие в первом
столбце, следует умножить на р. Формулы же 14 и 15 изменятся
значительнее. Так как F*(p) = pF(p)y то, подставляя в левой
части формулы 14 вместо F (р) выражение —~ и умножая на /?,
получим
Подставляя в левой части формулы 15
С /~\ _ Fl (Р) V /~\ __ ^2 (Р)
и умножая это произведение на /?, получим
t
15'. JL Fl (p) Ft (p) -V J /, (т) /2 (<-т) dr.
О
§ 10. Вспомогательное уравнение
для данного дифференциального уравнения
Пусть мы имеем линейное дифференциальное уравнение я-го
порядка с постоянными коэффициентами а0, а19 ..., ап_1} ап:
^^ ^ C1)
Требуется найти решение этого уравнения x = x(t) при t^O,
удовлетворяющее начальным условиям:
х @) = *в, *' @) = xi, ... f tf»-" @) = 4"}. C2)
Поставленную задачу ранее мы решали так: находили общее
решение уравнения C1), содержащее п произвольных постоянных;
потом постоянные определяли так, чтобы удовлетворялись началь-
начальные условия C2).
Здесь мы изложим более простой метод решения этой задачи—
метод операционного исчисления. Будем находить L-изображение
решения x(t) уравнения C1), удовлетворяющего условиям C2).
Это L-изображение обозначим через х(р)\ таким образом, ~х{р) -+
Предположим, что существуют изображения решения уравне-
уравнения C1) и его производных до порядка п (после разыскания
решения мы можем проверить справедливость этого дредположе-

412 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ |ГЛ. XIX
ния). Умножим все члены равенства C1) на е"~г\ где p = a + ib,
и проинтегрируем по t в пределах от 0 до +оо
+ оо +сс +оо
С dnx С dn~*- х Г*
J uln J dtn~~ l J
0 0 О
+ 00
= \ e~Pff{i)dt. C3)
о
В левой части равенства стоят L-изображения функции л:(/)иее
производных, справа L-изображение функции /(/), которое обозна-
обозначим через F (р). Следовательно, равенство C3) можно переписать
так:
Подставляя в это равенство вместо изображений функции и ее
производных выражения B7), B9), C0), получаем
X (р) -
хо} + а^(р) = F (р). C4)
Уравнение C4) называется вспомогательным уравнением, или
изображающим уравнением. В этом уравнении неизвестным яв-
является изображение х{р)у которое из него и определяется. Пре-
Преобразуем его, оставив в левой части члены, содержащие х(р):
C4')
Коэффициент при л:(/?) в левой части равенства C4') есть много-
многочлен п-й степени от /?, который получается, если в левую часть
уравнения C1) вместо производных поставить соответствующие
степени р. Обозначим его через уп(р):
Ф* (Р) = а*Рп + fliP" + • • • + <*n-iP + <*n- C5)
Правая часть уравнения C4') составляется следующим образом:
коэффициент an_i умножается на х0,
коэффициент ап_2 умножается на '
коэффициент аг умножается на рп~г
коэффициент aQ умножается на pnxQ+pn~'2x'Q+...+xiQn\

§lOj ВСПОМОГАТЕЛЬНОЕ УРАВНЕНИЕ 413
Все эти произведения складываются. Прибавляется еще изобра-
изображение правой части дифференциального уравнения F(p). Все
члены правой части равенства C4'), кроме F (/?), после приве-
приведения подобных членов образуют многочлен от р степени п — 1
с известными коэффициентами. Обозначим его через tyn4ml(p). Та-
Таким образом, уравнение C4') можно переписать так:
Из этого уравнения и определяем х(р):
х{р) = ЩМ + Ж. C6)
Такое определенное х (р) есть изображение решения х (t) урав-
уравнения C1), удовлетворяющего начальным условиям C2). Если
теперь мы найдем функцию x*(t)> изображение которой—функ-
которой—функция х(р), определенная равенством C6), то на основании теоремы
единственности, сформулированной в § 1, будет следовать, что
**(/) есть решение уравнения C1), удовлетворяющее условиям
C2), т. е.
*• @ = *<*)•
Если мы будем находить решение уравнения C1) при нуле-
нулевых начальных условиях: хо = х'о = х1 = . ¦. =х(оп~1} = 0, то в ра-
равенстве C6) будет $п-г1(р) = 0 и оно примет вид
или
Х {Р) =
Пример 1. Найти решение уравнения
+Xl
удовлетворяющее начальному условию: х~0 при i — 0.
Решение. Составляем вспомогательное уравнение х (р) (/?+1) =0-[ ,
«ли х(р)= , {t—. Разлагая стоящую справа дробь на элементарные, полу-
получим х(р)= . . Пользуясь формулами 1 и 4 таблицы I, находим
решение:' х (/) = 1 —е~*.
Пример 2. Найти решение уравнения
удовлетворяющее начальным условиям д:о = д:о=:О при ?=0.

414 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XIX
Решение. Напишем вспомогательное уравнение C4'): #"(р) (р2+9)=— ,
или х (р)=—. 2 д ¦. Разлагая эту дробь на элементарные, получим F(p) =э
— р/9 1/q
*= 2 i qH— • ^a основании формул 1 и 3 таблицы 1 находим решение:
1 1
х (t)=—-q-cos3^-[--q-.
Пример 3. Найти решение уравнения
удовлетворяющее начальным условиям #о = #о = О при ^ = 0.
Решение. Напишем вспомогательное уравнение C4'):
или
Разлагая эту дробь на элементарные дроби методом неопределенных коэффи-
коэффициентов, получим
-, ч 1 1 3 1 . 1 1
*W-2 pi 4 р^
По формулам 9, 1 и 4 таблицы 1 находим решение:
Пример 4. Найти решение уравнения
<ХЧ , о dx , - . .
— Jt.2-3r+bx = smti
удовлетворяющее начальным условиям хо = 1, хо = 2 при /==0,
Решение. Пишем вспомогательное уравнение C4'):
или
откуда находим Т (р):
Разлагая последнюю дробь правой части на элементарные, можно написать
11
ИЛИ
29 2 J_ р . 1
# "^Ю * р2+1 ^ 5

§111 ТЕОРЕМА РАЗЛОЖЕНИЯ 415
На основании формул 8, 7, 3 и 2 таблицы 1 получаем решение:
11 2Q 11
e-'tos 2f+^-*sln2f ^cost+jsin tt
или окончательно
A1 9Q \
iicos,2* + |5sta2*J-
1 1
rocosf+r8ln U
§11. Теорема разложения
Из формулы C6) предыдущего параграфа следует, что изобра-
изображение решения линейного дифференциального уравнения состоит
из двух членов: первый член есть правильная рациональная дробь
от /?, второй член—дробь, числителем которой является изобра-
изображение правой части уравнения F(p)y а знаменатель—многочлен
cpw(/?). Если F(p) — рациональная дробь, то второй член будет
рациональной дробью. Таким образом, нужно уметь находить
начальную функцию, изображением которой является правиль-
правильная рациональная дробь. Этим вопросом мы и займемся в на-
настоящем параграфе. Пусть L-изображение некоторой функции есть
правильная рациональная дробь от р:
^п-l (Р)
Требуется найти начальную функцию (оригинал). В § 7 гл. X т. 1
было показано, что всякую правильную рациональную дробь
можно представить в виде суммы элементарных дробей четырех
видов:
(
I- 2 . а+4-а'» где КОРНИ знаменателя комплексные, т. е.
*V. ( 2.^+fa \к 5 где ^ > 2, корни знаменателя комплексные.
Найдем начальные функции для выписанных элементарных
дробей. Для дроби I вида на основании формулы 4 таблицы 1
получаем
Для дроби II вида на основании формул 9 и 4 таблицы 1 по-
получаем
<*-1«" <37)

ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. XIX
Рассмотрим теперь дробь III вида. Произведем тождественные
преобразования:
Ар + В __
<-+?
Обозначая здесь первое и второе слагаемые через М и N соот-
соответственно, получим на основании формул 8 и 7 таблицы 1
М Л Ае~
^'cos (t Y^—^ )>
Таким образом, окончательно
Ар+в ^
Г
C8)
Рассматривать случай элементарной дроби IV вида мы здесь
не будем, так как зто сопряжено с большими вычислениями. Для
некоторых частных случаев мы этот вопрос рассмотрим ниже:
В случае необходимости читатель может обратиться к одному из
указанных в начале главы курсов.

ПРИМЕРЫ РЕШЕНИЯ ОПЕРАЦИОННЫМ МЕТОДОМ 417
§ 12. Примеры решения дифференциальных уравнений
и систем дифференциальных уравнений операционным методом
Пример, L Найти решение уравнения
d2x
_4-4*=sina*f
удовлетворяющее начальным условиям % = 0, х'0 = 0 при / = 0,
Решение. Составляем вспомогательное уравнение C4'):
или
5 , 5 _ 1 3 , 3
^Tj^+j2Zf4 5 * р2+9+10
откуда получается решение
~sin2/—4-sin3/.
i\) О
Пример 2. Найти решение уравнения
удовлетворяющее начальным условиям ло = 1, jco = 3, Jto^8 при /=0.
Решение. Составляем, вспомогательное "уравнение C4'):
находим
И разлагаем полученную рациональную дробь на элементарные:
2 -р+Ь _
'tPi ~
Пользуясь таблицей 1, пише*м решение
Пр»имер 3* Найти решение уравнения
удовлетворяющее начальньш условиям х~0, л:о==О при 2^=
Решение. Пишем вспомогательное уравнение {34'):
н. С. Пискунов, т. 2

418 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XIX
откуда после некоторых преобразований получим
-. , 51,51,8 1
Следовательно,
х (Q = _А sm t+Yssin 2t+Y D*sin 2'~'cos
Очевидно, что операционным методом можно решать и системы линейных
дифференциальных уравнений. Покажем это на примере.
Пример 4. Найти решение системы уравнений
Я ** .-.dy , dx dy
удовлетворяющее начальным условиям х — 0, ^ = 0_при ^ = 0.
Решение. Обозначим х (t) -?- х (р), у (t)+- у (р) и напишем систему
вспомогательных уравнений
Решая эту систему, находим
. -, . 4/7 + 3 1 1 33
Х{Р)- р(р+\)(Пр + 6)~~2р 5(/7 + 1) 10A1/7+6) *
1 Ji_ / 1 11 Л
A1/7 + 6) (/7+1)  i/7+l И/7 + 6У *
По изображениям находим начальные функции, т. е. искомые решения
системы,
Аналогично решаются и линейные системы высших порядков.
§ 13. Теорема свертывания
При решении дифференциальных уравнений* операционным
методом бывает полезна следующая
Теорема свертывания. Если Fxip) и F2(p) суть изо-
изображения функций ^(Z) и 12У),т. е. F± (/?)—> fj (t) и F2(p)-^
—V /2 (t), то Fi (p) F2 (p) есть изображение функции
т. е.
t
l{x)ft(t-x)dx. C9)
о

$133
ТЕОРЕМА СВЕРТЫВАНИЯ
419
Доказательства Найдем изображение функции
t
исходя из определения изображения:
Стоящий справа интеграл есть двукратный интеграл, который
берется по области, ограниченной прямыми % — О, x = t (рис. 398).
Изменим порядок интегрирования в этом инте-
интеграле, тогда получим
U
J
> Г +оо
Рис, 398,
Произведя замену переменной / — т — г во внутреннем интеграле,
• получим
+ 00 +00 +00
% о
Следовательно*
/ t
Итак.
Это есть формула 15 таблицы 1.
Замечание 1. Выражение J ft(т)/2 (f — т)dx называется
о
сверткой {складкой) двух функций ft(t) и /2(^). Операция полу-
получения свертки называется свертыванием двух функций, при этом
14*

420 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ {ГЛ. i XIX
Справедливость последнего равенства устанавливается путем - за-
замены переменной t—x = z в правом интеграле. -
Пример. Найти решение уравнения
удовлетворяющее начальным условиям лго = л:о = О при t =
; Решение. Пишем вспомогательное уравнение C4')..
где F (p) — изображение функции f (t). Следовательно, x(p)~~Yj-jF (р), но
¦ 2 -+ sint и F (р) -V / (t). Применяя формулу свертывания C9), обозначив
ггтт = F2 (Р)» F (Р) = fi W> случим
t
D0)
Замечание 2. На основании теоремы свертывания легко
находится изображение интеграла от данной функции, если изве-
известно изображение этой функции; а именно, если F(p)-^f(t), то
t
f(T)di. D1)
Действительно, если мы обозначим
' L(t) = f(t), М0=1, то F1(p) = F{p)y F2(p) = j.
Подставляя эти функции в формулу C9), получим формулу D1).
§ 14. Дифференциальные уравнения механических колебаний.
Дифференциальные уравнения теории электрических цепей
'Из механики известно, что колебания материальной точки
массы т описывается уравнением *)
здесь х — отклонение точки от некоторого положения, ft —жест-
—жестокость упругой системы, например пружины (рессоры), сила сопро-
сопротивления движению пропорциональна (с коэффициентом пропор-
*) См., например^ гл. XIII, § 26, где такое уравнение получено при рас-
рассмотрении колебания груза на рессоре.

$*5] РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ КОЛЕБАНИЙ 421
циональности к) первой1 степени скорости, fi(t) — внешняя, или
возмущающая, сила.
Решением уравнения типа D2) описываются малые колебания
и других механических систем с рдной степенью свободы, напри-
например крутильные колебания маховика на уп- ' ^
ругом валу, если х—угол поворота махови- Г L
ка, т — момент инерции маховика, k ~ кру- 1 *
тильная жесткость вала, a mf1(t)—момент |
внешних сил относительно оси вращения. _ ?|
Уравнения типа D2) .описывают не только I
механические колебания, но и явления в *
электрических цепях. dt
Пусть имеем электрическую цепь, сое- Рис. 399.
тоящую из индуктивности L, сопротивления
jR и емкости С, к которой приложена э. д. с. Е (рис. 399).
Обозначим через i ток в цепи, а через Q заряд конденсатора,
тогда, как известно из электротехники, г и Q удовлетворяют сле-
следующим уравнениям:
W-i D4)
Из уравнения D4) получаем
?Q = ^i /44'л
Подставляя D4) и D4') в уравнение D3), получаем для Q урав-
уравнение типа D2):
Дифференцируя обе части уравнения D3) и используя уравне-
уравнение D4), получаем уравнение для определения тока /:
dt ^ С * ~ dt # *
Уравнения D5) и D6) являются уравнениями типа D2).
§ 15. Решение дифференциального уравнения колебаний
Уравнение колебаний запишем в виде
где механический или физический смысл искомой функции хл
коэффициентов а1э а2 и функции /(/) легко устанавливается

422 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XIX
сравнением этого уравнения с уравнениями D2), D5), D6). Най-
Найдем решение уравнения D7), удовлетворяющее начальным усло-
условиям х = х0, х' = х'о при ? = 0.
Составим вспомогательное уравнение для уравнения D7):
х(р) (р* + alP + а2) = хор + х'0 + a,xQ + F(p), D8)
где F (/?) — изображение функции f(t). Из равенства D8) находим
F(p)
Итак, для решения Q(t) уравнения D5), удовлетворяющего
альным условиям Q = Qo, Q' = Q'o при / = 0, изображение будет
ть вид
o [
Е(р)
Характер решения существенно зависит от того, будут ли корни
трехчлена р2 + а1р-\-а2 комплексные, или действительные различ-
различные, или действительные равные. Подробно рассмотрим случай,
когда корни трехчлена комплексные, т. е. когда (ik-* —а2<0.
Остальные случаи рассматриваются аналогично.
Так как' изображение суммы двух функций равно сумме их
изображений, то на основании формулы C8) начальная функция
для первой дроби, стоящей в правой части D9), будет иметь вид
-t e
a:0cos
^Найдем далее начальную функцию, соответствующую дроби
Fjp)
Здесь воспользуемся теоремой свертывания, заметив, что

$16} ИССЛЕДОВАНИЕ СВОБОДНЫХ КОЛЕБАНИЙ
Следовательно, *по формуле C9) получаем
423
E1)
Итак, из D9), учитывая E0) и E1), получаем:
*(*) =
Если внешняя сила / (/) ^ 0, т. е. если мы имеем свободные
механические или' электрические колебания, то решение дается
первым слагаемым правой части выражения E2). Если началь-
начальные условия равны нулю: xo = x'Q = 0, то решение дается вторым
слагаемым правой части равенства E2). Рассмотрим эти случаи
подробнее.
§ 16. Исследование свободных колебаний
Пусть уравнение D7) описывает свободные колебания, т. е.
/ (t) = 0. Введем для удобства написания формул обозначения
^ = 2/2, а2 = &2, kl = k2 — n2. Тогда уравнение D7) примет вид
E3)
Решение этого уравнения хСВУ удовлетворяющее начальным
условиям х = х0, х' = х'о при t = 0, дается формулой E0) или пер-
первым слагаемым формулы E2):
к*coskxt
sin^
E4)
Обозначим л:0 = а, Xoj~x°n ~Ь. Очевидно, при любых a nb можно.
подобрать такие М и б, что будет a = Msin6, 6 = Afcos6, при
этом М2 = а2 + Ь2, tg6 = a/b. Формулу E4) перепишем так:
хсв = e~nt [M cos kxt sin б + М sin k±t cos б],

424 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ - [ГЛ. XIX
или окончательно решение можно переписать так:
*св = Va2 + Ь2 е-п* sin (k±t + S). - ч E5)
Решение E5) соответствует затухающим колебаниям. * '
Если 2п = а1 = 09 т. е. если отсутствует внутреннее трение, то
решение буде? иметь вид
sin
В этом случае имеют место гарионические колебания. (В гл. XIII,
§ 27, на рис. 276 и 278 даны графики гармонических и затухаю-
затухающих колебаний.)
§ 17. Исследование механических и электрических колебаний
в случае периодической внешней силы
При изучении упругих колебаний механических систем и осо-
особенно при изучении электрических колебаний приходится рас-
рассматривать различные виды внешней силы f(t). Рассмотрим под-
подробно случай периодической внешней силы. * Пусть уравнение D7)
имеет вид -
^+2n^ + k2x==Asm<dt. E6)
Для выяснения характера движения достаточно рассмотреть слу-
случай, когда х9-=х'0 = 0. Можно было бы получить решение урав-
уравнения по формуле E2), но здесь с методической точки зрения
удобнее получить решение, проделав все промежуточные вычис-
вычисления. ' • .
Напишем изображающее уравнение
откуда получаем
—, v Лео
*1Р
Рассмотрим случай, когда 2пфО (м2<&2). Стоящую справа
дробь разлагаем на элементарные дроби:
Л© Np+B . Cp.+b
Постоянные Nt В, С, D определяем методом неопределенных
коэффициентов. Пользуясь ффрмулой C8), из E7) найдем началь-
начальную функцию
-f e
~nt
1t] \ ; E9)

СЛУЧАЙ ПЕРИОДИЧЕСКОЙ ВНЕШНЕИ^СИЛЫ
425
здесь снова ^==\^к2-^п^. Это и есть решение уравнения E6),
удовлетворяющее начальным условиям: х0 = лг© = 0 при / — 0.
Рассмотрим частный случай, когда 2п = 0. Это соответствует
тому, что в механической, например, системе нет внутреннего
сопротивления, нет амортизатора. В случае электрического кон-
контура это соответствует тому, что R = 0, т. е. отсутствует внут-
внутреннее сопротивление цепи. Уравнение E6) в этом случае прини-
принимает вид
?L F0)
а решение этого уравнения, удовлетворяющее условиям х0 — .
=0 при / = 0, получится, если в фор- ад
муле E9) положить л —0:
о
Здесь имеем сумму двух гармонических
колебаний: собственных с частотой^,
/а А ^ ы
ХЬ \Ч — ?2__032 ~k
и вынужденных с частотой о>,
^@
А
А
Рис 400.
Для случая, когда fe^>w, характер колебаний изображен на
рис. 400. * . •
Вернемся снова к формуле E9). Если 2п > 0, что и имеет
место в рассмотренных механических и электрических системах,
то член, содержащий множитель e~nty представляющий затухаю-
затухающие собственные колебания, при t возрастающем быстро убывает.
При достаточно большом t характер колебаний будет определяться
членом, не содержащим множителя е~пХ, т. е. членом
~ e')sin Ы ~
Введем обозначения
где

426 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XIX
Решение F2) можно переписать так:
* @= , , * .„ sin N+«>•
* /(-*)'+**
Из формулы F4) следует, что частота k вынужденных колебаний •
не совпадает с частотой со внешней силы. Если внутреннее сопро-
сопротивление, характеризующееся числом п, мало, а частота со близка
к частоте k, то амплитуда колебаний может быть сделана как
угодн*о большой, так как знаменатель может быть как угодно
малым. При п = 0, со2 = &2 решение не выражается формулой F4).
' § 18. Решение уравнения колебаний в случае резонанса
Рассмотрим частный случай, когда ^==2п = 0, т. е. когда
сопротивление отсутствует, а частота внешней силы совпадает
с частотой собственных колебаний & = со. В этом случае уравне-
уравнение имеет вид
~p + k2x=Asmkt. F5)
Будем искать решение этого уравнения, удовлетворяющее началь-
начальным условиям хо = О, #o = O при ? = 0. Вспомогательное "уравнение
будет
откуда
— Ah
x(p)=-$4!w- . <66)
Мы получили правильную рациональную дробь IV вида, которую
в общем виде мы не рассматривали. Чтобы найти начальную
функцию для изображения F6),° воспользуемся следующим при-
приемом. Напишем тождество (формула 2 таблицы 1)
>
' е~** sin kt dt. F7)
о
Продифференцируем *) обе части этого равенства по k:
= \ e~Pft cos ktdt.
Пользуясь тождеством F7), это равенство можно переписать так:
~р* tcoskt—г-sin)
*) Интеграл, стоящий, справа, можно представить в.виде суммы двух интег-
интегралов действительной переменной, каждый из которых зависит от параметра к.

119]
ТЕОРЕМА ЗАПАЗДЫВАНИЯ
427
Отсюда непосредственно следует
Ak
А ( \ \
k [•Js'mkt — tcoskt\
(из этой формулы получается формула 13 таблицы 1). Итак, иско-
искомое решение уравнения F5) будет
F8)
x(t) = -^(—sin kt — t cos kt\
Изучим второе слагаемое этого решения
^ F8')
при увеличении t эта величина не является ограниченной. Ампли-
Амплитуда колебаний, соответствующих «формуле F8'), неограниченно
возрастает при неограниченном возрастании t. Следовательно, и
амплитуда колебаний, соответствующих формуле F8), неограни-
неограниченно возрастает. Это явление, имеющее место при совпадении
частоты собственных колебаний с частотой внешней силы, назы-
называется резонансом (см. также гл. XIII, § 28, рис. 280).
§ 19. Теорема запаздывания
Пусть функция f(t) при /<0 'тождественно равна нулю
(рис. 401, а). Тогда функция f(t — tQ) будет тождественно равна
нулю при t < 10 (рис. 401, б).
Т Р\
Рис, 401.
Докажем следующую теорему запаздывания:
Теорема. Если F(p) есть изображение функции f(t), то
e-pt«F(p) есть изображение функции f(t — ?0), т. е. если fit)*—
+±F{p), то
f(t-tJ*+e-p'.F(p). ' , F9)
Доказательство. По определению изображения имеем
00 t0 ' 00

428
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. XIX
Первый интеграл, стоящий в правой части равенства, равен нулю*
так как f(t—to) = O при / < t0. В последнем интеграле сделаем
замену переменной, полагая /—to = z: *
J
1 п
h
Рис. 402. =е~Рг* \ e~Pzf (z) dz = e~*
о
Таким образом, f(t—tQ)^~e"^oF(p).
Пример. В §2 было установлено для единичной функции Хевисайда,
что <т0 (t) ч-| . На основании доказанной теоремы следует, что для функции
t—/г), изображенной на рис. 402, L-изображением будет —e~?flt т. е, •
Oo(t—h)+i- — i
§ 20. Дельта-функция и ее изображение
Рассмотрим функцию
G0)
0 при / < О,
0
}
^
при h < /,
изображенную на рис. 403. ^
Если эту функцию трактовать как силу, действующую за про-
промежуток времени от 0 до /г, а* в остальное время равную нулю,
то, очевидно, импульс этой силы
будет равен единице.
На основании формул (8) и G0)
изображение этой функции будет
т. е.
-у
i
h
h '%
Рис. 403.
В механике бывает удобно рассматривать силы, действующие
очень короткий промежуток времени, как силы, действующие
мгновенно, но имеющие конечный импульс. Поэтому вводят функ-
функцию б(/) как предел функции ox(t, h) при Л—^0;
6@- lim ахA, /г)*). G3)
h-+ 0
*) Следует иметь в виду, что 6 (t) не есть функция в обычном'понимании.
(Многие авторы-физики функцию б (t) называют функцией Дирака.)

§203 ДЕЛЬТА-ФУНКЦИЯ И ЕЕ ИЗОБРАЖЕНИЕ 429
¦i.
Эту функцию называют единичной импульсной функцией, или
дельта-функцией.
Естественно положить -
5 l. ' G4)
-'00
Также пишут
о
$6(/)df = l. G5)
о
Отметим, что функция б (х) применяется не только в механике,
« во многих разделах математики, в частности при решении многих
задач уравнений математической физики.
Рассмотрим действие 6(t)y если ее представлять как силу.
Найдем решение уравнения
|f- = б (/), G6)
удовлетворяющее условиям
s = 0, -§- = 0 при. f = 0.
Из уравнения G6) находим, учитывая G5),
t
в(*)Л=1 . G7)
При любом ti в частности и при ? — 0. Следовательно, определяя
б (л:) равенством G3), можно трактовать эту функцию как силу,
сообщающую материальной точке с массой единица в момент
/ = 0 скорость, равную единице.
L-изображение :функции б (t) определим как предел изображе-
изображения функции el(ti h) |при А—>О:
L{6(x)Hlunр1
(здесь воспользовались правилом Лопиталя для нахождения пре-
предела). Итак,
- ^ - 6@-^1. ! G8)
Далее определяется функция б(^—10), которую трактуют как
силу, мгновенно, в момент t = t0, сообщающую единичной массе
скорость, равную единице. Очевидно, что на основании теоремы
запаздывания будем иметь
1 ' *(* —g+fe-*. G9)

430 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ ?ГЛ. XIX
Аналогично G5) можем написать
ld(t-to)dt=l. * « (80)
to
* На основании механического толкования дельта-функции сле-
следует, что присутствие дельта-функции в правой части уравнения
может быть заменено соответствующим изменением начальных усло-
условий. Покажем это на простом примере. Пусть имеем дифферен-
дифференциальное уравнение
•^г = /(/) + »(') . „ (81)
с начальными условиями xQ = 0, ,х'0 = 0 при t = 0. Вспомогательное
уравнение будет
p*x(p) = F(p)+l, (82)
откуда
Пользуясь формулами 9 и 15 таблицы, прлучаем
t<
о
К этому же результату мы бы пришли, если бы находили реше-
решение уравнения
' ~dF~~
с начальными условиями хо = О, хг0=1 при / = 0, В этом случае
вспомогательное уравнение имело бы вид
p2x(p)-^l=F(p). (84)
Оно эквивалентно вспомогательному уравнению (82), а следова-
следовательно, решение будет совпадать с решением (83).
В заключение отметим следующее важное свойство дельта-
функции. На основании равенств G4) и G5) можем написать
0 при —oo<t<0%
1 при 0^.t < + oo,
т. е. этот интеграл равняется единичной функции Хевисайда aQ (t).
Итак,
t
b(%)d%. (86)

УПРАЖНЕНИЯ К ГЛАВЕ XIX 431
Дифференцируя правую и левую, части равенства по t, получаем
условное равенство
а;(*) = в(/). . (87)
Для пояснения смысла условного равенства (87) рассмотрим
функцию oQ(t, ft), изображенную на
рис. 404. Очевидно,
o'0(t9 fc) = M'. ft) * (88)
(кроме точек ? = 0 и t — h). Переходя
к пределу при/i—*0 в равенстве (88),
видим,' что aQ (t, ft) —* a0 (/), и будем
писать
0о {t% ft)—*0о(О при ft—^0.
Правая часть равенства (88) аг(t, ft) —>б(t) при ft—^0, Таким
образом, равенство (88/ переходит в условное равенство (87).
Упражнения к- главе XIX
Найти решения следующих уравнений при указанных начальных условиях:
0, х = 1у х' =2 при ? = 0. Оте% х = 4е~*—Зе~2*.
2. ^ — ^±.=0, д; = 2, х'=Ъ, х"=\ при / = 0. Оли. х=1 —
3. —-^2а-^-+(«2+^2)'^ = 0,, д; = л:о, д:'=^ при / = 0. Ome, л: =
г [л:0^соз bt + (xQ—xoa) sin bt].
4. -jp—3-^+2л: = е5<, x = l, x'=2 при ^ = 0. Ome, л;=^
d2x /
5. -j72—\-m2x = acos nt, x = x0> x' ~xq при ^ = 0, Ome, x =
—s o-(cos «^—cos mt) + Xq cos mt -\—— sin mt,
m —ti tit
6. -j^—Ж^*2* x=z°' x==0 при ^=0' Ome* x==z2et—o-t3 — t2—2t—2'
' ~dF"TrX~~2 e ' X~X ~X ^~ ПрИ ~

ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. XIX
=xq = xq = Q при t = Q, Отв, х—\ —~е~*
о = ^о==^о = ^о =0 при / = 0. Отв%
10. Найти решение системы дифференциальных уравнений —тг-f-j/ = 1,
-^p--J-x = O, удовлетворяющее начальным условиям х0=1/о=^о=^о = 0 np i
432
8.
9.
d4
1 1
4F~''

ГЛАВА XX
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Каждодневный опыт убеждает нас в том, что в .обыденной
жизни, практических ситуациях, а также в научных исследова-
исследованиях постоянно приходится сталкиваться с положениями, когда
привычные нам закономерности строгого детерминизма уже не
имеют места. Приведем несколько примеров. Представим, что нас
интересует число вызовов, поступающих на станцию скорой помощи
'в течение суток.
Длительные наблюдения показывают, что нет возможности точно
прогнозировать, как много вызовов поступит на станцию в течение
ближайших суток. Это число подвержено значительным и притом
случайным колебаниям. Точно так же случайно то время, которое
придется затратить врачу, прибывшему по вызову больного.
Если поставить на испытания некоторое число N каких-нибудь
изделий, изготовленных, казалось бы, в одних и тех же условиях
и из тех же самых материалов, то время 'от начала испытаний до
приведения изделий в неработоспособное состояние оказывается
случайным, подвержено весьма сильному разбросу.
При стрельбе из орудия по цели наблюдается так называемое
рассеивание снарядов. Уклонение точки* попадания снаряда от
центра цели заранее указать нет возможности — оно случайно.
Одной констатации факта наличия случайности для уверенного
использования явлений природы или управления технологическими
процессами совершенно недостаточно, необходимо научиться коли-
количественно оценивать случайные события, прогнозировать их течение.
Этого теперь настойчиво требуют, как теоретические, так и практи-
практические задачи. Решением возникающих при этом вопросов и созда-
созданием общей математической теории занимаются две математические
дисциплины—теория вероятностей и математическая статистика.
В последние геды, благодаря в первую очередь работам совет-
советских ученых, происходит развитие теоретических основ теории
вероятностей, ее проникновение в другие, особенно во вновь раз-
развивающиеся науки. Здесь в первою очередь следует указать работы
А. Н. Колмогорова, Б. В. Гнеденко, Н. В. Смирнова и др.

434* ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ " [ГЛ. XX
§ 1. Случайное событие. Относительная частота
случайного события. Вероятность события, Предмет
теории вероятностей
Основным понятием^теории вероятностей является понятие слу-
случайного события. Случайным событием называется такое событие,
которое при осуществлении некоторых условий может произойти
или не произойти.
Пример 1. Появление герба при бросании монеты есть случайное со-
событие.
Пример 2. Попадание в данный объект или в данную площадь при
стрельбе по этому объекту из данного орудия есть случайное событие.
Пример 3. При изготовлении цилиндра с заданной величиной диаметра
20 см!получать ошибки меньше, чем 0.2 мм, при данных средствах произ-
производства есть случайное событие.
Определение 1. Относительной частотой (или просто
частотой) р* случайного события Д называется отношение числа т*
появления данного события к общему числу п* проведенных оди-
одинаковых испытаний, в каждом из которых могло появиться или
не появиться данное событие. Будем писать так:
Пример 4. Пусть по данному объекту из данного орудия при одинаков
вых условиях произведено 6 серий выстрелов:
в 1-й серии было 5 выстрелов, число попаданий 2,
во 2-й серии чбыло 10 выстрелов, .число попаданий б,
в 3-й серии было 12 выстрелов, число попаданий 7,
в 4-й серии было 50 выстрелов, число попаданий 27,
в 5-й серии было 100 выстрелов, число Попаданий 49,
в 6-й серии 200 выстрелов, число попаданий 102.
Событие А—попадание в цель. Относительная частота попадания в сериях
будет
2
в 1-й серии -=-—0,40,
во 2-й серии -^=0,60,
в 3-й серии -^- = 0,58,
27
в 4-й серии -^г-=0,54,
49
в 5*й серии Tqq = 0»49*
102
в 6-й серии 2оо™°>51.
Из наблюдений различных явлений следует, что если число
испытаний в каждой серии практически невелико, то относитель-
относительные частоты появления события А в каждой серии могут суще-

§1] СЛУЧАЙНОЕ СОБЫТИЕ 435
ственно отличаться одна от другой. Если же число опытов в сериях
велико, то, как правило, относительные частоты появления собы-
события А в различных сериях отличаются друг от друга мало и это
отличие тем меньше, чем больше испытаний в сериях. Говорят,
что относительная частота при большом числе испытаний все более
перестает носить случайный характер. Однако отметим, что.суще-
что.существуют такие события, у которых относительная частота не носит
устойчивый характер и ее величины в различных сериях, даже
очень больших, могут сильно отличаться друг от Друга.
Опыт показывает, что в подавляющем большинстве случаев
существует постоянное число р такое, что относительные частоты
появления события А при большом числе испытаний, кроме редких
случаев, мало отличаются от этого числа р.
Этот опытный факт символически записывают так;
P <2>
Число р называется вероятностью появления случайного собы-
события А. Последнюю фразу символически записывают так:
Р(А) = р. C)
Вероятность р является объективной характеристикой возмож-
возможности появления события А при данных испытаниях, определяю-
определяющейся характером события А.
Относительная частота при большом числе испытаний мало
отличается от вероятности, «кроме редких случаев», существова-
существованием которых часто можно'пренебречь.
Коротко словами соотношение B) формулируют так:
При неограниченном увеличении числа опытов п* относитель-
относительная частота события А сходится к вероятности р появления
этого события.
Замечание. В приведенных рассуждениях мы на основании
опытов постулировали соотношение B). Но постулируют и другие
естественные условия, следующие из опыта. Из них выводится
соотношение B), которое тогда уже будет теоремой. Это известная
в теории вероятностей теорема Я. Вернул ли A654—1705).
Так как вероятность является объективной характеристикой
возможности появления некоторого события, то для предсказания
характера протекания многих процессов, которые приходится рас-
рассматривать и в военном деле, и в организации производства, и
в экономике и т. д., нужно уметь определять вероятность появле-
появления некоторых сложных событий. Определение вероятности по-
появления события по вероятностям элементарных событий, опреде-
определяющих данное сложное событие, изучение вероятностных зако-
закономерностей различных случайных событий и является предметом
теории вероятностей.

436 « ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. XX
§ 2. Классическое определение вероятности
и непосредственный подсчет вероятностей . <
Во многих случаях вероятность рассматриваемого случайного
события может быть подсчитана, исходя из анализа рассматрива-
рассматриваемого испытания.
Для понимания дальнейшего изложения рассмотрим пример.
Пример I. Однородный куб, на гранях которого нанесены различные
числа от 1 до б, будем называть игральной костью. Рассматриваем случайное
событие—появление числа / A ^/<;6) на верхней грани при бросании играль-
игральной кости. Так как в силу симметрии кости события — появление любого чи-
числа от I до 6—^одинаково возможны, то их называют равновозможными. При
большом числе п бросаний кости можно ожидать, что число /, как и каждое
другое число от 1 до 6, появится на верхней грани примерно в — случаях.
Это подтверждается опытом.
Относительная частота будет близка к числу р*~ —. Поэтому считают,
¦что вероятность появления на верхней грани числа /, как н всякого другого
числа от I до 6, равна —.
Анализом случайных событий, вероятность которых подсчиты-
вается непосредственно, мы и займемся ниже.
Определение 1. Случайные события называются несовмест-
несовместными в данном испытании, если никакие два* из них не могут
появиться вместе.
Определение 2. Будем - говорить, что случайные события
образуют полную группу, если при каждом испытании может по-
появиться любое из них и не может появиться какое-либо иное со-
событие, несовместное с ними.
. Рассмотрим полную группу равновозможных несо-
несовместных случайных событий. Такие события будем на-
называть случаями (или шансами).
Событие (случай) такой группы называется благоприятствую-
благоприятствующим появлению события Л, если появление этого случая влечет
появление события А.
Пример 2, В урне находится 8 шаров, на каждом из которых постав-
поставлено по одной цифре'от I до 8. Шары с цифрами 1, 2, 3 красные, остальные
шары черные. Появление шара с цифрой I (так же как и появление шара с
цифрой 2 или 3) есть событие, благоприятствующее появлению красного шара.
Для рассматриваемого случая можно дать иное, чем в § 1,
определение вероятности.
Определение. 3. Вероятностью р события А называется
отношение числа т благоприятствующих случаев к числу всех
возможных случаев я, образующих полную группу равновозмож-
равновозможных"" несовместных событий, или символически

§2]
КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
437
Определение 4. Если какому-либо событию благоприятст-
благоприятствуют все п случаев, образующих полную группу равновозмож-
ных несовместных событий, то такое событие называется достовер-
достоверным; его вероятность р=1.
Событие, которому не благоприятствует ни один из п случаев,
образующих полную группу равновозможных несовместных собы-
событий, называется невозможным; его вероятность /?^=0.
Замечание 1. Противоположные утверждения в данном слу-
случае также верны. Однако в других случаях, например в случае
непрерывной случайной величины (§ 12), противоположные утвер-
утверждения могут быть и неверны, т. е. из того, что вероятность
какого-либо события равна 1 или 0, еще не следует, что это со-
событие достоверно или невозможно.
Из определения вероятности следует, что она удовлетворяет
соотношению
П р и м е р 3. Из колоды в 36 карт вынимается одна карта. Какова веро-
вероятность появления карты пиковой масти? ,
Решение. Здесь всего случаев п = 36. Событие А — появление карты
•пиковой масти. Число случаев, благоприятствующих событию Л, /и = 9.
Следовательно, р = 9/36 = 1 /4. ~
Пример 4. Бросаются одновременно две монеты. Какова вероятность
Выпадения герба на обеих монетах (т. е. двух гербов)?
Решение. Составим схему возможных случаев.
1-й случай
2-й случай
3-й случай
4-й случай-
Первая монета'
герб
герб
не герб
не герб
Вторая монета
герб
не герб .
герб
не герб
Всего случаев 4. Благоприятствующих случаев 1. -
Следовательно, вероятность выпадения герба на обеих монетах будет
Пример 5. Вероятность попадания в некоторую цель при стрельбе из
первого орудия равна 8/10, при стрельбе из другого орудия—7/10. Найти ве-
вероятность поражения цели при .одновременном выстреле обоих орудий. Цель
будет поражена, если будет хотя бы одно попадание из какого-либо орудия,-
Решение. Эта задача моделируется следующим образом. В двух урнах
находится по 10 шаров, пронумерованных от 1 до 10. В первой урне 8 крас-
красных и ^2 черных, во второй 7 красных и 3 черных. Вынимается по одному
шару из каждой урны. Какова вероятность, что среди вынутых двух шарсв
имеется хотя бы один красный? . . >
Так как каждый шар первой урны может быть вынут с любым шарсм
второй, то всего случаев 100: п= 100. «
Подсчитаем благоприятствующие случаи.

438 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. XX ,
При вынимании каждого из 8 красных шаров первой урны одновременно
с любым шаром второй урны в числе вынутых будет находиться по крайней
мере один красный шар. Таких случаев будет 10x8 = 80. При вынимании ка-
каждого из 2 черных шаров первой урны одновременно с любым из 7 красных
шаров второй урны в числе вынутых будет Один красный. Таких случаев бу-
будет 2x7=14. Таким образом, всего благоприятствующих случаев будет
80 + 1494
Вероятность того, что среди вынутых будет по крайней мере один крас-
красный шар, равна
т 94
/?=Т==Тоо-
Такова будет и вероятность поражения цели.
Замечание 2. В этом примере задачу о вероятности при-
стрельбе мы свели к задаче о вероятности появления того или
иного шара при вынимании шаров из урны. Многие задачи тео-
теории вероятности можно свести-к «схеме урн». Поэтому на задачи
о вынимании шаров из урн следует смотреть как на задачи обоб-
обобщенные.
Пример 6. В партии из 100 изделий 10 изделий бракованных. Какова
вероятность того, что среди взятых 4 изделий 3 будут не бракованные?
Решение. Взять 4 изделия из 100 можно следующим числом способов:
п = С\оо. Число случаев, когда среди этих 4 изделий будут 3 не бракованные,
равно m — Clo*C\o.
Искомая вероятность будет
Р~~п~ С$оо 4753 ~U'J'
§ 3. Сложение вероятностей; Противоположные
случайные события
Определение 1. Суммой двух.событий А± и А2 называется
событие С, состоящее в появлении хотя бы одного из этих событий.
Ниже будет рассматриваться вероятность суммы двух несовме-
несовместных событий Ai и Л2. Сумма этих событий обозначается
или
At или А2 *).
Справедлива следующая теорема, которая называется теоремой
о сложении вероятностей.
Теорема 1. Пусть при данном испытании (явлении, опыте)"
могут иметь место случайное событие Af с вероятностью Р (Лх)
и событие А2 с вероятностью Р(А2). События At и А2 несовмест-
*) Заметим, что в этом выражении слово «или» не носит характера исклю-
исключения, а означает^ что появится хотя бы одно из этих событий в соответствии
с определением 1.

СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ
439
ны. Тогда вероятность суммы событий, т.е. того, что произой-
произойдет или событие А± или событие А2> вычисляется по формуле
Р(А± или Л2) = Р(ЛХ) + Р(Л2). A)
Доказательство. Пусть
Так как события 'Аг и А2 несовместны, то при общем числе
случаев п число случаев, благоприятствующих появлению собы-
событий А± и Л2 одновременно, равно 0, а число случаев, благоприят-
благоприятствующих появлению или события Af или события Л2, равно
Следовательно,
или Л,)=
что и требовалось доказать.
Аналогичным образом можно доказать эту теорему для любо-
любого числа слагаемых:
или А2 или ... или A~) =
Последнее равенство записывается и так:
i=z 1
+Р(Л„). (Г)
<П
Замечание. Мы доказали теорему сложения для схемы слу-
случаев, когда вероятность определяется непосредственным подсче-
подсчетом. В дальнейшем будем считать, что теорема сложения вероят-
вероятностей справедлива и тогда, когда непос-
непосредственный подсчет вероятностей осу-
осуществить невозможно. Это утверждение
основано на следующих' соображениях.
Вероятности событий при большом чис-
числе испытаний близки (за редкими исклю-
исключениями) к относительным частотам, а
для относительных частот доказательст-
доказательство проводится так же, как и выше. Это
замечание будет относиться и к дока-
доказательству последующих теорем, кото-
которые мы будем доказывать, пользуясь
схемой урн.
Пример 1. Производится стрельба по некоторой области, состоящей
из трех непересекающихся зон (рис. 405). Вероятность попадания в зону I:
Р (AJ ^ТОО" ' в зону 11: Р ^ ^ТОО" > ^*30НУ Ш: р Из) =ТооГ • Какова
вероятность попасть в область D? Событие Л—попадание в область D. По
Рис. 405,

440 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ > [ГЛ. XX
формуле (Г) имеем
Р (^i) + P (А2)-f-P (Л3) = Too +Т00 + W = ТОО* • -
Определение 2. Два события называются противополож-
противоположными, если они несовместны и образуют полную группу.
Если одно событие обозначим через Л, то противоположное
событие обозначают через Л.
Пусть вероятность появления события Л есть /?, вероятность
непоявления события Л, т.е. вероятность появления события Л,
обозначим через P(A) = q.
Так как' при_испытаний обязательно произойдет или событие
А или событие Л, то на основании теоремы A) получаем:
i
m. с. сумма вероятностей противоположных событий равняется
единице:
^l- B)
Пример 2. Производится один выстрел по мишени. Попадание—собы-
Попадание—событие А. Вероятность попадания р: Р(Л) = /?. Определить вероятность промаха.
Промах есть событие А, противоположное событию А, поэтому вероятность
промаха q — l—р.
Пример 3. Производится некоторое измерение. Получение ошибки при
измерении, меньшей к> есть событие А. Пусть Р (Л) = р. Противоположное
событие—получение ошибки^ большей к или равной Я, есть событие X Ве-
Вероятность' этого-события Р (А) = q == I*—/7.
Следствие 1. Если случайные события А1У A2f ..., Ап обра-
образуют полную группу несовместных событий, то имеет место
равенство
Р(Л) + Р(Л) + +Р(ЛН1. C)
Доказательство. Так как события А1У Л2, ..., Ап обра-
образуют полную группу событий, то появление одного из этих собы-
событий есть событие достоверное. Следовательно,
Р(ЛХ или Л2 или ... или Ап)=1.
Преобразуя левую часть по формуле (Г), получим равенство C).
Определение 3. Случайные события Л и В называются
совместными, если при данном испытании могут произойти оба
эти события, т. е. произойдет совмещение событий Л и В.
Событие, заключающееся в совмещении событий Л и В, бу-
будем обозначать (Л и В) или (АВ). Вероятность совмещения собы-
событий Л и В будем обозначать Р(Л и В).
Теорема 2. Вероятность суммы совместных событий вычис-
вычисляется по формуле
Р(Л или В) = Р(Л) + Р(В)-Р(Л и В). .. D)

§41
УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ НЕЗАВИСИМЫХ СОБЫТИЙ
441
Справедливость формулы D) мы проиллюстрируем геометри-
геометрически. Предварительно введем следующее определение.
Определение 4. Пусть дана некоторая область D, пло-
площадь которой равна S. Рассмотрим область d, входящую в D.
Пусть ее площадь S. Тогда вероят-
вероятность попадания точки в область d>
считая ' достоверным попадание точ-
точки в ^бласть D, по определению,
равна S/S, т.е. p = S/S. Эту вероят-
вероятность называют^ геометрической веро-
вероятностью.
Тогда, считая, достоверным попа-
попадание точки в квадрат со стороной,
равной 1, имеем (рис. 406)
Р (А или В) = пл. abcda,
?{А) =пл. abfda\
?{В) =пл. bcdeb,
Р(Л и-В) -пл. debfd.
E)
Рис. 406,
Очевидно, что имеет место следующее равенство:"
пл. abcda= пл. abfda + ил. bcdeb — пл. debfd.
Подставляя в это равенство левые части равенств E), полу-
получим равенство D).
Аналогичным образом можно вычислить вероятность суммы
лкЬбого числа совместных случайных событий.
' Отметим, что теорему 2 можно доказать, исходя из сделанных
выше определений и правил операций.
§ 4. Умножение вероятностей независимых событий
Определение 1. Событие А называется ^независимым от
события В, если .вероятность появления события А не зависит
от того, произошло событие В или не произошло.
Теорема 1. Если случайные события А и В независимы, то
вероятность совмещения событий А и В равна произведению веро-
вероятностей появления событий А и В:
Р(Д и В) =
Р(В).
A)
Доказательство. Проведем доказательств этой теоремы
для схемы урн. В каждой из двух урн соответственно находятся
пг и п2 шаров. В 1-й урне mt красных шаров, остальные черные.
Во 2-й урне т2 красных, остальные черные. Из каждой урны
вынимается по одному шару. Какова вероятность того, что оба
вынутых шара окажутся красными? ! .

442 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. XX
Пусть событие Л —вынимание, красного шара из 1-й урны.
Событие В —вынимание красного шара из 2-й урны. Эти события
независимы. Очевидно,
Р(Л)=^Э Р(В) = %. B)
Всего возможных случаев одновременного вынимания по одно-
одному шару из каждой урны будет п±п2. Число случаев, благоприят-
благоприятствующих появлению красных шаров из обеих урн, будет тхт^
OOQOOOOQO
о о о о о о
Рис. 407,
Вероятность совмещения событий А и В будет
Р(Л и В).
_ гп\ ш2
Заменяя в этой формуле ^- и -1 их выражениями из B),
получаем равенство A). Иллюстрацию этой теоремы см. на рис. 407.
Если имеем п независимых событий Аъ Л2, ..., Ап, то анало-
аналогичным образом можно доказать справедливость равенства
P(At и Л2 и ... и Ап) = Р(А1) Р(Л2) ... ?(Ап). C)
Пример 1. Из двух танков стреляют по одной цели. Вероятность попа-
9 5
дания из 1-го танка -щ-, из 2-го — -=-. Из обоих танков делается одновре-
одновременно по одному выстрелу. Определить вероятность того, что будет два попа-
попадания в цель.
'9 5
Решение. Здесь Р (Л) = -гтг-, Р (В) = -тг ; Р (А и В)—вероятность двух
попаданий — находится по формуле A):
ч Пример 2, Безотказная работа прибора определяется безотказной рабо-
работой каждого из трех узлов, составляющих прибор. Вероятность безотказной
работы узлов за некоторый цикл соответственно равна /?1=*0,6; р2 = 0,7; /?3 =
ess 0,9. Найти вероятность безотказной работы прибора за указанный цикл.
Решение. По теореме умножения вероятностей C) будем иметь;
— 0^6- 0,7- 0,9 = 0,378,

§5f ЗАВИСИМЫЕ СОБЫТИЯ , 443
Замечание. Теорема 2 § 3 (формула D)) о вероятности
суммы совместных событий с учетом формулы A) запишется так:
?{А или Я) = Р(Л) + Р(Я)-Р(Л) Р(В). D)
Пример 3. Решить задачу, сформулированную в примере 5 § 2, поль-
пользуясь формулой D).
Решение. Событие А — попадание в цель из 1-го орудия. Событие В—
попадание в цель из 2-го орудия. Очевидно,
Р(Д или В)=_-(-___.—=_.
Естественно, что мы получили тот же результат, что и раньше.
Пример 4. Вероятность уничтожения цели при одном выстреле равна /?.
Определить число выстрелов я, необходимых для поражения цели с вероят-
вероятностью, большей или равной Q.
Решение. На основании теорем о сумме и произведении вероятностей
можем написать
Решая это неравенство относительно п,~ получаем:
П3э In(l-p) *
Задача с таким аналитическим решением легко формулируется в терминах
«схемы урн»,
§ 5. Зависимые события. Условная вероятность.
Полная вероятность
Определение 1. Событие А называется зависимым от со-
события В, если вероятность появления события А зависит от того,
произошло или не произошло событие В.
Вероятность того, что произошло событие А при условии, что
произошло событие В, будем обозначать Р(А/В) и называть услов-
условной вероятностью события А при условии В.
Пример 1. В урне находится 3 белых шара и 2 черных. Из .урны
вынимается один шар (первое вынимание), а затем второй (второе вынимание).
Событие В—появление белого шара при первом вынимании. Событие А—по-
А—появление белого шара при втором вынимании.
Очевидно, что вероятность события Л, если событие В произошло, будет
Р(Л/Я)=2/4=1/2.
Вероятность события А при условии, что событие В не произошло (при
первом вынимании появился черный шар), будет
Р (ЛIB) =3/4.
Видим, что

444 ЭЛЕМЕНТЫ ТЕОРИЙ ВЕРОЯТНОСТЕЙ [ГЛ. XX
Теорема 1. Вероятность совмещения двух событий равня-
равняется произведению вероятности одного из них на условную веро-
вероятность второго, вычисленную при условии, что первое событие
произошло, т.е.
и В) = Р(В) P(AjB). 1\)
Доказательство. Доказательство приведем для событий,
которые сводятся-к схеме урн (т.е. в случае, когда применимо
классическое определе-
определение вероятности).
Пусть в урне п ша-
шаров, при этом пх белых,
п2 черных. Пусть среди
пг белых шаров п\ ша-
шаров с { бтметкой «звез-
«звездочка»,, остальные чисто
белые (рис. 408).
Из урны вынимается один шар. Какова вероятность события
вынуть белый шар с отметкой «звездочка»?
Пусть В — событие, состоящее в появлении белого шара, А —
событие, состоящее в появлении шара с отметкой «звездочка».
Очевидно,
Р (*> = ¦?-. B)
Вероятность появления белого шара со «звездочкой)? при усло-
условии, что появился белый шар, будет
Вероятность появления белого шара со «звездочкой» есть
Р(А и В). Очевидно,
Но - ,
п п пг * ^ ' '
Подставляя в E) левые части выражений B), C) и D), полу-
получаем
Р(А ц В) = Р(В) Р(А/В).
Равенство A) доказано.
Если рассматриваемые события не укладываются в классичес-
классическую-схему, то формула A) служит для определения услов-
условной вероятности. А именно, условная вероятность* сббыпгия А
при условии осуществления события В определяется с помощью

. § 5] • > ЗАВИСИМЫЕ ¦ СОБЫТИЯ 445
формулы
Замечание 1. Применим последнюю формулу к выражению
?(В и А):
Р(Ви А) = ?{А) Р(В/А). , F)
В равенствах A) и F) левые части равны, так как это одна
и та же вероятность, следовательно, равны и правые. Поэтому
можем написать равенство
Р (А и В) ^ Р (В) Р (Л/5) = Р (А) Р (В/А). G)
Пример 2. Для случая примера 1, приведенного в начале этого пара-
параграфа, имеем Р(Я) = ---, Р (А/В) = -^. По формуле A) получаем Р (Л и В) =
3 13
^Т'Т^Ш' вероятность р (^ и Я) легко вычисляется и непосредственно.
Пример 3. Вероятность изготовления годного изделия данным станком
равна 0,9. Вероятность появления изделия 1-го сорта среди годных изделии
есть 0,8. Определить вероятность изготовления изделия 1-го сорта данным
станком. '
Решение. Событие В — изготовление годного изделия данным станком,
событие А—появление изделия 1-го сорта. Здесь Р (В) =0,9, Р(Л/Я)==0#
Подставляя в формулу (I), получаем искомую вероятность Р (А и B) = Q,9x
Х0,8 = 0,72.
Теорема 2. Если событие А может осуществиться только
при выполнении одного из событий В1% В2, ..., Вп, которые обра-
образуют полную группу несовместных событий, то вероятность
события А вычисляется по формуле
Р (А) = Р (В,) ?-(А1Вх) + Р (В2) Р (AJB2) + ... + Р (Вп) Р (А/Ва). (8)
Формулд (8) называется формулой полной вероятности.
Доказательство. Событие А может произойти при вы-
выполнении любого из совмещенных событий
(В, и Л), (В2 и Л), ...к\Вп и А).
Следовательно, по теореме о сложения вероятностей получаем
.Р(А) = Р(В1 и А)+Р(В2 и А)+...+Р(Вп и А).
Заменяя слагаемые правой части по формуле A), получим ра-
равенство (8).
Пример 4. По цели произведено три последовательных выстрела. Ве-
Вероятность попадания при первом выстреле ^ = 0,3, при втором /?2 = 0,6, при
третьем р3 — 0,8. При одном попадании вероятность поражения цели Xi?= 0,4,
при двух попаданиях й2 —0»?, при трех попаданиях Яз=1Д Определить ве-
вероятность шфаженйя цели при трех выстрелах (событие А).
Решение. Рассмотрим полную'группу несовместных событий:
#!—было одно попадание;
В2—было два попадания;

446 * ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ 1ГЛ. XX
Вз—было три попадания;
?4—не было ни одного попадания.
Определим вероятность каждого события. Одно попадание произойдет, если
или первый выстрел даст попадание, второй и третий—промах; или первый
выстрел—промах, второй попадание, третий промах; или первый выстрел —
промах, второй промах, третий—попадание. Поэтому по теореме умножения
и сложения вероятностей будем иметь для вероятности одного попадания вы-
выражение
Аналогично рассуждая, получим
A— ра) Рз + A— Pi) Р*Рз = 0,468,
з = 0,144,
Р (В,) = A -рО A -р2) A -рз) = 0,056.
Напишем условные вероятности поражения цели при осуществлении каж-
каждого из этих событий:
Р (Л/В,) = 0,4, Р (Л/ВО = 0,7, Р(Л/Я3)=1,0, Р(Л/Я4) = 0.
Подставляя полученные выражения в формулу (8), получим вероятность
поражения цели
Р (Л) = Р (ВО Р (Л/В0 + Р (ВО Р (Л/В2)+Р (В3) Р (А/В3) + ? (В,) Р (Л/В0 =
= 0,332.0,4+0,468-0,7+0,144.1,0+0,056-0 = 0,6044.
Замечание 2. Если событие А не зависит от события В7 то
Р(А/В)=Р(А),
и формула A) принимает вид:
Р(Л и Я) = Р(Я)Р(Л),
т, е. получаем формулу A) § 4.
§ 6. Вероятность гипотез. Формула БаДеса
Формулировка задачи. Как и в теореме 2 § 5, будем
рассматривать полную группу несовместных событий Въ В2;..., Вп,
вероятности появления которых суть Р(Вг), РE2), ..., Р(Вп)>
Событие А может произойти только вместе с каким-либо из со-
событий Въ В2, ¦.., Вп, крторые будем называть гипотезами.
Вероятность появления события А в соответствии с форму-
формулой (8) § 5 будет
Р (А) = Р (Вг) Р (А/Вг) + Р (В2) Р (А/В2) +...+Р (Вя) Р (А/Вп). A)
Допустим, что событие А произошло. То, что событие А прои-
произошло, изменит вероятности гипотез РEХ), .*,, Р(Вп). Требуется
определить условные вероятности осуществления этих гипотез
в предположении, что событие А произошло, т. е, определить
), P(BJA), ..., P(BJA).

§Щ ВЕРОЯТНОСТЬ ГИПОТЕЗ. ФОРМУЛА БАЙЕСА 447
Решение задачи. По формуле G) § 5 найдем вероятность
Р (А и BJ:
Р(Л и В1) =
откуда
Подставляя вместо Р(Л) его выражение A), получим
P(BJA)= /WpW >. - B)
2 P(Bt)
Аналогичным образом определяются
Р(В„/Л).
ад . C)
2 Р (В/) Р И/В/)
t=i
Формула B) называется формулой Байеса или теоремой ги-
гипотез.
Замечание. Из формулы C) следуе;г, что в выражении
вероятности Р (Bk/A) — вероятности осуществления гипотезы- Вк
при условии, чтр событие А произошло,—знаменатель не зависит
от номера k.
Пример 1. Пусть до опыта было четыре равновероятные гипотезы
#i, В., Вя, В4:Р(В1)=*Р(В1) = Р(В8)=Р(В4) = 0|25.
Условные вероятности появления события А соответственно равны
Р(А/Вг) = 0,7. Р (Л/5,) = 0,1,
Пусть в результате испытания, событие А произошло. Тогда по формулам C)
получаем
р т /л 0,25-0,7 0Л75 ^
г (Oilл)—о,25.0,7 + 0,25-0,1+0,25-0,1+0,25-0,02~ о,23 ~и'/0»
p(fi^)(I1
Здесь было Р(Вх) = 0,25, Р (В1/А) = 0,76 стало больше, потому что событие Л
произошло При этом вероятность Р(Л/5х) = 0,7 большая сравнительно с дру-
другими условными'Вероятностями.

448 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ t [ГЛ.
Пример 2.* Каждый из танков независимо сделал выстрел по- некото-"
рому объекту. Вероятность поражения цели первым танком pi = 0,8, вторым
р2 —0,4. Объект поражен одним попаданием. Определить вероятность того, что
объект -поражен первым танком.
Решение. Событие А — поражение объекта одним попаданием. До
стрельбы возможны следующие гипотезы:
В\—оба танка не попали,
В2—оба танка попали,
#з—первый танк попал, второй не попа л,-
jB4—первый не попал, второй попал.
"Определим вероятности этих гипотез по теореме умножения вероятностей:
P(Bi)«(l-Pi)(l-p2) = 0f2.0,6 = 0,12i
Р(В2) = р1р2 = 0,8.0,4 = 0,32,
Определим условные вероятности наступления события А:
Р (>!/?!) = 0, РИ/?2) = 0, Р(Л/Я8)=1, P(W
По формуле B) находим условную вероятность гипотез:
,32-0+0,48 -1+0,08 -l^O^B
Пример 3. 30% приборов собирает специалист высокой квалификации
и 70%—специалист средней квалификации. Надежность работы прибора, со-
собранного специалистом высокой квалификации, 0,90, надежность прибора,
собранного специалистом средней квалификации, 0,80. Взятый прибор ока&'лся
надежным. Определить вероятность того, что он собран специалистом высокой
квалификации.
Решение. Событие Л-«-безотказная работа прибора. Для проверки
прибора возможны гипотезы
#j—прибор собран специалистом высокой квалификации,
В2—прибор собран специалистом средней квалификации.
Выпишем вероятности этих гипотез:
0,3f P
Условные вероятности события А:
Определим вероятности гипотез Bi и В2 nptr условии, что событие А
произошло.
По формуле B) имеем * f
OJ-0,8 0,56

ДИСКРЕТНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
449
§ 7. Дискретная случайная величина. Закон распределения
дискретной случайной величины ,
V
Определение 1. Переменная величина х, принимающая
в результате испытания одно из конечной или бесконечной после-
последовательности значений xi9x2,.. ,ухк, .'.., называется дискретной
случайной величиной, если каждому Значению хк соответствует
определенная вероятность рк того, что переменная величина л:
примет значение хк.
Из определения следует, что каждому значению хк соответст-
соответствует вероятность рк. ~
Функциональная зависимость вероятности рк от хк называется
законом распределения вероятностей дискретной случайной вели-
величины х *).
Возможные значения слу-
случайной величины
Вероятности этих значений -
Pi
Р2
...
...
...
...
...
...
Xk
Pk -
...
Так же закон распределения может быть задан графически
в виде многоугольника распределения вероятностей, когда в пря-
прямоугольной системе координат строятся точки, с координатами
(хк, рк),п соединяются ломаной (рис. 409).
Закон распределения может быть задан и аналитически:
То, что случайная величина х примет одно из значений по-
последовательности Xf, х2У .:.
•.., я*, .. •, есть событие досто- Р\
верное, и потому должно вы-
выполняться условие
в случае конечной последова-
последовательности .N значений, или
00
A')
Рис. 409,
в случае бесконечной последовательности. Заметим, что значе-
значение случайной величины xh имеющее наибольшую вероятность,
*) Иногда коротко говорят «закон распределения случайной- величины».
15 н. с. Пискунов, т. 2

45а
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
(ГЛ. XX
называется модой. Случайная величина #, изображенная на
рис. 409, имеет моду х2.
Пример 1. Переменная величина х есть число очков, выпадающее на
верхней грани игральной кости при ее однократном бросании. Переменная х
может принять одно из следующих значений: 1, 2, 3, 4, 5, 6. Вероятность
выпадения каждого значения есть, 1/6. Следовательно, таблица распределения
этой случайной величины будет иметь вид
X
р
1
1
6
2
1
6"
3
1
6
4
1
5
1
6
6
1
6
П р и м е"р 2. Вероятность появления события А при каждом из бесконеч-
бесконечной последовательности испытаний равна р. Случайная величина х—номер
испытания, при котором произошло первый раз событие Л. Найти закон рас-
распределения случайной величины х.
Решен ие. Случайная величина х может принимать любое целое поло-
положительное значение 1, 2, 3, ... Вероятность рх того, что событие А произой-
произойдет при первом испытании, будет
Вероятность р2 того, что событие не произойдет при первом испытании,
а произойдет при втором, будет
р2 —Р(Л и А) = (\—р) р.
Вероятность /?3 того, что событие А не произойдет ни при первом, ни
при втором испытании, а произойдет при третьем, будет
р3 = Р(Л и Л и Л) = A—р) A—р)р = A—рур
и т. д.,
Pk~(l—Р)к~1Р* B)
Таблица распределения вероятностей будетv
X
Pk
1
р
2
0—Р)Р
3
A—РJР
...
...
...
...
k
...
...
Здесь также имеем:
Зада*1а о стрельбе до первого попадания. Рас-
Рассмотренная задача имеет приложение, в частности, к вопросам
стрельбы.
' Пусть производится стрельба до первого попадания. Вероят-
Вероятность попадания при каждом выстреле есть р.

ОТНОСИТЕЛЬНАЯ ЧАСТОТА
451
Случайная величина л: —номер выстрела, при котором про-
произошло первое попадание. Таблица распределения вероятностей
этой случайной величины будет та же, что и в примере 2.
Пример 3. Вероятность попадания при каждом выстреле /? = 0,8. Име-
Имеется три снаряда. Определить вероятность того, что будет израсходован один
снаряд, два снаряда, три снаряда, если стрельба ведется 'до первого попада-
попадания или промаха всеми тремя снарядами: составить таблицу распределения
случайной величины х—числа израсходованных снарядов.
Решение. Пусть х—случайная величина: число израсходованных сна-
снарядов; P(#=Xi)—вероятность того, что будет израсходовано д? снарядов.
Тогда Р (х= 1) = р = 0,8 равна вероятности попадания при одном (первом)
выстреле.
Р (д: = 2) = A— р) р = A —0,8) -0,8 = 0,16
— вероятность того, что при первом выстреле был промах, при втором вы-
стреде—попадание.
так как всего три снаряда и стрельбу прекращают независимо от того, будет
ли при третьем выстреле попадание или промах. Последнюю вероятность
можно было вычислить и как разность
1 — Р(л:=1) — Р(д:==2) = 1—0,8—0,16 = 0,04.
Таблица распределения будет иметь вид
X
р (*=**)
1
0,8
2
0,16
3
0,04
Замечание. Данную задачу можно сформулировать в терминах «схемы
урн», следовательно, она может иметь значение ; и при рассмотрении других
вопросов. Это замечание относится и к некоторым другим задачам.
§ 8. Относительная частота и вероятность относительной
частоты при повторных испытаниях
Пусть производится серия из п испытаний. В каждбм из испы-
испытаний может осуществляться событие А с вероятностью р. Пусть
х—случайная величина, означающая относительную частоту появ-
появления события А в серии из п испытаний. Требуется определить
закон распределения случайной величины х в серии из п испы-
испытаний.
Очевидно, что случайная величина х при п испытаниях при-
примет одно из следующих значений: 0//г, \/п, 2//г, ..., /г/л.
Теорема 1. Вероятность Р(х = т/п) того, что переменная
величина х примет значение т/п, т. е^что при п испытаниях
событие А появится т раз, а событие А (не появится событие А)
п—т раз, равняется C%pmqn~mx где С%—число сочетаний из п эле-
15*

452 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. XX
ментрв по т; р—вероятность появления события Л, р = ^
q—вероятность непоявления события Л, т. е. q=l—/? = Р(Л).
Доказательство. Событие Л появится т раз^ при п испы-
испытаниях, например, если чередование событий А я А будет таким:
АА...ААА...А,
т. е. в первых т испытаниях появляется событие Л, а в после-
последующих п—т испытаниях событие Л не появляется (появляется
событие Л). Так как
то по теореме умножения вероятность такого чередования собы-
событий Л и Л будет
Но событие Л может появиться т раз при п испытаниях и
при другой последовательности чередования событий Л и Л, на-
например, при таком чередовании: АА.. .ААА.. .АА. Нбобязательно
т—\ п-т t __
событие Л должно произойти т раз, а событие Л п—т раз.
Вероятность появления такого чередования событий Ли J будет
pnqn~mp = pmqn~m.
Сколько же различных чередований событий Л и Л может
быть при h испытаниях, в которых событие Л появится т раз?
Очевидно, что оно равно числу сочетаний из п элементов по т:
Таким образом; по теореме сложения получаем
или
Теорема доказана. ' "
Доказав теорему, мы тем самым определили закон распределе-
распределения случайной величины х, который мы выразим и в виде таблицы

§8]
ОТНОСИТЕЛЬНАЯ ЧАСТОТА
453
X
'И)
0
п
\-qn
1
п
2
п
...
...
т
п
Стртдп~т
п
п
\.рп
Полученный закон распределения называется биномиальным
законому потому что вероятности р(х = ~) равняются соответст-
соответствующим* членам разложения выражения (q + p)n по формуле бинома:
B)
/7Z=U
Как и следовало ожидать, сумма вероятностей всех возможных
значений переменной величины равна 1, так как (/?+?)"= \*= 1.
Замечание. При исследовании многих волросов бывает
нужно определить вероятность того, что событие А осуществится
«хотя бы один раз», т. е. относительная частота этого события
х ^ —:' Очевидно, что эта вероятность
равенства
-А определится из
= 1-9". C)
Из таблицы распределения также следует, что вероятность
р (х^ —) того, что событие произойдет не менее чем k раз, опре-
определится по формуле
п
* / ? \ V1
т=А
ИЛИ
k~\
\ nJ т==о
Пример 1. Изобразить графически биномиальный закон распределения
случайной величины х при /г = 8, Р=у » ^Т*
Решение. Определим все значения вероятностей, входящие в таблицу;
D ( П
Р 1*=87 =
Р
1
8 1 1
Т * 256=32'
(*=А)=с28. (±У=?1.18==1,
8>7»6 1
=32'

454
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
\! 87-65 1 35
) =
7
[ГЛ. XX
Л 4\ .4 П\! 87-65 1 35
[Х= Г)=Са ' \Т) =Ь2^4 * F=l28'
64'
1 1
Построим многоугольник распределения (рис. 410).
i д
Рис. 410.
Пример 2. Какова вероятность того, что событие А произойдет два
раза а) при 2 испытаниях; б) при 3 испытаниях; в) при 10 испытаниях,
если вероятность появления события при каждом испытании равняется 0,4?
Решение, а) Здесь п = 2, р = 0,4, ^ = 0,6:
ci/>v=4^ • 0>42=0>16;
б) здесь я = 3, р = 0,4, ^ = 0,6:
Р (*=-|) =С32/>У=^|. 0,42.0,6 = 0,288;
в) здесь я=10, р = 0Д, ^ = 0,6:
Р
Пример 3. По цели производится 5 независимых выстрелов. Вероят-
Вероятность попадания лри каждом выстреле равна 0,2. Для поражения цели до-
достаточно трех попаданий. Определить вероятность поражения цели.
Решение. Здесь п=^5, /? = 0,2, ^==0,8. Очевидно, что вероятность по-
поражения следует вычислять по формуле

§9]
или по формуле
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
455
По первой формуле имеем
5 = 0,05792 * 0,06.
Пример 4. Производится четыре независимых испытания. Вероятность
появления события А при каждом испытании 0,5. Определить вероятность
того, что событие Л появится не менее двух раз.
Решение. Здесь я = 4, /7 = 0,5, <7 = О,5:
или
Вычислим вероятность
Следовательно, по второй из формул получаем
Р Гд;^ ^ = 1 — [0,54+4-0,54] =0,6875 « 0,69.
Пример 5. Вероятность брака в данной партии деталей р = 0,1. Какова
вероятность того, что в партии из трех деталей будет яг = 0, 1, 2, 3 бракован-
бракованных деталей?
Решение.
-§-) =Clpq* = у-0,1 -0,92 = 0,243,
Р (* = -
Р (*=
Р (**=¦§¦) =Cj^ = l-0.18= 0,001.
§ 9. Математическое ожидание дискретной случайной величины
Пусть имеем дискретную случайную величину х с соответст-
соответствующим законом распределения
X
?(x=xk)
Pi
*2
Р2
...
...
Ч
Pk
...
*п
Рп

456 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ {ГЛ. XX
Определение 1. Математическим ожиданием дискретной
случайной величины х (будем его обозначать М [х] или тх) назы-
называется сумма произведений всех возможных значений случайной
величины на вероятности этих значений:
М [х] = хгрх+х2р% +... +xnpnf
или коротко
М[*]=2**Л. A)
п
~ При этом, как ранее указывалось, 2/??=1-
Если значения случайной величины образуют бесконечную по-
последовательность значений, то
ю*= 23 **/>*. ^ A')
Будем рассматривать только такие случайные величины, для
которых этот ряд сходится.
Установим связь математического ожидания случайной вели-
величины со средним арифметическим значением случайной величины
при большом числе испытаний, а именно покажем, что при большом
числе испытаний среднее арифметическое наблюдаемых значений
близко к ее математическому ожиданию, или в терминах, уста-
установленных в § 1, можно сказать, что среднее арифметическое
наблюдаемых значений случайной величины при неограниченном
возрастании числа испытаний стремится к ее математическому
ожиданию.
Пусть производится N независимых опытов. Предположим, что
значение хг появилось nt раз,
значение х% появилось п2
значение xv появилось nv раз.
Случайная величина х принимает значения *ff х2У ..., xv.
Вычислим среднее арифметическое полученных значений вели-
величины х (будем его обозначать через М[#] или тх):
"лГ+*-- +*v^r* B)
Но так как при большом числе испытаний N относительная
частота -^ стремится к вероятности появления значения хк, то

МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
457
При довольно естественных предположениях получается
*М—ММ- C)
Замечание 1. Если бы мы рассмотрели схему урн с N ша-
шарами, где пг шаров с числовой отметкой х19 п2 шаров с числом ха
и т. д., то «ожидаемое число» при вынимании одного шара будет
выражаться формулой B), т. е. равно тх.
Пример 1. Определить математическое ожидание случайной величины л
числа попаданий при трех выстрелах, если вероятность попадания при каждом
выстреле р = 0,4.
Решение. Случайная величина х может принять значения
дс1==О, #2 = 1, х3 = 2, дс4 = 3.
Составим таблицу распределения данной случайной величины.
* Вероятность этих значений находим пв теореме о повторных испытания»
(Л==3 р=0Д fl=06):
р (* = 1)=С?. 0,4- 0,62 =0,432,
Р(* = 3)=С|.0,43=0,064.
Таблица распределения случайной величины будет
X
р (*=**)
0
0,216
1
0,432
2
0,288
3
0,064
Математическое ожидание вычисляем по формуле A):
т* = 00,216+1 0,432 + 2 0,288+3 0,064 = 1,2 попаданий.
Пример 2. Производится один выстрел по объекту. Вероятность попа-
попадания равна р. Определить математическое ожидание случайной величины 4
числа попаданий.
Составляем" таблицу распределения случайной величины
• 1 •
Pk II 1 —р
1
р
Следовательног mJC = 0-(i—
Замечание 2. В дальнейшем будет установлено, что мате-
математическое ожидание М{лс] числа появления события А при п не-
независимых испытаниях равно произведению числа испытаний на
вероятность р появления события А при каждом испытании:'
ММ = пр. D)
Если в формуле D) п—число выстрелов, р—вероятность по*
падания, то решение задачи примера 1 будет следующее:
= яр = 3-0,4= 1,2 попаданий.

458
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
1ГЛ. XX
Если в формуле D) известны М[д;] и /?, то находится п—число
испытаний, дающих заданное математическое ожидание числа на-
наступления события:
Пример 3. Вероятность попадания при одном выстреле р — 0,2. Опре-
Определить расход снарядов, обеспечивающих математическое ожидание числа
попаданий, равное 5: ,
п = ^~2 = 25 снарядов.
(Отметим еще раз, что подобные задачи имеют место в различных иссле-
исследованиях. Там слово «попадание» заменяется словами «появление события»,
слово «выстрел»—словом «испытание»4.)
Пример 4. Определить математическое ожидание случайной величины xt
со следующей таблицей распределения:
X
Рк
1
р
2
<1-р)р
3
A-р)*р
...
...
k
A-р)*-1р
...
...
Смотри пример 2 § 7.
Решение: По формуле A) имеем (обозначая 1
Итак,
Заметим, что
•оо при р
Эти соотношения можно объяснить, исходя из вмысла задачи.
Действительно, если вероятность появления события А при
каждом испытании близка к 1 (р « 1), то можно ожидать,, что со-
событие А произойдет при одном (первом) испытании (тхж 1). Если
же вероятность р мала (р « 0), то можно ожидать, что для того,
чтобы произошло событие Л, потребуется произвести очень много
испытаний (тх « оо).
Математическое ожидание случайной величины х называется
центром распределения вероятностей случайной величины х.
Замечание 3. Название «центр распределения вероятностей»
введен по аналогии с названием «центр масс». Если на оси Ох
в точках с абсциссами xlt хг> ..., хп помещены массы р1э /?а,...

§9]
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
459
• .., рпУ то из аналитической геометрии известно, что абсцисса
центра этих масс определяется по формуле
Если
= 1, то
E)
Формула E) по виду совпадает с формулой A) для математи-
математического ожидания.
Итак, установлено, что центр масс и математическое ожида-
ожидание вычисляются по аналогичным формулам. Отсюда и название
«центр распределения вероятностей».
п
я?
h
Рис. 411.
Рис. 412.
Пусть дана случайная ^величина х с соответствующим законом
распределения (рйс. 411); пусть ее математическое ожидание тх.
Рассмотрим далее разность случайной величины х и ее математи-
математического ожидания х—тх.
Эту случайную величину будем называть центрированной слу-
случайной величиной или отклонением и обозначать л:0.
Очевидно, что закон распределения этой случайной величины л:0
будет
Pk
*i=*i — тх
Pi
*2=#2 — тх
Р2
...
...
•*& = #?—*П>Х
Pk
(рис. 412).

460 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ * * [ГЛ. XX
Найдем математическое ожидание центрированной случайной
величины:
п п п
М[х—тх]= 2 (Xk—mjpk^ 2 хкрк— 2 тхрк =*
Итак, математическое ожидание центрированной случайной
величины равно нулю.
Замечание 4. Иногда бывает целесообразно неслучайную
(достоверную) постоянную величину с рассматривать как случай-
случайную величину, которая с вероятностью 1 принимает значение <\
а другие значения принимает с вероятностью 0.
Тогда имеет смысл говорить о математическом-ожидании по-
постоянной:
M[c] = <?.l=cf F)
т. е. математическое ожидание постоянной равно самой постоянной.
§ 10. Дисперсия. Среднеквадратичное отклонение.
Понятие о моментах
к
Кроме математического ожидания случайной величины х, кото-
которое, определяет положение центра распределения вероятностей,
количественной характеристикой распределения случайной вели-
величины является дисперсия случайной величины х.
Дисперсию будем обозначать D [л:] или о*.
Слово «дисперсиям означает рассеивание. Дисперсия является
числовой характеристикой рассеивания, разброса значений слу-
случайной величины относительно ее математического ожидания.
Определение 1. Дисперсией случайной величины х назы-
называется математическое ожидание квадрата разности случайной вели-
величины л: и ее математического ожиданияДт. е. математическое ожи-
ожидание квадрата соответствующей центрированной,случайной вели-""
чины):
D[x] = Ni[(x-mxn A)
или
0[x]=l>(xk-mxyPk. B)
Дисперсия' имеет размерность квадрата случайной величины.
Иногда, для характеристики рассеивания, удобнее пользоваться
величиной, размерность которой совпадает с размерностью слу-
случайной величины. Такая величина—среднеквадратичное откло-
отклонение.

110]
ДИСПЕРСИЯ
461
Определение 2. Среднеквадратичным отклонением слу-
случайной величины называется корень квадратный из ее дисперсии:
или в развернутом виде
а
И =|/Jl <**-«*)•/»*.
.C)
Среднеквадратичное отклонение обозначают также ах.
.Замечание 1. При вычислении дисперсии формулу (Ц бы-
бывает удобно преобразовать так:
п п % п п
D[х] = 2 (xk-mxy pk - 2 *&>*-2 2
Ы
п
п
2 рн^
_ 1-mS, D)
т. е. дисперсия равна разности математического ожидания квад-
квадрата случайной величины и квадрата математического ожидания
случайной величины.
Пример 1. Производится один выстрел по объекту. Вероятность попа-
попадания р. Определить математическое ожидание, дисперсию и среднеквадратич*
ное отклонение. -
Решение. Строим таблицу значений числа попаданий
X
Рк
1 1 0
Р | Я
q = i — р. Следовательно,
о lx] =
E)
Чтобы представить смысл понятия дисперсии и среднеквадратич-
среднеквадратичного отклонения как характеристики рассеивания/случайной вели-
величины, рассмотрим примеры.
Пример 2. Случайная величина х задана следующим законом распре-
распределения (см. таблицу и рис. 413):
х | 2
Рк. | о.з •
3
0,4
4
0,3

462
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
{ГЛ. XX
Определить: 1) математическое ожидание, 2) дисперсию, 3) среднеквадра-
среднеквадратичное отклонение.
Решение
1. МЫ ==2-0,3+3 0Д+4-0,3 = 3,
2. р[л] = B~3J0,3+C~3J.0,4+
3. с [*]=VD[*] = ^0,6 = 0,7?.
Пример 3. Случайная величина х задана следующим законом распре-
распределения (см. таблицу и, рис. 414):
X II 1
Pk | 0,3
3 | 5
0,4 0,3
Определить: 1) математическое ожидание, 2) дисперсию, 3) среднеквадра-
среднеквадратичное отклонение.
ИЗ
р\
0,4
¦2 3
Рис. 413,
0,3
х
0,3
i 3
Рис. 414.
a-
Решение.
1. M[*] = l.0,3+3-0,4+50,3 = 3,
2. DM==(l-3J.o,3 + C~>3J.O4+(),,,
3. a[*] = l/*2,4=l,55.
Рассеивание, разброс случайной величины в первом примере меньше рас-
рассеивания случайной величины во втором примере (см. рис. 414 и 415). Диспер-
Дисперсии этих величин соответственно равны 0,6
и 2,4.
Пример 4; Случайная величина х за-
задана следующим законом распределения (см.
таблицу и рис. 415):
X
J р
3
1
3 а
Рис. 415.
. Определить: 1) математическае ожидание 2) дисперсию, 3) среднеквадра-
среднеквадратичное отклонение.
Решение.
2\ D[4=C-3J'l=0,
3. а[х]=-0.
Рассеивание значений этой' случайной величины отсутствует.

§П]
ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
463
Замечание 2. Если рассматривать постоянное число как
случайную величину, которая принимает значение с с вероятностью
1, то легко покааать, что D[c] = 0.
Доказательство. Было показано, что М [с] = с (см. E) § 9).
По формуле A) получаем D[c] = M[(c—сJ] = М[0] = 0, что и тре-
требовалось доказать.
Замечание 3. По аналогии с механической терминологией
математическое ожидание величин х—тх, (х—тхJ называют
центральным моментом первого и второго порядка случайной ве-
величины х. Рассматривают и центральный момент третьего порядка
п
Л (хь—тх)* Рн-
Если случайная величина распределена симметрично относительно
центра распределения вероятностей (рис. 411), то очевидно, что
ее центральный момент третьего порядка будет равен нулю. Если
центральный момент третьего порядка отличен от нуля, то слу-
случайная величина не может быть распределена симметрично.
§ II. Функции от случайных величин
Пусть случайная величина'* задана законом распределения
в виде таблицы
X
Pk
Xi
Pi
х2
Р2
...
...
Ч
Pk
...
...
Хп
Рп
Рассмотрим функцию от случайной величины х: '
Значения функции ^ = /(хл) будут значениями случайной ве-
величины у.
Если все значения yk = f(xk) различны, то закон распределе-
распределения случайной величины у задается таблицей
y=f(y)
Pk
#i = /(*i)
Pi
Л = /(«¦)
P*
•..
...
yk = fD)
Pk
...
...
yn = f(xn)
Pn
Бели среди значений у^ = /(хЛ) есть равные, то соответствую-
соответствующие столбцы следует объединить в один, сложив соответствующие
вероятности.

464
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
?ГЛ. XX
Математическое ожидание функции y=f(x) случайной величи-
величины х будет определяться по формуле, аналргичной формуле A) § 10:
' A)
Аналогичным образом определяется и дисперсиях функции:
^tA[f(x)]r]= 2 (f(xh)-mf{x)yPk.
Я 1
Пример. Случайная величина <р задана следующим законом распреде-
распределения:
ф
Рк
я
0,1
я ,
0,1
0
0,2
л
Т '
0,3
я
~2
0,3
Рассматривается функция этой случайной величины
у~А sinq>.
Составим таблицу распределения для_ случайной величины у:
У
Рк
—А
0,1
A V2
0,1
а
0,2
АУ
0,3
А
0,3
Найдем 'математическое ожидание функции:
.0,1+00,2+^-^.
Задачи подобного типа могут возникнуть при рассмотрении колебательных
процессов.
§ 12. Непрерывная случайная величина. Плотность
распределения непрерывной случайной величины. Вероятность
попадания случайной величины в заданный интервал
Для понимания данного вопроса рассмотрим пример.
, Пример. Измеряется величина износа цилиндра после некоторого пе-
периода эксплуатации. Эта величина определяется значением увеличения диа-
диаметра цилиндра» Обозначим ее х. Из существа задачи следует, что- величина ~х
может принимать любое значение из некоторого интервала (а, Ь) возможных
ее значений.

§12]
НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
465
Такую величину называют непрерывной случайной величиной.
Итак, рассмотрим непрерывную случайную величину *, задан-
заданную на некотором интервале (а, Ь), который может быть и беско-
бесконечным интервалом (— оо, +оо). Разделим этот интервал произ-
произвольными точками *0, х19 х2
хп на малые интервалы длины
И^
I
Рис-416.
Допустим, что нам известна вероятность того, чю случайная
величина^ попала в интервал (х(_19 х(). Эту вероятность мы
обозначим так: ?{хг_г<х <xt) и изобразим в виде площади пря-
прямоугольника с основанием A#/_i (рис. 416).
" Для каждого интервала (x,-_i, х{) определяется вероятность
^попадания случайной величины х в этот интервал и, следова-
следовательно, может быть построен соответствующий прямоугольник.
Таким образом, получаем ступен-
чатую ломаную.
Определение 1. Если су-
существует такая функция */ = /(#),
что
; х < х+Ах)
Ах
= /(*). 0)
то эт^ функция / (х) называется плотностью распределения вероят-
вероятностей случайной величины х или законом распределения. (Также
говорят «плотность распределения» или «плотность вероятности».)
Через х будем обозначать случайную непрерывную величину,
через х или хк значения этой случайной величины. Но иногда,
если это не мешает пониманию, и в первом случае черту будем
опускать. Кривая y — f(x) называется кривой распределения вероят-
вероятностей или кривой распределения (рис. 417). Пользуясь опреде-*
лением предела, из равенства A) с точностью до бесконечно малых
высшего порядка относительно Д# следует приближенное равенство
Р(х <x< j

466
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
{ГЛ. XX
Докажем далее следующую теорему.
Теорема' 1. Пусть f{x) есть плотность распределения слу-
случайной величины х. Тогда вероятность того, что значение случай-
ной величины х попадет в некоторый интервал (а, р), равна
определенному интегралу от 'функции \{х) в пределах от а до ft>
т. е. справедливо равенство
C)
Доказательство. Разобьем интервал (а, Р) точками a=xi,
= |3 на п малых интервалов (рис. 418). К каждому
О
Рис. 418.
из этих интервалов применим формулу B):
Р (хх < х < х2) ^ / (хг) &
P(x2<x<x3)^f (x2) Ах
(жладываем левые и правые части равенства. Очевидно, что слева
получим Р (а < х < Р). Итак,
Р(а <?<Р) ^23/(**) До-
Дополучили приближенное равенство. Переходя к пределу в пра-
пой части при тахДл;;—*0, йа основании свойств интегральных
сумм получим точное равенство
P(a<J<§)= lira 2/(*/)Д**.
max Лдг—>-0 i=sl
(Mli предполагаем, что f (x) такова, что справа стоящий предел
существует.) Но справа стоящий предел есть определенный инте-.

НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
грал от функции f(x) в пределах от а до р. Итак,
467
Теорема доказана.
Таким образом, зная плотность распределения случайной вели-
величины, мы можем определить вероятность того, что значение слу-
случайной величины попало в данный интервал. Геометрически эта
вероятность равняется площади соответствующей криволинейной
трапеции (рис. 419).
Замечание. В случае непрерывной случайной величины
вероятность события, состоящего в том, что х = х09 будет равна
нулю.
Действительно, положив в
равенстве B) x = xQ, получим
Р (х0 < х < хо+^x) ж f (x0) А*,
откуда
lim Р (х0 < И < хо
Дя-И)
О,
ИЛИ
Рис. 419,
(См. также замечание 1 на с. 437.) Поэтому в равенстве C)
и предыдущих мы можем писать не только Р (а < ;Г< Р), но и
так как
Если все возможные значения случайной величины х нахо-
находятся в интервале (a, b), то
ь
!. D)
так как достоверно, что значение случайной величины попадет
в интервал (а, &).
Если интервал возможных значений (—оо, +оо), то
lf(x)dx=h E)
Заметим, что если из существа рассматриваемой задачи сле-
следует, что функция / (х) определена на конечном интервале (а, 6),
то можно считать, что она определена на всем бесконечном

ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
?ГЛ. XX
интервале (—оо>(
но
вне интервала (а, Ь). В этом случае выполняется и равенство D),
и равенство E). Плотность распределения случайной величины
полностью определяет случайную величину.
§ 13. Функция распределения, или интегральный закон
распределения. Закон равномерного распределения вероятностей
Определение 1. Пусть f_(x) есть плотность распределения
некоторой случайной величины х (—оо/< х < +оо), тогда функция
х
0)
называется функцией распределения вероятностей, или инте-
интегральным законом распределения.
Для дискретной случайной величины функция распределения
равна сумме -вероятностей тех ее значений х^ которые меньше х:
F(x)= 2 pk.
xk<x
На основании равенства C) § 12 следует, что функция рас-
распределения F (х) есть вероятность того, что случайная величина х
примет значение, меньшее х
(рис. 420):
F(x)^P(-oo<~x<x). B)
Из рис. 420 следует, что при дан-
ном значении х значение функ-
функции распределения численно рав-
равняется площади ограниченной
кривой распределения, лежащей левее ординаты, проведенной
через точку лс.
. График функции F (х) называется интегральной кривой рас-
распределения (рис. 421).

§13]
ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
469
Переходя к пределу при х —+ +оо в равенстве A), с учетом
E) § 12 получаем
lim
im F(jc)= lim С/(*)<**=
Докажем далее следующую теорему.
Теорема 1. Вероятность попадания случайной величины х
в заданный интервал (а, р) равняется приращению функции рас-
распределения на этом интервале:
Доказательство. Выразим вероятность попадания случай-
случайной величиныJx в заданный интервал (а, Р). Формулу C) § 12
У^
перепишем так:
= J
(рис. 422). Пользуясь равенством A), можем написать
что и требовалось доказать (рис. 423).
Заметим, что плотность распределения / (х) и соответствующая
функция распределения F(x) связаны соотношением
* F'(x) = №. ~ i : C)
Это следует из равенства A) и теоремы о циффе?€нцировании
определенного интеграла по верхнему пределу.
Рассмотрим далее случайную величину с законом равномерного
распределения вероятностей. Закон распределения или плотность
распределения f(x) такой случайной величины задается следую-
следующим образом: /(х) = 0 при х < a, f(x) = c при а<л:<Ь, /(л:) = 0
при Ъ < х. На интервале (а, Ъ) плотндсть / (х) имеет постоянное
значение с (рис. 424), а вне этого интервала равна нулю. Такое
распределение также называют законом равномерной плотности.

470
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
?ГЛ. XX
+ 00
Из условия J / (х) dx = 1 находим значение с:
-00
* +09 Ь
следовательно,
Из последнего равенства следует, что интервал (а, 6), на котором
имеет место равномерное распределение, обязательно конечен.
Ц
я»
W
Рис. 423.
Рис. 424,
Определим вероятность того, что случайная величина х примет
значение, заключенное в интервале (а, р):
Итак, искомая вероятность
(это соотношение аналогично определению геометрической вероят-
вероятности для двумерного случая, приведенному на с. 441).
Определим интегральный закон распределения
Если д:<а, то f(x) = 0 и,' следовательно,
Если а<л:<&, то /(^) = ^i^ и» следовательно,

§14] ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ 471
Если b < х, то
/(*) = 0, $/(*)<** = О,
ъ
следовательно,
(рис. 425).
Приведем несколько конкретных случайных величин с законом
равномерной плотности.
Пример 1. При измерении некоторой величины производится округление
до ближайшего деления шкалы. Погрешность при округлении есть случайная
величина с равномерным распределением вероятностей. Если 2/—число неко-
некоторых единиц в одном делении шкалы, то плотность распределения этой слу-
случайной величины будет -,.
/(*) = 0 при *<—/,
/(*) = 1/2/ при — /<*</,
f(x) = O при / < х.
Здесь а = —/, & = /, с=1/2/.
Пример 2. Вращающееся симмет- Рис. 425.
ричное колесо останавливается вслед-
вследствие трения. Угол 9, образованный некоторым фиксированным подвижным
радиусом колеса с неподвижным радиусом после остановки колеса, есть слу-
случайная величина с плотностью распределения / (8) = 0 при 6 < 0, / (В) = ^—
при 0 < 9 < 2я, / @) = О при 2л < 9.
§ 14. Числовые характеристики непрерывной случайной величины
Аналогично тому, как это было сделано ранее для дискретной
случайной величины, рассмотрим числовые характеристики непре-
непрерывной случайной величины х с плотностью распределения f(x).
Определение 1. Математическим ожиданием непрерыв-
непрерывной случайной величины х с плотностью распределения f(x) на-
называется выражение
+ 00
М[х]= \xf(x)dx. A)
-со
Если случайная величина х может принимать значения только
на конечном отрезке [а, 6], то математическое ожидание
выразится формулой
ъ
(Г)
Формулу (Г) можно рассматривать как обобщение формулы A) § 9.

472 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ {ГЛ. XX
Действительно/ разобьем отрезок [а, Ь] на интервалы {xk_b xk).
В каждом из интервалов возьмем точку lk. Рассмотрим вспомо-
вспомогательную дискретную случайную величину |, которая может
принять значения
Пусть вероятности соответствующих значений дискретной слу-
случайной величины будут р19 р2У ..., ркУ ..., рп\
Математическое ожидание данной дискретной величины ? будет
или
М И = IJ (У Д^ + gj (I,)
Переходя к пределу при max Ддсй —>¦ 0, получаем
Ига 2 6*/&) А** =$*/<*)<**•
max Дх^ a
Выражение, стоящее справа, есть математическое ожидание р
рьтной случайной величины х, которая может принимать любое
значение лс, принадлежащее отрезку [а, Ь]. Аналогичное рассуж-
рассуждение можно провести и для бесконечного интервала, т. е. для
выражения A). Формулы A) и (*') аналогичны формуле A) § 9
для дискретной случайной величины. Математическое ожидание
также будем обозначать - тх.
Математическое ожидание называют центром распределения
вероятностей случайной величины х (рис. 426). Если кривая рас-
распределения симметрична относительно оси Oyf т, е. f(x)—функ-
f(x)—функция четная, то очевидно, что
М[*]= S xf(x)dx = 0.
— QO
В этом случае центр распределения вероятностей совпадает
с началом координат (рис. 427). Рассмотрим центрированную слу-
*) В то же 'время f (g^) Ад:^ есть вероятность того, что непрерывная слу-
случайная величина х примет значение из интервала' (*&-?, *#).

§141 ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ 473
чайную величину х—тх. Найдем ее математическое ожидание:
+ 00 +00 +00
M[jt—mj= j (x—mx)f(x)dx = \ xf(x)dx—mx ^f(x)dx=*
= mx—тхЛ = (X
Математическое ожидание центрированной случайной вели-
величины равно нулю.
Определение 2. Дисперсией случайной величины х назы-
называется математическое ожидание квадрата соответствующей цент-
центрированной случайной величины:
+ 00
x-mxrf(x)dx. B)
Формула B) аналогична формуле B) § 10.
Определение 3. Среднеквадратичным отклонением случай-
случайной величины х называется корень квадратный из дисперсии:
/"
О\х] = У
C)
Эта формула аналогична формуле C)"§ 10, При рассмотрении
конкретных примеров мы увидим, что, как и в случае дискретной
Рис. 426.
случайной величины, дисперсия и среднеквадратичное отклонение
характеризуют рассеивание значений случайной величины.
Определение 4. Значение случайной величины #, при
котором плотность * распределения имеет наибольшее, значение,
называется модой (будем ее обозначать Мо). Для случайной вели-
величины ху- кривая распределения которой изображена на рис. 426
и 427, мода совпадает сматематиче- * -
ским ожиданием.
Определение 5. Число, кото-
которое мы обозначим Ме> называется
медианой, если оно удовлетворяет
равенству
Me + оо
f(x)dx= §f(x)dx = ±. D)
Me
Рис. 428,

474 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. XX
(рис. 428). Последнее равенство можно переписать так:
т. е. равновероятно, что случайная величина х примет значение,
меньшее Ме и большее Ме. __
Заметим, что сама случайная величина х может значения Ме и
не принимать.
§ 15. Нормальный закон распределения.
Математическое ожидание нормального распределения
Изучение различных явлений показывает, что многие случай-
случайные величины, например, такие, как погрешности при измерениях,
боковое отклонение и отклонение по дальности точки попадания
от некоторого центра при стрельбе, величина износа деталей во
многих механизмах и т. д., имеют
плотность распределения вероятности,
выражающуюся формулой
1 {х~аJ
f/v\ _*__/>"" 2а2 ' /1\
В этом случае говорят, что слу-
случайная величина подчинена нормаль-
нормальному закону распределения (это распределение также называют за-
законом Гаусса). Кривая нормального распределения изображена на
рис. 429. Таблица значений функции A) при а = 0, а= 1 помещена
в конце книги (см. табл. 2). Аналогичная кривая подробно ис-
исследована в § 9 гл. V т. I.
Покажем сначала, что плотность распределения A) удовлетво-
удовлетворяет основному соотношению E) § 12:
+ 00
— 00
Действительно, вводя обозначение
можем написать
+ оо (х-аJ
— 00
так как
+ 00
(см. § 5 гл. XV).

15]
НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
475
Определим математическое ожидание случайной величины с нор-
нормальным законом распределения A). По формуле A) § 14 имеем
B)
Сделав замену переменной
подучаем
Следовательно,
2
Первый интеграл ^справа равен
Итак,
= а.
i Ce-'V' + ^-т^ f te-**dt.
J у п д
Вычислим второй интеграл:
C)
3-
Значение параметра а в формуле A) равно математическому ожи-
ожиданию рассматриваемой случайной величины. Точка х = а явля-
является центром распределения вероят-
вероятностей, или центром рассеивания. При
х = а функция f(x) имеет наибольшее
значение, поэтому значение х = а яв-
является модой случайной величины.
Так как кривая A) симметрична от-
относительно прямой х = а, то
J f(x)dx= \f(x)dx,
т. е. значение х=^а является медианой нормального распределе-
распределения. Если в формуле A) положим а = 0, то получим
о 2а»
D)
Соответствующая кривая симметрична относительно оси Оу.
Функция f(x) есть плотность нормального распределения случай-
случайной величины с центром распределения вероятностей, совпадаю-
совпадающим с началом координат (рис. 430), Числовые характеристики

476 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ' < [ГЛ. XX
случайных величин с законами распределения A) и D), опреде-
определяющие характер рассеивания значений случайной величины
относительно центра рассеивания, определяются формой кривой,
которая не зависит от величины а, й поэтому совпадают. Вели-
Величина а определяет величину сдвига кривой A) вправо (при а > 0)
или влево (при а < 0). Для некоторого сокращения письма мы
будем проводить/многие дальнейшие рассуждения применительно
к плотности распределения, определяемой формулой D).
§ 16. Дисперсия и среднеквадратичное отклонение
случайной величины, подчиненной нормальному закону
распределений
Пусть плотность распределения случайной величины х дается
формулой
Дисперсия непрерывной случайной величины определяется по
формуле B) § 14.
В нашем случае
0
Имеем
-г w
= f
J
Сделаем замену переменной -^=- = ?, тогда
Проинтегрировав по частям, получим
Так как
lim
то окончательно получаем
D[I] = o*. B)
Среднеквадратичное отклонение в соответствии с формулой C)
§ 14 будет

§171
ВЕРОЯТНОСТЬ ПОПАДАНИЯ В ЗАДАННЫЙ ИНТЕРВАЛ
477
Итак, дисперсия равняется параметру а2 в формуле плотно-
плотности распределения A). Мы уже говорили выше, что дисперсия
характеризует рассеивание значений случайной величины-относи-
величины-относительно центра рассеивания.
Посмотрим', как значение па-
параметра а2 влияет на форму
кривой распределения. На
рис. 431 изображены -кривые
распределения для значений
ст =у, ог= 1, сх = 2. Рассмат-
Рассматривая эти кривые, видим, что
чем меньше су, тем максимум
функции f(x) больше, веро-
вероятность значений, близких
к центру рассеивания (х = 0),
больше, вероятность значений, удаленных от начала, меньше.
Это обстоятельство выражают словами: чем меньше дисперсия а\_
тем меньше рассеивание значенир случайной величины.
§ 17. Вероятность попадания значения случайной величины
в заданный интервал. Функция Лапласа. Интегральная
функция распределения для нормального закона
В соответствии с формулой C) § 12_определим вероятность
того, что значение случайной величины х с плотностью распре-
распределения
попадает в интервал (а, Р): •
1 (*-*)*
или
(рис. 432). Сделаем замену переменной-
Х п __ ?
Получаем
A)
= y^ J е-*ft.

478
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
[ГЛ. XX
Справа сюящий интеграл не выражается через элементарные функ-
функции. Значения этого интеграла выражаются через значения инте-
интеграла вероятностей
X
-*dt. B)
Укажем некоторые свойства функции Ф (х), которыми мы будем
пользоваться ниже.
Рис. 432,
Рис. 433,
1. Ф(л:) определена при всех значениях х.
2. Ф@) = 0.
C)
4. Ф(лг) монотонно возрастает на интервале @, + °°).
5. Ф(х)—функция нечетная, так как
, Ф(—х) = — Ф(х).
6. График функции Ф(*) изображен на рис. 433.
Составлены подробные таблицы значений этой функции. Крат-
Краткая таблица приведена в конце книги (см. табл. 1).
Перепишим равенство (Г), пользуясь теоремой о разбиении
промежутка интегрирования:
о о VI
а VI
VI
Последнее равенство можно переписать так:
oVl
— \ e~tZdt +
а VI
У
dt

ВЕРОЯТНОСТЬ ПОПАДАНИЯ В ЗАДАННЫЙ ИНТЕРВАЛ
479
Пользуясь функцией Ф (х) (см. B)), окончательно выразим вероят-
вероятность попадания случайной величины х, подчиненной нормаль-
нормальному закону, в интервал (а, р):
При а = 0 получаем
Приравняв правые части равенств A) для случая а = 0 и равен-
равенства E), получаем
Часто приходится вычислять вероятность того, что значение слу-
случайной величины попадает в интервал (а — /, а + /), симметричный
Рис 434.
относительно точки х = а (рис. 434). В этом случае формула
D) принимает вид
Учитывал, что Ф ( -^=- j = — Ф f \ (см. формулу C)),
окончательно получаем
F)
Правая часть не зависит от положения центра рассеивания, сле-
следовательно, и при" а = 0 получаем
Р (-/<*</) =<D(~^). G)

480
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
1.ГЛ. XX
Пример 1. Случайная величи-
величина х подчинена нормальному закону
распределения с центром рассеивания
0=0,5 и дисперсией o2=-3-. Опре-
о
делить вероятность того, что значе-
значение случайной величины JT попадет в
интервал @,4; 0,6) (рис. 435).
Решение. Здесь —jr=r = 2.
Y 2
По формуле D) получаем
Р@,4 < F<0,6) =
1 1
Но Ф(—0,2)=—Ф @,2) (см. формулу C)), поэтому можем написать
Р,@,4 < х< 0,6) = ~[Ф @,2)+Ф @,2)] = Ф @,2).
По, таблице значений функции Ф {х) (см. табл. 1 в конце книги) находим
Р@,4< J<0,6) = 0,223.
Пример 2. Длина изготовляемой автоматом детали представляет собой
случайную величину, распределенную по нормальному закону с параметрами
М[#1 = 10, °*==2(Ю' Найти вероятность брака, если допустимые размеры де-
детали должны быть 10 ± 0,05.
Решение. В нашем случае а —10,
1
— =10, о=-
1
V 10 У" 2
ность брака рбр в соответствии с формулой D) выразится так:
— . Вероят-
Рбр = 1_р (9,95 < х < 10,05)= 1-—тг(Ф [Ю .A0,05—10)]—Ф [10- (9,95—10)]}=
= 1 — ^.{ф @,5) —Ф (—0,5)} = 1 —Ф @,5) = 1 —0,52 = 0,48.
Пример 3. Определить вероятность попадания в полосу шириной
2/ = 3,5'м, если ошибки стрельбы подчиняются нормальному закону распре-
распределения с параметрами а = 0, а=1,9.
Решение. В нашем случае,а = —1,75, C = 1,75, —7:=^==0,372. По фор-
s а у 2
муле G) получаем
Р(—1,75 <7< 1,75) = ФA,75.0,372) = Ф@,651) = 0,643.
Замечание. Вместо функции Ф(х) (B)) часто пользуются
функцией Лапласа
X f2
ф/дЛ __ * f e^~dt. (8)
Эта функция Лапласа связана с функцией Ф(я) простым соотно-

§]8] ВЕРОЯТНОЕ ОТКЛОНЕНИЕ 481
шением. Сделав в интеграле (8) замену -^=r- = z, получаем
X
V~2
Итак,
и, очевидно,
A0)
Формула E) с использованием функции Ф(х) и соотношения (9)
запишется так:
и при а = 1
Р (а < х < Р) = Ф ф) -Ф (а).
Таблица значений функции Лапласа Ф (л:) помещена в конце книги
(см. табл. 3).
Определим далее интегральную функцию нормального закона
распределения. По формуле A) § 13 имеем:
««' dx = P(-oo <x
Пользуясь формулой D) для случая а = —оо, Р = х, получаем.
но Ф(—оо)=—1 (см. формулу C)). Следовательно,
График функции F (х) при а = 0 изображен на рис. 436.
§ 18. Вероятное (срединное) отклонение или срединная ошибка
Во многих вопросах прикладной теории вероятностей, в част-
частности в теории стрельбы, а также в теории ошибок, пользуются
характеристикой рассеивания, которую называют вероятным, или
срединным отклонением. В теории стрельбы ее называют средин-
срединной ошибкой.
t? H. Ci Пискунов, т.' 2

482
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
[ГЛ. XX
Определение 1. Вероятным (срединным) отклонением на-
называется такое число ?, что вероятность того, что случайная
величина (ошибка, например), подчиненная нормальному закону
распределения
попадет в интервал (— ?, ?), равна 1/2 (рис. 437), т. е.
Р(-?<*<?)=1/2. A)
Для любой, случайной величины х, подчиняющейся нормаль-
нормальному закону распределения с центром рассеивания х = а, средин-
срединное отклонение Е (рис. 438) удовлетворяет соотношению
Р (а—Е<х<а + Е) = 1/2. B)
Выразим среднеквадратичное отклонение а через срединную
ошибку Е.
/\
0,25
0,25
-? О Е
Рис. 437,
я а
ДО
[Рис. 438.
Левую часть равенства A) выразим через функцию Ф(х):
j
По формуле G) § 17 получаем
C)
D)
В равенствах A) и D) левые части равны, следовательно, равны
и правые;
По таблице значений функции Ф(#) находим значение аргу-
аргумента х = 0>4769, для которого Ф(л:)=1/2. Следовательно,
-А_ = 0,4769.

-$ 19J ПРИВЕДЕННАЯ ФУНКЦИЯ ЛАПЛАСА 483
Это число 0,4769 принято обозначать через р;
_? ==р = 0,4769. F)
Отсюда
G)
§ 19, Выражение нормального закона распределения
через срединное отклонение. Приведенная функция Лапласа
Выражая параметр а через параметр Е по формуле G) § 18
и подставляя в D) § 15, получим выражение закона распределе-
распределения через срединное отклонение:
Вероятность попадания случайной величины (например, ошибки)
в интервал (а, Р) в соответствии с формулой E) § 17 будет
и в соответствии с формулой G) § 17
B) , C)
Числа -—¦ и -—, стоящие ъ правой части формулы B), опреде-
определяются характером задачи, р —известное число, р = 0,4769.
Чтобы избежать умножения на р, при каждом вычислении со-
составлены таблицы- для функций Ф(р#). Эту функцию обозна-
обозначают Ф(л:):
D)
/Ь (х) называют приведенной функцией Лапласа. Таблица значений
этой функции помещена в конце книги (см. табл. 1).
На основании B) § 17 функция Ф(х) определяется интегралом
Сделав замену переменой / = рг, получим
-**<1г. ¦ E)

484 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. XX
Выразим правую ч%стъ равенства B) через приведенную функцию
Лапласа:
В частности, вероятность попадания значения случайной ве-
величины в симметричный относительно центра рассеивания интер-
интервал (—/, /) в соответствии с формулой C) выразится так:
G)
- 48)
Заметим, что вероятность попадания случайной величины х в
интервал (a, fty, если математическое ожидание афО выразится
через срединную ошибку Е так (см. формулу D) § 17):
Через приведенную функцию Лапласа последнее равенство выра-
выразится /гак:
1[(!^)()] A0)
§ 20. Правило трех сигм. Шкала вероятностей
распределения ошибок
При проведении практических вычислений за единицу изме-
измерения отклонения случайной величины, подчиненной нормальному
закону от ее центра рассеивания (математического ожидания),
принимают среднеквадратичное отклонение а. Тогда на основа-
основании формулы G) § 17 получаются полезные при различных вы-
вычислениях равенства
Р(-сг<х< а) = ф(-*_) = 0,683,
Р (_2су < х < 2а) = Ф {V2) = 0,954,
Р (_ Зог < х < За) = Ф (JL-\ = 0,997.'
Эти результаты геометрически изображены на рис. 439.
Почти достоверно, что случайная величина (ошибка) не откло-
отклонится от математического ожидания по абсолютной величине больше
чем на За. Это предположение называют правилом трех сигм.
В теории стрельбы и при обработке различных статистиче-
статистических материалов бывает полезно знать вероятность попадания
случайной величины х в интервалы @, Е), (?, 2?), B?, 3?),

§20]
ПРАВИЛО ТРЕХ СИГМ
485
C?, 4?), DЕ, ?>?) при плотности распределения, определяемой по
формуле A) § 19. Знание этих вероятностей во многих случаях
сокращает вычисления и помогает при анализе явлений.
Рис. 440.
При вычислении этих вероятностей .будегй пользоваться форму-
формулой (8) § 19 и таблицей функции Ф(х):
Р@<х<Е) =
=0,2500,
= 1[ФC)-ФB)]=0,0672,
4?) = 1[Ф D)-ФC)]-0,0180,
Р D? < х< оо) = 1 [Ф(оо) -Ф D)] = 1 A -0,9930) =*0,0035.
Результаты вычислений геометрически изображены на рис. 440,
который называется шкалой рассеивания ошибок. Из этих расчетов
следует, что практически достоверно, что значение случайной вели-
величины попадает в интервал (—4?, 4?). Вероятность того, что зна-
значение случайной величины попадает вне этого интервала, меньше 0,01.
Пример 1. Производится один выстрел
по полосе шириной 100 м. -Прицеливание рас-
считывалось на среднюю линию полосы, ко-
торая перпендикулярна к плоскости полета
снаряда. Рассеивание подчиняется нормаль-
нормальному закону с вероятным отклонением по даль-
дальности ?" = 20 м. Определить вероятность попа-
попадания в полосу (ршГ. 441). Срединное отклоне-
отклонение по дальности в теории стрельбы обозначают'
Вд, боковое Вб.
Рис. 441.
Решение. Воспользуемся формулой G) § 19. В нашем случае /
Е = Вд = 20 м. Следовательно,
50 м,
Р(-50 <
50) =Ф №\ = Ф B,5) =0,9082
0,91.
Замечание. Приближенно можно было бы решить задачу, не пользуясь
таблицами функции Ф(*)> а воспользоваться шкалой рассеивания (рис. 440).

486 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. XX
В нашем случае / = 2,5?. Следовательно,
Р(_5'о< *"< 50)=2.@,25 + 0,16 + 0,04)= 0,90.
Пример 2. Опытом установлено, что ошибка прибора для измерения
дальности подчиняется нормальному закону со срединной ошибкой Е = 10 м.
Определить вероятность того, что определенная этим прибором дальность будет
отклоняться от истинной не более чем на 15 м.
Решение. В данном случае f=±=15 мь ?=10 м. По формуле G) § 19
получаем:
Р(-15<7< 15) = Ф('^=Ф A,5) = 0,6883 «0,69.
§ 21. Среднеарифметическая ошибка
Для характеристики ошибок вводят понятие среднеарифмети-
среднеарифметической ошибки, равной математическому ожиданию абсолютной
величины ошибок. Будем обозначать среднеарифметическую ошибку
через d. Определим среднеарифметическую ошибку, если ошибки
х подчиняются нормальному закону D) § 15. По формуле, ана-
аналогичной B) § 15, получаем (а = 0)
+ 00
f 1*1—U
2о
Итак, среднеарифметическая ошибка выражается через средне-
среднеквадратичное отклонение а так:
§ 22. Мера точности. Соотношение между характеристиками
распределения ошибок
При рассмотрении многих процессов, особенно в теории; стрельбы,
плотность распределения нормального закона записывают в форме
fix^rfee-**. A)
Сравнивая формулы D) § 15 и A), видим, что введенный пара-
параметр h выражается через параметр а так:
Величина h обратно пропорциональна а, т. е. среднеквадратич-
среднеквадратичной ошибке или среднеквадратичному отклонению. Чем меньше
дисперсия а2, т. е. чем меньше рассеивание, тем больше значение
Л. Поэтому h называют мерой точности.

§23]
ДВУМЕРНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
487
Из B) и A) § 21 получаем
C)
D)
Срединная ошибка Е выражается через меру точности h на
основании формулы G) § 18 и C):
F - р
E)
Иногда .бывает нужно одну характеристику распределения
ошибок выразить через другую. Поэтому бывают полезны следую-
следующие равенства:
iL = уГ^ =,1,2533, F)
р/2
Т = ^=1'1829.
§ 23. Двумерная случайная величина
С двумерными случайными величинами приходится иметь дело,
например, при рассмотрении процесса поражения объекта, нахо-
находящегося на плоскости хОу. Значение двумерной случайной вели-
величины определяется двумя числами х и у\ саму двумерную случай-
случайную величину будем обозначать (л:, у). Пусть х и у принимают
дискретные значения х{ и уу. Пусть каждой паре значений (xh
yj) из некоторой совокупности соответствует определенная вероят-
вероятность Pij. Мы можем составить таблицу распределения вероятно-
вероятностей дискретной двумерной случайной величины
XI -
yi Pii
Уг 1 Pi2
¦> !
Ут j Pirn
х*
P2i
Ры
Рш
...
...
...
хп
Pni
Рпг
Рпт

4gg ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Очевидно, что должно выполняться равенство
т п
[ГЛ. XX
0)
Определим, далее, непрерывную двумерную случайную величину..
Вероятность того, что значение двумерной [случайной^ величины
{х, у) удовлетворяет неравенствамх<х <х + Ах, у <у<у+Ау,
будем обозначать так: Р(х <х <х + Ах, у<у<у+Ау).
У
а-
Рис. 443.
Опредедение 1. Функция /(х, у) называется плотностью
распределения двумерной случайной величины (х9 у), если с точ-
точностью до бесконечно малых высшего порядка относительно, Др=
== \^Ах2 + Ау2 выполняется равенство
* P(x<x<x + Axt y<y<y + by)**f(x, у)АхАу. B)
Формула B) вполне аналогична формуле B) § 12.,
Рассмотрим прямоугольную ^систему координат хОу. Если
значения случайной величины (х, у) будем обозначать точками
плоскости с соответствующими координатами х и у, то выражение
Р (х < х < я + Ах, у < у <у + Ау) обозначает вероятность того,
что двумерная случайная величина (х, у) примет значение, обо-
обозначенное точкой, находящейся в заштрихованном прямоуголь-
прямоугольнике As-(рис. 442). Будем говорить, что «значение случайной
величины попало в область As»*).
ВероятностьJ»(х<1с<х + Ах, у<у<у + Ау) также будем
обозначать Р[(х, у)czAs]. В этих обозначениях равенство B)
можно переписать так:
Р[(*, y)cAs]&f(x9 у)As.
C)
Докажем далее следующую теорему, аналогичную теореме 1 § 12:
*) Площадку в равенстве C) можно было бы брать и произвольной формы.

§23]
ДВУМЕРНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
489
Теорема 1. Вероятность P[(^,p)cD] того, что двумерная
случайная величина (х, у) с плотностью распределения /(*, у)
попадет: в область D, выражается двойным интегралом от функ-
функции f (х, у) по области D, /п. е.
g)dxdy.
D)
Доказательство. Разбиваем область D, как это делалось
в теории двойных интегралов, на площадки As. Для каждой
площадки пишем равенство C) и складываем левые и правые части
полученных равенств. Так как ^As = D и 2Р[(*, */)clAs] =
= Р [(#,#) с D], то с точностью до бесконечно малых высшего
порядка относительно As получаем приближенное равенство
, • P[Ccf y)crD]«2/(*» #)As-
Переходя к пределу в правой части последнего равенства при
As—fO, справа получим двойной интеграл и на основании свойств
интегральной суммы точное равенство
(*f y)dxdy.
D есть прямоугольник, огра-
огра= Т> У = Ъ (Рис- 443), то
, y)dxdy. " 'E)
Теорема доказана.
Замечание 1. Если область
ниченный прямыми х = а, х = $, #
а V
Замечание 2. Аналогично равенству A) выполняется
равенство
+ 00+00
J fix, y)dxdy=\, F)
так как достоверно, что двумерная величина примет какое-то зна-
значение. Там, где функция f (х, у) не
определена по смыслу задачи, пола-
полагаем /(#, у) = 0.
Если область D является суммой
прямоугольников вида, изображенно-
изображенного на рис. 444, то вероятность по-
попадания случайной величины в такую -
область определяется как сумма ве-
вероятностей для отдельных прямоуголь- - рис. 444,

490
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
[ГЛ. XX
ников, т. е. как сумма определенных интегралов 'по каждому
прямоугольнику:
Пример. Плотность распределения двумерной случайной величины
задается формулой
Определить вероятность того, что значение случайной величины попадет
в прямоугольник, ограниченный прямыми х = 0, *=1, у— --.=•, у = у 3 .
Решение, По формуле E) получаем
Р Го < х< 1, -Тг=-< У <
1 У~з * v •
Iff d*d# 1 fd* f
t= V \ ¦ —;—st :==—*" \ —;—5" \
я2 J J (l+*2)(l + r/2) ^2J1+a;2J
0 1 0 1
Уз=
Уз
yf
Определение 2. Функция
г/ \_ f [ f(u
-
24•
G)
— 00 — 00
называется интегральной функцией ^распределения вероятностей
двумерной случайной величины (а:, у).
Очевидно, что интегральная функция распределения выражает
вероятность того, что х < *, у < у, т. е.
У
Ш
Геометрически функция распределения выражает вероятность того,
что двумерная случайная величина попала в бесконечный четырех-
четырехугольник, заштрихованный на
рис. 445.
На основании теоремы о диф-
дифференцировании определенного ин-
интеграла по параметру устанавли-
устанавливается связь между плотностью
распределения и интегральной функ-
функцией распределения:
(8)
Рис. 445.
= /(*, У).

§24]
НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ НА ПЛОСКОСТИ
491
Плотность вероятности двумерной случайной величины является
смешанной производной второго порядка от интегральной функции
распределения.
§ 24. Нормальный закон распределения на плоскости
Определение 1. Распределение двумерной случайной вели-
величины называется нормальным, если плотность распределения этой
величины выражается форму-
формулой,
fix, У) =
1
2лохоу
в 2°*
X
График этой функции есть
поверхность, изображенная на
рис. 446.
Центром рассеивания слу-
случайной величины с законом рас-
распределения A) является точка
@; 0)*). ах и о у называются главными среднеквадратичными от-
отклонениями.
Перепишем формулу A) так:
Рис. 446,
B)
Таким образом, f(x, у) можно рассматривать как произведение
двух плотностей нормальных распределений случайных величин
я и у. Как и в случае одномерной случайной величины, определим
главные вероятные отклонения двумерной случайной величины Ех
и Еу (см. формулу G> § 18):
C)
Подставляя ах и ау, выраженные через Ех и Еу, в формулу A),
получим
D)
*) Если центр рассеивания находится в точке (а; Ъ), то закон распределе-
распределения дается формулой
(х-аJ (у-Ь)»
fix. #)=к е
2а»
20*

492 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. XX
* Рассмотрим линий уровня поверхности D)
4r
ty
E)
(при этом будет f(x, y) = const). Линиями уровни являются эл-
эллипсы с полуосями, равными kEx и kEy. Центры эллипсов сов-
совпадают с центром рассеивания. Эти эллипсы называются эллип-
эллипсами рассеивания. Их оси называются осями рассеивания. Еди-
Единичным эллипсом рассеивания называется эллипс, у которого
полуоси равны "вероятным отклонениям Ех и Е . Уравнение еди-
единичного эллипса получится, если в уравнении E) положить k—\\
Полным эллипсом рассеивания называется эллипс, полуоси
которого равны \ЕХ и 4Еу. Уравнение этого эллипса
*2 | У2 -1 т
В следующем параграфе мы установим, что вероятность попа-
попадания двумерной случайной величины в полный эллипс рассеива-
рассеивания равна 0,97, т. е. практически попадание достоверно.
§ 25. Вероятность попадания двумерной случайной величины
в прямоугольник со сторонами, параллельными главным осям
рассеивания г при нормальном законе распределения
Пусть
По формуле E) § 23 (см. рис. 443) вероятность попадания слу-
случайной величины в прямоугольник, ограниченный прямыми х =
= а, # = р, у = у, у = 8, выражается так:
р б
0)
Представляя подынтегральную функцию в виде произведения двух
функций, можем написать
и на основании формулы F) § 19 окончательно получаем
C)

§251
ВЕРОЯТНОСТЬ ПОПАДАНИЯ В ПРЯМОУГОЛЬНИК
493
Если в последней формуле положить а = — /?, P = /i> 7 — — I*
б = /2, т. е. рассматривать прямоугольник с центром в начале ко-
координат, то на основании формулы G) § 19 формула C) примет вид
D)
Замечание. Задачу о вероятности попадания случайной
величины в прямоугольник со сторонами, параллельными осям
координат, можно было бы решать и так. Попадание в прямо-
прямоугольник есть сложное событие, состоящее в совпадении двух:
независимых событий— -попадания в полосу — k<x<li и попа-
попадания в полосу — 12<у<12- (Д&я краткости рассматриваем пря-
прямоугольник с центром в начале координат.) Пусть плотность
распределения случайной величины х есть
Плотность распределения случайной величины у есть
Вычисляем вероятности попадания _случайной величины в по-
полосу _/х < х< lt и в полосу — /2 < у < /2. По формуле G) § 19
получаем
Вероятность сложного собы-
события—попадания в прямо-
прямоугольник — будет равна про-
произведению вероятностей:
50
700
-50
Рис. 447,
Получили формулу D).
Пример. Производится стрельба по площади прямоугольника со сторо-
сторонами 200 м и 100 м, ограниченного линиями
* д: = —100, *=100,
у:=_50, у = 50.
Главные срединные отклонения соответственно равны Ех — Вд = 50 м, Еу~Вб~
= 10м. Найти вероятность попадания в прямоугольник при одном выстреле
(рис. 447).

494 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. XX
Решение. В нашем случае /х = 100, /2 = 50, ?'дг = 50, Еу — Ю. Подстав-
Подставляем эти значения в формулу D) и, пользуясь таблицей значения функции
Ф (х) (см. табл. 1 в конце книги), находим
р = ф A™\ ф (у|П=<&B) Ф E) = 0,8227-0,9993= 0,822b
§ 26. Вероятность попадания двумерной случайной величины
в эллипс рассеивания
В теории ошибок бывает нужно рассматривать следующую
задачу. Вычислить вероятность того, что случайная величина,
например ошибка на плоскости, попадет в эллипс. рассеивания
если плотнрсть распределения дается формулой D) § 24. По фор-
формуле D) § 23 получаем:
^^~F+l\ - B)
где область D9 ограничена эллипсом A). Сделаем замену пере-
переменных, полагая
при этом преобразовании эллипс D3 перейдет в круг
k\ • C)
Так как якобиан* преобразования равен 1 = ЕхЕу} то равенство
B) примет вид *ч
^?erdudv. D)
Dk
k
В последнем интеграле перейдем к полярным координатам
Тогда правая часть равенства D) принимает вид
2п k
Производя вычисления в правой части, получим выражение веро-
вероятности попадания в эллипс рассеивания:
1-*-р*\ . E)

§ 27] ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 495
Рассмотрим частные случаи. Вероятность попадания в единич-
единичный эллипс рассеивания получится, если положить в формуле E)
|*в1= 1-е-е* = 0,203. F)
Вероятность попадания в полный эллипс рассеивания G) § 24
получится, если в формуле E) положить ? = 4:
Р[(х, y)aDd]\k=4= 1-е-16<>2 = 0,974. G)
Рассмотрим частный случай, когда в формуле (Ф) § 24 Ех=*
i=Ey = E. Элдапс рассеивания E) § 24 превращается в круг
x2 + y2=:k2E2 (8)
с радиусом R == kE\ Вероятность попадания двумерной случайной
величины в ?руг радиуса R в соответствии с формулой E) будет
P[(x,l/)<zDR] = l-e E\ (9)
Определение 1. Радиальным вероятным отклонением на-
называется такое число ERi чта вероятность попадания двумерной
случайной величины в круг радиуса R = E% равняется 1/2.
Из определения следует, что величина R = ER определяется
из соотношения
Цо таблице значений показательной функции находим
§ 27» Задачи математической статистики.
Статистический материал
В результате наблюдений и регистрации массовых случайных
явлений получаются статистические данные или статистический
материал. В частности, статистическим материалом являются
ошибки различных измерений.
Если наблюдаемая величина есть случайная величина, то она
изучается методами теории вероятностей. Для понимания харак-
характера этой случайной величины нужно знать ее закон распреде-
распределения. Определение законов распределения рассматриваемых ве-
величин и оценка значений параметров распределения на основа-
основании наблюденных значений—задача математической статистики.
Еще одной задачей математической статистики является создание
методов обработки и анализа статистического материала с целью
получения определенных выводов, нужных для организации оп-
оптимального процесса, где участвую^ рассматриваемые величины.

496
ЭЛЕМЕНТЫ ТЕОРИЙ ВЕРОЯТНОСТЕЙ
[ГЛ. XX
Приведем примеры различных наблюдений явлений, в резуль-
результате которых получается статистический материал.
-Пример 1. При многократном измерении некоторого объекта с помощью
измерительного инструмента, в частности при определении ^дальности до неко-
некоторого1 объекта, получаются различные значения наблюдаемой величины. Эти
значения будем называть наблюденными значениями (так мы будем называть
всякое значение, полученное при изучении любого- явления).
Полученные таким образом значения требуют систематизации
и обработки, прежде чем на их основании можно было бы сделать
какие-либо выводы.
Как уже указывалось, разность 8 между наблюденным зна-
значением х и истинным значением наблюдаемой величины а(х—а = 6)
называется ошцбкой измерения. Сказанное выше можно выразить
в терминах ошибок. Ошибки измерения требуют математической
обработки с целью получения определенных выводов.
Пример 2. При массовом производстве приходится рассматривать вели-
величину отклонения некоторого размера полученного изделия (например, длины)
от заданного размера для полученных изделий (ошибка изготовления).
Пример 3. Разность между координатой точки попадания при стрельбе
и координатой точки прицеливания есть ошибка стрельбы (рассеивание). Эти
ошибки требуют математического исследования.
Пример 4. Результаты измерений величины отклонения размера детали
после эксплуатации от ее размеров до эксплуатации (проектных) требуют мате-
математического анализа. Эти отклонения также можно рассматривать как «ошибки.
Из приведенных примеров следует* что рассматриваемые вели-
величины суть случайные величины, а каждое наблюденное ' значение
следует рассматривать как частное значение случайной величины.
Так, например, ошибка по дальности (рассеивание) при стрель-
стрельбе определяется ошибкой при отвешивании заряда, ошибкой в
массе при изготовлении снаряда, ошибкой наводки, ошибкой при
определении дальности, изменением метеорологических условий и
т. д. Все это случайные величины, и рассеивание как результат
их совместного влияния является случайной величиной.
§ 28. Статистический ряд. Гистограмма
Статистический материал, получающийся в результате наблю-
наблюдений (измерений), помещается в таблице, состоящей из двух
строк. В первой строке отмечается номер "измерения i9 во вто-
второй— полученное значение xi измеряемой величины х
г
Xi
1
*i
2
х* -
3
*з
...
...
i
Xi
...
...
п
Хп

СТАТИСТИЧЕСКИЙ РЯД. ГИСТОГРАММА
497
Такая таблица называется простым статистическим рядом.
При большом числе измерений статистический материал, поме-
помещенный в такую таблицу, трудно обозрим и, следовательно, ана-
анализ его затруднен. Поэтому на основании полученного простого
статистического ряда составляется группировка. Это делается
следующим образом.
Весь интервал полученных значений величины х разобьем на
частичные равные интервалы (а0, ах), (aiy а2), ..., (ад,-1, а*) и под-
подсчитаем число значений тк величины х, попадающих в интервал
(p>k-i> ak)- Значения, попадающие на конец интервала, относят
или к левому, или к правому интервалам (иногда их относят и
к левому и к правому интервалам по половине их числа). Число
— = Р* \Ч
есть относительная частота, соответствующая интервалу {ак^ь ак).
Очевидно, что
На основании результатов такой обработки строим таблицу,
состоящую из трех строк. В первой строке указываем интервалы
в порядке возрастания ак% во второй строке соответствующие
им числа тк, в третьей строке—частоты pk = ^;
Интерв алы
mk
Pi
(aOf at)
mx
Pi
(au a2)
m2
Pi
...
...
...
mk
Pi
...
...
...
m%
Pi
Это и есть группировка. Группировку оформляют и геометри-
геометрически. Это делается следующим образом. На оси Ох отмечаем
точки a0, alf ..., аъ .,., ая. На отрезке \ак„1У ak] как на ос-
основании строим прямоугольник, площадь которого равна pi, По-
Полученная фигура называется гистограммой (рис. 448).
На основании группировки и гистограммы строится прибли-
приближенно статистическая функция распределения.
Дальнейшая обработка материала производится следующим
образом. Середины интервалов (ак_г> ak) обозначают хк и счи-
считают это значение значением результата измерения, которое
^ Н. С, Пискунов, т. 2

498
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
[ГЛ. XX
повторяется тк раз. После этого вместо таблицы, задающей
группировку, строится следующая таблица:
mk
Pi
т±
Pi
x2
m2
¦
P2
...
• • • •
...
mh
Pi
•. •
•..
...
Pi -
Данная обработка сделана на основании того, что все значе-
значения в интервале (актя^ ak) близки друг к другу и потому их счи-
считают равными абсциссе середины интервала х%.
0 az a3 a4 as aB аг as x
Рис. 448.
0,05
0,24
од
Ofl
m m m m
Рис, 449,
Пример. При 100 определениях дальности получены результаты, на
основании которых построена группировка;

$29]
ОПРЕДЕЛЕНИЕ ПОДХОДЯЩЕГО ЗНАЧЕНИЯ
499
Интервалы
тк
Pi
80-110
2
0,02
110-140
5
0,05
140-170
16
0,16
170-200
24
0,24
200-230
28
0,28
230-260
18
0,18
260-290
6
0,06
290-320
1
0,01
На основании группировки строим графическое изображение статистиче-
статистического ряда (гистограмму) (рис. 449).
Построим, далее следующую таблицу:
тк
Pi
95
2
0,02
125
5
0,05
155
16
0,16
185
24
0,24
215
28
0,28
245
18
0,18
' 275
6
0,06
305
1
0,01
§ 29. Определение подходящего значения измеряемой величины
Пусть при измерении некоторой 'величины получили резуль-
результаты измерения хи х2, . •., хп. Эти значения можно рассматри-
рассматривать как частные значения случайной величины х. За подходя-
подходящее значение определяемой величины принимают среднее ариф-
арифметическое полученных значений
<=^- О)
Величину тх называют статистическим средним.
Если число изменений п велико, то пользуются материалом
таблицы, рассмотренной в § 28, и ml вычисляют так:
тх
или, пользуясь обозначениями A) § 28,
B)
полученное значение называют средним езеешенньул.
Замечание. В дальнейшем результаты вычислений по фор-
формулам A) и B) будем обозначать одной и той же буквой. Это
замечание будет относиться и к формулам C)' и D).
17*

500 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕН [ГЛ. #?
Можно доказать, что статистическое среднее при некоторых
ограничениях стремится по вероятности при п—»-оо к математиче-
математическому ожиданию случайной величины х. Это утверждение следует
из теоремы Чебышева.
Определим, далее, статистическую дисперсию. Она опреде-
определяется так*):
Эта величина характеризует рассеивание значений наблюдаемой
величины.
Если пользоваться материалом таблицы § 28, то статистичес-
статистическая дисперсия определится по формуле
D* = ?{4-mlYpl D)
Эта формула аналогична формуле B) § 10.
Пример. Определить статистическое среднее и статистическую дисперсию
на основании статистических материалов примера § 28,
Решение. По формуле B) получаем
-95.0,02+125.0,05+155.0,16+185.0,24+
+215.0,28+245.0,18+275.0,06+305.0,01=201,20.
Пв формуле D) получаем
п
?, \Xfc 1— Mix/
= 952.0,02+1252^0,05+1552*0,16+1852.0,24+2152.0,28+2452.0,18+
+ 2752.0,06+3052.0,01 —201,20» = 1753,56.
§ 30. Определение параметров закона распределения.
Теорема Ляпунова. Теорема Лапласа
Пусть х—случайная величина, например результат • измере-
измерения, а—измеряемая величина, б—ошибка измерения. Тогда эти
величины связаны соотношением
6=1с—а9 х = а + 8. A)
*) На самом деле статистическую дисперсию лучше вычислять по другой
формуле, приведённой на с. 502.

§,30] ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ЗАКОНА РАСПРЕДЕЛЕНИЯ .501
Многочисленные опыты и наблюдения показывают, что ошибки
измерений после исключения систематической ошибки, т. е. такой
ошибки, которая постоянна при всех измерениях (например, ошибка
прибора), или такой, которая изменяется по известному закону
от измерения к измерению, и после исключения грубых ошибок
подчиняются нормальному закону распределения с центром рас-
распределения в начале координат. Это подтверждается и теорети-
теоретическими обоснованиями.
Если случайная величина является суммой большого числа
случайных величин, то при некоторых ограничениях эта сумма
подчиняется нормальному закону распределения. Это утвержде-
утверждение формулируется в виде так называемой центральной предель-
предельной теоремы, принадлежащей А.М.Ляпунову A857—1918). Мы
здесь сформулируем эту теорему в несколько упрощенном^ виде.
Теорема 1. Если независимые случайные величины хг, х2, ...
..., хп имеют один и тот же закон распределения с математи-
математическим ожиданием а {не нарушая общности, можно предполагать,
что а = 0) и дисперсией а2, то при неограниченном увеличении п
п
закон распределения суммы уп = '~Л— как угодно мало отли-
отличается от нормального (уп нормирована так, что М[уп] = 0,
D[yn]=l).
Практическая значимость теоремы Ляпунова заключается в сле-
следующем. Рассматривается случайная величина, например, откло-
отклонение некоторой величины от заданной. Это отклонение вызвано
действием многих факторов, каждый из которых дает некоторую
составляющую отклонения, например, в случае стрельбы откло-
отклонение точки попадания от точки прицеливания происходит из-за
ошибки наводки, ошибки определения дальности, ошибки изгото-
изготовления снаряда и т. д. Все составляющие нам даже не известны,
также как могут оказаться неизвестными законы распределения
составляющих случайных величин. Но из теоремы Ляпунова сле-
следует, что случайная величина—общее отклонение—подчиняется
нормальному закону.
Из теоремы Ляпунова следует, что если xlf х2, .. .,*хп—резуль-
.,*хп—результаты измерений некоторой величины (каждая из х]—случайная
величина), то случайная величина—среднее арифметическое
— при достаточно большом п подчиняется закону распределения,
как угодно близкому к нормальному, если случайные величины хх
подчиняются одному и тому же закону распределения.

502 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. XX
Теорема остается справедливой и для суммы случайных величин
с неодинаковыми законами распределения при некоторых допол-
дополнительных условиях, которые, как правило, для рассматриваемых
на практике-случайных величин выполняются. Как показывает
опыт, при числе слагаемых порядка 10 уже можно считать их
сумму нормально распределенной.
Обозначим через а и а2 приближенные значения математиче-
математического ожидания и дисперсии. Тогда можем ^аписать приближенно
законы распределения случайных величин б и J:
Параметр а на основании экспериментальных данных опреде-
определяется по формуле A) § 29;
Это следует из так называемой теоремы Чебышева A821—
1894). Не останавливаясь на доказательстве, укажем, что пара-
параметр а естественнее определять не по формуле C) § 29, а по
формуле
п
2 (*/-•?)•
2 t = 1 УК\
G ——- ' «' ' ' • 1*^7
П— 1 х '
Отметим, что правая часть в формуле E) и правая часть в фор-
формуле C) § 29 отличаются ~тиножителем * , который в практи-
практических задачах близок к 1.
Пример 1. Написать выражение закона распределения случайной вели-
величины на основании результатов измерений, приведенных в примере § 28, и
результатов вычислений, приведенных в примере § 29.
Решение. На основании вычислений, приведенных в примере § 29,
получаем
Подставляя в формулу C), получаем ч
(*-201)«
1 Г 2-1771

$ 30] ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ЗАКОНА РАСПРЕДЕЛЕНИЯ 503
Замечание. Если получена статистическая функция распре-
распределения для некоторой случайной величины х, то вопрос о том,
следует ли считать данную случайную величину подчиняющей-
подчиняющейся нормальному закону распределения или нет, иногда реша-
решают так.
Пусть имеем значения случайной величины xiy х2У . •¦, хп.
Определяем среднее арифметическое значение а по формуле D).
Определяем значения центрированной случайной величины
Уг> */2>*-*> Уп- Абсолютные величины значений yt располагают
в ряд в возрастающем порядке. Если п нечетное, то за средин-
срединное отклонение или срединную, ошибку ?ср принимают ту абсо-
абсолютную величину | уср | в составленном ряде абсолютных величин,
которая занимает —^—I- 1-е место, а если п—четное, то за ?ср
принимают среднее арифметическое абсолютных величин, стоящих
на местах с номерами у и -g- + 1.
Составим, далее, среднеарифметическую ошибку по формуле
По формуле E) определяем среднеквадратичное отклонение
G) -
Е Е
Далее определяем отношения —2: и _JL.
do
Для случайной величины, подчиненной нормальному закону,
Е Е
отношения -~рИ-^?- соответственно равны 0,8453 и 0,6745
Р F
(см. формулу F) § 22). Если отношения —^- и -^Д- отличаются
d a
от 0,8453 и 0,6745 на величину порядка 10%, то условно при-
принимают, что случайная величина у подчиняется нормальному
закону.
Следствием центральной предельной теоремы является важная
теорема Лапласа о вероятности того, что событие появится не
менее а раз и не более |5 раз. Приведем эту теорему без дока-
доказательства.
Теорема 2 (Лапласа). Если производится п независимых
испытаний, в каждом из которых вероятность появления собы-

504 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ ?ГЛ. XX
тия А есть /?, то справедливо соотношение
где т — число появлений события Л, <7 = 1 —р, Р (а < m < р) —
вероятность того, что число появлений события А заключено
между а и р.
Функция Ф(х) определена на с. 478.
Покажем применение теоремы Лапласа для решения задач.
Пример 2. Вероятность брака при производстве некоторых деталей
р = 0,01. Определить вероятность того, что в 1000 деталях окажется не более
20 бракованных.
Решение. В данном случае
« = 1000, р = 0,01, ? = 0,99, а = 0, E = 20.
Далее находим
а~пр - °-lL = 225
^2 25
По формуле (8) получаем:
Р@<т<20)==у[ФB,25) —Ф(— 2,25)] = Ф B,25).
По таблицам функции Ф (х) находим
P@<m< 20) = 0,9985.
Отметим, что теоремы Бернулли, Ляпунова, Чебышева, Лапласа, о кото-
которых говорилось выше, составляют так называемый закон больших чисел теории
вероятностей.
Упражнения к главе XX
1. Одновременно бросаются две игральные кости. Определить вероятность
того, что выпадет сумма очков, равная 5. Отв. 1/9.
2. В лотерее имеется 10 билетов: 5 выигрышей и 5 проигрышей. Берем
два билета. Какова вероятность выигрыша? Отв. 7/9.
3. Игральная кость бросается 5 раз. Какова вероятность того, что хоть
1 раз не появится 4 очка? Отв. 0,99987.
4. Вероятность попадания в самолет из винтовки равна 0,004. Сколько
стрелков должно стрелять одновременно, чтобы вероятность попадания стала
> 70%? Отв. п > 300.
5. Из двух орудий по одной цели произведено по выстрелу. Вероятность
попадания из первого орудия 0,7, из второго 0,6. Определить вероятность
хотя бы одного попадания. Отв. 0,88.
6. На 100 карточках написаны числа от 1 до 100. Определить вероятность
того^ что на случайно взятой карточке содержится цифра 5. Отв. 0,19.
7. Имеется 4 машины. Вероятность того, что машина" работает в произ-
произвольный момент /, равна 0,9. Определить вероятность того, что в момент t
работает хотя бы одна машина. Отв. 0,9999.
6. Вероятность попадания в цель р = 0,9. Определить вероятность того,
что при трех выстрелах будет три попадания. Отв. « 0,73.

УПРАЖНЕНИЯ К ГЛАВЕ XX 505
9. В первом ящике деталей первого сорта 30%, во втором 40%. Выни-
Вынимаются по одной детали из каждого ящика. Определить вероятность того,
что обе вынутые детали первого сорта. Отв. 0,12.
10. Механизм состоит из трех деталей. Вероятность брака 1-й детали
р1==0,008, вероятность брака 2-й детали /?2 = 0,012, вероятность брака 3-й де-
детали рз = 0,01. Определить вероятность брака при изготовлении всего меха-
механизма. Отв. 0,03.
11. Вероятность попадания при одном выстреле /7 = 0,6. Определить вероят-
вероятность того, что при трех выстрелах будет иметь место хотя бы одно попадание.
Отв. 0,936.
12. Среди 350 механизмов 160 первого сорта, 110—второго сорта и 80 —
третьего сорта. Вероятность брака среди механизмов первого сорта 0,01, среди
второго сорта 0,02, среди третьего сорта 0,04. Берется один механизм. Опре-
Определить вероятность того, что механизм исправный. Отв. 0,98.
13. Пусть известно, что вследствие ошибок, допускаемых при подготовке
стрельбы, центр рассеивания снарядов (ЦРС) при первом выстреле может
находиться по дальности в одной из пяти точек. Вероятность того, что ЦРС
будет находиться в этих точках, соответственно равны р1 = 0у\у р2 = 0,2,
р3=0,4, /?4 = 0,2, р5 = 0,1. Известно также, что если ЦРС будет находиться
в первой точке, то вероятность попадания "в цель_ по дальности будет равна
pi =0,15 и для остальных точек соответственно /?2 = 0,25, р3 = 0,60, /?4 = 0,25,
Р5 = 0,15.
На исходной установке прицела произведен выстрел, в результате кото-
которого получен по дальности промах. Определить, чему равна вероятность того,
что выстрел произведен на установке прицела, соответствующей каждой из
указанных пяти точек ЦРС, т. е. определить вероятности гипотез о различных
ошибках в положении ЦРС после испытания (выстрела). Отв. 0,85; 0,75; 0,40;
0,75; 0,85.
14. Игральная кость бросается 5 раз. Какова вероятность, что 2 раза
выпадет шестерка и 3 раза не шестерка? Отв. 625/3888.
15. Производится 6 выстрелов. Определить вероятность того, что не все
выстрелы дадут перелеты, если вероятность перелета р = 1/2, вероятность
недолета q=\/2 (стрельба по «узкой» цели). Отв. 31/32.
16. Для условий предыдущей задачи определить вероятность того, что
будет 3 перелета и 3 недолета. Отв. 5/16.
17. Найти математическое ожидание числа очков при одном бросании
игральной кости. Отв. 7/2.
18. Найти дисперсию случайной величины ху заданной таблицей распреде-
распределения
• 12
Р | 0,1
3
0,6
5
0,3
Отв. 1,05.
19. Вероятность появления события А при одном испытании равна 0,4.
Производится 5 независимых испытаний. Найти дисперсию числа появлений
события Л. Отв. 1,2.
20. Производится стрельба по мишени. Вероятность попадания 0,8.
Стрельба идет до первого попадания. Имеется 4 снаряда. Определить матема-
математическое ожидание числа израсходованных снарядов. Отв. 1,242.
21. При стрельбе по некоторой «тонкой» цели вероятность перелета р=1/4,
вероятность недолета # = 3/4. Определить вероятность комбинации из 2 пере-
перелетов и 4 недолетов при шести выстрелах. Отв. 0,297.
22. Вероятность того, что деталь имеет брак, р=0,01. Какова вероятность
того, что в партии из 10 деталей будет бракованных 0, 1, 2, 3 деталей?
Отв. 0,9045; 0,0904; 0,0041; 0,0011.

506
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
[ГЛ. XX
распределе-
распределевероятность
интервале A0, 50).
23. Найти вероятности получения хотя бы одного попадания в цель при
10 выстрелах, если вероятность попадания при одном выстреле р=0,15.
Отв. 1—0.851?» 0,603.
24. Случайная величина х задана интегральной функцией распределения
( 0 при х < 0,
/?(*)=-! х при 0«^*«^1,
( 1 при 1 < х.
Найти плотность распределения /(*), М [*],, D[x].
( 0 при х < 0, . ,
i Отв. f(x) = l 1 при 0<*<:1, М[дг]=-^-, D[*] = j2«
• V 0 при 1 < х.
25. Случайная величина х подчиняется нормальному закону
ния с математическим ожиданием 30 и дисперсией Ш0. Найти
того, что значение случайной величины заключено в
Отв. 0,954.
26. Случайная величина подчинена нормальному закону распределения
с дисперсией а2=0,16. Найти вероятность того, что значение случайной вели-
величины будет отличаться по абсолютной величине от математического ожидания
меньше, чем на 0,3. Отв. 0,5468.
27. Случайная величина ^подчинена нормальному закону распределения
с центром рассеивания а = 0,3 и мерой точности h = 2. Найти вероятность
попадания в интервал @,5; 2,0). Отв. 0,262.
28. Стрельба ведется по полосе шириной 4 м. Систематическая ошибка
наводки 1 м (с занижением). Вероятное отклонение 5 м. Найти вероятность
попадания в полосу при нормальном законе рассеивания. Отв. 0,211.
29. Стрельба ведется по прямоугольнику, ограниченному прямыми Х\ = 10 м,
*2 = 20 м, г/!=15м, (/2 = 35 м, в направлении прямой, делящей короткую
сторону пополам. Вероятные отклонения нормального распределения на пло-
плоскости Ех = 5 м, ?„ = 10 м. Найти вероятность попадания при одном выстреле.
Ств. 0,25.
30. Ошибка при изготовлении детали с заданной длиной 20 см есть слу-
случайная величина, подчиненная нормальному закону; а=0,2 см. Определить
вероятность того, что длина изготовленной детали будет отличагься от задан-
заданной меньше, чем на 0,3 см. Отв. 0,866.
31. В условиях примера 30 определить ошибку при изготовлении изделия,
которая не будет превзойдена с вероятностью 0,95. Отв. 0,392.
32. Случайная величина х распределена по нормальному закону с пара-
параметрами М[*]=5 и а = 2. Определить вероятность того, что случайная вели-
величина окажется в интервале A, 10). Сделать чертеж. Отв. 0,971.
33. Длина изготовляемой автоматом детали представляет собой случайную
величину, распределенную по нормальному закону с параметрами М [х] = 15,
а = 0,2. Найти вероятность брака, если допустимые размеры детали должны
быть 15 ± 0,3. Какую точность длины изготовляемой детали можно гаранти-
гарантировать с вероятностью 0,97? Сделать чертеж.
34. При'измерении некоторой величины получен следующий статистиче-
статистический ряд:
X
Относитель-
Относительная частота
1
20
2
15
3
10
4
5
Определить статистическое среднее и статистическую дисперсию. Отв. 2; 1.

УПРАЖНЕНИЯ К ГЛАВЕ XX
35. Результаты измерения даются таблицей
50?
х 0,18
Относите ль- *
ная частота
0,20
18
0,22
33
0,24
35
0,26
9
0,28
1
Определить статистическое среднее а, статистическую дисперсию а.
Отв. 0,226; 0,004.
36. Вероятность брака при производстве деталей /7 = 0,02. Найти вероят-
вероятность того, что в партии из 400 деталей окажется от 7 до 10 бракованных
деталей. Отв. 0,414.
37. Вероятность попадания в цель /7=1/2. Какова вероятность того, что
при 250 выстрелах число попаданий будет заключено между 100 и 150?
Отв. 0,998.
38. Вероятность брака при изготовлении некоторых деталей р = 0,02.
Определить вероятность того, что среди взятых 1000 штук деталей окажется
бракованных не более 25. Отв. 0,87.

ГЛАВА XXI
МАТРИЦЫ. МАТРИЧНАЯ ЗАПИСЬ СИСТЕМ И РЕШЕНИЙ
СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 1. Линейные преобразования. Матрица
Рассмотрим две плоскости Р и Q. Пусть в плоскости Р задана
прямоугольная система координат хг0х2 и в плоскости Q—система
координат ух0у2.
Плоскости Р и Q могут совмещаться. Также могут совмещаться
и системы координат. Рассмотрим систему уравнений
На основании равенств A) каждой точке М (хг\ х2) плоскости
хг0х2 соответствует точка М (уг\ у2) плоскости ух0у2.
Говорят, что уравнения A) определяют линейные преобразо-
преобразования координат, отображающие плоскость хг0х2 на плоскость
уг0у2 (не обязательно на
№ всю плоскость). Так как
уравнения A) линейные,
то отображение называется
линейным отображением.
0 -^- Если в плоскости хг0х2
* Hi мы рассмотрим некоторую
Рис. 450. область Sf, то с помощью
f равенств A) определяется
некоторая совокупность точек Ш плоскости уг0у2 (рис. 450).
Замечание. Отметим, что рассматривают и нелинейные
отображения y1 = <f(xiy x2), y2 = rty(Xi, x2).
Мы ограничимся здесь рассмотрением только линейных отобра-
отображений.
Отображение A) полностью определяется совокупностью коэф-
коэффициентов ап, а12, а21, а22.
Прямоугольная таблица, составленная из этих коэффициентов,
записанная так:
ИЛИ

§1]
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ- МАТРИЦА
509
называется матрицей отображения A). Символы || | или ( )
суть символы матрицы.
Матрицы обозначают и одной буквой, например А или
IIаи ai2\\
Определитель, составленный из элементов матрицы без их
перестановки (обозначим его А (Л)),
A = hiai2, C)
называется определителем матрицы.
Пример 1. Отображение
уг = хх cos а —#2 sjn а, у2 = ** sin с* +*2 cos а
есть поворот на угол а. При этом отображении каждая точка М с полярными
координатами (р; 0) переходит в точку М с полярными координатами (р; 9+а),
если системы координат xt0x2 и уг0у2 совмещены (рис. 451).
в
/
/
Рис.
451.
Рис. 452,
Матрица этого отображения
Пример 2. Отображение
cos a
sin а
соз а
есть растяжение вдоль оси Охх с коэффициентом растяжения к (рис. 452).
Матрица этого отображения
A\k Oil
Пример 3. Отображение
есть растяжение в к раз как в направлении
оси Охъ так в направлении оси Ох2 (рис. 453).
Матрица этого отображения
Л||о *1г
Пример 4. Преобразование
называется зеркальным отражением от оси
Ох2 (рис. 454).
Рис. 453,

510 МАТРИЦЫ [ГЛ. XXI
Матрица рассматриваемого преобразования имеет следующий вид;
|]—1 oil
I о п
Пример 5. Преобразование
называется сдвигом вдоль оси Охг (рис. 455).
, г *t
т т г т т т ^
Рис. 454.
Матрица этого преобразования
Рис, 455,
1 Ц
о 1 г
Можно рассматривать линейное преобразование с любым числом
переменных.
Так, преобразование
D)
Уз = аЬ1хг + а32х2+а33х9
есть отображение трехмерного пространства (хь х2, х3) в трех-
трехмерное пространство (у^ у2У у3). Матрицей этого преобразования
будет
| 1
«21 «22 «23 .
«31 «32 «33II
E)
Можно рассматривать линейные преобразования с неквадрат-
неквадратной матрицей, т. е. такой матрицей, где число строк не равняется
числу столбцов. Так, преобразование

f 21 ОБЩИЕ ОПРЕДЕЛЕНИЯ. СВЯЗАННЫЕ С ПОНЯТИЕМ МАТРИЦЫ 511
является отображением плоскости хг0х2 в некоторую совокуп-
совокупность точек в пространстве (у19 у2, у3).
Матрицей этого преобразования будет
1
«21 «22 J. G)
«31 «32 I
Рассматривают матрицы с любым числом строк и любым чис-
числом столбцов. Матрицы используются не только при линейных
преобразованиях, но и в других разделах. Поэтому матрица яв-
является самостоятельным математическим понятием, аналогичным
понятию определителя. Ниже сформулируем несколько определе-
определений, связанных с понятием матрицы.
§ 2. Общие определения, связанные с понятием матрицы
Определение 1. Прямоугольная таблица из тп чисел,
содержащая т строк и п столбцов,
|«11 «12 ••• «1л|
....... I, A)
II
называется матрицей. Коротко матрицу обозначают так:
4 = 1*1/1 (*=1, 2, ..., т; У=1, 2, ..., п), B)
где aif—члены матрицы.
Если в матрице число строк равняется числу столбцов tn = nf
то матрица называется квадратной:
1ац
Определение 2. Определитель, составленный из элементов
квадратной матрицыДбез перестановок), называется определителем
матрицы, будем его обозначать А (Л):
«Я «12 ••
«21 «22 ••
D)
«/if «/12 ... Щ
Заметим, что неквадратная матрица определителя не имеет.

512 МАТРИЦЫ* * [ГЛ, XXI
Определитель матрицы, полученной из матрицы А вычерки-
вычеркиванием 1-й строки и /-го столбца, умноженный на (—1)'+Л назы-
называется алгебраическим дополнением элемента atj и обозначается Ац.
Определение 3. Матрица А* называется транспонированной
по отношению к матрице Л, если столбцы матрицы А являются
строками матрицы Л*.
Пример. Пусть
1011 «12 И
«з! «зг!
Транспонированной матрицей Л* будет
д* II 0ii «21 «3i II
I «12 «22 «32 II . .
Определение 4. Квадратная матрица А называется сим-
симметричной относительно главной диагонали, если а^ = а;1. Оче-
Очевидно, что симметричная матрица совпадает со своей транспо-
транспонированной v
Определение 5. Квадратная матрица, у которой все эле-
элементы, не стоящие на главной диагонали, равны нулю, называется
дийгонйльной. Если элементы диагональной матрицы, стоящие' на
главной диагонали, равны единице, то матрица называется еди-
единичной. Будем ее обозначать буквой Е:
I 0 ОII
О 0
Определение 6. Рассматривают матрицы, состоящие из
одного столбца или из одной строки:
...yml F)
Первая матрица называется столбцевой, вторая строчной.
Определение 7. Две матрицы А и В считаются равными,
если они имеют одинаковое количество строк и столбцов и соот-
соответствующие их элементы равны, т. е.
А = В, G)
или
Ik/flHM (|=l,2,...,/n;/=l,2,..,,n), (8)
если
аи^Ьи (9)
Бывает удобно иногда отождествлять ётолбцевую матрицу
с вектором в пространстве соответствующего числа измерений,

§¦3]. 1 ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ 513
где элементы матрицы являются проекциями вектора на соответ-
соответствующие оси координат. Так, можем написать
Ы = *1/+*1У+**. (Ю)
1*3 I
Иногда и строчную матрицу удобно отождествлять с вектором.
§ 3. Обратное преобразование
Из уравнений A) § 1
, #2 = 021*1+022*2 0)
следует, что отображение плоскости хг0х2 на плоскость ух0у2
является однозначным, так как каждой точке плоскости хг0%л
соответствует единственная точка плоскости ух0у2.
Если определитель матрицы преобразования отличен от нуля:
или axla22—a21a12 Ф О, B)
то, как известно, система уравнений (J) имеет единственное ре-
решение относительно хг и х%\
У\ «12 I {«11 У\
«22 I v _ I«2L
«11 «12 Г Z «11 «12 '
I «21 «22 I I «21 «22 I
или в развернутом виде
Каждой точке М (уг\ у2) плоскости уг0у2 соответствует опре-
определенная точка М{хг\ х2) плоскости хх0х2. В этом случае ото-
отображение A) называется взаимно однозначным (невырожденным).
Преобразование C) координат (ух\ у2) в координаты (хх; х2)
называется обратным. В этом случае обратное отображение
является линейным. Заметим, .что линейное невырожденное ото-
отображение называется аффинным. Матрицей обратного преобразо-
преобразования является матрица (обозначим ее через Л"*1):
^в ~~Ql
Л Л II. D)
-«21 «11 ¦• к '
А А
Если определитель матрицы А равен нулю:

514 МАТРИЦЫ [ГЛ.
то матрица А и преобразование A) называются вырожденными.
Это преобразование не будет взаимно однозначным.
Докажем это. Рассмотрим два возможных случая:
1) Если ali = ai2 = a2i = a22 = 09 то при любых хх и х2 будут
t/x = 0, у2 = 0. В этом случае любая точка (хх; х2) плоскости хх0х2
переходит в начало координат плоскости уг0у2.
2) Пусть хотя бы один из коэффициентов преобразования
отличен от нуля, например а^фО.
Умножая первое из уравнений A) на a2i, второе на ап и про-
производя вычитание, получим с учетом равенства E)
= 021*1 + 022*2»
¦011#2=О. . F)
Итак, при любых х19 х2 для значений ух и у2 получаем равен-
равенство F), т. е. соответствующая точка плоскости хг0х2 попадает
на прямую F) плоскости yfiy2. Очевидно, что это отображение
не является взаимно однозначным, так как каждой точке прямой
F) плоскости уг0у2 соответствует совокупность точек плоскости
хг0Хъ, лежащих на прямой Уг — п^х^а^^
В обоих случаях отображение не является взаимно однозначным*
Пример 1. Преобразование
является взаимно однозначным, так как определитель А (Л) матрицы преобра-
преобразования Л отличен от нуля:
_¦ -з.
Обратное преобразование будет
1.1^12
Матрица обратного преобразования, в соответствии с формулой D) будет
.1 Л
3 3
1 _1
3 3
Пример 2; Линейное преобразование
y1=x1+2x2t у^^2х
является вырожденным, так как определитель матрицы преобразования
Это преобразование переводит все точки плоскости (*& *2) в прямую Уъ—Ъ
= 0 плоскости (#i, уа)«

§41 ДЕЙСТВИЯ НАД МАТРИЦАМИ. СЛОЖЕНИЕ МАТРИЦ 515
§ 4* Действия над матрицами. Сложение матриц
Определение 1, Суммой двух матриц Ца^Ц и 11&//ЦС оди-
одинаковым количеством строк и одинаковым количеством столбцов
называется матрица Ц^-Ду которой элементом et/является сумма
йц+bij соответствующих элементов матриц \atj\ и Ц&^-Ц, т. е.
lk/i+IIM=IM' 0)
если
=iCt/ (/=1> 2* •••» т> /=Ь 2, ..., д), B)
Ппимеп 1 И* a™\\-L.\\bn buiUn+Ьц a12+b12\\
Пример 1. |ад ^l + l^ 622|-||a21+62i a22+622||-
Аналогичным образом определяется разность двух матриц.
Целесообразность такого определения суммы двух матриц,
в частности, следует из представления вектора как столбцевой
матрицы.
Умножение матрицы на число. Чтобы умножить
матрицу на число Я, нужно умножить на это число каждый эле-
элемент матрицы:
Ч«*/Ы*М- C)
Если X целое, то формула C) получается как следствие пра-
правила сложения матриц.
Пример 2.
* II 021 022
Произведение двух матриц. Пусть имеем линейное
преобразование плоскости хх0х2 на плоскость yfiy^
II —— /У V I П Y I/ — /7 V I , /у V / 4\
«71 ~"~* 11 1 | *^12 2' к/2 *~"~ 21 1 I 22 2 - \ /
с матрицей преобразования
II - П
E)
Пусть, далее, произведено линейное преобразование плоскости
уг0у2 на плоскость гг0г2:
*г = ЬпУ1 + КУ» Ч = Ьлуг + ЬыУ2 F)
с матрицей преобразования
Требуется определить матрицу преобразования плоскости х1Ох2
на плоскость zx0z2. Подставляя выражения D) в равенства F)^
получаем
zt = bn (ailx1 + ai2x2)+bl2 {a21xt + a22x2)t

516
ИЛИ
МАТРИЦЫ
Ai) *i + (Мл+M22) **
21) *i + (Mu +
Матрица полученного преобразования будет
или коротко
С = Cl1 °12
\\C21 с22
|гл. хт
(8)
(9)
A0)
Матрицу (9) называют произведением матриц G), E) и пишут
1^11 ^12 1 ^И ^12 ^11^11 ~T^l2^2i ^11^12 "Т~ ^12^22 II Л1\
^21 ^22 I II ^л< "-""*" " h~*n**' -\-h~~n** h~«n«~-X-h л^~1г * '
или коротко
\а21 а22
Ь21а12 + Ь2
В-А = С.
A2)
- Сформулируем далее правило умножения двух матриц В и Л,'
если первая содержит т строк и k столбцов, а вторая k строк
и п столбцов.
Схематически оно показано в равенстве
... ь„
aii а>\ъ ... &\]
а21 а22 ... а2/
. A3)
Элемент ctj матрицы С, являющейся произведением матрицы В
на матрицу Л, равен сумме произведений элементов 1-й строки
матрицы В на соответствующие элементы /-го столбца матрицы
Л, т. е.
A=1, 2, ..., т; /=1, 2, ..., /г).
Пример 3. Пусть
В==
1 0
о о
0 о
1 о|Г
тогда
1) ВА =
2) АВ =
В данном примере
1 0
0 0
0 011
1 Oil
110 01! 1
И1 о! |
о о
о о
1 ° I] Л ° ° И
оо - Юг
В А Ф АВ.

ДЕЙСТВИЯ НАД МАТРИЦАМИ. СЛОЖЕНИЕ МАТРИЦ
517
Мы пришли к следующему выводу. При умножении матриц
не справедлив переместительный 'закон.
Пример 4. Даны матрицы
111 0 011
Д= 0 2 1
3 О О
10 1 Oil
2 0 1.
1 0 1И
Найти АВ и ВА.
Решение. По формуле A3) находим
10+02+01 Ы+00+00 10+01+01
АВ = 00+2.2+Ы 01+20+10 00+21 + 11
3-0+0.2+01 31+00+00 30+01+0.1
0J + 10+0-3 00 + 1-2+00 00+Ы+00
ВА= 2.1+00+1-3 20+02 + 10 20+01+10
1.1+0-0+1-3 10+02+10 ЬО+01+10
Пример 5. Найдем произведение матриц:
10 1 О
5 0 3
0 30
1° 2 1
5 О О
4 О О
ац а12
«21 «22
«23
'13 + а12^23 + ^1зЬзЗ
22^21+ а23^31 «21^12 + fl22^22 + a23^32 ^21^13 + ^22^23 + ^23^33
Путем непосредственной проверки можно убедиться в справед-
справедливости следующих соотношений для матриц (k—число, Л, В,
С—матрицы):
A4)
A5)
A6)
A7)
На основании правил умножения квадратной матрицы А на
число k и правила вынесения общего множителя элементов столб-
столбцов определителя для матрицы л-го порядка следует
= knA(A).
A8)
Так как при умножении двух квадратных матриц А и В по-
получается квадратная матрица, элементы которой образуются по
правилу умножения определителей, то очевидно, что справедливо
следующее равенство:
(Я). A9)
Умножение на единичную матрицу. Квадратная
матрица, у которой элементы, стоящие на главной диагонали,
равны единице, а все остальные элементы равны нулю (как ука-
указывалось выше), называется единичной матрицей.

518
На
т.
Так,
МАТРИЦЫ
единичной матрицей 2-го
41
основании правила умножения
е.
АЕ — 1п11 а±2 UP
|| #21 «22 || II ^
порядка
матриц
) l|| fla21
будет
получаем:
[ «12 |
. «22 I'
[ГЛ. XXI
B0)
-А, B1)
а также
ЕА = А. B2)
Легко видеть, что произведение квадратной матрицы любого
порядка на соответствующую единичную матрицу равняется пер-
первоначальной матрице, т. е. справедливы равенства B1) и B2).
Таким образом, при умножении матриц единичная матрица играет
роль единицы, поэтому и называется единичной.
Единичной матрице B0) соответствует преобразование
Такое преобразование называется тождественным. Обратно,
тождественному преобразованию соответствует единичная матрица.
Аналогичным образом определяется тождественное преобразова-
преобразование любого числа переменных.
§ 5. Преобразование вектора в другой вектор
с помощью матрицы
Пусть дан вектор
который запишем в виде столбцевой матрицы
1*з I
Произведем преобразование проекций этого вектора с помощью
матрицы
1а±± ai2 #хз||
«21 «22 «23 ; B)
«31 «32 «331|
У 2 = *ll*l + Я22*2 + Я23*3 Э C)
Получим новый вектор

f «1 ОБРАТНАЯ МАТРИЦА Ы9
который в виде столбцевой матрицы можно записать таю
1Уг1 | «u*i+а12х2+«13*31
1/2=| а21х!+а22х2+«2з*з . ' D)
Уз 1 ! ЯзЛ+Яз2*2+«83*з И
Пользуясь правилом умножения матриц, эту операцию преоб-
преобразования можно записать так:
1а11 * «12 «13 II | *1 II I «11*1 + «12*2 + «13*3 ||
«21 «22 «23 .|*2 == «21*1 + «22*2 + «23*3 L E)
«31 «32 «33 1 11*8 У 1 «31*1 + «32*2 + «33*3 1
т. е.
V = АХ. F)
При умножении квадратной матрицы на столбцевую получается
столбцевая матрица той же высоты.
Очевидно^ что преобразование трехмерного вектора X в век-
вектор Y—это другая формулировка преобразования трехмерного
пространства в трехмерное.
Отметим, что система равенств C) вытекает из матричного
равенства D) путем приравнивания элементов матриц, стоящих
слева и справа.
Равенство D) дает преобразование вектора X в вектор Y
с помощью матрицы Л.
Все проведенные рассуждения для вектора в трехмерном; про-
пространстве переносятся на преобразование векторов в пространстве
любого числа измерений.
§ 6, Обратная матрица
Пусть дан вектор Х- Произведем над ним преобразование
с помощью квадратной матрицы Л, получим вектор Y:
Г=АХ. A)
Пусть определитель матрицы А отличен от нуля: А (А) ФО.
Тогда существует обратное преобразование вектора Y в вектор X.
Это преобразование находится путем решения системы уравнений
C) § 5 относительно х±, х2У хъ. Матрица обратного преобразова-
преобразования называется обратной матрицей к Л и обозначается Л".
Таким образом, можем написать
X=A"lY. B)
Здесь X— столбцевая матрица, К—столбцевая матрица, АХ —
столбцевая матрица, А—квадратная матрица. Подставляя вме-
вместо Y в правой части равенства B) правую часть равенства A),
получаем
Х=А~*АХ. C)

520 - матрицы * [гл. xxi
Над вектором X последовательно произвели преобразование с мат-
матрицами Л и Л, т. е. произвели преобразование с матрицей,
равной произведению матриц (А~1А). В результате получилось
тождественное преобразование. Следовательно, матрица А А есть
единичная матрица:
Л-М = ?. D)
Равенство C) имеет вид
Х=ЕХ. E)
Теорема 1. Если матрица Л—обратная к матрице Л,
то и матрица А—обратная к матрице Л, т. е. справедливы
равенства
АА = АА = Е. F)
Доказательство. К обеим частям равенства C) применим
преобразование с помощью матрицы Л:
Пользуясь свойством сочетательности при умножении матриц,
последнее равенство можно переписать так:
Отсюда следует, что
АА-* = Е. G)
Утверждение доказано.
Из равенств D) и G) следует, что матрицы Л и Л"*1 взаимно
обратные. Из указанных равенств также следует
(А~1)-* = А. - (8)
Действительно, из равенств G) следует
Сравнивая последнее равенство с равенством D), аолучаем ра-
равенство (8).
§ 7. Нахождение матрицы, обратной данной
Пусть дана невырожденная матрица
Л =021 022 023 L A)
||031 032 033 ||
013
0. B)
0ii
02*
031
012
022
032'
013
023
038

5 7}
НАХОЖДЕНИЕ МАТРИЦЫ, ОБРАТНОЙ ДАННОЙ
521
Докажем, что обратной матрицей А~г будет матрица
Ац A2i А31
д д д
XXX
XXX
где Аи—алгебраическое дополнение элемента aif (см. § 2).
Найдем матрицу С, равную произведению матриц Л, А:
|
азз||
д
X
X
д
X
X
д
X
X
|
110 0
Действительно, на основании правила умножения матриц диаго-
диагональный член матрицы С равен сумме произведений элементов
строки определителя А на соответствующие им алгебраические
дополнения, деленной на определитель А, т. е. равен единице.
Например, элемент cxi определяется так:
Каждый недиагональный член равен сумме произведений элемен-
элементов некот9рой строки на алгебраические дополнения другой строки,
деленной на определитель А; например, элемент с23 опреде-
определяется так:
Таким образом, теорема доказана.
Замечание. Матрица
IA А А I
^13 Л23 -^33II
называется матрицей, присоединенной к А. Обратная матрица Л
через присоединенную Л выражается так:
л ~Д(Л)Л- W
Справедливость этого равенства следует из равенства C).
Пример. Дана матрица
II 2 011
0 3 1.
0 1 21
Найти обратную .матрицу Л*1 и присоединенную'матрицу А.

522
МАТРИЦЫ
{ГЛ. XX
Решение. Находим определитель
матрицы
Л (Л) = 5.
Находим алгебраические дополнения
Ли= 5, Л12 =
А л А —
/121 — —*! Л22—
Л31= 2, Л32 =
Следовательно, по формуле C)
л-1—
5
5 ~~
0
0 —-
0,
2,
-1,
4
5
2
5
Т
Лз
t Л13= 0,
Л23 =—1,
Лзз== ' 3.
2
5
1

3
5
По формуле D) находим присоединенную матрицу
115— 4 211
Л Jo 2—lL
НО —1 3
§ 8. Матричная запись системы линейных уравнений
Рассуждения будем проводить для случая трехмерного про-
пространства. Пусть имеем систему линейных уравнений
A)
B)
C)
D)
031*1 + 032*2 + 033*3 = d3 •
Рассмотрим три матрицы:
А = «21 «22 «23 ,
1 «31 «32 «33 ||
0 =
Тогда, пользуясь правилом умножения матриц, систему A)
можно записать в матричной форме так:
|«11 «12 «13П
«21 «22 «23
«31 «32 «33 1
х2 \\ = \
E)
Действительно, в последнем равенстве в левой части стоит
произведение двух матриц, которое равно столбцевой матрице,

191 РЕШЕНИЕ МАТРИЧНЫМ МЕТОДОМ &23
элементы которой определяются равенством E). Справа стоит
также столбцевая матрица. Две матрицы равны, если равны их
элементы. Приравнивая соответствующие элементы, получим си-
систему уравнений A). Матричное равенство E) коротко записы-
записывают так:
AX = D. F)
Пример. Записать в матричной форме систему уравнений
3*2+ *з = 9,
Решение. Напишем матрицу А системы, матрицу решений X и мат-
матрицу свободных членов D:
II 2 01 flrfl 151
0 3 1 , ЛГ=|*Х *> = 191.
0 1 2|| lUsll |,81
Данная система линейных уравнений в матричной форме запишется так:
1112О1'И1 II5!
0 3 41*2 Н9-
§ 9. Решение системы линейных уравнений матричным методом
Пусть определитель матрицы А отличен от нуля: А(Л)#0.
Умножив левую и правую части равенства F) § 8 слева на мат-
матрицу Л, обратную матрице Л, получим
Но Л-МХ-Л-Ф.. A)
Л-I А р ру V
поэтому из A) следует
«Л — /1 MJ* \^ь/
Последнее равенство с учетом равенства E) § 7 можно запи-
записать так:
или в развернутом виде
Производя умножение матриц, стоящих справа, получим
I*1! 1 |И1Л11+^21+^зЛз1|
*2 = Г7ТГ ^и+^и+Ми L E)
*з|| Д ( ; UiA+*A+dA

524
МАТРИЦЬ*
1ГЛ XXI
Приравнивая члены матриц, стоящих слева и справа, получаем
у _ «'lAl + «<2^2l + ^3^31
*i- д
I * Ji
F)
Решение F) можно записать в форме определителей:
d\
d2
dz
«и
«2i
«3i
«12 «13
«22 «23
«32 «33
«12 «13
«22 «23
«32 «33
Y —*•
- » *2
«11
«21
«31
«11
«2i
«3i
«*1
d2
dz
«12
«22
«32
«13
«23
«33
«13
«23
«33
- > *з
«11
«21
«3i
«11
«21
«31
«12
«22
«32
«12
«22
«32
di
d2
dn
«13
«23
«33
Пример 1. Решить систему уравнений
G)
матричным методом.
Решение. Найдем определитель матрицы системы
II 2 011
о з 1 =5:
О 1 2\\
Определим обратную матрицу по формуле C) § 7:
¦-4 i
Матрица D такова:
•-т
-I?!
Решение в матричной форме по формуле B) запишется так:
1
0
0
4
5
2
5
1
5
2
5
1
3
5
5
9
8
=
1.5-1-9+4.8
0.5+4.9--1-8

$10] ОРТОГОНАЛЬНЫЕ ОТОБРАЖЕНИЯ 525
Приравнивая строки матриц, стоящих слева и справа, получаем
о о
Пример 2. Решить систему уравнений
матричным методом.
Решение. Находим определитель матрицы системы
II1 2 1II
А(Л)= 2 1 1=1 ^0.
|| 1 3 1Ц
Находим обратную матрицу
Ih2 1 41
1 5 —1 —3 If
Пишем решение системы в матричной форме:
[яд|| ||—2 1 1|| ||0|| || 311
Приравнивая строки матриц, стоящих справа и слева, получаем
*i = 3, х2 = 2, дс3 = —7.
§ 10. Ортогональные отображения. Ортогональные матрицы
Пусть в трехмерном пространстве имеем две прямоугольные
системы координат (jclf х2У х3) и (х[у х2у х'3)у имеющие общее на-
начало О. Пусть точка М имеет координаты (х^ х2\ х3) и (х[\ xf^y x'z)
в первой и второй системах координат (можно начала координат
и не совмещать).
Обозначим через е1У е2, е3 единичные векторы на осях коор-
координат в первой системе координат, через е'и е2, е'3 единичные
векторы во второй системе координат. Векторы е19 е2, е3 являются
базисными векторами в системе (х19 х2, х3), векторы е'1У el, е'%
базисные в системе (x'l9 x2f лез).
Тогда вектор ОМ в первой системе координат запишется так:
^ ^^; A)
во второй системе:
OM = x[e[+xiez+x'9ei B)
Рассмотрим преобразование координат xiy х;2У хъ произвольной
точки М в координаты хи х%у х3 этой же точки. Можно сказать,

526 МАТРИЦЫ . [ГЛ. XXI
что будем рассматривать преобразование пространства (xi9 x2, я3)
в пространство (х'и х2у х'3).
Это преобразование обладает тем свойством, что отрезок длины/
переходит в отрезок той же длины L Треугольник переходит
в равный треугольник, следовательно, два вектора, выходящие
из одной точки с углом г|) между ними, переходят в два вектьра
той же длины с тем же углом ме5кду ними.
Преобразование, обладающее указанным свойством, называется
ортогональным.
Можно сказать, что при ортогональном преобразовании проис-
происходи! перемещение всего пространства как твердого тела или
перемещение и зеркальное отображение. Определим матрицу этого
преобразования.
Выразим единичные векторы е[, вг, ёъ через единичные век-
векторы е19 е2, е3:
2е2 + а32еЗУ C)
ei = сс13е1+а23
Здесь
!, e'2), als = cos(^lf e'3),
^2, e'2), a23 = cos(e2, e'9)t D)
a3i = cos (e3, e[)y a32 = cos (e3, ei), a33 = cos (e3, ei).
Девять направляющих косинусов запишем в виде матрицы
Iaii a2j a3i||
«le a22 «32 . E)
«13 «23 «33 11
Пользуясь соотношениями D), можем также написать
^2 ^ a2l^l + а22^2 + G& 23^3* F)
Очевидно, что матрица
|«11 «12 «131|
a2i а22 а2з G)
«31 «32 «33II
является транспонированной матрицей по отношению к матрице S.
Так как е'и е'29 ez—единичные взаимно перпендикулярные век-
векторы, то их векторно-скалярное произведение равно ±К Следо-
Следовательно,
«и
«12 «22 «32 = ±1. (8)
«33

ОРТОГОНАЛЬНЫЕ ОТОБРАЖЕНИЯ 527
Аналогично
«II «12 «13
(€162€3) — A (S*) = «21 «22 «2 3 =±1. *(9)
Вычислим произведение матриц
|«11 «21 «31 | || «11 «12 «13 | || 1 0 01|
«12 «22 «32 N«21 «22 «23 = 0 1 0 = ?. (Щ)
«13 «23 «33 I II «31 «32 «33 1 ||0 0 1 И
Действительно, если обозначить через % элементы матрицы
произведения, то получаем
A1)
С33 — ai3 "Т a23 "*Г a33 === * >
cia = aaa12 + a21a22 + a31a32 = e[e'2 = 0.
Аналогично
cj7 = e-e- = 0 при /^/ (/=1, 2, 3; / = l, 2, 3). A2)
Итак,
SS* = E. . A3)
Таким образом, транспонированная матрица S* совпадает
с обратной матрицей S:
S* = S~*. A4)
Матрица, удовлетворяющая условиям A3) или A4), т. е. обратная
своей транспонированной, называется ортогональной. Найдем да-
далее формулы преобразования координат (хг, х2, х3) в координаты
(x'lt лса, *з) и обратно. В силу формул C) и F) правые части ра-
равенств A) и B) можно выразить как через базис (е?, е2, в3), так
и через базис {е[, е'2у в3). Следовательно, можно написать равенство
A5)
Умножая последовательно все члены равенства A5) на вектор
е*и на вектор е'2> на вектор в§ и учитывая, что
в^в/ = 0 при гФ\%
e'iej=\ при /==/, A6)
получим
A7)
4 = «13^ + «23^2 + «33*3.

528 - матрицы [гл. XXI
Умножая члены равенства A5) последовательно на е±% е2> е3,
получим
*i = «i A + «12^2+а13*з,
*2 = «21 ^ + «22*2+«28*81 ' (I8)
*3 = а31^1 + а32^2 + «33*8-
Итак, матрицей ортогональных преобразований A7) является
матрица S, а матрицей обратного преобразования A8)—матрица S*.
Таким образом, доказано, что в декартовой системе координат
ортогональному преобразованию соответствует ортогональная мат-
матрица. Можно доказать, что если матрицы прямого и обратного
преобразования A7) и A8) удовлетворяют соотношению A3) или
A4), т. е. являются ортогональными, то и преобразование будет
ортогональным.
Если введем столбцевые матрицы
!*з II I'*3'»
то системы A7) и A8) можно записать так;
X' = SX, г ' B0)
X=S~lX'. B1)
Если введем матрицы, транспонированные к матрицам A9):
X* = |х^ х'2 х; ||, X* -1|хг х2 х31, B2)
то можем написать
X'* = X*S~\ X* = X'*S. B3)
§ 11. Собственный вектор линейного преобразования
Определение 1. Пусть дан вектор Х\
где
Если после преобразования вектора X с помощью матрицы
(см. B) § 5) получается вектор V:
B)
параллельный вектору X:
Х C)

СОБСТВЕННЫЙ ВЕКТОР 529
где Я—число, то вектор X называется собственным вектором
матрицы А или собственным вектором данного линейного преобра-
преобразования] число X называется собственным значением.
Найдем собственный вектор
== W
1хз I
для данного линейного преобразования или для данной матрицы Л.
Чтобы вектор X был собственным вектором матрицы Л, необ-
необходимо, чтобы выполнялись равенства B) и C). Приравнивая
правые части этих равенств, получаем:
АХ = ХХ D)
или
АХ^ХЕХ,
т. е.
(Л—ХЕ)Х = 0. E)
Из этого равенства следует, что вектор X определяется с
точностью до постоянного множителя.
В развернутом виде равенство D) записывается, очевидно, так:
011*1 + 012*2 + 013*3 = ^*1>
21 1 ] 22 2 | 23 3 X2у V /
а равенство E) запишется так:
@11- — Ц *1 + 012*2 + 013*3 = О,
021*1 + @22 —^)*2+ 023*3=0» С7)
031*1+ 032*2 + @33 — ^)*3 = 0.
Получили систему однородных линейных уравнений для оп-
определения координат х19 х2, х3 вектора X. Чтобы система G)
имела ненулевые решения, необходимо и достаточно, чтобы оп-
определитель системы был равен нулю:
L1 — X а12 013
«21 «22—^ «23 =0, (8)
или
А (Л—Х?) = 0. (9)
Это есть уравнение третьей степени относительной. Оно называ-
называется характеристическим уравнением матрицы*А. Из этого урав-
уравнения находятся собственные значения X.
Рассмотрим случай, когда все корни характеристического урав-
уравнения действительные и различные. Обозначим их через Хъ Х2, Х3.
18 Н. С. Пискунов, т. 2

530 МАТРИЦЫ [ГЛ. XXI
Каждому собственному значению % соответствует собственный
вектор, координаты которого определяются из системы G) при
соответствующем значении %. Обозначим собственные векторы
через т1э т2, т3. Можно показать, что эти векторы линейно не-
независимы, т. е. ни один из них не выражается через остальные.
Следовательно, любой вектор можно выразить через векторы т*,
т2, т3, т. е. их можно принять за базисные векторы.
Отметим без доказательства, что все корни характеристичес-
характеристического уравнения симметрической матрицы действительны.
Пример 1. Найти собственные векторы и соответствующие им собствен-
собственные значения матрицы
1в
Решение. Составим характеристическое уравнение и найдем собственные
значения:
Найдем собственный вектор, соответствующий собственному значению Я| =—1,
из соответствующей системы уравнений G):
A—Я1)д:1+ *2 = 0,
8*1+ C—&*)*, = 0, или
Решая эту систему, находим *x = m, *2 =—2т, где т—произвольное число.
Собственный вектор будет
тх = mi—2mJ.
Для собственного значения Я2=5 пишем систему уравнений
—4^+^2 = 0, 8*!—2^2=0.
Собственный вектор будет
Пример 2. Найти собственные значения и собственные векторы матрицы
17—2 01]
-2 6-2.
0 -2 5|
Решение. Напишем характеристическое уравнение
7—1 ~2 0
_2 6—к —2 =0, т.е. —А,3+Ш,2--99А,+162=0.
0 «2 5-Я
Корни этого уравнения суть A,i = 3, A^ = 6, Я3==9.
Для ki=3 собственный вектор определяется из системы уравнений
2—2*3 = 0, —2*2+2*з = 0.
Полагая *f = m, получаем Х2 = 2т, *3 = 2/п. Собственный вектор
тх = mi-\-2mJ+2mk.
Аналогично находим *
^Mj—itikt т3=mi+mj

§12] ' МАТРИЦА ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ 531
§ 12. Матрица линейного преобразования, при котором
базисные векторы являются собственными векторами
Определим, далее, матрицу линейного преобразования, когда
базисом являются собственные векторы xit т2, т3. При этом пре-
преобразовании должны выполняться соотношения
где т*, Та, Тз—образы векторов riy т2, хй.
Пусть матрица преобразования будет
1п'п п12 аЦ
a2l«22fi23 . B)
Определим члены этой матрицы. В базисе т^, т^ х% можем
написать
Так как вектор х± после преобразования с помощью матрицы
А' переходит в вектор Ti = Хгхг:
то можем написать
Следовательно,
| I ЦЦ!
О = а21 а22 а23 И C)
О | | Ц||
или в виде системы уравнений
D)
Из этой системы находим:
На основании соотношений
%1 = Х2т2, Тз = ksxu
аналогично найдем
18*

532 ^ МАТРИЦЫ [ГЛ. XXI
Таким образом, матрица преобразования имеет вид
IXi о Oil
ох, о|. E)
0 0 А*!
Линейное преобразование будет
У! = К*и
у'2 = Кх*> F)
Если Xi = X2 = X3 = X*y то линейное преобразование имеет вид
Такое преобразование называется преобразованием подобия с
коэффициентом ^*. При этом преобразовании каждый вектор про-
пространства является собственным вектором с собственным значени-
значением Я*.
§ 13. Преобразование матрицы линейного преобразования
при переходе от одного базиса к другому
Пусть X—произвольный вектор:
Iх! II
*2 \ = х1е1 + х2е2+х3е3, A)
1
заданный в базисе (е19 е2У ez). Вектор X преобразуется с по-
помощью матрицы А в вектор Y:
у _ у2 __
Lai '
Г= AY. C)
Введем в рассматриваемом пространстве новый базис (е[, 02, вз),
связанный со старым базисом формулами перехода
€г = U11€1 + ^21^2 Г ^31^8»
е'г = Ь1гег + Ьпег + Ьзъеш, D)
Пусть вектор X в новом базисе напишется так:
X' — х\ ех + #202 4" х'ъёъ = ^2 . E)
Можем написать равенство
F)

§13J „. ПРЕОБРАЗОВАНИЕ МАТРИЦЫ 533
где в правую часть подставлены выражения D). Приравнивая
коэффициенты при векторах е19 е2, е3 справа и слева, получим
равенства
*i - Ьпх[+Ь12х'2 + &13*з,
х2 = КЛ + b22xf2 + Ь29х'3, G)
или коротко
Х=ВХ', (8)
где
Ibyi b12 613|
^21*22*23. (9)
^31 ^32 ^331
Эта матрица невырожденная, имеет обратную матрицу В,
так как система G) имеет определенное решение относительно х'и
#2, х'ъ. Если в новом базисе запишем вектор Y:
то, очевидно, имеет место равенство
У=ВГ. A0)
Подставляя выражения (8) и A0) в C), получим
BY' = ABX'. A1)
Умножая обе части равенства на В"*1, получим
Г=В-МВХ'. A2)
Следовательно, матрица А' преобразования в новом базисе будет
Л' = ?-МВ. A3)
Пример. Пусть с помощью матрицы А
II 1 0 О
10 1
0 111
производится преобразование вектора в базисе {ей e2i e$. Определить матрицу
преобразования А' в базисе (e'v e2, е?), если
Решение. Здесь матрица В такова (см. формулы D) и (9)):
112 11]
2 11.
1 3 if
Найдем обратную матрицу (Д(В) = 1)
II— 2 1 111
B-i= _1 0 1L
5—1 ~3

5Э4 МАТРИЦЫ [ГЛ. XXI
Далее находим
1—1 —1 211
—1 0 1 .
4 2 —4|
Окончательно по формуле A3) находим
1—1 3 ОЙ
О 1 0 .
4 —2 2|
Докажем, далее, следующую теорему.
Теорема 1. Характеристический многочлен (левая часть
уравнения (8) § 11) не меняется в зависимости от выбора базиса
при данном линейном преобразовании.
Доказательство. Напишем два матричных равенства
где А и А'—матрицы, соответствующие различным базисам при
одном и том же линейном преобразовании, В—матрица перехода
от новых координат к старым, Е—единичная матрица.
На основании двух последних равенств получаем
А'—ХЕ^В-^А—ЩВ.
Переходя от матриц к определителям и пользуясь правилом
умножения матриц и определителей, получаем
А (Л'—Щ = А (Б (А—ХЕ) В) = А (В) А (А—Щ А (В).
Но
А (В-1) А (В) = А (В-ЧВ) = А (?) = 1.
Следовательно,
ti{A' — Щ = А(А—%Е).
Слева и справа стоят характеристические многочлены матриц
преобразования. Теорема доказана.
§ 14. Квадратичные формы и их преобразования
Определение 1. Квадратичной формой от нескольких
переменных называется однородный многочлен второй степени от
этих переменных.
Квадратичная форма от трех переменных хи х2, х3 имеет вид
F = аг1х\ + a22xl + ям*1 + 2^^ + 2аихххъ + 2а33х2х3, A)
где пц—заданные числа, коэффициенты 2 взяты для того, чтобы
получить более простые последующие формулы.

§14] ' КВАДРАТИЧНЫЕ ФОРМЫ И ИХ ПРЕОБРАЗОВАНИЯ 535
Равенство A) можно написать так:
F = хг (апх1 + а12х2 + alzxz) +
*,), B)
где аи (t=l, 2, 3; /=lf 2, 3)—заданные числа, при этом
012 = 021» 018 = 031» 023 = 032- C)
Матрица
|«ll «12 «13 II
«21 «22 «23 D)
«31 «32 «33 |
называется матрицей квадратичной формы A). Данная матрица
симметричная.
Будем считать (х19 х29 х3) координатами точки пространства
или координатами вектора в ортогональном базисе (el9 е2, е3),
где е19 е2, е3—единичные векторы.
Рассмотрим линейное преобразование в базисе (еи е29 ez):
x[ = allx1+a12x2+a13x3,
х'2 = алхг + а22х2+а23х3, E)
х3 = а31хг+а32х2
Матрица этого преобразования совпадает с матрицей квадратич-
квадратичной формы.
Определим далее два вектора
*i||
х± F)
А
Х' =
1
G)
Преобразование E) запишем в форме
Х'^АХ. (8)
Тогда квадратичную форму B) можно представить как ска-
скалярное произведение этих векторов:
(9)
Пусть ei, е'2, e3—ортогональные собственные векторы преоб-
преобразования (8), соответствующие собственным значениям Xif Я2, Я3.
Можно доказать, что если матрица симметрична, то существует
ортогональный базис, составленный из собственных векторов
матрицы. Произведем преобразование (8) в базисе (ei, e2, e'z).
Тогда матрица преобразования в этом базисе будет диагональной

536' ' ' матрицы ' Чгл. xxi
lj О О П
А =\о х, о|. A0)
II0 0 Xsl
Можно показать, что применяя это преобразование к квадра-
квадратичной форме A), можно привести последнюю к виду
(И)
Направления собственных векторов е'и el, el называются глав-
главными направлениями квадратичной формы.
§ 15. Ранг матрицы. Существование решений системы
линейных уравнений
Определение 1. Минором данной матрицы называется
определитель, составленный без перестановок из оставшихся эле-
элементов матрицы после вычеркивания из нее^нескольких строк и
столбцов.
Пример 1. Пусть дана матрица
Ia-ix a12 а13 а14|
«21 «22 «23 «24 •
«3f «32 «33 «34II
Миноры третьего порядка этой матрицы получаются после вычеркивания
одного столбца и замены знака матрицы [| || знаком определителя | |. Их че-
четыре. Миноры второго порядка получаются после вычеркивания двух столбцов
и одной строки, их 18. Миноров первого порядка 12.
Определение 2. Рангом матрицы А называется наивыс-
наивысший порядок отличного от нуля минора матрицы Л.
Пример 2. Легко проверить, что ранг матрицы
II —1 011
2 0 1
1 1 l|
равен 2.
Пример 3. Ранг матрицы
111 2 3
||3 6 9
равен 1.
Если матрица А квадратная порядка п, то ранг этой мат-
матрицы k удовлетворяет соотношению k^n. Как указывалось выше,
если k = /г, то матрица называется невырожденной, если k < п,
то матрица называется вырожденной.
Например, матрица
110 1 011
0 0 1
111 I oil

§!6J . ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ МАТРИЦ 53?
является невырожденной, так как Л (Л) = 1 ^ 0; матрица в примере 2 особая,
так как там л = 3, k=2.
Понятие ранга матрицы широко используется в теории систем
линейных уравнений. Имеет место следующая
Теорема 1. Пусть дана система линейных уравнений:
Введем в рассмотрение матрицу системы
|«11 «12 «13 ||
«21 «22 «23 B)
«31 «32 «331
и расширенную матрицу
|«и «12 «13 ЬА
«21 «22 «23 ЬЛ. C)
«31 «32 «33 ?з||
Система A) имеет решения, если ранг матрицы А равен ран-
рангу матрицы В. Система не имеет решений, если ранг матри-
матрицы А меньше ранга матрицы В. Если ранг матрицы А и ранг
матрицы В равен 3, то система имеет единственное решение.
Если ранг матриц А и В равен 2, то система имеет бес-
бесчисленное множество решений, при этом два неизвестных вы-
выражаются через третье, которое имеет произвольное значение.
Если ранг матриц А и В равен 1, то система имеет бес-
бесчисленное множество решений, при этом два неизвестных имеют
произвольные значения, а третье выражается через них.
Справедливость этой теоремы легко устанавливается на осно-
основании анализа решений системы уравнений, известного из алгеб-
алгебры. Эта теорема справедлива для системы любого числа уравнений.
§ 16. Дифференцирование и интегрирование матриц
Пусть дана матрица ||#//@11» гДе членами atj- (t) матрицы
являются функции некоторого аргумента t:
... aln(t)
am2(t) ... amn{t)
или коротко будем это записывать так:
A(t) = \au(t)\ (/=1, 2, ..., m; /=lf 2, ..., п). B)

538
МАТРИЦЫ
[ГЛ. XXI
Пусть члены матрицы имеют производные
dan @ damn (t)
dt » '••» dt '
Определение 1. Производной от матрицы A (t) называет-
dA (t)
ся матрица, обозначим ее через —-—¦, члены которой являются
производными от членов матрицы A (t), т. е.
dA(t)
dt '
datl
dt
da21
dt
dami
da12
dt "
da22
dt "
dam2
daln
1 ' dt
da2n
" dt
damn
dt dt
dt
C)
Заметим, что такое определение производной от матрицы по-
получается естественным путем, если наряду с введенными опера-
операциями вычитания матриц и умножения на число (см. § 4) при-
присоединить операцию предельного перехода:
щ
At
Символически коротко равенство C) можно записать так:
Определение 2. Интегралом от матрицы A (t) называется
матрица, обозначим ее через
t
\A(z)dz,
и
члены которой равны интегралам от членов данной матрицы:
t t
а1г (z)dz ... \ а1п (г) dz
t t
\an{z)dz ... \ain{z)dz
и t*
i t
]aml{z)dz ... \ama{z)dz
E)

5 171 МАТРИЧНАЯ ЗАПИСЬ СИСТЕМЫ
более кратко:
539
F)
§ 17, Матричная запись системы дифференциальных уравнений
и решений системы дифференциальных уравнений
с постоянными коэффициентами
Рассмотрим систему п линейных дифференциальных уравнений
€ п искомыми функциями x1{t)y x2(t)> ...yxn{t):
-j- — ciux1 -f- ct12x2 + •. •
A)
dxn
Коэффициенты at/—постоянные. Введем обозначение:
(О
B)
Это матрица решений или векторное решение системы A). Далее,
определим матрицу производных от решений:
dX
1Г
ЧГ
dx2
dt
dt
C)
Выпишем матрицу коэффициентов системы дифференциальных
уравнений
Я22
D)
Пользуясь прашлом умножения матриц (см. § 4), систему диф-
дифференциальных уравнений A) можно в матричной форме записать

540
так:
dxx 1
dt
dx2
dt
dxn
dt
=
МАТРИЦЫ
«ii «12 • • • «in
«21 «22 • • • «2/2
•
*1
*2
x,
[ГЛ. XXI
E)
или коротко на основании правила дифференцирования матриц
Пусть
G)
где а; — некоторые числа.
Совокупность решений системы дифференциальных уравнений
будем искать в форме (см. формулы B) § 30 гл. XIII)
Х=е**а. (8)
Подставляя (8) в F) и пользуясь правилом умножения матрицы
на число и правилом дифференцирования матриц, получаем
keMa=Ae^a9 (9)
откуда
ka=Aa, A0)
или
Аа—&а = 0.
Напомним, что в последнем равенстве А—матрица D), k—число,
а—столбцевая матрица G). Матрицу, стоящую в левой части
равенства A0), можно записать так:
(A—kE)a = 0, (И)
где Е—единичная матрица л-го порядка. В развернутом виде
равенство A1) перепишется так:
а12
«22
аЛ
_ Л
/10\
ап2 ... апп—k
Равенство A1) показывает, что вектор а с помощью матрицы А
преобразуется в параллельный ему вектор ka. Следовательно,
вектор а является собственным вектором матрицы Л, соответст-
соответствующий собственному значению k (см. § 11).

МАТРИЧНАЯ ЗАПИСЬ СИСТЕМЫ
541
В скалярной форме равенство A0) записывается как система
алгебраических уравнений (см. систему C) § 30 гл. XIII). Число k
должно определяться из уравнения E) § 30 гл. XIII, которое
в матричной форме можно записать так:
А (Л—Л?) = 0, A3)
т. е. определитель
ац—k ai2 ... ain
1 Я22—k ... a2n
_g
an2 ... ann—k
Пусть все корни уравнения A4) различны:
ь ь ь
Для каждого значения ?,. из системы A1) определяется матрица
значений а
(одно из этих значений произвольное). Решение системы A)
в матричной форме, следовательно, запишется так:
ч
B)
C2ek*
A5)
где Сi—произвольные постоянные.
В скалярной форме решения даются формулами F) § 30 гл. XIII.
Пример 1. Записать в матричной форме систему и решение системы
линейных дифференциальных уравнений
——-=2х\-\-2х2, jj =z %i Ч-Зл^.
at at
Решение. Напишем матрицу системы
'12 211
з|г
В матричной форме система уравнений запишется так (см. уравнение E)):
dXt
dt
dx2
'dt
2 2
1 3
п
IU2I
Составим характеристическое уравнение A4) и найдем его корни:
—/г 2
1 3—k
=0, т. е. ?2—56+4 = 0,

542
МАТРИЦЫ
[ГЛ. XXI
?\
следовательно, &i=l, k2 = 4. Составляем систему A2) для определения зна-
значений ai1*, оса0 для корня ^х=1:
B- \)а?}+ 2^2^ = 0,
Полагая ai1}=l, получаем а"^—-1/2.
Аналогичным образом находим ai2) и а?\ соответствующие корню &2 —4.
Получаем ai2)=l, а22>=1. Теперь можем написать решение системы в мат-
матричной форме (формула A5))
или в обычной форме
Пример 2. Записать в матричной форме систему и решение системы
дифференциальных уравнений
dx-i dx» dx$
dt dt dt
Решение. Напишем матрицу системы
II 0 0||
1 2 0 .
1 1 3||
Следовательно, в матричной форме система уравнений записывается так
(см. уравнение E)):
dt
dx^
dt
I1 0 1II I хг ||
1 2 0 . лг2 .
Составим характеристическое уравнение A4) и найдем его корни;
1—& 0 0
1 2—k О
1 1 3—k
= 1, т.е. A-*) B—*) C—*) = <),
следовательно,
Определим aiT), aiJ), a^, соответствующие корню ^i= 1 э из системы урав-
уравнений A2):
находим
Определим a(i\ a{?\ a(?\ соответствующие корню k2 = 2t из системы
находим

§18] МАТРИЧНАЯ ЗАПИСЬ ЛИНЕЙНОГО УРАВНЕНИЯ п-ТО ПОРЯДКА 543
Определяем ai3), аг3>, аC3), соответствующие корню ?3 = 3, из системы
-2а?> = 0> af-ai3) = 0, a
находим
Напишем в матричной форме решение системы (см. формулу A5))
I*1! II 1 ° °1 \\Ciei II
*,|=|-i 1 о
Хъ | | о —1 11
или в обычной форме
§ 18. Матричная запись линейного уравнения я-го порядка
Пусть имеем линейное дифференциальное уравнение n-го по-
порядка с постоянными коэффициентами
(о
Заметим, что из дальнейшего изложения будет следовать, что
такая нумерация коэффициентов удобна. Обозначим x = xt и,
далее,
~~v "ЗГ = ^ Т^' B)
dt
dXn — п 1
ЧГ"а^
Напишем матрицу коэффициентов этой системы
О 1 0 о ... о
оо 1 о ... о
C)
0 0 0 0 ... 1
аг а2 а3 а4 ••• ал
Тогда систему B), аналогично формуле E) § 17, можно запи-
записать так:
или коротко
dxx
ЧГ
dx2
dt
dxn-i
dt
dxn
dt
=
0 1 0
0 0 1
о
о
0 0 0
a± a2 a3
1
х2
хп-1
D)
— — AX
dt -лл-
E)

544 МАТРИЦЫ 1ГЛ. XX!
Дальнейшее решение проводится так же, как это было в § 17,
так как матричное уравнение E) является частным случаем урав-
уравнения F) § 17.
Пример. Записать в матричной форме уравнение
d4 dx .
Решение. Обозначим х = х±. Далее
dxt dx2
В матричной форме система уравнений запишется так:
dt
dx2
dt
llhl
Я Р\\ 11*2 I
§ 19. Решение систем линейных дифференциальных уравнений
с переменными коэффициентами методом последовательных
приближений с использованием матричной записи
Пусть требуется найти решение системы линейных дифферен-
дифференциальных уравнений с переменными коэффициентами
^ = alx (t) х± + ai2 (t)x2+...+ aln (t) xn,
^ = a21 (t) Xi + a22 (t)x2+...+ a2n (t) xny
удовлетворяющие начальным условиям
Хг = Xf0> Х2 = ^20» • • •» хп== Хп0 ПРИ t == ^о- B)
Если ввести в рассмотрение, наряду с матрицей коэффициен-
коэффициентов системы и матрицей решений, матрицу начальных значений
#20
то систему уравнений A) с начальными условиями B) запишем так:
ТГ D)
при начальных условиях
Х = Х0 при t = t0. E)
Здесь A(t)—снова матрица коэффициентов системы.

§191 ' МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ 545
Будем решать задачу методом последовательных приближений.
Для лучшего понимания дальнейшего материала применим
метод последовательных приближений сначала для одного линей-
линейного уравнения первого порядка (см. гл. XVI, § 26).
Требуется найти решение одного уравнения
при начальном условии
х = х0 при t = t0. G)
Будем предполагать, что a (t)—непрерывная функция.
Как указывалось в § 26 гл. XVI, решение дифференциального
уравнения F) при начальном условии G) сводится к решению
интегрального уравнения
x = xQ + \a(z)x(z)dz. (8)
to
Будем решать это уравнение методом последовательных при-
приближений:
to
t
W
Вводят для сокращения письма оператор S—оператор инте-
интегрирования
S( )=S( )dz. A0)
Используя оператор S, равенства (9) записывают так:
= x0+S (a (x, + S (ax,))),
(a (x0 + S (

546 МАТРИЦЫ [ГЛ. XXI
Раскрывая скобки, получаем:
Х/я = х0+Sax0 + Set Sax0 + Sa Sa Sax0 + .. .+SaSaSa.. .SaxQ.
m раз
Вынося х0 за скобки (х0—постоянная), получаем
xm = [l+Sa + SaSa+...+SaSa...Sa]xu. A1)
m раз
Выше (в § 26 гл. XVI) было доказано, что если a(t)—непре-
a(t)—непрерывная функция, то последовательность {хт\ сходится. Предел
этой последовательности есть сходящийся ряд:
..]*.. A2)
Замечание. Если a(t) = const, то формула A2) принимает
простой вид. Действительно, на основании A0) можем написать
Sa = aS\=a(t—t0),
Sa Sa = a'S (t—f,) = a2 (t~^ ,
SaSa...Sa = a>»-?=^
ml
m раз
В этом случае A2) принимает вид
ИЛИ
х = х6еа ('-'•>. A3)
Рассмотренный метод решения одного уравнения F) целиком пере-
переносится на решение системы A) при начальных условиях B).
В матричной форме система A) с начальными условиями B)
запишется так:
4г (Н)
при начальном условии
Х=Х0 при t = t0. A5)
Используя правило умножения матриц и интегрирования мат-
матриц, решение системы A4) при условии A5) сводится к решению
матричного интегрального уравнения
t
X{t) = Хо + J А (г) X (г) dz. A6)

§ 19] МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ 54/
Находим последовательные приближения
t
Хт @ = Хо + j А (г) Хт_г (z) dz. A7)
и
Путем последовательной подстановки последовательных прибли-
приближений под интеграл решение системы в матричной форме выра-
выразится так:
A (z1)(x0+ J А Ы(хй+ { Л (z3)(...)...
A (z1)(x0+ J А Ы(хй+
ИЛИ
t t zt
X(t) = XQ+ I A(z1)XQdz1+ S A (zj J А (г1Х&&г+ ... A8)
t0 to to
Используя оператор интегрирования S, равенства A8) можно
написать так:
X(i) = [E + SA + SASA+ .. .]ДГв. A9)
Оператор, стоящий в квадратных скобках, обозначают одной
буквой. Обозначим его через <?>^К Равенство A9) коротко запи-
записывают так:
X(t) = Sf(lXa. B0)
Интересно отметить следующее обстоятельство. Если коэффи-
коэффициенты системы A) постоянные, то, пользуясь правилом вынесе-
вынесения за знак матрицы общего множителя всех членов матрицы *),
можем написать
SASA = (*~^оJ А\
SASAS A = ^=^3 Л3 и т. д.
Формула A9) в случае постоянных коэффициентов примет вид
t. B1)
Последнее равенство символически записывают так:
4*-Ч>АХп. B2)
*) Мы оставляем без обсуждения вопрос о предельном переходе для опе-
операций над матрицами.

548
МАТРИЦЫ
[ГЛ. XXI
Упражнения к главе XXI
1. Для линейного преобразования t/i — 3x
рицу обратного преобразования. Отв. *г~~
— / о
2 = 7xt+5x2 найти мат-
мат2. Найти матрицу обратного преобразования
Отв.
II
-1 1
i—х2,
3. Найти произведение матриц
111 2 3
4. Даны матрицы А— 2 0 1
1 211 112 О
. Отв.
8 —2
18 -4
3 4| ||3 -
150 71!
1 23 . Найти матрицы АВ и
-1 0 2
II3 -1 1
14 4 191| || 26 3 2211
9 0 16 и 14 —1 81.
13 —2 201| || 5—4 — if
II 2 311
5 7 10 , Е—единичная матрица 3-го порядка. Определить
4 3 1||
13 2 3
5 9 10
4 3 3
11 2II !!
о л\\. Найти матрицу А2. Отв.
* 4И II
7. Пусть Л=||д ^1. Найти Л2+5Л. Отв.
1 1 1
8. Для матрицы А = 5 4 3
110 5 1
9. Решение системы уравнений
Ц
7 10 J
15 22
п ~~4
4
найти обратную. Отв. —25 9 — 2 .
15 -5 1
записать в матричной форме и найти
Отв. 1х2 = — 1 0 1 20 , .
10. Решение системы уравнений
x2,
—60.
10^ + 5*2+ лг3= 11,5
записать в матричной форме и найти х±у х2) х3.
0Ш.Ш
11
25
15
-4
9
—5
1||
—2 •
1
3 |
11
11,5

УПРАЖНЕНИЯ К ГЛАВЕ XXI 549
11. Найти собственные значения и собственные векторы матрицы
II 2—411
2 —2 —21.
-4 -2 11
Отв. &i = 6, ?2 = &з = — 3; т± = т1-\—^ mj—mk, т2—любой вектор, удов-
удовлетворяющий условию Т!Т2 = 0, т—произвольное число.
<п ТТ , м I! cos a sin а II л тт
12. Найти собственные векторы матрицы . . Отв. Не сущест-
существуют.
14 0 011
0 4 0 . Отв. Все векторы соб-
0 0 4||
ственные.
14. Решить матричным способом систему линейных дифференциальных
уравнений
d ^
dt
Отв. jci=

ПРИЛОЖЕНИЯ
Таблица I
Значения функции
X
2 Л
:7*Т
ё~~г* dt и приведенной функции Лапласа
Ф(х)
Ф(х)
Ф(х)
Ф(х)
0,00
0,05
0,Ш
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
1,00
1,05
1,10
1,15
1,20
1,25
1,30
1,35
0,0000
0,0564
0,П25
0,1680
0,2227
0,2763
0,3286
0,3794
0,4284
0,4755
0,5205
0,5633
0,6039
0,6420
0,6778
0,7112
0,7421
0,7707
0,7969
0,8209
0,8427
0,8624
0,8802
0,8961
0,9103
0,9229
0,9340
0,9438
564
561
555
547
536
523
508
490
471
450
428
406
381
358
334
309
286
262
240
218
197
178
159
142
126
111
98
85
0,0000
0,0269
0,0538
0,0806
0,1073
0,1339
0,1604
0,1866
0,2127
0,2385
0,2641
0,2893
0,3143
0,3389
0,3632
0,3870
0,4105
0,4336
0,4562
0,4783
0,5000
0,5212
0,5419
0,5620
0,5817
0,6008
0,6194
0,6375
269
269
268
267
266
265
262
261
258
256
252
250
246
243
238
235
231
226
221
217
212
207
201
197
191
186
181
175
1,40
1,45
1,50
1,55
1,60
1,65
1,70
1,75
1,80
1,85
1,90
1,95
2,00
2,05
2,10
2,15
2,20
2,25
2,30
2,35
2,40
2,45
2,50
2,55
2,60
2,65
2,70
2,75
0,9523
0,9597
0,9661
0,9716
0,9736
0,9804
0,9838
0,9867
0,9891
0,9911
0,9928
0,9942
0,9953
0,9963
0,9970
0,9976
0,9981
0,9985
0,9988
0,9991
0,9993
0,9995
0,9996
0,9997
0,9998
0,9998
0,9999
0,9999
74
64
55
47
41
34
29
24
20
17
14
11
10
7
6
5
4
3
3
2
2
1
1
1
О
1
О
о
0,6550
0,6719
0,6883
0,7042
0,7195
0,7342
0,7485
0,7621
0,7753
0,7879
0,8000
0,8116
0,8227
0,8332
0,8434
0,8530
0,8622
0,8709
0,8792
0,8871
0,8945
0,9016
0,9082
0,9146
0,9205
0,9261
0,9314
0,9364
169
164
159
153
147
143
136
132
126
121
116
111
105
102
96
92
87
83
79
74
71
66
64
59
56
53
50
46

ПРИЛОЖЕНИЯ
551
X
2,80
2,85
2,90
2,95
3,00
3,05
3,10
3,15
3,20
3,25
3,30
3,35
3,40
3,50
3,60
3,70
3,80
Ф<*)
0,9999
1,0000
А
i
1
Ф(х)
0,9410
0,9454
0,9495
0,9534
0,9570
0,9603
0,9635
0,9664
0,9691
0,9716
0,9740
0,9761
0,9782
0,9818
0,9848
0,9874
0,9896
л
АЛ
44
Л 1
41
QO
оУ
36
33
32
оо
zy
97
Z/
25
ОА
z4
91
Z1
91
ZI
36
30
26
99
19
X
3,90
4,00
4,10
4,20
4,30
4,40
4,50
4,60
4,70
4,80
4,90
5,00
5,10
5,20
5,30
5,40
Табл
Ф(Х)
ица
А
1 (продолжение)
Ф(х)
0,9915
0,9930
0,9943
0,9954
0,9963
0,9970
0,9976
0,9981
0,9985
0,9988
0,9991
0,9993
0,9994
0,9996
0,9997
0,9997
А
1 К
10
1 О
1о
1 1
11
9
7
6
о
л
4
о
О
г\
3
2
f
1
п
JL
I
1
и
Таблица 2
Значения функции /(х) = "^—*
X
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
fix)
0,3989
0,3984
0,3970
0,3945
0,3910
0,3867
0,3814
0,3752
0,3683
0,3605
0,3521
0,3429
0,3332
0,3230
0,3123
0,3011
0,2897
0,2780
0,2661
0,2541
X
,00
,05
,10
1,15
1,20
1,25
1,30
,35
1,40
1,45
1,50
1,55
1,60
1,65
1,70
1,75
1,80
1,85
1,90
1,95
0,2420
0,2299
0,2179
0,2059
0,1942
0,1826
0,1714
0,1604
0,1497
0,1394
0,1295
0,1200
0,1109
0,1023
0,0940
0,0863
0,0790
0,0721
0,0656
0,0596
X
2,00
2,05
2,10
2,15
2,20
2,25
2,30
2,35
2,40
2,45
2,50
2,55
2,60
2,65
2,70
2,75
2,80
2,85
2,90
2,95
fix)
0,0540
0,0488
0,0440
0,0396
0,0355
0,0317
0,0283
0,0252
0,0224
0,0198
0,0175
0,0154
0,0136
0,0119
0,0104
0,0091
0,0079
0,0069
0,0060
0,0051

552
ПРИЛОЖЕНИЯ
Таблица 2 (проволокенш)
X
3,00
3,05
3,10
3,15
3,20
3,25
3,30
fix)
0,0044
0,0038
0,0033
0,0028
0,0024
0,0020
0,0017
X
3,35
3,40
3,45
3,50
3,55
3,60
3,65
fix)
0,0015
0,0012
0,0010
0,0009
0,0007
0,0006
0,0005
X
3,70
3,75
3,80
3,85
3,90
3,95
4,00
fix)
0,0004
0,0004
0,0003
0,0002
0,0002
0,0002
0,0001
Таблица 3
Значения функции Ф (х) = ,— \ е 2 dz
X
0,00
0,01
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
Ф (х) х
0,0000
0,0040
0,0199
0,0398
0,0596
0,0793
0,0987
0,1179
0,1368
0,1554
0,1736
0,1915
0,2088
0,2257
0,2422
0,2580
0,2734
0,2881
0,3023
0,3159
0,95
1,00
1,05
1,10
1,15
1,20
1,25
1,30
1,35
1,40
1,45
1,50
1,55
1,60
1,65
1,70
1,75
1,80
1,85
Ф(х)
0,3289
0,3413
0,3531
0,3643
0,3749
0,3849
0,3944
0,4032
0,4115
0,4192
0,4265
0,4332
0,4394
0,4452
0,4505
0,4554
0,4599
0,4641
0,4678
X
1,90
2,00
2,10
2,20
2,30
2,40
2,50
2,60
2,70
2,80
2,90
3,00
3,20
3,40
3,60
3,80
4,00
4,50
5,00
Ф(*)
0,4713
0,4772
0,4821
0,4861
0,4893
0,4918
0,4938
0,4953
0,4965
0,4974
0,4981
0,49865
0,49931
0,49966
0,499841
0,499927
0,499968
0,499997
0,500000

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Амплитуда колебаний 97
— комплексная 98, 348, 354
Анализ гармонический 345
Вектор линейного преобразования соб-
собственный 529
— матрицы собственный 529
— пространства Ф 360
Векторы базисные 525
— ортогональные 358
Величина случайная двумерная 487
дискретная 449
непрерывная 465
равномерно распределенная 469
центрированная 459
Вероятность 435, 436
— геометрическая 441
— относительной частоты при повтор-
повторных испытаниях 453
— попадания двумерной случайной ве-
величины в эллипс рассеивания 494
случайной величины в заданный
интервал 466, 479
— условная 443—445
Вихрь 231
Вронскиан 69
Вычисление двойного интеграла 160
— значений sin x приближенное 283
— интеграла Пуассона 172—174
— коэффициентов тригонометрическо-
тригонометрического ряда 319, 321
— криволинейного интеграла 213
— логарифмов приближенное 288
— массы фигуры 189
— объема тела 161, 166, 195
— определенных интегралов с помо-
помощью рядов 290—292
— площади плоской области 167
поверхности 181
— поверхностного интеграла 227
— работы 209, 216
— тройного интеграла 194
— числа я 288
Вычитание сходящихся рядов почлен-
почленное 248
Гармоника 348
Гипотеза 446
Гистограмма 497
Градиент скалярной функции 236
Группа событий полная 436
Группировка 497
Движение стационарное 51
— установившееся 51
Дельта-функция 429
Диаметр области 190
— площадки 153
Дивергенция вектора 235
Дисперсия 460
— непрерывной случайной величины
473
— нормально распределенной слу-
случайной величины 476
— статистическая 500, 502
Дифференцирование изображения 407
— степенного ряда 279
— функциональных рядов почленное
273
Длина вектора 359
Дополнение алгебраическое 512
Жесткость рессоры 94
Задача Дирихле 385, 387
— Дирихле — Неймана 387
— краевая вторая 385
для уравнения Лапласа 385
первая 373, 385
для уравнения теплопровод-
теплопроводности 377
— Неймана 385, 387
— о второй космической скорости 64
математическом маятнике 62
распаде радия 23
стрельбе до первого попадания
450
— об электрических колебаниях в
проводах 367
Закон больших чисел 504
— Гаусса 474

554
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Закон Кулона 228
— равномерной плотности 469
— распределения вероятностей бино-
биномиальный 453
дискретной случайной вели-
величины 449
интегральный 468
нормальный 474
равномерно распределенной слу-
случайной величины 469
случайной величины 449
центрированной случайной вели-
величины 459
Замена переменных в двойном интегра-
интеграле 174—179
тройном интеграле 196—199
Значение интеграла главное 353
— определяемой величины подходящее
499
— собственное 370, 529
Значения наблюденные 496
— функции / (х) 551, 552
Ф (х) 550, 551
ф (х) 552
Ф (х) 550, 551
Изображение 401
— дельта-функции 429
— лапласово 401
— производной 409
— функции с измененным масштабом
независимой переменной 403* 404
Изоклина 21
Интеграл вероятностей 478
— двойной 153
в полярных координатах 170
— двукратный 155
— Дирихле 341
— дифференциального уравнения 17
общий 18
особый 46 '
• частный 18
п-го порядка общий 56
—, зависящий от параметра 201
— криволинейный 209, 211, 212
от полного дифференциала 223
по замкнутому контуру 210
— несобственный кратный 173
— от векторной функции 210
матрицы 538
— поверхностный 225, 226
— Пуассона 172, 383, 394
— трехкратный 191
— тройной 190
в сферических координатах 197,
198
цилиндрических координатах
196
— Фурье 350
Интеграл Фурье в комплексной форме
354
Интегрирование дифференциальных
уравнений с помощью рядов 292—
294
— почленное степенного ряда 279
функционального ряда 272
— уравнений в полных дифференциа-
дифференциалах 35
Интервал сходимости степенного ряда
276
Исследование свободных колебаний
423, 424
Колебание вынужденное 99
— гармоническое 97, 424
— затухающее 99, 424
— свободное 96, 423
Координаты криволинейные 175
в пространстве 198
— сферические 197
— центра масс линии 197
плоской фигуры 188
тела 200
— цилиндрические 196
Корень функции Бесселя 357
— характеристического уравнения 109
Косинус гиперболический комплексной
переменной 302
— комплексной переменной 302
Косинус-преобразование Фурье 351
Косинусы направляющие нормали 226
Коэффициенты биномиальные 287
— степенного ряда 275, 280
— тригонометрического ряда 318
— Фурье 319, 321
комплексные 348
по ортогональной системе функ-
функций 356
Кривая гладкая 67
— интегральная 19, 56, 117
— нормального распределения 474
— распределения 465
вероятностей 465
интегральная 468
— резонанса 101
Круг сходимости 301
Линейность изображения 404
Линия равного потенциала 52
— силовая 53
— тока 52
— цепная 15
— эквипотенциальная 52
Лист декартов 239
Ломаная Эйлера 128
Луч 168
Мажорируемость степенного ряда 278
Масса тела 189

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
555
Материал статистический 496
Матрица 511
— вырожденная 514, 536
— диагональная 512
— единичная 512, 517
— квадратичной формы 535
— квадратная 511
— невырожденная 536
— обратная 513, 519, 521
— ортогональная 527
— отображения 509
— присоединенная 521
— расширенная 537
— симметричная 512
— столбцевая 512
— строчная 512
— транспонированная 512
Матрицы равные 512
Медиана 473, 475
Мера точности 487
Метод Адамса 130
— вариации произвольных постоян-
постоянных 82, 91
— интегрирования дифференциальных
уравнений графический 66
систем дифференциальных урав-
уравнений первого порядка приближен-
приближенный 136
— неопределенных коэффициентов 294
— приближенного решения дифферен-
дифференциальных уравнений разностный 130
— разделения переменных 368
— Фурье решения задач математичес-
математической физики 368
— Эйлера численного решения диффе-
дифференциальных уравнений первого по-
порядка 127
Метрика пространства Ф 360
Минор 536
Многоугольные распределения вероят-
вероятностей 449
Множитель интегрирующий 38
Мода 450, 473, 475
Модуль вектора 359
Момент балки изгибающий 58
— инерции плоской фигуры относи-
относительно оси 185
точки 184
системы точек 184
тела 199
точки 184
— статический 189
— центральный второго порядка 463
первого порядка 463
третьего порядка 463
Набла-оператор 236
Направление интегрирования 209
Направления квадратичной формы
главные 536
Нахождение радиуса сходимости ряда
277
Независимость криволинейного интег-
интеграла от пути интегрирования в прост-
пространстве 232
на плоскости 220
Непрерывность суммы ряда 270
степеннбго ряда 278
Неравенство Бесселя 337
— Буняковского 187
— Шварца 187
Норма элемента 360
Область замкнутая 152
— интегрирования 153
•— правильная 155, 168
в направлении оси Ох 155
Ог/ 155
трехмерная 191
— сходимости ряда 266
степенного ряда с комплексной
переменной 300
Объем тела 161, 166, 195
— эллипсоида 195
Огибающая семейства кривых 40
Ожидание математическое дискретной
случайной величины 456
непрерывной случайной величи-
величины 471
нормально распределенной слу-
случайной величины 475
Оператор Гамильтона 236
— Лапласа 239, 376, 384
Определитель Вронского 69
— матрицы 509, 511
— функциональный 177
Оригинал 401
Оси рассеивания 492
Остаток ряда 267
Отклонение 459
— вероятное 481, 482
радиальное 495
— срединное 481, 482
— среднеквадратичное 460, 461
непрерывной случайной величи-
величины 473
нормально распределенной слу-
случайной величины 476
Отклонения главные вероятные 491
— среднеквадратичные 491
Отображение аффинное 513
— взаимно однозначное 513
— вырожденное 514
— линейное 508
— невырожденное 513
— обратное 513
— однозначное 513

556
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Отражение зеркальное от оси 509
Оценка двукратного интеграла 158
— погрешности приближенного реше-
решения 308
Ошибка изготовления 496
— измерения 496
— срединная 481
— среднеарифметическая 486
Парабола безопасности 43
Период колебаний 97
Плоскость фазовая 117
Плотность вероятности 465
— вещества поверхностная 183
средняя 183
— нормального распределения случай-
случайной величины 474, 476
— распределения вероятностей слу-
случайной величины 465
двумерной случайной величины
488
, нормально распреде-
распределенной 491
— спектральная 354
Площадь плоской области 167, 215, 216
— поверхности 180
— эллипса 216
Поворот 509
Подобие 532
Поле векторное безвихревое 238
потенциальное 237
соленоидальное 238
трубчатое 238
— направлений 20
Понижение порядка дифференциально-
дифференциального уравнения 59, 60
Порядок дифференциального уравне-
уравнения 16
Последовательность функций, ортого-
ортогональная на отрезке 360
Потенциал вектора 222
— поля тяготения 233
— скоростей 52
— стационарного электрического поля
388
Поток вектора через поверхность 236
— векторного поля через поверхность
225
— вихря через поверхность 231
Правило трех сигм 484
Предел последовательности комплекс-
комплексных чисел 299
Преобразование ортогональное 526
— тождественное 518
— Фурье 354
обратное 354
Преобразования координат линейные
508
Приближение в среднем 334
Приближение решения второе 303
нулевое 303
первое 303
Признак Даламбера 252, 253
— Коши 256
— разложимости функции в ряд Фурье
достаточный 321
— сходимости знакопеременного ряда
достаточный 263
ряда интегральный 257, 258
необходимый 248
Прогрессия геометрическая 246
Продолжение функции нечетное 333
четное 333
Произведение матриц 516
— скалярное 358
функций 359
Производная матрицы 538
— слева 343
— справа 343
Пространство евклидово л-мерное 358
— линейное функциональное с квадра-
квадратичной метрикой 360
— функций 359
— Еп 359
— Ф359
Равенство Ляпунова — Парсеваля 337
Радиус сходимости степенного ряда 276
с комплексной перемен-
переменной 301
Разложение в ряд Маклорена arcsin x
288
ch х 285
cos л: 285
е* 284
In A+х) 288
sh х 285
sin x 283
(\+х)т 287
фурье непериодической
функции 332, 333
нечетной функции 329,
330 Y
функции 321
четной функции 330
Разность вторая 130
— второго порядка 130
— матриц 515
— первая 130
— первого порядка 130
Ранг матрицы 536
Распределение двумерной случайной
величины нормальное 491
— температуры в однородном теле ста-
стационарное 384, 385
Распространение тепла в неограничен-
неограниченном стержне 379—384
Рассеивание 496

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
557
Расстояние между элементами прост-
пространства Ф 360
Растяжение 509
— вдоль оси 509
Расходимость ряда 245
Резонанс 103, 427
Решение дифференциального уравне-
уравнения 17
колебаний 421—423
комплексное 98
методом операционного ис-
исчисления 411—413
общее 18
особое 46, 49
частное 18
/i-го порядка общее 56
частное 56
— задачи Дирихле для кольца 390
круга 390—394
методом конечных разностей
394—396
о распространении тепла в неог-
неограниченном стержне 383, 384
— линейного дифференциального урав-
уравнения первого порядка 30
неоднородного дифференциаль-
дифференциального уравнения второго порядка
общее 81
— — с постоянны-
постоянными коэффициентами 85, 86
высшего порядка 91
с постоянными
коэффициентами 92, 93
однородного дифференциально-
дифференциального уравнения с постоянными коэффи-
коэффициентами общее 79
— однородного дифференциального
уравнения первого порядка 26
— первой краевой задачи 377—379
— системы дифференциальных уравне-
уравнений общее ПО
с постоянными коэффи-
коэффициентами матричным методом 539—
541
. 1 устойчивое по Ляпунову
114
линейных дифференциальных
уравнений с переменными коэффици-
коэффициентами матричным методом 544—547
однородных дифференциаль-
дифференциальных уравнений с постоянными коэф-
коэффициентами 108
уравнений матричным мето-
методом 523, 524
— уравнения колебаний в случае ре-
резонанса 426, 427
струны 368—372
Решения линейно зависимые 69
независимые 69
Ротор 231
Ряд абсолютно сходящийся 264
с комплексными членами 301
— биномиальный 287
— гармонический 249
— знакопеременный 263
— знакочередующийся 260
— из комплексных чисел 299
— мажорируемый 267
— Маклорена 283
— неабсолютно сходящийся 264
— простой статистический 497
— равномерно сходящийся 269
— расходящийся 245, 300
— с положительными членами 250
— степенной 275, 280
с комплексной переменной 300
— сходящийся 245, 300
— Тейлора 282
— тригонометрический 318
— условно сходящийся 264
— функциональный 266
— Фурье 321
в комплексной форме 347
для нечетных функций 330
функций с периодом 21 331
четных функций 330
по ортогональной системе функ-
функций 356
— числовой 245
Свертка функций 419
Свертывание функций 419
Свойства абсолютно сходящегося ряда
265
— двойного интеграла 153, 154
— двукратного интеграла 156—159
— криволинейного интеграла 210
— сходящихся рядов 246, 247
— трехкратного интеграла 192, 193
— условно сходящегося ряда 265
Свойство линейности изображения 404
Сдвиг вдоль оси 510
Седло 119
— вырожденное 125
Семейство кривых однопараметричес-
кое 40
— ортогональных траекторий 51
Сетка 394
Синус гиперболический комплексной
переменной 302
— комплексной переменной 301
Синус-преобразование Фурье 352
Система дифференциальных уравнений
автоионная 115
нормальная 103
первого порядка 103
— линейных дифференциальных урав-
уравнений 539, 544

558
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Система однородных дифференциаль-
дифференциальных уравнений с постоянными коэф-
коэффициентами 108
— ортогональных многочленов Ле-
жандра 357
функций полная 301
— функций Бесселя 357
, ортогональная на отрезке 355
полная 356
Складка функций 419
Скорость вращения вектора угловая 97
— распада радия 24
— распространения тепла 372
Сложение вероятностей несовместных
событий 438, 439
совместных событий 440
— сходящихся рядов почленное 247
Случай 436
—, благоприятствующий событию 436
Событие достоверное 437
— невозможное 437
— случайное 434
События зависимые 443
— независимые 441
— несовместные 436
— противоположные 440
— равновозможные 436
— совместные 440
Спектр 348
— дискретный 348
— непрерывный 354
Спираль логарифмическая 55
Сравнение рядов 250, 252
Среднее арифметическое значений слу-
случайной величины 456
— взвешенное 499
Сумма геометрической прогрессии 246
— интегральная 152
— матриц 515
— ряда 245
из комплексных чисел 300
частичная 245
— событий 438
Схема урн 438
Сходимость знакочередующегося ряда
261
— ряда 245, 300
абсолютная 264, 301
равномерная 269
условная 264
Фурье в среднем 356, 361
Таблица изображений 410
Теорема Абеля 275
— Бернулли 435
— гипотез 447
— единственности изображения 402
решения дифференциального
уравнения 308, 309
Теорема живых сил 233
— запаздывания 427
— Лапласа 503
— Лейбница 261
— Ляпунова 501
— о вычислении тройного интеграла
194 F
сложении вероятностей 438
сравнении рядов 250, 252
среднем для двукратного интег-
интеграла 159
трехкратного интеграла
— об оценке трехкратного интеграла
193
— Пеано 308
— разложения 415, 416
— свертывания 418
— смещения 405
— существования двойного интеграла
153
и единственности решения диф-
дифференциального уравнения 304
, „ п~го порядка 55
интеграла по поверхности 225
криволинейного интеграла 211
тройного интеграла 190
— центральная предельная 501
— Чебышева 500, 502
Теория вероятностей 435
Течение жидкости или газа потенци-
потенциальное 385
Точка области внутренняя 154
— обыкновенная 46
— особая 46
для дифференциального уравне-
уравнения 117
— пространства Ф 359, 360
— я-мерного евклидова пространства
358
Траектория дифференциального урав-
уравнения 117
— изогональная 50, 53
— ортогональная 50, 51
Угол между двумя векторами 359
Узел неустойчивый 118, 119
— устойчивый 117, 118
Узлы сетки 394
Уклонение наибольшее 334
— среднеквадратичное 334
Умножение вероятностей зависимых
событий 444
¦ независимых событий 441, 442
— матрицы на число 515
единичную матрицу 518
— сходящегося ряда на постоянный
множитель 247
Уравнение Бернулли 33

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
559
Уравнение Бесселя 295
— в конечных разностях 394
полных дифференциалах 35
— вида yW=:f(x) 56
— волновое 364—366
— вспомогательное 412
— вынужденных колебаний 95
— геометрического места особых точек
— гиперболического типа 364
— дифференциальное 13, 16
в частных производных 13, 16
второго порядка неоднородное
линейное 81
. с постоянными ко-
коэффициентами 84
однородное с постоян-
постоянными коэффициентами 74
высшего порядка неоднородное
линейное 90
изогональных траекторий 54
линейное без правой части 68
неоднородное 68
однородное 68
первого порядка 30
с правой частью 68
п-го порядка 68, 543
механических колебаний 94
обыкновенное 16
ортогональных траекторий 51
первого порядка 17
однородное 25
, приводящееся к однородному 27
с разделенными переменными 22
разделяющимися перемен-
переменными 23
цепной линии 59
д-го порядка 55
линейное однородное с по-
постоянными коэффициентами 79
— изображающее 412
— интегральное 303, 352
— Клеро 47
— колебаний струны 66
— крутильных колебаний стержня 396
— Лагранжа 49
— Лапласа 239, 364, 365, 384
в полярных координатах 389
цилиндрических координа-
координатах 389
на плоскости 355
— неразрывности течения сжимаемой
жидкости 386
— огибающей 40
— параболического типа 364
— продольных колебаний стержня 397
— разностное 394
— распространения тепла 373
в стержне 377
Уравнение распространения тепла
на плоскости 377
— свободных колебаний 95
— телеграфное 367, 368
— теплопроводности 364, 365, 373
в пространстве 376
— Фурье 364
— характеристическое 75, 529
для системы дифференциальных
уравнений 109
— эллиптического типа 364
Уравнения динамики материальной
точки основные 232
Условие граничное 366, 367, 373, 376
— линейной независимости решений
линейного дифференциального урав-
уравнения 71
— Липшица 305
— начальное 18, 373, 376
— независимости криволинейного ин-
интеграла от пути интегрирования на
плоскости 220
— полного дифференциала функции
трех переменных 232
— сходимости ряда с комплексными
членами 300
Условия краевые 367
— начальные 55, 366, 367
— независимости криволинейного ин-
интеграла от пути интегрирования в
пространстве 232
— сходимости ряда Фурье достаточ-
достаточные 343
Устойчивость решений системы диффе-
дифференциальных уравнений 114
Фаза начальная 97
Фокус неустойчивый 121, 122
— устойчивый 120, 121
Форма квадратичная 534
Формула Адамса 133
— Байеса 447
— Грина 219, 242
— Лиувилля 70
— Остроградского 235
— Остроградского — Гаусса 235
— полной вероятности 445
— преобразования координат в двой-
двойном интеграле 177
— Стокса 231
— Тейлора 282
— Эйлера 285, 286
для функций комплексной пере-
переменной 302
Функции линейно зависимые 79
независимые 79
—, ортогональные с весом р (х) 357
Функция абсолютно интегрируемая
349

560
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Функция Бесселя второго рода нуле-
нулевого порядка 299
д-го порядка 298
первого рода д-го порядка 298
р-го порядка 297
— гармоническая 239, 384
— Дирака 428
— единичная импульсная 429
— интегральная нормального закона
распределений 481
распределения вероятностей дву-
двумерной случайной величины 490
— комплексной переменной аналити-
аналитическая 301
показательная 301
— кусочно монотонная 321
непрерывная 338
— Лапласа 480
приведенная 483
— начальная 401
— нечетная 329
— однородная я-го измерения 25
— от случайной величины 463
— распределения вероятностей 468
— собственная 370
— спектральная 354
— Хевисайда единичная 402
— четная 329
— °о W 402
Центр 123
— распределения вероятностей
чайной величины 458, 472
— рассеивания двумерной нормально
распределенной случайной величины
491
Циркуляция вектора 211
Циссоида 145
Частота 434
— колебаний 97
— относительная 434, 451
Часть уравнения правая 68
Числа волновые 348, 354
Член матрицы 511
— ряда 245
Шанс 436
Шкала рассеивания ошибок 485
Элемент пространства Ф 359
— /i-мерного евклидова пространства
358
Эллипс инерции 188
— рассеивания 492
единичный 492
полный 492
Энергия движущейся точки кинетиче-
кинетическая 62
потенциальная 62
Якобиан 177, 198
L-изображение 401
— функции Хевисайда 402
— ch at 406
— cos t 403
слу- — e~at 405
— sh at 406
— sin t 403
— tn 408
у-оператор 236