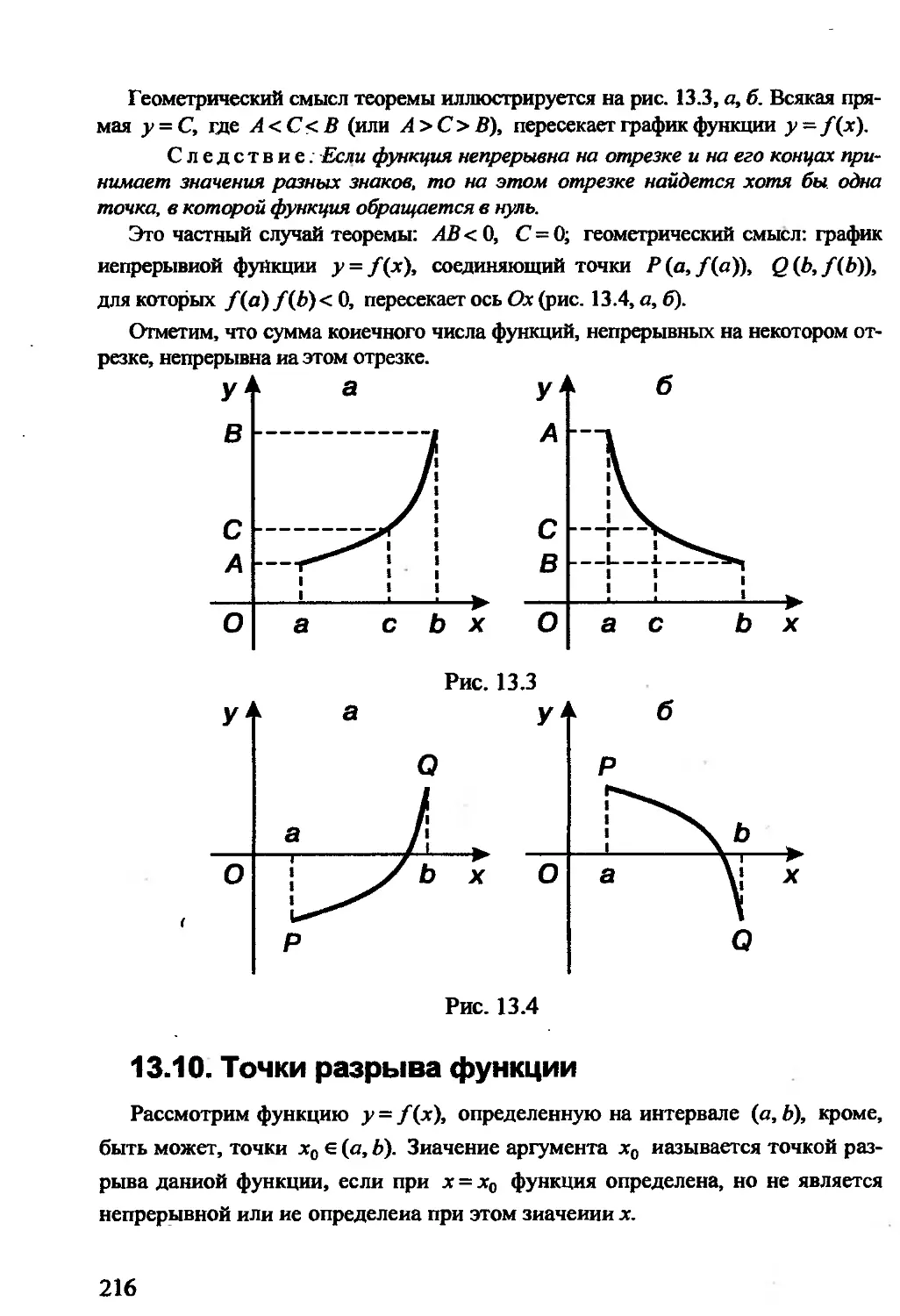
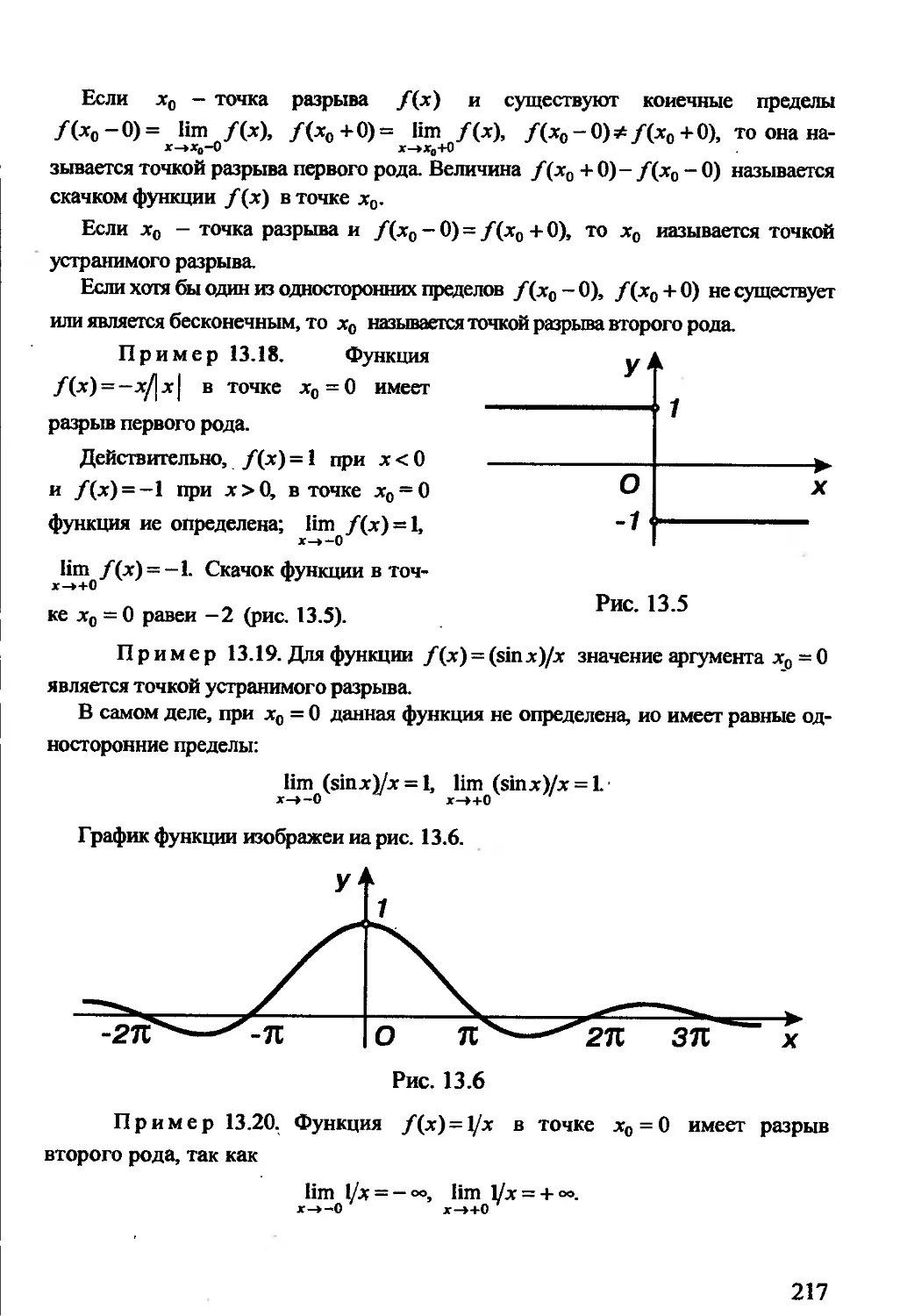
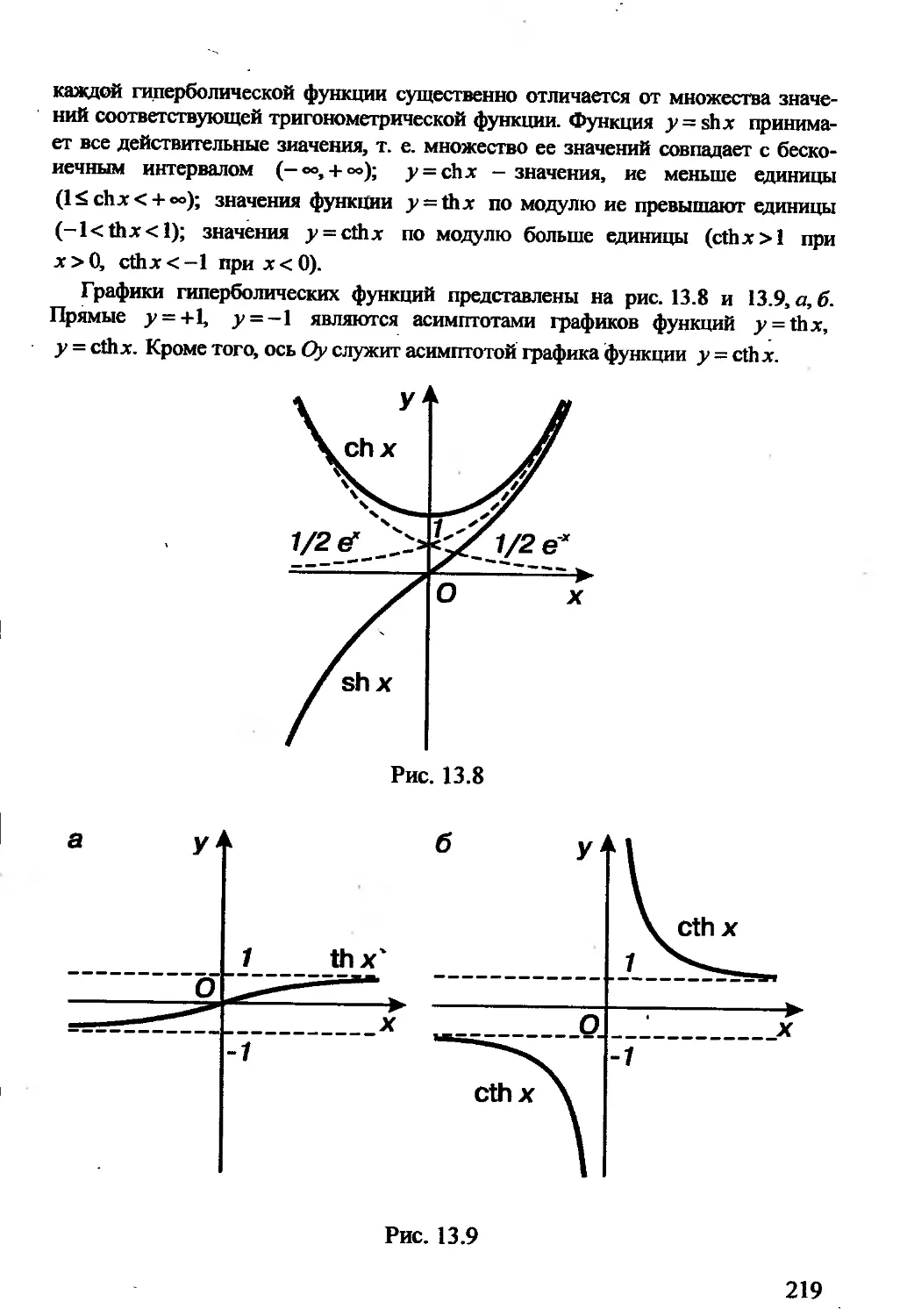
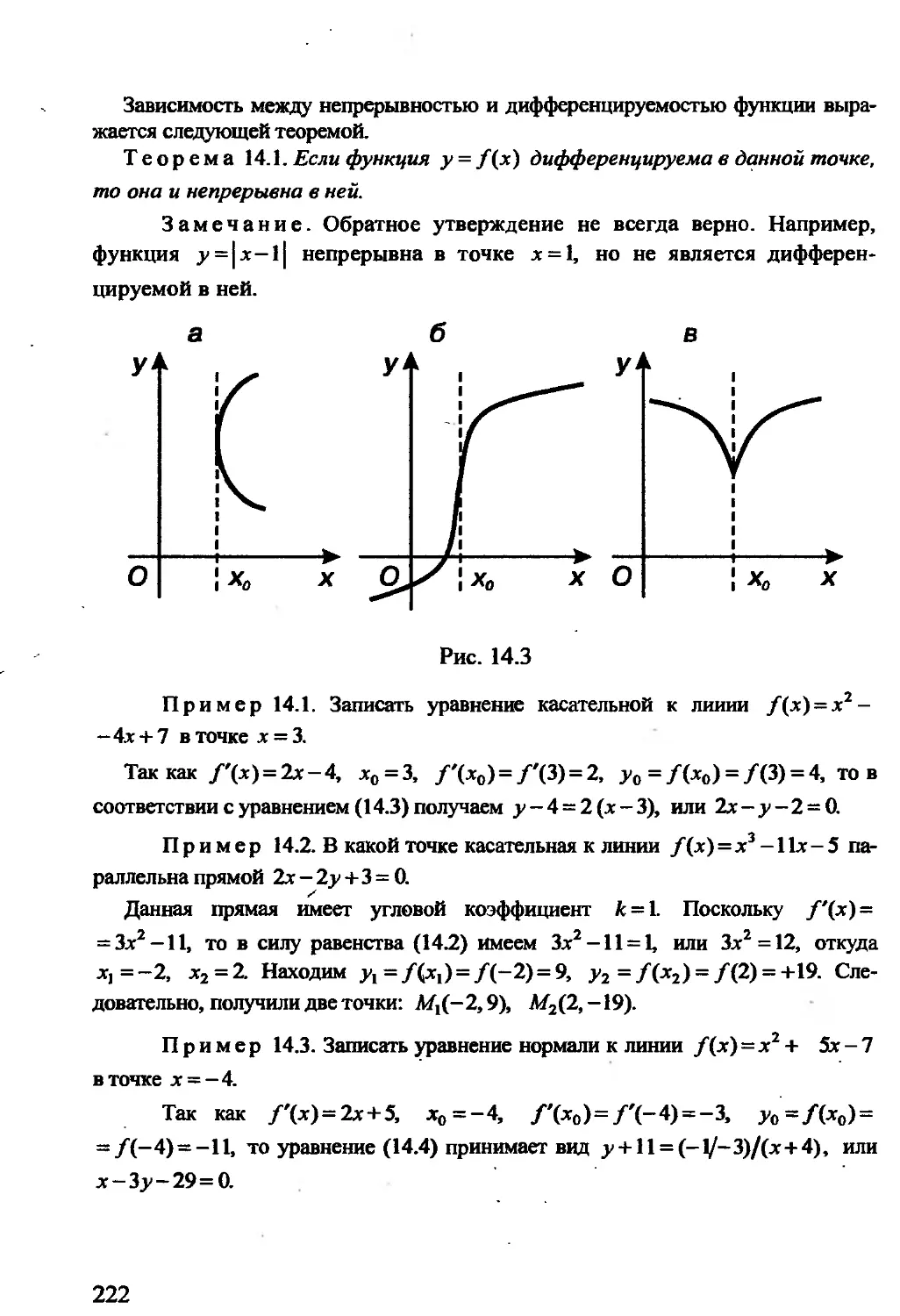
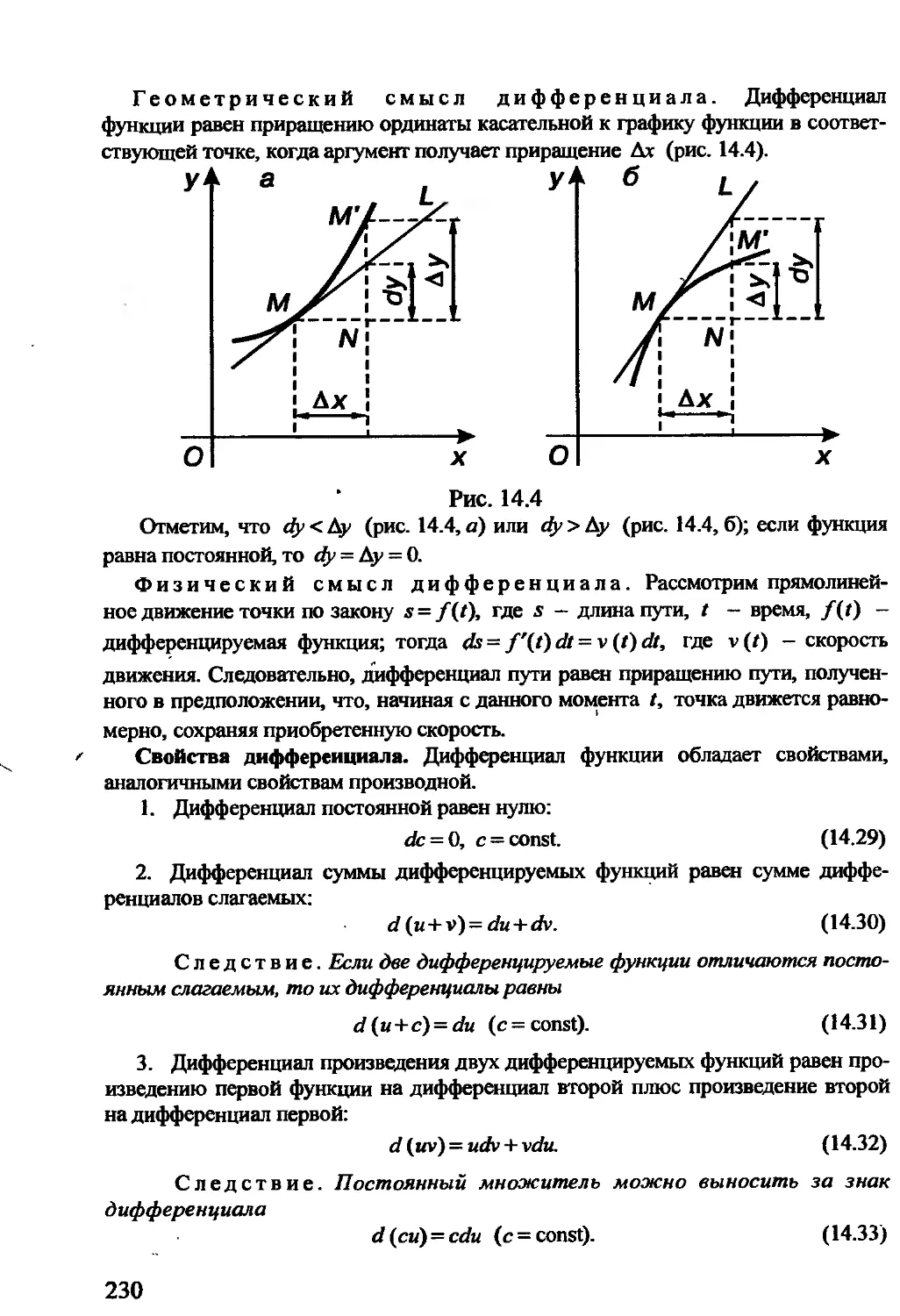
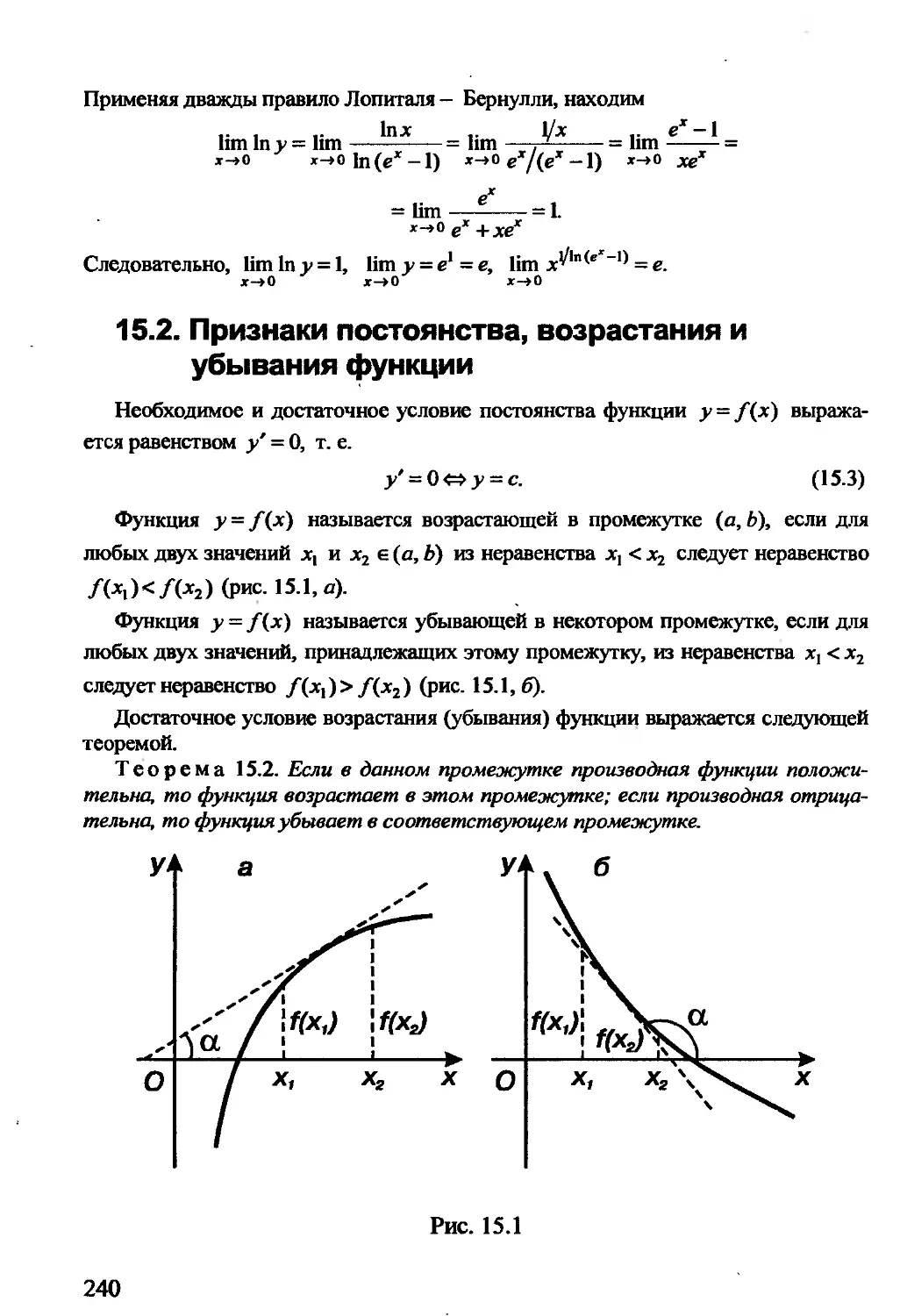
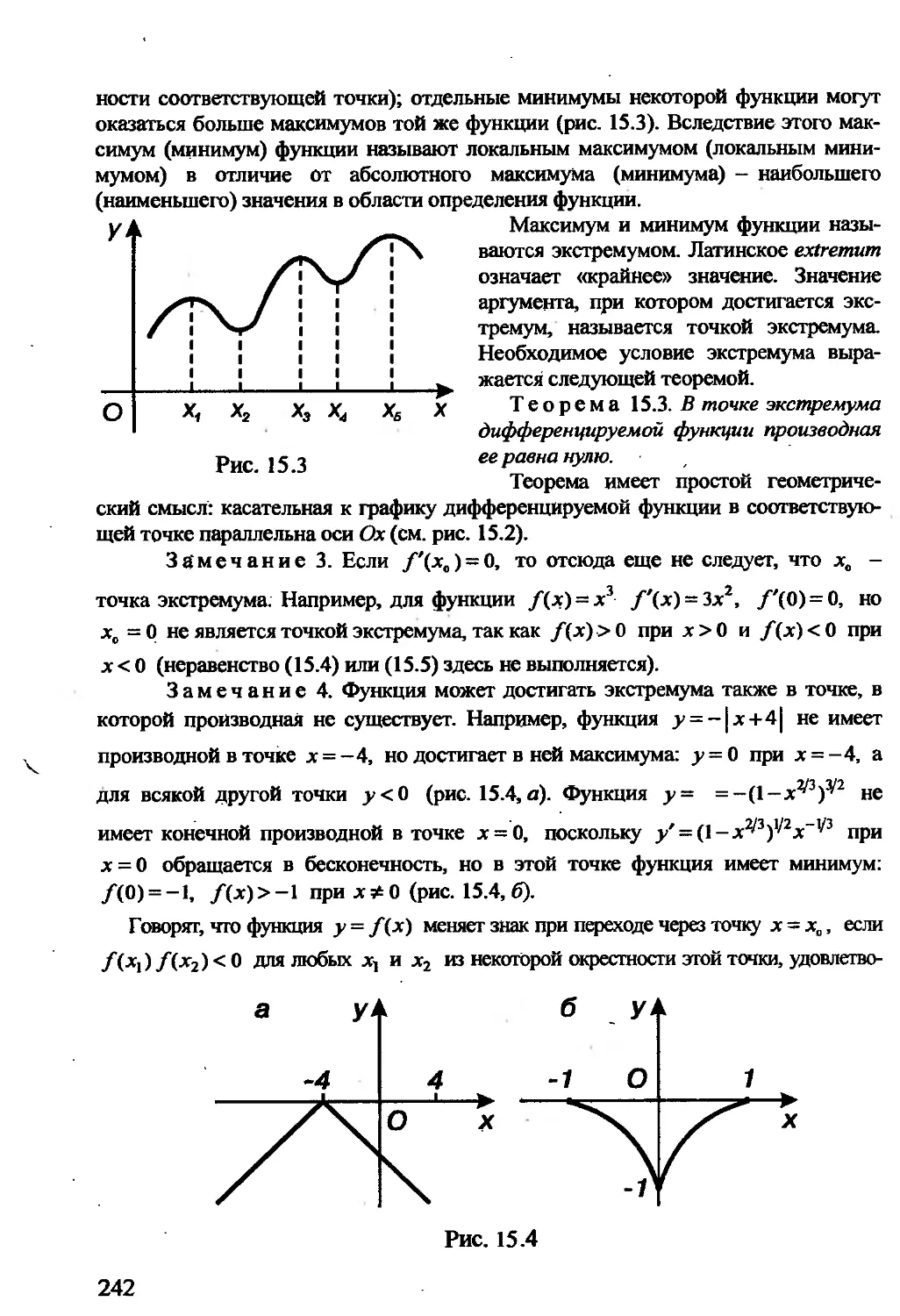
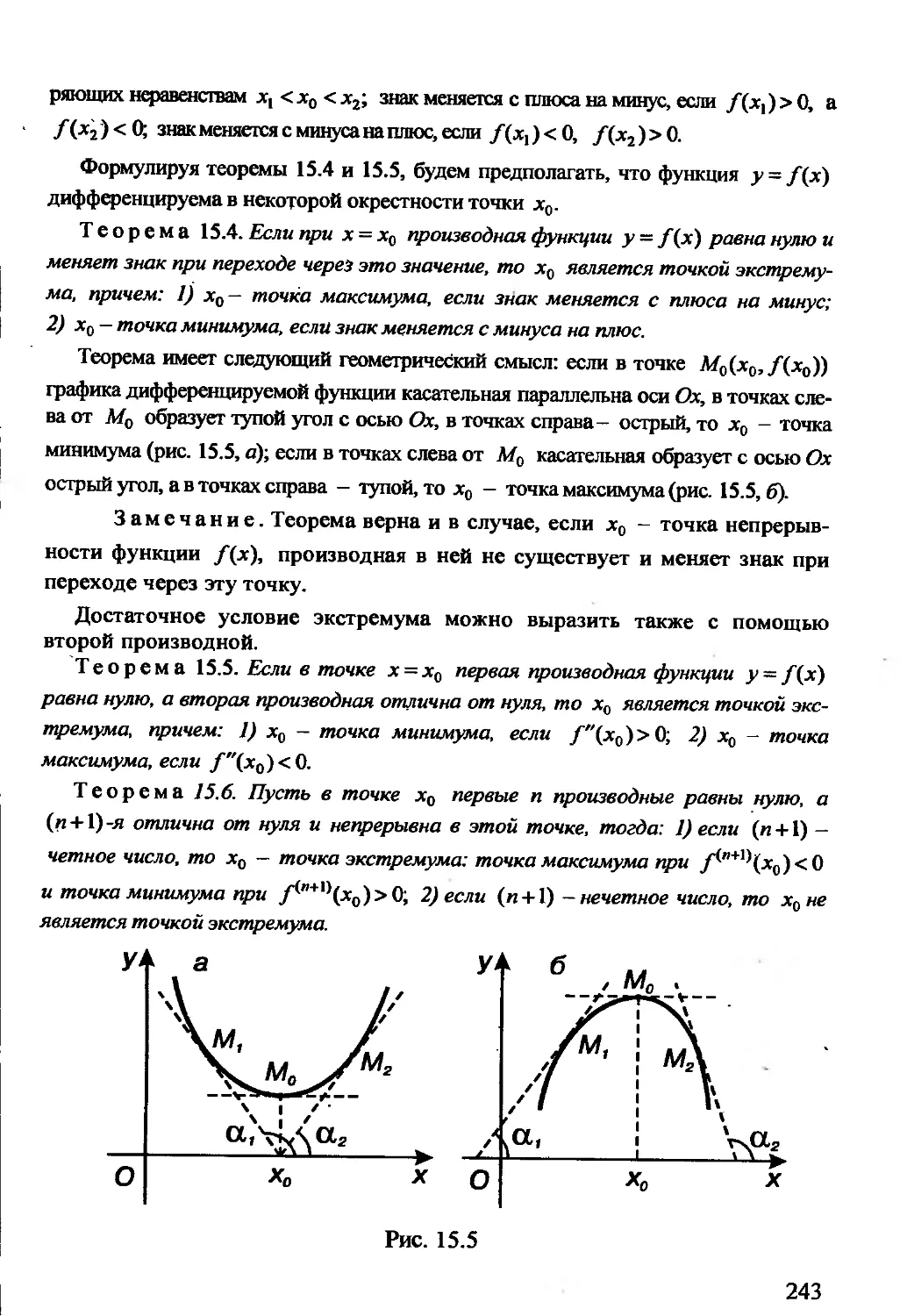
Автор: Гусак А.А. Гусак Г.М. Бричикова Е.А.
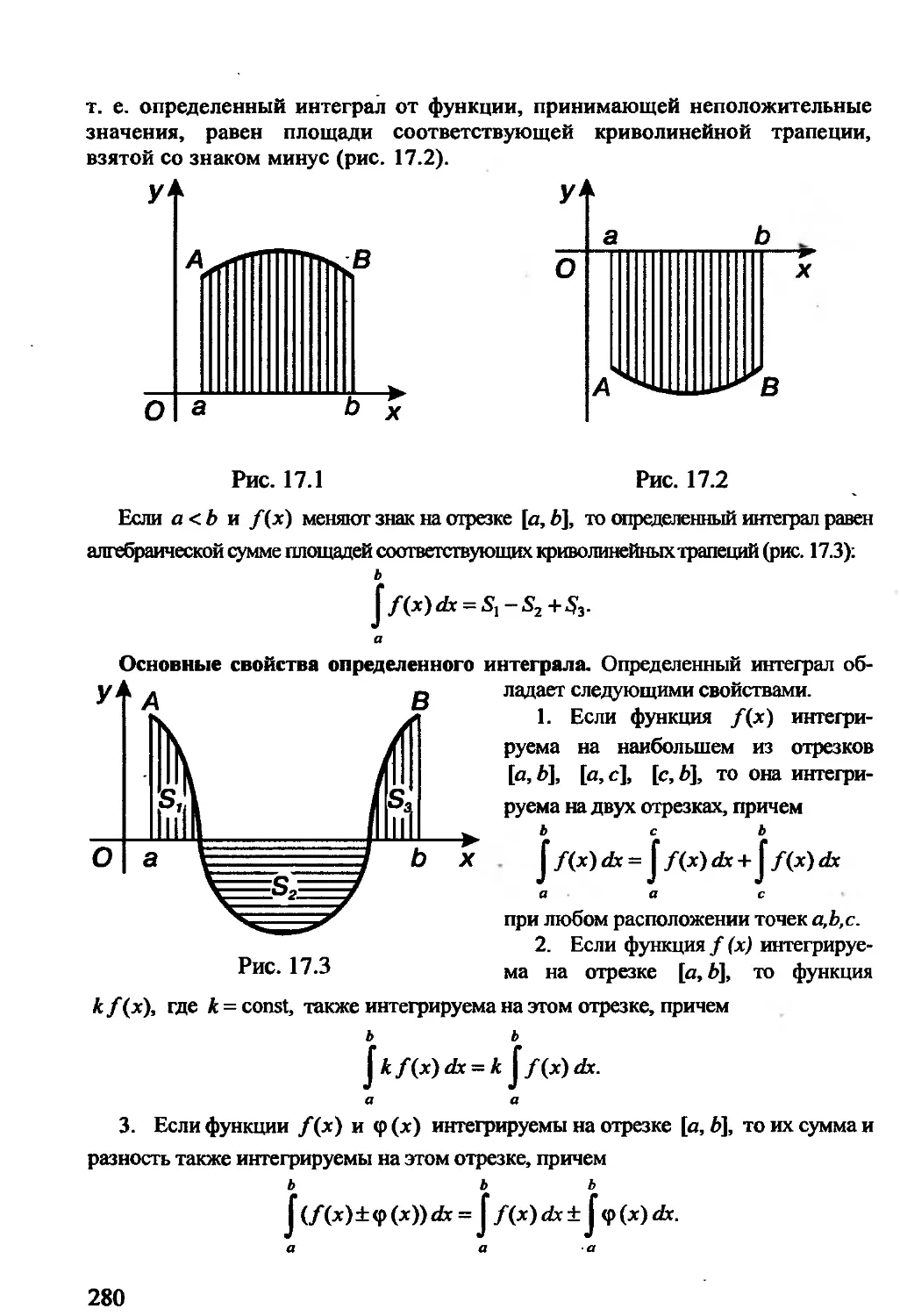
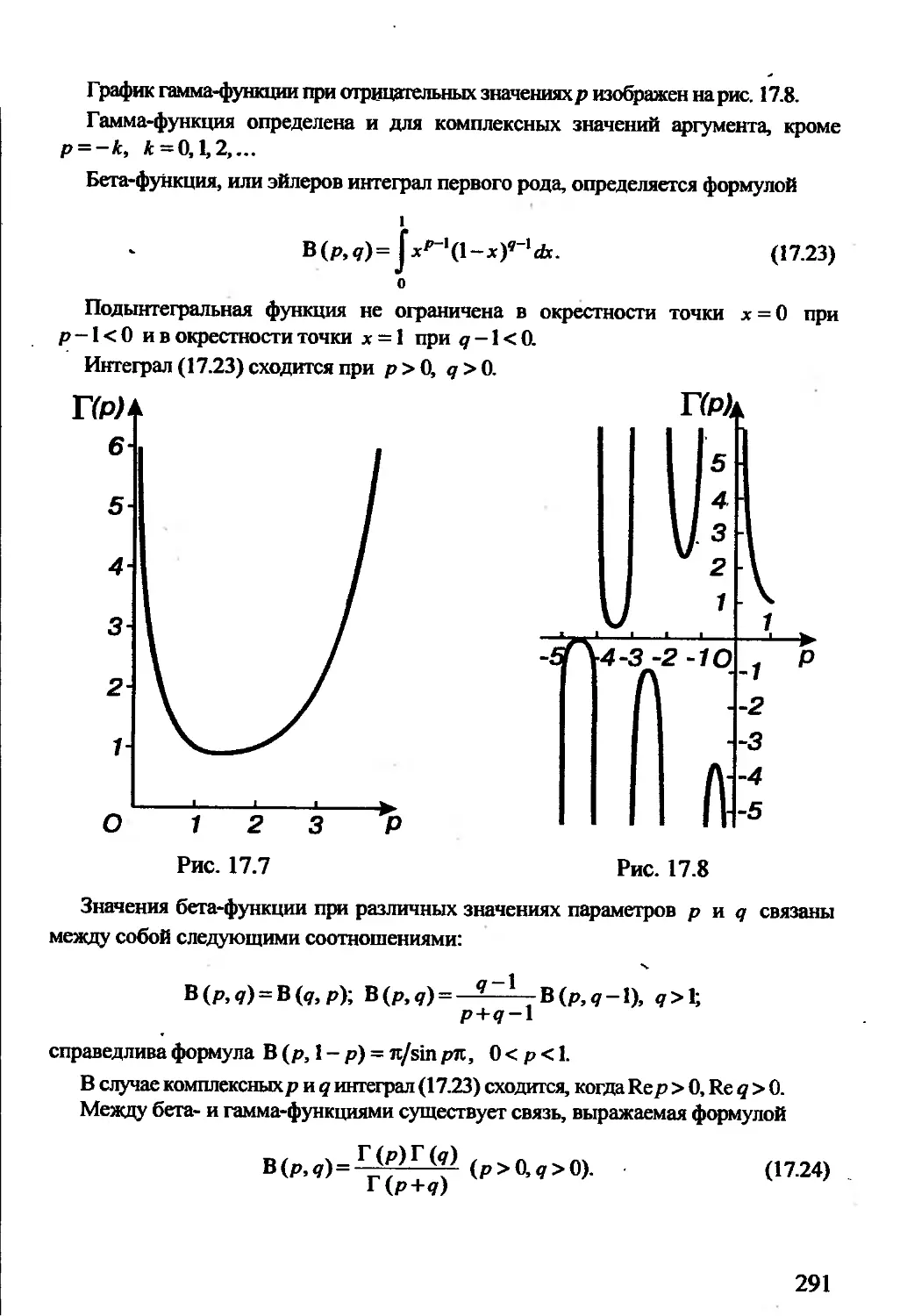
Теги: математика задачи по математике высшая математика издательство террасистемс
ISBN: 985-6317-51-7
Год: 1999
Текст
А.А. Гусак
Г.М. Гусак
Е.А. Бричикова
СПРАВОЧНИК
ПО ВЫСШЕЙ
МАТЕМАТИКЕ
МИНСК
ТетраСистемс
1999
УДК 51(035)
ББК 22.1 я2
Г 96
Авторы:
кандидат физико-математических наук, профессор А.А. Гусак;
кандидат физико-математических наук, доцент Г.М.Гусак;
старший преподаватель Е.А.Бричикова
Научный редактор:
доктор физико-математических наук, профессор П.И.Монастырный
Рецензенты:
доктор физико-математических наук, профессор М.Д. Мартыненко;
кандидат физико-математических наук, профессор А.А.Дадаян
Гусак А.А. и др.
Г 96 Справочник по высшей математике / А.А.Гусак,
Г.М.Гусак, Е.А.Бричикова. - Мн.: ТетраСистемс.
1999. - 640 с.
ISBN 985-6317-51-7
Справочник содержит теоретические сведения по многим разделам
математики: аналитической геометрии, алгебре, математическому анали-
зу, дифференциальным уравнениям, численным методам, теории вероят-
ностей и ее приложениям, теории функций комплексной переменной, опе-
рационному исчислению. Включает примеры применения теории к реше-
нию задач, иллюстрации, соответствующие исторические сведения.
Рассчитан на студентов, аспирантов и преподавателей вузов, а так-
же на инженерно-технических и научных работников.
УДК 51(035)
ББК 22.1 я 2
ISBN 985-6317-51-7
© НТООО "ТетраСистемс",
1999
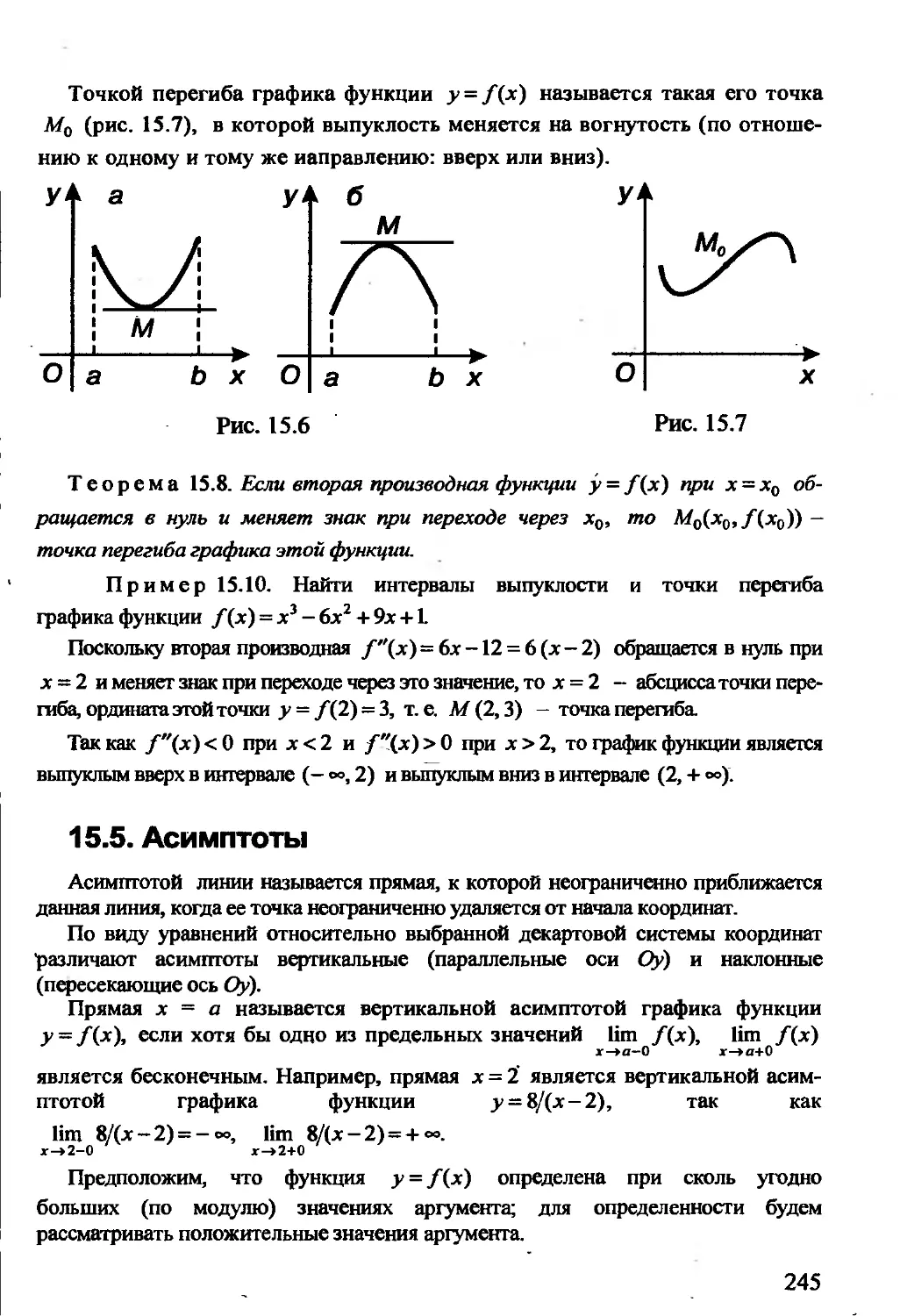
ПРЕДИСЛОВИЕ
Справочник включает следующие разделы высшей математики:
аналитическая геометрия (на плоскости и в пространстве), алгебра (мат-
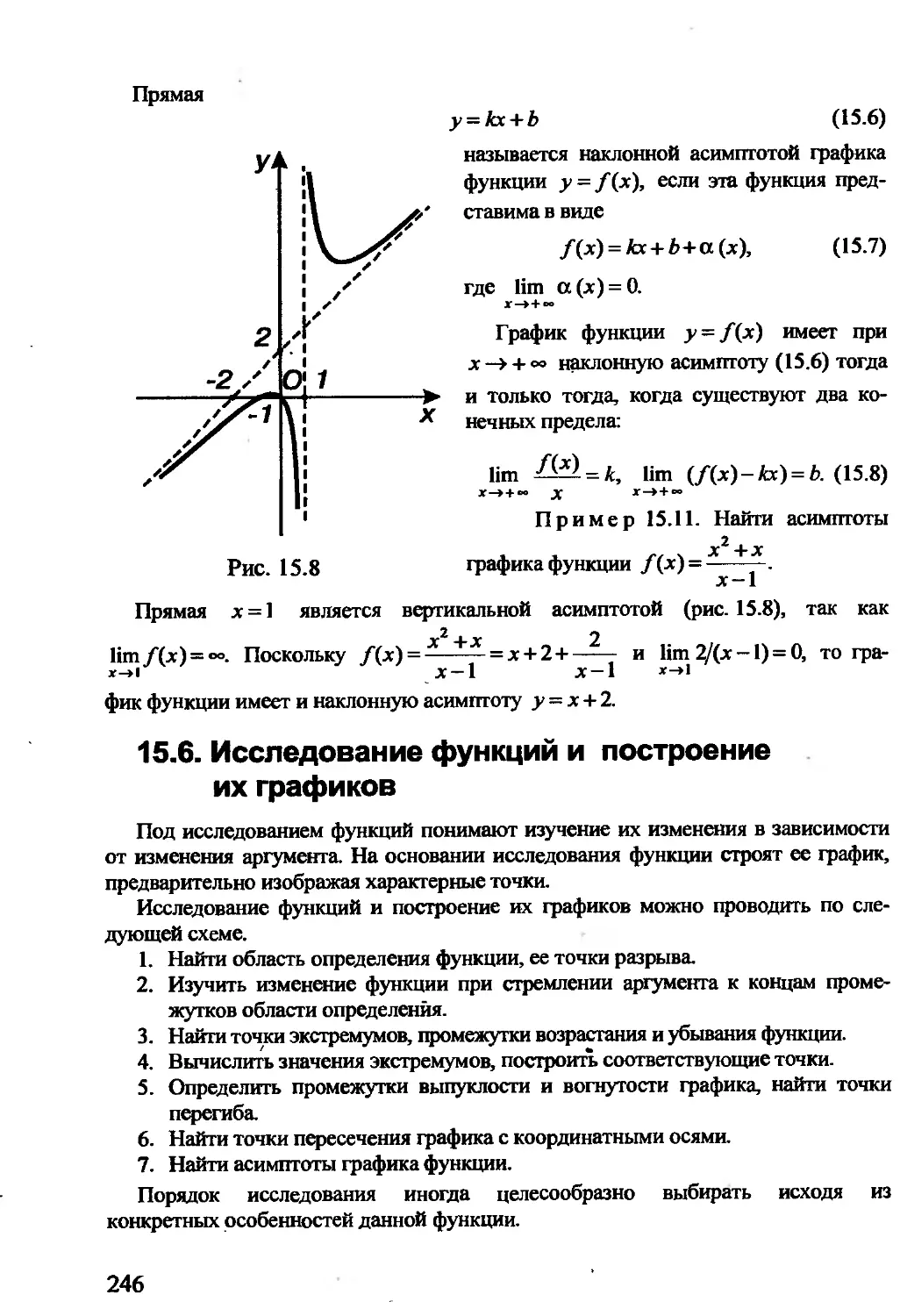
рицы и определители, линейные пространства, линейные операторы,
квадратичные формы, группы), дифференциальное исчисление и инте-
гральное исчисление (функций одной переменной и функций нескольких
переменных), ряды (числовые и функциональные, в том числе ряды Фу-
рье), дифференциальные уравнения (обыкновенные и с частными произ-
водными), численные методы (решения алгебраических, трансцендентных
и дифференциальных уравнений;.интегрирования и интерполирования
функций), элементы теории вероятностей и математической статистики (с
математической обработкой результатов измерений), элементы теории
функций комплексной переменной и операционного исчисления (с прило-
жением последнего к решению дифференциальных уравнений и их сис-
тем), начала векторного и тензорного анализа.
Справочник содержит теоретический материал без доказательств:
определения соответствующих понятий, формулы, уравнения; формули-
ровки теорем, основных задач, признаков; изложение математических ме-
тодов; свойства математический понятий, их смысл и приложения.
Во многих случаях указано, кто и когда предложил соответствую-
щий термин, символ для его обозначения, отмечено происхождение мате-
матического термина.
В каждом параграфе имеются примеры применения теории к реше-
нию практических задач. Наличие многочисленных примеров с подроб-
ными решениями может оказать существенную помощь студентам, зани-
мающимся по заочной форме обучения, при самостоятельном выполнении
ими контрольных работ, а также студентам дневных отделений при вы-
полнении домашних заданий и подготовке к зачетам и экзаменам.
Справочник снабжен иллюстративным материалом; в нем имеются
рисунки, поясняющие математические понятия, идеи методов, формулы,
уравнения, условия задач и примеров, а также чертежи кривых и поверх-
ностей, графики функций, таблицы.
Справочник включает два приложения: некоторые оригиналы и их
изображения, некоторые математические знаки и даты их возникновений.
Приложен также биографический словарь, содержащий краткие
сведения о жизни и деятельности математиков, имена которых встречают-
ся в справочнике.
Авторы
3
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Глава 1
КООРДИНАТЫ НА ПРЯМОЙ,
НА ПЛОСКОСТИ, В ПРОСТРАНСТВЕ
1.1. Координаты на прямой
На прямой зафиксируем одно из двух определяемых ею направлений и назовем
его положительным, другое - отрицательным. Прямую, на которой указано по-
ложительное направление, называют осью.
Отрезок, ограниченный точками А и В, называют направленным отрезком или
вектором, если указано, какая из данных точек является началом, какая — концом.
Направленный отрезок с началом в точке А и концом в точке В обозначают АВ.
Величиной направленного отрезка АВ некоторой оси называют его длину, взя-
тую со знаком плюс, когда направление этого отрезка совпадает с положительным
направлением данной оси, и со знаком минус, когда оно совпадает с отрицатель-
ным направлением оси. Величину направленного отрезка АВ обозначают АВ.
Координатной осью называют прямую, на которой зафиксированы начало от-
счета, положительное направление и выбран масштаб для измерения длин.
Координатой точки М координатной оси (рис. 1.1) называют величину ОМ на-
правленного отрезка ОМ, где О - начало координат. Если обозначить ко-
ординату точки М через х, то по определению х = ОМ.
• ------------- ----------------►
О Е М х
Рис. 1.1
Запись М(х) означает, что точка М имеет координату х.
Если даны две точки Mt(xt) и М2(х2), то величина направленного отрезка
М]М2 вычисляется по формуле
MtM2=x2-xt, *- (1.1)
а расстояние между ними - по формуле
р(А/,, А/2) = |а/1А/2| = |х2-х1|. <12)
4
Простым отношением трех различных точек Mt, М2, М, лежащих на одной
прямой и взятых в указанном порядке, называют число
MjM
ММ2 '
где MjM и ММ2 - величины направленных отрезков М,М и ММ2.
Если точка М принадлежит отрезку MjM2, простое отношение положительно
(/ > 0), так как числитель и знаменатель в последней формуле одного знака. В
этом случае говорят, что точкаМделит отрезок М,М2 внутренним образом. Если
точкаМ лежит вне отрезка MjM2, то /<0 (числитель и знаменатель в формуле
имеют противоположные знаки); точка М делит отрезок MjM2 внешним образом.
Если точки Л/, и М совпадают, то I = 0.
Пусть Л/Дх,), Л12(х2), М(х) — точки координатной оси Ох, тогда
~ мм2
(13)
(1.4)
откуда
2
(1.5)
Эта формула определяет координату точки М, делящей направленный отрезок
М]М2 в данном отношении I.
Если точка М совпадает с серединой отрезка MjM2, то I = 1, поэтому ее ко-
ордината определяется формулой
(1.6)
2
Пример 1.1. Даны две точки Л7,(4), Л/2(-3). Найти величину направленно-
го отрезка MjM2 и расстояние между точками.
В данном случае х1=4,л2 = -3; по формулам (1.1) и (1.2) находим
Л/(Л/2 =—3—4 = -7, р(Л/„ Л/2) = |-3-4| = 7.
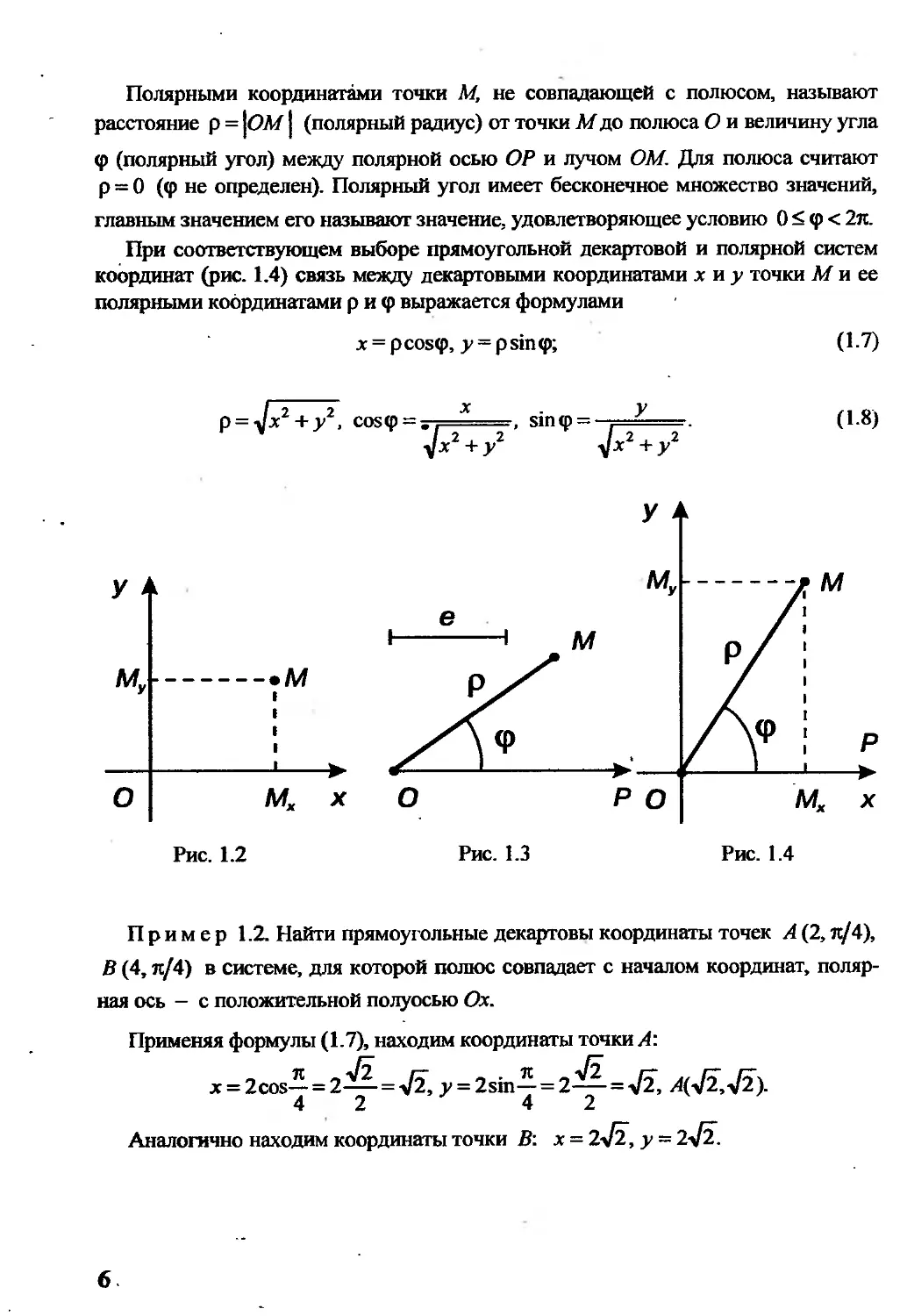
1.2. Координаты на плоскости
Прямоугольными декартовыми координатами точки М называют числа, опре-
деляемые формулами
х = ОМХ, у = ОМу,
где ОМХ — величина отрезка ОМЖ оси Ох, ОМу - величина направленного
отрезка ОМу оси Оу (рис. 1.2).
Полярная система координат на плоскости определяется точкой О
(полюс), исходящим из нее лучом ОР (полярная ось), масштабным отрезком
е и направлением отсчета углов (рис. 1.3).
5
Полярными координатами точки М, не совпадающей с полюсом, называют
расстояние р = |ОЛ/1 (полярный радиус) от точки М до полюса О и величину угла
<р (полярный угол) между полярной осью ОР и лучом ОМ. Для полюса считают
р — 0 (<р не определен). Полярный угол имеет бесконечное множество значений,
главным значением его называют значение, удовлетворяющее условию 0 < <р < 2л.
При соответствующем выборе прямоугольной декартовой и полярной систем
координат (рис. 1.4) связь между декартовыми координатами х и у точки М и ее
полярными координатами р и <р выражается формулами
jr = pcos<p, y = psin<p; (1.7)
Пример 1.2. Найти прямоугольные декартовы координаты точек Л(2, л/4),
В (4, л/4) в системе, для которой полюс совпадает с началом координат, поляр-
ная ось - с положительной полуосью Ох.
Применяя формулы (1.7), находим координаты точки Л:
X = 2cos- = 2— = 42, у = 2sin— = 2— = 42, А(42,42).
4 2 4 2
Аналогично находим координаты точки В: х = 142, у = 242.
6
1.3; Расстояние между двумя точками
на плоскости
В прямоугольной декартовой системе координат расстояние между двумя точ-
ками Af, (jr,, >j), Л/2(х2, у2) определяется формулой
р ( Л/р Л/2 ) = ^(л2 - )2 + (у2 - у, )2. (1-9)
В частном случае, когда одна из точек, например Mt, совпадает с началом ко-
ординат, формула (1.9) принимает вид
р(О,Л/2) = 7л2+у2. (1-Ю)
Пример 1.3. Вычислить расстояние между точками Л/,(6,-3), Л/2(9,-7)
и расстояние от точки М2 до начала координат.
По формулам (1.9) и (1.10) получаем
рЩ, Л/2> = 7(9-6)2+((-7)-(-3))2 =5, р(О, Л/2)= ^92+(-7)2 =7130.
Пример 1.4. Вычислить периметр треугольника с вершинами в точках
Л (-1,-3), В (2,-3), С (2,1).
По формуле (1.9) находим
а = р (В. С) = 7(2-2)2+(1-(-3))2 = 4,
b = р (А, С) = 7(2-(-1))2+(1-(-3))2 = 5,
с = р (А, В) = 7(2-(-I))2 +(-3-(-3))2 = 3.
Следовательно, Р - а+Ь+с=12.
1.4. Деление отрезка в данном отношении
Отношением, в котором точка М лежащая на прямой, проходящей через точки
Л/, и Л/2, делит отрезок М.М2, называют число/, определяемое формулой (1.3).
Если даны точки Л/,(х,, у,), Л/2(х2, у2), то координаты точки М(х, у), де-
лящей отрезок М,М2 в отношении /, определяются формулами
х,+Zx2 у,+/у2
х = -!-~,у = ——(111)
1 + / 1+/ U '
Когда точка М является серединой отрезка М,М2, то ее координаты вычис-
ляют по формулам
х = (х,+х2)/2, у = (у,+у2)/2.
(1.12)
7
Пример 1.5. Даны две точки Л/Д-1,-,2), Л/Д3,4). На прямой A/jA/2 най-
ти точку М, которая в три раза ближе к Мь чем к М2, и находится вне отрезка
М|М2. Найти середину этого отрезка.
Искомая точка Л/делит отрезок MjM2 в отношении / = —1/3. По формулам
(1.11), считая в них х, =-1, yt=-2, х2 = 3, у2 = 4, находим
—1+(-1/3)3 _ 3 -2+ (-1/3) 4
1 + (—1/3) .,У 1 + (—1/3)
= -5; Л/(-3,-5).
С помощью формул (1.12) находим точку W=(l,l) - середину отрезка МХМ2.
Пример 1.6. Найти координаты точки пересечения медиан треугольника с
вершинами в точках А (х,, у(), В(х2, у2), С(х3,у3).
Пусть S’ (х, у) - точка пересечения медиан АК, BL, СМ треугольника АВС
(рис. 1.5, а). Так как точка L- середина отрезка АС, то она имеет координаты
хг = (Х]+х3)/2, yt = (у, +у3)/2. Отрезок BL точкой S делится в отношении
/ = 2/1=2. Считая точку В первой, точку L второй, по формулам (1.11) находим
х2 +2(х, +х3)/2 _ X! + х2 +х3 _ у2 +2(^ + у3)/2 _ у, + у2 +у3
1+2 3 ’ У~ 1 + 2 3
Следовательно, координаты точки пересечения медиан треугольника по коор-
динатам его вершин определяются формулами
х = (Х]+х2+х3)/3, У = (У!+у2 + у3)/3.
(113)
&
1.5. Центр тяжести системы масс
Дана система масс ,т„, помещенных соответственно в точках
Л/((Х|, ух), М2(х2, у2),М„(х„,у„) некоторой плоскости. Формулы, выражаю-
щие координаты центра тяжести этой системы масс, имеют вид
х = ximl+x2m2+---+x„m„ у = +у2т2+ — +у„т„
т1+т2+---+ти т1+т2+—t-mn
или
п п
у, УЛ
*=1 *=|
где знаком Е обозначена сумма однотипных слагаемых.
Пример 1,7. В вершинах А (*„ у,), В(х2,у2), С (х3, у3) треугольника АВС
сосредоточены равные массы т. Найти центр тяжести этой материальной системы.
Формулы (1.14) при я = 3 принимают вид
х _ х^ +х2гп2 +xJmi _ ухтх + у2т2 + у^
щ т^+п^ + т^
Используя условие = т^, получаем
_ xtm+x2m + x3m _ m(xt +х2 + х3) _ х, + х2 + х3
т+т + т Зт 3
= У1ОТ + у2т + у3щ _ т(ух + у2 + у3) = у, +у2 +у3
т+т + т Зт 3
Замечание. Из последнего примера и формул (1.13) следует, что центр тя-
жести данной системы находится в точке пересечения медиан треугольника.
1.6. Площадь треугольника
Каковы бы ни были три точки A(xl,yl), В(х2,у2), С(х3,у3), площадь S
треугольника ЛВС вычисляется по формуле '
±5 = ^[(х2-х,)(у3-у1)-(х3-х1)(у2-у1)]. (1.15)
Правая часть формулы равна +S в.том случае, когда кратчайший поворот от-
резка АВ к отрезку АС положителен (рис. 1.5, а), и S, когда указанный поворот
отрицателен (рис. 1.5, б).
В формуле (1.15) берут знак плюс, когда выражение в квадратных скобках по-
ложительно, и минус, когда оно отрицательно.
9
Пример 1.8. Даны две точки А (3,5), В (6, - 2). На о.си Оу найти такую точ-
ку С, чтобы площадь треугольника ЛВС равнялась 15 квадратным единицам.
Пусть С (0, у) - искомая точка (х = 0, так как точка лежит на оси Оу). В фор-
мулу (1.15) подставим значения S’= 15, Л]=3, У] =5, х2=6, у2=—2, х3=0,
у3 = у и найдем у:
±15 = |[(6-3)(у-5)-(0-3)(-2-5)]=|[3(у-5)-21],
± 15 = ^-(Зу - 36), ± 30 = Зу - 36, у, = 2, у2 = 22.
Итак, условию задачи удовлетворяют координаты точек С](0,2), С2(0,22).
1.7. Уравнение линии в декартовых координатах
Уравнением линии относительно фиксированной системы координат называют
такое, уравнение с двумя переменными, которому удовлетворяют координаты лю-
бой точки этой линии и не удовлетворяют координаты ни одной точки, не лежа-
щей на данной линии.
Уравнение линии в декартовых координатах в общем виде записывается так:
F(x,y) = 0,
где F (х, у) — функция переменных х и у.
Пример 1.9. Составить уравнение множества точек, равноудаленных от двух
данных точек Л/] (-4,3) и Л/2(2,5).
Пусть М (х, у) - произвольная точка данного геометрического места. По ус-
ловию | Mt М | = | М2 М |. По формуле (1.9) получаем
|Л/,Л/| = 7(х + 4)2+(у-3)2, \M2M\ = J(x-2)2 + (у-5)2.
Подставляя эти выражения в равенство | Л/, Л/| — | Л/2Л/1, находим уравнение дан-
ного множества точек:
А/(х + 4)2+(у-3)2 = 7(х-2)2+(у-5)2.
Упростим это уравнение. Возведем в квадрат обе части уравнения и раскроем
скобки в подкоренных выражениях:
х2 + 8х +16 + у2 - бу + 9 = х2 - 4х + 4+у2 - 10у + 25.
Произведя преобразования, получим Зх + у—1 = 0. Это уравнение прямой линии.
Пример 1.10. Составить уравнение окружности радиуса R с центром в
точке С(а,Ь).
Пусть М (х, у) — произвольная точка данной окружности. По определению
окружности (как множества точек, равноудаленных от данной точки) для любой ее
10
точки имеем |Л/С| = Я. Выражая расстояние между точками М и С по формуле
\MC\ = J(x-a)2+(y-b)2 и подставляя его в левую часть данного равенства,
получим уравнение -J(x — а)2 + (у — b)2 = R, которое можно записать так:
(x — a)2+(y—b)2 = R2. (1.16)
Уравнение (1.16) является уравнением окружности радиуса R с центром в
точке С (а, Ь).
Если точка С совпадает с началом координат, то уравнение (1.16) принимает вид
x2+y2 = R2. (1.17)
Замечание. Если точка N (х, у) лежит внутри круга радиуса R с центром в
начале координат, то ее координаты удовлетворяют неравенству x2 + y2<R2;
если вне указанного круга, то неравенству х2 + у2 > R2.
Пример 1.11. Точка М движется так, что в любой момент времени ее рас-
стояние до точки /1(4,0) вдвое больше расстояния до точки В (1,0). Найти урав-
нение траектории движения точки М.
Текущие координаты точки М в прямоугольной декартовой системе координат
обозначим через х, у. По условию |М41 = 2|Л/В |. Выразим длины отрезков МА и
МВ через координаты соответствующих точек с помощью формулы (1.9):
\МА | = 7(х-4)2 + у2, |Л/В| = J(x-l)2 + y2.
Подставляя эти выражения в равенство |М41 = 2} МВ |, получаем уравнение траек-
тории движения точки М: yj(x- 4)2 + у2 = 2-j(x-1)2 + у2. Упростим это уравне-
ние, для чего возведем в квадрат обе части и приведем подобные члены
(х -4)2 + у2 = 4((х -1)2 + у2), х2 - 8х +16 + у2 = 4(х2 - 2х+1 + у2),
12 = 3х2+3у2, х2+у2=4.
Итак, траекторией движения точки М является окружность радиуса R = 2 с
центром в начале координат.
1.8. Пересечение линий
Координаты точек пересечения двух линий, заданных уравнениями
'F (х, у) = 0, Ф (х, у) = 0, находят из системы этих уравнений
F(x,y)=0, Ф(х,у) = 0. (1.18)
Число действительных решений равно числу точек пересечения. Если система
(1.18) не имеет действительных решений, то данные линии не пересекаются.
Пример 1.12. Найти точки пересечения линий х2 + у2 = 10, х + у - 4 = 0.
Из последнего уравнения выражаем у = —х + 4 и подставляем в первое урав-
11
нение: х2+(—х + 4)2 =10, 2x2 —8x + 6 = 0, x2 — 4x + 3 = 0, откуда x, =1, x2=3.
Подставим эти значения в уравнение у = -х + 4 и найдем у, = 3, у, = 1. Следова-
тельно, получены две точки пересечения Л/ (1,3), N (3,1).
Пример 1.13. Найти точки пересечения двух окружностей, заданных урав-
нениями (х - 5)2 + (у — 6)2 = 25, (х + 2)2 + (у - 6)2 =32.
Раскрывая скобки и приводя подобные члены, получаем систему уравнений
х2+у2 — 10х-12у + 36= 0,
х2 +у2 +4х-12у + 8 = 0.
Вычитая второе уравнение из первого, получаем —14х + 28 = 0, откуда х = 2.
Второе уравнение системы при х = 2 сводится к квадратному относительно у:
у2-12у + 20 = 0. Решив его, найдем yt =2, у2 =10. Следовательно, данные ок-
ружности пересекаются в точках Л/, (2,2), Л/2(2,10).
1.9. Уравнение линии в полярных координатах
Уравнение линии на плоскости в полярных координатах в общем виде
можно записать так:
F(P,<P) = O,
где F(p, <р) - функция переменных р и <р (р, <р - полярные координаты). Если это
уравнение разрешимо относительно р, то его можно представить в виде р = р (<р).
Пример 1.14. Составить уравнение прямой, перпендикулярной полярной
оси и отсекающей от нее отрезок, длина которого равна а.
Обозначим буквой А точку пересечения данной прямой с полярной осью ОР
(рис. 1.6). Пусть Л/(р, <р) - произвольная точка данной прямой. Из прямоуголь-
ного треугольника ОАМ находим, что pcoscp = а. Полученное уравнение является
искомым; ему удовлетворяют координаты любой точки данной прямой и не удов-
летворяют координаты ни одной точки, не принадлежащей этой прямой.
Рис. 1.7
Рис. 1.6
12
Пример 1.15. Составить уравнение окружности радиуса а, касающейся по-
лярной оси в полюсе, центр которой расположен выше полярной оси (рис. 1.7).
Пусть М (р, <р) - произвольная точка окружности, ОА - диаметр окружности,
равный 2а. Так как в треугольнике ОАМ угол при вершине М прямой, угол при
вершине О равен л/2-ф, то 2асоз(л/2-ф) = р, или р = 2аз1пф. Это искомое
уравнение данной окружности.
1.10. Параметрические уравнения линии
Уравнения вида
* = /(0>> = ф(0 (119)
называются параметрическими уравнениями линии, если при изменении t в неко-
тором промежутке формулы (1.19) дают координаты любой точки данной линии и
только таких точек.
Если линия задана уравнением р = р (ф) в полярных координатах, то ее пара-
метрические уравнения можно записать так:
Х = р(ф)СО5ф, у = р(ф)8Шф. (120)
В уравнениях (1.20) роль параметра играет полярный угол ф.
Пример 1.16. Составить параметрические уравнения окружности радиусаR
с центром в начале координат.
Пусть М (х, у) — произвольная точка данной окружности, t— величина угла,
образуемого отрезком ОМ и осью абсцисс, Р и Q - основания перпендикуляров,
опущенных из точки М на координатные оси (рис. 1.8). Так как по определению
х = ОР, у = OQ и OP = Rcost, OQ= Rsint, то х = Rcost, у = Rsint.
Следовательно, параметрические уравнения данной окружности имеют вид
x=7?cosf, у = 7?sinf, где0< t<2n.
Исключив из этих уравнений параметр t (для чего возведем в квадрат оба равен-
ства и почленно сложим), получим уравнение х2 +у2 = R2 (см. уравнение (1.17)).
Пример 1.17. Составить параметрические уравнения циклоиды. Циклоидой
называют линию, являющуюся траекторией фиксированной точки окружности
радиуса R, катящейся по прямой.
13
Указанную прямую примем за ось Ох декартовой прямоугольной системы ко-
ординат (рис. 1.9). Предположим, что фиксированная точка при начальном поло-
жении окружности находилась в начале координат, а после того как окружность
повернулась на угол t, заняла положение М.
Поскольку х = OP = ОК - РК, у = МР = СК - CN и ОК = МК = Rt,
PK=MN = Rsiat, СК = R, CN = Rcost, то х = Rt-7?sin/, у = R-Rcost, или
х = R(t-sinf), y=R(l-cos/). (1-21)
Уравнения (1.21) называются параметрическими уравнениями циклоиды.
1.11. Преобразования декартовых
прямоугольных координат на плоскости
Одна и та же точка имеет различные координаты в разных системах декартовых ко-
ординат. Существует связь между координатами точки в разных системах координат.
Параллельный перенос. Пусть даны две системы декартовых прямоугольных
координат с общим масштабным отрезком: Оху (старая) и OtXY (новая), соответ-
ствующие оси которых параллельны (рис. 1.10). Положительные полуоси имеют
координаты которой х = а, у = b (новые координаты ее равны нулю). Относительно
таких систем говорят, что одна получена из другой путем параллельного переноса
Старые координаты х, у точки М через ее новые координаты X, Y и старые ко-
ординаты а, b нового начала С\ выражаются формулами
x = X + a,y = Y+b, (1.22)
откуда
Х = х — а, Y = y-b. (1.23)
Поворот координатных осей. Новая система Ох'у' получена путем поворота
старой на угол а вокруг точки О (рис. 1.11). Старые декартовы прямоугольные х,у
14
точки Мчерез ее новые координаты х', у' выражаются формулами
х = х’ cos а —у' sin а, у = х' sin а -у' cos а. (1-24)
Чтобы выразить х', у" через х, у, необходимо разрешить систему (1.24) относи-'
тельно х', у'. Можно сделать проще: считать систему Ох'у' старой, тогда переход
к новой системе Оху совершается поворотом на угол (—а), поэтому в формулах
(1.24) достаточно поменять местами хи х',уи у', записать (-а) вместо а.
В общем случае, когда даны две системы Оху и Ох'у' (рис. 1.12), вводя про-
межуточную систему О'х"у" и применяя последовательно формулы (1.22) и
(1.24), получаем
x = x'cosa- у'sin a + a,
, . , (1.25)
у = х sina + y cosa + t>. *
Замечание. Система координат
Оху, в которой кратчайший поворот
положительной полуоси Ох до совпа-
дения с положительной полуосью Оу
совершается против часовой стрелки,
называется правой; если указанный
поворот совершается по часовой
стрелке, система называется левой.
Формулы (1.25) остаются прежними,
если обе системы координат являются
левыми. Если одна система правая,
другая левая, то в формулах (1.25) из-
менится знак перед у', так как в случае простейшего преобразования координат
разноименных систем формулы имеют вид х = х', у = -у'.
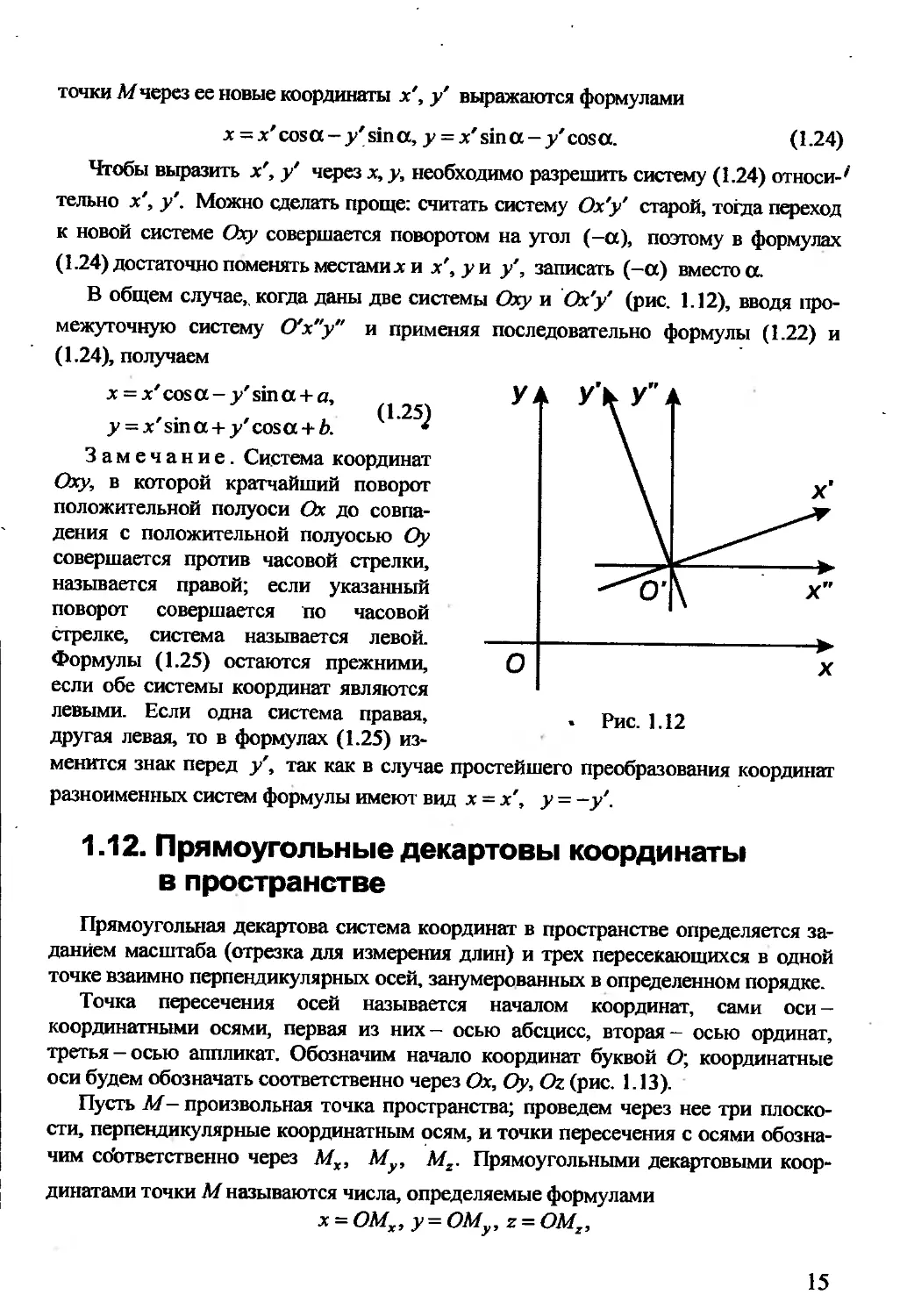
1.12. Прямоугольные декартовы координаты
в пространстве
Прямоугольная декартова система координат в пространстве определяется за-
данием масштаба (отрезка для измерения длин) и трех пересекающихся в одной
точке взаимно перпендикулярных осей, занумерованных в определенном порядке.
Точка пересечения осей называется началом координат, сами оси -
координатными осями, первая из них — осью абсцисс, вторая- осью ординат,
третья-осью аппликат. Обозначим начало координат буквой О; координатные
оси будем обозначать соответственно через Ох, Оу, Ог (рис. 1.13).
Пусть М- произвольная точка пространства; проведем через нее три плоско-
сти, перпендикулярные координатным осям, и точки пересечения с осями обозна-
чим со'ответственно через Мх, Му, Mz. Прямоугольными декартовыми коор-
динатами точки М называются числа, определяемые формулами
х = ОМХ, у = ОМу, z = OMZ,
15
где ОМХ, ОМу, ОМ2 — величины
направленных отрезков ОМХ,
ОМу, ОМХ соответствующих
координатных осей. Число х назы-
вается первой координатой или
абсциссой, число у - второй коор-
динатой или ординатой, число z -
третьей координатой или ап-
пликатой точки М.
Координатные плоскости Оху,
Oxz, Oyz делят все точки пространст-
ва, не принадлежащие этим плоско-
стям, на восемь частей, называемых
октантами.
Таблица 1.1
Координата Октант
I II III IV V VI VII VIII
X + - - + + - - +
У + + - - + + - -
Z + + + + - - -
Начиная с I октанта, в котором все координаты-положительны, пронумеруем ок-
танты I, II, III, IV верхнего полупространства (z > 0) против часовой стрелки (для
наблюдателя со стороны положительной оси Oz). В нижнем полупространстве
(z < 0) проведем соответствующую нумерацию октантов V, VI, VII, VIII так, что-
бы V находился под I, VI - под II, VII - под III, VIII - под IV. Знаки координат
точек в различных октантах приведены в табл. 1.1.
Очевидно, знаки координат однозначно определяют октант пространства.
1.13. Расстояние между двумя точками
в пространстве
Если у,,Z,), A/2(x2,y2,z2) “Две любые точки пространства, то рас-
стояние между ними определяется формулой
р (Л/„ Л/2) = J(x2 -хх)2 + (у2 - у, )2 + (z2 - z,)2. (1.26)-
В частном случае, когда точка Мх совпадает с началом координат
(Л1 = у1 = Zj = 0), то формула (1.26) принимает вид
р(.О, Л/2) = -^х2+у2+z2. (1.27)
16
Пример 1.18. Вычислить расстояние между точками Л/,(1,-2,2) и
Л/2(3, -1,4), а также расстояние от точки Л/2 до начала координат.
По формулам (1.26) и (1.27) соответственно получаем
р(М„ Л/2) = 7(3-1)2 + (-1 -(—2))2 + (4-2)2 = 3,
р (О, М2 ) = 7з2+(-1)2+42 = V26-
Замечание. Формулы (1.26) и (1.27) упрощаются, когда точки и М2
лежат в плоскости, параллельной одной из координатных плоскостей, или в самой
этой плоскости. В этом случае получаем формулы (1.9) и (1.10).
1.14. Цилиндрические асферические
координаты
В плоскости П фиксируем точку О и исходящий из нее луч ОР (рис. 1.14). Че-
рез точку О проведем прямую, перпендикулярную плоскости П, и укажем на ней
положительное направление; полученную ось обозначим Oz. Выберем масштаб
для измерения длин. Пусть М- произвольная точка пространства, N- ее проекция
на плоскость П, Mz — проекция на ось Oz. Обозначим через риф полярные коор-
динаты точки N в плоскости П относительно полюса О и полярной оси ОР. Ци-
линдрическими координатами точки М называются числа р, ф, z, где р, ф-
полярные координаты точки N (р > 0,0 < ф < 2л), z = ОМ. — величина направ-
ленного отрезка OMZ оси Oz. Запись М(р, ф, z) обозначает, что точка М имеет
цилиндрические координаты р, ф, z. Наименование «цилиндрические координаты»
17
объясняется тем, что координатная поверхность р = const (т. е. множество точек,
имеющих одну и ту же первую координату р) является цилиндром (на рис. 1.14 он
изображен штрихами).
Если выбрать систему прямоугольных декартовых координат так, как показано
на рис. 1.14, то декартовы координаты х, у, z точки М будут связаны с ее цилинд-
рическими координатами р, <р, z формулами
x = pcos<p, y = psin<p, z = z. (1.28)
Сферические координаты вводят следующим образом. Выберем масштаб для
измерения длин отрезков, фиксируем плоскость П с точкой О и полуосью Ох, ось
Oz, перпендикулярную плоскости П (рис. 1.15). Пусть М— произвольная точка
пространства (отличная от О), N— проекция ее на плоскость П, г- расстояние
точки Мдо начала координат, в —.угол, образуемый отрезком ОМ с осью Oz, <р-
угол, на который нужно повернуть ось Ох против часовой стрелки (если смотреть
со стороны положительного направления оси Oz), чтобы она совпала с лучом CW;
в называется широтой, <р — долготой.
Сферическими координатами точки М называются три числа г, 0, <р, опреде-
ленные выше. Если точка М имеет сферические координаты г, 0, <р, то пишут
М (г, 0, <р).
Наименование «сферические координаты» связано с тем, что координатная по-
верхность г = const (т.е. множество точек, имеющих одну и ту же координату г)
является сферой (на рис. 1.15 одна из таких сфер изображена штрихами); фикси-
ровав другое значение г, получим другую сферу.
Для того чтобы соответствие между точками пространства и тройками сфери-
ческих координат г, 0, <р было взаимно однозначным, обычно считают, что г, 0, <р
изменяются в следующих границах: 0 < г < +°°, 0 < 0 < л, 0 < <р < 2л. Если вы-
брать оси прямоугольной декартовой системы координат так, как указано на
рис. 1.15, то декартовы координаты х, у, z точки М связаны с ее сферическими
координатами г, 0, <р формулами
x=rsin0cos<p,y = rsin0sin<p, z = rcos0. (1-29)
18
Гпава 2
ЛИНИИ НА ПЛОСКОСТИ
Алгебраической линией (кривой) n-го порядка называют линию, определяемую
алгебраическим уравнением и-й степени относительно декартовых координат.
Линии первого порядка определяются уравнением Ах + Бу + С = 0 (А2 + В2 * 0),
а линии второго порядка - уравнением Ах2+Вху + Су2 + +Dx+Ey+F = 0
(Я2 + В2+С2*0).
Линии первого порядка - прямые.. К линиям второго порядка относятся ок-
ружность, эллипс, гипербола, парабола.
2.1. Прямая на плоскости
Прямую линию на плоскости относительно системы декартовых прямоуголь-
ных координат можно задать различными способами. Прямая однозначно опреде-
ляется углом, образуемым ею с осью Ох, и величиной направленного отрезка, от-
секаемого на оси Оу, координатами двух точек и т. п.
Различные виды уравнения прямой иа плоскости. Прямая, параллельная
оси Оу прямоугольной декартовой системы координат (рис. 2.1), пересекающая
ось Ох в точке А(а, 0), имеет уравнение
х = а. (2.1)
Угловым коэффициентом прямой называют тангенс угла а наклона ее к поло-
жительной полуоси Ох прямоугольной декартовой системы координат
fc = tga (0^а<л).
Угловой коэффициент прямой через координаты двух ее различных точек
(Х|, у,), М2 (х2, у2 ) определяется формулой
19
к_Уг~У\ <2-2>
Х2 — JC|
Уравнение прямой с угловым коэффициентом имеет вид
у = кх + Ь, (2.3)
где к — угловой коэффициент, b = OD — величина направленного отрезка ОВ,
отсекаемого на оси Оу (рис. 2.2).
Уравнение прямой, имеющей угловой коэффициент к и проходящей через дан-
ную точку М0(х0,у0), записывается так:
у-Уо = к(х-хо). (2.4)
Уравнение прямой проходящей через две данные точки М^х^у^,
М2(х2,у2):
у —у, х — х, ,
=-----L (*2 * xi > У2 * yt ) (2.5)
У2-У1 х2-х{
Параметрические уравнения прямой проходящей через эти точки:
x = xl+(x2-xl)t, у = У1+(у2~У1)(> (2.6)
где t принимает все действительные значения.
Уравнением прямой в отрезках называют уравнение
х/а + у/Ь = \, (2.7)
где а = ОА, b = ОВ — величины направленных отрезков, отсекаемых соответст-
венно на оси Ох и оси Оу-
Общим уравнением прямой называют уравнение,
Ах + Ву+С=0, (2.8)
в котором А тл В одновременно в нуль не обращаются, т.е. Л2 + В1 Ф 0.
Пример 2.1. Составить параметрические уравнения сторон треугольни-
ка, вершины которого находятся в точках А (2,3), В (4,7), С (6,9).
Составим сначала уравнения прямых, на которых лежат стороны АВ, ВС и АС
соответственно. Используя уравнение (2.5), получаем
у—3_х —2 у—3_х-2 у-3_х-2
7-3 - 4-2’ —4 2 ’ 2 " 1 ’
у-7 х-4 у-7 х — 4
—---=-----, ---=-----, у - 7 = х - 4;
9-7 6—4 2 2
у-3_х-2 у—3 _х —2 у-3 _х —2
9-3 " 6-2’ 6 - 4 3 “ 2
Обозначим буквой t равные отношения, получим параметрические урав-
нения этих прямых: x = 2 + t, y = 3 + 2t(AB); x = 4+t, y = 7+t(BC);
x=2 + 2t, y = 3+3t(AC).
20
Введя ограничения на изменение параметра t, получим уравнения соответст-
вующих сторон треугольника АВ, ВС, AC: x~2 + t, y = 3+2t (0</<1);
x = 4 + Z, y = 7 + t (O<Z<1); x = 2+2z, y = 3+3t (O<Z<1).
Пример 2.2. Найти величины отрезков, отсекаемых на осях координат
прямой, заданной уравнением 7х - Зу - 21 = 0.
Разделив это уравнение почленно на 21, получим
х/3-у/7-1 = 0, или х/3 + у/(-7) = 1.
Сравнивая полученное уравнение с уравнением (2.7), заключаем, что а = 3, b - 7.
Угол между двумя прямыми. Условия параллельности и перпендикуляр-
ности двух прямых. Тангенс угла между двумя прямыми (рис. 2.3)
y = ktx + bl,y = k2x + b2 (2.9)
вычисляется по формуле • . ~~ ki tg<P“ , , • (2.10) 1 + Мг ’
Необходимое и достаточное условие параллельности прямых, заданных уравне-
ниями вида (2.9), выражается равенством kl=k2, а условие их перпендику-
лярности - равенством
Если прямые заданы общими уравнениями
AjX + В]У + С\ =0,
А2х + В2у + С2 = 0,
то тангенс угла между ними определяется формулой
4^ - а2в1
tg«p = ^2----—.
+ В}В2
(2.11)
(2.12)
(2-13)
(214)
Необходимое и достаточное условие параллельности прямых, заданных
уравнениями (2.12) и (2.13), выражается
равенством
AjA^BjB^ (2.15)
или
Ai=lA2,Bi = lB2, (2.16)
а условие их перпендикулярности -
равенством
-AilBi=B2/A2, 1лляАхА2 + В}В2=(3. (2.17)
Отметим, что прямые Ах + Ву + С=(3,
Вх-Ау + С = 0 перпендикулярны в силу
условия (2.17).
21
Пример 2.3. Найти угол между прямыми, заданными уравнениями
5х+3у+15 = 0, х + 4у — 7 = 0.
Применяем формулу (2.14). Так как в данном случае At =5, В} = 3, А2 = 1,
Дг = 4, то
5-4-1-3 ,
tg<p =-------= 1 ф = 45 .
51 + 3-4
Замечание. При другой нумерации прямых (А, =1, В, =4, А2=5,
В2=3) получаем tg<р' = -1, <р' = 135°. Очевидно, <р + <р' = 180°.
Пример 2.4. Составить уравнение прямой, проходящей через точку
Л/(4,-5) и параллельной прямой Зх + 4у + 12 = 0.
Искомое уравнение имеет вад Зх + 4у + С = 0, где С пока не определено. Вид
уравнения следует из условия (2.16) при / = 1 (считаем соответствующие коэффи-
циенты равными). Чтобы найти значение С, необходимо подставить координаты
точки М в искомое уравнение (точка М лежит на прямой, поэтому ее координаты
должны удовлетворять уравнению этой прямой). Подставляя координаты х = 4,
у = -5 в уравнение Зх + 4у + С = 0, получаем 3-4+4-(-5)+С = 0, откуда С=8.
Таким образом, уравнение прямой имеет вцд Зх + 4у + 8 = 0.
Пример 2.5 Составить уравнение прямой, проходящей через точку
Л/(-3,2) и перпендикулярной прямой 4х + 5у-7 = 0.
Искомое уравнение имеет вад 5х—4 у + С = 0. Действительно, для прямых вы-
полнено условие (2.17): 4-5+5-(—4) = 0. Точка М(—3,2) лежит на прямой
5х — 4у + С = 0, поэтому ее координаты должны удовлетворять этому уравнению:
5(-3)-4-2+С = 0. Отсюда находим, что С = 23. Итак, уравнение прямой прини-
мает'вид 5х-4у + 23 = 0.
Пример 2.6. Вершины треугольника находятся в точках Л(3,4),
В (-2,1), С (-3,-5). Составить уравнение прямой, на которой лежит высота,
опущенная из вершины В на сторону АС.
Найдем сначала угловой коэффициент прямой, проходящей через точки А и С.
Считая точку А первой, точку С второй, т.е. полагая х} =3, yt = 4, х2 = -3,
у2=-5, по формуле (2.2) получаем =(—5-4)/(-3-3) = 3/2. Прямая, на кото-
рой лежит высота, опущенная из точки В на сторону АС, будет перпендикулярна
прямой, проходящей через точки А и С. Угловой коэффициент этой прямой обо-
значим через к^. Используя условие перпендикулярности двух прямых, заданное
формулой (2.11), находим к^ = l/fct, к^ = -2/3.
Составим уравнение прямой, проходящей через точку В (-2,1) и имеющей
заданный угловой коэффициент к^. Подставляя значения х0 = -2, у0 = 1,
к = -2/3 в уравнение (2.4), получаем у-1 = (-2/3)(х-(-2)),
3(у — 1) + 2(х + 2) = 0, 2х + Зу + 1 = 0.
22
Расстояние от точки до прямой. Уравнения биссектрис углов между двумя
прямыми. Расстояние от точки М0(х0,у0) до прямой Ax + By + C=Q вычис-
ляют по формуле
| Ах0 + Ву0 + С |
“7ZF-' (218)
Уравнения биссектрис углов между прямыми А}х + Bty + Cj = О,
А2х + В2у + С2 = 0 имеют вид
Atx + Bty + С] _ А2х + В2у + С2
№+в? + В2 (219)
Пример 2.7. Найти расстояние от точки Л/о(-7,4) до прямой, заданной
уравнением 4х — Зу —15 = 0. *
Воспользуемся формулой (2.18). Так как в данном случае х0=-7, у0 = 4,
А = 4, В = -3, С = -15, то
V«!+<-3)!
Пример 2.8. Дан треугольник с вершинами Р (2, — 1), Q (6, - 4),
R (10,3). Найти длину высоты, опущенной из точки Я.
Задача сводится к вычислению расстояния от точки R до прямой PQ. Запишем урав-
- жт у + 1 х-2
некие этой прямой. На основании уравнения (2.5) имеем —----=----, или
-4+1 6-2
Ззс + 4у — 2 = 0. Расстояние точки R (10,3) до этой прямой вычислим по формуле (2.18)
d =
| 310+4-3-2 | _
/з2+42 =&
Следовательно, длина высоты равна 8.
Замечание. Эту задачу можно решить и другими способами. Например,
длину искомой высоты можно вычислить, зная площадь треугольника PQR и длину
основания PQ. Эта же длина равна расстоянию между двумя точками R и М (М -
основание высоты, опущенной из точки R на PQ). В свою очередь координаты точки
М находятся в результате решения системы уравнений стороны PQ и высоты RM.
Пример 2.9. Составить уравнения биссектрис углов, образованных пря-
мыми Зх — 4 у - 7 = 0, 8х + бу — 1 = 0.
В соответствии с формулой (2.19) получаем
Зх-4у-7 8х + бу -1
^32 + (-4)2 л/82+62
23
Преобразуя эти уравнения, находим
Зх-4у-7 , 8х + 6у-1 . ,о
----------= ±----, 2 (Зх - 4у - 7) = ± (8х + бу -1).
Отсюда получаем уравнения биссектрис 2х + 14у + 13 = 0, 14х-2у-15=0.
Задачи, относящиеся к прямым. Рассмотрим примеры решения задач, в ус-
ловиях которых даны уравнения прямых.
Пример 2.10. Даны уравнения двух сторон параллелограмма
х + 2у + 2 = 0 и х + у - 4 = 0 и уравнение одной из диагоналей х - 2 = 0. Найти
координаты вершин параллелограмма.
Решая систему уравнений х + 2у + 2 = 0, х + у - 4 = 0, находим точку
А (10, - 6) — одну из вершин параллелограмма. Две другие вершины найдем как
точки пересечения данной диагонали со сторонами, т. е. определим их координаты
из систем уравнений х + 2у+2 = 0, х — 2 = 0; х + у — 4=0, х — 2 = 0. Это будут
точки В (2,2) и D (2, - 2). Середина диагонали BD находится в точке
S (2,0). Так как диагонали параллелограмма в точке пересечения делятся пополам,
то четвертая вершина С (х, у) может быть найдена как конец отрезка АС по извест-
ному концу А и середине S: (х + 10)/2 = 2, (у + (-6))/2 = 0. Отсюда получаем
х = —6, у = 6, т.е. точку С (-6,6) - четвертую вершину параллелограмма ABCD.
Пример 2.11. Составить уравнение линии, расстояние каждой точки кото-
рой до точки А (2,0) относится к ее расстоянию до прямой 5х + 8 = 0 как 5:4.
Пусть М (х, у) - произвольная точка данной линии, N- основание перпен-
дикуляра, проведенного через точку Л/к прямой 5х + 8=0, или х = -8/5. Рас-
стояния точки М до точки А и до прямой х = -8/5 определяются соответственно
формулами |М41 = д/(х-2)2 + у2, |AflV| = |x-(-8/5)| = |x + 8/5| (последнее ра-
венство следует также из формулы (2.18)). По условию задачи -J(x — 2)2 + у2:
|х + 8/5| = 5:4, откуда 4^/(х - 2)2 + у2 = 5|х + 8/51. Преобразуем это уравнение:
16(х2 - 4х + 4 + у2) = 25 (х2 + (16/5)х + 64/25),
16х2 - 64х + 64 + 16у2 = 25х2 + 80х + 64, 9х2 - 16у2 + 144х = 0.
Выделим полные квадраты в левой части полученного уравнения:
9(х2+ 16х + 64)—16у2-9-64 = 0, 9(х + 8)2-16у2 =9-64.
Последнее уравнение примет вид 9Х2 —16У2 =9-64, или А'2/б4-У2/36 = 1, если
перейти к новым координатам X = х + 8, Y = у.
Полученное уравнение определяет гиперболу с полуосями а = 8, b = 6 (см.
уравнение (2.25)).
24
2.2. Окружность
Каноническим уравнением окружности радиуса R с центром в точке С (а, Ь)
называют уравнение
(х — а)2 + (у—b)2 = R2. (2.20)
Когда центр окружности находится в начале координат, уравнение принимает
вид х2 + у2 -R2.
Если уравнение второй степени, не содержащее члена с произведением коор-
динат и имеющее равные коэффициенты при х2 и у2, т.е. уравнение
Ax2+Ay2+£>x+Ey+F=0, определяет некоторую линию, то эта линия - окружность.
Пример 2.12. Найти координаты центра и радиус окружности, опреде-
ляемой уравнением 4х2 + 4у2 - 8х + 12у - 3 = 0.
Разделив обе части уравнения на 4 и выделив полные квадраты, получим
4 9 9 3
(х2-2х+1)+у2+2-у+--1---- = 0,
2 4 4 4
или (х-1)2+(у + 3/2)2 = 4.
Сравнивая полученное уравнение с уравнением (2.20), заключаем,
что а = 1, Ь = -3/2, R = 2.
Пример 2.13. Какое множество точек плоскости определяет уравнение
х2 + у2-4х + 10у + 29 = 0?
Так как это уравнение сводится к уравнению (х - 2)2 + (у + 5)2 = 0, которому
удовлетворяют лишь координаты х='2, у = -5, то оно определяет единственную
точку С (2, -5).
2.3. Эллипс
Эллипсом называют геометрическое место точек плоскости, для каждой из ко-
торых сумма расстояний до двух данных точек (фокусов) той же плоскости есть
постоянная величина.
Каноническое уравнение эллипса
х2/а2 + y2/b2 = 1, (2.21)
где а = ОА — большая, b = ОВ — малая полуоси (рис. 2.4).
Координаты фокусов эллипса, определяемого уравнением (2.21): хх= — с,
>1=0; х2=с, у2 = 0, т. е. Tj(-c, 0), F2(c, 0), где
c = -Ja2-b2. (2.22)
Эксцентриситетом эллипса е называют отношение фокусного расстояния 2с к
длине большой оси 2а:
£ = с/а, £ = Jl-(b/a)2. (2.23)
25
Фокальными радиусами точки М эллипса называют отрезки прямых, соединяющих
эту точку с фокусами Ft и F2. Их длины и и г2 можно вычислить по формулам
Г1 = а + Ех,
Директрисами эллипса (2.21)
Рис. 2.4
г2 = а-ех. (2.24)
называют прямые, определяемые уравнениями
х=—а/Е, х = а/Е.
Пример 2.14. Какую линию опреде-
ляет уравнение Зх2 + 4у2 =12?
Разделим это уравнение почленно на.12:
х2/4+у2/3 = 1. Сравнивая полученное урав-
нение с уравнением (2.21), заключаем, что оно
определяет эллипс с полуосями а = 2, Ь = 4з.
Найдем фокусы этого эллипса. Из формулы
(2.22) следует, что с2=а2-Ь2-, поскольку в
данном случае а2 =4, Ь2=3, с2 =4—3 = 1,
с = 1. Следовательно, фокусы эллипса находятся в точках Tj(-1,0), F2(l, 0).
Пример 2.15. В прямоугольной декартовой системе координат постро-
ить линию, определяемую уравнением у = (— 2/3)79 ~х2.
Преобразуем это уравнение, возводя в квадрат обе его части:
у2 _ 9-х2 х^_+У^_ = 1
9’94’
-*7^7
/=1(9-х2),
9 4
Последнее уравнение определяет эллипс с полуосями а = 3, b = 2. Если решить
это уравнение относительно у, получим
у - -79-х2, у - -
3 3
В условии задачи дано второе из этих уравнений. Оно определяет не весь эл-
липс, а только ту его часть, для точек которой у < 0, т. е. половину эллипса,
расположенную ниже оси Ох.
Пример 2.16. Записать каноническое уравнение эллипса, проходящего
через точки М (3,2), N (3-J3/2, -J2).
Каноническое уравнение эллипса имеет вид х2/а2 + у2/b2 = 1. Так как точки Л/и
З2 22 ,
2 + >2 ~ 1’
а b
9 4
N лежат на эллипсе, то их координаты удовлетворяют уравнению эллипса:
(зТз/2)2 (Т?)2
а2 + Ь2
27 2_
а2' Ь2 ’ 2&г+Ь2 ’
Решая полученную систему уравнений, находим, что а2 = 18, Ь2 = 8.
Таким образом, получено каноническое уравнение эллипса х2/18+у2/8 = 1.
26
2.4. Гипербола
Гиперболой называется геометрическое место точек плоскости, для каждой из
которых модуль разности расстояний до двух данных точек (фокусов) той же
плоскости есть величина постоянная.
Каноническое уравнение гиперболы
x2/a2-//Z>2=l, (2.25)
где а = ОА — действительная, b = ОВ - мнимая полуоси (рис. 2.5).
Координаты фокусов гиперболы (2.25):
X] = — с, ^=0; х2 = с, у2 = 0, т. е.
F/-C, 0), F2(c, 0), где
c = -Ja2 + b2. (2.26)
Эксцентриситетом гиперболы называется
отношение фокусного расстояния 2с к длине
действительной оси 2а:
z = c/a. (2.27)
Асимптотами гиперболы называют пря-
мые, определяемые уравнениями
b b
у = —X, у =-X.
а а
(2.28)
Директрисами гиперболы называются прямые, определяемые уравнениями
х =—ajz, х = a/z. (2.29)
Гипербола с равными полуосями (Ъ = а) называется равносторонней, ее кано-
ническое уравнение имеет вид
х2-у2 = а2. (2.30)
Фокальные радиусы точки правой ветви гиперболы вычисляется по формулам
Г] = гх + а, г2 = гх - а-, (2.31)
фокальные радиусы точки левой ветви — по формулам
rt=-zx—a,r2=—zx + a: (2.32)
Пример 2.17. Какую линию определяет уравнение 9х2-4у2=36?
Разделив обе части уравнения на 36, получим х2/^-у2/9 = \. Сравнивая это
уравнение с уравнением (2.25), заключаем, что оно определяет гиперболу с дейст-
вительной полуосью а = 2 и мнимой полуосью b = 3.
Пример 2.18. Найти полуоси, координаты фокусов и эксцентриси-
тет гиперболы, заданной уравнением 5х2 — 4у2 = 20. Вычислить длины фо-
кальных радиусов точки М (-4, J15).
27
Разделив обе части уравнения на 20, получим х2/4-у2/5 = 1. Сравнивая это
уравнение с уравнением (2.25), заключаем, что а2 = 4, Ь2 = 5, т. е. а = 2, b = Js.
Из формулы (2.26) следует, что с2 = а2 +Ь2, с = 3, ^(-3,0), F2(3, 0). По форму-
ле (2.27) находим г = с/а = 3/2. Поскольку точка М лежит на левой ветви гипер-
болы, то при вычислении г, и г2 необходимо пользоваться формулами (2.32)
г, =(-3/2) (-4)-2 = 4, г2 =(-3/2) (-4)+2 = 8. Отметим, что
r2-ri = 8-4 = 4 = 2а.
Пример 2.19. Записать уравнения асимптот и директрис гиперболы
4х2-9у2=36.
Приводя уравнение гиперболы к каноническому виду (2.25), заключаем, что
а2 =9, Ь2 = 4, т.е. а = 3, b = 2. В соответствии с (2.28) записываем уравнения
асимптот у = (2/3)х, у = - (2/3) х. По формуле (2.26) находим с = V9+4 = л/Тз,
а по формуле (2.27) - эксцентриситет е = -Лз/з. Согласно (2.29), получаем
уравнения директрис х = -9/V13, х = 9/л/Тз.
2.5. Парабола
Параболой называется геометрическое место точек плоскости, равноудаленных от
данной точки (фокуса) и данной прямой (директрисы), лежащих в той же плоскости.
Уравнение параболы, симметричной относительно оси Ох и проходящей через
начало координат (рис. 2.6), имеет вад
у2 = 2рх, (2.33)
уравнение ее директрисы
х = —р/2. (2.34)
Парабола, определяемая уравнением (2.33), имеет фокус F (р/2,0), фокаль-
28
ный радиус ее точки М (х, у) вычисляется по формуле
г-х + р/2. , (2.35)
Парабола, симметричная относительно оси Оу и проходящая через начало ко-
ординат (рис. 2.7), определяется уравнением
х2=2«у- (2.36)
Фокус этой параболы находится в точке F (0, q/2), уравнение директрисы имеет вид
y = -q/2. Фокальный радиус ее точки М (х, у) выражается формулой r-y + q/1.
Замечание. Каждое из уравнений у2 =-2рх, х2 =~2qy определяет
параболу.
Пример 2.20. Найти координаты фокуса и уравнение директрисы пара-
болы у = 8х. Вычислить расстояние точки М (2,4) до фокуса.
Сравнивая уравнение у2 - 8х с уравнением (2.33), находим, что 2р = 8, отку-
да р = 4, р/2 = 2. В соответствие с формулой (2.34) получаем уравнение х = -2
директрйсы параболы, фокус параболы находится в точке F (2,0). Точка
М (2,4) лежит на параболе, так как ее координаты удовлетворяют уравнению
у2 = 8х. По формуле (2.3 5) находим фокальный радиус точки М: г = 2 + 2 = 4.
Пример 2.21. Найти координаты фокуса и уравнение директрисы пара-
болы х2 = 4у. Вычислить расстояние точки М (6,9) до фокуса.
Сравнивая уравнение х2 = 4у с уравнением (2.36), получаем 2q - 4, откуда
q-2, q/2 = \. Следовательно, фокус параболы находится в точке F (0,1), урав-
нение директрисы имеет вид у = — 1, а фокальный радиус трчки М: г = 9 + 1 = 10.
Пример 2.22. Составить уравнение параболы, симметричной относи-
тельно оси Ох и проходящей через точки М (5, 4), N (15, - 6).
Так как парабола симметрична относительно оси Ох, то в ее уравнение у вхо-
дит только во второй степени. Уравнение этой параболы имеет ввд
у2 = 2рх + с, где р и с — некоторые постоянные. Найдем рис, использовав усло-
вия задачи. Поскольку точки М и N лежат на параболе, то их координаты должны
удовлетворять ее уравнению 42 = 2р-5+с, (~6)2 = 2р15+с. Из уравнений
16 = 10р + с, 36 = 30р + с находим р = 1, с = 6.
Таким образом, данная парабола определяется уравнением у2 = 2х + 6.
2.6. Полярное уравнение эллипса,
гиперболы, параболы
Пусть у - дуга эллипса, гиперболы или параболы (рис. 2.8). Проведем через
фокус F прямую, перпендикулярную директрисе А, точку их пересечения обозна-
чим через А, проекцию точки М на эту прямую - буквой N. В точке F проведем
перпендикуляр к прямой AN (оси линии у), обозначим буквой Р точку ее пересече-
29
ния с дугой у, а длину отрезка FP - буквой р, т. е. |FP | = р, и назовем ее фокаль-
ным параметром линии у.
Пусть р и <р — полярные координаты точки М в системе координат с полюсом
в точке F и полярной осью FN, тогда
Р=-—------
1-ЕСО8ф
Уравнение (2.37) называется полярным уравнением эллипса, гиперболы, пара-
болы (это уравнение определяет одну из двух ветвей гиперболы).
(2-37)
Отметим, что для параболы фокальный пара-
метр совпадает с параметром р, входящим в урав-
нение (2.33), для эллипса и гиперболы, заданных
соответственно уравнениями (2.21) и (2.25), он
выражается формулой
р = Ь2/а. (2.38)
Пример 2.23; Какую линию определяет урав-
16
нение о =---------в полярных координатах?
5-3cos<p
Разделим на 5 числитель и знаменатель правой части
уравнения:
р=—.
l-(3/5)cos<p
Сравнивая полученное уравнение с уравнением
(2.37) и учитывая формулу (2.38), получаем р = Ь21а = 16/5, е = с/а = 3/5, откуда
а=5, Ь=4, с=3. Поскольку 0< е<1, то данное уравнение определяет эллипс с по-
луосями а = 5, Ь = 4.
9
Пример 2.24. Какую линию определяет уравнение р =------------ в по-
4-5cos<p
лярных координатах?
Разделив числитель и знаменатель правой части на 4, приведем это
уравнение к виду (2.37):
р.
l-(5/4)cos<p
Следовательно, р = Ь2/а=9/4, г=с/а = 5/4>\. Данное уравнение определяет
гиперболу с полуосями а = 4, 6 = 3.
30
2.7. Некоторые другие виды уравнений
линий второго порядка
Уравнение у = ах2 + Ьх + с приводится к виду X2 = 2qY и определяет парабо-
лу с осью, параллельной оси OtY.
Уравнение х = Ay2 + By + С приводится к виду Y2 = 2pX и определяет пара-
болу с осью, параллельной оси OtX.
Равносторонняя гипербола имеет уравнение (2.30), а в системе координат, ося-
ми которой являются ее асимптоты, определяется уравнением
АУ = С(С*0). (2.39)
Уравнение
ах + b . . , „
у =-----(ad-bc*Q,c*Q)
cx + d
приводится к виду (2.39) и определяет гиперболу.
Параметрические уравнения эллипса х2/а2 + у2/b2 = 1 имеют вид
x = acosZ, y = hsinz.
Параметрические уравнения гиперболы х2/а2 -y2/b2 = 1 имеют вид
х = о(/ + (1/4/)), y = h(Z-(l/4i)),
а также
х = пей/, у = 2>shf,
где ch г, sh/ - гиперболические функции аргумента t (см. п. 13.11).
Параметрические уравнения параболы х2 = 2qy можно записать так:
x = t, y-t2/2q.
Уравнение
у2 = 2рх+(Е2 -1) х2 (2.40)
определяет эллипс при 0 < £ < 1, гиперболу при Е > 1, параболу при £ = 1. В слу-
чае 0 < е < 1 это уравнение принимает вид
у2 = 2px-qx2,
где p = b2]a, q = b2/a2, а в случае £>1 у2 = 2px + qx2, гдер и q имеют те же
выражения.
Уравнение (2.40) называют уравнением эллипса, гиперболы, параболы, отне-
сенных к вершине; начало декартовой прямоугольной системы координат нахо-
дится в вершине линии - точке пересечения с координатной осью (рис. 2.9).
Эллипс, гиперболу, параболу называют каноническими сечениями. В сечении
конуса плоскостью, не проходящей через его вершину (рис. 2.10), получаются эти
линии, а именно эллипс (сечение одной полости конуса плоскостью, не перпенди-
31
кулярной его оси и не параллельно образующей), парабола (сечение плоскостью,
параллельной его образующей), гипербола (речение плоскостью обеих полостей
Пример 2.25. Построить линию, определяемую уравнением Зу =
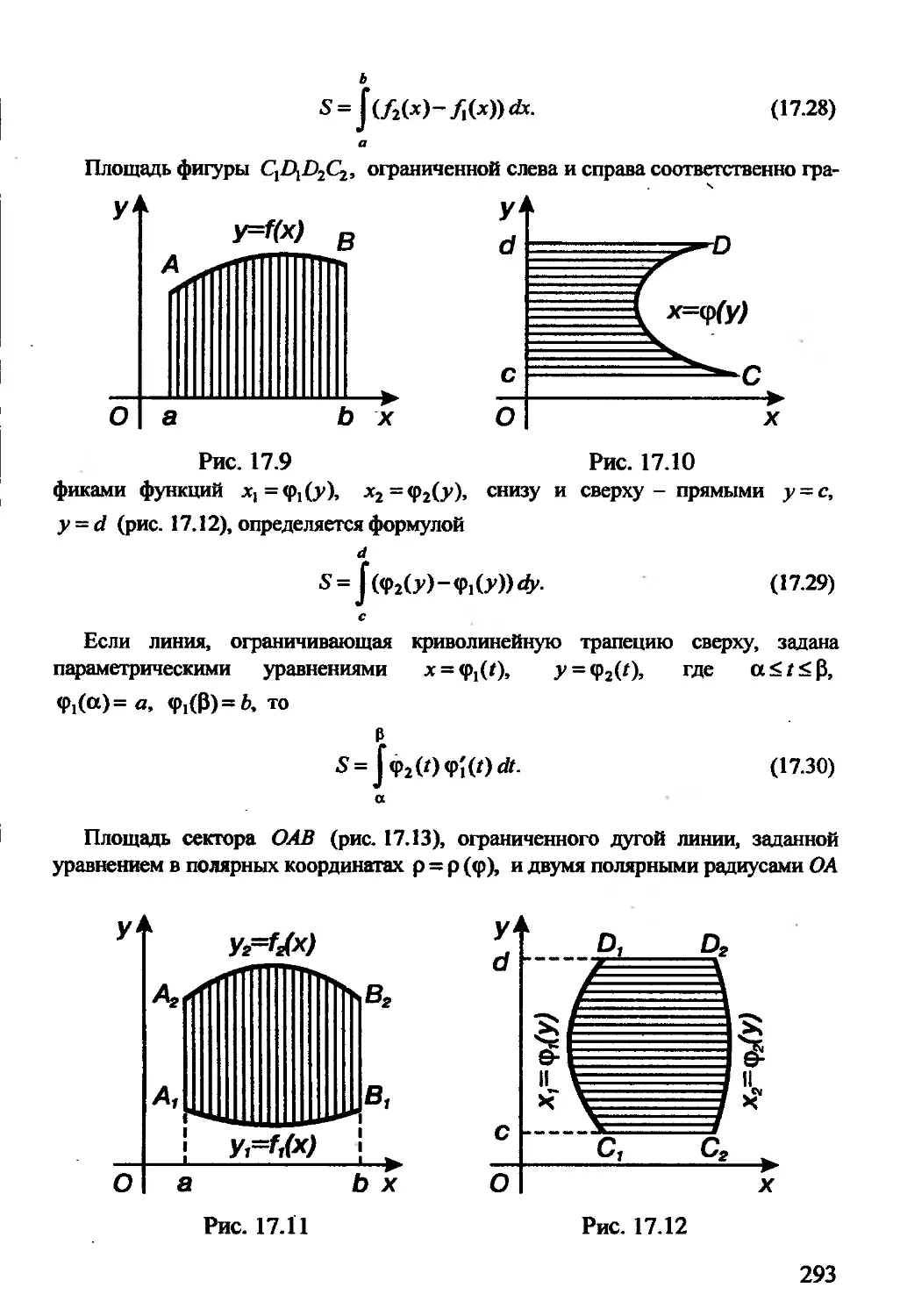
= х2-6х + 15.
Преобразуя это уравнение, получаем у = (1/3)((х2-6х+9)+6), у =
= (1/3) (х - З)2 + 2, у-2 = (1/3)(х-3)2. .
Перейдем к новым координатам по формулам Х = х-3, Y=y—2. В новых
координатах уравнение принимает вид Y = (1/3) X2, или Х2=ЗУ; оно определяет
параболу. Строим системы координат Оху и OtXY, последнею с началом в точке
О](3,2), и саму параболу - в новой системе координат по ее каноническому
уравнению (рис. 2.11).
Пример 2.26. Построить линию, определяемую уравнением
2х + 12
У=^т-
Преобразуя данное уравнение:
у(х+3)-2х —12 = 0, у (х+3)-2х - 6-6 = 0,
у(х + 3)-2(х+3)-6 = О, (х + 3)(у-2)= 6.
Переходя к новым координатам по формулам X = х + 3, Y = у-2, получаем
уравнение XY = 6, определяющее гиперболу. Строим линию в системе координат
OtXY (рис. 2.12), начало которой находится в точке ОД-3,2).
32
Рис. 2.12
Пример 2;27. Какую, линию определяет уравнение ху+х-2у-14 = О?
Преобразуем это уравнение: (ху+х)-(2у + 2)-12 = 0, х(у+1)-2(у +
+ 1)-12 = 0, (у + 1)(х —2)—12 = 0, (х-2)(у+1)=12.
Переходя к новым координатам по формулам Х = х-2, Y = y+l, получаем
уравнение XY = 12, которое определяет гиперболу.
2.8. Упрощение уравнения второй степени, не
содержащего члена с произведением
координат
Рассмотрим уравнение второй степени относительно прямоугольных декарто- •
вых координат, не содержащее члена с произведением координат ху.
Ax2 + Cy2+Dx + Ey + F = 0. (2.41)
Перейдем к новой системе координат OjXK полученной из исходной путем парал-
лельного переноса (см. рис. 1.10) начала в точку Ох(а,Ь), при котором старые координа-
ты (лу) точки М выражаются через ее новые координаты (X, Y) формулами (1.22).
Уравнение (2.41) путем выделения полных квадратов может быть приведено к
одному из следующих канонических уравнений:
Х2]а2+ Y2/b2 = 1, (2-42)
X2/a2 + Y2/b2 = Q, (2.43)
X2la2 + Y2lb2 = -1 (2.44)
в случае АС>0 (линии эллиптического типа);
X2la2-Y2fb2=\, - X2/a + Y2/b2 =1, (2.45)
X2/a2-Y2!b2 =0 (2.46)
в случае АС<0 (линии гиперболического типа);
2 Зак. 1
33
(2.47)
(2.48)
(2.49)
(2.50)
У2=2рХ,
Y2 = b\
У2=0, '
y2 = -z>2
в случае AC=0, A = 0 (линии параболического типа).
Если С=0, Л*0, то уравнение (2.41) приводится к виду X2 =2qY, если
Е * 0, и к одному из,уравнений X2 = а2, X2 — —а2, X2 = 0, когда Е= 0.
Уравнение (2.42) определяет эллипс, уравнения (2.45) - гиперболы (с дейст-
вительной осью 0}Х или ОХУ), уравнение (2.47) - параболу (с осью 0}Х),
уравнения (2.46) - пару пересекающихся прямых bX-aY = 0, bX + aY = Q,
уравнение (2.48) - пару параллельных прямых У **Ь, У = -Ь, уравнение (2.49) -
пару совпавших прямых У = 0, У = 0, уравнению (2.43) удовлетворяют координа-
ты единственной точки X = 0, У = 0, уравнениям (2.44) и (2.50) не удовлетворя-
ют координаты ни одной точки.
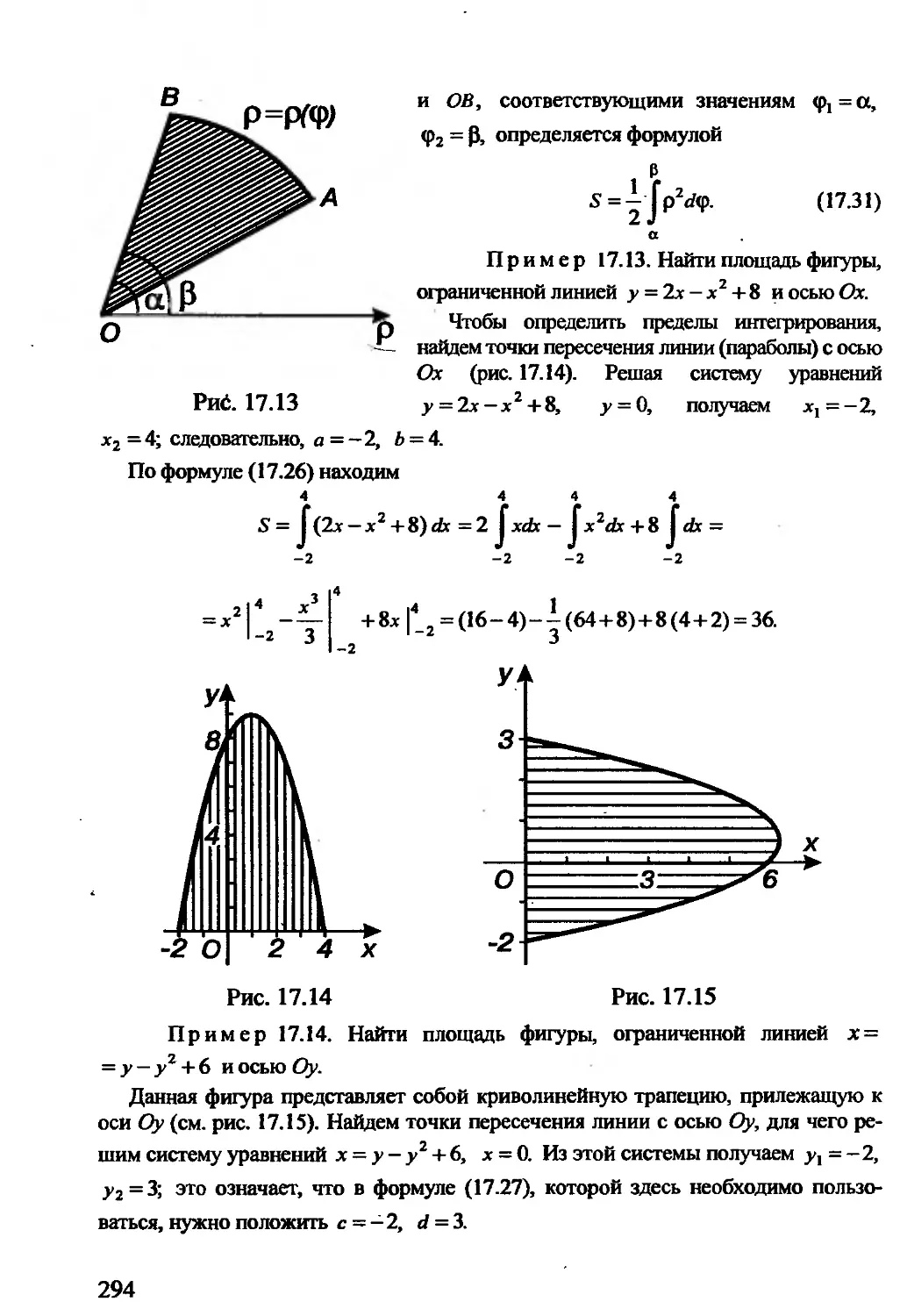
Пример 2.28. Построить линию, определяемую уравнением
9х2 -16/ - 36л-32у -124 = 0.
Преобразуем это уравнение:
9(х2-4х + 4)-16(/ +2у + 1)-36+16-124 = 0,
9(х-2)2-16(у+1)2-144= 0, (х-2)2/16-(у+ 1)2/9 = 1.
Перейдя к новым координатам по формулам Х = х-2, У = у+1, получим
уравнение Х2/16-У2/9 = 1> определяющее гиперболу с полуосями а -4, • b = 3
(рис. 2.13). Центр гиперболы находится в точке, для которой X — 0, У = 0. Так как
34
X=x-2, Y = y + \, то х—2 = 0, >+1 = 0, откуда х = 2, у = -1. Получена точка
Oi(2, -1), в которой находится начало новой системы координат.
Пример 2.29. Построить линию, определяемую уравнением
9х2 + 16у2 +36х —64у —44 = 0.
Выделяя полные квадраты в левой части уравнения, получаем
9(х2 + 4х+4)+16(у2-4у+4)-36-64-44 = 0,
‘9(х + 2/ + 16(у-2)2=144, (х + 2)2/1€+(у-2)?/9 = 1: 1
Переходя к новым координатам по формулам -X =.x,f2, У =, у.-2, последнему
уравнению придадим вид АГ2Дб+У2/9 = 1. Эго уравнение определяет эллипс с прлу-
осями а = 4, А,= 3 (рис. 2.14), Центр эллипса находится в точке, для которой X = 0,
У = 0, или х + 2=0; у-2= 0, откуда х =—2, у = 2, т. е. в точке 0^-2,2).
2.9. Упрощение общего уравнения второй степени
Общее уравнение второй степени относительно прямоугольных декартовых
координат х и у
Ах2+2Вху+Су2 +Dx + Ey+F = 0 . ч -.. ,(2.51)
при повороте координатных осей на угол а, для которого
ctg2a = (/l-C)/2B, (2.52)
преобразуется в уравнение А}х'2 + С\у'2 +jDjx'+ Ety' + F = 0, являющееся уравне-
нием вида (2.41).
Формулы преобразования координат имеют вид
х=x'cosa—y'sina, y = x'sina+y'cosa, (2.53)
причем
sina = ±1/(l-cos2a)/2, cos a = ±1/(l + cos2a)/2, (2.54)
_ ctg2a
cos2a = — .S (2.55)
±-Jl+ctg2a
гдеД§2о*01^{геляе1ся1формулс|йн(2.52)^ _ _ ’’У™
Уравнение (|.51) определяет ,йли пустое множество, или точку, или пару пря-
мы^/гйр^кающи&я, параллельных, совпавших), или одну из линий
(окружность, злщптс, гипербблу, параболу). Парупрямых называют распадающей-
ся линией второго порядка. -1 X
Пример 2.30. Построить линию, Определяемую уравнением '
5х2 — бху + 5у2 — 24х + 8у + 24 = 0.
Это частный случай уравнения (2.51), для которого Д=5, 2В = -6, С = 5,
35
D--24, E = 8, F=24. По формуле (2.52) имеем ctg2a = (5-5)/(-6)=0. Возь-
мем 2а = п/2, т. е. а = л/4, тогда sina = cosa = 4/2/2. Формулы (2.53) прини-
мают вид
л = (4/2/2) (х' - /), у = (4/2/2) (х' + У). (I)
Подставляя эти выражения в исходное уравнение, получаем
(5/2)(х'-У)2 -(6/2)(х'-У)(х' + У)+(5/2)(х' + У)2 -
-1VV2 (х'-/)+4Т2(х'+/)+24 = О,
(5/2)(х'2 -2хУ+ У2)-З(х'2 -У2)+(5/2)(х'2 + 2х'у'+у'2)-
-12/-j2(x' - у')+4-^2(х' + /)+ 24 = О,
2х'2 + 8у'2 - 8>/2х'+1бЛу + 24 = О,
х'2 + 4/2 - 4^2х' + &j2y'+12 = 0.
Преобразуем левую часть последнего уравнения, выделив в ней полные квадраты:
(х'2-4-Лх' + 8)+4(У2+272/+2)-8-8+12=0, (х'-2-Л)2+4(У+V2)2 =4.
Переходя к новым координатам по формулам
X = x'-2-j2, У = у' + у[2, (П)
последнее уравнение записываем так:
Хг + 4 У2 = 4, или Х2/4 + У 2/1 = 1. (Ш)
Каноническое уравнение (III) определяет эллипс с полуосями a = 2, Ь = 1. По-
строим этот эллипс относительно
новой системы декартовых прямо-
угольных координат О, ХУ. Угол
наклона оси ОхХ к оси Ох уже
известен a = 45°, осталось опре-
делить старые координаты точки
Ор В системе ОхХУ эта точка
' (центр эллипса) имеет координаты
X = б, У = 0. По формулам (II)
имеем х' — 2^2 =0, y'+-j2=0,
откуда х' = 2^2, у' = -2J2. С
помощью формул (I) находим координаты точки Ох в старой системе координат Оху.
х = (V2/2) (2^2- (-4/?)) = 3, у = (4/2/2) (2^2- 4/2 ) = 1, Ох(3,1).
Строим новую систему координат OxXY и сам эллипс по его канониче-
скому уравнению (III) (рис. 2,15).
2\
1-
О
Рис. 2.15
36
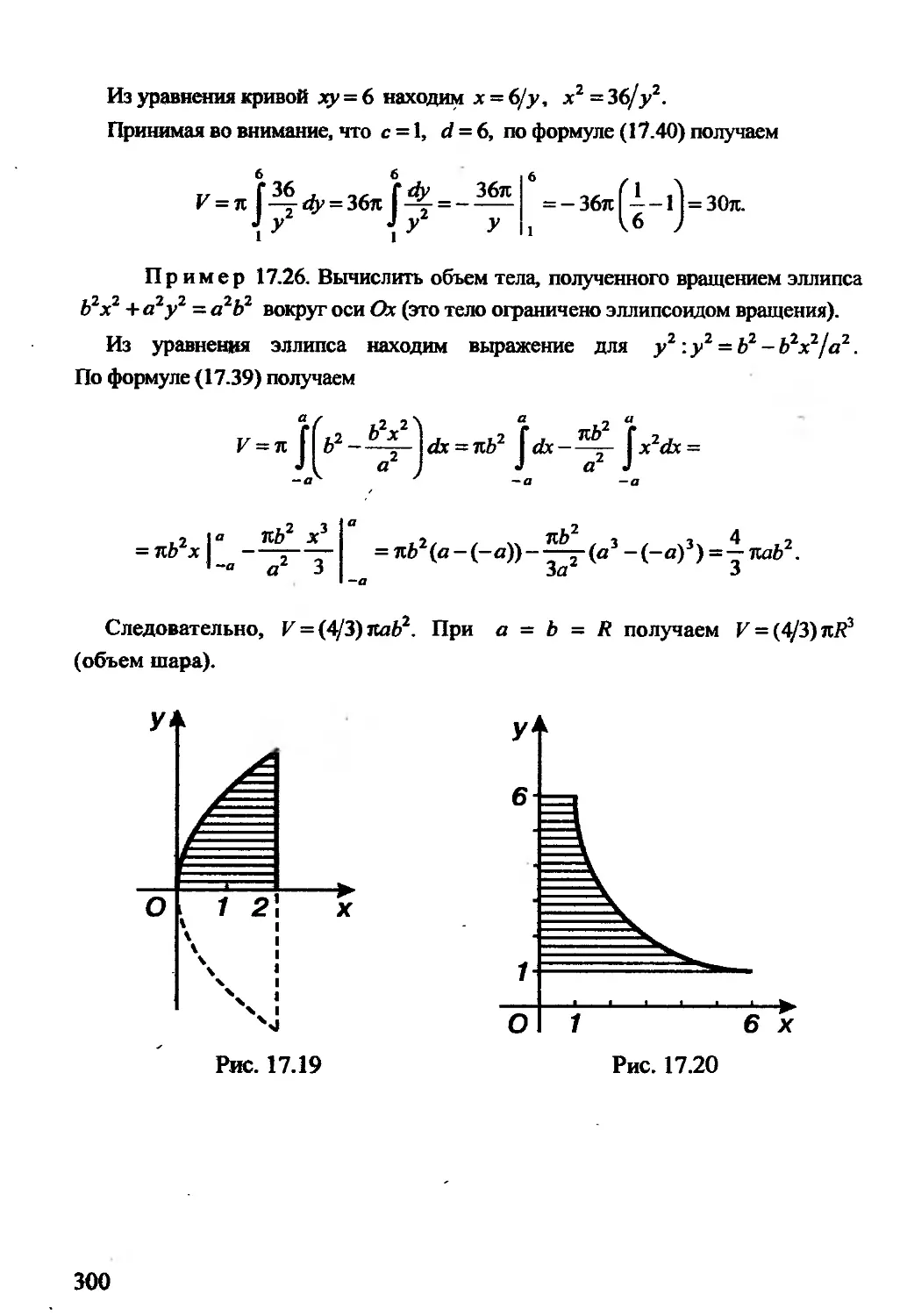
Пример 2.31. Построить линию, определяемую уравнением
Зх2+4ху — 4х — 8у = 0.
В данном случае А = 3, 2В = 4, С = 0. По формуле (2.52) Находим
ctg2a = (3-0)/4 = 3/4. В формулы (2.53) входят sina и cos а. Найдем их значе-
ния с помощью формул (2.54) и (2.55), в которых знак можно выбрать по своему
усмотрению. Выбрав везде знак плюс, получим
_ 3/4 3 11-3/5 1
71+.O/4)2 5 ’ 2 7?
2 1
cosa = -=, tga=—.
J5 2
Формулы (2.53) принимают вид
X = (1/75) (2x' - у'), у = (1/75 ) (х' + 2у‘). (IV)
Подставим эти выражения в исходное уравнение и преобразуем его:
Т (2х' - у ')2 4--^- (2х' - у') (х' + 2у ') —(2х' - у') —т=(х’+2у') = 0,
-(4х'2 -4х'у' + у'2)+-(2х'2 +4х у'-х'у'-2у'2)--!£х'—£у' = 0,
5 5 75 75
Перейдем к новым координатам по формулам
X=x'-VT5, Г = у' + б/Т5. (V)
Последнее уравнение в новых координатах примет вид
4 Л 2 - Г2 = -4, или - Х2/1 + Г2/4 = 1.
Эго каноническое уравнение определяет гиперболу с полуосями а = 1, 6 = 2,
причем действительной осью будет ось OtY. Построим гиперболу в новой системе
координат otXY. Найдем сначала старые координаты точки Ot, в которой нахо-
дится центр гиперболы. Для этой точки X = 0, Y = 0. По формулам (V) получаем
х' = ^75, у'—б/Т5. С помощью формул (IV) находим
37
1 ( 4 6 >
J5{45+ -J5)
0,(2,-2). Через точку О, про-
водим ось OtX, для которой tga = l/2, иось О,У. перпендикулярную оси О{Х.
В системе координат OtXY строим гиперболу по ее каноническому урав-
нению (рис. 2.16).
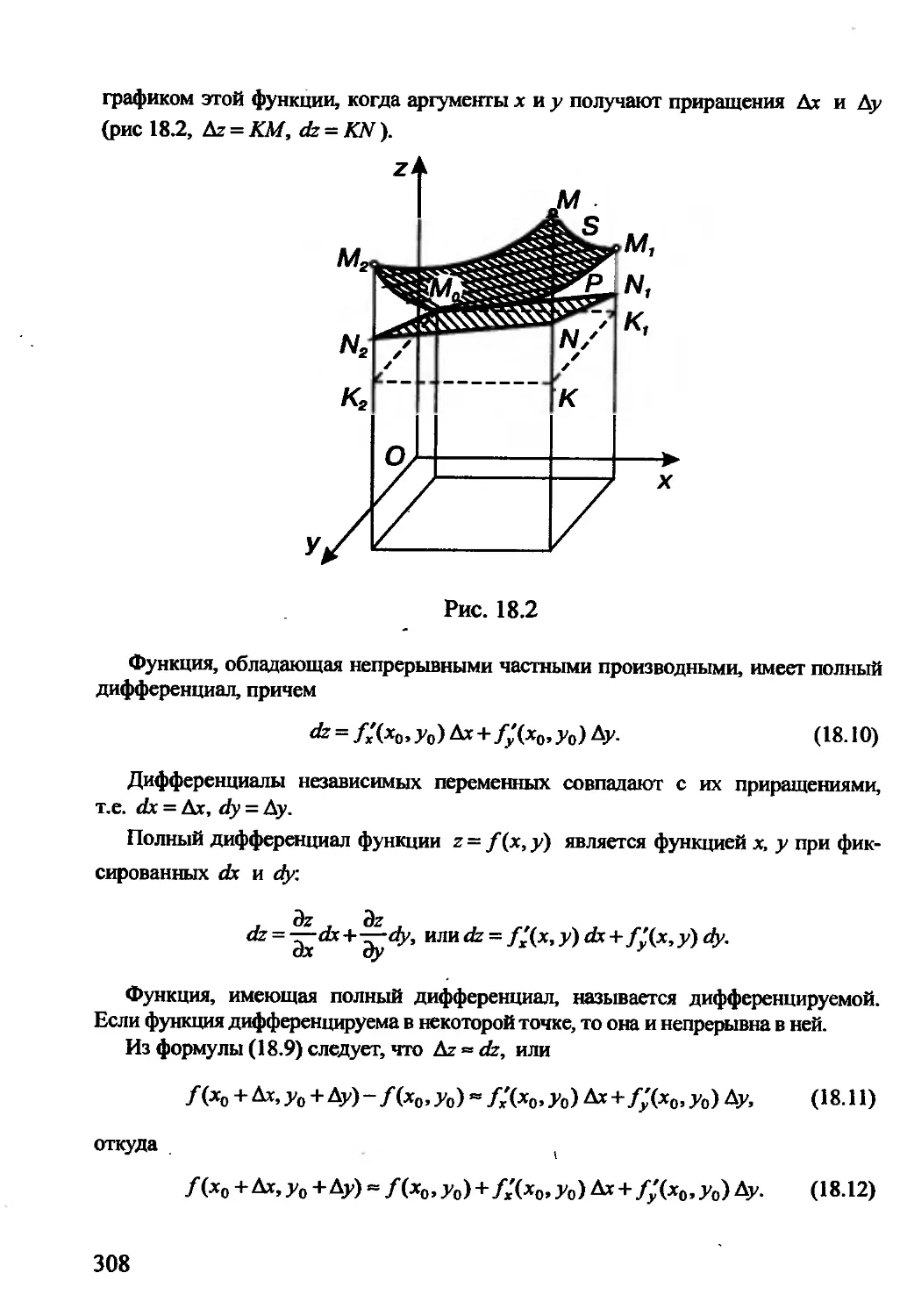
Пример 2.32. Построить линию, определяемую уравнением
х2 -2ху+у2 + 4х-8у + 7 = 0.
Поскольку Л = 1, 2В = -2, С = 1, то по формуле (2.52) ctg2a = (l-
—1)/(—2)= О, 2a = Jt/2, a = n/4. Формулы (2.53) принимают вид
х = (72/2)(х'*-У), y = (j2/2)(x'+y'). (VI)
Подставим эти выражения в исходное уравнение и преобразуем его:
(1/2) (х' - у')2 - (х' - У) (х'+У )+(1/2) (х'+у’)2 + 2^2 (х' - У) -
-4>/2 (х' + У)+7 = О,
2у’2 - 2-Лх' - 6^2/+7 = 0, (у' - 3 yfi/2)2 —Л(х'+ 1/^2) = 0.
Перейдем к новым координатам по формулам
Х = х‘+\1-Л, У = у’ -3-J2/2. <VI1)
В новых координатах последнее уравнение принимает вид
У2 - -J2X = 0, или У2 = J2X.
38
Это уравнение определяет параболу. Вершина параболы находится в точке, для
которой X = О, У = 0. Найдем старые координаты этой точки. По формулам (VII)
находим х' = -1/Л, у' = зД/2. С помощью формул (VI) получаем
J2
2
1_____3^
/2 V2
=-2,
1_+_3_
(2 -J2
= 1, Ц(-2,1).
V2
У=Т
Строим систему координат OtXY и параболу по ее каноническому уравнению (рис. 2.17).
2.10. Некоторые алгебраические линии
высших порядков
Декартов лист — линия, определяемая в прямоугольной декартовой системе
координат алгебраическим уравнением
х1 + у3 - Заху = 0 (а = const * 0).
В полярных координатах уравнение принимает вид
__За cos <p sirup
Р * 3 . з
cos <p+sin <р
Декартов лист можно задать и параметрическими уравнениями
x = 3at/(l + t3), y = 3at2/(l+t3).
Линия эта изображена на рис. 2.18.
Циссоида. Рассмотрим окружность с диаметром О А = 2а и касательную к ней
в точке А (рис. 2.19). Из точки О проведем луч ОВ, точку его пересечения с ок-
ружностью обозначим буквой С. На этом луче отложим отрезок |ОА/|=(ВС|.
;„з
39
Проведя другой луч и выполнив аналогичное построение, получим точку М}.
Таким способом можно построить сколько угодно точек. Множество точек
М, называют циссоидой. Построив достаточное число указанных точек и
соединив их плавной линией, получим циссоиду (см. рис. 2.19).
Уравнение циссоиды в декартовых прямоугольных координатах имеет вид
у2 =х3/(2а-х),
в полярных координатах
p = 2asin2<p/cos<p.
Параметрические уравнения циссоиды
2а 2а
?+1 Т(Т2+1)
или
х = 2а sin2 ф, у = 2а sin3 ф/созф,
где ф - полярный угол.
Строфоида. Рассмотрим точку А и прямую Д, не проходящую через данную
точку (рис. 2.20). Обозначим буквой С точку пересечения перпендикуляра к пря-
мой Д, проведенной в точке А, а длину отрезка АС-а, т. е. | АС] = а. Вокруг
точки А вращается луч, на котором откладываются отрезки ВМ} и ВМ2 от точки
В пересечения с данной прямой так, что | BMt | = | ВМ21 = | ВС |. Каждому положе-
нию луча соответствует пара точек Мх, М2, построенных указанным способом.
Множество пар точек Mt, М2 называют строфоидой. Точки Л/, и М2 при этом
называют сопряженными. Построив достаточное число точек и соединив их плав-
ной линией, получим строфоиду (см. рис. 2.20). Название «строфоида» происхо-
дит ст греческого слова <профТ|- поворот.
Уравнение строфоиды в полярных координатах
р = а (1 ± sin ф)/созф,
в декартовых координатах
2 (х-а)2х . I х
у = ------—, или у = ± (х - a) J-.
2а-х Ч2а-х
Параметрические уравнения строфоиды
х = а (1 ± sin ф), у = а (1 ± sin ф) sin ф/cos ф.
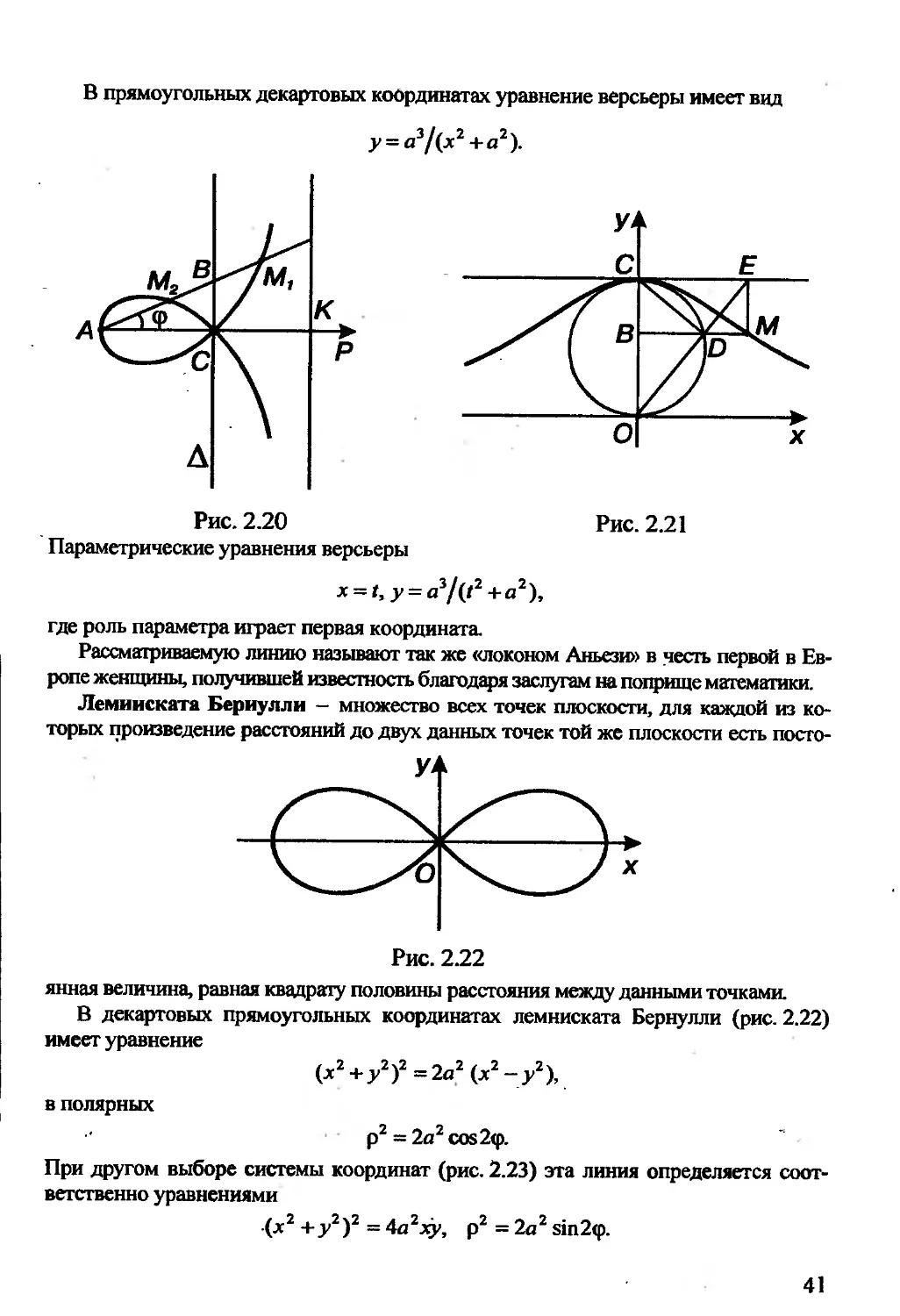
Версьера. Рассмотрим окружность с диаметром | ОС| = а и отрезок ВМ, по-
строений так, что |ОВ|:|BZ>| = |ОС|:|ВМ| (рис. 2.21). Множество точек М
называют версьерой.
40
В прямоугольных декартовых координатах уравнение версьеры имеет вид
Параметрические уравнения версьеры
х = I, у = a1/(I2 +а2),
где роль параметра играет первая координата.
Рассматриваемую линию называют так же «локоном Аньези» в честь первой в Ев-
ропе женщины, получившей известность благодаря заслугам на поприще математики.
Лемниската Бернулли — множество всех точек плоскости, для каждой из ко-
торых произведение расстояний до двух данных точек той же плоскости есть посто-
янная величина, равная квадрату половины расстояния между данными точками.
В декартовых прямоугольных координатах лемниската Бернулли (рис. 2.22)
имеет уравнение
(х2+у2)2 = 2о2 (х2-у2),
в полярных
p2 = 2a2cos2<p.
При другом выборе системы координат (рис. 2.23) эта линия определяется соот-
ветственно уравнениями
(х2 +у2)2 = 4а2ху, р2 = 2а2 sin2<p.
41
Название линии происходит от греческого слова - повязка, бант.
Линия названа по имени ученого, открывшего ее. Уравнение лемнискаты впервые
встречается в статье Я. Бернулли, опубликованной в 1694 г. в журнале «Acta eru-
ditorum» («Труды ученных»).
Овал Кассини - множество всех точек плоскости, для каждой из которых
произведение расстояний до двух данных точек той же плоскости есть постоянная
величина.
Уравнение овала Кассини в декартовых координатах
(х2 +уг)-2а1(х1 -у2) = Ь4-а4,
в полярных
p = a^cos2<p±ycos2<p((t)/a)-l).
Вид овала Кассини зависит от соотношения между постоянными а и Ь. В слу-
чае Ь> а овал имеет форму замкнутой линии, симметричной относительно осей
координат (рис. 2.24). При b = а получаем лемнискату Бернулли. В случае b < а
овал состоит из двух замкнутых линий.
Овалы Кассини названы в честь французского ученного, впервые рассмотрев-
шего их. Жан Доминик Кассини (1625 - 1712) открыл эти линии при попытке
Рис. 2.24
Конхоида. В плоскости фиксируем прямую и точку О, отстоящую от этой
прямой на расстоянии |ОЕ| = а (рис. 2.25, а). Проведем луч ОК, пересекающий
прямую LL, в точке К. На луче от точки К, по обе стороны от нее, отложены два
отрезка КМ и КМ, таких, что | КЛ/| = | КМ, | = I, где I - заданное число. Вращая
луч вокруг точки О (от 0 до 180° ) и проводя аналогичные построения (при одном
и том же значении 0. получим линию, описываемую точками М и М„ которую
называют конхоидой. Точку О при этом называют полюсом конхоиды, а прямую
42
LLf - ее базисом. Линия эта состоит из двух ветвей: одну ветвь описывает точка
М,другую- точка
Рис. 2.25
Уравнение конхоиды в полярных координатах
p = (a/sin<p)±/,
знак плюс - для верхней ветви, минус - для нижней. Форма конхоиды зависит
от соотношения между параметрами I и а. При / = а и 1>а линия имеет вид,
изображенный на рис. 2.25, б, в.
В прямоугольных декартовых координатах конхоида имеет уравнение
(х2+у2')(у-а)2-12у2=0.
Линию эту называют конхоидой Никомеда, по имени древнегреческого гео-
метра, впервые открывшего ее.
Улитка Паскаля. Рассмотрим окружность радиуса г с центром в точке С
(рис. 2.26). Выберем на данной окружности точку О. Представим себе, что вокруг
точки О вращается луч ОМ. В каждом его положении от точки N пересечения луча
и окружности откладываем отрезок |7VA/| = /, где I - заданное положительное
число. При повороте луча от 0 до 180° получим множество точек М. При даль-
нейшем' повороте луча от 180 до 360°, откладывая отрезок длины Z по направле-
нию луча, мы фактически будем откладывать его в сторону, противоположную
Рис. 2.26 Рис. 2.27 Рис. 2.28
43
прежней, т. е. | NMX | = I,и получим точки Мх. Множество точек М и Мх назы-
вают улиткой Паскаля.
Уравнения улитки Паскаля:
р = 2гcos<p ± I, (х2 + у1 - 2гх)2 - 12(х2 + у2) = 0.
Форма улитки Паскаля зависит от соотношения между параметрами г и I:
I < 2г (рис. 2.26), I = 2г (рис. 2.27), I > 2г (рис. 2.28).
Линия названа в честь Этьена Паскаля — французского математика-любителя,
отца знаменитого Блеза Паскаля.
Карднода - линия, описываемая точкой М окружности радиуса г, катящейся
по окружности с таким же радиусом (рис. 2.29). Параметрические уравнения кар-
диоды
x = 2rcos<—rcos2r, у = 2rsint-sin2t,
в полярных координатах
p = 2r (l-cos<p),
в декартовых координатах
(х2 + у2 + 2гх)2 = 4г2(х2 + у2).
Уравнение р = 2r (1+costp) также определяет кардиоду в полярной системе коор-
динат с полюсом в той же точке и противоположно направленной полярной осью.
Рис. 2.29 Рис. 2.30
Каппа - линия, представляющая собой множество точек касания касательных,
проведенных из данной точки к окружности заданного радиуса, центр которой пере-
мещается по фиксированной прямой, проходящей через эту точку (рис. 2.30).
Линия эта напоминает греческую букву К (кйппа), откуда и происходит ее название.
Параметрические уравнения каппы
х = a cos2 <p/sin <р, у = a cos<p,
44
в полярных координатах
p = actg<p,
в декартовых координатах
(х2 +у2)2 у2 — а2х2.
Роза - линия, заданная полярным уравнением p = asinJt<p или уравнением
р = в cos Хс<р, где а и к - положительные числа Роза целиком расположена в круге
радиуса а (р^а), так как | sinA<p|^l. Роза состоит из конгруэнтных лепестков,
симметричных относительно наибольших радиусов, каждый из которых равен а.
Количество этих лепестков зависит от числа к. Если к- целое число, то роза со-
стоит из к лепестков при нечетном к и из 2к лепестков при четном к (рис. 2.31, о,
б). Если к - рациональное число, причем к = т/п (п > 1), то роза состоит из т
лепестков в случае, когда тип- нечетные числа, или из 2т лепестков, если одно
из чисел будет четным. При этом в отличие от предыдущего случая каждый сле-
дующий лепесток будет частично покрывать предыдущий (рис. 2.31, в-е).
Если число к является иррациональным, то роза состоит из бесконечного мно-
жества лепестков, частично накладывающихся друг на друга.
Четырехлепестковой розой (см. рис. 2.31,6) называют линию, определяемую
полярным уравнением
p = esin2<p.
В декартовых координатах линия имеет уравнение
К=4/3 К=1/2 К=1/3
Рис. 2.31
45
Четырехлепестковая роза образуется множеством оснований перпендикуляров,
опущенных из вершины О прямого угла на отрезок постоянной длины, концы которого
скользят по двум взаимно перпендикулярным прямым, пересекающимся в точке О.
Трехлепестковой розой (см. рис. 2.31. а) называют линию, определяемую уравнением
p = asin3<p.
В декартовых координатах линия имеет уравнение
(x2+y2J2=a(3x2y-y3).
Астроида. Прямоугольник, две стороны которого лежат на двух взаимно перпен-
дикулярных прямых,; деформируется так, что его Жагональ сохраняет постоянную
длину Д Множество точек — оснований перпендикуляров, опущенных из вершины
прямоугольника на его диагональ, называют астроидой (рис. 2.32, а).-
~ Астроида ймеетйараметрические уравнения ...
x = acos3/, j> = asiti®'r.
Исключив из этих уравнений параметр t, получим уравнение астроиды в пря-
моугольных координатах:
’ х^+у^=^3.
Освобождаясь от дробных показателей, находим
(х2 + у2 -а2)3 + Т1х2у2а2 = 0.
Астроиду можно рассматривать как траекторию точки окружности- радиуса г
(рис. 2.32, б), катящейся по внутренней стороне другой окружности, радиус R ко-
торой в четыре раза больше г (R = 4г).
' НгфаметрИчес^ое у^ЙАнёниё асфбцдй в Мом'сЙ^чае
3 w t 1 „ 3t. 3 „ . t 1 „ . 3t
х = — Л cos—+— Л cos—, у = —Rsin-------Rsin—.
4 4 4 ... ,.4z- /..-Л 4 4 А.!-
46
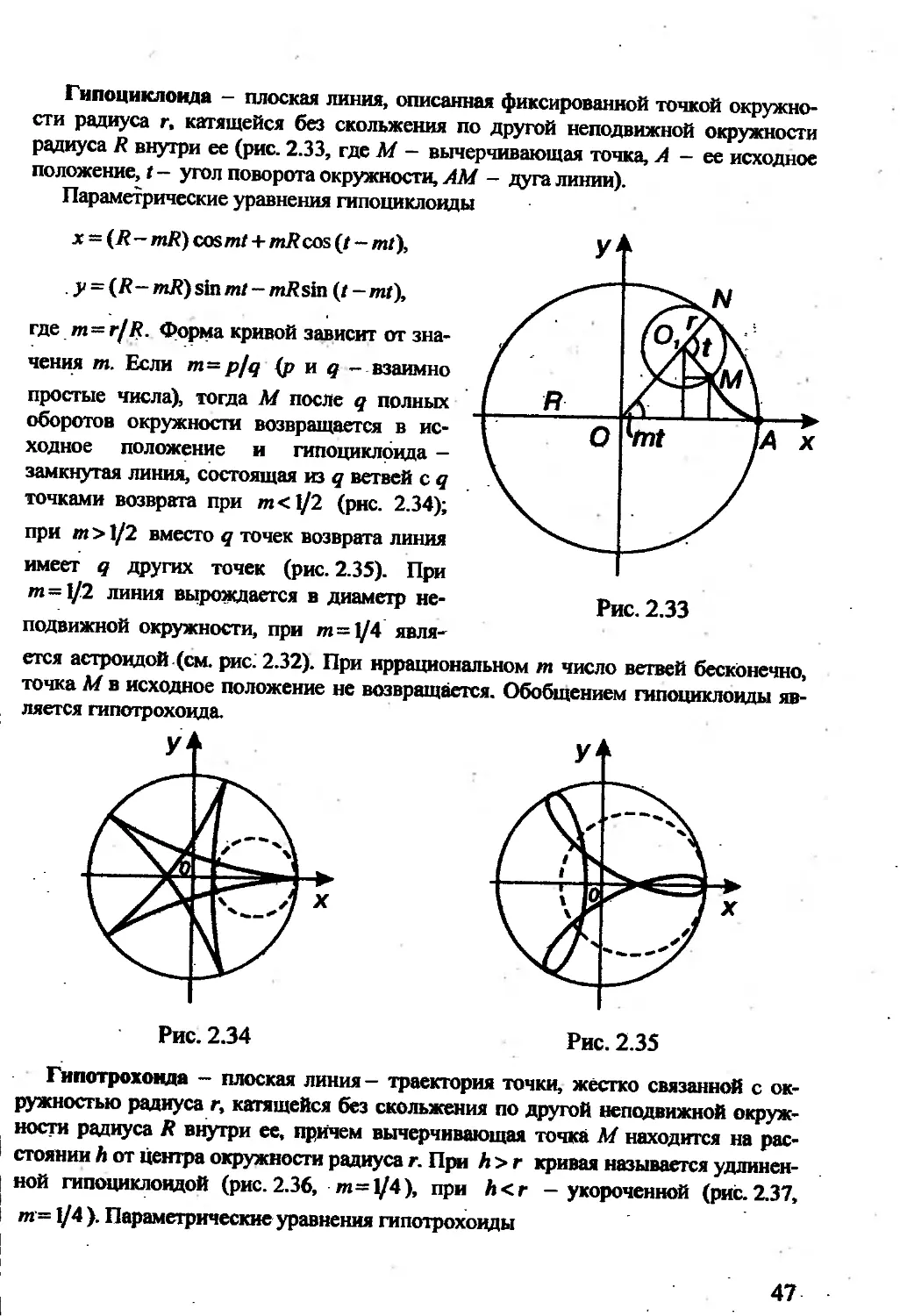
Гипоциклоида - плоская линия, описанная фиксированной точкой окружно-
сти радиуса г, катящейся без скольжения по другой неподвижной окружности
радиуса R внутри ее (рис. 2.33, где М — вычерчивающая точка, А - ее исходное
положение, t — угол поворота окружности, AM - дуга линии).
Параметрические уравнения гипоциклоиды
x-(R-mR) cos mt + mJ?cos (/ - mt),
y = (R-mR) sin mt - mJ? sin (t—mt),
где m=r/R. Форма кривой зависит от зна-
чения т. Если т= p/q (р и q - взаимно
простые числа), тогда М после q полных
оборотов окружности возвращается в ис-
ходное положение и гипоциклоида -
замкнутая линия, состоящая из q ветвей с q
точками возврата при т<Л]2 (рис. 2.34);
при т > 1/2 вместо q точек возврата линия
имеет q других точек (рис. 2.35). При
т-\/2 линия вырождается в диаметр не-
подвижной окружности, при т=1/4 явля-
ется астроидой (см. рис. 2.32). При иррациональном т число ветвей бесконечно,
точка М в исходное положение не возвращается. Обобщением гипоциклоиды яв-
Гипотрохоида - плоская линия - траектория точки, жестко связанной с ок-
ружностью радиуса г, катящейся без скольжения по другой неподвижной окруж-
ности радиуса R внутри ее, причем вычерчивающая точка М находится на рас-
стоянии h от центра окружности радиуса г. При h > г кривая называется удлинен-
ной гипоциклоидой (рис. 2.36, m=i/4), при h<r - укороченной (рис. 2.37,
т = 1/4 ). Параметрические уравнения гипотрохоиды
47
х = (Л-mR) cos mt + h cos (/ - mt),
x = (R- mR) sin mt — h sin (t — mt),
raem = r/R. При R = 2r линия является эллипсом, при h = R+r- розой (см. рис. 2.31).
Эпициклоида - плоская линия - траектория фиксированной точки окружно-
сти радиуса г, катящейся без скольжения по другой неподвижной окружности
радиуса R вне ее (рис. 2.38, где М - вычерчивающая точка, А - ее исходное
Рис. 2.38
положение, I- угол поворота окружности, AM -
дуга кривой).
Параметрические уравнения эпициклоиды
х = ( R + mR) cos mt - mR cos (t + mt),
y = (R+mR) sin mt - mRsvn (t + mt),
где m = r/R. Форма кривой зависит от значения т
(рис. 2.39, а; т = \/3, рис. 2.39, б; т = 2/3). Если
т = Р/ч (ptAq - взаимно простые числа), точка М
после q полных оборотов окружности возвращает-
ся в исходное положение и эпициклоида -
замкнутая линия, состоящая из q ветвей с q точка-
ми возврата. При т = 1 кривая является кардиодой
(см. рис. 2.29). При иррациональном т число ветвей бесконечно, точка М в исходное
положение не возвращается. Обобщением эпициклоиды является эпитрохоида.
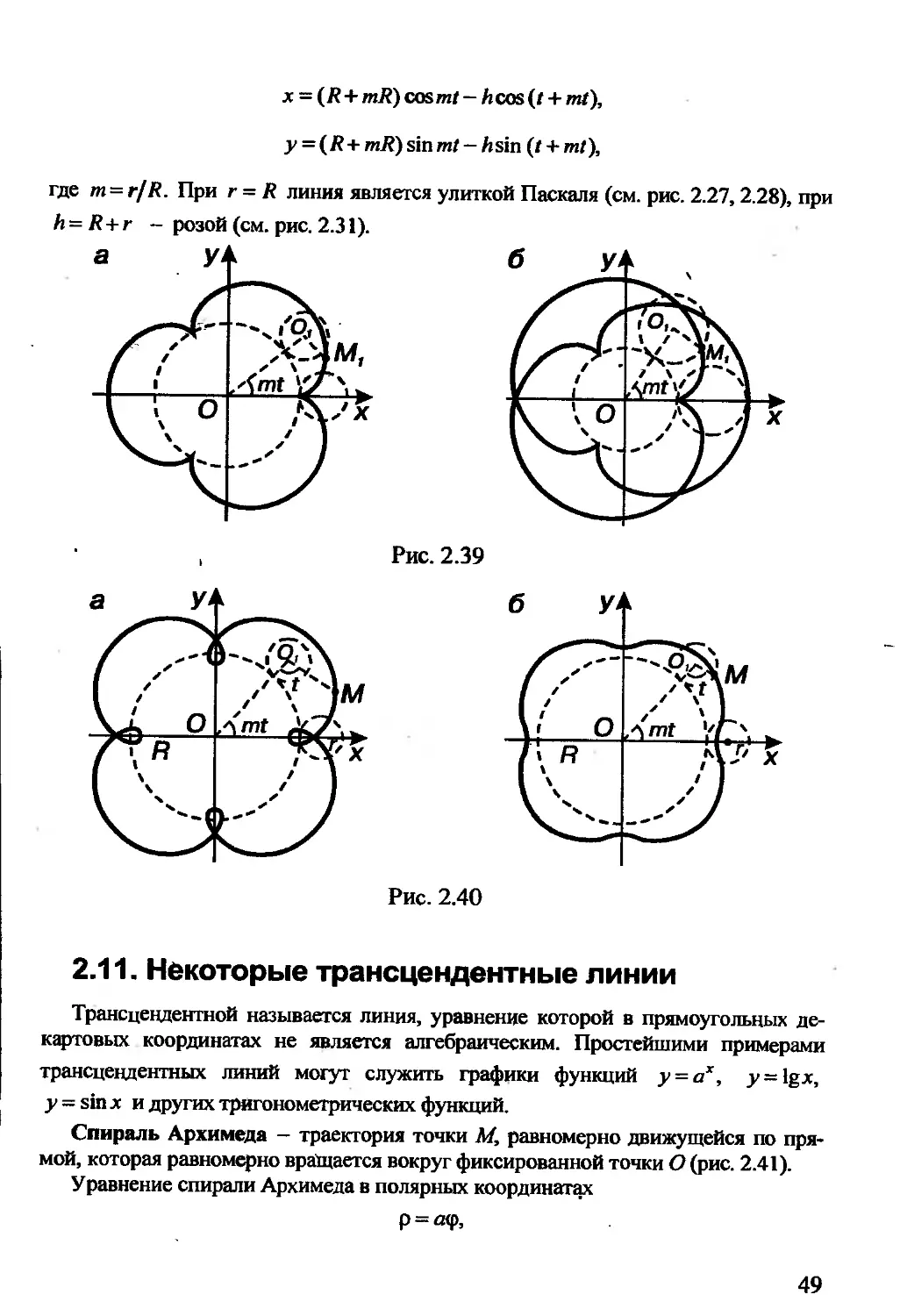
Эпитрохоида - плоская кривая - траектория точки, жестко связанной с про-
изводящей окружностью радиуса г, катящейся без скольжения по другой непод-
вижной окружности радиуса R вне ее, причем вычерчивающая точка М находится
на расстоянии h art центра производящей окружности. При , h > г линия называет-
ся удлиненной эпициклоидой (рис. 2.40,а; т=\/А), при h<r - укороченной
эпициклоидой (рис. 2.40, б; т = 1/4 ). Параметрические уравнения эпитрохоиды
48
х = (Я + mR) cos mt — A cos (t + mt),
у = (Я + mR) sin mt — Asin (t + mt),
где m = r/R. При r = R линия является улиткой Паскаля (см. рис. 2.27, 2.28), при
УА
2.11. Некоторые трансцендентные линии
Трансцендентной называется линия, уравнение которой в прямоугольных де-
картовых координатах не является алгебраическим. Простейшими примерами
трансцендентных линий могут служить графики функций у = ах, y=lgx,
у = sin х и других тригонометрических функций.
Спираль Архимеда - траектория точки Л/, равномерно движущейся по пря-
мой, которая равномерно вращается вокруг фиксированной точки О (рис. 2.41).
Уравнение спирали Архимеда в полярных координатах
р = а<р,
49
в декартовых координатах
jx2+y2 =aarctg(yfx).
Циклоида — траектория фиксированной точки окружности, которая без
скольжения катится по прямой
(см. пример 1.17, уравнения (1.21)).
Рассмотрим траекторию точки,, жестко
связанно)! с окружностью, катящейся по
прямой, но находящуюся не на самой окруж-
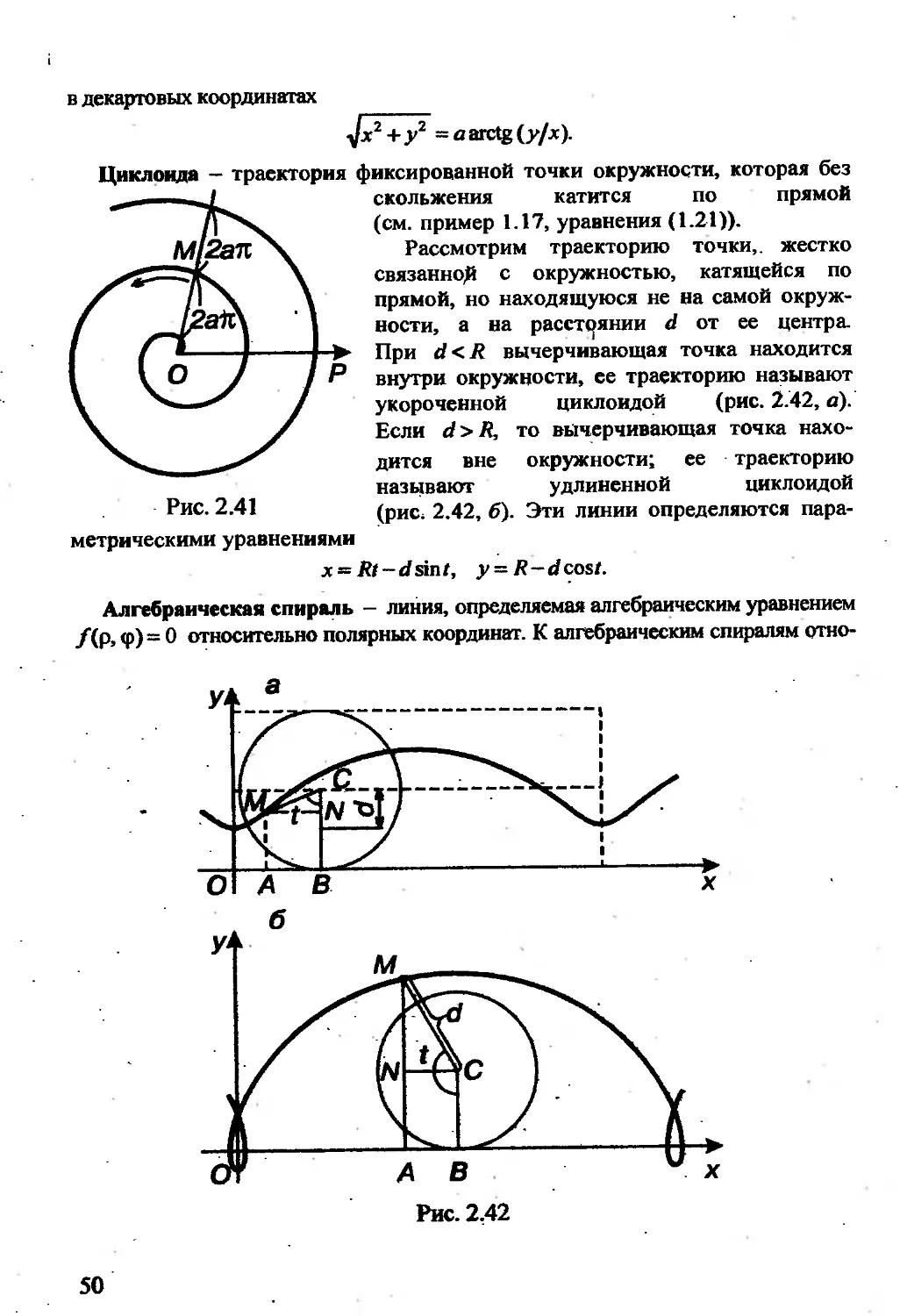
ности, а на расстоянии d от ее центра.
При d<R вычерчивающая точка находится
внутри окружности, ее траекторию называют
укороченной циклоидой (рис. 2.42, а).
Если d>R, то вычерчивающая точка нахо-
дится вне окружности; ее траекторию
называют удлиненной циклоидой
(рис, 2.42, 6). Эти линии определяются пара-
метрическими уравнениями
х = Rt-dsint, у= R-dcost.
Алгебраическая спираль - линия, определяемая алгебраическим уравнением
/(р, <р)= 0 относительно полярных координат. К алгебраическим спиралям отно-
50
сится спираль Архимеда, так как ее уравнение р = а<р является алгебраическим
уравнением первой степени относительно риф. Другими .простейшими алгебраи-
ческими спиралями являются линии, определяемые уравнениями:
р = а/ф (гиперболическая спираль, рис. 2.43);
р = (а/ф)+/, где/>0 (конхоида гиперболической спирали, рис. 2.44);
р = аф2 (егшраль Галилея, рис. 2.45);
р2=«2ф J /. f (спираль Ферма, рис; 2.46); ?
р = а^ф".+ 1, гДе 1 > 0 (парЖйТичёёкая ейираль, рис. 2.47); \ J
р = аД/ф' : 1 (жезл; рис. 2.48);
Логарифмической спираль (рис. 2.49) - линия, определяемая уравнением
р = в’ (а > 0, а * 1).
Логарифмическая спираль пересекает полярные радиусы всех своих точек под
одним и тем же углом. На этом свойстве основано ее применение в технике. Так, в
различных режущих инструментах и машинах вращающиеся ножи имеют' про-
филь, очерченный по дуге логарифмической спирали. В силу этого угол резания
остается постоянным. Логарифмическая спираль применяется в теории механиз-
мов при проектировании зубчатых колес с переменным передаточным числом (т.е.
отношением их угловых скоростей). В природе некоторые раковины очерчены по
логарифмической спирали (рис. 2.50).
Логарифмическая спираль впервые упоминается в письме Декарта к Мерсенну
от 12 сентября 1638 г. (опубликовано в 1657 г.). Независимо от Декарта логариф-
мическая спираль была открыта Торричелли, который выполнил ее спрямление и
квадратуру. Название «логарифмическая спираль» для данной линии предложил
Лопиталь, автор первого печатного учебника по дифференциальному исчислению.
Квадратриса. Дан отрезок AD длины 2а, середина которого находится в точке
О (рис. 2.51, а). Отрезок ОА равномерно вращается вокруг точки О с угловой ско-
ростью <о = я/27', а прямая КС, перпендикулярная AD, одновременно начинает
равномерно двигаться от точней А к точке'р'св^кордечсью v = а/Т, оставаясь па-
раллельной исходному направлению. Точка М пересечения вращающегося отрезка
и движущейся прямой вписывает линию, юАорую.Называют квгщратрисой.
Уравнение квадраггрисы в декартовых координатах
______________________________y = xctg(rtx/2aj,
в полярных координатах
А
р = а (Я-2<p)/ncos<p.
51
Рис. 2.50
52
Линия имеет бесконечное множество точек пересечения с осью ординат, так
ctg(nx/?a) = O при х = ±а, х = ±3а, х=±5а,... Квадратриса изображена на
рис. 2.51, б, а на рис. 2.51, а указана та часть линии, которая соответствует значе-
ниям аргумента х: - a S х £ а. Название линии дал Лейбниц.
Квадратрису впервые открыл Гиппий из Эллады (древнегреческий софист,
живший в V в. до н.э.) в поисках решения задачи о трисекции угла. К задаче о
квадратуре круга эту линию применил древнегреческий геометр Динострат IV в.
до н.э. В связи с этим линию называют квадратрисой Динострата.
Трактриса — линия, у которой длина касательной является постоянной вели-
чиной. Под длиной касательной понимают длину отрезка МТ, касательной между
точкой касания М и точкой Т пересечения с осью Ох (рис. 2.52). Трактриса имеет
параметрические уравнения
x = aintg(f/2) + acosr, y = asinz;
ее уравнение в прямоугольных декартовых координатах
х = ± (a In ((а +7а2 —у2 }/у)+Ja2 -у1).
Трактриса применяется в-одной из частей механизма карусельного токарного
станка (рис. 2.53). Линия вертикального профиля антифрикционной пяты этого
механизма обладает тем свойством, что длина ее касательной постоянна.
53
Трактриса сыграла выдающуюся роль в истории математики в связи с откры-
тием Н.И. Лобачевским новой геометрии и последующим развитием учения о не-
евклидовых геометриях. Геометрия Лобачевского реализуется на псевдосфере,
полученной вращением трактрисы вокруг ее асимптоты.
Трактриса была открыта в XVII в. Ее название происходит от латинского слова
tracto - тащу, влеку.
Цепная линия - кривая, форму которой принимает под действием силы тя-
жести нить с закрепленными концами (рис. 2.54). В прямоугольных декартовых
координатах цепная линия имеет уравнение
у = (а/2)(ех/а+е-х/о).
Длина дуги цепной линии от ее вершины до заданной точки равна про-
екции ординаты этой точки на касательную, проведенную в этой точке
(рис. 2.55, s= MN). Проекция ординаты произвольной точки цепной линии
на нормаль в этой точке является величиной постоянной, равной параметру
а цепной линии (а = ML).
Свойства цепной линии применяются в строительстве и технике. Они исполь-
зуются в расчетах, связанных с провисанием нитей-проводов, тросов и т.д. В
строительной технике применяется также линия свода, определяемая уравнением
у = с(ех/а+е-х/о).
Вопрос о форме линии провисания впервые рассмотрел Галилей (1638).
Он полагал, что линия провисания является параболой. Против этого позже
возражал Гюйгенс. Окончательное теоретическое решения вопроса о форме
линии провисания дали Лейбниц, Гюйгенс, Я. Бернулли.
54
Гпава 3
ВЕКТОРЫ
Понятие вектора возникло как математическая абстракция объектов, характе-
ризующихся величиной и направлением, например, таких как перемещение, ско-
рость и т. п. Термин «вектор» ввел У. Гамильтон (около 1845 г.), обозначения:
a - Ж. Арган (1806), АВ - А. Мёбиус, г - Коши (1853), а - О. Хевисайд (1891)
3.1. Основные понятия
Вектором называется направленный отрезок. Если начало вектора находится в
С
D
точке А, конец - в точке В, то вектор обозначается символом АВ или АВ. Нача-
ло вектора называют также точкой его приложения. Вектор иногда обозначается
одной строчной буквой жирного шрифта а, Ь и т. д., или такой же буквой светлого
шрифта с черточкой наверху a, Ь и т. д.
Модулем вектора а называется его длина, он обозначается через | а ] или про-
сто а. Модуль вектора — скалярная
неотрицательная величина.
Нуль-вектором (или нулевым век-
тором) называется вектор, начало и
конец которого совпадают. Нуль-
вектор обозначается символом 0. Его
модуль равен нулю, а направление не
определено.
Единичным вектором называется вектор, длина которого равна единице.
Векторы, лежащие на параллельных прямых или на одной прямой, называются
коллинеарными (рис. 3.1, CD и MN, КЬи MN, CD и KL ).
Коллинеарные векторы, имеющие одинаковые направления и равные длины,
называются равными (рис. 3.2, а, ВС = AD ). Так как векторы АВ и CD имеют
противоположные направления, то АВ* CD, хотя
Отметим, что
ОМ| * ОМ2, где М\ и
Мг - две различные
точки окружности ра-
диуса R с центром в
точке О (рис. 3.2, б),
поскольку векторы
ОМ, и ОМ2 имеют
разные направления.
К
L N
М
Рис. 3.1
а
В
Рис. 3.2
м,
55
Векторы, противоположно направленные и имеющие равные длины, называ-
ются противоположными (векторы АВ и CD на рис. 3.2, а). Вектор противопо-
ложный вектору а, обозначается через — а.
Векторы, лежащие в параллельных плоскостях (или в одной плоскости), назы-
ваются компланарными.
Вектор, точка приложения которого может быть выбрана произвольно, назы-
вается свободным.
3.2. Линейные операции над векторами
Линейными операциями над векторами называют сложение, вычитание, умно-
жение вектора на число.
Суммой векторов а и Ь называют третий вектор с, начало которого совпадает с
началом вектора а, а конец — с концом вектора Ь при условии, что вектор Ь отло-
жен из конца вектора а. Вектор с получается по правилу треугольника (рис. 3.3, а)
или параллелограмма (рис. 3.3, б).
Рис. 3.3
Аналогично определяется сумма трех и более векторов. Суммой и векторов
а|,а2,....ап называется вектор, начало которого совпадает с началом первого
вектора а(, конец — с концом последнего а„ при условии, что каждый после-
дующий вектор а4+1 отложен из конца предыдущего Яц (/г = 1,2, ...,и-1). Ука-
занный способ построения суммы называется правилом замыкающей.
Рис. 3.4
Сумма векторов обладает свойством переместительности (коммута-
тивности, рис. 3.4):
а+Ь=Ь+а
и свойством сочетательности (ассоциативности)
(а + Ь)+с = а + (Ь+с).
56
Сумма трех некомпланарных векторов а, Ь, с наряду с правилом замыкающей по-
лучается и по правилу параллелепипеда: сумма а + Ь + с равна вектору OD, где
О D - диагональ параллелепипеда, построенного на векторах ОА = а, ОВ = Ь,
ОС = с, отложенных из одной точки (рис. 3.5).
Рис. 3.6
Из определения суммы следует, что
а + О = а, а+(-а) = О.
Разностью а - Ь двух векторов а и Ь называется такой вектор d, который в
сумме с вектором Ь дает вектор а:
a-b = d, еслиЬ + д = а.
Чтобы получить разность а - Ь двух векторов а и Ь, необходимо отложить их
из одной точки и соединить конец второго вектора с концом первого (рис. 3.6, а).
Разность а - b равна сумме двух векторов а и (- Ь), где (- Ь) - вектор, про-
тивоположный вектору b (рис: 3.6, б), т. е.
а-Ь = а+(-Ь).
Векторы — диагонали параллелограмма ОАСВ (рис. 3.6, в), построенного на векто-
рах ОА = а, ОВ = Ь, являются соответственно суммой и разностью этих векторов.
57
Произведением вектора а на число а называется вектор
Ь = аа,
удовлетворяющий условиям: 1) | b| = | а| | а |; 2) b и а одинаково направлены при
а> 0; 3) Ь и а имеют противоположные направления при а<0 (рис. 3.7). Оче-
видно, Ь = 0, если а = 0 или а = 0.
а
2,5а
-За
Рис. 3.7
Произведение вектора на число обладает следующими свойствами:
а(ра) = (ар)а, a(a + b) = aa+ab, (а+р)а = аа+ра;
а(а1+а2 + --- + а„) = аа1+аа2 +-*аа„;
(а, +а2 + -"+аи)а=а1а+а2а+--аиа.
^Необходимое и достаточное условие коллинеарности векторов а и Ь выражает-
ся равенством
(3.1)
Ь = аа.
3.3. Проекция вектора на ось
В пространстве заданы вектор АВ и ось и (рис. 3.8). Пусть А, - проекция
точки А на ось и, Д - проекция точки В, т. е. основания перпендикуляров, опу-
щенных из данных точек на эту ось.
Проекцией вектора на
ось и
Рис. 3.8
называется величина направленного отрезка
(вектора) 4Д оси и. Проекция вектора АВ
на ось и обозначается через пр„АВ, т. е.
AtBt = ири АВ, вычисляется по формуле
пр, АВ = j АВ | cos<p,
гдеф — угол между вектором АВ и осью и.
Из равенства (3.2) следует, что если а = b то
пр,а = пр„Ь, (3.3)
(3.2)
т. е. равные векторы имеют равные проекции (на одну и ту же ось).
58
Проекция вектора на ось обладает следующими свойствами:
пр„(а + Ь) = пр„ b + пр„а, (3.4)
пр„(аа) = а пр, а, (3.5)
при(а, +а2 + — + а„) = приа1 +приа2 + — +приап. (3.6)
Если а1,а2,...,ал — произвольная конечная система векторов; а,,а2,• ••,ап -
произвольная система действительных чисел, то вектор
а = а1а1 +а2а2+ -- + а„аи
называется линейной комбинацией векторов этой системы.
Из равенств (3.4) — (3.6) следует, что
пр„(а1а1 +а2а2 + -а„а„)= сцпр^, +а2приа2 + -а„приап. (3.7)
3.4. Декартовы прямоугольные координаты
вектора в пространстве. Длина вектора.
Направляющие косинусы вектора
Рассмотрим в пространстве декартову прямоугольную систему координат. Ра-
диусом-вектором точки М называется вектор г = ОМ, точка приложения которого
совпадает с началом координат, а конец находится в точке М (рис. 3.9).
Декартовыми прямоугольными координатами X, Y, Z вектора г называются его
проекции на координатные оси
% = пргг, К = пр^,г, Z = npIr.
Каждая из записей
г = (X, Г, Z), г (X, У, Z), г = {X, Y, Z) (3.9)
означает что вектор г имеет координаты X, Y, Z.
Если х, у, г - декартовы прямоугольные координаты точки М, то
Х = х, Y = у, Z=z,
т. е. координаты радиуса-вектора ОМ
равны координатам точки М.
Введем в рассмотрение единичные
векторы i, j, к координатных осей (их
называют ортами) и векторы. ОА = Xi,
ОВ=П OC = Zk, где А, В, С-
V
вершины прямоугольного параллелепи-
педа, для которого ОМ является диаго-
налью (А, В, С - проекции точки М на
координатные оси; ОА = X, ОВ = Y,
ОС = Z - проекции вектора на коорди-
59
натные оси). По определению суммы ОМ = ОА+ОВ+ОС, поэтому
r = Ai + 4+Zk. (3.10)
Формула (3.10) выражает разложение вектора г по базисным векторам i, j, к.
Векторы стоящие в правой части формулы (3.10), называются составляющими или
компонентами вектора г.
На основании теоремы о квадрате диагонали прямоугольного параллелепипеда по-
лучаем формулу, выражающую длину вектора (3.9) или (3.10) через его координаты:
|r| = V%2 + r2 + Z2. (3.11)
Из равенства (3.3) следует, что равные векторы имеют равные координаты, по-
этому координаты вектора не зависят от точки его приложения. Координатами
любого вектора называются его проекции на координатные оси.
Направляющими косинусами вектора называются косинусы углов а, р, у, обра-
зуемых им с координатными осями.
Принимая во внимание формулу (3.2), для вектора (3.9) получаем
X = |r|cosa, y = |r|cosP, Z=|r|cosy. (3-12)
Из равенств (3.11) и (3.12) следуют формулы для направляющих, косинусов
вектора г:
X о Y Z
cosa=, ........., cosр= ., ч........., cosy — —,.. . СЗ 13>
4x2 + y2+z2 Jx2 + y2+z2 4x2 + y2+z2
откуда
cos2 a + cos2 p+cos2 у = 1.
Из формулы (3.12) следует, что координаты единичного вектора равны его на-
правляющим косинусам; т. е.
е = (cos a, cosp, cosy).
Пример 3.1. Дан вектор а = (2, -1, - 2). Найти его длину и единичный
ректор а0 направления вектора а.
По формуле (3.11) находим длину вектора |а| = 722+(-1)2+(-2)2=3, апо
формулам (3.13) - его направляющие косинусы
cosa = —,
3
о 1
cosp = -—,
2
cosy = -у,
1 -3.)
з’ Зу
60
3.5. Переход от векторных соотношений
к координатным
Если даны векторы (т. е. известны их координаты) и указаны определенные со-
отношения между ними, то они равносильны аналогичным числовым соотноше-
ниям между координатами.
Координаты произведения вектора на число. Пусть дан вектор
a = (Xl,Yi,Zl} ичисло а*0. Координаты X2,Y2,Z2 вектора Ь = аа:
Х2 = аХ„ Y2 = аЦ, Z2 = aZx. (3.14)
Отметим, что равенства (3.14) выражают необходимое и достаточное условие
коллинеарности двух векторов: а = (X,, Yt, Zt), b = (Х2, Y2, Z2). Если ни одно из
чисел Xt, Yx, Zx не равно нулю, то эти равенства можно записать так:
XJX^YJY^ZJZ,.
Векторы коллинеарны тогда и только тогда, когда пропорциональны их одно-
именные координаты.
Координаты суммы (разности) двух векторов. Пусть даны два вектора
a = (X|,^,Z1), b = (X2,1^,Z2), тогдаX, Y,Z - координаты вектора суммы а + Ь:
Х=Х, + Х2. Y = YX + Y2, Z = Zl+Z2,
Х' = Хх-Х2, Y' = YX-Y2, Z' = Z}-Z2,
где X', Y', Z' — координаты разности а - b.
Координаты вектора, заданного двумя точками. Начало вектора М,М2 на-
ходится в точке jl/|(X|,yl,Z|), коней - в точке М2(х2, у2, г2). Выражение для
его координат X*Y, Z через координаты точек Мх и М2:
X-x2-xx,Y=y2-yx,Z-z2-zx. (3.15)
Координаты линейной комбинации векторов. Заданы п векторов
a, =(Xl,Yi,Zi), a2=(X2,Y2,Z2),...,a„=(X„,Y„,Zll) и их линейная комбинация
а = а,а, +а2а2 + ---+аяа„.
Координаты X, Y, Z вектора а определяются формулами
Х = агХ1 +а2Х2 + — +а„Х„,
Г=а^+а2Г2 + - + а,Х.
Z == (XjZj + <x2Z2 + • + &>nZn.
Деление отрезка в данном отношении. Даны две точки в пространстве
A/1(Xi,y„Z|), M2(x2,y2,z2). Координаты точки М, делящей отрезок М,М2 в
отношении I:
xx+lx2 yi+ly2 zx+lz2
1+1 ’У 1+/ ’ 1+/
61
В частности, координаты середины отрезка определяются формулами
теме, X, Y, Z - в новой, тогда
x=Xi+X2_ У\+У2
2 ,У 2 ’ 2
Преобразование декартовых прямоуголь-
ных координат при параллельном переносе.
Рассмотрим две декартовы прямоугольные сис-
темы координат с одним и тем же масштабным
отрезком й одинаковыми направлениями одно-
именных координатных осей (рйс. ЗЛО). Начало
новой системы координат находится в точке
Ot(a,b, с). Пусть М — произвольная точка про-
странства, х,у, z т- ее координаты в старой сис-
х = Х+а, y=Y+b, z = Z+c,
или
Х = х-а, Y = y—b, Z = z-c.
(3-17)
П р и м е р 3.2. Даны две точки А (3, - 4,7), В (5, - 6,8). Найти координа-
ты вектора АВ и координаты точки Е — середины отрезка АВ.
По формулам (3.15) и (3.16) соответственно получаем
Х=5-3 = 2, У=-6—(-4) = —2, Z=8-7=l, АВ = (2,-2,1);
х = (5+3)/2 = 4, у = (- 6+(-4))/2 = -5, z = (8 + 7)/2 = 7,5, Е (4; - 5; 7,5).
Пример 3.3. Даны четыре точки А (5,6, - 8), В (8,10, - 3), С (1, - 2,4),
D (7,6,14). Коллинеарны ли векторы АВ и CD?
Так как АВ = (8-5,10-6,-3-(-8)) = (3,4,5), CD = (7-1,6-(-2),
14 - 4)=(6,8,10) и CD = 2АВ, т. е. выполнено равенство (3.1), то векторы АВ и
CD коллинеарны.
3.6. Скалярное произведение двух векторов
Скалярным произведением двух векторов а й ^называется число, равное про-
изведению их длин на косинус угламеж^у рими.Если обозначить скалярное про-
изведение через аЬ,то ....,, ............... , I.
'аЬ^=|а||ь|со8<р.‘" J . .. 1((ЗД8)
Так Как |b| cos<p = npab и | а | созф‘= пр „а (рйс. 3.11), то равенство (3.18) можно
представить в двух видах: - ' ''> '! ' •
ab = |a|ripab,‘ab = |b|npba.
Понятие скалярного произведения возникло в механике. Если вектор а изо-
бражает силу, точка приложения которой перемещается из начала в конец вектора
62
Ь, то работа w указанной силы определяется равенством w = | а 11 b | coscp.
Скалярным квадратом вектора а называется
скалярное произведение вектора а на себя:
а2 = ая = | а || а | cosO=| а |2,
т. е. скалярный квадрат вектора равен квадра-
ту его длины.
Векторы а и b перпендикулярны тогда и
только тогда, когда
ab = 0. (3.19)
Скалярное произведение обладает свойствами:
1) переместительности (коммутативности)
ab = ba.
2) сочетательности (ассоциативности) относительно числового множителя
(aa)b = a(ab),
3) распределительности (дистрибутивности) относительно суммы векторов
a (b+c)=ab+ac.
Скалярное произведение двух векторов
a = (Xl,j;,ZJ), b=(X2,Z2,Z2)
выражается формулой
ab=X1>f2 + r}r2+Z1Z2,
(3.20)
(3.21)
т.е. скалярное произведение двух векторов равно сумме произведений одноимен-
ных координат.
Замечание. Если Ь = а, то формула (3.21) принимает вид аа = А"2 +
+1/ + Z2. Поскольку аа = а2 = | а |2, то | а | = А"2 + lj2 + Z2 .
Косинус угла между векторами (3.20) определяется формулой
cos<p =
XlX2 + YlY2+Z}Z2
Jxf + Y* + Z? Jx% + Y2+Zf
(3-22)
Необходимое и достаточное условие перпендикулярности двух векторов (3.20)
выражается равенством
XtX2 + Y,Y2 + ZjZj = 0, (3.23)
оно следует из формул (3.19) и (3-21).
Если ось и образует с координатными осями углы а, р, у соответственно, то
проекция вектора s = (X, Y, Z) на эту ось определяется равенством
пржв = A'cosa + Kcosp+Zcosy.
63
Пример 3.4. Даны два вектора а = (8, - 7, - 2), b = (7, -11,8). Найти
угол между ними.
По формуле (3.22) получаем
8-7+(—7)(—П)+(-2)-8 117 -J2
cos<p= - 7 ' У ф = 45°.
д/82+(—7)2+(-2)2 д/72+(-11)2+ 82 H7-v2 2
Пример 3.5. Доказать, что векторы а = (2, - 4, 6), b = (3,3,1) пер-
пендикулярны.
По формуле (3.21) находим: ab = 2-3+(-4)-3+61 = 0. Так как выполнено ус-
ловие (3.19), то векторы а и b перпендикулярны.
3. 7. Правые и левые тройки векторов.
Правые и левые системы координат
Три некомпланарных вектора ОА = а, ОВ = Ь, ОС = с, взятых в указанном
порядке (а - первый вектор, Ь - второй, с - третий) и приложенных в одной
точке (рис. 3.12, а, б), называют тройкой векторов а, Ь, с. Будем смотреть с конца
вектора с на плоскость, определяемую векторами а и Ь. Если кратчайший поворот
Рис. 3.12
от вектора а к вектору Ь совершается против часовой стрелки, то тройка векторов
а, Ь, с называется правой*) (рис. 3.12, а), если указанный поворот совершается по
часовой стрелке, тройка а, Ь, с называется левой (рис. 3.12, б).
Две тройки, обе правые или обе левые, называются тройками одной ориента-
ции; если одна тройка является правой, а другая левой, то они называются трой-
ками различной ориентации.
При круговой перестановке векторе® (первый заменяется вторым, второй- третьим,
третий - первым,рис.3.12,в)ориентациятройкинеменяется(см.рис.3.12,а,б).
*) В случае правой тройки а, Ь, с векторы а, Ь, с располагаются так, как большой, указатель-
ный и средний пальцы правой руки; если тройка а, Ь, с является левой, то векторы а, Ь, с
располагаются так, как указанные пальцы левой руки.
64
Если поменять местами два вектора, то ориентация тройки меняется, например
если а, Ь, с — правая тройка, то тройка Ь, а, с (тех же векторов, взятых в порядке
Ь, а, с) будет левой.
Прямоугольная декартова система координат называется правой, если тройка
базисных векторов i, j, к правая; если эта тройка левая, то система координат на-
зывается левой.
3. 8. Векторное произведение двух векторов
Векторным произведением вектора а на вектор b называется третий вектор,
обозначаемый символом [а, Ь] и удовлетворяющий условиям:
1) | [а, Ь] | = | а 11 b| sin <р, где <р - угол между векторами а и Ь;
2) вектор [а, Ь] перпендикулярен каждому из векторов а и Ъ;
3) тройка векторов а, Ь, [а, Ь] имеет ту же ориентацию, что и!, j, к.
Для векторного произведения применяют и другие обозначения, например а х Ь.
Замечание. Если пользоваться только правыми системами координат,
то условие 3) можно заменить другим - тройка а, Ь, [а, Ь] является правой.
Понятие векторного произведения возникло в *
механике. Если вектор Ь изображает силу, прило-
женную в точке М, а = ОМ, то [а, Ь] выражает
момент силы Ь относительно точки О.
Из условия 1) следует, что модуль векторного i к
произведения [а, Ь] равен площади 5 параллело-
грамма, построенного на векторах а и b ®
(рис. 3.13), т. е.
|[a,b]| = S, (3.24) Ь Ъ
поэтому ЯS ф /
[a, b|=Se, S' /
гдее - единичный вектор направления вектора [а,Ь].
Равенство [,4=0 выражает необходимое и Рис. 3.13
достаточное условие коллинеарности двух векторов а и Ь; в частности, для любого
вектора а [а,а]=О.
Векторное произведение двух векторов обладает свойствами:
1) антиперестановочности множителей
[а,Ы = -[Ь,а];
2) сочетательности относительно скалярного множителя
[(аа), Ь] = а [а, Ь], [а, (рЬ) ] = ₽ [а, Ъ];
3) распределительности относительно сложения
[(a + b), с]= [a,c]+[b,с], [a,(b + c)]= [a, b]+[a,ej.
ЗЗак. 1
65
Векторное произведение [а, Ь] двух векторов
a = (Jfl,y1,Z1), b=(X2,y2,Zj) (3.25)
выражается формулой
h.b]
г,
z2
(3.26)
Эту формулу можно представить через символический определитель
третьего порядка
(3.27)
Замечание. Составим матрицу из координат векторов а и Ь
Х2
У, Z.
r2 Z2
Координаты векторного произведения [а, Ь] равны минорам второго порядка
этой матрицы, полученным путем поочередного вычеркивания первого, второго и
третьего столбцов, причем второй минор нужно взять со знаком минус.
Площадь параллелограмма, построенного на векторах (3.25), вычисляет-
ся по формуле
s- IP Zi Г+И1 Г+Н* 4
YI r2 zj I х2 z, I I х2 у2
которая следует из (3.11) и (3.24).
Площадь треугольника ЛВС определяется формулой
S = 1|[AB,AC]|. (3.29)
Формула (3.29) следует из (3.24), так как площадь треугольника ЛВС составля-
ет половину площади параллелограмма, построенного на векторах АВ и АС.
Пример 3.6. Даны два вектора а = (5,3, -4), b = (6,7, - 8). Найти ко-
ординаты векторного произведения [а, Ь].
П&формуле (3.27) получаем
i J к
5 3-4
6 7-8
[а,6] =
-4
-8
i-
5 -4
6 -8
k = 4i+16j + 17k,
3
7
j +
5
6
3
7
[a,b]=(4,16,17).
Пример 3.7. Вершины треугольника находятся в точках Л(1,1,3),
В(3,-1,6), С(5,1,-3). Вычислить его площадь.
66
С помощью формул (3.15) находим координаты векторов
АС. АВ = (2, - 2,3), АС = (4,0, -6). Так как
; , (-'• -? t .1 : ..
f -2 3 2 3 2-2
[АВ,АС]= _ , . = (12,24/8),?:
[ и —р 4 — о I J 4 О
АВ и
! . .‘uQld8
« *• j . .f ] * *
-ад4- Г
3.9. Смешанное произведение Трех векторов
Пусть даны три вектора а, Ь, с. Вектор а умножим векторно на Ь, векторное
произведение [а, Ь] умножим скалярно на с, в результате получаем число, кото-
рое называют векторно-скалярным произведением или смешанным произведением
[а, Ь]с трех векторов а, Ь, с.
Смешанное произведение [а, Ь] с трех некомпланарных векторов равно объе-
му параллелепипеда, построенного на векторах ОА = а, ОВ = Ь, ОС = с
(рис. 3.14), взятому со знаком плюс, если тройка (а, Ь, с) - правая, со знаком
минус, когда эта тройка - левая:
V = mod ([а, Ь] с). (3.30)
Векторы а, Ь, с компланарны тогда и только тогда, когда их смешанное произ-
ведение равно нулю, т. е.
[а, Ь] с = 0.
Смешанное произведение [а, Ь]с и
а [Ь, с] обозначают через abc:
abc = [а, Ь] с = а [Ь, с].
Если поменять местами два вектора, то
смешанное произведение изменит лишь
знак. Для трех векторов а, Ь, с: ,.
abc = bca = cab = -bac == -cba = acb
Смешанное произведение трех век-
торов
(332)
определяется формулой
а = (Х„ Yt, Z,), Ь = (Х2, У2, Zj), с = (Х3, Г3, Zj)
abc =
К Z,
r2
Гз
Zi
(3.33)
з
Из формул (3.30) и (3.33) следует, что объем параллелепипеда, построенного
67
на векторах (3.32), вычисляется по формуле
JT, }{ Zt
r = mod Х2 У2 Z, (3.34)
Х3 Г3 Z2
Объем треугольной пирамиды с вершинами в точках Мх(хиуигх),
>2>гг)> мз(*з> Уз> 2з), М4(х4,у4, z4) определяется формулой
*2~*1 Уз “Л 23~2\
*э“*| Уз~У\ г3-г,
*4~*1 Уа-Уз г4-2(
V = —mod
6
(3.35)
Необходимое и достаточное условие компланарности трех векторов (3.32) вы-
ражается равенством
У, А
Уз ^2 = 0, (3.36)
*з Уз z2
которое следует из равенств (3.31), (3.33).
Пример 3.8. Найт и объем параллелепипеда, построенного на векторах
а =(1,3,1), Ь = (2,1,3), с = (3,1,2).
По формуле (3.34) получаем
1 3 1 1 0 0
K = mod 2 1 3 = mod 2 -5 1 =13.
3 1 2 3 -8 -1
Пример 3.9. Доказать, что векторы а=(1, — 2,3), Ь = (4,-5,6),
с = (5, —7,9) компланарны.
Так как
1 -2 3 1 -2 3
4 -5 6 = 03-6 =0,
5 -7 9 0 3-6
т.е. выполнено условие (3.36), то данные векторы компланарны.
Пример 3.10. Вычислить объем треугольной пирамиды, вершины кото-
рой находятся в точках Л/, (6,1,4), Л/2(1, — 3,7), Л/З(7,1,3), Л/Д2.-2,-5).
В соответствии с формулой (3.35) находим
K = mod-2-
6
1-6
2-6
7-6
-3-1
-2-1
1-1
7-4
-5-4
3-4
, 1
= mod —
6
-5-4 3
-4 -3 -9
1 0 -1
23
3 '
68
3.10. Линейная зависимость векторов
Векторы а(, а2 я„ называются линейно зависимыми, если существуют дей-
ствительные числа а|,а2,...,ап из которых по меньшей мере одно отлично от
нуля, такие что
а,а1+о^а2+-+аяаи=а (3.37)
В противном случае (т. е. когда таких чисел не существует) векторы называют-
ся линейно независимыми; другими словами, векторы линейно независимы, если
равенство (3.37) выполняется лишь при
а|=а2 = ...=а„ = 0. (3.38)
Если один из векторов, например а,, является нулевым, то система
Я|, а2..ая окажется линейно зависимой, так как равенство (3.37) будет выпол-
нено при а, = 1, а2 = а3 =... = а„ = 0. Если часть векторов в|, а2 а* линейно
зависима, то и вся система а,,а2,.... а„ линейно зависима, поскольку из равенст-
ва a1a1+a2a2+--+atat =0 следует равенство' (3.37), в котором
at+l = ал+2 =... = а„ = 0.
Теорема 3.1. Векторы а(,а2.....а„ (и>1) линейно зависимы тогда и
только тогда, когда по меньшей мере один из них является линейной комбинаци-
ей остальных.
Теорема 3.2. Два вектора а и b линейно зависимы тогда и только тогда,
когда они коллинеарны.
Теорема 3.3. Если е, и е2 - два неколлинеарных вектора некоторой
плоскости, то любой третий вектор а той же плоскости можно единственным
образом разложить по ним, т.е. представить в виде а = xet + уе2.
Теорема 3.4. Три вектора а, Ь, с линейно зависимы тогда и только тогда,
когда они компланарны.
Теорема 3.5. Если векторы е(, е2, е3 некомпланарны, то любой вектор a
можно единственным образом разложить по ним, т.е.
а =хе, +уе2 +ze3.
Теорема 3.6. Всякие четыре вектора линейно зависимы.
Любая упорядоченная система трех линейно независимых (т.е. некомпланар-
ных) векторов а, Ь, с называется базисом. Согласно теореме 3.5, всякий вектор d
можно разложить по базису, т.е. представить в виде
d = xa + yb+zc. (3.39)
Числа х, у, z называют координатами вектора d в базисе а, Ь, с.
Пр им ер 3.11. Образуют ли базис векторы а = (8,2,3), b = (4,6,10),
с = (3,-2,1)?
69
Так как
abc =
8 2 3
4 6 10
3 -2 1
-18 3
-26 26 10
0 0 1
I
|-26
8
26
7 8
О 26
= 182,
т. е. смешанное произведение отлично от нуля, то векторы некомпланарны. Зна-
чит, они линейно независимы и образуют базис.
Пример 3.12. Даны векторы а = (1,1,-1), Ь = (2,-1,3), с=(1,-2,1),
d = (12, -9,11). Доказать, что векторы а, Ь, с образуют базис и найти координаты
вектора d в этом базисе.
Поскольку
1 1 -1
abc= 2-13
1 -2 1
0 0-1
5 2 3
2 -1 1
5 2
2 -1
= 9*0,
то векторы а, Ь, с линейно независимы (некомпланарны) и образуют базис. Вектор
d можно представить в виде d = ха +yb + zc (см. формулу (3.39)). Это равенство
равносильно следующим равенствам:
12 = x+2y+z, — 9=х-y-2z, \l = —x+3y+z,
так как равные векторы имеют равные координаты и координаты линейной коорди-
нации векторов равны соответствующим линейным комбинациям одноименных ко-
ординат (см. п. 3.5). Решив полученную систему уравнений, найдем х=2, у=3, z=4.
Итак, d = 2а + ЗЬ+ 4с, вектор d в данном базисе имеет координаты х=2, у=3, z=4.
3.11. Аффинные координаты
Фиксируем некоторую точку О заданной плоскости и выберем два неколлинеар-
ных вектора е1; е2, назовем эту точку началом координат, векторы е,, е2 -
базисными. От точки О отложим векторы ОЕ] = е, и ОЕ2 = е2, проведем прямые,
которым принадлежат векторы ОЕ, и ОЕ2, фиксируем на них положительные
Рис. 3.15
направления, совпадающие с направлениями
ОЕУ и ОЕ2 соответственно, получим две коор-
динатные оси Ох и Оу (рис. 3.15). Будем гово-
рить, что построена общая декартова или аф-
финная систем^! координат (О, е|; е2). Пусть а
- любой вектор данной плоскости, отложим из
точки О вектор ОА = а, тогда по теореме 3.3
a=xat+ya2- (3.40)
Числа х и у формулы (3.40) называются
общими декартовыми или аффинными координатами вектора а в системе
(О;е,,е2), они также называются аффинными координатами точки А в той
же системе, т. е. а = (х, у), А (х, у).
70
Так как ОА] = хе,, ОА2 =уе2, то х и у - величины направленных отрезков
ОА] и ОА2 координатных осей, |х| - длина отрезка ОА1, измеренная с помо-
щью масштабного отрезка ОЕц | у | - длина отрезка ОА2, измеренная с помо-
щью масштабного отрезка ОЕг. Другими словами, аффинными координатами
точки А (и вектора а = ОА ) называются числах и у, определяемые формулами
x = OAt, у = ОА2, ’
где ОАг, ОА2 - величины направленных отрезков ОА] и ОА2 координатных
осей ( At - проекция точки А на ось Ох, взятая параллельно оси Оу, А2 - проек-
ция точки А на ось Оу, взятая параллельно оси Ох; длины отрезков на каждой оси
измеряются с помощью своего масштабного отрезка).
Аналогично вводится аффинная система координат в пространстве. Фиксируем
начало координат - точку О, базис - три некомпланарных вектора е(, е2, е3,
отложим из точки О векторы ОЕ( = в], ОЕ2 =е2, ОЕ3 = е3, координатные оси
Ох, Оу, Oz. Если а - любой вектор, то, отложив из точки О вектор ОА = а, по
теореме 3.5 получим
а =хв]+уе2+ze3. (3.41)
Общими декартовыми или аффинными координатами вектора а (н точки А) на-
зываются числах, у, г в разложении (3.41).
Пусть At — проекция точки А на ось Ох, взятая параллельно координатной
плоскости Oyz (определяемой векторами е2, е3), т.е. точка пересечения оси Ох и
плоскости, проходящей через точку А и параллельной плоскости Oyz; А2 -
проекция точки А на ось Оу, взятая параллельно плоскости Oxz, А3 - проекция
точки А на ось Oz, взятая параллельно плоскости Оху, тогда ОА]=хе],
ОА2 = уе2, ОА3 = ze3.
Следовательно, х, у, z - проекции вектора ОА на координатные оси, т.е. вели-
чины направленных отрезков ОАИ ОА2, ОА3, длины отрезков на каждой коор-
динатной оси измеряются с помощью своего масштабного отрезка ( в] - на оси
Ох, е2 - на Оу, е3 - на Oz).
В частном случае векторы в], е2, е3 попарно перпендикулярны и имеют рав-
ные длины | е, | = | е21 = | е3 ] = 1, их называют ортами и обозначают i, j, к, система
координат называется прямоугольной.
Термин «орт» ввел О. Хевисайд (1892), обозначения в], е2, е3 - Г. Грассман
(1844), i,j, к - У. Гамильтон (1853).
71
Глава 4
ПОВЕРХНОСТИ И ЛИНИИ
В ПРОСТРАНСТВЕ
4.1. Уравнение поверхности.
Уравнения линии в пространстве
Уравнением поверхности в фиксированной системе координат называется та-
кое уравнение с тремя переменными, которому удовлетворяют координаты любой
точки данной поверхности и только они.
Из этого определения вытекает способ решения следующей простой задачи:
выяснить, лежит ли данная точка на поверхности, определяемой заданным урав-
нением. Для решения задачи необходимо подставить ее координаты в данное
уравнение, если получается числовое равенство, то точка лежит на поверхности, в
противном случае точка поверхности не принадлежит.
Всякое уравнение с тремя переменными х, у, z можно записать так:
F(x,y,z)=0, (4.1)
где F (х, у, z) - функция переменных х, у, z.
Из определения прямоугольных декартовых координат точки в пространстве
(см. п. 1.12) следует, что координатные плоскости Oyz, Oxz, Оху определяются соот-
ветственно уравнениями: х - 0, у = 0, z - 0 (х = 0 — уравнение плоскости Oyz и т.д.).
Линию в пространстве можно рассматривать как пересечение двух поверхно-
стей, поэтому она определяется двумя уравнениями. Пусть I - линия, по которой
пересекаются поверхности, определяемые уравнениями F(x,y,z) = O и
Ф(х, у, z) = 0, т.е. множество общих точек этих поверхностей._тогда координаты
любой точки линии I одновременно удовлетворяют обоим уравнениям:
F(x,y,z) = O, Ф(х, у, z) = 0. (4.2)
Пр и м е р 4.1. Составить уравнение сферы радиуса R с цешром в точке C(a,b,c).
Исходя из определения сферы как множества точек пространства, равноуда-
ленных от данной точки (центра), для произвольной ее точки M(x,y,z)
получаем р(С, М)= R. Так как
р (С, М) = 4(х-в)2 +(y-b)2 +(z-c)2, то 7(z - в)2 + (y -h)2 + (z - с)2 = R,
или
(х - в)2 + (у - fe)2 + (z - с)2 = й2. (4.3)
72
Для точки N, не лежащей на данной сфере, равенство р (С, /V) = R не будет выпол-
нено, поэтому ее координаты не удовлетворяют уравнению (4.3). Следовательно,
уравнение (4.3) является уравнением сферы радиуса R с центром в точке С (а ,Ь, с).
В частном случае, когда центр сферы находится в начале координат
( а = Ь = с = 0 ), уравнение (4.3) принимает вид
x2+y2+z2 = R2. (4.4)
Уравнение (4.4) называется каноническим уравнением сферы.
Пример 4.2. Уравнения
х2+у2 +z2 = 25, z = 0
определяют окружность радиуса R = 5, лежащую в плоскости Оху. Действитель-
но, первое уравнение определяет сферу радиуса R = 5 с центром в начале коорди-
нат, второе уравнение - координатную плоскость Оху.
Пример 4.3. Ось Ох прямоугольной декартовой системы координат в
пространстве определяется уравнениями у-0, z = 0.
Действительно, уравнение у=0 определяет координатную плоскость Oxz, а
уравнение z=0 - координатную плоскость Оху. Ось Ох является линией пересе-
чения координатных плоскостей Oxz и Оху (см. рис. 1.13).
Отметим, что ось Оу имеет уравнения х=0, z=0, а ось Oz — уравнения х=0, у=0.
Поверхность, определяемая алгебраическим уравнением и-й степени относи-
тельно декартовых координат, называется поверхностью и-го порядка. Сфера -
поверхность второго порядка, так как ее уравнение (см. (4.3) и (4.4)) является
уравнением второй степени относительно декартовых координат.
4.2. Параметрические уравнения линии
и поверхности
Параметрическими уравнениями линии в пространстве называются уравнения вида
X = ф, (0> У = Ч>2 (0> 2 = Фз (0. (4.5)
где ф|(/), ф2(0> Фз(О — функции некоторой переменной г (параметра), если
при каждом значении t из конечного или бесконечного промежутка они дают ко-
ординаты всех точек данной линии и только таких точек.
Параметрические уравнения часто применяются в механике для описания тра-
ектории движущейся точки, роль параметра t в таких случаях играет время.
Параметрическими уравнениями поверхности называются уравнения вида
X = f (и, V), у = /2(«, v), Z = /3(л, V), (4.6)
где f(u,v),f2(u, v),f3(u, v) - функции двух переменных и и v (параметров),
если при любых значениях и и v (меняющихся в некоторой области) они дают
координаты всех точек данной поверхности и только таких точек.
Правые части уравнений (4.6) содержат два параметра, а уравнения (4.5)-
только один параметр.
73
Пример 4.4. Составить параметрические уравнения винтовой линии.
Винтовой линией называется линия, описываемая точкой, равномерно движу-
щейся по образующей кругового цилиндра, который при этом вращается вокруг
своей оси с постоянной угловой скоростью.
Выберем ось вращения цилиндра в качестве оси Oz декартовой прямоугольной
системы координат в пространстве (рис. 4.1). Обозначим через v постоянную ско-
рость прямолинейного движения точки вдоль образующей, со - скорость враща-
тельного движения, R - радиус цилиндра. Пусть в начальный момент точка нахо-
дилась на осн Ох (совпадала с точкой А), а в момент времени г— в положении М.
Обозначим буквой N проекцию точки М на плоскость Оху, буквой Р- проекцию
точки N на ось Ох, буквой Q - проекцию точки N на ось Оу. Обозначим через <р
угол между ОР и ON, получаем x = OP = cos<p, у = 06 = Asin <р, z = NM = vt.
Поскольку <р = сос, то
х•= R cosat, у = Asin©/, z = vt. (4.7)
Уравнения (4.7) являются параметрическими уравнениями винтовой линии.
Пример 4.5. Составить параметрические уравнения сферы радиуса R.
Введем в рассмотрение систему декартовых прямоугольных координат с нача-
лом в центре сферы и систему сферических координат с началом в той же точке
(рис. 4.2). Пусть М — произвольная точка сферы, У - ее проекция на плоскость
Оху. Обозначим угол, образуемый вектором ОМ с осью Oz, через и (широта);
угол, образуемый вектором ON с осью Ох, через v (долгота). Принимая во внима-
ние определение декартовых координат (или связь между декартовыми и сфериче-
74
скими координатами, см. 1.13, формулы (1.29)), получаем параметрические урав-
нения сферы
x = Bsinwcosv, у = Ksinusinv, z = Rcosu, (4.8)
где 0<н<л, 0<г<2л.
Исключив из этих уравнений параметры и и v (для чего нужно возвести в квадрат обе
части каждого уравнения и почленно сложить), получим уравнение сферы (4.4).
4.3. Различные виды уравнения плоскости
Плоскость в пространстве можно задать различными способами (точкой и .век-
тором, перпендикулярном плоскости, тремя точками и т. д.), в зависимости от
этого рассматривают различные виды ее уравнения.
Уравнение плоскости, проходящей через данную точку и перпендикуляр-
ной данному вектору. Ненулевой вектор п, перпендикулярный плоскости, назы-
вают ее нормальным вектором. Если дана точка М0(х0, у0, z0) и нормальный
вектор п = (А, В, С) плоскости, то ее уравнение имеет вид
Л (x-xo)+B(y-yo)+C(z-zo) = 0.
(4.9)
В этом уравнении коэффициенты А, В, С являются координатами нормального вектора
Равенство (4.9) выражает необходимое и достаточное условие перпендикуляр-
ности двух векторов: п = (Л, В, С), M0M = (x-x0,y-j'0,z-z0), где M(x,y,z)
- любая точка плоскости (рис. 4.3).
Общее уравнение плоскости. Уравнение первой степени относительно декар-
товых координат
Ax + By + Cz + D — O,
где А, В, С одновременно в нуль не обращаются, т.е.
А2+В2 + С2*0, (4.11)
определяет плоскость в пространстве. Урав-
нение (4.10) называется общим уравнением
плоскости. Отметим частные случаи этого
уравнения.
Если £> = 0, то уравнение (4.10) при-
нимает вид
Ах + By + Cz = 0
и определяет плоскость, проходящую че-
рез начало координат (рис. 4.4, а; коорди-
наты х = у - г = 0 удовлетворяют данному
уравнению). ~
(4.Ю)
Если С = 0, то уравнение (4.10) принимает вид
Ax + By + D=0
н определяет плоскость, параллельную оси Oz (рис. 4.4, б); нормальный вектор
п = (Л, В, 0) перпендикулярен оси Oz, ибо С = 0.
75
Если С = 0, D = 0, то уравнение (4.10) принимает вид
Ах + Ву = 0
и определяет плоскость, проходящую через ось Oz (рис. 4.4, в; плоскость парал-
лельна оси Oz и проходит через начало координат; в этом случае А2 + В2 ФО в
силу условия (4.11)).
Если С=0, В = 0, то уравнение (4.10) принимает вид
Ax + D-О, йлих = в (а = -£>/Л)
и определяет плоскость, параллельную плоскости Oyz или перпендикулярную оси Ох
(рис. 4.4, г; нормальный вектор п = (А, 0,0) перпендикулярен плоскости Oyz).
Если С = 0, В = 0, D = 0, то уравнение (4.10) принимает вид
Ах- 0, илнх = 0 (так как Л # 0)
и определяет координатную плоскость Oyz.
Замечание. Если в уравнении (4.10) свободный член равен нулю (О = 0),
то плоскость проходит через начало координат; если коэффициент прн одной из
текущих координат равен нулю, то плоскость параллельна соответствующей коор-
динатной оси (например, если В=0, то плоскость параллельна оси Оу); еелй в нуль
обращаются свободный член и один из коэффициентов при текущей координате, то
плоскость проходит через соответствующую ось (если D = 0 н С = 0, то плоскость
проходит через ось Oz); если равны нулю два коэффициента при текущих коорди-
натах, то плоскость параллельна соответствующей координатной плоскости (когда
А = 0, В = О, плоскость параллельна плоскости Оху); если обращаются в нуль сво-
бодный член и два коэффициента при текущих координатах, то плоскость совпа-
дает с соответствующей координатной плоскостью (когда 0 = 0, А = 0, С.= О,
плоскость совпадает с плоскостью Охг).
Уравнение плоскости в отрезках, отсекаемых на осях координат. Если все
коэффициенты уравнения (4.10) и его свободный член отличны от нуля, то урав-
нение можно привести к виду
х/а + у/Ь + 2/с = \, (4.12)
где а = - D/А, Ь = - D/В, с = - D/С. Числа а, b и с означают величины направ-
Рис. 4.4
76
ленных отрезков, отсекаемых на осях координат. Этим объясняется название дан-
ного вида уравнения плоскости.
Нормальное уравнение плоскости. Уравнение
xcosa + ycosp + zcosy-p = 0, (4.13)
где а, р, у — углы, образованные нормальным вектором плоскости с координат-
ными осями Ох, Оу, Oz соответственно, р - длина перпендикуляра, опушенного
из начала координат на плоскость, называется нормальным (или нормированным)
уравнением плоскости. Чтобы привести общее уравнение плоскости к виду (4.13),
необходимо умножить его на нормирующий множитель
1
±т!а2 + В2 + С2 ’
где знак выбирается противоположным знаку D. После умножения уравнения
(4.10) на число |Л получаем нормированное уравнение плоскости
Ax + By+Cz+D
±Ja2+b2+c2
Уравнение плоскости, проходящей через три точки. Если даны три точки
^i(xi>3'i>zi)> ^г(22» >2» 2г)> Л/3(х3, Уз> 2з)> не лежащие на одной прямой, то
уравнение плоскости, проходящей через эти точки, имеет вид
Х-Х| У~Уз г-z,
х2-х1 У2-У1 г2-г. = 0.
х3-х1 У3-У1 Zj-Z,
(4.14)
Равенство (4.14) выражает необходимое и достаточное условие
(см.(3.36)) компланарности трех векторов М|М=(х-х(,у-у|,г-г1),
MlM2=(x2-xl,y2-yl,z2-zl), M1MJ=(xJ-xl,y}-yI,zJ-zl), где M(x,y,z)
- любая точка данной плоскости (рис. 4.5).
Уравнение плоскости, проходящей через две точки и параллельной дан-
ному вектору. Если задан вектор a = (a1,a2,eJ) и две точки M^Xi, yt, zt),
77
Л/2(х2, y2,z2), причем векторы а и М,М2 ,цеколлиреарны (рис. 4.6), то уравне-
ние плоскости, проходящей через эту точку параллельно вектору а, имеет вид
x-Xit у-у, ?“2i ?
*2“*i У2-У1 2i~2i *0' (4.15)
«•нь&ьн > :it.№“taA </,- пня/ -ti.
Равенство (4.15) выраи^аст необходимое и достаточное, условие компланарно-
сти трех векторов М|М = (*5-д:ь^м.|ь г-ifX < MtM2 = (x24(xi> Z2-Z1).
а = (а1,в2,в3), где ЛГ(х,у,'г) - любая точка данной плобкОСти.
Уравнение плоскости, проходящей через данную точку и параллельной
двум неколлинеарным векторам. Если даны два неколлинеарных вектора
(рис. 4.7) а = (в,, а2, а3), Ь = (6ц Ь2,Ь3), и точка M^xt, у,, z,), io уравнение плос-
кости, проходящей через данную точку параллельно векторам а и Ь, имеет вид
*-*1 У~У1 2~21
а| а2 а3 = 0. (4.16)
bi Фг
Равенство (4.16) выражает необходимое и достаточное условие компланарности
трех векторов: а, Ь, М(М, где М — произвольная точка данной плоскости.
Параметрические уравнения плоскости. Если даны два неколлинеарных век-
тора a = (eI,e2,a3), b = (6j, 62,6^), и точка А/ДхрУц?,), то параметрические
уравнения плоскости, проходящей через эту точку параллельно данным векторам,
имеют вид
x = xl+ual + v61, у = У| +ua2+vb2, z = z, +иа3 +vb3. (4-17)
Уравнения (4.17) следуют из равенства MlM = «a + vb, где M(x,y,z)~
/1----------------—--------7 любая точка плоскости (равенство
/ .у / M,M = ua+vb означает, что любой вектор
/ М.М можно разложить по векторам а и Ь).
в / Пример 4.6. Записать уравнение
/ плоскости,. проходящей через точку
___________ / л/о(2, -3,4) и имеющей нормальный вектор
Рис.4.7 «^6,-7).
Так как в данном случае х0 = 2, у0 = -3;
z0=4, А = 5, В = 6, С=-7, то уравнение (4.9) принимает вид
5(x-2)+6(y + 3)-7(z-4) = 0, или 5x + 6y-7z + 36 = 0.
Пример 4.7. Составить уравнение плоскости, проходящей через точку
Л/,(1, - 3,2) параллельно векторам а = (5, - 4,8), b = (6, -1,7).
Данные векторы неколлинеарны, так как их координаты не пропорциональны.
78
В соответствии с уравнением (4.16) получаем
Разлагая определитель по элементам первой строки, находим
1-4 8 Г 15 81 5-41
(х-1) . _ -(у+3) + (г-2) = 0,
Л I —1 / I , | О / | О “ 1 I
-20(x-l)+I3(y+3)+19(z-2)=0, 20x-13y-19z-21 = 0.
Пример 4.8. Найти величины отрезков, отсекаемых на осях координат
плоскостью Зх-4у + 5г-60 = 0.
Разделив обе части уравнения на 60 и преобразовав его, получим
х у z , х у z .
—+— = 1, или —+——+— = 1.
20 15 12 20 -15 12
Сравнивая последнее уравнение с уравнением (4.12), заключаем, что a = 20,
6 =-15, с = 12 Таковы величины отрезков, отсекаемых плоскостью соответст-
венно на осях Ох, Оу, Oz.
Пример 4.9., Составить уравнение плоскости, проходящей через три
точки Л/,(9,-1.1,5), М2(7,4,-2), Л/3(-7,13, - 3).
В соответствии с уравнением (4.14) получаем
x-9 у +11 z - 5 x-9 y + 11 z—5
7-9 4+11 -2-5 = 0, -2 15 -7
-7-9 13 + 11 -3-5 -16 24 -8
x-9 y + 11 z-5 x-9 y+11 z-5
= 8 -2 15 -7 = 0, -2 15 -7 = 0,
-2 3 -1 -2 3 -1
-’Н'-Ч-г зН
6(х—9)+12(y + ll)+24(z-5)=0, (х —9)+2(у+ ll)+4(z—5)=0,
x + 2y+4z-7 = 0.
79
4.4. Различные виды уравнений прямой
в пространстве
Прямую в пространстве можно задать различными способами (точкой и векто-
ром, параллельной ей; двумя точками и т. п.), в связи с чем рассматривают раз-
личные виды ее уравнений.
Векторно-параметрическое уравнение прямой- Направляющим вектором
прямой называется любой ненулевой вектор, параллельный ей. Если даны точка
Л/0(х0, у0, z0) и.направляющий вектор а = (at, а2, а3) прямой (рис. 4.8), то
г = г0+а/, (4.18)
где г = ОМ - радиус-вектор точки М(х, у, z), г0 = ОМ0 - радиус-вектор точки
Л/оОчъ Уо, zo), t — переменная величина (параметр). Уравнение (4.18) называется век-
торно-параметрическим уравнением прямой, проходящей через точку Мо и имею-
щей направляющий вектор а. Равенство (4.18) следует из определения суммы векто-
ров и необходимого и достаточного условия коллинеарности двух векторов.
Параметрические уравнения прямой. Переходя от векторного соотношения
(4.18) к координатным, получаем
x = x0+att,y = y0+a2t, z = zD+a3t. (4.19)
Эти уравнения называются параметрическими уравнениями прямой, проходящей
через точку Mrfxo, у о, zo) н имеющей направляющий вектор а = (а,, а2, а3).
Канонические уравнения прямой. Выражая параметр t из уравнений (4.19) н
приравнивая полученные выражения, находим, что
х~х0 _У~Уо _z-z0
а1 а2 а3
(4-20)
Уравнения (4.20) называются каноническими уравнениями прямой, проходящей че-
рез точку Л/о(ль> Уо, Zo) и имеющей направляющий вектор а = (at, а2, а3).
Уравнение прямой, проходящей через две точки. Если даны две точки
Л^(-х1>У1»г1)> Уг> гг)> т0 в качестве ее направляющего вектора можно
Рис. 4.8
взять вектор М,М2 = (х2 - х,, у2 - yt, z2 - z(),
поэтому уравнения (4.20) примут вид
*-*1.,=±-Л. = -£2.?к (4.21)
*2~*1 У2-У1 z2~zl
Пример 4.10. Записать параметрические
И канонические уравнения прямой, проходящей
через точку Л/о (7, -9, 8) параллельно вектору
а = (4,3,-2).
Так как в данном случае
*о = 7, Уо = ~9, го = 8, fl| = 4, а2 = 3,а3 = -2,
80
параметрические уравнения (4.19) принимают вид
х = 7+4/, у = -9 + 3/, z = 8~2/,;
а канонические уравнения (4.20) запишутся так:
х-7 у + 9 z-8
4 = 3 “ -2 '
Пример 4.11. Составить уравнения прямой; проходящей через точки
Mt(6, -5,4), Л/2(8,-7,9). Привести эти уравнения к параметрическому виду.
Поскольку Х]=®, yt=-5, z,=4, х2=8, У2=-7, z2=9, то уравнения (4.21) примут вид
х — 6 у+5 z—4 х — 6 у + 5 z-4
----= —-----=-----, или-----= ----=------.
8-6 -7+6 9-4 2-2 5
Обозначая равные отношения буквой t, получаем параметрические уравнения
данной прямой:
х = 6+2/, у = —5—2/, z = 4 + 5/.
4.5. Задачи, относящиеся к плоскостям
Взаимное расположение двух плоскостей. Даны две плоскости
А,х + В,у + C,z +£>, = 0, (4.22)
• А2х + В2у + C2z + £>2=0. (4.23)
Необходимое и достаточное условие параллельности этих плоскостей выража-
ется равенствами
а их совпадения - равенствами
А = ^. = ^.=^.. (4.25)
А Д G D,
Другими словами, плоскости параллельны тогда и только тогда, когда пропорциональ-
ны их коэффициенты при текущих координатах; например, плоскости
x+2y-3z-l = 0, Зх + бу—9z + 7=0 параллельны. Плоскости совпадают тогда и
только тогда, когда пропорциональны коэффициенты при текущих координатах и свобод-
ные члены; например, плоскости 2х - Зу+z - 4 = 0, 4х - бу+2z - 8 = 0 совпадают.
Если условие (4.24) не выполняется, то плоскости (4.22) и (4.23) пересекаются.
Угол между двумя плоскостями. Косинус угла между плоскостями (4.22) и
(4.23) определяется формулой
А/2 + RB,+QC-,
со8ф= j ‘ j 2 . (4.26)
Ja?+b?+Ci Ja2+b2+c2
Необходимое и достаточное условие перпендикулярности плоскостей (4.22) и
(4.23) выражается равенством
АуА2 + BiB2 +С|(?2 — О*
(4.27)
81
Расстояние от точки до плоскости. Расстояние-от точки Ме(х0, у0, z0) до
плоскости Ax + By+Cz + D=0 вычисляется по формуле
. |^о+ДУо + СгО+Д| '
а =J---J .........—Ч (4.28)
уА2 + В2+С2
Пример 4.12. Составить уравнение плоскости, проходящей через точку
Л/о(2,3, - 5) и параллельной плоскости х - 2у+4z -1 = 0.
Это уравнение будем искать в виде x-2y + 4z + D = 0, где£> - неизвестный
свободный член (в формуле (4.24) полагаем отношение равнымединице).
Так как плоскость проходит через точку Мо, то ее координаты должны удов-
летворять последнему уравнению: 2-2-3+4(-5)+£> = 0. 2-6-20+ +D = 0,
D=24. Следовательно, x-2y+4z+24 = 0 - искомое уравнение.
Пример 4.13. Найти угол между двумя плоскостями 11л-8у-7г +
+6 = 0; 4x-10y + z—5 = 0.
Косинус угла найдем по формуле (4.26), подставив в нее значения Л, = 11,
Д=-8, q =-7, Л =4, В2 = -10, С2=1:
cosq> = И-4+(—8)-(-10)+(-7)-1 = 44+80-7 в Л «.
/112 + (-8)2 + (-7? /42 + (-10)2 +12 ^234 VT17 2 ’ 4
Пример 4.14. Вычислить расстояние от точки Л/о(4,3,6) до плоскости
2х-у— 2z-8 = 0.
Подставив в формулу (4.28) значения х0 = 4, у0 = 3, z0 = 6, А = 2, В = -1,
С=-2, £>=-8, получим
d- |2-4-3-2-6-8| |-15|_5
/22 + (-1)2+(-2)2 3
Пример 4.15. Найти расстояние между параллельными плоскостями
x+2y-2z-l = 0, x + 2y-2z+5= 0.
Это расстояние равно расстоянию любой точки одной плоскости до дру-
гой. Выберем на первой плоскости произвольную точку. Приняв, например,
что у0 = 1, z0 = l, из уравнения x + 2y-2z-l = 0 найдем х0 = 1. По формуле
(4.28) находим расстояние от точки Л/о(1,1,1) до плоскости
х + 2у—2z + 5 = 0:
11+2-2+5[ 6 2
Jl2 + 22+(-2f 3
82
4.6. Задачи,ртнорящиесяк прямым,
в пространства,„
Угол между двумя прямыми - угол мезвду направляющими векторами этих
прямых Косинус угла между двумя прямьши ' -.’о
x = xl+alt, y = yt+a2l, z = zl+a3t;
•ij- . >1'XMXA1I '!: ,t ГЩ-j;: л/J
X .Шк.Щ
определяется формулой
Ji I j- niH’jil li 01 T ’ L3 l < C i >. J.l'.»’: Д JittWSi V.
ab a.b, + a2b, + aji,
Ve>2+«2+Й +^2+#
Равенство afy+a2t>2+a3b3l=0 выражает необходимое и достаточное условие
перпендикулярности прямых (4.29), (4.30). Необходимое и достаточное условие
параллельности этих прямых выражается равенствами Ь,=(ХЯ|, Ь2 = аа2,
Ь3 = <ха3, или
ab
Vai=Va2=Va3-
(4.29)
(4.ЭД,
> - (4.31)
(4-32)
Взаимное расположение двух прямых в пространстве. Для исследования
взаимного расположения прямых (4.29) и (4.30) рассматривается смешанное про-
изведение трех векторов а = (дц а2, а3\ b = (b{, b2, b3), М,М2 = (х2 -хь У2-У1,
Z2-Z1). Если аЬМ,М2*0, т.е.
«1
А
Х2 ~Х1
а2 а3
^2 ^3
У2-У1 Z2~Z1
(4.33)
то прямые являются скрещивающимися. Неравенство (4.33) означает, что векторы
а, Ь, М,М2 некомпланарны.'
Прямые (4.29) и (4.30) лежат в одной плоскости тогда и только тогда, когда
аЬМ]М2 = 0, т.е.
(4.34)
-••qr,
х2-х, y2-yl z2-Z{
Эти пряцые пересекаются, если первые две строки определителя не пропор-
циональны, т.е. не выполнено,^условие (4.32). Прямые параллельны, когда первые
две строки определителя пропорциональны. Прямые совпадают, если пропорцио-
нальны все строки определителя (4.34). •'
Замечание. Чтобы найти точку пересечения прямых (4.29) и
(4.30), необходимо решить систему их уравнений; при этом целесообразно
параметры обозначить различными буквами (так как одна и та же
точка пересечения прямых получается, как правило, при различных значе-
ниях параметра в уравнениях данных прямых).
83
Расстояние от точки до прямой. Расстояние от точки Мо (x0,y0,z0) до пря-
мой (4.29) вычисляется по формуле
d_|Kr,-r.),.l| (4J5)
Pl
где г0 и Г] - радиусы-векторы точек Мо и Мх, а- направляющий вектор пря-
мой (рис. 4.9).
Расстояние между двумя прямыми. Кратчайшее расстояние между двумя
прямыми (4.29) и (4.30) определяется формулой
. _|(г2-г1)аЦ
(4.36)
где Г], г2 - радиусы-векторы точек Ми М2; а, b — направляющие векторы
данных прямых (рис. 4.10).
Пример 4.16. Найти угол между двумя прямыми х = 3+2/, у- = 4 + 7/,
z — -5+8t; х = 2+8/, _у = 6-11/, z = -8—7t.
Первая прямая имеет направляющий вектор а = (2,7,8), вторая -
b = (8, -11, - 7). По формуле (4.31) находим
= 2 8+7 (-11)+8 (-7) = -117 =____1_
Ф /г2 + 72 + 82 \/82 + (-11)2 + (~7)2 -Л17 /234 Л
Следовательно, ф = 135°.
Пример 4.17. Доказать, что прямые х = 7+5/, y = -5-7t, z = -2-3/ и
х = /, у = /, г = -3 + 2/ пересекаются. Найти точку их пересечения.
Рассмотрим векторы М,М2 = (0- 7,0- (-5), - 3- (-2)) = (-7,5, -1),
а = (5,-7,-3), b = (l, 1,2) и их смешанное произведение
84
«ьм,м2 =
5 -7 -3
1 1 2
-7 5 -1
5 —12 -13
10 0 =0.
7 12 13
Поскольку смешанное произведение трех векторов равно нулю, то векторы ком-
планарны; значит, данные прямые лежат в одной плоскости. Так как направляю-
щие векторы а и b этих прямых неколлинеарны (их координаты не пропорцио-
нальны), то прямые пересекаются.
Чтобы найти точку пересечения, приравняем выражения для координат, пред-
варительно обозначив параметр буквой а в уравнениях второй прямой:
7 + 5t = s, -5-Tt — s, —2—3f = —3+2s.
Из первых двух уравнений следует, что 7+5< = -5-7т, откуда Г = -1; следова-
тельно, 5 = 2. При этих значениях t ns третье уравнение обращается в тождество.
Подставляя значение t = -1 в уравнения первой прямой (или s = 2 в уравнения
второй прямой x = s, y = s, z = —3+2s), находим x = 2, у = 2, z = l. Итак,
M (2,2,1) - точка пересечения данных прямых.
Пример 4.18. Найти расстояние от точки Л/о(2,-3,5) до прямой:
х = 5+2/, у = —4—t, z = 6—2t.
Найдем сначала векторное произведение, входящее в формулу (4.35):
г, - г0 = М0М! = (5- 2, - 4 - (-3), 6- 5) = (3, -1,1), а = (2, -1, - 2),
[(г, — г0), а] =
-11 3 1
-1 -2 ’ 2 -2
3 -1
2 -1
= (3,8, -1).
По формуле (4.35) получаем
д 7з2+82+(-1)2 J74
7г2+(-1)2+(-2)2 з
4.7. Задачи на прямую и плоскость
Прямая как линия пересечения двух плоскостей. Рассмотрим две плоско-
сти, заданные общими уравнениями (4.22) и (4.23). Если условие (4.24) не выпол-
нено (т. е. коэффициенты Alt В,, Ct не пропорциональны коэффициентам А2, В2,
С2), то плоскости пересекаются по прямой, определяемой уравнениями
Alx + B1y+Clz + Dl =0, А2х + В2у + C2z + D2 =0.
Эти уравнения приводятся к параметрическому виду
х=х0 +
В2
с2
t,y=y0-
4 с.
с2
t,z=z0 +
А
В2
t.
(4.37)
(4.38)
4
4
85
Данная прямая имеет направляющий вектор
а = [п1, п2] =
д
Вг
G _ 4 G А
^2 ^2 ^2
%
Вг
(4.39)
где П] = (Д, В,, Q), й2 = (А2, В2, С2) - нормальные векторы данных плоскостей.
Точка Л/0(х0, у0, z0) на прямой может быть выбрана произвольно; для этого не-
обходимо в системе (4.37) зафиксировать значение одной переменной (например,
z = z0 ), из полученной системы уравнений найти значения двух других перемен-
ных (х = х0, у = у0).
Пучок плоскостей — множество всех плоскостей, проходящих через одну и ту же
прямую. Уравнение пучка плоскостей, проходящих через прямую (4.37), имеет вид
а ( А,х + В)У + C,z + Dt)+Р (А2х + В2у + C2z + D2 ) = О,
где а и Р — любые действительные числа, причем хотя бы одно из них отлично от
нуля. Это уравнение можно привести к виду
Atx + Bty+Qz + £>] + X ( А2х + В2у + C2z + D2) = 0, (4.40)
где X = P/а, а * 0. Уравнение (4.40) определяет все плоскости пучка, за исклю-
чением той, которой соответствует а = 0, т.е. за исключением плоскости
А2х + В2у + C2z + D2 = 0.
Угол между прямой и плоскостью. Синус угла между прямой
х = х0+Д]/,y = y0+a2t, z = z0+a3t (4.41) (4.42)
И плоскостью Ax + By+Cz+D=0
определяется формулой | Aat + Вд2 + Сдз |
sin <р = (4-43)
1 1
Ja2+B2 + C2 -jaf +д2 + д*
(4.44)
(4.45)
(4.46)
(4.47)
Взаимное расположение прямой й плоскости. Прямая (4.41) и плоскость
(4.42) пересекаются, если
Aat + Вд2 + Са3 Ф 0;
перпендикулярны, когда
_£ = _S_=jC.
Д] д2 Оу.
параллельны, если
А Д] + Ва2 + Сд3 = 0, Аха + Ву0 + Cz0 + D Ф 0;
совпадают, когда
А д, + Ва2 + СДз = 0, Ах0 + Ву0 + Cz0 + D = 0.
Координаты точки пересечения прямой (4.41) и плоскости (4.42) нахо-
дятся из системы их уравнений.
86
Неравенство (4.44) означает, что нормальный вектор п =(Я, В, С) плоскости
(4.42) и направляющий вектор а = (ц,аг,а3) прямой (4.41) не перпендикулярны,
т.е. прямая и плоскость не параллельны.
Равенства(4.45) означают, что векторы пи а коллинеарны, т.е. прямая (4.41) и
плоскость (4.42) перпендикулярны.
Соотношения (4.46) показывают, что векторы п и а перпендикулярны, т.е.
прямая и плоскость параллельны, но точка Мо(*о>Уо»го) прямой (4.41) не при-
надлежит плоскости (4.42).
Равенства (4.47) означают, что векторы п и а перпендикулярны и точка
Л/0(х0, у0, z0) прямой принадлежит плоскости (прямая лежит в плоскости).
Пример 4.19. Уравнения прямой x + 2y+4z-7 = 0, 2x + y-z-5 = 0
привести к параметрическому виду.
Поскольку в этих уравнениях коэффициенты при текущих координатах непро-
порциональны, то плоскости, определяемые данными уравнениями, пересекаются.
Данные уравнения определяют прямую. Выберем на прямой точку. Полагая в этих
уравнениях, например, z0 = 2, получаем
х + 2у = -1, 2х+у = 7,
откуда Ло=5, уо=-3. На прямой зафиксирована точка Л/о(5, - 3,2). По формуле (4.39)
найдем направляющий вектор прямой. Так как n, = (1,2,4), п2 = (2,1, -1), то
а=[П|,п2]=
2 4 I _1 1 4
• -И |2 -1
= (-6,9,-3).
I 2
2 1
Параметрические уравнения (4.38) данной прямой принимают вид х = 5-6г, -
у = -3+9т, z = 2-3t.
Замечание. В качестве направляющего вектора можно взять
у а =(-2,3,-1), тогда х = 5-2/, y = -3 + 3t, z=2—t.
Пример 4.20. Найти угол между прямой x = -3-t, у = 5-г,
z = -4 + 2t и плоскостью 2x-4y+2z-9 = 0.
Применяя формулу (4.43) для случая а,=-1, e2=-1, в3=2, А=2, В=-4, С=2, находим
sin(p =
| 2(-1)-4(—1)+2-2|
^22 +(-4)2 + 22 7(-1)2 +(-02 + 22
= -7^ _ = !, <р = 30°.
л/24 э/б 2
Пример 4.21. Найти проекцию точки Л/(1,-2,4) на плоскость
5х — Зу + 6z + 35 = 0.
Этой проекцией является точка пересечения перпендикуляра к плоско-
сти, проходящей через точку М. Для прямой, перпендикулярной плоскости,
направляющим вектором будет п = (5, -3,6). Параметрические уравнения
«7
прямой, перпендикулярной плоскости и проходящей через точку М, примут
вид х = 1 + 5/, y = -2-3z, z = 4+6z.
Подставляя эти выражения в уравнение плоскости, находим:
5(1 + 50-3(-2-3/)+6(4+6Г)+35 = 0, 70/ + 70 = 0, г = -1.
При этом значении t из уравнений прямой получаем: х= 1 - 5 = - 4, у = -2 + 3 =
1, z = 4 - 6 = -2. Следовательно, точка N (- 4,1, - 2) - искомая проекция.
Пример 4.22. Вершины пирамццы находятся в точках Д(4,6,5), А2(6,9,4),
Л3 (2,10,10), Л4(7,5,9). Найти: 1)длинуребра А1Аг; 2) угол между ребрами AtA2 и
4 А; 3) площадь грани AlAjA-s, 4) объем пирамиды Л1Л2Я3И4; 5) уравнение плоскости
А1АгА3; 6) уравнения прямой А,А4; 7) угол между ребром AtA4 и гранью А|А2Аз;
8) уравнения высоты, опущенной из вершины А4 на грань AiA-fa.
Найдем сначала координаты векторов AtA2, AtA3, А,А4 и координаты век-
торного произведения [А]А2,А]А3]. По формуле (3.15) получаем
А,А2 = (6- 4,9- 6,4- 5) = (2,3, -1); А,А3 = (2-4,10- 6,10- 5) = (-2,4,5);
А, А4 = (7 - 4,5 - 6,9 - 5) = (3, -1,4).
С помощью формулы (3.26) находим
[А]А2, А|А3] —
3 -1
4 5
2 -1
-2 5
2 3
-2 4
= (19,-8,14).
1. Длина ребра AtA2 равна расстоянию между точками А{ и Аг, которое вы-
числим по формуле (1.26):
р (Д, A2)=V(6-4)2+(9-6)2+(4-5)2 = 714 = 3,74.
Тот же результат можно получить, найдя модуль вектора А, А2 по формуле (3.11).
2. Угол между ребрами Л,Л2 и AtA3 равен углу ф между векторами A,A2 = a,
А]А3 = Ь. В соответствии с формулой (3.22) получаем
ab 2(—2) + 3-4 —1 5 • 3 1
|a||b| 7г2+32+(-1)2 V(-2)2 + 42 + 52 ЗТТО ТТО
созф = 0,1195, ф » 83°31'.
3. Площадь грани AtA2A3 равна площади треугольника A/a2A3, которую вы-
числим по формуле (3.29), использовав формулу (3.11) для модуля вектора и ко-
ординаты вектора [AtA2, А(А3]:
S = j| [А,А2, А,А3] | = у 7192+(-8)2 + 142 = S-12,46.
88
4. Объем пирамиды Л]Л2И3И4 найдем по формуле (3.35):
1 6-4 9-6 4-5 2 3 -1
V = - mod 2-4 10-6 10-5 1 = —mod -2 4 5 _ 121 = 20—
6 6 6~ 6
7-4 5-6 9-5 3-14
5. Уравнение плоскости А}А2Аз как плоскости, проходящей через три точки
(см. (4.14)), принимает вид
x — 4 y-6 z-5
6-4 9-6 4-5 = 0,
2-4 10-6 10-5
х-4
2
-2
у-6 z—5
3 -1
4 5
= 0,
19(х —4)—8(у—6)+14(z—5) = 0, 19x-18y + 14z-98 = 0. (I)
6. Уравнения прямой Д]Д4 как прямой, проходящей через две точки
(см. (4.21)), запишутся так:
х — 4 _ у — 6_z-5 x — 4_y — 6_z—5
7-4~ 5-6 “9^5’ 3 " -1 4~’
или
х = 4+3/, у = 6—t, z = 5+4/. (II)
7. Угол между ребром АХА4 и /ранью Л^Лз равен углу ф между плоскостью
(I) и прямой (II). По формуле (4.43) находим
119-3-8-(-1) + 144| _ 121
Ф 7192+(-8)2+142 ^32+(-1)2 + 42 V621 -Лб ’
sin ф = 0,9522, ф = 72°13'.
8. Уравнения высоты, опущенной из вершины А4 на /рань А^Аз, можно за-
писать как уравнения прямой, проходящей через точку А4 и перпендикулярной
плоскости (I), имеющей нормальный вектор п = (19,-8,14), который для этой
прямой будет направляющим вектором. Уравнения (4.19) в данном случае прини-
мают вид х = 7 +19/, у = 5-8/, z = 9 + 14/.
4. 8. Цилиндрические поверхности.
Поверхности вращения
Цилиндрической называется поверхность, описываемая прямой (образующей),
движущейся вдоль некоторой линии (направляющей) и остающейся параллельной
исходному направлению (рис. 4.11). Уравнение цилиндрической поверхности,
образующие которой параллельны оси Oz, имеет вид
F(x,y) = 0. (4.48)
89
Особенность уравнения (4.48) состоит в том, что оно не содержит переменной г.
Есяи уравнение F (у, z) = О определяет некоторую поверхность, то ею является
цилиндрическая поверхность с образующей, параллельной оси Ох. Если уравнение
F (х, z) = О определяет некоторую поверхность, то ею является цилиндрическая
поверхность с образующей, параллельной оси Оу.
Поверхность, образованная вращением линии I
^ = /(z),y = <p(z)
(4.49)
вокруг оси Oz (рис. 4.12), определяется уравнением
jr2+/=/2(z)+<p2(z). (4.50)
Поверхность, образованная вращением линии х = /j(y), z- f2{y) вокруг оси Оу,
имеет уравнение х2 +z2 = f\{y)+f2{y)-
Поверхность, образованная вращением линии у = фДх), z = ф2(х) вокруг оси
Ох, определяется уравнением у2 +z2 = ф2(х) + ф|(х).
. Поверхностью вращения второго порядка называется поверхность, полученная
вращением линии второго порядка вокруг ее оси.
Эллипсоидом вращения называется поверхность, полученная вращением
эллипса вокруг одной из его осей. Уравнение эллипсоида вращения, полу-
ченного вращением эллипса у2/Ь2 + z2/c2 = 1, х = 0 вокруг оси Oz, имеет вид
х2//?2 + у2//?2 + z2/c2 = 1.
Однополосным гиперболоидом вращения называется поверхность, полученная враще-
нием гиперболы вокруг ее мнимой оси. Однополосный гиперболоид вращения, получен-
ный вращением гиперболы y2/b2-z2/c2 = 1, х = 0 вокруг оси Oz, имеет уравнение
x2/b2.+ y2lb2-z2/c2 = 1.
Двуполостным гиперболоидом вращения называется поверхность, по-
лученная вращением гиперболы вокруг ее действительной оси. Двуполо-
стный гиперболоид, полученный вращением гиперболы z2/c2 - y2fb2 = 1,
90
х = 0 вокруг оси Oz, определяется уравнением
х2/б2 + у2/б2 -z2/c2 =-1.
Параболоидом вращения называется поверхность, полученная вращением па-
раболы вокруг ее оси. Уравнение параболоида вращения, полученного вращением
параболы у2 = 2pz, х = 0 вокруг оси Oz, имеет вид
2 2
i-=2_=2z.
р р
Пример 4.23. Составить уравнение поверхности, полученной вращени-
ем линии х2/а2 - z2/c2 =0, у = 0 вокруг оси Oz.
Данные уравнения определяют пару пересекающихся прямых в плоскости Oxz,
проходящих через начало координат (являющихся пересечением плоскостей xJa -
z/c = 0, х/а + z!c = 0 с плоскостью Oxz). Приведем эти уравнения к виду (4.49):
x = + (a/c)z, у = 0.
В соответствии с уравнением (4.50) получаем
2 2 «2 2 X2 у2 Z2
х*+у2= z\ —+Z__—=0.
с а а с
Последнее уравнение является уравнением конуса вращения, получающегося при
вращении указанных прямых вокруг оси Oz.
4.9 . Поверхности второго порядка
Поверхностью второго порядка называется поверхность, Определяемая ал-
гебраическим уравнением второй степени относительно текущих координат х, у, z.
Канонические уравнения поверхностей второго порядка:
х2/а2 + у2/Ь2 + г2/с2 =\ (эллипсоид, рис. 4.13); (4.51)
x2l<?+y2lb2-z2lc2 = \ (однополосный гиперболоид, рис. 4.14); (4.52)
x2la2 + y2/b2-z2lc2=-\ (двуполостный гиперболоид, рис. 4.15); (4-53)
о И <4 1 сч + сч сч К (конус, рис. 4.16); (4.54)
х2 /а2 + у2 /b2 =2z (эллиптический параболоид, рис. 4.17); (4.55)
x2/a2-y2lb2=2z (гиперболический параболоид, рис. 4.18); (4.56)
91
л2/а2+/Д2 = 1 (эллиптический цилиндр, рис. 4.19); (4.57)
х2/Д2-//б2 = 1 (гиперболический цилийдр, рис. 4.20); (4.58)
х2 = 2ру (параболический цилиндр, рис. 4:21); (4.59)
х2/а2 — у2/b2—Q (пара пересекающихся плоскостей); (4.60)
х2/а2=\ (пара параллельных плоскостей); (4.61)
х2 = 0 (пара совпадающих плоскостей). (4-62)
Рис. 4.13
Рис. 4.14 Рис. 4.15
92
93
Замечание, 1 .Уравнение (4.51) прио,=/> = с = ./?принимаетвид
х2 +у2 +г2 = /г2 /. . (4.63) •
и определяет сферу радйусА )? с центром-в начале координат.’
Общее уравнениевторой степени относительно ас, у, г мож;етбыть:ириведаНо к
одному из уравнений (4.51) - (4.63) или к одному из следующих уравнений:
-,х2 /а2+у2 /b2.+z2 /с2=--1; .. (4.64)
x2/a2+y?/ft2|+^2/e.2qr:(JftOi v : -C i ;,. :.!(W)
i! х2/д2+у2/Р--1; Л‘ 7 (4.66)
x2/a2 +y2/b2 = Q',e 4 i4'
х2/д2=-1. (4.68)
Уравнениям (4.64), (4.66) и (4.68) не удовлетворяют координаты ни одной точ-
ки пространства; уравнению (4.65) удовлетворяют координаты единственной точ-
ки О (0,0,0); уравнению (4.67) удовлетворяют координаты точек, лежащих на
прямой х = 0, у = 0.
Замена ни е 2. Если уравнение
Ax2 + Ay2 + Az2 + Bx + Cy+Dz + F=0 (4.69)
(т.е. уравнение, у которого коэффициенты при квадратах координат равны между
собой, а коэффициенты при произведениях координат равны нулю) определяет
некоторую поверхность, то этой поверхностью является сфера. Уравнение (4.69) в
этом случае может быть приведено к виду
(x-a)2+(y-6)2 + (z-c)2 = /?2. (4.70)
Уравнение (4.70) является уравнением сферы радиуса А с центром в точке С(а, Ь, с).
Прямые, целиком лежащие на некоторой поверхности, называются прямоли-
нейными образующими данной поверхности.
Однополосный гиперболоид (4.52) имеет два семейства прямолинейных
образующих:
(х zA о(, уА (х z\ у А
а-------= рН-Z. , а------L=p 1+Z.I
\а с J \ bj \а с J \ Ь)
„(х z') (, у A afx z')(. у А
Р -+~те(х 1+- ,’ Р| —+— ha 11-— .
\а с) bj \а с J \ Ь)
Гиперболический параболоид (4.56) также имеет два семейства прямолиней-
ных образующих: ''><
(X а ' г,(Х ~
— , =Р*. Р —+т 1 = 2а,
a b) \ab)
„(х -H-OR йРх^-л,
а----— 1=2р, р —+— =<xz.
\а \а Р)
94
Пример 4.24. Определить вид и параметры поверхности второго поряд-
ка, заданной уравнением
Зх2 + 4у2 +f>z2 — 6х + 16у—36z+49 = 0.
Преобразуем это уравнение, выделив в левой части полные квадраты:
3(x2-2x + l)+4(y2+4y+4)+6(z2-6z + 9)-3-16-54 + 49=0,
3 (х -1)2 + 4 (у+2)2 + 6 (z - З)2 = 24.
Введем новые координаты по формулам (3.17):
X=x-l, Y=y+2, Z=z-3, (I)
тогда уравнение примет вид
ЗХ2 + 4У2 + 6Z2 = 24, или Х2/&+ У2/б+ Z2/4 = L
Полученное уравнение определяет эллипсоид (см. (4.51)), для которого а = 2^2,
b = Тб, с = 2. Центр эллипсоида находится в точке 0,(1, - 2,3); в новой системе
координат центром является точка с координатами X = О, У = О, Z = 0. Из этих ра-
венств и формул (I) находим х - 1, у = -2, z = 3, т.е. координаты точки Ох.
Пример 4.25. Определить вид и параметры поверхности
2х2+3у2 —6z2 —8x + 6y+12z —1 = 0.
Преобразуем это уравнение:
2(x2-4x+4)+3(y2+2y+l)-6(z2-2z + l)-8-3+6-l = 0,
2(x-2)2 + 3(y+l)2-6(z-l)2 = 6.
Переходя к новым координатам по формулам X ==х-2, Y = у+1, Z = z -1» полу-
чаем
2Х2 + ЗУ2 - 6Z2 = 6, или Х2/3 + У2/2 - Z2/l = 1.
Это уравнение определяет однополостный гиперболоид (см. (4.52)), для которого
а = 7з, Ь = -]2, с = 1, с центром в точке 0,(2,-1,1).
Пример 4.26. Доказать, что уравнение z - ху определяет гиперболиче-
ский параболоид.
Введем новые координаты по формулам х = Х— У, y=X+Y, z = Z, тогда
уравнение примет вид
Z=(X-Y)(X+Y), Z=X2-Y2.
Полученное уравнение является уравнением вида (4.56), для которого 2а2 = 1,
2b2 = 1; оно определяет гиперболический параболоид.
Пример 4.27. Доказать что уравнение х2 = yz определяет конус.
Переходя к новым координатам по формулам х = X, у = Z-Y, z = Z+Y, по-
лучаем X2 =(Z-y)(Z + y),X2 =Z2-y2, или X2 + y2-Z2=0.
Полученное уравнение является уравнением вида (4.54), для которого
а = Ь = с = I, оно определяет конус.
95
4.1 0. Некоторые другие поверхности
В плоскости Oxz (у=0) задана линия Z, своими параметрическими уравнениями
X = /(«), Z = ф («), (4.71)
не пересекающая ось Oz. Рассмотрим поверхность, полученную вращением этой
л^нии вокруг оси Oz.
Параметрические уравнения рассматриваемой поверхности вращения
имеют вид
х = /(h)'cosv, у= /(«)sinv, г = ф(и). (4.72)
Тор — поверхность, полученная вращением окружности вокруг оси, лежащей
в плоскости данной окружности и не пересекающей ее. Эта поверхность напоми-
нает спасательный круг, камеру автомобильной шины (рис. 4.22).
Рассмотрим тор, полученный вращением вокруг оси Oz окружности, заданной
параметрическими уравнениями
x = a + bcosu, у = 0, z = bsinu (b<a).
Эта окружность лежит в плоскости Oxz (у = 0) и определяется уравнениями вида
(4.71)»где f(u) = a+bcosh, ф(и) = 5$ти.
В соответствии с(4.72) получаем параметрические уравнения тора
х = (а+b cos и) cos v, у = (а + b cos и) sin v, z=b sin и. (4.73)
Катеноид — поверхность, полученная вращением цепной линии вокруг ее оси
(рис. 4.23). Рассмотрим катеноид, полученный вращением вокруг оси Oz цепной
линии, заданной параметрическими уравнениями
х = a ch (и/a), у = 0, z = и.
Эта линия расположена в плоскости Oxz (у = 0). Она определена уравнения-
ми вида (4.71), где /(и) = о ch (и/a), ф (и) = и. В соответствии с (4.72) находят
96
параметрические уравнения катеноида
x = och(u/fl)cosv, у-ach(u/n)sinv, z — u.
Исключая из этих уравнений параметры и, v, получаем
Jx2+y2 = (д/2) (ez/a + (4.74)
Катеноид является единственной минимальной поверхностью среди поверхно-
стей вращения. Минимальные поверхности возникли при решении следующей
задачи: среди всех поверхностей, проходящих через данную замкнутую простран-
ственную линию, найти ту, которая имеет минимальную площадь поверхности,
ограниченной данной линией. Отсюда происходит и название такой поверхности.
Бельгийский физик Плато предложил простой экспериментальный способ получе-
ния минимальных поверхностей посредством мыльных пленок, натянутых на про-
волочный каркас.
Катеноид обладает следующим свойством. Рассмотрим две окружности, полу-
ченные пересечением катеноида (4.74) соответственно плоскостями z = -с, z = с.
Любая поверхность, края которой совпадают с этими окружностями, имеет пло-
щадь большую, чем часть катеноида, расположенная между указаншши окружно-
стями. Мыльная пленка, соединяющая данные окружности под действием сил
внутреннего натяжения, принимает форму катеноида.
Геликоид - поверхность, описанная прямой, которая вращается с постоянной
угловой скоростью вокруг неподвижной оси, пересекает ось под постоянным уг-
лом а и одновременно перемещается поступательно с постоянной скоростью
вдоль этой оси. При а = 90° геликоид называют прямым (рис. 4.24, а), при
а # 90° геликоид называют косым (рис. 4.24, б).
Рассмотрим прямой геликоид, описанный прямой, перпендикулярной оси Oz
(см. рис. 4.24, в). Пусть M(x,y,z) - произвольная точка поверхности, Р- ее
проекция на плоскость Оху, Q, L - проекции точки Р соответственно на оси Ох,
Оу. Обозначим через и расстояние точки М до оси Oz (| MN ] =| ОР] = и), а через
v - угол, образуемый отрезком ОР с осью Ох.
Параметрические уравнения геликоида имеют вид
х = wcos v, у — usin v, z = av,
где а— некоторая постоянная.
Наглядное представление о положении отдельных прямых (лгучей) при
v = const Дают ступени винтовой лестницы.
Представление о-геликоиде можно составить, например, наблюдая движение
винта вертолета при его вертикальном взлете. Отметим, что первоначально верто-
леты называли геликоптерами;.винтокрылыми. Первый эскиз геликоида был нари-
сован еще Леонардо да Винчи.
Разнообразные геликоиды широко применяются на практике Это объясняется
следующим: геликоид образован сложением двух самых распрос траненных видов
4 Зак. 1
97
равномерного движения — прямолинейного и вращательного. Вследствие этого
геликоид можно применить там, где необходимо перейти от одного из указанных
вадов движения к другому, что имеет место практически в любой машине.
Псевдосфера - поверхность, полученная вращением трактрисы вокруг
ее асимптоты (рис. 4.25). Рассмотрим псевдосферу, полученную вра-
щением вокруг оси Oz трактрисы
х= asinu, у = 0, z = с (In tg (u/2)+cosk).
Эта трактриса лежит в плоскости Oxz (у = 0), ось Oz спужт ее асимптотой. Ли-
ния задана параметрическими уравнениями вида (4.71), где f(u) = asinu,
Рис. 4.24 Рис. 4.25
<р(и) = а(1п tg(«/2)+cos«). В соответствии с (4.72) получены параметрические
уравнения псевдосферы
x = «sin«cosv, у = asinusinv, z =a(lntg(«/2)+cos«).
Важность псевдосферы состоит в том, что на ней частично реализуется
плоская неевклидова геометрия Лобачевского. Этот удивительный факт
установил итальянский математик Эудженио Бельтрами в 1868 г., уже
после смерти Н.И. Лобачевского.
98
II
АЛГЕБРА
Гпава 5
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
5.1. Матрицы. Основные определения
Матрицей называется система т- ц чисел, расположенных в прямоугольной
таблице из т строк и и столбцов. Числа этой таблицы называются элементами
матрицы. Обозначения матрицы:
ЙП а,2 ... Оу,
«21 «22 О2п
Оп О12 ...
а21 а22 а2п
. Чя1 ат2 — ат>
„Чи! ат2 ••• атп >
Оц а12 ... а,„
О2] 022 ... а2п
ат1 От2 Цда
Элементы в(|,ап, ...,в/и составляют i-ю строку (1=1,2,элементы
alk, а2к,...,атк составляют к-й столбец (к = 1,2,.ал - элемент, принад-
лежащий i-й строке и Л-му столбцу матрицы, числа i, к называют индексами эле-
мента. Матрицу, имеющую т строк и я столбцов, называют матрицей размеров
тхп (читается т на и). Употребляются и более краткие обозначения матрицы
размеров тхп.
(^гл)тл» ||MW*
Матрицу обозначают также одной заглавной буквой, например
Две матрицы Am„=(aik)M„ 8^=^)^ называются равными, если
р = т, д = п и aik = bik (i=\,2,...,m, к = 1,2,...,п); другими словами, если
они одинаковых размеров и их соответствующие элементы равны.
99
Матрица, состоящая из одной строки, называется строчной матрицей, или мат-
рицей-строкой. Строчная матрица имеет вид
h «з - ««]•
Матрица
«2
имеющая один столбец, называется столбцовой матрицей, или матрицей-
столбцом.
Матрица, все элементы которой равны нулю, называется нулевой. Нулевую
матрицу обозначают буквой О:
о= 0 0 ... 0 0 0 ... 0 0 0 ... 0
Квадратной называется матрица, у которой число строк равно числу столбцов
(т = я), т. е. матрица вида
«11 «12
«21 «22 «2и
ап1 «и2 • •• апп .
Порядком квадратной матрицы называется число ее строк.
Будем говорить, что элементы аи,а22,...,ат, квадратной матрицы образу кл-
ее главную диагональ, а элементы а1и, а2и_(,..., аи1 - вторую диагональ.
Квадратная матрица называется симметрической, если а№ = аи, т. е. равны ее
элементы, симметричные относительно главной диагонали.
Диагональной называется квадратная матрица, у которой все элементы, не
принадлежащие главной диагонали, равны нулю, т. е. матрица
«и 0 ... 0 ‘
0 0
diag(aI1,a22,...,aniI) =
0 0 ... &пм
Скалярной называется диагональная матрица, у которой аи=с
(с = const) при 1 = 1,2,...,п.
100
Единичной называется диагональная матрица, у которой все элементы главной
диагонали равны единице. Единичную матрицу обозначают буквой Е:
Е =
1 0 . 0 ‘
0 1 0
0 0 1
Треугольной называется квадратная матрица, все элементы которой, располо-
женные по Одну сторону от главной диагонали, равны нулю. Различают соответст-
венно верхнюю и нижнюю треугольные матрицы:
«п ап «1з . • «1» ' «11 0 0 .. 0 ‘
0 «22 «23 «2н «21 а22 0 . .. 0
0 0 «зз . • «31 «32 «33 .. 0
0 0 0 • ат . «л2 «лЗ «л».
Матрица произвольных размеров вида
А =
Г «и «12 «13 ... «1г • • ^1и
0 «22 «23 ... «2г • • «2н
0 0 «33 «Зг • - «3»
0 0 0 &ГГ «гл
0 0 0 ... 0 0
называется
(5.1)
квазитреугольной (ступенчатой или
где а„*0 (i = l,2,..,,r),
трапециевидной).
Матрица Ат, полученная из данной матрицы А заменой каждой ее строки
столбцом с тем же номером, называется транспонированной относительно Л. Если
А — матрица размером тхп, тоАТ имеет размеры их т.
Например, если А =
, то Лт =
’ 1 3
8 6
4
7
1
3
4
8
б
7
101
Элементарными преобразованиями матрицы называют следующие преоб-
разования: 1) умножение строки (или столбца) матрицы на число, отличное от
нуля; 2) прибавление к элементам строки (столбца) соответственных элемен-
тов другой строки (столбца), умноженных на любое число; 3) перестановка
местами двух строк (столбцов).
Термин «матрица» был введен Д. Сильвестром в 1851 г.
5.2. Линейные действия над матрицами
Линейными действиями над матрицами называются сложение и вычитание
матриц, умножение матриц на число. Сложение и вычитание определяются только
для матриц одинаковых размеров.
Суммой двух матриц А = (aik)m„, В„п =(Ь^)„п называется такая матрица
С = (сй)тл, что
cik = ajk + bik (i = l, 2, k = l, 2, ...,и), (5.2)
т. e. матрица, элементы которой равны суммам соответствующих элементов мат-
риц слагаемых. Сумма двух матриц А иВ обозначается А + В.
Разностью двух матриц А = (а/к)т„, Bm/I=(bik)m„ называется матрица
D = № )mn> для которой
(i = 1,2,..., т; к = 1,2,..., и). (5.3)
Произведением матрицы А = (ал )тл на число а (или числа а на матрицу А) назы-
вается матрица Л = (^й)тл, для которой
btk = ааа (г = 1,2,...,т, к = 1,2,...,и), -(5.4)
т. е. матрица, полученная из данной умножением всех ее элементов на число а.
Произведение матрицы А на число а обозначается Аа (или аЛ).
Матрицу (-1)Л называют матрицей, противоположной матрице А, и
обозначают -А.
Замечание. Разность А-В двух матриц можно определить так:
А-В=А + (—В). (5.5)
Линейные действия над матрицами обладают следующими свойствами:
1)А + В = В+А; 2) (А +В) + С-А + (В + С); 3) А + О=А; 4) А + (-А)=О;
5) 1А = А; 6) а (РЛ) = (а₽) А- 7) а(Л + В) = аЛ + аВ; 8) (а + ₽) А = аЛ + рл, где
А, В, С - матрицы одних и тех же размеров; О - нулевая матрица; (-Л) -
матрица, противоположная матрице Л: а, р — любые действительные числа.
102
В соответствии с формулами (5.2) и (5.3) получаем 3-2
'1+8 3+2 9 51 ’ 1-8
А + В = 2+6 5+3 = 8 8 , А-В = 2-6 5-3
6+1 4+5 7 9 6-1 4-5
Пример 5.2. Даны две матрицы
5.3. Произведение матриц. Многочлены от матриц
Произведение определяется для квадратных матриц одного и того же порядка,
а также для прямоугольных матриц, у которых число столбцов матрицы множимо-
го равно числу строк матрицы множителя.
Произведением матрицы Атп = (ajk)mn на матрицу Д,/=(пЛ)„/ называется та-
кая матрица С„, = (Сд)^, для которой
п
Cik=aiiblk+ai2b2k+...+ai„bnk=^aiJbjk, (5.6)
7=1
т. е. элемент сл матрицы Ст/ равен- сумме произведений элементов i-й строки
матрицы А на соответствующие элементы А-rg столбца матрицы В„,. Матрица
Ст/ имеет т строк (как и матрица А) и I столбцов (как и матрица Вя/). Произве-
дение матрицы А на матрицу В обозначается АВ.
Замечание.Из того, что матрицу А можно умножить на В, не следует,
что матрицу В можно умножать на Я. В общем случае АВ * ВА. Если АВ = ВА, то
матрицы А кВ называются перестановочными или коммутативными.
При умножении матриц единичная матрица Е играет роль единицы, а нулевая
матрица О - роль нуля, так как АЕ = ЕА = А, АО=ОА = О.
Умножение матриц обладает следующими свойствами. Если имеют
смысл соответствующие действия, то выполняются равенства:
1) (ЯВ)С=Я(ВС); 2) а(АВ) = (аА)В, 3) (Л + В)С= АС+ВС;
4) С(А +В) = СА+СВ, где а - любое действительное число.
103
Отметим, что (АВ)' = В'А', где штрихом обозначена матрица, транспо-
нированная данной.
Целой положительной степенью A* (k > 1) квадратной матрицы А называется
произведение к матриц, каждая из которых равна А, т.е. А* = Ах Ах... х А. Мат-
Араз
рица А* имеет тот же порядок, что и матрица А. Нулевой степенью квадратной
матрицы А (А * 0) называется единичная матрица того же порядка, что и А, т. е.
Л° = Е. Первой степенью Л1 матрицы А называется сама матрица А, т. е. Л1 - А.
Многочленом (или полиномом) степени к (к-' целое неотрицательное число) от
квадратной матрицы А называется выражение вида
а*Л* + . + а2Л2 + а,А + а0А°,
где at (i = Q,\,2,...,k) - любые числа, причем ак *0. Обозначим многочлен от
матрицы Л через Р(Л), тогда по определению
Р (Л) = а*Л* + Л*’1 4-.. .4- а2Л2 + а, А+а0Л°,
ши
P(A) = atA* +at_lA*~l +...+а2А2 +atA+a0E. (5.7)
Из определения следует, что многочлен от матрицы можно получить, если в
обычный многочлен Р(х) = акх* + at_tx*~i +...+а1х + а0 вместо х подставить
квадратную матрицу (и учесть, что Л° = Е ).
Пусть дан многочлен Р(х). Если Р(А) является нулевой матрицей, т. е.
Р(А)=О, то матрица Л называется корнем многочлена Р(х), а многочлен Р(х)
— аннулирующим многочленом для матрицы Л.
Пример 5.3. Найти произведение АВ и ВА матриц
Обе матрицы являются квадратными матрицами одного и того же порядка
(второго), поэтому можно получить произведения АВ и ВА. Применяя формулу
(5.6) для случая т=и = 2, и=/ = 2, получаем
ЛВ =
-5
-6
7 1_Г 1(—5)4-2(—6) 1-74-2-8
8 ]“[3(-5)4-4(-6) 3-74-4-8
-17 23
-39 53
1 2
3 4
ВА =
-5
-6
7
8
1 21_Г (-5)14-7-3 (-5)24-7-4 1 Г16 18
3 4 J-[ (-6)14-8-3 (-6)24-8-4 18 20
Отметим, что АВ Ф ВА, т. е. результат умножения зависит от порядка множителей.
104
Пример 5.4. Даны две матрицы
1 2 — 4
5 7-8
О 1 -2
-1
-2
-3
-7
Найти произведение АВ. Можно ли получить произведение ВА?
Число столбцов матрицы А равно числу строк матрицы В (ширина матрицы А
равна высоте матрицы В), поэтому произведение АВ определено. Умножая строку
матрицы А на столбец матрицы В, по формуле (5.6) получаем
3-4+ 1-5 + 2-6 + (—4) 8
АВ = 6-4 + 5-5 + 7-6+(—8) 8
9-4 + 0 5+1-6 + (-2)8
3(—1)+1(—2) + 2 (—3)+(—4) (—7)
6(—1) + 5(—2) + 7(—3)+(-8)(-7)
9 (—1) + 0(—2) + 1 (—3) + (—2)(—7)
12+5 + 12-32 -3-2-6 + 28 -3 17
24+25 + 42-64 -6-10-21+56 27 19
36+0 + 6-16 -9 + 0-3 + 14 26 2
Произведение ВА не определено, так как число столбцов матрицы В не равно
числу строк матрицы А.
Пример 5.5. Найти многочлен Р(А), если Р(х)=х*- Зх+5 и Я = * .
В соответствии с определением многочлена от матрицы (см. формулу (5.7)) по-
лучаем Р(Я) = А2-ЗА + 5Е или
Р(Я) =
1 -1
2 -3
1 -1
2 -3
' -1 2'
— 4 7
2
-3
-1
-3
-3
-3
-9
-1
-3
-1
-3
О'
5
' 1 О'
0
1
-10
О'
1
5
21
1
2
3
6
1
2
1
2
5
0
+ 5
1
1
0
5.4. Определители и их свойства
Определителем квадратной матрицы второго порядка
«11 «12
. «21 «22 .
называется число, равное «рОгг ~«i2«2i и обозначаемое символом
2 й в а в в* , т. е. «11 «12 «21 «22 ~ «11«22 «12«2Г
(5.8)
105
Числа an, al2, a2l, a22 называются элементами определителя матрицы второго
порядка. Каждый элемент определителя обозначен буквой а с двумя индексами;
первый (1) обозначает номер строки, второй (2) - номер столбца, на пересечении
которых находится соответствующий элемент (например, элемент a2i принадле-
жит второй строке й первому столбцу определителя).
Определитель матрицы называют также детерминантом. Для определителя
матрицы употребляются следующие обозначения:
| А |, det A, det (ал), Д.
Определителем квадратной матрицы третьего порядка
«12 «13
«22 «2з
«32 «33
называют число
«11
«21
«31
«12
«22
«32
«13
«23
«33
«|1«22«33 +«12«23«31 + «2|«32«В
~«В«22«31 ~«12«21«33 — «23«32«1Г
(5.9)
Заметим, что каждое слагаемое алгебраической суммы в правой части этой
формулы представляет собой произведение элементов определителя, взятых по
одному и только по одному из каждой строки и каждого столбца Этому произве-
дению приписывается соответствующий знак. Чтобы запомнить, какие произведе-
ния следует брать со знаком плюс, какие со знаком минус, полезно правило, схе-
матически изображенное на рис. 5.1.
Рис. 5.1
Минором какого-либо элемента определителя называется определитель, полу-
ченный из данного вычеркиванием той строки и того столбца которым- принадле-
жит данный элемент. Минор элемента аа обозначим Мл.
Алгебраическим дополнением элемента аа определителя называется его ми-
нор, взятый со знаком (—1)/+*. Алгебраическое дополнение элемента а№ будем
обозначать через А1к. В соответствии с определением Аа = (-1)'+*Л/й.
106
Определители матриц второго порядка и третьего порядка короче называют
определителями второго и третьего порядка.
Свойства определителей:
1) определитель не изменится при замене всех его строк соответствующими
столбцами;
2) при перестановке двух соседних строк (столбцов) определитель меняет лишь знак;
3) определитель с двумя одинаковыми строками (столбцами) равен нулю;
4) множитель, общий для элементов некоторой строки (столбца), можно вы-
нести за знак определителя;
5) определитель равен нулю, если все элементы некоторой строки (столбца)
равны нулю;
6) определитель не изменится, если к элементам некоторой строки (столбца)
прибавить соответствующие элементы другой строки (столбца), предварительно
умножив их на один и тот же множитель;
7) определитель равен сумме произведений элементов любой строки (столбца)
на их алгебраические дополнения.
Например, det А = allAil +аъАъ +аьАи, т.е.
ап ah
а21 а-а
^11
а,
«л
«.1
а„
(5.10)
Эта формула выражает разложение определителя третьего порядка по элементам
первой строки.
По аналогии с формулой (5.10) вводятся определители четвертого порядка:
Цц аь ... а1я
«л - «1И = £(-!)** О1дА/1Д, (5.Ц)
................. *=г
^/12
ИЛИ
п
det^ = ^au4*,
*=i
где Аи - алгебраическое дополнение элемента а1к, п = 4; определители пятого
порядка и т. д.
Теорема 5.1 (теорема замещения). Суммы произведений произвольных
чисел bf,Ъг,..., Ь„ соответственно на алгебраические дополнения элементов
некоторого столбца (троки) матрицы порядка п равны определителю мат-
рицы, которая получается из данной заменой элементов этого столбца
(строки) числами
Теорема 5.2 (теорема аннулирования). Сумма произведений элементов
одного из столбцов (трок) матрицы на соответствующие алгебраические
дополнения элементов другого столбца (троки)равна нулю.
107
Теорема 5.3. Определитель произведения двух квадратных матриц А и В
одного порядка равен произведению определителей перемножаемых матриц:
det (АВ) = det А • det В.
Название «детерминант» предложил Гаусс. Современное изложение теории
определителей дал Коши. Обозначение определителя в виде квадратной таблицы
чисел с двумя вертикальными чертами ввел Кэли в 1841 г.
Пример 5.7. Вычислить определитель Д =
7 6
1 8
В соответствии с формулой (5.8) получаем Д = 7- 8 - 6 -1 = 50.
Пример 5.8. Вычислить определитель
4273 3273
4274 3274
Умножая первую строку на —1 и прибавляя ко второй, находим
4273 3273 I
4274 3274 “|
4273 3273
1 1
= 4273- 3273 = 1000.
Пример 5.9. Вычислить определитель третьего порядка
1
Д= 2
3
2 -4
6 -1
5 -8
тремя способами: 1)по определению; 2) по формуле (5.10); 3) преобразованием
его с помощью свойств.
1) Д = 1-6(—8)+2(—1)3+2-5(—4)—(—4)6-3—2-2(—8) —Г5(—1)= 15.
.6-1
5 -8
3) Умножая первую строку на (-2) и прибавляя ко второй, затем умножая
2) Д = 1
2 -1
3 -8
—4
= 1(-43)-2(-13)-4(-8) = !5.
— 2
2 6
3 5
первую строку на (— 3) и прибавляя к третьей, получаем
1
0
0
Д =
2 -4
2 7
-1 4
Разлагая этот определитель по элементам первого столбца, находим
2 7
-1 4
= 8—(—7) = 15.
108
Пример 5.10. Вычислить определитель матрицы
1 1 1 Г 1111
2 18 3 2 18 3
А = , т. е. detA -
3 2 12 3 2 12
4 2 4 1 4 2 4 1
Применяя формулу (5.11), получаем
1 8 3 2 8 3 2 1 3 2 1 8
det А = 2 1 2 — 3 1 2 + 3 2 2 - 3 2 1
2 4 1 4 4 1 4 2 1 4 2 4
Вычисляя определители третьего порядка, находим detA = 27 - 50 + (-5) - (-12)=-16.
Замечание. Этот определитель можно вычислить путем его преобра-
зований на основании свойств:
1111 2 18 3 3 2 12 4 2 4 1 = 10 0 0 2-161 3 -1 -2 -1 4-2 0-3 SS -1 6 1 -1 -2 -1 -2 0 -3 =
-1 6 1 -8 -2
0 -8 -2 = (-D -12 -5 = -16.
0 -12 -5
5.5. Обратная матрица
Матрицей, обратной квадратной матрице А, называется квадратная матрица
А~', удовлетворяющая равенствам
АА~' = А~'А = Е, (5.12)
где£- единичная матрица.
Квадратная матрица называется невырожденной или неособенной, если ее оп-
ределитель отличен от нуля. Если определитель матрицы равен нулю, то матрица
называется вырожденной или особенной.
Всякая невырожденная квадратная матрица
Й11 а12 ••• а1п
, fl21 а22 "• а2п
. °И1 ап2 ат
имеет единственную обратную матрицу
109
я->=-Ь
det/1
Ал
Аг
(5.14)
_ 4я ^2п ••• ^пп _
где Аи — алгебраическое дополнение элемента аа матрицы А. Отметим, что
алгебраические дополнения элементов каждой строки матрицы А в формуле (5.14)
записаны в столбец с тем же номером.
В случаях п = 2 и и=3 формулы (5.13) и (5.14) принимают соответственно вид
Ai
Аг
Аз
(5-15)
(5-16)
Теорема 5.4. Произвольную невырожденную матрицу А с помощью эле-
ментарных преобразований можно привести к единичной матрице Е:
А-УЕ. (5.17)
Теорема 5.5. Если к единичной матрице порядка п применить те же эле-
ментарные преобразования только над строками и в том же порядке, с помо-
щью которых невырожденная квадратная матрица А порядка п приводится к
единичной, то полученная при этом матрица будет-обратной матрице А.
Эта теорема дает способ нахождения матрицы, обратной данной, с помощью эле-
ментарных преобразований. При этом удобно записывать матрицы А и Е рядом, отде-
ляя их вертикальной чертой (рассматривать расширенную матрицу (А | £) ), и одно-
временно производить элементарные преобразования над строками матриц А и Е. В
результате преобразования строк матрица (А | Е) преобразуется в матрицу (£ | А~*):
(Л|Е)->(Е|Л-'). (5.18)
Этот метод вычисления обратной матрицы называют методом Жордана.
Замечание 1. Теорема 5.5. верна применительно к элементарным преобразова-
ниям над строками. Когда преобразования производятся над столбцами, то матрицу Е
„ j . :-1>. А
располагают под матрицей А, рассматривают расширенную матрицу —
I £.
тогда
Е
(5.19)
Е
.А
Замечание 2. Если в соотношении (5.18) на место единичной матрицы
справа от вертикальной черты поставить матрицу В, то в результате соответст-
вующих преобразований получим матрицу Я~*В:
(5.20)
ПО
Замечание !. Если в соотношении (5.19) на место единичной матрицы под
горизонтальной чертой поставить матрицу В, то в результате соответствующих
преобразований получим матрицу ВЛ-1:
Г—
[в
Е
(5.21)
.ВЛ1]’
Обратная матрица используется при решении матричных уравнений вида
AX=B,YA = B, (5.22)
где А, В - невырожденные квадратные матрицы одного и того же порядка. Эти
уравнения имеют соответственно решения
Х = Л-1В, Г=ВЛ-1. (5.23)
Матрицы А~ХВ и ВЛ-1 можно найти с помощью элементарных преобразова-
ний в соответствии с соотношениями (5.20) й (5.21).
Пример 5.11. Найти матрицу, обратную матрице А =
4 5‘
2 3 ’
Так как det Л = 2, т. е. det А *0, то матрица А имеет обратную. Поскольку
Л|]=3, Л|2=-2, Л2)=-5, Л22 =4, то по второй из формул (5.15) находим
3 -5‘
2-2 4
я-‘=1
1,5 -2,5 ‘
-1 2
Пример 5.12. Найти матрицу, обратную матрице
Л =
2
7
15
1
3
6
3'
10
20
Вычислим определитель данной матрицы:
2
7
15
1
3
6
3
Н)
20
0
1
3
1
3
6
0
1
2
1
3
1
2
= -(2-3)=1.
Так как det А * 0, то матрица А имеет обратную матрицу. Найдем алгебраиче-
ские дополнения элементов матрицы А:
10
20
3
6
= 0, Л12 = -
7
15
10
20
= 10, л„ =
7 3
15 6
= -3,
Л2,
Л31 —
1
3
1 3
6 20 •
3
10
—2, Л22 —
1, Лг ~
2
7
2
15
3
10
3
20
— -5, Л23 —
= 1. 4з =
2 1
7 3
2
15
1
6
= 3,
1.
111
По второй из формул (5.16) находим
я- = *
1
О
10
-3
-2
-5
3
Г
1
-1
0
10
-3
-2
-5
3
Г
1
-1
Пример 5.13. С помощью элементарных преобразований найти матрицу
А~', обратную матрице
Составляем матрицу (Л|Е) и преобразуем ее; приводя матрицу А
ной, матрица Е будет приведена к А"1:
к единич-
А =
1
1
2
1
2
2
1
2
1
1
1
2
1
2
2
1
2
1
0
0
-1
в результате следующих элементарных
Вторая матрица получена из первой
преобразований: элементы первой строки умножены на (—1) и сложены с элемен-
тами второй строки, элементы первой строки умножены на (-2) и сложены с
элементами третьей строки.
Умножив последнюю строку второй матрицы на (-Г), получим третью матри-
цу (матрица Л приведена к верхней треугольной форме).
Умножая третью строку на (-1) и прибавляя ее ко второй, а затем к первой
строке, получаем четвертую матрицу. Умножая ее вторую строку на (-1) и при-
бавляя к первой строке, получаем пятую матрицу: слева от черты- единичная
матрица, справа- матрица Л-1, обратная исходной матрице Л.
. Замечание. Элементарные преобразования производятся в два
этапа: 1) матрица А преобразуется к верхней треугольной форме с единич-
ными диагональными элементами (путем преобразования строк «сверху
вниз»); 2) полученная матрица преобразуется к единичной (путем преобра-
зования строк «Снизу вверх»). • • V
112
Пример 5.14. Даны две матрицы
3 1
1
2
3
6 2
А = 2 1
1 2
В = 6 1
8 -1
-1
1
4
Найти матрицу X, удовлетворяющую уравнению АХ = В.
Это уравнение разрешимо, так как det Л* 0, его решение Х = А~'в
(см. первую из формул (5.23)). Матрицу А~'В найдем с помощью элементарных
преобразований в соответствии с соотношением (5.20). Составляем матрицу
[А | В], преобразуем ее, приводя матрицу А к единичной:
3
2
1
1
1
2
1
2
3
6
6
8
2
1
1
3
2
1
8
6
6
1
О
О
2
1
-1
-1
1
4
2
-3
-5
3
—4
-8
8
-10
-18
-1
3
5
4
-7
-13
1
2
3
’ 1
О
о
2
2
-5
3
4
-8
-1
1
2
4
1
-1
8
8
-18
-1
-2
5
4
6
-13
2
1
-5
3
2
-8
8
4
-18
-1
-1
5
-1
-1
о
4
3
-13
4
3 -Э
1
2
1
О
О
О
1
-1
-1
0
-1
-1
о
г
1
1
1
0
0
1
о
о
3
2
2
8
4
2
4
3
2
1
о
о
2
1
0
3
2
1
8
4
1
1
О
о
2
1
О
5
2
I
1
0
0
1
2
1
о
1
о
о
о
1
1
-1
О
-1
1
1
Отсюда следует, что
1
2
1
А~'В=Х =
1
-1
0
-1
1
1
Называя шагом переход о^ одной матрицы к другой, дадим пояснения к выпол-
ненным преобразованиям. I inar - поменяли местами перйуЮ и третью строки
(чтобы an = 1). II шаг- перйую строку умножили на ^2 и прибавили ко второй;
первую строку умйЬжйли на’—З’ и прибавили к третьей. III шаг - третью строку
умножили на -1 й прибавили ко второй. IV шаг - йтбрую 'Строку умножили на
1/2. V шаг - вторую строку умножили на 5 и прибавили к третьей. VI шаг -
третью строку умножили на 1/2. VII шаг - третью строку умножили на -3 и при-
113
бавили к первой; третью строку умножили на - 2 и прибавили ко второй. VIII шаг -
вторую строку умножили на -2 и прибавили к первой.
5.6. Ранг матрицы
Рассмотрим матрицу размером m х и
А =
аП а12
а21 °22
«I»
а2п
_ ап1 ат2
Выберем в ней произвольно г различных строк и г различных столбцов, причём
1 < s < min (т, л), где min (т, п) - меньшее из чисел тип. Элементы, стоящие на
пересечении выбранных строк и столбцов, образуют матрицу порядка s. Определитель
этой матрицы называется минором порядка.? матрицы А. Например, если дана матрица
7 -3 1
2-6 3
4-5 9
6 5
8 О
1 2
то, взяв первую и третью строку, третий и пятый столбец, получим матрицу вто-
рого порядка и ее определитель
Этот определитель является минором второго порядка для исходной матрицы.
Аналогично можно получить другие миноры второго порядка, а также миноры
третьего порядка. Некоторые из миноров могут оказаться равными нулю.
Рангом матрицы называется наибольший из порядков ее миноров, отличных от
нуля. Ранг матрицы А обозначают одним из символов: гл, rang Л, г. Если все
миноры матрицы равны нулю, то ранг ее считается равным нулю.
Из определения ранга матрицы получаем следующие утверждения.
1. Ранг матрицы выражается целым числом, заключенным между 0 и мень-
шим из чисел т, п,т. е. О < г < min (m, n).
.... Ранг матрицы равен нулю тогда и только тогда, когда матрица нулевая.
3. Для квадратной матрицы л-го порядка г = п тогда и только тогда, когда
матрица невырожденная.
. При нахождении ранга матрицы можно пользоваться свойствами миноров. Если все
миноры порядка к данной матрицы равны нулю, то все миноры более высокого порядка
также равны нулю. Таким образом, если среди миноров порядка к данной матрицы есть
отличные от нуля, а все миноры порядка к +1 равны нулю или не существуют, то г = к.
Отметим некоторые очевидные свойства ранга матрицы..
1. Ранг матрицы, полученной из данной транспонированием^ равен
рангу исходной Матрицы.
114
2. Ранг матрицы не изменится, если вычеркнуть или приписать нулевую стро-
ку (т. е. строку, все элементы которой равны нулю) или нулевой столбец.
При элементарных преобразованиях ранг матрицы не меняется. С помощью
элементарных преобразований матрицу можно привести к квазитреугольной фор-
ме. Ранг квазитреугольной матрицы (5.1) равен г, поскольку ее минор с главной
диагональю ап,а22,...,агт равен произведению аиа12...агг *0, а все миноры
более высокого порядка равны нулю (как содержащие нулевые строки).
Пример 5.15. Найти ранг матрицы
2
3
0
0
0
0
0
0
0
5
7
0
А
Среди миноров второго порядка этой матрицы имеется один, отличный от нуля:
2 5
3 7
= -1*0.
Все миноры третьего порядка равны нулю. Следовательно, ранг данной матри-
цы равен двум (г = 2).
Пример 5.16. Найти ранг матрицы
А = 1 1 -1 -Г 12 3 4 8 7 6 5 —1 -1 1 1
Применяя элементарные преобразования, приводим данную матрицу к квазит-
реугольной форме:
1 1 -1 -Г ’ 1 1 -1 -Г 1 1 -1 -Г
1 2 3 4 0 1 4 5 0 1 4 5
8 7 6 5 0 -1 14 13 0 0 18 18
-1 -1 1 1 0 0 0 0 0 0 0 0
(Вторая матрица получена из первой путем поочередного умножения первой
строки на (-1), (-8), 1 и прибавления ко второй, третьей и четвертой строкам;
-1
4
18
третья матрица получена из второй путем прибавления второй строки к третьей.)
Ранг последней матрицы равен трем, так как имеется отличный от нуля минор
третьего порядка этой матрицы
. >1ЛЬ1 1, 1
О 1
О о
= 11 18 = 18*0,
а определитель самой матрицы (определитель четвертого порядка) равен нулю
(как содержащий нулевую строку). Следовательно, ранг исходной матрицы равен
трем (г = 3). '
115
Глава t?
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
6.1. Линейные системы. Основные определения
Системой уравнений называют множество уравнений с п неизвестными
(и >2), для которых требуется найти значения неизвестных, удовлетворяющих
одновременно всем уравнениям системы.
Системой т линейных уравнений с л неизвестными х1,х2,...,х„ иле линейной
системой, называется система вида
йцХ, +al2x2 + — +ainx„ =b„
a2ixi+a22x2+ — + a2„x„=b2,
(o.l)
+ am2*2 + - +a„„X„ = bm,
где a№,bj — числа Числа aa (i = 1,2, к = 1,2, ...,n) называются коэффи-
циентами, bt(i=l,2,...,m) - свободными членами. Коэффициенты обозначены
буквой а с двумя индексами i и к: первый (i) указывает номер уравнения, второй
(к) — номер неизвестной, к которой относится данный коэффициент. Число урав-
нений т может быть больше, равно или меньше числа неизвестных п.
Линейная система называется неоднородной, если среди свободных членов
имеются отличные от нуля. Если все свободные члены равны нулю, то линейная
система называется однородной. Однородная линейная система имеет вид
anxi +аЛх2 +-+а,„х„ =0,
a2i*i + аих2 + ••• +а2пх„ = О,
(6.2)
+а„2х2 ++ аятх„ = 0.
Решением линейной системы (6.1) называется упорядоченная совокупность и чисел
с{,с2,...,с„, (6.3)
подстановка которых вместо xt,x2,...,x„ соответственно (x^q, х2=с2,...
...,х„= сп) обращает в тождество каждое из уравнений этой системы.
Система, имеющая хотя бы одно решение, называется совместной, а система, не
имеющая ни одного решения, - несовместной. Отметим, что однородная система всегда
совместна, так как она имеет нулевое решение: xt = О, х2 ~Q,...,x„ = 0.
Совместная система, имеющая единственное решение, называется определенной.
Совместная система называется неопределенной, если она имеет более одного решения.
116
Две системы называются эквивалентными или равносильными, если любое ре-
шение одной из них является также решением другой и обратно, т. е. если они
имеют одно и то же множество решений. Любые две несовместные системы счи-
таются эквивалентными.
Элементарными преобразованиями линейной системы называются следующие
преобразования: 1) умножение уравнения системы на число, отличное от нуля;
2) прибавление к одному уравнению другого уравнения, умноженного на любое
число; 3) перестановка местами двух уравнений системы.
При элементарных преобразованиях линейной системы получают систему,
равносильную данной.
Выражение «решить линейную систему» означает выяснить, совместна она или
несовместна; в случае совместности - найти все ее решения.
6.2. Матричная запись линейной .системы
Линейную систему (6.1) можно записать в матричном виде. Матрица
ап ап ••• а4п
«21 «22 ••• а2п
. аяЛ ат2 атп _
составленная из коэффициентов линейных уравнений системы (6.1), называется
основной матрицей системы (или матрицей системы). Матрица
аП а12 а1п ^1
«21 й22 ••• а2п ^2 ,,
_ ат\ ат2 атп .
полученная из основной присоединением столбца свободных членов, называется
расширенной матрицей системы (6.1).
Рассмотрим столбцовые матрицы, составленные из неизвестных и свободных членов:
Поскольку матрица А согласована с матрицей X (число столбцов матрицы А равно
числу строк матрицы X ), то можно найти произведение
auxx+aax2+---+ainx„
.v о2{Х1+а22х2+- + а2,^„
an,ixi+om2x2+- + amnx„
117
Элементами этой столбцовой матрицы являются левые части уравнений системы
(6.1), поэтому на основании определения равенства матриц
АХ = В. (6.7)
Таким образом, система линейных уравнений (6.1) записана в виде одного мат-
ричного уравнения (6.7), где А, X, В определяются формулами (6.4) и (6.6); эта
запись системы называется матричной.
Каждой линейной системе (6.1) соответствует единственная пара матриц А, В к
обратно: каждой паре матриц - единственная линейная система. Система (6.1)
может быть записана и в таком виде
Если ) — решение системы (6.1), то матрица
(6.8)
(6.9)
называется векгор-решением этой системы. Матрица (6.9) удовлетворяет уравнению (6.7).
Пример 6.1. Представить в матричной форме линейную систему уравнений
2Х] +3х2 =8,
5-Xj +х2 = 7.
В данном случае формулы (6.4) и (6.6) запишутся так:
поэтому уравнение (6.7) принимает вад
2 31 Гх, 1 Г 8
5
Эта система имеет вектор-решение С =
1
2
Замечание. В соответствии с формулой (6.8) данная система
представима в виде
2
5
8
7
118
6.3. Невырожденные линейные системы
Определителем системы и линейных уравнений с п неизвестными х,, х2,..., х„
«11*1 + «12*2 + — + «1* **+”• + а1пх„ = Ь,,
«21*1 + «22*2 + • • + «2*** + • • + «2„*„ = Ь2,
(6.10)
«„1*1 + «„2*2 + • + «М** + • + «„„*„ = Ь„
называется определитель матрицы из коэффициентов уравнений этой системы:
«11 «12 «1* ••• «1„
д=021 аи а2к - а2п. (6.П)
«„1 «»2 «п» ат
Обозначим через Ек определитель, полученный заменой в определителе Д столбца
из коэффициентов при неизвестной хк столбцом свободных членов системы (6.10):
«И «12 . bt . •• «1„
«21 «22 b, . «2„ (6.12)
«„1 «„2 ь„ . atm
где £ = 1,2,..., и.
Линейная система (6.10) называется невырожденной, если ее определитель от-
личен от нуля (А * 0).
Теорема 6.1. Невырожденная линейная система (6.10) имеет единст-
венное решение
x,=A,/A. х2=Д2/Д, ..., хв=Д„/Д, (6.13)
гдеАи Д*(£ = 1,2..... п) определены соответственно формулами (6.11) и (6.12).
Эта теорема называется теоремой Крамера, а формулы (6.13) -
формулами Крамера.
Следствие из теоремы Крамера. Если однородная линейная система
«и*1 +«12*2 +• + «!„*„ = 0»
«21*1 +«22*2 + ”' + «2„*„ =°>
«„1*1+«„2*2+-+«№*„ =°
. имеет ненулевое решение, то ее определитель Д равен нулю.
Систему (6.10) и линейных уравнений с и неизвестными можно записать
в матричном виде
АХ = В, (6.14)
119
где
единственное решение
Х = А~'В, (6.16)
где А~' - матрица, обратная матрице А, & В определяется третьей из формул (6.15).
Пример 6.2. Решить систему уравнений
Х| +х2-4х3 = 1,
х, + 2х2 - Злг3 = 5,
Зх, - 2х2 + 4х3 = 4.
Составим определитель системы А и определители ДЛ (к = 1,2,3):
1 1 -4 1 1 -4
А = 1 2 -3 , А,= 5 2-3 J
3 -2 4 4-2 4
1 1 -4 1 1 1
= 1 5 -3 . дз = 1 2 5
3 4 4 3-2 4
Определитель системы Д = 21*0, т. е. данная система является невырожден-
ной, поэтому применимы теорема 6.1 и формулы (6.13). Вычислим определители
Aj,A2, А3; пользуемся формулами (6.13), полагая в них и = 3. Так как
А, =42, Д2=63, Д3 = 21, то
х, = Д|/А=—= 2, х2 = Д2/А=—= 3, х3 = Д3/Д=—= 1.
Пример 6.3. Решить систему уравнений
4х, — Зх2 +2х3 = 9,
2х, + 5х2 - Зх3 = 4,
5х,+ 6х2 —2х3 =18.
120
Вычисляем определитель матрицы Л, находим матрицу А~':
-11
-13
6 -1
-18 16
-39 26
По формуле (6.16) получаем решение системы
т. е. = 2, х2 = 3, х3 = 5.
6.4. Произвольные линейные системы
Рассмотрим линейную систему (6.1), ее основную матрицу А и расширенную
А, определяемую формулой (6.5).
Теорема 6.2. (Кронекера — Капелли). Для совместности системы (6.1) необхо-
димо и достаточно, чтобы ранг ее матрицы был равен рангу расширенной матрицы.
Теорема 6.3. Если ранг матрицы совместной системы равен числу неиз-
вестных, то система имеет единственное решение.
Теорема 6.4. Если ранг матрицы совместной системы меньше числа неиз-
вестных, то множество ее решений является бесконечным.
Базисным минором матрицы называется отличный от нуля ее минор, порядок
которого равен рангу этой матрицы. Базисными неизвестными совместной систе-
мы, ранг матрицы которой равен г, назовем г неизвестных, коэффициенты при
которых образуют базисный минор. Остальные неизвестные назовем свободными.
Из теорем 6.2 - 6.4 следует, что решение системы линейных уравнений можно
производить следующим образом.
1. Находят ранг г матрицы А системы и ранг г расширенной матрицы А.
Если г # г, то система несовместна.
2. Если г = г, то выделяют базисный минор и базисные неизвестные. Исход-
ную систему уравнений заменяют эквивалентной ей системой, состоящей из тех г
уравнений, в которые вошли элементы базисного минора.
Отметим, что в случае, когда число базисных неизвестных равно числу неизвестных
системы, система имеет единственное решение, которое можно найти по формулам
Крамера Если число базисных неизвестных меньше числа всех неизвестных, то из со-
ответствующей системы находят выражения базисных неизвестных через свободные,
используя, например, формулы Крамера Придавая свободным неизвестным произ-
вольные значения, получают бесконечное множество решений исходной системы.
121
Пример 6.4. Решить систему уравнений
х( - Зх2 + 2х3 = 1,
2хх +х2-4х3 = 5,
5xj — 8х2 + 2х3 = 8.
Поскольку
то система совместна. В матрице А минор
1 -3
2 1
ствует система уравнений х( —Зх2 =1-2х3, 2х, + х2 = 5+4х3, в которой х3, х2
- базисные неизвестные, х3 - свободная неизвестная. Решая эту систему по
формулам Крамера, находим
х3 = (10х3 +16)/7, х2 = (8х3 +3)/7,
отличен от нуля, ему соответ-
где х3 может принимать любые действительные значения.
6.5. Метод Гаусса
Пусть дана система (6.1) т линейных алгебраических уравнений с п не-
известными Х„ х2,..., хп.
Метод последовательного исключения неизвестных,, или метод Гаусса, приме-
няемый для решения системы (6.1), состоит в следующем.
Предполагая, что аи * 0 (это всегда можно сделать сменой нумерации
уравнений), умножая первое уравнение системы (6.1) на -а21/вп и прибав-
ляя ко второму, получаем уравнение, в котором коэффициент при х( обра-
щается в нуль. Умножая первое уравнение на -а3)/ан и прибавляя к треть-
ему, получаем уравнение, также не содержащее члена с х,. Аналогичным
путем преобразуем все остальные уравнения, в результате чего придем к
системе, эквивалентной исходной системе уравнений:
122
опх, + al2x2+3 + aXnxn=bl,
<Л+3 +а2„х„=%,
<*2+3 +<*„=<
(6.17)
<2*2+3 + <„*„ = <,
где а'к (z = 2,3,2 , т; к = 2,3,2 , п) — некоторые новые коэффициенты.
Полагая * 0 и оставляя неизменными первые два уравнения системы
(6.17), преобразуем ее так, чтобы в каждом из остальных уравнений коэффициент
при х2 обратился в нуль. Продолжая этот процесс, систему (6.17) можно привес-
ти к одной из следующих систем:
сп*1+с12*2+с13*з+3 +clnx„ = d1,
С22*2 +С23*3 +3 +С2„Х„ = d2,
сзз*з+3 + c3„x„ = d3, (6.18)
CnnXn dn9
где си * 0 (i = 1,2,2 , и), сй—некоторые коэффициенты, d, — свободные члены;
С11*1+с12*2+3 +ci***+3 +c,„x„=d„
с22*г+3 +с2***+3 + c2nx„=d2,
c***t+3 +ckfrx„=dk,
где к < и;
сп*1 +с12х2 +3 +clnx„=d„
^22*2 +3 + С2„Х„ = d2,
(6.20)
0 xn=dk,
где к<п.
Система (6.18) имеет единственное решение, значение х„ находится из по-
следнего уравнения, хп_х - из предпоследнего, Xj - из первого.
Система (6.19) имеет бесконечное множество решений. Из последнего уравне-
ния можно выразить одно из. неизвестных (например, хк ) через остальные п-к
неизвестных (хк+],хк+2,2 ,*„), входящих в это уравнение. Из предпоследнего
уравнения можно выразить xt_( через .эти неизвестные и т. д. В полученных фор-
мулах, выражающих хх,х2,2 ,хк_х,хк нерез хк+1,хк+2,2 ,х„, последние неиз-
вестные могут принимать любые значения.
123
Система (6.20) несовместна, так как никакие значения неизвестных не могут
удовлетворять ее последнему уравнению.
Итак, метод последовательного исключения неизвестных применим к любой
системе линейных уравнений. Решая систему этим методом, преобразования со-
вершаются не над уравнениями, а над матрицами, составленными из коэффициен-
тов при неизвестных и свободных членах.
Пример 6.S. Решить систему уравнений
jq — 2х2 — Зх3 — х4 = 2,
х( + х2 +.6х3 + Зх4 = —3» .
2х3 + Зх2 + 5х3 + 2х4 = 1,
х2 +х3 +х4 =3,
5х2 + 7х3 + 4х4 = 5.
Составляем матрицу и преобразуем ее: 1
1 -2 -3 -1 2' 1 -2 -3 -1 2'
1 1 6 3 -3 0 3 9 4 -5
2 3 5 2 1 0 7 11 4 -3 -
0 1 1 1 3 0 1 1 1 3
0 5 7 4 5 0 5 7 4 5
' 1 -2 -3 -1 2' 1 -2 -3 -1 2'
0 1 1 1 3 0 1 1 1 3
0 3 9 4 -5 —> 0 0 6 1 -14
0 7 11 4 -3 0 0 4 -3 -24
0 5 7 4 5 0 0 2 -1 -10
\ ’ - -•
1 -2 -3 -1 2‘ 1 -2 -3 -1 2"
0 1 1 1 3 0 1 1 1 3
0 0 2 -1 -10 0 0 2 -1 -10
0 0 4 -3 -24 0 0 0 -1 -4
0 0 6 1 -14 0 0 0 4 1б_
‘ 1 -2 -3 -1 2:
0 1 1 1 3
0 0 2 -1 -10
0 0 0 -1 —4
0 0 0 0 0
124
Последней матрице соответствует совместная система четырех уравнений с че-
тырьмя неизвестными:
х, -2х2 -Зх3-х4 = 2,
х2+х3+х4=3,
2х3-х4 = -10,
-х4=-4.
Решая эту систему, находим х4 = 4, 2х3 = -10+х4 =-10+4 =-6, х3 = -3,
х2 =3—х3—х4 =3—(-3)—4 = 2, х, = 2х2 + Зх3 +х4 +2= = 2-2 + 3(-3) + 4 + 2 = 1
Следовательно, исходная система имеет решение Xj = 1, х2 = 2, х3 = - 3, х4 = 4.
Пример 6.6. Решить систему уравнений
Х| +х2 +х3 +х4 = 4,
2Х| -х2 + Зх3 - 2х4 = 2,
Зх, + 2х2 + 4х3 - 6х4 = 3,
4х( + Зх2 + 5х3 — 5х4 = 6.
Записывая соответствующую матрицу и совершая преобразования, получаем
1
2
3
4
1
0
0
о
1 1 1 4 1 1 1 1 4'
-1 3 -2 2 —> 0 -3 1 -4 6
2 4 -6 3 0 -1 1 -9 9
3 5 -5 6 0 -1 1 -9 -10
1 1 1 4 1 1 1 1 4
-1 1 -9 -9 0 -1 1 - -9 -9
-1 1 -9 -10 0 0 0 0 -1
-3 1 -4 -6 0 0 -2 23 21
Третья матрица получена из предыдущей переменой местами последних трех
строк. Последней матрице соответствует система уравнений
Х| +х2 +х3 +х4 = 4,
—х2 +х3 -9х4 = -9,
0х4 =-1,
-2х3 + 23х4 = 21.
Эта система несовместна, так как никакие значения неизвестных не могут
удовлетворить ее третьему уравнению.
Следовательно, исходная система также несовместна.
Пример 6.7. Решить систему уравнений
X! +х2 -х3 +х4 = 2,
2х, - х2 + Зх3 - 4х4 = 0,
4х, + х2 + х3 - 2х4 = 4,
5Х( + 2х2 - х4 = 6.
125
Преобразуя матрицу, получаем
1 1 -1 1 2’ 1 1 -1 1 2"
2 -1 3 - -4 0 0 -3 5 -6 —4
4 1 1 - 2 4 0 -3 5 -6 —4
5 2 0 -1 6 . 0 -3 5 -6 — 4
' 1 1 -1 1 2
0 -3 5 . -6 -4
0 Л О в, 0; •
0 0 0 0 0
Таким образом, данная система сводится к системе двух уравнений относи-
тельно четырех неизвестных: • •
—Зх2 + 5х3 — 6х4 = —4,-,'
общее решение которой определяется формулами
2 2 4 5
х|=у-ухз+х4,х2 =,у+ух3-2х4,
где х3, х4 могут принимать любые действительные значения.
Пример 6.8. Решить систему уравнений
Х| — х2 + 7х3 — 2х4 = 2,
2xt — Зх2 + 8х3 — 4х4 = I,
6х( — 5х2 +1 Ъс3 —Зх4 =s —3.
Составляем матрицу и преобразуем ее:
1
2
4
6
-1
-3
2
-5
7
8
19
11
-2
—4
1
-3
2
1
8
-3
1
О
о
о
-1
-1
6
1
7
-6
-9
-31
-2
О
9
9
2
-3
О
-15
1 -1 7 -2 2' 1 -1 7 -2 2'
0 -1 -6 0 -3 0 -1 -6 0 -3
0 0 -45 9 -18 0 0 -45 9 -18
0 0 -37 9 -18 0 0 8 0 °
Последняя матрица получена в результате сложения третьей, умноженной на
(-1), и четвертой строк. Этой матрице соответствует система уравнений
Х| — х2+.7х3 — 2х4 =2,.
-х2 —6х3 = -3,
-45х3+9х4 = -18, !
8х3 = О,
имеющая решение х3 - О,х4=-2, х2=3,х,= 1.
126
Гпава 7
КОМПЛЕКСНЫЕ ЧИСЛА
7.1. Упорядоченные пары действительных
чисел и операции над ними
Пару (а, Ь) действительных чисел а и b называют упорядоченной, если указа-
но, какое из них считается первым, какое - вторым. Примеры упорядоченных
пар: (0,1); (2,3); (3,2). Отметим, что последние две пары различны, хотя и об-
разованы одними и теми же числами.
Каждую упорядоченную пару чисел обозначим одной буквой, введем понятие
равенства двух пар, определим действия над ними. Рассмотрим две упорядочен-
ные пары
a = (e,fe), ₽ = (с,4). (7.1)
Эти пары называют равными, если a = с, b = d, т. е.
((а, 6) = (с, (/))<=> (а = с, 6 =d). ' (7.2)
Суммой двух пар (7.1) называют упорядоченную пару
a+p = (a,b)+(c,d') = (a + c,b+d), (7.3)
а их произведением - упорядоченную пару
оф = (а, b)(c, d) = (ac- bd, bc+ad). (7.4)
Из соотношения (7.3) видно, что пара
О = (0,0) (7.5)
обладает тем свойством, что сложение ее с любой другой упорядоченной парой не
меняет исходной пары: (а, 6)+(0,0) = (а, 6). Пара (7.5) играет роль нуля при
сложении упорядоченных пар; назовем ее нуль-парой.
Разностью а-Р двух упорядоченных пар (7.1) называют такую упорядочен-
ную пару z = (x,y), что z+P = a.
Вычитание упорядоченных пар (7.1) определяется следующим образом:
a - р = (а, Ь)~ (с, d) = (a - с, b-d). (7.6)
Частным a/Р, где р #0, двух упорядоченных пар (7.1) называют такую упо-
рядоченную пару z = (х, у), что zP = a.
Если Р*0, т. е. c2+d2*0, то частное a/Р двух упорядоченных пар (7.1)
127
определяется формулой
ac+bd
be - ad \
TTd2)'
(7.7)
Из этой формулы следует, что если а = Р, т. е. а = с, b = d, то
1 =
с2 +d2 de—cd
2 , ,2 ’ 2 , ,2
с +a с +a
1 = (1,0).
Значит, роль единицы при делении двух упорядоченных пар выполняет упорядо-
ченная,пара
1 = (1,0).
Рассмотрим упорядоченные пары
а = (а, 0), b = (b,O).
(7.8)
(7.9)
Арифметические действия над упорядоченными парами вида (7.9) производят-
ся так, как и над действительными числами. Действительные числа отождествля-
ются с парами вида (7.9).
7.2. Понятие комплексного числа.
Алгебраическая форма комплексного числа
Комплексным числом называют упорядоченную пару (а, Ь) действительных
чисел а и Ь. Рассмотрим упорядоченную пару
/ = (0,1). (7.10)
Применяя формулу (7.4), получаем i2 = i • i = (0,1) (0,1) = (0 -1,0+0) = = (-1,0).
Поскольку (-1,0) = -1 (см. формулу (7.9)), то
/2=-1, i = ^A. (7.11)
Упорядоченную пару (7.10), удовлетворяющую соотношению (7.11), называют
мнимой единицей. С помощью мнимой единицы можно выразить любое ком-
плексное число а = (а, Ь), т. е. упорядоченную пару действительных чисел. В са-
мом деле, так как Ы = (Ь, 0) (0,1) = (0, Ь), то (а, Ь) = (а, 0) + (0, Ь) = = а + Ы, т. е.
(a, b) = а + bi. (7.12)
Поскольку (а,b) = а + bi, (а,Ь)=(0,£>)+(а,0) = Ы+а, то а + Ы= Ы + а. Значит,
в правой части формулы (7.12) можно менять местами слагаемые. Выражение
а + Ы называют алгебраической формой комплексного числа. Число а называют
действительной частью,' число b — мнимой частью комплексного числа а + Ы.
Обозначая комплексное число а + Ы одной буквой а, записывают
а = Rea, b= Im а, где Re - начальные буквЬ1 латинского слова realis
(действительный), Im - начальные буквы латинского слова imaginarius (мнимый).
128
Кроме этих обозначений, употребляют и другие, например: а = /?(а), b-I (а),
где a = a + bi.
Отметим частные случаи формулы (7.12). Если Ь = 0, то (а, 0) = а —
действительное число; если а = 0, то
(О, b) = bi. (7.13)
Число bi называют чисто мнимым или Просто мнимым.
Два комплексных числа а + Ы, с + di называют равными, когда а =с, b-d\
(а + Ы = с + di) e$(a = c,b- d).
Комплексное число равно нулю, когда равны нулю его действительная и мни-
мая части:
(а + Ы = 0) <=> (а = 0, b = 0).
Если дано комплексное число а = а+ Ы, то число а - Ы, отличающееся от а
только знаком при мнимой части, называют числом, сопряженным числу а, и обозна-
чают а. Числом, сопряженным а, будет, очевидно, число а, поэтому говорят о паре
сопряженных чисел. Действительные числа, и только они, сопряжем,! сами себе.
Обозначение i для мнимой единицы (i = J-1) ввел Эйлер в 1777г.
7.3. Геометрическое изображение
комплексных чисел
На плоскости выберем систему прямоугольных декартовых координат
(рис. 7.1). Комплексному числу (а,Ь)=а + Ы сопоставим точку М(а,Ь) этой
плоскости с координатами (а, Ь). Если Ь = 0, то
получим действительное число (а,0) = а, которое
изображается точкой Я (а, 0) на оси Ох. Вследствие
этого ось Ох называют действительной осью
(точками оси абсцисс изображаются действительные
числа). Если а = 0, то получаем чисто мнимое чис-
ло Ы, которое изображается точкой В(0, Ь), ле-
жащей на оси Оу. По этой причине ось ординат на-
зывают мнимой осью (точками этой оси изобража-
ются чисто мнимые числа). Отметим, что мнимая
единица i изображается точкой (0,1), расположенной на положительной полуоси
ординат и отстоящей от начала координат на расстояние, равное единице. Число
(-/) изображается на оси ординат точкой (0,-1), симметричной точке (0,1).
Любое комплексное число а = (а,Ь), где а*0, Ь*0, изображается точкой, не
лежащей на осях координат. Обратно, любой точке М (а, Ь) плоскости соответст-
вует комплексное число (а, Ь)=а + Ы. Таким образом, между множеством ком-
У
в
м
Рис. 7.1
г-
О
-г
5 Зак.I
129
плексных чисел и множеством точек плоскости установлено взаимно однозначное
соответствие. Плоскость, точки которой отождествлены с комплексными числами,
называют комплексной плоскостью.
Рассматривают также комплексную переменную z=x + iy, где х, у-
дейсгвительные переменные, i- мнимая единица Значения этой переменной-
комплексные числа, изображаемые точками комплексной плоскости.. Вследствие этого
комплексную плоскость называют также плоскостью, комплексной переменной.
7.4. Действия над комплексными числами
Из определения комплексного числа (как упорядоченной пары действительных
чисел) и определения арифметических действий над упорядоченными парами
(см. формулы (7.3), (7.4), (7.6), (7.7)) следует, что
(а + bi)+(с + di) = (a + c) + (b + d) i, (7-14)
(a+bi)-(c+di) = (a-c) + (b— d)i, (7.15)
(a + bi)(c + di) = (ac-bd) + (bc+ad)i, (7.16)
a+bi ac+bd be—ad . , 2 ,2
---2- + (c2+d2#0). (7.17)
c + dt c2+d2 c2+d2
Формула (7.14) определяет правило сложения двух комплексных чисел: чтобы
сложить два комплексных числа, необходимо сложить отдельно их действительные и
мнимые части. Формула (7.15) означает, что при вычитании одного комплексного
числа из другого необходимо вычесть отдельно их действительные и мнимые части.
Отметим, что сумма и произведение двух комплексно-сопряженных чисел
а = а + Ы, а = а—Ы являются действительными числами: сх + сх = 2а,
аа. = а2 +Ь2.
Арифметические действия над комплексными числами подчиняются тем же за-
конам, что и действия над действительными числами. Если а = а + Ы, ₽ = с + di,
y = e + fi - любые комплексные числа, то верны следующие равенства:
1) а + ₽ = ₽ + а; 2) (а + ₽)+у = а + (₽ + у); 3) а₽ = ₽а; 4) (а₽)у = а(Ру);
5) (а+₽)у = ау+₽у.
Полагая а = 1, Ь = 0 в формуле (7.17), получаем
Формулой (7.18) определяется число ₽ *, обратное комплексному числу ₽ =
= c + di (₽*0, т. е. с2+</2*0).
Натуральные степени мнимой единицы i принимают лишь четыре значения:
-1, —i, 1, i, определяемые формулами
I4* = 1, j4i+1 = i, i4k+2 = -1, »4*+3 = -i, (7.19)
где к = 0,1,2,...
130
При возведении комплексного числа а = а + Ы в степень п(л- натуральное
число) пользуются формулой бинома Ньютона:
(о + Ы)" = а” + па”~' a”~\bi)2 +
+ И~”~ У” ~ 2) а”~\Ы)3 + - +{Ы)”. (7.20)
В правой части этого равенства заменяют степени мнимой единицы по фор-
мулам (7.19) и .приводят .подобные члены, в результате подучают Некоторое
комплексное число с + di.
Квадратным корнем из комплексного числа называют комплексное число,
квадрат которого равен данному комплексному числу:
Ja+bi -u+iv, если (u+iv)2 =а+Ы. (7.21)
Числа и и v определяются из равенств
и2 = (a +-Ja2 +b2 )/2, V = (-a +-Ja2 +b2 )/1, (7.22)
причем и и v будут действительными, так как при любых а и b выражения
а + у/а2 + Ь2 и -a+-Ja2 +Ь2 являются положительными. Знаки и и v выбирают
так, чтобы выполнялось равенство 2uv = b. Извлечение квадратного корня из
комплексного числа а + Ы всегда возможно и дает два значения u,+lv(, +-Zv2,
различающихся лишь знаком.
Пример 7.1. Даны два комплексных числа 5+1 и 2+31. Найти их сум-
му, разность, произведение и частное.
В соответствии с формулами (7.14) — (7.17) получаем
(5+1)+(2+31)у(5+2)+(1+3)1=7+41,
(5+0 - (2+30 = (5 - 2) +(1 - 3) i = 3 - 21,
(5+0(2+31)= 10+151+21+312 = 7+171,
5+1 = (5+1)(2-31) = 10-151+21-312 = 13-131 =
2+31 (2+30(2-31) 4-912 13
Пример 7.2. Возвести в указанные степени данные комплексные числа:
(3+402, (1+21)3, (2+04-
Применяя формулы (7.19) и (7.20) при п = 2, п=3, и = 4, получаем
- (3+402 =32 +2 121+(41)2 = 9+241+1612 =-7+241,
(1+21)3 = 1 +61+1212 + 813 = 1+61-12- 81=-11 -24
(2+1)4 = 24 +4-231+6-412 +4-213 +14 = 16+321-24-81+1 = -7+ 241.
131
Пример 7.3. Извлечь корень квадратный из числа а = 9+40/.
Обозначим V9+40Z = и+iv. Поскольку в данном случае а = 9, 6 = 40, то
формулы (7.22) примут вид
и2 = (9+л/92+402)/2 = (9+41)/2 = 25;
v2 =(-9+V92+402)/2=(-9+41)/2 = 16.
Так как и2 - 25, v2 = 16, то ц = -5, «j = 5, v, = -4, v2 = 4. Получено два значения
кория: ц+У|« = —5—4i и a2+v2i = 5+4i.
Пример 7.4. Найти значение выражения z3 -2z2 + 5z при z-l-i.
Поскольку (1-О2 = l-2i+i2= l-2i—l = -2i, (1-i)3 =(l-i)2(l-i) =
= -2i(l—i) =-2i+2i2 =-2-21, to z3-2z2+5z =—2—2i—2(-2i)+5(l—i)=3-3i.
Пример 7.5. Показать, что комплексное число z = 1 - i является корнем
уравнения z3+2z2 -6z+8 = 0.
Так как z2 =(l-i)2 =—2i, z3 =(1—i)3 = —2—21, то z3+2z2-6z+8 =
= -2-2i+2(-2i)-6(l-i)+8 = 0, т.е. (1-i) - корень уравнения.
7.5. Модуль и аргумент комплексного числа.
Тригонометрическая форма комплексного
числа
Комплексное число и = а+Ы, заданное в алгебраической форме, можно пред-
ставить и в другом ваде. Изобразим число а точкой М (о, 6) комплексной плос-
кости. Рассмотрим радиус-вектор этой точки (рис. 7.2). Модулем комплексного
числа a = a+bi называют длину г радиуса-вектора ОМ точки М (о, 6), изобра-
жающей данное число. Модуль комплексного числа а обозначают символом | а |.
Следовательно, по определению
г = |ОМ|, г = |а|, |а|й0. (7.23)
Так как [ ОМ | = Vo2 + b2 (см. рис. 7.2), то
| а | = >/а2 + 62, | а + Ы | = >/а2 +62, г = л/а2 +Ьг, (7.24)
т.е. модуль комплексного числа равен арифметическому значению корня квадратного
из суммы квадратов его действительной и мнимой частей. Если 6 = 0, т. е. число а
является действительным, причем а = а, то формула (7.24) принимает вид | а | = 4а2.
Аргументом комплексного числа а-а+Ы называют величину угла <р наклона
радиуса-вектора г = ОМ точки М (а, Ь) к положительной полуоси Ох. Аргумент
комплексного числа а обозначают символом Arg а. Угол <р может принимать
132
любые действительные значения. Аргумент комплексного числа <х имеет бесконеч-
ное множество значений, отличающихся одно от другого на число, кратное 2л. Аргу-
мент не определен лишь для числа 0, модуль которого равен нулю. Среди значений
аргумента комплексного числа а # О существует одно и только одно, заключенное
между -лил, включая последнее значение. Его называют главным значением и обо-
значают arg а. Итак, аргумент комплексного числа удовлетворяет соотношениям
Arga = arga + 2nfc (к =0,±1,±2,...), -n<argaS^
С помощью модуля и аргумента комплексное число a = ,a + bi можно предста-
вить в другой форме. Поскольку
a = г cos ф, b = г sin ф, (7.25)
то
а+Ы = г (созф+гБШф) (г S0), (7.26)
где
г = ^а2 +Ьг, со5ф = o/Va2 +b2, sin<p = б/7«2 + fc2'. (7.27)
Выражение, стоящее в правой части формулы
(7.26), называют тригонометрической формой
комплексного числа. Отметим особенности три-
гонометрической формы: 1) первый множитель
- неотрицательное число, г^О; 2) записаны
косинус и синус одного и того же аргумента;
3) мнимая единица умножена на вшф.
Два комплексных числа, заданных в триго-
нометрической форме, равны тогда и только
тогда, когда их модули равны, а аргументы
отличаются на величину, кратную 2л. Следовательно, если
rt (со5ф| + isinф,) = г2 (созф2 + isinф2), (7.28)
то
Ц=г2, ф2=ф(+2Ал (£ = 0,±1,±2,...); (7.29)
и обратно, из равенств (7.29) следует формула (7.28).
Если комплексное число а = а + Ы задано в тригонометрической форме
а = г (сояф + isin ф), то комплексно-сопряженное число а = а— Ы записывается
вформе a=r(со5(-ф)+/5ш(—ф)); поэтому |a| = |а|, arga = -arga (рис.7.3).
уПр и м ер 7.6. Комплексное число а = 2-j2/(l-i) записать в алгебраиче-
ской и тригонометрической форме.
Умножая числитель и знаменатель данной дроби на число, сопряженное
знаменателю, получаем
2^2 2-^(1 + Q 272(1 + 0 2j2+i2j2 rz.fr
1-1 (1-0(1+П 1-г2 2 ' '
133
Это - алгебраическая форма данного числа:
a = -j2+i-j2.
Применяя формулы (7.27), находим
г = 7(-^)2+(-^)2 = 2, sin«p = b/r = -ji/l,
costp = a/r = V2/2, откуда главное значение
ф — л/4. Следовательно, тригонометрическая фор-
ма данного числа имеет
вид
а = 2(cos (л/4) + i sin (л/4)).
7.6. Действия над комплексными числами,
заданными в тригонометрической форме
Произведение двух комплексных чисел
z, = г(со5ф+/5Шф), z2 =p(cosy+ isiny), (7.30)
где r = |z| |, 9 = ArgZj, p = |z2 |, у = Argz2 находится по формуле
Z|Z2 =rp(cos(<p+y)+isin (Ф+Ф)). (7.31)
Из этой формулы следует, что
| Z|Z21 = | Z| 11 z21, ф+у = Arg (z,z2),
т. е. модуль произведения равен произведению модулей множителей, а сумма ар-
гументов множителей является аргументом их произведения.
Если z2 * 0, т. е. р * 0, то
—=—(со5(ф-у)+15т(ф-у)), (7.32)
z2 р
откуда
| zl /z2 I = | zl l/l z2 |> Ф “ V = (zl/z2 )
Эти формулы означают, что модуль частного равен модулю делимого, делен-
ному на модуль делителя, а разность аргументов делимого и делителя является
аргументом частного двух комплексных чисел.
Если г = г(со5ф+»5тф)иг*0, то
z~l =1/г = г-|(со5(-ф)+<5т(-ф)), (7.33)
откуда
|z_|| = |z|”', argz-1 =-argz,
т. e. модуль комплексного числа z-1, обратного числу г, равен обратной ве-
личине модуля числа г, а его главное значение аргумента отличается от глав-
ного значения аргумента z лишь знаком.
134
Еслип- натуральное число и z=r (cos<p + isin<p), то
z" = (г (cos<p+isin<p))” = r"(cosn<p+isinn<p), (7.34)
откуда |z" | = |z|", иф = Argz".
Формула (7.34) называется формулой Муавра. При г = 1 она принимает вид
(cos ф+i sin ф)" = cos иф+isin пф.
Корнем n-й степени из комплексного числа z называется такое комплексное
число а, что а" = z.
Извлечение корня n-й степени из комплексного числа z = г (созф+шпф) все-
гда возможно и дает п различных значений:
пГ( Ф . . Ф^ пг( Ф+2л . ф+2л')
а0 =ч/г cos—+ism — I, а. = Vr cos—-----+isin —------- ,
V n nJ \ n nJ
„г( Ф+4л . ф + 4яА
a2=Vr cos—-------+isin—------ ,..., (7.35)
V n n J
\ n n J
j—,-----7^—7 пГ( Ф+2£л . . ф+2АлА
Иг (С05ф + 181Пф) = vr cos-1---+ isin —-----|, (7.36)
V п nJ
где Л= 0,1,2,..., п-1.
Из формул видно, что все п значений корня и-й степени из комплексного числа
z расположены на окружности радиуса z | с центром в точке нуль и делят эту
окружность на п равных частей.
Отметим, что корень n-й степени из действительного числа также имеет п раз-
личных значений. Среди этих значений действительных будет два, одно или ни
одного в зависимости от знака а и четности п. Корень n-й степени из нуля имеет
только одно значение, равное нулю (Vo = 0).
Корни n-й степени из единицы определяются формулой
„г 2lai 2кп
VI = cos--+ isin------, (7.37)
л и
где £ = 0,1,2,...,п-1.
Пример 7.7. Найти значения квадратного корня из числа z = i.
Представим сначала это число в тригонометрической форме:
i = cos (л/2)+isin (л/2). В соответствии с формулой (7.36) имеем
п I п . . п л/2+2£л . . п/2+2кк , „ ,
V i = J cos—+1 sin — = cos —---+1 sin — ------, к = 0,1.
V 2 2 2 2
Следовательно,
п . . п -J2 .^2 5л . 5л
a0 = cos—bi sin — =----t-i—, a. =cos----t-isin — = -txn-
4 4 2 2 4 4 0
135
Пример 7.8. Найти все значения корня 6-й степени из числа —64.
Представим данное число в тригонометрической форме:
-64 = 64 (cos л + /sin л). Формула (7.36) принимает вид
л+2Ал л+гАл') , „ ,
-------+isin------- , А = 0,1,..., 5.
6 6 )
Замечая, что V64 = 2 и придавая к указанные значения, находим шесть ис-
комых значений:
ftf—64 = у/б4 [ cos
fn . . Л 1 it .
cos —Hsin — | = V3 +1,
a. = 2 cos —Ь isin — = 2i,
I 2 2 J
f 5Л . . 5лА it .
a, =2 cos-------t-ism — = —v3+i,
2 I 6 6 J
I 7Л . . 7Л1 it .
a, =2 cos------Ustn — =— V3 — I,
3 I 6 6 J
a, = 21 cos-f- isin —1 =.—2i,
I 2 2 J
( Пл НлА [- .
Ofc = 2 cos——+isin-- = v3-i.
V 6 6 J
Эти значения изображаются вершинами правильного шестиугольника, вписан-
ного в окружность радиуса Я = 2 (рис. 7.4.).
Пример 7.9. Решить уравнение z3 - 2 ^2/(1 - i) = 0.
Так как 2-72/(l-i) = 2(cos (n/4)+isin (л/4)), то
z = ^2 (cos (n/4)+lsin (л/4)).
Применяя формулу (7.36), получаем
Г? л . . л^ (л/4)+2Ал . . (л/4)+2Ал)
з| 2[ cos —t-isin — =v2 cos —--------l-isin-------I, k = 0,1,2.
f k 4 4 J k 3 3 )
Полагая в этой формуле к - 0, к = 1, к = 2, ндходим
я . . л^ Зг( (л/4)+2л . . . (л/4)+2л)
zn =V2 I cos-Hi sin — , z, = V2 cos —-----1-ism-------|=
0 V 12 12 J ’ V 3 3 J
зсГ Зя . . Зл') 3tr( 17л . Пл')
— 42 I cos —+ism — , z, =42 I cos--l-isin-- .
k4 4 ) I 12 12 J
136
Гпава 8
АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
8.1. Алгебраические многочлены
Алгебраическим многочленом степени и называется сумма целых неотрица-
тельных степеней переменной х, взятых с некоторыми числовыми коэффициента-
ми, т. е. выражение вида
a^x" + fl|XB-1 + — + а„чх + а„, а0* О.
Для сокращенной записи многочленов употребляют обозначения /(х),
Ф (*)> g (*) и т. п.
Два многочлена f(x) и g(x) считают равными и пишут f(x)=g(x) в том и
только в том случае, когда равны их коэффициенты при одинаковых степенях х.
Теорема 8.1. Для любых двух многочленов f(x) и ф (х) можно найти та-
кие многочлены q(x) и г(х), что
/(х) = ф(х)д(х)+г(х), (8.1)
причем степень г (х) меньше степени <р (х) или же г (х) = 0. Многочлены q (х)
и г (х) определяются однозначно.
Многочлен q(x) называется частным от деления /(х) на ф(х), а г(х) -
остатком от этого деления.
Замечание. Формулу (8.1) можно записать так:
ф (*) ф (*)
Если остаток от деления /(х) на <р(х) равен нулю, то многочлен ф(х) назы-
вается делителем многочлена /(х); в этом случае говорят, что /(х) делится на
<р (х) (или нацело делится на ф (х) ).
Многочлен ф(х) тогда и только тогда является делителем многочлена /(х),
когда существует многочлен у (х), удовлетворяющий равенству
/(х)=Ф(х)ф(х).
Многочлен Л(х) называется общим делителем для многочленов /(х) и
g (х), если он является делителем каждого из этих многочленов.
Два многочлена называются взаимно простыми, если они не имеют других об-
щих делителей, кроме многочленов нулевой степени (т. е. постоянных).
137
Наибольшим общим делителем отличных от нуля многочленов /(х) и g (х)
называется общий делитель d (х), который делится на любой другой общий де-
литель этих многочленов. Наибольший общий делитель многочленов /(х) и
g(x) обозначается так: (/(х), #(х)).
Наибольший общий делитель многочленов /(х) и g (х) можно найти с по-
мощью алгоритма Евклида. Если
/(x) = g(x)?1(x)+r1(x),
g(x) = r, (x)g2(x)+r2(x),
Л U) = r2(x)93(x) + r3(x),
(82)
г„ -г(х) = П -I (*) 9. (*)+r. (*)>
r,_i(x) = rl(x)gt+|(x),
то г,(х) = (/(х),#(х)).
Замечание. Наибольший общий делитель многочленов определен с
точностью до постоянного множителя: если d (х) — наибольший общий дели-
тель многочленов /(х) и g(x), то cd(x), где с - любое число, отличное от
нуля, также является их наибольшим общим делителем.
Пример 8.1. Найти частное q (х) и остаток г (х) прн делении много-
члена /(х) = х4 — х2 -2 на многочлен <р (х) = хэ -2х2 +х - 2. Выразить /(х)
через <р(х) и г(х).
Выполняя деление, находим
х4-х2-2
2x3 -2x2 +2x-2
±2x3tP4x2+2x:F4
2х2 + 2
Итак, д(х) = х + 2, г(х)=2х2+2, х4-х2-2=(х3-2х2+х-2)х
х(х+2)+2х2 + 2.
Пример 8.2. Найти общий наибольший делитель двух многочленов
/(х)=х4+2х2 —3 и ф(х) = х3-х2+2х-2.
138
Произведя деление f(x) на <р(х), получим первое из равенств (8.2):
х4+2х4-3=(х3-х2 + 2х-2)(х-1)+(х2-1), так как ^(х) = х-1 и г|(х)=х2-1.
Разделив <р (х) на г, (х), найдем второе из указанных равенств:
х3-х2 + 2х-2 = (х2-1)(х-1)+Зх-3, поскольку д2(х) = х-1 и г2(х)=3х-3.
Остаток г, (х) нацело делится на остаток г2 (х): х2-1 = (3х-3)х
Г1 г ч 1 1
х —хч— ; й3(х) =—х+—.
^3 3J 3 3
Следовательно, г2 (х) = Зх - 3 = 3 (х -1) является общим наибольшим делите-
лем данных многочленов. В соответствии с замечанием общим наибольшим дели-
телем будет также d(x) = х-1.
8.2. Корни многочлена. Теорема Безу
Значением многочлена
f(x) = аох” + atx”~' + • • • + a„_tx + а„ (8.3)
при х = с называется число
/(с) = аос" + a,c"-1 + — + а„_,с+а„.
Число с называется корнем многочлена /(х) или корнем уравнения /(х) = 0,
если /(с) = 0, т.е.
аос" + atc”~' + + а„чс +а„ = 0.
Теорема 8.2. (Безу). Остаток г от деления многочлена f(x) на линейный
многочлен х—с равен значению f(c) многочлена f(x) при х = с, т. е.
r = f(c). (8.4)
Следствие. Число с тогда и только тогда будет корнем многочлена
f(x\ когда f(х) делится нах-с.
Если многочлен /(х) задан формулой (8.3) и
/(х)=(х-с)</(х)+г,
где
q (х) = box"~' + ftjX"'2 + fejx”-3 + — + b„_2x + Vi.
то коэффициенты многочлена q (х) определяются формулами
Ь0=а0, bk=cbk_y+ak, £ = 1,2,...,л-1, (8.5)
а остаток г - по формуле г = cb„_} +а„.
Коэффициенты частного и остаток вычисляются по следующей схеме:
b0 cbo+a^b, cfe!+a2=h2 cb2+a3=b3 ... cb„_2+a„_t = b„_t cb^+a„=r.
Эту схему, называемую схемой Горнера, используют также для вычисле-
ния значений многочлена, йоскольку f(c) = r (см. формулу (8.4)).
139
Если с - корень многочлена f(x), т.е: /(с) = 0, то многочлен /(х) делится
на х—с. Может оказаться, что f(x) делится и на более высокие степени х-с.
Пусть существует такое натуральное число к, что f(x) нацело делится на
(х-с/, но уже не делится на (х—с/+1. В этом случае /(х) = = (х-с/ф(х),
причем число с не является корнем многочлена <р (х). Число к называется кратно-
стью корня с многочлена f(x), а число с - ^-кратным корнем этого многочлена.
Если к = \, то говорят, что число с - простой корень многочлена /(х).
Теорема 8.3. Всякий многочлен, степень которого не меньше единицы,
имеет хотя бы один корень (действительный или комплексный).
Эту теорему раньше называли «основной теоремой высшей алгебры».
Следствие. 1. Всякий многочлен п-й степени единственным образом, с
точностью до порядка сомножителей, разлагается в произведение п линейных
множителей: если <Х|,а2,...,ап - корни многочлена (8.3), то
/(х) = а0(х - а,) (х - а2)... (х - а„). (8.6)
Следствие.2. Всякий многочлен f(x) степени п > 1 имеет п корней,
считая равные и комплексные.
Следствие.З. Если многочлены f(x) и <р(х), степени которых не
превышают п, имеют равные значения более чем при п различных значениях пе-
ременной. то f(x) = <р (х).
Если многочлен
/(х) =х" +а|х'н + а2х"~г ++ а^х+а„, (8.7)
для которого о0 = 1, имеет корни а|,а2,...,а„, то его коэффициенты выражают-
ся формулами Виета:
а1=-(а|+а2+- + а„);
а2 = а,а2 +а,а3 + • • •+а,а„ + а2а3 + •• • +
а3 =-(а,а2а3 +а|а2а4+--+аи_2а„_|а„;
(8.8)
а„-1 =(-1)"-,(а1а2 ...а^.+а,^ ...а„_2а„+ -+а2а3 ...а„);
в„=(-1)"~,‘Х|«2
Эти формулы Означают следующее: в правой части k-ro равенства
{к = 1,2,..., и) находится сумма всевозможных произведений по к корней, взятая
со знаком плюс или минус в зависимости от четности или нечетности к.
Последняя из формул (8.8) свидетельствует о том, что корни многочлена (8.7)
являются делителями его свободного члена.
Формулы Виета дают возможность найти многочлен по корням.
Теорема 8.4. Если комплексное число а является корнем многочлена с дейст-
вительными коэффициентами, то его корнем будет также и сопряженное число а.
140
Следствие. I. Многочлен f(x) в этом случае делится на квадратный
трехчлен <р (х) = (х - а) (х - а) = х2 +px+qc действительными коэффициента-
ми р = -(а + а), д = аа.
Следствие. 2. Комплексные корни всякого многочлена с действитель-
ными коэффициентами попарно сопряжены.
Следствие. 3. Многочлен нечетной степени с действительными ко-
эффициентами имеет хотя бы один действительный корень. Если же действи-
тельных корней больше одного, то их будет нечетное число (так как комплекс-
ные корни попарно сопряжены).
Следствие. 4. Всякий многочлен с действительными коэффициентами
можно представить, причем единственным способом (с точностью до порядка
множителей), в виде произведения его старшего коэффициента и нескольких
многочленов с действительными коэффициентами, линейных вида х-с, соот-
ветствующих его действительным корням, и квадратных вида x2+px+q, со-
ответствующих парам его сопряженных комплексных корней.
Пример 8.3. Разделить многочлен /(х) = х5 - 2х3 + 2х2 - Зх + 5 на х -1.
Коэффициенты многочлена: а0 = 1, ах=0, а2=-2, <з3 = 2, о4=-3, as=5.
Коэффициенты частного q (х) = Ьох4 + 1\х3 + t^x2 + bjx + Ь4 и остаток г находим
по схеме Горнера, считая с = L
с 1 О —2 2 -з 5
1 1 11+0=1 1-1 —2 = —1 Г(—1)+2 = 1 1-1-3 = -2 1(-2)+5 = 3
Следовательно, частное q (х) = х4 + х3 - х2 + х - 2, а остаток г = 3.
Пример 8.4. Вычислить значение многочлена /(х) = 2х5-4х4 +
+5х’-26х2-17*+9 при х = 3.
По схеме Горнера находим:
с 2 -4 5 - 26 -17 9
3 2 3 2-4 = 2 3-2 + 5 = 11 3-11-26 = 7 3-7-17=4 3-4+9 = 21 '
Итак, г = 21; поскольку f(c) = r, то/(3) = 21.
Пример 8.5. Показать, что число х = 4 является корнем многочлена
/(х) = Зх4 - 2х3 - 47х2 + ЗОх - 8.
С помощью схемы Горнера находим, что г = /(4) = 0:
с 3 - 2 -47 30 -8
4 3 4-3 — 2 = 10 4-10 — 47 = —7 4(-7)+30 = 2 42-8=0
Так как г = 0, то /(4) = 0, х = 4 - корень многочлена.
Пример 8.6. Найти многочлен третьей степени, корни которого а, = 1,
0^=-2, а3=3.
141
Воспользуемся формулами Виета. При п = 3 многочлен (8.7) и формулы (8.8)
принимают соответственно вид
/(х) = х3 +а,х2 +а2х+а3,- о, = -(а1 +а2 +а3),
а2 = а,а2 +а1а3 +а2а3, а3 = -а,а2а3.
Йодставляя в последние три формулы значения корней, получаем а, =
=-(1-2 + 3) =-2, а2 = 1 (—2)+1-3+(—2)3 = -5, а3 =-1(-2)3 = 6. Следова-
тельно, f(x) ~ х3 - 2х2 - 5х+6.
Пример 8.7. Найти многочлен четвертой степени, имеющий корни
а, = -1, а2 = 2, ос, = 4, а4 = 5.
При л = 4 многочлен (8.7) и формулы (8.8) запишутся так:
/(х) = х4 + а,х3 + а2х2 +а3х + а4,
ах = - (а, +а2 +а3 +а4),
а2 = а,а2 +а,ос, +а,а4+а2а3 +а2а4 +а3а4,
а3 = - («iO^oCj +а,а2а4 +а,а3а4+а2<х3а4),
а4 = а|а2а3а4.
По эти формулам находим о, =-10, а2 = 27, а3=-2, а4 = -40. Итак,
/(х) = х4 - 10х3 + 27х2 - 2х - 40.
8.3. Квадратные уравнения
Алгебраическим уравнением n-й степени с одной переменной х называется
уравнение вида
т.е. а0<
аох" + аххп~' ч-1- а„_,х+а„ = 0, (8.9)
где а0, а,,..., а„_,, а„ — заданные числа, называемые коэффициентами.
Корнем алгебраического уравнения (8.9) называется такое значение перемен-
ной х = с, при котором оно обращается в тождество,
+ а1ся-1 + -а„_1с+а„ = 0.
Выражение «решить уравнение» означает найти все его корни.
Квадратным называется уравнение вида
ах2+Ьх+с = 0 (а*0).
Корни уравнения (8.10) вычисляются по формуле
(8.10)
*1.2 =
М2-4ос
2а
(8.11)
Выражение
D = i2-4oc
называется дискриминантом квадратного уравнения (8.10).
142
Если а, b, с - действительные числа, то квадратное уравнение (8.10) при
£>>0 имеет два различных действительных корня, при Ь=0 - два равных дей-
ствительных корня, при D < 0 — два комплексно-сопряженных корня.
Отметим, что коэффициенты квадратного уравнения (8.10) могут быть и ком-
плексными числами. Его корни также вычисляются по формулам (8..11). В этом
случае дискриминант будет комплексным числом.
Уравнение (8.10) можно привести к виду
х2 +px+q = 0. (8.12)
Корни этого уравнения вычисляются по формуле
Xl2=-£.±^-q, (8.13)
которая является частным случаем формулы (8.11).
Пример 8.8. Решить уравнение х2 - 4х +13 = 0.
По формуле (8.13) получаем х!2 = 2 +V4-13 = 2 ±^9. Это уравнение имеет
корни xt = 2 + 3», хг = 2 — 3i, где i =
Пример 8.9. Решить уравнение х2-(4+6»)х-5+10» = 0 с комплекс-
ными коэффициентами.
По формуле (8.13) находим х12 =(2 + 3»)±-^(2+3»)2 -(-5+10») =
= (2+3») ±т/4+12»!+9»2 +5-10» = (2 + 3») ± V2? = ( 2+3») ± (1 +»); х, =3+4»,х2 =1 +2».
8.4. Кубические уравнения
Кубическим называется уравнение
х3 +ах2+Ьх + с = 0. (8.14)
Это уравнение с помощью формулы х = z - а/3 можно привести к виду
z3 + pz+q = 0. (8.15)
Корни кубического уравнения (8.15) вычисляются по формуле z = и+v, где
(8.16)
или
(8.17)
Все три корня уравнения (8.15) определяются следующими формулами:
z, = Uj +V], z2 = ЦЕ + V|E2, z3 = »/i£2 +vie, (8.18)
где U] - любое из трех значений и, определяемых первой из формул (8.16), v, —
то из трех значений v, которое соответствует ц на основании равенства
143
3wv+p = 0,
• 1 . -Л 2 i . -Л
е =—+«—, е =---------1 —
2 2 .2 2,„ ...
- кубические корни из единицы.
Дискриминантом уравнения (8.15) называется выражение
(819)
(8.20)
( 2 3 А
Б = -4Р3- 27q1 =^-108 .
4 27 )
Уравнение (8.15) при D<0 имеет один действительный и два комплексно-
сопряженных корня: при D = 0 - три действительных корня, причем два равных;
при D > 0 - три различных действительных корня.
Замечание. Третий случай (D>0) называется неприводимым. В этом
случае все корни уравнения (8.15) с действительными коэффициентами являются
действительными, однако для нахождения их по формуле (8.17) следует извлекать
кубические корни из комплексных чисел.
Формула (8.17) называется формулой Кардано. Правило, соответствующее
этой формуле, впервые опубликовано в книге итальянского ученого Д. Кар-
дано «Великое искусство или о правилах алгебры» (1545). Это правило реше-
ния кубического уравнения было получено ранее (1535) другим итальянским
математиком Н. Тартальей.
Пример 8.10. Решить уравнение z3-6z + 9=0. Это уравнение вида
(8.15), для которого р = -6, q = 9. Составим выражение
<1\р'_92 (-6)3_81 „49
4 27 4 З3 4 4
По формулам (8.16) находим и и v:
Следовательно, ц=-1, у,=-2, равенство (8.19) выполняется. По формулам
(8.18) с учетом формул (8.20) находим
Z] =«,+v, =-3,
2 , ./ 1 .ч/з) , 1 .->/з) з 7з.
z2 = H,e+v.e =(-1) —+«— +(— 2) —-I— = — ч--------1,
2 2 ) [ 2 2)2 2
2 з -Л.
z3 = W1e +^6=-——I.
144
Замечание. Корни z2 и z3 можно найти и другим способом. Так как
zt=-3 - корень уравнения, то многочлен z3-6z+9 делится на (z+З). Произ-
ведя это деление, получим z3 - 6z+9 = (z+3) (z2 - 3z+3). Данное уравнение при-
мет вид (z + 3)(z2-3z+3) = 0, откуда z+3 = 0, z2-3z+3 = 0. Последнее урав-
нение имеет корни
Зе V3 3 V3
z, = —I--1, z, -------i.
2 2 2 3 2 2
Пример 8.11. Решит уравнение х3 — 5х2+8х-6 = 0.
Разложим на множители многочлен в левой части уравнения:
х3 -5х2 +8х-6 = х3 -Зх2 -2х2 +6х+2х —6 = х2(х —3)—2х (х—3)+2(х-3) =
= (х-3)(х2-2х + 2). Данное уравнение примет вид (x-3)(xz-2x + 2) = 0 и
распадается на два уравнения: х— 3 = 0, х2 -2х+2 = 0, которые имеют корни
8.5. Уравнения четвертой степени
Алгебраическое уравнение четвертой степени
х4 + ах3 + bx2 + сх + d = 0
с помощью подстановки х = z-a/4 можно привести к уравнению
z4 +pz2 +qz+r = 0, (8.21)
в котором коэффициент при г3 равен нулю.
Это уравнение можно записать так:
(z2 +р/2+а)2 - (2az2 - qz+(а2 + ра - г + р2/4)) = 0, (8.22)
где а - вспомогательный параметр. Значение параметра выберем так, чтобы вы-
читаемый многочлен был полным квадратом. В этом случае многочлен имеет два
равных корня, так как его дискриминант равен нулю, т. е.
92-4-2а(а2+ра-г+р2/4)=0. (8.23)
Уравнение (8.22) принимает вид
z z у
I z2+—+осо I -2а0 z—=0, (8.24)
к 2 ) V 4а0 J
где а0 - отличный от нуля корень уравнения (8.23).
Уравнение (8.24) распадается на два квадратных уравнения:
145
(8.25)
Корни этих уравнений будут корнями уравнения (8.21).
Пример 8.12. Решить уравнение z4-5z2 + 4=0.
Это уравнение вида (8.21), для которого р = -5, q = 0, г = 4. Уравнение
(8.23) в данном случае сводится к квадратному уравнению относительно парамет-
ра а:а2-5а—4+25/4=0, или а2-5а+9/4 = 0, которое имеет корни а}=9/2,
а2 = 1/2. При а0 = 1/2 уравнения (8.25) запишутся так: z2 - z - 2 = О,
z2 +z-2 = 0. Первое из них имеет, корни Z]=-l, z2=2, а второе - z,=l,
z2 = -2. Эти числа являются и корнями исходного уравнения.
Пример 8.13. Решить уравнение х4 +4х3 + 7х2 - 4х-8 = 0. Разложим на
множители многочлен в левой. части уравнения:
х4 +4х3 +7х2 — 4х —8 = (х4 — х2)+(4х3 — 4х)+(8х2 — 8) = х2(х2 — 1).+4х(х2 -1)+
+ 8 (х2 -1) = (х2 -1) (х2 + 4х+8).
Следовательно, уравнение примет вид (х2-1)(х2+4х+8) = 0, откуда
х2 —1 = 0, х2+4х + 8 = О, Х[=—1, х2 = 1, х3=—2+2»,: х4 = — 2 — 2i.
8.6. Решение алгебраических уравнений
способом разложения многочлена
на множители
Если Ора,,...,а„ - корни многочлена /(x) = o0xft+o1x"_|+••• +
+ о„_,х+а„, то уравнение (8.9) можно записать так:
ао(х-а|)(х-а2)...(х-а„) = 0.
Если а и а - сопряженные комплексные корни, то (х-а)(х-а) =
= х2 +px+q, raepnq - действительные числа (р = -(а+а), q=aa).
Предположим, что левая часть уравнения (8.9) разложена на множители вида
х-с и x2+px+q. Приравнивая нулю каждый множитель, получаем уравнения,
каждое из которых является линейным или квадратным. Корни этих уравнений
будут корнями уравнения (8.9).
Пример 8.14. Решить уравнение х3-2х-4 = 0.
Разлагаем на множители многочлен в левой части уравнения:
х3 — 2х —4 = х3 — 2х2+2х2-4х+2х-4 =
146
= х2(х - 2)+2х (х - 2)+2 (х - 2)=(х - 2) (х2 + 2х +2).
Данное уравнение принимает вид (х - 2) (х2 + 2х + 2) = О и распадается на два
уравнения: х — 2=0, х2 + 2х + 2 = О; первое из них имеет корень х, = 2, а второе
- два комплексно-сопряженных корня х2 = -1 - i, х3 = -1+i.
Пример 8.15. Решить уравнение х4-5х3 + 5х2 + 5х-6 = 0.
Так какх4- 5х+5х2+5х* 6 =х4-5х*+51?+5х-5-1 = (х4-1) + (-5х3+5х2)+(5х-5)=
=& -1 )(х2+1) -5х\х -1)+5(х -1)= (х2 -1М?+1) -5 (х -1) (х2 -1> (х2 -1)( х2+1 -5(х -1))=
(х2 -1)(х2 -5х+6), то (X2 -1) (х2 - 5х + 6) =.0, откуда х2-1 = 0, х2 — 5х+6=0,
X! = -1, х2 =1, х3 = 2, х4 = 3.
Пример 8.16. Решить уравнение х4+2х3-2х2-8х-8 = 0.
При разложении на множители используется результат примера 8.14.
Поскольку х4 + 2х3 - 2х2 - 8х - 8 = х4 + 2х3 - 2х2 - 4х - 4х - 8 = х3(х+2)-
-2х(х+2)-4(х+2)=(х+2)(х-2)(хг+2х+2)=0, откуда х+2 = 0, х-2 = 0,
х2 + 2х+2 = 0; Xj=—2, х2=2, x3 = -l-i, х4=—l+i.
Пример 8.17. Решить уравнение х5-х4-81х + 81 = 0. Так как х5-
-х4-81х + 81 = х4(х — 1)-81(х-1) = (х—1)(х4-81) = (х-1)(х2-9)(х2+9), то
(х-1)(х2-9)(х2+9) = 0, откуда х-1 = 0, х2-9=0, х2+9=О, х,=1,
х2 = —3, х3 = 3, х4 = -31, х5 = 31.
Замечание. Алгебраические уравнения n-й степени (и>5) в общем
случае в радикалах не решаются, т. е. не существует формул, которые давали бы
возможность вычислить корни уравнения по его коэффициентам. Это впервые
доказал норвежский математик Н.Х Абель. Однако имеются частные виды урав-
нений любой степени, разрешимые в радикалах (например, х" = а). Вопрос о том,
каково необходимое и достаточное условие для того, чтобы алгебраическое урав-
нение решалось в радикалах, исследовал французский математик Э. Галуа.
8.7. Разложение дробной рациональной
функции в сумму элементарных дробей
Целой рациональной функцией называют алгебраический многочлен. Дробной
рациональной функцией или рациональной дробью называется отношение двух
многочленов:
R (Х) = Р"(х) = аоХп+а3хп-' + -+а„_1х+ап
Й»(Л) box"+blx"~t+ —+bm_lx + bm
Если т>п, то рациональная дробь называется правильной.
Элементарными дробями называются рациональные дроби вида
А Вх+С
(х - с)" ’ (х2 + рх +q)m ’
147
где п, т- натуральные числа; с, р, q. А, В, С - действительные числа;
(р2/4)-9 < 0 (корни трехчлена х2 +рх+q являются комплексными).
Всякую правильную рациональную дробь можно разложить в сумму элемен-
тарных дробей на основании следующей теоремы.
Теорема 8.5. Если дана правильная рациональная дробь (8.26) и
Q(x) = (x-ci)”' ...(x-cr)"'(x2+pix+qi)mi ...(х2+psx+qJf*,
где Cj (i = l,2,...,г) - попарно различные действительные корни многочлена
Q(x) кратности nt; х2 + pkx+qk=(x—a.k)(x—a.k), где а* и а* (к —
= 1,2...s) - попарно различные при разных к корни многочлена Q (х) кратно-
сти тк, то существуют действительные числа
A" = п = 1,2,...,»,), В", <7(Jt = l,2,...,s; « = 1,2,...,»%)
такие, что
Р(х)_ 41 ч 4 , , 4"‘ +...
0(х) x-q (x-q)2 (x-q)"1
Btx+Cl , B2x+C2 , , В^х + СГ |
x2+Ax+9i (x2+plx+ql)2 (x2+plx+ql'fl
-Bjx+C? B2x+C^~'. . Bf-x+C?
x2+psx+qI (x2+psx+q1)2 (x2+psx+q1)a‘
Отметим, что каждому действительному корню с кратности I соответствует
сумма I элементарных дробей вида А/(х - с)":
4 +—4*—+ ...+_А_
х-с (х-с)2 (х-с/
а каждой паре комплексно-сопряженных корней а и а (таких, что
(х’-а)(х-а) = х2 +px+q) кратности т- сумма дробей вида
(Вх+с/(х2 +px+q)”:
ВуХ+С[ । В2х+С2 __________Втх+Ст
x2+px+q (х2 +px+q)2 (x2+px+q)m
Пример 8.18. Разложить в сумму элементарных дробей рациональную
дробь (7х2-х+1)/(х’+1).
148
Так как х3 +1 = (х +1) (х2 - х +1), то искомое разложение имеет вид
7x2j-x+1_ 7х2-х+1 _ А Вх+С
х3+1 (х+1)(х2-х+1) х+1 х2-х+1’
где коэффициенты А, В, С пока не определены. ,
Приводя к общему знаменателю правую часть и сравнивая коэффициенты при
одинаковых степенях х, получаем
7х2—х + 1 (Я + В)х2+(В + С-Л)х + Л + С
х3+1 х3+1
7х2-х + 1 = (Л + В)х2+(В+С-Л)х + (Л+С),
А + В=7, В+С-А = -1, А + С=1.
Из этой системы уравнений находим Л = 3, В = 4, С=-2. Следовательно,
7х2 —х + 1______________________3 4х-2
х’+1 х + 1 х2-х + Г
Пример 8.19. Разложить в сумму элементарных дробей рациональную
дробь (х2 + х + 1)/(х3 — Зх + 2).
Разлагая знаменатель на множители, получаем х3-Зх+2 = х3—х—
-2х-2 = х(х2-1)-2(х-1) = (х-1)(х(х + 1)-2) = (х-1)(х2-1)+(х-1) =
= (х-1)2(х+2).
Данную рациональную дробь представим в виде суммы элементарных дробей
х2+х + 1 _ А В С
х3-Зх + 2 х + 2 х-1 (х-1)2’
откуда
х2+х + 1 = Я(х —1)2 + В(х —1)(х + 2)+С(х + 2), (II)
или
х2+х+1 = (Л+В)х2+(В+С-2Л)х+(И-2В+2С).
Сравнивая коэффициенты при одинаковых степенях, получаем уравнения А+В -1,
В + С-2А=1, А-2В+2С =1, из которых находим Л = 1/3, В =2/3, С=1.
Следовательно, разложение (I) примет вид
х2+х + 1 1 2 1
х3 —Зх+2 3(х+2) 3(х —1) (х-1)2
Замечание. Коэффициенты А, В, С разложения (I) можно получить и
другим способом. Полагая в тождестве (II) х = 1, получаем 3 = С-3, С=1. Поло-
жив в этом тождестве х=-2, получим 3= Л(-3)2, откуда А = 1/3. Аналогично
при х = 0 находим 1 = А-2В+2С, В = 2/3.
149
Глава 9
ЛИНЕЙНЫЕ ПРОСТРАНСТВА
9.1. Линейное пространство. Подпространство
Линейным действительным пространством или векторным действительным
пространством называется множество V элементов х, у, z,..., для которых опреде-
лены операции сложения элементов и умножения элемента на действительное
число, удовлетворяющие следующим аксиомам: I. х + у = х + у,
II. (x + y)+z= x+(y+z), III. Существует нулевой элемент 0 такой, что х+О = х,
IV. Для каждого хеV существует противоположный элемент -х такой, что
х+(-х) = О, V. 1х = х, VI. а(Рх)=(ар)х, VII. а(х + у) = = ах+ау,
VIII. (а+р)х = ах+Рх.
Эти аксиомы выполняются соответственно для всех х, у, z е V, ol, р e"R.
Элементы действительного линейного пространства называются векторами.
Замечание. Аналогично определяется комплексное линейное про-
странство: вместо множества R действительных чисел рассматривается множестве
С комплексных чисел.
Из определения линейного пространства вытекают следующие утверждения.
1. В линейном пространстве имеется единственный нулевой элемент.
2. Для любого элемента х линейного пространства существует единственны
элемент -х.
3. Для элемента -х противоположным будет элемент х.
4. Для любого элементах произведение 0х = 0, где 0 - нуль, 0 - нулевой элемен
5. Для любого элементах (~1)х = ~х, где (- х) - элемент, противоположный х
6. Для любого числа а произведение аО = 0, где 0 — нулевой элемент.
7. Если ах = О и а * 0, то х = 0.
8. Если ах = 0 и х # 0, то а = 0.
Равенство ах = О выполняется тогда и только тогда, когда а = 0 или х = 0.
Замечание. Сумму х+(-у) обозначают х - у и называют разноси
элементов х и у.
Примеры линейных пространств.
1. Множество V3 всех свободных векторов а (о„а2,й3), для которых onj
делены сложение и умножение вектора на число так, как в п. 3.2, является лии
ным пространством. Отметим, что роль нулевого элемента здесь играет ну
вектор; для любого вектора а противоположным является -а. Аксиомы I - У
выполняются, о чем свидетельствуют формулы п. 3.2.
150
2. Множество всех матриц размером mxn, для которых определены сложе-
ние матриц и умножение матрицы на число соответственно формулами (5.2), (5.4).
Роль нулевого элемента здесь играет нулевая матрица; для матрицы (а1к)тп про-
тивоположной является матрица (~ал)т„. Аксиомы I - УШ выполняются
(см. п. 5.2, свойства 1-8 линейных операций над матрицами).
3. Множество {Р„(х)} всех алгебраических многочленов степени, не превы-
шающей натурального числа л, для которых операции сложения многочленов и
умножения многочлена на действительное число определены обычными правила-
ми. Нулевой элемент - многочлен, все коэффициенты которого равны нулю; для
многочлена Р„(х) = аох” + $x”~l -I и a„_tx + а„ противоположным будет
~ рЛх) = ~аох” - atx”~l---a„_tx-а„.
Замечание. Множество всех многочленов степени, точно равной нату-
ральному числу и, не является линейным пространством, так как сумма двух таких
многочленов может оказаться многочленом степени ниже л (т. е. не принадлежать
рассматриваемому множеству).
4. Множество А„ элементами которого являются упорядоченные совокупно-
сти л действительных чисел (х1,х2.-..,х„). Каждый элемент этого множества
будем обозначать одним символом, например х, у,..., и писать
х = (х„х2,...,х„), у=(у\,у2,---,у„),.- Действительные числа хх,х2,...,х„
называют координатами элемента х. Линейные операции над элементами Ап оп-
ределяются формулами х+у = ((х1+у1),(х2+у2 ),..., (х„+у„)), ах =
= (ах1,ах2,...,ахя). Отметим, что элемент 0 = (0,0,...,0) является нулевым,
элемент -х = (-х1,-х2,...,-х„) - противоположным элементу х =
= (x1,x2,...ix„).
5. Множество С [а, 6] всех функций x = x(t), определенных и непре-
рывных на отрезке [а, 6]. Операции сложения этих функций и умножения
функции на число определяются обычными правилами. Нулевым элементом
является функция x(z) = 0 для всех /е[о, 6]. Элементом, противоположным
*
элементу x(t), будет -х(Г).
Множество IV g V называется подпространством линейного пространства У,
если выполняются следующие условия: 1. В множестве W определены те же опе-
рации, что и в множестве У. 2. Если х,yeJV, то x+yeJV. 3. Если хе W, то
ах е W. Очевидно, всякое подпространство W линейного пространства У является
линейным пространством, т.е. в W выполняются аксиомы I - VIII. Прежде всего, в
W имеется нулевой элемент 0: если х е W, то Ох = 0 е W. Для любого элемента
xeW имеется противоположный элемент -х: если хе IV, то (—1)х =-хеW.
Отметим, что нулевой элемент 0 линейного пространства У образует подпро-
странство этого пространства, которое, называют нулевым подпространством.
151
Само линейное пространство V можно рассматривать как подпространство, этого
пространства. Эти подпространства называются тривиальными, а все другие, если
они имеются, - нетривиальными. Приведем примеры нетривиальных подпро-
странств. 1. Множество V2 всех свободных векторов я(а1,а2), параллельных
некоторой плоскости, для которых обычным образом определены операции сло-
жения векторов и умножения вектора на число, представляет подпространство
линейного пространства V3. 2. Множество Ц всех свободных векторов а (в!),
параллельных некоторой прямой, также является подпространством линейного
пространства V3. 3. Множество {P„_((x)} всех алгебраических многочленов сте-
пени, не превышающей натурального числа л-Ч, является подпространством
линейного пространства {Е„(х) }.
9.2. Линейная зависимость и линейная
независимость векторов линейного
пространства
Рассмотрим векторы (элементы) х,, х2,..., х„ линейного пространства. Вектор
у = а,х1 +а2х2 + -+а„х„, где ах,а2.....а„ - некоторые числа, называется
линейной комбинацией векторов х„х2,...,х„, а числа ах,а2............а„ -
коэффициентами этой линейной комбинации. Если все числа at (1=1,2,...,ri)
равны нулю, то линейная комбинация называется тривиальной. Если хотя бы одно
из чисел а, отлично от нуля, линейная комбинация называется нетривиальной.
Система векторов
х1,х2,...,х„ (9.1)
называется линейно зависимой, если существуют числа
сц.а,,....»/ (9.2)
не все равные нулю, такие, что
(XjXj + а2х2 + • • •+алхп - 0. (9.3)
Если таких чисел не существует, т. е. равенство (9.3) выполняется только в
случае
“1 = «2 =•=«» =°» (9-4)
то система векторов (9.1) называется линейно независимой.
Другими словами, векторы (9.1) называются линейно зависимыми, если существует
их нетривиальная линейная комбинация, равная нуль-вектору, и линейно независи-
мыми, если только их тривиальная линейная комбинация является нуль-вектором.
Из. определения линейной зависимости и линейной независимости векторов
вытекают следующие утверждения.
1. Всякая система векторов, содержащая нуль-вектор, является линейно зависимой.
2. Если к (к < п) векторов системы (9.1) линейно зависимы, то и вся система
линейно зависима.
152
3. Если из системы линейно независимых векторов х(, х2,хп отбросить г(г<п)
векторов, то оставшиеся векторы образуют также линейно независимую систему.
4. Если среди векторов системы (9.1) имеются такие векторы х* и хт, что
хЛ = Ххга, где Л - некоторое число, то система (9.1) линейно зависима.
Теорема 9.1. Векторы х,, х2,..., х„ линейно зависимы тогда и только то-
гда, когда хотя бы один из них является линейной комбинацией всех остальных.
Эта теорема выражает необходимое и достаточное условие линейной зависи-
мости п векторов х,, х2,..., х„.
Два вектора линейного пространства называются коллинеарными, если они
линейно зависимы, и неколлинеарными, если они линейно независимы. Три век-
тора линейного пространства называются компланарными, если они линейно за-
висимы, и некомпланарными, если они линейно независимы. Введенные понятия
коллинеарности и компланарности векторов линейного пространства совпадают с
известными из аналитической геометрии понятиями коллинеарности и компла-
нарности обычных векторов.
9.3. Размерность и базис линейного пространства.
Изоморфизм линейных пространств
Число л называется размерностью линейного пространства V, если выполняют-
ся следующие условия: 1) в V существует л линейно независимых векторов;
2) любая система л+1 векторов из V линейно зависима. Размерность линейного
пространства V обозначают dim Г (от французского слова dimension -
размерность). Если пространство состоит из одного нулевого элемента, то его
размерность считают равной нулю. Размерность линейного пространства- это
наибольшее возможное количество линейно независимых элементов в нем. Поня-
тие размерности согласуется с наглядным представлением о ней; так, пространст-
во У3 всех свободных векторов является трехмерным (dim У3 = 3), пространство
У2 — двумерным, пространство Ц - одномерным.
Базисом и-мерного линейного пространства Vn называется любая упорядочен-
ная система л линейно независимых векторов этого пространства. Приведем при-
меры базисов некоторых линейных пространств. Базис пространства V3 образует
любая тройка некомпланарных векторов, так как эти векторы линейно независимы
(см. теорему 3.4), и любая четверка векторов линейно зависима (см. теорему 3.6).
Базис пространства V2 образует два любых неколлинеарных вектора, поскольку они
линейно независимы (см. теорему 3:2), и любой вектор плоскости, определяемой
двумя векторами, можно разложить по ним (см. терему 3.3). Базисом линейного про-
странства Fj является любой ненулевой вектор, коллинеарный данной прямой.
Линейное пространство, в котором имеется базис, состоящий из конечного
числа векторов, называется конечномерным. Примерами конечномерных про-
странств являются пространства У2, У3, А„.
153
Линейное пространство А„ является л-мерным, а его базис образует система
векторов е, = (1,0,..., 0), е2=(0,1,0,...,0), е„ =(0,0, ...,.0,1).
Линейное пространство Называется бесконечномерным, если при любом нату-
ральном числе т в нем найдется т линейно независимых векторов. Примером бес-
конечномерного пространства может служить линейное пространство С (о, 6] всех
функций х = х (/), определенных и непрерывных на отрезке [а, Ь];
Два линейных пространства V и U называются изоморфными, когда между их
элементами можно установить взаимно однозначное соответствие такое, что если
х2<->у2, гДе х„ х2еК, yl,y2eU, то (х1+х2)«-»(у,+у2),
ах, <->ау,, где а - действительное число.
Теорема 9.2. Два линейных пространства изоморфны тогда и только то-
гда, когда они имеют одинаковую размерность.
В частности, пространство Г3 (всех свободных векторов) и пространство 4,
(всех упорядоченных троек действительных чисел) изоморфны. Отметим также,
что каждое конечномерное линейное пространство размерности п изоморфно ли-
нейному пространству Л„.
9.4. Координаты вектора линейного пространства
Теорема 9.3. Если е1,е2,...,е„ - базис линейного п-мерного пространст-
ва V„, то любой вектор х этого пространства линейно выражается через ба-
зисные векторы е],е2,...,е„, т. е.
х = а|е1+а2е2+-+а„е„. Z (9.5)
Коэффициенты а.1,а.2,...,ап этого разложения определяются однозначно.
Выражение (9.5) называется разложением вектора х по базису е„е2,...,е„.
Координатами вектора х в базисе е|,е2,...,е„ называют коэффициенты
а„а2,...,а„ в разложении этого вектора по данному базису, т. е. в формуле
(9.5). Если вектор х в некотором базисе имеет координаты а1,а2,...,аи, то пи-
шут х = (а1,а2,...,а„), или х(а„а2,...,а„).
Операции над векторами сводятся к операциям над их координатами на осно-
вании следующих свойств.
1. Вектор является нулевым вектором линейного пространства тогда и только
тогда, когда все его координаты в любом базисе равны нулю.
2. Координаты суммы двух векторов в некотором базисе равны сумме соот-
ветствующих координат данных векторов в том же базисе.
3. Координаты произведения вектора на число равны произведению соответ-
ствующих координат на это число (в одном и том же базисе).
4. Два вектора равны тогда и только тогда, когда равны их соответствующие
координаты в одном и том же базисе.
5. Вектор у является линейной комбинацией векторов х„ х2,..., х„ тогда и
154
только тогда, когда каждая координата вектора у является такой же линей-
ной комбинацией соответствующих координат этих векторов в одном и том
же базисе.
Пример 9.1. Пусть Д, - четырехмерное линейное пространство с базисом
е(,е2,е3,е4. Найти координаты векторов е3 и х = Зе, - 5е3 + 7е4 в этом базисе.
Представим каждый из векторов е3 и х в виде (9.5). Так как вз =
Ое, +0е2 +1е3 +0е4, то, вектор ej имеет координаты (0,0,1,0). Поскольку
х = Зе, + 0е2 -5е3 + 7е4, то вектор х имеет координаты (3,0, - 5,7).
Пример 9.2. В некотором базисе даны векторы х(1,2,-2,-1,3),
у (4,-3,-2,1,-1). Найти координаты вектора 5х-3у.
Так как 5х =(5,10,-10,-5,15), -3у = (-12,9,6,-3,3), то вектор
5х - Зу = 5х + (- Зу) имеет координаты (- 7,19, - 4, - 8,18).
9.5. Ранг системы векторов линейного
пространства
Рассмотрим систему т векторов
Я1 = (°||»в21’"-’°»|)
Я2 =(°12> в22»"‘> Дй)
(9.6)
Ят =(аия’а21и’-"’апт)
линейного п-мерного пространства, координаты которых заданы в одном и том же
базисе. Системе векторов (9.6) поставим в соответствие матрицу
°11 й12 ••• Й1Л1
. °и! ап2 апт .
в к-м столбце которой записаны координаты вектора at (к = 1,2,..., т). Матрицу
(9.7) называют матрицей системы векторов (9.6) в данном базисе, а ранг этой мат-
рицы - рангом системы векторов а„а2,..., а„. Обратно, если дана матрица
(9.7), то ей можно поставить в соответствие систему (9.6) т векторов линейного п-
мерного пространства. Согласно свойству 5 п. 9.4, будем говорить, что столбцы
матрицы (9.7) линейно зависимы, если векторы (9.6) линейно зависимы и обратно.
Теорема 9.4. Для того чтобы т векторов п-мерного линейного про-
странства были линейно независимы, необходимо и достаточно,- чтобы
ранг матрицы этой системы был равен т.
Следствие 1. Система п векторов п-мерного линейного про-
странства линейно независима тогда и только тогда, когда матрица
этой системы векторов является невырожденной.
155
Следствие 2. Если ранг матрицы системы т векторов линейного
пространства равен г, то максимальное число линейно независимых век-
торов этой системы равно г.
Пример 9,3. Найти максимальное число линейно независимых векторов
в системе а,(1,2,3,4), а3(8,7,6,5), а4(-1,-1,1,1).
Матрица данной системы векторов имеет вид
1 1 8 -Г
12 7-1
-13 6 1
-14 5 1
Так как ранг этой матрицы равен 3 (см. пример 5.16), то максимальное число
линейно независимых векторов этой системы равно 3.
Теорема 9.5. Максимальное число линейно независимых строк всякой мат-
рицы равно максимальному числу ее линейно независимых столбцов, т. е. равно
рангу этой матрицы.
9.6. Преобразование координат вектора
при изменении базиса
В линейном n-мерном пространстве V„ фиксируем два базиса
(9.8)
ере2> (9.9)
Матрицей перехода от базиса (9.8) к базису (9.9) называется матрица системы
векторов (9.9) в базисе (9.8). Каждый вектор системы (9.9) можно разложить по
базису (9.8). Пусть
®1 = *11®1 "*"*21®2 * *"*nl®n>
®2 = f12e1 + ^22*2 "* * *»2®п> ,а 1ПЧ
«„ — *1п®1 "*"*2л®2 "*
тогда матрица перехода от базиса (9.8) к базису (9.9) имеет вид
*п *12 *1»
Z21 *22 ••• *2»
. *П1 *Я2 ••• "*ля .
Матрица перехода от одного базиса к другому невырожденная (так как базис-
ные векторы линейно независимы). Всякую невырожденную матрицу л-го порядка
можно рассматривать как матрицу перехода от одного базиса и-мерного линейно-
го пространства к другому базису этого пространства. Очевидно, матрица Г"1,
обратная матрице (9.11), является матрицей перехода от базиса (9.9) к базису (9.8).
156
Теорема 9.6. Если xt,x2,...,x„ -
координаты вектора х в базисе е|,е2,...,е„;
х[,х2,...,х'„ - координаты того же вектора в
базисе ej,e2,...,e',mo
Х=ТХ\ (9.12)
где
Т - матрица, определяемая формулой (9.11).
Замечание. Теорема 9.6 выражает старые координаты х1,х2,...,х„
вектора х через его новые координаты. Чтобы получить формулы, выражающие
новые координаты через старые, умножим слева равенство (9.12) на матрицу Г-1,
обратную матрице Т, получим Т~1Х = 7’-1ГА’', Т~'Х = X' или X' = 7’-1Аг.
Пример 9.4. В пространстве V2 рассмотрим базис е1 = i, е2 = j, где i,
j - орты, и базис е[ = i', е2 = j', где Г, j' - орты, причем Г образует с i угол <р
(рис. 9.1). В данном случае i' = icos<p + jsintp, ’ j' = -isin<p+jcos<p.
Матрица перехода от базиса i, j к базису Г, J' имеет вид
cos<p -sincp
sintp costp
Если вектор а имеет координаты х, у в базисе i, j; х', у' - в базисе 1', j', то
х = х' cos<p—y'sin ф, у = х' sin ф + у' совф.
9.7. Евклидово пространство
Определение евклидова пространства. В линейном действительном про-
странстве V, кроме операций сложения векторов и умножения вектора на действи-
тельное число, введем еще одну операцию, которую назовем скалярным умноже-
нием векторов. Каждой упорядоченной паре векторов х, у е V поставим в соот-
ветствие действительное число, которое назовем их скалярным произведением и
обозначим (х, у). Потребуем, чтобы для любых х, у, zе V и любого числа аеR
выполнялись следующие аксиомы: I. (х, у) = (у, х), II. (х+у, z)= = (х, z)+(y, z),
III. (ах, у)=а(х, у), IV. (х,х)>0 для всех х#0, (х,х) = 0 для х = 0.
Очевидно, скалярное произведение равно нулю, если хотя бы один из векторов
нулевой: (0, у) = (Ох, у) = 0 (х, у) = 0.
157
Скалярное произведение (х, х) вектора х на себя называется скалярным квад-
ратом этого вектора и обозначается х2, т. е.
(х, х) = х2. (9.14)
Евклидовым пространством называется линейное действительное пространст-
во, в котором задана операция скалярного умножения векторов, удовлетворяющая
аксиомам I — IV. Если л-мерное линейное пространство является евклидовым, то
будем называть его евклидовым л-мерным пространством, а базис этого линейно-
го пространства - базисом евклидова Пространства.
Примеры евклидовых пространств. 1 В линейном пространстве Е3 скаляр-
ное произведение двух векторов а и b определим так, как в п. 3.6; аксиомы I — IV
для него будут выполнены (см. свойства скалярного произведения и определение
скалярного квадрата вектора).
Следовательно, линейное пространство У3 всех свободных векторов с обыч-
ным определением скалярного произведения является евклидовым пространством.
2. Рассмотрим л-мерное линейное пространство А„ упорядоченных совокупностей
л действительных чисел. Скалярное произведение двух его элементов х = (хь х2,..., х„),
у = (у,, у2,..., у„ ) по аналогии с формулой (3.21) определим соотношением
(*> у) = *1У| + ЪУг ++х«Уп- <9-15)
Легко видеть, что все аксиомы I - IV скалярного произведения при этом вы-
полняются. Таким образом, рассматриваемое линейное пространство со скалярным
произведением (9.15) является евклидовым пространством, его обозначают Е„.
3. В бесконечномерном линейном пространстве С [а, Ь] всех функций, не-
прерывных на отрезке (в, Ь], скалярное произведение двух его функций х(/),
у (г) определим формулой
ь
(х,у) = |х(Т) (9.16)
а
Непосредственной проверкой можно убедится в том, что аксиомы I - IV скаляр-
ь
кого произведения будут выполнены, в частности (х,х) = jx2(t)dt>0 при
х(0*0, (х,х) = 0 при х(/) = 0.
Следовательно, линейное пространство С [а, 6] с указанным определением скаляр-
ного произведения любых двух его элементов является евклидовым пространством.
Норма вектора евклидова пространств*. Нормой вектора евклидова про-
странства называется арифметическое значение корня из скалярного квадрата
этого вектора. Норму вектора х обозначим | х J, тогда по определению
Норма вектора обладает следующими свойствами: 1) |хЦ = О тогда и только тогда,
158
когда х = 0; 2) |ах|| = |а|||х J, где а-действительное число; 3) |(х, у)|^Цх|Цу||;
Неравенством Коши - Буняковского называют неравенство
(918)
а неравенством треугольника - неравенство
|х + у|<|х|+|у||. (9.19)
Запишем норму и неравенства (9.18), (9.19) для векторов (элементов) каждого
из рассмотренных выше евклидовых пространств.
В евклидовом пространстве У3 с обычным определением скалярного произведения
норма вектора совпадает с его длиной, т. е. Ца|| = |а|; это следует из формул
а2=|а|2 и (9.17). Неравенства (9.18) и (9.19) принимают соответственно вид
| (a, b)|<|a|-|b|, [ а + b|<|а|+|b|. Отметим, что неравенство | (а, Ь)|<|а|• |b|
следует из формулы (3.18). Неравенство |a+b|<|a|+|b| следует из определений
суммы векторов и длины вектора; оно имеет простой геометрический смысл (в тре-
угольнике сумма д лин двух сторон больше длины третьей стороны).
В евклидовом пространстве С [а, Ь] норма элемента x(t) определяется формулой
П
h(o||=J р(ол,
неравенства (9.18) и (9.19) принимают вид
ь
jx(f)y(t)dt<Z
b
[х2(Г)Л
b
[y2(t)dt,
ь
f(x(0 + y(r))2 dt <
b
\y2(j)dt.
b
[x\t)dt +
a
В евклидовом пространстве E„ co скалярным произведением (9.15) норма
элемента х = (х1э х2,..., х„ ) определяется формулой
||х|| = 1/х12+х22 + -’-+х2.
а неравенства (9.18) и (9.19) принимают вид
| ЗД +х2у2 + - + х„у„\<-jxt +xl + - + xt-jy2+y*+- + y2,
+У1)2 +(Х2 +у2У+ -+{х„ + у„)2 <
<7л,2+х2+- + х2+7у12 + У2+” + >2.
ISO
Угол между двумя векторами евклидова пространства. Углом между, двумя
векторами х и у евклидова пространства называется угол <р, для которого
(х. v5
cos<p = ц п-п jr (0 < ф < 2л). (9.20)
Отметим, что в пространстве V3 всех свободных векторов введенное понятие угла
совпадает с понятием угла, рассматриваемого в векторной алгебре.
Два вектора евклидова пространства называются ортогональными, если их скаляр-
ное произведение равно нулю. Очевидно, нуг^вой вектор ортогонален любому другому
вектору. В пространстве У3 ортогональность векторов означает их перпендикулярность.
Из определений следует, что ненулевые векторы х и у ортогональны тогда и
только тогда, когда созф = 0.
Равенство
| (х> У) | = йх I II УI <9-21)
выполняется тогда и только тогда, когда х и у коллинеарны ( у = ах ). Другими словами,
в формуле (9.18) равенство достигается лишь в случае коллинеарности векторов х и у.
Ортонормироваиный базис. Система векторов а(,а2,...,а„ называется ор-
тогональной, если эти векторы ортогональны, т. е. (aj,at) = 0 при i*k.
Теорема 9.7. Ортогональная система ненулевых векторов линейно независима.
Вектор а называется нормированным или единичным, если || а || = 1. Если а -
ненулевой вектор, то каждый из векторов
будет нормированным. Нахождение для данного вектора нормированного вектора
по формулам (9.22) называется нормированием данного вектора, а множитель
ц = 1/±||а|| - нормирующим множителем.
Система векторов е(, е2,..., е„ называется ортонормированной, если она орто-
гональна и каждый вектор является нормированным, т. е.
(е„е*) =
0, при i*k,
1, при i = k,
(9.23)
где i,& = 1,2,...,л.
Базис п-мерного евклидова пространства называется ортонормированным, если
базисные векторы образуют ортонормированную систему.
Теорема 9.8. Во всяком евклидовом п-мерном пространстве (п > 2) суще-
ствует ортонормироваиный базис.
Выражение скалярного произведения через координаты векторов в орто-
нормированием базисе. Пусть в n-мерном евклидовом пространстве фиксирован
ортонормироваиный базис е,, е2,..., е„ и даны векторы этого пространства
х = х1е1+х2е2 + -+х„е„, у = у1е| + у2е2 + — + у„е„. (9.24)
160
Скалярное произведение этих векторов выражается формулой
(х, у) = х, у, + х2 у2 + — +х„у„. (9.25)
Отсюда следует, что
|| х || = 7(х, х) = ф^+Хг+'+х*.
9.8. Унитарное пространство
Комплексное линейное пространство U называется унитарным пространством,
если каждой паре векторов х, у е U поставлено в соответствие комплексное чис-
ло, обозначаемое (х, у) и называемое скалярным произведением векторов х и у,
причем выполняются следующие аксиомы: I. (х, у) = (у, х),
П. (х+у, z) = (x, z)+(y, z), III. (ax, y) = a(x, у), IV. (x,x)>0 если x*0, для
всех x, у, zet/ и всех aeC (С - множества комплексных чисел).
Замечание. Черта означает комплексную сопряженность: (у,х) -
комплексное число, сопряженное комплексному числу (у, х).
Из аксиом скалярного произведения в унитарном пространстве вытекают сле-
дующие свойства:
1) (х, у+z) = (х, у)+(х, z) для любых х, у, z е U;
2) (х, ay) = а (х, у) для любых х, у е U и любого a е С;
3) (0, х) = (х, 0) = О для любого хе С7;
'к I Л к I
4) £аЛ, =£ ^аДО^).
< 1=1 7=1 ) i=l 7=1
Примером унитарного пространства является множество С„ упорядоченных
систем п комплексных чисел
x=(al,a2,...,a„), у = (Р1,Р2,...,р„),...,
для которых скалярное произведение определено формулой
(х, у) = а,р, + а2 р2 + - •+а„р„,
где р* — комплексное число, сопряженное числу Pt (к = 1,2,..., и).
Унитарным преобразованием комплексного линейного пространства называется
линейное преобразование, сохраняющее положительно определенную эрмитову форму
Х|Х] +х2х2 ч--*-х„хп, где х(,х2, координаты вектора пространства. В ор-
тонормированием базисе относительно эрмитова произведения, задаваемого этой фор-
мой, унитарное преобразование записывается унитарной матрицей, унитарной матри-
цей называется квадратная невырожденная матрица А, удовлетворяющая условию
А~' = Ат, где Л-1 - обратная матрица, Ат - транспонированная и комплексно-
сопряженная матрица. Определитель унитарной матрицы по модулю равен единице.
Все характеристические корни унитарной матрицы по модулю равны единицы. Всякая
(действительная) ортогональная матрица есть в то же время унитарная матрица.
6 Зак. 1
161
Глава 10
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
(ЛИНЕЙНЫЕ ОПЕРАТОРЫ)
10.1 . Линейное преобразование и его матрица
Если указано правило/, по которому каждому вектору х линейного простран-
ства V ставится в соответствие единственный вектор у этого пространства, то бу-
дем говорить, что в нем задано преобразование (отображение, оператор) / или
задано преобразование пространства V в себя, и писать /: V —> V. Говорят также,
что преобразование / переводит вектор х в вектор у, и пишут у = /(х). Вектор у
называют образом вектора х, а х - прообразом вектора у.
Преобразование, при котором каждый вектор имеет единственный прообраз,
называется взаимно однозначным (или биективным).
Преобразование / линейного пространства V называется линейным преобразо-
ванием (линейным оператором), если для любых векторов этого пространства
хь х2, х и любого действительного числа Л. выполняются условия
1)/(х, + х2) = /(х,)+/(х2); 2)/(Хх) = Х/(х).
(Если рассматривается комплексное пространство, то X - любое комплексное число.)
Из этих условий следует, что
/(ах1+рх2) = а/(х1)+р/(х2), (10.1)
где а, Р - любые числа (действительные или комплексные). Обратно, из равенст-
ва (Ю.1) следуют условия 1) и 2). Итак, линейное преобразование (линейный опе-
ратор) определяется равенством (10.1).
Отметим, что линейное преобразование переводит нулевой вектор в нулевой,
так как, согласно условию 2), /(0) = /(0х) = 0/(х) = 0.
Простейшим примером линейного преобразования является тождественное
преобразование или преобразование /(х) = х, т.е. преобразование, которое каж-
дому вектору линейного пространства ставит в соответствие тот же вектор. Ли-
нейное преобразование будет вполне определено, если заданы образы базисных
векторов рассматриваемого пространства.
Пусть/-линейное преобразование л-мерного линейного пространства, пере-
водящее базисные векторы е„ е2.е„ в векторы е{, е2,..., е'. Каждый из по-
следних векторов разложим по базису:
ej =а1|е|+а21е2+--+а„,е„,
е2 = °12е1 +а22е2 "* •'ал2*л
< = Я1„С| +а2„е2 +"+л,„,х„.
162
Матрица
а11 а12 а1п
А_ °21 а22 °2п
. °nl ал2 ”• ат .
в которой fc-й столбец состоит из координат
вектора ej. (к = 1,2,..., я), называется мат-
рицей линейного преобразования f в базисе
е2,...,е„; ранг г матрицы А называется
рангом преобразования f а число (я-г) -
дефектом этого преобразования. Итак, каждому линейному преобразованию я-
мерного линейного пространства соответствует матрица порядка п в данном бази-
се; и наоборот, каждой матрице порядка л соответствует линейное преобразование
л-мерного пространства.
Отметим, что матрица тождественного преобразования в любом базисе будет
единичной; обратно, любой единичной матрице я-го порядка соответствует тож-
дественное преобразование линейного я-мерного пространства.
Пример 10.1. В пространстве V2 всех свободных векторов на плоскости
определим преобразование поворота всех векторов вокруг начала координат на угол
<р. Каждому вектору х (рис. 10.1) этой плоскости ставим в соответствие вектор
у = /(х), полученный вращением вектора х на один и тот же угол ф. Это преобра-
зование является линейным, поскольку условия 1) и 2), определяющие линейное
преобразование, будут выполнены. Найдем матрицу этого линейного преобразова-
ния в базисе i, j. (рис. 10.2, а, б). Так как /(i) =ОА + ОВ= 1со5ф + ]5тф,
/(j)= ОС+ OD =-15Щф +)С05ф, то
163
10.2 . Линейное преобразование в координатах
Рассмотрим линейное преобразование f «-мерного линейного пространства, за-
данное в некотором базисе е„ е2,..., е„ матрицей
ап ап ••• а1п
«21 «22 — «2„ /1П-ч
_ ап\ ап2 ••• апп _
Координаты вектора х и его образа у = /(х) известны:
х = х,е, +х2е2 +-+х„е„, /(х) = у,е, +у2е2 + — +-у„е„. (10.3)
Зависимость между координатами векторов х и у выражается формулами
у, = апх, +а12х2 +-+а1пх„,
У2 =а21Х1 +а22Х2 >'а2пХп’ ппм
У„ = «„1*1 + «„2*2 +•••+«№*„
Формулы (10.4) можно записать в матричном виде
Y=AX, (10.5)
где А определяется формулой (10.2), аХи Y - формулами
Если переменные у,,у2, связаны с переменными xt,x2,...,x„ форму-
лами (10.4), то будем говорить, что задано линейное однородное преобразование
переменных с матрицей А, переводящее переменные xlsx2,...,x„ в переменные
у(, у2,..., у„. Оно обладает теми же свойствами, что и линейное преобразование
«-мерного линейного пространства. Линейное однородное преобразование пере-
менных (10.4) или (10.5) называется невырожденным, если det А Ф 0.
Замечание. При рассмотрении линейных преобразований (линейных
операторов) пользуются и другими обозначениями. Если у = /(х), где /-
линейное преобразование (линейный оператор) с матрицей А в некотором базисе,
то пишут у = Ах. Условия 1) и 2), определяющие линейное преобразование, мож-
но записать в виде А (х, +х2)= Лх, + Ах2, А(кх) = кАх.
164
10.3 . Зависимость между матрицами одного
и того же преобразования в различных
базисах. Подобные матрицы
В n-мерном 'линейном пространстве фиксируем два базиса: е,,е2.е„ и
е,, е2,..., е'; первый из них назовем старым, второй - новым. Предположим, что
известно преобразование, переводящие старый базис в новый.
Теорема 10.1. Если е|,е2,...,е„ и ej,e2,...,e' — два базиса линейного про-
странства, А - матрица линейного преобразования в старом базисе е„ е2,..., е„,
то матрица В этого преобразования в новом базисе е,, е2,..., е' имеет вид
В=Т~'АТ. (10.6)
где Т — матрица перехода от старого базиса к новому.
Следствие. Если линейное преобразование имеет невырожденную
матрицу в некотором базисе, то матрица этого преобразования будет невыро-
жденной в любом другом базисе.
Матрица В называется подобной матрице А, если существует невырожденная
квадратная матрица С, удовлетворяющая равенству В = С'АС.
Две квадратные матрицы А и В порядка п тогда и только тогда являются мат-
рицами одного и того же линейного преобразования пространства V„ в соответст-
вующих базисах, когда матрица В подобна матрице А.
Пример 10.2. В базисе e,,e2 преобразование/имеет матрицу
Найти матрицу преобразования/в базисе ej = 2е, + е2, е2 = бе, + 4е2.
Так как
2 61 r-i И 4 -61 = Г 2 -3
1 4J’ 2 L-1 2j [-0,5 1
то по формуле (10.6) получаем
10.4 . Характеристическое уравнение линейного
преобразования
Теорема 10.2. Если линейное преобразование f в базисе ev,e2,...,e„ имеет
матрицу Айв базисе е[, е2,..., е' - матрицу В, то
det (А - ХЕ) = det (В-ХЕ), (10.7)
где X — любое действительное число, Е - единичная матрица п-го порядка.
165
Отметим, что det (А - кЕ) является многочленом степени и относительно X и
называется характеристическим многочленом матрицы А или характеристическим
многочленом линейного преобразования f
Замечание. Равенство (10.7) означает, что характеристический много-
член линейного преобразования остается неизменным при переходе к новому ба-
зису; матрица линейного преобразования меняется.
Характеристическим уравнением линейного преобразования называется уравнение
det (Л-ХЕ) = 0, (10.8)
где А — матрица этого преобразования в некотором базисе. Очевидно, характери-
стическое уравнение не зависит от выбора базиса. Уравнение (10.8) называют
также характеристическим уравнением матрицы А, а корни уравнения -
характеристическими числами линейного преобразования f или характеристиче-
скими числами матрицы А.
Если линейное преобразование f в некотором базисе е|,е2,...,ея имеет
квадратную матрицу n-го порядка A = (ait), то характеристическое уравнение
(10.8) запишется так:
аи ап ••• а1п
а21 а22~^ ••• а2п
(10.9)
Левая часть равенства (10.9) является характеристическим многочленом
матрицы А; обозначим его Р„(к), тогда характеристическое уравнение
(10.9) примет вид Р„(Х) = 0.
Пример 10.3. Найти характеристический многочлен и характеристи-
ческие числа матрицы
4
Л= 2
-2
-2
1
В соответствии с определением характеристического многочлена получаем
Р„^)=
1
-1 -2
1-Х —2
-1 1-Х
Рп(Х) = (4-Х) (1-Х)2+4+2+2 (1-Х)+2(1-Х)-2 (4-Х) =-Х3 + бХ2-11Х+6.
Приравнивая этот многочлен нулю, находим характеристическое уравнение
-X3 +6Х2-11Х+6 = 0 или Х3-6Х2 +11Х—6 = 0. Разлагая левую часть этого
166
уравнения на множители X5-6Х2+11Х-6= X3-X2-5Х2+5Х+6Х-6 =
= Х2(Х— 1)-5Х (Х-'1) + 6(Х-1) = (Х-1) (X2 -5Х + 6), приводим данное уравне-
ние к виду (Х-1)(Х2-5Х + 6) = 0, откуда Х,=1, Х2 = 2, Х3=3. Эти корни -
характеристические числа данной матрицы.
10.5. Собственные векторы линейного
преобразования
Ненулевой вектор х линейного пространства называется собственным век-
тором линейного преобразования f этого пространства, если существует
число к такое, что
/(х)=*х, (10.10)
причем к - действительное число для действительного линейного пространства и
комплексное число в случае комплексного пространства. Число к называется соб-
ственным значением вектора х относительно преобразования/. Равенство (10.10)
можно записать в матричном виде
АХ = кХ, (10.11)
где А - матрица преобразования / в некотором базисе, X - матрица-столбец из
координат собственного вектора х в том же базисе. Ненулевая матрица-столбец X,
удовлетворяющая уравнению (10.11), называется собственным вектором-столбцом
матрицы А с собственным значением к.
Собственные векторы и собственные значения обладают следующими свойствами.
1. Собственный вектор линейного преобразования имеет единственное
собственное значение к.
2. Если х- собственный вектор линейного преобразования / с собственным
числом к и X - любое, отличное от нуля число, то Хх - также собственный век-
тор преобразования / с собственным значением к
3. Если х и у - линейно независимые собственные векторы линейного пре-
образования/ с одним и тем же собственным значением к, то х + у - также соб-
ственный вектор этого преобразования с собственным значением к.
4. Если х и у - собственные векторы линейного преобразования/с собствен-
ными числами к и т, причем к*т, то х и у линейно независимы.
Следствие. Если х1,х2,...,хт — линейно независимые собственные
векторы линейного преобразования f с одним и тем же собственным значением к,
то любая нетривиальная линейная комбинация этих векторов является собст-
венным вектором этого преобразования с собственным значением к.
Теорема 10.3. В комплексном линейном пространстве все корни
характеристического уравнения и только они являются собственными
значениями линейного преобразования.
167
Координаты собственного вектора х = (х1,х2,...,х„) находятся из систе-
мы уравнений (ап - к) х, + а|2х2 + • - + ainx„ = 0, а2Л+(<’22-*)л2+-+а2яхл=0, ч (10.12)
мы х, + а„2х2 + • • • + (а„„ - к) х„ = 0.
Эта система имеет ненулевое решение тогда и только тогда, когда ее определитель
равен нулю (см. следствие из теоремы Крамера), т. е.
а,,-* о12 ... а1п а21 а22~к ••• а2п а„1 а„2 ... ат-к = 0.
(10.13)
Это означает, что число к является корнем характеристического уравнения.
Замечания. 1. Уравнение (10.13) является алгебраическим уравнением ri-
ft степени относительно к. Такое уравнение имеет ровно п корней, считая равные и
комплексные. Среди корней этого уравнения может не оказаться действительных.
2. Собственными значениями линейного преобразования действительного
пространства являются только действительные корни характеристического уравнения.
Собственные значения линейного преобразования называются также собствен-
ными значениями матрицы этого преобразования. Собственное значение называется
m-кратным, если оно является m-кратным корнем характеристического уравнения.
Теорема 10.4. Корни характеристического уравнения действительной
симметрической матрицы являются действительными числами.
Следствие. Действительная симметрическая матрица имеет только
действительные собственные векторы.
Система (10.12) для определения координат собственного вектора в этом случае
имеет только действительные решения, так как а^ мк- действительные числа.
Теорема 10.5. Собственные векторы действительной симметрической
матрицы, соответствующие различным собственным значениям, ортогональны.
Пример 10.4. Найти действительные собственные значения и собствен-
ные векторы линейного преобразования с матрицей
4-5 7
-4 9
0 5
Составляем характеристическое уравнение матрицы А
4-Х -5 7
1 -4-Х 9
-4 0 5-Х
= 0 или Х3-5Х2+17Х-13 = 0.
168
Разложим на множители многочлен в левой части уравнения: К3 -
-512+171-13= 13-12-412 + 41+131-13=12(1-1)-41(1-1)+13(1-1) =
= (1-1)(12-41+13). Уравнение принимает вид (1-1)(12-41+13)= О, откуда
1,=1, 12=2—31, Х3 = 2+3i. Следовательно, линейное преобразование с данной
матрицей имеет только одно действительное собственное значение 1 = 1.
Для отыскания соответствующего собственного вектора используем систему
уравнений (10.12), которая принимает вид
(4-1)л, -5х2 +7х3 =0, Зх, -5х2 +7х3 =0,
х, -(4 + 1)х2 + 9х3 =0, и х, -5х2 + 9х3 = 0,
-4х, +(5-1) х3 = 0 -4х, + 4х3 = 0
при 1 = 1. Решая полученную систему, находим х, = х3, х2 = 2х3. Полагая х3 = 1,
получаем собственный вектор х = (1,2,1).
Замечание. Собственный вектор линейного преобразования определяет-
ся с точностью до произвольного множителя (см. свойство 2 собственного вектора).
10.6 . Приведение матрицы линейного
преобразования к диагональному виду
Теорема 10.6. Матрица линейногопреобразования имеет диагональный вид
а,, 0 ... 0
.0 0 ... а„„
тогда и только тогда, когда каждый базисный вектор является собственным
вектором этого преобразования.
Матрица А называется приводимой к диагональному виду, если существует не-
вырожденная матрица Т такая, что матрица Т~'АТ = В является диагональной.
Следовательно, если матрица А приводима к диагональному виду, то
' 1, 0 ... 0'
0 12 ... о
В =
О О ... 1„
где 1„ 12,..., 1п - характеристические числа матрицы А.
Теорема 10.7. Матрица А линейногопреобразования f п-мерного линей-
ного пространства приводима к диагональному виду тогда и только тогда ,
когда существует базис этого пространства , состоящий из собственных
векторов данного преобразования.
Если все собственные числа матрицы А попарно различны, то матрица
приводится к диагональному виду.
169
10.7 . Действия над линейными преобразованиями
Произведение преобразований. Рассмотрим преобразование/, переводящие
вектор х в вектор у, т. е. у = /(х). К вектору у применим преобразование g,
переводящие вектор у в вектор г, т. е. z = g (у). Так как у = /(х), то имеем
преобразование z=g(/(x)), переводящее вектор х в вектор z, причем z по-
лучен в результате последовательного применения преобразований / и g. Пре-
образование, заключающееся в последовательном применении преобразова-
ний / и g, называется произведением- преобразования / на преобразование g
или композицией этих преобразований и обозначается g ° / (или просто gf);
отметим, что справа записывается первое преобразование. Таким образом,
g°/(x) = g (/(*))• (10.15)
Произведение линейных преобразований является линейным преобразованием.
Теорема 10.8. Если в некотором базисе линейные преобразования/и g
имеют соответственно матрицы А и В, то их произведение gf в том же
базисе имеет матрицу ВА.
Сумма преобразований. Суммой преобразований / и g некоторого про-
странства называется преобразование h такое, что для любого вектора х
этого пространства
Л(х) = /(х)+£(х). (10.16)
Сумму преобразований/и g будем обозначать /+g. Очевидно /+g = g + f.
Теорема 10.9. Если линейные преобразования f и g в некотором базисе
имеют соответственно матрицы А и В, то преобразование /+g в том же
базисе имеет матрицу А + В.
Пример 10.5. Даны два линейных преобразования
х{ = 7х1 + 4х3, х" = х'2 — 6х3,
Х2 = ^Х2 -9х3, Х2 = Зх,' + 7Ху,
Ху = 3xt +Х2, хз=х1 +х2 ~х3-
Средствами матричного исчисления найти преобразование, выражающее
х" х2, х3 через х„ х2, х3.
Первое преобразование задано матрицей А, второе - матрицей В, где
А = ’7 0 4‘ 0 4-9 3 1 0 ев и 1 1 н- UJ о к- о К- л м; 1 1
170
Искомое преобразование в соответствии с теоремой 10.8. имеет матрицу ВА.
Умножив матрицу В на матрицу А, получим
0 1 -6' 7 0 4 -18 -2 -9
3 0 7 0 4 -9 = 42 7 12
1 1 -1 3 1 0 4 3 -5
Следовательно, искомое преобразование определяется формулами
Х]"=—18х] — 2х2 — 9х3, х2 = 42Л] + 7x2+12x3, х"=4х1 +Зх2—5х3.
10.8 . Невырожденные линейные преобразования.
Преобразование, обратное данному
Линейное преобразование называется невырожденным, если его матрица является не-
вырожденной; в противном случае линейное преобразование называется вырожденным.
Теорема 10.10. Линейное преобразование является невырожденным тогда
и только тогда, когда оно взаимно однозначно.
Следствие. Линейное невырожденное преобразование ненулевой век-
тор переводит в ненулевой; обратно также верно: если линейное преобразование
ненулевой вектор переводит в ненулевой, то оно будет невырожденным.
Теорема 10.11. Произведение двух линейных невырожденных преобразова-
ний есть невырожденное линейное преобразование. Преобразование <р называет-
ся обратным преобразованию/, если для любого вектора х
/<р(х) = <р/(х)=х, (10.17)
т. е. произведение этих преобразований является тождественным преобразовани-
ем. Из определения следует, что если <р — преобразование, обратное преобразова-
нию / то/— преобразование, обратное <р. Преобразования/и <р, удовлетворяющие
условию (10.17), называются взаимно обратными.
Линейное преобразование имеет обратное преобразование тогда и только то-
гда, когда оно является невырожденным.
Для любого невырожденного линейного преобразования с матрицей А в неко-
тором базисе существует единственное обратное преобразование с матрицей Л-1
в том же базисе.
Пример 10.6. Найти линейное преобразование, обратное преобразова-
нию J] =2Xj-х3, у2=-Зхх+х2+х3, y3=2xi-x2.
Это преобразование имеет матрицу А, определитель которой отличен от нуля,
поэтому для него существует обратное преобразование с матрицей Л-1. Так как
2 0 -Г 1 11
Л = -3 1 1 . л-' = 2 2 1
2-1 0 1 2 2
то обратное преобразование выражается формулами X] = yt + у2 + у3,
х2 = 2у! +2у2 + у3, х3 = + 2у2 + 2у3.
171
10.9 . Ортогональные матрицы
Матрица
в11 в12 ”• в1л
а21 а22 в2л
(10.18)
вл1 вл2 ••• ат
называется ортогональной, если соответствующая ей система векторов
Я1(а11»в21>-">вл1)’ Я2(в12>в22>"->вл2)’ •••’Ял(в1л»в2л>-”>влл) (10.19)
является ортонормированной.
Векторы (10.19) будут ортонормированиями (см. п. 9.7), если
п
к=1
i-J;
(10.20)
для любых i, J (irj = 1,2,..., п).
Примеры ортогональных матриц:
cosa —sina
sin a cosa
0,8 -0,6
-0,6 -0,8
1 0
0 1
Отметим, что единичная матрица любого порядка является ортогональной.
Теорема 10.12. Необходимое и достаточное условие ортогональности
матрицы А выражается равенством
АГА = Е, (10.21)
где А1 - матрица, полученная из матрицы А транспонированием, Е -
единичная матрица того же порядка, что и А.
Следствие 1. Модуль определителя ортогональной матрицы
равен единице.
Следствие 2. Ортогональная матрица является невырожденной
матрицей.
Следствие 3. Произведение двух ортогональных матриц есть ортого-
нальная матрица.
Следствие 4. Равенство Аг ~А~1 выражает необходимое и доста-
точное условие ортогональности матрицы А.
Следствие 5. Матрица, полученная транспонированием ортогональ-
ной матрицы, является ортогональной.
Следствие 6. Матрица, обратная ортогональной матрице, является
ортогональной.
172
Замечания.1. Из условия det/l = ±l не следует, что А-
[2 31
ортогональная матрица. Например, матрица А= , для которой detj = l, не
является ортогональной, так как А1 А * Е.
2. Сумма ортогональных матриц не является ортогональной матрицей.
3. Необходимое и достаточное условие ортогональности матрицы А мож-
но выразить равенством АА? = Е.
Теорема 10.13. Матрица перехода от одного ортонормированного базиса
к другому является ортогональной.
10.10 . Ортогональные преобразования
Линейное преобразование евклидова пространства называется ортогональным,
если в некотором ортонормированном базисе его матрица ортогональна.
Теорема 10.14. Линейное преобразование евклидова пространства являет-
ся ортогональным тогда и только тогда, когда оно ортонормироваиный базис
переводит в ортонормироваиный.
Теорема 10.15. Ортогональное преобразование не меняет скалярного про-
изведения векторов.
Следствие 1. При ортогональном преобразовании f остается неиз-
менной норма вектора, т.е. Ц х || = J /(х) Ц.
Следствие 2. При ортогональном преобразовании f остается неиз-
менным угол между векторами, т. е.
(х, У) (/(х), /(у))
11М-1|у|Гк«М1/.(у)1Г
Ортогональные преобразования обладают следующими свойствами.
1. Ортогональное преобразование является невырожденным.
2. Для любого ортогонального преобразования существует обратное преобра-
зование, являющееся ортогональным.
3. Если ортогональное преобразование имеет матрицу А, то обратное ему
преобразование имеет матрицу Лт.
4. Произведение двух ортогональных преобразований является ортогональ-
ным преобразованием.
173
Глава 11
КВАДРАТИЧНЫЕ ФОРМЫ
11 .1. Квадратичная форма и ее матрица
Квадратичной формой /(хъх2,...,х„) п действительных переменных
л?!, х2,..., х„ называется сумма вида
f(x\, х2,..., х„ ) = вцХ2 + в12Х!Х2 + — + alnxtx„ +
+ «21*2*1 + «22*2 ++ О2пХ2Х„ + ....
+ агЛх„х1 +а„2х„х2 + ---+атх^,
или
/(*i, х2,..., х„) = '^aljxix1, (11.2)
;=i j=\
где atj - некоторые числа, называемые коэффициентами. Не ограничивая общ-
ности, можно считать, что а у = а;Г
Квадратичная форма называется действительной или комплексной в зависимости
от того, являются ли ее коэффициенты соответственно действительными или ком-
плексными числами. Будем рассматривать действительные квадратичные формы.
Матрицей квадратичной формы называется матрица, составленная из ее
коэффициентов. Квадратичной форме (11.1) соответствует единственная
симметрическая матрица
«11 «12 ••• «1л
в21 а22 а2п ... ,,
_ «л1 «л2 ат .
И наоборот, всякой симметрической матрице (11.3) соответствует единственная
квадратичная форма с точностью до обозначения переменных.
Рангом квадратичной формы называют ранг ее матрицы. Квадратичная форма
п переменных называется невырожденной, если ее матрица невырожденная, т. е.
г = и, и вырожденной, если г <п.
Квадратичную форму (11.1) и переменных х2, ...,х„ можно записать в мат-
ричном виде. Действительно, если X- матрица-столбец из переменных
174
xl,x2,...,x„, Хт - матрица, полученная транспонированием матрицы X, т.е.
матрица-строка из тех же переменных, то
f(Xt,X2,...,X„)=XTAX, (11.4)
где А определяется формулой (11.3).
Пример 11.1. Записать матрицу квадратичной формы f(X\,X2,Xi) =
= Х\ — 6Л]Л2 - 8xjX3 + 7х2 + 4х2х3 - 5х3 и найти ее ранг.
В данном случае Дц = 1, й|2 ~ ^21 ~ ^13 ' ^31 = ^22 ~ 7, о2з =
= а32 = 2, а33 = -5, поэтому
1
-3
—4
-3
7
2
-4
2
-5
Вычислим определитель этой матрицы
detA =
1
-3
-4
-3 -4
7 2 =-35 + 24 + 24-112 + 45-4 = -58.
2 -5
Так как detA*O, то ранг матрицы равен трем (г = 3). Эта квадратичная форма
является невырожденной, поскольку г = п.
11 .2. Преобразование квадратичной формы при
линейном однородном преобразовании
переменных
Рассмотрим квадратичную форму (11.1). Перейдем к новым переменным
Ум Ут> •. Уп по формулам
х, = + bny2 ++ b}„y„,
х2 = А21>1 + b22y2 ++ Ь2„у„, „
хп = Ьп\У1 + Ьп2Уг + • • + ь„пУ„.
или в матричном виде
X = BY, (11.6)
175
форму ф (ух, у2,, у„) п переменных с некоторой матрицей С. В этом случае го-
ворят, что квадратичная форма f(xx, х2, переводится в квадратичную форму
Ф(у(, у2,...,уи) линейным однородным преобразованием (11.5). Линейное одно-
родное преобразование (11.6) называется невырожденным, если det В * 0.
Две квадратичные формы называются конгруэнтными, если существует невы-
рожденное линейное однородное преобразование, переводящее одну форму в дру-
гую. Если f(xx,x2,...,x„) и ф(у>1,у2,...,у„)конгруэнтны, то будем писать
Дх1,х2,...,хи)~ф(у1,у2,...,у„).
Свойства конгруэнтности квадратичных форм.
I- f(xx,x2,.... хл) ~/(Хр х2,..., х„) .
2. Если /(хрх2,...,х„)~ф(уру2,...,у„), q>(yx,y2,...,y„)~v(zx,z2,...,z„),
то /(хр х2,..., х„) ~у (z„z2,..., z„).
Теорема 11.1. Квадратичная форма f(xx,x2, ...,х„) с матрицей А линей-
ным однородным преобразованием X = BY переводится в квадратичную форму
ф(У1,у2>...,у„) сматрицей С=В1АВ.
Следствие 1. Определители матриц конгруэнтных невырожденных
действительных квадратичных форм имеют одинаковые знаки.
Следствие 2. Конгруэнтные квадратичные формы имеют одинаковые ранги.
11.3. Приведение действительной квадратичной
формы к нормальному виду
Квадратичная форма /(хрх2.....х„) называется канонической, если она не
содержит произведений различных переменных, т. е.
Г
f{xux2,...,x„)='^alixf (г<п). (11.8)
>=1
Каноническая квадратная форма называется нормальной (или имеет нормаль-
ный вид), если | аи | = 1 (г = 1,2,..., г), т. е. отличные от нуля коэффициенты при
квадратах переменных равны +1 или —1. Например, квадратичная форма
/(хр х2, х3, х4) = 6х^+4х3 -Зх4, для которой ап = 6, а22 = 0, а33 = 4, =—3,
имеет канонический вцд; квадратная форма /(хрХ2, х3,х4)=хр- —х3+х4 явля-
ется нормальной, так как ап =1, а22 = 0, а33=-1, а44 = 1.
Теорема 11.2. Любая квадратичная форма некоторым невырожденным
линейным преобразованием может быть приведена к каноническому виду
Ф (?1. >2 . • • • > Уп ) = Ь1 irf + Ь22У1 + - + ь„пУю
где У1’У2’---’Уп ~ новые переменные.
Некоторые из коэффициентов Ь„ могут оказаться равными нулю; число отличных
от нуля коэффициентов в этой формуле равно рангу г матрицы квадратичной формы ф.
176
Теорема 11.3. Любую действительную квадратичную форму линейным не-
вырожденным преобразованием можно привести к нормальному виду
z2,...,z„) = z12+z2+- + z2_1-z^-z2.
Число входящих сюда квадратов равно рангу формы.
11.4. Закон инерции квадратичных форм
Закон инерции квадратичных форм выражает
Теорема 11.4. Число положительных и число отрицательных квадратов в
нормальном виде, к которому приводится данная действительная квадратичная
форма невырожденным действительным линейным преобразованием, не зависит
от выбора преобразования.
Число положительных квадратов в нормальной форме, к которой приводится
данная действительная квадратичная форма, называют положительным индексом
инерции этой формы, число отрицательных квадратов - отрицательным индек-
сом инерции, разность между положительным и отрицательным индексами инер-
ции — сигнатурой формы/ Если известен ранг формы, то задание любого из трех
указанных выше чисел определяет два других.
Теорема 11.5. Две действительные квадратичные формы от п пере-
менных тогда и только тогда конгруэнтны, когда они имеют одинаковые
ранги и одинаковые сигнатуры.
11.5. Знакоопределенные квадратичные формы
Действительная квадратичная форма f(xx,x2,...,x„) называется положитель-
но-определенной, если она приводится к нормальному виду, состоящему из п по-
ложительных квадратов: f(xx, х2,..., х„) ~ <р (у2,..., уп ), где
Ф (Ур Уз.Ул) =>'12+У2+- + >'«> (Н.9)
т. е. если ранг и положительный индекс инерции равны числу неизвестных.
Систему значений х2,..., х„ назовем нулевой, если х, = х2 =... = = х„ = О,
и ненулевой, если хотя бы одно из них отлично от нуля.
Теорема 11.6. Действительная квадратичная форма f(xx,x2,...,xn) яв-
ляется положительно-определенной тогда и только тогда, когда она принимает
положительные значения при любой ненулевой системе значений переменных
хих2,...,х„.
Пусть дана квадратичная форма /(х1,х2,...,х„) с матрицей А = (ау). Глав-
ными минорами квадратичной формы/называются миноры
«п>
«11
«21
«12
«22
«11 «12 ••• «И
«21 «22 ••• а2к
«11 «12 " «1л
«21 «22 ••• «2л
аП а1с2 акк
«л1 «л2 ' * * • «/от
177
т. е. миноры порядка 1,2,..., п матрицы А, расположенные в левом верхнем углу;
последний из них совпадает с определителем матрицы.
Теорема 11.7. Квадратичная форма f{xux2,...,xH) с действительной
матрицей является положительно-определенной тогда и только тогда, когда
все ее главные миноры положительны.
Действительная квадратичная форма называется отрицательно-определенной, ес-
ли она является невырожденной и приводится к нормальному виду, содержащему
только отрицательные квадраты всех переменных; эту форму можно привести к виду
фО’1,Л»-»У.)в-^ ~У1------------------------------У*- (11.10)
Теорема 11.8. Квадратичная форма является отрицательно- определенной
тогда и только тогда, когда ее главные миноры четного порядка положительны,
а нечетного — отрицательны.
Положительно-определенные и отрицательно-определенные квадратичные
формы называются знакоопределенными квадратичными формами.
Вырожденные квадратичные формы, нормальный вид которых состоит из
квадратов одного знака, называются полуопределенными.
Неопределенными называются квадратичные формы, нормальный вид которых
содержит как положительные, так и отрицательные квадраты переменных.
Пример 11.2. Доказать, что квадратичная форма f(xx,x2,x3') =
= 6х2 + 5х2 + 7х3 - 4хрс2 + 4xjX3 положительно-определенная.
Запишем матрицу А этой квадратичной формы и определитель матрицы А:
6 -2 2‘ 6 -2 2
л = -2 5 0 , det Л = -2 5 0
2 0 7 2 0 7
= 26 и det Л = 162, т.е.
Так как главные миноры матрицы аи = 6,
все положительны, то данная квадратичная форма является положительно-определенной.
11.6. Приведение квадратичной формы
к каноническому виду ортогональным
преобразованием переменных
Теорема 11.9. Если существует ортогональное преобразование с матри-
цей С, приводящее действительную квадратичную форму /(х,, х2,..., х„ ) к ка-
ноническому виду
Ф (Тр >2> - ’ У„ ) = W + + +^„К2> (1111)
то А], Л2,..., — характеристические числа матрицы А квадратичной формы f
Теорема 11.10. Для любой действительной квадратичной формы сущест-
вует ортогональное преобразование, приводящее ее к каноническому виду.
Теорема 11.11. Для любой действительной симметрической матрицы А су-
ществует такая ортогональная матрица Т, что Т~1АТ — диагональная матрица.
178
Следствие. Любая действительная симметрическая матрица может
быть приведена к диагональному виду.
Теорема 11.12. Если линейное преобразование действительного линейного
пространства имеет действительную симметрическую матрицу в некотором
ортонормированном базисе, то существует ортонормированный базис, состоя-
щий из собственных векторов этого преобразования.
Из этих теорем следует правило нахождения ортогонального преобразования, при-
водящего квадратичную форму п переменных к каноническому виду. Эго правило со-
стоит в следующем: 1) записать матрицу данной квадратичной формы, найти ее собст-
венные значения и п попарно ортогональных собственных векторов, пронормировать
их; 2) составить матрицу из ортонормированных собственных векгор-столбцов;
3) записать искомое ортогональное преобразование с помощью последней матрицы.
Пример 11.3. Найти ортогональное преобразование, приводящее к
каноническому виду квадратичную форму двух переменных хь х2,
/(xt, х2) = 5Xj + 4^6х,х2 + 7х’.
Поскольку в данном случае ап = 5, = аг1 = 2-/б, = 7, то матрица А этой
квадратичной формы и ее характеристическое уравнение det (А - ХЕ) = 0 запишутся так:
Г 5 27б] 5-Х 2-/б „
2-J6 7 ’ 2з/б 7-Х
Характеристическое уравнение (5-Х)(7-Х)-24 = 0, или X’-12Х+ +11 = 0,
имеет корни Xj =1, X, =11, которые являются собственными значениями матрицы А.
Найдем собственные векторы, соответствующие полученным собственным
значениям. Координаты ($, /) этих векторов определяются из системы уравнений
(10.12), которая в данном случае имеет вид
(5-X)s+2V6t=0,0
2-7б5+(7-Х)/ = 0.
При Xj = 1, Х2 = 11 имеем две системы
4^ + 2-j6t = 0, -6s + 2-j6t = 0,
2у[бз + 6t = 0, 2-Убх — 4t = 0.
Из этих систем находим собственные векторы и = (- (з/б/2) t, t), v = ((т/б/з) t, t),
где t^O. Положив <!=-2, t2 =3, получим и = (4б, -2), v = (Тб,3).' Нормиро-
вав эти векторы, запишем их координаты в столбцы, составим матрицу В:
179
С помощью матрицы В записываем искомое ортогональное преобразование
или
Это преобразование приводит данную квадратичную форму к каноническому виду
<Р(У^У2) = У^+1^Уг-
11.7. Упрощение уравнений фигур второго
порядка на плоскости
Фигурой второго порядка на плоскости называется множество точек этой плоско-
сти, декартовы координаты которых удовлетворяют уравнению второй степени
ацх2 +2ai2xy + a22y2 + а13х + а23у + а33 = 0, (И 12)
где аи, а]2, а22 одновременно в нуль не обращаются. Отметим, что это множест-
во, в частности, может состоять из единственной точки или оказаться пустым.
Первые три члена левой части уравнения (11.12) образуют квадратичную фор-
му двух переменных = х, х2 = у:
f(x, у) = в! хх2 + 2аХ2ху+а22у2
с симметрической матрицей
ап а12
. °12 а22 .
По теореме 11.10 эту квадратичную форму ортогональным преобразованием мож-
но привести к каноническому виду
Л(^/) = ^'2+^2>''2
(1115)
с матрицей
с=р*
0
где А],Л2 - характеристические числа
ского уравнения матрицы А:
0
Л2
матрицы А, т. е. корни характеристиче-
(11.16)
ап~^ а12
а12 а22 **”
При этом ортогональном преобразовании уравнение (11.12) примет ввд
Х,х'2 + Х2у'2 + а'хзх‘ + а'^у' + а33 = 0. (11.18)
Это уравнение можно привести к каноническому виду путем выделения в левой
части полных квадратов.
Фигуру второго порядка, определяемую уравнением (11.12), называют
центральной, если detA#O, и нецентральной, когда detA = O.
= 0.
(11.17)
(11.13)
А =
(1114)
180
Отметим, что при ортогональном преобразовании переменных определитель
матрицы квадратичной формы не меняется, т. е. det С = det А. Так как
detC=XtX2 (см. (11.16)), то
det^ = X1X2. (11.19)
Пусть уравнение (11.18) определяет центральную фигуру, т. е. det А * 0. Здесь
возможны два случая: 1) ХД2 > 0 (числа X, и Х2 одного знака), фигура называ-
ется фигурой эллиптического типа; 2) ХД2 < 0 (числа X, и Х2 имеют разные
знаки), фигура называется фигурой гиперболического типа.
Если Х|Х2 * 0, то уравнение (11.18), выделив в его левой части полные квадра-
ты, можно привести к виду
- К )2 + М/ ~ М2 = Я
ИЛИ
Х,Х2+Х2Г2=9, (11.20)
где
X = x'-hl, Y^y'-hi. (П.21)
Формулы (11.21) выражают зависимость между координатами (х',у') и {X, Y)
при параллельном переносе координатных осей в точку XJ.
В случае > 0 уравнение (11.20) приводится к одному из канонических видов
%2/fl2 + r7fc2 = l, (11.22)
Х2/а2 + У2/б2=-1, (11.23)
Х2/а2 + Г2/б2=0 (11.24)
в зависимости от знаков 1, ид: 1) Х,д>0, 2) Х,д<0, 3) <? = 0.
Уравнение (11.22) определяет эллипс, уравнению (11.23) не удовлетворяют ко-
ординаты ни одной точки плоскости, уравнению (11.24) удовлетворяют координа-
ты одной точки (X = 0, Y = 0).
В случае ХД2 < 0 уравнение (11.20) приводится к одному из канонических видов
X2/a2-Y2/b2=l, (11.25)
X2/a2-Y2/b2=-l, (11.26)
X2la2-Y2lb2=Q (11.27)
в зависимости от знаков X, ид: 1) Xtg>0, 2) Ххд<0, 3) д = 0.
Уравнение (11.25) определяет гиперболу с действительной осью О:Х, уравне-
ние (11.26) - гиперболу с действительной осью O}Y, уравнение (11.27) - пару
пересекающихся прямых, так как оно распадается на два уравнения
£_£=0, *-Д=0, или уЛХ,Г=ЛХ.
a b а b а а
181
Обратимся к нецентральным фигурам, т.е. к случаю когда det ,4 = 0. В силу
(11.19) из равенства det А = 0 следует, что Х,Л2 = 0. Последнее равенство означа-
ет, что одно из чисел ХД2 равно нулю (оба числа , Х2 в нуль обратиться не
могут, так как это означало бы, что квадратичная форма (11.15) является вырож-
денной, чего быть не может, поскольку nf, + о,22 + а22 * 0 )• Если л23 * 0, то урав-
нение (11.18) можно привести к ввду Х1(х'-й|)2+а£3у'+д = 0 и записать так:
W-A.)2=-«w(/-^)- (11.28)
Осуществим параллельный перенос репера (Oj.eJ, е2) на вектор
ОО, = + Aje2, получим новую систему координат OtXY, причем X и У опре-
деляются формулами (11.21). Уравнение (11.28) приведем к ваду
X2 = 2pY. (11.29)
Уравнение (11.29) определяет параболу с осью OtY.
Если в уравнении (11.18) а23 = 0 (и Х2 = 0), то, выделив полный квадрат, его
можно записать так:
Х1(х'-Л|)2+9 = 0. (11.30)
Осуществив параллельный перенос репера (О,,е{, е2) на вектор ОО] = Aet,
т.е. выполнив преобразование X = x'—ht, Y = y', получим новую систему коор-
динат О, АТ, в которой уравнение (11.30) принимает один из видов:
Х2 = а2,Х2=-а2,Х2 = 0 (1131)
в зависимости от соотношения знаков чибел Х1 и q: ),tq > 0, X}q <0, q = 0. Пер-
вое из уравнений (11.31) определяет пару параллельных прямых X = а, X —-а,
второму уравнению не удовлетворяют координаты ни одной точки плоскости,
третье уравнение определяет пару совпавших прямых X = 0, X = 0.
Операция перехода от уравнения (11.12) к уравнению (11.18) называется отне-
сением фигуры к главным осям. Новые оси координат параллельны осям симмет-
рии фигуры. Главными направлениями фигуры, заданной уравнением (11.12), на-
зывают направления ортогональных собственных векторов матрицы квадратичной
формы, соответствующей этому уравнению.
Из теорем п. 11.6 следует, что существует декартова прямоугольная система
координат, в которой уравнение (11.12) принимает канонический ввд. Чтобы вы-
брать эту систему координат, необходимо сделать следующее.
1. Найти ортогональное преобразование, приводящее к каноническому виду
квадратичную форму, соответствующую данному уравнению.
2. С помощью этого преобразования определить главные направления фигу-
ры, т. е. векторы е{, е2 - ортонормированные собственные векторы матрицы
указанной квадратичной формы.
3. Найти уравнение фигуры в репере (О,, е{, е2).
4. Выделить полные квадраты в полученном уравнении.
5. Совершить параллельный перенос системы (£>],«{, с£) на соответствующий
вектор ОО, и составить каноническое уравнение фигуры в репере (Olse[,e2).
182
Пример 11.4. Какую линию на плоскости определяет уравнение
5х2 +4-Лху + 7у2 =22?
С помощью теории квадратичных форм приведем это уравнение к канониче-
скому виду. Левая часть уравнения - квадратичная форма f(x,y) =
5х2 +4-Лху + 7у2, которая с точность до обозначений переменных (xj=x,
х2 = У, У1 =х', у2 = у') (см. п. 11.6, пример 11.3) приведена к каноническому
виду <р(х', у')= х'2+11у'2 посредством ортогонального преобразования х =
= -^=-(Лх'+Лу'), у = -^=-(~Лх'+Лу').
Это преобразование данное уравнение переводит в уравнение
5 (Лх' + Лу ')2 )+(Лх' + Лу') (- Лх’ + Лу') +
+ у (-Лх’ + Лу')2 = 22, или х’2 +11/2 = 22.
Полученное уравнение определяет эллипс с полуосями а = Л1, b = Л-
11.8. Упрощение уравнений фигур второго
порядка в пространстве
Фигурой второго порядка в пространстве называется множество точек про-
странства, декартовы координаты которых удовлетворяют уравнению
аих2 + а22у2 + a33z2 + 2апху +2aI3xz + 2a23yz +
+ с14х + а24у + a34z + а44 = 0, (11.32)
где at । + fl22 + а33 + а12 + а13 + я23 0.
Сумма первых шести членов левой части уравнения (11.32) представляет собой
квадратичную форму трех переменных, х, у, z:
f(x, у, z) = a, ,х2 + а22у2 + a33z2 + 2о12ху + 2al3xz + 2aByz (11.33)
с симметрической матрицей
А =
«11
«12
.«13
«12
«22
«23
«в
«23
«33 .
(11.34)
Фигура второго порядка называется центральной, если det .<4*0, и нецен-
тральной, если det А = 0.
С помощью. ортогонального преобразования квадратичную форму (11.33)
можно привести к каноническому виду <р(х', у', z') = Х,х'2+Х2у'2+X3z'2, где
183
X^X^Xj - корни характеристического уравнения det (Л-ХЕ) = 0. Матрица
квадратичной формы ф =чр (х', у', z') принимает вид
X, 0 О'
С= 0 Х2 0 (11.35)
0 0 х3
Указанное ортогональное преобразование приводит уравнение (11.32) к виду
\х'2 + Х2у'2 + X3z'2 + а\Ах' + a'2iy' + a'34z' + а'^ = 0. (11.36)
Центральные фигуры. Если det A * 0, то det С = XjX2X3 * 0, так как
det Л = det С. Выделяя полные квадраты в левой части уравнения (11.36), можно
привести его к виду
Х^2+X2K2+X3Z2 = ц, (1137)
где X = x'—hl, Y=y'—h^ Z = z’-h3.
Поскольку Х]Х2Х3 * 0, то ни одно из чисел не равно нулю, все эти числа могут
иметь один знак (Х,Х2Х3 > 0) или только два из них одного знака.
1. Если все числа Х|,Х2,Х3 одного знака, то уравнение (11.37) можно при-
вести к одному из следующих канонических видов:
Х2/а2+ Y2jb2 +Z2/c2 = \, (11.38)
Х2[а2 + Y2/b2 + Z2/c2 = -1, (11.39)
Х2/а2 + Y2/b2 +Z2/c2 = 0 (11.40)
в зависимости от Х| и ц: Х)Ц > 0, Х|Ц <0, Ц = 0.
Уравнение (11.38) определяет эллипсоид, уравнению (11.39) не удовлетворяют
координаты ни одной точки пространства, уравнению (11.40) удовлетворяют ко-
ординаты единственной точки (X = 0, Y = 0, Z= 0).
2. Пусть знак одного из этих чисел противоположен знаку двух других: предполо-
жим,что Х,Х2 >0. Уравнение (11.37) можно привести к одному из канонических видов
X2la2 + Y2lb2-Z2lc2 = \, (H.41)
X2/a2 + Y2lb2 - Z2/c2 = -1, (11.42)
X2/a2 +Y2/b2 - Z2/c2 = 0 (11.43)
в зависимости от Xt и ц: Х]Ц > 0, Х(ц <0, ц = 0.
Уравнения (11.41) — (11.43) определяют соответственно однополосный гипер-
болоид, двуполостный гиперболоид и конус второго порядка.
184
Нецентральные фигуры. Если det А = 0, или Х|Х2Х3 = О, то одно или два из
этих чисел равны нулю.
1. Пусть А3 = 0, а34 * 0, тогда уравнение (11.36) приводится к виду
A1X2+A2r2+pZ=0. (11.44)
Если А,А2 > 0 и Л.!|х < 0, то имеем
X2/a2+Y2/b2=2Z; (11.45)
в случае 1,А2 < 0, IjP < 0 получаем
X2/a2-Y2lb2=2Z. (11.46)
Уравнения (11.45) и (11.46) определяют соответственно эллиптический и гипер-
болический параболоиды.
2. Пусть А3 = 0, а34 = 0, тогда имеем уравнение
l1A'2+%2r2+v = 0, (Н-47)
которое приводится к одному из следующих канонических видов:
Х2/а2+ Y2/b2 =\, (11.48)
X2/a2 + Y2lb2=-\, (11.49)
X2/a2-Y2lb2=\, (11.50)
X2/a2-Y2lb2=-\, (П51)
X2/a2-Y2jb2 =Q. (11.52)
Уравнение (11.48) определяет эллиптический цилиндр, каждое из уравне-
ний (11.51), (11.50) - гиперболический цилиндр, уравнение (11.52) - пару
пересекающихся плоскостей; уравнению (11.49) не удовлетворяют коорди-
наты ни одной точки.
3. Если А2=А3 = 0 и о24*0, то уравнение (11.36) приводится к виду
А, %2 +цУ= 0 или
X2 = 2pY (11.53)
и определяет параболический цилиндр.
4. Если А2=А3 = 0 и а24=0, то имеем уравнение A1A'2+v = 0, которое
приводится к одному из канонических видов
Х2=а2,Х2=-а2,Х2=0. (11.54)
Первое из уравнений (11.54) определяет пару параллельных плоскостей
(Х = а, Х = -а), третье, уравнение — пару совпавших плоскостей; второму
уравнению не удовлетворяют координаты ни одной точки пространства.
185
Пример 11.5. Какую поверхность определяет уравнение 6х2+5у2 +
+ 7г2 -4xy+4xz = 18?
Это уравнение вида (11.32), для которого аи = 6, а22 = 5, а33=7, а12=-2,
а13=2, а23 = 0, а14 = 024 = а34 = 0, а44=-18. Левая часть данного уравнения
является квадратичной формой f(x, y,z) = 6х2 +5у2 +7z2 -4ху+ + 4xz трех
переменных x,y,z (х = х,, у = х2, z = х3). Составим матрицу А этой квадратич-
ной формы и характеристическое уравнение матрицы А:
Характеристическое уравнение (6-А) (5-А) (7- А)-4(5-А)-
-4(7-А)=0, или A3-18А2 +99А-162 = 0 имеет корни А,=3, А2=6, А3=9,
(так как А3-18А2 +99А-162 = А3-ЗА2-15А2 +45А+54А-162 = А2 х
х (А - 3) - 15А(А- 3) +54 (А - 3) = (А - 3) (А2 - 15А +54)).
Следовательно, квадратичную форму f(x,y,z) можно привести к виду
<р(Х, У, Z) = 3X2+6У2+9Z2. В новых координатах X, Y, Z данное уравнение
имеет вид ЗХ2 +6У2 +9Z2 = 18, или
A'76+r2/3+Z2/2 = l,
оно определяет эллипсоид с полуосями о=у6, h = V3,
c = -j2.
186
Гпава 12
ГРУППЫ
12.1. Понятие группы. Основные определения
Группой называется множество G элементов а, Ь, с,...» для которых опреде-
лена операция (сложения или умножения), которая каждой упорядоченной паре
(а, Ь) элементов G ставит в соответствие единственный элемент с = а°Ь данного
множества, причем операция обладает следующими свойствами:
1) операция ассоциативна, т.е. для любых a, b, с е G
ао(Ьос)=(аоЬ)ос; (12.1)
2) в G существует нейтральный элемент е такой, что для любого элемента а е G
а°е = е°а = а; (12.2)
3) для каждого элемента а е G существует обратный ему элемент а-1 такой, что
аоа~1 = е, а"1 °а = е. (12.3)
Если, кроме того, для любых a,beG выполняется условие
до6 = 5од, (12.4)
то группа называется коммутативной или абелевой группой.
В любой группе нейтральный элемент определен однозначно; для каждого
элемента существует единственный обратный элемент.
Группа состоящая из конечного числа элементов, называется конечной. Число
элементов группы называют ее порядком. Группа, не являющаяся конечной, назы-
вается бесконечной.
Группа называется аддитивной или группой по сложению, когда групповая
операция, ставящая в соответствие паре элементов (о, Ь) элемент с = а о Ь, явля-
ется сложением. В этом случае символ операции ° заменяется знаком +;
с = а + Ь, нейтральный элемент называют нулем и обозначают символом 0;
а + 0= 0+я = а. Элемент, обратный к элементу а, называют противоположным и
обозначают -а : а +(—а) = (-о) +а = 0.
Группа называется мультипликативной или группой по умножению, когда группо-
вая операция, ставящая в соответствие упорядоченной паре (а, Ь) элемент с = а°Ь,
является умножением. В данном случае произведение а ° b обозначается а b или ab;
нейтральный элемент называется единицей и обозначается символом 1: а • 1 = 1 • в = а.
Произведение и элементов, равных а, называют n-й степенью элемента а и обо-
значают а". Отрицательные степени элемента а можно определить или как эле-
187
менты группы G, обратные положительным степеням, или как произведения соот-
ветствующего числа множителей, равных элементу в-1. Эти определения совпа-
дают, так как верно равенство
(и>0).
В любой группе G для степеней каждого элемента а при любых показателях т
и п (положительных, отрицательных или нулевых) выполняются равенства
„п „т „т„п__ „п+т /„п\т_„пт
। а а = а а = а , (а ) =а .
Если операция в группе называется сложением, то вместо степеней элемента а
говорят о кратных этого элемента и пишут па.
В каждой мультипликативной группе однозначно разрешимы уравнения
ах = Ь, уа = Ь, первое из них имеет решение х-а~1Ь, второе - у = Ьа~\
Если группа является коммутативной, то эти уравнения не различаются, они
имеют одинаковые решения x = y = a~'b.
12.2. Примеры групп
1. Множество всех целых чисел с операцией сложения образует аддитивную
группу. Действительно, сумма а + b двух целых чисел а и b также является целым
числом. В этом случае говорят, что множество целых чисел замкнуто относительно
операции сложения. Сложение целых чисел коммутативно: (a+b)+c = a+(b+c).
В данном множестве имеется нейтральный элемент, т.е. число 0 такое, что а + 0 = а
при любом целом числе а. Для каждого элемента целого числа а существует обрат-
ный элемент (противоположное число), т.е. такое число -а, что а + (-а) = 0. Рас-
сматриваемая группа является коммутативной, так как а + b = Ь+а.
Замечание 1. Множество всех целых чисел не образуют группу по ум-
ножению, так как обратные для целых чисел (отличных от -1 и 1) не являются
целыми числами. Например, для числа 2 обратное число 2-1 не принадлежит
множеству целых чисел.
2. Множество всех действительных чисел, отличных от нуля, с операцией ум-
ножения образует мультипликативную группу. Эта группа является коммутатив-
ной, так как ab = Ьа.
Замечание 2. Множество всех действительных чисел не образует
группу по умножению, поскольку для числа 0 нет обратного.
3. Множество всех векторов трехмерного пространства образует группу по
сложению. Эта группа является коммутативной (а + Ь = Ь+а).
4. Множество матриц размером тхи образует коммутативную группу по
сложению (А + В = В + А). Для матрицы А обратным элементом является матрица
(- А); нейтральный элемент - нулевая матрица О.
5. Множество всех невырожденных квадратных матриц порядка и образует
мультипликативную группу. Эта группа, которую называют полной линейной
группой, не является коммутативной (в общем случае АВ * ВА).
188
Замечание 3. Множество всех квадратных матриц порядка и не обра-
зует группу по умножению, так как для некоторых его элементов нет обратных
(вырожденная матрица не имеет обратной).
6. Множество всех невырожденных линейных преобразований линейного
пространства образует мультипликативную группу.
7. Множество, состоящее из двух чисел +1,-1, образует группу по умноже-
нию. Действительно, каждой из произведений (+!)(-!) =-1, (+1)(+1) = + 1,
(-1)(—1) = + 1 принадлежит данному множеству. Умножение ассоциативно. Су-
ществует единица - число +1, которое удовлетворяет условию (-.1) (+1) = -1,
(+1) (+1) = +1. Для каждого элемента существует обратный: каждое из этих двух
чисел совпадает со своим обратным.
Замечание 4. Множество, состоящее из двух чисел +1,-1, не образу-
ет группу по сложению, так как сумма (+1)+(-1) = 0, а число 0 не принадлежит
данному множеству. (В таком случае говорят, что данное множество не является
замкнутым относительно операции сложения).
8. Множество, состоящее из одного элемента 0, образует аддитивную группу.
Действительно, 0 + 0 = 0, сумма принадлежит данному множеству. Свойства опе-
рации сложения очевидны.
9. Множество, состоящее из одного элемента 1, образует мультиплика-
тивную группу.
Группа, образованная одним элементом, называется единичной.
12.3. Подгруппа
Подгруппой группу G называется подмножество Н ее элементов, образующее
группу относительно операции, определенной в G. Чтобы убедится в том, что
множество Н группы G является ее подгруппой, необходимо проверить, что:
1) произведение (сумма) любых двух элементов а,ЬеН принадлежит Н; 2)для
любого элемента аеН обратный элемент принадлежит Н. Этого будет достаточ-
но, так как ассоциативный закон выполняется для любых трех элементов G, в том
числе и для элементов Н, а нейтральный элемент е (1 или 0) будет принадлежать Н
(как произведение аа-1 или сумма а+(-а)).
Примеры подгрупп некоторых групп.
I. Множество всех действительных чисел является аддитивной группой.
Подгруппами аддитивной группы всех действительных чисел являются в част-
ности, следующие: 1) аддитивная группа рациональных чисел; 2) аддитивная
группа целых чисел; 3) аддитивная группа всех целых чисел, кратных числу к,
например аддитивная группа четных чисел.
Группа целых чисел является подгруппой группы рациональных чисел.
Замечание 1. Множество нечетных чисел не образует группу по сло-
жению, так как сумма двух нечетных чисел является четным числом (и не принад-
лежит данному множеству).
II. Мультипликативная группа всех действительных чисел, отличных от нуля, име-
ет, в частности, следующие подгруппы: 1) мультипликативную группу положительных
189
действительных чисел; 2) мультипликативную группу рациональных чисел, отличных
от нуля; 3) множество, состоящее из двух чисел +1,-1 с операцией умножения.
Замечание 2. Мультипликативная группа положительных действи-
тельных чисел не является подгруппой аддитивной группы всех действительных
чисел, так как групповые операции в рассматриваемых множествах- разные
(соответственно умножение, сложение).
Ш. Мультипликативная группа невырожденных матриц порядка п имеет, в ча-
стности, подгруппы: 1) группу ортогональных матриц; 2) группу диагональных
матриц; 3) группу матриц с положительным определителем; 4) группу матриц с
определителем, равным единицы (эта группа называется унимодулярной).
Пересечение двух подгрупп группы G является подгруппой в G. Например, в
аддитивной группе целых чисел пересечение подгруппы четных чисел и подгруп-
пы чисел, кратных трем, будет подгруппой чисел, кратных шести.
Каждая группа является своей подгруппой. Далее, каждая группа имеет еди-
ничную подгруппу, состоящую из одного нейтрального элемента (единицы или
нуля). Эти две подгруппы называются несобственными (или тривиальными) под-
группами. Остальные подгруппы называются собственными (или истинными)
подгруппами. В любой группе все подгруппы каждой группы являются в тоже время
подгруппами исходной группы. Например, аддитивная группа целых чисел является
подгруппой аддитивной группы рациональных чисел, которая в свою очередь есть
подгруппа аддитивной группы всех действительных чисел; аддитивная группа целых
чисел - подгруппа аддитивной группы всех действительных чисел.
12.4. Группы преобразований.
Симметрическая группа n-й степени
Преобразованием множества X называется взаимно однозначное отобра-
жение этого множества на себя. Преобразование множества X обозначим бук-
вой Р. Определение преобразования Р множества X означает следующее: лю-
бому элементу х е X ставится в соответствие единственный элемент х' = Рх
того же множества; х' называется образом элемента х, а х - прообразом х'.
Каждый элемент х' е X имеет единственный прообраз х е X.
Умножением преобразований называется последовательное их выполнение.
Произведение двух преобразований Р, Q обозначается PQ (справа записано то
преобразование, которое выполняется первым; по определению (QP) х = Q (Рх)).
Очевидно, произведение двух преобразований данного множества является преоб-
разованием данного множество. Отметим, что в общем случае умножение не явля-
ется коммутативным, т.е. QP * PQ. Можно показать, что произведение преобра-
зований подчиняется ассоциативному закону. Роль единицы при умножении пре-
образований выполняет тождественное преобразование Е, ставящее в соответст-
вие каждому элементу множества его самого. Для каждого преобразования Р суще-
ствует обратное преобразование Р~х, которое каждому элементу х" е X ставит в
соответствие его единственный прообраз х 6 X, причем РР' = Р~'Р= Е. Следова-
тельно, множество преобразований Р данного множества А" образует группу.
190
Если множество X конечно и состоит из п элементов, то всевозможные взаимно
однозначные отображения этого множества на себя называются подстановками.
Подстановку из п элементов можно обозначить так:
1 2 3 ... и
а, а2 а3 ... а„
где а1, а2 ,..., а„ - те же числа 1,2,3,..., п, обозначающие данные элементы и
записанные в другом порядке.
Примеры подстановок при п = 5:
1 2 3 4 5 ) ( 1 2 3 4 5
3 1 524 ^’^12345
1 2 3 4 5 ) f 2 14 5 3
3 4 5 2 1 4 3 2 1 5
Первая подстановка означает такое взаимно однозначное отображение множества
(1,2, 3,4, 5) на себя, при котором 1 переходит в 3, 2 — в 1 и т. д. Вторая подста-
новка называется тождественной, каждый элемент соответствует сам себе. Равен-
ство двух других подстановок показывает, что расположение столбцов в записи
подстановки не играет роли. Подстановки, отличающиеся только порядком следо-
вания столбцов, не считаются различными.
Умножением подстановок называют последовательное их выполнение (сначала
правого сомножителя, затем левого). Умножение подстановок ассоциативно, но не
коммутативно. Например, если
1 2 3 4 ^ ( 1 2 3 4
24 13 1^1234 1
то
PQ =
1 2 3
4 1 3
2 3 4 )
1 2 4 )
PQ*QP.
Единицей при умножении подстановок из п элементов служит тождественная
подстановка
12 3... и)
1 2 3 ... п J
Каждая подстановка из и элементов имеет обратную:
1 2 3 ... и V -f а‘ а2 а"
а, а2 а3 ... а„ J 1 2 з ... и
Чтобы получить подстановку, обратную данной, необходимо поменять местами строки.
191
Множество подстановок из п элементов относительно введенной операции ум-
ножения образует группу. Группа подстановок из я элементов называется симмет-
рической группой n-й степени и обозначается S„. Число подстановок из я элемен-
тов равно я!, поэтому группа S,, имеет порядок я!.
Рассмотрим группу подстановок из трех элементов а, Ь, с. Поскольку из трех элемен-
тов можно составить шесть различных перестановок abc, acb, bac, bca, cab, cba, то
и число различных подстановок для них равно шести (я = 3,3! = 1 • 2 3 = 6).
Обозначим эти подстановки следующим образом:
Ь с А ( а b с Л ( а b с
, Рг = , Р3 =
Ь с j \ а с b J с Ь а
b с\ ( а b с \ (а b с
>Л= , >-Рб= ,
ас) \b с а ) I с а о
Отметим, что Pt — тождественная подстановка; для каждой подстановки су-
ществует обратная:
РГ' = РГ' = Рг, РГ' = Рз, РГ' = Ра, РГ' = Р6, РГ' = Рз-
Группа S3 (симметрическая группа подстановок из 3 элементов) некоммута-
тивна, поскольку, например, Р„Р5 = Р2, Р5Р4 = Рз, т.е. P4PS*P5P4.
Таблица 12.1
р, Рх Рг Рз Ра Рз . Р6
Рх Рх Рг Рз Ра Рз Ръ
Рг Рг Рх Рз Р6 Рз Ра
Рз Рз Р6 Рх Рз Ра Рг
Ра Ра Рз Р6 Рх Рг Рз
Рз Рз Ра Рг Рз Р6 Рх
Р6 Рб Рз Ра Рг Рх Рз
Группу S3 можно представить следующей таблицей умножения, в которой
слева стоят левые множители р/г сверху - правые Pf, а на пересечении соот-
ветствующей строки и столбца - их произведение. Таблицы такого рода на-
зывают таблицами Кэли (табл. 12.1).
192
12.5. Группа вращений правильного
многоугольника. Циклические группы.
Группа симметрий правильного
треугольника
Пусть дан правильный и-угольник AtA2 ...А„ с центром в точке О (рис. 12.1,
и = 6). Рассмотрим всевозможные повороты плоскости вокруг точки О, при
которых этот правильный и-угольник совмещается сам с собой. Таких поворо-
тов будет и: а0 — поворот на угол ф0 = О
(тождественное преобразование); а, —
поворот на угол ф1=2л/и, а2 - поворот на
угол ф2 = = (2л/п)2,...,а„_) - поворот на
угол фл_, =(2тс/и)(и—1). Под умножением
поворотов будем понимать последовательное
их выполнение: ак ° a, = ак+1, причем
а*+л=«* при любом к (к = 0,1,2,..., и), в
частности а„ = а0. Умножение поворотов
является ассоциативным (и коммутативным).
Множество указанных поворотов правильно-
го многоугольника образует группу по умножению, роль единицы играет тож-
дественное преобразование - поворот а0. Для каждого элемента ак существу-
ет обратный элемент а*1 = а„_к (А = 0,1, 2,..., и-1), так как ак ^ая_к = а„ = а0,
т.е. ак оа„_к =а0, где а0 - единичный элемент.
Положим at = a, тогда а2 = аг,а3 = а3,...,а„_, = а” 1,а„=а'1. В этом случае
говорят, что группа образована степенями одного из своих элементов (или что она
порождается одним из своих элементов); таким элементом является элемент
а = а,. Группы, образованные степенями одного из своих элементов, называются
циклическими. Таким образом, группа вращения правильного
n-угольника является циклической группой порядка л, эта группа обозначается
Сп. Отметим, что аддитивная rpynria целых чисел также будет циклической, она
порождается одним из своих элементов - числом 1: 2 = 1+1, 3=(1 + 1)+1 ит. д.
Эта группа является бесконечной циклической группой, ее обозначают С„.
Пусть дан правильный треугольник АВС с центром в точке О (рис. 12.2). Рас-
смотрим все симметрии данной фигуры, т.е. те преобразования плоскости, при
которых этот треугольник переходит в себя (или самосовмещается). К ним отно-
сятся: три поворота ф0, ф], ф2 плоскости вокруг точки О соответственно на углы
0,2л/3,4л/3 (частный случай рассмотренных выше вращений правильного и-
7 3ак. 1
193
угольника при и=3); три осевых симметрии ф3, ф4,ф5, определяемых соот-
ветственно осями симметрии /, т, п, прохо-
дящими через вершину правильного тре-
угольника и середину его противоположной
стороны (см. рис. 12.2).
Будем характеризовать каждое самосовмеще-
ние <р подстановкой на множестве вершин
А, В, С правильного треугольника
АВС
«1 а2 а3
где а,, а2, а2 - те же буквы А, В, С, взятые в
некотором порядке. Принятое нами соответст-
вие между самосовмещениями треугольника и подстановками множества его
вершин дает
(АВС} (А В С} (АВС}
фо~[л В cJ’<₽,-[b С A В )'
(А В С} (АВС} (А В С}
фз=[л С в]’ф4“[с В л]’ф5-[в А С)
Множество самосовмещений ф0,ф|,ф2,ф3,ф4, Ф5 образует группу относитель-
ного умножения (последовательного выполнения двух самосовмещений). Роль еди-
ницы играет тождественное преобразование, каждый элемент данного преобразова-
ния имеет обратный. Эта группа называется группой симметрий треугольника.
12.6. Изоморфизм групп
Группы G] и G2 называются изоморфными, если между их элементами можно
установить взаимно однозначное соответствие, сохраняющее групповую опера-
цию, т.е. такое, что если х,,у, gG,, x2,_v2gG2 и х, <->х2, У1«-»У2> то
Х1°У1 <->х2°у2.
Симметрическая группа S3 трех элементов а,Ь,с и группа симметрий правиль-
ного треугольника с вершинами А, В, С изоморфны. Эти группы отличаются только
обозначениями элементов и названиями соответствующих преобразований. Цикли-
ческая группа порядка п изоморфна группе вращений правильного n-угольника; бес-
конечная циклическая группа изоморфна аддитивной группе целых чисел.
Если/- изоморфное отображение группы G, на G2, то f(?x) = t2, где
е„ е2 - единичные элементы групп Gt и G2 соответственно, и для любого
xteGt, /(х)",) = (/(х1))"'.
194
12.7. Разложение группы по подгруппе
Пусть дана группа G и некоторая ее> подгруппа Н. Фиксировав любой эле-
мент х е G, рассмотрим множество элементов х ° h, h- любой элемент Н. Это
множество хоН называется левым смежным классом группы G по подгруппе
Н, порожденным элементом х. Два любых смежных класса группы G по под-
группе Н или совпадают, или не имеют ни одного общего элемента.
Вся группа G распадается на непересекающиеся левые смежные классы по
подгруппе Н. Это разложение называется левосторонним разложением группы
G по подгруппе Н. Очевидно, одним из левых смежных классов этого разложе-
ния будет сама подгруппа Н, этот смежный класс порождается элементом е (или
любым элементом h&H, поскольку Л°Я = Я).
Аналогично вводится понятие правого смежного класса группы G по под-
группе Н, порожденного элементом х; это множество Н<>х, т. е. множество всех
элементов вида h°x, где х - фиксированный элемент G, h- любой элемент из
Н. Аналогичным образом получается правостороннее разложение группы G по
подгруппе Н. Если группа G абелева, то оба ее разложения по любой подгруппе
(левостороннее и правостороннее) совпадают. В этом случае говорят просто о
разложении группы по подгруппе. Приведем пример такого разложения.
Пусть G — аддитивная группа целых чисел и Н - ее подгруппа, состоящая
из всех чисел, кратных к. Разобьем группу G на классы, относя к одному классу
все те числа, которые при делении на к дают одинаковые остатки. Разложению
данной группы G по указанной подгруппе Н состоит из к различных смежных
классов, порождаемых соответственно числами 0,1,2,., к -1. В классе, по-
рождаемом числом I, где 0 < I < к -1, собраны все те числа, которые при делении
на число к дают остаток I.
Полученное разложение группы целых чисел по подгруппе чисел, кратных к,
при к = 3 можно представить следующим образом:
Н...-9-6-3 0 3 6 9...
1 + Я...-8-5-2 1 4 7 10...
2+Н...-7-4-1 2 5 8 11...
Замечание. В некоммутативной группе левостороннее и правосторон-
нее разложения могут оказаться различными. Обратимся к симметрической группе
S3 (см. п. 12.4). Из таблицы Кэли для этой группы видно, что множество элемен-
тов РХ,Р2 образует подгруппу, обозначим ее В = {Р3,Р2}. Левостороннее разложе-
ние группы S3 по подгруппе В состоит из классов В, Р5В= Р4В = {Р4,Р5},
Р3В=Р6В = {Р3,Р6}, а правостороннее - из классов В, ВР6 = ВР4={Р4,Р6},
ВР5 = ВР3 = {Р3, Р5}, т. е. эти разложения различны. Отметим, что левостороннее и
НК
правостороннее разложение этой группы по ее подгруппе третьего порядка
А = {Ри Р5, Р6} совпадают; каждое из них состоит из двух классов:
А = {Р1,Р5,Р6}, АР2 = Р2А = {Р2,Р3,Ра}.
Теорема 12.1 (Лагранжа). Порядок подгруппы конечной группы является
делителем порядка группы.
Следствие 1. Порядок любого элемента конечной группы является де-
лителем порядка группы.
Следствие 2. Всякая конечная группа, порядок которой есть простое
число, является циклической.
12.8. Нормальный делитель
Подгруппа Н группы G называется нормальным делителем этой группы (или
инвариантной подгруппой), если левостороннее и правостороннее разложения
этой группы по указанной подгруппе совпадают.
Из определения следует, что любая подгруппа коммутативной группы является
в ней нормальным делителем. Далее, в любой группе G сама группа и ее единич-
ная подгруппа будут нормальными делителями: разложение группы G по самой
этой группе состоит из одного элемента G, разложения группы G по единичной
подгруппе совпадают с разложением группы на отдельные элементы. Приведем
примеры нормальных делителей в некоммутативных группах.
1. В симметричной группе (см. п. 12.4) подгруппа Н= {/J, Р5, Р6} явля-
ется нормальным делителем, так как левостороннее и правостороннее разложения
совпадают, они состоят из двух классов: Н= {Д, Р5, Р6}, НР2 =
= Р2Н = {Р2,Р3,Р4}.
2. В мультипликативной группе невырожденных квадратных матриц порядка
и подгруппа матриц с определителем, равным единице, будет нормальным делите-
лем. Действительно, левый и правый смежные классы по этой подгруппе, порож-
даемые матрицей М, совпадают с классом всех матриц, определитель которых
равен определителю матрицы М (как известно, определитель произведения двух
матриц равен произведению определителей этих матриц).
Можно дать и другие определения нормального делителя, равносильные ис-
ходному. Приведем одно из них.
Подгруппа Н группы G называется нормальным делителем этой группы, ес-
ли хоН = Н°х для любого xeG, т. е. для любого xeG и элемента heH су-
ществуют /г,, Aj е Н такие, что х»Л = ^ »х, Лох = xoAj.
12.9. Классы сопряженных элементов
Элементы а и Л группы G называют сопряженными, если в G существует
хотя бы один такой элемент х, что
Л = х-1ах. (12.5)
В этом случае говорят, что элемент Ь получается из элемента а трансформирова-
196
нием с помощью элементах Из равенства (12.5) находим
a =xbx~l = (x-1)-1tor"1,
т.е. элемент а при этом получается из элемента b трансформированием
элементом х-1. .
Теорема 12.2. Подгруппа Н группы G тогда и только тогда будет нор-
мальным делителем в G, если вместе с любым своим элементом h она содержит
все элементы, сопряженные с ним в G.
Замечание. Нормальный делитель называют также инвариантной
подгруппой. Из теоремы 12.2 следует происхождение этого названия. Если
Н - нормальный делитель группы G, то трансформирование любого эле-
мента подгруппы Н с помощью элемента группы G дает снова элемент под-
группы Н (подгруппа Н остается неизменяемой по отношению к операции
трансформирования элементов Н ).
Теорема 12.3. Пересечение двух нормальных делителей группы является
нормальным делителем этой группы.
12.10. Фактор-группа
Фактор-группой группы G по нормальному делителю Н называется группа
всех смежных классов этой группы G по подгруппе Н.
Таким образом, с группой G можно связать некоторый набор новых групп -
ее фактор-групп по различным нормальным делителям.
Отметим, что фактор-группа абелевой группы является абелевой; фактор-
группа циклической группы — циклической группой.
Примеры фактор-групп.
1. Пусть G - аддитивная группа целых чисел, Н - подгруппа чисел,
делящихся на 3. Найдем фактор группу G/Н. Групповой операцией в дан-
ном случае является сложение. Число смежных классов равно трем
(см. пример в п. 12.7): множество чисел, делящихся на 3, два множества
чисел, дающих при делении на 3 соответственно остатки 1 и 2. Обозначим
эти смежные классы [0], [1], [2]. В этом множестве введем операцию
сложения следующим образом: сложив соответствующие числа в
квадратных скобках, определим, какой остаток при делении на 3 дает их
сумма, и будем считать суммой смежных классов тот, которому
принадлежит полученный остаток. Таблица умножения для фактор-группы
имеет вад [0]+[0] = [1 ]+[2] = [2]+[1] = [0], [0]+[ 1 ] = [1 ]+[0] = [2]+[2] = [1],
[0]+[2] = [2]+[0] = [1]+[1 ]= [2]. Отсюда видно, что фактор-группа абелева.
Кроме того, все смежные классы порождаются классом [1], они совпадают
со степенями этого класса: [1], [1 ]+[1]=[2], [1]+[1]+ [1] = [0]. Поскольку фак-
тор-группа порождена одним элементом, то она циклическая.
197
2. Пусть G — аддитивная группа целых чисел, И — подгруппа целых чи-
сел, кратных натуральному числу к. Фактор-группой G/Н является конечная
группа порядка к, состоящая из классов [0], [1], [2],...[Л-1]. Эта фактор-
группа циклическая, как и сама группа G.
3. Пусть G - мультипликативная группа всех невырожденных матриц
порядка п, Н - подгруппа матриц с определителем, равным единице. Фак-
тор-группа G/Н изоморфна мультипликативной группе отличных от
нуля действительных чисел.
12.11. Гомоморфизм групп
Если G и G' — группы и f: G —» G' — такое отображение, при котором для
любых элементов х, у группы G
/(ЛУ) = /«/(Л (12.6)
то f называется гомоморфным отображением или гомоморфизмом группы G
в группу G'. Отметим, что в определении гомоморфизма имеется в виду, что
каждый элемент группы G поставлен в соответствие хотя бы одному элемен-
ту группы G', но разным элементам из G может соответствовать один и тот
же элемент из G'. Другими словами, отображение группы G в группу G' не
предполагается взаимно однозначным, как в случае изоморфизма.
Очевидно, каждая группа гомоморфна себе самой, так как можно поло-
жить f(x) = х для всех х е G. Далее, каждая группа гомоморфна единичной
группе ( состоящей из одного нейтрального элемента е). Примером гомо-
морфного отображения групп может служить циклическая группа С6 шестого
порядка с элементами е, а, а2, а2, а4, а5, которая гомоморфна циклической
группе С2 второго порядка с элементами Е, А:
/(«) = Я«2) = Я«4) = Е, /(«) » /(«’) = /(«’)= А
Равенство (12.6) означает, что образ произведения двух элементов
равен произведению образов этих элементов (которые, впрочем, могут
называться по-разному в группах G и G’), поэтому говорят, что гомомор-
физм «сохраняет групповую операцию». Гомоморфизм групп сохраняет не
только групповую операцию, но также нейтральный и обратный элементы:
если/- гомоморфное отображение группы G в группу G', то f(e) = e’, где
е, е’ — нейтральные элементы групп G и G' соответственно.
Теорема 12.4. Каждая группа гомоморфна любой своей фактор-группе.
Обратно, если группа G гомоморфна группе G', то G’ изоморфна фактор-
группе G по некоторому нормальному делителю Н.
198
12.12. Представления групп
С точки зрения алгебры изоморфные группы не считаются различными. О
группе, изоморфной некоторой подгруппе группы подстановок, говорят, что она
представлена подстановками.
Теорема 12.5. (Кэли). Каждая конечная группа изоморфна некоторой
группе подстановок (т. е. всякую конечную группу можно представить
подстановками).
Следовательно, при описании любой конечной группы можно воспользоваться
преимуществами группы подстановок.
Для теории и приложений наиболее интересны линейные представления
конечных групп. Говоря о линейном представлении конечной группы G,
предполагают, что дано векторное пространство Vn, в котором действуют
линейные невырожденные преобразования. Эти преобразования образуют
группу G-, которой гомоморфна исходная группа G; при этом говорят, что
группа G' представляет группу G.
Гомоморфное отображение Г группы G в группу G' невырожденных линей-
ных преобразований п-мерного векторного пространства Vn называется линей-
ным представлением группы G.
Следовательно, если Г - линейное представление группы G группой G', то
каждому элементу aeG поставлено в соответствие невырожденное линейное
преобразование Г (а) е G' пространства V„ так, что для любых a,beG спра-
ведливо соотношение Г (ab) = Г (а) Г (£>). Как известно, при этом Г (е) = Е, где
е,Е- нейтральные элементы групп G, G' соответственно, и
Г(а~') = (Г(а))'1 для любого aeG.
Пространство V„, в котором действуют преобразования из группы G', назы-
вается пространством представления группы G. Размерность пространства Vn
называют размерностью (или степенью) рассматриваемого представления.
Вместо линейных преобразований часто рассматривают соответствующие
им матрицы.
199
Ill
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Глава 13
ФУНКЦИИ И ПРЕДЕЛЫ
13.1. Понятие функции. Основные определения
Рассмотрим множество X элементов х и множество Y элементов у. Если каж-
дому элементу хеХ по определенному правилу f поставлен в соответствие
единственный элемент у е Y, то говорят, что на множестве X задана функция
у = f(x) со значениями в множестве Y. Элементы х е X называются значения-
ми аргумента, а элементы у g Y - значениями функции. Множество X называют
областью определения функции, множество всех значений функции — областью
значений этой функции.
Замечание. Функцию, заданную на множестве X со значениями в мно-
жестве Y, называют также отображением множества X в множество Y. Если
множество Y является множеством значений функции, то рассматриваемую
функцию называют отображением множества X на множество Y.
Функцию, заданную на множестве X, называют также оператором, заданным на
множестве X, и обозначают символом /.
В случае, когда X и У - числовые множества, соответствующие функции на-
зываются числовыми функциями. Если рассматриваются действительные числа, то
функции называют действительными (вещественными) функциями одной дейст-
вительной (вещественной) переменной.
Употребляются следующие обозначения функции: у = fix), у = F (х),
у = Ф(х), у = <р(х), у = у{х) и т. п. Значение, которое функция y = f(x) при-
нимает при х = а, обозначается через /(а).
Функция и аргумент могут обозначатся также другими буквами, например
$ = /(/), u = f(y), r = r(t), х=х(Г)ит.д.
К простейшим областям определения функции относятся отрезок, ин-
тервал, полуинтервалы или совокупность указанных промежутков. Напри-
мер, для функции у = --у9-х2 областью определения является отрезок
[-3,3], а областью ее значений - отрезок [-3,0]; для функции у = х3 об-
ласть определения и область значений совпадают с интервалом (- о», + <»>).
200
Графиком функции у = /(л) называется множество точек плоскости, коорди-
наты которых удовлетворяют данной функциональной зависимости, т. е. точек
M(x,f(x)). Например, графиком функции у = —J16-x2 является полуокруж-
ность радиуса R = 4 с центром в начале координат, расположенная ниже оси Ох.
К традиционным основным способам задания функции относятся: аналитиче-
ский (с помощью одной или нескольких формул); графический (с помощью гра-
фика); табличный (с помощью таблицы значений).
Функция заданная формулой
> = /(*). (13-1)
правая часть которой не содержит у, называется явной функцией.
Функция у = у (х), определяемая уравнением
Г(х,у) = О, (13.2)
называется функцией, заданной неявно, или неявной функцией.
Отметим, что одно уравнение вида (13.2) может определять несколько функ-
ций. Например, уравнение х2 + у2 - R2 = 0 определяет две функции
У1 = fi(x) = -\Ir2-x2, у2 = /2(х) = -Jr2-x2.
Обратимся к функции (13.1). Каждому х&Х по определенному закону ста-
вится в соответствие единственное значение у е Y. С другой стороны, каждому
у е Y соответствует одно или несколько значений х е X.
В случае, когда каждому у е Y по некоторому закону <р соответствует только
одно значение х е X, получаем функцию
х = <р(у), (13.3)
заданную на множестве Y со значениями в множестве X. Функцию (13.3) назы-
вают обратной функцией по отношению к функции (13.1). Функции (13.1) и (13.3)
в этом случае называются взаимно обратными. Для взаимно обратных функций
выполняются тождества:
<Р(/(^))=^ хеХ; /(ф(у))=у, yeY.
Примеры взаимно обратных функций: у = Зх, x = log3y; у = 2х-3, х = (у + 3)/2.
Если придерживаться стандартных обозначений (у - функция, х—
аргумент), то обратную функцию (13.3) следует писать в виде у = ф(х). Напри-
мер, можно говорить, что функции у = Зх, y = log3x взаимно обратные.
Функцию, обратную к функции у =fix), удобно обозначать символом х = /"'(у).
Если у = f(u), ц = ф(х) - функции своих аргументов, причем область опре-
деления функции f содержит область значений ф, то каждому х из области опре-
деления функции ф соответствует у такое, что у = f(u), где и = ф(х). Эта функ-
ция, определяемая соответствием
r/(<₽W).
201
называется функцией от функции или сложной функцией. (Применяются также и
другие названия: композиция функций <р и f, суперпозиция функций ф и /.)
Например, если у = и, u = cosx, то у = (cosx)3 = cos3x.
Рассматривают также функции, являющиеся композициями более чем двух
функций. Так, функция w = sinlg(l+x2) представляет собой композицию сле-
дующих функций: w = sin и, u=\gv, v = l+z, z = x2.
Функция у = f(x) называется четной, если для любых х и -х из области ее
определения выполняется равенство f(-x) = f(x). Функция у = ф(х) называется
нечетной, если для любых хи -х из области ее определения выполняется равен-
ство ф(-х) = -ф(х). Например, у = х2, у = cosx - четные функции, ,у = х3,
y = sinx — нечетные функции.
Функция у = f(x) называется периодической, если существует число Т # О
такое, что при всех х и х + Т из области ее определения выполняется равенство
f(x + T) = f(x). Число Т в этом случае называется периодом функции. Всякая
периодическая функция имеет бесконечное множество периодов. Говоря о перио-
де функции у = f(x) (/(х)^ const), обычно имеют в виду наименьший положи-
тельный период: так, периодом функции y = sinx является число 2л, периодом
функции y = tgx - число л.
Функция у = /(х) называется ограниченной на множестве X, если существует
такое число С > 0, что для всех х е X выполняется неравенство | /(х) | < С.
Тригонометрические и обратные тригонометрические функции, функции
у = ха (а = const), у = ах (а > 0, а # 1), у = loga х (п > 0, a # 1) называются
основными элементарными функциями.
Элементарными функциями называются все функции, которые можно полу-
чить из основных элементарных функций с помощью алгебраических действий и
образования сложных функций. Например, функции у = lg cosx, y = x3+sinx,
У _ 2|eslnx+c°sx и т д являются элементарными.
Термин «функция» впервые появился в 1673 г. в одной из работ Лейбница. Под
функциями Лейбниц понимал некоторые отрезки прямых. И. Бернулли дал опре-
деление функции как аналитического выражения, состоящего из переменной и
постоянных величин (1718), он же применил обозначение «рх (без скобок). Обо-
значение /(х) впервые предложил Эйлер в 1734 г.
13.2. Предел последовательности
Числовой последовательностью (или последовательностью) называется функция
х„ = <р (и), п = 1,2,3,...,
определенная на множестве натуральных чисел. Каждое значение х„
(п = 1,2,3,...) называется элементом последовательности, а число п - его номером.
202
Числовую последовательность с элементом х„ обозначают либо х„,
« = 1,2,3,..., либо (xt,x2,...,x„,...), либо (х„).
Примеры числовых последовательностей: 1) (с) = (с,с,с,...);
fz-iy'-’A <11 1 \
2) М- = ’ - 7’ ; 3> (cos™) = (-’• !> -’> 1.
\ J \ 4 9 16 )
Числовая последовательность всегда содержит бесконечное множество эле-
ментов; среди них могут быть равные (см. примеры 1) и 3))-
Число а называется пределом последовательности (х„), если для любого чис-
ла е > О найдется такое натуральное число N, что при всех п > W выполняется
неравенство | х„ - а | < е.
Предел последовательности (х„) обозначают limx„=a; х„—при
п -» оо (читается: х„ стремится к а, когда п стремится к бесконечности).
Последовательность, имеющая предел, называется сходящейся. Последова-
тельность, у которой нет предела, называется расходящейся.
Интервал (а-Е, я + а) называется е-окрестностью точки а и обозначается О (а, е).
Определение предела имеет следующий геометрический смысл: число а явля-
ется пределом последовательности (х„), если в любой его £-окрестности содер-
жатся почти все члены (х„), или вне этой окрестности находится лишь конечное
число членов данной последовательности.
Из определения предела последовательности следует, что предел постоянной
равен этой постоянной lim с = с (с = const), поскольку в данном случае х„ = с,
я=с, |х„-я| = О<£ для любого е>0. Из определения следует также, что по-
следовательность может иметь только один предел.
Последовательность (х„) называется ограниченной сверху (снизу), если суще-
ствует такое число Л, что х„ < А (соответственно х„ > А) для всех номеров п.
Последовательность (х„), ограниченная сверху и снизу, называется просто
ограниченной.
Очевидно, последовательность (х„) ограничена тогда и только тогда, когда
существует такое число С > 0, что | х„ | < С для всех номеров п.
Например, последовательности (l/n), (l/n2), (cos(n«/2)) ограничены, после-
довательность (и2) ограничена снизу, но не ограничена сверху, последователь-
ность (и cos ли) не является ограниченной ни сверху, ни снизу.
Теорема 13.1. Если последовательность имеет предел, то она ограничена.
Число а называется верхней гранью последовательности (х„), если: 1) х„ < а
при всех п; 2) для любого £ > 0 существует такой номер N, что xN > а - £. Верх-
няя грань последовательности (х„) обозначается sup (х„) или supx„.
203
Аналогично определяется нижняя грань последовательности (х„) и обознача-
ется inf(x„) или infjc„.
В качестве примеров отметим, что sup | ——-| = 1, inf | ——-| = 0, inf(n2) = l,
V п ) \ п )
sup (и2 )=««>.
Последовательность (xj называется монотонно возрастающей (монотонно убываю-
щей), если л„ < хи+1 (соответственно х„ > х„+1) при всех п. Монотонно возрастающие
или монотонно убывающие последовательности называются просто монотонными.
Теорема 13.2. Всякая ограниченная сверху (снизу) монотонно возрастаю-
щая (монотонно убывающая) последовательность (х„) имеет предел, причем
lira х„ = sup (х„) (соответственно lim х„ = inf (х„)).
Если последовательности (а„) и (Ь„) имеют пределы, то пределы их суммы,
разности, произведения, частного существуют и находятся по формулам
lim (а„ +b„)= lim а„+ lim b„, (13.4)
lim (а„ -Ь„)= lim а„ - lim b„, (13-5)
lim (a„b„)= lim а„ lim Ь„, п-*** п—>°° (13.6)
/ х lim а„ lim 1 2il (lim b„ * 0). (13.7)
И—
Пример 13.1. Последовательность (8+1/и) сходится и имеет предел а=8.
Действительно, каково бы ни было число е > 0, найдется такое натураль-
ное число N, что |х„— о|=|(8+1/и)-8| = 1/и<е, 1/и<Е для n>N; неравен-
ство (1/и)<Е будет выполнено при всех n>N, если N>1/e, т. е. в качестве
А можно взять большее из двух последовательных натуральных чисел, между
которыми заключено число 1/е. Например, если £|=0,1, то А, =10; если
е2 = 0,01, то N2 = 100 и т. д.
Замечание. Одновременно показано, что последовательность (1/и)
имеет пределом нуль, т. е.
lim—= 0. (13.8)
п
Пример 13.2. Последовательность (cosли) является расходящейся.
В самом деле, каково бы ни было число а, вне его е-окрестности, например при
0<е'<1, заведомо лежит бесконечное множество элементов данной последова-
тельности (хотя среди них и много равных между собой); это означает, что а не
является ее пределом.
204
ГТ «-> -> тт м_ 1- 2д2-Зи + 5
Пример 13.3. Найти hm —z--------.
6n +4n-9
Разделив числитель и знаменатель дроби на и2 и применив формулы
(13.4) — (13.8), получим
о 2 а . с -> II с! 1 1*т (2—3/лг+5/лг2) ,
Нт 2и -Зи+5= ,im 2_-3/n + 5/n *___ ’Л.
"-»~6и2+4и-9 «->-6 + 4/и-9/и2 lim (6+4/и-9/и2) 3
13.3. Предел функции
Постоянная b называется пределом функции у = f(x) при х —> а (или в точ-
ке а), если для любого числа е > 0 существует такое число 8 > 0, что при всех х,
удовлетворяющих условию
О < | х — а | < 8,
выполняется неравенство
|/(х)-8|<е.
Предел функции /(х) при х, стремящемся к а, обозначают:
lim /(х)=Ь; f(x)-*b при х-ьа.
х-*а
Рассматривают также односторонние пределы функций: предел слева
lim /(x) = ij (х стремится к а, оставаясь меньше а; х<а) и предел справа
х-»о-0
lim /(х) = t>2 (х стремится к а, оставаясь больше а; х > а). Если односторонние цре-
х-»л+О
делы равны: lim /(х)= lim /(х)= Ь, то предел функции f(x) в точке а существу-
х->а-0 х-^>а+О
ет и равен Ь: lim /(х) - Ь. Если односторонние пределы различны или хотя бы один из
х-*а
них не существует, то не существует и предел функции в соответствующей точке.
Если с — постоянная величина, то lim с = с.
х—*а
Если функции /(х) и ср (х) имеют пределы при х -* а, то
lim (/(х)±<р(х)) = lim/(х)± lim <р(х), (13.9)
х—*а х—*а х—*а
lim (/(х)ср(х))= lim /(х) lim <р(х), (13.10)
х-*а х-ьа х-ьа
= -----(lim<p(x)*0). (13.11)
*-»°<p(x) lim<p(x)
x—ta
Из (13.10) следует, что
lim (c/(x))= c lim /(x) (c = const), (13.12)
x-*a x-^a
205
lim (/(х)У = (lim /(x))m, (13.13)
x—ya х—ьа
\waxm = am, (13.14)
x—*a
где m - натуральное число.
Если ^lim f(x) существует, то
lim rff(x) = Jlim/(x). (13.15)
x-ta yx-*a
Число А называется пределом функции у = /(х) при х, стремящемся к - «>
или + <*>, если для любого числа е > 0 можно указать положительное число N,
такое, что при всех значениях х, удовлетворяющих условию | х | > N, выполнялось
неравенство | f(x) - А | < е.
Пример 13.4.Найти lim(2х2-5х + 4).
х—>3
Применяя формулы (13.9), (13.12), (13.14), получаем
lim (2х2 —5х + 4) = lim (2х2)- lim (5х)+ lim 4 = 2-З2 -5-3+4 = 7.
х—>3 х—>3 х—>3 х—>3
Пример 13.5.Найти lim—:----------.
н Е х-2 3х2-8х+5
С помощью формулы (13.11) и формул, указанных в примере 13.4, находим
.. 6х2-9х+4 ]™(6л2-9* + 4) б-22-9-2 + 4
*-»2 3х2-8х+6 lim (Зх2 - 8х + 6) 3-22-8-2+6
х-»2
Пример 13.6. lim—£—* —- -г——.
*-»• х4 —2х3+2х2 — 1
При х = 1 числитель и знаменатель дроби равны нулю, имеем неопределен-
ность вида Чтобы раскрыть ее, предварительно преобразуем данную дробь,
разложив многочлены на множители:
х4-х3+х2-1 _ х3(х-1)+(х-1)(х + 1)
х4-2х3+2х2—1 (х2 —1)(х2+1)—2х2(х —1)
- (х-1)(х3 +х + 1) _ х3 +х +1
’ (х —1)((х+1)(х2+1)—2х2) ~ х3 —х?+х + Г
. Переходя к пределу, получаем
206
16-л’
Пример 13.7. Найти lim . - —.
—4 75+7-3
При х = 4 числитель и знаменатель дроби обращаются в нуль, имеем неопре-
0 „ ,
деленность вида —. Чтобы раскрыть эту неопределенность, предварительно пре-
образуем дробь:
16-л2 (16—х2)(75+х+3) = (16-л2) (75+7 + 3) =
77+7-3 (75+х-3)(75+х+3) 5+х-9
= (4-20(4+л)(75Н7+3) = _ {х + 4) + 3)
л-4
Переходя к пределу с использованием формулы (13.15), находим
1/7_____________ „2 _ ____
lim — — = -lim (х + 4)(75+х +3)=-8-6 = -48.
—^475+х-3 *-»4
13.4. Бесконечно малые функции и их свойства
Функция а = а (х) называется бесконечно малой при х —> а (или при х -» °°),
если ее предел равен нулю:
lim а (х) = О (lim а (х) = 0).
Х-Ю ХЧ“
Например, функция а (х) = (х-5)2 есть бесконечно малая при х -> 5, так как
lim a (х) = lim (х - 5)2 = 0; функция а (х) = 1/х является бесконечно малой при
х-»5 х—>5 ’
х-»оо, поскольку
lim а (х) = lim — = 0.
х—х—>™ х
Принимая во внимание определение предела функции, определение бесконеч-
но малой функции можно сформулировать следующим образом.
Функция а = а (х) называется бесконечно малой при х —> а, если, задав лю-
бое число е > 0, можно указать такое число 5 > 0, что для всех х, удовлетворяю-
щих условию 0 < | х - а | < 8, выполняется неравенство | а (х) | < е.
Свойства бесконечно малых выражаются следующими теоремами.
Теорема 13.3. Если функция у = у(х) имеет предел b при х—>а, то
у(х)=6+а(х), у = 6+а, (13.16)
где а = а (х) - бесконечно малая при х —> а. Обратное также верно: если вы-
полнено равенство (13.16), то limy(x) = b.
х-Ьа
Теорема 13.4. Алгебраическая сумма конечного числа бесконечно малых
функций при х —> а есть бесконечно малая функция при х -> а.
207
Теорема 13.5. Произведение бесконечно малой функции на ограниченную
функцию есть бесконечно малая функция.
Следствие 1. Произведение двух бесконечно малых функций есть бес-
конечно малая функция.
Следствие 2. Произведение бесконечно малой функции на постоянную
есть бесконечно малая функция.
13.5. Сравнение бесконечно малых функций
Бесконечно малые а (х) и р (х) при х -* а называются величинами одного
порядка, если их отношение имеет конечный предел, отличный от нуля, т. е.
1- а(х) г PW 1 i
hm = с, или hm (с#0).
»->»р(х) '-*»а(л) с
В этом случае пишут: а(х) = О(р(х)) при х-»а (читается: а(х) есть О
большое от р (х) при х -» а ).
Например, a(x) = sinx и р(х) = 3х при х-»0 являются бесконечно малыми
одного порядка, так как lima(x)/p(x) = l/3, sinx = O(3x) при х-»0.
Если предел отношения а (х)/р (х) при х -> а равен нулю (с = 0), то величина
ос(х) называется бесконечно малой высшего порядка по сравнению с Р(х) (величина
р (х) - бесконечно малая низшего порядка по сравнению с а (х) ). В данном случае
применяется обозначение а(х) = о(Р(х)) при х-»а (читается: а(х) есть о малое
от р (х) при х -> а). Например, х2 = o(sinx) при х -> 0, поскольку
х2 х
lim----= limx lim-----= 0-1 = 0.
х-»о sinx *-»о х-»о sinx
Функция р (х) называется бесконечно малой k-ro порядка относительно функ-
ции а(х), если р(х) и (а(х))* - бесконечно малые одного порядка, т. е.
lim Р^ = с (с#0).
—°(а(х))*
Например, если ос(х) = х, р(х) = х4, то при х-»0 Р(х) - бесконечно ма-
лая четвёртого порядка относительно бесконечно малой ос(х) (но бесконечно
малая второго порядка по сравнению с у (х) = х2).
Две бесконечно малые функции ос(х) и р(х) называются эквивалентными
(или равносильными) бесконечно малыми при х —> а, если предел их отношения
равен единице, т. е.
lim^^ = l, или lim Р = 1.
*-»<>р(х) *-»ea(x)
208
Эквивалентность бесконечно малых а(х) и р(х) обозначается символом -
а (х) - Р (х) при х -» а.
Из формул (13.17) и (13.22) (см. п. 13.8) следует, что при х —> О
x-sinx-tgx, 1п(1+х)~х.
Теорема 13.6. Бесконечно малые функции ос(х) и р(х) эквивалентны то-
гда и только тогда, когда их разность есть бесконечно малая высшего порядка
по сравнению с каждой из них.
Теорема 13.7. Если а(х) ~а{(х), р(х)~р((х) при х-ьа и существует
г а1(*) 1- сс(х)
lim , то существует lim—причем
х^Р,(х) Л ^Р(Х)
.. а(х) .. а, (х)
hm —— = hm '
*-»°Р(х) х-юр!(х)
Следствие. Если aj(x)-p(x), а2(х)~Р(х) при х-ьа, то
а( (х)~а2 (х) при х—ьа.
При нахождении предела отношения двух бесконечно малых функций каждую
из них (или только одну) можно заменить другой бесконечно малой, ей эквива-
лентной: если а(х)-а1(х), р(х)-р( (х), то
.. а(х) .. а. (х) .. а(х) .. а. (х)
lim - > = lim —L' — = lim = hm 1 v .
x-»op(x) x-»a p(x) x-»opj(x) I-*°P|(X)
Замечание. Если отношение <x(x)/p(x) двух бесконечно малых
функций при х —> а не имеет предела и не стремится к бесконечности, то беско-
нечно малые функции а (х) и р (х) несравнимы между собой. Например, несрав-
нимы при х—>0 бесконечно малые функции a(x) = xsin(l/x), Р(х) = х, так как
a(x) = xsin(l/x) = sjn 2
Р(х) х х
и sin (у/х) не имеет предела при х -» 0.
Пример 13.8. Доказать, что функции а(х) = 6х2/(1-х) н Р(х)= =х2
при х -> 0 являются бесконечно малыми одного порядка.
Найдем предел отношения двух данных функций:
lim 6х-----= 6 lim —— = 6.
*->°х2(1-х) «ol-х
Поскольку полученный предел отличен от нуля, то данные функции являются
бесконечно малыми одного порядка.
Пример 13.9. Доказать, что порядок функции a(x) = xs/(2+x2) выше,
чем порядок функции р(х) = х4 при х-»0.
209
Так как
X5 X
lim —------т— = lim-----5- = О,
««л (2+л ) ««2+л
то функция а(х) = х5/(2+х2) есть бесконечно малая высшего порядка, чем
функция р(х) = х4.
ГТ *-> ia тт 1- sin(x-3)
Пример 13.10. Найти hm ---------.
х->з х — 5х + 6
При х-»3 функции х-3, sin (х-3) являются эквивалентными бесконечно
малыми. Поскольку при замене бесконечно малой функции sin(х-3) эквива-
лентной ей функцией х-3 предел отношения не изменится, то
lim = lim =
х-»3х2-5х + 6 х-3(х-3)(х-2)
= lim----—3-----= lim —-— = 1.
(л - 3)(л - 2) х - 2
• - . ^.2 4
з
Пример 13.11.Найти lim
х->0
Так как (sinjt+л2-хА)~х, (2х-х3)~2х при х-»0, то
• 2 4 • «
sinx+x —х ,. sinx 1 .. sinx
lim —-----5----= Inn-----= — lim-----=
*-»o 2x-x x-»° 2x 2x->o x
2
2’
13.6. Бесконечно большие функции
Функция у = f(x) называется бесконечно большой при х -> а, если для любого
положительного числа N можно найти такое число 8 > 0, что при всех значениях х,
удовлетворяющих условию 0 < | х - а | < 8, выполняется неравенство | f(x) | > N.
Бесконечно большая функция не имеет предела при х -> а, но иногда условно
говорят, что ее предел равен бесконечности, и пишут: lim f(x) = °°, или
х—
f(x) -> о», при х -> а.
Если /(х) стремится к бесконечности при х -» а, принимая только положи-
тельные или только отрицательные значения, то соответственно пишут:
lim /(х) = + °°, lim /(х) = -°°.
х—х—>а
Если функция /(х) стремится к бесконечности при х-»<*>,
то пишут lim /(х) = °°.
х—
Примером бесконечно большой функции является функция f(x)=\jx при
х -> 0. В самом деле, при любом N > 0 неравенство 11/х | > N будет выполнено,
210
если | х | = | x - 01 < 1/N = 8. Эта функция принимает положительные значения при
х>0 ( lim /(х) = + <*>) и отрицательные - при х<0 ( lim /(х) = -°°).
х-»+0 х->-0
Функция /(х) = 1/(х-2)2 - бесконечно большая при х—>2. Действительно,
при любом W>0 неравенство 1/(х —2)2>N будет выполнено, если
(х-2)2<1/Л или |x-2|<l/Vjv =5. Данная функция принимает только положи-
тельные значения.
Если функция а = а (х) стремится к нулю при х —> а (или х —> и не обра-
щается в нуль, то функция у (х) = 1/а (х) стремится к бесконечности.
13.7. Основные теоремы о пределах функций
Теорема 13.8. Функция у = у(х) не может иметь более одного
предела при х-^а.
Теорема 13.9. Пусть функция у= f(x) определена в некотором проме-
жутке, содержащем точку а. Если при х —> а функция у - /(х) имеет поло-
жительный (отрицательный) предел, то найдется 8-окрестность точки а та-
кая, что для всех хеО(а, 8) функция положительна (отрицательна).
Эта теорема называется теоремой о сохранении знака функции, имеющей предел.
Теорема 13.10. Если функции и(х), v(x) определены в некоторой 8-
окрестности точки а, для всех хеО(а,8), хФа выполняется неравенство
и (х) < v (х) и функции имеют пределы при х —> а, то lim и (х) < lim v (х).
х—х-уа
Замечание. Теорему 13.10 кратко можно сформулировать
так: в неравенстве, обе части которого имеют пределы, можно перейти к
пределу, присоединив знак равенства. Например, 7+х2>7-х2, х*0;
lim(7+x2)= lim (7-х2) = 7.
х->0 х->0
Теорема 13.11. Пусть три функции и=м(х), у = у(х), v = v(x) опреде-
лены в некотором промежутке, содержащем точку а.
Если для любого х из этого промежутка выполняются неравенства
и(х)<у (х) < v (х) и функции и=и (х), v = v (х) имеют одинаковые пределы
при х —> а, то у = у (х) имеет тот же предел при х—ь а.
13.8. Некоторые важные пределы
Если угол а выражен в радианах, то
to^-l, |taa“.L (В.,7)
а-»0 а а-»0 а
?11
Числом е называется предел
/ I у lim|l+—I =е или lim (1 + а)^“ = е. (13.18) х->«*> ( х J сх—>0
При нахождении многих пределов применяются следующие пределы:
lim 1ое°<1+л) = iogo е, (13.19) х—»0 X lim^—^ = 1пд, (13.20) *-»о X .. (1+х)“-1 hm = а. (13.21) х—>0 х
Частными случаями формул (13.19) и (13.20) являются соответственно формулы:
lim ln(1+*)=i, (13 22)
х—»0 х
ех-1
lim-—l = t (13.23)
х—»0 х
При нахождении пределов вида lim (<p(x))vW = С необходимо иметь
х->а
в виду следующее:
1) если существуют конечные пределы lim <р (х) = A, lim у (х) = В, то С= Ав\ х—Ьа х-*а
2) если lim <р (х) = А Ф1 и lim у (х) = °°, то С находится с помощью формул х—>а х—>а ,, (0, если 0<Л<1, hm Л = i х-»+~ [+°°, если А>1, г (+<», если 0<Л<1, hm А =1 х->— [0, если Л>1;
3) если lim<p(x)=l, limy(x) = <*>, то, положив <р(х) = 1+а(х), где х—»а х—>а
а(х) —> 0 при х а, получим z ч . v . v lima(x)w(x) lim [©(x)-llw(x) С= lim {П + а(х)^аМ}аМ*м =е”“ х-*а f ь\х Пример 13.12. Найти lim 1 1. х->~( х)
При х—><*> выражение (1-(6/х))—>1, получаем неопределенность
вида 1“. Чтобы раскрыть ее, введем новую переменную по формуле
(-5/х) = а, откуда х = -Ь/а; а—>0, когда х—>°». Переходя к пределу
с использованием формул (13.13) и (13.18), находим
212
( h\
lim 11---1 = lim (1 + cc)'^a = lim [ (1 + a)^“]"A =
x J a-»0 a->0
= [lim(l + a)v“rd=e"d; lim fl--] = e"*.
CL->0 x—><» I X)
В частности, при b = -2 получаем lim
= e2, приЬ=3 lim fl- — j = e3.
*-»’Л xj
Пример 13.13. Найти lim
'Зх-2/
3x + 4 J
Разделив числитель и знаменатель на Зх и воспользовавшись результатом при-
мера 13.12, получим
lim
X—♦«“
Зх —2Y
.Зх + 4 J
lim
1-(2/3)/xY
l+(4/3)/xJ
= lim fl 1-lim f 1+^Y = e-^; Л3 = e‘2.
x J X J
Пример 13.14. Найти lim s‘n7'x
x-»0 X
Преобразуя эту дробь и применяя первую из формул (13.17), находим
lim = Нт 7sin7* = 7 lim S1^ = 7 -1 = 7.
х->0 X х->0 Ух *-»0 7х
Пример 13.15.Найти lim —1
У-»0 у
Преобразуя данную функцию, вводя новую переменную х = 2у и применяя
формулу (13.21), находим
Х-»0 у у-»0 2у
_.. (l+x)V2-l 1 ,
= 2 lim ----i---= 2-- = 1.
х-»о х 2
Пример 13.16.Найти lim
>-»о у
Преобразуя эту функцию, вводя новую переменную х=5у и применяя
формулу (13.22), получаем
lim Пт5^(1^ =
у-*0 у >->0 5у
... 1п(1+х) - , ,
= 5 lim—i---< = 5.1 = 5.
х-»0 JC
213
еу/3-1
Пример 13.17. Найти lim-------.
у
После соответствующих преобразований по формуле (13.23) находим
.. е^-1 .. еу/3-1
hm-------= hm ------— =
у—»о у у-*о Зу/З
1 ех—1 1 , 1
3*->о х 3 3
13.9. Непрерывность функции
Функция у = f(x), определенная на интервале (а, Ь), называется непрерыв-
ной в точке х0 е (а, Ь), если
lim /(х) = /(х0)
(т. е. предел функции равен ее значению при предельном значении аргумента).
Согласно определению предела функции, условие (13.24) равносильно сле-
(13.24)
дующему: для любого числа е>0 существует
такое число 8 > 0, что при всех х, удовлетво-
ряющих условию 0 < | х - а | < 8, выполняется
неравенство | f(x)~ f(x0) | < е.
Если х0 е (а, Ь) и хе (а, Ь), то разность
Д с = х - х0 называется приращением аргумента в
точке х0, а разность Ay = f(x)~ f(x0), или
Ay = /(х0+Ах)-f(x0), - приращением функ-
ции в той же точке (рис. 13.1); Ау -функция Ах.
Необходимое и достаточное условие непре-
рывности функции у = f(x) в точке х0 выра-
или
lim [/(х0+Дх)-/(х0)]= 0.
\х-»О
(13.25)
жается равенством
lim Ау = 0,
Дх->0
Итак, функция непрерывна в точке, если бесконечно малому приращению ар-
гумента в этой точке соответствует бесконечно малое приращение функции.
Замечание. Поскольку х0 = lim х, то формулу (13.24) можно перепи-
х-»х0
сать так: lim f(x) = f( lim x), т. e. для непрерывной функции символы предела и
Х-»Х„ Х-»Хд
функции перестановочны.
Теорема 13.12. Если функции f(x) и <р(х) непрерывны в точке х0, то
также непрерывны в этой точке их сумма /(х)+<р(х), разность /(х)-<р(х),
произведение /(х)<р(х), а также частное f(x)[y(x) при условии, что <р(х)#0.
214
Следствие 1. Целая рациональная функция Р„(х) = а0 +арс +
+а2х2 + • • • + а„хп непрерывна при всех х.
Следствие 2. Дробная рациональная функция
R <х) = = «о+а^ + «2^2 +- + аяхи
й,(*) bo+bpt + l^x2 + + bmxm
непрерывна при всех х, для которых знаменатель не обращается в нуль.
Теорема 13.13. Если функция <р(х) непрерывна в точке х0, а функция
f(y) непрерывна в точке у0 = <р (х0), то сложная функция F (х)= = /[<р(х)1
непрерывна в точке х0.
Функция называется непрерывной на интервале, если она непрерывна
в каждой точке этого интервала.
Если функция определена при х = а и при этом lim /(х) = /(а), то говорят,
х~»а+О
что f(x) в точке а непрерывна справа. Аналогично, если lim f(x) = f(b), то
x-»A-0
говорят, что в точке b эта функция непрерывна слева.
Функция называется непрерывной иа отрезке [а, 6], если она непрерывна в
Рис. 13.2
каждой его точке (в точке а - непрерывна справа, в точке Ь - непрерывна слева).
Отметим, что основные элементарные функции непрерывны в соответствую-
щей области определения.
Функции, непрерывные на отрезке, обладают рядом важных свойств, которые
выражаются следующими теоремами.
Теорема 13.14. Функция, непрерывная
на отрезке [а, 6], достигает в нем своего
наименьшего значения т и наибольшего значе-
ния М, т.е. существуют такие точки хь х2
этого отрезка, что f(xt)=m, f(x2)=M.
Эта теорема имеет простой геометрический
смысл (рис. 13.2).
Замечание. Функция, непрерывная
на интервале, этим свойством не обладает.
Например, функция у = 6х2 на интервале
(0,1) не достигает значений т = 0 и М = 6,
так как эти значения функция принимает в
точках х = 0 и х = 1, а последние данному интервалу не принадлежат.
Теорема 13.15. Если функция y-f(x) непрерывна на отрезке [а,Ь]
и на его концах принимает неравные значения f(a) — A, f(b)=B,
А* В, то каково бы ни было число С, заключенное между А и В,
найдется точка се [а, £>] такая, что f(c)=C.
215
Геометрический смысл теоремы иллюстрируется на рис. 13.3, а, б. Всякая пря-
мая у = С, где А < С< В (или А > С> В), пересекает график функции у - f(x).
Следствие. Если функция непрерывна на отрезке и на его концах при-
нимает значения разных знаков, то на этом отрезке найдется хотя бы одна
точка, в которой функция обращается в нуль.
Это частный случай теоремы: AB<Q, С = 0; геометрический смысл: график
непрерывной функции у = f(x), соединяющий точки P(a,f(a)), Q(b,f(b)),
для которых f(a) f(b) < 0, пересекает ось Ох (рис. 13.4, а, б).
Отметим, что сумма конечного числа функций, непрерывных на некотором от-
13.10. Точки разрыва функции
Рассмотрим функцию у = /(х), определенную на интервале (а,Ь), кроме,
быть может, точки х0 е (д, Ь). Значение аргумента х0 называется точкой раз-
рыва данной функции, если при х = х0 функция определена, но не является
непрерывной или ие определена при этом значении х.
216
Если х0 — точка разрыва f(x) и существуют конечные пределы
f (х0 - 0) = lim f (х), f (х0 + 0) = lim f (х), f (х0 - 0) * f(x0 + 0), то она на-
х—»хо-0 х—»xQ+0
зывается точкой разрыва первого рода. Величина f(x0 + 0)- f(x0 - 0) называется
скачком функции f (х) в точке х0.
Если х0 — точка разрыва и /(хо-0) = /(х0+0), то х0 называется точкой
устранимого разрыва.
Если хотя бы один из односторонних пределов /(хо-0), /(хо + 0) не существует
или является бесконечным, то х0 называется точкой разрыва второго рода.
Пример 13.18. Функция
/(х) = -х/|х| в точке х0 = 0 имеет
разрыв первого рода.
Действительно, f(x) = 1 при х < 0
и /(х) = -1 при х>0, в точке х0 = 0
функция ие определена; lim /(х) = 1,
X—»- О
lim /(х) = -1. Скачок функции в точ-
х—»+0
ке х0 = 0 равен -2 (рис. 13.5).
У' к
1 /
О -1 я* X
Рис. 13.5
Пример 13.19. Для функции /(x) = (sinx)/x значение аргумента х0 = 0
является точкой устранимого разрыва.
В самом деле, при х0 = 0 данная функция не определена, ио имеет равные од-
носторонние пределы:
lim (sinjc)/jr = 1, lim (sinx)/x = l.
x—>—0 x—>+0
Пример 13.20. Функция f(x)=l/x в точке xo = 0 имеет разрыв
второго рода, так как
lim 1/х = -<х>, lim 1/х = + <>о.
х—»- О х—>+0
217
Рис. 13.7
Пример 13.21. Для функции
/(х) = 3^ значение х0 = 0 является
точкой разрыва второго рода, так как
lim f(x) = + оо. Второй односторонний
х-»+0
предел конечен: lim f(x) = 0 (рис. 13.7).
х—>-0
13.11. Показательная функция. Гиперболические
функции
Показательной (экспоненциальной) называется функция у = а* (а > 0, а ФI).
Пусть а — е (см. формулу 13.18), в этом случае показательная (экспоненциальная)
функция обозначается у = ех = ехрх.
Показательную функцию с другим основанием можно привести к показатель-
ной функции с основанием е. Действительно, по определению логарифма
а = е|па, поэтому ах = (elna)x = efa, где к = In а.
Гиперболическим синусом называется функция, определяемая формулой
е* —е~х
shx = —-2 , (13.26)
гиперболическим косинусом - функция
chх = е* *е * . (13.27)
Гиперболический тангенс и гиперболический котангенс определяются соответ-
ственно формулами
shr ех-е~х
thx= = -------—, (13.28)
chx ех + е~х
chx ех +е~х
cthx =----=-------. (13.29)
shx ех—е~х
Функции, определяемые формулами (13.26) - (13.29), называются
ги перболичес кими.
Гиперболические функции имеют вполне определенные значения при всех зна-
чениях х, кроме функции у = cthx, которая в точке х = 0 обращается в бесконеч-
ность. Отметим, что sh 0 = 0, ch 0 = 1, как и для обычных синуса и косинуса.
Гиперболические функции не обладают важнейшим свойством тригонометри-
ческих функций - свойством периодичности. Кроме того, множество значений
218
каждой гиперболической функции существенно отличается от множества значе-
ний соответствующей тригонометрической функции. Функция у = shx принима-
ет все действительные значения, т. е. множество ее значений совпадает с беско-
нечным интервалом (—<»,+ <*>); y = chx - значения, не меньше единицы
(l^chx< + oo); значения функции y = thx по модулю не превышают единицы
(—1< thjc< 1); значения _y = cthx по модулю больше единицы (cthx>l при
х>0, cthx<-l прих<0).
Графики гиперболических функций представлены на рис. 13.8 и 13.9, а, б.
Прямые у = +1, у = —1 являются асимптотами графиков функций y = thx,
у = cthx. Кроме того, ось Оу служит асимптотой графика функции у = cth х.
Рис. 13.9
219
Глава 14
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
14.1. Понятие производной, ее геометрический
и физический смысл
Касательной к линии I в точке Мо называется прямая М0Т — предельное
положение (рис. 14.1) секущей М0М, когда точка А/стремится к Мо вдоль дан-
ной линии (т. е. угол устремится к нулю) произвольным образом.
Производной функции у = f(x) в точке х0 называется предел отношения при-
ращения этой функции к приращению аргумента, когда последнее стремится к нулю.
Производную функции у = f(x) в точке х0 обозначают символом /'(х0)
(читается: «эф штрих отхо») или у'(х0). Следовательно, по определению
/'Uo)= lim А*о+.Д*) или /(jfo)= lim (14.1)
Дх->0 Ду Дх-ьО Дх
Рис. 14.1
Употребляются и другие обозначе-
dy Ду .. Лх
ния: — = hm —, х = hm —,
dx Дх-»о Лх zu->o Д/
если х = f(t).
Термин «производная» (а также
«вторая производная») ввел Ж. Лагранж
(1797), ои же предложил обозначения
у’, f\x), f"(x) (1770, 1779). Обозна-
чение dy/dx впервые встречается у
Лейбница (1675).
Геометрический смысл производ-
ной. Производная функции у = f(x)
при х = х0 равна угловому коэффициенту касательной к графику данной функции
в точке М0(х0, f(x0)\ т.е.
/'(^0) = tga,
(14.2)
где а— угол наклона касательной к оси Ох прямоугольной декартовой системы
координат (рис. 14.2).
Уравнение касательной к линии у — f(x) в точке М0(х0,у0) принимает вид
У~Уо=/’(хо)(х-хо). (14.3)
220
Нормалью к кривой в некоторой ее точке называется перпендикуляр к каса-
тельной в той же точке. Если /(х0)* 0, то уравнение нормали к линии у - f(x) в
точке Л/0(х0, у0) запишется так:
У~Уо = --у~Ах~хо)- (14.4)
f(x0)
Физический смысл производной. Если х = /(<) - закон прямолинейного
движения точки, то х' = f'(t) — скорость этого движения в момент времени I.
Быстрота протекания физических, химических
и других процессов выражается с помощью про-
изводной.
Если отношение Ду/Дх при х—»х0 имеет
предел справа (или слева), то он называется про-
изводной справа (соответственно производной
слева). Такие пределы называются односторонни-
ми производными.
Односторонние производные функции /(х)
в точке х0 обозначается соответственно
символами /_'(х0), /+'(х0):
> г f(.xo + ^x)~f(.xo)
/_(х0)= hm ------------ - - производная слева;
Дх—»—О Дх
г,, ч •• /(х0+Дх)-/(х0)
Д(х0) = hm --у---------—- - производная справа.
Дх->+0 Дх
Очевидно, функция /(х), определенная в некоторой окрестности точки х0, имеет
производную /'(х0) тогда и только тогда, когда односторонние производные /_'(х0),
/+'(х0) существуют и равны между собой, причем /_'(х0)= /+'(х0) = /'(х0).
Если для некоторого значения х выполняется одно из условий
Ду Ду
hm -^- = +со, hm — = -<»,
Дх-»О Дх Дх—>0 Дх
то говорят, что в точке х существует бесконечная производная, равная
соответственно +°°,
Геометрическое истолкование производной как углового коэффициента каса-
тельной к графику распространяется и на этот случай: касательная в данном слу-
чае параллельна оси Оу (рис. 14.3, а - Ь).
Функция, имеющая производную в данной точке, называется дифференцируе-
мой в этой точке. Функция, имеющая производную в каждой точке данного про-
межутка, называется дифференцируемой в этом промежутке. Если промежуток
является замкнутым, то на концах его имеются односторонние производные.
Операция нахождения производной называется дифференцированием.
221
Зависимость между непрерывностью и дифференцируемостью функции выра-
жается следующей теоремой.
Теорема 14.1. Если функция у = f(x) дифференцируема в данной точке,
то она и непрерывна в ней.
Замечание. Обратное утверждение не всегда верно. Например,
функция у = |х—1| непрерывна в точке х = 1, но не является дифферен-
цируемой в ней.
Пример 14.1. Записать уравнение касательной к линии f(x) = x2 —
—4х + 7 в точке л = 3.
Так как f'(x) = 2х-4, х0 = 3, /'(*о) = /'(3) = 2, у0 = f(x0) = /(3) = 4, то в
соответствии с уравнением (14.3) получаем у-4 = 2(х-3), или 2х-у—2 = 0.
Пример 14.2. В какой точке касательная к линии /(л)=х3-11л-5 па-
раллельна прямой 2х—Ту+3 = 0.
Данная прямая имеет угловой коэффициент /с = 1. Поскольку f\x) =
= 3.x2 —11, то в силу равенства (14.2) имеем Зх2 —11 = 1, или Зх2=12, откуда
Xj=-2, х2 = 2. Находим =/(xi) = /(-2) = 9, у2 =/(х2) =/(2) =+19. Сле-
довательно, получили две точки: Л/] (-2,9), Л/2(2,-19).
Пример 14.3. Записать уравнение нормали к линии f(x)=x2+ 5х-7
в точке х = -4.
Так как f'(x)=2x+5, х0=-4, f(x0)= f(-4) = -3, уо=/(*о) =
= /(-4) = -11, то уравнение (14.4) принимает вид у + 11 = (-1/~3)/(х+4), или
х-Зу-29=0.
222
14.2. Основные правила дифференцирования
Производная алгебраической суммы функций выражается следующей теоремой.
Теорема 14.2. Производная суммы (разности) двух дифференцируемых
функций равна сумме (разности) производных этих функций:
(w±v)' = u'±v'. (14.5)
Следствие. Производная конечной алгебраической суммы дифферен-
цируемых функций равна такой же алгебраической сумме производных слагае-
мых. Например, (и— v + w)' = u' — v' + w'.
Производную произведения функций определяет
Теорема 14.3. Производная произведения двух дифференцируемых функций
равна произведению первой функции на производную второй плюс произведение
второй функции на производную первой, т. е.
(uv)’ = u'v + uv'. (14.6)
Следствие 1. Постоянный множитель можно выносить за знак про-
изводной (cv)' = cvz (с = const).
Следствие 2. Производная произведения нескольких дифференцируе-
мых функций равна сумме произведений производной каждой из них на все ос-
тальные. Например, (uvw)' = u'vw + uv'w + uvw'.
Производная частного двух функций выражается следующей теоремой.
Теорема 14.4. Производная частного двух дифференцируемых функций оп-
ределяется формулой
(”) <14”
Производную сложной функции выражает
Теорема 14.5. Если y = f(u) и « = <р(х) — дифференцируемые функции
своих аргументов, то производная сложной функции у = /(<р (х)) существует и
равна произведению производной этой функции по промежуточному аргументу
на производную промежуточного аргумента по независимой переменной, т. е.
Производная обратной функции. Если у = f(x) и х = <р (у) - взаимно об-
ратные дифференцируемые функции и у' * О, то
x;=-L. (14.9)
Ух
223
14.3. Основные формулы дифференцирования
Производные степенных и тригонометрических функций выражаются сле-
дующими формулами:
(х“)' = ах'
1
2 ’
(sin x)' = cosx, (cosx)' = - sin x,
, w 1 1
(tgx) =——, (ctgx) =—t^—.
cos x sm x
Если и = и (x) - дифференцируемая функция, то
(иа)' = аиа~'и',
(sin и)' = cos и • и', (cos и)’ = - sin и и’,
(tg«)' = —(ctgw)' = —.
COS X sin и
Пример 14.4. Найти производную функции у = л/1-х2.
Считая 1—х2 = и и применяя формулу (14.10), получаем
у = (1-х2Л / = 1(1-х2)-^(1-х2)' = ^т=^^.
2 2л/1-х2 л/1-х2
(14.10)
(14.П)
(14.12)
Пример 14.5. Найти производную функции у = sin —+cos —.
3 6
Применяя формулы (14.11), находим
. -л
-sin — —
616.
. Л I л
у = cos — —
зи
= —cos—= ——sin—.
Пример 14.6. Найти производную функции у = ctg2 Зх.
Так как у = v2, где v = ctg и, и = Зх, то формулу (14,8) применяем дважды. На
основании формулы (14.10) и второй из формул (14.12) получаем
, - . , 1 ,, v 6ctg3x
у = -2ctg3x . j - (Зх) =—7^—.
sin Зх sin Зх
Пример 14.7. Найти производную функции у = l/tg22x.
Так как y = l/w, w = v2, v = tgw, и = 2х, то у' = у» м»' *'•«'. Применяя
формулу (14.10) и первую из формул (14.12), находим
, 1 „ _ 1 _ 4 1 4cos2x
tg42x cos22x tg32x cos22x sin32x
224
Производные показательных и логарифмических функций выражаются
формулами
(ах)' = ах1па, (ех)' = ех,
п v 1 . 1
(log„ х) = - togo е = ——,
х х In а
(1пх)' = — (х>0), (1п|х|)' = — (х^О).
Если и = и (х) - дифференцируемая функция, то
(a")' = a“lnaw', (e“)' = eV, (14.13)
(log„M)' = -^—, (1пи)' = —. (14.14)
xlna и
Пример 14.8. Найти производную функции y = esm3x.
Применяя вторую из формул (14.13), находим
у' = e"n3x(sin3x)' = ейп3х cos3x (Зх)' = Зейо3х cos3x.
Пример 14.9. Найти производную функции у = In (1+х2). На основа-
нии второй из формул (14.14) получаем
(1+х2у_ 2х
1+х2 1+х2
Пример 14.10. Найти производную функции у = 1пл/х2+4х + 5. Так
1 ?
как у = —1п(х +4х + 5), то
(х2+4х + 5)' _ х + 2
У 2(х2 + 4х + 5) х2+4х+5
Производные обратных тригонометрических функций находят по формулам
, • V 1 V 1
(arcsinx) = , , (arccosx) =—, ,
71-х2 ТГх2
(arctgx)'= —Ц, (arcctgx)z = --J-y.
1+х2 1+х2
Если и = и (х) — дифференцируемая функция от х, то
(arcsinw)'= . и (arccosw)' = —(14.15)
л/1— и2 -yl —«2
(arctgw)' = ——, (arcctgw)' =-—(14.16)
1+ц2 1+w2
Пример 14.11. Найти производную функции у = arcsin-J1 - Зх +
+arccos-Vl-2x.
8 Зак. I
225
Применяя формулы (14.15), находим
(д/1-Зх)' (л/1-2хУ _ -3 1__
У ф-(1-Зх) д/1-(1-2х) 2д/1-Зх >/з7
-2 1 3 | 1
2л/1-2х -J2x 2л/зх-9х2 л/2х-4х2
1—X
Пример 14.12. Найти производную функции у = arctg-.
1+х
С помощью первой из формул (14.16) и формулы (14.7) получаем
, = 1= а+*)2 х
У 1+((1-х)/(1+х))2 ll+xj (1+х)2+(1-х)2
„Г-1(1+х)-1(1-хЙ_ -2 _______________1_
(1+х)2 J 2+2х2 1+х2’
Производные гиперболических функций находят по формулам
(shx)' = chx, (chx)' = shx,
(Л*)' = -Д—, (cthx)' = - —.
ch x sh x
Если u=u(x) - дифференцируемая функция, to
(sh u)' = ch и • iZ, (chi/)' = sh и • iZ,
(thw)' =
u'
ch2x ’
(cthw)' = —
sh x
(14.17)
(14.18)
Пример 14.13. Найти производную функции y = sh2x + ch3x
Применяя формулы (14.17), находим j/ = ch2x(2x)'+sh3x(3x)' =
= 2ch2x+3sh3x.
Пример 14.14. Найти производную функции у = th + cth .
В соответствии с формулами (14.18) получаем
, = (*/5)' _ (X/7)' = 1 _ 1
ch2(x/5) sh2(x/7) 5ch4x/5) 7sh2(x/7)‘
Производные неявных функций и функций, заданных параметрически.
Производная функции у=и". Если дифференцируемая функция у = у{х) зада-
на уравнением F(x, у)=0, то производная у' = у'(х) этой неявной функции
может быть найдена из уравнения F' = 0, где F = F(x,y) рассматривается как
сложная функция переменной х.
226
Если функция у = у(х) задана параметрически:
x = x(t), y = y(t) (а<Г<Р), (14.19)
где x(t), y(f) - дифференцируемые функции и У (О* 0, то ее производная у'х
определяется формулой
Уж = У//х1- (14.20)
Производная степенно-показательной функции и", где u,v —
дифференцируемые функции от х, находится с помощью предварительного лога-
рифмирования, которое приводит к формуле
(«”)' = и” ( v' In и+^-|. (14.21)
к и )
Пример 14.15. Найти производную функции, заданной уравнением
у sinx = cos (х-у).
Это уравнение определяет у = у (х) — функцию от х. Подставляя функцию
у = у(х) в данное уравнение, получаем тождество у (x)sinxs cos(x-y (х)).
Дифференцируем это тождество и из полученного уравнения находим у' = у’ (х):
y'sinx+ycosx = -sin(x-y)(l-y'), y'sinx + ycosx = -sin (х - у) + y'sin (х - у),
,, . , • , . , , у cosx + sin (х-у)
ycosx + sin(x-y) = y (sm(x-y)-smx), у =------------------.
sin (x-y)-sinx
Пример 14.16. Найти производную функции, заданной уравнениями
x — t-sin/, y = l-cos/.
Эта функция задана параметрически (см. (14.19)). Так как х(' = 1- -cos/,
у,'= sin Г, то по формуле (14.20) получаем у' = —= -ш- .
х, 1-cosr
Пример 14.17. Найти производную функции у = хыпх.
Логарифмируя это равенство по основанию е, получаем lny= sinxInх. Диф-
ференцируя, находим у'/у = cosx In х +sinx-(1/х), откуда у' =
= у (cosxlnx + sinx- (1/х)), у' = x”nx(cosxlnx + sinx/x).
Пример 14.18. Найти производную функции хх.
Это также функция у-и", где и = х, v=x. По формуле (14.21) получаем
у' = хх(1пх+1).
Производные высших порядков. Производной второго порядка, или второй
производной, функции у = /(х) называется производная от ее производной
у' = f\x) (которую называют первой производной).
Обозначения второй производной:
/'=(/)'. rw=(/w.
dx dx
227
(14.22)
Механический смысл второй производной. Если х = f (t)
- закон прямолинейного движения точки, то х" = f”(t) - ускорение этого дви-
жения в момент времени t.
Аналогично определяются и обозначаются производные третьего, четвертого и
более высоких порядков:
уш=(/'У=(/"МУ. у™ = (/"У. -. у(и)=(у(”‘,)У-
Производная n-го порядка обозначается и так:
dx” У '
Если функция задана параметрически: х = х (t), у = у (t), то ее вторая произ-
водная определяется формулой
„ У2У_х'у”~у'х" (
Ухх dx2 х'3 ’
Пример 14.19. Найти вторую производную функции у = х31пх
Так как у' = (х3)'1пх+х3(1пх)' = Зх21пх+х3(1/х) = Зх21пх+х2, то
у" = 6х In х+3jc 2 (1/jc)+2х, у" = 6х In х + 5х.
Пример 14.20. Найти вторую производную функции, заданной парамет-
рически: x = z-sinz, y = l-cosz.
Поскольку х' = 1 — cos t, y' = sin/, x" = sinr, у" = cost, то по формуле (14.22)
d2y (1 - cost) cost —sintsin t cost-1 1
получаем —= —---------------5---------------5- =--------5-.
dx2 (1-cos/)3 (1-cos)3 (1-cos/)2
Пример 14.21.Найти /"'(1) для функции f(x) = x4-5х3 + 6х2 - 7х+9.
Так как /'(*) = 4х3-15х2+12х-7, f"(x) = l2x2-30х+12, то
f"'(x) = 24х - 30. Следовательно, /"'(1) = -6.
14.4. Дифференциал функции
Понятие дифференциала. Применение дифференциала в приближенных
вычислениях. Рассмотрим функцию у = f(x), определенную в некотором про-
межутке (а, Ь), и ее приращение Ду = /(х +Дх)-/(х) в точке х0, где х0,
(х0+Ах)е(а,Ь).
Если приращение функции представимо в виде
Ду = ЛДх + о (Дх), (14.23)
где А - постоянная, о (Ах) - бесконечно малая высшего порядка по сравнению с
Дх, то слагаемое ААх называют дифференциалом функции f(x) в точке х0 и
228
обозначают dy или df(x0)-. dy = АЛх; функцию у = f(x) в этом случае называют
дифференцируемой в точке х0.
Если приращение функции у = f(x) представимо формулой (14.23), то
Л = f'(x): следовательно, dy = f'(x0)Ax. Так как
dx = Ax, (14.24)
т. е. дифференциал независимой переменной равен приращению этой переменной, то
dy = f'(xo )dx, cfy = y'„dx, (14.25)
откуда f'(xQ)-dy/dx, т. e. производная равна отношению дифференциала функ-
ции к дифференциалу независимой переменной.
Формулу (14.23) можно записать так:
Ду = dy + о (Дх). (14.26)
Дифференциал функции называют также главной линейной частью ее приращения.
Теорема 14.6. Бесконечно малое приращение функции эквивалентно ее
дифференциалу при всех значениях независимой переменной, для которых произ-
водная функции конечна и отлична от нуля.
Из равенства (14.26) при достаточно малых Дх получаем
Ду = dy, или f(x0+txx)-f(x)~ f'(x0)£>x, (14.27)
откуда
/(х0+Дх) = /(х0) + /'(х0) Дх. (14.28)
Формулы (14.27) и (14.28) применяются в приближенных вычислениях.
Пример 14.22. Вычислить значение дифференциала функции
f (х) = х4 - 5х2 + 7, когда аргумент х меняется от х = 2 до х = 2,1.
Найдем сначала выражение для дифференциала данной функции по формуле
(14.25): dy = (xo-5xo+7)'<l!x=(4xo + 10xo)<ix. Так как dx = Ax =
= xt-х0 =2,1-2 = 0,1, х0=2, то dy = (4 • 23 -10 • 2) 0,1 = 1,2.
Пример 14.23. Вычислить приближенно значение функции /(х) =
= Vl + 7x2 при х = 1,1.
Значение аргумента х = х0 + Дх представим в виде х = 1 + 0,1, где х0 = 1,
Дх = 0,1. При х0 = 1 легко вычисляются значения функции и ее производной
/'(*)= , -Л, = V1 + 7-12 = 2, />(1)=-г 141 =1
3^(1+7х2)2 3^(1 + 7-12)2 6
Эти значения входят в формулу ^1+7(1,1)2 °У1 + 7-12+- , 141 0,1, полу-
3 ^/(l+7 -l2)2
ченную из формулы (14.28). Следовательно, /(1,1) = 2 + 7/60 = 2,117.
229
Геометрический смысл дифференциала. Дифференциал
функции равен приращению ординаты касательной к графику функции в соответ-
ствующей точке, когда аргумент получает приращение Дх (рис. 14.4).
Рис. 14.4
Отметим, что ф<Ду (рис. 14.4, а) или dy>by (рис. 14.4,6); если функция
равна постоянной, то dy = Ду = О.
Физический смысл дифференциала. Рассмотрим прямолиней-
ное движение точки по закону s = f(t), где s — длина пути, t - время, f(t) —
дифференцируемая функция; тогда ds = f'(t) dt = v (t) dt, где v (/) - скорость
движения. Следовательно, дифференциал пути равен приращению пути, получен-
ного в предположении, что, начиная с данного момента t, точка движется равно-
мерно, сохраняя приобретенную скорость.
Свойства дифференциала. Дифференциал функции обладает свойствами,
аналогичными свойствам производной.
1. Дифференциал постоянной равен нулю:
de = 0, с = const. (14.29)
2. Дифференциал суммы дифференцируемых функций равен сумме диффе-
ренциалов слагаемых:
d (u+v)= du + dv. (14.30)
Следствие. Если две дифференцируемые функции отличаются посто-
янным слагаемым, то их дифференциалы равны
d(u+c) = du (с= const). (14.31)
3. Дифференциал произведения двух дифференцируемых функций равен про-
изведению первой функции на дифференциал второй плюс произведение второй
на дифференциал первой:
d (uv) = udv + vdu. (14.32)
Следствие. Постоянный множитель можно выносить за знак
дифференциала
d(cu) = cdu (с = const). (14.33)
230
4. Дифференциал частного u/v (v#0) двух дифференцируемых функций
и = и(х) и v = v(x) определяется формулой
vdu-udv
d - =------r. (14.34)
\у) v
5. Свойство независимости вида дифференциала от выбора независимой пе-
ременной (инвариантность формы дифференциала): дифференциал функции равен
произведению производной на дифференциал аргумента независимого-от того,
является ли этот аргумент независимой переменной или функцией другой незави-
симой переменной.
Основные дифференциалы:
I. dxa = аха xdx, II. d(ax) = ax\nadx,
ш. IV. d (sin x) = cosxtfe,
V. d (cosx) = - sinx<&, VI. d (tgx) = dx/ cos2 x,
VII. d (ctg x) = - dx/ sin2 x, VIII. rf(arcsinx)= tfa/Vl-x2
IX. d (arccosx) = - dx/-\/l - x2 , X. d (arctg x) = dx/ (1+x2 ),
XI. d (arcctgx) = - dx/(1+x2), ХП. d (shx) = chxtfc,
XIII. d (chx) = shx<&, XIV. d (thx) = tfa/ch2 x,
XV. d (cth x) = - tfa/sh2 x, XVI. df(u) = f'(u)du.
Дифференциалы высших порядков. Если х - независимая переменная и
У = f(x) - дифференцируемая функция, то dx = f'(x)dx, т. е. дифференциал
функции есть функция, зависящая от двух аргументов х и dx. Этот дифференциал
будем называть также дифференциалом первого порядка (или первым дифферен-
циалом). Считая dx постоянной, получаем, что df(x) - функция одной пере-
менной. Предположим, что функция у = f(x) имеет не только первую производ-
ную, но и и последовательных производных у" = f"(x),
Дифференциал от дифференциала функции у = f(x) называется вторым диф-
ференциалом или дифференциалом второго порядка этой функции и обозначается
d2у: d2y = d (cfy), причем
d2y = f"(x)dx2. (14.35)
Дифференциалом n-го порядка называется дифференциал от дифференциала
(п-1)-го порядка: dny = d (dn~'y):
dny = f{n\x)dx". (14.36)
Замечание. Формулы(14.35) и(14.36) при и> 1 справедливы, когдах
является независимой переменной.
231
14.5 . Основные теоремы дифференциального
исчисления
Теорема 14.7. (Лагранжа). Если функция f(x) непрерывна на отрезке [а, 6] и
дифференцируема в интервале (а,Ь), то существует такая точка се(а,Ь), что
f(b)-f(a) = f'(c)(b-a) (а<с<Ь).
Следствие 1. Если производная функции равна нулю в каждой точ-
ке некоторого промежутка, то функция есть тождественная постоянная в
этом промежутке.
Следствие 2. Если две функции имеют равные производные в не-
котором промежутке, то они отличаются в этом промежутке лишь
постоянным слагаемым.
Корнем (или нулем) функции у = f(x) называется такое значение х = х0
ее аргумента, при котором эта функция обращается в нуль. Геометрически
корень функции означает абсциссу точки, в которой график функции пере-
секает ось Ох или касается ее.
Теорема 14.8. (Ролля). Между двумя
различными корнями дифференцируемой
функции содержится по меньшей мере один
корень ее производной.
Замечание 1. Теорема имеет про-
стую геометрическую интерпретацию: меж-
ду значениями а и b имеется по меньшей
мере одно значение с такое, что в точке
С (с,/(c)) графика функции касательная к
графику параллельна оси Ох (рис. 14.5).
Замечание 2. Теорему можно сформулировать в более общем виде.
Если у = f(x) - функция, дифференцируемая на отрезке [а,Ь] и f(a) = f(b), то
между a u b найдется точка с, в которой производная равна нулю, т. е. f’(c) = 0.
Теорема 14.9. (Коши). Если у- /(х) и у = <р(х) - две функции, непре-
рывные на отрезке [a, Z>] и дифференцируемые в интервале (а, Ь), причем
ф'(л)*0 для любого хе(а,Ь), то между а и b найдется такая точка с, что
f(b)-f(a) _ f'(c)
<p(b)-<p(a) ф'(с)’
232
14.6 . Формула Тейлора
Формула
/(х) = /(а)+^(х-а)+^Ж(х-а)2 + - -+^^(х-а)и +
1! 2! п\
+ /^(fl+e(x-fl)) .
(п + 1)!
называется формулой Тейлора с остаточным членом в форме Лагранжа:
W = /(и+,)й). (14.38)
(и + 1)!
Если д = 0, то формула принимает вид
/^/(OJ+M+W+.^m^^x-
1! 2! и! (и + 1)!
(14.39)
где 0 < © < 1, и называется формулой Маклорена.
Формулу (14.37) можно записать в виде
/(х) = /(д)+(х - а) + • - + (х - а)" + о ((х - а)"), (14.40)
1! и!
где о((х-а)п) - бесконечно малая порядка выше n-го по сравнению с х-д; эта
форма остаточного члена была указана Пеано.
Замечание. Если в формулах (14.37) и (14.40) перенести в левые части
/(а) и обозначить (х-д) = Дх, тогда
ДГ(л) = /'(а) Дх + 2^1 Дх2 + • • • + дх" +-/—’Ч) Дх"*1,
2! и! (п + 1)!
V(a) = f\a) Дх+^- /"(а) Дх2 + • • • + Д /(п)(а) Дх" + о(Дх").
2! и!
Если в этих формулах Дх заменить на dx и принять во внимание формулы
(14.35), (14.36), то получим соответственно
дс(«)=«//(fl)+l rf2/(fl)+-+a rf"/(fl)+—
2! n\ (” + 1)1
Af(fl)=j/(fl)+l£f2/(fl)+-+-Lrf"/(fl)+o(Axn).
2 n\
233
Следовательно, если предположить, что Ах —» О, то по этим формулам из бес-
конечно малого прирашения функции А/Ха) можно выделить не только его глав-
ный член — первый дифференциал, но и члены более высоких порядков малости,
совпадающие (с точностью до факториалов в знаменателях) с последовательными
дифференциалами d2f(a), d3f(a),dnf(a).
14.7 . Формула Тейлора для некоторых функций
Формула (14.39) для функции /(х) = е* принимает вид
V V2 т" v"+1
е* = 1+-+--+---+—+——Л (о<е<1). (14.41)
1! 2! и! (и+1)!
Отметим, что при любом х остаточный член формулы (14.41) стремится к
нулю при неограниченном возрастании п, т. е.
„И+1
lim Л„(х) = lim---е* = 0.
(п 4-1)!
Разложение функции /(x) = sinx по формуле (14.39):
Xn+I . (г. (и + 1)7сЛ
+--------sin вх + ------— . (14.42)
(«4-1)1 V 2 J
Остаточный член
D Z X Л”+1 • (а . (И+1)Я^
Я„(х)=-------sm вх+i---------—
(и+1)! I 2 )
формулы (14.42) также стремится к нулю при п —> <».
Формула (14.39) для функции /(x)=cosx имеет вид
, х2 х4 х6 х" гт
cosx = 1-----ь--------(•••• + — cos--ь
2! 4! 6! п! 2
x"+l (а (и + 1)Я^ л-п
+--------cos вх+ -------— . (14.43)
(и+1)! V 2 )
Каково бы ни было х, остаточный член формулы (14.43) стремится
К нулю при И —> оо.
Для функции /(х) = (а+х)", где а - действительное число, и- натуральное
число, получаем
(а+х)" = а” + иа"-,х + а"-2х2 +
+ и (и-1) (и- 2) а„-зхз + + и (и-1) - 2 +л„
3! (и-1)!
Это равенство называется формулой бинома Ньютона.
234
14.8 . Приближенные формулы
Если в формуле (14.39) отбросить остаточный член, то получится прибли-
женная формула
/(W(O)A+W+..A», (1445)
1! 2! и!
заменяющая данную функцию многочленом и-й степени. Качество этой фор-
мулы оценивается двояко: указываются границы погрешности R„(x) с помо-
щью выражения (14.38) для остаточного члена либо порядок малости этой
погрешности при х —> 0 7^,(х) = о(х").
В случае функции f(x) = ex получаем приближенную формулу
. X х3 х3 хп
е . (14.46)
1! 2! 3! л!
Поскольку Rn(x) = ев":хя+1/(и+1)!, то например, при х>0 погрешность
оценивается неравенствами
0<7?„(х)<-^— хя+*. (14.47)
(и + 1)!
11 1 3
В частности, при х=1 получаем е* = 1 + + — + -+—, 0<Rn(x)< ----.
1! 2! и! (и + 1)!
Если взять п = 8 и произвести вычисления с пятью десятичными знаками, то
получим е = 2,71827. Здесь верны первые четыре знака, так как ошибка
не превосходит 3/9! или 0,00001.
Взяв /(x) = sinx и положив в равенстве (14.42) и = 2т, получим прибли-
женную формулу
х3 х5
sinx = х------к —
3! 5!
t (-ir-'x2”-1
(2m-1)! ’
(14.48)
остаточный членжоторой
R2n(x) = ?п(е^+(2от + 1)п/2) i)<" cos6x /г2"""
(2m+l)! (2m + l)!
оценивается соотношением
I |2m+l
И_______
(2/n+l)!
235
Для функции /(x) = cosx аналогично получаем
JC2 г4 х2т
cosx = l-—+----------+(-1) ——• (14.49)
2! 4! (2т)!
Погрешность приближенной формулы (14.49) выражается остаточным членом
*2m+lW = (-l)m+' cosOx
2т1 (2т+2)!
и оценивается неравенством
|2/и+2
Например, для формулы cosx = l---к— погрешность
2! 4!
|^(л)|^И_=2е!_.
1 4 1 6! 720
Пример 14.24. Вычислить е0,75 с точностью до 0,001.
Применяем формулу (14.46), полагая в ней х = 0,75 = 3/4. Поскольку х<1 и
е < 3, то из формулы (14.47) следует, что
I Л,(л) I < е<* xn+1 < —-—.
1 1 (и+1)! (и+1)!
3 1
Требование | R„(x) | < 0,001 будет выполнено, если - —— < уддд >
или (и+1)! >3000.
Это неравенство выполняется при и=6 (тогда (и+1)!= 7!= 5040).
Значит, для вычисления е0,75 с заданной точностью в формуле (14.46) нужно
075 , 3 1 З2 1 З3 1 З4 1 З5 ,
взять шесть слагаемых е' = 1 +—+-----------z- +---г +----г+-----г = ,+
4 2 42 6 43 24 44 120 45
+0,7500 + 0,2813 + 0,0703 + 0,0132 + 0,0019 = 2,1167, е0 75 =2,117.
236
Глава 15
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
15.1. Правило Лопиталя - Бернулли
При исследовании функций может появиться необходимость нахождения пре-
дела дроби /(х)/ф (х), числитель и знаменатель которой при х-+а стремятся к
нулю или к бесконечности. Нахождение таких пределов называют раскрытием
неопределенностей соответствующего вида. Основой его является правило Лопи-
таля - Бернулли, выражаемое следующей теоремой.
Теорема 15.1. Если функции f(x) и ф(х) дифференцируемы в окрестно-
сти точки х = а, обращаются в нуль в этой точке и существует предел отно-
шения f'(x)/<p' (х) при х -+а, тогда существует предел отношения самих
функций, равный пределу отношения производных
lim = lim (15 j)
х-ьа ф (л) x—ta ф' (л)
Замечание 1. Теорема верна и в том случае, когда функции /(х) и
Ф (х) не определены в точке х = а, но lim /(хЬ= 0, lim ф (х) = 0.
х->а х-да
Замечание 2. Теорема верна и в случае а = <», т. е. когда
lim /(х) = 0, lim ф (х) = 0.
Замечание 3. Если /'(а) = 0, ф'(а) = 0, функции f'(x), ф'(х) диф-
ференцируемы в окрестности точки х = а и существует предел отношения
f"{x)/ty"(x) при х —> а, то
.• /"(х)
lim J к ' = lim -=<- > <
<PZ (х) х->" ф" (*)
(15.2)
Другими словами, правило Лопиталя - Бернулли при выполнении соответст-
вующих условий можно применять несколько раз.
Правило Лопиталя — Бернулли применимо и при раскрытии неопределенно-
стей вида —, поскольку ее можно привести к неопределенности вида —, пред-
оо 0
ставив рассматриваемую дробь так:
/(*)_ 1 . 1
ф(х) ф(х) /(х)’
о °°
С помощью тождественных преобразований к основному виду — или — можно све-
0 °°
сти неопределенности других видов, таких, как 0 -<», <»-<», 1”, 0°, ~°.
237
Неопределенность вида 0-«>, т.е. произведение /(х)ф(х), где /(х)—>0,
<р (х) —> оо при х—> а, приводится к виду — или — по формулам
0 оо
/(х) Ф (х) = Дх): —Дх) Ф (х) = Ф (х): —,
ф(*) f(x)
а затем применяется правило Лопиталя - Бернулли.
Аналогично раскрывается неопределенность вида <»-<», т. е. находится пре-
дел lim (/(х)-ф(х)) при условии, что lim/(x) = o°, Нтф(х) = ~. С помощью
х-*а х-*а х-ьа
преобразования Дх)-ф(х) =--------------:---------- эта неопределенность
^ф(х) Дх)) /(х)ф(х)
сводится к неопределенности вида —.
Раскрыть неопределенность вида — значит найти предел lim (/(х))ф(х)
х-*а
при условии, что lim Дх) = 1, lim ф (х) =
х-*а х-*а
Раскрыть неопределенности вида 0°, <»0 - значит найти предел
lim (/(х))ф(х) при соответствующем условии: 1) lim/(x) = 0, 1нпф(х) = 0;
х-*а х-*а х-*а
2) lim /(х) = о°, 1йпф(х) = 0.
х-ъа х->а
Неопределенности 1”, 0°, раскрываются способом, в котором использу-
ется тождество (/(х))ф(х) =е»ГОк/(»)
При раскрытии этих неопределенностей данное выражение предварительно ло-
гарифмируют и находят предел его логарифма.
Правило, выражаемое теоремой 15.1, сформулировано швейцарским математи-
ком И. Бернулли (1667 - 1748) и опубликовано в 1696 г. в первом печатном
учебнике анализа бесконечно малых, написанном французским математиком
Г. Лопиталем (1661 - 1704).
__ е~х
Пример 15.1. Найти lim---------.
х-»о 1п (1 + х)
При х = 0 числитель
неопределенность вида
и
0
0
знаменатель дроби обращаются в нуль, имеем
Чтобы раскрыть ее, применяем правило
Лопиталя - Бернулли:
.. е —е .. е + е _
lim---------= hm-----------= 2.
In (1+х) *-»о 1/(1+х)
гг тт I- COSX-COS7X
Пример 15.2. Найти hm----------
*->о cosx-cos3x
238
Для раскрытия этой неопределенности вида — правило Лопиталя - Бернулли
необходимо применить дважды:
cosx-cos7x -sinx + 7sin7x -cosx+49cos7x
lim-----------= lim-------------= lim---------------=
x-»o cosx —cos3x »->o -sinx+3sin3x *-»o -cosx + 9cos3x
-1+49 ,
=-------— o.
-1+9
Пример 15.3. Найти lim I—---J—
x->o^ ex — l)
Здесь имеем неопределенность вида <»—Преобразуем данную разность
2 1 ех-1-х
х ех -1 х (ех -1)
При х = 0 в правой части этого равенства имеем неопределенность вида
Применяя дважды правило Лопиталя — Бернулли, находим:
.. [1 1 А .. ех-1-х .. ех-1
lim------------ hm------— = hm---------=
ex-lj х-»о хех-х *->°хех+ех-1
хех +ех +ех 2
Пример 15.4. Найти lim —, где и - натуральное число.
X —>+ gX
Применяя правило Лопиталя - Бернулли п раз, получаем
и(л-1)х"-2
lim —-----—
-»+- ех
и(и-1)...21
lim —-------------= 0.
X—>4-00 g*
Следовательно, при неограниченном возрастании аргумента степенная функ-
ция растет медленнее показательной функции.
Пример 15.5. Найти lim х^|п(е -1).
х—>0
При х = 0 получаем неопределенность вица 0°. Обозначим у = х^|п(е*-1) и
прологарифмируем это равенство по основанию е.
. 1 . 1пх
In у =--------In х =---------
ln(e -1) 1п(ех-1)
В правой части этого равенства при х = 0 имеем неопределенность вида —.
СО
239
Применяя дважды правило Лопиталя - Бернулли, находим
lim In у = lim —= lim —---------------= lim -----
х-»о *-»oln(ex-l) х-»о ех/(ех-1) х-»о Хех
= lim —------= 1.
х-»0 ех +хех
Следовательно, lim In у = 1, lim у = е1 = е, lim х^|п(е -|) = е.
х->0 х-»0 х->0
15.2. Признаки постоянства, возрастания и
убывания функции
Необходимое и достаточное условие постоянства функции у = f(x) выража-
ется равенством у' = 0, т. е.
/ = О«у = с. (15.3)
Функция у = f(x) называется возрастающей в промежутке (а, Ь), если для
любых двух значений х, и х2 G (а, Ь) из неравенства х1 < х2 следует неравенство
f(xi)<f(x2) (рис. 15.1, а).
Функция у = f{x) называется убывающей в некотором промежутке, если для
любых двух значений, принадлежащих этому промежутку, из неравенства х1 < х2
следует неравенство f(.xt)> f(x2) (рис. 15.1, б).
Достаточное условие возрастания (убывания) функции выражается следующей
теоремой.
Теорема 15.2. Если в данном промежутке производная функции положи-
тельна, то функция возрастает в этом промежутке; если производная отрица-
тельна, то функция убывает в соответствующем промежутке.
240
Замечание. Теорема имеет простой геометрический смысл. Если в не-
котором промежутке касательная к графику функции у = /(х) образует с осью Ох
острый угол a (tga>0), то функция возрастает в этом промежутке (рис. 15.1, а).
Если касательная к графику образует с осью Ох тупой угол a (tg а < 0), то функ-
ция убывает (рис. 15.1, б).
Пример 15.6. Найти промежутки возрастания и убывания функции
f (х) = х3 — 6х2 + 9х - 2.
Находим производную функции и разлагаем на множители соответствующий
квадратный трехчлен: /'(х) = Зх2 - 12х + 9 = - 4х +3), f'(x) = 3 (х -1) (х - 3).
Если х < 1 и х > 3, то f\x) > 0; функция возрастает в интервалах (- «, 1),
(3, + <»). Если 1 < х < 3, то f'(x) < 0; функция убывает в интервале (1,3).
15.3. Экстремум функции
Рассмотрим функцию у = f(x), областью определения которой является
промежуток (а, Ь).
Если можно указать такую 8-окрестность точки х,, принадлежащую проме-
жутку (а, Ь), что для всех х е О(хр8), х*хх, выполняется неравенство
f(x0>f(x), (15.4)
то У1 - fi (-*1) называют максимумом функции у = f(x) (рис. 15.2).
Максимум функции у- f(x) обо-
значим через max /(х).
Если можно указать такую 8-
окрестность точки х2, принадлежа-
щую промежутку (а, Ь), что для всех
х е О (х2,8), х * х2, выполняется
неравенство
f(x2) </(х), (15.5)
то Уг - f(x2) называют минимумом функции у = f(x) (см. рис. 15.2).
Минимум функции у = f(x) обозначим через. min /(х).
Другими словами, максимумом (минимумом) функции у = f(x) называют та-
кое ее значение, которое больше (меньше) всех других значений, принимаемых в
точках, достаточно близких к данной и отличных от нее.
Замечание 1. Максимум функции, определяемый неравенством
(15.4), называется строгим максимумом; нестрогий максимум определяется
неравенством /(х^ /(х2).
Замечание 2. Максимум и минимум функции имеют локальный харак-
тер (это наибольшее и наименьшее значения функции в достаточно малой окрест-
241
ности соответствующей точки); отдельные минимумы некоторой функции могут
оказаться больше максимумов той же функции (рис. 15.3). Вследствие этого мак-
симум (минимум) функции называют локальным максимумом (локальным мини-
мумом) в отличие от абсолютного максимума (минимума) - наибольшего
(наименьшего) значения в области определения функции.
Максимум и минимум функции назы-
ваются экстремумом. Латинское extremum
означает «крайнее» значение. Значение
аргумента, при котором достигается экс-
тремум, называется точкой экстремума.
Необходимое условие экстремума выра-
жается следующей теоремой.
Теорема 15.3. В точке экстремума
дифференцируемой функции производная
ее равна нулю.
Теорема имеет простой геометриче-
ский смысл: касательная к графику дифференцируемой функции в соответствую-
щей точке параллельна оси Ох (см. рис. 15.2).
Замечание 3. Если f'(x„) = Q, то отсюда еще не следует, что х„ -
точка экстремума. Например, для функции f(x) = х3 f'(x) = Зх2, /'(0) = 0, но
х0 =0 не является точкой экстремума, так как /(х)>0 при х>0 и /(х)<0 при
х < 0 (неравенство (15.4) или (15.5) здесь не выполняется).
Замечание 4. Функция может достигать экстремума также в точке, в
которой производная не существует. Например, функция у = -|х+4| не имеет
производной в точке х = -4, но достигает в ней максимума: у = 0 при х = -4, а
для всякой другой точки у<0 (рис. 15.4,а). Функция у= = -(1-х^3)^2 не
имеет конечной производной в точке х = 0, поскольку у' = (1-х^3)У2х~У3 при
х = 0 обращается в бесконечность, но в этой точке функция имеет минимум:
/(0) = -1, /(х)>-1 при х*0 (рис. 15.4,6).
Говорят, что функция у = /(х) меняет знак при переходе через точку х - х„, если
/(Х])/(х2) < 0 для любых X] и х2 из некоторой окрестности этой точки, удовлетво-
242
ряющих неравенствам х, <х0 < х2; знак меняется с плюса на минус, если f(xl)>0, а
/(х2 )< знак меняется с минуса на плюс, если /(х,)<0, /(х2)>0.
Формулируя теоремы 15.4 и 15.5, будем предполагать, что функция у = f(x)
дифференцируема в некоторой окрестности точки л0.
Теорема 15.4. Если при х = хъ производная функции у = f(x) равна нулю и
меняет знак при переходе через это значение, то х0 является точкой экстрему-
ма, причем: 1) х0- точка максимума, если знак меняется с плюса на минус;
2) xQ — точка минимума, если знак меняется с минуса на плюс.
Теорема имеет следующий геометрический смысл: если в точке М0(х0, f(x0))
графика дифференцируемой функции касательная параллельна оси Ох, в точках сле-
ва от Мо образует тупой угол с осью Ох, в точках справа- острый, то х0 - точка
минимума (рис. 15.5, а); если в точках слева от Л/о касательная образует с осью Ох
острый угол, а в точках справа - тупой, то х0 - точка максимума (рис. 15.5,6).
Замечание. Теорема верна и в случае, если х0 - точка непрерыв-
ности функции f(x), производная в ней не существует и меняет знак при
переходе через эту точку.
Достаточное условие экстремума можно выразить также с помощью
второй производной.
Теорема 15.5. Если в точке х = х0 первая производная функции у- f(x)
равна нулю, а вторая производная отлична от нуля, то х0 является точкой экс-
тремума, причем: 1) х0 - точка минимума, если f"(xo)>O; 2) х0 - точка
максимума, если f"(xo)<O.
Теорема 15.6. Пусть в точке х0 первые п производные равны нулю, а
(п +1) -я отлична от нуля и непрерывна в этой точке, тогда: 1) если (и + 1) —
четное число, то х0 — точка экстремума: точка максимума при /(и+1)(х0)<0
и точка минимума при /^”+|)(х0)>0; 2) если (и + 1) - нечетное число, то хоне
является точкой экстремума.
243
Пример 15.7. Найти экстремумы функции /(л) = л4 - Юл2 +15.
Поскольку f'(x) - 4л3 - 20л = 4л (л2 - 5), то точками, для которых f'(x) = О,
являются Л]=-л/5, л2=0, л3=л/5. Исследуем знак второй производной
/"(л) = 12л2-20 в этих точках: /"(—Т5) = 12-5-20>0, /"(-75) =
= 12-5-20>0, /"(0) = -20<0.
Следовательно, л,= —75, л2=-75 - точки минимума, л2=0 - точка мак-
симума; min/(x) = /(—75) = /(Т5) = 25-10-5+15 = -10, тах/л)=/0)= 15.
Пример 15.8. Вычислить значения экстремумов функции /(л) =
= л5-5л4+5л3+9.
Первая производная /'(л) = 5л4-20л3 + 15л2 = 5л2(л2-4л+3) обращается в
нуль при Л|=0, х$=1, л3=3. Вторая производная /"(л) = 20л3 - бОх2 + ЗОх в этих точках
принимает соответственно значения /"(0)=0, /"(1) = -10<0, /"(3) = 90>0.
Следовательно, л2 = 1 — точка максимума, л3 = 3 - точка минимума, причем
тах/(л) = /(!) = 10, тт/(л) = /(3) = -18. Чтобы исследовать точку л,=0,
обратимся к третьей производной /"'(л) = 60л2-120л+30. Поскольку
/'"(0) = 30 * 0, и +1 = 3, то л, = 0 не является точкой экстремума.
Пример 15.9. Найти точки экстремума функции /(л) = л4+4л3 +
+ 6л2 +4л + 3.
Первая производная /'(л) = 4л3 + 12л2 +12л+4 = 4 (л3 + Зл2 + Зл+1) равна ну-
лю в единственной точке л = -1. Находим выражения последующих производных
и их значения в критической точке л = -1: f"(x) - 12л2 + 24л +12, /"(-1) = 0,
/'"(л) = 24л+ 24, /"'(-1) = 0, /1У(л) = 24. Поскольку /IV(-l)>0 и и + 1 = 4
(четное число), то л = -1 - точка минимума, причем шт/(л) = /(—1) = 2.
15.4. Направления выпуклости, точки перегиба
График функции у = /(л) называется выпуклым вниз (вогнутым вверх) в дан-
ном промежутке, если он целиком расположен выше касательной в его произволь-
ной точке (рис. 15.6, а).
График функции у = /(л) называется выпуклым вверх (вогнутым вниз) в дан-
ном промежутке, если он целиком расположен ниже касательной в его произволь-
ной точке (рис. 15.6, б).
Теорема 15.7. Если вторая производная функции y = f(x) в данном
промежутке положительна, то график ее является выпуклым вниз
в этом промежутке; если /"(л)<0, то график функции является
выпуклым вверх в соответствующем промежутке.
244
Точкой перегиба графика функции у = f(x) называется такая его точка
Л/о (рис. 15.7), в которой выпуклость меняется на вогнутость (по отноше-
Теорема 15.8. Если вторая производная функции у = f(x) при х = х0 об-
ращается в нуль и меняет знак при переходе через х0, то ЛУ0(х0,/(х0)) —
точка перегиба графика этой функции.
Пример 15.10. Найти интервалы выпуклости и точки перегиба
графика функции f(x) = х3 - 6х2 + 9х + L
Поскольку вторая производная f"(x) = 6х -12 = 6 (х - 2) обращается в нуль при
х = 2 и меняет знак при переходе через это значение, то х = 2 - абсцисса точки пере-
гиба, ордината этой точки _у = /(2) = 3, т.е. М (2,3) — точка перегиба
Так как f"(x) < 0 при х < 2 и f"(x) > 0 при х > 2, то график функции является
выпуклым вверх в интервале (- 2) и выпуклым вниз в интервале (2, + ~).
15.5. Асимптоты
Асимптотой линии называется прямая, к которой неограниченно приближается
данная линия, когда ее точка неограниченно удаляется от начала координат.
По виду уравнений относительно выбранной декартовой системы координат
различают асимптоты вертикальные (параллельные оси Оу) и наклонные
(пересекающие ось Оу).
Прямая х = а называется вертикальной асимптотой графика функции
y = f(x), если хотя бы одно из предельных значений lim f(x), lim f(x)
x—>a-0 x->a+0
является бесконечным. Например, прямая х = 2’ является вертикальной асим-
птотой графика функции _у = 8/(х-2), так как
lim 8/(х — 2) = — оо, lim 8/(х — 2) = + «=.
х—>2-0 х—>2+0
Предположим, что функция y = f(x) определена при сколь угодно
больших (по модулю) значениях аргумента; для определенности будем
рассматривать положительные значения аргумента.
245
Прямая
y = kx + b
(15.6)
Прямая х = 1 является
называется наклонной асимптотой графика
функции у = f(x), если эта функция пред-
ставима в виде
f(x) = kx + b+a.(x), (15.7)
где lim а (х) = 0.
График функции у = f(x) имеет при
х —> + «о наклонную асимптоту (15.6) тогда
и только тогда, когда существуют два ко-
нечных предела:
lim f^l = k, lim (f(x)-kx)=b. (15.8)
Пример 15.11. Найти асимптоты
x^ + X
графика функции /(х) =-----.
вертикальной асимптотой (рис. 15.8), так как
х^ + х 7
lim/(x) = oo. Поскольку /(х) =------= х + 2 +—— и lim 2/(х -1) = 0, то гра-
х-»1 х-1 х-1 *-»i
фик функции имеет и наклонную асимптоту у = х + 2.
15.6. Исследование функций и построение
их графиков
Под исследованием функций понимают изучение их изменения в зависимости
от изменения аргумента. На основании исследования функции строят ее график,
предварительно изображая характерные точки.
Исследование функций и построение их графиков можно проводить по сле-
дующей схеме.
1. Найти область определения функции, ее точки разрыва.
2. Изучить изменение функции при стремлении аргумента к концам проме-
жутков области определения.
3. Найти точки экстремумов, промежутки возрастания и убывания функции.
4. Вычислить значения экстремумов, построить соответствующие точки.
5. Определить промежутки выпуклости и вогнутости графика, найти точки
перегиба.
6. Найти точки пересечения графика с координатными осями.
7. Найти асимптоты графика функции.
Порядок исследования иногда целесообразно выбирать исходя из
конкретных особенностей данной функции.
246
Если рассматриваемая функция четная или нечетная, то ее достаточно иссле-
довать при положительных значениях аргумента из области ее определения и при-
нять во внимание, что график четной функции симметричен относительно^ оси
ординат, а график нечетной - относительно начала координат.
Отметим также, что графики взаимно обратных функций симметричны относи-
тельно прямой, на которой лежит биссектриса первого координатного угла.
х2 +1
Пример 15.12. Исследовать функцию /(х) = —х—и построить ее график.
х -1
1. Функция не определена лишь при х = -1 и х = 1. Следовательно, область оп-
ределения состоит из трех интервалов: (-°°, -1), (-1,1), (1,+<*>), два из которых
являются бесконечными.
2. При стремлении аргумента к концам промежутков области определения со-
ответственно получаем
.. х2+1 , .. х2+1 х2+1
hm -*— = 1, hm —=-----= + °°, hm —z-----= -°°,
х-‘-“’Х2 —1 «-М/-1 х-»-1+0 х2-1
.. х2 + 1 х2 +1 .. х2+1 ,
hm —х = -°°, hm —=— = + °°, hm — = 1.
х-»|-0а2-1 х-»1+0х2-1 х-> + ~ х1 -1
3. Находим производные данной функции:
/'(*)=
-4х
(х2-1)2’
= 4(Зх2+1)
(х2-1)3 ’
Поскольку /'(х)>0 при х<-1 и -1<х<0, то функция возрастает в интер-
валах (-09,-1) и (—1,0). Так как f'(x)<0 при 0<х<1 и х>1, то функция
убывает в интервалах (0,1) и (1, + ~=).
Поскольку f'(x) = O приль=Ои f"(xQ) = /"(0)<0, тохо=0 - точка максимума.
Других критических точек нет, ибо f'(x) не определена только при х=-1 и х =1, но
в этих точках не определена и сама функция.
4. Вычисляем значение максимума функ-
ции тах/(х) = /(0) = -1.
5. Поскольку f"(x)>0 при х<-1 и
х > 1, то график функции является выпук-
лым вниз в интервалах (- °°, -1) и
(1,+ оо). Так как f"(x)<0 при -1<х<1,
то график функции является выпуклым
вверх в интервале (-1,1).
Точек перегиба график данной
функции не имеет, ибо вторая производ-
ная в нуль нигде не обращается и
не определена в тех же точках, в кото-
рых не определена и сама функция.
247
6. График функции не пересекает ось Ох, так как уравнение (л2 +1)/(л2 -1) = О
не имеет действительных корней. Если х=0 (уравнение оси Оу), то у = -1, в точке
В (0,-1) график пересекает ось Оу.
7. Йз п. 2 следует, что график функции имеет две вертикальные асимптоты
х = -1 и х = 1 и горизонтальную асимптоту у = 1. Последнее вытекает также из
х2 + 1 , 2 2
того, что = 1+—z------- и lim = Q.
х2-1 х2-1 х-*°°х2—1
Заметив еще, что f(x)>0 при х<-1 и х>1, f(x)<0 при -1<х<1, стро-
им график функции (рис. 15.9).
15.7. Задачи на наибольшие и наименьшие
значения
Наибольшим значением (абсолютным максимумом) функции у = f(x) на от-
резке [а, Ь] называют такое ее значение, которое больше всех других значений,
принимаемых функцией на данном отрезке. Чтобы найти наибольшее значение
функции на отрезке, необходимо вычислить значения максимумов на этом отрез-
ке, значения функции на концах отрезка, а также во всех точках отрезка, в кото-
рых производная не определена; из полученных чисел выбрать самое большое.
Аналогично определяется и разыскивается наименьшее значение функции
(абсолютный минимум).
В математике, физике, химии, технических и других науках, а также в повсе-
дневной жизни часто встречаются задачи на отыскание наибольших и наименьших
значений некоторых функций.
Общая схема решения таких задач состоит в следующем. Сначала устанавливает-
ся зависимость рассматриваемой величины у от некоторой независимой перемен-
ной величины х (обозначения, разумеется, могут быть другими). Из условия задачи
определяется промежуток, в котором может изменяться аргумент функции. Функция
у — f(x) исследуется с помощью теории, рассмотренной в предыдущих главах.
Пример 15.13. Найти наименьшее значение суммы двух положительных
чисел, произведение которых постоянно и равно а.
Обозначим искомые числа через х и у. По условию ху = а, где а > 0, поэтому
у = а/х. Сумма этих чисел з = х+у, s(x) = x+a/x является функцией перемен-
ной х, в соответствии с условием х > 0.
Находим производные функции s(x):s' (х) = 1-а/хг, s" = 2а/х3.
Приравнивая нулю первую производную, получаем уравнение 1 - ah?— 0, из
которого находим критические точки Xj=-Va, x2=Va; первое значение не
принадлежит области изменения аргумента данной функции.
Поскольку s"(7a)>0, то х = 7а - точка минимума,
причем mins(x) = s(Va) = 2Va.
248
Пример 15.14. Найти наибольшее и наименьшее значения функции
/(х) = х3 -12х + 7 на отрезке [0,3]. •»
Найдем сначала экстремумы данной функции: f\x) = Зх2 -12, f"(x) = 6х,
f'(x) = 0, Зх2 —12 = 0, Х]=-2, х2=2. Точках]=-2 не принадлежит данному
отрезку. Так как /"(2)>0, то х = 2 - точка минимума, причем
min/(х) = /(2) = -9. Находим значения функции на концах отрезка: Д0)=7,
/(3) = -2. Сравнивая эти три числа, заключаем, что наибольшее значение данной
функции на заданном отрезке равно 7, а наименьшее - 9.
Пример 15.15. Прямоугольник
вписан в эллипс с осями 2а и 2Ь. Каковы
должны быть стороны прямоугольника,
чтобы его площадь была наибольшей?
Рассмотрим прямоугольник ABCD, впи-
санный в данный эллипс (рис. 15.10), с ос-
нованием 2и и высотой 2v. Площадь пря-
моугольника определяется формулой
s = 2u-2v = 4uv, где v = (b/a)^a2 - и2
(получено из уравнения эллипса). Следова-
тельно, s = (Ab/а) и -Ja2 - и2 — функция
s' = (4Z>/a)(a2 —2и2)/-\/а2-и2 , то s'= 0 при
переменной и. Так как
и = а/л/2. Поскольку s' > 0 при
u<a/-j2 и s'<0 при и>а/-^2, то и = а/-^2 — точка максимума функции
s = s(u). Если u = a/-j2, то v = (b/a)-\la2 —и2 = b/-j2. Следовательно, площадь
прямоугольника будет наибольшей, когда его стороны равны 2аД/2, 2b/-j2
(тогда площадь равна 2аЬ).
15.8. Дифференциал длины дуги кривой
Пусть на отрезке [а, Ь] задана дифференцируемая функция у = f(x), графи-
ком которой является дуга АВ (рис. 15.11). Отрезок [а, Ь] разобьем на и частей
точками J^,x2,...,x„_I. Этим точкам будут соответствовать точки Mt,
М2,..., M„-i дуги АВ. Соединим их отрезками прямых. Ломаную
АМхМг ... M„_tB называют вписанной в дугу АВ. Периметр этой ломаной обо-
значим через Z„, т.е.
п
1„ = £| | (Л/о = Л, Л/„ = В).
249
Длиной дуги называется предел периметра вписанной в нее ломаной, когда
число звеньев Мк./Мк неограниченно возрастает, а длина наибольшего из них
стремится к нулю:
*=1
где X - длина наибольшего звена.
Будем отсчитывать длину дуги от некоторой ее точки, например, от точки А;
пусть в точке М (х, у) длина дуги AM равна /, а в точке М'(х + Дх, у + Ду)
длина дуги AM' равна /+Д/, где Д/ - длина дуги ММ' (рис. 15.12). Очевидно,
/ = / (х), бесконечно малая дуга линии и стягивающая ее хорда эквивалентны:
Дифференциал длины дуги плоской кривой, заданной уравнением у = f(x),
выражается формулой
dl = ^dx2 +dy2.
Эта формула имеет простой геометрический смысл: она выражает теорему Пифагора
для бесконечно, малого треугольника MTN (рис. 15.12, dl=MT, Ы- ММ').
Дифференциал дуги пространственной кривой выражается формулой
dl = -^jdx2 + dy2 + dz2.
15.9. Кривизна плоской кривой
Рассмотрим плоскую линию, определяемую уравнением у = f(x). Проведем
касательную к этой линии в ее точке М0(х0, у0); обозначим через а угол, образо-
250
ванный касательной с осью Ох (рис. 15.13). Пусть касательная в точке М образует
с осью Ох угол а + Да.
Угол Да между касательными в указанных точках называют углом смежно-
сти. Можно сказать, что при переходе из точки Мо в точку М данной линии каса-
тельная к ней повернулась на угол Ьа, которому будем приписывать соответст-
вующий знак в зависимости от направления поворота.
Средней кривизной дуги М0М данной линии называется абсолютное значе-
нйе отношения угла смежности Да к длине Д7 дуги М0М:
Да
л/ ’
Кривизной линии в данной точке Л/о на-
зывается предел средней кривизны дуги
М0М при М -> Мо:
Да
Лср
к= lim
Да
. (15.9)
Отметим, что для прямой к = 0, а для ок-
ружности радиуса R кривизна к = =1/R.
Кривизна линии, заданной уравнением у= fix'),
вточке Л/0(х0, у0) вычисляется по формулам
или к =
5^ (15.10)
к (1+(/(х0))2/2’^"Л (1 + Х2/2’
Если линия задана параметрическими уравнениями х = х (/), у = у (/), то с
учетом (14.2Q) и (14.22) формула (15.10) принимает вид
t — J_i_____±_L
(х'2+/2)*2’
Кривизна линии, заданной уравнением р = р (<р) в полярных координатах, вы-
числяется по формуле
(15.11)
| р2+2р'2 — рр"|
(15.12)
к (р'2+р2)*2
Пример 15.16. Найти кривизну косинусоиды у = cosx вточке ЛУо(0,1).
Поскольку у' = -sinx, у" = -cosx, кривизна косинусоиды в ее произвольной
точке определяется формулой
l-cosxj
(l+sin2x)^2
При х = 0 получаем к = 1/(1+0)^2 = 1.
, к = lim
251
15.10. Окружность кривизны. Центр и радиус
кривизны. Эволюта и эвольвента
Радиусом кривизны данной линии в данной ее точке называется величина R,
обратная кривизне к этой линии в рассматриваемой точке:
*=|,- (15.13)
* I У XX I
На нормали к кривой в точке М отложим отрезок МС = R в сторону вогнуто-
сти кривой (рис. 15.14). Точка С называется центром кривизны данной линии в
точке М. Окружность радиуса R с центром в точке С называется окружностью
кривизны этой линии в точке М. Очевидно, в данной точке М кривизна кривой и
кривизна окружности равны между собой.
Координаты центра кривизны определяются формулами
Х = х->^±£1, У = У+^р. (15.14)
Если кривая задана параметрическими уравнениями х=х(1)> У = у(Л то
формулы (15.14) с учетом равенств (14.20) и (14.22) примут вид
Х = х_У^±У^1, у = у + *'(*'2 + У'\ (15.15)
х'у"-х"у' Х'у"-Х"у'
Множество всех центров кривизны дан-
ной линии называется ее эволютой. По отно-
шению к своей эволюте исходная линия на-
зывается эвольвентой (или разверткой).
Если линия задана уравнением у = f(x),
то уравнения (15.14) можно рассматривать
как параметрические уравнения ее эволюты
(с параметром х).
В случае параметрического задания кри-
вой уравнения (15.15) являются параметриче-
скими уравнениями эволюты (входящие в
правые части этих уравнений величины зависят от параметра I).
15.11. Переменная векторная величина.
Вектор-функция скалярного аргумента
Рассмотрим точку M(x,y,z), движущуюся по некоторой линии у в про-
странстве (рис. 15.15). Радиус-вектор г = ОМ точки М будет иметь определенное
направление и длину в фиксированный момент времени Г. С течением
времени направление и длина вектора ОМ будут изменяться.
252
Таким образом, здесь имеем дело с перемен-
ным вектором ОМ или с переменной векторной
величиной
r = r(t),
(15.16)
зависящей от времени t. Равенство (15.16) называет-
ся векторным уравнением движения точки М.
Координаты переменного вектора
ОМ = г (Г) = {х (I), у (О, z (Г)} являются также пере-
менными величинами (скалярными), зависящими от
времени I:
x=x(t), y = y(f), z = z(t).
Рис. 15.15
(15.17)
Уравнения (15.17) являются параметрическими уравнениями рассматри-
ваемой линии у.
Переменная векторная величина и называется вектор-функцией (или
векторной функцией) скалярного аргумента I, если каждому значению
t0 е Т, где Т — некоторое множество действительных чисел, соответствует
определенный вектор U(r0); в этом случае пишут u = u(Z).
Если и = u (t), то и проекции их, иу, uz переменного вектора и на оси декар-
товой системы координат будут (скалярными) функциями аргумента t: их = ux(t),
uy=uy(t), uz = uz(f).
Пример вектор-функции скалярного аргумента Дает рассмотренный выше
случай радиус-вектора г = г(Г) точки, движущейся по некоторой линии в
пространстве.
Годографом переменной векторной величины называется геометрическое
место концов векторов всех ее отдельных значений при условии, что они от-
ложены из одной точки. Годографом постоянного век-
тора является точка (конец вектора). Годограф вектор-
функции и = и (г) представляет собой некоторую ли-
нию. Если вектор сохраняет постоянную длину, то его
годограф - линия, лежащая на сфере. Годографом ра-
диуса-вектора г = ОМ движущейся точки М является
траектория этой точки.
Пусть а- некоторый вектор (постоянный) и г = г(0 -
вектор-функция, определенная в некоторой окрестности
точки t0, кроме, быть может, самой точки t0.
Вектор а называется пределом вектор-функции
г = г (Г) при t —> Го, если для любого е > 0 существует
такое 8 = 8(е)>0, что |г(г)-а|<е для всех t, удовле-
творяющих неравенству |t-r0|<8, t*t0 (рис. 15.16).
Рис. 15.16
253
Обозначения предела вектор-функции:
lim г (Г) = а, (15.18)
г(г)->а при <->Г0.
Очевидно, равенство (15.18) эквивалентно равенству
lim | г (Г)-а | = 0. (15.19)
/—>/()
Если г (r,) = {x(r),y(f),z(r)} и о = (О|,о2,а3), то равенство (15.18) выполня-
ется тогда и только тогда, когда \
lim х (t) = Op lim у (t) = а2, lim z (I) = o3.
/—>/o t—>/0 t—>/0
Если вектор-функции Г| (г) и г2 (г) определены в некоторой окрестности точ-
ки t0 и существуют пределы
lim Г] (Г) = a, lim r2 (I) = Ь,
/—>/0 I—>/0
lim Г| (I) lim r2 (I) = а - b, [ lim г, (г), lim г2 (г) ] = [а, Ь],
t—*tQ t—btQ t—bt0
скалярная функция fit) имеет предел при t —> t0, то существуют также пределы
lim (Г| (t)+r2 (t)) = а + Ь,
/—>/{)
lim (J\t) г, (/))= lim f(t) lim г, (О,
/ —> t —> t0 t —> t0
lim Г) (r)r2 (r)=a b,
I—>ro
lim[r)(0,r2(0] = [a,b].
Вектор-функция r = г (Г), определенная в точке t0 и некоторой ее окрестно-
сти, называется непрерывной в этой точке, если lim г (t) = г (10).
Из эквивалентности условий (15.18) и (15.19) следует, что вектор-функция
г (Г) - {х (Г), у (0>2 (О} непрерывна в точке г0 тогда и только тогда, когда не-
прерывны в ней функции х (/), у (t), z (t).
15.12. Дифференцирование вектор-функций
Предел отношения приращения вектор-функции к приращению аргумента, ко-
гда последнее стремится к нулю, называется производной вектор-функции
и = u (v) в точке v:
,, , du .. k(v + Av)-k(v)
it (v) = — = hm —-----------
dv Av
Необходимым и достаточным условием существования производной вектор-
функции
u(v) = {x(v),y(v),z(v)} (15.20)
254
в некоторой точке является дифференцируемость функций х (v), у (v), z (v) в
этой точке; причем в данном случае
it' (v) = {х' (v), у' (v), z’ (v) }.
Правила дифференцирования вектор-функции аналогичны правилам обычного
дифференциального исчисления. Если u, = u, (v), u2 = u2 (v) -
дифференцируемые вектор-функции скалярного аргумента v, • с - постоянный
вектор, /(v) - дифференцируемая скалярная функция, к- постоянная скалярная
величина, w - скалярный аргумент, связанный с v формулой w = w(v), где
w (v) - дифференцируемая функция, то эти правила дифференцирования выра-
жаются следующими формулами:
1) — = 0, 2) rf(ui±u2)_rfui । ^U2
dv dv dv dv
3) dU^ = #ui+f^L,
dv dv dv
За) = 36) =
dv dv dv dv
.. d(u,u2) du2 du. . . d(cu.) du,
4) —L_2' = U|—2- + u,—L 4a) —i—L< = c—1
dv dv dv dv dv
5) d[Uj,u2]^
dv
du, du.
—- + —L, u,
dv dv
6)
du, _ du, dw
dv dw dv
Геометрический смысл производной
u'(v)*0: производная вектор-функции в дан-
ной точке есть вектор, направленный по каса-
тельной к годографу данной вектор-функции в
соответствующей точке (рис. 15.17).
Отметим, что при другом значении v получим
новое значение u' (v), т. е. производная вектор-
функции также является вектор-функцией. Век-
тор-функция, имеющая производную, называется
дифференцируемой.
Дифференциалом вектор-функции u = u(v)
называется произведение её производной на
дифференциал аргумента du = u'(v)dv, где
Рис. 15.17
dv = Av; отсюда u' = da/dv.
255
Пусть
г = г (Г), r = x(Oi+y(OJ+z(Ok -
векторное уравнение движения точки М в пространстве. Приращению At времени
t соответствует приращение Дг = М0М вектор-функции г = г (/). Отношение
Дг/Д/ называется вектором средней скорости, этот вектор направлен по прямой
М0М. Предел указанного отношения при Д/ -> 0 называется вектором скорости
в момент г0 (или вектором мгновенной скорости), обозначим его через v, т.е.
v = r'(O = ^. (15.21)
at
Следовательно, вектор мгновенной скорости (или вектор скорости) движущей-
ся точки направлен по касательной к ее траектории. Вектор г' (t) характеризует
направление и быстроту движения точки.
Если для вектор-функции г = г (/) в качестве параметра t выбрать длину дуги
s, отсчитываемой от некоторой точки Мо, то производная вектор-функции будет
равна единичному вектору, направленному по касательной. Обозначив этот вектор
через т, получим
^ = т, |т| = 1- (15.22)
ds 1 1
Второй производной вектор-функции и = и (v) называется производная от ее
производной u'(v): u" (v) = (u'(v))'.
Для функции (15.20) имеем
u"(v) = {x"(v),/'(v),z"(v)},
если существуют вторые производные функций х (v), у (v), z (v).
Аналогично определяются производные более высокого порядка для вектор-
функции u = u(v).
15.13. Уравнения касательной к
пространственной линии.
Кривизна пространственной линии
Рассмотрим пространственную линию у (рис. 15.18), заданную векторно-
параметрическим уравнением
Г = Г (0, Г (Z) = x(r)i+y(O j+z(t)k (15.23)
или параметрическими уравнениями
х = х(г), у = у(О, z = z(r),
256
где х (/), у {t), z (t) — дифференцируемые функции переменной t. Зафиксируем
значение t0 параметра t, ему соответствует точка M0(x^y0,z0), где х0=х(/0),
Уо=УМ, z0=z(r0).
Уравнения касательной к пространственной линии (15.24) в точке
M0(x0,y0,z0) имеют вид
*~*о _У~Уо 2~Ч П525)
*'Go) /Go) z'Go)
Нормальной плоскостью к пространствен-
ной линии в данной ее точке М называется
плоскость, проходящая через точку М и
перпендикулярная касательной к данной кри-
вой в той же точке.
Нормальная плоскость к линии (15.24) в точ-
ке Л/0(х0, _у0, z0) имеет уравнение
Рис. 15.18
х' (Г„) (х - х„) + у' (Го) (у - у0) + z'G0) (г - 4) = О. (15.26)
Если я — длина дуги, то единичный вектор касательной т к линии у опреде-
ляется формулой (15.22). Придав аргументу t приращение А/, получим точку М
линии у и соответствующий вектор касательной т + Дт. Степень изогнутости кри-
вой можно характеризовать скоростью поворота вектора т.
Кривизной к линии у в точке Мо называется модуль производной
функции т = т (s) в данной точке, т. е.
ds
вектор-
(15.27)
Это определение равносильно определению кривизны плоской кривой.
Кривизна линии, заданной уравнениями (15.24), выражается формулой
И3 ’
Кривизну линии можно выразить в координатах. Поскольку r(t)=
=М0. /0. zG)}. г'(0 = {х'(0. y'G). z'G)}. r"(t) = {х"(г), /G).z"G)}. то
(15.28)
[r',r"] =
i j k
х' у' z'
(15.29)
и
^(/z" - /*')2 + (x'z" - x"z')2 + (x/' - x"/)2
(x'2+/2+z'2/2
(1530)
9 Зак. 1
257
Отметим, что формула (15.11) является частным случаем формулы (15.30).
Пример 15.17. Записать уравнения касательной, уравнение нормальной
плоскости и вычислить кривизну линии г (/) = 2 sin2 ti + 2 cos2 rj+sin 2tk в точке,
для которой t0 = л/4.
Перейдем к параметрическим уравнениям данной линии
x = 2sin2r, y = 2cos2f, z = sin2/. (I)'
Найдем координаты точки Мо (xg,yo,Zo)- х0 =x(Z0) = 2sin2(n/4) =
= 2(Л/2)2=1, y0 = y(r0) = 2cos2(m/4)=l, z0 = z(Z0) = sin2(m/4) = l; Мо(1,1,1).
Найдем производные функций (I) и их значения при 10 = л/4:
x' = 2-2sinrcosr = 2sin2r, y' = -2sin2z, z' = 2cos2/; (П)
x'(r0) = 2sin2(n/4) = 2, y'(r0) = -2sin2(m/4) = -2, z'(ro) = O.
В соответствии с равенствами (15.25) получаем уравнения касательной
к данной линии
(x-l)/2 = (y-l)/(-2) = (z-l)/0, или (х-1)/2 = (у-1)/(-2), z-l = 0,
Подставляя соответствующие значения в формулу (15.26), находим уравнение
нормальной плоскости: l(x-l)-’l(y-l) + 0(z-l) = 0, или х-у = 0.
Для вычисления кривизны линии в точке Л/о(1,1,1) нужны значения
вторых производных функций (I) при Г0 = л/4. Так как. x" = 4cos2z, у" =
= -4cos2z, z" = -4sin2r, x"(fo) = O, y"(to)—O, z"(r0)=-4, то по
формуле (15.30) находим
к = ^/((-2) (-4)- 00)2 +(2 (-4)- 0- О)2 +(2- 0- 0 (-2^ = V128 = j_
(22 +(-2)2 + 02/2 8У2 2’
258
Глава 16
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
16.1. Неопределенный интеграл и его свойства.
Таблица основных неопределенных
интегралов
Функция F (х), определенная в промежутке (о, Ь), называется первообразной
данной функции /(х) в этом промежутке, если для любого значения х е (о, Б)
выполняется равенство
= (16.1)
Например, функция F(x) = x5 - первообразная функции /(х) = 5х4 в про-
межутке (-«>,+ <*>), поскольку (х5)' = 5х4 для всех х; функция F(x)=lnx -
первообразная функции /(х) = 1/х в промежутке (0, + •*>), так как (1пх)' = 1/х;
функция F (х) = arccosx — первообразная функции /(х)= = —l/Vl-х2 в ин-
тервале (-1,1), ибо (arccosx)' = - 1Д/1 - х2.
Если F(x) - первообразная функции /(х), то
Ф (х) = F (х) + С, (16.2)
где С - произвольная постоянная, также является ее первообразной.
Выражение (16.2), в котором функция F(x) удовлетворяет условию (16.1),
определяет множество всех первообразных данной функции /(х) в заданном
промежутке (о, Б).
Неопределенным интегралом от данной функции /(х) называется множество
всех ее первообразных:
J/(x)<fe = F(x)+C, (16.3)
где F'(x) = /(х). Знак I называется знаком неопределенного интеграла, функ-
ция /(х) - подынтегральной функцией, выражение f(x)dx -
подынтегральным выражением.
Операция нахождения первообразной данной функции называется
интегрированием.
Неопределенный интеграл обладает следующими основными свойствами.
259
1. Производная неопределенного интеграла равна подынтегральной функции;
дифференциал неопределенного интеграла равен подынтегральному выражению:
= /(*), (16.4)
d jf(x)dx = f(x)dx. (16.5)
2. Неопределенный интеграл от дифференциала некоторой функции равен
сумме этой функции и произвольной постоянной:
р<р(х) = <р(х)+ф. (16.6)
3. Постоянный множитель можно выносить за знак неопределенного интеграла:
jkf(x)dx = k^f(x)dx (к = const,к* 0). (16.7)
4. Если функции fi(x) и /2(Л) имеют первообразные, то функция
У1(х) + Л(х) также имеет первообразную, причем
J (/i W+/2(*)) dx = J" Л (•*) + J /г(*) dx. (16.8)
Таблицу простейших неопределенных интегралов нетрудно получить, восполь-
зовавшись тем, что интегрирование является операцией, обратной дифференциро-
ванию. Будем исходить из формулы (16.6), которую запишем следующим образом:
если dF (х) = f(x)dx, то ]7(х)<& = F (х)+С. Например, поскольку
d(sinx) = cosxdxr, то Jcosx«fr = sinx + C.
Применяя аналогичное рассуждение к каждой из формул основных дифференциа-
лов (см. п. 14.4), получаем следующие простейшие неопределенные интегралы:
1. Jl-d>c = Jd>c = x + C,
Г vo+1
2. Ixadx = -— + С (а*-1),
J а+1
4. (axdx = — + С (о>0),
J In а
5. J exdx = ех + С,
6. I cosjofo = sinx + С,
260
7. Jsinxd!x =—cosx + C,
8- f-^- = tgx + C,
J COS X
9. = -ctgx + C,
J sin X
10. f—, = arcsinx + C= - arccosx + C,
J
г dx
11. I--- = arctgx + €=-arcctgx + C,
J 1+x2
12. Jshxdfr = chx + C,
13. Jchx = shx + C,
14. f-~ = thx + C,
J ch2x
15. f—= -cthx + C.
J sh2x
Отметим, что все указанные формулы справедливы в тех промежутках, в кото-
рых определены соответствующие функции. Например, формула 3 справедлива
для любого промежутка, не содержащего точку х = 0; формула 10 - для интерва-
ла (-1,1) ит. п.
Замечание. В таблице основных интегралов вместох везде можно за-
писать и = и(х), где и(х) - любая дифференцируемая функция независимой
переменной х: jdu=u+C, J—= 1п|м| + С ит.д.
При использовании формул этой таблицы для преобразования подынтеграль-
ного выражения к виду f(x)dx = g(u)du применяются простейшие преобразова-
ния дифференциалов: 1) dx = d(x + b), где b = const, 2) dx= = — d(ax), а*0,
а
У) dx = (\]a}d(ax + b), а#0, 4) xdx = (1/2)d(х2 + b), 5) sinxdbc = d(-cosx),
6) cosxdx = d (sinx), 7) <p' (x) dx = t/ф (x).
Например,
J sin 5xdx = J sin 5x у d (5x) = у J sin 5xd (5x) = - +c,
U* - i , c
Jx2+1 J x2+l 2 J X2+1 2 •
261
К наиболее важным методам интегрирования относятся следующие:
1) непосредственное интегрирование; 2) метод замены переменной; 3) метод ин-
тегрирования по частям.
16.2. Непосредственное интегрирование
Непосредственное интегрирование основано на свойстве 4 неопределенного интеграла
Если функции fx(x), fzix)...fn(x) имеют первообразные в некотором про-
межутке, то функция /(х) = у;(х)ч-/2(х)ч-/3(х)ч-также имеет перво-
образную в том же промежутке, причем
J(/i(*)+/2W+••+/„(*)) dx = J f(x) dx + J/2(x) dx + — J f„(x) dx, (16.9)
т.е. неопределенный интеграл от алгебраической суммы конечного числа функций
равен такой же алгебраической сумме неопределенных интегралов от слагаемых.
Пример 16.1. Найти неопределенный интеграл
J(x3-6x24-4x-5)dr.
Пользуясь свойствами неопределенного интеграла, формулой (16.9) и первыми
двумя формулами простейших неопределенных интегралов, находим
J (х3 - 6х2 + 4х - 5) = J x3d>c - J 6х2с& + J 4x«fr - J 5с& =
= ^x3dx — 6 jx2dx + 4 jxdx—5 jdx = ~~6~+4^—5x + C =
= -—2x3+2x2-5x + C.
4
Замечание. Постоянное слагаемое не записано при нахождении каж-
дого интеграла алгебраической суммы, а лишь один раз, так как сумма произволь-
ных постоянных величин есть величина постоянная.
rf 1У
Пример 16.2. Найти интеграл I 1ч— dr.
J V х J
Преобразуя подынтегральную функцию и пользуясь первыми тремя формула-
ми неопределенных интегралов, получаем
+3J$+I$=I6&+3It+3P2(&+P3(&=
—2+1 —2 •» ,
= хч-31п|х|ч-3 —-ч-—ч-С=хч-31п|х|- ——Ц-ч-С.
1 1 -2ч-1 —2 1 1 х 2х2
262
Пример 16.3. Найти неопределенный интеграл | —+—z- dx.
Дх л/х х )
С помощью формул 2 и 3 простейших интегралов (при а = - — и а = -2) получаем
(Г—+-i--^-ldx = ff—+x-V2-x"2ldx = ln|x| + 2-7x +— + С.
Дх Vx х2; J к* J х
Пример 16.4. Найти интеграл Jtg2xdx.
Преобразуя подынтегральную функцию и пользуясь формулами интегра-
лов 1 и 8, находим
Г 7 . fsin2x . fl-cos2x , f dx f, _
I tgxdx = I--z— dx = I---5---dx = I--z---I dx = tgx-x+C.
3 3 cos x J cos x J cos x J
„ f cos2xdx
Пример 16.5. Найти интеграл I----z---z—.
J cos x sin x
Преобразуя подынтегральную функцию и пользуясь формулами 9, 8, получаем
f = f(cos2x-sin2x)^= f dx_ pfr = _ctgx_tgx + c
J cos x sin x J cos x sin x J sin x J cos x
J cos2(x/2) dx.
Поскольку cos2(x/2) = (1/2)(1 + cosx), to
J cos2(x/2) dx = J(1 + cosx) dx j
Пример 16.7. Найти интеграл J
Преобразуя подынтегральную функцию, с помощью формул 1 и 11 простей-
ших интегралов, находим
Пример 16.6. Найти интеграл
x2dx
. 1
j 1 1 •
cosxdx = — x ч— sinx + C.
2 2
f x2dx _ f (х2 +1)—1
J х2+1 J х2+1
dx
J J х2 +1
= x - arctgx + C.
16.3. Метод подстановки
Интегрирование путем введения новой переменной (метод подстановки)
основано на формуле
J/(x)dx = J/(<p(O)<p'(O^. (16.10)
где х = <р(Г) - дифференцируемая функция переменой I.
263
Пример 16.8. Найти интеграл
J л/1
x3dx
/1-х8’
Введем новую переменную t по формуле х4 = t, откуда 4x3dr = dt,
x3dx = ^dt, x8=(x4)2 = t2.
Переходя к новой переменной и используя формулу 10 простейших интегра-
лов, получаем
x3dx
/1-х8
dt 1
i=—= = — arcsin t + C.
4
1 • 4
— arcsinx
4
Пример 16.9. Найти интеграл If
J -Ji
— dt .
4 _ 1
/Г? 4
Возвращаясь к переменной х, находим
f * = — arcsin х4 + С.
4
Замечание. Результат можно проверить дифференцированием. Так как
11 4 , _ 4х3 _ х3
4 Jl-(x4)2 * 4л/1-х8 л/1-х8 ’
то на основании формулы (16.4) заключаем, что пример решен верно.
x3dx
'а2-х2'
В случае, когда подынтегральное выражение содержит -Ja2-х2, целесооб-
разно применить тригонометрическую подстановку х = a sin t или х = a cos t.
Положим x = asint, тогда dx = a cos tdt, поэтому
Г x3<±r _ f o3sin3t-ocosft/t _ f a3 sin3 t-acostdt _
J -Jo2-x2 Vo2 -o2sin2t ° cost
= a3 J sin3 tdt = a3 J sin21 sin tdt = -a3 J (1 - cos2t) d (cost) =
i f о a3 cos31 •>
= a J (cos t -1) d (cost) =-----a cost + C.
Заметив, что sin t = xJa, cost = -\/l-sin2t = ф-х2/а2 = -J(o2-x2)/o, получим
r^^=(VaEZ^_fl27^7+c.
Jj^2 3
Пример 16.10. Найти интеграл’ f .-—--г-.
J л/х2+а
264
Применим так называемую подстановку Эйлера у/х2 +а = t-х, где г -новая
переменная. Переписав это равенство в виде t = х+у/х2 +а и взяв дифференциа-
лы от его обеих частей, получим
, tdx
ах =
, — = [—= 1пЫ + С = 1п|х+л/х2+а |+С.
откуда
Итак,
f , = In I x + л/х2+а I + C.
Ц2+а I ।
(16.11)
16.4. Метод интегрирования по частям
Если и = и (х), v = v (х) - дифференцируемые функции от х, то из формулы
для дифференциала произведения двух функций d(uv) = udv+vdu получается
формула интегрирования по частям
judv = uv—jvdu. (16.12)
Эта формула применяется в случае, когда подынтегральная функция представ-
ляет собой произведение алгебраической и трансцендентной функций. В качестве
w обычно выбирается функция, которая упрощается дифференцированием, в ка-
честве dv — оставшаяся часть подынтегрального выражения, содержащая dx, из
которой можно определить V путем интегрирования.
В некоторых случаях для сведения данного интеграла к одной из формул про-
стейших интегралов формула (16.12) применяется несколько раз. Иногда искомый
интеграл определяется из алгебраического уравнения, получающегося с помощью
интегрирования по частям.
Пример 16.11. Найти интеграл Jx-3хdx.
Полагаем x = w, 3xdx = dv, откуда dx = du, v = 3x/ln3 (по формуле 4 про-
стейших интегралов). Подставляя эти выражения в формулу (16.12), получаем
fx.3^ = x-^-f^dx = ^-^ + C.
J 1пЗ J 1пЗ 1пЗ (1пЗ)2
265
Л
Замечание. Результат можно проверить дифференцированием:
(х-Зх 3х Ц _ 3х , х-Зх(1пЗ) ЗЧпЗ_л Г
[ 1пЗ (1пЗ)2 J ЛпЗ (1пЗ) (1пЗ)2
Пример 16.12. Найти интеграл J arctgxdx.
Полагая « = arctgx, dv = dx, находим du= dx/(l+x2), v=x.
По формуле (16.12) получаем
f , . f xdx . 1 fd(x2+l)
J arctgxdx = x arctgx - J ——= x arctgx - — J —- =
1 ,
= x arctgx-—In (x +1)+C.
Пример 16.13. Найти интеграл J x2 sin xdx.
Полагая u = x2, dv = sinxdx = d(-cosx), получаемdu-2xdx, v = -cosx.
Следовательно,
J x2 sin xdx = x2(- cosx) - J(- cosx)2xdx = -x2 cosx + 2 Jx cosxdx. (I)
Полученный интеграл снова находится интегрированием по частям. Его можно
найти и не вводя явно функции и и v:
Jxcosxdx = Jxd (sinx) = xsinx—J sin xdx = xsinx + cosx + Q.
Подставляя это выражение для интеграла в формулу (I), находим
Jx2 sinxdx =-х2 cosx + 2 Jx cosxdx =-х2 cosx + 2 (х sin х + cosx+С|) =
= -x2cosx+2(xsinx+cosx)+C (C=2Q).
Пример 16.14. Найти интеграл I (arccosx)2dx.
Полагая и = (arccosx)2,
dx = dv, получаем v = x, du =
= -2arccosxdx/Vl-x2 .
По формуле (16.12) имеем
J(arccosx)2dx = x(arccosx)2 + 2 Jxarccosxdx/-\/l-x2 .
Этот интеграл также находим методом интегрирования по частям:
и = arccosx, dv = xdx/-]\-x2 , du = -dx/^\-x2 , v = --Jl-x2,
f x^rccos-^ dx = - -\/l-x2 arccosx - f —— dx =
= - y/l—x2 arccosx - x + CP
266
Следовательно,
J(arccosx)2<±r = x(arccosx)2 -2^11-x2 arccosx-2x + C.
Пример 16.15. Найти интеграл Jет cosfixdlx.
Полагая u = eox, dv = cospxaEx, находим du = ae^dx, v = (l/P)sinpx; следо-
вательно,
J em cos pxdx = ею sin px - J sin px > ae^dx,
(I)
J em cos pxdx = i e*“ sin fix - J e*“ sin pxdx.
Интеграл в правой части равенства (I) также находим методом интегри-
рования по частям:
cospx+J-^ cospx aemdx =
J e*“ sinpxdx= Je*“ d (-cospx) = - ± ею
г"
cospx+^- fe°xcospxdx.
(П)
Подставив выражение (II) в равенство (I), получим
[-|e<“cosPx+|Je<“c<
Je” cospxdx.
J ею cospxdx = е*“ sinpx
= — еох sinpx +-^- ет cospx -
Р Р2
Перенося интеграл в левую часть, получаем уравнение
1+^] fe°xcospxdx = — етsinрх+~ес“cospx,
P2JJ Р Р
из которого находим
Г е*“ cos pxdx = —у?—у
J а2+р2
е*“ (a cos рх + Р sin рх )+С.
Пример 16.16. Найти интеграл J^/x2+adx.
V2 » 1 хал J
х +а, ax = ov, отсюда . = аи,
л/х2+а
(16.12) получаем
f Vx2 +а dx = xVx2 +а - [х
J J Vx2+a
Преобразуем интеграл в правой части
v=x. По формуле
267
#- _Г<Ц^А.|(^>А.а| * .
Vx+а J лрг+а J->Jxi+a J->Jxi+a
Следовательно,
jy/x2 +adx-a
откуда
2 Jy/x2 + adr = xy/x2 + a + a J , Jy/x2 +adx =
Так как последний интеграл определяется формулой (16.11), то
JVx2 + a<& = (xy/x2 +a +aln| x+y/x2 +a | )+C. (16.13)
Пример 16.17. Найти интеграл J ^a2 —x2 dx.
Применяя метод интегрирования по частям, получаем
Поскольку
то
откуда
а2 -х
.2
x2dx
а2—х2
.2
.2
. dx =
'а2-х2
[(a2-^~a2.dx.
.2
2 2
а —х
'а2-х2
dx
.2
а2-х2
а2—х2
'а2-х2
= arcsin —
а
a2 — x2dx =Х'
.2
^а2 -x2dx + a2 arcsin —,
о'
_ _______ 2
Г~2 2 а . X
’а -х Ч--------arcsin — + С.
2 а
(16.14)
2
Замечание. Этот интеграл
подстановки x = asinr.
с
можно найти
помощью
268
16.5. Интегрирование рациональных дробей
с квадратным трехчленом в знаменателе
Интеграл вида 7, = J dx/^px1 +qx+r) путем дополнения квадратного трехчле-
на до полного квадрата по формуле рх2 + дх + г = р ((х + к)2 ± а2 ) сводится к од-
ному из двух интегралов:
Г du
1 Ж w _
=— arctg — + С,
а а
du 1 , и-а
---r = V_|n --
и -а 2а и+а
где и = х + к.
Интеграл
тх+п
рх2 +gx+r
(16.15)
(16.16)
(16.17)
сводится к интегралу (16.15) или (16.16) и интегралу
f м^ = 11п|м2+а1+с (16.18)
J и + а 2 1 1
При нахождении неопределенного интеграла от рациональной функции с квад-
ратным трехчленом в знаменателе, т. е.
R (JC) = Р’М = a„x"+a„-ixn '+-+a2x2+aix+a0
Р2(х) ax2+bx+c
сначала производят деление; в результате получают /?(х)=(2„(х)+ (kx+l)/(ax?+bx+c), где
Qm(x) - многочлен, степень которого ниже степени многочлена Р„(х).
Первообразная от многочлена Qm(x) находится непосредственно, а от остатка
(fcx + 1)1 (ах2 +Ьх+с) - как интеграл вида (16.17).
Пример 16.18. Найти интеграл Г———-----------.
J х +4х-12
Дополняя квадратный трехчлен до полного квадрата и интегрируя на основа-
нии формулы (16.16) для случая, когда и = х+2, а = 4, находим
dx _ Г dx _ f dx
х2+4х—12 ~ J (х2+4х+4)-4-12 “ J (х + 2)2-16
(х+2)-4 +с=
(х + 2)+4
+ С.
--—г-г =— 1П
(х + 2)2-42 2-4
х-2
х + 6
= 11п
8
269
Пример 16.19. Найти интеграл J
dx
х2-6х+34
Выделяя полный квадрат и применяя формулу (16.15) для случая, когда
и = х-3, а = 5, находим
f dx _ Г____________dx________ Г dx
J x2-6x+34 = J (x2-6x+9)-9+34 J (x-3)2 + 25
Г d(x-3)
J (x-3)2+52
Пример 16.20. Найти f £*-+ .
J x2 +4x+20
Преобразуя подынтегральное выражение, получаем
f (х+8) 1 f 2x + 16 1 f(2x+4) + 12 J
I —z-----dx = — I —z----dx = — I —z---dx =
Jx2+4x + 20 2 Jx +4x+20 2 Jx2+4x+20
2. f (2x+4)d5c । f dx _ 1 f (x2 +4x + 20)' <& +
2Jx2+4x + 20 Jx2+4x+20 2 J x2+4x+20
+ 6 f-^±2)T = lln(x2 + 4x+20)+64arc^^+C=
J(x+2)2+42 2 ' 4 е 4
= —ln(x2 +4x+20)+^arctg^^+C.
П irni и fx4+5x3-3x2+7x + 3 ,
Пример 16.21. Найти J---5—j-----
Так как
x4+5x3-3x2 + 7x + 3
2x+7
x2 +1
TO
x4+5x’-3x2 + 7x + 3 , x3 5j. i z 2 -7 ,
------------------dx =--1— x - 4x + In (x +1)+7 arctgx + C.
xz+l 3 2
16.6. Интегрирование рациональных функций
Рассмотрим неопределенные интегралы ввда J R (х) dx, где R (х) -
правильная рациональная дробь, т. е.
r (Х) = AW = go +а1х +.а2^ +''' + a«-tx ' ±.а«х („ < ту
Qn(x) b0+blx+b2x2+-+ b„^xm + bmxn
Нахождение указанных интегралов основано на разложении рациональной
270
дроби в сумму элементарных дробей, т. е. дробей вида
А Вх + С
{х-а)0-’ (x1 + px + qf’
где а, 0 - натуральные числа; а, р, q, А, В, С - действительные числа;
р2/4 - q < 0 (корни трехчлена являются комплексными).
Это разложение определяется теоремой 8.5 (см. п. 8.7).
г 7х2 — х +1
Пример 16.22. Найти J---j—-— dx.
„ 7х2-х+1 3 4х-2 . _
Так как--------=-----1—------(см. пример 8.18), то
X *4" 1 X Ч"1 X — X Ч- 1
Г7х2-хч-1 д Г4(х+1) , 2 f(x2-x+l)'<fr _
J х3ч-1 J хЧ-1 J х2-хч-1
= 31п|х + 1|+21п|х2-х + 1| + С.
Пример 16.23. Найти Г - +Jc+^ dx.
Jx3-3x+2
Поскольку
х2+х + 1 _ 1 2 1
х3-Зхч-2 3(х+2) + 3(х-1) + (х-1)2
(см. пример 8.19), то
f х2+х+1 1 р(х + 2) 2 frf(x-l) f cf(x-l) _
Jx3-3x + 2 3J х+2 3J х-1 J (х-1)2
= iln|x+2|+-ln|x-l|-----— +С =
3 1 1 3 1 1 х-1
= |lnl(x + 2)(x-l)2|--Ц- + С.
3 1 । х-1
Пример 16.24. Найти интеграл [ —;----------=- —.
J х5-х4+2х3-2х2+х-1
Разлагая знаменатель на множители, получаем х5-х4+2х3-2х2+х-
-1 = х4(х-1)+2х2(х-1)+(х-1)=(х-1)(х4+2х2 +1) = (х-1)(х2 +1)2.В данном
случае разложение в сумму элементарных дробей должно иметь вид
______1_______ А + Вх + С Dx+E
(х-1)(х2+1)2 х-1 х2+1 (х2+1)2’
откуда
1 = А (х2 +1)2 + (Вх + С) (х -1) (х2 +1)+(Dx + £) (х -1).
Полагая в этом тождестве х = 1, находим 1 = А • 4, т. е. А = 1/4 - Придавая х со-
ответственно значения х = 0, х = -1, x = i = ^/-T, получаем уравнения
271
1 = A-C-E; 1 = 4A+4B—4C+2D—2E-, l = (Di+E)(i-l), или 1 =
= -D—Di+Ei-E, т.е. \ = -D-E + (E-D)i, откуда \ = -D-E, E-D = 0.
Решив полученные уравнения, найдем В = —1/4, С = —1/4, D = —1/2, Е=—1/2.
Таким образом,
Г________dx__________/Г 1 х + 1 х + 1
J х5-х4+2х3-2х2+х + 1 - J ^4 (х-1) ~ 4 (х2+1) ~ 2 (х2+1)2 J
_1_ ГЛ (х-1) 1 f xdx 1 Г dx
4 J х-1 4jx2+1 4jx2+1
1 f
2 J (x2 +1)2
1 „ 1 fd(x2+l) 1
- — arctgx —- I —з-—
4 4 J (x2+l)2
= ln|x—1|--1- ln(x2+l)-^arctgx+^
4 4-2 4 4
1 . 1 X _ 1 . |*-1|
4 s 4 1+x2 4
xdx
2 J (x2 +1)2
= lln|x-l|-|ln(x2+l)-
dx _
2 J (x2+l)2 “
1
1 , 1-x
— arctgx +----z---+ C.
2 6 4(x2+1)
_ ч Г dx „
Замечание. Интеграл I —z--------z- найден с помощью подстановки
J (x +1)
x = tgt. Так как dx = dt/cos21, to
f dx f tft/cos2/ Г 2.j. f l+cos2t
J(x2+1)2 J(tg2t+1)2 J J 2
1 1 „ 1 1 x
= — t +— sm2t = — arctgx +——5---F C
2 4 2 6 2x2+l
I sin2r = 2sintcost = 2 cos21 = 2tgrcos21 = 2x —^-5-].
V cost 1+x J
16.7. Интегрирование простейших
иррациональных функций
Неопределенный интеграл f , выделением полного квадрата в
J Ах2+Вх + С
подкоренном выражении и введением новой переменной и = х+Ь в зависимости
от знакаА приводится к одному из интегралов:
f = arcsin - + С, (16.19)
Ча2-и2
272
= 1п|м+7м2+а l + C. (16.20)
J л/м2 +а । 1
J yfu2+adu=л/и2+« + у 1п |
Неопределенный интеграл j -у Ах2 + Вх + Cdx в зависимости от знака А приво-
дится к одному из интегралов:
н+л/и2+а | + С, (16.21)
^а2-u2du = ^^ja2 -и2 +^-arcsin —+ С (16.22)
(см. формулы (16.13) и (16.14)).
Неопределенный интеграл f --j—, —dx приводится к интегралам вида
J ^Ах2+Вх + С
Ь£^=[^ = 1п|/(х)| + С,
J /(*) » /(*)
J dx=J (/(х)) - ^/(х) = (/(.^)1/2 + С=+ с.
Интеграл вида
(16.23)
(16.24)
(16.25)
где R—рациональная функция иpi^i,.... Ръ<к — целые числа, с помощью подстановки
где «-наименьшее общее кратное чисел >?*> приводится к
интегралу от рациональной функции.
Интеграл от дифференциального бинома
7 = |х”(а + 6х''У’<&, (16.27)
где т,п,р - рациональные числа; а,Ь - постоянные, отличные от нуля, сво-
дится к интегралу от рациональной функции в трех случаях:
1) когда р — целое число, — разложением на слагаемые по формуле бинома Нью-
тона при р>0; подстановкой x = tN, где W - общий знаменатель дробей тип;
2) когда (т+1)/я - целое число,-подстановкой a+bx" = ts, где s —
знаменатель дроби р;
3) когда (т+1)/и+-р - целое число, - подстановкой ах~" +b = ts.
Пример 16.25. Найти f ..............
л/Зх2 +6х+4
273
Так как 3x2+6x+4 = 3(x2+2x+l)-3+4=3(x+l)2+l = 3((x+l)2 + 1/3), то,
положив х +1 = и, по формуле (16.20) получим
Г dx _ 1 f d(x+l)
3 7зх2+6х+4 л/З J -/(х + 1)2 +1/3
= -^ In | (х+1)+J(x + 1)2 +1/3 | + С.
Пр и м е р 16.26. Найти J Vx2 + 6x+13t/x.
Поскольку х2+6х + 13 = (х2+6х+9)+4 = (х+3)2+4, то, полагая и= = х+3,
по формуле (16.21) находим
[ л/х2 + 6х + 13<&=^±2 д/(х+3)2 +4 +| In| (х+3)+д/(х+3)2 +4 |+С =
|х+3+л/х2+6х + 13 | + С.
2 '
= ^±^л/х2+6х + 13+21п
2
г 0-4х
Пример 16.27. Найти I ......— dx.
•Ч5 + 8Х-4Х2
Поскольку (5+8х - 4х2 )' = 8 - 8х = - 8 (х -1), 9 - 4х = -4х +4+5= -4 (х -1)+5,
5+8х—4х2 =—4((х2-2х + 1)-1)+5 = -4(х-1)2+9=4х х(9/4-(х-1)2), тона
основании формул (16.19) и (16.24) получаем
f , 9~4* dx= f -4(2С-1>+5 f ~^-^ +
J л/5+8х-4х2 3 л/5+8х-4х2 3 /5 + 8х-4х2
+ [ . *** -1 f ,< f ^(*-1) _
J л/5+8х-4х2 2 J л/5+8х-4х2 J 2^9/4-(х-1)2
= л/5+8х-4х2 + — arcsin —— + С.
2 3
Пр имер 16.28. Найти интеграл
dx
(х-1)л/х2-2-
/ Перейдем к новой переменной t по формуле x-l = VG откуда dx =
= -dt/t2, x2-2 = (l+2t-?)/t2.
Следовательно^
Г f dt Г d(t-l)
J (x-1)a/x2-2 J -71 + 2Г-Г2 J -JcV2)2-(t-l)2
- arcsin—t=- + C.
Возвращаясь к переменной x, находим
f dx . -J2 (x — 2)
3 (x —l)-\/x2 -2 2(x-l)
274
dx
Пр и м e p 16.29. Найти .
J 4^+з+Щх+з)2
Это интеграл вида (16.25), причем а = 1, b = 3, с = 0, d = l, р}/д} = = Ц2,
р21д2=2]3, п-6. Подстановка (16.26) принимает вид x+3=t6. Отсюда следу-
ет, что x=t6 — 3, dx = 6tsdt, -J(x+3) =(х+3)^2 =(t6)^2 = t3, ^/(x+3^ = t4,
t = (x + 3)V6, t2 =(х+3)У3. Таким образом,
Г_____А______= f 6tsdt 6 Г t5dt _ 6 Г t2dt _
J 7х+3+\|!(х+3)2 J '3+z4 J r3(l+O J 1+г
ч^Л=6)(,.1)Л+6^=
= 6y-6z+61n|l + z| + C=3(x + 3)V3-6(x+3)V6+ 61n| l+(x + 3)V6|+C.
Пример 16.30. Найти f
J Vx2
Переписав интеграл в виде Jх~^3(1 +x^3)^2dx и сравнив с интегралом (16.27),
заключаем, что т = — 2/3, и = 1/3, р = \/2. Так как (т+1)/и =
= (-2/3+1)/(1/3) = 1 есть целое число, то имеем второй случай интегрируемости
дифференциального бинома. Подстановка a + bx" = ts в данном случае примет
вид (l+xV3) = Z2, откуда x^3=z2-l, (l/3)x~^3dx = 2tdt, x~^3dx= =6tdt. Под-
ставив эти выражения в интеграл, получим
J х-2/3(1 +xV3)V2<& = J(1 +xV3)V2x~2l3dx = j t-6tdt = 6 j t2dt =
t3
= 6j + C=2(1+xV3)3/2+C.
16.8. Интегрирование некоторых
тригонометрических выражений
Неопределенные интегралы вида
I sinarsintadbc, I cosaxcasbxdx, I sinaxcosbxdx (16.28)
275
с помощью тригонометрических формул
sin a sin р = -i (cos (а - Р) - cos (а+р)),
cosa cosP=(cos (a - p)+cos (a+P)),
sin a cos p = у (sin (a - P)+sin (a+P))
приводятся к интегралам
f , , sinfac _ f . , , cos far „
I cosfacdx ----ь С; I sm kxdx -------1- C.
J kJ к
Неопределенные интегралы вида = Jsin"xcos"x<&, где т и и —натуральные
числа, находятся с помощью тригонометрических формул sin2x = (l-cos2x)/2,
cos2x = (l+cos2x)/2, sinxcosx = (sin2x)/2, если m и и четные.
Если хотя бы одно из чисел т и и - нечетное, то от нечетной степени отделяется
множитель и вводится новая переменная. В частности, если и = 2к +1, то
4>, п = J s*n”"х cos2**1 xdx = J sin" x cos2* xcosxdx =
= J sin"x (l-sin2x)* d (sinx)=J u"(l-u2)* du.
Последний интеграл находится непосредственно (как интеграл от алгебраиче-
ского многочлена).
Неопределенный интеграл J Я(sinx, cosx)dx, где R(sinx, cosx) - рацио-
нальная функция от sinx и cosx, путем введения новой переменной по формуле
“tg^ = f (16.29)
приводится к интегралу
^-4]-^-= |Ч(о л»
j i+t2ji+t2 j ч
где (г) - рациональная функция переменной t.
Пример 16.31. Найти интеграл Jsinl4xsin6xt/x.
Это первый из интегралов типа (16.28), в данном случае a = 14, b = 6.
Применяя первую из приведенных выше тригонометрических формул, преоб-
276
разуем подынтегральную функцию и интегрируем:
J sin 14х sin 6xdx =
J (cos 8x - cos 20.x) dx =
= — fcos8x«&-— fcos20xdx = — sin8x—— sin20x + C.
2 J 2 J 16 40
Пример 16.32. Найти интеграл Jcosl0xcos7x<&.
Преобразуя подынтегральное выражение, находим
[ cosl0xcos7xdx = — [ (cos3x + cosl7x)<7x =
If , . . 1 f , sin3x sinl7x „
= — I cos3xt£c+— I cosl7xdx =------------FC.
2 J 2 J 6 34
Пример 16.33. Найти J sin6 x cos5 xdx.
Поскольку одна из степеней является нечетной (и = 5), то интеграл можно
найти следующим образом:
J sin6 х cos5 xdx = J sin6 xcos4 x cosxtfo = J sin6 x (1- sin2 x)2 d (sinx) =
= J sin6 x (1 - 2sin2 x + sin4 x) d (sinx) = J (sin6 x - 2sin8 x + sin10 x) d (sin x) =
_ sin7 x _ 2sin9 x + sin11 x +
7 9 11 +
n tt f 5-sinx+3cosx .
Пример 16.34.Найти I--------------dx.
J 3+sinx-3cosx
Преобразуя подынтегральное выражение, получаем
Г 5-sinx+3cosx Г 8-(3+sinx-3cosx)
J 3+sinx-3cosx J 3+sinx-3cosx
= 8 f-----—------Г А
J 3+sinx-3cosx J
Чтобы найти первый интеграл, применим подстановку (16.29):
f___________= г_________зМ___________Л= г
J 3+sinx —3cosx J 3+2t/(l + t2) + 3(?-l)/(l + t2) J3t2+r
f (1 a \
-----— <* = lnl/l-ln|3t + l| + C = ln
3r+i; 11 1 1
tg(^/2)
3tg(x/2)+l
Следовательно,
f 5-sinx + 3cosx , o,
I--------------dx = 8 In
J 3+sinx-3cosx
tg(x/2)
3tg(x/2)+l
277
Глава 17
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
17.1. Определенный интеграл,
его геометрический смысл и свойства
Понятие определенного интеграла. Пусть дана функция у- f(x), опреде-
ленная на отрезке [а, Л], где а < Ь. Отрезок [а, Л] точками а = х0<
<xi<x2<...<x„_i<x„ = b разобьем на я элементарных отрезков [a,xj,
[х15х2],..., [*„_], £>], длины которых обозначим через ДхА, т. е. ДхА = хк -xA_j
(Л = 1,2,..., я, х0 = а, х„ = Ь). В каждом из элементарных отрезков [xH,xt] вы-
берем произвольно одну точку значение функции в этой точке /(^*) умно-
жим на длину отрезка Дхъ получим произведение /(^А) ДхА. Составим сумму
всех таких произведений
п
=£/($*) Дх*. <171)
*=i
Сумма (17.1) называется интегральной суммой для функции у = f(x)
на отрезке [а, Л].
Обозначим через А, длину наибольшего из элементарных отрезков [хЛ_,,хЛ]
(А = 1,2,..., я), т.е. А, = шахДх4 (Л = 1,2,..., я).
Число S называется пределом интегральной суммы (17.1), если для любого
числа е > 0 можно указать такое число 8 > 0, что при А < 8 выполняется нера-
венство |S„-S|<e независимо от выбора точек на отрезках [х^.х*].
Определенным интегралом от функции у = f(x) на отрезке [а, Л] называется
конечный предел ее интегральной суммы, когда число элементарных отрезков
неограниченно возрастает, а длина наибольшего из них стремится к нулю. Опре-
ь
деленный интеграл обозначается символом jf(x)dx (читается: определенный
а
интеграл от а до Л); /(х) называется подынтегральной функцией, х- перемен-
ной интегрирования, а - нижним, b - верхним пределами интегрирования.
Следовательно, по определению
г "
|/(х)А= Нт У/(£*)Дх*. (17.2)
J Х->0
а *=1
278
Из определения следует, что величина определенного интеграла не зависит от
обозначения переменной интегрирования, т.е.
ь ь ь
J /(х) dx = J f(t) dt = • • • = J f(u) du. (17.3)
a a a
Функция, для которой существует предел суммы (17.1), называется интегри-
руемой на отрезке [а, Ь].
Очевидно, если функция f(x) интегрируема на отрезке [а, 6], то она и ограни-
чена на этом отрезке. Обратное утверждение не верно: существуют ограниченные
функции, не являющиеся интегрируемыми. К ним относится функция Дирихле, рав-
ная единице в рациональных точках и нулю - в иррациональных. На любом отрезке
[a, Z>] эта функция ограничена, но не является интегрируемой на нем.
Соответственно по определению
а
J/(x)dx = O, (17.4)
а
где f(x) - любая функция;
Ь а
J/(x)dr = -J/(x)dx, (17.5)
а b
где f(x) - функция, интегрируемая на отрезке [/>, а] (Ь<а).
Справедливы следующие утверждения.
1. Если функция f(x) интегрируема на отрезке [a, ft], то она интегрируема
на любом отрезке [с, d], содержащемся в [а, />].
2. Если функция f(x) непрерывна на отрезке [a, Z>], то она и интегрируема
на этом отрезке.
3. Если функция f(x) имеет на отрезке [a, ft] конечное число точек разрыва
первого рода, то она интегрируема на [а, £>].
Геометрический смысл определенного интеграла. Если а < b, f(x)> 0, то
ь
|/(х)<& = 5,
а
т.е. определенный интеграл от функции у = f(x) по отрезку [а, Ь] равен площади
криволинейной трапеции, ограниченной сверху графиком функции у = f(x), слева
и справа - отрезками прямых х = а, х = Ь, снизу — отрезком оси Ох (рис. 17.1).
Если а<Ь и /(х)5 0, то
ь
j/(x) <& = -£,
279
т. е. определенный интеграл от функции, принимающей неположительные
значения, равен площади соответствующей криволинейной трапеции,
взятой со знаком минус (рис. 17.2).
Рис. 17.1
Рис. 17.2
Если а < b и /(х) меняют знак на отрезке [а, Ь], то определенный интеграл равен
алгебраической сумме площадей соответствующих криволинейных трапеций (рис. 17.3):
ь
J f(x)dx = ^1 — $2 +$з-
а
Основные свойства определенного интеграла. Определенный интеграл об-
Рис. 17.3
ладает следующими свойствами.
1. Если функция /(х) интегри-
руема на наибольшем из отрезков
[а, Л], [а, с], [с, Л], то она интегри-
руема на двух отрезках, причем
ь с ь
j f{x) dx = J Дх) dx+J Дх) dx
a a c
при любом расположении точек a,b,c.
2. Если функция f (х) интегрируе-
ма на отрезке [а, 6], то функция
Л f (х), где к = const, также интегрируема на этом отрезке, причем
ь ь
J к f(x) dx = k jf(x)dx.
а а
3. Если функции Дх) и <р (х) интегрируемы на отрезке [а, Л], то их сумма и
разность также интегрируемы на этом отрезке, причем
ь ь ь
j (Дл)± ф (*)) dx = J Дх) dx + J <р (х) dx.
а а а
280
4. Если функц ия fix) интегрируема на отрезке fah], где a<b, nfix)>0 для всех х е то
ъ
J/(x)d5c>0.
а
5. Если функции f(x), <р (х) интегрируемы на отрезке [а, 6], где а < Ь, и
f(x) < <р (х) для всех х е [а, 6], то
ъ ъ
J/(x)<&< |<p(x)dx.
а а
6. Если функция /(х) интегрируема на отрезке [а, 6], где а < Ь, то функция
|/(х)| также интегрируема на [а, />], причем
» ь
jf(x)dx < ||/(х)|Л.
а а
17.2. Определенный интеграл с переменным
верхним пределом.
Формула Ньютона - Лейбница
Рассмотрим функцию у = /(х), интегрируемую на отрезке [а, 6]. Если хе [а, Л],
то функция /(х) интегрируема также на любом отрезке [а, х]. Предположим, что х
меняется на отрезке [а, 6], тогда на этом отрезке определена функция
Ф(х)=|/(<)<*• (17.6)
а
(Переменную интегрирования обозначили буквой t, переменный верхний предел
— буквой х).
Теорема 17.1. Если функция y = f(x) интегрируема на отрезке [а, 6], то
функция (17.6) непрерывна на этом отрезке.
Теорема 17.2. Если подынтегральная функция непрерывна, то производная
определенного интеграла с переменным верхним пределом существует и равна
значению подынтегральной функции для этого предела, т.е.
Ф'(х) = /(х), или
=/(х).
\а /х
Следствие 1. Если функция fix) непрерывна на отрезке [а,Ь], то при любом х
ь
= -f(x), или ~ f/(Odz=-/(x).
ах J
281
Следствие 2. Определенный интеграл с переменным верхним пределом
является одной из первообразных для непрерывной подынтегральной функции.
Другими словами, для любой непрерывной функции существует первообразная.
Замечание. Интеграл с переменным верхним пределе»! интегрирова-
ния используется при определении многих функций. К таким функциям относятся,
например:
1) Si(x) = (интегральный синус);
о
2) Ci(x) = - dt (интегральный косинус);
3) li(x) = I-- (интегральный логарифм);
J 1п/
-о
4) Ei(x) = J— dt (интегральная показательная функция);
5) S(x) = Jsinr2eft, С(х) = Jcosz2A (интегралы Френеля);
о о
6) Ф(х) = -?= fe“'aJz (интеграл вероятностей).
л/л J
о
Эти функции не являются элементарными; первообразные указанных подынте-
гральных функций не выражаются через элементарные функции.
Все приведенные функции хорошо изучены, для них составлены таблицы зна-
чений, эти функции находят широкое применение.
Связь между определенными и неопределенными интегралами выражает сле-
дующая теорема Ньютона — Лейбница, называемая основной теоремой интеграль-
ного исчисления.
Теорема 17.3. Огределенный интеграл от непрерывной функции равен разности
значений любой ее первообразной для верхнего и нижнего предела интегрирования:
ь
^f(x)dx-=F(b)—F(a), (17.7)
где F'(x)=f(x).
Формула (17.7) называется формулой Ньютона - Лейбница; ее можно пе-
реписать в ввде
ь
j/(х)dx = F(х)|*, F(x)\ba=F(b)-F(a),
282
левая часть второй формулы читается так: «двойная подстановка от а до b для
функции F(x)».
4
Пример 17.1. Вычислить интеграл J (32+28л - 9х2) dx.
2
Принимая во внимание свойства определенного интеграла, получаем
4 4 4 4
J (32+28л—9х2 ) dx = J 32t/x+J 28xd5r - J 9x2dr =
2 2 2 2
4 4 4
= 32 j dx+28 j xdx - 9 j x2dx = 32.x | * +
2 2 2
X2
+ 28 —
2
= 32(4-2)+14(42-22)-3(43-23) = 64.
2
1^2
Пример 17.2. Вычислить интеграл J cos4 <pd<p.
-HZ2
Переменная интегрирования обозначена буквой <р. Преобразуя подынтеграль-
ную функцию, получаем
/• ~ \2 .
4 ( 1 + COS 2ф ] о 2 о х
cos <р = 1---—— I = —(l+2cos2«p + cos 2<р).
Следовательно,
1^2 к/2
Jcos4<pj<p = -i J(l + 2cos2<p + cos22<p)c/<p =
->У2 -я/2
г]2 я/2 к/2
= i J^+-i Jcos2<prf(2<p)+— J(l + cos4<p)d<p =
-я/2 -к)2 -я/2
1 1 я/2 1 . - । rj2 1 I >уг 1 . . । k/2 3
— Ф ,,+—sm2<p ,.+ — <p ,.+—sm4<p „=—л.
4 T 1 -*/2 4 T । -*/2 g Y I -*/2 32 1g
17.3. Замена переменной в определенном
интеграле. Интегрирование по частям
Теорема 17.4. Если выполнены условия: 1) функция f(x) непрерывна на
отрезке [а, £>]; 2) отрезок [a, Z>] является множеством значений функции
х = ф (/), определенной на отрезке а < t < р и имеющей на нем непрерывную
производную: 3) ф (а) = а, ф (р) = Ь, то справедлива формула
283
ь Р
fix) dx = J/(<p (0) ф' (0 dt. (17.8)
a a
Теорема 17.5. Если функции u = и (x), v = v(x) имеют непрерывные про-
изводные на отрезке [а, &], то справедлива формула
ь ь
J и (х) v' (x)dx = и (х) v (х) | * - J v (x) и (x)dx. (17.9)
a a
2
Пример 17.3. Вычислить интеграл Jxy'2-xdx.
i
Введем новую переменную по формуле Г = л/2-х, из которой получим
tz = 2—x, x = 2-tz, dx = -2tdt.
Вычислим новые пределы интегрирования с помощью формулы t = -\/2-х. По-
скольку при х - 1 t = л/2 —1 = 1, то a = 1; далее, при х = 2 t = 0, поэтому 3 = 0.
Формула (17.8) принимает вид
2 0 0
Jx-JT-^xdx = J(2- г2) t (~2tdt) = [(2г4 -4?) dt.
1 1
Вычисляя последний интеграл, находим
О 0 О 5
j(2t4 — 4t2)dt = 2 f t4dt - 4 j t2dt = 2
1 1 1
2
Следовательно, Jx-^2-xdx = 14/15.
i
2
Пр и м e p 17.4. Вычислить интеграл jxS/8-2x2<£r.
•Л
Введем новую переменную по формуле x = 2sinZ. Поскольку dx = 2costdt,
t = arcsin (x/2), Г, = л/4 при x = л/2, t2 = л/2 при x = 2, то
2
"/2
J (2sinz)2^8-2(2sin/)2 2cosrdi =
J2 я/4
Ф ______________
= J 4 sin2 r\/8-8sin2r 2 cos tdt = J16-/2 sin21 cos2 tdt -
= f4^sin22zt* = 2-^ [ (1 - cos 4t) dt = 2-^2
i L V 4 >^4 2
*/4
«/4
284
2я
Пример 17.5. Вычислить интеграл Jxsin(x/2)«fc.
о
Интегрируя по частям, находим
2? 2я 2я
+ 2 I cos— dx = -2xcos — + 4sin — =4л.
J 2 2 о 2 0
я/2
Пример 17.6. Вычислить интеграл J/2sintdt.
о
Дважды интегрируя по частям, получаем
я/2 я/2 я/2
J t2 sinZdf =- J t2d (cos t)=-t2 cost |o + ^2t costdt =
0 0 0
k/2 я/2
= 2 jtd (sint)=2tsint |^2-2 Jsintdi = u+2cost |^2 = it-2.
о 0
17.4. Оценка определенного интеграла.
Теорема о среднем
Теорема 17.6. Если функция f(x) интегрируема на отрезке [а, 6], где
а<Ь, и для всех х е [a, i] выполняется неравенство т< f(x)< М, то
ь
m(b-a)<^f(x')dx<M(b-a). (17.10)
а
С помощью неравенств (17.10) можно оценить определенный интеграл, т.е.
указать границы, между которыми заключено его значение. Неравенства (17.10)
выражают оценку определенного интеграла.
Теорема 17.7. Если функция f(x) интегрируема на отрезке [а, Ь] и для
всех х е[а, Ь\‘выполняются неравенства т< f(x)<M, то
ь
|/(х)А=ц(6-а), (17.11)
где т<р< М.
Эта теорема называется теоремой о среднем.
285
Замечание. В случае, когда функция /(х) непрерывна на отрезке
[а, £>], равенство (17.11) принимает вид
ь
J f(x)dx = f(c)(b — a), (17.12)
а
где с е [а, Л].
Число ц = /(с), определяемое формулой
(17.12), называется средним значением функции
/(х) на отрезке [а, 6].
Равенство (17.12) имеет следующий геометриче-
ский смысл: площадь криволинейной трапеции,
ограниченной непрерывной линией у = /(х)
Рис 17 4 (/(х)>0), равна площади прямоугольника с тем
же основанием и высотой, равной ординате некото-
рой точки этой линии (рис. 17.4).
к
„ ~ Г dt
Пр и м е р 17.6. Оценить интеграл I . - ^==.
* дР+(9/16)sin2/
Поскольку подынтегральная функция f(t)= (/д/1+(9/16) sin21 в данном про-
межутке [0, л] имеет наименьшее значение т = 4/5 и наибольшее М =1, то в
соответствии с формулой (17.10) получаем
4 .Г Л
л < I < л.
5 {д/1+(9/16) sin2/
17.5. Несобственные интегралы
При введении понятия определенного интеграла предполагалось, что выпол-
няются условия: 1) пределы интегрирования а и b являются конечными;
2) подынтегральная функция /(х) ограничена на отрезке [а, 6]. В этом случае
определенный интеграл называют собственным. Если хотя бы одно из указанных
условий не выполняется, то интеграл называют несобственным.
Интегралы с бесконечными пределами. Пусть функция y = f(x) непрерывна
при любом х > а. Рассмотрим интеграл с переменным верхним пределом:
ь
I (b) = j f(x)dx. (17.13)
а
Предположим, что при b —> + °° функция (17.13) имеет конечный предел; этот
предел называется сходящимся несобственным интегралом от функции /(х) по
286
промежутку [а, + <*>) и обозначается так:
+ °° ь
[f(x)dx = lim [/(x)dx. (17.14)
J b~>+*>J
a a
Если предел (17.14) не существует или равен бесконечности, то несобственный
интеграл называется расходящимся.
Геометрически несобственный интеграл от неотрицательной функции выражает пло-
щадь бесконечной криволинейной трапеции, ограниченной сверху графиком функции
у = f (х), слева — отрезком прямой х=а, снизу- осью Ох (рис. 17.5); в случае сходяще-
гося интеграла эта площадь является конечной, в случае расходящегося - бесконечной.
Если F (х) - первообразная для f(x), то
+~ ь
[f(x)dx = lim f/(x)tfe = lim (F(6)- F(o)) = F (+<»)-F(a),
J b~++°o J b
a a
где F (+«>) = lim F (b).
b—t+co
Аналогично определяется несобственный интеграл с бесконечным нижним пределом
ь ь
f /(х) dx = lim [ /(х) dx
j a->-ooj
и несобственный интеграл с обоими бесконечными пределами
+ ** с 4-ов
J /(X) dx = J /(X) dx + J /(х) dx,
где с - любая точка из интервала (- •», + <»).
Теорема 17.8. Если при х>а выполнены неравенства 0<ф(х)< f(x) и
J/(x)dx сходится, то сходится и J" ф (х) dx» причем ^(х)<£с< J/(*)<&;
о а а а
если J ф (х) dx расходится, то расходится и J/(x)dr.
а а
Геометрическое значение этой теоремы иллюстрируется на рис. 17.6.
Рис. 17.5
287
Теорема 17.9. Если в промежутке (а, + °°) функция f(x) меняет знак и
J| f(x) | dx сходится, то сходится также J /(х) dx.
а а
Интегралы от неограниченных функций. Если функция у - f(x) неограни-
ченна в окрестности точки с отрезка [a, h] и непрерывна при а<х<с и
с < х < Ь, то несобственный интеграл от этой функции определяется формулой b С-Е Ь
1 f(x) dx = lim I f(x) dx + lim 1 f(x) dx, J E—>0 J T]~>0 J a a c+T] где e>0, T|>0. В случае c = b или с—а получаем b b-ъ (17.16)
J f(x) dx = Inn J f(x) dx, a a b b (17.17)
f /(x) dx = lim f /(x) dx. J n->o J a а+т] (17.18)
Несобственные интегралы (17.17) и (17.18) называются сходящимися, если су-
ществует конечный предел соответствующего определенного интеграла; в про-
тивном случае интегралы называются расходящимися.
Несобственный интеграл (17.16) называется сходящимся, если существуют оба
предела в правой части.
Для интегралов от неограниченных функций справедливы теоремы, аналогич-
ные теоремам 17.8 и 17.9. Они применяются для исследования вопроса о сходимо-
сти несобственных интегралов и оценки их значений.
Пример 17.7. Исследовать, сходится ли несобственный интеграл
J х2+х+1
-1
Преобразуем подынтегральную функцию, выделив в знаменателе полный квадрат:
1 1_______ 1
х2 + х+1 х2 + 2.1х+1_1+1 (х + 1/2)2+3/4*
2 4 4
Применяя формулы (16.15) и (17.15), находим
7 = 7 t/(*+1/2) = -1- arctg +" =
Jx2+x + l J (х + 1/2)2+ь/з/2)2 л/з/г л/з/2
arctg (+°°)—arctg
-1+1/2 2 (п Л^_ 4л
л/з/2 J л/зк.2 + б) Зл/з’
Итак несобственный интеграл сходится и его значение равно 4 л/з-Тз (=2,4184).
288
Пример. 17.8. Исследовать при каких значениях а > 0 сходится несоб-
ь
ственный интеграл I-----— (Ь>а).
а
Если а = 1, то
ь ь
( dx fd(x-a)
I----= hm I —--------= hm In (x - а) =
J x-a e-»o J x-a e-+o a+E
a a+e
= lim (In (b - a) - In (a + e - a)) = In (b - a) - lim In e = + *>.
е-Л> e->0
Следовательно, при a = 1 несобственный интеграл расходится. Если a * 1, то
ь ь
[—— = lim [(x-a)~ad(x —a) = lim—!—(x-a)l-“| =
J (x-a) e-*° J lo+e
a a+e
, =lim-J—((b-a)'"“-e,-“).
e->0 i — a
Этот предел будет бесконечным при l-a<0, или ool; он будет равен постоянной
(fe-a)1-“/(l-a) при l-ооО, или а<1. Итак, данный интеграл сходится при а<1.
Пример 17.9. Исследовать, сходится ли несобственный
Г dx
интеграл J .
Так как
1 1 _ 1 1
л/1+х8 ^х8(1+1/х8) х4^1 + 1/х8 хА
и
то сходится и данный интеграл.
Пример 17.10. Исследовать, три каких а сходится несобственный интеграл f—
J х“
i
Если а*1, то
оо Ь ,
(dx (dx x'“+1
I — = hm I — = hm ----------
Jx 4-»+~J x *-»+“—a+1
i i
Следовательно,
b
= lim —(Z>’“+,-l).
1 —01
приа>1’ S^=+°° приа<1
1 1
10 Зак. 1
289
_ , Г dx , I-
В случае а = 1 J — = Inx | f
>. Итак несобственный интеграл сходится при col.
17.6. Интегралы Эйлера
Гамма-функция, или эйлеров интеграл второго рода, определяется формулой
r(p) = Je'V,c£c. (17.19)
о
Этот интеграл является несобственным, так как верхний предел бесконечен; кроме
того, при р-1<0 подынтегральная функция не ограничена в окрестности точки х = 0.
Интеграл (17.19) сходится при р>0. Каждому положительному значению р соответст-
вует вполне определенное значение Г (р). Функция Г (р) не является элементарной.
С Помощью метода интегрирования по частям можно доказать, что
Г(р+1) = рГ(р). (17.20)
При р = 1 интеграл находится непосредственно:
Подставляя в формулу (17.20) значения р = 1,2,...,и, получаем
Г(2) = 1Г(1) = 1 = 1!, Г(3) = 2Г(2) = 21 = 2!, Г(4) = ЗГ(3) = 3-2-1 = 3!.
Г(и+1) = и(и-1)...2-1 = и!. (17.21)
Итак, при натуральных значениях аргумента гамма-функция совпадает с фак-
ториалом, т.е. с функцией /(и) = и!. Но гамма-функция определена не только
при натуральных и, но и при любых положительных значениях аргумента. Из
формулы (17.21) следует, что можно считать 01 = Г (1) = 1. График гамма-функции
изображен на рис. 17.7.
Гамма-функция определяется и при отрицательных значениях р. В этот случае
необходимо применить формулу (17.21), переписав её в виде
Г(р)=Г(р+1\ (17.22)
Р
Если -1<р<0, то 0<р+1<1, поэтому правая часть формулы (17.22)
имеет смысл, ею и определяется Г (р) при этих значениях р; отметим, что в
таком случае Г (р) < 0. .Продолжая аналогичные рассуждения, убеждаемся в
тед^что гамма-функция определена для всех отрицательных значений р,
кроме р = -к, где Л = 1,2,3,^., и кроме р = 0.
290
График гамма-функции при отрицательных значениях р изображен на рис. 17.8.
Гамма-функция определена и для комплексных значений аргумента, кроме
р = -к, *=0,1,2,...
Бета-функция, или эйлеров интеграл первого рода, определяется формулой
1
В(р,?)= (17.23)
о
Подынтегральная функция не ограничена в окрестности точки х = 0 при
р -1 < 0 ив окрестности точки х = 1 при q -1 < 0.
Интеграл (17.23) сходится при р>0, q>0.
Рис. 17.7
Рис. 17.8
Значения бета-функции при различных значениях параметров р и q связаны
между собой следующими соотношениями:
В(р,<7) = В(<7,р); В (р, </) = —^—^—В (р, g — 1), q>\,
p + q-\
справедлива формула В (р, 1 - р) = л/sin рл, 0 < р < 1.
В случае комплексныхр и q интеграл (17.23) сходится, когда Rep > 0, Re q > 0.
Между бета- и гамма-функциями существует связь, выражаемая формулой
В(Р, <?) =
г(р)г(?)
г (₽+<?)
(р > 0, q > 0).
(17.24)
291
Пример 17.11. Вычислить Г (1/2) с помощью формулы(17.24).
Полагая в формуле (17.24) р = q = 1/2, получаем
Г2
:’V2(l-x)"V2= j
О
dx
d(х 1/2) _(2х-1)|* =л, Г2
о Л о •у'74)_(-х-1/2)2
Так как Г(р)>0 при р>0, то Г (1/2) = д/л = 1,772.
dx
л.
р 17.12. Вычислить Je *2dx.
о
При вычислении этого интеграла используем результаты примера 17.11.
Полагая x = -Jt, находим
Приме
о
Следовательно,
1 Ге-'Г^Л = 1 fe-'t<V2)-'A = lr
2 J 2 J 2
О о
/л
2
(17.25)
17.7. Площадь криволинейной фигуры
Площадь криволинейной трапеции аАВЬ, ограниченной сверху графиком
функции у = f (х), слева и справа - прямыми х = а и х = b соответственно,
снизу - осью Ох (рис. 17.9), вычисляется по формуле
S = ^f(x)dx. (17.26)
а
Площадь криволинейно трапеции cCDd (рис. 17.10), ограниченной справа
графиком функции х = <р (у), сверху и снизу - соответственно прямыми у = d,
у = с, слева - осью Оу, определяется формулой
d
S = J<p(y)dy. (17.27)
' с
Площадь криволинейной фигуры AlA2B2Bi, ограниченной сверху графиком
функции y2 = f2(x), снизу - графиком функции У\= f\{x), слева и справа -
прямыми х = а, х = Ь (рис. 17.11), вычисляется по формуле
о
о
292
ь
s=j(/2(x)-/;w)<fe.
(17.28)
Площадь фигуры CjZ^D^Q, ограниченной слева и справа соответственно гра-
Рис. 17.9
фиками функций X|=<Pj(y), х2=<р2(у),
у = d (рис. 17.12), определяется формулой
d
s = |(<Р2(У)-<Р1(У))Ф'-
(17.29)
Если линия, ограничивающая криволинейную
параметрическими уравнениями х = ф](Г),
<Pi(«)= а, <₽!(₽)=£>, то
трапецию сверху, задана
у = Ф2(г), где а</<₽,
5 = |<p2(O<Pi(O«fr-
(17.30)
Площадь сектора ОАВ (рис. 17.13), ограниченного дугой линии, заданной
уравнением в полярных координатах р = р (<р), и двумя полярными радиусами ОА
293
Ри<5. 17.13
и ОВ, соответствующими значениям <р, = а,
<р2 = Р, определяется формулой
S=|Jp2Ap. (17.31)
а
Пример 17.13. Найти площадь фигуры,
ограниченной линией у = 2х-х2+8 и осью Ох.
Чтобы определить пределы интегрирования,
найдем точки пересечения линии (параболы) с осью
Ох (рис. 17.14). Решая систему уравнений
у = 2х-х2 +8, у = 0, получаем х,=-2,
х2 = 4; следовательно, а = — 2, b = 4.
По формуле (17.26) находим
4 4 4 4
S' = J(2x—х2 +8)dr = 2 Jxdr ~ +8 Jdr =
-2 -2 —2 —2
Рис. 17.14 Рис. 17.15
Пример 17.14. Найти площадь фигуры, ограниченной линией х =
= у-у2 + 6 и осью Оу.
Данная фигура представляет собой криволинейную трапецию, прилежащую к
оси Оу (см. рис. 17.15). Найдем точки пересечения линии с осью Оу, для чего ре-
шим систему уравнений х = у — у2 + 6, х = 0. Из этой системы получаем у, = — 2,
у2 = 3; это означает, что в формуле (17.27), которой здесь необходимо пользо-
ваться, нужно положить с = - 2, 4 = 3.
294
Следовательно,
3 2
s = j(y-y2 +6)ify = ^-
-2
3 3
_У_
3
-2
з
+6р|12
-2
|(9-4)-|(27+8)+6(3+2) = 20
Пример 17.5. Вычислить площадь
х2+4у2=8, х2-4у = 0.
Данная фигура ограничена сверху дугой
эллипса х2+4у2 =8, снизу - дугой пара-
болы х2 =4у (рис. 17.16).
Площадь вычислим по формуле (17.28).
Решая систему уравнений зЗ+Лу2^, х2=4у,
находим Х|=-2, х2=2 - абсциссы точек пе-
ресечения заданных линий; следовательно,
о=-2,Ь=2.' Каждое из уравнений разрешаем
относительно у: ух=з?14, у2 = Vs-x2/2.
(В формуле (17.28) через у2 = f2(x)
обозначена функция, график которой
ограничивает фигуру сверху.)
Таким образом, искомая площадь
V8—х2 х2
5
б‘
ограниченной линиями
фигуры,
2
2
2
«Ьс = —j-\/8-x2«bc-j.. „.
-2 -2
Для вычисления первого интеграла применим подстановку х = 2-^2 sin Г, тогда
dx = 2-J2 costdt, а = -л/4, Р = л/4.
2 _____ */4
s,=i |78-х2«Ес = | j-78-8sin2t2^ =
-2 -х/4
= 2 Jf
-^4
2 4
- 2\
Поскольку
2
S2=jfx2dx =
-2
то S = S| — S2 = л+2—4/3 = л+2/3.
sin2r
= n+2.
1^.
4 3
2
1 4
= — (8 + 8) =—,
12 3
-2
295
Пример 17.16. Вычислить площадь области, ограниченной эллипсом
x = acosT, y = 6sinT.
В силу симметрии эллипса относительно координатных осей достаточно вы-
числить площадь части области, лежащей в первой четверти, и результат умно-
жить на 4. Заметим, что в этом случае х меняется от 0 до а, поэтому t будет ме-
няться от л/2 до 0. По формуле (17.30) находим
О >9'2
S = 4j(6sinf)(-«sinr)*fr = 4a6 Jsin2tdT =
ц/2 0
>^2
Г 1 - cos 2/
J 2
о
, _ , ( sin 2т
dt = 2ab\t------
I 2
= nab,. S = ПаЬ.
о
Замечание. В частном случае, когда а = b = R, получаем S’ = л/?2 -
площадь круга радиуса R.
Пример 17.17. Вычислить площадь области, ограниченной лемни-
скатой р2 = a2 sin2<p.
Принимая во внимание симметрию линии относительно ее оси (см. п. 2.10), по
формуле (17.31) получаем
~S= |*-i«2sin2(pJ<p = ia2 Jsin2<p</(2<р) =
о
2
п/4 « „ 2
„ = —, S = а .
0 4
О
°2 о I
= - — cos2<p |
17.8. Длина дуги кривой
Если линия задана параметрическими уравнениями
х = р1(Г), у = <р2(Т), г = Ф3(О (a<t<P), (17.32)
где <р,(Т) (« = 1,2,3) - дифференцируемые функции аргумента Т, то дифферен-
циал длины ее дуги выражается формулой
ds = ^x'2+y,2+z'2dt. (17.33)
Интегрируя равенство (17.33) по промежутку [<х,р], получаем формулу для
вычисления длины дуги линии (17.32):
₽
s = ^x'2+y'2+z'2dt. (17.34)
а
Если линия (1732) лежит в плоскости Оху, то z = 0 при всех t е [а, 0], поэтому
s=yx'2+y,2dt. (17.35)
296
В случае, когда плоская линия задана уравнением y = f(x) (a<,x<,b'), где
f(x) - дифференцируемая функция, последняя формула принимает вид
ь
s = ^i + y,2dx. (17.36)
а
Если плоская линия задана уравнением р = р (<р) (а < t < р) в полярных
координатах, то
₽
s = J-^p2+p'2d<p. (17.37)
а
Пример 17.18. Вычислить длину дуги линии у = Insinx между точка-
ми, для которых Х| = л/3, х2 = л/2.
Искомую длину вычисляем по формуле (17.36).
Поскольку у = Insinx, y' = cosx/sinx, то
_______________________________________ Ф
s = f Jl+(cosx/sin x)2 dx - f =
J______________________________________J sin x
z л/2
= Г sin*<fr _ f (cosx) _ 1 |n I-COSX _
J sin2x J cos2x-l 2 1+cosx
я/з n/3
= --ln- = lln3 = 0,5493.
2 3 2
Пример 17.19. Найти длину дуги линии х = 4 (cos/+ /sin/), у =
= 4 (sin/-/cos/) (OSt<.л/2).
Применяем формулу (17.35), полагая в ней а = 0, р = л/2.
Так как x' = 4(-sin/ + sin/ + /cos/)=4/cos/, у'= 4 (cos/-cos/+/sin/) =
= 4/ sin /, т]х,2+у'2 = -J16/2 cos2 / +16/2 sin2 / = 4/, to
1^2
s = J 4/d/ = 2/2 | ”/2 = л2/2.
о
Пример 17.20. Вычислить длину дуги винтовой линии x = acos/,
у = a sin /, z=bt между точками, для которых / = 0, / = р.
Поскольку х' = - a sin /, у' = a cos /, z' = b, jx'2 +y'2 +z'2 = -Ja2 +b2, то
по формуле (17.34) находим
₽ ______ __________ p
s = J 7e2 +b2dt = Vfl2 +b2t = -Ja2 +62p.
о °
297
Пример 17.21. Найти длину кардиоды p = 2a(l-cos<p).
Так как p' = 2asin<p, р2+р'2 =4a2sinz<p+4a2(l-cos<p)2 = 8а2(1-
- cos<p) = 16а2 sin2 —, то по формуле (17.37) получаем
Я я \
s=2 | 4а sin — dm = 16а Г sin — d — 1 = -16аcos —
J 2 J 2 Uj 2
о 0
= 16а.
о
17.9. Объем тела. Площадь поверхности вращения
Если задана функция S = S(x) (а < х < Ь), определяющая площадь попереч-
ного сечения тела плоскостью, перпендикулярной оси Ох, то его объем вычисля-
ется по формуле
ъ
V = js(x)dx. (17.38)
а
Объем тела, полученного вращением вокруг оси Ох криволинейной трапеции
АаЬВ (рис. 17.17), где АВ - дуга кривой у = f(x), вычисляется по формуле
ъ ъ
Уж =п jУ2dx, или Vx = л J f\x)dx. (17.39)
а а
Объем тела, полученного вращением вокруг оси Оу криволинейной трапеции
CcdD (рис. 17.18), где CD - дуга кривой х = <р(у), определяется формулой
298
Площадь поверхности, образованной вращением вокруг оси Ох дуги кривой
y~f(x) (a<x<b), определяется формулой
S = 2л J y-Ji + y'2dx.
а
(17.41)
Пример 17.22. Вычислить площадь поверхности, образованной вра-
щением вокруг оси Ох дуги линии y = chx, где 0<х<1 (поверхность эта
называется катеноидом).
Так как y' = shx, то по формуле (17.41) с учетом равенства ch2x- sh2x=l
получаем
1 ______________
S = 2л j chx^/l + sh2xdx = 2л
о
J ch х ch xdx = 2л J-i (ch 2x +1) dx =
о
о
= л J ch 2xdx + л J dx = 71
о 0
ля112
2
+л = 8,84.
Пример 17.23. Вычислить объем тела, полученного вращением во-
круг оси Ох криволинейной трапеции, ограниченной параболой у2 = 6х,
прямой х = 2 и осью Ох.
В соответствии с условием задачи находим пределы интегрирования а = О,
6 = 2 (рис. 17.19).
По формуле (17.39) получаем
2 2
И = л J y2dx = п J 6xdx = Злх21 ° = 12л.
о о
Пример 17.24. Найти объем тела, полученного вращением вокруг оси Оу
криволинейной трапеции, ограниченной параболой х2 = 4у, прямой у = 4 и осью Оу.
Замечая, что пределы интегрирования с = 0, d — 4, по формуле (17.40) находим
4 4
V = x2dy = л J 4ydy = 2лу21 ° = 32л.
о о
Пример 17.25. Найти объем тела, полученного вращением вокруг оси
Оу криволинейной трапеции, ограниченной гиперболой ху = 6, прямыми у = 1,
у = 6 и осью Оу (см. рис. 17.20).
299
Из уравнения кривой ху = 6 находим x = f>/y, x2=3f>/y2.
Принимая во внимание, что с = 1, d = 6, по формуле (17.40) получаем
£ 6
rz f 36 , f dy 36л
6
= -36л
= 30л.
Пример 17.26. Вычислить объем тела, полученного вращением эллипса
Ь2х2 + а2у2 = а2Ь2 вокруг оси Ох (это тело ограничено эллипсоидом вращения).
Из уравнения эллипса находим выражение для у2 -у2 = Ь2-Ь2х2/а2.
По формуле (17.39) получаем
Г = л
. nb2 Г 2
ах----j- J х ах =
nb2 х3
а2 3
= л62(а - (-а)) - (а3 - (-а)3) = 4 ™b2.
5а 5
Следовательно, К = (4/3) nab2. При
а = b = R получаем К = (4/3)лЯ3
(объем шара).
300
Глава 18
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
18.1. Множества в n-мерном пространстве
Упорядоченную совокупность и действительных чисел х^х^,...,х„ называют
точкой, а сами эти числа - ее координатами. Запись М (х,, х2,... ,х„) означает,
что точка М имеет координаты xbx2,...,x„. Множество всевозможных точек
называется арифметическим (координатным) и-мерным пространством и обозна-
чается символом А" или А„.
Арифметическое и-мерное пространство А" называется и-мерным евклидовым
пространством, если для любых двух точек М '(х', х2,..., х'), М"(х", х2,... ,х'Э,
принадлежащих А”, определено расстояние по формуле
р(М', М") = ^(хГ-х,')2 +(х2"-х')2 +-. + (х;-х„')2.
Евклидово и-мерное пространство обозначается через Е” или Е„.
Примеры множеств в и-мерном евклидовом пространстве Еп.
1. Если для координат всех точек множества {М} выполняется неравенство
р (М, Mq)< R , или
(X] -х®)2 +(х2 -х°)2 +-.+(х„ -х„°)2 < R2,
то {Л/} называется открытым и-мерным шаром.
2. Множество {Л/} точек М (хр х2,...,х„), координаты которых удовлетво-
ряют неравенству р (Л/, Мо) < R, или
(х. -х°)2 +(х2 -х20)2 + ...+(х„ -х„°)2 < R2,
называется замкнутым и-мерным шаром радиуса R с центром в точке
М0(х°,х2°,...,х°).
3. Множество {М} точекЛ/(х1,х2,...,х„), для которых р(М, Мо)= R, или
(х. -Xj0)2 +(х2 -х20)2 + ... + (х„ -х„°)2 = R2,
называется (и-1)-мерной сферой радиуса R с центром в точке
М0(х°,х02,...,х°„).
301
4. Множество точек М (xt,x2,...,xn), координаты которых заданы как не-
прерывные функции х, = X/(t) (i = 1,2,..., п), определенные на некотором отрезке
[a, Z>], называется непрерывной кривой в пространстве Е". Аргумент t называется
параметром кривой. Точка А{хх(а),х2(а),...,х„{а)) называется началом, точка
B(xI(ft),x2(h),...,xn(f>)) - концом данной кривой.
Множество точек М «-мерного евклидова пространства Еп, для каждой из ко-
торых расстояние до фиксированной точки Мо меньше е > 0, называется е-
окрестностью точки Мо. Другими словами, е-окрестностью точки Мо называет-
ся «-мерный открытый шар радиуса е с центром в точке Л/о.
Пусть {Л/} - некоторое множество точек «-мерного евклидова пространства
Еп. Точка А называется предельной точкой (или точкой сгущения) множества
{Л/}, если любая ее окрестность содержит по крайней мере одну точку этого
множества, отличную от А. Предельная точка может принадлежать или не принад-
лежать ему. Например, точки X] = 3, х2 = 7 являются предельными для отрезка
[3,7] и интервала (3,7), но первому они принадлежат, а второму не принадле-
жат. Множество, содержащее все свои предельные точки, называется замкнутым.
Если существует окрестность точки В множества {М} , не содержащая никаких
других точек этого множества, кроме самой точки В, то эта точка называется изо-
лированной точкой множества {М}.
Точка М множества {М} называется внутренней точкой этого множества, ес-
ли существует такая ее Е-окрестность, все точки которой принадлежат множеству
{Л/}. Открытым множеством называется множество, все точки которого внут-
ренние. Множество называется связным, если любые две его точки можно соеди-
нить в нем непрерывной кривой. Областью называется открытое связное множество.
Точка М называется граничной точкой множества {Л/}, если любая ее Е-окрестность
содержит как точки множества { М}, так и точки, не принадлежащие ему.
Совокупность всех граничных точек множества {М} называется его границей.
Если к области присоединить его границу, то полученное множество называется
замкнутой областью. Например, множество точек М (х, у) плоскости Оху, для
которых х2 + у2 < 1, является замкнутой областью; к области, определяемой не-
равенством х2 + у2 < 1, присоединены все его граничные точки, т.е. точки окруж-
ности х2+у2=1. .
Множество называется ограниченным, если все его точки находятся внутри
некоторого «-мерного шара.
Диаметром ограниченного множества {Л/} называется верхняя грань расстоя-
ний между его любыми двумя точками.
Число А называется верхней гранью числового множества {X}, если:
1) х<А для всех хеХ; 2) для любого числа Е>0 существует такое хе еХ, что
302
хе> А-е. Верхняя грань множества X обозначается через supJf или supx. На-
хбЛ1.
пример, для сегмента X = [1,8] supx = 8; для интервала X = (2,9) sup Л = 9.
Число а называется нижней гранью числового множества X, если:
1) х > а для всех х g X; 2) для любого числа е > 0 существует такое хЕ е X, что
хе<а+Е. Нижняя грань множества X обозначается через inf А" или inf х. На-
хеХ
пример, если X = (4,5), то inf X = 4; если X = [6,7], то inf X = 6.
Всякое непустое множество действительных чисел, ограниченное сверху, име-
ет конечную верхнюю грань, а ограниченное снизу — конечную нижнюю грань. У
всякого множества действительных чисел верхняя (нижняя) грань единственна.
18.2. Понятие функции нескольких переменных
Функция, определенная на некотором множестве X арифметического п-
мерного пространства, называется функцией п аргументов
У = /(Л1,-’Ч..*«)>
где х1,х2,...,х„ - координаты точки М (хих2,...,х„) данного множества. В
этом случае говорят, что задана функция точки М, и пишут у = f(M), или
у = /(х), где x = (xi,x2,...,x„).
Рассмотрим случаи, когда п-2 и п = 3. Предположим, что X - некоторое
множество точек плоскости, Y — подмножество множества всех действительных
чисел. Так как в фиксированной декартовой прямоугольной системе координат
ОХ]Х2 каждой точке М соответствует упорядоченная пара действительных чисел
х(, х2 - ее координаты, то функция, заданная на указанном множестве X, являет-
ся функцией двух аргументов, т.е. у = /(x^Xj), где х1гх2 — координаты точки
М (Х|,х2). Если координаты точки М обозначить буквами х и у, а функцию -
буквой z, то z = /(х, у). Переменные х и у при этом называются аргументами функ-
ции z или независимыми переменными. Значение функции z = /(х, у), которое она
принимает при х = а, у = Ь, обозначается через /(а, Ь).
Область определения функции двух переменных представляет собой некоторое
множество точек плоскости.
Графиком функции z = f(x,y) называется множество точек N (х,у,/(х,у)),
т.е. некоторое множество точек пространства._ Например, график функции
z - х - у представляет собой плоскость в пространстве, проходящую через начало
координат и пересекающую координатную плоскость Оху по прямой, образующей
равные углы с осями Ох и Оу; геометрическим изображением функции z = х2 + у2
является поверхность параболоида вращения, а функции z = ^9-x2 -у2 -
полусфера радиуса R = 3 с центром в начале координат, расположенная выше
303
плоскости Оху. Отметим, что первые две функции определены на всей плоскости
Оху, третья - в круге радиуса R = 3 с центром в начале координат, т.е. в области,
заданной неравенством х2 + у2 < 9.
Функцию
г = /(х,у) (18.1)
можно представить так: z - f(x, у) = 0, или в более общем виде
F(x,y,z) = O. (18.2)
Функция, заданная формулой (18.1), называется явной, функция, определяемая
уравнением (18.2), называется неявной.
Действительная функция, определенная на некотором множестве {X} точек
пространства, т.е. точек М (х, у, z), где х, у, z - декартовы координаты, называ-
ется функцией трех переменных х, у, z. Функцию трех переменных х, у, z обо-
значим буквой и, тогда м = f(x,y,z). Значение функции и = f(x,y,z) при х = а,
y = b, z = с обозначается через f(a,b,c). Областью определения функции трех
переменных является некоторое множество точек пространства. Например, об-
ласть определения функции и = ^/1—х2 -у2 —z2 представляет собой шар радиуса
R = 1 с центром в начале координат, областью определения функции
и = 1 /д/1-х2 —у2 —z2 является множество точек, лежащих внутри указанного ша-
ра (граничные точки, т.е. точки сферы х2 +у2 + z2 = 1, исключаются).
18.3. Предел и непрерывность функции
нескольких переменных
Полное приращение функции двух переменных z = Дх, у) в точке М(х, у) опре-
деляется формулой
Дз = /(х+Дх,у+Ду)-/(х,у), (18.3)
а ее частные приращения (по х и у соответственно) в той же точке — формулами
Дхг = /(х+Дх,у)-/(х,у), (18.4)
Д>,г = /(х,у+Ду)-/(х,у), (18.5)
х, у, х+Дх, у+Ду принадлежат области определения функции.
Аналогично определяются полное и частные приращения функции
большего числа переменных.
Замечание. Частное приращение функции по одному из аргументов
есть разность между двумя ее значениями, когда приращение получает только
данный аргумент; полное прйращение функции - разность между двумя значе-
ниями, когда приращения получают все ее аргументы.
304
Число А называется пределом функции и = f(M) при М, стремящемся к
М0,если для любого е>0 существует .такое 8 > 0, что при всех М, расстояние
которых до точки Мо меньше 8, т.е.
0<р(М, Мо)<8, (18.6)
выполняется неравенство
|/(М)-л|<е. (18.7)
Функция и = /(М) называется непрерывной в точке Л/о, если выполняется условие
lim/(Af) = /(M0). (18.8)
Необходимое и достаточное условие непрерывности функции и = f(M) в точ-
ке Мо выражается равенством
Ит Ди = 0, или lim (/(Л/)-/(Л/о)) = О,
Др—>0 Др—>0
где Др = р (М, Мо), Ди = /(М)-/(Мо).
Теорема 18.1. (об устойчивости знака непрерывной функции).
Если функция u = f(M) непрерывна в точке Мое.Х и то суще-
ствует 8-окрестность точки Мо, в которой f(M) не обращается в нуль и
имеет знак, совпадающий со знаком
Теорема 18.2. Если функция z = f(x,y) непрерывна в ограниченной
замкнутой области, то она ограничена в этой области и достигает в
ней своего наименьшего и наибольшего значения.
Если в некоторой точке Мо не выполнено условие (18.8), то эта точка называ-
ется точкой разрыва функции и — f( М).
Точки разрыва функции двух переменных могут заполнять отдельные линии (линии
разрыва). Например, для функции u = 1 / (х2 +у2 -1) линией разрыва является окруж-
ность х2 + у2 -1 = 0 в плоскости Оху. Точки разрыва функции трех переменных могут
заполнять отдельные поверхности (поверхность разрыва). Так, для функции
u= l/(z—х2 —у2) поверхностью разрыва является параболоид вращения z = x2+y2.
18.4. Частные производные функции
нескольких переменных
Частной производной функции нескольких переменных по одной из
них в фиксированной точке называется предел отношения соответствую-
щего частного приращения этой функции к приращению данной перемен-
ной, когда последнее стремится к нулю.
305
Для функции z = f(x,y) частные производные в точке М0(х0, у0) по* и у со-
ответственно определяются формулами:
fdz] .. /(х0+Дх,у0)-/(х0 у0)
— = lim-------------------------,
f—I = lim ^X°’Уо + ~ ^X°’ У°)
I dy J 4>>-»o Ду
4 z MO
Употребляются , и другие обозначения: z’x(x0,y0),f‘(x0,y0),
z'y(x0,y0), fy(x0,y0).
Частная производная функции z = f(x,y) по переменной * выражает скорость
изменения функции в данном направлении (у = у0) или скорость изменения
функции f(x,y0) одной переменной.
Частные производные функции z = f(x,y) имеют следующую геометриче-
скую интерпретацию:
fx(xo> Уо) = «, 4'(*о, Уо) = tg ₽>
где а — угол между осью О* и касательной в точке N (х0,у0, f(x0,y0)) к линии
пересечения поверхности z = /(*,у) и плоскости у = у0, Р - угол между осью
Оу и касательной в той же точке к линии пересечения данной поверхности с плос-
костью * = *0 (рис 18.1).
Очевидно,
Л ж=хо dy
т.е. частная производная в данной точке равна производной функции одной пере-
менной, вычисленной при соответствующем значении аргумента, поэтому при
нахождении частных производных пользуются обычными правилами дифферен-
цирования.
При переходе от точки М0(х0,у0) к точке М(Х,у) получим новые значения
частных производных. Следовательно, частные производные функции f(x,y)
также являются некоторыми функциями двух переменных:
= Гу(.х,у).
дх ду
Пример 18.1. Найти значения частных производных функции
z = /(*,y) = 2*3+3*2y+6*y-y3 вточке Л70(-1,2).
306
Считая у постоянной и дифференцируя z, как функцию х, находим
Рис. 18.1
частную производную по х, вычисляем ее значение в точке Мо:
z' = (2х3)' + (3х2у)' +(6ху)' -(у3)' = 6х2 + 6ху+бу—0 = 6(х2 +ху + у);
Л'(~1,2) = 6 ((-1)2 + (-1) 2 + 2) = 6.
Считая х постоянной и дифференцируя z, как функцию у, находим
частную производную по у и ее значение в точке Мо:
z’y = (2х3)’+(3х2у)'+(6ху)' -(у3); = 0 + Зх2 + 6х - Зу2 = 3 (л2 + 2х - у2);
2) = 3 ((-1)2+ 2(- 1) - 22) = -15.
18.5. Полный дифференциал функции
нескольких переменных
Если полное приращение функции z = /(x,y) в точке М0(х0,у0) предста-
вимо в виде
Дг = РДх + £Му+ еДр,
где Р, Q - постоянные, Др = ^/Дх2+Ду2 и е—>0 при Др-эО, то РДх+0Ду
называют полным дифференциалом данной функции в этой точке и обозначают
через dz: dz= РДх + (?Ду. Следовательно,
Дг = <&+еДр, е->0при Др—>0. (18.9)
Полный дифференциал функции двух переменных равен приращению аппли-
каты z касательной плоскости в точке Л/0(х0, у0, z0) к поверхности, являющейся
307
графиком этой функции, когда аргументы х и у получают приращения Ах и Ау
(рис 18,2, Az = КМ, dz = KN).
Рис. 18.2
Функция, обладающая непрерывными частными производными, имеет полный
дифференциал, причем
dz = f&c0,y0) Ах+4'(х0,у0) ДУ- (18- Ю)
Дифференциалы независимых переменных совпадают с их приращениями,
т.е. dx = Ax, dy = Ay.
Полный дифференциал функции z = f(x,y) является функцией х, у при фик-
сированных dx и dy:
dz dz
dz = —dx+—dy, или dz = f'(x, у) dx +f’(x, y) dy.
ax ay
Функция, имеющая полный дифференциал, называется дифференцируемой.
Если функция дифференцируема в некоторой точке, то она и непрерывна в ней.
Из формулы (18.9) следует, что Az = <зЬ, или
f(x0 + Дх, у0 + Ay) - f(x0, у0) = f'(x0, у0) Ах+f'(x0, у0) Ду, (18.11)
откуда ,
/(х0 + Ах,у0 +Ау) •= /(х0,у0) + /х'(х0,у0) Лх + //(х0,у0) Ау. (18.12)
308
Если все первые частные производные функции и = f(xt,x2,... ,х„) непрерыв- .
ны, то полный дифференциал выражается формулой
, ди , ди , ди ,
du--—dxA+—dx2 + ...+——dx„. (18.13)
CW]
Каждое слагаемое правой части этой формулы называется частным дифферециалом.
В частности, полный дифференциал функции трех переменных вычисляется по
формуле
du = ^—dx+z^~-dy + ^—-dz. (18.14)
дх ду dz
Пример 18.2. Дана функция z = /(x,y) = x2+3ху-6х и две точки
А (4; 1), В (3,96; 1,03). Требуется: 1) вычислить значение z функции в точке В; 2)
вычислить приближенное значение функции в точке В исходя из значения z0
функции в точке А, заменив приращение функции при переходе от точки А к точке
В дифференциалом.
Вычисляем значения данной функции в точках А и В:
^ = /(^) = /(^o.№) = /(4,l) = 42+3-1-4-6 4 = 4, z=/(B) = /(xI,y,) =
= /(3,96; 1,03) = (3,96)2 + 3 3,96 1,03 - 6 3,96 = 4,158.
Находим приращения аргументов: Дх = х,-х0 = 3,96- 4,00=-0,04,
Ду = У1— У о = 1»03 -1,00 = 0,03; значения частных производных
/Х'(х,у) = 2х + 3у-6, f' = 3x в точке А: Л(х0,у0) = =
= 2-4+31-6=5, fy(x0,y0) = f'(4,1) = 3-4=12; значение дифференциала в
точке А по формуле (18.10): dz = 5 (—0,04) + 12 0,03 = 0,16; значение функции в
точке В по формуле (18.12): z, = f(xityA)- /(3,96; 1,03) = 4+0,16 =4,16.
Пример 18.3. Вычислить приближенно gO-'^-Co.s)2
2 2
Рассмотрим функцию z = ех ~у . Искомое число можно считать приращенным
значением этой функции при х = 1, у = 1, Ах = 0,1, Ду = -0,1. Поскольку
f(x,y) = ex ~у = е° = 1, Az «= dz = 2ех ~у (xdx - ydy) = 2е° (0,1+0,1) = 2-0,2 = 0,4, то
е(1.1)2-(0.9)2!=е1-1+Дг==1 + ()4=1>4
Пример 18.4. Вычислить полный дифференциал функции w = xyz при
переходе от точки М(6;4;2) к точке АД5,92; 3,95; 2,07).
Так как и' = yz, и'у = xz, иг = ху, то в соответствии с формулой (18.14)
du = yzdx+xzdy+xydz. Подставив в эту формулу значения х = 6, у = 4, z = 2,
dx = Дх = 5,92 - 6 = -0,08, dy = by = 3,95-4 = -0,05, dz = Az = 2,07 - 2 = 0,07,
получим du = 4 2 (-0,08) + 6 - 2 (-0,05) + 6 4 • 0,07 = - Q,64 - 0,6+1,68 = 0,44.
Пример 18.5. Как изменится диагональ прямоугольника со сторонами а = 8
см, 6 = 6 см, если сторону а уменьшить на Змм, а сторону Ь увеличить на 7 мм?
309
Диагональ прямоугольника / через его стороны а и Ь выражается формулой
/ = 4а2 +Ь2 . Введем в рассмотрение функцию z = д/х2 +у2. Поскольку
х = 8,у = 6, Дх = -0,3, Ду = 0,7, = то 8 <^3 * *> + 6 °-7 = = 0,18.
Jx2+y2 № +62
Следовательно, диагональ увеличится на 0,18 см.
18.6. Частные производные и дифференциалы
высших порядков. Формула Тейлора
Частные производные функции нескольких переменных называют также частны-
ми производными первого порядка или первыми частными производными.
Частными производными второго порядка (или вторыми частными производ-
ными) данной функции называются соответствующие частные производные от ее
первых частных производных.
Для функции z = f(x,y) по определению имеем
d2z_ Э
дх2 дх
(^]=(/;(*, у»;=/£(*, у),
Vox J
d2z д
ду2 ду
= (fy(.x, у)Уу = f"(x, у),
d2z__________
ЭхОу ду (.Эх
э2?__________
дудх дх ^ду
~ = (А'(х, у))' = f"(x, у),
~ 1 = (/Дх, у)К = f"(x, у).
Вторые частные производные обозначаются также символами
z" z" z” z” Производные z", z" называются смешанными частными
л л лу ул уу л лу ул
производными.
Частные производные появились в трудах И. Ньютона, Г. Лейбница, Я. Бернулли
и И. Бернулли. Обозначения —, — ввел Лежандр (1786), f', z' -
ox ox
32z 32z
Ж. Лагранж (1797,1801), —г, —-----К. Якоби (1837).
дх дхду
Теорема 18.3. Если функция z = f(x,y) и ее смешанные производные
z’y, z’p определены в некоторой окрестности точки М0(х0,у0) и непрерывны в
этой точке, то f”(x0,у0) = f"(x0, у0).
Дифференцируя частные производные второго порядка как по х, так и по у, полу-
чаем частные производные третьего порядка или третьи частные производные:
310
93z d3z d3? d3z d3z d3z d3z d3z
Эх3 ’ dx2dy ’ dxdydx ’ dxdy2 ’ dydx2 ’ dydxdy ’ dy2dx ’ ду3
Вообще, частная производная я-го порядка функции z = f(x,y) есть первая
частная производная от ее частной производной (я -1) -го порядка.
Аналогично определяются и вычисляются частные производные второго и
высших порядков от функции трех и большего числа переменных.
Полным дифференциалом второго порядка некоторой функции называется
полный дифференциал от ее полного дифференциала.
Полным дифференциалом я-го порядка называется полный дифференциал от
полного дифференциала (и -1) -го порядка. Если z-f(x, у), dz = z'xdx +z'ydy, то
d2z = d (dz) = z" dx2 + 2z"ydxdy+z"ydy2,
d3z-d (d2z) = ^-dx3+3^^-dx2dy + 3-^Tdxcfy2 + 3~dy\...,
dx dx dy dxdy dy
d”z = У C* dj dx^dy^ C*
& dx^dy* I "
k=O * x
я(я-1)-[Я-(A:-1)]'
k\
Эту формулу записывают и в следующем символическом виде:
Формула Тейлора для функции двух переменных
/о. у) /«,. t)+v
к'- (« + 1)!
ИЛИ
а™»
где М'(а+6Лх, Ь+вЛу) — точка области S.
Формула Тейлора для функции большего числа переменных
и — f(M), М(х1,х2,...,х„), аналогична формуле (18.16).
Замеч ан ие. При и=1 формула (18.15) принимает вид
f(x, у) = f(a, b) + (/Да, Ь) Ах + /Да, Ь) Ду) +
П) Дх2 +2/"(t n) ЛхЛу+f"^, n) Ay2),
где £ = а + 6Ах, Т) = 6+0Ду, 0<6< 1.
Пример 18.6. Дана функция z = x3 +2х2у-8ху2 +у3. Найти ее
частные производные второго порядка. Находим сначала первые производные:
z; = Зх2+4ху-8у2, г; = 2х2- 16лу+3у2.
311
Пользуясь определениями и правилами дифференцирования, получаем
z" = 6х+4у, z" =4х-16у, z'^ = 4х-16у, z^, = -1бх+6у.
- 2 < д3и
Пример 18.7. Дана функция и = х ycos3t+y z . Найти
dxdydt
д4и • д5и
dy2dz2 ’ dz5 ’
Дифференцируя по одной из переменных, считаем все другие постоянными:
Эи „ Э2и „ „ Эи , . «
— = 2xycos3r, ——- = 2xcos3r, ——— = -6xsin3r;
Эх дхду dxdydt
ди 2 „ _ 5 Э2и п « Э3и 4 Э4и з
«»3, + 2„ , ^.2, , ;
^? = 120Л Й-120Л
oz dz dz dz az
Пример 18.8. Дана функция z = ln(x2 +у2 +2х + 1). Показать, что
Л» • —z/ — Л
zxr ~^Zyy ~ 0‘
Найдем частные производные первого и второго порядка:
dz (х2+у2+2х+1)'х 2х+2
дх х2+у2+2х+1 х2 +у2 +2х+Г
dz (х2 + у2 + 2х +1)'____2у_____
ду х2+у2+2х + 1 х2+у2+2х + 1’
d2z ( 2х + 2 "I ' = 2(х2 + у2 + 2х +1)-(2х +2) (2х + 2) =
.Эх2 -^х2+у2+2х + !“ (х2+у2+2х + 1)2
2у2-2х2-4х-2
(х2 +у2 +2х+1)2 ’
Э2г _ Э f 2у "I_ 2(х2+у2+2х+1)-2у2у = 2х2-2у2+4х+2
Эу2 ду [х2 +у2 +2х + 1) (х2 +у2 +2х + 1)2 (х2 +у2 +2х+1)2
Составим сумму z" +z^, вторых частных производных и убедимся, что она
тождественно равна нулю:.
Э2г Э2г 2у2 - 2х2 - 4х - 2 2х2-2у2+4х+2
Эхг+Эу2 (х2 +у2 +2х+1)2 (х2 +у2 +2х+1)2
312
18.7. Дифференцирование неявных и
сложных функций
Функция « переменных х1,х2,...,хп называется неявной, если она задана
уравнением
F(jc,,jc2,..„x„,u) = 0, (18.17)
не разрешенным относительно и.
Частные производные неявной функции, заданной уравнением (18.17), нахо-
дятся по формулам
du _ F't ди _ ^х2 ди _
dx, F' ’ дх2 F' ’ ’ дх„ F'
В частности, если у - функция одной переменной х, заданная
уравнением F(x,y) = G, то
у' = -:(18.18)
еслиг — функция двух переменных х, у, заданная уравнением F(x,y,z) = O, то
dz F' dz _ F"
дх~~~^’^~~~f;'
Если u = F(v,,v2,...,v„), где v, =/,(х1,х2,...,х„),
v2 = f2(xl,x2,...,x„), = f„(xl,x2,...x„y, то функция и называется сложной
функцией независимых переменных х1,х2,...,х„. Переменные v,,v2,...,v„ назы-
ваются промежуточными аргументами.
Частная производная-сложной функции по одной из независимых переменных
равна сумме произведений ее частных производных по<промежуточным аргумен-
там на частные производные этих аргументов по данной независимой переменной:
du ^1 du dx2 _ du dv, du du dv2 du + dv„ du + 3v«
dx, dv2 dv, । du dx, dv2 dx, ’ dx2 ’ (18.19)
dvi dx2 dv2 dx2 '
du du dv. du dv2 du
dx„ dv, dx„ dv2 dx„ dx„ ’
Если все промежуточные аргументы являются функциями одной независимой
переменной /, то функция будет сложной функцией от t. Полная производная этой
функции находится по формуле
du ди dv. ди dv7 ди dv„
— =--------+--------*-+...+-------.
dt dv, dt dv2 dt dv„ dt
313
18.8. Экстремум функции нескольких
переменных
Максимумом (минимумом) функции z = fix,у) в точке М0(х0,у0) называется та-
кое ее значение f(x0,y0), которое больше (меньше) всех других ее значений, принимае-
мых в точках М ix,y), достаточно близких к точке Мо и отличных от нее.
Максимум и минимум функции называется ее экстремумом. Точка, в которой
достигается экстремум, называется точкой экстремума.
Экстремум функции трех и большего числа переменных определяется аналогично.
Необходимые условия экстремума. В точке экстремума дифференцируемой
функции нескольких переменных частные производные ее равны нулю.
Если М0(х0,у0) - точка экстремума дифференцируемой функции z=fx,y), то
Д'(*о. Уо) = 0> /;(*о.Уо) = 0- (18.20)
-Из этой системы уравнений находятся стационарные точки. Система (18.20)
эквивалентна одному уравнению
df(x0,y0)^Q. (18.21)
В общем случае в точке экстремума М0{х0,у0) функции z = fix, у) выполня-
ется равенство (18.21) или df(x0,y0) не существует.
Достаточные условия экстремума. Пусть М0(х0,у0) - стационарная точка,
т.е. точка, для которой выполняется равенство (18.21):
1)если
d2fix0, у0) < 0 (при dx2 +dy2 > 0), (18.22)
то fixo,yo) ~ максимум функции z = fix, у);
2)если
d2f(x0, у0) > 0 (при dx2 +dy2 > 0), (18.23)
то f(x0,y0) — минимум функции z = fix, у).
Эти условия эквивалентны следующим: пусть fzix0,y0) = C), fy(x0,y0) = Q и
A = f"(x0,y0), B = f"ix0,y0), C=f"ix0,y0\ (18.24)
Ь = АС-В2, (18.25)
тогда:
1) если Д>0, то функция fix, у) имеет экстремум в точке Л/о: максимум
при А < 0 (или С < 0), минимум при А > 0 (или С > 0);
2) если Д < 0, то экстремума в точке Мо нет.
Для функции трех и большего числа переменных необходимые условия
экстремума аналогичны условиям (18.20), а достаточные условия аналогич-
ны условиям (18.22), (18.23).
314
Рис. 18.3
Пример 18.9. Найти экстремум функции fix, у )= хг+ у2- 4х+6у+17.
Поскольку f' = 2х - 4, // = 2у+6, f" = 2,f" = 0, f” = 2, // = 0, fy =0 при
х = 2, у = -3, Д = 2 • 2 - 0 = 4 > О, Л = 2 > 0, то в точке Л/О(2,-3) функция имеет
минимум, причем min/(x, у) = /(2,-3) = 4.
Пример 18.10. Найти наибольшее и наименьшее значения функции
z = f(x,y) = 3-2х2 -ху-у2 в замкнутой области, заданной системой нера-
венств: х < 1, у>0, у<х.
Область представляет собой треугольник О АВ (рис. 18.3), причем
О (0,0), А (1,0), В(1,1). Находим экстремум
функции: /х' = -4х-у, f'=-x-2y;flc' = 0,fi' = 0
при х = 0, у = О, /" = -4,/" = /;' = -1, /" = -2,
Ь = АС-В2 = (—4)(—2) —(—I)2 =7>0, Л = -4<0,
в точке (0,0) функция достигает максимума:
max /(х, у) = f (0,0) = 3. Найдем экстремумы на гра-
нице области: на стороне ОА (у = 0) функция
z = /(х, 0) = 3 - 2х2 = <р (х) зависит от одной пере-
менной х;<р'(х) = —4х, ф"(х) = —4, ф'(х) = 0
при х = 0; ф"(0) = - 4 < 0, х = 0 - точка максимума: ф (0) = /(0,0) = 3. На пря-
мойЛв (х = 1) функция z = /(l,у) = 3-2-у- —у2 — 1-у-у2 = у(у) зависит
только от у; ф'(у) = -1 - 2у, у '(у) = 0 при у = -1/2, но эта точка не принадле-
жит отрезку АВ. На стороне ОВ (у = х) функция зависит только от х:
z = /(x,x)= = 3-2xz-xz-x2 = 3—4х2 =ф(х), ф'(х) = -8х, ф"(х) = -8, ф = 0
при х = 0, ф"(0) = — 8 < 0, /(0,0) = 3. Вычисляем значения функции в точках А и
В: /(J) = /(1,0) = 1, /(в) = /(1,1) = -1. Следовательно, в заданной области наи-
меньшее значение данной функции равно -1, а Наибольшее равно 3.
Пример 18.11. Найти наибольшее и наименьшее значения функции
z = xz+yz-2x-2y+4 в круге х2 +у2 5 4.
Данная функция имеет минимум в точке М (1,1), лежащей в заданной области,
причем min (х, у) = /(1,1) = 2.
Исследуем изменение функции на границе области, т.е. на окружности
х2 +у2 = 4. Воспользуемся параметрическими уравнениями этой окружности
х = 2cos/, у = 2sin/(0< / < 2л). На данной окружности функция становится
функцией одной переменной t: z = z(/) = 4cosz/ + 4sin2/-4cos/-4sin/+4 =
= 8- 4 cos/- 4 sin Л Поскольку z'(0 = 4sin/ - 4cos/, z'(/) = 4sin/ - 4cos/ = 0,
tg/ = 1, z, = n/4, t2 = (5/4) л, z"(Z) = 4cos+ 4 sin/, z"(/j) > 0, z"(/2) <0, to /j -
315
точка минимума, t2 - точка максимума, причем minz (Г) = z (л/4) =
= 8-4^2-2,344, maxz (г) = z((5/4) л) =8+4-/2 -13,656.
Рассматривая полученные экстремальные значения функции, заключаем, что в
указанном круге наибольшее значение функции равно 8+4^2 =13,656, достигается
оно в точке N (-2, -2), лежащей на границе окружности; наименьшее значение
функции равно 2, достигается в точке минимума М (1,1).
18.9. Условный экстремум
Если разыскивается экстремум функции многих переменных, которые связаны
между собой одним или несколькими уравнениями (число уравнений должно быть
меньше числа переменных), то говорят об условном экстремуме. При решении
задачи можно пользоваться методом неопределенных множителей Лагранжа.
Чтобы найти условный экстремум функции z = f(x, у) при наличии уравнения
связи <р(х,у) = 0, составляют функцию Лагранжа
/г(л,у) = /(х,у) + Х.ф(х, j/), (18.26)
где X - неопределенный постоянный множитель, и ищут ее экстремум. Необхо-
димые условия экстремума функции (18.26) выражаются системой трех уравнений
с тремя неизвестными х, у, X:
£.£+А0, (18.27)
дх дх дх ду ду ду
Вопрос о существовании и характере условного экстремума решается на осно-
вании изучения знака второго дифференциала функции Лагранжа
d2F = F"dx2 +2F"dxdy,+ F"dy2 для испытуемой системы значений х, у, X, полу-
ченной из системы (18.27) при условии, что dx и dy связаны уравнением
^-dx+^-dy = Q (dx2 +dy2 *0).
йх ду
Функция f(x,y) имеет условный максимум, если d2F<0, и условный мини-
мум, если d2F> 0.
Аналогично находится условный экстремум функции трех или большего числа
переменных при наличии уравнений связи.
Если, например, требуется найти экстремум функции f(x,y,z) при условиях
<р (х, у, z) = 0, у (х, у, z) = 0, (18.28)
то вводят функцию
F (х, у, z) = f(x, у, z)+Х<р (х, у, z)+цу(х, у, г)
икуравнениям(18.28)присоединяютещетри уравнения: /^' = 0, F' = 0, F' = 0.
316
Пример 18.12. Найти экстремум функции z = 9-8x-6y при условии,
что ее аргументы удовлетворяют уравнению х2 +у2 = 25.
Геометрически задача сводится к нахождению экстремальных значений
аппликаты z точек пересечения плоскости z = 9-8x-6y с круговым цилин-
дром х2+у2=25.
Составляем функцию Лагранжа, определяемую формулой (18.26):
F (х, у) = 9 — 8х - бу + X (х2 + у2 - 25), находим ее частные производные
F" = - 8 + 2Хх, F' - - 6+2Ху. Система уравнений (18.27) принимает вид
-8+2Хх = 0, -6+2Ху = 0, х2+у2 =25,
или
Ах-4 = 0,Ху-3 = О, х2+у2=25.
Решив эту систему, получим: 1)Х., = 1, х, = 4, у, =3; 2) Х2=-1, х2=-4,
у2 = -3. Находим вторые частные производные: F" = 2Х, F" = О, F" = 2Х и
второй дифференциал d2F = X (dx2 +dy2). Так как id2F>Q при
X, = 1, х, = 4, у, = 3, то функция /(х,у) в точке (4,3) имеет условный минимум,
причем min/(x,y) = /(4,3) = -41. Поскольку d2F<0 при Х2=-1, х2=-4,
у2=-3, то в точке (-4,-3) функция имеет условный максимум /(-4,-3) = 59.
18.10. Касательная плоскость и нормаль
к поверхности
Касательной плоскостью к поверхности в данной точке М (точке касания) на-
зывается плоскость, в которой лежат касательные в этой точке к всевозможным
кривым, проведенным на данной поверхности через указанную точку.
Нормалью к поверхности называется перпендикуляр к касательной плоскости в
точке касания. Координаты вектора нормали п = (а, Ь, с) к поверхности
F(x,y,z) = 0 (18.29)
в точке M0(x0,y0,z0) пропорциональны значениям соответствующих частных
производных функции F(x,y,z) в этой точке: a = X(Fx)0, b = "k(F^)0,
с = X (F^o, где (Fx')0 = F'(x0,y0, z0), (F')o = F'(x0, y0, z0), (F/)o =
= ^Vo.X'o.z0). \
Координаты вектора n входят в уравнение касательной плоскости к поверхно-
сти в точке M0(x0,y0,z0):
(Fx')o(->c-xo) + (f;')o(y-yo) + (^)o(z-Zo) = O, . (18.30)
317
а также в уравнение нормали к данной поверхности в той же точке:
ГОо (^)о ГОо
Пример 18.13. Записать уравнения нормали и касательной плоскости к
поверхности z = x2 +у2 в точке Л/о(1,—2,5).
Поскольку F(х,у,z) = х2 +у2 —z, F’ = 2x, F" = 2y, F' = -\, x0 = 1, y0 = -2,
z0 = 5, F'(x0,y0,z0) = 2, F'(x0,y0,z0) = -4, то на основании уравнений (18.30),
(18.31) получаем 2(x-l)-4(y+2)-(z-5) = 0, 2x-4y-z-5 = 0 (уравнение
x. ч У + 2 Z~S Z ,
касательной плоскости),-= ----=----- (уравнения нормали).
2-4-1
18.11. Семейства линий и их огибающие.
Семейства поверхностей и их огибающие
Однопараметрическим семейством линий, лежащих в плоскости Оху, называ-
ется множество линий, определяемое уравнением
F(x,y,C) = 0, (18.32)
в котором параметр С может принимать различные действительные
значения (при каждом фиксированном значении С получаем определенную
линию семейства).
Огибающей семейства линий называется такая линия, которая в каждой точке
касается некоторой линии семейства.
Множество всех точек, удовлетворяющих системе уравнений
F (х, у, С) = 0, F'(x, у, С) = 0, (18.33)
называется дискриминантной линией семейства (18.32).
Если в точках дискриминантной линии частные производные F'hF’
одновременно в нуль не обращаются, то дискриминантная линия совпадает
с огибающей семейства.
Множество линий, определяемое уравнением
F (х,у,С1,Сг,...,С„) = 0,
где С,,С2,...,С„ - независимые параметры, называется «-параметрическим се-
мейством линий (параметры называются независимыми или существенными, если
их число нельзя уменьшить путем введения новых параметров).
Однопараметрическим семейством поверхностей называется множество по-
верхностей, определяемое уравнением
318
F (x,y,z,C) — G. (18.34)
Огибающей семейства поверхностей называется поверхность, которая в каж-
дой своей точке касается некоторой поверхности семейства.
Огибающая семейства поверхностей (18.34) удовлетворяет системе
уравнений
F (х,y,z,C) = 0, F£(x, y,z,C) = 0. (18.35)
Пример 18.14. Найти огибающую однопараметрического семейства ли-
ний х2 + (у-С)2 = А2.
Система уравнений (18.33) запишется так:
х2+(у-С)2-Я2 =0, 2(у-С) = 0.
Из этой системы находим, что
х2 - R2 = 0, или х = -R, х = R.
Прямые x~-R,x-R являются огибающей
данного однопараметрического семейства ли-
ний — множества окружностей радиуса R с
центрами на оси Оу (рис 18.4).
Пример 18.15. Найти огибающую одно-
параметрического семейства поверхностей
x2+y2+(z-C)2=R2.
Система уравнений (18.35) принимает вид
x2+y2+(z-C)2-R2=0, 2(z-C) = 0,
откуда следует, что х2 +у2 = R2.
Круговой цилиндр радиуса R, ось которого
совпадает с осью Oz, является огибающей
данного однопараметрического семейства
сфер радиуса R, центр каждой из которых на-
ходится на оси Oz.
Рис. 18.4
319
Глава 19
ДВОЙНОЙ ИНТЕГРАЛ
19.1. Понятие двойного интеграла,
его геометрический и механический смысл
На плоскости Оху рассмотрим область S площади S, ограниченную замкнутой кривой у
(рис 19.1), Пусть в области S определена функция z = f(x,y). Разобьем область S сетью
линий на конечное число областей (AS, ),(AS2 ),..., (AS„), площади которых
AS], AS2,. -., AS„. В каждой i-й элементарной области (AS,) выберем произвольную
точку Mt(X',y,), значение функции в этой точке /(х,,у,) умножим на площадь AS,
соответствующей области и все произведения сложим. Полученная сумма
п
4 = ^’У^
1=1
называется интегральной суммой функции f (х, у) в области S.
Двойным интегралом от функции f(x,y) по области S называется конечный
предел / интегральной суммы 1„ при X —> О, где X - наибольший из
диаметров элементарных областей (AS,):
п
I=Kniy'f(xl,yi)bSl. (19.1)
Рис. 19.1
Рис. 19.2
320
Обозначения двойного интеграла: I = J J f(x, у) dS, I = J J f (х, y)dxdy.
s s
Функция z = f(x,y), для которой предел (19.1) существует и конечен, называ-
ется интегрируемой.
Если функция z-f(x,y) непрерывна в области S, то она интегрируема
в этой области.
Геометрический смысл двойного интеграла. Если /(х,у)>0, то двойной
интеграл от функции z = f(x, у) по области S равен объему тела, ограниченного
сверху поверхностью z = f(x,y), с боков - цилиндрической поверхностью, об-
разующие которой параллельны оси Oz, а направляющей служит контур у фигуры
S, снизу - плоскостью z = 0 (рис 19.2).
Механический смысл двойного интеграла. Двойной интеграл от функции
z = f(x, у) > 0 по области S представляет собой массу фигуры S, если подынте-
гральную функцию f(x,y) считать плотностью этой фигуры в точке М(х,у).
Свойства двойного интеграла.
1.
JJ cf (х, у) dS = сJJ f(x, у) dS (с = const).
S S
jj (/(*> у) ± (ф (x, y))dS = JJ f(x, y) dS ± JJ Ф (x, y) dS.
s
Если f(x,y)<q(x,y), to
2.
3.
4.
s
s s
JJ f(.x, y) ds < JJ<P (x, y) dS.
s s
JJ/(x,y)dS <JJ|/(x,y)|rfS.
JJ f(x, y) dS = JJ /(x, y) dS +JJ /(x, y) dS,
S ' St s2
где Sj и S2 — области, на которые разбита область 5.
6. Если в области S т < f(x,y)<M, то
5.
mS<]]f(x,y)dS<MS,
s
откуда
JJ/(х.у) dS = р5 (т< ц < М).
s
Пример 19.1. Оценить двойные интегралы
I = ff j = ff_______dxdy_______
' V J15-X2-у2 ’ 2 V 25+sin2(x+y)+cos2/
11 Зак. 1
(19-2)
321
где S2 - квадрат jx|+|y|5 5, S, - круг х2+у2 516.
Оценим первый интеграл. Областью интегрирования является круг радиуса
R = 4, площадь которого S = 16л. Так как в данной области функция
f(x,y) = 4^25-х2~у2 удовлетворяет соотношениям 1Д/25-0 5
51/^25-х2-у2 < 1/V25-16, т.е. 1/551/^25-х2-у2 <1/3, то в соответствии
с неравенствами (19.2) получаем (16/5) л 5 Ц 5 (16/3) л.
Переходим к оценке второго интеграла. Областью интегрирования является квадрат
с вершинами А(-5,0), В(0,5), С(5,0), £>(0,-5). Длина его стороны а = 5л/2, а площадь
S=50. Поскольку 1/275 1/(25+sin2 (х+у) + cos2 у) 5 51/25, то 1,85512 52.
19.2. Вычисление двойного интеграла
в декартовых прямоугольных координатах
Различают два основных вида области интегрирования:
1) область первого вида т.е. область А1А2В2В1, ограниченную слева и
справа прямыми х = а, х = Ь (а < Ь) соответственно, снизу - кривой у = <PiW.
сверху - кривой у=<р2(х) (<р( (х) 5 <р2 (х)), каждая из которых пересекается с
вертикалью х = а (а 5 а 5 Ь) только в одной точке (рис. 19.3);
2) область второго вида S2, т.е. область ClDlD2C2, ограниченную снизу и
сверху прямыми у=с, y = d соответственно, слева - кривой х = у,(у), справа
- кривой х = у2(у) (у,(у) 5 у2(у)), каждая из которых пересекается с горизон-
талью у = Р (с 5 р 5 d) только в одной точке (рис. 19.4).
3 ам еч ан и е. В некоторых случаях точки At и Л2, Bt и В2, С} и С2,
Dt и D2 могут сливаться в одну.
Если для функции /(х,у), определенной в области 5,, существует двойной
интеграл, а при каждом постоянном значении х из [а, Ь] простой интеграл
92<»)
£(х)= J/(x,y)^,
91 (*)
то существует также и повторный интеграл
i 91W Ь 92(х)
Jdr J /(x,y)<fy = j{ j/(x,y)dy}dx
a 9i(x) а <Р|(х)
и выполняется равенство
Ь 4>j(x)
dS = jdx jf(x,y)<fy. (19.3)
S a <pi(x)
322