Текст
Л. А. ПАРС
АНАЛИТИЧЕСКАЯ
ДИНАМИКА
Перевод с английского
К. А. ЛУРЬЕ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВ А 19 7 1
531
П18
УДК 531.3
Аналитическая динамика. Парс Л. А., Главная редакция физико-
математической литературы изд-ва «Наука», 1971 г., 636 стр.
В содержание книги включен не только традиционный материал
курсов аналитической механики. Значительное место уделено применению
к задачам механики методов качественной теории дифференциальных
уравнений, на современном уровне трактуются вопросы о разделяемое™
переменных в уравнении Гамильтона — Якоби, дается рассмотрение
эргодических теорем, включая теорему Пуанкаре о возвращении; нашло
свое место несколько отличное от принятого и приспособленное к задачам
динамики изложение теории устойчивости движения, включающее теоремы
Ляпунова. В заключительных главах, посвященных ограниченной задаче
трех тел и задаче трех тел, автору в небольшом объеме удалось дать хоро-
хорошее представление о постановках и трудностях этой классической в исто-
истории точных наук проблемы.
Илл. 124, библ. 50 ссылок.
L. A. PARS
A Treatise on
ANALYTICAL
DYNAMICS
HEINEMANN
LONDON
2-4-2
11B-71
ОГЛАВЛЕНИЕ
От издательства 10
Из предисловия автора 11
Глава I. Движение материальной точки 15
§ 1.1. Свободная материальная точка , 15
§ 1.2. Прямолинейное движение материально]'! точки в силовом поле ... 17
§ 1.3. Либрациошюе движение 24
| 1.4. Заданная сила не может быть функцией от ускорения : . . 26
§ 1.5. Несвободная материальная точка (случай I) 27
§ 1.6. Несвободная материальная точка (случай 11) 28
§ 1.7. Несвободная материальная точка (случай III) 30
§ 1.8. Голономные и неголономные системы . 31
§ 1.9. Случай двух связей 32
Глава II. Механические системы 34
§ 2.1. Система двух материальных точек 34
§ 2.2. Система материальных точек 35
§ 2.3. Катастатическая система 38
§ 2.4. Реакции связей 38
§ 2.5. К понятию о механической системе 39
Глава Ш. Первая форма основного уравнения 41
§ 3.1. Основное уравнение 41
§ 3.2. Сохранение импульса 42
§ 3.3. Катастатическая система и первая форма уравнения энергии .... 43
§ 3.4. Консервативные силы и вторая форма уравнения энергии 44
§ 3.5. Третья форма уравнения энергии 46
§ 3.6. Сохранение энергии 47
§ 3.7. Принцип Гамильтона 47
§ 3.8. Варьированный путь 49
§ 3.9. Распределенные системы 50
Глава IV. Вторая и третья формы основного уравнения 54
§ 4.1. Вторая форма основного уравнения 54
§ 4.2. Третья форма основного уравнения 55
§ 4.3. Принцип Гаусса наименьшего принуждения 56
§ 4.4. Приложения принципа Гаусса 56
§ 4.5. Физический смысл принципа Гаусса 58
Глава V. Лагранжевы координаты 59
§ 5.1. Выбор лагранжевых координат 59
§ 5.2. Некоторые классические задачи 61
§ 5.3. Сферический маятник 71
§ 5.4. Задача двух тел 74
§ 5.5. Уравнение Кеплера . 76
§ 5.6. Столкновение 77
§ 5.7. Лагранжевы координаты для голономной системы 78
§ 5.8. Лагранжевы координаты для неголономной системы 80
§ 5.9. Качение тела 81
§ 5.10. Достижимость 83
§ 5.11. Варьированный путь в принципе Гамильтона 84
§ 5.12. Обзор полученных результатов 85
ОГЛАВЛЕНИЕ
Глава VI. Уравнения Лаграюка 87
§ 6.1. Четвертая форма основного уравнения. Лагранжезы координаты . . 87
§ 6.2. Уравнения Лагранжа 89
§ 6.3. Вывод уравнений Лагранжа из принципа Гамильтона 90
§ 6.4. Форма уравнений Лагранжа % 92
§ 6.5. Консервативные системы и другие системы, обладающие потенциаль-
потенциальной функцией 93
§ 6.6. Функция Лагранжа 95
§ 6.7. Интеграл Якоби 97
§ 6.8. Явная форма интеграла Якоби 98
§ 6.9. Об одной ошибке 101
§ 6.10. Обобщенный импульс 101
§ 6.11. Циклические координаты 102
§ 6.12. Инвариантность уравнений Лагранжа 103
Глава VII. Теория поворотов 104
§ 7.1. Движение твердого тела 104
§ 7.2. Теорема Эйлера 104
§ 7.3. Матрица I и вектор Т 106
§ 7.4. Обобщение теоремы Эйлера 108
§ 7.5. Теорема Шаля 109
§ 7.6. Формула поворота 109
§ 7.7. Полуобороты и отражения 111
§ 7.8. Кватернионная форма записи формулы поворота 112
§ 7.9. Сложение вращений 113
§ 7.10. Угловая скорость 117
§ 7.11. Ориентация твердого тела в пространстве. Углы Эйлера 117
| 7.12. Ориентация твердого тела в пространстве. Углы <pi, <p2, фз 119
% 7.13. Повороты около движущихся осей 119
§ 7.14. Повороты около неподвижных осей 120
§ 7.15. Определение угловой скорости с помощью матриц I и I 120
§ 7.16. Составляющие вектора угловой скорости 121
Глава VIII. Приложения уравнений Лагранжа 124
§ 8.1. Дифференциальные уравнения 124
§ 8.2. Формулы ускорения в ортогональных координатах 125
§ 8.3. Обезьяна и противовес 126
§ 8.4. Кинетическая энергия твердого тела 126
§ 8.5. Задача о движении в двух измерениях 128
§ 8.6. Вращающийся волчок; основные уравнения 129
§ 8.7. Вращающийся волчок; другое решение 130
§ 8.8. Гироскопические силы 131
§ 8.9. Вращающийся волчок; исследование движения 131
§ 8.10. Численный пример 134
§ 8.11. Стержень во вращающейся плоскости 136
§ 8.12. Качение диска 137
Глава IX. Теория колебаний г 140
§ 9.1. Колебания около положения равновесия 140
§ 9.2. Теория преобразования к главным координатам 150
§ 9.3. Приложение теории 154
§ 9.4. Наложение связи 157
§ 9.5. Принцип Релея 158
§ 9.6. Устойчивость установившегося движения 160
§ 9.7. Колебания в окрестности установившегося движения 164
§ 9.8. Гироскоп Фуко 167
§ 9.9. Спящий волчок 169
§ 9.10. Вынужденные колебания 174
Глава X. Дальнейшие приложения уравнений Лагранжа 176
§ 10.1. Исключение координат 176
§ 10.2. Исключение одной координаты 178
§ 10.3. Гироскопическая устойчивость 179
§ 10.4. Явное выражение для Л в общем случае 181
• § 10.5. Вращающийся волчок 182
ОГЛАВЛЕНИЕ О
§ 10.6. Линейные члены в функции L 183
§ 10.7. Движение относительно подвижной системы отсчета 187
§ 10.8. Движение частицы вблизи заданной точки на поверхности Земли . . 189
§ 10.9. Маятник Фуко 190
§ 10.10. Движение снаряда 192
§ 10.11. Диссипативная функция Релея 196
§ 10.12. Гироскопическая система с диссипацией 198
§ 10.13. Уравнения Гамильтона 200
§ 10.14. Уравнение энергии и явное выражение для Н 202
§ 10.15. Главный триэдр 205
Глава XI. Переменная масса 207
§ 11.1. Частица переменной массы. Функция Лагранжа 207
§ 11.2. Кинетическая энергия 208
§ 11.3. Функция Гамильтона 209
§ 11.4. Движущийся электрон 209
§ 11.5. Электрон в электромагнитном поло 211
Глава XII. Уравнения Гиббса — Аппеля 214
§ 12.1. Неголономные системы 214
§ 12.2. Квазикоординаты 214
§ 12.3. Пятая форма основного уравнения 216
§ 12.4. Определение ускорения 217
§ 12.5. Уравнения Гиббса — Аппеля 219
Глава XIII. Приложения уравнений Гиббса — Аппеля 220
§ 13.1. Плоское движение частицы 220
§ 13.2. Аналог теоремы Кёнига 221
§ 13.3. Плоское движение 221
§ 13.4. Движение твердого тела 222
§ 13.5. Шар на вращающейся плоскости 224
§ 13.6. Шар на вращающейся наклонной плоскости 226
§ 13.7. Качение шара по неподвижной поверхности 228
§ 13.8. Вращающийся волчок 230
§ 13.9. Качение монеты (тонкого диска) 232
§ 13.10. Уравнения Эйлера 233
§ 13.11. Свободное тело; случай осевой симметрии 234
§ 13.12. Свободное тело; общий случай 235
§ 13.13. Ориентация свободного тела 238
§ 13.14. Теоремы Пуансо и Сильвестра 240
§ 13.15. Качение эллипсоида по шероховатой горизонтальной плоскости . . 241
§ 13.16. Устойчивость вращающегося эллипсоида ' 242
Глава XIV. Теория удара 244
§ 14.1. Ударный импульс, 244
§ 14.2. Импульсивные связи 246
§ 14.3. Движение системы, на которую действуют ударные импульсы. Основ-
Основные уравнения теории удара 247
§ 14.4. Катастатическая система 248
§ 14.5. Принцип наименьшего принуждения в теории удара 249
§ 14.6. Катастатическая система. Теорема о суперпозиции 250
§ 14.7. Катастатическая система. Шесть теорем об энергии 251
§ 14.8. Лагранжевы координаты и квазикоординаты 255
§ 14.9. Лагранжева форма уравнений движения в теории удара 257
§ 14.10. Другие доказательства теорем об энергии 258
§ 14.11. Приложения теории удара 260
§ 14.12. Импульсивное движение непрерывных систем 264
Глава XV. Шестая форма основного уравнения 269
§ 15.1. Шестая форма основного уравнения 269
§ 15.2. Непосредственные выводы 269
§ 15.3. Функция Рауса 271
§ 15.4. Теорема: ~ (pr bqr) = bL 272
§ 15.5. Главная функция 274
ОГЛАВЛЕНИЕ
§ 15.6. Примеры использования- главной функции 275
§ 15.7. Доказательство равенства dS/dt0 — По 276
§ 15.8. Свойства главной функции 277
§ 15.9. Примеры непосредственного вычисления главной функции 281
Глава XVI. Теорема Гамильтона — Якоби 283
§ 16.1. Уравнение Гамильтона в частных производных 283
§ 16.2. Теорема Гамильтона—Якоби (доказательство первое) 284
§ 16.3. Теорема об эквивалентности 286
§ 16.4. Теорема Гамильтона — Якоби (доказательство второе) 289
§ 16.5. Замечания по теореме Гамильтона — Якоби 290
§ 16.6. Однородное ноле 291
§ 16.7. Гармонический осциллятор 292
§ 16.8. Частица в переменном поле At 295
§ 16.9. Центральная орбита 295
§ 16.10. Сферический маятник , 296
§ 16.11. Вращающийся волчок 297
§ 16.12. Стержень на вращающейся плоскости 298
§ 16.13. Электрон в центральном поле 299
§ 16.14. Пфаффова форма рг dqr — II dt 301
Глава XVII. Системы с двумя степенями свободы, допускающие разделение
переменных 303
§ 17.1. Разделение переменных 303
§ 17.2. Условия разделимости переменных в системах с двумя степенями сво-
свободы 303
§ 17.3. Изучение движения системы 305
§ 17.4. Классификация траекторий 308
§ 17.5. Устойчивость 309
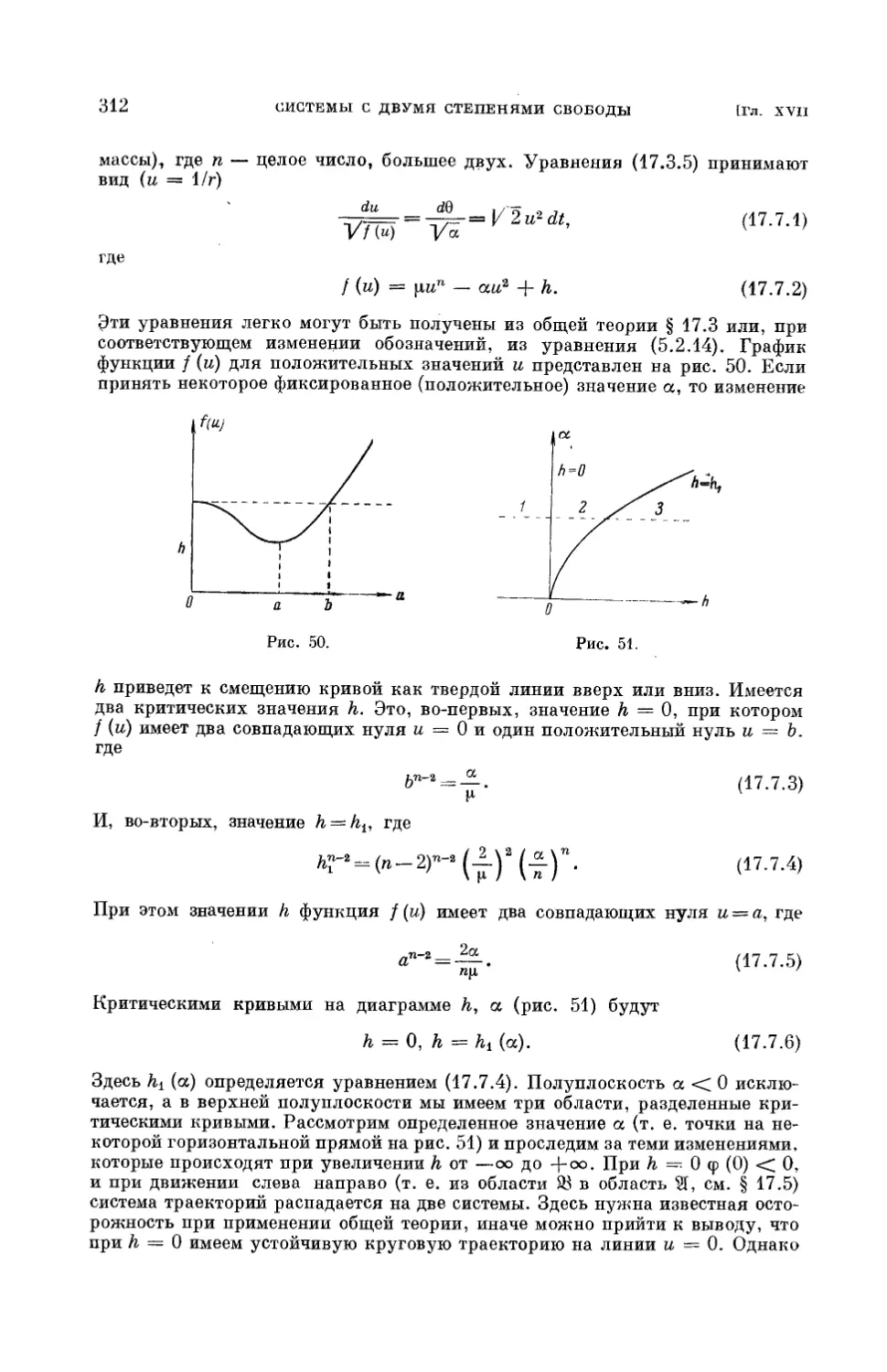
§ 17.6. Приложения теории 311
§ 17.7. Притяжение к центру по закону k/rn+1 311
§ 17.8. Притяжение к центру по закону к/г6 314
§ 17.9. Ньютоновское притяжение и однородное поле 317
§ 17.10. Два неподвижных притягивающих центра 320
§ 17.11. Ограниченные траектории 323
§ 17.12. Уравнения орбит 325
§ 17.13. Неограниченные орбиты 326
§ 17.14. Системы, допускающие разделение переменных более чем одним спо-
способом 327
Глава XVIII. Системы с п степенями свободы, допускающие разделение переменных 329
§ 18.1. Система Лиувилля 329
§ 18.2. Теорема Штеккеля 330
§ 18.3. Исследование интегралов . . . . > 333
§ 18.4. Дополнительные замечания к теореме Штеккеля - . . . 334
§ 18.5. Ква.шпериодические движения 335
§ 18.6. Углоные переменные 338
§ 18.7. Стандартный куб 339
§ 18.8. Постоянные 1Г Ш
§ 18.9. Соотношения между q n v 3-53
§ 18.10. Малые колебания 343
§ 18.11. Сферический маятник 345
§ 18.12. Задача двух тел 347
§ 18.13. Интерпретация параметров аи Р 349
§ 18.14. Выражение г как функции от t 35t>
§ 18.15. Угловые переменные 352
§ 18.16. Постоянные 1Т 352
§ 18.17. Возмущения 355
§ 18.18. Неортогональные и ненатуральные разделимые системы 355
Глава XIX. Системы с одной степенью свободы, движение в окрестности особой
точки 357
§ 19.1. Дифференциальные уравнения 357
§ 19.2. Движение частицы по прямой 361
§ 19.3. Система с одной степенью свободы 363
§ 19.4. Движение в окрестности особой точки. Линейное приближение . . . 364
ОГЛАВЛЕНИЕ
§ 19.5. Устойчивость равновесия. Асимптотическая устойчивость и неустой-
неустойчивость 370
§ 19.6. Движение в окрестности особой точки. Общая теория 371
§ 19.7. Движение в окрестности узла 373
§ 19.8. Движение в окрестности седловой точки 375
§ 19.9. Движение в окрестности фокуса 378
§ 19.10. Движение в окрестности центра 379
§ 19.11. Связь линейного приближения с общей теорией 382
Тлава XX. Системы с одной степенью свободы. Циклические характеристики . . . 385
§ 20.1. Индекс кривой и индекс особой точки 385
§ 20.2. Положительное предельное множество 387
§ 20.3. Отрезок без контакта 389
§ 20.4. Отрезок без контакта, проходящий через точку множества Л .... 390
§ 20.5. Структура множества Л 391
§ 20.6. Теорема Пуанкаре — Бендиксона 392
§ 20.7. Приложение к системе частного вида 394
§ 20.8. Существование предельного цикла 395
§ 20.9. Уравнение Ван-дер-Поля 399
Тлава XXI. Системы с п степенями свободы. Свойства характеристик 401
§ 21.1. Интегралы системы дифференциальных уравнений 401
§ 21.2. Преобразование к новым координатам 405
§ 21.3. Оператор Tt 406
§ 21.4. Решение в форме степенных рядов 406
§ 21.5. Формула для X (ж) — X (а) 410
§ 21.6. Интегральные инварианты 410
§ 21.7. Интегральные инварианты порядка m 413
§ 21.8. Свойства множителей 415
§ 21.9. Последний множитель Якоби 417
§ 21.10. Линейная система 418
§ 21.11. Устойчивость равновесия 419
§ 21.12. Дискретная устойчивость 421
§ 21.13. Устойчивость преобразований 422
§ 21.14. Приложение к дифференциальным уравнениям 424
§ 21.15. Теорема Пуанкаре — Ляпунова 425
§ 21.16. Критический случай 428
Тлава XXII. Уравнения Гамильтона 432
§ 22.1. Уравнения Гамильтона '. 432
§ 22.2. Скобки Пуассона 433
§ 22.3. Теорема Пуассона 434
§ 22.4. Использование известного интеграла 435
§ 22.5. Линейный интегральный инвариант Пуанкаре 437
1 22.6. Теорема Лиувилля 439
§ 22.7. Теорема возвращения (теорема Пуанкаре) 439
§ 22.8. Примеры инвариантных областей 441
§ 22.9. Эргодические теоремы 441
§ 22.10. Конкретные примеры 443
§ 22.11. Множество Ks 444
§ 22.12. Собственные отрезки 445
§ 22.13. Доказательство эргодической теоремы; первый этап 446
§ 22.14. Доказательство эргодической теоремы; второй этап 447
§ 22.15. Метрическая неразложимость 448
§ 22.16. Интегралы уравнений движения 451
§ 22.17. Следствие теоремы Лиувилля 451
§ 22.18. Последний множитель 452
Тлава XXIII. Движение в окрестности заданного движения. Устойчивость движения 457
§ 23.1. Уравнения в вариациях 457
§ 23.2. Решение уравнений в вариациях 459
§ 23.3. Случай постоянных коэффициентов 462
§ 23.4. Случай периодических коэффициентов 464
§ 23.5. Нулевые показатели 467
§ 23.6. Уравнения в вариациях для системы Гамильтона 469
8 ОГЛАВЛЕНИЕ
§ 23.7. Устойчивость траекторий A) 471
§ 23.8. Устойчивость траекторий B) 478
§ 23.9. Устойчивость периодических орбит 479
§ 23.10. Вынужденные колебания 481
Глава XXIV. Контактные преобразования 487
§ 24.1. Контактные преобразования 487
§ 24.2. Формулы контактного преобразования 489
§ 24.3. Другие формулы 491
§ 24.4. Обобщенное точечное преобразование и другие однородные контакт-
контактные преобразования 493
§ 24.5. Специальная форма уравнений преобразований. Бесконечно малые
контактные преобразования 494
§ 24.6. Обобщение теоремы Лиувилля 495
§ 24.7. Условия контактности преобразования, скобки Лагранжа 495
§ 24.8. Соотношения между двумя системами производных 496
§ 24.9. Условия контактности преобразования, выраженные с помощью ско-
скобок Пуассона . 497
§ 24.10. Соотношения между скобками Лагранжа и скобками Пуассона . . . 498
§ 24.11. Приложение к контактному преобразованию 498
§ 24.12. Инвариантность скобки Пуассона 498
§ 24.13. Другая форма условий контактности преобразования 499
§ 24.14. Функции, находящиеся в инволюции 500
§ 24.15. Некоторые примеры 501
Глава XXV. Теория преобразований 504
§ 25.1. Уравнения движения после контактных преобразований 504
§ 25.2. Вариация элементов траектории 506
§ 25.3. Вариация эллиптических элементов 510
§ 25.4. Другие доказательства теоремы Якоби 513
§ 25.5. Постоянство скобок Лагранжа 517
§ 25.6. Бесконечно малые контактные преобразования 517
§ 25.7. Интегралы в инволюции 519
§ 25.8. Теорема Ли о системах в инволюции 521
§ 25.9. Интегралы, линейные относительно импульсов 522
§ 25.10. Случай, когда функция Гамильтона является однородной квадратич-
квадратичной формой 524
Глава XXVI. Вариационные принципы 529
§ 26.1. Принцип Гамильтона ' . . . . 529
§ 26.2. Теорема Ливенса 531
§ 26.3. Точки минимума и седловые точки 533
§ 26.4. Асинхронное варьирование. Принцип Гёльдера 534
§ 26.5. Принцип Фосса 535
§ 26.6. Обобщение принципа Гамильтона 537
§ 26.7. Замена независимой переменной 537
§ 26.8. Нормальная форма системы с двумя степенями свободы 539
§ 26.9. Система Лиувилля 540
§ 26.10. Конформные преобразования 542
Глава XXVII. Принцип наименьшего действия 544
§ 27.1. Вариация действия 544
§ 27.2. Принцип наименьшего действия 545
§ 27.3. Принцип наименьшего действия в форме Якоби 547
§ 27.4. Теорема Уиттекера 550
§ 27.5. Исключение координат 552
§ 27.6. Характеристическая функция 552
§ 27.7. Пространство конфигураций 553
§ 27.8. Система с двумя степенями свободы 555
§ 27.9. Теорема Кельвина 556
§ 27.10. Однородное поле 558
§ 27.11. Задача Тэта. Непосредственное решение 559
§ 27.12. Задача Тэта. Теория огибающих 560
ОГЛАВЛЕНИЕ
Глава XXVIII. Ограниченная задача трех тел 562.
§ 28.1. Задача трех тел 562
§ 28.2. Ограниченная задача. Уравнения движения 563
§ 28.3. Положения равновесия 564
§ 28.4. Положения равновесия на прямой А В 565
§ 28.5. Положения равновесия, не лежащие на прямот"! А В 567
§ 28.6. Поверхность z = U 567
§ 28.7. Движение вблизи положения равновесия 569
§ 28.8. Теория движения Луны 570
Глава XXIX. Задача трех тел 573
§ 29.1. Классические интегралы 573
§ 29.2. Случай, когда вектор момента количеств движения равен нулю . . . 575
§ 29.3. Три точки Лагранжа 57&
§ 29.4. Решения, для которых треугольник Лагранжа сохраняет свою форму 578
§ 29.5. Случай плоского движения 579
§ 29.6. Координаты относительно частицы А3 581
§ 29.7. Движение в окрестности равновесного решения 582
§ 29.8. Сведение к системе шести уравнений 584
§ 29.9. Устойчивость трех точек Лагранжа 586
§ 29.10. Преобразованная форма уравнений движения 587
§ 29.11. Другой подход к задаче трех точек Лагранжа 589
§ 29.12. Сведение к системе восьми уравнений 591
§ 29.13. Невозможность тройных столкновений 595
§ 29.14. Плоское движение. Другой способ приведения к системе птестого
порядка 597
§ 29.15. Равновесные решения 600
Глава XXX. Периодические орбиты 602
§ 30.1. Периодические орбиты 602
§ 30.2. Периодическое движение в окрестности особой точки 602
§ 30.3. Условия вещественности 605
§ 30.4. Уравнения Гамильтона 606
§ 30.5. Сходимость 609
§ 30.6. Три точки Лагранжа 611
§ 30.7. Системы, содержащие параметр 613
§ 30.8. Приложение к ограниченной задаче трех тел 616
§ 30.9. Метод неподвижной точки 619
§ 30.10. Теорема Пуанкаре о кольце _ 619
§ 30.11. Периодические орбиты и теорема о кольце ' 620
§ 30.12. Доказательство теоремы Пуанкаре о кольце 625
Библиография 628
Именной указазатель 631
Предметный указатель , 633
ОТ ИЗДАТЕЛЬСТВА
Публикацией перевода «Аналитической динамики» Л. А. Парса издатель-
издательство «Наука» представляет современному читателю труд, подобный тракта-
трактатам Рауса. Аппеля, Уиттекера, Суслова, на изучении которых основывалось
механико-математическое образование предшествующих поколений.
С этими классическими сочинениями книгу Парса роднят неторопли-
неторопливость изложения, точность исходных определений, изящество доказательств,
тщательно отобранные, иллюстрирующие теоретические рассуждения.задачи.
Конечно, и сам предмет изложения. Было бы несправедливым не отметить
оригинальности подхода автора к изложению хорошо известных положений,
новизну ряда рассуждений и доказательств; многие из них представляют
ценные педагогические находки.
В содержание книги включен не только традиционный материал кур-
курсов аналитической механики. Значительное место уделено применению
к задачам механики методов качественной теории дифференциальных урав-
уравнений, на современном уровне трактуются вопросы о разделимости перемен-
переменных в уравнении Гамильтона — Якоби, дается рассмотрение эргодических
теорем, включая теорему Пуанкаре о возвращении; нашло свое место несколь-
несколько отличное от принятого и приспособленное к задачам динамики изложение
теории устойчивости движения, включающее теоремы Ляпунова. В заклю-
заключительных главах, посвященных ограниченной задаче трех тел и задаче
трех тел, автору в небольшом объеме удалось дать хорошее представление
о постановках и трудностях этой классической в истории точных наук проб-
проблемы. Книга заканчивается теорией периодических орбит. Использование
здесь (и в некоторых других местах) простейших понятий и рассуждений
теории множеств не может затруднить внимательного читателя.
Следует предвидеть, что «Аналитическая динамика» Л. А. Парса займет
прочное место среди основных руководств по механике.
ИЗ ПРЕДИСЛОВИЯ АВТОРА
Механика точки как наука была основана Галилеем в начале семнад-
семнадцатого столетия и после его смерти развивалась Гюйгенсом. Основные
принципы были установлены и сформулированы Ньютоном, чье великое
сочинение «Математические начала натуральной философии» [1] появилось
в 1687 г. В 1743 г. Даламбер [2] распространил законы Ньютона на задачи
механики твердого тела. Основания аналитической механики были зало-
заложены Эйлером уже в 1736 г. [3], но выдающимся событием в ранней истории
этой науки стал выход в свет «Аналитической механики» Лагранжа
в 1788 г. [4]. Развитие аналитической механики со времен Лагранжа связано
с именами многих прославленных математиков. Среди тех, кому принадле-
принадлежат наиболее фундаментальные открытия в этой области, в первую очередь
следует назвать Лапласа, Гамильтона, Якоби, Гаусса и Пуанкаре.
Цель настоящего сочинения — дать сжатое, последовательное и доста-
достаточно полное изложение современного состояния предмета. Аналитическая
"механика основывается на одном результате Лагранжа, который мы будем
называть основным уравнением. Этот результат устанавливается в гл. III
после необходимого предварительного обсуждения. Чтобы изложение приоб-
приобрело возможно более гибкую и изящную форму, основное уравнение необ-
необходимо представить в нескольких различных видах. Именно так строится
изложение в этой книге. Каждая из этих различных форм (всего их шесть)
примечательна своими собственными особыми достоинствами, и каждая из
них, по мнению автора, является верной отправной точкой для развития
определенной ветви механики. Автор старался ясно указать условия, при
которых справедлива каждая из таких форм, и круг проблем, для решения
которых каждая из них является наиболее подходящей. Повышенный инте-
интерес к этим вопросам объясняется тем фундаментальным значением, какое
они имеют для осознания предмета в целом. Стоит однажды понять их, как
все в целом становится ясным и предстает в простом и естественном свете.
Различные формы этого уравнения позволяют получить основные
уравнения для различных разделов механики; при этом мы сталкиваемся
с серьезной трудностью, связанной с огромным объемом материала. Выбор
сведений и фактов составлял одну из самых больших трудностей для автора,
стремившегося дать систематическое изложение предмета. Трудность эта
лишь подчеркивается тем особым положением, которое механика занимает
в иерархии физических наук.
Принципы механики важны не только для тех, кто изучает эту науку,
чтобы постичь ее самое, но и для инженеров, астрономов и физиков. Каждую
из этих групп специалистов интересуют в первую очередь свои вопросы.
Инженер, например, обращает большее внимание на динамику твердого
тела, теорию упругости и учение о колебаниях; астроном интересуется глав-
главным образом специальными задачами небесной механики; физика интере-
интересуют те разделы механики, из которых легко установить связь со статисти-
статистической механикой и квантовой теорией. Вероятно, не существует такого
выбора материала и такого построения изложения, которые полностью
удовлетворили бы всех читателей. Тем не менее автор надеется, что читатели,
12 .ИЗ ПРЕДИСЛОВИЯ АВТОРА
принадлежащие к каждой из этих столь различных групп, найдут здесь
изложение основных фактов, которое соответствует их специфическим инте-
интересам. Автор стремился развивать каждую тему таким образом, чтобы
у читателя не возникло чувства разочарования; даже если и не оказалось
возможным дать ответ на тот или иной вопрос, интересующий чита-
читателя, то он найдет здесь все необходимое, чтобы сделать это самостоя-
самостоятельно.
Различные вопросы теории автор иллюстрировал конкретными приме-
примерами; голое изложение абстрактной теории могло бы показаться читателю
оторванным от жизни и неинтересным. Применение теории к конкретным
задачам есть лучшее средство продемонстрировать полезность и жизнен-
жизненность науки. Желая ограничить объем книги разумными пределами, автор
старался устоять перед соблазном включить в текст вопросы, которые мог-
могли бы увести изложение в сторону от основных идей; в текст, однако, вклю-
включен ряд замечательных по своей красоте результатов, имеющих историческое
значение, которые связаны непосредственно с основным изложением. (К ним,
по-видимому, следует отнести шесть теорем об энергии § 14.7 и, возможно,
значительную часть теории удара.) Кроме того, автор старался не выходить
за рамки чистой механики и потому не касался вопросов, связанных с элект-
электроникой и квантовой теорией, а также задач инженерной практики, хотя
это легко можно было бы сделать во многих местах. В качестве известной
компенсации он позволил себе дать по два независимых доказательства
некоторых наиболее важных теорем.
«On a deja plusieurs Traites de Mecanique» *) — такими словами начи-
начинается предисловие к «Аналитической механике» Лагранжа, и, конечно,
в настоящее время сочинений по механике гораздо больше, чем в 1788 г.
Во многих из них вопросы, изложенные в этой книге лишь в общих чертах,
рассмотрены весьма подробно. Так, например, теория вращающегося волчка
кратко изложена в § 8.9, подробное же изложение этого вопроса занимает
у Клейна и Зоммерфельда [33] четыре тома. Гл. IX посвящена классической
теории колебаний, а в гл. XIX кратко рассматриваются некоторые задачи
нелинейных колебаний. Между тем в последние годы общая теория нелиней-
нелинейных систем привлекла большое внимание ученых, и появилось множество
книг и статей, где эти вопросы излагаются значительно более подробно.
В работе [46] библиографический указатель только последних публикаций
занимает около семидесяти страниц. (Превосходный обзор современного
состояния предмета дан Минорским в работе [43].)
В гл. XXII дается доказательство эргодической теоремы, но фундамен-
фундаментальная эргодическая теорема динамики является лишь отправной точкой
для хорошо разработанной в настоящее время абстрактной теории. Хопф
в своей работе [47] 1937 г. цитирует более пятидесяти работ по эргодической
теории, и это число к настоящему времени выросло в огромной степени **).
Ни одно сочинение по механике не будет полным без задачи трех тел —
проблемы, оказавшей на развитие этой науки, по-видимому, большее влия-
влияние, чем любая другая.
Главы XXVIII и XXIX служат кратким введением в эту проблему.
Более подробное рассмотрение увело бы нас слишком далеко в сферу инте-
интересов астрономов.
В вопросе о терминах и обозначениях автор придерживается консерва-
консервативных позиций. Например, часто используется термин центр тяжести,
хотя, строго говоря, он оправдан только в той задаче, где он возник,—
в задаче о твердом теле в однородном поле тяжести. По традиции через q
*) «По механике уже имеется много трудов» (франц.). (Прим. ред.)
**) См., например, библиографию, приведенную в работе [49] на стр. 731—826.
ИЗ ПРЕДИСЛОВИЯ АВТОРА 13
•обозначается лагранжева координата, через L — функция Лагранжа, через
Н — функция Гамильтона и через S — главная функция. Отступления
от общепринятых обозначений делаются по особым причинам лишь в немно-
немногих местах, где излагаются второстепенные вопросы.
В этой книге автор сравнительно редко делает ссылки на другие работы.
Это объясняется, с одной стороны, желанием не прерывать изложение мате-
материала и, с другой стороны, еще одной причиной, характерной именно для
излагаемого здесь предмета. Дело в том, что литература по механике столь
•обширна, что список публикаций по какому-либо частному вопросу, даже
¦без претензии на полноту, оказался бы во многих случаях очень громоздким.
Можно было бы ограничиться двумя-тремя наиболее важными ссылками,
но практически это не всегда легко сделать, особенно тогда, когда затраги-
затрагиваются вопросы приоритета.
Вопросы о приоритете часто бывают спорными. С одной стороны, многие
результаты были получены почти одновременно двумя различными авторами
независимо друг от друга. С другой стороны, даже в том случае, когда пер-
первое явное упоминание о результате содержится в какой-либо ссылке, появив-
появившийся ранее результат иногда бывает настолько близок к нему, что вопрос
<о приоритете можно с основанием оспаривать. Такого рода трудности возни-
возникают в особенности в связи с работами середины девятнадцатого столетия,
когда создавалось основное здание аналитической механики. Замечатель-
Замечательным примером тесно связанных теорий, выдвинутых почти в одно и то же
время двумя разными авторами независимо друг от друга, служит цент-
центральная теорема, которую автор (как и большинство английских математи-
математиков) называет теоремой Гамильтона — Якоби; такое название дано в память
о двух знаменитых авторах, одновременно работавших над одним и тем же
кругом идей. Другим примером фундаментальной теории, разработанной
двумя различными учеными независимо друг от друга (хотя на этот раз и не
одновременно), служат уравнения Гиббса — Аппеля. Когда Уиллард Гиббс
открыл эти уравнения, они не произвели глубокого впечатления, важность
их была оценена лишь после того, как двадцать лет спустя Аппель открыл
их вновь. Можно привести еще много других примеров, когда разные ученые
независимо друг от друга приходили к одному и тому же результату.
Вообще говоря, книгу следовало бы начать с истолкования понятий
массы и силы и с логического обоснования законов движения Ньютона, все
это — вопросы фундаментальной важности. Но это потребовало бы много
места и, кроме того, эти вопросы, по всей вероятности, известны большин-
большинству читателей. Поэтому после некоторых колебаний автор решил начать
с практических вопросов, предположив, что логическая основа теории
читателям уже известна *).
Несколько слов о содержании книги. Очевидно, изложение было бы
проще и компактнее, если бы все внимание сосредоточить на голономных
системах. Однако такое ограничение дало бы искаженное представление
о предмете в целом. В то же время автор учитывал, что на практике мы обыч-
обычно имеем дело с голономными системами, и потому уделил неголономным
системам сравнительно немного места. Особое внимание было обращено
на отдельные классические задачи динамики твердого тела, которые, по мне-
мнению автора, еще недостаточно полно освещены в литературе. Это мнение
(о недостаточном внимании к динамике твердого тела) послужило причиной
того, что в книгу включен раздел о теории поворотов твердого тела (гл. VII).
Можно возразить, что эти вопросы составляют скорее предмет теории групп
и вряд ли их следует включать в руководство по механике. Возможно, что
*) Читатель, интересующийся аксиоматическим построением механики, может
обратиться к статье: G. Н а ш е 1, Die Axiome der Mechanik. См. [24], стр. 1—42.
14 ИЗ ПРЕДИСЛОВИЯ АВТОРА
решение автора в большей степени было продиктовано внутренней красотой
теории, нежели практическими потребностями изложения.
При работе над систематическим и подробным изложением предмета
возникает естественное желание сделать некоторые теоретические обобще-
обобщения, привести новые или более простые доказательства. Некоторые из них
были опубликованы автором отдельно, иные появились в других работах
автора, а часть впервые увидит свет в этой книге.
Автор считает себя во многом обязанным ряду ученых, прежде всего
Раусу и Аппелю. Галльское изящество и ясность «Аналитической механики»
Аппеля [21] способствовали пробуждению у автора интереса к аналитиче-
аналитической механике; читатели, знакомые с этой книгой, почувствуют, вероятно,
то влияние, какое она оказала на его восприятие предмета. Знаменитая книга
Рауса [20], впервые опубликованная в 1860 г. и выдержавшая в последующие
годы много изданий, и сейчас оказывает громадное влияние на преподава-
преподавание механики; богатство содержания этой книги поистине поразительно.
Раус (которого часто недооценивали как математика), когда писал свою
книгу, был близок к открытию фундаментальных теорий. Многие важней-
важнейшие результаты были добавлены им в более поздние издания в виде прило-
приложений.
Обозревая историю создания механики за два столетия, мы видим триум-
триумфальное развитие ее, постоянно расширяющийся круг приложений, огром-
огромное разнообразие и гибкость применяемых методов, неизбежное смещение
интересов в сторону той или иной области по мере развития науки. Трудно
удержаться от восхищения этим примером неисчерпаемой силы человече-
человеческого духа. Очень многие задачи, казавшиеся неразрешимыми, раскрыли
наконец свои тайны, а во многих других, решенных не до конца, достигнуто
важное и значительное продвижение. И все же, как ни поражает нас величие
наших достижений, мы должны ясно представлять себе объем и разнообра-
разнообразие еще нерешенных проблем. Мы и поныне напоминаем собой детей, играю-
играющих на берегу огромного и неисследованного океана истины.
В последние годы среди математиков наметилось заметное ослабление
интереса к классической механике. Это объясняется рядом причин. К их чис-
числу следует отнести возросший интерес к теории относительности и связан-
связанное с этим понижение престижа механики Ньютона, коренное изменение
взгляда на физику, переход от старой идеи чистого детерминизма к новой
идее о статистическом характере событий и связанное с этим развитие стати-
статистической механики, интерес, вызванный новыми открытиями в квантовой
теории и в атомной физике, а также то, что многие математики, занимаю-
занимающиеся прикладными задачами, предпочитают абстрактным теориям числен-
численные решения с последующей опытной проверкой.
По мнению автора, этим современным направлениям, самим по себе
достойным всяческого поощрения, часто недостает изящества классических
теорий. Автор надеется, что его книга в какой-то мере будет способствовать
возрождению интереса к аналитической динамике как к таковой.
Кембридж-, JJ. А. Парс
июня 1964 г.
Глава I
ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
§ 1.1. Свободная материальная точка. Движение свободной частицы-
(материальной точки) под действием заданной силы определяется вторым
законом Ньютона, который можно выразить в традиционной форме:
Р = т/. A.1.1)
Б качестве системы отсчета выбирается ньютонова, или инерциалъная
система; существование такой системы представляет основной постулат
ньютоновой механики. Р в формуле A.1.1) обозначает заданную силу, мно-
множитель т — массу частицы и / — ее ускорение (по отношению к выбранной
системе отсчета). Если через х, у, z обозначить прямоугольные координаты
частицы в момент t, отнесенные к осям, жестко связанным с системой отсче-
отсчета, а через X, Y, Z — составляющие заданной силы вдоль этих осей, то дви-
движение частицы будет описываться уравнениями
тх = X, тг/'= Y, rriz = Z, A.1.2),
эквивалентными A.1.1).
В уравнениях A.1.2) составляющие X, Y, Z — известные функции семи
• • •
переменных: х, у, z; x, у, z; t. Эти функции определены в некоторой обла-
области D семимерного пространства (х, у, z; x, у, z; t)\ в простейшем случае
они заданы для всех вещественных значений этих семи переменных. Следует,
однако, отметить, что задачи, в которых X, Y, Z зависят от t, встречаются
сравнительно редко, в большей части случаев эти функции зависят лишь.
• • •
от х, у, z; х, у, z. В еще более специальном, но часто встречающемся случае
X, Y, Z являются заданными функциями трех переменных: х, у, z. В этом
случае говорят, что частица движется в силовом поле.
В ньютоновой системе отсчета прямоугольный триэдр осей находится в покое,
и мы для краткости такие оси будем называть неподвижными. Если жесткий прямоуголь-
прямоугольный триэдр движется относительно неподвижных осей, то эти новые оси мы будем назы-
называть подвижными. Позже (§ 10.7) мы рассмотрим влияние движения осей на движение
механической системы, каким оно представляется наблюдателю, связанному с движу-
движущимися осями.
В случае, когда новый триэдр движется относительно основного равномерно и без
вращения, он определяет новую ньютонову систему отсчета. Уравнения движения сохра-
сохраняют при этом свою форму A.1.1) или A.1.2), хотя выражения для X, Y, Z теперь должны
быть представлены через новые координаты, их первые производные и время. (В задаче
трех тел, где действующие силы зависят только от их относительных положений, урав-
уравнения движения имеют одну и ту же форму в любой ньютоновой системе.)
Параметр т в уравнениях движения есть положительная постоянная.
Во всех случаях, когда не будет оговорено противное, будет предполагаться,
что масса частицы остается неизменной во время движения. Позже, однако
(в гл. XI), мы встретимся с задачами, в которых т будет известной функцией
скорости V хг -f- у2 -\- z2. JB подобных задачах точки переменной массы
16 ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ [Гл. I
.уравнения A.1.2) заменяются следующими:
±{mi) = X, ~(my) = Y, ±{m'z) = Z A.1.3)
Уравнения движения A.1.3) явно и однозначно выражают ускорения
х, у, z как функции семи переменных: х, у, z; x, у, z; t. В дальнейшем
мы увидим, что аналогичное положение сохраняется и в общей теории дина-
динамических систем. Для классической механики характерно, что с помощью
уравнения движения ускорение выражается как явная функция положения,
скорости и времени.
В случае движения свободной материальной точки все необходимые
сведения динамического характера даются законом Ньютона. Задача сводит-
сводится к интегрированию системы трех совокупных обыкновенных дифферен-
дифференциальных уравнений второго порядка. Вторые производные входят в-эти
уравнения линейно.
Если функции X, Y, Z принадлежат классу*) С\ в области D пере-
• • •
менных (х, у, z; х, у, z; t), то уравнения определяют значения х, у, z
в момент t, если для момента т заданы значения ха, у0, z0; и0, v0, w0 пере-
• • •
менных х, у, z; х, у, z. При этом точка (х0, у0, zc; щ, v0, w0; т) принад-
принадлежит области D и решение справедливо для некоторого интервала време-
времени, содержащего момент t = т. В простейших случаях решение сохраняет
силу для всех вещественных значений t.
Если ввести новые переменные
• • .
и = х, v = у, w — z, A.1.4)
то три дифференциальных уравнения второго порядка A.1.2) можно заме-
заменить шестью дифференциальными уравнениями первого порядка:
х = и, y = v, z = w, I
• X • Y ' Z \
u = —¦, v = —, iv = —
m m m
в которых X, Y, Z являются теперь функциями х. у, z; и, v, w, t Урав-
Уравнения A.1.5) можно записать в более компактной форме:
х = X. A.1.6)
Здесь х обозначает матрицу-столбец
Х\
У
z
и
V
W
*) Мы будем говорить,.что функция одной или нескольких переменных принадлежит
классу Ср в области D изменения независимых переменных, если все ее производные
порядка р существуют и непрерывны в D.
S 1.2] ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ В СИЛОВОМ ПОЛЕ 17
X — матрицу-столбец
V
W
т
У_
т
Строго говоря, между вектором X и матрицей-столбцом, элементы кото-
которой являются составляющими вектора, следует проводить различие, однако
мы часто будем вектор и матрицу-столбец считать синонимами, и это не при-
приведет к какой-либо путанице. Удобства ради мы иногда будем писать состав-
составляющие вектора в строку, а не вертикально и будем пользоваться фигурны-
фигурными скобками вместо круглых, чтобы подчеркнуть матричный характер
вектора. Так, вместо х мы можем написать {х, у, z; и, v, w}, а вместо X
{и, v, w, X/m, Y/m, Zlm).
В дальнейшем нам часто будет встречаться уравнение вида A.1.6).
В общем случае х будет обозначать вектор {xj, xz, . . ., хт}, & X — вектор
{Х-\, Х2, ¦ ¦ ., Хт}. Составляющие ХТ вектора X будут, вообще говоря,
зависеть от m -f- 1 переменных: xi7 x2
xm; t. Кратко это можно запи-
записать в виде X = X (х; t). Во многих случаях, однако (как это уже отме-
отмечалось в случае одной свободной частицы), переменная t не входит в выра-
выражение для X, т. е. X = Х (х). В этом случае говорят, что система автономна.
Уравнения A.1.2) определяют движение частицы в обычном простран-
пространстве. Аналогично, уравнения A.1.5) определяют движение изображающей
точки с координатами х, у, z, и, v, w в пространстве шести измерений.
Система A.1.5) содержит шесть зависимых переменных, тогда как систе-
система A.1.2) содержит три зависимые переменные. Важным преимуществом
уравнений A_1.5) является то, что положение изображающей точки в шести-
шестимерном пространстве в момент f определяет ее положение в момент t, по край-
крайней мере для некоторого интервала значений t, включающего момент t = т.
В дальнейшем мы часто будем прибегать к подобного рода замене п диффе-
дифференциальных уравнений второго порядка 2п уравнениями первого порядка.
§ 1.2. Прямолинейное движение материальной точки в силовом поле.
Простейшей и в то же время весьма важной задачей является задача о дви-
движении материальной точки по прямой линии Ох \ силовом поле. В этом
случае
X = F(x), A.2.1)
где F(x) — заданная функция независимой переменной х, принадлежащая
классу Ci в некоторой области значений х; в простейших случаях функция
F(x) определена для всех вещественных значений х.
Введем потенциальную функцию V(x):
A.2.2)
где а — любое подходящее число, лежащее в области определения F(x).
Таким образом, V(a) -¦- 0, V(x) ? C2 и
X = F(x)=-^. A.2.3)
2 Л. А. Парс
18 ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ [Гл. I
Кинетическая энергия Т материальной точки определяется формулой
Г = -1рм:2. A.2.4)
Уравнение движения имеет вид
mx='X = F{x). A.2.5)
Символ F(x) в правой части уравнения A.2.5) обозначает теперь величи-
величину функции F(x) в точке х, в которой точка находится в момент t (в противо-
противоположность A.2.1), где F(x) есть функция независимой переменной х). Анало-
Аналогичным образом, если V (х) представляет собой значение в точке х (t), в кото-
которой частица находится в момент t (в противоположность A.2.2), где V (х)
есть функция независимой переменной х), то можем написать
dV dV • с / \ "
Умножая A.2.5) на х, находим, что -тг{Т + V) = 0, откуда
Т + V = h, A.2.6)
где h — постоянная.
Уравнение A.2.6) представляет собой известное уравнение энергии, или
интеграл энергии. Уравнение второго порядка A.2.5), выражающее а; как
функцию отх, заменяется, таким образом, уравнением первого порядка A.2.6),
выражающим х2 как функцию от х. Для рассматриваемой задачи характерно
*
то, что одному значению х соответствуют два значения х, одинаковые по вели-
величине, но различающиеся знаком. Поскольку Т ^ 0, из A.2.6) следует, что
материальная точка никогда не выходит за пределы области V ^.h.
Если уравнение второго порядка A.2.5) заменить двумя уравнениями первого
порядка, то будем иметь
х=и, u = Z?L. A-2.7)
Для наших непосредственных целей в этом нет необходимости, но в других случаях
такой прием оказывается очень удобным. Уравнение энергии представляет собой урав-
уравнение траектории изображающей точки в плоскости хи:
h. A.2.8)
Уравнение энергии
±mx = h-V A.2.9)
проходит через всю теорию прямолинейного движения материальной точки
в силовом поле. Более того, уравнение вида
х2 = <р(х), A.2.10)
в ¦ котором ф (х) ? С% в соответствующей области х, фигурирует во многих
задачах динамики. По этой причине следует кратко остановиться на задаче
о,б интегрировании уравнения A.2.10). Мы увидим, что характер движения
можно определить по графику функции ср (х).
Рассмотрим сначала один особый случай. Пусть имеется'точка хц такая,
что, в ней ф (х) и ф' (х) одновременно обращаются в нуль. Иначе говоря,
в этой точке кривая и = Ф (х) касается оси Ох и эта точка является положе-
§ 1.2] ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ В СИЛОВОМ ПОЛЕ 19
нием равновесия. Если в момент t = 0 х = зд (и, следовательно, х = 0),
то всегда х = хо и точка находится в положении равновесия.
Кроме этого исключительного случая существуют четыре возможных
варианта поведения точки в зависимости от t:
1. Точка совершает непрерывные колебания вдоль оси х между точками
х = а ж х ='Ь, и ее движение является периодическим; такое движение
называется либрационным движением.
2. х->-а, когда ?-»-оо; такое движение называется лимитационным
движением *).
3. х-*- оо (или а;-»- — оо), когда t-*~ оо.
4. ж-»- оо (или ж-»- — оо), когда i —»- io-
Покажем, каким образом эти четыре типа движений получаются из урав-
уравнения A.2.10). Обратимся для этого к графику функции у = ф (ж). Ордина-
Ордината у для всякого значения х дает соответствующее значение ж2, а производ-
ная dyldx указывает соответствующее значение 2х. Движение может осуще-
осуществляться только на тех участках оси х, где ср (х) ^ 0. Предположим, что
О / x, \ U x0 0 ' х,
a) b) cj
Рис. 1.
при t = 0 х = Хо, функция ф (хо) > 0 (а не ф (х0) = 0) и что в этот момент
а; >¦ 0, т. е. х — Уф (х0). Для достаточно малых значений t скорость * поло-
положительна, и соотношение между tux для этих значений t имеет Вид
I. Предположим сначала, что точка х0 Лежит между двумя последова-
последовательными простыми вещественными нулями a, b функции ф (х), причем а <; Ъ.
График у = ф (х) для этого случая показан на рис. 1, а; кривая пересекает
ось х в точках а и Ь, и ф (х) > 0 при а < х < Ь, причем в точке a dq>/dx > О,
а в точке Ъ dy/dx < 0. Поскольку b — простой нуль функции <р (х), интеграл
в правой части A.2.11) сходится при х-^-b, так что материальная точка
достигает точки b за конечное время. В точке-fe она приходит в состояние
* •
покоя, но лишь мгновенного (поскольку х <С 0), и затем начинает двигаться
влево. Подобным же образом устанавливаем, что материальная точка дости-
достигает точки а за конечное время, на мгновение останавливается и затем начи-
начинает двигаться вправо. В начальную точку она возвращается с той же (поло-
(положительной) скоростью, с какой она начала свое движение; это происходит
за время
ь
—^= = 2 [-й=- A.2.12)
Уф(Е) * ""-'"
*) Либрационное движение и лимитационное движение, а также обзор теории
с несколько иных позиций см. в книге: К. Ш а р лье, Небесная механика, М., иэд-во
«Наука», 1966.
2*
20 ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ [Гл. 1
после старта. (В первом интеграле в формуле A.2.12) \ возрастает от а до Ь
и затем убывает от Ъ до а; радикал берется со знаком плюс, когда | возра-
возрастает, и со знаком минус, когда | убывает. Во втором интеграле радикал
берется со знаком плюс.) Движение в интервале от t = <т до t = 2ст пред-
представляет собой простое повторение движения в интервале от t = 0 до
t = о*. Это же справедливо для движения в интервале от t = го* до t =
= (г -f 1) ст, где г — любое целое положительное число. Движение периоди-
периодическое с периодом о*.
До сих пор мы предполагали, что ср (х0) > 0, но ясно, что такое же
периодическое движение будет иметь место, если точка начинает движение
из состояния покоя в точке а или Ъ.
Наконец, такое же движение будет и в том случае, когда в момент
t --= 0 ф (х0) > 0 и х < 0 (х = - |/ф {х0)).
П. Предположим теперь, что, удаляясь от хо, точка приближается
к двойному (или более высокой кратности) нулю с функции ф (х). Кривая
Ф (х) касается оси Ох в точке х = с (рис. 1, Ъ). В этом случае интеграл
в правой части A.2.11) расходится при х—>-с, и х —>- с при t-*-oo.
В случае, иллюстрированном на рис. 1, с, х0 лежит между простым
нулем а функции ф (х) и двойным нулем с этой фупкции: а < х0 < с.
Если в момент f = 0 а; < 0 (ж = — ]fq> (x0)), то х сначала убывает и части-
частица достигает точки а за конечное время; остановившись в этой точке на мгно-
мгновение, она затем движется вправо, и х —>- с при i->- oo.
Если, наконец, ф (х) > 0 при х > хо, то точка продолжает двигаться
вправо (при условии, что в начальный момент х > 0), и уравнение A.2.11)
удовлетворяется во все время движения. При этом имеются две возможности.
III. Если интеграл в правой части A.2.11) расходится при х->-оо,
то с ростом ( х->оо.
IV. Если же интеграл сходится при х -> оо к значению t<y, то при
t —у- ?о х —*- оо.
Легко видеть, что ничто не изменяется и в том случае, когда х =sC 0
при t = 0, за исключением того, что при t ->- оо или t -^- t0 x может стре-
стремиться не к +°°, а к —оо. Классификация возможных случаев на этом
завершается. Во всякой частной задаче достаточно посмотреть на график
функции ф (х), чтобы установить тип движения. В том частном случае,
с которого мы начали рассмотрение этой задачи, функция ф (х) имеет вид
2(h — F); для любого заданного h график V (х) определяет характер дви-
движения.
Рассмотрим теперь несколько простых примеров прямолинейного дви-
движения точки в силовом поле. Эти примеры элементарны и легко могут быть
решены и без общей теории. Однако, отыскивая выражение х от t, полезно
заранее знать тип осуществляющегося движения.
Пример 1.2А. Гармонический осциллятор. Дейст-
Действующая на частицу притягивающая сила направлена к фиксированной
точке О оси Ох, и величина ее пропорциональна расстоянию от точки О.
Приняв точку О за начало координат, можем написать
X = — тп2х, A.2.13)
где п — положительная постоянная. Уравнение движения можно написать
в виде
х + пгх = 0. A.2.14)
Решение этого линейного уравнения с постоянными коэффициентами
легко получить, не обращаясь к общей теории; оно имеет вид
х = a cos nt 4- (b/n) sin nt, A.2.15)
§ 1.2] ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ В СИЛОВОМ ПОЛЕ 21
Здесь через а обозначено начальное (в момент t = 0) значение х, а через Ь
начальное значение х. Формулу A.2.15) можно также записать в форме
х = с cos {nt -- a), A.2.16)
где
а а — угол в пределах 0 ^ а < 2л, определяемый равенствами
Ь
с cos а = а, csmcx =—.
п
Уравнение A.2.16) описывает движение по оси Ох проекции на нее точ-
точки, движущейся по окружности с постоянной угловой скоростью п. Движе-
Движение периодическое с периодом 2л/п.
Задача была решена нами непосредственно, рассмотрим теперь ее с точ-
точки зрения общей теории. Считая V ==¦ 0 в точке О. имеем V = утя?.
Уравнение энергии A.2.9) принимает вид
X ¦+ П X = . 11. Z. 1 / )
т
Постоянная h, очевидно, положительна. Если h — 0, то мы имеем тривиаль-
тривиальный случай, когда частица покоится в точке О: х = 0 все время. Если
А
h положительно и равно h = -к-тп%сг, где с> 0, то функция у = h — V
имеет вид
у = — тпг (с2 — х2) A.2.18)
и движение, очевидно, представляет собой либрацию между значениями ±с.
Гармонический осциллятор является прототипом всех либрационных дви-
движений. Из формулы A.2.12) легко находится период либрации.
Чтобы проинтегрировать уравнение
~2 „2 1Г1 „2\ (Л О <1О\
введем вместо х параметр 9, определяемый формулой х = с cos 9. Без потери
общности можно принять, что 8 всегда возрастает вместе с t. Подставляя
х = с cos 6 в A.2.19), находим, что 9а = и2, откуда 6 = п и9 = л/ — а.
Таким образом, мы вновь приходим к решению A.2.16).
Прежде чем закончить рассмотрение задачи о гармоническом осцилляторе, просле-
проследим еще раз за ходом рассуждений в связи с заменой одного уравнения второго поряд-
порядка A.2.14) двумя уравнениями первого порядка (§ 1.1). Эти уравнения имеют вид
х = и, и= —п2х. A.2.20)
Траектория изображающей точки в плоскости хи представляет собой эллипс
Точка проходит его по движению часовой стрелки. Еще проще в качестве перемен-
переменной взять у ~ х/п. Уравнения при этом записываются в форме
х = пу, у = —пх. A.2.22)
Траекторией изображающей точки в плоскости ху является окружность, проходимая
по ходу часовой стрелки с постоянной угловой скоростью п. В результате мы приходим
к формуле A.2.16). Можно было бы с самого начала заменить независимую переменную t
переменной т = nt, после чего исходное дифференциальное уравнение A.2.14) при-
принимает вид
х" + х — 0. A.2.23)
22 ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ [Гл. I
Штрихами здесь обозначено дифференцирование по т. Это уравнение эквивалентно систе-
системе уравнений
х' - у, у' = -х, A,2.24)
из которых видно, что изображающая точка движется по окружности с угловой скоро-
скоростью, равной единице, и с периодом по т, равным 2я.
Если материальная точка, находящаяся в силовом поле, выведена
из состояния покоя в точке а, в которой функция V (х) класса С2 имеет
минимум, то ее движение приближенно является гармоническим. Для невоз-
невозмущенного движения уравнение энергии A.2.9) имеет вид
-i тх2 = V (а) - V (х) A.2.25)
и кривая V (а) — V (х) касается оси Ох в точке х — а. В точке х = а
функция V (а) — V (х) имеет максимум, и потому кривая в окрестности
этой точки лежит под осью Ох. Если постоянная полной энергии h возра-
возрастает от значения V (а) до значения V (а) -\- 8h, где 8h — малое положитель-
положительное число, то получаем либрацию между двумя значениями, лежащими
вблизи а. Равновесие такого типа называется устойчивым. Уравнение энер-
энергии для возмущенного движения записывается в виде
| F(i). A.2.26)
Подставляя а + | вместо х, получаем
4^ )-F(a)}. A.2.27)
Величина ? остается малой во все время движения, поэтому можно написать
приближенное равенство
1т|2 = бЛ-1г(оN2. A.2.28)
Сравнивая A.2.28) и A.2.19), видим, что возмущенное движение при-
приближенно можно трактовать как гармоническое колебание с периодом 2л/п,
где пг = V" (а)/т, и амплитудой Y'lbhlV" (a).
Пример 1.2В. Однородное силовое поле, В этом
примере сила постоянна по величине и направлению, например, X == тс,
где с > 0. Уравнение движения в этом случае имеет пид
i'= с. A.2.29)
Решение представляется отрезком ряда Тейлора
x = a + bt+~ct2, A.2.30)
где а и Ъ — начальные значения х и х. Равенство A.2.30) может быть
переписано в следующей форме:
x-xo = \c(t-tof, A.2.31)
где хд = а — (Ь2/2с), t0 = — Ыс. В момент I = 10 имее.м х — х0; в последую-
последующие моменты х ^ х0. Уравтгеттие энергии записывается в форме
±х* = с(х-х0). A.2.32)
Этот пример относится к случаю III, так как х —>¦ оо при t-*- <х>.
§ 1.2] ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ В СИЛОВОМ ПОЛЕ 23
Пример 1.2С. Рассматривается поле сил отталкивания, пропорцио-
пропорциональных расстоянию от точки О: .
X = тп2х. A.2.33)
Уравнение движения имеет вид
"х - п2х = 0, A.2.34)
а решение его представляется формулой
х — a ch nt + (b/n) sh nt. A.2.35)
где а и Ъ — значения х и х в момент t = 0. Уравнение энергии записы-
записывается в форме
±-(x2-n2x2) = h. A.2.36)
Если в начальный момент х = а, х = — па, то h = 0 и график функции
h — V представляет собой параболу
у = ±п*з*. A.2.37)
Имеем лимитационное движение, в котором х->-0 при t-y-oo,— пример,
относящийся к случаю II. Решение уравнения A.2.34) при данных началь-
начальных условиях имеет вид
x = ae;ni, A.2.38)
и1->0 при t —»- оо, как это следует из теории.
Если в начальный момент х — а, х = 0, то решением будет
х = a ch n* A.2.39)
и мы будем иметь случай III. Частица уходит в бесконечность гораздо
быстрее, чем в однородном поле. В данном случае х = О (ent), тогда как
в случав однородного поля х = О (t2).
Пример 1.2D. Притяжение по закону \im/rn. При а; > 0
действующая сила равна X = — \im/xn, где п — целое число, большее
единицы. Если частица удаляется от начала координат, начав движение
из точки х = а со скоростью, которой она достигла бы, двигаясь из состоя-
состояния покоя из бесконечности (так что h = 0), то имеем
Формула показывает, что в соответствии с теорией частица движется
в бесконечность. Действительно,
2
? = a(l + to)n+1, A.2.41)
где К = —^-— 1/ .1" п+1. Мы снова имеем случай III. Частица движется
в бесконечность медленнее, чем в однородном поле, так как теперь х =
2
()
Пример 1.2Е. Рассмотрим поле
X = т {- п2х + Зп2х2/Bа)}. п > 0, a > 0. A.2.42)
24
ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
1Гл.
Пусть частица начинает свое движение в момент t = 0 из точки х — а.
где она находилась в состоянии покоя. Решение будет иметь вид
и х -> оо при t ->
энергии имеет вид
A.2.43)
л/п. Этот пример относится к случаю IV. Уравнение
1 1
у х2 = у-
(я — а).
A.2.44)
§ 1.3. Либрационное движение. Рассмотрим более подробно либрацион-
ное движение (случай I). В движении, определяемом уравнением
х% = ф (х),
A.2.1U)
начальное значение х лежит между последовательными простыми вещест-
вещественными нулями а, Ъ функции ф (х). Можно написать
При этом в замкнутом промежутке а
ние A.2.10) принимает теперь форму
ф (х) = (Ъ — х) (х — а) 1|з (х).
х ^ Ъ имеем
(х)
= F - г) (г — а) ф (ж).
A.3.1)
0. Уравне-
УравнеA.3.2)
Знак х зависит от самой задачи, так как при колебательном движении
частица движется попеременно то вправо, то влево. Знак в уравнении
dx
V«P(*)
A.3.3)
должен выбираться таким образом, чтобы при изменении х между предель-
предельными значениями а и Ъ правая часть уравнения A.3.3) всегда была поло-
положительна. Поэтому, когда х возрастает,
следует выбирать знак плюс, а когда х
убывает — знак минус. С этим мы уже
встречались в § 1.2 и встретимся еще
позже.
Для того чтобы избежать в дальней-
дальнейшем возможной путаницы со знаком, целе-
целесообразно ввести новую угловую перемен-
переменную 6, непрерывно возрастающую вместе
с t. Мы будем рассматривать либрацию
как движение проекции на ось Ох точки,
совершающей вращение по окружности.
Точки х = а и х = Ъ будут концами диа-
диаметра этой окружности. Когда точка Q (рис. 2) движется по окружности
в одном и том же направлении, точка Р совершает колебания между точ-
точками А и В. Переменные i и 8 связаны между собой соотношением
Рис. 2.
а
cos 0,
где
а — р = а, а 4- р = Ь
(Ъ - х) (х - а) = р2 sin2 6.
A.3.4)
A.3.5)
A.3.0)
§ 1.3] ЛИБРАЦИОННОЕ ДВИЖЕНИЕ 25
Уравнение A.3.2) принимает теперь вид 02 — г|э (а — Р cos 6), откуда
a-p cos6). A.3.7)
Вопрос о знаке, таким образом, отпадает, поскольку величина 0 положи-
положительна. Если бы функция г|з (х) была постоянна, то постоянным было бы
и значение 0; это мы имеем в частном случае гармонического движения.
Можно написать
X /f\\ /Л О ОЧ
(е). (>
(а-р cos 6)
Функция % @) — четная, везде положительная и периодическая с перио-
периодом 2л. Переменные ( и 0 связаны между собой соотношением
е
*-*<.=-= jx(?)#- A-3.9)
о
Здесь t0 — значение t, при котором х = а; без потери общности можно поло-
положить t0 = 0. Заметим, что 0 = 0 при х = а, а z > 0 в течение полупериода
0< << уа. Период а определяется формулой
2я я
ст= [%(t)<% = 2\%(t)dl. A.3.10)
о о
Можно написать a — 2л/л, где п — среднее значение 0 *).
Чтобы закончить решение задачи, найдем явное выражение х от t.
Поскольку х — четная функция от t с периодом 2п!п. ее можно предста-
представить в общем случае в виде ряда Фурье:
x = -^-ao-\-al cosn?-fa2 cos2n? + . .. A.3.11)
Нам нужно определить коэффициенты а0, а\, а2, ... С этой целью сначала
разложим % F) в ряд Фурье:
X (в) = i сь-bet cos в+ с2 cos 28 f ... A.3.12>
Здесь
*) Период можно также выразить формулой
ь
К(х)
У(Ь—х)(х—а)
dx,
в которой вместо ф (х) стоит 1/{Я (х)}2. Из нее можно получить приближенное выраже-
выражение для периода: я {к (а)-\-К F)}. Это выражение можно также записать в виде-
я F—аI/2 {[ф'(а)]~1//24-[—ф'F)]~1/'2}. Оно дает точное значение периода, если
к (а — р cos 6) линейным образом зависит от 6.
26 ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ 1Гл. X
Имеем
е
I = \ у (?) й? = —- с 0 -+- с sin 9 -I —с sin 28 -1 —с sin 39 4- A3 13)
о
Отсюда
д* = 9 + б A.3.14)
и
оо
б = б(9) = п 2 (Cr/r)sinrd. A.3.15)
r=i
Уравнение A.3.14) связывает ( и 0. Положим ф = nt; тогда точка R
на рис. 1.2, где /iACR = ф, будет равномерно двигаться по окружности.
Но 9 = ф — б и угол б геометрически представляет отклонение рассмат-
рассматриваемого либрационного движения от строго гармонического. Угол б обра-
обращается в нуль, и точка Q совпадает с R, когда R проходит через точки А
и В, т. е. когда t равно целому числу полупериодов.
Теперь определим коэффициенты аг. Поскольку
x = Yao + aicos4l ra2cos2(p+ . .., A.3.16)
мы имеем
я ь
2 С 2 С
аг = — \ х cos гф dq> = \ sin гф dx =
0 а
Я Я
= — -?; \ sinr(psinQdQ = -^- \ {cos(np~fЭ) — соэ(гф — 0)}сЮ A.3.17)
о о
и, так как ф = 9 ~f- б, получаем
л
+ гб] — cos [(r— l)9 + r6]}d9. A.3.18)
Величина б есть известная функция от 6, определяемая формулой A.3.15).
Таким образом, коэффициенты ат в правой части A.3.16) определены, на чем
решение задачи заканчивается.
§ 1.4. Заданная сила не может быть функцией от ускорения. В § 1.1 мы видели,
что заданная сила есть функция от положения, скорости и времени. Некоторые авторы *)
пробовали построить более общую теорию, в которой X, Y, Z зависят не только от пере-
переменных х, у, z; х, у, z; t, но еще от ускорений х, у, z. Эта идея, однако, несовместима
« ньютоновой механикой и противоречит одному из ее важнейших постулатов. Для дока-
доказательства достаточно рассмотреть задачу о прямолинейном движении точки. Пусть точка
массы га совершает движение вдоль оси Ох. Рассмотрим две силы: mq> ('/) и mty (/), где
• • •
/ = х — ускорение точки. Функции ф и if> могут зависеть также от х, и = х и ?, но сейчас
нас в первую очередь интересует зависимость их от /. Рассмотрим три случая. В первом
из них пусть точка находится под действием силы т<р, во втором — под действием силы тф
и в третьем — под действием силы т (ф + if>)- Значения х, и, t пусть будут одними и теми
же во всех трех случаях. Обозначая через /ь /2, /з ускорения в каждом из этих случаев,
находим
h = ф (/i), A-4.1)
h = * (/2), A-4.2)
/3 = Ф (h) + Ф (/з). A-4.3)
*) Например, Дж. Д. В и р к г о ф, Динамические системы, Гостехиздат, 1941,
•стр. 17.
§ 1.5] НЕСВОБОДНАЯ МАТЕРИАЛЬНАЯ ТОЧКА (СЛУЧАЙ I) 27
Первое, что обращает на себя внимание,— это то, что уравнение типа A.4.1) не
обязательно определяет /i единственным образом, что само по себе чуждо ньютоновой
механике. Но даже если на это не обращать внимания и считать, что /1( /2 и /3 определяют-
определяются однозначно, то остаются еще гораздо более серьезные противоречия.
Фундаментальным постулатом ньютоновой механики является утверждение, что
две силы, приложенные к материальной точке, производят такое же действие, как одна
сила, равная их векторной сумме. Эквивалентно этому каждая сила сообщает точке
такое же ускорение, какое она сообщила бы при отсутствии другой силы. Таким образом,
/з = А + /я. A-4.4)
Из этого равенства и равенства A.4.3) получаем
h + h = ф (U + /2) + * (/1 + /2). A-4-5)
Теперь легко видеть, что в общем случае уравнения A.4.1), A.4.2) и A.4.5) несовме-
несовместны. Ибо A.4.1) содержит только значение <р для Д, а A.4.2) — значение if) для /2, причем
ничего нельзя сказать о значениях ф или ф для /j + /2.
В качестве конкретного примера рассмотрим простой случай, когда функции ф и у
линейны:
<р (/) = Af + B,
Ч>(/) = Cf+D.
Можно считать, что А и С не равны нулю, а также единице и, стало быть, существуют
единственные решения для /j и /2. Уравнения A.4.1), A.4.2) и A.4.5), однако, будут
совместны только в том случае, если
ВС A - С) + DA A - А) = 0.
Таким образом, силы, зависящие от ускорения, в ньютоновой динамике неприем-
неприемлемы. Однако не исключено, что они могут встретиться в электродинамике, где выска-
высказанный выше постулат не имеет места.
§ 1.5. Несвободная материальная точка (случай I). Предположим теперь,
что на частицу по-прежнему действует заданная сила (X, Y, Z), но частица
несвободна и вынуждена находиться на заданной гладкой поверхности.
Пусть эта связь будет двухсторонняя (неосвобождающая), а не односторонняя
(освобождающая), когда частица может покинуть поверхность, по которой
она движется. Двухсторонняя связь выражается равенством, тогда как
односторонняя связь — неравенством.
Пусть, далее, ф (х, у, z) = 0, ф ? С2, будет уравнением поверхности.
Тогда координаты частицы х, у, z должны во все моменты времени удовлет-
удовлетворять соотношению
Ф (х, у, z) = 0. A.5.1)
Это условие можно выразить и иным способом. Можно считать, что
составляющие скорости х, у, z связаны между собой однородным линейным
уравнением
*Li + .*Ly+*L; = o, A.5.2)
дх ду " dz v
коэффициенты которого — заданные функции переменных х, у, z класса С\.
Иначе говоря, однородное линейное уравнение
j(te4fdjH45-dZ = 0 A-5.3)
дх • ду * ' dz v '
связывает дифференциалы dx, dy, dz возможного бесконечно малого пере-
перемещения частицы. Нет необходимости подчеркивать, что A.5.3) — точное
уравнение. Оно в точности эквивалентно A.5.2). Каждое их трех уравне-
уравнений A.5.1), A.5.2), A.5.3) мы будем называть уравнением связи. По причи-
причинам, которые вскоре станут ясными, последнее из них — уравнение Пфаф-
Пфаффа — является наиболее удобным.
Заметим, что уравнение связи — будем говорить в данном случае
об уравнении A.5.2) — удовлетворяется всеми возможными составляющими
28 ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ Гл. I
скорости х, у, z, которые могла бы иметь частица, находящаяся в точке
х, у, z. Частица может начать движение из этой точки с любой скоростью,
удовлетворяющей уравнению связи. Когда мы рассматриваем какую-либо
конкретную задачу, в которой частица проходит через точку х, у, z в мо-
момент t, то одна из этих скоростей является действительной. Уравнение
связи, однако, удовлетворяется всеми гипотетическими скоростями, которые
частица могла бы иметь.
Совокупность перемещений dx, dy, dz, которые частица может совершить
за время dt, двигаясь из точки х, у, z, назовем возможными перемещениями
Перемещение, которое частица совершает в действительности за время dt.
находится среди возможных перемещений.
Механизм, посредством которого действительное движение осуществля-
осуществляется в соответствии с уравнением связи, хорошо известен. На частицу
действует дополнительная сила — реакция поверхности. Эта сила направ-
направлена по нормали к поверхности — именно это имеют в виду, когда говорят,
что поверхность гладкая. Это единственное ограничение, наложенное a priori:
величина этой силы никакому ограничению не подчинена. Поверхность
может вызывать нормальную реакцию любой величины (и знака). Величина
этой реакции будет такой, что частица, двигаясь под действием обеих при-
приложенных к ней сил, будет все время оставаться на поверхности.
Реакцию поверхности на частицу называют реакцией связи. Рассмотрим
более подробно природу этой силы. В нашей задаче единственным наложен-
наложенным на реакцию ограничением является требование, чтобы она была нор-
нормальна к поверхности. Пытаясь обобщить это требование, естественно спро-
спросить: «Какова общая характеристика реакции связи, частным примером
которой является реакция поверхности?». Ответ хорошо известен: он дается
принципом виртуальной работы в статике. Реакция связи не совершает
работы на любом возможном перемещении. Справедливость этого утвержде-
утверждения очевидна. Если составляющие, силы реакции обозначить через X', Y'.
Z', то будем иметь
Y' V 7'
А — г _-_?__ (\ с: А\
дх ~ду~ dz
откуда
X'dx + Y'dy + Z'dz = 0 A.5.5)
для любого перемещения dx, dy, dz, удовлетворяющего уравнению свя-
связи A.5.3).
В этом простом примере каждая из действующих сил принадлежит
к одному из двух классов: классу заданных сил и классу реакций связи.
Заметим, между прочим, что в элементарной механике силы часто класси-
классифицируют по другому признаку: их разделяют на внешние и внутренние.
Имеются системы, для которых разделение сил на заданные силы и реакции
связи оказывается несущественным. Однако такие системы в этой книге
рассматриваться не будут.
§ 1.6. Несвободная материальная точка (случай II). Усложним немного
задачу. Пусть теперь частица движется не по фиксированной гладкой поверх-
поверхности, а по изменяющейся гладкой поверхности г|з (х, у, z, t) = 0, г|з ? Сг-
Три формы уравнения связи запишутся следующим образом:
$(х, у, z, 0=0, A.6.1)
§ 1.6] НЕСВОБОДНАЯ МАТЕРИАЛЬНАЯ ТОЧКА (СЛУЧАЙ II) 29
Эти уравнения существенно отличаются от соответствующих уравнений § 1.5.
Прежде всего, коэффициенты новых уравнений зависят, кроме х, у и z,
еще и от t, но это отличие не основное. Фундаментальное различие между
уравнениями A.5.2) и A.6.2) состоит в том, что первое из них есть однород-
однородное линейное уравнение, связывающее составляющие скорости х, г/, z, тогда
как второе не является однородным. Аналогично, уравнение A.6.3) отлича-
отличается от уравнения A.5.3) наличием слагаемого, содержащего dt.
Реакция связи остается нормальной к поверхности, так что
X' Y' Z'
Я«и Л.и Я«и ' ^l.O.^
дх ду dz
но теперь уже неверно утверждение о том, что работа реакции связи на любом
возможном перемещении равна нулю. Мы здесь имеем другой класс переме-
перемещений Ьх, 5у, 6z, удовлетворяющих уравнению
Эти перемещения мы будем называть виртуальными перемещениями; они
существенно отличаются от возможных перемещений. Работа реакции связи
на любом виртуальном перемещении равна нулю. Соответствующие скоро-
• • •
сти х, у, z называются виртуальными скоростями; они удовлетворяют урав-
уравнению
Легко понять физический смысл виртуальных перемещений: это —
те перемещения, которые были бы возможны на поверхности, если в момент t
эту поверхность мгновенно остановить. Приведем простой пример. Пусть
частица перемещается по полу кабины лифта, который поднимается со ско-
скоростью W. Направляя ось z вертикально вверх, мы видим, что возможные
перемещения удовлетворяют равенству
dz — W dt = 0,
тогда как виртуальные перемещения удовлетворяют равенству
8z = 0.
Или через скорости: для возможных скоростей имеем
2 = W,
а для виртуальных скоростей
*z = 0.
Мы видим, что скорости различны: вертикальная составляющая возможных
скоростей равна W, а вертикальная составляющая виртуальных скоростей
равна нулю.
Различие между возможными и виртуальными перемещениями (или
между возможными и виртуальными скоростями) для этого примера весьма
существенно. Этого различия мы не имели в § 1.5, где оба типа перемеще-
перемещений (скоростей) совпадали. Заметим, что уравнение A.6,5) для виртуальных
перемещений очень просто можно получить из уравнения A.6.3) для возмож-
возможных перемещений: достаточно в последнем опустить слагаемое, содержа-
содержащее dt, и заменить dx, dy, dz на 8х, 8у, bz.
30 ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ [Гл. I
§ 1.7. Несвободная материальная точка (случай III). После того как
мы рассмотрели два примера, сделаем одно обобщение.
В приведенных примерах левая часть уравнения связи Пфаффа является
точным дифференциалом, но это обстоятельство ни в коей мере не является
существенным для общего понятия о связях. Уравнение может содержать
любую форму Пфаффа, не обязательно такую, которая допускает интегри-
интегрирующий множитель. В общем случае уравнение связи мы будем записывать
в следующей форме:
a dx + Ъ dy + с dz + р dt = 0, A.7.1)
где а, Ь, с, р — заданные функции переменных х, у, z, t, принадлежащие
классу С±. Перемещения, удовлетворяющие уравнению A.7-1), суть возмож-
возможные перемещения. Виртуальные перемещения удовлетворяют уравнению
а 8х + b 8у + с 8z = 0. A.7.2)
Вместо возможных и виртуальных перемещений можно оперировать
возможными и виртуальными скоростями. Возможные скорости удовлетво-
удовлетворяют уравнению
ах + by + cz + p = 0, A.7.3)
а виртуальные скорости — уравнению
ах + by + cz = 0. A.7.4)
Практически уравнения Пфаффа A.7.1) и A.7.2) обычно более удобны,
чем уравнения A.7.3) и A.7.4).
Сформулируем теперь задачу в общем виде. Материальная точка нахо-
находится под действием заданной силы (X, Y, Z) и реакции связи (X', У,Z').
Реакция связи такова, что работа ее на любом виртуальном перемещении
равна нулю, и движение при действии указанных выше двух сил является
возможным, т. е. действительное движение удовлетворяет уравнению A.7.3).
Теперь легко убедиться, что в общем случае движение может быть
определено. Поскольку
Х'8х + Y'8y + Z'8z = 0 A.7.5)
для всех 8х, 8у, 8z, удовлетворяющих A.7.2), будем иметь
V V 7f
а Ъ с v '
ИЛИ
X' = Ха, У = ХЪ, Z' = Хс. A.7.7)
Таким образом, переменные х, у, z удовлетворяют следующим урав-
уравнениям:
тх = X + Ха, A.7.8)
ту = Y + ХЪ, A.7.9)
m'z = Z + Хс, A.7.10)
а'х + b'y + cz + р = 0. A.7.3)
В общем случае этих четырех уравнений достаточно для определения
четырех неизвестных х, у, z, X как функций независимой переменной t.
Для нахождения решения нужно знать значения х, у, z и х, у, z (удовлет-
(удовлетворяющие A.7.3)) в момент t = 0.
§: 1.8] ГОЛОНОМНЫЕ И НЕГОЛОНОМНЫЕ СИСТЕМЫ 31
Сделаем еще пару замечаний. Геометрически уравнение A.7.2) показы-
показывает, что виртуальное перемещение лежит в плоскости, перпендикулярной
к вектору (а, Ь, с), тогда как из уравнения A.7.6) следует, что реакция
связи направлена вдоль этого вектора. Физический смысл множителя тоже
ясен: он пропорционален величине реакции связи. Реакция связи равна
а2 + Ъг + с2.
Как правило, возможные перемещения и виртуальные перемещения
различаются, однако если р тождественно равнр нулю, то они совпадают.
В этом случае система носит название катастатической. Заметим, что
в катастатической системе коэффициенты а, Ъ, с могут зависеть не только
от х, у, z, но и от t. Для катастатической системы характерно, что 1) воз-
• • •
можные и виртуальные перемещения идентичны и 2) скорость {х, у, z) = О
является возможной скоростью. Система, не являющаяся катастатической,
называется акатастатической.
§ 1.8. Голономные и неголономные системы. Если уравнение связи
Пфаффа A.7.1) интегрируемо (после умножения на соответствующий инте-
интегрирующий множитель), то система называется голономной *). Уравнение
связи в этом случае можно записать в конечной форме:
Ц(х, у, z, t) = 0. A.8.1)
Если уравнение A.7.1) неигнтегрируемо, то система называется неголо-
номной.
Чтобы ответить на вопрос о том, в чем состоит основное различие между
голономными и неголономными системами, достаточно рассмотреть катаста-
тические системы, ограничившись простым случаем, когда коэффициенты
а, Ъ, с не зависят от t.
Если пфаффова форма a dx + b dy + с dz допускает интегрирующий
множитель, то система голономна и уравнение связи записывается в виде
Ф (х, у, z) = const. A.8.2)
Отсюда следует, что из всякой заданной точки (скажем, из начала коорди-
координат) можно достигнуть лишь двухпараметрического множества точек,
а именно множества точек поверхности
Ф (х, у, z) = ф @, 0, 0). A.8.3)
С другой стороны, если система неголономна, то достижимо трехпара-
метрическое множество точек. Пусть уравнение связи задано, например,
в форме
dy — zdx = 0, A.8.4)
не допускающей, очевидно, интегрирующего множителя. В этом случае
можно указать путь, удовлетворяющий условию A.8.4) и ведущий из начала
координат в произвольную точку х2, У2, 22- Для доказательства рассмотрим
путь
y = f(x), z = f'(x), A.8.5)
считая / (х) ? С2. Уравнение связи A.8.4), очевидно, удовлетворяется, и оста-
остается лишь подобрать функцию / (х) таким образом, чтобы удовлетворялись
*) Термин «голономный» происходит от греческих слов okot, (целый, по смыслу
интегрируемый) и v6[xo? (закон). Различие между голономными и неголономными систе-
системами подробно проанализировал Генрих Герц. Будучи человеком редкой гениальности,
он за свою короткую жизнь (он умер в возрасте неполных тридцати семи лет) открыл
электромагнитные волны и написал книгу по основам механики [6]. И то и другое при-
принадлежит к числу важнейших научных достижений.
32 ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ [Гл. I
условия
/ @) = 0, /' @) = 0; / (х2) = у2, /' (х2) = z2. A.8.6)
Из простых геометрических соображений следует, что существует
бесконечное множество таких функций. В частности, поставленным условиям
удовлетворяет любая функция семейства
/ (х) = (Зг/2 — z2x) (xlxzY — Bг/2 — z2x2) {xlx2f +
+ Ах2(х2 — хJ+Б sin2 (nx/x2). A.8.7)
Разность между числом координат и числом уравнений связи назы-
называется числом степеней свободы системы. В рассматриваемом примере мы
имеем три координаты и одно уравнение связи, так что число степеней сво-
свободы равно двум. Важным свойством голономной системы является дости-
достижимость двухпараметрического множества положений из данной началь-
начальной точки. Если же система неголономна, то достижимо трехпараметрическое
множество положений, хотя система по-прежнему обладает двумя степенями
свободы.
Приведенное рассуждение носит общий характер, несмотря на то что
рассмотренное уравнение связи имело специальный вид A.8.4). Общее
неинтегрируемое уравнение Пфаффа с помощью подходящей подстановки
может быть приведено к форме A.8.4) *).
Попутно отметим, что неголономные системы, состоящие из одной точки, практиче-
практически редко встречаются. Простейшим примером, возможно, может служить кривая пресле-
преследования. Точка Q движется по оси Ох по заданному закону Ъ, (?). Частица, положение
которой в момент t определяется координатами х, у, движется в плоскости ху таким
образом, что вектор ее скорости в каждый момент времени направлен в точку Q. Уравне-
Уравнение связи
у dx + (s — х) dy = 0 A.8.8)
не допускает интегрирующего множителя (за исключением тривиального случая, когда
§ постоянно), и система является неголономной.
§ 1.9. Случай двух связей. Рассмотрим теперь частицу, движущуюся в простран-
пространстве под действием заданной силы (X, Y, Z), в случае, когда на нее наложены две связи,
выражаемые уравнениями
со = a dx + Ь dy+ с dz+ p dt = 0 A.9.1)
и
ш' = a' dx + V dy + с' dz+ р dt = 0. A.9.2)
Коэффициенты а, а', ... в этих уравнениях являются заданными функциями х, у, z, t,
принадлежащими классу С\. Здесь возможны три случая.
1. Система уравнений Пфаффа вполне интегрируема, т. е. эквивалентна двум урав-
уравнениям вида
df=O, df' = O. A.9.3)
Уравнения связи могут быть записаны в виде
/ = с, /' = с', A.9.4)
и система является голономной.
2. Существует одна и только одна интегрируемая комбинация уравнений A.9.1)
и A.9.2). В этом случае можно указать множители \i, \i' такие, что сумма [хш + ц'со'
является точным дифференциалом, причем нельзя указать другую интегрируемую комби-
комбинацию, которая была бы независима от первой. (Пфаффова форма ф (/) (\iw + ц'ш')
также представляет собой точный дифференциал, но она эквивалентна предыдущей
форме.)
Уравнения связи могут быть представлены в форме одного конечного соотношенпя
и одного уравнения Пфаффа:
/ = с, ш = 0. A.9.5)
Система является неголономной.
*) Это следует из теоремы Пфаффа; доказательство см., например, в книге: Е. G о и г-
s a t, Probleme de Plaff. Paris. 1922, гл. I.
§ 1.9]
СЛУЧАЙ ДВУХ СВЯЗЕЙ
33
3. Не существует ни одной интегрируемой комбинации, и первоначальная форма
уравнений связи A.9.1), A.9.2) не может быть упрощена. Система неголономна.
Система имеет одну степень свободы. В случае 3 из данной точки можно достигнуть
трехпараметрического множества положений, в случае 2 — двухпараметрического множе-
множества и в случае 1 — однопараметрического множества. Случай 1 мы имеем, например,
когда бусинка скользит по проволоке известной постоянной или переменной формы.
Виртуальные перемещения удовлетворяют уравнениям
а дх + bdy+cdz = O, A.9.6)
а Ьх + Ъ' Ьу + с' 6z = 0. A.9.7)
Работа реакции связи (X', Y', Z') на любом виртуальном перемещении равна нулю:
Х'дх + Y'6y + Z'dz = 0 A.9.8)
при любых Ьх, Ьц, bz, удовлетворяющих уравнениям A.9.6) и A.9.7). Поэтому существуют
множители X, X' такие, что
Яя + А'а', ¦>
Xb + X'b't I
Xc+X'c'. г
A.9.9)
' = Xc+X'c'.
Движение частицы под действием силы (X + X', Y + Y', Z + Z') согласуется
с уравнениями связи A.9.1) и A.9.2). Легко видеть, что движение в общем случае может
быть определено до конца. В самом деле, система няти дифференциальных уравнений
\
A-9-Ю)
'c', \
ах -\- by 4- cz -\- р = 0,
a'x + b'y + c'z + p'^O
позволяет определить х, у, z, Я, X' как функции от t. Ясно, что множители X, X' про-
пропорциональны реакциям двух связей.
В случае трех связей задача становится тривиальной. Три уравнения связи
ax-Jrby-\-cz-\-p = O, \
a"x + b"u4-c"z + p"^=0 *
A.9.11)
определяют х, у, z как функции от х, у, z, t. Мы имеем уравнения первого порядка,
и положение частицы в момент t = 0 определит ее положения в последующие моменты
времени. Уравнения, аналогичные A.9.10), служат лишь для того, чтобы выразить
множители А, X', X", пропорциональные реакциям связи, через составляющие X, Y, Z
заданной силы.
Глава II
МЕХАНИЧЕСКИЕ СИСТЕМЫ
§ 2.1. Система двух материальных точек. В предыдущей главе мы рассмотрели
движение материальной точки, и теперь казалось бы естественным, следуя историческому
развитию механики, перейти к рассмотрению движения твердого тела; именно такого
порядка обычно и придерживаются. В нашем курсе аналитической механики мы, однако,
отступим от сложившейся традиции и от движения материальной точки перейдем непо-
непосредственно к движению механической системы. Твердое тело есть, разумеется, частный
случай механической системы, и в дальнейшем мы его часто будем использовать в каче-
качестве примера.
Основные принципы механики были даны Ньютоном для материальной точки в его
знаменитом сочинении «Математические начала натуральной философии» в 1687 г. Систе-
Систематическое же изучение динамики твердого тела началось приблизительно через полсто-
полстолетия *). В классической механике под твердым телом понимают совокупность материаль-
материальных точек, укрепленных на жестком невесомом «каркасе». Аналогично, под механической
системой в общем случае понимают любую совокупность материальных точек, находя-
находящуюся под действием заданных сил и подчиненную различного рода механическим связям.
Начнем с простого примера. Пусть система состоит из двух материальных точек Pi
и Р2, соединенных легким стержнем длиной а, причем а есть заданная функция времени;
функция a (t) принадлежит классу С4. Для упрощения формул примем, что система
совершдет движение в плоскости z = 0, так что мы будем иметь дело с пространством двух
измерений. Пусть массы частиц равны mi и т2, а заданные силы равны (Х4, У4) и
(Х2, Y2); кроме того, на частицы действует реакция стержня. Координаты частиц
удовлетворяют уравнению связи
(х2 - xtf + (у2 - Vif = а», B.1.1)
а возможные перемещения — уравнению
(х2 — xi) (dx2 — dxi) + (у2 — уг) (dy2 — dyt) — аа dU {2.1.2)
Система имеет три степени свободы.
Рассмотрим теперь уравнения движения
B.1.3)
Реакции связи (Х[, Y[), (X'%, Y'2) обусловлены усилием в стержне. Принимая его рав-
равным Ка, находим
vi V' V V
У2 — У1 x2—Xi У2—У1
B 14
Сумма работ реакций связи равна нулю на любом перемещении бхь byit дх2, ду2, удовле-
удовлетворяющем условию
(х2 - Х1) Fх2 - 6*,) + (у2 - Vi) Fу2 - 6yt) = 0. B.1.5)
Такие перемещения называются виртуальными (см. § 1.6). Физически они означают
перемещения точек при неизменной длине стержня.
*) Работа Даламбера «Traite de dynamique» была опубликована в 1743 г. В русском
переводе [2] она вышла в 1950 г. (Прим. перев.)
§ 2.2] СИСТЕМА МАТЕРИАЛЬНЫХ ТОЧЕК 35
Очевидно, что в общем случае движение может быть определено до конца. Система
пяти дифференциальных уравнений
= X1 — X (х2 —
= Х2-\-'к (Ж2—
B.1.6)
достаточна для определения xt, y4, x2, У2,< Я как функций t.
Мы видим, что картина та же, что в § 1.6. Силы реакции не совершают работы на
любом виртуальном перемещении, и движение системы при действии двух систем сил
(заданных сил и реакций связи) происходит так, что удовлетворяются уравнения связи.
Другим примером системы из двух точек, отличным от только что рассмотренного,
является система из двух свободных точек, совершающая плоское движение под действием
различных сил, включая силы взаимного притяжения. В этом случае связи отсутствуют
и все силы, в том числе силы взаимного притяжения, относятся к заданным силам. Такая
система имеет четыре степени свободы.
Обе системы являются голономными. Вернемся теперь к задаче о частицах, соеди-
соединенных стержнем, и ограничимся рассмотрением того случая, когда длина стержня а
остается постоянной. Это — простейшая модель твердого тела, состоящего всего из двух
частиц. Предположим, что связь такова, что скорость частицы Pi направлена в каждый
момент времени вдоль стержня, так что реакция связи, действующая на Pi, перпендику-
перпендикулярна К стержню. (Такая связь приближенно реализуется в планиметре, где колесико
с острой кромкой может катиться по листу бумаги, но не может скользить в сторону.)
В этом случае имеем два уравнения связи:
(*2 - *i)a + (J/2 - Ш)% = °?, B.1.7)
(У2 — Vi) dxi — (х2 — xi) dyt = 0. B.1.8
Уравнение Пфаффа B.1.8) неинтегрируемо, и система неголономна.
Система имеет две степени свободы, но тем не менее при движении из данной точки
достижимо трехпараметрическое множество положений. Действительно, любое конечное
положение может быть достигнуто из любого начального. Доказательство легко получает-
получается из простых геометрических соображений. С другой стороны, положение системы можно
характеризовать тремя переменными ц, у\, z, где
z=l±zJb- B.1.9)
X2—Xt
есть тангенс угла между осью Ох и стержнем Р\Р2. Уравнение связи Пфаффа прини-
принимает вид
dyi — z dxi = 0. B.1.10)
Такая форма уравнения связи уже рассматривалась в § 1.8, и мы видели там, что
любое конечное положение системы может быть достигнуто из любого начального поло-
положения.
§ 2.2. Система материальных точек. Мы рассмотрели несколько простых
примеров механических систем и проиллюстрировали некоторые фундамен-
фундаментальные понятия динамики. Перейдем теперь к общей теории механических
систем.
Рассмотрим конечное число v частиц и примем, что каждая частица сохра-
сохраняет в процессе движения свою индивидуальность, так что о каждой из них
можно сказать: «Вот частица, которая в момент t = 0 была там-то, а сейчас
находится здесь». Таким образом, мы можем пронумеровать все частицы
и раз навсегда приписать им номера 1, 2, . . ., v. Массу каждой частицы
мы будем считать постоянной (хотя это предположение и не является суще-
существенным для самого понятия механической системы; позже, в гл. XI, мы
рассмотрим случай, когда масса частицы известным образом зависит от ее
скорости). Координаты частиц относительно неподвижной прямоугольной
системы осей будем обозначать через Х\, х2, ¦ . ., xN, где N — 3v, так что
3*
36 МЕХАНИЧЕСКИЕ СИСТЕМЫ [Гл. II
частица под номером г будет иметь координаты хзт-2, ^зг-ь х3г. Массу этой
частицы будем обозначать через от3г_2, тзт_х или т3т. Такой способ обо-
обозначения практически оказывается более удобным.
В тех случаях, когда мы захотим сосредоточить свое внимание на v
частицах, а не на N координатах, мы будем координаты частицы массы т
обозначать через х, у, z, а суммирование по v частицам — через 2. Таким
образом, выражения
2 т (xbx + yby + z8z) B.2.1)
2 тТхТЬхТ B.2.2)
будут обозначать одно и то же. Последнее выражение можно записать немно-
немного проще, если отбросить индексы; тогда будем иметь
Smjp&c B.2.3)
Такую сокращенную форму записи (с отброшенными индексами) мы будем
применять, не опасаясь путаницы, когда будем подразумевать суммирова-
суммирование по N.
Частицы находятся под действием заданных сил Xlt Х2, .... XN;
составляющие силы, действующей на r-ю частицу, будут Хзт-2, X3T-i, X3r.
Задать силы — значит задать их как функции х, х и t.
Иногда Xi, х2, . . ., xN удобно рассматривать как координаты изобра-
изображающей точки в ./V-мерном пространстве. Эту точку, или вектор {хи х2, . . ¦
. . ., xN} мы будем обозначать символом х. Подобным же образом, сила
• •
{Xi, Xz, . . ., XN} будет обозначаться через X, скорость {xi, x2, ...
• •
. . ., xN} — через х или и и т. д.
Возможные перемещения частиц не являются произвольными (за исклю-
исключением задачи v тел, где мы имеем совокупность v свободных частиц): они
связаны L уравнениями связи
N
%ATBdxl + Ardt = 0, г=1,2, ..., L<N. B.2.4)
Коэффициенты Ars, AT — функции класса С\, определенные в некоторой
области значений xi: x2, . . ., xN; t. Уравнения B.2.4) предполагаются
независимыми, а число их — наименьшим. Это означает, что ранг матрицы
из коэффициентов равен L (хотя практически для отдельных значений ж, t
ранг матрицы может быть меньше L). В уравнениях
ЗЛЛ + Л-О, г = 1,2, ...,Д B.2.5)
s=l
* •
можно задать N — L значений х; остальные L значений х определятся из урав-
уравнений. Величина
Л = N - L B.2.6)
определяет число степеней свободы системы; оно равно числу составляющих
скорости, которые могут быть заданы произвольно.
В простейшем и наиболее распространенном случае система уравнений
Пфаффа B.2.4) вполне интегрируема, т. е. эквивалентна L уравнениям вида
dfT = 0, г = 1, 2, . . ., L, B.2.7)
(j 2.2] СИСТЕМА МАТЕРИАЛЬНЫХ ТОЧЕК 37
где
/г = /г (xii Х2> • • -1 xn'i t).
В этом случае система называется голономнои и уравнения связи могут быть
записаны в виде
U = ст. B.2.8)
Практически уравнения связи часто задаются не в форме B.2.4), а в фор-
форме B.2.8), причем постоянные сг имеют заданные значения.
Каковы бы ни были действующие на систему силы, движение ее под-
подчиняется уравнениям связи B.2.5). Процедура, с помощью которой это дости-
достигается, была проиллюстрирована ранее на примерах. Вводятся реакции
связи Х[, Х'2, . . ., X'N (или, короче, реакция связи X'), подчиненные усло-
условию, что они не совершают работы на любом виртуальном перемещении.
Виртуальное перемещение определяется как любое перемещение 6zi, 8x2, ¦ ¦ ¦
. . ., 8хк, удовлетворяющее уравнениям
%ATJ>xt = 0, г =1,2, ...,?. B.2.9)
8=1
Поэтому
j]X's8zs-=0 B.2.10)
8=1
для любого перемещения (8xi: 8х2, ¦ ¦ ., 8xN), удовлетворяющего B.2.9.)
Реакции связи получаются такими, что движение под действием совокупной
системы сил удовлетворяет уравнениям B.2.5).
Изложенная теория позволяет определить движение в общем случае.
Уравнения B.2.10) и B.2.9) показывают, что величины Х[, Х'г, . . ., X'N
могут быть выражены с помощью L множителей Хт:
X's=j\XTATS, 8 = 1,2, ...,N. B.2.11)
r=l
Уравнения движения
i»A = Xs + XI s = 1, 2, . . ., N. B.2.12)
принимают вид
? » *=1,2, ...,N. B.2.13)
r=l
К ним следует присоединить L уравнений связи
N
^+4 = 0, г = 1,2, .... L. B.2.5)
8=1
Система N -\- L уравнений B.2.13) и B.2.5) определяет N -\- L переменных
Xi, х2, . . ., xN; Яь к2, . . ., KL как функции от t. Теоретически можно опре-
определить движение в некотором интервале времени, содержащем момент t = 0,
если заданы значения переменных х ш х при t = 0.
Мы получили уравнения движения произвольной механической системы
в простой и ясной форме. Тем не менее для практики эта форма уравнений
движения не очень удобна. В конкретных задачах нас, как правило, не инте-
интересуют величины К (связанные с величиной реакций связи); по этой причине
мы в следующей главе представим основные уравнения в другой форме,
не вводя множители Я.
38 МЕХАНИЧЕСКИЕ СИСТЕМЫ [Гл. II
§ 2.3. Катастатическая ¦ ;тема. Если в уравнениях связи B.2.4) или
B.2.5) коэффициенты Ат тождественно равны нулю, то система называется
катпастпатической. В § 1.7 мы уже ввели это понятие для случая одной
частицы. Для катастатических систем характерно, что 1) виртуальные пере-
перемещения совпадают с возможными (или, что то же, виртуальные скорости
совпадают с возможными скоростями) и 2) класс виртуальных или возможных
скоростей включает скорости
хТ = 0, г = 1, 2, . . ., N, B.3.1)
т. е. система может находиться в состоянии покоя.
Система, не являющаяся катастатической, называется акапгастатиче-
ской; это понятие уже было введено нами в § 1.7 для случая одной частицы.
§ 2.4. Реакции связей. Применяя теорию, изложенную в предыдущем параграфе,
к конкретным задачам, необходимо уметь выделять силы, относящиеся к категории реак-
реакций связи. На практике это обычно не представляет трудности, так как эти силы нам уже
знакомы из принципа виртуальной работы в статике. Тем не менее представляется полез-
полезным рассмотреть сейчас типы реакций связи, наиболее часто встречающиеся в классиче-
классических задачах. Это придаст абстрактной теории конкретность и приблизит ее к практике.
Сила, действующая на частицу со стороны внешнего агента, является реакцией
связи лишь в том случае, если она не совершает работы на любом виртуальном пере-
перемещении, т. е. если при любом виртуальном перемещении частица перемещается перпен-
перпендикулярно к силе. Это иллюстрируется ниже примерами 1) — 4).
С другой стороны, силы взаимодействия между двумя частицами, принадлежащими
системе, лишь тогда относятся к категории реакций связи, когда сумма работ действия
и противодействия на произвольном виртуальном перемещении равна нулю. Это иллю-
иллюстрируется примерами 5) — 8).
1) Частица, принадлежащая системе, принуждена двигаться по гладкой поверх-
поверхности, которая находится в покое или совершает движение под влиянием внешней силы.
Действие поверхности на частицу проявляется в силе реакции связи: при виртуальном
перемещении частица движется по заданной поверхности, т. е. перпендикулярно к силе.
2) Частица, принадлежащая системе, совершает движение, вызванное внешним
воздействием. Сила, действующая на частицу извне, есть реакция связи. Классическим
примером служит система, представляющая собой твердое тело, одна точка которого
вынуждена двигаться заданным образом.
3) Твердое тело, принадлежащее системе, скользит по гладкой поверхности, кото-
которая находится в покое или совершает движение. Действие гладкой поверхности на тело
представляет собой реакцию связи.
4) Твердое тело, принадлежащее системе, катится без скольжения по поверхности,
находящейся в покое или совершающей движение. В этом случае поверхность обычно
называют идеально шероховатой. Действие такой поверхности на тело представляет собой
реакцию связи.
5) Усилие в стержне, соединяющем две частицы системы и имеющем длину, изме-
изменяющуюся со временем по заданному закону, принадлежит к реакциям связи. Силы,
с которыми стержень действует на частицы, равны по величине и противоположны по
направлению, и при любом виртуальном перемещении составляющие перемещения обеих
частиц в направлении стержня одинаковы.
Простейшим примером является случай, когда расстояние между обеими частицами
остается неизменным. Это условие соблюдается для частиц твердого тела, и система вну-
внутренних реакций в этом случае может быть представлена в виде системы попарно равных
и противоположно направленных сил взаимодействия между частицами.
При виртуальном перемещении твердое тело остается твердым. Но ничто не запре-
запрещает нам рассматривать перемещения деформируемых тел. Следует только помнить, что
в этом случае работа внутренних сил не будет равна нулю.
Другим примером могут служить два шарнирно соединенных твердых тела. Действие
и противодействие (рассматриваемые вместе, а не каждое в отдельности) принадлежат
к реакциям связи.
6) Частица, принадлежащая системе, скользит по гладкой поверхности твердого
тела, которое также принадлежит системе. Действие и противодействие между частицей
и телом относятся к реакциям связи.
7) Действие и противодействие между гладкими поверхностями соприкосновения
двух твердых тел, принадлежащих одной системе, являются реакциями связи.
8) Действие и противодействие между идеально шероховатыми поверхностями
соприкосновения двух твердых тел, принадлежащих одной системе, являются реакция-
реакциями связи.
§ 2.5] К ПОНЯТИЮ О МЕХАНИЧЕСКОЙ СИСТЕМЕ -39
9) Приведенный выше перечень не является исчерпывающим: перечислены только
наиболее часто встречающиеся случаи. Все силы, порождаемые теми или иными типами
связей, относятся к категории реакций связей, если они удовлетворяют основному усло-
условию, а именно если сумма работ их на любом виртуальном перемещении системы рав-
равна нулю.
§ 2.5. К понятию о механической системе. Данное нами определение механической
системы представляет собой обобщение, основанное на ряде конкретных примеров. Нужно,
однако, отметить, что подобное обобщение связано с некоторым произволом в выборе;
оно не есть что-то однозначно предопределенное природой физического мира. Сделанный
нами выбор в целом является одним из наиболее удачных, так как позволяет развить
теорию, достаточно мощную для решения интересующих нас задач. Однако интересно
исследовать и другие возможные определения механической системы, охватывающие
более или менее широкий круг явлений.
Расширение области приложения этого определения может быть достигнуто различ-
различными способами.
1) Мы предполагали до сих пор, что все действующие на частицы системы силы суть
либо заданные силы, либо реакции связи. Можно, однако, дать более широкое определе-
определение, включив такие системы, для которых это разделение сил не имеет места. Рассмотрим,
например, частицу, скользящую по шероховатой поверхности. Реакция такой поверхно-
поверхности на частицу имеет касательную составляющую, направленную противоположно движе-
движению. Ее величина равна величине нормальной составляющей, умноженной на [х, причем
и представляет собой физическую постоянную, зависящую от природы рассматриваемой
поверхности. (В большей части практических задач величина \i принимается одинаковой
для всех точек поверхности.) Реакция поверхности на частицу не является ни заданной
силой, ни реакцией связи, и потому эта задача не охватывается развитой здесь теорией.
(Это не значит, конечно, что подобные задачи нельзя решить.)
2) Наложенные на систему связи мы выражали посредством равенств, но можно было
бы также рассмотреть связи, выражаемые неравенствами. Такие связи называются одно-
односторонними или освобождающими. Простой пример односторонней связи представляет
частица, скользящая по гладкому горизонтальному столу; она может покинуть стол, но
не может пройти сквозь стол. Если ось z направить вертикально вверх, то эту связь можно
выразить неравенством z ^ 0. Принятое нами ранее определение исключает односторон-
односторонние связи, и системы с такими связями нельзя непосредственно исследовать с помощью
методов этой книги. (Можно было бы, конечно, видоизменить теорию соответствующим
образом.)
3) Уравнения связи были заданы нами в форме
• • •
/ (xi, х2, . . ., xN; xi, х2, . . ., xN; t) ¦= 0, B.5.1)
где функции / линейны по аргументам xt, х2, . . ., xN (см. B.2.5)). Кроме того, пред-
предполагалось, что уравнения для виртуальных перемещений вытекают из уравнений для
возможных перемещений (см. B.2.9)). Можно было бы отказаться от ограничения, свя-
связанного с линейностью функций, и считать, что функции / в B.5.1) имеют более общий
вид. В этом случае виртуальные перемещения будут определяться независимыми уравне-
уравнениями и не будут непосредственно следовать из уравнений связи; такие уравнения должны
иметь форму B.2.9).
4) Предположение о том, что реакции связи не совершают работы на произвольном
виртуальном перемещении, можно было бы заменить другим, более широким, например,
предположением, что работа их на любом возможном перемещении измеряется скалярным
произведением перемещения и некоторой дополнительной силы, зависящей от системы.
Уравнение
N
2 X's6xa = 0 B.2.10)
заменилось бы тогда соотношением
2 X's6xs= § ХУЬХ„ B.5.2)
s=l s=l
в котором составляющие X"s суть заданные функции переменных х, х и t.
Сузить область приложения определения механической системы можно по крайней
мере двумя путями.
1) Можно ограничиться рассмотрением систем, которые являются катастатиче-
скими (§ 2.3) и для которых коэффициенты Ars не зависят от t. Уравнения связей B.2.4)
40 МЕХАНИЧЕСКИЕ СИСТЕМЫ Ltti. II
тогда заменились бы уравнениями
N
г-¦¦--!, 2, ..., L, B.5.3)
в которых коэффициенты Ars зависят от xlt х2, ¦ ¦ ., xN.
2) Можно ограничиться рассмотрением голономных систем. Связи в »том случае
выражаются L уравнениями
1т{хи х2, ..., xN; t) = cr. B.2.8)
Такое ограничение привело бы к упрощению теории, но исключило бы и.ч рассмо-
рассмотрения многие важные и интересные задачи.
Вдальнейшем мы будем придерживаться определения механической системы, дан-
данного в § 2.2. Нетрудно сообразить, как следует видоизменить теорию в соответствии
с только что перечисленными ограничениями; значительно труднее установить влияние
какое окажет на теорию расширение основных предпосылок, рассмотренных в начале
этого параграфа.
Глава III
ПЕРВАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ
' § 3.1. Основное уравнение. Рассмотрим механическую систему, опре-
определенную в § 2.2. Имеем N уравнений движения
т^'г = ХТ+ Х'т, г = 1, 2, . . ., N. B.2.12)
Реакции связи Х'г удовлетворяют условию
N
2х;&гг-о B.2.Ю)
для любого виртуального перемещения 6aii, бж2, . . ., 8xN. Отсюда немед-
немедленно вытекает основное уравнение механической системы
%(mrXr-XrNxT = 0. C.1.1)
Это уравнение справедливо для любого виртуального перемещения. Одно-
Одновременно оно является обобщением принципа виртуальной работы в статике
и принципа Даламбера для твердого тела. Важное значение имеет то, что-
это уравнение не содержит реакций связи. Впервые основное уравнение было^
получено в 1760 г. Лагранжем; см. [4]. Оно является основным уравнением
излагаемой нами теории. Мы представим его в нескольких различных фор-
формах и форму C.1.1) будем называть первой формой основного уравнения.
Основное уравнение можно также без труда получить из уравнений
движения B.2.13), приведенных в § 2.2. Умножая г-е уравнение
m=l
= l,2, ...,7V, B.2.13]
на 6хт и суммируя от г = 1 до r = N, находим
N N N
S (mrxr-XrNxT= 2 MS Amrbxr). C.1.2)
r=l m=l r=l
Поскольку 8xi, 8x2, ¦ ¦ ., 8xN — виртуальные перемещения, правая
часть в силу B.2.9) обращается в нуль, и мы вновь приходим к C.1.1).
Пользуясь обозначениями § 2.2, можно записать основное уравне-
уравнение C.1.1) в следующей форме:
S {{nix - X) 8х + (my- Y) 8у + (mz - Z) 62} = 0 C.1.3)
или, в сокращенных обозначениях,
*"— X) 8х = 0. C.1.4)
42 ПЕРВАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ [Гл. III
Напомним, что сокращенные обозначения мы употребляем лишь тогда,
когда суммирование производится по N координатам.
Эту главу мы посвящаем непосредственным приложениям уравне-
уравнения C.1.1).
§ 3.2. Сохранение импульса. Среди виртуальных перемещений может
оказаться такое, при котором вся система как твердое тело перемещается
вдоль оси х без вращения. Тогда для каждой частицы в уравнении C.1.3)
можно положить
Ьх = а, Ьу = 0, bz = 0, C.2.1)
где а — произвольное вещественное число. Уравнение C.1.3) приобретает
при этом форму
Smx = SX. C.2.2)
Этот результат можно упростить. В правой части C.2.2) можно отбро-
отбросить все внутренние силы, так как они попарно равны и противоположны.
В результате получаем равенство
Smx = S'X, C.2.3)
в котором символ ,S" обозначает суммирование по заданным внешним силам.
Сумму в правой части C.2.3) можно было бы, конечно, заменить на сум-
сумму всех внешних сил. В уравнение C.2.3) внешние силы, являющиеся реак-
реакциями связи, не входят, и отсутствие их оправдывается тем, что класс вир-
виртуальных перемещений системы содержит перемещения C.2.1).
В простейшем случае правая часть уравнения C.2.3) равна нулю:
Snix = 0. C.2.4)
"Следовательно,
Smx = const.; C.2.5)
Это равенство выражает теорему о сохранении импульса. Поскольку
Smx = (Sm) I, C.2.6)
где |, г), ? — координаты центра тяжести (центра масс) G системы, равен-
равенство C.2.5) можно переписать в эквивалентной форме:
i = const. C.2.7)
В частном случае, когда система представляет собой твердое тело и сум-
сумма проекций заданных сил на ось х равна нулю, составляющая скорости
центра тяжести G вдоль этой оси остается постоянной. В задаче v тел, где
все заданные силы являются внутренними силами, центр тяжести движется
равномерно и прямолинейно. Можно пользоваться ньютоновой системой
отсчета, в которой центр тяжести находится в покое.
Подобно предыдущему, можно так выбрать класс виртуальных пере-
перемещений, чтобы он включал бесконечно малый поворот всей системы как
твердого тела вокруг оси Oz. В этом случае в уравнении C.1.3) для каж-
каждой частицы можно положить
бх = — у 69, Ьу = х 69, bz = 0. C.2.8)
Тогда будем иметь
Sm (х'у — ух) = S (xY — уХ). C.2.9)
§ 3.3] КАТАСТАТИЧЕСКАЯ СИСТЕМА И ПЕРВАЯ ФОРМА УРАВНЕНИЯ ЭНЕРГИИ 43
Опуская, как и ранее, все внутренние силы в правой части, получаем
Sm {ху — ух) = S' (xY - уХ). C.2.10)
Если сумма моментов внешних сил относительно оси Oz равна нулю, то
xy — y'x) = Q C.2.11)
и, следовательно,
Sm (ху — ух) = const. C.2.12)
Равенство C.2.12) выражает теорему о сохранении момента количеств дви-
движения.
В качестве примера рассмотрим частицу, движущуюся в плоскости
z — 0 под действием центральной силы с центром в точке О; момент ее отно-
относительно центра, таким образом, будет равен нулю. Имеем
ху — ух = const. C.2.13)
Полученный результат выражает теорему площадей: быстрота изменения
площади, ометаемой радиус-вектором точки, остается постоянной.
Другим примером, для которого справедливо равенство C.2.13), может
служить частица, скользящая под действием силы тяжести по гладкой
поверхности вращения, имеющей вертикальную ось Oz. Если в качестве
поверхности вращения взять сферу с центром на оси Oz, то мы будем иметь
сферический маятник.
§ 3.3. Катастатическая система и первая форма уравнения энергии.
В случае катастатической системы — т. е. когда коэффициенты АТ в уравне-
уравнении связи B.2.4) тождественно равны нулю — класс виртуальных скоростей
совпадает с классом возможных скоростей. В частности, действительная
скорость системы является виртуальной скоростью, и в основном уравне-
уравнении C.1.1) вместо Ьхт можно написать хт. Тогда получим уравнение
Л1 m N
2 mTxTxr= 2 Хтхт, C.3.1)
r=l r=l
или
¦§¦=2
r=l
где
Л'
T'-=^^mrxl C.3.3)
r=l
— кинетическая энергия системы. Ее можно записать в следующих эквива-
эквивалентных формах:
f={5m(^4J44 C.3.4)
Т = \^тх\ C.3.5)
Таким образом, кинетическая энергия равна половине суммы произведений
масс точек на квадрат их скоростей.
44 ПЕРВАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ 1Гл. III
Уравнение C.3.2) представляет собой первую, или простейшую, форму
уравнения энергии. Оно выражает тот факт, что скорость изменения кинети-
кинетической энергии равнао скорости, с которой совершается работа заданных
сил. Уравнение справедливо для любой катастатической системы, включая
системы, у которых коэффициенты Ars в уравнениях связи зависят от t.
§ 3.4. Консервативные силы и вторая форма уравнения энергии. До сих
пор мы под х понимали действительные координаты точек с,истемы в момент t
и искали х как функции от t. Рассмотрим теперь все поле координат х.
а не совокупность значений, принимаемых системой в процессе движения.
Координаты х будут временно играть роль независимых переменных.
Пусть заданные силы Х4, Х2, ¦ - ., XN зависят только от х и не зависят
от х и t. Во многих случаях форма Пфаффа 2 %r dxr, фигурирующая в основ-
ном уравнении C.1.1), является полным дифференциалом однородной одно-
однозначной функции — V аргументов хи х2, ¦ . ., xN:
N
2 XrdxT=—dV. C.4.1)
r=l
При этом говорят, что заданные силы консервативны (или что механиче-
механическая система консервативна), а функцию V называют потенциальной энер-
энергией заданных сил (или системы).
Если заданные силы консервативны, то для произвольного замкнутого
контура в ./У-мерном пространстве х справедливо равенство
N
2у J,- п /о / о\
г=1
Этот результат следует непосредственно из C.4.1). Легко видеть, что, и об-
обратно, существование функции V, удовлетворяющей условию C.4.1), выте-
вытекает из C.4.2). В самом деле, значение функции V в точке Р пространства
N
равно интегралу — j ^J XTdxT, взятому по произвольной кривой, соеди-
J r=i
няющей неподвижное начало координат О с точкой Р.
Если система консервативна, то основное уравнение C.1.1) можно запи-
записать в следующей форме:
N
mrxrbxr-\-oV = 0. C.4.3)
В § 1.2 был приведен простой пример консервативной системы, состоя-
состоящей из одной частицы. Другой простой пример представляет частица, дви-
движущаяся в силовом поле —VF. Если поле однородно и вектор напряжен-
напряженности его равен mg и направлен в отрицательную сторону оси Oz, то потен-
потенциальная энергия равна
V = mgz.
Для поля сил притяжения ц>(г) к началу координат О (г = |^а;2+ у2-\- г2)
имеем
§ 3.4] КОНСЕРВАТИВНЫЕ СИЛЫ И ВТОРАЯ ФОРМА УРАВНЕНИЯ ЭНЕРГИИ 45
Другими частными случаями являются 1) изотропный осциллятор, для
которого ф (г) == тп2г, V = -jmnh2, и 2) притяжение по закону Ньютона,
для которого ф (г) = \wi/r2, V = — \am/r. Во всех этих случаях постоянной
интегрирования, можно придать какое угоднр значение; практический инте-
интерес представляет лишь изменение V при переходе системы из одного положе-
положения в другое. Для систем, содержащих много частиц, примером консерва-
консервативной силы может служить сила притяжения между двумя частицами,
когда она зависит от расстояния г между частицами. Если сила притяжения
равна ф (г), то потенциальная энергия определяется интегралом I ф (|) d\.
В частности, еслиф (г) = к (г — о), то потенциальная энергия равна -х- к (г —
— аJ; если ф (г) дается ньютоновским притяжением уМтп/r2, то потенциаль-
потенциальная энергия равна — yJHm/r. В случае трех взаимно притягивающихся
частиц имеем
где nil, niz, m3 — массы частиц, a r^;- — расстояние между частицами i и j.
Обобщение на случай v тел представляется очевидным.
Вернемся теперь к катастатической механической системе и предполо-
предположим, что заданные силы консервативны и потенциальная энергия равна V.
Подставим в выражение для функции V значения координат xt, х2, . . ., xN,
принимаемые в момент t при некотором действительном движении системы.
Теперь V представляет собой не значение потенциальной энергии в произ-
произвольной точке, а ее значение в определенной точке в момент t. При этом
N N
dt — 2j дхт Хг~~ 2
r=l r=l
Учитывая C.3.2), получаем
0. C.4.4)
Отсюда
T + V = h, C.4.5)
где h — постоянная. Уравнение C.4.5) определяет вторую, или классическую,
форму уравнения энергии, или интеграл энергии. Для катастатической систе-
системы, находящейся под действием заданных консервативных сил, сумма кине-
кинетической и потенциальной энергий системы сохраняет постоянное значение
при любом движении системы; значение h в каждом движении определяется
начальными условиями.
Поверхность V = h в iV-мерном пространстве хи х2, ¦ . ., xN называют
поверхностью постоянной энергии для данного движения. Так как Т ^ О,
то в течение всего времени движения системы V sj h.
На первый взгляд может показаться странным, что классическая форма уравнения
энергии сохраняет силу для таких систем, у которых коэффициенты Ars в уравнениях
связи зависят от t. Хотя в большей части случаев, представляющих практический интерес,
;>ти коэффициенты и не зависят от t, все же интересно проиллюстрировать случай зависи-
зависимости коэффициентов от t на простом конкретном примере. Рассмотрим плоское движение
частицы массы ш, находящейся в однородном силовом поле @, mg), при наличии связи
вида t dx — dy = 0. Предположим, что в момент t = 0 частица находится в точ-
точке @, 0) и имеет начальную скорость (и, 0). Уравнения движения будут иметь вид
mic—X', m'y=mg+Y'. C.4.6)
46 ПЕРВАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ [Гл. III
Кроме того,
X' + tY' = 0, у = t'x. C.4.7)
Интегрируя, получаем
± l), C.4.8)
-g)Q, y =
где sh 0 = t. Непосредственной проверкой убеждаемся, что уравнение энергии
^т(х*+у*) — mgy^^mu^ C.4.9)
удовлетворяется.
Прежде чем закончить рассмотрение классической формы уравнения энергии,
заметим, что предположение, принятое нами относительно функций ХТ (= Хг (ж)).
является строго говоря, более сильным, чем это действительно необходимо. Мы предпо-
предполагали, что выражение 2 %г &хт есть точный дифференциал для произвольных вариаций
r=i
dxit dx2, ¦ ¦ ., dxN, тогда как достаточно было считать его точным дифференциалом для
произвольного перемещения системы. (Строго говоря, мы имеем дело с произвольным
виртуальным перемещением, но в данном случае можно опустить слово «виртуальный»,
поскольку речь идет о катастатической системе, для которой виртуальные и возможные
перемещения совпадают.) Приведем простой пример. Предположим, что частица совер-
совершает движение в силовом поле X, Y, Z. Согласно теореме Пфаффа можно представить
пфаффову форму X dx + Y dy + Z dz в виде —dV + 6 (ftp, где V, 0 и ф — функции от
х, у, z. Вообще говоря, таким путем мы еще не получаем уравнения энергии в классичр-
ской форме C.4.5). Но если система подчинена связи
dq> = 0, C.4.10)
то для произвольного (виртуального) перемещения имеем
X dx + Y dy + Z dz = —dV. C.4.11)
Отсюда следует, что классическая форма уравнения энергии C.4.5) сохраняет силу.
Можно отметить, наконец, что встречаются системы, в которых задан-
заданные силы Xi, Xz, . . ., XN зависят как от t, так и от ас и для которых
N
2 Xrdxr=-dsV, C.4.12)
r=l
где V = V (xi, хг, . . ., xN, t) и символ dsV выражает пространственный
N
дифференциал V. —— dxT при фиксированном t. (Простым примером служит
r=l
движение заряженной частицы в однородном магнитном поле, напряжен-
напряженность которого изменяется со временем.) В данном случае мы не имеем клас-
классического интеграла энергии, тем не менее свойство, выражаемое соотноше-
соотношением (ЗЛЛ2у, приводит к упрощению уравнений движения (§ 6.5).
§ 3.5. Третья форма уравнения энергии. Может случиться, что заданные
силы в целом не консервативны, но система образована из двух подсистем,
одна из которых является консервативной. В этом случае можно написать
Хг = Хп + Хг2, C.5.1)
причем слагаемое Xri .зависит от xi, х2, . . ., xN и система сил Xri консер-
консервативна, так что
N
J)Xndxr=-dV. C.5.2)
, r=l
§ 3.7] ПРИНЦИП ГАМИЛЬТОНА 47
При этих условиях уравнение C.3.2) для катастатической системы
приобретает вид
N N N
dT v,V ' i Vv ' dV i "^ v *
-fif — 2j AtiXt + 2j Лг2хг =¦ of + 2j At2^t-
r=l r=l r=l
Отсюда
N
-^r(T + V)=^Xr2xr. C.5.3)
r=l
Мы получили третью форму уравнения энергии. Очевидно, эта форма
включает две предыдущие как частные случаи. Она выражает тот факт,
что скорость изменения полной энергии, кинетической плюс потенциальной,
равна мощности остальных сил, т. е. сил, не даюЩих вклада в потенциаль-
потенциальную энергию V; мы можем смотреть на механическую систему и консерватив-
консервативные силы как на нечто физически целое, для которого остальные силы явля-
являются посторонними.
§ 3.6. Сохранение энергии. Формула C.4.5), выражающая классический
интеграл энергии, играет важную роль во всей механике. Ее значение
не ограничивается рамками классической механики и распространяется
буквально на все области физических наук. Например, работа, затрачивае-
затрачиваемая на растяжение струны, переходит в энергию натянутой струны. Если
один конец струны закреплен, а другой соединен с частицей, то при осво-
освобождении струны запасенная в ней энергия переходит в кинетическую
энергию частицы. Общий закон о сохранении энергии занимает столь важное
место в нашем представлении о физическом мире, что, даже встречаясь с ди-
динамической задачей, в которой энергия не сохраняется, мы предпочитаем
говорить, что энергия не уничтожается, а переходит в другую форму, отлич-
отличную от кинетической или потенциальной энергии механической системы
(например, в тепло). Тем не менее, несмотря на всеобъемлющий характер
этого принципа для физики в целом, не следует придавать уравнению C.4.5)
большее значение, чем оно имеет в действительности. Мы будем рассматри-
рассматривать его как чрезвычайно простой первый интеграл уравнений движения.
§ 3.7. Принцип Гамильтона *). Основное уравнение дает возможность
без труда получить изящную теорему, известную под названием принципа
Гамильтона. Рассмотрим движение механической системы в промежутке
времени от to до t\. Рассмотрим затем для каждого момента времени виртуаль-
виртуальное перемещение б^, бх2, ¦ ¦ ., bxN из положения хг, х2, . . ., xN, занима-
занимаемого в действительном движении. Виртуальное перемещение произвольно,
за исключением того, что его составляющие 8х\, Ьх2, . ¦ ., bxN суть функ-
функции от t, принадлежащие классу С2 и обращающиеся в нуль в моменты t^
и t\. О последовательности положений ас + бас можно говорить как о варьиро-
варьированном пути; следует, однако, отдавать себе ясный отчет, что это не есть
возможный путь, т. е. путь, удовлетворяющий уравнениям связи. В самом
деле, в случае неголономной системы варьированный путь, вообще говоря,
не является возможным (§ 3.8).
Обозначим через ЬТ разность между значением Т в момент t на варьиро-
варьированном пути и значением Т в тот же момент в действительном движении.
Пользуясь сокращенными обозначениями (§ 2.2), находим
6Г = у 2 т{(х + 6жJ-х2} = 2 тх б^ + Т 2
*) Принцип Гамильтона содержится в его первом знаменитом сочинении
1834 г. [16].
48 ПЕРВАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ [Гл. III
где суммирование совершается по всем N координатам. Предположим теперь,
что величины 8х и 8х — малые порядка е, и отбросим слагаемые порядка е2.
Тогда справедливо соотношение
ЬТ —^тхЬх C.7.1)
и, поскольку вариации синхронны,
bx — -j--bx. C.7.2)
Отсюда
- 1 71 IIVJL KjUy III 1 7. fllti- '~j,~ \\J**sj \ль
to to
= 2 mx $x x ~~ \ 2 mx
(o
Первое слагаемое в правой части равно нулю, так как в моменты t0 и ts
8х обращается в нуль. В результате получаем
dt= - j |^ {тх-Х) ЬхХ dt. C.7.3)
t0 (о
Поскольку бас есть виртуальное перемещение, правая часть в этом равен-
равенстве в силу основного уравнения C.1.1) обращается в нуль, и мы приходим
к равенству
п
j ( 2 ) C.7.4)
Оно выражает известный принцип Гамильтона. Если заданные силы консер-
консервативны, то C.7.4) можно записать в виде
J 6(Г —7)& = 0. C.7.5)
«о
Применяя принцип Гамильтона, следует помнить, что концевые точки,
а также начальный и конечный моменты времени фиксированы.
Таким образом, мы доказали, что, отправляясь от действительного движения и варьи-
варьируя путь указанным выше способом, мы приходим к равенству C.7.4), которое выражает
необходимое условие движения. Это условие, однако, является также и достаточным.
Если х (t) есть геометрически возможное движение системы, т. е. путь в TV-мерном про-
пространстве, удовлетворяющий условиям B.2.5), и если равенство C.7.4) справедливо для
произвольной вариации описанного типа, то исходное движение является действительным
{динамически возможным) движением системы. Для доказательства заметим, что усло-
условие C.7.4) означает, что правая часть равенства C.7.3) обращается в нуль для всех вариа-
вариаций дх описанного выше типа. Ранг матрицы (Ars) в уравнениях B.2.9) равен L, поэтому
наиболее общее виртуальное перемещение дх в момент t является линейной комбинацией
к независимых перемещений ба5A), бж<2), . . ., 6aJ<h), так что r-я компонента 6х, т. е. Ьхг
может быть представлена в форме
h
8=1
В результате получаем
JV
2 Х° [ 2 ^г~ХТ) 6*<*>] | dt = 0. C.7.7)
s=l г=1
§ 3.8] ВАРЬИРОВАННЫЙ ПУТЬ 49
Множители X — функции от t, непрерывные в промежутке [t0, tj и обращающиеся в нуль
в моменты t0 и (t, а в остальном произвольные; поэтому коэффициент при каждом К
в подынтегральной функции C.7.7) должен быть равен нулю. Это показывает, что в каж-
каждый момент времени удовлетворяется основное уравнение C.1.1), и, следовательно, исход-
исходное движение является динамически возможным.
Если система голономна, то вместо C.7.5) можем написать
r — V)dt = O. C.7.8)
J
'о
В этом случае значение интеграла \ (Т — V) dt, принимаемое в действитель-
(о ¦ ¦
ном движении, стационарно по отношению к его значениям в близких к нему
движениях с одними и теми же концевыми значениями координат и одними
и теми же значениями начального и конечного моментов времени. Если,
однако, система не является голономной, то от уравнения C.7.5) нельзя
перейти к C.7.8), если только не трактовать последнее условно как экви-
эквивалентное C.7.5) в некотором смысле. Если же система неголономна и C.7.8)
интерпретируется естественным образом как условие стационарности интег-
A
рала \ (Т — V) dt по отношению к геометрически возможным соседним путям
(о
с теми же концевыми точками и теми же начальным и конечным моментами
времени, то утверждение C.7.8) перестает быть верным. К этому вопросу
мы еще вернемся в гл. XXVI.
Принцип Гамильтона представляет большой теоретический интерес,
но практическое значение его для решения задач невелико. По существу,
он выражает основное уравнение в проинтегрированном виде. Результаты,
получаемые с помощью принципа Гамильтона, практически обычно могут
быть получены более быстрым путем непосредственно из основного уравне-
уравнения. В § 3.9 приведены два примера, относящиеся к системам с непрерывно
распределенной массой; они это достаточно ясно иллюстрируют. Результа-
Результаты, полученные в § 3.9 из основного уравнения, могут быть получены и из
принципа Гамильтона, но, как легко видеть, первый путь является более
коротким.
§ 3.8. Варьированный путь. Используемый в принципе Гамильтона
варьированный путь, вообще говоря, не является возможным, если система
неголономна, иначе говоря, система не может следовать по варьированному
пути без нарушения наложенных на нее связей. Для доказательства этого
утверждения достаточно рассмотреть простой конкретный пример.
Пусть частица движется в пространстве, и пусть на нее наложена связь,
выражаемая уравнением
со =з a dx + Ъ dy + с dz = 0, C.8.1)
где а, Ъ и с — функции от х, у, z класса Си и форма Пфаффа со не допускает
интегрирующего множителя. Исходная траектория, несомненно, удовлетво-
удовлетворяет условию C.8.1). Это же, согласно предположению, справедливо для
вариаций траектории. Таким образом, *имеем
ах + by + cz = 0, C.8.2)
а 8х + Ъ Ьу + с бг = 0. C.8.3)
4 л. Л. Паре
50 ПЕРВАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ [Гл. III
Спрашивается, удовлетворяет ли варьированный путь этим условиям?
Предположим, что это так, т. е. что справедливо равенство
б (ах + by + cz) = 0. C.8.4)
Условие C.8.3) соблюдается в любой момент времени, так что
-^¦(а8х+Ъ&у + с&г) = 0. C.8.5)
Вычитая C.8.4) из C.8.5) и пользуясь C.7.2), находим
1^-Ьх-хЬа) + (^-8y-y8b) + (-^6z-z6c) =0, C.8.6)
или, подробнее,
Но согласно C.8.2) и C.8.3)
ydz—zdy zbx— x6z xby — уЬх
*
и поэтому (оставляя в стороне тривиальный случай, когда Ьх/х — Ьу/у =---
= бг/г и перемещение происходит вдоль самой исходной траектории), учиты-
учитывая C.8.6) и C.8.7), находим *)
I дс дЬ\ ,1 да дс \ I дЪ да \ „ /ч о о\
\ ду dz I ' \ dz дх I ' V дх ду I ч '
Но равенство C.8.8) невозможно, поскольку уравнение C.8.1) неин-
тегрируемо. Предположение, что варьированный путь геометрически возмо-
возможен, приводит, таким образом, к противоречию **).
В случае голономной системы этой трудности не возникает и варьиро-
варьированный путь всегда оказывается возможным.
§ 3.9. Распределенные системы. В классической механике изучаются
главным образом системы, имеющие конечное число степеней свободы, о них
в основном и будет идти речь в этой книге. Тем не менее естественно пред-
предположить, основываясь на физических соображениях, что основное уравне-
уравнение справедливо также и для распределенных систем, имеющих бесконечное
число степеней свободы, например движущейся жидкости или колеблющей-
колеблющейся струны.
В таких задачах суммирование в основном уравнении заменяется интег-
интегрированием. В этом параграфе мы рассмотрим два таких примера. Сначала
рассмотрим задачу классической гидродинамики.
1) Идеальная (невязкая) несжимаемая жидкость находится под дей-
действием заданных сил и заключена между внутренней и внешней границами,
*) Уравнение C.8.8) является условием существования интегрирующего множителя
для формы Пфаффа C.8.1). (Прим. перев.)
**) Приведенный здесь пример (показывающий, что варьированный путь для неголо-
номиой системы, вообще говоря, не является возможяым путем) представляется наиболее
естественным. Его рассматривали многие ученые, работавшие в этой области механики.
Он содержится, например, в известной работе Гёльдера о вариационных принципах дина-
динамики: О. Гёльдер, О принципах Гамильтона и Мопертюи, в сборнике «Вариационные
принципы механики» под ред. Л. С Полака, М., Физматгиз, 1959. Другие примеры
см. в § 5.11.
§ 3.9] ' РАСПРЕДЕЛЕННЫЕ СИСТЕМЫ 51
которые либо находятся в покое, либо совершают движение. Движение
границ должно быть таким, чтобы заключенный между ними объем оставался
неизменным; это условие автоматически выполняется, если границы пред-
представляют собой твердые поверхности.
Но здесь мы наталкиваемся на трудность. Движение жидкости пол-
полностью определяется движением ее границ, каковы бы ни были действующие
на жидкость силы. Что же в таком случае можно получить из основного
уравнения?
Оказывается, что основное уравнение устанавливает существование
функции давления, при помощи которой полностью описываются внутрен-
внутренние напряжения в жидкости.
Основное уравнение для непрерывных систем имеет вид
{V-X)u + (g-Y)v + (h-Z)w}dT = O. C.9J)
В этом уравнении р обозначает плотность жидкости (не обязательно одно-
однородной), f,g,h — составляющие ускорения, X, Y, Z — составляющие
заданной силы на единицу массы жидкости, и, v, w — составляющие произ-
произвольной виртуальной скорости. Интегрирование производится по всему
пространству, занятому жидкостью. Уравнение C.9.1) можно записать
в векторной форме:
\p-Udx = 0. C.9.2)
Здесь Р есть вектор {р (/ — X), р (g — У), р (h — Z)}, а виртуальная ско-
скорость U такова, что div TJ = 0 и нормальная составляющая Un на гранич-
граничной поверхности S обращается в нуль. Если
C.9.3)
то удовлетворяется уравнение неразрывности. Полагая
A = Q Уф, C.9.4)
где 0 и ф — скалярные функции класса Сг, получаем
U — rot А — V0 х Уф. C.9.5)
Линии тока поля виртуальных скоростей (с фиксированными гранич-
граничными поверхностями) представляют собой линии пересечения поверхностей
0 = const и ф = const, так что если в качестве 0 мы выбираем функцию,
которая на поверхности S обращается в нуль, то на этой поверхности обра-
обращается в нуль и Un.
Основное уравнение C.9.2) принимает теперь вид
J (P-votA)dx = 0. C.9.6)
С помощью векторного тождества
div (РЖ A) = A'TotP — P-rotA C.9.7)
уравнение C.9.6) можно привести к виду
f (A -rot P) dx = f div (P X A) dx. C.9.8)
Интеграл в правой части этого равенства обращается в нуль, так как он равен
интегралу от нормальной составляющей вектора Р х А по границе S,
а последний равен нулю, поскольку вектор А на границе S обращается
в нуль. Таким образом,
¦ = 0, C.9.9)
4*
52 ПЕРВАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ [Гл. III
и это равенство справедливо для всех функций 0 класса С2, обращающихся
в нуль на поверхности S. Поэтому в каждой точке жидкости
V(p.rotl> = 0. C.9.10)
Отсюда легко вывести, что всюду в жидкости
rot JP = 0. C.9.11)
(Можно, например, положить ф = х; тогда из C.9.10) видно, что составляю-
составляющая х вектора rot P равна нулю.)
Поскольку равенство C.9.11) справедливо в любой точке жидкости,
существует скалярная функция р такая, что
JP == — grad p, C.9.12)
и, следовательно,
P ду '
C.9.13)
p dz
Таким образом, мы получили уравнения движения жидкости; здесь р —
функция давления.
2) В качестве второго примера сплошной системы рассмотрим задачу
о колеблющейся струне. Однородная упругая струна натянута силой Р;
концы струны х = 0 и х = I неподвижно закреплены на оси Ох. Струна при-
принимается идеально гибкой, и рассматриваются малые поперечные колебания
в плоскости z = 0. Натяжение струны в процессе ее движения остается посто-
постоянным.
Изменяя надлежащим образом уравнение C.4.3), можем написать для
сплошной системы
i
V = 0. C.9.14)
Здесь р — масса (постоянная) единицы длины, а у (х, t) — поперечное пере-
перемещение струны. Уравнение C.9.14) справедливо для любого момента t = U,
а виртуальное перемещение Ьу (х) принадлежит классу С2 в промежутке
0 ^ х ^ Z, причем в точках х = 0тих — 1Ьу = О. Кроме того,
О к = ir ОЛ, \o.\j.lD)
где Я. — длина струны в смещенном положении в момент t\.
i
К= \ Y^ + y'^dx C.9.16)
I
(производная ду/дх обозначена здесь через у'). Уравнение C.9.14) можно
записать теперь в виде
2 I
р Г y6ydx + P \ y'8y'dx = 0. C.9.17)
о {
Так как Ьу' = -^— Ьу, то, интегрируя по частям и учитывая, что при
х = 0 и х = 1 8у~0, находим
j (У- сУ) by dx = 0. C.9.18)
§ 3.9] РАСПРЕДЕЛЕННЫЕ СИСТЕМЫ 53
Здесь с2 = Pip, а у'' обозначает производную д2у/дх2. Равенство C.9.18)
верно в любой момент времени для любого бг/ описанного выше типа. Отсюда
следует, что функция у (х, t) должна удовлетворять дифференциальному
уравнению
Это — волновое уравнение, описывающее поперечные колебания струны.
Мы его получили для струны конечной длины I, но оно справедливо и для
бесконечной или полубесконечной струны. Уравнение получило название
волнового благодаря тому, что ему удовлетворяет решение / (х — ct), где
/ (х) — произвольная функция класса С2. Таким образом, решение
у = f(x — ct) C.9.20)
представляет волну, распространяющуюся по струне в направлении возра-
возрастания х. Решение
y=f(z + ct) C.9.21)
представляет волну, распространяющуюся в противоположном направлении.
Глава IV
ВТОРАЯ И ТРЕТЬЯ ФОРМЫ ОСНОВНОГО УРАВНЕНИЯ
§ 4.1. Вторая форма основного уравнения. При любом возможном дви-
движении системы удовлетворяются уравнения связи
N
2Ла + Л = 0, г=ь1,2, ...,?. B.2.5)
s=l
Пусть
хг + Ахи х2 + Ах2, . . ., хп + Ахп
будут какие-нибудь другие возможные скорости в том же положении систе-
системы и в тот же момент времени. Они также удовлетворяют уравнению
+ AT = 0, r=l,2, ...,L. D.1.1)
8=1
Из уравнений B.2.5) и D.1.1) получаем
N
2ЛАс. = 0, r = l,2,...,L. D.1.2)
8=1
Конечные приращения скорости Axit Ax2, . . ., AxN удовлетворяют урав-
уравнениям B.2.9) для виртуальных перемещений; поэтому в основном уравне-
уравнении C.1.1) можно вместо 8хг написать Ахт. Таким путем приходим к урав-
уравнению
^j (mTxr — Xr) AxT = 0, D.1.3)
r=l
представляющему собой вторую форму основного уравнения. Его можно
записать в эквивалентном виде:
S {(тх — X) Ах + (ту — Y) Ay + (mz — Z) Az} = 0. D.1.4)
Во второй форме основного уравнения конфигурацию системы и момент
времени мы предполагаем заданными и рассматриваем два состояния системы
при одной и той же конфигурации и в один и тот же момент времени, отли-
отличающиеся лишь скоростями, причем возможные значения скорости отличают-
отличаются на конечную, а не на бесконечно малую величину. В простейшем случае Ах
представляет собой бесконечно малую разность между близкой к действи-
действительной возможной скоростью и действительной скоростью *). Однако резуль-
результат справедлив и в более общем случае, когда Ах — конечная разность
между двумя любыми возможными скоростями.
Из уравнения D.1.3) легко получить уравнение энергии для катаста-
тической системы. Для этого достаточно в уравнение D.1.3) вместо Ах под-
подставить действительную скорость ж; проделав это, мы получим уравне-
уравнение C.3.2).
*) Этот случай был рассмотрен Ф. Э. В. Журдэном в 1908 г.
§ 4.21 ТРЕТЬЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ 55
Вторая форма основного уравнения находит применение в теории удара}
этот вопрос будет рассмотрен в гл. XIV.
§ 4.2. Третья форма основного уравнения. При любом возможном дви-
движении системы в каждый момент времени удовлетворяются уравнения
связи
N
5МгвЯ« + Л = 0, г=1,2, ...,?. B.2.5)
s=l
Дифференцируя их по t, получаем
N
s=l
Оператор -=— означает
N
Если теперь рассмотреть два возможных движения системы при одной
и той же конфигурации в момент t и одинаковых скоростях, но различных
ускорениях х и х + Ах, то, помимо D.2.1), будем иметь
JV
--^ = 0, г = 1,2, ..., L. D.2.3)
Из уравнений D.2.1) и D.2.3) получаем
N
Конечные приращения ускорения Axj, Az2, . . ., AxN удовлетворяют
уравнениям B.2.9) для виртуальных перемещений; поэтому в основном урав-
уравнении C.1.1) вместо 8хг можно написать Ахг. Проделав это, получим соот-
соотношение
r=l
D.2.4)
представляющее третью форму основного уравнения. Его можно записать
также в виде
S {{nix — X) Ах+ (ту — У) А'у'+ (mz — Z) Az) = 0. D.2.5)
В третьей форме основного уравнения конфигурация системы, скорость
и время считаются заданными и рассматриваются два состояния системы,
отличающиеся только ускорениями, причем возможные приращения уско-
ускорения имеют конечную величину, а не бесконечно малую. В простейшем
случае Ах представляет собой бесконечно малую разность между близким
к действительному возможным ускорением и действительным ускорением*).
Однако результат справедлив и в более общем случае, когда Ах — конечная
разность между двумя любыми возможными ускорениями.
В этой форме уравнение применяли Гаусс и Гиббс.
56 ВТОРАЯ И ТРЕТЬЯ ФОРМЫ ОСНОВНОГО УРАВНЕНИЯ [Гл. IV
t' Итак, в первой форме основного уравнения рассматривается бесконечно
малое виртуальное перемещение из заданной конфигурации системы, во вто-
второй форме координаты не варьируются и рассматривается возможное при-
приращение (не обязательно малое) скорости и в третьей форме координаты
й скорости не варьируются и рассматривается возможное приращение (не обя-
обязательно малое) ускорения.
§ 4.3. Принцип Гаусса наименьшего принуждения *). Пусть заданы
конфигурация и скорость системы в момент времени t. Напишем выражение
(^) D.3.1)
r=l
•••• •• ••
зависящее от хх, х2, ¦ ¦ ., xN, и будем рассматривать те значения эс, которые
возможны при заданных конфигурации и скорости системы. Принцип Гаусса
утверждает, что в этом классе значений х выражение С для истинного уско-
ускорения минимально. Иными словами, для истинного ускорения выражение С
принимает меньшее значение, чем для любого другого возможного ускорения.
Эта теорема была открыта Гауссом в 1829 г. Доказательство ее очень
• • • • • •
просто. Пусть х— истинное ускорение, а ж -\- Дэс — любое другое возмож-
возможное ускорение. Пользуясь сокращенными обозначениями, можем написать
= у 2 т (Дж)в+ 2 (тх-Х) Ах. D.3.2)
Последняя сумма в силу D.2.4) обращается в нуль. Таким образом,
АС > 0, D.3.3)
• •
если только Аас отлично от нуля.
Уравнения движения заданной системы получаются как следствие более
слабого условия, а именно условия стационарности С для истинного дви-
движения. Чтобы получить эти уравнения, достаточно 'написать равенство
6С = 0. D.3.4)
Отметим, что в принципе Гаусса мы имеем дело с простой алгебраиче-
алгебраической задачей о минимизации квадратичной формы. Осуществляя эту миними-
минимизацию, мы получаем дифференциальные уравнения движения.
§ 4.4. Приложения принципа Гаусса. Принцип Гаусса тесным образом
связан с уравнениями движения в форме Гиббса — Аппеля, которые будут
рассмотрены в гл. XII и XIII; там же будут приведены решения более слож-
сложных задач. Здесь же мы ограничимся несколькими простыми примерами.
Пример 4.4А. Машина Атвуда. Две массы М и т соединены
легкой нерастяжимой нитью, перекинутой через гладкий блок, и движутся
по вертикали. Определить движение масс.
Если/ — ускорение массы т, движущейся вверх, и массы М, движущей-
движущейся вниз, то можем написать
±g)*}. D.4.1)
*) Оригинальное изложение принципа Гаусса наименьшего принуждения см.
в работе: К. Г а у с с, Об одном новом общем принципе механики, в сборнике «Вариацион-
«Вариационные принципы механики» под ред. Л. С. Полака, М., Физматгиз, 1959.
§ 4.4]
ПРИЛОЖЕНИЯ ПРИНЦИПА ГАУССА
57
Отсюда
Выражение С достигает минимума при
, М—т
D.4.2)
так что ускорение имеет постоянное значение. Еще проще этот результат
получается из условия
df u'
выражающего стационарность функции С.
Пример 4.4В. Обезьяна и противовес. Пусть теперь
вместо груза массы т на конце нити находится обезьяна той же массы,
и пусть она лезет вверх по нити. Положение обезьяны относительно нити
в момент t зададим функцией ф (t) класса Сг и будем предполагать, что пер-
первоначально система находилась в покое и что ф @) == ср @) = 0.
Если через z обозначить вертикальную координату обезьяны (рассмат-
(рассматриваемой как материальная точка), а через ?, — координату противовеса
в момент t, то выражение С запишется в следующей форме:
± V . D.4.4)
D.4.5)
Пусть при г = 0 z = ? = 0; тогда z + ? = ф и
С = 1 {т (z+ g)* + М (ф -V + gf).
Требуется определить значение z, минимизирующее выражение С. Оно нахо-
находится из уравнения
(М+т)'г = Му-\-(М — m)g. D.4.6)
Решение этого дифференциального уравнения имеет вид
(М+т)г = Мц> + ~(М—т) gt2. D.4.7)
В частном случае, когда М = т, получаем z= 5 =тФ> т- е- обезьяна
и противовес находятся на одной и той же высоте.
Пример 4.4С. Частица на движущейся наклон-
наклонной плоскости. Клин массы М скользит по столу, а частица массы т
движется по наклонной плоскости клина, образующей с плоскостью стола
угол а. Все поверхности гладкие* Движение происходит в вертикальной
плоскости, проходящей через линию наибольшего наклона. Найти движение
частицы.
Если через / обозначить ускорение клина в момент t, а через /' — уско-
ускорение частицы относительно клина в этот же момент времени, то выражение
для С запишется в виде
| 1 gJ}. D.4.8)
D.4.9)
Из уравнений dC/df = O и dC/df = 0 находим
та cos a M-\-m
Следовательно, / и /' постоянны.
58 ВТОРАЯ И ТРЕТЬЯ ФОРМЫ ОСНОВНОГО УРАВНЕНИЯ [Гл. IV
§ 4.5. Физический смысл принципа Гаусса. Рассмотрим систему, заданную в момент
• • •
t координатами ху, х2, ¦ ¦ ., xN и скоростями х4, х2, . . ., xN. Требуется определить уско-
• • ¦
рения xt, x2, ¦ ¦ ., xN.
Пусть а — положение некоторой частицы в момент *, а с — ее положение в момент
t + dt в действительном движении. Обозначим через Ъ положение этой частицы в момент
t -j- dt, которое она занимала бы, если бы не было наложено связей, т. е. под действием
одних только заданных сил. (В общем случае конфигурация положений Ь, конечно,
невозможна.) Тогда составляющая ас по оси х приближенно будет равна
D.5.1)
а составляющая ab по оси х—
г<й + -г dt2. D.5.2)
2 m
Отсюда
2Sfti (bc^z^dt^C, D.5.3)
и физический смысл принципа Гаусса заключается в том, что действительное ускорение
минимизирует величину 25m (beJ, при любом другом ускорении эта величина была бы
больше. Если, следуя Гауссу, сумму 2Sm (beJ принять за меру отклонения системы от
того движения, которое она имела бы при отсутствии связей, то можно сказать, что систе-
система имеет движение, наиболее близкое к свободному.
Глава V
ЛАГРАНЖЕВЫ КООРДИНАТЫ
§ 5.1. Выбор лагранжевых координат *). До сих пор мы пользовались
декартовыми координатами. В дальнейшем мы не будем себя связывать
ограничениями в выборе системы координат и перейдем к координатам более
общего типа. Введение таких координат может быть сопряжено с известными
трудностями, однако это — трудности скорее алгебраического характера,
чем динамического. Нужно отличать трудности, присущие самому изучаемо-
изучаемому явлению, от трудностей, связанных с выбранной системой координат.
Выбор лагранжевых координат производится следующим образом.
Выбираются п параметров qt, q2, . . ., qn, значения которых определяют
конфигурацию системы в момент времени t. Декартовы координаты Х\, х2, ...
. . ., xN точек системы будут некоторыми функциями от q и t. (В большей
части случаев координаты х являются функциями только от q и не зависят
от t.) Выбор координат qu q2, . . ., qn должен быть произведен таким обра-
образом, чтобы их значения представляли все возможные конфигурации систе-
системы, а не некоторую совокупность возможных конфигураций.
Как мы увидим, для голономной системы число п можно взять равным
числу степеней свободы к. Для неголономной системы наименьшее значе-
значение п равно к + I, где I есть инвариант системы, определяемый уравнениями
связи.
В дальнейшем (§§ 5.7 и 5.8) будет указана формальная процедура пере-
перехода от декартовых координат к лагранжевым. Однако в ряде задач выбор
лагранжевых координат напрашивается сам, и потому нет необходимости
обращаться к формальным методам, развитым для общей механической
системы.
Ниже приводятся несколько примеров.
1) Простой маятник. Тяжелая точка движется без трения
по окружности в вертикальной плоскости. Такое движение можно осущест-
осуществить, например, заставив бусинку скользить по гладкой проволоке, изогну-
изогнутой в форме окружности радиуса а. Или же можно частицу соединить с кон-
концом невесомого стержня длины а, другой конец которого шарнирно закреп-
закреплен в точке О, так что стержень может свободно качаться в вертикальной
плоскости около этой точки. Положение частицы на окружности будет опре-
определяться углом Э, отсчитываемым от наинизшей точки окружности. Декар-
Декартовы координаты частицы х, у будут связаны с лагранжевой координатой 0
формулами
х = a sin 0, у = о cos 0. E.1.1)
Ось Ох здесь горизонтальна, а ось Оу направлена вертикально вниз.
2) Центральная орбита. Частица совершает плоское движе-
движение под действием силы, все время направленной в начало координат О.
В качестве лагранжевых координат возьмем полярные координаты г, 0.
Декартовы координаты х, у будут связаны с лагранжевыми координатами
формулами
х = г cos 0, у = г sin 0. E.1.2)
*) Лагранжевы координаты впервые были введены в работе: Ж. Л. Л а г р а н ж,
Аналитическая механика, т. I, пер. с франц. Гостехиздат, 1950. Мы используем здесь
обозначения <7i, ?2> <7з> ¦ • ¦ вместо обозначений |, i|), ф, которыми пользовался Лагранж.
60 ЛАГРАНЖЕВЫ КООРДИНАТЫ [Гл. V
3) Сферический маятник. Материальная точка Р скользит
под действием силы тяжести по гладкой поверхности сферы радиуса а с цент-
центром в точке О. В качестве лагранжевых координат выберем полярные углы 0,
Ф, где 0 — угол между вектором ОР и направленной вверх вертикальной
осью Oz, а ф — азимутальный угол между плоскостью POz и координатной
плоскостью xOz. В данном случае
х = a sin 0 cos ф, у = a sin 0 sin ф, z = a cos 0. E.1.3)
4) Твердая пластинка, движущаяся в своей
плоскости. В качестве лагранжевых координат возьмем координаты \,
у\ центра тяжести (центра масс) G пластинки относительно неподвижной
системы отсчета и угол 6, образуемый прямой Gx', проведенной на пластин-
пластинке, с неподвижной осью Ох. Если о, Ъ — координаты некоторой точки пла-
пластинки в системе Gx'y', связанной с самой пластинкой, то будем иметь
х = ? -\- a cos 6 — Ъ sin 0, 1
5) Твердое тело, движущееся в пространстве.
Система является голономной с шестью степенями свободы. В качестве
лагранжевых координат можно выбрать координаты |, tj, ? центра тяжести G
относительно неподвижной системы Oxyz и три угла 6i, 62, 63, определяющие
ориентацию тела.
Возьмем прямоугольный триэдр G123, связанный с телом (обычно в каче-
качестве осей 61, G2, G3 выбирают главные оси инерции тела в точке G), и матри-
матрицу направляющих косинусов I
(h mi пЛ
h Щ, nz )• E.1.5)
13 т3 щ/
Элементами первой строки этой матрицы служат направляющие косинусы
оси G1 по отношению к осям системы Oxyz, элементами второй строки —
направляющие косинусы оси G2, и элементами третьей строки — направляю-
направляющие косинусы оси G3. Элементы матрицы I являются известными функциями
от углов 9i, 02, 03; явные выражения для этих функций будут приведены
позже (§ 7.11) для двух способов выбора углов Qt, 02, 63. Для точки с коор-
координатами а, Ъ, с в системе G123 справедливы формулы
E.1.6)
у = т] + т^а + тф + mzc,
z — ? + ща + пф + щс.
Их можно записать в матричной форме;
. E.1.7)
Здесь х — вектор {х, у, г}, % — вектор {|, т], ?}, 'а — вектор {а, Ъ, с),
а V — матрица, полученная из I транспонированием.
В ряде случаев триэдр G123, связанный с телом, удобней обозначать
через GABC, а матрицу I записывать в виде
E.1.8)
§ 5.2] НЕКОТОРЫЕ КЛАССИЧЕСКИЕ ЗАДАЧИ 61
6) В предыдущих примерах мы имели голономные системы и число п
лагранжевых координат равнялось числу к степеней свободы механической
системы. В заключение приведем простой пример неголономной системы.
Стержень Р^Рг совершает плоское движение. Наложенная идеальная
связь такова, что точка Pi может двигаться только вдоль направления Р\Рг
(см. § 2.1). В качестве лагранжевых координат выберем координаты хи у^
точки Pi по отношению к неподвижным осям Оху и угол 9 наклона отрез-
отрезка Р1Р2 к оси Ох. Возможные перемещения удовлетворяют уравнению
(см. B.1.10))
cos 9 dyi — sin 9 dxi = 0. E.1.9)
Это уравнение не допускает интегрирующего множителя. Система имеет
две степени свободы (к = 2, I = 1), но число лагранжевых координат равно
трем (тг = Те + I = 3). Декартовы координаты точки, находящейся на стерж-
стержне на расстоянии а от точки Pi, выражаются формулами
х — xt + a cos 9, у = г/i + a sin 9. E.1.10)
Несмотря на то, что система имеет лишь две степени свободы, множество
достижимых конфигураций является трехпараметрическим. В самом деле,
систему из любого начального положения можно перевести в любое конеч-
конечное. Это было доказано уже в § 2.1.
§ 5.2. Некоторые классические задачи. Позже (в § 6.2) мы выведем
уравнения Лагранжа, описывающие движение механической системы в лаг-
лагранжевых координатах. Однако уже сейчас мы можем решить некоторые
важные задачи, не пользуясь уравнениями Лагранжа. Рассмотрим пять
задач. Четыре из них (примеры 5.2А, 5.2В, 5.2С и § 5.3) могут быть решены
с помощью одних только законов сохранения энергии C.4.5) и сохранения
момента количества движения C.2.12). В последней задаче (§§ 5.4, 5.5, 5.6)
мы используем также уравнения движения в декартовых координатах.
Пример 5.2А. Простой маятник. Тяжелая точка движется
без трения по окружности радиуса а в вертикальной плоскости. Система
голономна с одной степенью свободы. В качестве лагранжевой координаты
возьмем угол 9, отсчитываемый от наинизшей точки окружности. Заданной
силой здесь является вес частицы, а реакцией связи — нормальная реакция
проволоки (если представить, что бусинка скользит по гладкой проволоке)
или натяжение стержня (если считать, что частица закреплена на конце
невесомого стержня, другой конец которого шарнирно закреплен в неподвиж-
неподвижной точке). Потенциальная энергия равна mgz, где z — высота частицы отно-
относительно центра окружности. Уравнение энергии имеет вид
упга29*2 —mga cos Q = h. E.2.1)
Положим h == mgar\, где т) — безразмерная величина, а ац — высота энер-
энергетического уровня Я над центром окружности (рис. 3). В этих обозначениях
уравнение E.2.1) переписывается в виде
-|-92 = re2(T) + cos9), n* = j-. E.2.2)
Это уравнение принадлежит к типу A.2.10), и решение его уже было нами
исследовано. Если т) < — 1, то движение невозможно. График правой части
уравнения E.2.2), приведенный на рис. 4, показывает, что могут иметь
место четыре следующих случая:
1) т) = — 1; частица находится в покое в положении устойчивого рав-
равновесия при 9 = 0;
62
ЛАГРАНЖЕВЫ КООРДИНАТЫ
[Гл. V
2) — 1 < т) < 1; частица совершает либрационное движение в пределах
от —а до а, т. е. совершает типичное для маятника движение;
3) т) = 1; частица находится в покое в положении неустойчивого равно-
равновесия при 9 = я или совершает лимитационное движение, при котором
0-> я (или —я), когда t-*-oo;
Рис. 3.
Рис. 4.
4) т) > 1; угол 0 непрерывно возрастает вместе с t (если в начальный
момент 9 > 0).
Рассмотрим эти случаи более подробно.
1) При изменении т) от —1 до —1 + бт) имеют место малые колебания
около положения 9 = 0 с периодом 2я/и и амплитудой }^26т] (см. пример 1.2А).
Полагая
1 1
sin у 0 = sin у a sin ф,
находим
Фа = п2A — k2sm2(p), к = sin у а. E.2.3)
Решение, удовлетворяющее условию 9 = ф = 0 при t = 0, имеет вид
sin ф = sn nt. E.2.4)
Таким образом, окончательно получаем
sin у 9 = sin -^ a sn. nt = к snnt, E.2.5)
где К1 у A -\- т)) = (со/2пJ, а со обозначает угловую скорость в момент,
когда 6 — 0. Период о равен АК/п. Заметим, что с ростом а от 0 до я период о
монотонно возрастает от 2я/тг до оо.
3) т) = 1. Рассмотрим лимитационное движение, приняв 9 = 0, 9>0
в момент t = 0. Имеем
02 = 2гс2 A + cos 9) = 4тг2 cos2 -| 0.
Отсюда
E.2.6)
§ 5.2] НЕКОТОРЫЕ КЛАССИЧЕСКИЕ ЗАДАЧИ 63
Этот результат можно представить в более удобной форме. Пользуясь
равенством
sec-J 0+ tg у 9 = <?»',
находим
откуда
и окончательно
sin-|-0 = thni. E.2.7)
Последняя форма E.2.7), по-видимому, наиболее удобна. Заметим, что (как
уже известно из общей теории) 0 —> я при t —> <х>.
Если положить 9 = я— 9', то Xg-^-Q' — \lshnt и приближенно 0' = 4е~п(.
1 ¦ / 1 \
4) т)>1. В этом случае имеем у92==ге2 (т)+1 — 2 sin2 -^ 91
. — ( —)
E-2.8)
= 2 -^-( 1 — &2sina у9) , где к2— . — ( —) > и окончательно
При этом, как и ранее, предполагалось, что 9 = 0 при t = 0.
Движение является периодическим. 0 непрерывно возрастает, но явля-
является циклической координатой: значения 9, 0 + 2я, 0 + 4я, . . . эквива-
эквивалентны, поскольку соответствуют одному и тому же положению системы.
Период равен 2Kkln.
Таким образом, для трех последних случаев имеем
2)
3)
4)
E.2.9)
В заключение напишем дифференциальное уравнение, описывающее
рассматриваемое движение:
9* + п2 sin 9 = 0. E.2.10)
Его можно вывести из уравнения E.2.1) или получить непосредственно.
И обратно, из уравнения E.2.10) легко вывести уравнение E.2.1). Если рас-
рассматривать малые колебания около положения устойчивого рановесия 9 = 0,
то приближенная форма уравнения совпадает с уравнением гармонического
движения
e + w29 = 0. E.2.11)
Период колебаний, как уже отмечалось, приближенно равен 2я/тг.
Зависимость 0 от t, получаемая в результате решения уравнения E.2.10),
представлена графически на рис. 5 для различных положительных значе-
значений со. При со, превышающих критическое значение 2п, переменная 9 всег-
всегда возрастает с ростом t. В этом случае вместо значения 8 в промежутке
64
ЛАГРАНЖЕВЫ КООРДИНАТЫ
[Гл. V
[Bтг — 1) я, Bтг + 1) я) можно взять соответствующее значение 6 в проме-
промежутке (—я, я), представляющее ту же самую точку окружности, что и дела-
делалось при построении графика.
Рис. 5
Приближенное вычисление периода*). В случае 2),
когда маятник совершает колебания с амплитудой а, период равен 4К/п,
a k = sin -^ а. Этот результат является точным, однако существуют раз-
личные приближенные способы вычисления периода, в которых не исполь-
используются эллиптические функции.
Прежде всего заметим, что для малых колебаний хорошим приближе-
приближением для периода служит 2я/ге, если а достаточно мало. Если а представляет
собой острый угол, то
а а
= re2 (cos 9 — cos а) = rea f sin х dx = п>
в
хdx. E.2.12)
Рассмотрим ту четверть периода, в которой значения 0 и 0 положительны.
Когда х увеличивается от 0 до а, отношение (sin x)lx монотонно убывает от 1
до (sin a)/a, так что при заданном 0 имеем
E.2.13)
1 ;, „ sin a f , sin a 1 „ , , m,
-5-62:>re2 \ xdx = --5-re2 (a2—92).
2 " ^'" a J •"" a 2
Таким образом, величина четверти периода
0
E.2.14)
E.2.15)
*) Приближенный способ вычисления периода колебания простого маятника
с помощью обычных арифметических и геометрических методов впервые предложил
А. Е. Ингам.
§ 5.2] НЕКОТОРЫЕ КЛАССИЧЕСКИЕ ЗАДАЧИ 65
заключена между пределами
а . а
— \ , и 1/ -г^ \ — , E.2.16)
п J Т/сс2 б2 ' sina п J т/а2 Q2 х
0 у о у
а значение а—между пределами
2я 2я -. /~ a ,r n ,п\
— и —1/ —: . E.2.17)
и п У sin а х '
Если амплитуда составляет 5°, то значение 1/ -^— приближенно равно
г SID. Ot
1,0007 и классическое значение 2п1п отличается от точного менее чем на одну
десятую процента.
Можно получить более точную оценку периода, если воспользоваться
одной теоремой, относящейся к арифметическому и геометрическому средним
значениям. Пусть а и Ъ — два заданных положительных числа, таких, что
а > Ъ ;> 0. Образуем две бесконечные последовательности {аг} и {br}
по следующему правилу: а0 = a, bo = b; при r^l в, представляет собой
среднее арифметическое чисел aT_i и Ът_\, а6г — среднее геометрическое этих
же чисел. Последовательность {аг} тогда будет монотонно убывающей,
а {Ьг} — монотонно возрастающей, и при г —у- оо обе эти последовательности
стремятся к одному и тому же пределу jx. Для каждого значения г справед-
справедливы неравенства аг >¦ jx > bT, и величина аг+1 аппроксимирует ц с ошиб-
1 / , ч
кои, меньшей чем -=- (аг — ог).
Рассмотрим теперь интеграл
я/2
/(а, 6)= f d9 E.2.18)
о
С помощью подстановки
- п 2а sin ш г о . „.
sin 9 = —, , . ,— J . „ E.2.19)
a-|-b-f-(a— 6) sin2 ф \ ;
докажем, что
/ (а, Ъ) = J (ai, bi). E.2.20)
Продолжая этот процесс, убедимся, что для всех значений г
/ (а, Ъ) = J (ar, Ъг). E.2.21)
Значение / (ar, br) лежит между пределами -^— и -хт— , каждый из кото-
которых стремится к значению -=—; таким образом,
J(a, b) = -~. E.2.22)
Для того чтобы оценить быстроту сходимости, можно воспользоваться
равенствами
8ar+i (or - Ьг) = (ar-! - ViJ E.2.23)
и
l)\ E.2.24)
Первое из них получается сразу, если заметить, что левая и правая части
порознь равны 4 (а? — Ъ\).
Пользуясь этими результатами, найдем приближенное значение перио-
периода оа, соответствующего амплитуде а @ < а < п). Обозначая через о
5 л. А. Парс
66
ЛАГРАНЖЕВЫ КООРДИНАТЫ
[Гл. V
период малых колебаний, получаем из E.2.3)
л/ 2
2*l — JL f dQ
где k — sm-^a, и, следовательно,
E.2.25)
E.2.26)
причем а=1 и о = к' — cos у а. Первые несколько членов последователь-
последовательностей {ат} и {6Г} имеют следующий вид:
17 *¦
v 1 ^*0 — COS fj ™?
1 /
= ~2 (
cosYa) =cos 4 а' "i=(cos-2'
i/2
1 \
s у а)
If , 1 , / 1 \ 1/2-1 1 / 1 V 1/4
=--у j cos2-^a-|- I cosset] j- , b2 = cos^ a I cos у a|
141/442
E.2.27)
В качестве приближенного значения для 1/[х можно взять 1/аг или \/Ът.
Чтобы оценить величину относительной ошибки, введем параметры бг и ег:
= ~{1-ег). E.2.28)
= ат (аг — Ът) иаг + 6г+1>аг+6г = 2ar+it
E.2.29)
Тогда, учитывая соотношения а\ —
находим
Полагая г=2 и пользуясь E.2.23), можем написать
Г 1 _ у
0<62
8аз
V
Здесь
Кроме того,
и, следовательно,
in^a)8, D = 2e642=-2e (cos-iaL cos^-a.
E.2.31)
0< eL =
0 < е2 < б2
26 cos -тг а
E.2.32)
E.2.33)
Обозначим правую часть последнего неравенства через т). Это неравенство
справедливо для 0<а<я, но при а, слишком близких к я, оно стано-
вится бесполезным. Если же 0 <а^.уя, что представляет наиболее инте-
интересный случай, то правая часть неравенства E.2.33) будет максимальной
§ 5.2] НЕКОТОРЫЕ КЛАССИЧЕСКИЕ ЗАДАЧИ 67
1
при а = -2-я; в этом случае
cos2Ta 8in4« l E.2.34)
1/2+1 " Т/2— 1 2 /2
70
1 2» (V+l)e ~ 29(99+70 1/2) 2">.
поскольку (99J — G0 У 2J= 1 > 0. Окончательно будем иметь
Здесь
Для большей части приложений такая точность вполне достаточна, но если
требуется более высокая точность, можно взять 1/а3, что даст ошибку
г
cos — a I cos-tj-cc
0<е2<б2<-п< 70р00 . E.2.37)
^- 2-10Ю •
Пример 5.2В. Центральная орбита. Выберем центр при-
притяжения за начало координат, а в качестве лагранжевых координат возьмем
полярные координаты точки г, 0. Силовыми линиями здесь будут радиусы,
а эквипотенциальными линиями (ортогональными семейству силовых
линий) — окружности г = const. Потенциальная функция будет зависеть
поэтому только от г; обозначим ее через пг93 (г), так что 93 будет потенциаль-
потенциальной энергией единицы массы. Сила притяжения mdiS/dr также будет зави-
зависеть только от г. Если мы имеем поле сил притяжения к точке О, то 93 (г)
является монотонно возрастающей функцией от г.
Имеем интеграл энергии и интеграл момента количества движения:
E.2.38)
Предположим для определенности, что а — положительное число, так что 8
возрастает вместе с t. В поле сил притяжения орбита располагается внутри
окружности 93 = h, если такая окружность существует. Исключая 9, на-
находим
г2 = 2й-2$-^-. E.2.39)
Это уравнение принадлежит к типу A.2.10), и решение его нами уже изу-
изучалось. В простейших случаях начальное значение г лежит между последо-
последовательными простыми вещественными' нулями . 7*1 и г2 функции /(г), где
через / (г) обозначена правая часть уравнения E.2.39) и 0 <; г-, < г2. В ра-
радиальном направлении движение представляет собой либрацию между
пределами г4 и г2, называемыми апсидальными расстояниями, и орбита
попеременно касается окружностей радиусов г = ri и г = г2. Точки каса-
касания, в которых г достигает минимального и максимального значений, назы-
называются апсидами; та из них, в которой г = rt, называется перигелием, а та,
5*
68 ЛАГРАНЖЕВЫ КООРДИНАТЫ
в которой г = г2, называется афелием. Угловая скорость 0 изменяется от наи-
наименьшего значения а!г\ (в афелии) до наибольшего значения alr\ (в пери-
перигелии). Угол, на который поворачивается радиус-вектор между двумя после-
последовательными апсидами, называется апсидалъным углом.
Связь между t и г выражается следующим соотношением:
i- <5-2-40>
Знак здесь выбирается согласно правилу, указанному в § 1.3. Таким обра-
образом, если частицы в момент t = tQ находится в перигелии, то
(знак в правой части для краткости записи опущен).
Связь между г и 0 может быть представлена в форме
E.2.42)
причем знак перед корнем определяется так, как указывалось выше. Если
в перигелии 0 = 90, то уравнение орбиты будет иметь вид
~\ /4 /?\
Адсидальный угол равен
Г2
' [^7==~- E-2-44)
Орбита представляет собой простую замкнутую кривую с одним перигелием
и одним афелием, если i|> = я. Если отношение т|)/я есть число рациональ-
рациональное, т. е.
4НЬ <5-2-45>
где р и q — целые числа, не имеющие общего множителя, то орбита является
периодической с периодом
Особый интерес представляют два частных случая. В изотропном осцил-
осцилляторе притяжение пропорционально расстоянию от точки О, функция 93
имеет вид 93 = у п2г2 и орбита представляет собой эллипс с центром в точ-
точке О. Апсидальный угол равен у я. В случае же притяжения точки по зако-
закону Ньютона сила обратно пропорциональна квадрату расстояния от точки О
и 93 = —• jx/r. Орбитой является коническое сечение, один из фокусов кото-
которого расположен в точке О. Если начальная скорость не превышает вели-
величины у 2jx/r0, где г0 — начальное расстояние от точки О, то это сечение
есть эллипс. Апсидальный угол равен я. Особенностью обеих задач — задачи
об изотропном осцилляторе и задачи о движении в гравитационном поле
по эллиптической орбите — является то, что орбита всегда периодическая,
каковы бы ни были начальные условия.
Остановимся на этих задачах немного подробнее.
5.2] НЕКОТОРЫЕ КЛАССИЧЕСКИЕ ЗАДАЧИ 69
1) Изотропный осциллятор. Имеем
5 Bг2)(г2Ь2)
5 7г-г2)(г2-Ь2). E.2.47)
Здесь расстояние до афелия г2 обозначено через а, а расстояние до периге-
перигелия rt — через Ъ; а > Ъ > 0. Дифференциальное уравнение орбиты имеет вид
Полагая у=1/г2, получаем его в виде
==4 (у2 — v)(v — vt), E.2.49)
E.2.50)
1 1т?
где у1 = — и У2 = "р"- ^сли положить
то найдем, что <р = ±2@ — 8о), и уравнение орбиты перепишется в виде
i-=y2sin2(e-eo) + ^cos2(e-e0). E.2.51)
Осуществляя поворот осей на угол 90, ему можно придать форму уравнения
эллипса с центром в точке О:
_??_д у! л /ко со\
Имеем
Г2г2 = W2 (д« _ Г2) (Г2 _ &2) E.2.53)
Отсюда
г2 = a2 cos2 тг (t — t0) + b* sin2 n (t — t0). E.2.54)
Эксцентрический угол п (t —¦ t0) точки на эллипсе, в которой находит-
находится частица, возрастает пропорционально времени *).
Вычисление в декартовых координатах в этой задаче было бы проще,
чем в полярных. ;
2) Движение точки в гравитационном поле. В этом
случае
г2 = Bhr2 + 2цг - а2)/?-2 E.2.55)
и h < 0; движение представляет собой либрацию между г4 и г2 @ < п < г2),
где rt и г2 — нули выражения 2/ir2 + 2\ir — а2. Дифференциальное урав-
уравнение орбиты (если отношение г/0 заменить на dr/dQ) будет иметь вид
Чтобы проинтегрировать это уравнение, введем параметр 'ф, определив его
следующим соотношением:
Находим (-jg-) =1, i|>=±F — So)- Орбитой, таки^. ^зом, служит кривая
*) Эксцентрический угол («аномалия») — угол между большой осью эллипса
и радиус-вектором точки на окружности радиуса а с той же абсциссой х = a cos n (t — t0),
что и движущаяся частица. См. рис. 5.5. {Прим. ред.)
70 ЛАГРАНЖЕВЫ КООРДИНАТЫ [Гл. V
причем угол G отсчитывается от перигелия. Если, как обычно, написать
г, = а A - е), г2 = а A + е), E.2.59)
то уравнение примет вид
^ os9, E.2.60)
где р = а A — е1). Мы получили уравнение эллипса с эксцентриситетом е
и фокальным параметром р. Поскольку г4 + г2 = — ц/h, постоянная энер-
энергии h равна
h = — ц,/Bа). E.2.61)
Координата г определяется из уравнения
г2 = ц (г2 - г) (г - пI{аг2). E.2.62)
Введем параметр w:
1 1
г — у (rs + ri) 2" (r2~ri) cos w = a{\ — ecosw), E.2.63)
так что w есть эксцентрический угол, отсчитываемый от перигелия. Имеем
}/~~dt = rdiv = a(l—ecosw) dw. E.2.64)
Интегрируя, получаем
п (t — t0) — w — е sin w, E.2.65)
где через п обозначена величина ]/ fi/a3 — среднее движение. Соотноше-
Соотношение E.2.65) известно как уравнение Кеплера; оно выражает связь между
положением тела на эллиптической орбите и временем.
Пример 5.2С. Теорема Ньютона о вращении ор-
орбиты. Рассмотрим теперь движение, возникающее при наложении на гра-
гравитационное поле дополнительного притяжения mv/r3. Чтобы решить эту
задачу, заменим функцию Ж на функцию
а функцию / (г) — на функцию /4 (г):
/1(г) = 2й1-2ЯЗ + -^—3-, • E.2.67)
где hi, aL — постоянные энергии и момента количества движения в новом
движении. Если положить
^ = h, a\ = а2 -|- v, E.2.68)
то функции /i (г) и / (г) окажутся одинаковыми. Чтобы убедиться в том, что
движение с такими значениями hi и at возможно, рассмотрим апсиду перво-
первоначальной орбиты, в которой г = с и скорость равна и.
Если в той же начальной точке сообщить частице под прямым углом
к радиус-вектору скорость, равную щ:
ul = + v/c2, E.2.69)
то будем иметь
hi = 4" "i + * (с) - ^т, = 4- и2 -1- Ж (й) = h, )
1 х v ' lci 2 ' w } E.2.70)
a= = cX = c2«M-v = a2 + v, J
и условия E.2.68) будут удовлетворяться.
¦5 5.3] СФЕРИЧЕСКИЙ МАЯТНИК 71
Если в обеих задачах при t = О принять 0 = 0, то связь между (иг
"будет одной и той же. Если в первоначальной задаче орбита задается урав-
уравнением
г = Ф @), E.2.71)
то в новой задаче она будет описываться соотношением
E.2.72)
где &а = 2 . < 1. Чтобы достигнуть значения г, соответствующего 9 = 0О
в первой орбите, радиус-вектор во второй орбите должен повернуться
на больший угол: во/к. Поэтому влияние дополнительного притяжения
можно представить как вращение первоначальной орбиты.
§ 5.3. Сферический маятник. Точка движется под действием силы тяже-
тяжести по гладкой сфере радиуса а. В качестве лагранжевых координат возьмем
полярные углы 0, ф радиус-вектора, причем отсчет угла 0 будем производить
от вертикали, направленной вверх. Уравнения энергии и момента количества
движения запишутся в виде
у та2 @2 + sin2 0ф2) -\-mga cos 9 = const = mgah, E.3.1)
sin2 9 ф = const = Y~2ga/a, E.3.2)
где h и а — безразмерные параметры (не являющиеся действительными зна-
значениями постоянных энергии и момента количества движения). Будем пред-
предполагать, что ф ^ 0. Высота энергетического уровня над центром сферы
равна ah. При h<C — 1 движение невозможно; кроме того, требуется, что-
чтобы а ^ 0.
Решение почти не отличается от решения в примере 5.2В. Исключая ф
из E.3.1) и E.3.2), находим
^()- E.3.3)
Обозначив cos0 через z, запишем это уравнение в следующей форме:
^z2 = /(z), E.3.4)
где
/ (z) = (h — z) A — z2) — a. E.3.5)
Уравнение E.3.4) связывает z и t и принадлежит к уже знакомому нам
типу A.2.10).
Чтобы определить траекторию точки на сфере, необходимо иметь соот-
соотношение, связывающее ф и г; такое соотношение имеет вид
1 dt п / 2ffct "I/ ol dz ,r о "Ь\
l — z* Г а 1 — z- yf(z)
Полученные результаты можно представить в следующей компактной
форме:
¦Л/ —dt — —— — ,_ . E.3.7)
У « У/B) Va V
Рассмотрим движение, соответствующее заданным значениям h и а.
Нужно, чтобы h > — 1, а > 0. Если h = — 1, то единственным возможным
72
ЛАГРАНЖЕВЫ КООРДИНАТЫ
[Гл. V
значением а является нуль, в этом случае точка находится в покое в наиниз-
наинизшем положении на сфере.
Построим график полинома третьей степени / (z) (рис. 6). Кривая / (г)
имеет максимум в точке г = z0:
E.3.8)
.При возрастании h от —1 до оо z0 увеличивается от —1 до 0. Ордината кри-
кривой в точке z0 равна
/ (?о) = i|) {К) — а, E.3.9)
где
,1, th\ ^ I7Z.2 I Q\3/2
Чтобы движение было возможно, необходимо, чтобы выполнялось неравен-
неравенство / (z0) > 0, т. е. чтобы
0<a<i|j(fc). E.3.10)
Весьма удобный способ классификации различных возможных движений
можно получить, построив вспомогательную диаграмму в координатах h, a
А
Рис. 6.
Рис. 7.
(рис. 7). На этом рисунке изображена кривая а = i|> (h). Допустимые зна-
значения к, а, удовлетворяющие неравенствам E.3.10), соответствуют точкам,
расположенным в незаштрихованной области плоскости, а также на грани-
границе этой области. При построении кривой следует иметь в виду, что при
h —>- оо
E.3.11)
Классификацию орбит теперь произвести просто. Имеется три класса
кривых, удовлетворяющих следующим условиям:
Рассмотрим последовательно эти три возможности.
1) a = 0. Этот случай соответствует задаче о простом маятнике, рас-
рассмотренной в примере 5.2А.
2) О <С a <Cty (h). Кривая третьего порядка три раза пересекает ось z
(рис. 6), причем
— 1 < z3 < so < z2 < 1 < zj. E.3.12)
Координата z3 отрицательна, — 1 < z3 < z0 < 0; координата z2 может быть
как положительной, так и отрицательной. Движение вдоль оси z есть либра-
либрация между z3 и z2. Траектория точки на сфере располагается между двумя
§ 5.3J СФЕРИЧЕСКИЙ МАЯТНИК 73
горизонтальными окружностями, поочередно касаясь их. Если р, опреде-
р, определяемое формулой
р==±[ У^ь_ t E.3.13>
есть число рациональное, то движение является периодическим. Полагая
Р = p/Qi гДе Р и Я — положительные целые числа, не имеющие общего-
множителя, получаем период равным
Н-?=. E.3.14).
В самом деле, приращение <р при изменении z от z3 до z2 и обратно до z3 равно-
Z2 ._
2 f V
zJ (l-
и орбита является периодической, если это приращение равно 2п, умножен-
умноженному на некоторый рациональный множитель, т. е. если оно равно, скажем,
(p/q) 2л; период равен времени, в течение которого происходит q полных
колебаний между z3 и z2.
Найдем теперь явное соотношение между t ж z. Имеем
z'2 = 4 (г - zt) (z - z2) (z - 23), E.3.15)
где через z' обозначена производная dz/dx, а т — новая безразмерная вре-
временная переменная, равная т = Т/ ^- t.
Перепишем уравнение E.3.15) в виде
Обозначим
Л ft Л
-3- , е2 = z2 — -g-, е3 = z3 — -3-
и
и введем функцию ^(z). Если начало отсчета времени выбрать таким обра-
образом, чтобы при ? = т = 0 z = z3 (т.е. z o- = e3l ' то ^УДем иметь
E.3.17)
E-3-18)
Тогда значение ср в момент t найдется из соотношения
Жр = тЙг<*т, E-3-19)
в правую часть которого вместо z следует подставить его выражение из E.3.17).
74 ЛАГРАНЖЕВЫ КООРДИНАТЫ [Гл. V
3) а = if> (h). Этот случай относится к задаче о коническом маятнике.
Частица движется по окружности в горизонтальной плоскости z = z0.
Период о равен 2я У(— azolg), т. е. 2я ]/'big, где Ъ — расстояние от центра
сферы до плоскости, в которой происходит движение. Движение устойчиво
в том смысле, что малое возмущение приводит к движению типа 2), ограни-
ограниченному узкой полосой на сфере в окрестности первоначальной круговой
траектории.
В заключение отметим, что аномальную точку h = —• 1, а = 0 можно
считать предельной для каждого из трех случаев. Частица находится в по-
покое в положении устойчивого равновесия в наинизшей точке сферы.
§ 5.4. Задача двух тел. Две частицы Р1 и Р2 движутся в пространстве
под действием сил взаимного притяжения. Обозначим массы частиц через т^
и т2, а расстояние Р\Р2 через г. Сила, действующая на частицу Pi, равна
¦¦ymim2/r2 и направлена от Р4 к Р2; через у здесь обозначена гравитационная
постоянная. Сила, действующая на частицу Р2, равна ymim2/r2 и направлена
от Р2 к Pi. Поэтому ускорение частицы Р2 относительно частицы Pi в любой
момент времени равно у (mi + m2)/r2 и направлено от Р2 к Р±. Относитель-
Относительное движение таково же, как движение частицы Рг с ускорением, равным
7 (mi H~ т2)/г2 и направленным в каждый момент в фиксированную точку Pi.
Орбита (в относительном движении), очевидно, является плоской; положение
плоскости определяется начальным положением прямой Р±Р2 и начальной
(относительной) скоростью частицы Р2 (если только она не направлена вдоль
PiPzi в последнем случае движение прямолинейно).
Если известно движение частицы Р2 относительно Рь то движение
ее относительно центра масс G определится из соотношения
rip mi р р
2 mi-\-m2
В задаче двух тел (если Вселенную считать состоящей всего из двух
частиц) центр масс G движется равномерно и прямолинейно. Если известно
движение центра масс G, а также движение Р2 относительно G, то можно
определить движение Р2 в пространстве; совершенно так же, разумеется,
можно определить движение частицы Pi. Поскольку точка G движется
равномерно, можно воспользоваться ньютоновой системой отсчета (часто
так и поступают); центр масс в ней будет находиться в покое.
Рассмотрим теперь движение частицы Р2 относительно Pi. Движение
это таково, что ускорение Р2 направлено к фиксированной точке и равно
\i/r2, где jx = у (mi ~Ь мг). Выберем неподвижный центр притяжения в ка-
качестве начала координат, а плоскость движения примем за плоскость z = 0.
¦Эта задача кратко уже рассматривалась нами в § 5.2 как иллюстрация
к общей теории центральных орбит, здесь мы решение получим более про-
простым путем и подвергнем его более детальному анализу. Уравнения движе-
движения имеют вид
'*'=-¦? cos G, у = - Ь sin G, E.4.1)
где х, у — декартовы координаты, а г, 9 — полярные координаты. Сохране-
Сохранение момента количеств движения выражается уравнением
г29 = а = const. E.4.2)
Примем для определенности, что а > 0 (случай а = 0, соответствующий
прямолинейному движению, оставим в стороне), Из уравнений E.4.1),
f 5.4] ЗАДАЧА ДВУХ ТЕЛ 75
E.4.2) получаем
cosB, j/ ^ E.4.3)
Интегрируя, находим
? ? B), E.4.4)
где А в. В — постоянные, определяемые начальными условиями.
Далее имеем
ху — ух = а. E.4.5)
Подставляя выражения для х и г/ из E.4.4), приходим к соотношению
-?- ж (cos е + Б) —? у (- sin 9 + Л) = а. E.4.6)
Поскольку х cos 8 + г/ sin 0 = г, уравнение E.4.6) можно переписать в виде
г = - Вх + Ау + (а2/». E.4.7)
Таким образом, орбита представляет собой геометрическое место точек,
расстояние которых от точки О пропорционально расстоянию до кривой
- Вх + Ау + (а2/ц) = 0, E.4.8)
т. е. орбитой служит коническое сечение с фокусом в точке О и директрисой,
выражаемой уравнением E.4.8). Эксцентриситет е равен ]/ А2 + В2.
Длина хорды кривой E.4.7), параллельной директрисе, равна 2a2/jx,
так что если удвоенный фокальный параметр конического сечения обозна-
обозначить через 2р, то моншо написать
a2 = \ip. E.4.9)
Далее, с помощью E.4.4) находим
= 1 А ? & + у*) —j| (ху - ух) -
Z, /r2 i ,,2\ rl /г: А л л \
— полная энергия, сохраняющая постоянное значение. Таким образом,
в соответствии с неравенством h ^ О
е^1. E.4.12)
Наконец, подставляя значение а'2 = |гр в соотношение E.4.10), находим
A-JL^-l). E.4.13)
76
ЛАГРАНЖЕВЫ КООРДИНАТЫ
.'Гл. V
Для эллиптической орбиты е<1, р = аA—е2) и, следовательно,
*=-&, E-4.14)
где 2а — длина большой оси эллипса *). Для параболической орбиты е — I и
h = 0. E.4.15)
Для гиперболической орбиты е > 1, р = а (е2 — 1) и
E-4.16)
= ¦?¦¦
Формулы E.4.9) и E.4.14) (или E.4.16)) являются классическими формула-
формулами, выражающими форму и размеры орбиты через постоянную энергии h
и постоянную момента количеств движения а.
§ 5.5. Уравнение Кеплера. Из теоремы о сохранении момента количеств
движения следует, что быстрота изменения площади, ометаемой радиус-
1
вектором, постоянна: за каждую секунду ометается площадь, равная-^- а.
В случае центральной орбиты эта площадь пропорциональна времени, что
позволяет получить соотношение между коорди-
координатой частицы на орбите и временем.
Рассмотрим эллиптическую орбиту. Период <т
равен 2А/а, где А — площадь эллипса, так что
1— ез 2л,
= -=F, E.5.1)
2лаЬ
а = =
где среднее движение п равно j
Время прохождения частицы от перигелия А
до точки Р эллипса определяется из соотношения
4 = 4-' E-5-2)
Рис. 8.
где б — площадь эллиптического сектора ASP.
Эллипс можно рассматривать как ортогональную
проекцию некоторой вспомогательной окружности (рис. 8). Как известно,
отношение площадей при ортогональном проектировании не меняется. Таким
образом, если Q — точка окружности, проекция которой есть Р, то
t
а
E.5.3)
где б' — площадь кругового сектора ASQ, а А' — площадь круга. Площадь
сектора ASQ равна площади сектора ACQ минус площадь треугольника
CSQ:
1 1
б' = у a?w —j a2e sin w,
E.5.4)
где w — эксцентрический угол в Р, составленный отрезками CQ и С А.
Таким образом, приходим к равенству
А'
w—е sinu)
2л
E.5.5)
*) Приводимое здесь, а также в §§ 5.5 и 5.6 краткое исследование эллиптического
движения можно было бы в значительной степени расширить. Но даже с учетом добавле-
добавлений, сделанных в § 18.12, оно не может удовлетворить специалиста-астронома. Подробное
изложение этого вопроса можно найти в курсах астрономии; см., например, книгу [29],
гл. IV.
§ 5.6] СТОЛКНОВЕНИЕ 77
которое с учетом E.5.1) дает
nt = w — e sin w. E.5.6)
Это соотношение носит название уравнения Кеплера; в § 5.2 оно нами было
получено другим способом. Уравнение Кеплера устанавливает связь между
координатой частицы на эллиптической орбите и временем.
Приведенный вывод уравнения Кеплера, возможно, является наиболее естествен-
естественным, поскольку в нем используется эксцентрический угол. Однако уравнение Кеплера
можно получить и не основываясь на геометрии эллипса. Один такой способ нами уже был
указан в § 5.2. Приведем еще более простой вывод. Если за координатные оси взять оси
эллипса, то координаты его точки будут равны a cos w, Ь sin w. Если теперь перейти
к новым осям, параллельным этим, но с началом в точке S, то будем иметь
х = a (cos w — е), у = Ь sin w E.5.7)
п
nbn = а = ху — ух — ab A — е cos w) w, E.5.8)
или
п = A — е cos w) w, E.5.9)
и мы снова приходим к формуле E.5.6).
Полярные координаты г, 9 легко выразить через угол w. Отсчитывая
углы от линии SA, получаем
г = а A — е cos w), E.5.10)
± ±-w, E.5.11)
¦-Y\
« Соотношение между г и t можно получить, например,
1 С
исключая w из E.5.6) и E.5.10) (см. § 18.14).
§ 5.6. Столкновение. Вернемся к задаче двух тел. Рассмотрим случай,
•когда а = 0: частица (в относительном движении) движется по прямой,
проходящей через точку О. Без потери общности эту прямую можно выбрать
и качестве оси Ох. Уравнение энергии (при х > 0) имеет вид
Остановимся подробнее на случае, когда h < 0, например, h = — jx/Ba),
а > 0 (по аналогии с рассмотренным выше эллиптическим движением).
Если в начальный момент и х и х положительны, то наибольшее удаление
частицы от точки О равно 2а. Чтобы исследовать связь между координатой
частицы и временем, введем новую переменную 0, определяемую из урав-
уравнения
х = а A + cos 0). E.6.2)
При х = 2а переменная 0 равна нулю, и можно считать, что с ростом t эта
переменная монотонно возрастает до столкновения с частицей в точке О,
когда 0 = л. Подставляя выражение для х из E.6.2) в уравнение
находим
A + cos ЭJ 92 = пг. E.6.4)
Отсюда, учитывая, что 0 > 0, получаем
A + cos 6) ё = п, E.6.5)
78 ЛАГРАНЖЕВЫ КООРДИНАТЫ [Гл. V
и, следовательно,
9 + sin 9 = nt, E.6.6)
причем при t = О имеем 9 = 0 и х = 2а.
Уравнение E.6.6) справедливо, собственно говоря, только для значе-
значений 0, удовлетворяющих условию — п < 9 < я, поскольку х-*- — оо,
когда х -> 0. Однако иногда предполагают, что движение продолжается
после столкновения, и тогда считают, что равенство E.6.6) сохраняет силу
и после столкновения. Такое предположение представляется наиболее есте-
естественным. Если бы а не равнялось нулю, а было бы малой положительной
величиной, то орбита представляла бы собой очень тонкий вытянутый эллипс
и мы имели бы периодическое движение, при котором в каждом периоде
существовало бы положение, близкое к столкновению. Это предположение
означает, что характер поведения частицы сохраняется и в предельном
случае прямолинейного движения.
Полагая 9 = п + ф, t — (п/п) + т, получаем
! = 1-Cdsq>, E.6.7)
т = ф — sin ф. E.6.8)
Столкновение происходит при х = т = ф = 0.
Если переменную ф считать комплексной, то правые части равенств
E.6.7) и E.6.8) будут целыми функциями, и, исключив ф, мы получим х
как аналитическую функцию от т. Разложение этой функции в степенной
ряд в окрестности точки т = 0 имеет вид
п=1
При т = 0 функция х (т) имеет алгебраическую точку разветвления,
в которой соединяются три листа соответствующей римановой поверхности.
Функция х (т) действительна лишь на одном из этих трех листов, и суще-
существует одно вещественное аналитическое продолжение за особую точку т = 0.
Эту функцию и выбирают для описания движения после момента столкно-
столкновения. Выбранная ветвь х (т) является четной функцией от т.
Высказанные выше соображения относятся и к задаче трех тел. Может
случиться, что в силу начальных условий два из трех тел столкнутся друг
с другом в некоторый момент t — t0. Для описания дальнейшего движения
нужно принять подходящее предположение, это делается только что указан-
указанным способом. Ясно, что в течение небольшого промежутка времени после
момента столкновения влияние третьего тела будет пренебрежимо мало,
и в течение этого промежутка времени задачу можно рассматривать как
задачу двух тел.
§ 5.7. Лагранжевы координаты для голономной системы. Вернемся:
теперь к задаче о переходе от декартовых координат к лагранжевым, кото-
которую мы начали рассматривать в § 5.1. Допустим сначала, что уравнения
связи B.2.4) вполне интегрируемы, т. е. что они эквивалентны L уравнени-
уравнениям вида
dfT = 0, г = 1, 2, . . ., L, E 7.1)
где
U = fr(Xi, x2, . . ., жд; t), E.7.2)
причем fT ? Со. В этом случае система является голономной.
§ 5.7] ЛАГРАНЖЕВЫ КООРДИНАТЫ ДЛЯ ГОЛОНОМНОЙ СИСТЕМЫ 79
Рассмотрим преобразование
qT = fT, r = l, 2, ..., N, E.7.3)
в котором первые L функций / суть функции E.7.2), определяемые уравне-
уравнениями связи, а остальные к = N — L функций / представляют собой под-
подходящим образом подобранные функции от аргументов Xi, x2, ¦ ¦ ., xN; t,
принадлежащие классу С2. Если D — достаточно малая область простран-
пространства Xi, x2, . . ., xN; t, в которой якобиан
а(/"/2 fN\ E.7.4)
х2, .-., xN)
отличен от нуля, то уравнения E.7.3) определяют взаимно однозначное
соответствие между областью D пространства х, t и областью А простран-
пространства q, t. Уравнения E.7.3) могут быть разрешены относительно xt, x2, • • ¦
. . ., xN. Получаемые при этом функции от аргументов q и t принадлежат
классу Ci в области А. В большей части случаев, представляющих практи-
практический интерес, переменные х зависят только от q и не зависят от t.
Уравнения связи в новых переменных принимают простую форму:
qr = ат, г = 1, 2, . . ., L. E.7.5)
(Действительно, в большей части случаев уравнения связи с самого начала
могут быть представлены в этой форме, причем а — абсолютные постоянные,
не зависящие от начальных условий.) Если значения постоянных аг в урав-
уравнениях E.7.5) установлены, остальные к переменных q определяют положе-
положение системы. Переменные х выражаются как явные функции от к координат
Ql+i, Ql+2, ¦ • ¦, Qn и времени, что является важным свойством лагранже-
вых координат. Уравнений связи теперь нет, перемещение, представляемое
произвольными дифференциалами dqL+i, dqL+z, ¦ . ., dqN, dt, является
возможным, и
JV
dxT= 2j J^d9s + -gfdt, r=l, 2, ...,N. E.7.6)
s=L+l
Рассмотрим теперь виртуальные перемещения. Виртуальные переме-
перемещения 8xi, Ьх2, ...,bxN удовлетворяют уравнениям
JV
2 ^6a:s = 0, r=l, 2, ..., L. E.7.7)
Уравнения E.7.7) удовлетворяются выражениями
JV
S^= S P^-bQm, s = l, 2 iV, E.7.8)
m=L+l
при произвольных значениях б^х,+ 1, 6gL+2, ...,bqN, поскольку
JV
8=1
если г ^ L и m > L. Более того, это — виртуальное перемещение в наибо-
наиболее общем виде. Виртуальные перемещения определяются произвольными
приращениями bqL+i, ?>qL+1, . . ., bqN, причем время t не варьируется.
Описанный выше процесс позволяет осуществить формальный переход
от декартовых координат к лагранжевым, однако на практике применяют
¦80 ЛАГРАНЖВВЫ КООРДИНАТЫ [Гл. V
значительно более простой способ преобразования координат. Как уже отме-
отмечено ранее (§ 5.1), в большей части случаев выбор лагранжевых координат
может быть произведен непосредственно.
§ 5.8. Лагранжевы координаты для неголономной системы. Предполо-
Предположим теперь, что уравнения связи B.2.4) не являются вполне интегрируемыми.
Пусть число независимых линейных комбинаций, допускающих интегри-
интегрирующий множитель, будет равно L — I. Тогда уравнения связи могут быть
записаны в виде
dfr = 0, г = 1, 2, . . ., L - I, E.8.1)
Юг = 0, г = 1, 2, . . ., I, E.8.2)
где со — пфаффовы формы от дифференциалов dxu dx2, . . ., dxN, dt. Число I
является инвариантом системы, и не существует какой-либо интегрируемой
комбинации уравнений связи, независимой от E.8.1).
Рассмотрим теперь преобразование
qr = fT, r = 1, 2, . . ., N, E.8.3)
в котором /i, /г, • - ., /ь-г — функции, стоящие в левой части уравнений
E.8.1), а последние I ¦+ к функций / представляют собой подходящим обра-
образом выбранные функции от аргументов Ху, х2, . . ., xN, t, принадлежащие
классу С2. Функции /1; /2, . . ., fN от аргументов х1: х2, ¦ ¦ ., xN, t незави-
независимы и принадлежат классу С2. Как и ранее, преобразование E.8.3) будем
считать обратимым, так что для соответствующей области qt, q2, ¦ ¦ ., <7л*, t
переменные х будут однозначными функциями q та. t.
В новых переменных первые L — I уравнений связи будут иметь про-
простой вид:
qT = ar, r = 1, 2, . . ., L - I. E.8.4)
Если постоянные ат зафиксированы, последние к + I переменных q опреде-
определяют положение системы. Однако теперь остаются I уравнений связи E.8.2),
которые не допускают интегрируемых комбинаций. В новых переменных
эти уравнения представляются в следующей форме:
N
^B/adq, + Brdt = 0, r=l,2,...,l. E.8.5)
Эти I уравнений Пфаффа не допускают интегрируемых комбинаций. Посколь-
Поскольку <7ь 42i ¦ ¦ -1 Ql-i постоянны, соотношения E.8.5) эквивалентны уравне-
уравнениям Пфаффа с к + I + 1 членами:
2 Brsdqs+Brdt = 0, r=i,2, ...,/. E.8.6)
Коэффициенты Brs, Br представляют собой известные функции от аргумен-
аргументов <7, t, принадлежащие классу Су.
Таким образом, для неголономной системы не представляется возмож-
возможным выбрать лаграгокевы координаты так, чтобы число их равнялось чис-
числу степеней свободы. Наименьшее возможное число лагранжевых координат
больше числа степеней свободы на число уравнений связи, не допускающих
интегрируемых комбинаций.
Возможные перемещения системы определяются равенствами
§ э.9] КАЧЕНИЕ ТЕЛА 81
Входящие сюда к -\-1 -\-1 дифференциалов
2> • • • > dqN, dt
связаны лишь соотношениями E.8.6). Виртуальные перемещения системы
выражаются соотношениями
Ьхг = 2 Ws8qs' E-8l8)
ж=Ь-1+1
причем к -f-1 дифференциалов связаны условиями
2 Brs8qs = 0, г =1,2 I. E.8.9)
s=L-H-l
Чтобы убедиться в том, что виртуальные перемещения действительно
определяются соотношениями E.8.8) и E.8.9), нужно доказать, что они удов-
удовлетворяют уравнениям
2^бхг = 0, m=l, 2, ...,L-l, E.8.10)
r=l
И
JV
2 А„г6а:г = 0, m = l, 2, ...,Z E.8.11)
r=l
(см. B.2.9)). Для уравнений E.8.10) это очевидно; что касается уравне-
уравнений E.8.11), то они выполняются в силу равенств
JV
Brs=^Arm^, s = L-l + l, L-l + 2 N.
m=l
Как и в голономных системах, введение лагранжевых координат прак-
практически производится более простым способом. В каждой конкретной задаче
обычно нетрудно выбрать эти координаты наиболее удобным образом.
§ 5.9. Качение тела. Ранее были указаны два простых, хотя и несколько
искусственных примера неголономных систем: кривая преследования (§ 1.8)
и планиметр (§ 2.1). Наиболее часто с неголономными системами мы встре-
встречаемся в задачах, связанных с качением одного тела по другому. Рассмотрим
твердое тело, положение и ориентация которого в пространстве определяют-
определяются шестью координатами: |, г\, ?, 0Ь 02, 03 (см. § 5.1, п. 5). Для заданной
частицы тела
х = Ъ + а1± + Ы2+ cl3, E.9.1)
и для произвольного перемещения d|, dx\, dt,, dQi, сЮ2, dQ3 имеем
dx = dl + a dk + b dl2 + с dl3 E.9.2)
и два аналогичных соотношения. В равенстве E.9.2) координаты а, Ъ и с
постоянны. Если частица находится в покое, то
dl + a dk + Ъ dl2 + cdl3 = 0. E.9.3)
Если уравнение E.9.3) относится все время к одной и той же частице
тела, то его можно проинтегрировать; проделав это, получим
| + ah + Ы2 + cl3 = const E.9.4)
6 Л. А. Парс
82 ЛАГРАНЖЕВЫ КООРДИНАТЫ [Гл. V
и два аналогичных равенства. В этом случае тело имеет одну неподвижную
точку, система является голономной с тремя степенями свободы и остается
рассмотреть лишь вопрос об ориентации тела при его вращении около непо-
неподвижной точки. Если же соотношение E.9.3) в различные моменты времени
относится к различным частицам (например, к частицам, находящимся в точ-
точке контакта тела с поверхностью, по которой оно катится), то уравне-
уравнение E.9.3) и два аналогичных уравнения не являются вполне интегрируемы-
интегрируемыми и система в целом оказывается неголономной.
Аналогичные замечания справедливы и в том случае, когда частица
(а, Ъ, с) не находится в покое, а движется с заданной скоростью (U, V, W),
причем U, V, W — известные функции от t. Уравнение E.9.3) заменится
при этом следующим:
d\ + adh + Ъ dl2 + cdl3= U dt. E.9.5)
Подобно предыдущему, если a, b, с — координаты одной и той же частицы,
то система голономна. В этом случае мы имеем твердое тело, одна точка кото-
которого совершает заданное движение. Если же, например, а, Ь, с — коорди-
координаты точки контакта тела с движущейся поверхностью, по которой катится
тело, то в различные моменты времени а, Ь, с принимают различные зна-
значения, и система оказывается неголономной.
В качестве иллюстрации рассмотрим классический пример качения
сферы радиуса р по идеально шероховатой горизонтальной плоскости.
Предположим, что плоскость вращается с угловой скоростью Q = Q (t)
около точки О, лежащей в этой же плоскости. Выберем неподвижную систе-
систему координат с началом в точке О и осью Oz, направленной вертикально
вверх. Положение тела в момент t будем определять координатами |, г\ точ-
точки контакта (так что центр сферы будет иметь координаты |, т), р), а ориен-
ориентацию тела — эйлеровыми углами Э, ср, aj). (Подробнее об углах Эйлера будет
сказано в § 7.11, а сейчас для наших целей нам нужны будут лишь опреде-
определение этих углов и матрица G.11.1).) Первое условие качения E.9.5) запи-
записывается в виде
d\ + a dlt + b dl2 + с dl3 = — t]Q dt, E.9.6)
и так как а, Ь, с суть координаты точки касания сферы с плоскостью, то
(а, Ь, с) = — р (щ, пг, п3), E.9.7)
где р — радиус сферы. Таким образом, условие E.9.6) принимает вид
dl — p (nidli + n2dl2 + n3dl3) = — Tjfi dt. E.9.8)
Подчеркнем, что при составлении равенства E.9.6) координаты а, Ъ, с счи-
считаются постоянными, поскольку речь идет о движении частицы, фиксиро-
фиксированной в сфере. Но в различные моменты времени мы имеем дело с различ-
различными частицами, и, чтобы получить уравнение E.9.8), справедливое во все
моменты времени, координаты а, Ъ, с следует заменить новыми перемен-
переменными согласно соотношению E.9.7). При выполнении преобразования E.9.8)
путем непосредственной подстановки значений 1и ти . . ., п3 в Э, ф, aj)
не возникает сколько-нибудь серьезных трудностей. Тем не менее вычисле-
вычисления можно упростить, если учесть следующее. Направляющие косинусы
оси Ох по отношению к движущейся системе G123 равны Z1? l%, l3. Поэтому
вектор L = {1\, 1%, 13} является постоянным, и, следовательно,
Х+о)Х 7v = 0, E.9.9)
где !(й '— угловая скорость тела или, что то же, движущихся осей G123.
Обращаясь теперь к выражению n^dl^ -f- n2dl2 + n3dl3, фигурирующему
§ 5Л0] ДОСТИЖИМОСТЬ 83
в уравнении E.9.8), можем написать
nji + njz-} п313 = Ж.? = 1?-A1Хы) = ы-AГх?) = ы-М, E.9.10)
где через Ж обозначен вектор {щ, п2, п3}, а через М — вектор {ть т2,
т3}. Скалярное произведение т-М представляет собой составляющую юу
вектора угловой скорости вдоль оси Оу. Равенство E.9.8) принимает теперь
вид
<Щ — puydt = — T]Q dt. E.9.11)
G другой стороны,
W;/ = cos фЭ + sin 9 sin срг|), E.9.12)
и соотношение E.9.8) окончательно записывается в виде
d? — р cos ф dQ — р sin 6 sin ф йг|) = — x\Q dt. E.9.13)
Мы получили первое из двух уравнений связи для неголономной системы.
Заметим, что равенство E.9.11) можно получить, выбрав систему координат с нача-
началом в точке G и осями, сохраняющими неизменное направление и параллельными соответ-
соответственно осям Ох, Оу, Oz. Тогда первое условие качения запишется в форме
| - pcov = -T)Q, E.9.14)
эквивалентной E.9.11). Этот путь, правда, несколько короче предыдущего, но мы им
не воспользовались, так как хотели проиллюстрировать изложенный выше метод.
Аналогичным образом получаем второе условие качения:
dx\ — р sin ф dQ + р sin 0 cos ф dty = ?й dt. E.9.15)
Третье условие заключается в том, что ?, — р.
Легко видеть, что уравнения Пфаффа E.9.13) и E.9.15) не допускают
интегрируемых комбинаций. Система неголономна и имеет три степени
свободы; наименьшее число лагранжевых координат, необходимых для
определения положения и ориентации системы, равно пяти. В качестве
таких координат можно выбрать ?, г\, 0, ф, о|з. В данном примере п = 5,
к = 3, 1 = 2.
§ 5.10. Достижимость. Рассмотрим теперь случай, когда сфера катится
по неподвижной горизонтальной плоскости. Тогда уравнения связи будут
иметь вид
,d? — р cos ф dQ — р sin Э sin ф daj) = 0, E.10.1)
dr\ — р sin ф dQ -\- p sin Э cos ф dip = 0. E.10.2)
Мы имеем неголономную систему с тремя степенями свободы. Однако про-
пространство конфигураций, достижимых из заданного положения, будет пяти-
пятимерным. В самом деле, систему из любой исходной конфигурации можно
перевести в любую другую, определяемую произвольными значениями
координат |, т], 8, ф, г|). Это уже отмечалось нами на примере более про-
простых неголономных систем (§§ 1.8 и 2.1). В этом параграфе доказательство
достижимости любой конечной конфигурации из любой начальной мы про-
проведем следующим образом. Пусть в начальной конфигурации Pt точка А
сферы находится в контакте с точкой А' плоскости, а в конечной конфигу-
конфигурации Р2 точка В сферы находится в контакте с точкой В' плоскости. Рассмот-
Рассмотрим дугу АВ большого круга; обозначим ее длину через ра, а длина линии:
А 'В' пусть будет р Bпп + Р), где п — целое число и 0 ^ (} < 2я. Продол-
Продолжим (если это нужно) дугу АВ на сфере до точки С так, чтобы длина дуги АС
равнялась рр1; пусть D будет серединой дуги ВС. Чтобы от конфигурации Рх
6*
84 ЛАГРАНЖЕВЫ КООРДИНАТЫ [Гл. V
перейти к конфигурации Р2, повернем сферу сначала вокруг диаметра,
проходящего через точку А', так, чтобы дуга АБ оказалась в вертикальной
плоскости, проходящей через отрезок А В'. Затем перекатим сферу к точ-
точке В', повернув на угол 2пп + -^ (а + C) так, чтобы точка D сферы пришла
в соприкосновение с точкой D' плоскости. После этого повернем сферу на
угол я вокруг диаметра, проходящего через точку D', и затем перекатим
ее на угол у (Р — а) до совпадения точки В сферы с точкой В' плоскости.
Наконец, поворачивая сферу около диаметра, проходящего через точку В',
переведем ее в требуемое положение Р2. Эти пять операций, разумеется,
можно осуществить за конечный промежуток времени, и координаты в про-
процессе этих движений будут иметь непрерывные вторые производные по вре-
времени. (Если отрезок кривой повернуть на угол у за конечный промежу-
промежуток времени от t = .0 до t = т, вращая его с угловой скоростью, равной
30у?2 (т — ?J/т5, то угловая скорость и угловое ускорение как в момент t = 0,
так и в момент t = % при этом будут равны нулю.)
§ 5.11. Варьированный путь в принципе Гамильтона. В принципе Гамиль-
Гамильтона (§ 3.7) варьированный путь получается из истинного пути посредством
виртуального перемещения в каждый момент времени. Для неголономной
системы варьированный путь, вообще говоря, невозможен. Это утверждение
нами уже было доказано для одной просто*й неголономной системы (§ 3.8).
Докажем его теперь еще для двух случаев, а именно: 1) для планиметра
|(§ 5.1, п. 6) и 2) для сферы, катящейся по плоскости (§ 5.10).
1) Истинное движение удовлетворяет уравнению
у\ — tg в Ж! = 0, E.11.1)
ш перемещение является виртуальным, так что
8yi — tg в Ьх, = 0. E.11.2)
Варьированный путь возможен тогда и только тогда, когда
8 (У1 - tg Э ъ) = 0. E.11.3)
Поскольку равенство E.11.2) выполняется в каждый момент времени, соот-
соотношение E.11.3) эквивалентно условию
xl) = 0 E.11.4)
или, что то же,
sec2 Э (в 8х! — ij6e) = 0. E.11.5)
Варьированный путь возможен тогда и только тогда, когда
^=Ф, E.11.6)
е xi
что в общем случае не имеет места.
2) Для сферы уравнения связи служат условиями качения E.10.1)
и E.10.2). Рассмотрим простой случай, когда исходное движение представ-
представляет собой качение вдоль оси Ох без вращения около вертикальной оси.
Если рассматривать перемещение, при котором в каждый момент времени
центр сферы смещается на бесконечно малое расстояние ра под прямым углом
к плоскости у = 0, то новый варьированный путь возможен. Дело в том, что
5 5.12] ОБЗОР ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ 85
точки контакта на сфере лежат на окружности длиной 2яр cos а, что с точ-
точностью до малых первого порядка относительно а равно 2пр. В общем же
случае варьированный путь невозможен без проскальзывания.
В исходном движении
е = Ф = |я, т)-0, ? = И>, E.11.7)
и вариация такова, что
8% —р 8^ = 0, 6т]-рбе = О. E.11.8)
Уравнения связи E.10.1) и E.10.2) удовлетворяются на варьированном
пути тогда и только тогда, когда
8 (| _ р cos ф 0 — р sin Э sin ф -ф) = 0, E.11.9)
8 (т| — р sin ф 0 + р sin 6 cos q>ij>) = 0, E.11.10)
что равносильно (вспомним значения переменных в исходном движении)
уравнениям
Эти уравнения не удовлетворяются, за исключением упомянутого выше
случая, когда бф = 0.
Таким образом, как и в более простом примере § 3.8, варьированный
путь невозможен без нарушения уравнений связи. Вряд ли нужно напоми-
напоминать читателю, что этот факт ни в коей мере не нарушает принципа Гамиль-
Гамильтона.
§ 5.12. Обзор полученных результатов. Резюмируем кратко наши выводы
относительно лагранжевых координат. Изменив очевидным образом обозна-
обозначения, можно определить лагранжевы координаты qt, д2, ¦ ¦ ., дп так, что
переменные будут выражаться явным образом через q и t:
vT = хт (ди д2, . . ., qn; t), r = 1, 2, . . ., Лг, E.12.1)
и все возможные конфигурации системы будут охватываться соответствую-
соответствующими значениями д^, д2, . . ., дп. t в некоторой области D пространства q, t.
В достаточно малой области этого пространства (хотя и не всегда во всей
области D) соотношение между переменными q и х будет взаимно однозначным.
В последующих примерах будет предполагаться, что функции
хт (Qii 4ii • • •¦> Qni t) принадлежат классу С2 в области D. В большей части
случаев, представляющих практический интерес, переменные х зависят
только от у и не зависят от t.
Если система голономна, то наименьшее возможное значение п равно
числу к степеней свободы системы. Если же система неголономна, то наи-
наименьшее возможное значение п равно к + I, где I — число уравнений связи
п
^]BTSdga + Brdt = 0, r = l, 2, ..., I, E.12.2)
s=l
причем эти уравнения не допускают интегрируемых комбинаций. Коэффи-
Коэффициенты в уравнениях E.12.2) принадлежат к классу С4. Возможные пере-
перемещения определяются формулами
п
dXr^^-^-dgs + ^dt, r = l, 2, ..., N. E.12.3)
86 ЛАГРАНЖЕВЫ КООРДИНАТЫ [Гл. V
Входящие сюда дифференциалы dqi, dq2, . . ., dqn, dt удовлетворяют усло-
условиям E.12.2). Виртуальные перемещения даются равенствами
n
oxr = _2] -=— Sgrs, /"=1, 2, ..., iV. E.12.4)
Дифференциалы бдг15 6д2, • • ¦, 8qn удовлетворяют условиям
2 5rs6gs = 0, r = l, 2, ..., Z. E.12.5)
Фярмулы E.12.3) и E.12.4) справедливы, разумеется, и для голономных
систем, но в этом случае дифференциалы не подчинены никаким ограниче-
ограничениям.
В любом случае число лагранжевых координат при желании можно
взять больше минимального числа, скажем, на р координат. При этом к пфаф-
пфаффовым уравнениям связи (если таковые имеются) добавятся еще р соотно-
соотношений. Эти соотношения можно представить в форме конечных уравнений
вида
'Fr (qu q2, . . ., qn; t) = 0, г = 1, 2, . . ., р E.12.6)
(а не уравнений Пфаффа). Функции Fr будем считать имеющими непрерыв-
непрерывные первые производные в некоторой области значений qu Q21 • • ¦? <7n» t.
В случае, когда число лагранжевых координат превышает минимальное,
принято говорить об избыточных координатах. Избыточные координаты
вводят, например, в тех случаях, когда желают перейти к новой системе,
накладывая связи на старую систему; при этом может оказаться удобным
сохранить координаты, описывающие старую систему, хотя число их и не
является наименьшим возможным числом для новой системы.
Во многих случаях совокупность qt, q2, . . ., qn удобно рассматривать
как изображающую точку в пространстве п измерений. Движение этой точ-
точки дает наглядное представление о движении механической системы, посколь-
поскольку движение системы (т. е. последовательность ее конфигураций) находится
в соответствии с движением изображающей точки в re-мерном пространстве.
Иногда, удобства ради, мы будем пользоваться обозначением q вместо
{<?ь <?2, • • -, qn) и q вместо {qu q2, . . ., qn}.
Глава VI
УРАВНЕНИЯ ЛАГРАНЖА
§ 6.1. Четвертая форма основного уравнения. Лагранжевы координаты.
Следующим нашим шагом будет представление основного уравнения в лаг-
ранжевых координатах: первую форму C.1.1) основного уравнения мы запи-
запишем в переменных q вместо переменных х. Характерным свойством лагран-
жевых координат является то, что переменные х могут быть представлены
как явные функции от qt, q2, . . ., qn, t. Мы постоянно будем предполагать,
что эти функции принадлежат классу С2 в соответствующей области D изме-
изменения ?i, qz, ¦ . ., qn, t.
Поскольку
хт = хт (qu q2, . . ., qn; t), r = 1, 2, . . ., N, F.1.1)
имеем
n
Z _ Ki dxr * i дхт л о N ¦ Cfi 1 9^
s=l
т. е. производные хт связаны с q линейными соотношениями, коэффициенты
в которых зависят от qx, q2, . . ., qn, t.
Две следующие леммы выражают простые свойства функций в правых
частях равенств F.1.2).
Лемма 1.
дх^__ дх^^ F.1.3)
Лемма 2.
9хг___^_/дхг_\ F.14)
dqs dt \ dqs ) \ • ¦ /
Первое равенство очевидно, для доказательства второго заметим, что
~dq7== 2j Tqsdqm ?m+ dqs dt =
m=l
2d2xr • дЧт _ d I дхт \
dqm dqs Qm + dt dqs dt \ dqs) •
__ d ( dxT '
dqmdqs 4m~r dt dqs ~"
Порядок дифференцирования можно менять, поскольку xT{qb q2, ..., qn; t)?C2
в области D.
Если я,, из F.1.2) подставить в формулу кинетической энергии
N
Т = ~2 2j mrxr, C.3.3)
88 УРАВНЕНИЯ ЛАГРАНЖА [Гл. VI
• • •
то получим полином ? второй степени относительно qu дг, ..., qn с коэф-
коэффициентами, зависящими от qu q2, ..., qn, t. Полином ? может быть пред-
представлен в форме
ZT T F.1.5)
где Т2 обозначает однородную квадратичную функцию от q:
п п
r2={S 2 «»?,¦?., (a. 1.6)
71! — однородную линейную функцию от q:
71,= S«r?r, F.1.7)
r=l
а То является функцией от qu q2, ..., qn, t. Нетрудно видеть, что, отбра-
отбрасывая слагаемое -^- в правой части формулы F.1.2), мы приходим
к выражению для Т, совпадающему с Г2. Поэтому Т2 представляет собой
определенно-положительную квадратичную форму от q при всех значениях
JV
qt, q2, ..., qn, t. Выражение Го= 2 mr (~§г) неотрицательно для всех
г=1
значений qu q2, ..., qn, t.
Обратимся теперь к основному уравнению C.1.1). Для виртуальных
перемещений имеем
п
ба:г = 2-^6^' г-1, 2, .... ЛГ, E.12.4)
s=l
и уравнение C.1.1) приобретает вид
п N
2 {Ц {mr'xr-XT) ^-} bqs = 0. F.1.8)
1 1
* * dx
Х
dx
Преобразуем выражение Хг-—-. С помощью лемм F.1.3) и F.1.4) получаем
Xr
r dqs - dt \Xt dqs ) Xr dt \ dqs
Коэффициент при 6qs в уравнении F.1.8) получается равным
где
N
г=1
Но выражение F.1.9) теперь имеет вид
4 (?¦)-¦?-& <•¦»¦">
§ 0.21 УРАВНЕНИЯ ЛАГРАНЖА 8&
и окончательно получаем
Это четвертая форма основного уравнения.
Укажем физический смысл величин Q. Сумма
Qi8qi + Q28q2 + ...+Qn8qn
выражает работу, совершаемую заданными силами на виртуальном переме-
перемещении 6<7i, 8q2, ..., 8qn. Величины Q называются обобщенными силами.
§ 6.2. Уравнения Лагранжа. Уравнение F.1.12) справедливо для любого
виртуального перемещения 8qt, 8q2, ..., 8qn. Предположим сначала, что
система голономна и число лагранжевых координат минимально, т. е. п = к.
Тогда уравнение F.1.12) справедливо для любых значений 8qu 8q2, •¦¦, 8qnr
и мы получаем уравнения движения Лагранжа
d l д% \ д% „ . о ,„„.,
T
aqr
Предположим теперь, что система неголономна и число лагранжевых
координат минимально, т. е. п = к+1. Имеем I уравнений связи
п
^Brsdqs + Brdt = O, r = l, 2, ..., I. E.12.2)
8=1
Уравнение F.1.12) теперь справедливо не для произвольных 8q, а для 8qt
удовлетворяющих условиям
п
25rs6?s = 0, r=l, 2, ..., I. E.12.5)
s=l
Уравнения движения запишутся теперь в форме
г
| = ^+ 2^mBmr, г = 1, 2, ...,», F.2.2)
содержащей Z множителей Я1? Я2! •••> ^г- Присоединяя к уравнениям F.2.2)
уравнения связи
п
^Brsqs + BT = 0, r = 1, 2, .... Z, F.2.3)
s=l
получаем систему n + Z уравнений для определения 'п + Z неизвестных
<? и Я как функций времени. Множители Я линейно связаны с реакциями
связи; например, в задаче о качении сферы они связаны с реакцией плоскости
в точке контакта с ней сферы.
Покажем, как изменяются уравнения при наличии избыточных коор-
координат. Пусть имеется р таких координат и р связывающих их соотношений
^г (qu Яг, • • •, qn; 0 = 0, г = 1, 2, . . ., р. E.12.6)
В этом случае в правую часть F.2.1) или F.2.2) добавляются слагаемые
v
2l*f-§?-, г=1, 2, ..., п. F.2.4)
t=i
Множители [Xi, [х2, . . ., \ip представляют р лишних неизвестных, для опре-
определения которых имеем р дополнительных уравнений E.12.6).
SO УРАВНЕНИЯ ЛАГРАНЖА [Гл. VI
Уравнения F.2.1) и F.2.2) были получены Лагранжем в 1760 г.
С их помощью можно описать движение любой механической системы.
Сначала выбираются лагранжевы координаты qT, затем составляется функ-
функция X — кинетическая энергия в виде полинома от q (с коэффициентами,
зависящими от q и, возможно, от t), и, наконец, пишется выражение для
работы, совершаемой заданными силами на произвольном виртуальном пере-
перемещении, в виде дифференциальной формы 2 Qr&Qr- Уравнения Лагранжа
занимают центральное место в его знаменитом сочинении «Mecanique Analy-
tique» [4], опубликованном в 1788 г. Это сочинение следует отнести к эпо-
эпохальным трудам во всей истории математики. Лагранж писал, что его метод
позволил свести динамическую задачу к задаче чистого анализа, так что
оказалось излишним приводить всякий раз геометрические соображения:
¦«On ne trouvera point de Figures dans cet Ouvrage» *). Сочинение Лагранжа
является основным источником идей аналитической механики и по праву
считается одним из величайших духовных достижений человечества.
§ 6.3. Вывод уравнений Лагранжа из принципа Гамильтона. В § 3.7 мы
получили принцип Гамильтона в следующей форме:
j ( ) C.7.4)
to r=l
Здесь б обозначает перемещение из точки действительной траектории в точку
варьированной траектории, соответствующую тому же моменту времени,
так что
Ьхт^^-Ьхт. F.3.1)
Вариация бж представляет собой виртуальное перемещение, которое
произвольно, за исключением того условия, что каждая составляющая 8хг
является функцией от t класса С2: обращающейся в нуль в моменты tg и h.
Принцип Гамильтона выражает свойство механической системы, не зави-
зависящее от системы координат, используемой для описания этой системы.
Попытаемся теперь выразить это свойство в лагранжевых координатах qT.
Рассмотрим траекторию изображающей точки в пространстве q и выра-
выразим принцип Гамильтона вместо переменных х в переменных q. Строим
варьированный путь, выбирая в каждый момент времени виртуальное пере-
перемещение 8q и получая точку на варьированной траектории, соответствую-
соответствующую этому моменту времени. Это виртуальное перемещение произвольно,
за исключением того условия, что каждая вариация 8qr представляется
функцией времени класса С2, обращающейся в нуль в моменты t0 и ti.
Поскольку вариация синхронна,
^г = -^-бдт, г=1, 2, ..., п. F.3.2)
Соотношения F.3.1) и F.3.2) эквивалентны. Это цочти очевидно, если
связь между q и х не содержит t, но это справедливо также и в общем слу-
случае, когда функции хт = zT (qi: q2, ¦ . ., qn; t) обладают свойствами, ука-
указанными в § 6.1. Доказательство проводится очень просто с помощью лемм
*) «В этом сочинении не найдется рисунков» (франц.). (Прим. ред.)
§ 6.3] ВЫВОД УРАВНЕНИЙ ЛАГРАН5КА ИЗ ПРИНЦИПА ГАМИЛЬТОНА 91
F.1.3) и F.1.4). Имеем
П
&r=2^%, r = l, 2, ..., N, E.12.4)
s=l
Если рассмотреть перемещение 8q, удовлетворяющее F.3.2), то с учетом
F.1.3), F.1.4) и F.3.2) получим
Перемещение 8q, удовлетворяющее F.3.2), удовлетворяет, таким образом,
и F.3.1), и обратно, поскольку между q жх существует взаимно однозначное
соответствие, перемещение 8х удовлетворяет F.3.2), если оно удовлетворя-
удовлетворяет F.3.1).
В принципе Гамильтона действительное движение системы сравнивается
с варьированным движением при одних и тех же конфигурациях системы
в начальный и конечный моменты времени и одинаковых самих этих момен-
моментах времени. Поэтому, если мы хотим выразить этот принцип с помощью
лагранжевых координат qi7 qz, ¦ ¦ ., qn, то нужно потребовать, чтобы поло-
положение системы в начальный и конечный моменты и самые эти моменты оста-
оставались неизменными (хотя соотношения между q я х содержат t). Принцип
Гамильтона, таким образом, принимает следующую форму:
r )dt =
F.3.4)
Мы увидим, что уравнение F.3.4) приводит непосредственно к уравнениям
Лагранжа. В самом деле, как уже отмечалось ранее, принцип Гамильтона
по существу представляет собой интегральную форму основного уравнения.
Вывод уравнений Лагранжа из принципа Гамильтона осуществляется тем
же путем, что и вывод этих уравнений непосредственно из основного урав-
уравнения.
Преобразуя первый член в левой части уравнения F.3.4) и исполь-
используя F.3.2), находим
Qr6qr) d/=
)
to r=l t0 r=\
«1
r=l
92 УРАВНЕНИЯ ЛАГРАНЖА [Гл. VI
Поскольку каждая вариация 6<?г в моменты t0 и tt обращается в нуль, урав-
уравнения F.3.4) и F.3.5) приводят к равенству
o r= 1
Если система голономна и п =.к, то [уравнение F.3.6) справедливо для
произвольных значений 8qi, 6q2, ¦ ¦ ¦, &qn (при условии, что 8qr ? С2). Соглас-
Согласно известной лемме вариационного исчисления коэффициент при каждом 8qr
в подынтегральной функции тождественно обращается в нуль, и мы полу-
получаем уравнения Лагранжа
d 1 д% \ д% „ . „ .....
*"ЫГ/ "г^^ ' ' "¦' "' ( >
Если система неголономна и п = к-\-1, то уравнение F.3.6) справедливо
лишь при условии, что вариации 8qt, bq2, ..., 6qn удовлетворяют уравне-
уравнениям
EW?S = O, г = 1, 2, ...,1. E.12.5)
Отсюда
4(^)^ r r«l, 2, .... п. F.2.2)
К этим уравнениям присоединяются I уравнений связи
п
2^rsgs-f5r = O, r=l, 2, ..., I. F.2.3)
8=1
Как указывалось в §§ 3.8 и 5.11, если система неголономна, то варьиро-
варьированный путь в общем случае не удовлетворяет уравнениям связи.
§ 6.4. Форма уравнений Лагранжа. Для голономной системы г -е урав-
уравнение Лагранжа записывается в форме
• • • • • •
ariqi + ar2q2 + . . . + arnqn — срг. F.4.1)
Правая часть cpr зависит только от q, q и t: уравнения Лагранжа линейны
относительно вторых производных q. Кроме того, коэффициенты aTs суть
коэффициенты определенно-положительной квадратичной формы Т2, причем
определитель ||яГ8|1 не обращается в нуль ни при каких значениях q и t,
так что уравнения F.4.1) можно разрешить относительно q:
• • • • ¦
qr =i|v (qi, q2, . . ., qn; qu q2, . . ., qn; t), r = 1, 2, . . ., n. F.4.2)
Функции aj)r зависят только от q, q и t. Для классической механики харак-
характерно то обстоятельство, что с помощью уравнений движения ускорение
явным образом выражается через координаты, скорости и время. Этот факт
уже отмечался нами в § 1.1, когда мы рассматривали движение свободной
материальной 'точки.
6.5] КОНСЕРВАТИВНЫЕ СИСТЕМЫ 93
Если обозначить qT = сог, то систему п уравнений второго порядкаF.4.2)
можно заменить системой 2п уравнений первого порядка:
г = 1, 2, . . ., п. F.4.3)
Уравнения теперь приводятся к виду
ж = X F.4.4)
где х ж X — матрицы-столбцы, или векторы с 2п составляющими, причем
X — функция от х и t. Форма F.4.4) играет важную роль, и в дальнейшем
мы часто будем ею пользоваться. Мы уже встречались с ней в § 1.1, когда
рассматривали движение одной частицы. Уравнения F.4.3) или F.4.4)
можно рассматривать как уравнения, описывающие движение изображающей
точки в пространстве 2га измерений. Заметим, что первая группа уравнений —
чисто геометрическая: эти уравнения просто определяют переменные coj.
и совершенно не связаны с принципами механики. Они не изменятся, если
на систему будут действовать другие заданные силы. Напротив, последние п
уравнений зависят от законов движения и заданной системы сил. В прило-
приложениях, однако, обе эти группы уравнений объединяются в единую систе-
систему вида F.4.4), и указанное различие этих групп теряет свое значение.
Значительно более удобно привести уравнения движения к форме F.4.4)
с помощью уравнений Гамильтона, которые будут рассмотрены в § 10.13
и в последующих главах.
Возвращаясь к уравнениям Лагранжа второго порядка, выразим урав-
уравнения движения явным образом через Т% и Т±, что нам потребуется в даль-
дальнейшем. Согласно F.1.6) г
п п
Т =-— V V а а а
2 2 2л 2л rs4T"a
2
r=l
d I дТ2\ дТг __ sp
dt \ я* / дат 2л
$Т з— i S— 1
Далее, согласно F.1.7)
r=l
И
? ^Г = ^Г + S V«?.. F.4.6)
где
dar das
§ 6.5. Консервативные системы и другие системы, обладающие потен-
потенциальной функцией. Предположим, что заданные силы Хт зависят только
от а; и не зависят ни от х, ни от t и что для любого виртуального
94 УРАВНЕНИЯ ЛАГРАНЖА [Гл. VI
JV
перемещения бас форма Пфаффа 2 Хт6хг является полным дифференциалом
г=1
— 8V, где V — однородная функция от переменных xlt x2, ..., xN, принад-
принадлежащая классу Сх. В этом случае заданные силы называют консервативны-
консервативными (см. § 3.4), а функцию V — потенциальной энергией. Предположим, далее,,
что соотношения между q и х не содержат /. Тогда
N п N п
г—\ s=l г=1 е=1
И
п
2 Qs&Qs= —635, F.5.2)
где
V(xi, х2, ..., xN) = 23(qu q2, ..., qn). F.5.3)
Четвертая форма основного уравнения F.1.12) принимает следующий вид:
Уравнения Лагранжа F.2.1) и F.2.2), соответственно для голономных
и неголономных систем, записываются теперь в виде
—^r^—d^+Zl1^^ r = l, 2,..., л. F.5.6)
т= 1
В некоторых случаях кроме консервативных сил имеются еще другие
силы ХТ. К их числу могут относиться, например, неконсервативные силы,
зависящие от положения, или силы, зависящие от скоростей. Если, подоб-
подобно F.1.10),
й=2*'ж- F-5-7>
г=1
так что работа добавочных сил на виртуальном перемещении равна
п
2 Qs^Qs, то уравнение F.5.4) нужно заменить уравнением
l
2 Г d I д% \ д% . дЪ К
s=l
г=1 ^ ^^
охватывающим формы F.1.12) и F.5.4). Уравнения Лагранжа, соответ-
соответственно для голономных и неголономных систем, принимают теперь вид
Ж==-^7 + ^' г = 1' 2' •••' п' F'5-9)
^7=-^7 + ^+2 л-5'"'-' г=1, 2, .... п.- F.5.10)
m=i
§ 6.6] ФУНКЦИЯ ЛАГРАНЖА 95
Форма F.5.4) справедлива также и в других случаях. Предположим,
что заданные силы Хт зависят как от t, так и от я, а соотношения, связыва-
связывающие q и х, также содержат t:
хт = хт (qu q2, . . ., qn; t). F.5.11)
Может случиться (см. § 3.4), что для некоторого произвольного виртуаль-
виртуального перемещения 8х
N
2 Xr8zr=-6SF, F.5.12)
r=l
где дифференциал в правой части вычисляется при неизменном /:
N
6>у=2-щ;8хг. F.5.13)
Если теперь
У(х±,х2, ...,xN; t) = №(quq2, ...,?„; t), F.5.14)
то будем иметь
^j^s-f-*- (б-5л5>
r=l s=l r=l s=l
2 №=-6,®, F-5.16)
s=l
n
где Os* = J>j-=—o?s вычисляется при неизменном t. В этом случае
8=1
уравнение F.5.4) остается справедливым.
Наиболее простым и часто встречающимся случаем является тот, когда
1) соотношения между q и х не содержат t, 2) заданные силы консервативны
и 3) система голономна, и лагранжевы координаты выбраны так, что п = к.
В этом случае
п п
71 _^^л/7л /'fi ^ 1 7Y
— -f 2 — ^г 2Li /Li ursqr4s ^o.o.i (/
r=l s=l
и коэффициенты ars зависят только от q. Последнее справедливо также
и для Й5, и уравнение F.5.4) выполняется для произвольных значений
Sgi, 6<72, . . ., ?>qn. Такая система называется натуральной системой.
§ 6.6. Функция Лагранжа. В этом параграфе мы примем новую систему
обозначений. До сих пор, описывая положение и движение системы с помощью
координат х и скоростей х, мы кинетическую и потенциальную энергии
обозначали соответственно через Т и V.
Когда мы рассматривали четвертую форму основного уравнения и урав-
уравнения Лагранжа, мы во избежание возможной путаницы соответствующие
функции, выраженные через q и q, обозначали через ? и 23. Теперь можно
без ущерба для понимания отбросить эти символы и для обозначения кине-
кинетической и потенциальной энергий, выраженных через q и q (а также,
возможно, и t), пользоваться буквами Т и V. Таким образом, для случаев,
96 УРАВНЕНИЯ ЛАГРАНЖА [Гл. VI
описанных в § 6.5, четвертая форма основного уравнения запишется в виде
Если разность Т — V обозначить через L, то уравнение F.6.1) можно
будет записать в следующей форме (поскольку функция V не зависит от д):
Если система голономна и п = к, то уравнения движения будут иметь вид
d ПдЬ \ _ дЬ
dt V^7"/ dir ' r=l, 2, ..., п. F.6.3)
Если же система неголономна и п = к-\-1, то уравнения движения будут
иметь вид
4(-^)=-^Г* 2 ЯА" г = 1,2, .., п. F.6.4)
1Т m=l
К этим п уравнениям нужно присоединить I уравнений связи
j] = 0, r=l,2,...,l. F.2.3)
8=1
Функцию Лагранжа L называют кинетическим потенциалом механи-
механической системы. Зная кинетический потенциал, можно написать уравнения
движения системы, так что фактически он полностью определяет всевозмож-
всевозможные движения механической системы. В дальнейшем мы встретимся еще
с другими функциями, описывающими движения системы.
Результаты, выражаемые уравнениями F.6.3) и F.6.4), можно распро-
распространить и на некоторые случаи, когда заданные силы зависят от скоростей.
Если работа заданных сил на произвольном виртуальном перемещении может
быть выражена в форме
r=l
где V зависит от q и q (а также, возможно, и от t), то уравнение F.6.2),
в котором L = Т — V, по-прежнему сохраняет силу. Уравнения F.6.3)
и F.6.4) также остаются справедливыми.
Нужно, однако, сделать следующее предостережение. Функция V может
зависеть от q лишь линейно, т. е.
— afli — a2q2 — ... — anqn + Vo, F.6.6)
где а и Vo зависят только от q (и, быть может, от t). В противном случае
заданные силы были бы функциями от составляющих ускорения, что, как
мы видели в § 1.4, невозможно в рамках ньютоновой механики.
Для натуральной системы функция Лагранжа имеет вид L = Т — V,
где Т — однородная квадратичная функция от q. В других случаях Т может
содержать члены, линейные относительно q, которые, следовательно, войдут
и в выражение для L. В дальнейшем (§ 10.6) мы рассмотрим влияние этих
членов на уравнения движения.
§ 6.7.] ИНТЕГРАЛ ЯКОБИ 97
§ 6.7. Интеграл Якоби. Допустим, что система, описываемая функцией
Лагранжа L, удовлетворяет двум следующим условиям!
1) L не содержит явно t;
2) скорость q в действительном движении является виртуальной ско-
скоростью.
В этом случае вместо 8qr в уравнении F.6.2) можно написать qr. Тогда
оно примет вид
Левую часть этого уравнения можно преобразовать к виду
после чего, интегрируя уравнение F.7.1), получаем
п
^qr^L-L = h, F.7.2)
г=1 дЧг
где h — постоянная. Соотношение F.7.2) известно |как интеграл Якоби.
Его называют иногда также интегралом энергии или уравнением энергии,
поскольку в случае натуральной системы
п
^q'TJL = 2T F.7.3)
r=l d1r
и F.7.2) эквивалентно равенству
T + V=h. F.7.4)
Рассмотрим условия, при которых существует интеграл вида F.7.2).
Условие 1), разумеется, будет выполнено, если ни Т, ни V не зависят от t.
Кроме того, Т не зависит явно от t, если соотношения между х и q не
содержат времени. Эта возможность, однако, не единственная; иногда
Т не содержит явно t даже в. том случае, когда переменные х зависят от q
и от t. Очевидным примером может служить равномерно вращающаяся систе-
система координат. Предположим, что система координат Ox'y'z' вращается
с постоянной угловой скоростью вокруг оси От!, совпадающей с осью Oz
неподвижной системы Oxyz. Тогда для произвольно выбранной точки систе-
системы будем иметь
х = х' coscof — у' sincof, ^
у = х' sin a>t-\-у' cosart, [ F.7.5)
2 = 2', j
где ю — постоянная угловая скорость. Поэтому
x2 + y2~r'z2 = (x' — y'(oJ+(y' +х'аJ + z'2 F.7.6)
и, следовательно,
Т = у Sm {(х' - у'®)* + (у' + x'(o)z + z'2} =
= ^Sm(x'2+y'2 + z'2)^(oSm(x'y'-y'x')+^-(^Sm(x^+y'2). F.7.7)
7 Л. А. Парс
(oSm(x'y'-y'x') =
98 УРАВНЕНИЯ ЛАГРАНЖА [Гл. VI
Предположим теперь, что лагранжевы координаты выбраны так, что
декартовы координаты во вращающейся системе зависят только от q и не за-
зависят от времени. Тогда
F.7.8)
где Т2 — квадратичная форма от q с коэффициентами, зависящими от q,
Tt — линейная форма* от q с коэффициентами, зависящими от q, и То —
функция от q. Таким образом, функция
Г = Т2 + 71! + То F.7.9)
не содержит t, хотя соотношения между q и х содержат t.
Далее, работа заданных сил на виртуальном перемещении равна
S (X 8х + Y 8у + Z 8z) = S (Х'бх' + Y'8y' + Z'8z'). F.7.10)
Если заданные силы, вычисленные во вращающейся системе координат,
консервативны, то работа равна — 6F, где V = V (дгь q2, . . ., qn). Практи-
Практически важен случай, когда имеет место симметрия относительно оси враще-
вращения Oz. В простейшем случае ось вращения вертикальна, а заданными
силами являются силы тяжести.
Условие 2), очевидно, будет выполнено, если система голономна и п = к.
Оно выполняется также и для неголономной системы, если коэффициенты Вт
в уравнениях связи F.2.3) все равны нулю. Последнее, очевидно, имеет
место, когда система является катастатической (§ 2.3) и соотношения меж-
между х и q не содержат t, например, в случае качения сферы по неподвиж-
неподвижной идеально шероховатой поверхности под действием силы тяжести.
§ 6.8. Явная форма интеграла Якоби. Предположим, что условия для
существования интеграла Якоби выполнены, т. е. L не содержит явно t
и действительная скорость является виртуальной. Тогда
п
-%fr*L-L = h, F.7.2)
где
L = Ta + T1 + T0-V. F.8.1)
Согласно теореме Эйлера об однородных функциях
п
%qr^=2T2 + T1. F.8.2)
r=l дЧт
Тогда равенство F.7.2) можно представить в виде
Тг + V - То = h. F.8.3)
Мы получили явную форму интеграла Якоби.
Слагаемые То и — V входят в функцию Лагранжа равноправно, и невоз-
невозможно выделить роль каждого из них в уравнениях движения. В истории
развития теории магнитной энергии это обстоятельство сыграло, к слову
говоря, не последнюю роль. Поэтому не вызывает удивления, что в левую
часть равенства F.8.3) эти величины входят в комбинации V — То. Суще-
§ 6.8] ЯВНАЯ ФОРМА ИНТЕГРАЛА ЯКОБИ 99
ственно, что в интеграл Якоби не входит 7\. Обратимся к примеру с вращаю-
вращающейся системой координат, рассмотренному § 6.7. Интеграл энергии в этом
случае такой же, как в случае, когда оси не вращаются, но к заданным силам
добавлены центробежные силы, иными словами, к V добавлено
-^Sm(o2(x'* + y'2). F.8.4)
Как уже было сказано, члены с Тх не входят в соотношение F.8.3).
В некоторых случаях можно пойти дальше и доказать, что они вообще
не оказывают влияния на движение и их можно отбросить в выражениях
для L. Это имеет место тогда, когда Тг имеет вид
п
4/(?!.?«. ••-.?*) = 2-^T?r. F.8.5)
В этом случае каждое из выражений
d (STi\ дТх
dt \ g-r ) аЧт
тождественно обращается в нуль (в чем нетрудно убедиться с помощью
леммы F.1.4) § 6.1). Если Tt имеет форму F.8.5), то оно обращается в нуль
при воздействии лагранжева оператора
d д д
Этот результат имеет важное прикладное значение в задаче о движении
системы во вращающихся осях. Заметим, что если
71! = coSw (zy — у'х')
имеет форму F.8.5), то влияние вращения на движение относительно вра-
вращающихся осей полностью учитывается введением центробежных сил.
Это верно, в частности, для любой системы с одной степенью свободы. Этот
факт очевиден: в случае одной степени свободы интеграл Якоби дает полное
решение задачи, и этот интеграл не зависит от Т^.
В качестве конкретного примера рассмотрим скольжение бусинки по глад-
гладкой жесткой проволоке (не обязательно имеющей форму плоской кривой),
которая вращается с постоянной угловой скоростью ю около вертикаль-
вертикальной оси. Для описания движения бусинки относительно проволоки можно
забыть о вращении проволоки и ввести добавочное поле центробежных сил
яггсо2, где г — расстояние от оси вращения; это эквивалентно добавле-
нию к V слагаемого g- ягг2ш2. Важный частный случай разбирается ниже
в примере 6.8.
Прежде чем закончить изложение этого вопроса, укажем на одно более
общее положение. Добавление выражения
-lff(qi,q2, ...,gr;t) F.8.6)
к функции Лагранжа L не оказывает влияния на уравнение движения.
Это опять-таки следует из леммы F.1.4). Члены в выражении для L, имею-
имеющие форму F.8.6), несущественны и просто могут быть отброшены. Этот'
результат является также следствием принципа Гамильтона.
7*
100
УРАВНЕНИЯ ЛАГРАНЖА
[Гл. VI
Пример 6.8. Движение точки по вращающейся
окружности. Пусть бусинка скользит по гладкому проволочному
кольцу радиуса а, а кольцо вращается около вертикального диаметра с по-
постоянной угловой скоростью со. Рассмотрим движение бусинки относитель-
относительно проволоки.
Пусть Э будет угловым перемещением бусинки из наинизшего ее поло-
положения на проволоке (см. пример 5.2А). Интеграл Якоби будет иметь вид
у ma2Q2 — mga cos 9 — у та2®2 sin2 Э = mgar\
или, что то же,
У ё2 = пг (т) + cos 9) + у со2 sin2 9,
F.8.7)
где п2 = gla. Это уравнение принадлежит к типу A.2.10); мы видели, что
характер движения для различных значений т] можно определить по графи-
графику функции, стоящей в правой части уравнения. Если со = 0, то мы при-
приходим к задаче о плоском маятнике и уравнение F.8.7) приводится к E.2.2).
При малых значениях со график мало отличается от представленного на
рис. 4 и возможные типы движения, вообще говоря, близки к типам дви-
движения плоского маятника. Критическое значение со равно п, и при со > п
возможные типы движения существенно
отличаются от движений плоского маят-
маятника. Условие со >» п означает, разумеется,
что период вращения меньше периода ма-
малых колебаний маятника. Рассмотрим поэ-
СО'
,2 =
тому случай со > п и положим
угол. Пра-
F.8.7) запишется
Рис. 9.
= n2 sec а, где а — острый
вая часть уравнения
теперь в виде
==п2 (т) -j-cos 9+-О- sec a sin2 9) =
= у п2 sec а {2т) cos а + 1 + cos2 a —
— (cos 9 —cos аJ}; F.8.8)
график этой функции представлен на
рис. 9 *). Кривая имеет максимумы в точ-
точках 9 = ± а и минимум при 9 = 0. Воз-
Возможны шесть типов движения в зависи-
зависимости от значений т); все они показаны на рисунке. (Вместо того чтобы
с увеличением т] поднимать кривую, мы на графике обходимся одной кри-
кривой, ось х располагая тем ниже, чем больше ¦ц.)
1) т, = _ 1 _ Я, где Я = A - cos aJ/B cos а) = (со2 - ге2J/Bтг2со2).
Это — наименьшее возможное значение т). Бусинка находится в покое (отно-
(относительно проволоки) в положении устойчивого равновесия при 9 = а или
при 9 = — а. Период малых колебаний (относительно проволоки) при нару-
шении равиовесия равен 2n/(cosina).
2) —1 — Л<т)< — 1. Движение представляет собой либрацию меж-
между пределами 94 и 92 (см. рисунок) или между —9i и —92, причем
О < 94 < а < 92
< у Я.
•) График построен для случая <а2 = 2»2, яри этом 03 = у я.
§ 6.10] ОБОБЩЕННЫЙ ИМПУЛЬС 101
3) т] = — 1. Бусинка находится в. покое в положении неустойчивого
равновесия 9 = 0 либо совершает лимитационное движение, при котором
9 сначала, возможно, возрастает до значения 93, но затем монотонно убывает,
стремясь к нулю при t—> оо.
4) — 1<Ст]<С1- В этом случае мы имеем либрационное движение
между пределами —р и р* (см. рисунок), близкое, вообще говоря, к либра-
ционному движению обычного плоского маятника.
5) т] = 1. Бусинка покоится в положении неустойчивого равновесия
9 = я (или, что то же, 9 = — я) либо совершает лимитационное движение,
при котором при t —>¦ оо 9 —>¦ я или 0 —>- — я.
6) т] > 1. Если в начальный момент 9 > 0, то 9 все время возрастает
вместе с t.
Этим перечнем исчерпываются возможные движения в рассматриваемой
задаче. Тип движения зависит от того, в каком интервале значений лежит
параметр г\, и в каждом случае из уравнения F.8.7) можно получить явное
соотношение между 9 и t.
§ 6.9. Об одной ошибке. Укажем на одну распространенную ошибку *), связанную
с получением уравнений Лагранжа из интеграла Якоби. Из уравнения F.7.2) вытекает, что
1(|^Н. F.9.1)
или, что то же,
По сути дела, это означает всего лишь изменение порядка действий при выводе интеграла
Якоби из уравнений Лагранжа.
Из уравнения F.9.2) нельзя вывести уравнения Лагранжа. Для этого нужно было
бы быть уверенным, что уравнение
справедливо для произвольных значений Я,4, Я2, ¦ ¦ ., Я^, тогда как равенство F.9.2)
показывает только то, что уравнение F.9.3) выполняется тогда, когда каждое значение Я,г
равно соответствующему значению qT в действительном движении.
§ 6.10. Обобщенный импульс. Частные производные dL/dqr, входящие
в уравнения Лагранжа, называют обобщенными импульсами или просто
импульсами; их обычно обозначают через рг:
Рг = ~. F.10.1)
dqr
Импульсы линейно зависят от обобщенных скоростей gb q2, ¦ . ., qn; для
натуральной системы они являются однородными линейными функциями
от обобщенных скоростей с коэффициентами, зависящими от д.
Позже мы увидим, что состояние системы в данный момент иногда бывает
удобнее описывать с помощью q и р (координат и импульсов), а не с по-
помощью q и q (координат и скоростей).
*) См., например, Дж Д. Б и р к г о ф, Динамические системы [35], стр. 22.
102 УРАВНЕНИЯ ЛАГРАНЖА [Гл. VI
Приведем два простых примера.
1) Пусть частица движется в консервативном поле с потенциалом V.
В этом случае функция Лагранжа имеет вид
L = ^m(x2 + y2+z*)~Vf F.10.2)
где х, у, z — обычные декартовы координаты. Обобщенный импульс, соот-
соответствующий координате х, будет равен
-^- = тх, F.10.3)
дх
т. е. будет равен проекции количества движения на ось Ох. В задачах,
подобных этой, где лагранжевы координаты не нумеруются, мы иногда
будем обобщенный импульс, соответствующий лагранжевой координате q,
обозначать через pq; например, в рассматриваемой задаче
' Px=*L = m?. F.10.4)
дх
2) Пусть частица совершает плоское движение под действием централь-
центрального поля притяжения <р (г) к точке О. Функция Лагранжа в полярных коор-
координатах будет иметь вид
? = lm(r2+r2e2)-F, F.10.5)
где
V = V(r)= J<p(?)dg. F.10.6)
га
В этом случае обобщенный импульс
Рв=Ц- = тА F.10.7)
будет равен моменту количества движения относительно точки О.
§ 6.11. Циклические координаты. В § 6.7 мы нашли первый интеграл
уравнений движения для систем определенного типа. Можно сразу указать
еще один первый интеграл, если среди координат, описывающих систему,
имеется так называемая циклическая координата. Координату gi называют
циклической, если она не входит в выражение для L (но gt, конечно, может
входить в это выражение). Соответствующее уравнение Лагранжа тогда
принимает вид
Отсюда
~== const. F.11.2)
Мы получили первый интеграл уравнений движения; он выражает
постоянство обобщенного импульса pi, соответствующего циклической коор-
координате <?!.•
Pi = const = Pj. F.11.3)
Это соотношение называют циклическим интегралом.
§ 6.12] ИНВАРИАНТНОСТЬ УРАВНЕНИЙ ЛАГРАНЖА 103
Если в примере 1) § 6.10 V не зависит от х, то х — циклическая коорди-
координата. В этом случае действующая на частицу сила всегда перпендикулярна
к оси Ох. Соответствующий циклический интеграл
рх = тпх = р
выражает сохранение проекции количества движения на ось Ох.
В примере 2) § 6.10 координата 9 является циклической и соответствую-
соответствующий циклический интеграл
Ре =
выражает сохранение момента количества движения относительно точки О.
§ 6.12. Инвариантность уравнений Лагранжа. Тот факт, что уравнения Лагранжа
для голономной системы имеют одну и ту же форму, каковы бы ни были описывающие
систему лагранжевы координаты, является очевидным, поскольку эти уравнения выво-
выводятся из основного уравнения (§ 6.2) или из принципа Гамильтона (§ 6.3). Тем не менее
представляет интерес непосредственное доказательство инвариантности уравнений
Лагранжа.
Рассмотрим взаимно однозначное преобразование лагранжевых координат gi, q2,
..., qn к новым координатам q'lt q'2, ..., q'n, связанным с первыми соотношениями
?, = /r(?i, q'i q'n, t), r=t, 2, ..., n, F.12.1)
гДе fr 6 ^2- Нам понадобятся две леммы, аналогичные F.1.3) и F.1.4), а именно:
dqr dqr dqT d I dqT \
то
Если
L(q, q',t) = L'(q',q',t), F.12.3)
dq'r Z| dqs dq'r + 2j ^ dq'r ~Zj 8qs dq'r +^ g^ dt \ dq'r
.^1-= vj^j^=y - j^._ F.12.5)
"?Г s=l "?S "9r s=l "?«
Отсюда
П 71
d I SL/\ dL' d l-^y dL dqs\ -\-\ dL dqs
A. (HL\^LLLA. lx —Ll±\_\
dt \ d'q'T I dq'r~ dt \2l ^ dq'r ) Ь dqs dq'r
^ qr )
Определитель
нении.
dqs
dq'r
s—1 ** s—1 *s
не обращается в нуль, откуда и следует инвариантность урав-
Глава VII
ТЕОРИЯ ПОВОРОТОВ
§ 7.1. Движение твердого тела. При исследовании движения твердого
тела с помощью уравнений Лагранжа кинетическую энергию тела мы выра-
выражаем через лагранжевы координаты, выбранные для описания его поло-
положения и ориентации в пространстве. Те же формулы используются и при
исследовании движения механических систем, содержащих твердые тела.
Поэтому рассмотрим подробнее теорию движения твердого тела.
Мы не ограничимся составлением функции Лагранжа для твердого тела.
Наше исследование будет значительно шире, и мы получим ряд важных
теорем, относящихся к перемещению и движению твердого тела. Использо-
Использование некоторых из этих результатов для составления уравнений Лагранжа
является лишь одним из многочисленных их приложений.
Рассмотрим механическую систему, состоящую из одного твердого тела.
Положение твердого тела в пространстве определяется положением некото-
некоторой фиксированной в нем точки, например центра тяжести G, и ориентацией
тела. В соответствии с этим кинетическую энергию тела можно представить
в виде суммы двух частей, одна из которых определяется движением центра
тяжести G, а другая — движением относительно центра тяжести, т. е. изме-
изменением ориентации тела при центре тяжести, принимаемом неподвижным
(теорема Кёнига). Имеем
Т = ±Sm(i* + y*+'z>)=±Sm{(l, + a)*+ (Ц+&+ ?+i)% G.1.1)
где координаты а, [}, у определяют положение частицы относительно центра
тяжести ?, т), ?. Поскольку Sma = Sm$ = Smy = 0, приходим к теореме
Кёнига:
В этом равенстве М = Sm есть масса тела. Кинетическая энергия представ-
представлена в виде суммы двух частей. Первая из них выражает кинетическую
энергию в случае, если бы вся масса тела была сосредоточена в его центре
тяжести G, а вторая — кинетическую энергию вращения тела вокруг центра
тяжести G как вокруг неподвижной точки.
Чтобы определить изменение положения тела, необходимо сначала
определить перемещение точки G, а затем изменение ориентации тела.
Разделим две эти операции и начнем с изучения второй из них: изменения
ориентации. Итак, мы переходим к исследованию движения твердого тела
с одной закрепленной точкой.
§ 7.2. Теорема Эйлера. Согласно этой теореме (полученной Эйлером
в 1776 г.) всякое перемещение тела с одной закрепленной точкой О представ-
представляет собой вращение. Иными словами, любое изменение ориентации тела
можно произвести путем поворота тела около некоторой оси, проходящей
через точку О.
§ 7.2] ТЕОРЕМА ЭЙЛЕРА 105
Ориентация тела определяется направлениями двух линий ОА, ОВ,
фиксированных в теле. Отрезки ОА и ОВ удобно взять единичной длины,
тогда точки А и В будут фиксированными точками тела на единичном рас-
расстоянии от неподвижной точки О. Представим себе две сферы с центром
в общей точке О: сферу радиуса единица, неподвижную в пространстве,
и бесконечно тонкую сферическую оболочку с внутренним радиусом едини-
единица, неизменно связанную с телом и движущуюся вместе с ним.
Предположим, что при некотором перемещении тела точка А оболочки
переходит в точку В, а точка оболочки, находившаяся ранее в В, переходит
в точку С (отрезок О А при этом выбран произвольно, а отрезок ОВ опреде-
определен только что указанным условием). Плоскость ABC пересекает неподвиж-
неподвижную сферу по окружности (рис. 10). Пусть L — какой-либо полюс этой окруж-
окружности. Равнобедренные треугольники LAB и LBC равны: дуги АВ и ВС
равны, поскольку представляют одну и ту же дугу
движущейся сферической оболочки в двух положе-
положениях. Следовательно, дуга А В может быть переве-
переведена в положение ВС путем поворота около оси OL
на угол ALB.
Отметим некоторые особые случаи. Если точка В
совпадает с точкой А, то теорема очевидна и пере-
перемещение представляет собой поворот около оси ОА.
Если В не совпадает с А, но С совпадает с А, то
в этом случае имеются две возможности. 1) Если
точки А, О, В не лежат на одной прямой, то через
точки А и В проходит один большой круг и переме- рис 10.
щение представляет собой полуоборот (т. е. поворот
на угол я) вокруг оси ОМ, где М — середина любой
из дуг А В большого круга. 2) Если же точки А, О, В лежат на одной пря-
прямой, то предыдущие рассуждения теряют силу. В этом особом случае
точки А и В располагаются на противоположных концах диаметра обо-
оболочки и направлений ОА и ОВ недостаточно для определения ориента-
ориентации тела. Через точки А и В теперь проходит не одна-единственная дуга
большого круга. В этом случае поступим следующим образом. Возьмем
какую-нибудь точку А' оболочки; она может быть произвольна, за исклю-
исключением того, что не должна совпадать с точкой А и не должна быть диамет-
диаметрально противоположной ей. При этом направления О А и О А' полностью
определяют ориентацию тела. Построим точки В' и С, связанные с А'
точно так же, как точки В и С связаны с А. Точка С" совпадает при этом
с А' (так как иначе точка С не совпадала бы с А). Если точки А', О, В'
не лежат на одной прямой, то доказательство завершается так, как мы пока-
показали выше. Если А', О, В' расположены па одной прямой, то перемещение
представляет собой полуоборот около оси OL, где L — любой полюс дуги
большого круга ABA'В''. Мы видим, что трудности возникают в случае,
когда поворот равен полуобороту; с этим мы еще встретимся в дальнейшем.
Теорема Эйлера эквивалентна утверждению, что для любых двух ориен-
ориентации тела можно указать единственную фиксированную в теле прямую OL,
направление которой (равно как и направление вращения) остается неизмен-
неизменным. Любая прямая, фиксированная в теле и параллельная OL, остается
после вращения параллельной первоначальному направлению. Сечение тела
плоскостью, перпендикулярной к OL, может быть переведено в конечное
положение путем перемещения в своей собственной плоскости.
Основываясь на этой новой точке зрения, можно дать другое доказа-
доказательство теоремы Эйлера. Отрезок ОА можно перевести в новое положение
ОА' совершая полуоборот около оси ОМ, где М— середина дуги АА' боль-
большого круга. После этого тело можно перевести в конечное положение путем
106
ТЕОРИЯ ПОВОРОТОВ
[Гл. VII
Рис. 11.
поворота, скажем, на угол ср около оси ОА'. Можно считать, что дуга
<л и | ср | ^С я. Но при полуобороте около ОМ и последующем повороте
на угол ф около О А' одна прямая тела остает-
остается неподвижной. Для доказательства этого
построим сферические треугольники A'ML и
A'ML', как показано на рис. И. Дуга L'ML
перпендикулярна к биссектрисе АА', и каж-
дый из углов LA'M, MA'L' равен уф. Рисунок
относится к случаю, когда вращение около О А'
на угол, меньший я, происходит в положитель-
положительном направлении. Полуоборот около М пере-
переводит точку Р на движущейся оболочке из
первоначального положения L в положение L',
а поворот около А' переводит точку Р в положение L. Поэтому прямая ОР
в твердом теле остается неподвижной, и два эти перемещения в совокуп-
совокупности эквивалентны одному повороту около этой прямой.
§ 7.3. Матрица I и вектор Т. Рассмотрим теперь перемещение тела
и теорему о существовании неподвижной прямой с другой точки зрения.
Возьмем фиксированный в теле прямоугольный триэдр OY ^, OY2, OY3
и рассмотрим матрицу направляющих косинусов осей OYU OY2, OY3 no
отношению к неподвижным осям OXt, OX2, ОХ3. Оба триэдра будем пред-
предполагать правыми. (Иногда будет удобнее пользоваться другими обозначе-
обозначениями, а именно оси подвижного триэдра обозначать через ОА, ОВ, ОС,
а оси неподвижного — через Ox, Oy, Oz.) Матрица направляющих косину-
косинусов имеет вид
G.3.1)
Элементы г-ж строки lri, lr2, 1т3 суть направляющие косинусы оси OYT по
отношению к триэдру ОХ\, ОХ2, ОХ3. Первый столбец матрицы дает направ-
направляющие косинусы оси OXi по отношению к триэдру OY\, OY2, OY3. Вооб-
Вообще элемент lrs выражает косинус угла между OYT и OXS.
Если xt, х2, х3 — координаты точки в системе OXi, ОХ2, OX3, a у±,
Уг, Уз — ее координаты в системе OY±, OY2, OY3, то
У = 1эс,
G.3.2)
где х — матрица-столбец {хи х2, х3), а. у — матрица-столбец {г/ь y2, у3}.
Если тело перемещается из первоначального положения, при котором
оси OYi, OY2, OY3 совпадают с осями OXi, OX2, ОХ3, то точка, фиксирован-
фиксированная в теле и находившаяся ранее в положении у, переходит в положение х
по отношению, конечно, к неподвижной системе OXiX2X3.
Матрица I является ортогональной матрицей размером 3x3:
17 1 \ Л 77' 7'7 7" /7 5 41
| ' ^^ I *) vb =^ v v = JL , [I .O.OJ
где Г обозначает транспонированную матрицу I; одно из собственных зна-
значений этой матрицы равно -|~1. Таким образом, существует ненулевой век-
вектор х такой, что
у = х. G.3.4)
Это равенство показывает, что существует прямая в теле, которая при пово-
повороте тела остается неподвижной.
$ 7.3] МАТРИЦА I И ВЕКТОР Т 107
Для доказательства того, что существует собственное значение, рав-
равное +1, рассмотрим функцию
Имеем
Отсюда
17 11 Т ТI 17" 7 1
\l\\l —1 \ — \±—1\.
Следовательно,
/ A) = (-1K/ A), / A) = 0.
Можно пойти дальше и получить с помощью матрицы I явные формулы
для угла поворота и направляющих косинусов оси вращения. (Мы имеем
в виду направляющие косинусы по отношению к неподвижной системе
OZiZ2X3, хотя на самом деле они не отли-
отличаются от направляющих косинусов по отно-
отношению к осям OYiY2Y3.) Уравнение
у = 1х G.3.2)
определяет изменение положения фиксиро-
фиксированной частицы тела, перешедшей из поло-
положения R в положение S. Координаты точки R
(в неподвижных ося х OXiXzX3) равны
yii Vii Уз: а координаты точки S равны Xi,
х2, х3. Уравнение G.3.2) можно представить
в эквивалентной форме:
х-у = К(х + у), G.3.5)
где^Гматрипа^ — I) (I +1)-1 = (I-\- l)~l(I— Рис- 12-
— I). Очевидно, матрица К существует при
условии, что —1 не является собственным значением матрицы I*). Кроме
того, матрица К кососимметрическая. Для доказательства рассмотрим равен-
равенство
K(I+l) = I — l. G.3.6)
Умножая его справа на I', находим
K{Z'+I) = l' — I. G.3.7)
Транспонируя матрицы, получаем
(l+I)K' = l — I. G.3.8)
Следовательно,
K' = (l + I)-1(l-I)=-K, G.3.9)
и, стало быть, матрица К является кососимметрической:
/О т т \
К=\ Т, 0 -ТЛ. G.3.10)
\-Тг Tt 0 /
Произведение матриц Кш, (где m = -^ (ас + у)\ представляет собой
матрицу-столбец векторного произведения IX »>*-, где вектор Т имеет
составляющие {7\, Тг, Т3). На рис. 12 прямая ОА имеет направление
*) Если осуществляется один полуоборот, то собственными значениями будут 1,
-1, -1.
108 ТЕОРИЯ ПОВОРОТОВ [Гл . VII
вектора Т, точка М есть средняя точка отрезка RS, перпендикулярного
к плоскости, содержащей векторы Т и m (поскольку -^RS = Т X т\ ,
а Р является точкой пересечения прямой ОА с плоскостью, проходящей
через точку R и перпендикулярной к прямой ОА.
Из соотношений
^{x-y) = TY.m, G.3.11)
| MS | = | T j | m | sin ф = | T11PM | G.3.12)
следует, что
|T| = tgla, G.3.13)
где через a обозначен угол RPS; можно считать, что 0<;а<;я. Переме-
Перемещение из точки R в точку S достигается путем поворота на угол а около
оси О А.
Таким образом, матрица I определяет вектор Т:
T=(tg-ia)ra, G.3.14)
где п — единичный вектор вдоль оси вращения, а a — угол поворота. Собст-
Собственно говоря, ось вращения и угол поворота определяются матрицей I.
Вектор поворота Т будет играть важную роль в дальнейшем.
Если теперь через г обозначить радиус-вектор частицы тела (по отноше-
отношению к неподвижным осям) до перемещения, а через s — радиус-вектор той
же частицы после перемещения, то уравнение G.3.11) можно представить
в следующей форме:
в—г = Тх(в + г), G.3.15)
где Т — вектор поворота. Это соотношение теряет силу, если а есть нечетное
кратное от я; в частности, оно неверно для полуоборота. Но в обычных
случаях можно предполагать (как уже указывалось ранее), что 0 < a < я.
Любое значение а (не нечетное кратное от л) можно представить в форме
2&я + 0, где к — целое число, а | 9 | < it. Если 0 > 0, то поворот на угол
2&я + 9 эквивалентен повороту на угол 0. Если 0 < 0, то поворот на угол
2&я + 0 около оси ОА эквивалентен повороту на угол —0 около оси АО. При
замене а на 2я — а, а и на —п вектор Т остается неизменным (как и следо-
следовало ожидать, поскольку этот вектор определяет перемещение).
Пример 7.3. Найти ось вращения и угол поворота в случав, когда после пере-
перемещения ось OYi совпадает с осью ОХ2, ось OY2 — с осью ОХ3 и ось OY3 — с осью OXt.
В этом случае
/0 1 0\ /0—1 1\
s=1 ooil, в:= 1 о —l I,
\1 0 0/ V-1 1 0/
так что вектор Т равен {1, 1, 1}. Ось вращения наклонена к осям ОХи ОХ2, ОХ3 под
одинаковыми углами, а tg — a = "[/3, a = -n- и- В этом простом примере результат оче-
очевиден и без вычислений. Ось вращения можно найти, исходя из того, что она имеет
направление собственного вектора, соответствующего собственному значению +1,
а величину угла поворота — исходя из того, что остальные собственные значения равны
ега и е~га. (Матрица I имеет те же собственные значения, что и матрица Ru см. ниже
формулу G.6.6).)
§ 7.4. Обобщение теоремы Эйлера. Теорема о том, что прямая, прове-
проведенная в теле, при повороте тела остается неподвижной, эквивалентна утверж-
утверждению, что отображение единичной сферы на себя, получаемое при любом
5 7.6] ФОРМУЛА ПОВОРОТА 109
перемещении скользящей по сфере оболочки (§ 7.2), обладает неподвижной
точкой. Между тем неподвижная точка существует для любого непрерывного
отображения сферы на себя при условии, что это отображение непрерыв-
непрерывным образом может быть переведено в тождественное. С этой точки зрения
теорему Эйлера можно рассматривать как частный случай весьма общего
результата. Более того, аналогичное утверждение можно высказать и для
случая, когда тело не является твердым, если только непрерывное измене-
изменение его формы таково, что проведенные через точку О прямые линии остают-
остаются прямыми. При любом перемещении тела, при котором выполняется это
условие, существует прямая, проходящая через точку О и остающаяся
неподвижной.
§ 7.5. Теорема Шаля. Откажемся на время от условия, что твердое тело
имеет одну неподвижную точку, и рассмотрим общий случай перемещения
тела. Докажем теорему, полученную Шалем в 1830 г.: любое перемещение
тела может быть осуществлено путем поступательного перемещения вдоль
некоторого направления и вращения около этого направления. Такое пере-
перемещение, как известно, называется винтовым*). Его мы получаем, напри-
например, навертывая гайку на болт.
Произвольное перемещение тела можно осуществить также путем посту-
поступательного перемещения, при котором некоторая точка его переходит из
положения О в положение О', и последующего поворота тела около оси,
проходящей через точку О'. Направление этой оси остается при этом неиз-
неизменным, т. е. не зависит от того, какая точка тела выбрана для выполнения
первого перемещения. Теорему Шаля можно получить из уравнения G.3.15),
но проще и лучше доказать ее чисто геометрическим способом. В теле суще-
существует система связанных с ним плоскостей, остающихся параллельными себе
после произвольного перемещения. Эти плоскости перпендикулярны к оси
вращения. Рассмотрим в одной из таких плоскостей, например в плоско-
плоскости со, треугольник PQR. Пусть он после перемещения займет положение
P'Q'R' в плоскости со', параллельной плоскости со. Путем поступательного
перемещения вдоль оси вращения плоскость со можно совместить с пло-
плоскостью со'. При этом треугольник PQR займет в плоскости «а' положе-
положение P"Q"R". Треугольник P"Q"R" можно перевести в положение P'Q'R'
путем чистого вращения около оси Я, параллельной оси вращения. Таким
образом, наиболее общее перемещение достигается путем поступательного
перемещения вдоль направления Я и вращения около оси X.
§ 7.6. Формула поворота. Вернемся теперь к случаю, когда тело имеет
неподвижную точку О, и рассмотрим перемещение такого тела. Мы видели,
что перемещение в этом случае можно представить как поворот на угол а
около оси О А. Фиксированная точка тела переходит при этом из своего пер-
первоначального положения R в конечное положение S. Предположим, что
ось ОА и угол поворота а известны. Возьмем точку тела с начальным поло-
положением R и найдем ее положение S после поворота.
Обозначим вектор OR через г, а вектор OS через «; векторы г и s
играют ту же роль, что и матрицы-столбцы у и х в § 7.3. Пусть п будет
*) Аналогом винтового движения может служить приведенная (к динаме) система
сил, приложенных к твердому телу. Возьмем в качестве центра приведения произвольную
точку О. Пространственная система сил может быть приведена к силе F, приложенной
в точке О, и к паре N. Центр О можно выбрать так, чтобы ось пары N была параллельна
линии действия силы F, т. е. чтобы плоскость пары была перпендикулярна к направле-
направлению силы. В этом случае совокупность силы и пары называют динамой. Подробнее см.,
иапример, книгу: R. S. Ball, A Treatise on the Theory of Screws, Cambridge, 1900.
110
ТЕОРИЯ ПОВОРОТОВ
[Гл. VII
единичным вектором вдоль оси вращения ОА. Установим формулу поворота
Здесь у = cos a, a = sin а. Пользуясь вектором поворота T=(tgya)»i,
введенным в § 7.3, запишем формулу поворота в следующем виде:
2
(T-r)T+Txr},
G.6.2)
где
Формулу поворота можно вывести многими способами. Ниже мы про-
проведем доказательство тремя различными способами.
1) Будем исходить из уравнения G.3.15):
Разрешим это уравнение относительно s. Для этого умножим левую
и правую части уравнения векторно на Т. Про-
А делав это, будем иметь
TX{s — r)—-Tx{Tx (s + r)} = {T-(s + r)} T —
— t2(s + r) = 2(T-r)T — t2 (s + г). G.6.3)
При этом мы использовали соотношение
T-(s+r) = 2(T-r). G.6.4)
Складывая G.3.15) и G.6.3), получаем
A +t2) s = A — t2) r + 2 (Т-r) Т + 2 (Т X г),
что эквивалентно G.6.2).
2) Получим теперь формулу поворота непо-
непосредственно из геометрических соображений.
Пусть Р будет основанием перпендикуляра из
точки R на прямую ОА, a N — основанием
перпендикуляра, проведенного из точки S на прямую PR (рис. 13). Пря-
Прямая ATS перпендикулярна к плоскости POR, и
п X г = г ?in 1|з • w = piv,
где r = \r\, p = PR, а w—единичный вектор в направлении NS.
Теперь имеем
Рис. 13.
sin a (n X г) = р sin a • w = NS
и окончательно
s = г + RN + NS = г — A — cos a) {r — (n-r) n} + sin a (и X r) =
— Vr + A — V) (n •'') n-\-anXr,
что и требовалось доказать.
3) Формулу поворота можно получить, вводя новые оси Оу(угуг таким
образом, чтобы ось Оу± была осью вращения. Докажем сначала лемму,
которая нам часто будет нужна в дальнейшем.
Лемма. Если триэдр OY^Y^Yъ поворачивается, па угол а около оси OYU
то матрица направляющих косинусов в новом положении, обозначаемая
§ 7.7] ПОЛУОБОРОТЫ И ОТРАЖЕНИЯ 111
через ?i, дается уравнением
?1 = л1г, G.6.5)
где .Kj — ортогональная матрица:
A0 0 \
О cos a sin а I. G.6.6)
О —sin а cos а/
Заметим, что направляющие косинусы прямой" равны координатам
точки этой прямой, находящейся на единичном расстоянии от точки О.
Из равенства у — 1х следует, что х = Гу, и, следовательно,
/10 0 \
1[ = Г I 0 cosa — since | = Z'l^. G.6.7)
\ 0 sin a cos a /
Формула G.6.5) получается отсюда транспонированием.
Теперь, пользуясь леммой, выведем формулу поворота. Заменяя век-
вектор г матрицей-столбцом х, а вектор s матрицей-столбцом х\, получаем
G.6.8)
откуда
х% =¦ 1[1х = 1'Л[1х = Wx, G.6.9)
где
W=l'M'1Z =
( mim2 М1м
hzhi Пг WisJ + ol hs 0 -1Н\. G.6.10)
(hi mim2 М1мз
\ ^13^11 'l3^12 Нз
Ось вращения, определяющая единичный вектор п, имеет направляющие
косинусы 1ц, liz, li3- В векторной форме формула G.6.9) имеет вид
(п-г)п+ап X г,
что и требовалось показать.
§ 7.7. Полуобороты и отражения. Любой поворот тела можно также
осуществить, например, путем двух полуоборотов (т. е. поворотов на угол л)
около двух пересекающихся прямых. Пусть О А, ОБ —две прямые, прохо-
проходящие через точку О и образующие между собой угол -^а. Полуоборот
около ОА и последующий полуоборот около ОБ эквивалентны повороту
на угол а (в направлении от ОА к ОБ) около оси OL, перпендикулярной
как к ОА, так и к ОБ. Докажем это. Согласно теореме Эйлера (§ 7.2) два
полуоборота эквивалентны одному повороту, и этот поворот должен проис-
происходить около оси OL, так как точки на прямой OL при этих полуоборотах
не получают перемещения. Точка, первоначально находившаяся на пря-
прямой ОА, при первом полуобороте остается неподвижной, а при втором полу-
полуобороте поворачивается на угол аи оказывается на прямой О А' (рис. 14, а).
Теорема, таким образом, доказана.
112
ТЕОРИЯ ПОВОРОТОВ
[Гл. VIB
Если; через и, v обозначить единичные векторы вдоль направлений ОА,
ОБ, а через п, как и ранее, единичный вектор вдоль вектора поворота Т,
направленного по оси вращения OL, то будем иметь
и X v^sm-^a-n ¦¦
G.7.1)
A'
a)
Рис. 14.
Полуоборот около оси а и последующий полуоборот около параллель-
параллельной оси Ъ эквивалентны поступательному перемещению тела. Оно совершает-
совершается от а к Ъ по прямой, перпендикулярной к а и Ъ, и равно удвоенному
расстоянию между осями а и Ъ. Это понятно, так как тело не изменяет
своей ориентации, а направление и величина перемещения становятся оче-
очевидными, если рассмотреть точку тела, первоначально находившуюся
на оси а.
Рассмотрим теперь результат двух последовательных полуоборотов
около скрещивающихся осей а и Ъ. Пусть АВ будет общим перпендикуля-
перпендикуляром к этим осям (причем точка А расположена на оси а, а точка В —
на оси Ь), и пусть а' будет осью, проходящей через точку В параллельно
оси а (рис. 14, Ь). Можно ввести
/„ . два полуоборота около оси а', не
изменяя конечного результата.
Тогда полуоборот около оси а, за
которым следует полуоборот около
оси а', переместит тело в направ-
направлении АВ на расстояние 2АВ.
а Затем полуоборот около оси а' и
последующий полуоборот около
оси Ъ произведут поворот тела
около оси АВ на угол а, равный
удвоенному углу между осями а
и Ъ. В результате мы получим
винтовое перемещение вдоль оси АВ. Таким образом, любое перемещение
твердого тела можно осуществить посредством последовательных полуобо-
полуоборотов около двух надлежащим образом выбранных осей.
Кроме того, поворот тела можно осуществить посредством последова-
последовательных отражений в двух плоскостях. Одного отражения, естественно,
недостаточно, так как при этом получается обратное отражение, но при
повторном отражении мы получаем правильное положение тела, и, таким
образом, два последовательных отражения дают возможное перемещение.
Это перемещение представляет собой поворот тела около линии пересечения
плоскостей отражения; угол поворота равен удвоенному углу между пло-
плоскостями.
Основываясь на эквивалентности вращения двум полуоборотам или
двум отражениям, можно дать другие доказательства формулы поворота,
что может представить интерес для читателя.
§ 7.8. Кватернионная форма записи формулы поворота. С помощью
скалярной величины а и вектора А. с составляющими X, Y, Z можно
построить кватернион:
q = a + Xi + YJ + Zk. G.8.1)
Иногда бывает удобно, не боясь, что это приведет к путанице, обозначать
символом А как вектор X, Y, Z, так и ассоциированный кватернион
О + Xt + Yj + Zk,
так что
G.8.2)
§ 7.9] СЛОЖЕНИЕ ВРАЩЕНИЙ 113
Составляя произведение
qq' = (a + A)(a' + A'),
находим
qq' = {aa' — А-А') + а'А+аА' +А ХА'. G.8.3)
Векторы в правой части этого равенства следует рассматривать как ассо-
ассоциированные кватернионы.
Для изучения вращений нам понадобится кватернион
q = c + ti+itf + Vc = c(l+T). G.8.4)
Здесь с = cos тг ос, a J-, т), ? — составляющие вектора, имеющего величи-
ну sin-^-a и направленного по оси вращения. Параметры с, |, ti, ?, фигу-
рирующие в выражении для д, впервые использовал Эйлер в 1776 г. Заме-
Заметим, что q представляет единичный кватернион, а
gri = c(l—Я7)« G.8.5)
Если вращение переводит res, то
s = qrq-\ G.8.6)
где г следует понимать как кватернион xi + yi + zk. Для доказательства
этого основного соотношения необходимо показать, что
s(l+T) = (l+T)r. G.8.7)
Пользуясь G.8.3), это равенство можно переписать в виде
— (*-T) + s+«X T= — (T-r) + r + TXr.
Скалярные величины слева и справа равны здесь, поскольку Т'Г = T-s,
а векторы равны в силу соотношения G.3.15).
§ 7.9. Сложение вращений. Рассмотрим два последовательных вращения:
поворот на угол а около оси ОА и последующий поворот на угол $
около оси ОБ. В результате мы получаем поворот
на угол у около оси ОС; величина у и положе-
положение оси ОС подлежат определению.
1. Начнем с простого геометрического реше-
решения. Пусть ОА и ОБ имеют единичную длину,
так что точки А и В расположены на единичной
сфере с центром в точке О. Построим на ней
сферический треугольник ABC (рие. 15) с углами
1 1
А =--тг а и В = -w-f>. Результирующее перемеще-
ние есть вращение около оси ОС. В самом деле,
первое вращение переносит частицу тела, нахо-
находившуюся первоначально в точке С, в точку С,
а второе вращение возвращает эту частицу
обратно в точку С. Заметим, что в изображен-
изображенном треугольнике ABC вершины обходятся по ходу часовой стрелки
и поворот около оси О А происходит не от АВ к АС, а от АС к АВ.
Для определения у построим треугольник А'ВС, представляющий собой
зеркальное отображение треугольника ABC относительно ВС. При первом
повороте частица тела, находившаяся в точке А, остается неподвижной,
при втором повороте она переходит в точку А', и, следовательно, угол у
оказывается равным углу АСА'. Таким образом, у = 2 (я — С) или, что
то же, у = — 2С, поскольку поворот на угол 2п возвращает тело в перво-
первоначальное положение.
8 Л. А. Парс
114 ТЕОРИЯ ПОВОРОТОВ [Гл. VII
Полученный результат можно представить в более наглядной форме.
Если ABC — сферический треугольник (с обходом вершин по движению
часовой стрелки, если смотреть снаружи сферы), то поворот на угол 2А
около оси ОА и последующие повороты на угол 2В около оси ОВ и на угол 2С
около оси ОС возвращают тело в его первоначальное положение. Эта теорема
была доказана Гамильтоном в 1844 г.
Рассмотрим сферический треугольник и, пользуясь обычными обозна-
обозначениями сферической тригонометрии, напишем
cos С = — cos A cos В + sin A sin В cos X.
Отсюда получаем
1 11 11
cos -g-у = cos -g- ос cos ~2" р — sin -g- a sin у р cos A, G.9.1)
где X — угол между двумя осями вращения.
Следует иметь в виду, что эти два поворота не коммутативны. Если
их производить в обратном порядке, то осью результирующего вращения
будет ось ОС.
2. Формула результирующего поворота. Пусть век-
вектор поворота Ti, имеющий величину tgTa и направленный по О А, харак-
теризует первое вращение, а вектор поворота Т%, имеющий величину tg-^- Р
и направленный по ОВ, характеризует второе вращение. Результирующее
вращение на угол у около оси ОС можно описать вектором поворота Т3,
имеющим величину tg -^-у и направленным по ОС. Результат последователь-
ного выполнения двух вращений однозначно определяется формулой резуль-
результирующего поворота
Т3 = (Т1 + Т2-Т1ХТ2)/A-Т1.Т2). G.9.2)
Эта формула перестает быть справедливой, если Т^-Тч = 1; в этом случае
угол у составляет целое кратное от я.
В частном случае, когда оси двух последовательных вращений образуют
между собой прямой угол, Ti-T2 = 0 и формула результирующего поворота
принимает более простой вид:
Тг^Т^Тг-Т,ХТг. G.9.3)
Формула G.9.2) показывает, что вектор Т3 не компланарен с векторами Ti и Т2
и чтс, как уже отмечалось выше, результат двух последовательных вращений зависит
от того, в каком порядке они осуществляются- Поэтому ясно, что величину tg — 6 (где
z
9 —• угол поворота) в определении вектора поворота нельзя заменить какой-либо другой
функцией от 9 таким образом, чтобы результат (физическая сумма) двух вращений пред-
представлялся векторной суммой двух векторов. Вращения можно характеризовать различ-
различными способами при помощи направленных величин вдоль осей вращения, но эти направ-
направленные величины не будут векторами в обычном смысле, поскольку они не удовлетворяют
правилу сложения векторов. Таким образом, «вектор поворота», по существу, не являет-
является вектором.
Доказательство, использующее полуобороты.
Как мы видели в § 7.7, полуоборот около единичного вектора и и после-
последующий полуоборот около единичного вектора v равносильны повороту
тела на угол 9 около вектора и xv, причем у9 — угол между векторами и.
§7.9] СЛОЖЕНИЕ ВРАЩЕНИЙ 115
и v. При этом вектор поворота Т определяется формулой
uxv = cT, G.9.4)
где с= cos -^-9. Таким образом, если v—любой вектор, перпендикуляр-
ный к Ti, то можно найти единичный вектор и такой, что первое вращение
будет эквивалентно полуобороту около вектора и и последующему полу-
полуобороту около вектора г,
m = c1(v —Tjxv), G.9.5)
где ci = cos -^-а. Аналогично, если v — любой единичный вектор, перпен-
дикулярный к Тг, то второе вращение будет эквивалентно полуобороту око-
около вектора v и последующему полуобороту около вектора га:
w^c2(v-\-T2Xv). G.9.6)
Выберем теперь в качестве вектора v единичный вектор, перпендику-
перпендикулярный одновременно к Т\ и к Т2. Результирующее перемещение будет
осуществляться путем полуоборота около вектора и, следующего за ним
полуоборота около v, еще одного полуоборота около vsi, наконец, полуобо-
полуоборота около га. Два последовательных полуоборота около v не производят
никакого перемещения, и потому их можно не учитывать. Тогда результи-
результирующее перемещение будет осуществляться посредством полуоборота около и
и следующего за ним полуоборота около w. Таким образом
с%Тг = uxw = с?г {(v — TiXv)x(v+T2X v)} =
= с^ {v X (Т2 X v) — (Ti Xv)Xv—{TiXv)x (T2 X v)} =
= ад№ + Т«-Г,хТ,I G.9.7)
поскольку
(Tj X i«) X (Т2 X v) == Тх X Т2. G.9.8)
Из формулы G.9.1) находим
C3/ctc2 = l —tgYatgyPcosA, = l —ТГТ2, G.9.9)
откуда получаем
2тз = (Т1 + Т2-Т1хТ2)/A-Т,-Т2). G.9.2)
Доказательство, использующее кватернионы. Для пер-
первого поворота используем кватернион (см. § 7.8)
ff^eifl + Tj), G.9.10)
а для второго — кватернион
д2 = с2A + Т2). G.9.11)
При первом повороте точка тела, имевшая первоначально радиус-век-
радиус-вектор г, переходит в положение, определяемое г, а при втором повороте —
в положение, определяемое s; при этом
r = 4№? G.9.12)
и
1 Лг1 = Язгд?, G.9.13)
где
G.9.14)
116 ТЕОРИЯ ПОВОРОТОВ [Гл. VII
Кватернион q3, определяющий результирующее вращение, равен
3). G-9.15)
Сравнивая формулы G.9.14) и G.9.15), находим
ca = clCa(l-TrTt) G.9.16)
и
c3T3 = clC2(T1+T2-T1XT3). G.9.17)
Соотношения G.9.16) и G.9.17) тоже приводят нас к равенству G.9.2).
Совершив повороты в обратном порядке, мы получим формулу, отли-
отличающуюся от G.9.2) лишь знаком перед векторным произведением в правой
части. Как уже указывалось, различие в выражениях для Т3 связано с изме-
изменением направления вектора Т± X Т2.
Пример 7.9А. Найти результат трех последовательных поворотов:
поворота на угол г|э около оси Oz, за которым следуют поворот на угол 9
около оси Оу, а затем поворот на угол ф около оси Oz.
Положим tt = tg у 9, t2 =-- tg у Ф, t3 = tg у i|x Операции, осуществляемые
T,[ = @, 0, t3) и Т2 = @, tu 0), эквивалентны операции, осуществляемой
Т' = (*ifs, U, t3), G.9.18)
а операции, осуществляемые Т' ,м Т3 = @, 0, t2),— операции, осуществ-
осуществляемой
Т = {- U (h - t3), h A + t2ta), h + t3}/(l - t2t3). G.9.19)
Этот результат легко получить также и с помощью кватернионов. Имеем
Ч = Wt1\ = (с2 + s2k) (d + Sij) (сз + s3k) =
stc2c3) j + (cic2s3 + CiSZc3) к =
= clC2c3{(l - t2tj) + ф3 - h)i + *t(l + i2i3) 7 + (t2 + t3) к}, G.9.20)
11111
где с^совуЭ, Ял = 8ту9; с3 = cos у ф, s2 = sin у ф; c3 = cosy^>, s3 —
= sinYi|3. Полученная нами формула эквивалентна соотношению
q = cos у у + sin -| у (Н + т/ + пк), G.9.21)
в котором I, m, n — направляющие косинусы оси результирующего враще-
вращения, а у — угол результирующего поворота. Величина вектора Т равна
tg у у, а направление его определяется направляющими косинусами I, m, п.
Сравнивая G.9.20) и G.9.21), приходим к G.9.19).
Отметим, что
1 + | Т |2 = A 4- *•) A f ф A + ф/A - Vs)8, G-9.22)
и формула поворота, определяемого вектором Т, приобретает вид (см. G.6.2))
1 l {r+(T-r)T+(Txr)}. G.9.23)
Пример 7.9В. Найти результат трех последовательных поворотов:
поворота на угол ф3 около оси Oz, за которым следуют поворот на угол ф2
около оси Оу и поворот на угол ф4 около оси Ох.
§7.11]
ОРИЕНТАЦИЯ ТЕЛА В ПРОСТРАНСТВЕ. УГЛЫ ЭЙЛЕРА
117
Поступая, как в предыдущем примере, находим
Т = (tt + «2*8. h - ht3, t3 + ht2)l(\ - tit2t3),
где ?r = tgycpr- Формула поворота имеет вид
G.9.24)
G.9.25)
§ 7.10. Угловая скорость. Если в формуле G.9.2) результирующего
поворота углы а и р считать малыми и пренебречь квадратами и произ-
произведениями этих величин, то формула приобретет простой вид:
T3 = ^i + 2V G.10.1)
В этом случае повороты коммутативны.
Из соотношения G.10.1) легко установить векторный характер угловой
скорости. Если угловую скорость представить как вектор ш, направленный
по оси вращения и равный по величине угловой скорости со, то сложение
двух угловых скоростей будет подчиняться правилу сложения векторов:
@3 = ©! +ш2. G.10.2)
Можно, разумеется, получить формулу G.10.2) и элементарным путем,
не обращаясь к формуле результирующего поворота. Например, при выводе
ее можно основываться на геометрических соображениях, приведенных
в § 7.9, п. 1. Положим
а =
и будем стремить 8t к нулю. Из рис. 15 находим
1
sin-75-а
Но так как при 8t
иметь
0 точка С стремится к точке Со на АВ, то будем
щ
G.10.4)
Далее, при б?-»-0 формула G.9.1) принимает вид
<Вз = ai+ CO2+ 2co1co2cosA, G.10.5)
и формулы G.10.4) и G.10.5) приводят к соотно- __
шению G.10.2). *? «
§ 7.11. Ориентация твердого тела в пространст-
пространстве. Углы Эйлера. Рассмотрим теперь способы ориен-
ориентации подвижного триэдра ОАВС относительно не-
неподвижного триэдра Oxyz. Оси О А, ОВ, ОС будем
считать фиксированными в теле и образующими правый ортогональный
триэдр. Хорошо известен способ определения ориентации триэдра ОАВС от-
относительно Oxyz с помощью углов Эйлера 0, ср, 1|э; через 9 и ср обозначены
полярные углы оси ОС, а через ty — угол между плоскостью zOC и плос-
плоскостью СО А, принимающий нулевое значение, когда точка А лежит на ду-
дуге большого круга zC (рис. 16).
Рис. 16.
118 ТЕОРИЯ ПОВОРОТОВ [Гл. VII
Матрица направляющих косинусов имеет вид
(cos 9 cos ф cos г|:—sincpsini|3 cos8sincpcos\|;+cos(psin\|: —sin9cosi|A
—cos9cosфsinг|:—sincpcosip —cos9sn^sini|)-f созфсозг|: sinGsin^ I.
sin 9 cos ф sin 0 sin ф cos 9 /
G.11.1)
Как легко видеть, элементы первой строки представляют собой проек-
проекции на оси Ох. Оу, Oz единичного вектора вдоль оси О А. Элементы второй
строки получаются из элементов первой путем замены в них г|з на г|э +-^-я.
Матрицу направляющих косинусов можно представить в более компакт-
компактной форме:
(
— ctc2s3 — s2c3 —с^2я3+с2с3 sts3\. G.11.2)
Здесь индексы 1. 2, 3 относятся соответственно к углам 9, ф, 1|э; через с,
обозначен cos 9, через s± обозначен sin 9 и т. д.
Выбирая в качестве исходного положения триэдра ОАВС то его поло-
положение, когда он совпадает с Oxyz, мы можем перевести его в конечное
положение одним из двух следующих способов:
a) 1. Производим поворот на угол ф около оси ОС = Oz, после чего
триэдр ОАВС принимает положение ORSz (рис. 16). 2. Совершаем поворот
на угол 0 около нового положения оси ОВ, т.е. около оси OS; при этом точ-
точка С достигает своего конечного положения и триэдр ОАВС принимает
положение OTSC. 3. Производим поворот на угол г|э около нового поло-
положения оси ОС. в результате чего триэдр ОАВС переходит в конечное поло-
положение .
b) Поворот на угол г|э около оси Oz, за которым следуют поворот на
угол 0 около оси Оу и поворот на угол ф около оси Oz.
Разумеется, каждая из последовательностей операций а), Ь) эквивалент-
эквивалентна единственному повороту Т, определяемому формулой G.9.19)*).
*) Эквивалентность последовательностей операций а) и Ь) является следствием
теоремы: последовательность конечных поворотов, определяемых векторами
эквивалентна последовательности
где ('х — единичный вектор, в который переходит ej при повороте Т2 (А. И. Лурье,
Прикл. матем. и мех. 21, № 4, 1957).
Последовательности операций а) и Ь) даются поворотами:
а) Si = к tg -|-, S2=j* tg -|, S3 = к' tg -|-;
б) Ti=ktg^-, T2=itg-|, T3 = fctg-|-.
Здесь j, к-—единичные векторы осей Оу, Oz; к' — единичный вектор на ОС; j*—еди-
j*—единичный вектор, в который переходит j при повороте Т3. В соответствии с упомянутой
теоремой последовательность Т2, Т$ эквивалентна Si, S2, так что последовательность Tit
Т2, Т3 эквивалентна Тi. Si, S2, но последняя в силу той же теоремы эквивалентна
Si, S2, S3 (последнее следует из того, что в результате последовательности поворотов
Si, S2 единичный вектор к переходит в к'). {Прим. перев.)
7.13]
ПОВОРОТЫ ОКОЛО ДВИЖУЩИХСЯ ОСЕЙ
119
§ 7.12. Ориентация твердого тела в пространстве. Углы <р17 <р2, <р3. Дру-
Другой, более симметричный способ определения ориентации триэдра ОАВС
заключается в следующем. Пусть сначала триэдр ОАВС совпадает с триэд-
триэдром Oxyz. Переведем его в конечное положение, производя последовательно
следующие операции: поворот на угол ф1 около оси О А = Ох, затем пово-
поворот на угол ф2 около оси ОБ в новом положении и, наконец, поворот
на угол ф3 около оси ОС в новом положении
(рис. 17). Матрица направляющих косинусов, опре-
определяющих положение триэдра ОАВС, будет иметь вид
I» G.12.1)
}
где ст обозначает cos фГ7 a sT обозначает sin фг.
Элементы первой строки выражают проекции на х
оси Ox, Oy, Oz единичного вектора вдоль оси О А.
Вторая строка получается из первой заменой ср3 на
Ц>з + V2rc.
с- •
§ 7.13. Повороты около движущихся осей. Рас-
смотрим теперь другой способ получения матрицы
G.12.1). Как мы видели в § 7.6, повороту на угол 9 около оси ОА соответ-
соответствует переход от матрицы I к матрице R^l, где .Ki = _Rt (9) — ортогональ-
ортогональная матрица
0 0
Rt F) = | 0 cos 9 sin 9
.0 —sin9 cos9,
G.13.1)
Аналогично, при повороте на угол 0 около оси ОВ мы переходим от I
к R2Z, где R2 — ортогональная матрица
(cos9 0 —sine1
0 1 0
sin 9 0 cos 9
G.13.2)
а при повороте на угол 8 около оси ОС — от I к R$l, где R3— ортогональ-
ортогональная матрица
cos 9 sin0 0\
,йзF)=| —sin 9 cos 9 0 I. G.13.3)
0 0 1/
Если сначала триэдр ОАВС совпадает с неподвижным триэдром Oxyz, то
начальное значение матрицы I равно I. Поэтому, если конечное положение
триэдра ОАВС достигается посредством поворотов на углы <pt, q>2, ф3
(см. § 7.12), то конечное значение I будет равно
(ф3) Пг (Ф2)
G.13.4)
что совпадает с G.12.1).
Этот же способ можно, разумеется, применить и для получения матрицы
направляющих косинусов, выраженных через углы Эйлера. В этом случае
120 ТЕОРИЯ ПОВОРОТОВ [Гл. VII
матрица будет иметь вид
R3(q)R2(Q)R3(y), G.13.5)
и мы вновь придем к матрице G.11.2).
§ 7.14. Повороты около неподвижных осей. Если тело поворачивается
на угол 0 около неподвижной оси Ох, то связанный с телом триэдр ОАВС
переходит в новое положение и матрица I направляющих косинусов заме-
заменяется новой матрицей, равной, очевидно, IRi @). То же можно сказать
и в отношении поворотов около осей Оу и Oz.
Поворот на угол q>3 около оси Oz, за которым следуют поворот на угол ср2
около оси Оу и поворот на угол qpi около оси Ох, описывается следующей
матрицей направляющих косинусов (первоначально I =У1):
-Вз (Фз)-В* (<Pa)--Ri (Фд), G.14.1)
что в точности совпадает с G.13.4).
Таким образом, если подвижной триэдр ОАВС первоначально совпадает
с неподвижным триэдром Oxyz, то повороты, совершаемые последовательно
около осей О А, ОВ, ОС, дают тот же результат, что и повороты около
осей Ох, Оу, Oz, совершаемые в обратном порядке.
Доказанная выше замечательная теорема позволяет, вместо поворотов
около мгновенных положений подвижных осей, рассматривать повороты
около неподвижных осей. Частный случай этой теоремы мы имели в кон-
це § 7.11.
Пользуясь этой теоремой, можно в примерах 7.9А и 7.9В выразить
вектор поворота Т, переводящий триэдр ОАВС из начального положения
в конечное, через углы Эйлера и через углы cpi, cp2, ср3- Соответствующие
формулы поворота дают еще один способ выражения метрицы I через углы
Эйлера или через углы cpi, срг, срз) но практически этот путь оказывается
менее удобным, чем рассмотренный ранее. Если, например, в формуле G.9.25)
в качестве вектора /• выбрать вектор A, 0, 0), то равенство
G.14.2)
определит элементы первой строки матрицы G.12.1).
•
§ 7.15. Определение угловой скорости с помощью матриц I и I. Допу-
Допустим, что твердое тело переводится из данного положения в новое посред-
посредством трех последовательных поворотов: поворота на угол ф1 около оси О А,
затем поворота на угол фг около нового положения оси ОВ и поворота
на угол ф3 около нового положения оси ОС. Как мы видели в § 7.13, мат-
матрица направляющих косинусов для конечного положения триэдра имеет вид
, G.15.1)
причем в общем случае эти операции не коммутативны.
Если, однако, углы поворота бесконечно малы и равны, скажем* бфь
бфг, бфз, так что квадратами и произведениями этих величин можно пре-
пренебречь, то порядок осуществления поворотов безразличен. Имеем
G.15.2)
§ 7.16] СОСТАВЛЯЮЩИЕ ВЕКТОРА УГЛОВОЙ СКОРОСТИ 121"
Следовательно,
(О бф3 — бф2\
-бфз 0 бф! \1. G.15.3)
бф2 — бфх 0 /
Таким образом,
-|^ + йг = О. G.15.4)
Здесь -J7- (или сокращенно I) — матрица, составленная из производных от
элементов матрицы I, a Q — кососимметрическая матрица
(О — со3 <°2 \
со3 0 — щ\, G.15.5)
— со2 coj О/
где (Oi, (о2, со3— составляющие вектора угловой скорости по осям ОА,
ОБ, ОС.
Геометрический смысл уравнения G.15.4) очевиден. Так, например,
элементы первого столбца матрицы I представляют собой составляющие
по осям триэдра ОАВС единичного вектора вдоль фиксированного направ-
направления Ох. Равенство нулю элементов первого столбца слева в G.15.4) экви-
эквивалентно известному результату
1( + (|)Хм = 0. G.15.6)
В этой формуле и — единичный вектор вдоль оси Ох, аи — угловая ско-
скорость относительно триэдра Oxyz.
Так как матрица I ортогональна, то из G.15.4) получаем
Й=— IV. G.15.7)
Это уравнение выражает угловую скорость через матрицы I и I. Нетрудно
непосредственно убедиться в том, что IV представляет собой кососимметри-
ческую матрицу.
§ 7.16. Составляющие вектора угловой скорости. Определим теперь
составляющие вектора угловой скорости твердого тела по направлениям ОА,
ОБ, ОС. Сначала будем предполагать, что ориентация тела определяется
углами Эйлера, а затем рассмотрим ориентацию тела с помощью углов <рь
Фг, Фз-
1. Углы Эйлера. Угловая скорость есть векторная сумма трех
векторов: вектора, равного по величине ф и направленного по оси Oz,
т
вектора, равного по величине 0 и направленного по оси OS, и вектора,
равного по величине яр и направленного по оси ОС (рис. 16). Обозначая
через a»i, (Ог? юз составляющие вектора угловой скорости соответственно
по осям ОА, ОБ, ОС, можем написать
со± == 9 sin г|5 — ф sin 0 cos i|5,
co2 = 0cosi|5-[- cpsmGsiniJj, \ G.16.1))
C03= ф COS 0+1M.
122 ТЕОРИЯ ПОВОРОТОВ [Гл. VII
Несимметричный характер углов Эйлера порождает следующий любо-
любопытный парадокс. Если в некоторый момент времени триэдр ОАВС совпада-
совпадает с триэдром Oxyz, так что 0 = ф = яр = 0, то формулы G.16.1) дают
Oil = О, С02 = 6, СО3 = ф + 'Ф-
Составляющая coj оказывается равной нулю, каковы бы ни были заданные
нами конечные значения 0, ф и г|з. Поэтому пользоваться углами Эйлера
в тех задачах, где триэдр ОАВС в некоторый момент совпадает с триэдром
Oxyz, не очень удобно, за исключением тех случаев, когда в этот момент
вектор угловой скорости лежит в плоскости Oyz. Вообще, если 6 = 0,
то из формул G.16.1) следует, что a»i = co2 tgi|), что в общем случае неверно.
2. У г л ы фь ф2, ф3- В этом случае угловая скорость представляет
векторную сумму трех следующих векторов: вектора, равного по величи-
величине ф1 и направленного вдоль оси Ох, вектора, равного по величине ф2 и на-
направленного вдоль оси 00, и вектора, равного по величине ф3 и направлен-
направленного вдоль оси ОС (рис. 17). Обозначая через coi, co2, со3 составляющие
вектора угловой скорости соответственно по осям О А, ОБ, ОС, будем иметь
со2= —
G.16.2)
тде сг = со8ф,-, s,.--~ sin ф,..
Здесь мы также встречаемся с некоторыми парадоксами, например,
при с2 = 0.
При ф! = ф2 = ф3 = 0 составляющие вектора угловой скорости рав-
равны фь ф2, ф3, как и следовало ожидать.
3. Полученные выше результаты можно вывести также из форму-
формулы G.15.7) для Q. Выбирая в качестве переменных углы фь ф2. ф3, будем
иметь
2(Ф2)Лг1(ф1) G.13.4)
О=-7Г. G.15.7)
Отсюда
Q = — ((fiR3R2 ~ + ЧгВь -^~ Rt + щ -^ R2RX) R[B.,B3 =
^^Л^-ф^Вз-^ВЖ-Фз-^Д;. G.16.3)
где аргументами матриц-функций Rt и R[ служат ср,.
Матрица J?, @) удовлетворяет соотношению
/0 0 0\
^R[= 0 0 1. G.16.4)
\0 -1 О/
Аналогично
/О 0 —1\
G.16.5)
7.16] СОСТАВЛЯЮЩИЕ ВЕКТОРА УГЛОВОЙ СКОРОСТИ 123
О 1 0\
г;=| -loo. G.16.6)
ооо/
Используя эти результаты, можно формулу G.16.3) переписать в следую-
следующем виде:
0 — (*аФ1+Фз) — <
Й=| VPi+Фз О -(с8СзФ1 + ЯзФ2) Г G-16-7)
1 — с3ф2
Таким образом, мы снова получаем соотношения G.16.2), однако метод,
изложенный в п. 1, является более простым.
Глава VIII
ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА
§ 8.1. Дифференциальные уравнения. Рассмотрим теперь приложения
лагранжевых уравнений движения к некоторым конкретным механиче-
механическим системам. Начнем с консервативной голономной системы с к степе-
степенями свободы. Положение системы в момент t задается лагранжевыми коор-
координатами qlt q2, . . ., qn, причем наименьшее возможное значение п равно к.
Будем предполагать, что координаты выбраны именно таким образом,
т. е. что п = к. Составим функцию Лагранжа L (§ 6.6), L = Т — V. Урав-
Уравнения движения запишутся в форме
Мы имеем систему п совокупных обыкновенных дифференциальных урав-
уравнений второго порядка относительно п неизвестных функций q^ (t), q2 (t), ...
. . ., qn (t). Система F.6.3), вообще говоря, определяет величины q как
функции от t, во всяком случае в некотором интервале времени, если в мо-
момент t = О известны значения q и q.
Когда мы говорим о решении динамической задачи, мы имеем в виду
определение величин q как функций t для всех вещественных значений t
или по крайней мере для некоторого интервала значений t, когда величины
•
Qr — Что и сог = qr0 в момент t = 0 заданы произвольным образом. Полу-
Получить такие решения удается лишь для немногих достаточно простых задач.
Типичным примером могут служить малые колебания (гл. IX).
Однако обычно приходится довольствоваться менее полным решением.
Но даже в том случае, когда не представляется возможным получить явные
формулы, определяющие величины q как функции 2п + 1 параметров
Яю, ?2(ъ • • -I ?nOi ©10. «го, • • ., @,10, t, все же можно установить общий
характер движения и выяснить некоторые важные характеристики его.
Кроме того, с помощью численных методов интегрирования или разложения
в степенные ряды (§ 21.4) можно получить приближенные решения, справед-
справедливые для достаточно малых значений t.
Аналогичные замечания можно сделать и в отношении неголономных
систем, хотя в этом случае дело обстоит несколько сложнее. В неголономных
системах наименьшее возможное значение п равно к Н- I, причем имеются I
уравнений связи
п
2 5rsgs + 5Г = 0, г = 1,2, ..., I. F.2.3)
s=l
Уравнения движения имеют вид
i
-ir+S KmPm» r=i,2,...,n. F.6.4)
Всего мы имеем п -\- I уравнений и п + I функций от t, подлежащих опре-
определению, а именно функции qt, q2, . . ., qn, К, Я2, • . ¦, ^.
§ 8.2] ФОРМУЛЫ УСКОРЕНИЯ В ОРТОГОНАЛЬНЫХ КООРДИНАТАХ 125
Наконец, если имеется р избыточных координат и р соотношений
Fr (qu q2, . . ., gn; t) = 0, r = 1, 2, . . ., p, E.12.6)
то к правым частям уравнений F.6.3) или F.6.4) следует добавить слагаемые
2^-g-, r = l,2, ...,п. F.2.4)
Появляются р дополнительных неизвестных, именно множителей щ, р,2, . . •
. . ., |хр, и р дополнительных уравнений E.12.6).
Рассмотрим теперь применение уравнений Лагранжа к некоторым част-
частным задачам.
§ 8.2. Формулы ускорения в ортогональных координатах. Положение
точки, движущейся в пространстве, будем определять ортогональными кри-
криволинейными координатами а, р, у. Квадрат линейного элемента ds в этих
координатах будет иметь следующее выражение:
ds2 = АЧа? + B2df>2 + СЧу2. (8.2.1)
Коэффициенты А, В, С здесь являются функциями от переменных а, р, у,
принадлежащими классу Cj. В каждой точке пространства определены три
главных взаимно ортогональных направления. Например, в точке (а0, ро, То)
первое главное направление задается касательной к кривой р = C0, у = у0,
причем а вдоль этого направления возрастает. Это направление мы иногда
будем называть «-направлением.
Для частицы единичной массы имеем
Г = у(Л2а2 + ?2р24-С272)- (8.2.2)
Если на эту частицу действует сила с составляющими X, Y, Z по главным
направлениям, то работа этой силы на виртуальном перемещении будет
равна
ХА da + YB dp -i- ZC dy. (8.2.3)
Первое уравнение Лагранжа имеет вид
^)ХА. (8.2.4)
Составляющая ускорения вдоль а-направления имеет следующее выраже-
выражение:
пли подробнее:
v л" , п' I дА ' 1 дА А . дА "\ 1 / л дА \ I d дВ а-; . г< дС 'Л
\ да ' <?Р г ' ду ' / Л \ 5а >9а г да. ' j
(8.2.6)
Составляющие ускорения по направлениям В и у выражаются аналогич-
вни образом.
Отметим два важных частных случая:
1) Для цилиндрических координат г, 6. z имеем
ds2 = dr2 + rW + иг2 (8.2.7)
126 ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА [Гл. VIII
и составляющие ускорения равны
. z . (8.2.8)
2) Для сферических координат г, Э, ф имеем
ds2 = йгг -f rW -\- r2 sin2 9 dif (8.2.9)
и составляющие ускорения равны
V—r@2 + sin20(p2), "j
гЭ + 2гЭ — г cos 0 sin Э ф2, > (8.2.10)
7-sin Эф 4- 2 (г sin 0 +г cos 00) ф. )
§ 8.3. Обезьяна и противовес. Рассмотрим снова пример 4.4В. Через
гладкий блок переброшена легкая гибкая нерастяжимая нить, на одном
конце которой укреплен груз массы М, а по другому концу взбирается вверх
обезьяна массы т, причем ее перемещение относительно нити задано как
функция времени ф (t). Как и ранее, будем предполагать, что ф ? С2, ц> @) =
= ф @) = 0 и что в начальный момент система находилась в покое.
Этот пример относится к типу задач, рассмотренных в § 6.5: работа
заданных сил на виртуальном перемещении равна —6SF, где V явно зави-
зависит от t, но символ 6S указывает, что перемещение рассматривается при
фиксированном t. Если через z обозначить высоту подъема обезьяны за вре-
время t, то высота противовеса будет равна с + ф — z- Имеем
Т = i- {mz2 + М (Ф - zJ}, (8.3.1)
у _ /Н.СТ2 __ Af ?f (ф z). (8 3 9)
Уравнение Лагранжа имеет вид
и мы снова приходим к формуле D.4.7):
(m + M) z = Мф + -7J- (М — in) gt2,
так как при t = 0 величины ф, ф, z, z обращаются в нуль.
§ 8.4. Кинетическая энергия твердого тела. Допустим сначала, что тело
имеет неподвижную точку О. Если ОА, ОВ, ОС — главные оси инерции
в точке О, a coj, co2, о>з — составляющие вектора угловой скорости по осям
О А, ОВ, ОС, то можно написать
Т = -тг Sm{((i>.2c — со3&J + (ща — cojcJ-}- (<*>$ — со2аJ}. (8.4.1)
Здесь а, Ь, с — координаты частицы тела по осям ОА, ОВ, ОС. Поскольку
эти оси фиксированы в теле, величины а, Ъ, с постоянны. Так как
Smbc = Smca = Smab = 0, (8.4.2)
то выражение (8.4.1) переписывается в виде
Т = -1 Sm {(Ь2 -f с2) а» + (с2 + a2) ©J + («2 + ^2) со^} = 1 (Лео? + В<% + Ссо^),
(8.4.3)
§ 8.4] КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТВЕРДОГО ТЕЛА 127"
где А, В, С — моменты инерции тела относительно осей ОА, ОВ, ОС,
т. е. главные моменты инерции тела в точке О.
Пусть теперь тело совершает движение в пространстве. Обозначим
через |, т], ? координаты центра тяжести G (относительно неподвижной
системы Oxyz), и пусть главными осями инерции в точке G будут GA, GB, GC.
Если a»i, а>2, аз — составляющие угловой скорости по осям GA, GB, GC,
то по теореме Кёнига (§ 7.1) имеем
T=±M(i>+44-i*)+Y(A(ai+Bat+c<aD- (8-4-4)
Чтобы воспользоваться этой формулой для составления уравнений Лаграп-
жа, величины @i, а>о, со3 следует выразить через лагранжевы координаты,
например углы Эйлера или углы фь <р2, <р3 (§ 7.16).
Указанный выше способ составления выражения для Т отличается простотой
и наглядностью, хотя на первый взгляд может показаться, что он не связан прямо с перво-
первоначальным определением Т (§ 3.3):
5B + Й + 22). (8.4.5)
Между тем следует отметить, что практически весьма удобно делать непосредственные
выводы из формулы (8.4.5). Пусть
* = I + ah + Ы2 + cl3. (8.4.6)
Обозначив направляющие косинусы оси GA через li: mj, ni и т. д., составим матрицу I
(см. § 7.3):
/к щ пл
m2 пЛ. (8.4.7).
Направляющие косинусы являются некоторыми простыми функциями лагранжевых
координат (§§ 7.11, 7.12). Имеем
x^i + ak+bh + c'h. (8.4.8).
Аналогичные формулы получаем для у и z. Поскольку
Sma = Smb = Smc = 0, Smbc = Smca = Smab = 0, (8.4.9)-
формула (8.4.5) для Т принимает вид
Y Y (8.4.10У
Выразим теперь Zj через 9, ф, ip или <pit ф2> фз- Вычисления, которые необходим»
при этом проделать, не особенно сложны, но их можно еще более упростить, если заме-
заметить, что Zj, l2, 13 определяют единичный вектор постоянного направления, так что
/1 = /2ш3— /Зсо2. (8.4.11>
Таким образом,
1
¦ 1 9 2 J.
и мы сразу приходим к (8.4.4).
128
ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА
[Гл. VIII
§ 8.5. Задача о движении в двух измерениях. В качестве примера дви-
движения в двух измерениях рассмотрим следующую задачу. Тонкая однород-
однородная цилиндрическая оболочка массы М и радиуса Ъ катится по горизон-
горизонтальной плоскости, а другая цилиндрическая оболочка массы т и радиу-
радиуса а катится внутри первой. Все поверхности считаются идеально шерохо-
шероховатыми, так что качение происходит без скольжения.
Описанная система голономна и имеет две степени свободы. На рис. 18
изображено поперечное сечение оболочек плоскостью, перпендикулярной
к их осям; центр первого цилиндра обозначен через С, центр второго —
через D. Точка В фиксирована на первом цилиндре, точка А —-на втором;
в начальный момент точка В совпадает с точкой О, принадлежащей пло-
плоскости, и точка А совпадает с В. В качестве лагранжевых координат возьмем
угол Э между отрезком СВ и направленной вниз
вертикалью в точке С и угол <р между отрезком CD
и этой же вертикалью; углы 9 и <р отсчитываются
в противоположных направлениях (см. рисунок).
Условие отсутствия скольжения записывается в виде
а (ф + г|)) = Ъ (9 + ф)
или
аар = 69 + сф, (8.5.1)
где с ¦¦=-- Ъ — а. В процессе движения поверхности,
вообще говоря, могут отделиться друг от друга,
но мы, чтобы не усложнять задачу, будем пред-
предполагать, что этого не происходит (это можно обе-
обеспечить, например, с помощью некоторого невесо-
невесомого механизма). Будем предполагать, что движе-
ние начинается из состояния покоя, в котором ф = а, причем 0 << а < -^- л.
Без ограничения общности можно считать, что в начальный момент 6 = 0.
Имеем
Т = у МЬЮ2 + у МЪЩ2 + у m
+ с2ф2 + 2Ьс9ф cos ф) -f -|
~ т (Ь2дг + с2ф2 + 2бс9ф cos <р) + у т F9
), (8.5.2)
F= — mgccosy. (8.5.3)
Интеграл импульса, соответствующий циклической координате 9, имеет
вид
2(М + т)Ьё + тсфA + со8ф) = 0, (8.5.4)
и мы сразу получаем, что
2 (М Лс т) 69 + тс (ц> + sin ф) = тс (а + sin a). (8.5.5)
Уравнение (8.5.5) определяет явным образом 6, если известна функция ф.
"Найдем последнюю.
Уравнение энергии записывается в форме
(М +т) bW + тс\2 + mbcQ ф A + созф) = mgc (соэф — cos а). (8.5.6)
Исключая 9 из уравнений (8.5.4) и (8.5.6) (с помощью очевидного тожде-
тождества
Ч —
а
а.г°- + 2hxy + by*- = {(ял: + %J + (аЪ -
§ 8.6] ВРАЩАЮЩИЙСЯ ВОЛЧОК; ОСНОВНЫЕ УРАВНЕНИЯ 129
или каким-либо иным способом), находим
Ф2 {1 — р2 A + cos фJ} = п2 (cos ф — cos a), (8.5.7)
где
Уравнение (8.5.7) определяет связь между ф и t. Очевидно, движение
носит периодический характер и ф колеблется между пределами а и —а.
Период колебаний равен
и
cos ф —
^ v '
§ 8.6. Вращающийся волчок; основные уравнения. Волчок представ-
представляет собой твердое тело, обладающее осевой симметрией; острие его О, рас-
расположенное на оси, остается неподвижным, и вращение его происходит вок-
вокруг точки О под действием силы тяжести. Свяжем с телом триэдр ОАВС,
направив ось ОС по оси симметрии; тогда оси О А, ОБ, ОС будут главными
осями инерции в точке О, а моменты инерции относительно осей О А и ОБ
будут одинаковы. Центр тяжести G лежит на оси ОС. Обозначим главные
моменты инерции в острие через А, А, С, массу волчка — через М, а рас-
расстояние OG — через I. При С = 0 мы приходим к задаче о сферическом маят-
маятнике, рассмотренной в § 5.3.
С чисто динамической точки зрения условие симметричности тела отно-
относительно оси является излишним. Уравнения, которые мы выведем, будут
справедливы для любого тела, эллипсоид инерции которого в точке G
является сфероидом с точкой О па его оси.
Вводя углы Эйлера для определения ориентации триэдра ОАВС и направ-
направляя ось Oz вертикально вверх, напишем выражения для кинетической
и потенциальной энергии тела:
\ ¦ • 1 •
Г = у Л F sini|5— фйтбсоз^+у А (
(8.6.1)
V = Mgl cosQ. (8.6.2)
Уравнение Лагранжа для 6 запишется в виде
А (8 — ^2sm0cos9)fC(ii) + (p cos0) ф sin 9 = Mg/sin 9, (8.6.3)
а интегралы импульсов, соответствующие циклическим координатам ф и ij),
будут иметь вид
A sin2 0 ф + С cos 8 (ij) + ф cos 9) = const = 2Ак, (8.6.4)
if> + ф cos 0 = const = п. (8.6.5)
Уравнение (8.6.4) выражает постоянство момента количеств движения
относительно оси Oz (величина его обозначена через 2АХ), а уравне-
уравнение (8.6.5) — постоянство спина, т. е. составляющей угловой скорости вдоль
оси волчка (величина его обозначена через п). Мы будем считать, что п > 0;
в большей части случаев, представляющих практический интерес, это число
довольно велико.
Я Л. А. Парс
130 ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА [Гл. VIII
Уравнения, определяющие 0 и <р как функции от t, т. е. уравнения,
описывающие движение оси волчка, приобретают вид
*8 — sin 9 (cosO ф2 — 2pif+ q) = 0, (8.6.6)
• sin2 9 ф + 2p cos 0 = 2%. (8.6.7)
Здесь 2р = Cn/A, q = MgllA; параметры ряд положительны.
Получим теперь интеграл энергии. Это можно сделать непосредственно
из уравнений движения либо с помощью общей теоремы (§6.7). Его можно
представить в форме '
02 + sin2 6 ф2 + 2q cos 0 = 2ц. (8.6.8)
Для некоторых целей уравнение (8.6.8) оказывается более удобным,
чем (8.6.6). Исключая ф из (8.6.7) и (8.6.8), приходим к уравнению
» ()A*»)-2(Л-.рг)а. (8.6.9)
где z = cos 0. Обозначим полином третьей степени в правой части (8.6.9) через
/ (z). Зависимость z от t может быть выражена посредством ^-функции Вейер-
штрасса, как в случае сферического маятника (к которому сводится наша
задача, если р = 0). Далее,
Мы приходим к трехпараметрической совокупности движений (не рас-
рассматривая фазовые постоянные, зависящие от выбора начала отсчета t, ц>, г|з)
от параметров р, к, \i.
§ 8.7. Вращающийся волчок; другое решение. Получим теперь резуль-
результаты предыдущего параграфа другим способом. Будем предполагать, что
спин сохраняет постоянное значение п. Тогда, если через и обозначить еди-
единичный вектор вдоль оси ОС, то вектор момента количеств движения отно-
относительно точки О будет равен
Спи + Аи х и (8.7.1)
и уравнение движения будет иметь вид
Спи -\- Аи X и = Mglu х v, (8.7.2)
где v — единичный вектор вдоль линии действия силы тяжести. Если теперь
обозначить через х, у, z составляющие вектора и и направить ось Oz верти-
вертикально вверх, так что v = {0, 0, —1}, то будем иметь
A (yz - z'y) + Cnx = — Mgly, (8.7.3)
A (zx — x'z) + Сп'у = Mglx, (8.7.4)
А (ху - ух) + Ста = 0. (8.7.5)
Из (8.7.5) сразу получаем
А {ху — ух) + Cnz = const. (8.7.6)
Это соотношение эквивалентно (8.6.7). Умножая уравнения (8.7.3) — (8.7.5)
• • • • • •
соответственно на у — z, z — х, х — у и складывая, находим
А {(хх + уу + zz) (х + у + z) — {х + у + z) (хх + у у + zz)} =
= Mgl {(x + y + z)'z- (хх + уу + zz)}. (8.7.7)
§ 8.9] ВРАЩАЮЩИЙСЯ ВОЛЧОК; ИССЛЕДОВАНИЕ ДВИЖЕНИЯ 131
¦ • •
Так как хх -\- уу + zz = 0, уравнение (8.7.7) упрощается и принимает вид
(' ''') = O. (8.7.8)
Отсюда
Y А (х2 + у2 + z2) + Mglz = const, (8.7.9)
что эквивалентно (8.6.8).
§ 8.8. Гироскопические силы. Рассмотрим движение волчка, на который
действует единственная сила F, приложенная в точке G (кроме реакции связи
в точке О). Пользуясь обозначениями § 8.7, напишем
Спи + Аихи =1и X F. (8.8.1)
Умножая обе части этого равенства векторно на и и обозначая 1и = г (так
что г равен вектору OG), находим
^r{r-(u.r)u} = {F-(u.F)u} + -^(uxir). (8.8.2)
• • ¦ •
Выражение {г — (и-г) и} в левой части равенства определяет составляющую
ускорения точки G, перпендикулярную к OG, т. е. составляющую, лежащую
в касательной плоскости к сфере, по которой движется точка G. Аналогичным
образом, выражение {F—(u-F) и} в правой части определяет составляющую
силы F, лежащую в касательной плоскости. Но составляющая ускорения
и составляющая силы не совпадают по направлению, если только точка G
не находится в данный момент в покое. Если г =^=0 и параметр п достаточно
велик, то в правой части (8.8.2) доминирует последнее векторное слагаемое,
перпендикулярное как к OG, так и к скорости точки G.
Движение точки G можно представить как движение частицы массы А/Р,
скользящей по гладкой сфере. Но такое движение будет вызываться не одной
силой F, а еще силой, перпендикулярной к скорости и пропорциональной ей.
Силы подобного рода постоянно встречаются в задачах* в которых рассмат-
рассматривается движение волчков и гироскопов, и называются гироскопическими
силами.
§ 8.9. Вращающийся волчок; исследование движения. Возвратимся
к задаче о движении волчка, рассмотренной в § 8.6. Угол, который ось волчка
составляет с вертикалью, и величина ф определяются уравнениями
±'z* = f(z) = (li
[
J
(„,
где z = cos 9. Рассмотрим полином третьей степени / (z). Имеем
/ (-1) = -2 (Л + Pf.< 0, / A) = -2 (I - рJ < 0. (8.9.2)
Еслиг2 > 0 при некотором z в интервале (—1, 1), то функция / (z) имеет три
действительных корня z4, z2, z3 таких, что
—Kz^Zz^Kz! (8.9.3)
(рис. 19).
9*
132
ПРИЛОЖЕНИЯ УРАВНЕНИИ ЛАГРАНЖА
[Гл. VIII
Возьмем точку Р на оси волчка, находящуюся йа единичном расстоянии
от острия О; движение ее происходит в сферическом поясе единичной сферы,
ограниченном окружностями z = z3 и z = z2. Если z2 и z3 совпадают, то дви-
движение является установившимся и точка Р равномерно движется по окруж-
окружности z = z3 на единичной сфере. Выясним, какие установившиеся движе-
движения возможны при 0 = а, если а — острый угол. Обозначим значение ср
в установившемся движепии через Q. Уравнение (8.6.6) показывает, что Q
является корнем квадратного уравнения
F (Q) = cos aQ2 - 2рп + д = 0. (8.9.4)
Это уравнение имеет два действительных
положительных корня Qi и Q2 @< Qi <C &г).
если р2 > q cos а. Мы примем, что р2 > (?¦
так что условие р2 > q cos a будет удовле-
удовлетворяться при всех а. Условие р2 > q удов-
удовлетворяется в подавляющем большинстве
случаев, представляющих практический инте-
интерес, так как в этих случаях параметр р ве-
велик. (Если qlp2 — величина малая, то мень-
меньший корень приближенно равен q/2p, а больший корень равен 2/?/cos а. Эти
величины выходят за область, определяемую действительными значениями:
д/2р меньше, чем Qi, а 2plcos а больше, чем Q2.)
Не входя в детали, можно общий характер движения в области сфериче-
сферического пояса (в предположении, что р2 > q) представить следующим образом.
Пусть в начальный момент точка Р перемещается в горизонтальной плоско-
плоскости по касательной к окружности z = cos а, где 0 < а < -^ л. Тогда в на-
Рис. 19.
чальный момент 0 = 0, ср = Q и, следовательно,
2% = 2р cos a + Q sin2a,
2jlx — 2q cos a + Q2 sin2a.
Далее.
и начальное значение z равно
V= -g- (y z2) -- - q A - z2) - 2z (ц - qz) + 4p (Я. -
(8.9.5)
(8.9.6)
(8.9.7)
—q sm2a — cos a (Q2 sin2 a) + 2p {Q sin2 a) =
=¦. - sin2a (cos aQ2-2PQ + q) = -sin2 aF(Q). (8.9.8)
Мы получаем, что в начальный момент z > 0, если Q лежит между зна-
значениями Qi и Qzi равными значениям <р в установившихся движениях при
0 = а. Если Q лежит между Qi и Q2, то z = cos а соответствует нижней
из двух граничных окружностей, т. е. z3 = cos а. Заметим, что % и ц. поло-
положительны.
Рассмотрим, как изменяется движение при возрастании Q от Q\ до й2-
Рассмотрим последовательность движений, когда нижняя окружность z =
= z3 = cos а фиксирована и угол а острый, так что z3 > 0. Основной вопрос
заключается в том, обращается ли величина ср в нуль и меняет ли она зпак
в процессе движения. Соотношение (8.6.10) показывает, что знак <р совпадает
со знаком Я, — pz. Поэтому, если к > р, то ф не может обратиться в нуль.
Если же 1) к < р и 2) "kip лежит между z2 и z3, то ф обращается в нуль во
S 8.9] • ВРАЩАЮЩИЙСЯ ВОЛЧОК; ИССЛЕДОВАНИЕ ДВИЖЕНИЯ 133
время движения. Далее,
2 (р — %) = 2р A — cos a) — п sin2a =
= A _ cos а) {2р — п A + cos а)}, (8.9.9)
так что условие 1) эквивалентно неравенству
п< . ,2р -. (8.9.10)
1 + cos a
Условие 2) удовлетворяется, если / (Х/р) > 0, т. е. если рц > qX; поскольку
X и \i задаются выражениями (8.9.5), (8.9.6), это условие эквивалентно
неравенству
п > qlp. (8.9.11)
Отметим теперь на рис. 20 точки на оси Q, соответствующие этим кри-
критическим значениям: это — точка В, где Q = qlp, и точка С, где Q =
= 2р/A + cos а). Каждое из этих значений лежит менаду Q\ и Q2; второе
из них больше первого, поскольку (как легко
проверить) значения F (—) и F { . . р ] отри-
* г / \ р I \1 + cos а / у
цательны и
2р _±_ 2p2-g(l + cosa) Q
1 + cos а р р A + cos a)
Поэтому, если график пересекает ось Q в точке А
(где Q = Qi) и в точке D (где Q = Q2), то точки
А, В, С, D располагаются в указанном на ри- рис. 20.
сунке порядке.
Представим значение О, для рассматриваемого движения изображающей
точкой W, занимающей все положения на отрезке AD. Когда W занимает
положения А или D (т. е. Q принимает значения Q4 или Q2), тогда z2 совпа-
совпадает с z3 и точка Р движется по горизонтальной окружности. Когда же точка
W занимает положение В, тогда
Q = — , 2Х = 2pcosa + — sin2a, 2ц = 2а cos a + -^- sin2 a (8.9.12)
р 1 р pJ ч с
и
А = JL = cos a + -Л- sin2 a = z2 = cos p. (8.9.13)
Этот случай является критическим, и <р обращается в нуль при z = z2.
Полином третьего порядка /(z) имеет вид
a)(cosP — z) ((—— cosa)— z) . (8.9.14)
Траектория точки Р имеет точки заострения на верхней окружности.
Это почти очевидно, поскольку при г = г2 точка Р находится в покое. Если
волчок начинает свое движение из состояния, в котором его ось находится
в покое при 0 = Р, то ось начинает удаляться от вертикали. Формально это
следует из такого рассмотрения: пусть траектория точки Р пересекает мери-
меридиан под углом х, тогда
(8.9.15)
cos
134 ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА [Гл. VIII
В общем случае в нуле функции / (z) угол % =-^-п. Но если (как это
имеет место в рассматриваемом случае) нуль совпадает с "kip, то в этой точке
X = 0 и траектория точки Р имеет точки заострения на линии z = z2.
Если точка W занимает положение С, то
TT^ |f?^ (8-9.16)
и
i> {(^2)} (8.9.17)
В этом случае z2 = 1 и точка Р проходит во время движения наивыс-
наивысшую точку единичной сферы. Отметим, что <р в процессе движения не обра-
обращается в нуль. В самом деле,
Ф = Т^- (8.9.18)
Теперь можно представить, как изменяется движение оси волчка или,
что то же, точки Р на единичной сфере, когда Q возрастает от Qi до Q2.
При перемещении точки W из положения А в положение С (рис. 20) z2
at Ь) si d)
Рис. 21.
увеличивается от z3 до 1, проходя через критическое значение cos |5, когда W
проходит через положение В; при дальнейшем перемещении точки W из по-
положения В в D z2 убывает от 1 до z3. Для значений Q, лежащих в области ВС,
Ф меняет знак в процессе движения и траектория точки Р делает петли.
Рисунок 21, a — d иллюстрирует изменение характера движения при возрас-
возрастании Q от Qi до Qz- Рис. 21,а соответствует случаю, когда точка И7 лежит
между А и В, а траектория точки Р проходит между двумя окружностями
на единичной сфере, касаясь их поочередно. Рис. 21, Ъ соответствует случаю,
когда точка W занимает положение В; траектория имеет точки заострения;
движение этого рода имеет место тогда, когда ось волчка начинает движение
из состояния покоя при 9 = р. Рис. 21, с отвечает случаю, когда W лежит
между В ж С; траектория, как показано, делает петли. Когда точка W зани-
занимает положение С, точка Р проходит через наивысшее положение на единич-
единичной сфере. Если же W лежит между С и D, то мы снова приходим к движению
в сферическом поясе, при котором ср остается положительной (рис. 21, d).
§ 8.10. Численный пример. В качестве иллюстрации изложенной выше
3 1
теории рассмотрим пример, в котором положимр2 =-^Ч и 2з = -о"' a =
= -g-я = 60°. Уравнение (8.9.4) в этом случае примет следующий вид:
3Q2 — 12рп + 4р2 = 0. (8.10.1)
§ 8.10 ЧИСЛЕННЫЙ ПРИМЕР 135
Корни приближенно равны
Qt = 0,367р, fi2 = 3,633р. (8.10.2)
Если W занимает положение Б, то Q = -jP и cos р ==-?-, р = 41°24'. Если
И7 занимает положение С, то й =-^р.
Рассмотрим сначала случай, когда точка W совпадает с точкой В. При
этом
*2 = А, я = |р, и = |? (8-10.3)
и
/(*)=<?D-г) (*-4) (l-z)- <8-10-4>
Кроме того,
так что ф > 0 ( ф = 0 при z = z2 = -v- i.
Чтобы получить более ясное представление о движении, определим при-
приращение ф между двумя последовательными точками заострения. Имеем
dz
(-т) (Ь)
Поэтому, если обозначить это приращение через 2у, то получим
-J—1/ ^]
1 —z2 I/ / 1
3/4
Т=|та1/ ГГ-ПГ—Г*- («-ЮЛ)
1/2
Грубую оценку величины у можно произвести следующим путем. Заметим,
что если 0 <С а < Ь, то
=^" dz=="T^~a)"- (8.10.8)
Другой сомножитель в подынтегральном выражении (8.10.7) представляет
собой монотонную функцию. Поэтому величина 2у заключена между значе-
значениями (]А)/6)я и (8)^21/49) я и заведомо лежит между пределами ^ли-тя.
Истинное значение величины 2у в этом примере равно 83°45'.
Рассмотрим теперь движение, соответствующее случаю, когда точка W
занимает положение С. При этом
z2 = l, K = p, ц = -|г» (8.10.9)
3-z), (8.10.10)
136 ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА [Гл. VIII
И
cp = 2p/(l + z), (8.10.11)
dw # 2p ~у 3
]/ -z)(z-y) (З-z) (l + z)j/ A-г) (г—у) C-z)
При возрастании z от у до 1 величина <р получает приращение
(8.10.12)
f (8.10,13)
Б правой части этого равенства следует положить z = -r—7"CoS 9- Множитель
(-к-, 1)
— z в интервале I-g-, 11 изменяется монотонно, так что значение
V лежит между пределами я|/б/4 и 2я|^30/15 и, стало быть, между пре-
3 3
делами -=-я и -т-Jt. Истинное значение у равно 119°48'.
§ 8.11. Стержень во вращающейся плоскости. Предположим, что стержень совер-
совершает движение по гладкой плоскости, которая вращается с угловой скоростью со около
горизонтальной оси, лежащей в самой плоскости. Пусть 0%, Оц — оси, связанные с пло-
плоскостью, причем за ось О\ возьмем неподвижную горизонтальную ось вращения, а ось Оц
расположим ниже горизонтальной оси под углом со? к ней. Если угол наклона
стержня к оси О\ в некоторый момент t обозначить через 9, то можно написать
L = — (|2+Т12 + со2т\2) +-у &3 (92+ш2 sin2 O) + gr) sin м, (8.11.1)
где g, т) — координаты центра тяжести G стержня, а М№ — его момент инерции относи-
относительно оси, проходящей черея G перпендикулярно к стержню. Эта задача интересна тем,
что выражение для L имеет вид суммы трех отдельных функций Лагранжа, каждая из
которых зависит лишь от одной координаты, и поэтому движение по каждой координате
не зависит от движения по остальным координатам. Система является полностью разде-
разделимой: ее можно трактовать как три независимые системы. Явление полной разделимости
наиболее ярко выступает в теории малых колебаний, излагаемой в следующей главе.
В дальнейшем (гл. XVII и XVIII) мы рассмотрим разделимые, но не полностью раздели-
разделимые системы; в таких системах изменение одной из координат хотя и не вполне автономно,
но все же в некотором смысле (более подробно см. ниже) оно происходит независимо от
других. (Следует заметить, что рассматриваемая нами здесь система не является раздели-
разделимой системой в обычном смысле, поскольку теория разделимых систем, излагаемая
в гл. XVII и XVIII, относится только к таким системам, для которых функция Лагранжа
не .содержит t\ в нашем случае время t входит явным образом в выражение для L-)
Уравнения движения имеют вид
|=0, г)—oJr] = gsincui, в = со cos 9 sin 6. (8.11.2)
Значение § остается постоянным (что, впрочем, очевидно), а значение т) в некоторый
момент t равно
8 е
-l-shcui+-2?-2 (sh crt—sin Ш), (8.11.3)
где а и 6 — значения г\ и т| в момент t = 0. Уравнение для 6 можно представить в виде
ф"+ «2 sin ф = 0, (8.11.4)
где ф = л — 29. Мы получили уравнение E.2.10), описывающее, движение простого
маятника.
§ 8.12]
КАЧЕНИЕ ДИСКА
137
§ 8.12. Качение диска. До сих пор применение уравнений Лагранжа
ограничивалось голономными системами. Рассмотрим теперь приложение
этих уравнений к неголономной системе, а именно к однородному диску или
однородному круглому обручу, катящемуся по шероховатой горизонтальной
плоскости. Система имеет три степени свободы, но для определения ее конфи-
конфигурации требуется пять лагранжевых координат. Дифференциалы этих пяти
координат, представляющие виртуальное перемещение, должны удовлетво-
удовлетворять двум пфаффовым уравнениям связи, а уравнения Лагранжа будут
содержать два множителя (§ 6.2).
Возьмем неподвижную систему координат Oxyz, причем ось От, направим
вертикально вверх, а точку О выберем в плоскости, по которой катится диск.
Ориентацию диска определим эйлеровыми углами Э, ф, яр, а ось GC системы
Рис. 22.
GABC (связанной с диском) направим по оси симметрии диска. Координатами
центра тяжести G будут ?, r\, a sin 9, где а — радиус диска. Функция Лаг-
Лагранжа запишется в виде
L = -i M (|2 + if + a? cos2 0 в8) + у А @2 + Ф2 sin2 6) +
yose)a — MgasinQ, (8.12.1)'
где М — масса диска, А, А, С — его главные моменты инерции в точке G,
причем С = 2А.
При виртуальном перемещении дифференциалы d|, dr\, dQ, dip, dip свя-
связаны двумя соотношениями (условиями качения), а именно:
dl cos ф ¦+ dr\ sin ф — a dQ sin 0 = 0, (8.12.2)-
— dl, sin ф + dt\ cos ф + a dap + a dip cos 0 = 0. (8.12.3).
В рассматриваемой задаче виртуальные перемещения, разумеется, совпадают
с возможными перемещениями. Уравнения (8.12.2) и (8.12.3) можно получить
различными способами. Можно, например, применить один из приемов,
использованных в § 5.9 для составления уравнений качения сферы. Однако
проще всего ввести подвижные оси 0123 (не связанные с диском), как
указано на рис. 22, и так как точка К диска в данный момент находится
в покое, то скорость точки G будет иметь составляющие 0, —ясоз, а<*>2 или
0, —а (г|з + ф cos 0), a0. Поэтому составляющие скорости точки G по-
138 ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА [Гл. VIII
направлениям ОР, 02 будут равны aQ sin 6, —а (ар + ф cos 0). Приравнивая
эти величины составляющим I cos ф + т] sin ф, —? sin ф + т] cos ф, полу-
получаем условия (8.12.2), (8.12.3)'.
С помощью функции Лагранжа (8.12.1) и уравнений связи (8.12.2),
{8.12.3) составляем уравнения движения:
М'% = X cos ф — ц sin ф, (8.12.4)
Мх\ — X sin ф + ц cos ф, (8.12.5)
-^ (Ma2 cos2 0 0 + Ав) = — Ma2 cos 0 sin 0 02 + A cos 0 sin 9 ф2 —
— Ссо3 Ф> sin 9 — Mga cos 0 — Ха sin 0, (8.12.6)
-^- (A sin2 0 ф + С cos 0 оK) = ца cos 0, (8.12.7)
-|- (С©,) = ца. (8.12.8)
Здесь через со3 обозначена величина ар + ф cos 0. Всего мы имеем семь урав-
уравнений: пять уравнений (8.12.4) — (8.12.8) и условия качения
? cos ф + т] sin ф = a sin 0 0, (8.12.9)
—? sin ф + ti cos ф = —асо3. (8.12.10)
Полученные нами семь уравнений определяют семь неизвестных: ?, т], 9, ф,
лр, X, ц.
Физический смысл величин X, ц очевиден: из уравнений (8.12.4), (8.12.5)
получаем
М (i cos ф + tj sin ф) = X, (8.12.11)
М ( — *? sin ф + т]' cos ф) = ц, (8.12.12)
и, таким образом, X, ц выражают составляющие реакции связи в точке кон-
контакта К вдоль осей ОР и 02.
Легко выразить X и ц через 9, ф, гр и их производные; в самом деле,
из (8.12.9), (8.12.10) имеем
? cos ф+"т] sin ф+(—? sin ф+т] cos ф) ц>=а (sin 0 0 + cos 9 02), (8.12.13)
¦• •• • • • •
—? sin ф + ti cos ф — (? cos ф + т] sin ф) ф = —асо3. (8.12.14)
Учитывая (8.12.9) — (8.12.12), получаем
X = Ma (sin 0 ё+ cos 0 02 + со3<р), (8.12.15)
ц =Ма (sin 6 0ф — ш3). (8.12.16)
Подставляя теперь эти выражения 1i|ib уравнения (8.12.6) и (8.12.8)
¦и исключая [I из (8.12.7) и (8.12.8), находим
(А + Ма2) 0 = А(р2 cos 0 sin 0 — (С + Ma2) со3Ц> sin 9 — Mga cos 9,
(8.12.17)
(С + Ma2)a3 = Ма2ёф sin 0, (8.12.18)
-^-(^4(psin20) = Cco30sin0. (8.12.19)
Эти три уравнения содержат три переменные: 0, ф^ со3.
§ 8.12] КАЧЕНИЕ ДИСКА 139
Теперь можно составить дифференциальные уравнения, выражающие
(о3 и ф как функции от 0. Обозначая cos 0 через р, запишем уравнения (8.12.18)
и (8.12.19) в форме
(8.12.20)
^ (8.12.21)
а
Здесь А = кМа2 и С = 2кМа2. Исключая <р, находим
3 = 0. (8.12.22)
Это дифференциальное уравнение типа Лежандра определяет со3 как функ-
2 4
цию от р. Значение коэффициента ¦ равно 1 для обруча и -=- для дис-
диска. Исключая ©з из (8.12.20) и (8.12.21), получаем
где через ? обозначено A — рг) ср. Дифференциальное уравнение (8.12.23)
•
определяет ?, а следовательно, и ф как функцию от р.
Из уравнения (8.12.17) можно получить условие для установившегося
движения, при котором диск составляет с горизонтальной плоскостью угол
а, а центр его движется по окружности радиуса Ъ со скоростью ban. Величина
Ф в установившемся движении равна со; значение со определяется
из уравнения
{Bк + 1) Ъ + ка cos a}co2 = g ctg a, (8.12.24)
при выводе которого используется равенство — асо3 = &со.
Рассмотренная задача иллюстрирует применение уравнений «Лагранжа
к неголономным системам. Мы видели, что это практически вполне возможно.
Однако, вообще говоря, метод Лагранжа не особенно удобен для задач такого
рода. Для неголономных систем более удобным и плодотворным является
другой метод, основанный на уравнениях Гиббса — Аппеля; с этим методом
мы познакомимся в гл. XII и XIII. .
Глава IX
ТЕОРИЯ КОЛЕБАНИЙ
§ 9.1. Колебания около положения равновесия. Свой метод Лагранж
с особо выдающимся успехом применил к теории малых колебаний механиче-
механической системы около положения устойчивого равновесия. Правда, применяе-
применяемые там уравнения описывают, движение приближенно, но, несмотря на это.
представляют большой интерес, поскольку, как уже отмечалось ранее в § 8.1.
эти уравнения относятся к числу полностью разрешимых: задаваясь значе-
значениями q и q при t = 0, можно получить явные формулы, дающие решения
уравнений для всех последующих значений t.
Рассмотрим натуральную систему (§ 6.5) с функцией кинетической
энергии
и функцией потенциальной энергии
V =V(gu q2, ¦ ¦ -, qn). (9.1.2)
В точке Qi, q%, . . ., qn, в которой функция V имеет минимум, система может
находиться в состоянии устойчивого равновесия. Отсчет координат удобно
производить от этой точки, тогда положению равновесия будет соответство-
соответствовать точка О, где q\ — q% = . . . = qn = 0. Без потери общности можно
принять, что в ней V = 0. Повсюду в окрестности О, за исключением самой
этой точки, V > 0. Уравнение V = С для достаточно малых значений С
представляет замкнутое (п — 1)-мерное многообразие S (С), внутренность
которого, / (С)-область, характеризуется неравенством F<C и расположе-
расположена в малой окрестности точки О. Если функцию V разложить в ряд Тейлора
в окрестности начала координат, то главные члены разложения
образуют определенно-положительную квадратичную форму. Для достаточно
малых значений С многообразие S (С) мало отличается от эллипсоида с цен-
центром в точке О.
Имеем интеграл энергии
Т + V =С. (9.1.4)
Если система начинает свое движение в непосредственной близости от точки
О с малой начальной скоростью, то постоянная С мала. В этом случае q ш q
во все время движения будут оставаться малыми и равновесие в точке О
будет устойчивым. В самом деле, поскольку Т 2> 0, движение происходит
в области
F<C. (9.1.5)
Изображающая точка располагается в области / (С) или в исключительном
случае (если во время движения эта точка останавливается) — на поверх-
поверхности S (С). Это указывает на то, что значения qt, q2, . . ., qn остаются
§ 9.1] КОЛЕБАНИЯ ОКОЛО ПОЛОЖЕНИЯ РАВНОВЕСИЯ 141
малыми в процессе всего движения. Далее, поскольку во время движения
V ^ О, справедливо неравенство
Т < С, (9.1.6)
и, следовательно, величины qi, Цъ, ¦ ¦ ¦-, дп также остаются малыми. Поэтому
достаточно хорошее приближение к действительному движению можно
получить, сохранив в уравнениях движения лишь слагаемые первого порядка
относительно д, q и д. В этом заключается так называемое линейное прибли-
приближение. Определяемое этим приближением движение тем ближе к точному,
чем меньше значение С.
r-е уравнение Лагранжа может быть записано в следующей форме
(см. F.4.5)):
5— 1 U= I V-- 1
Мы сохраним лишь члены первого порядка относительно q, g и д. Тогда в
левой части уравнения (9.1.7) будем иметь
angi+ аГ2д2+ ... +агпд„. (9.1.8)
Кроме того, можно считать, что коэффициенты ars в этом выражении имеют
постоянные значения, равные их значениям в положении равновесия. В пра-
правой части уравнения (9.1.7) мы оставим лишь члены первого порядка в раз-
разложении в ряд Тейлора по q\, д^.- .... дп.
Таким образом, для получения линейного приближения можно соста-
составить уравнения Лагралжа по выражениям ГиУ, каждое из которых пред-
представляет квадратичную форму с постоянными коэффициентами. Коэффици-
Коэффициенты в выражении для Т можно взять равными их значениям в положении
равновесия; иными словами, для наших целей достаточно найти выражение
для Т в момент, когда система проходит положение равновесия. Функцию V
можно представить членами второго порядка в разложении Тейлора в окрест-
окрестности точки О, т. е. квадратичной формой вида (9.1.3). Таким образом, теория
колебаний будет основываться на уравнениях Лагранжа, когда Т и V
задаются определенно-положительными квадратичными формами с постоян-
постоянными коэффициентами. Мы будем пользоваться теми же обозначениями, что
и ранее, а именно:
причем, как уже говорилось, коэффициенты ars постоянны. Для функции
V примем приближенное выражение (9.1.3):
7==т22Ь™^' (9.1.10)
в котором коэффициенты brs постоянны. В результате мы приходим к системе
линейных уравнений с постоянными коэффициентами
8=1
=l,2, ...,«. (9.1.11)
Если матрицу {ars) обозначить через Л, матрицу {brs) — через Л и вектор
(матрицу-столбец) {дч, д2, . . ., дп] — через q, то уравнения (9.1.11) можно
записать в матричной форме:
Q. (9.1.12)
142 ТЕОРИЯ КОЛЕБАНИЙ [Гл. IX
С помощью действительного неособого линейного преобразования квад-
квадратичные формы (9.1.9) и (9.1.10) можно одновременно привести к суммам
квадратов с положительными коэффициентами. Одновременное приведение
двух квадратичных форм к суммам квадратов всегда возможно, если по край-
крайней мере одна из форм определенно-положительная. (То обстоятельство, что
в нашем случае одна из форм содержит q, а другая q, несущественно, так как
линейное преобразование q влечет за собой такое же преобразование q.)
Можно найти новые координаты |ь |2> • • •, 1п> связанные с qu q2, . . ., gn
линейными соотношениями, такие, что
1
I
J
i I (9-1.13)
v=у(Кр%1+Кр%1 +...+Kplll). J
Коэффициенты к и р в этих формулах суть вещественные положительные
постоянные. При желании можно было бы пойти еще дальше и представить Т
в виде квадратичной формы, все коэффициенты которой равны единице,
однако для динамической задачи это несущественно.
В координатах | r-е уравнение движения имеет вид
IV + Р2т1т = 0. (9.1.14)
Оно содержит только одну координату \т. Таким образом, система уравне-
уравнений распадается на п полностью независимых систем.
Если в момент t = 0 Ъ,т равно аг и |г равно рг, то
Ът = ат cos prt + (pr/pr) sin prt. (9.1.15)
Это решение получено совершенно независимо от остальных |.
Координаты ii, |г5 • • .) ?п называются главными или нормальными
координатами колебательной системы; колебание, при котором изменяется
лишь одна главная координата, а остальные все время равны нулю, называет-
называется главным колебанием. Мы говорим, что в главном колебании соответствую-
соответствующая главная координата возбуждена, а остальные координаты находятся
в покое. Как видно из формулы (9.1.14), в r-м главном колебании координата
|г изменяется по гармоническому закону с периодом 2п/рТ. Всего имеется п
таких периодов, не обязательно различных; их называют собственными перио-
периодами или периодами свободных колебаний системы. Периоды свободных коле-
колебаний являются инвариантами системы и не зависят от лагранжевых коор-
координат, выбранных первоначально для описания системы. Главное колебание
с наибольшим периодом и, стало быть, с наименьшей частотой, т. е. колеба-
колебание с наименьшим р, называется основным колебанием. Поскольку q зависят
от | линейно, любое колебание может быть представлено как суперпозиция
главных колебаний.
Движение системы в общем случае, в противоположность описанному
выше, обычно не является периодическим, однако в одном случае движение
всегда будет периодическим независимо от начальных условий. Это имеет
место тогда, когда отношение любой пары величин р представляет собой
рациональное число. Если существуют целые числа Шх, т%, . . ., тп (не име-
имеющие общего множителя) такие, что
то любое колебание системы является периодическим с периодом 2л/со. Если,
однако, отношение одной пары величин р, скажем pt и pj, иррационально,
§ 9.1] КОЛЕБАНИЯ ОКОЛО ПОЛОЖЕНИЯ РАВНОВЕСИЯ 143
то любое движение, в котором возбуждаются ?-е и /-е главные колебания г
не может быть периодическим. Но можно, однако, всегда указать целые числа
тх, т2, . . ., тпп такие, что равенство (9.1.16) будет выполнено приближенно,
и, таким образом, в широком смысле каждое движение приближенно является
периодическим. В самом деле, каждая переменная дт представляет собой
почти периодическую функцию от t. Для того чтобы приближение к периоди-
периодическому движению было достаточно хорошим, приближенный период 2л/о>
может оказаться весьма большим.
В главном колебании, скажем в первом главном колебании, координаты
|2, Ез> • . •, ?п »се время равны нулю; отсюда следует, что отношения Qi '¦
:q2: . . . :qn постоянны. В самом деле, если q и \ связаны соотношениями
= mnli + m12l2 + ..
= "bill + "*22?3 + .. . + m2
(9.1.17)
то в первом главном колебании
-2i- = ^L= ...=-^- (9.1.18)
ти m2i mni v
и каждая координата qT изменяется по гармоническому закону с периодом
2n/pt:
• • ¦ • • •
-^ = ^=...=-^=-р*. (9.1.19)
Ч\ Чъ Чп ч
В главном колебании наблюдаемая конфигурация системы, определяемая
отношениями q\ : q2 : . . .: qn, остается неизменной, а сами координаты
изменяются по гармоническому закону с периодом соответствующего главно-
главного колебания.
Преобразование (9.1.17) можно записать в следующей форме:
q = S%. (9.1.20)
Здесь q— вектор (матрица-столбец) {ql, q2, . . . , qn}, %—вектор {gj, |г, • • •
...,?„}, а $ — квадратная матрица (mrs).
Решение конкретных задач, по крайней мере в тех случаях, когда перио-
периоды главных колебаний различны, не вызывает особых затруднений. Один
из возможных путей решения используется ниже в примере 9.1 А. Он состоит
в следующем. Сначала определяют периоды главных колебаний и отношения
qi : q2. . . . :qn для каждого такого колебания. Таким образом находят эле-
элементы матрицы 8 и с помощью преобразования (9.1.17) приводят уравнения
движения к форме (9.1.14). После этого, можно выразить решение через пере-
переменные |ь ?2, • • • > 1п> если знать начальные значения | и ?; последние
можно определить из начальных значений q и q. Итак, для любого момента
времени можно найти значения q, зависящие линейным образом от ?, если
известны начальные значения q и q. Таким образом, задача полностью решает-
решается при любых начальных условиях.
Значения коэффициентов К, входящих в (9.1.13), не определяются опи-
описанной выше процедурой, так как мы нашли лишь отношения элементов
в каждом столбце матрицы 8. Соответствующая неопределенность имеет
место и в отношении переменных |. Это обстоятельство, однако, совершенно
несущественно с практической точки зрения. Преобразование
Ъг = (МЬ г = 1, 2, .... п, (9.1.21)
144
ТЕОРИЯ КОЛЕБАНИЙ
iTh. IX
в котором ц — постоянные, а г\ — главные координаты,
выборе fi приводит выражения для Т и V к виду
при надлежащем
(9.1.22)
г=1
г=1
Этой формой часто пользуются при теоретических исследованиях, но прак-
практически можно обойтись без перехода от (9.1.13) к (9.1.22). Входящие в выра-
выражения (9.1.22) главные координаты т] определяются единственным образом
(с точностью до знака), если все р различны.
Сделаем еще одно существенное замечание. Форма (9.1.10) должна быть
определенно-положительной; если V — лишь знакопостоянная (полуопре-
(полуопределенная) форма, то изложенная выше теория теряет силу. Например, если
одна из переменных J-, скажем |ь не
входит в V, то соответствующее уравне-
• •
ние движения имеет вид |4 = 0. Отсюда
следует, что ii = «i + pV, и перемен-
переменная |i в общем случае не остается ма-
малой в течение всего движения.
Рассмотрим теперь два конкретных
примера; во втором из них система
имеет лишь две степени свободы и реше-
решение поэтому значительно упрощается.
Пример 9.1А. Невесомая струна длиной 4а натянута силой Р между
двумя фиксированными точками. На струне закреплены точечные массы
пг, -=- тп, m на равных расстояниях друг от друга и от концов струны (рис. 23).
о
Система совершает поперечные колебания в своей плоскости. Требуется
найти движение системы.
Представим себе, что движение совершается на гладкой поверхности
стола. Натяжение Р будем считать большим и изменением его будем пренеб-
пренебрегать.
Пусть х, у, z обозначают смещения частиц в некоторый момент t. Урав-
Уравнения движения частиц с точностью до величин первого порядка относитель-
относительно х, у. z запишутся в виде
Рис. 23.
Эти уравнения можно переписать в следующей эквивалентной форме:
(9.1.23)
где п?=-Р/2та.
Можно, конечно, получить уравнения движения и с помощью метода
Лагранжа. Удлинение первого участка струны с точностью до величин вто-
второго порядка относительно х равно хг/2а, Учитывая аналогичным образом
§ 9.1]
КОЛЕБАНИЯ ОКОЛО ПОЛОЖЕНИЯ РАВНОВЕСИЯ
145
удлинения остальных участков струны, получаем
Кроме того,
Если составить теперь уравнения Лагранжа, то легко убедиться, что они
совпадают с уравнениями движения (9.1.23).
Рис. 24.
Для главного колебания с периодом 2п/р имеем
iL = A = JL = р2
х у z "
Подставляя х, у, z в уравнения движения, получаем
2п2х + ( у рг — 4и2) у + 2n?z = О,
(9.1.24)
(9.1.25)
Эти уравнения будут совместны, если
О
= 0.
(9.1.26)
О 2га* р2 — 4га2
Отсюда, как и следовало ожидать, получаем три положительных значения р2:
„2 „2 П2_/И2 „2. С„2 /Q \ Ч!)
Для первого, или основного, главного колебания р2 = га2, и уравнения
(9.1.25) для отношений x:y:z образуют (совместную) систему
-Зх+2у =0, ^1
3x — iy + 3z = 0, I (9.1.28)
так что для первого главного колебания
2 3 2 '
Аналогично, для второго главного колебания р2 = 4ге2 и ^г = -н"==—7:
а для третьего р2 = 6га2 и ~г = ТГ7 = ~г ¦ Формы всех трех колебаний
(несколько напоминающие формы первых трех колебаний однородной непре-
непрерывной струны) показаны на рис. 24.
Любое движение, в котором третье главное колебание отсутствует, явля-
является периодическим с периодом 2л/га.
10 Л. А. Парс
146
ТЕОРИЯ КОЛЕБАНИЙ
[Гл. IX
Преобразование к главным координатам J-, r\, | имеет вид
(9.1.29)
Отсюда
(9.1.30)
Легко проверить, что Т и F, выраженные через |, т|, ?, имеют вид суммы квад-
квадратов:
(9.1.31)
V = у тп* B0?2 + 8т]2 + 20^2).
Теперь можно дать полное решение задачи линейного приближения при
любых заданных начальных условиях. Значение ? в некоторый момент t
дается, например, формулой
| = a cos p^ + — sin p^,
где а и Р — значения | и | при ^ = 0.
Для конкретности предположим, что в начальный момент система нахо-
находится в покое в положении равновесия и движение вызывается малым попе-
поперечным импульсом величиной ти, приложенным к первой частице. В началь-
начальный момент имеем
1
1
(9.1.32)
В любой последующий момент времени будем иметь
Ъ * Vt ^
ж окончательное решение будет иметь вид
3u / 1 .
lsi
1 .
si
где
Pi _ Pi _ Pi _ о _ P
1 ~" 4 ~ 6 ~Г
(9.1.33)
(9.1.34)
(9.1.35)
Пример 9.IB. Невесомая струна AD длиной 4a натянута силой Р
между двумя фиксированными точками. В середине струны В укреплена
точечная масса т; другая точечная масса 2т укреплена в точке С, делящей
§ 9.1] КОЛЕБАНИЯ ОКОЛО ПОЛОЖЕНИЯ РАВНОВЕСИЯ 147
пополам отрезок между В и D. Система совершает малые поперечные колеба-
колебания в плоскости, проходящей через точки А и D.
Доказать, что движение системы является периодическим с периодом
2л/п, где и2 = Р/2та, и найти ее движение при условии, что в момент t = О
каждая частица получает отклонение Ъ от прямой AD, а начальные скорости
равны нулю.
Обозначим смещение частицы В через х, а смещение частицы С через у.
Уравнения движения имеют вид
Как и в предыдущем примере, эти уравнения легко получить из уравнений
Лагранжа; с принятой точностью приближения имеем
где пг = Р/2ат. Уравнения Лагранжа имеют вид
'х'+пЦЗх-2у) = 0, у + п*Bу — х) = 0. (9.1.36)
Система имеет всего лишь две степени свободы, что упрощает решение.
Рассмотрим два способа решения этой задачи.
1) Как в предыдущем примере, для главного колебания имеем х =
• • • • • •
= —р2х и у = —ргу. Подставляя эти значения х и у в уравнения движения,
находим
(р2 — Зп2) х + 2пгу = О, п2х + (р2 — 2п2)у = 0. (9.1.37)
Этим уравнениям удовлетворяет ненулевой вектор {х, у} при условии, что
(р2 - 2п2) (р2 - Зп2) - 2п* = 0. (9.1.38)
Значения р2 в двух главных колебаниях равны
Р\ = п2, Р\ = 4п2. (9.1.39)
В первом главном колебании — х + у = 0, а во втором х + 2у — 0.
Можно было бы, аналогично предыдущему примеру, перейти к главным
координатам, однако в этом нет необходимости, поскольку в случае двух
степеней свободы результат очевиден. Когда система совершает первое глав-
главное колебание, вторая главная координата равна нулю, а когда система совер-
совершает второе главное колебание, первая главная координата равна нулю.
Поэтому первая и вторая главные координаты \ и г\ могут быть взяты в форме
I = х + 2у, т) = х - у, (9.1.40)
откуда
z = |(E+2ri), г/ = 1(|_г1). (9.1.41)
Как легко проверить, в этих координатах Т и V представляются суммами
квадратов:
Т = ±-тA2+2ц% V = ±-mn2(l2 + 8rf). (9.1.42)
2) Умножая второе уравнение движения на Я, и складывая с первым,
получаем
х + 1у + п2 {C - к) х + (-2 + 2Я,) у] = 0. (9.1.43)
10*
148 ТЕОРИЯ КОЛЕБАНИЙ [Гл. IX
Это равенство принимает вид 8 + р26 = 0 при
Следовательно, к = 2 или —1, Если к = 2, то получаем уравнение
i'+ 2у + >г2 (х + 2у) = 0; (9.1.45)
вели же к == —1,-то получаем уравнение
(х- у) + 4га2 (х - у) = 0. (9.1.46)
Таким образом, мы находим как главные координаты, так и соответствующие
периоды. Главные координаты равны Ъ,=±х-\-2уж'х\ = х — у. Имеем
|'+ n2t = 0, \\ + Ьп\ =а 0. (9.1.47)
Периоды главных колебаний равны 2п1п и 2я/2и;, поскольку первый
из них в два раза больше второго, любое движение системы является перио-
периодическим с периодом 2п1п.
В начальный момент имеем
х = у = Ь, х ='у = 0 (9.1.48)
или
I = 36, т| = 0, ( = т)'= 0. (9.1.49)
Следовательно,
I = ЪЪ cos nt, r\ = 0 (9.1.50)
и
х = у — focos nt. (9.1.51)
Пример 9.1С. Связанные системы. Пусть на стене висят
двое маятниковых часов. Приведем один из маятников в колебание с ампли-
амплитудой а. Тогда может случиться, что спустя некоторое время амплитуда коле-
колебаний этого маятника уменьшится почти до нуля, а второй маятник придет
в колебание с амплитудой а. Спустя еще период времени второй маятник
¦остановится, а первый придет в колебание с первоначальной амплитудой а.
Таким образом, колебание будет поочередно передаваться от одного маятни-
маятника к другому. Аналогичное явление происходит в рассматриваемом ниже
примере.
Тяжелый стержень АВ массы М подвешен в горизонтальном положении
да концы А и В на двух невесомых нитях длиной а каждая. К точке А подве-
подвешена на невесомой нити длиной а частица С массы т, такая же частица на та-
такой же нити подвешена к точке В. Система совершает малые колебания в вер-
вертикальной плоскости около положения равновесия.
Если угол, который нити, удерживающие стержень, составляют с вер-
вертикалью, обозначить через 6, а углы отклонения маятников от вертикали —
через ф и тр, то с принятой точностью приближения можно написать
л .Л . . А .
=-- т Ма282 + у таг (9 + фJ+-j ma (е + 'Ф) >
, ! ! (9-1-52)
V = -j MgaW + у mga (92 + Ф2) + у mga (82 + ^2).
9.1] КОЛЕБАНИЯ ОКОЛО ПОЛОЖЕНИЯ РАВНОВЕСИЯ 149
Уравнения движения запишутся в виде
2кЩ + Ф + т|) + 2/с2тг29 = 0, ^
9 + ф +«2Ф =0' Г (9.1.53)
9 +ф+»Ч -О, J
где А;2 = -н )-1 и и2 = — . Отсюда
Ф —^*4-ге2(ф —il?) = 0, (9.1.54)
так что одна из главных координат равна (ф —ф). Если второе и третье
уравнения сложить и умножить на А; и прибавить или вычесть первое урав-
уравнение, то получим
BА9 + Ф + ф) = 0,
(к —
т|= Ф —-
Эти формулы определяют две другие главные координаты. Таким образом,
главными координатами будут
& = 2&9+<р+Ч>,
(9.1.56)
-^.
к к
Кроме того, pt — T~T7n2j Р? = л2) Р?~г—т712- Нас будет интересовать случай,
когда отношение М/т велико (и, следовательно, к велико); в этом случае»
как и следовало ожидать, все три периода почти одинаковы. Разрешая
уравнения (9.1.56) относительно 0, ф, г|з, получаем
(9.1.57)
4-ф = Е — 2-п — С-
Рассмотрим теперь движение, определяемое следующими начальными
условиями:
6 = а/2Л;, Ф = а, -ф = 0; 6 = ф = ^ = 0. (9.1.58)
При этом
| = 2а cos pi<, I] = а cos p2f, ? — 0 (9.1.59)
и, следовательно,
Ф = уа (cos/jjf+cospgf), т|) = у o^cos/jjf — cos p20- (9.1.60)
Предположим теперь, что отношение МIm велико. Тогда j>i — п, a pt
несколько меньше, чем п; запишем его в виде pi = п — 2v, где v — малая
величина. Переменные ф Hif можно представить в форме
Ф = a cos v? cos (n — v) t, 1|з = a sin vt sin (n — v) t. (9.1.61)
Движение по координате ф можно считать гармоническим с периодом
2п/(п — v) (который мало отличается от периода 2л/п свободных колебаний
каждого из маятников, когда стержень А В находится в покое) и медленно
изменяющейся амплитудой с большим периодом 2jt/v. Движение по коор-
координате т|) принадлежит к тому же типу. При этом, однако, амплитуда ф-коле-
баний максимальна тогда (t = 0, л/v, 2n/v, . . .), когда амплитуда ¦ф-коле-
бания минимальна, и наоборот. Колебание медленно передается от первого
маятника ко второму, затем обратно — от второго к первому и т. д.
150 ТЕОРИЯ КОЛЕБАНИЙ [Гл. IX
§ 9.2. Теория преобразования к главным координатам. До сих пор лишь
предполагалось, что преобразование к главным координатам существует,
в настоящем параграфе мы дадим доказательство существования этого преоб-
преобразования.
Напомним, что матрицы Ал В суть вещественные симметричные матрицы,
ассоциированные с определенно-положительными квадратичными формами.
Уравнение относительно р2,
\р2А — В | = 0, (9.2.1)
называется уравнением периодов. Все его корни вещественны и положитель-
положительны. В самом деле, если pf — корень уравнения (9.2.1), то существует ненуле-
ненулевой вектор (матрица-столбец) иг такой, что
(р2тА — В)иг = 0. (9.2.2)
Отсюда получаем
п п (9.2.3)
(вектор ит получается из иг заменой каждой его составляющей комплексно-
сопряженной величиной). Это соотношение показывает, что р\ вещественны
и положительны. Корни ри р\, . . ., р? уравнения периодов являются соб-
собственными значениями *), а вектор иТ, удовлетворяющий уравнению (9.2.2),
— собственным вектором, соответствующим собственному значению р\. Так
как pf — число вещественное, то и вектор иг можно считать вещественным,
что мы всегда и будем предполагать в дальнейшем. Положительный квадрат-
квадратный корень из собственного значения pi обозначим через рТ.
Докажем теперь теорему о том, что существует действительное неособое
преобразование, приводящее Т и V к суммам квадратов. Применим метод
индукции: считая теорему верной для п — 1 переменных, докажем справед-
справедливость ее для п переменных.
Возьмем какое-нибудь собственное значение р\ (не обязательно простой
корень уравнения периодов), и пусть щ будет соответствующим вещественным
ненулевым собственным вектором, так что
{р\А — B)Ui = 0. (9.2.4)
Тогда единственное однородное уравнение
и[Аи = 0 (9.2.5)
*) Лагранж в первом издании своей «Mecanique Analytique» в 1788 г. и во втором
издании в 1811 г., вышедшем за три года до его смерти, а также Лаплас в «Mecanique
Celeste» (Premiere Partie, Livre II, Art. 57) ошибочно утверждали, что в случае равных
собственных значений обязательно появляются члены вида t cos pt или te^f и что поэтому
для устойчивости необходимо, чтобы собственные значения были все различны. В § 23.3
будет показано, что такие члены действительно иногда появляются, когда два одинаковых
собственных значения равны. Но в рассматриваемом здесь случае эти члены не появляют-
появляются и малые колебания происходят около положения, в котором потенциальная энергия
имеет минимум. Это легко усмотреть непосредственно из уравнения энергии (§ 9.1).
На эту ошибку Лагранжа и Лапласа указали еще Вейерштрасс в 1858 г. и Раус в 1877 г.
Хорошо известны комментарии Томсона и Тэта («Treatise on Natural Philosophy», 1912,
p. I, Art. 343m): «Странно, что Лагранж не заметил этой своей ошибки в течение двадцати
трех лет. Вероятно, он обнаружил бы ее уже при написании статьи для последнего изда-
издания, если бы имел обыкновение иллюстрировать свои замечательные аналитические
результаты примерами. В этом случае он, конечно, заметил бы, что вывод о неустойчиво-
неустойчивости равновесия частицы, находящейся на дне гладкого сосуда, имеющего форму тела
вращения около вертикальной оси, не может быть справедливым».
[Одновременно с Вейерштрассом на ошибку Лагранжа указал О. И. Сомов. См. кни-
книгу Я. Л. Геронимуса «Очерки о работах корифеев русской механики», Гостехиздат,
1952.— Прим- перев.]
§9.2]
ТЕОРИЯ ПРЕОБРАЗОВАНИЯ К ГЛАВНЫМ КООРДИНАТАМ
151
будет иметь п — 1 линейно независимых решений, скажем u = v2, vs, ..., vn.
Пусть Т будет матрицей, первый столбец которой составлен из компонент
вектора щ, а остальные столбцы — из компонент векторов v2, v3, ..., vn:
Матрица Т неособенная, и матрица Т''AT имеет вид
Ц 0 0 ... 0>
Т'АТ=\ 0 Ai | (9.2.7)
,0
Действительно, r-й элемент первой строки при г> 1 равен u'rAvr, a r-й эле-
элемент первого столбца при г> 1 равен v'rAui, и оба эти элемента равны
нулю.
Аналогичное утверждение справедливо и в отношении матрицы В;
так как
р\Ащ = .
то
Таким образом,
= 0, г = 2,3,
о\Кг 0 0 ... 0\
0
0 Bt
О
п.
(9.2.8)
(9.2.9)
(9.2.10)
Матрицы At и Bt являются матрицами определенно-положительных
форм (полученных из форм с матрицами Т'АТ, Т'ВТ при первой пере-
переменной, взятой равной нулю). Согласно нашей гипотезе, существует неосо-
неособенная матрица TJ^ такая, что матрицы TJ'xAiU^ и JJ'xBfJ^ являются диаго-
диагональными. Если обозначить
где U — матрица вида
I 1 0 0 ... 0\
о
о ut
то преобразование
приведет Т и V к сумме квадратов. В самом деле,
q'Aq=l'S'ASl
kt 0 0
о
0
0\
(9.2.11)
(9.2.12)
(9.2.13)
(9.2.14)
(9.2.15)
152
ТЕОРИЯ КОЛЕБАНИЙ
[Гл. IX
а это есть диагональная матрица Л:
Точно так же
где Р—диагональная матрица
>р\
р\
(9.2.16)
(9.2.17)
(9.2.18)
ЛР =
Таким образом, Т и V приводятся к виду
(9.2.19)
(9.2.20)
Здесь | — главные координаты.
Из доказанной теоремы получаем важные следствия.
1) Как уже отмечалось, уравнения движения можно представить в форме
~ir + P%r = 0, r=l, 2, ...,п. (9.2.21)
Это суть уравнения Лагранжа, составленные по Г и V в форме (9.2.20).
Уравнения движения (9.2.21) можно представить и в ином виде. Запишем их в мат-
матричной форме (9.1.12):
A'q'-\-Bq = 0, (9.2.22)
где q—вектор» или матрица-столбец {qiy q2, ..., qn}. Посредством преобразования (9.2.13)
получаем
(9.2.23)
(9.2.24)
и так как
S'AS=A, S'BS=AB,
то из (9.2.23) следует, что
A(V+-PS)=0.
Поскольку матрица А неособенная, это эквивалентно уравнению
которому соответствуют п уравнений (9.2.21).
(9.2.25)
(9.2.26)
§ 9.2] ТЕОРИЯ ПРЕОБРАЗОВАНИЯ К ГЛАВНЫМ КООРДИНАТАМ 153
2) Существует п линейно независимых собственных векторов, причем
каждому корню кратности к уравнения периодов (9.2.1) соответствует к
таких векторов. Обозначая через ит г-ж столбец матрицы 8, находим из (9.2.24)
u'rAus = 0, r=?S; u'rAuT = K; )
u'rBus = 0, гфв; u'TBur = Kpr- J
Следовательно, ут, определяемый по формуле
(pU-B)ur = yT, (9.2.28)
удовлетворяет уравнению
u'syT = 0 (9.2.29)
при всех s. Так как векторы ад1? щ, . .., ип (столбцы неособенной матрицы S)
линейно независимы, из уравнения (9.2.29) следует, что
х'уг = 0 (9.2.30)
для всех х. В частности,
УтУг^О, (9.2.31)
откуда получаем (поскольку ут — действительный вектор), что уг = 04
Таким образом,
(plA — B)uT = 0, (9.2.2)
так что столбцами матрицы S являются п линейно независимых собственных
векторов.
Уравнение (9.2.1) и уравнение
|р2Л-Лр| = 0 (9.2.32)
имеют одни и те же корни; они равны диагональным элементам матрицы JP,
а именно р\, р\, . . ., р\. Поэтому, если, например, корень р\ = р\ = ...
... = р\ имеет кратность к, то соответствующие к столбцов матрицы 8
образуют систему А; линейно независимых собственных векторов, отвечающих
А;-кратному собственному значению.
Из (9.2.24) следует, что если нормировать собственные векторы иг так,
чтобы
= 1, г=1, 2, ...,п, (9.2.33)
то каждое кг будет равно единице и выражения для Т и V примут форму
(9.1.22).
3) Найденные описанным выше способом п линейно независимых соб-
собственных векторов ит удовлетворяют условиям ортогональности:
u'TAus = 0, r^=s, (9.2.34)
u'rBus = 0, r^=s. (9.2.35)
Заметим, что между задачами, в которых корни уравнения периодов
простые, и задачами, в которых эти корни кратные, имеется существенная
разница.
Решим теперь задачу другим способом, основывая решение не на алгебре
квадратичных форм, а на уравнениях движения. Если корни уравнения пери-
периодов простые, то уравнение (9.2.2) определяет собственные значения един-
единственным образом с точностью до скалярного множителя; условия ортого-
ортогональности (9.2.34), (9.2.35) при этом выполняются автоматически.
154 ТЕОРИЯ КОЛЕБАНИЙ [Гл. IX
В самом деле, из (9.2.2) следует, что
pl(u'sAuT)=--u'sBur (9.2.36)
и аналогично
р\ (u'rAUs) = u'TBus. (9.2.37)
В силу симметричности матриц А и В имеем
u'sAuT = u'TAus, u'sBur = UrBus (9.2.38)
и из (9.2.36), (9.2.37) получаем
(pl-pl)u'rAus = Q. (9.2.39)
Условие (9.2.34) вытекает из (9.2.39), поскольку pf — р% =^0, а условие
(9.2.35) — из (9.2.37), Точно так же доказывается, что в любом случае,
независимо от кратности корней уравнения периодов, два собственных век-
вектора, соответствующих различным собственным значениям, всегда удовлет-
удовлетворяют условиям (9.2.34), (9.2.35).
Рассмотрим теперь случай, когда уравнение периодов имеет кратные
корни. Если р^ есть ^-кратный корень, то к линейно независимых собствен-
собственных векторов ui, U2, ¦ ¦ •', Uh, построенных по решениям уравнения
(ДА —В) и = 0, (9.2.40)
не обязательно удовлетворяют условиям (9.2.34), (9.2.35). Однако по задан-
заданной системе векторов гц, и->., . . ., wft можно с помощью известного процес-
процесса *) построить ортогональную систему wi, Wz, . . ., wh. Для этого положим
г
гег = щ, wr+1 = ur+i— 2 а^и8, (9.2.41)
s=l
где
as = w'sAuT+i/w'sAws. (9.2.42)
Система wl7 w2, ¦¦-, w^ удовлетворяет условиям ортогональности. Практи-
Практически векторы w строятся последовательно: если векторы wit wSl ...,wr,
где г<Ск, уже построены, то в качестве wT+1 можно взять любое решение
уравнения (9.2.40), удовлетворяющее условию
w'sAu = 0, e=l,2, ...,г. (9.2.43)
4) Если уравнение периодов имеет лишь простые корни, то главные
координаты т], входящие в (9.1.22), определяются с точностью до знака. Если
же уравнение периодов имеет кратные корни, то это утверждение перестает
быть справедливым. Например, если р\ = р\, то Т и V могут быть приведены
к виду
и мы по-прежнему будем иметь главные координаты, если заменим r)i и г\2
на переменные ?4, ^2 по формулам
T]j = ^i cos а + ?2 sin ос, тJ = Si s^n a — S2 c°s a-
§ 9.3. Приложение теории. Теория преобразования к главным коорди-
координатам, изложенная в § 9.2, позволяет применить новый метод к решению кон-
конкретных задач. Принципиального отличия от способа § 9.1, конечно, нет, и,
*) Процесс ортогонализации Грама — Шмидта.
I 9.3] ПРИЛОЖЕНИЕ ТЕОРИИ 155
вообще говоря, он приводит к цели медленнее, чем старый метод, однако он
имеет то преимущество, что может быть непосредственно применен к таким
задачам, для которых уравнения периодов имеют кратные корни.
Как и ранее, решаем сначала уравнение периодов
\Р*А - В | = 0. (9.3.1)
Пусть pi, pi, . . ., Рп будут его корни; расположим их в порядке возрастания:
Р* < pi < . . . < Pi- (9.3.2)
Определим действительный собственный вектор ит, соответствующий
каждому собственному значению р\. В случае простых собственных зна-
значений никаких трудностей при этом не возникает: собственные векторы опре-
определяются однозначно (с точностью до скалярного множителя), и любая их
пара удовлетворяет условиям ортогональности (9.2.34), (9.2.35). Если же
уравнение периодов имеет кратные корни, решение усложняется, к собствен-
собственных векторов, соответствующих ^-кратному корню, должны быть выбраны
так, чтобы они образовали независимую систему векторов и чтобы каждая
их пара удовлетворяла условиям ортогональности (см. § 9.2, п. 3). Практиче-
Практически бывает достаточно удовлетворить условию (9.2.34); условие (9.2.35)
тогда выполняется автоматически.
Рассмотрим теперь матрицу S, элементами r-го столбца которой являются
действительные ненулевые собственные векторы ит-
8=(щ, и2, . .., ип). (9.3.3)
Преобразование
q = 8\ (9.3.4)
осуществляет переход к главным координатам. Полное решение задачи про-
производится так же, как и ранее.
Все сказанное выше вытекает из теории, изложенной в § 9.2, но может быть получено
и непосредственно.
Убедимся сначала, что выведенные нами векторы щ, и^, ¦ ¦ ¦, ип линейно незави-
независимы. В самом деле, из того, что
ur+l = aiu1Jra2uz-)r ...4-aj.ur, (9.3.5)
следует, что
п
u'r+1Aur+i='^1 as(u'r+1Aus). (9.3.6)
s=l
Но последнее равенство заведомо неверно, поскольку левая часть его положительна,
а правая равна нулю. Следовательно, столбцы матрицы S независимы и матрица неосо-
неособенная.
Уравнения движения могут быть представлены в форме
Ад + Вд = 0. (9.3.7)
Далее,
u и2, ..., wn) = (Bui, Bu2, ..., Вип) =
= (р\Ащ, р\Аиг, ..., р\Аип) = {Аии Аиг, ...
= А(щ, и2, ..., un)P=ASP, (9.3.8)
где, как и ранее, Р обозначает диагональную матрицу
jP=| ' I. (9.3.9)
156 ТЕОРИЯ КОЛЕБАНИЙ [Гл. IX
Воспользуемся формулой (9.3.7), чтобы записать уравнение движения (9.3.4) через
переменные |. Проделав это, получим
i+0 (9.3.10>
или, принимая во внимание (9.3.8),
AS('i+F%)=0. (9.3.11>
Матрица AS неособенная (поскольку матрица S неособенная), и из (9.3.11) мы полу-
получаем уравнение
V (9.3.12)
эквивалентное системе п уравнений
lr+ Phr= 0, г= 1, 2, . . ., п. (9.3.13)
Стало быть, | — главные координаты, что и требовалось доказать.
Как указывалось в § 9.2, преобразование (9.3.4) приводит выражения для Т и V
к суммам квадратов. Этот факт тоже легко доказать непосредственно, поскольку
2T = q'Aq=t'S'Asi (9.3.14)
и матрица S'AS диагональна. В самом деле, полагая
S'AS = (cTS), (9.3.15).
находим
crs = u'TAus, (9.3.16)
и если г ф s, то в силу условий ортогональности crs = 0. Матрица S'AS представляет
собой диагональную матрицу А:
\
л=
(9.3.17)
к)
в которой
lr^u'rAur (9.3.18)
вещественны и положительны. Таким образом,
2Г=|'Л|= 2 КЬ- (9-3.19)
Аналогично
2V = q'Bq = l'S'BS%, (9.3.20)
и так как согласно (9.3.8)
S'BS= S'ASP, (9.3.21)
то S'BS есть диагональная матрица
АГ=
(9.3.22)
2V= 2 Kpflh (9.3.23)
r=l
3 9.4] НАЛОЖЕНИЕ СВЯЗИ 157
Если мы нормируем собственные векторы ит так, чтобы
u'rAur = l, r = i,2,...,n, (9.3.24)
то каждое Я,г равно единице и Т и V принимают форму (9.1.22).
Пример 9.3. Найдем преобразование к главным координатам, если
1
). J
(9.3.25)
2V = и2 Fg2 + 5ql + iq% + 8g2g3 + 8 jtfj + 10qtq2). '
Для этого случая имеем
/3 2 1'
4 = 1 2 2 1 |, В = п*\ 5 5 4 |. (9.3.26)
\1 1 1
Уравнение периодов имеет вид
(р« _ и2J (р2 _ An2) = 0, (9.3.27)
•откуда
pi = p* D ns, р* = 4/г2. (9.3.28)
Для р2 = р\ собственные векторы удовлетворяют единственному уравнению
?i + ?г + ?з = ° (9.3.29)
и решениями, удовлетворяющими условию ортогональности, будут A, —1, 0)
и @,1,-1).
Для р2 = Рд уравнения для собственных векторов имеют вид
6?1 + Зд2 = 0, 3g, + 3q2 = 0 (9.3.30)
и собственным вектором будет @, 0, 1).
Преобразование к главным координатам имеет вид
/ 1 0 0\
д= -1 1 0 1. (9.3.31)
V 0-11/
Действительно, собственные векторы нормированы и
2Т=\
,}
§ 9.4. Наложение связи. Если на колебательную систему с п степенями
свободы наложить одну связь, то получим новую колебательную систему
сп — 1 степенями свободы. При этом система будет обладать следующим
свойством: значения п — 1 периодов свободных колебаний этой системы будут
заключены между последовательными значениями периодов свободных колеба-
колебаний первоначальной системы. В частности, основная частота системы при
наложении связи увеличивается.
Для доказательства рассмотрим исходную систему в главных координа-
координатах; имеем
(9.4.1)
158 ТЕОРИЯ КОЛЕБАНИЙ [Гл. IX
Предполагается, что все периоды различны и р\ < р\ < ... < р?_4 <; р\.
Уравнение связи возьмем в форме
. . . + Anqn = 0. (9.4.2)
Для системы с наложенной связью удобно воспользоваться теми же самыми
координатами; в результате мы придем к голономной системе с избыточными
координатами (§ 5.8). Уравнения движения несвободной системы будут иметь
вид
Чт + Р'тЯг = Я^г, г = 1, 2, . . ., п, (9.4.3)
где Я, — неопределенный множитель. Уравнением связи будет (9.4.2). Для
главного колебания несвободной системы с периодом 2п/р имеем
• ¦ • • • •
?1 Яг Яп К
откуда, учитывая (9.4.3), получаем
(-рл+Р$ qT = ЬАТ. (9.4.5)
С помощью уравнения связи (9.4.2) получаем уравнение периодов
Если ни один из коэффициентов Аг не обращается в нуль и исходная система
не имеет одинаковых периодов, то один из корней р2 лежит между р\ и р\,
один — между р\ и р\ и т. д.
Если один из коэффициентов Ат равен нулю, то соответствующая коор-
координата остается главной и период главного колебания не изменяется. Если
два периода исходной системы одинаковы, то их общее значение является
одновременно и периодом несвободной системы.
§ 9.5. Принцип Релея. Если на колебательную систему с п степенями
свободы наложить п — 1 связей, то получим систему с одной степенью сво-
свободы. Физически это означает, что мы задаем форму колебаний системы.
Возникает вопрос: каков период колебаний такой системы?
Введем главные координаты для исходной системы; тогда будем иметь
U ¦¦¦+&),
} (9.5.1)
Уравнения связи представим в виде
iL==^.= ...=is.. (9.5.2)
Обозначим общую величину этих отношений через 8; эта величина будет
играть роль единственной лагранжевой координаты несвободной системы.
Для такой системы будем иметь
г =4 («;+«!+...+«?) в*, I
\ (9.5.3)
V = \ (pjaj + р\а\ + ...+ PWn) в2. J
Период колебаний несвободной системы будет равен 2я/р, где
§ 9.5] ПРИНЦИП РЕЛЕЯ 159
Если правую часть этого равенства рассматривать как функцию от аи
а2, . . ., а„, то нетрудно убедиться, что эта функция приобретает стационар-
стационарное значение, если все а, кроме одной, равны нулю. Таким образом, получаем
следующую теорему: период колебаний несвободной системы, рассматривае-
рассматриваемый как функция от связей, имеет стационарное значение, если исходная сис-
система вынуждена совершать одно из своих главных колебаний. Эта теорема
составляет содержание принципа Релея.
В некоторых задачах можно, основываясь на соображениях симметрии,
получить общее представление о характере главных колебаний; принцип
Релея тогда позволяет найти периоды и получить полное решение задачи
(пример 9.5А). В других случаях удается угадать форму какого-либо одного
колебания, обычно основного. Свойство стационарности главных колебаний
показывает, что достаточно хорошая оценка формы главного колебания позво-
позволяет, вообще говоря, получить хорошее приближение для соответствующего
периода. (Если отношения а2/а1? a3lai, . . ., ап/а4 имеют порядок О (г), то
величина р2 — р\, полученная по формуле (9.5.4), имеет порядок О (е2).) Это
свойство иллюстрируется в примере 9.5В.
Пример 9.5А. Рассмотрим снова пример 9.1А, в котором
Если систему заставить совершать такие колебания, для которых
т = т=7' (9'5-6>
то период их будет равен 2л/р, где
п2 _ 4п2(«2 + Р2 + У2-«Р-Ру) .
Р — 7 • (У.О.1)>
Очевидно, что будет главным колебание, для которого х + z = у = 0^
полагая Р = 0, а = —у, находим
р* = pl = 4и2. (9.5.8)
Далее разыскиваются главные колебания, для которых х = z; получаем^
полагая а = у:
_р2_ 2а*-2аР + Р» _ (За-2рJ + (а+рJ
6ге2 За2 + 2р2 (За—2РJ +6(а + РJ ' \v.o.vr
Это выражение стационарно при -^- = -^- и -g-= —1. Соответствующие зна-
Р « Р
чения р2 равны р\ = пг и р23 = 6п2.
Таким образом, мы получили значения р\, р\, р\, которые раньше нахо-
находили непосредственным вычислением; закончить решение задачи можно так
же, как в примере 9.1А.
Принцип Релея представляет собой практически удобный способ реше-
решения задач, когда известны формы главных колебаний или когда общее пред-
представление о них можно получить из физических соображений.
Пример 9.5В. В качестве простого примера произведем рас.чет перио-
периода главного колебания, когда приближенно известна его форма. Рассмотрим
однородную гибкую струну, натянутую достаточно большой силой. Пусть
концы струны закреплены в двух фиксированных точках и она совершает
поперечные колебания. Обозначим длину струны через I, ее плотность —
через р, натяжение — через Р и поперечное смещение — через у = у (х, t).
160 ТЕОРИЯ КОЛЕБАНИЙ [Гл. IX
В этом случае мы имеем непрерывную систему (см. § 3.9), и, строго гово-
говоря, предыдущие результаты, полученные для систем с конечным числом сте-
степеней свободы, здесь неприменимы. Однако, основываясь на общих физи-
физических соображениях, эти результаты можно распространить на непрерыв-
непрерывный случай. С требуемой степенью точности можно написать
i i
{^f (9.5.10)
Основное колебание симметрично относительно середины струны х = -я-1.
Поэтому рассмотрим колебание струны, при котором она принимает форму
дуги параболы, симметричной относительно точки х = -^ I. Тогда будем
иметь
у = Ах (I — х) 9, (9.5.11)
где 8 = 0 (t). При этой форме струны кинетическая и потенциальная энер-
энергии будут иметь следующие выражения:
V
^ j (9.5.12)
Отсюда получаем р2 = 10с2/Р. Точная форма описывается уравнением
у = AQ sin {nxll), (9.5.13)
и р2 = п2с2/12, так что наш, вообще говоря, довольно грубый расчет, произ-
произведенный на основе принципа Релея, дал значение р2, отличающееся от точ-
точного всего лишь на 1,3%.
§ 9.6. Устойчивость установившегося движения. Понятие об устой-
устойчивости мы до сих пор связывали с отклонениями от положения равновесия,
однако его можно обобщить, если рассматривать отклонения от заданного
движения.
Положение равновесия устойчиво, если при достаточно малом отклоне-
отклонении система остается вблизи этого положения и скорость ее при этом остается
малой. Чтобы выразить это формально, введем функцию г = г (t):
= У
1=1
Здесь <Xi, «2, • • •, осп — координаты, относящиеся к положению равновесия.
Положение а устойчиво, если любому сколь угодно малому положительному
числу е можно поставить в соответствие положительное число х = х (е)
такое, что если г @) < к, то г (t) < е при t > 0 *).
Дадим теперь определение устойчивости движения: движение является
устойчивым, если, получив малое возмущение, оно остается близким, в из-
известном смысле, к невозмущенному движению. Понятие об устойчивом дви-
движении сложнее, чем понятие об устойчивом равновесии; общую теорию устой-
устойчивости движения мы рассмотрим в гл. XXIII. Однако имеется класс задач,
теория которых достаточно проста. Для них можно указать простой способ
проверки устойчивости движения, аналогичный способу проверки устойчи-
устойчивости равновесия по минимуму потенциальной энергии.
п п
*) В качестве функции г (г) можно взять также функцию 2 I Чь ~ а$ I + 2
1 l
§ 9.6]
УСТОЙЧИВОСТЬ УСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ
161
Рассмотрим гироскопическую систему, т. е. натуральную систему,
несколько лагранжевых координат которой являются циклическими (§ 6.11).
Пусть qu q2, . . ., qm — циклические координаты, a qm+u qm + 2, • ¦ •, qn —
нециклические, или явные координаты. Нам известны т + 1 первых инте-
интегралов системы, именно т циклических интегралов, соответствующих т
циклическим координатам:
dqr
и интеграл энергии
, r = l, 2, ..., m,
T + V = С
(9.6.1)
(9 6.2)
Движение, при котором скорости qi7 q2, ¦ • •, qm и координаты qm+i,
gm + 2, • • -, qn имеют постоянные значения, является установившимся. При
этом движении явные координаты удовлетворяют уравнениям
-~,
т + 2,
п.
(9.6.3)
• • •
Функция То получается из Т, если величинам дч, q2, . . ., qm придать по-
постоянные значения, соответствующие установившемуся движению, а вели-
величины qm+i, qm + 2, ¦ ¦ ч Чп положить равными нулю.
Примерами установившегося движения могут служить движение части-
частицы в центральном поле по круговой орбите, круговое движение сферического
маятника и установившаяся прецессия вращающегося волчка.
Пусть мы имеем установившееся движение, в котором циклические инте-
интегралы равны Pi, р2, • • ¦, Рт, а явные координаты равны am+i, am+2t • ¦ ¦
. . ., ап. Рассмотрим возмущенное движение, при котором р остаются неиз-
неизменными, а начальные значения величин
Стп+i |)
|?т+г|» • • ч \Яп\
малы. Если они будут оставаться малыми в течение всего времени движения,
то мы будем говорить, что иходное установившееся движение является устой-
устойчивым. Более точно, установившееся движение называется устойчивым, если
для любого заданного положительного числа е можно указать положитель-
положительное число х (е) такое, что если г @) < х, то г (t) < 8 при t > 0; функция
г {t) имеет вид
'¦@
s=m-t-l
(9-6.4)
Циклические интегралы (9.6.1) можно записать в следующей форме:
Pi-
P2-
m+zQm+2 ~Ь
+2 I • • • ~Г йт, nQn)•
(9.6.5)
11 Л. А. Парс
162 ТЕОРИЯ КОЛЕБАНИЙ [Гл. IX
Правые части этих равенств для краткости запишем в виде
Pi-fib p2-f?2, . . ., pm-Bm. (9.6.6)
Матрица (ars) размером т х т неособенная, поэтому уравнения (9.6.5)
• • ¦
можно разрешить относительно q\, qz, ¦ ¦ ., qm- Если обратную матрицу
обозначить через (drs): то можно написать
Яг = drl (Pi - Bt) + dr2 (p2 - Вг) + . . . + dTm (pra - Bm),
r = 1, 2, . . ., m. (9.6.7)
• • •
Кинетическую энергию Т можно выразить не через qu q2, ...,qm, а че-
через р. Тогда будем иметь
Д77 • AT • AT
V 9m+2 — Ь • • • + Яп — =
n n
фг + i>T){an (p4 — jDi) + ar2 (p3 — ts2) -j- ... -\- arm (pm — tsT,
n n
+r=2+lsJ+1
mm mm n n
/t i "TsPrPs"™" ^j .^j Urs-Br-Bs "г ^j ^j ftrsQrQs —
m m
^i arsprps-f-zi , (y.o.o)
где через Т обозначена квадратичная форма от gm+i, qm+2, ¦ • ч 1п\ она опре-
определенно-положительна, так как Т ^0, если каждое р положить равным нулю.
Уравнение энергии (9.6.2) принимает теперь вид
~Т + W = С. (9.6.9)
Здесь
m m
ТТ7 T/TZ /ft ft ft Л \ — \1 \ 1 x7 ft ft 1 T/* /Q R 4 d\
• • — KK ^pi, P2j • • •) Рш? ynHl) :/wi+2» • • •} Qut — "о" / i / | Q^rsPrPs ~i ' • \У.О. XUy
r=ls=l
Таким образом, во время движения
W^C, (9.6.11)
и рассуждения, аналогичные проведённым при исследовании колебаний около
положения равновесия (§ 9.1), показывают, что установившееся движение
является устойчивым, если функция W достигает в точке (am+i, am+2, . . .
. . ., an) минимума.
Функция W стационарна в установившемся движении независимо от то-
того, устойчиво оно или нет. В самом деле, уравнения
|^ = 0, г = т + 1, т+2, ...,п, (9.6.12)
эквивалентны уравнениям (9.6.3). Для доказательства заметим, что
т
W= 2 ёгРг — Ta+V. (9.6.13)
г=1
§ 9.61 УСТОЙЧИВОСТЬ УСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ 163
Рассматривая малые отклонения от установившегося движения, имеем
r=l r r=m+l
m n
= > <7ropr+ > ——z — oqr. (9.6.14)
r— 1 r—m-\-1
Следовательно,
dW^d(V-To) r = m+l, m+2, ...,n, (9.6.15)
откуда видно, что уравнения (9.6.12) эквивалентны уравнениям (9.6.3).
Теперь ясно, как находить установившиеся движения и исследовать
их устойчивость. В выражении для Т -\-V мы от qi, q2, ¦ ¦ . ., qm перейдем
к Pi, p2, • • ¦, Pm, a qm+u qm+2, ¦ ¦ -, qn положим равными нулю. В резуль-
результате получим W = W (Pi, Рг, • • ., Рт! ?т+ь Чт+г, • • •> ?п)- В установив-
установившемся движении W, как функция от qm+i, qm+2, ¦ . ., qni принимает стацио-
стационарное значение; если W имеет минимум, то движение устойчиво.
Пример 9.6А. Центральное поле. Частица движется под
действием притяжения к центру с силой \ylrn на единицу массы.
Имеем
~i-^l- (9-6.16)
Координата 0 является циклической, и соответствующий циклический
интеграл имеет вид
г26 = р, (9.6.17)
откуда
В установившемся движении (круговая орбита) функция W имеет ста-
стационарное значение:
Движение устойчиво, если
^=?-^>0. (9.6.20)
В силу равенства (9.6.19) условие (9.6.20) эквивалентно неравенству п < 3,
что и является условием устойчивости. Равенство (9.6.19) очевидно и из
элементарных соображений, поскольку для круговой орбиты
г02 = |д,/ги. (9.6.21)
Пример 9.6В. Конический маятник. Для сферического
маятника (§ 5.3) при измерении угла 0 от направленной вниз вертикали имеем
Т V F==y?na2(e2+sm2eqJ)—mgaccsQ (9.6.22)
или
(9.6.23)
11*
164 ТЕОРИЯ КОЛЕБАНИЙ [Гл. IX
Координата <р является циклической, и соответствующий циклический инте-
интеграл равен
sin26 ф = р. (9.6.24)
Отсюда получаем
&-cos9' (9-6-25)
cos 6 ,
(sin2 6 + 3 cos2 9) 2
г« cos
и установившееся движение является устойчивым. Устойчивость его можно
доказать на основании § 5.2 без ссылки на общую теорию. В установившемся
движении нули z3 и z2 функции / (z) совпадают и кривая / (z) касается оси
Oz в точке z = z3 (см. рис. 5). Влияние малого возмущения сказывается
в том, что оно изменяет кривую таким образом, что она пересекает ось Oz
в двух почти совпадающих точках. Движение при этом происходит в узком
сферическом поясе вблизи первоначальной окружности.
Пример 9.6С. Прецессия вращающегося волчка.
Как мы видели в § 8.6, имеются два возможных установившихся движения
волчка, ось которого наклонена под любым заданным углом а к направленной
вверх вертикали, при условии, что р2 > q. Рассуждения, подобные только
что проведенным для сферического маятника, показывают, без ссылок на об-
общую теорию, что эти установившиеся движения устойчивы. Для установив-
установившегося движения кривая / (z) на рис. 19 касается оси Oz; малое возмущение
изменяет этот график таким образом, что он пересекает ось Oz в двух почти
совпадающих точках.
Получим теперь этот результат из общей теории. Имеем
Т + V = ~ А@4-sin2 0 ф2) + у С (ур + ф cos 0J + Mgl cos в. (9.6.28)
Циклические интегралы, соответствующие циклическим координатам ф
иг|), имеют вид
A sin20cp + С 0ф + ф cos 0) cos 0 = 2Лк, (9.6.29)
С (ф + Ф cos 9) = Сп. (9.6.30)
Для W получаем следующее выражение:
W о (*¦ — Pcos eJ i Q , Сп% /с, а ол\
Л- = 2 /пзе +gcos0+15r, (9.6-31)
где, как и ранее, через 2р обозначено Сп/А, а через q обозначено Mgl/А.
Обозначая, кроме того, cos 0 через z, получаем
j! 2p,f (9.6.32)
и установившееся движение будет устойчивым. Обращение в нуль производ-
производной dWIdz в установившемся движении равносильно условию (8.9.4).
§ 9.7. Колебания в окрестности установившегося движения. Если уста-
установившееся движение устойчиво, так что вызываемое малыми возмущениями
отклонение от установившегося движения остается все время малым, то мож-
можно получить приближение к возмущенному движению, положив в уравнени-
§ 9.7] КОЛЕБАНИЯ В ОКРЕСТНОСТИ УСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ 165
ях движения
д\ = wr + Чг, г = 1, 2, . . ., то, (9.7.1)
qr=ar+%r, r = m+l, т + 2, ..., п (9.7.2)
(через сог обозначено постоянное значение qr, г = 1, 2, . . ., т, в установив-
установившемся движении) и сохранив в них лишь члены первого порядка относитель-
относительно | И Т].
В качестве примера найдем первое приближение к возмущенному движе-
движению в трех классических задачах, рассмотренных в § 9.6. Напомним, что,
строго говоря, теория относится к возмущению, при котором j3r сохраняют
те же значения, которые они имели в первоначальном установившемся дви-
движении. Однако практически это ограничение несущественно, так как малые
изменения этих постоянных означают лишь переход к колебаниям около
соседнего состояния установившегося движения.
Пример 9.7А. Центральное поле (д,/гп; возмущение
круговой орбиты. Частица движется по окружности радиуса г =а
со скоростью и под действием притяжения к центру с силой [х/ги, где
п <С 3. Найдем движение, вызванное малой радиальной скоростью ки, направ-
направленной наружу и сообщенной в момент t = 0.
Имеем
V_r02=-JL
r \ (9.7.3)
Исключая 9, находим
Полагая г = а+% и сохраняя в разложении лишь члены первого порядка
относительно ?, получаем
|+ра| = 0, (9.7.5)
где
ра--=C — п)ц/ап+1. (9.7.6)
Отсюда находим
^ ^sinpL (9.7.7)
Значение г в некоторый момент t определяется из формулы
(9.7.8)
Далее, пренебрегая членами порядка А,2, имеем
9= % ==<0A~f
—соа р<). (9.7.10)
где co = ]/fx/an+1 обозначает угловую скорость установившегося движения.
Мы приняли, что 0 = 0 при t = 0. Приближенное уравнение возмущенной
орбиты записывается в виде •
-\—jh=
~]/3—п
(9.7.11)
166 ТЕОРИЯ КОЛЕБАНИЙ [Гл. IX
Апсидальные расстояния равны а A ± — ) , а апсидальный угол равен
V I/о— га'
я/]/3 — п. В двух хорошо известных случаях, п = —1 и п = 2, эта формула
апсидального угла является точной.
Пример 9.7В. Сферический маятник; колебания
в окрестности конического движения. Если угол Э
отсчитывать от вертикали, направленной вниз, то функции Т и V для сфери-
сферического маятника будут иметь следующий вид:
Г = у(ёя + зт«вфа), V=-n2cosQ, (9.7.12)
где п2 = gla. Первоначально груз маятника двигался по горизонтальной
1 *
окружности 0 = а, 0<а<-^-зх, и <р = /г ]/ sec а. Предположим, что
в момент t = О груз получил малый импульс, направленный наружу и ле-
жащий в меридиональной плоскости, так что в начальный момент 0 имело
малое значение к. Из уравнений Лагранжа находим
os 0 sin 0 ф2 — п2 sin 0, 1
\ (9.7.13)
q> = nsin2a]/rsec а,. )
0 = COS 0 !
sin2 0'
Исключая ф, получаем
*q i о • /sin0 cos0sin3a\ л /ппл/.\
8 4-n2sina гто- =U. (У./.14)
1 \sma cosasm30 / Ч '
Полагая 0 = a + g и сохраняя в разложении лишь члены первого порядка
относительно \, находим
g + p2l = 0, (9.7.15)
где
р2 = п2 (sec a + 3 cos a). (9.7.16)
Следовательно,
!= —sinpf.
Экстремальные значения 0 равны <x-±{'klp). Если в момент t — О считать
Ф = 0, то будем иметь
(9.7.17)
Траектория груза на сфере будет описываться уравнением
AA;cp, (9.7.18)
Р
где
к2 = 1+3 cos2 a.
Пример 9.7С. Нутация волчка. Уравнения, описывающие
движение оси волчка, имеют вид (см. § 8.6)
ё - sin 0 (cos 0Ф2 — 2/нр + q) = 0, (9.7.19)
¦ sm209 + 2p cos 0 = 21. (9.7.20)
Мы предполагаем, что р2 > q. Первоначально ось волчка имела установив-
установившуюся прецессию, при которой 9 = а, 0 < а < -у л, а ср = Q, где Q —
§ 9.8] ГИРОСКОП ФУКО 167
один из корней квадратного уравнения
cos аи2- 2рп + q = 0. (9.7.21)
Рассмотрим возмущение, при котором ри! остаются неизменными. В момент
t = 0 примем 0 = а, ф = Q, 0 = ?, где ? — малая величина. Полагая
в уравнении (9.7.20) 6 = a + ^<P = fi + il, получаем с точностью до членов
первого порядка относительно ? и т|
2(p-Qcosa) g (9?22)
1
sine.
так что г\1\ остается постоянным во все время движения. Вычисляя линейное
приближение для уравнения (9.7.19), замечаем, что выражение в скобках
имеет первый порядок малости в силу (9.7.21), поэтому множитель sin0
можно заменить на sin a, после чего легко находим приближенное уравнение:
'% + Q2 sin2 a| + 2 sin a (p — Q cos a) ц = 0. (9.7.23)
Исключая т) с помощью (9.7.22), находим
'I + %Ч = 0, (9.7.24)
где
х2 = Q2 sin2cc + 4 (р — Q cos aJ = fi2 sin2 a + 4p2 — Aq cos a. (9.7.25)
Если скорость вращения волчка очень велика, то х имеет порядок 2р =
= CnlA. С принятой точностью приближения период нутации (т. е. колеба-
колебания около установившегося прецессионного движения) равен 2я/х. Зависи-
Зависимость 0 от i имеет вид
0 = a+-^-sinxi!, (9.7.26)
и, таким образом, угол наклона 0 оси волчка к направленной вверх вертикали
изменяется в пределах a ± (?/х).
§ 9.8. Гироскоп Фуко. Рассмотрим вращающийся волчок, подвешенный
к неподвижной точке О; пусть центр тяжести его G находится на одной вер-
вертикали с точкой О и вращение происходит около его оси. Если волчку сооб-
сообщить малое возмущение, то его ось OG сохранит направление, близкое к вер-
вертикальному. Это имеет место независимо от скорости вращения и следует
из уравнения энергии, которое можно записать в форме, аналогичной (8.6.8):
е2 +sin2 0 ф2 — 2q cos 0 = 2ц. (9.8.1)
Когда ось стационарна, 2\х, = —2q; если эту величину немного изменить,
положив 2[х = —2q cos a, где а — малая величина, то для возмущенного
движения получим
02 +sin20 ф2 — 2q cosje = —2qcos a (9.8.2)
и во все время движения будем иметь 0 ^ а.
При изучении возмущенного движения в окрестности направленной
вниз вертикали удобно ось Ох направить вертикально вниз и избежать, таким
образом, неприятностей, связанных с неопределенностью <р в состоянии
покоя, возникающей, когда ось Oz направлена вертикально. Тогда будем
иметь
= -?A @2+sin20 ф2)+ -^-С(^ + ф cos ЭJ + Mgl sin 0 cos ф. (9.8.3)
?i Li
168 ТЕОРИЯ КОЛЕБАНИЙ [Гл. IX
Полагая, как обычно,
ij)-f Ф cos 0 =/г (9.8.4)
и используя это равенство при составлении уравнений Лагранжа для 0 и ф,
получаем
А (ё — ф2 cos 0 sin 0) + Спц> sin 0 — Mgl i
igl cos 0 cos ф = 0, "I
| (9.8.5)
A (ф sin 0 + 20ф cos 0) — CnQ + Mgl
Во втором из этих уравнений произведено сокращение на множитель sin 0;
он отличен от нуля (sin 9 близок к единице).
Чтобы рассмотреть возмущенное движение в окрестности вертикали,
направленной вниз, положим 0=-=-я — z, ц> = у. Тогда с точностью до ве-
величин первого порядка относительно у и z направляющие косинусы оси волч-
волчка будут равны A, у, z). Приближенные уравнения движения, составленные
с такой же точностью, будут иметь вид
Эти уравнения совпадают с уравнениями движения частицы в плоскости
yz под действием линейно изменяющейся притягивающей силы и гироскопи-
гироскопической силы (§ 8.8). Полагая w = у + iz и обозначая, как и ранее, р —
= Сп/2А и q = MgllA, находим, что w удовлетворяет дифференциальному
уравнению
iv — 2ipw + qw = 0. (9.8.7)
Решение этого уравнения имеет вид
w = Аег <s+p) l + Be-1 <s-p) f, (9.8.8)
где
* = W + q, (9-8.9)
а коэффициенты А, В, вообще говоря, комплексные. При малом возмущении,
когда | и; | и | w\ в начальный момент малы, | w \ все время остается малым
и линейное приближение достаточно хорошо аппроксимирует действительное
движение, по крайней мере для не слишком больших значений t.
Уравнения (9.8.6) можно очень просто получить с помощью метода, описанного
в § 8.7. Имеем
Спи+АиХ. u = MgluX v. (8.7.2)
Поскольку вектор v имеет теперь компоненты {1, 0, 0}, векторное уравнение (8.7.2)
эквивалентно трем скалярным уравнениям
A {yz — z'y) + Спх = 0, ^
A{zx'—xz)+Cn'y = Mglz, \ (9.8.10)
A(xy — yx)-\-Cnz——Mgly, '
где и есть вектор (х, у, z). В нашей задаче у и z малы, а х близок к единице; учитывая
это, мы приходим к уравнениям (9.8.6).
Рассмотрим решение уравнения (9.8.7) в двух частных случаях; началь-
начальные значения w и w обозначим соответственно через Wq и Vq.
§ 9.9]
СПЯЩИЙ ВОЛЧОК
169
1) w0 = 0, v0 вещественно и положительно (и, разумеется, мало); в мо-
момент t — О ось волчка имеет вертикальное направление.
Решение имеет вид
w = ae^t sin st (a = vo/s). (9.8.11)
Траектория имеет форму розетки и в полярных координатах описывается
уравнением
г = a sin kQ, (9.8.12)
где к = sip > 1. Траектория изображена на рис. 25, она построена для
случая, когда скорость вращения мала и к, следовательно, велико. Если
Рис. 25.
Рис. 26.
скорость вращения велика и к лишь немного превышает единицу, то форма
траектории близка к окружности.
2) v0 = О, w0 = а, причем а вещественно и положительно; ось волчка
начинает движение из состояния покоя вблизи вертикали.
Решение имеет вид
w = -f- {(* - р) el
2s
(s + p)
(9.8.13)
и траектория представляет собой гипоциклоиду. Такую кривую описывает
точка окружности радиуса &,&<-=- а, катящаяся внутри окружности радиу-
радиуса а (рис. 26). В обозначениях, указанных на рисунке, можем написать
w = (а — Ъ) е~м + be1 <а-ь> е. (9.8.14)
Если положить здесь
и =
s — p
а, о = -
2s
(9.8.15)
то мы получим формулу (9.8.13).
§ 9.9. Спящий волчок. Если волчок находится в покое в положении,
когда ось его вертикальна, а центр тяжести расположен выше точки подвеса,
то равновесие его не будет устойчивым. Но, как хорошо известно, если при-
привести волчок в быстрое вращение, то вертикальное положение его станет
устойчивым. Более точно, достаточным условием устойчивости будет р2 > q.
Если это условие выполняется и если начальное смещение оси от вертикали
и начальная угловая скорость малы, то они будут малыми в течение всего
времени движения. В этом случае (когда р2 > q) линейная аппроксимация
служит хорошим приближением к действительному движению в окрестности
положения равновесия.
Из опыта известно, что вертикальное положение спящего волчка устой-
устойчиво, если скорость вращения достаточно велика. Формальное доказатель-
170 ТЕОРИЯ КОЛЕБАНИЙ [Гл. IX
ство устойчивости можно провести с помощью метода, аналогичного тому,
которым мы пользовались при получении интеграла энергии в теории малых
колебаний (§ 9.1). Если через ж, у, z обозначить направляющие косинусы
оси волчка и ось Ох направить вертикально вверх, то интегралы анергии
и кинетического момента относительно оси Ох запишутся в форме (см. § 8.7)
(x2 + 2+2)\ = const, (9.9.1)
yz — zz/ + 2px = const. (9.9.2)
Ho
x2 + y2 + z2 = 1. (9.9.3)
Положим 1 = 1-)-Еи будем отсчет производить от положения равновесия;
тогда |, г/, z в окрестности положения равновесия будут малы. Интегралы
{9.9.1) и (9.9.2) теперь примут вид
1(|2+^2,_|_22) + ^ = const, (9.9.4)
yz — zi/ + 2p? = const. (9.9.5)
Кроме того,
I2 + у2 + z2 + 2| = 0. (9.9.6)
Теперь можно образовать интеграл, имеющий вид определенно-положитель-
определенно-положительной квадратичной формы от переменных |, i/, z, |, i/, z. Из соотношений
{9.9.4) и (9.9.5) получаем новый интеграл
/?2 i *21 2\1 ? /" *lO?\ /^ /Q Q 1\
который в силу (9.9.6) эквивалентен следующему:
fz2) = C. (9.9.8)
¦ • •
Если |, у, z, ?, г/, z в начальный момент малы, то постоянная С тоже мала.
Если р2 > д, то левая часть равенства (9.9.8) является определенно-поло-
определенно-положительной квадратичной формой. Отсюда следует (см. § 9.1), что \, у, z, |,
у, z остаются малыми в течение всего времени движения. Можно указать
границы изменения переменных, например:
Таким образом, устойчивость заведомо доказана; поэтому, если началь-
начальное возмущение мало, линейная аппроксимация дает достаточно хорошее
приближение к движению (по крайней мере, для не слишком большого про-
промежутка времени).
Существует и другой подход к рассматриваемой задаче. Мы остановимся
на нем, так как он типичен для многих задач и сыграл важную роль в исто-
истории динамики.
Пусть известно положение равновесия механической системы. Выберем
лагранжевы координаты qT так, чтобы они в этом положении равнялись нулю.
(Или q могут обозначать, как здесь, явные координаты в гироскопической
системе; имеется положение кажущегося равновесия, и q выбираются
так, чтобы в этом положении они равнялись нулю.) Требуется определить,
является ли положение равновесия q = 0 устойчивым; иными словами, если
9.9] СПЯЩИЙ ВОЛЧОК 171
q и q в момент t = 0 малы, то будут ли они малыми в течение всего времени
движения? Чтобы получить ответ на этот вопрос, составляют приближенные
линейные уравнения движения. Если мы имеем независимое доказательство,
что отклонение должно оставаться малым, как, например, в данной задаче
или в задаче о малых колебаниях около положения, соответствующего мини-
минимуму потенциальной энергии, то линейная аппроксимация служит доста-
достаточно хорошим приближением к возмущенному движению. Если, однако,
мы не имеем такого независимого доказательства, то следует проявлять
осторожность. Если линейное приближение показывает устойчивость (т. е.
при малости начальных значений q и q остаются малыми в течение всего вре-
времени движения), то говорят, что положение равновесия устойчиво по первому
приближению. Трудность заключается в том, что устойчивость по первому
приближению еще не означает, что мы получим устойчивость, когда от ли-
линейного приближения перейдем к точным уравнениям.
Для исследования вопроса об устойчивости положения равновесия вве-
введем п лагранжевых координат qu q2, . ¦ ., qn, определяющих отклонение
от этого положения (см. § 9.1), и составим п дифференциальных уравнений
второго порядка. Устойчивость требует, чтобы как q, так и q оставались малы-
малыми. Или же можно составить систему In уравнений первого порядка (относи-
(относительно q и q или q ш р). Тогда устойчивость будет требовать лишь малости
отклонений от положения равновесия. Для механической системы это тре-
требование означает малость как скоростей, так и отклонений. Если п уравнений
второго порядка заменить на т = In уравнений первого порядка, то послед-
последние запишутся в форме F.4.4):
хг — ХТ \Х\, Х2, • ¦ ., хт), г = 1, 2, . . ., т.
Положениям равновесия соответствуют особые точки векторного поля
ЛГ, т. е. точки, где все составляющие X обращаются в нуль. Поместим начало
координат в такую точку. Поскольку уравнения имеют первый порядок,
последующее движение будет определяться положением изображающей
точки (х\, хг, . . ., хт) в момент t = 0. Положим
г (*) = Vxl
Пусть г @) мало; спрашивается, будет ли г (t) мало при ?> 0? Предположим,
что функции Хг разложены в степенные ряды по ii, х2, . . ., хт. Поскольку
особая точка расположена в начале координат, постоянного члена не будет.
Сохраняя лишь члены первой степени, получаем линейное приближение.
Если определяемое линейным приближением движение устойчиво, то поло-
положение равновесия устойчиво по первому приближению.
В последнем случае естественно было бы ожидать устойчивости; однако
это не всегда так. Нетрудно привести примеры, убеждающие нас в этом.
Пусть, например, движение изображающей точки в плоскости ху описывает-
описывается уравнениями первого порядка
х = — у + гх, у = х + п/, (9.9.9)
где г = У х2 + J/2- Линейное приближение
х = -У, У~=х (9.9.10)
имеет решение
г = г0, 6 = 90 + t, (9.9.11)
172 ТЕОРИЯ КОЛЕБАНИЙ [Гл. IX
где г и 0 — полярные координаты, и в рамках этого приближения начало
координат представляет, очевидно, положение устойчивого равновесия.
Если, однако, учесть члены второго порядка, то получим
г'г = х'х + уу = г3, г = г2. (9.9.12)
Отсюда
г = 1/(а - t), (9.9.13)
где а = 1/г0. Таким образом, если t -*¦ а, то г-*- оо. Как бы ни было мало
г0 > 0, г непрерывно возрастает и за конечный промежуток времени дости-
достигает бесконечного значения.
С другой стороны, если линейное приближение показывает неустойчи-
неустойчивость, то равновесие действительно неустойчиво. На первый взгляд может
показаться, что переход от линейного приближения к точным уравнениям
может превратить неустойчивый случай в устойчивый, однако в действитель-
действительности это может случиться лишь в исключительных обстоятельствах *).
В некоторых случаях определяемое линейным приближением движение
оказывается таким, что все q и q стремятся к нулю, когда t стремится к беско-
бесконечности. В этих случаях говорят об асимптотической устойчивости по пер-
первому приближению. Асимптотическая устойчивость сохраняется и при пере-
переходе от линейного приближения к точным уравнениям: если q и q в началь-
начальный момент малы, то они стремятся к нулю, когда t стремится к бесконечно-
ности.
Резюмируя, можем сказать, что если линейное приближение дает неустой-
неустойчивость или асимптотическую устойчивость, то в общем случае то же самое
мы будем иметь и при переходе к точным уравнениям. Что касается обычной
устойчивости, то нельзя утверждать, что она всегда следует из линейного
приближения. Эти вопросы мы рассмотрим подробнее в гл. XIX и XXI,
где приведем доказательства сформулированных только сейчас положений.
Вернемся теперь к задаче о спящем волчке. Направим ось Ох вертикаль-
вертикально вверх (в § 9.8 ось Ох мы направляли вертикально вниз) с целью избежать
неприятностей, связанных с неопределенностью <р в положении кажущегося
равновесия. Если направляющие косинусы оси волчка обозначить череа
A, у, z), то линейное приближение к уравнениям движения, полученное
одним из указанных в § 9.8 способов, запишется в виде
w — 2ipw - qw = 0, (9.9.14)
где w = у -\- iz. Оно отличается от уравнения (9.8.7) лишь знаком послед-
последнего члена в левой части. Если р2 < q, то решение не остается малым; если
же р2 > q, то решение имеет вид
w = Ae^+si* + Be^v-^t, (9.9.15)
где s = у рг — q, а коэффициенты А, В могут быть комплексными. Если
р2>ди|и>|и|ц;|в начальный момент малы, то эти величины остаются
малыми во все время движения, что следует из ранее известного факта устой-
устойчивости (существование знакоопределенного интеграла (9.9.8)).
Чтобы проиллюстрировать движение, описываемое уравнением (9.9.14),
рассмотрим снова задачу § 8.9. Пусть в начальный момент точка Р оси волчка
движется горизонтально, так что можно принять, что w = а и w = ikd при
t = 0; параметры auk будем считать вещественными и положительными.
*) Исключительный случай такого рода приводится в примере 19.НС. (В этом
примере характеристическое уравнение системы двух уравнений линейного приближения
имеет двойной нулевой корень.— Прим. перев.)
§ 9.9]
СПЯЩИЙ ВОЛЧОК
173
Возьмем (как в § 8.9) такой интервал значений к, чтобы ось волчка поднима-
поднималась из начального положения; тогда траектория точки Р будет лежать внупь-
ри окружности г — а. Ранее, в § 8.9, мы рассматривали эту задачу, основы-
основываясь на точных уравнениях, но решение носило в основном описательный
характер; сейчас мы используем прибли-
приближенные уравнения, справедливые только
для малых значений \ w \, но решение
этих уравнений будет точным.
Решение уравнения (9.9.14), удовле-
удовлетворяющее заданным начальным условиям,
имеет вид
}. (9.9.16)
Рис. 27.
Траекторией точки Р служит эпитрохоида.
Если диск радиуса [3 катится по непод-
неподвижной окружности радиуса а (рис. 27), то точка Р диска, отстоящая
от его центра на расстоянии у, описывает кривую, определяемую уравнением
Если положить
w = (a
p + s — k
p+s '
р— s
к—
(9.9.17)
(9.9.18)
то оно совпадет с уравнением (9.9.16). Переменные t и <р связаны между
собой соотношением
<р _ 2s (p+s) 1
t p+ s — к а
(9.9.19)
Следуя тому же порядку изложения, что и в § 8.9, рассмотрим различные
видоизменения движения, связанные с изменением к от р — s до р + s.
Имеем четыре критических случая; обозначим их (как в § 9.8) через А, В,
С и D:
А) к = р — s; В) к = р — {s2/p); С) к = р; D) к = р + s.
В случае А движение представляет собой медленную прецессию по окружно-
окружности г = а. Между А и В мы имеем либрацию, ограниченную окружностями
Рис. 28.
Рис. 29.
г = а и г = {(р — k)/s} а (рис. 28). В случае В траекторией служит эпици-
эпициклоида с точками заострения на окружности г = (s/p) а (рис. 29). Между В
и С траектория представляет собой кривую с петлями, заключенную между
174
ТЕОРИЯ КОЛЕБАНИЙ
[Гл. IX
окружностями г = а и г = {(р — к)Is} а (рис. 30). В случае С мы имеем кри-
кривую г — a cos (sip) 9, проходящую через точку О (рис. 31). Между С и D мы
Рис. 30.
Рис. 31.
вновь имеем либрацию, ограниченную двумя окружностями (рис. 32), и,
наконец, в случае D мы имеем быструю прецессию по окружности г = а-.
Сюда относятся и две частные задачи, касающиеся гироскопа Фуко:
1) когда ось проходит через вертикаль и 2) когда ось начинает движение из со-
состояния покоя, находясь в наклонном положении.
Обе эти задачи охватываются описанной выше
классификацией: первая относится к случаю С,
вторая — к случаю В. Читателю, возможно, будет
интересно получить решения независимо, как это
сделано в § 9.8 для гироскопа Фуко.
§ 9.10. Вынужденные колебания. В §§ 9.1—9.3
мы изучали свободные колебания около положе-
положения устойчивого равновесия. Теперь мы рассмо-
рассмотрим вынужденные колебания, возникающие тогда,
^^^ ^-'' когда на систему действуют силы, периодически
изменяющиеся с течением времени.
Рис. 32. Рассмотрим гармонический осциллятор, на
который действует внешняя сила, пропорциональ-
пропорциональная sin pt. Уравнение движения такого осциллятора запишется в форме-
х + п2х = с sin pt.
Если р фп, то решение этого уравнения имеет вид
С 1 / Т)С \
х = —5 j-sin pit-fa cos nt A— ( и ^-—=-) sin nt.
(9.10.1)
(9.10.2>
Здесь через а к и обозначены соответственно значения х и х при t = 0. Пер-
Первый член решения выражает вынужденное колебание с периодом 2п/р, а
остальные члены — свободные колебания с периодом 2п/п. Если р имеет
значение, близкое к п, то явление, при котором амплитуда вынужденных
колебаний становится большой по сравнению с амплитудой с внешней силы,
называется резонансом. Иногда этот термин употребляют лишь в том случае,
когда р точно равняется п. В последнем случае (р = п) решение имеет вид.
с 1 /
= —2~ tcos nt 4~а cos nt Н— (и
с
i nt
(9.10.3)-
§9.10] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ 175
С
и вынужденное колебание — к- t cos nt можно трактовать как синусоидаль-
синусоидальное колебание с периодом 2л/п и амплитудой, непрерывно возрастающей
вместе с t *).
Практически, однако, уравнение (9.10.1) всегда является приближенным,
справедливым лишь для малых значений х, и найденное нами решение нельзя
считать достоверным в случае резонанса, когда амплитуда вынужденных
колебаний велика. Это обстоятельство особенно следует иметь в виду,тогда,
когда рассматривается резонанс при р = п, поскольку в этом случае- ампли-
амплитуда возрастает со временем неограниченно.
Кроме того, на системы практически всегда действуют какие-либо силы
трения. Влияние трения проявляется в том, что свободные колебания в конце
концов затухают и остаются только вынужденные колебания. Рассмотрим
гармонический осциллятор, на который кроме внешней периодической силы
действует сила трения, пропорциональная первой степени скорости. Урав-
Уравнение движения будет иметь вид
х + 2кх ¦+ п2х = с sin pt. (9.10.4)
При этом предполагается, что 0 < к ¦< п. Свободные колебания будут опи-
описываться членами вида e~ht cos \it и e~hl sin \it, где [х = у n2 — к2. Их можно
трактовать как синусоидальные колебания с периодом 2п/ц и амплитудой,
пропорциональной множителю е~м и потому быстро стремящейся к нулю.
Свободные колебания скоро становятся пренебрежимо малыми («затухают»),
и остаются вынужденные колебания с периодом 2п/р, описываемые уравне-
уравнением
x = -^sm(pt — a), (9.10.5)
где R cos а = п2 — р2, R sin a = 2рк. Даже тогда, когда в задачах на коле-
колебание трение не входит явно в уравнения движения, важно найти и изучить
периодические решения, имеющие период дополнительной силы. Это связано
с тем, что даже при самом ничтожном трении свободные колебания в конце
концов становятся пренебрежимо малыми.
С переходом от простого случая линейных колебаний к вынужденным
колебаниям системы, описываемым нелинейными уравнениями, задача
сильно усложняется. В § 23.10 мы рассмотрим одну из таких задач.
*) По вопросу о правомерности такой трактовки вынужденных колебаний ,см.
Л. И. Мандельштам, Лекции по колебаниям. Полное собрание трудов, т. IV,
Изд-во АН СССР, 1955. (Прим. перев.)
Глава X
ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА
§ 10.1. Исключение координат. Рассмотрим голономную систему с п
степенями свободы, описываемую п лагранжевыми координатами qi, q2, • • •
. . ., qn, функция Лагранжа L которой не содержит t. Остановимся более
подробно на случае, когда некоторые из координат системы являются цикли-
циклическими (§ 6.11).
Пусть qi, q2, ¦ ¦ •, qm @ < т < п) —циклические координаты. Посколь-
Поскольку они не входят в функцию Лагранжа, первые т уравнений Лагранжа дают
циклические интегралы
-^ = Р„ г = 1,2, ...,т. A0.1.1)
dqr
Постоянные рг здесь определяются начальными условиями. Из уравнений
A0.1.1), линейных относительно qu q2, ¦ . ., q-n, можно выразить gb q2, ...
. . ., qm как линейные функции от рь р2, • • ., Pm, qm+i, 9m+2, • • -,qn-
qr = tyr (Pj, p2, . . ., рт, qm+u qm+2, ¦ ¦., qn, Qm+i, Qm+2: ¦ ¦ •> Qn), r = l, 2, . . .,m.
A0.1.2)
Подставляя теперь qb q2, ..., qm из A0.1.2) в функцию
2?^2Р? ()
r=1 dqr r=1
получаем функцию R:
R = R (qm+l, qm+2, ...,qn', qm+i, Qm+z, --^Чп, Pi, Pa. ••-,Pm)- A0.1.4)
Функцию R называют функцией Рауса; она образуется из функции A0.1.3)
путем замены в ней т первых q на р.
Если первоначальная система натуральная, так что
п п
Т = 1\ = т 2 2 ar^rqs,
Г= 1 8= 1
то уравнения A0.1.2) принимают вид
m n
qr=^]drsf>s- 2 drsq*, r=l,2, ...,m, A0.1.5)
s— 1 s^=m+1
где коэффициенты drs для s^.m выражаются так же, как в формуле (9.6.7),
а для s>m равны
m
drs= 2 drlais.
i=l
Функцию Рауса можно записать в виде
-V; A0.1.6)
10.1] ИСКЛЮЧЕНИЕ КООРДИНАТ 177
здесь T's — однородная форма степени s от qm+\, qm+2, ¦ ¦ •, <7п> коэффици-
коэффициенты которой представляют собой степени B — s) от рь р2, • • ¦, Рт- Квадра-
Квадратичная форма Т'2 не является, конечно, первоначальной функцией кинети-
кинетической энергии; тем не менее она по-прежнему представляет определен-
определенно-положительную форму, так как, когда все р равны нулю, она принимает
значение кинетической энергии.
Докажем, что R играет роль функции Лагранжа для механической систе-
системы с координатами qm+i, qm + 2, ¦ ¦ •> qn (так называемые явные координаты).
Мы свели, таким образом, первоначальную задачу к задаче для системы с
п—т степенями свободы; процесс такого сведения называют исключением
координат. Циклические координаты появляются обычно в системах, [вклю-
[включающих гироскопы; поэтому системы, содержащие циклические коордипаты,
иногда называют гироскопическими системами *) (§ 9.6).
Заметим, что вовсе не обязательно исключать все циклические коорди-
координаты. Ясно, что координаты qi, #21 • ¦ -i qm должны быть циклическими, но
среди остальных координат qm+i, qm+2, ¦ ¦ • > Чп также могут быть цикличе-
циклические. Например, в известной задаче о спящем волчке движение оси удобно
изучать, применяя процесс исключения лишь к одной координате^, так что
функция Лагранжа будет содержать координаты 0 и <р. Подобная процедура
в ряде случаев оказывается полезной, несмотря на то что координата ср
тоже является циклической, если ось Oz вертикальна.
Покажем теперь, что функция R может применяться в качестве функции
Лагранжа с координатами qm+i, qm+2, ¦ ¦ •, qn- Составим полную вариацию
функции R (варьируя также и постоянные рь р2, • • •, Рт> но не варьируя
время t); тогда будем иметь
2л да-r ^J „* "r
r=l
= 2 (ir
r=m+l дЧг г=1
Отсюда находим
OR dL OR дЬ
Ъг 9qr dqr dqr
и
l, то +-2, .... п, A0.1.8)
Ят=—^7- r = l,2,...,m. (Ю.1
С помощью уравнений движения Лагранжа для qm+u qm+21 • • •,
из A0.1.8) получаем
dt v „
dqr
A0.1.10)
что и требовалось доказать.
Обычно нас не очень интересуют значения циклических координат qi,
<72, • • ., qm B момент t, но если решение уравнений A0.1.10) получено, то
значения #ь q%, . . ., qm^> момент t могут быть найдены из A0.1.9).
*) Более подробно гироскопические системы рассмотрены Томсоном и Тэтом [22].
Функция Рауса была впервые введена Раусом в его работе «The Stability of Motion»,
London, 1877.
12 Л. А. Паре
178 ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА [Гл. X
§ 10.2. Исключение одной координаты. Рассмотрим натуральную систе-
систему, для которой
п п
r=ls=l
Пусть координата q^ будет циклической. Нас будет интересовать вид функ-
функции Рауса при исключении циклической координаты q\.
Процесс можно упростить, если заметить, что
п
Pi=S%s?s A0.2.2)
s=l
и, следовательно,
2anT—pl = 2anS, A0.2.3)
где S — однородная квадратичная форма п—1 переменных q2, q3, •.., qn-
п п
r=2 s=2
^ A0.2.5)
Циклический интеграл имеет вид
Pl = p. A0.2.6)
Имеем
Г - pjt _ V = S + J- р» - -А (Р - aJz - ai3q3 - ... - olngn) - F. A0.2:7)
Отсюда находим функцию Рауса:
( ^) A0.2.8)
Как отмечалось (§ 10.1), S представляет собой определенно-положитель-
определенно-положительную форму.
Исходная система представляла натуральную систему с п степенями
свободы. После исключения циклической координаты мы получили систему
с п — 1 степенями свободы, но уже не натуральную, содержащую линейные
члены:
6
Т[ = -~ {al2q2 + ai3q3 + ... + ainqn).
"и
Особый интерес представляет часто встречающийся в практике случай,
когда величина ац постоянна (и, разумеется, положительна). Тогда функция
Рауса A0.2.8) для исследования движения в явных координатах q2, q3, • • •
. . . , qn имеет вид
R = S + со (a12q2 + ai3q3 + . . . + ainq'n) _ V. A0.2.9)
Здесь йцсо написано вместо р. Допустим теперь, что постоянная ац велика
по сравнению с другими (переменными) коэффициентами ars. Тогда скорость
gi будет почти постоянна и равна со, а коэффициенты brs в силу A0.2.5) будут
почти равны соответствующим коэффициентам aTs. Поэтому, если пц — боль-
большая положительная постоянная, то функция Рауса A0.2.9) почти равна
(с точностью до постоянных членов) исходной функции Лагранжа, если в ней
qi заменить на постоянную величину со.
§ 10.3] ГИРОСКОПИЧЕСКАЯ УСТОЙЧИВОСТЬ 179
Линейные члены в выражении для функции Лагранжа могут появиться либо при
составлении функции Рауса, либо тогда, когда на систему наложено движение с заданной
постоянной скоростью <j>i = со. В рассмотренном выше случае, когда «ц постоянно и вели-
велико, эти две, казалось бы, несвязанные причины приводят к одному и тому же результату,
а именно к одной и той же функции Лагранжа для изучения движения в явных коорди-
координатах.
Рассмотрим в качестве примера систему, связанную с массивным телом, способным
вращаться около некоторой оси. Пусть Ox'y'z' будет системой координат, связанной
с вращающимся телом, причем за ось Oz' выберем ось вращения. Поступая так же, как
мы поступали при составлении выражения F.7.7) для кинетической энергии, несмотря
на то, что здесь угловая скорость переменна, тогда как там она была постоянна, находим
Ь=Ъ + вц+^№+-^С№—V, A0.2.10)
где % — кинетическая энергия относительного движения относительно вращающегося
тела), У] = Sm (х'у' — у'х') — кинетический момент относительно оси Oz' в относитель-
относительном движении, /— (переменный) момент инерции системы относительно оси Oz', а С —
момент инерции вращающегося тела относительно оси Oz'. Система имеет п степеней сво-
свободы и описывается п координатами: координатой 6 и п — 1 лагранжевыми координатами
?2» ?з, • • •, 9П> определяющими положение системы относительно вращающегося тела.
Если соотношения, связывающие х и q, не содержат t, то % есть однородная квадратичная
форма от переменных <j>2> <?з, • • •, <?ти а 'Ч — линейная форма от этих же переменных.
Координата 6 является циклической,
()9. A0.2.11)
и dL/дЬ имеет постоянное значение; обозначим его через С(?>. Тогда функция Рауса
будет иметь вид
Tfla-r. A0.2.12)
Это точное выражение для R- Предположим теперь, что С очень велико, и произведем
разложение в ряд по степеням 1/С; отбросив члены порядка НС и вытае, получим
i? = 2:+G»H-y/aJ—2LCaJ-F- A0.2.13)
Это выражение отличается лишь на постоянную от функции Лагранжа A0.2.10), в кото-
которой 0 заменено на со.
Уравнение энергии F.8.3), полученное из функции Рауса A0.2.13), будет иметь вид
1
24- У — у I®2 = const. A0.2.14)
Его можно получить как предельный случай из уравнения энергии для исходной системы.
В самом деле, согласно A0.2.10) его можно переписать в виде
Z + f)r\ + ±-(C + I)№+V = const. A0.2.15)
Подставляя сюда в из уравнения A0.2.11):
: Са> — г\
9= с + 1 , A0.2.16)
и, как и ранее, отбрасывая в разложении члены порядка 1/С, получаем формулу A0.2.14).
§ 10.3. Гироскопическая устойчивость. В задаче о спящем волчке
(§ 9.9) мы уже встречались с гироскопической устойчивостью; сейчас мы
коротко остановимся на общей теории, из которой гироскопическая устой-
устойчивость следует как частный случай.
Рассмотрим снова, как в § 10.2, систему, имеющую одну циклическую
координату gi; коэффициент ап пусть будет постоянным. Движение системы
сп — 1 степенями свободы, описываемой явными координатами, определяет-
12*
180 ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА [Гл. X
ся с помощью функции Рауса
R = S -\—'— (Й12?2~Ь а1з9з~1~ • • • ~\~ атЯп) — V. A0.2.8)
Тогда точка (q2, q3, . . ., qn), в которой все производные dV/dq2, dV/dq3, ...
. . ., dVldqn обращаются в нуль, является положением кажущегося равно-
равновесия. Это — положение равновесия в явных координатах для всех значений
р. Нашей целью будет изучить устойчивость по первому рриближению этого
кажущегося равновесия.
В точке р 0 (#20! ?30i • • -, Qno)i B которой функция V имеет минимум,
равновесие, несомненно, устойчивое. Без потери общности можно принять,
что V = 0 в точке Ро. Из уравнения энергии F.8.3) тогда имеем
S + V =* С, A0.3.1)
и так как S — определенно-положительная форма, то при всех t
V^C. A0.3.2)
При достаточно малых значениях С это означает, что движение происходит
в малой окрестности точки Ро, так что равновесие в точке Ро является устой-
устойчивым.
Если точка Ро является точкой максимума функции V или седловой точ-
точкой, то движение неустойчиво, если |3 = 0. Но в некоторых случаях можно
достигнуть устойчивости или по крайней мере устойчивости по первому при-
приближению, если придать параметру р достаточно большое значение. В этом
случае говорят о гироскопической устойчивости; с ним мы встречаемся в зада-
задаче о спящем волчке.
Как и в теории малых колебаний, примем за начало отсчета положение
равновесия. При исследовании устойчивости по первому приближению
достаточно применить выражение для R, составленное с точностью до членов
второго порядка по q и q.
Чтобы пояснить основную идею, рассмотрим простой случай, когда
система имеет всего две явные координаты. Перейдем к координатам, в кото-
которых S и V представляются суммами квадратов; при р — 0 это главные коор-
координаты. Преобразование наверняка существует, поскольку ?> — определен-
определенно-положительная форма. Обозначив новые координаты через хжу, напишем
R — ~2 (х2т~ J/2) +P (&?+ w) —«г (^а;2 + ^#2)- A0.3.3)
При этом ? и ц нам требуется знать лишь с точностью до членов первого поряд-
порядка по а; и у. Линейные приближения для уравнений движения в явных коор-
координатах запишутся в виде
х — щ-\-кх = 0,
... _ [ (Ю.3.4)
где
— некоторый постоянный множитель. Решения уравнений A0.3.4) содержат
множители e±pit, e±P2t, где pi и pi являются корнями квадратного урав-
уравнения
ptjr% —хр
= 0 A0.3.6)
§ 10.4]
ЯВНОЕ ВЫРАЖЕНИЕ ДЛЯ Я В ОБЩЕМ СЛУЧАЕ
181
или
р* + (А, + ц, + х2) р2 + V = 0. A0.3.7)
Условие устойчивости по первому приближению заключается в том, чтобы
это квадратное относительно р2 уравнение имело вещественные отрицатель-
отрицательные корни; для этого в сдою очередь требуется, чтобы
Л (Ю.3.8)
Ж A0.3.9)
Из неравенства A0.3.8) следует, что к и [i должны быть либо одновремен-
одновременно положительными, либо одновременно отрицательными. Это означает, что
обе степени свободы, рассматриваемые в отдельности, при fS = 0 устойчивы
или обе неустойчивы в нулевой точке. Потенциальная энергия должна иметь
либо минимум, либо максимум, но не седловую точку. Условие A0.3.9),
очевидно, выполняется, если и к и ц положительны. В этом случае функция V
в нулевой точке имеет минимум, и, как уже отмечалось, равновесие при этом
устойчиво при всех значениях f>. Условие A0.3.9) может выполняться и тогда,
когда к и |х отрицательны, а именно когда
Из этого неравенства следует, что если обе степени свободы при fS = 0
неустойчивы, то неустойчивое положение можно превратить в устойчивое
(в смысле устойчивости по первому приближению), если придать р достаточно
большое значение. Неустойчивое положение становится устойчивым, если
гироскопу сообщить достаточно быстрое вращение.
§ 10.4. Явное выражение для R в общем случае. В § 10.2 мы приводили явное выра-
выражение для функции Рауса R в простом случае, когда имеется одна циклическая коорди-
координата. Сейчас мы укажем способ получения явного выражения для R в общем случав
натуральной системы, в которой т первых координат циклические. Предполагаемый
метод несколько громоздок и потому имеет скорее теоретический, нежели практический
интерес.
Как и в § 6.10, напишем
дТ
Следовательно,
Чт=
г = 1, 2, ..., п.
г=1,2, ...,п,
8=1
где (crs) — матрица, обратная матрице (ars). Матрица (cTS) симметрична. Далее,
Следовательно,
r=l
A0.4.1)
A0.4.2)
A0.4.3)
*+2Рт*2+...+ЯпРп- (Ю-4-4)
В правой части равенства д4, д2, ..., Чт следует выразить через р4, р2, •¦•) Рт- Рас-
Рассмотрим определитель с re -f-1 строками и столбцами
Оц
а21
«ml
0
0
0
Pi
«22
am2
0
0
0
Р2
• • ¦ alm
• ¦ • в-гт
¦¦ • атт
... 0
... 0
... о
Рт
— °1, т+1
«2, т+1
' «т, т+1
-J
0
0
Рт+1
а1, т+2
°2, т+2
«т, т+2
0
— 1
0
Рт+2
• •¦ —«1,71
••• — «2, П
• ¦ ¦ ат, п
0
0
1
Рп
Pi
/>2
Рт
•
Ят+1
<?га+2
In
\-2(R + V)
A0.4.5)
182 ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА [Гл. X
который, очевидно, равен нулю. Если r-й столбец для г = m + 1, т -\- 2, ..., п заме-
п
нить на \ (crS X s-ж столбец), то последняя строка в полученном определителе будет
s=l
иметь вид
Pi, Р~2. ¦ ¦ •. Рт> Чт+l, Чт+2, ¦ ¦ •> 9тг> —2 (R + V).
Приравняв определитель нулю и разложив его по элементам последней строки (заменив
при этом рг на Рг), получим явное выражение для R + V. Оно представляет собой, как
уже отмечалось, ^однородную квадратичную форму от Рь Р2> • • •> Рт. ?т+ь Чт+2, ¦ ¦ ¦
*
• • •, in-
§ 10.5. Вращающийся волчок. Если ориентацию триэдра, связанного
с волчком, определить при помощи углов Эйлера, то, как и в § 8.6, будем
иметь
ycos0J-F. A0.5.1)
Если 1) ось Oz направить вертикально вверх, то получим
V = Mgl cos 0 A0.5.2)
и обе координаты ф и i|) будут циклическими. Если 2) ось Ох направить верти-
вертикально вверх, то получим
V = Mgl sin 0 cos ф A0.5.3)
и циклической будет только координата i|).
В случае 1) можно исключить обе координаты фиг|зи составить функцию
Лагранжа только с одной координатой 0. Тогда будем иметь
рф = A sin2 0 ф + С cos 9 (гр + Ф cos 6) = рь A0.5.4)
р^ = С (г|) + ф cos 9) =* р2 A0.5.5)
и
2 (Л + F) = ёр9 -ФРФ--ФР* =
= А& — ф {Л sin2 0 ф + С cos 0 (г|5 + ф cos 0)} — Сг|э (i|j + ф cos 0) =
= А& — A sin2 9 ф2 — С (ijj-+ ф cos 0J =
^i1 A0.5.6)
В обозначениях § 8.6
4?, A0.5.7)
и мы находим (опуская постоянный член) с точностью до постоянного поло-
положительного множителя
e^ A0.5.8)
Интеграл энергии (§ 6.7), определяющий соотношение между t и 0 в про-
процессе движения, имеет вид
^ ii, A0.5.9)
эквивалентный (8.6.9).
§ 10.6] ЛИНЕЙНЫЕ ЧЛЕНЫ В ФУНКЦИИ L 183
В случае 2) (и также, конечно, в случае 1)) можно исключить координату
¦ф и составить функцию Рауса с двумя координатами 6 и ф:
R^L- p^, A0.5.10)
где •
р^ = С (ф + ф cos 9) = р. A0.5.11)
Здесь
R = -|- A (92+sin2 9 <р2) -1- Рф cos 9— V. A0.5.12)
Постоянный член мы отбросили. Эту функцию Лагранжа можно использо-
использовать для изучения движения оси; если V = Mgl cos 9, то мы снова получаем
результаты § 8.6; если же V = Mgl sin 9 cos ф, то приходим к результатам
§ 9.9.
§ 10.6. Линейные члены в функции L. В случае натуральной системы
(§ 6.5) Т является однородной квадратичной функцией от q. Функция Ла-
Лагранжа, составленная по методу Рауса, содержит, однако, еще слагаемые,
линейные относительно q:
azqz + . . . + anqn, A0.6.1)
где п обозначает теперь число явных координат, т. е. эффективное число сте-
степеней свободы системы, для которой R играет роль функции Лагранжа. Выше
(в §§ 6.1 и 6.6) уже отмечалось, что такого рода линейные члены появляются
и в других случаях, например в некоторых задачах, где фигурируют силы,
зависящие от скорости; в дальнейшем нам еще встретятся примеры, когда
в L входят линейные члены.
Функция Ti добавляет к левой части r-го уравнения Лагранжа выра-
выражение
(
dt \ZI ~ dqT
oqr
ИЛИ
дат
dt
^Yris, A0.6.2)
где
Y7.s==^r.__^l= _Ysr. A0.6.3)
Если коэффициенты а зависят только от q и не зависят от t (что имеет место,
например, если функция Рауса составлена путем исключения координат из
из натуральной системы), то линейная форма Т4 порождает в уравнениях
движения антисимметричные линейные члены, называемые гироскопическими
членами. Вектор, r-я составляющая которого равна Qr,
п
^r=-EWs. A0.6.4)
п .
не совершает работы во время движения, поскольку V QTqr = 0. Поэтому
„ ¦ r=1
линейные члены в функции Лагранжа не входят в уравнение энергии; с этим
фактом мы уже встречались ранее (§ 6.8).
Мы видели выше, каким образом появляются л нейные члены вида
A0.6.1) в функции Лагранжа (для явных координат), образованной с помощью
184 ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА [Гл. X
процесса исключения. Рассмотрим теперь случай, когда линейные члены
в функции Лагранжа появляются из-за наличия сил, зависящих от скорости.
Возьмем в качестве примера задачу о движении материальной точки относи-
относительно неподвижной прямоугольной системы координат. Предположим, что
функция L содержит линейные члены:
Т,. = Рх + Qy -j- Rz A0.6.5)
или, что то же,
T^-F-v, A0.6.6)
где F — вектор {Р, Q, Я}, v — вектор {х, у, z}, a P, Q, Д —функции от х,
у, z; t, принадлежащие классу Ct. Полная функция Лагранжа имеет вид
+ (Px+Qy+Rz) — V, A0.6.7)
где V — V (х, у, z; t). Напишем уравнения движения
m'*'=--?--ijr+(k-^) (lo-6-8)
и два аналогичных; через |, ц, ? здесь обозначены составляющие rotF:
ё^ ду dz ' ^~ dz дх ' ^^ дх ду • (Ш.Ю.У)
В векторной форме уравнение движения можно записать так:
mr=-- -gradV — ~ + vxrotF. A0.6.10)
Таким образом, если на частицу действует сила, порождаемая потенциаль-
ной функцией V, и сила вида — -^—\- v X rot F, то функция Лагранжа имеет
форму A0.6.7).
Рассмотрим некоторые важные частные случаи.
1) Частица находится под действием силы притяжения к точке О (или
отталкивания от этой точки), причем величина силы притяжения (отталкива-
(отталкивания) пропорциональна г, так что
7 = у7П^2=утА:(ж3 + г/2 + 23), A0.6.11)
где к > 0 для случая притяжения и к <. 0 для случая отталкивания. Пусть,
кроме того, имеется еще гироскопическая сила G X v, где G — постоянный
вектор. В этом случае вектор Fne зависит от t и G = — rot F, так что состав-
составляющие F являются линейными функциями от х, у, z с постоянными коэффи-
коэффициентами. Если, в частности,
F = {тру, - трх, 0}, A0.6.12)
G=—iotF = {0,0,2mp} A0.6.13)
и уравнения движения записываются в форме
х -j- 2py -\-кх = 0,
I
A0.6.14)
§ 10.6] ЛИНЕЙНЫЕ ЧЛЕНЫ В ФУНКЦИИ L 185
Последнее уравнение этой системы автономно; если принять, что в началь-
начальный момент частица движется в плоскости z = 0. так что при ? = 0z = z = 0,
то все время будем иметь z = 0. Первые два уравнения можно заменить одним
уравнением относительно комплексной переменной w = х + Лу:
w — lip'w + kw = 0. A0.6.15)
С этим уравнением мы уже встречались дважды: (9.8.7) для к > 0 и (9.9.14)
для к <; 0. Знак к, конечно, существен: между задачей о притяжении и зада-
задачей об отталкивании имеется существенная разница. Что же касается знака
р, то он не играет особенно важной роли, поскольку замена р на —р и tua
—t приводит к тому же самому уравнению. Положительная полутраектория
(траектория для положительных значений t) в одной задаче такая же, как
отрицательная полутраектория (траектория для отрицательных значений
t) в другой задаче, отличающейся знаком р. Будем считать, что р > 0 *).
Представляет интерес случай, когда р2 -\- к > 0. Это всегда выполняется
для притяжения (к^> 0), а при р2 > | к | и в случае отталкивания {к <; 0);
как отмечалось в § 9.9, это есть условие устойчивости. Будем считать, что
условие выполняется, и положим ра -f- к = s2, s > 0. Тогда при к > 0
s > р, а при к <с 0 s <l р. Решение имеет вид
и; = -й'{[(*-Р)и7о-и>о] e*<-H»*-H(s +P) ^о+ tool e-1<'-«'}, A0.6.16)
где w0 и у0 — значения соответственно и? и w при i = 0. Некоторые примеры
движения, описываемого уравнением A0.6.16), нами уже рассматривались
(в § 9.8 для к > 0 и в § 9.9 для к <z 0).
2) Рассмотрим движение заряженной частицы в электромагнитном поле.
Сила поля, действующая на частицу, равна в гауссовых единицах
— egradQ— ^{A — v x rot A}, A0.6.17)
где е — заряд, который несет частица, Q — скалярный потенциал и А —
векторный потенциал поля. Как мы уже видели (уравнение A0.6.10)), член
F-v в выражении для L порождает силу
действующую на частицу. Поэтому действие электромагнитного поля можно
учесть, если в функцию Лагранжа L ввести члены
— (Q+-A-V. A0.6.18)
С
С
Пример 10.6А. Теорема Лармора. Рассмотрим массивную
заряженную частицу, движущуюся в поле механических и электрических
сил, симметричных относительно оси Oz. Как изменится движение частицы
при наложении слабого однородного магнитного поля напряженностью у
в направлении Oz?
Имеем
А=±у{-у,х,0] A0.6.19)
*) Изменение знака р сводится к замене ? на —i, что в конечном счете скажется лишь
на знаке координаты у. Из рассуждения в тексте следует, что суждение об устойчивости
или неустойчивости движения, описываемого уравнением A0.6.15), одинаково пригодно
как при t >. 0, так и при t < 0. (Прим. перев.)
186 ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА [Гл. X
z*) + ±-2L(xy-y'x)-V-e7i, A0.6.20)
где у и Q представляют собой функции от хг + у2 и z. Сравним функцию
A0.6.20) с функцией Лагранжа (§ 6.7) при тех же механическом и электро-
электростатическом полях, но без магнитного поля, причем будем считать, что коор-.
динатные оси вращаются около Oz с угловой скоростью со. Имеем
L = 4"т (*2 + У% + z2) + mco(.п/ — ух) — F — eQ + ~т(х2 + у2) со2. A0.6.21)
2
Если положить
со = еу12тс
и считать со столь малой, что в A0.6.21) можно пренебречь членами порядка
со2, то выражения A0.6.20) и A0.6.21) совпадут. Движение в магнитном поле
напряженностью у оказывается таким же, как движение относительно вра-
вращающихся осей при отсутствии этого поля. Наложение слабого однородного
магнитного поля вдоль оси симметрии заданных механического и электроста-
электростатического полей равносильно наложению на исходное движение вращения с угло-
угловой скоростью — со. Это утверждение составляет содержание теоремы Лар-
мора. Если заряд е отрицательный, то получаем правое вращение около оси
симметрии.
Пример 10.6В. Скрещивающиеся поля. Заряженная
частица совершает движение под действием однородного электрического поля
и перпендикулярного ему однородного магнитного поля. Найдем траекторию
частицы, начинающей движение из состояния покоя.
Пусть заряд частицы будет —е (так что если заряженной частицей явля-
является электрон, то е положительно), вектор напряженности электрического
поля пусть будет {—Е, 0, 0} и магнитного поля {0, 0, у}. Тогда
L = у т {х* + У2 + z2) - у -J- (ху - ух) + гЕх A0.6.22)
или
Т / О I О [ 9\ 7 / \ 1 /Л Г\ d Г»О\
•k — "о" (х ~гУ i~z )—' тк \ХУ — Vх)~r §xi AU.O./O)
где k = zy/mc, g = &Elm. Уравнения движения запишутся в виде
x = g — ky, 'y'=kx, У=0. A0.6.24)
Если частица начинает свое движение из начала координат из состояния
покоя, то z все время будет равно нулю и движение в плоскости г = 0 будет
описываться уравнением
w = g + ikw, A0.6.25)
где w = х + iy. Решение, удовлетворяющее условиям w = w = 0 при t = 0,
имеет вид
u; = -l-(l_eif")-fi-^-(fe)- A0.6.26)
Траекторией частицы является циклоида
х = а A — cos 9), у = а (9 -sin 9), A0.6.27)
где •
1 _ 8 „ га?с2
А — , о —
8у<
§ 10.7] ДВИЖЕНИЕ ОТНОСИТЕЛЬНО ПОДВИЖНОЙ СИСТЕМЫ ОТСЧЕТА 187
и 0 = kt t= (eylmc) t. Циклоида имеет точки заострения на оси Оу; наиболь-
наибольшее расстояние от этой оси во время движения равно
2к = 2тЕс2/гу*. A0.6.28)
§ 10.7. Движение относительно подвижной системы отсчета. В случае
натуральной системы соотношения, связывающие х и q, не содержат явно t
(через х, как обычно, обозначены координаты частиц относительно неподвиж-
неподвижного прямоугольного триэдра, т. е. триэдра, жестко связанного с ньютоновой
системой отсчета). Рассмотрим теперь более подробно некоторые задачи, в ко-
которых соотношения между xviq содержат t. Это будет иметь место при простом
и естественном выборе лагранжевых координат, если на некоторую часть
системы наложено движение или если используются подвижные оси, причем
выбор координат q произведен так, что координаты х' частиц относительно
подвижных осей являются функциями одних только q. Примером может слу-
служить случай, когда подвижные оси связаны с твердым телом, совершающим
заданное движение.
Рассмотрим движение относительно системы отсчета F' движение кото-
которой относительно неподвижной системы F (ньютоновой системы) задано.
Системой отсчета F' служит триэдр, неизменно связанный с твердым телом,
совершающим заданное движение относительно системы F. Один простой
случай подобного рода уже был рассмотрен нами в § 6.7.
Пусть {и, v, w} определяют вектор скорости начала О' подвижного три-
триэдра, а {91?62, 93} — вектор угловой скорости этого триэдра относительно
неподвижной системы F; составляющие указаны вдоль мгновенных положе-
положений подвижных осей. Тогда
2Г = Sm{(u + 'x-yQ3 + z92J +... + ...}. A0.7.1)
Для удобства мы здесь опустили штрихи в обозначениях координат относи-
относительно подвижных осей. Таким образом,
2Г = Sm (х2 + 'у2 + z2) + Sm (и2 + v2 + ш2) +
+ Sm {(yQ3 - z92J+ ... + • • •} + 2Sm {и (х - yQ3 + z92) +
+ ... + •••} + 2Sm {x'(-yQ3 + zQ2)+ ... + ...}. A0.7.2)
Здесь и, v, w, 0i, 92, 93 представляют известные функции от t. Выражению
A0.7.2) можно придать более удобную форму. С этой целью рассмотрим под-
подробнее отдельные члены, входящие в эту формулу.
Член
Sm (хг + у2 + za), A0.7.3)
который мы обозначим через 2?, равен удвоенной кажущейся кинетической
энергии движения относительно системы отсчета F', иными словами, ? —
это кинетическая энергия системы, как ее оценил бы наблюдатель, движущий-
движущийся вместе с системой F' и потому считающий ее неподвижной.
В выражении
Sm (u2 + v2 + w2) = М (и2 + v2 + w2) = MU2 A0.7.4)
через М = Sm обозначена полная масса системы, а через U = | JJ \ — ско-
скорость точки О'.
Член
Sm {(г/03 - z92J + (z94 - Ж93J+ (xQ2 - гАJ } A0.7.5)
равен /со2, где ю — угловая скорость (94, 92, 93) системы отсчета F', со =
= | to |, а / — момент инерции всей системы в рассматриваемый момент
времени относительно оси, проходящей через точку О' в направлении <о.
188 ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА [Гл. X
В выражении
= М [и?+ (vQ3 —wQ2) %\ +¦ ... + ....=
+ ?(!/;- u92 + vQi)} = M-^(B-U)-M (В •/) A0.7.6)
R = {?, T], ?} обозначает радиус-вектор центра масс G системы, XI— ско-
скорость точки О' (т. е. вектор {и, v, w}) и/ — ускорение точки О'. Все векторы
R, U, /' измеряются относительно неподвижного триэдра, совпадающего
с мгновенным положением подвижного триэдра.
В выражении
sm{x( — yQ3 + zQ2) + ... + . ..} = 915rm(!/z — zy\-\- ...+ ...=
(*» • -П') (Ю.7.7)
V == {"Hii Чг-i "Пз) представляет вектор кажущегося момента количеств дви-
движения, т. е. момента количеств движения, как его оценил бы наблюдатель,
связанный с системой отсчета F' и потому считающий ее неподвижной.
Таким образом, можем написать
Т = г + ^Ми^ + ~1^ + М-^(В-и)-М(Ц./)+((о.ц'). A0.7.8)
При составлении функции Лагранжа член-к-Aff/2, а также член М — (R-U),
имеющий форму F.8.6), можно опустить; тогда окончательно будем иметь
L = Z + (w.i\') — V A0.7.9)
и
F' = F + M(J?./)-l/co2, A0.7.10)
где V — функция потенциальной энергии. В наиболее интересном для нас
случае функция V зависит от положения системы относительно подвижной
системы отсчета F'.
Введем лагранжевы координаты qt, q2, . . ., qn, где п — число степеней
свободы голономной системы в ее движении относительно системы F'; пере-
переменные q таковы, что соотношения между хидне содержат t. В этом случае
? оказывается определенно-положительной квадратичной формой перемен-
• •
ных q, а выражение (а>-Т]') — однородной линейной формой переменных q;
коэффициенты этой линейной формы в общем случае зависят как от t, так и от q.
Теперь можно установить влияние движения подвижной системы отсчета
на движение механической системы, каким оно представляется наблюдателю,
связанному с ней и потому считающему ее неподвижной. Это влияние заклю-
заключается в следующем:
a) в центре масс G системы действует сила, равная —Mf;
b) «кажущаяся» потенциальная энергия отличается от V на величину
«-I®2, вследствие чего появляются центробежные силы;
c) возникают силы, обусловленные членом (<о-т]') в выражении для L;
если t не входит в этот член, то они представляют собой гироскопические силы.
§ 10.8] ДВИЖЕНИЕ ВБЛИЗИ ЗАДАННОЙ ТОЧКИ НА ПОВЕРХНОСТИ ЗЕМЛИ 18&
Отметим некоторые частные случаи.
1) Если <о=0 и/ = 0, то движение подвижной системы отсчета не сказы-
сказывается вовсе на уравнениях движения. Это явление хорошо известно. Систе-
Система отсчета, движущаяся равномерно, прямолинейно и поступательно отно-
относительно ньютоновой системы, сама является ньютоновой. Это утверждение
часто называют ньютоновым принципом относительности *).
2) Если <о=0, то движение подвижной системы отсчета проявляется
только в том, что возникает однородное поле ускорений — /, которое дает
силу —Mf, приложенную в центре масс G. Отсюда, в частности, получается
известная теорема о движении твердого тела: если одна точка твердого тела
совершает заданное движение, то движение тела относительно этой точки
происходит таким образом, как если бы эта точка была неподвижна и кроме
других сил на центр масс тела действовала бы еще сила — Mf.
3) Если/ =0, то движение подвижной системы отсчета сказывается в том,
что появляются центробежные и гироскопические силы. Частный случай,
когда вектор а» остается постоянным, уже рассматривался нами (§ 6.7). Гиро-
Гироскопических сил не возникает, если (w*rj') является полной производной
-т- / (</; t) это; всегда имеет место, если число степеней свободы равно единице.
Эти силы отсутствуют также и в том случае, когда вектор i\' во все время
движения перпендикулярен к со. В этих случаях влияние вращения системы
отсчета сводится лишь к появлению центробежных сил.
4) Теорема Кориолиса. Если система состоит только из одной
частицы, массу которой для удобства примем равной единице, то можно
написать
Т = | (i2 + у* + z2) -f {8j (y'z-zy) + 92 (z'x-x'z) + 93 (xy-yi)}-
где через а, р, у обозначены составляющие вектора /. Составляющая век-
вектора ускорения по оси х равна
^J ( A0.7.12)
озо
где
(p1 = a — yQ3 + zQ2 — xa2 + Qi(r-(ii). A0.7.13)
Здесь ф! представляет собой ^-составляющую ускорения точки, фиксирован-
фиксированной в подвижной системе осей. Таким образом, мы приходим к следующему
результату: ускорение движущейся частицы равно векторной сумме трех сла-
слагаемых: 1) ускорения той точки подвижного пространства, где находится
в данный момент частица, 2) ускорения г относительно подвижных осей,
3) гироскопического члена —Ът X (о.
В этом заключается теорема Кориолиса. Особо важное значение имеет
гироскопический член; он не имеет аналога в соответствующей теореме, отно-
относящейся к скорости движущейся частицы. Теорему Кориолиса мы получили
как частный случай общей теории движения в подвижной системе отсчета;
но ее, разумеется, можно получить без особого труда и непосредственно,
не обращаясь к общей теории.
§ 10.8. Движение частицы вблизи заданной точки на поверхности Земли.
С самого начала заметим, что внешнее однородное поле не влияет на движе-
движение частицы относительно Земли, поскольку оно действует как на частицу,
*) Этот принцип общепринято называть принципом Галилея. (Прим. ред.)
190
ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА
Гл. X
так и на Землю с силами одного направления (хотя это направление может
меняться с течением времени) и пропорциональными массам. Поэтому,
сохраняя высокую степень точности, можно пренебречь гравитационным
эффектом удаленных масс. Кроме того, мы будем пренебрегать влиянием
небольшого отклонения формы Земли от сфериче-
сферической и примем, что распределение плотности ве-
вещества Земли характеризуется сферической сим-
симметрией, так что внешнее гравитационное поле
будет таким же, как у точечной массы, находя-
находящейся в ее центре. При изучении относительного
движения центр Земли С можно считать находя-
находящимся в покое.
Обозначим широту заданной точки О на по-
поверхности Земли через X. Ось Oz можно было бы
направить вдоль радиуса Земли, ось Ох — на югт
а ось Оу — на восток. Однако удобнее повернуть
систему немного около оси Оу, направив Oz вверх
вдоль линии отвеса, т. е. по линии кажущейся силы
тяжести. Тогда ось Oz будет располагаться в ме-
меридиональной плоскости и будет составлять с нормалью к оси Земли угол
9 = К + р, где р — небольшой угол отклонения линии отвеса от истинной
вертикали. Для Лондона, расположенного на широте к = 51°30', угол Р
составляет всего 6'. Плоскость z = 0, строго говоря, не является горизон-
горизонтальной (т. е. касательной плоскостью к сфере), но для точек, близких
к точке О, отклонение весьма мало (рис. 33).
Если скорость вращения Земли обозначить через <о и считать постоянной,
то можно написать
L = Z + (a-ri') — V'. A0.8.1)
Положив массу частицы равной единице, перепишем это выражение в сле-
следующей форме:
Рис. 33.
L = т (ж2 + у2 + г2) - со cos 9 (yz - zy) + со sin 9 (ху - ух) - V,
где to = |
и R есть вектор {х, у, z). Через V здесь обозначена потенциальная функция
кажущегося гравитационного поля. В первом приближении V =gz, где
g — ускорение силы тяжести по измерениям наблюдателя, связанного с под-
подвижной системой отсчета F'. Для задачи о маятнике Фуко, где масштаб дви-
движения вообще мал, а для вертикального движения в особенности, прибли-
приближение V = gz является достаточно точным. Напомним, что со весьма мала
(приблизительно 7,27-Ю сек'1).
§ 10.9. Маятник Фуко *). Опыт с маятником Фуко, при котором произ-
производится наблюдение за поворотом плоскости качания простого маятника
относительно Земли, служит подтверждением ее вращения. Подвесим неболь-
небольшой груз к неподвижной точке на легкой нити длиной I. Выбрав начало коор-
координат в положении равновесия, можем с достаточной степенью точности
написать
V'— ж — — (х*-+-и2) СЮ 9 1 >
*) Более точное исследование движения маятника Фуко см. в статье:
T.J.I'A.Bromwich, Proc. L.M.S., 2, vol 13, стр. 224—235.
§ 10.9]
МАЯТНИК ФУКО
191
Отбрасывая в функции Лагранжа члены порядка z2, coz, coz, получаем для нее
следующее приближенное выражение:
р (Ху-ух)-~п
A0.9.2)
где р = со sin 9, п2 = gll. Заметим, что совсем не обязательно придерживать-
придерживаться первоначальных направлений осей х и у; их можно повернуть на нужный t
угол около оси Oz, не изменяя формы функ-
функции L.
Уравнения движения имеют вид
х—
2ру + п?х--=0, }
2рх + п?у = 0. J
(Ю.9.3)
Положив w = x-\-iy, заменим их одним урав-
уравнением
w+2ipw + n2w = 0. (Ю.9.4)
УравнениеA0.9.4) аналогично уравнению(9.8.7),
описывающему движение оси гироскопа Фуко
(§ 9.8), и отличается от него лишь знаком коэф-
коэффициента при w. Подобное уравнение встречалось нам также в § 10.6. Рас-
Рис. 34.
смотрим движение маятника из состояния покоя: при ( =
где а вещественно и положительно. Решение имеет вид
и? =
2s
4- (s — p) e-
где
тг2 + Р2.
= а и w = 0,
A0.9.5)
A0.9.6)
Траектория маятника (рис. 34) представляет собой гипоциклоиду
w = (а — Ь)
где
Ъ =
s—p
2s
а,
9 = -^*.
а
A0.9.7)
A0.9.8)
Поскольку р мало, а Ъ лишь немного меньше -^- а, последовательные дуги
Li
гипоциклоиды близки к прямым. Время полного периода качания («туда
и обратно») равно 2n/s; оно лишь немного меньше, чем время 2п/п, соответст-
соответствующее случаю, когда отсутствует вращение. Значение w в момент 2л/s равно
(см. A0.9.5)) ае-'Bяр/в)? тйк что плоскость качания поворачивается за это
время в отрицательном направлении на угол 2npls. Таким образом, эта плос-
плоскость вращается по ходу часовой стрелки со средней угловой скоростью р.
Решение A0.9.5) можно переписать в форме
* ?, A0.9.9)
где
w =
¦' a cos st -f- i — a sin st,
A0.9.10)
так что траекторией точки ? является вытянутый эллипс, большая полуось
которого равна а, а малая равна {pls)a и, стало быть, мала по сравнению с а.
Можно сказать, что точка w описывает вращающийся эллипс. Но это описа-
описание «вряд ли выражает весьма простую идею о гипоциклоиде».
192
ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА
[Гл. X
§ 10.10. Движение снаряда. В задаче о маятнике Фуко мы считали
V = gz, поскольку изменение координаты z было мало. Этим выражением
для V можно пользоваться в некоторых случаях и тогда, когда движение
имеет больший масштаб, например при изучений движения снаряда. Однако
в этом случае это приближение будет более грубым. Для более точного расче-
расчета произведем сравнительную оценку членов, которыми мы пренебрегли в пер-
первом приближении, и найдем те из них, которые играют существенную роль.
Как и ранее, Землю будем считать шаром, скорость вращения ее — посто-
постоянной и центр ее — неподвижным. Мы уже ука-
указывали, что со мало (около 7,27-10~5 сек'1). Имеем
(§ 10.7)
G^ j/ Z = ?+((».ti') — V, A0.10.1)
где
A0.10.2)
Ьш'
Рис. 35.
Массу снаряда мы для удобства приняли равной
единице. Пользуясь обозначениями рис. 35,
направляя ось Oz' вдоль радиуса Земли и обозначая расстояние тела от центра
Земли С через г, а расстояние его от точки О через р == [ К |, можем написать
Члены —V — (-R*/) вносят, таким образом, в функцию L следующее выра-
выражение:
= { _ (G —
cos х) z'
sin
} + -J-Cz'2-p2)-
-~Ez'3-3pV), A0.10.4)
где b = acosX, G = \x/a2. Членами порядка Gp^/a3 мы пренебрегли.
Линейные члены в выражении A0.10.4) равны, очевидно, — gz (ось Oz,
как и ранее, выбрана, вдоль линии отвеса). Кроме того,
^ш2 sin
G = g cos p + feco2 cos X = g A + e),
где
e = (aaP/g) cos21 — A — cos p1) = ctg A, sin p" — 1 + cos p\
поскольку
sin p" = (aaf/g) cos k sin k.
A0.10.5)
A0.10.6)
A0.10.7)
A0.10.8)
Таким образом, приближенное (с точностью до членов порядка р") значение е
равно
е = р ctg k, A0.10.9)
и, стало быть, Р и е, как функции от со, имеют один и тот же порядок малости.
Связь между малыми величинами Ьсо2 и р иллюстрируется на рис. 35.
8 10.10] ДВИЖЕНИЕ СНАРЯДА 193
Члены второго порядка в выражении A0.10.4) после перехода к осям
Oxyz запишутся в виде
-|- Cz'2 — р2) = ^- {3 (z cos р4- х sin РJ — ж2 — г/2 — z2} =
где ? = tg|S. Это выражение можно записать еще в форме
Отбрасывая таены второго порядка в выражениях для 8 ?, получаем
.|_BZ2-_z2-z/2L-y^{8Bz2-z2-*/2) + ВД. A0.10.12)
Члены третьего порядка в пределах принятой степени точности остаются
неизменными при изменении осей, и мы имеем
— yvBzs — Зж2г — Зг/2г). A0.10.13)
Собирая все члены, окончательно получаем
L — — (хй+ г/2 4- z2) — со cos 9 (yz — zy) + со sin 9 (ху — ух) —
га_ Ж2 __ у2) _¦_ А. сй2г/2+ у со2 (z cos 9 + х sin 9J +
Отсюда находим уравнения движения
х — 2со sin 9 у = — — х + со2 sin 9 (х sin 9 4- z cos 0) —
g
y-\-2a>sin9x4- 2cocos0 z = — — .V-1 «>2г/ — — ei/H—|-г/г,
A0.10.15)
z — 2co cos 0 у — — g 4- — z 4- to2 cos 9 (ж sin 9 4- z cos 9) 4-
+ f Bez + 3?z) - ^ Bz2 - x2 - j/2).
Полученные уравнения имеют скорее теоретический, нежели практиче-
практический интерес, поскольку описывают движение снаряда в пустоте. Сопротив-
Сопротивление воздуха оказывает на движение снаряда значительно большее влияние,
чем введенные выше малые поправки.
1) Первое приближение, при котором не учитывается вращение Земли
и гравитационное поле принимается однородным, приводит к элементарной
параболической теории полета снаряда. Уравнения движения в этом случае
имеют простой вид:
'х = 'у'=0, 'z'=—g. A0.10.16)
Если в момент 2 = 0 снаряд вылетает из начала координат со скоростью
(щ, v0, w0), то решение имеет вид
x = uot, y — vot, z = wot—^-gt2. A0.10.17)
13 л. А. Парс
194 ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА [Гл. X
2) Во втором приближении учитываются члены порядка со, а другие
малые члены отбрасываются. При этом получаем
'х — 2cosin9^O, A0.10.18)
V +¦ 2cosin Qx + 2со cos 9z = 0, A0.10.19)
'z — 2cocoaQy=—g. A0.10.20)
Это — классические уравнения, описывающие движение снаряда отно-
относительно вращающейся Земли. Интегрирование уравнений A0.10.18) —
A0.10.20) производится достаточно просто. Однако следует помнить, что они
приближенные и потому решение их описывает движение лишь с точностью
до величин порядка со или, если формула их не содержит, то с точностью
до наинизшей степени со.
Прежде чем приступить к интегрированию, отметим еще одно обстоятель-
обстоятельство. Форма уравнений позволяет произвести замену независимой переменной
и от t перейти к т = со?. При этом со исключается из уравнений, кроме сла-
слагаемого g/co2. Решение дает нам х, у, z как функции от т = coZ, и формулы
будут содержать в качестве линейных множителей параметры Uo, Vo, Wo, Г,
равные соответственно u0/co, vqI'со, wo/a, g/co2. Переменная at безразмерна,
а каждый из параметров Uq, Vo, Wo, Г имеет размерность длины.
Перейдем теперь к решению уравнений A0.10.18) — A0.10.20). Из урав-
уравнений A0.10.18) и A0.10.20) имеем
х = и0 + 2сог/ sin 9, z = w0 — gt + 2сог/ cos 9. A0.10.21)
Подставляя эти выражения для хж z в уравнение A0.10.19), получаем диффе-
дифференциальное уравнение относительно у:
"у + 4со2г/ = —2со (и0 sin 9 + w0 cos 9) + Bgco cos 9) t. A0.10.22)
Отсюда
\ I it in \
у =-*& sin 2Ш — у (~-sin9-)--^-cos9) A — cos2coi) +
+ ^2 cos9 Bfitf —sin 2oa*). A0.10.23)
Подставляя теперь найденное у в уравнения A0.10.21) и интегрируя, полу-
получаем окончательное решение, выраженное через со?:
A0.10.24)
где
P = l— cos2co?, (? = 2coif — sin 2^t, R = 1 — cos 2co? — уBсо^2. A0.10.25)
Старшие члены в выражениях для Р, Q, R равны соответственно 2 (со?J,
§ 10.10]
ДВИЖЕНИЕ СНАРЯДА
195
Рассмотрим два частных случая:
а) Если не все и0, v0, w0 равны нулю, то, сохраняя члены порядка со
и пренебрегая членами более высокого порядка, получаем более точное реше-
решение, чем A0.10.17):
, х = uot -f (v0 sin 9) at2,
у = vQt — (u0 sin 9 + w0 cos 9) cat2 -\- -^ (g cos 9) at3,
z = wot— у gt2 + (y0 cos 9) cat2.
A0.10.26)
При сравнительно небольших значениях t эти формулы дают вполне
достаточную степень точности для большей части приложений. Решение
можно выразить также через переменную т:
х — Uox -{- F0t2 sin 9,
у = Vox — (Uo sin 9 + WQ cos 9) т2 + -i- Гг3 cos 9,
A0.10.27)
Рассмотрим теперь другой способ получения решения A0.10.26), справедливый
с точностью до членов порядка со. Уравнение движения в векторной форме имеет вид
х г + <а X (со X г) =д.
A0.10.28)
Чтобы найти приближенное решение, справедливое с точностью до членов порядка со,
поступим следующим образом. Отбросив в уравнении A0.10.28) члены порядка со2,
будем иметь
У+2са хг = д.
Если при t~0 r = 0 и г = и, то после интегрирования получим
г =u-\-gt.
Пренебрегая здесь членами порядка со, находим первое приближение:
A0.10.29)
A0.10.30)
A0.10.31)
Чтобы найти второе приближение (а это как раз нам и требуется), подставим выраже-
выражение A0.10.31) в отброшенный нами малый член в уравнении A0.10.30). Таким образом,
с точностью до членов порядка со будем иметь
— 2» х
Окончательно получаем
r = ut+— gfi— (
A0.10.32)
A0.10.33)
Полагая и={щ, v0, w0}, g={0, 0, —g}, co={ — cocosO, 0, cosinG}, видим, что реше-
решение A0.10.33) эквивалентно решению A0.10.26).
б) Если частица начинает движение из состояния покоя (начало коорди-
координат мы помещаем над поверхностью Земли), так что все щ, v0, Wq равны нулю,
то главные члены решения имеют вид
х = -jjr (g cos 9 sin 9) со2*!4 = i- Гт4 cos 9 sin 9,
1 1
y = — (g cos 9) co?3 = -5- Гт3 cos 9,
z= -y
A0.10.34)
13*
196 ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА ГГл. X
Как и следовало ожидать, наиболее существенным оказывается отклонение
от вертикали к востоку. В самом деле, поскольку
у = i со/sine, A0.10.35)
отклонение к югу мало по сравнению с отклонением к востоку.
3) Вернемся теперь к уравнениям A0.10.15) и произведем сравнительную
оценку различных членов, которыми мы пренебрегли в п. 2. Выясним, какие
из этих членов наиболее существенны для более точного расчета. Для это-
этого необходимо определить численные значения различных коэффициен-
коэффициентов. Рассмотрим более подробно первое уравнение и по-прежнему будем
считать Я, = 51°30' (так что р будет приближенно равно 6'). Имеем
2со sin 9 = 1,14- ЮЛ -f-=l,54-10-<\
со2 sin2 9 = 3,25• 10~9, ю2 cos 9 sin 9 = 2,57 • 10~9,
Что касается последнего члена в правой части первого уравнения A0.10.15),
, , 3g *
то коэффициент при х равен -| z, и даже если z имеет порядок одной мили
2
(так что — == опер) > то и тогда этот коэффициент равен всего лишь около
1,17 • Ю-9.
Итак, можно заключить, что для более точного расчета самым важным
является первый член в правой части, а именно — (g/a) x; он важнее, чем
члены порядка со2, члеиы, содержащие ей?, или члены порядка #(р/яJ.
Аналогичные замечания можно сделать и в отношении второго и третьего
уравнений A0.10.15). Таким образом, уравнения третьего приближения для
задачи о полете снаряда запишутся в следующем виде:
х — 2<и sin 9 у = — п\х,
У_|_ 2и sin 9 х+ 2со cos 9 z = — п2у, У A0.10.36)
z = 2<и cos 9 у = —g+ 2n2z,
где ri1 --=¦ g/a.
§ 10.11. Диссипативная функция Релея. Если среди заданных сил
имеются силы, зависящие от скорости, то они могут оказать влияние на чле-
члены QT в уравнениях Лагранжа F.2.1). В некоторых случаях, когда силы явля-
являются гироскопическими (например, в задаче о движении заряженной частицы
в магнитном поле, сМ. § 10.6), они могут быть учтены путем присоединения
к выражению для L соответствующих линейных членов. В этом параграфе
мы рассмотрим другой класс задач, связанных с силами, зависящими от ско-
скорости. Речь будет идти о силах сопротивления, или диссипативных силах,
действующих на каждую частицу в направлении, противоположном ее ско-
скорости. Мы ограничимся исследованием простого случая, когда сила сопротив-
сопротивления пропорциональна скорости. Уравнения движения B.2.12) запишутся
теперь в форме
т'ТхТ = ХТ + Х'г - кг'хт, г = 1, 2, .... N, A0.11.1)
причем коэффициенты кг, подобно коэффициентам тпт, будут иметь одно и то
же значение для трех членов, относящихся к одной частице: к3г_2 = к3г_{ =
= кЯг. Коэффициенты &, подобно коэффициентам гп, положительны, но, в от-
§ 10.11] ДИССИПАТИВНАЯ ФУНКЦИЯ РЕЛЕЯ 197
личие от т, они могут зависеть как от х, так и от г. Так как при произвольном
виртуальном перемещении
2х;ва:г = 0, B.2.10)
то основное уравнение C.1.1) принимает теперь вид
N N
2 (тгхг - ХТ) Ьхт + 2 krXr&Cr = 0. A0.11.2)
г=1 г=1
Предположим, что система голономна и имеет п степеней свободы, и вве-
введем лагранжевы координаты qt, q2, . . ., qn. Рассмотрим простой случай,
когда переменные х зависят только от q и не зависят от t, а силы Хг (т. е. за-
заданные силы, не являющиеся диссипативными) консервативны. Первое сла-
слагаемое в левой части равенства A0.11.2) известным образом (§ 6.1) выражает-
выражается через лагранжевы координаты, остается рассмотреть второе слагаемое
N
2 ктхг8хт. Согласно лемме 1 § 6.1 имеем
8= 1 8= 1 U'S
Отсюда
N n N .
KrXTOXr— 2j \ 2j Kr X'~T-J °Qs- (IV.11.1)
Г=1 8=1 Г«1 5<?S
Введем диссипативную функцию Релея F, представляющую собой сумму
-о- 2 ^гжг) выраженную через q и д. Эта функция в известном смысле анало-
г=1
гична функции кинетической энергии Т: она представляет собой однородную
квадратичную форму переменных q с коэффициентами, зависящими от q,
и является определенно-положительной при всех значениях q. Уравнение
A0.11.4) можно теперь представить в следующей форме:
JV n
2J.JS, — V Л?_ к„ СЮ ЦБ)
Г=1 8=1 ^S
Основное уравнение A0.11.2) после преобразования первого слагаемого (§ 6.1)
принимает вид
п
) г У оаг = 0. A0.11.6)
оЯт ^Ят
Оно справедливо для произвольных значений бд; таким образом, мы полу-
получаем п уравнений движения
d
4
Физический смысл функции F очевиден: численное значение F в любой
момент времени равно половине скорости потери энергии, расходуемой на пре-
преодоление трения. Это истолкование подтверждается и соотношением A0.11.7):
умножая r-е уравнение на qr и суммируя по г от 1 до п, находим (см. § 6.7)
2=-2F. A0.11.8)
r=l d1r
198 ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА [Гл. X
В качестве примера рассмотрим колебания системы около положения
устойчивого равновесия при наличии диссипативных сил рассматриваемого
типа. Диссипация, очевидно, способствует устойчивости. Как обычно, при-
примем, что в точке О функция V равна нулю, так что (поскольку V имеет в точке
О минимум) V > 0 в окрестности точки О, но не в самой этой точке. Если при
t = 0 энергия Т + V имеет значение С, то согласно A0.11.8) при f>0 T +
+ V < С; следовательно, при t > 0 V < С и равновесие устойчиво.
Приведенные рассуждения, однако, не являются полными. В общем слу-
случае при t —у оо смещение стремится к нулю и колебание затухает. Когда
смещение стремится к нулю, говорят об асимптотической устойчивости;
когда же оно сохраняется малым (см. § 9.9), то говорят просто об устойчи-
устойчивости.
Докажем, что наличие диссипативных сил превращает обычную устой-
устойчивость в асимптотическую. Рассмотрим для простоты систему с двумя сте-
степенями свободы. Пусть х и у — главные координаты системы без затухания,
так что
у ygV)- A0.11.9)
Введем теперь диссипативные силы, соответствующие диссипативной функции
^ , A0.11.10)
где А, Н, В с достаточной степенью точности можно считать равными их
значениям в положении равновесия. Уравнения движения запишутся в виде
+ Hx = O. J
A0.11.11)
> + By+q*y+Hx = <
Заметим, что если форма F лишь знакопостоянная, то движение может
и не быть асимптотически устойчивым, например, если А = Н = 0, то дви-
движение по координате х будет представлять гармоническое колебание. Если,
однако, F— определенно-положительная форма, то обе переменные х и у
стремятся к нулю при ?—>- оо. В самом деле, решения уравнений A0.11.11)
строятся как линейные комбинации членов е1^, el2t, е1^' и eXit, где ki, к2,
к3, kt суть корни уравнения четвертой степени
(Я," + Ак + р2) (к2 + Вк + q) — Я2*2 = 0, A0.11.12)
причем все они имеют отрицательные вещественные части. В самом деле, пусть
/ (к) обозначает левую часть уравнения A0.11.12). Функция / (z) не имеет
действительных или чисто мнимых нулей, и изменение amf (z) при обходе
контура, состоящего из отрезка действительной положительной полуоси,
дуги большого круга в первом квадранте и отрезка положительной мнимой
полуоси, равно нулю. Поэтому уравнение A0.11.12) не имеет корней в первом
квадранте. Поскольку коэффициенты в уравнении действительны, его корни
комплексно-сопряженные, и, следовательно, справа от мнимой оси уравне-
уравнение не имеет корней. Таким образом, все четыре корня лежат слева от мнимой
оси и действительные части их отрицательны.
§ 10.12. Гироскопическая система с диссипацией. Рассмотрим голоном-
ную систему с п степенями свободы, в которой т первых лагранжевых коор-
координат qi, q2, . • ., qm являются циклическими. Предположим, что система
обладает диссипацией типа Релея, влияющей только на явные координаты,
так что
F= 2 2 frsQrqs, A0.12.1)
r=m-\-1 s=m+1
§ 10.12] ГИРОСКОПИЧЕСКАЯ СИСТЕМА С ДИССИПАЦИЕЙ 199
где коэффициенты /„ зависят от (qm+i, qm+2, ¦ ¦ ¦ , In)- Первые т уравнений
Лагранжа дают
4^ = Рг, г=1,2, .... т. A0.12.2)
dqr
т •
Составляем функцию Рауса, для чего L — V $rqr выражаем через qm+i,
r=l
gra+2, . . . , qn\ qm+u qm+2, ¦ ¦ -, Qn, Pi, P2, • • ., Pm (см. § 10.1). С помощью
уравнений A0.11.7) уравнения движения в явных координатах можно запи-
записать в виде
_(_-_-_ = —, г = т+1, т+2, ..., п. A0.12.3)
dqr
Примером системы такого рода может служить система, содержащая гиро-
гироскопы с подшипниками без трения, когда движение платформы, на которой
укреплен гироскоп, испытывает трение релеевского типа.
Рассмотрим теперь проблему гироскопической устойчивости и выясним,
каково влияние диссипации по явным координатам. Если V, как функция
от явных координат, имеет в положении равновесия минимум, то диссипация,
как и следовало ожидать, повышает устойчивость. В общем случае мы имеем
асимптотическую устойчивость по явным координатам. Если же V имеет
максимум в положении равновесия, то дело обстоит иначе. Даже тогда, когда
при отсутствии диссипации имеет место устойчивость для достаточно боль-
больших значений Р (§ 10.3), введение диссипации вызывает неустойчивость.
Чтобы убедиться в этом, рассмотрим снова задачу о спящем волчке
{§. 9.9) и предположим, что имеется пара сил трения с моментом ка>, препят-
препятствующим вращению оси волчка и пропорциональным угловой скорости со.
Будем считать, что к постоянно и не зависит от положения оси. Диссипатив-
ная функция имеет вид
1 i • •
или, приближенно,
F = ±k& + z*), A0.12.5)
причем направляющие косинусы оси выбраны равными A, у, z), как в § 9.9.
Допустим на минуту, что у и z малы (фактически это не выполняется). Урав-
Уравнения движения будут иметь вид (см. (9.9.1))
1'
J
2pz-qy=-2sy,
z — 2ру —qz=— 2sz,
где 2s = к/А > 0. Полагая, как и ранее, w = у + iz, получаем
w — 2i(p + is) w — qw = 0. A0.12.7)
Даже если считать, что р2 > q + s2 (вместо р2 > q), то окажется, что верти-
вертикальное положение оси волчка неустойчиво. Решение содержит слагаемые
exp i {(р + is) ± (а + *Р)} t = ехр {(—* + р) + i (p ± a)} t, A0.12.8)
где а > р > s > 0, и одно* слагаемое имеет множитель e<P~s)'. Сделанное
ранее предположение о том, что ось волчка остается вблизи направленной
вверх вертикали, не выполняется, и вертикальное положение оси является
неустойчивым. (Как уже отмечалось, линейное приближение оказывается
200 ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА ?Гл. X
достаточным для установления неустойчивости, тогда как в противополож-
противоположном случае, когда | w | остается малым, устойчивость не может быть гаранти-
гарантирована на основании линейного приближения.) Значения аир определяются
формулами
2а2 =V(jfi-q- S2J + 4pV + {р2 _ q _ s2); | (Ю12
- q -¦ s2J + 4p2s2 - (pz - q - s2) J
2 (p2-s2) = у (p*-q+ s2J+ 4gs2- (p2-g + s2) > 0. A0.12.10)
§ 10.13. Уравнения Гамильтона. Мы уже отмечали (§ 6.4), что п урав-
уравнений Лагранжа второго порядка для голономной системы можно заменить
2/г уравнениями первого порядка, имеющими вид
х = Х. F.4.4)
Здесь х в. X — векторы (матрицы-столбцы). Этого, очевидно, можно достиг-
достигнуть, выбрав в качестве переменных п координат qr та п скоростей со,. = qr.
Но значительно более удобную и важную форму уравнений первого порядка
мы получим, если в качестве переменных возьмем п координат qr и п импуль-
импульсов рг (§ 6.10).
Предположим сначала, что система голономна и консервативна и обла-
обладает п степенями свободы. Имеем
Рг = ~, г=1,2, .... п. A0.13.1)
dqr
Выразим из этих уравнений q через р. Скорости q являются линейными функ-
функциями от р с коэффициентами, зависящими от q (иногда также от t). Подстав-
Подставляя эти выражения для q в соотношение
п п
2?г-^ L=^prqr-L, A0.13.2)
получаем функцию от р, q та t. Эта функция называется функцией Гамильтона
и обозначается через Н. Таким образом, мы получаем функцию Гамильтона
из соотношения A0.13.2) после замены в нем q на р. Она представляет собой
квадратичную форму от р с коэффициентами, зависящими от q и t. Функция
Гамильтона
Н = И (qu q2, . ¦ ., qn; Pi, рг„ ¦ ¦ ¦, Pn; t) A0.13.3)
зависит от переменных q и р, тогда как функция Лагранжа (§ 6.6) зависела
от q и q. Кратко функцию A0.13.3) можно записать так:
Н = H(q; p; t). _ A0.13.4)
Рассмотрим теперь произвольную вариацию q та. q (или соответственно-
произвольную вариацию q и р), при которой t не варьируется. Имеем
п
*тт ^Л I s* , ' с dL s dL s' \
г=1 ЧГ д9г
п
•= 2 (<lrbPr-~8qr) ¦ A0.13.5)
§ 10.13] УРАВНЕНИЯ ГАМИЛЬТОНА 201
A0.13.6)
A0.13.7)
Отсюда
Переходя к
*
Qr =
уравнениям
Р
dH
~~ дрг'
dL
dqT
движения
г dt \
dL
dqr
\
dH
dqr
dL
dqr '
видим, что они эквивалентны системе 2п уравнений
ОН ' дН . п ,.„,„„,
qr = Tp7' Pr=~~^q7' г=1,2, .... га. A0.13.8)
Это — уравнения движения Гамильтона, полученные им в 1834 г. Уравне-
Уравнения Гамильтона играют исключительно важную роль в аналитической
механике. Они имеют форму F.4.4), но отличаются от нее тем, что 2п входя-
входящих в них зависимых переменных сгруппированы в п пар (qT, pr), а правые
части имеют форму, указанную в уравнениях A0.13.8).
Прежде всего отметим, что две группы уравненииA0.13.8) неодинаковы
по своему содержанию. Первые п уравнений
l = f- A0.13.9)
получены исключительно на основе определения функции В и совершенно
не связаны с законами динамики. Они эквивалентны п уравнениям, опреде-
определяющим переменные р:
Рт = -^-- A0.13.10).
dqT
В самом деле, уравнения A0.13.9) определяют q как линейные функции от р,
а уравнения A0.13.10) определяют/) как линейные функции от q. Если раз-
разрешить уравнения A0.13.9) относительно р, то получим соотношения
A0.13.10), а разрешая последние относительно q, придем вновь к уравнениям
A0.13.9). Динамические закономерности находят отражение лишь во второй
грулле уравнений A0.13.8):
Рг=~. A0.13.11)
То обстоятельство, что две группы уравнений Гамильтона различаются по со-
содержанию, несущественно для приложений, и их можно считать совершенно-
равноправными.
С помощью функции Гамильтона можно составить уравнения движения,
она заключает в себе полное описание возможных движений механической
системы.
Уравнения Гамильтона A0.13.8) были выведены нами для голономной
консервативной системы, однако нетрудно видеть, что они могут быть полу-
получены и для механических систем других типов.
1) Если система не является голономной, то, пользуясь обозначениями
§ 6.2, можно написать
i
2 ^5™-' г=1'2' •••'п-
m=l
К этим уравнениям присоединяются I дополнительных уравнений связи
п
о, r = i,2, .... г. (io.i3.i3)
s=l
202 ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА [Гл. X
2) Если система голономна и имеет п степеней свободы и если помимо сил,
обладающих потенциальной функцией V, имеются еще другие заданные силы,
то в обозначениях § 6.5 будем иметь
г=1, 2, ...,»•
Предполагается, что функции QT зависят только от q и не зависят от q. (В об-
общем случае, когда Q зависят также и от q, уравнения не имеют формы х =
= X, но их можно привести к этой форме, если каждая функция Qr есть
линейная форма от q с коэффициентами, зависящими только от q.)
3) Если система голономна и имеет п степеней свободы и если имеются
силы трения типа сил Релея (§ 10.11), то уравнения движения записываются
в следующей форме:
*r=-dj7* ^""^г~^7' г=и2>••"ге- A0-13-15)
Поскольку F есть однородная квадратичная форма от q, эти уравнения можно
привести к виду х = X.
4) Варианты 2) и 3) легко обобщаются на случай неголономной системы.
Для этого достаточно добавить к правым частям уравнений для рт слагаемые
i
2 КпВтт и присоединить к полученным уравнениям I уравнений связи
m = l
<io.i3.i3).
Функцию Гамильтона Н мы получили из функции Лагранжа L. Можно
решить и обратную задачу — найти функцию L, зная функцию Н. В самом
п
деле, L представляет собой функцию вида 2 РгЯг — Н, в которой р заменены
на q, а такую замену легко сделать с помощью уравнений qr = дН1дрг.
§ 10.14. Уравнение энергии и явное выражение для Н. Для голономной
консервативной системы функция Н в самом общем случае зависит от q, p и t,
хотя в большей части конкретных примеров t отсутствует. Полная производ-
производная от Н по t равна
-л-=-1г+21*г9г+2 жР" A0л4Л)
и в силу уравнений Гамильтона
= ^- A0 14 2)
Таким образом, если Н не зависит явно от t, то эта функция сохраняет посто-
постоянное значение во все время движения:
Н = h. A0.14.3)
Этот результат есть не что иное, как интеграл Якоби (§ 6.7). (Напомним, что
если L не зависит явно от t, то и Н не зависит явно от t, и наоборот.)
Получим теперь явное выражение для функции Н. Для натуральной
системы
п п
Г = Г^уЦ2 W A0.14.4)
r=l s=l
§ 10.14]
УРАВНЕНИЕ ЭНЕРГИИ И ЯВНОЕ ВЫРАЖЕНИЕ ДЛЯ Я
203
2
r=l
A0.14.5)
так что Н совпадает с полной энергией T-\-V, причем Т выражено через р
вместо q. Поскольку
находим, что
pr= Zi arsqs
4r= Zj
s=l
r = 1, 2, ..., п,
Г=1,2,...,П,
A0.14.6)
A0.14.7)
где, как и в § 10.4, (crs) обозначает матрицу, обратную матрице (ars). Учи-
п
тывая, что 2Т — 2 PrQr, напишем явное выражение для Н в следующей
г=1
форме:
п п
A0.14.8)
Г=1 6=1
Переход в функции Т от q к р производится аналогично тому, как осу-
осуществляется переход от точечных координат к линейным в уравнении кони-
конического сечения в однородных координатах. Кроме того, Т можно выразить
через р с помощью уравнения
«И
«21
«711
Pi
«12
«22
ап2
Р2
¦ • ¦ а1п
• ¦ • п%п
• • • «П71
... Рп
Pi
Pi
Pn
IT
= 0.
A0.14.9)
Определитель размером (n + 1) X (n + 1) равен нулю, так как, умножая
r-й столбец на qr и суммируя от г = 1 до г = и, мы получаем последний стол-
столбец. Разлагая определитель, находим явное выражение для Т в виде квадра-
квадратичной формы от р.
Особый интерес представляет простой частный случай, когда система
отнесена к ортогональным координатам; при этом матрица (aTS) диагональна.
Если
п
L = ^ry,a.yr-V, A0.14.10)
то
pr =
г=1
A0.14.11)
A0.14.12)
Мы видим, что в этом случае выражение для Н составляется сразу.
204 ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА [Гл. X
Рассмотрим теперь более общий случай ненатуральной системы
L = Т2 + Tt + То - V. A0.14.13)
В этом случае, как и в § 6.8, можем написать
i + T0-V) = T2+V-T0 A0.14.14)
и Н равно выражению Т2 -\- V — То, в котором q заменены на р. Полагая,
согласно формулам F.1.6) и F.1.7),
1Ь II
= ~2~ 2 2 а™ЯгЯа, Л
Г=1 8=1 Г=1
находим
Поэтому
r^l,2,...,n, A0.14.15)
s=l
¦¦ 2jCrs(Pe-as). A0.14.16)
8=1
n n n
¦ S Qr(Pr — Or)—- 2 H crs(/?r — ar)(ps — as), A0.14.17)
r=l r=l s=l
и выражение для i/ записывается в следующей окончательной форме:
п п
Я = 4-2 2 cn(Pr-ar)(p,-a.)+V-T0. A0.14.18)
Г=1 8=1
Таким образом, функция Н представляется в виде суммы Н2 + Hi + НОь
где Нт — форма степени г относительно р. Опуская для краткости знак
суммы, можем написать
1 1
Л2 — ~crsPrPs, Нi-— — crsarps, Но = уcTSards-\-V — То.
В качестве примера рассмотрим заряженную частицу, движущуюся
в поле механических и электромагнитных сил. Согласно A0.6.18)
? = |т(г2 + уЧ22) + 7(^-|- А«У+ Az'z) — V — eQ, A0.14.19)
где Q — скалярный потенциал, а {Ах, Ау, Az} — векторный потенциал
электромагнитного поля. В обозначениях F.10.4) имеем
px = mx + -jAx A0.14.20)
и два аналогичных уравнения. Выражение для Н имеет вид
S 10.15] ГЛАВНЫЙ ТРИЭДР 205
§ 10.15. Главный триэдр. Рассмотрим снова движение механической
системы относительно подвижной системы отсчета F' (§ 10.7). Обсуждаемый
здесь вопрос не затрагивался нами в § 10.7, так как это увело бы изложение
далеко в сторону. Будем пользоваться обозначениями § 10.7. Обозначим через
р' кажущийся импульс:
A0.15.1)
а через h' — кажущийся момент количеств движения:
h[ = Sm(yz— zy), h'2 — Sm(zx— xz), h'3 = Sm(xy— ух). A0.15.2)
Таким образом, р' и ft' — это импульс и момент количеств движения
системы, какими они представляются для наблюдателя, находящегося в сис-
системе F'.
Систему F' можно выбрать так, чтобы р' = h' =0. Тогда для любой
системы, неподвижной относительно F', также будем иметь р' = й/ = 0.
Для доказательства, что подвижную систему можно выбрать так, чтобы
р' = Ь! =0, заметим прежде всего, что условие р' = 0 будет выполнено, если
выбрать систему отсчета так, чтобы центр тяжести G находился относительно
нее в покое. Проще всего взять точку G за начало подвижной системы коор-
координат. Тогда составляющая /г, истинного момента количеств движения h
(в отличие от кажущегося момента количеств движения Л') будет иметь сле-
следующий вид:
h1 = Sm{y(w+z — хд2 + г/6,) — z{v+ y — zQt + х63)} =
=:/г; + Л91-#62-С93, A0.15.3)
где А, В, С, F, G, II— осевые и центробежные моменты инерции системы
в рассматриваемый момент времени. Равенство h' = 0 поэтому возможно
лишь тогда, когда
AQi — Я92 — GQ^ = klt л
— HQl+BQ2 — FQ3 = h2, \ A0.15.4)
_ G6, — FQ2 + С83 = h3." J
Эта система уравнений имеет единственное решение 64, 92, Э3, так как опре-
определитель из коэффициентов отличен от нуля; эти коэффициенты определяют
эллипсоид инерции всей системы.
Таким образом, хотя частицы системы совершают движение относитель-
относительно «неподвижной» системы отсчета F, можно указать такую подвижную сис-
систему отсчета F', в которой р' и h' все время будут равны нулю. Эту систему
назовем главным триэдром.
Если F' есть главный триэдр и начало подвижной системы отсчета выбра-
выбрано в точке G, то формула A0.7.8) запишется в виде
Т^Х + уЛШЧ-уТю2 A0.15.5)
и будет представлять обобщение теоремы Кёнига. Мы видим, что ? < Т.
Взяв произвольную (не обязательно ньютоновскую) систему отсчета F.
можно показать, что для главного триэдра значение ? меньше, чем для
любой другой системы отсчета. Таким образом, главный триэдр представляет
систему отсчета, в которой кажущаяся кинетическая энергия имеет наимень-
наименьшее возможное значение.
Ньютоновская космология основана на концепции абсолютного пространства,
евклидова по своей структуре, абсолютного времени и неподвижной в пространстве
системы отсчета. Оставаясь в рамках этих понятий, можно в качестве системы отсчета
206 ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА [Гл. X
взять главный триэдр для всей материальной Вселенной. Если Вселенную считать состоя-
состоящей из некоторого числа массивных удаленных звезд, взаимное расположение которых
остается неизменным, и некоторого числа солнечных систем и комет, то звезды относи-
относительно главного триэдра будут находиться почти в покое, поскольку главный триэдр
обеспечивает наименьшее возможное значение кинетической энергии. Таким образом,
в этой системе звезды оказываются неподвижными.
Интересно теперь попробовать отказаться от ньютоновской системы отсчета как
независимой гипотезы и отождествить ее с главным триэдром для всей материальной
Вселенной. Если это сделать, то третий закон Ньютона окажется следствием второго
закона, а не независимым утверждением. В самом деле, рассмотрим некоторую материаль-
материальную систему, совершающую движение, и отнесем ее движение к триэдру, жестко связанному
с главным триэдром. Тогда из условий р' = ft' = 0 получим
Smz = 0, 1
у'—ух) = 0. J
A.0.15.6)
Sm(yz—zy) ^=0, Sm(zx—a;z) = 0, Sm{xy-
Считая второй закон Ньютона справедливым, приходим к выводу, что система всех
действующих на частицы сил эквивалентна нулю (если бы частицы составляли твердое
тело, то это тело находилось бы в равновесии). Система сил, состоящая из равных по
величине и противоположно направленных сил, приложенных к каждым двум частицам
(действующих вдоль прямой, их соединяющей), очевидно, эквивалентна нулю. И обратно,
любую систему сил, эквивалентную нулю, можно представить в .виде совокупности пар
равных по величине и противоположно направленных сил (если только все частицы
системы не расположены вдоль одной прямой, что мы исключаем). Чтобы убедиться
в этом, следует сначала рассмотреть случай трех (не лежащих на одной прямой) частиц
и затем провести доказательство методом индукции. Пусть имеется произвольная система
как угодно движущихся частиц. Выберем главный триэдр в качестве системы отсчета.
Если принять, что второй закон Ньютона справедлив, то третий (закон равенства действия
и противодействия) отсюда получается как следствие *).
*) Дальнейшее развитие идей этого параграфа содержится у J. le R о u x, Principes
mathematiques de la theorie de la Gravitation, Gauthier-Villars. Paris, 1931.
Глава XI
ПЕРЕМЕННАЯ МАССА
§ 11.1. Частица переменной массы. Функция Лагранжа. В специальной
теории относительности масса частицы считается переменной, зависящей
от скорости частицы. Если масса частицы в состоянии покоя равна ту, то при
движении со скоростью v ее масса будет определяться выражением
где с — скорость света. В большей части практических случаев отношение
vie мало и т можно считать равным т0. Отличие становится заметным лишь
тогда, когда vie приближается к единице: при v —*- с т —*- оо.
Поэтому необходимо исследовать, какие изменения претерпит развитая
ранее теория, если массу частицы считать функцией скорости: т = ср (v).
Теоретически нет необходимости требовать, чтобы функция ц>(ь>) была одной
и той же для всех частиц, хотя обычно в приложениях зависимость ср (v) при-
принимается в виде A1.1.1) для всех частиц.
В случае точки переменной массы второй закон Ньютона JP = mf запи-
записывают в форме JP =-т-(тог'): произведение массы на ускорение заменяют
производной от импульса. Логические основания для такой замены даются
теорией относительности. Первое, что бросается в глаза, это то, что в общем
случае направление ускорения не совпадает с направлением силы. В самом
деле,
P = mf-\-mv. A1.1.2)
Уравнения движения свободной частицы в неподвижных прямоугольных
осях координат имеют вид
±(тх) = Х, jL(my)-=Y, -^{mz)--=Z. A1.1.3)
Рассмотрим систему частиц переменной массы. В обозначениях § 2.2
уравнения движения B.2.12) заменятся следующими:
-^¦(т^г) = ХТ+Х'Т, r=l,2, ...,N. A1.1.3)
Для произвольного виртуального перемещения имеем
N
/1 Л.гОХг = и.
Основное уравнение C.1.1) запишется теперь в виде
N
2 {-згК*г)-Хг}в*г = О. A1.1.4)
г=1
Если-массы частиц постоянны, то уравнение A1.1.4) принимает, разумеется,
форму C.1.1).
208 ПЕРЕМЕННАЯ МАССА 1Гл. XI
Рассмотрим теперь голономную консервативную систему с п степенями
свободы. Введем лагранжевы координаты qi, q2, . . ., qn. Соотношение
n
&xr= T^ j-^&Zs и уравнение A1.1.4), справедливое для любой системы зна-
•i-J oqs
e= 1
чений 6gt, 6g2j ¦ • ч &Qm позволяют написать следующие уравнения:
. S-^^)-^^—?¦' *=1.2, ...,п. A1.1.5)
г=1
Применим к ним преобразование § 6.1. Для этого воспользуемся доказанными
ранее леммами, а именно:
^т_^дх^ F.1.3)
¦dqs
С помощью этих лемм уравнения A1.1.5) можно записать в форме
N . N
A1.1.6)
7
ИЛИ
-r 5my——I— Smv ^r— =—5—. A1.1.7)
Мы пишем символ S, поскольку суммирование производим по v частицам,
а не по N координатам. Это удобнее, так как масса каждой частицы зависит
от ее скорости.
Введем функцию
\ A1.1.8)
или, точнее.
Т7* С \ го /-г^ т Ат (\\ \ Q\
о
Уравнения A1.1.7) тогда запишутся в виде
d /JT*_,_^L=_W в=а1 2 in. A1.1Л0)
* V д-и ) . dg. dgs V
.Уравнения движения можно записать в форме Лагранжа, если положить
L = Т* — V. A1.1.11)
Отметим, что в общем случае Т* не является квадратичной формой от q,
как ото имело место в случае постоянных масс.
§ 11.2. Кинетическая энергия. Предположим теперь, что все координаты
хг зависят только от q и не зависят от I. Введем функцию Т — кинетическуя;
энергию, которую определим так, чтобы удовлетворялось уравнение энергии
в первой форме C.3.2):
^ A1.2.1)
11.4] ДВИЖУЩИЙСЯ ЭЛЕКТРОН 209
При замене Ьхг на хт основное уравнение A1.1.4) остается справедливым,
так что из A1.2.1) получаем
dT „
~dT-b
A1.2.2)
Отсюда
T = S \ v-^-(mv)dt = S (mv2 — f mvdv) = Smv2—T*. A1.2.3)
Определяемая этим соотношением функция Т есть функция кинетической
энергии. Если действующие на систему силы консервативны и обладают потен-
потенциалом V, то справедливо уравнение, аналогичное уравнению энергии:
Т + V = С. A1.2.4)
В случае постоянных масс выражение для Т принимает обычный вид
— Smv2, что было очевидно с самого начала.
§ 11.3, -Функция Гамильтона. Составим теперь выражение для функции
Гамильтона. Имеем
A1.3.1)
ддг dqT dqT
и, следовательно,
' ~ ' ' в /1 .„х „, modv + v =
T-\-V, A1.3.2)
Мы здесь воспользовались тем, что v2 представляет собой однородную квад-
ратичную функцию от q. Таким образом,
Н = Т + V, A1.3.3)
где Т следует выразить через q и р. Заметим, что Н не имеет той формы, к ко-
которой мы привыкли в задачах с постоянными массами. Теперь Т не является
квадратичной функцией от р.
§ 11.4. Движущийся электрон. Рассмотрим движущийся в пространстве
электрон. Имеем
т=—JP9. . A1.4.1)
/4
Следовательно,
V
/. »* Г / ,.9. -\
A1.4.2)
14 Л. А. Парс
208 ПЕРЕМЕННАЯ МАССА [Гл. XI
Рассмотрим теперь голономную консервативную систему с п степенями
свободы. Введем лагранжевы координаты gb q2, . . ., qn. Соотношение
п
&xr= V. T-^&qs и уравнение A1.1.4), справедливое для любой системы зна-
•*-J oqs
s= l
чений 6gn> &4i, ¦ ¦ ¦¦> ^Чт позволяют написать следующие уравнения:
N
2d , * ч дхг д\ . „ iл л л г-\
-jt(™rxr)-a?=—eX' i:=l12 "¦ A1Л'5)
Применим к ним преобразование § 6.1. Для этого воспользуемся доказанными
ранее леммами, а именно:
дхг_^дхт_ F.1.3)
¦a».
¦С помощью этих лемм уравнения A1.1.5) можно записать в форме
44
<lt I -^J '"-т . i /л ч»т~т а„ а„—, s— 1» 2, . . ., П,
r=l
ИЛИ
dv \ с dv dV ... . „.
\Smv—5—. A1.1.7)
dqJ dqs dqs
Мы пишем символ 5, поскольку суммирование производим по v частицам,
я не по N координатам. Это удобнее, так как масса каждой частицы зависит
от ее скорости.
Введем функцию
Т* = S f mv da A1.1.8)
или, точнее.
V
T* = S [ (f>(x)zdx. A1.1.9)
о
Уравнения A1.1.7) тогда запишутся в виде
Уравнения движения можно записать в форме Лагранжа, если положить
L = Т* - F. A1.1.11)
Отметим, что в общем случае Т* не является квадратичной формой от q,
как это имело место в случае постоянных масс.
§ 11.2. Кинетическая энергия. Предположим теперь, что все координаты
хг зависят только от q и не зависят от t. Введем функцию Т — кинетическую
энергию, которую определим так, чтобы удовлетворялось уравнение энергии
s первой форме C.3.2):
AT • • •
^L z). A1.2.1)
§ 11.5] ЭЛЕКТРОН В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ 211
полученные из уравнения _Р = -т- (mv) или из уравнений Лагранжа, имеют вид
у 1 ;г ¦
где через р обозначено выражение у 1 ;г ¦ Здесь g обозначает отношение
для определенности предполагается, что g > 0, так что е и Е одного знака. Интегри-
Интегрируя уравнения A1.4.13), получаем
X Un у
Г= n ' n =?*• A1.4.14)
О On О '
где ро—у 1 ^Г ¦ Возводя в квадрат равенства A1.4.14) и складывая, а также
используя равенство у2 = с2A — р2), находим
с2 с2
-?2~ = -pT + g2«2 = g2(a2 + Z2), A1.4.15)
где
а=~^^~7^й^^л- (И.4.16)
Теперь уже нетрудно довести решение до конца. Из формулы A1.4.15) видно, что
вместо времени t удобно ввести новую независимую переменную 6:
Уравнения A1.4.14) тогда можно записать в форме
dx сщ dy
-^= —= «oa, -^- = Cashe. A1.4.18)
Отсюда
x = щав, у= са (chQ — 1). A1.4.19)
Траекторией электрона служит кривая
Она получается из цепной линии
— = ch-^ 1, A1.4.21)
если ординату у увеличить в отношении с/и0.
§ 11.5. Электрон в электромагнитном поле. Функция Лагранжа в этом
случае имеет вид (см. A0.6.18))
где, как и ранее, W = V + ей, Q — скалярный потенциал ж Л — векторный
потенциал электромагнитного поля.
Составим теперь выражение для функции Гамильтона в координатах х,
у, z. Имеем
PX = 1L. = J*?- + ±AX A1.5.2)
дх "
и два аналогичных уравнения; в них AX,AV,AZ —составляющие вектора Л,
1 5- • Да
1 5- • Далее находим
A1.5.3)
14*
212 ПЕРЕМЕННАЯ МАССА [Гл. XI
и, поскольку
окончательно получаем
(У A1.5.5)
В качестве примера рассмотрим задачу о движении электрона в скрещивающихся
электрическом и магнитном полях. Пусть электрическое поле имеет составляющие
{—Е, 0, 0}, а магнитное поле — составляющие {0, 0, у}; заряд электрона обозначим
через —8. Векторный потенциал равен -у у {—У, х, 0}, и
L = moe2(l-p) —^-(ху~ух) + еЕх. A1.5.6)
Из уравнений Лагранжа (или непосредственно) получаем уравнения движения
~ky, A1.5.7)
где g = eE/m0, к = гу/тос, причем ш g ж к принимаются положительными. Если элек-
электрон первоначально двигался в плоскости z = 0, то он все время будет двигаться в этой
плоскости.
Рассмотрим классическую задачу о движении электрона при следующих начальных
условиях: пусть в момент t = 0 он находится в начале координат и скорость его равна
нулю. Находим сразу первые интегралы уравнений A1.5.7) и A1.5.8):
• ¦
J = gt-ky, j = kx. A1.5.10)
Чтобы довести интегрирование до конца, умножим уравнения A1.5.7) и A1.5.8) соответ-
соответственно на х/р и у/р и сложим. Проделав это, получим
d I 1 у2 \ вх
1г(т^г) р ¦ A1-5Л1)
Учитывая, что У2~е2A—р2), находим
1 с2 \ вх
Отсюда
с2 •
—^гр = г* (И.5.13)
и, следовательно,
~- = c2+gx, A1.5.14)
Равенство A1.5.14) позволяет представить уравнения A1.5.10) в следующей форме:
х (с2 + gx) = с2 (gt - ky), A1.5.15)
'у (с2 + gx) = сЧх. A1.5.16)
11.5] ЭЛЕКТРОН В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ 213
Дифференцируя уравнение A1.5.15) по (в исключая у с помощью уравнения A1.5.16),
получаем
(е2 + ртJ х'+ g (с2 + gx) z2 = c*g (c2 + gx) - cVx. A1.5.17)
Это соотношение, связывающее * и х, можно переписать в эквивалентной форме:
gZ)x. A1.5.18)
Отсюда после интегрирования получаем
(с2 + g*J *а = c*x{2c*g - (е2А2 - g2) x). A1.5.19)
Мы предполагаем, что ск > g, что эквивалентно неравенству у > Е, а последнее
условие выполняется практически во всех интересующих нас случаях.
Определим теперь траекторию электрона. Из A1.5.19) и A1.5.16) находим
где
г=_1^_ A1.5.21)
(И-5-22)
Чтобы получить параметрические уравнения траектории, налишем
х = 2а sin2 В = а A — cos 29). A1.5.23)
Из уравнения A1.5.20) тогда находим
dy = p tg в dx = Aap sin2 9 tffl = 2ap A — cos 26) d9,
и, следовательно,
у = pa B9 — sin 29). A1.5.24)
Уравнения A1.5.23) и A1.5.24) выражают траекторию электрона в параметрической
форме. Если бы параметр р (который больше единицы) имел значение, равное единице,
то траекторией была бы циклоида с точками возврата, расположенными на оси Оу.
Мы видели ранее (пример 10.6В), что если масса электрона постоянна, то траекторией
электрона действительно является циклоида такого типа. Если же учесть изменение
массы, то циклоидальная траектория изменится вследствие увеличения параметра р
в направлении у. Наибольшее удаление электрона от оси Оу в процессе движения равно
Соответствующее удаление частицы постоянной массы т равно (см. A0.6.28))
(И.5.26)
Глава XII
УРАВНЕНИЯ ГИББСА—АППЕЛЯ
§ 12.1. Неголономные системы. Мы видели ранее, каким образом можно
применить уравнения Лагранжа к случаю неголономной системы, и в качест-
качестве примера рассмотрели в § 8.12 качение круглого диска. Однако уравнения
Лагранжа не очень удобны для изучения пеголопомных систем, и в этой главе
мы рассмотрим уравнения движения в новой форме, которая особенно удобна
в тех случаях, когда система неголономна (хотя, разумеется, уравнения эти
справедливы и для голономных систем). Начнем изложение с понятия о ква-
квазикоординатах .
Массы частиц, составляющих систему, теперь будем считать постоянными.
§ 12.2. Квазикоординаты. Лагранжевы координаты обладают тем свой-
свойством, что переменные х являются явными функциями от q и t. Весьма удобно,
особенно в случае неголономных систем, ввести координаты более общего
типа. В этих координатах каждая переменная хт является линейной функцией
от q, но эти функции в общем случае не являются полными производными
по времени. Каждое хт может быть представлено в виде линейной функции
от к переменных q, где к — число степеней свободы системы.
Рассмотрим неголономную систему с к степенями свободы и I уравнения-
уравнениями связи. Для описания этой системы необходимы к + I лагранжевых коор-
дднат <71? <72, . . . ., Qu+i- Возможные перемещения системы удовлетворяют
уравнению (см. § 5.7).
h+i
O=^BTSdqs + Brdt, r=l,2,...,l, A2.2.1)
8=1
где коэффициенты Brs, Вт суть функции от ql: q2, . . ., gft+z; t, имеющие
непрерывные первые производные в соответствующей области D изменения
переменных q1: q2, ¦ ¦ ., qh+Г, t.
Введем р новых величин 915 82, . • ., 8Р, где р — произвольное целое
число. Величины 0 не определены как функции от q и t, но их дифференциалы
представляют собой пфаффовы формы от q и t:
h+l
dQr=^]Crsdqs+Crdt, r = 1, 2, ..., p. A2.2.2)
8=1
Коэффициенты Crs, Ст здесь суть функции от gb qz, . . ., qq+i; t, имеющие
непрерывные первые производные в области D. Выражения в правых частях
равенств A2.2.1) и A2.2.2) представляют I -\- p независимых форм Пфаффа;
в общем случае они не являются полными дифференциалами. Величины
0 называют квазикоординатами. Будем далее писать 8Г = qh+t+T, так что
будем иметь п переменных qt, q2, . . ., qn, где п — к + I + P-, из которых
первые к + I представляют собой лаграпжевы координаты, а остальные р —
квазикоординаты; при этом
h+i
dqM+r=l]Crsdqs+Crdt, r = 1, 2, ..., р. A2.2.3)
8=1
§ 12.2] КВАЗИКООРДИНАТЫ 215
Разрешим теперь I + р уравнений A2.2.1) и A2.2.3) относительно I -f- p
дифференциалов dq, выразив их через оставшиеся к дифференциалов. Эти
предпочтительные к дифференциалов, через которые выражены остальные,
могут быть дифференциалами либо лагранжевых координат, либо квазикоор-
квазикоординат. Если эти выделенные координаты временно обозначить через cpi, фг, . .
- . ., фй, то для координаты qr, к ним не принадлежащей, будем иметь
ft
dqr = 2 Drs dtp. + Dr dt. A2.2.4)
8=1
Всего будем иметь I -j- p таких уравнений. Уравнения A2.2.4) в точности
эквивалентны системам A2.2.1) и A2.2.3). Следует подчеркнуть, что коэф-
коэффициенты Drs, Dr зависят От всех лагранжевых координат q и от времени t,
а отнюдь не от ф4, ф2, . . ., ф^; t.
Координата хт зависит от дь q2, . . ., qu+i', t, следовательно,
k+i
^r = ^^dqs + ^-dt, r = l,2, ..., N. A2.2.5)
s=l
Выразим дифференциал каждой из невыделенных координат в правой части
A2.2.5) через d(pi, d(pz, . . ., dy^, воспользовавшись для этого равенством
A2.2.4). В результате dxv выразится в виде линейной функции от Лр1; ^ф2, .. •
. . ., d(pk, dt; коэффициенты этой линейной формы будут содержать все лагран-
жевы координаты q и время t.
Изменим наши обозначения. В дальнейшем к выделенных координат
(которые могут быть либо лагранжевыми, либо квазикоординатами) будем
обозначать через gi, q2, . ¦ ., qu, а остальные I -\- р координат — через qu+i,
qu+2, • • -i Чп- Формула для dxT тогда примет вид
k
dxT^^arsdq,+ardt, r=l,2,...,N, A2.2.6)
8=1
а A2.2.4) запишется в виде
h
dqr= ^$rsdqs + $rdt, г^к + 1, к + 2, ..., п. A2.2.7)
8=1
Формулы A2.2.6) и A2.2.7) являются основными для развиваемой здесь
• • • *
теории. Производные хг можно выразить через к скоростей gl5 g2> ¦ • ч Qh-
Аналогично через них можно выразить и qr для г > к. Но в каждом случае
коэффициенты ars, ar, prs, pr содернгат координаты q, отличные от к выделен-
выделенных координат; в общем случае эти коэффициенты содержат все лагранжевы
координаты q и время t. Полученные формулы весьма удобны. Составляющие
скорости я,» (для всех N декартовых координат частиц) и qT (для невыделен-
невыделенных координат q) выражаются через систему составляющих скоростей по чис-
числу степеней свободы системы. Скорости gb q2, . . ., qh могут иметь произволь-
произвольные значения, но если эти значения заданы, то тем самым определены скоро-
скорости всей системы.
Виртуальные перемещения выражаются через произвольные приращения
6<7i, 8g2, . . ., 8qh следующим образом:
ft
6xr=2a«6gs, r = l,2, ..., N, A2.2.8)
8=1
h
%=SM?S. r = k + l, k-\ 2, ..., n. A2.2.9)
8=1
216 УРАВНЕНИЯ ГИББСА — АППЕЛЯ [Гл. XII
Приведем простые примеры.
1) Частица совершает плоское движение. Напишем
dq = х dy — у dx,
где х, у — декартовы координаты. Здесь q представляет удвоенную площадь,
ометаемую радиус-вектором, начиная с некоторого момента t0, и является
квазикоординатой.
2) В практике часто встречается случай, когда квазикоординатой являет-
является «полный поворот» твердого тела, начиная с момента t = t0, около заданной
оси, неподвижной или движущейся. Например, в задаче о волчке «полный
поворот» около оси волчка равен q. В общепринятых обозначениях (§ 8.6)
dq = d\p + cos 9 dq>.
Правая часть этого уравнения, очевидно, не является полным дифференциа-
дифференциалом, и q представляет собой квазикоординату.
§ 12.3. Пятая форма основного уравнения. Вычислим работу, совер-
совершаемую заданными силами на виртуальном перемещении. Выражение для
этой работы, фигурирующее в первой форме C.1.1) основного уравнения,
N
имеет вид 2 ХтЬхг. Подставляя сюда 8хг из A2.2.8), получаем
N ft N ft
2 XT6xr = 2 ( 2 Xrars) 8qs = 2 Qsbq*, A2.3.1)
Г=1 S=l Г=1 8=1
где
N
(?4=EU». A2.3.2)
r=l
Рассмотрим теперь соответствующее выражение, входящее во вторую
N
форму D.1.3) основного уравнения, а именно 2 Хг Ахг, где Ахг есть конечное.
г=1
а не бесконечно малое приращение скорости, совместимое с положением систе-
системы в данный момент времени. Из уравнения A2.2.6) для любой возможной
системы скоростей получаем
h
жг= Sar.ff. + ar, r = 1,2, ..., N. A2.3.3)
s=l
Если мы рассмотрим другую возможную систему скоростей q-^-Aq при
той же конфигурации системы, то будем иметь
П h
xr+Axr= 2 aTS(qs + Aqs)+ar, r =1,2, ...,N. A2.3.4)
s=l
Следовательно,
k
Axr = 2 a,TSAq's, r=l,2, ...,N. A2.3.5)
s-=l
Таким образом,
JV ft iV ft
2 XrAxr =2B XraTS) Aqs - 2 QsAq's, A2.3.6)
r—l s=l r=l s=l
где Q — те же коэффициенты A2.3.2), что и в первой форме основного урав-
уравнения.
§ 12.4] ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ 217
Рассмотрим, наконец, третью форму D.2.4) основного уравнения.
Из A2.3.3), дифференцируя, получаем
ft ft
х;=2а^+2т^ + ^Г' г=1,2, ..., TV, A2.3.7)
s=l s=l
n
где — обозначает оператор -тт-+ ^ <7т~з—• Если мы рассмотрим другую
m=l
возможную систему ускорений q-\-k.q при той же конфигурации системы
и тех же скоростях, то будем иметь
ft ft
i; + Ai; = 2a«('i + A?J + 2-%s-?. + -^:-, r = l,2, -.., N. A2.3.8)
8=1 8=1
Следовательно,
ft
Ai'rr= 2а„Д?« г = 1,2, ..., Ж A2.3.9)
s=l
Таким образом,
S ХгЛ^г = 2 ( S Xrars) Aq's = 2 <?A A2.3.10)
r=l s=l r=l s=l
и сюда опять входят те же коэффициенты QT.
Третья форма D.2.4) основного уравнения приводит теперь к соотно-
соотношению
п .... и
S mrxrAxr — 2 &Дд8' = 0, A2.3.11)
Г=1 8=1
представляющему собой пятую форму основного уравнения.
§ 12.4. Определение ускорения. Введем функцию Гиббса @
JV
\ 2 т^ A2.4.1)
г=1
/J • • • • • «
(или ~y Sm {хг + у2 + z2)), которую с помощью формул A2.3.7) выразим
через <?i, g2) • • •> QV- Функция Гиббса будет представлять собой полином от
G2 + Gt + Go, A2.4.2)
где G-i — однородная квадратичная функция от q^, q2, . . ., qh, Gi — одно-
однородная линейная функция от gb q2, . . ., qh; &Ga не зависит от q. Обычно G2
легко находится, так как коэффициенты здесь те же, что и у квадратичных
членов в выражении для Т, представленном в виде функции от qi, q2, . . ., qk.
Члены Gi должны быть определены независимо, а члены Go несущественны,
и их можно вообще опустить. Основная задача, таким образом, заключается
в определении Gu
Коэффициенты функции @ в общем случае зависят от всех переменных
¦ • • •
q, q, а не только от первых А;. При желании q^+i, <Zft+2> • • •> Чп
218 УРАВНЕНИЯ ГИББСА — АППЕЛЯ [Гл. XII
исключить с помощью уравнении
h
Чг== SPris + Рг, г = А + 1, к + 2, ..., п, A2.4.3)
s=l
получаемых из A2.2.7), однако эта процедура не дает каких-либо заметных
преимуществ. Уравнения A2.4.3) тем не менее будут встречаться нам в даль-
дальнейшем в общей совокупности уравнений.
Рассмотрим теперь систему, конфигурация и скорость которой заданы
в момент t. Мы хотим получить уравнения для определения ускорений частиц
системы. Этого легко достигнуть при помощи следующей простой и важной
теоремы. Ускорение системы таково, что выражение
®-2&?;, A2-4.4)
8=1
рассматриваемое как функция от qlt q2, . . ., qh, имеет минимум. Применяя
эту теорему, координаты и составляющие скоростей следует считать постоян-
постоянными; фактически мы имеем дело с квадратичной функцией с постоянными
коэффициентами.
Доказательство теоремы очень простое. Если через q обозначить ускоре-
ускорение в действительном движении, а через q -\-Aq — ускорение в любом другом
возможном движении, то будет справедливо следующее равенство:
ft n N h
д (@ - 2 Qs9s) ={2m'?¦+А^J-т 2 т^г- 2 &д?» =
8=1 Г-1 Г=1 8=1
IV N h
= \ ^ mr (Дх> + ( 2 'mrXrAxr - 2 Q.bq.) ¦ A2.4.5)
Г= 1 Г~ I 8=1
Последняя скобка в правой части тождественно равна нулю, как это следует
из пятой формы A2.3.11) основного уравнения. Следовательно, если Дзс
то
Д (@ - 2 <?JS) > 0, A2.4.6)
8=1
и теорема, таким образом, доказана.
Эта теорема тесно связана с принципом наименьшего принуждения
Гаусса (§ 4.3). В самом деле, имеем
C = 4-2mr(i'r-?J. A2.4.7)
r=l
а это с точностью до членов, не содержащих ускорений, то же самое, что
N
®-^Хт'хг. A2.4.8)
г=1
N h
Выражение 2 Xrxr отличается от У] QsQs лишь членами, не зависящими
Г=1 8=1
от ускорений. Таким образом, A2.4.4) отличается от С только членами, не со-
содержащими ускорений, и, следовательно, теорема A2.4.6) может быть полу-
получена из принципа наименьшего принуждения Гаусса.
§ 12.5] УРАВНЕНИЯ ГИББСА — АППЕЛЯ 219
§ 12.5. Уравнения Гиббса — Аппеля. Доказанная выше теорема
k
(§ 12.4) о том, что выражение @ —-2 QsQs в действительном движении имеет
8= 1
минимум, позволяет составить уравнения движения. Для этого достаточно
написать условия стационарности. Тогда получим уравнения
¦^r = Qr, r = l,2, .... к, A2.5.1)
ддг
называемые уравнениями Гиббса — Аппеля *). Их можно было бы получить
из пятой формы A2.3.11) основного уравнения, если бы мы рассматривали
бесконечно малые, а не конечные приращения. Уравнения A2.5.1) впервые
были получены Уиллардом Гиббсом в 1879 г. и подробно исследованы Аппе-
лем двадцать лет спустя. Яспо, что при составлении уравнений движения
члены в выражении для @, не содержащие q, можно опустить. К дифферен-
дифференциальным уравнениям движения следует добавить п — к = I -\- р уравнений
геометрических связей
h
?г=- SPr.?.+Pr, г = к + 1, A+2, -.., п, A2.5.2)
полученных из A2.2.7).
Уравнения Гиббса — Аппеля представляют наиболее простую и в то
же время наиболее общую форму уравнений движения. Исключительно
простые по форме, они с равным успехом могут быть применены как к голо-
номным, так и к неголономным системам и позволяют легко вводить квазико-
квазикоординаты.
При пользовании этими уравнениями сначала определяют число степе-
степеней свободы системы к и составляют так называемую «кинетическую энергию
N
1 v * * * *
ускорений» у 2j rnrx2r, выраженную через к ускорений q. В результате полу-
г=1
чают функцию @. В общем случае в нее входят все п координат q и скоростей
q, но существенно то, чтобы в нее входили лишь к выделенных ускорений q.
Выделенные к координат q могут быть как лагранжевы, так и квазикоорди-
квазикоординаты, в зависимости от удобства. Далее рассматривается работа заданных
сил на виртуальном перемещении; выражение для этой работы представляет-
'h
ся в форме 2 Qs^Qs- Уравнения движения имеют вид A2.5.1), к ним добавля-
ются п — к геометрических уравнений A2.5.2), и из совокупной системы
дифференциальных уравнений определяются п переменных qi7 q^-, ¦ • -, qn
как функции от t.
*) История вывода уравнений Гиббса — Аппеля весьма примечательна. Эти урав-
уравнения были получены Уиллардом Гиббсом в 1879 г. в его работе: On the fundamental
formulae of Dynamics, American Journal of Mathematics, II, стр. 49—64; Collected papers,
vol. II, 1928. Гиббс установил свои уравнения для голономных систем, но, по-видимому,
понимал, что они справедливы и для неголономных систем. В то время его метод не полу-
получил должной оценки, и открытие Гиббса, казалось, не вызвало особого интереса. В 1896 г.
Аппель опубликовал первое издание своей «Mecanique Rationelle» [21], в которое вкралась
серьезная ошибка. Функцию Лагранжа для неголономной системы Аппель выражал
через к составляющих скорости qr и по отой функции строил уравнения Лагранжа.
(Подобное заблуждение не раз встречалось в истории механики, см., например,
А. В. В a s s e t t, Motion of one solid on another, Quarterly Journal of Pure and Applied
Mathematics, XLVIII, 1920, стр. 310—320.) После выхода в свет первого издания Ап-
иель обнаружил свою ошибку и занялся поисками такой формы уравпений движения,
которые были бы в равной степени приложимы как к голономным, так и к неголономным си-
системам. Уравнения Гиббса — Аппеля были опубликованы в «Comptes Rendus» в 1899 г.,
а также во втором издании «Mecanique Rationelle» в 1904 г.
Глава XIII
ПРИЛОЖЕНИЯ УРАВНЕНИЙ ГИББСА-АППЕЛЯ
§ 13.1. Плоское движение частицы. Применим сначала уравнения
Гиббса — Аппеля к исследованию плоского движения частицы. В качестве
координат возьмем г, q:
г2 = х2 + у2, dq = xdy — у dx. A3.1.1)
Здесь г — лагранжева координата, a q — квазикоордината. Имеем
гг = хх + уу, q = ху — ух. A3.1.2)
Следовательно,
r2r2 + g2 = г2 (х2 + у2). A3.1.3)
Далее,
г'г + г2 = хх + уу'+ х'2 + у'2. A3.1.4)
Учитывая A3.1.3), находим
=гг — ^-. A3.1.5)
С другой стороны,
ху — ух =q, A3.1.6)
так что из A3.1.5) и A3.1.6) следует, что
r2(x2 + y2) = q2+ (rr'—jrJ. A3.1.7)
Таким образом, окончательно получаем
Поскольку члены, не зависящие от ускорения, можно опустить, вместо
A3.1.8) можно написать
@ = ут (У2-¦?¦ fr'+ ~q2). A3.1.9)
Выражение для @ можно вывести и непосредственно, если заметить,
что радиальная составляющая ускорения равна
а окружная составляющая равна q/r.
Если радиальную и окружную составляющие силы обозначить соответ-
соответственно через R и S, то работа, совершаемая на виртуальном перемещении,
будет равна
^8q A3.1.10)
$ 13.3] ПЛОСКОЕ ДВИЖЕНИЕ 221
и уравнения Гиббса — Аппеля примут вид
т ('¦*-""?') =Я' ™<i--=rS- A3.1.11)
В задаче о движении по центральным орбитам силовое поле радиальное
(S = 0), и мы имеем первый интеграл q = а. Первое уравнение принимает
теперь вид
т (г —-2?)=Д, A3.1.12)
и если ,Д= —т-у-, то сразу получаем известный первый интеграл E.2.39):
j.24. 2V -\- а = 2h
§ 13.2. Аналог теоремы Кёнига. Для любой механической системы
справедлива теорема об ускорениях, аналогичная известной теореме Кёнига
{7.1.2) о скоростях. Функцию Гиббса @ можно представить в виде суммы
двух слагаемых: одного, включающего только ускорение центра тяжести G
системы, и другого, зависящего только от ускорений частиц системы относи-
относительно центра тяжести. Полагая
х = I + a, i/ = T] + p, z = ?+y,
где х, у, z — декартовы координаты частицы, получаем (см. § 7.1) следующее
выражение для функции Гиббса:
@ = ±М $ + i[* + i*) + ±Sm(a*+pa + y*)- A3.2.1)
Это следует из основного свойства центра тяжести, согласно которому
• • • • » •
Sma = Sm$ = Smy = 0.
Интересен частный случай, когда система представляет собой одно твер-
твердое тело. Если система состоит из нескольких твердых тел, то обычно удоб-
удобнее (как и в случае теоремы Кёнига) применять теорему к каждому твердому
телу в отдельности, а не ко всей системе в целом.
§ 13.3. Плоское движение. Для твердой пластинки, движущейся в своей
плоскости, имеем
@ = у МР +1 Sm (rW+rW), A3.3.1)
где / — ускорение центра тяжести G, а г, 8 — полярные координаты относи-
относительно системы осей, сохраняющих неизменное направление, с началом в цен-
центре тяжести. Опуская несущественные слагаемые, можем написать
@ = уМ/Му/ё2- A3.3.2)
Здесь через / обозначен момент инерции пластинки относительно центра
тяжести.
В качестве конкретного примера рассмотрим качение однородного твер-
твердого цилиндра радиуса а по внутренней поверхности неподвижного полого
цилиндра радиуса Ъ. Оси цилиндров пусть будут горизонтальны, поверхно-
поверхности их будем считать шероховатыми, исключающими проскальзывание,
222
ПРИЛОЖЕНИЯ УРАВНЕНИЙ ГИББСА — АППЕЛЯ
[Гл. XIII
и пусть во все время качения цилиндры касаются друг друга. В данном слу-
случае к = 1. Точка А' на поверхности катящегося цилиндра (рис. 36) в поло-
положении равновесия совпадала с наинизшей точкой А
неподвижного цилиндра, так что длина дуги А'В
окружности катящегося цилиндра равна длине
дуги АВ окружности неподвижного цилиндра.
Условие чистого качения в обозначениях рис. 36
запишется в следующем виде:
а F + ф) = 66, или аф = с9, A3.3.3)
где с = Ъ — а. Функция Гиббса имеет вид
& = у М (с292 + с29*) + у DМаЛ ф2. A3.3.4)
Рис. 36.
Выразим ее через одну составляющую ускоре-
ускорения (поскольку к = 1). Опуская несущественные слагаемые, находим
4
A3.3.5)
Работа заданных сил (силы тяжести) на виртуальном перемещении равна
Mg8(c cos Э) = — Mgc sin 9 69. A3.3.6)
Уравнение движения запишется в виде
или
¦Afc29= —Mgc sin 9
9 + 4-sin9 = 0.
О С
A3.3.7)
Оно показывает, что угол 9 изменяется так же, как угол отклонения маятни-
„3
ка длиной -тг с от направленной вниз вертикали.
§ 13.4. Движение твердого тела. Для нахождения функции Гиббса вос-
воспользуемся теоремой § 13.2. Сначала вычислим @ для твердого тела с одной
неподвижной точкой. Возьмем подвижную прямоугольную систему коорди-
координат с началом в неподвижной точке О. Пусть 6 будет вектор угловой скорости
этой системы, а со — вектор угловой скорости тела. Радиус-вектор произволь-
произвольной частицы тела обозначим через -г, скорость ее — через и и ускорение —
через /. Все эти векторы измеряются относительно подвижной системы коор-
координат (точнее говоря, относительно неподвижной системы, совпадающей
в каждый данный момент с подвижной системой). Имеем следующие соотно-
соотношения:
:г = сохг, A3.4.1)
= fi>X[(fi> — 9) xr]+(axr+Qx (axr) =
= о X (со X г) + (о X г + [в + (со X г) + (о X (г X 9)] =
= (со-г)» — coV — r Хф, A3.4.2)
§ 13.4] ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА 223
где
со. A3.4.3)
Составляющая ускорения по оси х равна
zy+a>3z) at — (со* -f w* + со*) x — уср3 ¦+ гф2 =
IйJ — фз) + г(й)зйI+фа). A3.4.4)
До сих пор движение системы отсчета мы никак не связывали с движе-
движением тела. В дальнейшем нам будет удобно систему координат выбрать таким
образом, чтобы оси ее совпадали с главными осями инерции тела и моменты
инерции тела относительно этих осей были постоянны. При таком выборе
системы отсчета будем иметь
2@ - Sm {[z2 (<в2соз - Ф4J + у2 (<ва<вз + <PiJl+ ... + ...}. A3.4.5)
В этом соотношении мы сохранили лишь члены, содержащие ф1( члены же,
не содержащие составляющих вектора <р, мы опустили. Кроме того, мы учли,
что
Smyz = Smzx = Smxy = 0. A3.4.6)
Раскрывая скобки в равенстве A3.4.5) и отбрасывая члены, не содержащие
составляющих ф, находим те члены в выражении для 2@, которые зависят
от ф4:
(у2 + z2) — 2(о2й)зф15т. (z2 — г/2). A3.4.7)
Окончательно получаем
2(А-В)(о,а2ср3, A3.4.8)
где А, В, С — моменты инерции тела относительно осей координат.
В приложениях при пользовании теоремой § 13.2 за начало координат
обычно выбирают центр тяжести тела (если только тело не имеет одной непод-
неподвижной точки). Рассмотрим некоторые частные случаи.
1) Однородный твердый шар, куб либо вообще любое тело, эллипсоид
инерции которого в точке О представляет сферу. В этом случае А = В = С
и движение системы координат может1 быть взято произвольно, независимо
от движения тела. Функция Гиббса (для движения относительно точки О)
имеет вид
@=4^(Ф1 + Ф1+Ф2з). A3.4.9)
2) Тело вращения, например однородный прямой цилиндр или вращаю-
вращающийся волчок, для которого А = В =^=С. Ось 03 системы координат все
время должна быть направлена вдоль оси симметрии; тогда 64 = ©i, 6? = йJг
но, вообще говоря, 93 =j? co3. В этом случае
ф1 = «1 + «2 («з — 9з). Фг = ю2 — со^соз— 9з). фз = «з A3.4.10)
и A3.4.8) принимает вид
± -Са3)(а>1ая-<ояа1)}, A3.4.11)
где некоторые несущественные члены мы опустили.
Иногда бывает удобно этот результат представить в другой форме. Для
точки Р, находящейся на оси симметрии на единичном расстоянии от точки О,
224 ПРИЛОЖЕНИЯ УРАВНЕНИЙ ГИББСА — АШ1ЕЛЯ [Гл. XIII
скорость и ускорение равны
и = {аг, —colf 0}, A3.4.12)
0I83, —
-К + со22)}, A3.4.13)
и мы можем написать
©=-i-4/»+iCffl;-Casg.(«tX/), A3.4.14)
где / = |/|, а через ? обозначен вектор ОР, т. е. вектор с составляющими
{0, 0, 1}. Можно также написать следующее выражение для @;
® = ±Af* + ±Ctfa-C<u3f-{txu). A3.4.15)
3) В общем случае, когда А, В и С различны, следует пользоваться сис-
системой координат, связанной с телом, с осями вдоль главных осей инерции
тела и с началом в центре тяжести О. В этом случае 6 = со, ф = {а±, со2, со3}
и, следовательно,
= -i {А(а\ + Бй)* + С(а\ — 2 (В —С)
A3.4.16)
§ 13.5. Шар на вращающейся плоскости. Рассмотрим качение шара
по шероховатой горизонтальной плоскости, которая вращается около фикси-
фиксированной в ней точки О с заданной угловой скоростью Q. Угловая скорость Q
может быть не постоянна и являться заданной функцией от t, принадлежащей
классу Ci (как в примере § 5.5). Можно рассматривать однородный твердый
шар, однородную сферическую оболочку либо вообще любое тело сферической
формы, центр тяжести G которого лежит в его геометрическом центре, а эл-
эллипсоид инерции в точке G представляет сферу. Воспользуемся системой
координат Oxyz с осями вдоль фиксированных направлений и началом в точке
О; ось Oz направим перпендикулярно к плоскости. Выберем затем систему
G123 с осями, параллельными осям системы Oxyz, так что в рассматриваемой
задаче будем иметь Gj = Э2 = 63 = 0. Координаты центра катящегося шара
обозначим через х, у, а; здесь а — радиус шара. Условия качения запишутся
в виде
z-<uoa=-Lu, , A3.5.1)
^-Qy, I
У +
Рассматриваемая система неголономна и имеет три степени свободы. Для ее
описания возьмем пять координат: х, у, qu q2, q3, причем
а • •
qt = щ, q2 = со2 , q3 = «3. A3.5.2)
В нашем случае & = 3, i = 2 и из пяти упомянутых выше координат х, у
являются лагранжевыми координатами, a qt, q2, q3 представляют собой ква-
квазикоординаты. Если положение шара определить с помощью углов Эйлера
8, ф,г|), то будем иметь п = 8. Возможные вариации координат удовлетворяют
соотношениям
dx — а dq2 + Qy dt = 0, 1 A3 5 3)
t = O. J
a dqi — Q
Составим теперь выражение для функции Гиббса @. Имеем
2@ = М (У2 + У2) + A (q\+qU- Ъ- A3.5.4)
§ 13.5] ШАР НА ВРАЩАЮЩЕЙСЯ ПЛОСКОСТИ 225
Правую часть этого равенства нужно выразить через три составляющие
ускорения, скажем через х, у, q3. Для этого воспользуемся соотношениями
A3.5.5)
a<?i = —y-\-Qx-]-Qx.
Отсюда получаем
2@ = M (x2 -\- у2) -\—?¦ (z-]-Qy-j-QyJ-\ g" (У — &x — Qx)z-]~Aql. A3.5.6)
В этом простом случае @ оказывается зависящей лишь от трех выделенных
координат х, у, q3, но в общем случае, как уже отмечалось (§ 12.4), функция
@ зависит и от остальных координат и скоростей.
Рассмотрим теперь работу, совершаемую заданными силами на виртуаль-
виртуальном перемещении. На этом перемещении
б^ = —byla, bq2 = bxla. A3.5.7)
Если система действующих на шар внешних сил эквивалентна силе (X, Y, Z),
приложенной в центре шара, и паре (Р, Q. R), то работа этих сил на вирту-
виртуальном перемещении равна
X6r+Y&y + P8ql + Q8q2 + Rdq3 =
A3.5.8)
Ясно, что существенным является лишь момент этой системы сил относитель-
относительно точки соприкосновения шара и плоскости; составляющие этого момента
вошли в выражение A3.5.8). Уравнения движения имеют вид
^, A3.5.9)
Му+ -^ (У-Qi-uc) = Г-^-. A3.5.10)
Aq3 = R. A3.5.11)
Рассмотрим в качестве примера частный случай, когда плоскость вра-
вращается с постоянной угловой скоростью (Q = 0), а система внешних сил,
действующих на шар, эквивалентна силе (Ж|, Мч\, MQ, приложенной в цен-
центре шара (Р = Q — R — 0).
Из A3.5.11) следует, что со3 = Яз = const, и уравнения движения центра
шара записываются в виде
Bz'+AQy = Ma%,
Ма% 1
A3.5.12)
где В — А + Ма? — момент инерции относительно касательной к поверх-
поверхности шара. Для однородного твердого шара имеем
Уравнения движения принимают вид
2 ¦ 5
A3.5.14)
I
• * 2 • 5
У — уйа: = тт|.
15 л. А. Парс
226 ПРИЛОЖЕНИЯ УРАВНЕНИЙ ГИББСА — АППЕЛЯ [Гл. XIII
Они совпадают с уравнениями движения частицы единичной массы под дей-
действием 1) силы ( у |,у ц\ и 2) гироскопической силы у Q| v |, перпендику-
перпендикулярной к вектору скорости v и пропорциональной | v |.
Рассмотрим случай однородного поля: ? = const, t] = 0. Если шар тяже-
тяжелый, а плоскость качения не горизонтальна, а наклонена под углом а к гори-
горизонту, то, направляя ось Ох вдоль линии наибольшего наклона, находим, что
§ = g sin а. Полагая х + iy = z, полу-
ц-у0 . чаем уравнения A3.5.14) в виде
• • •
z — iv.z = К. A3.5.15)
Здесь х и К — вещественные постоянные.
2 5
х = уй и Я = -=-1. Решение этого урав-
_ __ нения имеет вид
A3.5.16)
Рис. 37. где z0 = Zt—o, w0 = z(==0 Кривая пред-
представляет собой трохоиду, описываемую
при качении окружности по линии, перпендикулярной к силовым лини-
линиям поля; в случае наклонной вращающейся плоскости эта линия горизон-
горизонтальна. Значение z0 несущественно: движение относительно начальной точки
зависит только от wo. В частном случае, когда и; о = 0, получаем циклоиду
z _ Zo = р A _ еш) + ip(xt), A3.5.17)
где р = —Я/х2 (рис. 37). Радиус катящейся окружности равен р, в случае
35 г .
наклонной вращающейся плоскости он равен -т- о5~ sm a"
§ 13.6. Шар на вращающейся наклонной плоскости. Пусть плоскость,
наклоненная под углом а к горизонту, вращается с постоянной угловой ско-
скоростью Q около вертикальной оси, а однородный тяжелый твердый шар массы
М и радиуса а катится по ней. В этом случае'& = 3, I = 2. Поместим начало
координат О в точку пересечения плоскости с осью вращения, ось Оу напра-
направим вдоль линии наибольшего наклона, ось Oz — перпендикулярно к плос-
плоскости, а ось Ох — по горизонтали в плоскости. Тогда будем иметь
6i = 0, 02 = Qsincc, 93 = Qcosa. A3.6.1)
Составляющие ускорения центра шара G с координатами х, у, z будут равны
и аналогично для /2 и /3. В рассматриваемом случае z — a, fy = 0 и наши
формулы принимают вид
h = х — 2ув3 -хп\
A3.6.3)
Последняя из формул не содержит составляющих ускорения и потому не пред-
представляет сейчас для нас интереса. Теперь можно написать ту часть функции
Гиббса, которая зависит от движения центра тяжести шара. Чтобы напи-
написать остальную часть, необходимо вычислить фь ср2 и ср3. Условия качения
§ 13.6] ШАР НА ВРАЩАЮЩЕЙСЯ НАКЛОННОЙ ПЛОСКОСТИ 227
записываются в виде
Их можно получить, рассматривая относительное движение шара. Если
скорость центра шара имеет составляющие u,'v, w, то, рассматривая движе-
движение той частицы шара, которая в данный момент касается плоскости, можем
написать
и — асо2= — z/03,
A3.6.5)
Из движения точки касания, т. е. основания перпендикуляра, опущенного
из центра шара на плоскость, находим
и — а02 = ? —1/03, |
V = y+XQ3, I A3.6.6)
w= —xQ2. \
Условия качения A3.6.4) непосредственно следуют из A3.6.5) и A3.6.6).
Таким образом,
— а(а>1 — <й203 + со302) = —у — |
A3.6.7)
где ? = асо3.
Функцию Гиббса теперь можно выразить через составляющие ускорения
х, У, Ь
Од/ • • • • • •
-~ = (х - 2*/03 - аЯ»)» +(у+ 2^63 - г/в| + а92езJ +
+ 4 (V- г/63)з + -| ('г/"+ ж93 - Ь2 + аЭ293J + 4 (V+ г/92J. A3.6.8)
Чтобы вычислить работу заданных сил на виртуальном перемещении,
можно рассмотреть момент силы тяжести относительно точки соприкоснове-
соприкосновения. Напомним, что при виртуальном перемещении плоскость остается
в покое. Еще проще, если заметить, что совершаемая работа равна —6F,
где V — Mgy sin а. Таким образом, работа заданных сил на виртуальном
перемещении будет равна
— (Mg sin a) 6y. A3.6.9)
Теперь можно написать уравнения движения:
^ 0, A3.6.10)
- ув23 + а0293 + -| (у+хв3 - ^92 + а9203) = - g sin а, A3.6.11)
S + »8e = 0. A3.6.12)
Из A3.6.12) находим
I + 1/02 = const. A3.6.13)
15*
228 ПРИЛОЖЕНИЯ УРАВНЕНИЙ ГИББСА — АППЕЛЯ [Гл. XIII
Исключая ? из A3.6.13) и A3.6.11), получаем уравнения, определяющие
х и у как функции от t. Их можно представить в следующей форме:
/+T] = 0. J
7y+12Qxcosa — Gcos2a — 2)Q2y +
Входящая сюда постоянная т] определяется следующим образом:
т] = Eg — 2апп + laQ2 cos a — 2Ш2 sin a) sin a, A3.6.15)
где b есть значение у при ? = 0, an — значение со3 в этот момент времени.
Если 7 cos2a Ф2, то, изменяя начало координат, можно получить линейные
однородные уравнения с постоянными коэффициентами.
Уравнения A3.6.14) можно проинтегрировать до конца, если задаться
начальными значениями х, у, х, у. Задача § 13.5, в которой X = Y = О,
является частным случаем рассматриваемой; она получается при a = 0.
Сравнение результатов провести нетрудно, хотя в § 13.5 ответ получен в не-
несколько иной форме, поскольку оси там не вращались.
§ 13.7. Качение шара по неподвижной поверхности. Будем предпола-
предполагать, что поверхности идеально шероховатые, чтобы не допустить скольже-
скольжения. Таким образом, будем считать, что имеет место чистое качение. Возьмем
подвижные оси координат Gl, G2, G3 с началом в центре шара G. Будем пред-
предполагать, что шар твердый и однородный или во всяком случае, что центр
тяжести его совпадает с геометрическим центром, а эллипсоид инерции в этой
точке представляет собой сферу. Ось G3 направим вдоль прямой, соединяющей
точку соприкосновения шара с центром шара; тогда координаты точки сопри-
соприкосновения будут @, 0, —а), где а — радиус шара. Условия качения запи-
запишутся в виде
щ = асо2, и2 = —ащ, u3 = 0, A3.7.1)
где и — скорость центра тяжести G, а ю — угловая скорость шара. Состав-
Составляющие ускорения точки будут равны
/i = ui — Мз + «з02 = a (co2
/2 = u2 — u301+u103= — а(а1 — (o2e3), ^ A3.7.2)
/з = Щ — и,в2 + u2Qi = — a (co292 + afij..
Составляющая /3 несущественна, так как не содержит (ог. Следовательно
в = у Л-(ф;+ф1+фЭ +^№(«1-«20зJ + уМа2(«2 + <й10зJ- A3.7.3)
Если момент заданных сил относительно точки соприкосновения обозна-
обозначить через Ж, те работа, совершаемая на виртуальном перемещении, будет
равна
ВД1 + N28q2 + N38qs, A3.7.4)
где qT = сог. Число степеней свободы системы равно трем, и функция @
• •
переменные q, так что уравнения движения запи-
запирме:
^- = 7Vr, г =1,2,3. A3.7.5)
d
выражена нами через три переменные q, так что уравнения движения запи-
записываются в следующей форме:
13.7]
КАЧЕНИЕ ШАРА ПО НЕПОДВИЖНОЙ ПОВЕРХНОСТИ
229
Отсюда получаем
! + Ma2 (cuj — (й2е3) -= Nlt
2 + Ма? (щ + щв3) = ^2,
A(f3=N3.
A3.7.6)
Обозначив сумму А + Ма? через В (тогда В будет моментом инерции шара
относительно касательной), перепишем урав-
нения движения. A3.7.6) в форме Zf.Z^ceZ^ *
катящейся сферы
плоскостью Ш
! —'(о293) +
В (<iJ + «163) —
А (со3 — а А
A3.7.7)
I ,^ & \ ЛТ
-\- (?>2\}ц = Л» 3.
Рассмотрим конкретный пример: каче-
качение однородного твердого шара радиуса а х'
по внешней стороне неподвижной сфериче- рис. 38.
ской поверхности радиуса с — а. Выберем
оси так, как показано на рис. 38 (ось G2 горизонтальна). Имеем
со< ==: — У)« С0о ==~ — Уг• у±о. § *oj
Nt = 0, N2 = Mga sinQ, N3^-0. A3.7.9)
Последнее уравнение A3.7.7) показывает, что (о3 = const, скажем
со3 = п.
Два первых уравнения A3.7.7) теперь принимают вид
A3.7.10)
В -^ F2 + Э^з) — АпВг = Mga sin 9.
Угловая скорость подвижной системы осей имеет составляющие
• • •
6i = —ф sin 9, 92 = 9, 63 = ф cos 9.
Для однородного твердого шара имеем
Подставляя эти значения в A3.7.11), получаем
1с (ф sin 9 + 29ф cos 9) — 2аге9 = О,
1с (9 — ф2 cos 9 sin 9) -f- 2апц> sin 9 = bg sin 9.
Эти уравнения определяют значения 9 и ф для любого момента
Умножая уравнение A3.7.14) на sin 9 и интегрируя, получаем
A3.7.11)
A3.7.12)
A3.7.13)
A3.7.14)
A3.7.15)
времени.
7сф sina9 + Ian cos 9 = const.
A3.7.16)
230
ПРИЛОЖЕНИЯ УРАВНЕНИЙ ГИББСА — А1ШЕЛЯ
[Гл. XIII
Уравнения A3.7.15) и A3.7.16) идентичны с уравнениями (8.6.6) и (8.6.7),
описывающими движение оси вращающегося волчка. При р = anile, q =
= 5g/7c и постоянной в правой части A3.7.16), равной 1АсК, они в точности
совпадают. Кроме того, известно, что уравнения движения оси вращающего-
вращающегося волчка являются уравнениями Лагранжа, полученными из функции Рауса
при исключении циклической координаты ajj. Уравнение же A3.7.15) есть
уравнение Лагранжа для 8, а соотношение A3.7.16) — интеграл количества
движения для ф, полученный из функции Лагранжа
Z = i- с (92 + sin2 0 ф2) + 2геаф cos 9 — 5g cos 0.
A3.7.17)
§ 13.8. Вращающийся волчок. Обратимся теперь к задачам о движении
твердого тела, имеющего ось симметрии. Начнем с известной задачи о вращаю-
вращающемся волчке, рассматривавшейся нами в §§ 8.6 — 8.10 на основе метода Лаг-
Лагранжа. До сих пор уравнения Гиббса — Аппеля мы использовали только
в неголономных системах, где наиболее ярко проявляются их преимущества.
Разумеется, их можно применить и к голономным системам, в частности
к задаче о волчке. Помещая начало координат О в острие волчка и направляя
ось 03 вдоль оси волчка, можем написать (см.
2 A3.4.11))
-ovuj). A3.8.1)
Уравнения движения будут иметь вид
А щ - (AQ3 - Ссо3) со2 = Ni, A3.8.2)
Aaz+(AQ3 — Са3) ац = N2, A3.8.3)
Сй3 = N3 A3.8.4)
(здесь qr = cor). Работа заданных сил на вир-
виртуальном перемещении будет равна N^8qi +
-j- N28q2 + N38q3.
Рассмотрим в качестве примера классический случай, когда заданными
силами являются силы тяжести. Пусть 0, ф — полярные углы оси 03 волчка
относительно неподвижной системы Oxyz, в которой ось Oz направлена вер-
вертикально вверх, а ось 02 горизонтальна (рис. 39). Тогда будем иметь
Рис. 39.
= —ф sin 6, со2 = 6, 63 = Ф cos 8,
V! = О, N2 = Mgl sin 8, N3 = 0.
A3.8.5)
A3.8.6)
Здесь l обозначает расстояние между центром тяжести G и острием волчка.
Из A3.8.4) следует, что (о3 = const, скажем
@3 = П.
A3.8.7)
Это справедливо и в любой другой задаче, в которой момент заданных сил
относительно оси волчка равен нулю. Уравнения A3.8.2) и A3.8.3) теперь
принимают вид
A3.8.8)
А (ф sin 9 + 2Эф cos 9) — Сгев = О,
АВ — (Aq> cos 0 — Сп) ф sin 9 = Mgl sin 9.
A3.8.9)
§ 13.8] ВРАЩАЮЩИЙСЯ ВОЛЧОК 231
Умножая уравнение A3.8.8) на sin 8 и интегрируя, получаем
Ay sin2 8 + С п cos в = const. A3.8.10)
Мы видим, что уравнения A3.8.9) и A3.8.10) совпадают с уравнениями (8.6.6)
и (8.6.7); дальнейший анализ производится так же, как в §§ 8.6—8.10.
Если исходить из другой формы функции @, а именно из формы A3.4.15),
то получающиеся уравнения будут иметь вид, указанный в § 8.7. В этом слу-
случае будем иметь
© = 1л/»+1с<^-С<ВзЛFх«*), A3.8.11)
или
@ = у A (i2 + у* + z2) + у Cw\ - Сщ (х {y'z - zy) + у (z'x - xz) + z\xy - ух)},
A3.8.12)
где х, у, z— направляющие косинусы оси волчка, т. е. составляющие век-
вектора %. Пользуясь выражением A3.8.12), следует помнить, что величины х,
у, z не являются независимыми. В самом деле,
'у'+ z'z'+-(x* + y'* + z2) = 0. A3.8.13)
Равенством A3.8.13) можно воспользоваться для того, чтобы привести
A3.8.12) к форме, содержащей лишь три необходимые составляющие уско-
ускорения. Более симметричное выражение получается, если ввести неопределен-
неопределенный множитель Лагранжа. Работа сил тяжести на виртуальном перемещении
равна — Mgffiz, так что уравнения движения записываются в виде
• • • • ч
Ах — Ссо3 (yz — zy) = кх,
Az — Сщ (ху — ух) — kz — Mgl,
Сщ = 0.
Последнее уравнение дает известный интеграл (о3 = п, тогда остальные
уравнения принимают вид
Ах — Сп {y'z — zy) = кх, A3.8.15)
Ay — Сп {z'x - xz) = ку, A3.8.16)
Az — Сп {ху — ух) = kz — Mgl. A3.8.17)
Теперь легко прийти к ранее выведенным формулам. Из уравнений
A3.8.15) — A3.8.17) непосредственно следуют уравнения (8.7.3) — (8.7.5).
В частном случае спящего волчка х и у малы, a z в первом приближении мож-
можно считать равным единице. Тогда с принятой степенью точности будем иметь
¦ к = Mgl, и уравнения A3.8.15), A3.8.16) примут вид
Ах + Спу
Ау
эквивалентный (9.9.14)..
x + Cny-Mglx-0, I
y — Cnx—Mgly = 0, J
232 ПРИЛОЖЕНИЯ УРАВНЕНИЙ ГИББСА — АГЩЕЛЯ 1Гл. ХШ
§ 13.9. Качение монеты (тонкого диска). Система, рассмотренная
в § 13.8, была голономна, а, как уже отмечалось, преимущества уравнений
Гиббса — Аппеля проявляются наиболее ярко в неголономных системах.
В этом параграфе мы рассмотрим задачу о качении диска или обода по шеро-
шероховатой горизонтальной плоскости. Эта задача исследовалась нами с помощью
метода Лагранжа в §8.12. Если обозначить через и скорость центра тяжести
G диска, а через/—его ускорение, то, пользуясь обозначениями рис. 22,
можно написать
щ = О, и2 = —а(о3, иг = аи2 A3.9.1)
/-Г-Гб8+«У--Г^ + (Ваа>) 1 A3 9 2)
а «з щ а , /-
/з ^= М3 — ^^02 4~ ^2^1 ^^ ^ (^*2 — k*3^l) * J
Здесь 9j — (ov 92 = co2. Таким образом, получаем следующее выражение для
функции Гиббса:
1 1 *
(э = у М а2 ((о2 — «з^!J + у -^fl2 (юз + ®1^2J +
4-у Л («>i4' Ю2) +Y^'CU3+ (^3 — Ссо3) ((й^ — cojCOj). A3.9.3)
Работа силы тяжести в единицу времени равна —Mga cos 6 (о2, так что урав-
уравнения движения записываются в виде
AcOi — AQ3(o2 4- С(о2(о3 = О,
(Л 4- Ма2) а2 4- -483©! — (С4- -Ма2) ©3©! = — Mga cos 0, ^ A3.9.4)
(С 4- Ма2) со3 + Л/а2©^ — О
(здесь qT = cor).
Если теперь полярные углы оси G3 относительно неподвижных прямо-
прямоугольных осей (рис. 22) обозначить через 9, ф, то будем иметь
«1 — —ф sin 8, со2 = 0, Шз = Ф cos 8. A3.9.5)
• • •
(Напомним, что 03 ф (о3: действительно, со3==0з+'Ф='Ф + Ф COS 0-) Под-
Подставляя эти значения в уравнения A3.9.4), получаем
(А + Ма2) 8 — Ац>2 cos Э sin 8 + (С + Ма2) со3ф sin 8 +
+ Mga cos 6=0, A3.9.6)
А (ф sin 6 + 28ф cos Э) — Ссо30 = 0, A3.9.7)
(С + Ма2) со'з - Ма28ф sin 8 = 0. A3.9.8)
Полученные уравнения эквивалентны уравнениям (8.12.17) — (8.12.19),
найденным ранее с помощью метода Лагранжа. Одно из приложений этих
уравнений мы уже рассмотрели. В качестве второго примера определим усло-
условие устойчивости (по первому приближению) диска или обода, катящегося
по прямой. При качении окружности по оси Оу с постоянной скоростью aQ
1
имеем 6 = у я, ф = 0, со3 = —?2- Рассмотрим малое возмущение и напишем
соответствующие уравнения первого приближения. Из уравнения A3.9.8)
§ 13.10] УРАВНЕНИЯ ЭЙЛКРА 233
видно, что величина со3 остается постоянной; можно считать, что она сохра-
сохраняет значение—Q невозмущенного движения. Полагая 9 = -^-я + | и сохра-
Li
няя лишь члены первого порядка относительно \ и ф, находим
(к + 1) Ё - Bк + 1) ОФ - n2l = 0, A3.9.9)
Ф + 2Щ == .0, A3.9.10)
где А = ту- С = &Ма2 и ге2 = — . Из уравнения A3.9.10) следует, что
Li Q/
Ф + 2Й| = const. A3.9.11)
Подставляя выражение для ф из A3.9.11) в A3.9.9), получаем
(к + 1) Ё + {2 Bк + 1)п2 — п2} % = const. A3.9.12)
Устойчивость по первому приближению будет обеспечиваться, если
a2Q2 > ga/Dk + 2). A3.9.13)
Для диска будем иметь a2Q2 > ga/3, а для обруча a2Q2 > ga/4. Для монеты
достоинством в 1 пенни (радиус которой равен 19/32 дюйма) критическая
скорость составляет около 0,73 фут/сек.
§ 13.10. Уравнения Эйлера. Обратимся теперь к некоторым задачам
о движении твердого тела, в которых оси координат мы свяжем с телом. Нач-
Начнем с задачи о движении тела в пространстве под действием заданной системы
сил. Возьмем систему координат G123 с началом в центре тяжести G и осями
Gl, G2, G3, направленными по главным осям инерции в точке G. Рассматривае-
Рассматриваемая система голономна и имеет шесть степеней свободы; в качестве шести
координат выберем координаты |, т), ? центра тяжести G относительно непо-
неподвижной системы Oxyz и координаты qt, q2, q3, производные которых ql, q2,
q3 представляют собой составляющие вектора угловой скорости тела по осям
Gl, G2, Gd. Из этих шести координат ?, т], ? являются лагранжевыми, <?lr q2,
q3 в общем случае представляют собой квазикоординаты. Функция Гиббса
имеет вид (см. § 13.2 и A3.4.16))
Действующие на тело силы эквивалентны силе, приложенной в точке G,
и некоторой паре. Пусть X, Y, Z — составляющие главного вектора по осям
Ox, Oy, Oz, a Ni, N2, N3 — составляющие главного момента по осям Gl, G2,
G3. Уравнения движения запишутся в следующей форме:
A3.10.2)
A3.10.3)
I
Ссо3 — (А— В)
Мы видим, что уравнения распадаются на две группы: первая группа
уравнений A3.10.2) описывает движение центра тяжести G, вторая группа
A3.10.3) — изменение ориентации тела. Этот факт составляет содержание
классической теоремы о независимости параллельных переносов и вращений.
Движение центра тяжести тела описывается так же, как движение материаль-
материальной точки массы М под действием силы, равной главному вектору всех сил,
234 ПРИЛОЖЕНИЯ УРАВНЕНИЙ ГИББСА — АППЕЛЯ 1Гл. XIII
действующих на твердое тело. Уравнения A3.10.3), описывающие вращение
твердого тела, представляют знаменитые уравнения Эйлера, полученные им
в 1758 г. *).
Уравнения Эйлера A3.10.3) можно применить также к задаче о вращении
тела около неподвижной точки О. В качестве осей 0123 в этом случае берутся
главные оси инерции в точке 0, а символы А, В, С обозначают моменты инер-
инерции тела относительно этих осей.
§ 13.11. Свободное тело; случай осевой симметрии. Одной из классиче-
классических задач динамики твердого тела является задача о свободном движении
твердого тела, т. е. о движении тела при отсутствии сил. Центр тяжести в этом
«лучае движется прямолинейно и равномерно, а вращение тела описывается
уравнениями
Aai — (В — С) (й2(о3 = О,
Вщ — {С-А)щщ = 0, \ A3.11.1)
Сщ— (А —В) cOjCOg = 0.
Эти уравнения справедливы и в других случаях. Если действующие
на тело силы приводятся к равнодействующей, приложенной в центре тяже-
хзти, то уравнения A3.11.1) будут справедливы, так как при этом N = 0;
важным частным случаем является задача о движении снаряда в (однород-
(однородном) гравитационном поле Земли. Уравнения A3.11.1) сохраняют силу так-
также в случае вращения твердого тела около неподвижной точки О, если момент
заданных сил относительно этой точки равен нулю.
Рассмотрим теперь различные случаи движения, описываемого уравне-
уравнениями A3.11.1). Если тело обладает сферической симметрией и, стало быть,
А = В — С, то задача решается просто. (Напомним, что оси жестко свя-
связаны с телом и движутся вместе с ним.) Из A3.11.1) сразу следует, что (о =
= const, т. е. тело вращается с постоянной угловой скоростью около непод-
неподвижной оси.
v Далее, рассмотрим тело, обладающее осевой симметрией (А = В =^=С),
например диск, или гироскоп, или же свободно вращающийся волчок. (В за-
задаче о вращении тела около неподвижной точки в поле силы тяжести непод-
неподвижная точка должна совпадать с центром тяжести.) Из третьего уравнения
Эйлера следует, что со3 = const; пусть
щ = п. A3.11.2)
Два первых уравнения тогда запишутся в виде
©! _ %а2 = 0, A3.11.3)
(о'2 _ Яол == 0, A3.11.4)
где X = п (С — А)/А. Предположим для определенности, что п > 0. Пола-
Полагая он + ico2 = z, заменим уравнения A3.11.3), A3.11.4) одним эквивалент-
эквивалентным уравнением в комплексных переменных:
z — ilz = O. A3.11.5)
*) Вряд ли нужно напоминать читателю, что уравнения Эйлера, полученные в этом
параграфе как следствие уравнений Гиббса — Аппеля, легко могут быть выведены
с помощью элементарных методов. Эти уравнения Эйлера содержатся в его книге [3]
1765 г. Примечательно то, что Эйлер открыл свои уравнения задолго до того, как пользо-
пользование подвижными осями стало обычным для математиков, и сразу осознал значение
•своего открытия.
§ 13.12]
СВОБОДНОЕ ТЕЛО; ОБЩИЙ СЛУЧАЙ
235
Отсюда
z = ре^С-'о), A3.11.6)
где р, t0 — вещественные постоянные и р>0. Без потери общности можно
считать, что t0 — 0; тогда
= р cos Kt, (o2 = р sin Kt, со3 = re.
A3.11.7)
На основании соотношений A3.11.7) нетрудно получить представление
о характере движения. Вектор (а±, со2, (о3) угловой скорости и вектор (^Icoi,
-4(о2, С(о3) момента количеств движения лежат в плоскости, проходящей
P(L=a.
Рис. 40.
Рис. 41.
через ось симметрии G3, которая вращается относительно тела с угловой
скоростью X. Ось вращения образует угол а с осью G3, а вектор момента
количеств движения составляет с этой осью угол Р; углы аир определяются
формулами
tg а = р/ге, tg р = Ар/Сп. A3.11.8)
Угловая скорость \^р2 + ге2 остается при этом постоянной.
Пусть С > А; тогда К > 0 и а > р. Ось вращения составляет постоян-
постоянный угол (а — р) с вектором момента количеств движения, который остается
неизменным; таким образом, ось вращения служит образующей прямого
кругового конуса, фиксированного в пространстве, с углом раствора (а — Р).
Одновременно ось вращения составляет постоянный угол а с осью G3 и опи-
описывает в твердом теле конус с углом раствора а. Таким образом, движение
может быть представлено как качение конуса с раствором а по внутренней
поверхности неподвижного конуса с раствором (а — р) (рис. 40).
Пусть теперь С < А; тогда Я < 0, скажем, X = —\а (\х > 0), и а < р.
В этом случае конус с углом раствора а, неизменно связанный с телом, ка-
катится по наружной поверхности неподвижного конуса с углом раствора
(р - а) (рис. 41).
В каждом из этих случаев ось гироскопа описывает конус с уг-
углом раствора р около вектора момента количеств движения с периодом
§ 13.12. Свободное тело; общий случай. Рассмотрим теперь движение,
описываемое уравнениями A3.11.1), в случае, когда А, В и С различны. Для
определенности предположим, что А > В > С. Умножая уравнения Эйлера
236 ПРИЛОЖЕНИЯ УРАВНЕНИЙ ГИББСА — АППЕЛЯ [Гл. XIII
A3.11.1) соответственно на щ, (о2, (о3 и складывая, получаем первый инте-
интеграл:
Аа?4-В(о1-\-С(о1 — 2Т, A3.12.1)
а умножая на Awb 5со2, Си>3 и складывая, получаем еще один первый
интеграл:
А*а>1 + ВЧо1 + С*а>* = 1)*. A3.12.2)
Полученные соотношения выражают постоянство кинетической энергии вра-
вращательного движения и постоянство величины момента количеств движения.
Представим их в следующей форме:
A3.12.3)
A3.12.4)
где D ш Q — положительные постоянные, D = г|2/2Г и Q = 2Т/г\. Если coi,
(о2, со3 считать декартовыми координатами изображающей точки, то траек-
траекторией этой точки будет линия пересечения двух эллипсоидов. Так как
то А ^ D ^ С. Случаи равенства не представляют особого интереса. Так,
например, из условия А = D следует, что со2 = со3 — 0 в течение всего вре-
времени движения, которое в этом случае представляет собой равномерное вра-
вращение с угловой скоростью +Q около оси G1. Поэтому, оставляя в стороне
случаи равенства, будем предполагать, что А > D > С. Разрешим уравне-
уравнения A3.12.3), A3.12.4) относительно со^ и со|, выразив эти величины через со|-
Проделав это, получим
2 В (В—С), а. 2 В(А — В),а. 2. /лчлпа\
1==А~ТЛ^С){ — 2'' ^з — q (А —С) ^ —С°2'' (lo.l/.D,)
где положительные постоянные аир определяются равенствами
а =В(В-С)"' Р ТВ(А-В)и- A6Л1.1)
Из второго уравнения Эйлера
Ва2= — (A — C)a3at A3.12.8)
теперь получаем
Дг (А —В) (В —С) . 2 „, ,о2 2\ /ло \п q\
а>2 — -д? \а —со2; (р —ю2;. ^xo.iz.a;
Это уравнение принадлежит к знакомому нам типу (см. § 1.2) и определяет
со2 в зависимости от t. Обозначим полином четвертой степени в правой части
равенства A3.12.9) через / (ю2). Нужно рассмотреть два случая: если а = р",
то полином имеет нули второй кратности; если а -ф р, то — простые нули.
1) а = р. Так как
р2 a9_z D{A-C)(B-D) ^ A3.12.10)
то равенство а = р имеет место лишь в том случае, когда D = В. Отсюда
получается соотношение
¦Л2 = 2ВТ, A3.12.11)
связывающее момент количеств движения т] и кинетическую энергию Т.
Если выполняется равенство A3.12.11), то а — р1 = Q и уравнение A3.12.9)
13.12]
СВОБОДНОЕ ТЕЛО; ОБЩИЙ СЛУЧАЙ
237
принимает вид
•% (A-B)(B-C)
^a--1 AC
A3.12.12)
График правой части уравнения A3.12.12) представлен на рис. 42. Согласно
результатам § 1.2, в данном случае по перемен-
\кж со2 осуществляется лимитационное движение,
так что при ?-»-оо либо со2 —»¦ +Q, либо
(о2—>- —?2.
Линия пересечения эллипсоидов A3.12.3) и
A3.12.4) лежит в плоскостях
A3.12.13)
и состоит из двух эллипсов. Вектор о в началь-
начальный момент располагается в одной из этих пло-
плоскостей. Предположим для определенности, что при t = О
О, со2 = 0, (о3 > О,
или, более подробно,
A3.12.14)
, = 0, щ=,+ау 2!±-П. A3.12.15)
Из уравнения A3.12.8) следует, что (о2 первоначально возрастает, следова-
следовательно, со2 все время монотонно возрастает, стремясь к Q при t—*- оо. Чтобы
определить (о2 как функцию от t, положим
(о2 = Q th 8.
Подставляя это выражение в уравнение A3.12.12), находим
в = nt,
где
(А-В) {В-С)
АС
Таким образом,
со2 = Q th nt,
и из A3.12.6) находим coi и со3:
A3.12.16)
A3.12.17)
A3.12.18)
A3.12.19)
. A3.12.20)
¦Знаки этих величин определяются начальными значениями: «i всегда отри-
отрицательно, а <й3 всегда положительно.- При t —*- оо величины <»i и со3 стремятся
к нулю, так что движение приближается
к равномерному вращению с угловой ско-
скоростью Q около оси G2.
2) а Ф р. При этом условии D фВ.
Полином /(со2) в правой части равенства
A3.12.9) имеет четыре простых нуля (рис.43),
и так как величина | со2 | меньше, чем наи-
наименьшая из величин а и р, то мы имеем ли-
либрацию по переменной со2 между значениями
±ос (если а < Р) или между значениями ±{5
(если р < а). Чтобы пояснить это, предположим для определенности, что
а < Р; это неравенство выполняется, если D <ZB. Таким образом, будем
238 ПРИЛОЖЕНИЯ УРАВНЕНИЙ ГИББСА — АППЕЛЯ [Гл. XIII
иметь
A>B>D>C. A3.12.21)
При этих условиях <а2 колеблется между пределами ±а, ол обращается
в нуль, когда со2 = ±а, а со| никогда не оказывается меньше, чем
№ а) у МЧ19 9Л
С{А-С)^ а> - с(В-С) ' A3.12.22)
так что (о3 сохраняет один и тот же знак в течение всего времени движения;
для определенности будем считать, что при t = 0 со3 > 0, и, следовательно,
всегда со3 > 0.
Величина со2, как мы видели, колеблется между пределами ± а. Начало
отсчета времени моншо выбрать так, чтобы при t = 0.
со2 = 0, со2 > 0.
Так как
Ва>2 = —(А — С) созСй!,
то в мо лт t = 0 имеем «i < 0. Начальные условия подобны тем, что были
приняты ранее (см. A3.12.14)). Чтобы проинтегрировать уравнение A3.12.9),
положим
со2 = a sn и, A3.12.23)
причем
к - 02 ~ (A-D)(B-C) • A3.12.24)
Подставляя в A3.12.9), получаем
где п > 0. Таким образом, при принятых начальных условиях будем иметь
и = nt A3.12.26)
и
со2 = a sn nt. A3.12.27)
Из A3.12.6) следует, что
С, , . j-, UU U.XJ. I Vis \J \A-LX I lT • ( \.(j • Л IL/ • ^-.iJ)'
Окончательно получаем
где р > а > у > 0. Полное решение для со будет иметь вид
(й4 = —у en n?, to2 = a sn n?, со3 = б dn nt. A3.12.30)
Величина «i колеблется между пределами у и —у с периодом АК/п, сог
колеблется между пределами а и —а с тем же периодом 4К/п, а со3 изменяется
между пределами
с периодом 2К1п.
§ 13.13. Ориентация свободного тела. Свободное движение твердого
тела описывается уравнениями A3.11.1), и из этих уравнений мы определили
§ 13.13] ОРИЕНТАЦИЯ СВОБОДНОГО ТЕЛА 239
угловую скорость тела в каждый момент времени, что дает своего рода внут-
внутреннее описание движения. Этот результат, однако, нельзя считать полным
решением задачи, так как он не дает представления о том, что мы наблюдаем
в действительности, т. е. не определяет истинной конфигурации системы в мо-
момент t. Это внешнее описание движения дается углами Эйлера в момент t
относительно некоторой неподвижной системы координат.
Предположим, что центр тяжести G находится в покое, и упростим вы-
вычисления, направив ось Oz фиксированной системы координат' (О === G)
вдоль вектора момента количеств движения, который, как мы знаем, остается
постоянным. Составляющие вектора момента количеств движения по осям
01, 02, 03 тогда определятся следующими формулами (см. G.11.1)):
Acdi = DQ cos zt = —DQ sin 9 cosojj, A3.13.1)
Ba2 = DQ cosz2 = DQ sin 9 sinajj, A3.13.2)
Cco3 = DQ cos z3 = DQ cos 9. A3.13.3)
Уравнение A3.13.3) вместе с решением A3.12.30) определяют угол 0
в зависимости от времени:
Так как
//а ._ (А— С) (В — D) /1Я 1Я S\
с, ., fC (A — D)
то cos 9 принимает значения, лежащие между верхним пределом 1/ тггз—тА
, /С (В—П) п „
и нижним пределом 1/ „ <в—с\' и имеет период 2л/ге.
<в—с\'
Определим теперь ijj как функцию от t:
_-./ГВ (А-С) sn nt <i4i4a\
-У A(B-C)cnnt' (ld.ld.b)
Как и следовало ожидать, г|з монотонно возрастает, причем за время 4К/п
увеличивается на 2я.
Затем найдем ф как функцию от t. Угловая скорость вращения около
оси ОТ (рис. 16) равна
— Ф sin 9 = (Oj cos if — (o2 sin г|з = —^i-J^.. A3.13.7)
Следовательно,
Подставляя значение со3 из формулы A3.12.28) и выполняя несложные
преобразования, получаем
(А - С) sn* nt+(В-С) en* nt (ЩЩп\
B(A-C)m*nt+A(B-C)<ai*nt ' A3.13.9)
Скорость ф изменяется между значениями DQIA и DQ/B, так что она всегда
положительна. Правая часть равенства A3.13.9) периодична с периодом
2К/п, так что
240 ПРИЛОЖЕНИЯ УРАВНЕНИЙ ГИББСА — АГШЕЛЯ [Гл. XIII
Следовательно,
и при возрастании t на 2К1п угол ф получает постоянное приращение ф0.
7~)О 9 JC
Значение ф0 можно найти, интегрируя A3.13.9); оно лежит между—^
Ш 2К_
После того как углы 9, ф, if определены как функции от t, можно по фор-
формулам G.11.1) определить зависимость от времени всех девяти направляю-
направляющих косинусов подвижной системы координат.
§ 13.14. Теоремы Пуансо и Сильвестра. Как и ранее, будем предполагать,
что центр тяжести G находится в покое. Рассмотрим эллипсоид, связанный
с телом и движущийся вместе с ним; пусть уравнение его в системе G123
имеет вид
Ах2 + By2 + Cz* = DQ2. A3.14.1)
Перпендикуляр, опущенный из G на плоскость, касательную к эллипсоиду
в точке P(coi, со2, со3), имеет длину Q, а направляющие косинусы нормали к
эллипсоиду в точке (со1( со2, со3), равны
Ащ/DQ, Baz/DQ, Сщ/DQ. A3.14.2)
Так как вектор момента количеств движения постоянен, касательная
плоскость к эллипсоиду в точке Р (col7 «2, со3) будет неподвижна; обозначим
ее через со. Таким образом, при свободном движении тела эллипсоид A3.14.1)
будет катиться по плоскости со; центр эллипсоида при этом будет оставаться
неподвижным. Угловая скорость будет равна расстоянию г от центра G
эллипсоида до точки Р касания с плоскостью со. В этом состоит теорема
Пуансо.
Сильвестр заметил, что если бы эллипсоид A3.14.1) представлял собой
однородное твердое тело, свободно закрепленное в точке G, и катился бы
по плоскости со без воздействия на него сил (кроме реакций в точках G и Р),
то это качение происходило бы точно так же, как происходит качение эллип-
эллипсоида, связанного со свободно движущимся телом (если, конечно, в обоих
случаях одна и та же начальная угловая скорость). Система имеет только
одну степень свободы, и нам остается показать, что когда твердый эллипсоид,
закрепленный в центре, катится по шероховатой плоскости, со пропорцио-
пропорционально г. Если массу эллипсоида обозначить через М, а полуоси его — через
а, Ъ. с, то кинетическая энергия будет иметь следующее выражение:
1U
10 r2 " ' ' * / • , \ i / >• {'-¦¦>
С другой стороны,
¦ {(b* + с2) х* + (с2 + а2) у2 + (а2 + b2) z2} -----
Где p — (постоянное) расстояние от неподвижного центра эллипсоида до ка-
касательной плоскости. Поскольку Т постоянно, со пропорционально г, что
и требовалось доказать.
S 13.1-М КАЧЕНИЕ ЭЛЛИПСОИДА ПО ШЕРОХОВАТОЙ ПЛОСКОСТИ 241
§ 13.15. Качение эллипсоида по шероховатой горизонтальной пло-
плоскости. В качестве последнего примера использования уравнений Гиббса —
Аппеля рассмотрим задачу о качении однородного твердого эллипсоида по ше-
шероховатой плоскости. Направим оси координат вдоль осей эллипсоида (кото-
(которые являются главными осями инерции в центре G). Скорость точки G обо-
обозначим через и, v. w, направляющие косинусы вертикали (направленной
вниз) — через I, т, п, а координаты точки соприкосновения эллипсоида
с плоскостью — через х, у, z. Условия качения запишутся в виде
у —zaI+a;(»3 = 0, | A3.15.1)
w — хщ-\- z/ft»! = 0. J
Вычислим сначала составляющие /4, /2, /з ускорения точки G. Имеем
/i = и — у ю3 + w&2- A3.15.2)
Подставляя и, v, w из A3.15.1), находим
/i = 2/Мз — ZC02 + г/«з — 2ю2 + х (и>\ + и>\ + ю|) — ю4 (xmt + ущ + zca3)- A3.15.3)
Вводя координаты q±, q2, q3 (причем qT = юГ), напишем выражение для
функции Гиббса:
® = ±-M(fl + fl+ft) + {{Awl-2(B-C)ti>&3w1}+...+ ..., A3.15.4)
в правую часть которого подставим выражение для f\ из A3.15.3) и выраже-
выражения для /2 и /3 из аналогичных формул.
Величины Qi, Q2, Q3 найти нетрудно, поскольку Q есть момент силы
тяжести относительно точки касания. Следовательно,
QK = Mg {—ny + mz). A3.15.5)
Может представить интерес и другой способ получения соотношения
A3.15.5). Имеем
_6У = -Mg Sp, A3.15.6)
где р — высота точки G, определяемая от горизонтальной плоскости. Далее,
— р = lu-\-mv-\-nw= 2 ЦУ®з— гщ) = S (— ny-\-mz) «ц. A3.15.7)
Таким образов,
—87 = MgJ] (-ny + mz) 6g,, A3.15.8)
и мы снова получаем формулу A3.15.5).
Так как Z, т, п определяют фиксированное направление в пространстве,
то
I —тщ -j- тш2 = 0, j
т-га©1-1-йвз = 0, \ A3.15.9)
п-Шг + тщ^0 )
Из элементарных геометрических соображений получаем
1 = -^-, m = ^r^ n=r^"' A3.15.10)
где й, Ь. с—полуоси эллипсоида.
16 Л. А. Парс
242 ПРИЛОЖЕНИЯ УРАВНЕНИИ ГИББСА - АППЕЛЯ [Гл. ХШ
Уравнения движения имеют вид
-^~ = Qr- A3.15.11)
Первое из этих уравнений подробно записывается следующим образом:
Му{х<^-]
+ Л©! — (В — С) <й2<й3 = Mg( — ny + mz) A3.15.12)
или, после преобразований,
¦ • • • ^
(Mr2 +. A) (Oj — Мх (ztt>i + у(о2 + zaK) +-Л/rroo'i —
— М(х — ущ + 2<й2) (жа>1 + г/ю2 + z(o3) — (В — С) (о2а>3 —
= Mg (—пу + пи), A3.15.13)
где г2 = z2 + у2 + 22. Уравнение A3.15.13) и два аналогичных составляют
искомую систему уравнений движения эллипсоида.
§ 13.16. Устойчивость вращающегося эллипсоида. В качестве примера
применения уравнений движения A3.15.13) рассмотрим задачу об эллипсои-
эллипсоиде, вращающемся около своей оси а с угловой скоростью ю. Спрашивается,
при каких условиях это движение устойчиво по первому приближению отно-
относительно малых возмущений? Предполагая, что возмущенное движение мало
отличается от невозмущенного, будем считать т, п, са2, ю3 малыми величина-
величинами одного порядка, что позволит нам составить уравнения движения с необ-
необходимой степенью точности. Итак, пренебрегая членами второго порядка,
будем иметь
Z = 1, ж = г = а, у = Ъгт1а, z = c2n/a. A3.16.1)
Из первого уравнения A3.15.13) получаем wt = 0, так что ац —¦ const; будем
предполагать, что щ равно значению ю в невозмущенном движении. Урав-
Уравнения A3.15.9) теперь запишутся в форме
п -j- cam, I
— m+care, J
A3.16.2)
справедливой с принятой степенью точности.
С помощью этих уравнений и соотношения А = М (Ь2 + с2)/5 и т. д.
перепишем второе и третье уравнения движения в виде
Fа2 +Ъ2)т — A2а2 — 5с2)care + (Ъ2 — а2) Fca2 +1?) m
где А,2 равно 5g/a. Период колебаний находится из уравнений
П °' 1 A3.16.3)
71 = 0, J
/ A3.16.4)
— рл ip — р2 ip
после исключения т/п. Проделав это, будем иметь
l(b2 + 6a2) p2 - (Ь2 - а2) Fю2 + к2)] [(с2 + 6а2) р2 -
_(С2 _ а2) (боJ + к2)] — EЬ2 — 12а2) Eс2 — 12а2) ю2р2 = 0. A3.16.5)
Достаточным условием устойчивости по первому приближению будет вещест-
вещественность и положительность корней уравнения A3.16.5).
§ 13.16] УСТОЙЧИВОСТЬ ВРАЩАЮЩЕГОСЯ ЭЛЛИПСОИДА 243
Прежде всего заметим, что оба корня не могут быть положительны, если
не выполнено неравенство
(Ь2 _ а2) (с2 — а2) > 0, A3.16.6)
так что (Ь2 — а2) и (с2 — а2) должны быть либо одновременно положительны,
либо одновременно отрицательны. Поэтому устойчивым может быть лишь
вращение эллипсоида либо около короткой, либо около длинной оси.
1) Если а есть короткая полуось эллипсоида, то уравнение A3.16.5)
можно представить в виде
+ 369V) «2 + (PV + Т202) ^2} Р2 + eV F«2 + ^2J = О,
A3.16.7)
гДе Pi Y> б, ф — положительные числа, определяемые соотношениями
Р2 = Ь2 + 6а2) у2 = С2 _|_ 6а25 02 = Ъ2 _ ^ ф2 = С2 _ ^2 A3.16.8)
Достаточное условие устойчивости по первому приближению, таким обра-
образом, состоит в том, чтобы значения р2, определяемые из уравнения
A3.16.7), были вещественны и положительны. Коэффициент при р2 в уравнении
A3.16.7), разумеется, отрицателен, и требуемое условие сводится к неравен-
неравенству
(РУ + 369V) ю2 + (р2ф2 + Т292) W > 2Рт9ф Fю2 +Х2), A3.16.9)
которое можно переписать в форме
(РТ — 69фJю2 + фФ — yQJX2 > 0, A3.16.10)
а это последнее неравенство, как легко видеть, выполняется, и, следователь-
следовательно, вращение эллипсоида около короткой оси устойчиво при всех значениях со.
2) Если а есть длинная полуось, то уравнение A3.16.5) можно предста-
представить в форме
PVP4 - {(PV + 36GV) ю2 - (р2ф2 + Y292) ^2} P2 + 02ф2 Fю2 + А2J = 0,
A3.16.11)
где теперь
Р2 = Ь2 _|_ 6^2^ у2 = С2 _|_ 6а2) Q2 = а2 _ ?2^ ф2 = ^2 _ ?2 A3.16.12)
и р, 7, 9, ф — положительные числа. Значения р2 будут вещественны и поло-
положительны при выполнении следующих условий:
+ 36GV) (о2 - (р2ф2 + Т292) № > 0, A3.16.13)
+ 3602Ф2) ю2 — (р2ф2 + т292) X2 > 2р70Ф Fю2 + X2). A3.16.14)
Последнее неравенство влечет за собой первое, так что для устойчивости
достаточно, чтобы
(PV - 60ФJ(й2 > (рФ + увJХ2. A3.16.15)
Но ру > 68ф, так что движение будет устойчивым, если | ю | > Q, где
?^ i/g HQ 16 16)
Итак, мы пришли к следующему результату. Если а есть меньшая из по-
полуосей а, Ь, с, то движение устойчиво по первому приближению при всех
значениях угловой скорости (как этого и следовало ожидать). Если а есть
средняя полуось, то движение всегда неустойчиво. И наконец, если а —
длинная полуось, то устойчивость имеет место для значений угловой скоро-
скорости, превышающих некоторое критическое значение Q.
16*-
Глава XIV
ТЕОРИЯ УДАРА
§ 14.1. Ударный импульс. В этой главе мы перейдем к изучению очень
быстрых (внезапных) изменений движения, происходящих при действии
на систему ударных импульсов. Под ударными импульсами мы будем пони-
понимать предельный случай действия больших сил в течение коротких проме-
промежутков времени. Уравнение движения свободной частицы имеет вид
тх = Х. A4.1.1)
Если X есть известная функция от t, то можно написать
«2
т(и2-щ) = j Xdt, A4.1.2)
где через иТ обозначено значение х в момент t = tT. Мы будем рассматривать
случай, когда величина т = ?2 — h мала, функция X в промежутке времени
(hi ti + т) велика, а интеграл
j Xdt^P A4.1.3)
н
имеет конечное значение; величину Р будем называть составляющей
импульса.
Выше мы определили ударный импульс как предельный случай действия
большой силы в течение малого промежутка времени. Физически правильней
будет рассматривать не строгий математический предел при т —*- О, а считать
т очень малым, но конечным промежутком времени, т. е. считать т физически
малым, но не математически малым. Во всех практических случаях % можно
считать пренебрежимо малой величиной. За время от t\ до ti + т конфигура-
конфигурация системы изменяться не будет, тогда как скорость в момент г4 = 0 будет
изменяться скачком. В задаче, в которой других сил, кроме ударных, нет,
координаты сохраняют постоянные значения, скорости в момент ti — О
задаются и требуется определить скорости в момент ^ + 0. Поскольку коор-
координата х остается неизменной, вместо х удобнее писать и.
Уравнения A4.1.2) и A4.1.3) вместе с соответствующими уравнениями
для координат у, z образуют систему уравнений
т(и — и0) = Р, т (v — v0) = Q, m (w — w0) = В, A4.1.4)
где {Р, Q, R} — ударный импульс, действующий на частицу в момент tt,
{и0, v0, Wo) — скорость частицы в момент tt — 0 (т. е. непосредственно перед
приложением импульса), а {и, v, w) — скорость частицы в момент ^ + 0
(т. е. непосредственно после приложения импульса). Уравнения A4.1.4)
являются основными уравнениями в теории удара. Если частица перед при-
приложением ударного импульса находилась в покое, то уравнения A4.1.4)
принимают вид
ти = Р, mv = Q. mw — R, A4.1.5V
§ 14.1] УДАРНЫЙ ИМПУЛЬС 245
т. е. импульс равен количеству движения, сообщенному частице, находив-
находившейся первоначально в покое. Этот результат аналогичен второму закону
Ньютона: аналогом силы здесь является импульс силы, а аналогом произве-
произведения массы на ускорение — количество движения.
Подход, при котором сила является основным понятием, а импульс — производным,
наиболее естествен и соответствует предыдущему изложению. Возможен, однако, и дру-
другой подход. Можно импульс считать основным понятием, а силу — производным. При
такой точке зрения конечная сила, действующая в течение некоторого интервала времени,
представляется как предельный случай действия большого числа малых импульсов
в моменты, распределенные по всему интервалу.
Рассмотрим движение твердого тела, на которое действует ударный
импульс. Так как заданные силы в течение короткого промежутка времени
принимают большие значения, то реакции связи в течение этого времени
также должны быть велики. Итак, мы будем предполагать, что реакции связи
велики; кроме того, будем считать, что тело остается твердым. Эти предполо-
предположения представляют дальнейшую идеализацию реальных (не абсолютно
твердых) тел. Фактически под действием конечных сил и тем более под дей-
действием ударных сил все тела получают деформации. В рассматриваемой нами
идеализированной теории тела не деформируются как при воздействии конеч-
конечных сил, так и при воздействии ударных сил.
Если через X' обозначить реакцию связи, действующую в течение вре-
мени от tt до ti + т, то интеграл \ X' dt =P' будет иметь конечное значение;
мы будем называть его ударным импульсом сил реакции. Он является анало-
аналогом реакции связи в задачах с конечными силами. Мы будем предполагать,
что при воздействии этих импульсов тело не деформируется, т. е. остается
абсолютно твердым. В более общем случае, при переходе от задачи движения
одного тела к задаче о движении системы тел, мы будем иметь в виду, что
на систему могут действовать соответствующие ударные импульсы сил
реакции.
Рассмотрим общий случай механической системы, на которую действуют
ударные импульсы. Начнем с задачи, в которой заданные силы (и соответст-
соответственно реакции связи) в течение малого промежутка времени т принимают
большие значения. Поскольку координаты частиц системы в течение этого
промежутка времени практически не изменяются, остаются постоянными
и коэффициенты Ars, AT в уравнениях связи B.2.4), что сильно упрощает
исследование.
В теории удара удобно пользоваться второй формой D.1.3) основного
уравнения:
S (mrxr-XT)Aur = 0. A4.1.6)
r=l
Конечные вариации скорости Аи удовлетворяют уравнению D.1.2):
N
2Л.Ди. = 0, г = 1,2, .... L, A4.1.7)
г—1
и так как коэффициенты ATS постоянны, то можно указать системы Ащ,
Ам2, . . ., AuN, удовлетворяющие уравнениям A4.1.7) в течение короткого
промежутка времени от t± до tt + т.
Мы воспользовались второй формой основного уравнения, до сих пор
почти не употреблявшейся, так как с эстетической и логической точек зрения
удобнее оперировать с вариациями скорости, нежели с виртуальными пере-
перемещениями; это объясняется тем, что в рассматриваемых задачах координаты
частиц остаются постоянными.
246 ТЕОРИЯ УДАРА [Гл. XIV
Задачи на удар в математическом отношении проще, чем задачи с конеч-
конечными силами. Уравнения для определения скоростей в момент ^ + 0 являют-
являются линейными алгебраическими уравнениями, тогда как задачи с конечными
силами приводятся к дифференциальным уравнениями. В общем случае
решение задач на удар не встречает особых затруднений.
§ 14.2. Импульсные связи. В предыдущем параграфе мы рассматривали
задачу, в которой механическая система, подвергаемая действию ударных
импульсов, принадлежала к типу, рассматривавшемуся в § 2.2.
Рассмотрим теперь некоторые новые типы систем, не встречающиеся
в задачах с конечными силами.
В уравнениях связи B.2.4), изучавшихся до сих пор, коэффициенты
ATS, AT считались функциями, принадлежащими классу С\\ это были непре-
непрерывные функции положения и времени. Введем теперь связи, описываемые
уравнениями
j]Ersxs+Er^0, r = 1, 2, ...,//, A4.2.1)
s=l
в которых коэффициенты ETS, Er терпят разрывы в момент ty. Подобные связи
будем называть импульсивными. Коэффициенты уравнения A4.2.1) непрерыв-
непрерывны до момента ty и после этого момента, но в момент t± они претерпевают
разрыв. Фактически в этом случае мы имеем две системы (постоянных) значе-
значений коэффициентов: значения при ty — 0 и значения при tt + 0.
Практически наиболее часто встречаются связи двух следующих типов:
1) Связи первого типа. Эти связи описываются уравнениями
N
2 Ers'xs = 0, r = l, 2, ..., L',
и накладываются внезапно в момент tx. Коэффициенты Ет в уравнениях
A4.2.1) при этом тождественно равны нулю, а коэффициенты Ers равны нулю
в момент t± — 0. Наложение связи такого рода фактически уменьшает число
степеней свободы системы.
Простым примером связи первого типа может служить движущаяся
частица, ударяющаяся в момент ?4 о гладкую неупругую неподвижную
плоскость х = х0. Связь в этом случае описывается уравнением г = 0в мо-
момент ti + 0.
2) Связи второго типа. Эти связи определяются уравнениями
A4.2.1), в которых коэффициенты ETS непрерывны (фактически постоянны),
а все коэффициенты Ет равны нулю в момент tx — 0 и, вообще говоря, отлич-
отличны от нуля в момент t\ + 0. При этом число степеней свободы системы остает-
остается неизменным.
В качестве простого примера связи второго типа укажем на движение
по гладкой плоскости х — х0, которая в момент tt внезапно приходит в движе-
движение со скоростью U в направлении оси Ох. Уравнение связи х = 0 в момент
h — 0 уступает место уравнению х — U = 0 в момент ti + 0.
Теоретически можно представить себе задачу, в которой заданные
импульсы и импульсивные связи прикладываются одновременно в момент
ti. Однако на практике чаще всего возникают задачи двух типов: 1) задачи,
в которых на систему действуют заданные ударные импульсы, а наложенные
связи конечны (т. е. не импульсивные); 2) задачи, в которых па систему не дей-
действуют ударные импульсы активных сил, но имеются импульсивные связи.
Однако при выводе основного уравнения движения системы мы для удобства
будем считать, что заданные импульсы и импульсивные связи действуют
5 14.S] ДВИЖЕНИЕ СИСТЕМЫ, НА КОТОРУЮ ДЕЙСТВУЮТ УДАРНЫЕ ИМПУЛЬСЫ 247
в один и тот же момент времени; это позволит охватить оба класса задач еди-
единой теорией. (Конкретная иллюстрация одновременного действия заданных
импульсов и импульсивных связей дается в § 14.6, где говорится о теоремах
Карно и Бертрана.)
Рассматриваемые здесь импульсивные связи, разумеется, не следует путать с импуль-
импульсами реакций связи, о которых была речь в § 14.1.
§ 14.3. Движение системы, на которую действуют ударные импульсы.
Основное уравнение теории удара. При выводе основного уравнения в случае
конечных сил мы рассматривали сначала простейшую систему, состоящую
из одной частицы. Здесь мы сразу перейдем к общему случаю механической
системы. Задача будет трактоваться как предельный случай задачи с конеч-
конечными силами, и, как уже указывалось, заданные импульсы и импульсивные
связи будут вводиться одновременно.
Рассмотрим промежуток времени от tt до ti + т, в течение которого
на систему действуют конечные силы. Этот промежуток времени будем счи-
считать столь малым, что коэффициенты в конечных уравнениях связи
Е4к8 + 4 = 0, г=1, 2, ..., L, A4.3.1)
г=1
в течение этого времени можно принять постоянными. Уравнения импуль-
импульсивных связей можно получить из конечных уравнений
N
2Я«и. + еР = 0, г = 1, 2, ..., L', A4.3.2)
s=l
в которых функция времени 8Г изменяется за время от ^ до ^ + т от значения
N
— S Ers OOii-o Д° нуля в случае связей первого типа и от нуля до (Er)t1+0 в
8=1
случае связей второго типа. Вторая форма D.1.3) основного уравнения за-
запишется теперь в виде
N
S(mri"-Ir)A«, = 0, A4.3.3)
r=l
где Аи—(конечная) вариация скорости и ее составляющие Ащ, Аи2, ¦ ¦ .
.... AuN удовлетворяют уравнениям
N
^]АгзАи8 = 0, г = 1, 2, ..., L, A4.3.4)
8=1
N
^jErsAus = 0, г=1, 2, ..., L'. A4.3.5)
г=1
Коэффициенты Ars, Ers в этих линейных уравнениях постоянны, так что
можно найти вариации At*, общие для всего интервала от tt до ^ + т. Выбе-
Выберем любую такую вариацию Аи. Подставляя ее составляющие в уравнение
A4.3.3) и интегрируя в пределах от t± до t\ + т, находим
JV
^{mr(ur-urQ)-Pr}Aur = 0, A4.3.6)
s=l
tl+т
где Рт — заданная составляющая импульса 1 Хт dt. Величина % здесь считает-
/1
ся пренебрежимо малой, а ито и иг обозначают значения хт в моменты ti — О
и tt + 0. Уравнение A4.3.6) будем называть основным уравнением движения
системы.
248 ТЕОРИЯ УДАРА [Гл. XIV
В случае неимпульсивных связей основное уравнение можно написать, используя
вместо больших конечных сил, действующих в течение короткого промежутка времени,
соответствующие импульсы. Рассуждения остаются в этом случае точно такими же, как
при выводе основного уравнения в случае конечных сил (§ 3.1). Если через Рг обозначить
составляющую заданного импульса активных сил, а через Р'т — составляющую импульса
реакции связи, то можно написать
тт (иг - иг0) = Рг + Р'г, г= 1, 2, . . ., N. A4.3.7)
Импульсы реакции связи удовлетворяют теперь уравнению
2^гЛмг = 0, A4.3.8)
г=1
и из уравнений A4.3.7) и A4.3.8) следует уравнение A4.3.6). Такой метод, однако, не
очень удобен в случае, когда имеются импульсивные связи.
§ 14.4. Катастатическая система. При использовании основного урав-
уравнения A4.3.6) важно знать класс Аи, для которых это уравнение справедливо.
Такие вариации удовлетворяют равенствам A4.3.4), A4.3.5). Рассмотрим их
более подробно для случая катастатических систем.
1) В случае отсутствия импульсивных связей уравнения A4.3.4), удовлет-
удовлетворяемые вариациями скоростей, идентичны с уравнениями, удовлетворяе-
удовлетворяемыми самими скоростями:
j]Arsus = 0, r=l, 2, ..., L. A4.4.1)
s=l
С другой стороны, уравнения A4.4.1) и A4.1.7) идентичны, поскольку
нулевая скорость принадлежит к классу возможных скоростей. Поэтому
в основном уравнении можно писать JJ вместо Аи, считая U(Ui, U2, ¦ ¦ ¦
. . ., UN) любым допустимым вектором скорости. Тогда основное уравнение
примет весьма удобную форму:
JV
2 тТ (иг - ит0) Uг = 2 PfUr A4.4.2)
или, если опустить индексы,
2 m (и - и0) U = 2 ри. A4.4.3)
2) Рассмотрим теперь катастатическую систему, на которую наложена
связь первого типа. Уравнения, которым удовлетворяет Аи, в точности совпа-
совпадают с уравнениями, которым удовлетворяет V, где V — любой вектор
скорости, допустимый для системы с наложенными связями. Основное урав-
уравнение при этом записывается так:
JV
2 mT(ur-un)UT = Q. A4.4.4)
Классом допустимых значений JJ является класс допустимых скоростей
в момент ti + 0.
3) Наконец, рассмотрим случай, когда на систему наложена связь второго
типа. Система с такими связями, конечно, уже не будет катастатической
после наложения связи. Все коэффициенты ЕТ в уравнениях A4.2.1) равны
нулю в момент tx — 0, и уравнения A4.3.4), A4.3.5), которым удовлетворяет
At*, в точности совпадают с уравнениями, которым удовлетворяют скорости,
допустимые в момент, непосредственно предшествующий наложению связи.
Основное уравнение записывается в форме
j]mr(ur-ur0)Ur = 0, A4.4.5)
§ 14.5] ПРИНЦИП НАИМЕНЬШЕГО ПРИНУЖДЕНИЯ В ТЕОРИИ УДАРА 249
причем классом допустимых значений V является класс возможных скоростей
в момент ty — 0.
§ 14.5. Принцип наименьшего принуждения в теории удара. Рассмот-
Рассмотрим катастатическую систему и будем предполагать, что в момент t\ прилага-
прилагаются заданные импульсы или накладываются связи первого типа или же осу-
осуществляется и то и другое одновременно. Докажем, что значения скоростей и
в момент t± -{- 0 (т. е. непосредственно после приложения импульсов) опреде-
определяются из условия, что выражение
рассматриваемое как функция от и, принимает минимум в классе скоростей,
допустимых в момент tx + 0 (и0, как обычно, обозначает систему скоростей,
в момент ti — 0, т. е. непосредственно перед приложением импульсов). Эта
теорема аналогична принципу наименьшего принуждения Гаусса в случае
конечных сил (§ 4.3).
Доказательство очень простое. Если и — действительная система ско-
скоростей в момент ti -f- 0, а и + Аи— любая другая возможная система скоро-
скоростей в этот же момент времени, то имеем
= 2™ ("-"о—^") Au + 4"Sm(A"K- A4.5.2)
Отсюда, учитывая A4.3.6), получаем
A© = i-2m(A"J>0, A4.5.3)
если только
Наиболее важным является случай, когда на систему наложены связи
первого типа; для этого случая теорема утверждает, что выражение
6 = y2m(u-u0J A4.5.4)
имеет минимум при истинном значении скорости и в классе скоростей, воз-
возможных для системы с наложенными связями.
Подобно аналогичной теореме § 4.3, доказанная теорема дает более чем
достаточную информацию для решения поставленной задачи; условия ста-
стационарности функции © приводят к системе линейных уравнений относи-
относительно составляющих вектора и.
В качестве простого примера рассмотрим следующую задачу.
Пример 14.5. Четыре однородных стержня, массы М и длиной I
каждый, шарнирно соединены друг с другом своими концами и образуют
раму; две противоположные вершины этой рамы соединены легкой нерастя-
нерастяжимой струной длиной Zf/^2 (так что, когда струна натянута, рама имеет
форму квадрата). Система движется по гладкой горизонтальной плоскости.
Первоначально струна не натянута, но в момент tx она натягивается. Требует-
Требуется определить движение системы непосредственно после приложения
импульса.
Кинетическая энергия одного стержня равна -^ М (м2+ u-v -\-vz +
+ Зш2), где векторы unv представляют собой составляющие скорости концов
стержня по направлениям, перпендикулярным к стержню, a w — скорость
вдоль стержня.
.250
ТЕОРИЯ УДАРА
[Гл. XIV
В рассматриваемой задаче скорости вдоль стержней обозначим через
и, v, w, х (рис. 44). Тогда кинетическая энергия стержня АВ будет
равна
1
¦i- M (и* — uw + wz +
6
A4.5.5)
Ряс. 44.
Написав соответствующие формулы для других стерж-
стержней, получим
© = -g-iW{5(M — M0J-j-5(v — ?>0J + 5 (w — woJ+5 (x —
-zo)a-2(u-uo)(a>-u>o)-2(i>-i>o)(*-*o)}. A4.5.6)
где и0, v0, w0, x0 — значения скоростей непосред-
непосредственно перед моментом натяжения струны.
Уравнение связи запишется в форме
u — v + w — x = 0. A4.5.7)
Условия стационарности функции ? при наличии связи A4.5.7) дают
5и — w — E«0 — w0) — X,
5w — и — Eш0 — и0) = X,
5х — v — Eх0 — vo)-= —X.
A4.5.8)
Отсюда находим
где
1 »
и — uo = w — w0 = -г л,
_, 1.
V Vq — X Хд'— - -т- А,
= — (щ — v0 + w0 — х0).
A4.5.9)
A4.5.10)
§ 14.6. Катастатическая система. Теорема о суперпозиции. Предполо-
Предположим, что положение и скорость системы заданы. Пусть система импульсов
Pi сообщает ей скорость щ, а система импульсов Р2—скорость и2- Требует-
Требуется найти скорость и3 при одновременном приложении обеих систем импуль-
импульсов 1\ + Р2.
Уравнения A4.4.2) дают (мы пользуемся сокращенными обозначениями)
2 m (щ - и0) U = S
2 m (u2 - щ) U = 2
2 m (щ - и0) U = 2
A4.6.1)
A4.6.2)
A4.6.3)
¦Эти уравнения удовлетворяются при одних и тех же значениях U, а именно
при скоростях, возможных в системе в ее положении в момент t\. Отсюда
следует, что для одних и тех же значений U
и2 — и0 — и3) U = 0.
A4.6.4)
Следовательно,
и3 = Щ + и2 — и0. A4.6.5)
Наиболее важным является случай, когда система первоначально нахо-
находилась в покое. Тогда
и3 = Щ + и2, A4.6.6)
так что суперпозиция импульсов влечет за собой суперпозицию скоростей.
§ 14.7] КАТАСТАТИЧЕСКАЯ СИСТЕМА. ШЕСТЬ ТЕОРЕМ ОБ ЭНЕРГИИ 251
§ 14.7. Катастатическая система. Шесть теорем об энергии. Рассмот-
Рассмотрим теперь ряд изящных теорем, касающихся кинетической энергии системы
при действии на нее ударных импульсов. В сокращенных обозначениях основ-
основные уравнения A4.4.3) и A4.4.4) записываются в виде
2 т (и — и0) U = 2 PU, A4.7.1)
2 т (и — щ) U = 0. A4.7.2)
1) Приращение энергии системы без импуль-
импульсивных связей. Имеем
2 т (и — щ) U = 2 PU, A4.7.1)
где U — любая система скоростей, возможная в момент t\. К ней принадле-
принадлежат, в частности, векторы и0 и и, а также вектор Ямо+(хм. В частности, мож-
можно взять вектор С = -^ (м+ и0), тогда получим
^21p A4.7.3)
ИЛИ
Приращение кинетической энергии равно сумме скалярных произведений
каждого импульса на среднее арифметическое скоростей точки его приложе-
приложения непосредственно перед приложением импульса и после него.
В частности, если система первоначально находилась в покое, то сооб-
сообщенная ей энергия равна-^-2 Ри-> или, если суммирование производить
по частицам,
A4.7.5)
2) Теорема Карно о потере энергии при наложе-
наложении связи первого типа. При наложении такой связи потерян-
потерянная энергия равна энергии потерянных скоростей. Потерянной скоростью
частицы называется векторная разность ее скоростей до и после наложения
связей. Имеем
2^ {и — uo)U = 0. A4.7.2)
Это равенство справедливо (§ 14.4) для любой системы скоростей 77, допусти-
допустимой непосредственно после наложения связи, т. е. в момент ^ -+- 0. В част-
частности, можно взять U =м, тогда будем иметь
2mu (и — и0) = 0. A4.7.6)
Но
и(и-ио)^±{и*-и1+(и-ио)*}, A4.7.7)
так что A4.7.6) равносильно равенству
Т 2 m<-\li ™»2 = | S т ("-"оJ A4-7.8)
или
То-Т = Яо. A4.7.9)
Здесь То есть кинетическая энергия в момент, непосредственно предшествую-
предшествующий наложению связи, Т — кинетическая энергия сразу после наложения
252 ТЕОРИЯ УДАРА [Гл. XIV
связи, a Ro — кинетическая энергия потерянных скоростей, равная
Яо=!2т^-"оJ- A4.7.10)
Интересно отметить, что теорему Карно можно вывести из двух предыдущих теорем.
Пусть JPq — система импульсов, сообщающая покоившейся системе движение со скоро-
скоростью щ, а Р'— система импульсов сил реакции при наложенной связи. Если импульс Р'
будет приложен к покоящейся системе, то он вызовет относительное движение со скоро-
скоростью и —щ, и энергия этого движения будет равна /J Р' —¦>—^- Приращение же энер-
\П _ И+Ил
гии системы при наложенной связи равно ZjP —~о' чт0 отличается от предыдущем
величины лишь знаком, так как согласно A4.3.8) 2 Р'и — 0.
Следует остановиться на одном обстоятельстве, которое может вызвать недоразуме-
недоразумения. Мы видели в § 14.5, что движение непосредственно поело наложения связи опреде-
определяется из условия минимума величины
С другой стороны, согласно теореме Карно потеря энергии равна
Но отсюда совсем не следует, что движение в момент tt -(- 0 таково, что потеря энергии
минимальна.
3) Выигрыш энергии при наложении связи вто-
второго типа. При наложении такой связи энергия системы возрастает
на величину, равную энергии приобретенных скоростей. Имеем
2 т (и — и0) U = 0. A4.7.2)
Это равенство справедливо (§ 14.4) для любой системы скоростей С, допусти-
допустимой непосредственно перед наложением связи, т. е. в момент ti — 0. В част-
частности, можно взять U =и0. Тогда будем иметь
^тио(и — и0) =• 0. A4.7.11)
Аргументы, аналогичные A4.7.7), показывают, что
Т — То = R. A4.7.12)
Справедливость теорем 2) и 3) очевидна непосредственно из тривиаль-
тривиальных примеров связей первого и второго типов, приведенных в § 14.2.
4) Т е о р е м а Бертрана*). Предположим, что система, первона-
первоначально находившаяся в покое в некотором положении, приводится в движение
заданной системой импульсов. Повторим мысленно этот эксперимент при
тех же условиях, но с той лишь разницей, что теперь систему подчиним
дополнительным (конечным) связям. Согласно теореме Бертрана, энергия Т{
системы во втором случае меньше энергии Т системы в первом случае на величи-
величину энергии потерянных скоростей (т. е. скоростей и — щ).
*) Эту теорему обычно называют теоремой Бертрана, хотя установить теперь про-
происхождение этого названия не так-то легко. Ее называл так еще Штурм (Comptes Rendus,
XIII, 1841, стр. 1046). Штурм показал, что теоремы Карно и Бертрана, по существу,
выражают одно и то же. Тоорома Кельвина приводится в «Proc. Royal Society of Edin-
Edinburgh», 1863, стр. 113, и в книге Томсона и Тэта «Natural Philosophy», 1912, стр. 286.
Теорема о том, что выигрыш энергии в теореме Кельвина превышает потерю энергии в тео-
теореме Бертрана, принадлежит Тейлору: G. I. Т а у 1 о г, Proc. London Math. Soc, Series 2,
Vol. 21, стр. 413.
§ 14.7] КАТАСТАТИЧЕСКАЯ СИСТЕМА. ШЕСТЬ ТЕОРЕМ ОБ ЭНЕРГИИ 253
Из A4.7.1) следует, что
2 muU = 2 ^?7, A4.7.13)
2 тщи = 2 />*7. A4.7.14)
Оба эти уравнения справедливы при U = Mi, следовательно,
2 /reuj (и — uj) = 0. A4.7.15)
Учитывая A4.7.7), получаем
Т — Tt = Rx > 0. A4.7.16)
Формулируя эту теорему, мы предполагали, что во втором опыте удар приклады-
прикладывается к системе, на которую наложены конечные связи. Однако результат будет тем же
самым, если импульсивная связь первого типа накладывается одновременно с ударом.
Это обстоятельство позволяет трактовать теорему Бертрана как видоизменение теоре-
теоремы Карно. В самом деле, в теореме Карно система приводится в движение заданными
импульсами, а импульсивная связь первого типа накладывается сразу же после .этого.
В теореме же Бертрана (в условиях второго опыта) можно считать, что связь первого типа
накладывается одновременно с приложением импульсов. В обоих случаях результат
один и тот же, поэтому и содержание обеих теорем одинаково.
Теорему Бертрана иногда формулируют для двух условий эксперимента,
соответствующих различным связям. Но результаты при этом не независимы:
система, на которую наложено меньше связей,— это просто «система», какой
она является в первом эксперименте приведенного выше доказательства.
5) Теорема Кельвина. Предположим, что система, находив-
находившаяся в заданном положении в покое, приводится в движение ударными
импульсами, приложенными в определенных точках; скорости (но не импуль-
импульсы) в точках удара будем считать заданными. Теорема Кельвина устанавли-
устанавливает, что при этих условиях энергия системы меньше, чем в любом другом дви-
движении, при котором указанные точки имеют заданные скорости.
Согласно A4.7.1) имеем
2 muU = 2 PU. A4.7.17)
Обозначим через и2 любую другую систему скоростей, при которой указан-
указанные точки имеют заданные значения скорости. Полагая U = и — и2, нахо-
находим
2 ти (и — щ) = 2 Р (и - иг)- A4.7.18)
Правая часть этого равенства равна нулю, так как Р обращается в нуль
всюду, где разность (и — и2) отлична от нуля. Поэтому
2 ти (и — и2) = 0 A4.7.19)
и, следовательно,
Т2 — Т = R2. A4.7.20)
Замечание 1. Теорема остается в силе и тогда, когда направление
удара в каждой точке, где он прилагается, задано, а также задана составляю-
составляющая скорости вдоль этого направления. В самом деле, при этом условии ска-
скалярные произведения Ри + Qv + Rw и Ри2 + Qv2 + Rw2 в каждой точке
удара одинаковы, откуда и следует теорема.
Замечание 2. Теорема легко обобщается на случай, когда система
в начальный момент не находится в покое. В этом случае имеем
2 пг(и — щ) {и — и2) = 0. A4.7.21)
что можно переписать в виде
2 m (и - щ) {{и - щ) - (и2 — ц0)} = 0. A4.7.22)
254 ТЕОРИЯ УДАРА [Гл. XIV
Обычным путем находим
±-^т(и2-и0)*-±-^т(и-щ)* = ±-^т(и-и2J>0. A4.7.23)
Теорема утверждает, что энергия потерянных скоростей при действи-
действительном движении минимальна.
Замечание 3. Теореме Кельвина можно придать форму, весьма
близкую к теореме Бертрана. Для этого приведем рассматриваемую свобод-
свободную систему в движение, задав соответствующим точкам определенные ско-
скорости. Пусть приобретенная энергия системы будет равна Т±. Затем повторим
мысленно эксперимент, на этот раз с системой, на которую наложены связи.
Приобретенную энергию системы в этом случае обозначим через Т2. Тогда
будем иметь Т2 > Tt. Наложение связи увеличивает энергию системы.
Связь между теоремами Бертрана и Кельвина можно продемонстрировать на сле-
следующем простом примере. Предположим, что стержень АВ, первоначально находившийся
в покое, приведен в движение ударом, перпендикулярным к стержню в точке В. Повторим
этот опыт при условии, что точка С стержня закреплена неподвижно. Если удар в точке В
в обоих опытах будет одним и тем же, то наложение связи уменьшит энергию стержня.
Если же в обоих опытах будет одинакова скорость в точке В, то наложение связи увеличит
энергию. (Если точка С находится близко от точки В, то выигрыш в энергии при одной
и той же скорости в точке В может быть весьма большим.)
Важно отметить, что связи, упоминаемые в замечании 3 к теореме Кель-
Кельвина, не вполне произвольны: они должны согласовываться с заданными
скоростями соответствующих точек. Фиксирование одной из таких точек
может служить простым примером запрещенных связей.
6) Теорема Тейлора о связи между теоремами
Бертрана и Кельвина. Произведем мысленно три опыта: а), Ь)
и с). В каждом из них будем предполагать, что в начальный момент система
находится в покое в некотором заданном положении.
а) В некоторых точках системы прикладываются ударные импульсы,
сообщающие системе кинетическую энергию Т.
б) Система подчинена связям и подвергается действию тех же ударных
импульсов, что и в опыте а). Приобретенная кинетическая энергия системы
в этом случае пусть будет равна 7V По теореме Бертрана Т — 7\ = i?i > 0.
с) Система подчинена тем же связям, что и в случае Ь), и к тем же точ-
точкам, что и в случае а), прикладываются ударные импульсы такие, что скоро-
скорости этих точек становятся равными тем, что были в случае а); иными словами,
эти точки получают такое же движение, как в случае а). Согласно теореме
Кельвина Т2 — Т = R2 > 0.
Теорема Тейлора утверждает, что R2 > R\, т. е. что энергетический
выигрыш в теореме Кельвина больше, чем потеря энергии в теореме Бертрана.
Для доказательства достаточно заметить, что в уравнениях A4.7.13) и A4.7.14),
используемых при доказательстве теоремы Бертрана, можно положить
U = и2, равно как и U = и и при этом получаем
2 т(и — щ) (и2 — щ) = 0. A4.7.24)
Это уравнение можно записать в форме
2 т (щ — и) {(щ — и) — (и2 — и)} = 0, A4.7.25)
после чего обычным путем (см. A4.7.7)) находим
Я4 _ #2 + R12 = о, A4.7.26)
где ¦
#i2 = y2m(-^iJ- A4.7.27)
§14.8] ЛАГРАНЖЕВЫ КООРДИНАТЫ И КВАЗИКООРДИНАТЫ 255
Отсюда получаем
R2 — R1== Rl2 > 0, A4.7.28)
что и требовалось доказать.
§ 14.8. Лагранжевы координаты и квазикоординаты. До сих пор при
изложении теории удара мы пользовались исключительно декартовыми
координатами, подобно тому как это делалось в гл. I — IV при изложении
теории в случае конечных сил. В этом параграфе введем координаты более-
общего типа. Ими могут быть как лагранжевы координаты, так и квазико-
квазикоординаты. В теории удара можно свободно пользоваться квазикоордината-
квазикоординатами, подобно тому как мы пользовались ими в уравнениях Гиббса — Аппе-
ля. Имеем
k
dxr^^arsdqs + ardt, r = l, 2, ..., N, A2.2.6)
s=l
где к — число степеней свободы системы (или, в задачах со связями первого-
типа, число степеней свободы до момента наложения связи). Уравнения
A2.2.7) в теории удара не требуются.
Из уравнений A2.2.6) получаем
ft
ur= ^ars(ds + ar, r = l,2,...,N, A4.8.1)
где юг — составляющая скорости qT. Из A4.8.1) находим
ft
2 A4.8.2)
2
s=l
h
uT — ur0= 2 ccrs(o3s — <0SO), A4.8.3)
s=l
причем коэффициенты ars считаются теперь постоянными.
Обратимся к основному уравнению A4.3.6):
п п
^тг(иг-ито)Аиг=^РгАиг. A4.8.4)
г=1 г=1
Правая часть этого уравнения равна
ft и п
S ( 2 РгОт,) A(»s = S Q.A«>., A4.8.5)
8=1 Г=1 5=1
где
N
Qs= 2 Pra™ A4.8.6)
r=l
есть обобщенная составляющая импульса. Величины Q могут быть найдены
точно таким же образом, как величины Q в уравнениях Гиббса — Аппеля
(§ 12.3). Именно, воспользуемся соотношением
IV h
^Prbxr^^Qsdgs. A4.8.7)
r=l s=l
В наиболее распространенном случае, когда все коэффициенты ат в A4.8.1)
равны нулю, имеем
jv k
2 Prur= 2 Qs(»s. A4.8.8)
r=l s—.1
256 ТЕОРИЯ УДАРА [Гл. XIV
Выражая правую часть A4.8.4) через к величин Дю, получаем
N k
2 тпг (ur — ur0) Aur= 2 QA^s- A4.8.9)
r=l s=l
Этот результат аналогичен пятой форме основного уравнения A2.3.11)
в случае конечных сил.
Введем функцию ffi:
N
U=^^mr(ur-urof. A4.8.10)
r=l
С помощью соотношений A4.8.3) ее можно выразить через разности (ац — (о1о),
(ю2 — «>2о)> ¦ • • > (<»й — ©йо)- Проделав это, получим однородную квад-
квадратичную функцию от этих разностей. Если коэффициенты осг все равны
нулю, то ffi зависит от (а>г — юг0) таким же образом, как Т зависит от юг;
в любом случае функцию Ж можно построить по членам Тч в выражении для
Т. Левая часть уравнения A4.8.9) равна
k N
s=i r=l
ft N ft
s=l r=l s=l
Поэтому его можно записать в эквивалентной форме:
к h
2 -j?- Aws = 2 QsAw- A4.8.12)
5=1 S=l
Чтобы получить уравнение движения в момент ^ + 0, достаточно, как
обычно, применить бесконечно малые вариации; тогда уравнение A4.8.12)
примет вид
h
6Ш = 2 ®s5as. A4.8.13)
*=i
В случае отсутствия импульсивных связей, когда вариации 6u)i,6cj>2, ...
. . ., бюй независимы, уравнение A4.8.13) приводится к уравнениям
~ = &s, «=1,2,..., A. A4.8.14)
В случае импульсивных связей первого типа, например связи, выражае-
выражаемой одним уравнением
bieoi + Ь2ю2+. . .+bhah = 0, A4.8.15)
движение в момент t± + 0 определяется условием 6Э{ = 0 и уравнением
связи A4.8.15); соответствующие уравнения имеют вид
~ = US, 8 = 1, 2, ..., к. A4.8.16)
Множитель Я пропорционален величине импульса, создаваемого импуль-
импульсивной связью.
Уравнения движения, получаемые из равенства
dl)»-0 A4-8Л7)
14.9] ЛАГРАНЖЕВА ФОРМА УРАВНЕНИЙ ДВИЖЕНИЯ В ТЕОРИИ УДАРА 257
(в котором бюг бесконечно малы), совпадают с условиями стационарности
выражения
h
3? - 2 Q^.. A4.8.18)
8—1
Это выражение в действительном движении имеет минимум. В самом деле,
ft
()
8=1
JV N h
=т 2 Иг (Ur+Диг ~~Ur°J -i2m'(u'- u>-oJ—2
8=1 Г=1 «=1
JV JV JV
= y2m>-(AUrJ + {S тг(иг-иго)Аиг-^ аДсоЛ. A4.8.19)
r=l r=l s=l
Отсюда, учитывая A4.8.9), получаем
ft JV
)у2(А«гJ>0. A4.8.20)
8=1 Г=1
Доказательство на этом заканчивается. Полученный результат аналоги-
аналогичен неравенству A4.5.3), подобно тому как неравенство A2.4.6) аналогично
принципу наименьшего принуждения Гаусса.
§ 14.9. Лагранжева форма уравнений движения в теории удара. Урав-
Уравнения движения можно получить из функции кинетической энергии Т, выра-
выраженной через col7 (о2, • • ., «й, вместо того чтобы выводить их из функции
9?, представленной через разности (о>1 — ю10), (а>2 — ®2о)> • • •> (Mft — шйо)-
Функцию Т, равную
JV
у2т^' A4.9.1)
г=1
следует выразить через щ, ш2> • • •> ©ь с помощью равенств A4.8.1). Имеем
JV
« vi , . дат дТ
так как производные -^ имеют одно и то же значение до удара и после удара.
Таким образом,
-^_ = — , A4.9.3)
дТ г дТ
где — обозначает приращение величины — , т. е'. разность между ее значе-
значениями в моменты ti + 0 и Ц — 0. Поэтому уравнения A4.8.14) и A4.8.16)
можно записать в форме Лагранжа:
.Д., «=1,2, ..., к, A4.9.4)
^_|-ЯА„ «=1,2, ..., к. ¦ A4.9.5)
Если система начинает движение из состояния покоя, то функция 4R
совпадает с Г и уравнения проще всего выводятся из соотношения
ft
ЬТ = 2 &М>- A4.9.6)
17 Л. А. Парс
258 ТЕОРИЯ УДАРА [ГЛ. XIV
В случае отсутствия импульсивных связей для системы, которая
в начальный момент находилась в покое, имеем
Р^-щ-О» A4-9.7)
где ps — составляющие обобщенного импульса, введенные в § 6.10 (там q
являлись лагранжевыми координатами, здесь же они могут быть квазикоор-
квазикоординатами). Каждая составляющая ps равна соответствующей составляющей
обобщенного импульса, необходимой для приведения в движение системы,
находившейся в покое.
§ 14.10. Другие доказательства теорем об энергии. Доказательства
теорем об энергии, которые мы дали в §§ 14.6 и 14.7, могут быть проведены
и в лагранжевых координатах. Дадим их для некоторых из теорем. Будем
предполагать, что все аг в формуле A4.8.1) равны нулю. При этом условии
Т является однородной квадратичной функцией от ©:
h h
Г = т2 S'WW A4.10.1)
r=l s=l
И
ft
Pr=S«ra»». A4.10.2)
Уравнение Лагранжа в теории удара записывается в виде
&т = рг - Pro- A4.10.3)
1) Для доказательства теоремы о суперпозиции (§ 14.6)*будем исходить
из равенств
ft
Qr= 2вгв(ю.-а«>), г = 1,2, ..., к, A4.10.4)
8=1
ft
Q;=Se«K-w«),> r=l,2, .... к, A4.10.5)
где to — скорость, сообщаемая импульсом Q, a ft/ — скорость, сообщаемая
импульсом ?}'. Следовательно,
h
Qr + ^= S «г«{К + ©!-©«,)-©ад), г = 1,2, ..., к, A4.10.6)
s=l
и скорость, сообщаемая импульсом Q + Й', равна
(й + ы' — (й0. A4.10.7)
Полученный результат эквивалентен теореме § 14.6, так как иг — линейные
и однородные функции от ю. Если, в частности, система первоначально нахо-
находилась в покое, то суперпозиция импульсов влечет за собой суперпозицию
скоростей.
2) Если система, находившаяся первоначально в покое, приводится
в движение заданной системой импульсов, то в силу A4.10.3) кинетическая
энергия ее имеет выражение
ft
r=l r=l
h
или выражение A4.7.5), так как скалярное произведение 2 йгюг представ-
г=1
ляет собой инвариант.
ft ft
=4- 2 °^=iS Q^ A4-10-8>
§ 14.10] ДРУГИЕ ДОКАЗАТЕЛЬСТВА^ТЕОРЕМ ОБ ЭНЕРГИИ 259
3) Если в момент приложения импульсов система находится в движении,
то
ft
Т — То = y 2 (WrPr ~ &гоРто) =
ft
2 . A4.10.9)
г=1
ft ft
у
г=1 г=1
С другой стороны,
ft k
И Pr<Oro = Ц /WV A4.10.10)
г=1 г=1
(Этот результат еще понадобится нам позже.) Учитывая A4.10.10), получаем
h
T-T0 = ^Qr co'-+@'-o,, A4.10.11)
r=l
что эквивалентно A4.7.4).
4) Для доказательства теоремы Бертрана предположим, что составляю-
составляющие обобщенного импульса Qr равны нулю при г>/и что во втором опыте
связи имеют вид юг = 0 при г > /.
Для первого опыта
n ^ • Г A4.10.12)
а для второго опыта
п * ^ • Г A4.10.13)
(штрихом обозначены величины, относящиеся ко второму опыту).
Имеем
ft ft
- ©;)+2 (P' - p'r) &'r—у 2 o°^ - p^) •
r=l r=l r=l
Второе" и третье слагаемые правой части равны нулю: второе в силу того,
что рт — р'т = 0 при г <; / и со'. = 0 при г>/, а третье в силу равенства
A4.10.10). В результате получаем
Т - Г = R > 0. A4.10.15)
5) Чтобы доказать теорему Кельвина, будем считать величины и>г задан-
заданными при г ^ /, а величины Qr равными нулю при г > ;. Если отнести ю'
к любому другому движению, возможному при заданных значениях o>i,
(о2, . . ., (?>], то можно будет написать
ft
г=1
ft ft ft
= - т 2 (P' - ^ (Шг - ю^) + 2 p- (ш<- -^)+12 ^'¦ш^ - p^--)- A4-10-!6)
г=1 г=1 г=1
17*
260 ТЕОРИЯ УДАРА [Гл. XIV
Здесь тоже второе и третье слагаемые правой части обращаются в нульз
второе в силу того, что юг > (л'г при г ^ ; и рт = 0 при г > ;, а третье в силу
равенства A4.10.10). В результате получаем
Г - Т = R > 0. A4.10.17)
§ 14.11. Приложения теории удара. Рассмотрим теперь несколько
конкретных примеров, иллюстрирующих изложенную выше теорию.
Пример 14.НА. Три однородных стержня АВ, ВС, CD, массы
М каждый, шарнирно соединены в точках В и С и располагаются по одной
прямой на гладкой горизонталь-
горизонтальны 2, \у В н°й плоскости. Система приводит-
А* 1 ¦ т ся в движение ударом в точку А,
| Т Т совершаемым в этой плоскости
'J под прямым углом к линии стерж-
Рис. 45. ней. Требуется найти движение
системы после удара и проиллю-
проиллюстрировать применение теорем Бертрана, Кельвина и Тейлора в том слу-
случае, когда конец D цепочки из стержней закреплен неподвижно.
В случае отсутствия импульсивных связей можно пользоваться уравне-
уравнением A4.9.6), 8Т — J bv; функцию Т представим в виде
Т = i M {{v2 - vx + х2) + (х2 - ху + у') +¦ (z/2 - yz + г2)} =
= -g- М (у2 — vx + 2х2 — ху + 2у2 — yz + z2) A4.11.1)
(см. рис. 45). Имеем
2v — x = 6J/M, —v + 4x — y = 0, 1
_ 4 _z = 0 - +2z =0 1 A4.11.2)
Отсюда
z _ У ... * _ " 6//M 2/ ... ,. оч
1 2 ~ 7 26 ' 45 ~ 15ilf "
Сообщенная стержням энергия согласно A4.7.5) равна
1 г 15 ,, „ 26 /2
Учитывая теперь уравнение связи z = 0, получаем
Т=|м(г;г- ra + 2z2 — ж!/+2г/2). A4.11.5)
Из условия ЬТ = / бь> находим
2у — х = 6//М, — v + 4z — i/ = 0, — х + 4у = 0. A4.11.6)
Отсюда
У _ * _ " _ 6//М _ 3/ (\L\M\
(itiii)
1 4 15 26 ~ 13М -
Сообщенная энергия равна
4^ ^2
1) Если величина / в обоих случаях одна и та же, то превышение энер-
энергии в первом случае по сравнению со вторым равно
§ 14.11]
ПРИЛОЖЕНИЯ ТЕОРИИ УДАРА
261
или, если выразить через скорость v0 точки А в первом случае,
Я — —i5_ Mn2
A4.11.10)
2) Если в обоих случаях v = v0, то уменьшение энергии в первом опыте
по сравнению со вторым будет равно
Следовательно,
К—В=
15
4680 70 304
3163 680 Mv°'
A4.11.11)
A4.11.12)
Пример 14.11В. Двенадцать одинаковых однородных стержней,
массы М каждый, шарнирно соединены своими концами друг с другом
так, что образуют пространственную ферму. В начальный момент эта
ферма имеет кубическую форму и находится в покое, причем одна верши-
вершина О куба закреплена. Система приводится в дви-
движение импульсом, приложенным к противополож-
противоположной вершине D; составляющие этого импульса
по направлениям ребер куба обозначим через X,
Y, Z. Определить движение этой фермы после
приложения импульса и вычислить сообщенную
ей энергию. '
Воспользуемся теоремой о суперпозиции
(§ 14.6) и рассмотрим сначала влияние одной
лишь составляющей X. Имеем (рис. 46)
л
1 "Я • I В I , П. . \о> (\Il 11 13}
Из условия, что ЬТ = Х8 (и2 + и3), находим
и2 = и3 = SX/B5M). A4.11.14)
Для остальных составляющих получаем аналогичные выраженияз
Wi = w2 = 3Z/B5M)
Сообщенная энергия равна
¦.}
A4.11.15)
. A4.11.16)
Пример 14.НС. Ромб массы М, образованный четырьмя шарнирно
соединенными одинаковыми стержнями АВ, ВС, CD, DA длиной 2а каждый,
движется как твердое тело в направлении диагонали АС со скоростью и.
Угол ромба при вершине А равен 2а. Внезапно к точке А присоединяется
частица массы тп, первоначально находившаяся в покое. Доказать, что каж-
каждый стержень придет во вращение с угловой скоростью
@ = 3 mu sin ос/Bах),
а потерянная при этом кинетическая энергия будет равна -^ЫтигЫ, где
х = М + теA + 3sin2a).
Обозначим скорость центра тяжести G фермы непосредственно после
приложения импульса через v. Тогда кинетическая энергия системы запишется
262 ТЕОРИЯ УДАРА [Гл. XIV
в виде
|ym(i;—2acosinaJ. A4.11,17)
Отсюда получаем
Ш = уМ(р — MK+|-Ma2(u2 + Ym(y-2a(osinaJ. A4.11.18)
(Угловая скорость каждого стержня, а также скорость массы w в момент
ti — 0 по условию равны нулю.) Из условия A4.8.13), 6fR = 0, находим
М (v — и) + т (v — 2а(л sin a) = 0, A4.11.19)
^ Мя2со — 2та sin a(v — 2aco sin a) — 0. A4.11.20)
Уравнение A4.11.19) выражает сохранение количества движения.
Из уравнений A4.11.19), A4.11.20) получаем
2аа> v— 2aco sin a v— и
Ът sin a M — m
~ Af + 3msm2a ~M+m(l +3sin2a) = IT* A4.11.21)
Отсюда
со = 3mu sin a/Bax). A4.11.22)
По теореме Карно находим, что потеря кинетической энергии равна
значению функции 8J при v тя. со-, соответствующих моменту ti + 0:
Ш = -к- [и ——\-v -z—^со-^—) = —ы-^— =
= -^Ми(и-и) = ~Мти?Ы. A4.11.23)
Пример 14.11D. Рассмотрим систему, кинетическая энергия кото-
которой, выраженная через coi,< co2, . . ., ah, содержит лишь квадратичные
члены:
ft
r = {2ffl^- A4.11.24)
г=1
Предположим, что система приводится в движение импульсом и что Qr =
= Qr0 при г ^ j и Q, = 0 при г > /. Определим движение системы после
приложения импульсов и сообщенную ей энергию. Затем рассмотрим ту же
систему в случае, когда на нее наложены конечные связи, выражаемые урав-
уравнением
&!©! + Ь2со2 + . . . + bkak = 0, A4.11.25)
и сравним энергии 1) при одинаковых импульсах и 2) при одинаковых /
первых скоростях.
Хотя в данном примере рассматриваются конечные связи, наложенные
на систему до момента приложения импульсов, однако результаты будут
такие же, как в случае, когда импульсивная связь накладывается одновре-
одновременно с импульсами (см. § 17.4, п. 4).
$ 14.11] ПРИЛОЖЕНИЯ ТЕОРИИ УДАРА 263
В случае отсутствия импульсивных связей
3
8Т = 2 Qr6cor.
r=l
Поэтому, если приобретенная скорость системы равна ait ос2, . . ., ah, то
аг = ^rQPO (г < j); ат = 0 (г > /). A4.11.26)
Кинетическая энергия системы равна
Го = | 2 4^0=1 2 -|г- A4.11.27)
r=l r=l
Рассмотрим теперь систему, на которую наложена связь.
1) Если импульсы не изменяются, то
щ = Агпп + %АТЪТ (г < /); юг = ЫТЪТ {г > /)• A4.11.28)
Параметр Я определяется из условия A4.11.25):
i h
2 АгЫ = 0. A4.11.29)
1
г=1 г=1
Сообщенная энергия в этом случае равна
3 3
Ту -у 2 Qro<»r=»Y 2 Ого(
г=1 г=1
= i-2 ^?o-y B^AQroO(S ^2г)-Г0-5, A4.11.30)
r=l r=l r=l
где
з ft
я=4BМгOB^?). (i4.ii.3i)
r=l r=l
2) Если система приводится в движение другой системой импульсов Q
такой, что Qr = 0 при г > j, и если импульсы таковы, что сог = осг при г ^ ;,
то
аг = Лгйг + ЫА (г < /¦); сог = ЫгЬг (г > /)• A4.11.32)
Кинетическая энергия в этом случае равна
з i з
Г2={1;Йгаг = {B а?/Л,)—i*2 &<-а" A4.11.33)
г=1 г=1 г=1
и так как
l ) A4.11.34)
r=l r=j-t-l
ТО
j fe h
Я2Ьг«г=- 2 «?Мг=-Я2( 2 Arbl)- A4.11.35)
r=l r=j+l r=j+l
Отсюда определяем Я:
>,= -BbPoI.)/( 2 AM). A4.11.36)
r=l r=i+l
264
ТЕОРИЯ УДАРА
[Гл. XIV
Таким образом,
r=l
r=l
где
, A4.11.37)
A4.11.38)
Легко убедиться, что К^> Б. В самом деле,
A4.11.39)
( S
г=1
Пример 14.НЕ. В заключение рассмотрим пример связи второго
типа. Возьмем ферму, состоящую из четырех одинаковых стержней (пример
14.5), и предположим, что сначала она двигалась как твердое тело. Если угол
ADC обозначить через 9, то в момент tt — 0 будем иметь 9 = -я- п, 9 — 0.
Пусть, далее, в момент ti величина 9 внезапно получает значение ср; можно
предположить, например, что толчок производит насекомое (массой которого
можно пренебречь), сидящее на раме в точке D. В обозначениях примера 14.5
уравнения импульсивной связи запишутся в виде
= tt-{-0. J
A4 И 40)
и— v + w — ж =
и — v-{-w — x =
Соотношение 88J = 0 будет справедливо для вариаций, связанных условием
&u — 8v + 8w — 8x = 0. A4.11.41)
Уравнения A4.5.8) также соблюдаются. Учитывая уравнения A4.11.40),
получаем
% = Iff. A4.11.42)
Окончательно находим
и — щ = w — w0 — -г
V — V0 = X — Хо= — -^
A4.11.43)
Выигрыш в энергии равен энергии приобретенных скоростей (§ 14.6,
п. 3) -77- М1\*, что, впрочем, легко получить и непосредственно.
Рассмотренная задача в известном смысле является обратной по отно-
отношению к задаче, разобранной в примере 14.5. Там мы имели связь первого
типа и величина 9 резко убывала от <р0 Д° нуля, здесь связь принадлежит
ко второму типу и значение 9 резко увеличивается от нуля до ср.
§ 14.12. Импульсивное движение непрерывных систем. Мы уже выска-
высказывали точку зрения, что основное уравнение для случая конечных сил при-
ложимо к непрерывным системам; в § 3.9 это положение было проиллюстри-
проиллюстрировано на конкретных примерах. Эта точка зрения основывалась на физиче-
физических соображениях.
Здесь мы выскажем аналогичное предположение о том, что основное
уравнение A4.3.6) теории удара сохраняет силу и для непрерывных систем,
§ 14.12] ИМПУЛЬСИВНОЕ ДВИЖЕНИЕ НЕПРЕРЫВНЫХ СИСТЕМ 265
с той лишь разницей, что там, где это нужно, суммирование заменяется
интегриров анием.
Рассмотрим некоторые примеры.
1) Несжимаемая жидкость. Рассмотрим однородную иде-
идеальную несжимаемую жидкость. Пусть имеются внутренние и внешние гра-
границы. Границы либо представляют собой твердые поверхности, либо явля-
являются деформируемыми; в последнем случае изменение их должно происходить
таким образом, чтобы ограничиваемый ими объем оставался неизменным.
Если движение границ в некоторый момент ti претерпевает разрыв (например,
если жидкость находится в покое в замкнутом сосуде и этому сосуду внезапно
сообщается резкий толчок), то движение жидкости также будет разрывным.
Задача заключается в том, чтобы определить мгновенное изменение движения.
Обозначим составляющие вектора скорости q относительно неподвиж-
неподвижной прямоугольной системы координат через и, v, w, а (постоянную) плот-
плотность жидкости -г- через р. В жидкости устанавливается импульсивное дав-
давление со, подобно тому как в системе с конечным числом степеней свободы
возникают импульсы связей. Основное уравнение A4.3.6) принимает вид
\ р {(и — щ) Аи-{- (v — v0) Av+ (w — w0) Aw} dx— — \ (uAqndS. A4.12.1)
Объемный интеграл берется по всему пространству, занятому жидкостью,
а поверхностный интеграл — по ограничивающим поверхностям. Через qn
обозначена "составляющая скорости вдоль внешней нормали. Символ А обо-
обозначает конечное (не бесконечно малое) приращение, возможное в момент
<i + 0. Если направляющие косинусы внешней нормали обозначить через
I, тп, п, то правую часть уравнения A4.12.1) можно представить в виде
— I «>(lAu-\-mAv-{-nAw) dS = — i {-*— Аи-\--^— Av-\-—^-Aw\ dr —
T- <14J2-2>
Второй член правой части равенства равен нулю, так как div q =
= div (q + Aq) = 0. Из уравнений A4.12.1) и A4.12.2) получаем
-f [p(u;--u;0) + jg-j Ди?} йт = 0. A4.12.3)
Это равенство справедливо для произвольных значений Aq, удовлетворяю-
удовлетворяющих условиям div Aq = О, Aqn = 0. Таким образом,
я , A4.12.4)
Мы получили уравнения импульсивного движения жидкости. Если в момент
ti — 0. движение было безвихревое, то оно будет безвихревое и в момент
ti -\- 0. Движение, начинающееся из состояния покоя, является безвихревым,
так что q = — grad <p. Импульсивное давление со связано с потенциалом
скоростей возникшего движения соотношением
ю = рср. A4.12.5)
266
ТЕОРИЯ УДАРА
[Гл: XIV
Все эти выводы справедливы лишь для классического случая идеальной
несжимаемой жидкости.
Некоторые хорошо известные теоремы классической гидродинамики, доказываемые
обычно с помощью формулы Грина, легко могут быть получены из общих теорем теории
удара. Предположим, что движение начинается из состояния покоя от резкого толчка
жестких границ. Энергия системы при этом будет равна (§ 14.7, п. 1)
' " f^u A4.12.6)
Интегралы здесь берутся по граничным поверхностям, а индекс п относится к внешней
нормали. Сообщенная энергия является наименьшей из всех возможных при заданных
значениях нормальной скорости в точках границы. Это следует из замечания 1 к теоре-
теореме Кельвина (§ 14.7, п. 5), так как в каждой точке границы задано как направление
импульса, так и составляющая скорости в этом направлении.
2) Неупругая струна (нить). Неупругая струна АВ, лежа-
лежащая на гладкой горизонтальной плоско-
плоскости, приводится в движение импульсом /,
направленным по касательной к струне
в точке В. Найти движение струны после
приложения импульса.
Пусть s — длина струны между точ-
точками А и Р, а "ф — угол между каса-
касательными к струне в этих точках. Будем
предполагать, что радиус кривизны р =
= dsldty положителен и конечен и пред-
представляет собой дифференцируемую функ-
функцию от г|э во всех точках дуги АВ. Обо-
Обозначим через и, v тангенциальную и нор-
нормальную составляющие скорости точки Р
(рис. 47). Если Я — линейная плотность
Р, то основное уравнение A4.3.6) запишется в форме
Рис. 47.
струны в точке
ds = J Аив,
A4.12.7)
где символ А, как обычно, обозначает конечную (не бесконечно малую) вари-
вариацию, а ив — значение и в точке В.
Поскольку струна нерастяжима, имеем
du
Аи = -тт- Аи,
и уравнение A4.12.7) записывается в виде
о
-^— (Аи)\
A4.12.8)
A4.12.9)
Здесь а обозначает величину угла i|) в точке В. Интегрируя по частям,
находим
а
XpvAu
в
ри— ~-(%pv)\
Ha концах струны выполняются следующие условия:
(%pv)A = 0, (kpv)B = /,
= JAuB. A4.12.10)
A4.12.11)
S 14.12] ИМПУЛЬСИВНОЕ ДВИЖЕНИЕ НЕПРЕРЫВНЫХ СИСТЕМ 267
и так как равенство A4.12.10) выполняется для произвольных Аи, то можем
написать
Яры = JJL (Яру). A4.12.12)
Функция и удовлетворяет дифференциальному уравнению
A4.12.13)
Что же касается функции v, то для нее имеем дифференциальное соот-
соотношение
З^Ы} A4Л2Л4)
эквивалентное однородному линейному уравнению
v" + xv' + Ы' - 1) v = 0, A4.12.15)
где х = «— т— (Хр) — заданная функция от г|э; штрихом обозначено диффе-
дифференцирование по 1)з. Нас интересует решение уравнения A4.12.15), удовлет-
удовлетворяющее условиям на концах A4.12.11). Заметим, что если радиус кривиз-
кривизны струны в точке Б равен нулю, например, когда Б является точкой заостре-
заострения дуги циклоиды, это решение не имеет места.
Другой случай мы имеем, когда конец А не свободен, а вынужден дви-
двигаться в направлении нормали к, кривой в точке А (другие направления
невозможны). Условиями на концах тогда будут
иА = 0, {Xpv)B = J. A4.12.16)
Рассмотрим два конкретных примера движения однородной струны, когда к =
= const, я = р'/р-
а) Струна имеет форму дуги окружности, и угол г|) изменяется от ¦ф = 0 до г|5 = а.
Уравнение для г> запишется в виде
v" — v = 0. A4.12.17)
Решение его будет иметь вид
?&#& A4Л2-18>
где М— масса струны. Из A4.12.12) находим
и=и>^1?^±. A4.12.19)
Энергия струны будет равна
: JL- а cth ее. A4.12.20)
Интересно отметить, что это значение больше, чем-^- (J2/M), что и следовало ожи-
ожидать на основании теоремы Бертрана; мы должны были бы наложить на движение связь,
ваставив струну двигаться внутри гладкой трубы; тогда ее энергия была бы равна
~ (Я/ДО-
Если конец А не свободен, а принужден двигаться в направлении нормали к стру-
струне, то дешение записывается в виде
f^± ^^± A4.12.21)
M cha '
A4.12.22)
268 ТЕОРИЯ УДАРА [Гл. Х1?
В этом случае энергия струны равна
T W A4.12.23)
и она меньше того значения, которое дает формула A4.12.20). Таким образом, мы еще раз
проиллюстрировали теорему Бертрана.
Ь) Струна имеет форму дуги цепной линии
s = с tgip, A4.12.24)
где угол ip изменяется от ip = 0 до гр = а. В этом случае р = с sec2 гр, у, = 2 tg ip и диффе-
дифференциальное уравнение для v принимает вид
v" + 2v' tg гр + B tg2 чр + 1) v = 0. A4.12.25)
Решением его будет
v = (С -Ь Лр) cos тр. A4.12.26)
Из условия A4.12.12) получаем
и = (С + Dip) simp + D cos тр. A4.12.27)
В случае свободной струны условия на концах A4.12.11) принимают вид
A4.12.28)
' ОС
Если же точка А принуждена двигаться по нормали, то условия на концах
A4.12.16) дают
^, D=0. A4.12.29)
В этом случае
M=Csinip, v=Ccosij5 A4.12.30)
и все точки струны движутся с одинаковой скоростью С в одном направлении — в направ-
направлении нормали к кривой в точке А.
Глава XV
ШЕСТАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ
§ 15.1. Шестая форма основного уравнения. В гл. XII и XIII мы рас-
рассматривали механические системы весьма общего типа. В этой главе речь
будет идти о более частном классе систем, а именно о консервативных голо-
номных системах. Выберем лагранжевы координаты qi, q2, . . ., qn, число
которых равно числу степеней свободы системы, и вспомним, что виртуаль-
виртуальными перемещениями мы назвали перемещения, задаваемые произвольными
значениями 8qi, 8q2, . . . , 8qn. Четвертая форма основного уравнения (§ 6.1)
может быть записана так:
п
\J |_ / А_Л—1_^ j Sgv = 0, A5.1.1)
г=1 дЯт 9г
и вследствие произвольности вариаций 8q^, 8q2, • • • > 8qn она эквивалентна
п уравнениям движения Лагранжа.
Обозначим составляющую обобщенного импульса dLldqT через рт (§ 6.10),
а вариацию функции Лагранжа при произвольных вариациях q и q is. неиз-
неизменном t — через 8L. Тогда будем иметь
п п
С 1* ^ \ I O-Lj С i UJ-J г, \ 'V" 1 / OjL/ q, . С \ / Л Г Л е\\
ЬЬ— >. I -z—8qr-\ 8qT\ — >, |-г—oqT-\-pToqT\ . A5.1.2)
^J \ oqr л / ¦^™ \ uQr /
r=l °Яг r=i
Из A5.1.1) и A5.1.2) получаем
n
(pT8qr-{-pT8qT) = 8L. A5.1.3)
r=l
Это есть шестая форма основного уравнения. Она справедлива при произ-
произвольных значениях 8q и 8q. Опуская знак суммирования, ее можно сокра-
сокращенно записать в виде
pr8qT 4- pT8qr — 8L. A5.1.4)
Шестая форма основного уравнения весьма удобна для описания движе-
движения динамических систем рассматриваемого типа. Сначала мы покажем,
каким образом с помощью ее можно получить доказанные ранее теоремы,
а затем перейдем к выводу некоторых других важных результатов.
§ 15.2.. Непосредственные выводы. Шестая форма A5.1.4) основного
уравнения была получена нами из уравнений. Лагранжа; теперь решим обрат-
обратную задачу — выведем уравнения Лагранжа из уравнения A5.1.4). Так как
уравнение A5.1.4) справедливо для любых значений 8q и 8q, то
Pr = iLf рТ = -^~, г =1,2, ..., п. A5.2.1)
Отсюда
-^-, г=1,2, ..., п. A5.2.2)
270 ШЕСТАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ [Гл. XV
Представим теперь уравнение A5.1.4) в форме
дт8рг — pTbqT = б (prqr — Ц, A5.2.3)
Обозначим через Н функцию pTqT — L, выраженную через д, р и t (§ 10.13).
Уравнения, определяющие р,
Рг = —^, '" = 1,2, ..., п,
dqT
линейны по q. Из них можно найти q как функции от q, p и t, причем зависи-
зависимость отр линейна. Исключив затем q в выражении prqT — L, получим функ-
функцию Н. В исходном уравнении A5.1.4) вариации q is q были произвольны,
поэтому произвольны будут и вариации q is p в уравнении
qr8pr-pT8qr=^8H. A5.2.4)
Следовательно,
8Н дН . „ //1С „ _.
УГ==Ж' Рг=~~д^' г = 1,2, ...,«. A5.2.5)
Мы получили уравнения Гамильтона.
Как уже отмечалось (§ 10.13), 2ге уравнений A5.2.5) образуют систему
уравнений первого порядка вида
х = Х,
где х и X — матрицы-столбцы, или векторы, с 2п составляющими. Составля-
Составляющая Хт вектора X зависит от хи х2, . . ., х2п и, возможно, от t. Функция
Н является новой описывающей (дескриптивной, descriptive) функцией
механической системы, т. е. функцией, по которой могут быть построены
уравнения движения, так что она неявно содержит в себе полное описание
возможных движений. Некоторые обобщения уравнений A5.2.5) уже рас-
рассматривались в § 10.13, а явное выражение для Н было получено в § 10.14.
Пространство 2п измерений, точки которого определяются 2п координа-
координатами <7i, q2, . . ., qn, Pi, P2, ¦ ¦ •, Pni называется фазовым пространством;
движение механической системы можно рассматривать как движение изоб-
изображающей точки в фазовом пространстве. Структуру фазового пространства
можно представить как 2ге-мерное евклидово пространство с прямоугольными
координатами qu q2, . . ., qn, pi, pz, . . ., pn. ¦
Функции Лагранжа и Гамильтона не являются единственно возможными дескрип-
дескриптивными функциями, хотя они и являются, конечно, наиболее важными. Из шестой формы
основного уравнения можно получить и другие формы уравнений движения. Так, напри-
например, уравнение можно написать в виде
дгбрг + ?гбрг = б {РАг+РтЧг—Ц- A5.2.6)
Если функция X = prqr + prqT — L выражена через р и р, мы получаем уравнения
движения
Чт = Ц~, ?r = -f^-. r=l,2, .... и, A5.2.7)
дрг дРг
типа уравнений Лагранжа; в самом деле, из них следует, что
d дХ дХ
dt д- дРт
г =1,2, .... п. A5.2.8)
§ 15.3] ФУНКЦИЯ РАУСА 271
Процесс построения функции X хотя теоретически и возможен, но для практических
целей непригоден. В самом деле, требуется решить уравнения
^ '=1.2 п, A5.2.9)
• •
относительно q и q (выраженных через р и р), а это возможно лишь в очень ограниченном
числе простых случаев: уравнения A5.2.9), как правило, нелинейны относительно д.
Примером, когда этот процесс удается провести, может служить задача о малых колебав
ниях. Если
п
ь- 2 2j (?г
г=1
то соответствующая функция X имеет вид
71
=4 s (-&*+л
г=1
и уравнения движения A5.2.7) оказываются эквивалентными уравнениям Лагранжа.
Теоретически можно построить также аналогичную дескриптивную функцию,
зависящую от q и р. Напишем уравнение A5.1.4) в форме
qrbPr-Pr6Qr = &(Pr<lr-L). A5.2.10)
Если через Y обозначить функцию prqr — L, выраженную через q и р, то уравнения движе-
движения запишутся в виде
Д ^ A5.2.11)
dpr dqr
В этом случае нужно исключить q, выразив их через р с помощью уравнений
что практически в большей части случаев опять-таки оказывается невыполнимым.
§ 15.3. Функция Рауса. Дескриптивную функцию можно построить
таким образом, чтобы некоторые из уравнений движения, скажем первые т
пар, имели гамильтонову форму, а остальные — лагранжеву. Сделать это
достаточно просто. Откажемся на время от принятой формы записи сумми-
суммирования и представим уравнение A5.1.4) в виде
п т т
S (Ргв?г + Ргб?г)- 2 (рМг+Яг&Рг) =6 (L- 2 prqr). A5.3.1)
¦ r=l r=l r=l
m
Обозначим через R функцию (L — 2 Pt4t)i b которой пг первых скоростей
r=l
?ь <7г> • • • 1m заменены на импульсы pi, p2, • ¦ ., pm- Тогда уравнения дви-
движения запишутся в виде
5г=~"^7' Pr = ~dq7' r=1'2' •••,№., A5.3.2)
Рг=-д—, Рг = —т-, г = т+1, т + 2, ...,п. A5.3.3)
Первые т пар уравнений движения здесь имеют гамильтонову форму (роль
функции Н играет функция —R), а остальные п — т пар — лагранжеву
форму (роль функции L играет функция R). Чтобы построить функцию Я,
272 ШЕСТАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ [Гл. XV
нужно решить т линейных уравнений
Pr = —-, ? = 1,2, •••? ТП,
• • *
относительно дгь д2> • • •» <7mi выразив последние через р4, />2, . . ., Рт>
gm+2, . . ., ?п и g, а также, возможно, ?.
Наиболее важным является случай, рассмотренный Раусом, когда пер-
первые т координат являются циклическими (см. § 10.1). В этом случае первые
т импульсов pi, р2, ¦ ¦ ¦, рт в процессе движения остаются постоянными
и функция R играет роль функции Лагранжа для системы с п — га степеня-
степенями свободы, описываемой координатами qm+i, qm+2, ¦ ¦ ¦¦, Чп- Некоторые при-
приложения были рассмотрены в § 10.1 и последующих.
§ 15.4. Теорема: ~rr{prbqr) — 6L. Уравнение A5.1.4) допускает иное
at
истолкование, отличающееся от данного выше. Будем судить о движении сис-
системы по движению изображающей точки в пространстве п измерений с коор-
координатами <7i> <72i • • ч Чп- Начнем с описания истинной траектории системы,
т. е. траектории в q -пространстве, удовлетворяющей уравнениям движения.
В каждый момент времени рассмотрим вариацию, соответствующую переходу
от точки qu q2, . . ., qn к толке qi + &qt, q2 + 8q2, . . .,jn + 6?„. Варьиро-
Варьированная траектория в общем случае не является истинной траекторией систе-
системы, т. е. не удовлетворяет уравнениям движения. Геометрически она, конеч-
конечно, возможна, поскольку рассматриваемая система голономна. Вариации
при этом произвольны и подчинены лишь одному условию, что каждая из ва-
вариаций 8qr есть функция от t класса С2- Поскольку вариации синхронны,
можем (опуская знак суммирования) написать
бдг = Аб9г, г=1,2, ..., п. A5.4.1)
Тогда уравнение A5.1.4) примет вид
¦|-(Ргв?г) = 6?. A5.4.2)
Скорость изменения скалярного произведения pr8qr равна вариации L, обуслов-
обусловленной синхронным варьированием 8q и 8q.
Воспользуемся теперь уравнением A5.4.2) для вывода принципа Гамиль-
Гамильтона. Правда, этот вывод, в отличие от приведенного в § 3.7, будет справедлив
только для голономных консервативных систем. Имеем
<i
f 8Ldt = pri8qTi — Pro8qrO, A5.4.3)
(о
где через qT0, рГо обозначены величины qT, pr в момент ?0, а через qT%, pri —
те же величины в момент ^. Если в моменты t0 и tx вариация бд обращается
в нуль, то
ч
J6?*=»O, A5.4.4)
to
что и выражает принцип Гамильтона.
§15.4] TEOEEMA: d (i>r 6qT) =; 6L 273
Уравнения A5.4.3), A5.4.4) можно записать еще в следующей форме:
б \ Ldt — prj8qn — Pro&Qrot A5.4.5)
to
0, A5.4.6)
to
причем исходный интеграл здесь берется вдоль дуги действительной траек-
траектории в ^-пространстве (т. е. вдоль пути, удовлетворяющего уравнениям
движения), а варьированный интеграл — вдоль допустимого пути, построен-
построенного так, как указывалось выше. Как уже отмечалось, этот путь, вообще
говоря, не является действительной траекторией.
Уравнение A5.4.2) справедливо для произвольного варьированного
пути, требуется только, чтобы соответствующие точ.ки исходного и нового
путей относились к одному и тому же моменту времени и чтобы каждое
&7г 6 С\; при этом новый путь вовсе не обязан быть действительной траекто-
траекторией.
Наложим теперь дальнейшее ограничение и потребуем, чтобы варьиро-
варьированный путь являлся действительной траекторией, соответствующей слегка
изменившимся начальным условиям. Оператор б будет теперь означать пере-
переход к точке на соседней действительной траектории, соответствующей тому
же моменту времени.
Рассмотрим сначала случай, когда L не содержит t, так что при заданных начальных
значениях q и q мы получаем одну и ту же траекторию независимо от начального момента
времени, и положение на траектории зависит только от промежутка времени, прошед-
прошедшего с момента старта. Обозначим теперь через б вариацию, соответствующую переходу
из одного положения на одной и той же траектории к другому после небольшого постоян-
постоянного интервала времени т. Варьируемым путем будет при этом та же исходная траектория,
но точки ее будут проходиться на т секунд раньше, чем точки действительной траектории.
При ятих условиях
dL
6?г = т?г, 6?г = т?г, 6L = T-^-, A5.4.7)
н из уравнения A5.4.2) получаем интеграл Якоби (§ 6 7):
-дГ(Мг-Ь)=0. A5.4.8)
Рассмотрим теперь траектории, начинающиеся в момент t = 0 из точек
замкнутой кривой у0 gr-пространства. Скорости будем считать изменяющими-
изменяющимися непрерывно при переходе от одной точки кривой к другой. Спустя время t
изображающие точки составят другую замкнутую кривую у. Для двух сосед-
соседних траекторий будем иметь
4 6L. A5.4.2)
так что для замкнутой кривой у получим
= 0. A5.4.9)
Криволинейный интеграл ф pr8qr сохраняет свое значение, когда криваяу дви-
движется описанным выше образом. Движению кривой в ^-пространстве соответ-
соответствуют возможные движения механической системы. Этот результат имеет
сходство с известными теоремами классической гидродинамики о сохранении
циркуляции скорости.
18 Л. А. Парс
274 ШЕСТАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ [Гл. XV
Полученный результат интересен еще с одной точки зрения. Каждая точ-
точка простой замкнутой кривой Го фазового пространства (§ 15.2) является
началом определенной траектории, выходящей из нее в момент t = 0. Изоб-
Изображающие точки, взятые на этих траекториях в момент t, составляют замкну-
замкнутую кривую Г, полностью определяемую заданной кривой Го. Значение кри-
криволинейного интеграла m prdqr, взятого по кривой Г, остается постоянным.
Этот интеграл называют интегральным инвариантом уравнений, описываю-
описывающих движение системы, в данном случае уравнений Гамильтона. Сказанное
справедливо только для интегралов, взятых по замкнутой кривой; в этом
смысле интегральный инвариант называют относительным. Речь идет об
известном интегральном инварианте Пуанкаре. Существование этого
интегрального инварианта выражает фундаментальное свойство гамильто-
новых систем. В дальнейшем, при более детальном рассмотрении уравнений
Гамильтона, мы дадим более подробный анализ этого, а также других инте-
интегральных инвариантов.
§ 15.5. Главная функция. Введем теперь так называемую главную
функцию Гамильтона *). Идея главной функции подсказана методами, при-
применяемыми в геометрической оптике. Главная функция позволяет получить
динамически возможные движения системы.
и
В явной форме главная функция S представляет собой интеграл \ L dt,
взятый вдоль действительной траектории (т. е. вдоль пути в ^-пространстве,
удовлетворяющего уравнениям движения) и выраженный через начальные
и конечные значения координат, а также начальное и конечное значения вре-
времени:
S = S (q10, q2o, ¦ • •» Япо\ Ян, ?2i» • • •, Яш', h, h), A5.5.1)
или, короче,
S = S (qT0; qH; t0, Ь). A5.5.2)
Чтобы построить главную функцию, можно поступить следующим образом. Допу-
Допустим сначала, что нам удалось найти интегралы уравнений движения Лагранжа, так что
каждая координата qr является известной однозначной функцией от п переменных qr0,
п переменных (ог0, а также моментов времени (си4 (через (лг0 мы обозначили значение qr
в момент *о)- Итак, пусть известны функции
¦" ?s = <Ps (Зго! шг0; t0, t), s¦= 1, 2, . . ., п. A5.5.3)
Теперь можно выразить функцию L через 2ге + 1 параметров (qr0; шг0; t0) и переменную *.
Взяв интеграл от этой функции в пределах от t0 до tt, выразим его через п параметров дг0,
п параметров сог0 и tQ и t±:
h
=2 (?ro; «го! <о. h)- A5.5.4)
Рассмотрим точку qn, g2i, ¦ ¦ -, qni, достигаемую в момент tt. Имеем
?si = <Ps (Sro! «W tOt ti), s = 1, 2, . . ., re. A5.5.5)
С помощью этих уравнений можно исключить сог0 из A5.5.4), выразив их через qTi. Про-
Проделав это, получим искомую функцию S:
2(?го; «го; «о. «i) = ^Cro; ы; {о< Ч)- A5.5.6)
Мы видим, что сог0 играют лишь вспомогательную роль и не фигурируют в оконча-
окончательном результате. Для этой же цели можно было бы использовать любую другую под-
подходящую систему параметров (например, ге величин рг0 или сог1). В результате мы пришли
бы к одной и той же функции S независимо от того, какой системой параметров пользо-
пользовались при ее составлении. Тем не менее для конкретности мы будем в дальнейшем счи-
*) Главная функция была введена впервые во второй известной работе Гамильтона
[16] в .1834 г.
§ 15.6] ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ ГЛАВНОЙ ФУНКЦИИ 275
тать, что функция S построена описанным выше способом. Отметим, что если функция L
не зависит явно от t, то q и q являются функциями от разности (t — t0) и t0 и ti входят
в выражение для S только в виде разности {ti — t0).
Выясним теперь характер зависимости ? от ее 2п + 2 аргументов. Фик-
Фиксируя сначала t0 и ti и рассматривая только вариации терминальных точек,
получаем из A5.4.5)
SS = Pri 6gri — Pro&Qroi A5.5.7)
где pro» Pn — составляющие обобщенного импульса в моменты to и t\. Состав-
Составляющие импульса в терминальных точках траектории можно найти из глав-
главной функции: они равны частным производным — dS/dqr0 и dS/dqn.
Далее рассмотрим вариацию времени t\. Если через L± обозначить зна-
значение L на траектории в момент tit то будем иметь
Следовательно,
~7п~— —Priori + bi =¦- —Л,, A5.5.9)
где Hi — значение функции Гамильтона Н в заданном движении в момент tx.
Из соображений симметрии следует, что
-|^ = #о, A5.5.10)
где Но — значение функции Н в заданном движении в момент t0. (Формаль-
(Формальное доказательство этого результата не совсем тривиально, если иметь в виду
описанный выше способ построения главной функции. Возникающие здесь
трудности можно обойти, если по-другому выбрать систему вспомогательных
параметров; к этому вопросу мы еще вернемся в § 15.7.) Таким образом, для
самой общей вариации по всем 2п + 2 аргументам мы получаем важную фор-
формулу:
dS = рп dqri — pro dqr0 — Ht dti + Ho dt0. A5.5.11)
§ 15.6. Примеры использования главной функции. Мы видели, что
главная функция зависит от 2п -\- 2 независимых переменных: координат
начальной и конечной точек в ^-пространстве и начального и конечного
моментов времени. В простейших случаях (см. ниже пример 1)) этим перемен-
переменным можно задать произвольные значения, так что, сообщив движение из
точки q0 в момент t0, можно достигнуть цели — точки qi — в момент tt.
В подобных случаях функция ? существует и является (однозначной) диф-
дифференцируемой функцией при всех вещественных значениях аргументов.
В более сложных случаях это не имеет места, что, однако, не противоречит
общей теории, поскольку практически мы всегда начинаем с заданной дуги
известной траектории. Это соответствует определенной точке
в {2п -\- 2)-мерном пространстве, для которой определенное значение S опре-
определяется заданной траекторией, и мы имеем дело только с вариацией S в не-
непосредственной окрестности точки A5.6.1).
Приведем несколько конкретных примеров.
1) Движение частицы в плоскости z=0 в однородном
силовом поле @, —g). Если через и0, v0 обозначить составляющие скорости в точ-
точке х0, у0, то можно написать
—X0 = U0{ti—10), л
18*
276
ШЕСТАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ
[Гл. XV
Если разность tt — t0 не равна нулю, то эти уравнения определяют и0. v0 единственным
образом. Существует единственное решение для произвольных положений терминальных
точек и для произвольных неравных значений t0 и ti. Следовательно, S существует
и является однозначной функцией шести своих аргументов.
2) Гармонический осциллятор. Уравнение движения имеет вид
Уравнение
= х0 cos n
10) + — sin п {ti —10)
A5.6.3)
A5.6.4)
однозначно определяет и0, если только п (f4 — t0) не кратно я. За исключением этого слу-
случая, существует единственная траектория для произвольных значений четырех аргумен-
аргументов и S является однозначной функцией от х0, xit t0, t,. Это ясно видно из рис. 48, на кото-
котором показаны движения, начинающиеся в точке х0 в момент t0. Если же п {tt — t0) = гя,
Рис. 48.
то траектории не существует, если только не выполняется условие ж4 = (—1)г х0; в послед-
последнем случае существует бесконечное множество траекторий. Поэтому, если п {tt — t0)
кратно я, то функция S, вообще говоря, не определена.
Рассмотрим более общую задачу, а именно малые колебания около положения
устойчивого равновесия (§ 9.1). В нормальных координатах имеем
Рг
sin ;>,.(*!-
= 1, 2, ..., п,
A5.6.5)
где сого есть значение |г в момент t0. Эти уравнения однозначно определяют coio, ffl20t • • •
. . ., шп0, если только ни одно из чисел pr (<j — t0) не является кратным я. За исключе-
исключением таких случаев, траектория однозначно определяется терминальными точками и вре-
временем перехода и S является однозначной функцией. •
3) Простой маятник. Для простоты положим Ц = 0 и 90 = 0, так что
начальному положению груза будет соответствовать наинизшее его положение. Зависи-
Зависимость 9 от t для различных начальных скоростей представлена на рис. 5. Если ti про-
произвольно, a 9i произвольно в пределах —я < 9j < я, то траектория, разумеется, не будет
единственной. Единственность траектории можно гарантировать, если принять следующие
ограничения: а) рассматривать лишь периодические движения с амплитудой, меньшей я,
исключив из рассмотрения траектории, где 9 изменяется монотонно; Ь) рассматривать
только положительные начальные значения 9; с) считать, что конечное значение 9j дости-
достигается за время, меньшее, чем один полный период.
§ 15.7. Доказательство равенства dS/dt0 = Но. Перейдем к доказательству равен-
равенства A5.5.10), причем будем предполагать, что функция 5 построена по способу, описан-
описанному в § 15.5. Докажем сначала следующую лемму.
§ 15.8J
СВОЙСТВА ГЛАВНОЙ ФУНКЦИИ 277
Лемма. Функции фг, определяемые уравнением A5.5.3), обращаются в нуль, если
подвергнуть их действию оператора
4^^' A5-7Л)
где Ого обозначает qT в момент t = t0 (знак суммирования для краткости опущен).
Справедливость этого утверждения становится очевидной, если варьировать опре-
определяющие траекторию параметры таким образом, чтобы их значения определяли ту же
самую траекторию. Чтобы получить формальное доказательство, замечаем, что при
произвольном значении tt в некоторой окрестности t0
<?s (?ro'> ®ro> tQ, t) =
= <?s {фг kmO\ W,«o; *o. *l); Фг (9m<>; fflmd 4, h)\ *it <}• A5.7.2)
Дифференцируя частным образом по ti и полагая затем ti — t0, получаем доказательство
леммы.
Теперь нетрудно доказать равенство A5.5.10). В силу соотношений A5.5.4) и A5.5.6)
имеем
A5-7-3)
где L, как и в A5.5.4), выражено через qr0, сого, *о> *• Далее,
:«, A5.7.4)
«о
_a2_^ js_aqri_ = г _а^Л_ A575)
(о
Умножая три последних уравнения соответственно на 1, cos0) aso и складывая, получаем
~^""Шб0'^"+с'?г1 \"^Г + С°80 8qs0 +as0 ЙШ^/
to
Согласно доказанной лемме, оператор A5.7.1) обращает qrl в нуль. Это справедливо
и для L, следовательно,
_^?_=_ffl J^L—L= со —L =Н A5 7 7)
что и требовалось доказать.
§ 15.8. Свойства главной функции. Знание функции S имело бы огромное
значение для изучения динамической системы, если бы ее можно было
по интуиции или изобретательности составить без того, чтобы сначала знать
интегралы уравнений движения Лагранжа. Рассмотрим, например, соотно-
соотношения
¦^r=-Pro, r=l,2, ...,n. A5.8.1)
Они определяют qri в зависимости от t± (и параметров qr0; pr0; t0). Соотноше-
Соотношения A5.8.1) представляют собой интегралы уравнений Лагранжа и определя-
определяют движение в ^-пространстве. Они дают нам, таким образом, общее решение
задачи Лагранжа. Следует подчеркнуть, что уравнения A5.8.1), дают дей-
действительное явное выражение движения в ^-пространстве, а не являются
278
ШЕСТАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ
[Гл. XV
лишь новой формой дифференциальных уравнений для определения этого
движения. Аналогично, соотношения
as
Рп,
г = 1,2, ...,«,
A5.8.2)
выражают рг1 через qri (а также qr0, t0 и t{). Две системы A5.8.1) и A5.8.2)
определяют qri ш pri как функции tt (и параметров qr0; pr0, t0). Они представ-
представляют собой интегралы уравнений Гамильтона и определяют движение систе-
системы в фазовом пространстве. Таким образом, они дают нам общее решение
задачи Гамильтона.
Отметим еще некоторые свойства функции S.
1) Если функция L не зависит явно от t, то ?0 и ti входят в выражение
для S лишь в комбинации (^ — t0). При этом (как нам уже известно из § 10.14)
Hi = Но и формула A5.5.11) принимает следующий вид:
dS = рЛ dqri — Pro dqr0 — Hid (tt — t0). A5.8.3)
2) Функция ? имеет непрерывные вторые производные, и определитель
dqi0 dqn dqi0 dq2i
d?20 <5?21 ' ' ' ^?20 дЯп1
дЯп.0 dq2i ' ' ' dqnO i
A5.8.4)
или, короче, определитель
, не обращается тождественно в нуль.
I dqrOdqsi [
В самом деле, в противном случае существовало бы функциональное соотно-
dS
шение, связывающее ^— и qr0 (а также t0 и ti). Это указывало бы на зависимо-
мость между pri и qT0 (а также t0 и ti), что противоречит предположению о не-
независимости этих переменных.
3) Теорема Л и у в и л л я. Якобиан
(?и> ?2Ь ¦ 1 Чт, Ри.
?20.
PlO>
0» ¦ • •. Рпо)
A5.8.5)
равен (плюс) единице. Это означает, что преобразование от (qro, Pro) K (in,
Pri), осуществляемое интегралами уравнений Гамильтона (при фиксирован-
фиксированных t0 и ti), обладает свойством сохранения протяженности (объема, меры)
фазового пространства.
Для доказательства теоремы Лиувилля выразим все величины через про-
промежуточные переменные qr0, qri- Записывая определитель A5.8.5) сокращен-
сокращенно как
д (qri; Pn)
<?(?ro; Pro) '
будем иметь
Рп)
Рп)
(-l)r
д (Рп)
д (qso)
Pro)
pr0)
A5.8.6)
(qsi)
§ 15.8] СВОЙСТВА ГЛАВНОЙ ФУНКЦИИ 279
Здесь „ ;Рг, обозначает определитель, в котором элемент г-ж строки и s-ro
о (Я so)
столбца равен д^г1 . Но правая часть равенства A5.8.6) равна
сВД
II dqsidqr0
что и требовалось доказать.
4) Соотношения A5.8.1), A5.8.2), дающие решение задачи Гамильтона,
выражают qri и pTi через 2п параметров qr0 и рг0. Однако эта система парамет-
параметров не всегда является наиболее удобной. Предположим, что мы хотим
перейти к новой системе 2п параметров ar, j3r, представляющих собой неза-
независимые функции от qr0 и рг0 с непрерывными первыми производными и удов-
удовлетворяющих условию
Pr dar = рго dqT0 A5.8.7)
(знак суммирования для краткости опущен). Такой переход от (qr0, pro)
к (аг, рг) называется однородным контактным преобразованием. В дальней-
дальнейшем нам часто будет встречаться преобразование этого типа.
Выразим теперь функцию S через 2п -\- 2 переменных {qT\, aT; t0, tf):
S (qT0; Чгп t0, h) = S' (<zr; qTl; t0, П). A5.8.8)
Согласно формуле A5.5.11) имеем
dS' = prl dqrl — pr daT — Hi dtt + Ho dt0. A5.8.9)
Из формулы A5.8.9) можно получить результаты, аналогичные тем, что были
получены из формулы A5.5.11). Уравнения
¦|?1= _Р г=1,2, ...,п, A5.8.10)
дают решение задачи Лагранжа. Они позволяют выразить qn через а, |3 и t0
и ij. Присоединяя уравнения
""• = Рп, г=1,2, ...,в, A5.8.11)
получаем две системы A5.8.10) и A5.8.11), дающие решение задачи Гамиль-
Гамильтона. Они позволяют выразить qrl и рг1 через а, р и t0 и ^.
Описанный выше процесс преобразования несколько более тонкий, чем это может
показаться на первый взгляд. В самом деле, чтобы выразить gr0, pr0 через (a/, qrl; tOj tj),
необходимо воспользоваться уравнениями
аг = ат (gs0, ps0), r = 1, 2, . . ., п, A5.8.12)
dS
Pro= — ~si—:=Pro(?eoj 9si> *o> ^i)> г= 1, 2, ...,п. A5.8.13)
dq
rl
Заметим попутно, что п функций в правой части A5.8.12) нельзя задавать произвольно:
они должны удовлетворять определенным условиям, которые будут указаны в дальней-
дальнейшем. С помощью уравнений A5.8.12), A5.8.13) образуем функцию S', перейдя в выраже-
выражении для S от переменных дт0 к переменным а. Для каждого дг0 в S нужно написать фор-
формулы перехода:
Яго = Яго (««; 9«i; *o, Ч)- A5.8.14)
На первый взгляд может показаться странным, что производные dS/dgrl и dS'/dqrl дают
одно и то же выражение для pTi. Решение этого парадокса найти нетрудно: оно связано
с условием A5.8.7). Имеем
5G7-0
dqr
I д?гО ,„ , dqr0 dqr0 u \
-f- -—— dqsi + -—— dt0 H -— dij I
dgsi dt0 dt^ /
dqn +~ dto'+ ^- dtt. A5.8.15)
280 ШЕСТАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ [Гл. XV
Но
в силу A5.8.7) сводится просто к — (Зг йаг; поэтому коэффициент при каждом диффе-
дифференциале dqsi в A5.8.16) тождественно равен нулю. Таким образом, кажущееся противо-
противоречие исчезает.
5) Преобразование (аг, (Зг) в (qTi; pTi) сохраняет меру:
*(fri;ft-i)=lj A5.8.17)
В самом деле, при переходе от (аТ, (Зг) к (qT0, prQ) мера сохраняется; это
доказывается аналогично тому, как это делалось выше в п. 3. Этим же свой-
свойством обладает преобразование (qr0, рг0) в (qri, pri) при фиксированных зна-
значениях t0, t±. Поэтому произведение этих двух преобразований, т. е. переход
от (аг, рг) к (qrl, Pri), также является преобразованием, при котором сохра-
сохраняется мера.
6) Периодические траектории. Рассмотрим теперь сис-
систему, для которой существует семейство периодических траекторий.
В некоторых системах все траектории являются периодическими. Напри-
Например, как уже отмечалось в гл. IX, если мы имеем колебательную систему, для
которой отношение двух любых периодов есть число рациональное, все дви-
движения являются периодическими. Обозначим периоды свободных колебаний
через 2л/[хг (г = 1, 2, . . ., п). Если существуют целые положительные чис-
числа тщ, тп2, . . ., тп такие, что
-Ki- = -^2.= ...=J2_ = S, A5.8.18)
то все движения будут периодическими с периодом 2я/со. Это утверждение
справедливо независимо от начальных условий. Простым примером может
служить изотропный осциллятор. В других системах периодическими явля-
являются все траектории, которые начинаются в некоторой области фазового про-
пространства. Если, например, частица движется к центру под действием ньюто-
ньютоновского притяжения \мп/г2, то траектория, начинающаяся в момент t = О
из точки х, у, z, рх, ру, pz фазового пространства, будет периодической, если
начальная точка лежит в области
(*2 + 02+za)(p? + PS + P»<4n2- A5.8.19)
В этом примере (ньютоновская орбита) период зависит от начальных усло-
условий, тогда как в предыдущем примере (колебательная система) он от них
не зависел.
Имеются системы, обладающие как периодическими, так и непериодиче-
непериодическими траекториями.
Рассмотрим натуральную систему, обладающую однопараметрическим
семейством периодических траекторий. Построим функцию S для одной
из них, т. е. для какой-либо замкнутой траектории. Так как начальная и ко-
конечная точки в данном случае совпадают, то равенство A5.5.2) принимает
вид
S = S (qra; a),
где а — период. Но функция S фактически не может зависеть от qr0, посколь-
поскольку ничто не изменится, если в качестве начальной будет взята какая-либо
другая точка замкнутой траектории; поэтому
S = S (а). A5.8.20)
§ 15.9] ПРИМЕРЫ НЕПОСРЕДСТВЕННОГО ВЫЧИСЛЕНИЯ ГЛАВНОЙ ФУНКЦИИ 281
Перейдем теперь к соседней кривой семейства периодических траекторий,
тогда формула A5.5.11) запишется в виде
dS = —h da,
где h есть (постоянное) значение Н на рассматриваемой периодической тра-
траектории. Таким образом,
fc=—ii. A5.8.21)
Мы получили, что в семействе периодических траекторий постоянная энер-
энергии h зависит только от периода а.
§ 15.9. Примеры непосредственного вычисления главной функции. Най-
Найдем главную функцию для нескольких простых частных случаев.
1) Однородное поле. Частица массы т движется в плоскости под действием
однородного поля @, —mg). Движение, как и в случае A5.6.2), определяется формулами
_ , „ A5.9.1).
Здесь V — gy и
t-to)'K J
j
'о
Результат интегрирования следует выразить через (х0, у0, xif yt, t0, t%). Проделан этог
будем иметь
UJ+(yoJ}-4; 8 (h-t0) (У1+ уо)—^ gHh-kK. A5.9.3).
Легко проверить, что функция S обладает перечисленными ранее свойствами.
Например, уравнения A5.8.1) дают нам решение задачи Лагранжа о движении в пло-
плоскости ху:
dS
дх°
Uq — —— ^—'• ^"~ 7— у
"x° h~~ ° I A5.9.4>
2) Гармонический осциллятор. Для этого случая имеем
х = х0 cos n(t— to)-\- — sin га (i—10) A5.9.5)-
n
(г2_„гг2)й. A5.9.6)
(о
Последний результат должен быть выражен через х0, х^. Выполняя элементарное инте-
интегрирование, получаем
Этот результат верен при условии, что п (tt — t0) не кратно я. Как мы знаем (§ 15.6,-
п. 2), в этом исключительном случае функции S не существует, если только не выполняет-
выполняется дополнительное условие х% = (—1)г х0 (в противном случае 5 = 0, ибо, согласно
известной теореме, для любого целого числа полупериодов гармонического осциллятора-
1 = ~V).
Легко проверить, что соотношения A5.8.1), A5.8.2) дают интегралы уравнений
движения Гамильтона. Например,
^ n*lt) , A5.9.8)
что эквивалентно соотношению между t и х, с которого мы начинали.
282 ШЕСТАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ [Гл. XV
3) Рассмотрим простой пример, в котором функция L явно зависит от t, так что S
зависит от t0 и *,, а не только от их разности ti — t0. Рассмотрим частицу, совершающую
движение по прямой в силовом поле, равномерно усиливающемся со временем. Конкрет-
Конкретным примером может служить движение магнитной массы в переменном магнитном поле.
Потенциал на единицу массы такого поля равен —Atx, где А = const. Имеем
'x = At, A5.9.9)
x = uo + ±A(fi-t&), A5.9.10)
x = z0 + u0(t-t0) + -^A(t-t0)*(t + 2t0). A5.9.11)
Теперь можно выразить
L = ^-'x2+Atx A5.9.12)
h
как функцию от t. Вычисляя интеграл \ L dt и выражая затем щ через х0, получаем
•следующее выражение для главной функции:
-L.42(*i-*oK(^+7Vo+4Ǥ)- A5.9.13)
Мы снова можем легко убедиться в том,-что функция S обладает всеми указанными ранее
•свойствами.
4) Периодические траектории. Составим функцию S для замкну-
замкнутой периодической траектории. Для гармонического осциллятора 5 = 0, что и следовало
•ожидать, так как здесь мы имеем исключительный случай, когда величина а постоянна,
имеет одно и то же значение для всех периодических траекторий.
Для ньютоновской эллиптической орбиты имеем
Здесь 2а — большая ось эллипса, а Т и V — средние по времени значения Ги7. Следо-
Следовательно, для замкнутой орбиты
||301/3. A5.9.15)
Уравнение A5.8.21) в этом случае легко проверить; в самом деле,
^=4№2/3=#-=->, A5.9.16)
da 2 \ а ) 2а v '
{Формулы A5.9.14) для средних значений Т и V можно получить многими способами.
Докажем лишь одну из них, другая может быть тогда получена из уравнения Т + V = h.
Выразим rat через эксцентрический угол <р:
г = а*A — е cos ф), nt = ф — е sin ф (п = 2п/о).
Отсюда получаем
а 2л
!
о J \ г I па j a
о О
что и требовалось доказать.)
Глава XVI
ТЕОРЕМА ГАМИЛЬТОНА—ЯКОБИ
§ 16.1. Уравнение Гамильтона в частных производных. Как уже отме-
отмечалось в § 15.8, главная функция играла бы весьма важную роль в исследо-
исследовании динамических систем, если бы мы могли построить ее без предвари-
предварительного определения интегралов уравнений движения. В этой главе мы ука-
укажем метод, с помощью которого можно построить если не функцию S, то по
крайней мере другие функции, полезные для описания движения системы.
Без потери общности можно всюду в дальнейшем считать t0 = 0. В слу-
случае, когда L не зависит от t, a S зависит от разности ti — t0, это очевидно.
Но это верно и в общем случае, когда L зависит явно от t, так как при произ-
произвольно взятой начальной точке в ^-пространстве предположение t0 = 0
не ограничивает совокупности всех возможных движений.
Мы допустим большую свободу в выборе параметров, определяющих
траекторию системы (§ 15.8, п. 4). Вместо начальных значений координат
и импульсов (qr0, pr0) мы в качестве параметров, определяющих траекторию
в фазовом пространстве, возьмем (аг, рг). Эти величины являются функциями
от qr0, pr0 с непрерывными первыми производными, однако они не произволь-
произвольны и должны (см. § 15.8) удовлетворять условию
Pr dar = pro dqr0. A6.1.1)
Когда мы вводили впервые понятие о главной функции, мы траекторию опре-
определяли начальной и конечной координатами и моментами времени t0 и t\.
Теперь мы станем на другую точку зрения и будем считать, что траектория
определяется величинами a, gri и Ц (t0 равно нулю), а функцию S будем выря-
выряжать через эти 2п + 1 переменных (см. § 15.8, п. 4). Опустим для удобства
индекс 1 в обозначениях координат конечной точки, а также в символах ti
ж Hi л будем теперь конечную точку определять координатами (qi, q2, ¦ ¦ ¦
. . ., qn, pi, рг, . . ., pn), а время достижения ее будем обозначать просто
через t. Таким образом,
S = S (qt, q2: . ¦ ., qn; at, a2, . . ., an; t) A6.1.2)
и
dS = pr dqr — Pr dar — H dt A6.1.3)
(знак суммы для краткости записи опущен). Отсюда получаем
-g-=_prt r=l,2, ..., п, A6.1.4)
-р- = Рт, г=1,2, ..., п, A6.1.5)
-§г=-я- A6л-6)
Как уже отмечалось, п уравнений A6.1.4) дают решение задачи Лагран-
жа, так как с их помощью можно выразить каждое qr через t, а и Р, а 2п
уравнений A6.1.4) и A6.1.5) дают решение задачи Гамильтона, так как с их
помощью можно выразить qT и рг через t, а и р.
284 ТЕОРЕМА ГАМИЛЬТОНА — ЯКОБИ [Гл. XVI
Функция Гамильтона Н, входящая в правую часть равенства A6.1.6),
есть известная функция от q, p и t:
Н = Н (qu q2, . . ., qn; pit рг, . . ., pn; t), A6.1.7)
или, короче,
H = H(q; p; t). A6.1.8)
Заменяя в правой части равенства A6.1.6) рг на -—, получаем тогда для S
oqr
следующее дифференциальное уравнение:
dS 4-Н(а а а ¦ dS dS dS-f\-0 Мб 1 91
at \JI' "' > .? •> (jq^ i Qq^ i ? Qq^ ' / ч '
или, короче,
dS
Это есть дифференциальное уравнение Гамильтона. Оно представляет собой
нелинейное уравнение в частных производных первого порядка. Главная
функция, выраженная через q и t и п параметров а, является полным инте-
интегралом этого уравнения.
Существует, как известно, множество полных интегралов уравнений
в частных производных, и нет гарантии, что найденный нами полный инте-
интеграл дифференциального уравнения Гамильтона будет представлять иско-
искомую главную функцию. Но тогда возникает вопрос: может ли любой полный
интеграл быть полезен для наших целей? Ответ на этот вопрос оказывается
утвердительным, и это обстоятельство составляет сущность теоремы Гамиль-
Гамильтона — Якоби.
Мы приведем два доказательства этой теоремы: первое будет основано
на непосредственной проверке, а второе — связано с эквивалентностью сис-
системы уравнений Гамильтона некоторому уравнению Пфаффа.
§ 16.2. Теорема Гамильтона — Якоби (доказательство первое). Если
S = S (qu q2, . . ., qn; au a2, . . ., ап; t), A6.2.1)
или, короче,
S = S (q; a; t) A6.2.2)
представляет полный интеграл дифференциального уравнения Гамильтона
в частных производных
^- + Н (q; 4?-; t)=0, A6.2.3)
то интегралы гамилътоновых уравнений движения даются соотношениями
¦g-=-pr, r=l,2, ..., п. A6.2.4)
¦Щ^ = Рг, г=1,2, ..., п, A6.2.5)
где через р обозначены п новых произвольных постоянных. Уравнения A6.2.4)
и A6.2.5) определяют q и р как функции от t, зависящие еще от 2п произволь-
произвольных постоянных а и р. Уравнения A6.2.4) дают решение задачи Лагранжа:
определяют движение в g-пространстве. Уравнения же A6.2.4) вместе
с A6.2.5) дают решение задачи Гамильтона, т. е. определяют движение в фа-
фазовом пространстве.
Полный интеграл есть функция класса С2, содержащая п произвольных
постоянных <Xi, а2, . . ., ап (а также аддитивную постоянную ссп+1), причем
определитель
A6.2.6)
5 56.2] ТЕОРЕМА ГАМИЛЬТОНА — ЯКОБИ (ДОКАЗАТЕЛЬСТВО ПЕРВОЕ) 285
элемент r-и строки и s-ro столбца которого равен ^—— , нигде в области изме-
изменения ддане обращается в нуль.
Докажем, что функции
qr = qT (a; р; t), A6.2.7)
рг = рт(а; р; t), A6.2.8)
определяемые из уравнений A6.2.4), A6.2.5), удовлетворяют уравнениям
Гамильтона при произвольных значениях а и р или, во всяком случае, при
их произвольных значениях в некоторой области (а, Р).
Функция S удовлетворяет уравнению A6.2.3) при всех значениях
q, a, t в соответствующей области, так что, подставляя в это уравнение пол-
полный интеграл и дифференцируя полученное тождество по at, находим
да.\ dt ' jLA d<Xi dqr
r=l
(через HVr здесь обозначена частная производная дН/дрг). Кроме того,
уравнение
-g-=-p, A6.2.10)
тождественно удовлетворяется, если вместо функций q подставить их значе-
значение A6.2.7). Тогда после дифференцирования по t получим
~яГя \-У\1Г-я Jr = °- A6.2.11)
at aai ^—i oqr oa.\ at \ /
Символом —- здесь обозначена скорость, которая ранее обозначалась через
-~; это потребовалось в связи с тем, что в данном случае qr, кроме t, зависит
еще от параметров а и р. Иными словами, мы теперь рассматриваем совокуп-
совокупность траекторий, а не отдельную траекторию. Поскольку S ? С2, имеем
и из уравнений A6.2.9) и A6.2.11) находим
Всего имеем п таких уравнений, по одному для каждого а. Определитель
A6.2.6) из коэффициентов не равен нулю, следовательно,
r=l,2, .... п. A6.2.14)
Подставляя полный интеграл в уравнение A6.2.3) и дифференцируя тож-
тождество по #1, находим
dS . Л , Z, d*S тт I dS
" dq '
r=l
Уравнение
Pi—Ёг A6-2-16)
286 ТЕОРЕМА ГАМИЛЬТОНА — ЯКОБИ [Гл. XVJ
удовлетворяется тождественно, если вместо pi и q подставить их выражения
через а, р и t. Проделав это и продифференцировав результат по t, получим
dpi d*S ^n d*S dqr (<\P,<)<\1\
dt dtdqt ^ Zj dqrdqi dt ' {iv.t.llf
d°-S
dqi dt
и с помощью A6.2.15) и A6.2.14) получаем уравнение A6.2.17) в виде
Аналогичным образом получаем п уравнений
r = 1,2, .... в. A6.2.20)
Уравнения A6.2.14) и A6.2.20) показывают, что функции qT и рг, опре-
определяемые соотношениями A6.2.7), A6.2.8), удовлетворяют уравнениям
Гамильтона
dt ~~ dpr1 dt ~ ~dq~^> Г-L,^ •••. П, (Ш.1Й.В/
при произвольных значениях аир, что и доказывает теорему.
Итак, с помощью любого полного интеграла дифференциального урав-
уравнения Гамильтона в частных производных можно получить полное решение
задачи Гамильтона, т. е. интегралы гамильтоновых уравнений движения.
Дифференциальное уравнение для функции S впервые было получено Гамиль-
Гамильтоном в 1834 г., а доказательство всей теоремы было дано Якоби в 1837 г. *).
§ 16.3. Теорема об эквивалентности. Главная функция S,
S = S (qt, q2, . . ., qn\ qt0, ?2<ь • • ¦> Qno', t) = S (q; qQ; t), A6.3.1)
обладает тем свойством (см. A5.5.11)), что
dS = pr dqr — Pro dqrQ — H dt, A6.3.2)
где через Н обозначена функция Гамильтона, заданная как функция от (qiy
q2, . ¦ ., qn; Pi, p2, ¦ . ., pn', t). Если в соотношение A6.3.1) вместо qr под-
подставить их значения, выраженные через qr0, pro и t, то получим функцию о|з:
S (q; q0; t) = о|з (q0; p0; t), A6.3.3)
и уравнение A6.3.2) примет вид
рт dqT — Н dt = cftj) + pr0 dqr0. A6.3.4)
Пфаффова форма pr dqT — H dt, выраженная через qr0, pro и t, представляет
собой сумму полного дифференциала А|з (где о|з = oji (q0; p0; t)) и пфаффовой
формы pro dqr0, не содержащей времени.
В более общем случае, определяя траекторию (в фазовом пространстве)
значениями Ъг подходящих параметров 7ь Yz> • • •? Y2n (взятых вместо
*) Дифференциальное уравнение Гамильтона в частных производных, а также
частный случай теоремы Гамильтона — Якоби, когда постоянные аир имеют смысл
начальных значений фазовых координат } в р, встречаются в работе Гамильтона [16],
1834 г. В более общем виде, при большом произволе в выборе параметров аир, теорема
была доказана Якоби в 1837 г. (Crelle's Journal, XXVII, стр. 97). См. также «Лекции»
Якоби [17], стр. 157.
§ 16.3] ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОСТИ 287
параметров qr0 и рго), получаем соотношение
п 2п
2 Pr dqT - Н dt = dip + 2 #s dye, A6.3.5)
Г"»1 8=1
в котором^ =1^G; 0> a функции if зависят лишь от у. 2га величин у являют-
являются независимыми функциями от qr0 и рг0 и определяют траекторию точно
2и
так же, как ее определяют параметры qr0 и рг0. Форма 2 ^s dys есть не что
8=1
П
иное, как форма 2 Pro dqr0, выраженная в новых параметрах. Этот результат,
г=1
собственно говоря, нами уже был получен в § 15.8, п. 4, когда мы форму
п п
2 Pro dqrQ заменили на форму 2 Pi- dar, однако при этом мы ограничивали
г=М г=1
выбор новых параметров а и р требованием, чтобы соответствующее преобра-
преобразование было однородным контактным преобразованием. Здесь же выбор
параметров у не стеснен никакими ограничениями. Отметим, что форма
2n n
2 Ks dys, по существу, является не более общей, нежели форма 2 Рг dar,
8=1 Г=1
поскольку первая из них всегда может быть сведена ко второй с помощью-
теоремы Пфаффа.
Уравнение Пфаффа A6.3.5) в точности эквивалентно 2п дифференциаль-
дифференциальным уравнениям Гамильтона. Изучение главной функции показало, что реше-
решения уравнений Гамильтона удовлетворяют уравнению A6.3.5); остается
доказать обратное, что функции
Qr (v; t), pr (у, t), A6.3.6)
удовлетворяющие соотношению A6.3.5), удовлетворяют также и уравнениям
Гамильтона. Однако целесообразней, по-видимому, дать самостоятельное
доказательство всей теоремы.
Теорема об эквивалентности. Пусть функции
?r = ?r(Yi, 72, •••, Ъп, t), r=l, 2, ..., п, 1 A6 3 7)
Pr = Pr (У 1,Уь, • ¦ •>• У2п', t), . г = 1,2, ...., га, J
образуют систему 2п функций от у. и t; величины qr, dqr/dt, pr, dprldt принад-
принадлежат к классу Ci в области А переменных (yi, 7г> • • •> 72п) и в интервале /
изменения t, а якобиан
( п)_ A6 3 8>
д(Уи ?2. ••-, ?2п)
отличен от нуля для G1, 7г> • • •> 7гп) 6 А и ^ € ^>
1) Если Н (q; p; t) есть заданная функция от 2га + 1 переменных, принад-
принадлежащая к классу С% (в области пространства (q, p), на которую для каждого
t из I отображается область А при помощи соотношений A6.3.7)), а пере-
переменные q и р при всех у из А тождественно удовлетворяют дифференциальным
уравнениям
dqr _ дН дрг дН _ . ? ,, R о п\
то имеет место равенство
рг dqr — Hdt = dty + Ks dys, A6.3.10)
288 ТЕОРЕМА ГАМИЛЬТОНА — ЯКОБИ [Гл. XVI
где гр = гр (-у; Об ^г> а коэффициенты Ks зависят только от у. (Повторяю-
(Повторяющийся индекс г означает суммирование от г = 1 до г = п, а повторяющийся
индекс s — суммирование от s = 1 до s = 2п.)
2) Пусть существует функция Н (q; р; t) ? C\ такая, что пфаффова
форма рТ dqr — Н dt, записанная в переменных у, t, имеет вид dip + Ks dys,
где гр = гр (-у; t) ? С2, а функции Ks зависят только от у. Тогда функции
qr, pT тождественно удовлетворяют дифференциальным уравнениям
dt " дрТ ' at ~~ dgr ' r~1'z' •••> ге' UD.o.y;
/г/)ц всеж у из области А.
Доказательство первое (прямая теорема). Запи-
Запишем форму рТ dqr — Н dt в переменных у, t в виде U dt -\- Us dys, где
U = pT2$f—H, A6.3.11)
#. = Рг|^, s==l,2, ..., 2л A6.3.12)
(здесь, как и раньше, знак суммы для краткости опущен).
Докажем, что
dU __ dUs
dys дТ'
Из соотношения A6.3.11) получаем
dU _ dpr dqr . дЦг dH dqT dH dpT
A6.3.13)
dys dYs dt ' rr Qysdt dqT dys dpr
D I Г16 3 14)
поскольку qr, pT удовлетворяют равенствам A6.3.9). И так как
Ph = -g%-, A6.3.15)
dysdt dtdys y
TO
«L ^^|?^i. A6.3.16)
dt y '
dys ^ dtdys ' dt dys dt
Введем теперь функцию о|з = oji (у; t) такую, что
•f*-=tf. A6.3.17)
Тогда
^ _ A6 3 18)
at dys dysdt dtdys (iv.o.io)
и, следовательно,
Ue=-Q-+K., A6.3.19)
где A's есть функция, зависящая только от у и не зависящая от t. Окон-
Окончательно находим
prdqr-Hdt = ^dt-f- (-^+Ks)dys-^dy+Ksdy8, A6.3.10)
что и требовалось доказать.
Доказательство второе (обратная теорема).
Поскольку
pr dqr — Н dt = dtp + Ks dys, A6.3.20)
§ 16.4] ТЕОРЕМА ГАМИЛЬТОНА — ЯКОБИ (ДОКАЗАТЕЛЬСТВО ВТОРОЕ) 289
имеем
^^ 8 = 1,2, ..., 2п. A6.3.22)
Учитывая, что
_
получаем
at )- dys- dqr ays aPr
Но так как
dt dys dys dt '
то уравнение A6.3.23) можно переписать в виде
рг , дН \ дрг I dqr дН
Всего мы имеем In таких уравнений, по одному для каждого у. Опреде-
Определитель из коэффициентов отличен от нуля, и, следовательно,
dqr _дН_ дрг дН МЙЧО*
дТ-дРт> дТ 1^- (lb.d.j)
Теорема об эквивалентности, таким образом, полностью доказана.
§ 16.4. Теорема Гамильтона — Якоби (доказательство второе). Теорему
Гамильтона — Йкоби можно вывести непосредственно из теоремы об эк-
эквивалентности. Пусть S = S (<?; ос; t) будет полным интегралом уравнения
Гамильтона в частных производных
W
Выразим q и р через а, Р, t с помощью формул
dS
Р
г=1'2'
-Рг = ^ г = 1,2, ..., и. A6.4.3)
В результате получим общее решение уравнений Гамильтона. Для доказа-
доказательства представим форму pr dqr — Н dt в переменных а, р, t, тогда будем
иметь
Рг dqr-Hdt = ~-dqr + -^dt = dS--~- dar««ty + Рг daTt A6.4.4)
где через oji обозначена функция S, выраженная в переменных а, |3 , t. Вели-
Величины q и р являются независимыми функциями от (а; |3; t); действительно
(см. § 15.8, п. 3),
9 (gr; Рг) _ 1 -lfi , сч
5 (аг; рг) 1ф (Ш.4.Ь)
Из равенства A6.4.4) в силу обратной теоремы об эквивалентности следует,
что qT, pT удовлетворяют уравнениям движения Гамильтона. Теорема, таким
образом, доказана.
19 Л, А. Парс
290 ТЕОРЕМА ГАМИЛЬТОНА — ЯКОБИ [Гл. XVI
§ 16.5. Замечания по теореме Гамильтона — Якоби. Эта изящная тео-
теорема, доказанная в §§ 16.2 и 16.4, имеет фундаментальное значение как для
теории, так и для приложений. До сих пор, исследуя динамическую систему
какого-либо частного вида, мы составляли уравнения движения, после чего
задача сводилась к интегрированию этих уравнений. Совершенно иначе
обстоит дело в методе Гамильтона — Якоби. Как только найден один полный
интеграл уравнения Гамильтона в частных производных, сразу могут быть
написаны интегралы уравнений движения. Вопрос заключается лишь в том,
насколько просто может быть найден полный интеграл. Однако, как будет
показано, для большей части задач классической механики нахождение пол-
полного интеграла не вызывает каких-либо затруднений.
Прежде чем переходить к решению конкретных задач, укажем некоторые
классы динамических систем, для которых решение упрощается. Это, преж-
прежде всего, случай, когда функции L и Н не зависят явно от t,
Н = Н (qu q2, . . .,- qn; Pi, Рг, • • ., Pn) = H (q; p), A6.5.1)
и существует интеграл энергии
Н = h. A6.5.2)
Чтобы получить полный интеграл, положим
S = —Ы + К, A6.5.3)
где h = ai — одна из произвольных постоянных, а К — функция от (qlt
?2> • • ч Qn), в которую входят h и п — 1 других произвольных постоянных
а2, а3, • • ., а„. Уравнение Гамильтона в частных производных записывает-
записывается теперь в форме
(Щ)К A6.5.4)
и требуется построить полный интеграл этого уравнения, содержащий п — 1
новых произвольных постоянных, ни одна из которых не является аддитив-
аддитивной. Интегралы уравнений движения запишутся в виде
t-to = ^, A6.5.5)
-Р'=1еЬ г==2'3' •••'"• A6-5-6)
Рг = -^-. г = 1,2, ..., п, A6.5.7)
где tB написано вместо р4.
Решение, как мы видим, представляется в исключительно простой форме.
Уравнения A6.5.6) определяют траекторию в g-пространстве, не определяя
скорости перемещения по ней, а уравнение A6.5.5) дает связь между положе-
положением на траектории и временем. Решение задачи Лагранжа разбивается,
таким образом, на два этапа. Уравнения A6.5.7) заканчивают решение задачи
Гамильтона.
Постоянная h = at определяется значением (сохраняющейся) энергии
системы, а постоянная to = Pi зависит исключительно от выбора начала
отсчета времени i.
Большинство систем, встречающихся в приложениях, консервативны,
и поэтому теорема Гамильтона — Якоби чаще всего применяется в указан-
указанной выше форме. Практически обычно начинают не с дифференциального
уравнения Гамильтона, а с модифицированного уравнения в частных про-
производных A6.5.4).
Далее, если Н не содержит явно t и если одна из координат, скажем qn,
является циклической, то можно произвести дальнейшее упрощение. Поло-
Положим в равенстве A6.5.3)
К = yqn + К', A6.5.8)
§ 16.6] ОДНОРОДНОЕ ПОЛЕ 291
где К' зависит от (gb qz, . . ., qn-i), от h = аи от у = ап и от п — 2 осталь-
остальных произвольных постоянных а2, ос3, . . ., an_i. Координата д„ не входит
в Ж, и функция .ЙГ' является полным интегралом уравнения
и I дК' дК' дК' \ г, /л а к п\
Интегралы гамильтоновых уравнений движения имеют вид
'-*° = T' A6.5.10)
г = 2,3 в-1, A6.5.11)
quo = ?, + -—. A6.5.12)
рг = ^-, г=1,2, .... п-1, A6.5.13)
/7n = Y A6.5.14)
(здесь —р„ обозначено через д„0)- Постоянная 7 = «п определяется, очевидно,
значением (сохраняющегося) импульса, соответствующего циклической
координате qn, а постоянная qn0 — —Р„ зависит лишь от выбора начала
отсчета координаты qn. Значение qn в момент t нас обычно не интересует,
и уравнение A6.5.12) поэтому не рассматривается.
Наконец, часто К удается представить в виде суммы функций, каждая
из которых зависит лишь от одной координаты q (и, разумеется, от постоян-
постоянных а или части их). Если для уравнения A6.5.4) существует полный инте-
интеграл такого вида, то говорят, что система допускает разделение выбранных
координат. К таким системам относятся почти все системы элементарной
динамики. Возможность разделения переменных зависит как от самой систе-
системы, так и от выбранных для ее описания лагранжевых координат.
§ 16.6. Однородное поле. Рассмотрим теперь приложения теоремы
Гамильтона — Якоби к решению конкретных задач. Начнем с исследования
трех простых примеров, для которых в § 15.9 мы нашли явный вид главной
функции. Эта функция сама представляет полный интеграл уравнения
Гамильтона в частных производных, но те полные интегралы, которые мы
получим для каждого из рассматриваемых случаев, фактически не будут
главными функциями.
Рассмотрим движение частицы в плоскости ху под действием однородного
поля @, —g). Считая массу частицы равной единице, можем написать
\ y. A6.6.1)
Уравнение Гамильтона в частных производных запишется в виде
Требуется найти решение этого уравнения, содержащее две произволь-
произвольные постоянные. Легко убедиться, что найденная в § 15.9 главная функция
^ ^^g2t3 A6.6:3)
удовлетворяет уравнению A6.6.2) при произвольных значениях х0 и у0.
Наша задача, однако, состоит в том, чтобы указать, как найти полный
интеграл. Поскольку функция Н нб содержит t, а координата х является цик-'
лической, можем написать
S = —Ы + ах + ф (у). A6.6.4)
19*
292 ТЕОРЕМА ГАМИЛЬТОНА — ЯКОБИ [Гл. XVI
Подставляя это выражение в уравнение A6.6.2), получаем
ф'2 = 2й - 2gy - а2 = 2g (к - у), A6.6.5)
где
h = \a*+gk. A6.6.6)
(Легко установить геометрический смысл параметра к: это — наибольшая
высота, достигаемая движущейся частицей.) Для ср имеем выражение
h , h-y
ф= f \r2g(k-z)dz = )/~2g j Vudu. A6.6.7)
v о
(При желании можно, конечно, вычислить последний интеграл, но в этом нет
необходимости.) Таким образом, мы получаем полный интеграл, содержащий
два параметра а и к:
h-y
\ Vu A6.6.8)
A6.6.9)
Движение в плоскости ху описывается уравнениями
которые, как легко видеть, совпадают с известными элементарными форму-
формулами.
Уравнения A6.6.9) можно переписать в виде
, * л f A6.6.10)
Тогда станет ясным смысл введенных параметров:
а = щ, у = v0,
Здесь хо, У о — координаты начальной точки в момент t — 0, а и0, v0 —
начальные скорости. Заметим, что
^ (l\^) + y A6.6.12)
л
k-y = -^(y-gtY A6.6.13)
(постоянная к, как уже указывалось, равна наибольшей высоте подъема).
§ 16.7. Гармонический осциллятор. В этом случае
(р»+яа:2) A6.7.1)
и уравнение Гамильтона в частных производных имеет вид
Легко проверить, что найденная ранее главная функция
A6.7.3)
§ 16.7] ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР 293
удовлетворяет уравнению A6.7.2) при всех значениях а. Здесь а = ж0 есть
начальное значение х; мы будем считать, что а > 0.
Чтобы найти полный интеграл, положим
S=—jn2a4+q>{x). A6.7.4)
Это выражение удовлетворяет уравнению A6.7.2), если
ф'2 = п2 (а2 - х2). A6.7.5)
Для ф примем выражение
X
<p = n\Va?IIyidy. A6.7.6)
о
Следовательно,
X
^ j Va*-y*dy. A6.7.7)
j
о
Из теоремы Гамильтона — Якоби получаем
J
о
что можно записать в обычной форме:
х = a sin n (t — t0), A6.7.9)
где Р = n?at0.
Выясним, как связаны между собой оба полученных полных интеграла. Рассмотрим
сначала решение
1 пха
50 = у п (*а + Ф) ctg nt - -^ипп + а' A6.7.10)
и положим в нем
а' = Ф (а, а, а'), A6.7.11)
считая, что функция Ф ? Ci, а в остальном произвольна. Тогда правая часть A6.7.10)
будет иметь вид F (x, t, а, а, а'). Из теории дифференциальных уравнений в частных про-
производных первого порядка известно, что если решить уравнение
— = 0 A6.7.12)
да
относительно а и подставить это значение в F, то мы получим новый полный интеграл-
Надо показать, что при надлежащем выборе функции Ф мы придем этим путем к функ-
функции A6.7.7) с аддитивной постоянной а'.
Положим
a
а'=п\ ~[/a2—y2dy + a' (a > a > 0). A6.7.13)
о
Тогда уравнение A6.7.12) запишется в следующей форме:
actgrei 1- Л/ф— а2 = 0. A6.7.14)
sin nt v
Это уравнение нужно решить относительно а и результат подставить в F- Перепишем
уравнение A6.7.14) в виде
х = a cos nt + T/a2 — a2 sin nt A6.7.15)
и положим а = a sin 6, тогда будем иметь
x = a sin (n* + 9) = a sin if, A6.7.16)
294 ТЕОРЕМА ГАМИЛЬТОНА — ЯКОБИ [Гл. XVI
где г|з = nt + 6. Таким образом,
F = — пх* ctg nt+^-na* ctg nt !г2—+1. па? BQ +sin 28) +а'=
cj di SlU fit 4
1 1
= -s- rea2 sin2 -ф ctg nt+~^- not? sin2 9 ctg nt—
di di
— s.^a2 sin 6 sin ^+~ rea2 B9 + sin 26) +a'. A6.7.17)
Ho
1 1
¦j rea2 sin2 6 ctg nt+-r no? sin 29 =
= 4" rea2 sin e (sine otg ref+cos 9) = na2 sin 9 sin ijj, A6.7.18)
z z sin nt
так что функция A6.7.17) принимает вид
F = — па? sin2 г|з ctg nt— ™а% sin 6 sin -ф-{- -г па2 B6) + а' =
/га2 sin г|з . . , 1 /га2 sin гЬ .
= 2 sin яГ (Sm ^ °0S rei~sin 6) + па Bе) + а = 2 sinHt C0S ^ Sm №' +
1 11
+-7-/га2 Bijj—2/г*) + а' = — у/г2а2*+ — rea2 Bi|) + si
'=5 + a'. A6.7.19)
Таким образом, подставив в A6.7.17) значение а, найденное из уравнения A6.7.14), мы
действительно получили новый полный интеграл.
В заключение остановимся коротко на одном обстоятельстве, имеющем
важное значение для приложений теоремы Гамильтона — Якоби. Мы видели,
что выражение — у п2а4 + ср (х) является полным интегралом уравнения
A6.7.2) при условии, что функция ср удовлетворяет дифференциальному
уравнению
Ф'2 = п2 (а2 — х2), A6.7.5)
и приняли ф в виде A6.7.6), причем нижний предел интеграла взяли равным
нулю. В качестве нижнего предела можно было бы взять один из нулей
функции, стоящей под радикалом, например —а. В дальнейшем нам часто
будут встречаться случаи, когда полный интеграл содержит слагаемое
Ф (q), причем ф удовлетворяет дифференциальному уравнению вида
Ф'а = / (?)
(функция / (q) содержит, разумеется, еще параметры а). Таким образом,
Ф
= J V7(S}da:,
и в качестве нижнего предела интегрирования можно взять либо абсолютную
постоянную, либо простой нуль а функции / (q). Обычно выбирают вторую
возможность, и в этом случае нижний предел интегрирования оказывается
зависящим от а. Но при вычислении частной производной dS/da дифферен-
дифференцирование, как и прежде, производится только под знаком интеграла; от того,
что нижний предел есть функция аг, новые члены не появляются, поскольку
подынтегральная функция при а обращается в нуль.
Операция дифференцирования по аг под знаком интеграла приводит к не-
несобственному интегралу, в котором подынтегральная функция обращается
в бесконечность на одном из пределов интегрирования. (Например, интеграл
§ 16.9] ЦЕНТРАЛЬНАЯ ОРБИТА 295
в правой части равенства A6.7.8) будет несобственным, если нижний предел
интегрирования взять равным —а.) Но интеграл сходится, так что правило
вычисления производной путем дифференцирования под знаком интеграла
остается в силе *). В этой задаче мы фактически уже встречались со сходя-
сходящимися несобственными интегралами: в уравнении A6.7.8) х мог принимать
значения а и —а, и при этих значениях х интеграл в правой части становился
несобственным, уравнение же A6.7,8) оставалось справедливым и для этих
значений х.
§ 16.8 Частица в переменном поле At. Для системы, рассмотренной в § 15.9, п. 3,
имеем
Я = 4-Р2 — Atx. A6.8.1)
Уравнение Гамильтона в частных производных записывается в виде
Легко проверить, что главная функция
L ^ A6.8.3)
полученная в § 15.9, удовлетворяет уравнению A6.8.2) при всех значениях х0.
Найдем полный интеграл. Положим
^ x — <p(t). A6.8.4)
Это будет полным интегралом, если
' Ф=4^2'5+1ГЛагз+1Га2'- A6-8'5)
Решение задачи Лагранжа дается уравнением
_Р = -Ё^ = ж_а*-jAp, A6.8.6)
совпадающим с A5.9.11) при t0 = 0.
§ 16.9. Центральная орбита. Применим метод Гамильтона — Якоби
к решению некоторых хорошо известных задач динамики. Рассмотрим сна-
сначала задачу о движении частицы в центральном поле с потенциалом V (г).
Выбрав в качестве лагранжевых координат г, 0, представим функцию
Н в виде
) A6.9.1)
(Напомним, что для натуральной системы
Н = Т + V
и в ортогональных криволинейных координатах (§ 10.14) функция Т может
быть выражена через переменные р.) Модифицированное уравнение в част-
частных производных A6.5.4) запишется в виде
Требуется найти решение, которое бы, кроме h, содержало еще произвольную
постоянную а. Поскольку координата 0 циклическая, полагаем
К = сс0 + R, A6.9.3)
*) См., например, Ш.-Ж. дела Валле-Пуссен, Курс анализа бесконечно
малых, Л.— М., Гостехиздат, 1933, том II, гл. I, § 23.
296 ТЕОРЕМА ГАМИЛЬТОНА — ЯКОБИ [Гл. XVI
где R есть функция от г. Функция A6.9.3) удовлетворяет уравнению A6.9.2),
если
/?'2. о г, от/ а (i(\ Q л\
Обозначим правую часть уравнения A6.9.4) через /(г). Тогда
К=--аВ + j j/2A-2F(g)—|J-dg = a8+ JK/(g)dg. A6.9.5)
a a
Здесь а есть простой нуль функции / (г) (см. § 16.7); в большей части случаев
движение представляет собой либрацию по г между двумя простыми нулями
а и Ъ функции / (г), причем / (г) > 0, когда а < г < 6. Решение задачи Лаг-
ранжа (движение частицы в плоскости) дается уравнениями
A6.9.7)
Мы получили решение, найденное нами ранее в примере 5.2В; уравнение
A6.9.6) совпадает с E.2.41), а уравнение A6.9.7) — с E.2.43).
Сделаем одно замечание относительно обозначений. В интегралах, встре-
встречающихся в формулах A6.9.5) — A6.9.7), буква г в одних случаях обозначает
переменную интегрирования, а в других — верхний предел. Например,
формула A6.9.6) иногда записывается так:
Конечно, не очень хорошо, что одна и та же буква применяется в различных
смыслах, но на это можно пойти ради удобства, надеясь, что это не явится
источником недоразумений.
§ 16.10. Сферический маятник. Будем пользоваться обозначениями,
принятыми в примере 5.2А, и угол 0 будем отсчитывать от направленной
вверх вертикали. Тогда будем иметь
r = -ima2@2 + sin20(p2), V = mga cos 0 = тпа2п2 cos 6, A6.10.1)
где n2 = g/a. Опуская положительный множитель та2, можем написать
A6.10.2)
A6.10.3)
Модифицированное уравнение в частных производных будет иметь вид
Решение его ищем в виде
К = ссср + в, A6.10.5)
§ 16.11] ВРАЩАЮЩИЙСЯ ВОЛЧОК 297
где в определяется из уравнения
в'2 = 2й—2re2cos0 ^Jq~. A6.10.6)
Обозначив правую часть уравнения A6.10.6) через / @), получим полный
интеграл в следующем виде:
е
VWdt. A6.10.7)
Нижний предел интеграла равен абсолютной постоянной или является прос-
простым нулем функции / @).
Интегралы лагранжевых уравнений движения имеют вид
дК - ? ^ Л
V У A6.10.8)
Если здесь положить h = n2h', а2 = 2гс2а', то получим
е
A6.10.9)
Ф-Ьр=1/^*
где
F(Q)==h' — cosQ--~j, A6.10.10)
что находится в полном согласии с результатами § 5.2.
§ 16.11. Вращающийся волчок. Будем определять положение тела
с помощью углов Эйлера (см. § 8.6), причем ось Oz направим вертикально
вверх. Тогда будем иметь
Т = \А @a + sm2092)+4c(^+<Pcos0J' V = MglcosQ. A6.11.1)
Выбранные нами координаты не ортогональны, так что выразить Т через
переменные р сразу не удается. Можем написать
рв = Ав, ^ ^ A6.11.2)
Pv = A sin2 бср + С cos 0 (ij) + ф cos 0), A6.11.3)
p^ = С D + Ф cos 0). A6.11.4)
Следовательно,
A sin2 0ф = pv — p$ cos 0. A6.11.5)
Таким образом, получаем
^ * ^ osQ, A6.11.6)
и модифицированное уравнение в частных производных записывается в форме
2 1 I дК дК Qv2 1 / дК \2
A6.11.7)
298 ТЕОРЕМА ГАМИЛЬТОНА — ЯКОБИ [Гл. -XVI
Координаты ф и ty являются циклическими, поэтому решение ищем в виде
К = а2ф + сс3г|з ¦+ в. A6.11.8)
Оно удовлетворяет уравнению A6.11.7), если
6" = 2А (h-Mglcos 9) - (а»-^°os9 J - 4 а\. A6.11.9)
Обозначая правую часть уравнения A6.11.9) через /@), получаем следую-
следующее выражение для полного интеграла:
е
Я = а2ф+а3а1>+ J/7A)<*1, A6.11.10)
е0
где б0 есть абсолютная постоянная или простой нуль функции / @).
Решение задачи Лагранжа" дается формулами
е
g Д. , A6.11.11)
/(Б)
_Д^ A6.11.12)
2 J sin| У/(|)
Pdif ? С A cos | . ^. d| ,.e .. ^о\
3 = ^ = ^-) {—аз-ш4"(а2"азСО8|)}17щ* A6Л1ЛЗ)
^ )
Второе из этих соотношений устанавливает связь между 0 и ф, т. е. положе-
положение оси волчка в пространстве, а первое дает зависимость между 0 и t. Послед-
Последнее соотношение, связывающее oji и 9, обычно не представляет интереса.
Формула A6.11.11), связывающая t и 9, может быть записана в следую-
следующей форме:
A2Q2=f(Q). A6.11.14)
Обозначив cos 9 через z, преобразуем ее к виду
Если положить (см, S 8.6)
v h — ^-^Ay., A6.11.16)
то уравнение A6.11.15) перейдет в (8.6.9).
§ 16.12. Стержень на вращающейся плоскости. В качестве следующего примера
рассмотрим систему, исследовавшуюся нами в § 8.11. Стержень движется по гладкой
плоскости, которая равномерно вращается вокруг горизонтальной оси, фиксированной
в этой плоскости. Эта задача проще решается с помощью уравнений Лагранжа, но инте-
интересно также решить ее методом Гамильтона — Якоби. Согласно (8.11.1) имеем
Я =T2 + V-T0 = Y (pf + p« +^ре2)-тсо^--2-*2<й2зт2 9-етзт т. A6.12.1)
Дифференциальное уравнение Гамильтона имеет вид
Выражение
S= сч? + е+ F(r\,t) A6.12.3)
есть полный интеграл, если функция в удовлетворяет уравнению
в'2 = А:2 (а| + &асо2 sin2 6), A6.12.4)
§ 16.13] ЭЛЕКТРОН В ЦЕНТРАЛЬНОМ ПОЛЕ 299
« функция F — уравнению
OP I др v 2
+[) +? + l222o)i = O. [A6.12.5)
Последнее имеет решение вида
i A6.12.6)
/ = i.C0
где ф и г); — функции от ?, удовлетворяющие уравнениям
ф -f соф = g sin со* A6.12.7)
0. A6.12.8)
Таким образом,
~S~ (sin wJ—cos at) A6.12.9)
и полный интеграл имеет вид
6
Уа.%
О
A6.12.10)
¦(мы здесь воспользовались обозначениями § 16.9). Решение задачи Лагранжа дается урав-
уравнениями
_р1 = ___ =?_(*!*, A6.12.11)
(f-g^-dt, A6.12.12)
о
в
\ , —а-Л. A6.12.13)
J ya| + A2co2sin2e 3 v ;
Уравнение A6.12.11) приводит, как и следовало ожидать, к равномерному движению
по g, а уравнение A6.12.13) приводит к соотношению
e2 = (u2sm2e + (al//c2), A6.12.14)
¦откуда получаем
е'= со2 cose sine A6.12.15)
в полном согласии с (8.11.2). Остается найти зависимость т) от t. Из уравнения A6.12.12)
получаем
~ sh ш~^ sin ш> A6.12.16)
что эквивалентно (8.11.3).
§ 16.13. Электрон в центральном поле. Предположим, что электрон,
масса которого переменна (см. A1.1.1)), движется в плоскости под действием
притяжения к началу координат; потенциал поля обозначим через V (г).
В полярных координатах функция Гамильтона (см. A1.4.12)) запишется
в виде
Н = с]/Гт'с*+р1 + -±гр1 -щс'+V. A6.13.1)
Это — не обычное выражение, в котором Н есть квадратичная функция от р,
но тем не менее метод Гамильтона — Якоби остается справедливым. Модифи-
300
ТЕОРЕМА ГАМИЛЬТОНА — ЯКОБИ
[Гл. XVI:
цированное уравнение в частных производных имеет вид
A6.13.2)
A6.13.3)
A6.13.4)
Обозначая правую часть A6.13.4) через / (г), получаем следующее выражение
для полного интеграла:
Полный интеграл ищем в виде
К = а0 + R.
Это выражение удовлетворяет уравнению A6.13.2), если
f ]Vf(r)
dr
A6.13.5)'
(мы здесь воспользовались обозначениями § 16.9).
Решение задачи Гамильтона дается уравнениями
t-t -il__L
1 l°~ dh - C2
moc*
7 И
¦dr.
— 6 = __ = в— \ ¦—"_ dr,
da J l/f(r)
A6.13.6)'
I = -^7T- = 0C.
Но согласно A1.4.9) имеем
mor
A6.13.7)
Рассмотрим подробнее случай ньютоновского притяжения, когда.
F = —(х/г, ц = Ze2 > 0. Функция / (г) в этом случае имеет вид
о+^-)т-«2A-7&L- A6-13-8>
Будем считать, что h <C 0; если частица начинает движение со скоростью и
из точки, находящейся на расстоянии к от точки О, то согласно A1.4.5) будем,
иметь
h = mQc2
и условие /г. < 0 будет выполняться, если
1 +
кш0
l 2 •
A6.13.9)
A6.13.10)
(При с—>- оо мы приходим к известному условию, определяющему эллипти-
эллиптическую орбиту в случае постоянной массы: шйки% < 2ц.) Можно принять,,
что 2пг0 + (й/са) > 0 и са > ц; эти неравенства обычно всегда выполняются,
вследствие того что с велико. При этих условиях функция / (г), зависящая
от Иг по квадратичному закону, имеет два вещественных положительных
нуля и
({4)(^) A6ЛЗЛ1>
§ 16.14] ПФАФФОВА ФОРМА VTdqr — Н dt 301
где
^=1—?г A6.13.12)
Уравнение траектории имеет вид
г
Я(8 + Р)={ ^^ тт2. A6.13.13)
Полагая
i» (J J)| (JL)B1>, A6.13.14)
i= (J_ + J_)+| (J___L
находим
Я(в + Р)=я|з, A6.13.15)
и уравнение принимает вид
При К = 1 это есть уравнение эллипса. В действительности же Я< 1,
и траектория оказывается незамкнутой; для того чтобы значение г повтори-
повторилось, угол 0 должен увеличиться на 2яД (> 2я).
Если начальная точка, отстоящая от начала О на расстоянии к, есть
апсида, то формулы упрощаются: к становится равным одному из апсидаль-
ных расстояний г4 или г2, и мы эту величину берем в качестве нижнего преде-
предела интегралов, кроме того, t0 = 0, р = 0,
^ A6.13.17)
. A6.13.18)
Если
mok
то апсидальное расстояние к будет расстоянием до перигелия; при с ->- оо
это неравенство принимает хорошо известную форму: токи2 > [л.
§ 16.14. Пфаффова форма pr dqr — И dt. Вернемся к теореме об экви-
эквивалентности (§ 16.3). Мы видели, что уравнение Пфаффа
рТ dqr — Н dt = dip + со A6.14.1)
эквивалентно гамильтоновым уравнениям движения и, обратно, из уравне-
уравнений Гамильтона следует уравнение A6.14.1). Были решены уравнения отно-
относительно q и р, причем решение содержало 2га независимых параметров Yi,
72i • • ¦, 72п- От этих же параметров зависят коэффициенты Ks пфаффовой
формы со:
со== 2 Ksdys. A6.14.2)
8=1
По теореме Пфаффа форму со можно представить как форму от п переменных:
п
со= 2 prdar, A6.14.3)
r=l
302
ТЕОРЕМА ГАМИЛЬТОНА — ЯКОБИ
[Гл. XVI
где а и Р — надлежащим образом выбранные функции от у. Эти новые пара-
параметры вводятся вместо прежних параметров у, и траектория в фазовом про-
пространстве определяется численными значениями аи^ или численными зна-
значениями у.
Пфаффова форма, стоящая в левой части равенства A6.14.1), имеет важ-
важное значение в теории движения в фазовом пространстве. Для изучения общей
формы Пфаффа
r=l
A6.14.4)
где коэффициенты Хг суть функции класса Ct от т. независимых переменных
xt. x2, . . ., хт, большую роль играет система уравнений Пфаффа
где
2 aTSdxs = O r = l, 2, ..., m, A6.14.5)
epe = i?z: _**•-. A6.14.6)
dxs dxT v '
(Гурса обозначал эту систему через Sx.) В нашем случае, когда т — 2п + 1,
переменными служат qt, q2, . . ., qn; px, p2, . . ., рп; t и форма Q имеет вид
Q = 2 Pr dqT — Я dt.
r=l
Кососимметрическая матрица (ars) имеет вид
A6.14.7)
-1
дН
да.
0
-1
дН
dq2
— 1
дН
oqn
1
дН
dpi
\
0
дН
дРг
1
дН
дРп
дН -
дН
дН
дН
дН
дН
дРп
о
Уравнения A6.14.5) для пфаффовой формы A6.14.7) записываются в виде
dpr-\--r—dt = O, r = 1, 2, ..., п, I
дРг
= l, 2, .... га,
A6.14.9)
2
г=1
ОН
Первые In уравнений представляют уравнения Гамильтона для динамиче-
динамической системы. Последнее уравнение не является независимым от остальных,
поскольку определитель матрицы есть кососимметрический определитель
нечетного порядка и потому равен нулю. Если функция Н не содержит явно
t, то последнее уравнение эквивалентно интегралу энергии Н = h.
Глава XVII
СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ,
ДОПУСКАЮЩИЕ РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ
§ 17.1. Разделение переменных. Некоторые механические системы, опи-
описываемые определенной системой лагранжевых координат, допускают разде-
разделение переменных. Иными словами, написанное для такой системы модифи-
модифицированное уравнение в частных производных A6.5.4) имеет полный инте-
интеграл в виде суммы п функций, каждая из которых зависит от одной из п
координат. Подобные системы обладают рядом важных и интересных свойств,
изучение которыхч составит предмет этой главы. Возможность разделения
переменных зависит как от самой изучаемой системы, так и от выбранной для
ее описания системы координат. Естественно, возникает вопрос: каковы усло-
условия, при которых возможно разделение переменных, и каковы свойства сис-
систем, допускающих это разделение? В дальнейшем мы ограничимся рассмот-
рассмотрением натуральных систем с п степенями свободы, для описания которых
используются п лагранжевых координат.
Разделимые системы встречаются главным образом в теории малых коле-
колебаний (гл. IX), когда выбранные лагранжевы координаты являются нормаль-
нормальными. Движение по каждой координате в этом случае совершенно не зависит
от движения по другим координатам, и система фактически распадается
на п независимых систем. Подобного рода полная разделимость встречается
и в других задачах (см. пример в § 8.11). Однако в общем случае в раздели-
разделимых системах это не имеет места. Мы не можем изолировать одну какую-либо
координату и изучать ее изменение, как для системы с одной степенью свог
боды. Тем не менее при изучении любой разделимой системы можно в извест-
известном смысле приблизиться к подобному идеальному разделению. Как станет
далее ясно, изменение одной координаты можно в определенной степени
рассматривать независимо от поведения других координат. Смысл этого*
пока не очень четкого утверждения станет ясен несколько позже (в § 17.3).
. Мы уже рассматривали ранее движение консервативной системы с одной
степенью свободы; типичной задачей этого рода является прямолинейное дви-
движение частицы в силовом поле. Основное дифференциальное уравнение, опи-
описывающее движение частицы (§ 1.2), имеет вид
**2 = / (х),
и, как уже указывалось, о характере движения можно судить по виду функ-
функции f (х). Решение основывается на теории дифференциальных уравнений
этого вида. В случае одной степени свободы функция / (х) содержит только-
один параметр, а в общем случае разделимой системы с п степенями свободы
мы имеем п параметров, входящих линейно в / (х).
§ 17.2. Условия разделимости переменных в системах с двумя степе-
степенями свободы. Мы начнем с рассмотрения важного частного случая систем
с двумя степенями свободы и ограничимся изучением ортогональных систем,
т. е. таких, для которых выражение кинетической энергии Т содержит только
квадраты и не содержит произведений. Прежде всего установим необходимые
и достаточные условия разделимости, затем, считая эти условия выполнен-
выполненными, получим основные характеристики возможных при этом движений
системы.
304 СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [Гл. XVII
Пусть х и у — лагранжевы координаты. Составим функцию Гамильтона
± + V, A7.2.1)
где а, Ъ, V — заданные функции от х, у; предполагается, что эти функции
принадлежат классу С4 в рассматриваемой области изменения х, у. Выведем
сначала необходимые условия разделимости. Если система допускает разде-
разделение переменных, то модифицированное уравнение в частных производных
* A7-2-2)
допускает полный интеграл вида
F (х, h, a) + G (у, h, a), A7.2.3)
где а — вторая произвольная постоянная. Таким образом, в рассматривае-
рассматриваемой области значений х, у, h, а тождественно выполняется равенство
If)}-"- <17-2-4»
Напишем его в упрощенной форме:
ав + Ь<Р « h — V. A7.2.5)
Здесь 0 = Tiir) зависит только от х (а также от h и а), а ф = -^ (у-) 2
зависит только от у (а также от А и а). Из равенства A7.2.5) получаем
ев! + Ьщ = 1, A7.2.6)
ав2 + Ьф2 = 0. A7.2.7)
Индекс 1 в этих формулах обозначает дифференцирование по h, а индекс
2 — дифференцирование по а. Напомним, что величины а и Ъ положительны
при всех значениях х, у; они являются коэффициентами в формуле кинети-
кинетической энергии. Из равенства A7.2.7) видно, что ни 02, ни ф2 не могут тожде-
тождественно равняться нулю, а из равенства A7.2.6) следует, что величины 8j
и ф1 не могут быть одновременно нулями. Кроме того, выражение
/dF_ dG\
d(9 Ф) dF dG \ дх ' ду ) rt7,ov
-^» — — —^_ A7.2.8)
не может тождественно равняться нулю, так как сумма F + G представляет
полный интеграл уравнения A7.2.2). Возьмем теперь какие-либо подходя-
подходящие фиксированные значения h и а; они должны быть такими, чтобы ни одна
из величин 02, фг, 01фг — 9гф1 не обращалась в нуль при всех значениях х
та. у, и также чтобы 0i и ф1 не обращались обе в нуль при всех значениях х и у.
Затем решим уравнения A7.2.5) — A7.2.7) относительно а, Ъ и V. Тогда
•будем иметь
hQi — 6 h(fi — ф
у
Ф2
_ф1 x+y
ф2
гдо |, X — функции только от х, а п, У — функции только от у. Эти величи-
величины не должны зависеть от выбранных нами фиксированных значений h и а,
для чего h и а должны линейно входить в 0 и ф; в дальнейшем мы увидим,что
§ 17.3] ИЗУЧЕНИЕ ДВИЖЕНИЯ СИСТЕМЫ 305
именно так и обстоит дело. Далее, имеем
1
а и
г, °2 г ..- „ .„.
е2 i
1
A7.2.11)
02 Ф2
Здесь Р = Р (х) и Q = Q (у); функции Р и Q также не должны зависеть от
принятых значений А и а.
Таким образом, если система допускает разделение переменных, то функ-
функция И должна иметь Следующий вид:
4 = 2(Х+Y) (РР* + QP'ti + Т$Г' A7.2.12)
где X, Р, ? суть функции только от х, а У, Q, -ц суть функции только от у.
Докажем теперь, что эти условия являются и достаточными, т.е. что
система, для которой
A7.2.13)
допускает разделение переменных. Для такой системы модифицированное
уравнение в частных производных записывается в форме
ТС (f )*+!+,}=*. (.7.2.14)
и полный интеграл требуемого вида F -\- G мы можем получить, положив
A7.2.15)
а- A7.2.16)
Таким образом, получаем полный интеграл
i\-a)dy. A7.2.17)
Входящие сюда интегралы интерпретируются обычным образом, например,
в первом из них верхний предел равен х, а нижний предел равен абсолютной
постоянной или простому нулю функции, стоящей под знаком радикала.
Обращаясь снова к доказательству необходимости, замечаем, что в при-
принятых там обозначениях
0 = (hX - I + аIР, Ф = (hY — л - «)/<?, A7.2.18)
что подтверждает формулы A7.2.9) — A7.2.11).
§ 17.3. Изучение движения системы. Интегралы уравнений движения
имеют вид
x d.r+ [ Y dij, A7.3.1)
1 dx-t 1 d,j A7.3.2)
У2Р (hX — l + a) J yiQ {hY — ч\ — а)
20 л. А. Парс
306 СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [Гл. XVII
Для решения задачи Лагранжа, описания движения в пространстве х, у, тре-
требуются лишь уравнения A7.3.1), A7.3.2); их можно записать кратко так:
dx_ dy _ dt H7 , «
где
R = R(x) = 2P (hX — ?+ а) A7.3.6)
и
5 = S (у) = 2<? (hY - г] — а). A7.3.7)
Уравнения A7.3.5), надлежащим образом интерпретированные, позво-
позволяют свести интегрирование уравнений Лагранжа к квадратурам. Заметим,
что произвольные постоянные h, а линейно входят в R и S.
Положим
-jfy- = dr. A7.3.8)
Переменную т можно интерпретировать как «искусственное время», отсчи-
отсчитываемое часами, движущимися вместе с изображающей точкой в простран-
пространстве х, у. Скорость хода этих часов зависит от их положения в пространстве,
и так как сумма X + Y всегда положительна, то т всегда возрастает вместе
с t. Далее имеем
% , ^ = dr, A7.3.9)
-i / П ' -I / с '
у Si [/о
так что
/&V (-^-\2 = 5. A7.3.10)
Эти уравнения можно интерпретировать подобно тому, как это было сделано
в случае одной степени свободы (§ 1.2). Действительно, соотношение между
х ж х здесь такое же, как между х и t в § 1.2. Нужно, однако, помнить, что
соотношение между переменными (и т зависит от х и у, так что движения
по х и по у фактически не независимы. Тем не менее в известном смысле эти
движения можно рассматривать как независимые. Они были бы полностью
независимы, если бы сумма X + Y оставалась постоянной (что потребовало
бы, разумеется, чтобы X ж Y были постоянны по отдельности). Если сумма
X + Y изменяется не слишком сильно, то х и у можно считать почти незави-
независимыми. В этом заключается смысл несколько туманного утверждения,
высказанного в § 17.1.
Предположим теперь, что сумма X -\- Y, которая, как мы знаем, поло-
положительна, ограничена сверху для всех значений х и у или по крайней мере
для значений, достигаемых в процессе рассматриваемого движения, т. е. бу-
будем считать, что существует постоянная А такая, что для всех t
0<Х + Y^A. A7.3.11)
Тогда т —>- оо вместе с t. В этом случае общий характер движения по каждой
координате очевиден. Если, например, начальное значение х лежит между
последовательными простыми нулями а^, Ь^ функции В, то изменение х носит
характер колебаний между этими значениями а± и bi. Движение такого
типа мы будем по-прежнему называть либрацией несмотря на то, что оно уже
не является периодическим по t (хотя и периодично по т). Как и в случае
17.3]
ИЗУЧЕНИЕ ДВИЖЕНИЯ СИСТЕМЫ
307
одной степени свободы, знак радикала \/ R в A7.3.5) выбирается положитель-
положительным, когда х возрастает, и отрицательным, когда х убывает. То обстоятель-
обстоятельство, что мы здесь имеем двузначную функцию, нас не должно смущать:
это связано с самой сущностью задачи. Если же начальное значение х распо-
расположено вблизи двойного нуля с функции R, то при стремлении t (и т) к беско-
бесконечности х —>- с; этот случай соответствует лимитационному движению.
Аналогичные соображения можно высказать, конечно, и в отношении коор-
координаты у.
Рассуждения изменятся, если сумма X + Y не ограничена. Предполо-
Предположим, например, что в рассматриваемом движении X + Y стремится к беско-
бесконечности вместе с t. (Обычно это
имеет место, когда х или у обра-
обращается в бесконечность вместе
с t.) Если интеграл
ь
dt
Рис. 49.
сходится, то при t-^ оо пере-
переменная т стремится к конечному
пределу т0, т. е. «искусственное
время» т должно остановиться!
Легко сообразить, как следует
видоизменить предыдущие вы-
выводы для этого случая. Если
начальное значение х лежит
между последовательными про-
простыми вещественными нулями
а, Ъ функции R, то вместо неограниченно продолжающейся либрации мы
получаем, что при t, стремящемся к бесконечности, х стремится к пределу I
(a^l-^b) (быть может, после некоторого числа колебаний). Если же х
находится вблизи двойного нуля с функции R, то х с ростом t стремится к пре-
пределу, лежащему в окрестности с. Движения такого типа можно назвать псев-
долимитационными движениями.
Если по каждой из координат имеет место либрация и, кроме того, число
(х, определяемое формулой
A7.3.12)
рационально, то движение является периодическим. Если ц, = p/q, где р
и q — целые числа, не имеющие общего множителя, то после q либрации
по координате х и р либрации по координате у система возвратится в перво-
первоначальное положение, т. е. примет первоначальные значения координат
и скоростей. Период этого движения будет равен
\у. A7.3.13)
Если [X есть число иррациональное, то движение не будет периодическим,
а траектория будет располагаться вся внутри прямоугольника (а4 ^ х ^ fet,
а2 ^ У ^ Ь2) плоскости ху, оставаясь незамкнутой (рис. 49). Такое движение
называют квазипериодическим. Более подробное изучение квазипериодических
движений связано с введением так называемых угловых переменных. Это
исследование мы отложим до рассмотрения общего случая п переменных.
(В § 1.3 был указан один простой пример введения угловой переменной для
системы с одной степенью свободы.)
20*
308 СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [Гл. Х\>11
Так как обе функции, и R и S, содержат А и а, то, казалось бы, естест-
естественно ожидать, что путем выбора начальных условий всегда можно получить
как периодические, так и апериодические движения. Такая гипотеза, однако,
оказывается несостоятельной. Мы знаем, что существуют системы, которые
всегда совершают периодические движения, и системы, которые никогда
не движутся периодически. Оба типа систем встречаются в теории малых
колебаний. Если отношение периодов есть число рациональное, то траекто-
траектория системы всегда периодична, каковы бы ни были начальные условия;
если же это отношение есть число иррациональное, то траектория никогда
не является периодической (исключая, разумеется, тот случай, когда система
совершает главные колебания). Другой достаточно ясный пример — это
ньютоновская орбита, которая всегда периодична, каковы бы ни были вели-
величина и направление начальной скорости планеты (если, конечно, начальная
скорость не превышает того значения, которое она имела бы при движении
из бесконечности в начальную точку под действием притяжения к центру).
В § 18.8 мы вернемся к этому вопросу и выясним причину встречающейся
здесь особенности.
§ 17.4. Классификация траекторий. Мы видели, что общее представле-
представление о виде траекторий в пространстве х, у можно получить, изучая веществен-
вещественные нули функций R и S. Если начальное значение х лежит между двумя
последовательными простыми нулями я4, ?>i функции R, то в общем случае
движение представляет собой либрацию между а^ и Ъй если же х лежит в ок-
окрестности двойного нуля функции R, то в общем случае мы имеем лимитаци-
онное движение. Аналогичные замечания можно сделать и в отношении дру-
другой лагранжевой координаты у. Исключение составляет случай, когда инте-
грал \ х,у dt сходится.
Остановимся на одном обстоятельстве, требующем пояснения. Функции Л и S
зависят лишь от двух постоянных: h и а, между тем общее решение уравнений движения
Лагранжа или Гамильтона для системы с двумя степенями свободы должно содержать
четыре постоянные. Выясним значение двух опущенных постоянных, а также установим,
почему они играют второстепенную роль в теории классификации траекторий.
Значение одной из этих постоянных очевидно: это — временная постоянная, зави-
зависящая от выбранного начала отсчета времени- Если функции х = ф (?), у = г|) (t) удовле-
удовлетворяют уравнениям движения, то этим же уравнениям удовлетворяют и функции х =
= ср (S — t0), у = г|) (t — t0), и значение t0 не влияет ни на траекторию, ни на скорость,
с какой она проходится. Вторая опущенная постоянная представляет собой фазовую
постоянную; она появляется при интегрировании уравнения, определяющего траекторию,
Значение этой постоянной оказывает влияние на форму траектории. (В самом деле,
в общем случае при заданных h и а через соответствующую начальную точку х, у проходят
две траектории. Пусть, например, А и а выбраны так, что а( й &< Являются последователь-
последовательными простыми вещественными нулями функции R, причем й > 0 между а4 и bi, a а2
и 62 являются последовательными простыми вещественными нулями функции S, причем
S > 0 между а2 и Ъг. Тогда, начиная с любой точки х0, у0, расположенной внутри прямо-
прямоугольника
at ^ х ^ &i, а2 ^ у ^ &2,
мы получаем две проходящие через эту точку траектории, удовлетворяющие уравне-
уравнению A7.4.1). Если бы знаменатели были однозначными функциями, то существовала бы
всего одна такая траектория. Но мы имеем дело здесь с ^-пространством, а не с фазовым
пространством. Через данную начальную точку проходит бесконечное число траекторий,
но лишь две из них отвечают заданным значениям h и а.) Общий характер траектории
определяется, однако, лишь нулями функций R и S, т. е. постоянными h и а. Поэтому
эти две постоянные играют основную роль в вопросе о классификации траекторий.
§ 17.5] УСТОЙЧИВОСТЬ 309
Рассмотрим сначала движение по одной из координатных кривых, ска-
скажем по кривой х = а. Такая траектория, как можно ожидать, представит
особый интерес, так как выбранные координаты таковы, что система обладает
ясно выраженным свойством разделимости. Для движений по кривой х = а
• • •
нам нужно, чтобы и х, и х обращались в нуль при х = а, а это требует, чтобы
а было двукратным нулем функции R. Из формул
.. 1 • • } A7.4.2)
(Х + Yfx = \ В! - (X + Y) {Х'х + Y 'у) х (
(формула для х справедлива и тогда, когда х = 0) видно, что при х — а
функции R и R' обращаются в нуль. Поэтому, если координатная кривая
х = const является траекторией, то значения h и а должны быть выбраны
так, чтобы функция R имела двукратный нуль. Для этого нужно, чтобы h
и а удовлетворяли определенному соотношению вида A (h, а) = 0.
Классификацию траекторий в пространстве х, у можно теперь провести,
пользуясь вспомогательной диаграммой, в которой в качестве осей взяты h
и а. Выбирая определенную точку на этой диаграмме, мы находим соответ-
соответствующие функции R и S. И хотя, как мы видели, это не определяет единст-
единственной траектории, однако все полученные таким образом траектории отно-
относятся к одному и тому же типу (или типам), с одними и теми же пределами
либрации (если движение является либрационным). Условие, что функция
R имеет двукратный нуль, выражается кривой или кривыми вида
A (h, a) = 0. A7.4.3)
Их называют критическими кривыми; существуют также критические кри-
кривые, соответствующие совпадающим нулям функции S. Этими критическими
кривыми плоскость ha разбивается на ряд областей, и траектории, представ-
представленные точками одной и той же области, принадлежат к одному и тому же
общему типу кривых, хотя пределы либрации (в случае либрационного дви-
движения) для различных точек области будут различны. Тип траекторий изме-
изменяется лишь с переходом в другую область, т. е. при пересечении критиче-
критической кривой.
Некоторые из областей могут не представлять интереса с точки зрения
динамики, если точкам А, а в них не соответствуют реальные траектории.
Эти исключаемые области характеризуются тем, что значения h, а в них тако-
таковы, что функция R (или S) отрицательна при всех значениях х (или у).
В § 17.6 мы укажем еще на один случай возникновения таких областей.
§ 17.5. Устойчивость. Рассмотрим теперь влияние малых возмущений,
обусловленных небольшими изменениями величин h и а. Если траектория
соответствует точке h, а, расположенной внутри области (т. е. не лежащей
на критической кривой), то малое возмущение приводит к соседней траекто-
траектории того же типа. Подобные траектории мы будем называть устойчивыми,
употребляя этот термин в широком смысле, т. е. не считая, что это обязатель-
обязательно должно означать, что возмущенная траектория лежит в окрестности невоз-
невозмущенной траектории. В этом смысле термин «устойчивость» означает лишь
то, что траектория возмущенного движения относится к тому же типу кривых,
что и исходная траектория.
Если же траектория соответствует точке h, а, лежащей на критической
кривой, то одна из функций R или S имеет двойной нуль. Пусть, например,
R = (х - а)* ф (х), A7.5.1)
310 СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [Гл. XVII-
где ф (а) =?= 0. Если теперь дать малое возмущение, изменив немного значе-
значения h и а, то правая часть A7.5.1) запишется в форме
(х - п1) (х - а2) ф (х), A7.5.2)
где ах и а2 почти равны а, а функция if> <(х) мало отличается от ф (х) для зна-
значений х, близких к а. В общем случае при перемещениях точки h, а в одну
сторону 21 от критической кривой величины а^ и а2 будут вещественны и раз-
различны, а при перемещениях в другую сторону 23 от критической кривой вели-
величины й! и а2 будут комплексны.
Легко видеть, что поведение будет существенно, различаться в зависимо-
зависимости от знака функции ф (а).
1) Предположим сначала, что ф (а) < 0. Для этих значений h, а движе-
движением по кривой х = а будет единственное возможное движение в окрестно-
окрестности х = а, так как в точке х, у, для которой R < 0, никакое движение невоз-
невозможно. Если имеется малое возмущение, то для значений х, близких к а,
г|) (х) < 0, так что если аь а2 вещественны, то возмущенное движение пред-
представляет собой либрацию между <Zj и а2, а если а1? а2 комплексны, то в окрест-
окрестности х = а никакое движение невозможно. Отсюда можно получить два
следствия. Во-первых, траектория возмущенного движения (в пространстве
{х, у)) заключена между кривыми х = а1 и х = а2, причем а4 и а2 близки к а.
В важном частном случае, когда кривые х = const представляют выпуклые
замкнутые кривые, возмущенная траектория лежит в узком поясе в окре-
окрестности невозмущенной траектории х = а. Эта невозмущенная траектория
устойчива не только в введенном выше широком смысле этого слова, но и в
более точном смысле, а именно, возмущенная траектория располагается
в непосредственной близости от невозмущенной при всех значениях t.
Во-вторых, при переходе критической кривой со стороны 21 на сторону
23 система траекторий вырождается: траектории располагаются в зонах,
которые, сужаясь, стягиваются к отдельным кривым по мере того, как изоб-
изображающая точка на диаграмме h, а приближается к критической кривой;
по другую сторону от критической кривой этих траекторий не существует.
Мы уже отмечали выше, что на диаграмме h, а могут существовать исключае-
исключаемые области такого рода, внутренним точкам которых не соответствуют
реальные траектории.
2) Если ф (а) > 0, то картина становится совсем иной. Движение, соот-
соответствующее таким значениям h, а, может быть либо движением вдоль кри-
кривой х = а, либо лимитационным движением, при котором х —> а при t —>- оо,
так что при больших значениях t траектория приближается к кривой х = а.
Если мы рассматриваем малые возмущения, то вблизи х = a if> (x) > 0.
Если возмущение выводит точку h, а в сторону 21 от критической кривой,
так что величины а^ и а2 оказываются вещественными, то х во все время дви-
движения должно иметь значения, лежащие за пределами интервала (ait a2);
при этом возможны две траектории: одна, для которой х ^ at, и другая, для
которой х^>а2. Если же возмущение выводит точку А, а в сторону 23 от кри-
критической кривой, так что величины а{ и а2 оказываются комплексными, то вы-
выражение A7.5.2) вблизи х = а положительно, нуля нет и границы для ж-дви-
жения тоже нет в окрестности х = а. Таким образом, как и ранее, при пере-
пересечении критической кривой и переходе со стороны Ж на сторону 23 система
траекторий исчезает: две отдельные системы сливаются в одну. Первона-
Первоначальное движение, будь то движение по кривой х = а или лимитационное
движение, является неустойчивым даже в широком понимании этого тер-
термина: малое возмущение приводит к траекториям совершенно иного типа.
Остается рассмотреть случай, когда точка h, а является трехкратным
нулем функции R:
{X + Yf'x* = (х- аK х (х). A7.5.3)
§ 17.7] ПРИТЯЖЕНИЕ К ЦЕНТРУ ПО ЗАКОНУ h/rn+1 311
Движение вдоль кривой х = а возможно; равным образом возможно и ли-
митационное движение, при котором х = а является предельной кривой
сверху, если % (а) > 0, и снизу, если % (а) < 0. Предположим для опреде-
определенности, что % (а) > 0. При малых возмущениях правая часть A7.5.3)
заменяется выражением
(а: - а4) (х - а2) (х - а3) р (х). A7.5.4)
Если а1? а2, аз вещественны и at < а2 < аз> т0 Для х> близких к а, будем иметь
х > а3 или а2 > ^ > аь A7.5.5)
Если at и «2 комплексные, то возможен лишь случай х > а3. В первом случае
(когда а±, а2, а3 вещественны) возможна либрация между пределами п\ и а2,
но также возможно нелокальное движение, имеющее а3 своей нижней грани-
границей. Подобное нелокальное движение является единственно возможным
во втором случае. Исходное движение при этом неустойчиво.
Наконец, могут найтись точки, в которых критические кривые функции
R и критические кривые функции S пересекаются. В таких точках h, а обе
функции R и S имеют двукратные нули; такая точка является точкой равно-
равновесия, система в этом положении может находиться в покое. Если точка h, a
такова, что
= (*-«)• Ф<*),
, 1
, J
l '
то тогда х = а, у = Ь будет точкой равновесия, и это равновесие будет
устойчивым (в обычном статическом смысле), если ф (а) < 0 и г|) (Ь) < 0.
§ 17.6. Приложения теории. Изложенная выше теория дает общее
представление о типах возможных траекторий и методах их классификации.
Применив ее к конкретным примерам, всегда можно ясно представить физи-
физический смысл выбранных координат. Формальное применение теории может
привести к неправильным выводам. Например, может случиться, что одна
из лагранжевых координат ограничена и значения этой координаты вне
отмеченной области лишены физического смысла (так, в теории центральных
орбит радиус-вектор г всегда неотрицателен). Существование подобного рода
ограничений на координаты может привести к появлению новых исключае-
исключаемых областей на диаграмме h, а. Формально в этих областях траектории
существуют, но значения одной из координат выходят за физически допусти-
допустимые пределы. Кроме того, ограничения на координаты могут повлечь за собой
некоторое видоизменение теории устойчивости. Для иллюстрации сказанного
предположим, что функция R имеет трехкратный нуль а, который является
предельным значением координаты х, х ^ а. Если % (а) > 0, то возможно
лишь устойчивое движение вдоль кривой х = а, лимитационное же движение
невозможно. Но если а есть двукратный нуль функции R и является предель-
предельным значением для х, то теория устойчивости не претерпевает никаких
изменений.
Еще до изложения общей теории нами был приведен один пример класси-
классификации траекторий. Мы имеем в виду задачу о сферическом маятнике (§ 5.3).
На рис. 7 изображена диаграмма h, а. Критическими кривыми являются
кривые a = 0 и а = ф (h). Мы видели, что траектории подразделяются на три
типа в зависимости от того, располагается ли точка h, а внутри допустимой
области или находится на одной из критических кривых, ее ограничивающих.
§ 17.7. Притяжение к центру по закону к/гп+1. Пусть частица движется
в плоскости в поле притягивающих сил с потенциалом —ц/г" (на единицу
312
СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
[Гл. XVII
массы), где п — целое число, большее двух. Уравнения A7.3.5) принимают
вид {и = 1/г)
du dQ ir2n*rlt (M 7 -h
?i to VLlj yl I . I ш If
где
V7W)~Va~V "" ""
f (и) = ушп — аи2 + h.
A7.7.2)
Эти уравнения легко могут быть получены из общей теории § 17.3 или, при
соответствующем изменении обозначений, из уравнения E.2.14). График
функции / (и) для положительных значений и представлен на рис. 50. Если
принять некоторое фиксированное (положительное) значение а, то изменение
Рис. 51.
h приведет к смещению кривой как твердой линии вверх или вниз. Имеется
два критических значения h. Это, во-первых, значение h = 0, при котором
/ (и) имеет два совпадающих нуля и = 0 и один положительный нуль и = Ъ.
где
Ьп'2 = —. A7.7.3)
И, во-вторых, значение /i = /г1? где
A7.7.4)
При этом значении h функция / (и) имеет два совпадающих нуля и —а, где
гер,
Критическими кривыми на диаграмме h, а (рис. 51) будут
h = 0, h = hi. (a).
A7.7.5)
A7.7.6)
Здесь hi (а) определяется уравнением A7.7.4). Полуплоскость а < 0 исклю-
исключается, а в верхней полуплоскости мы имеем три области, разделенные кри-
критическими кривыми. Рассмотрим определенное значение а (т. е. точки на не-
некоторой горизонтальной прямой на рис. 51) и проследим за теми изменениями,
которые происходят при увеличении h от —оо до +оо. При h — 0 ер @) < 0,
и при движении слева направо (т. е. из области Ж в область §1, см. § 17.5)
система траекторий распадается на две системы. Здесь нужна известная осто-
осторожность при применении общей теории, иначе можно прийти к выводу, что
при h = 0 имеем устойчивую круговую траекторию на линии и = 0. Однако
S 17Л]
ПРИТЯЖЕНИЕ К ЦЕНТРУ ПО ЗАКОНУ h/rn+1
313
это не имеет физического смысла, ибо и = 1/г; более того, теория устойчиво-
устойчивости неприложима к этому случаю, поскольку малым изменениям и здесь
вовсе не соответствуют малые перемещения в пространстве. Как указывалось
в § 17.6, следует иметь в виду возможность такого рода аномалий, обусловлен-
обусловленных свойствами выбранной системы координат. При h = hi ф (а) > 0 (знак
Ф (а) совпадает со знаком /" (а)), и нри переходе слева направо (т. е. из обла-
области §1 в область 25) система траекторий исчезает.
Прежде чем перейти к классификации возможных типов траекторий на
плоскости, заметим, что интеграл 1 —т===- сходится в нуле и в бесконеч-
ности. Отсюда следует, что величина 0 стремится к конечному пределу, когда
траектория уходит в бесконечность или прибли-
приближается к притягивающему центру. Кроме того, /'
каждая траектория, уходящая в бесконечность, /
имеет асимптоту, поскольку dQIdu стремится к ко-
конечному пределу, когда и стремится к нулю. '
Теперь можно перейти к классификации i
траекторий. Обозначим три области, указанные \
на рис. 51, цифрами 1, 2, 3, а разграничивающие \ /
их кривые — цифрами 12 и 23. \ /
1. /i<0; и возрастает от нижнего предела и0 "--___-''
до оо, причем Wo > Ъ. В этом случае существует рис- 52.
лишь один тип траектории, в виде розетки, распо-
расположенной внутри окружности г = l/w0 (рис. 52). Угол ф определяется
формулой
UQ
У/ (и)
A7.7.7)
12. h = 0. Как уже отмечалось, это — аномальный случай. Существует
лишь одна траектория, розетка, вписанная в окружность
г — 1/6. Ее уравнением будет
1/ЧЬг)
0:
dx
A7.7.8)
Для ге = 4 (притяжение по закону г~ь) это есть окружность i
7- = i-cosG.
2. О < h < hi. Каждой точке области соответствуют
две траектории: розетка при м>м2 и траектория типа
гиперболы при и ^ щ (на рис. 53 показана только траек-
траектория второго типа). Гиперболическая траектория имеет
внешнее касание с окружностью г = l/wt и при больших Рис. 53.
значениях h и а она близка к прямой.
23. h = hi. Траектория представляет либо окружность г = На (движе-
(движение неустойчивое), либо спираль, наворачивающуюся на эту окружность
снаружи или изнутри; в этих случаях имеем лимитационное движение
(рис. 54).
3. h > hi. Траектория одним концом уходит в бесконечность, а другим
концом идет к притягивающему центру (рис. 55). Предельным случаем
является прямая, проходящая через притягивающий центр.
314
СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
[Гл. XVII
Наиболее примечательным, пожалуй, является тот факт, что при п > 2
все возможные траектории принадлежат, по существу, к одному и тому же
типу.
Рис. 54.
Рис. 55.
В следующем параграфе мы укажем точную форму траекторий для слу-
случая п = 4.
§ 17.8. Притяжение к центру по закону к/г5. Теперь, после того как
мы произвели классификацию всех возможных траекторий, можно перейти
непосредственно к интегрированию; детальное вычисление всегда предпоч-
предпочтительно осуществлять после качественного исследования. В случае централь-
центрального поля с потенциалом V = —\i/rn уравнения интегрируются при п = —2,
—1, 1, 2 в тригонометрических или экспоненциальных функциях, а при
п = —6, —4, 3, 4, 6 — в эллиптических функциях. (Теория предыдущего
параграфа применима, разумеется, лишь в случаях, когда п больше двух.)
Рассмотрим случай, когда притяжение пропорционально г
-Б
т. е.
п = 4.
В этом случае имеем
причем
/ (и) — [ш4 — аи2 + h,
A7.8.1)
A7.8.2)
Критическая кривая h — hi является параболой а2 = 4|ifo. При иллюстра-
иллюстрации теоретических выводов мы ограничимся рассмотрением центральной
области 2 (рис. 51) и ее границ 0 ^ h ^ fet или 0 ^ J3 ^ -т, где h = a2j3/j,i.
Нам будет удобно перейти от и к г; тогда уравнения A7.7.1) запишутся в виде
dr
vt<
A7.8.3)
/здесь мы без ущерба для общности изменили знак первого радикала).
Рассмотрим траектории для |3, лежащих в области 0 ^ § ^=Т-
12. р = 0. Дифференциальное уравнение траектории в плоскости гЭ
запишется в виде
17.8]
ПРИТЯЖЕНИЕ К ЦЕНТРУ ПО ЗАКОНУ ft/r°
315
где с = 1/Ь; траектория (типа розетки) представляет окружность
г = с cos 9. A7.8.5)
2. О < р < -г . В этом случае
dr \ 2 сев , „ , и аВ , „ 2\ , ,, о\
-jo-) =—- г г2+ — = ——(г2 — г?) (Н — г,),
где
A7.8.6)
A7.8.7)
Имеем две траектории: траекторию типа розетки, расположенную внутри
окружности г = ri, и незамкнутую траекторию типа гиперболы, расположен-
расположенную вне окружности г = г2.
1) Траектория типа розетки; 0 ^ г ^ rj. Применяем подстановку г =
= Г! sn у, /с = /
При этом
1+6'
г\ —
A7.8.8)
A7.8.9)
и уравнение A7.8.6) принимает вид
а уравнение орбиты записывается в виде
г = n sn Я8. A7.8.11)
Заметим, что г достигает своего максимального значения г\ при 8 = 90, где
f + к9. A7.8.12)
80 = К/К = К
При к —>- 1 угол 80-> сю и траектория приближается по форме к спирали,
которая при р —> -J- наворачивается
изнутри на окружность.
Численный пример.
Пусть р = 4/25, к = 1/2, X2 = 4/5.
Тогда
• К = 1,6857, % = 0,8944,
г| = 4г2 = 5^/а A7.8.13)
и угол 8о составляет приблизитель-
приблизительно 108° (рис. 56).
2) Незамкнутая траектория, с'
г^г2. Для того чтобы закончить
интегрирование, воспользуемся подстановкой, в которой г2 — г\ пропор-
пропорционально s2/(l — s2), где s — sn v; вводя соответствующий множитель про-
пропорциональности и полагая, как и ранее, к = rjr2, будем иметь
Тогда
A7.8.14)
A7.8.15)
316 СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [Гл. XVII
r = r,-?f. A7.8.16)
В результате получаем
dr i ги г*) snv М7 Я 17^
Подставляя в дифференциальное уравнение траектории A7.8.6), получаем
у = Л8. Уравнением траектории будет
dn Л0 .. _ с, , о.
ГГ A7.8.18)
При 8-> Эо здесь г-> оо. Траектория, соответствующая указанным выше
численным данным, изображена на рис. 56.
Уравнения можно выразить также не через эллиптические функции Якоби, а через
кции Вейерштрасса.
В уравнении A7.8.6)
полагаем
"=¦¦$¦ Kg")" A7-8-20'
При этом получаем
/ du \ 2 / dr \2 I I dr \2 I 2гсф \ 2 / dr \ 2
где
11 11 1
'1 = ТГ+Т6' е2 = Т"~"'6' '3= ~"§"' A7.8.22)
1 1
так что et > — > е2 > —»-. Для траектории типа розетки
D О
v = f @ — ш2), A7.8.23)
так что у достигает максимального значения е2 при 0 = a>i. Уравнение траектории записы-
записывается в форме
^i { т} A7.8.24)
Для незамкнутой траектории
v = ^> @ — ац) A7.8.25)
и v достигает минимального значения et при 0 = 0 и стремится к бесконечности при
0 -»- СО]. Уравнение траектории имеет вид
} A7.8.26)
Возвращаясь к систематической классификации траекторий, рассмотрим
точки h, а, лежащие на границе 23 рис. 51.
23. р = 1/4; дифференциальное уравнение траектории может быть
записано в форме
(Y A7-8.27)
§ 17.9] НЬЮТОНОВСКОЕ ПРИТЯЖЕНИЕ И ОДНОРОДНОЕ ПОЛЕ 317
Возможны три случая:
1) Если в начальный момент г = гь то траектория представляет собой
окружность г = г4.
2) Если в начальный момент г < гг и г возрастает вместе с 0, то
где ф = 0/]/2. Траекторией является спираль
г = п th ф = rj th (9/J/2), A7.8.29)
наворачивающаяся изнутри на окружность г = г4.
3) Если в начальный момент г > г4 иг убывает с ростом 0, то
и траектория представляет собой.спираль
г = r4 cth ф = Г! cth @/^2),
наворачивающуюся снаружи на окружность г = ri.
Читатель, желающий продолжить исследование, может самостоятельно
составить уравнения траекторий, соответствующих значениям h, а, лежа-
лежащим в областях 1 и 3 рис. 51.
§ 17.9. Ньютоновское притяжение и однородное поле. Пусть частица движется
в плоскости ху под действием двух полей: поля сил притяжения т\х/г2 к началу координат
и однородного поля {—mg, 0). Потенциал такого поля (на единицу массы) равен
— ——f- gx. Введем параболические координаты и, v:
Кривая и = с представляет собой параболу с фокусом в точке О и вершиной в точке (с, 0),
а кривая v = с — параболу с фокусом в точке О и вершиной в точке (—с, 0). Два эти
семейства парабол образуют семейства ортогональных кривых. Области изменения пере-
переменных и и v следующие: 0 ^ и < сю, 0 ^ v < сю. Напишем обратные формулы:
х = и — v, у2 = Auv, г = и+ v. A7.9.2)
Опуская положительный множитель т, можем теперь написать
) A7-9'3)
_i:_{gB2_g(l,2 + b2)}, A7.9.4)
где б2 = \ilg. (Точкой равновесия в заданном силовом поле будет точка х — ~-Ъ. у — 0.)
Таким образом.
Мы видим, что функция Н имеет форму A7.2.12), причем
Х = Р=и, l = gifi; Y = Q = v, ц = —g (у2 + Ь2). A7.9.6)
Следовательно, при выбранных координатах система удовлетворяет условиям
разделимости, и интегралы уравнений движения находятся из соотношений
йи dv dt
A79Л)
где
R = — 2и {gu2 — hu — a), A7.9.8)
S = 2г; (gi? + hu + ^62 - а). A7.9.9)
Перейдем теперь к классификации траекторий. Как и в общей теории (§ 17.4),
здесь можно воспользоваться плоскостью ha, однако удобнее применить более простой
метод. Кубический полином R должен иметь все нули вещественными. В самом деле, если
318
СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
[Гл. XVII
бы квадратичная форма
gv? — hu — a
имела комплексные нули, то полином R был бы отрицательным для всех положительных
значений и и никакое движение не было бы возможно. Следовательно, нулями полинома
R б 0 ^ П
д
R будут иь и2, 0, причем их и и2 — числа вещественные, Mi
й
, у
Поэтому для классифи-
классифиК
р у ф
кации траекторий можно вместо плоскости h, а воспользоваться плоскостью мь и2. Крити-
Критические кривые определить нетрудно, однако сделанные в § 17.5 замечания относительно пе-
пересечения критических кривых в плоскости h, а применить здесь непосредственно нельзя.
Итак, определим сначала критические кривые. Для R это кривые и± = 0, м2 = О,
щ = м2. Область щ < О исключается, так как щ < 0 означало бы, что R < 0 для всех
положительных значений м. Таким образом, ui ^ 0; при м4 >¦ 0 имеем либрацию между
пределами щ и и2, если и2 > 0, и между пределами и4 и 0, если и2 < 0. Критическими
кривыми для S будут Vi = 0, v2 =-- 0, Vi = v2. Интерпретируем теперь это на плоскости
щ, и2. Величины v±, v2 являются корнями уравнения
v2 + (щ + и2) и + (щи2 + Ь2) = 0. A7.9.10)
Следовательно, v^ или v2 обращается в нуль, если точка (щ, и2) лежит на гиперболе
Щи2 + Ъ2 = 0. A7.9.11)
Далее, i>t и и2 вещественны и различны, если
щ — и2 > 2Ь; A7.9.12)
вещественны и равны, если
щ — м2 = 2Ь, A7.9.13)
и комплексны, если
м, — и2 < 2Ь. A7.9.14)
Полученные кривые изображены на рис. 57. Уравнение A7.9.13) определяет касательную
к гиперболе A7.9.11) в точке F, —Ь).
и-и
— х
Рис. 57.
Рис. 58.
Для классификации траекторий нужно рассмотреть четыре области и разделяющие
их граничные кривые. Ниже приводится таблица нулей функций R и S:
Область 1. mi > u2 > 0; i>lt i>2 комплексные или 0 >¦ vt > i>2;
2. «l > 0 > u2; i?j, f2 комплексные или 0 >¦ у4 > y2;
3. ui > о > u2; fi > f2 > 0;
4. Mi > 0 > м2; i>j >¦ 0 > y2.
Теперь легко указать пределы изменения м, когда точка (щ, м2) располагается вну-
внутри любой из четырех областей; аналогичные сведения можно получить и относительно и.
В области 1 по координате и имеем либрацию между пределами ut и м2; в областях 2, 3,
4 м совершает либрацию между пределами «i и 0. Переменная v в областях 1 и 2 убывает
от сю до 0 (на полной траектории), а затем снова возрастает до с»; в области 3 имеются
две возможности: а) либрация между v2 и 0 и Ь) убывание от с» до vt и затем возрастание
до оо; в области 4 v ведет себя так же, как в области 3, случай Ь). Наибольший интерес
представляет единственный случай ограниченной траектории (область 3, случай а),
показанный на рис. 58. В этом случае
й<0, 0<а<?Ь2, A7.9.15)
§ 17.9] НЬЮТОНОВСКОЕ ПРИТЯЖЕНИЕ И ОДНОРОДНОЕ ПОЛЕ 319
а в начальный момент
О < v < v2. A7.9.16)
Условие h < О эквивалентно условию
^W*<-?r-gz, A7.9.17)
где W — начальная скорость, а х, у — начальные координаты точки. Условие A7.9.17)
при g = О обращается в известное неравенство для ньютоновской эллиптической орбиты.
Условию A7.9.17) нельзя удовлетворить, если
гх>Ъ2, A7.9.18)
т. е. если начальная точка расположена справа от кривой гх = Ъ2.
Уравнение траектории можно записать в параметрической форме с помощью
^-функций Вейерштрасса с одним вещественным периодом 2coi и с одним чисто мнимым
периодом 2со3. Можем написать
A7.9.19)
yiu (щ — и) {и — иг) ~[/4и (ui — v) (v2—v)
Для и нужна ^-функция с
-¦&(¦?+.)•
а для v нужна ^-функция с
Уравнения траектории в параметрической форме имеют вид
^ ^ >3 + Q-00). A7.9.22)
Здесь 0 вещественно, первой ^-функции соответствуют инварианты A7.9.20), а второй —
инварианты A7.9.21).
Остановимся коротко на вопросе о траекториях, соответствующих точкам на гра-
границах области 3 (рис. 57). Этим точкам соответствуют движения по параболам и = const
или v = const или же лимитационные движения, приближающиеся к движениям по этим
кривым.
Для граничной кривой 23 (разделяющей области 2 и 3) имеем
R = 2gu{(b — к) — и}{и + (Ъ + к)}, S = 2go (v — кJ, A7.9.23)
где 0 < к < 6. Возможным движением будет движение по дуге параболы v = к, рас-
расположенной внутри параболы и = Ъ — к. Это движение неустойчиво, как и лимитацион-
ное движение к этой дуге.
Для граничной кривой 34 имеем
R = 2gu (Ье~в — и) (и + Ьее), S = 2gv* {v — 2b sh 0), A7.9.24)
где 0 > 0. Частица движется по линии v = 0 (положительная часть оси х между х = 0
и х= Ье ); движение не будет представлять либрацию, поскольку в точке О силовое поле
имеет особенность.
Для точек, расположенных на отрицательной части оси и2, ограничивающей
область 3, имеем
R = —2gu2 (и + 2Ь ch0), S = 2gv (Ье~в — v) (bee — v), A7.9.25)
где 0 > 0. Мы имеем устойчивое движение по линии и = 0 (отрицательная часть оси х
между л; = —6е~е и х = 0). Движение опять-таки не будет либрацией вследствие особен-
особенности силового поля в точке О.
Наконец, рассмотрим специальные точки А и В на рис. 57. В точке А имеем
R = — 2gui (и+ 2Ь), S = 2gv(v—bJ, A7.9.26)>
что соответствует неустойчивому равновесию в нейтральной точке и = 0, v — Ъ (т. е. х =
= —Ь, у = 0). Возможно также движение вдоль отрицательной части оси х, при котором
х-*-—Ъ, когда * —>- оо; частица начинает движение с одной из сторон от нейтральной
точки с энергией, как раз достаточной для ее достижения.
В точке В имеем
R = 2gu (б* - м2), S = 2gv3. A7.9.27)
Если и первоначально возрастает, то оно достигает значения Ь, а затем уменьшается
до нуля, u-движение происходит по линии v — 0 (положительная часть оси х) либо пред-
представляет лимитациопное движение к и = 0. Оба эти движения неустойчивы.
320
СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
[Гл. XVII
Читатель, который пожелает продолжить классификацию траекторий для других
областей и граничных кривых рис. 57, сможет проделать это самостоятельно.
В случае g = О мы имеем одно только поле ньютоновского притяжения. Заметим,
что в этом случае задача допускает разделение переменных как в полярных, так и в пара-
параболических координатах (§ 17.14).
§ 17.10. Два неподвижных притягивающих центра *). Рассмотрим дви-
движение планеты массы то в поле сил двух притягивающих центров с массами
т и т'; движение происходит в плоскости, проходящей через оба центра.
Эта задача представляет большой интерес, поскольку может рассматриваться
как некоторый частный случай задачи трех тел. Впервые она была подробно
рассмотрена Лежандром в связи с его
у исследованиями по теории эллиптиче-
эллиптических функций. Пусть гиг' будут рас-
\^~Р стояниями планеты до масс т и т'\
введем конфокальные (эллипсоидаль-
(эллипсоидальные) координаты Я и ц:
т
~~Т х = у(г+г'), ц = у(г-г'). A7.10.1)
Рис. 59.
IL---C
Кривая Я = const будет представлять
эллипс, в фокусах которого располо-
расположены притягивающие массы, а кривая [л = const — ветвь гиперболы с теми
же фокусами. Обозначим через 2с расстояние между притягивающими цен-
центрами. Координата Я ограничена снизу (Я;>с), а координата \i ограничена
как снизу, так и сверху (с^|л^>—с).
Выбрав оси декартовой системы координат так, как показано на рис. 59,
с началом посередине расстояния между притягивающими центрами, будем
иметь
Отсюда
г» = (Х _ су + у\ г'2 = (х + сJ + у\
= ±. (Г'2 + Г2) =
и, следовательно.
Дифференцируя, получаем
(Х2
A7.10.2)
A7.10.3)
A7.10.4)
A7.10.5)
A7.10.6)
Отсюда ршходим
A7.10.7)
A7.10.8)
*) Другое изложение задачи о притяжении к двум неподвижным центрам см.
в «Лекциях» Якоби [17], стр. 221—231, и в книге: К. Ш а р л ь е. Небесная механика, М.,
изд-во «Наука», 196R.
S 17.10] ДВА НЕПОДВИЖНЫХ ПРИТЯГИВАЮЩИХ ЦЕНТРА 321
и, далее.
где
к = у (т + т), к' =у(т — т). A7.10.10)
Предположим для определенности, что т^>т', тогда
к>к'>0. A7.10.11)
Опуская положительный множитель т0, получаем
= ~2 \ X2— z ) {( )№+(с —М- ) Рц}— ,а__ 2 A7.10.12)
и видим, что функция Гамильтона относится к типу A7.2.12), допускающему
разделение переменных.
Интегралы лагранжевых уравнений движения можно записать в форме
A7.3.5):
ds __ ф _ й_) A7.10.13)
где
r = 2 (X2 — c2) {hi2 + kl + a), A7.10.14)
S = —2{c2 — \x2) (V + k'\x + a). A7.10.15)
Введем следующие обозначения:
L = h№ + kl + a, A7.10.16)
M = feu2 + к'ц + a.. A7.10.17)
В процессе движения будем иметь
L>0, M^O. A7.10.18)
Пусть Xi, X2 — нули функции L, а (xi, (X2 — нули функции М. Величины
%i, 12, очевидно, вещественны. В самом деле, если бы li, Xz были комплекс-
комплексными, то к2 < 4afe и, стало быть, к'2 < iah, так что [^ и jx^ также были бы
комплексными. Последнее, однако, невозможно, так как если бы и L и М
имели комплексные нули, то обе эти функции имели бы тот же знак, что и h,
и одно из неравенств A7.10.18) не выполнялось бы. Вещественность Xit X2
будет служить основой для классификации траекторий. Вместо плоскости
h, а (§ 17.4) мы воспользуемся плоскостью Xi, Хг.
Из условий A7.10.18) следует, что если h < 0, то X заключено в интерва-
интервале (Xi, Х2), а ц лежит вне интервала (^ь ц2), если fj,4 и \а2 вещественны; если
же h > 0, то X лежит вне интервала (a.i, X2), а (х заключено внутри интервала
(Ць М-з)- Комплексные значения (Xi и jx2 при h > 0 невозможны.
Определим теперь критические кривые на диаграмме Xi, X2, причем будем
считать, что Х^Х2- Величины Ц1 и \а2 суть корни уравнения
.г2 — -^-(Х1 + Х2)х + Х1Х2 = 0. A7.10.19)
Они равны друг другу, если
(Я, + Ъ2J = AXiX2 (klk'f. A7.10.20)
Положив
ch9 = ^r A7.10.21)
или, что то же,
¦^- = th«4e. A7.10.22)
представим уравнение A7.10.20) в форме
¦^- = е±2е. A7.10.23)
21 Л. А. Парс
322
СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
[Гл. XVII
Оно определяет две прямые в плоскости
Это — две критические кривые.
Далее, если
с одинаковым наклоном к осям.
т. е. если точка
j, Х2) лежит на гиперболе
(А* — ск'/к) (К2 - ск'/к) = -с2 th20,
A7.10.24)
A7.10.25)
то либо jai = с, либо (х2 = с.
Прямые A7.10.23), проходящие через начало координат, касаются
гиперболы, причем прямая Xi = Я,2е2е касается нижней ветви гиперболы
в точке (сее, се~в). Нужно определить еще (считая }*1>-ц2), какая ветвь
гиперболы A7.10.25) отвечает fx4 = с и какая ц2 = с. Если (х2 = с, то jxi +
+ \к2 ^ 2с и Я4 + Я2 ^ 2ск/к' = 2с ch 0, так что условие }л2 = с соответ-
соответствует той части гиперболы, которая расположена справа от точки (сее, се~е).
Аналогичные рассуждения показывают, что равенствам }*i = —с, \а2 = —с
соответствуют части гиперболы
(ki + ск'/к) (К2 + ск'/к) = —с2 th 20. A7.10.26)
Обе гиперболы A7.10.25) и A7.10.26) проходят через точку (с, —с).
На этом заканчивается исследование критических кривых, соответст-
соответствующих нулям функции S (рис. 60). Нулям функции R будут соответство-
соответствовать критические кривые Хх — к2, %\ = с, К2 = с. Однако некоторые из об-
областей будут исключаемыми.
Л
компт
т
/
г\/
ксные
\
^;
И-f'C
/y-i
1
комплексные
———
>LL>'C Л=
-Л
-с
Рис. 60.
Рис. 61.
Если h < 0, то % лежит в интервале (Яь К2), и поскольку К ^ с, область
%i < с исключается. Если fe < 0, то ц лежит вне интервала ((гь \х2), и посколь-
поскольку с ^ (г ^ — с, следует исключить область, для которой \ii > с > —с >
> (г2. Так как ц± + }л2 > 0, то выполнение условия — с > (г2 влечет за собой
выполнение условия jai > с.
Если h > 0, то, как мы уже видели, комплексные значения jai, (X2 исклю-
исключаются. Но если jii, \a2 вещественны, то \а лежит между этими значениями,
так что области \iz > с, —с > \>ц исключаются. Однако в этом случае условие
(г2 > с не является следствием второго условия, так как \>ц -\- ц2 < 0.
Если не считать исключаемые области, полуплоскость Ki ^ Xz разделя-
разделяется критическими кривыми на восемь частей (рис. 61). Им соответствуют
§17.11]
ОГРАНИЧЕННЫЕ ТРАЕКТОРИИ ¦
323
восемь основных типов орбит. Кроме этих восьми основных типов имеются
еще другие типы, соответствующие некоторым особым точкам на рис. 61.
Это — точки на критических кривых, изолированные точки, для которых
три нуля функции R или S совпадают, и точки пересечения критических
кривых функций R и S (т. е. точки, для которых соответствующие формы
R и S имеют двукратные нули).
Вспомним, что для того, чтобы было возможно движение по эллипсу
X — Хо, Хо должно быть двукратным нулем функции R. Следовательно, при
движении по линии X = Хо > с Хо должно быть двукратным нулем функции
L, тогда как при движении по линии X = с (прямая, соединяющая центры
притяжения) с должно быть простым нулем функции L. Аналогично, при
движении по линии jx = fx0, где | ц0 | < с, и.о должно быть двойным нулем
функции М, а при движении по линии ц = с (или ц = —с) с (или —с) должно
быть простым нулем функции М.
§ 17.11. Ограниченные траектории. Ограничимся рассмотрением случая
h < 0. Тогда Хг > с и траектория располагается внутри эллипса X = Xi.
Если Hi, \a2 вещественны, то \а лежит вне интервала (hi, ц2). Учитывая это,
Рис. 62.
Рис. 63.
Рис. 64.
легко представить четыре типа возможных траекторий. В области 1 Xi > Х2 > с
и движение по координате X представляет либрацию между пределами
^i и Х2. В областях 2, 3, 4 Xi > с > Х2 и движение по координате X есть либ-
либрация между пределами Я] и с. В областях 1 и 2 нули функции М либо ком-
комплексные, либо вещественные (в последнем случае ^ >¦ \а2 > с). Движением
по координате \л является либрация между пределами с и —с. В области 3
с > M-i > Hz > —с и движение по координате \х может быть либо (а) либра-
либрацией между пределами с и (xi, либо (Ъ) либрацией между пределами Ц2 и—с.
В области 4 Hi > с > М-2 > —с и движение по координате н есть либрация
между пределами ц2 и —с.
Таким образом, области 1 соответствуют траектории, представляющие
собой выпуклые кривые, не обязательно замкнутые, расположенные в кольце
между эллипсами X = Х\ и X = Х2 (рис. 62). Замкнутые траектории и перио-
периодические движения мы будем иметь тогда, когда отношение
7,2
I dh/-\/R
Ч
A7.11.1)
есть число рациональное.
Области 2 соответствуют траектории, имеющие форму восьмерки, охва-
охватывающей оба центра (рис. 63).
Движение, соответствующее области 3, представляет обращение планеты
вокруг одного из притягивающих центров (рис. 64). При переходе из обла-
области 2 в область 3 траектория, имевшая форму восьмерки, разбивается на две
21*
324 СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [Гл. XVIT
отдельные кривые, одна из которых исчезает при переходе из области 3
в область 4. В этой последней области планета обращается вокруг притяги-
притягивающего центра с большей массой (т).
Чтобы закончить классификацию траекторий в случае h < О, следует рассмотреть
еще точки границ областей, указанных на рис. 61. Исследование разделим на три части.
1) Кривая 23, разделяющая области 2 и 3, является критической кривой, для кото-
которой |л4 = |х2; значения двойного нуля лежат между некоторым значением (Хо и с. Функ-
Функция М имеет два нуля, которые при hi = с, h2 = се'2в равны ц0, так что
к'
В самом деле, точка А, = с, \i = |х0, лежащая на прямой, соединяющей притягивающие
центры, является точкой равновесия, поскольку в этой точке
1/т У^ Ут + У^ _ Ут-У^Р ,,. ., „.
__==___= _ _ _ A/.11.2)
и, следовательно,
Ут-У^=се-* = ^ A7Л13)
У\У'
Укажем теперь основные результаты для точек на критических кривых 12, 23,
34, 42.
Критическая кривая 12. В этом случае величины ц,4, \i2 либо комплексны, либо
вещественны и больше с; движение по координате ц является либрацией между преде-
пределами с и —с. Далее, hi > h2 = с и
R = 2А' (А, — сJ (А, + с) (hi — h),
причем h' = — h > 0. Движение по координате h либо есть движение по линии h= с,
либо является лимитационным движением, причем соответствующая траектория под-
подходит к линии h = с сверху. Первое из этих движений происходит по прямой, соединяю-
соединяющей притягивающие центры, и не является истинной либрацией из-за особенностей поля
в центрах. Второе же движение происходит по спирали, лежащей внутри эллипса h — hi
и касающейся его. Все эти орбиты, однако, неустойчивы и на практике не встречаются.
Критические кривые 23, 34, 42. Для этих кривых hi > с > Я2 и движение по коор-
координате h есть либрация между пределами hi и с.
Критическая кривая 23. Для этой кривой с > Ц) = \i2 > Цо и
5 = Ш (с2 - ц2) (ц - ц4J.
Движение по координате ц либо есть движение по кривой \i — р', представляющей гипер-
гиперболу, пересекающую ось между центром т' и точкой равновесия, либо является лимита-
лимитационным движением с любой стороны от этой гиперболы. В первом случае движение носит
характер колебаний, ограниченных эллипсом h = hi. Оба типа движения неустойчивы.
Критическая кривая 34. Для этой кривой |ii = с > Цг > - с и
S = 2Ь! (с - цJ (ц + с) (ц2 - ц).
В этом случае имеются две возможности, а) Движение по координате ц может представ-
представлять либрацию между пределами \х2 и —с, так что планета будет обращаться вокруг цен-
центра т. Орбите этого типа соответствуют точки с обеих сторон от граничной кривой, а также
точки на самой кривой; квадратичный член в выражении для М не влияет на характер
орбиты. Ь) Движение по координате ц может представлять изолированное устойчивое
движение по линии ц = с; при этом планета является спутником центра т'. Движение
по координате h не является истинной либрацией, поскольку спутник сталкивается
с массой /га'.
Критическая кривая 42. В этом случае \ii > [х2 = с и
S = 2А' (с - цK (с + ц) (ц, - ц).
Движение по координате [х, как и в предыдущем случае, есть движение по линии ц = с,
но в данном случае оно неустойчиво или же является лимитационным; в последнем случае
траектория приближается к линии \i = с снизу, подобно тому как это имело место для
критической кривой 23.
2) Рассмотрим теперь критические кривые, обозначенные на рис. 61 буквами а,
Ъ, с, d. Вдоль кривых а и Ъ величины и.4 и [х2 комплексны, и движение по координате [i
представляет собой либрацию между пределами с и —с.
Кривая a. hi = h2 > с и
R = —2А' (Я2 - с2) (А, - А,4J.
17.12] УРАВНЕНИЯ ОРБИТ
325
Ей соответствует изолированное устойчивое периодическое движение по эллипсу Л, — М.
Эллипс является возможной орбитой как при движении в поле каждого из притягиваю-
притягивающих центров, так и при движении в поле обоих притягивающих центров. (Читатель может
доказать это утверждение независимо от общей теории.)
Кривая Ъ. с — kt > k2 и
R = —2ti (к - сJ (к + с) (к — к2).
В этом случае имеем изолированное устойчивое движение по линии, соединяющей при-
притягивающие центры, заканчивающееся столкновением с одной из притягивающих масс.
Кривая с. с = А,] > к2 и
Л = —2W (к - сJ (к + с) (к- кг),
С > |Xl > Цо > ^2 > ~с
И
S = 2h' (с2 — ]х2) ((х — щ) ([х — ц2).
Подобно случаю Ъ, движение по координате к есть изолированное устойчивое движе-
движение вдоль к = с. Движение по координате (х совершается либо между пределами с, |хь
либо между пределами |х2, —с. Планета является спутником одной из притягивающих
масс; движение начинается из точки вблизи одной массы по направлению к другой
и никогда не достигает точки равновесия. Планета сталкивается с притягивающей мас-
массой, вблизи которой началось ее движение.
Кривая d. ki > с > к2. Движение по координате к есть либрация между преде-
пределами kt и с. Кроме того,
fXl > С > Ц2 = — С
S = -2&' ([х + сJ (ц. — с) (ц. — щ).
Движение по координате ц есть изолированное устойчивое движение вдоль линии (х = —с;
планета является спутником массы т.
3) Остается рассмотреть несколько особых точек на рис. 61.
Начнем с точки, общей для областей 2, 3, 4. В этой точке ki = се , к2 = се~ ,
и движение по к является либрацией между Я4 и с. Далее, (Xi = |х2 = с и
S = 2h' (с — (хK (с -\- (х).
Движение либо происходит вдоль линии \i = с, либо является лимитационным; в послед-
последнем случае траектория приближается снизу к линии (х = с. Эти движения неустойчивы.
Можно считать, что рассматриваемая точка принадлежит кривой 42, которая в этом
месте разветвляется на две кривые: 23 и 34.
В точке аЪ величины ц4 *и ц2 комплексны, и движение по координате [х является
либрацией между пределами с и —с. Кроме того, ki = А2 = с и
Л = —2h' (к + с) (к- сK.
Движение происходит вдоль линий, соединяющей центры притяжения, и является устой-
устойчивым, несмотря на кубический множитель в выражении для Л, так как координата к
ограничена. Здесь мы имеем особый случай, упоминавшийся в § 17.6.
В точке be пересекаются критические кривые R и S, при этом Я4 = g и (Xi = |х2 —
= |х0. В этой точке'
Л = — 2ti (к — сJ (А, + с) (А, — кг),
S = 2А' (с2 - ц3) ((I - дем-
демдвижение по координате А, есть изолированное движение вдоль линии А, = с. Что же
касается координаты (х, то имеем либо [х = цо> либо (х -*¦ (Хо сверху или снизу. Планета
либо находится в покое в точке равновесия, либо стремится к ней в пределе с той или
иной стороны, причем движение начинается из точки вблизи одного притягивающего
центра по направлению к другому с энергией, как раз достаточной для достижения точки
равновесия. Как положение равновесия, так и лимитационное движение являются
неустойчивыми.
§ 17.12. Уравнения орбит. После того как мы закончили классифика-
классификацию возможных типов орбит, можно перейти к непосредственному интегри-
интегрированию уравнений. Рассмотрим в качестве примера область 1 (рис. 62),
для которой траектория, вообще говоря незамкнутая, охватывает оба притя-
притягивающих центра и лежит внутри эллиптического кольца %i ^ X ^ Х2. Тра-
Траектория планеты определяется из дифференциального уравнения
dX ¦= ф , A7.12.1)
-к)(к-к2)(к-с)(к + с) y^-^^ + cjdxj-^^-p.)
326 СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [Гл. XVII
в котором А4 > А2 > с > —с и (i! > ц2 > с > - с. Движение по координате
А представляет собой либрацию между пределами At и А2, а по координате
ц — либрацию между пределами с и —с.
Приравнивая каждую часть уравнения A7.12.1) величине 2dQ, можем выразить к
и \i через 0 множеством способов, используя эллиптические функции Якоби или Вейер-
штрасса. В результате получим /уравнения кривой в параметрической форме к = к @),
IX = ц @). Для иллюстрации приведем один из способов интегрирования.
Применяя подстановку
^ ^, A7.12.2)
запишем левую часть уравнения A7.12.1) в следующей форме:
2 dx A7.12.3)
V(h~e) (Я2 + с) V(iTx*) A-А%г2)
где
^k^L^. A7.12.4),
(X,j — с) (кг + с)
Таким образом,
x = snu, A7.12.5)
где
— с)
Аналогично, с помощью подстановки
можно правую часть уравнения A7.12.1) записать в форме
2 t\-& -I ' A7Л2>8)
где
Следовательно,
у — sn и,
i-де
:)((Х2 + С)F—60), A7.12.10)
з у — (ц.1-^)_сп2_у_ A7.12.11)
Мы получили уравнения траектории в виде X = к F), ц = [г F). Параметр &2 для
эллиптических функций Якоби в выражении A7.12.3) определяется формулой A7.12.4),
а соответствующий параметр х2 в выражении A7.12.8) — формулой A7.12.9).
§ 17.13. Неограниченные орбиты. Рассмотрим теперь орбиты, соответ-
соответствующие положительным значениям h, т. е. орбиты, соответствующие точкам
областей 5, 6, 7, 8 на рис. 61. В этих случаях величины }j,i, ц2 вещественны,
а А2 и ц2 отрицательны. В процессе движения параметр А принимает значения,
лежащие вне интервала (Ai, а2), а (г — значения внутри интервала (ц1: ц2).
Значения А не ограничены сверху, а их нижняя граница равна большему
из чисел А4 и с. За исключением одного тривиального случая (когда а4 = с
и А первоначально убывает, мы имеем неустойчивое лимитационное движение
§ 17.14] СИСТЕМЫ, ДОПУСКАЮЩИЕ РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ 327
к К = с), величина К возрастает вместе с t. Более того, % —*¦ оо с ростом t.
Для доказательства этого достаточно заметить, что
^r yg=g rf, 17ЛЗЛ)
и последний интеграл справа расходится.
Поведение переменной [а требует более внимательного рассмотрения.
Имеем
A7ЛЗ-2)
и интеграл в правой части сходится при Я -*- оо. Мы имеем пример псевдоли-
митационного движения (§ 17.3). Если функция S имеет простые нули, то
после конечного числа (которое может быть и нулем) колебаний наступает
псевдолимитационное движение к пределу, заключенному между двумя после-
последовательными простыми нулями. Если же один из нулей функции S двукрат-
двукратный, то мы имеем псевдолимитационное движение к предельному значению
вблизи двукратного нуля.
За исключением упомянутого выше тривиального случая (который имеет
место тогда, когда Ki = с, а функция R имеет двойной нуль), все орбиты при
h > О оказываются неограниченными. Такие орбиты менее интересны, неже-
нежели ограниченные, и поэтому мы остановимся только на одном частном случае.
Рассмотрим точку, расположенную внутри области 5 на рис. 61. Для
точек этой области Я4 > с и орбита располагается вне эллипса к = Я4, при-
чем X неограниченно возрастает после возможного (при К < 0 в начальный
момент) первоначального убывания до значения Xj. В этом случае (Xj > с >
> — с > (j,2, и на первый взгляд можно было ожидать либрации по коорди-
координате (х между пределами с и —с. Между тем это не так, ибо, как мы видели,
движение по координате \х является псевдолимитационным и после конечного
числа колебаний между пределами с и —с величина ц стремится к u,j. Орбита
представляет собой спираль, касающуюся снаружи эллипса 1 = 1ih после
конечного числа витков уходящую в бесконечность и приближающуюся к од-
одной из конфокальных гипербол.
§ 17.14. Системы, допускающие разделение переменных более чем
одним способом. Как уже отмечалось в § 17.1, свойство разделимости пере-
переменных определяется как самой динамической системой, так и принятыми
для ее описания лагранжевыми координатами. В некоторых задачах может
случиться, что, выбирая по-разному лагранжевы координаты, мы получим
несколько случаев разделения переменных для одной и той же динамической
системы.
Простым примером может служить задача о ньютоновых орбитах, т. е.
задача о плоском движении частицы под действием притяжения к центру
с силой, обратно пропорциональной квадрату расстояния. Разделение пере-
переменных можно осуществить, воспользовавшись полярными координатами
с началом в притягивающем центре (§ 16.9). Тот же самый результат мы полу-
получаем, если используем параболические координаты. (См. § 17.9, где рассмот-
рассмотрен случай движения в поле притяжения к центру с наложенным на него
однородным полем. В этом случае, как мы видели, система допускает разделе-
разделение переменных в параболических координатах. Ясно, что это свойство
сохраняется и при отсутствии однородного поля.) Имеется еще и третья воз-
возможность разделения переменных — выбор конфокальных (эллипсоидаль-
(эллипсоидальных) координат. В самом деле, чтобы получить задачу о ньютоновом притя-
притяжении к одному центру, достаточно в формулах § 17.10 положить т! = 0.
328 СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ 1ГЛ. XVIJ
Решение в полярных координатах уже рассматривалось нами в примере 5.2В;
более подробно мы на нем остановимся в § 18.12 и далее. Рассмотрим решение в параболи-
параболических координатах. Имеем
Система относится к тину A7.2.13), причем
X = Р = и, Y = Q = v, l + i]= — ц. A7.14.2)
Функции Я и S имеют вид
где с + к = —[i/h. Рассмотрим случай, когда движение не есть движение вдоль пря-
прямой, проходящей через точку О. Пусть h < 0, скажем, h = —ц/Bя); тогда с и к положи-
положительны и с + к = 2а, Дифференциальное уравнение орбиты имеет вид
du dv ,„..,
A7.14 4)
~Vu(c — u) ~\/v(k — v)
Если ввести параметры ф и яр, связанные с и и v формулами
1 1
м = -к-сA —cosip), у = -к- к A — cosi|)), A7.14.5)
то уравнение A7.14.4) примет вид dtp = +Лр и выражение ф + \р будет постоянным.
•Положим
tp =F\p = 2x, A7.14.6)
л (в противном случае движение совершалось бы
у О). Таким образом,
cos ф cos г|) + sin ф sin \p = cos 2x. A7.14.7)
причем х не равно нулю и не кратно л (в противном случае движение совершалось бы
по прямой, проходящей через точку О). Таким образом,
Учитывая формулы
-к-ссовф = — с — и, -у с sin ф = ~\/и (с — и),
t ! ,f
Y = -<r k — v, —ksinty—~\/v(k — v), j
находим
(few + cv — ck sin2 xJ = ickuv cos2 x = cky2 cos2 x. A7.14.9)
Уравнение орбиты записывается теперь так:
ku + cv — ck sin2 x = ± V^ J/ cos x A7.14.10)
/ 1 1
ИЛИ (ПОСКОЛЬКУ U — -;r-{r+x) И у=— (г—
-7y(c + k)r = —(c — k)x±~[/ck у cos x-f eft sin^ и. A7.14.11)
Li &
Уравнение A7.14.11) эквивалентно соотношению
т = ер, A7.14.12)
в котором р обозначает длину перпендикуляра, опущенного из точки х, у на линию X,
-~-(с — к)х± Vcfcj/cosx + cA;sin2x = 0. A7.14.13)
Для точек, лежащих по одну сторону от Я с точкой О, знак р берется положительный.
Параметр е определяется из формулы
Ca + *a + &*cos2x f A7.14.14>
с2 + /с2 -(- 2cft
Орбита представляет собой эллипс с фокусом в точке О и директрисой Я.
Глава XVIII
СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ,
ДОПУСКАЮЩИЕ РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ
§ 18.1. Система Лиувилля *). В § 17.2 мы видели, что система с двумя
степенями свободы допускает разделение переменных, если ее кинетическая
и потенциальная энергии имеют следующие выражения:
A8.1.1)
V — 5 i- 'rl
~~ X + Y
где X, P, | — функции только от x, а У, Q, к] — функции только от у. Обоб-
Обобщим эти выражения на случай системы с п степенями свободы. Тогда будем
иметь
2(xi+x2i...+xn)
где Хт, PT, \T являются функциями от qr. Подобные системы называют сис-
системами Лиувилля, и, естественно, встает вопрос о возможности разделения
переменных в таких системах.
Покажем, что переменные разделяются. Модифицированное уравнение
в частных производных для системы A8.1.2) может быть записано в форме
Сразу получаем полный интеграл
К = Kt +К2+. . . + Кп. A8.1.4)
Функции КТ = Кт (qr) определяются из уравнений
A8л-5>
= щХт-1т-аг, г = 2,3, .... п, A8.1.6)
где через ао обозначена сумма <х2 -\- <х3-\- . . . -\- ап. Среди п произвольных
постоянных al5 а2, . . ., ап постоянная энергии <Xi = h играет особую роль.
В обозначениях, принятых в § 16.9, полный интеграл записывается в виде
j yp A8.1.7)
r=2
*) Система Лиувилля впервые рассматривалась в Journal de math., XIV, 1849r
стр. 257. Интегрирование можно выполнить непосредственно с помощью уравнений
Лагранжа, не прибегая к теореме Гамильтона — Якоби; см., например, Уиттекер [27].
Другое элементарное доказательство см. далее в этой книге (§ 26.9).
330 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ ?Гл. XVIII
Таким образом, система допускает разделение переменных, и интегралы лаг-
ранжевых уравнений движения имеют вид
„ Г Xj dqi , чп Г XTdqT
r=2 [ A8.1.8)
— ps= I — \ — ,
•'Уф! (?l) " Уфе (9s)
где
ф!Ы = 2Р1(аД1-^+а0),
<pr(qr) = 2Pr(a1Xr-tT-ar), г=ь2, 3, .. ., п.
Интегралы уравнений Гамильтона получаются путем присоединения
к уравнениям A8.1.8) уравнений
Рг = ™-~1ЛЙЙ. A8.1.10)
Мы поступаем здесь так же, как и в случае системы с двумя степенями
свободы. Интегралы лагранжевых уравнений движения записываем в следую-
следующей краткой форме:
d d Ы dt _dr A8.1.11)
Здесь т играет роль «искусственного времени» (см. § 17.3). Уравнения
A8.1.11), между прочим, можно сразу получить из A8.1.8) или, еще проще,
путем сравнения A8.1.10) с уравнениями
Х^ A8.1.12)
Общий характер движения можно представить себе совершенно так же,
как и в простом случае двух степеней свободы. Появление радикалов в зна-
знаменателях соотношений A8.1.11) не является неожиданным. В случае либ-
рационного движения знак перед радикалом Уфг (qT) выбирается следующим
образом: если qr возрастает, берется знак плюс, а если qr убывает — то знак
минус. Более подробное исследование будет проведено в следующем пара-
параграфе, где рассматривается более общая система, чем система Лиувилля.
§ 18.2. Теорема Штеккеля *). В этом параграфе мы рассмотрим цен-
центральную теорему теории разделимых систем. Естественно поставить вопрос:
какова наиболее общая форма разделимой системы? Исчерпывающего ответа
на этот вопрос пока нет. Но если ограничиться рассмотрением ортогональных
систем (т. е. таких систем, у которых выражение для Т содержит только квад-
ратичные члены по q или р и не содержит произведений), то ответ дается тео-
теоремой Штеккеля, которую мы сейчас докажем. Рассмотренная выше система
Лиувилля принадлежит к классу разделимых ортогональных систем, но не
является ортогональной системой самого общего вида.
*) См. P. S t а с k e I, Ueber die Integration der Hamilton-Jacobi'schen Differential-
gleichung mittels Separation der Variabeln, Habilitationsschrift, Halle, 1891. Другие
работы Штеккеля о его теореме см. в Comptes Rendus, 1893, стр. 485—487, 1284—1286;
Comptes Rendus, 1895, стр. 489—492. Теорему Штеккеля можно получить непосредствен-
непосредственно из уравнений Лагранжа без ссылки на теорему Гамильтона — Якоби; см., например,
An elementary proof of Stackel's theorem, American Mathematical Monthly, Vol. LVI,
No. 6, стр. 394—396.
18.2].
ТЕОРЕМА ШТЕККЕЛЯ
331
Рассмотрим систему, для которой
Т = у
г=1
n
-1 у A
A8.2.1)
Заметим, что qr = сгрг. Коэффициенты ст и потенциальная функция V являют-
являются заданными функциями лагранжевых координат qt, q2, . . ., qn, принадле-
принадлежащими к классу Ci в соответствующей области пространства; кроме того,
сг>0.
Теорема Штеккеля утверждает, что система допускает разделение пере-
переменных тогда и только тогда, когда существуют неособая матрица (urs) раз-
размером п X п, элементы которой uTS зависят только от qT, и матрица-стол-
матрица-столбец {wi, W2, ¦ . ., wn), где wr зависят только от qr, такие, что
п
' ' Т TS 1'
г=1
п
2 CTWT = V.
s=l, 2, . .., п,
A8.2.2)
A8.2.3)
Прежде чем переходить к доказательству теоремы, заметим следующее.
Условие A8.2.2) можно записать так:
с'и = A, 0, 0, . . ., 0). A8.2.4)
Здесь и обозначает матрицу (uTS), ас — матрицу-столбец {с4, с2, . . ., сп).
В матрицах и и w r-я строка содержит только одну координату qT. Если v —
матрица, обратная матрице и, то сГ и V имеют следующие выражения:
п
cr = vir, F== 2 virWr- A8.2.5)
r=l
Перейдем теперь к доказательству теоремы. Сначала докажем, что усло-
условия A8.2.2), A8.2.3) являются необходимыми. Предположим, что переменные
разделяются, т. е. что модифицированное уравнение в частных производных
г=1
A8.2.6)
A8.2.7)
имеет полный интеграл вида
К = Кх + К2 + ... + Кп,
где
Кг = Kr (qr, au а2, . . ., ап). A8.2.8)
Подставим это выражение полного интеграла в уравнение A8.2.6); оно будет
удовлетворяться тождественно для всех значений q и а в соответствующей
области. Дифференцируя частным образом по каждому а, получаем
^ дК дШ
2'
г=1
dqr
дК
dqT
да,
д'-
да*
dqT
•'К
;dqr
X ,
= 0,
= 2,3, ..., п.
A8.2.9)
Коэффициент при сТ в каждом из этих уравнений зависит только от qT,
поскольку К имеет форму A8.2.7); определитель из этих коэффициентов равен
дК дК дК
dqx dq2
дат dqs
A8.2.10)
Он отличен от нуля, поскольку К есть полный интеграл.
332 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ [Гл. XVIII
Возьмем теперь некоторую систему значений al5 a2, . . ., an такую, что-
чтобы определитель А не обращался в нуль. Тогда уравнения A8.2.9) примут
форму
п
У г и — 1
У crurs = 0, s = 2 3 га
r=l
A8.2.11)
т. е. будут иметь форму A8.2.2) с ||urS||^=0. Далее.
п п
7 = а 1у с/-^\2= Усг1агмг 1 / дКг \2\ A8 2.12)
r=l T г=1
п
т. е. имеет вид 2 cTwr. Таким образом, мы доказали необходимость указанных
условий для того, чтобы система допускала разделение переменных.
Докажем теперь, что эти условия и достаточна. Затем, считая, что эти
условия выполняются, перейдем к нахождению интегралов уравнений дви-
движения и исследованию движения.
Модифицированное уравнение в частных производных имеет вид
п
l2c'(yJ + F"a" A8.2.13)
где a4 = h есть одна из произвольных постоянных, входящих в выражение
полного интеграла. Так как по нашему предположению условия A8.2.2),
A8.2.3) выполняются, то уравнение A8.2.13) можно записать в следующей
форме:
п п
1 XI / дК \2 , v-i
г=1 г=1
п п п
= a "S* с и 4-а V сци-1- 4-a ^? с и A8 2 14)
r=l r=l r=i
где a2, a3, .... а„—произвольные постоянные. Его можно записать также
в виде
{у (^) ... + anwrn-o}=0. A8.2.15)
Теперь очевидно, что сумма
К± + Кг + . . . + tfn, A8.2.16)
в которой функции КТ определяются из уравнений
+ • • • +anUpn -wT), A8.2.17)
представляет полный интеграл.
Обозначим правую часть уравнения A8.2.17) через /r (gy). Эта функция
зависит только от r-й координаты и содержит постоянные at, a2, . . ., an,
которые входят в ее выражение линейно. Кроме того,
Kr=\ Vfr Ы dgr, A8.2.18)
<j 18.3] ИССЛЕДОВАНИЕ ИНТЕГРАЛОВ 333
или, точнее,
т=[ Vfr {x) dx. A8.2.19)
Нижний предел интеграла берется, как обычно, равным либо абсолютной
постоянной, либо значению простого нуля функции /г (дг).
Интегралами уравнений движения будут
:_pr = -f^L = у Г -Щк^г, A8.2.20)
..., n, A8.2.21)
r=1 - v ,,ЛЯг)
р8 = -|^- = К77Ы. s=l,2, .... га. A8.2.22)
Решение динамической задачи, таким образом, сводится к квадратурам.
Уравнение A8.2.21) определяет траекторию в g-пространстве (безотноситель-
(безотносительно ко времени). Уравнения A8.2.20), A8.2.21) дают решение задачи Лагран-
жа о движении в g-пространстве, а уравнения A8.2.20) — A8.2.22) — реше-
решение задачи Гамильтона о движении в фазовом пространстве.
Укажем на некоторые свойства полученного решения. Постоянная энер-
энергии а4 в дальнейшем будет играть особую роль, r-я составляющая обобщенно-
обобщенного импульса рг есть функция г-ж координаты qr; в случае либрации она явля-
является двузначной функцией qr. r-я составляющая скорости qr определяется
формулой
qr = c,.pr = cT Vfr (Яг) A8.2.23)
и зависит не только от qT; в случае либрации она двузначна и знак ее совпа-
совпадает со знаком рг.
§ 18.3. Исследование интегралов. Из уравнения A8.2.23) получаем
j!* crdt = dXrt г=1,2, ...,». A8.3.1)
Здесь тг есть «местное» время, введенное в § 17.3, с той лишь разницей, что
теперь для каждой координаты требуются свои часы. Поскольку сТ ^ 0,
знак перед радикалом берется положительным, если qr возрастает с t, и отри-
отрицательным в противном случае. Если ст не обращается в нуль, сг ^ Ат > 0,
и функция /г (qr) непрерывна, то представление об общем характере gv-Движе-
ния можно получить из уравнения A8.3.1). «Местное» время хг стремится
к бесконечности вместе с t, и характер изменения qr зависит от расположения
вещественных нулей функции /г (<?,.)• Если в начальный момент qr располо-
расположено между последовательными простыми вещественными нулями аг, Ъг
функции /г (qr) (так что fT (qr) > 0 при ат <iqr < br), то движение по коор-
координате qr является либрацией. Если же qr в начальный момент лежит вблизи
двойного нуля аг функции /r (qr), то мы имеем лимитационное движение, при
котором qr —>¦ аг, когда i->- oo. Либрация представляет собой колебательное
движение между пределами ат и br, продолжающееся неограниченно долгое
время; в общем случае оно не является периодическим по t. Как и в случае
системы с двумя степенями свободы (§ 17.3), движение по одной координате
в некотором смысле можно рассматривать независимо от движений по осталь-
остальным координатам; это является характерным свойством разделимых систем.
334 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ [Гл. XVIII
Уравнения A8.3.1) можно вывести и другим способом. Из уравнений
A8.2.20), A8.2.21) следует, что
2Ч7Г^Т = 0' « = 2,3, ...,». A8.3.2)
г~ У/г (9т-)
Сравнивая эти уравнения с A8.2.2), приходим к уравнениям A8.3.1).
Остановимся коротко на случае, когда сг может обращаться в нуль. Может случить-
случиться, что при t -*- оо ст -*¦ 0 или что ст обращается в нуль в некоторой точке q, обычно в точ-
точке, лежащей на границе той области ^-пространства, для которой q имеет физическое
истолкование.
Предположим сначала, что ст -»- 0 (в действительном движении), когда ?->-оо.
Тогда тг может стремиться к конечному пределу, когда t ->• сю (см. § 17.3), и в этом слу-
случае ^-движение есть псевдолимитационное движение. Если в начальный момент дг рас-
располагается в интервале между последовательными простыми вещественными нулями аг,
Ьг функции fT (qT), то qr не совершает либрации, продолжающейся неограниченно долгое
время, как это можно было ожидать, а вместо этого с ростом t стремится к пределу I
(ат ^ I ^ Ъг) после, быть может, конечного числа колебаний. Если же qr первоначально
находится в окрестности кратного нуля функции fT (qr), то qr стремится к пределу вблизи
кратного нуля.
Мы знаем, что ст > 0 и в общем случае ст (зависящее от всех д, кроме qT) положи-
положительно. Но может существовать точка q, в которой сг обращается в нуль, и тогда наши
выводы относительно ^-движения, сделанные на основании уравнений A8.3.1), могут
претерпеть изменения. В качестве примера рассмотрим случай, когда ст имеет вид
(дг — qro) i|V, где г|)г (qt, q2, . . ., qn) ^ Ar >> 0. При этом каждый элемент urs r-й строки
матрицы и имеет, вообще говоря, простой полюс в точке qr0 (это следует из уравне-
уравнений A8.2.2)). Функция fr (qr) уже не является непрерывной и имеет простой полюс в точ-
точке qr0. Уравнение A8.3.1) записывается теперь так:
dqr —^rdt. A8.3.3)
У(<7г-<?го)г/гЫ
Функция под знаком радикала имеет в точке qr0 простой нуль. Отсюда следует, что qr(t
может служить одним из пределов либрационного движения для qT, хотя qr0 является
полюсом, а не нулем функции /г (дг). С этим случаем мы встречаемся, например, в задаче
о ньютоновом притяжении к двум центрам (§ 17.10). Уравнение A8.3.1) для Я, прини-
принимает вид
rzpdt- A8-3-4)
Здесь % = с является простым нулем функции с± и простым полюсом функции /4 (Я),
и уравнение A8.3.4) соответствует уравнению A7.10.13), в котором с есть простой нуль
функции R.
Особенности такого типа обычно нетрудно обнаружить в конкретных задачах.
§ 18.4. Дополнительные замечания к теореме Штеккеля. 1) Теорему Штеккеля мож-
можно выразить через п первых интегралов уравнений движения Лагранжа для системы,
определяемой формулами A8.2.1) — A8.2.3). В самом деле, уравнения A8.2.23) можно
представить в форме
1 о2
^ + г + ++. A8.4.1)
Отсюда получаем
n
= ag, s=l,2, ..., re,
где v — матрица, обратная матрице и (см. A8.2.5)).
§ 18.5] . КВАЗИПЕРИОДИЧЕСКИЕ ДВИЖЕНИЯ 335
2) Система Лиувилля представляет собой частный случай системы Штеккеля;.
чтобы убедиться в этом, положим wr = %r/Pr и напишем матрицу и в форме
I/Pi 1/Pl... 1/iv
^2/^2 —1/^2 0 ... 0
X3/P3 0 -l/^з... О I. A8.4.3)
кХп/Рп О 0 ... -i/Pnt
п
3) Если Т = — У, сгрг, как в A8.2.1), то можно удовлетворить условиям теоремы
г=1
Штеккеля, положив
С1 =1, С2 = фЬ С3 = ф1ф2, Ci = ф1ф2ф3, . . ., «71 = ф1ф2 . . . фп_1, A8.4.4>
где фг — функция от qr; матрица и при этом будет иметь вид
A8.4.5)
Система допускает разделение переменных, если V имеет следующее выражение:
V = Wi + ф1"^2 + ф1ф2^3 + • • • + ф!ф2 • • • 4>n-iWn- A8.4.6)'
4) Теорему Штеккеля можно записать так, чтобы формулы были близки к темг
п
что были получены для системы Лиувилля (§ 18.1). В самом деле, поскольку ~S^ crurl = I,.
r=l
можем написать
1
0
0
0
0
Ф]
— 1
0
0
0
0
Ф2
\
0
0
0 ...
0 ...
4>з ¦¦•
0 ...
0 ...
0
0
0
Фп-1
— 1
A8.4.7)
Сходство с A8.1.2) очевидно. Эти формулы, однако, не имеют каких-либо практических
преимуществ.
§ 18.5. Квазипериодические движения. Рассмотрим систему типа Штек-
Штеккеля и остановимся более подробно на простейшем (и наиболее распро-
распространенном) случае, когда движение по каждой координате представляет
собой либрацию. Будем предполагать, что коэффициенты сг не обращаются
в нуль, а функции /г (qr) непрерывны. Каждое qr в начальный момент лежит
между простыми вещественными нулями ат, Ъг функции /г (qr) (предполага-
(предполагается, что аг < br), и колебания qT происходят между пределами ат, Ъг. Возь-
Возьмем аг в качестве нижнего предела интегрирования в формуле A8.2.19)
для Кт. В течение движения будем иметь
—^— = crdt. A8.5.1)
v/r ы
Знак радикала берется положительным, когда qT возрастает, и отрицатель-
отрицательным, когда qr убывает. Согласно A8.2.22) имеем
p! = /,Wi A8-5.2)
336
СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ
[Гл. ХУШ
и каждое рг является двузначной функцией от соответствующего qT\ характер
этой зависимости показан на рис. 65. Движение изображающей точки в д-про-
странстве совершается внутри прямоуголь-
прямоугольного параллелепипеда
ат <9V < Ьт, г = 1, 2,
п.
Движение изображающей точки в фа-
фазовом пространстве происходит в области,
получающейся путем расширения этого па-
параллелепипеда за счет р, вычисляемых по
формулам A8.5.2) (рис. 65). Движение этого
типа называется квазипериодическим; ниже
мы дадим объяснение этому термину.
Рассмотрим преобразование лагранжевых координат qr к новым коорди-
координатам Qr, определяемым уравнениями
Рис. 65.
d4r
,2, .. ., n,
A8.5.3)
или, более точно, уравнениями
— Zj -./ —ахт,
s = 1, 2, . . ., re.
A8.5.4)
Лагранжева координата qr лежит в интервале ат ^ qr ^ br, и при преоб-
преобразовании координат предполагается, что каждое qr совершает колебание
между пределами ат и Ъг (как в действительном движении). Радикал yfr(xr)
берется положительным, если хт возрастает, и отрицательным, если хт убы-
убывает. Таким образом, 8 оказывается неоднозначной функцией от q и имеет
дискретную систему значений, зави-
зависящую от траектории, по которой
изображающая точка переходит из
положения а в положение q.
Разберем простой пример. Положим
п = 2 и рассмотрим четыре траектории,
соединяющие точки (аь а2) и Р (qlt q2)
(рис. 66). Вдоль каждой из них х2 возра-
возрастает от а2 до q2. Вдоль кривых 1 и 2it
возрастает монотонно от а4 до д4, и значе-
значение 0ь 92 для них одинаково. Но для кри-
кривой 3 (где xi сначала возрастает от 6ь а за-
затем убывает до д4 )оно отлично, как и для
кривой 4 (где Xi сначала возрастает до Ь4.
затем убывает до аь после чего снова воз-
растает до qi).
Предположим теперь, что коор-
координата qr проходит полный цикл
своих значений и возвращается в
свою первоначальную точку, в то время как остальные координаты q оста-
остаются неизменными. В этом случае 9S получает приращение
Рис. 66.
§итя1
(Яг)
A8.5.5)
S 18.5] КВАЗИЛЕРИОДИЧЕСКИЕ ДВИЖЕНИЯ 337
которое можно записать также в форме
^г- A8-5.6)
Vtiq)
Таким образом, если 0l5 02, . . ., вп получают приращения соответственно
cori, (ог2, . . ., com> то мы возвращаемся к исходной точке g-мерного паралле-
параллелепипеда с теми же самыми скоростями. Функции
?, = <Pr(elt 02, • •., ej A8.5.7)
имеют свойство
фг @J, 02, . . ., 0П) = фг @! + @,1, 02 + «S2, . . ., 0» + ©,„). A8.5.8)
Всего имеется п таких систем периодов. Предположим, что эти системы
линейно независимы, т. е. || (ors || фО. Тогда две точки пространства 0 будут
эквивалентны одной и той же точке пространства q и даже одной и той же точ-
точке фазового пространства, если их относительные положения описываются
одним из векторов йг (с составляющими cori, сог2, ¦ . ., соГГ1). Векторы Qr,
г = 1, 2, . . ., п, линейно независимы. Более того, две точки Р\ и Р2 0-про-
странства эквивалентны одной и той же точке фазового пространства, если
п
положение точки Р% относительно Р4 описывается вектором 2 Щ&г, гДе
г=1
m — целые числа, положительные, отрицательные или нули.
Таким образом, можно разбить 8-пространство на периодические ячейки
п
с узлами, определяемыми векторами ^mTQr для всех целых значений /%,
таг- ¦ ¦ •> тпп- Ячейки обладают тем свойством, что конгруэнтные точки в двух
любых ячейках представляют одну и ту же конфигурацию и одну и ту же
скорость динамической системы. Соотношение между переменными } и 9
не является симметричным; так, например, если дг возрастает от gr0 до Ът
и затем убывает до дт0 (в то время как остальные координаты q остаются неиз-
неизменными), то в результате мы попадаем в другую точку 0-ячейки, представ-
представляющую ту же д-точку, но с другой скоростью. Действительно, каждая точка
параллелепипеда в ^-пространстве соответствует 2п точкам в 0-ячейке,
а каждая из этих 0-точек представляет одну из 2™ возможных систем скоро-
скоростей. Мы видим, что 0-ячейка дает более точное представление движения,
нежели параллелепипед в g-пространстве, поскольку каждая точка в ней
представляет как определенную конфигурацию системы, так и определенную
скорость ее.
Так как конгруэнтные точки в различных 0-ячейках эквивалентны, то
естественно сосредоточить внимание на рассмотрении одной стандартной
ячейки и каждой точке 0-пространства поставить в соответствие конгруэнт-
конгруэнтную ей точку в стандартной ячейке. Будем считать, что одна из вершин стан-
стандартной ячейки расположена в начале координат (соответствующем точке а
в g-пространстве), а в качестве ребер, проходящих через эту вершину, возь-
возьмем векторы йг.
Поясним сказанное простым примером, когда п = 2. Движение изображающей
точки в плоскости (g1? q2) ограничено прямоугольником (рис. 49), и соответствующую
изображающую точку в плоскости (в4, 82) можно перенести в стандартную ячейку. Движе-
Движение в плоскости @i, 82) описывается очень просто: изображающая точка движется с еди-
единичной скоростью параллельно оси 6^:
? -_.-. . A8.5.9)
22 л. А. Парс
338
СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ
[Гл. XVIII
и различные отрезки этой линии нужно заменить на конгруэнтные отрезки в стандартной
ячейке (рис. 67). Вообще говоря, они не перекрываются и с увеличением числа отображае-
отображаемых отрезков покрывают стандартную ячейку все более и более плотно. Но если отноше-
отношение @22/<»i2 есть число рациональное, то с течением времени отрезки будут проходиться
повторно. В этом случае траектория в стандартной 9-ячейке будет состоять пз конечного
числа отрезков, проходимых снова и снова; траектория в параллелепипеде д-простран-
ства будет замкнутой, периодической. Позже мы получим общее условие периодичности,
и тогда данный пример можно будет рассматривать как частный случай.
§ 18.6. Угловые переменные. Вернемся к задаче с п степенями свободы.
Введенные в § 18.5 координаты 0Г сами по себе не играют особенно большой
роли, основное значение для теории имеют некоторые линейные комбинации
этих координат, называемые угловыми переменными. Роль координат 0 заклю-
заключается в том, что они облегчают переход к угловым переменным.
Рассмотрим неособое линейное преобразование
e, = a>1,i;1 + a>Mi;2+ ... + <on.i;.= 2 ts>nvr, «=1,2, ..., п. A8.6.1)
г=1
В матричной форме его можно записать в виде
A8.6.2)
где в — матрица-столбец {0i, 02, . . ., 0n}, v — матрица-столбец {v±, v%, ...
. . ., vn}, а. а — матрица (соге) размером re X re.
Если vr увеличивает свое значение на единицу, в то время как остальные
v остаются неизменными, то 0l5 02, . . ., Qn возрастают соответственно на юг1,
соГ2> • • •) о™? т. е. на соответствующие периоды, a q, q и р остаются без
изменений. Эти последние переменные являются периодическими функциями
от v с периодом, равным единице по каждому v. Величины v называют угло-
угловыми переменными (хотя такое наименование было бы более подходящим для
переменных wT = 2nvr, имеющих период 2я по каждому w). Если величины
2nvT интерпретировать как угловые переменные на re-мерном торе, то будет
существовать взаимно однозначное соответствие между точками этого тора
и соответствующей областью фазового пространства. В общем случае коор-
координаты q могут быть представлены в форме рядов Фурье по v:
qr =
, v2
\-vni>n)
A8.6.3)
где индекс v принимает все целые значения,
или нуль.
положительные, отрицательные
§ 18.7] СТАНДАРТНЫЙ КУБ 339
Движение в пространстве v является равномерным и прямолинейным:
п
у8 = И-1801 + М'2Л-г •••-!-И-П80» = S УтА, s-=l,2, ..., га. A8.6.4)
Здесь через (u.rs) обозначена матрица, обратная матрице (corg). ]Тодставляя
вместо 6 их значения в момент t, а именно:
84 = t — рь 0S = —р„ s = 2, 3, . . ., га, A8.6.5)
получаем
у, = ца* + fie, A8.6.6)
где вместо \iis использован символ jas, а через Ss обозначено выражение
г=1
A8.6.7)
Постоянные u.l5 (г2, . . ., и.„ называют частотами движения. Если величину
2nvT рассматривать как угол, составленный вращающимся вектором с непод-
неподвижным направлением, то ц.,. будет выражать число оборотов в секунду.
Конфигурация системы в произвольный момент t определяется уравне-
уравнением
qr = 1|зг (nit + Si, \\2t + S2, . . ., nnt + 6n). A8.6,8).
Каждая функция г|)г периодична по любому из своих аргументов с периодом,
равным единице. Однако, как уже указывалось ранее, функции qr, вообще
говоря, не являются периодическими по t. Координаты q будут периодиче-
периодическими функциями t с периодом а в том случае, если все величины
будут целыми числами. Такой множитель существует только тогда, когда
все отношения u.2/(Ai, М-з/м-ь • • ч fij^i суть числа рациональные. Замкнутая
периодическая орбита получается лишь при условии, что частоты связаны
п — 1 независимыми линейными соотношениями с целыми коэффициентами.
Если указанное условие не выполняется, изображающая точка в про-
пространстве v никогда не возвращается в первоначальное положение; то же
самое можно сказать и относительно фазового пространства. Но даже если
это условие не выполняется, т. е. не существует множителя т такого, что все
величины Tfij, т.ц.2, . . ., т(г,г представляют собой целые числа, то все же мож-
можно выбрать такое произвольное (большое) число т, что все эти величины будут
сколь угодно мало отличаться от целых чисел. Это — одна из форм, выражаю-
выражающих теорему Дирихле. Вследствие равномерной непрерывности q и р (как
функций от v) аналогичное утверждение можно высказать и относительно
фазового пространства. Можно указать такое, достаточно большое, значение
времени т, по истечении которого изображающая точка в фазовом простран-
пространстве окажется в заданной окрестности е своего исходного положения. Это
объясняет термин «квазипериодическое движение».
§ 18.7. Стандартный куб. Теперь становится очевидным, что в у-про-
странстве мы имеем периодическую структуру, аналогичную структуре в
6-пространстве. Две точки в ^-пространстве соответствуют одной и той же точ-
точке в фазовом пространстве, если их относительное перемещение определяется
п
вектором 2 mrUr, где т — целые числа, a U — единичные векторы, парал-
г=1
дельные координатным осям. Все пространство v, таким образом, можно раз-
разбить на ячейки в форме куба единичного размера так, что конгруэнтные точки
в двух любых ячейках будут эквивалентны, т. е. будут соответствовать одной
22*
340
СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ
[Гл. XVIII
и той же точке фазового пространства. Поэтому естественно сосредоточить
внимание на рассмотрении стандартного единичного куба и отнести отрезок
траектории, лежащий в каком-либо кубе, к конгруэнтному отрезку в стан-
стандартном кубе. Траектория будет состоять из параллельных отрезков прямых,
проходящих через стандартный куб.
Расположим точку Ро (84, б2, ¦ • ., бп), соответствующую моменту вре-
времени t = 0, в вершине стандартного куба. Пары противоположных граней
стандартного куба являются (п — 1)-мерными плоскостями, определяемыми
уравнениями
vT = бг, vr = 8Г + 1, г = 1, 2, . . ., п. A8.7.1)
Положение изображающей точки в некоторый момент t относительно точки
Ро определяется формулами
vr _ бг = (\irf), г = 1, 2, . . ., га, A8.7.2)
где через (х) = х — [х] обозначена дробная
часть числа х. Как мы видели, изображаю-
изображающая точка никогда не возвращается в свое
исходное положение Ро, если только часто-
частоты цг не связаны п — 1 линейными соотно-
соотношениями с целыми коэффициентами.
Если имеется п^ таких соотношений,
причем 0 < щ < п — 1, то движение носит
исключительный характер; в таких случаях
говорят, что движение является вырождаю-
вырождающимся. Поясним это. Предположим сна-
сначала, что щ = 1, т. е. что существует одно
соотношение вида
¦Vlfil + V2M-2+ • ¦ • + VnfAn = 0, A8.7.3)
Рис. 68.
в котором v — целые числа, не все равные
нулю. Легко дать геометрическую интерпре-
интерпретацию этому соотношению: оно выражает, что траектория в д-простран-
стве ограничена многообразием меньшего измерения, чем п. В самом деле,
п п п
0=1 И vr|ir}*= 2 vr[fMl+ 2 "MM. A8.7.4)
r=l
r=l
откуда следует, что 2 vr (fx,-^) есть целое число, положительное, отрицатель-
г=1
ное или нуль, и изображающая точка в силу A8.7.2) лежит в одной из плос-
плоскостей
2 ^ (у, - бг) = 0, +1,±2, . . . A8.7.5)
Отрезки, изображающие орбиту, в этом случае не проходят вблизи всех точек
куба, а ограничены системой (конечного числа) эквидистантных параллель-
параллельных плоскостей. На рис. 68 иллюстрируется случай п = 3, когда имеется
одно соотношение вида A8.7.3). Аналогично (для системы с п степенями сво-
свободы), если имеется щ независимых соотношений, то отрезки ограничены
многообразием (п — щ) измерений.
Если нет соотношений типа A8.7.3), то отрезки траектории плотно запол-
заполняют стандартный куб. Если Xi, К2, . . ., Кп — произвольная точка единич-
единичного куба, а е — заданное сколь угодно малое положительное число, то мож-
можно указать такое (достаточно большое) число т, чтобы
| (и,гт) — К | < е, г = 1, 2, . . ., п.
Это неравенство выражает теорему Кронекера. Изображающая точка беско-
бесконечно много раз проходит в произвольной близости от любой точки единич-
5 18.8] ПОСТОЯННЫЕ Ir 341
ного куба. Аналогичное утверждение справедливо и в отношении соответ-
соответствующей области фазового пространства. Мы получили результат, уже
доказанный ранее в § 18.6. Если движение является вырожденным, то тра-
траектория изображающей точки плотно заполняет соответствующее многооб-
многообразие ^-пространства (см., например, рис. 68).
§ 18.8. Постоянные 1Г. Общий характер движения определяется рас-
распределением вещественных нулей функций fr (gr), что в свою очередь зависит
от значений постоянных аь а2, . . ., ап. Хотя для определения траектории
необходимо задать 2/г параметров аГ, рг, однако задание одних лишь постоян-
постоянных а уже позволяет определить общий характер траектории. Это обстоя-
обстоятельство уже отмечалось нами при исследовании двумерной задачи, где ука-
указывалось на существенную роль постоянных h, a (§ 17.4). В n-мерной задаче
постоянная р4 зависит лишь от выбора начала отсчета времени, а фазовые
постоянные рг (г > 1) не оказывают влияния на пределы либрации и, сле-
следовательно, не сказываются на общем характере движения.
Рассмотрим теперь частоты \ir. Их значения определяются постоянными
cors. В самом деле, \ii = jxlr, где (\irs) — матрица, обратная матрице (cors),
и величины
,, , N A8.8.1J
Vfr {Яг)
будут определены, коль скоро известны параметры а и, стало быть, пределы
либрации по координате qr. Поэтому элементы матриц (cors) и (\irs) являются
известными функциями а, и, в частности, частоты \ir являются известными
функциями а. Возникает вопрос: в какой мере задание начальных условий
определяет частоты? В частности, возможны ли такие движения динамиче-
динамической системы, когда частоты \ir пропорциональны целым числам? Иными
словами, существуют ли периодические движения?
Чтобы ответить на эти вопросы, введем вместо а новые постоянные 1Г.
Постоянную 1Т примем равной приращению функции Кг, когда координата
qT проходит полный цикл своих значений. Таким образом,
A8.8.2)
Введенные постоянные / образуют новую систему параметров, зависящих
от первоначальных параметров а; из равенства A8.8.1) следует, что
cors = -|^. A8.8.3)
A8.8.4)
Представив а как функции /, будем иметь
да.
и, в частности,
^ = -!^1. A8.8.5)
Постоянная а1; как можно было ожидать, играет здесь особую роль: а^ есть
постоянная энергии.
Таким образом, мы приходим к следующему простому правилу для ква-
квазипериодических движений систем типа Штеккеля: если постоянная энергии
СЦ выражена через параметры I, то частоты системы определяются как
частные производные dajdlr.
В общем случае следует ожидать, что уравнения A8.8.5) при заданных
\i (по крайней мере при jx, заданных в некоторой области) могут быть решены
342 СИСТЕМЫ С я СТЕПЕНЯМИ СВОБОДЫ [Гл. XVIII
относительно /. Это означает, что при надлежащем выборе начальных усло-
условий мы можем придать частотам системы любые значения. В общем случае
это утверждение справедливо, однако имеется важное исключение.
Может оказаться, что а± будет зависеть от линейной комбинации пара-
параметров /, т. е. <%! = F (z), где
z = kji -!- к212 + . . . + кп1п, A8.8.6)
а коэффициенты кг являются фиксированными абсолютными постоянными.
В этом случае, каковы бы ни были начальные условия, справедливы
равенства
17==~а7^ "'¦ =="*7' A8.ь./)
Эти формулы раз навсегда определяют отношения частот друг к другу, и эти
отношения нельзя изменить никаким выбором начальных условий. Тем
самым устанавливается определенная степень вырождения системы. В част-
частном случае, когда отношение двух любых коэффициентов к есть число рацио-
рациональное, движение всегда является периодическим; при этом между коэффи-
коэффициентами к существуют п — 1 линейных соотношений
v^ + vzk2 -[-... + vnkn = О A8.8.8)
с целыми vr. В другом частном случае, когда между к не существует ни одного
соотношения типа A8.8.8), движение системы никогда не будет периодическим
(за исключением главных колебаний в колебательных системах). В промежу-
промежуточном случае, когда имеется щ независимых линейных соотношений A8.8.8),
причем 0 < щ < п — 1, степень вырождения системы не зависит от началь-
начальных условий.
В § 17.3 были приведены два примера подобных явлений.
1) В теории малых колебаний (гл. IX), где
A8.8.9)
движение всегда периодично, когда отношение любой пары значений т есть
число рациональное, и никогда не периодично (за исключением главных коле-
колебаний), если между nti, т2, ¦ • ., тп не существует линейного однородного
соотношения с целыми коэффициентами. Действительно, в этом случае сц
зависит от комбинации mJi -\~ пг2/2+ . . . + тп1п и, следовательно,
A8.8.10)
(Ч __ V-2 _ М-П
"'1 '"г тП
2) Второй пример относится к движению планеты в пространстве под
действием ньютоновского притяжения к центру. Вопрос о том, почему орбита
(если она ограничена) должна быть всегда периодической, возник в начале
изучения общих динамических систем. В этой задаче параметр а4 зависит
от /i + /г + /з, и, следовательно, каковы бы ни были начальные условия,
будем иметь
Щ = Ц2 = Из- A8.8.11)
Другой особый случай мы имеем, когда at зависит не от одной линейной формы z,
а от р независимых линейных форм г4, z2, • • •, zp:
zr --= knh + kr2l2 + . . . + krnln, n = 1, 2, . . ., p, A8.8.12)
где 0 < p < n — 1. При этом \х связаны п — p независимыми линейными соотношениями
vrt|ii + v,.2(i2 + . . . + vmnn = 0, г = 1, 2, ...,(»- P)- A8.8.13)
§ 18.10] МАЛЫЕ КОЛЕБАНИЯ 343
Если коэффициенты krs рациональны, то коэффициенты vrs также рациональны и можно
считать их целыми числами. Тем самым устанавливается степень вырождения системы
независимо от начальных условий.
§ 18.9. Соотношения между q и г. Величины q являются периодиче-
периодическими функциями от v с периодом, равным единице, по каждому v. Чтобы
получить соответствующие зависимости в явной форме, заметим, что из соот-
соотношений A8.5.4) и A8.6.1) следует, что
и 1г п
V Г -UrsM dxT=^ «>rsVr, *-=1,2, ..., П. A8.9.1)
Разрешая эти линейные уравнения относительно v, находим
п
я «г 2 HsZ"t-s {хт)
"'¦=-¦^1 \ S=1/ dxn Z== 1,2, ..., п. A8.9.2)
Отсюда следует, что при прохождении qm полного цикла своих значений ь>;
получает приращение 6^.
Соотношения между q ж v можно представить в значительно более про-
простой форме, если перейти к параметрам 1Г. Подставим в К параметры а,
выраженные через /. Тогда мы получим функцию вида К' (qir q^, ¦ ¦ ¦, qn\
h, I2, . . ., /„), т. е.
К (q; a) - K' {q; I). A8.9.3)
Далее, учитывая A8.8.3), находим
e*=-? = S^-S7=2^-S7' . = 1,2,...,». A8.9.4)
С другой стороны,
n
9S= S <?rsvr, s = l, 2, .. .,n. A8.9.5)
r=l
Из формул A8.9.4) и A8.9.5) получаем
vr = ^, г-1,2,..., п. A8.9.6)
Эти уравнения представляют собой особенно простую форму соотношений
между q и v.
§ 18.10. Малые колебания. Применим теперь теорию квазипериодиче-
квазипериодических движений к ряду конкретных динамических систем.
Рассмотрим сначала полностью разделимую систему, а именно колебательную
систему, отнесенную к главным координатам (гл. IX). Хотя этот пример и элементарен,
однако он хорошо иллюстрирует полученные теоретические результаты.
Кинетическая и потенциальная энергии системы в этом случае выражаются фор-
формулами
г=1 г=1 г=1
Модифицированное уравнение в частных производных имеет вид
г=1
344 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ [Гл. XVIII
Полный интеграл равен Ki-\-K2-\-.. .-\-Кп, где Кг опеределяется из уравнения
(l^J==m?(e*-#' A8Л0-3)
причем
п
1г2гаХ-=а1. A8.10.4)
аи—1 остальных параметров а2, аз, ...,ап выражаются формулами
— т\а\ = а\ — а2— а3— ... — а„, ^
} A8.10.5)
2-^ = аг,г = 2,3 ». J
Таким образом,
KT = mr \ ~\/a\ — x*dx. A8.10.6)
0
Следовательно,
1г = ътга\. A8.10.7)
Из формул A8.10.4) и A8.10.7) получаем
4 ... +гап/„). A8.10.8)
Таким образом, мы имеем особый случай, отмеченный в § 18.8. Частоты системы имеют
значения
^=-^-=-Ж' -1,2,..., п. A8.10.9)
Чтобы найти явное соотношение между q и и, воспользуемся способом, описанным
в § 18.9. Имеем
— x*dx A8.10.10)
о
и, следовательно,
дК' дКт 1 dx 1 С dx Qr
У, лтт
где qr = ar sin Or. Функция gr выражается через угловые переменные следующим
образом:
A8.10.12)
qT=y ^-sm2nvr.
У nmT
В рассматриваемом случае каждая координата qT зависит только от соответствующей
переменной vr, в общем случае это, разумеется, не имеет места.
С помощью соотношений A8.10.5) и A8.10.7) легко выразить / через а:
2я Л
1\ — —-(«1 — а2—аз — ... — аЛ), |
Щ | A8.10.13)
/ - П а г-23 п
а также а через /:
1 ^
A8.10.14)
.=±ш1 г = 2 3 в I
2я г г> ' * )
§ 18.11]
СФЕРИЧЕСКИЙ МАЯТНИК
345.
Матрицы & и ц легко составить, исходя из определения элементов cors или по-
формулам A8.8.3), A8.8.4). Получаем
' 2я 2л 2л 2л'
«0 =
0
"*"П
0 0 0 •••-2я-
Значения переменных у в некоторый момент t равны
2л
2я
га2
nil
о
2я
О
т3
2я ••
т3
2я
2л
• 2л
. О
. О
A8.10.15),
A8.10.16).
а значения переменных q равны
(*—Pi —Э*), -' = 2, 3, ...,п,
A8.10.17).
sin m» <*— Pi —
s = 2,3, ..., п.
§ 18.11. Сферический маятник. Рассмотрим вновь задачу о сферическом маятни-
маятнике (§ 5.3), на этот раз с точки зрения теории квазипериодических движений. Движение
носит характер либрации по каждой координате. Если в качестве одной из координат
взять азимутальный угол <р, то мы будем иметь особый случай. В самом деле, в этом слу-
случае координата <р не колеблется между двумя предельными значениями, а все время воз-
возрастает. Однако если ввести координату s = sin <p, то будем иметь колебания между пре-
пределами + 1 и —1.
Практически нет необходимости полностью отказаться от использования монотон-
монотонно изменяющейся переменной <р, но нельзя при этом упускать из виду, что требуется
внести несущественное изменение в общую теорию. Имеем (см. § 5.3)
= mgecos6.
A8.11.1)
Угол 6 отсчитывается здесь от вертикали, направленной вверх. Полагая, как и ранее,
г = cos 9 и вводя безразмерное время т = t ~[/g/2a, можем написать (опуская положи-
положительный множитель)
A8.11.2)
(штрихом здесь обозначено дифференцирование по т).
Таким образом, система имеет стандартную форму A7.2.13) разделимой системы
с двумя степенями свободы, и если за координаты ж, у принять ф, z, то будем иметь
X = 0, Р = 2, g = 0, У = 1 — г2, Q = 2 A — г2J, т) = z A — г2). A8.11.3)
Таким образом,
r = 4а, S = 4 A — z2J {(h — z) (I - z2) - а} = 4 A — 22J / {?) A8.11.4)
346 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ [Гл. XVIII
A8.11.5)
Интегралы уравнений движения Лагранжа будут иметь вид
, . . \ A8.11.6)
— В — —— — f
2 УаФ J 2A —z^) У/' J
Поскольку мы имеем либрацию, выбор знака радикала У/ (г) производится обычным
образом: когда z возрастает, берется положительный знак, а когда z убывает — отрица-
отрицательный. Координата <р, как мы видели, непрерывно возрастает, поэтому удобней перейти
к новой переменной s = sin <p. Обозначим интегралы, содержащие У/(г), через А и В:
1=J уг- B=J d-
или, точнее,
Z Z
С d.r f dx
A8.11.7)
При колебании г между пределами z3 и z2 эти функции непрерывно возрастают. Они
многозначны (см. § 18.5), так что значение А (или В) зависит не только от величины z,
но и от числа совершенных колебаний, а также от того, возрастает ли переменная г или
убывает. Имеем
. ^ -- „ Г dz „С & „ ? dz
An —
§dz
Вычислим элементы матрицы (cors):
" Li I
12 Уа ' 22 2 °' J
Следовательно,
m-=J^-^-, Ц2 = ^"- A8.11.10)
Периодическое движение имеет место при условии, что отношение щ/ц.2 есть число
рациональное, и это согласуется с E.3.13). /i и /2, соответствующие i^i и ЛГ2, выражаются
-формулами
/1==2яУа, /2^<?>7~4-d2- A8.11.11)
Интересно проверить формулу jxr = dhldlr непосредственным вычислением. Соот-
Соотношение между h и /i и /2 можно записать в виде
A8.11.12)
Дифференцируя это равенство по 1^ и по /2, находим
!• A8.11.13)
•откуда получаем A8.11.10).
§ 18.12] ЗАДАЧА ДВУХ ТЕЛ 347
Найдем теперь явные выражения для угловых переменных. Уравнения A8.6.1)
имеют вид
Отсюда следует, что
„, * ф+*°у° D-4-) •
1 2я Y ' 2я \ ^40 ?0 / '
Как и следовало ожидать, эти формулы показывают, что когда qr проходит цикл своих
значений, в то время как остальные q остаются без изменения, vr увеличивается на еди-
единицу. Следует иметь в виду, что сказать, что ф проходит цикл своих значений,— это
то же самое, что сказать, что <р возрастает на 2я.
Соотношения между и и q можно получить также по способу, описанному в § 18.9.
Имеем
4^ lj^z' A8.11.16)
Z3
где
F = (А' - z) (I - z2) - (/i/2nJ, A8.11.17)
а через ti обозначено h, выраженное через /4 и /2 с помощью соотношения A8.11.12).
Легко убедиться в том, что уравнения vr = дК'ldlr вновь приводят нас к форму-
формулам A8.11.15).
Наконец, если положить
И + ) A8.11.18)
(см. E.2.40)) и при t~-x — Q считать z = 23, то будем иметь
А= [ —^ = 2т, А0=Аа1. A8.11.19)
С помощью формул A8.11.15) получаем, что и2 ~ А/Ао ~- т/Bан), и, так как (.i2 =
--- 1/Bcu4), находим, что v2 = ЦгТ.
§ 18.12. Задача двух тел. Пусть солнце S массы М и планета Р массы тп1
движутся в пространстве под действием сил взаимного притяжения yMmJr2.
Движение планеты относительно Солнца происходит так, как если бы Солнце
находилось в покое, а планета двигалась с ускорением у (М + m^/r2, направ-
направленным вдол^ь прямой PS. Траекторией в относительном движении планеты
будет коническое сечение, в фокусе которого находится Солнце. В § 5.4 было
дано элементарное решение этой задачи. В этом и последующем параграфах
мы снова рассмотрим относительное движение планеты, на этот раз с позиций
теории квазипериодических движений. Мы ограничимся случаем эллиптиче-
эллиптических орбит, что позволит нам достаточно полно проиллюстрировать различ-
различные аспекты теории.
Движение планеты Р относительно Солнца S характеризуется следую-
следующей функцией Гамильтона:
где \i — у (М + пг^. Мы здесь пользуемся сферическими полярными коор-
координатами и угол Э отсчитываем не от полюса, а от экватора, как это принято
в астрономии. Приняв г, 9, ср соответственно за gb q2, ?з> будем искать полный
интеграл К либо путем непосредственного решения модифицированного
уравнения в частных производных, либо с помощью теоремы Штеккеля.
348 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ [Гл. XVIII
Следуя первому из этих способов, запишем уравнение в частных производных:
1 Паку
1 ,дК у 1 (дК\гЛ ц
2
Решение его ищем в форме
К = а3ф + R + в, A8.12.3)
где R = R (г), 0 = в (9). Подставляя его в уравнение A8.12.2), получаем
0. A8.12.4)
Левая часть этого равенства представляет сумму функции от г и функции
от Э; следовательно, каждая из них должна быть постоянной. Функция от 6,.
очевидно, положительна, так что можно написать
^oW (^) -а2 A8.12.5)
и", следовательно,
i?'2 = 2a1+-^----i-, 6'2 = al %г. A8.12.6)
1 ' г г2 2 cos2 0 v '
Полный интеграл теперь находится сразу. Без сколько-нибудь существенной
потери общности параметры а2 и а3 можно считать положительными, тогда
из формулы для в'2 следует, что а2 > а3. В интересующем нас случае а4 < О,
квадратичная форма 2atr2 + 2\ir — a\ имеет два вещественных положитель-
положительных нуля ги г2 @ < г4 •< г2) и движение по координате г представляет собой
либрацию между пределами г4 и г2. В дальнейшем мы будем предполагать,
что параметры at, a2, a3 удовлетворяют неравенствам
a2 > a3 > 0 > at. A8.12.7)
Выбирая теперь обычным образом нижние пределы интегралов, будем
иметь
г 9
К= \ yr2a1 + ^—^-dr+ J j/al—^. dQ + a3cp. A8.12.8)
п о
Интегралы лагранжевых уравнений движения имеют вид
г
f-p, = - aro =-, A8.12.9)
ri
= - у a2dr/:2 , + у a2'9 . , A8.12.10)
-Рз= -f °»^соа29=. + ф: A8.12.11)
cos2 6
Эти уравнения являются основными в излагаемой теории. Движение по коор-
координатам г и Э представляет либрацию, а координата ф все время возрастает.
С подобным явлением мы уже встречались ранее, в § 18.11,; так же как и там,
здесь удобно заменить ср новой переменной s = sin ср. После такой замены
¦§ 18.13]
ИНТЕРПРЕТАЦИЯ ПАРАМЕТРОВ ос И
349
лзторое слагаемое правой части уравнения A8.12.11) запишется в виде
ds
Г ds
и мы будем иметь либрацию по s между пределами +1 и —1.
Отвлечемся на время и выясним, в чем состоит отличие полученного нами результата
•от решения, получаемого с помощью теоремы Штеккеля. Одно из таких отличий очевид-
очевидно: в решении Штеккеля параметры а входят линейно в выражения, стоящие под радика-
-лом. Мы имеем
/1 -1/7-2 0 ч /-(Х/
м=10 1 — 1/COS26], м» = 1 О
Vo о 1 / V о
A8.12.12)
в
dr-u
Ф
A8.12.13)
п О
{параметры здесь для отличия их от предыдущих снабжены штрихами). Эти две группы
параметров связаны между собой формулами
Преобразование параметров (а,
¦зованием (см. § 15.8):
2
Р3=Рз/«з-
в (a', fS') является однородным контактным преобра-
; da'r =
8r dar.
A8.12.15)
r=i r=l
•Значение этого факта станет ясным позднее.
§ 18.13. Интерпретация параметров аир. Равенство A8.12.11) можно
лзреписать в следующей форме:
sec29 dQ
!(tg(
A8.13.1)
Следовательно,
tg В = |/"-^§-— 1 зш(ф+Рз)- A8.13.2)
Мы получили линейное соотношение между направляющими косинусами
'(cos Э cos ф, cos Э sin ф, sin Э), откуда следует, что
траектория планеты плоская. Это, впрочем, оче-
очевидно и из элементарных соображений. Если
через ф0 обозначить долготу восходящего узла,
а через i — наклон орбиты (т. е. наклон плоско-
плоскости орбиты к плоскости экватора z = 0), то с по-
помощью известных формул сферической тригоно-
тригонометрии (рис. 69) получим
tg Э = tg i sin (ф — ф0). A8.13.3)
Сравнивая A8.13.2) и A8.13.3), находим
Рз = — фо> Сз/«2 = cos i. A8.13.4)
Обращаясь теперь к соотношению A8.12.10),
видим, что каждый интеграл справа имеет очень простой смысл:
= г|;, A8.13.5)
i\ r I \ r r2 '
350 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ [Гл. XVIIT
где
При вычислении интеграла
9
a2dQ
\
A8.13.7)
воспользуемся подстановкой
sin Э = sin г sin и. A8.13.8)
Здесь и обозначает угловое смещение относительно восходящего узла, изме-
измеряемое в плоскости орбиты. Получаем
е е и
(* a2dB (" cos 9 ей) I* sin i cos и du ,.о .„ ,..
\ , =—= \ — \ , = и. A8.13.9)
J Va.% — aisec^e ^ i/cos26 — cos2 j ]Q Vsin2 г — sin2 9 '
Равенство A8.12.10) принимает теперь простую форму:
г|э = и + р2, A8.13.10)
и так как при г = гг i|; = 0, то
р2 = —Щ, A8.13.11)
где и0 — значение и в перигелии. Из формул A8.13.6) и A8.13.10) получаем
уравнение орбиты в своей плоскости:
f 4 (+i) +1 (^-^)cos с-"»)- A8ЛЗЛ2>
f =4
Это есть уравнение эллипса. Вводя обычные обозначения а, е для большой
полуоси и эксцентриситета, получаем
П = сA - в), г2 = сA + <?), A8.13.13)
и так как ri, r2 суть нули полинома 2atr2 + 2^хг — а\, то
_i. = r1+-r8 = 2a, -^ = 7-^ = ^A-^). A8.13.14)
Следовательно,
at = — н-/Bв), a2 = /^, A8.13.15)
где р = а A — е2) есть фокальный параметр эллипса.
Мы выяснили, таким образом, смысл всех параметров a, P, за исключе-
исключением Pi. Формула A8.12.9) показывает, что Pj = t0, т. е. определяет момент-
нахождения планеты в перигелии. Окончательно получаем
а, = -11/Bа), р1 = /0, "j
аа = Кн<Р. р2=—u0, v A8.13.16>
ab = V\ip cos i, P3= — Фо- i
Параметры а зависят лишь от а, е, и г. Шесть постоянных а, е, i, t0, и0, ф0
называют эллиптическими элементами.
§ 18.14. Выражение г как функции от t. Поскольку уравнение A8.12.9)
содержит только t и г, можно воспользоваться способом § 1.3, развитым для
систем с одной степенью свободы, и выразить г в виде функции от t. Отметим,
между прочим," что этот способ впервые был применен именно в задаче о дви-
движении планеты.
§ 18.14] ВЫРАЖЕНИЕ г КАК ФУНКЦИИ ОТ t 351
Уравнение A8.12.9) можно переписать в следующей форме:
t-to=\-7= r,dr =']/-[ / Tdr A8.14.1)
J V(-2ai) V(r2—r)(r-rj) * V- J У(г2 —r)(r —rj)
Имеем
1 1
r=rj cos2 yW-frj sin2 -z-w = a(\. —ecosu;), A8.14.2)
так что w представляет эксцентрический угол (в перигелии w = 0); в астроно-
астрономии эту величину называют эксцентрической аномалией. В этих обозначени-
обозначениях уравнение A8.14.1) принимает вид
V)
[rdw l/ (w-esmw). A8.14.3)
Отсюда получаем уравнение Кеплера, связывающее положение планеты на ор-
орбите со временем:
w — е sin w = n (t — t0), A8.14.4)
где n = jAjx/a3. Период обращения по эллипсу равен 2л/п, где среднее движе-
движение п представляет среднее по времени значение угловой скорости радиус-
вектора планеты; вращаясь равномерно с этой угловой скоростью, радиус-
вектор совершает один оборот за период обращения планеты. Уравнение
Кеплера было получено нами раньше (см. E.2.65) и E.5.6)).
Чтобы найти явную зависимость между (и г, представим г в виде ряда
Фурье:
— = -2-60+ 2 ^cos si, A8.14.5)
s=l
где I обозначает n(t — t0), а коэффициент bs определяется по формуле
, 2 f г , ,„ 2 Г г . Л» 2 п г' 1 . 7 ,
о. = — \—cos s/ at =-— —sinst I —sin si or =
nja ' я L«s Jo я J as
0 a(l-e)
2 С
= \ sin si (ae sin u?) du? =
nas J v '
0
= — \ (cos(sl-\-w) — cos (si — w)\dw, A8.14.6)
JtSJ14 v " v '
0
и так как из A8.14.4) l = w — esinu;, то получаем
зт
bs = —\ {cos [(s-\-1) w — se sin w] — cos [(s — 1) w — se sin w]} dw ~
0
— — (J , (se) — J , (se)\ C18 14 7)
где /,г (л") —функция Бесселя:
я
1 1*
/„ (а) = — \ cos {пВ — х sin 9) dQ =
о
(»/»)" Г, (ФI , (^/2L
~ п\ \ 1-(ге-
Таким образом, мы выразили г как функцию от t.
352 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ [Гл. XVIII
Для простых расчетов можно вместо явного соотношения воспользовать-
воспользоваться уравнениями A8.14.2) и A8.14.4) и выразить г через t с помощью проме-
промежуточной переменной w. Аналогичным способом можно выразить и через w:
, U— Игр -i/^l + ei 1 /ЛО л / с\\
tg—__o. = |/ _I_tgTu;, A8.14.9)
и, следовательно, косвенным образом через t.
§ 18.15. Угловые переменные. Формулы A8.12.9) —A8.12.11) опреде-
определяют элементы матрицы (a>rs). Переменная г в течение одного цикла изменяет-
изменяется от Г! до г2 и обратно, переменная Э — от —i до -\-.i и обратно, а переменная
Ф возрастает за один цикл на 2я. Таким образом, из формул A8.12.9) —
<18.12.11) имеем
сои = 2я/я, со21 = 0, .<о31 = 0, ^|
ю12=—2я, ю22 = 2я, оK2 = 0, [¦ A8.15.1)
со13 = 0, ?02з= — 2я, о)зз = 2я. J
Вводя угловые переменные (§ 18.6), получаем
^|
;2, [ A8.15.2)
J
•Следовательно,
} A8.15.3)
}
- j
2nv3 = ? + и0 + Фо
Частоты Hi, |д.2, Цз равны между собой, их общее значение составляет
п/2п. Координаты г, 9, ф являются периодическими функциями от v с перио-
периодом, равным единице, по каждой переменной. Таким образом, все они, как
и следовало ожидать, являются функциями от i с периодом 2я/и. Заданная
функция от г, Э, ф может быть выражена как функция от I, и0, ф0 с периодом
:2я по каждой из этих переменных.
§ 18.16. Постоянные I,.. Эти параметры с помощью формулы A8.12.8)
можно выразить через а, а стало быть, через эллиптические элементы а, е, i.
Найдем сначала /4:
V^2^1V(r2-r)(r-r1)^. A8.16.1)
п
Интегрирование можно произвести различными способами. Используя'
эксцентрическую аномалию, получаем
г = а A — е cos w), г — г4 = ае A — cos w), r2 — г = ае A + cos w),
A8.16.2)
и интеграл равняется
/, = /¦(=2^ t ,(Г51ПЦ))\^-2Л{^-]/^}. A8.16.3)
1 ' v J/ J a A — e cos w) r r-^J ч
0
Выразив правую часть через а, найдем
^ A8Л6-4)
18.16]
ПОСТОЯННЫЕ
353
Другой возможный способ мы приведем здесь в качестве иллюстрации приемов
интегрирования, хотя в данном случае он особых преимуществ не имеет. Рассматривая
г как комплексную переменную, произведем интегрирование
по контуру. Чтобы сделать подынтегральную функцию одно-
однозначной, произведем в плоскости разрез от ri до г2. Непо-
Непосредственно ниже разреза радикал будем считать поло-
положительным. Выражение A8.16.1) для It можно трактовать
как интеграл по простому замкнутому контуру С, охваты-
охватывающему разрез (рис. 70):
г
/-1 = У-2а1 V(r2~r)
с
A8.16.5)
рис
Обозначим через Г окружность , большого радиуса
с центром в точке О, а через у — малую окружность с
центром в той же точке; тогда подынтегральная функция
будет регулярна в замкнутой области, ограниченной снаружи
окружностью Г, а изнутри — контуром С и окружностью у. Можем написать
Г- С f
A8.16.6)
J J
с г v
Здесь интегралы берутся по контурам, проходимым в положительном направлении
(против часовой стрелки). Имеем
A8.16.7)
J У(г»-г)(г-Г1)?-=*-1 J V(r2-r) A4-г)-
Подынтегральная функция имеет простой полюс в начале координат с вычетом утуг2,
так что интеграл будет равен
— i-2ni Vnr2'= 2л Ут\г~г. A8.16.8)
Для интеграла по большой окружности получаем
{ri-r)(r-rl)^r=l \ V(r-ri){r-r2)^- = i
A8.16.9)
v'
Здесь мы перешли к новой переменной t = 1/г и обозначили через у' малую окружность
с центром в точке t = 0. В начале координат подынтегральная функция имеет полюс
второго порядка с вычетом-^- (rj + r2), так что интеграл A8.16.9) равен
... 1
Окончательно получаем
h = V-2O! {п (Г1 + г2) - 2я
-2я
У-2а,
A8 16.10)
A8.16.11)
что совпадает с полученным выше результатом.
Далее, имеем
Применив подстановку
23 Л. А. Парс
sin 8 = sin i sin u,
A8.16.12)
A8.13.8)
354 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ [Гл. XVIII
преобразуем этот интеграл к виду
= 2a2 [ (l--. .cf2' )du = 2а2я A - cos i) = 2я (а, - a3). A8.16.13)
j \ l — sin i sin и /
Вводя эллиптические элементы, находим
cosi). A8.16.14)
Наконец,
osi. A8.16.15)
Итак, имеем
lj?A = 2я(а2-а3), /3 = 2яа3. A8.16.16)
у — 2aj
Отсюда следует, что
Ii + I2+h = 2nyi/^^2^i, A8.16.17)
и, следовательно,
a, =* _2яу/(Л + /2 + /зJ. A8.16.18)
Мы здесь имеем пример особого случая, который упоминался в § 18.8.
Постоянная энергии aj зависит от единственной линейной формы от /, и воп-
вопрос о периодичности или непериодичности движения решается независимо
от начальных условий. В самом деле, в рассматриваемом случае все частоты
системы одинаковы и, поскольку at < 0, движение всегда периодично.
Общая величина частот равна
или
^3/2 i/| = ^T- A8.16.20)
Мы, таким образом, пришли к результату, уже полученному нами в § 18.15.
Переменные v можно выразить через величины, определяющие положение планеты.
Для этой цели заменим в формулах A8.15.3) величину I на w — e sin w, тогда получим
2яи1 = и; — е sin w, )
2nv2 = w — esinw + щ, \ A8.16.21)
2nv3 = w — esin №-| J
Эти формулы эквивалентны соотношениям, связывающим переменные q и и; они легко
выводятся на основе теории, изложенной в § 18.9. Чтобы получить выражение для К',
достаточно заменить параметры а. в формулах A8.12.8) их значениями, выраженными
через /:
2я2и2 1 1
= «2 = ТйГ('2 + /з) «з = -2^/3.. A8.16.22)
Тогда формулы A8.16.21) непосредственно следуют из уравнений A8.9.6).
§ 18.18] НЕОРТОГОНАЛЬНЫЕ И НЕНАТУРАЛЬНЫЕ РАЗДЕЛИМЫЕ СИСТЕМЫ 355
§ 18.17. Возмущения. До сих пор мы рассматривали движение одной
планеты относительно Солнца. Выясним теперь, какое влияние на это дви-
движение окажет наличие второй планеты.
Орбитой относительного движения первой планеты, строго говоря,
теперь уже не будет эллипс. Если, однако, вторая планета имеет достаточно
малую массу и удалена на достаточно большое расстояние, то ее влияние
на движение первой планеты будет мало. Поэтому можно считать, что эллип-
эллиптическая орбита первой планеты под влиянием возмущающего действия вто-
второй планеты медленно изменяет свои параметры. Исследование этих возмуще-
возмущений составляет основную задачу небесной механики. В настоящей книге мы
не имеем возможности подробно останавливаться на этих вопросах, хотя
позднее, в § 25.3, им будет уделено известное место. Здесь нее мы ограничимся
тем, что составим выражение для возмущающей функции R.
Обозначим массу Солнца через М, массу первой планеты — через т^
(см. § 18.12), а массу второй планеты — через т2. Пусть расстояния планет
Рис. 71.
от Солнца будут равны соответственно /-j и г2, а расстояние между планетами
г12. Ускорения Солнца и первой планеты выражаются суммами векторов,
показанных на рис. 71, а. На рис. 71, Ъ показано ускорение первой планеты
относительно Солнца. Обозначая через xit yt, zt и х2, z/2, z2 координаты пер-
первой и второй планет относительно Солнца, можем написать следующее
уравнение:
xt ут2 х2 утг хх—х2_ Э
Входящий сюда «гравитационный потенциал» U = — V равен
и= T(Jf+mi)> A8.17.2)
a R имеет выражение
jJ *1*+УУ+»М A8.17.3)
Аналогичные уравнения мы будем иметь и для координат у± и zlt а также
для координат второй планеты. При яг2 = 0 возмущающий член R пропадает,
и мы получаем знакомую нам задачу двух тел. Если масса тге2 мала, а расстоя-
расстояния г2 и ГB остаются в процессе движения достаточно большими, то влияние
возмущающего члена R можно рассматривать как постепенное изменение
эллиптического движения. В § 25.3 мы еще вернемся к этому вопросу,
§ 18.18. Неортогональные и ненатуральные разделимые системы. Системы, для
которых справедлива теорема Штеккеля, принадлежит к классу натуральных и орто-
ортогональных систем. Функция кинетической энергии Т для таких систем представляет
однородное квадратичное выражение от q и р; более того, это выражение содержит одни
23*
356 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ [Гл. XVIII
лишь квадраты. Существуют, однако, разделимые системы, которые не являются ни орто-
ортогональными, ни даже натуральными системами (так что для этих систем функция Т имеет
вид Г2 + Ту -f То).
Выше (в § 16.11) мы уже встречались с примером натуральной, но неортогональной
системы, допускающей разделение переменных; такой системой являлся вращающийся
волчок. Выбирая в качестве координат эйлеровы углы и считая функцию V зависящей
только от 9 (как это имеет место в обычных условиях, когда волчок движется под дей-
действием силы тяжести, а ось Oz направлена вертикально вверх), получаем систему, в кото-
которой переменные разделяются. В этой задаче обе координаты <р и г|) являются цикличе-
циклическими, что весьма существенно для вопроса о возможности разделения переменных.
Если исключить только координату г|) и составить функцию Рауса, то получится
ненатуральная система с двумя степенями свободы. Эта система также допускает раз-
разделение, если считать, что функция V зависит только от 9. В соответствии с форму-
формулой A0.5.12) имеем
y — V. A8.18.1)
Составим функцию Гамильтона. Определив импульсы по формулам
pe = AQ, рф = A sin26q)+ P cos 6, A8.1&.2)
Найдем
Й =±.А (fc+sirfB ^)+V = -^jpl+ 2A*.n2Q (рф-pcose^+F. A8.18.3)
Модифицированное уравнение в частных производных имеет вид
та (?)''+ы±ш (¦?-'—)''+"-•.• <'»¦'«>
Полный интеграл имеет форму
K = a2(f + f(Q), A8.18.5)
где функция / (9) удовлетворяет уравнению
(a^°s9J. A8.18.6)
Таким образом, ненатуральная системы A8.18.1) допускает разделение переменных.
Глава XIX
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ, ДВИЖЕНИЕ
В ОКРЕСТНОСТИ ОСОБОЙ ТОЧКИ
§ 19.1. Дифференциальные уравнения*). В предыдущих главах были
установлены некоторые принципы, дающие возможность решать ряд дина-
динамических задач или по крайней мере существенно продвинуться в этом напра-
направлении. Ряд задач относится к системам, которые обладают определенными
свойствами, упрощающими исследование, например свойством разделимости
переменных (гл. XVII и XVIII). Настоящая глава посвящена одной общей
задаче теории дифференциальных уравнений, имеющей непосредственное
отношение к классической механике.
Уравнения движения голономной системы кратко могут быть записаны
в следующей векторной форме F.4.4):
х = X. A9.1.1)
Здесь х = {хи х2, . . ., хт), X = {Хи Х2, . . ., Хт} и Хг = Хг (хи х2, ...
. . ., хт; t). Число т = 2га, т. е. равно удвоенному числу степеней свободы
механической системы. В скалярной форме уравнения имеют вид
хг = ХТ, ' г = 1, 2, . . ., т. A9.1.2)
В задачах динамики система т зависимых переменных разбивается на п
связанных менаду собою пар. В уравнениях Лагранжа ими являются пере-
переменные q и со, и уравнения имеют форму F.4.3):
qr = ©г, о>г = i|v, г = 1, 2, . . ., п.
В уравнениях Гамильтона такими парами переменных служат q и р (см<
A0.3.8)):
дг = дН/дрг, р\ = —dH/dqr, г = 1, 2, . . ., п.
Для наших целей в этой и следующей главе подразделение т перемен-
ных на пары не понадобится.
В большей части задач, представляющих практический интерес, функции-
ХТ зависят только от ж и не зависят от t. Системы такого рода называются
автономными. Неавтономную систему A9.1.2) с т зависимыми переменными
можно рассматривать как автономную систему с т. + 1 зависимыми пере-
переменными:
хт = Хт(х1у х2у ..., xm; xm+i), r=l, Z, .. ., т, I
} A9.1.3)
Хтл-i = !• '
Свойства решений системы A9.1.2) определяются свойствами функций ХТ; чем
больше предположений сделано относительно этих функций, тем больше соображений
можно высказать относительно решений. Напомним коротко основные результаты из
теории дифференциальных уравнений. Сначала будем предполагать, что все переменные
*) Доказательства теорем этого параграфа можно найти у Коддингтона и Левин-
сона [40]. Литература по общей теории нелинейных систем весьма обширна; см., напри-
например, [42—46], а также S. Lefschetz, Lectures on Differential Equations (Princeton,
1948); S. Lefshetz (ed.), Contributions to the Theory of Non-linear Oscillations
(Princeton, 1950). Пример A9.7.12) принадлежит Суиннертону — Дайеру.
358
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[Гл. XIX
вещественны, а затем покажем, что некоторые результаты можно распространить и на
случай комплексных переменных.
1) Основная теорема существования для уравнений A9.1.2) впервые была доказана
Пеано в 1885 г. Предположим, что функции X однозначны и непрерывны в области R,
которая является связным открытым множеством вещественного (т + 1)-мерного евкли-
евклидова пространства (хи х2, . . ., хт; t). Пусть (аь а2, . . ., ат\ х) будет точкой простран-
пространства R. Основной результат заключается в том, что существует решение уравне-
уравнений A9.1.2), проходящее через точку (а4, а2, . . ., ат; т). Точнее, существуют положи-
рщ р
тельное число хит функций
времени /,
у (i, 2,
{t), хг (t),
t—
хт (t), определенных на промежутке
и обладающих следующими свойствами:
a) хГ (т) = а/,
b) xr (f) существует и непрерывна в /;
c) точка [xj (t), x2 (t), . . ., хт (t); t] лежит в области R, если
d) ф () A912)
? /;
j (), 2 (), , т (); ]
) функции xr (t) удовлетворяют уравнениям A9.1.2).
Промежуток времени / можно взять замкнутым, если условиться считать, что про-
производные хТ (t) на концах промежутка равны их односторонним значениям.
Выше речь шла о фиксированной начальной точке («i, а2, • • •> °hn'y x) области R.
В более общем случае можно считать, что начальная точка выбирается произвольно среди
иочек некоторой подобласти области R; при этом решение будет зависеть не только от t,
но от m + 2 параметров: t\ аи а2, . . ., ат; т. Получаем
хг = фг (t;
a2,
. ., ат; т), г = 1, 2,
2) Основная теорема существования ничего не говорит о единственности решения.
В общем случае решение не является единственным, если только функции X не подчине-
подчинены некоторым дополнительным ограничениям. Для доказательства достаточно рассмо-
рассмотреть простой пример, в котором т = 1:
х = У\х~\.
Областью R в данном случае будет вся плоскость (t, x). В полуплоскости х
имеет вид
1
4
а в полуплоскости х <; О
0 решение
Кроме того, имеем решение х = 0, справедливое для всех t. Зависимость х от t для этих
решений показана графически на рис. 72. Из рисунка видно, что решение, соответствую-
соответствующее начальной точке (т, а), не является
единственным (одно из возможных решений
отмечено на рисунке жирной линией).
Если а Ф 0, то в некоторой окрестности
точки (т, а) решение единственно; если же
а = 0, то окрестности (т, а), в которой
решение единственно, не существует.
3) Промежуток времени / в формули-
формулировке основной теоремы существования в
общем случае не является наибольшим про-
промежутком, в котором существует решение,
проходящее через точку (oci, a.2, • • •, ami
т). Обычно этот промежуток можно
расширить влево и вправо и получить
решение, определенное на максимальном
открытом интервале а < t <; Ъ, называе-
называемом естественным интервалом определения
Рис. 72. решения. При этом числа а и Ъ зависят от
выбора точки (cci, а2, . . ., о^; /) и вы-
выбранной ветви решения, если оно не един-
единственно. В рассмотренном примере а может равняться —оо, а Ь может равняться +°°»
так что имеются четыре типа естественного интервала определения решения.
Если функции ХТ (xit хъ ..., xm; t) ограничены в области R, то при стремлении
t к конечной граничной точке естественного интервала (если такая точка существует)
§ 19.1] ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 359
решение [xi (f), х2 (t), . . •, хт (t); t] стремится к точке, расположенной на границе
области Л.
4) Положение существенно упрощается, если дополнительно предположить, что
функции Хг принадлежат к классу С\ в области Л. Это предположение приводит к сле-
следующим важным следствиям:
a) Решение, проходящее через точку («i, а2, . . ., ат; т),
хТ = <pr {t; «1, а2, . . ., ат; т),
является единственным.
b) Рассмотрим совокупность решений, проходящих через точки {а.\, а2, • • •> am> T)
подобласти D области R. Из сделанного предположения (о том, что каждое Хт ? C\
в области Л) следует ряд свойств решений как функций от (а4, а2, . . ., ат; т). Именно,
функции <рг имеют первые производные dcpr/3as и д<рг/дт и эти производные непрерывны
в области Е, определяемой условием
(«ь «2, • • -, «т; т) 6 D, а < t < Ъ.
c) Вторые производные d\r/dt2 и d2<pr/dt das = d\Tldas dt существуют и непре-
непрерывны в области Е.
5) В некоторых задачах функции X содержат параметры Xi, Я2, . . ., Хр. Обычно
приходится иметь дело со случаем, когда значения (Xlt Л2, . . ., %р) принадлежат неко-
некоторой области L, например окрестности выбранной точки (А^, Х$, . . ., Щ,). Решения
будут зависеть от параметров X (а также, конечно, от (, а и т):
хт = фг (f, a1( a2, . . ., am; т; Ки Х2, . . ., Хр), г = 1, 2, . . ., т.
Это решение определено в интервале а < t <; 6, причем пределы а и Ь зависят теперь,
помимо а и т, еще от параметров Я. Если считать, что функции Хг принадлежат классу d
в области Е, определяемой условием
(«1, а2, , . ., ат; т) ? D, а < * < Ь, (Яь Я2, . . ., Хр) g L,
то первые производные d<pr/dt, дц>г/да,, д<рг/дт, d<pr/dXs и вторые производные д\г/д№,
d\rldt das = d2<pr/das dt и d\r/dt dXs = d\rldXs dt существуют и непрерывны в обла-
области Е.
В дальнейшем, если не будет оговорено противное, всюду будет предполагаться,
что функции ХТ удовлетворяют условиям, сформулированным выше в пп. 4) и 5), так
что можно считать, что решения qpr обладают соответствующими свойствами дифферен-
цируемости.
Вернемся теперь к исследованию уравнений A9.1.2). Будем их рассмат-
рассматривать как уравнения, описывающие движение изображающей точки (xi,
х2, ¦" • ., хт) в ^-мерном пространстве; движение этой точки является ото-
отображением движения динамической системы (не только в д-пространстве,
но и в фазовом пространстве). Рассматриваемое пг-мерное пространство можно
считать евклидовым пространством с прямоугольными координатами ж1?
X<i, . . ., -Хт.
Иногда уравнения A9.1.2) удобно рассматривать не как уравнения, опи-
описывающие движение изображающей точки, а как уравнения, определяющие
движение жидкости в те-мерном пространстве. Скорость жидкости в точке
{xi, хг, . . ., хт} в некоторый момент t будет {Хь Хг, ¦ ¦ ¦, Хт}. Такое
представление позволяет нам вместо одного движения рассматривать целую
совокупность возможных движений (или по крайней мере движений, начи-
начинающихся в некоторой области (т + 1)-мерного пространства (ас, t)). Это
особенно важно в случае автономной системы; движение жидкости при этом
оказывается установившимся, т. е. скорость жидкости в любой заданной
точке одна и та же для всех значений времени t.
Иногда уравнения A9.1.2) удобно записывать в следующей форме:
^- = ^1=...=-^». = *. [A9.1.4)
Эта форма записи особенно полезна в случае автономной системы.
Решения уравнений A9.1.2) имеют вид
xr = qv (t; au a2, . . ., ат; т), г = 1, 2, . . ., т. A9.1.5)
360 СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [Гл. XIX
Если функции X обладают указанными выше свойствами, то существует
единственное движение изображающей точки, при котором х в момент t = т
принимает значение ос. Кривые в (т + 1)-мерном пространстве (ас, t), опре-
определяемые уравнениями A9.1.5), называются характеристиками.
В случае автономной системы обычно принимают т = 0 (что не нарушает
общности), так что х = а при t = 0. Функции Х\, Х2, . . ., Хт определяют
векторное поле в m-мерном пространстве х. Кривые в пространстве х, кото-
которые описывает изображающая точка безотносительно ко времени, называются
траекториями. Траектории представляют собой проекции характеристик
на пространство х. Уравнения A9.1.5), определяющие характеристики, одно-
одновременно дают параметрическое представление траекторий (через параметр t).
Кривые, определяемые уравнениями
* d d A9.1.6)
называются силовыми линиями. Через каждую обыкновенную точку поля
проходит единственная силовая линия, но через особые точки могут проходить
несколько силовых линий (например, через точку, в которой Х\ = Х2=~- ¦ ¦ ¦
. .. = Хт=0).
Траектории представляют собой дуги силовых линий, хотя, строго гово-
говоря, эти кривые не тождественны. Например, если а — особая точка, то начи-
начинающаяся в ней траектория есть сама точка. Силовая линия может проходить
через особую точку, тогда как соответствующая траектория никогда ее не до-
достигает. Задача отыскания характеристик распадается на-два этапа: опреде-
определение траекторий и установление связи между положением точки на траекто-
траектории и временем. После того как траектории найдены, второй из этих этапов
осуществляется просто, по крайней мере теоретически. Предположим, что
траектория задана в виде
хТ = г|)г (xi), г = 2, 3, . . . , т. A9.1.7)
Тогда связь между положением точки на траектории и временем определяется
из уравнения
Щ-=М, A9.1.8)
где
Х = Х(аг1) = Х1(ж1, *h, %, ...,^т). A9.1.9)
В случае автономной системы, если выходящая из точки а в момент
t = 0 характеристика задается уравнениями
хТ = фг (t; аь а2, . . ., аго), г = 1, 2, . . ., ш, A9.1.10)
то другая характеристика описывается уравнениями
хт = фг (t — t0; аи а2, . . ., ат), г = 1, 2, . . ., т. A9.1.11)
Все характеристики A9.1.11), соответствующие различным значениям
tQ, расположены на одной и той же траектории; различие между ними состоит
лишь в том, что изображающая точка при своем движении по разным харак-
характеристикам проходит данное положение на траектории в различные моменты
времени.
В случае автономной системы, если движение точки начинается в момент
t = 0 из положения А в m-мерном пространстве, то последующие (при
t ^ 0) положения изображающей точки составляют положительную полу-
полухарактеристику, исходящую из точки А. Аналогично, положения, занимае-
занимаемые изображающей точкой в моменты t ^ 0, при условии, что в момент t = О
§ 19.2] ДВИЖЕНИЕ ЧАСТИЦЫ ПО ПРЯМОЙ 361
она попадает в положение А, составляют отрицательную полухарактеристи-
полухарактеристику, начинающуюся в точке А *).
Решения уравнений A9.1.2) обладают рядом важных и интересных
свойств, в особенности для автономной системы; с некоторыми из них мы
познакомимся в гл. XXI. Однако единственным случаем, для которого в на-
настоящее время развита достаточно полная теория, является случай автоном-
автономной системы при т = 2. Именно этот случай будет предметом рассмотрения
этой и следующей глав. Простейшим примером может служить прямолинейное
движение частицы под действием силы, зависящей от а: и а: (но не от t). Возни-
Возникает вопрос: почему нельзя обобщить полученные результаты на случай
т >» 2? Невозможность такого обобщения связана, в частности, с тем обсто-
обстоятельством, что, согласно теореме Жордана, простая замкнутая кривая Г,
расположенная в плоскости П, делит область П — Г на две отдельные обла-
области, внутреннюю и внешнюю, с общей границей Г. В пространстве более чем
двух измерений подобная теорема не имеет места.
§ 19.2. Движение частицы по прямой. Обозначим через х смещение частицы в неко-
некоторый момент t относительно фиксированного начала координат О, выбранного на пря-
прямой. Если через т обозначить массу частицы, а через mF — действующую на нее силу, где
F = F(x, х, t), A9.2.1)
то уравнение движения будет иметь вид
У = F. A9.2.2)
Заменим это уравнение двумя уравнениями первого порядка типа A9.1.2), тогда будем
иметь
* = У, У = F (х, у, *). A9.2.3)
Если функция F не содержит ?, то система будет автономной.
Выше мы уже встречались с несколькими примерами подобных систем. В § 1.2
была рассмотрена задача о движении точки в силовом поле, когда функция F зависит
только от х.
Движение частицы под действием силы, зависящей от скорости (например, движе-
движение, в сопротивляющейся среде), также представляет собой простую задачу. Уравнение
движения в этом случае имеет вид
x'=f(x), A9.2.4)
и если сила обусловлена сопротивлением среды, то функция / (х) обращается в нуль
вместе с х и является монотонно убывающей. Представляет интерес случай, когда усло-
условие xf (x) <С 0 не выполняется; в этих случаях говорят об отрицательном трении. Урав-
Уравнение A9.2.4) эквивалентно системе двух уравнений:
*=V, » = /(»), A9.2.5)
причем второе из них не связано с первым, так как содержит только переменные у ш t.
Траектории в плоскости ху можно определить из уравнения
iHtH A9-2-6>
Кроме того, имеем
() A9-2-7)
и для сопротивляющейся среды правая часть отрицательна (за исключением случая
у = 0), так что кинетическая энергия движения всегда убывает с ростом t.
*) Сделаем одно терминологическое замечание. Поскольку речь идет о кривых в про-
пространстве as, а не в пространстве (ж, t), логичнее было бы говорить о положительных
и отрицательных полутраекториях, а не о полухарактеристиках. Тем не менее в даль-
дальнейшем мы будем придерживаться введенных здесь терминов.
362 СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [Гл. XIX
Классической задачей, приводящейся к уравнениям типа A9.2.1), является задача
о движении частицы в однородном силовом поле при сопротивлении, пропорциональном
скорости. Уравнение движения в этом случае имеет вид
"х = — g — к'х, A9.2.8)
где х измеряется в направлении, противоположном направлению поля. Решение, удо-
влетворяющее начальным условиям: при t = 0 х = х0, х = у0, имеет вид
к (х- х0) = (с + уй) A - егЫ) _ с (kt), A9.2.9
где с есть терминальная скорость g/k. Траектория в плоскости ху описывается урав-
уравнением
(^±Уу A9.2.10)
Прежде чем перейти к общей теории, остановимся на вопросе о движении в сопро-
сопротивляющейся среде под действием сил неоднородного поля общего вида. В этом случае
функция F задается суммой функции от х и функции от х и уравнение движения записы-
записывается в форме
x=—^- + f(x). A9.2.11)
Отсюда следует, что
^^ } A9.2.12)
и если сила mf (x) обусловлена сопротивлением среды, то правая часть уравнения отри-
отрицательна, и энергия Т -\- V монотонно убывает.
Рассмотрим в качестве примера осциллятор в среде с сопротивлением, пропор-
пропорциональным скорости. Уравнение движения такого осциллятора имеет вид
х + 2к'х + пах = 0. A9.2.13)
Будем рассматривать случай «слабого» сопротивления, когда 0 < к < п. Решением,
удовлетворяющим начальным условиям: х = а, х = и при t = 0, будет
х = е-М (a cospf + ^bi? sinpA , A9.2.14)
где р = ~\/пъ — к2. Выбрав подходящим образом начало отсчета времени, запишем реше-
решение в виде
х = Ае-Ы Sin pt. A9.2.15)
Отсюда
у = 'х = АегЫ (р cos pt — к sin pt). A9.2.16)
Определив острый угол а соотношениями
cos а sin а 1 , „ _.
—— = —- _, AЧ.глп
перепишем решение в следующей форме:
x = Ae-6tgasmd, у = пАе~в ^а cos (9 -fa), A9.2.18)
где 9 = pt. Эти уравнения определяют спиральную кривую, приближающуюся к точ-
точке О (рис. 73); она обладает свойством, выражаемым формулой
_ -ntga Н0 2 1сп
Колебания осциллятора, совершаемые вдоль прямой, затухают, и изображающая точка
стремится к положению О, соответствующему состоянию покоя.
Задача о вынужденных колебаниях осциллятора при наличии затухания
рассматривалась нами в § 9.10.
Движения, подобные только что описанному, составляют широкий класс задач,
и прототипом для них служит осциллятор. Пусть X (х) обозначает силу притяжения
к точке О, а / (х) — сопротивление трения. Функция X (х) монотонно убывает
f 19.3]
СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
363
убывает, обращаясь в нуль вместе с х; функция / (х) также монотонно убывает и обращает-
обращается в нуль при х = 0. Можно считать, что V @) = 0, так что V (х) > 0 при i^tOi моно-
монотонно возрастает с ростом х. При этих условиях движение представляет собой затухаю-
затухающее колебание, как это имело место в рассмотренном выше примере. Для доказательства
заметим, что с ростом t энергия — у2 -\- V монотонно убывает и при t ->- оо стремится
Li
к предельному значению С ^ 0. Случай С > 0, однако, невозможен. В самом деле, если
предположить, что С > 0, то мы имели бы
С A9.2.20)
и это соответствовало бы периодическому колебанию с постоянной энергией С на отрез-
ке (xt, х2) оси х,
хг. Соответствующей траекторией в плоскости ху была бы
замкнутая овальная кривая, подобная кривой Г
(проведенной сплошной линией на рис. 74). С дру-
другой стороны, если выражение -х- у2 + V монотонно
убывает, приближаясь к значению С, то изобра-
изображающая точка в плоскости ху описывает спираль,
Рис. 73.
Рис. 74.
стремящуюся к кривой Г (пунктирная кривая на рис. 74). При этом за промежуток
времени между двумя последовательными минимумами х энергия убывает на величину,
превышающую К, где
К=— '<
dr.
,A9.2.21)
Через у здесь обозначена положительная функция от х, график которой представляет
часть кривой Г в верхней полуплоскости. Но К > 0, так что спустя конечное число коле-
колебаний (между двумя последовательными минимальными значениями х) энергия будет
меньше С, каково бы ни было ее начальное значение. Таким образом, предположение,
что С > 0 приводит к противоречию, откуда следует, что С = 0. Траектория изображаю-
изображающей точки в плоскости ху имеет форму спирали, приближающейся к точке О (спираль
имеет вид, показанный на рис. 73); двигаясь вдоль оси х, частица стремится к положе-
положению равновесия О- Все эти результаты интуитивно понятньь
§ 19.3. Система с одной степенью свободы. Перейдем теперь от простых
частных случаев к рассмотрению автономной системы общего вида при т = 2.
Имеем векторное поле _F(обозначаемое в общем случае через X), составляю-
составляющие которого Р, Q принадлежат к классу d в области D плоскости ху. Урав-
Уравнения движения имеют вид
х = Р (х, у), у = Q(x,y) A9.3.1)
(движение системы мы представляем движением изображающей точки в плос-
плоскости ху).
364 СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [Гл. XIX
Точка х, у называется обыкновенной или регулярной, если для нее выпол-
выполняется неравенство Р2 + Q* > 0; если же Р = Q = 0, то она называется
особой точкой. В дальнейшем мы будем рассматривать лишь такие векторные
поля, для которых особые точки являются изолированными и якобиан }¦ ' у
отличен от нуля.
Траекториями будут дуги силовых линий, определяемых уравнениями
?~|. A9-3.2)
При этом, как уже отмечалось, через всякую регулярную точку проходит
одна-единственная силовая линия. Заданной точке А области D соответствует
единственное движение изображающей точки, при котором в момент t = 0
она занимает положение А. Если А есть особая точка, то проходящая через
нее траектория вырождается в самое эту точку, так что имеет место состоя- •
ние покоя. Если же А есть обыкновенная точка, то изображающая точка
удаляется от А вдоль проходящей через А силовой линии, с которой совпадает
соответствующая траектория.
Ниже мы увидим, что особые точки (дающие положения равновесия)
и замкнутые силовые линии (дающие периодические орбиты) играют особую
роль при изучении движения системы. Начнем с изучения движения в окрест-
окрестности особой точки.
§ 19.4. Движение в окрестности особой точки. Линейное приближение.
Возьмем начало координат в особой точке. Производя разложение в окрест-
окрестности особой точки (г = ]/"ж2 + У2 мало), будем иметь
, 1
, J
11 (я, У)
причем ad — be =?=0 и величины г/г, r\lr стремятся к нулю вместе с г. (В про-
простых случаях е и т) имеют порядок О (г2).) Естественно ожидать, что линейное
приближение (т. е. приближение, определяемое одними только линейными
членами, без учета членов, содержащих е и г\) даст нам возможность судить
о поведении движения и в общем случае. Поэтому начнем с рассмотрения
более простой задачи, когда уравнения имеют вид
х = ах -+- by,
A9.4.2)
y = cx-\-dy, )
или, в матричной записи,
х = Ах. A9.4.3)
Здесь х обозначает матрицу-столбец {х, у}, а А—неособенную матрицу
'а Ъ^
Как мы увидим, результаты исследования существенно зависят от соб-
собственных значений матрицы Л, определяемых как корни уравнения
\К1—А\ = 0 A9.4.4)
или, что то же,
%? — X (а + d) + (ad — be) = 0. A9.4.5)
$ 19.4] ДВИЖЕНИЕ В ОКРЕСТНОСТИ ОСОБОЙ ТОЧКИ. ЛИНЕЙНОЕ ПРИБЛИЖЕНИЕ 365
Если произвести линейное преобразование
х = Си, A9.4.6)
где С — неособенная матрица, а и есть вектор (матрица-столбец) {и, v},
то уравнение A9.4.3) перейдет в следующее:
и = Ви, A9.4.7)
где через В обозначена матрица С~гАС Матрицу С можно выбрать так, чтобы
матрица В имела простой вид — так называемую нормальную форму Жор-
дана. Этот выбор производится следующим образом.
а) Если корни А,ь Х2 вещественны и различны, то существует вещест-
вещественное линейное преобразование такое, что матрица В принимает вид
о J <19-4-8>
(вспомним преобразование к нормальным координатам в теории малых коле-
колебаний, см. § 9.2).
Ь) Если корни А,ь Х2 вещественны и одинаковы, то существует вещест-
вещественное линейное преобразование такое, что матрица В принимает форму
(о J
A9.4.9)
или форму
(n'lV A9.4.10)
с) Если корни Я,1, А,2 комплексны и Я,2 = Я,ь то существует комплексное
линейное преобразование такое, что матрица В принимает форму
UxJ-
A9.4.11)
Последнее эквивалентно утверждению, что с помощью надлежащего вещест-
вещественного линейного преобразования можно привести матрицу В к виду
/а -64
IP *У
A9.4.-12)
тде %i = а + Ф-
Рассмотрим характер движения в различных случаях.
1) Собственные значения вещественны и одно-
одного знака. Рассмотрим отдельно случай, когда они различны и случай,
когда они одинаковы.
1а) Собственные значения вещественны, не рав-
равны друг другу и имеют одинаковые знаки. Для опре-
определенности предположим, что собственные значения отрицательны, т. е.
Xi < А,2 < 0. Преобразованная система имеет вид
и = Xtu, v = X2v. A9.4.13)
Решение можно представить в форме
и = woe^i( = uoe-vii, v = уйех'г — уое^^г, A9.4.14)
где \it = —kt, |л4 > |л2 > (К
Малым значениям ух2-\-у2 соответствует малые значения у u2-\-v2 и
если У х2 + уг -V 0, то и У и2 -\- v2 -*- 0, так что расстояние изображающей
366
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[Гл. XIX
точки от начала координат Оща-t—v оо стремится к нулю. В таких слу-
случаях мы будем говорить, что траектория стремится к точке О. Далее, направ-
направление касательной к траектории при t -v оо и г -v 0 стремится к некоторому
.предельному направлению; мы будем говорить, что при этом траектория
входит в точку О. Чтобы доказать, что касательная к траектории стремится
занять предельное направление, рассмотрим отношение
J">*. A9.4.15)
Если v0 =fi=O, то оно стремится либо к +оо, либо к —оо. Таким образом, тра-
траектория входит в точку О вдоль положительного или отрицательного направ-
направления оси v. Если v0 = 0, то траектория представляет собой отрезок оси и
между и = и0 и и = 0. Таким образом,
вдоль оси и в точку О входят две траекто-
траектории (или, точнее, две системы полутраекто-
полутраекторий, поскольку изображающая точка дви-
движется к точке О вдоль положительного на-
направления оси и при всех положительных
значениях и0, а не только при каком-нибудь
одном значении). Мы имеем здесь случай,
описанный выше, в § 19.1. Траектория вхо-
входит в точку О, но сама эта точка не принадле-
принадлежит траектории, а является лишь предельной
точкой.
Таким образом, если Хг <С Х2 < 0, то
все положительные полухарактеристики вхо-
входят в точку О, из них две (или, точнее, две-
системы) входят в эту точку вдоль оси цт
а остальные — вдоль оси v (рис. 75). (Если
перейти к первоначальным переменным (х, у),.
тЪ направления, по которым кривые входят
в точку О, уже не будут составлять прямого угла.) Особенность такого типа
называют устойчивым узлом. Если Х± > Х2 > 0, мы имеем неустойчивый
узел; в этом случае в точку О входят отрицательные полухарактеристики.
1Ь) Собственные значения вещественны и равны
друг другу, и матрица
Рис. 75.
V с d—kj
имеет нулевой ранг. В этом случае b = с = 0, а = d =
нения имеют вид
х = %iX, 'у = Х1У,
и если Xi <С 0, например Х\ = —\х.и то решением будет
х =
Траекториями являются прямые
у =
х0
A9.4.16)
Xt. Урав-
A9.4.17)
A9.4.18)
A9.4.19)
и все положительные полухарактеристики входят в точку О. Эта точка снова
оказывается устойчивым узлом, но на этот раз, в отличие от случая 1а),
положительные полухарактеристики входят в точку О по всевозможным
направлениям (рис. 76). Если ^ > 0, то получаем неустойчивый узел. Осо-
Особенность этого типа редко встречается в практических задачах.
§ 19.4] ДВИЖЕНИЕ В ОКРЕСТНОСТИ ОСОБОЙ ТОЧКИ. ЛИНЕЙНОЕ ПРИБЛИЖЕНИЕ 367
1с) Собственные значения вещественны и рав-
равны друг другу, и ранг матрицы
fa-X1 b \ A9.4.20)
A9.4.21)
\ с d-j
равен единице. Матрицу можно привести к виду
-С? О-
Уравнения запишутся следующим образом:
и — Xiit, + v, v = XiV. A9.4.22)
Если Xi < 0, например Xt = — fxb то решение будет иметь вид
/ i j\ и i ii / (Л Q /i 9Q\
и = (u0 + vo4 е~^'¦ > у = ''о6'^1! \,1У-4-^«5;
и положительные полухарактеристики будут стремиться к точке О. Если
Рис. 76.
Рис. 77.
= 0, то траектория является частью оси и. Если v0
то отношение
- = —^— A9.4.24)
стремится к нулю, когда i-> oo, и положительная полухарактеристика вхо-
входит в точку О вдоль оси Ои. Мы снова имеем устойчивый узел, и все полуха-
полухарактеристики входят в точку О по направлению оси и (рис. 77). Если Я,4 > 0,
то получаем неустойчивый узел.
Итак, можно утверждать, что если собственные значения вещественны
и отрицательны, то особая точка является устойчивым узлом, если же эти
значения вещественны и положительны, то особая точка является неустой-
неустойчивым узлом.
2) Собственные значения вещественны и раз-
различны по знаку, скажем, Xt <c 0 <С А,2. Уравнения имеют вид
A9.4.25)
A9.4.26)
и = _ (х1М, v = X2v.
Решением будет
и = иое-М, v = vat***.
К точке О подходят лишь положительные полухарактеристики, для
которых v0 = 0. Остальные траектории представляют собой кривые типа
368
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[Гл. XIX
гипербол (точные гиперболы получаются при Xt — |j,i), а также (при и0 = 0)
ось v; изображающая точка движется по этим кривым в бесконечность
(рис. 78). Особенность этого типа называется седловой точкой или седлом.
Рис. 78.
Рис. 79.
3) Собственные значения являются комплекс-
комплексно-сопряженными (равны а ± *Р, а ^= 0). Вещественное
линейное преобразование в этом случае приводит к уравнениям
v = Р" + av, A9.4.27)
и = аи - Pi;,
или, в более компактной форме,
w = (а +
где w = и + iv- Решение имеет вид
w =
w, A9.4.28)
o pe^eW-'»), A9.4.29)
причем р и ^ вещественны, а и;0 = ре-*Р'». Переходя от декартовых координат
(и, у) к полярным "(г, 6), получаем
г = pea*, е = Р (* - *d). A9.4.30)
Если a < 0, то г -v 0 при ? -»- оо; при этом траектории стремятся к точке
О, но не входят в нее. Кривые имеют форму спиралей (логарифмических спи-
спиралей, если координаты прямоугольные), закручивающихся около точки О
в положительном направлении, если Р > 0 (рис. 79).
Особенность этого типа называется спиральной точкой или фокусом.
Фокус устойчив, если a < 0. Если a > 0, то получаем неустойчивый фокус;
в этом случае к точке О приближаются отрицательные полухарактеристики;
/•-»¦ 0 при t-*- —оо.
Пример 19.4А. Классический пример устойчивого фокуса мы имеем в случае
затухающих колебаний. Эта задача нами уже рассматривалась в § 19.2, здесь мы вкратце
повторим решение с целью проиллюстрировать выводы общей теории. Уравнения движе-
движения имеют вид
Собственные значения
перепишем уравнения
х —
равны —к J
и ~
в форме
У, У
zip.
= кх -
•
и = —ки —
II,
где
+¦ У'
pv,
— П А
Р =
V
V =
¦ — бпу
-- yV ¦
= Рх,
= ри —
- л2.
• kv.
Вводя
новые переменные
A9.4.32)
A9.4.33)
19.4J ДВИЖЕНИЕ В ОКРЕСТНОСТИ ОСОБОЙ ТОЧКИ. ЛИНЕЙНОЕ ПРИБЛИЖЕНИЕ 369
В полярных координатах (и = г cos 6, v = r sin 6) имеем
г = — кг, 6 = р.
Решение имеет вид
г = гое-Ы, 6 = р<.
Мы приняли, что 6 = 0 при t = 0. Таким образом,
i, у = roe~fti! sin pi.
Следовательно,
v
A9.
A9.
A9,
A9
A9
A.
Л.
.4.
.4
.4
34)
35)
36)
.37)
.38)
x = — = Ae~bt sin pt,
P
kv
y= и =Ае~м (p sin pi—«cos pt),
где A = го/р. Мы получили формулы A9.2.15), A9.2.16); траектория в плоскости ху
показана на рис. 73.
4) Собственные значения чисто мнимы (равны
± гР). Этот случай мы получаем из предыдущего при а = 0. Уравнения име-
имеют вид
'и = — рУ, v = Ри. A9.4.39)
Решением будет
г = г0, 0 = р (* — д. A9.4.40)
В плоскости му траектории представляют собой окружности, а в плоскости
ху — эллипсы. Мы имеем здесь исключительный случай, когда все траекто-
траектории являются замкнутыми и, следовательно, все орбиты периодические.
Особенность такого типа называется вихревой точкой или центром.
Пример 19.4В. Классический пример вихревой точки дает гармонический
осциллятор (пример 1.2А). Движение его описывается уравнением второго порядка
"х + А = 0 A9.4.41)
или двумя уравнениями первого порядка
'х = у, у = —/Ас. A9.4.42)
Собственные значения равны ±г. Полагая и = пх, v = у, получаем
'и = nv, v = —пи. A9.4.43)
Решением в плоскости uv (и = г cos 9, v = r sin 6) будет
г = Го> 0 = —п (i _ t0). A9.4.44)
Отсюда получаем известное решение в координатах х, у:
х = с cos п (t — tn),
¦ ,, *, г A9.4.45)
у= —ncsmn(t — tQ). J
Траекториями в плоскости ху являются эллипсы
п2х2 + у% = const. A9.4.46)
Пример 19.4С. Для системы
'х = х + у, У = —2х ~ у A9.4.47)
собственные значения равны ±i. Траектории находим из уравнения
Bх + у) 'х + (х + у) у = 0. A9.4.48)
24 л. А. Парс
370
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[Гл. XIX
Решая его, получаем
2хг + 2ху + у2 = const. A9.4.49)
Следовательно, траекториями являются эллипсы (рис. 80). (Чтобы построить траектории,
заметим, что
" (V5-D2 '
причем tga=l/2("|/5—l).)
Эта система фактически эквивалентна предыдущей, так как уравнения, можно
записать в виде
а
и = v, i>= —и, A9.4.50)
где и = х и v = х -\- у. Решение будет иметь вид
и = с cos (t — *„)> г> = — с sin (г — <„). A9.4.51)
Траекториями в плоскости иу будут окружности
иг _|_ у2 = Const. A9.4.52)
Уравнения A9.4.52) и A9.4.49), очевидно, эквива-
эквивалентны.
§ 19.5. Устойчивость равновесия. Асимп-
Асимптотическая устойчивость и неустойчивость.
Особые точки поля, или точки равновесия,
представляют собой те точки, в которых изо-
бражающая точка может находиться в покое.
Продолжим исследование устойчивости системы,
которое мы начали в гл. IX.
Мы будем говорить, что положение равно-
равновесия, соответствующее особой точке О, устой-
устойчиво, если траектория, начинающаяся в окре-
окрестности точки О, остается вблизи нее и в дальнейшем. Пусть г (t) — расстоя-
расстояние изображающей точки от точки О в некоторый момент Р.
Рис. 80.
= | х (t) | =
У2
Дадим строгое определение устойчивости: равновесие является устойчивым,
если для любого е > 0 существует положительное число х = х (е) такое, что
если г @) <С х, то г (t) <; е при t ^- 0 *).
В этом определении не указывается точная величина х (е); если считать
ее наибольшей из возможных, то х (е) будет монотонной функцией от е
и х (е) —> 0 вместе с е. Если равновесие в точке О устойчиво по отношению
к любому достаточно малому х, то существует положительное число е такое,
что при г @) < х имеет место неравенство г (t) <C г при t >- 0.
В теории малых колебаний мы исходили из уравнений Лагранжа, которые пред-
представляют собой уравнения второго порядка. Здесь же мы имеем уравнения первого
порядка, и поэтому при определении устойчивости нужно иметь в виду, что малость
г означает как малость самого отклонения, так и малость скорости динамической
системы. Рассмотрим, например, простой случай, когда х представляет лагранжеву
координату динамической системы с одной степенью свободы и первое из уравне-
•
ний A9.3.1) имеет вид х = у. Особые точки (х0, 0) дают конфигурации х = х0, при кото-
которых система может находиться в покое; при этом требование малости величины г =
= У (х — х0J -)- ха означает не только малость отклонения системы от положения
равновесия, но также и малость скорости.
*) Существует более точное определение устойчивости, согласно которому тре-
требуется, чтобы при г @) < х имело место неравенство г (?) < е при всех значениях t
(т. е. как при t <; 0, так и при t ^ 0). Это уточнение, впрочем, не имеет большого значе-
значения для динамики, и мы не будем придерживаться его в этой книге.
§ 19.6] ДВИЖЕНИЕ В ОКРЕСТНОСТИ ОСОБОЙ ТОЧКИ. ОБЩАЯ ТЕОРИЯ 371
В некоторых приведенных выше примерах рассматривалось более силь-
сильное условие, нежели условие устойчивости, а именно, чтобы траектории,
начинающиеся вблизи от точки О, приближались к этой точке; при этом дви-
движение системы затухало и изображающая точка стремилась к состоянию
покоя в особой точке. В подобных случаях говорят об асимптотической
устойчивости. Равновесие называется асимптотически устойчивым, если
оно устойчиво в обычном смысле и если, кроме того, существует положитель-
положительное число х такое, что если г @) < х, то г (t) -v 0 при t -*- оо.
Неустойчивость означает отсутствие устойчивости. Следовательно, рав-
равновесие в точке О неустойчиво тогда и только тогда, когда существует поло-
положительное число х такое, что можно указать траекторию, начинающуюся
в произвольной близости от точки О, такую, что для некоторых положитель-
положительных значений t выполняется неравенство г (t) > х.
Заметим, что это определение неустойчивости не требует, чтобы г (t) > x для всех
достаточно больших значений I или даже для некоторых произвольно больших t, хотя
во многих конкретных примерах то или иное из этих условий обычно выполняется.
В § 19.4 мы рассмотрели все возможные типы особых точек линейной
системы. Одним из них является вихревая точка. Вихревая точка устойчива.
Траектории в окрестности такой точки представляют семейство подобных
эллипсов с центром в точке О; рассматривая эллипс с большой полуосью,
равной е, мы можем взять в.качестве х (е) малую полуось этого эллипса.
Устойчивые узлы и фокусы одновременно устойчивы и асимптотически. Сед-
ловые точки, а также неустойчивые узлы и фокусы неустойчивы. (Чтобы
получить уравнения в форме, в какой мы их писали в § 19.4, следует приме-
применить линейное преобразование
х = Си, A9.4.6)
где С — вещественная неособенная матрица размером 2x2. Для того чтобы
сделать заключения относительно устойчивости в различных случаях,
достаточно заметить, что | х | = 0 тогда и только тогда, когда | и | = 0,
и | ж | мало тогда и только тогда, когда мало | и |.)
Все это относится к случаю линейного приближения, поэтому возникает
естественный вопрос: можно ли судить об устойчивости по результатам иссле-
исследования линейного приближения? Как станет видно из дальнейшего, в рас-
рассматриваемом случае, когда т = 2, это можно сделать, за исключением
случая вихревой точки, когда имеется устойчивость в линейном приближе-
приближении. В последнем случае исследование точных уравнений может показать
как устойчивость, так и неустойчивость *).
Определения устойчивости, асимптотической устойчивости и неустой-
неустойчивости допускают, как мы увидим, распространение на случай, когда
т> 2. Позже (в § 23.7) будет произведено также обобщение понятия устой-
устойчивости на случай движения механической системы, когда вместо вырожден-
вырожденных траекторий, состоящих из изолированных равновесных точек, рассмат-
рассматриваются собственно траектории. (Один частный пример на исследование
устойчивости движения был приведен в § 9.6.)
§ 19.6. Движение в окрестности особой точки. Общая теория. Перейдем
теперь к общей теории движения в окрестности изолированной особенности
поля F. Поместим начало координат, как и в § 19.4, в особую точку. Тогда
*) Другим исключением является случай нулевого собственного значения, до сих
пор не рассматривавшийся. В этом .случае линейное приближение не дает представления
о действительном поведении системы (см. ниже примеры 19.11В и 19.НС).
24*
372 СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [Тл. XIX
уравнения запишутся в форме
x = ax-\-by+e(x,y), \ A9.6.1)
Здесь ad — 6с ^0 и е/r и T)/r-v 0 вместе с г.
Обозначим через J^o поле, определяемое одними только линейными чле-
членами:
Ро = ах + by, Qo = ex + dy. A9.6.2)
Вблизи точки О поле F мало отличается от Fo, точнее, при г—>-О
| F\ /| Fo I -> 1 и i|> -v 0, где г|) — угол между Fo и I*7. Это утверждение почти
очевидно. Чтобы доказать его формально, заметим, что
F0(r,Q)--=rFQ(l, В) A9.6.3)
и отношение | Fo \/г не обращается в нуль. В самом деле, \ F0\/r^> с^> О,
где с —нижняя граница |.F0| на единичном круге. Кроме того, при г—>0
| F-Fo |/г = ]/> + tiVr-> 0. A9.6.4)
Таким образом, | ^—Fo |/| JF01—>0, когда г—»0. Далее,
|^| = |^0 + ^-^0| = |^0| + X|JP-ir0|, A9.6.5)
где | Я |-^1, следовательно,
и первое утверждение, таким образом, доказано. Доказательство второго
утверждения следует из условия
sini|;<l^~Jo1 -»0. A9.6.7)
Иногда рассматривают радиальную и трансверсальную составляющие
поля F; обозначим их соответственно через R и S, а составляющие^ — через
#о и So.
Поле Fo мы исследовали в § 19.4; выясним теперь, в какой степени дви-
движение в окрестности точки О в поле F отличается от движения в окрестности
этой точки в поле J^o- Однако теперь, в отличие от поля!^, мы ограничимся
характеристиками, начинающимися вблизи точки О.
Как мы увидим, движение в окрестности узла, седла или фокуса подобно
соответствующему движению для поля Fo. Исключение составляет вихревая
точка. В этом случае линейных членов недостаточно, чтобы решить вопрос
об устойчивости. Это является несколько неожиданным, в особенности если
учесть, что сюда относится задача о малых колебаниях (гл. IX). Однако в слу-
случае малых колебаний мы располагаем некоторыми дополнительными данны-
данными, получаемыми из уравнения энергии, факт устойчивости мы знаем зара-
заранее, и линейная теория в этом случае дает хорошее приближение к действи-
действительному движению. Но в общем случае оснований для такого рода утверж-
утверждений нет.
Рассмотрим сначала положительную полухарактеристику, которая стре-
стремится к точке О и входит в нее. Если при f-v oo у/х —>• Z, то одновременно
ylx-^r- l, и поскольку
i + d + g j
$ 19.7]
ДВИЖЕНИЕ В ОКРЕСТНОСТИ УЗЛА
373
находим
c + dl
A9.6.9)
Вектор {1, 1} представляет собственный вектор матрицы Л. Таким образом,
если собственные значения Хх и Х2 вещественны и различны, то могут сущест-
существовать лишь два направления (или четыре, если различать положительные
и отрицательные), по которым траектории входят в точку О; если же собствен-
собственные значения комплексно-сопряженные, то ни одна траектория не может
входить в точку О.
Рассмотрим теперь движение в окрестности особых точек различных
типов.
§ 19.7. Движение в окрестности узла. Соответствующим аффинным
преобразованием координат уравнения можно привести к виду
jX -f
е(я, у), 1
A9.7.1)
О вместе с г.
Здесь мы вместо и, v ввели новые переменные х, у и е/r и ц/г-
Рассмотрим более подробно случай Xi < Я,2 < 0.
Введем в новой плоскости ху полярные координаты, тогда для радиаль-
радиальной составляющей будем иметь
RJr = — (hi cos2 0 + |Л2 sin2 9) < —|л2 < 0, A9.7.2)
где \it = —kt (см. A9.4.14)). Отсюда следует, что существуют расстояние
г0 и положительное число ц такие, что для г ¦<; г0
д/г < _,х < 0. A9.7.3)
Рассмотрим теперь характеристику (г (t), 9 (t)), начинающуюся в точке
внутри круга радиуса г0, г @) <С г0. Поскольку г = R < 0, изображающая
точка располагается в этом круге и при t> 0, и
1 ЙГ R ^ /л г\ п /\
Следовательно,
г (t) < г @)
A9.7.5)
Таким образом, если t —v оо, то г (t) —>- 0, и
каждая положительная полухарактеристика,
начинающаяся в достаточно малой окрестности
точки О, приближается к О. Более того, траек-
траектория входит в точку О либо вдоль оси Оу, либо
вдоль оси Ох. В самом деле, можно пока-
показать, что отношение у (t)/x (t) при t-*- оо стре- рИс^ 81.
мится либо к -f-oo, либо к —оо, либо к нулю.
Для этой цели возьмем угол б и рассмотрим углы At = At (б) раствором 26
каждый (рис. 81). Для поперечной составляющей имеем
SJr = (|j,i — fx2) cos 8 sin 9, A9.7.6)
так что вне углов Аг будем иметь
|?0 \1г > (ц! — fx2) cos б sin б > 0. A9.7.7)
Следовательно, существуют расстояние г^ = гх (б), гх ^г0, и положитель-
положительное число |д/ такие, что в точках вне областей А1 и внутри круга радиуса г.
374 СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [Гл. XIX
выполняется неравенство
| S |/r > fx' > 0. A9.7.8)
Вообще говоря, чем меньшее значение мы берем для б, тем'меньшее зна-
значение нужно для Гц. Области, расположенные внутри круга радиуса г^ вне
секторов Аг, будем обозначать через 5Ь Вг, В3, 54 (рис. 81). Угловая ско-
скорость 0 изображающей точки равна S/r; в областях В^ и В3 имеем
в>|х'>0, A9.7.9)
а в областях В2 и Вк
в<—ц'<0. A9.7.10)
Рассмотрим положительную полухарактеристику, начинающуюся
в точке области Вг. Так как rx ^L r0, то траектория стремится к точке О,
и поскольку в области Bt 9 > ц', изображающая точка входит в область А2.
Но, оказавшись в области А2, изображающая точка остается в ней. Для дока-
доказательства достаточно указать направление поля F в точках на границе сек-
сектора. Траектория может пересекать ось Оу. Далее, заменим б на уй и рас-
рассмотрим точку на той же траектории в момент времени t, выбранный так,
чтобы r(t)<Zri (у б ) . Если точка в этот момент еще не находится в области
Аг (у б), то, рассуждая, как и выше, заключаем, что она попадет туда и оста-
останется там.
Таким образом, применяя повторно этот метод, мы видим, что при любом
заданном х\ > 0, как бы мало оно ни было, существует время т = т (т)) такое,
что при t > т
4-я-т]<8(г)<уЯ + г|, A9.7.11)
и траектория входит в точку О вдоль положительной оси у.
Если изображающая точка начинает движение в момент t = 0 из обла-
области В2, то траектория опять-таки входит в точку О вдоль положительной оси
у. Если она начинает движение из области В3 или 54, то траектория входит
в точку О вдоль отрицательной оси у. Каждая положительная полухаракте-
полухарактеристика, которая не входит в точку О вдоль оси х, входит в нее вдоль оси у.
Остается открытым вопрос, существует ли траектория, которая входит
в точку О вдоль оси х. На этот вопрос можно дать утвердительный ответ. Для
доказательства рассмотрим дугу CD окружности г = гь лежащую в области
Ai. Предположим, что в момент t — 0 изображающая точка начинает свое
движение из некоторого положения на дуге CD. Если ни одна из начинающих-
начинающихся на дуге CD положительных полухарактеристик не входит в точку О вдоль
оси х, то все эти кривые входят в точку О вдоль оси у сверху или снизу. Одни
из них попадут в область А2 (и войдут в точку О вдоль положительной оси у),
другие попадут в область At (и войдут в точку О вдоль отрицательной оси у).
Поэтому на дуге CD можно указать два непустых множества точек, в зави-
зависимости от того, входит ли траектория в область Аг или Ак. Эти множества
являются открытыми, поскольку решение изменяется непрерывным образом
в зависимости от начальной точки, так что на дуге CD существует хотя бы
одна точка, которая не принадлежит ни одному из этих множеств. Эта точка
дает начало траектории, входящей в точку О по направлению оси Ох. (Сущест-
(Существует, однако, важное отличие от линейного случая, состоящее в том, что тра-
траектория, входящая в точку О вдоль оси Ох, не. обязательно является единст-
единственной *). Так, например, система
'х = —2а:, 'у = —у — За:2 sin (лу/2х2) A9.7.12)
*) Если дч\1ду ->- 0 вместе с г, то имеет место единственность.
§ 19.8] ДВИЖЕНИЕ В ОКРЕСТНОСТИ СЕДЛОВОЙ ТОЧКИ 375
имеет бесконечное множество траекторий, входящих в точку О вдоль оси
Ох, в частности кривые у = 0 и у = х2.)
Итак, поведение в окрестности узла в основном такое же, как и в рассмот-
рассмотренном ранее линейном приближении.
Случай, когда Хх = Х2, можно исследовать аналогичным образом; устой-
устойчивость узла определяется одними лишь линейными членами. В обычных
случаях, когда е и т) имеют порядок О (г2), узел остается узлом. В более
общем случае, когда г/г—>-0, г]/г—»-0, узел может превратиться в фокус.
Пример 19.7. Рассмотрим систему, движение которой описывается
уравнениями
х = —[1х + е, у = —цу -f т), A9.7.13)
где ц > 0 и
е = -sine/(r), ti = cos6/(r), A9.7.14)
Если в начальный момент г = г0 < г±, то
г = —цг, г = гое~»{ A9.7.15)
и траектория стремится к точке О. Кроме того, имеем
6= * = k == /._L=-. A9.7.16)
Интегрируя, получаем
8-eo = ^]/^+ln^-, A9.7.17)
так что особенностью полного поля является фокус. Согласно линейному
приближению особенность представляет собой устойчивый узел.
§ 19.8. Движение в окрестности седловой точки. Запишем уравнения
в форме
* = М+в(*. У),
где ki < 0 < %2- Имеем
R0/r = X2 sin26 — jj,! cos2 9 = (hi + Я2) sin29 — fxt =
= ^2 — (и + Я,2) cos2 e. A9.8.2)
Можно указать такой угол б и такую положительную постоянную К, чтобы
R0/r>K>0 для областей A2, Ai} "I
/
R0/r<i—К <0 для областей Аи Аг
(обозначения см. на рис. 82). Кроме того, имеем
SQ/r = (|л4 + к2) cos 0 sin 6, A9.8.4)
так что
S0/r > (uj + X2) cos б sin б > 0 для областей В., В3, "I
а - d n i A9.8.5)
для областей В2, В±. )
376 СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [Гл. XIX
Аналогичные результаты можно получить и для Rlr и Sir, если рассмат-
рассматривать точки в достаточной близости от точки О. Существуют расстояние
гх = Г! (б) и положительные числа к, к' такие, что если г ¦< гь то
r = R> Ат->0 для областей A2, At, I ... o „.
\ A9.8.6)
для областей Аь А3 J
6 = S/r > Л' > 0 для областей Z^, Z?3,
Q = S/r<Z—&'<<0 для областей 2?2, Д,.
Рассмотрим траекторию, начинающуюся в области В±. Поскольку в этой
области 8 > /с', изображающая точка перейдет в область Аг (если только
перед этим она не выйдет за пределы круга
г = Г[). Как и ранее, оказавшись в обла-
области А 2, изображающая точка останется в этой
области. Но в области А2
r> kr, r>roeht, A9.8.8)
что указывает на то, что при дальнейшем
движений изображающая точка покинет круг.
Итак, либо точка попадает в область А2 и
затем выходит за пределы круга г = г1; либо
она покидает этот круг прежде, чем вхо-
входит в область А2. Особая точка неустой-
неустойчива, что совпадает с результатом, получен-
полученным при линейном приближении.
Рис- 82- Как и в случае линейного приближе-
приближения, существует одна-единственная траекто-
траектория, которая входит в точку О по направлению положительной оси х.
Для доказательства рассмотрим траектории, начинающиеся в точках дуги
CD окружности г = гг. Траектория с началом в точке D попадает в область
Bi, после чего она покидает пределы круга в точке, расположенной выше
оси Ох (как мы видели выше). Аналогично, траектория, начинающаяся в точ-
точке С, попадает в область 54 и потом выходит из пределов круга в точке ниже
оси Ох. Если теперь предположить, что все траектории, начинающиеся в точ-
точках дуги CD, принадлежат к одной из двух этих групп (т. е. они покидают
пределы круга либо в верхней, либо в нижней полуплоскости), то придем
к противоречию. На дуге CD имеем два открытых множества, следовательно,
существует хотя бы одна разделяющая их точка, которая не принадлежит
ни к одному из этих множеств; начинающаяся в этой точке траектория не от-
относится ни к одной из указанных групп. Эта траектория не покидает преде-
пределов области Ai и, следовательно, входит в точку О вдоль оси Ох. Но с помо-
помощью тех же рассуждений можно доказать, что существует по крайней мере
одна траектория, входящая в точку О слева по оси Ох.
Пример 19.8А. Простой маятник. В качестве примера рассмотрим
простой маятник вблизи положения неустойчивого равновесия. Если отсчитывать зна-
значения 6 от верхней точки окружности, то уравнение движения запишется в форме
б' - п* sin 6 = 0, пг = gla. A9.8.9)
Оно эквивалентно двум уравнениям первого порядка:
ё=ф, ф= гс2 sine. A9.8.10)
Напишем линейное приближение:
ё = ф, ф = п2в. A9.8.11)
19.8]
ДВИЖЕНИЕ В ОКРЕСТНОСТИ СЕДЛОВОЙ ТОЧКИ
37?
Собственные значения равны +ге, особая точка представляет собой седло. Из предыду-
предыдущего нам известно, что существует траектория, которая входит в особую точку с двух
противоположных сторон; в соответствующих лимитационных движениях маятник дости-
достигает верхней точки окружности.
На рис. 83 показаны траектории для общего случая (не только для случая движе-
движения вблизи особой точки). Особенности расположены на линии ф = 0 в точках 6 = 0
и 6 = ±гея; точки 6 = 0 и 6 = ±гея (где л
четное) являются седлами, точками неустой-
неустойчивого равновесия, а 6 = я и 6 = +гея (где п
нечетное) представляют собой вихревые точки,
точки устойчивого равновесия. Уравнения
траекторий имеют вид
?2=uJ_4re2cos2-i 6, A9.8.12)
где (о — угловая скорость в нижней точке
окружности; уравнение A9.8.12), разумеется,
эквивалентно уравнению энергии. Для коле-
колебательных движений | со | < 2п, для движе-
движений, в которых 6 непрерывно возрастает или
убывает, | со | > 2ге. В критическом случае,
когда энергетический уровень касается окружности в ее верхней точке, | со [ = 2ге.
Разделяющая кривая, или сепаратриса, определяется уравнением ф = —2п sin — 9>
1
(кривая ф = 2п sin -j- 6, изображенная на рисунке пунктиром, соответствует движе-
движению, когда при t —>- оо 6 -*¦ 2я снизу; физически это движение не отличается от лимита-
ционного движения, в котором при t -*¦ оо 6 —>- 0 снизу, так что фактически пунктирная
кривая также является частью сепаратрисы).
Пример 19.8В. Маятник в сопротивляющейся среде. Рас-
Рассмотрим теперь случай, когда маятник движется в сопротивляющейся среде. Пусть,
например, бусинка скользит по гладкой вертикальной проволочной окружности, испы-
испытывая сопротивление, пропорциональное скорости. Отсчитывая 6 от верхней точки
окружности, запишем уравнение движения в форме
Рис. 83.
е + 2*е — rfi sin e = о.
Оно эквивалентно двум уравнениям первого порядка:
9 = ф, ф = п2 sin Э — 2й
Первое приближение будет иметь вид
A9.8.13)
A9.8.14У
= Ф, ф = п2% — 2Аф.
A9.8.15)
Собственные значения равны —к ± р, где р = ~\/к2 + п2. Точка 6 = ф = 0 является
седловой точкой. Существует траектория, которая входит в это седло с двух сторон.
В любой точке окружности можно сообщить бусинке такую начальную скорость,
которая будет как раз достаточна для того, чтобы бусинка достигла верхней точки, хотя'
время для этого может потребоваться бесконечно большое. Это чувствуется интуитивно.
Можно представить, что существует критическое значение начальной скорости, ниже
которого бусинка не дойдет до верхней точки окружности, а выше которой — пройдет ее.
Интересно рассмотреть совокупность траекторий в общем случае (а не только вблизи
седловой точки). Заменив 6 на х и выбрав соответствующий масштаб времени, можно
уравнение записать в следующей форме:
"х + 'х — р sin х = 0, A9.8.16)
где р = п2Цк2; соответствующие уравнения первого порядка будут иметь вид
х — У, У = Р sin х — у. A9.8.17)
В подобных задачах обычно удается построить силовые линии графически.
Построим сначала (рис. 84) кривую у = р sin x. Перпендикуляр к оси Ох, опущенный:
378
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[Гл. XIX
из произвольной точки А, пересечет синусоиду в точке В, а ось Ох в точке N. На оси Ох
выберем точку С, лежащую слева (справа) от точки N на расстоянии АВ, если точка А
расположена выше (ниже) точки В.
Вектор поля в точке А имеет направ-
ление, перпендикулярное к С А. На
рис. 85 показаны силовые линии этого
поля, которые являются траекториями
Рис. 85.
рассматриваемой динамической задачи. Точка неустойчивого равновесия F = ф = 0)
является седлом, а точка устойчивого равновесия (Э = л, ф = 0) — устойчивым фокусом.
§ 19.9. Движение в окрестности фокуса. Приведем уравнения к нор-
нормальной форме:
(*, У),
(х, У).
A9.9.1)
Здесь а, ± if} — собственные значения, а е и т) таковы, что отношения г/г,
¦ц/r стремятся к нулю вместе с г. Для определенности предположим, что
а < 0 и р > 0. Далее, Ro = ar, So = pY, так что траекториями поля Fo
будут спирали, закручивающиеся в положительном направлении около
точки О. В точках, достаточно близких к точке О, поле F мало отличается
otIjFq) так что при г < г0 имеем
Rlr < _& < 0, S/r > к' > 0. A9.9.2)
Положительная полухарактеристика, начинающаяся в точке круга
г <С г0, снова оказывается спиралью, закручивающейся около точки О;
при этом при t —у оо г (t) —v 0 и 0 (t) —>• оо. Мы вновь приходим к выводу, что
характер поведения траекторий вблизи особой точки определяется одними
только линейными членами. Если а <С 0, то особая точка устойчива; если
<х > 0, то неустойчива.
Этот случай иллюстрируется также примером 19.8В. Если отсчитывать Э от нижней
точки окружности, то уравнение движения запишется так:
е + 2&е + пг sin б = о.
Соответствующие уравнения первого порядка будут иметь вид
6 =
= — пг sin 9 — 2А:ф.
A9.9.3)
A9.9.4)
Собственные значения равны — k ± ip, где р = ^/гс2 — к2. На рис. 85 показаны траек-
траектории этой системы; интересующая нас особенность располагается на этот раз не в начале
координат, а в точке (л, 0).
5 19.10] ДВИЖЕНИЕ В ОКРЕСТНОСТИ ЦЕНТРА 379
§ 19.10. Движение в окрестности центра. Здесь мы рассмотрим крити-
критический случай. Выше было установлено, что в окрестности особых точек
типа узла, седла и фокуса движение происходит, по существу, так же, как
если бы оно описывалось соответствующим линейным приближением. Одна-
Однако для особой точки типа центра это не имеет места. В этом случае линейное
приближение дает устойчивость, в то время как точные уравнения могут
привести либо к устойчивому, либо к асимптотически устойчивому, либо,
наконец, к неустойчивому движению.
Запишем исходные уравнения в нормальной форме:
в (х, у), 1
", У). )
A9.10.1)
г/ = Рх + г] (х,
Введем полярные координаты; используя соотношения гг = хх-\-уу, г29 =
= ху — ух, получаем
1_ хе-{-уц
A9.10.2)
Решение уравнений линейного приближения имеет вид
г = Го, 9 = 90 -\- fit.
Формула для 6 остается в силе и для точных уравнений, если е/х =
= г\/у.
Пример 19.10А. Исследуем сначала линейные уравнения
'х = у, у = —х, A9.10.3)
описывающие, очевидно, колебания гармонического осциллятора. Начало
координат является особой точкой типа центра, Р = —1, и решение имеет
вид
г = г0, 0 = 0О — t. A9.10.4)
Посмотрим, как изменится решение, если в выражения для составляющих
вектора поля добавить члены второго порядка, и приведем примеры для
каждого из трех возможных здесь случаев. (В каждом из приводимых ниже
примеров соблюдается условие е/х = х\1у, так что во всех случаях уравнение
0 = 0О — t остается в силе.)
1) Уравнения имеют вид
х = у — ху, у — —х — у2. A9.10.5)
Отсюда получаем
г = —гу = —г2 sin (90 — t).
Решая, находим
1 1
= cos F0 — t) — cos90 = cos9 — cos90.
Траекториями являются конические сечения г = е A — х) с фокусом в точке
О и директрисой х = 1. При малых значениях г0 траектории представляют
собой эллипсы, и вопрос об устойчивости решается так же, как в случае
линейного приближения. Для всякого заданного положительного е < -о-
380
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[Гл. XIX
мы можем взять к (е) = -т е (определение символов е и к дано в § 19.5).
На рис. 86 показаны траектории, пересекающие прямую у = 0 в точках
а: = 0,1, 0,2, 0,3, 0,4, 0,5, 0,6 и 0,7.
2) Уравнения имеют вид
х — у — хг, у — —х — уг. A9.10.6)
Отсюда получаем
г = -г2
Решая, находим
.г и при if —v оо г —>• 0. Устойчивость не только
сохранилась, но стала еще более сильной: мы
получили асимптотическую устойчивость.
3) Уравнения имеют вид
х = у + хг, у = -х + уг. A9.10.7)
Отсюда получаем
г = г2
Решая, находим
Рис. 86.
г0
В этом случае при t —>•— г—*- оо, так что особая точка оказывается
неустойчивой. (Этот пример мы уже приводили в § 9.9.)
В случаях 2) и 3) траектории имеют вид гиперболических спиралей.
Пример 19.10В. Рассмотрим в свете изложенной теории задачу о колебаниях
гармонического осциллятора в сопротивляющейся среде (эта задача уже рассматривалась
нами в § 19.2).
Уравнения движения
У+ f (х) + х = 0 A9.10.8)
приводится к двум уравнениям первого порядка:
х = у, y=-x-f (у).
A9.10.9)
Функция / (у) обращается в нуль вместе с у и монотонно возрастает, так что yf (у) всюду
положительно, за исключением у = 0, и монотонно возрастает, когда у возрастает или
убывает от нуля. Начало координат представляет особую точку типа центра. Далее,
• • •
тг = хх + уу = —yf (у),
так что г непрерывно убывает и при t -*¦ оо стремится к предельному значению I (I ^ 0).
Но выше мы видели (§ 19.2), что случай I > 0 невозможен, так что г -*¦ 0 и особая точка
асимптотически устойчива.
Пример 19.ЮС. Рассмотренная выше система может и не быть асимптотически
устойчивой, если снять требование, чтобы / (у) имело тот же знак, что и у.
Рассмотрим, например, движение, определяемое уравнением
'х+х*+х = 0. A9.10.10)
Уравнения первого порядка имеют вид
'х = у, у=-х-уК A9.10.11)
Начало координат представляет особую точку типа центра, причем р = —1. В полярных
координатах имеем
§ 19.10]
ДВИЖЕНИЕ В ОКРЕСТНОСТИ ЦЕНТРА
381
Если t заменить на —*, а у на —г/, то уравнения сохранят свою форму. Отсюда
следует, что траектории симметричны относительно оси Ох. Рассмотрим траекторию,
начинающуюся в точке (—Ъ, 0), считая Ъ > 0. Изображающая точка попадает в верхнюю
полуплоскость; пока она там находится, выполняются неравенства х > 0 (так что
л: > —!>) и г < 0 (так что г < 6). Кроме того, при малых значениях Ъ величина 6 моно-
монотонно убывает; предположив для определенности, что Ъ < 1/2, получим, что 6 < —1/2.
Траектория не может войти в точку О, так что она вновь пересекается с осью Ох справа
от О. Благодаря симметрии траектория в нижней полуплоскости является зеркальным
отображением траектории в верхней полупло-
полуплоскости, так что в целом получаются овальные
замкнутые кривые. В этом случае устойчивость,
получаемая из линейного приближения, сохра-
сохраняется как обыкновенная устойчивость, в про-
противоположность предыдущему случаю асимпто-
асимптотической устойчивости.
В этой задаче траектории можно получить
в явном виде. Интересно исследовать полное
решение, не ограничиваясь случаем малых воз-
возмущений из положения равновесия. Уравнение
A9.10.10) эквивалентно следующему:
A9.10.12)
Это линейное дифференциальное уравнение пер-
первого порядка относительно г/2. Характеристикой,
проходящей через точку (о, 0), будет
-т-*-(т-)
что можно записать также в виде
A9.10.13)
ег{а-х> — 1}. A9.10.14)
„ Рис. 87.
Правая часть уравнения показывает, что при
О < а < 1/2 мы имеем по координате х либра-
либрацию и траекторией в плоскости ху является замкнутая кривая. Движение в этом
случае является периодическим: переменная х совершает колебания в пределах а ^ х ^
^ —b (fc > 0), причем а и Ъ связаны между собой соотношением
A + 2Ь) е~2Ъ = A — 2а) е2а.
{Если величина а мала и положительна, то Ъ приближенно равно а -f- -=- a2 -f- -g-
16
9
и период составляет
2я A .+ 1 а2) *)
Отметим, что 6-»-оо, когда а -*• 1/2. Если
л равно критическому значению 1/2, траектория принимает форму параболы у2 ~f- ж = 1/2
их-»- —оо при ? -»- оо. Если о > 1/2, траектории оказываются незамкнутыми и при ?,
стремящемся к конечному пределу t0, х -»- —оо. На рис. 87 показаны соответствующие
кривые для значений а = 0,1, 0,2, 0,3, 0,4, 0,5, 0,6, 0,7 (см. рис 86). При построении
этих кривых следует иметь в виду, что замкнутые траектории в точках их пересечения
с параболой у2 + х = 0 имеют горизонтальные касательные, а максимальное значение ш
переменной у определяется из уравнения
— 2а
или
w \2 2
-) =l+T
Для незамкнутых траекторий 6 = 0 на кривой х2 -\- у2 -f- xy% = 0.
Пример 19.10D. В качестве еще одного примера движения в окрестности центра
рассмотрим систему
r-,,.L.r ir\ A9.10.15)
*) См. примечание на стр. 25.
382 СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [Гл. XIX
Для этой системы Э = Эо — t при любой форме / (г) и г = rf (г). Случаи / (г) = ±г нами
уже рассматривались в примере 19.10А, поэтому сейчас мы рассмотрим три следующих
случая:
1) / (г) = г (а — г), а > 0. Если в начальный момент г = г0, 0 < г0 < а, то г > О
и при t ->¦ оо г -»- а. Траектория представляет собой спираль, накручивающуюся изнутри
на окружность г = а. Имеем
где через р обозначена разность 1. Особая точка типа центра, находящаяся в начале
координат, неустойчива. Если г0 > а, то г < 0 и г -> я при t ->¦ оо; траектория представ-
представляет собой спираль, накручивающуюся снаружи на окружность г = а.
2) / (г) = г sin (я/г). В этом случае г = г2 sin (я/г) и существует семейство перио-
периодических траекторий, а именно окружностей г = 1/п, где п — целое положительное
число. Если г0 = 1/п, то траекторией служит окружность г = 1/п.
Если г0 > 1, то г > 0 и г -коо вместе с ?. Если 1 > г0 > 1/2, то г < 0 и г -> 1/2,
когда ? -»- оо; траекторией является спираль, накручивающаяся снаружи на окруж-
окружность г = 1/2. Если 1/2 > г0 > 1/3, то г > 0 и г -*¦ 1/2, когда ? ->• оо; траекторией
является спираль, накручивающаяся изнутри на окружность г = 1/2. Вообще, если
0 < г0 < 1 и г0 не имеет вида 1/п, то траектория представляет собой спираль, накручи-
накручивающуюся изнутри или снаружи на ближайшую окружность, радиус которой равен
обратной величине четного целого числа. Добавление членов высшего порядка не изме-
изменяет устойчивости, установленной линейным приближением: она не становится асимпто-
асимптотической. Не все траектории вблизи точки О являются периодическими (как это было
в примере 19.10А, 1) и в примере 19.ЮС). Читатель может попробовать самостоятельна
* JX
рассмотреть уравнение г2 = г* sin2 — , применяя теорию, развитую в гл. I при выводе
уравнения A.2.10).
1 1
3) / (г) = г2. В этом случае —= = 2 (t0 — t) и г ->- оо, когда t ->- t0 = — . Траекто-
г ^го
рией является спираль г2 F — 6j) = 1/2, где 6i = 60 — 'о- Особая точка типа центра
неустойчива (см. пример 19.10А, 3)).
Если ввести обозначения | = х — iy, r\ = x -j- iy, то уравнения примут вид
Тогда
и, следовательно,
t) Я — е2*(во-0
*'' Б
что совпадает с полученным ранее решением. Аналогичным образом можно поступить-
и в случае более общей системы
| = XI + |х| (|т))п, т| = —Л.-П + цт) (|т))".
§ 19.11. Связь линейного приближения с общей теорией. В предыдущих
параграфах мы рассмотрели вопрос об устойчивости положения равновесия
в связи с задачей о линейном приближении. Было найдено, что если линей-
линейное приближение показывает асимптотическую устойчивость, то к этому же-
результату мы приходим и в случае учета нелинейных членов. Аналогично,
если линейное приближение показывает неустойчивость, то этот результат
сохраняется и при учете нелинейных членов. Что же касается обыкновен-
обыкновенной устойчивости, то она, вообще говоря, не сохраняется при переходе
от линейного приближения к точным уравнениям.
Рассмотрим еще три примера. В первом из них система имеет две особые-
точки — типа центра и типа седла — и траектории разделяются на три клас-
класса сепаратрисой — силовой линией, проходящей через седловую точку.
§ 19,19]
СВЯЗЬ ЛИНЕЙНОГО ПРИБЛИЖЕНИЯ С ОБЩЕЙ ТЕОРИЕЙ
383
Второй и третий примеры относятся к исключительному случаю, когда в осо-
особой точке якобиан обращается в нуль.
Пример 19.НА. Частица единичной массы движется по прямой под действием
силы
-»+. ,f ., A9.11.1)
а+Ъ—х'
причем 0 <[ а <[ 6 ж х <^а-\-Ь. Уравнения имеют вид
• • аЪ
а + Ъ — х '
A9.11.2)
Правая часть второго уравнения обращается в нуль в точках а и 6. Поле обладает двумя
особенностями: центром в точке А (а, 0) и седлом в точке В F, 0). Потенциальная функ-
функция имеет вид
A9.11.4)
и траектории определяются из уравнения энергии
График функции — V имеет вид, показанный на рис. 88. Подобно § 1.2, форма кри-
кривой определяет характер движения для всех значений С. Траектории показаны на рис. 89.
Точка А (центр), относительно кото-
которой линейное приближение показывает
обыкновенную устойчивость (см. пример
19.10А, 1) и пример 19.ЮС), остается
-—а+Ъ —
1
Рис.
Рис 89.
устойчивой и при учете нелинейных членов. Подтверждается также вывод, получен-
полученный в § 19.8, что движение в окрестности седла сохраняет свой характер при переходе
от уравнений линейного приближения к точным уравнениям.
Сепаратриса, которая является силовой линией, проходящей через седловую точку
В, пересекает себя в этой точке. Седловая точка сама есть точечная траектория, кроме
того, она является предельной точкой входящих в нее траекторий — дуг сепаратрисы.
Уравнение сепаратрисы имеет вид
In
A9.11.5)
Эта кривая еще раз пересекает ось х, слева или справа от начала координат в зависимости
от величины Ъ1а. Критический случай, когда пересечение происходит точно в начале
координат, имеет место тогда, когда величина (а + ЬIа удовлетворяет уравнению
т. е. приблизительно при х = 3,51 или Ъ/а = 2,51. Если Ь/а превышает это критическое
значение, то сепаратриса пересекает ось Ох слева от начала координат; рис. 89 относится
к случаю, когда Ъ = За.
384 СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ [Гл. XIX
Пример 19.11В. До сих пор мы рассматривали системы с изолированными осо-
особыми точками, причем предполагали, что якобиан д (Р, Q)ld (х, у) в этих точках отличен
от нуля. Сейчас мы рассмотрим два примера, относящиеся к исключительному случаю,
когда якобиан в особой точке обращается в нуль и изложенная выше теория неприменима.
Рассмотрим систему
я = ж2_з,«) у=2ху. A9.11.6)
Правые части этих уравнений не содержат линейных членов, и решение уравнений
линейного приближения имеет вид х = х0, у = у0. Соответствующая этому приближению
особая точка является устойчивой, и согласно определению устойчивости, данному
в § 19.5, можно положить х = е.
Рассмотрим теперь точные уравнения. Пользуясь формулами A9.10.2), запишем
эти уравнения в полярных координатах:
г = хг, Ь = у. A9.11.7)
Отсюда легко находится уравнение траектории: г = к sin 8. Положение точки на траек-
траектории в некоторый момент t определяется уравнением 6 = к sin2 6. Изображающая точка
описывает окружность, касающуюся вси Ох в точке О; положение точки на окружности
в момент t определяется уравнением
ы = ctg е0 — ctg e. 19.H.8)
В конце концов точка возвращается в положение О, поскольку 6 монотонно возрастает
и стремится к я, когда t —>- оо. Тем не менее особая точка не является устойчивой. В самом
деле, в произвольной близости от точки О можно выбрать такую начальную точку, чтобы
в последующем движении изображающая точка удалилась от точки О сколь угодно дале-
далеко; например, если 60 — малое положительное число, а 7-0 = Т/sin 60, то к = l/~|/sin 60,
т. е. очень велико.
Рассмотрим случай, когда траектория начинается в точке, лежащей на оси х. Если
начальная точка имеет координаты {х0, 0), то характеристика определяется уравнениями
V = - 1, y=0. A9.11.9)
X Xq
Если х0 > 0, то координата х монотонно возрастает и стремится к бесконечности, когда
t стремится к 1/^о- Если х0 < 0, то х монотонно убывает и стремится к нулю, когда t стре-
стремится к бесконечности.
Пример 19.11 С. Если отказаться от условия, что якобиан в особой точке
не равен нулю, то утверждение о том, что неустойчивость по линейному приближению
влечет за собой неустойчивость из точных уравнений, теряет силу. В качестве примера
рассмотрим систему
х = у — xs, 'у = 0. A9.11.10)
Движение, определяемое линейным приближением, очевидно, неустойчиво. В то же время
движение, определяемое точными уравнениями, является устойчивым. В самом деле, если
в начальный момент у — у0, то у = г/о и в дальнейшем, а х при t —>- оо стремится к пре-
предельному значению уУ3 *).
*) См. подстрочное примечание в п. 9.9. (Прим перев.)
Глава XX
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ.
ЦИКЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ
§ 20.1. Индекс кривой и индекс особой точки. В этой главе мы продол-
продолжим изучение периодических движений, которые возможны в системе
х = Р(х, у), y = Q(x, у). B0.1.1)
Траектории периодических движений суть простые замкнутые кривые.
Они являются замкнутыми силовыми линиями поля (P,Q), если таковые
существуют.
Известны случаи, когда все силовые линии поля являются замкнутыми.
Рассмотрим прямолинейное движение частицы в силовом поле. Уравнением
траектории будет
~y* = C-V, B0.1.2)
и если V = у п2х2 (гармонический осциллятор) или, вообще, если с увеличе-
увеличением х от —оо до + °° функция V монотонно убывает от +°° до некоторого
минимума, а затем монотонно возрастает до +оо, то все силовые линии явля-
являются замкнутыми, а все возможные движения — периодическими. Этот слу-
случай, однако, является исключительным. Во многих важных случаях суще-
существует только одна циклическая траектория, причем почти все траектории
имеют форму спиралей, приближающихся к периодической траектории.
Система, так сказать, имеет тенденцию к периодическому движению.
Мы будем пользоваться термином циклическая траектория вместо
замкнутая траектория, так как в доказательствах теорем настоящей главы
будет применяться теория точечных множеств и термин замкнутая будет
употребляться в том смысле, в каком он обычно употребляется в теории мно-
множеств.
Особые точки, изучавшиеся в предыдущей главе, представляют собой
вырожденные случаи циклических характеристик.
Рассмотрим простую замкнутую кривую Г, не проходящую через особые
точки; пусть точка р проходит всю эту кривую, двигаясь в положительном
направлении (против хода часовой стрелки). Обозначим через 0 (р) наклон
силы поля F к осяОх в точке р. Если точка р, двигаясь по кривой в положи-
положительном направлении, против хода часовой стрелки, совершает один полный
оборот, то 0 (р), изменяясь непрерывно с изменением р, получает приращение
2rat, где п — целое положительное или отрицательное число или нуль. Число
п называется индексом кривой для заданного поля. Изменение 0 при переме-
перемещении точки р по кривой Г можно представить посредством отображения
кривой Г на единичную окружность. Если через и (р) обозначить единичный
вектор .-=п F, то индекс будет равен числу полных оборотов вектора и при
одном обходе точки р по кривой Г.
Если кривая Г фиксирована, а векторное поле F непрерывно изменяется,
но так, что на кривой Г не появляется особых точек, то индекс кривой остается
без изменения. Обратно, если зафиксировать поле и непрерывно деформиро-
деформировать кривую Г, но так, чтобы она оставалась простой замкнутой кривой,
25 л. д. Парс
386 ЦИКЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ [Гл. XX
не проходящей через особую точку, то индекс не изменится. Это непосред-
непосредственно следует из того простого факта, что переменная, которая может при-
принимать лишь дискретные значения, при непрерывном изменении может лишь
оставаться постоянной.
Рассмотрим теперь изолированную особую точку q. Окружим ее малым
кружком у; радиус кружка возьмем столь малым, чтобы ни внутри его, ни на
его границе, кроме q, не было других особых точек. Тогда индекс кривой
у будет иметь вполне определенное значение, не зависящее от радиуса круж-
кружка, поскольку с изменением радиуса в нем не появляется других особых точек.
Это число называют индексом особой точки q.
Понятие индекса встречается в теории функций комплексной переменной. Если
регулярная функция / (z) определяется векторным полем F,
f(z)=P+ iQ, B0.1.3)
то индекс кривой Г равен числу N нулей функции / (z) (с учетом их кратности), располо-
расположенных внутри кривой Г. Если / (г) регулярна внутри Г и на ее границе, за исключением
конечного числа полюсов внутри этой области, то индекс равен Jv — М, где М — число
полюсов (с учетом кратности), расположенных внутри Г.
Нетрудно определить индекс для каждого типа особых точек, рассмот-
рассмотренных в предыдущей главе. Как и ранее, поместим начало координат в осо-
особой точке поля. Тогда будем иметь
Р = ах + by + e, Q = сх + dy + j], B0.1.4)
причем ad — be, значение /0 якобиана ¦ в точке О, отлично от нуля. Для
определения индекса можно вместо поля F рассматривать поле ]F0, так как
угол г|з между F и Fo при приближении к точке О стремится к нулю (§ 19.6).
Рассмотрим малый кружок у с центром вОи поле
Р0 = ах + Ьу, Q0 = cx + dy. B0.1.5)
Отображение
(х, у) -> (Ро, <?о), B0.1.6)
где (Ро, Qo) интерпретируются как прямоугольные координаты на вспомо-
вспомогательной диаграмме, переводит круг у на плоскости ху в эллипс на плоско-
плоскости (Ро, Qo), причем если /0>0, то положительному направлению обхода
круга соответствует положительное направление обхода эллипса, а если
Jo < 0 — отрицательное направление. Через /0 мы обозначили
B017)
0 д(х, у) L д{х, у) _|(о, 0)
Следовательно, при /0 > 0 индекс особой точки равен +1, а при Jo < О
равен —1. С другой стороны, /0 равно произведению собственных значений
матрицы А (§ 19.4); это произведение положительно для узла, фокуса и цент-
центра и отрицательно для седла. Таким образом, индекс любой допустимой осо-
особой точки (при /0 =5^=0) равен +1 (+1 для узла, фокуса и центра и —1 для
седла).
Если замкнутая кривая Г лежит в односвязной области поля F без осо-
особых точек, то ее индекс равен нулю. В самом деле, такую кривую можно,
не изменяя индекса, путем непрерывной деформации стянуть в точку. Если
Г — простая замкнутая кривая, не имеющая на себе особенностей, а имею-
имеющая лишь допустимые изолированные особые точки внутри ограничиваемой
ею области, то индекс для кривой Г равен сумме индексов охватываемых ею
особых точек. Число особых точек в области, ограничиваемой кривой, долж-
должно быть конечным. При этом условии сформулированное утверждение легко
§ 20.2] ПОЛОЖИТЕЛЬНОЕ ПРЕДЕЛЬНОЕ МНОЖЕСТВО 387
доказать. Рассмотрим, например, кривую, изображенную на рис. 90. Индекс
этой кривой равен нулю; с другой стороны, он равен индексу Г минус сумма
индексов отдельных петель. Таким образом, индекс для кривой Г равен N —
— S, где S — число седловых точек, а N — число особенностей других
типов, содержащихся в области, ограниченной
кривой Г.
В важном частном случае, когда Г является
циклической траекторией, ее индекс равен еди-
единице (назависимо от того, совершается ли дви-
движение по ходу часовой стрелки или против).
Таким образом, для циклической траектории
N — S = 1. B0.1.8)
Отсюда следует, что не существует цикличе- р д„
ских траекторий, которые бы не охватывали
особых точек или охватывали бы одни лишь
точки типа седла. Простейшим является случай, когда в области, ограни-
ограниченной циклической траекторией, имеется всего одна изолированная осо-
особая точка (отличная по типу от седла); в этом случае N = 1 и S = 0.
§ 20.2. Положительное предельное множество. Рассмотрим ограничен-
ограниченную положительную полухарактеристику С, расположенную в области D
(§ 19.3). Будем отмечать положение изображающей точки на полухарактери-
полухарактеристике С в момент t посредством вектора р (t), p (t) = {x (t), у (t)}, так что
р (t) ? D и | р (t) | < К при г;>0. Обозначим через I точку такую, что
I = Jim p (tn), B0.2.1)
Tlr->OO
где последовательность {tn} задается неравенствами
0'<*i<f2<*3 • • • B0.2.2)
и tn -*¦ сю вместе с п.
Множество таких точек I называется положительным предельным множе-
множеством или множеством предельных точек для рассматриваемой траектории;
обозначим его через Л. Точки I множества Л называются Л-точками. Л-точки
кривой С являются предельными точками (точками сгущения) этой кривой,
но не все предельные точки С принадлежат к числу Л-точек.
Л-точка кривой С может лежать на этой кривой, а может и не лежать
на ней. В некоторых простых случаях положительное предельное множество
находится без труда. Если при t -> оо р (t) стремится к устойчивой особой
точке ро, то Л == р0. Если полухарактеристика С циклическая, то каждая
ее точка является Л-точкой и других Л-точек не существует. Таким образом,
если С — циклическая полухарактеристика, то Л = С. В дальнейшем мы
увидим, что во многих случаях множество Л само составляет циклическую
траекторию, а С представляет собой спираль, приближающуюся к Л, когда t
стремится к бесконечности.
Рассмотрим теперь основные свойства положительного предельного мно-
множества Л. К ним относятся следующие свойства: 1) множество Л не является
пустым; 2) множество является замкнутым; 3) множество является связным;
4) если I G Л, то вся траектория, проходящая через I (т. е. и положительная
и отрицательная полухарактеристики, начинающиеся в точке I), принадле-
принадлежит множеству Л.
Мы уже отмечали выше, что свойство 1) справедливо для циклической
характеристики. Пусть теперь С не является циклической. Рассмотрим мно-
множество точек р A), р B), р C), . . . Оно является бесконечным и ограничен-
ограниченным, причем все элементы его различны и существует по крайней мере одна
25*
388 ЦИКЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ [Гл. XX
предельная точка, которая является Л-точкой С. Доказательство свойства
2) аналогично доказательству известного факта, что производное множество
заданного множества является замкнутым.
Для доказательства свойства 3) нужно показать, что Л не может состоять
из двух (или более) непустых замкнутых множеств, не имеющих общих точек.
Предположим противное: пусть Л состоит из двух не связанных между собой
непустых множеств А и В. Тогда эти множества отделены друг от друга;
обозначим расстояние между ними через б. Пусть точка а принадлежит мно-
множеству А, а точка Ъ — множеству В. Возьмем любое положительное число
t0. Тогда можно указать такое число t±, большее чем t0, чтобы выполнялось
неравенство
d{a,p(t1)}<±8, B0.2.3)
а также такое число t2, большее чем t±, чтобы выполнялось неравенство
d{b,p(t2)}<±b. B0.2.4)
Из неравенства B0.2.3) следует, что
d{p(h),A}<±-8, B0.2.5)
и, следовательно,
d{p(tJ,B}>±b B0.2.6)
d {p (*,), А) - d {p (h), В} < 0. B0.2.7)
Аналогично
d{p(t2), A}-d{p(t2), B}>0, B0.2.8)
так что функция
Ф (<) = d{p (t), A)-d {p (t), В} B0.2.9)
отрицательна при ^ и положительна при t2. В силу непрерывности функции
Ф (t) существует такое число 0, лежащее между ti и t2, для которого ф @) = 0.
При любом выборе t0 можно указать такое 0, большее t0, для которого
d{p(Q), A} = d{p(Q), В}. B0.2.10)
Таким образом, можно построить возрастающую последовательность
0i, 02, в3, • • •, стремящуюся к бесконечности и обладающую тем свойством,
что
d{p(Qn), A) =d{p(en), В}. B0.2.11)
Пусть ро — предельная точка множества {р @П)}; тогда р0 6 Л и
d (p0> A)=d (ро, В). B0.2.12)
Однако последнее равенство невозможно, так как точка р0 принадлежит
либо множеству А, либо множеству В. Итак, предположение о том, что Л
состоит из двух отдельных множеств, привело к противоречию; аналогично
доказывается, что Л не может состоять из нескольких множеств. Таким
образом, Л является непустым замкнутым связным множеством.
Наконец, чтобы доказать свойство 4), обозначим через р {t) траекторию,
выходящую из точки I, так что р @) = I. Рассмотрим последовательность
{?„}, монотонно возрастающую до бесконечности и такую, что lim p {tn) = I.
n-wo
Пусть t — заданное положительное или отрицательное число. Тогда
(*n) = p@) B0.2.13)
ОТРЕЗОК
lim p(
П->-оо
БЕЗ
КОНТАКТА
t)=p(t),
§ 20.3] ОТРЕЗОК БЕЗ КОНТАКТА 389
и, следовательно,
B0.2.14)
так как решения дифференциальных уравнений для всех конечных t зависят
непрерывным образом от начальных значений. Поэтому р (t) ? Л для всех t,
что и завершает доказательство.
Итак, резюмируя сказанное, можно утверждать, что если множество Л
не состоит из одной-единственной особой точки, то оно является непустым
замкнутым множеством, образованным из полных траекторий.
§ 20.3. Отрезок без контакта. Отрезком без контакта будем называть
конечный замкнутый отрезок прямой, обладающий тем свойством, что ни в од-
одной его точке нормальная к нему составляющая поля F не обращается в нуль.
Иными словами, отрезок без контакта не касается ни одной траектории и не
проходит ни через одну особую точку. Отрезок без контакта, проходящий
через точку р0, представляет отрезок, для которого эта точка является внут-
внутренней. Ясно, что через всякую обыкновенную точку можно провести беско-
бесконечное число отрезков без контакта. Установим основные свойства таких
отрезков.
1) Если положительная полухарактеристика С пересекает отрезок без
контакта S больше одного раза, то она пересекает его всегда в одном и том же
направлении. В самом деле, если бы С пересекала S в точках Pi и Р2 с разных
сторон, то нормальная составляющая вектора F имела бы в этих точках про-
противоположные знаки, и так как она изменяется вдоль S непрерывным обра-
образом, то нашлась бы точка между Pt и Р2, в которой нормальная составляющая
F обращалась бы в нуль. Однако последнее невозможно, поскольку S являет-
является отрезком без контакта.
2) За конечный промежуток времени траектория С может пересекать
отрезок S лишь конечное число раз. Предположим противное: пусть в проме-
промежутке a^f^p имеется бесконечное число моментов {tn} таких, что
Р tin) € S. В этом случае никакие две точки р (tr), p (ts) не совпадают. Если
бы такое совпадение имело место, то траектория либо представляла бы собой
особую точку, лежащую на S, но это невозможно по условию, либо была бы
циклической. В последнем случае траектория имела бы период о и число
пересечений ее с отрезком S в интервале [а, р] было бы конечным. Таким
образом, все точки р (tn) различны.
Значения {tn} имеют предельную точку t0, a ^ tQ ^ р, и р (tQ) ? S.
Можно выбрать точку tn как угодно близко к точке t0, так чтобы хорда
Р tio) P (tn) стремилась принять направление касательной к траектории С
в точке р (t0). Тогда в точке р (tQ) кривая С касалась бы отрезка S, но это
невозможно в силу определения отрезка без контакта. Таким образом, пред-
предположение о том, что траектория за конечный промежуток времени пересе-
пересекает отрезок без контакта бесконечное число раз, приводит к противоречию.
3) Если ро — точка, лежащая вблизи отрезка без контакта S, то про-
проходящая через эту точку траектория пересекает отрезок S. Прежде всего
уточним формулировку теоремы. Пусть q — внутренняя точка S, а е —
заданное положительное число. Тогда существует положительное число
б = б (е) такое, что если d (q, p0) < б, то начинающаяся в точке р0 положи-
положительная или отрицательная полухарактеристика пересечет отрезок S через
промежуток времени, не превышающий длительности интервала (—е, е);
если р (t) есть траектория, для которой р @) = р0, то существует число Э
такое, что —е < Э < е и р (Э) 6 S.
Прежде чем переходить к доказательству, введем новые переменные
путем аффинного преобразования, при котором отрезок S переходит в отре-
390 ЦИКЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ [Гл. XX
зок Xi =sC x =sC х2 на оси х, х± < 0 < а^, а точка q — в начало координат.
Траектория, начинающаяся при 1 = 0 в точке р0 = (х0, у0), представляет
собой кривую р (t; x0, у0). Обозначим составляющие через
х (t; х0, г/о), У (t; х0, г/о)-
Требуется доказать, что при достаточно малом У х\ + у\ уравнение
У (t; х0, г/о) = 0 B0.3.1)
имеет решение
t = ф (х0, г/о), B0.3.2)
причем это решение таково, что | t | < е и точка х (ср; х0, г/о) лежит внутри
(Xi, х2). Производная
-§ГУ(*> *o> Уо)
не обращается в нуль в точке t = Xq = г/0 = 0, так что при достаточно малом
У х\ + у\ решение наверняка существует. Кроме того, ср @, 0) = 0 и функ-
функция ф непрерывна по (х0, у0), так что | ф (х0, у0) | мало, если мало У х\ + у\.
Наконец, если t и Ух\ + у\ малы, то мало и х, что завершает доказательство.
§ 20.4. Отрезок без контакта, проходящий через точку множества Л.
Пусть С — положительная полухарактеристика, для которой предельное
множество Л не сводится к одной особой точке. Обозначим через I обыкно-
обыкновенную точку множества Л, а через S — отрезок без контакта, проходящий
через I. Всякому заданному положительному числу е соответствует положи-
положительное б (е) такое, что если траектория начинается при t — т из точки, уда-
удаленной от I меньше чем на б, то эта траектория пересекает отрезок S в неко-
некоторый момент времени, заключенный в интервале (t — е, т + е) (§ 20.3, п. 3).
Далее, каково бы ни было произвольно большое число t0, существует еще
большее число f такое, что
d {p (О, 1} < б-
Следовательно, за промежуток времени (t' — г, t' -\- г) кривая С должна
пересекать отрезок S. Таким образом, существует бесконечное множество
значений t, для которых точки р (t) лежат на отрезке S. За конечный отре-
отрезок времени происходит конечное число пересечений, поэтому моменты
пересечения можно перенумеровать так, чтобы
h<t2< t3. . .
При этом tn стремится к бесконечности вместе с п. Обозначим точку р (tr)
на отрезке S через рг. Имеются две возможности. 1) Если точка р2 совпадает
с рг, то траектория С является циклической и все точки pt, p2, J>3, • • • совпа-
совпадают. 2) Если точки р2 и Pi различаются, то точка р3 отличается от pt и р2
и точка р2 располагается между точками pt и р3. Здесь необходимо обратить-
обратиться к теореме Жордана. Рассмотрим простую замкнутую кривую Г, составлен-
составленную из дуги р\р2 траектории С и отрезка pzPi прямой S. Если изображающая
точка попадает внутрь области, ограниченной кривой Г, то она там и остает-
остается, поскольку она не может пересечь ни дугу pip2 траектории С, ни прямо-
прямолинейный отрезок p2pi- Поэтому точка р2 лежит между точками pt и р3
(рис. 91, а). Аналогично, если изображающая точка оказывается вне области,
ограниченной кривой Г, то она там и остается, и опять-таки точка р2 лежит
между точками р4 и р3 (рис. 91, Ь).
Таким образом, точки pt, p2, р3, ... на отрезке S либо все совпадают,
либо все различны; в последнем случае они образуют монотонную последо-
последовательность. Эта последовательность, будучи монотонной и ограниченной,
20.5]
СТРУКТУРА МНОЖЕСТВА Л
391
имеет предел, который принадлежит множеству Л и, следовательно, может
быть только точкой I. В силу единственности предельной точки других точек
множества Л, отличных от I, на отрезке S быть не может.
Результаты, изложенные выше, можно сформулировать в виде следую-
следующей теоремы. Пусть I — обыкновенная точка множества Л, которое является
положительным предельным множеством траектории С, a S — отрезок без
Ь)
Рис. 91.
контакта, проходящий через точку I. Тогда, во-первых, на отрезке S нет
точек множества А, отличных от I, и, во-вторых, траектория С является
циклической тогда и только тогда, когда она пересекает отрезок S лишь
в одной точке.
§ 20.5. Структура множества Л. Предположим снова, что предельное
множество Л положительной полухарактеристики С не сводится к особой
точке. Теперь мы знаем, что траектория, начинающаяся в точке множества
Л, целиком принадлежит этому множеству. Предположим, что множество
Л содержит траекторию С, предельное множество которой (положительное
или отрицательное) не сводится к одной особой точке. Тогда траектория С
является циклической и Л = С.
Докажем сначала, что С есть циклическая траектория. Пусть/) — обык-
обыкновенная точка, скажем, положительного предельного множества Л' кривой
С. Множество Л' составляет часть Л (поскольку С принадлежит Л и это
множество замкнуто), так что р ? Л. Пусть S будет отрезок без контакта,
проходящий через точку р. Тогда S пересекает Л в единственной точке р.
Таким образом, S пересекает С в одной-единственной точке р, и, следова-
следовательно, траектория С является циклической.
Докажем теперь, что С == А. Предположим противное: пусть Е —
множество точек, принадлежащих Л и не лежащих на С". Множества Л и С"
замкнуты, а множество Е открыто; поэтому существует предельная точка
q множества Е, которая не лежит в Е. Но точка q лежит в Л, так как это мно-
множество замкнуто, следовательно, q?C Рассмотрим теперь отрезок без кон-
контакта S', проходящий через точку q (которая является обыкновенной точкой
и лежит на С). Пусть р' — точка множества Е, лежащая достаточно близко
от точки q. Тогда р' будет обыкновенной точкой и проходящая через нее
характеристика будет пересекать отрезок S' в точке q', которая будет отлична
от д, так как характеристики не пересекаются. Но q ? Л, так как р' 6 Л,
и, следовательно, вся характеристика, проходящая через точку р', принад-
принадлежит множеству Л. Таким образом, отрезок iS" содержит две различные
точки q и q', принадлежащие множеству Л, а это, как мы видели, невоз-
невозможно. Следовательно, множество Е должно быть пустым и С = Л. Мно-
Множество Л сводится к циклической траектории.
392 ЦИКЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ [Гл. XX
Если траектория С циклическая, то С = Л. Пусть С — не циклическая
траектория. Рассмотрим отрезок без контакта S, проходящий через точку р
множества Л. Последовательность точек пересечения pi, P2, />3, . . . кривой
С с отрезком S сходится к точке р (§ 20.4), так что С представляет спираль,
приближающуюся к множеству Л при f-> оо. В этом случае циклическая
траектория Л называется предельным циклом.
Остается рассмотреть исключительный случай, когда множество Л
не сводится к особой точке, но таково, что каждая траектория, полностью
лежащая в Л, обладает тем свойством, что ее положительное предельное
множество является особой точкой и ее отрицательное предельное множество
является особой точкой. В этом исключительном случае множество Л явля-
является псевдоциклической траекторией, т. е. представляет собой замкнутую
кривую, составленную из траекторий, каждая из которых начинается и за-
заканчивается в особой точке. Эти особые точки являются седловыми. Простей-
Простейшим случаем псевдоциклической траектории является тот, когда одна тра-
траектория выходит из седловой точки и возвращается в нее. В другом простом
случае имеются две различные седловые точки, которые соединяются двумя
различными траекториями. Выше были приведены примеры обоих этих слу-
случаев: сепаратриса на рис. 89 дает пример первого случая, а сепаратриса
на рис. 83 — пример второго случая.
§ 20.6. Теорема Пуанкаре — Бендиксона. Результаты, полученные
выше, можно представить в виде следующей теоремы. Рассмотрим ограничен-
ограниченную положительную полухарактеристику С, расположенную в области D,
и предположим, что положительное предельное множество А этой полуха-
полухарактеристики не сводится к особой точке. Тогда либо полухарактеристика
С является циклической и А = С, либо А представляет собой циклическую
траекторию (в исключительном случае псевдоциклическую) и С является спи-
спиралью, приближающейся к А, когда ? —> сю.
Рассмотрим некоторые дополнительные результаты, имеющие отношение к теореме
Пуанкаре — Бендиксона. Подробного и полного исследования мы проводить здесь не бу-
будем, так как это увело бы нас далеко в сторону. Напомним, что мы рассматриваем силовое
поле, определенное в § 19.3, в котором имеются лишь изолированные особые точки, в каж-
каждой из которых д (Р, Q)ld (x, у) ф 0.
1) Выше мы видели, что положительное предельное множество траектории С может
состоять из одной-единственной особой точки I и при t -*¦ оо траектория стремится к I
или, возможно, входит в нее. Этот результат можно трактовать как частный случай тео-
теоремы Пуанкаре — Бендиксона, если особую точку I рассматривать как вырожденную
форму предельного цикла.
2) Если существует замкнутая область R, не содержащая особых точек и такая, что
в каждой точке ее границы вектор поля F направлен внутрь области, то в такой области
имеется по крайней мере одна циклическая траектория. (Предполагается, что граница
области состоит из кривых с непрерывно изменяющимся наклоном касательной, за исклю-
исключением конечного числа угловых точек.) В самом деле, любая положительная полухарак-
полухарактеристика, начинающаяся в области R, остается в этой области и при t ^ 0; эта положи-
положительная полухарактеристика либо является циклической, либо стремится к предельному
циклу. К тому же выводу мы приходим и в том случае, когда во всех точках границы
вектор поля F направлен наружу. Для доказательства достаточно рассмотреть отрица-
отрицательные полухарактеристики, начинающиеся в точках области R. Из сказанного, разу-
разумеется, не следует, что в области Л имеется лишь одна циклическая траектория. (Область
R не может быть односвязной. Если бы, например, область Л состояла из простой замкну-
замкнутой кривой Г и ограничиваемой ею области, а вектор Fb каждой точке Г был бы направлен
внутрь этой области, то индекс (§ 20.1) кривой Г был бы равен единице, так что в области
была бы по крайней мере одна особая точка.)
3) Предположим, что положительная полухарактеристика С представляет собой
спираль, которая стремится изнутри к предельному циклу Л. Если р0 — любая точка
внутри Л и достаточно близкая к Л, то положительная полухарактеристика, начинающая-
начинающаяся в точке р0, стремится к Л. Докажем это.
Пусть q — точка кривой Л, S — отрезок без контакта, проходящий через точку q,
а Аг> Pn+i — Две последовательные точки пересечения кривой С с отрезком S, соответст-
соответствующие заданному (достаточно большому) значению га. Рассмотрим кольцевую область,
§ 20.6] ТЕОРЕМА ПУАНКАРЕ — БЕНДИКСОНА 393
ограниченную снаружи кривой Л, а изнутри — простой замкнутой кривой, составленной
из дуги pnpn+i кривой С и отрезка pn+ipn прямой S (рис. 92). При достаточно большом п
эта область не имеет особых точек, так что положительная полухарактеристика С, начи-
начинающаяся из точки р0 внутри этой области, в ней и остается. По мере того как кривая С
стремится к Л, кривая С" стремится к тому же предельному циклу. В самом деле, последо-
последовательные точки пересечения С" с отрезком S лежат в интервалах pnpni.i, pn+iPn+2,
Pn+zPn+s, ¦ ¦ ¦, так как две траектории не могут пересечься одна с другой. Следовательно,
при t ->- оо кривая С стремится к Л.
4) Если к предельному циклу Л изнутри стремится положительная полухаракте-
полухарактеристика, то к нему не может изнутри стремиться отрицательная полухарактеристика.
Рассмотрим, как и в п. 3), отрезок без контакта S, проходящий через точку q кривой Л.
Последовательные точки пересечения pi, p2, Рз> ¦ ¦ • положительной полухарактеристики
с отрезком S стремятся к точке q, и, стало быть, после-
последовательные точки пересечения отрицательной полуха-
полухарактеристики удаляются от точки q. В этом случае пре-
предельный цикл Л называется устойчивым изнутри.
5) Если существует циклическая траектория Г
такая, что изнутри к ней не приближается ни поло-
положительная, ни отрицательная полухйрактеристика, то
в области, ограниченной кривой Г, и вблизи нее про-
проходит еще одна циклическая траектория.
Для доказательства рассмотрим точку q на кри-
кривой Г и отрезок без контакта S, проходящий через эту
точку. Пусть р0 — точка на отрезке S, лежащая
внутри области, ограниченной Г, вблизи от q. Рассмо-
Рассмотрим положительную полухарактеристику, начинаю-
начинающуюся в точке р0. Изображающая точка либо возвра-
возвращается в первоначальное положение р0, и тогда теорема р qq
доказана, либо попадает на отрезок S в некоторую
точку pi. Если эта точка лежит между р0 и q, то сле-
следующая точка пересечения р2 окажется между р4 и q, и т. д. Последовательность {рп }
будет сходиться к предельной точке, расположенной на отрезке poq. Этой предельной точ-
точкой не может быть точка q, ибо тогда проходящая через точку р0 положительная полу-
полухарактеристика стремилась бы к траектории Г, что по условию не имеет места. Поэтому
точки рп стремятся к пределу I, заключенному между р0 и q, а траектория стремится
к предельному циклу Л, проходящему через точку I. (Если точка р4 не лежит между ра
и q, то следует воспользоваться отрицательной полухарактеристикой, проходящей через
точку р0.)
6) Рассмотрим случай, когда Г является циклической траекторией и в ограничивае-
ограничиваемой ею области имеется одна особая точка р0, которая является узлом или фокусом. Возь-
Возьмем точку q вблизи от р0. Если особая точка неустойчива, то положительная полухарак-
полухарактеристика, начинающаяся в точке q, не может стремиться к точке р0. Следовательно, она
должна стремиться к предельному циклу, который либо совпадает с Г, либо является
другой циклической траекторией, расположенной внутри области, ограниченной кривой
Г. Отрицательная полухарактеристика, начинающаяся в точке q, при этом стремится
к точке р0 и, возможно, входит в нее.
Если предельный цикд для положительной полухарактеристики, начинающейся
в точке q, совпадает с самой кривой Г, то в области, ограниченной этой кривой, не может
быть других циклических траекторий. В противном случае положительная полухаракте-
полухарактеристика, начинающаяся в q, стремилась бы к одной из них, а не к Г. В этом случае Г назы-
называют наименьшей циклической траекторией, охватывающей точку р0. Из рассуждений,
подобных тем, что мы проводили в п. 3), следует, что положительная полухарактеристика,
начинающаяся в любой точке q', не совпадающей с р0 и лежащей внутри области, ограни-
ограниченной кривой Г, стремится к этой кривой, тогда как отрицательная полухарактеристика,
начинающаяся в q', стремится к точке р0.
Аналогичное положение имеет место и тогда, когда точка /H устойчива. В этом слу-
случае положительная полухарактеристика, начинающаяся в точке q', стремится к точке-
р0, а соответствующая отрицательная полухарактеристика стремится к Г.
7) В других возможных случаях может иметься конечное число циклических траек-
траекторий, охватывающих одну особую точку р0, или счетное множество циклических траек-
траекторий. Как мы видели, если р0 есть особая течка типа центра, то все траектории могут быть
циклическими.
Если точка р0 окружена конечным числом циклических траекторий и является
неустойчивой, то наименьшая циклическая траектория, охватывающая р0, должна быть
устойчива изнутри. В исключительном случае она может оказаться полуустлйчивой, т. е.
устойчивой изнутри и неустойчивой снаружи. Этот последний случай встречается очень
редко, и, как правило, наименьшая циклическая траектория устойчива, т. е. устойчива
с обеих сторон. В общем случае последовательные циклические траектории либо устойчи-
устойчивы, либо неустойчивы.
394 ЦИКЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ [Гл. XX
§ 20.7. Приложение к системе частного вида. Затухающие гармониче-
гармонические колебания (§ 19.2), как известно, описываются уравнением
У + 2кх + п2х = 0, п>к>0. B0.7.1)
С ростом t амплитуда колебаний убывает по экспоненциальному закону.
Если уравнение B0.7.1) заменить эквивалентной системой двух уравнений
первого порядка, то начало координат будет устойчивым фокусом (§ 19.4).
Если, однако, в уравнении B0.7.1) считать к отрицательным (и>0>А:),
то получим систему с отрицательным трением и колебания будут неограни-
неограниченно возрастать по амплитуде. Начало координат для эквивалентной сис-
системы двух уравнений первого порядка будет неустойчивым фокусом.
Выбирая подходящим образом масштаб времени, можно, без потери
общности, положить в уравнении B0.7.1) п = 1.
Заменим теперь в уравнении B0.7.1) постоянную к, положительную
или отрицательную, некоторой функцией от х и г, которая может принимать
как положительные, так и отрицательные значения. В этом случае колебания
будут то затухать, то, наоборот, возбуждаться. При этом может случиться,
что движение будет периодическим при достаточно малых отклонениях
от положения равновесия или будет стремиться к периодическому, при кото-
котором полная потеря энергии будет равна нулю. Первый из этих случаев мы
имели в примере 19.ЮС. В качестве иллюстрации второго случая рассмотрим
прямолинейное движение частицы, описываемое уравнением
•г + |л {х2 + 'х2 — а2) х + х = 0, B0.7.2)
в котором |л > 0, а > 0. При г > а (г = у хг + х2) трение приводит к зату-
затуханию колебаний, а при г < а —- к нарастанию колебаний. Естественно
ожидать, что система будет стремиться к режиму гармонических колебаний
с амплитудой а, где х2 + х2 = а2, и трение при этом будет равно нулю. То,
что это предположение оправдывается, непосредственно следует из теории.
Соответствующие уравнения первого порядка имеют вид х — Р, у — Q,
где
Р = У, Q = -х - V- (г2 - а2) у. B0.7.3)
Радиальная составляющая поля равна
R = —? (г* _ а2) г sin26. B0.7.4)
Рассмотрим кольцо а < г < р, где 0<Са<а-<р. В точках внутрен-
внутренней окружности кольца г = а поле направлено в наружную сторону, а в точ-
точках внешней окружности г = Р — во внутреннюю сторону (за исключением,
конечно, точек на линии у = 0). Поэтому положительная полухарактери-
полухарактеристика, начинающаяся в точке кольцевой области, либо является циклической
(что имеет место, когда в начальный момент г = а), либо стремится к пре-
предельному циклу (§ 20.6, п. 2), которым является окружность г = а.
Значительно более важный пример доставляет уравнение Ван-дер-Поля
'х + |л (х2 — 1) х + х = 0, |л > 0. B0.7.5)
Когда | х | > 1, происходит затухание; когда ] х ( < 1 — нарастание
колебаний. Можно ожидать, что система будет стремиться к режиму перио-
периодических колебаний и обе эти противоположные тенденции в результате
не окажут влияния. И действительно, в дальнейшем мы увидим, что эквива-
эквивалентная система уравнений первого порядка обладает одним предельным
циклом.
§ 20.8] СУЩЕСТВОВАНИЕ ПРЕДЕЛЬНОГО ЦИКЛА 395
Рассмотрим вместо B0.7.5) уравнение более общего вида, а именно:
'x+f(x)'x + x = 0, B0.7.6)
где / (х) ? Си причем / (х) — четная функция и такая, что если F (х) =
х
= \ /(?) d\, то существует такое положительное число Ъ, что при 0 < х < Ъ
о
F (х) отрицательно, а при х> Ъ F (х) положительно и монотонно возрастает*).
(В частном случае уравнения B0.7.5) имеем
и b = )
Рассмотрим уравнение
"z + F(z)+z = 0, B0.7.7)
которое, по существу, эквивалентно уравнению B0.7.6). В самом деле, если
z есть решение уравнения B0.7.7), то z есть решение уравнения B0.7.6).
Кроме того, если х удовлетворяет уравнению B0.7.6), то функция
z = 'x + F(x) B0.7.8)
является решением уравнения B0.7.7). Для доказательства замечаем, что
z = 'х + f (х) х = — х B0.7.9)
и, следовательно,
z' + F (z) + z = — х + F {—x) + 'x + F (x), B0.7.10)
что равно нулю, так как F (х) — нечетная функция. Периодическому реше-
решению одного из уравнений B0.7.6) и B0.7.7) соответствует периодическое
решение другого с тем же периодом..
§ 20.8. Существование предельного цикла. Рассмотрим уравнение
B0.7.7), причем зависимую переменную будем обозначать не г, а х:
'х + F (х) + х = 0. B0.8.1)
Как обычно, запишем эквивалентную систему двух уравнений первого поряд-
порядка: х = Р, у = Q, где
P = y,Q = -x-F (у). B0.8.2)
Начало координат является единственной особой точкой и представляет
собой, либо неустойчивый узел, либо неустойчивый фокус. Как выяснится
в дальнейшем, существует одна-единственная циклическая силовая линия
а все положительные полухарактеристики стремятся к одному предельному
циклу. Система обнаруживает стремление к установлению периодических
колебаний независимо от начальных условий движения (исключая тривиаль-
тривиальный случай, когда в начальный момент х = х = 0).
*) Результаты сохраняют силу и для более общего уравнения
"х + f (x)'x+ g {х) = 0,
в котором g (х) — нечетная функция и такая, что интеграл I g (x) dx расходится. В этой
книге мы ограничимся, однако, рассмотрением лишь частного случая, когда g (x) = х.
396
ЦИКЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ
[Гл. XX
Существование предельного цикла будет доказано, если будет найдена
замкнутая кривая, охватывающая точку О, которая обладает тем свойством,
что вектор F в каждой ее точке направлен внутрь области, ограничиваемой
этой кривой. При этом, как и в § 20.6, существование предельного цикла
будет следовать из теоремы Пуанкаре — Бендиксона. Однако, мы приведем
здесь другое доказательство, которое одновременно будет гарантировать
и единственность решения.
Направление поля в каждой точке можно определить с помощью графи-
графического построения, подобного тому, которым мы пользовались в § 19.8.
Изобразим на чертеже кривую L, определяемую уравнением
x = -F (у). B0.8.3)
Направление поля в любой точке А найдется тогда из следующего построе-
построения. Проведем через точку А горизонтальную прямую, она пересечет кривую
L в точке В. Вертикальная прямая, про-
проходящая через точку В, пересечет ось Ох
в некоторой точке N. Тогда вектор поля
в точке А будет направлен перпендику-
перпендикулярно к отрезку NA.
Теперь легко представить общий ха-
характер поля. В точках верхней полупло-
полуплоскости горизонтальная составляющая Р
направлена вправо, а в точках нижней
полуплоскости — влево. Слева от кри-
кривой L вертикальная составляющая Q на-
направлена вверх, а справа от нее — вниз.
На кривой L поле горизонтально, а на оси
Ох — вертикально.
Рассмотрим теперь траекторию, про-
проходящую через произвольно выбранную
начальную точку (х0, у0). Пусть для опре-
определенности эта точка располагается в верх-
верхней полуплоскости слева от кривой L. Точка (xt, 0) на отрицательной
полуоси х соединяется дугой траектории с точкой (х2, 0) на положительной
полуоси х. Эта дуга в верхней своей точке пересекается с кривой L.
В этой точке ордината траектории достигает значение ?, затем траектория
снижается (рис. 93). Это почти что очевидно из общего характера поля, но
нужно дать и формальное доказательство. Когда изображающая точка уда-
удаляется от точки (хо, Уо), координаты х и у возрастают, так что х ^ у а > 0
и изображающая точка пересекает линию L. При пересечении производная
•
у изменяет знак с положительного на отрицательный, так как
Рис. 93.
= -у-1 (У) У
B0.8.4)
и в точке пересечения у = —? < 0. Изображающая точка может пересечь
кривую L только один раз в верхней полуплоскости (поскольку пересечение
должно происходить слева направо), и траектория ее не может касаться кри-
кривой L, так как в точке на кривой L касательная к траектории горизонтальна.
Поэтому горизонтальное смещение точки от кривой L, равное х + F(y),
никогда не обращается в нуль, если оно уже достигло положительного значе-
значения. С другой стороны, х -\- F (у) = —у, так что спустя небольшое время т
1
после пересечения будем иметь у <. — у ?т, х + F (у) > у ?т > 0. На той
части траектории, которая расположена справа от L, производная у < 0
не принимает нулевого значения, и изображающая точка достигает оси Ох.
§ 20.8] СУЩЕСТВОВАНИЕ ПРЕДЕЛЬНОГО ЦИКЛА 397
После пересечения с осью Ох траектория продолжается в нижней полу-
полуплоскости и снова пересекает кривую L, а также отрицательную полуось х.
Рассмотрим теперь дугу траектории, проходящую в верхней полупло-
полуплоскости и соединяющую точку (xi, 0), xt < 0, с точкой (х2, 0), х2 > 0. Эта дуга
определяется ординатой ? наивысшей точки (в которой она пересекается
с кривой L). Обозначим эту дугу через Cj и будем считать х\ = хг (?), х2 =
= х2 (Q. Функции Х\ (?) и ^2 (?) монотонны (так как траектории не пересе-
пересекаются) и изменяются в зависимости от Z, непрерывным образом: при возра-
возрастании ? от 0 до оо функция х^ изменяется от 0 до —оо, а функция х2 — от
0 до -г оо.
Если теперь заменить х на —х, а у на —у, то уравнения не изменятся;
поэтому кривая, симметричная дуге С^ относительно начала О, также явля-
является дугой траектории. Отсюда следует, что траектория является цикличе-
циклической в том и только в том случае, когда х2 — —Х\.
Возвращаясь теперь к уравнениям х = Р, у = О, где Р и Q определяют-
определяются формулами B0.8.2), находим
хх + у'у = -F (у) у = -F (у) х. B0.8.5)
Следовательно,
[\} B0.8.6)
Мы получили, как легко видеть, уравнение энергии в третьей форме (см. § 3.5).
Интегрируя вдоль дуги Cj, получаем
-L(xl-xl)= - J F(y)dx. B0.8.7)
XI
X2
Обозначим для краткости интеграл — \ F (у) dx через Я (?). Тогда можно
утверждать, что лш будем иметь циклическую траекторию тогда и только
тогда, когда Я (?) = 0.
Покажем, что функция Я (Q обращается в нуль лишь при одном поло-
положительном значении ?. Докажем сначала справедливость следующих поло-
положений:
1) если ? < Ь, то Я (?) > 0;
2) если ?2 > Si > Ь, то Я (?2) < Я (?i), так что с ростом ? (при ? > Ь)
функция Я (Q монотонно убывает;
3) при ?-> оо Я(?)-н- —оо.
Из этих утверждений будет вытекать, что функция Я (Q лишь один-
единственный раз принимает нулевое значение.
Перейдем к их доказательству.
1) Если ? < Ь, то вдоль кривой С% у <С b ж F (у) <С 0. Отсюда
. B0.8.8)
2) Выберем ?, и ?2 так> чтобы ?2>?1>Ь. Пользуясь обозначениями
рис. 94, напишем
Bi Ь
FB/)-J-^. B0.8.9)
398
ЦИКЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ
[Гл. XX
Вдоль траектории имеем
dx__x_ У
~dy~ -y ~ -x-F{y)
B0.8.10)
Правая часть равенства в точках Pt и Р2 положительна, причем в точке Р2
значение ее меньше, чем в точке Р^.
Аг А,
dy
Отсюда
Рис. 94.
B0.8.11)
. B0.8.12)
Рассуждая аналогичным образом, полу-
получаем, что
Х>2 JH
-\F(y)dx<-\F(y)dx. B0.8.13)
1 бг
Остается сравнить интегралы, взятые вдоль дуг В1С1 и В2С2. На этих
дугах F (у) > 0 и
с2
F(y)dx,
B2
ибо при у > Ъ функция F (у) монотонно возрастает вместе с у.
Таким образом,
Г>2
- J
- J
= Я, (SJ,
B0.8.14)
B0.8.15)
что завершает доказательство второго утверждения.
3) Перейдем теперь к большим значениям Z,. Доли, которые вносят дуги
А2В2 и C2D2 в значение интеграла — \ F (у) dx, положительны и ограничены,
а доля дуги В2С2 при ? -> оо стремится к минус бесконечности. Для доказа-
доказательства выберем фиксированное число с > Ъ, и пусть линия у = с пересека-
пересекает дугу Cj2 (при ?2 > с) в точках М2 и 7V2. Тогда
С2 iV2
J F (у) dx>^F(у) dx>F(с) M2N2 B0.8.16)
в2 м2
и длина отрезка M2N2 стремится к бесконечности вместе с ? (ибо для любой
заданной точки на линии у = с мы можем найти проходящую через нее тра-
траекторию). В результате получаем, что А, (?)-»-—оо, когда ?-> оо.
Мы доказали таким образом, что функция Я (?) обращается в нуль при
одном-единственном положительном значении Z, и, следовательно, сущест-
существует лишь одна циклическая траектория Г. При t —>¦ оо любая положитель-
положительная полухарактеристика стремится к Г. Начало координат представляет
собой неустойчивую особую точку, и всякая траектория, начинающаяся
внутри области, ограниченной кривой Г, стремится к этой кривой изнутри.
Для траектории, начинающейся вне указанной области, имеем х2 < (—Xi),
20.9]
УРАВНЕНИЕ ВАН-ДЕР-ПОЛЯ
399
и при t -н» оо эта траектория стремится к предельному циклу. Но предельным
циклом может быть только кривая Г, поскольку других циклических траек-
траекторий не существует.
Существование единственного предельного цикла, к которому стремятся
все положительные полухарактеристики, нами было доказано для уравнений
первого порядка, получаемых из уравнения B0.8.1). Это остается в силе и для
уравнения B0.7.6) и, в частности, для уравнения Ван-дер-Поля B0.7.5).
§ 20.9. Уравнение Ван-дер-Поля. Изучение теоремы Пуанкаре — Бен-
диксона мы закончим рассмотрением уравнения Ван-дер-Поля B0.7.5)
х + \i (х2 - 1) х + х = 0,
к которому применим изложенную выше теорию.
Уравнение, соответствующее B0.7.7), имеет вид
0,
B0.9.1)
х = 0, B0.9.2)
а эквивалентная система уравнений первого порядка записывается в виде
B0.9.3)
Эта система, как мы знаем, обладает одним-единственным предельным цик-
циклом. Движение, описываемое уравнением B0.9.2), стремится к некоторому
периодическому колебанию.
Представляется интересным приближенно определить форму предельного цикла
в двух крайних случаях, когда (х очень мало и когда \i очень велико.
1) Если \i очень мало, то уравнение B0.9.2) почти не отличается от уравнения
гармонического движения. Если бы и. равнялось нулю, то траекториями для системы
B0.9.3) были бы окружности; если же ц очень
мало, то единственная оставшаяся цикличе-
циклическая траектория будет весьма близка к окруж-
окружности. Радиус R этой окружности можно найти
Рис. 95.
Рис. 96.
из энергетических соображений (см. B0.8.6)); интеграл I F (у) dx за полный период должен
быть равен нулю. Таким образом,
B0.9.4)
Интеграл здесь берется вдоль полуокружности радиуса R в верхней полуплоскости. Ради-
Радиус R почти кругового предельного цикла получается равным двум. Это есть амплитуда
колебания для х (а также для у). Траектории имеют вид спиралей, медленно приближаю-
приближающихся к предельному циклу (рис. 95); движение по координате х представляет почти гар-
гармоническое колебание с амплитудой, медленно возрастающей (или убывающей) до значе-
значения, равного двум (рис. 96).
2) Если [х имеет очень большое значение, то форму предельного цикла приближенно
можно определить из геометрических соображений. В точках кривой L,
B0.9.5)
400
ЦИКЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ
[Гл. XX
поле F имеет горизонтальное направление. По мере удаления от кривой L направление
поля быстро приближается к вертикальному (поскольку |х велико), причем слева от L
вектор F направлен вверх, а справа от I — вниз. Если изображающая точка начинает
свое движение из точки R слева от кривой L в верхней полуплоскости (рис. 97), то сначала
она движется почти вертикально вверх, а
затем, приблизившись к кривой L, — почти
горизонтально. В точках кривой L' (получае-
(получаемой из кривой L сдвигом ее вправо на неболь-
небольшое расстояние) вектор поля F принимает
, почти вертикальное направление (вниз), и
Рис. 97.
Рис. 98.
изображающая точка остается в полосе между кривыми L и L'. Она движется почти что
/2 \
вдоль кривой L, пока не приблизится к крайней точке В ( -=- |х, 1), после чего перемещается
почти что по вертикали вниз, пока вновь не достигнет кривой L. После пересечения с этой
кривой вблизи точки С (-п-(х, —2 ) изображающая точка опять почти что следует вдоль
/2 \
кривой L, пока не достигнет ближайшей окрестности точки D I — -^-(х, —1 ). Затем она, дви-
гаясь почти вертикально, снова достигает кривой L вблизи точки А I =- (х, 2 1 . В резуль-
результате при больших значениях fx предельный цикл оказывается весьма близким по форме
к кривой ABCD, состоящей из двух вертикальных отрезков и двух дуг кривой L.
Изменение у в зависимости от t в периодическом движении на предельном цикле
показано на рис. 98. Время прохождения почти вертикальных участков мало, и так как
dt = dx/y, то период с приближенно можно выразить следующей формулой:
= 2 f —dx = 2 [ -^G/2_l)&/ = (xC_
J У J У
B0.9.6)
Таким образом, приближенно а равно 1,6 (х. Таково приближенное значение периода пре-
предельного периодического .движения, описываемого уравнением Цан-дер-Поля.
Г л -cue a XXI
СИСТЕМЫ С П СТЕПЕНЯМИ СВОБОДЫ.
СВОЙСТВА ХАРАКТЕРИСТИК
§ 21.1. Интегралы системы дифференциальных уравнений. Теперь,
после того как мы изучили основные свойства автономной системы второго
порядка (т = 2), перейдем к системе общего вида
хТ = Хт (хи аг2, . . ., xm; t), г = 1, 2, . . ., т. B1.1.1)
Известны многие интересные и важные свойства характеристик этих
уравнений; некоторые из них мы рассмотрим в этой главе. Однако, как мы
уже отмечали, случай произвольного т (даже в предположении автономности
системы) изучен менее подробно, чем случай системы второго порядка, рас-
рассмотренный в двух предыдущих главах.
Число т равно удвоенному числу степеней свободы системы (т — 2п).
Сначала мы будем предполагать, что все переменные вещественны, но позже
мы иногда будем считать их комплексными. Часто бывает удобным уравне-
уравнения записывать в форме A9.1.4):
^— = ^= • ¦ • ~-v— = ar. (ZJ..1.Z;
Решения этих уравнений имеют вид
хТ = фг (t; аи а2, . . ., ат; т), г = 1, 2, . . ., т, B1.1.3)
где а есть вектор х при t — т. Как уже указывалось, чем точнее определить
функции Хг, тем полнее можно представить решения уравнений (§ 19.1).
Функции ХТ будем считать принадлежащими к классу Ci в некоторой области
R пространства xif х2, ¦ . ., xm, t. Отсюда следует, что решения срг обладают
соответствующими свойствами дифференцируемости. Иногда мы будем делать
более сильные предположения. В частности, в некоторых случаях будем счи-
считать Хг аналитическими функциями от т -}- 1 комплексных переменных х\,
х2, . • ., хт, t в некоторой области их изменения; тогда соответствующие
решения будут аналитическими функциями от т + 2 комплексных перемен-
переменных t, а4, «2, . . ., <хт, т в определенной области пространства.
Наиболее важным и чаще всего встречающимся случаем является случай
автономной системы, когда функции ХТ не зависят от t:
Хг = Хг («„ хг, . - ., хт), г = 1, 2, .... т. B1.1.4)
Предполагается, что эти функции по крайней мере имеют непрерывные пер-
первые производные в области D пространства переменных Xi, х2, . . ., хт.
Можно без потери общности положить т = 0, так что а будет обозначать век-
вектор х в момент t — 0. Если изображающая точка начинает свое движение
в момент t = 0 из положения а области D, то в момент t (если | t \ не слишком
велико) она достигнет точки х этой же области, и соответствующая характе-
характеристика будет определяться уравнениями типа A9.1.10):
хТ = фг (I; аь а2, . . ., ат), г = 1, 2, . . ., пг. B1.1.5)
Траектории изображающей точки, т. е. проекции характеристик на
^-пространство, представляют дуги силовых линий поля. Эти кривые
26 л. А. Парс
402 СИСТЕМЫ С П СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК [Гл. XXI
определяются уравнениями
пХл и,Хъ иХгп /с\А л г*\
Если а — обыкновенная точка области D, то через нее проходит одна-
единственная траектория, по крайней мере в некоторой окрестности а; если
же а — особая точка, то она сама и будет траекторией; однако возможен
случай, когда через а проходит множество силовых линий (см. рис. 75—77).
Решение задачи о нахождении характеристик можно разбить на два этапа:
сначала определить траектории, а затем искать зависимость между положе-
положением изображающей точки на траектории и временем t. Если траектории
известны, то второй этап не представляет трудностей, по крайней мере в тео-
теоретическом отношении (см. начало § 19.1 и окончание § 21.2).
Разрешая уравнения B1.1.5) относительно аь а2, . . ., ат, получаем
«г = фг (—t; Xt, х2, . . ., хт), г = 1, 2, . .., т. B1.1.7)
Свойство обратимости функций фг, обнаруживаемое из равенств
B1.1.5) и B1.1.7), является важным отличительным свойством автономных
систем.
Возвратимся теперь к общему (неавтономному) случаю и рассмотрим
функцию / (х\, х2, . . ., хт; t), принадлежащую к некоторой области класса
С\ и обладающую тем свойством, что она остается постоянной в силу диффе-
дифференциальных уравнений B1.1.1). Иными словами, при движении изображаю-
изображающей точки в соответствии с дифференциальными уравнениями имеет место
соотношение
/ (хи хг, . . . ., хт; t) = с, B1.1.8)
где (xi, xz, . . ., хт) — положение изображающей точки в некоторый момент
t, и оно сохраняется для всех характеристик, хотя постоянная с на различ-
различных характеристиках принимает различные значения. Соотношение B1.1.8)
называется интегралом системы дифференциальных уравнений B1.1.1)
или B1.1.2). Функция / удовлетворяет уравнению в частных производных
teT-rAs ~^п" ' ¦+Xm~dx^s=0' B1.1.9)
и обратно, любое решение уравнения B1.1.9) представляет собой интеграл
системы B1.1.1) Интеграл, зависящий только от (х±, хг, ¦ ¦ ., хт) и не зави-
зависящий от t, удовлетворяет уравнению
В этом случае его называют пространственным интегралом.
Если система автономна, то пространственные интегралы системы
B1.1.2) являются интегралами системы B1.1.6); любое решение уравнения
B1.1.10) есть интеграл системы B1.1.6) и пространственный интеграл системы
B1.1.2). Если система автономна и / есть интеграл системы B1.1.2), завися-
зависящий от.?, то dfldt также есть интеграл этой системы. Аналогично, d^fldf1 тоже
является интегралом, и т. д., при условии, что частные производные суть
функции класса Cj.
Можно, разумеется, указать функции, которые сохраняют постоянное значение
на некоторых (но не на всех) характеристиках; такие функции не относят к интегралам.
Тривиальным примером может служить система уравнений
dx dy da dv
§ 21.1J ИНТЕГРАЛЫ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 403
где g—постоянная. Система имеет интегралы
Кроме того, на тех характеристиках, на которых в начальный момент и = 0, / = х
остается постоянным, но это не имеет места на всех характеристиках, и поэтому соотно-
соотношение / = х не является интегралом.
Обозначим через Q линейный оператор
фигурирующий в уравнениях B1.1.9) и B1.1.10). Пространственные инте-
интегралы системы B1.1.2) удовлетворяют условию
Q/ = 0, B1.1.12)
т. е. оператор Q обращает функции от хи х2, . . ., хт в нуль. Интегралы,
включая те, что зависят от времени, удовлетворяют условию
=°- B1Л-13)
Систему уравнений B1.1.1) или B1.1.2) можно записать также в форме
хТ = Qxf, г = 1, 2, . . ., тп, B1.1.14)
или в форме, сходной с B1.1.13):
0, r = l,2, ...,m. B1.1.15)
Как уже указывалось (§ 19.1), иногда бывает полезно уравнения B1.1.1)
рассматривать не как уравнения движения изображающей точки, а как урав-
уравнения движения жидкости; Это позволяет представить всю совокупность
возможных движений или по крайней мере движений, которые начинаются
в некоторой области, а не ограничиться одним возможным движением дина-
динамической системы. Линии тока в установившемся движении жидкости совпа-
совпадают с траекториями; они являются также силовыми линиями поля X. Если
f (Xi, x2, • ¦ ., хт) есть пространственный интеграл автономной системы,
то уравнения / = с определяют (для некоторого интервала значений с)
многообразия, содержащие линии тока. В классической гидродинамике опе-
оператор -s—1-й обычно обозначают через у- . Величина -^ выражает скорость
изменения функции / (х\, х2, . ¦ ., хт; t) в переменной точке, занимаемой
изображающей точкой. Интегралы системы B1.1.1) удовлетворяют условию
^7=0, B1.1.16)
которое показывает, что поверхности/ = const движутся вместе с жидкостью.
Если автономная система достаточно проста, то можно найти более чем
одно решение уравнения B1.1.10); всего может оказаться т — 1 независимых
решений /i, /2, • ¦ ¦, /m-i- В этом случае каждая траектория представляет
линию пересечения т — 1 поверхностей, определяемых уравнениями вида
/г = сг. Всего может быть не более т — 1 независимых пространственных
интегралов. Однако в общем случае нельзя гарантировать существование
т — 1 однозначных или конечнозначных пространственных интегралов.
Если мы можем найти т — 1 независимых решений уравнения B1.1.10),
то для получения общего решения достаточно знать одно решение уравнения
{21.1.9), содержащее t.
26*
404 СИСТЕМЫ С п СТЕПКНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК [Гл. XXI
Рассмотрим в качестве примера колебательную систему с двумя степенями свободы
х = и, и= —ргх, 'у = v, Ь = — q2y, B1Л.17)
где р и q — положительные постоянные; т = 4. Уравнения траекторий
имеют, как известно, интегралы
ргх* + и* = const, q2y* + i>2 = const. B1.1.19)
Если отношение р/д есть число рациональное, то существует третий пространствен-
пространственный интеграл, представляющий алгебраическую функцию от (х, у, и, v); при иррацио-
лальных p/q интеграла не существует.
Введем новые переменные х, у, |, tj:
р*|2 __ ргх2 _|_ Ц2) ^2 _ g2^2 _j_ y2_ B1.1.20)
В этих переменных уравнения B1.1.16) принимают вид
dj _ rfr] _ cfa __ rfy B1121)
0 0 ~i /*•«>' о -i /' n ЙГ " \ • * /
B1.1.22)
Отсюда получаем \ = а, т) = Ь и
Если отношение p/q есть число иррациональное, то кривая, определяемая уравне-
уравнениями B1.1.22), плотно заполняет прямоугольник со сторонами х = ± а, у=±Ь
(см. рис. 49); при этом конечнозначного интеграла системы B1.1.22) не существует.
Рассмотренный пример поучителен еще в одном отношении. Мы видели, что если
имеется интеграл /, зависящий от времени, то частная производная df/dt также представ-
представляет собой интеграл; то же верно и для d*f/dt2 и т. д. Может показаться, что, имея один
такой интеграл, мы указанным путем сможем найти т. независимых интегралов и в ре-
результате получим полное решение задачи. Однако получающиеся при этом интегралы
совсем не обязательно будут независимы. Так, например, соотношение
/ = рх sin pt -f и cos pt B1.1.23)
есть интеграл уравнений B1»1.15). Производная
df/dt = р (рх cos pt — и sin pt) B1.1.24)
образует еще один независимый интеграл. Эти два интеграла определяют х п и как функ-
функции от t. Но уже вторая производная d2f/dt2 отличается от / только множителем и, стало
быть, не является интегралом, не зависящим от уже найденных.
В дальнейшем ради краткости мы иногда вместо фг (t; о^, а2, . . ., <хт)
будем писать фг (t; а). Частную производную dq>r/das мы будем обозначать
через фГ8. Функции фГ8 (t; at, a2, . . ., am), или в сокращенном обозначении
фгв (t', a), определяются единственным образом исходными дифференциаль-
дифференциальными уравнениями B1.1.1).
Если выражения B1.1.7) для переменных ai, a2, • . •, ат подставить в правую часть
равенств B1.1.3), то получится тождество, содержащее функции ц>/.
хГ = Фг {t; Ф1 (-<; ж), ф2 (-*; ж), . . ., Фт (-*; ж)}. B1.1.25)
Дифференцируя частным образом по t и учитывая, что
я d
—-фг It; а) = ХТ(а>), -%- фг( — t; ж) = — Хг (а), B1.1.26)
приходим к равенству
m
Хг (ж) = 2 фГ4 (<; a) Xs (a). B1.1.27)
8=1
Другое доказательство этого соотношения будет дано в § 21.5 (см. уравнение B1.5.4)).
§21.2] ПРЕОБРАЗОВАНИЕ К НОВЫМ КООРДИНАТАМ 405
§ 21.2. Преобразование к новым координатам. Запишем уравне-
уравнения B1.1.1) в новых координатах yt, yz, . . ., ут, задав их формулами
уТ = FT (хи x2, . . ., xm), r = 1, 2, . . ., m. B1.2.1)
Функции Fr будем считать принадлежащими к классу С2 в соответствующей
области D пространства х; в автономном случае эта область совпадает с об-
областью!), введенной ранее для системы B1.1.4). Предполагается, что якобиан
2' ' * ''^~ в области D не обращается в нуль. При этих условиях пре-
о \х^,х2, . . . , хт)
образование B1.2.1) представляет отображение области/) пространствахв об-
область Е пространства у; если область!) не слишком велика, то это отображе-
отображение является взаимно однозначным соответствием, непрерывным и дважды
дифференцируемым в обоих направлениях.
Уравнения B1.1.2),
аХ{ dx2 dZm ¦,. ,па с\ п\
~?Т'— z==- ~^7—== . . • === ~^~ = Ufr, \L*Y.L*.&)
преобразуются в следующие:
dyi dy2 dym j. 1пм о о\
-у- ^-— ... ——— — at, {61.4.O)
Y
2
где через YT обозначено Q^r, выраженное через координаты у и время t.
Уравнения B1.2.2) и B1.2.3) устанавливают соответствие между движе-
движениями в пространстве жив пространстве у. Пусть Хо — некоторая точка в об-
области D, а. у о — соответствующая ей точка в области Е. Далее, пусть х —
точка, достигаемая в момент t на траектории системы B1.2.2), начинающейся
в точке х0, а у — точка, достигаемая в момент t на траектории системы
B1.2.3), начинающейся в точке у0. Тогда х и у будут соответственными точ-
точками для всех значений t, при которых х 6 D.
Пусть теперь F± — пространственный интеграл системы B1.2.2). Тогда
Yi = 0, и при движении в ^-пространстве координата у± сохраняет постоян-
постоянное значение, скажем, yt = p\. Тогда система B1.2.3) может быть заменена
системой
dy2 _ dy3 __ dym , ft>. n/ч
x a * а * m
причем функции Y'r получаются из функций Yr путем замены г/4 на р4. Таким
образом, воспользовавшись известным интегралом системы B1.2.2), мы
уменьшили число координат с т до т — 1. Подобно этому, если известны ц
независимых пространственных интегралов Fi, F2, . . ., F^, то можно эти
функции выбрать в качестве \i первых составляющих в преобразовании
B1.1.1) и таким образом уменьшить число координат стдот — \i.
Рассмотрим частный случай автономной системы, для которой известны
т — 1 независимых пространственных интегралов Ft, F2, ¦ ¦ ., Fm_i. Как
отмечалось выше, траектории системы определяются как линии пересечения
поверхностей FT = рг. Рассмотрим траекторию, соответствующую некоторой
фиксированной системе значений рь р2, • • •> Pm-ь и найдем соотношение,
связывающее положение точки на траектории со временем. Это соотношение
дается уравнением
Ф*—Я, B1.2.5)
в котором Х'т получается из Хт, если его выразить через (Pi, f52, • • •> Pm-i>
хт) с помощью формул
Fr = рг, г = 1, 2, . . ., т - 1. B1.2.6)
406 СИСТЕМЫ С ПЧСТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК [Гл. ХХГ
Высказанные утверждения вполне очевидны; формальное доказательство
можно получить, применив преобразование
Z } B1.2.7)
У т. — Хт- )
§ 21.3. Оператор Tt. Рассмотрим автономную систему. Характеристики,
представляемые уравнениями B1.1.5), определяют преобразование а в х,
зависящее от t:
x = Tta. B1.3.1)
Оператор Tt преобразует точку а, занимаемую изображающей точкой
в момент t == 0, в точку х, занимаемую изображающей точкой в момент t.
Предполагается, что якобиан
д(ф1. ф2. ••-. фго)
а (ОС!, а2, ..., От)
не обращается в нуль ни при одном допустимом значении а и t. (Ниже мы
увидим, что в важном частном случае уравнений Гамильтона этот якобиан
имеет значение, равное единице.) Рассмотрим подобласть Ео области D
(соответствующей уравнениям B1.1.4)), и пусть а ? Ео- Тогда преобразование
Tt при достаточно малых t определит топологическое отображение Ео на об-
область Et. Оператор То будет определять тождественное преобразование,
а оператор Г_( — обратное преобразование, отображающее область Et на
Eq. Два последовательных преобразования, задаваемые операторами Г^,
Tt2, обладают свойством коммутативности и эквивалентны одному преобра-
преобразованию, осуществляемому оператором
B1.3.2)
Кроме того, оператор Tt обладает свойством ассоциативности:
Tt3(Tt2Ttl)^(ThTt2)Ttv B1.3.3)
Таким образом, мы имеем непрерывную однопараметрическую группу пре-
преобразований пространства х в себя.
В важном частном случае уравнений Гамильтона 2п переменных груп-
группируются в п пар (qr, pr), и соответствующее преобразование, обладающее
особыми свойствами, называется контактным преобразованием. Преобра-
Преобразования этого вида будут рассмотрены нами в гл. XXIV.
§ 21.4. Решение в форме степенных рядов. Рассмотрим автономную
систему, обладающую тем свойством, что в области D функции Хг имеют
производные всех порядков. Введем функцию / (х), зависящую от времени.
Здесь х — положение изображающей точки в момент t. Тогда будем иметь
С другой стороны,
JL f — 'У ILr —V х д^ — Qf B1 4 I)
-§^ = Xr = Qzr, B1.4.2)
следовательно,
§ 21.4] РЕШЕНИЕ В ФОРМЕ СТЕПЕННЫХ РЯДОВ 407
и вообще
1^Г = Йп*г. B1.4.4)
Если аг = а при ? = 0, то, предположив, что ряд Тейлора сходится, найдем
Xr = (xrH + t(QxrH + -^(Q?xrH+ ...=ar + toar + -|co2ar + ... B1.4.5)
Здесь a> обозначает оператор
т
2^г(а„оа>..., о™)-^. B1.4.6)
г=1
Равенство B1.4.5) можно записать в компактной форме
хТ = etcaar, г = 1, 2, .... m, B1.4.7)
представляющей решение уравнений хТ = Хг (зс).
Ряд для хт наверняка сходится,*если Qnxr ограничено (для всех п) на тра-
траектории, соединяющей а их. Таким образом, вообще говоря, при фиксиро-
фиксированном а ряд будет сходиться внутри круга сходимости радиуса | t \ = рг.
Решение будет справедливо для всех координат zt, х2, . . ., хт, если | ? | <
< р (а), где р — наименьшее из чисел рь р2, . . ., рт.
В более общем случае начальная точка может не быть фиксирована,
а лежать в некоторой области Rq. Тогда радиус сходимости | t | не должен
превышать наименьшего значения р (а) для а в области Ro.
Приведем другое доказательство того, что ряд B1.4.5) является решением. Согласно
{21.1.7) qv (—*; xi, x2, ¦ ¦ ., хт) есть интеграл уравнений B1.1.1); поэтому в соответ-
соответствии с B1.1.13)
(^) <Рг (-*;*!, *2, ...,*т) = 0. B1.4.8)
Следовательно,
(|) г(*;«1, хг, ...,хт) = 0 B1.4.9)
2 ccm)=O. B1.4.10)
Таким образом, функция фг (t; аь аг, ..., ат) удовлетворяет уравнению
-^=софг. B1.4.11)
Но если Хг — бесконечно дифференцируемые функции, то это уравнение, очевидно, удо-
удовлетворяется рядом
аТ-{-ШаТ-\--~у ш2аг+.... B1.4.12)
который при ( = 0 имеет значение аг. Таким образом, выражение B1.4.12) равно хг,
и мы снова получаем B1.4.5).
Решение в форме степенного ряда при достаточно малых t дает явное
выражение для оператора Tt:
Tt = e(M. B1.4.13)
Отсюда легко установить основное групповое свойство. Возьмем любую ана-
аналитическую функцию / (xi, х2, . . ., хт) и проследим за ее изменением при
движении точки х вдоль траектории. Имеем
,+ *L о*/(„)+..., B1.4.14)
408 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК [Гл. XXI
так что функция не будет изменяться только в том случае, когда
oa/(olf о2, . . ., ат) = 0, B1.4.15)
т. е. только тогда, когда / (х) удовлетворяет уравнению B1.1.11). Таким
образом, инвариантные функции являются интегралами уравнений B1.1.6),
т. е. они являются пространственными интегралами системы B1.1.2). Мы по-
получили (теперь уже с иной точки зрения) подтверждение того, что интегралы
B1.1.6) определяют многообразия, образованные из траекторий.
В простейших случаях степенные ряды сходятся для всех значений t
(см. ниже примеры 21.4А, В). Однако в общем случае решение сохраняет
силу только для достаточно малых значений t.
Пример 21.4А. Гармонический осциллятор. Уравнения име-
имеют вид
, х = и, и = — п?х. B1.4.16)
Ищется решение, удовлетворяющее условиям: х = а, и — Р при t = 0. В рассматриваемом
случае оператор со равен
co^JL.^J.. B1.4.17)
и решение имеет вид
x^(i + ta> + ~a>2-{....\ а, Л
з Г B1.4.18)
Далее, имеем
25:=Й
и т. д. Таким образом,
Аналогично
и = — па sin nt + p cos nt. B1.4.21)
¦
Последний результат, разумеется, проще получается из соотношения и = х. Мы пришли
к хорошо известному решению. Заметим, что решения обладают свойством обратимости
(см. B1.1.5) и B1.1.7)):
а = х cos nt——
— sin ni, Л
n \ B1.4.22)
и cos nt. )
$ = nx sin nt-{-
B рассматриваемом элементарном случае все результаты получаются из простых
соображений (см. пример 19.4В). Положим и = пу, тогда уравнения запишутся в форме
х = пу, 'у = — пх B1.4.23)
и преобразование Tt сведется к простому повороту на угол nt по ходу часовой стрелки.
Поэтому, чтобы получить явные формулы, достаточно повернуть оси координат против
хода часовой стрелки на угол nt и представить координаты начальной точки в новых осях.
Проделав это, получим
х = х0 cos nt + Уо sin nt,
у= —х0 sin nt + !/0 cos nt
j B1.4.24)
что эквивалентно B1.4.20), B1.4.21).
Пример 21.4В. Однородное поле. Этот случай еще проще предыдуще-
предыдущего, поскольку ряды представляют здесь конечные суммы. Имеем
• • • • • •
^ = «4, х2 = х5, х3 = х6, xi = 0, xi = 01 xe = g B1.4.25)
S 21.4]
РЕШЕНИЕ В ФОРМЕ СТЕПЕННЫХ РЯДОВ
409
Таким образом,
Отсюда приходим к известному решению
1
Укажем снова на свойство обратимости решений: выразив а через (ж, t), мы придем
к тем же самым формулам, но в которых ж и а поменялись местами, а t заменилось на —*.
Пример 21.4С. Ньютоновская орбита. В этом случае имеем
хь = a5,
B1.4.26)
B1.4.27)
--?., B1.4.29)
где |, т) обозначают соответственно рг, рд. Предполагается, что в начальный момент
(г, 0, |, т])= (а,'р, 7, S). B1.4.30)
Уравнения движения Гамильтона записываются в виде
Оператор <в равен
Для нахождения r = r(t) имеем
B1.4.31)
B1.4.32)
и т. д. В результате получаем
B1.4.33)
»+• ¦ ¦ <"-^>
Это выражение дает приближенное значение г для малых t. Однако в общем случае удоб-
удобнее пользоваться разложением в ряд Фурье (§ 18.14).
Чтобы определить 0 = 0 (t), напишем сначала
а4
I F2
\ аз
2б
I
а* + а*
263
а"
B1.4.35)
410 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК [Гл. XXI
и т. д. В результате получаем
9 = Р+ » t-^-t'+{&- + -&-~)t•+... B1.4.36)
'а2 а3 ' \ а4 За5 За6 /
Решение для | определяется из уравнения ? = г, а решение для т) имеет простой вид:
т] = 6.
§ 21.5. Формула для X (х) — X (а). Решения уравнений B1.1.1) даются
формулами B1.1.5), в которых а есть значение х при t = 0; при этом пред-
предполагается, что функции ф принадлежат к классу С2. Как обычно, на уравне-
уравнения мы смотрим как на соотношения, описывающие движение изображающей
точки, начинающееся из положения а в момент 1 = 0 и достигающее поло-
положения х в момент t. Как ив § 21.1, частную производную дц>г/дая мы будем
обозначать сокращенно через фГ8.
Предположим, что в момент t = 0 изображающая точка достигает поло-
положения 1,
Ь = фг(б; «1, а2, • • ., ат). B1.5.1)
Движение, начинающееся из точки а в момент t = 0, эквивалентно движе-
движению, начинающемуся из точки | в момент t = 8, поэтому
Фг (О + t; а) = Фг (*; |). B1.5.2)
Дифференцируя это равенство частным образом по 8, получаем
m
Хг {<р(8+ *; а)} = 2 <Prs (t; I) Xs {ер F; а)}. B1.5.3)
Полагая здесь 0 = 0, находим
m
^(ав) = S Фг8 (*; «) ^ («)• B1.5.4)
8=1
Этот результат нами уже был получен в § 21.1 другим методом. Таким
образом,
m
Хг (х) - Хг (а) = 2 {Фг* (*; а) - 8rs} Xs (а). B1.5.5)
s=l
Обозначим через F=JF(t',a) матрицу размером тхт, элементы кото-
которой имеют вид
/г. = Фг.(« «)-А,. B1.5.6)
Тогда предыдущий результат запишется в виде
Х(ав) —JT(o) = F(«; o)JC(o). B1.5.7)
§ 21.6. Интегральные инварианты*). Рассмотрим снова автономную
систему. Оператор Tt определяет преобразование, переводящее точку а —
положение изображающей точки в момент t = 0 — в точку х, занимаемую
изображающей точкой в момент t. Будем рассматривать теперь не одну началь-
начальную точку а, а совокупность точек, образующих кривую у0. Будем предпо-
предполагать, что эта кривая имеет непрерывно изменяющуюся касательную всюду,
за исключением, быть может, конечного числа угловых точек. Преобразова-
Преобразование Tt, определяемое дифференциальными уравнениями B1.1.1), переводит
каждую точку а, лежащую в момент t = 0 на кривой уОч в точку х, соответ-
соответствующую моменту t; эти последние точки в совокупности и образуют кривую
*) Интегральные инварианты были введены Пуанкаре (Acta Mathematica, XIII,
1890). Они нашли широкое применение в т. III его «Methodes nouvelles» [18]. См. также
Э. К а р т а н, Лекции об интегральных инвариантах, М., Гостехиздат, 1940.
S 21.6] ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ 411
•у. Если на уравнения B1.1.1) смотреть как на уравнения, определяющие
движение жидкости (см. § 21.1), то кривая у будет кривой, движущейся вместе
с жидкостью, а уо — се положением, занимаемым в момент t = 0.
Предположим теперь, что существует векторное поле Р — Р (х) с состав-
составляющими Ри Р2, . . ., Рт (РТ ? Сг) такое, что
\ P1dxi + P2dx2 + .. .+Pmdxm = \ P1dxl + P2dx2+ ... +Pmdxm B1.6.1)
vo v
для всех значений t и всех возможных кривых у0. При этих условиях кри-
криволинейный интеграл
m
\ P-dx=[ ^jPrdxr B1.6.2)
V V r=l
называют интегральным инвариантом уравнений B1.1.1). Если интеграл
остается инвариантным для всех кривых — разомкнутых и замкнутых,—
то его называют абсолютным интегральным инвариантом. Если же значение
интеграла сохраняется постоянным только для замкнутых кривых, то его
называют относительным интегральным инвариантом.
Тривиальный пример относительного интегрального инварианта мы имеем, когда
Р есть градиент однозначной потенциальной функции. В этом случае интеграл ф P-dx
вдоль любой замкнутой кривой в любой момент времени равен нулю. Другой пример
можно привести из классической гидродинамики. Рассмотрим установившееся движение
жидкости, тогда составляющие скорости и, v, w будут зависеть только от х, у, z. Объем-
Объемные силы, действующие на жидкость, будем считать потенциальными. При этих условиях
циркуляция скорости
и dx + v dy + w dz, B1.6.3)
взятая по замкнутой кривой, движущейся вместе с жидкостью, сохраняет постоянное
значение во времени.
Найдем теперь необходимые и достаточные условия того, чтобы интеграл
\ P'dx представлял собой интегральный инвариант. Для этого введем пара-
параметр и, изменяющийся от 0 до 1, и выразим через него кривую у. Выбор
параметра и подчиним дополнительному требованию, чтобы фиксированному
значению и отвечали точки, лежащие при любом t на одной и той же траекто-
траектории. Таким образом,
хТ = хт (t, и), г = 1, 2, . . ., т. B1.6.4)
Функции в правой части принадлежат к классу С\- При фиксированном зна-
значении t, когда и пробегает значения от 0 до 1, уравнения B1.6.4) определяют
кривую у. Если же фиксировано значение и, то уравнения определяют тра-
траекторию и
^=ХГ, г = 1,2, ...,т. B1.6.5)
Иными словами, кривые и = const представляют собой траектории, а кривые
t = const — мгновенные положения кривой у, движущейся вместе с жид-
жидкостью.
Рассмотрим теперь криволинейный интеграл
T^-du B1.6.6)
412 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК [Гл. XXI
(знак суммы мы здесь опускаем). Имеем
Dt J dt \ T du ) J \ dxs s du ~ T du
0
1
= Г (№rx.°^ + Prgz.?z.)du= f (^Xs+Ps^-)^du. B1.6.7)
J \ dxs s du ' T dxs du I J \ dxs * ' * dxr / ди ч '
0 0
Правую часть этого равенства можно представить в форме криволиней-
криволинейного интеграла вдоль кривой у:
IH (?
V
где
6=1
Необходимое и достаточное условие того, чтобы интеграл / был абсолют-
абсолютным интегральным инвариантом, состоит в том, чтобы выражение
QrdxT B1.6.10)
V
равнялось' нулю при любом выборе кривой у. Относительный интегральный
инвариант мы имеем в том случае, если интеграл ф QT dxT равен нулю для
т
всех замкнутых кривых, т. е. если выражение 2 Qr dxT является полным
r—i
дифференциалом однозначной функции от хи х2, ¦ ¦ ., хт.
Приведенные выше результаты можно получить весьма коротким путем, если вос-
воспользоваться представлением о движении жидкости. Рассмотрим линейный элемент das,
движущийся вместе с жидкостью. Тогда
/р fl^ \ __ ^ -Т^. |_ р , *7-г /91 6 11V
Далее,
¦Щ^-=-^-Х8, B1.6.12)-
-j—dxT = dXT= -dxs. B1.6.13)
Следовательно,
^dxs, B1.6.14)
и мы снова приходим к уже полученному ранее результату.
В качестве простого примера рассмотрим систему
0 — Фу
i 21.7] ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ ПОРЯДКА m 413
Интеграл ф udx-\-vdy представляет относительный интегральный инвариант. Это
^ 4
сразу следует из того, что выражение 2 Qr dxT есть точный дифференциал; кроме того,
г=1
это непосредственно видно из решения
x = xo+uot, y = y0cosnt + —v0sinnt, I B6 6 16)
U=Mg, V= —nyg Sill Tlt-\-VQ COS Jit. j
До сих пор мы, рассматривали интегральные инварианты лишь первого
порядка. Но можно рассмотреть интегральные инварианты более высоких
порядков: 2-го, 3-го, . . ., т-то, в которых область интегрирования представ-
представляет многообразие 2, 3, . . ., пг измерений, движущееся вместе с жидкостью.
Для классической динамики наиболее важны крайние случаи, когда много-
многообразие интегрирования имеет размерность либо 1, либо пг.
Всякому относительному интегральному инварианту порядка г соответ-
соответствует абсолютный интегральный инвариант порядка (г + 1). Это следует
из обобщенной теоремы Стокса.
Теорию интегральных инвариантов можно распространить на случай,
когда система неавтономна и когда функции Рг содержат t. Выражение
B1.6.10) заменится при этом следующим:
x" B1.6.17)
v
и интеграл / будет представлять абсолютный интегральный инвариант, если
выражение B1.6.17) обращается в нуль при любом выборе кривой у. Если
m
2 (~sf ~Ь Qr) dxr есть точный дифференциал, то мы будем иметь относитель-
ный интегральный инвариант.
В качестве тривиального примера, когда функции Р содержат t, можно опять-таки
рассмотреть систему B1.6.15). Для этой системы абсолютным интегральным инвариантом
-является \ dx — * du. В этом можно убедиться либо с помощью общего критерия (из обра-
обращения в нуль выражения B1.6.17)), либо непосредственно из решения B1.6.16).
§ 21.7. Интегральные инварианты порядка т. Начнем со случая авто-
.номной системы. Предварительно докажем следующую лемму.
Лемма. Обозначим через J определитель Якоби:
ц, х2, ..., хт) ,0. _ ..
<а через Д — дивергенцию векторного поля X:
Тогда
^ = /Д. B1.7.3)
Производная определителя может быть представлена в виде суммы пг
определителей, получаемых путем последовательного дифференцирования
элементов каждой строки. Таким образом, dJIdt может быть представлено
в виде суммы т определителей, первый из которых равен
д (xj, хг, ..., хт) д (Хи хъ ..., хт) /2\ 7 4)
д («ь а2, ..., обта) ~ д (аи а2, ..., ат) '
414 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК [Гл. XXI
г-й элемент первой строки этого определителя равен
дат ~А dxs дат • V*i./.o,
Вычитая из элементов первой строки соответствующие элементы s-й строки,
умноженные на dXJdxs (где s пробегает все значения от 2 до ш), мы не изме-
изменяем величины определителя. В образованном таким образом определителе
r-й элемент первой строки будет равен -г^-т-^ . так что первый из m определи-
телей, полученных при дифференцировании, будет равен -г-* J. Рассуждая
подобным образом и дальше, приходим к равенству
/, B1.7.6)
что и доказывает лемму.
Рассмотрим теперь замкнутую область Ео конечного объема Ао. Пусть
эта область переводится в область Et преобразованием Tt. Если А — объем
области Et, то
А \ d d d \ / d d d i<^\ n n\
= \ dxx dx2 . • • dxm = \ / dat daz ... dam.
E E
Пространство х считается здесь евклидовым. В результате получаем
-jj- = I -г:- dai da2 ... dam — \ A/ dat da2 ... dam = \ A dxr dx2 ... dxm.
Eo Eo E(
B1.7.8)
Уравнение B1.7.8) дает наглядную геометрическую интерпретацию
понятию дивергенции векторного поля X. Применяя полученный результат
к малому объему Et m-мерного пространства, приходим к формуле
Д = Т^« B1-7.9)
где V — удельный объем жидкости в точке х. Для т = 3 этот результат хоро-
хорошо известен в классической гидродинамике.
Найдем теперь необходимые и достаточные условия того, чтобы интеграл
/= \ Mdxtdx2 ...dxm B1.7.10)
к
был интегральным инвариантом. Скалярную функцию М от xlt х2, ..., хт
будем считать принадлежащей к классу Сх.
Имеем
/= f Mdxidx2 ...dxm= [ MJda^da2 ... dam. B1.7.11)
Et Eo
Следовательно,
-W=\lt (MJ) da± йа2 • • • da™- B1.7.12)
Пользуясь формулой B1.7.3), находим
m
^)^J^^{MXr). B1.7.13)-
r=l ¦ r=l
5 21.8] СВОЙСТВА МНОЖИТЕЛЕЙ 415
Равенство B1.7.12) можно переписать теперь в виде
: ) I 2 ~~&Г (МХг)} J dai daz • • • da™ —
Eg v== 1
m
_ f J у " (MX ) \ dx dx . .. dx B1.7.14)
DI_
Dt
г г=1
Итак, окончательно DI/Dt = O, при произвольном выборе Et в том
и только в том случае, если
^ JL J B1.7.15)
Функции М (xi, х2, . . ., хт), удовлетворяющие линейному уравнению
в частных производных B1.7.15), Якоби назвал множителями для системы
B1.1.1) *). Уравнение, которому удовлетворяют множители, можно записать
в одной из следующих форм:
div (MX) = 0, B1.7.16)
М div X + QM = 0. B1.7.17)
К этому же результату можно прийти и с помощью равенства B1.7.9). Рассмотрим
бесконечно малую область ^-пространства объема V- Имеем
г=1
Отсюда получается требуемый результат.
Система B1.6.15) дает простой пример интегрального инварианта порядка т. Таким
инвариантом является интеграл
\ \ Н
dxdydudv. B1.7.19)
Это следует из уравнения B1.7.15) или непосредственно из решения B1.6.16).
Теорию можно обобщить на неавтономные системы и подынтегральные
функции М, зависящие не только от хи х2, . ¦ ., хт, но и от t. Формула
B1.7.3) сохраняет силу и в неавтономном случае; если функция М содержит t,
то условие B1.7.15) заменяется следующим:
™кк(МХ) + +k{MX)=°- B1-7-20)
+к{МХд+к
Тем не менее мы сохраним термин множитель лишь для тех функций М,
которые не содержат t.
§ 21.8. Свойства множителей. Рассмотрим автономную систему: функ-
функции ХТ в правых частях уравнений B1.1.1) не зависят от t. Доказанные выше
положения позволяют вывести ряд важных свойств автономных систем.
1) Если % (xi, х2, . . ., хт) есть явное выражение для удельного объема
V, то 1/% представляет собой множитель.
2) Если найдены два независимых между собой множителя Mit M2,
то их отношение М\1М2 представляет интеграл системы дифференциальных
уравнений. Это следует из того факта, что оба выражения М\У и M2V остают-
остаются вдоль траектории постоянными (см. B1.7.18)), следовательно, остается
*) Теория множителей изложена в «Лекциях» Якоби [17].
416 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК [Гл. XXI
постоянным и их отношение MJM2. Или, иначе, из равенства B1.7.17) имеем
^^O; B1.8.1)
отсюда следует, что
(^H. B1.8.2)
3) Если А = 0, то М = 1 является множителем; сам объем я-простран-
¦ства представляет собой интегральный инвариант. (Это справедливо также
и для неавтономных систем, в которых А = 0.)
Дифференциальное уравнение, которому удовлетворяют множители,
имеет простой вид:
пМ = 0, B1.8.3)
так что множители представляют собой не что иное, как пространственные
интегралы. К этому результату можно прийти и другим путем. Если М —
пространственный интеграл, то он сохраняет свое значение вдоль траектории,
и так как А = 0, то и V сохраняет свое значение вдоль траектории. Поэтому
остается постоянным и произведение MV, откуда следует, что выражение
I M dxi dx2 . ¦ . dxm представляет собой интегральный инвариант.
4) Если т = 2, то множители являются интегрирующими множителями
уравнения
Х2 dXi - Xt dx2 = 0. B1.8.4)
В самом деле, интегрирующие множители \i удовлетворяют уравнению
5? = 0, B1.8.5)
а это уравнение совпадает с уравнением для множителей.
В частности, если т = 2 и А = 0, то единица является множителем
и одновременно интегрирующим множителем, т. е. выражение Х2 dxi —
— Хх dx2 есть полный дифференциал dtp. Функция^ является функцией тока
Лагранжа; она играет важную роль в изучении плоских течений несжимае-
несжимаемой жидкости.
5) Рассмотрим преобразование к новым переменным yt, у2, . • ¦, ymi
введенное нами в § 21.2.
В уравнениях преобразования
уТ = Fr (xi, x2, . . ., xm), r = 1, 2, . . ., пг, B1.8.6)
функции Fr принадлежат к классу С2 в области D пространства х; якобиан
У2, -...Ут) пл о п\
B18Л)
J~ d(Xl,x2,...,Xm) B1-8Л)
в области D не обращается в нуль. Преобразование устанавливает взаимно
однозначное соответствие между областью D пространства х и областью Е
пространства у.
Докажем, что если М является множителем для исходной системы, то
(M/J)' является множителем преобразованной системы. Штрих здесь указы-
указывает на то, что выражение дается в новых переменных г/4, у2, . . ., ут-
Эту теорему нетрудно доказать непосредственным вычислением *), одна-
однако значительно проще воспользоваться развитым выше гидродинамическим
представлением. Мы видели, что соответствие существует не только между
*) См., например, Е. Т. У и т т е к е р, Аналитическая динамика, М.— Л., ОНТИ,
1937, стр. 308.
§21.9.] ПОСЛЕДНИЙ МНОЖИТЕЛЬ ЯКОБИ 417
двумя пространствами, но и между двумя движениями (§ 21.2). Изображаю-
Изображающие точки х и у в этих двух пространствах занимают соответствующее отно-
относительное положение в момент t — О и, двигаясь вместе с соответствующими
жидкостями, сохраняют это взаимное положение в течение всего времени.
В силу этого из B1.7.18) имеем
^^(^)(^) B1.8.8)
где штрихи указывают на то, что выражения даются в переменных z/i, у2, ¦ . .
. . ., ут. Теорема, таким образом, доказана.
§ 21.9. Последний множитель Якоби. Рассмотрим уравнения траекто-
траекторий автономной системы
dXj __ dx2 _ __ dxm <2j g ^ч
и допустим, что нам известны т — 2 пространственных интегралов
fr = cr, г = 1, 2, . . ., т - 2, B1.9.2)
этих уравнений. Для определения траекторий требуется проинтегрировать
уравнение
X'mdxm_i-X'm_idxm = 0, B1.9.3)
в котором функции Х'т, Xm-i находятся из Хт, Xm_i при переходе
к си с2, . . ., ст_2, жт_!, хт с помощью соотношений B1.9.2).
Если известен множитель для исходной системы, то можно определить
интегрирующий множитель уравнения B1.9.3). Соответствующее правило
дается известной теоремой Якоби о последнем множителе. Пусть М —
множитель исходной системы -B1.9.1), тогда интегрирующий множитель
уравнения B1.9.3) дается выражением {MlК)', где
К= ?,(/ь f*> •¦••*>»-*> , B1.9.4)
д(хи хъ ...,Хт-.2) к '
а штрих указывает на то, что величина выражается через си Сг, . • -, ст_г,
xm_i, хт. Таким образом (т — 1)-й,интеграл определяется выражением
tra-i = { {MlК)' (X'ndXn-i-X'^dXm), B1.9.5)
что и завершает решение системы B1.9.1): все траектории найдены.
Доказательство теоремы Якоби весьма простое. Перейдем к новым пере-
переменным уг с помощью формул
2/1 = А. Уг = /г, • • ., У т.-г = fm-г, Ут-i = zm_i, Ут = хт. B1.9.В)
В пространстве у движение происходит в плоскостях
J/i = с17 уг — с2, . . ., ут_г — ст-г- B1.9.7)
При этом функции Yu Y2, ¦ ¦ ., Ут-г тождественно равны нулю. Кроме того,
для преобразования B1.9.6) / = К. Преобразованная система имеет вид
о о ••• о х'т_х~ х'т- V1*-0'
и если М — множитель для исходной системы, то {MlК)' будет множителем
для преобразованной системы (§ 21.8, п. 5). Поэтому {MlК)' является инте-
интегрирующим множителем уравнения B1.9.3) (§ 21.8, п. 4), что и требовалось
доказать.
Не следует, однако, переоценивать полученный результат. Как мы виде-
видели, нет гарантии, что существуют т — 2 независимых однозначных про-
27 д. А. Парс
418 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК [Гл. XXI
странственных интеграла. Если же они существуют, то интегрирование урав-
уравнения B1.9.3) может оказаться достаточно простым и без специального пра-
правила для отыскания интегрирующего множителя.
Теорема легко обобщается на тот случай, когда требуется найти т-ж
интеграл системы (автономной или неавтономной), если известны т — 1 ее
интегралов и один множитель, удовлетворяющий уравнению B1.7.20). В са-
самом деле, как уже указывалось, неавтономную систему с т координатами
можно трактовать как автономную систему с т + 1 координатами. Уравне-
Уравнения B1.9.1) заменятся теперь следующими:
cfai dx2 __ dxm dt
причем функции X могут содержать t. Правило Якоби определяет инте-
интегрирующий множитель уравнения
dxm — X'mdt = O,
где штрих указывает на переход к переменным хт и t и т — 1 постоянным
сь с2, . . ., cm_t.
§ 21.10. Линейная система. Перейдем теперь от системы общего вида
х\ = ХТ, г = 1, 2, . . ., т, B1.1.1)
к системе специального вида, правые части Хт которой представляют линей-
линейные однородные функции от переменных Xi, х2, . . ., хт, коэффициенты
которых суть заданные вещественные функции от t с непрерывными первыми
производными:
Хг = аг1Ж! + aT2x2+. . .+armxm, г = 1, 2, . . ., р. B1.10.1)
Эти уравнения можно кратко записать в следующей форме:
х = Ах, B1.10.2)
где х — матрица-столбец {xt, х2, . . ., хт}, а А — матрица размером т х т
с элементами вида aTS = ars(t).
В дальнейшем (гл. XXIII) мы дадим решение уравнения B1.10.2) в об-
общем случае, здесь же мы основное внимание уделим частному случаю, когда
элементы ars постоянны (система автономна). При этих условиях решение
системы, как легко видеть, запишется в виде
х = е*Ла* B1.10.3)
где а есть значение х при t = 0, а символ etA обозначает матрицу
Jm-f tA + (t*/2\) A* + (ts/3l) A3+ ... B1.10.4)
Действительно, выражение B1.10.3) удовлетворяет уравнению B1.10.2)
и при t = 0 обращает as в а. Вопрос о сходимости также не вызывает затруд-
затруднений. Если | ars | < К для всех значений г и s, то \а^ | < m^^iP (где
а<р> — типичный элемент матрицы Ар), откуда следует, что каждый элемент
матрицы etA при t > 0 не превышает выражения
1 _}. Kt + тКг (t2l2\) + m?Kz («3/3!)+ . . . = (т — 1 + emKt)/m. B1.10.5)
Этот ряд мажорируется заведомо сходящимся экспоненциальным рядом
и, следовательно, равномерно сходится в любом промежутке 0^ ?^C tt.
r-я составляющая правой части B1.10.3) представляет собой частный
случай (когда ХГ есть линейная однородная функция от хи х2, . . ., хт)
степенного ряда для хТ, полученного нами ранее (в § 21.4) другим способом.
§ 21.11] УСТОЙЧИВОСТЬ РАВНОВЕСИЯ 419
§ 21.11. Устойчивость равновесия. Вернемся теперь к общему случаю
автономной системы, движение которой определяется уравнениями
хт = Хт (хи х2, . . ., хт), г = 1, 2, . . ., т, B1.1.1)
и рассмотрим более подробно движение, начинающееся в окрестности особой
точки поля (т. е. точки, в которой Х\ = Х2= . . . = Хт = 0). Поместим
начало координат в особой точке, как это мы делали в гл. XIX для частного
случая т = 2, и будем предполагать, что функции Хг, обращающиеся в точке
О в нуль, могут быть разложены в ряд в окрестности этой точки:
Хг = arlXi + aT2x2-\- . . . +armxm + 0Г, B1.11.1)
где 0Г = 8Г (#!, х2, . . ., хт) таковы, что Qr/R —>~ 0 вместе с R, где R = | х | =
= У х\ -\-x\-\- . . . + хт. Во многих случаях функции 9Г удается представить
в виде степенных рядов, начинающихся с членов второй степени и сходящих-
сходящихся при R <C Ro.
Символ R обозначает расстояние от точки (ж4, х2, ¦ ¦ ., хт) до начала
координат О в вещественном (евклидовом) пространстве (xi, х2, . . ., хт).
Если допустить комплексные значения х, то выражение для R следует взять
в виде R — Y\ Xi |2 + | x2 |2+. . .+1 xm |2. Можно также в обоих случаях
(вещественных и комплексных х) взять вместо R функцию R', равную | xt |+
+ I ^2 I+- ¦ -+I хт\. В данном случае подходят оба варианта, ибо величина
R' мала в том и только в том случае, если мала величина R, и R' = 0 тогда
и только тогда, когда R = 0.
Определение устойчивости и другие связанные с этим определения ана-
аналогичны приведенным в § 19.5 для рассмотренного там частного случая.
Будем обозначать через R (t) значение R в точке (хг, х2, . . ., хт) в момент t
(иными словами, R (t) будет обозначать расстояние изображающей точки
от точки О в момент t).
Будем называть равновесие устойчивым, если для заданного 8 > 0 можно
указать положительное число х = х (е) такое, что если R @) < х, то R {t) <
< 8 для всех t ^ 0. Иными словами, если равновесие в точке О устойчиво, то
любому как угодно малому положительному числу х соответствует положи-
положительное число е такое, что неравенство R @) < х влечет за собой неравенство
R (t) <; е для всех t ^ 0.
Равновесие называется асимптотически устойчивым, если оно устой-
устойчиво и если, кроме того, существует положительное число х такое, что если
R @) <х, то R (t)-+ 0 при t-+ +oo.
Неустойчивость означает отсутствие устойчивости. Иными словами, рав-
равновесие в точке О неустойчиво, если существует положительное число х такое,
что можно указать характеристики, начинающиеся как угодно близко от точ-
точки О и такие, что для некоторого положительного значения t выполняется
неравенство R (t) > х.
Подобно тому как мы поступали в § 19.4, начнем с рассмотрения линей-
линейного приближения, т. е. заменим функции ХТ в уравнениях B1.1.1) линейны-
m
ми членами разложений, а именно 2 arsxs- Уравнения тогда примут вид
х = Ах. B1.10.2)
Рассмотрим сначала случай, когда матрицу А с помощью неособого пре-
преобразования удается привести к диагональной форме. Осуществляя линейное
преобразование зс = Си, приводим уравнения к виду
B1.11.2)
27*-
420 СИСТКМЫ С п СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК [Гл. XXI
Матрицу С выберем так, чтобы матрица С~ХАС была диагональной
матрицей Л, диагональные элементы которой равны собственным значе-
значениям ?ц, Яг, . . ., Я,т матрицы А. Так как элементы матрицы С могут ока-
оказаться комплексными, то и могут быть комплексными даже тогда,
когда х вещественны. Обозначим расстояние точки и от начала О через S =
— V | ы-1 12-+ \и2 |2+. . .+ | ит |2. Величина S мала лишь в том случае, если
мало расстояние R, и S = 0 тогда и только тогда, когда R--0. (Как и выше,
можно вместо S ввести величину S', равную | щ | + | и2 |+. . .+ | ит |.)
Уравнения B1.11.2) записываются теперь в следующей форме:
иг = Хгиг, г = 1, 2, . . ., т. B1.11.3)
Решения имеют вид
иг = аге*-п, г = 1, 2, . . ., т, B1.11.4)
где аг есть значение иТ при t = 0.
В случае, когда матрица ,4. может быть приведена к диагональному виду,
очевидно, что условия устойчивости сохраняют форму, данную в § 19.5.
Если собственные значения матрицы А имеют вещественные части отрицатель-
отрицательные и нулевые, то равновесие устойчиво. Если все вещественные части соб-
собственных значений отрицательны, то равновесие устойчиво асимптотически.
Если хотя бы одно собственное значение имеет положительную вещественную
часть, то равновесие неустойчиво.
В гл. IX мы рассмотрели несколько с иной точки зрения классическую задачу о ма-
малых колебаниях системы около точки g-пространства, в которой потенциальная энергия V
минимальна. В свете изложенной выше теории эта задача относится к случаю, когда
m = 2я, матрица может быть диагонализирована, собственные значения суть чисто мни-
мнимые числа + ipi, ±ip2, ¦ • •, ±ФП и равновесие устойчиво.
Однако иногда исследование устойчивости для случая m > 2 приводит
к результатам, отличным от случая m = 2. Предположим, что матрицу А
нельзя диагонализовать (это имеет место тогда, когда среди собственных зна-
значений есть кратные и элементарные делители не являются простыми); при
этом система может оказаться неустойчивой, если среди кратных собственных
значений будет хотя бы одно чисто мнимое, даже если все остальные собствен-
собственные значения имеют отрицательные или нулевые вещественные части. Дей-
Действительно, при этих условиях в формулах для х могут появиться члены
tN cos Pi и tN sin f>t. Формальное доказательство мы отложим до § 23.3, а здесь
ограничимся рассмотрением простого примера.
Пример 21.11. Рассмотрим в качестве примера систему (т = 4)
#! = Х2, Х2 = Х3, Х3 = Xt, Xk = —7l4?i — 2п*Х3, B1.11.5)
считая п вещественным положительным числом. Собственные значения равны in, in, —in,
—in. Решение содержит члены cos nt, sin nt, t cos nt, t sin nt. В явной форме имеем
1 1
xj =-=- {2 cos nt+nt sin nt) ai + — Csinref — nt cos nt) a2+
1 1
-\--п~~ч~ (nt: sinnt)a3~\--^~Y (sin nt—nt cos nt)^ B1.11.6)
и аналогично для х2 = xt, x3 = x2 и xt = x3. Ясно, что начало координат является точкой
неустойчивого равновесия. Пусть, например, ocj = а2 = а4 = 0, тогда
xt — -2^2- (nt sin nt) a3.
Положим га?=|Лг-|--я-| я, где iV — целое положительное число, тогда будем иметь
j> 21.12] ДИСКРЕТНАЯ УСТОЙЧИВОСТЬ 421
Путем надлежащего выбора N правая часть может быть сделана сколь угодно большой,
как бы мало ни было при этом значение | а | = | сс3 I -
Отметим, что в данном случае (и во многих других подобных случаях) тот факт, что
начало координат О является точкой неустойчивого равновесия, еще не означает, что
R (t) принимает большие значения для любых малых значений | а |. Если аз = —ra2aj
и сс4 = — п2а2, то имеем
х^ = а.\ cos nt-\ - sin nt, x2 — —reai sinnt + a2 cos nt,
n
x% = — re2ai cos nt— rea2 sin nt, xt = n3aj sin nt— n2a2 cos nt,
и неравенство | аз | < в соблюдается при всех t, если [ a | достаточно мало.
§ 21.12. Дискретная устойчивость. Перейдем теперь от линейного при-
приближения к точным уравнениям B1.1.1). Предположим, что в определениях
устойчивости и неустойчивости, данных в § 21.11, допускаются не все неотри-
неотрицательные значения t, а только дискретные моменты времени 0, т, 2т, Зт, ....
где х — раз и навсегда фиксированная положительная постоянная. Точку
х (кх) на траектории, начинающуюся в ас @), называют иногда /ет-образом
точки х @). Если рассматривать только указанные дискретные моменты вре-
времени, то мы придем к новому определению понятия устойчивости.
Равновесие называется устойчивым, если для заданного е > 0 можно
указать такое положительное число х — х (е), что если R @) < х, то R (кх) <
< б при всех целых положительных значениях к.
Равновесие называется асимптотически устойчивым, если оно устой-
устойчиво и если, кроме того, существует положительное число х такое, что если
R @) < х, то R (кх) —>- 0, когда к стремится к бесконечности, пробегая целые
положительные значения.
Неустойчивость означает отсутствие устойчивости. Иными словами, рав-
равновесие является неустойчивым, если можно указать положительное число х
такое, что существуют траектории, начинающиеся в произвольной близости
от точки О и такие, что для некоторого целого положительного к выполняется
неравенство R (кх) > х.
Введенное ранее (в § 21.11) понятие устойчивости можно условиться
называть С-устойчивостью (имея в виду непрерывное изменение t), а новое
понятие устойчивости — /^-устойчивостью *) (имея в виду дискретный харак-
характер изменения t).
Докажем теперь, что оба определения устойчивости означают, по сущест-
существу, одно и то же: С-устойчивость означает ^-устойчивость, а ^-устойчивость
означает С-устойчивость. Аналогичные утверждения справедливы и в отно-
отношении асимптотической устойчивости, а также неустойчивости. Доказатель-
Доказательство этих утверждений основано на следующей лемме. Пусть х (t), как и ранее,
обозначает траекторию, начинающуюся в точке х @). Если в момент t = 0
изображающая точка находится в положении х @), та в момент t она занимает
положение x(t). За промежуток времени 0 ^ t ^.x изображающая точка
проходит отрезок траектории, который мы будем называть т-сегментом, начи-
начинающимся в ас @). Возьмем положительное число г, и пусть S (г) будет множе-
множеством точек всех т-сегментов, начинающихся в точках ас(О) внутри гиперсфе-
гиперсферы радиуса г, описанной вокруг точки О. Пусть г' будет верхней гранью рас-
расстояний точек множества S (г) от точки О. При указанных условиях г' будет
непрерывной монотонно возрастающей функцией от г, обращающейся в нуль
вместе с г. Положим г = f (г'); функция / (г1) непрерывна и монотонно воз-
возрастает, причем / @) = 0 и 0 < / (г') ^ г', если г' > 0. (В частном случае
линейного приближения / (г) = Кг', причем К = const и 0 < К < 1.)
Эквивалентность двух понятий устойчивости теперь почти очевидна.
Тем не менее приведем формальное доказательство.
*) Автор образует эти термины из первых букв английских слов «continuous»—
непрерывный и «discrete» — дискретный. (Прим. ред.)
422 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК [Гл. XXI
Устойчив ость. То, что С-устойчивость означает ^-устойчивость,
очевидно. Остается доказать, что из ^-устойчивости следует С-устойчивость.
Предположим, что имеет место D-устойчивость. Возьмем положительное чис-
число е, и пусть х (е) есть число, фигурирующее в определении D-устойчивости
{т. е. такое, что если R @) < х, то Д (кх) < е при целых положительных
значениях к). Положим х' = / (х) и выберем точку х @) так, чтобы | ас @) | <
<х'.
т-сегмент, начинающийся в точке х @), расположен внутри сферы радиу-
радиуса х вокруг точки О. Тогда траектория, начинающаяся в точке х (9), где
0 ^ 9 < т, при всех целых положительных к обладает тем свойством, что
| х (9 + кх )| < е. Поэтому, если | х @)| < х', то при всех положительных
? выполняется неравенство \x(t)\<C&, откуда следует С-устойчивость.
Асимптотическая устойчивость. То, что асимптоти-
асимптотическая С-устойчивость означает асимптотическую D-устойчивость, очевидно.
Остается доказать, что асимптотическая D-устойчивость означает асимптоти-
асимптотическую С-устойчивость. Предположим, что имеет место асимптотическая
D-устойчивость, и пусть х есть число, фигурирующее в ее определении (т. е.
такое, что если R @) < х, то R (кх) ->¦ 0, когда к стремится к бесконечности,
пробегая целые положительные значения). Положим х' = / (х), и пусть
х @) есть любая точка такая, что | х @)| < х'.
т-сегмент, начинающийся в точке х @), расположен внутри гиперсферы
радиуса х вокруг точки О. Тогда траектория, начинающаяся в точке х (9),
где 0 ^ 9 < т, обладает тем свойством, что | х (9 + кх)\ -> 0, когда к стре-
стремится к бесконечности, пробегая целые положительные значения. Поэтому,
если | ас @)| < х', то \ х (f) ]-*¦ 0 при t-+ + оо, откуда следует асимптотиче-
асимптотическая С-устойчивость.
Неустойчивость. То, что D-неустойчивость означает С-неустой-
чивость, очевидно. Остается доказать, что С-неустойчивость означает .D-не-
.D-неустойчивость. Предположим, что имеет место С-неустойчивость. Тогда суще-
существует положительное число х такое, что, как бы мало ни было е > 0, можно
указать точку х @) такую, что если | х @) [ < г , г = / (е), то для некото-
некоторого 6 из интервала 0 ^ 9 ^ т выполняется неравенство | х (9 -f kx)\ > х,
где к — целое положительное число, т-сегмент, начинающийся в точке
ж. @), расположен внутри гиперсферы радиуса е вокруг точки О, так что рас-
расстояние между точками ас (9) и О меньше заданного числа е. Через к шагов
точка ас (9) окажемся, однако, за пределами окружности радиуса х с центром
в точке О, откуда и следует ^-неустойчивость.
Таким образом, мы доказали эквивалентность двух определений устой-
устойчивости и в дальнейшем можем не делать различия между С-устойчивостью
и ^-устойчивостью, а говорить просто об устойчивости. Для того чтобы уста-
установить устойчивость какой-либо конкретной механической системы, можно
воспользоваться любым удобным критерием, считая переменную t либо
непрерывной, либо дискретной. Длительность т основного интервала опреде-
определяется нашим выбором; в ряде случаев эта величина естественно определяет-
определяется самой задачей, в иных случаях можно положить т = 1.
§ 21.13. Устойчивость преобразований. Рассмотрим непрерывное пре-
преобразование, устанавливающее соответствие между точками ж и у; оператор
преобразования обозначим через Т:
Тх = у. B1.13.1)
Оператор Т определен для точек ж, принадлежащих области D. Во всех
рассматриваемых ниже случаях область D содержит начало координат, кото-
которое считается неподвижной точкой преобразования ТО = 0. Можно ввести
определение устойчивости аналогично тому, как это было сделано в § 21.12
§ 21.13] УСТОЙЧИВОСТЬ ПРЕОБРАЗОВАНИЙ 423
при рассмотрении дискретного случая. Грубо говоря, будем считать оператор
Т устойчивым, если величина | Тпх | мала, когда мало | х |. Точное опреде-
определение можно сформулировать следующим образом.
Определяемое оператором Т преобразование называется устойчивым
(или, иначе, оператор Т называется устойчивым), если для заданного е > О
можно указать положительное х = х (е) такое, что если | х | < х, то
| Тпх | < е для всех целых положительных чисел п.
Преобразование асимптотически устойчиво, если оно устойчиво и если,
кроме того, существует положительное число х такое, что если | х | < х,
то | Тпх |->-0, когда и—>- оо.
Если преобразование не обладает свойством устойчивости, то говорят,
что оно неустойчиво, т. е. преобразование неустойчиво тогда и только тогда,
когда существует положительное число х такое, что можно указать точки х
с произвольно малым | х |, для которых | Тпх |>х при некотором целом
положительном значении п.
Рассмотрим в качестве примера линейное преобразование
у = Вх, B1.13.2)
где В — неособенная матрица размером m X m с постоянными элементами
bTS. Предположим, что матрица В может быть приведена к диагональной фор-
форме. Введем новые переменные и, v, определяемые формулами х = Си, у =
= Cv, где С — неособенная матрица; уравнение B1.13.2) тогда перепишется
в виде
v = C~xBCu. B1.13.3)
Выбор матрицы С подчиним требованию, чтобы матрица С~ХВС была
диагональной, элементами этой матрицы М будут собственные значения \ii,
jo,2, ¦ • •, \Ут матрицы В. Преобразование принимает теперь простую форму
v = Ми, r-е уравнение записывается в виде
vT = \iruT. B1.13.4)
Таким образом, r-я составляющая оператора Тпи равна ц"мг. Условие устой-
устойчивости (а также асимптотической устойчивости и неустойчивости) преобра-
преобразования следует теперь немедленно. Преобразование, осуществляемое опера-
оператором Т, является устойчивым, если | |хг | ^ 1 при всех значениях г из сово-
совокупности 1,2, . . ., т; оно асимптотически устойчиво, если | \ir | < 1 при
всех этих г, и оно неустойчиво, если | \ir | > 1 для какого-нибудь значения г.
Приведем еще два примера, оба для преобразования с одной переменной.
Пример 21.13А. Рассмотрим преобразование
Тх = х + хг.
Начало координат является (единственной) неподвижной точкой преобразования;
эта точка неустойчива. Обозначим выражение Тпа через хп.
1) Если а > 0, то хл ->-оэ вместе с п. Последовательность а, хи х2, ... монотонно
возрастает, и при п > 1
n-i > 1 -г- а,
следовательно,
xn > a A + a)"
gin-)-oo вместе с re.
2) Если a = 0, то xj = г2 =... .=0.
3) Если 0 > a > —1, то хп ->- 0 при ге ->- оо. В самом деле, полагая a =
находим
х, = -р A - р).
Отсюда
424 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК [Гл. XXI
и аналогично
0>хп> — 1
для всех п. Последовательность а, х1, х2, . . . монотонно возрастает и ограничена, так
что хп —»- I при и —>- оо; устремляя п к бесконечности в уравнении
•^n = %n-i "Г ХП— 1;
находим, что 1=0.
4) Если а = —1, то х± = х2 = . . .= 0.
5) Если —1 > а, то ii > 0 и % ->- оо (как в случае 1)).
Таким образом, если 0 J> a J> —1, то хп ->- 0, в противном случае хп ->- оо.
Пример 21.13В. Рассмотрим дробно-линейное преобразование
В общем случае имеются две неподвижные точки р и q, которые определяются как корни
уравнения
сх2 + (d — а) х — Ь = 0.
Величины хп_1 и хп связаны между собой соотношением
жл —9 жл-1— 9 '
1'Дв
cp + d ¦
Предположим, что (d — aJ -f- 46с >0и1|^0. При этих условиях корни
р ж q вещественны ж различны и | X \ Ф 1. Числа р и q можно расположить так, чтобы
| Л, | < 1. Имеем
Если а Ф q, то отсюда следует, что хп -^- р при и —»- оо. Неподвижная точка р асимптоти-
асимптотически устойчива, тогда как точка q неустойчива.
В исключительном случае, когда (d — аJ + 46с >0иа+й=0, имеем X, = — 1;
при этом хп = а, если п — число четное, и хп= , ,, если п—число нечетное. В этом
са-\-а
случае обе неподвижные точки устойчивы, но ни одна из них не является асимптотически
устойчивой.
§ 21.14. Приложение к дифференциальным уравнениям. Вернемся
к системе дифференциальных уравнений B1.1.1): хт — Хг. Эта система авто-
автономна. Как и в § 21.11, будем считать начало координат особой точкой.
Движение, определяемое этими дифференциальными уравнениями, можно
представить с помощью преобразования, осуществляемого оператором Tt
(§ 21.3):
x = Tta, B1.3.1)
где а есть значение х в момент t = 0. Фиксируя положительное значение т
переменной t, получаем преобразование Т = Тх, которое имеет неподвижную
точку О. Как было показано, для исследования устойчивости можно выбрать
дискретные значения t: 0, т, 2т, Зт, . . . Поэтому устойчивость равновесия
в точке О — это то же самое, что устойчивость преобразования Т; аналогич-
аналогичное заключение можно сделать и относительно асимптотической устойчиво-
устойчивости, а также относительно неустойчивости.
Рассмотрим линейное приближение к дифференциальным уравнениям
х = Ах. B1.10.2)
При этом мы получим подтверждение найденных выше результатов.
21.15J ТЕОРЕМА ПУАНКАРЕ — ЛЯПУНОВА 425>
Соответствующее линейное преобразование имеет вид
B1.14.1)-
Матрица В задается формулой (см. B1.10.3))
В = ехЛ. B1.14.2)
Если Хт — собственное значение матрицы Л, то соответствующее собствен-
собственное значение матрицы В равно цг = ех%т. Рассматривая случай, когда мат-
матрицы Л ж В могут быть приведены к диагональной форме, и обозначая веще-
вещественную часть Хг через рг, можно выразить условия устойчивости (неустой-
(неустойчивости) через рг или | \ir \.
Устойчивость: рг ^ 0, | [хг | ^ 1 для всех значений г.
Асимптотическая устойчивость: рг < 0, | цт | < 1 для всех значений г.
Неустойчивость: рг >> 0, | [ir | > 1 для некоторого значения г.
Эти результаты нами уже были получены раньше, в § 21.11 и в § 21.13.
Если матрицу Л не удается диагонализовать, то исследование услож-
усложняется. Как мы видели, в этом случае выполнения условия рг ^ 0 (или, что
то же, [ \lt | :?С 1) для всех г уже недостаточно для того, чтобы гарантировать-
устойчивость: кратные чисто мнимые собственные значения Хг могут привести
к неустойчивости. Но другие условия остаются без изменений. Если все-
Рг < 0 (или все | [iT | <; 1), то имеем асимптотическую устойчивость; если
хотя бы одно значение рг > 0 (или одно | \ir | > 1), то имеем неустойчивость.
Доказательство см. ниже, в § 23.3.
§ 21.15. Теорема Пуанкаре — Ляпунова. Перейдем теперь от линейного
приближения (для движения в окрестности особой точки О)
х = Ах, B1.10.2)'
которому соответствует преобразование
х = Ва, B1.14.1)
к точным уравнениям
хт = Хт, г = 1, 2, . . ., те. B1.1.1)
Им соответствует преобразование х = Тха,
хт = срг (т; щ, а2, . . . , ат), г = 1, 2, . . , т. B1.15.1)
Функции срг будем считать принадлежащими к классу С2.
Собственные значения для линейного приближения к преобразованию х = Та
не зависят от выбора координат. Для доказательства перейдем к новой системе координат
причем if @) = 0 и все функции t|;r принадлежат к классу С2. Преобразование можно
записать в форме y = U$. Пусть Л есть матрица для линейного приближения к Т:
(индекс нуль указывает, что значение берется при а = 0).
Пусть 2J—матрица для линейного приближения к U:
а С—матрица
dxs } о \ das ) о "
426 СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК [Гл. XXI
Тогда
откуда следует, что матрицы А и В имеют одинаковые собственные значения и эле-
элементарные делители.
Перейдем теперь к теореме Пуанкаре — Ляпунова. Ограничимся рассмот-
рассмотрением только таких преобразований, для которых удается диагонализовать
матрицу А линейного приближения. Теорема утверждает, что в этом случае
вопрос об устойчивости решается на основе линейного приближения, за исклю-
исключением критического случая, когда некоторые из чисел X являются чисто мни-
мнимыми. Если все рг < 0, то равновесие асимптотически устойчиво; если хотя
бы одно рг > 0, то равновесие неустойчиво.
Именно такой результат, конечно, и следовало ожидать, учитывая выво-
выводы гл. XIX, относящиеся к случаю т — 2. Для этого случая было уста-
установлено, что если собственные значения для линейного приближения Fo
чисто мнимые, то особая точка поля Fo устойчива; если же рассматривать
эту точку как особенность поля .F, то можно получить как устойчивость, так
и неустойчивость. Чтобы решить вопрос об устойчивости, можно восполь-
воспользоваться преобразованием Т = Тх, как это показано в § 21.14.
1) Асимптотическая устойчивость. Предположим,
что все рг < 0, | [хг | < 1 (где %r = pr -\- iar — собственные значения матри-
матрицы A, a \lt = ex%f — собственные значения матрицы В). Линейному приб-
приближению соответствует линейное преобразование Т:
х = Ва. B1.14.1)
Предположим, что матрицу В можно диагонализировать путем подходящего
преобразования, тогда уравнения B1.14.1) можно записать в форме
хт = \iTaT, г = 1, 2, . . ., т. B1.15.2)
Преобразование при этом обладает следующим свойством:
\Ва\<к\а\, B1.15.3)
где к < 1 — число, лежащее между наибольшим из | цг | и 1. Докажем сна-
сначала простую лемму: если
|_Ba|<Z|a|, B1.15.4)
где О <J < 1, то |Дпа| —> 0 при п —> оо. В самом деле, имеем
|J?2a|<Z|.Ba|<Z2|a| B1.15.5)
и вообще
\Впа\<1п\а\. B1.15.6)
Последнее выражение стремится к нулю, когда п стремится к бесконечности.
Преобразование
х = Та, B1.15.7)
дающее при t=-x решение точных уравнений, обладает тем свойством, что
|Го —До| = 0(|о|). B1.15.8)
Это свойство следует из того, что функции ср имеют непрерывные вторые про-
производные (фактически оно имеет место и при более общих предположениях).
Отсюда заключаем, что существует положительное число е0 такое, что если
! а |< е0, то
<^=^|а| B1.15.9)
5 21.151 ТЕОРЕМА ПУАНКАРЕ — ЛЯПУНОВА 427
B1.15.10)
где 0 < I < 1. Следовательно, согласно лемме | Тпа \ —*• 0, откуда следует
асимптотическая устойчивость.
2) Неустойчивость. Предположим теперь, что хотя бы одно
значение рг > 0, так что соответствующее | jir | > 1. Как и ранее, матрицу
В считаем представленной в диагональной форме.
Для доказательства неустойчивости оператора Т поступим следующим
образом. Введем вещественную квадратичную форму
<?(ж)=2A-Ы2Ж12- B1.15.11)
Имеем
Q(x)-Q(Bx) = S A-|цг|2J|^|2. B1.15.12)
г=1
Правая часть представляет определенно-положительную форму, так что
существует положительная постоянная с такая, что при всех х
Q{x) — Q(Bx)>2c\x\*. B1.15.13)
Из соотношений
\Тх\ — \Вх\ = О(\х\), \Вх\ = О(\х\) B1.15.14)
следует, что
Q(Tx) — Q(Bx) = O(\x\z). B1.15.15)
И'з B1.15.13) и B1.15.15) приходим к неравенству
Q{x) — Q{Tx)>c\x\\ B1.15.16)
справедливому при малых значениях | х |, например при | х | < х.
Далее, поскольку по крайней мере одно из | [ir | превышает единицу,
можно указать точку а, причем | а | произвольно мало, такую, что Q (а)
будет отрицательным, например, Q (а) < — а < 0. Далее доказательство
проведем от противного. Предположим, что каждая из величин \ а \, \ Та \,
| Т2а |, ... не превышает х, и покажем, что это предположение приводит
к противоречию.
Поскольку | Тпа |<х при всех значениях п, из условия B1.15.16)
следует, что
-а><?(а)><?(Га)> ...>(? (Тпа) B1.15.17)
при всех п. Так как из неравенства Q (х) < —а следует | х \ > Ъ, Ъ > 0,
то находим, что | Тпа | > Ъ при всех значениях и. Обращаясь снова к усло-
условию B1.15.16), получаем неравенство
Q {Га) - Q (Г+1а) > с | Га |2 > с&2, B1.15.18)
справедливое при всех г.
Напишем теперь неравенства B1.15.18) для г = 0, 1,2, . . ., /г — 1
и сложим их; проделав это, будем иметь
— <?(Гпа)> — Q(a) + ncb2>a + ncb2, B1.15.19)
откуда следует, что Q (Тпа) -> —оо при гс—>- оо. Однако это противоречит
предположению о том, что | Тпа \ < х, поскольку неравенство | ас | < х
показывает, что величина | Q (х) | ограничена. Прийдя к противоречию, мы
тем самым доказали теорему.
428 СИСТЕМЫ Gn СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК [Гл XXI
Доказанная теорема устанавливает достаточные условия асимптотической устой-
устойчивости и неустойчивости. Можно указать также необходимые условия устойчивости.
Рассмотрим линейное преобразование х=Ва (где матрица В не обязательно диагональная,
но может быть приведена к диагональному виду). Произведение собственных значений
матрицы В будет равно | В |, определителю матрицы В. Необходимое условие устойчи-
устойчивости заключается в том, чтобы | В | ^ 1. Для линейного приближения к преобразова-
преобразованию B1.15.1) элементы brs матрицы В должны быть равны значениям частных производ-
производных dyr/das в точке а = 0. Таким образом, для устойчивости преобразования B1.15.1)
необходимо, чтобы якобиан
d( ф2, ¦•., фт)
д{аи а2, ..., ат)
при о= 0 не превышал по абсолютной величине единиц]
Следствие. Рассмотрим преобразование Т, для которого матрица
А линейного приближения имеет собственные значения, не превышающие
единицы, | \ir | < 1 при г = 1, 2, . . ., т. Оператор Т асимптотически
устойчив. Пусть к — число, лежащее между наибольшим из | \ir | и единицей.
Тогда существуют положительные числа т] и с такие, что если | х | < т], то
\Тпх\<скп B1.15.20)
при п = 1, 2, 3, ...
Для доказательства введем преобразование U:
Ux = -^Tx: B1.15.21)
Тогда
/7n-v _ ¦* тппг (9\ 1е; 99\
U JU— , 1 JL. \иI.. I.O.бел)
Матрицей для линейного приближения к U является -г- А; собственные
значения ее равны \iT/k, причем все они не превышают единицы. Поэтом'у
преобразование U устойчиво, и можно указать такие п, с, что
| Unx | < с B1.15.23)
при всех целых положительных значениях п. Неравенство B1.15.20) следует
непосредственно из B1.15.22).
§ 21.16. Критический случай. Теорема Пуанкаре — Ляпунова ничего
не говорит нам о критическом случае, когда некоторые из Хг имеют чисто
мнимые значения.
Если m = 2, то критический случай соответствует особой точке типа
центра; мы видели в § 19.4, что хотя линейное приближение Fo дает устойчи-
устойчивость, точное поле F может дать как устойчивость, так и неустойчивость.
Случай m > 2 отличается от случая m = 2 тем, что при наличии кратных
чисто мнимых корней Кг неустойчивость можно получить уже в линейном
приближении (§ 21.11). Даже в том случае, когда линейное приближение дает
устойчивость, точное поле может дать как устойчивость, так и неустойчивость.
Мы приведем пример каждой из этой возможностей в случае m = 4. В первом
из этих примеров рассматриваются малые колебания около положения, где
потенциальная энергия V имеет минимум. Равновесие в этом случае, как
известно, устойчиво (гл. IX).
Пример 21.16А. Маятник на упругой нити. Эта задача
отличается от обычной задачи о колебании маятника тем, что неупругая нить
заменена упругой, подчиняющейся закону Гука. Система имеет две степени
свободы и m = 4.
Пусть а — длина нерастянутой струны, а {а + с) — длина растянутой
струны в положении статического равновесия. Если г — длина струны в не-
некоторый момент t, а 9 — угол ее отклонения от направленной вниз вертикали,
21.16] КРИТИЧЕСКИЙ СЛУЧАЙ 429
то кинетическая и потенциальная энергии системы запишутся следующим
образом:
B1.16.1)
V=-grcosQ + -^-(r—af, B1.16.2)
где импульсы рг и pq обозначены соответственно через {• и т). Функция
Гамильтона равна Г + F, а уравнения движения Гамильтона имеют вид
• L е ¦ B1.16.3)
? — -iL_i_^^naf)— — (г — а), т]= -
В положении равновесия 9 = | = г] = 0, г = а-|-с; положив r = a-\-c-\-s, мы
придем к следующим уравнениям линейного приближения:
• ,. А 1
Дй+СJ ¦ B1.16.4)
Как и следовало ожидать, собственные значения равны ±i у —
и± iy —~. (В данном случае нет необходимости вычислять определи-
определитель четвертого порядка, поскольку уравнения линейного приближения рас-
распадаются на две группы, одна из которых содержит только s и ?, а другая —
только 9 и т|; в самом деле, имеем
7 + -?s = 0, *Э +-4—9 = 0.) B1.16.5)
Рассмотрим теперь точное поле F. Потенциальная энергия V имеет мини-
минимум Vo в положении равновесия. При малых положительных значениях е
кривые V = Vo + e представляют собой простые замкнутые выпуклые кри-
кривые вокруг точки равновесия г = а -\- с, 9 = 0. Если постоянная энергии
равна Vo + s, то в течение всего движения будем иметь
V - 70^ е, Г < е, B1.16.6)
так что частица не выйдет за пределы кривой V — Vo + e, и кинетическая
энергия будет оставаться малой. Поэтому будут малы и величины Э, s, 5; 1"Ь
откуда следует, что равновесие является устойчивым.
В явной форме уравнение кривой V — Vo + e записывается в виде
r(l— cos9) + -^-(r — ЬJ= -^-/с2, B1.16.7)
где i = й + с i е = gk2/Bc).
Экстремальные значения г па кривой достигаются при Э = 0 и равны
b ± к. Что касается значений 9, то они заключены между пределами ±90,
которые определяются из уравнения
B1.16.8)
(если г — \^Ь2 — &2, то 6 —± 90). Если груз подвешен на струне, а не на
430
СИСТЕМЫ С п СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК [Гл. XX]
пружине, то при к<С с струна будет, разумеется, натянута во все время дви-
движения. Кривые B1.16.7) для значений к/с = 1/2, 1, 3/2, 2 представлены нн
рис. 99. Введем прямоугольные координаты и, v, начало возьмем в поло-
положении равновесия, а ось и направим вертикально вниз. В этих координатах
уравнение B1.16.7) запишется в виде
[2 (Ъ — c)(r-u) = u2 + v2 + 2Ь2 — 26с — к2 B1.16.9)
или
м +-r-y —/с Wuv "+" "льГ^ Dм — f )— . . . (Zl.lb.10)
Пример' 21.16В. Рассмотрим систему, для которой т = 4, а функция
Гамильтона имеет вид
Н = ±
B1.16.11)
Pi =- — Mi — «(?i92 — P1P2),
Параметры п и а будем считать вещественными и положительными. Урав-
Уравнения движения будут иметь вид
B1.16.12)
Собственные значения матрицы линейного приближения Fo равны + in,
± 2т, и движение определяется следующими формулами:
qt = % cos ntJrbi sin rc?,
q2 = a2 cos 2nt — b2sin2nt, i B1.16.13)
Pj = by cos 72f — aj sin nt,
Pi. == ^2 C0S ^Wi -(- Я2 sin 2^
B1.16.14)
где au a2, bt, Ъ2 суть значения qu q2, pu p2 при
Решение можно записать также в виде
t = A sin
t = A cos
p2=
§ 21.16] КРИТИЧЕСКИЙ СЛУЧАЙ 431
Все полученные орбиты периодичны с периодом 2л/ге, и особая точка
по первому приближению устойчива.
Рассмотрим теперь точное поле _F. Уравнения B1.16.12) удовлетворяют-
удовлетворяются функциями
(t[_M sm2
( o) V B1.16.15)
1
c
при всех значениях t0 и б. Если t0 велико, то в момент t = 0 изображающая
точка находится вблизи от точки О, но для значений ?, близких к t0, она отсто-
отстоит от точки О на большом расстоянии. Точное поле показывает, что особая
точка неустойчива. Рассмотрим конкретный пример. Пусть в момент t = 0
<7i = 4i = Pi ——ai Pi = 0- Решение дается формулами B1.16.15), в кото-
которых at0 = 1/а и б = я/4:
B1,16.16)
К этой задаче мы вернемся позже, в § 30.4.
Глава XXII
УРАВНЕНИЯ ГАМИЛЬТОНА
§ 22.1. Уравнения Гамильтона. В предыдущей главе мы рассматривали
систему дифференциальных уравнений
х\ = Хт, г = 1, 2, . . ., т. B2.1.1)
К этой форме различными способами можно привести уравнения движе-
движения голономной системы с п степенями свободы (т = 2п). Наиболее важную
роль играют уравнения Гамильтона
^ = -^7' ^=-^Г' г=1,2,...,п. B2.1.2)
Определению подлежат 2п функций от t:
4l, 42, ¦ ¦ -, Яп', Pi, Р2, ¦ ¦ -, Рп-
Здесь
хт = Чт, %п+т == Рт, г — 1? 2, . . ., П.
Имеем 2п функций Хт:
дН_ дН__ дН . _ дН_ дН ___ дН
dpi ' др2 ' ' ' '' дрп ' dgi ' dg2 ' ' dqn
так что
X —IE. X — — — г—1 2
В автономном случае, с которым нам придется чаще всего иметь дело,
функция Н не содержит t:
Н = Н (qi, q2, . . ., qn; pu p2, . . ., рп). B2.1.3)
Предполагается, что Н ? С2 в области D пространства переменных (g4, q2, ...
• • •> In', Pi, Pz, ¦ ¦ ¦, Рп)-
Как уже указывалось в § 10.14, если система автономна, то Н является
ее интегралом. Доказывается этот важный факт весьма просто. Имеем
п
dH
^yl™qr + _^Lp\. B2.1.4)
r=l
В силу уравнений B2.1.2) это выражение равно нулю. Итак, Я = const = h
во все время движения. Траектории располагаются на поверхностях Я = h.
Гамильтоновы уравнения движения можно записать в матричной форме:
x = ZHx, B2.1.5)
где х — матрица-столбец, или вектор с составляющими {qu q2, ..., qn;
, rT ( дН дН дН дН дН дН
Pi, Pi, ¦¦-, Рп}, Нх — вектор
a Z — матрица размером 2га X 2п:
т оП) B2л-6)
— 1 п и /
§ 22.2] СКОБКИ ПУАССОНА 433
Матрица Z удовлетворяет очевидным равенствам
Z' = Z-*=—Z, \Z\ = 1. B2.1.7)
§ 22.2. Скобки Пуассона. Интегралы F уравнений Гамильтона удовлет-
удовлетворяют уравнению
~ + ?lF = 0. B2.2.1)
Входящий сюда линейный оператор Q определяется формулой
dF дН 9F дН\_ъ д (F, Н) ,99 9 9,
) 2 (гггг)
- 2л \dgr дрг ~Ж Ж) ~ 2л
dgr дрг ~Ж Ж) ~ 2л d(gr,Pr)
г=1 г=1
Если и и v — функции от (qu q2, . . ., qn; pt, p2, . . ., pn; t), принадле-
принадлежащие классу Сг, или, сокращенно, функции от (q; p; t), то выражение
а( ) B2.2.3)
Л
^ <5(?г> Рт)
г=1
представляющее собой сумму п определителей Якоби, называют скобкой
Пуассона и обозначают через (u, v). Таким образом,
UF = (F, Н), B2.2.4)
и интегралы уравнений Гамильтона удовлетворяют уравнению
|Я) = 0. B2.2.5)
Собственно уравнения Гамильтона также можно записать с помощью
скобок Пуассона:
хт = пхг = (хг, Н), г = 1,2, . . ., In. B2.2.6)
Скобки Пуассона играют важную роль как в классической механике,
так и в квантовой механике. Познакомимся с их основными свойствами.
Пусть и, v, w — функции от (g; p; t) класса С2, а с — некоторая постоянная.
Скобки Пуассона обладают следующими очевидными свойствами:
{и, и) = (и, с) = (с, и) = 0,
(v,u) = ( — u,v) = (u,—v)=—(u,v), l> B2.2.7)
д , . I ди \ , / dv
(uv)[ v) + (u
При использовании скобок Пуассона нужно помнить, что существен-
существенное значение имеет порядок записи переменных: (v, и) = — (и, v).
Наиболее важное свойство скобок Пуассона выражается теоремой,
известной под названием тождества Пуассона или тождества Якоби:
(и, (v, w)) + (v, (w, и)) + (ц;, (и, v)) = 0. B2.2.8)
Для доказательства заметим прежде всего, что если А и В — два линей-
линейных оператора вида
^ 2^
Г=1 г=1
с коэффициентами Аг, Вг класса Ci и если функция / ? Сг, то выражение
ABf — BAf B2.2.10)
28 л. А. Парс
434 УРАВНЕНИЯ ГАМИЛЬТОНА [Гл. XXII
зависит линейным образом от первых производных функции / и не содержит
вторых производных этой функции. Если теперь написать подробные выра-
выражения для скобок Пуассона в левой части тождества B2.2.8), то мы увидим,
что каждое из слагаемых представляет произведение двух производных пер-
первого порядка и одной производной второго порядка. Поэтому достаточно
доказать, что коэффициент при каждой из вторых производных равен нулю.
Рассмотрим вторые производные функции и; они содержатся в первом и треть-
третьем слагаемых суммы B2.2.8). Кроме того,
(v, и) = Vu, (w, и) = Wu, B2.2.11)
где V и W — линейные операторы указанного выше типа. Имеем
(v, (w, и)) + {w, (и, v)) = (v, (w, и)) — (w, (v, и)) = VWu — WVu.
B2.2.12)
Правая часть не содержит вторых производных функции и, откуда и следует
теорема.
§ 22.3. Теорема ПуасСона. Если ср, г|э — интегралы уравнений Гамильто-
Гамильтона, принадлежащие классу С2, то (ф, г)з) также является интегралом.
Доказательство весьма простое. Имеем
§ Я) = 0, ^L+(q,H) = 0. B2.3.1)
Следовательно,
= -((Ф, Я), ^)-(9, (ф, Я))+((Ф> 1|з), #) =
= (ф, (Ф, Я)) + (Ф, (Н, я|>)) + (Я, (ф, Ф)). B2.3.2)
Согласно тождеству Пуассона B2.2.8) полученное выражение обращает-
обращается в нуль. Таким образом, (ф, ф) представляет собой интеграл.
Теорема Пуассона не столь плодотворна, как это может показаться на первый
взгляд. По двум известным интегралам можно определить третий интеграл, затем четвер-
четвертый и т. д. Однако в ряде случаев вновь получаемый интеграл оказывается тождествен-
тождественным нулем или зависит от уже найденных интегралов. Очевидно, что процесс составле-
составления новых интегралов не может продолжаться до бесконечности, поскольку существует
не более 2ге независимых интегралов.
Предположим, что // не содержит t и, стало быть, представляет собой интеграл.
Если ф есть другой пространственный интеграл, то скобка (ф, Н) тождественно равна нулю,
и теорема Пуассона в этом случае ничего нового не дает. Если же ф есть интеграл, завися-
зависящий от t, то
(Ф, Н)=-^-, B2.3.3)
и мы снова приходим к известному факту (§ 21.1), что dq>/dt представляет собой интеграл.
Но иногда теорема Пуассона позволяет получать интеграл, не зависящий от исход-
исходных. В качестве примера рассмотрим движение частицы под действием притяжения к цен-
центру О. Сила притяжения пусть будет функцией расстояния г от точки О- Возьмем прямо-
прямоугольные координаты qlt q2, дз, начало координат поместим в центре О. Тогда будем иметь
±(p{+Pl + Pl) + V, B2.3.4)
где V есть функция г. Массу частицы мы положили равной единице. Если
ф1 s= ?2Рз — ЧзР2, B2.3.5)
то (фь Н) = 0 и ф4 есть интеграл уравнений Гамильтона. Аналогично
ф2 = ?зР1 — ?1Рз B2.3.6)
§ 22.4] ИСПОЛЬЗОВАНИЕ ИЗВЕСТНОГО ИНТЕГРАЛА 435
также есть интеграл. Эти два интеграла суть интегралы момента количеств движения.
Согласно теореме Пуассона (<pi, ф2) также есть интеграл, и
так как два других определителя обращаются в нуль. Далее,
4|j^ B2.3.8)
> Рз)
и новый интеграл есть третий интеграл момента количеств движения.
§ 22.4. Использование известного интеграла. В § 21.2 мы видели, что
известный интеграл можно использовать для понижения порядка системы
уравнений, т. е. первоначальную систему уравнений можно заменить другой,
с числом зависимых переменных на единицу меньше. Если первоначальная
система уравнений имеет гамильтонову форму, то можно не только понизить
порядок системы, но также и сохранить гамильтонову форму уравнений.
Точнее, 2 (п — 1) уравнений новой системы будут иметь форму Гамильтона,
а одно уравнение — не будет.
В качестве простого примера рассмотрим интеграл количества движе-
движения, соответствующий некоторой циклической координате. Предположим,
что функция Н не зависит от координаты д4:
Н = Н (g2, q3, . . ., qn; ри р2, . . ., рп; t). B2.4.1)
Тогда величина pi остается в процессе движения постоянной:
Pi = Р, B2.4.2)
и система приводится к гамильтоновой с 2 (п — 1) зависимыми переменными:
dq2 _ dq3 __ _ dp2 __ dp:i __ __, /99 4 4Y
дН' ~ дН' ~" дН' ~ дН' ~ 1- к^.ъ.э)
dpz dp?, dq2 dq3
Функция Я' получается из Н, если в последней положить pi равным р. Кроме
того, мы имеем еще одно уравнение, связывающее координату qi и время t,
С ОН' ,.
а именно qt = \ -тк- at.
Если система автономна, то для понижения порядка системы можно
использовать интеграл энергии
Н (qi, q2, . . ., qn; pu Pz, • • -, Рп) = h. B2.4.4)
Предположим, что координата qi не является циклической, и пусть
уравнение B2.4.4) может быть разрешено относительно qt:
Ч\ = ф (?2» <1г, ¦ ¦ ¦ . Чп, Р2, Рз, ¦ ¦ • , Рп', h; Pi). B2.4.5)
Если эту функцию подставить в соотношение B2.4.4), то получим тождество.
Дифференцируя его частным образом по рг (г = 2, 3, . . ., и), получаем
™ + Мр- = 0. B2.4.6)
дрг dqi dpi- - - v '
Следовательно,
дН
dqr qr дрг д<р /90 Л 7\
dp, • дН дрг v '
Pi
28*
436 УРАВНЕНИЯ ГАМИЛЬТОНА [Гл. XXII
Аналогично, подставляя функцию ф вместо qi в соотношение B2.4.4)
ж дифференцируя по qr (г = 2, 3, ..., п), находим
Ш +|й_<Эф_ B2.4.8)
dqr dq^ dqr v
Отсюда
^pr Рг dgr Эф (92 4 Q)
Таким образом, функцию ср можно взять в качестве новой функции Га-
Гамильтона с 2 (п—1) зависимыми переменными qz, q3, • • ¦ , qn\ Pi, Рз, • ¦ ¦ ,Pn
и независимой переменной pi (роль которой обычно выполняет время t).
Новая система уравнений не является автономной, поскольку функция ср
содержит новую независимую переменную. Остающимся уравнением явля-
является уравнение энергии в форме B2.4.4) или B2.4.5).
Практически преимущества этого метода проявляются тогда, когда функция Н
линейным образом зависит от д4. В качестве простого примера рассмотрим случай, когда
B2.4.10)
Здесь х, у — лагранжевы координаты, | = рх, т) = ру, a fc, g — положительные постоян-
постоянные. Если уравнение Н = h разрешить относительно х ж получить х = ф {у; r\; h; |), то
будем иметь
¦ —. B2.4.11)
Функцию ф можно взять в качестве гамильтоновой функции для системы с одной
степенью свободы; зависимыми переменными будут у ж ц = ру, а независимой перемен-
переменной будет %. Уравнения будут иметь вид
_|_|е_а, B2.4.12)
*l=_^- = A(g_fcj,). B2.4.13)
Решение этих уравнений элементарно. Из B2.4.12) и B2.4.13) получаем
4!1 = A_-^^--_-A_^1ti, B2.4.14)
dc," g g dtj 8 8
откуда находим
T^JL-i-^cos — E + Bsin — E. B2.4.15)
kg 8
Выражение для у получаем из B2.4.13). На этом решение второй задачи (нахожде-
(нахождение у ж т] как функций |) заканчивается. Для решения исходной задачи имеем
I = 8, I = g.o + St. B2.4.16)
Для х находим х = ф. (Непосредственное решение также элементарно.)
Аналогичным образом, если разрешить уравнение Н = h, например,
относительно pt, то получим
Pi. = —^ (?2, Яз, ¦ • •> Яп', Рг, Рз, ¦ ¦ ¦, Рп, h; qt). B2.4.17)
Рассуждая подобно тому, как это мы делали выше, легко показать, что
функцию \|) можно взять в качестве гамильтоновой функции новой системы
сп — 1 степенями свободы и с независимой переменной q\:
dqr д\р dpr ch|j г, о ,оо / 4 о\
§ 22.5] ЛИНЕЙНЫЙ ИНТЕГРАЛЬНЫЙ ИНВАРИАНТ ПУАНКАРЕ 437
Но так как Н = h есть уравнение второй степени относительно рх, то
выражение для г|э содержит иррациональность и потому не очень удобно.
Если бы исходная функция Гамильтона Н не содержала qi, то эта перемен-
переменная не вошла бы и в выражение для г|), и в результате новая система имела
бы «интеграл энергии»
г|) = Pi. B2.4.19)
Этот новый интеграл представляет собой, разумеется, интеграл количества
движения, соответствующий циклической координате qt.
Доказанные выше теоремы о понижении порядка уравнений с помощью интеграла
энергии можно получить и другим способом, который представляет самостоятельный
интерес. Этот способ основан на теореме эквивалентности (§ 16.3). Для определенности
остановимся на первом из рассмотренных выше случаев, когда новая функция Гамильто-
Гамильтона получается путем решения уравнения Я = h относительно переменной gt (см. B2.4.5)).
Если задачу рашать с помощью теоремы Гамильтона — Якоби, то в решение войдут
2ге параметров аг, Рг, где at есть постоянная энергия h, a р4 — постоянная 1й, связанная
с началом отсчета времени (§ 16.5). Тогда будем иметь
2 Рг<*«г. B2.4.20)
г=1 г=1
или, что то же,
2 Prdqr-qidp, = d(if + ht-qipi) + yi p,rdar + (H-h)dt-(t-t0)dh. ' B2.4.21)
r=2 r=2
Будем теперь рассматривать не все возможные движения, а только такие, для кото-
которых постоянная энергии h имеет одно и то же значение; таким образом, она будет играть
роль абсолютной постоянной. Все рассматриваемые траектории будут располагаться
на многообразии Н = h, и это многообразие теперь будет объектом нашего рассмотрения
вместо всего фазового пространства. Имеем
п п
2 PrdqT-qidpir=d(ty + ht-qm)+ ^ М«г- B2.4.22)
т—2 г=2
Согласно теореме эквивалентности переменные д2. ?з, • • -, qn'' Рг* Рз. • • •> Рп удовлетво-
удовлетворяют уравнениям Гамильтона с гамильтоновой функцией д4 и независимой переменной
Pi (вместо <). Функцию qx надлежит представить в форме B2.4.5) с помощью уравнения
Н = h. Таким путем мы снова придем к желаемому результату.
§ 22.5. Линейный интегральный инвариант Пуанкаре. В этом параграфе
п
мы докажем известную теорему Пуанкаре: линейный интеграл <т> ^pr dqT
r=l
представляет собой относительный интегральный инвариант уравнений
Гамильтона. Доказательство можно провести либо основываясь на общих
рассуждениях § 21.5, либо непосредственно. Пользуясь обозначениями § 21.5
и вводя обозначение a>rs для разности -~ — -J^ , напишем следующее соот-
oxs охТ
ношение:
K.) = Z. B2.5.1)
Отсюда
2п
так что форма Пфаффа 2 QrdxT представляет собой полный дифференциал
г=1
— dH. Теорема вытекает из § 21.5. Непосредственное доказательство также
438 УРАВНЕНИЯ ГАМИЛЬТОНА [Гл. XXII
весьма простое; оно проводится либо путем введения параметра и на замкну-
замкнутой кривой у (как в B1.5.7)), либо путем рассмотрения линейного элемента
(как в B1.6.14)). Следуя первому способу и опуская знак суммирования,
находим
1
/JL -I \ ®Ят 1 /по с о\
= (Viprdqr^= \ рг ~5—du. (//.о.о)
v о
Дифференцируя по t, получаем
П1_ Г Г дРг dqr д I дН \ \ ,
JJt J I. Ос аи ои \ opr I )
О
Jf дН даг . д I дН \ дН дрг ~| ,
{ г—- —Z-1—\- -гг— I рг -з— 1 j ^— > du =
(_ dqr ди ди \г дрг j дрг ди J
о
Из относительного интегрального инварианта Пуанкаре можно получить
абсолютный интегральный инвариант второго порядка:
J \ dqx dpt 4- dq2 dp2 + ... + dqn dpn. B2.5.5)
Это следует непосредственно из теоремы Стокса. Интеграл B2.5.5) берется
по площади одной стороны двусторонней поверхности, движущейся вместе
с жидкостью.
Справедлива и обратная теорема Пуанкаре. Именно, если существует
относительный интегральный инвариант ф prdqr, то Zn переменных qr, pr
удовлетворяют уравнениям, имеющим гамильтонову форму. Для доказатель-
доказательства введем, как и выше, параметр и. Тогда будем иметь
1
DI DC , Г д I dqr \ ,
о
i
дрг dgr dgr дрг \ , д I dqr \ Л , .„„ ^ „,
]
О
Последний член в подынтегральном выражении справа дает нуль, так как
" ТТ DI А
интегрирование производится по замкнутой кривой. Из условия -yr- = U
(отбрасывая параметр и) получаем равенство
rdqr-'qrdpr = O, B2.5.7)
которое выполняется в любой момент вдоль любой замкнутой. кривой.
Отсюда следует, что выражение pr dqr — qT dpT представляет собой полный
пространственный дифференциал- — dsH, где Н = Н (q; p; t) *). Таким
образом, во время движения величины qr, pr изменяются так, что
что и требовалось доказать.
*) Символ ds означает, что при вычислении дифференциала переменная t в выраже-
выражении для Я считается фиксированной. {Прим. перев.)
§ 22.7] ТЕОРЕМА ВОЗВРАЩЕНИЯ (ТЕОРЕМА ПУАНКАРЕ) 439
Полученный результат показывает, что любая система дифференциальных уравне-
уравнений вида
хт = Хг, г = 1, 2, . . ., т, B2.5.9)
для которой существует линейный интегральный инвариант, может быть полностью или
частично приведена к гамильтоновой форме. Это утверждение тесно связано с теоремой
Пфаффа о линейной дифференциальной форме. Предположим, что система имеет относи-
относительный линейный интегральный инвариант ф о), где о) обозначает форму Пфаффа
li dxt + 6а dx2 + . . . + Ira dxm, B2.5.10)
причем каждая из функций gr (x\, х2, . . ., хт) принадлежит к классу С±. По теореме
Пфаффа форму ш путем надлежащего выбора переменных можно привести к одному из
следующих видов:
Pi tyi + p2 dq2 + • • • + PvdQv B2.5.11)
или
Pi dqt + p2 dq2 + . . . + pvdgB + dqv+i, B2.5.12)
в зависимости от того, является ли класс формы а четным Bv) или нечетным Bv + 1).
Если форма о) неособенная, то ее класс равен т; если форма а особенная, то ее класс
меньше т.
Перейдем теперь от переменных гь х2, . . ., хт к новым переменным д1г q2, ...
• • • , Чп'< Pi' Ръ-> ¦¦¦ > Pni если т четное Bп), или к переменным ft, q2, . .. , qn; p4, p2, ..., pn;
§v
^ Prdqr будет относительным интегральным
r=l
инвариантом для преобразованных уравнений, и в новых переменных 2v дифферен-
дифференциальных уравнений могут быть записаны в гамильтоновой форме.
§ 22.6. Теорема Лиувилля. Для уравнений Гамильтона дивергенция
поля Д равна нулю. Отсюда следует (см. § 21.8, п. 3), что объем {протяжен-
{протяженность) фазового пространства является инвариантом преобразования, опре-
определяемого дифференциальными уравнениями. Иными словами, «фазовая жид-
жидкость несжимаема». В этом состоит известная теорема Лиувилля, играющая
важнейшую роль в кинетической теории газов. Как известно, множителями
системы являются ее пространственные интегралы, они удовлетворяют ус-
условию
QM == {М, Н) = 0. B2.6.1)
Если М — пространственный интеграл, то интеграл \ М dV является аб-
абсолютным интегральным инвариантом порядка 2п. Это следует из § 21.8,
п. 3. (Мы здесь для краткости через \ М dV обозначили интеграл
[ \ ... \ Mdqx dq2 . . . dqn dpi dpz. . . dpn.)
§ 22.7. Теорема возвращения (теорема Пуанкаре). Рассмотрим авто-
автономную систему
Хг = ХГ, г = 1, 2, . . ., т, B2.7.1)
обладающую двумя следующими свойствами:
1) А = 0, т. е. объем пространства переменных инвариантен относитель-
относительно преобразования 7\, определяемого решениями уравнений B2.7.1) (иначе
говоря, «жидкость несжимаема»). Как отмечалось выше, в наиболее интерес-
интересном для нас случае уравнений Гамильтона это условие выполняется.
2) Существует замкнутая область Q конечного объема mQ, такая, что
начинающиеся в ней характеристики целиком располагаются в ней («жид-
(«жидкость движется в замкнутом сосуде»). Такая область преобразованием Tt
переводится в самое себя и поэтому называется инвариантной областью.
Теорема Пуанкаре устанавливает, что если а есть любая сколь угодно
малая замкнутая подобласть области Q, то существуют характеристики,
440 УРАВНЕНИЯ ГАМИЛЬТОНА [Гл. XXII
которые бесконечное число раз пересекают область а. Точнее, для любого
сколь угодно большого значения ti можно указать такие движения системы,
при которых изображающая точка для некоторого t^> ti окажется в области а.
Для доказательства возьмем какую-нибудь замкнутую подобласть А
области Q и рассмотрим изображающие точки (или частицы жидкости), кото-
которые в момент t = 0 лежат в А. Пусть в момент t = 9 > 0 эти точки образуют
множество В, так что В = Т$А. Множество В можно считать Э-образом мно-
множества 4, а множество А — 9-прообразом В (см. § 2:1.12). Если А задано, то
множество В однозначно определяется числом 9, и наоборот, если задано В,
то множество А однозначно определяется значением 9. Более того, поскольку
движение является установившимся, изображающие точки, лежащие в мо-
момент t = t0 в А, в момент t = t0 + 9 располагаются в В, и наоборот, точки,
лежащие в момент t = t0 в В, в момент t = t0 — 9 располагаются в А.
Рассмотрим теперь заданную замкнутую подобласть а и возьмем какое-
нибудь положительное число т, например т = 1. Обозначим (т, 2т, Зт, . . .)-
прообразы а через а4, а2, а3, . . . Все множества а, а4, а2, а3, . . . имеют
одинаковый объем та и содержатся в множестве Q. Если N > mfi/ma, то
области a, oci, а2, . . ., осд-_1 не могут не иметь общих точек. По крайней
мере одна пара таких областей, скажем аг и as (r ;> s), будет иметь общую
часть Р, объем которой т§ отличен от нуля.
Отсюда следует, что и области а и ар (р =- г — &¦) имеют общую часть а'
того же объема т§. В самом деле, область ар является sx-образом области <хг,
а область а — sx-образом области as.
Возьмем теперь в качестве исходной области вместо а область а' и снова
повторим предыдущие рассуждения, приняв тот же основной интервал вре-
времени т, что и выше. Тогда найдется такое целое число р', что а' и его р'х-
прообраз а'Р' будут иметь общую часть а" конечного объема.
Продолжая таким образом, мы можем построить совокупность вложен-
вложенных областей а, а', а", . . ., каждая из которых содержится в предыдущей.
Эта последовательность сходится к предельному множеству К, которое пред-
представляет собой либо точку, либо замкнутую область и принадлежит всем
областям а, а', а", . . . Области а, а', а",. . . обладают тем свойством, что
изображающие точки, лежащие в момент t = t0 в области а(Г1+1), в момент
t = t0 + р{П)г располагаются в области a(Tl).
Рассмотрим теперь характеристику, начинающуюся в точке Ро области
К; изображающая точка Р в момент t = 0 находится в положении Ро.
Поскольку точка Р в момент t — О лежит в области а', в момент t=px она
будет находиться в области а. Аналогичным образом, если в момент t = 0
точка Р лежит в области а", то в момент t = р'х она окажется в области а' и,
следовательно, в момент t = (р' + р") х попадет в область а. Находясь в мо-
момент t = 0 в области а'", изображающая точка в момент t = p"x попадет
в область а", в момент t = (р' + р") т — в область а' и в момент ?= (р +
+ Р' + Р") х — в область а. Продолжая эти рассуждения, мы приходим
к выводу, что точка Р находится в области а в следующие моменты времени:
t = 0, t = px, t={p-\- р') т, t = {р + р' + р") х и вообще при t = (р +
-)- р'-\-. ¦ .+/?<П)) т. С ростом п сумма (р + />'+. . .+р(П>) стремится к бес-
бесконечности, поскольку все р — целые положительные числа. Изображающая
точка бесконечное число раз возвращается в область а, что и требовалось
доказать.
Выше мы рассматривали положения точки Р лишь для дискретных
моментов времени: 0, т, 2т, . . ., но теорема, очевидно, справедлива и тогда,
когда t изменяется непрерывно.
Движение, при котором система бесконечное число раз возвращается
в окрестность начального состояния, Пуанкаре называл «устойчивым в смыс-
смысле Пуассона».
§ 22.9] ЭГОДИЧЕСКИЕ ТЕОРЕМЫ 441
Отметим, что основная идея в доказательстве теоремы Пуанкаре заклю-
заключается в использовании теоремы Лиувилля о сохранении меры при преобра-
преобразовании с помощью оператора Tt. Никакие другие свойства уравнений
Гамильтона здесь не используются.
Ранее, при изучении квазипериодических движений (§ 18. 6), мы уже встречались
с теоремой, близкой по своему характеру к теореме Пуанкаре. Было показано, что изобра-
изображающая точка проходит бесконечное число раз в произвольной близости от своего на-
начального положения в фазовом пространстве.
Теорему Пуанкаре можно считать отправным пунктом в новом подходе
к задачам классической динамики. До сих пор мы полагали, что решить
задачу динамики ¦— это означает найти зависимость положения системы
от времени t и заданных начальных значений координат и скоростей частиц.
Для большей части задач, однако, такое решение получить не удается. Имен-
Именно это обстоятельство вызвало столь большой интерес к теореме Пуанкаре и
обусловило развитие связанных с нею теоретических вопросов. Основное вни-
внимание теперь уделяется не изучению индивидуальных свойств характеристик,
а исследованию статистических свойств целого семейства характеристик.
§ 22.8. Примеры инвариантных областей. Рассмотрим систему, для которой функ-
функция Гамильтона ограничена снизу в фазовом пространстве. Можно считать, что точная
нижняя грань функции Гамильтона равна нулю: этого всегда можно добиться, если при-
прибавить к этой функции надлежащим образом выбранную постоянную (что не изменяет
уравнения движения) или изменить произвольную постоянную в функции V. Будем пред-
предполагать также, что «поверхность» Н = h (h > 0) является замкнутой. Но функция Н
представляет собой интеграл уравнений Гамильтона, так что поверхность Н = h (h > 0)
является инвариантной областью. Замкнутая область, ограниченная двумя такими поверх-
поверхностями (т. е. множество точек ж, для которых /ц < Я (ж) < h2), также представляет
собой инвариантную область.
В качестве простейшего примера рассмотрим гармонический осциллятор
q = р, р = —д B2.8.1)
(единица времени нами выбрана так, чтобы период колебаний составлял 2л). Эта система
имеет одну степень свободы, фазовое пространство является двумерным, и траектории
Н = const представляют собой окружности
\{qi+Pi) = K h>0, B2.8.2)
Изображающая точка равномерно движется по ходу часовой стрелки вдоль каждой
из этих окружностей с угловой скоростью, равной единице. Окружность г = R (где г2 =
= Ф + Р2) ПРИ R > 0 является инвариантной областью: действительно, эта область со-
содержит как раз одну траекторию. Область R\ ^ r ^ R2 также является инвариантной.
Соответствующее движение жидкости представляет вращение ее как твердого тела, и
в качестве инвариантной области Q можно взять любую окружность R = Rt, или любой
круг R ^ Ri, или же круговое кольцо Ri ^ г ^ Лг-
§ 22.9. Эргодические теоремы. Теорема Пуанкаре (теорема возвраще-
возвращения) устанавливает существование таких движений, когда изображающая
точка бесконечное число раз возвращается в исходную область а. Более
глубокие свойства этих движений связаны с выяснением следующего вопроса:
какую долю времени своего движения изображающая точка находится в об-
области а? Аналогичный вопрос возникает и тогда, когда мы имеем дело с дис-
дискретными моментами пт. Именно, спрашивается, какая часть этих моментов ха-
характеризуется попаданием изображающей точки в область а? *) Ответ на эти
и аналогичные вопросы дается так называемыми эргодическими теоремами**).
*) См. определения С-устойчивости и ^-устойчивости в § 21.12.
**) Эргодическая теорема впервые была доказана Дж. Г. Биркгофом, Ргос.
Nat. Academy of Sciences, Vol., 17, 1931, стр. 656. Несколько более слабый результат
незадолго до этого был установлен Дж. Нейманом. Доказательство, приведенное в тексте,
принадлежит А. Н. Колмогорову. Оригинальное доказательство для случая, когда усред-
усреднение производится по дискретным значениям t, см. в работе Ф. Рисса: F. R i e s z, Com-
Comment. Math. Helv., Vol. 17, 1945, стр. 221.
442 УРАВНЕНИЯ ГАМИЛЬТОНА [Гл. XXII
Прежде чем переходить к рассмотрению этих теорем, приведем некото-
некоторые сведения об интегрировании по точечным множествам. При этом нам
придется пользоваться понятием о мере Лебега точечного множества вместо
более простого представления об объеме (протяженности), которым мы удов-
удовлетворялись до сих пор. В соответствии с этим в дальнейшем (до конца § 22.17)
мы будем рассматривать интегралы Лебега, а не интегралы Римана, которы-
которыми обычно пользуются в других разделах классической динамики.
Рассмотрим преобразование Tt, определяемое решениями автономной
системы
хт = Хг, г = 1, 2, . . ., т. B2.9.1)
Предположим, что div Ж = 0, так что преобразование сохраняет меру.
Рассмотрим инвариантную область Q, имеющую конечную меру тО,. Пусть
/ (Р) — функция положения, определенная в области Q и суммируемая,в этой
области. Обозначим через Pt точку, в которую переходит точка Р в резуль-
результате преобразования Tt. Иными словами, если движение изображающей точки
начинается в момент t = О из положения Р и определяется уравнением
B2.9.1), то в момент t эта точка приходит в положение Pt.
Будем рассматривать среднее по времени значение функции / (Р) на от-
отрезке траектории (например, траектории, начинающейся в точке А), прохо-
проходимом изображающей точкой с момента t = а до момента t = Ъ (a<ib).
Положим
ь
dt. B2.9.2)
Существование величины \уъа {А) почти для всех точек А области Q
следует из суммируемости функции / (Р) в силу теоремы Фубини. В дальней-
дальнейшем мы исключим из рассмотрения множества точек А меры нуль, для кото-
которых эта величина может не существовать. Основной результат, который
составляет содержание эргодической теоремы, заключается в том, что вели-
величина [х^ (А) при Ъ —>• оо стремится к пределу ф (^1) почти для всех точек А
области Q.
Если, в частности, / (Р) есть характеристическая функция области а
(т. е. / (Р) равно единице для точек Р, лежащих в области а, и нулю для точек
Р, расположенных в области Q — а), то ф (А) выражает долю времени, в те-
течение которого изображающая точка, начавшая движение в момент t = О
из положения А, находится в области а.
Прежде всего заметим, что если существует предел ф (А) для какой-
нибудь точки А, то существует и предел ф (Ав) для любой точки Ав на траек-
траектории, проходящей через А, причем для всех этих точек он имеет одно и то же
значение. Для доказательства того, что при заданном фиксированном значе-
значении Э существует ф (Aq), покажем, что
е+ь
\ \ f{At)dt B2.9.3)
стремится к пределу, когда Ъ —> оо . Имеем
е+ь е+ь е
j f(At)dt = ~ j f{At)dt-\\f{At)dt =
е+ь е
dt. B2.9.4)
§ 22.10]
КОНКРЕТНЫЕ ПРИМЕРЫ
443
При Ъ —>- оо первый член правой части стремится к ф (А), а второй — к нулю.
Таким образом, предел ф (Ав) существует и ф (Ад) = ф (А).
В дальнейшем мы увидим, что при известных условиях справедливо
и более сильное утверждение, а именно что величина ф {Р) постоянна не толь-
только на траектории, но и во всей области Q. Это свойство инвариантных обла-
областей играет фундаментальную роль в статистической механике. Впервые оно
было высказано в форме правдоподобной гипотезы в кинетической теории
газов, где эргодическая теорема используется весьма широко. Нетрудно
видеть, что это свойство (постоянство функции ф (Р) в области Q) не имеет
места для уравнений Гамильтона в классической динамике: Для того чтобы
оно выполнялось, необходимо, чтобы система обладала некоторыми особыми
свойствами, о которых речь будет ниже (§ 22.15).
§ 22.10. Конкретные примеры. Прежде чем переходить к доказательству эргодиче-
ской теоремы, приведем несколько примеров.
Начнем с простого случая, когда изображающая точка Р движется по окружности
по направлению часовой стрелки с постоянной (единичной) угловой скоростью. 1) Если t
изменяется непрерывно и в качестве области а берется дуга с углом раствора C, то спра-
справедливость теоремы Пуанкаре (теоремы возвращения) очевидна. Далее, если % (*) есть
доля интервала времени от 0 до (, в течение ко-
которого изображающая точка находится в области а,
то отношение % (ЪIЪ, очевидно, стремится к преде-
пределу р72я, и этот предел не зависит от положения
начальной точки А на окружности. 2) Если мы
имеем дискретную последовательность моментов
времени t = О, т, 2т, ... (§ 22.7) и обозначим
через v (п) число точек А, Ах, А%х, '. . ., А(п_^х,
лежащих в области а, то отношение v (n)ln при
п ->- оо будет стремиться к тому же пределу р/2я
при условии, что отношение т/2я есть число ирра-
иррациональное. Действительно, при этом условии точ-
точки А, Ах, А2.x, . ¦ ., отстоящие на угловых рас-
расстояниях 0, т, 2т, ... от точки А, стремятся к рав-
равномерному распределению по окружности. Предел
не зависит ни от положения точки А па окружно-
окружности, ни от величины основного интервала т, если
только х не является соизмеримым с 2я.
Рассмотрим теперь простой пример гармони-
гармонического осциллятора, о котором уже шла речь
в конце § 22.8. Пусть множеством Q будет круг радиуса R с центром в точке О, и
пусть А —¦ точка внутри этого круга. Проходящая через А характеристика является
окружностью. Доля времени, в течение которого изображающая точка находится в зам-
замкнутой области а, стремится к пределу р72л, где C — угол, стягиваемый дугой CD окруж-
окружности, проходящей через точку А (рис. 100). Предел, как мы видели, не зависит от поло-
положения точки А на характеристике. Результат останется без изменений, если взять пре-
предел v (п)/п, где v (п) —¦ число точек А, Ах, А2Х, ¦ ¦ • , A(n_DX, лежащих в области а,
при условии, что отношение т/2я есть число иррациональное. Результат не зависит ни от
положения точки А на характеристике, ни от величины интервала т.
Следует отметить, однако, что в этом случае предел для различных характеристик
имеет различные значения: он не остается постоянным во всей области Q.
Предположим теперь, что для рассматриваемой системы функция / (Р) не является
характеристической функцией области а. Положим / (Р) равной q2. Если точка А имеет
координаты ?i, pi, то точка At будет определяться координатами
Рис. 100.
pisint, \
t-\-Pi cos t, i
g = g1cost-\-pisin
р=—?j sin
и среднее значение функции / (Р) на характеристике будет равно
ь
qlpx cos t sin t-\-pj sin2 t)dt =
B2.10.1)
ь
1 Г
-г \ (ql
о
B2.10.2)
444 УРАВНЕНИЯ ГАМИЛЬТОНА [Гл. XXII
1
При Ь ->- оо эта величина стремится к -р- {q\ + pf) *). Мы вновь обнаруживаем, что предел
один и тот же для всех положений точки А на характеристике, но не одинаков во всей
области Q. Результат не изменится, если взять дискретные точки А, Ах, . . ., A(n_i)x;
Л
среднее значение q2 в этих точках стремится к тому же самому пределу — {q\ + p{), если
только т не равно целому кратному я.
§ 22.11. Множество Ks. Перейдем теперь к доказательству эргодической
теоремы. Доказательство проведем в два этапа. Сначала докажем, что вели-
величина [\% (р) почти для всех точек Р множества Q стремится к некоторому
пределу, когда параметр Ъ растет до бесконечности, принимая целые значения.
Затем мы от этого ограничения откажемся и докажем, что предел существует
и тогда, когда Ъ стремится к бесконечности, возрастая непрерывно.
Рассмотрим.величину \i%(P), считая п целым числом. Требуется дока-
доказать, что эта величина стремится к некоторому пределу почти для всех Р.
Предположим противное: пусть имеется подмножество L множества Q, име-
имеющее положительную меру mL и такое, что для точек Р ? L величина \i™ (P)
не стремится ни к какому пределу. Докажем сначала две следующие леммы.
Лемма 1. Существуют два вещественных числа а и $, а < |5, и под-
подмножество К множества L, имеющее конечную положительную меру тК
и такое, что если Р ? К, то
lim |i» (Р)< а, НпГ ^ (Р) > р. B2.11.1)
Для доказательства рассмотрим множество всех интервалов с рацио-
рациональными граничными точками. Так как это множество счетное, то его эле-
элементы можно расположить таким образом, чтобы и-й интервал б„. имел гра-
граничные точки ап, рп. Если Р ? L, то
и, следовательно, среди интервалов бп найдется такой (скажем, бр),
для которого
Обозначим через Lp множество точек L, связанных с интервалом
Множества Ьг и Lj при i ф]'не имеют общих точек, и
L= U Lp.
i
Так как mL > 0, то mLp >0 по крайней мере для одного р, скажем
р = q. В качестве множества К мы можем взять Lq с a = aq и |5 = j3g.
Лемма 2. Пусть s — целое положительное число. Обозначим через К&
подмножество точек Р множества К (см. лемму 1), для которых неравенство
выполняется по крайней мере для одного значения п ^ s. Тогда для достаточ-
достаточно больших значений s будем иметь
mKs>0. B2.11.2)
Так как при достаточно большом s каждая точка Р ? К принадлежит
всем Ks, то
К= U Ks.
8=1
*) Этот результат следует из известного свойства гармонического движения: Т =
§ 22.12] СОБСТВЕННЫЕ ОТРЕЗКИ 445
С другой стороны,
Ks
Следовательно,
тК= lim mKs.
8-ЮО
Из неравенства тК > 0 следует, что mKs > 0 при достаточно большом s.
Лемма 2, таким образом, полностью доказана.
В дальнейшем мы будем считать s фиксированным целым положитель-
положительным числом, для которого выполнено условие mKs > 0.
§ 22.12. Собственные отрезки. Введем понятие собственного отрезка,
точнее, собственного отрезка точки Р для числа |5 (см. леммы 1 и 2). Возь-
Возьмем точку Р множества К, и пусть а — целое число, положительное, отри-
отрицательное или нуль. Рассмотрим числа \i%+1 (P), \i%+* (Р), ц.„+3 (Р), . . .
Если \i\ (P) есть первое из этих чисел, превышающее |5, то отрезок (а, Ъ) мы
будем называть собственным отрезком точки Р. Таким образом, собствен-
собственный отрезок (а, Ъ) обладает тем свойством, что
где с — любое целое число, заключенное между а и Ъ.
Лемма 3. Два собственных отрезка (at, bt) и (az, b2) точки Р не могут
частично перекрывать друг друга. Допустим, например, что at < а2 < &i <
< Ьг. Тогда мы имели бы
(bt - «О К\=(а* - «О К1+(fei - а2> К\-
Но это невозможно, поскольку левая часть больше, чем (&t — аг) fi, а правая
часть меньше (или равна), чем
(az — at + fej — а2) р = (bj — at) p.
Собственный отрезок точки Р мы будем называть максимальным отрез-
отрезком ранга s, если его длина не превышает s и если он не содержится ни в ка-
каком другом собственном отрезке точки Р, длина которого не превышает s.
Лемма 4. Всякий собственный отрезок, длина которого не превышает
s, содержится в одном и только в одном максимальном собственном отрезке
ранга s. Для доказательства заметим, что среди всех собственных отрезков,
длина которых не превышает s и которые содержат данный отрезок, имеется
один отрезок максимальной длины. Ясно, что этот отрезок и есть макси-
максимальный отрезок ранга s. Существует лишь один такой отрезок; если бы их
было два, то они имели бы общие точки, поскольку оба они содержат заданный
отрезок. Но в этом случае либо один из них содержался бы в другом и потому
не был бы максимальным отрезком ранга s, либо они имели бы общую часть,
что, как мы видели, невозможно. Таким образом, лемма доказана.
Лемма 5. Для того чтобы точка Р принадлежала множеству Ks,
необходимо и достаточно, чтобы эта точка имела максимальный отрезок
{а, Ь) ранга s такой, что а ^ 0 < Ъ.
Необходимость условия. Пусть Р ? Ks и п есть наимень-
наименьшее целое положительное число, для которого \\% (Р) > р, так что п ^ s.
Тогда отрезок @, п) будет собственным отрезком точки Р, и единственный
максимальный отрезок ранга s, который содержит его, удовлетворяет усло-
условиям леммы.
Достаточность условия. Предположим, что точка Р имеет
максимальный отрезок {а, Ь) ранга s такой, что a gel 0 < Ъ. Докажем, что
^о (Р) > Р- Отсюда будет вытекать, что Р ? Ks, поскольку Ъ ^.Ъ — а ^ s.
Если а = 0, то неравенство [А*» (Р) > |5 немедленно следует из того, что
отрезок (а, Ъ) является собственным отрезком точки Р. Предположим, что
446 УРАВНЕНИЯ ГАМИЛЬТОНА [Гл, XXII
а < 0. Если (ijj (Р) ^ р, то существует собственный отрезок (О, Ь'), где Ъ' > Ъ,
и он частично перекрывает отрезок (а, Ъ). Но это невозможно в силу леммы 3.
Следовательно, \у\ (Р) > р, и лемма, таким образом, доказана,
§ 22.13. Доказательство эргодической теоремы; первый этап. Для вели-
величин, связанных с максимальными отрезками ранга s, а ^ 0 < b (лемма 5),
удобно ввести новые обозначения. Положим
а = — р, Ъ — а = д. B2.13.1)
Так как
а < О, Ъ — а < s, B2.13.2)
то будем иметь
0<p<g<s. B2.13.3)
Всякой паре целых чисел (р, q), удовлетворяющих неравенству B2.13.3),
поставим в соответствие подмножество Kpq тех точек множества Ks, которые
связаны с отрезком (—р, —р + q) в смысле леммы 5. Заметим, что подмно-
подмножества Kpq, соответствующие различным парам целых чисел (р, q), не имеют
общих точек. Через р единиц времени множество KOq переходит в множество
Kpq'-
TpKoq = Kpq, B2.13.4)
так что
mKoq = mKvq. B2.13.5)
Далее, для любой суммируемой функции ф (Р) имеем
<p(P)dV= J <p{PP)dV. B2.13.6)
K
С помощью этих соотношений находим
s q— I s q— I
3=1 P=0 Kpg g=l p=0 KOq
s q—1 1 s q~ 1 P+l
j J J j
= 2 2 J'dv J f(pP+№= 2 2 JdV j
' P=« ^09 ° ' ""
q s
. dv]HPt)dt=^
w 9=1 q
s g-1
= P2 2m^ = P(m^)' B2.137)
g=l p=0
До сих пор s считалось фиксированным целым положительным числом.
Но равенство B2.13.7) остается в силе для всех достаточно больших s, и,
устремляя s к бесконечности, находим
J). B2.13.8)
к
Проведем теперь аналогичные рассуждения для нижнего предела обла-
области а (лемма 1). Поскольку
B2.13.9)
§ 22.14] ДОКАЗАТЕЛЬСТВО ЭРГОДИЧЕСКОЙ ТЕОРЕМЫ; ВТОРОЙ ЭТАП 447
мы можем совершенно так же доказать, что
\\il(P)dV4?a(mK). B2.13.10)
к
Но соотношения B2.13.8) и B2.12.10) противоречат друг другу, так как
а < р, из чего заключаем, что предположение, что
т (L) > 0,
неверно. Иными словами, величина [х" (Р) стремится к пределу ф (Р) почти
для всех точек Р множества Q.
§ 22.14. Доказательство эргодической теоремы; второй этап. Теперь
нам остается доказать, что величина \i^ (P) стремится к пределу и в том слу-
случае, когда Ъ растет до бесконечности, изменяясь непрерывным образом.
Для этого нам потребуется рассмотреть среднее значение функции | / (Р) |
на отрезке характеристики, проходимом изображающей точкой за время
между моментами f = пи t = п -\- I; оно равно
п+1
®п(Р)= j \f(Pt)\dt. B2.14.1)
П
Замечаем сразу, что
еп (Р) = е0 (рп). B2.14.2)
Докажем следующую лемму.
Лемма 6. Отношение Qn (P)ln при п, стремящемся к бесконечности,
стремится к нулю почти для всех точек Р множества Q. Пусть е — произ-
произвольное фиксированное положительное число, an — целое положительное
число. Обозначим через ЕПг п множество точек Q, для которых
Э„ (Р) > гп, B2.14.3)
и пусть Еп< 0 — множество точек Q, характеризуемых неравенством
60 (Р) > еп. B2.14.4)
Преобразование Тп, определяющее перемещение изображающей точки
за время t = n, переводит множество Еп>0 в множество ЕП!П, так что
тЕп, п = тЕп> 0. B2.14.5)
Докажем, что ряд
%тЕп,п, B2.14.6)
п=1
или, что то же, ряд
оо
1]тЕп>0 B2.14.7)
п=1
является сходящимся. Пусть s — целое положительное число. Если Fs есть
множество точек Q, для которых
1)е, B2.14.8)
то справедливо очевидное равенство
?n,o= U Л. B2.14.9)
s=n
448 УРАВНЕНИЯ ГАМИЛЬТОНА [Гл. XXII
Тогда ряд B2.14.7) можно переписать в форме
J
) ;
\f{Pt)\dt = \ j Л J \f(Pt)\dV. B2.14.10)
0 Й
J
s= 1 s= 1 se < 9o(P) ;? (e+1) 8
1 1
^^ j J
Q 0 0 Й
Поскольку область Q инвариантна, а преобразование Tt сохраняет меру,
последнее выражение равно
1
I j<ftj|/(i>)|tfF=4 ]\f{P)\dV. B2.14.11)
ОЙ Й
Но эта величина имеет конечное значение, так как функция / (Р) суммируема
в области Q. Сходимость ряда B2.14.6), таким образом, доказана.
Отсюда следует, что все точки Q, за исключением, быть может, точек
множества меры нуль, принадлежат не более чем конечному числу множеств
Еп> п (п = 1, 2, 3, . . .). Поэтому почти для всех точек Р множества Q можно
указать число N — N (Р) такое, что для любого п^> N будет выполняться
неравенство
-Эп(Р)<еп. B2.14.12)
Так как е произвольно, то отсюда следует лемма 6.
Теперь легко получить доказательство эргодической теоремы для слу-
случая, когда Ъ-*-оо, изменяясь непрерывным образом.
Пусть п — наибольшее целое число, не превышающее Ъ; тогда п/Ь—>- 1,
когда b —>¦ оо. Имеем
n+1
Й< j |/(^)|Л = 8л(Р). B2.14.13)
n n и
Следовательно,
;1э„(Р) = ^-^-. B2.14.14)
Выражение справа, согласно лемме 6, стремится к нулю, когда Ь—*оо,
Таким образом, разность
Рьо(Р)—$Р*(Р) B2.14.15)
при Ъ —> оо стремится к нулю, откуда следует, что \уь0 (Р) и ^™ (Р) имеют
один и тот же предел ф (Р).
§ 22.15. Метрическая неразложимость. Мы видели, что предел
ь
=1ш{( f(Pt)dt B2.15.1)
существует почти для всех точек Р инвариантной области Q и что функция
Ф (Р) постоянна вдоль траектории. Как уже указывалось, при определенных
условиях функция ф {Р) сохраняет постоянное значение во всей области,
§ 22.15] МЕТРИЧЕСКАЯ НЕРАЗЛОЖИМОСТЬ 449
но примеры § 22.10 показывают, что в классической механике это, вообще го-
говоря, не имеет места. В этом параграфе мы рассмотрим условия, которые долж-
должны выполняться для того, чтобы функция ф (Р) была постоянна в области й.
Будем называть инвариантную область й метрически неразложимой,
если ее нельзя представить в виде
Q = Qt U й2, B2.15.2)
где инвариантные области Й4 и Й2 не имеют общих точек и обладают положи-
положительной мерой. Докажем, что если область Q метрически неразложима, то
1) функция ф (Р). почти всюду в Q постоянна и 2) величина этой постоянной
определяется выражением
il B2.15.3)
Важность последнего результата состоит в том, что среднее по времени
значение на характеристике заменяется средним по пространству (по обла-
области Q).
Докажем сначала, что функция ф (Р) почти всюду в области Й постоянна.
Разделим вещественную ось х на отрезки
^<х^Ц±, B2.15.4)
считая к целым числом (не обязательно положительным). Будем называть
такой отрезок существенным отрезком, если множество точек Р области Q,
для которых значения ф (Р) принадлежат отрезку, имеет положительную
меру. Если для любого п существует только один существенный отрезок
6П-, то отрезок бп+1 содержится в бп и последовательность отрезков 8п (п =
= 1,2, . . .) имеет единственную общую точку а. При этом ф (Р) = а почти
всюду в области й. С другой стороны, если для некоторого п можно указать
два существенных отрезка, то найдется число р, обладающее тем свойством,
что область Й может быть разделена на две части Й1 и Й2 такие, что для точек
fii будем иметь ф (Р) > р, а для точек й2 будем иметь ф (Р) ^ |5. Но множе-
множества Й1 и Й2 представляют собой инвариантные области, не имеющие общих
точек, поскольку функция ф (Р) постоянная на характеристике. Таким
образом, мы пришли к противоречию с предположением о метрической не-
неразложимости области Й. Следовательно, функция ф {Р) постоянна во всей
области Й, т. е.
Ф (Р) = а B2.15.5)
почти для всех точек Й.
Остается доказать, что а = А, где
B2.15.6)
Интуитивно это ясно. Нетрудно получить и формальное доказательство.
Для этого заметим прежде всего, что для любого положительного Ь
ъ
j ]x\ (P) dV = -1 ( dt J / (Pt) dV, B2.15.7)
а о q
Но так как Й является инвариантной областью, то в силу теоремы Лиу-
вилля имеем
B2.15.8)
29 л. А. Парс
450 УРАВНЕНИЯ ГАМИЛЬТОНА [Гл. XXII
и из формул B2.15.7) и B2.15.8) находим
J \i*(P)dV= J f{P)dV = A(mQ). B2.15.9)
Я й
Таким образом, интеграл \ |д& (Р) dV фактически не зависит от Ъ, и, чтобы
а
доказать равенство а — А, достаточно показать, что интеграл
V B2.15.10)
а
стремится к нулю при Ъ —>¦ оо, но поскольку он не зависит от Ь, то его значе-
значение может быть только нулем.
Возьмем некоторое положительное число е. Пусть Qj (b) — множество
точек Р области Q такое, что
\а — Ро(р)\<Ь B2.15.11)
a Q2(&)— множество точек Р области Q такое, что
\*-$(Р)\>*- B2.15.12)
При этих условиях будем иметь
{а-ц$(/>)}dF|< J \a-V>(P)\dV +
Qi(b)
o-nS(/>)|d7<e(mQ)+|a|(mfl2(b))+ J |цЬ(/>)|йК. B2.15.13)
Q(b)
j J
Q2(b) Q2(b)
Разность ^ (Р) — а при & -> оо стремится к нулю почти для всех точек
области Q, и так как сходимость почти всюду означает сходимость по мере,
то mQz (&) -> 0, когда Ъ ->¦ оо.
Для последнего слагаемого в правой части B2.15.13) имеем оценку
ь ь
j |ng(/>)|dF<4-Jd* j |/(Pt)|d7 = 4-idi J 1/(^I^' B2.15.14)
Я2(Ь) 0 Я2(Ь) О nJ(b)
где через Q^F) обозначена область, в которую переходит область Й2 (&)
за время t. Но mQ2F) = тпг (Ь) и mQ2 (b) стремится к нулю, когда b -*- схз,
так что интеграл \ | [х§ (Р) | dV при достаточно большом b может быть
Й(Ь)
2()
сделан меньше е. Окончательно получаем, что существует такое число Ьо,
что при b > b0
e, J ||ig(P)|d7<e B2.15.15)
Q2(b)
и, следовательно, при fe > &0.
| + l)e. B2.15.16)
Так как левая часть не зависит от Ь, то она может равняться только нулю,
что и завершает доказательство.
Условие метрической неразложимости существенно для постоянства функции <р (Р)
в области Q. Простым примером, в котором это условие заведомо не выполняется, может
служить гармонический осциллятор, рассмотренный в § 22.10. Возьмем какую-либо кон-
концентрическую окружность радиуса Rlt 0 < Ri < R, тогда область Q (r ^ R) разделится
на две инвариантные области Q4 @ < г < ДО и Q2 (Ri < r < R), каждая ненулевой
меры. Как уже указывалось, в этом примере функция <р (Р) постоянна вдоль характери-
характеристик, но не постоянна во всей области Q.
§ 22.17] СЛЕДСТВИЕ ТЕОРЕМЫ ЛИУВИЛЛЯ 451
§ 22.16. Интегралы уравнений движения. Согласно теореме § 22.15
требуется, чтобы рассматриваемая инвариантная область была метрически
неразложимой. Если уравнения движения допускают однозначный интеграл
г)), то область а ^ а|;> ^ Ъ будет инвариантной областью. Однако ясно, что она
не будет метрически неразложимой, поскольку представляет объединение
инвариантных областей asCiji^c, с < г|) s^ Ь, где с — любое число, заклю-
заключенное между а и Ъ. Тем не менее существование такого интеграла позволяет
перейти в теореме Лиувилля от интегрирования по m-мерному пространству
к интегрированию по (т — 1)-мерному пространству.
Рассмотрим в качестве примера автономную гамильтонову систему, для
которой координата qn является циклической. При этом рп представляет
собой интеграл и траектории располагаются в плоскостях рп = const. Рас-
Рассмотрим плоскость со, заданную уравнением рп = р. Движение системы опре-
определяет преобразование точки Ро плоскости со в точку Р той же плоскости
(здесь PQ — положение изображающей точки в момент t = 0, a P — поло-
положение ее в момент t). В результате область Uo плоскости со переходит в задан-
заданный момент t в область U той же плоскости.
Это преобразование в Bга — 1)-мерной плоскости со сохраняет меру.
Иными словами, теорема Лиувилля остается справедливой в Bга — ^-мер-
^-мерном пространстве. Для доказательства рассмотрим цилиндр с основанием
Uo, ограниченный плоскостями рп = р и рп = р + е. Согласно теореме
Лиувилля объем этого цилиндра является инвариантом, откуда следует,
что mU — mU0.
Возьмем более общий случай: пусть -ф есть однозначный интеграл урав-
уравнений движения. Обозначим через dv элемент объема многообразия г|з = р.
Тогда, повторяя те же рассуждения, что и раньше, убеждаемся, что интеграл
¦ dv
| grad
остается инвариантным при преобразованиях, определяемых движением.
Наиболее важным является случай, когда г|з есть функция Гамильтона Н.
Тогда интеграл \ dv сам не является инвариантом, но существование инва-
риантного интеграла I ф dv с положительной подынтегральной функцией ф
может оказаться столь же полезным, как и существование объемной инвари-
инвариантности в теореме Лиувилля.
§ 22.17. Следствие теоремы Лиувилля. В предыдущем параграфе мы
использовали факт существования однозначного интеграла уравнений
движения для получения инвариантного интеграла по области 2п — 1
измерений. Выясним теперь условия, при которых существует инвариант-
инвариантный интеграл по области 2га — 2 измерений.
Рассмотрим автономную систему Гамильтона, допускающую периоди-
периодическое решение. Допустим, что периодическая траектория начинается в мо-
момент t = 0 в точке А фазового пространства и возвращается в эту точку
в момент t = 0; координатами точки А пусть будут (аь а2, . . ., ап, рь
р2> • • ч Рп)- Предположим, далее, что производная dH/dqi в точке А не обра-
обращается в нуль, так что траектория не касается плоскости со, уравнение которой
Pi = Pi-
Обозначим через Uo малую окрестность точки А в плоскости со и рас-
рассмотрим траекторию, начинающуюся в момент t = 0 из точки Ро области Uo.
Спустя время т изображающая точка возвратится в плоскость со, в точку Р,
близкую к Ро; время т будет мало отличаться от ст. Траектория, начинаю-
29*
452 УРАВНЕНИЯ ГАМИЛЬТОНА [Гл. XXII
щаяся в точке Ро, может многократно возвращаться в плоскость со, но тем
не менее точка Р точно определяется упомянутым выше свойством непрерыв-
непрерывности. По мере того как точка Ро принимает всевозможные положения в об-
области Uo, точка Р описывает область U в плоскости со, и в результате дви-
движение определяет топологическое отображение области Uo на область U.
Точка А является неподвижной точкой этого отображения.
Рассмотрим интервал времени от t = 0 до t = t0. Траектории, выходя-
выходящие в момент i = 0 из точек области Uo, заполняют в течение этого вре-
времени цилиндр Со с основанием UQ. Аналогично, траектории, начинающиеся
в момент t = 0 в точках области U, образуют за время @, t0) цилиндр С с ос-
основанием U. Если обозначить через R трубку, образуемую траекториями,
начинающимися вДи оканчивающимися в Р, то согласно теореме Лиувилля
область R -\- С — Со будет иметь тот же объем (меру в пространстве 2и),
что и R, так что С будет иметь тот же обт>ем, что и Со. Полагая t0 = 0, видим,
что интеграл
) —5гГ dqi ^2 '"" dqn dpz dpz ''" dpn B2.17.1)
остается при преобразовании инвариантным.
Используем теперь тот факт, что Н есть интеграл уравнений движения.
Перейдем от переменных qi, qz, . . ., qn, рг, р3, . . ., рп к переменным Н,
q2, q3, . . ., qn, р%, р3, . . ., рп и возьмем в качестве Uo произведение про-
пространств: Bп — 2)-мерной области Ао пространства {q^, q3-> • ¦ •> Qm Vii
p3, . . ., pn) и интервала (-й — б, Но + б) переменной Н. Область Ао явля-
является малой окрестностью точки (а2, а3, . . ., осп, $2, р3> • • •> P™)i a HQ есть
значение Н в точке А. Но Н сохраняет постоянное значение вдоль траекто-
траектории, откуда следует, что U является прямым произведением Bп — 2)-мер-
ной области А пространства (q2, ?з> • • •> ?т Рг> Рз> • • •> Рп) и интервала
(Но — б, Но + б) переменной Н. Интеграл B2.17.1) равен
- 26 dq2 dq3 ... dqn dp2 dp3 ... dpn, B2.17.2)
д
откуда следует, что интеграл
\ dq2 dq3 . .. dqn dp2 dp3 ... dpn B2.17.3)
д
является инвариантом.
В этом и заключается следствие теоремы Лиувилля, которое мы хотели
вывести.
Доказательство можно несколько сократить, если воспользоваться теоремой § 22.4.
Систему можно привести к гамильтоновой с функцией Гамильтона B2.4.5). Новыми зави-
зависимыми переменными будут д2, ?з, ¦ • •> 4ni Pz> Рз> • • • > Pni независимой переменной
будет pi. Система будет неавтономна, поскольку функция Гамильтона ф содержит ри одна-
однако это не исключает возможности применения теоремы Лиувилля, и полученное выше
следствие является специальным случаем теоремы Лиувилля для преобразованной
системы.
§ 22.18. Последний множитель. Рассмотрим приложение теоремы Якоби
о последнем множителе (§ 21.9) к автономным гамильтоновым системам.
Для системы Гамильтона единица является множителем, причем простей-
простейшим. Рассмотрим сначала вопрос об определении траекторий. Теорема Яко-
•би утверждает, что если известны т — 2 интегралов системы
^а>^.= ,..в^!' B2.18.1)
§ 22.18] ПОСЛЕДНИЙ МНОЖИТЕЛЬ 453
и если с помощью этих интегралов задача сведена к интегрированию одного
уравнения
X'ndxm-i-X'n-idxm = 0, B2.18.2)
то интегрирующий множитель определяется из правила Якоби.
Применим этот результат к исследованию автономной гамильтоновой
системы с двумя степенями свободы. Рассмотрим систему уравнений
dqt __ dq2 _ dpi _ dp2 /99<1ЙЧ\
он "~ дн
dpi др2 dqx dq2
где
Н = H{qu q2, Pu Pz)-
Если известны три интеграла уравнений B2.18.3), то можно определить
траектории изображающей точки в фазовом пространстве. Один такой инте-
,грал нам известен: это — интеграл Якоби Н = h. Допустим, что мы знаем
еще один пространственный интеграл F = а, где
F = F (qu qz, p±, p2).
Правило Якоби дает тогда возможность найти третий интеграл. Мы увидим,
что это можно проделать весьма изящным образом.
Рассмотрим в области D фазового пространства два известных интеграла:
m,4»i>i,i>j I B2.18.4)
причем предполагается, что H^Ct, F^Ct и что якобиан
J=dJH'F\ B2.18.5)
д (Pi, Рг) v '
не обращается в области D в нуль. Правило Якоби дает третий интеграл:
B2Л8-6)
где коэффициенты в подынтегральной функции выражены через qt, q2, h, a.
Предположим, что уравнения B2.18.4) разрешены относительно ри р2-
¦Pi = U (Яи Яг, h, а), р2 = /2 (qu q2, h, a). B2.18.7)
Подставляя эти выражения в уравнения B2.18.4) и дифференцируя до а
полученные тождества, находим
Отсюда
дН дН —J '
дрг dpi
и третий интеграл B2.18.6) принимает вид
dfj , OF df2 _ л
да дрг да '
dfi df2
да да I B2.18.9)
ir-dqi-\-~ dq2 = const. B2.18.10)
da ^ll да чг \ • /
454 УРАВНЕНИЯ ГАМИЛЬТОНА [Гл. XXII
Следовательно, форма Пфаффа
/i <ki + h dq2 B2.18.11)
от qi q2 является полным дифференциалом, что нетрудно доказать непосред-
непосредственно, не прибегая к теореме Якоби. В самом деле, заменим pi, рг в равен-
равенствах B2.18.4) их выражениями через функции /1; /2 и продифференцируем
полученные тождества по qi. Проделав это, получим
дН _^_ ,_
да. ~^~ гЬо да, *"U) !
B2.18.12)
= 0. '
B2.18.13)
B2.18.14)
0. B2.18.15)
При выводе этого равенства мы использовали тот факт, что скобка Пуассона
(Н, F) обращается в нуль, так как F есть интеграл уравнений.
Таким образом, форма fidqi + f2dqz есть точный дифференциал dK
функции К,
К = K(quqz,h,a), B2.18.16)
так что третий интеграл можно записать в виде
dK
Исключая из
Аналогичным
Следовательно
dqi dpi dq^
dF dF dfi
dqi ' dpi dqi
этих уравнений dfjdqv
dh
dq{
образом находим
dfi _
dqz
dh dfi
1 dpz dqi
, dF df2
' dpz dqi
получаем
d (#, F)
d(qu Pi)
j
д (H, F]
d (?2. Рг)
_j
_ (Я- F) -
da
const. B2.18.17)
Определение траекторий, таким образом, закончено. Однако в рассмат-
рассматриваемой задаче можно пойти дальше и построить еще один, четвертый
интеграл, который, разумеется, будет зависеть от t. Рассуждая подобно тому,
как мы это делали при выводе соотношения B2.18.9), находим
dpz дрх
Приравнивая выражения B2.18.3) дифференциалу времени dt, получаем
Ql dPi ?2
др2 Ql dPi _ dfi ,
dkaqi+ dh
dpi dp2
и находим четвертый интеграл системы Гамильтона
4г = ^+ const. B2.18.20)
§ 22.18] ПОСЛЕДНИЙ МНОЖИТЕЛЬ 455
Итак, разрешая уравнения B2.18.4) относительно pt, p2, мы можем
составить линейную форму pi dqi + p2 dq2, которая будет точным дифферен-
дифференциалом dK\ тогда остальные интегралы будут иметь вид
дК Л
дК \ B2.18.21)
да v J
Полученное решение весьма примечательно. Оно имеет в точности такую
же форму, какая получается при решении задачи с помощью теоремы Гамиль-
Гамильтона — Якоби. Связь между двумя этими способами решения обусловлена
тем, что К (#i, q2, h, а) есть полный интеграл модифицированного уравнения
в частных производных A6.5.6).
Во многих конкретных приложениях вторым интегралом является инте-
интеграл количества движения, соответствующий циклической координате q2.
В этом случае исходными известными интегралами являются
Н (?1, Pi, p2) =h, p2 = а, B2.18.22)
и
dK = г|з dqt + a dq2. B2.18.23)
Функция я|) = -ф (qi, h, а) находится из решения уравнения
H(qupu a) =h B2.18.24)
относительно pt:
Pi=y(qi,h,a). B2.18.25)
Два остальных интеграла определяются с помощью только что доказан-
доказанной теоремы; они имеют вид
*-*„. j|?-d?i + ?a=-P. B2.18.26)
Пример 22.18А. Центральная орбита; применение поляр-
полярных координат. Для этой задачи
l+-^pl)+V, B2.18.27)
где V = V{r). Имеем интегралы энергии и момента количества движения:
Н = h, pg = а; функция я|) имеет вид
я|з(г, h, a) = y2h-2V-^=:VW)- B2.18.28)
С помощью интегралов B2.18.26) находим известные формулы
' B2Л8-29)
Г1 Г1
полученные нами ранее в примере 5.2В.
Пример 22.18В. Центральная орбита; примене-
применение декартовых координат. Получим теперь решение этой
задачи в декартовых координатах, воспользовавшись правилом Якоби.
Имеем
H = ~(u* + v2) + V. B2.18.30)
Здесь и, v введены вместо рх, pv. Известными интегралами будут
±.(uz+v*) + V = h, B2.18.31)
xv — уи = а. B2.18.32)
456 УРАВНЕНИЯ ГАМИЛЬТОНА [Гл. ХХП
Согласно доказанной выше теореме, если разрешить эти уравнения отно-
относительно и я v я подставить их в выражение и dx + v dy, то мы получим точ-
точный дифференциал dK; остальные интегралы тогда будут иметь вид B2.18.21).
Рассмотрим выражение хи + yv, которое обозначим через у. Тогда будем
иметь
U = JE=«L, v=yKp?L B2.18.33)
Формулы для и и v получаются, если у выразить через х, у, h, а. Имеем
{хи + yvf + (xv — yuf = г2 (u2 -f г;2). B2.18.34)
Используя B2.18.31), получаем
Y2 = r2Bfe-2F—J)=r2/(r). B2.18.35)
Теперь находим
dK = —~!-dx-\—^—dy, B2.18.36)
где через Г обозначено г]/5/(г). Окончательно получаем
Q, B2.18.37)
что совпадает с полученным ранее решением.
Пример 22.18С. Сферический маятник. Пользуясь сфе-
сферическими координатами (см. § 5.3) и опуская постоянное слагаемое mga
в выражении для L, получаем
^) B2.18.38)
где n2 = g/a. Известными интегралами будут
Н = h, рф = а. B2.18.39)
Пользуясь обозначением B2.18.25), запишем функцию а|) в виде
г|з(Э, h, a) = y/"A(fe — cosB) — j^q-==V7WJ- B2.18.40)
Функция К будет иметь вид
К=[У7Щйв + а(р. B2.18.41)
Интегралы B2.18.26) примут форму
Ф J Т/ТТв) ' J
Полученные результаты совпадают с формулами § 5.3. (Чтобы в этом убе-
убедиться, достаточно вместо а2 написать 2ос/?г2.)
Глава XXIII
ДВИЖЕНИЕ В ОКРЕСТНОСТИ ЗАДАННОГО ДВИЖЕНИЯ.
УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
§ 23.1. Уравнения в вариациях. Уравнения движения механической
системы (например, уравнения Гамильтона) имеют форму A9.1.1): х = Х-
В этой главе мы начнем с рассмотрения автономных систем, для которых
X = X (ж). Записывая уравнения для составляющих, получаем систему
в форме B1.1.3):
х'т = Хт (хи х2, . . ., хт), г = 1, 2, . . ., т. B3.1.1)
Функции Хг принадлежат к классу 6\ в некоторой области D простран-
пространства х. Уравнения B3.1.1) определяют движение изображающей точки в т-
мерном пространстве (xi, x-l, ¦ ¦ ., хт). Если эта точка начинает свое дви-
движение из точки а области D в момент t = 0, то ее положение в момент t,
а < t < Ъ, будет определяться уравнениями вида ас = <р (t; а) или, в обо-
обозначениях B1.1.4),
хг = qv (t; аи а2, . . ., ат), г = 1,2, . . ., т. B3.1.2)
Функции фт- имеют непрерывные первые производные dq>r/dt, dq>r/das в обла-
области Е, определяемой условием
a?D, a<t<b.
Вторые производные d2tpT/dt2, d2q>r/dt das = d2cpr/das dt также будем считать
непрерывными в указанной области (§ 19.1). Решение задачи состоит в опре-
определении функций фг. Эти функции удается найти лишь в немногих простых
случаях. В общем случае решение в этом смысле получить не удается, хотя
во многих астрономических приложениях можно получить приближенные
решения с высокой степенью точности.
Поскольку во многих задачах не представляется возможным получить
явные выражения для функций фг, важно указать те классы задач, решение
которых облегчается, если использовать некоторые упрощающие обстоятель-
обстоятельства. Важной проблемой является задача построения характеристик, распо-
расположенных в окрестности заданной характеристики. При этом нам известны
величины ас для всех положительных значений t при определенном заданном
значении начальной точки а, но нам неизвестны функции фг для какого-либо
интервала значений а. Задача заключается в том, чтобы определить, точно-
или приближенно, характеристику, начинающуюся в точке а + б, близкой
к точке а.
Обозначим известное решение, которое часто называют невозмущенным,.
через ас; таким образом, при t = 0 хТ — ат и хт = Хт {xi, xz, . . ., xm).
Близкую, или возмущенную, характеристику обозначил! через х + у, тогда
в момент t = 0 будем иметь уг = 8Г, и
хг + Ут = Xr{xi + уи хг + г/2, . . ., хт + ут), г = 1, 2, . . ., т.
B3.1.3>
-458 устойчивость движения [гл. ххщ
Таким образом, смещение // относительно невозмущенной характеристи-
характеристики удовлетворяет уравнениям
Ут = Уг (уи г/г, • • -, ут\ О, г = 1, 2, . . ., т, B3.1.4)
где
Уг (г/i, г/2, ¦ ¦ м Ут, t) = Xr (xt + уи хг + уг, . . ., хт + ут) —
-Хг(хих2, . . ., хп). B3.1.5)
Символы Xi, х2, ¦ ¦ ., хт в правой части B3.1.5) обозначают известные функ-
функции от t, а именно значения координат невозмущенного движения в момент t.
Система B3.1.4), в отличие от B3.1.1), конечно, не является автономной.
Обозначим через | у | величину ]/"| уг |а + | у2 |2+ . . . +| ут \г и соот-
соответственно через | б | — выражение \r\ 6j |2 + | б2|2+. . -+|бт |а *). Пред-
Предположим, что величина | 6 | мала. Как известно, решение дифференциаль-
дифференциальных уравнений B3.1.1) изменяется в зависимости от начальных данных
непрерывным образом; поэтому величина | у | будет мала вместе с | б |, по
крайней мере для достаточно малой области значений t. В некоторых част-
частных случаях величина | у | остается малой для всех положительных значе-
значений t.
Ниже (в § 23.7) мы вернемся к уравнениям B3.1.4), сейчас же нашей
непосредственной целью будет изучение не точных уравнений, а уравнений
линейного приближения. Если разложить правые части уравнений B3.1.5)
в ряды по степеням уТ и ограничиться линейными членами, то мы получим
следующие уравнения линейного приближения:
m
i=]>>rS?s, r=l,2, ...,m. B3.1.6)
8=1
Мы обозначили здесь зависимую переменную через %т, а обозначение уг
сохранили для составляющих вектора у, удовлетворяющего точным уравне-
уравнениям B3.1.4). Таким образом, вектор | удовлетворяет линейной системе
{23.1.6). Коэффициенты ars являются известными функциями от t: они равны
частным производным dXT/dxs, вычисленным в точке (xi, х2, . . ., хт), зани-
занимаемой изображающей точкой в момент t на невозмущенной характеристике.
Уравнения B3.1.6) называют уравнениями в вариациях, иногда — урав-
уравнениями в вариациях Якоби или Пуанкаре. Они связаны с точными уравне-
уравнениями B3.1.4) точно так же, как уравнения линейного приближения связаны
с точными уравнениями в задаче о движении в окрестности особой точки
(§ 21.11). Уравнения в вариациях можно записать в матричной форме:
1 = А1, ' B3.1.7)
где | есть матрица-столбец {Нь |г, . . ., ?„,}, а А — матрица размером
т X т, элементы которой aTS суть известные функции от t.
В следующем параграфе мы найдем решение | уравнений B3.1.7), при-
принимающее значение б при t = 0. Если это решение таково, что величина | | |
остается малой вместе с | б | в течение всего времени, то соответствующее
невозмущенное движение называют устойчивым по первому приближению
или устойчивым в бесконечно малом.
Имеются два важных частных случая, в которых элементы ars матрицы
А постоянны. Первый из этих случаев относится к движению в окрестности
особой точки; он, в частности, включает в себя классическую теорию малых
колебаний около положения устойчивого равновесия. Во втором из этих
случаев невозмущенное движение является установившимся (§ 9.6). При этом
*) Отметим, что, как и в § 21.11, функция | yi | + | у2 I + • ¦ • + \ Ут \ имеет
А основном ту же область применения, что и | у |.
§ 23.2] РЕШЕНИЕ УРАВНЕНИЙ В ВАРИАЦИЯХ 459
движении явные (нециклические) координаты и количества движения сохра-
сохраняют постоянные значения, а циклические координаты (которые не остаются
постоянными) не входят в формулы, определяющие элементы матрицы ars.
Решение уравнений в вариациях B3.1.7) для случая, когда элементы матри-
матрицы Л постоянны, уже было найдено нами в § 21.10.
Если известно общее решение B3.1.2) уравнений движения, то решение уравнений
в вариациях B3.1.7) при заданном начальном значении 6 находится, очевидно, без осо-
особого труда. Эти уравнения удовлетворяются функциями
5r = -|g-, г = 1,2, ...,,п, B3.1.8)
где индекс s может иметь любое из значений 1,2. . . ., т. Это утверждение становится
очевидным, если в уравнения B3.1.1) вместо х,. подставить шг и продифференцировать
частным образом по ag, учитывая при этом, что d2(pr/dt das=d2(pr/das dt. Геометрический
смысл этого очевиден. Обозначим матрицу (d<pr/das) через &, каждый столбец ее удовлет-
удовлетворяет уравнению B3.1.7), следовательно,
S=AS. B3.1.9)
(Как обычно, S обозначает здесь матрицу, которая получается из S дифференцирова-
дифференцированием по времени каждого элемента.) Отсюда следует, что решением уравнений в вариа-
вариациях будет | = &6, и так как S=Im при i = 0, то полученное решение как раз и будет
решением, для которого при t=0 | = 6.
§ 23.2. Решение уравнений в вариациях. В этом параграфе мы получим
решение уравнений в вариациях B3.1.6), удовлетворяющее в момент t = 0
заданному начальному условию | = 6. Воспользуемся методом последова-
последовательных приближений.
Рассмотрим матрицу R (t), заданную рядом
Л («) = Do+ 2>i@ + -»2 (*)+•-., B3.2.1)
в котором первое слагаемое равно
D0 = Im, B3.2.2)
а последующие слагаемые определяются по правилу
Dm = АПп B3.2.3)
причем
Пг+1@) = 0 B3.2.4)
(матрица _Dr+i получается из матрицы Dr+i дифференцированием каждого
элемента).
Отсюда следует, что
jR@) = D0 = 2m . B3.2.5)
и
JR(t) = AB(t). B3.2.6)
J2(?N удовлетворяет системе B3.1.6) и в момент < = 0 имеет значение б,
так что искомым решением будет
l = JR(t)b. B3.2.7)
Как и следовало ожидать, | линейным образом зависит от 6. (Матрица
R(t) фактически есть матрица S (dq>r/das), встречавшаяся нам в § 23.1.)
Элементы матрицы Jt представляются в форме бесконечных рядов, в
связи с чем возникает вопрос о сходимости. Рассмотрим интервал 0 ^ t ^ t\ и
определим число К таким образом, чтобы для всех т2 элементов ars матрицы А
460 УСТОЙЧИВОСТЬ ДВИЖЕНИЯ [Гл. XXIII
выполнялось неравенство
| ars (t)\<K B3.2.8)
во всем интервале 0 ^ t gel t±. Обозначая через d^l типичный элемент мат-
матрицы Dr(t), напишем следующие очевидные равенства:
t
dSl = auv, d$l = *\ auv (9) dQ. B3.2.9)
о
Отсюда получаем оценку
\d&\<Kt, B3.2.10)
справедливую в интервале 04^.t^.t1.
Аналогично
I d%l | = | 2 auw d$l | < тКЧ B3.2.11)
и
B3.2.12)
Продолжая рассуждения, находим, что в интервале O^t^ti
m\d«l\<{mKt)r/r\ * B3.2.13)
Отсюда следует, что ряды для элементов матрицы R мажорируются
экспоненциальными рядами с постоянными членами и, следовательно, рав-
равномерно сходятся в интервале 0 ^ t ^ t\.
Отметим некоторые свойства определителя Якоби
|||- = -|72f- B3.2.14)
д (б) д (a) v '
(Для краткости мы здесь через d(g)/dF) обозначили 3(|4, ?2,..., ^,т)/д(81, б2,..., бт).)
Как и в § 21.7, имеем
^B3.2.15)
откуда
J PF)ci6
/ = в° . B3.2.16)
(Эту формулу можно вывести непосредственно из B3.2.6), не ссылаясь на ре-
результаты § 21.7.) Функцию р (t) можно рассматривать как дивергенцию Л
векторного поля J5T в момент t в невозмущенном движении. Если для системы
величина А тождественно равна нулю (как это имеет место, например, для
системы Гамильтона), то в течение всего времени / = 1 (см. § 22.6).
В частном случае, когда элементы ars матрицы Л постоянны, имеем
DT = {f/r\)Ar B3.2.17)
и
R = Im+tA + (t2/2\)A2+{t3/3\)As+...=е'л. B3.2.18)
Решение B3.2.7) в этом случае (т. е. когда элементы матрицы А
постоянны) принимает вид
1 = е'л6, B3.2.19)
уже знакомый нам из § 21.10.
§ 23.2] РЕШЕНИЕ УРАВНЕНИЙ В ВАРИАЦИЯХ 461
Рассмотрим два простых конкретных примера приложения решения B3.2.7),
в частности решения B3.2.19), уравнений в вариациях.
Пример 23.2А. Гармонический осциллятор. Выше уже отмеча-
отмечалось, что в задаче о малых колебаниях элементы матрицы А постоянны. В частном случае
системы с одной степенью свободы уравнения имеют вид
It = Ь, U = -«2li B3.2.20)
п матрица А имеет форму
А=\
¦Следовательно,
^= ("о* -Л»)' А3= ((-%~Т ) • Л4= ((~оИ2J (_%.) и т- д- <23-2-22>
Таким образом
п
к — п sin nt cos nt
Решение имеет вид
?i =S< cos ?г^-1—— sin nt,
re f B3.2.24)
|й ——n&i Sin nt-\-&2 cos nt-
Решение становится еще более простым, если матрицу привести к диагональной
форме, введя новые переменные и^ ± s|2. Как уже отмечалось в § 21.10, степенные ряды
B3.2.23) были получены нами в § 21.4 другим методом.
Пример 23.2В. Ньютоновская орбита. Имеем
Уравнения движения имеют вид
} B3.2.26)
р-р ^= ——[— Pq j Z-*fl =~~ *-*• I
Величины г, 8, рг, р$ играют здесь роль переменных xi% x2, х3, хк\ матрица А имеет форму
0 0 10
г»
где Р — постоянное значение рд в невозмущенном движении, а г — значение в момент t
в невозмущенном движении. Если невозмущенная орбита представляет собой эллипс
с периодом 0, то элементы матрицы А являются известными периодическими функциями
от t с периодом а.
Рассмотрим, в частности, случай, когда невозмущенная орбита представляет собой
окружность радиуса а; пусть она описывается телом, совершающим вращение с угловой
скоростью со = Т/^/я3- Движение в этом случае является установившимся, и элементы
матрицы А сохраняют постоянные значения:
0 0 10
А = \ п й \. B3.2.28)
_Ш2 00 —
а
0 0 0 0
462 УСТОЙЧИВОСТЬ ДВИЖЕНИЯ [Гл. XXIII
Уравнения в вариациях имеют вид
Решением этих уравнений будет
s 9
ti = 61 coscot-j- —-sinoM-J 64 A —coscoi),
со асо
g2= 61 sin cot-U62 -A —cos cot) ~C(ot — 4 sin cot),
a aco a-co j- (Zo.Z.Sv)
2
?3= —соб( sin (ot-\- 63 cos сог-j S4 sin сог,
Заметим, что величины | ?1 I, 1 ?3 I. I ?4 I остаются малыми вместе с | б | в течение
всего времени, а I |г I -»¦ °°> когда t —>- 00 (исключая случай, когда 64 = 0). В важном
частном случае, когда (di, 62, 63, 64) = @, 0, и, 0), решение имеет вид
и . 2и
со дсо **
§ 23.3. Случай постоянных коэффициентов. Рассмотрим уравнения
\ = Л%, B3.3.1)
и пусть элементы матрицы А будут постоянны. Как мы видели, решение
в этом случае имеет вид
1 = е'-46. B3.3.2)
Этот результат легко получается, если матрица А имеет диагональную форму. Тог-
Тогда уравнения имеют вид
ir = Kir, r = 1, 2 т, B3.3.3)
где Яг = аТг. Система распадается на m независимых уравнений. Решением будет
\г = еагдг, B3.3.4)
что совпадает с B3.3.2); поскольку матрица etA является диагональной:
etkl 0 ... 0
0 eAl •¦¦ ° ' B3.3.5)
О 0 ... еа"
Если в уравнениях B3.3.1) произвести преобразование | = Сц, где
матрица С неособенная, то получим
B3.3.6)
Матрицу С можно выбрать таким образом, чтобы матрица С~гАС имела
нормальную форму Жордана J. Тогда
\ = Jy\. B3.3.7)
Если все собственные значения матрицы А различны или если они не все
различны, но элементарные делители все простые, то матрица J является
диагональной и уравнения в вариациях могут быть представлены в форме
B3.3.3).
В общем случае имеем
А - CJC-1 B3.3.8)
и
B3.3.9)
23.3]
СЛУЧАЙ ПОСТОЯННЫХ КОЭФФИЦИЕНТОВ
463-
Далее,
fJT0 0 0 ...
О Ji 0 ...
B3.3.10)
О
0
где Jo — диагональная матрица, диагональные элементы которой Я1; к2,. . -
.. ., Xq не обязательно все различны, и
/ A9+s 1 0 ... О О
О V« 1 ¦ • • О О
к. B3.3.11)-
О
о
о о
о о
1
о я,
q+s/
Матрица JH имеет rs строк и столбцов, и
Далее имеем
' etjro 0 0 ...
О etJi О ...
е1" =
0 0 0
B3.3.12)-
B3.3.13),
Матрицу elJ° нетрудно вычислить. В самом деле, как мы видели, эта1
матрица имеет диагональную форму с диагональными элементами е(Я»,
еа2,..., eaq.
Вычислим матрицу etJa. Имеем
где
(О 1 0 0 ... О 0\
О 0 1 0 ... О О
О 0 0 0 ... О 1
0 0 0 ... О О;
B3.3.14).
B3.3.15>
есть Л1атрица, все элементы которой, кроме тех, что расположены непосред-
непосредственно справа от главной диагонали, равны нулю. Матрица K2S получается
из Ks путем сдвига всех единиц на один элемент вправо, матрица Kss — путем
сдвига всех единиц на два элемента вправо и т. д. Матрица Krss является
нулевой; такой же будет и матрица К^ при N > rs. Таким образом, степен-
степенной ряд для eiK* является конечным и
B3.3.16)
О
О
О
.
1
О
О
2! ' '
t . .
О . .
О . .
¦ (г,-2)!
1
О
(г.-1I
t
1
464 УСТОЙЧИВОСТЬ ДВИЖЕНИЯ [Гл. XXIII
Но
etjs = e\+JetKti B3.3.17)
и, таким образом, все матрицы в B3.3.13) вычислены. Окончательно матрица
etA находится из B3.3.9).
В качестве простого примера рассмотрим случай т = 4, причем будем считать,,что
матрица А имеет нормальную форму Жордана J:
B3.3.18)
\ 0 0 0 A3/
Тогда
/ ettl 0 0 0 \
B3.3.19)
еы = CetJC-i. B3.3.9)
Таким образом, если матрицу ^4 удается представить в диагональной
форме (т. е. если эта матрица имеет простые элементарные делители), то реше-
решение системы B3.3.1) имеет вид
т
Ь=У]ЛГэе^. B3.3.20)
В частности, если постоянные к все чисто мнимые, то решение содержит
лишь синусы и косинусы, аргумент которых пропорционален it. В этом случае
величина | | |, будучи малой в начальный момент, остается малой и в даль-
дальнейшем, так что исходное движение устойчиво по первому приближению.
В общем случае решение содержит члены вида tNeM. Если все посто-
постоянные X имеют отрицательные вещественные части, то | Ъ, | —>¦ 0 при t —>¦ оо,
и система асимптотически устойчива по первому приближению. (Это следует
из тог факта, что при положительных N ж к выражение tNe~M стремится
к нулю, когда t —*- оо.)
Если хотя бы одно X имеет положительную вещественную часть, то мы
имеем неустойчивость по первому приближению! отклонение, определяемое
линейным приближением, не остается малым. Если имеется кратное чисто
мнимое Я и соответствующий элементарный делитель не является простым, то
решение уравнений Якоби содержит члены вида tN cos Pit, tN sin Pit, что
опять-таки дает неустойчивость по первому приближению.
§ 23.4. Случай периодических коэффициентов. Вернемся к рассмотре-
рассмотрению общего случая уравнений в вариациях
1 = 41, B3.4.1)
где коэффициенты ars являются известными функциями от t.
Матрица F (t) размером гахм, столбцы которой представляют т линей-
линейно независимых решений | уравнений в вариациях, называется фундамен-
фундаментальной матрицей. Фундаментальная матрица F (f) удовлетворяет уравне-
нению
F{t) = A{t)F{t). B3.4.2)
S 23.4] СЛУЧАЙ ПЕРИОДИЧЕСКИХ КОЭФФИЦИЕНТОВ 465
Если F {t) — фундаментальная матрица, то любая другая фундаменталь-
фундаментальная матрица может быть представлена в виде F(t) С, где С — неособая мат-
матрица размером т X т с постоянными элементами crs. Это следует из того, что
любое решение линейной системы B3.4.1) может быть выражено в виде линей-
линейной комбинации (с постоянными коэффициентами) т независимых решений.
В частности, матрица _R (t) (см. § 23.2) является фундаментальной матрицей:
ее первый столбец, например, представляет решение, удовлетворяющее
начальным условиям {1, 0, 0, . . ., 0}. Итак, любая фундаментальная мат-
матрица имеет форму Л (t) С.
Рассмотрим теперь случай, когда исходная характеристика является
периодической орбитой с периодом а. (Разумеется, если а есть период, то 2а,
За, . . . также являются периодами. Обычно, хотя и не всегда, мы будем
понимать под а наименьший период.) Элементы ars матрицы^, при этом явля-
являются периодическими функциями от t с периодом а, так что для всех значе-
значений t имеем
A(t+o)=A(t). B3.4.3)
Если F (t)— фундаментальная матрица, то таковой будет и матрица F(t-\-a);
поэтому существует неособенная матрица М такая, что
F(t + e) = F(t)M. B3.4.4)
Матрица М называется матрицей монодромии фундаментальной матри-
матрицы F(t). Для фундаментальной матрицы S(t) матрица монодромии равна
К (а); это сразу следует из того факта, что S @) = Im.
Выясним, какова матрица монодромии Лг другой фундаментальной
матрицы G (t) = F(t) С. Имеем
G(t + a) = F(t + a)C = F(t) MC = О (t)С^МС. B3.4.5)
Следовательно, фундаментальной матрице О (t) соответствует матрица
монодромии
Х^С^МС. B3.4.6)
Если М есть матрица монодромии для фундаментальной матрицы, то
матрица Ж будет матрицей монодромии для другой фундаментальной матри-
матрицы тогда и только тогда, когда N имеет вид С~ХМС. Поэтому все матрицы
монодромии имеют одни и те же собственные значения и элементарные дели-
делители, и все они приводятся к одной и той же нормальной форме Жордана.
Собственные значения щ, ^ • • •» Цт называют множителями. Ни один
из множителей не обращается в нуль, поскольку
0. B3.4.7)
Для нахождения множителей можно воспользоваться матрицей монодромии
R(a).
Пусть М — матрица монодромии фундаментальной матрицы F (t); всегда
можно найти матрицу К (не обязательно вещественную) такую, что будет
выполняться равенство
М = еоА". B3.4.8)
Если собственные значения матрицы К равный, Х2, . . ., Хт, то собствен-
собственными значениями матрицы М будут еоЛ>, е0^»,. . ., ем"»,
\ Цг = е<ыт. B3.4.9)
Числа %i, %г, . . ., Хт Пуанкаре "называл характеристическими пока-
показателями заданной периодической орбиты.
Наиболее важное свойство системы B3.4.2), матрица которой A (t)
периодична с периодом а, заключается в том, что любая ее фундаментальная
30 Л. А. Парс
466 УСТОЙЧИВОСТЬ ДВИЖЕНИЯ [Гл. XXIII
матрица F (t) может быть представлена в форме Р (t) etK, где Р — неособен-
неособенная матрица, элементы которой являются непрерывными периодическими
функциями от i с периодом а, а Ж — постоянная матрица.
Таким образом, фундаментальная матрица F (t) представляется в виде
произведения периодической матрицы и фундаментальной матрицы для
системы уравнений в вариациях с постоянными коэффициентами.
Для доказательства замечаем, что
a) = F(t) M= F{t)e°K'. B3.4.10)
Положим
P(t) = F(t)e~tK. B3.4.11)
Тогда
ЦЩ) e~tK = P (t), B3.4.12)
откуда видно, что матрица Р (t) является периодической. Эта матрица неосо-
неособенная, поскольку матрицы F(t) и etK неособенные. Из B3.4.11) тогда полу-
получаем, что
K, B3.4.13)
что и требовалось доказать. Характеристические показатели Xi, X2, • • -, Хт
однозначно определяются для заданной периодической матрицы А, но ма-
матрица К не определяется матрицей F (t) единственным образом.
Чтобы получить решение в явном виде, следует привести матрицу К
к нормальной форме Жордана. Пусть i есть неособенная матрица такая, что
LXKL=J, B3.4.14)
где J—матрица в нормальной форме B3.3.10). Тогда
F(t) = P(t)etK = P(t)etLJL-1 = P(t)LetJIr1, B3.4.15)
и, следовательно, фундаментальная матрица F (t) L имеет форму
Q(t)e^, B3.4.16)
где Q {t) есть периодическая матрица Р (t) L. Множитель etJ уже был вычис-
вычислен нами в § 23.3.
Рассуждения упрощаются, если ограничиться рассмотрением случая, когда нор-
нормальная форма матрицы монодромии является диагональной. При этом для любой фунда-
фундаментальной матрицы F (t) будем иметь
щ 0 ... 0 \
^2'" ° I. B3.4.17)
0 0 ... Ihn/
Обозначим первый столбец матрицы F (t) через |lf тогда
St (t+o) =mSi @ = eMlii (*), B3.4.18)
и, следовательно,
е-Ы*+<т)|1(г+ст)=:е-^|1@. B3.4.19)
Таким образом, функция е~ ii (t) является периодической с периодом а, и мы можем
написать
Si@ = *a'1V(«). B3.4.20)
где
Ф1 (* + <*) = <Pi (О-
§ 23.5] НУЛЕВЫЕ ПОКАЗАТЕЛИ 467
Рассуждая подобно тому, как это мы делали в § 23.3, где рассматривался
случай постоянной матрицы^., можно из B3.4.16) установить тип решений
для различных случаев. Если все характеристические показатели Кг имеют
отрицательные вещественные части, то во всех случаях движение асимптоти-
асимптотически устойчиво по первому приближению. (Это следует из того, что если N
и к — положительные числа, то tNe~ht -> 0, когда ?-> оо.) Если все пока-
показатели % — числа чисто мнимые, а нормальная форма матрицы монодромии
диагональна, то движение по первому приближению устойчиво. Если жо при
чисто мнимых показателях к матрица монодромии не приводится к диагональ-
диагональной форме, то решение содержит члены вида ф (t) tN cos Pit, ф (t) tN sin $t
(где ф (t) — периодическая функция с периодом а), и соответствующее дви-
движение не является устойчивым по первому приближению. Наконец, если хотя
бы один показатель к имеет положительную вещественную часть, то движе-
движение также неустойчиво по первому приближению.
Обратимся к случаю, когда элементы матрицы Л постоянны. Мы опре-
определили характеристические показатели только для периодической матрицы Л.
Однако из § 23.3 следует, что если матрица А ^постоянна, то ее, собственные
значения играют в решении уравнений в вариациях такую же роль, что и ха-
характеристические показатели в случае, когда матрица А является периоди-
периодической. Поэтому термином «характеристический показатель» можно пользо-
пользоваться и в том случае, когда элементы матрицы А постоянны. В задачах, в ко-
которых А есть постоянная матрица, характеристические показатели являются
ее собственными значениями.
§ 23.5. Нулевые показатели. В задаче о движении в окрестности перио-
периодической орбиты один из характеристических показателей всегда равен нулю.
(В задаче о движении в окрестности положения равновесия это не имеет
места.) В самом деле, так как заданное периодическое движение удовлетво-
удовлетворяет уравнениям
хг = Хт, B3.5.1)
то имеем
«г =2 "ЙГ^= S *"*•' B3.5.2)
8= 1 8= 1
и уравнения в вариациях удовлетворяются функциями
Ь = х„ г = 1, 2, . . ., т. B3.5.3)
Таким образом, уравнения в вариациях имеют чисто периодическое решение
с периодом о, что возможно лишь при условии, если одно из К равно нулю.
Предположим, далее, что исходная периодическая орбита соответствует
значению а = 0 в однопараметрическом семействе периодических орбит
) 2, ..., т, B3.5.4)
где % — % {а), о = х @). Тогда
/Л9+ 1, а) =/г@, а). B3.5.5)
Решение уравнений в вариациях можно получить путем дифференциро-
дифференцирования уравнений B3.5.4) по а. Имеем
^) r = l,2, .... m, B3.5.6)
где fTi обозначает производную от /г по i-му аргументу. В этом случае реше-
решение, кроме периодических членов, содержит члены вида fop (it), где ф (t) —
30*
468 УСТОЙЧИВОСТЬ ДВИЖЕНИЯ [Гл. ХХШ
периодическая функция. Результаты § 23.4 показывают, что в этом случае два
характеристических показателя оказываются равными нулю. (Если т' @) =
= 0, аргументация теряет силу, но результат остается справедливым, так
как в этом случае имеются два независмых периодических решения уравне-
уравнений в вариациях: хт и дхт1да.)
Примером такого однопараметрического семейства периодических орбит может
служить семейство круговых орбит в центральном силовом поле с потенциалом V (г).
Для этого случая (см. пример 23.2В) имеем
и уравнения движения записываются в виде
г = р 9 = —
i . Г2 [ B3-5.8)
Матрица А имеет вид
О О 1 О \
~75~ ° ° 7
or , <23-5-9)
— V(r) О О Яг
О 0 0 0/
где через р обозначено постоянное значение ре, а через г — значение в момент t в перво-
первоначальном движении.
Если первоначальное движение представляет собой вращение по окружности радиу-
радиуса а с угловой скоростью со, то асо2 = V (а) и Р = а2со = ~\/asV (а). Элементы матри-
матрицы А при этом постоянны,
О 0 10
а а.%
I^I_F»(aH0^
а а
0 0 0 0
и характеристические показатели вычисляются как корни уравнения
= 0, B3.5.11)
Два корня этого уравнения равны нулю, а два Других при произвольном а равны
нулю в том и только в том случае, если
3 F(a)-|-F"(a) = 0 B3.5.12)
для всех значений а. При этом
V («) = -§-, B3.5.13)
т. е. притяжение обратно пропорционально кубу расстояния.
Рассмотрим более подробно случай притяжения по закону ц/гп, где п — целое
число. В этом случае
к'И=-?г, Г'<г)=-»75НГ' ю2 = ^' 1
B3.5.14)
() ()
и характеристические показатели находятся из уравнения
X2 {А,2 + C - п) со2} = 0. B3.5.15)
§ 23.6] УРАВНЕНИЯ В ВАРИАЦИЯХ ДЛЯ СИСТЕМЫ ГАМИЛЬТОНА 469
Для различных значений п имеем:
п = — 1 А, = @, 0, 2гсо, -2ш),
п = 2 А, = (О, О, гсо, — гсо),
п = 3 Я = @, 0, 0, 0),
п > 3 А, = (О, 0, а, —а).
В последнем случае а — число вещественное и положительное: а — со"]
ная форма Жордана матрицы А имеет вид:
пф— 1, пфЪ /010 0'
0
О
¦ 0 0 0 —р
где р чисто мнимое, если п < 3, и вещественное, если и > 3.
§ 23.6. Уравнения в вариациях для системы Гамильтона. Если исходные
уравнения движения имеют гамильтонову форму и допускают периодиче-
периодическое решение, то два характеристических показателя равны нулю. Кроме
того, если \i есть собственное значение матрицы монодромии, то 1/р. и \i также
являются собственными значениями. Таким образом, если характеристиче-
характеристический показатель Я не является ни вещественным, ни чисто мнимым, то другие
характеристические показатели равны —Я, Я и —Я. Если же характеристи-
характеристический показатель Я является вещественным или чисто мнимым, то другой
характеристический показатель равен —Я.
В частности, для системы с двумя степенями свободы характеристические
показатели равны @, 0, а, —а) или @, 0, ia, —га), где а — число вещест-
вещественное (см. § 23.5).
Перейдем к доказательству этих важных утверждений. Исходные урав-
уравнения, которым удовлетворяет заданное периодическое движение, имеют вид
qr = ~-, рг = —~ г=1,2, .... п. B3.6.1)
Здесь Н = Н (qi, q2, . . ., qn\ Pi, Рг, ¦ ¦ •, Pn) 6 Сг. Обозначим через qT +
+ Ir, Рг + ^г координаты и импульсы в возмущенном движении. Уравне-
Уравнения в вариациях запишутся в виде
r-Psr s УгвЦз, r=l, 2, ..., га > B3.6.2)
(знак суммы мы для краткости записи опускаем).
Величины ars = asr, p*rs, yrs = ysr равны
rJH rUH r&Tf
&rs == » Mrs == Yrs ^ ~~ у (^o.b.o)
где после дифференцирования подставляются значения q и р в первоначаль-
первоначальном движении.
470 УСТОЙЧИВОСТЬ ДВИЖЕНИЯ [Гл. ХХШ
Уравнения B3.6.2) имеют гамильтонову форму, роль переменных q и р
играют здесь | и ц. Функция Гамильтона имеет вид
1 1
<$? = у Vrslrls + $rslr4s + -у yrs4rT]s, B3.6.4)
где, как и выще, повторяющиеся индексы означают суммирование. Если
вектор с составляющими (?,i, ?2, • • •, in» Чи Чъ, • ¦ •, т|п) обозначить через
g и записать уравнения Гамильтона в форме B2.1.5), то будем иметь
B3.6.5)
где Z, как обычно, обозначает матрицу
-1.0 Г <23Ж6)
a S — симметрическую периодическую матрицу размером 2га X 2га.
Докажем теперь, что если g, x — два независимых решения уравнений
в вариациях B3.6.5), то функция
Ф = ?'?х B3.6.7)
сохраняет постоянное значение. В самом деле, производная от этого выражения
<p = g'Za*+ g'Zx = ^'S'Z'Z'x-'r ZfZZSv. B3.6.8)
равна нулю, поскольку матрица 8 симметрическая и Z' = — Z. (Развернутое
выражение для ф имеет вид
п
где ?ь g2, . . ., \п, щ, Tj2, • • ., f]n обозначают составляющие вектора . g,
a |j, |2, . . ., |^, r|j, т]2, . . ,, г\'п — составляющие вектора х.) Итак, функ-
функция ф остается постоянной; отсюда следует, что
g'Zx = 6'Ze, B3.6.10)
где 6 и е обозначают соответственно значения g и х при t = 0.
Возьмем, в частности, векторы g, x в момент времени t = o. Тогда
g = J?(aN = M6, к = В(а)е = Ме, B3.6.11)
где М, через которое мы обозначили It (a), представляет матрицу монодромии
фундаментальной матрицы R(t) (см. § 23.4). Из B3.6.10) имеем
b'M'ZMe = 6'Ze, B3.6.12)
и так как это справедливо для произвольных значений б, е, то матрица М
обладает следующим свойством:
M'ZM=Z. B3.6.13)
Такая матрица называется симплектической.
Напомним, что все матрицы монодромии имеют одни и те же собственные
значения. Если \i есть собственное значение симплектической матрицы М
(которая является матрицей монодромии фундаментальной матрицы It (t)),
то 1/ц также является собственным значением. В самом деле, если [i —
собственное значение матрицы Ш, то
|M'-uJ2n| = 0. • B3.6.14)
Отсюда
B3.6.15)
J 23.7] УСТОЙЧИВОСТЬ ТРАЕКТОРИЙ A) 471
и, следовательно, в силу B3.6.13)
\Z — (iZMj = 0. B3.6.16)
В результате получаем
М —~12п =0, B3.6.17)
откуда видно, что 1/ц. есть собственное значение матрицы М.
Вспоминая, что ц.г = еаЯг, легко приходим к теореме, сформулирован-
сформулированной в начале параграфа.
Как мы выяснили в § 23.5, один из характеристических показателей X
равен нулю. Теперь мы установили, что все ненулевые показатели встреча-
встречаются парами: Хт и —Хг. Но так как общее число всех показателей является
четным, то нулевых показателей должно быть два. Кроме того, поскольку
матрица М вещественная, ее собственным значением, вместе с ц, будет ком-
комплексно-сопряженное число (.1. В результате получаем, что если X есть харак-
характеристический показатель, который не является ни вещественным, ни чисто
мнимым, то X также будет характеристическим показателем. Теорема, таким
образом, доказана-.
§ 23.7. Устойчивость траекторий A). Впервые понятие устойчивости
было установлено для системы, выведенной из положения равновесия (§ 9.1).
В § 9.9 мы это понятие применили при исследовании равновесия гироскопи-
гироскопической, системы, а в § 9.6—при исследовании установившегося движения
гироскопической системы. Наконец, при изучении уравнений в вариациях
(§ 23.1) мы ввели понятие устойчивости движения по первому приближению.
Возникает вопрос: можно ли каким-либо разумным способом обобщить
понятие устойчивости на общий случай движения и что следует тогда иметь
в виду, говоря об устойчивости движения, а не об устойчивости равновесия?
Напомним, что мы рассматриваем кривые в фазовом пространстве 2ге
измерений, а не в re-мерном ^-пространстве. Во- многих случаях невозмущен-
невозмущенная исходная характеристика представляет собой периодическую орбиту.
Будем пользоваться обозначениями § 23.1. Рассматриваемые нами орбиты
представляют собой траектории уравнений B3.1.1):
хг = Хг (хи х2, . . ., хт), г = 1, 2, . . ., т, B3.7.1)
или, в сокращенном виде, уравнения
х = Х(х). B3.7.2)
Решение х, принимающее при t — 0 значение а, может быть представ-
представлено в виде B3.1.2):
хг = Фг (t; ai, az, . . ., ат), г = 1, 2, . . ., т, B3.7.3)
или, короче,
x = (f(t;a). B3.7.4)
Если немного изменить начальные условия и от точки а перейти к близ-
близкой точке а -\~ б и обозначить через х + у соответствующую точку на траек-
траектории в момент t (см. § 23.1), то можно будет написать
а + б) — ф(*; а). B3.7.5)
При непрерывном изменении начальных данных решение системы диф-
дифференциальных уравнений также изменяется непрерывным образом; поэтому,
если t не слишком велико, то \ у {t) \ мало вместе с | б |. Точнее, для всякого
положительного числа г можно указать положительные числа х = х (г)
472 устойчивость движения [гл. ххш
и t0 = t0 (е) такие, что если | б | < х, то для всех t в промежутке @, t0) выпол-
выполняется неравенство | у (t) | -< 8.
Можно было бы дать такое формальное определение устойчивости дви-
движения. Движение называется устойчивым, если конечный интервал @, tQ)
можно заменить бесконечным интервалом @, оо). Если мы примем такое
определение, то придем к следующей формулировке: траектория <р (t; a)
является устойчивой, если для любого е > О можно указать такое положи-
положительное х = х (г), что если | 6 | < и, то | <р (it; а + 8) — <р (t; a) | < е для
всех положительных it. Траекторию, удовлетворяющую этому условию, назы-
называют устойчивой по Ляпунову.
Если решение B3.7.4) известно не только , ~ какой-либо одной опреде-
определенной начальной точки ос, а для всех начальных .очек в некоторой окрест-
окрестности точки а, то легко проверить, выполняется ли критерий устойчивости
по Ляпунову. Однако в общем случае мы знаем решение B3.7.4) для какого-то
одного определенного а, а не для совокупности начальных точек (§ 23.1).
Возмущение у (t) определяется как решение уравнений B3.1.4),
уТ = YT (г/ь г/2, . . ., ут; t), г = 1, 2, . . ., т, B3.7.6)
принимающее при t = О значение 6. Правые части уравнений B3.7.6),
как и в B3.1.5), равны
Уг (Уи Уг, ¦ ¦ ., Ут; t) = ХТ (хг + уи хг + г/2, . . ., хт + ут) —
- ХТ (хи хг, . . ., хт), B3.7.7)
где хТ — известные функции от it, а именно значения координат в невозмущен-
невозмущенном движении в момент it. Основной вопрос заключается в следующем: извест-
известно, что | б | мало, означает ли это, что | у \ также мало при всех значениях
<> О?
Исследуя задачу о спящем волчке (§ 9.9), мы пришли к выводу об устой-
устойчивости положения равновесия; это заключение мы вывели из Существования
интеграла, имеющего вид определенно-положительной квадратичной формы
от перемепных \, у, z, |, у, z. (В том исследовании рассматривались урав-
уравнения Лагранжа, а не Гамильтона и шесть переменных |, г/, z, |, г/, z играли
роль переменных yt, у%, j/з» Z/4-> Уь-i Уб-) Подобным же образом, в теории малых
колебаний около положения равновесия, в котором потенциальная функция
имеет минимум, заключение об устойчивости вытекало из рассмотрения
интеграла энергии. Этот интеграл не является определенно-положительной
квадратичной формой (за исключением случая, когда коэффициенты в выра-
выражении для Т постоянны, а потенциал V представляет собой точно, а не при-
приближенно, определенно-положительную квадратичную форму), но обладает
некоторыми существенными свойствами такой формы. (Переменные qt, q2, ¦ ¦ ¦
¦ • -i Qn, ?ь Чг, ¦ ¦ ¦, Яп играют при этом роль уи у2, . . ., ут- Малость
| у | означает малость | q \, а также малость | q |.) В некоторых случаях
можно воспользоваться этим же методом и установить устойчивость по Ляпу-
Ляпунову невозмущенного движения, составляя интеграл уравнений B3.7.6),
который представляет собой либо определенно-положительную квадратич-
квадратичную форму от переменных уи у2, . . ., ут, либо функцию, обладающую
основными свойствами такой формы. Можно также распространить эту теорию
на случай, когда функции, кроме переменных г/4, г/2> • • •> 2/m> содержат еще
it, а также на случай, когда функции не являются интегралами уравнений
B3.7.6), но монотонно убывают по мере того, как происходит движение.
В дальнейшем мы будем иметь дело с функциями, которые по своим свой-
свойствам аналогичны определенно-положительным квадратичным формам.
Будем говорить, что функция / (г/i, у2, • • ., ym)i или, короче, / (у), является
23.7]
УСТОЙЧИВОСТЬ ТРАЕКТОРИЙ A)
47$
определенно-положительной функцией, если в окрестности точки у = 0 она
принадлежит к классу С\ и обладает следующими свойствами:
1) при г = 0 / (у) = 0; существует положительное число х такое, что
если 0 < г ^ х, то / (^/) > 0. Здесь и дальше г обозначает | у | =
[ 1 У
2) можно указать положительное число к такое, что если 0 < ci < с2 ^
^ &, то поверхность / (?/) = ct лежит строго внутри поверхности / (у) = с2;
обычно при достаточно малых значениях с поверхности / (у) = с являются
замкнутыми (т — 1)-мерными поверхностями *).
Некоторые свойства определенно-положительных функций вытекают
непосредственно из их определения. Обозначим через R = R (/) наименьшее
значение г для точек на поверхности / (у) = к; пусть 0 < R ^ х. Выберем
число а, удовлетворяющее неравенству
^ /?, и обозначим через та (/) и
соответственно точную нижнюю
и точную верхнюю грань функ-
/ (у) на сфере г — а. Тогда
0<а
Ma{f)
грань
ции
Рис. 101.
0 <. та (/) ^ Ма (/), и при заданной функ-
функции / величины та (/) и ЛТа (/) являются
монотонными функциями от а и стремятся
к нулю вместе с а. Если г sgl а, то / (у) ^
<.Ма (/), а если г > а, то / (?/) > та (/).
Далее, неравенство / (у) ^ mo (/) озна-
означает, что г ^ а, а неравенство / (у) ^
>ЛТО (/) — что г ^ а. Если $/ изменяется
таким образом, что / (у) -»¦ 0, то г—»-0.
(Общая картина кривых / ($/) = с для случая т = 2 представлена на рис. 101.
Сплошными линиями на рисунке показаны кривые с = та (/) и с = ЛГО (/).)
В качестве простого примера для т = 2 можно указать функцию / (j/) =
= аг/J + &у22, где 0 < а < f; при этом та (/) == аа2 и Ма (/) = ра2.
Распространим теперь понятие асимптотической устойчивости, введен-
введенное нами в § 19.5, на случай возмущенного движения. Невозмущенную тра-
траекторию х (t) будем называть асимптотически устойчивой, если существует
такое положительное число х, что для всех значений б, лежащих в области
| б | < х, г —>¦ 0 при t-+ оо, т. е. возмущенное движение при t—>- <х> стремит-
стремится к невозмущенному движению.
Расширим понятие определенно-положительной функции таким обра-
образом, чтобы оно охватывало функции, зависящие не только от у±, уг, . . .
. . ., ут, но еще и от it. Будем говорить, что функция g (yt, y2, ¦ ¦ ., ут; t),
или, короче, g (у; t), определенно-положительная, если g {у, 0) является
определенно-положительной функцией и если существует определенно-
положительная функция h {у) такая, что если г ^ R (h) и t ^ 0, то g (у; t) ^
> h (у).
Вернемся теперь к критерию устойчивости по Ляпунову. Он определяет-
определяется следующей теоремой и следствиями из нее.
Теорема Ляпунова. Если уравнения B3.7.6) возмущенного-
движения допускают определенно-положительный пространственный инте-
интеграл / (у), то невозмущенное движение х (i) устойчиво.
Рассмотрим интеграл / (у) — / (б). Выберем какое-нибудь е > 0 и поло-
положим с = mB(f). Пусть, далее, х есть положительное число, определяемое
равенством с = Мн (/). Тогда, если | б | ^ х, то / (у) = / (б) ^ Мк (/) =
= тг (/) и, следовательно, г ^ г. Теорема, таким образом, доказана.
*) Термин «определенно-положительная функция» иногда применяют к функциям,
удовлетворяющим менее жестким условиям, а именно вместо условия 2) накладывают
более слабое требование, чтобы малость / (у) влекла за собой малость | у \.
474 устойчивость движения [гл. ххщ
Следствие 1. Если определенно-положительная функция / {у) не
является интегралом уравнений B3.7.6), но обладает тем свойством, что
функция
т
F(y;t)^-^YS-§L B3.7.8)
8=1
положительна при достаточно малых г для всех положительных t, то невоз-
невозмущенное движение х (t) устойчиво.
При изменении у вдоль траектории, определяемой уравнения-
уравнениями B3.7.6) и начинающейся в точке 6, имеем
¦Zrf(v)=-f(v;t)<0, B3.7.9)
•откуда следует, что / (у) < / F). Это неравенство справедливо при всех t
и заменяет равенство / (у) = / F). Если | 6 | < х, то
/Ы</(б)<тв(/) B3.7.10)
и г ^ е при t > 0.
Следствие 2. Если функции f (у) и F (у; t) являются определенно-
положительными, то невозмущенное движение х (f) асимптотически устой-
устойчиво. (В следствии 1 функция F (у; t) предполагалась лишь положительной
для достаточно малых г.)
Нужно доказать, что существует положительное число х такое, что
для любых | б | в области | б | < х г-> 0 при ?—>- оо. Как мы знаем (см.
•следствие 1), существует такое х, что если | б | ^ х, то / (у) непрерывно убы-
убывает, когда у перемещается вдоль траектории, определяемой уравнения-
уравнениями B3.7.6), и, следовательно, стремится к пределу L = L (б), где L ^ 0.
Предположим, что при некотором частном выборе 6 L > 0. Тогда для всех
положительных t j{y) ^ L, и, следовательно, г ^ а, где а — положительное
число, определяемое уравнением Ма (/) = L. Пусть h (у) есть определенно-
положительная функция, соответствующая F (у; t). Тогда из неравенства
г ^ а будем иметь F (у; t) ^ h (у) ^ X, где К = та (К) > 0. Таким образом,
при перемещении у вдоль траектории, определяемой уравнениями B3.7.6),
имеем
^Xt. B3.7.11).
Но это невозможно, поскольку правая часть при достаточно больших значе-
значениях t отрицательна. Отсюда следует, что L = 0,T.e./(j/)->0 при it —>- оо,
и, следовательно, г—>~0. Невозмущенное движение x(i), таким образом,
асимптотически устойчиво.
Распространим теперь теорию на случай функций, зависящих не только
от уи г/2, . . ., ут, но и от t.
Следствие 3. Если определенно-положительная функция g (у; t)
является интегралом уравнений B3.7.6), то невозмущенное движение х (t)
устойчиво.
Рассмотрим интеграл g (у; f) = g (б; 0). Существует определенно-поло-
определенно-положительная функция h (у) такая, что
h(vL?g(y,t) = gF;0). B3.7.12)
Функция g {у; 0) определенно-положительная, следовательно, можно
указать такое положительное число х, что если | б | ^ х, то g (б; 0) ^ тв (h).
Тогда в течение всего движения
h (у) < те (h), B3.7.13)
•откуда следует, что г ^ 8.
§ 23.7] УСТОЙЧИВОСТЬ ТРАЕКТОРИЙ A) 475
Следствие 4. Если определенно-положительная функция g (у; t)
такова, что
т
положительно при всех достаточно малых г для всех положительных t, то
невозмущенное движение х (t) устойчиво.
В этом случае функция g (у; t) постоянно убывает, когда у перемещается
вдоль траектории B3.7.6), и мы приходим к тому же результату, что
и в следствии 1.
Наконец, произведем простое обобщение следствия 2, приводящее к кри-
критерию асимптотической устойчивости. Этот критерий требует наложения
дополнительного ограничения на определенно-положительную функцию
g (у; t). Любая определенно-положительная функция / {у) обладает тем
свойством, что, как бы мало ни было е > 0, существует такое положительное
х = х (е), что если г < х, то / (у) < 8. Правда, в общем случае это утвержде-
утверждение неверно *), однако мы будем рассматривать только такие функции
g {у; t), которые обладают указанным свойством для всех t, т. е. функции,
для которых неравенство г < х влечет за собой g (у; t) <.e для всех t. Если
определенно-положительная функция обладает этим свойством, то говорят,
что она имеет бесконечно малую верхнюю грань.
Следствие 5. Если определенно-положительная функция g {у; t)
имеет бесконечно малую верхнюю грань и если функция G {у; t) определенно-
положительная, то невозмущенное движение х (t) асимптотически устойчиво.
Обозначим через h (у) определенно-положительную функцию, соответ-
соответствующую g (у; t) (см. следствие 3), а через Н (у) — определенно-положи-
определенно-положительную функцию, соответствующую G {у; t). Как и в следствии 3, выберем
число х таким, чтобы при | б | ^ х g (б; 0) ^ тг (h) и, стало быть, г ^ е.
Если | б | ^ х, то при перемещении у вдоль траектории, начинающейся
в б, g {у; t) монотонно убывает и стремится к пределу L, где L ^ 0. Пред-
Предположим, что L > 0 для некоторого б. Тогда g {у; t) ^ L, и потому (в силу
того, что g (у; t) имеет бесконечно малую верхнюю грань) существует поло-
положительное число т] такое, что г ^ г\. Отсюда следует, что в течение всего
движения
г)<г<8. B3.7.15)
Обозначим через % точную нижнюю грань определенно-положительной
функции Н (у) в замкнутой области, определяемой условием B3.7.15).
Тогда можем написать
G (у; t) > Н (у) > I > 0 . B3.7.16)
и
g (У, t)= gF; 0) - JGdt<g (б; 0) - It. B3.7.17)
Однако последнее неравенство невозможно, поскольку его правая часть
при достаточно больших значениях t отрицательна. Отсюда следует, что вели-
величина L может быть только нулем, и так как g {у; t) имеет бесконечно малую
верхнюю грань, то г —>- 0.
Приведем несколько примеров систем, устойчивых по Ляпунову. В первом и во вто-
втором примерах мы найдем общее решение уравнений движения, а в третьем примере вос-
воспользуемся теоремой Ляпунова.
Пример 23.7А. Гармонический осциллятор. При надлежащем
выборе масштаба времени выражения для кинетической и потенциальной энергий, а так-
Простым примером тому может служить функция g (у; t) = г2 + sin2 (rt).
476 УСТОЙЧИВОСТЬ ДВИЖЕНИЯ [Гл. ХХШ
же для функции Гамильтона будут иметь следующий вид:
^ = у<72, v=Yq2' я = 4(?2+р2)' B3.7.18)
Уравнения движения запишутся в виде
Я = Р, Р = ~Я- B3.7.19)
Решением этих уравнений будет
q = a cos t -\- p sin t, p = —a sin f + P cos t, B3.7.20)
где через а, р обозначены начальные значения переменных q, p. Для траектории, начинаю-
начинающейся в соседней точка (ос', Р'), будем иметь
?'-? = (a'-a)cost+(P'-P)sint, 1 ,,,,,,,
р' —р=—(a'—a)sin«+(P' —P)cos« J ^o./.^i)
Г2 = (?/ _ ?J + (p> _ pJ = (a, _ aJ + (p- _ pJ. B3.7.22)
Последняя формула показывает, что расстояние между изображающими точками
в невозмущенном движении и в возмущенном движении остается неизменным во времени;
этот результат геометрически очевиден, поскольку изображающие точки движутся по кон-
концентрическим окружностям с одинаковой угловой скоростью. Движение устойчиво в смыс-
смысле Ляпунова, и мы можем положить х = е.
В более общем случае, когда
т=\ (?!+91+ • ¦ • +к) =4-
У = у К<?2 + »»|?1+... f
B3.7.23).
уравнения движения принимают форму
qr = рт, р'г = -то??г, г = 1, 2, . . ., п. B3.7.24)
При этом написанные уравнения мы рассматриваем как точные, а не как приближенные,
как это мы делали в теории малых колебаний. Решение имеет вид
qr = ar cos mrt-\--^-sin mTt, pr=—mrar sinmrt-\-fiT cosmrt, B3.7.25)
mr
где начальная точка определяется координатами (a]? a2, • . ., an, р4, Рг. • • •, Рп)- Для
траектории, начинающейся в близкой точке (а[, а.'г, . . ., а,'п, §[, Pj. . . ., $'п), будем иметь
о/ о
g'r-gr = (<x'r-*r)coSmrt+^=-±sinmrt, | ^ щ
р'г — Рт— —Mr (<%'т — ar) s'n mr* + (Pr — Pr) cosmrt. )
Следовательно,
" ^ ~ ~ ч ч B3.7.27)
B3.7.28)
}
где К/~[/2 есть наибольшее из чисел mr и l/mr. Критерий устойчивости по Ляпунову
выполняется, и мы можем положить х = г/К.
Пример 23.7В. Рассмотрим движение, определяемое уравнениями
где г = ~[/х2 -\- у2 и а > 0. В полярных координатах имеем
V = a - г, 6=1. B3.7.30)
S 23.7] УСТОЙЧИВОСТЬ ТРАЕКТОРИЙ A) 477
Траектории этого движения устойчивы по Ляпунову. Рассмотрим, например, перио-
периодическую орбиту г = а, 6 = t, проходящую через начальную точку (а, 0). Через близкую
к ней точку (а -f- Si, б2) будет проходить орбита
r = a + 6ie-<, О = б2-г-г. B3.7.31)
В возмущенном движении при t -*¦ оо г -»- я, так что расстояние между изображаю-
изображающими точками на спиральной орбите и на круговой орбите непрерывно убывает и стре-
стремится к пределу 2я sin -=- | б2 |. Периодическая орбита устойчива по Ляпунову, и мы мо-
Z
жем положить х = е.
Пример 23.7С. Рассмотрим задачу, в которой уравнения B3.7.6) возмущенного
движения имеют вид
У1'~ wi v 1,1 \- -si -»¦«' | /по п оо\
где 0 <; а < Р и 0 < а < 6. Возьмем определенно-положительную функцию
' f=ay$+ М- B3.7.33)
Тогда соответствующая функция F будет иметь вид
F = 2 (ау\ + Рг/D A - ау\ - Ъу\). , B3.7.34)
Если г2 < 1/6, то F > 0; внутри круга г2 = 1/B6) функция F определенно-положитель-
определенно-положительна. (Записывая F в полярных координатах, будем иметь
F = 2r2 (a cos2 9 + р sin26) {1 — г2 (а cos29 + 6 sin29)} B3.7.35)
и
-^— = 2 (а cos2 в + Р sina 9) {1 -2г2 (а coSa G + 6 sin2 9)}. B3.7.36)
Если
2<
nae) ' B3.7.37)
та dFId (гг) > 0. Неравенство B3.7.37) выполняется для всех 6, если г2 < 1/B6).) Невоз-
Невозмущенное движение х (t) асимптотически устойчиво в смысле Ляпунова (см. следствие 2).
На первый взгляд может показаться, что понятие устойчивости по
Ляпунову является естественным обобщением устойчивости, рассматривав-
рассматривавшейся нами для положения равновесия (которое можно трактовать как
вырожденную характеристику). Но для классической динамики это понятие
оказывается не всегда пригодным, поскольку оно связано со слишком силь-
сильными требованиями, накладываемыми на систему. Правда, выше мы привели
несколько примеров, для которых имеет место устойчивость в указанном
•смысле, однако даже для весьма простых систем, для которых интуитивное
представление об устойчивости не вызывает сомнений, критерий устойчи-
устойчивости по Ляпунову не выполняется. Рассмотрим, например, частицу, дви-
движущуюся прямолинейно в силовом поле. Согласно определению устойчиво-
устойчивости по Ляпунову движение в однородном поле неустойчиво; это же относится
и к обычному либрационному движению (если не считать некоторых три-
тривиальных исключений, таких, как колебания гармонического осциллятора).
Если однородное поле имеет направление вдоль оси Ох, то невозмущенной
характеристикой, проходящей через начальную точку (а, и), будет
x = a+ut+±-ct2, у = иЛси B3.7.38)
•где у обозначает х, а с > 0 — постоянное ускорение поля. Если через х', у'
¦обозначить координаты точек возмущенной характеристики, проходящей
через близкую начальную точку (а + б4, и + б2), то будем иметь
+ б,/. / — у = бг. B3.7.39)
478 устойчивость движения [гл. ххш
и | ф {t; а + б) — ф (t; a) | будет стремиться к бесконечности вместе с t
всегда, за исключением случая б2 = 0.
В случае либрационного движения период возмущенного движения
(которое также является периодическим) в общем случае отличается от перио-
периода невозмущенного движения, так что | х (t; а + б) — х (t; a) | не может
все время оставаться малым, и, стало быть, и | ф {t; а + б) — ф {t; a) |
не будет малым. В других, менее простых случаях (например, в ограничен-
ограниченной задаче трех тел, см. гл. XXVIII) лишь очень немногие характеристики
оказываются устойчивыми по Ляпунову.
§ 23.8. Устойчивость траекторий B). Поскольку понятие устойчиво-
устойчивости по Ляпунову не является исчерпывающим для задач классической дина-
динамики, мы будем пользоваться другим определением устойчивости. Существует
много различных определений, одно из простейших состоит в следующем:
траектория С (в фазовом пространстве) устойчива, если траектория С",
начинающаяся в точке фазового пространства, достаточно близкой к началь-
начальной точке траектории С, такова, что всякая точка траектории С находится
вблизи от некоторой точки траектории С. Это условие является более сла-
слабым, нежели предыдущее, поскольку хотя здесь и требуется, чтобы точка
Ф (t; а + 6) на траектории С была близка к некоторой точке траектории С,
однако эти точки не обязательно должны проходиться в один и тот же момент
времени. Устойчивость такого типа принято называть орбитальной устой-
устойчивостью .
Критерий орбитальной устойчивости можно выразить в следующих
формах.
1) Характеристика ф (t; а) устойчива, если для заданного е > 0 суще-
существует положительное число х = и (е) такое, что если | б | < х, то всякому
положительному числу t можно поставить в соответствие такое положи-
положительное t' = t' (t; б), что
\y(t; а + 6)-ф(?'; а)|<е. B3.8.1)
2) Обозначим через d (у, С) расстояние точки у от положительной
полухарактеристики С (иными словами, d — точная нижняя грань расстоя-
расстояний точки у от точки у' на кривой С). Характеристика С, составленная их
точек ф {t; а) для t ^ 0, устойчива, если для всякого заданного е > 0 можно
указать такое положительное х, что d (ф (f, а + б), С) < е для всех положи-
положительных значений t, если | б | < х.
Рассмотренные выше движение в однородном поле и либрационное
движение являются устойчивыми в указанном смысле. Рассмотрим движение
в однородном поле; введем новую независимую переменную f (считая
t > | б2 \/с):
f = t + 62/c. B3.8.2>
Тогда будем иметь (см. уравнения B3.7.38))
x(t\ a+b)-x(f; aH^-^fu-fi-e,) , у (t; a + b)-y(t'; a) = 0,
B3.8.3)
и орбитальная устойчивость очевидна. Нетрудно провести формальное дока-
доказательство и для либрационного движения, но еще проще воспользоваться
непосредственными геометрическими соображениями. В исходном либра-
ционном движении траектория в плоскости ху (где у = х) является простой
замкнутой выпуклой кривой, симметричной относительно оси Ох (см. рис. 74)г
траектория же в возмущенном движении представляет замкнутую выпук-
выпуклую кривую, почти совпадающую с первой, так что ( орбитальная устойчи-
устойчивость очевидна.
§ 23.9] УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ ОРБИТ 479>
Другим примером может служить круговая орбита в поле ньютоновско-
ньютоновского притяжения. Легко видеть, что траектория (в фазовом пространстве)
неустойчива в смысле Ляпунова, но обладает орбитальной устойчивостью.
В качестве еще одного примера рассмотрим систему
х = —уг, У = хт, B3.8.4)
где г = "|/z2 -\- у2. Решением, соответствующим начальной точке (a cos p, a sin f5), будет
х = a cos (at + ft, у = а sin (at + Р), B3.8.5>
и движение будет представлять равномерное вращение по окружности с периодом 2п1а.
Равновесие в точке О будет устойчивым. Круговые траектории неустойчивы по Ляпунову,
но обладают свойством орбитальной устойчивости.
Понятие орбитальной устойчивости можно расширить и включить в него
аналог асимптотической устойчивости. Будем называть траекторию С асимп-
асимптотически устойчивой в орбитальном смысле, если при t—>• °° d (ц> (?; а+б),
С) -»¦ 0 всякий раз, когда | б | <С х. Например, в теории предельных циклов-
(гл. XX) мы установили, что в окрестности устойчивого предельного цикла
траектории имеют вид спиралей, приближающихся к предельному циклу;,
таким образом, устойчивый предельный цикл асимптотически устойчив
в орбитальном смысле. Конкретной иллюстрацией может служить при-
пример 23.7В, в котором система обладает как асимптотической устойчивостью-
в орбитальном смысле, так и устойчивостью (но не асимптотической) в смысле
Ляпунова *).
Существует еще много других определений устойчивости движения.
Можно, например, принять определение, аналогичное орбитальной устой-
устойчивости, но связанное не с фазовым пространством, а с траекторией в q-npo-
странстве. Согласно этому определению движение является устойчивым,
если траектория в ^-пространстве, соответствующая слегка измененным
начальным условиям, располагается вблизи от невозмущенной траектории.
Наглядный пример орбитальной устойчивости такого типа приведен в § 17.5,
п. 1; невозмущенное движение в этом примере представляет движение по
замкнутой кривой х = а, причем ф (а) < 0. Некоторые другие определения
устойчивости приводились нами в § 17.5 и в § 22.7.
§ 23.9. Устойчивость периодических орбит. Как мы видели в § 23.5,
в задаче о движении в окрестности периодической-орбиты один характери-
характеристический показатель равен нулю. Здесь мы докажем,, что если все остальные
характеристические показатели имеют отрицательные вещественные части,
то периодическая орбита асимптотически устойчива в орбитальном смысле.
Возьмем точку О на периодической орбите за начало координат и напра-
направим ось хт вдоль касательной к орбите в точке О. Тогда в этой точке и в окре-
окрестности ее будем иметь Хт > 0. Рассмотрим траекторию, начинающуюся
при t = 0 в точке Р вблизи от точки О. Эта траектория пересечет плоскость
хт = 0, переходя от значений хт <; 0 к значениям хт > 0, поскольку
в окрестности точки О Хт > 0. Обозначим координаты точки пересечения
через (aj, a2, . . ., am_i, 0), а время пересечения (положительное или отри-
отрицательное) — через 9. Введем (т — 1)-мерный вектор а = (аь а2, . - .
. . ., am_i); в рассматриваемой задаче |ос | и 9 будут малы. Предположим,
что в момент a + 0' характеристика снова пересекает плоскость хт = О
в точке а', переходя на этот раз от значений гт<0к значениям хт > 0;
здесь а обозначает период периодического движения, а величины | а \
*) Этот пример наводит на мысль, что и в общем случае асимптотическая устойчи-
устойчивость в орбитальном смысле влечет за собой устойчивость по Ляпунову. Эта точка зрения
находит подтверждение в том, что скорость возрастания сдвига времени | V ¦— t\ в пер-
первом приближении пропорциональна величине | <р (t; а -\- 6) — <р (t'; а) |, которая в свою
очередь убывает по экспоненциальному закону.
480
УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
[Гл. XXIJ
и I 9' I являются малыми. Характеристика много раз пересекает плоскость
хт = О, но пересечение в точке ос' (спустя время, равное почти а) точно
определяется из соображений непрерывности. На рис. 102 иллюстрируется
случай т = 2.
Точка а полностью определяется точкой а, а = С/а, причем опера-
оператор U в качестве неподвижной точки имеет точку ос = 0. Матрица А линей-
линейного приближения к U (имеющая т — 1 строк
и т — 1 столбцов) имеет вид
А = (da'r/dasH. B3.9.1)
Кроме того, разность 9' — 9 зависит только
от а:
0' = 9 + г|з (аь а2, . . ., ат_4) = 0 + ty (а).
B3.9.2)
Функция i|) обращается в нуль при
а = 0 и имеет непрерывные первые произ-
производные, и поэтому существует постоянная К
такая, что если | а | достаточно мало, то
Рис. 102.
Пусть теперь характеристика, начинающая в точке Р, определяется
т параметрами аь а2, . . ., am_i, 0. Если Т есть оператор преобразования
(а, 0) в (а', 0'), то матрица линейного приближения к этому оператору
имеет вид
'а1! да[ д
да j
о
0
да.'
да.1
да.2
дв'
1
B3.9.Я)
и характеристический полином этой матрицы равен (ц — 1) Р (\л), где Р (ц)—
характеристический полином (степени т — 1) матрицы А. Обозначим нули
полинома Р {\х) через уц, ц2, ¦ . ., fim_i. Тогда характеристические показа-
показатели периодической орбиты будут равны 0, Х1; Х2, . . ., Ят_4, где е^ = \лг
(§ 23.4), и так как вещественные части показателей Я,г отрицательны, то
| цТ | < 1 при г = 1, 2, . . ., m — 1. Следовательно, преобразование U
асимптотически устойчиво и | Una |-> 0 при п->оо.
Итак, периодическая орбита асимптотически устойчива в орбитальном
смысле. К этому выводу мы пришли из рассуждений, проводившихся для
дискретной системы точек на траектории возмущенного движения, но
результаты остаются в силе и в общем случае, поскольку для любого конеч-
конечного промежутка времени характеристика изменяется непрерывным обра-
образом в зависимости от начальных данных.
Обозначим через гест + 9<»> момент re-го пересечения плоскости хт = 0 характери-
характеристикой. Докажем, что величина 9<п> ограничена; разность | V — t \ (в определении орби-
орбитальной устойчивости) не возрастает неограниченно.
Для целых положительных значений г имеем
где 9<°» — в, и. следовательно.
B3.9.4)
B3.9.5)
2
г=0
§ 23.10] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ 481
Далее, имеем
|
I < К | Па | B3.9.6)
и
| Г^а | < скг, с > О, 0 < ft < 1, B3.9.7)
для всех г при условии, что | а | достаточно мало. Неравенство B3.9.7) вытекает из след-
следствия из теоремы Пуанкаре — Ляпунова (§ 21.15). В результате получаем
п— 1 оо
|e<n>|<|9| + tfc ^ kr<\Q\ + Kc ^ Ar=|9| + tfc/(l —ft), B3.9.8)
r=0 r=0
что и требовалось доказать.
§ 23.10. Вынужденные колебания*). Выше (в § 9.10) мы уже рассмат-
рассматривали вынужденные колебания осциллятора с затуханием. Уравнение
движения такой системы является линейным. Переход к исследованию
вынужденных колебаний нелинейных систем связан с весьма большими
трудностями, и обычно, чтобы достигнуть прогресса, приходится вводить
упрощающие предположения, которые часто бывает трудно оправдать.
Поясним это на примере движения математического маятника (пример 5.2А),
на который действует дополнительная малая горизонтальная сила таг sin pt,
где е — малый параметр. Уравнение движения маятника запишется в виде
maQ = —mg sin 6 + таг sin pt cos 6, B3.10.1)
или
ё + re2 sin 6 = e cos 9 sin pt, n2 = g/a. B3.10.2)
Напомним, что период свободных колебаний с малой амплитудой а
лишь немного превышает 2я/п; при увеличении амплитуды а от нуля до п
период о" непрерывно возрастает от 2к/п до оо. Точнее, сг = АК/п, где к =
. 1
= sin y a-
Рассмотрим по отдельности нерезонансный случай, когда разность
| ге2 — р2 | не является малой, и резонансный случай, когда параметр р
близок к п.
1) Рассмотрим сначала нерезонансный случай. Решение соответствую-
соответствующего однородного уравнения B3.10.2) определяет свободные колебания.
Однако они не представляют для нас интереса, поскольку в механической
системе практически всегда имеется трение, и потому свободные колебания
затухают. Частное решение, которое стремится к периодической функции
с периодом 2п/р, выражает вынужденное колебание. Вынужденное колебание
малой амплитуды всегда существует; если же р < п, то существуют два
вынужденных колебания конечной амплитуды.
Чтобы исследовать вынужденные колебания малой амплитуды, возьмем
линейное приближение к уравнению B3.10.2):
9 + к29 = е sin pt. B3.10.3)
*) Вынужденные колебания имеют важное значение в астрономии и в технике. Раз-
Различные рассмотренные здесь примеры можно найти у Е. W. Brown (Rice Institute Pam-
Pamphlets, 1932; Elements of the Theory of Resonance, Cambridge, 1932; Planetary Theory,
by E. W. Brown and C. A. Shook, Cambridge, 1933); см. также Н. Jeffreys (Quarter-
(Quarterly Journal of Mechanics and Applied Mathematics, XII, 1959, стр. 124) иЕ. A. Struble
(Quarterly Journal of Mechanics and Applied Mathematics, XV, 1962, стр. 245).
(Рассматриваемой в этом параграфе задаче о колебаниях системы с одной степенью
свободы, близкой к консервативной (х -f- / (х) = ei|) (x, x, t, г), ty (x, x, t, e) =
= ij) (х, х, t + Т, е)), посвящено подробное исследование А. М. К а ц а, Прикл. матем.
и мех., 19, стр. 13—32, 1955.— Прим. перев.)
31 Л. А. Парс
482 устойчивость движения. [гл. ххш
Решением этого уравнения будет
в = -^-Я-*™Р*- B3.10.4)
Оно дает приближенное выражение для вынужденного колебания конечной
амплитуды.
Далее, если р < п, то существуют свободные колебания конечной ампли-
амплитуды а, имеющие период 2л/р. (Возьмем, например, такое значение р, чтобы
амплитуда свободного колебания с, периодом 2п/р была равна 60°. Тогда
к = sin -i a = 1/2, К = 1,6858 и pin = я/2# = 3,1416/3,3716, что грубо
равняется 27/29.) Существование свободного колебания с периодом 2п/р
предполагает возможность вынужденного колебания примерно такой же
амплитуды. Представим свободное колебание в форме
е = ф (*).
Функция <р (t) нечетна, периодична с периодом 2п/р и имеет амплитуду а;
явное выражение для <р (t) дается формулой E.2.9). Будем теперь искать
решение уравнения B3.10.2) в форме ф {?) + у, где у — малая величина
порядка е. Подставляя в B3.10.2), получаем приближение, верное с точно-
точностью до членов первого порядка относительно е:
• •
у + п2у cos ф (t) = е cos ф (t) sin pt. B3.10.5)
Если у удовлетворяет этому уравнению, то <р (t) -+- У и —ф (i) + у
будут приближенными решениями уравнения B3.10.2).
Частное решение уравнения B3.10.5) можно представить в форме
Аи (t) + Bv (t), где и = ф (t) — четная функция, a v — нечетная функция;
¦ •
выражение uv — vu остается постоянным, и путем соответствующего выбора
функции г; можно добиться, чтобы эта постоянная равнялась единице. Общее
решение уравнения B3.10.5) запишется тогда в виде
t
у = Аи (t) + Bv(t) — e^{u(t)v (I) — v(t)u (I)} cos <p (?) sin pi d|. B3.10.6)
о
Если положить А = 0, то правая часть B3.10.6) будет нечетной функ-
функцией от t, причем благодаря тому, что v{nlp) =ih 0, мы можем выбрать постоян-
постоянную В так, чтобы у обращался в нуль при nip (следовательно, также и при
—nip). Тогда
у (nip) = у (—п/р), у (nip) — у (—nip),
и поэтому решение являемся периодическим с периодом 2п/р. Решения
±ф it) + у представляют два вынужденных колебания амплитуды а и являют-
являются приближенными (с точностью до членов порядка е) решениями уравне-
уравнения B3.10.2).
Итак, если п2 — р2 положительно и не слишком мало, то мы имеем три
вынужденных колебания: одно малой амплитуды и два колебания с ампли-
амплитудой, близкой к а.
Хотя мы молчаливо предполагали, что свободные колебания затухают, однако
в уравнении B3.10.2) мы не имели члена, указывающего на наличие трения. Важно отме-
отметить, что вынужденные колебания амплитуды, близкой к а, сохраняются и тогда, когда
имеется малое трение. Если ввести малый линейный член, обусловленный наличием тре-
трения, то уравнение примет вид
9* + беё + п2 sin 6 = е cos 6 sin pt, B3.10.7)
§ 23.10] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ 483
где положительный множитель 6 не слишком велик. Функция ф (t — tB) имеет период
• •
2я/р и удовлетворяет уравнению ф + п2 sin ф = 0. Для того чтобы получить периодиче-
периодическое решение уравнения B3.10.7), близкое к ф (t — t0), необходимо, чтобы
2я/р
0=Г1-82 — «2 cos е!2Я/Р=е [ (Q cos Q sin pt—bfc)dt.
о
Таким образом, приближенно будем иметь
2л/р 2л/р
Ь [ q>2(t)dt= [ <p(i)cos<p(i) sin p(t+to)dt. B3.10.8)
J J
о о
Если интеграл в правой части не обращается тождественно в нуль, то B3.10.8)
дает как раз два значения t0 при условии, что параметр 6 не превышает некоторого предель-
предельного значения; эти два значения соответствуют двум вынужденным колебаниям, амплиту-
амплитуда которых близка к ранее найденной а.
2) Рассмотрим теперь случай резонанса, когда п2 — р2 мало. Записывая
уравнение B3.10.2) в форме
ё + P2Q = п2 (8 — sin 9) — (п2 — р2) 9 + е cos 8 sin pt, B3.10.9)
видим, что нелинейный возмущающий член п2 (9 — sin 9) имеет тот же поря-
порядок, что и наибольшая из величин (га2 — р2) 9 и е sin pt. Предположим, что
все эти три величины имеют один и тот же порядок; тогда 9 = 0 (е1/3)
и п2 — р2 = О (е2/3), и, обозначая &г/3 через г\, получаем Q — О (ч\112)
иге2 — р2 = О (г\). Положим п% = р2 A + кц); подставляя выражения 8 =
= zri1/2 и е = т]3/2 в уравнение B3.10.2) и сохраняя лишь члены первого
порядка относительно г\, получаем
B3.10.10)
В этом уравнении г\ мало, но к пе обязательно мало.
При г| = 0 уравнение B3.10.10) имеет решение z = a sin (pt — ф),
где а и ф — произвольные постоянные. Если г\ #0, то решение ищется
в форме
z = a sin (pt — ф) + TjZi + TJz2 + . . ., B3.10.11)
где а и ф на этот раз считаются переменными величинами. Эти величины мы
найдем сначала с точностью до т], затем с точностью до т]2 и т. д.; одновре-
одновременно, проводя вычисления с точностью до г\, мы определим zit проводя
вычисления с точностью до т]2, определим z2 и т. д. Наличие членов вида
r\Zi + TJz2 + . . . указывает на нелинейный характер левой части уравне-
уравнения B3.10.2). Действительно, решение невозмущенного уравнения 8 +
-f- re2 sin 8 = 0 можно записать в форме B3.10.il), считая, однако, вели-
величины а и ф постоянными. Медленное изменение а и ф связано с наличием
возмущающего члена в правой части уравнения B3.10.2).
Если выражение B3.10.11) для z подставить в уравнение B3.10.10),
то с точностью до членов порядка г\ получим
Bра — 2аф — аир) С + Bрщ + 'а — щ2) F+r\ (zt + p%) =
= P2r\ |(-^a-sin<p)C+ (-g-a3 — ka + -^ cosy} S — -^a3sm3(pt— ф)| ,
B3.10.12)
где через С и S обозначены соответственно cos (pt — ф) и sin (pt — ф). Урав-
Уравнение будет удовлетворяться, если
• • • • •
2ра — 2аф — аф==т1зтф, B3.10.13)
cos ф) . B3.10.14)
31*
484
УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
[Гл. XXIII
При этом
-Ф). B3.10.15)
Уравнения B3.10.13) и B3.10.14) определяют зависимость функций а
и ф от времени; их называют уравнениями в вариациях. Как станет ясно даль-
дальше, эти уравнения определяют медленные долгопериодические вариации.
Уравнение B3.10.15) называется пертурбационным уравнением; оно опре-
определяет короткопериодические вариации. Если бы, например, а и ф были
постоянны, то уравнение B3.10.15) имело бы решение
Zl = T§2 «3sin3(p? —ф). B3.10.16)
Производные а и ф имеют порядок г\, поэтому, с точностью до величин
этого порядка, уравнения B3.10.13) и B3.10.14) можно заменить более
простыми:
a = ^-sin(p, B3.10.17)
ф==-Ш-1й3--й:а+4гсо8ф). B3.10.18)
Эти уравнения определяют медленную вариацию величин а и ф.
Уравнения B3.10.17) и B3.10.18) имеют знакомую нам форму A9.3.1).
Представим изменение а и ф на диаграмме' как движение изображающей
точки; а, ф будут полярными координатами изо-
изображающей точки в момент]!. Особые точки поля
лежат на луче ф = 0; соответствующие значения
координаты а находятся из уравнения
L = 0, B3.10.19)
которое, будучи уравнением третьей степени,
имеет либо один, либо три вещественных корня.
Таким образом, будем иметь либо одну особую
точку, либо три особые точки. (Заметим, что
уравнения
> = я, Ti
¦ка ^- =
Рис. 103.
также определяют те же точки.)
Особые точки соответствуют решениям B3.10.16), B3.10.17), в которых
<а и ф постоянны. Эти решения представляют так называемые стационарные
колебания, в которых главный член ряда B3.10.11) является чисто синусои-
синусоидальным: z = a sin (pt — ф), где а и ф постоянны, причем а является веще-
вещественным корнем уравнения B3.10.19). Зависимость а от к показана на
рис. 103. Отбрасывая член с а3 в левой части B3.10.19), получаем для а
выражение а = 1/(&р2), совпадающее с элементарным решением B3.10.4),
полученным для колебаний с малой амплитудой. Уравнение B3.10.19) имеет
либо три вещественных корня, либо один, в зависимости от того, превышает
ли параметр к некоторое критическое значение к0 или нет. Если к < к0,
то имеется одно стационарное колебание; если к > к0, то —• три стационар-
стационарных колебания. Значение к0 равно 3/B5/Зр4/3).
Перейдем теперь от стационарных колебаний к общему случаю, когда
амплитуда а и фаза ф медленно изменяются в соответствии с уравнения-
уравнениями B3.10.17), B3.10.18). Эти уравнения допускают первый интеграл
4ra4-4-^2 + 4-cos9 = c. B3.10.20)
§ 23.10]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
485
Кривые, определяемые этим уравнением, представлены на диаграмме как
траектории изображающей точки. Они показаны на рис. 104 и рис. 105;
первый из них относится к случаю, когда
имеется один вещественный корень, а вто-
второй — к случаю, когда имеются три ве-
вещественных корня. Скорость движения
изображающей точки по траектории опре-
определяется уравнениями B3.10.17) и
B3.10.18).
Особым точкам на графиках соответ-
соответствуют стационарные колебания; поведе-
поведение кривых в окрестности особой точки
отражает изменение параметров движе-
движения, связанное с малым возмущением ста-
стационарного колебания. Поэтому для опре-
определения устойчивости или неустойчивости
стационарных колебаний (в смысле § 23.8)
можно воспользоваться результатами гл.
XIX. Так, на рис. 104 имеется одна осо-
особая точка типа центра, и, следовательно, р ,.,
соответствующее стационарное колебание
устойчиво. На рис. 105 имеются три осо-
особые точки. Две из них являются центрами, и соответствующие им стацио-
стационарные колебания устойчивы, третья представляет собой седло, и ей
Рис. 105.
соответствует неустойчивое колебание. На рис. 103 показаны амплитуды ста-
стационарных колебаний, сплошная линия соответствует устойчивым колеба-
колебаниям, пунктирная — неустойчивым.
486 УСТОЙЧИВОСТЬ ДВИЖЕНИЯ [Гл. ХХШ
Рассмотрим вариации величин а и ср в окрестности устойчивого стацио-
стационарного колебания; возьмем, например, вариацию, определяемую кривой Г
на рис. 104. Эта кривая замкнутая, так что вариация является периодиче-
периодической. Такие долгопериодические вариации параметров а и ф называются
биениями. Таким образом, с точностью до величин порядка т) движение
маятника можно представить как суперпозицию периодического движения
z = a sin (pt — ф) с периодом 2п/р, амплитуда а и фаза ф в котором медлен-
медленно изменяются с большим периодом 2, и добавочного движения, которое
приближенно можно считать короткопериодическим с периодом 2я/3/з.
Для определения периода 2 подставим в уравнение B3.10.17) выраже-
выражение для ф, полученное из B3.10.20). Проделав это, будем иметь
где через s обозначено а2 и
i=Jl/(e), B3.10.21)
B3.10.22)
Период 2 выражается через эллиптический интеграл:
°2
2 = ^j -щ-. B3.10.23)
где а)Ий2 — соответственно минимальное и максимальное значения а (дости-
(достигаемые в точках Ai и Az, рис. 104).
Если теперь (путем надлежащего выбора масштаба времени) придать р значение,
равное единице, то корни уравнения B3.10.19), дающие значения х в особых точках, ока-
окажутся равными
—2а, а— Р, а + р,
/4 1 / 1 \
а2 ; соответствующее значение к будет равно -^- ( а2 } . Кривые
на рис. 104 построены для случая а = 1/2, значение к для этих кривых равно —7/8,
и имеется одна особая точка (—1, 0). Кривые на рис. 105 построены для случая а = 2,
к = 7/4, и имеются три особые точки: (—4, 0), B—1/2", 0), B+/% 0).
В этих расчетах не принималось во внимание влияние трения; учет его может при-
привести к тому, что вместо центра мы получим устойчивый или неустойчивый фокус.
Исследование устойчивости можно было бы продолжить до членов поряд-
порядка г|2, г|3, . . ., однако это приводит к громоздким вычислениям.
Глава XXIV
КОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ
§ 24.1. Контактные преобразования. Движение динамической системы
определяет непрерывную группу преобразований фазового пространства
(§ 21.3). Эти преобразования переводят изображающую точку из положения
<7io> <7го' - • •> Япо' Рю> Pzo, ¦ • ¦¦> Рпо,
занимаемого ею в момент t = 0, в положение
Яи ?2» • • •, ?тм Pb P2, ¦ • ч Pni
занимаемое в момент t. Функции, определяющие преобразование, являются
решениями уравнений Гамильтона; они имеют вид
qr = фг (gi0, ?2о> • • •» Япо'^ Р«> Рго> • • ч PnoJ 0. г = 1, 2, . . ., ге,
B4.1.1)
Рг = фп+r (?Ю> ?20> • ч QnO; PlO) Р2о> • • ч РпО? ')> ?" = 1, 2, . . ., П.
B4.1.2)
Предполагается, что функции <р принадлежат к классу Сг, когда точка
(?ю, ?го» • • ч 9W. Рю> Рго' • • ч Рпо) леншт в некоторой области D, a t-
в интервале времени / (который во многих случаях является бесконечным:
—оо <; t < оо). Для краткости мы часто будем писать
qr = фг (q0; р0; i), рг = Ф„+г (я0, Ро\ *)•
Следует помнить, что мы имеем дело с 2/г-мерным пространством особого
рода — пространством п пар переменных (gi, pi), (q2, Рг), . . ., (qn, pn)-
Рассматриваемые преобразования сохраняют меру:
L B4Л.з)
^ (?ro; Pro) v
Далее, поскольку левая часть B4.1.3) не обращается в нуль, мы можем
разрешить уравнения B4.1.1), B4.1.2) относительно qr0 и рг0 и получить
в результате уравнения обратного преобразования:
Яго =4>r(q; p; t), г = 1, 2, . . ., п, B4.1.4)
Рг0 = г|>п+г (д; р; «), г = 1, 2, . . ., п. B4.1.5)
Уравнения B4.1.1), B4.1.2) определяют оператор Tt (§ 21.3), а уравне-
уравнения B4.1.4), B4.1.5) — обратный оператор (Г^). В автономном случае,
когда Н не содержит t, обратный оператор равен T-t и
Ч>. (?; р; 0 = ф8 (г; р; -*), s = 1, 2, ..., 2п. B4.1.6)
Эти соотношения можно представить в иной форме, что иногда оказывается
полезным. Например, мы можем, вообще говоря, разрешить уравне-
уравнения B4.1.4) относительно р, выразив их через д, д0 и t. Проделав это, будем
иметь
Рг = Ъ (я; Яо, f), г = 1, 2, . . ., п. B4.1.7)
488 КОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ [Гл. XXIV
Такая операция возможна при условии, что якобиан
d(pi, Рг, ¦¦¦, Рп)
не равен тождественно нулю. То, что в общем случае такое решение возмож-
возможно, ясно из того факта, что обычно движение полностью определяется зада-
заданием времени и концевых точек в g-пространстве (§ 15.6). Исключая р0
из уравнений B4.1.1), B4.1.2), приходим к уравнениям B4.1.4) и B4.1.7).
Точно таким же образом мы можем, вообще говоря, из уравне-
уравнений B4.1.5) выразить р через q, p0 и t.
Напомним еще одно фундаментальное свойство преобразования B4.1.1),
B4.1.2). Если S = S {q; q0; t) есть главная функция (§ 15.5), то
PrdqT= pTOdqro + Н dt + dS, B4.1.8)
где повторяющийся индекс г означает суммирование от 1 до п. В дальнейшем
мы будем предполагать, что функция Н (в правой части B4.1.8)) выражена
через переменные (g; qQ; t) с помощью соотношений B4.1.7). Уравнение B4.1.8)
показывает, что преобразование B4.1.1), B4.1.2) таково, что при фиксиро-
фиксированном значении t выражение
рг dqr — Pro dqr0 B4.1.9)
представляет полный дифференциал однозначной функции от переменных
(?! <7о> t); это свойство характерно для преобразований, определяемых урав-
уравнениями Гамильтона. Мы будем называть любое преобразование, обладаю-
обладающее этим свойством, контактным преобразованием. Если, в частности,
форма B4.1.9) тождественно равняется нулю, то мы будем говорить об одно-
однородном контактном преобразовании. (Такое преобразование уже встреча-
встречалось нам в § 15.8.) Очевидно, что контактные преобразования образуют
группу, и криволинейный интеграл Пуанкаре m Рг dqr является инва-
инвариантом этой группы.
Таким образом, движение динамической системы в фазовом простран-
пространстве порождает контактное преобразование, благодаря чему контактное
преобразование и нашло впервые применение в механике.
Из равенства B4.1.8) легко получить формулы для контактного пре-
преобразования, определяемого движением заданной динамической ' системы.
Сравнивая коэффициенты при вариациях, находим
dS
Чг
dS
Pro == —
dt
B4.1.10)
Эти формулы уже были получены нами в § 15.8 и в § 16.1. Там они опреде-
определяли решение задачи Гамильтона; здесь же они определяют контактное
преобразование. Таким образом, они выражают по существу одно и то же,
но с разных точек зрения.
Равенства B4.1.10) получаются из B4.1.8) лишь при условии, что между
переменными q, q0 и t нет никакого тождественного соотношения. Но послед-
последнее условие, очевидно, выполняется, ибо в противном случае это означало
бы существование тождественного соотношения между переменными q0, p0
и t, что невозможно в силу независимости этих переменных. Однако следует
иметь в виду, что в иных случаях подобные тождественные соотношения
могут иметь место; ниже мы приведем несколько таких примеров.
§ 24.2J ФОРМУЛЫ КОНТАКТНОГО ПРЕОБРАЗОВАНИЯ 489
Рассуждая в обратном порядке, возьмем произвольную функцию
S = S {q; q0; t) класса Са; формулы
! ? <24-1Л1>
определяют в общем случае некоторое контактное преобразование. (В сле-
следующем параграфе мы укажем условие, которому должна удовлетворять
функция S.)
Ранее (в § 15.8) нам уже представлялся случай для перехода к новым
параметрам («i, а2, . . ., сс„; р4, р2, • • •, Рп)> являющимся функциями
от переменных q0 и р0 и связанным с ними однородным контактным преобра-
преобразованием, так что
pr dar = Рто dqro. B4.1.12)
Численные значения параметров а и Р определяют орбиту в фазовом
пространстве так же, как и значения параметров q0 и р0. Преобразование
переменных (а; Р) в переменные (q; p) представляет произведение двух
контактных преобразований. В самом деле, имеем
pr dqr = p\ dar + H' dt + dS', B4.1.13)
где штрихи означают, что соответствующая величина выражена через q,
а и t. Некоторые замечания относительно двух формул dSI'dqT и dS'ldqT,
выражающих каждая рг, нами уже были сделаны в § 15.8, п. 4.
§ 24.2. Формулы контактного преобразования. Рассмотрим преобра-
преобразование переменных
Ql, Яг, ¦ ¦ •) 4ni Ри Р2, • ¦ ¦, Рп
к переменным
Qi, Qz, ¦ ¦ •, Qni Pii Pzi • • •! P-ni
определяемое уравнениями
Qt = q>r{qi, ?2. • • •. 4n, Pu Pz, ¦ ¦ ., Pn\ t), r = 1, 2, . . ., n, B4.2.1)
PT = ф„+г (gb qz, ¦ ¦ ., qn\ Pi, Pz, ¦ ¦ ¦, Pn\ t), r = 1, 2, . . ., n. B4.2.2)
Эти формулы мы часто будем записывать в следующей компактной форме:
Qr = Фг (q; p; t), Pr = ф„+г (g; p; t).
Функции ф принадлежат к классу С2, когда переменные {q, p) лежат
в области D, а переменная t находится в некотором интервале /. Для каждого
значения t в интервале / уравнения преобразования определяют топологи-
топологическое отображение области D на область Et пространства (Q; Р); при этом
преобразование допускает обращение, а именно:
qr=^r(Q; P; t), B4.2.3)
Pr = %+r (Q; P; t). B4.2.4)
Эти формулы справедливы при условии, что точка (Q, Р) лежит в обла-
области Et, a t — в интервале /. В частном случае, рассмотренном в § 24.1,
функции ф и г|з определялись движением определенной динамической систе-
системы; теперь мы не будем делать никаких предположений подобного рода.
Действительно, во многих важных для практики случаях функции ф и \\>,
входящие в формулы B4.2.1), B4.2.2) и B4.2.3), B4.2.4), не содержат t.
Простым примером контактного преобразования такого типа могут служить
формулы B4.1.1), B4.1.2), ,,есди величину t считать в них постоянной.
В дальнейшем, при исследовании задачи трех тел (гл. XXIX), мы встре-
встретимся со многими другими примерами подобных преобразований, уравне-
уравнения которых не содержат t.
490 КОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ [Гл. XXIV
Предположим теперь, что преобразование, заданное формулами B4.2.1),
B4.2.2), является контактным. Возьмем пфаффову форму Рт dQr и выразим
ее через переменные (q; p; t) с помощью формул B4.1.1), B4.1.2). Проделав
это, будем иметь
Pr dQr = Pr dqr +R dt — dW, B4.2.5)
где R и W — функции от (q; p; t). Рассмотрим два возможных случая:
1) Если якобиан
Pi,...,Pn) K '
не обращается тождественно в нуль, то уравнения B4.2.1) можно разрешить
относительно /з1; р2, . . ., рп, выразив их через {q; Q\ t); функции R и W
также можно представить в зависимости от (q; Q; t). Между переменными q,
Q и t не существует никакого тождественного соотношения, и контактное
преобразование задается формулами
Рг = ^г- г=1,2,...,п, B4.2.7)
рг=—т-> г =1,2, .... п, B4.2.8)
L
dt
B4.2.9)
где теперь символы R и W обозначают функции от переменных (q; Q; t)
и функция W ? С3 в соответствующей области пространства (q; Q; t). Фор-
Формулы B4.2.7) и B4.2.8) определяют контактное преобразование посредством
производящей функции W (q; Q; t).
Обратно, если дана произвольная функция W (q; Q; t), то уравне-
уравнения B4.2.7) и B4.2.8) определяют контактное преобразование при условии,
что матрица
(Ч) B4-2Л°)
не является особенной. Действительно, в этом случае уравнения B4.2.7)
можно разрешить относительно переменных Q, выразив последние через
(q; p; t); в результате мы придем к формулам B4.2.1). Подставляя получен-
полученные выражения для Q в B4.2.7), мы тождественно удовлетворим этим равен-
равенствам, следовательно,
ЭЦ? j 6p. B4.2.11)
dQsdqr dpm r
Таким образом, матрица, обратная неособенной матрице B4.2.10), равна
(d(pr/dps) и, стало быть, сама является неособенной матрицей. Поэтому
якобиан B4.2.6) не равен нулю, откуда следует, что формулы B4.2.7)
и B4.2.8) определяют контактное преобразование.
2) Если якобиан B4.2.6) тождественно равен нулю, то существует по
крайней мере одно тождественное соотношение, связывающее переменные
q, Q и t. Предположим сначала, что матрица {d(pr/dps) имеет ранг (п — 1).
Тогда между этими переменными имеется одно и только одно тождественное
соотношение; запишем его в форме
Q (?i. ?2, - • -, Qn, Qu <?2, . - -, Qn, t) = 0. B4.2.12)
Теперь функции R и W будут выражаться через переменные (q, Q, t)
уже не единственным образом и, следовательно, формулы B4.2.7) — B4.2.9)
§ 24.3] ДРУГИЕ ФОРМУЛЫ 491
перестанут быть справедливыми и должны быть заменены следующими:
PrSS^- + X-^-, r=l,2, ..., п, B4.2.13)
Рт==—^--.Х~, г=1,2. .... и, B4.2.14)
dQr dQr ..., v /
Bs^+j,^, B4.2.15)
где А, — неопределенный множитель. Аналогично, если матрица (дц>г1др3)
имеет ранг (п — I), то переменные q, Q ж t связаны I тождествами и соот-
соответствующие формулы преобразования содержат I множителей A-i, А,2, . . ., А,г.
§ 24.3. Другие формулы. Некоторых неудобств, связанных с введением
множителей, можно избежать, если немного изменить ход решения. Рассмо-
Рассмотрим еще раз случай, когда якобиан B4.2.6) тождественно равен нулю, так
что переменные q, Q ж t связаны по крайней мере одним тождественным соот-
соотношением. Но будем предполагать, что якобиан
С (ф1, ф2) • ' • I фп) /О/ О л \
d(9l. 92, .... 9n) v '
не равен тождественно нулю. Тогда уравнения B4.2.1) можно разрешить
относительно переменных q, выразив их через р, Q ж t. Если теперь уравне-
уравнение B4.2.5) записать в форме
рт dQr = —qT dpr + R dt — dU, B4.3.2)
положив U = W — Я.тРт1 и функции R ж U выразить через переменные
(р; Q\ t), то мы придем к следующим формулам:
?«¦=—-^-, г = 1,2, ..., п, B4.3.3)
dU г=1,2, .... и, B4.3.4)
R = -^T- B4.3.5)
Таким образом, контактное преобразование выражено нами посредством
производящей функции U (p; Q; t).
Итак, мы рассмотрели два способа получения контактных преобразова-
преобразований с помощью производящих функций; можно указать еще два способа
получения преобразований этого типа. Рассмотрим контактное преобразова-
преобразование, в котором переменные х\, xz- . . ., хп ж Xi, X2, ¦ ¦ ., Хп не связаны
никакими тождественными соотношениями (малыми буквами х здесь обозна-
обозначены либо все переменные д, либо все переменные р, а большими буквами
X — либо все Q, либо все Р). Возьмем в фундаментальном соотношении
B4.2.1) х ж X в качестве независимых переменных. Легко проверить, что
формулы
±Ут = ^-1 г = 1,2, ..., п, B4.3.6)
±Yr = -~, r = l,2,...,n, B4.3.7)
i?=~ B4.3.8)
содержат в себе как ранее полученные соотношения B4.2.7), B4.2.8) и B4.3.3),
B4.3.4), так и две группы соотношений, которые еще не были нами полу-
получены. В этих формулах U = U (х; X; t) 6 С3, а у ж Y обозначают системы
переменных, не входящих в U; выбор знака производится согласно
492 КОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ [Гл. XXIV
мнемоническому правилу: плюс ставится перед р (или Р). Формулы B4.3.6),
B4.3.7) определяют контактное преобразование при условии, что функция U
принадлежит к классу С3, в остальном же она произвольна, если не считать
требования, чтобы матрица (d2U/dxr dXs) была неособенной (см. § 24.2).
Практически наиболее часто встречаются случаи, когда в качестве
переменных х и X берутся р и Q или q и Р. В первом из этих случаев пре-
преобразование определяется формулами B4.3.3), B4.3.4), которые можно запи-
записать в эквивалентной форме
r)W rlW
причем R = —dW/dt. (Единственное преимущество формы B4.3.3), B4.3.4),
со знаком минус в правой части, заключается в том, что при этом сохраняет-
сохраняется соотношение R = -\-dUldt, что, конечно, совершенно несущественно в слу-
случае, когда преобразование не содержит t.) Во втором случае преобразование
определяется уравнениями
*=¦§-• ь=ж,' B4-ЗЛ0)
причем RdUldt.
С точки зрения абстрактной теории обычно несущественно, в какой именно форме
записаны уравнения преобразований. Действительно, различные формы этих уравнений
тесно связаны друг с другом. Предположим, например, что мы переходим от перемен-
переменных (д, р) к переменным (Q, Р) с помощью контактного иреобразования, получаемого
посредством производящей функции U (q\ Q; t) и определяемого формулами
Рассмотрим затем контактное преобразование от переменных (Q, Р) к переменным {Qr, P'),
описываемое формулами
¦Qr = P'T, Pr=~Qr- B4.3.12)
Тогда переход от переменных (q, р) к переменным (Q', Р') можно осуществить с помощью
производящей функции U (д; P'\ t) по формулам
Отсюда легко установить связь между первой группой формул B4.2.7) — B4.2.9)
(где производящая функция содержит q и Q) и последней группой B4.3.10) (где произво-
производящая функция содержит q и Р).
Сделаем еще одно замечание, касающееся теоремы Гамильтона — Якоби. Мы виде-
видели (§ 16.2), что если S (q; a; t) представляет собой полный интеграл уравнения в частных
производных Гамильтона, то решение задачи Лагранжа можно получить из п уравнений
dS = const. B4.3.14)
Постоянную в правой части мы ранее обозначали через —Рг (см. A6.2.4)). Уравнения
B4.3.14) показывают, что преобразование переменных (qu\ р0) в переменные (а; Р) являет-
является контактным преобразованием; при этом естественно считать аг лагранжевой координа-
координатой, а Рг — соответствующей составляющей импульса. Если же постоянную в правой
части B4.3.14) принять равной +РГ, то контактным преобразованием будет преобразова-
преобразование переменных (q0; ро) в переменные ф; а), и Рг будет играть роль лагранжевой коорди-
координаты, а аг — составляющей импульса. Поэтому, если мы желаем, чтобы правая часть
B4.3.14) выражалась координатой, а не импульсом, то мы должны эту постоянную поло-
положить равной +Рг- В теории движения планет, например, постоянные в правых частях
уравнений B4.3.14) обычно имеют смысл углов и Р естественно считать координатами,
а не импульсами; тогда уравнения следует записывать в форме
dS hPr- B4.3.15)
daT ' rr-
Нужно, однако, иметь в виду, что при пользовании контактными преобразованиями,
по существу, стираются различия между координатами и импульсами. Так, например,
$ 24.4] ОБОБЩЕННОЕ ТОЧЕЧНОЕ ПРЕОБРАЗОВАНИЕ 493
в формулах B4.3.12) «координаты» Qr и «составляющие импульса» Р'г представляют одни
и те же физические величины.
В этой книге мы будем придерживаться стандартной формы записи теоремы Гамиль-
Гамильтона — Якоби A6.2.4):
¦1^ — Рг. B4.3.16)
§ 24.4. Обобщенное точечное преобразование и другие однородные
контактные преобразования. Рассмотрим точечное преобразование
qr = Fr (Qu Q2, . . ., Qn), r = 1, 2, . . ., n, B4.4.1)
выражающее переход от одной системы лагранжевых координат к другой;
функции F образуют здесь систему п независимых функций от (Qi: Q2, . . .
. . ., Qn), принадлежащих каждая к классу С2. Будем рассматривать нату-
натуральную систему и обозначим соответствующие импульсы, как обычно,
символами р и Р. Тогда преобразование переменных (q; р) в переменные
(Q; Р) будет однородным контактным преобразованием; его называют рас-
расширенным или обобщенным точечным преобразованием. Это следует из того
факта, что скалярное произведение prqr, где q — любая скорость (не обяза-
обязательно скорость, связанная с импульсомр), является инвариантом. (Строго
говоря, если воспользоваться тензорными обозначениями, то следовало бы
писать qr вместо qr, поскольку q — ковариантный вектор.)
Таким образом, PrQr = prqr, и, следовательно,
РТ dQr = Рг dqr, B4.4.2)
так что преобразование является однородным контактным преобразованием.
Нетрудно написать явные формулы этого преобразования. Если
2 Г = arjqrqs = ArsQrQs, B4.4.3)
то
Рг = АЛ = а^^^аи^д, = Р1 |g-. B4.4.4)
Соотношения B4.4.1) и B4.4.4) определяют контактное преобразование.
Как и следовало ожидать из физических соображений, величины Р являются
линейными однородными функциями от р. Уравнения преобразования не
содержат времени.
Разумеется, не составляет труда вывести эти формулы с помощью общего
метода § 24.3. В рассматриваемом случае величины q и Q не являются неза-
независимыми; в самом деле, между этими величинами имеется ровно п незави-
независимых соотношений B4.4.1). Ранг матрицы B4.2.6) равен нулю. С другой
стороны, величины р, Q и t не связаны никакими соотношениями, ибо в про-
противном случае существовала бы связь между независимыми переменными
(qi, q2, . . ., qn; Pi, p2, ¦ ¦ •, Pn', t)- Поэтому уравнения преобразования мож-
можно взять в форме B4.3.3), B4.3.4); в самом деле, если
U = -pTFr, B4.4.5)
то формулы B4.3.3), B4.3.4) принимают вид
qr = Fr, Pr = Pi^, B4.4.6)
совпадающий с B4.4.1) и B4.4.4).
Если производящую функцию взять зависящей от q и Q (что, очевидно, в данном слу-
случае нзудобно и делается лишь с целью иллюстрации), то для любого фиксированного
494
КОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ
[Гл. XXIV
значения t будем иметь
откуда
Рт dQr = рт
(dqT - dFr),
яр.
i
B4.4.7)
B4.4.8)
Таким образом, множителями Хг являются импульсы рг.
Рассуждения легко распространяются на случай расширенного точеч-
точечного преобразования, содержащего t; в этом случае функции Fr в форму-
формулах B4.4.1) также будут зависеть от t. Мы по-прежнему можем пользоваться
производящей функцией B4.4.5); формулы B4.4.6) не изменяют своего вида,
хотя теперь содержат t.
Аналогичным образом исследуется и тот случай, когда Q явно выражены
как функции q (и, возможно, t). Уравнения B4.4.1) заменяются при этом
следующими:
Qr = U (ди ?2, • • м qn; t). B4.4.9)
Производящая функция задается выражением
U = Prfr. B4.4.10)
Уравнения преобразования B4.3.10) принимают вид
Pr = PtjtL, Qr = fr. B4.4.11)
В расширенном точечном преобразовании, не содержащем t (и являющемся частным
случаем однородного контактного преобразования), имеется п тождественных соотноше-
соотношений между переменными q и Q. Фактически для любого однородного контактного преоб-
преобразования, не содержащего t, можно указать по крайней мере одно тождественное соот-
соотношение, связывающее переменные q и Q- Для доказательства достаточно заметить, что
уравнение
Рг dQr = Pr dqr B4.4.12)
влечет за собой в соотношений
л.
Отсюда следует, "что определитель
B4.4.13)
B4.4.14)
тождественно равен нулю, а это в свою очередь означает, что между переменными q и Q
существует соотношение (§ 24.2).
§ 24.5. Специальная форма уравнений преобразований. Бесконечно
малые контактные преобразования. Рассмотрим контактное преобразование,
в котором переменные q и Р (и, возможно, t) не связаны никаким тождествен-
тождественным соотношением. Положим в общих уравнениях преобразования B4.3.6) —
B4.3.8)
U = qrPr + М, B4.5.1)
где М — М (q; P; t). Тогда будем иметь
Qq
~,
B4.5.2)
B4.5.4)
(Аналогичные формулы получаются и в том случае, когда производящая
функция зависит от переменных р, Q и t.)
§ 24.7] УСЛОВИЯ КОНТАКТНОСТИ ПРЕОБРАЗОВАНИЯ, СКОБКИ ЛАГРАНЖА 495
Формулы B4.5.2), B4.5.3) представляют особый интерес вследствие их
сходства с уравнениями движения Гамильтона. Вспомним, что впервые
рассмотренные нами контактные преобразования определялись движением
динамической системы. Теперь мы видим, что и в общем случае контактные
преобразования определяются уравнениями сходной структуры.
Это сходство становится еще более разительным, если правые части
уравнений B4.5.2) — B4.5.4) считать малыми величинами; для этого доста-
достаточно положить, например, М = \мр, где \х — малый параметр.
Если пренебрегать членами порядка (д,2, то нет необходимости делать
различие между величинами, выражаемыми малыми и большими буквами
в членах, умножаемых на (д.. Учитывая это, мы приходим к уравнениям
B4.5.6)
в которых ф = ф (g; p; t). Определяемое этими уравнениями преобразо-
преобразование называется бесконечно малым контактным преобразованием. Его можно
интерпретировать как изменение положения в фазовом пространстве, кото-
которое происходит в течение малого промежутка времени от t до t + \i для дина-
динамической системы с гамильтоновой функцией, равной ф.
§ 24.6. Обобщение теоремы Лиувилля. Свойство сохранения меры при
преобразованиях, определяемых уравнениями Гамильтона (последние, как
мы видели, определяют контактные преобразования), сохраняется и для кон-
контактных преобразований общего вида. В самом деле, докажем, что якобиан
d(Qu (?2, •-., Qn, Pi, Рг, ...,Рп) /24 б 1)
d(q\, 92, ••-, <7n> Pi. P2. ••¦¦. Pn)
имеет значение, равное единице. Для определенности возьмем случай, когда
переменные q и Q не связаны никакими тождественными соотношениями.
Преобразование определяется уравнениями B4.2.7), B4.2.8), в которых
независимыми переменными являются q и Q. Записывая якобиан B4.6.1)
кратко в форме д (Q; РIд {q; p), получаем
d(Q; Р)_ d(Q;P) I д(д; р) , ,,n д(Р) I d(p) _ \ dQ ) / \ dg (> ?>
d[q,p) d(q;Q)ld{q;Q) K Ч d(q)\d{Q) dq / д (Q) *>l**-"-*/
где, например, символ д (Р)/д (q) обозначает определитель д (Рь Р2, ¦ ¦ ¦
. . ., Рп)/д (q-y, q2, . ., qn). Теорема, таким образом, доказана. В других
случаях доказательство проводится аналогичным образом.
§ 24.7. Условия контактности преобразования, скобки Лагранжа.
Пусть каждая из переменных gb q2, . ¦ ., qn, Pi, Рг, • ¦ •, Рп является функ-
функцией класса С2 от N аргументов и, v, w, ... Рассмотрим сумму п определи-
определителей Якоби
д^ Р!] ¦ B4.7.1)
д (и, v) v '
Эту сумму называют скобкой Лагранжа и обозначают обычно символом
[и, v]. В данный момент нас будет интересовать случай, когда N = 2п + 1;
в качестве аргументов и, v, w, ... выберем Q±, Q%, . . ., Qn, Pi, P2, ¦ ¦ ¦
. . ., Pn; t. Для того чтобы преобразование переменных (q; p) к переменным
(Q; Р) было контактным, необходимо и достаточно, чтобы выполнялись
496 КОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ [Гл. XXIV
равенства
[Qr, Q$}= О, [РТ, Р.] = 0, [QT, Р.] = б? B4.7.2)
для всех пар целых чисел г, s в последовательности 1,. 2, . . ., п при любом
фиксированном значении t.
Доказательство следует немедленно. Принимая во внимание основное
равенство B4.2.5) и выбирая Q и Р за независимые переменные, находим,
что для контактности преобразования необходимо и достаточно, чтобы
выражение
(Pt Щ^-Pr) dQr+(Pi ¦§-) dPr B4.7.3)
было полным дифференциалом при любом фиксированном значении t. Но это
выражение представляет полный дифференциал лишь в том случае, если
выполняются равенства
д
дР«
p
4" dQr \Pl dP,
что равносильно B4.7.2).
§ 24.8. Соотношения между двумя системами производных. Предполо-
Предположим, что область D пространства- (q; p) при фиксированном значении t
преобразуется в область Е пространства (Q; Р) посредством контактного
преобразования. При этом производные от функций Q и Р по переменным
(q; p), взятые в точке области D, связаны простым образом с производными
от функций (q; p) по переменным (Q; Р), взятыми в соответствующей точке
области Е, а именно:
i5zL=_^. _dQL==__dq1_ B4 8 1)
dq$ дР r ? dps dPr
дРг dps дРг _ dqs .„, „ „.
Доказательство весьма просто получается из условий для скобок Лагранжа,
•выведенных в предыдущем параграфе. Пусть г — любое целое число из
последовательности 1, 2, . . ., п; рассмотрим форму Пфаффа
' dpi ^ dgt ^ dpi
*9 ар1 =
ж 7dPs) = t<?s' Pr]dQs +[Ps' Pr]dPs = dQr- B4'8>3)
Отсюда следуют формулы B4.8.1). Соотношения B4.8.2) аналогичным обра-
образом получаются из равенства
Формулы B4.8.1), B4.8.2) можно вывести простым и изящным образом, рассматри-
рассматривая так называемый билинейный ковариант. Рассмотрим две произвольные вариации dx
и 6ж точки ж0 = (?«, 920. • • •> 9по, Рю, Р20, ¦ ¦ •> Рпо) фазового пространства. Обозначим
через dX и 6.Х соответствующие вариации преобразованной точки Хо = (Qi0, Qi0, . . .
¦ ¦ •, Qno, Pio, ^20, • • ¦. Рпо)- Тогда справедливо равенство
dQrbPr — dPTbQr = dqrbpr — dpr6gr B4.8.5)
(знак суммы мы для краткости записи здесь опускаем).
Выражения в левой и правой частях равенства B4.8.5) представляют каждое били-
билинейный ковариант.
§ 24.9] УСЛОВИЯ КОНТАКТНОСТИ ПРЕОБРАЗОВАНИЯ 497
Равенство B4.8.5) непосредственно следует из самого определения контактного пре-
преобразования. Остановимся более подробно на значении символов d и б. Рассмотрим дву-
двумерное многообразие М, содержащее точку х0 и векторы dx и бж. Будем определять поло-
положение точки на многообразии М координатами |, г\; координаты qit q2, . . ., qn, pi, p2, ¦ ¦ •
. . ., рп точки ж поверхности М будут функциями от (g, r|), принадлежащими классу С2.
При этом кривая ц = const в точке ж0 будет иметь направление вдоль dx, а кривая | =
= const в той же точке — направление вдоль бж. Поэтому перемещение dx в точке ж0
будет иметь составляющие dxs = (dxs/d?,H dg, s = 1, 2, . . ., re, а перемещение баз — со-
составляющие bxs = (дха1дцH br\. Символы d и б мы сохраним и для обозначения перемеще-
перемещений в точках ж, близких к точке х0, так что формулы dxs = (dxJdQ d| и 6a;s = (дх8/дц) 6ц
будут справедливы и в общем случае. Вариации dg, br\ будем считать раз и навсегда фик-
фиксированными, так что 6dg = dдц = 0. Отсюда следует, что 6da;r = dbxr и, вообще, для
любой функции / от (<jflt q2, . .-., qn, pu p2, . . ., рп) класса С
bdf = d&f. B4.8.6)
Теперь легко получить желаемый результат. Пользуясь основным свойством B4.2.5)
контактного преобразования, находим
б (Pr dQr) — d (PT bQr) = б (рт dqr — dw) — d (Pr 6qr — &w), B4.8.7)
откуда, учитывая B4.8.6), сразу получаем B4.8.5).
Для того чтобы вывести соотношения B4.8.1), B4.8.2) из билинейного коварианта,
обозначим через d вариацию, обусловленную изменением одной лишь координаты qs,
а через б — вариацию, обусловленную изменением одной только координаты Qr. Тогда
в каждой части равенства B4.8.5) останется по одному члену, и мы будем иметь
—dPT 6Qr = dqs6ps (суммирование не производится), B4.8.8)
откуда
дРт ^ др.
Y^- dqsoQr = dqs-^y-bQr (суммирование не производится) B4.8.9)
и
^=—ж-- B48-10>
dqs dQr
Остальные формулы B4.8.1), B4.8.2) получаются совершенно аналогичным путем.
С помощью билинейного коварианта можно получить также условия контактности
преобразования, выраженные нами ранее через скобки Лагранжа (§ 24.7). Если правую
часть равенства B4.8.5) выразить через dQ и dP, а также bQ и ЬР, то получим
Коэффициент при выражении dQr6Ps — dPs6Qr равен [Qr, Ps], коэффициент при
dQr&Qs равен [Qr, Qs], а коэффициент при dPr6Ps равен [Pr, Ps]. Сравнивая коэффициенты
при соответствующих выражениях в левой и правой частях уравнения, приходим к фор-
формулам B4.7.2).
§ 24.9. Условия контактности преобразования, выраженные с помощью
скобок Пуассона. Установленные в § 24.8 соотношения между двумя систе-
системами производных позволяют выразить условия контактности преобразова-
преобразования с помощью скобок Пуассона (§ 22.2). Действительно,
\п пл— dqi dpi dPi dqi — dPr dPs i dPr dPs — ( p p\ с?л q-n
Точно так же
[Qr, P.] = (Qs, Pr), iPr, Ps] = (Qr, Qs)- B4.9.2)
Отсюда следует, что если преобразование переменных (д; р) в переменные
(Q; Р) является контактным, то
(Qr, Qs) = 0, (Рг, Р.) = 0, «?г, Р.) = б?. B4.9.3)
Ниже мы увидим, что эти равенства являются не только необходимыми,
но и достаточными условиями контактности.
32 л. А, Парс
498 КОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ [Гл. XXIV
§ 24.10. Соотношения между скобками Лагранжа и скобками Пуассона.
Предположим, что величины qt, q2, . ¦ ., qn, Pi, p2, ¦ ¦ ., pn образуют в обла-
области D фазового пространства систему In независимых функций класса С2
от. 2п переменных щ, и2, • ¦ -, и2п. Пусть эти функции осуществляют топо-
топологическое отображение области D фазового пространства на область Е
пространства и. (Мы здесь не считаем, что это преобразование обязательно
является контактным.) Фундаментальное соотношение, связывающее скобки
Лагранжа со скобками Пуассона, имеет вид
2и
2 [ur, us](uT, uk) = 8s» B4.10.1)
Доказывается это просто. Левая часть B4Л0.1) равна
/ dq{ dpj dpi dgt \ I dur duh duh dur \ _ I dqi dur \ dpi duh
) ) \ )
_ I
\
dur dus dur dus ) \ dqj dpj dqj dpj ) \ dur dqj ) du
duh I dpt dur \ dqt duh ,
) ^
_ / dqi duT \ dpj duh I
V duT dpj I dus dqj \ dur dqj ) dus dpj "^
)^L^lLt B4.10.2)
dus dqj ч '
где индекс г указывает на суммирование от 1 до 2п, индексы i ж j — на сум-
суммирование от 1 до п. Второе и третье слагаемые в правой части B4.10.2),
очевидно, обращаются в нуль, а первое и четвертое дают
p,l?L^^L^ = 8l B4.10.3)
dpi dus ¦ dqt dus y '
Теорема, таким образом, доказана.
Если скобку Лагранжа [ur, us] обозначить через Xrs, а скобку Пуассона
(ur, us) — через a>rs, то равенство B4.10.1) можно будет очень просто выра-
выразить через матрицы X, и ю размером Ъг X In с элементами Xrs и wrs. В матрич-
матричной форме равенство B4.10.1) тогда будет иметь вид'
Гю = 1~2п. B4.10.4)
§ 24.11. Приложение к контактному преобразованию. Рассмотрим част-
частный случай, когда в качестве щ, иг, . . ., и2п берутся Qu Q2, . . ., Qn,
Pi, P2 , . ¦ -, -РП! входящие в уравнения контактного преобразования.
Благодаря свойствам B4.7.2) скобок Лагранжа матрица X принимает вид
-in о
и, следовательно,
« = (X')-1 = Z. B4.11.2)
Таким образом, условия B4.9.3) для скобок Пуассона совершенно экви-
эквивалентны соответствующим условиям для скобок Лагранжа. Подобно им,
соотношения B4.9.3) образуют систему необходимых и достаточных условий
контактности преобразования.
§ 24.12. Инвариантность скобки Пуассона. Скобка Пуассона двух функ-
функций при контактном преобразовании остается инвариантной, или подроб-
подробнее, если переход от {q; p) к (Q; Р) осуществляется с помощью контактного
преобразования и если
и (q; P) = U (Q; P), v (g; p) = V (Q; Р), B4.12.1)
§ 24.13] ДРУГАЯ ФОРМА УСЛОВИЙ КОНТАКТНОСТИ ПРЕОБРАЗОВАНИЯ 499
ТО
(и, v) = (U, V), B4.12.2)
где (U, V) обозначает скобку Пуассона с независимыми переменными (Q; Р),
п
а именно 2 д (U, V)/d (Qr, Рт). Если в уравнения преобразования входит
г=1
t, то равенство B4.12.2) выполняется для любого заданного значения t.
Этот результат легко получается из условий B4.9.3) для скобок Пуассона.
Имеем
. v ди dv dv ди
( v)
Pr dqT dpT
— I dU dQi | dU dPj \ I dV dQj dV dPj
\ dQi dqr dPi dqT ) \ dQj dpr dPj dpr
_ / dU dQi , dU dPj \ / dV dQj dV dPj \ _
V dQi dpr + dPi dpr ) \ dQj dqr + dP] dqr j ~
§ 24.13. Другая форма условий контактности преобразования. Заменим
символы
?1» ?2, • • ч ?п. Pi, Рг, ¦ ' м Рп
на
Х\, Х2, . • •, Хп, bC^_|_i, xn_j_2i • • *i "^2ti
(см. § 22.1), а символы
Qi, Q2, ¦ ¦ •> Qn, Pi, Р2, • ¦ •> Рп
на
1, Л-2, • • ч лп- Лтг + 11 лп + 2, • • •, ¦л-2п-
Рассмотрим квадратную матрицу М размером In X 2n с элементами
dXrldxs. Ее можно представить в форме
(А В\
m=(cd)' B4ЛЗЛ)
где А, В, С, D — матрицы размером пхп с элементами
_
~"^7' urs~ dps •
Тогда
/AB' — BA' AD' — BC'
\'-I)A' CD'-DC
((Qr, <?.)) («?„ p.))
((
= \(
Это равенство показывает, что необходимые и достаточные условия контакт-
контактности преобразования можно представить в форме
MZM'=Z. B4.13.4)
Условию B4.13.4) удовлетворяют как матрица М, так и обратная?
матрица m с элементами dxr/dXs. Для того чтобы убедиться в этом, доста-
достаточно умножить обе части равенства B4.13.4) слева на m и справа на т'.
32*
500 НОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ [Гл. XXIV
С другой стороны, этот результат связан с тем, что само преобразование
(Q, Р) в (q, p) является контактным.
Итак,
mZm'=Z. B4.13.5)
Если теперь перейти к обратным матрицам, то получим
M'ZM = Z, B4.13.6)
откуда следует, что условие, которому удовлетворяет матрица М, удовле-
удовлетворяется и транспонированной матрицей. Сказанное выше справедливо
и для матрицы т, которая является транспонированной обратной матри-
матрицей; имеем
m'Zm = Z. B4.13.7)
Все четыре условия B4.13.4) — B4.13.7) эквивалентны друг другу: каждое
из них влечет за собой три остальных. Матрица М, обладающая таким свой-
свойством, называется симплектической матрицей (см. § 23.6). Если М есть
симплектическая матрица, то это относится и к транспонированной
и к обратной матрицам.
Рассмотрим в качестве примера линейное преобразование
х=СХ B4.13.8)
с неособой матрицей С, элементы которой постоянны. В этом случае т = С
и преобразование является контактным тогда и только тогда, когда выпол-
выполняется матричное равенство
C'ZC = Z. B4.13.9)
§ 24.14. Функции, находящиеся в инволюции. Мы видели, что если
преобразование (q; р) в (Q; Р) является контактным, то п составляющих
(Qi, <?2, ¦ • ¦> (?п)> как функции от (q; р; t), удовлетворяют условию
{Qt, Qs) = 0- Если система функций такова, что скобка Пуассона любых
двух функций тождественно равна нулю, то говорят, что эти функции нахо-
находятся в инволюции.
Ясно, что произвольные п функций от (q; p; t) не могут служить первы-
первыми п составляющими Qi, Q2, ¦ ¦ ., Qn контактного преобразования, так как
эти функции должны находиться в инволюции. Естественно, возникает
вопрос: пусть даны п функций Qi, Q2 ¦ ¦ ¦ Qni находящихся в инволюции;
спрашивается, можно ли указать п других функций Pi, Р2, . . ., Рп таких,
чтобы преобразование (q; p) в (Q; Р) было контактным?
В простейшем случае расширенного точечного преобразования (§ 24.4)
ответ на этот вопрос, разумеется, будет утвердительным; такой же ответ
можно дать i в ряде других случаев, которые будут рассмотрены ниже.
Рассмотрим п функций <pi, фг, ¦ . ., <р„, находящихся в инволюции,
и предположим, что якобиан
/ *(Ф1' Ф2,...,Фп) B4.14.1)
д(ри Pz, ¦¦¦, Рп)
не равен тождественно нулю. Переменные q, Q и t не связаны никаким тожде-
тождественным соотношением, и мы можем разрешить п уравнений
Qr = фг (q; Р; t) B4.14.2)
-относительно р^, р%, . ¦ ., рп. Проделав это, получим
Рг = Цг (?; Q; t), г = 1, 2, . . ., п. B4.14.3)
Докажем, что для всех пар г и s справедливы равенства
-5^ = -5^'. B4.14.4)
¦dqs- dqT v '
S 24.15] НЕКОТОРЫЕ ПРИМЕРЫ 501
Подставляя в B4.14.2) вместо рг функции г|зг, получаем тождество относи-
относительно переменных (q; Q; t):
Фг (q; у; t)-Q,=O, i = 1, 2, . . ., п. B4.14.5)
Дифференцируя это тождество частным. образом по qs, находим
*р—?р-2к. = 0, , = 1,2, ...,п. B4.14.6)
dga dpr dqs v '
Если теперь умножить полученное равенство на d(fj/dps и просуммировать
по s от 1 до п, то получим
dps dqs
Вычтем из этого уравнения такое же уравнение, в котором переставлены
индексы i и j; используя условие (ср*, Ф7-) = С, найдем
dffj dyj dtyr d^j дщ д\]рг ^q
дрг dps dqs dpr dps
B4 14 8)
Если во втором члене слева поменять местами повторяющиеся индексы г
и s, то полученное равенство можно представить в форме
^L*PL(°$!L-l$i.)=o. B4.14.9)
дрт dps \ dqs dqr ) v '
Всего мы имеем п2 таких уравнений (соответственно числу пар значений г
и ;'), и из этой системы линейных однородных уравнений можно найти Пг
неизвестных величин
dqs dqr
Определитель из коэффициентов этой системы равен /2п и не равен нулю;
следовательно, для всех пар чисел г и s справедливы равенства
4^ 4г^. B4.14.10)
dqT v '
4 = 4г.
dqs dqT
Отсюда следует, что существует функция W —W(q; Q; t) такая, что
Pr = ^r{q; <?; 1) = -^-, r=l,2,...,n, B4.14.11)
а матрица I -^——=р) является неособои (в противном случае между перемен-
\ oqr okIs I
ними q, p и t существовало бы тождественное соотношение). Поэтому,
если положить
Р'-=—М-' г=1,2, ...,га, B4.14.12)
то уравнения B4.14.11), B4.14.12) определят контактное преобразование
(см. B4.2.7), B4.2.8)), что и требовалось доказать.
§ 24.15. Некоторые примеры. Рассмотрим сначала систему с одной степенью свобо-
свободы. В этом случае вопрос решается просто: единственным условием контактности преоб-
преобразования является требование о сохранении меры, а именно:
Как можно видеть, это есть условие для скобок Пуассона (§ 24.9). Можно также
заметить, что интеграл Qp p dq вдоль простой замкнутой кривой в фазовом пространстве
(т. е. в плоскости qp) равен (со знаком минус) площади, ограниченной этой кривой; неиз-
неизменность площади означает, что выражение Р dQ — р dq является полным дифферен-
дифференциалом.
502 КОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ [Гл. XXIV
Линейное преобразование
Q=aq+bp + c, Р = a'q+ Ъ'р + с' B4.15.2)
с коэффициентами а, Ъ, с, а', Ь', с', зависящими от времени, является контактным лишь
в том случае, если
аЪ' - Ъа' = 1. B4.15.3)
Простой способ нахождения контактного преобразования мы получаем, рассматри-
рассматривая движение динамических систем. При этом переменные (q, p) определяют координаты
начальной точки, а переменные (Q, Р) — координаты изображающей точки в момент t.
Уравнения таких преобразований, соответствующих действительным движениям, обра-
обращаются в тождества при t = 0; если зафиксировать значение t =f= 0, то получим контакт-
контактное преобразование, не зависящее от времени. Следующие два примера контактных пре-
преобразований соответствуют хорошо известным задачам прямолинейного движения:
Q=q+pt+\e?i, P = P+gt, B4.15.4)
Q = q cos nt + (pin) sin nt, P = —nq sin nt -\- p cos nt. B4.15.5)
Другими простыми примерами линейных контактных преобразований могут служить
Q = Q-q0, P=P-Po< B4.15.6)
Q = a<?, P = p/a, " B4.15.7)
Q = ap, P=—q/a, B4.15.8)
р. B4.15.9)
Последовательно применяя эти преобразования, можно получать другие преобра-
преобразования. Отметим два важных частных случая преобразования B4.15.8), которые полу-
получаются при а = ±1, а именно:
Q = p, P=-q, B4.15.10)
Q = -р, р = д. B4.15.11)
Преобразование
Q = f(q) cos р, Р = / (?) sin p B4.15.12)
является контактным при условии, если //' =1, /2 = 2 (q -\- а); тогда получаем
Q="|/2 (q + a)cosp, P = -\/2(q + a) sin p. B4.15.13)
Это можно записать также в форме
(ij) B4.15.14)
Легко убедиться, что выражение Р dQ — p dq представляет собой полный дифференциал.
В самом деле,
Р dQ — р dq = d {(cos p sin p — р) (q + a)}. B4.15.15)
Формулы B4.15.13) можно также вывести из производящей функции U (p, Q) (см.
B4.3.3), B4.3.4)); для этого достаточно взять
Q2tg + B4.15.16)
Объединяя B4.15.13) и B4.15.10), получаем контактное преобразование
P= — ~\/2(p+a)sinq. B4.15.17)
Преобразование
Q = e*Pf (q), P = e-bPg (q) B4.15.18)
является контактным, если
-ft ifg' + gf) = 1, -kfg = q + a. B4.15.19)
В частности, формулы
B4.15.20)
определяют контактное преобразование.
Понятие контактного преобразования мы до сих пор применяли лишь к веществен-
вещественным переменным. Это понятие допускает распространение и на тот случай, когда пере-
переменные (q; p) и (Q; Р) могут принимать комплексные значения. В конкретных приложе-
приложениях окончательные результаты мы будем записывать в вещественной форме. Рассмотрим
§ 24.15] НЕКОТОРЫЕ ПРИМЕРЫ 503
простой пример. Положим в формулах B4.15.9) а = 1, Р = —i/n, где п —• вещественное
положительное число. Тогда будем иметь
=— (i/n)(p + inq), ~\/2P = p—inq. B4.15.21)
Если в формулах B4.15.20) положить k=i, то получим контактное преобразование
P = ie-lP "l/g + o. B4.15.22)
К этому результату можно также прийти, объединяя формулы B4.15.9) при а = 1 и 0 = i
и формулы B4.15.13).
Рассмотренные выше примеры относились к системам с одной степенью свободы,
обратимся теперь к системам с п степенями свободы. Простой пример дает расширенное
точечное преобразование (§ 24.4). В качестве иллюстрации рассмотрим переход от декар-
декартовых координат к полярным в случае плоского движения точки. В этом случае
<7i = х, д2 = у, Qi = г, Q2 = 9 B4.15.23)
и формулы B4.4.6) имеют вид
=sine, -,
= r(— pxsin&-\-pycosQ). J
Pr = Px cos Q + Py sine, p9 = r(— pxsin&-\-py
Контактные преобразования встречаются и во многих других случаях. Движение дина-
динамической системы определяет контактное преобразование (д0; р0) в (q; p). Кроме того, если
мы будем фиксировать траекторию в фазовом пространстве с помощью параметров (а; [3),
связанных с (q0; р0) соотношениями pr daT = рт0 dqr0, то преобразование от (а; р) к (д; р)
будет контактным (§ 24.1). В самом деле, подобное контактное преобразование мы полу-
получаем всякий раз, когда решаем задачу динамики с помощью теоремы Гамильтона — Яко-
би (§ 25.2). Можно, наконец, определить контактное преобразование с помощью произво-
производящей функции (§ 24.3); в дальнейшем, при исследовании задачи трех тел (гл. XXIX),
мы приведем много примеров контактных преобразований.
Глава XXV
ТЕОРИЯ ПРЕОБРАЗОВАНИЙ
§ 25.1. Уравнения движения после контактных преобразований. Рассмот-
Рассмотрим те видоизменения, которым подвергаются уравнения движения механи-
механической системы при переходе от старых переменных к новым посредством
контактного преобразования. Пусть динамическая система характеризуется
функцией Гамильтона Н (qt, q2, . . ., qn; pu р2, . . ., рп; t). Уравнения
движения запишем в виде
Ь-Ж> ^="^-' г = 1,2,...,п. B5.1.1)
Перейдем к новым переменным Qt, Q2, . . ., <?„, Pi, Р2, • • , Рп, связанным
со старыми контактным преобразованием, таким, что
Рт dQT = pT dqT + R dt — dW. B5.1.2)
Согласно известной теореме Якоби уравнения движения в новых пере-
переменных сохраняют гамилыпонову форму *).
Доказательство этой теоремы получается весьма просто из теоремы
эквивалентности (§ 16.3) и основного свойства контактного преобразова-
преобразования B5.1.2). Предположим, что решения уравнений B5.1.1) выражены через
2п независимых параметров -yi» Уг, ¦ • ¦, У2п (см. § 16.3). Тогда будем иметь
рТ dqT — Н dt = dip + со, B5.1.3)
где со есть пфаффова форма 2 &s ^Ys> причем К суть функции у. Кроме
8=1
того, равенство B5.1.3) показывает, что переменные q ш р удовлетворяют
уравнениям B5.1.1).
Чтобы описать движение в новых переменных Q и Р, нужно эти пере-
переменные выразить через параметры у и t посредством q и р. Из B5.1.3)
и B5.1.2) имеем
Рт dQr — (Н + R) dt = d (г|) — W) + со, B5.1.4)
и теорема Якоби теперь следует из второй части теоремы эквивалентности.
Новыми уравнениями движения будут
Qr^^r, РТ=--Щ^, г=1,2,...,п, B5.1.5)
где символом Н* обозначена сумма функций Н + R, выраженная через пере-
переменные Q, Р и t, что и составляет содержание теоремы Якоби.
Если контактное преобразование задается производящей функцией U
(см. B4.3.6), B4.3.7)), то новая функция Гамильтона Н* равняется сумме
Н + (dU/dt), выраженной через Q, Р и t. В частности, если уравнения' пре-
преобразования не содержат t, то новые уравнения Гамильтона в переменных
(Q; Р) получаются из функции Гамильтона Н*, которая равна исходной
функции Гамильтона Н, выраженной в новых переменных.
*) Доказательство того, что уравнения Гамильтона при контактных преобразова-
преобразованиях сохраняют свою форму, дано Якоби (Comptes Rendus, 1837, стр. 61).
g 25.1] УРАВНЕНИЯ ДВИЖЕНИЯ ПОСЛЕ КОНТАКТНЫХ ПРЕОБРАЗОВАНИЙ 505
Рассмотрим несколько частных случаев.
Если применить преобразование
qT^PT, pr = -QT, r = 1,2,..., п, B5.1.6)
уже встречавшееся нам в § 24.3 и в § 24.15, то новая функция Гамильтона
будет равна Н (Р; —Q\ t). В теории преобразований стирается различие
между координатами и импульсами; в частности, лагранжева координата
может играть роль составляющей импульса.
Рассмотрим другой важный частный случай. Пусть точка (<Zi, a^, .
. . ., ап; &i, Ъг, ¦ ¦ ¦ Ьп) будет стационарной точкой автономной системы
с гамильтоновой функцией Н, так что формулы qr = ат, рт = Ът будут опре-
определять равновесное решение уравнений Гамильтона. Рассмотрим произво-
производящую функцию
2 ()( ) B5.1.7)
r=l
Получаемое из нее контактное преобразование будет определяться уравне-
уравнениями
Чт = ат + Qr, pr = bT + Рт. B5.1.8)
Мы видим, что {Q; Р) характеризует отклонение от равновесного реше-
решения. Новая функция Гамильтона Н* имеет вид Н (а + Q; Ь + Р). Если
Н есть аналитическая функция, то, представляя ее в виде степенного ряда
по переменным Qr и Рг, найдем, что Н* не будет содержать линейных членов.
Линейное приближение к уравнениям движения мы получим, если в Н*
сохраним лишь члены второго порядка.
Рассмотрим более общий случай. Пусть qT = ur (t), pr = vT (t) будет
известным решением уравнений Гамильтона для автономной системы. Про-
Производящая функция
"%
U=2j (Qr-ur)(Pr + vr) B5.1.9)
r=l
дает контактное преобразование
gr = иг + Qr, Pr = Уг + Pr. B5.1.10)
Мы снова видим, что (Q; Р) характеризует отклонение от известного реше-
решения. Новая функция Гамильтона имеет вид
п п
H(u+Q; v+P)+ 2 QrVr- 2 PrUr, B5.1.11)
а уравнения движения записываются в форме
gr(u; v),
где через Hq обозначена частная производная dHldqT, а через Hv — про-
производная дН1дрг (см. § 16.2). Линейное приближение (т. е. уравнения в вариа-
вариациях) можно получить, раскладывая функцию Н (и -\- Q; v + Р) в ряд по
степеням Q и Р и сохраняя одни только квадратичные члены. Разумеется,
линейное приближение можно получить весьма просто и не пользуясь тео-
теорией контактных преобразований (см. B3.1.4)).
Преобразования B5.1.8) и B5.1.10) представляют расширенные точечные преобра-
преобразования весьма частного вида. В этих преобразованиях не только q являются функциями
от (Qi, Qz, ¦ ¦ -, Qn), но и р являются функциями от (Pi, Р2, ¦ ¦ ., Рп); далее, каждое qr
есть функция от соответствующего Qr и от if, а каждое рт — функция от соответствующего
Рг и от t.
506 ТЕОРИЯ ПРЕОБРАЗОВАНИЙ [Гл. XXV
Приведем еще один простой пример контактного преобразования, для
которого уравнения преобразования содержат t. Рассмотрим частицу еди-
единичной массы, движущуюся в плоскости под действием силы притяжения
к центру О. В неподвижных прямоугольных осях будем иметь
г = Ух* + z/a.
Применим контактное преобразование, получаемое из производящей
функции
U = Рх (я cos (at -\- у sin at) + PY {у cos (at — x sin co?), B5.1.14)
где о) — постоянная. Уравнения преобразования будут иметь вид
у sin со?, Y =
Рх = Рх cos cot — Pysincof, pj, == Рх sin at -f- ^*y cos
? B5 1 15)
s coi. J
Новой функцией Гамильтона будет сумма Н-{-(dU/dt), выраженная
через (X, Y, Px, PY):
H* = ^{P*x + PV)-<u(XPt-YPx) + V. B5.1.16)
Геометрический смысл такой замены очевиден: (X, Y) представляют
собой координаты частицы в системе осей, равномерно вращающихся с угло-
угловой скоростью со. В этих осях
, B5.1.17)
B5.1.18)
а функция Н* равна сумме T2-\-V — To, выраженной через (Рх, Рт) (вместо
X и У):
Н* = | {(Рх + УсоJ + (Рт - Xwy} + V - \ ^ (X* + У2) =
Y + V. B5.1.19)
Мы снова получили формулу B5.1.16).
§ 25.2. Вариация элементов траектории. Предположим, что нам уда-
удалось с помощью теоремы Гамильтона — Якоби найти решение уравнений
движения системы с функцией Гамильтона Н. Рассмотрим теперь другую
задачу, когда функция Гамильтона равна Н -\--К. Решение этой новой зада-
задачи получается, как мы покажем, путем интегрирования уравнений движения
гамильтоновой системы чрезвычайно простого вида.
Пусть S = S (qi, q2, • • •, qn', ai, cc2, • • •» an; t) есть известный пол-
полный интеграл уравнения в частных производных Гамильтона для исходной
системы. Рассмотрим преобразование (q; p) в (а; Р), определяемое уравне-
уравнениями
OS -ч
Яг gs г = 1,2,..., п. \ B5.2.1)
§ 25.2] ВАРИАЦИЯ ЭЛЕМЕНТОВ ТРАЕКТОРИИ 507
Это преобразование является контактным, поскольку
Рг da? = dc&r =¦ —dS -\—^—dq-p -j dt=^prdc[r — Н dt — dS. B5.2.2)
Рассмотрим теперь задачу, когда функция Гамильтона равна Н + К,
и составим уравнения движения в новых переменных (а; р). По теореме
Якоби (§ 25.1) новые уравнения движения будут иметь вид
• _ дК*
д\гш г = 1,2, ...,п, [ B5.2.3)
где К* обозначает функцию К, выраженную через а, (} и t. Это как раз мы
и хотели доказать.
Сделаем несколько замечаний, относящихся к полученному результату.
1) Если К = О, то, как показывают формулы B5.2.3), величины аир
постоянны, и мы получаем в точности теорему Гамильтона — Якоби.
2) Если К =Ф О, то решение новой задачи представляется в весьма инте-
интересной форме. В исходной задаче движение описывалось переменными q
и р, выраженными через t ш 2п постоянных (а; Р) Решение новой задачи
дается точно такими же формулами, что и решение исходной, с той лишь
разницей, что постоянные (а; Р) заменяются общим решением уравнений
B5.2.3). Это общее решение будет содержать 2п новых постоянных.
Новую задачу теперь можно интерпретировать следующим образом.
Можно считать, что в каждый момент времени движение происходит вдоль
одной из траекторий первоначальной задачи, но элементы (а; (}) этих траек-
траекторий не остаются постоянными (как это было в первоначальной задаче),
а изменяются с течением времени. Вместо того; чтобы переход от функции
Гамильтона Н к Н + К рассматривать как совершенно новую задачу, мы
теперь характеризуем влияние дополнительного члена К как непрерывное
изменение первоначального движения. Функцию К можно назвать пертур-
пертурбационной функцией. (В небесной механике возмущающая функция R обычно
представляет собой дополнительное слагаемое в выражении гравитацион-
гравитационного потенциала и К = —R.)
3) Доказанная выше теорема является точной. Однако она оказывается
особенно полезной в тех случаях, когда возмущение мало, т. е. когда К
содержит малый параметр ц, и требуется лишь приближенное решение для
малых значений ц.. Именно в этом случае представление о непрерывном
изменении исходного движения является особенно важным.
Пример 25.2А. Проиллюстрируем полученный результат на простом примере.
Возьмем в качестве исходной системы гармонический осциллятор, для которого
Я = у(л2?2+р2). B5.2.4)
Рассмотрим движение, которое возникает при наложении однородного поля g
К = —gq. B5.2.5)
Это движение легко получить из элементарных соображений, но мы его найдем с помо-
помощью только что доказанной теоремы.
Теорема Гамильтона — Якоби (§ 16.7) дает следующее решение исходной задачи:
q = a sin \nt f— ) ,
> B5.2.6)
р = па cos I nt — г .
\ па I
508 ТЕОРИЯ ПРЕОБРАЗОВАНИЙ [Гл. XXV
По доказанному выше задача о возмущенном движении имеет такое, же решение, но;
теперь а и Р являются общими решениями уравнений
где
•г- >"%¦•
= — gasin (nt—?~\ . B5.2.8)
Мы получили новую задачу Гамильтона. Решение ее удобно искать непосредственно,
не прибегая к теореме Гамильтона — Якоби. Имеем
в I В \
а =— cos I nt — I ,
п \ па !
S B5.2.9)
/ P\gP/ Р \
\ na I na \ na I
о
Обозначая разность nt — через 0, получаем
па
1
—j—L р=
па2 па
(g'sine +
B5.2.10)
= иЧ—(JLcos0^ — (gsine + —
1 па2 \ п I па \ па
Чтобы проинтегрировать уравнения B5.2.9), положим
A, = asin6, n = reacosG. B5.2.11)
Имеем
%—<х sin 6 + aG cosG =
= —cosGsinG + acose (n ^— sine) =nacosQ = u, B5.2.12)
n ' \ na I r '
• • •
|x = na cos 0 — naQ sin 0 =
= n cos G ( — cos 0 1 — n a sin G In — sin 0 ] =
\ n I \ na I
= g — n2asinQ = g — n^K. B5.2.13)
Следовательно,
X=-^+A sin n(t—t0), p= nA cos n(t — t0), B5.2.14)
и решением задачи о возмущенном движении будет q = Я, р = ц.
Пример 25.2В. Простой маятник; второе приближение.
Отсчитывая угол 0 от направленной вниз вертикали, находим (см. пример 5.2А)
L— cos 9), B5.2.15)
или, полагая n2 = gja и ma2 = l,
r=i-92, F = 7i2(l — cos 6). B5.2.16)
Тогда р = 0, и функция Гамильтона принимает вид
p + n (l — cose). B5.2.17)
Если амплитуда колебаний маятника мала, то в первом приближении можно написать
1ге202. B5.2.18)
•§ 25.2] ВАРИАЦИЯ ЭЛЕМЕНТОВ ТРАЕКТОРИИ 509
В качестве второго приближения можно взять задачу с функцией Гамильтона
Н+К, где
К=—^пЮК B5.2.19)
Если с помощью теоремы Гамильтона — Якоби получить решение первой задачи
{задачи о гармоническом осцилляторе), то решение второй задачи будет отличаться только
тем, что аир более не будут постоянными, а будут определяться общим решением урав-
уравнений B5.2.3).
Для первого приближения уравнение в частных производных Гамильтона имеет вид
и полный интеграл равен
<S= — nat+ l /2;га —и2ф2йф. B5.2.21)
О
{Для наших целей это выражение несколько удобнее, нежели A6.7.7).) Решением задачи
¦будет р = dS/dQ, р = —dS/da, откуда находим
B5.2.22)
р = ~)/2па cos (nt—Р).
Решение задачи второго приближения дается этими же формулами, но символы а
а Р теперь обозначают решение уравнений B5.2.3), в которых
К*= — -|- a2 sin* (nt— P) = — ^ а2 {3— 4 cos 2 (nt— p) -f cos 4 (nt— p)}. B5.2.23)
Таким образом,
06 = ^ a2 {2 sin 2 (rc*—P) — sin4(wf—P)}, "j
B5.2.24)
1
Р =7г7 а {3— 4 cos 2 (nt— P) + cos 4 (nt— p)}.
Если амплитуда колебаний мала, то мала и величина а, а производная а равна про-
произведению а2 на периодический множитель; поэтому величину а можно считать постоян-
постоянной. В соответствии с этим главный член в выражении для р можно записать в виде
Р' + " at> гДе Р' ~ постоянная. Таким образом, следующее (после B5.2.22)) прибли-
о
жение для G дается формулой
e = |/-^-sin {(и — -g- ol\ t—P'| B5.2.25)
или, если ввести амплитуду А,
6 = .4sin jra(l —-^-Л t+p' |. B5.2.26)
Период колебания приближенно равен
{В § 5.2 мы нашли .лучшие приближения, например, приближение at для величины
дает следующее выражение для периода:
B5-2-28)
Приближенно оно совпадает с B5.2.27).)
Подойдем теперь- к решению задачи о маятнике с иной точки зрения. Возьмем
функцию Гамильтона B5.2.23) и перейдем от переменных (а, Р) к переменным (а1, Р')
510 ТЕОРИЯ ПРЕОБРАЗОВАНИЙ [Гл. XXV
с помощью контактного преобразования, определяемого производящей функцией U[{a, Р'):
l3nt—2sin2(wi— р') + —sin4(wi — р') L. B5.2.29
J7 = ap+__
Тогда будем иметь
-^ = -^ {3- 4 cos 2 (ni— P') + cos 4 (ret- p')}. B5.2.31)
В новых переменных функция Гамильтона будет иметь вид K*-\-{dU/dt). Таким образом,
К* +-^ = JL «2 {4 [cos 2 (nt— P)-cos 2 (nt— p')] —
— [cos 4 (/if — p)— cos 4 (/if — p')]}, B5.2.32
причем правую часть надлежит выразить через а', Р', f. Но а мало отличается от а',
ар — от Р'; поэтому новая функция Гамильтона близка к нулю и а' и р' почти постоян-
постоянны. Отсюда, как и ранее, приходим к равенству р = р' -)—g- at.
о
§ 25.3. Вариация эллиптических элементов. Задача о движении двух
тел (например, Солнца и планеты) под действием сил взаимного притяжения
может быть рассмотрена на основе изложенной выше теории. Здесь требует-
требуется выяснить, каково изменение во времени эллиптических элементов а, е,
i, t0, uQ, ф0 (§ 18.13), вызванное малым возмущением.
В свое время мы уже определили с помощью теоремы Гамильтона —
Якоби связь эллиптических элементов с величинами аир. Она выражается
следующими формулами (см. A8.13.16)):
Pi = |
B5.3.1)
. — e2)cosi, P3= — ф0.
Разрешая эти уравнения относительно эллиптических элементов, получаем
^ , _я *
B5.3.2)
1 . О-з о
COS Ь —~ . Фп — — Рч*
«2
Зададимся пертурбационной функцией К* (а; Р; t); выражая ее через
переменные а, е, i, t0, и0, ф0 и t, получаем возмущающую функцию R:
К* (а; Р; t) = — R (a, e, i, tQ, u0, ф0; t). B5.3.3)
Составим теперь уравнения, определяющие зависимость величин а, е,
i, t0, щ, ф0 от времени. Для этого перейдем в уравнениях B5.2.3) к эллип-
эллиптическим элементам. Этот переход произведем в два этапа3 сначала выразим
производные а, . . . через а, . . ., т. е. через дК*/да1, . . ,, а затем выразим
величины дК*1да.1, . . . через dRIda, . . .
25.3]
ВАРИАЦИЯ ЭЛЛИПТИЧЕСКИХ ЭЛЕМЕНТОВ
511
Таким образом, осуществляя первый этап, получаем
;_ ц д _ 2а2 dK*
дК*
. . di
- SHI I -тг- =
cos i
V]M A -
1
A — е2)
щ= — P2 =
A dK*
Ч>°==-Рз = -а5Г-
Осуществляя второй этап, получаем
dK* dR da dR de ц с
da
de
ал:* ад а« ад аг
аа2 di
Щ да ц2е de
_ _2а^_ dR _ о A-е2)
[х аа [ле
2a!a2 аД а3 аД
М.2е ае a! sin j ai
аД дг
1 ад
ctgt ад
Уца A — e'i) di
dR
да3
дК*
Эр! "
ал:*
ар2 ~
dK*
di дщ
dR
dt0 '
dR
¦ duo>
dR
ар3 аф0'
Из этих формул
; K2 Sin
находим
2
a=
* a
di
* У(Х
; _ 2a2
"o e ^/
t a;
;a2 5д
jx dt0
A-е2;
lie
ctgi
0A—Й
ад
aa '
/l-e
1
sin i
) ад
i~V[xa A — e
1 ,/1
dt0 e У
dR
.2) a;
o(l-
(i.
2 ад
de
*o sin i"]/
-&) dR
s ae '
ctg
V|ia(l
ад
.2)
— <
ца
1
i
г* ад
du0 '
ад
A-е2) Сфо
ад
.2) а/ '
sin
B5.3.4)
B5.3.5)
B5.3.6)
512 ТЕОРИЯ ПРЕОБРАЗОВАНИЙ [Гл. XXV
Эти уравнения определяют изменение эллиптических элементов со вре-
временем *).
Исследуем сначала возмущение движения планеты, вызываемое нали-
наличием другой планеты. В § 18.7 мы нашли выражение для возмущающей функ-
функции R через координаты обеих планет относительно Солнца, и, чтобы исполь-
использовать его в уравнениях B5.3.6), следует перейти к эллиптическим элемен-
элементам планет. Всего получается двенадцать уравнений, поскольку элементы
а', е', i', t'o, u'o, (p'n второй планеты также немного изменяются со временем.
Исследование этой системы уравнений составляет одну из важнейших задач
небесной механики; не имея возможности привести его здесь во всей пол-
полноте, ограничимся несколькими замечаниями.
Так как массы планет mi и т2 малы по сравнению с массой Солнца М,
то решения уравнений можно искать в форме
а'2+ ..., B5.3.7)
и аналогично для остальных элементов. Здесь а0 обозначает начальное зна-
значение а; «! имеет первый порядок относительно mJM и т2/М; а2 — второй
порядок и т. д. Об этих величинах можно говорить как о возмущениях пер-
первого и второго порядка, и аналогично для других элементов. Если мы хотим
ограничиться возмущениями первого порядка, то вычисления упрощаются,
поскольку функция R сама имеет первый порядок и в правых частях урав-
уравнений B5.3.6) элементы обеих планет можно считать постоянными и равными
их начальным значениям. Правые части B5.3.6) с принятой степенью точ-
точности можно считать известными функциями от t, и решение этих уравне-
уравнений может быть найдено по способу механических квадратур.
Наиболее распространенный способ отыскания решения общей задачи
состоит в разложении функции R в ряд вида 2 CcosD, где
v[V + v2u0 + v'2u'Q + v3q>0 + v^. B5.3.8)
Здесь v и v' — целые числа, положительные, отрицательные или нули,
а коэффициенты С зависят от шести параметров: а, а', е, е , i, V. Во многих
приложениях достаточно бывает нескольких членов, чтобы получить высо-
высокую точность приближения. Тем не менее некоторые теоретические вопросы,
например вопрос о сходимости рядов, остаются пока нерешенными.
В более общих задачах о движении планет функция К* задается рядом
К* =т ^ cs («) cos Ds, , B5.3.9)
s
где т — малый постоянный параметр, коэффициенты С зависят от а, а функции Ds опре-
определяются выражениями
*\, = 2v«fo + /l*i' B5.3.10)
i
где v — целые числа, положительные, отрицательные или равные нулю. Будем предпо-
предполагать сначала, что ни одно из чисел ns не равно нулю. Вариации параметров а и Р опре-
определяются уравнениями B5.2.3).
*) Уравнения B5.3.6) имеют форму, несколько отличающуюся от принятой среди
астрономов. Они определяют изменение эллиптических элементов в зависимости от вре-
времени и не очень удобны для теории движения планет. Если функцию R представить в фор-
форме B5.3.8), то, учитывая, что п зависит от а, будем иметь
dR xi дС „ . дп -л п ¦ г.
да ^-i да да ZJ *
То обстоятельство, что в некоторые члены входит множитель t, вызывает определенные
трудности. Со способами преодоления этих трудностей в астрономии можно познакомить-
познакомиться в работе: Tisserand, Traite de Mecanique Celeste, Tome I, Ch. XI.
S 25.4] ДРУГИЕ ДОКАЗАТЕЛЬСТВА ТЕОРЕМЫ ЯКОБИ 513
В этой задаче удобно перейти от переменных (а; E) к переменным (а'; р") посредст-
посредством контактного преобразования с производящей функцией U (а'; Р):
и^-У.а'^-т 2— С, (о') sin Д.. B5.3.11)
i s
Уравнения B4.3.3), B4.3.4) принимают при этом вид
-33- B5.3.12)
Отсюда получаем
аТ -^a'r+m V — Cs (a') cos Ds,
4—i ns
B5.3.13)
Кроме того,
•|-=-m2c» («') c<>s Ds. B5.3.14)
s
Новой функцией Гамильтона будет функция
™ 2 {?„(«) — Сs (a')} cos Dg, B5.3.15)
записанная в переменных а', р" и i. Здесь а{. отличаются от аг (а Р{. — от pV) на величину
порядка тп, поэтому новая функция Гамильтона имеет порядок т2.
Если в разложении функции К* содержатся члены t л, = 0, то соответствующие
члены в B5.3.11) следует опустить. Кроме того, бывает удобно опустить также и долго»
периодические члены, т. е. члены с малыми, но отличными от нуля значениями ns. Важно
отметить, что короткопериодические члены порядка т исчезают из выражения функции
Гамильтона в результате канонического преобразования.
§ 25.4. Другие доказательства теоремы Якоби. В § 25.1 мы привели
доказательство теоремы Якоби об инвариантности формы уравнений движе-
движения по отношению к контактным преобразованиям. Это доказательство осно-
основывалось на теореме эквивалентности и, возможно, является простейшим.
Тем не менее ввиду важности теоремы Якоби мы приведем еще два доказа-
доказательства ее, каждое из которых представляет самостоятельный интерес.
Одно из них связано с рассмотрением производящих функций контактных
преобразований (§ 24.2 и § 24.3) и включает в себя некоторые приемы,
которые окажутся полезными впоследствии. Другое доказательство осно-
основано на использовании симплектического свойства матрицы М (§ 24.13);
оно показывает, между прочим, что контактное преобразование не является
самым общим преобразованием, при котором уравнения Гамильтона сохра-
сохраняют свою форму.
Второе доказательство теоремы Якоби. Будем определять
контактное преобразование с помощью производящей функции. Для определенности
возьмем случай, когда преобразование не связано с какими-либо предварительными тож-
тождественными соотношениями между переменными q, Q и t. В этом случае уравнения т/рр-
образования записываются в форме B4.2.7) — B4.2.9):
Докажем сначала две леммы.
Лемма 1. Предположим, что общее решение уравнений Гамцльтона имеет, вид
?r=qv(Yi.Y*...,Y»r,*), r Л^....п\ B5.4.2)
33 Л. л. Парс
514 ТЕОРИЯ ПРЕОБРАЗОВАНИЙ [Гл. XXV
где функции ср принадлежат к классу С2 области. D пространства (yit у2, . . ., у2п; t).
Пусть, далее,
Н (q; p; t) = G (уи у2, . . ., у2п; t). B5.4.3)
Тогда G g С2 и
-^¦ = [*,7il. t = l,2, ..., 2и. B5.4.4)
Доказательство следует немедленно, поскольку
8G
__ дН ддг дН дрТ _ dqr дрг дрг dqr
;>„ д.. i д„ з.. л* д„. Л4. з.. >
dyt dqr dyt dpr dyt dt dyt dt dyt
где повторяющийся индекс г означает суммирование от 1 до п. Лемма, таким образом,,
доказана.
Лемма 2. Обратно, пусть qit q%, . . ., qn; pi, p2) • • •> Pn суть Ъп независимых
функций класса С2 от переменных yi, y2, ¦ . ., yzn> t- Если существует функция
G (yi, y2, . . ., у2п', t) такая, что
^--.[t,yt\, i-=l,2, ..., In, B5.4.4)
то переменные q и р удовлетворяют уравнениям Гамильтона
dqr _дН дрг _ дН_
n,
в которых функция Н получается из функции G, если последнюю выразить через q, p и t:
G(y; t) = H(q; p; t). B5.4.7)
Разрешим уравнения B5.4.2) относительно переменных у, выразив их, таким обра-
образом, через q, p и t, и составим функцию Л в соответствии с B5.4.7). Тогда будем иметь
dG _ dH dqT dH dpr
—— — —— — ¦ —i ~ —™ . 1 ^jU.*±.U /
dyt dqr dyt dpT dyt
С другой стороны, из B5.4.4) получаем
^__^Яг_^Рг^__^Р^^Яг_ B549)
dy^ dt dy^ dt dy^
Сравнивая B5.4.8) и B5.4.9), находим
Всего имеем 2п таких соотношений, по одному для каждого из индексов i; определи-
определитель этой системы 2п однородных уравнений не равен нулю, откуда и следует утвержде-
утверждение леммы.
Читатель, без сомнения, заметит тесную аналогию между доказанными леммами
и двумя частями теоремы эквивалентности (§ 16.3). Приводимое ниже доказательство тео-
теоремы Якоби по существу мало отличается от доказательства, данного в § 25.1, различие
между ними заключается лишь в деталях.
Перейдем теперь к доказательству теоремы Якоби. Переменные g4, q2, . . ., qn,
Pi, p2, . . ., рп, определяемые соотношениями B5.4.2), удовлетворяют уравнениям
Гамильтона B5.4.6). Перейдем в них кновым переменным Qt, Q2, . . ., Qn, Pi, P2, . . ., Pn
с помощью контактного преобразования B5.4.1). Выразим функцию W через у и t:
W (<?; Q;t) = F (y; *)• B5.4.11)
Тогда для i, принимающих любое из значений 1, 2, . . ., 2п, будем иметь
dF _ dW dqr , dW dQr _ dqr „ dQr .
dyt aqT dyt dQr dyt dyt dyt
и
dF dW dqr , dW dQr . dW dqr _ dQr , dW ,„_ . ,„,
dt dqr dt "•" dQr dt ^ dt ~Fr dt T dt ^ dt ' y >
Функция F ? C2, и, следовательно,
-ггд—=-—jr-. B5.4.14)
oi dyt dyt dt
§ 25.4] ДРУГИЕ ДОКАЗАТЕЛЬСТВА ТЕОРЕМЫ ЯКОБИ 515
Из B5.4.12) и B5.4.13) получаем
Таким образом,
dQr дРг дРг dQr dqr дрт дрг ддг
— ....
dt dyt dt dyt dt dyt dt dyt ~ dyt dt
_ OH dPr dH dgr 3W _ д I dW \_ dG
dpr dyt + dqr dyt + dyt dt - dyt \" + dt I' dyt '
dW
мму H-\-—^—, выраженную че
чить скобки Лагранжа для (Q; Р), то будем иметь
dW
где G обозначает сумму H-\-—^—, выраженную через у и t. Если через [[t, yt]] обозна-
обознаB5.4.17)
Отсюда, в соответствии с леммой 2, заключаем, что переменные Qu Q2, ..., Qn,
^2' •••> Рп удовлетворяют уравнениям Гамильтона
dW
где H* обозначает сумму Н -f- —— , записанную в переменных Q, Р и t. Теорема Якоби,
ОС
таким образом, доказана.
Аналогично проводится доказательство и в других случаях. Допустим, например,
что между переменными q, P и t нет никаких тождественных соотношений, и возьмем кон-
контактное преобразование с производящей функцией U (q; P\ t), определяемое уравнения-
Q2f ffip
ми B4.3.9). Если U (q; P; t) = F (у; t), то уравнения ———= -—— приведут к форму-
формуем oyi oyidt
лам B5.4.17), откуда и следует утверждение теоремы.
Третье доказательство теоремы Якоби. Мы виде-
видели в § 22.1, что уравнения Гамильтона могут быть записаны в форме
x = ZHx, B5.4.19)
где х — матрица-столбец, составленная из элементов хг, а Шх — матрица-
столбец, составленная из элементов дН1дхт. Перейдем к новым переменным
Ai, Л 2, . . ., Л 2п.
Хт = фг (хи х2, . . ., х2п; t), г = 1, 2, . . ., 2га, B5.4.20)
причем будем считать это преобразование обратимым в некоторой области
пространства (х; t). Тогда будем иметь
х — -^--\-тХ, НХ — М'КХ, B5.4.21)
где через К обозначена функция Гамильтона, выраженная через переменные
Xi, Х2, . . ., Х2п, U
Н(хи х2, . . ., х2п; t) =К(Хи Хг, . . ., Х2п; t). B5.4.22)
Здесь т обозначает матрицу (dxT/dXs), а М — матрицу {dXr!dxs) (см. § 24.13).
Таким образом,
Л/—?jXlx — —дт—г НИ А.—?jJXL Л-х, \ijOA.LiO)
и, следовательно,
1Х. B5.4.24)
33*
516 ТЕОРИЯ ПРЕОБРАЗОВАНИЙ [Гл. XXV
В новых переменных уравнения движения запишутся в-форме
-JMi5JM д^-М-^- B5.4.25)
или
, ,,, дх
B5.4.26)
До сих пор мы не делали никаких предположений относительно харак-
характера преобразования координат. Теперь мы предположим, что это преобра-
преобразование является контактным. Для контактного преобразования
MZM' = Z B5.4.27)
и уравнения движения в новых переменных принимают гамильтонову форму
B5.4.28)
дх
при условии, что матрица-столбец т'Zi — имеет вид Lx. Доказать это
весьма просто. Если временно обозначить Z -^- через и, то указанное
условие будет состоять в том, что для всех значений г и s
д
dXs
/
dui
дХп
dxi '
дХГ1
dxi
дХ„
\ ^
1 дХТ
диг
дХ„
I dxi
\U' dXs
dxt
дХ. '
B5.4.29)
или, что то же,
Последнее равенство выполняется в том случае, если матрица m'Zmt
(где nit получается из т дифференцированием каждого элемента частным
образом по t) является симметрической, т. е.
m'Zmt = m'tZ'm. B5.4.31)
Так как Z' = —Z, то условие B5.4.31) эквивалентно следующему:
0. B5.4.32)
Это означает, что матрица ¦nn'Zm не зависит от времени, что, несомнен-
несомненно, имеет место в силу B4.13.7). Теорема Якоби, таким образом, доказана.
Рассмотрим преобразование, удовлетворяющее более общему условию,
нежели B5.4.27), а именно:
MZM' = XZ, B5.4.33)
где Я —скалярный множитель, отличный от нуля. При этом справедливо
равенство
mZm' = ~Z B5.4.34)
и новые уравнения движения сохраняют, как и прежде, гамильтонову фор-
форму B5.4.28). Условие B5.4.33) представляет обобщение условия B5.4.27);
поэтому, вообще говоря, целесообразно расширить понятие контактного
преобразования и включить в него более широкий класс преобразований,
удовлетворяющих условию B5.4.33). Однако мы сохраним это,название за
преобразованиями, для которых X = +1.
Обратно, если мы будем исходить из общего преобразования B5.4.20)
и будем искать условия, при которых новые уравнения движения B5.4.26)
сохраняют форму Гамильтона, то придем к выводу, что преобразование
§25.6] БЕСКОНЕЧНО МАЛЫЕ КОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ 517
должно удовлетворять условию B5.4.33). Действительно, правая часть урав-
уравнения B5.4.26) должна иметь форму ZHx для любой функции Гамильто-
Гамильтона Н, откуда следует, что такую форму должен иметь каждый член этой
части. Отсюда приходим к равенству B5.4.33).
§ 25.5. Постоянство скобок Лагранжа. Если общее решение уравнений Гамильтона
для заданной динамической системы имеет вид
V2, •••. Y2n; *). \ B5.5.1)
Y 7! t) )
то скобка Лагранжа [yi, yj] сохраняет постоянное значение в течение всего времени дви-
движения.
Как мы знаем, эта теорема справедлива, когда параметры у представляют начальные
значения переменных q ж р; в самом деле, в этом случае переменные (q0; p0) и (q; p) связа-
связаны уравнениями контактного преобразования, и мы имеем
[?joi 4jo\ = \-Pio, Pjo] = 0, [qi0, pJ0] = б|. B5.5.2)
Отсюда можно получить доказательство и для общего случая. Однако проще вос-
воспользоваться билинейным ковариантом (§ 24.8). Как известно, выражение
dqrbpr — dprbqr B5.5.3)
при контактных преобразованиях сохраняется неизменным; в частности, оно остается
постоянным во время движения механической системы. Обозначим через d вариацию
траектории в фазовом пространстве, обусловленную изменением одного только yt, а через
б — вариацию траектории, обусловленную изменением одного только yj. Тогда будем
иметь
= [Yi> 7j] dy^yj (не суммируется), B5.5.4)
откуда и следует сформулированная выше теорема.
К этому результату можно прийти и из рассуждений § 25.4, касающихся второго
способа доказательства теоремы Якоби. Как и в B5.4.3), положим
Н (q\ p; t) = G (у; t), B5.5.5)
при этом G g С2 и
(см. B5.4.4)). Легко убедиться в справедливости тождества
[
ж[ъ> ^]+^т[t' т*]+4г[ур t]==0' B5-5'7)
которое аналогично тождеству Пуассона (§ 22.2). Отсюда получаем
д ,_д д д dG д dG _„
Ж17*' Ч*1 "'ду^[ ' yji~ d7j [t> yii~~dy~~dy~~~dy~J dyt '
Теорема, таким образом, доказана.
§ 25.6. Бесконечно малые контактные преобразования. Уравнения
дргд B5.6.1)
в которых [х — малый параметр и <р ? С2, определяют контактное преобра-
преобразование, если пренебречь членами порядка и2 (§ 24.5). Расстояние на фазо-
фазовой плоскости между точками (q; p) и (Q; Р) является малой величиной
порядка [х. Во всех последующих выкладках величинами порядка и2 мы будем
пренебрегать; поэтому в членах, в которые входит (я в качестве множителя,
518 ТЕОРИЯ ПРЕОБРАЗОВАНИЙ ГГл. XXV
можно не делать различия между старыми и новыми переменными, что суще-
существенно упрощает вычисления.
Рассмотрим некоторую функцию /,(gb д2, ¦ ¦ ., qn\ Pi, Pi, ¦ ¦, Рп, t)
(или, короче, / (q; p; f)) от переменных q, p и t; пусть она принадлежит
к классу С2. Легко указать простую формулу для приращения этой функ-
функции при переходе от (q; р;) к (Q; Р) при фиксированном t. С точностью
до величин порядка и. имеем
f{Q\P\ t)-f(q;p; t) = (QT-qT)-%L+iPT-pT)-IL =
_.. df ^Ф „ d'f df _..// m\ /OK fi ov
В соответствии со сказанным выше, в выражении и. (/, ф) нет необходимости
делать различие между старыми и новыми переменными.
Рассмотрим систему с функцией Гамильтона Н (q; p; t) и подвергнем
ее бесконечно малому контактному преобразованию B5.6.1). После пре-
преобразования система будет иметь функцию Гамильтона Н*, равную
^ B5.6.3)
и выраженную через (Q; Р; t) (§ 25.1). Согласно B5.6.2) будем иметь
#*(<?; Р; t) = H(Q; P; *)-ц(#, Ф) + ,х-^ =
{^ } B5.6.4)
Во втором члене правой части этого равенства можно вместо qr, pT написать
Qr, Pr, в результате получим требуемое выражение для функции Н* в новых
переменных QT, PT.
Особый интерес представляет следующий частный случай. Предполо-
Предположим, что функция ф (g; p; f) есть интеграл исходной гамильтоновой системы.
Тогда, согласно B2.2.5), выражение
-^+(Ф,#) B5.6.5)
будет тождественным нулем, и новая функция Гамильтона по форме не будет
отличаться от старой; разница будет состоять лишь в том, что вместо старых
переменных мы будем иметь соответствующие новые переменные. Поэтому
в рассматриваемом; случае семейство траекторий в пространстве (Q, Р) не
отличается от семейства траекторий в пространстве (q, p). Преобразование
переводит всякую траекторию системы в другую (близкую) траекторию.
В этом случае говорят, что система допускает преобразование.
Можно дать новое, весьма изящное доказательство теоремы Пуассона
(§ 22.3). Возьмем в качестве функции ф известный интеграл исходной систе-
системы Гамильтона, при этом семейство траекторий в фазовом пространстве
преобразуется само в себя, т. е. каждая траектория преобразуется в другую,
близкую траекторию системы. Если т|) (g; p; t) есть другой интеграл уравне-
уравнений Гамильтона, то приращение его при контактном преобразовании
(т. е. разность г|з (Q; P; t) — г|з (q; p; t)) будет равно и. (г|з, ф); эта последняя
величина остается постоянной, поскольку преобразованная траектория
является одновременно траекторией исходной системы. Таким образом,
(ф, ф) является функцией от (g; p; t), которая сохраняет постоянное значе-
значение вдоль траекторий гамильтоновой системы, иными словами, если ф и
¦ф — известные интегралы уравнений Гамильтона, то (г|з, ср) также будет инте-
интегралом этих уравнений, и теорема Пуассона, таким образом, доказана.
§ 25.7] ИНТЕГРАЛЫ В ИНВОЛЮЦИИ 519
§ 25.7. Интегралы в инволюции. Ранее (в § 24.14) было показано, что
если мы имеем систему из п функций фг (g; p; t) класса С2, находящихся
в инволюции (т. е. таких, что скобка Пуассона любой пары функций тожде-
тождественно равна нулю), и если якобиан
i, ф2, ••-, Фп)
д{Ри Р2, •••> Рп)
не обращается тождественно в нуль в соответствующей области простран-
пространства (q; p; t), то существует контактное преобразование, переводящее
(д; р) в (Q\ P), в котором
Qr = ц>г (g; p; t), г = 1, 2, . . ., п. B5.7.1)
Мы видели, что если уравнения B5.7.1) разрешить относительно р и полу-
получить соотношения вида
Рг = ч>г (?; <?; t), B5.7.2)
то будем иметь
-Jk = -Jk, B5.7.3)
dqs dqT v '
откуда следует, что существует функция W (q; Q; t) такая, что
Ъ = Щ-. B5.7.4)
Соответствующее контактное преобразование задается уравнениями
dW п . Ж . о
B5.7.5)
Выясним теперь, как изменятся эти результаты, если в качестве функ-
функций ф взять п интегралов динамической системы с функцией Гамильтона Н.
Как известно, в новых переменных {Q; Р) уравнения движения имеют гамиль-
SW
тонову форму и характеризуются функцией И*, равной сумме Н -\—— ,
записанной в переменных Q, Р и t. Но Q, будучи интегралами, не изменяются
при движении, откуда следует, что Н + -or не может содержать ни одного
Р. Мало того, мы всегда можем выбрать такое контактное преобразование,
которому соответствует функция Н*, тождественно равная нулю. Отсюда
следует, что Р, как и Q, остаются неизменными в процессе движения. Следо-
Следовательно, если известны п интегралов, находящихся в инволюции, то суще-
существуют еще п однозначных интегралов. Совокупность 2п интегралов дает
возможность построить полное решение задачи.
Докажем сначала, что функция G (q; Q; f), получающаяся из
Н (q; p; t) путем исключения рг с помощью B5.7.2), удовлетворяет урав-
уравнениям
^ + ^ = 0, г=1,2, ...,». B5.7.6)
Если в правой части B5.7.2) заменить Qr их выражениями B5.7.1), то полу-
получим тождественные соотношения относительно переменных (q; p; t); продиф-
продифференцировав их по qs, ps, t, получим
*fcL + ^L*EL = 0. B5.7.7)
dqs r dQt dqs K '
Wdp7~ " ( }
Поскольку фг являются интегралами уравнений движения, то
^+(фь Я) = 0. B5.7.10)
520 ТЕОРИЯ ПРЕОБРАЗОВАНИЙ [Гл. XXV
Используя соотношение B5.7.9), получаем
dt - dQt \ dqs dps dq, dp
откуда с помощью B5.7.7) и B5.7.8) находим
д$г _ дН «% дН
~di -^7^7-^7- B5./.12)
Но, с другой стороны,
K** + *L*k.. B5.7.13)
dqr dqr ' дра dqr v '
Правые части B5.7.12) и B5.7.13) в силу B5.7.3) отличаются только знаками,
откуда следует B5.7.6).
Теперь легко доказать теорему. Из равенств B5.7.3) и B5.7.6) следует,
что существует функция W (q; Q; t) такая, что
Если теперь совершить контактное преобразование, получаемое из произ-
производящей функции W (см. формулы B5.7.5)), то новая функция Гамильтона
Н* будет равна сумме G + ir, записанной в переменных (Q; P; t).
Но согласно B5.7.14) функция Н* тождественно равна нулю, откуда и сле-
следует теорема. Функции Р от (q; p; •?) образуют п новых интегралов исход-
исходных уравнений Гамильтона. Эти интегралы находятся в инволюции (в силу
условий для скобок Пуассона, выполняющихся при контактных преобразо-
преобразованиях, см. § 24.9).
Теорему можно представить в несколько иной форме. Разрешим урав-
уравнения
Фг (q\ P; t) = ar, r = 1, 2, . . ., га, B5.7.15)
относительно р, выразив их в виде
Рг = г|)г (q; a; t), r = 1, 2, . . ., п. B5.7.16)
Подставив теперь эти выражения для рг в Н (q; p; t), образуем функцию
G = G(q; a; t). B5.7.17)
Тогда выражение
yrdqr — Gdt B5.7.18)
будет полным дифференциалом dW функции W (q; a; t), а остальные
п интегралов гамильтоновой системы определятся формулами
-Рг = |^, г=1,2, -.., п. B5.7.19)
Теперь становится очевидной тесная связь доказанной теоремы с теоре-
теоремой Гамильтона — Якоби. Зная п интегралов в инволюции, мы можем
построить функцию W по полному дифференциалу B5.7.18), и так как
if^H, B5.7.20)
то функция W действительно представляет полный интеграл уравнения
Гамильтона в частных производных.
Теорема принимает еще более простой вид, когда функции Я и ф н&
содержат t. В этом случае мы имеем п интегралов в инволюции
фг (g; p) = ссг, г = 1, 2, . . ., п, B5.7.21)
где
ф1?=#(?;р), B5.7.22)
§ 25.8] ТЕОРЕМА ЛИ О СИСТЕМАХ В ИНВОЛЮЦИИ 521
a at обозначает постоянную энергии. (Интегралы <р2, ф3, . . ., <рп"находятся^
в инволюции с ф! = Н и, следовательно, друг с другом.) Разрешая уравне-
уравнения B5.7.21) относительно р, находим
Рг =tr(g; a), B5.7.23)-
причем функции я|)г равны
Ь = ^, B5.7.24).
где K=K(q; а). Функция W равна —а$-\-К, и остальные п интегралов;
имеют вид
дК
t — t(j, I
B5.7.25>
Эти уравнения имеют вид, аналогичный уравнениям A6.5.5) — A6.5.7),
полученным из теоремы Гамильтона — Якоби. Частный случай п = 2
нами был исследован раньше с помощью теоремы о последнем множителе
(§ 22.13).
§ 25.8. Теорема Ли о системах в инволюции. В предыдущем параграфе
мы рассматривали систему функций щ, и2, . , ., uN класса С2 в некоторой*
области!) от переменных (^i, g2> • ¦ • > Яп\ Pt, Т>г-< • • •> Vn\ t), причем скобка
Пуассона (ur, us) любой пары этих функций тождественно равнялась нулю.
Такую систему функций мы называли системой в инволюции.
Докажем теперь следующую теорему. Если функции
v — v (щ, и2, . . ., uN), w = w (щ, и2, . .'., uN) B5.8.1)'
от переменных (щ, и2, . . ., uN) принадлежат к классу С2 в области значе-
значений и, соответствующей области D значений переменных (q; p; t), то
(у, w) = 0. B5.8.2)-
Доказательство легко получить путем непосредственного дифференци-
дифференцирования, однако для наших целей предпочтительнее воспользоваться тео-
теорией контактных преобразований. Напомним, что бесконечно малое кон-
контактное преобразование B5.6.1) переводит функцию / в самое себя, если
(ф, /) = 0.
Рассмотрим бесконечно малое контактное преобразование, когда ф = щ.
Это преобразование переводит каждую из функций иг в самое себя; то же-
относится и к функции v. Следовательно, (щ, и) = 0, и точно так же
(ur, v) = 0, г = 1, 2, . . ., N.
Рассмотрим теперь бесконечно малое контактное преобразование, когда
Ф = v. При этом преобразовании каждая из функций щ, и2, . . ., uN пере-
переходит в самое себя; то же относится и к функции w. Следовательно, (v, w) =
= 0, и теорема, таким образом, доказана.
Эту теорему можно выразить несколько в иной форме, что часто оказы-
оказывается удобным. Предположим, что уравнения v = 0, w = 0 являются след-
следствием уравнений ut = 0, и2 = 0, . . ., uN = 0. Тогда {v, w) = 0. В такой
формулировке эта теорема известна как теорема Ли.
Воспользуемся теоремой Ли для доказательства одного утверждения,
уже доказанного нами ранее в § 24.14 и § 25.7; теорема Ли в сильной сте-
степени упрощает все рассуждения. Пусть имеются п функций ф(, <р2, . . ., фп,
522 ТЕОРИЯ ПРЕОБРАЗОВАНИЙ |Гл. XXV
находящихся в инволюции. Если разрешить уравнения
От - Фг (q; p; t) = 0 B5.8.3)
относительно переменных р и представить их в форме
Рг - ¦Фг ig; <?; t) = о, B5.8.4)
то будем иметь
Это равенство было выведено нами в § 24.14 путем довольно длинных
рассуждений; теперь можно показать, что оно является непосредственным
•следствием теоремы Ли. В самом деле, если параметры Q рассматривать
как постоянные, то уравнения B5.8.4) оказываются следствиями уравне-
уравнений B5.8.3). Далее, так как левые части уравнений B5.8.3) образуют систему
в инволюции, то этим же свойством обладают и левые части уравне-
уравнений B5.8.4). Следовательно,
q_ d{pr—^r) d(ps—\ps) d(ps—\ps) d(pr — ipr) __
dq d dq d
dqt dpi dqt
= $ + 6=^+ Ц B5g6)
dqi dqt . dqs dqr y '
и равенство B5.8.5), таким образом, доказано.
Другой аналогичный результат такого же типа относится к теореме
Гамильтона — Якоби. Предположим, что для заданной динамической систе-
системы с функцией Гамильтона Н нам известен полный интеграл S (q; a; it)
уравнения Гамильтона в частных производных. Разрешим уравнения
Рг-~ = О, г=1,2, ...,п, . B5.8.7)
•относительно а и представим их в виде
аг = фг (q; p; t), г = 1, 2, . . ., п. B5.8.8)
Функции я|) являются интегралами гамильтоновых уравнений движе-
движения, и эти интегралы находятся в инволюции. В самом деле, легко прове-
проверить, что левые части уравнений B5.8.7) образуют систему в инволюции;
требуемый результат следует тогда из теоремы Ли.
§ 25.9. Интегралы, линейные относительно импульсов. Если среди
лагранжевых координат, описывающих динамическую систему, имеется
циклическая координата (скажем, qn), то соответствующий импульс рп
при движении сохраняет свое значение неизменным. Докажем, что, и обрат-
обратно, любая автономная система, имеющая пространственный интеграл,
линейный относительно импульсов, при надлежащем выборе лагранжевых
координат может быть описана как система с циклической координатой.
Пусть известный интеграл задается выражением
• • ¦ + ЦпРп, B5.9.1)
где я|) — известные функции от q. Доказательство теоремы связано с построе-
построением расширенного точечного преобразования переменных (q; p) в пере-
переменные (Q; Р), при котором
Рп = ЬРг + te + • • ¦ + ЪпРп- B5.9.2)
Возможность построения такого преобразования определяется в свою оче-
очередь свойствами линейных уравнений первого порядка в частных произ-
производных.
S 25.9] ИНТЕГРАЛЫ, ЛИНЕЙНЫЕ ОТНОСИТЕЛЬНО ИМПУЛЬСОВ 523
Рассмотрим уравнения
i?i_=rf?L=_=_*»_ B5.9.3)
определяющие семейство кривых в ^-пространстве. Решения этих уравнений
можно определить как линии пересечения интегральных поверхностей,
соответствующих п — 1 независимым интегралам уравнения в частных
производных
, dz , , dz . , dz ,-. or ^ ,.
Введем для этих интегралов обозначения
Фг (?i, 42, • ¦ ¦, Яп) = const, г = 1, 2, . . ., п — 1, B5.9.5)
и рассмотрим точечное преобразование
QT = Фг, г = 1, 2, . . ., п, B5.9.6)
в котором первые п — 1 функций фг являются функциями B5.9.5).
Остается определить функцию ф„. Выберем Qn = ф„ таким образом,
чтобы при движении вдоль одной из интегральных кривых, определяемых
уравнениями B5.9.3)., выполнялись соотношения
Можно, например, взять в качестве Qn интеграл уравнения
d& = -f4 B5.9.8)
где через W} обозначена функция ij)^ записанная в переменных gi: Qu
Q2,...,Qn-i. Отметим, что функция ф„ является интегралом уравнения
в частных производных
Предположим теперь, что преобразование B5.9.6) обратимо и пере-
переменные q можно выразить через переменные Q в соответствующей области
(^-пространства:
qT = FT(QuQ2,...,Qn), г = 1, 2, ...,». B5.9.10)
При этом
^ = 1>г, г=1,2,...,п. B5.9.11)
Последнее следует из того, что функции Qi, Q2, ¦ ¦ ¦, Qn-i удовлетво-
удовлетворяют уравнению B5.9.4), a Qn — уравнению B5.9.9). Геометрически это
ясно из системы B5.9.7), если рассмотреть движение вдоль одной из инте-
интегральных кривых системы B5.9.3); при таком движении Qt, Q2, . . ., Qn-i
остаются постоянными.
Теперь уже легко доказать теорему. Рассмотрим расширенное точечное
преобразование B4.4.6):
qT = FT, PT = Pi^-. B5.9.12)
В новых переменных будем иметь
^ B5.9.13)
524 ТЕОРИЯ ПРЕОБРАЗОВАНИЙ [Гл. XXV
так что величина Рп при движении остается постоянной,-и, стало быть,
соответствующая координата Qn является циклической, что и требовалось
доказать.
§ 25.10. Случай, когда функция Гамильтона является однородной квад-
квадратичной формой *). В теории малых колебаний, когда применяются главные
координаты, функция Гамильтона имеет вид
^ B5.10.1)
г=1
В результате контактного преобразования
У 2 Qr= — (i/пт) (Рг + inTgr), V2 Рг--=рг — inTqT, г = 1,2, ...,п,
B5.10.2)
получаем новую функцию Гамильтона:
#*= 2 inrQvPr. B5.10.3)
r=l
Уравнения движения принимают простой вид:
Qr = inrQr, Pr = —inrPr, r = 1, 2, . . ., п. B5.10.4)
Функция Гамильтона B5.10.1) представляет сумму двух независимых
однородных квадратичных форм, одна из которых содержит только пере-
переменные д, а другая — только переменные р. Покажем, что функцию Гамиль-
Гамильтона можно привести к виду B5.10.3) всякий раз, когда Н является однород-
однородной квадратичной формой 2п переменных {q^, q2, ¦ ¦ ., qn, р±, Рг, . ¦ ., рп)-
Функция Гамильтона такого типа встречается, например, в уравнениях
в вариациях (см. B3.6.4)).
Будем пользоваться обозначениями § 24.13 и заменим переменные
?i> Чг, ¦ ¦ •. Чп, Ри Р2, ¦ ¦ ч Рп
переменными
Х\, Xi, . . ., Хп, Хп_|_ 1, Хп _)_2, ¦ • •) Хт,
где т = 2п. Однородную квадратичную форму Н можно представить в виде
Н = ^-х'8х, B5.10.5)
где х — вектор-столбец, г-ж элемент которого равен хТ, & 8 — вещественная
симметричная матрица размером m x m. Докажем, что можно подобрать
такую матрицу К с постоянными элементами, чтобы линейное преобразо-
преобразование
х = Ку B5.10.6)
было контактным преобразованием, приводящим функцию Н к виду
2P2+ . . . + KnQnPn. B5.10.7)
r=l
Если это удастся сделать, то дальнейшее решение задачи станет
простым. Уравнения движения имеют вид
Qr = KQr, Pr = -W B5.10.8)
*) Метод, изложенный в этом параграфе, принадлежит А. Дж. Уорду.
§25.10] ФУНКЦИЯ ГАМИЛЬТОНА - ОДНОРОДНАЯ КВАДРАТИЧНАЯ ФОРМА 525
Решением этих уравнений будет
QT = ATe%r\ рт = вге-%г\ B5.10.9)
где Ат и Вт обозначают соответственно величины Qr и Рг при t — 0. Если
один из показателей Кт, скажем A,j, чисто мнимый, то существует периодиче-
периодическое движение системы, при котором все Q2, Q3, ¦ ¦ ¦, Qn\ Pz, P3, ¦ ¦ ¦, Pn
равны нулю.
Обратимся теперь к задаче отыскания контактного преобразования,
приводящего функцию Гамильтона к форме B5.10.7). Требуется построить
матрицу К размером тп X m (m = 2п) такую, чтобы
K'ZK=Z B5.10.10)
и
[) B5.10.11)
где L—диагональная матрица размером пхп:
B5.10.12)
Рассмотрим собственные значения матрицы A=Z8, т. е. корни
ь Я,а, ...,hm уравнения /(Я) = 0, где
Xlm\. B5.10.13)
Имеем
Z(S+XZ) = ZS-Um, B5.10.14)
и так как |Z|== 1, то
f(X) = \8+KZ\. B5.10.15)
Поскольку матрица 8 неособенная, ни один из корней Kt, Я,2, . . ., "km
не равен нулю; будем предполагать, что все они различны.
Полином / (К) содержит только четные степени К. Это следует из того,
что матрица 8 — симметрическая, а матрица Z — кососимметрическая.
Следовательно,
(8 + Щ' = 8 — %Z, B5.10.16)
откуда следует, что / (К) есть четная функция:
f(X)=f(-X). B5.10.17)
Корни образуют пары ±К (г = 1, 2, . . ., п). Расположим их в сле-
следующем порядке:
так что при г ^ п будем иметь Кп+Г = —Хг. Ни один из корней Х\, Я2, . . ., Кп
не равен нулю, и среди них нет также двух одинаковых или двух равных
по величине, но противоположных по знаку.
Существуют 2п линейно независимых собственных векторов сг, сп+г
(г = 1. 2 п) таких, что
8сг = - XrZer, Sen+r = KZc,l+r B5.10.18)
а также
r — Z8Cr = krCr, Acn+r~-=Z8cn+r= — >-rc,l+r- B5.10.19)
526 ТЕОРИЯ ПРЕОБРАЗОВАНИЙ [Гл. XXV
Обозначим через В матрицу размером т х т с элементами Ьц:
bij^clScj. B5.10.20)
Тогда, если г^п и s^n, то
brs = c'rScs = — %ac'rZe8. B5.10.21)
С другой стороны,
brs = c'sSCr = — Kc'sZcr = Xrc'rZcs, B5.10.22)
и так как %Тф — ks, то brs = 0. Точно так же можно показать, что Ьп+Г! n+s = 0.
Далее,
Ьт, n+s = c'rScn+s = Xsc'rZcn+s = Cn+rScr — —%rc'n+sZcr — Xrc'rZcn+s. B5.10.23)
Отсюда видно, что если г =fi=s, то br, n+s = 0. Точно так же, если г фв,
то bn+TtS = 0 и так далее, поскольку матрица Z — кососимметрическая и
, Ьп+Т, s = -Ьа, п+г. B5.10.24)
Обозначим через К матрицу (с4, с2, . . ., ст), а через С — матри-
матрицу K'ZK. Элемент сц матрицы С равен
dj^c'iZcj, B5.10.25)
откуда следует, что матрица С — кососимметрическая. В самом деле,
B5.10.26)
где I) — диагональная матрица размером п X п:
B5.10.27)
dr = c'rZcn+r. B5.10.28)
Умножим теперь сг (или cn+r, или каждый из них) на подходящим
образом выбранный (комплексный) скалярный множитель так, чтобы полу-
получить dr = 1. Если проделать эту процедуру для всех значений г из последо-
последовательности 1,2, . . ., п, то получим С = Z, и матрица К будет удовле-
удовлетворять условию симплектичности B5.10.10).
Кроме того, имеем
К'8К = Е, B5.10.29)
где матрица Е имеет элементы вида
etj = c'iSCj = — Xjc'iZCj B5.10.30)
и, следовательно, представляет собой симметрическую матрицу
0]. B5.10.31)
Таким образом, матрица К обладает требуемыми свойствами B5.10.10)
и B5.10.11); преобразование х = Ку является контактным, а новая функ-
функция Гамильтона
Н* = y'K'SKy B5.10.32)
имеет желаемую форму B5.10.7).
25.10]
ФУНКЦИЯ ГАМИЛЬТОНА - ОДНОРОДНАЯ КВАДРАТИЧНАЯ ФОРМА
527
Вернемся к уравнению / (Я) = 0. Поскольку коэффициенты полинома
/ (К) вещественны, его корни являются комплексно-сопряженными. Если
собственное значение Хи (к ^ п) не является ни вещественным, ни чисто
мнимым, то существует собственное значение %t (где I = I (к) ^ п) такое,
что %i = 7ch. Далее,
{A-hIm)ch = 0, B5.10.33)'
откуда
(А - lhlm) "ch = (A - AzJm) ch = 0, B5.10.34)
и так как матрица (А — Kilm) имеет ранг (т—1), то сг отличается от Ck
лишь скалярным множителем:
B5.10.35)
Аналогичным образом получаем, что
сА = ргсг B5.10.36)
и Ргрй = 1. При желании моншо нормировать собственные векторы (умноже-
(умножением на подходящие скалярные множители) таким образом, чтобы выполня-
выполнялись равенства | pft | = | рг | = 1, но это не всегда целесообразно делать.
Решение для у дается формулами
r=l, 2, . ..,?ra,
B5.10.37)
и, следовательно,
r=l r=l
Слагаемые
A^e h Ch-{-Аге l Ci, B5.10.39)
входящие в выражение B5.10.38) для х, дают в сумме вещественное число,,
если
Ah = phAh B5.10.40)
Если одно из собственных значений Kh (к ^ п) есть чисто мнимое число
щ, где (д. вещественно, то Kn+h — —i\a и cn+k отличается от ск только ска-
скалярным множителем. Если при этом выбрать сп+^ равным сь, то c^Zcn+h
будет чисто мнимым. Если одно из собственных значений Kf, (к ^ п) веще-
вещественно, то Ап+/( также будет вещественным, и мы можем выбрать соответ-
соответствующие собственные значения вещественными. При таком выборе сумма
соответствующих слагаемых в выражении B5.10.38) для х будет веществен-
вещественной, если вещественны коэффициенты Ah и An+h.
Пример 25.10. В качестве примера рассмотрим случай, когда п = 3,
а матрица 8 имеет вид
1
0
0
1
0
0
0
1
0
0
0
0
0
0
1
0
0
0
1
0
0
2
0
0
0
0
0
0
0
1
0
0
0
0
1
0
.528
ТЕОРИЯ ПРЕОБРАЗОВАНИЙ
Гл. XXV
Собственные значения определяются из уравнения
(Я2 + 1) (W + 1) = О
и, стало быть, располагаются на единичной окружности в комплексной
Л-плоскости (рис. 106).
Матрица (с4, с2,
ваны, имеет вид
Рис. 106.
с6), собственные векторы которой не нормиро-
"A + 0 о о A —
о A + о A-0 о
о A — 0 A + 0 °
-1 0 0-1
0 /2/2 0
0 i /2 —г/2 0
Для таких векторов имеем
Умножая на подходящим образом выбранные скалярные множители, полу-
получаем dl = d2 = d3=l, после чего матрицу К можно записать в виде
0 О
-A + 0 -A-0
-A-0 -A + 0
о о
/2 /2
i/2 -i/2.
К
Г1
0
0
—A—0/2
0
0
0
0
i
0
0
I
¦
A
A
/2
/2
0
-о
+ 0
V2
Г/2
0
A + 0
A-0
0
0
1/2
0
0
-A + 0/8
-A-0/8
0
/2/8
i /2/8
-A-0/8
-A + 0/8
0
/2/8
-г /2/8 _
Глава XXVI
ВАРИАЦИОННЫЕ ПРИНЦИПЫ
§ 26.1. Принцип Гамильтона. Простейший из вариационных принци-
принципов динамики — принцип Гамильтона — уже был установлен нами в § 3.7.
Этот принцип допускает формулировку в любых координатах, в § 6.3 мы
выразили его в лагранжевых координатах и вывели из него лагранжевы
уравнения движения.
Напомним формулировку принципа Гамильтона. Будем определять
положение системы лагранжевыми координатами g4, q2, . . ., дп, причем
выберем наименьшее возможное значение п. Если система голономна, то
п = к, где к, как обычно, обозначает число степеней свободы системы. Если
же система неголономна, то п = к + I, где I — число независимых неинте-
грируемых связей. Принцип Гамильтона утверждает, что
6Ldt = 0, B6.1.1)
где символ б обозначает перемещение из точки (дч, #2> • • ¦¦> qn) на истинной
траектории в ^-пространстве в точку (дч + бдч, q2 + 8q2, ¦ • •> qn + Sqn)
на варьированной траектории, причем оба положения соответствуют одному
и тому же моменту времени. Таким образом, 6</ представляет собой виртуаль-
виртуальное перемещение в момент t. Вариации бду как функции от t принадлежат
к классу С2 и обращаются в нуль в моменты t0 и ^. Следовательно, точ-
точки Ро и Рх фиксированы в ^-пространстве. Напомним, что для неголономной
системы варьированный путь в общем случае не является геометрически
возможным путем, т. е. в общем случае он не удовлетворяет уравнениям
связей (§ 3.8, § 5.11).
Результаты существенно упрощаются, если система голономна. В этом
случае уравнение B6.1.1) можно заменить следующим:
= 0. B6.1.2)
'о
Значение интеграла I L dt, взятого вдоль траектории в ^-пространстве,
сравнивается с его значением вдоль соседней кривой, соединяющей те же
самые концевые точки и проходимой за то же самое время. Если мы перейдем
к (п + 1)-мерному пространству {t, qi, qz, • ¦ ¦, qn), то получим обычную
{не параметрическую) задачу вариационного исчисления при фиксированных
концевых точках. Рассмотрим семейство кривых
qi(t), q2(t), ..., qn(t), B6.1.3)
соединяющих точку Ro,
*0) ?io> ?2о> ¦ ¦ ¦> <7по> B6.1.4)
с точкой i?i,
h, Ян, ?2i Япи B6.1.5)
34 Л, А. Парс
530 ВАРИАЦИОННЫЕ ПРИНЦИПЫ [Гл. XXVI
причем qr (t) ? С2. Кривая в {п + 1)-мерном пространстве,-соответствующая
действительному движению, отличается тем, что вдоль нее интеграл \ L dt
имеет стационарное значение. Во многих случаях, правда не во всех, этот
интеграл в действительном движении принимает минимальное значение.
Если система неголономна, то формы B6.1.1) и B6.1.2) уже не являют-
являются эквивалентными и следует пользоваться первоначальным уравне-
уравнением B6.1.1). В самом деле, для неголономной системы было бы неверным'
интерпретировать равенство B6.1.2) обычным образом, считая, что сравни-
сравниваются близкие геометрически возможные пути.
Для доказательства последнего утверждения достаточно рассмотреть простой при-
пример. Предположим, что частица совершает движение в пространстве при наличии един-
единственной (неинтегрируемой) связи
z dx — dy = 0. B6.1.6)
Эта система неголономна (к = 2, I = 1, п = 3). Для простоты будем предполагать,
что никаких активных сил нет и единственной силой, действующей на частицу, является
реакция связи. Мы знаем, что несмотря на то, что система имеет две степени свободы,
частица может из заданной точки попасть в точки, составляющие многообразие трех изме-
измерений, по геометрически возможному пути. В самом деле, в § 1.8 было показано, что
любой точки пространства можно достигнуть, отправляясь из любой другой точки. С дру-
другой стороны, динамически возможные траектории способны перевести частицу лишь
в точки некоторого двумерного многообразия.
Поясним основную идею. Для этого рассмотрим движение частицы, начинающееся
в момент t = 0 из начала координат со скоростью (и, 0, w). Уравнения движения будут
иметь вид
'х = Xz, V = —Я, 7=0. B6.1.7)
Присоединим к ним уравнение связи
zx'—'y = 0. B6.1.8)
Интегрируя, получаем (для w Ф 0)
х = — 9, у = — (ch6 — I), z = sh6, B6.1.9)
где переменная 9, заменившая время, определяется из уравнения
she = wt. B6.1.10)
В этом примере точка Ро находится в начале координат О, а точка Pi должна быть
некоторой точкой на линейчатой поверхности Г, заданной уравнениями B6.1.9); положе-
положение точки на этой поверхности определяется параметрами u/w и 9. Как и следовало ожи-
ожидать, при движении из точки О можно достигнуть лишь точек, лежащих на некоторой
двумерной поверхности. Выбирая подходящим образом начальную скорость, можно
перевести частицу из точки О в любую точку на поверхности Г за заданный промежуток
времени.
Предположим теперь, что мы зафиксировали точку Ро (выбрав ее в точке О), точку
Pi, а также моменты выхода частицы из точки О и прихода ее в точку Pi. Если точка Pi
не принадлежит поверхности Г, то динамическая задача не имеет решения, хотя, как мы
знаем, существуют геометрически возможные пути, соединяющие точку О с точкой Pi.
Если же точка Pi принадлежит поверхности Г, то существует динамически возможное
движение, при котором частица, выходя из точки О в момент t0, приходит в точку Pt
t\
в момент tit однако это движение не доставляет интегралу \ L dt стационарного значе-
<о
ния в классе геометрически возможных путей.
Для доказательства этого утверждения воспользуемся известной теоремой вариа-
вариационного исчисления. Геометрически возможный путь, удовлетворяющий заданным
Н
граничным условиям и доставляющий-интегралу \ L dt стационарное значение при срав-
*о
нении с соседними t0 геометрически возможными путями, должен удовлетворять прави-
правилу множителей. Это требует, чтобы * движение описывалось уравнениями Лагранжа,
§ 26.2] ТЕОРЕМА ЛИВЕНСА 531
составленными по функции Лагранжа
1 .
B
где (г есть функция от t, подлежащая определению. Эти уравнения имеют вид
B6.1.11)
^ 7й B6.1.12)
К ним следует присоединить уравнение связи B6.1.8). Движение, определяемое уравне-
уравнениями B6.1.9), не удовлетворяет уравнениям B6.1.12) ни при каком ц, откуда следует,
что движение системы не удовлетворяет условию B6.1.12), но оно, конечно, удовлетворяет
условию B6.1.1).
Интересно доказать непосредственно, не прибегая к правилу множителей, что инте-
h
грал 1 L dt не является стационарным для действительного движения по сравнению
о
с движениями вдоль соседних геометрически возможных путей. Для этой цели рассмотрим
геометрически возможный путь, который зададим уравнениями
9) ' B6ЛЛЗ>
где к обозначает отношение и/w, параметр 9 определяется формулой B6.1.10), а штрих
обозначает дифференцирование по 9. Функции a (9) и |3 (9) принадлежат к классу С3,
и, кроме того, функции а, C, а', C' принимают нулевые значения при 9 = 0 и 6 = 6),
где 9j определяется из уравнения sh 9j = wtt. В интересующем нас случае функции a
d
и C, а также их производные малы. Обозначим через 6/ приращение интеграла \ L dt
oJ
при переходе от невозмущенного пути B6.1.9) к варьированному пути B6.1.13). Имеем
z'2 + 2/'2 + z'2)d9. B6.1.14)
Если бы интеграл принимал на невозмущенном пути стационарное значение, то линейные
члены в выражении для б/ обращались бы в нуль. В действительности же они равны
в! в!
(a'secb9+P'tli9)d9+m— \ (— a' ch 9 — a" sh 9 + Р") й9 =
о о
61
= вш J (a'sech6 + P'th9)d9 B6.1.15)
о
и, вообще говоря, в нуль не обращаются.
Таким образом, мы доказали, что для голономных систем обе формы B6.1.1)
и B6.1.2) принципа Гамильтона справедливы. Если же системы неголономны, то прин-
принцип Гамильтона выражается только равенством B6.1.1).
§ 26.2. Теорема Ливенса. В этом параграфе мы будем рассматривать
только голономные системы. В § 6.3 мы вывели уравнения Лагранжа из
принципа Гамильтона. Естественно попытаться вывести аналогичным путем
уравнения Гамильтона; такая попытка приводит к весьма интересным резуль-
результатам. Однако при таком выводе требуется известная осторожность, посколь-
поскольку вариации величин q и со нельзя считать независимыми. В самом деле,
если вариация 8q задана в каждый момент времени, то вариация <о опре-
определяется уравнениями
6юг = ^6-?г, г =1,2,.,., п. B6.2.1)
Чтобы преодолеть это затруднение, обратимся вновь к правилу множителей.
34*
532 ВАРИАЦИОННЫЕ ПРИНЦИПЫ [Гл. XXVI
Будем характеризовать движение системы перемещением изображающей
точки в 2п-мерном пространстве {qu qz, . . ., qn, ац, со2, • • •, юп)- Из усло-
условия B6.1.2) следует, что интеграл I L (q; ш; t) dt принимает стационарное
значение в семействе кривых, удовлетворяющих п дифференциальным
уравнениям
q'T = юг, г = 1, 2, . . ., п. B6.2.2)
В концевых точках значения переменных q и независимой переменной t
фиксированы, а значения со остаются свободными. Поскольку мы рассма-
рассматриваем лишь такие кривые, которые удовлетворяют уравнениям B6.2.2),
а вариации синхронны, можно утверждать, что условия B6.2.1) наверняка
удовлетворяются.
Согласно правилу множителей интеграл
J [b(q;
ш; t) + 2 Кг (?>—«М} dt B6.2.3)
(где знак 2 обозначает суммирование от 1 до п) принимает стационарное
значение при произвольных вариациях переменных q и со; при этом функ-
функции К {t) подлежат определению. Условия стационарности записываются
в форме 2п уравнений
к которым следует присоединить п уравнений B6.2.2). Разумеется, из этих
уравнений можно сразу получить уравнения Лагранжа. Но для нас сейчас
важно другое, а именно:
J
'о
принимает стационарное значение по отношению к произвольным вариа-
вариациям пути в пространстве (q, со). Но такие вариации эквивалентны произ-
произвольным вариациям переменных q и р, и, выражая результат через понятия
фазового пространства, можем сформулировать следующую теорему: инте-
интеграл
^(t B6.2.6)
принимает стационарное значение при произвольной вариации переменных q
и р. В этом состоит теорема Ливенса *). Символом Н под знаком интеграла
обозначена функция
S^-g.-L, B6.2.7)
записанная в переменных q, p. Для этого уравнения
Pr = -g; B6.2.8)
нужно разрешить относительно со (см. § 10.13). Время и переменные q фик-
фиксированы в концевых точках, а переменные р свободны. Таким образом,
*) Доказательство теоремш см. также в работе: G. H. Livens, On Hamilton's
Principle and the Modified Function in Analytical Dynamics, Proc. Royal. Soc. Edinburgh,
XXXIX, 1919, стр. 113.
§ 26.3] ТОЧКИ МИНИМУМА И СЕДЛОВЫЕ ТОЧКИ 533
мы имеем задачу в пространстве переменных t, q\, q%, . ¦ ., qn, pi, P2, ¦ • •¦, Pn
со свободными концевыми точками. Но условия на концах не вносят ничего
нового, поскольку подынтегральная функция не содержит рт.
Уравнения Эйлера — Лагранжа, выражающие необходимые условия
стационарности функционала B6.2.6), представляют собой не что иное, как
уравнения Гамильтона
*"- = -^Г' л=—^Г' r=t,2,...,n. B6.2.9)
§ 26.3. Точки минимума и седловые точки. Рассмотрим голономную систему с п
степенями свободы. Движение системы характеризуется тем, что траектория q = q (t)
в пространстве t, qi, q2, . . ., qn доставляет стационарное значение интегралу \ L dt
по сравнению с его значениями на соседних кривых q = q (f)-\- bq (t), соединяющих те же
концевые точки. Соответствующее движение в пространстве переменных t, qlt q2, ...
. . ., qn, pi, p2, . . ., pn происходит вдоль кривой q = q (t), p = p (t), которая доставляет
стационарное значение интегралу > (—Н -\- ^prqr) dt по сравнению с его значениями
на соседних кривых q = q (t) -\- &q (t), p = p (t) + bp (t) при фиксированных концевых
значениях переменных t и q и свободных концевых значениях р. Оба указанных интегра-
интеграла имеют, разумеется, одинаковые значения для действительного движения в каждом
частном случае. Однако, как указывал в свое время Гильберт, в то время как первый
интеграл может достигать минимума, второй интеграл для той же задачи может не иметь
ни максимума, ни минимума.
Для иллюстрации этого утверждения достаточно рассмотреть простой пример пря-
прямолинейного движения частицы единичной массы в однородном поле g. Перемещение
частицы за время t равно
x=ut + -^gtz. B6.3.1)
Пусть в момент i = 0 х = 0, а в момент i = 9 x= иб-Ь-^- g92. To, что интеграл
е
С # 1 .
1 Ldt, где L = -q- xz-\-gx, для действительного движения будет иметь минимум, можно
Jo 2
легко доказать, если воспользоваться основным достаточным условием, известным из
вариационного исчисления. Однако проще дать непосредственное доказательство. Срав-
Сравним действительное движение, описываемое уравнением B6.3.1), с соседним движением,
для которого
x = ut+^-gt* + a(t), B6.3.2)
где а @ ? С2 и а @) = а (9) = 0. Для этого варьированного движения имеем
е е
7 + 67= j (jx*+gx)dt=^ {4-(" + ^+aJ+g (Mi + 4"^2+a)} dt- B6-3-3)
0 0
Следовательно,
G ее
6/= J YY^ + {u. + gt)'a. + ga} df=j Y^dt+(u + St)oi Q
0 0 0
(так как a @) = a (9) = 0). Таким образом, 67 >> 0, если только a (t) не равно тождест-
е
венно нулю. Движение B6.3.1) доставляет минимум интегралу i L dt по сравнению с его
0
значениями для всех других движений с теми же концевыми точками в д-пространстве
и с теми же начальным и конечным моментами времени.
е
Рассмотрим теперь интеграл \ (—77-)- ^j prqT I dt вдоль кривой в пространстве
1
t, q, р. В нашем случае Н = — p2—-gx, и интеграл, который надлежит рассмотреть,
= [ -|-a2df B6.3.4)
534 ВАРИАЦИОННЫЕ ПРИНЦИПЫ [Гл. XXVI
равен
е
/= j (— -jpi + gx + px}dt B6.3.5)
о
и берется вдоль кривой в пространстве t, х, р. Запишем интеграл в форме
9
B6.3.7)
о
В действительном движении
В варьированном движении, для которого
a:-.ut + y^2 + aW, P = « + g«+PW, B6.3.8)
где a (f) обращается в нуль при i = 0 и 2 = 9, а Р (t) в эти моменты времени не обяза-
обязательно равно нулю, имеем
6
б/
Г 1 •
= I — { —(ft —«J-f «2W*. B6.3.9)
i 2
Таким образом, б/ < 0, если |3 =? 0, a = 0, и б/ > 0, если |3 = а и a =^= 0. Интеграл /
при функции B6.3.7) имеет стационарное значение, но это значение не является ни макси-
максимумом, ни минимумом.
§ 26.4. Асинхронное варьирование. Принцип Гёльдера *). В принципе
Гамильтона операция варьирования производилась для одного и того же
момента времени: точке Р (в ^-пространстве) на действительной траектории
в момент t ставилась в соответствие точка Р' на варьированной траектории
соответствующая тому же самому моменту времени. Это было возможно,
так как в принципе Гамильтона задаются не только концевые точки, но
и соответствующие им моменты времени, так что движение по исходному
и варьированному путям совершается за одно и то же время. Теперь мы рас-
рассмотрим случай, когда точке q на исходной траектории, соответствующей
положению системы в момент t, ставится в соответствие точка q + 8q на
варьированной траектории, характеризующей положение системы в момент
I + bt. Будем предполагать, что вариации б^, 8д%, • • ., bqn, 81 являются
функциями времени, принадлежащими к классу Сг.
Рассматривая асинхронные вариации, мы принимаем, что соотноше-
соотношения F.1.1) между х и q не содержат I, так что конфигурация системы для
любого t определяется одной и той же точкой в д-пространстве.
*i
Вычислим теперь интеграл i 8L dt, имея в виду, что нижний предел д@),
'о
занимаемый системой в момент t0, смещается в положение ql0) -\- 8q@>,
занимаемое системой в момент t0 + 8t0: а верхний предел дA), соответст-
соответствующий моменту ty, смещается в положение qA) + 6gA), соответствующее
моменту ti + 8ti- Система при этом не обязательно является голономной.
Имеем
^ 8Ldt= I (¦^8t+2i-^-8qr+2i-^-8qr) dt, B6.4.1)
*) Известная работа Гёльдера о вариационных принципах опубликована в «Gottin-
ger Nachrichten», 1896, стр. 122.
$ 26.5] ПРИНЦИП ФОССА 535
где знак 2 означает суммирование от 1 до п. Далее,
Подставляя это выражение для 8qr в B6.4.1), находим после интегриро-
интегрирования
-J[2 {¦*¦(?)-¦&} Ч*- <26-«>
Рассмотрим последний интеграл в правой части этого равенства. Если
8q есть виртуальное перемещение в момент t, то в силу основного уравнения
в его четвертой форме F.1.11) подынтегральная функция равна нулю. При
этом
'~ ' ЯГ ~ ". B6.4.4)
Предположим теперь, что виртуальное перемещение 8q в моменты t0
и ti выбрано нами равным нулю, так что конфигурация системы в эти момен-
моменты является заданной. Тогда мы приходим к следующему результату:
+ B ^f-) w6t-
Это равенство выражает принцип Гёлъдера.
Укажем условия, при которых выполняется принцип Гёльдера. В каж-
каждый момент времени выбирается виртуальное перемещение 8q по отношению
к действительному движению; составляющие 8qr являются функциями от t
класса С2, обращающимися в нуль в моменты t0 и t±. Затем выбирается
функция 8t от t, также принадлежащая к классу С2- В варьированном дви-
движении точка q -f- 8q проходится в момент t + 8t, причем вариация б? не
обязательно равна нулю в моменты t0 и t\. В случае, когда система неголо-
номна, варьированный путь, вообще говоря, не будет удовлетворять урав-
уравнениям связей. Если функция 8t тождественно равна нулю, то мы снова
приходим к принципу Гамильтона.
§ 26.5. Принцип Фосса *). В принципе Гёльдера вариация 8q пред-
представляет собой виртуальное перемещение в момент t, тогда как соответст-
соответствующая точка q + 8q проходится в момент t + 8t. Чтобы избежать этого
положения, предпринимались попытки сформулировать вариационный прин-
принцип таким образом, чтобы 8# было возможным перемещением в интервале
времени 8t. Один из таких вариационных принципов приводится ниже.
Заметим сначала, что если F<?i, 8q2, ¦ • ¦, 8qn) обозначает возможное
перемещение за промежуток времени (t, t + 8t), a (gl5 q2, . . ., qn) — воз-
возможную скорость в момент t, то
(8qi — qi8t, 8q2 — q28t, . . ., 8qn — qn8t) B6.5.1)
*) О принципе Фосса см. А. Фосс, О принципах Гамильтона и Мопертюи, сборник
«Вариационные принципы механики» под ред. Л. С. Полака, М., Физматгиз, 1959.
536 ВАРИАЦИОННЫЕ ПРИНЦИПЫ [Гл. XXVI
будет виртуальным перемещением. Доказательство следует немедленно.
В самом деле, согласно E.12.2) имеем
. . r=l,2,...,Z.
8=1
Следовательно,
2j Brs(8qs — qs8t)=O, r=l,2, ...,l,
8=1
так что B6.5.1) удовлетворяет условиям E.12.5) для виртуального переме-
перемещения.
Рассмотрим теперь траекторию системы в ^-пространстве и варьиро-
варьированный путь. Точке q на исходной траектории в момент t поставим в соот-
соответствие точку q + бд на варьированной траектории в момент t + 8t. Вычис-
h
лим соответствующее приращение интеграла \ L dt. Имеем
tl t!
б j Ldt= j (8L+L~6t)dt =
*Q t(}
tl
Коэффициент при 8t в подынтегральном выражении равен
-*=%{¦*(-?;)--<&}*'' B6-5-3)
откуда получаем
б f Ldt =
to
-f[2
где через Z? обозначено выражение B<7r -^) • Если теперь бо есть еоз-
можное перемещение за время б?, то выражение 8qr — qrbt будет определять
составляющую виртуального перемещения и подынтегральная функция
последнего интеграла в правой части равенства B6.5.4) будет равна нулю
§ 26.7] ЗАМЕНА НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ 537
в каждый момент времени. При этом
б f Ldt= (У, — bqr—Ebt\ *\ B6.5.5)
Если вариации 6qu 8q%, ...,6gn, 8t в моменты toutx выбрать равными
нулю, то будем иметь
h
\ O. B6.5.6)
В этом заключается принцип Фосса. Для голономной системы полученный
результат равносилен принципу Гамильтона в его второй форме B6.1.2).
Отметим поразительное сходство между формулой B6.5.5) и класси-
классической формулой A5.5.11) для вариации главной функции. Изучая в § 15.5
главную функцию, мы рассматривали изменение ее, связанное с переходом
к соседней траектории системы; здесь же на вариацию не накладывается
подобное ограничение. Поэтому ясно, что формула A5.5.11) представляет
частный случай более общего результата B6.5.5).
§ 26.6. Обобщение принципа Гамильтона. При доказательстве предыду-
предыдущей теоремы мы фиксировали не только концевые точки, но также и началь-
начальный и конечный моменты времени. Первое из этих требований несуществен-
несущественно, что же касается второго, то оно связано с серьезными неудобствами.
Однако если наложить на систему соответствующие ограничения, то можно
получить вариационный принцип, в котором начальный и конечный моменты
времени будут изменяться желаемым образом.
Предположим, что выполняются следующие условия: система является
катастатической, соотношения между х и q не содержат t, и, кроме того,
функция L не содержит явно t. В этом случае класс виртуальных перемеще-
перемещений совпадает с классом возможных перемещений и существует интеграл
Е = h. Поэтому, если зафиксировать концевые точки, но не фиксировать
начальный и конечный моменты времени, то из уравнения B6.5.5) получим
б [ (L + )dt ( E)8t
J 'о
to
Отсюда находим
B6.6.1)
h
б \ (L + h)dt = O. B6.6.2)
'о
При этом существенно, что моменты времени, соответствующие концевым
точкам, не являются фиксированными. Интересно отметить (имея в виду
наложенные на систему ограничения), что к результату B6.6.2) можно
также прийти, исходя из принципа Гёльдера.
§ 26.7. Замена независимой переменной. Важное и существенное свой-
свойство вариационных принципов заключается в том, что их легко можно выра-
выразить в любых выбранных координатах. Это обстоятельство уже отмечалось
нами ранее (в § 6.3) при выводе уравнений Лагранжа из принципа Гамиль-
Гамильтона. Обобщение принципа Гамильтона B6.6.2) дает возможность пойти
дальше в этом направлении и произвести замену независимой переменной.
Введем вместо t новую независимую переменную Э, связанную с t соотно-
соотношением
dt = и dQ, B6.7.1)
538 ВАРИАЦИОННЫЕ ПРИНЦИПЫ [Гл. XXVI
в котором и обозначает заданную положительную функцию от q, принадле-
принадлежащую к классу С\. Переменную 0 можно считать новым (искусственным)
временем, измеряемым по часам, связанным с изображающей точкой в д-про-
странстве, скорость хода которых является заданной функцией положения
в пространстве. С понятием искусственного времени мы уже встречались
в §§ 17.3, 18.1 и 18.3. Из принципа Гамильтона в его обобщенной форме
B6.6.2) следует, что
в!
б j u(L + h)dQ = 0, B6.7.2)
во
причем концевые точки в ^-пространстве фиксированы, а концевые значе-
значения 9 свободны. Поэтому, если мы выразим функцию L через q и q', где
q'r = dqr/d9, то сможем получить уравнения движения с 0 в качестве неза-
независимой переменной. Этими уравнениями будут уравнения Эйлера — Лаг-
ранжа вариационной задачи B6.7.2) или, что то же, уравнения Лагранжа
для системы с функцией Лагранжа
Л = и (Z/ + К), B6.7.3)
где через L' обозначена функция L, записанная в переменных q вместо q.
При этом, однако, следует помнить, что не все решения этих уравнений
представляют возможные движения, а лишь те из них, для которых Е — h.
Уравнения определяют траекторию в ^-пространстве, но не устанавливают
непосредственно связи между положением точки на траектории и временем.
Найдем выражение для функции Л. Напишем, как обычно,
Т - Т2 + Tt + То,
где (см. F.1.6))
и (см. F.1.7))
Ti = 2 ат4т-
Выражения Т'г и Т'х в переменных q[, q'2, .. ., q'n-записываем точно таким же
образом:
|2 2, К^агф. B6.7.4)
Имеем
r2 = 0V; = -J, г1 = 0>; = А. B6.7.5)
Теперь находим
A = u(T2 + Tt + T0 — V-\-h) B6.7.6)
и окончательно
A^^+T'. + uiTo-V + h). B6.7.7)
Следует иметь в виду, что только такие движения, для которых
IiTo = h, B6.7.8)
отвечают динамической задаче. Если система неголономна, то в уравнения
движения войдут I множителей %, как это имело, место в F.6.4). В простей-
простейшем и наиболее распространенном случае натуральной системы множите-
§ 26.8] НОРМАЛЬНАЯ ФОРМА СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ 539
ли Я не появляются и в выражения B6.7.7) и B6.7.8) не входят слагае-
слагаемые Т'г и То, так что
Л = Л. + и(Л —7) B6.7.9)
и ограничение B6.7.8) принимает вид
§ u. B6.7.10)
Интересно непосредственно убедиться в том, что уравнениям движения, получен-
полученным с помощью функции B6.7.7), действительно удовлетворяют движения системы
с энергией h.
Имеем
ff = «^, -р = ^. B6.7.11)
К ддг dgr d(}r
B6.7.12)
dq'r dgr ' dqT " dqT '
Отсюда
ял \ i йт \ ат. a /77_j_t7.\
B6.7.13)
B6.7.14)
так как коэффициент при —— равен нулю в силу B6.7.8). Окончательно получаем
"Яг
Правая часть этого равенства обращается в нуль, поскольку движение удовлетворяет
уравнениям Лагранжа.
§ 26.8. Нормальная форма системы с двумя степенями свободы. Рас-
Рассмотрим голономную систему с двумя степенями свободы, для которой
^2 = у (ацв1+2а12адг + а2а^), T1 = a1q1 +a2q2. B6.8.1)
Путем надлежащей замены переменных (переходом к так называемым изотер-
изотермическим или изометрическим координатам) выражение для Т2 удается
представить в форме
\U(Q\ + Q% B6.8.2)
где U = U ((?!, Q2) > 0. Представляется удобным сохранить для новых коор-
координат обозначения qi и q2; тогда будем иметь
T2-^u(q'Uq'l), 7'1 = ag1 + P?.. B6.8.3)
Воспользуемся теперь теоремой § 26.7, выбрав в качестве новой незави-
независимой переменной 9, связанное с t соотношением dt — udQ. Из B6.7.7)
находим
fPri-Y. B6.8.4)
540 ВАРИАЦИОННЫЕ ПРИНЦИПЫ [Гл. XXVI
где
y==u(V-T0-h), B6.8.5)
а V и То выражены в новых координатах. Уравнениями движения теперь
будут
ri=-to;-|*-. ?==&—?-. B6.8.6)
где
(&?) <26А7>
Траектории, соответствующие энергии h, определяются интегралами
системы B6.8.6), удовлетворяющими условию
1-(<7? + #)+Т = 0. B6.8.8)
Систему B6.8.6) иногда называют нормальной формой системы с двумя
степенями свободы. Эти уравнения описывают плоское движение частицы
под действием силы консервативного поля с потенциалом у и гироскопиче-
гироскопической силы величиной ?у, направленной под прямым углом к скорости V.
Здесь гироскопическая сила более общего типа, чем в § 8.8 и § 9.8, посколь-
поскольку множитель ? не является постоянным и зависит от qt и q%. Если исходная
система является натуральной, то ? = 0 и общая задача сводится к задаче
о плоском движении частицы в поле консервативных сил.
§ 26.9. Система Лиувилля. Теорема § 26.7 особенно удобна для изуче-
изучения системы Лиувилля, рассмотренной нами в § 18.1. Система Лиувилля
является натуральной системой с п степенями свободы. В простейшем слу-
случае имеем
T~Tt = ±-us, V = —, B6.9.1)
где
s=qt + qi+ + ql и = Х1 + Х+ +Х \ B6 9 2)
а Хг, |г являются функциями от qr; и и w представляют суммы функций,
каждая из которых зависит от соответствующей координаты. Как и в § 26.7,
введем новую независимую переменную 0, связанную с t соотношением
dt = и dQ. Тогда будем иметь
A = ±(q'1* + q'*+... + q'n2)+hu-w. B6.9.3)
Интеграл энергии B6.7.8) запишется в форме
(q?+gr2+ + g'2) ыш B6.9.4)
Функция Лагранжа B6.9.3) обнаруживает замечательное свойство: она
лолностью распадается на п независимых функций Лагранжа вида
±q? + hXr-tr. B6.9.5)
Соответствующее уравнение движения
q; = -^-(hXT-lr) B6.9.6)
, допускает интеграл энергии
^q'/^hXr-lr + cr, B6.9.7)
26.9] СИСТЕМА ЛИУВИЛЛЯ 541
где согласно B6.9.4) 2сг = 0- Траектории в ^-пространстве для движений
с энергией h могут быть найдены путем интегрирования уравнения
dqr = dQ B6.9.8)
и выражения каждого qT через 0.
Сказанное выше без труда распространяется на системы более общего
типа, для которых
T = i-uS, F = —,
где
B6.9.9)
S=^'ql/Pr, B6.9.10)
а Рт есть функция от qr. (Это обобщение является достаточно очевидным;
чтобы получить его, нужно перейти к новым координатам QT, связанным
со старыми соотношениями
f? B6.9.11)
При этом S принимает вид 2^r» a u и w по-прежнему представляют суммы
функций, каждая из которых зависит от соответствующей координаты.)
Вводя, как и ранее, новую переменную 8, связанную со старой соотноше-
соотношением dt = и dQ, получаем для системы B6.9.9)
Л = у2т7 + /ш~ш- B6.9.12)
Мы снова обнаруживаем, что функция Лагранжа распадается на п незави-
независимых функций вида
±-^- + hXT-lr. B6.9.13)
Интеграл энергии B6.7.8) в данном случае принимает вид
Т2Т7 = /Ш~Ш' B6.9.14)
я интегралы энергии для отдельных систем —
± Zr+cr), B6.9.15)
причем 2 сг = 0- Зависимость каждой из переменных qr от 0 можно полу-
получить, интегрируя уравнение
dqr = ^0 B6.9.16)
кХ1 + )
Этот результат уже был получен нами ранее (см. A8.1.10)).
На первый взгляд может показаться, что в рассмотренных примерах
осуществляется полное разделение системы на п независимых систем, подобно
тому как это имело место в теории малых колебаний, когда использовались
нормальные координаты. Однако такое разделение является в известном
смысле кажущимся. Действительно, мы можем получить соотношение меж-
между каждым gr и 0 независимо от остальных qr (см. B6.9.8) и B6.9.16)), но этого
не удается сделать для соотношений между qr и временем. Следует иметь
в виду, что 0 не является истинным временем, соотношение между 9 и f
включает в себя все q, поскольку dQ = dtlu.
542
ВАРИАЦИОННЫЕ ПРИНЦИПЫ
[Гл. XXVI
§ 26.10. Конформные преобразования. Рассмотрим систему с функцией
Лагранжа
L = ±{i* + i*)-V(x,y). B6.10.1)
В качестве такой системы естественно принять материальную точку, дви-
движение которой происходит в плоскости ху под действием сил консерватив-
консервативного поля, причем х ж у — обычные декартовы координаты. Можно, разу-
разумеется, принять и более сложную систему, для которой х и у будут лагран-
жевыми координатами.
Если перейти к новым переменным |, г) с помощью конформного преоб-
преобразования
х+ iy = z=/(?) =/(? + in), B6.10.2)
задаваемого функцией /(?), регулярной в некоторой области ?, то будем
иметь
| dz | = М | d%\, где М = | /' (О |, B6.10.3)
и
B6.10.4)
где
U, Ti) = Ffey). B6.10.5)
Применим теперь теорему § 26.7 к системе B6.10.4), положив и = М2.
Новая функция Лагранжа B6.7.7) для движений с энергией h будет иметь
вид
~ i"
B6.10.6)
а интеграл энергии B6.7.8) за-
запишется в виде
B6.10.7)
Рассмотрим в качестве при-
Рис. 107. мера преобразование
z = ?2, B6.10.8)
отображающее правую полуплоскость t, на плоскость z с разрезом вдоль
отрицательной вещественной оси. При этом
М2 = 4 \1 |2 = 4 | z | = 4г,
где, как обычно,
г2 = х2 + у2.
Функция Лагранжа запишется теперь в форме
A (fe'2 +
B6.10.9)
B6.10.10)
а интеграл энергии будет иметь следующее выражение:
B6.10.11)
B6.10.12)
Кривые \ = const иг] = const в ^-плоскости отображаются в два семейства
конфокальных парабол, пересекающих друг друга под прямым углом
(рис. 107). Эти семейства парабол уже встречались нам в § 17.9.
Преобразование B6.10.8) особенно удобно для исследования задачи
о движении в поле ньютоновского притяжения, когда V = — у./г. В этом
§ 26.10] КОНФОРМНЫЕ ПРЕОБРАЗОВАНИЯ 543
случае
Л-у(Г2 + г]'2) + 4Лг + 4^ = 1(Г2 + 'П'2)+4Л(Е2+'П2)-+4^ B6.10.13)
и мы снова получаем разделение системы на две независимых. Уравнения
движения имеют вид
I" = 8hl, ц" = 8hr\, B6.10.14)
а интеграл энергии имеет следующее выражение:
1'\+ т)'2 - Sh (g« + г]2) = 8ц. B6.10.15)
1
Как хорошо известно, характер решения существенным образом зави-
зависит от знака h. Рассмотрим более подробно случай, когда h < 0, положив,
например, 8/t = — р2, где р — вещественное положительное число. Общее
решение получить нетрудно. Оно будет иметь более простой вид, если «выст-
«выстрелить из вершины параболы», иными словами, положить Ъ,' = ц — 0 при
6=0. Тогда будем иметь
I = a cos pQ, ц = р sin pQ, B6.10.16)
причем
а2 + рг = _ р/к = 2а. B6.10.17)
Выбор этого обозначения продиктован тем, что при движении по эллипти-
эллиптической орбите энергия равна —\il2a, где 2а обозначает большую ось эллипса.
Положим
а2 = а A - е), р2 = а A + -е), \е |< 1. B6.10.18)
(Если в качестве начальной точки выбран перигелий, то е>0.) Тогда будем
иметь
х = |2 — тJ = аA — е) cos2 р8 — оA-|-е) sin2p0 = a(cos v — e),
B6.10.19)
г = |2 + Цг — а A — е) cos2 pQ + а A + е) sin2 pQ = а A — е cos v),
где i; = 2р8.
Рассмотрим теперь зависимость положения частицы на орбите от вре-
времени. Имеем '
dt = 4r dQ = 4а A — е cos v) dvllp, B6.10.20)
t — to = — {v — esinv). B6.10.21)
Принимая во внимание формулу р2 = A[i/a, находим
v — е sin v = п (t — t0), B6.10.22)
где п2 = ц/а3. Ясно, что величина v представляет собой эксцентрическую
аномалию, а уравнение B6.10.22) является уравнением Кеплера.
Напишем уравнение орбиты в полярных координатах, отсчитывая
полярный угол ф от оси Ох:
±:aA7e2) . B6.10.23)
Это есть уравнение эллипса; если е > 0, то перигелий расположен на поло-
положительной оси х (ф = 0).
В ходе вывода надо было предположить, что движение происходит
по части кривой B6.10.16), расположенной в правой полуплоскости ?,
соответствующей орбите в z-плоскости, не пересекающей линии разреза.
Теперь в этом ограничении нет нужды.
Глава XXVII
ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ
§ 27.1. Вариация действия. В этой главе мы рассмотрим вариационный
принцип иного типа — так называемый принцип наименьшего действия.
Мы будем предполагать, что выполняются условия, сформулированные
в § 26.6, а именно что система является катастатической, связи между х
и q не зависят от t и функция L не содержит время. При этом исчезает раз-
различие между возможными и виртуальными перемещениями и, кроме того,
существует интеграл энергии Е = h:
E=%qr^—L, B7.1.1)
где знак 2 означает суммирование от г=1 до г = п.
Отличительной чертой излагаемой здесь теории является то, что на
варьируемые движения накладывается ограничение, состоящее в том, что
для них Е сохраняет постоянное значение. Варьированное движение полу-
получают, сообщая в каждый момент t виртуальное перемещение 8q относительно
действительного движения, причем положению q -\- 8q соответствует момент
времени t + Ы. В общем случае продолжительность варьированного дви-
движения отличается от продолжительности исходного движения. Варьиро-
Варьированное движение в общем случае не является динамически возможным дви-
движением, а в случае неголономной системы оно не является даже геометри-
геометрически возможным. Единственное ограничение, которому подчинено это
движение, заключается в требовании постоянства полной энергии. Мы будем
по-прежнему предполагать, что вариации 8q и 8t являются функциями от t
класса Cz-
Определим действие &С как интеграл
h
й*=| B?r-^)dt, B7.1.2)
вычисляемый вдоль траектории в ^-пространстве. Выражение B7.1.2) экви-
эквивалентно следующему:
'1
= J
dt. B7.1.3)
'о
Для натуральной системы последний интеграл записывается в форме
h
8C=J2Tdt. B7.1.4)
«о
Основная теорема состоит в том, что при указанной выше вариации
h
dqr
l+(*i-*o)M, B7.1.5)
to
где h-\-8h есть (постоянное) значение Е на варьированном пути. Приведем
два доказательства этого результата.
27.2] ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ 545
1) Согласно B6.4.4) имеем
Но
6? = 6B<7r^)-6L = 6fc, B7.1.7)
так что B7.1.6) принимает форму
B7.1.8)
Последнее эквивалентно
Теорема, таким образом, доказана.
2) Из уравнения B6.5.5) имеем
— h(8tt — 8t0). B7.1.10)
Но вдоль исходного пути
dqr
Аналогичное соотношение будет справедливо и для варьированного пути,
если постоянную h заменить на h-\-8h. Таким образом, соотношение B7.1.10)
принимает вид
dqT
*»
B7.1.11)
что и доказывает теорему.
§ 27.2. Принцип наименьшего действия. Из основной теоремы B7.1.5)
получаем, что при фиксированных концевых точках и 8/t = 0
Ш = 0. B7.2.1)
В этом заключается принцип наименьшего действия. Таким образом, для
истинной траектории действие имеет стационарное значение по сравнению
с его значениями на варьированных траекториях с теми же концевыми точ-
точками (в ^-пространстве) и той же энергией.
Этот принцип проще всего проинтерпретировать на примере голоном-
ной системы, когда не возникает затруднений, связанных с возможностью
нарушения уравнений связей. Рассмотрим семейство х путей, соединяющих
начальное и конечное положения системы и характеризуемых одним и тем
же значением энергии Е, равным h. Для действительного пути действие
имеет стационарное значение по сравнению с теми значениями, которые оно
принимает для других кривых рассматриваемого семейства.
35 л. А. Парс
546 ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ [Гл. XXVII
Принцип наименьшего действия обычно приписывают Мопертюи *),
чье сочинение «Essai de Gosmologie» вышло в свет в 1751 г". В действитель-
действительности же высказывания Мопертюи основывались на метафизических сообра-
соображениях и носили туманный и ненаучный характер. Впервые в удовлетвори-
удовлетворительной форме принцип наименьшего действия был сформулирован Эйлером.
Подобно принципу Гамильтона (§ 3.7), принцип наименьшего действия выражает
необходимые и достаточные условия движения. Поэтому из него можно вывести уравне-
уравнения движения. Однако это сделать значительно трудней, чем из принципа Гамильтона,
вследствие ограничения Е = h, накладываемого на движения вдоль варьированных
путей. В этом случае мы имеем вариационную задачу Лагранжа. Мы приведем здесь этот
вывод для натуральной системы. Согласно принципу наименьшего действия функционал
\ 2Т dt принимает стационарное значение в классе кривых
ii @1 Чг (*). ¦ • •> in О.
удовлетворяющих дифференциальному уравнению
Т+ V~h = 0. B7.2.2)
Будем рассматривать кривые в (п + 1)-мерном пространстве (t, qit q2, . . ., qn)
при фиксированных начальных значениях t0, qx (t0), q2 (t0), . . ., qn (t0) и фиксированных
конечных значениях gr4 (t^, q2 (?4), . . ., qn (*i), но свободном конечном значении времени tt.
В решении задачи Лагранжа используется правило множителей, на которое мы уже
ссылались в §§ 26.1 и 26.2. Требуется составить условия стационарности функционала
Г
F dt, где
'° F= 2T+ Х(Т+ V— К), B7.2.3)
а К есть функция от t, подлежащая определению. Условием на верхнем пределе будет **)
при t=ti.
Ч
Необходимые условия стационарности функционала \ F dt даются уравнениями
Эйлера:
=1'2 "¦ B7-2-5)
*) Мопертюи был президентом Берлинской Академии во время царствования Фрид-
Фридриха Великого. В его «Essai de Cosmologie» содержался в весьма туманной форме прин-
принцип наименьшего действия, но истинным создателем этой теории следует считать Эйлера.
Журдэн в своей книге «The principle of Least Action» (The Open Court Publishing Co.,
Chicago, 1913) пишет: «То, что Мопертюи сделал неубедительно и сложно, Эйлер сделал
с подлинным искусством, просто и убедительно». Работы Мопертюи подвергались критике
со стороны его современников, в том числе со стороны гаагского профессора Кёнига.
Дискуссия между Мопертюи и Кёнигом перешла в спор между Фридрихом Великим и
Вольтером (подобно тому как боги в «Илиаде» продолжают распри смертных!): Фридрих
принял сторону Мопертюи, Вольтер — сторону Кёнига. Этот спор в конце концов пере-
перешел в ссору, и Фридрих и Вольтер окончательно порвали друг с другом. Присущие Мопер-
Мопертюи самомнение и эксцентричность служили прекрасным поводом для насмешек со сторо-
стороны Вольтера; остроумная и блестящая «История доктора Акакия и уроженца Сен-Мало»
явилась уничтожающей сатирой на Мопертюи. К сожалению, принцип наименьшего
действия был открыт намного раньше, чем значительно более простой принцип
Гамильтона. Это обстоятельство нашло отражение в известных работах Гамильтона 1834 г.
Первая из них посвящена характеристической функции, которая естественным образом
связана с принципом наименьшего действия; что же касается главной функции, связан-
связанной с принципом Гамильтона, то она появилась лишь во второй работе.
**) Это — известное в вариационном исчислении условие трансверсальности
t {1=о,
причем по условию 6го = О. (Прим* перев.)
27.3] ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ В ФОРМЕ ЯКОБИ 547
Их можно записать в форме
'-<•» -
Умножая r-е уравнение на дг и суммируя по г от 1 до ге, получаем
"9г
Следовательно,
где —г- обозначает сумму V -j—gr, а—- сумму V I—— qr-\ —qr). Таким
at +—i oqr ai ^—i \ oqr „ /
oqr
образом,
B + X)^r(T + V) = 2(l + X)^r-2T ^L. B7.2.9)
Левая часть этого равенства тождественно равна нулю, а правая часть эквивалентна
выражению
-2 A + к) -?L-2T^=-2-fL (Г+М1). B7.2.10)
Следовательно, величина A + X) Т остается постоянной вдоль траектории, и концевое
условие B7.2.4) показывает, что эта постоянная равна нулю. Поэтому К = —1 для всех
значений /. Отсюда следует, что уравнения B7.2.6) равносильны уравнениям движения
Лагранжа.
§ 27.3. Принцип наименьшего действия в форме Якоби. Трудности,
связанные с ограничением, накладываемым на вариации в принципе наи-
наименьшего действия, иллюстрированные выше, заставили искать новую
форму принципа, свободную от упомянутого ограничения. Оказалось, что
такая форма принципа получается достаточно просто.
Рассмотрим голономную систему с п степенями свободы и предположим
сначала, что система натуральная. Как для исходного, так и для варьиро-
варьированного движения будем иметь
Т = h — V = V T {h — V). B7.3.1)
Согласно принципу наименьшего действия функционал
JV)dt B7.3.2)
«о
принимает стационарное значение в классе движений с постоянной энер-
энергией h. Теперь, однако, это последнее ограничение (требование о постоян-
постоянстве энергии всех сравниваемых движений) не является существенным.
В самом деле, подынтегральная функция в выражении B7.3.2) является
однородной функцией первой степени относительно скоростей, так что зна-
значение интеграла зависит только от траектории системы в д-пространстве
и не зависит от скорости движения вдоль этой траектории. Таким образом,
мы приходим к следующей теореме: интеграл
н
J V — V) dt
35*
548 ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ [Гл. XXVII
в действительном движении принижает стационарное значение по сравнению
с его значениями для соседних движений, соединяющих те же концевые точки
в q-пространстве. В этом заключается принцип наименьшего действия
в форме Якоби. Задача об определении траектории изображающей точки
в g-пространстве свелась, таким образом, к обычной задаче вариационного
исчисления с фиксированными концами.
Для задачи о движении частицы в пространстве под действием сил кон-
консервативного поля с потенциалом V выражение B7.3.2) принимает вид
б J V2(h — V)ds = 0, B7.3.3)
где s — длина дуги. Эта форма записи напоминает принцип Ферма в оптике.
Принцип Ферма утверждает, что луч света из точки А идет в точку .В таким
образом, что время прохождения им расстояния от А до В имеет минималь-
минимальное (или по крайней мере стационарное) значение. Этот принцип справедлив
даже в тех случаях, когда световой луч претерпевает внезапные изменения
направления, как это бывает, например, при отражении от зеркала или
при встрече с поверхностью линзы с резко отличающимся показателем
преломления. В динамике чаще всего приходится встречаться с задачами,
аналогичными распространению света в среде с непрерывно изменяющимся
показателем преломления \jl. Скорость света в такой среде пропорциональ-
пропорциональна 1/[х, и путь, для которого время распространения света является наи-
наименьшим, определяется из условия минимума функционала
I \ids.
Таким образом, задача динамики об определении траектории движения
частицы совпадает с задачей оптики об отыскании формы светового луча,
если силовое поле и постоянная энергии в первой из них связаны с показа-
показателем преломления во второй соотношением
— V.
Если система не является натуральной, то выражение B7.3.2) заменяет-
заменяется следующим:
h
\ {2 VT2(h-V+TQ) + T,} dt. B7.3.4)
В качестве простого примера рассмотрим задачу о плоском движении частицы
в однородном поле. Траекториями движения являются кривые, доставляющие стацио-
стационарное значение интегралу \ ~|/2 (h—V) ds. Для однородного поля напряженности g,
направленного вдоль оси О у, потенциал имеет выражение V= —gy и интеграл прини-
принимает вид \ У 2 (h-\-gy) ds. Выбирая теперь ось Ох в качестве нулевого уровня энергии,
находим, что /г=0, и задача сводится к отысканию экстремалей интеграла
f YJds= f Y y(i+y'2)dx. B7.3.5)
Подынтегральная функция / не содержит х, поэтому получаем хорошо известный
первый интеграл
| B7.3.6)
откуда находим
у = Ъ A + у'2) = Ъ sec2г|з (Ь > 0), B7.3.7)
где tg г); = у' выражает наклон траектории к оси х. Имеем
dx = ctg г|з dy = 26 sec3 t]j *|з, B7.3.8)
§ 27.3] ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ В ФОРМЕ ЯКОБИ 549
откуда получаем *)
х — д= 26 tgi|). B7.3.S)
Исключая я|> из B7.3.7) и B7.3.9), находим уравнение траекторий
(х — аK = 46 (г/ — 6). B7.3.10)
Ими являются параболы, расположенные в верхней полуплоскости и имеющие ось Ох
в качестве директрисы.
Принцип наименьшего действия в форме Якоби показывает, что в слу-
случае натуральной системы функция
V = 2VT(h - V) B7.3.11)
может быть использована в качестве функции Лагр^яжа и из нее могут быть
получены уравнения движения, которым удовлетворяют движения с энер-
энергией h. В этом нетрудно убедиться непосредственным вычислением. Заметим
при этом, что п дифференциальных уравнений, получающихся из функции
Лагранжа B7.3.11), не являются независимыми; этот факт хорошо известен
в теории параметрических задач вариационного исчисления. Уравнения
определяют только траектории в д-пространстве для движений с энергией h.
Чтобы определить скорость движения изображающей точки вдоль траекто-
траектории, нужно учесть, что полная энергия Т + V равна h.
Для доказательства того, что уравнения, полученные из функции Лаг-
Лагранжа B7.3.11), не независимы, достаточно заметить, что, умножая г-е
уравнение на qr и суммируя по г от 1 до п, мы получаем (см. § 6.7)
Правая часть этого равенства тождественно равна нулю, поскольку функ-
функция L' — однородная функция первой степени от переменных д.
В качестве простого примера использования функции Лагранжа B7.3.11) рассмот-
рассмотрим снова задачу о плоском движении частицы в однородном поле g, направленном
вдоль оси Оу. В этом случае
B7.3 13)
и координата я является циклической. Поэтому из уравнения движения относительно
координаты х получаем
-]/2{h + gy) X = const, B7.3.14)
что эквивалентно B7.3.7). Как мы уже отмечали, уравнение для координаты у не незави-
независимо, так что одного уравнения достаточно для определения траектории.
Так как функционал B7.3.2) зависит только от пути изображающей
точки в д-пространстве и не зависит от скорости ее движения вдоль него,
то независимую переменную t можно заменить на новую переменную \.
В качестве такой переменной можно взять, например, одну из координат q.
Введем функцию Т', являющуюся однородной квадратичной формой пере-
переменных q[, q'2, . . ., q'n-, где q'r = dqTld\. Если
|^' B7.3.15)
*) Можно было бы также проинтегрировать уравнение by'2 = у — 6, применив
подстановку у — 6 = z2.
550 ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ [Гл. XXVII
то
4 ;. B7.3.16)
Для промежутка времени, в течение которого переменная | монотонно
изменяется вместе с t, имеем
h ii
\2VT(h-V)dt= \2\^T'(h-V)dl, B7.3.17)
to lo
В соответствии с принципом наименьшего действия в форме Якоби
можно теперь выражение
Л = 2]/ Г (h — V) B7.3.18)
принять в качестве новой функции Лагранжа с независимой переменной |,
введенной вместо времени. Соответствующие уравнения движения по-преж-
по-прежнему будут определять только траекторию движения, но не скорость пере-
перемещения вдоль нее.
В качестве простого примера рассмотрим плоское движение частицы под действи-
действием притяжения к центру, когда известна потенциальная функция F = F(r). В поляр-
полярных координатах будем иметь
Т=4-Й+г2ё2). B7.3.19)
Li
Полагая ?=г, получаем
/" 9'2)(A-F). B7.3.20)
Координата Э является циклической, и первый интеграл
-^7-= а B7.3.21)
приводит к хорошо известному дифференциальному уравнению орбиты (см. E.2.42))
0'2 = а2^г4 . B7.3.22)
§ 27.4. Теорема Уиттекера *). Интересно попытаться дать элементарный
вывод принципа наименьшего действия в форме Якоби для простого случая
плоского движения частицы в поле консервативных сил. Рассмотрим в пло-
плоскости дугу С. Обозначим через s длину этой дуги между начальной точ-
точкой А и текущей точкой Р, а через 0 — наклон внешней нормали в точке Р
к оси Ох. Будем предполагать, что вдоль кривой С угол 6 все время возра-
возрастает вместе с s и является дифференцируемой функцией от s. В частности,
если кривая замкнута, то она выпуклая.
Найдем вариацию функционала
/= J Y2(h—V)ds B7.4.1)
при переходе от кривой С к кривой С, получающейся из С путем смещения
ее на расстояние Ьр в направлении внешней нормали. Предполагается, что
смещение 8р непрерывно изменяется в зависимости от s. Вариация функцио-
функционала равна
6/=--. [ ~6F Л-c-f j Y2{h — V)bds. B7.4.2)
Но
-8V = N бр, B7.4.3)
*) См. E. T. W h i t t a k e r, Monthly Notices R. A. S., LXII, 1902, стр. 186.
§ 27.4] • ТЕОРЕМА УИТТЕКЕРА 551
где N — составляющая силы поля вдоль внешней нормали, а
8ds = 8р dQ = 8р ds/p, B7.4.4)
где р — радиус кривизны кривой С в точке Р. В результате получаем
6/=Л -_1^ЛАГ+ 2{h~V)Xbpds. B7.4.5)
J /2 (h- V) \ Р /
Используем сначала эту формулу для вывода принципа наименьшего
действия в форме Якоби в одном частном случае. Предположим, что дуга
кривой С между точками А и В является частью траектории, и положим
вариацию 8р = 8р (s) в точках А и В равной нулю. Обозначая скорость
частицы через v, можем написать
ar=_ggl=-2(*-r)t B7.4.6)
Р р v
и, следовательно, подынтегральная функция в B7.4.5) обращается в нуль
в каждой точке кривой С. Отсюда следует, что 81 = 0. Таким образом,
мы пришли к результату Якоби.
Теперь используем формулу B7.4.5) для доказательства теоремы Уит-
текера о существовании простых периодичесих траекторий. Выберем зна-
значение h таким, чтобы во всей рассматриваемой области выполнялось нера-
неравенство h > V- Пусть С — простая замкнутая выпуклая кривая указанного
выше типа; рассмотрим функцию
ff'=N+2{h~V) B7.4.7)
в точках этой кривой. Если всюду вдоль кривой выполняются неравенства
W < 0 и 8р > 0, то согласно B7.4.5) 81 < 0. Таким образом, при этих
условиях значение функционала / уменьшается при переходе от кривой С
к соседней простой замкнутой кривой, окружающей С. Предположим
теперь, что существует другая простая замкнутая выпуклая кривая D, окру-
окружающая кривую С и такая, что во всех ее точках W > 0. Тогда, если в каж-
каждой точке кривой D 8р < 0, то 81 < 0, и значение / уменьшается при пере-
переходе от кривой D к соседней простой замкнутой кривой, лежащей целиком
внутри области, ограниченной кривой D.
Рассмотрим, далее, значения функционала / на простых замкнутых
кривых Г семейства х, расположенных внутри кольца, ограниченного кри-
кривыми С и D. Предположим, что это кольцо не содержит особых точек функ-
функции V. Мы видели, что значения / убывают при перемещении кривой Г
наружу от кривой С или внутрь от кривой D. Предполагая, что значения /
на кривых семейства х ограничены и что точная нижняя грань этих значе-
значений т достигается на некоторой кривой семейства, приходим к выводу, что
существует по крайней мере одна кривая Го, для которой / (Го) = т. На этой
кривой функционал / достигает минимального значения. Очевидно, что
кривая Го не может совпадать как с кривой С, так и с кривой D ни целиком,
ни какой-либо частью. Таким образом, если на кривой С W < 0, а на кри-
кривой D W > 0, то в кольцевой области, ограниченной этими кривыми, суще-
существует по крайней мере одна периодическая траектория.
Рассмотрим, в частности, случай, когда кривые С и О сами являются
периодическими траекториями, причем кривой С соответствует энергия hi,
а кривой D — энергия Ъг, где h\ > h2. Пусть'h — любое число, лежащее
в интервале между /ц и h%:
hi>h> h2.
Тогда вдоль кривой С W < 0, а вдоль кривой D W > 0, и, следовательно,
по доказанной только что теореме существует замкнутая траектория
552 ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ [Гл. XXVII
с энергией h, расположенная в кольцевой области, ограниченной кривыми С
и D. Мы приходим, таким образом, к однопараметрическому семейству пе-
периодических орбит (см. § 15.8, п. 6).
§ 27.5. Исключение координат. Теория исключения координат, развитая в § 10.1,
может быть выведена из вариационного принципа, аналогичного принципу наименьшего
действия. Мы будем рассматривать функционал, который принимает стационарное значе-
значение не во всем классе кривых сравнения, соединяющих концевые точки, а лишь в классе
кривых, подчиненных известному ограничению. В этом параграфе мы выведем снова
некоторые полученные ранее формулы (см. § 10.1), и хотя здесь мы не получим никаких
новых результатов, однако рассуждения, приводящиеся нише, представляют известный
самостоятельный интерес. Возьмем голономную систему с п степенями свободы, причем
первые т координат qit g2, . ¦ ., qm будем считать циклическими.
Рассмотрим интеграл
, <L I у gr dL
t0 dt V=i dqT
Для вариации этого интеграла, обусловленной переходом к соседнему пути в д-про-
странстве, получаем по B6.5.5) следующее выражение:
B7.5.2)
\J^+ldqr ~i ydqr' ¦> '°
Но
•^• = РГ, г = 1,2, ...,т, B7.5.3)
dqr
причем теперь мы ограничиваем варьированное движение таким образом, чтобы эти равен-
равенства оставались справедливыми. Первые т составляющих импульса в этом движении
остаются постоянными, равными их значениям в исходном движении. Учитывая это
ограничение, находим
t\ m
Отсюда легко получаем требуемый результат. Выражаем подынтегральную функ-
• • •
цию в левой части B7.5.4) через рь Р2, . . ., Pm, qm+u qm+2, ¦ ¦ ¦> ?ти исключаем первые
т составляющих скорости и вводим вместо них соответствующие составляющие импульса
с помощью соотношений B7.5.3) (см. § 10.1). После этого под знаком интеграла будет
стоять функция Рауса R, зависящая от явных координат qm+i, qm+2, • ¦ ¦, Яп и их про-
• • •
изводных qm+i, Ят+2' ¦ • ч Яп и содержащая, разумеется, постоянные р. Если теперь
зафиксировать концевые значения явных (не циклических) координат, а также начальный
и конечный моменты времени, то получим
h
б f Rdt = O. B7.5.5)
Уравнения Рауса A0.1.9) выводятся отсюда точно таким же образом, каким урав-
уравнения Лагранжа получаются из принципа Гамильтона. Изложенный вывод принадлежит
Лармору.
§ 27.6. Характеристическая функция. Обратимся к основному резуль-
результату B7.1.5). Ограничимся рассмотрением натуральной системы с и степе-
степенями свободы. В этом случае будем иметь
L = Т — V, B7.6.1)
§ 27.7] ПРОСТРАНСТВО КОНФИГУРАЦИЙ 553
где
^- B7-6-2>
Напомним, что варьирование производится в предположении, что вдоль
кривых сравнения энергия остается постоянной, равной h + бй. Это огра-
ограничение вариаций, в сущности, не является чересчур искусственным: мы
просто требуем, чтобы изображающая точка двигалась вдоль варьирован-
варьированного пути в g-пространстве со скоростью, удовлетворяющей условию Т +
+ V = h -\- bh, причем время движения по этому пути нами не ограни-
ограничивается.
Основная формула B7.1.5) была выведена нами в предположении, что
варьирование совершается относительно динамически возможного пути
(т. е. пути, удовлетворяющего уравнениям движения). Варьированный путь
при этом не является, вообще говоря, динамически возможным путем, но
мы остановимся на том частном случае, когда этот путь является динамиче-
динамически возможным. Варьированным движением при этом будет движение систе-
системы с немного измененными начальными значениями координат и скоростей.
Определим характеристическую функцию Гамильтона. Эта функция
определяется интегралом действия К, взятым вдоль действительного пути
и выраженным через начальные и конечные координаты и постоянную энер-
энергии h. Обозначим характеристическую функцию через К (qi0, <?2oi • • ч <7по!
?н» 5211 • • •, Чпи й). Основное уравнение B7.1.5) определяет вариацию-
характеристической функции при произвольных вариациях ее 2п + 1 аргу-
аргументов. Это соотношение аналогично классической формуле A5.5.11) для
вариации главной функции. Обозначая dLldqr через рг, можем написать
dK = 2 Рп dqrl — 2 Pro dqm + (*i — *o) dh. B7.6.3)
Соотношение
** = Ш <27-6-4>
служит аналогом соотношения A6.5.7) и определяет значение составляющей
импульса в конечной точке в зависимости от qr±, qrQ и h. В модифицирован-
модифицированной теореме Гамильтона — Якоби A6.5.5) — A6.5.7) характеристическая
функция К выполняет роль, аналогичную роли главной функции S в основ-
основной теореме Гамильтона — Якоби.
Сравнение характеристической функции Гамильтона с главной функ-
функцией показывает, что последняя обладает большей простотой. Поясним это
на простом примере. Рассмотрим плоское движение частицы в однородном
поле. Если задать начальную точку х0, у0 и конечную точку ж1? г/i, а также
начальный и конечный моменты времени t0 и tit то движение частицы тем
самым будет полностью определено. Отсюда следует, что функция S будет
однозначной функцией пяти аргументов: х0, у0, х±, у^, tt — t0 — и будет
определена для всех значений аргументов. (В § 15.9 мы ее вычисляли.)
Если же мы зададим точки х0, у0 и х±, у\ и постоянную энергии h, то можем
получить либо две траектории, либо одну, либо ни одной. Таким образом,
функция К будет многозначной функцией своих пяти аргументов: х0, у0, х^,
i/i, h, и определена она будет лишь для некоторых значений аргументов.
Выражение для К для рассматриваемой задачи будет дано позже (§ 27.10).
§ 27.7. Пространство конфигураций. Как мы видели в § 27.3, принцип
наименьшего действия в форме Якоби позволяет свести задачу об определе-
определении траектории частицы, движущейся в силовом поле, к простой вариацион-
вариационной задаче. Действительная траектория частицы доставляет минимальное
554 ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ [Гл. XXVII
(или по крайней мере стационарное) значение интегралу
J V2(h-V)ds. B7.7.1)
Сейчас мы рассмотрим аналогичное преобразование задачи в случае систе-
системы более общего вида.
Пусть мы имеем натуральную систему, для которой
Г==т22а^' B7.7.2)
причем коэффициенты аг$ суть функции от переменных (gi, q2, . . ., qn),
принадлежащие к классу d. Введем в g-пространстве риманову метрику,
определив элементарное расстояние между двумя соседними точками q
и q -\- dq формулой
^2 = 2И*г.<Мд.« B7.7.3)
Если ^-пространство обладает метрикой B7.7.3), то его называют про-
пространством конфигураций. Возвращаясь к задаче о движении системы v то-
точек, можем написать
N
ds2 = ^]mrdx*. B7 Л А)
г=1
После того как мы определили бесконечно малые расстояния в про-
пространстве конфигураций (формула B7.7.3)), можно перейти к вычислению
конечных расстояний между точками. Определим длину спрямляемой кри-
кривой в пространстве с помощью интегрирования вдоль этой кривой и введем
понятие расстояния между двумя любыми конфигурациями как нижнюю
грань (наибольшую нижнюю границу) длин спрямляемых кривых, соеди-
соединяющих эти две конфигурации. Расстояние между двумя конфигурациями Р±
и Pi обозначим через | Р\Рг I- Теперь можно легко определить понятие
окрестности. Пусть Ро — некоторая конфигурация, а 8 — положительное
число. Множество точек Р таких, что
\Р0Р К е, B7.7.5)
назовем сферической окрестностью Ро. Любое множество конфигураций Р,
которое содержит сферическую окрестность Ро, будем называть окрест-
окрестностью Ро. Располагая понятием окрестности в пространстве конфигураций,
мы можем изучать его топологические свойства.
Кинетическая энергия системы определяется формулой
T = -~'s\ B7.7.6)
Она имеет такой вид, словно изображающая точка есть частица единичной
массы, движущаяся в пространстве. Но это, конечно, еще не дает полной
картины. Аналогия между динамической системой и точкой, движущейся
в пространстве конфигураций, распространяется также и на уравнение
движения, r-е уравнение движения Лагранжа для системы имеет вид
2 arsqs+ 22 [uy' r]Vuqv= — -g^t B7.1.7)
где, подобно F.4.5), через [uv, r] обозначен первый символ Кристоффеля,
хотя, строго говоря, следовало бы вместо qT писать дг, как это принято
в тензорном анализе. Левая часть равенства B7.7.7) представляет не что
иное, как ковариантную составляющую ускорения в пространстве конфигу-
конфигураций. Уравнение движения Лагранжа для системы в точности совпадает
с уравнением, выражающим второй закон Ньютона для частицы единичной
¦§ 27.8] СИСТЕМА С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ 555
массы, движущейся в пространстве конфигураций под действием поля
с потенциалом V.
Принцип наименьшего действия в форме Якоби B7.3.2) для общего
случая динамической системы принимает следующий вид:
V)ds = 0. B7.7.8)
Это равенство имеет точно такую же форму, как и в простом случае движения
частицы в обычном пространстве, отличие состоит в том, что теперь интегри-
интегрирование производится вдоль кривой в пространстве конфигураций и s здесь
обозначает длину дуги этой кривой.
§ 27.8. Система с двумя степенями свободы. Для некоторых простых систем с двумя
степенями свободы можно указать поверхность (в обычном евклидовом пространстве),
которая гомеоморфна всему пространству конфигураций, иными словами, существует
взаимно однозначное отображе-
отображение пространства конфигураций у
на указанную поверхность. Рас-
Рассмотрим два простых примера.
1) Твердая пластина дви-
движется в своей плоскости таким
образом, что некоторая ее точка А
перемещается вдоль заданной пря-
прямой Ох. Положение пластины в
момент t можно определить двумя
лагранжевыми координатами: х и Рис. 108.
6, где х есть расстояние ОА,
а 6 — угол между осью Ох и
отрезком AG, соединяющим точку А с центром тяжести пластины G (рис. 108). Простран-
Пространство конфигураций в данном случае гомеоморфно поверхности кругового цилиндра
с цилиндрическими координатами х, 9, причем х отсчитывается вдоль оси цилиндра,
а Э — от неподвижной плоскости, проходящей через ось.
Если точка А может свободно перемещаться по всей длине оси х, то цилиндр будет
иметь бесконечную длину. Если же имеются ограничения, выражаемые неравенствами
Xi < х < хг B7.8.1)
или
xi < х < х2, B7.8.2)
то в этом случае длина цилиндра ограничена плоскостями, нормальными к его оси. Пре-
Пределы в. неравенствах B7.8.1) иногда называют неупругими упорами, а в неравенствах
B7.8.2) — упругими упорами.
Интересно отметить, что при ином выборе лагранжевых координат в данной задаче
можно добиться фактического равенства линейных элементов пространства конфигура-
конфигураций и его топологического эквивалента — поверхности цилиндра. Имеем
Г = -|-М {x*-2axQ sin 9 + (а2+/>2) &}, B7.8.3)
где а обозначает длину отрезка A G, а Мрг — момент инерции пластины относительно цен-
центра масс G. Для пространства конфигураций имеем (полагая М = 1)
ds3 = <fe2 — la sin 9 dx dQ + (a2 + p2) <Ю2. B7.8.4)
Перейдем теперь к новым лагранжевым координатам ?, <р, связанным со старыми
соотношениями
9
_fL_)
B7.8.5)
так что | есть координата х точки G, а ср есть монотонно возрастающая функция от 9,
причем значению 9 = 2л соответствует значение ф = 2я. Равенство B7.8.4) при этом
принимает вид
ds2 = dl* + Ь2Лр2, B7.8.G)
где
Ь = -5- Уа^+рТ B7.8.7)
556 ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ [Гл. XXVII
Элемент длины в пространстве конфигураций |, ср равен элементу длины отрезка
на цилиндре радиуса Ъ с Ь, ср, | в качестве цилиндрических координат. Если нет заданных
сил (V = 0 в уравнении B7.7.8)), траектории в пространстве конфигураций соответствуют
геодезическим линиям на поверхности цилиндра; если последний развернуть на пло-
плоскость, то геодезические линии перейдут в прямые.
2) Рассмотрим двойной маятник, составленный из двух стержней АВ, ВС, соеди-
соединенных вместе в точке В, и свободно подвешенный в неподвижной точке А. Такая система
может совершать движение в вертикальной плоскости, проходящей через точку А. (Вме-
(Вместо двух стержней мы могли бы взять легкую струну ABC, подвешенную в неподвижной
точке А, с массивными грузами в точках В и С.) В качестве лагранжевых координат
возьмем углы Э и ср, которые стержни АВ и ВС составляют с направленной вниз верти-
вертикалью. Пространство конфигураций такой системы гомеоморфно поверхности тора; при
этом Э играет роль азимутального угла, а ср — углового перемещения в круговом попереч-
поперечном сечении, отсчитываемого от центральной плоскости тора.
§ 27.9. Теорема Кельвина. Вернемся к рассмотрению системы с п сте-
степенями свободы, пространство конфигураций которой имеет метрическую
структуру, определяемую формулой B7.7.3). Можно дать очень простую
интерпретацию импульса (pi, р%, . . ., рп) такой системы. Имеем
п
pr=^arsqs, B7.9.1)
s=l
откуда следует, что импульс есть ковариантный вектор, соответствующий
вектору скорости (qit q2, . . ., qn), который является контравариантным.
Условие ортогональности смещения dq и скорости q выражается равенством
%%anqJqr = 0, B7.9.2)
или, короче,
2prd?r = 0. B7.9.3)
Рассмотрим в пространстве конфигураций семейство траекторий, харак-
характеризуемых одной и той же энергией h. В этом случае формула B7.6.3) для
вариации характеристической функции принимает вид
dK = ^Рп dqTi - S^ro dqr0. B7.9.4)
Предположим теперь, что траектории с энергией h все выходят из'задан-
ной точки Ро (qi0, q2o, ¦ . ., qno) пространства конфигураций. Начальная
скорость при этом для всех траекторий одинакова по величине, поскольку
^L's^==T = h-V, B7.9.5)
но различна по направлению. Имеем
dK = Sph dqrU B7.9.6)
и если (dqi, dq2, . . ., dqn) представляют перемещение вдоль поверхности
К = const == к, то
Ърп dqH = 0, B7.9.7)
откуда следует, что траектория пересекает поверхность под прямым углом.
Поверхность К = к представляет геометрическое место точек Pi, принад-
принадлежащих различным траекториям и таких, что интеграл действия \ 2Tdt,
взятый вдоль соответствующих траекторий от точки Ро до точки Pi, имеет
одно и то же значение к. Поверхности К = к называют поверхностями рав-
равного действия относительно точки Pq. Таким образом, мы приходим к выво-
выводу, что семейство траекторий постоянной энергии, начинающихся в данной
§ 27.9] ТЕОРЕМА КЕЛЬВИНА 557
точке, ортогонально поверхностям равного действия относительно этой же
точки. Это утверждение составляет первую часть теоремы Кельвина.
Рассмотрим теперь точки (qi0, q2o, . . ., <?по)> принадлежащие «поверх-
«поверхности» Го:
ф (?ю, ?2о. • • •, ?„о) = 0, B7.9.8)
где фб С\. Возьмем в пространстве конфигураций траектории с заданной
энергией h, выходящие из точек Го перпендикулярно к этой поверхности
с одной ее стороны. Если dq0 есть вектор перемещения по поверхности Го,
то согласно условию перпендикулярности
г0 dqrQ = 0, B7.9.9)
и уравнение dK = 0 снова показывает, что
2Pri dqTi = 0. B7.9.10)
Траектории пересекают поверхности К = к под прямым углом. Семей-
Семейство траекторий, характеризуемых одной и той же энергией и выходящих
из точек поверхности Го под прямым углом к ней, ортогонально поверхно-
поверхностям Г^, причем приращение функции действия между этими поверхностя-
поверхностями одинаково для всех траекторий. В этом состоит вторая часть теоремы
Кельвина.
Поверхность Г^ является огибающей поверхностей равного действия
К = к относительно точек поверхности Го. Поверхность равного действия
К — к относительно точки Ро задается уравнением вида
К (qi0, q20, . • м qno> ?н» ?2i» • • •> Qni) = к, B7.9.11)
где (glt, «/21» • • •* Qni) — текущие координаты. Для точек огиЗаюдзя ihm
21^=0 B7-9-12)
при условии
2-^-^ = 0. B7.9.13)
Отсюда получаем соотношение
*/ *3Lconst, B7.9.14)
показывающее, что (ковариантный) вектор dK/dqr0 имеет направление нор-
нормали к поверхности Го- Точка касания поверхности B7.9.11) с огибающей
расположена на траектории, выходящей с поверхности Го под прямым углом
к ней.
Укажем на тесную связь между полученными результатами и принци-
принципом Гюйгенса в оптике. Траектории частицы в оптике соответствует световой
луч, а поверхности равного действия — волновой фронт. Волновой фронт
является огибающей частичных волновых фронтов, расходящихся от точек,
которые лежали на поверхности волнового фронта в предшествующий момент
времени. Различие заключается в том, что в задачах динамики мы имеем
дело с приращением функционала действия, а в задачах оптики — с при-
приращением времени.
Как правило (за исключением простейших случаев), определить поверхности рав-
равного действия бывает весьма трудно. Приведем два примера, не требующих сложных
вычислений.
1) Частица движется в обычном трехмерном пространстве без действия на нее сил.
Траекториями являются прямые, скорость вдоль которых равна v = ~\/2h. Интеграл
558 ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ [Гл. XXVII
действия равен
[ 2Tdt = vH = z;r = г V~2h,
где г — длина отрезка от точки Ро до точки Pi. Поверхностями равного действия отно-
относительно точки Ро являются сферы с центром в этой точке; поверхность К = к представ-
представляет сферу радиуса k/~[/2h. Если за исходную принять произвольную поверхность Го,
то поверхностями Tk равного действия будут параллельные поверхности, получающиеся
из Го путем смещения ее вдоль нормали на расстояние k/~\/2h.
2) Частица движется по гладкой поверхности при отсутствии активных сил. Траек-
Траекториями в этом случае будут геодезические линии, а поверхностями равного действия
относительно точки Ро — геодевические круги с центром в Ро-
§ 27.10. Однородное поле. Перейдем теперь к задаче, упоминавшейся
в конце § 27.6. Определим характеристическую функцию и, следовательно,
уравнение поверхностей равного действия для задачи о плоском движении
частицы единичной массы в однородном поле сил. Пространство конфигура-
конфигураций для этого случая есть не что иное, как обычная евклидова плоскость,
в которой движется частица. Направим ось Оу вдоль поля, а за поверхность
нулевой энергии возьмем ось Ох; тогда будем иметь V = — gy и h = 0.
Обозначая через и, v составляющие начальной скорости в точке Ро (х0, уо)г
можем написать
x — xo = ut, y-yo = vt + ±-gt*. B7.10.1)
Отсюда получаем
е е
К= ^2Tdt= \(u2+v2+2vgt+g2t2)dt B7.10.2)
о о
или
K--=(u2+v2)Q+vgQ2 + -^-g2Q3, B7.10.3)
где мы положили t0 = 0, t\ = 6. Далее,
u« + у2 = 2gy0, B7.10.4)
и, исключая и и v из правой части B7.10.3), представляем К как функцию»
от Э:
gy0Q + gQ (у, - г/о - 4
к = 2gy0Q + gQ (у, - г/о - 4 г02) + т ^ = ?0 (г/i+г/о) - 4 г203 = ^~т
B7.10.5)
где через s обозначена сумма j/i + j/o-
Выражая 0 через х0, у0, хь уь получаем
2gy0Q2 = {и2 + у*) б2 = (а* - хоJ+ {у, - у0 - \ g&y =
= (Xl-Xoy+(y1-yoJ-gQ2(y1-yo) + ±.gW, B7.10.6)
что можно представить в форме
#204 - AgsQ2 + Ar2 = 0, B7.10.7)
где
г2 = {ху - х0J + (ух - у0J. B7.10.8)
На рис. 109 парабола s = г представляет огибающую G; вещественным
положительным значениям 6 соответствует условие s ^ г. Действительно,,
разрешая уравнение B7.10.7) относительно 0, получаем
?02 = 2s ± 2 /s^r2 = (V^T^ ± V^^)\ B7.10.9)
§ 27.11]
ЗАДАЧА ТЭТА. НЕПОСРЕДСТВЕННОЕ РЕШЕНИЕ
55»
откуда при s>r находим два значения Э:
Ys+r + Ys — г, "I
J/7+7—УТ^г, J
при этом gQ]Q2 = 2г. Таким образом,
и, следовательно,
B7.10.10)
3-е- г^- B7.10.11)
= (s + rK/2±(s-rK/2. B7.10.12)
Двузначный ответ не является неожиданным (см. § 27.6). Если, напри-
например, положить (xi, yi) = (xQ, у0), так что s = 2у0, г = 0, то одно из значений
Z обратится в нуль, а другое будет равно -|- Y2g!/V2- Первому из этих значе-
значений отвечает отсутствие движения, а второму — прямолинейное движение,
при котором частица в началь-
начальный момент движется навстречу
полю.
Рис. 109.
Рис. 110.
Поверхностями равного действия относительно точки Ро будут кривые,
определяемые уравнениями
(s + гK'2 ± 0? — гK/2 = const. B7.10.13)
Согласно первой части теоремы Кельвина эти кривые ортогональны семей-
семейству траекторий (рис. 110). Нижний знак при этом соответствует точке пере-
пересечения с траекторией до момента соприкосновения ее с огибающей, а верх-
верхний знак — точке пересечения после соприкосновения с огибающей. Кривые
равного действия имеют точки заострения, расположенные на огибающей
параболе.
§ 27.11. Задача Тэта. Непосредственное решение. Рассмотрим теперь пример,
иллюстрирующий вторую часть теоремы Кельвина (§ 27.9). (Поскольку мы будем решать
плоскую задачу, роль поверхностей равного действия будут играть кривые.) Рассмотрим
снова задачу о движении частицы в однородном поле, и пусть начальной кривой будет
прямая, параллельная направлению поля.
Направим ось Оу вдоль поля и будем считать прямую у = 0 линией нулевой энер-
энергии, а прямую х = 0 — линией, с которой частица начинает движение.
Определим траектории частиц, начинающих свое движение из точек @, у0) со ско-
скоростью (и, 0), где и2 = 2gy0. Вычисления аналогичны тем, которые мы проводили в преды-
предыдущем параграфе. Имеем
х= ut, y= yo + ±gt* B7.11.1)
560
ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ
[Гл. XXVII
K= \ (u2 + g2z2) dt = u2Q-\ g203 = _L_j g-203 . B7 112)
I -393
причем, как и ранее, мы положили здесь to = O, ^ = 0. Уравнение для 9 имеет вид
B7.11.3)
или
Следовательно,
Отсюда находим 6:
где ради краткости
2=Ui ±
Выражение для К имеет вид
обозначено через |, a
B7.11.4)
B7.11.5)
B7.11.6)
— xi—через т|.
39 "^
±тK). B7.11.7)
Поверхности (в данном случае кривые) равного действия (рис. 111) описываются
уравнением
(г/1 + xiK/2 ± (г/i — xjK/2 = const. B7.11.8)
Траекториями частиц являются параболы
х? = 4у0 (г/i - г/о), B7.11.9)
что можно записать также в форме
I ± л = 2Уг7о". B7.11.Ю)
Параболы B7.11.9) касаются линий
г/i = ±Хь а кривые равного действия
B7.11.8) имеют точки заострения, распо-
расположенные на этих линиях..
§ 27.12. Задача Тэта. Теория оги-
Рис. 111. бающих. Интересно получить решение
задачи Тэта с помощью теории огибаю-
огибающих. Как мы уже видели, поверхность
равного действия Tk, порождаемая поверхностью Го, служит огибающей поверхностей
равного действия относительно отдельных точек Го (§ 27.9). Здесь, однако, имеется
некоторая тонкость. Поскольку в точке @, у0) траектории направлены горизонтально,
допускается лишь меньшее из двух возможных значений времени достижения точек
(xi, г/j), и, как ив § 27.10, мы можем написать
B7.12.1)
B7.12.2)
где теперь
-г/оJ. B8.12.3)
а к представляет приращение функции действия при переходе вдоль траектории из точ-
точки @, г/о) в точку (xi, yt). Для нахождения огибающей нужно исключить у0 из уравне-
уравнения B7.12.2) и уравнения
д " • K/2_(s_rK/2}=0- B7.12.4)
Легко убедиться непосредственной проверкой, что последнее уравнение эквивалентно
S 27.12]
ЗАДАЧА ТЭТА. ТЕОРИЯ ОГИБАЮЩИХ
561
уравнению траектории; поэтому его можно заменить более простым:
х\ = 4г/0 (г/i - г/о)-
B7.12.5)
Как уже отмечалось, огибающей этого семейства парабол служит пара прямых
у\ = х\; точка касания определяется формулой у^ = 2у0.
На дуге АВ (рис. 112) имеем у0 < yt < 2у0, а на дуге „
ВС 2у0 <Vi- у L
Теперь нужно исключить у0 из уравнений B7.12.2) и
B7.12.5). Проделав это. будем иметь
откуда, учитывая B7.12.5), находим
^T7i = 2Ув.
Таким образом,
.'/1 —Z/o— * — 2(/o = s—У*2— ri =
B7.12.0)
B7.12.7)
B7.12.8)
Рис. 112.
где У«+г обозначено через к, а У«— г—через |я. Далее, из уравнения
Уо) = (М1~2уо)* B7.12.9)
находим
У\ — xl =
-г/1 на дуге АВ,
2у0 на дуге ВС.
Следовательно, вдоль дуги АВ
а вдоль дуги ВС
B7.12.10)
B7.12.11)
B7.12.12)
B7.12.13)
Теперь легко составить уравнение огибающей. Рассмотрим каждый случай в отдель-
отдельности. Для дуги АВ имеем
I B7.12.14)
>). B7.12.15)
B7.12.16)
B7.12.17)
. B7.12.18)
B7.12.19)
и, следовательно,
Окончательно получаем
Аналогично, для дуги ВС
2) = -Ld-^ 2 (|2
VS
i ~ Уо = -J
1
и, следовательно,
ГЗ окончательном виде будем иметь
3ft
Формулы B7.12.16) и B7.12.19) эквивалентны уравнениям B7.11.7) при К = к, что
мы и хотели доказать.
36 Л. Л. Парс
Глава XXVIII
ОГРАНИЧЕННАЯ ЗАДАЧА ТРЕХ ТЕЛ
§ 28.1. Задача трех тел. Задача трех тел принадлежит к числу наи-
наиболее известных проблем классической динамики. В ней рассматривается
движение трех частиц в пространстве под действием сил взаимного притяже-
притяжения и требуется определить их положения в любой момент времени, если
в момент t = 0 заданы их координаты и скорости. Изучение этой задачи
оказало огромное влияние на развитие всей динамики. Многие из наиболее
важных результатов этой науки в большей или меньшей степени связаны
с задачей трех тел.
Решение задачи двух тел, кратко изложенное в § 5.4 и далее, представ-
представляет одно из самых больших достижений ньютоновой механики. В указан-
указанном выше смысле эту задачу можно считать полностью решенной, т. е. мы
можем определить положения частиц в любой момент времени, если известны
координаты этих частиц и их скорости в момент t = 0. Что же касается
задачи трех тел, то ее нельзя считать решенной в этом смысле. Однако для
многих частных случаев этой задачи, возникающих в астрономии, удается
построить приближенное решение с весьма высокой степенью точности.
Небесные тела приближенно можно считать имеющими сферическую форму
со сферически симметричным распределением массы; взаимное притяжение
таких тел таково же, как у частиц, расположенных в их центрах. Если
в качестве трех тел рассматриваются Солнце и две планеты, то основным
упрощающим условием является то, что массы т^ и т^ планет малы по срав-
сравнению с массой М Солнца, так что членами третьего порядка относительно
mJM и тпг1М обычно можно пренебречь. (Например, масса Земли составляет
менее чем 1/300 000 массы Солнца.) Если же рассматривается движение
Солнца (М), планеты (ш) и ее спутника (\i), то отношения пг/М и ц/М всегда
малы и, кроме того, \\,1тп мало, хотя порядок малости последнего отношения
и отличается от порядка малости пг/М. (Например, масса Луны составляет
около 1/80 массы Земли.) Другое обстоятельство, облегчающее построение
приближенных решений, заключается в том, что эксцентриситет планетных
орбит, как правило, весьма мал (для орбиты Земли он составляет приблизи-
приблизительно 1/60).
В предыдущих главах мы пробовали применить два подхода к решению
задачи трех тел. В § 17.10 рассматривалось движение планеты в поле двух
притягивающих центров. Если считать, что это движение происходит в непо-
неподвижной плоскости, проходящей через притягивающие центры, то можно,
как мы видели, дать исчерпывающую классификацию траекторий. Более
того, можно найти уравнения траекторий, выразив их через эллиптические
функции. Трудности, с которыми мы сталкиваемся в этой сравнительно
простой задаче, дают представление о сложности проблемы в общем случае.
В § 25.3 мы рассматривали вариации эллиптических элементов. При этом
сначала изучалось движение одной планеты относительно Солнца, а затем
рассматривались те возмущения, которые обусловлены наличием второй
планеты. Второй этап в этих • рассуждениях не носил характера самостоя-
самостоятельной задачи: возмущенное движение рассматривалось как непрерывное
видоизменение исходного эллиптического движения. Этот метод эффективен,
поскольку массы планет весьма малы по сравнению с массой Солнца.
§ 28.2] ОГРАНИЧЕННАЯ ЗАДАЧА. УРАВНЕНИЯ ДВИЖЕНИЯ 563
§ 28.2. Ограниченная задача. Уравнения движения. Органиченная
задача трех тел заключается в следующем. Частица А массы а и частица В
массы р движутся под действием сил взаимного притяжения. Центр масс G
обеих частиц движется равномерно и прямоли-
прямолинейно, так что без потери общности можно счи-
считать, что он находится в покое. Начальные усло-
условия таковы, что орбита частицы В относительно А
представляет собой окружность с центром в А,
следовательно, каждая частица движется относи-
относительно центра масс G по окружности. Рассмотрим
частицу Р пренебрежимо малой массы (так назы-
называемый планетоид); пусть эта частица совер-
совершает движение в одной плоскости с А и В. Мы
будем считать, что она движется под действием Рис. 113.
притяжения частиц А ж В, но ее собственная
масса т столь мала, что она не оказывает склько-нибудь заметного влияния
на движения А и В. Задача состоит в том, чтобы определить движение
частицы Р.
Возьмем вращающиеся оси с началом в точке G и осью х, направлен-
направленной вдоль прямой GB (рис. 113). Обозначим длину отрезка АВ через I, а уг-
угловую скорость вращения — через со; величина со будет определяться по
формуле
(+P) B8.2.i)
По отношению к вращающимся осям частица А будет находиться в покое
в положении (—а, 0), а частица В — в покое в положении (Ь, 0), где а и Ъ
определяются по формулам
Не нарушая общности, можно принять, что а > р > 0. Считая, что
частица Р (х, у) не влияет на движение частиц А и В, можем написать
^^ B8.2.3)
где г обозначает длину отрезка АР, as — длину отрезка ВР:
г2 = (х + аJ + У2, s2 = (х - ЪJ + у2. B8.2.4)
Опуская положительный множитель т, можем написать
Ь = ~(х2+у*) + (о(ху-ух) + ±-аЦх* + у2) + ^+&. B8.2.5)
Функция L имеет вид Т2 + Т\ + То — V. При отсутствии членов Ti и То
мы имели бы задачу о движении в поле притяжения двух неподвижных
центров, рассмотренную нами в § 17.10 и далее. Заметим, что функция L
не содержит явно t\ интеграл Якоби F.8.3) имеет вид
41-^-? = й. B8.2.6)
Введем обозначение
T0-V = yU, B8.2.7)
где
±-?±?(х2 + у2) + -2- -1 1. B8.2.8)
36*:
564 ОГРАНИЧЕННАЯ ЗАДАЧА ТРЕХ ТЕЛ [Гл. XXVIII
Уравнения движения запишутся в виде
у-,
ди \ B8.2.9)
Эти уравнения показывают, что движение происходит так же, как дви-
движение частицы единичной массы в поле консервативных сил с потенциа-
потенциалом —yU при наложенных гироскопических силах. Из интеграла Якоби
B8.2.6) следует, что во все время движения yU + h > 0; следовательно,
движение может происходить лишь при
U>U0, B8.2.10)
где U о = — hi у.
Поскольку
Ьг2 _|_ as2 = i (xi _|_ у2) + ab(a+ b), B8.2.11)
выражение для U можно представить в переменных г и s. Тогда будем иметь
*-^ + М + ^+±-^|. B8.2.12)
Полагая r — pl, s = ol, находим
Эта формула удобна для построения кривых U = const. В областях у > 0 и у < 0 мож-
можно р и а принять за независимые переменные, но вдоль оси у = 0 переменные р и о
связаны между собой. Если ось у = 0 разделить на три части: ?Й\ (— оо < х < — а),
¦$2 (— а <С х <С Ъ) и ^з (Ь < х < °°)i т0 будем иметь
сг—р=1 в области Ми ~)
ст+р = 1 в области М2* \ B8.2.14)
р—ст = 1 в области Мг- '
§ 28.3. Положения равновесия. В точках, где функция U принимает
стационарное значение, планетоид может находиться в покое относительно
вращающихся осей. Если представить себе поверхность
z = U, B8.3.1)
то положениями равновесия будут те ее точки, в которых касательная пло-
плоскость параллельна плоскости z = 0. В точках А и В поверхность B8.3.1)
уходит в бесконечность и при х2 + У2 —>- °° приближенно представляет пара-
параболоид
2n - B8.3.2)
Далее имеем
dU
дх
или
B8.3.6)
§ 28.4] ПОЛОЖЕНИЯ РАВНОВЕСИЯ НА ПРЯМОЙ АВ 565
где для краткости обозначено
Ч*?-&- {28-3-7)
Вторые производные (они нам понадобятся ниже) имеют следующие
выражения:
941 _г , За(х + аK Зр(х-Ь)« B8 3 8}
&U _ дЮ __3а(х + а)у 3${х — Ь)у B8 3 9)
дхду~~ ду дх~ гь ~Т~ [«а ' К • ¦ )
™ W W B8.3.10)
r5 I S5
йТТ йТТ
В точках равновесия ^- = -^- = 0. Согласно B8.3.6) отсюда следует, что
либо у = 0, либо Х = 0. Рассмотрим оба случая.
§ 28.4. Положения равновесия на прямой АВ. При у = 0 имеем г =
= \ х -\- а \, s ¦= \ х — Ъ \ и, следовательно, исключая особые точки А ж В,
Таким образом, d2U/dx2 > 0 при у = 0. Рассмотрим поведение функции
U {х, 0) при возрастании х от —оо до +00- При х = — аиж = Ь она обра-
обращается в бесконечность и, кроме того, стремится к бесконечности вместе
с | х \. Производная dUldx монотонно возрастает от —оо до +оо в каждой
из трех областей: М\ (— оо <; х < — а), Мг (— а < х <; Ъ) и М$ (Ъ <
<а;<оо). Следовательно, в каждой из этих областей производная dUldx
один раз принимает нулевое значение, и функция U достигает при этом
минимума. Соответствующие точки JVt (х = щ), N2 (х = Пг), Л^з (х = Пз)
являются положениями равновесия. Этот факт физически совершенно оче-
очевиден, если U считать потенциалом.
Положение равновесия Ni находится на расстоянии, не превышающем I,
от точки А, а положение равновесия Ns — на расстоянии, не превышаю-
превышающем I, от точки В. Чтобы доказать это, замечаем, что для трех указанных
выше областей
• = (-1,1,1), *=(_!, -1,1), B8.4.2)
х + а-
так что, например, в области J?j
oU ее -т— p.ct.p /оо / о\
-н- = —н^- х + -о- + sr • B8.4.3)
to г3 г2 х2
Следовательно, для точки области J?1? в которой
r==it s = 2l, B8.4.4)
tx-f-p
будем иметь
откуда вытекает, что точка Ni расположена между х = — а — /их = — а.
Точно так же доказывается, что точка N3 лежит между x = bnx=b-rl.
Что касается точки 7^2, то она располагается между G и В. Действительно,
для точки G имеем
аи
дх
566
ОГРАНИЧЕННАЯ ЗАДАЧА ТРЕХ ТЕЛ
[Гл. XXVIII
График функции U (х, 0) показан на рис. 114.
Имея в виду дальнейшие приложения, отметим, что в каждой из то-
точек Nlf Nz, N3
d'U- n dU " dU - B8.4.7)
Первое из этих условий было доказано выше (см. B8.4.1)), а второе
вытекает из B8.3.9). Для того чтобы доказать третье, заметим, что в точ-
точке Ni согласно B8.3.10) —-- = X, и так как в этой точке -т— = 0, то из соот-
соотношения B8.3.5) получаем
дЮ , аЫ I 1
Это выражение в точке Nt отрицательно, по-
поскольку в этой точке х<.0 и r<Cs. Для точ-
точки iV3 доказательство аналогично. Для точки N2
имеем
гз
9Л
Рис. 114.
и это выражение отрицательно, так как в обла-
области М% и г и s не превышают I.
Обратимся к графику функции U (х, 0) (рис. 114). В точках iVl5 JV2
и JV3 функция имеет минимум, причем можно показать, что
U (пг) > U (п3), U (п3) > U (щ)
B8.4.10)
(мы по-прежнему считаем, что а > р > 0). Для этого возьмем в области Мг
точку <2з (х = 9з)' расстояние которой от точки 5 равно расстоянию точ-
точки N2 от точки В. Положив N2B = BQ3 = ft, будем иметь
и Ы-
(ь-*)'+т^+1}
B8.4.11)
Отсюда следует, что С/ (п2) > С/ (<?3)- Но, с другой стороны, U (qa) ^ U (п3),
поскольку в точке N3 функция U имеет меньшее значение, чем в любой
другой точке области <523> чт0 и доказывает первое из неравенств B8.4.10).
Возьмем теперь в области Mi точку Qi (x = gt), находящуюся от точ-
точки G на том же расстоянии, что и точка JVV Положив QiG = GN3 ~ к, будем
иметь
U(n3)-U(qi):
2cw
2—62/ "
B8.4.12)
Отсюда следует, что U {п3) > U (gi). Но, с другой стороны, U {qi) >
^ U (щ), поскольку в точке N± функция U имеет меньшее значение, чем
в любой другой точке области Ми таким образом, второе неравенство B8.4.10)
доказано.
S 28.6]
ПОВЕРХНОСТЬ z = и
567
§ 28.5. Положения равновесия, не лежащие на прямой АВ: Перейдем
теперь к рассмотрению второй возможности, которую мы указывали в кон-
конце § 28.3, а именно предположим, что % — 0. Отсюда следует, что dUldy = 0,
и так как, кроме того, в каждой равновесной точке dU/dx = 0, то из B8.3.5)
получаем, что г = s. Из формулы B8.3.7) теперь находим, что г = s = I.
Таким образом, имеется еще два положения равновесия iV4 и N5 в вершинах
равносторонних треугольников с основанием АВ. Точка iV4 имеет коорди-
координаты (^|у, КЗу) , а точка 7V5 — координаты (^ъ-^ , — КЗу)-
Вторые производные функции U в точках JV4 и Nb определяются фор-
формулами B8.3.8) — B8.3.10). В каждой из этих точек
B8.5.1)
откуда получаем
дЮ 3 сс-
д'Щ
9 ге
4
дх* 4 /з ' дхду"' — 4" I* ' дуг 4 /з ¦• B8.5.2)
Верхний знак в этих формулах относится к точке Nt, а нижний — к точке N5.
Интересно установить существование равновесных точек 7V4 и ^5 на основании эле-
элементарных соображений. Предположим, например, что планетоид находится в положе-
положении N^. В этом положении составляющая действующей на планетоид результирующей
силы по направлению, перпендикулярному к GN^,
равна нулю, так как (см. обозначения на рис. 115)
B8.5.3)
Последнее равенство вытекает из соотношения
sin 0j AG р
sin 9, ~~ GB
а
B8.5.4)
Возьмем на отрезке N^B точку К такую, чтобы
прямая GK была параллельна прямой AN±\ тогда
B8.5.5)
Рис. 115.
На единицу массы планетоида в направлении N±G будет действовать сила
cos Gj) = ^(« + P) GNi== GA4.w2. B8.5.6)
2| cos в^У^ cos G2
Отсюда и следует искомый результат.
§ 28.6. Поверхность я = TJ. В каждой из пяти точек Nt касательная
плоскость к поверхности г = U параллельна плоскости г = 0. В положе-
положениях равновесия, лежащих на прямой АВ, имеем (см.1 B8.4.7))
B8.6.1)
дх'г ду2 \ дх ду
Неравенство показывает, чт.о эти положения равновесия являются седло-
выми точками, а не точками минимума. Что касается точек JV4 и N6, то
для них имеем (см-. 28.5.2))
дЮ _ „ дЮ д'Щ 1 дЮ \ а 27аР
дх*
0,
дх*
¦>0,
B8.6.2)
\ дхду
так что они представляют собой точки минимума. Имеем очевидные нера-
неравенства
U2>U3>Ui>Ull = Ub, B8.6.3)
568
ОГРАНИЧЕННАЯ ЗАДАЧА ТРЕХ ТЕЛ
[Гл. XXVHI
где Ui обозначает величину функции U в соответствующей точке Nt. Теперь
легко представить форму поверхности z = U (х, у).
Мы видели (см. B8.2.10)), что при заданном значении постоянной энер-
энергии h движение может происходить лишь в области U > и0, где ?/„ -=
= _ hly. Исследуем границы этой области при различных значе-
1) Если Uo > Uг, то область ограничивается изнутри выпуклыми
замкнутыми кривыми, охватывающими точки А и В, а снаружи — боль-
большой выпуклой замкнутой кривой (рис. 116, а). Если Uo очень велико, то эти
к=2,2
Рис. 116.
овальные кривые близки по форме к окружностям. Областями возможных
движений являются области внутри малых овалов и вне большого овала.
Если планетоид совершает движение внутри одного из малых овалов, то
он является спутником одного
из центров А или В; при этом
гравитационное притяжение со-
соответствующего центра является
основным фактором, определя-
определяющим движение планетоида.
В 2) Если Uг > ?/0 > *7з> ТР
область возможных движений
ограничена лишь двумя кри-
кривыми (рис. 116, Ь). Наибольший
интерес представляет случай,
когда планетоид движется во
^=1,8 Х=1,6 внутренней области. Вычисле-
рис. Ц7. ния, проведенные в § 17.11, по-
показывают, что в этом случае
траекториями будут кривые типа лемнискат, и планетоид при этом как бы
является спутником обоих притягивающих центров.
3) Если U3 > Uo > Uи то область возможных движений ограничена
одной-единственной кривой (рис. 117, а).
4) Если Z7i > Uo > U^ то имеются две замкнутые граничные кривые
(рис. 117, Ь), и движение возможно только вне областей, ограниченных
этими кривыми.
5) Если С/4 > Uо, то граничных кривых не существует. Областью
U>U0 возможных движений является вся плоскость.
В общем случае наибольший интерес представляют варианты 1) и Z),
для которых Uo > U3-
а)
"'
§ 28.7] ДВИЖЕНИЕ ВБЛИЗИ ПОЛОЖЕНИЯ РАВНОВЕСИЯ 569
Кривые, изображенные на рисунках, соответствуют случаю, когда
а = 2р\ а X имеет значения 2,2; 2,0; 1,8 и 1,6; здесь (см. B8.2.13))
B8.6.4>
§ 28.7. Движение вблизи положения равновесия. Возникает вопрос:
являются ли положения равновесия устойчивыми и существуют ли такие
движения планетоида, при которых он все время остается вблизи какой-либо-
из точек Nt?
Обозначим через Хо, г/0 координаты какой-нибудь точки Nt и положим
в уравнениях движения
х = хо + 1, г/ = г/0+Г). B8.7.1)
Разлагая правые части уравнений движения в ряды по степеням ? и г] и со-
сохраняя только члены первого порядка, получаем следующие уравнения
линейного приближения:
Вг\), 1
; ¦ B8.7.2>
' У
В этих уравнениях постоянные А, В и С выражают значения производных
ао/Т A'ZTT А%ТТ
-Г9-. д и -g-g- в точке х0, г/0. Уравнения B8.7.2) представляют собой
уравнения в вариациях § 23.1, хотя в данном случае рассматриваются откло-
отклонения относительно положения равновесия, а не относительно известной
траектории.
Решение уравнений B8.7.2) — линейных уравнений с постоянными
коэффициентами — составляется из членов, содержащих в качестве мно-
множителя est, где s — корень уравнения
s2 — у А — 2(os — yB
2т- В s2- С = °' B8.7.3)
или
.V4 - {у {А + С) — 4со2} s2 + у2 (АС — В2) = 0. B8.7.4)
Это — квадратное уравнение относительно s2, и для устойчивости по перво-
первому приближению корни его должны быть вещественны и отрицательны.
С самого начала ясно, что по крайней мере одно из положений равнове-
равновесия Ni, N2, N3 не будет устойчивым. В самом деле, согласно B8.6.1) АС —
— В2 <С 0, так что одно из значений s2 положительно, а другое отрицательно.
Величины s имеют вид либо ±р, либо ±ф', где р и р — вещественные поло-
положительные числа.
Рассмотрим теперь одну из точек iV4, Nb. Для этих точек уравне-
уравнение B8.7.4) принимает вид
<Л 4- (п _|_ РЛ -1- «2 i HZ пЛ У1_ Г) /28 7 Ч1»
(Мы сюда подставили найденные ранее значения постоянных А, В ж С,
см. B8.5.2).) Для того чтобы s2 было вещественно и отрицательно, нужно,
чтобы
а2 — 25аф + р2 > 0, B8.7.6)
а это неравенство в свою очередь будет выполняться при условии, если
отношение а/р превышает больший корень уравнения
х2 - 2Ъх + 1 = 0, B8.7.7)
570 ОГРАНИЧЕННАЯ ЗАДАЧА ТРЕХ ТЕЛ [Гл. XXVIII
который равен 24,96... Таким образом, положения равновесия iV4 и JV5
будут устойчивы по первому приближению, если масса в точке А прибли-
приблизительно в 25 раз больше массы в точке В. Если, например, в точке А нахо-
находится Солнце, а в точке В — одна из планет, то это условие, разумеется,
будет выполняться.
Сделаем по поводу полученных результатов два замечания. Во-первых,
устойчивость по первому приближению еще не означает устойчивости при
рассмотрении точных уравнений (гл. XIX). Кроме того, в этом случае мы
лишены возможности вывести суждение об устойчивости из интеграла энер-
энергии, как это мы делали в теории малых колебаний (гл. IX). Во-вторых, если
система устойчива при рассмотрении точных уравнений, а также в первом
приближении, то это связано с влиянием линейных членов Ti в выраже-
выражении для L. Благодаря им в уравнениях движения появляются гироскопи-
гироскопические члены. При отсутствии слагаемых Ti мы имели бы задачу о движении
в поле консервативных сил, а для такого поля потенциальная функция
в точках 7V4 и N6 имеет максимум, и эти точки являются положениями неу-
неустойчивого равновесия.
Линеаризованные уравнения движения B8.7.2) являются уравнениями Лагранжа.
полученными из функции Лагранжа
Соответствующая функция Гамильтона имеет выражение
1 1
H = -z- {@4-сот1J-Нф — со|J} — — у (,4|2_|_27?|т] + Ст]2), B8.7.9)
Z ' Z
где через 0, ф обозначены составляющие импульса р|, р.ц- Гамильтоновы уравнения
движения имеют вид
"' т~'Л " " B8.7.10)
§ 28.8. Теория движения Луны. Рассмотрим более подробно случай,
когда планетоидом является спутник тела В, так что отношение sll остается
малым в течение всего времени движения. Возьмем новые координаты ?,
г] с началом в точке В и положим
х = Ь + I, у = г). B8.8.1)
Функция Лагранжа B8.2.5) запишется в форме
где
r« = Z2 + Щ + I2 + if, s2 = g2 + гJ. B8.8.3)
В выражении B8.8.2) мы опустили постоянное слагаемое, а также слагае-
слагаемое cofrn, которое не оказывает влияния на движение (см. § 6.8).
Выражение B8.8.2) является точным. Примем теперь некоторые при-
приближения, справедливые в случае, когда отношение sll остается малым
в процессе движения. Кроме того, будем считать малым и отношение р/а.
{Как уже отмечалось, если в точке А находится Солнце, а в точке В — Зем-
Земля, то отношение р/ос составляет около 1/300 000. Для справедливости изла-
излагаемой ниже теории нужно еще допустить, что орбита Земли является кру-
круговой.) Рассмотрим слагаемые
S 28.8] ТЕОРИЯ ДВИЖЕНИЯ ЛУНЫ 571
входящие в выражение B8.8.2). Разлагая 1/г в ряд по степеням *|/Z и г\Ц
и отбрасывая члены порядка (s/lK, получаем
Та? 1 Т(а+Р) /?8 | -8ч , Wj 6 J!±I!l_L3ii
± JL\ -
2 P I ~~
— ~-[~ "I" 75" Vb + Л j т ~275~ 5 ¦ \*o.o.o)
Произведем дальнейшие упрощения в полученной формуле. Прежде
всего, слагаемое, пропорциональное р«2, можно отбросить, как пренебрежи-
пренебрежимо малое по сравнению со слагаемым, пропорциональным а§2, поскольку
отношение р/а мало, а отношение s/l в течение всего времени также остается
малым. Оставшийся член можно записать в виде-
ЗуК S2 _ А а 2?2 /08 Я К1)
и с достаточной для нас степенью точности коэффициент —-р-д- можно при-
а-рр
нять равным единице. В результате выражение в приближенно будет равно
у со2!2 и функция Лагранжа будет иметь вид
Отличие от ньютоновской задачи состоит в присутствии слагаемых
¦ * 3
о) (?т) — т)|) и у со2!2. Уравнения движения, соответствующие функции B8.8.7),
имеют вид
X— 2cori — Зсй2?= — ур
т] -f- 2со| = — yPt)/s3
Интеграл Якоби принимает форму
!¦ B8.8.8)
Теперь мы имеем лишь два положения равновесия: Л^ и N3. Эти точки
находятся на прямой АВ и имеют координаты
A&)'. 4 = 0. B8.8.10)
Далее имеем
УР . Р /я- Р р
Зш2 ~ З(а+Р) l ~ За
и можем написать
Уравнения движения можно представить в эквивалентной форме, при
которой мы не будем иметь особенности в точке ,9 = 0. Умножая уравнения
B8.8.8) соответственно на т), \ и вычитая, получаем
й - т)Б 4- 2со (g| + Т1л) + 3co2gT) = 0. B8.8.12)
Умножая же эти уравнения соответственно на | и т] и складывая, находим
;" 4ё —I^^A- B8.8.13)
572 ОГРАНИЧЕННАЯ ЗАДАЧА ТРЕХ ТЕЛ |.Гл. XXVIII
Наиболее важным приложением является случай, когда в точке А
находится Солнце, в точке В — Земля, а планетоидом является Луна.
При этом можно считать, что орбита Земли при ее движении вокруг Солнца
достаточно близка к круговой и что масса Луны пренебрежимо мала. Урав-
Уравнения B8.8.8) являются уравнениями Хилла; они чрезвычайно важны для
исследования движения Луны. Ввиду недостатка места мы не можем дать
здесь подробного изложения основных результатов. Отметим только, что
основная цель астронома заключается в отыскании периодических движений.
Периодическое движение с периодом о можно представить в форме рядов
оо оо
1= 2 а„ cos Bя+1) т, т]= 2 b/iSinBn-H)T,
где т — новая переменная (т = 2nt/o). Подстановка этих рядов в уравне-
уравнения B8.8.8) или B8.8.12), B8.8.13) дает возможность определить (завися-
(зависящие от о) коэффициенты ап, Ъп.
Глава XXIX
ЗАДАЧА ТРЕХ ТЕЛ
§ 29.1. Классические интегралы*). Три частицы Av Az, A3, имеющие
массы соответственно mi, гп2, т3, движутся в пространстве под действием
сил взаимного притяжения. В момент t = О заданы координаты и скорости
частиц. Требуется определить положения частиц в любой момент времени.
Возьмем неподвижную систему прямоугольных осей и обозначим теку-
текущие координаты частиц АТ через хт, yr, zT. Координаты центра масс G этих
частиц обозначим через X, У, Z. Тогда будем иметь
3 3 3
МХ=^тгГг, МУ= 2 Шгуг, MZ='%mrzT, B9.1.1)
r=l г—1 r=l
где М есть масса системы
М = т1 + т2 + т3. B9.1.2)
Положим
хТ = X + От, у г = У + pr, zr = Z + Уг, B9.1.3)
т. е. пусть аг, рг, уг будут координатами частиц Ат относительно поступа-
поступательно движущейся системы с началом в точке G.
Функцию Т кинетической энергии системы можно представить в одной
из следующих форм:
з
т=т 2 Шг (^+&+2^' B9 ¦1 -4)
г=1
|^ i-2/n'-(^ + P'+V?), B9.1.5)
где уГ5 есть скорость частицы As относительно частицы Ат,
vis = (ж,-ХгJ 4- (».- г/'гJ+ (г.- zrJ = (as-arJ + (P.-р-> -f-(у,-^rJ. B9.1.7)
При выводе формулы B9.1.6) мы воспользовались элементарным алгебраи-
алгебраическим тождеством
(mi+m2+m3) {m&\ -f- m2xl + m^l) =
• • • • •
— (/n^j -f пг2ж2 H- m3xaJ -f
, — x3)'2+ m1tn2(x2 — xiJ. B9.1.8)
Потенциальная энергия системы равна —U, где
U-у /ЭД_и^1,^\ Г29 1 9)
Х \ ri ' г2 ^ г3 Г \ • ¦ ¦• I
*) См. Н. В г u n s, Ueber die Integrale des Vielkorper-Problems, Berichte der Konig-
lich Sachsisehen Gesellschaft der Wissenschaften zu Leipzig. 1887. стр. 1—39.
574 ЗАДАЧА ТРЕХ ТЕЛ [Гл. XXIX
Здесь rj обозначает длину отрезка А2А3 и
- у2J + (z3 - z2J = (a3 - а2J+ (р8 - Р2J + (у3 - 72J- B9.1.10)
Аналогично определяются г2 и г3.
Рассматриваемая система голономна и имеет девять степеней свободы.
Для ее описания .нужно девять уравнений Лагранжа или восемнадцать
уравнений Гамильтона. Уравнения Лагранжа имеют вид
аи •• аи •• аи . „ „ /ОГ1 . ...
гпУ = -щ^, mTZr = -^, r = l, 2, 3, B9.1.11)
я уравнения Гамильтона—
mTxT = lr, ттуг = т\т, тг%т = 1т, ^)
i - dU • _ dU Г - dU г_4 9 ч f B9-1Л2)
ёг~"^Г7 ^--^Г' tr~"^7' r-1' z' й' J
где через gd, T]i, 1и 1г, Лг» Сг, 5з, "Из* ?з обозначены составляющие
импульса.
Существует десять классических интегралов уравнений Лагранжа
и соответственно десять классических интегралов уравнений Гамильтона.
Шесть из них выражают то, что центр масс G движется равномерно и прямо-
прямолинейно:
Х = и0, Y = Fo, Z = Wo, B9.1.13)
X = Uot + Хо, Y = Vot+ Уо, Z = Woi + Zo. B9.1.14)
Условие постоянства момента количеств движения относительно начала
координат дает еще три интеграла:
з
2 mr(yrzr — zryr) = a
r=l
з
2 /nr (zrzr — xr'zr) = Ъ,'\ B9.1.15)
r=l I
3 I
Их мржно переписать в следующей форме:
з
М (YZ - ZY) + 2 гпг фтуг - Тт-Рг) = а,
2 Оу V) B9.1.16)
г=1
3
УХ) + ^ тпг (а^г - ргаг) = с.
г=1
Последним классическим интегралом является интеграл энергии
Т - U = h. B9.1.17)
Эти десять интегралов представлены нами в лагранжевои форме и выраже-
выражены через координаты и скорости. Запишем теперь их в форме Гамильтона,
S 29.2] СЛУЧАЙ, КОГДА МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ РАВЕН НУЛЮ 575
через координаты и импульсы:
Zi + Zi + b = MW0, )
mixi -f- m2x2 -f m3x3 = Л/ (t-У -f Xo),
^1 + ™2*/2 + "M3 = ^ (JV + Yo),
з зз
S (Уг?г — ZrT)r) = a, 2 (^r — xrlr) = b, S (^rT)r — УгЬ) = С,
r=l r=l r=l
B9.1.18)
r=l
Десять интегралов B9.1.18) уравнений Гамильтона независимы между собой и пред-
представляют алгебраические соотношения между координатами, импульсами я временем-
Возникает вопрос: не существует ли других алгебраических интегралов, не зависящих
от уже найденных? Ответ на этот вопрос дается замечательной теоремой, доказанной
Брунсом в 1887 г. Оказывается, что новых алгебраических интегралов не существует:
любой алгебраический интеграл уравнений Гамильтона для задачи трех тел представ-
представляет комбинацию десяти классических интегралов.
Поскольку центр масс G движется равномерно и прямолинейно, мы
можем перейти к ньютоновской системе отсчета с началом в точке G. Иначе
говоря, можно без потери общности считать, что центр масс находится
в покое. Именно это мы и будем постоянно предполагать в дальнейшем.
Ориентацию осей можно выбрать так, чтобы ось Gz была направлена вдоль
вектора момента количеств движения; при этом две другие составляющие
этого вектора будут равны нулю.
§ 29.2. Случай, когда вектор момента количеств движения равен нулю.
При известных условиях каждая из постоянных а, Ь, с в формулах B9.1.15)
может оказаться равной нулю. Для этого необходимо, чтобы движение
частиц происходило в одной плоскости с G и, кроме того, чтобы в момент
t = 0 момент количеств движения относительно начала О был равен нулю-
Чтобы доказать, что при условии а2 + Ъ2 + с2 = 0 движение проис-
происходит в одной плоскости, поместим начало координат в точку G, а пло-
плоскость, в которой лежат частицы в момент t = 0, возьмем за плоскость z = 0.
Если вектор момента количеств движения относительно некоторой точки
равен нулю, то он равен нулю и относительно всех других точек (начало G
находится в покое), и, следовательно, три составляющие этого вектора,
стоящие в левых частях уравнений B9.1.15), равны нулю при любой ориен-
ориентации осей. Обращение в нуль первых двух составляющих дает (поскольку
24 = z2 = z3 = 0 при t = 0)
тм^ + щм^з
ITljXjZi -\- TT12X2Z2
так что при t = 0 составляющие скорости zit z2, z3 связаны соотношениями
B9".2.2)
z2Jrm3x3z3 = 0, j
или
AGP2P3
B9.2.3)
Л76 ЗАДАЧА ТРЕХ ТЕЛ [Гл. XXIX
где символом aGP2P^ обозначена площадь треугольника GP2P3 и т. д.
Из B9.2.3) заключаем, что
21 = 22 = z3-w. B9.2.4)
Отсюда следует, что составляющая Скорости центра масс трех частиц в на-
направлении Gz равна и. Но центр масс находится в покое, следовательно,
и = 0. Векторы скоростей частиц в момент t = 0 все лежат в плоскости
% = 0, следовательно, движение частиц и в дальнейшем будет происходить
в этой плоскости. (Обратно, если движение частиц происходит в плоско-
плоскости 2 = 0, то две первые составляющие вектора момента количеств движения
равны нулю; это условие является достаточным, но отнюдь не необходимым.)
Третья составляющая момента количеств движения обращается в нуль
при условии, что
m-2 (x2y2 — y2x2) + m3 (хьу3 — y3x3) = 0. B9.2.5)
Оно выполняется лишь в исключительных случаях. Если известны коорди-
координаты всех частиц на плоскости, а также скорости двух первых частиц,
то условие B9.2.5) выполняется тогда и только тогда, когда скорость третьей
частицы такова, что импульс тп3 (х3у3 — УзРз) имеет значение, определяемое
равенством B9.2.5). Мы этот особый случай оставим в стороне и будем счи-
считать, что а2 + Ь2 + с2 > 0.
§ 29.3. Три точки Лагранжа. Лагранж указал на то, что в ряде случаев
удается получить точные решения уравнений движения. В частности, имеют-
имеются две задачи, в которых расстояния г4, г2, г3 сохраняют постоянные зна-
значения в течение всего времени движения. В первой из этих задач частицы
располагаются в вершинах треугольника постоянного размера и постоян-
постоянной формы, а во второй задаче они располагаются вдоль одной прямой.
Начнем с выяснения вопроса о том, возможно ли вообще такое движение
системы, при котором треугольник А^А2А3 вращается в собственной пло-
плоскости с постоянной угловой скоростью со вокруг точки G, находящейся
в покое. Равнодействующая всех сил, действующих на частицу А3, в любой
д момент времени должна быть равна m3GA3(?>2 и
направлена вдоль прямой A3G; следовательно,
должны выполняться условия
B9.3.1)
B9.3.2)
Через Я обозначен центр масс частиц Ах и А2, а
через 01; 02 —углы НА3А2, АгАгН (рис. 118).
Далее имеем
fi Sill v7i Л г*2 ЛЪ^ / cif\ о о\
:—К—===—л—7Т =~ t [?<J*O.o)
т?. sin D2 A^H m2
ис- ' откуда, учитывая B9.3.1), получаем, что г± = г2.
Аналогичным образом, рассматривая движение
частицы А2, приходим к выводу, что гг = г3. Следовательно, чтобы было
возможно такое движение, треугольник А\А2А3 должен быть равносторон-
равносторонним: Обозначим длину его стороны через I.
Обратимся теперь ко второму уравнению B9.3.2). Если провести в тре-
треугольнике AiA2A3 отрезок НК параллельно стороне AiA3 (см. рисунок),
то будем иметь
НК = НА2 ~ mi I, KA3 = AtH = m.2 I, B9.3.4)
§ 29.3] ТРИ ТОЧКИ ЛАГРАНЖЛ 577
откуда
НА3 = ЯК cos 02 + КА3 cos 6j = (mi cos 02 + m% cos 6^ 1/{т^ + т2). B9.3.5)
Равенство B9.3.2) теперь принимает вид
5^ B9.3.6)
или
0,2 = уМП3. B9.3.7)
Ясно, что аналогичные условия будут выполняться и для двух осталь-
остальных частиц. Таким образом, мы доказали возможность движения системы,
при котором частицы располагаются в вершинах равностороннего треуголь-
треугольника со стороной I, вращающегося с угловой скоростью VyMll3. Размер
стороны I может быть любым, угловая скорость при этом пропорциональ-
пропорциональна 1~3/2 (что с очевидностью следует из теории размерностей).
Докажем теперь, что возможно также движение частиц, когда все они
расположены на одной прямой, проходящей через центр масс G и равномерно
вращающейся в плоскости. Обозначим расстояния точек Ai, А2, А3 от цент-
центра G через Х\, х2, х3. Без потери общности можно предположить, что xi <L
< х2 <х3, при этом xf <0их3>0. Обозначив угловую скорость через со,
будем иметь
<29-3-9>
B9.3.10)
Заметим, что соотношение B9.3.9) справедливо как при положительном х2,
так и при отрицательном х2. Сразу убеждаемся, что
rriiXi + гп2х2 + тп?с3 — 0. B9.3.11)
Легко видеть, что равенства B9.3.8) — B9.3.10) определяют отноше-
отношения г\ : г2 : г3. Положим Ti/r3 = k, тогда
-ТГ- B9ЗЛ2)
и мы будем иметь
mi . 2+3
— х2 (fc+1)-^'1" fe2'
x2—xi m3 m3 ))
B9.3.13)
Отсюда получаем уравнение пятой степени относительно к:
Aщ + т2) къ + {Ът,1 + 2т2) к* + C^ + т2) к3 —
— {т2 + Ът3) к2 — Bт2 + Зт3) к — (т2 + т3) = 0. B9.3.14)
Это уравнение имеет только один вещественный корень; будучи положитель-
положительным, он определяет единственное значение к для отношения Г\1г3. Расстоя-
Расстояние г3 может быть любым, и при этом со2 пропорционально г~33. Если вели-
величина г3 задана, то значения Х\, х2 и х3 легко находятся. Имеем
kxi — (к + 1) хг + х3 = 0. B9.3.15)
Отсюда, учитывая B9.3.11), получаем
Mfl Мх2 _ МХ3 _ Г1 ^_ Г2 _ Г3 ,„п , ,т
— {т2+{к+1)т3} пн — ктз ~~ (к+\)пц-\-ктг к ' А+1 1 * \*v-o-lv)
37 л. А. Парс
578 ЗАДАЧА ТРЕХ ТЕЛ [Гл. XXIX
Из B9.3.8) и B9.3.10) находим
Ы2_ Y Г 1 _, , ^ + i l I ,2q о 17ч
i l(*+l)s * ' *2(* + l) 2 r (A+lK 3J ' ^У-о.1'>
Этот результат, разумеется, можно представить и в других формах.
Выше предполагалось, что частица А% располагается между At и А3.
Существуют еще два решения, соответствующие случаям, когда промежу-
промежуточное положение занимает частица А± или частица А3.
§ 29.4. Решения, для которых треугольник Лагранжа сохраняет свою
форму. Равносторонний треугольник в решении Лагранжа остается неиз-
неизменным как по размерам, так и по форме. Лагранж поставил следующий
вопрос: «Существуют ли такие решения, для которых частицы располага-
располагаются в вершинах треугольника, неизменного по форме, но изменяющего
свои размеры?» Чтобы ответить на этот вопрос, возьмем неподвижную пря-
прямоугольную систему координат и предположим, что частицы расположены
в точках с комплексными координатами
wr = хт + iyr = crw, r = 1,2,3, .B9.4.1)
где с — комплексные постоянные, аи? — комплексная функция времени t.
Уравнения движения тогда будут иметь вид
} B9А2)
и два аналогичных уравнения. Для того чтобы решение имело форму B9.4.1),
необходимо, чтобы
с^ = у \т2 , с»-с'„ +ГОзт^^г1 т-^г B9.4.3)
I |c2—ci|3 ' •J|c3 — Ci|sJ \w\* v '
и т. д. Следовательно, если существуют постоянные сь с2, с3 такие, что
-VLCr^y^m. |СС;1СС;Г ' = 1,2,3, B9.4.4)
где (л — вещественное положительное число, то любое решение уравнения
^-li^jT B9.4.5)
удовлетворяет уравнениям движения B9.4.2).
Некоторые решения этих уравнений нам уже известны, например реше-
решения вида wr = сгеш, где cl5 c2, с3 — значения координат точек Лагранжа
при t = 0, отсчитываемых от точки G. В первом из рассмотренных выше
случаев точки с±, с%, с3 образуют вершины равностороннего треугольника,
причем со2 = уМ/l3. Следовательно, указанные значения с\, с^, с3 удовлетво-
удовлетворяют уравнению B9.4.3) при \i = yM/l3.
Уравнение B9.4.5) описывает движение частицы в ньютоновском поле
тяготения, а для этой задачи нам хорошо известно решение. Таким образом,
мы получили решение задачи трех тел, в котором каждая частица описывает
коническое сечение с одним из фокусов, расположенным в центре масс;
при этом центр масс находится в покое.
Частицы по-прежнему располагаются в вершинах треугольника, кото-
который все время остается равносторонним. Конические сечения, описываемые
каждой частицей, имеют один и тот же эксцентриситет. Если сечения пред-
представляют собой эллипсы, то движение имеет периодический характер.
Большой интерес представляет случай, когда период движения по эллипсу
равен 2я/ю, т. е. совпадает с периодом вращения треугольника Лагранжа. Для этого слу-
случая движение' относительно осей, вращающихся с угловой скоростью со, также является
§ 29.5] СЛУЧАЙ ПЛОСКОГО ДВИЖЕНИЯ 579
периодическим с периодом 2я/со. Рассмотрим более подробно случай, когда частицы пер-
первоначально движутся по окружностям, а затем каждая из них получает небольшой
импульс, после чего траектории становятся эллиптическими. Эксцентриситет эллипсов е
при этом мал, а период обращения каждой частицы равен первоначальному периоду
обращения по окружности. При этих условиях каждая частица (относительно вращаю-
вращающихся осей) остается вблизи своего первоначального положения. Чтобы исследовать
движение относительно вращающихся осей, выберем оси Ох, Оу так, чтобы ось Ох состав-
составляла угол wt с большой осью эллипса. Координаты частицы относительно вращающихся
осей запишутся тогда в виде
x = a(coscp — e) cos со;-f 6 sin ф sin (of,
у =—a(cos(p — е) sva.K>t-\-b sincp cos Ш,] '
где а и b — полуоси эллипса, а ф — угол, образуемый радиус-вектором с большой
осью эллипса. Но для эллиптического движения, если считать, что в момент t = О
частица находится в перигелии, будем иметь (§ 5.5)
cot = ф — е sin ф, B9.4.7)
и формулы B9.4.6) тогда примут вид
х = о(созф — е) сов(ф — е sin ф) + 6 sin ф эт(ф — esinqi), .„
у=—а(совф — е)вт(ф — е sin ф) + 6 sin ф cos (ф — евтф). J
Эти формулы являются точными независимо от того, мал эксцентриситет е или нет.
Однако сейчас нас интересует лишь случай, когда он мал. Разлагая выражения в правых
частях B9.4.8) в ряды по степеням е и сохраняя только члены первого порядка, полу-
получаем
х = а A — е cos ф), у = 2ае sin ф. B9.4.9)
Приближенно траекторией частицы относительно вращающихся осей будет эллипс
с центром в точке (а, 0). Длина большой оси этого эллипса в два раза больше длины
малой оси.
Подобным же образом можно убедиться в существовании решений во вто-
втором случае Лагранжа, когда частицы коллинеарны во время движения.
При таких движениях значение к = rjrs определяется из уравнения B9.3.14),
а значение ц = со2 — из уравнения B9.3.17).
Кроме того, существует решение, в котором частицы постоянно дви-
движутся вдоль прямой. Отношение п/г3 в этом случае по-прежнему равно к.
Это решение было известно еще Эйлеру, который тоже получил для к урав-
уравнение пятой степени B9.3.14).
Изложенная теория без труда распространяется на случай плоского движения
п тел. Если удается получить решение, для которого центр масс G находится в покое,
а тела расположены в вершинах равномерно вращающегося многоугольника постоянных
размеров и неизменной формы, то можно указать решения (в частности, периодиче-
периодические), в которых тела располагаются в вершинах многоугольника неизменной формы,
но изменяющихся размеров. Простейшим является тот случай, когда все тела имеют
одинаковую массу т. Очевидно, что существует решение, в котором частицы распола-
располагаются в вершинах правильного многоугольника, вращающегося с постоянной угловой
скоростью. Пусть а — радиус круга, описанного около многоугольника, тогда угловая
скорость будет равна
о>2=^-, B9.4.10)
где
71-1
A=T2iiniW* B9-4Л1)
s=l
С помощью рассуждений, аналогичных тем, что проводились выше для случая
в = 3, можно показать, что существуют решения, соответствующие правильному много-
многоугольнику изменяющихся размеров.
§ 29.5. Случай плоского движения. Исследуем в более общей форме-
случай плоского движения трех частиц. Возьмем систему осей, вращающих-
вращающихся вокруг неподвижного начала О с постоянной угловой скоростью со. Если
37*
580 ЗАДАЧА ТРЕХ ТЕЛ [Гл. XXIX
через Xi, г/ь х2, y^i xzi Уз обозначить координаты часхиц относительно
вращающихся осей, то функция кинетической энергии запишется в виде
3
У = {2т^^-*)!+(Уг + (охг)8}, B9.5.1)
а потенциальная энергия будет равна — U, где
И
\ ri г2 г3 / >
— У2J, rl=(xi—
J
B9-5J)
Для составления функции Гамильтона нужно
3 3
Т2-и-Т0 = ±%тТ(х1 + у*)-±-^^тг(х* + у1)-и B9=5.4)
г==1 г-=1
выразить через импульсы, исключив скорости (§ 10.14). Обозначая составляю-
составляющие импульсов рХг и рУт соответственно через |г, г\г, будем иметь
%Т = тТ(хг — щг), х\т = тт(уг-^ыхт) B9.5.5)
и, следовательно,
— со (ж^! — yiii + жат12 —у2|2+а:зТ1з —Уз1з) —^- B9.5.6)
Уравнения движения имеют вид
|г = ?ОТ)г+_, т,г=_ш|г+_, |
где г= 1, 2, 3.
Коэффициент при —со в формуле B9.5.6) для Я, равный
з
2(*гТ1,-0г|г), B9.5.8)
г=1
представляет собой момент количеств движения системы относительно
точки О. Уравнения B9.5.7) показывают, что эта величина в течение всего
движения остается постоянной.
Возникает вопрос: существует ли такое решение, в котором частицы
остаются в покое относительно вращающихся осей? Подобное решение
можно назвать равновесным решением. Если равновесное решение суще-
существует, то оно обращает правые части уравнений B9.5.7) в нули, откуда
следует, что
¦^- + mra>2xr = 0, ~ + тга2ут = 0. B9.5.9)
Обратно, если существуют значения Х\, г/i, хг, у^, х3, у3, удовлетворяю-
удовлетворяющие уравнениям B9.5.9), то существует равновесное решение, для кото-
которого величина ?г имеет значение — тТауг, а величина ч]г — значение
т,га>хт. Таким образом, равновесные решения определяются теми точками
§ 29.6] КООРДИНАТЫ ОТНОСИТЕЛЬНО ЧАСТИЦЫ А, 581
пространства {xt, yt, х2, у2, %3i Уз), в которых функция
з
U + ^tf^mrixl+yl) B9.5.10)
принимает стационарные значения.
Ясно, что в равновесном решении центр масс трех частиц расположен
в точке О и находится в покое. Это почти сразу вытекает из уравнений B9.5.9).
В самом деле, если записывать подробно, то эти уравнения будут иметь вид
У B9.5.11)
T {^-(У1-Уз)+^(у1-уя)} J
и т. д. Мы видим, что
miXi + m2xz + т3х3 = 0, B9.5.12)
nnyi + m2yz + т3у3 = 0, B9.5.13)
и, следовательно, центр масс трех частиц находится в покое в точке О.
Проведем теперь ось х через точку, занимаемую частицей А3 (что можно
сделать без потери общности); при этом х3 > 0, у3 = 0. Тогда из последне-
последнего уравнения для у B9.5.11) получаем
= 0, B9:5.14)
'2 '1
и так как
mij/i + т2у2 = 0, B9.5.15)
то
т1У1 (-i---i)-O. B9.5.16)
Таким образом, либо г4 = г2, либо уг = 0. Если г± = г2 = ?, то уравне-
уравнение B9.5.11) для х вместе с уравнением B9.5.12) приводят к равенству
со2 = уМ/Р (см. B9.3.7)), и тогда уравнение B9.5.11) для у вместе с B9.5.15)
дают г3 = I.
Если уг — 0, то и z/2 = 0, так что все три частицы располагаются на
одной прямой. Предполагая, что частица А2 находится между Аг и А3 и что
А3 имеет положительную координату х, можем написать
хг < 0, х3 > 0, г4 = :г3 — я2, г2 = х3 — хи г3 = х2 — xi. B9.5.17)
Формулы B9.5.11) для х теперь совпадают с B9.3.8) — B9.3.10).
Таким образом, мы получили все равновесные решения; в этих решениях
частицы располагаются либо на одной прямой, либо в вершинах равносто-
равностороннего треугольника.
§ 29.6. Координаты относительно частицы А$. Вернемся к общей тео-
теории плоского движения, причем будем пользоваться обозначениями § 29.5.
В частности, функцию Гамильтона возьмем в форме B9.5.6).
Введем координаты частиц At и А2 относительно частицы А3:
qi = xi — x3, g2 = yi~y3, -I
д3 = .г2— х3, qi = y2 — y3, I B9.6.1)
^5 = ^3, ?6=*/з- J
Относительно частицы А3 частица Ai имеет координаты (gb q2), а частица
А2 — координаты (q3, g4)- Формулы B9.6.1) определяют контактное пре-
преобразование, которое является расширенным точечным преобразованием с
582 ЗАДАЧА ТРЕХ ТЕЛ [Гл XXIX
производящей функцией
W = pi (xi — х3) + р2 (j/i — Уз) + р3 (хг — х3) +
+ Pi (г/г — Уз) + Рь^з + РбУз- B9.6.2)
Уравнения преобразования
<*¦ = !?¦, Ь = ^, Ъ=--~- г=1,2, .... 6; я=1, 2, 3, B9.6.3)
дают B9.6.1) и соотношения
ll = Pl> Л1=/>2. ^2 = ^3, 112=^4, ) B9 6 4)
ls=—Pi—P3 + Pi, ч\з=—Рц — Р1 + Ря- J
Поскольку W не содержит t, новая функция Гамильтона будет иметь вид
— q2Pi + QsPi — ЧьРз + q&Pe — q&Pb) — U, B9.6.5)
где \ir = 1/m.r, а функция U равна
и==у(Л^ + И^.+Л^11.у B9.6.6)
причем
-^J- B9.6.7)
§ 29.7. Движение в окрестности равновесного решения. Воспользуемся
функцией Гамильтона B9.6.5) для изучения вопроса об устойчивости (в смыс-
смысле первого приближения) системы трех точек Лагранжа. Рассмотрим снача-
сначала равновесное решение во вращающихся осях, причем для определенности
возьмем решение, в котором частицы располагаются в вершинах равносто-
равностороннего треугольника. Допустим, что существует решение уравнений дви-
движения, которое мало отличается от равновесного решения. Пусть (q°, p°)
есть равновесное решение. Положим
Яг = q°r + ur, Pr=P°r+vr, г = 1, 2, . . ., 6. B9.7.1)
Формулы B9.7.1) определяют контактное преобразование. Новая функ-
функция Гамильтона, записанная в переменных ur, vr, не содержит линейных
слагаемых. Так как и, v остаются малыми, то первое приближение мы полу-
получим, если в уравнениях движения сохраним лишь линейные члены, что
равносильно сохранению одних только квадратичных членов Hz в функции
Гамильтона. Указанное первое приближение определяется уравнениями
^ = 4?' ^=-"SS r=l,2..., 6. B9.7.2)
Выберем оси координат так, чтобы
??=-?S = T*' & = & = ?rl. B9.7.3)
Квадратичные слагаемые в правой части B9.6.5) не затрудняют состав-
составления функции Я2: нужно просто заменить переменные {qT, pT) на перемен-
переменные (ит, vT). (Заметим, что нет нужды вычислять невозмущенные значения Рт
переменных рт.) Для вычисления членов Hz, обусловленных функцией U,
имеем
(±У(^ )\ B9.7.4)
1)Г1/2. B9.7.5)
29.7]
ДВИЖЕНИЕ В ОКРЕСТНОСТИ РАВНОВЕСНОГО РЕШЕНИЯ
583
Квадратичными членами разложения \/ri будут
1 t
;). B9.7.6)
Рассуждая аналогичным образом относительно переменных г2, г3, полу-
получаем следующее выражение для членов второго порядка, обусловленных
функцией U:
где
М
B9.7.7)
B9.7.8)
Таким образом, линейное приближение мы получаем из функции
Гамильтона
— vaJ} —
— u4v3-\- ubve — uevb) — U2. B9.7.9)
Теперь мы можем вычислить правые части уравнений B9.7.2); эти
уравнения имеют вид
B9.7.10)
где w есть вектор {щ, щ, ..., u6, vlt и„, ...,ve). Чтобы решить вопрос об
устойчивости по первому приближению, необходимо знать собственные
значения матрицы А. Имеем
— С
В
1}
-С
B9.7.11')
где В, С, D — матрицы размером 4x4 вида
B9.7.12)
С =
1
со
0
0
— со
X
0
0
0
0
к
со
0
0
— со
К
B9.7.13).
О
0
B9.7.14)
о
Цч + Н-з U [х3
О (х2 + [i3 О
Н-з 0 Н-г + Н-з,
Вычисление определителя размером 8x8 в правой части B9.7.11)
довольно затруднительно, однако задачу можно упростить, если воспользо-
воспользоваться следующим приемом. Имеем
0
Н-з
0
(—С DW J4 0\ / 0 1)\
{-в -с) [п-ч iJ = {-B-ci>-w -с) •
<29-7-15>
584 ЗАДАЧА ТРЕХ ТЕЛ [Гл. XXIX
B9.7.16)
B9.7.17)
B9.7.18)
B9.7.19)
Следовательно,
(Л2 —со2 — 2А.СО 0 0 \
2Г W--0*. • <»•'¦»>
О 0 2Асо А2-со2/
Теперь определитель | DB-\-DCD^C | размером 4x4 можно вычис-
вычислить непосредственно. Выполнив необходимые выкладки, придем к сле-
следующему уравнению для собственных значений матрицы А:
V (к2 + со2K (Л4 + со2А.2 + йсо4) = 0, B9.7.21)
где
г, _ 27 т2пз+т3т1 -[-mtw2 ,9Q 7 99.
/ъ —у } ; : гх » V &и • I *?ч->)
А. 1т. _L_ m ~ _1_ т „ \ 4 * '
В силу B9.7.11) уравнение
о = ц,2[х3 Ч- М-зН-i Ч- ^#2 =
Если бы все корни уравнения B9.7.21) были простые и чисто мнимые,
то можно было бы заключить, что исходное равновесное решение устойчиво
по крайней мере в первом приближении. Однако на данной стадии исследо-
исследования такого заключения сделать нельзя вследствие наличия множителя А,2
и повторения множителя (X2 + со2) в левой части уравнения B9.7.21). В сле-
следующем параграфе мы покажем, каким образом порядок системы можно
понизить с 12 до 6. Для приведенной системы собственные значения будут
определяться уравнением шестой степени
(к2 + со2) (k4 + со2^2 + А; со4) = 0. B9.7.23)
Это уравнение уже не содержит нежелательных множителей.
§ 29.8. Сведение к системе шести уравнений. Рассмотрим снова функ-
функцию Гамильтона B9.6.5). Прежде всего заметим, что функция U не содер-
содержит qb и (fo (что, конечно, очевидно геометрически). Два последних уравне-
уравнения Гамильтона имеют вид
Ре - «р6 =0, р&+ сор6 = 0. B9.8.1)
Составляющие импульса равны
" It + ?2 + ?з = Рь, Л* + 112 + tjs = Pe. B9.8.2)
так что уравнения B9.8.1) выражают сохранение импульса. Если центр
масс G системы находится в покое, то
р5 = Рв = 0 B9.8.3)
в течение всего времени движения. Если начальные условия таковы, что
центр масс G находится в покое, а начало координат О совпадает с G, то
координаты q5, qa могут быть найдены по известным q±, q2, Gз> Яь, с помощью
29.8]
СВЕДЕНИЕ К СИСТЕМЕ ШЕСТИ УРАВНЕНИЙ
585
формул
Mq5 = — rriiqi — m2q3, Mq6 = — mxq2 — m2qk. B9.8.4)
Эти уравнения непосредственно следуют из B9.6.1) и B9.5.12), B9.5.13).
Таким образом, если центр масс G находится в покое и начало коорди-
координат О выбрано в точке G, то число уравнений системы может быть понижено
до восьми. Переменные grl7 q2, q3, Ць, Pi, Рг> Рз> Pi определяются из уравне-
уравнений Гамильтона, соответствующих функции Гамильтона
-U. B9.8.5)
Покажем теперь, как- осуществить дальнейшее понижение числа урав-
уравнений — с восьми до шести. Это делается с помощью процедуры, предло-
предложенной Якоби и известной как исключение узлов *). Коэффициент при —со
в выражении B9.8.5) равен моменту количеств движения системы относи-
относительно точки О. Как показывают уравнения движения, эта величина сохра-
сохраняет постоянное значение. Основная идея метода Якоби заключается в при-
применении такого контактного преобразования, в котором выражение для
момента количеств движения
является одной из новых переменных. С этой
целью произведем точечное преобразование
где
С = cos <?4, S = sin Qk. B9.8.8)
Рис. 119.
Геометрический смысл такого преобразо-
преобразования очевиден: (Qi, Qi) являются полярными
координатами точки (qit q2) в подвижных осях, a (Q2, Q3) представляют
составляющие вектора (q3, q^), параллельную и перпендикулярную век-
вектору (qx, q2) (рис. 119). Чтобы определить контактное преобразование — рас-
расширенное точечное преобразование B9.8.7), требуется следующая произво-
производящая функция:
W = PlCQi + p2SQt + p3 (CQ2 - SQ3) + pk (SQ2 + CQ3). B9.8.9)
Уравнения преобразования имеют вид
dW „ dW
qr=iWr'
г =1,2,3,4,
B9.8.10)
откуда следует, что преобразование определяется уравнениями B9.8.7)
и уравнениями
pa = CPa-SP3, P4 =
где через К обозначено выражение (Р4 — <?2^з + QaP^/Qi- Заметим, что
Ра = qiP2 — q2Pi + q3Pi — ?4Рз B9.8.12)
есть постоянный момент количеств движения. Это является отличительной
особенностью преобразования Якоби. Новая функция Гамильтона имеет
*) Это название больше подходит для общей пространственной задачи (см. ниже
§ 29.12).
586 ЗАДАЧА ТРЕХ ТЕЛ [Гл. XXIX
следующее выражение:
B9.8.13)
Это выражение не содержит Q^ и, следовательно, Рк остается постоян-
постоянным в процессе всего движения:
Р4 = Г. B9.8.14)
Мы снова получили уже известный нам результат. Система, таким
образом, свелась к системе с шестью переменными; для функции Гамиль-
Гамильтона мы получили выражение
где К обозначает теперь (Г — QzPs-^rQsP^IQi- Если эту систему шестого
порядка проинтегрировать, то оставшуюся переменную Qt можно будет
найти квадратурой из уравнения
<?4 = faK + Цз (^з + K)}/Qt - со. B9.8.16)
§ 29.9. Устойчивость трех точек Лагранжа. Вернемся к задаче, рас-
рассмотренной в § 29.7. Речь там шла об устойчивости равновесного решения
в случае, когда частицы находятся в покое (относительно вращающихся
осей) в вершинах равностороннего треугольника. Прежде всего заметим,
что если возмущения выводят центр тяжести системы из состояния покоя,
то нельзя рассчитывать на устойчивость, так как при этом система уходила
бы все дальше и дальше от первоначального положения. Поэтому ограничим-
ограничимся рассмотрением лишь таких возмущений, при которых центр масс G остает-
остается в покое. При таких возмущениях задачу можно свести к шестому поряд-
порядку (§ 29.8); собственные значения соответствующей задачи первого прибли-
приближения будут определяться как корни уравнения
(Я2 + со2) (К* + соаЛ2 + йсо4) = 0, B9.9.1)
где, как и в B9.7.22),
21 fft^ + w3w + ww B9 9 2)
Таким образом, система будет устойчива по первому приближению,
если корни уравнения
х2 + ойс + кол4 = 0 B9.9.3)
вещественны и отрицательны; последнее имеет место при
*<-!". B9.9.4)
т. е. когда
27 (mzm3 + m3nii + гп^гп^ < (rot + тг + ^зJ- B9.9.5)
Смысл неравенства B9.9.5) станет более ясным, если привести следующую геомет-
геометрическую интерпретацию. Возьмем (mi, тг, тз) за декартовы координаты вспомогатель-
вспомогательного пространства. Условие B9.9.5) можно переписать так:
a, B9.9.6)
о
причем
B9.9.7)
§ 29.10]
ПРЕОБРАЗОВАННАЯ ФОРМА УРАВНЕНИЙ ДВИЖЕНИЯ
587
Последнее уравнение определяет сферу радиуса а с центром в начале координат О,
а уравнение
з Уз
B9.9.8)
определяет плоскость со, расстояние которой от точки О составляет три пятых ее рас-
расстояния от плоскости, параллельной ш и касательной к сфере. Неравенство B9.9.6)
показывает, что точка (лц, т%, т3) лежит на той части сферы, которая расположена
в положитель номоктанте и ограничена координатными плоскостями и плоскостью со.
Указанная область на сфере состоит из трех отдельных частей, каждая из которых огра-
ограничена дугами двух больших кругов и малой окружностью вблизи точек (а, 0, 0),
(О, а, 0), @, 0, а) соответственно, так что одна масса должна быть намного больше осталь-
остальных. Если пц — наибольшая из трех масс, то достаточным условием устойчивости будет
пц > 26 (т2 + т3). B9.9.9)
Если величины тоь т2, т3 удовлетворяют неравенству B9.9.5), то реше-
решение для равностороннего треугольника Лагранжа будет устойчиво по пер-
первому приближению. Однако, как мы видели, это еще не означает устойчи-
устойчивости при переходе от линейного приближения к точным уравнениям дви-
движения.
§ 29.10- Преобразованная форма уравнений движения. Перейдем
теперь от движения в плоскости к общему случаю. Откажемся на время
от предположения, что центр масс G находится
в покое. Обозначим вектор А±А2 через и, а век-
вектор НА3 (где/f — центр масс двух частиц Ai и
А2) — через v (рис. 120). Вектор А2Аг равен
+ v, а вектор А^Аг равен а2и + v, где
*1 —
B9.10.1)
Обозначим теперь составляющие и через х,
у, z, а составляющие v — через |, т|, ?. Выра-
Выразим Т через эти координаты по формуле B9.1.6).
Опуская временно члены, обусловленные движе-
движением центра масс, запишем те слагаемые в выра-
выражении для Т, которые связаны с относительным движением в направле-
направлении оси х:
а2х
Рис. 120.
— 1 Г Г
где
r
B9.10.3)
Присоединяя соответствующие выражения для координат у и z, полу-
получаем следующую компактную формулу:
). B9.10.4)
+ ^ + '-^2), B9.10.5)
Далее имеем
Г2
588 ЗАДАЧА ТРЕХ ТЕЛ [Гл. XXIX.
где
КJ, >B9.10.6)
Лагранжевы уравнения движения имеют вид
1У± Л. Itr J IlbX — n , М'Ц " -.*- ( ^(У ш Jl\J a i F
дХ ох г дс,
и аналогично для координат у ж z.
Прежде всего заметим, что функция U не зависит от X, Y, Z, поэтому
из первого уравнения B9.10.7) следует, что X = 0. Точно так же получаем,
что
X = У = 'Z = 0, B9.10.8)
и, следовательно, центр масс G совершает равномерное прямолинейное дви-
движение. Векторы и и v, определяющие относительное положение частиц,
удовлетворяют уравнениям Лагранжа, получаемым из кинетической энергии
77 = i-TO(i2-(-^24-z2) + yH-(i2 + 'n2+?2) B9.10.9)
и потенциальной функции U B9.10.5). В результате приходим к задаче
с шестью степенями свободы вместо девяти. В самом деле, мы уже видели,
что без потери общности можно считать, что центр масс G находится в покое.
Второе и третье уравнения B9.10.7) теперь принимают вид
т'х = — Ах + В%, \х% = Вх — С\, B9.10.10)
где
т2'
B9.10.11)
)
Присоединяя соответствующие уравнения для у, z, т], ?, получаем
векторные уравнения
mu=—Au + Bv, \iv = Bu — Cv. B9.10.12)
Если и ж v найдены, то положения частиц относительно центра масс G
определяются векторами
— сс2и — Qv, atu — Qv, qw, B9.10.13)
где
9=^, ф=т' + т^ B9.10.14)
Если интегралы B9.1.15) момента количеств движения выразить через
и и v, они приним-ют изящную форму. Момент количеств движения отно-
относительно оси Ох записывается в виде
М М
rl 4) '
— z2y2) + m3 (y3z3 — z3y3) =
= mi{(Y-a2y-Qn)(Z-a2z-ei)-{Z-a2z-Qt>)(Y-a2y'-(pr])} +
§ 29.11] ДРУГОЙ ПОДХОД К ЗАДАЧЕ ТРЕХ ТОЧЕК ЛАГРАНЖА 589
-zy) + (т$* + m202 + т3ф2) (л?- Бл) =
= М {YZ-ZY) +m(y'z~zy) + р^-Ш- B9.10.15)
Интегралы момента количеств движения B9.1.15) тогда принимают
следующую форму:
М (YZ - ZY) + m(yz- zy) ,-f \i (т? - ?tj) = а,
B9.10.16)
Поскольку центр масс G движется равномерно и прямолинейно, сла-
слагаемые М (YZ — ZY) и [m(yz — zy)-}-\i fat— &п)] сами по себе сохраняют
постоянные значения. В этом нетрудно убедиться и непосредственно. В са-
самом деле, имеем
^[m(yz — zy) + p(i\i — ?r\)] = m(yz — zy)+\iDt, — t,r\)=:
/Я Я Я Я i
7, B9.10.17)
но это равно нулю, поскольку оператор
д д . д Т д
обращает величины г±, г2, г3 в нуль.
Описанный выше процесс позволяет существенно упростить задачу трех
тел. Ее теперь можно трактовать как задачу двух тел, из которых одно имеет
массу m и расположено в точке х, у, z, а другое имеет массу |я и расположено
в точке |, т), ?. Действующие на тела силы обладают потенциалом —U,
где U определяется формулой B9.10.5). Хотя силы и не направлены вдоль
линии, соединяющей частицы, тем не менее главный момент этих сил отно-
относительно начала координат
их( — Au + Bv) + vX(Bu — Cv) B9.10.18)
равен нулю, и, следовательно, момент количеств движения системы отно-
относительно начала координат сохраняет постоянное значение.
§ 29.11. Другой подход к задаче трех точек Лагранжа. В качестве первого прило-
приложения уравнений B9.10.12) рассмотрим снова задачу, когда ги г2, гз сохраняют постоян-
постоянные значения. В этом случае выражения и-и, u-v, v-v остаются постоянными. Будут
постоянны также коэффициенты А, В, С в уравнении B9.10.12), прячем А и С поло-
положительны и, кроме того,
^^^) B9.11.1)
\ Г2Г3 r3rl rV2 I
Так как и-и = const, то
и-и = 0, и-и + и-и = 0 B9.11.2)
и, следовательно,
mu-u + u-(~Au~\-Bv) = 0. B9.11.3)
Отсюда, учитывая, что «¦M = const, u-v = const, получаем w-w = const и
ii-u=6! B9.11.4)
590 ЗАДАЧА ТРЕХ ТЕЛ [Гл. XXIX
Таким образом,
«•(—Au + Bv) = 0, B9.11.5)
и, следовательно,
Bu-v = 0. B9.11.6)
Отсюда следует, что либо В = 0, либо u-v = 0 во все время движения.
1) Если В = 0, то Г( = г2 = 1 и векторы и ш v удовлетворяют уравнениям вида
м + п2м = 0, V+p2t, = 0, B9.11.7)
где пир — положительные числа. Каждое из этих уравнений описывает движение
изотропного осциллятора. Поскольку ] и \ постоянно, решение записывается в виде
u = u0cosnt-\-ul sin nt, B9.11.8)
где векторы и0 и щ равны по величине и направлены под прямым углом друг к другу.
Если вектор и на вспомогательной плоскости (и0, ut) обозначить через ОР, то точка Р
будет описывать па этой плоскости окружность с постоянной угловой скоростью п.
Аналогично
v = v0cos pt-{-v1 sin.pt, B9.11.9)
причем векторы да0, »t равны по величине и направлены под прямым углом друг к другу.
Постоянство скалярного произведения и -ъ показывает, что векторы щ, щ, v0, ^компла-
^компланарны и р = п (при этом предполагается, что вращение от v0 к г\ происходит в том
же направлении, что и вращение от и0 к щ). Уравнение п2 = р2 в развернутой форме
имеет вид
(gi+^ ^) + M + m' B9.11.10)
откуда следует, что г3 = I, т. е. треугольник равносторонний. Он вращается с угловой
скоростью п, где г? = уМ/l3 (см. B9.3.7)).
2) Если В фО, то м-» = и»да = 0, откуда следует, что векторы «. и v параллельны
и частицы расположены на одной прямой. Предположим противное: пусть векторы и
и v не параллельны. Тогда, поскольку u-v = u-u = 0, вектор и перпендикулярен к пло-
плоскости векторов и и v; то же самое справедливо и относительно вектора да. Таким об-
образом, учитывая постоянство \и\ и |да|, заключаем, что
v = pu, B9.11.11)
• • • а
где р — постоянный скалярный множитель. Следовательно, v = pu, откуда
m(Bu — Cv) = pii(^Au + Bv). - B9.11.12)
Но последнее равенство невозможно, поскольку из него следует, что АС — В2 = 0,
а это противоречит условию B9.11.1). Таким образом, векторы v и и коллинеарны (да =
= ри) и частицы располагаются на одной прямой. Соотношение B9.11.12) приводит
к квадратному уравнению относительно р:
и,Вр2 — (цА — тС) р — тВ = 0. - B9.11.13)
Можно также вывести уравнение пятой степени для величины к = rjr3, хотя непо-
непосредственный метод, изложенный в § 29.3, проще. Предполагая р > at (что не нарушает
общности, а лишь устанавливает определенный порядок расположения частиц на прямой)
и учитывая, что | и \ = r3, | v | = г4 + air3, получаем
«1Г.3 + Г! = рг3, B9.11.14)
откуда следует, что
р = к+ ai B9.11.15)
и
»2 = ri + гз = (* + 1) г3. B9.11.16)
§ 29.12] СВЕДЕНИЕ К СИСТЕМЕ ВОСЬМИ УРАВНЕНИЙ 591
Коэффициенты в уравнении B9.11.13) имеют теперь следующие выражения:
А у faim3 а2т3
т r% \ к3 (А+1K ' J
/ 1 1 \
U8 (/с + 1K / '
)•
Подставляя их в уравнение
(?|) | = 0, B9-11,18)
получаем уравнение седьмой степени относительно к:
к (к + 1) {(пц + m2) fc6 + Cmj + 2m2) A* + Cmi + таг) А3 — (т2 + 3??г3) Р —
— Bт2 + Зт3) к — (т2 + та3)} = 0. B9.11.19)
Отбрасывая корни к = 0, —1, которые соответствуют случаю совпадения двух частиц,
мы приходим снова к уравнению B9.3.14).
§ 29.12. Сведение к системе восьми уравнений. Вернемся к рассуждениям
§ 29.10. Мы видели, что задача трех тел фактически может быть сведена
к задаче двух тел: частицы массы т, сосредоточенной в точке {х, г/, г), и части-
частицы массы (Л, расположенной в точке (|, т), ?); при этом действующие на
частицы силы обладают потенциалом —U. Движение частиц описывается
системой двенадцати уравнений Гамильтона. В настоящем параграфе мы
сократим число этих уравнений до восьмой, для чего воспользуемся теорией
контактных преобразований.
Перейдем к другим обозначениям: вместо (х, у, z) будем писать (gb q2,
qs), а вместо (?, г\, ?) будем писать (q^, g5, qu). Функция Гамильтона для
системы будет иметь следующее выражение:
H = ±(pl + Pl + P$+-^(PI + Pl + Pl)-U, B9.12.1)
в котором
U = y^rn^s+m^L + m^y B9.12.2)
а ri> rs, r3 определяются формулами
102 + Ibf + ( — °Чд3 -г ЯеJ, )
(a2q3 + qey, \ B9.12.3)
Вспомним, что
Pi —Mi, ^5= Мб, Рб = ^6-
Понижение порядка произведем в два этапа. Сначала перейдем от
(q; p) к новым переменным (Q; Р) с помощью контактного преобразования,
определяемого уравнениями
^ = Ж' Рг = Ж' г=1>2'--, B9.12.5)
592
ЗАДАЧА ТРЕХ ТЕЛ
[Гл. XXIX
причем производящую функцию W возьмем в виде
W = W (p; Q) = (pi cos Q3 + р2 sin Q3) Qi cos Q2 + pQt sin Q2 +
+ (Pi cos Qs + p6 sin Qe) Qk cos <?6 + aQt sin <?s, ' B9.12.6)
где
p> = (-pisinQ3 + p2CosQ3y + ^, , B9 12 7)
= (-Pi sin
cos <
!:}
Заметим, что функция W есть сумма двух выражений, причем второе
получается из первого путем замены индексов 1, 2, 3 соответственно на
индексы 4, 5, 6. Имеем
sin
= (p± cos
(~PlSing8+f>aCOSg3)
sing,
(?3 + p2 sin (?3) cos (?2 -r p sin Q2,
(P cos <?з + Pt sin (?3) sin (?2 +¦ p cos (?2},
2cosQ3) „
J,
i cos
B9.12.8)
/2g 12 9)
и аналогичные формулы с индексами 4, 5, 6.
Поясним физический смысл введенных координат. Прежде всего заме-
заметим, что
откуда видно, что
задаче двух тел, т
B9.12.10)
есть расстояние точки т от точки О в эквивалентной
Д
e. расстояние г3 в исходной задаче трех тел. Далее рас-
рассмотрим движение частицы т в эквивалентной
задаче двух тел. Пусть радиус-вектор От пересе-
пересекает единичную сферу в точке М; предположим,
что плоскость со, содержащая начало О и элемент
траектории частицы т, пересекает дугу большого
круга z = О единичной сферы в точке А. Тогда Q3
будет долготой узла А и AM = Q2 (рис. 121).
Чтобы убедиться в этом, покажем, что если на
рис. 121 угол хА обозначить через Q3, а угол
AM — через Q2, то формулы преобразования сов-
совпадут с B9.12.8). Точку дуги большого круга
z = 0 с долготой-7J- я -\- Q3 обозначим через В;
пусть плоскость со пересекает дугу большого кру-
круга zB в точке N. Составляющие импульса частицы т
вдоль осей Ox, Oy, Oz равны pt, p2, р3; поэтому составляющая его вдоль ОВ
равна (—pi sin Qs + р2 cos Q3), и так как вектор импульса лежит в пло-
плоскости со, то
sin0^^lSin<?3+/>2CO^3)/P' } B9Л2Л1)
где через 0 обозначен угол BN. Единичный вектор в направлении ОМ имеет
составляющую cos Q2 по оси О А, составляющую sin Q2 cos 9 по оси ОВ
и составляющую sin Q2 sin 0 по оси Oz. Составляющие этого вектора по осям
яс" '
§ 29.12] СВЕДЕНИЕ К СИСТЕМЕ ВОСЬМИ УРАВНЕНИЙ 593
Ox, Oy, Oz соответственно равны
cos Q2 cos Q3 — sin Q2 cos 0 sin Q3,
cos Q2 sin Q3 + sin Qz cos 0 cos Q3,
sin Q2 sin 9.
Приравнивая эти выражения величинам qi/Qi, qJQi, Яз/Qii получаем
равенства B9.12.8).
Физический смысл величин Р ясен из соотношений B9.12.9). Импульс
частицы т есть векторная сумма вектора (pi cos Q3 + р2 sin Q3), направлен-
направленного вдоль О А, и вектора р, направленного вдоль ON. Отсюда следует,
что Р4 есть составляющая импульса в направлении ОМ, Pi = mQy. Далее,
Р2 равняется величине вектора момента количеств движения относительно
точки О (этот вектор имеет направление ON', где N' обозначает полюс сфе-
сферы, экваториальная плоскость которой есть со). Наконец, Р3 = Р2 cos 0
есть момент количества движения частицы т относительно оси Oz.
Формулы преобразования B9.12.8), B9.12.9) и соответствующие форму-
формулы с индексами 4, 5, 6 показывают, что
l + Pl^Pl + щ B9.12.12)
= с2с&С-Ьc2s5S cos (p — s^c^S cos9 +s2s5C cos 0 cos cp-4 s2s5 sin0 sin cp, B9.12.13)
где cr = cos Qr, sr = sin Qr, С = cos {Q3 — Q6), S = sin (Q3 — Qe), а угол ф
определен для индексов 4, 5, б точно так же, как угол 0 — для индексов 1, 2, 3.
Кроме того, поскольку
cos0-^, cos<p = -^, B9.12.14)
переменные q можно выразить через Q и Р, так что функцию Н B9.12.1)
также можно представить в переменных Q и Р.
Чтобы выразить составляющие момента количеств движения в новых
переменных, воспользуемся формулами
— g3jtV=-^2 sin 9 sin <?з, Л
— <1iPa= -P2 sine cos <2з, 1 B9.12.15)
вытекающими из B9.12.8), B9.12.9). Последняя из этих формул уже упо-
упоминалась ранее, а две остальные легко выводятся непосредственно из чер-
чертежа. Интегралы момента количеств движения имеют вид
Р2 sin 9 sin Q3 -\-Рь sin ф sin Q6 = а, Л
— P2sin0cos<?3 — P5 sin ф cos (?6 = Ь, \ B9.12.16)
Р3+Р6 = с. J
На этом завершается первый этап решения поставленной задачи. Заме-
Заметим, что рассмотренное нами преобразование не является расширенным
точечным преобразованием, поскольку переменные Qi, Q2, Q3 нельзя выра-
выразить через одни только переменные дь q2, q3-
Перейдем теперь ко второму этапу. Воспользуемся интегралами момента
количеств движения. Направим ось Oz вдоль (постоянного) вектора момента
1/ь 38 Л. А. Парс
594 ЗАДАЧА ТРЕХ ТЕЛ [Гл. XXIX
количеств движения, так что будем иметь а = Ъ = 0, и совершим контакт-
контактное преобразование, в котором третья составляющая Р3 + Р6 будет един-
единственной переменной импульса.
Равенство нулю двух первых выражений B9.12.16) показывает, что
sin (Q3 — Qe) = 0. Без потери общности можно принять Q3 = Q$, и, следо-
следовательно,
Р2 sin 9 = — Р5 sin ф, B9.12.17)
что ясно из геометрических соображений.
Теперь откажемся от принятого ранее деления формул на две группы:
на формулы для индексов 1, 2, 3 и формулы для индексов 4, 5, 6. Перейдем
от переменных (Q; Р) к переменным \q'; р') с помощью уравнений преобразо-
преобразования
Qr==™L, Pr^lUfr' B9.12.18)
где
W = W (Р; q') = Ч[Рг + q'2P4 + q'3P2 + q,Pb + q'6 (Ps - Рв) + д'в (Р3 + Рв).
B9.12.19)
В результате будем иметь
B9.12.20)
Оба использованных нами преобразования не зависят от t, поэтому
для получения новых уравнений движения достаточно выразить функцию Н,
имеющую вид B9.12.1), через q' и р'.
Прежде всего, заметим, что координата q'a циклическая, что нетрудно
было предвидеть, поскольку величина р'я остается постоянной в течение
всего времени движения. Положим р'е = р. Далее, q'b = 0 в продолжение
всего времени, и из формул B9.12.17) и B9.12.14) следует, что для любого t
/>2 _ р2 = pa __ p2( B9.12.21)
откуда
р'* — р? = Р22 — Р\ = (Р3 + Рв) (Ро — Рв) -^ $р'у B9.12.22)
Это значение переменной р'ъ можно ввести в выражение для Н до того, как
будут написаны уравнения движения. В самом деле, обозначая составлен-
составленную так функцию через Н' (q[, q'2, q3, qv q'h, p'v p'2, р'г, р'4, р'л), а любую
из переменных q[, q'2, q3, q[, p[, p'z, p'3, p'4 — временно через tJj, будем иметь
дН' дН . дН dpi /Оп л о оо\
дН *
так что ¦^-т- = дг5 будет равно нулю в течение всего времени. Отсюда следует,
что при составлении функции Гамильтона (которая во всяком случае
не содержит q'e) можно положить q'& = 0, р'й = р и
Р'* = (Р?-Р'*№- B9.12.24)
В результате получаем функцию Гамильтона от восьми переменных: q[, q'2,
9з> Qi'Pi'Pz' P'31 P'f Задача, таким образом, свелась к системе восьмого поряд-
порядка. После того как система проинтегрирована, циклическая координата q'e
§ 29.13] НЕВОЗМОЖНОСТЬ ТРОЙНЫХ СТОЛКНОВЕНИЙ 595
находится квадратурой из уравнения
"я'^-Щ-- B9.12.25)
Единственное затруднение при составлении функции Я связано с пре-
преобразованием суммы cos 0 cos ф 4- sin 0 sin ф в правой части равенст-
равенства B9.12.13). Учитывая B9.12.17), находим
cos 0 cos ф -f- sin 0 sin ф — cos 0 cos ф —^ sin2 0 =
1&{Р**-ъ+ъ)=ш®ж-р''-р?)- B9Л2-26)
Итак, уравнения движения составляются с помощью следующей функ-
функции Гамильтона:
Н= 1 („* | Ра\ i 1 /р« | Pi) Ym^3 утзггц упцт2 BQ ^о 27)
2т К^1' q\) ' 2ц V 2 ~ q\ ) rt r2 Ь У ' ' '
(штрихи мы отбросили). Здесь
(cos g3 cos g4 + ^~~p*'~Pi sin g3 sin g4) + gl,
/ B*-»»-^ ч B9.12.28)
(cosg3cosg44 H ^ ^4iJ | J
Для понижения порядка системы до шестого, вообще говоря, можно было
бы воспользоваться интегралом энергии (см. § 22.4), но в данном случае
эта процедура привела бы к значительным вычислительным трудностям.
§ 29.13. Невозможность тройных столкновений. Рассмотрим задачу трех
тел в предположении, что центр масс G находится в покое. Введем функ-
функцию R:
MR2 = тгтгг\ + т3т^г + т^гг\. B9.13.1)
Эта функция неотрицательна и симметрична по отношению к трем телам.
В обозначениях § 29.10 (где была сформулирована эквивалентная задача
двух тел) получаем (см. B9.10.6))
Д« = mr2 + Ц-Р2' B9.13.2)
где
г* = | и |2 = х* + у2 + z\ р2 = | v |2 = |2 + У]2 + ?2- B9.13.3)
Кинетическая энергия определяется формулой
^ ъ +Ь, B9.13.4)
а интеграл энергии имеет вид
Т = Л + U. , B9.13.5)
Интегралы момента количеств движения определяются равенствами
m(y'z — zy) + \i(rii — tT\) = a, B9.13.6)
m(zi-xz) + n(^-li) = b, B9.13.7)
in (ijr-yi)+ |i(|T|-Tii) = с. B9.13.8)
Далее имеем
±f R2 = 2m (xx + уу + zz + х* + У2 + z2) + 2ц {Ц + г]т1 +- ?? +12 4- т]2 + ?2).
B9.13.9)
38*
596 ЗАДАЧА ТРЕХ ТЕЛ [Гл. XXIX
С другой стороны, в силу B9.10.7)
т(хх+ уу + zz)
ибо функция U однородна степени —1 относительно переменных х, у, z,
|, т], ?. Равенство B9.13.10) вместе с B9.13.5) приводят к формуле Лагранжа
^ B9.13.11)
Далее имеем
RR = тг'г + н-РР, B9.13.12)
так что
R2R2 = (jnr2 + jup2) (mra + цр2) — пц1 (гр - ргJ. B9.13.13)
Следовательно,
jf2 = mr'2 + N>_jgL(rp_p;.J. B9.13.14)
Кроме того,
(а-» + г/2 + а«) (х2 + у* + z2) = (жж + уу + zzJ +
+ {Q/z-zyJ + (zi-zzJ + (^-z/iJ}, B9.13.15)
откуда
^^-L-^ iX2J+(x^-j/iJ}. B9.13.16)
Подставляя это выражение для г2 и аналогичное выражение для р2
в правую часть B9.13.14) и учитывая B9.13.5), приходим к формуле Зунд-
мана
R2 = 2h + 2U - S, B9.13.17)
где
s = тг {(У* - ЧУ + (zx - xzf + (xy - y'xf) +
+ -^-{(г]?-^J+(^-Ша + Ш11-т1т + 5г(гр-ргJ. B9.13.18)
Исключая U из B9.13.17) и B9.13.11), получаем
2RR + R*-2h = S. B9.13.19)
Рассмотрим теперь S как функцию семи переменных (yz — zy),
(zx — xz), ..., (|т) — т]|), (гр — pr), подчиняющуюся соотношениям B9.13.6) —
B9.13.8). Наименьшее значение, которое может иметь выражение
J±(yz-zy)*+-?i{T&-u[)* B9.13.20)
при дополнительном условии B9.13.6), равно a2/R2. Это очевидно из элемен-
элементарного тождества
2. B9.13.21)
Отсюда и из аналогичных формул приходим к неравенству
S > 62/Д2, B9.13.22)
§ 29.14] ПЛОСКОЕ ДВИЖЕНИЕ 597
где
б2 = а2 + Ъ2 + с2. B9.13.23)
Так как случай а =¦ Ъ = с = 0 мы исключили (§ 29.2), то б > 0. Из фор-
формул B9.13.19) и B9.13.22) находим
2RR + R2 — 2fe > 62/i?2. B9.13.24)
Если теперь ввести обозначение
F = RR-2hR + -^, B9.13.25)
то будем иметь
k( ^y B9.13.26)
Неравенство B9.13.24) показывает, что функция F возрастает (или
по крайней мере не убывает) с возрастанием R и убывает (или по крайней
мере не возрастает) с убыванием R.
Теперь нетрудно показать, что столкновение трех частиц невозможно,
если б > 0. Предположим противное: пусть R -*- 0, когда t —*- t0 со стороны
меньших значений. Тогда F -> оо при t -*- t0. Далее, формула B9.13.11)
показывает, что d2 (R2)/dt2 -*- оо при t -> t0, и, следовательно, d2 (R2)ldt2 > 0,
если t достаточно близко к t0, например, лежит в интервале /, определяемом
неравенствами t\ ^ t < t0. В интервале / производная d (R2)/dt растет
вместе с t, откуда следует, что в этом интервале d {R2)ldt ^ 0. В самом деле,
если бы в некоторой точке t2 интервала / выполнялось неравенство
d (R2)ldt > 0, то оно выполнялось бы и в интервале 12 ^ t < tQ, что невоз-
невозможно, так как i?->0 при ?-> t0. Таким образом, R < 0 в интервале /,
и, следовательно, в этом интервале F ^ 0, что приводит к противоречию,
поскольку F-*- оо при t—>¦ t0.
Если 6 = 0, то тройное столкновение возможно. В качестве простей-
простейшего примера можно привести случай, когда три частицы одинаковой массы
начинают свое движение, находясь в вершинах равностороннего треуголь-
треугольника.
Столкновение двух частиц возможно и при б > 0. После такого столк-
столкновения частицы движутся так, как описано в § 5.6. (В течение короткого
промежутка времени, включающего момент столкновения, влияние третьей
частицы пренебрежимо мало по сравнению с взаимным притяжением стал-
сталкивающихся частиц, и в течение этого промежутка времени задача факти-
фактически становится задачей двух тел.) Особенности в формулах, соответ-
соответствующие столкновению двух частиц, не являются существенными; они могут
быть устранены посредством надлежащего выбора новой независимой пере-
переменной. Этот результат содержится в известной работе Зундмана 1912 г.
Зундман показал, что координаты трех частиц и время могут быть пред-
представлены в виде функций комплексной переменной т, регулярных внутри
единичного круга | т | = 1. Координаты при этом определяются степен-
степенными рядами по т, сходящимися для всех значений времени. Единственным
случаем, на который эта теория не распространяется, является случай
тройного столкновения.
§ 29.14. Плоское движение. Другой способ приведения к системе шестого
порядка. В § 29.8 мы показали, что уравнения движения в задаче трех тел
в случае плоского движения допускают понижение до шестого порядка.
Этот результат можно получить и другим путем, если исходить из уравне-
уравнений в форме, приведенной в § 29.10.
1/2 38 Л. А. Парс
598 ЗАДАЧА ТРЕХ ТЕЛ [Гл. XXIX
Будем предполагать, что центр масс G находится в покое и движение
происходит в плоскости z = 0. В обозначениях § 29.10 будем иметь
7I = -2-m(^ + ^) + y|x(la + V). B9.14.1)
и= (гп^Щ^тзЩ !щт2\ B9 14 2)
V V Г4 ' Г2 ~ Г3 ) ' V • • /
где
r* = (-Kl:r + ^ + (-aii/+T]J, ^j
2 ( ) } B9.14.3)
Возьмем систему осей, вращающихся с постоянной угловой скоро-
скоростью со вокруг оси Oz. Если через {q±, q%) и (qs, Зч) обозначить составляю-
составляющие векторов и я v в этих осях, то можно будет написать
Т = ±т{{дг-(одя)* + 4 + содЛ +±р {(д3-Щ,J + (д4+ЩвJ}, B9.14.4)
причем формулы для rt, r2, г3 не изменят своего вида:
B9.14.5)
Последнее утверждение очевидно геометрически и легко может быть про-
проверено непосредственно.
Чтобы составить выражение для функции Гамильтона, нужно в выра-
выражении
^ ^-^m^iql+q^-^^iql + q^-U B9.14.6)
перейти от q к р с помощью формул
= m(q2 + щ±), \ B9 14 7)
Проделав это, получим функцию Гамильтона в виде
^ ^ -адз)-^. B9.14.8)
Коэффициент при —со в правой части равенства,
B9.14.9)
определяет момент количеств движения относительно точки G (см. B9.10.15)).
С помощью уравнений Гамильтона легко убедиться, что выражение B9.14.9)
сохраняет постоянное значение во все время движения. Этим обстоятель-
обстоятельством мы воспользуемся для понижения порядка системы. Аналогичную
процедуру мы уже применяли в § 29.8.
Составляющие вектора и во вращающейся системе осей равны gi, q%.
Введем полярные координаты Qi, Q^ с помощью формул
<7i = CQu q2 = SQU B9.14.10)
где
С = cos <?4, S = sin &. B9.14.11)
29.14]
ПЛОСКОЕ ДВИЖЕНИЕ
599
Обозначим составляющие вектора v, параллельную и перпендикулярную
к вектору и, соответственно через Q2 и Q3 (рис. 122). Тогда будем иметь
qa = CQ2 - SQ3, ?4 = SQ2 + CQ3. B9.14.12)
Необходимым контактным преобразованием будет расширенное точечное
преобразование, определяемое уравне-
уравнениями \
SW
dW
dQr'
г=1,2, 3,4,
B9.14.13)
где производящая функция W имеет вид
W = piCQi + p2SQi + p3 (CQ2 — SQ3) +
CQ3). B9.14.14)
Рис. 122.
Таким образом, уравнениями, опре-
определяющими преобразование, будут уравнения B9.14.10) — B9.14.12) и
B9.14.15)
л ПТ) ОТ) j, ОТ)
где через К обозначено выражение (Р4 — Q2Ps
Заметим, что
dW
Р4 = ~ = — PlSQt + p2CQi +ps(—SQ2 — CQ3)
== ч 1Р2 — Ч2Р1~1~ЯзРк — 4iP3 \6v-i^-lu)
определяет момент количеств движения относительно точки G. Поскольку
контактное преобразование не содержит t, новая функция Гамильтона полу-
получается из старой простым переходом к новым переменным:
H = y-(P\+ К2)+~(Р22 +Р23) — юР4 — U. B9.14.17)
Эта функция несколько проще, чем B9.8.13), полученная ранее другим
методом.
Далее имеем
B9.14.18)
= (- a?Qi + CQ2 - SQ3y + (- a.SQ, + SQ2 + CQ3f =
(aaSQi + SQ2 + CQ3f =
± + CQ2 -
Следовательно, функция Н не содержит Qk и Р4 = 0. Таким образом,
Р4 остается постоянным в течение всего времени движения, что, впрочем,
мы уже видели раньше. Положим
Р4 = Г. B9.14.19)
В результате получаем систему шестого порядка относительно переменных
Qu <?2i (?3i Pi, Pz, Рз и функцию Гамильтона
# = 4- (PU- К*) +4- (PI + PD-U, B9.14.20)
где теперь К обозначает выражение (Г — Q2P3 +
38*
600
ЗАДАЧА ТРЕХ ТЕЛ
[Гл. XXIX
После того как система проинтегрирована, оставшаяся переменная —
угол Qk — находится квадратурой из уравнения
Q^^(T-Q2P3+Q3P2)-w. B9.14.21)
__ § 29.15. Равновесные решения. В качестве простого примера применения изложен-
изложенной теории рассмотрим снова вопрос о существовании равновесных решений, т. е. таких
решении, в которых частицы находятся в покое относительно вращающихся осей. Преж-
Прежде всего заметим, что согласно B9.14.21), если такое решение существует, то
<й = Kl(mQi). B9.15.1)
Уравнения движения для системы шестого порядка B9.14.20) имеют вид
B9л5-2)
m Qi ^ 9Qi '
1 KP2 dU
m О, + dOt
В равновесном решении правые части этих уравнений обращаются в нуль, и в силу
B9.15.1) будем иметь
Следовательно,
«»¦»*
B9.15.4)
Равновесным решениям соответствуют точки в пространстве (Qj, Qj, Q3), в которых
Функция
(Ql + Ql+Ql)efl B9.15.5)
имеет стационарное значение.
Уравнения B9.15.4) в развернутом виде записываются следующим образом:
=0,
=0, B9.15.6)
B9.15.7)
B9.15.8)
Из последнего уравнения слеДует, что либо
либо
(?з = 0.
B9.15.10)
Предположим, что имеет место условие B9.15.9). Тогда, подставляя это выраже-
выражение для (Ш2 в левую часть уравнения B9.15.7), находим
0- B9.15.11)
Так как Qi = r3 Ф 0, то отсюда следует, что rj = т^. Положим
Г1 = г2 = г. B9.15.12)
§ 29.15] РАВНОВЕСНЫЕ РЕШЕНИЯ 601
Тогда из уравнения B9.15.9) получаем
0J = ^^-. B9.15.13)
Подставляя это выражение для со2 в левую часть B9.15.6), находим
~1Г = -]з—h—JZ—• B9.15.14)
Таким образом,
г3 = I, B9.15.15)
т. е. мы получили равносторонний треугольник Лагранжа.
Предположим теперь, что имеет место условие B9.15.10). Тогда все три частицы
располагаются вдоль одной прямой. Считая, как и ранее, что частица А 2 расположена
между At и Аз, можем написать
<?i = '"з, <?2 = ri + оцгз, (?з = 0, г2 = Ti + г3. B9.15.16)
В обозначениях B9.3.12) будем иметь
Ц-. B9.15.17)
к к+1 1 '
Уравнение B9.15.8) удовлетворяется, поскольку (?з = 0, и из уравнений B9.15.6),
B9.15.7) получаем
Разделив второе из этих уравнений на первое и принимая во внимание B9.15.17),
получаем
Это соотношение эквивалентно уравнению пятой степени B9.3.14). Таким образом, мы
снова получили уже известный результат, согласно которому равновесные решения
исчерпываются равносторонним треугольником Лагранжа и случаем, когда частицы
располагаются на одной прямой.
Глава XXX
ПЕРИОДИЧЕСКИЕ ОРБИТЫ
§ 30.1. Периодические орбиты. Как правило, уравнения движения дина-
динамической системы при произвольных начальных условиях не удается про-
проинтегрировать до конца. Так обстоит дело, в частности, и для задачи
трех тел. Мы видели (§ 17.10), что даже классификация возможных типов
траекторий в общем случае встречает большие трудности. Однако иногда
мы в состоянии найти периодические орбиты или по крайней мере доказать
их существование. Пуанкаре в своей классической работе о задаче трех тел
придавал особое значение отысканию периодических решений и считал это
отправным пунктом для решения общей задачи о классификации и интегри-
интегрировании *). Траектории могут быть периодическими как в абсолютном
смысле (по отношению к неподвижным осям), так и в относительном смысле
(по отношению к осям, движущимся определенным образом). Например,
в ограниченной задаче трех тел мы говорим о периодических траекториях
частиц относительно вращающихся осей.
§ 30.2. Периодическое движение в окрестности особой точки. В гл. XIX
было рассмотрено движение автономной динамической системы с одной
степенью свободы вблизи положения равновесия (особой точки). Сначала
рассматривалось линейное приближение, т. е. приближение, которое полу-
получается из уравнений движения
хг = Хг, г = 1, 2, C0.2.1)
в которых в правых частях сохранены одни только линейные члены, начало
координат выбрано в особой точке и функции Хг не содержат постоянных
слагаемых. В линейном приближении уравнения движения записываются
в форме
х = Ах, C0.2.2)
где Л — матрица размером 2x2, элементами которой являются вещест-
вещественные постоянные.
Основной вопрос состоит в следующем: что можно сказать об устойчи-
устойчивости движения, определяемого уравнениями C0.2.1), если движение устой-
устойчиво в линейном приближении C0.2.2)?
Особый интерес представляет случай точки типа центра; в этом случае
матрица А имеет чисто мнимые собственные значения. Система с одной
степенью свободы устойчива по первому приближению, но это свойство,
как мы видели, не всегда сохраняется при переходе к точным уравнениям.
В общем случае системы с п степенями свободы уравнения движения
записываются в форме
хт = Хг, г = 1, 2, . . ., тп, C0.2.3)
*) «Се qui nous rend ces solutions periodiques si precieuses, c'est qu'elles sont, pour
ainsi dire, la seule breche par ou nous puissions essayer de penetrer dans une place jusqu'ici
reputee inabordable». (Эти периодические решения столь для нас привлекательны пото-
потому, что они представляют, так сказать, единственную брешь, через которую можно
пытаться проникнуть в место, до сих пор считавшееся недоступным.)
i 30.2] ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ В ОКРЕСТНОСТИ ОСОБОЙ ТОЧКИ 603
где т — In. Если начало координат выбрано в положении равновесия,
то все функции ХТ при х^ = хг = ... = хт = 0 обращаются в нули.
Уравнения линейного приближения имеют вид (см. § 21.11)
х = Ах, C0.2.4)
где теперь А обозначает матрицу размером тхт. Если все собственные
значения этой матрицы являются простыми и чисто мнимыми числами,
то начало координат в линейном приближении представляет положение
устойчивого равновесия. Однако частный случай т = 2 показывает, что
при переходе от приближенных уравнений к точным мы этого можем не
получить.
Тем не менее можно указать такое свойство устойчивого положения
равновесия, которое сохраняется при переходе к точным уравнениям. Для
системы Гамильтона, имеющей пару сопряженных чисто мнимых собствен-
собственных значений ±фо> эг0 свойство заключается в том, что в окрестности
положения равновесия существует семейство периодических движений.
Элементы этого семейства зависят от вещественного параметра р; они суще-
существуют для достаточно малых значений р и при р -> 0 стремятся к равновес-
равновесному решению (при котором изображающая точка находится в покое в нача-
начале координат). Период а (р) при р->-0 стремится к значению 2я/^0.
Рассмотрим вместо системы Гамильтона систему общего вида C0.2.3).
Правые части Хг при х = 0 обращаются в нуль. Предположим, что каждая
из функций Хг при достаточно малых | х | может быть представлена степен-
степенным рядом по переменным (х±, х2, . . ., хт) с вещественными коэффициен-
коэффициентами и без постоянного члена. Линейное приближение имеет вид C0.2.4).
Будем предполагать, что матрица А обладает следующими свойствами.
Все собственные значения Xlr Xz, . . ., Хт этой матрицы различны; два
из них, например Xi и Х2, являются равными по величине и противополож-
противоположными по знаку мнимыми числами: ^ = — Яз = ?[х0; наконец, ни одно
из отношений X3M,i, XJXi, . . ., 'kml'ki не является целым числом.
Рассмотрим уравнение линейного приближения C0.2.4). Совершая
неособое линейное преобразование
C0.2.5)
получаем
у=-€~гАСу. C0.2.6)
Матрицу С выберем так, чтобы матрица С~гАС была диагональной матри-
матрицей L:
¦к
к
L = \ \ | C0.2.7)
Уравнения движения принимают теперь вид
C0.2.8)
и движение, при котором
ух--ае^, z/a = Pe-^, г/3 = 2/4=-..=г/т = 0, C0.2.9)
является периодическим с периодом 2л/^0. Комплексные коэффициенты а,
¦6 при этом выбираются так, чтобы величины х были вещественны.
604 ПЕРИОДИЧЕСКИЕ ОРБИТЫ [Гл. XXX
Если теперь применить это же самое линейное преобразование к точ-
точным уравнениям C0.2.3), то получим уравнения
'ук = Ъ-нУк + gh, к = 1,2, . . ., т, C0.2.10)
в которых gk обозначают степенные ряды по переменным (у±, уг, . . ., ут),
начинающиеся с членов второй степени. Чтобы доказать существование
периодических решений, подобных решениям C0.2.9), воспользуемся прие-
приемом, аналогичным известному способу вариации произвольных постоянных.
Предположим, что существует решение, при котором каждая из функций у^
представляется как функция двух переменных |, т] с помощью следующих
формул:
2««?У, C0.2.11)
aUW, C0.2.12)
yk = Zk = 2 ahrslrns, к>2, C0.2.13)
причем ряды для Zi, z2, . . ., zm начинаются с членов второй степени. Отно-
Относительно этих рядов предположим следующее. Будем считать, что a\s = 0,
если г = s + 1, так что ряд для г4 не содержит членов вида | (?т))8 и, следо-
следовательно, ряд для dzjd% не содержит членов вида (St])s. Аналогично, будем
предполагать, что а% = 0, если s=r+l, так что ряд для z2 не содержит
членов вида (grj)rTi, а ряд для дъг1дх\ не содержит членов вида {?,ц)г. При-
Причины, заставляющие нас вводить эти ограничения, выяснятся позже.
Будем предполагать, далее, что вспомогательные переменные | и т)
являются функциями от времени, удовлетворяющими дифференциальным
уравнениям
t = ul, 'х[ = щ, C0.2.14)
где и есть функция от произведения переменных %r\, разложение которой
в ряд по степеням \ц начинается с постоянного члена Кх:
и = Я* + ЩЪ\ + u2l\* + . . ., C0.2.15)
& v — функция от |т), разложение которой начинается с постоянного чле-
члена }^2-
v = Я.2 + vi\i\ + v2l\* + . . . C0.2.16)
Предполагая, что эти ряды сходятся для достаточно малых значений \
и г), представляем уравнения C0.2.10) в следующей форме:
ul^+vy\^ = %kyh + gh, к = 1,2, ...,т. C0.2.17)
Если подставить сюда соответствующие разложения для у^, и, v и срав-
сравнить коэффициенты при подобных членах ?'r|s, то можно будет определить
все коэффициенты a^s, ur, vr.
Уравнение C0.2.17) для к = 1 имеет вид
ul + ul -ф + щ -^ -
или, в развернутой форме,
+ ¦ ¦ ¦)+ (S ra\sVrf) (Я, + UjS
..)-X1^a1rslrvf = gl. C0.2.18)
Аналогичным образом, второе уравнение дает
l*^+...)+(%ra*tlrif)(k1+u1li\+...) +
+ (S *4Гт13) (^2+ WiSt, + ...)- Л-2 S «?8Гт15 = ft. C0.2.19)
30.3] УСЛОВИЯ ВЕЩЕСТВЕННОСТИ 605
Остальные уравнения приводят к формулам
+ B saUY) (К + v&l +...)- h 2 arS?V = gft. C0.2.20)
Вместо функций gft в правые части этих уравнений нужно подставить соот-
соответствующие ряды по степеням уи у2, ¦ ¦ ., ут.
Левая часть уравнения C0.2.18) не содержит членов вида |s+1r|s нигде,
кроме как в выражении ?и, а левая часть C0.2.19) не содержит членов
вида %TV['+1 нигде, кроме как в выражении r\v. Неизвестные коэффициенты
находятся теперь шаг за шагом путем приравнивания коэффициентов. Если
найдены все коэффициенты a*, (ft = 1, 2, . . ., иг) для г + s < N и коэф-
коэффициенты иТ, vr для 2г < N — 1," то коэффициенты а*, для г + s = N можно
найти, сравнивая коэффициенты при |гт|г. Оставляя в стороне случаи
г — s = l при к = 1 и г — s = — 1 при к = 2, получаем
[(г _ в) ^ _ Xk) a*s = p, C0.2.21)
где р — полином относительно уже найденных коэффициентов. Коэффи-
Коэффициент при a^s в левой части последнего уравнения никогда не обращается
в нуль. Действительно, если ft = 1, то г — s^=l,a если ft = 2, то г — s Ф — 1.
Если же ft > 2, то выражение [(г — s) Xi — Kk] не может равняться нулю,
так как ни одно из отношений Xh/Xi не является целым числом. Наконец,
коэффициенты ит находятся путем приравнивания коэффициентов при ?г+1т]г
в уравнении C0.2.18), что позволяет выразить ит через уже известные коэф-
коэффициенты. Аналогичным путем из уравнения C0.2.19) можно определить
коэффициенты vr. Таким образом, мы построили степенные ряды для m + 2
переменных у^, и, v; вопрос о сходимости этих рядов будет предметом даль-
дальнейшего рассмотрения.
§ 30.3. Условия вещественности. Уравнения C0.2.1) можно записать
в следующей форме:
х=/(ж), C0.3.1)
где f(x) есть вектор {Хи Х2, ..., Хт}, причем/"(ж) вещественно, если вещест-
вещественны хь х2, ...,хт. Преобразование х = Су приводит уравнение C0.3.1)
к виду
У = С~У(Су), C0.3.2)
и уравнение C0.2.17) принимает форму
Обозначим через yh, и, v ряды, которые получаются из разложений
для z/й, и, v при замене коэффициентов комплексно-сопряженными.
Из C0.3.3) тогда получаем
Щ ^ C0.3.4)
ябо f(x) вещественно, когда вещественно х.
Определим матрицу Т с помощью формулы
С = СТ, Т = С1С. C0.3.5)
Правую часть уравнения C0.3.4) тогда можно записать в виде
T^C^fiCTy). C0.3.6)
39 л. А. Паре
606 ПЕРИОДИЧЕСКИЕ ОРБИТЫ [Гл. XXX
Отсюда видно, что уравнение C0.3.3) останется в силе, если заменить у
на Ту, и на и и v на v.
Рассмотрим преобразование w = Ту. Ему эквивалентно преобразо-
преобразование Cw = Су, которое показывает, что
wh = pkyi C0.3.7)
(мы здесь воспользовались обозначениями § 25.10). В частности, имеем
Wi = Р1У2, w2 = р2г/1 C0.3.8)
и Pip2 = 1- Две первые составляющие Ту равны
pil/2 = pin + ... C0.3.9)
и
Р2^1 = Р2 I + • • • C0.3.10)
Остальные составляющие имеют разложения, начинающиеся с квадратич-
квадратичных членов по переменным |, ц.
Уравнение C0.3.3) будет удовлетворяться, если
y(t,i\), и(Ъ,т\), v(l,n) C0.3.11)
заменить соответственно на
Ту (pill, p2?), ^ (pill, р2Е), mCpjT], р2|). C0.3.12)
Отсюда в силу единственности решения, удовлетворяющего заданным усло-
условиям, получаем
Су (I, г]) = Су (рл Pag), и (§, г]) = v (plT|, p2S). C0.3.13)
Далее имеем
яв(?, Ti) = Cy(g, Ti). C0.3.14)
Равенства C0.3.13) показывают, что х будет вещественным, если
I = PiT|. n = p2S- C0.3.15)
Отметим важный частный случай, когда все собственные значения Я), Я2, ...
. . ., Хп, — hi, — Л2, . . ., —Х„ чисто мнимые, а собственные векторы, образующие столб-
столбцы матрицы С, нормированы, так что все множители рг равны единице, и (га + г)-й стол-
столбец матрицы С (для г = 1, 2, . . ., п) имеет элементы, сопряженные соответствующим
элементам r-го столбца. При этих условиях Ту есть вектор (yn+i, уп+г, • ¦ ¦, у~гп*
У и У г, • ¦ •. Уп)' а Т есть матрица
/0 In\
\ln О)*
§ 30.4. Уравнения Гамильтона. Особый интерес представляет случай,
когда уравнения C0.2.1) имеют гамильтонову форму и существует пара
чисто мнимых собственных значений, одинаковых по величине и противо-
противоположных по знаку. Начнем с того, что совершим линейное преобразование
(см. § 25.10) и приведем члены низшего (второго) порядка в функции Гамиль-
Гамильтона к виду
- • • + КЯпРп- C0.4.1)
Собственными значениями будут Xi, Kz, . . ., ^п, —Х\, —^2> • • •>—ХпУ
а фундаментальной парой собственных. значений теперь будут Ki, Xn+i
(где Ki = — hn+i = фо) вместо ?ц, Я2, составлявших фундаментальную пару
в предыдущих параграфах. Когда члены Н2 в функции Н имеют форму
C0.4.1), уравнения движения принимают вид C0.2.10).
§ 30.4] УРАВНЕНИЯ ГАМИЛЬТОНА 607
Обозначим через К результат замены в формуле для Н величин q и р
их выражениями через ?, ц:
Н (q; p) = K (?, т|). C0.4.2)
Из уравнения энергии получаем
— = 1%— + щ — = 0. C0.4.3)
Напомним, что и я v суть функции от со = |т]. Легко видеть, что К также
будет функцией со. Если эту функцию представить в форме степенного ряда
по | и г), то единственным членом второго порядка будет }^|т]. Но если К
имеет вид
Ш + S ЬгЛ\\ C0.4.4)
где г + s > 2, то из уравнения C0.4.3) получаем
(А..+ 2 ИгГУ) (*,&!,+ S r/crsrris) +
+ (- К+ S ^гГ-Пг) (Я-^Л + S *йг4гт1в) = 0. C0.4.5)
Определяя коэффициенты шаг за шагом, обнаруживаем, что krs = 0, если
r=/=s. Таким образом, К есть функция от со, скажем ф(со), и уравне-
уравнение C0.4.3) принимает вид
«>*Е. = О. C0.4.6)
Следовательно,
и + v = 0, C0.4.7)
что очевидно также из C0.4.5).
Далее имеем
IF = If Gi) = (« + ") 5Л = 0, C0.4.8)
и, стало быть, со сохраняет в процессе движения постоянное значение;
и я v = — и, являющиеся функциями со, также постоянны. Следовательно,
I = loeut, ц = ^ое1". C0.4.9)
Если |0, тH выбрать так, чтобы ^0 = pjT]0, то, как и в § 30.3, и —
= w (|, т]) = и (?0, щ) и v = v (|, т)) == у (?о> Ло) будут комплексно-сопря-
комплексно-сопряженными, и так как и + v === 0, то будем иметь
м = tjut, у = — ф. C0.4.10)
Уравнения
5 = !сЛ л = цое-^ C0.4.11)
при достаточно малых 11 [ определяют семейство периодических решений
уравнений Гамильтона. Выражение |oei|i( можно записать в форме peW-'o),
где р — вещественное и положительное число; тогда, изменив начало отсче-
отсчета времени, будем иметь
I = peW, ц = рр2е-{^. C0.4.12)
(Матрицу С можно взять в такой форме, чтобы р2 = 1.) Период равен 2я/(г,
и так как
и = щ = i[x0 + go-qo (Ul +...), C0.4.13)
то при р —>¦ 0 период 2jt/u. стремится к значению 2зт/|а,0. При этом периоди-
периодическое движение стремится к равновесному решению. Координаты хт могут
39*
608 ПЕРИОДИЧЕСКИЕ ОРБИТЫ [Гл. XXX
быть выражены рядами Фурье вида
у ао + 2 (flv cos уИ^+&v sin v\it).
Для случая п = 1 мы уже указывали ряд примеров семейств периоди-
периодических траекторий в окрестности особой точки типа центра: пример 19.10АA)
(рис. 86), пример 19.ЮС (рис. 87), пример 19.НА (рис. 89). В приме-
примере 19.10АA) период каждого из периодических движений точно (а не при-
приближенно) равен 2я/[х0. В примере 19.ЮС период приближенно равен
2я A+-^-а2) и при а—*-0 стремится к 2я.
Доказанная теорема относится к системам, которые либо имеют форму
Гамильтона, либо могут быть приведены к ней. В других случаях семейства
периодических орбит может и не существовать (см. пример 19.10АB), при-
пример 19.10АC) или пример 19.10В).
Пример 30.4. Простой иллюстрацией для п = 2 может служить
случай, когда функция Гамильтона имеет вид B1.16.11):
Н = j п («й +- pj) - n (q\ + pi) +1 a {q\q2 -Чгр\- 2qlPlp2), C0.4.14)
где и>0 и а>0. Уравнениями движения являются
ql = npi — a{q2pi-\-qip2), pt= — nqi — a(q1q2 — pip2), )
. . ! } C0.4.15)
q2 = — 2npz — aqipu рг = 2nq2 —^a{q\ — p\). j
Начало координат представляет собой особую точку типа центра и, как
было показано, является положением неустойчивого равновесия. Собствен-
Собственные значения равны
1Х = 2m, l2 = in, —lu —l2, C0.4.16)
и необходимые условия, как видим, выполняются: отношение X2/Xi = 1/2
не является целым числом. В окрестности начала координат сущест-
существует семейство периодических орбит с периодами, равными приближенно п/п.
Легко непосредственно убедиться в существовании такого семейства.
В самом деле, уравнения движения C0.4.15) удовлетворяются, если qt и pt
тождественно равны нулю, a q2 и р2 удовлетворяют уравнениям
q2 = — 2пр2, 'р2 = 2щ2. C0.4.17)
Таким образом, имеем семейство периодических траекторий, для которых
q2 = a2 cos 2nt — Ъ2 sin 2nt, pz = b2cos2nt-\-a2sia2nt. I
В этом простом случае период каждого из движений точно (а не прибли-
приближенно) равен я/га, кроме того, траектории существуют для сколь угодно
больших значений q2 и р2, а не только вблизи начала О.
Если же вместо hi взять Х2 в качестве фундаментального собственного
значения, то положение полностью изменится. Изложенная теория в этом
случае неприменима, поскольку Ki/X2 = 2; поэтому нет оснований ожидать
наличия периодических решений с периодами, близкими к 2я/га. Действи-
Действительно, легко видеть, что таких решений не существует: не может быть
периодического решения, если в начальный момент (а стало быть, и в тече-
течение всего времени) не выполняются условия qt = р^ = 0.
§ 30.5] СХОДИМОСТЬ 609
Полагая 0 = q\ -\- p\, ф = q\ + р\, находим
0 = а2 D0Ф + 02). C0.4.19)
В справедливости этого равенства легко убедиться непосредственно из диф-
дифференциальных уравнений для д4, plt q^, р%. Отсюда следует, что 0 >> 0
в течение всего движения, так как если бы в какой-нибудь момент оказа-
оказалось, что 0 = 0, то оно оставалось бы нулем все время. Итак, 0>О, и движе-
движение не может быть периодическим.
§ 30.5. Сходимость. В этом параграфе мы докажем сходимость рядов
функций yh (ft = 1, 2, . . ., т), и, v по степеням ?, ц для достаточно малых
значений | | |, | т| |. Рассуждения будем вести для случая гамильтоновой
системы, когда и + v = 0. Воспользуемся обозначениями § 30.2 (A-i = — А.2);
пусть d\s — коэффициент при |rr)s в разложении функции g^, полученном
путем замены z/i, у2, ¦ ¦ ¦, уп соответствующими рядами по степеням ?, г).
Сравнение коэффициентов при |rTf в формулах C0.2.18) — C0.2.20) при-
приводит к следующим соотношениям:
[(г —в)*, —А*]а? + (г —sJ«voiLv.s-v = <&, k = l,2,...,m. C0.5.1)
Суммирование по v здесь производится от v = 1 до v = min (r, s). Случаи
ft = 1, г — s = l и ft = 2, s — г = 1 являются аномальными. В первом
из них первый член в левой части C0.5.1) заменяется на us, а во втором
случае он заменяется на vT = — иТ; сравнивая в C0.2.18) коэффициенты
при ?г+1'п'', а в C0.2.19) коэффициенты при |гт]г+1, получаем
u, = #+i,r=-d?>r+1. C0.5,2)
За исключением этих двух случаев, коэффициент при ars в C0.5.1)
никогда не обращается в нуль, и существует положительная постоянная с±,
не зависящая от ft, r, s и такая, что
:ct. C0.5.3)
Из C0.5.1) тогда получаем
I «rs |-^С1 j C?rs | + C± 2 | Mv^r-v, s-v|- C0.5.4)
Далее имеем
\ur\ = \dl+itr\ = \drtr+i\- C0.5.5)
Обозначим pHflL
через Zh. Если этот ряд сходится, то сходится и ряд для yh. Аналогичным
образом, обозначим ряд
2 I «г IS Y
через U, а ряд
через <?й. Ряды Zh, U, Gh получаются из zk, и — Хь gh заменой коэффициен-
коэффициентов в степенных рядах их абсолютными значениями. Наконец, пусть Y.h
обозначает ряд, полученный из ряда для yh заменой коэффициентов их
абсолютными величинами. Умножая C0.5.4), C0.5.5) на ?rrjs и суммируя
610 ПЕРИОДИЧЕСКИЕ ОРБИТЫ [Гл. XXX
по к, г, s, получаем
(I + -ц) U + Z < с, (G + UZ), C0.5.6)
где
G = d + G2 + . . . + Gm, Z = Z, + Z2+ . . . +Zm. C0.5.7)
Условие C0.5.6) является основным для дальнейших рассуждений.
Символ -< обозначает, что ряд в правой части является мажорирующим
для ряда, стоящего слева. Символ мажоранты относится только к коэф-
коэффициентам в формальном разложении в степенной ряд; применение этого
символа не требует, чтобы ряды сходились.
Построим теперь мажоранту для ряда G. Функции Хг (хи х2, . . ., хт)
предполагаются регулярными в окрестности точки х = 0, и, следовательно,
т функций gh (x/i, у2, ¦ . ., ут) также регулярны в окрестности точки у = 0.
То же самое относится к функциям G% (z/i, y2, • • ., j/m), получающимся
из функций gh (yi, z/a, . . ., ут) заменой коэффициентов в их разложениях
по степеням yt, у2, . . ., ут соответствующими абсолютными значениями.
Ряды для функций G% начинаются с квадратичных членов; отсюда следует,
что существует положительная постоянная а такая, что
2 G*k (yi. Y2,...,Ym)<^ (aW)n = -^щг, C0.5.8)
ft=l n=2
где
W = Y1 + Y2+ ... +Ym = g + n+Z. C0.5.9)
Отметим, что выражение в правой части равенства C0.5.8) пока рас-
рассматривается нами только, как сокращенное обозначение геометрического
ряда, без какого-либо предположения о его сходимости. (Если ряд Z оказы-
оказывается сходящимся в окрестности точки (?, т}) = @, 0), то геометрический
ряд также сходится в некоторой, быть может меньшей, окрестности этой
точки.) Символ ¦«< в соотношении C0.5.8) относится (исключительно) к крат-
кратному степенному ряду по Уь Y2, . . ., Ym, но, так как все коэффициенты
этого ряда положительны, мы можем понимать этот символ в обычном смыс-
смысле, когда обе части представлены в виде рядов по степеням |, ц. Кроме того,
из определения d^s следует, что ряды Gk и G% по степеням |, ц связаны
условием
Gh<G*h(Y1, Y2,...,Ym). C0.5.10)
Из C0.5.6) —C0.5.10) получаем
( ^ttlXZ ) C0-5Л1>
Остается установить сходимость рядов U и Z в окрестности точки
(I, tj) = @, 0). Вследствие неотрицательности всех коэффициентов достаточ-
достаточно доказать сходимость рядов лишь для частного случая | = т|. Если поло-
положить | = т|, то левая часть C0.5.11) примет вид 2\V + Z; обозначим
2\U + Z = ?Р. C0.5.12)
Функция Р задается степенным рядом без постоянного члена. При | = г\
будем иметь
21 + Z < 2| A + Р) C0.5.13)
и
UZ<±IP*<41P\ C0.5.14)
§ 30.6] ТРИ ТОЧКИ ЛАГРАНЖА 611
Из C0.5.11) находим
Положив
1 + P+IP = Q, C0.5.16)
получаем мажорирующие соотношения
1 + IP<Q, IP<Q\ l{i-YPf<l + Qi. C0.5.17)
Далее имеем
где а — наибольшее из двух положительных чисел с2 и с3. Для наших целей
достаточно доказать сходимость ряда Q для малых положительных значе-
значениях |.
Рассмотрим уравнение
в котором R есть степенной ряд по ?. Положим
^=2 «гГ, Д=2РгГ- C0.5.20)
г=1 г=1
Коэффициенты рг легко определяются шаг за шагом путем сравнения
коэффициентов при одинаковых степенях | в соотношении 2Л = а| + осД2;
В самом деле,
P1 = i-a, p2 = 4«3, рз = ^а5, ... C0.5.21)
Кроме того, шаг за шагом можно доказать, что аг ^ рг, так что ряд R
мажорирует ряд Q и сходимость первого из этих рядов влечет за собой
сходимость второго. Если же сходится ряд Q, то сходится ряд Р, а отсюда
в свою очередь следует сходимость рядов Z и U.
Равенство C0.5.19) можно переписать в виде
A — аиJ = 1 - а% C0.5.22)
откуда
2aR<(l-aR)-*-l= ^ C0.5.23)
и, следовательно, ряд R сходится, если | ? | < I/a2. Теорема, таким обра-
образом, доказана.
§ 30.6. Три точки Лагранжа. Применим теорему § 30.2 к исследованию
равновесного решения, в котором три частицы располагаются в вершинах
равностороннего треугольника и находятся в покое. Уравнения движения
возьмем в преобразованной форме § 29.8. Собственные значения линеари-
линеаризованной задачи о возмущенном движении найдем из уравнения
(I2 + оJ) (к* + <о2^2 + Лео*) = 0, C0.6.1)
в котором
к m2m3 + 'n3ml+mim2 .„„ „ „
" \ •. • )
612 ПЕРИОДИЧЕСКИЕ ОРБИТЫ [Гл. XXX
Собственными значениями будут
Xi = ia>, ^2» ^з> —^i) —^2> —^з- C0.6.3)
Ни одно из отношений ^г/^ь ^3/?ч БРИ этом не является целым числом. Дейст-
Действительно, в случае неустойчивого равновесия (к > V4) числа %2 и Х3 не явля-
являются чисто мнимыми, а в случае устойчивого равновесия (к < 1/4), когда
К2 и ^з — чисто мнимые, равные т2 и ш3, имеем
2<^<со2 C0.6.4)
и k2/hi и X3/Xi лежат в интервале от 0 до 1. Таким образом, условия теоре-
теоремы § 30.2 выполнены, и в окрестности равновесного решения существует
семейство периодических движений (относительно вращающихся осей)
с периодами, близкими к 2я/со.
Эти периодические движения нам уже известны, они были предметом
нашего рассмотрения в § 29.4. Речь идет о решениях типа треугольника
Лагранжа, форма которого остается неизменной. Частицы при этом движут-
движутся в пространстве с периодом 2я/со по эллипсам, близким к окружностям;
движение их относительно вращающихся осей в окрестности равновесного
положения приближенно является эллиптическим. В этом случае периоды
точно (а не приближенно) равны 2я/со.
Если выполнено условие устойчивости к < 1/4, то в окрестности равно-
равновесного решения существует еще одно семейство периодических движений
с периодами, близкими к 2п1щ. При этом ни одна из величин со/ге3, пг1п3
не является целым числом, так как
К-5-<2, 0<-^-<1. C0.6.5)
Следовательно, условия теоремы § 30.2 выполняются. Существование
этих периодических решений является новым результатом: он не следует
из рассуждений § 29.4.
Наконец, если к < V4, то вблизи равновесного решения имеется третье
семейство периодических движений, периоды которых близки к 2п/п2, при
этом ни (л1п2, ни п3/п2 не должно быть целым числом. Отношение со/и2 равно
целому числу v > 1, если
1 = = ve. C0.6.6)
Отсюда
к= v2~1 . C0.6.7)
Отношение п3/п2 является целым числом v > 1, если
= = v2. C0.6.8)
Отсюда
Таким образом, третье семейство периодических движений существует
в окрестности равновесного решения тогда, когда к не является рациональ-
рациональным числом вида C0.6.7) или C0.6.9).
§ 30.7] СИСТЕМЫ, СОДЕРЖАЩИЕ ПАРАМЕТР 613
§ 30.7. Системы, содержащие параметр. Рассмотрим системы, для кото-
которых функции Хт в уравнениях движения содержат параметр ц. Уравнения
записываем в форме
хт = Хт (хи Х2, . . ., хт; (х) = ХТ (х; jx). C0.7.1)
Функции Хг предполагаются регулярными в некоторой области изменения
(комплексных) переменных Xi, х2, • • ., хт, [х. Пуанкаре поставил следую-
следующий вопрос: «Предположим, что для некоторого значения параметра ц^
периодическое решение существует. Можно ли тогда утверждать, что периоди-
периодические решения существуют для значений ц, достаточно близких к р.0?>>-
Без потери общности можно считать значение \i0 равным нулю, тогда задача
Пуанкаре принимает следующую формулировку: «Предположим, что при
(х = 0 существует периодическое решение. Существуют ли тогда периоди-
периодические решения при достаточно малых значениях [х?»
Рассмотрим в качестве иллюстрации ограниченную задачу трех тел-
(гл. XXVIII). Предположим, что при фиксированных значениях парамет-
параметров а + Р и I мы в состоянии изменять величину отношения р7а так, чтобы
угловая скорость со при этом имела постоянное значение у (а + $)/Р (см.
B8.2.1)). Положим (о, = р/(а + f>). Значение [i = 0 соответствует р = 0,
так что при [х = 0 задача о движении планетоида становится эквивалентной
задаче о движении частицы в поле ньютоновского притяжения к неподвижно-
неподвижному центру. В этом случае периодическое движение, разумеется, существует
(во вращающейся системе координат). Существуют, например, эллиптиче-
эллиптические орбиты (относительно фиксированных осей) с периодом обращения
2я/со, и, что особенно важно для наших целей, существуют равномерные
круговые движения около центра А (который при [i = 0 совпадает с G).
Спрашивается, существуют ли периодические движения для достаточно
малых положительных значений |Л?
Общее решение уравнений движения возьмем в виде (см. B1.1.4))
xr = q>r(x°v a», ...,x°m; ji; t) = <pr(x°; ц; t), C0.7.2)
где хй есть вектор х при t = 0. Будем пользоваться обозначениями § 21.5,
в частности, производную d<pr!dx°s обозначим через cprs. Начнем с известного-
периодического решения (для [х = 0); оно не является равновесным реше-
решением: если [I = 0, то решение, начинающееся из точки А, х° =а, является
периодическим с периодом а. Тогда для любого значения t будем иметь
Х(а; 0)^=0, C0.7.3)
Фг(а; 0; 0) = аР1 г = 1,2 ю, C0.7.4)
Фг(а; 0; t + a) = q>r(a; 0; *), г = 1,2, ...,т. C0.7.5)
Последнее из этих соотношений можно упростить. В самом деле, ска-
сказать, что равенство C0.7.5) выполняется для всех значений t,— это то же-
самое, что сказать, что оно выполняется для одного какого-нибудь значе-
значения t. Это является следствием единственности решения. Поэтому уравне-
уравнение C0.7.5) можно заменить более простым:
фг (а; 0, а) = аг| г = 1, 2, . . ., т, C0.7.6)
Пуанкаре первый поставил вопрос: «Существуют ли периодические
решения с тем же периодом о, если в уравнениях движения \х имеет не нуле-
нулевое значение, а малое значение, отличное от нуля?» Такие орбиты сущест-
существуют, если при заданном [х =^=0 можно найти такие рь p2i • • •» Pmi что
будут выполняться га следующих уравнений:
Фг (Р; (i; 0) = р„ г = 1, 2, . . ., т. C0.7.7)
614 ПЕРИОДИЧЕСКИЕ ОРБИТЫ Гл. XXX
Если [1—0, то, как мы знаем, уравнения C0.7.7) имеют решения рг = ат,
и для достаточно малых ц мы можем найти решения, если определитель
матрицы
(Фг5 (Р; ц; *) - 6rs) C0.7.8)
отличен от нуля для р =а, [х = 0, Г=± а.' Обозначим эту матрицу через F:
Us = <Prs («; 0, а) - 6rs. C0.7.9)
Таким образом, если
\1Г\ФО, C0.7.10)
то уравнения C0.7.7) можно разрешить относительно р4, р2, • • •> Рт-
Разности рг — аг являются функциями от ^, и при jut = 0 они равны нулю,
так что каждую из них можно представить в виде ряда по степеням уь без
постоянного члена.
Эти рассуждения, однако, бесполезны, поскольку на самом деле | F \ — 0.
Полагая в равенстве B1.5.7) t = а, получаем
FX(a; 0) = 0. C0.7.11)
В правой части этого равенства стоит нулевой вектор-столбец. Так как
X (а; 0) не равно нулю, то
\F\ = 0. C0.7.12)
Таким образом, изложенный метод не позволяет сделать вывода о суще-
существовании периодических решений с периодом а для значений ц, близких
к [х = 0.
Причину того, что | F | = 0, легко усмотреть из § 21.5. Она состоит,
в сущности, в том, что мы можем изменять точку А, в которой начинается
орбита, от а до любой точки на орбите. Это показывает, что трудность,
связанную с обращением в нуль | F |, можно обойти, если ограничить пере-
перемещение точки А плоскостью, проходящей через а и нормальной к орбите,
или вообще любой поверхностью, которая не касается орбиты в точке а.
Условие C0.7.3) показывает, что не все составляющие Хт (а; 0) равны нулю,
и, не уменьшая общности, можно считать, что
Xm(a;0) =jfc0. C0.7.13)
(При желании можно пойти еще дальше. Мы можем выбрать местную прямо-
прямоугольную систему координат, направив ось хт вдоль касательной к орбите
в точке а, т. е. вдоль вектора X в этой точке. Тогда все составляющие век-
вектора X, за исключением Хт, будут равны нулю. Практически, однако, вряд
ли стоит поступать таким образом.)
Поставим теперь вопрос о существовании при ц =^=0 периодической
орбиты с начальной точкой Р такой, что рт = ат, но рг =f=. ar для всех зна-
значений г, меньших т. Мы по-прежнему должны удовлетворить т условиям
Фг (Р; р; т) = рг C0.7.14)
и условию рт = ат. Это означает, что период изменяет свое значение с а
на т. Всего имеем т неизвестных: Pi, Рг, • . ., Pm-i, т. В случае [х = 0,
как мы знаем, существует решение аь а2, . . ., ат-\, о. Составим матри-
матрицу G-, т — 1 первых столбцов которой те же, что у матрицы F, а последним
столбцом служит вектор X (а; 0). Если- определитель | G | этой матрицы
не равен нулю, то можно найти решения (при ц = 0 все разности Pi — al7
р2 — а2, . . ., pm-i — am_i, r — о обращаются в нуль).
Можно указать примеры, в которых выполняется условие | G- | ^=0
и для достаточно малых [X ф0 существуют периодические решения с пе-
периодом, близким к а. Однако в случаях, представляющих практический
интерес, обычно | (? | = 0, и изложенный метод опять-таки не дает ответа
на вопрос о существовании периодических орбит при [х, отличном от нуля.
§ 30.7] СИСТЕМЫ, СОДЕРЖАЩИЕ ПАРАМЕТР 615
Обращение в нуль | <2 | происходит тогда, когда существует интеграл
Якоби или вообще какой-нибудь однозначный пространственный интеграл.
Пусть / (xi, х2, . . ., хт; [х) есть такой интеграл. Частную производную
dfldxT обозначим через /г. Предположим, что х — а не является стационар-
стационарной точкой функции / (х; 0), т. е. не все производные /г (а; 0) равны нулю.
Тогда в силу B1.1.9) и C0.7.13) т — 1 первых производных /г (а; 0) не могут
все равняться нулю, и, расположив переменные в определенном порядке,
мы всегда можем считать, что
/m-i(o;0) ^=0. C0.7.15)
Функция / сохраняет постоянное значение на орбите, так что для
Любых Р, [X, t
/{Ф(Р; и.; 0, [*} = /(Р; |х). C0.7.16)
Дифференцируя по ps, находим
2 U (х; (х) Фг8 (Р; [х; t) = U (P; (x), s = 1, 2, .... m. C0.7.17)
r=l
Положив в этом равенстве Р = а, u. = 0, t = a, перепишем его в следующей
форме:
m
2 fr (а; 0){Ф„(а; 0; о)-6Г8} = 0, C0.7.18)
г—1
или
J>^=0, C0.7.19)
где D обозначает матрицу-строку, г-ж элемент которой равен /г(а; 0).
С другой стороны, из уравнения B1.1.9) имеем
JDX{a; 0) = 0 C0.7.20)
и из C0.7.19) и C0.7.20) находим
0. C0.7.21)
Отсюда в силу того, что D =^=0, получаем, что \ G- | = 0, что и требовалось
доказать.
До сих пор нам не удавалось доказать существования периодических
орбит для [х ф0, но, несколько изменив подход к решению этого вопроса,
мы можем провести это доказательство. Рассмотрим сначала вопрос о суще-
существовании периодических решений с периодом о. Как и ранее, положим
Рт = «т и разрешим т — 1 уравнений C0.7.7), где г фт — 1, относи-
относительно т — 1 переменных р1? р2, • • ., Pm-i- В результате мы их выразим
как функции от [х. Разности pi — «i, Рг — а2, ¦ ¦ -, Pm-i — am-i> как
обычно, представим в виде рядов по степеням [х без постоянных членов.
Для того чтобы такое решение было возможно, необходимо, чтобы \Н \ ф0,
где матрица Н получается из JT путем отбрасывания (т — 1)-й строки и иг-го
столбца. Если удовлетворяются все уравнения C0.7.7), кроме одного, то это
последнее уравнение будет удовлетворяться автоматически благодаря инте-
интегралу Якоби. Это утверждение геометрически совершенно очевидно. Чтобы
получить формальное доказательство, обозначим фг (Р; [х; о) через рг. Тогда
будем иметь рг = рг для всех г, кроме г = т — 1. Поскольку / (х; \i) есть
интеграл,
0 = / (Р; (х) - / (Р; |i) = (pm_i - pm_i) /m_i (I; ц), C0.7.22)
616 ПЕРИОДИЧЕСКИЕ ОРБИТЫ [Гл. XXX
где рг = рг = рг для всех г, кроме г = т — 1, причем pm_t лежит между
Pm-i и рт. Но /m_t (а; 0) =^=0, так что для достаточно малых (А имеем
/m-i (Р; ц) Ф®- Отсюда следует, что pm_t = pm_i, и оставшееся уравне-
уравнение C0.7.7) также удовлетворяется. Таким образом, если | Н \ фО, то для
ц фО существуют периодические орбиты с периодом а.
Наконец, если [х фО, то существуют периодические решения с задан-
заданным периодом т, где т — а достаточно мало, но не равно нулю, и такие,
для которых постоянное значение интеграла / (х; ц) то же, что и для
первоначальной периодической орбиты. Присоединим к т — 1 уравнениям
C0.7.14), где гфт — 1, уравнение
/ (р; ц) = / (а; 0). C0.7.23)
Разрешив эти т уравнений относительно т переменных р1( р2, • • •> Pm-ь тг
найдем, что разности pt — аь р2 — а2, ¦ ¦ ., f>m-i — ат_15 т — о представ-
представляются рядами по степеням jo, без постоянных членов. Решение возможно
при условии, если определитель \ К \ ф0, причем матрица К. получается
из матрицы
Х(а; 0)
о
при отбрасывании {т — 1)-й строки и пг-го столбца. Но (т — 1)-я строка
линейным образом зависит от остальных строк (см. C0.7.19) и C0.7.20)),
а т-т столбец линейным образом зависит от остальных столбцов (см. C0.7.11")
и C0.7.20)). Поэтому наше условие заключается в том, чтобы матрица C0.7.24)
имела ранг т. Если это условие выполнено, то при \i ф0 существуют перио-
периодические орбиты с периодом t фа.
На первый взгляд может показаться, что проведенное исследование
малопрдгодно для практических целей, так как для составления матрицы F
требуется знать решение C0.7.2) уравнений движения. Но это, однако,
не совсем так. Фактически нам требуется знать лишь значения фгв при р = а,
[х = 0, t = с, для чего достаточно знать решение уравнений линейного
приближения (уравнений в вариациях) для случая \i = 0. Последнее же
решение всегда может быть построено (гл. XXIII). Таким образом, теория
Пуанкаре дает нам практически удобный метод доказательства существо-
существования периодических решений.
§ 30.8. Приложение к ограниченной задаче трех тел. Предположим, что
величины а + Р и I фиксированы, следовательно, фиксировано и значение
ю = -у (а + Р)/К Выберем \х, равным р/(а + Р). Случай [х = 0 соответст-
соответствует движению в поле ньютоновского притяжения к неподвижному
центру. Для этого случая уравнения движения в обозначениях § 28.2 име-
имеют вид
X — ZCOZ/ = i , ,
. f C0.8.1)
где
W — — m2 f r2 -I- v2) -A- cciz — HO 8 9\
5 30.8] ПРИЛОЖЕНИЕ К ОГРАНИЧЕННОЙ ЗАДАЧЕ ТРЕХ ТЕЛ 617
Обозначив производные х и у соответственно через и и v, напишем
эквивалентную систему уравнений первого порядка:
х = и, )
х C0.8.3)
т6
Равномерное вращение по окружности радиуса А; описывается уравне-
уравнениями
х = ks, у = — кс, и — ркс, v = pks, C0.8.4)
где
с = cos pt, s — sin pt. C0.8.5)
Это движение возможно, если выполняется условие
к2 (р + соJ = Z3со2. C0.8.6)
Условие C0.8.6) очевидно из элементарных соображений, в справедли-
справедливости его можно убедиться также непосредственной подстановкой в уравне-
уравнения движения. Период движения относительно вращающихся осей равен
о = 2п/\р |.
Равновесное решение р = 0 следует исключить, так же как и случаи
р — — со и р = — 2ю. Случай р = — со требует бесконечно большого
значения к, а в случае р = — 2со имеем к = I, и если ц =^=0, то точка В
•с координатами (A — ^) I, 0) является особой и при [х -> 0 стремится к точ-
точке на окружности г = I.
Обозначим х, у, и, v через xit x2, х3, хк и составим уравнения в вариа-
вариациях. С этой целью положим
xi = ks + z/i, x2 = — кс + г/г. хг = ркс + у3, хк = pks + г/4- C0.8.7)
Так как
г2 = к2 + 2к (yiS - у2с) + (у\ + yl), C0.8.8)
то
4(-З^М+-...). C0.8.9)
Теперь нетрудно написать уравнения в вариациях:
1 C0.8.10)
соJ s(yts I
J/4 = — (Р2 + 2рсо) г/2 — 2сог/3 — 3 (р + соJ с (yts — z/2c). j
Введем новые переменные z:
Zj = i/1s —i/2c, Z2 = j/1c+y2s. z3=i/3S — i/4c, • z4=i/3C+z/4s. C0.8.11)
В новых переменных уравнения будут иметь вид
z, = pz2 + z3, z3 =- Bр2 + 4рсо + Зсо2) z, + (р + }
2t = — jDZj 4 Z4, Z4=-(p+ 2CO) (pz2 + Z3), J
618
ПЕРИОДИЧЕСКИЕ ОРБИТЫ
[Гл. XXX
z4 = (p + 3(o) A + (p + 2o>) (QC + <pS).
Здесь
С = cos (p + <o) ?, 5 = sin (p + (o) ?,
а постоянные А, В, 0, ф определяются равенствами
t = (p + 2u))v2 —•
- a,) e = - (p + 3(o) ¦
т. е. будут линейными уравнениями с постоянными коэффициентами. Эта
система имеет следующее решение:
C0.8.13)
C0.8.14)
C0.8.15)
где уг есть начальное значение уг. Матрица (p + (o)i имеет вид
-2рA-С)
-pS
-р (Р+2С0) S
-Р(Р-со) A-С)
О
3 (р+со) (р+2со)ст-
-2 (р+Зсо) S
(Р+Зш) A-С)
(Р+2и) (р+Зш) A-С)
Зр (р+со) (р+2ш) ст—
- (р-ш) (р+Зсо) S
-рй (р+со) (р+2ш)
-3 (р+а) O+4S
2 A-С)
-2 A-С) S
-2 (р+2со) A-С) (р+2ш) S
-Зр (р+со) 0+ (р-а) A-С)
+2 (р-ш) S
pk (р+со) О
pk (р+со)
О
О
p2ft (р+СО)
О
где, в отличие от предыдущего,
(О
С — cos (р + о)) о = cos 2зх — ,
(О
C0.8.16)
C0.8.17)
Теперь нетрудно проверить результаты общей теории. Матрица F полу-
получается из матрицы L путем отбрасывания пятой строки и пятого столбца.
Как и следовало ожидать, третья строка матрицы F не независима от осталь-
остальных строк, а четвертый столбец не независим от остальных столбцов. Опре-
Определитель матрицы Н размером 3x3, получающейся при отбрасывании
третьей строки и четвертого столбца матрицы JF, равен
— 24я sin2
соя
Таким образом, если
C0.8.18)
C0.8.19)
где v — целое положительное число, то при достаточно малых ц существуют
периодические решения с периодом о. Значение р = —ю было нами исклю-
исключено, так же как и значения р = 0 и р = — 2 оз.
Далее, матрица G-, получающаяся из L путем отбрасывания пятой стро-
строки и четвертого столбца, очевидно, является особой, как это и следует
из общей теории. Если в матрице L отбросить третью строку и четвертый
столбец, то получится матрица К; ее определитель имеет значение
соя
C0.8.20)
§30.10] ТЕОРЕМА ПУАНКАРЕ О КОЛЬЦЕ 619
Как и ранее, параметр р не должен принимать значений, указанных в фор-
формуле C0.8.19), тогда при достаточно малом [х будут существовать периоди-
периодические движения с периодом т Ф а.
В обоих рассмотренных случаях речь идет о решениях, периодических
относительно вращающихся осей.
§ 30.9. Метод неподвижной точки. В § 30.8 мы доказали, что при опре-
определенных условиях для достаточно малых значений параметра \i существуют
периодические орбиты. Из этого доказательства не следует, вообще говоря,,
что такие орбиты существуют для больших зна-
значений [х. Пуанкаре исследовал этот вопрос с
помощью теории преобразований, имеющих не-
неподвижную точку.
Нетрудно видеть, что теория таких пре-
преобразований имеет непосредственное отноше-
отношение к вопросу о существовании периодических
решений. Рассмотрим обычные уравнения
хт = Хг (х), г = 1, 2, . . ., т, C0.9.1)
правые части которых суть функции класса С^
в области D пространства (xi, х2, . . ., хт).
Возьмем плоскость со, определяемую уравнением
%т = <ят; эта плоскость параллельна плоскости рИс. 123.
хт = 0. Обозначим через А множество точек со,
для которых Хт > 0, а через р —множество точек А, обладающих тем свой-
свойством, что траектории с началом в этих точках целиком расположены
в области D. Обозначим, далее, через Р точку множества р и рассмотрим
движение изображающей точки по траектории с началом в Р.
Движение этой точки происходит в области хт > 0 (поскольку в точ-
точке Р Хт > 0). В дальнейшем, возможно, точка перейдет из области хт > О
в область хт < 0 (при этом ее траектория пересечет плоскость со в точке,
не принадлежащей А), а затем вновь попадет в область хт > 0, причем
на этот раз пересечет плоскость м в точке Р' множества А (см. рис. 123,
иллюстрирующий случай т = 2). Преобразование точки Р в точку Рг
(обозначим его Р' = ТР) является топологическим отображением области р
в область р' множества А.
Если отображение Р' = ТР имеет неподвижную точку Ро, для которой
ТР0 = Ро, C0.9.2)
то орбита, проходящая через Ро, является периодической. Или, в более
общем виде, если существует точка Ро такая, что для некоторого целого
положительного числа п
ТпР0 = Ро, C0.9.3)
то проходящая через Ро орбита является периодической.
Если div X = 0 (что для уравнений Гамильтона всегда выполняется),
то интеграл
Xm dxt dx2... dxm_u CQ.9.4)
взятый по области р, при преобразовании Т остается инвариантным. Дока-
Доказательство этого утверждения было дано ранее (см. § 22.17, формула B2.17.1)).
§ 30.10. Теорема Пуанкаре о кольце. Существует одна теорема о непод-
неподвижной точке, которая особенно тесно связана с именем Пуанкаре. Эту
€20 ПЕРИОДИЧЕСКИЕ ОРБИТЫ [Гл. XXX
теорему иногда называют последней теоремой Пуанкаре или теоремой Пуан-
Пуанкаре о кольце. Изучая задачу трех тел, Пуанкаре пришел к мысли о суще-
существовании бесконечного множества периодических орбит (во вращающейся
¦системе осей) не только для малых, но и для каких угодно значений \л =
= р/(а + Р)- Пуанкаре не дал строгого доказательства этой теоремы, хотя
у него не было сомнений в ее справедливости; доказательство было дано
Дж. Д. Биркгофом уже после смерти Пуанкаре. Эта теорема состоит в сле-
следующем.
Рассмотрим кольцевую область, ограниченную окружностями г = а
я г — Ь, где 0 < а < Ь. Определим топологическое отображение замкнутой
области а ^ г ^ Ъ на себя с помощью уравнений
г' = Ф (г, 9), 0' = г|> (г, 0). C0.10.1)
Это отображение обладает следующими свойствами:
1) оно сохраняет меру;
2) каждая из граничных окружностей при отображении переходит
в себя, т. е. ф (а, 8) = а и ф (Ь, 8) = Ъ;
3) точки окружности г = а при отображении передвигаются против
хода часовой стрелки, а точки окружности г = Ъ — по ходу часовой стрел-
стрелки, что означает, что -ф (а, 8) > 9, а ф F, 8) < 8.
Теорема утверждает, что при выполнении этих условий отображение
имеет две неподвижные точки.
На первый взгляд возникает трудность в связи с тем, что функция
¦ф (г, 9) определена сначала лишь по mod 2jx. Однако фактически это обстоя-
обстоятельство не является существенным, так как если функция г|з (г, 6) задана
в одной точке кольца, то в силу непрерывности ее значения становятся
известными везде.
Теорема остается верной и тогда, когда условие о сохранении меры
заменяется более слабым требованием о существовании инвариантного
интеграла с положительной подынтегральной функцией. Условие о сохра-
сохранении меры можно заменить еще более слабым условием, что никакая под-
подобласть кольцевой области не преобразуется в часть себя самой.
Интуитивные соображения, которые навели Пуанкаре на мысль о связи
теоремы о кольце с вопросом о существовании периодических орбит, не очень
убедительны и во многих отношениях спорны, но, несмотря на это, в следую-
следующем параграфе мы приведем аргументацию Пуанкаре ввиду ее особой важ-
важности для понимания вопроса и значительного исторического интереса.
§ 30.11. Периодические орбиты и теорема о кольце*). Рассмотрим
динамическую систему с двумя степенями свободы. Положение системы
будем описывать с помощью лагранжевых координат х, у. Движению систе-
системы отвечает перемещение изображающей точки (х, у) в плоскости z = 0.
Предположим, что система допускает интеграл вида
¦^&+ij2)+W = h, C0.11.1)
где W — заданная функция от (х, у).
При этих условиях движение системы происходит в области р, опреде-
определяемой неравенством W < h. Будем рассматривать такие значения h, для
которых область р располагается внутри простой замкнутой выпуклой
кривой а.
*) При изложении этого параграфа автор основывался на статье Пуанкаре, вышед-
вышедшей в 1912 г., незадолго до его смерти: Sur un theoreme de geometrie, Rend. Circ. mat.
Palermo, 33, 1912, стр. 375—407. Эта работа весьма примечательна. Пуанкаре был убеж-
убежден в справедливости теоремы о кольце, он доказал ее для ряда частных случаев, но
общего доказательства не получил, предоставив это сделать другим математикам.
§ 30.11] ПЕРИОДИЧЕСКИЕ ОРБИТЫ И ТЕОРЕМА О КОЛЬЦЕ 621
Основной интерес для нас представляет ограниченная задача трех тел,
когда рассматривается движение планетоида относительно вращающихся
осей (§ 28.2). Для этой задачи существует интеграл требуемого типа, а имен-
именно интеграл B8.2.6), и W = —yll. Если —h>yU3, то область W < h
состоит частью из одной или двух внутренних областей, ограниченных
снаружи замкнутыми выпуклыми кривыми, а частью из внешней области,
ограниченной изнутри замкнутой выпуклой кривой (рис. 116а, Ь). В каж-
каждом из этих случаев внутреннюю область можно взять в качестве области р.
Скорость частицы в точках области р по величине определяется форму-
формулой C0.11.1), что же касается направления скорости, то оно произвольно.
Обозначим через г|з угол, образуемый вектором скорости с осью Ох, и будем
считать, что 0 ^г|з < 2я. Тем самым каждой точке области Р мы поставим
в соответствие бесконечное множество элементов, понимая под этим терми-
термином совокупность величины вектора скорости и наклона этого вектора
к оси Ох. В каждой точке граничной кривой а скорость равна нулю, так
что точке этой кривой фактически соответствует один-единственный элемент.
Это замечание мы используем ниже при геометрической интерпретации.
Прежде всего совершим топологическое отображение области р на
область р', представляющую собой внутренность круга, границей которого
является окружность а' — образ кривой а. Рассмотрим движение изобра-
изображающей точки в преобразованной области р' (см. § 21.2). Пусть М — точка
области Р'; обозначим через М' ее образ, полученный в результате инверсии
относительно окружности а'. В плоскости, перпендикулярной к плоско-
плоскости Р', построим окружность Г на отрезке ММ' как на диаметре. Всякому
направлению траектории, проходящей через точку М (т. е. всякому эле-
элементу в точке М), поставим в соответствие определенную точку окружно-
окружности Г. При этом, например, значение г|/ = 0 будет соответствовать точке М',
значение г|/ = я — точке М, а значения 0 <г|/ < л отвечают точкам окруж-
окружности Г, для которых z > 0. (Уравнением плоскости Р' будет z = 0; через г|/
обозначен угол наклона траектории в преобразованном движении к оси Ох.)
Если точка М ? р', то ей соответствует бесконечно много точек; если же
М?а', то одна точка. Каждому элементу соответствует одна точка прост-
пространства, и, обратно, каждой точке пространства соответствует один-един-
один-единственный элемент.
Траекториям здесь поставлены в соответствие кривые С, образующие
семейство к пространственных кривых; через каждую точку пространства
проходит одна и только одна такая кривая С. Заметим, что при изменении
направления движения на обратное картина траекторий изменяется. Замк-
Замкнутым кривым С соответствуют периодические орбиты.
Предположим, что имеется периодическая траектория Go, устойчивая
по первому приближению (§ 23.1). Выберем единицу времени такой, чтобы
период был равен 2я. Обозначим через Со замкнутую кривую семейства к,
соответствующую траектории Go, и построим поверхность S, натянутую
на кривую Со; участок этой поверхности, ограниченный кривой Со, обозна-
обозначим через А. Предположим, что область А односвязная и является областью
без контакта, т. е. ни одна кривая С не касается поверхности S в точках А
(сравните с понятием отрезка без контакта в § 20.3).
Возьмем точку Р в области А. Через эту точку проходит только одна
кривая С. Будем двигаться вдоль этой кривой до нового пересечения с по-
поверхностью А в точке Р'\ эту точку назовем последующей точкой по отно-
отношению к Р. Преобразование Т, переводящее точку Р в точку Р', представ-
представляет топологическое отображение области А на себя.
Может показаться, что для некоторого положения Q точки Р преобразо-
преобразование Т будет разрывным. Однако это невозможно. В самом деле, возьмем
последовательность точек Р, Р', Р", Р"', . . ., в которых траектория С
40 Л. А. Папе
622 ПЕРИОДИЧГСКИЕ ОРБИТЫ [Гл. XXX
пересекает область А, и предположим, что при перемещении точки Р из поло-
положения Q точки Р' и Р" сначала совпадают, а затем становятся мнимыми,
так что последующей точкой для Р оказывается точка Р'". Но это невозмож-
невозможно, потому что поверхность А является областью без контакта. По той же
причине между точками Р и Р' не могут появиться две новые точки пере-
пересечения, т. е. последующей точкой для Р не может стать точка Р^ вместо
точки Р'. Кроме того, при перемещении точки Р из положения Q точка Р'
не может пересечь траекторию Со, так как через точку этой кривой, кроме
нее самой, никакой другой траектории не проходит.
Преобразование Т обладает положительным интегральным инвариан-
инвариантом; доказательство этого утверждения аналогично доказательству § 22.17.
Если точка Р совпадает с Р' или с любой из других последующих точек Р",
Р'", . . ., то кривая С оказывается замкнутой, а изображаемая ею траек-
траектория — периодической.
Рассмотрим преобразование Т для точек Р, близких к границе Со обла-
области А. Пусть Ci — кривая класса К, проходящая через точку Р, т. е. кри-
кривая, соответствующая траектории Gt, которая проходит в непосредственной
близости от Gq. Чтобы составить приближенные уравнения кривой d, обра-
обратимся к методам § 23.4. Выберем такую систему координат и, v, w, чтобы
1) положение точки на траектории зависело только от и, v, а направление
элемента траектории — также и от w, 2) уравнение траектории Со имело
вид v = w = 0, а переменная и при полном обходе замкнутой кривой Со
изменялась от 0 до 2я. При движении вдоль кривой Со имеем
* = в+ф(и), C0.11.2)
где ф (и) — периодическая функция с периодом 2я.
Если характеристические показатели устойчивой периодической орби-
орбиты Go равны 0, 0, га, —га, то уравнения кривой С4 можно записать в виде
(см. § 23.5)
psin(T+Ti), -^- = p1sin(T+Ti) + p2cos(T+^), C0.11.3)
где а и и — постоянные интегрирования, причем а мало, а через т обозна-
обозначено at, так что
т = аи -f- смр (и), C0.11.4)
откуда видно, что т все время возрастает вместе с и.
Точки пересечения кривых Gt и GQ получим, положив v = 0. Тогда
будем иметь
т + т) = Nn, C0.11.5)
где N — целое число. Если М± — одна из таких точек, а М2 — следующая
за ней точка пересечения, то точку М% называют кинетическим фокусом
точки Mi. Значения ti и т2 переменной т в точках М\ и Мг кривой Cj связа-
связаны между собой соотношением
Т2 _ Tl = л. C0.11.6)
Поверхность S, на которой расположена область А, определится урав-
уравнением
F (и, v, w) = 0. C0.11.7)
Разложение функции F по степеням v и w не содержит постоянного
члена, поскольку кривая Со (v = w = 0) расположена на поверхно-
поверхности C0.11.7). Поэтому линеаризованное уравнение этой поверхности имеет
вид
.&iv + gzw = 0, C0.11.8)
§30.11] ПЕРИОДИЧЕСКИЕ ОРБИТЫ И ТЕОРЕМА" О_КОЛЬЦЕ 623
где gt и gi — периодические функции от и. Чтобы найти точки пересечения
кривой Ci с поверхностью А, подставим выражения C0.11.3) для v и w
в уравнение C0.11.8). Проделав это, получим
Pi sin (т + ц) + рг cos (т + ц) = 0, C0.11.9)
где pi и рч — периодические функции от и. Уравнение C0.11.9) можно пред-
представить в эквивалентной форме
i? sin (т + К + г\) = 0, C0.11.10)
где А, = arctg/?2/pi- Следовательно, А. является функцией от и, производная
которой есть периодическая функция. Поэтому А, можно представить в виде
ти + г|з (и), где т — целое число, a -xj? (и) — периодическая функция. Точки
пересечения кривой Ci с поверхностью Л определяются уравнением C0.11.10),
и, следовательно, величина т + А, + т) кратна я. Но поскольку область А
ограничена кривой Со и за пределы этой кривой не распространяется,
сумма т + А. + г) кратна четному числу я:
т + Я + т] = 2/ст, C0.11.11).
где А; — целое число. Если Pi и Рг — Две последовательные точки пересе-
пересечения, то имеем
(т2 + Кг) - (п + V) = 2я, C0.11.12)
где т2, А-2 относятся к точке Р2, a tj, A-i —¦ к точке Р±.
Функция т + А, есть монотонная функция от и. Докажем это. Обозна-
Обозначим левую часть равенства C0.11.10) через / (и, v, w). Если найдется такое
значение и, при котором / = /' = 0, т. е. при котором
C0 11 1
iTsin(T+A, + Ti) + i?(T' + A,')cos(T+A.-bTi)==0 ' v
то на кривой Сi будет иметься точка, которой она касается поверхности А.
Если для некоторого значения щ переменной и функция %' -\- А/ обра-
обращается в нуль, то, взяв для г) значение в этой точке, равное —(т + А,),
мы удовлетворили бы обоим уравнениям C0.11.13). . Но это невозможно,
поскольку поверхность А есть поверхность без контакта. Отсюда следует,
что функция %' + А/ никогда в нуль не обращается, т. е. сохраняет свой
знак; без ограничения общности его можно принять положительным.
Введем вместо и новую переменную
ji = -??-, C0.11.14)
которая монотонно возрастает вместе сии увеличивается на 2я при одном
полном обходе кривой Со. Положение точки на кривой Со можно фиксиро-
фиксировать, вместо и, параметром \i. Если точка Р4 находится вблизи кривой Со,
а Р2 есть последующая точка для Pi, то будем иметь
^-^1 = -^. C0.11.15)
где [Xi есть значение ц в точке Pt, а (д,2 — значение ц в точке Р2.
Рассмотрим теперь топологическое отображение области А на внутрен-
внутренность круга и, применяя полярные координаты, отобразим кривую Со на
окружность г = Ъ, вдоль которой 0 = [I. Преобразование Т переводит
окружность г = Ъ в себя, и при этом каждая точка окружности перемещает-
перемещается на угол 2я/(а + ш). Такое преобразование имеет нечетное число непо-
неподвижных точек, каждой из которых соответствует периодическая орбита.
40*
624 ПЕРИОДИЧЕСКИЕ ОРБИТЫ [Гл. XXX
Из этих орбит по крайней мере одна устойчива по первому -приближению;
пусть это будет орбита, соответствующая неподвижной точке Ро. Совершим
еще одно топологическое отображение круга на себя такое, чтобы точка Ро
перешла в центр круга, а точки окружности подверглись бы такому же
преобразованию, что и прежде. В результате получим преобразование Т,
которое оставляет центр круга неизменным, а границу его отображает
на себя, причем все точки границы передвигаются против хода часовой
стрелки на один и тот же угол.
Рассмотрим теперь действие этого преобразования на точки, лежащие
в непосредственной близости от центра круга.
Пусть С'о есть периодическая орбита, проходящая через точку Ро.
Возьмем систему координат и', v', и/. Эти координаты отличаются от введен-
введенных ранее для кривой Со, поскольку теперь поверхность S, содержащая
область А, имеет уравнение и' = 0. При таком выборе координат уже невоз-
невозможно определить положение точки на траектории заданием одних лишь
значений и' и v', а изменение направления элемента — изменением одной
только переменной w'. Но это сейчас не имеет большого значения. Кривая С,
проходящая вблизи от С'о, описывается уравнениями
? ^ . C0.11.16)
Здесь а мало, а т' равно
т' = К +ф(и'), C0.11.17)
где г|) (и') — периодическая функция и', а характеристические показатели
устойчивой периодической орбиты С'о равны 0, 0, ф, —ifl. Если и' изменяет
свое значение на 2я, то х' изменяет свое значение на 2яр. Можно выбрать
полярные координаты таким образом, чтобы для точек, близких к Ро
(т. е. для малых значений г), имели место приближенные равенства
-^ = p'sin9, -^-*» pj sin e+pj cos9, C0.ll.18)
где р', pj, Рз берутся для и' — 0.
Если точка Р расположена вблизи от центра Ро, то при переходе от Р
к последующей для нее точке Р' переменная и' возрастает на 2я, а 9 —
на 2яр\ или, поскольку 9 определено только по mod 2я, ее приращение может
•составлять 2я (р + и), где п — целое число. При этом, если значение п
известно для какой-нибудь одной точки, то в силу непрерывности оно извест-
известно и для всех точек.
Рассмотрим теперь преобразование Тр, где р — целое положительное
число. Это преобразование переводит внутреннюю часть круга в себя, а его
границу — в границу преобразованного круга. Преобразование Тр обладает
положительным интегральным инвариантом. Если Т (г, 9) = (г', 9'), то, как
мы знаем, на окружности г = Ъ мы будем иметь
9' —9 = 2я—?—, C0.11.19)
а вблизи от точки г = 0
6' — 9 = 2лр (р + п). C0.11.20)
Преобразование останется прежним, если 9' заменить на 9", где 9" =
= 6' — 2qn, a q — целое число; при этом на окружности г = Ъ будем иметь
C0.11.21)
§ 30.12] ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ПУАНКАРЕ О КОЛЬЦЕ 625
а вблизи от точки г = О
9" - 9 = 2я {р (р + п) - q). C0.11.22)
Выберем число п так, чтобы выполнялось условие (а + т) (р + п) ф1.
Тогда можно указать бесконечно много пар значений р, q таких, что либо
C0.11.23)
C0.11.24)
а-\-т
либо
I<
а-\-т р
Таким образом, условия теоремы Пуанкаре (для случая, когда внутрен-
внутренний радиус кольца стремится к нулю) оказываются выполненными. Поэтому,
если теорема верна и если существует одна устойчивая периодическая орби-
орбита Go, то существует бесконечно много таких периодических орбит.
§ 30.12. Доказательство теоремы Пуанкаре о кольце*). Приведем теперь
доказательство теоремы, сформулированной в § 30.10. Отобразим кольцо
а ^ г s^ Ъ на полосу 0 ^ у ^ 1 плоскости ху с помощью уравнений
х=2^' У = !*=Ж- C0.12.1)
Преобразование Т сохраняет меру и в новых переменных. Полагая
Т (х, у) = (*', у'), C0.12.2)
замечаем, что при у = 0
х' > х, у' = 0, C0.12.3)
а при у = 1
z'<:r, #' = 1. C0.12.4)
Если полосу разбить на прямоугольники линиями х = п (п — целое
число), то получится периодическая структура, так как конгруэнтные точки
различных прямоугольников отвечают одной и той же точке кольца.
Докажем прежде всего, что преобразование Т имеет одну неподвижную
точку.
В этом доказательстве используются все три условия § 30.10; если хотя бы одно
из них не выполняется, теорема может оказаться неверной. Проиллюстрируем это на
примере преобразования, при котором сначала каждая концентрическая окружность
поворачивается в положительном направлении, если г > — (а-\- Ъ), и в отрицательном,
если г < -5- (а +Ь), а затем точки этих окружностей смещаются радиально вовне. В ка-
честве конкретного примера можно взять
r' = r+ 2(bi_a) {(b-r)(i—a)}, C0.12.5)
где к > 0. Это преобразование не имеет неподвижной точки, поскольку 0' =^= 0, если
только г не равно -^ (а + Ь), и если г = ¦_- (а -)- Ъ), г' > г.
Если точку с координатами х, у обозначить через р, а точку с коорди-
координатами х', у' — через р', то равенство C0.12.2) можно записать в форме
Тр = р'. Приступая к доказательству, предположим, что преобразование
*) См. G. D. Birkhoff, Proof of Poincare's geometric theorem, Trans. Amer.
Math. Soc, 14, 1913, стр. 14—22.
626
ПЕРИОДИЧЕСКИЕ ОРБИТЫ
[Гл. XXX
Рис. 124.
не имеет неподвижной точки, и покажем, что это предположение приводит
к противоречию. Обозначим вектор рр' через Vp, величина его равна R {р),
а угол, составляемый им с осью Ох, равен г|з (р).
Поскольку преобразование не имеет неподвижной точки, величина R (р)
имеет положительную нижнюю грань Н. Угол г|з (р) определен по mod 2я;
на нижней границе полосы Lo (у = 0) г|з имеет значение 2тп, а на верх-
верхней границе полосы L% {у = 1) угол г|з равен Bп + 1) л, где тип — целые
числа. Без ущерба в общности можно принять, что для всех точек пря-
прямой Lo т = 0. При этом угол'г|з (р) будет определен в силу непрерывности
для всех точек полосы 0 < у < 1, и функция г|з (р) будет однозначной
и непрерывной функцией
у своего аргумента. В част-
частности, число п имеет одно
и то же значение для всех
точек прямой Li. Рассмо-
Рассмотрим два пути A0Ai и B0Bi,
соединяющие точку на пря-
прямой Lo с точкой на пря-
прямой L\. Предположим, что
каждый из этих путей пе-
пересекает любую из пря-
прямых у = у0 только в одной
точке. Переведем эти пути
друг в друга непрерывной
деформацией, перемещая
соответствующие точки по
горизонтали. Приращение функции г|з (р) при перемещении точки р вдоль
кривой от Lo до Li изменяется непрерывно, и, следовательно, значение ijj (р)
на прямой Li при непрерывной деформации не может измениться скачком
от одного нечетного кратного значения я до другого.
Фактически мы имеем п = 0; значение функции г|з во всех точках Li
равно я. Это является основным пунктом всего доказательства.
Чтобы показать, что п = 0, совершим преобразование U, отличающееся
от преобразования Т последующим вертикальным перемещением е, где
0 < е < Н:
и(х,у)~(х',у'+г). C0.12.6)
Это преобразование сохраняет площадь и не имеет неподвижной точки,
оно переводит полосу 0 < у < 1 в полосу е < у < 1 + е.
Преобразование U переводит прямую Lo в прямую Ку, задаваемую
уравнением у = е; прямую KY оно переводит в кривую К2, нигде не пере-
пересекающую Ки и т. д. (рис. 124). Полоса So между Lo и Kt отображается
на полосу Si между К^ и Кг, и т. д. Кривые Ки К2, К3, . . . периодически
повторяются в каждом единичном интервале по координате у, и площадь
полосы Sr между прямыми х = 0 и х = 1 равна е. Площадь (в интервале
0 < х < 1) под кривой Кт равна re, так что для достаточно больших целых г
кривая Кг должна иметь точки, расположенные над прямой Lu Пусть п —
наименьшее целое число, обладающее таким свойством. Тогда можно ука-
указать точку р0 на прямой Lo такую, что Unp0 окажется либо на прямой Lu
либо выше ее.
Рассмотрим теперь прямую, соединяющую точку р0 на прямой Lo с точ-
точкой Up0 на прямой Ki. Преобразование U переводит точки этого отрезка
в точки дуги, расположенной в полосе Si и соединяющей точку прямой Kt
с точкой линии К2- Эта дуга переводится преобразованием U в дугу, лежа-
лежащую в полосе S2, и т. д. В результате получаем простую кривую Г, соеди-
§ 30.12] ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ПУАНКАРЕ О КОЛЬЦЕ 627
няющую точку р0 на прямой Lo с точкой Unpo, лежащей на прямой Lj или
выше ее.
Рассмотрим теперь поведение функции if (p) при перемещении точки р
вдоль кривой Г от р0 до Un~1p0. Если е мало, то функция г|з (р) мала и поло-
положительна, когда точка р занимает положение р0, и имеет значение, близкое
к Bп -\- 1) я, когда р занимает положение Ua~xp0. Рассмотрим изменение
наклона хорды, соединяющей точки р и Up при перемещении точки р
вдоль кривой Г. При этом на каждом этапе нижний конец хорды распола-
располагается в полосе Sr, а верхний конец — в полосе Sr+1 или нижний конец —
на линии Кг, а верхний конец — на линии Kr+i.
Изменение наклона хорды можно определить в два этапа следующим
образом. На первом этапе нижний конец хорды фиксирован в точке р0,
а верхний конец q перемещается из положения Up0 в положение Uap0.
На втором этапе верхний конец хорды фиксирован в точке Unp0, а нижний
конец q перемещается из положения р0 в положение Un~xp0. На каждом
из этих этапов приращение наклона хорды не превышает я, суммарное
приращение поэтому не превышает 2я, так что число п может быть равно
только нулю. Таким образом, для точек прямой Li г|з (р) — я, что и требо-
требовалось доказать.
Аналогичным образом, рассматривая обратное преобразование Т~г,
можно доказать, что изменение наклона хорды, соединяющей точки р и T~xpt
при перемещении точки р от Lo до L\ равно —я. Но изменение наклона
хорды, проведенной из р в Тр, в точности равно изменению наклона хорды,
проведенной из Тр в р. Мы пришли, таким образом, к противоречию, кото-
которое указывает, что предположение об отсутствии неподвижных точек неверно.
Для доказательства существования двух неподвижных точек достаточно
заметить, что изменение функции г|з (р) при обходе точкой р единичной окруж-
окружности равно нулю. С другой стороны, если точка р обходит простой замкну-
замкнутый контур, охватывающий одну неподвижную точку, то изменение функ-
функции if> (р) составляет ±2я (§ 20.1). Поэтому внутри единичного круга рас-
расположены по крайней мере две неподвижные точки.
БИБЛИОГРАФИЯ
I. Основные сочинения
1. Newton I., Philosophiae naturalis principia mathematica (первое издание, London,
1687). Имеется множество изданий и переводов; см., в частности, «Sir Isaac Newton's
Mathematical Principles of Natural Philosophy», под ред. F. Cajori (Cambridge, 1934).
[Имеется русский перевод: Н ь ю т о н И., Математические начала натуральной фило-
философии. Перевод с латинского с примечаниями и пояснениями А. Н. Крылова. Собра-
Собрание трудов акад. А. Н. Крылова, т. VII, Изд-во АН СССР, Москва — Ленинград,
1936.
2. d' A I e m b е г t J. le R., Traite de dynamique (Paris, 1743). [Имеется русский пере-
перевод: Даламбер Ж., Динамика. Гостехиздат, Москва, 1950.]
3. Е u I e r L., Mechanica, sive motus scientia analytice exposita (С.-Петербург, 1736)
и Theoria motus corporum solidorum seu rigidorum (Greifswald, 1765). [Имеется рус-
русский перевод: Эйлер Леонард, Основы динамики точки. ОНТИ, Москва,
1938.]
4. Lagrange J. L., Mecanique Analytique (Paris, 1788). [Имеется русский перевод:
Лагранж Ж., Аналитическая механика, т. 1, 2. Гостехиздат, Москва,
1950.]
II. Исторические обзоры, критические статьи
5. М а с h E., Die Mechanik in ihrer Entwicklung historisch-kritisch dargestellt (Leipzig
1883). [Имеется русский перевод: Max Э., Механика в ее историко-критическом раз-
развитии, С.-Петербург, 1907.]
6. Hertz H., Die Principien der Mechanik in neuem Zusammenhange dargestellt (Leip-
(Leipzig, 1894). [Имеется русский перевод: Герц Г., Принципы механики, изложенные
в новой связи. Изд-во АН СССР, Москва, 1959.]
7. D ug a s R., Histoire de Mecanique (Neuchatel, 1950).
III. Ссылки на оригинальные работы
8. Cayley A., Report on the Recent Progress of Theoretical Dynamics, 1857, а также
Report on Special Problems, 1862 (Collected Papers, Cambridge, 1890, т. Ill, стр. 156—
204 и т. IV, стр. 513-593).
9. Royal Society Index (см. Catalogue of Scientific Papers, 1800—1900), т. II, Mechanics.
10. International Catalogue of Scientific Literature, В (Mechanics). Охватывает период
с 1900 г. по 1913 г.
И. Jahrbuch iiber die Fortschritte der Mathematik, 1862—1942.
12. Revue semestrielle des publications mathematiques, 1893—1932.
13. Mathematical Reviews, 1940.
Литература специально no задаче трех тел
14. Whittaker E. Т., Report on the progress of the solution of the problem of Three
Bodies (British Association Report, 1899).
15. Lovett E. O., Generalizations of the problem of several bodies (Quarterly Journal
of Mathematics, XLII, 1911, стр. 252—315). Содержит ссылки на работы, опубликован-
опубликованные между 1898 и 1908 гг.
IV. Позднейшие сочинения
16. Hamilton W. R., On a general method in Dynamics; Second Essay on a general
method in Dynamics, 1834 (Collected Papers, т. II, Cambridge, 1940, стр. 103—211).
[Имеется русский перевод в сборнике «Вариационные принципы механики» под редак-
редакцией Л. С. Полака, стр. 175—288. Физматгиз, Москва, 1959.]
17. J а с о b i C.G.J., Vorlesungen iiber Dynamik (Berlin, 1884). [Имеется русский пере-
перевод: Я к о б и К., Лекции по динамике, ОНТИ, Ленинград, 1936.]
БИБЛИОГРАФИЯ 629
18. Poinc are H., Les methodes nouvelles de la Mecanique Celeste C тома, Paris, 1892—
1899).
19. G i b b s J. W i 11 a r d., Collected Works, т. II (New York, 1928).
20. Ronth E. J., Elementary Rigid Dynamics и Advanced Rigid D3rnamics (первое
издание, London, 1860). Имеется много последующих изданий.
21. А р р е 11 P., Traite de Mecanique Rationelle, т. II (Paris, 1896). [Имеется русский
перевод: Аппель П., Теоретическая механика, т. I, II.
Физматгиз, Москва, I960.]
V. Дальнейшие ссылки
a) 22. Т h о m s о n W. (Lord Kelvin) and T a i t P. G., Treatise on Natural Philosophy
(Cambridge, т. I, 1879, т. II, 1883; новое издание, 1912).
23. Encyklopadie der Mathematischen Wissenschaften, т. IV. 1 и IV. 2 (Leipzig,
1901—1908).
24. Handbuch der Physik, т. V, Grundlagen der Mechanik, Mechanik der Punkte und
starren Korper (Berlin, 1927).
25. Lord R а у 1 e i g h, Theory of Sound (London, т. I, 1878, т. II, 1879). [Имеется
русский перевод: С т р э т т Дж. В. (лорд Рэлей), Теория звука, т. I, П. Гостех-
издат, Москва, 1941—1944.]
26. Jeffreys H. and Jeffreys B.C., Methods of Mathematical Physics (Cam-
(Cambridge, 1946; изд. 3-е, 1956). [Имеется русский перевод: Джеффрейс X. и
Джеффрейс В., Методы математической физики, «Мир», 1970.]
b) 27. Whittaker E. Т., A treatise on the analytical dynamics of particles and rigid
bodies, with an introduction to the problem of three bodies (Cambridge, 1904;
изд. 4-е, 1937). [Имеется русский перевод: Уиттекер Е.Т., Аналитическая
динамика, Гостехиздат, Москва, 1937.]
28. Levi-Civita Т., Amaldi U., Lezioni di Meccanica Razionale (Bologna,
\ 922). [Имеется русский перевод: Леви-Чивита Т. и Амальди У.,
Курс теоретической механики, т. I, ч. I, II; т. II, ч. I, П. ИЛ, Москва, 1951 —
1952.]
29. Wintner A., The Analytical Foundations of Celestial Mechanics (Princeton,
1941). [Имеется русский перевод: Уинтнер А., Аналитические основы небес-
небесной механики. «Наука», Москва, 1967.]
30. S i e g е 1 С. L., Vorlesungen iiber Himmelsmechanik (Berlin, 1956). [Имеется
русский перевод: 3 и г е л ь К. Л., Лекции по небесной механике, ИЛ, Москва,
1959.]
31. Moulton F. R., Periodic Orbits (Washington, 1920).
с) 32. Routh E. J., A Treatise on Dynamics of.,a Particle (Cambridge, 1898).
33. К 1 e i n F. und Sommerfeld A., t)ber der Theorie des Kreisels (четыре
тома, Leipzig, 1897—1910).
34. Lamb H., Higher Mechanics (Cambridge, 1920; изд. 2-е, 1929). [Имеется рус-
русский перевод: Л а м б Г., Теоретическая механика, т. III, ОНТИ, Москва,
1936.]
35. В i r k h о f f G. D., Dynamical Systems (New York, 1927). [Имеется русский
перевод: Б и р к г о ф Дж. Д., Динамические системы. Гостехиздат, Москва,
1941.]
36. Goldstein H., Classical Mechanics (Cambridge Mass., 1951). [Имеется русский
перевод: Голдстейн Г., Классическая механика. Гостехиздат, Москва,
1957.]
37. Sommerfeld A., Vorlesungen iiber Theoretische Physik, т. I, Mechanik
(Leipzig, 1942). [Имеется русский перевод: Зоммерфельд А., Механика,
ИЛ, Москва, 1947.]
38. Peres J., Mecanique Generate (Paris, 1953).
39. Lanczos C., The Variational Principles of Mechanics (Toronto, 1949).
[Имеется русский перевод: Л а н ц о ш К. Вариационные принципы механики.
«Мир», Москва, 1965.]
d) 40. С о d d i n g t о n E. A. and Levinson N., Theory of ordinary differential
equations (New York, 1955). [Имеется русский перевод: Коддингтон Э. А.
иЛевинсон Н., Теория обыкновенных дифференциальных уравнений. ИЛ,
Москва, 1958.]
41. Л я п у н о в А. М., Общая задача об устойчивости движения. ОНТИ, Москва,
1935.
42. Stoker J. J., Nonlinear Vibrations (New York, 1950). [Имеется русский пере-
перевод: Стокер Дж., Нелинейные колебания в механических и электрических
системах, ИЛ, Москва, 1952.]
43. Minorsky N., Nonlinear Oscillations (Princeton, 1962).
44. Крылов Н. М. и Боголюбов Н. Н., Введение в нелинейную механику.
Изд. АН УССР, Киев, 1937.
630 БИБЛИОГРАФИЯ
45. L a S a 1 1 е J. and Lefschetz S., Stability by Liapounov's Direct Method
(New York, 1961). [Имеется русский перевод: Ла-Салль Ж., Л е ф ш е ц
С., Исследование устойчивости прямым методом Ляпунова. «Мир», Москва,
1964.]
46. С е s а г i L., Asymptotic behavior and stability problems in ordinary differential
equations (Berlin, 1959). [Имеется русский перевод: Ч е з а р и Л., Асимптоти-
Асимптотическое поведение и устойчивость решений обыкновенных дифференциальных урав-
уравнений. «Мир», Москва, 1964.]
е) 47. Н о р f E., Ergodentheorie (Berlin, 1937).
48. Н а 1 m о s P. R., Lectures on Ergodic Theory (New York, 1956).
49. D u n f о r d N. and Schwartz J. Т., Linear Operators, часть I (New York,
1958). [Имеется русский переревод: Данфорд Н. и Шварц Дж. Т., Линей-
Линейные операторы, общая теория. ИЛ., Москва, 1962.]
50. J а с о b s К., Neuere Methoden und Ergebnisse der Ergodentheorie (Berlin,
1961).
ИМЕННОЙ УКАЗАТЕЛЬ
Амальди У. (Amaldi U.) 629
Аппель П. (Appell P. E.) 13, 14, 56, 139,
219—221,. 232, 234, 241, 255, 629
Бассет A. (Bassett А. В.) 219
Бендиксон И. (Bendixon J.) 393, 396, 399
Бертран Ж. (Bertrand J. L. F.) 247, 252—
254, 259, 260, 267, 268
Биркгоф Дж. Д. (Birkhoff G. D.) 26, 101,
441, 620, 625, 629
Боголюбов Н. Н. 629
Болл P. (Ball R. S.) 109
Браун Э. (Brown E. W.) 481
Бромвич Т. (Bromwich T. J. ГА) 190
Брунс Г. (Brims E. Н.) 571, 575
Дирихле Г. (Dirichlet G. P. L.) 339
Дюга P. (Dugas R.) 629
Жордан К. (Jordan С.) 361, 390, 462, 464,
466
Журдэн Ф. (Jourdain F.) 54, 546
Зигель К. (Siegel С. L.) 629
Зоммерфельд A. (Sommerfeld A.) 12, 629
Зундман (Sundmann) 597
Ингам А. Е. (Ingham A. E.) 64
Валле-Пуссен Ш. Ж. (Valle-Poussin Ch. J.)
295
Ван-дер-Поль Б. (Van-der-Pol В.) 394, 399
Вейерштрасс К. (Weierstrass К.) 150, 326
Вольтер (Voltaire F. М.) 546
Галилей Г. (Galilei G.) И, 189
Гамель Г. (Hamel G.) 13
Гамильтон У. P. (Hamilton W. R.) И,
13, 47—50, 84, 85, 90, 91, 93, 99, 103,
114, 200—202, 210, 211, 270, 272, 274,
275, 278, 279, 281, 283—295, 298—302,
308, 321, 329, 330, 333, 347, 356, 406,
409, 429, 432—437, 439, 441, 443, 451,
452, 454, 455, 457, 460, 469, 470, 472,
476, 487, 488, 492, 493, 503—510, 513—
522, 524—526, 529, 531, 533—535, 537,
538, 546, 553, 574, 575, 580-586, 591,
594, 595, 598, 599, 603, 606—608, 619,
628
Гаусс К. (Gauss К. F.) 11, 54, 56, 58, 218,
257
Гельдер О. (Holder L. О.) 50, 534, 535, 537
Геронимус Я. Л. 150
Герц Г. (Hertz H. R.) 31, 628
Гиббс У. (Gibbs J. W.) 13, 54, 56, 139,
219—222, 224, 226, 232, 234, 241, 255,
628
Гильберт Д. (Hilbert D.) 533
Голдстейн Г. (Goldstein H.) 629
Гурса Э. (Goursat E.) 32
Гюйгенс X. (Huyghens С.) И, 537
Даламбер Ж. (D'Alembert J. le R.) 11, 34,
628
Данфорд Н. (Dunford N.) 629
Джеффрейс Б. (Jeffreys В.) 629
Джеффрейс Г. (Jeffreys H.) 481, 629
Карно Л. (Carnot L. N. М.) 247, 251—253
Картан Э. (Cartan E. Y.) 410
Кац А. М. 481
Келлер И. (Kepler J.) 70, 76, 77, 351
Кениг С. (Koenig S.) 104, 205, 221, 546
Клейн Ф. (Klein F.) 12, 629
Коддингтон Э. (Coddington E. А.) 357, 629
Колмогоров А. Н. 442
Кориолис (Coriolis) 189
Кристоффель Э. (Christoffel E. В.) 554
Кронекер (Kronecker) 340
Крылов Н. М. 629
Кэли A. (Cayley A.) 628
Лагранж Ж. Л. (Lagrange J. L.) 11—13,
41, 59, 61, 87, 89, 90, 92—99, 101—104,
124—127, 129, 136—141, 144, 145, 147,
150,176—179,183—186,188,191,199, 200,
202, 207, 210—212, 214, 219, 230—232,
257, 258, 269—272, 277, 279, 296, 298,
306, 308, 329, 330, 333, 334, 346, 472,
492, 495—498, 515, 517, 530—533, 537—
542, 546, 547, 549, 550, 552, 554, 570,
571, 574, 576, 578, 579, 582, 586—589,
601, 611, 628
Ламб Г. (Lamb H.) 629
Ланцош К. (Lanczos С.) 629
Лаплас П. (Laplace P. S.) И, 150
Лармор Дж. (Larmor J.) 185, 186, 552
Ла-Салль Ж. (La Salle J.) 629
Лебег A. (Lebesque H.) 442
Левинсон Н. (Levinson N.) 357, 629
Леви-Чивита Т. (Levi-Civita Т.) 629
Лежандр А. М. (Legendre A. M.) 302
Ле Ру Ж. (le Roux J.) 206
Лершец С. (Lefschetz S.) 357, 629
Ли С. (Lie M. S.) 521, 522
Ливенс (Livens) 531, 532
632
ИМЕННОЙ УКАЗАТЕЛЬ
Лиувилль Ж. (Liouville J.) 278, 329, 335,
439, 441, 449, 451, 452, 540
Ловетт Э. (Lovett E. О.) 628
Лурье А. И. 118
Ляпунов А. М. 425, 426, 428, 472, 473,
475, 477-479, 481, 629
Мак Э. (Mach E.) 628
Мандельштам Л. И. 175
Минорский Н. (Minorsky N.) 12, 629
Мопертюи П. (Maupertuis P. L. М.) 50, 546
Мультон Ф. (Moulton F. R.) 629
Ньютон И. (Newton I.) 11, 15, 34, 70, 206,
207, 245, 554, 628
Пеано (Реапо) 358
Перес Ж. (Peres J.) 629
Полак Л. С. 50, 56, 535
Пуанкаре A. (Poincare J. H.) 11, 392, 396,
399, 410, 425, 426, 428, 437—441, 458,
465, 481, 488, 602, 619, 620, 625, 628
Пуансо Л. (Poinsot L.) 240
Пуассон С. (Poisson S. D.) 433, 434, 440,
497—501, 518—520.
Пфафф Ф. (Pfaff J. F.) 27, 30—32, 35, 36,
46, 49, 50, 86, 94, 287, 301, 302, 437,
439, 454
Раус Э. (Routh E. J.) 14, 150, 176—181,
183, 199, 230, 270, 552, 628, 629
Риман Б. (Riemann В.) 442
Рис Ф. (Riesz F.) 442
Сильвестр (Sylvester) 240
Сомов О. И. 150
Стокер Дж. (Stoker J. J.) 629
Стоке Дж. (Stokes G. G.) 413
Страбл P. (Struble R.) 481
Стрэтт Дж. В. (Лорд Релей) (Strutt J. W.,
Lord Rayleigh) 158—160, 196—198, 629
Суиннертон-Дайер (Swinnerton-Dyer) 357
Тейлор Дж. (Taylor G. I.) 252, 254, 260
Тиссеран (Tisserand) 512
Томсон У. (Лорд Кельвин) (Thomson W.,
Lord Kelvin) 150, 177, 252—254, 259,
260, 266, 556, 557, 559, 629
Тэт П. (Tait P. G.) 150, 177, 559, 560, 629
Уинтнер A. (Wintner A.) 629
Уиттекер Э. (Whittaker E. T.) 329, 417,
550, 628
Уорд A. (Ward A. J.) 524
Ферма П. (Fermat P.) 548
Фосс A. (Voss A. E.) 535, 537
Фридрих Великий 546
Фуко Л. (Foucault L.) 167, 190, 192
Фурье (Fourier) 338, 351, 409
Халмош П. (Halmos P. R.) 629
Хилл (Hill) 572
Хопф Э. (Hopf E.) 12, 629
Чезари Л. (Cesari L.) 629
Шаль (Chasles) 109
Шарлье К. (Charlier С.) 19, 320
Шварц Дж. (Schwartz J. T.) 629
Штеккель П. (Stackel P.) 330, 331, 334,
335, 341, 347, 355
Штурм Ф. (Sturm F.) 252
Шук К. (Shook С. А.) 481
Эйлер Л. (Euler L.) 11, 104, 105, 108, 109,
117, 119, 121, 122, 129, 182, 233, 234,
236, 297, 546, 579, 628
Якоби К. (Jacobi С. G. J.) 11, 13, 97—99,
101, 202, 283, 284, 286, 289-291, 293-
295, 298, 299, 326, 329, 330, 413, 415,
417, 433—435, 437, 452—455, 458, 460,
492, 493, 495, 503, 504, 506—510, 513—
517, 521, 522, 547—551, 553, 555, 585,
615, 628
Якобе К. (Jacobs К.) 629
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Вариация элементов траектории 506
— эллиптических элементов 510—513
Варьированный путь в принципе Гамиль-
Гамильтона 49, 84
Возмущения 355
Волчок вращающийся 129—136
— —, нутация 166
— —, прецессия 164
— —, приложение теоремы Гамильтона —
Якоби 297
— —, приложение уравнений Гиббса —
Аппеля 230
— — спящий 169—174
— —, функция Рауса 183
Гироскоп Фуко 167—169
Движение импульсивное в случае непре-
непрерывных систем 264—268
— квазипериодическое 307, 335—343
— либрационное 19, 24—26, 306
— лимитационное 19, 307
— относительно подвижной системы от-
отсчета 187—196
— под действием ударных импульсов 247—
264
— прямолинейное в силовом поле 17
— снаряда 192—196
Достижимость в неголономных системах
31, 35, 83
Задача двух тел 74—77
— — —, приложение теории разделимых
систем 347—354
— трех тел 573—601
— — —, невозможность тройных столк-
столкновений 595—597
— — — ограниченная 562—572
— — —, сведение к системе восьми урав-
уравнений первого порядка в общем случае
591—595
— — —, сведение к системе шести урав-
уравнений первого порядка в случае плоского
движения 584—586, 597—600
— Тэта 559—561
Замена независимой переменной в урав-
уравнениях Лагранжа 537
Импульс обобщенный 101
Инварианты интегральные 274, 410—415,
437—439
Индекс кривой и особой точки 385
Интеграл Якоби 97—101
Интегралы в инволюции 519—521
— линейные относительно импульсов 522—¦
524
Исключение координат 176—179, 271, 552
— узлов 585
Качение диска 137—139, 232
— сферы 224—230
— тел как пример неголономных систем
. 81-83
— эллипсоида 241—243
Квазикоординаты 214—216
Классификация траекторий 308—317
Ковариант билинейный 496, 517
Колебание основное 142
Колебания в окрестности положения рав-
равновесия 140—149
— — — установившегося движения 164—
167
— вынужденные 174, 481—486
Координаты лагранжевы 59—61, 80—81,
255
— нормальные 142, 150—154
— ортогональные, формулы ускорения
в них 125
— циклические 102
Кривые критические 309
Масса переменная 207—213
Матрица монодромии 465
— симплектическая 470, 500
Маятник конический 163
— —, колебания в окрестности устано-
установившегося движения 166
— —, устойчивость установившегося дви-
движения 164
— на упругой нити 428
— простой 61—63
— — во вращающихся осях 100
— — в среде с сопротивлением 377
— — , второе приближение 508
— — как пример движения в окрестности
особой точки 376
— —, приближенное вычисление периода
64—66
— сферический 60, 71—74
— —, приложение теоремы Гамильтона —
Якоби 296
— —, приложение теоремы Штеккеля
345-347
— —, приложение теории последнего мно-
множителя 455
— Фуко 190
Множество предельное положительное
387-389
634
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Множители в теории уравнений в вариа-
вариациях 465
— — — — движения 415—417
Множитель последний Якоби 417
— — —, приложение к гамильтоновой си-
системе с двумя степенями свободы 452—
456
Неразложимость метрическая 448
Области инвариантные 439
Орбиты периодические 602—627
Ориентация твердого тела, углы Эйлера
и углы ф1? ф2, ф3 Н7
Осциллятор в среде с сопротивлением 362
— гармонический 20—22
— —, применение теоремы Гамильтона —
Якоби 292—295
— —, решение в форме степенных рядов
408
— —, уравнения в вариациях 461
— —, устойчивость по Ляпунову 475
— изотропный 69
Отражения 111
Переменные угловые 24, 338, 352
Перемещения виртуальные и возможные
28, 29, 36
Показатели характеристические 465, 467
Поле гравитационное; движение в нем
69, 74—76, 461, 543
— однородное 22
— —, движение в нем как пример на
приложение теоремы Гамильтона — Яко-
Якоби 291
— —, решение в форме рядов 409
— —, характеристическая функция для
движения в нем 558—559
— силовое 15
Полуобороты 105, 111, 114
Поля скрещивающиеся 186
— —, движение электрона 212
Преобразования контактные 487—503
— — бесконечно малые 494, 517
— — однородные 488
— —, производящая функция 490
, формулы 489—493
— конформные 542
— обобщенные точечные 493
Приближение линейное 141
Принцип Гамильтона 47—49
— —, невозможность варьированного пу-
пути в общем случае 49, 84, 529
— —, обобщение 537
— —, приложение к распределенным си-
системам 50—53
— Гаусса наименьшего принуждения 56,
218
— — — — в теории удара 249
— Гельдера 534
— наименьшего действия 545—547
— — — в форме Якоби 547—550
— Релея в теории малых колебаний 158—
160
— Фосса 535
Притяжение ньютоновское и однородное
поле 317—320
Силы консервативные и потенциальные
функции 44, 93
Система голономная и неголономная 31, 37,
78—81, 214
— катастатическая 31, 38, 43, 248—255
— Лиувилля 329, 540—542
— механическая 34—40
— отсчета ньютонова (инерциальная) 15
— с одной степенью свободы; движение
в окрестности особой точки 363—384
Системы, допускающие разделение пере-
переменных 291, 303—356
— — — — более чем одним способом
327
¦— — — —, неортогональные и ненату-
ненатуральные 355
— связанные 148
— с двумя степенями свободы 303—328
— era степенями свободы 329—356
Скобки Лагранжа 495—498, 517
— Пуассона 433, 497—499
Скорость угловая 117, 120—123
Сохранение импульса 42
— момента количеств движения 43
— энергии 47
Степенные ряды 406
Стержень во вращающейся плоскости 136,
298
Тело твердое, движение в двух измере-
измерениях 128—129, 221
— —, — в пространстве 222—224
Теорема Бертрана 252
— Гамильтона — Якоби 283
— Гиббса 221
— Карно 251
— Кельвина в теории удара 253
— — об орбитах в пространстве конфигу-
конфигураций 556—558
— Кенига 104
— —, аналог для функции Гиббса 221
— Кориолиса 189
— Лармора 185
— Ливенса 531
— Лиувилля 278
— —, обобщение на контактные преобра-
преобразования 495
— —, следствие из нее 451
— Ляпунова 473
— Ньютона о вращении орбиты 70
— площадей 43
— Пуанкаре — Бендиксона 392—393
— Пуанкаре — Ляпунова 448—450
— Пуанкаре о возвращении 439
о кольце 619, 625—627
— Пуансо 240
— Пуассона 434
— Сильвестра 240
— Уиттекера 551
— Шаля 109
— Штеккеля 330—333
— Эйлера в теории поворотов 104—106
, обобщение 108, 109
— эквивалентности 286—289, 437, 504
— эргодическая 441—448
— Якоби о сохранении гамильтоновой
формы уравнений при контактных пре-
преобразованиях 504—506, 513—517
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
635
Теория колебаний 140
— поворота 104—123
— —, вектор поворота 108
— —, сложение вращений 113
— —, формула поворота 109—111
— —, — —, кватернионная форма запи-
записи 112-113
— —, формула результирующего поворо-
поворота 114—117
— преобразований 504—528
—fудара 244
Траектории 360
Три точки Лагранжа 576—578, 589—591,
600—601, 611—612
— — —, решения, для которых треуголь-
треугольник Лагранжа сохраняет форму 578—
579
Триэдр главный 205—206
Углы Эйлера 117
Уравнение Ван-дер-Поля 394, 399—400
— Гамильтона в частных производных 283
— Кеплера 70, 76
— основное, первая форма 41
— —, вторая форма 54
— —, третья форма 555
— —, четвертая форма 87
— —, пятая форма 216
— —, шестая форма 269
— Хилла движения Луны 572
— энергии 18, 43—47, 97, 202
Уравнения в вариациях 457
— — — для системы Гамильтона 469—
471
— — —, их решение 459
— Гамильтона 200—202, 432—456
— Гиббса — Аппеля 219
— Лагранжа 89
— — в теории удара 257
— —, вывод из принципа Гамильтона
90-92
— —, инвариантность 103
— связей, импульсные связи 246
Уравнения связей, наложение связей на
колебательную систему 157
— —, реакции связей 27—31
— Эйлера движения твердого тела 233
Устойчивость асимптотическая 370, 419
— гироскопическая 179, 199
— движения 471
— дискретная 421—422
— орбитальная 478
— периодических орбит 479—481
— по Ляпунову 472—478
— по первому приближению 171, 458
— преобразований 422—424
— равновесия 140
— системы с двумя степенями свободы,
допускающей разделение переменных
309
— трех точек Лагранжа 587
— установившегося движения 160—164
Функции в инволюции 500
— дескриптивные 270
Функция Гамильтона 200
главная 274—282
— —, приведение некоторых типов к виду
2 524—528
2
— диссипативная Релея 196
— Лагранжа 95
— Рауса 176, 181
Характеристики 360
— циклические 385
Электрон в скрещивающихся полях 212
— — электрическом поле 210
— — электромагнитном поле 211
— движущийся 209
—, — под действием притяжения к центру
299
Энергия кинетическая системы 43, 88
— — твердого тела 126
Л. А. Парс
Аналитическая динамика
М., 1971 г., 636 стр. с илл.
Редактор А. Н. Рубашов
Техн. редактор В. Н. Кондакова
Корректоры Т. С. Плетнева, Н. Б. Румянцева
Сдано в набор 4/VI 1971 г. Подписано к печати 29/Х 1971 г. Бумага
70x1081/16- Физ. печ. л. 39,75. Условн. печ. л. 55,65. Уч.-изд. л. 48,82.
Тираж 5000 экз. Цена книги 3 р. 92 к. Заказ 1011.
Издательство «Наука»
Главная редакция физико-математической литературы.
117071, Москва, В-71, Ленинский проспект, 15.
Московская типография № 16 Главполиграфпрома
Комитета по печати при Совете Министров СССР.
Москва, Трехпрудный пер., 9.