Текст
А. Г. МЛАДОВ
Системы
дифференциальных
уравнений
и устойчивость
движения
по ляпунову
Допущено
Министерством высшего и среднего
специального образования СССР
в качестве учебного пособия
для студентов высших технических
учебных заведений
ИЗДАТЕЛЬСТВО «ВЫСШАЯ ШКОЛА»
МОСКВА—1966
АННОТАЦИЯ
Предлагаемое учебное пособие предназначено для
студентов втузов, которые специализируются по автоматизации
производственных процессов, оно вполне пригодно для
студентов всех видов обучения, в том числе и для заочников;
может быть полезным для инженеров и преподавателей.
В пособии даны начальные сведения о системах
обыкновенных дифференциальных уравнений, понятие об описании
движений (физических процессов) с помощью систем
дифференциальных уравнений, понятие фазового пространства
системы, понятия устойчивости и неустойчивости движения по
Ляпунову, критерии устойчивости и неустойчивости для
линейных систем, линеаризация системы, кратко изложены
понятия технической устойчивости; в порядке дополнительного
материала дано представление о втором методе Ляпунова и
о теоремах Ляпунова и Четаева; разобран ряд примеров.
К пособию приложено контрольное задание № 16 для
студентов-заочников.
-3
66
ПРЕДИСЛОВИЕ
Студентам, которые специализируются по автоматизации
производственных процессов, перед прохождением курса «Теория
автоматического регулирования и управления» необходимо в
дополнение к основной программе по высшей математике изучить
следующие главы: «Теория функций комплексного переменного»
(22 час. лекций и 10 час. упражнений), «Преобразование
Лапласа» (12 час. лекций и 10 час. упражнений), «Системы
дифференциальных уравнений и устойчивость движения по Ляпунову»
(28 час. лекций и 18 час. упражнений).
Предлагаемое руководство, в котором излагается последняя
иэ этих трех глав, предназначено в качестве учебного пособия
для студентов указанной специальности всех видов обучения, в
том числе и для заочников. В обязательную программу включен
материал § 1 —17 этого подобия, за исключением мелкого
шрифта. Этот материал можно изучать либо в том порядке, как он
изложен в пособии, либо в таком порядке: § 1—3, 10—12, 4—9,
13—17. Материал § 18—20 и мелкий шрифт § 2, 3, 5, 11, 17
может быть изучен факультативно. Примеры из § 2—5, 8, 10
следует использовать на лекциях, а примеры из § 2—5, 7, 8, 9, 15,
16 — на упражнениях.
Настоящее пособие составлено на основе лекций и
упражнений по обсуждаемой теме, которые я провожу в течение
девяти лет со студентами 2—5 курсов Московского института
химического машиностроения. Первоначальным источником для
моих лекций послужили шесть лекций об устойчивости
движения, которые прочитал профессор П. А. Безсонов студентам
5 курса МИХМа в 1955 г. В последующие годы в моих лекциях
и занятиях со студентами этот материал был существенно
переработан и получил значительное развитие как по содержанию,
так и по объему. В результате этого в предлагаемом пособии
образовались § 2, 3, 5, 7, 10, 11, 14, 15, большая часть
содержания § 1, 4, 8, 19, примерно половина содержания § 6, 9, 12, 13,
16, 17, 18, 20 и контрольное задание № 16 для заочников.
3
С любезного согласия профессора П. А. Безсонова материал
его лекций использован при составлении этого пособия.
Большую техническую работу по подготовке рукописи к печати и в
процессе печатания пособия выполнила Г. М. Печникова.
Полезные советы по улучшению текста пособия дали доктор
физ.-матем. наук Г. Л. Лунц и старший преподаватель В. С. Берман.
Я приношу мою большую искреннюю благодарность профессору
П. А. Безсонову, Г. М. Печниковой, доктору физ.-матем. наук
Г. Л. Лунцу и старшему преподавателю В. С. Берману.
Я благодарю также рецензентов моей рукописи доцента
И. А. Брина, профессора М. И. Вишика, профессора А. Ф.
Леонтьева, доктора технических наук профессора Н. К. Куликова,
научного редактора кандидата физ.-матем. наук М. И. Зеликина
за весьма ценные'замечания, которые были очень полезны при
доработке пособия.
Л. Младое
15 марта 1965 г.
§ 1. ВВЕДЕНИЕ
Теория устойчивости движения является важнейшей
математической основой теории автоматического регулирования. В свою
очередь теория автоматического регулирования служит
теоретическим обоснованием практики автоматического
регулирования и управления.
Автоматическое регулирование производственных процессов
и различных типов машин (в трм числе тепловых,
электрических, электронных) является мощным средством, без которого
немыслима современная техника. Автоматическое управление
работой котельных установок, электростанций, электрических
сетей, электроприводов скоростных прокатных станов,
автоматизация процессов химической, нефтеперерабатывающей,
металлургической и металлообрабатывающей промышленности,
автоматизация движения на транспорте и полетов в авиации — вот
некоторые примеры из техники, где автоматическое
регулирование нашло широкое применение. Автоматическое регулирование
необходимо всюду, где невозможно или нецелесообразно
ручное управление, т. е. в тех случаях, когда нужна большая
скорость и точность управления, особенно при большом объеме
информации, поступающей от управляемого объекта. Это в
значительной мере относится к приведенным выше примерам и
особенно к управлению ракетами, космическими кораблями без
человека, а также процессами, связанными с атомной энергией
и ядерной физикой.
Совокупность регулируемых объектов и автоматических
регулирующих устройств 'называется системой автоматического
регулирования. Система автоматического регулирования
называется устойчивой, если происходящие в ней процессы мало
изменяются под действием внешних возмущающих воздействий;
система автоматического регулирования называется
неустойчивой, если происходящие в ней процессы очень сильно
изменяются даже под действием очень малых внешних возмущающих
воздействий.
Так, в аппарате, в котором происходит некоторая
химическая реакция, нужно поддерживать определенный режим тем-
5
пературы, давления, концентраций исходных веществ и
продуктов реакции. При этом желательно сохранять оптимальный
режим, т. е. наиболее производительный, наиболее экономичный
и дающий наивысшее качество продукции. Такой режим
стараются осуществить с помощью регулирования подачи или отвода
тепла, работы компрессоров или вакуум-насосов, подачи
исходных веществ и отвода продуктов реакции.
Если под действием каких-либо малых внешних
возмущающих воздействий некоторые из параметров, т. е. температура,
давление, концентрации, отклоняются от заданного режима, то
вступают в действие соответствующие автоматические
регуляторы, чтобы вернуть параметры к заданным значениям. Но эти
регуляторы могут приостановить свое действие с опозданием,
вследствие чего параметры успеют отклониться в
противоположном направлении. Снова действуют регуляторы, но опять с
опозданием, что приводит к новым отклонениям параметров в
другую сторону. Таким образом, в аппарате получаются
колебательные отклонения от заданного режима.
Если в системе имеются гасители отклонений и если они
работают достаточно хорошо, то отклонения от заданного
режима будут оставаться малыми, т. е. получающийся процесс будет
мало отличаться от заданного режима. В этом случае заданный
оптимальный режим является устойчивым.
Если же гасители отклонений работают плохо или их
вообще нет, то отклонения от заданного режима с течением времени
могут стать очень большими, т. е. получающийся процесс будет
сильно отличаться от заданного режима. Для такой системы
заданный режим является неустойчивым.
Тем более система может стать неустойчивой, если имеются
сильные внешние возмущающие воздействия, поступающие
внезапно или непрерывно. Например, отключение теплообменника
или насоса подводящей или отводящей линии, выход из строя
какого-нибудь регулятора могут настолько нарушить режим в
аппарате, что весь процесс станет неустойчивым.
Конечно, здесь дается лишь схематическое представление об
устойчивости и неустойчивости движения. Строгие определения
этих понятий будут даны в § 8, 9.
Устойчивость системы автоматического регулирования
является одним из главных требований, предъявляемых к ней.
Поэтому основная задача теории устойчивости движения состоит
в нахождении признаков устойчивости и неустойчивости
движений материальных систем. Это делается посредством анализа
того, как влияют на движения материальных систем их
внутреннее строение и внешние возмущающие воздействия.
Академик А. М. Ляпунов (1857—1918) создал весьма общую
и глубокую математическую теорию устойчивости движения,
которую он изложил в своей важнейшей работе «Общая задача об
устойчивости движения» [5], опубликованной в 1892 году. Этими
вопросами, кроме Ляпунова, занимались Раус, А. Пуанкаре,
Н. Е. Жуковский, а из наших современников Н. Г. Четаев [11],
И. Г. Малкин [6], Н. Н. Красовский [4], Л. С. Понтрягин,
В. Г. Болтянский, Р. В. Гамкрелидзе, Е. Ф. Мищенко [8] и
многие другие. (Здесь и ниже в квадратных скобках указаны
номера книг из списка литературы, помещенного в конце этого
пособия.)
Основной математический аппарат теории устойчивости
движения — это системы дифференциальных уравнений. Поэтому
системам дифференциальных урагвнении посвящены не только
§ 2, 3, 11, 12, но по .существу и почти .все остальные
параграфы нашего пособия.
§ 2. СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ (ОСНОВНЫЕ ПОНЯТИЯ)
Системой обыкновенных дифференциальных уравнений
называется совокупность дифференциальных уравнений, которые
содержат общие для всей этой совокупности искомые функции
одной независимой переменной и их производные до
некоторых порядков.
Независимую переменную мы будем обозначать буквой t,
так как в дальнейшем ее роль будет играть время. В каждое
уравнение системы для каждой искомой функции могут входить
производные либо до одного и того же порядка, либо до
различных порядков. Число уравнений и число искомых функций
в системе могут либо совпадать, либо не совпадать. Чаще всего
рассматриваются системы, в которых число уравнений и число
искомых функций совпадают.
Напишем в общем виде систему п дифференциальных
уравнений с п искомыми функциями у\, t/2, ..., уп независимой
переменной t:
Л Р; У^Уи Уи • • • , y\kit)\ У*, У%, У* • • . , #2М; ... ]
• ••; Уп>уЛ>'Уп>.-- >^1я)] = о
^2 [*; Ух, Уг, £i, ... , У^2%)\ Уг, У2, уя у?2г)\ ... \
• и и и vink™)] = 0 1' <2Л>
• • • > i/л» i/л» £//i» • • • > Уп »J vr I
Fn ['; Ух, Ух, Уг ytn)\ Уг, Уг, Уг У^; ... \
• ••; Уп'Уп'Уп уппп)] = о }
7
Здесь и в дальнейшем через у^ yjt ..., y/ft) обозначаются
производные соответствующих порядков от функций уз по t.
Подчеркнем, что функции Fu F2, ..., Fn — это известные функции
аргументов, перечисленных в квадратных скобках, а неизвестными,
искомыми, являются только уи Уъ ..♦, Уп-
Пусть в системе (2.1)
max ka = kly max ki2 = k2,
/-1,2 n /=l,2,...,/i
max kin = kn.
/=1,2,...,д
Ясно, что ku k2, ..., kn — это наивысшие порядки входящих в
систему (2Л) производных функций уи У% ..., Уп соответственно.
Число kx называется порядком системы (2.1) относительно
Уи число &2 — порядком системы (2.1) относительно у2, ..., число
kn — порядком системы (2.1) относительно уп.
Число K=ki+k2,+...+kn называется порядком системы (2.1);
во избежание недоразумений мы будем называть это число К
суммарным порядком системы (2.1).
При некоторых условиях (рассмотрение которых ввиду их
сложности выходит за рамки нашего курса) система (2.1)
может быть разрешена относительно старших производных
искомых функций01Л|),У2^\ ..м0яя\ т. е. может быть записана в виде
У\
{кг)=<кК\уиу19уг9
>У\Х \ Уъ> Уъ> Угу
у Уп* Уп> Уп>
, ^-°]
У{2г) = Q2 [t\ Ух Уху Уху • • • > УГ "I Уг> У%, Уъ>
У2 у
i У2 у
> Уп* Уп* Уп>
,^"-,)]
Уп
«V
,(*,-!).
Qn № Ук Уи Уи • ■ •. у\' ; у*, у%> у*, • • •. у\
„(**-».
. (2.2)
• • • 9 Уп> Уп> Уп> •
Эта система имеет суммарный порядок
К = кг + к2+...+кп.
Пример. Рассмотрим систему двух дифференциальных
уравнений с двумя искомыми функциями уи У*.
У г (Ух)3 — Ух*у% — У г sin ух = ОI
(2.3)
*Ук (Ух)3 + У&У2 — Ух ^os #2= 0]
Очевидно, в этой системе &i = 2, &2=3, причем обе старшие
производные у\ и у2 содержатся в каждом уравнении системы
(2.3).
8
Покажем, что систему (2.3) можно разрешить относительно
старших производных. В оба уравнения системы (2.3) старшие
производные входят в виде одинаковых комбинаций (у\)3 и е&*
Относительно неизвестных (t/i)3 и еу* система (2.3) является
линейной алгебраической системой. Выпишем определитель из
коэффициентов при этих неизвестных:
Уг — Уг
*Ух У%
= *У±У1 + УъУг-
При условии, что этот определитель отличен от нуля, система
(2.3) разрешается так:
,3 =
(Уг)
Уг
е72 = А1У±
yzsinyt — yi
yxcosy2 у2
y2s\ny1
y\cosy2
_. у1у2 sinyi + (у{)2cosy2
tyiili + УгУг ty&x + у2у2
= ^iCOSf/2 — tyly2 sin yx
tyiyi + УгУъ tyitji + У2У2
Извлечем кубический корень из обеих частей первого уравнения
и прологарифмируем обе части второго уравнения (здесь мы
берем лишь действительные значения корня и логарифма):
Уг
— •[/ Ш
УгУ2Ь\пух+ (уг)2 cos y2
tyiyi-jry^
"' =in y&i&*yt--ty1ytslny1
tyik + У2У2
г
(2.4)
Это и есть результат разрешения системы ,(2.3) относительно
старших производных у\ и уг.
Для дальнейшего особенно важен случай, когда в систему
дифференциальных уравнений входят только первые
производные искомых функций. В этом случае ki=k2=...=kn=l и
система (2.2) принимает вид:
yi=Qi(t,yi,y2> ••• >Уп)
Уъ = <2Л*>У1>У2>... ,Уп)
Уп = Яп(*>У1>У*> ... >Уп)
(2.5)
Этот вид системы называется нормальной формой системы
дифференциальных уравнений. Очевидно, система в нормальной
форме (2.5) имеет суммарный порядок п.
9
К нормальной форме может быть приведена система (2.2)
при любых ku &2, ..., kn. Для этого наряду со старыми
искомыми функциями уи У2> .♦., Уп нужно принять за новые
самостоятельные искомые функции все их производные, входящие в
правые части системы (2.2).
Введем обозначения для этих новых искомых функций:
[ (2.62)
У\ = Уп
У1 = Уп
Ух = Уis
/'-'> - *м.-1 .
■ (2.6»)
Уп = Ут
Уп = УпЪ
Уп = Упг
У?»-» =
У2 = .
Уъ = .
Уг =
Лк,-\)
У2
>
]
Уп,кп-1
Ун
Угг
У&
= У2,к,-\
(2.6„).
Продифференцируем один раз равенства
(2.60, (2-62) (2.6„):
У1 = Уп
Ух = Уп
</Г° - Уи<-2
yt* = yi.*,-i J
Уг = #21
' Уг = f22 |
. (2.7^ 1
У^ = У2А-2
У2г) = ЙА-1 J
У« = Ут
Уп = #«2
(2.7„)
(2,7.)
Далее берем первое равенство (2.6i), а затем сравниваем
первое равенство (2.7i) ico вторым равенством (2.6i), второе из
(2.7i) —с третьим из (2.6i) и, наконец, предпоследнее из (2.70
с последним из (2.6i). В результате этого получается система
уравнений
Ю
#1 = Уи
Уи = Ун
Ут'= из
#1,*,-2 = #1,4,-1
(2А) \
Это система (k\—1) дифференциальных уравнений первого
порядка с k\ искомыми функциями
Уху Уп> #i2> • •• » yui-i-
Такое же сравнение равенств (2.72) и (2.62), ..., (2.7П) и •
(2.6П) дает подобные же системы, состоящие из (k2— 1), ..., J
(&n—1) дифференциальных уравнений первого порядка: [
У 2 = У 21
У21 ^ У22
У22 = #23
У2,кг-2 = f/2,^-1
(2-8а)
#« = У,л
Уп1 = #«8
УгЛ — УпЗ
Уп,кп-2 = Уп,ка-1
(2-8») .
Делаем замену в правых частях уравнений системы (2.2), ис- .
пользуя равенства (2.6i), (2.62), ..., (2,6П), и >в левых частях. I
используя последние из равенств (2.7i), (2.72), ..., (2.7П):
У1Л-1 = Qi (t; У1У Уи, у12, • •. , Уиъ-г;
• • • i Уя» #я1> #я2» • • • * Уп£п—\)
У2,к2-\ = Q2(tu, Уху Ухху Угы • • • » У\,кг-\\
• • • J #л> #Л1> */Л2> • • • » Уп,кп—\)
(2.9) ;
Уя,*я-1 = Q„ (*; Ун Уп, Уп* • • • I #ut-r, • • •
• • • > #/l> #/llt #/l2» • • • » yn,kn—l)
Это система п дифференциальных уравнений первого порядка
с &i + &2+... + &n искомыми функциями.
Совокупность систем (2.8i), (2.82), ..., (2.8П) и (2.9)
образует систему ki+k2 + ... + kn дифференциальных уравнений
первого порядка с тем же числом искомых функций. Bice уравнения
этой системы разрешены относительно производных, следова- [
И;
тельно, мы получили нормальную форму системы
дифференциальных уравнений.
Если описанную замену сделать не в системе (2.2), а в
системе (2.1) и затем присоединить .системы (2.8i), (2.82), ♦..,
(2.8П), то, конечно, тоже получится система дифференциальных
уравнений первого порядка, но не в нормальной форме.
Важно подчеркнуть, что как исходные системы (2.2) и (2.1),
так и полученная из них путем описанного преобразования
система уравнений первого порядка, имеют один и тот же
суммарный порядок K=k} + k2+ ... +kn.
Системой линейных дифференциальных уравнений
называется система, которая состоит иэ уравнений первой степени
относительно совокупности всех искомых функций и всех
их производных, входящих в эту систему. Такую систему
называют также линейной системой дифференциальных уравнений.
Так, например, система (3.2) § 3 линейная, а рассмотренные
выше системы (2.3) и (2.4) нелинейные.
Замечание. В случае линейной системы дифференциальных уравнений
условия разрешимости ее относительно старших производных упрощаются.
Проще всего это выяснить для системы линейных дифференциальных
уравнений первого порядка.
Пусть дана система п линейных дифференциальных уравнений первого
порядка с п искомыми функциями в виде, не разрешенном относительно
производных:
(аи^ + а12у2 + ... + а1пуп) + (рц#! + р12у2 + ... + р1пуп) + h = О
(а21уг + а22у2 + .. . + а2пуп) + ф21у1 + $22у2 + •. • + ЪгпУп) + h2 «= О
(<Wi + art2#5 + ... + аппуп) + фп1у1 + рп2у2 + ... + рппуп) + hn=0
. (2Л0)
Здесь уи У2> ...» Уп—искомые функции независимой переменной t\ yu У2, ...
♦••» Уп—их первые производные по t\ коэффициенты а^, (З/д и свободные
члены hi
(t=l, 2, ... , п; k=l, 2, ... , я) —
заданные функции от / или, в частности, постоянные. Поэтому определитель
из коэффициентов при уи У2, ...» Уп, т. е. определитель
au a12 ... alrt
a2l a22 • • • °2/l ,
= a,
ЛЯ1 «Я2 • • • аП
который раскрывается по тому же правилу, как и определитель третьего
порядка (подробнее об этом см. § 10), есть известная функция от t или постоянная
величина. При всех значениях ty для которых а=^0, систему (2.10) можно
разрешить относительно у\, У2, ..., Уп как систему линейных алгебраических
уравнений, т. е. записать в виде:
12
У\ = Yn^i + Yi2^2 + •. • + ЧмУп + h |
Уг = Y2i#i + Y^#2 + • • • + ЧгпУп + h \
(2.И)
Уп = УтУ1 + УюУг + ■.. + УппУп + /J
Конечно, здесь у// являются соответствующими комбинациями функций а^
и Р^, а /у — комбинациями а^ и /*/.
Совершенно аналогично можно убедиться в том, что система п линейных
дифференциальных уравнений любого порядка с п искомыми функциями
может быть разрешена относительно старших производных, если определитель
из коэффициентов при старших производных отличен от нуля, причем слова
«старшие производные искомых функций» здесь имеют, конечно, тот же смысл,
как и в общем случае систем (2.1), (2.2).
§ 3. О РЕШЕНИЯХ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
Решением системы п дифференциальных уравнений с п
искомыми функциями называется система п функций
й = л(о| (ЗЛ)
Уп=УпУ)>
подстановка которых в систему уравнений вместо искомых
функций превращает ее в систему тождеств относительно
независимой переменной t.
Подчеркнем при этом, что функции (3.1), образующие
решение, нужно подставлять в дифференциальные уравнения, строго
соблюдая их нумерацию как в системе уравнений, так и в
системе (3.1); те же функции (3.1), подставленные в систему
уравнений без соблюдения нумерации, могут не обратить эти
уравнения в тождества, т. е. могут не образовать решение. Функции
(3.1), образующие решение системы дифференциальных
уравнений, часто называют компонентами решения, точнее первой,
второй, ..., /1-й компонентами решения.
Известно, что одно дифференциальное уравнение может
иметь много решений, даже бесконечно много решений. Это
положение распространяется и на системы дифференциальных
уравнений.
Пример 1. Пусть дана система дифференциальных
уравнений
13
01 = Уг—Уз
02 = 0i + Уз
(3.2)
+ С8е-'
03 = 01 + 02
Возьмем систему функций
0i= Сх
Уш = -С1 + С^-Суе-' [, (3.3)
где Си Сг, Сз — произвольные постоянные. Для каждой тройки
числовых значений постоянных Cit C2, Сз из равенств (3.3)
получается тройка функций, которые при подстановке их (с
соблюдением номеров) в систему (3.2) превращают ее в систему
тождеств. Следовательно, система (3.3) представляет собой
совокупность решений системы (3.2).
Рассмотрим подробнее вопрос о решениях системы п
дифференциальных уравнений первого порядка с п искомыми
функциями, записанной в общем виде:
Л (<; 01. у» 02.02; • • •; у„, уп) = °
F* (<; 01, у\; 02.02; • • •; 0„. уа) = о
РЯ(Ь 0i. 01*. 02- 02; • • •; уя. Уп) = °
или в нормальной форме
01 = Ql(t, 01,02 Уп)
02 = Qi (*. 01. 02 Уп)
(3.4)
(3.5)
Уп - Qn (ft 0i. 02, • • •. Уп)
При изложении этого вопроса мы увидим, что свойства
одного дифференциального уравнения первого порядка и свойства
системы дифференциальных уравнений первого порядка во
многом аналогичны.
Часто приходится рассматривать такое решение системы
(3.4) или (3.5), что функции, образующие это решение,
принимают заданные значения при некотором значении t=U.
01 tt>) = 010
02 #о) = 020
Уп(*о)=УпО
(3.6)
14
Эти условия называются начальными условиями или системой
начальных условий, а такое решение называется частным
решением системы уравнений (3.4) или (3.5), соответствующим или
удовлетворяющим системе начальных условий (3.6).
Система начальных условий вида (3.6), которой
соответствует хотя бы одно частное решение системы дифференциальных
уравнений (3.4) или (3.5), называется допустимой для этой
системы уравнений, а в противном случае — недопустимой.
Так, в приведенном выше, примере 1 начальные условия
вида
Уг (to) = Ую
Уг (to) = #20
Уз (to) = Узо J
(3.7)
с любой четверкой чисел t0i y10, уго, #зо допустимы для
системы уравнений (3.2).
В самом деле, подставляя любые числа t0, уюУ #2о, узо вместо
t, Уи #2, Уг в равенства '(3.3), Мы получаем систему трех
линейных алгебраических уравнений с тремя неизвестными Сь С2„ С3:
Ухо = Сг + Сае-<* )
У2о = —С1 + С2е*°—Све-*>
Узо = —Сг + С2е*о
(3.8)
Каждой четверке чисел /о, Ую, */2о, узо соответствует
единственное решение Сю, С2о, Сзо системы (3.8), так как в ней
определитель из коэффициентов при неизвестных не равен нулю:
1 0 *-*•
— 1 е*° — е~'°
— 1 <к 0
= 1.
Подставляя Сю, С2о, Сзо, т- е- решение системы (3.8), вместо
Ci> Сг., Сз в равенства (3.3), мы получаем частное решение
системы (3.2), соответствующее начальным условиям (3.7).
Пример 2. Пусть дана система уравнений:
Уг
У*
V у г
-V
г
Уг
У1
(3.9)
15
Возьмем систему функций:
Л = (^ + С1)С1
t + Cx
(ЗЛО)
где С\ и С2 — произвольные постоянные, но С2ф0. Для каждой
пары числовых значений Сь С2 из равенств (3.10) получается
пара функций, которые при подстановке их в систему (3.9)
превращают ее в систему тождеств. Следовательно, система (ЗЛО)
представляет собой совокупность решений системы (3.9).
Очевидно, уравнения (3.9) теряют смысл при #i = 0 и #2=0,
т. е. на осях координат плоскости у и у%. Далее, если принимать
во внимание лишь действительные значения t, yu у2, С\, С2, то
уравнения (3.9) имеют смысл только при совпадении знаков
ух и #2, т. е. внутри первой четверти и внутри третьей четверти
плоскости #i, г/2, и не имеют смысла во второй и четвертой
четвертях.
Так как правые части уравнений (3.9) положительны
(корень взят со знаком « + »), то и у\у у2 должны быть
положительны, но из равенств (ЗЛО) следует
Vi =
Уг =
с2
1
с,
и, значит, Сг>0.
Рассмотрим начальные условия вида
Ух (h) = Ум
У* (to) = У».
(3.11)
Из сказанного ясно, что эти начальные условия
недопустимы для системы (3.9), если в тройке чисел to, yw> у?о одно или
оба числа ую, у2о равны нулю либо ую и у2о имеют разные
знаки.
Покажем, что при любой тройке чисел to, Ум, #20, в которой
Ум, #2о не равны нулю и имеют одинаковые знаки, начальные
условия (3.11) допустимы для системы (3.9). Для этого
подставим t=t0, #1=#ю, уг=У2о из условий (3.11) в систему функций
(ЗЛО):
fto^o + CJCV
#20 — -
16
Для каждой тройки чисел t0, г/ю, */2о, в которой #1оУ2о>0, эта
система имеет свое единственное решение:
С10 = Ую l/^ - U = У20l/^ - 'о )
V УЮ V #20
>.
Подставляя Ci = Ci0, C2 = C2o в систему (ЗЛО), мы получаем
частное решение системы (3.9), соответствующее начальным
условиям (3.11).
Как узнать, какие начальные условия для данной системы
дифференциальных уравнений первого порядка допустимы и
какие недопустимы? Мы дадим упрощенную формулировку
теоремы, которая отвечает на этот вопрос.
Теорема существования и единственности
частного решения нормальной системы
дифференциальных уравнений.
Пусть заданы система п дифференциальных уравнений
первого порядка с п искомыми функциями в нормальной форме
(3.5) и система начальных условий (3.6).
1) Если точка M0(t0, #10, #2л, ..., Упо) находится внутри
(п + 1)-мерной области переменных ty у\, у2, ..., уп> в которой
непрерывны функции Qi, Q2, ..., Qn> то существует частное
решение системы (3.5), удовлетворяющее условиям (3.6), т. е.
начальные условия (3.6) допустимы для системы (3.5).
2) Если, кроме того, в этой (п + 1) -мерной области функции
Qi имеют непрерывные частные производные
-%&- t = 1, 2, ... ,лг; / = 1,2 я,
то указанное частное решение единственное.
Более общую и точную формулировку этой теоремы, а также
ее доказательство можно найти, например, в [10] (гл. IV, § 1,
п. 2, стр. 142—149). В примере 1 любые начальные условия (3.7)
допустимы для системы (3.2) именно потому, что правые части
уравнений (3.2) непрерывны и даже дифференцируемы при всех
значениях уи у2, у3.
В примере 2 для системы (3.9), как мы видели, допустимы
только такие начальные условия (3.11), в которых r/ю и #2э не
равны нулю и имеют одинаковые знаки. Это объясняется тем,
что только внутри первой и третьей четвертей плоскости у и У*
правые части уравнений (3.9) действительны, непрерывны и
даже дифференцируемы.
Из приведенных примеров мы видим, что система
дифференциальных уравнений первого порядка имеет совокупность
частных решений, зависящую от произвольных постоянных.
17
Общим решением системы п дифференциальных уравнений
первого порядка с п искомыми функциями называется
совокупность ее частных решений, зависящая от п различных
произвольных постоянных так, что каждой допустимой
системе начальных условий соответствуют определенная система
значений этих постоянных и определенное частное решение из
указанной совокупности. Точнее говоря, общим решением системы
п дифференциальных уравнений первого порядка с п искомыми
функциями, заданной в виде (3.4) или (3.5), называется
система п функций
yi = yi(t,ClfCt9...,Cn))
Уг — й(^1»Ц) • • • > Сп/
Уп = Уп(*>С1>С*>--- >Сп) )
(3.12)
которая
1) удовлетворяет системе дифференциальных уравнений
(3.4) или (3.5) при любых значениях произвольных
постоянных C\f Сг, ..., Сп\
2) для каждой допустимой системы начальных условий
вида (3.6) значения постоянных Сь С2, ..., Сп можно подобрать
так, что функции- (3.12) будут удовлетворять этим условиям
(3.6).
Здесь произвольные постоянные Си Сг, ..., Сп называются
различными в том смысле, что в общем решении их число не
может быть уменьшено.
Так, в примере 1 система функций (3.3) образует общее
решение системы уравнений (3.2), а в примере 2 система
функций (3.10) представляет собой общее решение системы
уравнений (3.9).
Рассмотрим теперь вопрос о решениях системы п
дифференциальных уравнений с п искомыми функциями, заданной в
виде (2.1) или (2.2), в которую входят старшие производные у№\
У2 , • • • , Уп п •
Начальные условия для выделения частного решения
системы (2.1) или (2.2) состоят в задании значений искомых
функций и всех их производных до порядков (ki—1), (k2—1), ...,
(kn—1) включительно при некотором значении t=tQ:
Ул. (to) = Ую Уг (h) = Уго •.. Уп (*о) = У по
У\ ^о) = Ую Уг (to) = Уго - - * Уп (fo) = УПо
№-1ЧЬ) = У&-1} y{2k>-l)(to) = y$-l) ... tti*-l4U)=y$rrl)
(3.13)
18
Число условий в системе (3.13) равно суммарному порядку
системы уравнений (2.1) или (2.2). Заданные числа в правых
частях равенств (3.13) называются компонентами начальных
условий.
Задача отыскания частного решения системы (2.1) или (2.2),
удовлетворяющего начальным условиям (3.13), и, в частности,—
частного решения системы (3.4) или (3.5), соответствующего
начальным условиям (3.6), называется задачей Коши.
Для системы уравнений вида (2.2) имеет место теорема
существования и единственности частного решения, аналогичная
приведенной выше теореме для нормальной формы системы
дифференциальных уравнений. Это станет понятным, если
вспомнить, что в § 2 было показано, как система (2.2)
приводится к нормальной форме.
Общим решением системы п дифференциальных уравнений
с п искомыми функциями, заданной в виде (2.1) или (2.2),
называется совокупность ее частных решений, зависящая от
(k\ + k2+... +kn) различных произвольных постоянных так,
что каждой допустимой системе начальных условий вида
(3.13) соответствуют определенная система значений этих
постоянных и определенное частное решение иа указанной
совокупности.
Как фактически найти общее решение системы
дифференциальных уравнений? При выполнении двух условий, которые
сейчас выяснятся, это удается сделать путем приведения
системы дифференциальных уравнений к одному дифференциальному
уравнению более высокого порядка (чем уравнения данной
системы) с одной искомой функцией.
Прежде всего заметим, что не всякая система
дифференциальных уравнений может быть сведена к одному уравнению.
Приведем два примера систем, не сводящихся к одному
уравнению.
Пример 3. Система
Уг^Уг 1
Уг= Уг\
распадается на два независимых уравнения, так как первое из
них не содержит #2, а второе не содержит у\. Общее решение
этой системы получается интегрированием каждого уравнения
в отдельности:
У1 = С^ j
#2= С^У
19
Пример 4. Система
У±= У2
У 2 = У\
Уз = Уз)
распадается на подсистему из двух уравнений
У\ = У А
Уъ = У1 Г
не содержащих #3, и отдельное уравнение */з=Уз, не
содержащее у\ и у2.
Покажем, как приводится к одному дифференциальному
уравнению с одной искомой функцией, например уи система п
дифференциальных уравнений первого порядка с п искомыми
функциями, заданная в нормальной форме:
#l=Ql(*>#l.#2> -->>Уп)
y% = Q2(t,yi>y*,... ,уп)
Уп = <2п(*>У1>У2, ... ,y«)i
(3.14)
Для этого продифференцируем по I первое из уравнений (3.14):
;; __ dQi » dQt • , dQt • , , dQx • ,„ - -.
dt
tyi
ду2
дуп
Подставляем сюда вместо у и #2, ..., уп их выражения Qi, Q2, ...,
Qn из системы (3.14):
Вводя краткое обозначение для правой части этого уравнения,
напишем его в виде
Дифференцируя полученное уравнение и поступая аналогично
предыдущему, найдем
У1 = Я8(*,У1.У2. ••• 'у^-
20
Продолжая далее таким же образом, получим, наконец,
уравнение
y\n) = Rn(t,yi,y* Ю-
Итак, мы получаем следующую систему:
#i = Qi (*.</i. #>> ••• ,У„)
У1=Яг(*,Уг,У2, ■■■ ,Уп)
Ух = Яз(^. Уи У* . Уп) \. (3.16)
y\n-l)=Rn-At,yi,y„...,yn)
y\n) = RAt,yi,y* Уп)
Теперь из п уравнений этой системы нужно исключить п—1
функций 1/2, Уз, ..., Уп- Для этого из первых (п—1) уравнений
системы (3.16) щайдем (если это возможно) г/2, #з, ..., уп,
выразив их через t, y\ и производные
y2 = s2{t,ylfk>k,
y3 = sa(t,y1\k,k>
У\ )
, уГ1))
уГ1))
(3.17)
yn = sn(t>yi>yi>yi>
Подставляя эти выражения в последнее из уравнений (3.16),
получим уравнение n-го порядка с одной искомой функцией у\\
yj«> = s (*, ylf ylf л уГ"1}). (3.18)
Найдем (если возможно) общее решение этого уравнения:
yi=!h(t,Cl9C%9 ...,СЯ). (3.19)
Дифференцируя последнее выражение (п—1) раз, найдем
производные уи Уи ..., */i(n-1) как функции от t, Cu С2, ..., Сп.
Подставляя эти функции в уравнения (3.17), получаем #2, Уз,—>
У п.
У* == Уъ ('» ^1> ^2» • • ■ > ^я)
Уз ~ Уз (*> Q» Q» • • • » ^п) | /3 20)
y« = yn(t.cltct,...,cn)
21
Система функций (3.19), (3.20) образует общее решение
заданной системы дифференциальных уравнений (3.14).
Таким образом, общее решение системы (3.14) получается
изложенным способом при выполнении двух условий: (п—1)
первых уравнений системы (3.16) разрешимы относительно у?,
Уг, ..., Уп и возможно найти общее решение уравнения (3.18).
Читателю рекомендуется обнаружить, что к системе (3.2),
приведенной в примере 1, этот метод применим лишь
относительно #2, но не относительно у\ и #3, и объяснить, почему
именно. Систему (3.9) из примера 2 можно свести к одному
уравнению и относительно у\ и относительно #2, но общее решение
системы (3.9) проще получается без этого.
Замечание 1. Может случиться, что функции #2, Уг, ..., Уп
исключатся не из всех п уравнений системы (3.16), а из
системы, которая получается из системы (3.16) отбрасыванием
одного или нескольких последних (а возможно и не только
последних) ее уравнений. Тогда мы получим дифференциальное
уравнение с искомой функцией t/i, порядок которого ниже п.
При этом может также случиться, что вместо всей системы (3.17) удастся
написать выражение лишь некоторых из функций t/г» </з, ..., Уп через ty yu t/i,...
..., t/j *>где k<n—1. Следовательно, указанным выше способом в этом случае
мы найдем не все искомые функции. Чтобы найти остальные искомые
функции, нужно подставить найденные функции лишь в те уравнения 'исходной
системы (3.14), которые содержат производные еще не найденных функций,
и к полученной нормальной системе применить описанный выше метод.
Замечание 2. Как в уравнении (3.15), так и в уравнениях,
получающихся при последующих дифференцированиях, можно
не заменять у\ через Qi(t, уи #2, ..., Уп)- Тогда вместо системы
(3.16) получится система, £-е уравнение которой в правой части
содержит
УиУи ••• . У$/—° 0 = 1,2, ... ,л).
Исключая из этой системы #2, #з, ..., Уп, все равно придем к
уравнению (3.18).
Замечание 3. Описанный метод можно применять и к системе
дифференциальных уравнений выше первого порядка, заданной в виде (2.2), т. е.
в виде, разрешенном относительно старших производных.
Замечание 4. Если система (3.14) или (2.2) линейна
относительно искомых функций, то и уравнение (3.18) и
уравнение, к которому приводится система (2.2), также являются
линейными.
Впрочем для систем линейных дифференциальных уравнений
с постоянными коэффициентами имеется и другой более
простой метод нахождения общего решения, который особенно
22
удобен при п>2. В § 12 этот метод будет рассмотрен для
линейных систем первого порядка.
Замечание 5. Кратко остановимся на случае, когда число
уравнений и число искомых функций в системе не совпадают.
Рассмотрим систему т уравнений с п искомыми функциями при
тфп.
Если т<я, то система уравнений будет неопределенной в
том смысле, что в качестве каких-либо п—т компонент
решения можно брать произвольные (достаточное число раз
дифференцируемые) функции и уже в зависимости от них находить
остальные т компонент.
Если т>п, то система уравнений может оказаться
несовместной, т. е. не имеющей ни одного решения.
§ 4. ОПИСАНИЕ ДВИЖЕНИЙ
С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
1. Механическое движение материальной точки
Рассмотрим движение материальной точки, имеющей
постоянную массу т.
Пусть прямоугольная декартова система координат,
относительно которой изучается движение точки, определена началом
координат О и единичными координатными векторами еъ е2, е3.
Координаты точки в этой системе обозначим через уи t)i, У*.
Тогда радиус-вектор, а также векторы скорости и ускорения
движущейся точки выразятся так:
r = yiex + y2e2+y3e3\
^УА + Й^ + УА
Г = #1*1 + #2*2 + #3*з)
(4.1)
Обозначим через F равнодействующую всех сил,
действующих на движущуюся материальную точку, а через, Fu F2, F3
проекции этой равнодействующей на еи е2, #з, так что
F = F1el + F2e2 + FBe3. (4.2)
Пусть известно, как выражается вектор F через ttr, r, и,
следовательно, Fu F2, F3 являются известными функциями
F = F{ttr;+)
23
Л = Л (t, ylt ylt yt, y\, y3, ys))
^2 = Рг(t, ylt Уi, Уг, Уг, У3, Уз)
?з = Ft (f, ylt ylt y%, у\, Уз, у3)
(4.3)
Тогда уравнение движения материальной точки в векторной
форме имеет вид:
mr = F(t, r, г).
(4.4)
Используя выражения (4.1) — (4.3), можно переписать одно
векторное уравнение (4.4) в виде системы трех скалярных
дифференциальных уравнений второго порядка:
"Ч/х = Fi Р. Ук Ук Уъ>'Уг> Уз, Уз)
™Уг = *«('. Уи Уъ Уг, Уг, Уз, Уз)
ту» = рз (t, yx, ylt Уг, Уг, Уз, Уз)
(4.5)
Каждое частное решение этой системы дает закон некоторого
конкретного движения. Общему решению системы (4.5)
соответствует совокупность движений или, как говорят, класс
движений, причем этот класс движений зависит от шести
произвольных постоянных. Подчеркнем при этом, что одна и та же
система (4.5) описывает каждое из этих движений; поэтому говорят,
что одна система дифференциальных уравнений описывает
класс движений. Для того чтобы из класса движений
выделить конкретное движение, нужно в некоторый момент t=to
задать начальные условия
(т. е. положение и скорость точки в момент to). В
координатной форме получается система из шести начальных условий
01 Со) = Ум 0iCo) = 0io
02 (to) = 020 02 Со) = 020
03 Со) =030 03 Со) = 030 )
(4.6)
При этом точку M0(t0, 0ю, 0ю, 020, 020, 0зо, 0зо) нужно брать
внутри области непрерывности функций Fu F2, Fa. Частное
решение системы (4.5), соответствующее условиям (4.6), дает закон
этого конкретного движения.
24
В дальнейшем в качестве момента U в условиях (4.6) мы
будем брать начальный момент £ = 0, т. е. момент, начиная с
которого отсчитывается время при изучении движений; при этом
числа #ю, #20, #зо и r/ю, #гэ, Уъъ называются соответственно на-
чальными координатами и проекциями начальной скорости
движущейся точки.
Если точка движется в одной плоскости, то векторы ее
скорости и ускорения, т. е. векторы г и г, а также
равнодействующая всех сил, действующих на точку, все время находятся в
этой плоскости. В этом случае векторы^, e% удобнее всего взять
в той же плоскости. При этом уъ = 0, у3 == 0,Уз == 0, F3 == 0;
следовательно, в выражениях (4.1) и (4.2) отпадут третьи
слагаемые, а вместо системы трех уравнений (4.5) получится система
двух уравнений:
Щ\ = Fi (*. Уъ Уи Уг> Уъ) 1 /4>5/ч
my2 = F*{t,yu УъУг* #а) I
в правые части которых, как и в выражения (4.3), не будут
входить #з, #з. Класс движений, описываемых системой (4.5'),
зависит от четырех произвольных постоянных. Для выделения
каждого конкретного движения требуются четыре начальных
условия из шести условий (4.6).
Если точка движется по прямой, то векторы ее {скорости и
ускорения, а также равнодействующая всех сил, действующих
на точку, все время расположены на этой прямой. Очевидно,
в этом случае вектор в\ удобнее всего взять на той же прямой.
При этом в выражениях (4.1) и (4.2) останутся только первые
слагаемые, в которых индекс 1 можно не писать, а векторное
уравнение движения (4.4) заменится одним скалярным
уравнением
my = F(t,yty). (4.5")
Класс движений, описываемых этим уравнением, зависит от
двух произвольных постоянных. Каждое конкретное движение
выделяется с помощью двух начальных условий:
У (*о) = Уо 1
У(*о) = Уо I
Наряду с у и у 2, У г можно принять за самостоятельные
искомые функции и у и У 2, Уз, вводя для них обозначение
yi = Vi
Уъ = Щ
Уз = у3 )
(4.7)
25
Дифференцируя эти равенства
#i = 0i
У 2 =Л
и делая замену в системах уравнений (4.5) и (4.5'), получаем
системы:
mv1 = Л (/, уи vl9 у2, v2l y3l v3)
тщ = F2 (f, уъ vlt y2t v2i y3, v3)
™>v3 = F3 (t, ylt vl9 y2, v2t уЗУ v3)
mvl = F1(t, yl9vu y2tv2) |
mv2=F2(t,ylfvl,y2,v2) J
(4.7')
(4.7")
При этом систему (4.7") нужно рассматривать совместно с
системой уравнений (4.7), а систему (4.7") — совместно с первыми
двумя уравнениями системы (4,7). Такая же замена в
уравнении (4.5") приводит к системе
у = и \
mv = F(t,y,v) J
Таким образом, движение материальной точки описывается
системой дифференциальных уравнений второго или первого
порядка либо одним дифференциальным уравнением второго
порядка, если ускорение не постоянно. Между тем можно
проверить, что для описания равномерного и равноускоренного
движений можно не прибегать к дифференциальным уравнениям.
Теперь рассмотрим физический пример прямолинейного
движения материальной точки, который будет использован и в
дальнейшем (см. § 5, 7, 8).
Пример 1. Пусть на вертикальной пружине подвешен
железный шарик массы т, который будем считать материальной
точкой.
Рассмотрим движение шарика но вертикальной прямой,
которую и примем за координатную ось. За начало координат О
на этой оси примем точку, в которой находится неподвижный
шарик, когда его вес уравновешивается упругой силой
пружины, а какие-либо другие силы отсутствуют (рис. 1).
Положительное направление на оси возьмем вниз.
Если шарик отклонить вверх или вниз от точки О и затем
отпустить или толкнуть его вверх или вниз, то он придет в
движение.
26
Обозначим через у отклонение шарика от точки О в момент t:
y-yit).
жш
Мы будем допускать лишь такие отклонения шарика от
точки О, при которьих не превосходится предел пропорциональной
упругости пружины. При этом условии упругая сила пружины,
стремящаяся вернуть шарик к точке О, пропорциональна его
отклонению и всегда направлена по вертикали в сторону,
противоположную отклонению. Действительно,
когда шарик отклоняется вниз от точки О, то
у принимает положительные значения, а
упругая сила действует вверх, если же шарик
отклоняется вверх от точки О, то у принимает
отрицательные значения, а упругая сила
направлена вниз. Таким образом, проекция
этой упругой силы на вертикальную ось
выразится так:
/упР = — аУ>
здесь положительная постоянная а зависит
от упругости пружины.
Напомним, что у и у дают проекции
скорости и ускорения шарика на вертикаль.
Пусть на шарик действует вертикальная сила,
препятствующая движению и
пропорциональная скорости, например, сила сопротивления среды,
происходит движение. Эта сила направлена противоположно
скорости движения, поэтому ее проекция на вертикаль
выразится так:
Рис. 1
в которой
/<
сопр
-Ъу,
где |3 — положительная постоянная.
Наконец, пусть на шарик действует вертикальная активная
сила, способствующая движению и пропорциональная скорости.
Очевидно, проекцию этой силы на вертикаль можно записать так:
/а,
У У,
где у — положительная постоянная. Такую активную силу
можно создать, например, с помощью вертикального магнитного
поля, напряженность которого пропорциональна скорости
шарика и, следовательно, изменяется синхронно с изменением этой
скорости. Однако здесь мы не рассматриваем конструкцию
установки, в которой осуществляется такое магнитное поле.
Постоянные <х, р, у считаются известными.
Так как векторы скорости и ускорения шарика и всех сил,
Действующих на него, направлены по вертикали, то при состав-
27
лении уравнения движения шарика мы сразу перейдем от
соотношения между этими векторами к соотношению между их
проекциями. Таким образом, уравнение движения шарика имеет
вид:
тУ = /упр + /сопр + /актив, Т. е. ту = — Щ — (5ij + ytj.
Перенесем все члены уравнения в левую часть и разделим
на т:
0.
м
обоз]
У +
*ачения:
а
т
= (02
_Р_
((С
т
>0), -
а
т
т
У-
У-
= 2k.
Тогда уравнение движения примет вид:
y + 2ky + tfy = Q. (4.8)
Характер движения шарика зависит от того, будет ли & = 0,
k>0 или &<0, а также от того, будет ли \k\ <co, \k\ =co или
Щ >со.
Разберем некоторые из этих случаев.
1. k = 0. В этом случае сила сопротивления в точности
уравновешивается активной силой (Р=у)- Уравнение (4.8) при этом
принимает вид:
£ + ©»у = 0. (4.9)
Характеристическое уравнение г2+со2 = 0 имеет чисто мнимые
корни Г1,2= ±cof. Поэтому общее решение уравнения (4.9)
пишем в виде:
у = сг с os at + C2 sin at. (4.10)
Это равенство определяет класс движений, описываемых
уравнением (4.9). Чтобы из этого класса выделить какое-нибудь
конкретное движение, зададим начальные условия:
(4.11)
У(0) = Уо )
Дифференцируем равенство (4.10):
у = — Схсо sin at + C2G)~cos arf. (4.12)
Подставляя в (4.10) и (4.12) t = 0 и используя начальные усло-
Уо
т, и а ли дим <-»l=£/0» ^2 =
28
вия, находим С\=уо, С2 = —. Конкретное движение выражается
О)
частным решением уравнения (4.9) при начальных
условиях (4.11):
У = Уо cos ©f+ -^- sin co^. (4.13)
(О
Выясним характер движений, входящих в класс (4.10). Для
этого введем вместо произвольных постоянных Сь Сг новые
произвольные постоянные Л и ф с помощью следующих
соотношений:
А = + У~С21 + С22; sin ер = -^Ц cosq> = -^-,
так как
Преобразуем равенство (4.10) так:
у = Л/'3-cos otf + — sincoA
т. е. у = A (sin ф cos Ы + cos ф sin otf),
и, наконец,
# = A sin(arf + q>). (4Л 4)
Движения, выражаемые синусоидальной функцией (4.14),—
это простые гармонические колебания с постоянной
амплитудой Л, начальной фазой ф и частотой со. Каждой системе
начальных условий вида (4.11) соответствуют свои значения Л и ф.
Итак, класс-движений (4.10) или (4.14) — это класс простых
гармонических колебаний
2. кф09 |£|<ю.
В этом случае сила сопротивления и активная сила не
уравновешиваются (k¥=0, т. е. $Фу), одна превосходит другую, но
так, что Щ <со.
Пишем характеристическое уравнение для уравнения (4.8)
г2 + 2kr + со2 = 0
и находим его корни п,2 = —k ± Y& — со2. Эти корни
комплексные, так как | k \ < со, поэтому, вводя обозначение v = + ]/со2 — &2,
перепишем их так: Г\,2 = —k±vi.
Общее решение уравнения (4.8) пишем в виде:
у = е"ы(Сг cos ^ + С2 sin vt). (4.15)
29
Из этого класса движений выделим конкретное движение
с помощью начальных условий вида (4.11). Дифференцируем
равенство (4.15):
у = — ке~ы (Сг cos xt + C2 sin \t) + e~~kt (— Cxv sin vt + Cav cos \t).
(4.16)
Подставляя в (4.15) и (4.16) £ = 0 и используя условия (4.11),
находим Ci=yo\
Уо = ~ hCx + C2v, откуда С2 = *> + **.
Искомое конкретное движение выражается частным
решением уравнения (4.8) при условиях (4.11)
у = e-kt (у0 cos v/ + y° + ky° sin vt). (4.17)
Чтобы выяснить характер движений, входящих в класс (4.15),
перепишем тригонометрический двучлен в этой формуле точно
так же, как при переходе от равенства (4.10) к равенству (4.14),
после чего выражение (4.15) принимает вид:
у = Ае-и sin(vt+<?). (4.18)
Отсюда видно, что движения, образующие клаас (4.15),
(4.18), — это колебательные движения с частотой v, начальной
фазой фи переменной амплитудой Ae~kt.
Если &>0, т. е. если сила сопротивления превосходит
активную силу (P>y)> то амплитуда Ае~ы быстро убывает с
течением времени, поэтому при k>0 движения класса (4.15), (4.18)
являются затухающими гармоническими колебаниями.
Если &<0, т. е. если активная гала превосходит силу
сопротивления (y>P), to амплитуда Ае~ы неограниченно возрастает
со временем. Поэтому при k>0 движения класса (4.15), (4.18)
представляют собой неограниченно нарастающие гармонические
колебания.
Конечно, неограниченное возрастание амплитуды физически
невозможно, так как при достаточно больших значениях
амплитуды движение совершенно изменится или прекратится либо
потому, что будет превзойден предел пропорциональной упругости,
затем предел упругости и пружина получат необратимую
деформацию, либо потому, что шарик достигнет одного из
полюсов магнита.
30
„.* -7Ч»> 1У
2. Примеры движений,
отличных от механического движения
Рассмотрим еще три примера.
Пример 2. Закон распада радиоактивных элементов состоит
в том, что скорость распада пропорциональна количеству нерас-
павшегося элемента. Зная период полураспада 8, т. е. время,
в течение которого распадается половина первоначального
количества элемента, выразить закон распада в конечной, т. е. не
дифференциальной, форме.
Пусть у— количество нераспавшегося элемента в момент
времени t, а уо — первоначальное количество элемента при£=0.
Скорость распада, т. е.——, пропорциональна у. Следовательно,
дифференциальное уравнение, описывающее процесс распада,
можно написать в виде:
-^ =-&*/. (4.19)
Здесь k — пока неизвестная положительная константа, знак
минус поставлен потому, что — <0, так как у убывает с течением
at
времени.
Общее решение уравнения (4.19) имеет вид:
у = Се-**.
Используя начальное условие y(0)=y0i получаем С=*/о, так
что
У=Уъ<ГН. (4.20)
Для нахождения k используем условие полураспада у (0) =
= -—-. Подстановка t = 0, у = -^- в равенство (4.20) дает
-f = ytfi-k\ откуда 4-Jii
Подставляя это значение k в равенство (4.20), окончательно
получаем
*_
У = Уо2 ' .
При каждом конкретном значении уо это равенство
выражает конкретный закон распада, а при всевозможных значениях
Уо — класс таких законов.
31
Пример 3. На рис. 2 дана схема электрической цепи,
которую образуют четыре последовательно соединенных звена:
звено ab — индуктивность, имеющая самоиндукцию L; звено be —
активное (омическое) сопротивление R\ звено cd — конденсатор,
имеющий емкость С; звено da —
электродвижущая .сила (э.д.с.) E=E(t).
Согласно . определениям, которые
даются в физике, величины L, R, С
положительны. Пусть L, R, С —
заданные постоянные, a
E=E(t)—заданная функция времени t или, в
частности, постоянная. Цепь, изображенная
на рис. 2, называется простым LRCE
контуром. Положительным
направлением тока в контуре считается
направление движения часовой стрелки.
Поскольку в (Простом контуре нет
никаких разветвлений цепи, то во всех его
звеньях течет одинаковый ток, величину которого обозначим
через 1=1 (t). Итак,
1аЬ = he = lcd = Ida:=I = 1 (О-
Обозначим через Q = Q(t) электрический заряд на верхней
пластинке конденсатора.
Пусть в некоторый момент t=t0 заданы заряд конденсатора
и сила тока в контуре:
Рис. 2
(4.21)
Требуется найти величины заряда Q = Q(t) и тока 1=1(t) как
функции времени.
Заметим, что эти функции связаны соотношением
Q V) = Q (t0) + j / W dx, откуда Q (t) = I (t). (4.22)
Разность потенциалов в каких-либо двух точках контура,
отсчитанная в положительном направлении, называется падением
напряжения на соответствующем участке контура.
Иэ курса физики известно, что падение напряжения на
индуктивности, омическом сопротивлении и емкости выражается
соответственно так:
Va-Vb = Uab=LI, Vb-Vc = Ubc = RI, Vc-Vd = Ucd=~Q. j
32
С
Сложение этих равенств дает
Va-Vd = ti + RI + ±.Q.
Той же разности потенциалов равно напряжение, создаваемое
э. Д. е.:
Va-Va=Uad = E.
Приравнивая полученные выражения для Va—Vd и учитывая
уравнение (4.22), получаем систему двух дифференциальных
уравнений первого порядка с двумя искомыми функциями Q и/:
(4.23)
Используя первое уравнение, можно сделать замену /=Q, /=Q
во втором уравнении этой системы, в результате чего она
сводится к одному дифференциальному уравнению второго порядка
LQ + RQ + ^Q
(4.24)
Как система (4.23), так и уравнение
(4.24) описывают один и тот же класс
процессов в электрической цепи,
изображенной на рис. 2. Этот класс
зависит от двух произвольных постоянных.
Каждый конкретный процесс из этого
класса выделяется с помощью
системы двух начальных условий вида
(4.21). Уравнение (4.24)—это
линейное дифференциальное уравнение
второго порядка с постоянными
коэффициентами. Как известно, для его
интегрирования сначала нужно найти общее решение
соответствующего уравнения без свободного члена:
(4.25)
Уравнение (4.25) описывает класс процессов в электрической
Цепи, изображенной на рис. 3, т. е. полученной из прежней цепи
(см. рис. 2) в результате исключения звена da и соединения
точек d и а.
Характер общего решения уравнения (4.25) зависит от
соотношения между величинами L, R, С, точнее от знака или
обращения в нуль выражения R2C—4 L. Подбор частного решения
* А. Г. Младов i i 33
уравнения (4.24) зависит от вида свободного члена E = E(t)9
Например, представляют интерес случаи постоянной э. д. с.
E(t) =Ео = const и синусоидальной е. д. с. E(t) = Е0 sin (а^+ф).
После отыскания функции Q = Q(t) ток находится
дифференцированием:
Q (0 = /(/)•
Читателю рекомендуется разобрать все указанные случаи
и сделать соответствующие выкладки.
Пример 4. Пусть в момент £=0 в аппарат загружены два
вещества, после чего между ними происходит химическая
реакция, скорость которой пропорциональна концентрации каждого
из этих веществ. Пусть в ходе реакции в аппарат не
добавляются никакие вещества.
Обозначим через y\—y\{t) и У2—У2Ц) концентрации
реагирующих веществ в момент t
Требуется найти эти концентрации как функции времени,
если заданы начальные концентрации, т. е. концентрации обоих
веществ в момент t = 0:
*<°>=М. (4.26)
У*Ф)=Уы J
Очевидно, по своему физическому смыслу #ю, #20, Уг(£), Jfe(f)
не отрицательны. Если хотя бы одно из чисел у\о,У2о равно нулю,
то никакой реакции нет. Если же ую>0 и jfoo>0, то идет
реакция, в ходе которой реагирующие вещества расходуются.
Следовательно, их концентрации должны убывать с течением
времени, а производные концентраций y\(t) и jfe(f)» которые как
раз и выражают скорость реакции, должны быть
отрицательными.
Таким образом, скорость реакции, пропорциональная
концентрации каждого из реагирующих веществ, выразится так:
Уг^—кгУгУг 1 /427)
Уж^—ЬщУ&г I
Здесь k\ и k2 — заданные положительные постоянные.
Система дифференциальных уравнений (4.27) описывает
класс химических реакций, зависящий от двух произвольных
постоянных. Каждый конкретный процесс из этого класса
выделяется с помощью начальных условий вида (4.26).
Для интегрирования системы (4.27) разделим ее первое
уравнение на второе:
-*---£-. откуда ■&--£-.
у2 «2 #1 «2
34
Интегрируя, получаем
Ж. = Ж+Сг. (4.28)
«1 «2
Используя начальные условия (4.26), находим
£ = Ую У20 __ к$у10 — feijfeo /л 9Q\
При таком значении Ci равенство (4.28) принимает вид:
Ум — У\ = J/2Q — У г /^ qq\
Далее сделаем замену искомых функций, вводя обозначения
уг = kxult у2 = k2u2t kxk2 = k. (4.31)
Тогда система (4.27) и равенство (4.28) примут вид:
й^-ы^л (4<32)(„2=Ul_Cit
и2 = — кихиг J
Подстановка ti2=U\—С\ в первое уравнение системы (4.32) дает
уравнение щ=—kui(u\—Ci), в котором переменные
разделяются:
dUl --Ш. (4.33)
"i ("1 — Ci)
В случае Ci=^=0, т. е. при к2ую—k{y2oФ0, сделаем
разложение на простейшие дроби, интегрирование и потенцирование:
dUl d"i=_£Cl<tf,
«1 — d «i
In («! — Ci) — In «! = — kCJ 4- In C2,
"1-Cl =C2e~*V. (4.34)
"i
Отсюда и из равенства u%=ti\—С\ получаем часть общего
решения системы (4.32):
"i =
Сг
1—Сгб-*0»'
_ саг*7»'
(4.35)
2* 35
Используя (4.26), (4.29), (4.31), из (4.34) находим С2 = -^-,
ЬцУю
а затем из (4.35) получаем соответствующее частное* решение
системы (4.27), которому придадим вид:
Уг =
Уг
(4.36)
Если же Сх = 0, т. е. если k2y10 — kxy20 = 0, или -^- = -^-,
то ых = ы2, и из уравнения (4.33) сразу получаем
— = — = Ы + С3.
В силу условий (4.26) находим
С,=
#10
а затем с помощью равенств (4.31) получаем соответствующее
частное решение системы (4.27):
Уг
Ую
кгУ\.4 + 1
Ь\У<^ + 1 J
(4.37)
Можно проверить, что решение (4.37) является предельным
случаем решения (4.36) при k2yw—kiy20-*0.
Бели &2#ю—*|У2о>0, т. е. Ci>0, то из равенств (4.35) видно,
что при t -* оо
уг = klUl -> КС, = **"> ~ k^ = ft, - -^ Ук, > 0,
у2 = k2u2 -* 0.
Если k2yw—kiy20<iOt т. е. Ci<0, то из равенств (4.35) видно, 1
что при t—>оо
Уг-+0,
у2 -> — /г2С! =
У20-
•?-У*>0.
Если fef/io—fti^2o = 0, т. е. Ci = 0, то из равенств (4.37) видно, щ
что при £—>оо
уг-*09 ^2-*0.
36
T»tlv- -Т^ЛЗ-КХ^С" п$ " "W1 -I - ~.ЛЯ5Л.^.^ *. ^TS*i.3LA * »
Вместе с тем формулы (4.36), (4.37), подтверждая монотонное
убывание концентраций, показывают, что у\ и \)г ни при каком
значении t не достигают перечисленных пределов. Поэтому
описанные химические реакции, начавшись в момент /=0,
теоретически никогда не закончатся.
Радиоактивный распад, процессы в электрической цепи,
химические реакции, рассмотренные в примерах 2, 3, 4,
представляют собой виды движений, отличные от механического
движения. Из приведенных примеров видно, что некоторые
немеханические движения описываются дифференциальными
уравнениями и системами дифференциальных уравнений первого и
второго порядков.
Ряд примеров описания механического движения и других
видов движения с помощью дифференциальных уравнений
первого и второго порядков можно найти в [1], гл. XIV, § 1—4; [2],
гл. X; [3], гл. I, § 6, гл. II, § И, гл. III, § 17, гл IV, § 20; [7],
гл. XIII, § 26—30; [12], гл. I, § 9, гл. II, § 8, гл. IV, § 1, 3, 4, 6, 7.
3. Движения материальной системы
Перейдем к описанию движения материальной
системы с помощью дифференциальных уравнений. Материальная
система — это либо система связанных между собой
материальных точек в каком-нибудь приборе или механизме, либо система
связанных между собой физических объектов, вообще говоря,
различной природы, например в какой-нибудь лабораторной или
промышленной установке. Движение системы материальных
точек— это обычное механическое перемещение. Движение
системы физических объектов — это какой-либо физический процесс,
происходящий в ней, который характеризуется изменением в
пространстве и во времени некоторых физических величин
(например, плотности массы или заряда, напряженности
гравитационного, электрического или магнитного поля, электрического
напряжения или силы тока, температуры, давления, вязкости,
концентрации реагирующих веществ, линейной и угловой
скорости и ускорения, вращающих моментов и моментов инерции)
в различных частях этой системы. Итак, движением
материальной системы можно считать всякий происходящий в ней
физический пространственно-временной процесс, а не только
механическое движение.
Выше мы видели, что движение материальной точки и
физические процессы, характеризуемые одной или двумя функциями,
шгут описываться дифференциальными уравнениями и
системами дифференциальных уравнений второго и первого
порядков. Это положение распространяется и на описание движения
37
многих материальных систем, т. е. на описание многих
физических процессов. Мы будем рассматривать только такие
движения материальных систем, которые могут быть описаны
системами обыкновенных дифференциальных
уравнений второго и первого порядков, в которых независимой
переменной служит время t.
Пусть движение такой материальной системы, т. е.
некоторый физический процесс, характеризуется р физическими
величинами у\у у-2, ..., Ур, которые являются искомыми функциями
времени ty причем в случае механического движения системы
материальных точек это просто все или некоторые координаты
этих точек. Скорости и ускорения изменения этих величин
характеризуются соответственно производными у и #2, ..., Ур и
Уи У% ..♦, Ур> причем в случае механического движения это
просто соответствующие проекции скоростей и ускорений
движущихся точек.
Итак, пусть движение этой материальной системы
описывается системой р дифференциальных уравнений, вообще говоря,
второго и первого порядков с р искомыми функциями t/i, #2„ ...,
Ур. Пусть искомые функции уи Уг, ..., Ур занумерованы так, что
т из них, а именно у\, у2, ..., уш входят в систему уравнений
вместе со своими первыми и вторыми производными, а
остальные р—т функций Ут+\, Ут+2, ., Ур — только с первыми
производными. Это значит, что каждая вторая производная
Уи У% •••» Уш содержится в одном или нескольких уравнениях
системы. Таким образом, система дифференциальных уравнений,
которая описывает движение материальной системы,
характеризуемое р функциями, имеет вид:
Fi(t',yi, Уг/i/i', У2> УъУг, •
Ут+2 у Ут+ъ'> *
F*(i\yi> УиУъУъ* Уг/Уъ ••
Ут-}-2> Ут+2 у • ■
• > У щу У ту Ут> УтМ-ч Ут+1>
.; уР> уР) = о
• I Ушу У ту Ут* У m+U УГ/и+1>
.; Уру ур) = о
. (4.38)
Fp{t\ Уи У\у УГу У2у У2у У2у • • • ; У ту У ту У ту Ут+Ъ Ут+Ъ
Ут+2у Ут+2\ • • • i Уру Ур) = °
Эта система имеет второй порядок относительно каждой из
т функций у\, //2, ..♦, Ут и первый порядок относительно
каждой из остальных р—т функций ут+и Ут+2, ..., Ур\
следовательно, эта система имеет суммарный порядок 2т + (р—т)=т+р.
Заметим, что в различных конкретных случаях число т в
38
системе (4.38) может принимать всевозможные (целые)
значения из промежутка 0^т<р. Если ап = 0, то система (4.38)
совсем не содержит вторых производных искомых функций. Если
т=Р, то система (4.38) содержит вторые производные всех
искомых функций у и У2, ..., Ур, так что среди них нет функций,
входящих в систему только с первыми производными. В
различных случаях р и т, а следовательно, и т + р могут быть и
четными и нечетными.
Система уравнений (4.38) описывает не одно движение, а
класс движений (физических процессов), зависящий от т+р
произвольных постоянных. Чтобы из этого класса выделить
конкретное движение, нужно в соответствии с формулой (3.13) § 3
задать систему т+р начальных условий:
#i('o) = #i<>;
у* (*о) = Ую\
Ут Со) = Уто\
Ут+1^о) = Ут+1,0
У1^о) = Ую
y*(to) = У to
УтУо)=:УтО
(4.39)
УР(*о) = Уро
и найти частное решение системы (4.38), удовлетворяющее этим
условиям.
§ 5. ФАЗОВЫЕ ТРАЕКТОРИИ И ИНТЕГРАЛЬНЫЕ
КРИВЫЕ (ПРИМЕРЫ)
Пример 1. Используем пример 1 из § 4, в котором было
рассмотрено движение груза на пружине. Разберем отдельно
случаи k = 0 и �.
1. При & = 0 уравнение движения груза имеет вид:
£ + соУ=;0, (4.9)
а при начальных условиях
У(0) = л !; (4.Н)
У(0) = Уо J
его частное решение выглядит так:
У = Уо cos ®t + -^~ sin со/.
(О
(4.13)
39
Функция (4.13) описывает реальное, т. е. истинное,
действительное, прямолинейное движение груза.
Принимая у за новую искомую функцию и вводя
обозначения
(5.1)
преобразуем уравнение (4.9) в систему уравнений первого
порядка:
*1=*а }. (5.2)
При этом начальные условия (4.11) примут вид:
*<°> = «М (5.3)
*i(0) = y0 I
Тогда согласно обозначениям (5.1) частное решение
системы (5.2), удовлетворяющее начальным условиям (5.3),
получается из" функции (4.13) и ее производной:
Zjl = у0 cos corf + — sin (at
0)
Z2 = — y0(x) Sin (dt + Уо COS <dt
(5.4)
Из двух уравнений (5.4) исключим t. Для этого возведем
в квадрат выражения Z\ и — и затем сложим результаты:
г;
,2
^о
г2 4- —- = и2 4- -^- = Р2
1 (О2 ° 'Л* ° '
откуда
А
(5.5)
Здесь Po = -f]/^ + ^|->0>
р2 (соро)2
поскольку мы изучаем движе-
ние груза, тогда как при у0 = Уо~0 груз оставался бы
неподвижным, что видно и из равенства (4.13).
Дадим два связанных между собой геометрических, точнее
кинематических, толкования уравнений (5.4).
Сначала возьмем декартову систему координат на
плоскости, причем обозначим эти координаты через ги 22 и направим
40
ось z\ вниз (например, потому, что в примере 1 § 4 ось «у» была
направлена вниз, а у = г{), а ось 22 вправо. Тогда уравнения
Mo(y0>i)
ня
еллипс с полуосями р0 и соро, а
ПрИ (0=1 — окружность радиуса
р0. На рисунке 4, а изображен
такой эллипс для случая со>1.
Уравнения (5.4) выражают
зависимость от времени текущих
координат точки М (t)7 которая
начинает свое движение в момент
/=0 от точки М0 (уо> У о) и
движется по эллипсу или
окружности (5.5). В силу уравнения £i=£2
из системы (5.2)^ ясно, что три
z2<0 Z\ убывает* а при 22>0 Z\
возрастает, т. е. в обоих случаях
точка М (t) движется по
кривой (5.5) по направлению
часовой стрелки (см. рис. 4, а).
Подчеркнем, что в наших
рассуждениях участвуют два
движения: реальное колебательное
движение груза по прямой,
выраженное равенством (4.13),
и соответствующее ему движение
точки М (t) по кривой (5.5),
выраженное уравнениями (5.4).
Так как реальное движение
груза совершается по прямой, а
не по кривой, то криволинейное
движение точки М (t)
называется фиктивным, т. е.
вымышленным, движением,
соответствующим реальному.
Отметим также и то, что
реальное движение описывается частным решением уравнения
(4.9) при начальных условиях (4.11), а соответствующее ему
фиктивное движение описывается частным решением системы
(5.2) при начальных условиях (5.3), причем система (5.2) и
условия (5.3) получены преобразованием уравнения (4.9) и
условий (4.11).
Точка M(t), совершающая фиктивное движение, называется
изображающей точкой. Траектория изображающей точки, т. е.
41
Рис. 4
- ^sFraa-sBrafess^ *»ячяаш»
кривая (5.5), называется фазовой траекторией системы
уравнений (5.2), соответствующей начальным условиям (5.3) или
начальной точке Мо(уо9 уо).
Изменяя как угодно (в физически допустимых пределах)
начальные условия (4.11) и (5.3), т. е. изменяя как угодно
положение начальной точки М0, получаем всевозможные реальные
движения (4.13) и соответствующие им всевозможные
фиктивные движения (5.4). Траектории всех этих фиктивных
движений представляют собой семейство подобных и подобно
расположенных концентрических эллипсов (или окружностей) вида
(5.5).
При различных положениях точки М0(у0, у0) траектории
этого семейства, соответствующие различным значениям ро, не
имеют общих точек, а траектории, соответствующие одному и тому
же значению ро, проходят по одной и той же кривой (5.5).
Семейство всех фазовых траекторий системы уравнений
(5.2) называется ее фазовым портретом, а плоскость zu z2y на
которой расположено это семейство, — фазовой? плоскостью.
Чтобы дать второе толкование уравнений (5.4), возьмем
правую декартову систему координат в трехмерном пространстве,
принимая за координаты переменные ty zu z2 (рис. 4, б).
В пространстве ty zu z2 первое из уравнений (5.4)
представляет собой синусоидальный цилиндр с образующими,
параллельными оси 22; второе из уравнений (5.4) изображает другой
синусоидальный цилиндр с образующими, параллельными оси
zu уравнение (5.5) есть уравнение эллиптического или
кругового цилиндра с образующими, параллельными оси t.
В пространстве t, Z\y z2 система уравнений (5.4) изображает
линию пересечения первых двух цилиндров, которая, конечно,
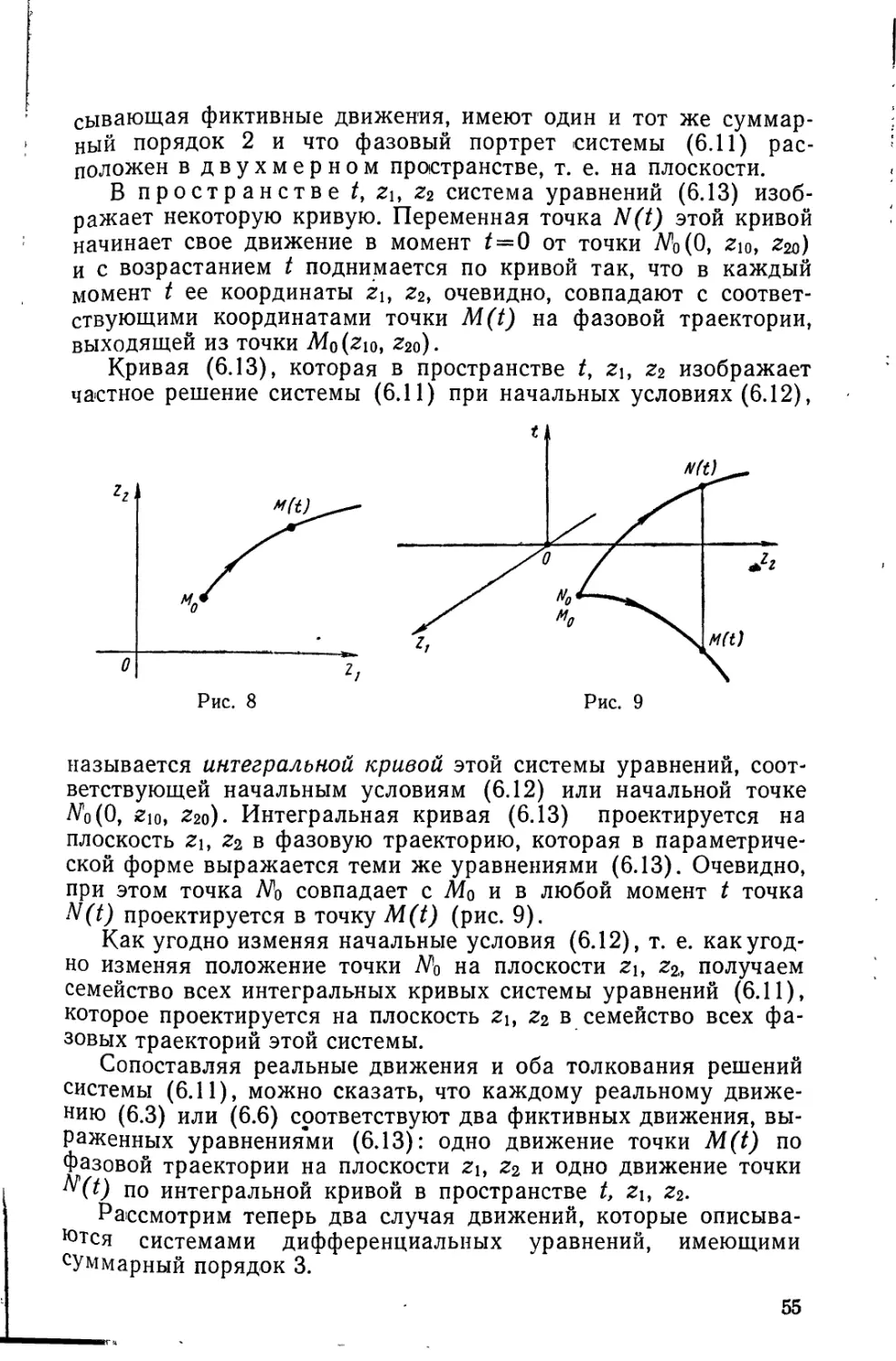
лежит и на цилиндре (5.5). Переменная точка N(t) этой линии
пересечения начинает свое движение в момент t = 0 от точки
М)(0, #о, Уо) и с возрастанием t поднимается по этой линии так,
что в каждый момент t ее координаты zu z2} очевидно,
совпадают с соответствующими координатами точки M(t) на
фазовой траектории, выходящей из точки М0(уо, #0). Так как точка
M(t) движется по направлению часовой стрелки, то траектория
точки N(t) представляет собой левую винтовую линию на
цилиндре (5.5), выходящую из точки N0 (см. рис. 4, б).
Винтовая линия (5.4), которая в пространстве t, Z\t z2
изображает частное решение системы (5.2) при начальных
условиях (5.3), называется интегральной кривой этой системы
уравнений, соответствующей начальным условиям (5.3) или
начальной точке N0(0, Уоу #о).
Из сказанного ясно, что интегральная кривая (5.4)
проектируется на плоскость Zi, z2 в фазовую траекторию, которая в
параметрической форме выражается теми же уравнениями (5.4),
42
а в координатной форме уравнением (5.5). Очевидно, при этом
точка No совпадает с точкой М0 и в любой момент t точка N (t)
проектируется в точку M(t). Таким образом, на рис. 4, б
картина в плоскости Z\f z2 совпадает с рис. 4, а.
Как угодно изменяя начальные условия (5.3), т. е. как
угодно изменяя положение точки N0 на плоскости z\, z2, мы
получаем семейство всех интегральных кривых системы уравнений
(5.2), которое проектируется на плоскость zu z% в семейство
всех фазовых траекторий системы (5.2).
Для системы уравнений (5.2) во всем пространстве t, zu z2
выполнены все условия теоремы существования и
единственности частного решения. Поэтому интегральные кривые системы
(5.2) нигде не пересекаются. В !самом деле, если предположить,
что через некоторую точку N\(tu гц9 z2X) проходит более чем
одна интегральная кривая, то это означало бы, что система
(5.2) имеет более чем одно частное решение, удовлетворяющее
начальным условиям:
*1 (* l) = *11
гг ('1) = z%\
что противоречило бы утверждению о единственности такого
решения.
Сопоставляя реальные движения груза и оба толкования
решений системы (5.2), можно сказать, что каждому реальному
прямолинейному движению (4.13) соответствуют два фиктивных
движения, выраженных уравнениями (5.4): одно движение
точки M(t) по фазовой траектории на плоскости zu z2 и одно
движение точки N(t) по интегральной кривой в пространстве
t> zu z2.
При различных положениях точки iV0(0, у0, у0)
интегральные кривые системы (5.2), соответствующие различным
значениям р0 = I/ у*-\ ^-, проектируются на плоскость zu z2 в
различные кривые (5.5), а интегральные кривые,
соответствующие одному и тому же значению р0, проектируются в одну и ту
же кривую (5.5).
2. Проведем аналогичные рассуждения для случая кФО,
Ul<(0.
Уравнение движения груза при этом имеет вид:
у + 2ку + <й*у = 0, (4.8)
а при начальных условиях
У(0) = Уо
УФ) = Уо
(4.11)
43
его частное решение выглядит так:
у = е~-** (
у0 cos \t +
Уо +
V /
(4.17)
Функция (4.17) описывает реальное прямолинейное движение
груза.
Принимая у за новую искомую функцию и вводя
обозначения
(5.1)
преобразуем уравнение (4.8) в систему уравнений первого
порядка:
(5.6)
2kz2 j
При этом начальные условия (4.11) примут вид:
*i(0)=ye )
2.(0)=Уо I
Тогда согласно обозначениям (5.1) частное решение
системы (5.6), удовлетворяющее начальным условиям (5.3),
получается из функции (4.17) и ее производной:
(5.3)
гх = e~kt (у0 cos vt + Уо + ку° sin tf)
■—ker»(
y0 cos vt
Уо +
t*^sinvt)
V /
+
+ e~kt [— y0v sin vt + (y0 + ky0) cos \t]
(5.7)
Исключить t из двух уравнений (5.7) возможно, но ниже
мы увидим, что это получается сложнее, чем в случае k = 0.
Преобразуем систему (5.7) так: заменим через Z\ его
выражение в первом члене выражения z<i и затем разделим на v,
после чего можем написать:
*2
± *5l_ = e-kt (_ Уо sin v* + i^±^ cos v*) •
(5.8)
Далее возведем в квадрат уравнение, выражающее Z\ и
последнее уравнение, и затем сложим результаты:
Z2 + (*2+^i)2 = е-ш ^2 + (Уо + kyo)2^ = p|^-2«f (5.9)
44
откуда
<р*Г*)»
+
Здесь
ft = ]/<« + ■
(Уо + kyQy
fa + fai)'
>о,
(5.10)
так как уо и уо не равны нулю совместно.
Перейдем к кинематическим толкованиям системы
уравнений (5.7).
Для первого толкования возьмем систему координат z\f z2
на плоскости, направив ось zx вниз, а ось z% вправо. Тогда
уравнения (5.7) можно считать параметрическими уравнениями
некоторой кривой на плоскости zu z2, в которых параметром
служит время t. Уравнение (5.10), которое здесь рассматривается
только как следствие уравнений (5.7), помогает выяснить вид
этой кривой. В самом деле, уравнение (5.10) напоминает
уравнение эллипса, но «полуоси» этого «эллипса» 9ке~ы и vp^e-71'
не постоянны, а зависят от t\ с возрастанием t при k>0 они
неограниченно убывают, а при k<0 неограниченно возрастают.
Поэтому в действительности уравнения (5.7), (5.10) определяют
на плоскости 2Ь z<i не эллипс или окружность, а
логарифмическую спираль (точнее эллиптико-логарифмичаскую спираль).
Выясним более строго вид кривой (5.7). Для этого, учитывая значение р^,
положим
и
введем на
плоскости
9k
новые
Zl
Ч
coscp
Уо + fyo
vp*
координаты
= *1
V
*1 +
1
— z2
V
sincp
Тогда первому из уравнений (5.7), уравнениям (5.8) и (5.9) можно придать
вид:
Zi=19ke **cos((p —v/)
z^ = Pke~kt sin (ф — v0
(5.П)
(5.12)
С помощью обозначения р = у 1>\ -f zj перепишем уравнение (5.12) так:
Р2 = р|е ш, откуда
■9ke
-kt
(5.1з;
45
В силу (5.13) и с помощью обозначения 0=<р—vt уравнения (5.11)
принимают вид:
г\ = р cos 0 1
z2 = p sin 0 J
Следовательно, р, 0 являются обычными полярными координатами на плоско-
^ ^ Ф —0
сти zu z2. Наконец, подставляя/= .в уравнение (5.13), получаем урав-
*(в-Ф)
нение кривой (5.7) в полярных координатах ?=Pke v , которое
представляет собой уравнение логарифмической спирали.
Заметим, что уравнение этой спирали без участия / можно
получить, выразив е~м и t из уравнения (5.9) и подставив их
в любое из уравнений (5.7).
Уравнения (5.7) выражают зависимость от времени текущих
координат точки M(t), которая начинает свое движение в
момент t=0 от точки М0(уо, у0) и движется по спирали. В силу
уравнения Z\ — z2 из системы (5.6), как и выше,
обнаруживается, что точка M(t) движется по спирали (5.7) по направлению
часовой стрелки.
Таким образом, при k>0 кривая (5.7)—это
логарифмическая спираль (вернее полуспираль), которая'начинается в момент
/ = 0 в точке М0(уо, yQ) и при возрастании t свертывается к
началу координат, так что точка M(t) совершает по ней
бесконечно много оборотов, никогда (т. е. ни при каком t) не
достигая начала координат (см. рис. 5, а), а при k<0 кривая (5.7) —
это логарифмическая спираль (вернее полуспираль), которая
также начинается в момент t = 0 в точке М0 и при возрастанииtf
неограниченно развертывается (см. рию. 6, а).
Заметим, что изменению t от момента t = 0 в отрицательном
направлении соответствовали бы другие части этих спиралей —
развертывающаяся при k>0 и свертывающаяся при k<0, но
они не имеют физического смысла, так как время t не может
убывать. Кроме того, поскольку мы считаем, что реальное
движение груза, а значит, и движение точки M(t) начинаются в
момент / = 0, а не раньше, то не нужно рассматривать
возрастание t в промежутках вида t\^A<b.
Как и выше, обратим внимание на то, что реальному
движению груза, выраженному равенством (4.17), соответствует
фиктивное движение изображающей точки M(t) по спирали
(5.7).
Траектория точки M(t)y т. е. полуспираль (5.7) при /^0,
называется фазовой траекторией системы уравнений (5.6),
соответствующей начальным условиям (5.3) или начальной точке
AfoQ/o, 4fo).
46
Изменяя как угодно начальные условия (4.11) и (5.3), т. е.
как угодно изменяя положение начальной точки Af0> получаем
всевозможные реальные движения (4.17) и соответствующие им
всевозможные фиктивные движения (5.7).
*)
Рис. 5
Рис. 6
Возьмем на плоскости какую-нибудь точку Мх (zllt z21) и затем
точку М% (zne v ; z21e v).
Рассмотрим вспомогательное семейство полных спиралей вида
(5.7), (5.10) при — oo<f< + oo, соответствующих тем точкам
47
М0(Уо, Уо), которые заполняют прямолинейный отрезок М{М2.
Легко проверить, что точки М\ и М2 лежат на одном луче,
выходящем из начала координат, и вместе с тем на соседних
витках одной спирали вида (5.7), (5.10). Поэтому все остальные
спирали этого семейства соответствуют всем промежуточным
точкам отрезка М\М2. Взятое семейство спиралей заполняет
всю плоскость Z\y z2, за исключением начала координат. Все эти
спирали подобны, подобно расположены и имеют полюс в
начале координат. Траектории всех фиктивных движений (5.7) на
плоскости zuz2 образуют семейство полуспиралей вида (5.7),
(5.10) (при ^0), которые располагаются на вспомогательном
семействе полных спиралей. Очевидно, при различных
положениях точки М0(у0, уо) траектории, проходящие по различным
спиралям, не имеют общих точек, а каждые две траектории,
проходящие по одной и той же спирали, совпадают, начиная с
некоторой точки.
Как и выше, семейство всех фазовых траекторий системы
уравнений (5.6) называется ее фазовым портретом, а плоскость
zu z2t на которой расположено это семейство, — фазовой
плоскостью.
Для второго толкования системы (5.7) возьмем правую де-
картову систему координат в трехмерном пространстве t, zu z2.
В пространстве t, z\f z2 первое из уравнений (5.7) представляет
собой экспоненциально-синусоидальный цилиндр с
образующими, параллельными оси z2\ второе из уравнений (5.7)
изображает другой такой цилиндр с образующими, параллельными
оси Z\. Как сказано выше, с помощью уравнения (5.9) можно
исключить t из уравнений (5.7); полученное при этом уравнение
представляет цилиндр с образующими, параллельными оси t,
причем это спиральный цилиндр, так как его направляющей
служит полуспиральная фазовая траектория в плоскости zu z2.
В пространстве t, Z\9 z2 система уравнений (5.7) изображает
линию пересечения первых двух цилиндров, которая, конечно,
лежит и на указанном спиральном цилиндре. Переменная точка
N(t) этой линии пересечения начинает свое движение в момент
t = 0 от точки Af0(0, #o, Уо) и с возрастанием t поднимается по
этой линии так, что в каждый момент / ее координаты гь z2,
очевидно, совпадают с соответствующими координатами точки
M(t) на фазовой траектории, выходящей из точки М0(#о, Уо).
Так как точка M(t) движется по направлению часовой стрелки,
то траектория точки N(t) представляет собой левую винтовую
линию на спиральном цилиндре, выходящую из точки N0. Мы
берем лишь ту часть спирального цилиндра, которая начинается
с образующей, проходящей через точку jV0, и соответствует
значениям t^O (как и на фазовой траектории). Поэтому при k>0
это неограниченно свертывающаяся к оси t часть спирального
48
цилиндра, а при k<0 — развертывающаяся часть спирального
цилиндра; следовательно, с возрастанием t точка N(t),
поднимаясь по спиральной винтовой линии (5.7), при k>0
неограниченно приближается к оси /, а при £<0 неограниченно
удаляется от оси t (см. рис. 5, б, 6, б).
♦ Спиральная винтовая линия (5.7), которая в пространстве
t, Z\y z2 изображает частное решение системы (5.6) при
начальных условиях (5.3), называется интегральной кривой этой
системы уравнений, соответствующей начальным условиям (5.3)
или начальной точке N0(0y у0, у0).
Ясно, что интегральная кривая (5.7) проектируется на
плоскость Zit z2 в фазовую траекторию, которая в параметрической
форме выражается теми же уравнениями (5.7). Очевидно, при
этом точка Л/о совпадает с точкой М0 и в любой момент t точка
N(t) проектируется в точку M(t). Таким образом, на рис. 5, б
и 6, б картина в плоскости zu z2 совпадает соответственно с
рис. 5, а и 6, а.
Как угодно изменяя начальные условия (5.3), т. е. как
угодно изменяя положение точки N0 на плоскости zu z2i получаем
семейство всех интегральных кривых системы уравнений (5.6),
которое проектируется на плоскость zu z2 в семейство всех
фазовых траекторий системы (5.6). Как и выше, доказывается, что
интегральные кривые системы (5.6) нигде не пересекаются.
Сопоставляя реальные движения груза и оба толкования
решений системы (5.6), можно сказать, что каждому реальному
прямолинейному движению (4.17) соответствуют два фиктивных
движения, выраженных уравнениями (5.7): одно движение
точки M(t) по фазовой траектории на плоскости zu z2 и одно
движение точки N(t) по интегральной кривой в пространстве
U Z\f Z2.
Пример 2. Вернемся к примеру 4 § 4, где рассматривались
химические реакции, описываемые нормальной системой диф-'
ференциальных уравнений:
Уг = — КУ\У\
У* = — &2#1#2
Там было обнаружено, что у\ и у2 связаны соотношением
|i-=f- + Cx. (4.28)
При начальных условиях
0i(O) = yio
УА°) = Уы
49
(4.27)
(4.26)
равенство (4.28) принимает вид:
Ую — У\
t/20 — У*
(4.30)
а система (4.27) имеет частное решение, выраженное
формулами (4.36) либо (4.37).
На плоскости с декартовыми координатами j/i, j/2 и в
трехмерном пространстве с координатами t, уи у% дадим два
кинематических изображения каждого частного решения системы
(4.27), т. е. каждой конкретной
химической реакции из этого класса.
На плоскости уи Уч
уравнение (4.28) выражает семейство
параллельных прямых, а уравнение
(4.30) выражает прямую АВ из
этого семейства (рис. 7, а), которая
проходит через точку М0 (*/ю, г/го),
изображающую начальные
условия (4.26).
Если ую>0 и #2о>0, то согласно
анализу, проведенному в конце
примера 4 § 4, у\ и #2 в формулах (4.36)
и (4.37) при всех 0^<оо
удовлетворяют условиям:
Ую>У1>°
У20>У*>°
Следовательно, в этом случае
равенства (4.36) и (4.37)
изображают переменную точку М (t),
которая в момент t = 0
находится в точке М0, а затем
движется по интервалу М0Е прямой
(4.30) по направлению к точке Е. При t-+oo точка M(t)
стремится к точке Е, но никогда, т. е. ни при каком t, не достигает
точки Е. Полузамкнутый интервал М0Е (без точки Е)
называется фазовой траекторией системы уравнений (4.27),
соответствующей начальным условиям (4.26) или начальной точке
Мо(ую, #2о). Движение точки M(t) по интервалу М0Е является
фиктивным движением, которое соответствует реальному
движению, т. е. химической реакции. Изменяя как угодно в
физически допустимых пределах начальные концентрации ую, #2о и
соответственно перемещая точку М0, получаем всевозможные
химические реакции изучаемого класса и соответствующие им
всевозможные фиктивные движения точки M(t) по фазовым
траекториям. Множество всех этих фазовых траекторий — это мно-
Рис. 7
50
жество всех полузамкнутых интервалов вида М0Е (с физически
допустимыми точками Мо), расположенных на семействе
прямых (4.28).
Если одно или оба из чисел r/ю, #20 равны нулю, т. е. точка
Мо расположена на одной из координатных осей или в начале
координат, то из равенств (4.36) или (4.37) видно, что при всех
t>0 точка M(t) остается в точке Мо. Следовательно, каждая
физически допустимая точка Мо, расположенная на
неотрицательных частях осей координат, сама является фазовой
траекторией системы (4.27). Множество всех фазовых траекторий
системы (4.27) называется ее фазовым портретом, а
заполненная им часть плоскости уи у2 называется фазовой плоскостью
системы (4.27).
В трехмерном пространстве t, уи у2 уравнение (4.28)
выражает семейство плоскостей, перпендикулярных к плоскости
уи у2 и параллельных между собой, а уравнение (4.30)
выражает плоскость AEF из этого семейства (рис. 7, б), которая
проходит через точку N0(0, уюУ #20).
Если г/ю>0 и #2о>0, то первое из уравнений (4.36)
представляет собой некоторую цилиндрическую поверхность,
параллельную оси #2, а второе — сходную с ней цилиндрическую
поверхность, параллельную оси у\. То же можно сказать и об
уравнениях (4.37). Линия пересечения цилиндров (4.36) или (4.37)
лежит на соответствующей плоскости AEF (4.30), на рис. 7, б это
кривая NqG. В силу уравнений (4.36) или (4.37) координаты
Уи #2 переменной точки N(t) кривой N0G совпадают ic
координатами точки M(t) на соответствующей фазовой траектории М0Е.
Поэтому в момент /=0 точка N(t) находится в точке
No(0, #ю, #2о), совпадающей с Мо, затем N(t) поднимается по
кривой NoG, причем в каждый момент точка N(t)
проектируется в точку M(t)t а вся кривая N0G проектируется на всю
фазовую траекторию М0Е. Следовательно, при t->oo точка N(t)
асимптотически приближается к полупрямой EF (см. рис. 7, б).
Кривая M)G называется интегральной кривой системы
уравнений (4.27), соответствующей начальным условиям (4.26).
Движение точки N(t) по интегральной кривой также является
фиктивным движением, которое соответствует реальной
химической реакции.
Если одно или оба из чисел */ю, ую равны нулю, т. е. точка
М)(0, yl0t #20) находится на одной из осей или в начале
координат, то соответствующей интегральной кривой системы (4.27)
служит вертикальная полупрямая, выходящая из точки No.
Всевозможным физически допустимым начальным условиям
вВДа (4.26) соответствуют всевозможные интегральные кривые
Указанных видов. Различные интегральные кривые системы
(4.27) не имеют общих точек, так как для этой системы при
всех t, yu у2 выполнены условия теоремы существования и един-
51
ственности частного решения. Семейство интегральных кривых
системы (4.27) проектируется на плоскость уи у2 в фазовый \
портрет этой системы.
§ 6. ФАЗОВОЕ ПРОСТРАНСТВО (ОБЩИЕ ОПРЕДЕЛЕНИЯ)
1. Случаи, когда д=2и/1=3
Начнем с двух простейших случаев.
1) Класс реальных движений (физических процессов)
описывается одним дифференциальным уравнением второго
порядка
F(t,y,!/,y) = 0. (6.1)
Пусть при начальных условиях
У(0) = Ув
УФ)=Уо
получается частное решение уравнения (6.1)
У^<УУ,Уо>Уо), (6.3)
(6.2)
1
которое выражает конкретное реальное движение.
2) Класс реальных движений (физических процессов)
описывается системой двух дифференциальных уравнений первого
порядка
Р1(*,УиУиУнУ2)=0 1
Пусть при начальных условиях
Уг (0) = Ую
получается частное решение системы (6.4)
(6.4)
(6.5)
(6.6)
которое выражает конкретное реальное движение.
Для единства дальнейших формулировок введем единые
обозначения для обоих случаев:
1) У = *г
(6.7)
52
принимая у за новую искомую функцию;
2) Уг = гх yie = *10| (б8)
У г = %ъ Уъо == ^20 i
В обозначениях (6.7) уравнение (6.1) преобразуется в
систему двух уравнений первого порядка:
*1 = *2
В обозначениях (6.8) система (6.4) перепишется так:
Fi{t>zx/z1% z2, za) = 0j
Объединим оба случая (6.9) и (6.10) в одну запись:
Gi(t,zltzlt z2, z2)=0
G2(t9zlyzlt z2, z2) = 0
Начальные условия (6.2). и (6.5) в обозначениях (6.7) и (6.8)
примут единый вид:
*i(0)=*10
(6.9)
(6.10)
(6.11)
(6Л2)
*i(0)=*20J
Частное решение системы (6.11) при начальных условиях
(6.12) напишем так:
г\ = Фг ('» zi0, z20) | (6 13)
*2 = Ф2(*. *Ю»*2о) J
Конечно, в первом случае
ф1(*,*ю.*»о) = *('. //0, у0)
Ф2(*> *к» 220) = ог(^,^0, #0)
а во втором случае
Ф1 (t9 z10, z20) = ot(tt y10, y20)
Ф2 (t> Zio, z20) == a2 (t, y10, y20)
Как и в примерах, рассмотренных в § 5, дадим два
кинематических толкования уравнений (6.13).
На плоскости z\, z% уравнения (6.13) считаем
параметрическими уравнениями некоторой кривой, в которых параметром
служит время t. В силу условий (6.12) переменная точка M(t)
53
- **.^етл, ,. з
этой кривой начинает свое движение в момент £=0 от точки I
Mq(Zio, Z2o). I
Подчеркнем, что реальное движение (6.3)—это либо меха- 1
ническое движение материальной точки по оси у> либо не меха- 1
ническое движение, а некоторый физический процесс, характе- ж
ризуемый одной функцией. Поэтому функции (6.13), т. е. част- 1
ное решение системы (6.11), в данном случае совпадающей с 1
системой (6.9), при начальных условиях (6.12), описывают ж
фиктивное движение точки M(t) в плоскости zu 22, которое I
соответствует реальному движению (6.3). I
Реальное движение (6.6.) — это либо некоторый физический 1
процесс, характеризуемый двумя функциями, либо механическое I
движение некоторого тела, либо механическое движение одной I
или двух материальных точек, причем уи у% могут быть не коор- щ
динатами, а проекциями скоростей этих точек. Поэтому суть ж
перехода от системы уравнений (6.4) к системе (6.10) или (6.11) 1
состоит, конечно, не в изменении обозначений (z вместо у), а ж
в том, что численные значения уи Уг реальных физических вели- Я
чин принимаются за координаты Z\, z2 точки M(t) на плоскости. 8
Вследствие этого реальному движению (6.6) любого иэ пере- Ц
численных здесь видов ставится в соответствие движение (6.13) щ
точки M(t) по плоскости z\f z2, которое, таким образом, являет- щ
ся фиктивным движением, соответствующим реальному движе- Я
нию (6.6). 1
Итак, реальному движению (6.3) или (6.6) соответствует Ц
[в единых обозначениях (6.7), (6.8), (6.11)] фиктивное движение Ш
(6.13) на плоскости zu z2. Точка M(t), совершающая фиктивное 1
движение, называется изображающей точкой. Фиктивное дви- 1
жение (6.13) точки M(t) выражается частным решением систе- 1
мы (6.11) при начальных условиях (6.12). Траектория изобра- J
жающей точки, т. е. кривая (6.13) (при t^O) на плоскости ш
Zu Z2y называется фазовой траекторией системы уравнений Ш
(6.11), соответствующей начальным условиям (6.12) или началь- Щ
ной точке M0(zio, z2q) (рис. 8). I
Как угодно изменяя физически допустимые начальные уело- Л
вия (6.2) и (6.5), а значит и (6.12), т. е. как угодно изменяя I
положение точки М0, получаем всевозможные реальные движе- j
ния (6.3) и (6.6) и соответствующие им всевозможные фиктив- I
ные движения (6.13). 1
Семейство всех фазовых траекторий системы уравнений Щ
(6.11) называется ее фазовым портретом, а плоскость z\9 z2y на I
которой расположено это семейство, называется фазовой пло- I
скостью. Часто называют фазовой плоскостью системы (6.11) I
лишь ту часть плоскости Z\9 Z2, которая заполнена фазовым I
портретом этой системы уравнений. |
Обратим внимание на то, что уравнение (6.1) и система
(6.4), описывающие реальные движения, и система (6.11), опи-
54
сывающая фиктивные движения, имеют один и тот же
суммарный порядок 2 и что фазовый портрет системы (6.11)
расположен в двухмерном пространстве, т. е. на плоскости.
В пространстве t, z\t z2 система уравнений (6.13)
изображает некоторую кривую. Переменная точка N(t) этой кривой
начинает свое движение в момент £=0 от точки М)(0, Z\0y z2Q)
и с возрастанием t поднимается по кривой так, что в каждый
момент t ее координаты zu z2y очевидно, совпадают с
соответствующими координатами точки M(t) на фазовой траектории,
выходящей из точки M0(zl0y z20).
Кривая (6.13), которая в пространстве /, Z\y z2 изображает
частное решение системы (6.11) при начальных условиях (6.12),
Рис. 8
Рис. 9
называется интегральной кривой этой системы уравнений,
соответствующей начальным условиям (6.12) или начальной точке
М)(0, ею, z20). Интегральная кривая (6.13) проектируется на
плоскость 2i, 22 в фазовую траекторию, которая в
параметрической форме выражается теми же уравнениями (6.13). Очевидно,
при этом точка ОД> совпадает с MQ и в любой момент t точка
N(t) проектируется в точку M(t) (рис. 9).
Как угодно изменяя начальные условия (6.12), т. е. как
угодно изменяя положение точки М) на плоскости Z\y z2iy получаем
семейство всех интегральных кривых системы уравнений (6.11),
которое проектируется на плоскость zu z2 в семейство всех
фазовых траекторий этой системы.
Сопоставляя реальные движения и оба толкования решений
системы (6.11), можно сказать, что каждому реальному
движению (6.3) или (6.6) соответствуют два фиктивных движения,
выраженных уравнениями (6.13): одно движение точки M(t) по
фазовой траектории на плоскости z\y z2 и одно движение точки
№(t) по интегральной кривой в пространстве t, zu z2.
Рассмотрим теперь два случая движений, которые
описывайся системами дифференциальных уравнений, имеющими
суммарный порядок 3.
55
3) Класс реальных движений описывается системой двух
уравнений:
№\УиУ1*У1\У*/Уг)=Ъ 1
f*(ti Уи Hi* hi у* у*) =о Г
Пусть при начальных условиях
Л (0) = 0W Ух(0)=Ую\
02(О)=02О I
получается частное решение системы (6.14)
0i = *i('.0io. 0м. У2о)\
0i = *M'»0io.0io. 0*о)1
которое выражает конкретное реальное движение.
4) Класс реальных движений описывается системой трех
уравнений первого порядка:
(6.14)
(6.15)
(6.16)
(6.17)
(6.18)
Pi (*. Уи У\> У*> У» Уз, Уз) = 0 ]
Ft(t,yi, У1,У%,у\, Уз,Уз) = 0
F*(t, Уг, Ух, У%, У*. Уз, Уз) =fi J
Пусть при начальных условиях
УЛ0)=Уы
Уш(0) = Ут
Уз (0) = У30 J
получается частное решение системы (6.17)
Ух = °>х (*, Ухо, Уго, Узо)
Уъ = щУ,у10,у29,у30)
Уз = ^з^,Ухо,У%о,Узо)
Опять введем единые обозначения для 3-го и 4-го случаев:
3) ух = гх у10 = z10 1
Ух — 22 Ухо = Z20
Уг = 2з У%о = 2зо -
принимая yt за новую искомую функцию;
4) Ух = гг Ую = 210
У2 = г2 г/20 = 2а0 }• (6.21)
Уз = 2з Узо — 2зо
56
(6.19)
(6.20)
цъглнв-я- «tS*»* i
«.■ч?з^ v?-' "хч-л f ~аиян
В обозначениях (6.20) система (6.14) преобразуется
му трех уравнений:
гг —гг
i 1 (*> ^1» ^2> Z2> Z3» Z3/ = 0 .
/2 (*> ^1» 22> 22> Z3> Za) == 0 j
В обозначениях (6.21) система (6.17) перепишется так:
^1 (*» Zl> Zl> Z2> Z2> ^3> ^з) = 0
■*2 (*> ^1» ^1> ^2> ^2» ^-3» ^3/ == "
**3 ('» %l> Zl> ^2> ^2» ^3> 23) = U
Объединим оба случая (6.22) и (6.23) в одну запись:
^l(t, Zi, 2Х, 22, ^2» ^3» 2з) == 0
^2 (* » *1» ^lt Z2> Z2> ^3» 2з) " О
(JZA\t> Zl> ^1» ^2» Z2> ^3> Z3/ == ^ /
Начальные условия (6.15) и (6.18) в обозначениях
(6.21) примут единый вид:
*i(0)=*io)
22(0)=220 •
*3 (0) = 230 ]
Частное решение системы (6.24) при начальных
(6.25) напишем так:
zx == фх (г, г1о, 2г2о> 2зо)
^2 = Ф2 ('» ^10» ^20» ^Зо)
ZB == Фз (* > Zl0> ^20» ^зо)
Конечно, в третьем случае
Фх = 4>i
Ф2==г|>1
ФЗ = ^2
в систе-
(6.22)
(6.23)
(6.24)
(6.20) и
(6.25)
условиях
(6.26)
57
а в четвертом случае
ф2 = соа .
Фз^со3 J
Дадим два кинематических толкования уравнений (6.26).
В трехмерном пространстве zu z2l z3 уравнения (6.26)
считаем параметрическими уравнениями некоторой кривой, в
которых параметром служит время t. В силу условий (6.25)
переменная точка M(t) этой кривой начинает свое движение в
момент t = 0 ОТ ТОЧКИ M0(Ziof 220, 2зо).
Реальные движения (6.16) и (6.19) могут быть некоторыми
физическими процессами либо движениями некоторых тел;
кроме того, эти реальные движения могут быть механическими
движениями одной, двух или трех материальных точек, причем в
системе (6.14) у2, а в системе (6.17) уи у2, уг могут быть не
координатами, а проекциями
скоростей этих точек. Как и выше,
суть перехода от системы (6.17)
к системе (6.23) состоит в том,
что численные значения у и i?/2, Уъ
реальных физических величин
принимаются за координаты zu
~*% z2> Zz точки М (t) в трехмерном
г* пространстве.
Таким образом, движение
(6.26) точки М(1) в пространстве
Z\, 22, 23 является фиктивным
Рис, 10 движением, соответствующим
реальному движению (6.16) или
(6.19) любого из перечисленных здесь видов. Как и выше,
точка M(t), совершающая фиктивное движение, называется
изображающей точкой. Фиктивное движение (6.26) точки М (t)
выражается частным решением системы (6.24) при начальных
условиях (6.25). Траектория изображающей точки, т. е.
кривая (6.26) (при t^O) в (пространстве Z\9 z2> z3, называется
фазовой траекторией системы уравнений (6.24), соответствующей
начальным условиям (6.25) или начальной точке М0 (z{0j 22o, 2зо)
(рис. 10).
Как угодно изменяя физически допустимые начальные
условия (6.15) и (6.18), а значит и (6.25), т. е. как угодно изменяя
положение точки Мо, получаем всевозможные реальные
движения (6.16) и (6.19) и соответствующие им всевозможные
фиктивные движения (6.26).
Семейство всех фазовых траекторий системы уравнений
(6.24) называется ее фазовым портретом, а трехмерное про-
58
странство zi, Z2, 23, в котором расположено это семейство,—
фазовым пространством. Часто называют фазовым
пространством системы (6.24) лишь ту часть пространства z\, z2t 23,
которая заполнена фазовым портретом этой системы уравнений.
Обратим внимание на то, что системы (6.14) и (6.17),
описывающие реальные движения, и система (6.24), описывающая
фиктивные движения, имеют один и тот же суммарный
порядок 3 и что фазовый портрет системы (6.24) расположен в
трехмерном пространстве.
Второе толкование системы (6.26) получается в
четырехмерном пространстве /, zu 22, 23.
Точки четырехмерного пространства — это всевозможные
упорядоченные четверки чисел. Все геометрические и
кинематические понятия и образы четырехмерного пространства — это
формальные обобщения соответствующих понятий и образов
трехмерного пространства. При этом сохраняется вся обычная
терминология. Однако делать чертежи в четырехмерном
пространстве невозможно.
В пространстве t, Z\y z2f 23 система уравнений (6.26)
изображает некоторую кривую. Переменная точка N(t) этой кривой
начинает свое движение в момент £ = 0 от точки М)(0, Zw, 220,230)
и с возрастанием / движется по кривой так, что в каждый
момент t ее координаты z\f z2f 23, очевидно, совпадают с
соответствующей координатами из точки M(t) на фазовой траектории,
выходящей из точки M0(zw, 22о, 2зо). Кривая (6.26), которая в
пространстве t, Z\y z2i 23 изображает частное решение системы
(6.24) при начальных условиях (6.25), называется интегральной
кривой этой системы уравнений, соответствующей начальным
условиям (6.25) или начальной точке Л/о(0, Zw, z2Q, 230).
Можно сказать, что интегральная кривая (6.26)
проектируется в пространство z\f z2, 23 в фазовую траекторию, которая
в параметрической форме выражается теми же уравнениями
(6.26). При этом точка М> совпадает с М0 и в любой момент t
точка N(t) проектируется в точку M(t). Как угодно изменяя
начальные условия (6.25), т. е. как угодно изменяя положение
точки М) в пространстве 2Ь 22, 23, получаем семейство всех
интегральных кривых системы уравнений (6.24), которое
проектируется в пространство z\, z2y 23 в семейство всех фазовых
траекторий этой системы.
Сопоставляя реальные движения и оба толкования, решений
системы (6.24), можно сказать, что каждому реальному
движению (6.16) или (6.19) соответствуют два фиктивных движения,
выраженных уравнениями (6.26): одно движение точки М(t) по
фазовой траектории в трехмерном пространстве 2Ь z2t z3 и одно
Движение точки J\P(t) по интегральной кривой в четырехмерном
пространстве t, zu 22, 23.
59
2. Обобщение на любое п
Теперь перейдем к общему случаю движения материальной
системы, который был рассмотрен в § 4.
Пусть класс реальных движений описывается системой р
уравнений:
^1 {t\ Уъ Уъ Уъ 02» 02» Уъ\ • • • i Ут> Ут> Ут> Ут+Ъ Ут+Ъ ^
Ут+2> Ут+Ъ* • • • > Ур> Ур) = °
F%{t\ Уъ Уъ Уъ 02» Уъ, Уъ\ ...; 0т, Уту Ут\ 0ш+ь Ут\ъ
Ут+2>Ут+2> -••'>Ур>Ур) = °
(6.27)
Fp(t\ Уъ Уъ Уъ 02» 02» 02'» • • •; У щу Ут> У ту Ут+ъУт+Ъ
Ут+2> Ут+2* • • • '» Ур> 0р) = °
Эта система имеет суммарный порядок п = т+р.
Пусть задана допустимая система начальных условий:
01 (0)= #10
02 (0)= 020
0m(°)=0mO
Ут+1 (°) = Ут+1.0
Ут+Ъ (0) = 0т+2,О
01 (0)= 0Ю
02 (0)= 020
0т(О)=0.
т0
0,(0) = 0,
ро
(6.28)
Частное решение системы (6.27) при начальных условиях
(6.28) выражает конкретное реальное движение:
01 = ^1 (t> 010» 010» • • » 0mO» 0mO» Ут+1.0, • • • , 0рО)
02 = ^2 С 010» 010» ...» 0тО» 0тО» Ут+1,0, ...» 0рО)
Ур = 'Фр С» 010» 010» • • • » 0тО» 0тО» Уот+1.0, • - ., 0рО)
. (6.29)
60
Преобразуем систему (6.27) в систему уравнений первого
порядка тем же методом, которым в § 2 система (2.2) была
приведена к системе (2.8i), (2.8г), ..., (2.8П), (2.9). Для этого
наряду со старыми искомыми функциями, УиУъ—,Уъ примем за
новые самостоятельные искомые функции первые производные
функций уи У2, ..., Ут- При этом удобно ввести единые
обозначения для всех т+р искомых функций:
У1 = ?1
Уг = *з
Уз=?ь
yk = z2k-i
Ут = г2гп-|
1
.
(6.30)
Ут+1 = 22т+1
Уп
г+2 = z2m+2
— %т-\-р
Ух = z2
У% = z4
Уз = 2о
Vk = ztk
Ут = Z2m J
• .
(6.31)
(6.32)
Продифференцируем один раз все эти равенства:
yi = *i
Уг = гз
yk=Z2k-A
Ут = Z2m-\
\ (6.33)
У1 = г2
k = z4
У к = ггк
Ут ~~ 22ст
(6.34)
(6.35)
Сравнение равенств (6.33) и (6.31) дает систему т
уравнений первого порядка:
61
»« «-.--.С VH. гга,-^ "".r;t
Z± — 22
Z3 — 24
z<ik-\ = 2<
(6.36)
2k
22m—1 — 22m
Далее делаем замену (6.30), (6.31), (6.32), (6.34), (6.35) в
исходной системе (6.27):
22, Z%\ 23, Z4, Z±\ . . .| 22m—1» 22m, 22m', 22m-fi> 22m-|_i|
^2m+2) 22m+2j . . • I 2m-|_p, 2/H-fp) = 0
F% \t\ 2i, 22, Z2| £3, 24, Z4J . . .; 22m—Ь 22m, 22m; 22m+b 22m-fb
22m+2> 22m-|-2) • • • I 2m-\-p> Zm-\-p) = 0
Fp\f\ 2j, Z2, 22; Z3, Z4, Z4; ...; 22m—1> 22m, 22m", 22m-fb 22m+l>
22m+2i 22m+2> • • • J Zm+pi Zm+p) — 0
(6.37)
;
Системы (6.36) и (6.37) вместе образуют систему m+p
дифференциальных уравнений первого порядка с т+р искомыми
функциями 2i, 22, ..., 2т+р. Систему (6.36), (6.37) можно
записать кратко:
22£-1 = 22£
/*/ (г; ...; Z2k—\y %2к> 22/j", ... j 22m-j_i, 2f2m+i; ... J 2ш_(_р, zm+p) = 0
& = 1, 2, ..., m
/ = 1,2, ...,p
Такую краткую запись мы будем часто применять и в
дальнейшем.
Введем еще обозначения:
yko = 22*-i,o
t/ko = 22*,о
k = 1, 2, ..., m
Ут+\,0 = 22m+l,0
*/m+2,0 = 22m+2,0
#p,0 = 2m-fpto
62
Тогда при преобразовании системы (6.27) в систему (6.36),
(6.37) начальные условия (6.28), очевидно, перейдут в такие:
*i(0) = #io = 2io
*2 (0) = Ую = г2о
*з (0) = Ум = *зо
*4 (0) = У*> = z40
*2т-1 (0) =[уто — Z2m-1,0
z2m (°) = У то = z2m,0
Z2m+1 (0) = Ут+1,0 = 2ат+1,0
2т+р (°) = УрО = *т+р,0
(6.38)
Если т = 0, т. е. если система (6.27) совсем не содержит
вторых производных искомых функций, то без каких-либо
преобразований и введения новых искомых функций она является
системой уравнений первого порядка.
Если т=р, т. е. если система (6.27) содержит вторые
производные всех искомых функций уи у2, ..., ур, то система (6.36),
(6.37) состоит из 2р уравнений.
Очевидно, при т>0 уравнения системы (6.36) являются
неполными; при этом неполны и уравнения системы (6.37), так
как в них отсутствуют zu Zz, ..., Згт-ь
Объединяя все случаи 0^т<р и используя обозначение
п = т+р, т. е. отвлекаясь от частного вида системы (6.36),
(6.37), напишем ее в общем виде:
Gi(*;2b*i; г*, k> ...;zn9zn)=0
^ G2 (t\ Zij Zi\ z2, г2; ...; zn, zn) = 0
Gn (t; zl9 zx; z2, za; ...; zn% zn) = 0
(6.39)
Напомним, что в различных случаях число п = т+р может быть
четным или нечетным.
Мы будем рассматривать только такие случаи, когда систе-
63
ма (6.39) может быть приведена к нормальной форме, т. е.
разрешена относительно производных:
2i = Qi(f,zlf z2, ...,*„)
гя = 0я(Л2ьгЯ1 ...,гл) j
(6.40)
Впрочем для этого необходимо и достаточно потребовать, чтобы
система (6.37) могла быть разрешена относительно
производных, так как система (6.36) уже разрешена относительно
производных.
Всюду в дальнейшем (и, в частности, в рассмотренных выше
случаях) мы будем считать, -что для системы (6.40) и начальных
условий (6.38), которые получились из системы (6.27) и
начальных условий (6.28), выполнены все условия теоремы
существования и единственности частного решения.
Пусть частное решение системы (6.40) при начальных
условиях (6.38) имеет вид:
Z1 — фх (f, 210, 220, . . . , 2п0) ]
22 = Фг (*> Zio> ^20> • • •» zno)
Zn = Фл (*» 2Ю» 220» • • • t Zno) )
(6.41)
Дадим два кинематических толкования уравнений (6.41) в
n-мерном пространстве zu z2, ..., 2пив (п+l)-мерном
пространстве tf zu *г> .-, *п- При этом относительно многомерного
пространства |с числом измерений больше трех можно дать
пояснение, вполне аналогичное сделанному выше о четырехмерном
пространстве.
В n-мерном пространстве z\f z%, ..., zn уравнения (6.41)
считаем параметрическими уравнениями некоторой кривой, в
которых параметром служит время t. В силу условий (6.38)
переменная точка M(t) этой кривой начинает свое движение в
момент £ = 0 ОТ ТОЧКИ Мо(2ю, 220, ..., Zn0).
Реальное движение (6.29) может быть некоторым
физическим процессом либо движением системы некоторых тел; кроме
того, это реальное движение может быть механическим
движением системы s материальных точек (—— <s^p), причем в си-
о
стеме (6.27) в случае т<р функции ут+и Ут+2, ..., уР могут
быть не координатами, а проекциями скоростей этих точек.
При т=0 переход от системы (6.27) к системе (6.39)
формально состоит лишь в замене буквы у буквой г, но, как и вы*
64
ше, суть этого перехода в том, что численные значения реальных-
физических величин уи Уг, ..., Ур мы принимаем за
координаты ги 22, ..., zn (я=р, так как т=0) точки M(t) в
n-мерном пространстве.
Таким образом, движение (6.41) точки M(t) в пространстве
zu 22, ..., zn является фиктивным движением,
соответствующим реальному движению (6.29) любого из перечисленных здесь
видов. Точка M(t), совершающая фиктивное движение,
называется изображающей точкой. Фиктивное движение (6.41)
точки M(t) выражается частным решением системы (6.40) при
начальных .условиях (6.38). Траектория изображающей точки, т.е.
кривая (6.41) (при t^O) в л-мерном пространстве zu 22, ..., zn,
называется фазовой траекторией системы уравнений (6.40),
соответствующей начальным условиям (6.38) или начальной
точке М0(2ю, 22о, >.., 2п0). Как угодно изменяя физически
допустимые начальные условия (6.28), а значит, и (6.38), т. е. как
угодно изменяя положение точки М0, получаем всевозможные
реальные движения (6.29) и соответствующие им всевозможные
фиктивные движения (6.41).
Семейство всех фазовых траекторий системы уравнений
(6.40) называется ее фазовым портретом, а n-мерное
пространство 2Ь 22, ..., 2П, в котором расположено это семейство, —
фазовым пространством. Часто называют фазовым пространством
системы (6.40) лишь ту часть пространства 2Ь 22, ..., 2П, которая
заполнена фазовым портретом этой системы уравнений.
Обратим внимание на то, что система (6.27), которая
описывает класс реальных движений, и соответствующая ей
система (6.40), которая описывает класс фиктивных движений, имеют
один и тот же суммарный порядок п = пг+р и что числа
измерений фазового пространства, в котором совершаются
фиктивные движения (6.41), также равно п = т+р, т. е. оно на т
единиц больше, чем число функций у\> у% ..., ур, выражающих
реальные движения вида (6.29).
В (я+1)-мерном пространстве t, zu z2t ..., zn система
уравнений (6.41) изображает некоторую кривую. Переменная точка
N(t) этой кривой начинает свое движение в момент t = 0 от
точки М)(0, 2ю, 22о, ..., 2по) и с возрастанием t движется по кривой
так, что в каждый момент t ее координаты zu z% ..., 2П,
очевидно, совпадают с соответствующими координатами точки M(t)
на фазовой траектории, выходящей из точки М0(210, 2го, ..., 2п0).
Кривая (6.41), которая в пространстве /, z\, z% ..., zn
изображает частное решение системы (6.40) при начальных условиях
(6.38), называется интегральной кривой этой системы
уравнений, соответствующей начальным условиям (6.38) или
начальной точке Afo(0, zi0i 220, ..., zn0).
Можно сказать, что интегральная кривая (6.41)
проектируется в пространство 2Ь 22, ..., zn в фазовую траекторию, кото-
3 А. Г. Мл адов
65
рая в параметрической форме выражается теми, же
уравнениями (6.41). При этом точка Л/о совпадает с М0 и в любой
момент t точка N(t) проектируется в точку M(t). Как угодно
изменяя начальные условия (6.38), т. е. как угодно изменяя
положение точки Л/о в пространстве z{f z2i ..., zn, получаем
семейство всех интегральных кривых системы уравнений (6.40),
которое проектируется в пространство zu z2i ..., zn в семейство
всех фазовых траекторий этой системы.
Интегральные кривые системы (6.40) нигде не имеют общих
точек, так как выше было сказано, что для этой системы и
любых допустимых условий (6.38) выполнены все условия
теоремы существования и единственности частного решения.
Сопоставляя реальные движения и оба толкования решений
системы (6.40), можно сказать, что каждому реальному
движению (6.29) соответствуют два фиктивных движения,
выраженных уравнениями (6.41): одно движение точки M(t) по фазовой
траектории в я-мерном пространстве Z\, z2, ..., zn и одно движе- -
нйе точки N(t) по интегральной кривой в (п+1)-мерном про- |§
странстве t> zu z2y ..., zn. .*]
Выясним, чем вызван переход от системы уравнений (6.27),
которая описывает класс реальных движений вида (6.29) с
помощью р функций у и У2, ..., Ур, к системе уравнений (6.40),
которая описывает класс фиктивных движений вида (6.41)
в фазовом пространстве zu z% ..., zn п=т+р измерений.
Может показаться, что Зтим переходом мы лишь усложняем
задачу изучения движений, так как при т>0 фиктивные
движения в фазовом пространстве могут быть сложнее, чем
соответствующие реальные движения (см. пример 1 § 5).
Однако следует подчеркнуть, что любому реальному
движению материальной системы, в том числе и не механическому, |j
всегда соответствует механическое фиктивное движение |
изображающей точки. Так что в этом смысле фиктивное
движение почти всегда проще реального.
Главное же состоит в следующем. Обратим внимание на то,
что при т>0 функции уи #2, ..., Ур входят в систему уравнений
(6.27) неравноправно: уи \)ч, ..., Ут входят с первыми и
вторыми производными, а ут+и Ут+2, ..., Ур только с первыми
производными; в то же время все функции zu z2, ..., zn (n =
= т+р) входят в систему уравнений (6.40) равноправно, т. е.
только с первыми производными. Это дает возможность
применять единые .методы изучения свойств сразу всех функций
Zu z2 ..., zn, тогда как методы изучения свойств функций ||
Уи #2, ..., Ут И Ут+U Ут+2, ..., Ур ДОЛЖНЫ бЫТЬ раЗЛИЧНЫ. *
Вместе с тем в дальнейшем, особенно в § 8, мы увидим, что,
зная характер фиктивных движений в фазовом пространстве,
можно делать выводы о характере соответствующих реальных
движений.
66
§ 7. СТАЦИОНАРНОЕ И НЕСТАЦИОНАРНОЕ ДВИЖЕНИЯ
В § 6 мы видели, что системе дифференциальных
уравнений (6.27), которая описывает класс реальных движений,
соответствует нормальная система дифференциальных уравнений
(6.40), которая в фазовом пространстве Z\, z2t ..., zn описывает
класс фиктивных движений, соответствующих реальным. Как
известно, эта нормальная система имеет вид:
Zl — Ql (^> 2ъ г2> • • • > zn)
Zot = V2 {t, Zi, Z2i . . . , Zn)
Zn — Qn ('» zb Z2> • • • i zn) ,
Каждое частное решение этой системы выражает конкретное
фиктивное движение изображающей точки M(t) по
соответствующей фазовой траектории.
Весь класс движений, описываемый системой (7.1), можно
рассматривать как поток некоторой сплошной среды, например
жидкости, частицы которой совершают движение по
всевозможным фазовым траекториям системы (7.1).
Пусть система координат в пространстве zu z2, ..., zn
определена началом О и единичными попарно-ортогональными
векторами еъ е2у ..., #п. Тогда радиус-вектор и вектор скорости
какой-либо частицы потока выразятся так:
г = г1ег + г%е%+ ...+гпеп; г = г1е1 + г%ег+ ...+znen.
Следовательно, левые части, а значит, и правые части
уравнений (7.1) выражают проекции скоростей частиц потока.
Таким образом, вся система (7.1) определяет поле
скоростей при всех тех значениях t, z\, z2y ..., zn, при которых
непрерывны функции Qi, Q2, ..., Qn. Это поле скоростей
определено в той области пространства Z\y z2y ..., zny которая занята
потоком и вместе с тем фазовым портретом системы- (7.1) и
рассматривается на некотором промежутке времени, например
на полуоси £>0, поскольку реальные и фиктивные движения мы
изучаем при *>0.
Из выражений функций Qu Q2, ..., Qn видно, что скорости
частиц потока, проходящих через каждую фиксированную точку
области пространства Z\f z2i ..., znt занятой потоком, зависят,
вообще говоря, от координат каждой такой точки и от времени.
Между тем возможен случай, когда скорости частиц,
проходящих через каждую фиксированную точку, зависят только от
координат этих точек, но в каждой такой точке не изменяются
с течением времени. В этом случае в правые части уравнений
(7.1)
3*
67
-■*■
(7.1) время t не входит непосредственно или, как говорят, явно
(входит лишь через посредство ги z2f ..., zn), т. е. система (7.1)
принимает вид:
zi — 9i(^i» 2з» • • • >zn) |
гг — Чъ(zu *2> - > - >zn) i (7.2)
Движение потока, в котором скорости всех частиц,
проходящих через каждую фиксированную *гочку области, занятой
потоком, зависят только от координат этих точек и в каждой
такой точке не изменяются с" течением времени, называется
стационарным движением. Таким образом, стационарное
движение описывается системой уравнений вида (7.2).
Движение потока, в котором скорости частиц, проходящих
хотя бы через одну фиксированную точку, зависят не только от
координат этой точки, а в этой точке изменяются с течением Ц
времени, называется нестационарным движением.
Следовательно, нестационарное движение описывается системой уравнений
вида (7.1), в которой хотя бы одно уравнение содержит t
непосредственно.
Следует заметить, что если в какой-то фиксированной точке
скорости частиц изменяются с течением времени, то в силу
непрерывности функций Qi, Q2, ..., Qn и в некоторой окрестности
этой точки скорости частиц изменяются со временем; иначе
говоря, если движение потока нестационарно в какой-нибудь
точке, то оно нестационарно и в некоторой окрестности этой точки.
Можно сказать, что стационарным движением называется Щ
такое движение, поле скоростей которого не изменяется с
течением времени, а нестационарным движением называется
движение, поле скоростей которого изменяется с течением времени.
При стационарном движении траектории частиц, т. е.
фазовые траектории системы (7.2), проходящие через каждую
'фиксированную точку, совпадают между собой; при этом
фазовые траектории с различными начальными точками либо
совпадают между собой, начиная с некоторой точки, либо вообще
не имеют общих точек. Напомним, что в § 5 были рассмотрены
примеры движений, которые, очевидно, являются
стационарными, причем фазовые траектории этих движений, расположенные
на эллипсах, спиралях и прямых, обладают только что
указанным свойством. При нестационарном движении хотя бы через
некоторые точки могут проходить несовпадающие траектории,
даже целые пучки несовпадающих траекторий. При этом по
различным траекториям, проходящим через одну и ту же точку,
68
частицы потока проходят в различные моменты времени и
поэтому никогда не сталкиваются между собой.
В силу предположений, принятых в § 6 для систем (7.1)
и (7.2) и для всех допустимых начальных условий, выполнены
все условия теоремы существования и единственности частного
решения. Поэтому интегральные кривые этих систем (в
пространстве t} Z\f z2f ..., zn) нигде не имеют общих точек. Но эти
интегральные кривые проектируются в фазовые траектории,
которые в одном случае могут частично совпадать, а в другом
случае пересекаться или касаться.
В заключение этого параграфа рассмотрим два примера.
Пример 1. Пусть стационарное движение описывается
системой уравнений
21 = 4 } • (7.3)
Продифференцируем первое из этих уравнений:
z1 = z2.
Подставляя из второго уравнения, получаем уравнение
zl — z1=0.
Его характеристическое уравнение г2—1=0 имеет корни
П,2,= ±1.
Следовательно,
Схё + С2е~*
(7.4)
Это общее решение системы (7.3), которое в параметрической
форме изображает семейство фазовых траекторий этой системы
на плоскости zu z2.
Чтобы исключить t и получить уравнение этого семейства в
координатной форме, возведем в квадрат каждое из уравнений
(7.4) и вычтем результаты:
Вводя обозначение 4CiC2 = C, окончательно получаем уравнение
фазового портрета системы (7.3):
z\-zl = С. (7.5)
Это семейство равносторонних гипербол (рис. 11), общими
асимптотами которых служат биссектрисы координатных углов,
которые сами входят в семейство при С = 0.
Из общего решения (7.4) видно, что начальным условиям
22(0)=0 J
соответствует частное решение
соответствующая фазовая траектория состоит только из.одной
точки — начала координат.
Рис. 11
Начальным условиям
*i(0) = a 1
z2(0)=a J
соответствуют в формуле (7.4) значения
Сг = а 1
С2 = 0 J
и частное решение
z2 = aet J '
отсюда уравнение соответствующей фазовой траектории Z\=z2;
при а>6 она лежит на биссектрисе первой четверти, при а<0 —
на биссектрисе третьей четверти.
70
Начальным условиям
22(0) = -а)
соответствуют в формуле (7.4) значения Ci = 0, С2 = а и частное
решение
гг = ае~*
гг = — о*?-'
отсюда уравнение соответствующей фазовой траектории
2i+22=0; при а>0 она лежит на биссектрисе четвертой
четверти, при а<0 — на биссектрисе второй четверти.
Начальным условиям
M0) = z10
*а(0) = г20
в которых |г10| Ф |г20|, соответствует фазовая траектория,
которая лежит на ветви гиперболы, проходящей через точку
Mo(z\o, 22o). Стрелки на рис. 11 указывают направления
движений .точки M(t) по перечисленным линиям; это следует как из
уравнения z\—z2i так и из уравнения z2~Zi.
Подчеркнем, что если движение потока рассматривается при
/>0, то траектория каждой конкретной частицы покрывает не
всю линию семейства (7.5), по которой она проходит, а лишь
часть этой линии от начальной точки Мо(2ю, z20), обращенную
в сторону, указанную стрелками на рис. 11. Если же движение
потока рассматривать при всех — оо < t < оо, то траектория
каждой конкретной частицы полностью покрывает
соответствующую линию семейства (7.5).
Пример 2. Пусть нестационарное движение описывается
системой уравнений
гг = г2
г2 ТГТТ^ "г *
е+1)2 t+\
(7.6)
Заметим, что коэффициенты второго уравнения имеют разрыв
при £=—1. Поэтому движение, описываемое этой системой,
нельзя рассматривать на всей оси t\ мы рассмотрим его при/^0.
Подставим 22 = 2i в правую часть второго уравнения:
i = 2*i t 2*i
2 tf+l)2 *-М '
71
Перепишем это уравнение так:
2 dt\t + l)
Отсюда
2 / + 1 ^
Подставляя сюда Z2 = zu получаем линейное уравнение первого
порядка со свободным членом С:
Zi-y^—C. (7.7)
Ищем общее решение этого уравнения методом вариации
постоянной. Соответствующее уравнение без свободного члена
z =о имеет общее решение z=k(t+l)2. Общее решение
уравнения (7.7) ищем в виде Z\=k{t) (t+\)2. Подставляя это
выражение в уравнение (7.7), находим
Вводя обозначение С2 =—С, напишем общее решение
системы (7.6):
2Ti=c1(*:+i)*+c1(*+i) I 8
г2 = 2Сгу + 1) + С, Г
Система (7.8) в параметрической форме изображает
семейство всех фазовых траекторий системы (7.6) на плоскости zuz2.
Чтобы исключить t и получить уравнение этого семейства
в координатной форме, выразим (£+1) из второго уравнения
системы (7.8), что возможно при С\фЬу и подставим в первое
уравнение:
/ + 1 =
%2 — ^2™
ад
1
После упрощений уравнение фазового портрета системы (7.6)
принимает вид:
4Сггх =£ — (%. (7.9)
Это семейство линий, зависящее от двух произвольных
постоянных.
72
Ш
s '«ueaFa-WTv^-H;
. .* .. ■.аз-т^.ы-ъы ^«ячяи^яявк*, 4WW3aKWWMee
При С{фО линии семейства (7.9) — это параболы, для
которых ось Z\ служит общей осью симметрии; при Ci>0 ветви этих
парабол обращены вправо, а вершины лежат не правее начала
координат; при Ci<0 ветви этих парабол обращены влево,
а вершины лежат не левее начала координат (рис. 12).
При С\ = 0 система (7.8) дает
*i=Ct(*+l)
Без участия t уравнение линий (7.10) имеет вид 22 = С2. Это
прямые, параллельные оси Z\.
Заметим, что эти прямые содержатся в семействе (7.9) при
Ci = 0, несмотря на то, что уравнение (7.9) было получено при
Рис. 12
С^О. Таким образом, если в уравнении (7.9) не исключать
значение Ci = 0, то оно выражает весь фазовый портрет
системы (7.6) (рис. 12). Стрелки на рис. 12 указывают направления
движений частиц потока по перечисленным линиям, что следует
из уравнения z{ = z2 системы (7.6).
Так как семейство (7.9) двухпараметрическое, т. е. зависит
от двух произвольных постоянных, то через каждую точку
плоскости z\t Z2 проходит целый пучок линий этого семейства.
Поэтому, чтобы узнать, по какой траектории проходит через
заданную точку какая-либо конкретная частица потока, нужно
задать еще момент ее прохождения через заданную точку. Это
можно делать как для начального момента £ = 0, так и для
любого другого момента t\>0.
Выясним, по каким линиям семейства (7.9) будут двигаться
73
(7.10)
sffiwa6TSafiH3L*sai'»<se»^«iSii' ,^ т чч»<~#-(
частицы потока, выходящие в момент < = 0 из заданных точек
плоскости. Как угодно задавая начальные условия
М0) = г10
z2(0)=z20
мы можем найти соответствующие значения постоянных Си С2.
В самом деле, подставляя в общее решение (7.8) /=0и
заданные Zw, 22o, получаем
*10== ^ + 6, \ (7П)
откуда
Сх =** — *& | (7Л2)
С2 = 2z10 — z20 J
Это значит, что каждая частица потока выходит из той точки,
в которой она находится в момент t = 0, по вполне определенной
траектории.
Из формул (7.8) и (7.10) видно, что при С\ = 0 траекториями
являются полупрямые. В свою очередь из формулы (7.12)
видно, что Ci = 0, если 2io=22o» так что при 2ю=22о>0 начальные
точки траекторий лежат на биссектрисе первой четверти, а при
2io=22o<0 — на биссектрисе третьей четверти. Далее из формул
(7.12) и (7.8) видно, что если 22о>2ю, т. е. если начальные
точки траекторий лежат над биссектрисой первой и третьей
четвертей, то Ci>0 и 22 = 2 Ci>0, так что траекториями являются
части парабол, обращенных ветвями вправо, расположенные
выше начальной точки; если 22о<2ю, т. е. если начальные точки
траекторий лежат под биссектрисой первой и третьей четвертей,
то Ci<0 и 22=2Ci<0, так что траекториями являются части
парабол, обращенных ветвями влево, расположенные ниже
начальной точки. Траектории частиц, начинающих свое движение
в момент *=0, изображены на рис. 12 сплошными линиями.
Как угодно задавая условия
Zl(*i) = Zu
22 (tx) = Z21
в любой момент 1\Ф—1 также можно найти значения
постоянных Си С2. Действительно, в силу этих условий из общего
решения (7.8) получаем
*u = c1(;1 + i)2 + c2&+;i)
*n=2Cx(tx+l) + C%
}■
74
откуда
г21 *11
22ц
'l + l
— z
21
(7.13)
Найдем, например, траектории, проходящие через точку
5(0; 1), по которым частицы потока проходят в моменты
Рис. 13
Подставляя в систему (7.13)
zn = О, z2i = 1, t\ = 1,
находим
c1==-i-. ct = -i
и получаем уравнение соответствующей траектории
2z1 = z\~ 1.
Подставляя в систему (7.13)
находим
Сх , С8 — 1
и получаем уравнение соответствующей траектории
4 2 «
75
Пользуясь системой (7.11), легко проверить, что в момент
£ = 0 частицы на этих траекториях находятся соответственно в
точках
А(-|;о), А(--Ь-т)
Эти траектории изображены на рис. 13.
Замечание. Термины стационарное и
нестационарное движения часто переводят как установившееся
и неустановившееся движения. Ни в коем случае нельзя
смешивать их с понятиями устойчивого и неустойчивого
движений, которые будут введены в следующем параграфе.
§ 8. УСТОЙЧИВОСТЬ И НЕУСТОЙЧИВОСТЬ РАВНОВЕСИЯ.
УСТОЙЧИВОСТЬ И НЕУСТОЙЧИВОСТЬ ДВИЖЕНИЯ
1. Устойчивость и неустойчивость равновесия
Для составления этих понятий рассмотрим сначала
систему q материальных точек Ми M2f ..., Mjt ..., Mqy которая
находится в равновесии, т. е. неподвижна относительно некоторой
системы координат.
I
Рис. 14
Пусть положение равновесия этих точек определяется их
постоянными радиусами-векторами r10, r20, ...,rj0,...,r90 (рис. 14).
В некоторый момент, который примем за момент t = 0
(начальный момент), сместим точки нашей системы на векторы
76
I
skus:<i-£«*«l -л .^.ч^и,^-^
ТТЛ --*-.»r-"-b*rT"S!wv\-- с
^f-ч.-^™ --о ■>*. «-wet -зж«?~экл*еетана«
Д/-10,... ,Ary0,..., Аг^о (начальные смещения) и сообщим точкам
скорости Дг>10, Д^го, • • • > Д^о> • • •, Д^о (начальные скорости).
Следует подчеркнуть, что физически невозможно мгновенно
сместить точки на какие-то векторы, для этого требуется
некоторое время; также невозможно мгновенно сообщить точкам
какие-то скорости, так как для этого нужно сообщить точкам
соответствующие импульсы, которые должны действовать
некоторое время. Поэтому, чтобы осуществить указанные смещения
и скорости точек в момент £=0, нужно начать делать это
заблаговременно, до момента £ = 0, и закончить в момент t = 0.
Заметим, что векторы rj0, Дг;0, Дг>у0 для каждого номера /
вообще могут быть неколлинеарными и даже некомпланарными.
Требуется только, чтобы все векторы
Д/> Д^о / = 1,2, ... ,9
допускались связями, которые имеются между точками Ми
Итак, в момент t=0 система Ми М2, ..., Мд выведена из
первоначального состояния равновесия. Поэтому при />0 она,
вообще говоря, придет в движение. Следовательно, при />0
отклонения точек от первоначального положения равновесия и их
скорости будут функциями времени, которые мы обозначим так:
Дг,(<) и Д^(0 . / = 1, 2, ... , д.
С помощью этих функций и определяется устойчивость и
неустойчивость равновесия.
Чтобы дать общие определения устойчивости и
неустойчивости равновесия, рассмотрим любую материальную систему,
характеризуемую р физическими величинами, равновесие
которой определяется постоянными значениями Ию, и2о, .♦., Що, ..., ир0
этих величин.
В некоторый момент, который примем за начальный момент
^ = 0, изменим значения Этих величин на Д^ю, Д«2о, ..., Д«го, ...,
Мр0 (начальные отклонения) и, если это физически возможно,
сообщим некоторые скорости их изменения ДакьД^о,..., Д^го,...,
Дуро (начальные скорости). Как и выше, «мгновенные»
отклонения и «мгновенные» скорости в момент /=0 следует понимать
как отклонения и скорости, которые осуществляются в течение
некоторого времени до момента t = 0 и заканчиваются при £ = 0.
Впрочем, в некоторых случаях (особенно в оптике и
электронике) начальные отклонения и начальные скорости можно
считать практически мгновенными. Все Да*о, Д^го, t=l, 2, ..., р
должны быть физически допустимыми.
Так, в примерах 1—4 § 4 мы видели, что равновесие, как
частный случай движения, может входить в класс движений,
который описывается дифференциальным уравнением или систе-
77
мой дифференциальных уравнений. Вообще, если система
уравнений (4.38) § 4 описывает класс движений, который содержит
некоторое положение равновесия, то физически допустимые
начальные отклонения от равновесия можно задавать для всех
функций уи У2, ..., уР, входящих в систему (4.38), а начальные
скорости в случае т<р можно задавать лишь для уи Уъ .«, #™»
но нельзя задавать их для ут+и #?п+2, ..., у?\ при этом
начальными скоростями являются начальные отклонения для у\, #2, ...,
ут. Читателю рекомендуется проследить это на примерах
1-4 § 4.
Материальная система, которая в момент /==0 выведена из
состояния равновесия, вообще говоря, придет в движение при
/>0. Поэтому при />0 отклонения физических величин,
характеризующих материальную систему, от их первоначальных
значений и скорости их изменения будут функциями времени,
которые мы обозначим через
ДиДО и At>,(f) 1 = 1, 2, ... , р.
С помощью этих функций мы составим определения
устойчивости и неустойчивости равновесия материальной системы.
Сущность этих определений состоит в следующем: равновесие
называется устойчивым, если при любых достаточно малых
начальных отклонениях и начальных скоростях все отклонения и
скорости во все последующее время остаются малыми;
равновесие называется неустойчивым, если даже при сколь угодно
малых начальных отклонениях и начальных скоростях, хотя бы
некоторые отклонения или скорости в последующее время не
остаются малыми.
Подчеркнем, что устойчивость или неустойчивость
равновесия материальной системы — это свойство системы, которое
обусловлено ее строением и не может быть устранено без
изменения строения системы.
Теперь мы можем дать точные определения.
Равновесие материальной системы называется устойчивым,
если для каждого заранее заданного положительного
числа е можно подобрать положительное число т|, зависящее от
е, Ti = ri(е), такое, что при любых начальных отклонениях и
начальных скоростях, удовлетворяющих условию
1А"<°1<М / = 1,2, ... ,р,
|At>tol<4J
все отклонения и скорости во все последующее время 7> 0
удовлетворяют условию
|Ди,(*)|<е
|Ао,(*)|<в
78
• * = 1, 2,
Равновесие материальной системы называется устойчивым
асимптотически, если оно устойчиво и, кроме того, все
отклонения скорости удовлетворяют условию
limA«i(0=0
t-*oo
UmAvi(t) = 0
t-±QQ
Равновесие называется устойчивым неасимптотически, если
оно устойчиво, но хотя бы некоторые отклонения или скорости
не стремятся к нулю при t-+- со.
Равновесие материальной системы называется неустойчивым,
если хотя бы для одного положительного числа е и для
каждого даже сколь угодно малого положительного числа т), хотя бы
при некоторых начальных отклонениях и начальных скоростях,
удовлетворяющих условию
|А«»1<П) t-_, 2 о
|Af*ol<4 1
хотя бы некоторые отклонения или скорости по меньшей мере
в некоторые моменты ts>0 удовлетворяют условию | Ди&(^)| >е
ИЛИ| &Vi(ts) j >8.
Заметим, что все эти определения применимы и к
рассмотренной выше системе материальных точек, так как в качестве
Attn, Д^го, Д«г(0> Дуг(0 можно брать длины или проекции
векторов Дг,о, Дг>;0> Д^(0, A*V(0-
Приведем два примера.
Пример 1. Пусть твердое тело закреплено в такой
установке, которая допускает вращение тела во Bicex направлениях,
но при этом оставляет неподвижной одну точку тела. Положим,
что вся установка окружена воздухом. Пусть так закрепленное
тело находится в равновесии за счет того, что его неподвижная
точка и центр тяжести расположены на одной вертикали.
Если центр тяжести тела расположен под неподвижной
точкой, то любая система точек этого тела, а значит, и все тело
находятся в устойчивом равновесии. Без учета сил трения и
сопротивления воздуха это равновесие устойчиво неасимптоти-
чески, а с учетом этих сил устойчиво асимптотически.
Если центр тяжести тела расположен над неподвижной
точкой, то любая система точек этого тела, а значит, и все тело
находятся в неустойчивом равновесии, так как при малейшем
отклонении или толчке тело опрокинется.
Пример 2. Пусть массивный шарик, который примем за
материальную точку, лежит на твердой поверхности, имеющей
форму чаши, например на сфере или на эллиптическом
параболоиде.
i = lt 2, ... , р.
79
Если шарик лежит на вогнутой стороне чаши, в ее низшей
точке, то он находится в устойчивом равновесии. Без учета сил
трения и сопротивления среды это равновесие устойчиво-
неасимптотически, а с учетом этих сил устойчиво асимптотически.
Если шарик лежит на выпуклой стороне чаши, в ее высшей
точке, то он находится в неустойчивом равновесии, так как при
малейшем отклонении или толчке скатится с купола.
2. Устойчивость и неустойчивость движения
по Ляпунову
Пусть класс реальных движений материальной системы
описывается системой дифференциальных уравнений такого вида,
который был рассмотрен в § 4 и 6:
Pi(t\ Уг> Уъ Уг\ Уг, #2, У*\ ... '• Ут> Ут, Ут\
Ут+1> Ут+1> Ут+2> 'Ут+Ъ> • • • "> Ур> f/p) = °
/ = 1, 2, ... , р
(8.1)
Пусть, как и в § 6, эта система уравнений приведена к
нормальной форме:
ii = Qi(ff zl9 z2t ... , zn)\
Z2 == 42 {*» ZU Z2> • • • » Zn)
Zn — Qfl V> Z\> Z2> • • • » Zn) J
(8.2)
В фазовом пространстве п=т+р измерений система (8.2)
описывает класс фиктивных движений, соответствующих
реальным.
Выделим из класса реальных движений одно конкретное
движение и назовем его невозмущенным движением. На практике
в качестве невозмущенного движения обычно выбирается такое
движение, т. е. такой режим физического или
производственного процесса, который желательно осуществить как можно
точнее. Отклонения от невозмущенного движения, которые обычно
вызываются внешними возмущающими воздействиями на
материальную систему, в этом случае нежелательны.
Фиктивное движение, которое соответствует
невозмущенному реальному движению, называется невозмущенным
фиктивным движением, а в дальнейшем просто невозмущенным
движением.
Начальные условия, которым удовлетворяет невозмущенное
фиктивное движение, называются невозмущенными начальными
условиями и считаются известными, заданными:
*i (0) = г10
z2 (0) = z20
*n(0)=zl
пО
(8.3)
Невозмущенное движение выражается частным решением
системы уравнений (8.2) при невозмущенных начальных условиях
(8.3); мы даем две записи этого частного решения: подробную,
которая отражает зависимость решения от начальных условий,
и краткую, которая удобна для дальнейших выкладок:
zx = фх (t, z10, г20, ... , zn0) = <px (t)
4 =■ Ф2 (U 2ю, 220, ... , zn0) = ф2 (t)
*Я = ФЯ('| *10> *20> • •• . *Яо)=ФЯ(0 J
(8.4)
Невозмущенное движение (8.4), как и невозмущенное реальное
движение, считается известным.
Как было сказано выше, материальная система испытывает
внешние возмущающие воздействия.
В нашем курсе всюду, кроме п. 3 § 8, изучается только
такой случай, когда внешние возмущающие воздействия на
материальную систему обладают следующими двумя свойствами:
1°. Все внешние возмущающие воздействия на материальную
систему навсегда прекращаются не позже
момента £=0.
2°. Под влиянием внешних возмущающих воздействий
движение материальной системы изменяется, но так, что не из-
меняютсяуравнения движения (8.1), а значит, и
уравнения (8.2).
Между тем реальные материальные системы могут
испытывать внешние возмущающие воздействия и после момента £=0,
Случай, когда все внешние возмущающие воздействия навсегда
прекращаются не позже некоторого момента t = t\y можно свести
к случаю, указанному в свойстве 1°; для этого достаточно
сдвинуть шкалу времени, т. е. перевести часы так, чтобы прежнему
моменту t=t\ соответствовал в новом времени момент ^ = 0.
Случай, когда нет такого момента, после которого внешние
возмущающие воздействия навсегда прекратились бы, а также случай,
когда под влиянием внешних возмущающих воздействий
изменяются и уравнения движения, мы кратко рассмотрим лишь
в п. 3 § 8.
Реальное движение, которое совершает материальная
система после прекращения внешних возмущающих воздействий,
81
Sn-0"sV*>J** <Ч
обладающих свойствами 1° и 2°, и соответствующее ему фиктив- |
ное движение называются соответственно возмущенным реаль- \
ным движением и возмущенным фиктивным движением относи- - |
тельно выбранного невозмущенного движения. I
Так как внешние возмущающие воздействия обладают свой- I
ствами 1° и 2°, а вюе движения мы изучаем лишь при £>0, то J
все возмущенные реальные движения содержатся в классе дви- [
жений, описываемых системой уравнений (8.1), а все возму- |
щенные фиктивные движения содержатся в классе движений, I
описываемых системой уравнений (8.2). Иначе говоря, каждое I
возмущенное реальное движение является некоторым частным |
решением системы (8.1), а соответствующее ему возмущенное |
фиктдвное движение — соответствующим частным решением си- -~|
стемы (8.2). Каждому возмущенному движению соответствуют
свои начальные условия, которые называются возмущенными
начальными условиями (соответственно реальными и в
фазовом пространстве). Возмущенные начальные условия должны
быть физически допустимыми для материальной системы.
Разности соответствующих компонент, возмущенных и
невозмущенных начальных условий называются возмущениями
начальных условий, а также начальными возмущениями или
начальными отклонениями (соответственно реальными и в
фазовом пространстве); обозначим их так:
&у10 = Аг10
&yl0 = Az20
Д#20 = Az30
Ау20 = Дг40
Д*/тО = Д^2т—1,0
Д*/т-Н,0 = AZ2m+l,0
A*/m-f2,0 = Д 22т+2,0
&Ур,о = Агт+р»о
Таким образом, результат внешних возмущающих
воздействий, обладающих свойствами Г и 2°, проявляется в
момент t = 0 только в виде начальных возмущений.
Эти начальные возмущения физически не могут получиться
мгновенно; их осуществление происходит в течение некоторого
промежутка времени и заканчивается не позже момента f=0.
(8.5)
32
Обозначим через zl9 z2, ..., zn координаты точки,
изображающей возмущенное движение. С помощью этого обозначения
возмущенные начальные условия запишутся так:
^i (0) = Zio + Az10 |
*2 (0) = 220 + &Z2Q I
^(°) = гя0 + А2яо J
Разности соответствующих координат точки, изображающей
возмущенное движение, и точки, изображающей иевозмущен-
ное движение (8.4), составленные для каждого момента t >0,
называются возмущениями (или отклонениями) для каждого
момента £>0, а в приложениях к системам автоматического
регулирования — расстройкой системы:
?2(0-
2/(0-
*»(')-
-Ф1(0 =
- Фа (0 =
-ф,(0 =
-фло-
= A*i(0 |
= t±zAt)
= д2,(0 I
= Дгя(0 1
Возмущения для каждого момента /> 0 являются
функциями времени, которые при t=0 имеют значения (8.5).
Из системы (8.7) можно выразить функции, описывающие
возмущенное движение, т. е. частное решение системы (8.2),
соответствующее возмущенным начальным условиям (8.6):
M0 = q>i(9 + A*i(0 ]
*я(0 = фя(0+ **«(<) J
Напомним, что для системы уравнений (8.2) и для любых
допустимых начальных условий при t=0 мы потребовали
выполнения всех условий теоремы существования и
единственности частного решения. Поэтому при отсутствии начальных
возмущений возмущенные начальные условия (8.6) совпадают
с невозмущенными начальными условиями (8.3), возмущенное
Движение совпадает с невозмущенным движением (8.4), а воз-
83
мущения для любого момента i>Q отсутствуют, т. е.
тождественно равны нулю.
Таким образом, возмущения для каждого момента />0
являются следствием только начальных возмущений, которые, как
известно, являются результатом внешних возмущающих
воздействий, обладающих свойствами Г, 2°.
Все записи мы делаем преимущественно в координатах
фазового пространства zu z2, ..., zn, так как это удобно для
дальнейшего.
Теперь мы можем перейти к определениям устойчивости и
неустойчивости движения по Ляпунову, которые составляются
с помощью начальных возмущений (8.5) и возмущений (8.7)
для каждого момента £>0.
Сущность этих определений состоит в следующем:
невозмущенное движение называется устойчивым, если при любых
достаточно малых начальных возмущениях все возмущения в
каждый момент t^O остаются малыми; невозмущенное
движение называется неустойчивым, если даже при сколь угодно
малых начальных возмущениях, хотя бы некоторые компоненты
возмущений при t>0 не остаются малыми. При этом
невозмущенное реальное движение называется устойчивым, если ему
соответствует устойчивое фиктивное движение; невозмущенное
реальное движение называется неустойчивым, если ему
соответствует неустойчивое фиктивное движение. Поэтому
определения устойчивости и неустойчивости относятся и к
невозмущенному реальному движению, хотя они проще формулируются
в тгерминах фиктивного движения.
Важно подчеркнуть, что устойчивость или неустойчивость
невозмущенного движения материальной системы является
свойством самой системы и того ее движения, которое принято за
невозмущенное; это свойство обусловлено строением этой
системы и не может быть устранено без изменения ее строения,
но во многих случаях это свойство для одной и той же
материальной системы может быть различным при различном
выборе невозмущенного движения. Впрочем, в следующем параграфе
будет показано, что если система (8.2) линейная, то
устойчивость или неустойчивость движения не зависит от выбора
невозмущенного движения.
Теперь мы дадим точные определения устойчивости и
неустойчивости движения по Ляпунову.
Невозмущенное движение называется устойчивым по
Ляпунову, если для каждого заранее заданного положительного
числа е можно подобрать положительное число г\, зависящее
от е, г| = т|(е) такое, что при любых начальных возмущениях,
удовлетворяющих условию
Що1<Ч * = 1. 2, ... , п,
84
все возмущения при всех t^O удовлетворяют условию
|Az,(f)l<e i = l, 2, ... , п.
Невозмущенное движение называется асимптотически
устойчивым по Ляпунову, если оно устойчиво и, кроме того, все
возмущения при />0 удовлетворяют условию
limAzi(t)=0 i = l, 2, ... , п.
Невозмущенное движение называется неасимптотически
устойчивым по Ляпунову, если оно устойчиво, но хотя бы
некоторые компоненты возмущений не стремятся к нулю при
*-*оо.
Невозмущенное движение называется неустойчивым по
Ляпунову, если хотя бы для одного положительного числа е и для
каждого даже сколь угодно малого положительного числа rj
хотя бы при некоторых начальных возмущениях,
удовлетворяющих условию
|A*/ol<4 * = 1, 2, ... , л,
хотя бы некоторые компоненты возмущений по меньшей мере в
некоторые моменты ts>0 удовлетворяют условию |Аг^(^)| >е.
Подчеркнем, что во всех этих определениях компоненты
начальных возмущений должны быть лишь достаточно малыми,
но они независимы между собой, т. е. никаких других
ограничений условий или связей на них не наложено, и,
следовательно, между ними не обязаны выполняться какие-либо
соотношения.
Пример. Вернемся к различным случаям движения груза на
пружине, которые были рассмотрены в § 4, 5. При этом согласно
общим определениям устойчивости и неустойчивости движения
мы будем исследовать соответствующие фиктивные движения
на фазовой плоскости zu z2l.
1) Если &=0, т. е. если сила сопротивления в точности
уравновешивается активной силой, то из § 5 мы знаем, что класс
фиктивных движений описывается системой уравнений
(8.8)
Пусть заданы начальные условия, которые мы примем за
невозмущенные:
гЛО) = Уо = г10\ (89)
*г (0) = У о = z20 I
85
игежжнзяючЯлм^а.ЕР'Ж-ь.*' тл кяячг1аиняяЕяииУлЛ5а-чкаг^
Используя формулу (5.4) § 5, напишем частное решение
системы (8.8) при начальных условиях (8.9), которое выражает
невозмущенное движение
zt = z10 cos tot Ц—— sin tot
CD
z2 = — z10 со sin tot + z20 cos tot
(8.10)
Введем обозначения для начальных возмущений и
возмущений для каждого момента t^O:
}■
Дг10 — х10
Az1(t) = xl)
Az2(0 = *2J
Напишем возмущенные начальные условия:
, £ (0) = z10 + Аг10 = г10 + х10
гг (0) = 220 + Д^20 = z20 + «^20 )
Используя ту же формулу (5.4), напишем частное решение
системы (8.8) при начальных условиях (8.13), которое выражает
возмущенное движение:
220 +*20
(8.11)
(8.12)
(8.13)
2i = (z10 + xl0)costot +
sin tot
(О
z2 = — (z±l + x10) to sin tot + (z20 + *20) cos orf J
(8.14)
Вычитая из функций (8.14) соответствующие функции (8.10)
и используя обозначение (8.12), получим возмущения для
каждого момента t^0:
Azt (t) = хх — х10 cos tot +
*20
sin (of
Az2 (t) = x2 = — x10 to sin tot + x2Q cos tot j
(8.15)
Докажем, что движение (8.10) устойчиво. Для этого сделаем
оценку возмущений (8.15):
|ЛМ01<1*ю1 +
1*20 I
|A*»(9KI*wh + l
(8.16)
Зададим произвольное положительное число е и покажем,
что можно подобрать положительное число г\ так, чтобы были
выполнены все требования, содержащиеся в определении устой-
86
чивости движения. В самом деле, при малых |*10|
могут быть выполнены условия
и **о
1*ю1 +
1*20 1
Ю
<е
или (после деления второго неравенства на со):
!*2о1 ^п
Чо1
I *м I +
1*20 I
в
(8.17')
(8.17")
При ю = 1 эти два условия превращаются в одно:
l*iol + l*2ol<e.
Поэтому, если взять г\ = —, то при |*ю|<Л и |*20|<ti в
силу оценок (8.16) будут выполнены условия:
|Az!(0|<e и |Az.(f)|<e.
При ю«<1 из двух условий (8.17') и (8.17") первое
более жестким. Поэтому, если взять v\ = -^—, то при
является
1*мКч
и 1*2о|<Л в СИЛУ оценок (8.16) получим:
|ДМ0|<
|А*(<)1<
80)
2
8G)2
е . 8 . 8
2 2^2
4-
80)
2^2
2 ' 2
При ю>1 из двух условий (8.17') и (8.17") более
является второе. Поэтому, если взять ti = , то при
2d)
и 1*20 К Л в СИЛУ оценок (8.16) получим:
жестким
|A«i(ft|<-
2(0
2©2
<е . е
■ =в,
2 2
|A*i(0l<"f +
2ш
<
^ 2
Таким образом, устойчивость движения (8.10) доказана. Но
эта устойчивость неасимптотическая. В самом деле,
возмущения (8,15) можно переписать как синусоидальные функции
вида Asm((dt+q>) подобно тому, как это было сделано в фор-
мУле (4.14) § 4; следовательно, они не стремятся к нулю при
87
Заметим, что функции (8.15) имеют тот же вид, что и
функции (8.10). Но в § 5 было установлено, что функции (5.4)
такого же вида выражают движение точки по эллипсу, имеющему
центр в начале координат. Это наглядно показывает, что в
формуле (8.15) |*i | и \х2\ ограничены большей полуосью
соответствующего эллипса, которую можно сделать как угодно
малой при достаточной близости к началу координат точки
/Со(*ю, *2?) и что хх и х2 не стремятся к нулю при t-+oo.
2) Если 0< \k\ <со, т. е. если сила сопротивления не
уравновешивается активной силой, то из § 5 известно, что класс
фиктивных движений описывается системой уравнений:
*1=*3 1 (8.18)
iav= — со2*! — 2kz% J
Обозначения (8.9), (8.11), (8.12), (8.13), используемые
ниже, имеют тот же смысл, как и в случае k = 0.
Используя формулу (5.7) § 5, напишем частное решение
системы (8.18) при начальных условиях (8.9), которое выражает
невозмущенное движение:
1 fz10 cos v* + *"» + **" sin vA
= /r-«i
— ke-ktf:
z10 cos vt +
V
Z20 + kzl0
sin vt
h
+ e~kt [— z10 v sin vt + (z20 + kz10) cos vt]
(8.19)
Используя ту же формулу (5.7), напишем частное решение
системы (8.18) при начальных условиях (8.13), которое выражает
возмущенное движение:
= ег* |
(Zio + *io)cosvf +
(Z20+"*20) + £(Zl0 + *l0)
sin vt
£ = _ ke-k* Г(г10 + x10) cos v/ + fa»+ ^)+ *(*» + *") sin vtj +
+ erki I— (z,0 + x10) v sin vt + ((z20 + x20) + k (z10 + *10)) cos vt]
(8.20)
Вычитая из функций (8.20) соответствующие функции (8.19),
получим возмущения для каждого момента t^O:
Д^ /А __ ^ _ Л— ktf » г.г,о ^ 1 *20 + &*10
AZ2(t):
х± = ег** fx10 cos vt +
x10 cos vt +
sin v/j
** + **"» sin vt
+ erki\— xxo v sin vt + (x20 + kxl0) cos vt]
)+
(8.21)
Покажем, что при k>0 движение (8.19) устойчиво. Для
этого сделаем оценку возмущений (8.21):
lA2l(OI<e-w(l^iol+ '*»' + *'*»')
.Д2,(0|<в-«Г*(|ДГ1в
1 +
|*2ol + *Uiol
+ \x10\y + (\xn\ + k\xu\)]
)+]■ (8-22)
Задавая произвольное положительное число е, и в этом
случае можно подобрать положительное число ц так, чтобы были
выполнены все требования, содержащиеся в определении
устойчивости движения. Перепишем оценки (8.22) так:
1^(91 <e-*(±^L|*le| + _L|^0|) j
L v v j )
При малых \х10\ и |д;20| могут быть выполнены условия:
—!— *ю И *«о <в
V V
(8.23)
(A + V)"
*ioH ~ l*«ol<e
или (после умножения на v и деления второго неравенства на
k+v)
(*+v)|*io| + l*.ol<ev
ev
k + v
(8.24)
При k + v = 1 эти два условия превращаются в одно:
l*iol+l*2ol<ev.
6V
Поэтому, если взять ц = , то при | х101< т) и | х20 | < т] в силу
оценок (8.23) будут выполнены условия:
lAzxWKe и |Az1(0|<e>
так как при k > 0 и t > 0 e~kt < 1.
При £ + v<l из двух условий (8.24) первое является более
6V
жестким. Поэтому, если взять rj =* , то при | xJ0 | < т] и
1*20 К Л в СИЛУ оценок (8.23) получим-
89
При k+ v> 1 из двух условий (8.24) более жестким является
второе. Поэтому, если взять т) = — , то при |*м|<4 и
1*юКч B СИЛУ оценок (8.23) получим:
|A*i(0K ! + ! О,
|А^(01< —+ 5 <в.
Таким образом, устойчивость движения (8.19) доказана.
Мало того, при k>0 легко обнаружить даже
асимптотическую устойчивость движения (8.19). В самом деле, при k>0
lime-w=0; поэтому при любых хю и х2о правые части, а значит,
t-юо
и левые части неравенств (8.22) стремятся к нулю при /-мх>.
Следовательно, при k>0 возмущения (8.21) обладают
свойством
' lim кгх (0=0, lim Az2 (0 = 0.
Наконец, заметим, что функции (8.21) имеют тот же вид, что
и функции (8.19). Но в § 5 было установлено, что функции
(5.7) такого же вида выражают движение точки по
полуспирали, которая при k>0 свертывается к началу координат (см.
рис. 5, а), а при k<0 неограниченно развертывается (см. рис.
6, а). При k>0 точка с координатами (хи х2), выражающими
возмущения (8.21), двигаясь по свертывающейся полуспирали,
стремится к началу координат, т. е. Xr-й), Хг->0 при /-*оо, что
означает асимптотическую устойчивость движения. При k<0
точка с координатами (8.21), двигаясь' по развертывающейся
полуспирали, неограниченно удаляется от начала координат,
т. е. Х\ и Х2 не остаются ограниченными при /->-оо, а это
означает неустойчивость движения.
Подобным, же рассуждением доказывается асимптотическая
устойчивость всех движений (физических процессов) в
примерах 2 и 3 § 4. Совсем другим путем можно доказать неасимпт^-
тическую устойчивость всех движений (химических реакций) в
примере 4 § 4 и в примере 2 § 5.
Замечание. Обратим внимание на большое сходство
между определениями устойчивости и неустойчивости равновесия и
определениями устойчивости и неустойчивости движения. Это
сходство не случайно, поскольку равновесие материальной си-
90
стемы можно рассматривать как простейший частный случай
движения. К тому же материальная система, находящаяся в
равновесии, т. е. покое, относительно одной системы координат,
может не находиться в покое относительно другой системы
координат, и наоборот.
В следующем параграфе будет показано, что анализ
характера движения, т. е. его устойчивости или неустойчивости, всегда
можно свести к анализу характера равновесия.
3. Техническая устойчивость
и неустойчивость движения
В этом пункте мы кратко рассмотрим понятие технической
устойчивости и неустойчивости движения, которое в технических
приложениях имеет даже большее значение, чем устойчивость
и неустойчивость по Ляпунову. Для того чтобы ввести
определения технической устойчивости и Неустойчивости движения, мы
используем начало предыдущего пункта (§ 8, п. 2) до формулы
(8.4) включительно, сохраняя смысл всех терминов и
обозначений. Однако теперь мы (внесем существенные изменения по
сравнению с пунктом 2. Прежде всего здесь мы будем
рассматривать реальные движения (8.1), фиктивные движения (8.2) и
невозмущенное движение (8.4) не на полуоси 0<!f<oo, а на
конечном отрезке времени, так как реальные технические
процессы обычно совершаются в течение конечного отрезка
времени. Мы будем считать, что этот конечный отрезок времени имеет
вид O^f^T, так как это легко сделать посредством сдвига
шкалы времени.
Далее в отличие от свойств Г, 2° пункта 2 здесь мы будем
рассматривать внешние возмущающие воздействия со
следующими свойствами:
Г. Материальная система может испытывать внешние
возмущающие воздействия не только при ^0, но и на всем отрезке
О^Г^Г или на какой-либо его части.
2'. Если имеются внешние возмущающие воздействия при
^0, то они могут изменять не только начальные условия (8.3),
но и уравнения движения (8.1), а значит, и (8.2).
3'. Если имеются внешние возмущающие воздействия при
0<^Г, то они изменяют уравнения движения (8.1) и (8.2).
Под влиянием внешних возмущающих воздействий со
свойствами 1', 2', 3' получаются возмущенные реальные движения и
соответствующие им возмущенные фиктивные движения, которые,
вообще говоря, не содержатся в классах (8.1) и (8.2).
Обозначим через Z\, Z2, ..., Zn фазовые координаты этих возмущенных
фиктивных движений. Какие-либо внешние возмущающие воз-
91
действия при t^.0 вызывают начальные возмущения, которые
мы обозначим через
М
AZ
ю
20
AZ,
/гО
(8.25)
Соответствующие возмущенные начальные условия запишутся
так:
£i(0) = z10 + AZ10
£2(0)=z20 + AZ20
Zn(0)=zn0+bZn0
(8.26)
Соответствующее возмущенное движение, которое
удовлетворяет условиям (8.26) и вызывается также некоторыми
внешними возмущающими воздействиями при 0<^Г, можно записать
так:
*i = q>i(0 + A*i(0
Zn = <(n(t) + bZn(t)
(8.27)
Здесь первые слагаемые, т. е. ф*(0 1=1, 2, ..., я, образуют
невозмущениое движение (8.4). Вторые слагаемые, т. е.
функции AZi(t) i=l, 2, ..., п, называются возмущениями движения;
при t = 0 они принимают значения (8.25).
Функции (8.27) образуют решение системы
дифференциальных уравнений, которая, вообще говоря, отличается от системы
(8.2):
Zi — Qi (ty Zlt Za, ..., Zn) + Pi (t, Zi, Z2, ..., Zn)
Z2 == Q% {t, Zi, Z2, ..., Zn) + P% ('» Zi, Z2, ..., Zrt)
. (8.28)
Здесь функции Qk(t, Zb Z2, ..., Zn) k=l, 2, ..., /г совпадают с
правыми частями уравнений (8.2), в которых переменные z<
заменены переменными Z*. Функции Pk(t, Zb Z2, ..., Zn) fc=l, 2, ..., л
называются возмущениями дифференциальных уравнений (8.2)
или кратко возмущениями уравнений. Каждые внешние
возмущающие воздействия со свойствами 1', 2', 3' вызывают свои на-
92
*~г*шкжж<г>7пжшшш?яиляъжх^шялг*ж»*:н1:*-я> ;,.;ж.-./ тг»^л»'ядм**..л^а1*'№5Л!,1,ам.Р
чальиые возмущения AZt-0, возмущения движения AZi(t) и
возмущения уравнений Pk{t, Zu ^2, ..., Zn), следовательно, им
соответствуют свое возмущенное движение вида (8.27) и своя
возмущенная система вида (8.28). Все возмущения уравнений
Pk(t, Zu Z2, ..., Zn) и соответствующие возмущенные системы
вида (8.28) рассматриваются на отрезке времени O^t^T и з
некоторой n-мерной замкнутой области D0 фазового
пространства, внутри которой проходит фазовая траектория
невозмущенного движения (8.4).
В технических приложениях обычно бывают известны или
заданы ограничения, которых не превосходят все начальные
возмущения и возмущения уравнений. Ограничения для начальных
возмущений задаются в виде серии неотрицательных
постоянных r|i t=l, 2, ..., п, так что любые допустимые начальные
возмущения обязательно удовлетворяют условию
|А*/о1<Л< *=1,2, ...,л. (8.29)
Ограничения для возмущений уравнений задаются на отрезке
0^£<Г в виде серии неотрицательных функций hk(t) k =
= 1, 2, ..., п, так что на отрезке 0^<<Г и в замкнутой области
Do любые допустимые возмущения уравнений обязательно
удовлетворяют условию
\Pk(t9ZltZ%9...,Za)\<hk(t) k = 1,2 л. (8.30)
Техническое требование, предъявляемое к невозмущенному
движению (8.4), состоит в том, что задаются ограничения,
которых не должны превосходить возмущения этого движения, т. е.
отклонения от него. Эти ограничения задаются на отрезке
0=^<Г в виде серии неотрицательных функций Ei(t) i =
— 1, 2, ..., п, так что на отрезке 0^<Г любые допустимые
возмущения движения должны удовлетворять условию
|AZ,(f)l<M0 * = 1,2,...,л. (8.31)
Нередко серии функций hk(t) и &i(t) могут быть заменены
сериями неотрицательных постоянных hk &=1, 2, ..., л и е* i=
= 1,2, .... л.
В зависимости от строения материальной системы, выбора
невозмущенного движения (8.4) и характера внешних
возмущающих воздействий при выполнении условий (8.29), (8.30)
требование (8.31) либо выполняется, либо не выполняется. Это и
приводит к понятию технической устойчивости и технической
неустойчивости движения.
Невозмущенное движение называется технически устойчивым
на отрезке 0^^<Г относительно ограничений щ> hh(t)t Ei(t)y
если при любых начальных возмущениях, удовлетворяющих
условию | AZfol^Th i=l, 2, ..., л, и любых возмущениях урав-
93
нений, которые при 0 ^t <Т и в области Do удовлетворяют
условию
\Pk(t9Zl9Z^...1Zn\^hk(t) ft =1,2,..., л,
для всех возмущений движения на всем отрезке 0^£<Т будет
выполнено требование
|Дад|<М0 t = l,2, ...,/г.
Невозмущенное движение называется технически неустойчивым
на отрезке 0 < t < Т относительно ограничений r\l9 hk (t)9 st (t)> если
при любых начальных юзмущениях, удовлетворяющих условию
| AZi0 К Л/ * = 1, 2, ..., л, и любых возмущениях уравнений,
которые при 0 < t < Т и в области D0 удовлетворяют условию
| Pk (t9 Zl9Z2, ...,Zn)\<hk(t) k = 1, 2, ..., n9 хотя бы для
некоторых возмущений движения и хотя бы в некоторые моменты
0<^<Г будет |Дад)|>е/(д.
Эти определения существенно отличаются от определений
устойчивости и неустойчивости движения по Ляпунову не
только конечным отрезком времени O^t^T (вместо полупрямой
0^Zt<oo) и свойствами Г, 2', 3' внешних возмущающих
воздействий, которые вызывают возмущения уравнений. Главное
отличие состоит в том, что ограничения т]* и hk(t) здесь задаются
независимо от &i(t)9 а не подбираются по заданным ei(t).
Аналогия с определениями устойчивости и неустойчивости движения
по Ляпунову появляется лишь в тех случаях, когда мы можем
распорядиться ограничениями щ и hk(t), т. е. подобрать их
достаточно малыми и удовлетворить требованию (8.31), либо, взяв
их как угодно малыми, обнаружить невыполнение требования
(8.31). Если при этом свойства 1', 2', 3' сводятся к свойствам
1°, 2° п. 2 на отрезке 0^<Т, то эта аналогия будет еще более
полной. В самом деле, так будет, если все внешние
возмущающие воздействия навсегда прекращаются не позже момента
£=0 и не изменяют уравнений движения (8.1) и (8.2).
Нередко бывает, что технический процесс протекает на
конечном отрезке времени O^f <Г, а условия теоремы
существования и единственности частного решения для системы
уравнений (8.2) выполняются на полуоси 0^£<оо. При этом заметим,
что если какой-либо процесс протекает на очень большом
отрезке времени 0^<Г, то иногда бывает удобно заменять этот
отрезок полуосью 0^Zt<<x> и рассматривать как бы предельный
случай (при Г-^оо) только что введенных определений
технической устойчивости и неустойчивости движения.
Из сказанного видно, что существует немало частных
случаев, когда анализ технической устойчивости и неустойчивости
движения можно свести к анализу устойчивости и
неустойчивости движения по Ляпунову. Общие же методы анализа техни-
94
ческой устойчивости и неустойчивости движения очень сложны,
вследствие чего не могут рассматриваться в нашем курсе.
Поэтому всюду в дальнейшем (§ 9, 13—20) мы будем заниматься
только устойчивостью и неустойчивостью движения по
Ляпунову и тесно связанной с ними условной устойчивостью (§ 13—15,
19 и 20).
Различные варианты определений технической устойчивости
и неустойчивости движения изложены, например, в [13].
Различные обобщения определений устойчивости и неустойчивости
движения по Ляпунову рассматриваются в [4]. В этих книгах
излагаются соответствующие методы анализа устойчивости и
неустойчивости движения.
§ 9. ПРЕОБРАЗОВАНИЕ СИСТЕМЫ, ОПИСЫВАЮЩЕЙ
КЛАСС ДВИЖЕНИЙ, В СИСТЕМУ ВОЗМУЩЕНИЙ
Пусть некоторому классу реальных движений материальной
системы соответствует класс фиктивных движений в фазовом
пространстве, который описывается нормальной системой
дифференциальных уравнений:
h = Q i V> *и 4 . • •.. *«) i = 1. 2,..., п. (9.1)
Пусть заданы невозмущенные начальные условия
*i(0) = *i0
4(0)=z20
Zn(°)=*n0 )
(9.2)
и невозмущенное движение, которое выражается частным
решением системы (9.1) при невозмущенных начальных условиях
(9.2):
Zi = <Pi V, z10, z20 zn0) = <px (t)
z2 = ф2 if, Zio, zi0 zn0) = <p2 (0
z„ = % (*, zw. г20 zn0) = <p„ (/)
(9.3)
Следовательно, при подстановке функций (9.3) (с
соблюдением их номеров) в систему уравнений (9.1) получается система
тождеств относительно независимой переменной t:
Ф/(0вв|['.ф1(0^(')..-..Ф|,(0] *=1,2,...,п. (9.4)
95
Напомним, что мы рассматриваем только такие внешние
возмущающие воздействия, которые обладают свойствами Г, 2°
§ 8, п. 2, так что в момент £ = 0 результат их действия на
материальную систему-проявляется только в виде начальных
возмущений.
Для соответствующих начальных возмущений в фазовом
пространстве наряду с обозначениями § 8 введем и новые
обозначения:
Asm = х
Дг
ю
20
Дг.
710
1/»0
(9.5)
Тогда возмущенные начальные условия запишутся так:
*i (0) = г10 + Az10 = z10 + д:10
Z2 ("/ = ^20 "т AZ2o ~ Z20 + «#20
£(°)=**o + A*,
л0
сл0
+ *,
710
(9.6)
В силу свойств 1° и 2° соответствующее возмущенное
движение выражается частным решением той же системы уравнений
(9.1), но при возмущенных начальных условиях (9.6).
Для возмущений в любой момент f^0 также введем новые
обозначения:
?i(0-9iW=A*i(f) = *i(0
«i(0 —Ф*(0 = Aft (0 = *»(') j.
~zn(t)-<?n(t) = Azn(t) = xn(t)\
(9.7)
Следовательно, возмущенное движение, т. е. частное
решение системы (9.1) при возмущенных начальных условиях (9.6),
выражается функциями, каждая из которых состоит из двух
слагаемых:
li(f)=q>i(f) + *i(0
ft(0 = <M0 + *i(0
(9.8)
96
■Енигпиь.'жли№:г>-й«г ^-„вгчад
Здесь первые слагаемые — это заданные функции (9.3), которые
образуют невозмущенное движение и удовлетворяют начальным
условиям (9.2), а вторые слагаемые —это обычно неизвестные
функции, которые должны выражать возмущения для любого
момента t^O и принимать значения (9.5) при £=0, иначе
говоря, удовлетворять начальным условиям (9.5).
Теперь мы должны найти функции X\(t)9 x2(t)y ..., xn(t) так,
чтобы функции (9.8), изображающие возмущенное движение,
удовлетворяли системе уравнений (9.1). Подставляя функции
(9.8) в уравнения (9.1), получаем систему уравнений с
неизвестными функциями Х\ (t), х2 (t), ..., хп (t):
ф, (0 + *i (0 = Qt Р; Ф1 (0 + * (0; ф2 (0 +
+ xt(t);...\vn(t) + xa(t)]i = if29...tn
(9.9)
Вычитая из уравнений (9.9) соответствующие тождества
(9.4), получаем систему уравнений с теми же неизвестными
функциями X\(t), X2(t), ..., xn(t):
xt (f) = Qt \t\ Ф1 (t) + * (0; ф2 (t) + *2 (0; ...;
ФЛ0 + М0]-адф1(0,ф2(а...,фЛ')]
> II I I. I „ —^ I I s
#,['.*i(0.*s(0. ....*«(*)] ' = 1.2 /i
(9.10)
Заметим, что правые части уравнений (9.1), т. е. функции
Qi(t, Zu ^2, .-, 2n), — это известные функции переменных t, zu
Z2, ..., zn. Кроме того, функции ф1 (^), фг(0» —i фп(0»
образующие невозмущенное движение (9.3), — это известные функции
от t. Поэтому правые части тождеств (9.4) также являются
известными функциями от t. В правые части уравнений (9.9) и
(9.10) переменное / входит непосредственно через посредство
функций ф1 (^), фг(0» —t фп(0 и через посредство функций
X\(t), ^2,(0, ..., xn(t). При этом известно, как входит t
непосредственно и через посредство <pi(/)> ф2(0> •••> фп(0> но неизвестно,
как входит t через посредство Xi(t)9 X2(t)9 ..., xn(t). Наконец,
известно, как входят в правые части уравнений (9.9) и (9.10)
сами Xi(t), x2,(t), ..., xn(t). Поэтому, если не обращать внимания
на то, что Xi(t), X2(t), ..., xn(t) зависят от t и считать их просто
аргументами Х\, Х2, ..., хп правых частей уравнений (9.9) и (9.10),
то эти правые части будут известными функциями аргументов
'» хи х2> ..., хп. Правые части уравнений (9.10) мы кратко
обозначили через Hi[t, X\ (t), X2 (t), ..., хп (t)]f так что систему
уравнений (9.10) можно кратко переписать так:
xi(t)=Hi[t9xl(t),x2(t)9. ..,*„(<)] ' = 1.2 я. (9.11)
4 А. Г. Мл адов
97
Система уравнений (9.10) или в краткой записи (9.11)
называется системой возмущений относительно невозмущенного
движения (9.3), так как искомые функции *i(0» х2 (')» —» xn(t) этой
системы должны описывать возмущения при ^0, т. е.
отклонения от невозмущенного движения (9.3). Вид правых частей
системы возмущений (9.10) или (9.11), особенно вид
непосредственного вхождения / в состав функций #t[f, X\ (t),
X2(t), ..., xn(t)]t вообще говоря, зависит от.выбора
невозмущенного движения (9.3).
Переход от системы (9.1) и невозмущенного движения (9.3)
к системе (9.10) или (9.11) называется преобразованием
системы, описывающей класс движений, в систему возмущений
относительно данного невозмущенного движения или, короче,
преобразованием системы движений в систему возмущений
(относительно данного невозмущенного движения).
Напомним, что для системы (9.1) и любых допустимых
начальных условий при £=0 выполнены все условия теоремы
существования и единственности частного решения. Поэтому для
системы возмущений (9.10) и любых допустимых начальных
возмущений (9.5), которые здесь играют роль начальных
условий, также выполнены все условия этой теоремы.
Легко проверить, что среди других решений система
возмущений (9.10) или (9.11) имеет тождественно нулевое частное
решение:
^(О-о
*я(<)и0
(9.12)
*я(*)-0
В самом деле, непосредственно видно, что подстановка этих
функций в правые части уравнений (9.10), а значит и (9.11)
дает тождественные нули. Очевидно, производные функций
(9.12) —это тождественные нули, так что подстановка их в
левые части уравнений (9.10) и (9.11) также дает тождественные
нули.
Таким образом, в результате подстановки функций (9.12) в
систему уравнений (9.11) получается система тождеств
относительно t:
Oef//,(*, 0,0, ...,0) 1 = 1,2, ...,л. (9.13)
Очевидно, нулевое частное решение (9.12) системы (9.11)
удовлетворяет нулевым начальным условиям:
*!(<))= 0
*2(0)=0
*„(0) = о
98
(9.14)
Ч •- ,*VW\K«S>* -
причем в силу единственности частного решения,
соответствующего данным начальным условиям, нулевым начальным
условиям (9.14) соответствует только одно частное решение системы
(9.11), а именно нулевое частное решение (9.12).
Нулевые начальные условия (9.14) означают отсутствие
начальных возмущений, а соответствующее нулевое частное
решение (9.12) системы возмущений (9.11) означает отсутствие
возмущений при t>0. Итак, мы снова убедились в том, что если
внешние возмущающие воздействия обладают свойствами 1° и
2°, то при отсутствии начальных возмущений не будет никаких
возмущений во все последующее время (>0 и в течение всего
времени движение останется невозмущенным.
Рассмотрим очень важный частный случай системы
уравнений (9.1), а именно систему линейных уравнений:
it = «л(t)zx + ai2(t)z2+ ...+ ain(t)zn + ft(t) \ (9 15)
i = 1, 2, .. .9n J
в которой коэффициенты a^t) и свободные члены fi(t)—это
известные функции от t либо, в частности, постоянные.
Применим к линейной системе (9.15) рассуждение,
проведенное при переходе от системы (9.1) к системе возмущений (9.10),
сохраняя смысл обозначений (9.2), (9.3), (9.5) —(9.8). При
подстановке функций (9.8) в систему (9.15) получается система
уравнений, выполняющая в этом случае роль системы (9.9):
Ъ (0 + Ъ (*) = an (0 [Ф1 .(<) + *i (*)] + ai2 (t) [Фа (t) + *2 (*)] + ... J
~ + *in®to*(t) + *n(t)] + fi(t) * = l,2,...,/i J
(9.16)
При подстановке функций (9.3) в систему (9.15) получается
система тождеств, выполняющая роль тождеств (9.4) :
Ф, (0 в ап (t) fh (0 + ал (0 фа (0 + ... + ain (t) Фл (*) + /, (*) | (дл ?)
*=1,2,...,л|'
Вычитая из уравнений (9.16) соответствующие тождества
(9.17), получаем систему возмущений для случая линейной
системы:
xi(t)=ail(t)x1(t) + ai2(t)x2(t)+...+ain(t)xn(t) 1 (9Л8)
i = l,2 п J
Как видим, система (9.18) отличается от системы (9.15)
лишь отсутствием свободных членов (которые уничтожились при
вычитании) и тем, что вместо функций zu z2, ..., znt
описывающих все возмущенное или невозмущенное движение, в систему
4*
99
(9.18) входят функции xx(t)y x2(t)t ..., xn(t)y описывающие
возмущения. При этом очень важно подчеркнуть, что система
возмущений (9.18) совсем не зависит от функций cpi(0> фг(0> •••>
Фп(0» образующих невозмущенное движение. Итак, в случае
линейной системы движений система возмущений не зависит
от выбора невозмущенного движения, и, следовательно, в этом
случае можно говорить просто о преобразовании системы
движений в систему возмущений, не упоминая при этом о выборе
невозмущенного движения.
Таким образом, получилось простое правило: в случае
линейной системы движений для составления системы возмущений
достаточно отбросить свободные члены и заменить букву z
буквой х\ при этом последняя замена, формально не существенная,
делается для того, чтобы не спутать движения класса (9.15) с
возмущениями, т. е. с отклонениями от одного из этих
движений, причем безразлично от какого именно.
Теперь мы дадим геометрическое, вернее кинематическое,
толкование преобразования системы движений в систему
возмущений в фазовом пространстве. Для этого рассмотрим в
n-мерном пространстве две декартовы системы координат
A*u z2, ..., 2п] и X{xh X2, ..., хп], координаты в которых связаны
соотношениями:
*i = q>i (ty+ ч
*2 = Ф2 (0 + Ч
(9.19)
причем здесь ф1(/)> фг(0» —> фп(0 —это функции, образующие
невозмущенное движение (9.3).
Пусть система Z— это система координат, относительно
которой рассматривается класс движений (9.1) или (9.15)
условно назовем ее старой или неподвижной. Систему X назовем
новой или подвижной, так как сейчас увидим, что она движется
относительно системы Z. Прежде всего из соотношений (9.19)
видно, что соответствующие оси систем Z и X параллельны и
одинаково направлены. Так как координаты zu z2„ ..., zn
получаются прибавлением к координатам хи х2, ..., хп членов
Ф1 (/) f фг(0, ..., Фп(0» зависящих от времени, то система X
движется относительно системы Z, все время оставаясь
параллельной системе Z. При этом движении в каждый момент времени
t^O началу координат системы X, т. е. точке
хг = 0
х2=0
100
соответствует в системе Z подвижная точка M(t) с
координатами
*! = q>i(0
*2 = Ф2 (О
г. е. точка, изображающая невозмущенное движение (9.3) и,
следовательно, движущаяся по фазовой траектории, которая в
момент £ = 0 выходит из точки Afo(zio, ^20, ..., zno),
изображающей невозмущенные начальные условия (9.2).
Таким образом, система X движется параллельно
неподвижной системе Z так, что в каждый момент f^O начало координат
системы X находится на траектории невозмущенного движения,
точнее, находится в точке M(t), т. е. совершает невозмущенное
flput>0
При f=*0
Рис. 15
движение. На рис. 15 (для случая п = 3) изображена схема
движения системы X относительно системы Z.
Сравним формулы (9.19) и (9.8), которые очень похожи друг
на друга. Однако существенное различие между ними состоит в
том, что в формуле (9.19) х\, #2, ..., хп могут принимать какие
угодно значения, а в формуле (9.8) xx(t)y x2(t), ..., xn(t)
являются такими функциями от t, которые образуют решение
системы возмущений (9.11) или (9.18).
В системе X в каждый момент t^O функции X\(t), ^(0» •••>
*п (t), образующие частное решение системы возмущений при
начальных возмущениях (9.5), определяют положение
движущейся точки K(t), которая называется точкой, изображающей
возмущения. Траектория точки K(t) в пространстве X
называется фазовой траекторией возмущений, соответствующей
начальным возмущениям (9.5) или начальной точке Ко(х\0у х2о, ..., хп0)
(см. рис. 16).
101
Поэтому в пространстве Z возмущенное движение (9.8) при
возмущенных начальных условиях (9.6) можно толковать как
сложное, т. е. составное движение точки M(t), в котором
переносным движением является невозмущенное движение (9.3), так
как его совершает подвижная система Х> а относительным
движением (относительно системы X) является движение точки
K(t) по фазовой траектории возмущений.
т)
tlput^O
Рис. 16
Mft) Xt
При t >0
Рис. 17
В системе Z начальную точку фазовой траектории
возмущенного движения, т. е. точку, изображающую возмущенные
начальные условия (9.6), обозначим через Alo(ziq+*io; ^20+^20; ...;
Zno+Xno); в системе X в момент tf=0 с точкой Afo совпадает
точка Ко(хю, *2о, ..., *по). Координаты точки M(t) определяются
функциями (9.8), изображающими возмущенное движение.
На рис. 17 изображена схема, в которой возмущенное
движение представлено в виде только что описанного составного
движения, причем дано два положения подвижной системы X: в
момент <=0 и в некоторый момент t>0. При этом дуга
траектории невозмущенного движения от начального момента до
этого момента t>0 проведена одной тонкой линией, а далее тонким
102
пунктиром; дуга траектории возмущенного движения проведена
жирной линией, а далее жирным пунктиром; дуга траектории
возмущений в системе X проведена двойной тонкой линией, а
далее двойным тонким пунктиром.
В силу определений § 8 характер равновесия и
невозмущенного движения (т. е. их устойчивость или неустойчивость)
исследуется по поведению возмущений при tf-*oo. В нашем
рассуждении возмущения, т. е. отклонения от невозмущенного
движения (9.3), определяются в системе Z отклонениями точки
M(t) от точки M(t)t но в системе X эти отклонения совпадают
с отклонениями точки K(t) от начала координат. При этом
обратим взимание на то, что в пространстве X фазовая
траектория, соответствующая нулевому решению (9.12) системы
возмущений (9.11), состоит из одной точки покоя, т. е.
неподвижной точки, находящейся в начале координат системы X. Таким
образом, изучать характер невозмущенного движения (9.3) в
неподвижной системе Z это все равно, что изучать характер
равновесия точки, находящейся в начале координат подвижной
системы X.
Рассмотрим пример преобразования системы движений в
систему возмущений и его толкования в фазовом пространстве.
Пример. Пусть на фазовой плоскости 2Ь z% класс движений
описывается системой линейных дифференциальных уравнений:
Zl = Z2
г2 = — 4гг + № + 2
Чтобы найти общее решение этой системы, сведем ее к
одному уравнению второго порядка. Для этого
продифференцируем второе уравнение
2t=—iii + 9t
и подставим сюда Zi=z2l из первого уравнения:
51 + 4z1 = «. (9.21)
Общее решение соответствующего однородного уравнения будет:
уг = Cicos 2t + C2 sin 2t.
Частное решение уравнения (9.21) ищем в виде
z\ = At + B.
Подстановкой находим, что Б = 0; Л =2; г* = 2/.
Следовательно, общее решение уравнения (9.21) запишется так:
z2 = d cos 2t + С2 sin 2/ + 2t. (9.22)
103
^змкг sw*.aw3ra«R-4PP^**K«r>'i(*a5SJw;i*.AS'
(9.20)
Для нахождения zx подставляем выражение гг во второе
уравнение данной системы:
— 2Сг sin 2t + 2C2 cos 2t + 2 = — Azx + At2 + 2,
откуда
z1 = —C1 sin 2t — — C2 cos 2/ + t\ (9.23)
Функции (9.23) и (9.22) образуют общее решение данной
системы (9.20):
гх= — Сг sin 2t — — С2 cos 2* + *2
г2 = Сх cos 2* + С2 sin 2* + 2*
ые условия
*i(0)=*w
(9.24)
Пусть заданы начальные условия, которые мы будем считать
невозмущенными:
(9.25)
M°) = Z2oI
Чтобы получить соответствующее частное решение, найдем
С\ и С2. Из (9.22) получаем Ci = Z2o, а из (9.23) находим С2 =
=—2zio. Напишем частное решение системы (9.20) при
начальных условиях (9.25), которое выражает невозмущенное
движение:
*i = ^ю cos 2* + — z20 sin 2t + t2 )
10 2 20 ^ . (9.26)
z2 = — 2z10sin 2f + г20cos2t -\-2t)
Преобразуем данную систему движений (9.20) в систему
возмущений. Так как система (9.20) линейная, то это
преобразование сводится к отбрасыванию свободных членов и замене
буквы z буквой х:
*}= Ч ]. (9.27)
Х2 == ■ 4^j J
Зададим начальные возмущения
*i(0) = *iol (928)
Ч (°) = *20 1
Тогда возмущения при t^O изображаются частным решением
системы (9.27) при начальных условиях (9.28).
Уравнения системы (9.27) отличаются от уравнений (9.20)
только отсутствием свободных членов, поэтому упомянутое част-
104
ное решение системы (9.27) отличается от функций (9.26) лишь
отсутствием алгебраических членов и, следовательно, имеет вид:
xi = хю cos 2^ Ч аг20 sin 2t
х2 = — 2х10 sin 2t + л:20 cos 2t
(9.29)
Эти равенства являются параметрическими уравнениями
фазовой траектории возмущений с начальной точкой /Со(*ю, ху>).
Исключим t из уравнений (9.29), возводя в квадрат выраже-
х2
ния Х\ и —— и затем складывая результаты:
4
или
А
Хп
Р2о
(2р0)2
= 1. (9.30)
Следовательно, на плоскости хи х2 точка K(t) с координатами
(9.29), изображающая возмущения при /^0, выходя в момент
t = 0 из точки /Со, движется по эллипсу (9.30), причем в силу
уравнения Х\=х2 по направлению часовой стрелки (см. рис. 18).
Координаты точки M(t)f изображающей возмущенное
движение, складываются из функций (9.26) и (9.29):
*1 = (*io + *м) cos 2t + — (z20 + х20) sin 2* + *2
гг = — 2 (z10 + *10) sin 2* + (г20 + *20)"cos 2t + 2t)
причем фазовая траектория возмущенного движения
начинается в момент £=0 в точке Мо(гю+Х\о\ -г2о+лг2о).
Таким образом, в фазовой плоскости zi, z2 возмущенное
движение точки M(t) изображается сложным движением,
составленным из двух движений: движения точки K(t) по эллипсу
(9.30) в системе координат хи х2 и одновременно такого
движения самой системы х\, х2, параллельного системе z\, z2y при
котором начало координат системы х\, х2 все время находится
в точке M(t), совершающей невозмущенное движение (9.26).
Упрощенная схема этого составного движения изображена
на рис. 19, причем упрощение состоит в том, что на схеме не
дается истинная форма фазовых траекторий невозмущенного,
а значит, и возмущенного движений. На схеме видно, что
фазовые траектории невозмущенного и возмущенного движений
пересекаются. Это соответствует сказанному в § 7, так как данная
система (9.20) описывает нестационарное движение.
105
Легко проверить, что невозмущенное движение (9.26)
устойчиво неасимптотически. В самом деле, мы видели, что на
плоскости хи *2 возмущения (9.29) изображаются движением
точки К(t) по эллипсу (см. рис. 18). Следовательно, они не
стремятся к нулю при t-+oo, но ограничены большей полуосью
эллипса (9.30), которая может быть сделана как угодно малой
при достаточной близости точки /Со(*ю, #2о) к началу
координат.
г,
Рис. 19
_. Замечание 1. Согласно § 7 система (9.1) описывает класс
движений, который в фазовом пространстве Z(zu z% ..., zn)
образует стационарное либо нестационарное движение. Подобно
этому система возмущений (9.11) описывает класс движений,
который в фазовом пространстве возмущений Х(хи х2„ ..., хп)
также образует стационарное либо нестационарное движение.
Если в правые части всех уравнений системы возмущений
(9.11) время / не входит непосредственно, то возмущения
называются стационарными. Если в правую часть хотя бы одного
уравнения системы возмущений (9.11) время t входит
непосредственно, то возмущения называются нестационарными. При этом
как стационарному, так и нестационарному движению (9.1) в
различных случаях могут соответствовать и стационарные и
нестационарные возмущения (9.11).
В связи к: этим вернемся к линейной системе (9.15). Если
хотя бы один из коэффициентов системы (9.15) зависит от t,
то и движение (9.15) и возмущения (9.18) нестационарны. Если
все коэффициенты системы (9.15) постоянны, а хотя бы один
из свободных членов зависит от t, то движение (9.15)
нестационарно, а возмущения (9.18) стационарны. Очевидно, это
положение осуществляется в рассмотренном выше примере (9.20).
т
Если все коэффициенты и все свободные члены системы (9.15)
постоянны (в частности, свободные члены могут отсутствовать),
то и движение (9.15) и возмущения (9.18) стационарны. В
частности, это применимо к движению, рассмотренному в примере 1
§ 4 и в примере 1 § 5.
Случай, когда движение (9.1) стационарно, а возмущения
(9.11) нестационарны, может осуществиться только для
нелинейной системы (9.1).
3 а м еч а ни е 2. Определения устойчивости и
неустойчивости движения по Ляпунову, которые были даны в § 8, можно
сформулировать также, используя понятие решения системы
возмущений, т. е. используя функции (9.7), образующие
частное решение системы (9.11) при начальных возмущениях (9.5).
Невозмущенное движение называется устойчивым по
Ляпунову, если для каждого заранее заданного положительного
числа е можно подобрать положительное число т], зависящее от е,
Ti = Ti(e) такое, что при любых начальных возмущениях,
удовлетворяющих условию
l*/ol<4 * = 1,2, ... ,л,
все компоненты решений системы возмущений при всех t^O
удовлетворяют условию | xi (t) | < 8 i= 1, 2, .., п.
Невозмущенное движение называется асимптотически устой-
чивым по Ляпунову, если оно устойчиво и, кроме того, все
компоненты решений системы возмущений удовлетворяют условию
limxi(t) =ь0 i = 1, 2, ... , п.
t~*OQ
Невозмущенное движение называется неасимптотически
устойчивым по Ляпунову, если оно устойчиво, но хотя бы
некоторые компоненты решений системы возмущений не стремятся
к нулю при t-+oo.
Невозмущенное движение называется неустойчивым по
Ляпунову, если хотя бы для одного положительного числа е и для
каждого даже сколь угодно малого положительного числа т|
хотя бы при некоторых начальных возмущениях,
удовлетворяющих условию |*/0|<т) 1 = 1, 2, ..., п, хотя бы некоторые
компоненты решений системы возмущений, по меньшей мере в
некоторые моменты ts>0 удовлетворяют условию K(?s)|>e.
Подчеркнем, что во всех этих определениях между
начальными возмущениями не обязаны выполняться какие-либо
соотношения; поэтому устойчивость или неустойчивость движения
по Ляпунову определяется поведением всей совокупности
решений, т.е. поведением общего решения системы
возмущений при £->-оо.
107
§ 10. ОБ ОПРЕДЕЛИТЕЛЕ ЛЮБОГО ПОРЯДКА
В начале этого параграфа мы остановимся на понятии
определителя любого порядка п.
Пусть задана квадратная матрица, т. е. квадратная таблица
элементов, состоящая из п столбцов и п строк:
/Ян <7i2 ... Яг^
Q =4 <J*l ?22 • • • Я*п
W Яп2 . . . Я
Элементы этой таблицы могут быть постоянными числами либо
функциями одного или нескольких аргументов. Определитель
n-го порядка из элементов матрицы Q или определитель
матрицы Q — это функция, составленная из всех элементов этой
матрицы по правилам, аналогичным правилу полного раскрытия
определителя третьего порядка (см. [9], ч. I, гл. VI, § 3). Эта
функция, т. е. определитель я-го порядка матрицы Q,
обозначается так:
Яп Й12
Яп ?22
Яш
Ягп
Япх Я,
Л2
(10.1)
При этом элементы, столбцы и строки матрицы Q называются
также элементами, столбцами и строками определителя (10.1).
Развернутое выражение функции q, т. е. определителя (ЮЛ)
n-го порядка, получается в результате его полного раскрытия,
причем его можно начать раскрывать по элементам любой
строки или любого столбца. Так, определитель (10.1) представляется
по элементам, например /-й строки, в виде суммы
<7 = 2(-i)/+4A,
А=1
(10.2)
где Mjk — миноры элементов q^ т. е. определители (п—1)-го
порядка, каждый из которых получается из определителя (10.1)
вычеркиванием /-ой строки и &-го столбца, &=1, 2, ..., п.
Далее каждый из определителей Mjk по тому же правилу
представляется аналогичной суммой, состоящей из (п—1)
определителей (п—2)-го порядка. После подстановки этих сумм в
сумму (10.2) получается сумма п(п—1) слагаемых, каждое из
которых представляет собой произведение некоторого
определителя (п—2)-го порядка на некоторые два элемента
определителя (10.1) и с некоторым знаком.
108
После третьего шага таким же образом получается сумма
п(п—1)(п—2) слагаемых, каждое из которых представляет
собой произведение некоторого определителя (п—3)-го порядка
на некоторые три элемента определителя (10.1) с некоторым
знаком. Продолжение этого процесса приводит к тому, что
количество слагаемых возрастает, а порядок определителей в
каждом из них соответственно убывает пока не понизится до
третьего, второго и, наконец, первого порядка.
В результате полного раскрытия определителя (10.1)
получается сумма из /г! слагаемых, каждое из которых является
произведением некоторых п элементов исходного определителя
(10.1) с некоторым знаком. При этом все п элементов
определителя (10.1), участвующие в каждом таком произведении,
обязательно оказываются взятыми из различных строк и различных
столбцов, а значит, из всех п строк и всех п столбцов
определителя (10.1).
Все эти п\ различных комбинаций по п элементов можно
получить, если, например, во всех произведениях писать первые
индексы элементов (т. е. индексы строк) в, натуральном
порядке, а над вторыми индексами (т. е. индексами столбцов)
совершать всевозможные перестановки. Так, в выражении
Яи^д2,к2Чг,к3 ...qniknn чисел ku k2, fay ..., kn являются некоторой
перестановкой чисел 1, 2, 3, ..., п. Заметим, что среди всех
комбинаций есть главная комбинация <7п <722<7зз... qnn, т. е.
произведение всех элементов главной диагонали определителя.
Из сказанного ясно, что если все элементы определителя
(10.1) являются постоянными числами, то и его величина q
постоянна; если хотя бы некоторые элементы определителя (10.1)
являются функциями каких-то аргументов, то и его величина q
есть функция тех же аргументов.
Определитель, который получается из определителя (10.1)
вычеркиванием /-го столбца и /-й строки, называется
диагональным минором (п—1)-го порядка, соответствующим элементу
Определитель любого порядка п обладает свойствами,
вполне аналогичными свойствам определителя третьего порядка
(см.[9],ч. I, гл. VI, §4).
Линейной комбинацией т столбцов таблицы или
определителя с номерами ku &2, .., km называется столбец, который
получается в результате умножения этих столбцов на некоторые
постоянные числовые коэффициенты akl, aki ... akfn и
последующего сложения полученных столбцов.
Столбец, все элементы которого равны нулю, называется
нулевым столбцом. Столбцы таблицы или определителя с
номерами k\, &2, ..., km называются линейно зависимыми, если
нулевой столбец может быть получен в виде такой линейной комби-
109
нации этих столбцов, в которой хотя бы некоторые из
коэффициентов ftkt, <**2, ..., <*£т Ьтличны от нуля. Столбцы
таблицы или определителя с номерами k\9 k2, ..., km называются
линейно независимыми между собой, если нулевой столбец
является только такой линейной комбинацией этих столбцов, в
которой все коэффициенты akl, akt9 ... , akm равны нулю.
Очень важно подчеркнуть, что если элементы столбцов
являются функциями каких-то аргументов, то обязательно должна
указываться область изменения этих аргументов, в которой
рассматривается линейная зависимость или независимость таких
столбцов; при этом нулевой столбец, участвующий в
определениях линейной зависимости и линейной независимости столбцов,
должен быть тождественно нулевым, т. е. должен
оставаться нулевым во всей этой области изменения.аргументов.
Если в таблице или определителе имеется несколько
пропорциональных (с постоянными коэффициентами
пропорциональности) столбцов, среди которых, в частности, могут быть и
одинаковые, то все эти столбцы, взятые вместе, а также любые из
них в количестве не меньше двух, очевидно, линейно зависимы;
в этом случае и все п столбцов таблицы или определителя
линейно зависимы. Очевидно, если в определителе с постоянными
элементами есть хотя бы один нулевой столбец, то определитель
равен нулю; если в определителе с функциональными
элементами есть хотя бы один тождественно нулевой столбец, то
определитель тождественно равен нулю; при этом все столбцы
определителя, взятые вместе, линейно зависимы, так как линейная
комбинация с ненулевым коэффициентом при нулевом или
тождественно нулевом столбце и с нулевыми коэффициентами при
всех остальных столбцах является нулевым или тождественно
нулевым столбцом.
Все сказанное о столбцах таблицы или определителя
распространяется и на его строки.
Приведем без доказательства следующие положения:
(1а). Если в определителе п-го порядка с постоянными
элементами найдется отличный от нуля определитель,
составленный из элементов каких-либо т^п столбцов и некоторых
т их строк, то в исходном определителе эти т столбцов, а
также эти т строк линейно независимы.
(16). Если в определителе п-го порядка с постоянными
элементами линейно независимы какие-либо m^Ln столбцов, то
найдется отличный от нуля определитель m-го порядка,
составленный из элементов этих т столбцов и некоторых т их строк,
и вследствие теоремы (1а) в исходном определителе эти т строк
будут линейно независимы. Эта теорема остается в силе при
обмене ролями столбцов и строк.
(1в). Если в определителе п-го порядка с
функционально
ными элементами найдется отличный от тождественного нуля
определитель, составленный из элементов каких-либо m^Zn
столбцов и некоторых т их строк, то в исходном определителе
эти т столбцов, а также эти т строк линейно независимы и не
получаются одни из других умножением на переменные
функциональные множители и сложением.
(1г). Пусть в определителе л-го порядка с
функциональными элементами линейно независимы какие-либо т^.п
столбцов. Если ни один такой столбец не получается умноже:
нием некоторых этих столбцов на переменные функциональные
множители и сложением, то найдется отличный от
тождественного нуля определитель m-го порядка, составленный из
элементов этих т столбцов и некоторых т их строк, и вследствие
теоремы (1в) в исходном определителе эти т строк обладают
такими же свойствами. Если же хотя бы один такой столбец
получается умножением этих столбцов на функциональные
множители и сложением, то все определители m-го порядка,
составленные из элементов этих т столбцов и любых т их строк,
тождественно равны нулю. Эта теорема остается в силе при
обмене ролями столбцов и строк.
Пример 1.
(/+1) t e*
1 t e*
2 2t 2e*
= 0.
(10.3)
Все столбцы этого определителя линейно независимы на оси
ty но второй столбец отличается от третьего лишь множителем
te-K Второй столбец отличается от первого не только
множителем t, благодаря чему определители второго порядка,
полученные из определителя (10.3) вычеркиванием третьего столбца и
второй или третьей строки, отличны от тождественного нуля.
Пример 2.
t sint
t2 tsint
e* te* etsint
s0.
(10.4)
Все столбцы, а также все строки этого определителя линейно
независимы на оси t, но все они попарно различаются лишь
множителями. Поэтому не только определитель (10.4), но и все
его миноры второго порядка тождественно равны нулю.
(2а). Во всяком определителе с постоянными
элементами наибольшее число линейно независимых столбцов равно
наибольшему числу линейно независимых строк. Это число
называется рангом определителя.
(26). В определителе с функциональными элементами
наибольшее число линейно независимых столбцов может не сов-
Ш
атеЕггЖИйдав^го**^ -
падать с наибольшим числом линейно независимых строк.
Однако в силу теоремы (1г) обязательно совпадают наибольшее
число столбцов и наибольшее число строк, которые не
получаются умножением других столбцов и соответственно строк на
переменные функциональные множители и сложением.
Например, в определителе (10.3) линейно независимы три
столбца и только две строки. Число столбцов и строк,
различающихся не только множителями, в определителе (10.3) равно
двум, а в определителе (10.4) —единице.
В каждой фиксированной точке области изменения
аргументов функциональный определитель становится числовым и имеет
некоторый ранг в смысле (2а), но в различных точках области
ранги соответствующих числовых определителей могут быть и
различными.
Пример 3. В определителе
t t
И2
t*-t
оба столбца и обе строки линейно независимы; при t = 0 nt==±l
ранг определителя^ равен единице, а при всех остальных
значениях t ранг равен двум.
(За). Для того чтобы определитель с постоянными
элементами был отличен от нуля, необходимо и достаточно, чтобы все
его столбцы, а значит и все его строки были линейно
независимы, т. е. чтобы ранг определителя равнялся его порядку. Это
является следствием из (1а), (16) и (2а).
(36). Для того чтобы определитель с
функциональными элементами был отличен от тождественного нуля,
необходимо и достаточно, чтобы все его столбцы, а также все его строки
были линейно независимы и не получались умножением других
столбцов и соответственно строк на переменные
функциональные множители и сложением. Для этого необходимо и
достаточно, чтобы ранг определителя был равен его порядку хотя бы
в одной точке области изменения аргументов. Это является
следствием из (1в), (1г) и (26).
(4а). Для того чтобы определитель с постоянными
элементами был равен нулю, необходимо и достаточно, чтобы все
его столбцы, взятые вместе, а значит и все его строки, взятые
вместе, были линейно зависимы, т. е. чтобы ранг определителя
был меньше его порядка. Это является следствием из (За).
(46). Для того чтобы определитель с
функциональными элементами был тождественно равен нулю, необходимо и
достаточно, чтобы его столбцы или строки либо столбцы и
строки не удовлетворяли хотя бы одному из четырех условий
теоремы (36), т. е. чтобы во всей области изменения аргументов
ранг определителя был меньше его порядка. Это является
следствием из (36).
И2
§ 11. ОСНОВНЫЕ СВОЙСТВА РЕШЕНИЙ НОРМАЛЬНОЙ СИСТЕМЫ
ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Здесь мы рассмотрим некоторые важнейшие свойства
решений такой системы.
Теорема 1. Пусть задана нормальная система линейных
однородных дифференциальных уравнений
Х1 — а11ХХ + а\2Х2 + • • • + а1пХп
Х2 ~ #21 *1 I #22*2 "Г • ■ • "Г а2пХп
Хп — ап1Х1 + ап*Х% + • • • + аппХп '
(11.1)
в которой коэффициенты ajk /=1, 2, ..., п\ й=1, 2, ..., п являются
заданными непрерывными функциями от t в некотором
интервале a<t<b либо, в частности, постоянны, а хх> х2у ..., хп —
искомые функции независимой переменной L Тогда справедливы
следующие утверждения:
1) Существует п линейно независимых на интервале a<t<b
частных решений системы (11.1), причем функции, образующие
каждое из этих решений, записаны в столбцы, в которых
первым индексом обозначен номер компоненты, а вторым индексом
номер решения:
хп (t) х12 (t) .
*21 (0 *22 (0 •
• • X2k (<) • • . Х2п (О
% (О Х)2 (0 • • • *jk (0 ■ • • Хзп (О
(11.2)
2) Каждый столбец таблицы (11.2), умноженный на какую
угодно постоянную, сумма двух или нескольких столбцов, а
значит и любая линейная комбинация столбцов таблицы (11.2)
также являются решениями системы (11.1).
3) Определитель таблицы (11.2), составленной из п линейно
независимых частных решений системы (11.1), не обращается в
нуль ни при одном значении t из интервала a<t<b и,
следовательно, в силу положения (36) § 10 яг только все столбцы, но
и все строки таблицы (11.2) линейно независимы на интервале
a<t<b.
4) Общим решением системы (11.1) является линейная
комбинация решений (11.2) с произвольными постоянными
коэффициентами:
ИЗ
xi-^Ckxlk(t)
/i
X2 ~ 2 W*% W
Замечание. Подчеркнем, что утверждение 3) справед- fj
ливо для таблицы (11.2), составленной из/z линейно неза- #1
висимых частных решений системы (11.1), а не для *
всякой квадратной таблицы функций, состоящей из п линейно
независимых столбцов. Например, определитель (10.3) тождест- J
венно равен нулю, хотя все его столбцы линейно независимы
на оси L J
Мы докажем утверждения 1, 2, 4, а утверждение 3 примем
без доказательства ввиду его сложности (см. [10], гл. VII, § 2, *1
п. 2, стр. 276).
Доказательство. Прежде всего заметим, что для
системы (11.1) и каких угодно начальных условий,
заданных при любом t=t$ из интервала a<t<b, выполнены все уело- :%
вия теоремы существования и единственности частного решения. ^
Чтобы доказать существование п линейно независимых част- М
ных решений (11.2) системы (11.1), зададим квадратную табли- Л
цу чисел с отличным от нуля определителем; примем эти U
числа за значения функций (11.2) при некотором t=t0 и
поэтому обозначим их так:
хп (^о) *i2 (^о) • • • хи vo) • • • xin "о/
*21 (^о) *22 (*0/ • • r X2k (^o) • • • X2n (ч))
Xjl (^>) Xj2 (^o) • • • Xjk (^o) • • • Xjn (h)
XnX (*o) Xn2 (h) • • • Xnk \h) • • • Xan (*o) , ,
Так как каждый столбец этой таблицы образует допустимую
систему начальных условий, то п столбцам таблицы (11.4)
соответствуют п частных решений системы (11.1); пусть они
записаны в виде столбцов таблицы (11.2). Определитель, состав- г*
114
(11.3)
(11.4)
ленный из этих функций (11.2), не является тождественным
нулем, так как при t=t$ он равен отличному от нуля
определителю таблицы (11.4). Поэтому в силу положения (36) § 10 все ;
столбцы, а также все строки таблицы (11.2) линейно незави- \
симы. |
Справедливость утверждения 2) вытекает из однородности !
и линейности уравнений системы (11.1). В самом деле, непо- j
средственной подстановкой легко проверить, что функции ка- j
кого-либо столбца таблицы (11.2) как до умножения, так и по- {
еле умножения на постоянную С обращают систему уравнений j
(11.1) в систему тождеств. ]
Покажем, что если сложить соответствующие компоненты \
каких-нибудь двух столбцов таблицы (11.2), то полученный \
столбец тоже является решением системы (11.1). !
Подставляя в систему (11.1) функции, например, £-го столб- \
ца, получаем систему тождеств \
*jk^ajlXlk+aVX2k+ ... +Цп*пк /=1.2, ... ,Л. |
Подставляя в систему (11.1) функции другого, /-го столбца, по- j
лучаем другую систему тождеств '
^3fl,i% + Va/+'-'+fliA/ /=1,2, ... ,/г.
Складывая почленно соответствующие тождества этих систем, |
получаем, очевидно, систему тождеств \
Xjk + *jl S ЯД (*1* + Хи) + й& (*2ft + %) + j
+ ...+ajn(xnk + xnl) / = 1,2, ...,п. ;
i
Это и доказывает высказанное утверждение. Легко видеть, что \
таким же свойством обладают суммы нескольких столбцов и *
всех п столбцов таблицы (11.2). ;
Очевидно, оба эти свойства (т. е. решение, умноженное на J
постоянную, есть также решение и сумма решений есть также !
решение) можно объединить в одно: всякая линейная комбина- s
ция столбцов таблицы (11.2) является решением системы (11.1). \
Впрочем этим свойством обладают не только столбцы (11.2), ;
но и какие угодно решения системы (11.1). з
Чтобы доказать утверждение 4, умножим функции первого j
столбца таблицы (11.2) на произвольную постоянную Си функ- j
ции второго столбца — на произвольную постоянную Сг, вообще !
функции &-го столбца — на произвольную постоянную Съ, и, на- j
конец, функции гс-го столбца — на произвольную постоянную ;
Сп и затем сложим соответствующие компоненты полученных \
столбцов. В результате этих действий получается столбец »
функций (11.3).
115 i
Из доказанного утверждения 2) ясно, что функции (11.3)
удовлетворяют системе (11.1), т. е. образуют ее решение.
Остается доказать, что это решение общее, т. е. что каждая
допустимая система начальных условий однозначно определяет
значения произвольных постоянных Си С2у..., Сп, входящих в
функции (11.3), и тем самым однозначно определяет частное
решение системы (11.1), удовлетворяющее этим условиям.
Пусть задана какая угодно система начальных
условий:
хг \*о) — хю
Х2 (^о) = Х20
xj \h) "* xjo
*п(*о)=х,
ПО
(11.5)
которая, как мы видели, при a<t0<b допустима для системы
(11.1).
Подставляя в функции (11.3)
< = *о.
xj0 /= 1,2, ... , n,
из условий (11.5) получаем систему алгебраических линейных
уравнений с неизвестными Си С2,..., Сп:
**о=2 Ckxjk(t0) / = 1,2 л
или в развернутом виде:
(to) + • • • + Ckxlk (t0) + ... + Спхи (/о)
*20 = W^21 (^o) + Q*22 (^о) + • • • + CkX2h (t0) + . . . + CnX2tl ('О/
*jo = сххп (to) + c2xj2 (t0) + ... + ckxjk (t0) + ... + с„*,.и (g
Xn0 = ^lXnl (t0) + Czxn2(t0)+...+ (t,)+...+C„xaa(t0))
(11.6)
Согласно утверждению З) (которое мы приняли без
доказательства) определитель таблицы (11.2) отличен от нуля на
всем интервале a<t<b.
В системе (11.6) определитель из коэффициентов при
Си С2, ..., Сп равен значению определителя таблицы (П.2) при
t=U и, следовательно, также отличен от нуля. Поэтому каждо-
116
му столбцу свободных членов Xjo /=1, 2,..., п, т. е. каждой
системе начальных условий (11.5), соответствует свое
единственное решение системы (11.6), которое мы обозначим через Сю,
Сго,..., Cko,..., С по. Подстановка чисел Cko k=\9 2,..., п в
функции (11.3) дает частное решение системы уравнений (11.1) при
начальных условиях (11.5).
Таким образом, доказано, что функции (11.3) образуют
общее решение системы уравнений (11.1).
Таблица функций, составленная из п линейно независимых
частных решений нормальной системы п линейных однородных
дифференциальных уравнений, называется фундаментальной
системой решений этой системы уравнений.
Теорема 2. Пусть все коэффициенты нормальной системы
линейных однородных дифференциальных уравнений
^ = вуЛ + а*Л+ ■•■ +°1пХп / = 1,2,... 9п (11.7)
действительны и являются заданными функциями от t или
постоянными, и пусть эта система имеет комплексное решение
xi = ui + ivx)
%2 == ^2 "Т ^2
Xj = щ + iVj
(11.8)
xn = un+ivn\
Тогда отдельно действительные части функций (11.8), т. е.
иг
и*
ui
образуют решение и отдельно мнимые части этих
функций, т. е.
Vl
образуют решение системы (11.7).
В самом деле, подстановка функций (11.8) в систему
уравнений (11.7) дает систему комплексных тождеств:
117
Щ + iVj m ajX (иг + ivj) + aj2 (u2 + iv2) + ... + ajn (un + ivn)
или j = 1, 2, ... , n,
щ + ty e (ajxux + aj2u2 + ... + ajnun) +
+ 4*fiVi+*j*v%+ • • • +*in*>J (1L9)
/ = 1,2 л.
Но для тождественного совпадения комплексных функций
необходимо и достаточно отдельно тождественное совпадение их
действительных частей и отдельно тождественное совпадение
их мнимых частей. Поэтому система комплексных тождеств
(11.9) распадается на две системы действительных тождеств:
uj = ajlu1 + aj2u2 + ... +ajnun / = 1,2, ... , я, (11.10)
^е^1 + аЙ+ ••• + a]nvn / = 1,2 П. (11.11)
Это и убеждает нас в справедливости утверждения теоремы.
Следствие. Если в условиях теоремы 2 система (11.7)
имеет решение (11.8), то и столбец комплексно-сопряженных
функций
хг = иг — iv-i
х2
и« — iv.
также образует решение системы (11.7).
Это легко проверить, умножая почленно на / тождества
(11.11) и затем вычитая полученные тождества из
соответствующих тождеств (НЛО).
Теперь рассмотрим нормальную систему линейных неоднородных
дифференциальных уравнений:
Ч = ап *i + 012*2 + • • • + ат*п + h
Z2 = 021*1 + «22*2+ • • • + <htlZn + h
(11.12)
*/i = ЯлА + Ял2*2 + ... + annzn + fn
Система, которая получается из системы (11.12) в результате
отбрасывания свободных членов ft, f2, ♦.., fn* называется однородной системой,
соответствующей неоднородной системе (11.12). Очевидно, соответствующие
коэффициенты обеих систем совпадают. Искомые функции обеих систем можно
обозначать одной и той же буквой или различными буквами.
Теорема 3. Пусть задана нормальная система линейных неоднородных
дифференциальных уравнений (11.12), в которой коэффициенты ajk и
свободные члены fj /=1, 2, ..., п\ £=1, 2, ..., п являются заданными непрерывными
функциями от t в некотором интервале a<t<b либо, в частности, постоянны.
118
TSRCAa-W-MIS.
!>"V* r-V^W-n.-.'V
«■'if ^WSSV^jTofiSK
e i~-^«*6^ -w.j*i«i.«-*Hirawa**s«iSB>w,5«
Тогда общее решение неоднородной системы (11.12) может быть представлено
в виде суммы общего решения соответствующей однородной системы и какого-
нибудь частного решения неоднородной системы (11.12).
Доказательство. Пусть неоднородной системе (11.12) соответствует
однородная система (11.1), которая имеет общее решение (11.3), составленное
из ее фундаментальной системы решений (11.2). Следовательно, при
подстановке функций (11.3) в систему уравнений (11.1) получается система тождеств:
2 CkiJk(f) = ah 2 Скхь (t) + aj2 2 Ckx2k(t)+ ... +
k=i k=i k=i
n
+ ajn^Ckxnk(t) /=1,2, ... , n. ill.13)
*=l
Пусть известно какое-нибудь частное решение неоднородной системы
(11.12):
У\ = Ух (О
У* = Ут, (О
У) = Уз (О
(11.14)
Уп = Уп (О
Значит, при подстановке функций (11.14) в систему уравнений (11.12)
получается система-тождеств:
^(0 = ^^(0 + ^2^(0+ ... + <4nyn(t) + fj /=1,2,..., л. (11.15)
Складывая соответствующие тождества систем (11.13) и (11.15), получаем
также систему тождеств:
«ю + 2с*^« = «/1[у1(о+ 2c**i*w] +
k=\
k=i
+ ч« [л(0 + 2 ck**(')] + ... + вуЛ [и. (0 + 2 c**«* W] + /;
&=1 fc=l
• / = 1, 2, ..
, л.
Это значит, что столбец функций, полученный сложением соответствующих
компонент столбцов (11.3) и (11.14), образует решение неоднородной системы
(11.12):
*1 = Л(9+ 2С*хи(/)
А=1
г2= i/2(0+ 2СА(/)
А=1
гл = </Л0 + 2jc**«*W
(11.16)
119
.^^лви*^жзалл»-Жй- гттк-.чиглда-Ажжляияжэ!
Остается доказать, что это общее решение неоднородной
системы (11.12).
Для системы (11.12) и каких угодно начальных условий,
заданных при любом t=to из интервала a <t <by выполнены все условия теоремы
существования и единственности частного решения.
Пусть задана какая угодно система начальных условий (a<to<b):
zi (to) = zio
22 (^о) = Z20
(11.17)
2/1 (to) — zn0
Подставляя в функции (11.16) t=*U, Zj = Zj0 /=1, 2, ..., п из условий (11.17)
и перенося влево yj(U) /=1, 2 я, получаем систему алгебраических
линейных уравнений с неизвестными Сь Сг, ..., С п:
*ю — У\ (to) = C1xn (t0) + C2*i2 (to) + • • • + Cnxin (t0)
220 — У* (t0) = Ci*2l (to) + C2*22 (to) + . • • + СпХгп (U) , /1 , 1 04
(11.10)
zno — Уп (to) — Ci xm (to) + C2Xfi2 (to) + ... + Cnxnn (to)
Согласно утверждению З теоремы 1 определитель из коэффициентов при
неизвестных Си С2, ..., Сп отличен от нуля. Поэтому каждому столбцу
свободных членов 2/о—Уз (to) /=1, 2, ..., п, т. е. каждой системе начальных
условий (11.17) и каждому частному решению (11.14), соответствует свое
единственное решение системы (11.18), которое мы обозначим через
С\о, С2о, ..., Ckoy ..., С по. Подстановка чисел С^о k = 1, 2, ..., п в функции
(11.16) дает частное решение системы уравнений (11.12) при начальных
условиях (11.17). Таким образом, доказано, что функции (11.16) образуют общее
решение системы уравнений (11.12).
§ 12. НАХОЖДЕНИЕ ОБЩЕГО РЕШЕНИЯ НОРМАЛЬНОЙ СИСТЕМЫ
ЛИНЕЙНЫХ ОДНОРОДНЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Пусть задана система уравнений вида, указанного в
заглавии параграфа:
Xi — #ii*i + #12*2 "t"
+ аихп
хъ — Oai-^i *г аггх2 Ч~ • • • ~Ь агп xi
xa = a,a.x1 + aiax,+ ... +аппхп
(12.1)
в которой коэффициенты щк /=1, 2,..., п; k=l9 2,..., п
постоянны, т. е. не зависят от t, а хи *2, •♦., хп — это искомые функции
независимой переменной L
120
Систему (12.1) можно рассматривать либо как систему,
описывающую класс движений точки M(t) в n-мерном
пространстве, либо как систему возмущений для такого класса движений.
В этом параграфе мы дадим метод нахождения общего
решения системы (12.1), не приводя ее к одному уравнению более
высокого порядка.
Сначала будем - искать частное решение системы (12.1) в
форме
хх = Bxert
х* = Въег*
*п = Впе>
,rt
(12.2)
где г, В\, В2,..., Вп пока неизвестные числа.
Подставляя функции (12.2) с соблюдением номеров в
систему (12.1), сокращая на множитель ert, не равный нулю, и
перенося все члены в одну сторону, получаем
(ап — г)В1 + а12Вй + ... + аиВп = 0\
а21В1 + (а22 —г)52+ ...+ataBn=0
апХВх + апфг + • • • + (а,* - г) Вп = О
(12.3)
Для дальнейшего очень важно, чтобы в системе (12.3)
члены с В{ были написаны в первом столбце, члены с В2 во втором
столбце и т. д. и, наконец, члены с Вп в п-ом столбце. При
несоблюдении этого порядка все дальнейшее рассуждение было
бы неправильным.
Система (12.3) как система алгебраических линейных
однородных уравнений относительно неизвестных В\9 В2,...,Вп при
любом г имеет очевидное нулевое решение Bi = B2= ... =Bn = 0.
Но тогда функции (12.2) тождественно равны нулю:
л;2==0
причем, очевидно, они образуют частное решение системы (12.1).
Тождественно нулевое решение системы (12.1) означает
либо состояние покоя точки М в начале координат, либо
отсутствие возмущений относительно какого-либо движения,
принятого за невозмущенное. Однако нас интересует состояние
движения при наличии возмущений. Поэтому мы должны искать
ненулевые решения системы (12.1), т. е. такие системы
функций вида (12.2), среди которых обязательно есть функции,
121
отличные от тождественного нуля. Это необходимо и для
получения фундаментальной системы решений, из
которой затем составляется общее решение системы (12.1). Для
этого необходимо выяснить, при каких значениях г система
(12.3) имеет ненулевые решения, т. е. решения, состоящие из
чисел В\, В2,..., Вп, среди которых есть отличные от нуля.
Напомним известное положение о системе п линейных
алгебраических уравнений с п неизвестными (см. [9], ч. I, гл. VI,
§ 5—7, где эти положения даны для я = 3).
Для того чтобы система линейных алгебраических
уравнений имела единственное решение, необходимо и
достаточно, чтобы определитель из коэффициентов при неизвестных был
отличен от нуля; в частности, если эта система
однородная, то этим единственным решением является нулевое
решение. Поэтому для того чтобы система линейных
однородных уравнений имела, кроме очевидного нулевого решения, еще
ненулевые решения, необходимо и достаточно, чтобы
определитель из коэффициентов при неизвестных был равен
нулю.
Таким образом, система (12.3) может иметь ненулевое
решение только в том случае, если определитель из
коэффициентов при неизвестных равен нулю:
(ап — г) а12 ... а1п
021 (022 —>*) •••
Я(г)^
*2я
= 0- (12.4)
ani ат ••• (апп~г)
Применяя прием, описанный в § 10, раскроем определитель
(12.4), чтобы понять, как его величина зависит от г и что
существуют такие значения г, при которых он равен нулю.
Главная комбинация его элементов имеет вид (ац—г) (агг—/") ...
— (о«пп — г). При раскрытии всех скобок получится член с самой
высокой степенью г, а именно (—1)"гп и члены с более низкими
степенями г. Все остальные комбинации элементов
определителя (12.4) могут содержать не все, а только некоторые
элементы его главной диагонали и поэтому дают члены со степенями г
ниже п.
В результате полного раскрытия определителя (12.4) и
приведения подобных членов, т. е. объединения коэффициентов при
каждой степени г, мы убеждаемся, что определитель (12.4)
является многочленом степени п от переменной г со старшим
членом (—\)пгп. Умножая этот многочлен на (—1)п, т. е.
никак не изменяя его при четном п, либо умножая на (—1) при
нечетном я, можно переписать уравнение (12.4) в виде
следующего алгебраического уравнения л-й степени относительно г:
г* + ДА*-' + iV-2 + • • • + Ап-2Г* + 4-i г + Ап = 0. (12.5)
122
ЯИНГЖЯРГЭТГН№ЧВ jsj-s *r*f гг -Хат ЛЯЯИвяг уГСЛОС- явКЖОдавЯ'ГИЮТС. ?«EK<OTh ?"Т#*-.Й*7»-Ю^ *rfi35S^T»±iHfT^f»*-2Wa*H?«!&
Здесь коэффициенты А\, А2, ...,ЛП являются определенными
комбинациями (которых мы не будем выписывать явно) коэф- I
фициентов ajk системы (12.1). |
Алгебраическое уравнение (12.4) или в развернутом виде j
(12.5) называется характеристическим уравнением системы ]
дифференциальных уравнений (12.1), а его левая часть назы- |
вается характеристическим многочленом системы (12.1). j
Как известно, корнем алгебраического уравнения (12.5) или j
корнем многочлена, являющегося левой частью этого уравне- ;
ния, называется такое значение переменной г, при котором этот j
многочлен имеет значение нуль. Для того чтобы число г0 было j
корнем многочлена, необходимо и достаточно, чтобы этот много- j
член делился без остатка на (г—го). Если число г0 является I
корнем многочлена и многочлен делится без остатка на (г—ro)m, |
но не делится на (г—r0)m+1, то г0 называется m-кратным кор- \
нем этого многочлена, а число m называется кратностью этого \
корня. Корни многочлена, имеющие кратность т= 1, называют- j
ся однократными или простыми корнями. Корни многочлена, j
имеющие кратности больше единицы, вообще называются крат- \
HblMU. • ':> ■ •*-"'• ;
Из сказанного следует, что в разложении многочлена на |
множители простому корню Г\ соответствует множитель (г—г\), \
а m-кратному корню г2 соответствует множитель (г—r2)m, !
т. е. множитель (г—г2), повторяющийся пг раз. В этом смысле j
о кратных корнях многочлена говорят как о повторяющихся j
равных корнях. i
Приведем без доказательства основную теорему ;
алгебры: алгебраическое уравнение п-й степени имеет ровно \
п корней, если каждый корень считать столько раз, какова его \
кратность. I
Для каждого алгебраического уравнения n-й степени осу- |
ществляется одна из двух возможностей: либо уравнение имеет .
п различных корней и, следовательно, все они однократные, j
простые, либо хотя бы некоторые корни уравнения кратные и, |
следовательно, различных корней меньше, чем п. |
Рассмотрим вопрос о нахождении общего решения системы |
дифференциальных уравнений (12.1), когда для ее
характеристического уравнения (12.4) или (12.5) осуществляется каждый ;
из двух указанных случаев.
1. Характеристическое уравнение (12.4), (12.5) системы
(12.1) имеет п различных корней, и, следовательно, все они
однократные, простые.
Обозначим эти корни через ги г2,..., г*,..., rn. {
Подставим в систему (12.3) вместо г корень г*, а искомым
числам Ви #2,..., Вп припишем второй индекс k в знак того, что
мы ищем их, используя корень rk:
123
.«д-ад^яиивиягадг^к^^^д^ллюу *^-яе?т»А mcsss;tti
(an —rk)Blk + a12B%k +
+ "lnBnk
0
+ ««яД.*.= 0
a„iBlk + an2B2k+ ... +(ann — rk)B,
nk
0
(12.6)
Определитель этой системы равен нулю, так как rh есть
корень уравнения (12.4):
Я(гк) =
(*п — гк)
*12
(<*н — Гк) •••
*1я
*2л
*«1
**«2
(e«« — h)
0. (12.7)
Отметим без доказательства (см. [10], гл. VII, § 2, п. 4,
стр. 284—285), что для различных гь &= 1, 2, ...,п в каждом
определителе вида (12.7) хотя бы один диагональный
минор (п—1) порядка отличен от нуля и,
следовательно, все определители вида (12.7) имеют один и тот же
ранг (п—1).
В силу положений (1а) и (2а) § 10, выбирая в каждом
определителе вида (12.7) какой-нибудь отличный от нуля минор
(п—1)-го порядка (причем даже при каждом k этот выбор
может оказаться не единственным), мы тем самым выбираем (п—1)
линейно независимых столбцов и (п—1) линейно независимых ,
строк в каждом из определителей (12.7).
Чтобы найти ненулевое решение системы (12.6),
соответствующее одному из rft, возьмем из нее только те (п—1) линейно
независимых уравнений, которые соответствуют (п—1)
выбранным строкам определителя (12.7), и отбросим одно оставшееся
уравнение, которое является линейной комбинацией взятых
уравнений. В полученной системе (п—1) уравнений выделим
отличный от нуля определитель порядка (п—1) из
коэффициентов, соответствующих выбранным выше (п—1) столбцам
определителя (12.7). Вместе с этим среди неизвестных В\к} B2k>..., Bnh
выделятся те (п—1) неизвестных, которые стоят при
выделенных коэффициентах. Оставшейся неизвестной дадим какое
угодно ненулевое значение и в зависимости от него
найдем значения выделенных неизвестных.
Так получается (причем для каждого k не единственным
образом) ненулевое решение системы (12.6), которое при r=rh
является ненулевым решением системы (12.3). Таким способом
последовательно находятся ненулевые решения системы (12.3),
соответствующие каждому корню характеристического
уравнения.
Напишем квадратную таблицу чисел Bjk из п строк и п
столбцов, в которой каждый столбец представляет собой нену-
124
левое решение системы (12.3), причем вторые индексы у чисел
Bjh совпадают с номерами тех корней rk, которым
соответствуют эти решения системы (12.3):
£ц ^12 • • • Blk ... В1а 1
£>21 -Оо2 • • ■ °2k • • • В2п
Bj± Bj2 ... Bjk ... Bjn
Bnl Впг ... Bnk ... Впп
Используя корни характеристического уравнения и
соответствующие им столбцы таблицы (12.8), составим таблицу из п
столбцов функций вида (12.2), причем вторые индексы у
функций Xjk совпадают с номерами тех корней rkj которым
соответствуют эти столбцы:
Xn=B11er*t
х.1=Впег'{
х,л=Вп1е^
*12 = ^12 &* .
•^22 = -^22 &* •
Хр = ВреГ'* .
хп% = Впгег* .
• .х1к = В1кегк( .
..Хи = Въкегь' .
..%=%ег*' ..
•• xnk=Bnker*'.
..х1п = В1пегп*\
.х2п = Вгпег«*
х- — В. егп*
Из самого построения ясно, что каждый столбец таблицы
(12.9) является частным решением системы дифференциальных
уравнений (12.1).
Докажем, что функции ег^ при различных rh k= 1, 2,..., п
линейно независимы на всей оси t. Прежде всего
очевидно, что тождество аег'=0 возможно только при а=0.
Поэтому тождество ще г**+ а2ег^ = 0 невозможно, если один из
коэффициентов ai или с*2 равен нулю, а другой не равен
нулю. Покажем, что это тождество возможно только при ai='
"=02 = 0. Для этого перепишем его так:
аг = — a2e(r*—rJf
и затем продифференцируем:
125
Это возможно только при сс2 = 0; но тогда и ai = 0. Далее по
доказанному тождество а\ег** + №*** +аз^ =0 невозможно,
если один или два из коэффициентов си, «2, а3 равны нулю, а
остальные не равны нулю. Чтобы показать, что оно возможно
только при ai = a2 = a3=0 перепишем его в виде
аг ES — a2e^""r^f — a8elr»-r*)t
и продифференцируем:
0 в <х2 (гх - г2) *'--'.» + <х3 (гг - г3) е^~г^.
Это возможно только при а2 = аз = 0; но тогда и txi = 0.
Продолжая таким же образом, мы убеждаемся в
справедливости утверждения. Ясно, что рассуждение остается в силе,
если один из гА, например ги равен нулю.
Докажем теперь, что все столбцы функций таблицы (12.9)
линейно независимы на всей оси t. Иначе говоря, нужно
доказать, что система тождеств
ьВпеГ* + а2Впе'** +...+ akBlkerk* + ... + апВ1п ег»< ^ 0 |
а1Впе"* + <ьРш*Г** + ... +akB2kerbf + ... +ааВ2пег^шО
а1В^ + а2В^ + ... +akBilfirff+ ... +a^/^0
о1Вя1^ + а1Вя^.'+ ... +акВпкег1?+...+апВппегп*^0 J
возможна только при ai = a2 = ... = afc=... = an=0.
В самом деле, в силу линейной независимости функций егь*
&=1, 2,..., п каждое из этих тождеств возможно только в том
случае, если все коэффициенты при этих функциях равны нулю,
т. е. a,kBjk=0 k—\% 2,..., п; /=1, 2,..., п. Но все эти равенства
выполняются только при ai = a2 = ...='afc = ... = an = 0, так как в
каждом столбце таблицы (12.8), а значит и при каждом
ад k=l, 2,..., п хотя бы одно из чисел Bjk отлично от нуля.
Таким образом, все столбцы таблицы (12.9) представляют
собой п линейно независимых частных решений
системы (12.1). Согласно определению § 11 таблица функций (12.9),
составленная из п линейно независимых частных решений
системы уравнений (12.1), является фундаментальной
системой решений системы (12.1).
В силу утверждения 3 теоремы 1 § 11 определитель таблицы
функций (12.9) не обращается в нуль ни при каком значении L
В частности, при £=0 определитель таблицы (12.9) совпадает
с определителем таблицы (12.8), который, следовательно,
отличен от нуля.
126
Теперь умножим функции первого столбца таблицы (12.9)
на произвольную постоянную Су, функции второго столбца —
на произвольную постоянную С2, вообще функции &-го
столбца— на произвольную постоянную Ck и, наконец, функции
п-то столбца — на произвольную постоянную Сп и затем сложим
соответствующие компоненты полученных столбцов.
В результате этих действий получается столбец функций,
которые мы обозначим просто через х\, Хг,..., х^..., хп и
напишем его кратко и подробно;
п л
xi = 2j ^ Xl
4k
*2 — V Си Xi
k**k
k=\
xi — Yi CkXjk
k=\
Xn — J] Ckxnk
k=\
k=l
rj
x2= "£CkB*berb]
k=\
CbB
Prkf
fe=l
(12.10)
(12.11)
В рассматриваемом случае, т. е. когда все корни
характеристического уравнения простые, в силу утверждения 4 теоремы 1
§ 11 функции (12.11) на всей оси £ образуют общее
решение системы дифференциальных уравнений (12.1). Легко
проверить, что для системы уравнений (12.1) и любых
начальных условий выполнены все условия теоремы существования и
127
№smessiKHk3irvataJt*a*£-4£Sirta
единственности частного решения, т. е. что любые начальные
условия допустимы для системы (12.1).
В примере 1 § 3 для системы уравнений (3.2) было написано
общее решение (3.3), которое может быть получено только что
изложенным методом. Читателю рекомендуется проделать
соответствующие выкладки.
2. Хотя бы некоторые корни характеристического уравнения
(12.4), (12.5) системы дифференциальных уравнений (12.1)
кратные и, следовательно, различных корней меньше, чем п.
Пусть корень г\ имеет кратность ти корень г2—кратность
т2, ..., корень ги — кратность mki ..., корень rs — кратность mSy
причем 5<п. В силу основной теоремы алгебры
s
т1+т2+ ... +mk+ ... +ms= yS£mk = n.
С помощью каждого из корней г\9 г% ..., rs можно найти по
одному частному решению системы уравнений (12.1) в
прежнем виде (12.2), т. е. в виде показательных функций с
постоянными коэффициентами, и тем же способом, как в
случае простых корней характеристического уравнения. Так
получится s<n линейно независимых решений системы (12.1).
Возможно ли в случае кратных корней найти больше, чем s
линейно независимых частных решений системы (12.1) в
прежнем виде (12.2)? Ответ на этот вопрос дает теорема, которую
мы приведем без доказательства (см. (10], гл. VII, § 2, п. 4,
стр. 288—289).
Теорема. Пусть характеристическое уравнение (12.4), (12.5)
системы дифференциальных уравнений (12.1) имеет s<n раз-
личных корней ги г<г,..., rki..., rs, соответственно кратностей т\,
т2,..., tKk,..., /ras. Пусть при подстановке корней rh в систему
(12.3) получаются системы вида (12.6), для которых
определители q(rk) вида (12.7) имеют соответственно ранги nk
£=1, 2,..., s. Тогда справедливы следующие утверждения:
п—Пк^тъ. Л=1, 2, ..., s\ по каждому корню rk можно найти
ровно п—nk линейно независимых частных решений системы
(12.1) в виде (12.2), г. е. всего
s s ~Щ *П -*
£> — %)< %mk*=n
таких решений.
Однако для нахождения всех этих решений вида (12.2)
нужно в каждом определителе q{rh) найти отличный от нуля
определитель наибольшего порядка, так как этот порядок и есть
ранг nk k=ly 2,..., s; но это связано с громоздкими выкладками,
особенно при /г^4. Поэтому мы дадим упрощенную схему
нахождения п линейно независимых частных решений системы
128
(12.1) методом неопределенных коэффициентов.
Напомним, что п таких решений нужны для получения
фундаментальной системы решений, из которой затем составляется
общее решение системы (12.1).
По каждому корню rk характеристического уравнения надо
найти ровно rrik линейно независимых частных решений системы
(12.1). Поскольку нет гарантии найти все такие решения в виде
(12.2), будем усложнять множители при показательной
функции; именно будем брать в качестве этих множителей
многочлены от t последовательно возрастающих степеней подобно
тому, как это делалось при решении одного линейного
уравнения с постоянными коэффициентами в случае кратных корней
его характеристического уравнения.
Итак, по корню г\ ищем т\ решений в виде:
*ii = Ян #* *и = Pit (t) ** Ьж = Ргм W *** • • • *i.m. = PXtMt (t) *** j
х21 = В21 &** х22 = Р22 (t) е* х2з = Рад (t) erJ ... x2tmt = /Vm, (t) erJ
Хц = В,,, en* xj2 = Pj2 (t) *i* xj3 = Pj3 (t) e*... X/tmi = P,,mi (t) er** I
xnl = Bal e* xn2 - Pn2 (t) e^t Xn3 = Pn3 (t) *J... Хп^ = P„,mi (ty** I
(«Лад
Здесь Bji — постоянные, которые находятся так же, как и в
случае простых корней; P$(t) /=1, 2,..., п — это многочлены
первой степени, Pjz(t) —многочлены второй степени и, наконец,
P/mt (0 — многочлены mi — 1 степени от t пока с
неопределенными коэффициентами.
Каждый столбец таблицы (12.12i) должен быть решением
системы дифференциальных уравнений (12.1). Поэтому для
нахождения коэффициентов многочленов какого-либо столбца
таблицы (12.12i) нужно подставить функции этого столбца в
систему уравнений (12.1), следя за первым индексом, сократить
на ег** и затем в получившихся равенствах приравнять
коэффициенты при одинаковых степенях ty в результате чего
получается система числовых уравнений относительно искомых
коэффициентов многочленов.
Ниже (см. § 15) на примерах мы увидим, что эта система
определяет искомые коэффициенты не единственным
образом, т. е. остается довольно большая свобода выбора.
Вследствие этого часто (особенно, если п—nj>l) удается найти
многочлены более низких степеней, чем предполагалось. Таким
образом, если столбцы таблицы (12.12i) являются решениями
системы (12.1), то многочлены Pj2(t), Pjz{t)9...f P/,mt(t) имеют
5 А. Г. Младов 129
степени соответственно не выше первой, не выше
второй и, наконец, не выше (т{—1).
Точно также по корню г2 находим т2 решений:
XUi+mi = fli,i+wier»'A:if2+m1 =P\,2+m1(t)er*t. . .Xhm^mi=PUm^mi{t)er^)
*2,1+ю, = B2tl+mi С2* X2,2+mx = P2,2+ml(t)er*t. . .X2,m2+mi=P2,m2+m1(t)er*t\
XIA+mt = BjA+mier*f X;t2+mi =P/,2+mt(t)er*t. . .^/.mi+m1=P/i»n1+w1(0«ri' I
Xnti+mt = Bn,l+mier*tXnt2+m1=Pnt2+mi(t)er*t . . .*n,m1+m1=/Vm1+m1(0^I4
(12.12,)
ЗдеСЬ B/A+mi — ПОСТОЯННЫе; P/,2+mt (t), Р/.3+Ш, (0 --Pf,m2+mt(t) —
многочлены степеней не выше первой, не выше второй, не выше
(пг2 — 1) соответственно.
Таким же образом находим решения по остальным корням и,
наконец, находим ms решений по корню rs:
X\t\-\-n-ms = Bi,i-]-n-mse s *1,2+л-/я9 = Pi,2+n—m^)^ s I
Xj,\+n—ms = fi/.i+zi—m^ £ **
*лЛ+я—m = Вп,\+п—т^е s
. . . #1,л =
« • • «Я/,я =
Xf,2+n-ms = P/t2+n-ms (0 * ^
*л,2+л-т5 = Рл,2+л-т^ (0 * Г<у
= Pu(0*v
= P/,*(0*V
... Xntn = PnAt)erJ J
Здесь 'Д/^+л-^— постоянные; P/t2+n-ms(t)t Pf>z+n-ms (t) ... ,
P/,n (t) — многочлены степеней не выше первой, не выше второй,...,
не выше (ms — 1) соответственно.
Подчеркнем, что каждую таблицу (12.12д) й=1, 2,..., 5
можно и нужно построить так, чтобы в ней все решения,
т. е. все столбцы были линейно независимы на оси t.
Отметим при этом, что из приведенной выше теоремы вытекает
130
следующее: по корню rky для которого п—nk<mky можно
построить таблицу (12.12ft), в которой п—nk первых столбцов
состоят из функции erkf с постоянными коэффициентами, и
лишь в последних mk+nk—п столбцах множителями при erk*
служат многочлены степеней не выше чем т^ + Пь,—п\ по
корню rk, для которого п—nk = tnk, можно построить таблицу
(12.12^), в которой все множители при ег£ постоянны.
Объединим таблицы (12.12i), (12.122),..., (12.12s) в одну
таблицу (12.12 1,2,...,e)i состоящую из тх+т2+ ... +ms=n
столбцов, каждый из которых является частным решением системы
(12.1). Как и в случае простых корней, легко проверить, что
любая линейная комбинация столбцов этой объединенной
таблицы также является решением системы (12.1). Из линейной
независимости столбцов каждой таблицы (12.12ft) й=1, 2,..., s
следует линейная независимость на оси t всех п
столбцов объединенной таблицы (12.12 i, 2 s).
Таблица (12.121, 2, .... $ ), обладающая всеми
перечисленными свойствами, является фундаментальной
системой решений для системы дифференциальных уравнений
(12.1) в случае кратных корней характеристического уравнения.
Согласно утверждению 3 теоремы 1 § 11 определитель таблицы
функций (12.12i, гл.., s) не обращается в нуль ни при каком
значении t.
Далее действуем так же, как при составлении функций
(12.10) из функций таблицы (12.9), т. е. умножаем столбцы
таблицы (12.121, 2, .... s) на произвольные постоянные С\9 Сг,..., Сп
и затем покомпонентно складываем получившиеся столбцы:
п
xi = 2 ^kxik
х2 — 2 Ckx*k
xj — 2 ^ьхлк
Xn — 2 ^kXi
nk
*=1
(12.13)
Так составленные функции (12.13) образуют общее
решение системы уравнений (12.1).
Теперь обратим внимание на то, что как среди простых, так
и среди кратных корней характеристического уравнения могут
быть комплексные корни. Пусть, например, имеется ком-
5*
131
плексный корень rk = ak + фл. Тогда функции xjk = Bjkerb*
или Xjk — Pjk{t)^kty из которых состоит соответствующее
частное решение, также являются комплексными, т. е. принимают
комплексные значения. Это происходит не только за счет
комплексной функции е& = eaf^(cos§kt -J- isin§kt)9 , но и
потому, что Bjh и коэффициенты многочленов Pjk(t), вообще говоря,
комплексны.
Между тем, если все коэффициенты а& системы (12.1)
действительны, то из любого комплексного решения этой системы
можно получить даже два действительных решения.
Возможность этого видна из теоремы 2 § 11.
Кроме того, заметим, что если все коэффициенты
характеристического уравнения (12.5) действительны и уравнение имеет
комплексные корни, то все эти корни группируются в
комплексно-сопряженные _п а р ы; так, вместе с корнем
rk — cLk + ifik имеется и корень Га=сьа—Фа, причем той же
кратности. Если корню rk = ak + i$k соответствует решение
*ik = uik + ivlk
X2k = U2k + iV2k
*nk
= unk + iv}
'nk
(12.14;
системы (12.1), то можно доказать, что столбец функций
vu
*ik'
•IV
Ik
X2k ~U2k W2k
Xnk — Unk tVnk
(12.15)
который в силу следствия из теоремы 2 § 11 является решением
системы (12.1), будет решением, соответствующим корню
fk = «А—Фа.
Если все коэффициенты системы (12.1) действительны, то по
теореме 2 § И действительные и мнимые части столбцов (12.14)
и (12.15) также являются решениями системы (12.1). Очевидно,
действительные части столбцов (12.14) и (12.15) совпадают, а
мнимые части отличаются только знаком, но это различие
несущественно ввиду однородности уравнений (12.1). Поэтому
существенно различны только два столбца:
«1*
U2k
(12.16)
"я*
132
\ WVH it TVp-'ЯЬ- гС ь.З!ГЛ^
г ^чж-.^жт-йчиптяг-*
(12.17)
*>nk
причем можно доказать, что они линейно независимы на всей
оси L
Заменяя в фундаментальной системе (12.9) или
(12.12 1,2 s) каждую пару комплексно-сопряженных
решений (12.14), (12.15) соответствующей парой действительных
решений (12.16), (12.17), можно всю фундаментальную
систему решений составить только из действительных
функций. Тогда и общее решение системы (12.1) получится в
действительной форме.
Наконец, отметим, что если при действительных
коэффициентах системы (12.1) ее характеристическое уравнение имеет
комплексные корни rk = ak + i$k и rh = ak—*'Рь, то
соответствующие комплексные решения (12.14), (12.15) и
действительные решения (12,16), (12.17), полученные выделением
действительных и мнимых частей комплексных решений, а также
линейные комбинации решений системы (12.1) с участием
указанных решений имеют колебательный характер. Ясно,
что эти колебания вызваны функциями
e(*k±ih)t = e<V(cos у ±isin pfcf), eVcosP^, e^sin^t,
которые участвуют в перечисленных решениях.
§ 13. КРИТЕРИИ УСТОЙЧИВОСТИ И НЕУСТОЙЧИВОСТИ ДВИЖЕНИЙ,
ОПИСЫВАЕМЫХ НОРМАЛЬНОЙ СИСТЕМОЙ
ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (КРИТЕРИИ
ВЫРАЖЕНЫ ЧЕРЕЗ КОРНИ ХАРАКТЕРИСТИЧЕСКОГО
УРАВНЕНИЯ СИСТЕМЫ ВОЗМУЩЕНИЙ)
1. Критерии устойчивости и неустойчивости
по Ляпунову
Пусть класс движений описывается нормальной системой
линейных, вообще говоря, неоднородных дифференциальных
уравнений с постоянными коэффициентами:
zy - ajXzx + aj2?t+ ... + ajnzn + Д (*)7 = 1, 2, ... , п. (13.1)
Здесь ajk /=1, 2,..., п\ /е=1, 2,..., п — постоянные, a fj(t)
/=1, 2,..., п — заданные функции от /, непрерывные при
0<*<оо,
133
F^'a^s»» А«гз",
Из § 9 известно/что если какое-нибудь (безразлично какое)
движение из класса (13.1) принять за невозмущенное, то
системой возмущений относительно этого движения
является однородная система, соответствующая данной
системе (13.1):
*j = ajixi + я,А + • • ■ + ajnxn / = 1, 2, .... л. (13.2)
Устойчивость или неустойчивость по Ляпунову движений
класса (13.1) определяется поведением всей совокупности
решений, т. е. поведением общего решения системы
возмущений (13.2) при £-^оо.
В данном случае система возмущений (13.2) имеет тот же
вид, как и система (12.1) предыдущего параграфа, где с
помощью корней характеристического уравнения этой системы
для нее была получена фундаментальная система решений
(12.9) или (12.12i, 2, .... s ) и составлено соответствующее
общее решение (12.10) или (12.13).
В этом параграфе мы получим критерии, т. е. признаки,
устойчивости и неустойчивости движений, описываемых
системой (13.1), причем эти критерии будут выражены через корни
характеристического уравнения системы возмущений (13.2).
Поэтому при выводе этих критериев мы все время будем
использовать только что приведенные результаты § 12.
В § 14 и § 16 будут рассмотрены критерии устойчивости и
неустойчивости движений, описываемых системой вида (13.1),
выраженные через коэффициенты характеристического
уравнения системы возмущений.
Мы рассмотрим пять случаев корней характеристического
уравнения системы возмущений '(13.2), каждый из которых дает
соответствующий признак устойчивости или неустойчивости по
Ляпунову движений класса (13.1).
Теорема 1. Если все корни характеристического уравнения
системы возмущений (13.2) имеют отрицательные
действительные части,то все движения класса (\ЗЛ)асимптотинески
устойчивы по Ляпунову.
Доказательство.
а) Действительные отрицательные корни
Если корень rk<0 простой, то в фундаментальной системе
решений (12.9) или (12.121, 2 s) ему соответствует столбец
функций вида Xjk = Bjkerkf, которые, очевидно, стремятся к
нулю при £-*оо.
Если корень гк<0 имеет кратность тк>\, то в
фундаментальной системе решений (12.12 i, 2»...,«) ему соответствуют тк
столбцов функций вида
134
xjk = P,Jk(t)erbf, (13.3)
где Pjk(t) —многочлены степеней не выше (mk—1) с
действительными коэффициентами в случае действительных
коэффициентов системы (13.1).
Заметим, что здесь и далее в этом параграфе в случае
корня rk кратности mk мы пишем для простоты второй индекс k
у функций Xjk и многочленов Pjk(t), соответствующих этому
корню, хотя в действительности этот индекс не совпадает с kf
а пробегает тк значений.
Возьмем любую из функций (13.3), и пусть в ней многочлен
Pjk(t) имеет некоторую степень 0<Х^тк—1.
Так как при t-+oo | Pjk(t) | ->oo, a/ft -И), то Xjk
представляет собой неопределенность вида оо-О. Для раскрытия этой
неопределенности перепишем Xjk в виде дроби % =—■J?r\ ■,
сю
которая является неопределенностью вида — , и применим к
со
ней к раз правило Лопиталя. Тогда, обозначая через Ьц
коэффициент при tK в многочлене Pjk(t), получаем
lim*ifc=lim-£^ = lim—^р—7=0.
б) Комплексные корни с отрицательной
действительной частью
Если корень rk = ak + i$k, где аА<0 и Ра#0, простой, то в
фундаментальной системе решений (12.9) или (12.121. 2, ..., s)
ему соответствует столбец функций вида Xjk=Bjkerk , где Bjkj
вообще говоря, комплексные постоянные. С помощью формулы
Эйлера можем написать
xjk = B^(«*+'V = B^e'h* = Bjkea* (cos У + I sin №
Ho
I eP* I = I cos p^ + i sin $kt I = yWp^ + sirfp^ - 1,
следовательно,
Ы = |В,*1А'.
Поэтому
lim | xjk | = 0, а значит и lim xjk = 0.
f-ЮО ' f-*00
135
Если корень rh = ak + i$h, где а&<0 и Рь#0, имеет кратность
тк>19 то в фундаментальной системе решений (12.12 i, 2, ..л s)
ему соответствуют mk столбцов функций вида
*,* = fy«)e(e*+",*M. (13.4)
где Pjfe(0—многочлены степеней не выше {mh— 1), вообще
говоря, с комплексными коэффициентами.
Очевидно, при t-^ot>
| в<W' | = eV | e'V | = eV -* О,
а значит и e(a*+/V -► 0.
Возьмем любую из функций (13.4) и пусть в ней многочлен
Pjk(t), вообще говоря, с комплексными коэффициентами
имеет некоторую степень 0<Я^т^—1. Чтобы выяснить, как
ведет себя при t-+oo модуль этого многочлена, напишем его в
развернутом виде, опуская для простоты индексы /, k у его
коэффициентов:
Pik (0 = Vх + &/"1 + ht%~2 +...+ ьк-2р + &,_! t + &я,
причем Ь0фО. Вынесем из многочлена множитель t%:
^-*(*+ -*- + -*-+•••+•£• + -£- +
+ -М=МЛ(0. (13.5)
где через Sjk(t) обозначено выражение в скобках при t%.
Очевидно,
limS^O^o^O, (13.6)
Следовательно, | Pjk (t) \=fr\ Sjk (/) | ~> oo при t -* oo.
Напишем выражение модуля взятой функции (13.4):
Ixjk | = |P]k (t) I • I e«*W| = | Sjk (0 |<W . (13.7)
Из сказанного ясно, что | х& | представляет собой
неопределенность вида оо-О; преобразовав ее в неопределенность
вида —, легко раскрыть ее, применяя К раз правило Лопиталя:
оо
136
lim |*.fc| = lim|S,fc(OI-Um-
t->oo t->oo t->oo
1601 - lim — W_^=|ftn|.0 = 0.
Следовательно, и
lim xjk = 0.
f-»oo
Заметим, что к самой комплексной функции (13.4),
переписанной в виде
правило Лопиталя не применимо. В самом деле (см.,
например, {7], гл. II, §10; гл. IV, § 1, 3, 4, 5) правило Лопиталя
получено с помощью теоремы Коши, доказанной с помощью
теоремы Ролля, в доказательстве которой используется теорема
о наибольшем и наименьшем значениях функции,
непрерывной на отрезке; последнее имеет смысл лишь для
функций, принимающих только действительные значения,
так как для комплексных чисел понятия «больше» и «меньше»
не определяются.
Итак, мы доказали, что в фундаментальной системе (12.9)
или (12.12 1, 2, ...-, s) все функции xjh, соответствующие корням
с отрицательными действительными частями (простым,
кратным, действительным, комплексным), стремятся к нулю при
f-^oo. Следовательно, и все компоненты общего решения (12.10)
или (12.13) системы возмущений (13.2) при всех значениях
произвольных постоянных Си С2, ..., Сп стремятся к нулю
при £->оо.
Остается доказать, что все движения класса (13.1)
устойчивы по Ляпунову и тогда теорема будет доказана.
Напомним, что значения произвольных постоянных Сь
С2,..., Сп находятся по начальным условиям. В данном случае
роль начальных условий выполняют начальные возмущения,
которые мы обозначим так:
*г (°) = *м
#2 V-V = -^20
х„ (Р) = *„о
:(1з.8)
Подставляя ^=0 в общее решение (12.10) или (12.13) системы
Бозмущений (13.2) и используя начальные возмущения (13.8),
получаем систему алгебраических линейных уравнений с
неизвестными Си С2,..., Сп:
137
%=2Cft%(0) / = 1,2,
k=l
или в развернутом виде
*10 = С1*Ц(0) + СЛ1(0) +
^• = Сл1(0) + С1дсм(0) +
+ Ckxlk(0) +
+ СЛк(0) +
+ Спх1п(0))
+ CnxZn(0)
[.(13.9)
Ъо = ClXjl (0),+ C2xj2 (0) + ... + Ckxjk (0) + ... + Cnxjn (0)
*„o = ClXnl (0) + Сгхп2 (0) + ... + Ckxnk (0) + ... + Cnxnn[0))
Вспомним, что согласно утверждению 3 теоремы 1 § 11
определитель таблицы (12.9) или (12.121, а,.... s) не обращается в
нуль ни при каком значении t, в том числе и при 7=0. Поэтому
в системе (13.9) определитель из коэффициентов при Си
С2,..., С„ отличен от нуля, и для каждого столбца свободных
членов, т. е. при каждых начальных возмущениях (13.8),
система (13.9) имеет единственное решение Сю, С2э,.... Сп0.
Выпишем определитель системы '(13.9):
W-
*п(0)
*21(0)
*д(0)
*м(0)
*22<0)
*;2(0)
(0)
Чк
Чл
v2n
(0)
(0)
,(0)
*.-,(0)
")П '
*«i(0) *„а(0)
*-nk
(0)
,(0)
¥=0.
Для каждого k=l, 2,..., п составим определитель Доь,
который получается из определителя w заменой его А-го столбца
столбцом свободных членов системы (13.9):
Хц (0) х12 (0) ... *,,*_, (0) х10 xttk+i (0) ... xln (0)
х21 (0) х22 (0) ... x2,k-\ (0) дг20 х2,к+\ (0) ... х2п (0)
«»*■=
*ii(0) *„(°) ... xM_,(0) (0)
(0)
(0)ж„2(0) ... *„.*-, (0) (0) ... *„„(<>)
Как в § 10, обозначим через Mjk минор (п—1)-го порядка
определителя wy соответствующий элементу Xjk(0), и раскроем
определитель Wk по элементам его &-го столбца:
Щ = (~ l)l+k*ioMlk + (- \f+kx2QMik +
+ ...+(- l)l+kxjuMik +...+(_ l)n+kx„0Mnk.
138
По правилу решения системы алгебраических линейных 1
уравнений (см. [9], ч. I, гл. VI, § 5—7, где это правило дано для .
п = 3) получаем решение системы (13.9):
С» = f = ~l(- mkx10Mlk+(- 1Г+»х20М2к +
+ ... +(-\y+kXj0Mjk+ ... +(-l)n+ltXnoMnk]
Дг = 1, 2 n
Очевидно,
(13.10)
\С»\<Г7\\*»\'\Млк\ + \х9л\-\Ми\ +
\w\
+ ...+\xj0\.\Mjk\+...+\xn0\.\Mnk\]
k = 1, 2, ,.. ,n
(13.11)
Отсюда видно, что при малых | х& \ /=1, 2, ...,п малы и \СМ\
й=1, 2,..., л.
Из полученных выше оценок ясно, что в условиях теоремы
модули всех функций Xjk(t) таблицы (12.9) или (12.12 i, 2 $)
ограничены на полуоси t^zO.
Оценим компоненты общего решения (12.10) или (12.13)
системы возмущений (13.2) при малых начальных
возмущениях (13.8):
1^1=|2С,0%(0|<2|С,о|-|%(01
k=i k=i
(13.12)
/ = 1,2,
,п
Из оценок (13.11) и (13.12) видно, что при любых достаточно
малых | Xjo | /=1, 2,..., /г, а значит при достаточно малых | См\
k=l, 2,...,л малы и| Xj | /=1, 2,..., п при всех t^Q. Это и
означает, что все движения класса (13.1) устойчивы по
Ляпунову.
Но выше было доказано, что все функции Xj /=1, 2,..., я,
образующие общее решение системы возмущений (13.2),
стремятся к нулю при /-^оо. Следовательно, все движения класса
(13.1) асимптотически устойчивы по Ляпунову.
Таким образом, теорема 1 доказана.
Теорема 2. Если хотя бы один корень характеристического
уравнения системы возмущений (13.2) имеет положительную
действительную часть, то все движения класса (13.1)
неустойчивы по Ляпунову.
139
Док аз ател ьство
а) Действительный положительный корень
Если корень rk > О простой, то в фундаментальной системе
(12.9) или (12.12i,2,...,s) ему соответствует столбец функций вида
xjk = Bjkerb*. Очевидно, | xjk | = | Bjk \ егь* ~> оо при / -> оо.
Если корень rk > 0 имеет кратность тк > 1, то в таблице
(12.12j,2 s) ему соответствуют mk столбцов функций вида
xjk = Pjk(t)ek\ где Pjk(t) — многочлены степеней не выше mk — 1
с действительными коэффициентами.
Возьмем любую из этих функций и пусть в ней многочлен
Pjk (t) имеет некоторую степень 0 < к < mk — 1. Так как при
t -» оо | Pjk (t) | -> оо и егь* -> оо, то и | л:^ | -* оо.
б) Комплексный корень с положительной
действительной частью
Если корень rk = ak + i$kt где ak>0 и §кф0> простой, то в
фундаментальной системе (12.9) или (12.12i,2 s) ему соответствует
столбец функций вида xjk = Bjkerk\ где Bjk, вообще говоря, комп
лексные постоянные. Как и выше, можем написать
\х№\ = \В,к\.\е<°ь+**\ = \В,11\еЧг*оо
при f->oo, так как afe^>0.
Если корень rk = ah + i$k9 где %>0 и $кф0, имеет
кратность т^>1, то в таблице (12.12i,2,...,s) ему соответствуют mk
столбцов функций вида xjk = Pjk(t)e(a^h)\ где Pjk(t) —
многочлены степеней не выше (mk—1), вообще говоря, с
комплексными коэффициентами.
Возьмем любую из этих функций, и пусть в ней многочлен
Pjk(t) имеет некоторую степень 0<Х^т&—1. Представляя
Pjk(t) в виде (13.5), Xjk в виде (13.7) и учитывая равенство
(13.6), видим, что |^jfe|-^oo при f-м», так как а&>0.
Итак, мы доказали, что в фундаментальной системе (12.9)
или (12.12 1, 2, ..., s) модули всех функций Xjk, соответствующих
корням с положительными действительными частями,
неограниченно возрастают при t-+oo и значит сами эти функции не
остаются ограниченными при £-*оо. Поэтому все компоненты
общего решения (12.10) или (12.13) при ненулевых
значениях хотя бы одной из произвольных постоянных С\, С2,..., Сп,
являющихся коэффициентами при неограниченных яд, также
не остаются ограниченными при /->оо. Это и
означает, что все движения класса (13.1) неустойчивы по
Ляпунову. Таким образом, теорема 2 доказана.
Теорема 3. Если характеристическое уравнение системы воз-
мущений (13.2) имеет простые корни с нулевой действи-
140
тельной частью, т. е. простой нулевой корень или простые чисто
мнимые корни, либо простой нулевой корень и простые чисто
мнимые корни, а все остальные его корни (если они имеются)
имеют отрицательные действительные части, то все движения
класса (13.1) неасимптотически устойчивы по Ляпунову.
Доказательство. Прежде всего из доказательства
теоремы 1 видно, что в фундаментальной системе (12.9) или
(12.12 i,2, ..., s) все функции Xjk, соответствующие корням с
отрицательными действительными частями (если такие
имеются), стремятся к нулю при t->oo и поэтому не могут вызвать
неустойчивости движений.
Если имеется простой корень rk = 0t то в фундаментальной
системе (12.9) или (12.12 i, 2 «) ему соответствует столбец
xjk = Bjk<** = Bjk / = lt2 я
действительных постоянных.
Если имеется простой чисто мнимый корень /ъ = 1"Рь, то в
фундаментальной системе (12.9) или (12.121, 2, ..., s) ему
соответствует столбец функций
xjk = Bjkelh< = *м (cos У + i sin У).
Очевидно, модули всех этих функций постоянны:
K*l=l%l -|cosjy + /siny\=,\Bjk\.
Заметим, что согласно сказанному в конце § 12, если все
коэффициенты системы (13.1_) действительны, то наряду с
корнем rk=i$k имеется корень гА=—*'рА; причем, очевидно, гкФгк\
конечно, корню г& соответствует решение, тоже состоящее из
функций с постоянными модулями.
Итак, в таблице (12.9) или (12.121, 2 s ) все функции х^
соответствующие простому нулевому корню и простым чисто
мнимым корням, имеют постоянные модули и, следовательно,
ограничены, но не стремятся к нулю при t-+oo.
Поэтому и все компоненты общего решения (12.10) или (12.13)
системы возмущений (13.2) при всех значениях Си С2,..., Сп
ограничены по модулю при £-*оо. Однако при
ненулевых значениях хотя бы одной из произвольных постоянных,
которые являются коэффициентами при функциях #д, не
стремящихся к нулю при f-м», компоненты общего решения также
не стремятся к нулю при t-+oot Следовательно,
движения класса (13.1) не являются асимптотически
устойчивыми по Ляпунову.
Остается доказать, что все движения класса (13.1)
устойчивы по Ляпунову. Но это делается точно так же, как в конце
доказательства теоремы 1. Таким образом, теорема 3 доказана.
141
Теорема 4. Пусть корни характеристического уравнения
системы возмущений (13.2) удовлетворяют условиям:
1) имеется один или несколько кратных корней с нулевой
действительной частью (т. е. кратный нулевой или кратные
чисто мнимые корни, либо кратный нулевой и кратные чисто
мнимые корни) и пусть для каждого такого корня г& его
кратность mk и ранг nk соответствующего определителя q{rk) вида
(12.7) связаны равенством п—nk=mk;
2) среди остальных корней (если они имеются) могут быть
только простые корни с нулевой действительной частью, а
также простые и кратные корни с отрицательными
действительными частями.
Тогда все движения класса (13.1) неасимптотически
устойчивы по Ляпунову.
Доказательство. В силу теоремы, сформулированной
в § 12, часть фундаментальной системы решений системы
возмущений (13.2), полученная по кратному корню г&, для которого
п—nk = mky т. е. соответствующая таблица (12.12&), целиком
состоит из функций вида Xjk = Bjkerk , где все Bjk постоянны.
В данном случае такими кратными корнями могут быть только
га = 0 и Га = 1'Рл. Следовательно, соответствующие им таблицы
(12.12^) состоят лишь из функций Xjk = Bjheot = Bjk и Xjk =
= Bjkel^k, т. е. из функций с постоянными модулями,
которые были рассмотрены в доказательстве теоремы 3. Второе
условие теоремы 4 вполне аналогично условию теоремы 3.
Поэтому окончание доказательства теоремы 4 совпадает с
доказательством теоремы 3.
Теорема 5. Пусть корни характеристического уравнения
системы возмущений (13.2) удовлетворяют условиям:
1) имеется хотя бы один кратный корень с нулевой
действительной частью (т. е. кратный нулевой или кратные чисто
мнимые корни, либо кратный нулевой и кратные чисто мнимые
корни) и пусть для каждого такого корня rk его кратность тъ
и ранг nk соответствующего определителя q{rk) вида (12.7) под-
чинены неравенству п—пи<ти\
2) среди остальных корней (если они имеются) могут быть
только кратные корни с нулевой действительной частью, для
каждого из которых кратности ши и ранги nk соответствующих
определителей q{rh) связаны равенствами п—пи = т^ а также
простые корни с нулевой действительной частью, простые и
кратные корни с отрицательными действительными частями.
Тогда все движения класса (13.1) неустойчивы по
Ляпунову.
Доказательство. Прежде всего из доказательств
теорем 1, 3, 4 ясно, что все функции х#, которые в
фундаментальной системе (12.12 i, 2 s) соответствуют корням, удовлетво-
142
ряющим второму условию теоремы 5, не могут вызвать
неустойчивости движений.
Рассмотрим часть фундаментальной системы (12.12i, 2 s),
построенную по корням, удовлетворяющим первому условию
теоремы 5.
Если имеется корень rk = 0 кратности тк>1, для которого
п — nk<.mk, то в фундаментальной системе (12.12i,2,....s) ему
соответствует п — nk столбцов, составленных из постоянных xjk =
= Bjke°t = Bjk и mk + nk — n столбцов функций вида xjk =
= Pjk(t)eot = Pjk(t)> т. е. многочленов степеней не выше
(tnk + nk — n)<Cmk—l с действительными коэффициентами. Для
тех многочленов, которые имеют степень выше нуля, известно,
что | xjk | = | Pjk (t) I -> 00 при t -» 00.
Если имеется корень rk — i$k кратности mk > 1, для которого
п — nk<^mk, то в таблице (12.12Ь2, ..,s) ему соответствует п — nk
столбцов функций xjk = Bjkelty с постоянными модулями и mk +
+ tik — п столбцов функций вида x^k = P^k (t)e1^, где Pjk(t)~
многочлены степеней не выше mk-\-nk — п<Стк — 1, вообще говоря,
с комплексными коэффициентами.
Возьмем любую из этих функций, в которой Pjk имеет
некоторую степень Я>0. Представляя этот многочлен в виде (13.5)
и используя (13.6), получаем
Ц*1 = \Р»Ше**\ = \Pjk(t)\ == \Sik(t)\t»-+00
при t -*оо.
Итак, мы доказали, что в фундаментальной системе
(12.12 1, 2, ..., s) все функции х#, соответствующие кратному
нулевому корню и кратным чисто мнимым корням, в которых
многочлены Pjh(t) имеют степени выше нуля, неограничены по
модулю при t-^oo. Поэтому все компоненты общего решения
(12.13) при ненулевых значениях хотя бы одной из
произвольных постоянных С\9 Сг,..., Сп, являющихся коэффициентами
при неограниченных Xja, также не остаются
ограниченными при t-+oo. Это и означает, что все движения класса
(13.1) неустойчивы по Ляпунову. Таким образом,
теорема 5 доказана.
Теорема 6 (следствие из теорем 2, 3, 4, 5). Если все
движения класса (13.1) асимптотически устойчивы по Ляпунову,
то все корни характеристического уравнения системы
возмущений (13.2) имеют отрицательные действительные части.
В самом деле, из теорем 2, 3, 4, 5 видно, что если хотя бы
один корень характеристического уравнения имеет
неотрицательную действительную часть, то движения класса (13.1) не
могут быть асимптотически устойчивыми по Ляпунову. Это и
доказывает теорему 6.
143
Теорема 7 (следствие из теорем 1, 2, 5). Если все движения
класса (13.1) неасимптотически устойчивы по Ляпунову, то:
1) все корни характеристического уравнения системы
возмущений (13.2) имеют неполоэюительные действительные
части;
2) имеется хотя бы один корень с нулевой
действительной частью;
3) среди корней с нулевой действительной частью могут
быть простые и только такие кратные, для которых п—nh = m^
В самом деле, из теорем 2 и 5 видно, что при наличии хотя
бы одного корня с положительной действительной частью или
кратного корня с нулевой действительной частью, для которого
п—nk<mki все движения класса (13Л) неустойчивы по
Ляпунову. С другой стороны, в силу теоремы 1 при отсутствии корней
с неотрицательными действительными частями все движения
класса (13.1) асимптотически устойчивы. Сопоставление этих
фактов и доказывает теорему 7.
Теорема 8 (следствие из теорем 1, 3, 4). Если все движения
класса (13.1) неустойчивы по Ляпунову, то
характеристическое уравнение системы возмущений (13.2) имеет хотя бы один
корень с положительной действительной частью или хотя бы
один кратный корень с нулевой действительной частью, для
которого п—nk<mki либо и то и другое.
В самом деле, из теорем 1, 3, 4 видно, что при отсутствии
корней с положительными действительными частями и кратных
корней с нулевой действительной частью, для которых
п—nk<mki все движения класса (13.1) устойчивы по Ляпунову.
Это и доказывает теорему 8.
Сделаем краткий обзор доказанных теорем.
Теоремы 1, 3 и 4 дают достаточные признаки того, что
все движения класса (13.1) устойчивы по Ляпунову
соответственно асимптотически и неасимптотически..
Теоремы 2 и 5 дают достаточные признаки того, что
все движения класса (13.1) неустойчивы по Ляпунову.
Теоремы 6 и 7 дают необходимые признаки того, что
все движения класса (13.1) устойчивы по Ляпунову
соответственно асимптотически и неасимптотически.
Теоремы 6 и 1 вместе дают необходимый и
достаточный признак того, что все движения класса (13.1)
асимптотически устойчивы по Ляпунову.
Теоремы 7 и 3, 4 вместе дают необходимый и
достаточный признак того, что все движения класса (13.1)
неасимптотически устойчивы по Ляпунову.
Теоремы 8 и 2, 5 вместе дают необходимый и
достаточный признак того, что все движения класса (13.1)
неустойчивы по Ляпунову.
144
-ягпя-льл.»*-чв-. . -«.*■.-.. т ....-,-. ™ ^ "»»А~*^.И«ГГ»Ч»ТО1^Ч«ГНЖ«аММ&=*ТЖ
Srew^AAJfi-"-1*?' -L«ftjf>v
2. Критерии устойчивости и неустойчивости
с учетом условной устойчивости
Напомним, что в определениях устойчивости и
неустойчивости движения по Ляпунову компоненты начальных
возмущений должны быть лишь достаточно малыми, но они независимы
между собой, т. е. никаких других ограничений условий или
связей на них не наложено и, следовательно, между ними не
обязаны выполняться какие-либо соотношения.
Между тем в некоторых физических системах на начальные
возмущения бывают наложены некоторые условия или связи,
которые аналитически выражаются некоторыми соотношениями
между компонентами начальных возмущений. В этих случаях
между произвольными постоянными, входящими в общее
решение системы возмущений, устанавливаются соответствующие
зависимости и тогда все возмущения при f^O описываются не
всем общим решением системы возмущений, а лишь некоторой
его частью. В некоторых случаях при /->оо поведение этой части
общего решения может отличаться от поведения всего общего
решения системы возмущений.
Ввиду этого возникают понятия условной, или
связанной, устойчивости и условной, или связанной,
асимптотической устойчивости движений.
Если без учета связей между начальными возмущениями
движение неустойчиво по Ляпунову, а с учетом этих
связей возмущения при t-+oo ведут себя как при устойчивом
движении, то такое движение при наличии связей
называется условно, или связанно, устойчивым.
Если без учета связей между начальными возмущениями
движение не является асимптотически
устойчивым по Ляпунову, а с учетом этих связей все
возмущения при t-+<x> стремятся к нулю, то такое движение при
наличии связей называется условно, или связанно,
асимптотически устойчивым.
Таким образом, характеристика устойчивости или
неустойчивости движения только по Ляпунову еще не выясняет, может
ли это движение при наличии некоторых связей, наложенных
на начальные возмущения, быть условно устойчивым или
условно асимптотически устойчивым. В связи с этим для дальнейшего
удобно ввести термины «обязательно» и «вообще
говоря».
Движение называется обязательно устойчивым, если
при любых достаточно малых начальных возмущениях все
возмущения при £-^оо ведут себя как при устойчивом
движении.
Движение называется обязательно асимптотически
устойчивым, если при любых достаточно малых начальных возмуще-
145
ниях все возмущения при t-+oo ведут себя как при
асимптотически устойчивом движении, т. е. стремятся к нулю при t-*~oo.
Движение называется обязательно неасимптотически
устойчивым, &слп при любых достаточно малых начальных
возмущениях все возмущения при t-+oo ведут себя как при
неасимптотически устойчивом движении.
Движение называется обязательно неустойчивым, если при
любых даже сколь угодно малых начальных возмущениях,
возмущения при t->oo ведут себя как при неустойчивом
движении.
Движение называется, вообще говоря, неустойчивым, если
при некоторых связях, наложенных на начальные
возмущения, оно становится условно устойчивым ((причем условно
кеасимптотически устойчивым или условно асимптотически
устойчивым).
Движение называется, вообще говоря, неасимптотически
устойчивым, если при некоторых связях, наложенных на
начальные возмущения, оно становится условно асимптотически
устойчивым.
Сопоставление этих определений с определениями
устойчивости и неустойчивости движений по Ляпунову дает следующее.
Для обязательной устойчивости движения необходима и
достаточна его устойчивость по Ляпунову, т. е. понятия
обязательной устойчивости и устойчивости по Ляпунову совпадают.
Для обязательной асимптотической устойчивости движения
необходима и достаточна его асимптотическая устойчивость по
Ляпунову, т. е. понятия обязательной асимптотической
устойчивости и асимптотической устойчивости по Ляпунову
совпадают.
Для неасимптотической устойчивости движения по Ляпунову
необходимо и достаточно, чтобы движение было либо
обязательно неасимптотически устойчиво, либо, вообще говоря,
неасимптотически устойчиво, т. е. обязательная
неасимптотическая устойчивость и, вообще говоря, неасимптотическая
устойчивость являются различными частными случаями
неасимптотической устойчивости по Ляпунову.
Для неустойчивости движения по Ляпунову необходимо и
достаточно, чтобы оно было либо обязательно неустойчивым,
либо, вообще говоря, неустойчивым, т. е. обязательная
неустойчивость и, вообще говоря, неустойчивость являются различными
частными случаями неустойчивости по Ляпунову.
В этом параграфе, а также в § 14, 15 мы рассмотрим все эти
понятия не в самом общем виде, а лишь применительно к
движениям класса (13.1).
Из п. 1 § 13 известно, что значения произвольных
постоянных Си Сг, •••» Сп, входящих в общее решение соответствующей
системы возмущений (13.2), выражаются через начальные воз-
146
мущения (13.8) по формулам (13.10). Возможны случаи, что
при некоторых начальных возмущениях некоторые Cfe0 равны
нулю. Это может произойти лишь при выполнении определенных
соотношений между компонентами начальных возмущений,
причем аналитически эти соотношения получаются при замене
нулями соответствующих Сио в левых частях равенств (13.10).
Теоретически это может привести к тому, что в условиях
теорем 2 или 5, т. е. при неустойчивости по Ляпунову всех
движений класса (13.1), эти движения иногда могут стать условно
неасимптотически или асимптотически устойчивыми, а в
условиях теорем 3 или 4, т. е. при неасимптотической устойчивости
по Ляпунову всех движений класса (13.1), эти движения иногда
могут стать условно асимптотически устойчивыми.
Однако очень важно подчеркнуть, что в реальных
физических системах соотношения между начальными возмущениями,
требуемые для получения условной устойчивости или условной
асимптотической устойчивости, являются аналитическим
выражением реальных связей между начальными возмущениями.
Но в большинстве приложений конструктивное осуществление
этих связей между начальными возмущениями является просто
ненужным, либо нецелесообразным, либо невозможным, а в
некоторых приложениях даже стараются по возможности
избавиться от связей между начальными возмущениями.
Поэтому движения, вообще говоря, неустойчивые, следует
считать практически неустойчивыми, а движения,
вообще говоря, неасимптотически устойчивые,
следует считать на практике неасимптотически
устойчивыми.
В заключение этого параграфа мы сформулируем критерии
устойчивости и неустойчивости движений класса (13.1),
перечисляя все теоретически возможные случаи.
I. Для того чтобы ©се движения класса (13.1) были
асимптотически устойчивы по Ляпунову (т. е. обязательно
асимптотически устойчивы), необходимо и достаточно, чтобы все корни
характеристического уравнения системы возмущений (13.2)
имели отрицательные действительные части.
II. Пусть хотя бы один из корней характеристического
уравнения системы возмущений (13.2) имеет положительную
действительную часть. Тогда:
а) Для того чтобы все движения класса (13.1) были
обязательно неустойчивы, необходимо и достаточно, чтобы все
корни характеристического уравнения имели положительные
действительные части.
б) Если, кроме корней с положительными действительными
частями, имеется хотя бы один корень с нулевой действительной
частью, но нет корней с отрицательными действительными
частями, то все движения класса (13.1), вообще говоря, неустой-
147
чивы, причем они могут быть условно неасимптотически устой*
чивыми, но не могут быть условно асимптотически
устойчивыми.
в) Если, кроме корней с положительными действительными
частями, имеется хотя бы один корень с отрицательной
действительной частью, но нет корней с нулевой действительной
частью, то все движения класса (13.1), вообще говоря,
неустойчивы, причем они могут быть условно асимптотически
устойчивыми, но не могут быть условно неасимптотически
устойчивыми.
г) Если, кроме корней с положительными действительными,
частями, имеется хотя бы один корень с нулевой
действительной частью и хотя бы один корень с отрицательной
действительной частью, то все движения класса (13.1), вообще говоря,
неустойчивы, причем они могут быть как условно
неасимптотически устойчивыми, так и условно асимптотически устойчивыми.
III. Пусть характеристическое уравнение системы
возмущений (13.2) имеет один или несколько простых корней с
нулевой действительной частью (т. е. простой нулевой корень или
простые чисто мнимые корни, либо простой нулевой и простые
чисто мнимые корни), а все остальные корни (если они
имеются) имеют отрицательные действительные части. Тогда:
а) Для того чтобы все движения класса (13.1) были
обязательно неасимптотически устойчивы, необходимо и достаточно,
чтобы все корни характеристического уравнения были
простые и имели нулевую действительную часть.
б) Для того чтобы все движения класса (13.1) были
обязательно устойчивы, но, вообще говоря, неасимптотически (а
значит могли быть условно асимптотически устойчивыми),
необходимо и достаточно, чтобы, кроме простых корней с нулевой
действительной частью, имелся хотя бы один корень с
отрицательной действительной частью.
IV. Пусть характеристическое уравнение системы
возмущений (13.2) имеет один или несколько кратных корней с нулевой
действительной частью, для каждого из которых п—п^ — т^
а среди остальных корней (если они имеются) могут быть
только простые корни с нулевой действительной частью, а также
простые и кратные корни с отрицательными действительными!
частями. Тогда:
а) Для того чтобы все движения класса (13.1) были
обязательно неасимптотически устойчивы, необходимо и достаточно,
чтобы все корни характеристического уравнения имели
нулевую действительную часть.
б) Для того чтобы все движения класса (13.1) были
обязательно устойчивы, но, вообще говоря, неасимптотически (а
значит могли быть условно асимптотически устойчивыми),
необходимо и достаточно, чтобы, кроме указанных корней с нулевой
действительной частью, имелся хотя бы один корень с
отрицательной действительной частью.
V. Пусть характеристическое уравнение системы
возмущений (13.2) имеет один или несколько кратных корней с нулевой
действительной частью, для каждого из которых п—/zfe<mfe,
а среди остальных корней (если они имеются) могут быть
только кратные корни с нулевой действительной частью, для
которых п—nk = mkj а также простые корни с нулевой
действительной частью, простые и кратные корни с отрицательными
действительными частями. Тогда:
а) Для того чтобы все движения класса (13.1) были, вообще
говоря, неустойчивы и могли быть условно неасимптотически
устойчивыми, но не могли быть условно асимптотически
устойчивыми, необходимо и достаточно, чтобы все корни имели ну-
левую действительную часть.
б) Для того чтобы все движения класса (13.1) были,
вообще говоря, неустойчивы и могли быть как условно
неасимптотически устойчивыми, так и условно асимптотически
устойчивыми, необходимо и достаточно, чтобы хотя бы один корень
имел отрицательную действительную часть.
Все перечисленные критерии вытекают из доказанных выше
теорем 1—8 и введенных затем определений. Критерий I
является очевидным объединением теорем 1 и 6, а критерии II—V
представляют собой соответствующие детализации теорем 2—5,
7, 8. Для того чтобы обнаружить условную неасимптотическую
или асимптотическую устойчивость движений в случаях II
(б, в, г), III (б), IV (б), V (а, б), необходимо и достаточно
приравнять нулю соответствующие произвольные постоянные в
общем решении системы возмущений.
§ 14. КРИТЕРИИ УСТОЙЧИВОСТИ И НЕУСТОЙЧИВОСТИ ДВИЖЕНИЙ,
ОПИСЫВАЕМЫХ НОРМАЛЬНОЙ СИСТЕМОЙ ДВУХ ЛИНЕЙНЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ (КРИТЕРИИ ВЫРАЖЕНЫ ЧЕРЕЗ
КОЭФФИЦИЕНТЫ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ
СИСТЕМЫ ВОЗМУЩЕНИЙ)
Пусть класс движений описывается системой уравнений
вида, указанного в заглавии параграфа:
zx = allZl + a12z2 + Д (t)
z2 = a21zx + a22z2 + f2 (t)
Коэффициенты an, ai2, агь 022 действительны и не зависят от
времени, но могут зависеть от некоторых параметров, также не
зависящих от времени; свободные члены f\(t)9 /г(0 —заданные
функции времени, непрерывные при 0^<оо.
(14.1)
149
Согласно § 9, система возмущений, соответствующая
движениям класса (14.1), получается путем отбрасывания свободных
членов системы (14.1):
«#2 = ^21*^1 i #22*^2
(14.2)
Очевидно, системы (14.1), (14.2) представляют собой
частный случай (при п=2) систем (13.1), (13.2) предыдущего
параграфа. Поэтому к ним применимы (с учетом того, что
я=2) соответствующие рассуждения и результаты § 10—13.
Как в § 12, ищем частное решение системы (14.2) в виде
Xl = В^* |
х2 = B2ert J '
Подставляя эти функции в систему (14.2), сокращая на ert и
перенося все члены в одну сторону, получаем систему
уравнений относительно неизвестных Вх и В2:
(а11 — г)В1+а12В2 = 0
я21#1 + («га — г)В2 = 0
(14.3)
Нам нужно найти ненулевое решение этой системы, т. е. пару
чисел Ви В2, из которых по крайней мере одно отлично от
нуля. Для этого определитель из коэффициентов при В\ и В2
должен быть равен нулю:
?(/•)=
(flu —г)
«21
«12
= 0.
Развертывая этот определитель, получаем характеристическое
уравнение системы возмущений (14.2) в виде
г2 — («п + а22) г + (оца,, — апа1ъ) = 0.
В соответствии с § 12 введем обозначения:
А2 — Яц#22 «2i#12
ац а12
#21 «22
Тогда характеристическое уравнение можно переписать так:
г* + Ахг+А2 = 0. (14.4)
Его коэффициенты и корни связаны известными
соотношениями:
150
A = — ('l + Г%)
(14.5)
2 Г 4
Ла — ГхГ2 J
Если Г\фг2, то, подставляя их поочередно в систему (14.3)
и находя ее решения, соответствующие этим корням, мы
получаем фундаментальную систему решений:
*и = ВпеГ** хХ2 = В12ег**
Ч\ = B2i^tf х22 = В22е**
и общее решение системы возмущений (14.2):
хг = dBneri* 4- С2В12ег*<
х2 = СхВг1еГг* + С2В22ег>*
В случае Г\ = г2 рассмотрим определитель:
(an — п) «i2
«21 («22 — fl)
Если определитель д(г\) имеет ранг ni = 0, для чего
необходимо и достаточно выполнение условий
(14.7)
(14.8)
?('!) =
0.
«12 = а21 = 0
то в силу теоремы § 12 можно найти два линейно независимых
частных решения системы (14.2) в виде (14.7) и ее общее
решение в виде (14.8).
Если определитель q(rx) имеет ранг /ii = l, т. е. если хотя бы
один его элемент отличен от нуля, то первый столбец
фундаментальной системы строится так же, как в таблице (14.7), а
второй столбец надо искать в виде произведений е'1* на
линейные двучлены. Таким образом, в этом случае фундаментальная
система имеет вид:
*11 = ВцС'1* *12 = («' + Ь) &**
*2i = B2ierit x22 = ict + d) ег**
(14.9)
Чтобы найти коэффициенты a, b9 c9 d подставим х12 и х22 из
таблицы (14.9) вместо хх и х2 в систему (14.2):
аег** + гг (at + Ь) ег*< = ап (at + Ь) ег**+ al2 (ct + d) erJ |
сег>* + r± (ct + d) ert* = a2l (at + b) er^ + a22 (ct + d) erJ J "
151
(14.10)
Сокращаем на ег** и переносим все члены в одну сторону:
(ап — rt) (at + b) + an (ct + d) — a=-0
а21 (at + b) + (aZ2 — гг) (ct + d)—c = 0
Коэффициенты a, b, c, d надо подобрать так, чтобы многочлены
первой степени относительно t в левых частях этих уравнений
обращались в нуль тождественно по t. Для этого необходимо и
достаточно, чтобы в этих многочленах коэффициенты при
каждой степени t были равны нулю. Собирая в этих уравнениях
коэффициенты при /, а также члены, не содержащие t, и
приравнивая их нулю, мы получаем четыре уравнения относительно
неизвестных а, 6, с, d, причем не все уравнения являются
существенно различными. Хотя бы одно из чисел а и с должно
быть отлично от нуля; одно из чисел b и d можно выбрать
произвольно.
После того как коэффициенты а, &, с, d найдены, умножая
первый столбец таблицы (14.9) на С\, второй столбец на С2 и
складывая по строкам, получаем общее решение системы
возмущений (14.2) в случае Г\ = г2 и rt\ = l:
хг = СгВц?** + С2 (at + Ь) erJ
x2 = C1B21erJ + C2(ct + d)er>*
Теперь, используя критерии I—V § 13, получим критерии
устойчивости и неустойчивости движений класса (14.1),
выраженные через коэффициенты Аи А2 характеристического
уравнения (14.4) системы возмущений (14.2).
Как мы сейчас увидим, устойчивость или неустойчивость
движений класса (14.1) по существу зависит от з н а ков
коэффициентов Ль А2 и от обращения или необращения их в нуль, но
не зависит от их абсолютных величин, причем главную роль в
этом играет коэффициент А2. При этом придется рассмотреть
одиннадцать комбинаций знаков и абсолютных величин А\ и A2i
которые будут группироваться в восемь теорем.
А. Для того чтобы все движения класса (14.1) были
асимптотически устойчивы по Ляпунову, т. е. обязательно
асимптотически устойчивы, необходимо и достаточно выполнение условий
*>°Ч. (14.11)
Аг>0 I
Доказательство достаточности. Докажем, что
если выполнены условия (14.11), то все движения класса (14.1)
асимптотически устойчивы по Ляпунову.
При выполнении условий (14.11) рассмотрим три случая:
А2 л / Л*
1) -i.-^X), тогда f>+y -j—-
152
««ft. **.-ft. ■. _.. „,_^„, -^.^«_™.-„ .„.„„__ ^Т^ПЛ>й*«яяЙЯ(„жв
■f wk.«^v-«k-»^j4„ «re-n „
и формула (14.5) дает
причем ri>r2.
А\
2) Л2 = 0, тогда формула (14.5) дает
А\
3) Л<0, тогда формула (14.5) дает комплексные корни
с отрицательной действительной частью:
ri,2 = _A±ty4—f •
Итак, во всех трех случаях все корни характеристического
уравнения (14.4) имеют отрицательные действительные части.
Следовательно, в силу теоремы 1 § 13 (которая является
частью критерия I) все движения класса (14.1) асимптотически
устойчивы по Ляпунову.
Доказательство необходимости. Докажем, что
если все движения класса (14.1) асимптотически устойчивы по
Ляпунову, то выполняются условия (14.11).
В силу теоремы 6 § 13 (которая является также частью
критерия I) все корни характеристического уравнения (14.4) имеют
отрицательные действительные части. Если Г\ и г2
действительные отрицательные, то из формул (14.6) с очевидностью
вытекает выполнение условий (14.11). Если гх и г2 комплексные, то
они должны быть сопряженными, так как коэффициенты
системы (14.1), а значит и коэффициенты А\ и А2 действительные.
Итак, пусть
/i = ai + tPi. /i = Oi —Фь
причем <xi<0, Pi=t^O, тогда формулы (14.6) дают
Л = -2о1>0, Ла = а2+р2>0.
Таким образом, теорема доказана.
Б. Для того чтобы все движения класса (14.1) были
обязательно неустойчивы, необходимо и. достаточно выполнение уело- \
вий |
(14.12) |
153 i
г---Щ(„ьааш11. штчнтштнит\ «и1 и»' и >№^в^««1^^пгт1^а&лу¥аяеш^т<^ш1^мешшм^^«^ж^^ i
Л<0
Доказательство достаточности. Докажем, что
если выполнены условия (14.12), то все движения класса (14.1)
обязательно неустойчивы.
При выполнении условий (14.12) рассмотрим три случая:
(14.5) дает
-Л2>0, тогда 1£]_
Сп ' при
r2>0j
л/ 4
> + 1/ —- — Ла и формула
чем гх > га.
А2
2) —!—Л^О» тогда формула (14,5) дает
ri = r2 = -A>0.
4 л
3) Л2<0, тогда формула (14.5) дает комплексные
корни с положительной действительной частью.
Итак, во всех трех случаях все корни характеристического
уравнения (14.4) имеют положительные действительные части.
Следовательно, в силу критерия II,а § 13, все движения класса
(14.1) обязательно неустойчивы.
Доказательство необходимости. Докажем, что
если все движения класса (14.1) обязательно неустойчивы, то
выполняются условия (14.12).
В силу того же критерия II,а все корни характеристического
уравнения (14.4) имеют положительные действительные части.
Далее доказательство заканчивается совершенно аналогично
доказательству теоремы А.
В. Если выполнены условия
Л>о 1
Л-оЬ (14ЛЗ)
то все движения класса (14.1) обязательно неасимптотически
устойчивы.
Доказательство. При выполнении условий (14.13)
формула (14.5) принимает вид:
Ггл= ±VZIAt= ±*УЪ>
т. е. корни получаются простые чисто мнимые. Поэтому в силу
критерия III,a § 13 все движения класса (14.1) обязательно
неасимптотически устойчивы.
154
Г. Для того чтобы все движения класса (14.1) были
обязательно устойчивы, но, вообще говоря, неасимптотически и
значит могли быть условно асимптотически устойчивыми
необходимо и достаточно выполнение условий
Л>о°)- <Ш4>
Доказательство достаточности. Докажем, что
если выполнены условия (14.14), то все движения класса (14.1)
обязательно устойчивы, но, вообще говоря, неасимптотически.
При выполнении условий (14.14) характеристическое
уравнение (14.4) принимает вид г2+А\г=0 и, следовательно, имеет
корни ri = 0, r2=—А\<0. Поэтому в силу критерия III,б все
движения класса (14.1) обязательно устойчивы, но, вообще говоря,
неасимптотически.
Условная асимптотическая устойчивость получается из
общего решения (14.8) при Ci = 0. Соотношение между
начальными возмущениями х\о, #2э, которое необходимо и достаточно для
этого, получается в результате подстановки в равенства (14.8)
Ci=0, £=0, X\=X\0t Х2=Хы и затем исключения С2 из
полученных равенств:
•^10 = ^2^12
*20 == ^2^22
ОТКуда 522*10 = В12X20.
Доказательство необходимости. Докажем, что
если все движения класса (14.1) обязательно устойчивы, но,
вообще говоря, неасимптотически, то выполняются условия (14.14).
В силу критерия III,б один из корней характеристического
уравнения должен иметь нулевую действительную часть, а
другой отрицательную действительную часть (так как квадратное
уравнение имеет всего два корня). Поэтому эти корни не могут
быть комплексно-сопряженными и, следовательно,
действительны: о = 0, г2<0. Но тогда формулы (14.6) дают ^i>0, Л2=0.
Таким образом, теорема доказана.
Д. Если выполнены условия
А2 = 0 \
Л<0 Г
(14.15)
то все движения класса (14.1), вообще говоря, неустойчивы,
причем они могут быть условно неасимптотически устойчивыми,
но не могут быть условно асимптотически устойчивыми.
Доказательство. При выполнении условий (14.15)
характеристическое уравнение (14.4) принимает вид г2+А\Г=0 и,
следовательно, имеет корни п = 0, r2 =—^i>0. Поэтому, в силу
155
критерия И,б § 13 все движения класса (14.1), вообще говоря,
неустойчивы, причем они могут быть условно неасимптотически
устойчивыми, но не могут быть условно асимптотически
устойчивыми.
Условная неасимптотическая устойчивость получается из
общего решения (14.8) при С2 = 0. Соотношение между
начальными возмущениями Хю, х2о> которое необходимо и достаточно для
этого, получается в результате подстановки в равенства (14.8)
С2 = 0, £ = 0, xi = *iof #2=*2o и затем исключения С\ из
полученных равенств:
х1о = CiBn
Х20 = ^1^21
ОТКуДа 521^10 = ^11-^20.
Е. Если выполнены условия
Л-о
(14.16)
т. е. если характеристическое уравнение (14.4) имеет кратный
нулевой корень ri = r2 = 0, то возможны два случая:
Ei) Для того чтобы при выполнении условий (14.16) все
движения класса (14J) были обязательно неасимптотически
устойчивыми, необходимо и достаточно, чтобы все коэффициенты Яп,
#12, я21, а22 системы (14.2) были равны нулю.
Е2) Для того чтобы при выполнении условий (14.16) все
движения класса (14.1) были, вообще говоря, неустойчивы и
могли быть условно неасимптотически устойчивыми, но не могли
быть условно асимптотически устойчивыми, необходимо и
достаточно, чтобы хотя бы один из коэффициентов ап, а\2, #2i, #22
системы (14.2) был отличен от нуля.
Доказательство теоремы Ei. Равенство нулю всех
коэффициентов системы (14.2) равносильно тому, что
определитель
q(ri)^g(0)
#11 #12
#21 #22
0
имеет ранг fi\=0. Тогда справедливость теоремы Ei вытекает из
критерия IV,a § 13. Впрочем, достаточность почти очевидна, так
как в этом случае система (14.2) принимает вид:
хх=^0
х2 = 0
156
.... FWWWETJ^iSa „Г Z.C HP T ~Нл***г ЧЬгТЖ.
.'<*.-> '-Л. £„ ШСЗЯ- -ЯГ?.**», jfr^b
owmwka— ююткнэк&гзакф- ^у-жя&ъ-ъ
и имеет общее решение
xi — С1
Д£2 = (^g
Доказательство теоремы Е2. Отличие от нуля
хотя бы одного из коэффициентов системы (14.2) равносильно
тому, что определитель
Я(г1)=д(0) =
аХ1 а12
#21 #22
-О
имеет ранг щ = 1. Для того чтобы в случае (14.16) все
движения класса (14.1) были, вообще говоря, неустойчивы и
могли быть условно неасимптотически устойчивыми,
необходимо и достаточно, чтобы общее решение системы возмущений
(14.2) имело вид (14.10), в котором хотя бы одно из чисел а ис
отлично от нуля. Но для этого необходимо и достаточно
условие п\ = 1. Достаточность следует из теоремы § 12, а
необходимость видна из теоремы Е\. Конечно, теорема Е2 вытекает и из
критерия V,a § 13.
Условная неасимптотическая устойчивость получается из
общего решения (14.10) при С2=0. Соотношение между
начальными возмущениями хю, #2о, необходимое и достаточное для
этого, получается в результате подстановки в равенства (14.10)
С2 = 0, £ = 0, #1=#ю, Х2 = х2о и затем исключения С\ из
полученных равенств:
х10 = СхВц
откуда В21х10 = Впх20.
Обратим внимание на то, что в теоремах Д и Е2 условия
различные, а утверждение одно и то же. Однако причины
неустойчивости в этих теоремах различны: в теореме Д
неустойчивость вызвана положительным корнем, а в теореме Е2—
кратным нулевым корнем. В более широком смысле это относится
также к теоремам 2 и 5 и_критериям II, V, § 13.
Ж. Если А2<0У то при любом значении коэффициента А\ все
движения класса (14.1), вообще говоря, неустойчивы, причем
они могут быть условно асимптотически устойчивыми, но не
могут быть условно неасимптотически устойчивыми.
Доказательство. При Л2<0 и при любом значении А ь
очевидно, справедливо неравенство
1А!;< + 1/ А
V4
157
Следовательно, формула (14.5) в этом случае дает ri>0, r2<0,
т. е. действительные корни различных знаков. Поэтому в силу
критерия II,в все движения класса (14.1), вообще говоря,
неустойчивы, причем они могут быть условно асимптотически
устойчивыми, но не могут быть условно неасимптотически
устойчивыми.
Условная асимптотическая устойчивость получается из
общего решения (14.8) при С\ = 0. Соотношение между
начальными возмущениями #ю, #20, необходимое и достаточное для этого,
получается в результате подстановки в равенства (14.8) Cj=0,
£=0, x\ = X\q, #2=Я2о и затем исключения Сг из полученных
равенств:
ХЮ == ^2^12 \
откуда В22х10 = В12х20.
Сопоставляя доказанные теоремы А—Ж, мы видим, что при
А2>0 (теоремы А, Б, В) все движения класса (14.1)
обязательно устойчивы или обязательно неустойчивы.
При Л2=0 в случаях Г и Ei все движения класса (14.1)
также обязательно устойчивы.
Во всех остальных случаях при Л2<0 (теоремы Д, Е2, Ж)
все движения класса (14.1), вообще говоря, неустойчивы,
т. е. практически неустойчивы.
§ 15. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ С ПОМОЩЬЮ КРИТЕРИЕВ,
ПОЛУЧЕННЫХ В § 14
Рассмотрим примеры с одинаковой постановкой задач, в
которых встретятся различные случаи корней
характеристического уравнения системы возмущений.
Постановка задачи
Пусть класс движений описывается системой уравнений
вида:
2i = an(a, P)2! + a12(a, P)za + A(0 )
z2 = a21 (a, p) zx + a22 (a, (5) z2 + f2 (t) J '
причем аир — параметры, не зависящие от времени.
а) При всех значениях аир выяснить характер движений
заданного класса, т. е. их устойчивость (обязательную,
условную, асимптотическую, неасимптотическую) или неустойчивость
(обязательную и вообще говоря).
158
б) Выяснить, при каких значениях аир возмущения имеют
колебательный характер.
в) При заданных фиксированных значениях аир выяснить
характер движений данного класса; если при этом возможна
условная устойчивость, то найти соотношение между
начальными возмущениями, при котором она получается. При заданных
начальных возмущениях х\о, х2о найти возмущения как функции
времени.
Решая примеры на эту постановку задачи, мы будем
пользоваться рассуждениями и результатами § 14.
Пример 1.
z1 = az1 + ^ + fl(t) \ 1бл
2« = -3z1-2z1 + /i(0 Г
а = 3; р = —8;
xi0 = — 0,1; #20 = ^»1 •
Решение. Пишем систему возмущений для движений
класса (15.1):
х1 = ах1 + $х2 1 (15 2)
Х2 == ОХ\ ^>Х2 )
Ищем частное решение системы (15.2) в виде:
Xl = Вхен
х2 — &Ф
Подставляя эти функции в систему (15.2), сокращая на ert и
перенося все члены в одну сторону, получаем
(а-г)Вг + ^Вж = 0 |
— 3B1 + (-2-r)B1 = 0 J
Чтобы найти ненулевое решение этой системы, приравняем
нулю определитель из коэффициентов при В\9 В2:
(о-г) р
-3 (-2-г)
0.
Развертывая этот определитель, получаем характеристическое
уравнение системы возмущений (15.2):
г2+(2 — а)г + (3р — 2а) =0. (15.4)
159
Вводя обозначения
перепишем уравнение (15.4) так:
r2 + A1r + A2 = 0t его корни п,2 = — — ± 1/ —L—Л2.
2 ' 4
Подставим сюда выражения (15.5):
г,>2 = ^±/-^-+(2а-ЗР),
или
Ги2 = (а-2)±/(а + 2р-12р _ (15 6)
Теперь мы будем решать каждую часть задачи а, б, в.
а) Будем рассматривать параметры аир как координаты
точек плоскости, которую назовем плоскостью параметров.
Нельзя смешивать плоскость параметров а, р с фазовой
плоскостью х\, х2у на которой изображаются решения системы
возмущений.
Коэффициенты Ах и А2 характеристического уравнения,
выраженные формулами (15.5), являются функциями переменных
а, р, которые определены и непрерывны на всей плоскости xt, p.
В § 14 мы видели, что характер движений класса (15.1)
зависит от знаков Аи А2 и от обращения или необращения их в
нуль, причем главную роль в этом играет коэффициент А2.
Поэтому начнем с исследования коэффициента А2.
Найдем геометрическое место точек плоскости а, р, на
котором Л2 = 0, так как это даст нам возможность найти области
положительных и отрицательных значений А2. Так как Л2 = 3р—
—2а, то равенство Л2 = 0 выражается уравнением Зр—2а = 0,
т. е. р= — а, которое представляет собой прямую КО PL на
о —
плоскости а, р (рис. 20).
Отметим, что поскольку функция Л2 = 3р—2а непрерывна
на всей плоскости а, Р, то она может изменить знак только при
переходе точки (а, р) через прямую KLy и, следовательно, А2
сохраняет знак в каждой полуплоскости, расположенной по
одну сторону от прямой KL.
Условие А2<0 выражается неравенством Зр—-2а<0, т. е.
2
Р < — а. Точки, координаты которых удовлетворяют этому
о
160
условию, заполняют полуплоскость под наклонной прямой KL.
Это легко проверить, подставляя координаты какой-нибудь
точки этой полуплоскости, например <х=1, Р = 0, в выражение
Л2 = 3р—2а, что дает Л2 =—2. При всех парах значений а, р,
при которых Л2<0, в силу критерия Ж § 14 все движения
класса (15.1), вообще говоря, неустойчивы и могут быть условно
асимптотически устойчивыми; на рис. 20 полуплоскость под
прямой KLy соответствующая этим значениям а, р, отмечена
прерывистой горизонтальной штриховкой. Напомним, что при
Л2<0 значение коэффициента А\ не влияет на характер
движений класса (15.1).
Условие Л2>0 выражается неравенством Зр—2а>0, т. е.
2
Р> — а. Точки, координаты которых удовлетворяют этому уело-
о
вию, заполняют полуплоскость над наклонной прямой KL. Это
легко проверить, подставляя координаты какой-нибудь точки
этой полуплоскости, например а=0, р=1, в выражение Л2, что
дает Л2 = 3.
Из критериев А, Б, В § 14 видно, что при Л2>0 характер
движений класса (15.1) существенно зависит от знака или
обращения в нуль коэффициента А\. Поэтому теперь мы найдем
геометрическое место точек, на котором Л1 = 0, а затем области,
в которых A\>Q и Ai<0. Так как Л1=2—а, то равенство Ai = Q
выражается уравнением 2—а=0, т. е. а=2, которое
представляет собой прямую MPN. На рис. 20 полупрямая РМ (без
точки Р), расположенная в области, где Л2<0, начерчена
пунктиром, поскольку она не нужна для решения задачи, так как при
Л2<0 характер движений класса (15.1) не зависит от
значений Ль
Условие А\<0 равносильно неравенству 2—а<0, т. е. а>2,
которое, очевидно, выражает собой полуплоскость справа от
прямой MN.
Условие Л1>0 равносильно неравенству 2—а>0, т. е. а<2,
которое выражает собой полуплоскость слева от пря!Мой MN.
6 А. Г. Младов
161
Теперь нам известны все области положительных и
отрицательных значений Л2 и А\.
При всех парах значений аир, соответствующих
внутренности тупого угла KPN (содержащего всю вторую четверть
плоскости а, р), выполнены условия Лг>0 и A\>Qy которые в
силу критерия А § 14 обеспечивают обязательную
асимптотическую устойчивость всех движений класса (15.1). На рис. 20
область внутри угла KPNy соответствующая обязательной
асимптотической устойчивости движений, отмечена сплошной
вертикальной штриховкой.
При всех значениях а, р, соответствующих внутренности
острого угла LPN, выполнены условия Лг>0 и ^i<0, которые
в силу критерия Б § 14 обеспечивают обязательную
неустойчивость всех движений класса (15.1). На рис. 20 область внутри
угла LPN, соответствующая обязательной неустойчивости
движений, отмечена сплошной горизонтальной штриховкой.
Остается выяснить характер движений при тех значениях
а, р, которые соответствуют полупрямым PN, PK, PL. Ha
полупрямой PN (без точки Р) выполнены условия Лг>0 и Ai = 0,
которые в силу критерия В § 14 обеспечивают обязательную
неасимптотическую устойчивость всех движений класса (15.1).
На полупрямой РК (без точки Р) выполнены условия Л2=0 и
-4i>0, при которых в силу критерия Г § 14 все движения
класса (15.1) обязательно устойчивы, но, вообще говоря,
неасимптотически и значит могут быть условно асимптотически
устойчивыми. На полупрямой PL (без точки Р) выполнены условия
А2=0 и Ai<0, при которых в силу критерия Д § 14 все
движения класса (15.1), вообще говоря, неустойчивы и могут быть
условно неасимптотически устойчивыми.
Наконец, в точке Р (2; ) выполнены условия Л2 = 0 и
о
Ах = 0, при которых в силу критерия Е2 § 14 все движения
класса (15.1), вообще говоря, неустойчивы и могут быть условно
неасимптотически устойчивыми.
б) Согласно сказанному в конце § 12, для того чтобы
решения системы возмущений (15.2) имели колебательный характер,
необходимо и достаточно, чтобы характеристическое уравнение
(15.4) имело комплексные корни. Для этого необходимо и
достаточно, чтобы подкоренное выражение в формуле (15.6),
которое мы обозначим через F, было отрицательным.
Очевидно, F=(a+2)2—12р есть функция, непрерывная на
всей плоскости а, р. Геометрическое место точек, на котором
f=0, имеет уравнение (а+2)2—12р = 0, т. е. р=-~-(а+2)2,
которое представляет собой параболу QRPS (см. рис. 20) с
вершиной в точке R(—2; 0) и с вертикальной осью симметрии.
Легко проверить, что прямая KL является касательной к этой
162
параболе в точке Р. Из формулы (15.6) ясно, что при F=0, т. е. [
на параболе QRS и только на ней, характеристическое уравне- j
а —2 I
ние имеет кратные корни ri,2 = . |
Функция F сохраняет знак в каждой области, лежащей по J
одну сторону от параболы QRS, и может изменить знак только !
при переходе через эту параболу. Условие F<0 равносильно !
1 ?
неравенству (а + 2)2—12р<0, т. е. Р> — (а+2)2, которое вы- j
полняется в области, расположенной над параболой QRS (эта j
область, содержащая фокус параболы, называется внутренно- i
стью параболы). Выполнение условия F<0 во внутренности па- |
раболы QRS проверяется подстановкой координат какой-нибудь j
точки этой области, например а = —2, р=1, в выражение F, что |
дает F=—12. В области под параболой QRS (эта область, со- i
держащая директрису параболы, называется внешностью пара- !
болы) F>0. Это проверяется подстановкой координат какой- j
нибудь точки этой области, например а = —2, р =—1, в выраже- »
ние F, что дает F=12. |
Итак, при всех значениях а, Р, которые соответствуют внут- \
ренности параболы QRS, решения системы возмущений (15.2) I
имеют колебательный характер. Заметим, что область
колебательных возмущений, т. е. внутренность параболы QRS, содер- j
жит часть области обязательной асимптотической устойчивости ;
(область внутри контура QRPN), полупрямую PN, соответст- j
вующую обязательной неасимптотической устойчивости, и часть
области обязательной неустойчивости (область внутри контура I
NPS) движений класса (15.1). J
в) При заданных значениях а = 3, р = —8 найдем корни ха- j
рактеристического уравнения (15.4) и общее решение системы '
возмущений (15.2). Для этого подставим а = 3, Р = —8 в систе- •
мы (15.2), (15.3) и в уравнение (15.4): \
Х% === д%1 ^%2
(3 — r)'Bi — 8B2 = 0
-ЗВ1 + (-2-г)В1-0
г» —г —30 = 0.
Корни последнего уравнения rj = 6, Гг = —5.
Найдем ненулевые решения системы (15.8), соответствую- .
щие этим корням. Подставим в систему (15.8) rj = 6 и неизвест- |
ным В\, В2 припишем второй индекс 1: '
— 35и — 8521 = 0 |
— ЗВц — 8В21 = 0 j ' ;
6* 163 |
(15.7)
(15.8)
Получилась система из двух одинаковых уравнений, так что по
существу это одно уравнение с двумя неизвестными 5ц, В2и
Поэтому одному из неизвестных можно дать любое ненулевое
значение и в зависимости от этого найти второе неизвестное.
Например, возьмем Вц = 8, тогда В2\ = — 3. Подставим в
систему (15.8) г2 = —5 и припишем неизвестным В\, В2 второй
индекс 2:
8В12 — 8В22 — О
— 35i2 + 3J322 = 0
Получилась система уравнений с пропорциональными
коэффициентами. Сокращая первое уравнение на 8, а второе на —3,
получаем одно и то же уравнение В\2—^22 = 0, или B\2=B22.
Любое отличное от нуля число можно взять в качестве общего
значения ВХ2, В22. Проще всего взять Bi2 = 522=l.
Составляем фундаментальную систему решений системы
возмущений (15.7):
(15.9)
Очевидно, каждый столбец этой таблицы образует частное
решение системы (15.7). Умножая первый столбец таблицы
(15.9) на Си второй — на С2 и складывая по строкам, получаем
общее решение системы (15.7):
х2 = — ЗС^' + С*-5'J
Теперь ответим на вопросы пункта «в» нашей задачи.
На плоскости а, р точка а = 3, р =—8 находится под прямой
KL, т. е. в области, где А2<0. Поэтому в силу критерия Ж§ 14
при <х=3, р=—8 все движения класса (15.1), вообще говоря,
неустойчивы, но могут быть условно асимптотически
устойчивыми. Конечно, это согласуется и с критерием II,в § 13, так как
при <х=3, р = —8 характеристическое уравнение имеет корни
г1==6>0, г2=—5<0. Впрочем, это видно и непосредственно по
поведению функций таблицы (15.9). В самом деле, при t-^co
г1 = 6
хп = 8е«
хп = — ЗеР*
г2 = — 5
*i2 = е~ы |
хг% = е~^ \
41'
>°°> |*2i|-*°°> *i2-*0, *22-*0.
Поэтому условная асимптотическая устойчивость получается из
общего решения (15.10) при Ci = 0. Соотношение между
начальными возмущениями, необходимое и достаточное для этого,
получается в результате подстановки в равенство (15.10) Ci = 0,
164
£ = 0, x\ = Xy:, x2==x2i и затем исключения С2 из полученных
равенств:
•^10 == ^2
•^20 == ^2
откуда *10 = л:20.
Наконец, при заданных начальных возмущениях х\о = —0,1,
Х2о = —0,1 (которые как раз удовлетворяют только что
полученному соотношению) найдем возмущения как функции времени.
Очевидно, при этом Ci = 0, C2 = —0,1. Это же можно получить,
подставляя £ = 0 и заданные начальные возмущения в общее
решение (15.10).
Итак, при начальных возмущениях *ю = —0,1, лг2о = —0,1
получаем частное решение системы возмущений (15.7):
*i = — 0,1е~5'
*я = —0,le~w
Пример 2.
z1=az1 — г2 + Л(0 | (15.11)
а = 2; р«2;
1_ . _ J_
•^10 Р > -^20 — л •
О 3
Решение. Пишем систему возмущений для движений
класса (15.11):
х1=ах1 — хг , (15.12)
ЛГ2 = Л^ -р рАГ2
Ищем частное решение системы (15.12) в виде
хг = Bxert
Х% — &%&
После подстановки этих функций в систему (15.12) и
упрощений получаем
Чтобы найти ненулевое решение этой системы, приравняем
нулю определитель из коэффициентов при Ви В2:
(а-г) -1
1 (Р-г)
= 0.
165
Развертывая этот определитель, получаем характеристическое
уравнение системы возмущений (15.12):
[г3 — (а 4- р) г -Ь (ар + I)
Вводя обозначения
Л = -(« + Р) |
Л2 = ар+1 Г
перепишем уравнение (15.14) так:
= 0.
(15.14)
(15.15)
л, л/ А\
г2 + Агг+А2 = 0, его корни rh2 = L ± I/ — Ла.
2 ' 4
Подставим сюда выражения (15.15):
л±!_ ± |//Ji±i)i_ap_1>
/"1,2 =
или
ru==(a+P)±T/>-P)*-4 ^ (1516)
а) Будем рассматривать параметры аир как координаты
точек плоскости. Коэффициенты А\ и Л2 характеристического
уравнения, выраженные формулами (15.15), являются
функциями, которые определены и непрерывны на всей плоскости а, р.
Найдем геометрическое место точек плоскости а, р, на
котором Л2=0, так как это даст нам возможность найти области,
в которых А2>0 и Л2<0. Поскольку Л2 = аР + 1, то равенство
Л2 = 0 выражается уравнением <хр+1=0, т. е. р = . Это
a
уравнение представляет собой гиперболу, расположенную во
второй и четвертой четвертях плоскости а, р, асимптотами
которой служат оси аир (рис. 21).
Эта гипербола разбивает всю плоскость a, p на три области:
внутренность гиперболы, т. е. две области, которые
расположены со стороны вогнутости гиперболы и содержат ее фокусы, и
внешность гиперболы, т. е. область, которая расположена
между ветвями гиперболы и содержит ее асимптоты. В каждой из
этих трех областей функция Л2 = аР+1 сохраняет знак, так как
ввиду ее непрерывности на всей плоскости a, P она может
изменить знак только при переходе через гиперболу.
Условие Л2<0 выражается неравенством ap+КО. Точки,
координаты которых удовлетворяют этому условию, заполняют
внутренность гиперболы. Для области, лежащей внутри ветви
KPL, это проверяется подстановкой, например, а = —2, р = 2 в
166
ЫгзГ*«-:Л£ХаЯг*ЪГ r&-~i£..zr7*ij;. -'-''/**,. I, *л ЛЛК "»i~~T-i^« 'V- r> -» SBFlT J »*^ 15^=1 4»i b-.^-.vy , -wvjje ■» iH>ft7i«7 S JaRT^ -^йЗЖ^ч-ввЮСНВ
выражение Л2, что дает А2 =—3. Для области, лежащей внутри
ветви MQN это проверяется подстановкой, например, а=2,
р =—2 в выражение Л2, что дает Л2 =—3.
При всех значениях а, р, при которых Л2<0, в силу
критерия Ж § 14 все движения класса (15.11), вообще говоря,
неустойчивы и могут быть условно асимптотически устойчивыми;
на рис. 21 внутренность гиперболы, соответствующая этим
значениям а, р, отмечена прерывистой горизонтальной штриховкой.
Условие Л2>0 выражается неравенством сф+1>0. Точки,
координаты которых удовлетворяют этому условию, заполняют
внешность гиперболы. Это проверяется подстановкой, например,
<х=0, р = 0 в выражение Л2, что дает Л2=1. При Л2>0 надо
учитывать знак или обращение в нуль коэффициента А\.
Найдем геометрическое место точек, на котором -4i = 0, а
затем области, в которых ^i>0 и Ai<0. Так как А\ ——(а+Р), то
равенство ^i = 0 выражается уравнением а+р=0, т. е. Р =—а,
которое представляет собой биссектрису второй и четвертой
четвертей плоскости а, р. На рис. 21 полупрямая PR (без
точки Р) и полупрямая QS (без точки Q), расположенные в
областях, где Л2<0, начерчены пунктиром, поскольку они не нужны
для решения задачи, так как при Л2<0 характер движений
класса (15.11) не зависит от значений А\.
Условие i4i<0 равносильно неравенству а+р>0, т. е.
Р>—а, которое выражает собой полуплоскость над прямой RS.
Это проверяется подстановкой, например, а=0, р=1 в
выражение А\9 что дает А\=—1.
Условие Л1>0 равносильно неравенству а+р<0, т. е.
Р<—а, которое выражает собой полуплоскость под прямой RS.
Это проверяется подстановкой, например а=0, р =—1, в выра-
167
■»v."-v JE. ч -гЛ^-Гч
-.Л-ЖМ*.^**!* *<■>&:
жение Ль что дает А\=1. Теперь нам известны все области
положительных и отрицательных значений А2 и Ах.
При всех значениях а, р, соответствующих области,
ограниченной контуром KPQM и содержащей третью четверть
плоскости а, р, выполнены условия А2>0У Ai>0, которые в силу
критерия А § 14 обеспечивают обязательную асимптотическую
устойчивость всех движений класса (15.11). На рис. 21 эта
область отмечена сплошной вертикальной штриховкой.
При всех значениях а, р, соответствующих области,
ограниченной контуром LPQN и содержащей первую четверть
плоскости а, р, выполнены условия А2>0 и ^i<0, которые в силу
критерия Б § 14 обеспечивают обязательную неустойчивость всех
движений класса (15.11). На рис. 21 эта область отмечена
сплошной горизонтальной штриховкой.
Остается выяснить характер движений при тех значениях
а, р, которые соответствуют точкам гиперболы и отрезка PQ.
На интервале PQ (без точек Р и Q) выполнены условия А2>0
и Ai = Ot которые в силу критерия В § 14 обеспечивают
обязательную неасимптотическую устойчивость всех движений
класса (15.11). На полуветвях РК и QM (без точек Р и Q)
выполнены условия А2=0 и ^i>0, при которых в силу критерия Г
§ 14 все движения класса (15.11) обязательно устойчивы, но,
вообще говоря, неасимптотичеаки и значит могут быть условно
асимптотически устойчивыми. На полуветвях PL и QN (без
точек Р и Q) выполнены условия Л2 = 0 и А\<0, при которых в
силу критерия Д § 14 все движения класса (15.11), вообще
говоря, неустойчивы и могут быть условно неасимптотически
устойчивыми. Наконец, в точках Р(—1,1) и Q(l,—1) выполнены
условия Л2 = 0 и Л i = 0, при которых в силу критерия Е2 § 14 все
движения класса (15.11), вообще говоря, неустойчивы и могут
быть условно неасимптотически устойчивыми.
б) Чтобы решения системы возмущений (15.12) имели
колебательный характер, т. е. чтобы корни характеристического
уравнения (15.14) были комплексными, необходимо и
достаточно, чтобы подкоренное выражение в формуле (15.16), которое
мы обозначим через F, было отрицательным.
Очевидно, F= (a—p)2—4 есть функция, непрерывная на всей
плоскости а, р. Геометрическое место точек, на котором F=0,
имеет уравнение (Р—а)2—4 = 0, распадающееся на два
уравнения р—а=±2, т. е. р = а±2, которые представляют собой пару
параллельных прямых TPU и VQW (см. рис. 21). Из формулы
(15.16) ясно, что при F = Q, т. е. на прямых TPU и VQW и
только на них, характеристическое уравнение имеет кратные корни
г12= Е-. Прямые TU и VW разбивают плоскость а, р на три
области, в каждой из которых функция F сохраняет знак и
может изменить его только при переходе через эти прямые.
168
Условие F<0 равносильно неравенству (а—13)2—4<0,
которое выполняется в полосе между прямыми TU и VW. Это
проверяется подстановкой, например, а = 0, р = 0 в выражение F,
что дает F = —4.
Условие /7>0 выполняется в полуплоскостях над прямой TU
и под прямой VW. Для полуплоскости над прямой TU это
проверяется подстановкой, например, а = —2, р = 2 в выражение F,
что даег F=12. Для полуплоскости под прямой VW это
проверяется подстановкой, например, а = 2, f} = —2 в выражение F,
что дает F = \2.
Итак, при всех значениях а, р, которые соответствуют
полосе между прямыми TU и VW, решения системы возмущений
(15.12) имеют колебательный характер. Область колебательных
созмущений, т. е. полоса между прямыми TU и VW, содержит
часть области обязательной асимптотической устойчивости
(полуполосу внутри контура TPQV), интервал PQ, соответст*
вующий обязательной неасимптотической устойчивости, и часть
области обязательной неустойчивости (полуполосу внутри
контура UPQW) движений класса (15.11).
в) При заданных значениях а = 2, р = 2 найдем корни
характеристического уравнения '(15.14) и общее решение системы
возмущений (15.12). Для этого подставим <х = 2, р = 2 в системы
(15.12), (15.13) и в уравнение (15.Ь
Х-\_ == £Х± •—~ Х%
Х% == Х± *-р- ЛХп
(2-г)В±-В% =
В±+(2-г)Вш =
г2— 4г + 5 =
Корни последнего уравнения
тх = 2 + /, г2 =:
Найдем ненулевые решения системы (15.18),
соответствующие этим корням. Подставим в систему (15.18) rx = 2 + i и
неизвестным Ви В2 припишем второй индекс 1:
-iBn-B21 = 0)
Blx-iB21=0 J
Получилась система уравнений с пропорциональными
коэффициентами (при умножении первого уравнения на i получается
второе, а при умножении второго на —i получается первое
уравнение), так что по существу это одно уравнение с двумя
неизвестными 5ц, 52.1. Поэтому одному из неизвестных можно дать
i \
■О
of
0.
l — i.
(15.17)
(15.18)
169
любое ненулевое значение. Например, возьмем Вц = /, тогда
Подставим в систему (15.18) г2=2—i и припишем
неизвестным Ви 52 второй индекс 2:
iB12 — В22 == О
В12 + iB22 = О
Опять получилась система уравнений с пропорциональными
коэффициентами, так что по существу это одно уравнение с
двумя неизвестными В\2у 5гг. Берем 5i2=—/, тогда #22 = 1.
Заметим, что для комплексно-сопряженных корней мы
подобрали комплексно-сопряженные решения системы (15.18), но
можно было выбрать и другие решения.
Составляем фундаментальную систему решений системы
возмущений (15.17):
хп = iefiWt = ie2t (cos t +1 sin t)y
x21 = eV+W = e2t (cos t + i sin t)y
r2 = 2 — i
x12 = — ie P-w = — ie*t (cos t — i sin t)y
x2% = eV-w = e2t (cos t — i sin t).
Введем обычные обозначения для действительных и мнимых
частей этих комплексных функций:
хп = ип + ivn, х12 = и1а + tola,
ЛГ21 = #21 4" ^21 > -^22 == М22 + *^22
и выпишем отдельно эти действительные и мнимые части:
ип = — e2t sin f vn = e2' cos f
u2l = e2t cos f tf8i'= **'sin'
и1а = — e2/ sin f v12 = — e2t cos t
u22 = e2t cos t v22 = — ea'sin f
Очевидно,
Wll ~ W12> ^11 — ^12»
u21 = u22, v21 = i>22»
т. е. действительные части^столбцов
и
*21 *22
совпадают, а мнимые части отличаются только знаком
170
(15.19')
(15.19")
Таким образом, по комплексно-сопряженным корням Г\$ —
= 2±i найдены комплексно-сопряженные решения системы
(15.18) и комплексно-сопряженные решения системы
возмущений (15.17). Если взять не комплексно-сопряженные решения
системы (15.18), соответствующие корням ri?2 = 2±/, то столбцы
Wll» f. W12»
будут пропорциональны между собой, а столбцы
Vll, и Vl2i
— между собой.
Согласно теореме 2 § 11 каждый столбец таблиц (15.19') и
(15.19") образует частное решение системы (15.17).
Определители таблиц (15.19') и (15.19") равны ^ eAt, т. е. отличны от
нуля при всех значениях t. Следовательно, как таблица (15.19'),
так и таблица (15.19") состоят из линейно независимых
решений системы (15.17), поэтому каждая из них может быть
принята за фундаментальную систему решений для системы (15.17).
Возьмем, например, таблицу (15.19'), полученную по корню
гi = 2 + i9 и составим из нее общее решение системы (15.17). Для
этого умножим первый столбец таблицы (15.19') на Си второй
столбец на С2 и затем сложим по строкам:
xi = Citin + С21)ц 1
х2 = С1и21 + C2CJ2i J
т. е.
хх = e2t (— d sin t + C2 cos t) j 20
x2 = e2t(C1cost + C%sint) J
Теперь ответим на вопросы пункта «в» нашей задачи.
На плоскости а, р точка а=2, р = 2 находится в области, где
А2>0, ^i<0. Поэтому в силу критерия Б § 14 при а=2, р=2
все движения класса (15.11) обязательно неустойчивы.
Конечно, это согласуется и с критерием II,а § 13, так как при а=2,
Р = 2 оба корня характеристического уравнения имеют
положительную действительную часть: ri,2 = 2±i. Это видно и
непосредственно по поведению функций (15.19'), (15.19"), (15.20),
которые не остаются ограниченными при f->oo.
Наконец, при заданных начальных возмущениях Х\о = — —.,
5
*2о= т~ найдем возмущения как функции времени. Подставим
t = 0 и заданные начальные возмущения в общее решение
(15.20):
_ 1 _с .1- г
Т-0*' 3 ~ Ll'
Итак, при начальных возмущениях
Xl0~~~T
*2о —
получаем частное решение системы возмущений (15.17):
1
ч ='_е« f J- sinf + — cos t \
хл =-
Хл
Пример 3.
= e2t [— cos t sin t )
V 3 5 J
ii = «i + P2i+/i(0 |
*2 = — zx — az2 + f2(t)\
a = l; p = 5;
_ l _ 1
4 2
(15.21)
Решение. Пишем систему возмущений для движений
класса (15.21):
хх = о*! + (к2 |
Ищем частное решение системы (15.22) в виде
(15.22)
>rt
xi = В\е)
х% — вф
После подстановки этих функций в систему (15.22) и
упрощений получаем
(а— г)В1 + рВ1=0
— В1 + (—а — г)В2=0
(15.23)
172
Чтобы найти ненулевое решение этой системы, приравняем
нулю определитель из коэффициентов при В\9 В2:
(а-г) P
-1 (-о-г)
0.
Развертывая этот определитель, получаем характеристическое
уравнение системы возмущений (15.22):
г2 + ф — <х2) = 0.
Коэффициенты этого уравнения выражаются так:
Л2-р — а2
Корни уравнения (15.24)
ri,2=±/a2-ji.
(15.24)
(15.25)
(15.26)
а) Будем рассматривать параметры аир как координаты
точек плоскости. Коэффициенты А\ и Л2 характеристического
уравнения, выраженные формулами (15.25), являются
функциями, которые определены и непрерывны на всей плоскости
а, р, причем ^i==0.
Найдем геометрическое место точек плоскости а, р, на
котором Л2 = 0, и затем найдем области, в которых Л2>0 и Л2<0.
Поскольку Л2 = Р—а2, то равенство А2—0 выражается
уравнением р—а2=0, т. е. р = а2,
которое представляет собой
хорошо известную .параболу KOL
(рис. 22). Эта парабола
разбивает плоскость a, р на две
области, в каждой из которых
функция А2 сохраняет знак,
так как ввиду ее
непрерывности на всей плоскости a, P она
может изменить знак только
при переходе через параболу.
Условие Л2 < 0 выражается
неравенством р—а2<0, т. е.
Р<а2. Точки, координаты кото- Рис 22
рых удовлетворяют этому
условию, заполняют внешность параболы, т. е. область,
расположенную под параболой. Это проверяется подстановкой,
например, а=0, р ='— 1 в выражение Л2, что дает Л2=—1. При всех
значениях а, р, при которькх Л2<0, в силу критерия Ж § 14 все
движения класса (15.21), вообще говоря, неустойчивы и могут
быть условно асимптотически устойчивыми; на рис. 22 внеш-
173
ность параболы, соответствующая этим значениям а, р,
отмечена прерывистой горизонтальной штриховкой.
Условие Л2>0 выражается неравенством р—а2>0, т. е.
Р>а2. Точки, координаты которых удовлетворяют этому
условию, заполняют внутренность параболы, т. е. область,
расположенную над параболой. Это проверяется подстановкой,
например, а=0, р = 1 в выражение Л2, что дает Л2=1.
При Л2>0 надо учитывать знак или обращение в нуль
коэффициента А\. Но в этом примере Л^О.
Во внутренности параболы KOL выполняются условия
Л2>0 и ^i = 0, которые в силу критерия В § 14 обеспечивают
обязательную неасимптотическую устойчивость всех движений
класса (15.21). На рис. 22 эта область отмечена сплошной
наклонной штриховкой.
На самой параболе KOL выполнены условия Л2 = 0 и А\ = 0,
при которых в силу критерия Е2 § 14 все движения класса
(15.21), вообще говоря, неустойчивы и могут быть условно
неасимптотически устойчивыми.
б) Чтобы решения системы возмущений (15.22) имели
колебательный характер, т. е. чтобы корни характеристического
уравнения (15.24) были комплексными, необходимо и
достаточно, чтобы подкоренное выражение в формуле (15.26), которое
мы обозначим через F, было отрицательным. Очевидно, в этом
примере F=—Л2 = а2—р. Поэтому условие F=0 равносильно
условию Л2=0, и геометрическое место точек, на котором F=0,
совпадает с рассмотренной выше параболой KOL (см. рис.22). ц
В данном случае условие F<0 равносильно условию Л2>0, ко- ||
торое, как мы знаем, выполняется только во внутренности
параболы KOL. Итак, при всех значениях а, р, которые
соответствуют внутренности параболы KOL, характеристическое
уравнение (15.24) имеет комплексные, точнее, чисто мнихмые, корни и
при этом решения системы возмущений (15.22) имеют
колебательный характер. В данном случае область колебательных
возмущений совпадает с областью обязательной
неасимптотической устойчивости движений класса (15.21).
в) При заданных значениях а=1, р = 5 найдем корни
характеристического уравнения (15.24) к общее решение системы
возмущений (15.22).
Подставим <х=1, р==5 в системы (15.22), (15.23) и в
уравнение (15.24):
х1 = х1 + 5х2 1 (1527)
Х% = Х^ Х% J
(1-г)51+5В2 = 0 )
г2 + 4 = 0.
174
тзжу"» *а-^чч41"- --- \^ , •»,« -» ci&t?*t*.
•>*- YW*S=>V?« *в^'»*1Ю
Корни последнего уравнения
rx = 2i\ r2 = — 2i.
Найдем ненулевые решения системы (15.28),
соответствующие этим корням. Подставим в систему (15.28) r\=2i и
неизвестным Ви В2 припишем второй индекс 1:
(1-20Ви + 5В21 = 0 |
-5и-(1 + 20521 = 0Г
Получилась система уравнений с пропорциональными
коэффициентами. Например, при умножении второго уравнения на
— (1—2/) получается первое, а при умножении первого на
5~ (1 +2г) получается второе уравнение, так что по существу
это одно уравнение с двумя неизвестными 5ц, В2\. Поэтому
одной из неизвестных можно дать любое ненулевое значение.
Например, возьмем 5ц = 1+2г, тогда B2i =—1.
Подставим в систему (15.28) r2 =—2i и припишем
неизвестным Ви В2 второй индекс 2:
(1+20Я12 + 5В22 = 0 J
-512 + (-i + 2t)522=;o г
Опять получилась система уравнений с пропорциональными
коэффициентами, так что по существу это одно уравнение с
двумя-неизвестными #12, ^22. Берем #12—1—2i, тогда В22 =—1.
Составляем фундаментальную систему решений системы
возмущений (15.27):
тх = 21
хп = (1 + 20 гш = (1 + 20 (cos 2t + i sin 20,
xn = — e2it = — (cos 2t -f i sin 20,
r2 = — 21
*12 = (1 — 20 e~w = (1 — 20 (cos 2t — I sin 20,
x22 = — erm = — (cos 2t — i sin 20-
Выделим действительные и мнимые части функций х\и ^21-
ип = cos 2t — 2 sin 2/ vn = sin 2t + 2 cos 2£
u21 = — cos 2* v2l = — sin 2£
Выделим действительные и мнимые части функций Х\2> х22:
ип = cos 2/ — 2 sin 2f d12 = — sin 2t — 2 cos 2t
w22 = — cos 2t v22 = sin 2*
175
(15,29')
(15.29")
**^тавпя=я5*пляякг jw*>**4iiW "*s«»>s>w^7->i.«*a^ ^
Очевидно, первые столбцы этих таблиц совпадают, а вторые
отличаются только знаком.
Согласно теореме 2 § 11 каждый столбец таблиц (15.29') и
(15.29") образует частное решение системы (15.27).
Определители таблиц (15.29') и (15.29") равны ±2, т. е. отличны от
нуля при всех значениях t. Следовательно, как таблица (15.29'),
так и таблица (15.29") состоят из линейно независимых
решений системы (15.27), поэтому каждая из них может быть
принята за фундаментальную систему решений для системы (15.27).
Возьмем, например, таблицу (15.29'), полученную по корню
ri=2£, и составим из нее общее решение системы возмущений
(15.27). Для этого умножим первый столбец таблицы (15.297)
на Си второй столбец на С2 и затем сложим по строкам:
хг = Сг (cos 2* — 2 sin 2t) + Са (sin 2* + 2 cos 2t)
х2 = — Сг cos 2t — Ca sin 2/
Теперь ответим на вопросы пункта «в» нашей задачи.
На плоскости а, р точка а=1, Р = 5 находится в области, где
А2>0, А\ = 0. Поэтому в силу критерия В § 14 при а=1, р = 5
все движения класса (15.21) обязательно неасимптотически
устойчивы. Конечно, это согласуется и с критерием III,a § 13,
так как при а=1, р = 5 оба корня характеристического
уравнения простые и имеют нулевую действительную часть rit2=±2L
Это видно и непосредственно по поведению функций (15.29'),
(15.29"), (15.30), которые при t-+oo ограничены по модулю, но
не стремятся к нулю.
Наконец, при заданных начальных возмущениях х10 = ~,
#20= — у найдем возмущения как функции времени. Подставим
£=0 и заданные начальные возмущения в общее решение
(15.30):
4
п 1 п 1
откуда Сг = у, С2 = — у.
Итак при начальных возмущениях
_ 1
*20 — — о
(15.30)
176
получаем частное решение системы возмущений (15.27):
1 9
хх = — cos 2t sin 2t
1 4 8
x2
Пример 4.
— cos 2t + — sin 2t
2 8
*i = a*i + P*e + /i(0
*l = *l+P*I + /l(0
a = -3; p = -l;
(15.31)
*10 — "T"» *20 ~
Решение. Пишем систему возмущений для движений
класса (15.31):
(15.32)
х1 = ах1 + $х2)
х2-=хх + ^х2 |
Ищем частное решение системы (15.32) в виде:
хг = Вур*
х2 = B2ert
После подстановки этих функций в систему (15.32) и
упрощений получаем:
(а-г)В1 + ^В,=0
В1 + ф-г)В2=0
(15.33)
Чтобы найти ненулевое решение этой системы, приравняем
нулю определитель из коэффициентов при Ви В2:
(а-г) Р
1 (р-г)
0.
Развертывая этот определитель, получаем
характеристическое уравнение системы возмущений (15.32):
r2-(a + p)r + (ap-p)=0.
Вводя обозначения
А = -(а + р)
Ла =ap —p
(15.34)
(15.35)
177
перепишем уравнение (15.34) так:
г2 + Агг + А2 = 0, его корни г1)2 = — у ± 1/ -^- — Л-
Подставим сюда выражения (15.35):
или
(а + Р)±У («~Р)2 + 4р
ri,2 = (15.do)
а) Будем рассматривать параметры аир как координаты
точек плоскости. Коэффициенты А\ и А2 характеристического
уравнения, выраженные формулами (15.35), являются
функциями, которые определены и непрерывны на всей плоскости
а, р.
Найдем геометрическое место точек плоскости а, р, на
котором Л2=0, и затем области, в которых Л2>0 и Л2<0. Так как
Л2=ар—р= (а—1)Р, то равенство Л2 = 0 выражается уравнением
(а—1)р=0, которое распадается на два независимых уравнения
а—1=0, р = 0, т. е. а=1, р = 0. Очевидно, эти уравнения
представляют собой совокупность двух прямых KL и MN (прямая
Р = 0 совпадает с осью а), которые изображены на рис. 23.
Прямые KL и MN разбивают плоскость а, р на четыре прямых угла:
NPL, LPM, MPK, KPNy в каждом из которых функция
А2=(а—1)р сохраняет знак, так как она может изменить знак
только при переходе через прямую KL или MN.
Условие Л2<0 выражается неравенством (а—1)Р<0. Точки,
координаты которых удовлетворяют этому условию, заполняют
внутренности углов LPM и KPN. Для области внутри угла LPM
это проверяется подстановкой, например, а=0, р=1 в
выражение Л2, что дает Л2 = — 1. Для области внутри угла KPN это
проверяется подстановкой, например, а=2, р =—1 в
выражение Л2, что дает А2=—1.
При всех значениях а, р, при которых Л2<0, в силу
критерия Ж § 14 все движения класса (15.31), вообще говоря,
неустойчивы и могут быть условно асимптотически устойчивыми;
на рис. 23 внутренности углов LPM и KPN, соответствующие
этим значениям а, р, отмечены прерывистой горизонтальной
штриховкой.
Условие Л2>0 выражается неравенством (а—1)Р>0. Точки,
координаты которых удовлетворяют этому условию, заполняют
внутренности углов NPL и MP К. Для области внутри угла NPL
это проверяется подстановкой, например, а = 2, р=1 в выраже-
178
ние i42, что дает Л2=1. Для области внутри угла MP К это
проверяется подстановкой, например, а = 0, р =—1 в выражение Л2,
что дает Л2=1.
При А2>0 надо учитывать знак или обращение в нуль
коэффициента А\.
Рис, 23
Найдем геометрическое место точек, на котором А\=0, а
затем области, в которых Лх>0 и ^i<0. Так как А\ =— (а+р),
то равенство Лх = 0 выражается уравнением а+р=0, т. е.
Р = —а, которое представляет собой биссектрису второй и
четвертой четвертей плоскости а, р. На рис. 23 полупрямая OR
(без точки О) и полупрямая QS (без точки Q), расположенные
в областях, где Л2<0, начерчены пунктиром, поскольку они не
нужны для решения задачи, так как при Л2<0 характер
движений класса (15.31) не зависит от значений А\.
Условие А{<0 равносильно неравенству а + р>0, т. е. Р>—а,
которое выражает собой полуплоскость над прямой /?S. Это
проверяется подстановкой, например, а=0, р=1 в
выражение Аи что дает А\ = — 1. Условие А\>0 равносильно
неравенству а + р<0, т. е. Р<—а, которое выражает собой
полуплоскость под прямой RS. Это проверяется подстановкой, например,
а=0, р =—1 в выражение Аи что дает Ах=1.
Теперь нам известны все области положительных и
отрицательных значений А2 и А\.
При всех значениях а, р, соответствующих области,
ограниченной контуром MOQK и содержащей третью четверть
плоскости а, р, выполнены условия Л2>0 и Ах>0, которые в силу
критерия А § 14 обеспечивают обязательную асимптотическую
179
ги«сщйдза8«*»ак«>р*ивгчгаад*^Егг«^ ччяк.»
устойчивость всех движений класса (15.31). На рис. 23 эта
область отмечена сплошной вертикальной штриховкой.
При всех значениях а, р, .соответствующих внутренности
треугольника OPQ и внутренности угла NPL, выполнены условия
Л2>0 и А\<0, которые в силу критерия Б § 14 обеспечивают
обязательную неустойчивость всех движений класса (15.31).
На рис. 23 эти области отмечены сплошной горизонтальной
штриховкой.
Остается выяснить характер движений при тех значениях
а, р, которые соответствуют точкам прямых KLy MN и отрезка
OQ. На интервале OQ (без точек О и Q) выполнены условия
А2>0 и А 1 = 0, которые в силу критерия В § 14 обеспечивают
обязательную неасимптотическую устойчивость всех движений
класса (15.31). На полупрямых ОМ и QK (без точек О и Q)
выполнены условия Л2 = 0 и Аг>0, при которых в силу
критерия Г § 14 все движения класса (15.31) обязательно устойчивы,
но, вообще говоря, неасимптотически и, значит, могут быть
условно асимптотически устойчивыми. На полупрямых ON и QL
(без точек О и Q) выполнены условия А2 = 0 и -4i<0, при
которых в силу критерия Д § 14 все движения класса (15.31),
вообще говоря, неустойчивы и могут быть условно неасимптотически
устойчивыми.
Наконец, в точках О и Q (1, —1) выполнены условия Л2=0
и Л 1 = 0, при которых в силу критерия Е2 § 14 все движения
класса (15.31), вообще говоря, неустойчивы и могут быть
условно неасимптотически устойчивыми.
б) Чтобы решения системы возмущений (15.32) имели
колебательный характер, т. е. чтобы корни характеристического
уравнения (15.34) были комплексными, необходимо и
достаточно, чтобы подкоренное выражение в формуле (15.36),
которое мы обозначим через F, было отрицательным. Ясно, что
F=(a—р)2+4р есть функция, непрерывная на всей
плоскости а, р.
Геометрическое место точек, на котором F=0, имеет
уравнение (а—р)2 + 4р = 0. Чтобы выяснить форму этой кривой
второго порядка, возьмем вспомогательную систему координат
а', Р', которые связаны с координатами а, р так:
а' = а — р|
Р' = а + РГ
Осью а' (которая имеет уравнение Р/==0, т. е. <х + р = 0)
является прямая RS (см. рис. 23), а осью Р' (которая имеет
уравнение а/=0, т. е. а—Р = 0) служит биссектриса первой и третьей
четвертей плоскости а, р. В результате замены получаем
уравнение
(а')2 + 2 (Р' - а') = 0, или Р' = ±- - \ (а' - Х)\
180
Это уравнение представляет собой параболу UOVQW
(см. рис. 23) с осью симметрии TVPT (имеющей уравнение
а'=1, т. е. В = а—1) и с вершиной в точке V с координатами
1 3 1
а'=1, Р'=—, т. е. а=— > Р = • Вся парабола, кроме
точек О и Q, лежит внутри угла МРК, а в точках О и Q касается
сторон этого угла.
Внутри параболы UVW выполнено условие F<0. Это
проверяется подстановкой, например, а = —, р = в
выражение F, что дает F =—1. Во внешности параболы /7>0. Это
проверяется подстановкой, например, а = 0, р=1 в выражение F,
что дает F=5.
Таким образом, при всех значениях а, р, которые
соответствуют внутренности параболы UVW, характеристическое
уравнение (15.34) имеет комплексные корни. В точках параболы
характеристическое уравнение имеет действительные кратные
корни, а во внешности параболы — действительные различные
корни.
в) При заданных значениях а = —3, р = — 1 найдем корни
характеристического уравнения (15.34) и общее решение
системы возмущений (15.32). Для этого подставим а = —3, р = — 1
в системы (15.32), (15.33) и в уравнение (15.34):
(15.37)
(-З-г^-Ъ-О) 38)
вг + (-\-г)В2 = о\'
Г2 + 4г + 4 = 0.
Последнее уравнение имеет кратный корень Г\)2 = —2.
Найдем одно ненулевое решение системы (15.38),
соответствующее этому корню. Подставим в систему (15.38) Г\ = —2
и неизвестным Ви В2 припишем второй индекс 1:
— 5ц —521= 0
Вп + В21 = 0
Получилась система уравнений с пропорциональными
коэффициентами. Поэтому одной из неизвестных можно дать любое
ненулевое значение. Например, возьмем 5ц = 1, тогда #21 =—1.
Получить другое решение системы (15.38), не
пропорциональное найденному, невозможно, так как ее определитель при
г=—2 имеет ранг ti\ = \. Следовательно, получится только одно
181
линейно независимое частное решение системы (15.37) в виде
показательных функций с постоянными коэффициентами:
XllZ=e~2t A. 05.39')
x21 = —e-2tj
Второе частное решение системы (15.37), линейно
независимое с решением (15.390, ищем в виде:
xlt=(at+b)er*
\/ xlt=(at+b)er* 1
I xn = (d+d)er* J
Чтобы найти коэффициенты а, &, с, rf, подставляем эти
функции в систему (15.37):
ae~2t — 2 (at + b) er* = —3(at + b) e~* — (ct + d) er* i
cer* — 2 (ct + d) e-* = (at + b) er* — (ct + d) e~2t
Сокращая на e~2i и перенося все члены в одну сторону,
перепишем эту систему так:
(at + b) + (ct + d) + a = 0 j
(at + b) + (ct + d) — c = 0
Собирая в этих уравнениях коэффициенты при t, а также члены,
не содержащие ty и приравнивая их нулю, мы получаем четыре
уравнения относительно 'неизвестных a, b9 cy d:
а + с=0
а + с = 0
b+d+a=0
b+d—c=0
Числа а и с должны быть отличны от нуля, в остальном же
одно из них можно выбрать произвольно. Например, берем а=1,
тогда с =—1. Подставляем эти значения а и с в два последних
уравнения системы:
b+d+l= 0
b+d+l=0
Одно из чисел Ъ и d можно выбрать совершенно произвольно.
Например, возьмем 6=0, тогда d=—1. Подставляем найденные
значения а, 6, с, d в Х\% и #22:
у — fp-*t
12 ■ (15.39")
x*t = -(t+l)er*'
182
г атяг^иигогак^вжуч»
Столбцы (15.39') и (15.39") образуют фундаментальную
систему решений для системы (15.37). Умножая функции (15.39')
на Си функции (15.39") на С2 и затем складывая покомпонентно,
получаем общее решение системы (15.37):
x1 = Cle-*' + Ctter*'
*„ = —d^-" —C^f + l)*-*'
Теперь ответим на вопросы пункта «в» нашей задачи.
На плоскости а, р точка а =—3, Р =—1 находится на
параболе UVW, точнее, на ее части f/O, которая лежит в области,
где Л2>0 и А\>0. Поэтому в силу критерия А § 14 при а=—3,
р==—1 все движения класса (15.31) обязательно
асимптотически устойчивы. Конечно, это согласуется и с критерием I § 13,
так как при <х=—3, р =—1 оба корня характеристического
уравнения отрицательны: п,2=—2. Это видно и непосредственно
по поведению функций (15.39'), (15.39"), (15.40), которые
стремятся к нулю при t-+oo.
Наконец, при заданных начальных возмущениях х10 = —,
о
х20 = найдем возмущения как функции времени. Подставим
6
/*-=0и заданные начальные возмущения в общее решение (15.40):
J--C )
з ~Cl
?»
—— = сг с2
Ь ;
откуда Сг = —, Са = . Итак, при начальных возмущениях
3 6
_ 1 )
*10~Т
_ 1 [
о /
получаем частное решение системы «возмущений (15.37):
'"(т'-тН'
Пример 5.
^ = ~pz» + (2o-4)z, + /,(/)
183
(15.40)
(15.41)
4 ft 4
a = —, 6 = —
3 * v 3
_ 1 __ 1
Решение. Пишем систему возмущений для движений
класса (15.41):
*i = a*i + P*i | (15.42)
х% = — pxx + (2a — 4) х2 J
Ищем частное решение системы (15.42) в виде:
Xl = Bxert
После подстановки этих функций в систему (15.42) и
упрощений получаем
(а-г)£1 + рЯ2 = 0 )
— ^+(20-4 —г)В, = 0 )•'
Чтобы найти ненулевое решение этой системы, приравняем
нулю определитель из коэффициентов при В\, В2:
(«-г) р
— Р (2а — 4 — г)
0.
Развертывая этот определитель, получаем характеристическое
уравнение системы возмущений (15.42):
г2 + (4 — За) г + (2а2 — 4а + р2) = 0. (15.44)
Вводя обозначения
Ах = 4 — За
Л2 = 2а2 — 4а + р2
перепишем уравнение (15.44) так:
(15.45)
гг _|_ Агг + А% = 0, его корни п.2 = — — ± ]/ —! Л •
Подставим сюда выражения (15.45):
Г1Л = Jl=± ± |/(3^1)L_2a2 + 4a3p2,
или
Г,,2= (8а-4)±/(а-4)»-4У . (15 46)
184
а) Будем рассматривать параметры аир как координаты
точек плоскости. Коэффициенты А{ и А2 характеристического
уравнения, выраженные формулами (15.45), являются
функциями, которые определены и непрерывны на всей плоскости
а, Р.
Найдем геометрическое место точек плоскости а, Р, на
котором Л2 = 0, и затем области, в которых Л2>0 и А2<0.
Рис. 24
Так как Л2 = 2а2—4а+р2, то равенство А2 — 0 выражается
Р2
уравнением 2 а2—4а + р2 = 0, или (а—1)2+-^~ = 1. Это
уравнение представляет собой эллипс, осями симметрии которого
служат _прямые р = 0 и а=1, а полуоси соответственно равны 1
и У 2 . На рис. 24 это эллипс LMONy который разбивает всю
плоскость а, р на две области: внутренность и внешность
эллипса.
Во внутренности эллипса выполняется условие Л2<0. Это
проверяется подстановкой, например, а=1, р = 0 в выражение Л2,
что дает А2 =—2. При всех значениях а, р, при которых Л2<0,
в силу критерия Ж § 14 все движения класса (15.41), вообще
говоря, неустойчивы и могут быть условно асимптотически
устойчивыми; на рис. 24 внутренность эллипса LMON,
соответствующая этим значениям а, р, отмечена прерывистой
горизонтальной штриховкой.
Во внешности эллипса выполняется условие А2>0. Это
проверяется подстановкой, например, а = 0, р=1 в выражение Л2,
что дает Л2=1. При Л2>0 надо учитывать знак или обращение
в нуль коэффициента А\.
Найдем геометрическое место точек, на котором А{ = 0, а
затем области, в которых Ai>0 и A\<0t Так как А\=А—За, то
185
равенство i4i = 0 выражается уравнением 4—3а=0, т. е. а =—,
о
которое представляет собой прямую RPQS.
На рис. 24 интервал PQ этой прямой, расположенный в
области, где Л2<0, начерчен пунктиром, поскольку он не нужен
для решения задачи, так как при Л2<0 характер движений
класса (15.41) не зависит от значений Ль
Условие А\>0 равносильно неравенству 4—3а>0, т. е.
а<С —, которое выражает собой полуплоскость слева от пря-
мой RS. Условие ^i<0 равносильно неравенству 4—3а<0, т. е.
а> —, которое выражает собой полуплоскость справа от
о
прямой RS.
Теперь нам известны все области положительных и
отрицательных значений А2 и А\.
При всех значениях а, р, соответствующих области,
ограниченной контуром RPNOMQS и содержащей вторую и третью
четверти плоскости а, р, выполнены условия А2>0 и i4i>0,
которые в силу критерия А § 14 обеспечивают обязательную
асимптотическую устойчивость всех движений класса (15.41).
На рис. 24 эта область отмечена сплошной вертикальной
штриховкой.
При всех значениях а, р, соответствующих области,
ограниченной контуром RPLQS и лежащей справа от него, выполнены
условия Л2>0 и i4i<0, которые в силу критерия Б § 14
обеспечивают обязательную неустойчивость всех движений класса
(15.41). На рис. 24 эта область отмечена сплошной
горизонтальной штриховкой.
Остается выяснить характер движений при тех значениях
а, р, которые соответствуют точкам полупрямых PR, QS и дугам
эллипса PNOMQ и PLQ. На полупрямых PR и QS (без точек
Р и Q) выполнены условия Л2>0 и i4i = 0, которые в силу
критерия В § 14 обеспечивают обязательную неасимптотическую
устойчивость всех движений класса (15.41). На дуге эллипса
PNOMQ (без точек Р и Q) выполнены условия Л2=0 и ^i>0,
при которых в силу критерия Г § 14 все движения класса
(15.41) обязательно устойчивы, но, вообще говоря,
неасимптотически и, значит, могут быть условно асимптотически
устойчивыми. На дуге эллипса PLQ (без точек Р и Q)
выполнены;условия Л2 = 0 и А\<0У при которых в силу критерия Д § 14 все
движения класса (15.41), вообще говоря, неустойчивы и могут быть
условно неасимптотически устойчивыми.
Наконец, в точках Р ( —; ] и Q (—; — | выполнены
условия Л2=0 и i4i = 0, при которых в силу критерия Е2 § 14 все
186
движения класса (15.41), вообще говоря, неустойчивы и могут
быть условно неасимптотически устойчивыми.
б) Чтобы решения системы возмущений (15.42) имели
колебательный характер, т. е. чтобы корни характеристического
уравнения (15.44) были комплексными, необходимо и
достаточно, чтобы подкоренное выражение в формуле (15.46),
которое мы обозначим через F, было отрицательным. Очевидно,
F=(a—4)2—4р2 есть функция, непрерывная на всей плоскости
а, р. Геометрическое место, на котором F = 0f имеет уравнение
распадающееся
на два уравнения
(а—4)2 — 4р2 = 0,
Р=~±^—(а—4). Эти уравнения представляют собой пару прямых
TPKU и VQKW, которые пересекаются в точке К(4; 0) и
касаются эллипса соответственно в точках Р и Q. Прямые TU
и VW разбивают всю плоскость а, р на четыре области, в
каждой из которых F сохраняет знак. Внутри углов VKU и TKW
выполнено условие F<0. Это проверяется подстановкой,
например, а=4, р=±1 в выражение /\ что дает F=—4. Внутри углов
ТКУ и UKW выполнено условие F>0. Для угла TKV это
проверяется подстановкой, например, <х=0, р = 0 в выражение F, что
дает F=16. Для угла UKW это проверяется подстановкой,
например, а=5, Р=0, что дает F=\.
Таким образом, при всех значениях а, р, которые
соответствуют внутренности углов VKU и TKW, характеристическое
уравнение (15.44) имеет комплексные корни. В точках прямых
TU и VW характеристическое уравнение имеет действительные
кратные корни, а внутри углов TKV и UKW — действительные
различные корни.
в) При заданных значениях а = —, р = — найдем корни
«3 о
характеристического уравнения (15.44) и общее решение
системы возмущений (15.42). Для этого подставим <*=—/£=—
о о
в системы (15.42), (15.43) и в уравнение (15.44):
• _ 4 .4
Х1 — — Х1 П Г" Х2
Хп
— хх —
3
(т-г)в'+т*-°
з 1 V з
г \В, = О
г3 = 0.
(15.47)
(15.48)
187
я&$>и**т?гг fs/swfm-i "^^ечв'тдв^^тажггл^-аз? г»,. .^jhs^H'jrs ■*-"■«* t v
Последнее уравнение имеет кратный нулевой корень rit2 = 0.
Найдем одно ненулевое решение системы (15.48),
соответствующее этому корню. Подставим в систему (15.48) г{ = 0 и
неизвестным Ви В2 припишем второй индекс 1:
~T5u~T5al = 0 J
Одной из неизвестных можно дать любое ненулевое значение.
Например, возьмем Вп = 1, тогда B2i =— 1. Получить другое
решение системы (15.48), не пропорциональное найденному,
невозможно, так как ее определитель при г=0 имеет ранг П\ = \.
Следовательно, получится только одно линейно независимое
частное решение системы (15.47) вида:
Xn=ept = i | (15.49')
Второе частное решение системы (15.47), линейно
независимое с решением (15.49'), ищем в виде:
x12 = (at + b)eot = at + b |
Хм = (ct + d) eot =ct + d J
Чтобы найти коэффициенты а, b, с, dy подставляем эти функции
в систему (15.47):
a = ±(at + b)+±(ct + d) |
c = -±(at + b)-±(ct + d) J
Перенося все члены в одну сторону, перепишем эту систему так:
±(at + b) + ±(d + d)-a = o)
±(at + b)+±(ct + d) + c = 0 j
Собирая в этих уравнениях коэффициенты при t, а также члены,
188
не содержащие /, и приравнивая их нулю, получаем четыре
уравнения относительно неизвестных а, Ь} с, d:
4 . 4
— аА с
3^3
о
— аЦ с = 0
— b+ —d — a = 0
з з
J-b+ —d + c = 0
Числа а и с должны быть отличны от нуля, в остальном же одно
из них можно выбрать произвольно. Например, берем а=1,
тогда с =—1. Подставляем эти значения а и с в два последних
уравнения системы:
jLb+±d — l =0
3 3
±b+±d~l
3 3
о
Одно из чисел bud можно выбрать совершенно произвольно.
Например, возьмем 6 = 0, тогда d=*—. Подставляем найденные
4
значения а, 6, с, d в х\2 и #22-
«#19 = *
v12
Х22 — * ЯТ
(15.49")
Столбцы (15.49') и (15.49") образуют фундаментальную
систему решений для системы (15.47). Умножая функции (15.49')
на С], функции (15.49") на С2 и затем складывая
покомпонентно, получаем общее решение системы (15.47):
Х\ = Ci + C2t ]
xt = -Ct + Ca(-t+±y) }' (15"50)
Теперь ответим на вопросы пункта «в» нашей задачи.
4 4
На плоскости а, р точка а=—, Р^'з"— это T04Ka Q, в
которой, как мы видели, выполнены условия А2 = 0 и Ai = 0. Поэто-
4 4
му в силу критерия Е2 § 14 при <*=~^", р = —все движения
класса (15.41), вообще говоря, неустойчивы, но могут быть
условно неасимптотически устойчивыми. Конечно, это согла-
189
4 4
суется и с критерием V,a § 13, так как при а — —, ji= —квад-
о о
ратное уравнение (15.44) имеет кратный нулевой корень, для
которого п\=1. При этом неустойчивость движений видна и
непосредственно, поскольку при £->оо абсолютные величины
функций (15.49") и функций (15.50) при С2ф0 неограниченно
возрастают. Поэтому условная неасимптотическая устойчивость
получается из общего решения (15.50) при С2 = 0. Соотношение
между начальными возмущениями, необходимое и достаточное
для этого, получается в результате подстановки в равенство
(15.50) С2=0, #1=#ю, #2=*2о и затем исключения С{ из
полученных равенств:
х10 = Сх
х20 = Ci
откуда Хю+Х2о=0-
Наконец, при заданных начальных возмущениях Хю = —,
*2о= — найдем возмущения как функции времени. Подставим
t=0 и заданные начальные возмущения в общее решение
(15.50):
2 х
4-=~сх+'
откуда Сг =—, С2 = 1. Итак, при начальных возмущениях
х10 — ■
*20
получаем частное решение системы возмущений (15.47):
xi=t + —
*2 = —* + —
4
Замечание. После изучения § 2—6, 8—15
студент-заочник может приступить к выполнению контрольного задания №16
«Устойчивость движения по Ляпунову», которое помещено в
конце этого пособия (см. стр. 220).
190
yi>r-T»rVf«-b, <
«l«*i, тх*г«>«:
§ 16. НЕОБХОДИМЫЙ ПРИЗНАК АСИМПТОТИЧЕСКОЙ
УСТОЙЧИВОСТИ И КРИТЕРИЙ РАУСА-ГУРВИЦА
Пусть класс движений описывается системой
дифференциальных уравнений
zj - aiXzx + а&% + ... + ainzn + /;- (t) J ^ ^
j = 1, 2, ... , n j
с действительными постоянными коэффициентами.
Пусть для соответствующей системы возмущений
/= 1. 2 л
характеристическое уравнение написано так, что коэффициент
при гп равен 1:
гп + Alf*-t + ЛаГп-2 + в ш в + Лл_2 Г2 + Ля_х Г+Ап=0. (16.3)
Напомним, что левая часть уравнения (16.3) называется
характеристическим многочленом системы (16.2).
При п=\ и п = 2 всегда легко вычислить корни
характеристического уравнения и с помощью этих корней выяснить
характер движений класса (16.1), пользуясь критериями § 13. Но при
п>2 вычисление корней характеристического уравнения (16.3)
становится затруднительным. Поэтому при /г>2 желательно
получить признаки, позволяющие судить о характере движений
класса (16.1) не по корням, а по коэффициентам
характеристического уравнения (16.3). Для случая п=2 такие
признаки были получены в § 14.
Здесь мы рассмотрим еще два признака, выраженных через
коэффициенты характеристического уравнения (16.3) и
справедливых для любого п.
1. Необходимый признак асимптотической устойчивости
движений, описываемых нормальной системой линейных
дифференциальных уравнений с действительными постоянными
коэффициентами
Теорема 1. Если все движения класса, описываемого
системой уравнений (16Л) с действительными постоянными
коэффициентами, асимптотически устойчивы по Ляпунову, то все
коэффициенты характеристического уравнения (16.3) системы
возмущений (16.2), написанного так, что коэффициент при гп
равен 1, строго положительны:
Аг>0, Л2>0, ... , Л„>0. (16.4)
191
(16.2)
Доказательство. Так как все коэффициенты систем
(16.1) и (16.2) действительны, то и все коэффициенты
характеристического уравнения (16.3) также действительны (см. §12).
Поэтому если характеристическое уравнение (16.3) имеет
комплексные корни, то они группируются в
комплексно-сопряженные пары; так, вместе с корнем Гь = а&+/Рь имеется и корень
fk = a>k—фк, причем той же кратности.
Так как по условию все движения класса (16.1)
асимптотически устойчивы по Ляпунову, то в силу критерия I § 13
действительные корни характеристического уравнения (16.3)
отрицательны", а все комплексные корни имеют отрицательные
действительные части.
Пусть характеристическое уравнение имеет действительные
корни
гх = —аг кратности ти
г2 = —аг кратности /и2,
г;- = —а,- кратности mj9
rp = —ap кратности тру
где а;.>0 /= 1, 2, ... , р
и комплексные корни
Гр+i = <*р+1 + Фр+i >>i = V-i — Фр+i кратности тр+1
гр+г = «р+2 + Фр+2 ~гр+2 = ар+2 — фр+2 кратности /пр+2,
Ъ = ak + Фа rk = ak — i$k кратности mk,
Гр+q = %+q + lh+a Гр+д = a^q — i$p+g КраТНОСТИ ГПр+д,
где ал<0 k = p+ 1, p + 2, ... , p + q.
Ясно, что
P Р+Я
S Щ + 2 £ mk = n
В разложении характеристического многочлена на множители
действительному корню г,- = — а,, кратности т^ соответствует
множитель (г — Г])т'= (г + а^ /= 1, 2, ... , р, а паре комп-
192
лексно-сопряженных корней rk = ak -f- Ф*. rk — ak — Ф* кратности
mk — множитель
К'1 ~ rk) (г - 7k)]mk = [г» - (rft + 7,) г + r, 7fcf* =
= [гг - 2aAr + (a! + pf)ffc = (r« + V + сЛ)т*,
где bft = -2afc>0, c, = af+pf>0 6 = p + 1, p + 2,...,p + q.
Таким образом, разложение характеристического многочлена
на множители может быть записано так:
г» + Л1г*-1 + Л1/*-,+ ... + 4-/2 + Аяг.1г + Ап =
= (г + ai)m« (г + о,)».... (г + a,)m*... (г + ap)"V x
х (г* + Ьр+1 г + cp+1)mp+i (г2 + Ьр+2 г + ср+2)то+* • ■ ■
...(/* + V + ck)mk ...(,* + &р+? г + cp+q)mp+<>.
Напомним., что ау > О / = 1,2 р
6*>0, сЛ>0 Л = Р+1, Р+2 Р + <7.
Поэтому, раскрывая все скобки и приводя подобные
члены, мы убеждаемся, что все коэффициенты!
характеристического многочлена (когда он не разложен на множители) строго
положительны:
Л>0, Л2>0, .... 4>0- (16.4)
Теорема доказана.
Полученный необходимый признак асимптотической
устойчивости движений класса (16.1) при п = 2 является и
достаточным, что видно из критерия А § 14. Очевидно, этот признак
является достаточным и при л=1. Но при /г>2 этот
необходимый признак не является достаточным, т. е. если все
коэффициенты характеристического уравнения, написанного в виде
(16.3), положительны, то движения класса (16.1) могут не быть
асимптотически устойчивыми и, следовательно, могут быть
неасимптотически устойчивыми или неустойчивыми.
Следствием необходимого признака асимптотической
устойчивости является достаточный признак невозможности
асимптотической устойчивости по Ляпунову: если хотя бы один из
коэффициентов характеристического уравнения системы возмущений
(16.2), записанного в виде (16.3), не положителен, то хотя бы
один из его корней имеет неотрицательную действительную
часть, т. е. движения класса (16.1) не могут быть
асимптотически устойчивы по Ляпунову.
7 А. Г. Мл адов 193
2. Критерий Рауса — Гурвица для многочлена.
Необходимый и достаточный признак асимптотической
устойчивости движений
Критерий Рауса—Гурвица, который мы сформулируем ниже,
дает возможность, не вычисляя корней многочлена, судить о
знаках действительных частей его корней только с помощью
коэффициентов этого многочлена.
Пусть задан многочлен степени п от переменной г с
действительными коэффициентами, записанный так, что коэффициент
при гп равен 1:
г" + Агг*-1 + Л2г"-2 + ... + Ап-2г* + Аа-гг + Ап. (16.5)
Построим таблицу из п строк и п столбцов, некоторыми
элементами которой будут служить коэффициенты многочлена
(16.5). Главную диагональ этой таблицы (т. е. диагональ,
направленную слева сверху вниз направо) составим из чисел Аи
Л2, Лз>..., Лп_ь Ап. Чтобы построить строки таблицы, возьмем
конечную последовательность чисел:
О, 0, ... , О, Ап9 Ап—х, ... , AkJ ... , Л2, Ах, 1,0, 0, .. • ,0.
л —1 раз л —2 раз
В качестве строк таблицы берем отрезки этой
последовательности длиной в п элементов. Причем строка с номером «k»
представляет собой такой отрезок, в котором элемент Ah находится
на £-ом месте и значит попадает на главную диагональ
таблицы.
Таким образом, таблица имеет следующий вид:
[Л^ООффффО О
\А3 Аг Ах 1 0 0 • • О О
IЛ 4* 43 А2 Аг 1 0 • О О
О
о
•
о
о
Ао'
о
- \
(16.6)
Как видим, строки таблицы построены из всех коэффициентов
многочлена (16.5), взятых с убывающими индексами, причем
элемент 1 здесь участвует как коэффициент при гп в многочлене
(16.5). Строки, в которых остаются свободные места после
элементов Аи 1 или перед элементами Ап, дополнены нулями.
Таблица (16.6) называется матрицей
Рауса—Гурвица для многочлена (16.5).
194
■ Жйвтягтд:^-* •
Из элементов матрицы (16.6) построим определители
порядков 1, 2, 3, ..., (л— 1), п:
1А, II '* ' °
I -"3 **% J
Дх = Л1( Д2 =
А3 =
А 1
А3 Аъ Ai
А$ /Ц А3
Д4 получается окаймлением определителя Аз элементами
4-й строки и 4-го столбца матрицы (16.6); вообще, Д/г+1
получается окаймлением определителя Д& элементами
(&+1)-йстроки и (&+1)-го столбца матрицы (16.6); следовательно,
Л 1 0 0 • • • • О
\А3 А2 Аг 1 О О • • О
K-i =
А% /Ц А3 А% А± 1 U
О 0 • • ф 0 0 Ап Ап-г I
получается при отбрасывании последней строки и последнего
столбца матрицы (16.6); наконец, раскрывая Дп, т. е.
определитель всей матрицы (16.6), по элементам последней строки и
учитывая, что вся она, кроме элемента Лп, состоит из нулей,
получаем An = kn-iAn.
Определители Дь Дг, Дз,.., Дп-ь Дп называются главными
диагональными минорами матрицы Рауса—Гурвица (16.6), так
как их главные диагонали являются отрезками главной
диагонали этой матрицы, начинающимися с элемента А\.
Теперь мы можем сформулировать следующую теорему.
Теорема 2 (критерий Рауса—Гурвица для многочлена).
Пусть многочлен п-й степени с действительными
коэффициентами задан в виде (16.5), т, е. написан так, что коэффициент
при гп равен 1. Для того чтобы все корни этого многочлена
имели строго отрицательные действительные части, необхо-
димо и достаточно, чтобы все главные диагональные миноры
матрицы Рауса—Гурвица (16.6), составленной для заданного
многочлена (16.5), были строго положительны:
Дх>0, Д2>0 Дя-1>0, Д„>0. (16.7)
Мы не даем доказательства этой теоремы ввиду его
сложности.
Следствие из теорем 1 и 2. Если для многочлена
(16.5) выполнены условия (16.7), то для него выполнены и
условия (16.4), т. е. все его коэффициенты положительны; обратное
утверждение при л>2, вообще говоря, не имеет места.
7*
195
--18ГЛ*?»* »14WJ* *i* ~f Я-ЯР"*-Т.»»,«*гй..Л «ЛяЛЭТ-^л"*!*.
Проследим, какой вид принимают условия (16.7) для
многочленов второй и третьей степеней.
Для многочлена г2+А\г+А2 эти условия имеют вид:
Д1 = Л1>0, Д2
А 1
О Л2
ЛЛ>0,
т. е.
Лх>0
А>оГ
что совпадает с критерием А § 14.
Для многочлена г3+А\г2+А2г+А3 условия (16.7) имеют
вид:
Ai = A>0, Д2 =
А 1
^3 ^2
Ах 1 О
Л3 А% Ai
о о 4
= АА-л3>о
Д2Л3 > О
т. е.
А>о
АА-А>0[.
л3>о
(16.8)
Теперь мы сформулируем очень важное следствие из
теоремы 2.
Необходимый и достаточный признак
асимптотической устойчивости движений
Пусть класс движений описывается нормальной системой
линейных дифференциальных уравнений (16.1) с
действительными постоянными коэффициентами. Пусть характеристическое
уравнение соответствующей системы возмущений (16.2)
написано в виде (16.3), т. е. с коэффициентом при гп, равным 1.
Тогда для того, чтобы все движения класса (16.1) были
асимптотически устойчивы по Ляпунову, необходимо и
достаточно, чтобы коэффициенты характеристического уравнения
(16.3) удовлетворяли условиям (16.7), т. е. чтобы все главные
диагональные миноры матрицы Рауса—Гурвица (16.6),
построенной для характеристического многочлена системы
возмущений, были строго положительны.
Справедливость этого признака непосредственно вытекает
из теоремы 2 этого параграфа и критерия I § 13.
196
Пользуясь условиями (16.7), можно найти область
асимптотической устойчивости движений класса (16.1) в пространстве
коэффициентов Аи Л2,..., Ап характеристического уравнения
(16.3).
Пример. Пусть класс движений описывается системой
уравнений
z1 = z1 — z2 + az3 + Д (t)
z2 = 2z1 — 2z2 — z3 + f2(t)
z3 = Zi + 2z2 + /з (О
(16.9)
где а — параметр, не зависящий от времени.
Выяснить, при каких значениях а движения заданного класса
асимптотически устойчивы по Ляпунову.
Решение. Пишем систему возмущений для движений
класса (16.9):
Хл Хл
' %2 "Т" ®%3
Х2 — ZdX-i £Х2 Х3
#3 = %1 \ ™2
Согласно § 12 характеристическое уравнение этой системы
имеет вид:
|(1—г) —1 a
2 —(2 +г) — 1 | = 0
1 2 —г
или в развернутом виде
г3 + г2 + (2 — а) г — (6а + 3) = 0
Аг = 1, А2 = 2 — а, А3 = — 3 (2а + 1).
Выше мы видели, что при п = 3 критерий Рауса—Гурвица, а
значит и признак асимптотической устойчивости принимают вид
(16.8).
В нашем примере первое из этих условий уже выполнено, а
два остальные сводятся к следующим:
(2 —a) + 3(2a+l)>0
— 3(2a+l)>0
т. е.
5а + 5 > 0
2а + 1 < 0
откуда
а<
197
Эти неравенства не противоречивы и их можно объединить в
одно двойное неравенство —1<а< —.
В полученном интервале значений а движения класса (16.9)
асимптотически устойчивы по Ляпунову.
§ 17. ЛИНЕАРИЗАЦИЯ СИСТЕМЫ ВОЗМУЩЕНИЙ
1. О формуле Тейлора — Маклорена и ряде Тейлора—Маклорена
для функций двух и нескольких переменных
Предварительно сформулируем некоторые общие
определения, связанные с областями любого числа измерений.
Область G\ называется звездообразной относительно своей
внутренней точки Л, если прямолинейный отрезок, соединяющий
точку А с каждой внутренней точкой области Gu целиком лежит
внутри G\.
Область G2 называется выпуклой, если прямолинейный
отрезок, соединяющий каждые две внутренние точки области G2,
целиком лежит внутри G2. Очевидно, выпуклая область
является звездообразной относительно каждой своей точки.
Сначала кратко изложим доказательство формулы Тейлора
для функции двух переменных. Подробное доказательство
дается в {2], ч. II, гл. XI, § 1, п. 155 (170), а схема другого
доказательства — в [7], гл. VIII, § 16.
Пусть задана функция f(x, у), которая в некоторой области
G плоскости х, у имеет непрерывные частные производные всех
порядков и всех комбинаций до (т+l) порядка включительно,
где т заданное целое положительное число.
Возьмем внутри области G какую угодно фиксированную
точку Л (а, 6), а переменную точку области G обозначим через
Р(ху у). Обозначим через GA ту часть области G, которая
звездообразна относительно взятой точки А\ в частности, GA может
совпасть со всей областью G.
В области GA мы представим функцию f(xt у) в виде
выражения, составленного из степеней разностей (я—а) и (у—Ь).
Поэтому для этих разностей удобно ввести краткие
обозначения: (x—a)=hf (y—b)=l, так что f(x, y)=f(a+h; b + l).
Для вывода формулы Тейлора временно фиксируем
произвольные значения /г, /, но так, чтобы точка P(a + ht b+l) лежала
внутри области GA} а затем возьмем вспомогательную
независимую переменную т и зависящую от т переменную точку
Q(x=a+hx', y = b + k).
198
При изменении т точка Q движется по прямой, проходящей
через точки А и P(a+h\ b+l).
Если т пробегает отрезок 0<т<1, то точка Q пробегает от- j
резок АР, очевидно, лежащий внутри области GAi а значит, и
внутри G. Поэтому для каждого положения точки P(a+h; b+l),
ВЗЯТОЙ Внутри GA, НаЙДуТСЯ ЧИСЛа Ti=Ti (Л, /) <0 И Т2 = Т2(Л, /) > 1 ;
такие, что при изменении т в интервале Ti<t<T2 точка Q будет \
пробегать интервал MAPN, лежащий внутри G.
Построим вспомогательную функцию переменной т: ф(т) —
=/(а+Ат; b + lx). В интервале ti<t<T2 функция ф(т)=/(я, у)
(поскольку х=а+кт, y = b+li) имеет непрерывные производ- \
ные до (т+1)-го порядка включительно: j
'1ММяХ^[тп) •Лх-*/*Х = 1,2,...|т+1,
где Cl = это биномиальные коэффициенты, т. е. чис- -
(k — k)\k\ ^ ;
ла сочетаний из Я элементов по &, и принято с£ = 1. j
Таким образом, в интервале Ti<t<T2 функция ф(т) может ,
быть представлена формулой Маклорена m-го порядка с оста- *
точным членом в форме Лагранжа, который выражается через |
значение (/и+1) производной функции ф(т) в некоторой точке :
вт, где 0<в<1: ;
5
ф (t) = ф (0) + уч^Ж т* + ф(т+1) w xm+K ;
W YW ' ^ ^! ^ (т + 1)!
Подставим в это равенство т = 1: ;
,(1).tro+2£a+^a. от..,;
Учтем, что при т=0 точка Q совпадает с точкой А (а, Ь), при \
т=1 точка Q совпадает с точкой P(a+h; b+l), так что |
ф(1)=/(а+А; b+l); значению т=Э соответствует некоторая!
точка S(a+hQ; b+lQ), лежащая на отрезке АР где-то между :
точками А и Р. Тогда равенство (17.1) можно переписать так: !
т к / я
«.+* »+о-/л»,+2[^(^5;)л^'] +
«+1
(«+!)!
•2^(5^)^"'- <•">
199 *
геэнртотнежАЬйывзкягуге'З' «jsw»v«»-k-*
Вспоминая, что h = x—a, l = y—bt перепишем это равенство так:
m-fl
Равенства (17.2) и (17.3) представляют собой различные записи
формулы Тейлора т-го порядка для функции f(x, у) в
окрестности точки А(ау Ь).
Если область G такова, что точку А можно взять в начале
координат, то формула Тейлора (17.3) превращается в формулу
Маклорена:
ЙL Я Йо \дх дУк /о.» -1
m+l
Н ! У! Сш+1 ( *" ^ 1 Jtm+'-V- (17.4)
Пусть при этом Р(х, у) есть произвольная точка области Go;
тогда S(Qx, Qy), где 0<8<1 — это некоторая промежуточная
точка отрезка ОР.
Последние члены в формулах (17.2), (17.3), (17.4)
называются дополнительными или остаточными членами формулы
Тейлора или соответственно Маклорена, записанными в форме
Лагранжа.
Если в области G функция f(x, у) имеет частные производные
всех порядков и всех комбинаций, то в звездообразных
областях GA и Go соответствующие формулы (17.3) и (17.4) могут
быть написаны для любого даже сколь угодно большого т,
а в области G могут быть написаны соответствующие
бесконечные ряды, которые называются рядами Тейлора и Маклорена
функции f(x, у).
Приведем формулировку теоремы о разложимости функции
в ряд Тейлора или Маклорена.
Для того чтобы в области DA функция f(x, у) была
разложима в ряд Тейлора:
«*-«*-/c.4+[(^-)uc-«o+(-f-X.«-4] +
1 U *f_\ ,,_я«±о/ d2f
200
2! |_\ дх2 Ja,b \ дхду Ja,b
(17.6)
+(fa.<*-»)!j+-+
или в области D0 f{x,y) была разложима в ряд Маклорена:
/м-/м+[(^+({у +
+±-\(щ *+2(-щ xy+im И + ...+
^ 2! [V ^2 /о.о \ длсву /о,о ^ \ dp /o,o J
m!^o Wm~V/o,o
необходимо и достаточно выполнение двух условий:
1) в области DA или D0f(x, у) имеет частные производные
всех порядков и всех комбинаций;
2) в области DA или D0 остаточный член соответствующей
формулы (17.3) или (17.4) стремится к нулю при т-+оо.
Для дальнейшего удобно несколько изменить символику.
Как известно, символы , означают действия однократ-
дх ду
ного частного дифференцирования по х и по у и называются
операторами однократного частного дифференцирования по х и по у.
Действия многократного частного дифференцирования можно обоз-
д д ~ дР
начать в виде степеней операторов и . Так, вместо
дх ду дхр
можно писать ) , вместо *— писать [ .
\дх J ' ду<* \ду J
«Умножение» функции на такие операторы, если они
написаны слева от функции, означает просто соответствующее
дифференцирование этой функции.
Например,
d«f(x,y)
(■£)-/(,, „-*£*. ffl,*.*
ду*
Если какие-нибудь функции написаны и справа и слева от
оператора дифференцирования, то это означает такой порядок
действий: сначала оператор действует на функцию, написанную
справа от него, а затем результат этого дифференцирования
умножается на функцию, написанную слева.
201
Например,
Если при этом у функции, написанной справа от оператора,
имеется нижний индекс, указывающий какую-либо точку, то
это означает, что в результат действия оператора на функцию,
написанную справа от него, т. е. в ее частную производную,
нужно подставить координаты указанной точки, а затем
полученное число умножить на функцию, написанную слева от
оператора, но в нее не делать этой подстановки.
С помощью этой символики можно запиеать общие члены
рядов (17.5) и (17.6):
т
k=o
1
•m—kfik __
аналогично записываются и остаточные члены формул (17.2),
(17.3), (17.4).
Эту символику особенно удобно применять к функциям
многих переменных.
Пусть в некоторой n-мерной области G задана функция
f(*u *2, ..., хп), имеющая в этой области непрерывные частные
производные всех порядков и всех комбинаций до (т+1)-го
порядка включительно. Обозначим через Р(х\, х2, ..., хп)
переменную точку области G.
Возьмем внутри области G какую угодно фиксированную
точку А (аи а2, ..., ап) и введем обозначение хх—а{ =/i^'= 1,2, ...,/г.
Образуем составной оператор
1 dxi 2 дхъ п дхп £л l dxt
Очевидно, действие этого оператора на функцию f(xu x2>..., хп)
состоит в нахождении первых частных производных этой функ-
202
ции, умножении их на соответствующие Ы и затем сложении
результатов,
т. е. !
или
(*"t+v£+-+Vsr)'-
= b*+h,JL + ...+KjL
oxi дх2 дхп
Рассмотрим целые положительные степени этого оператора
V * дхг ^ 2 дх2 ^ ^ п дхп J \ZJ l dXi J
Развернутые выражения таких операторов получаются так же,
как развернутые выражения степеней суммы п слагаемых: (
В звездообразной области Ga, содержащейся в G (или совпа- !
дающей с ней), при указанных условиях функция f(x\, #2, ... :
...,xn)=f(P) может быть представлена формулой Тейлора I
нр) - /и>+ [£<*,-*,) -J-] п+i|j> -ч ±рА+...
*=1 i=l
П
т+1
m! I ^-J4 l u dXi J 'A (m+1)! L^ <?*i J
гдеЯ^ + вЛь а, + вй2;...;ая + вйЛ) O<0<1-
это некоторая промежуточная точка отрезка АР.
Если точка А совпадает с началом координат пространства
хи Х2,..., хПу то формула Тейлора превращается в формулу
Маклорена
/т-/то+(2«£)/.+±(Б« £)■/.+
/=1 t=l
+ —!—fV*!-^ T+I/s, (17.7)
^ (m+1)! liiJ ' ддг, >/ 's' K
/=1
203
китлчб ягя^ггетал «•& ■аав.'чргы,- w» w&zb* «sis «&? .-««л i -i лк
где 5(8x1, 6x2,..., вхп) 0<6<1 — это некоторая промежуточная
точка отрезка ОР.
Доказательство этих формул проводится тем же методом,
как доказательство формул (17.2), (17.3), (17.4).
Если в области G функция f(x\, x2>..., хп) имеет частные
производные всех порядков и всех комбинаций, то для нее
можно составить соответствующий ряд Тейлора или
Маклорена. ,
Теорема о разложимости функции п переменных .в ряд
Тейлора или Маклорена вполне аналогична сформулированной
выше теореме для функции двух переменных.
Функция, которая в некоторой области DA разложима в свой
ряд Тейлора, называется аналитической в этой области.
2. Линеаризация системы возмущений.
Критерии устойчивости и неустойчивости
по первым приближениям
Пусть в n-мерной области G фазового пространства ги
22, ..., zn задан класс движений, который описывается
нелинейной нормальной системой дифференциальных уравнений
*j = Qi{t,zl9z2t...,2n) /=1,2 л, (17.8)
и пусть в области G для системы (17.8) выполнены все условия
теоремы существования и единственности частного решения.
Пусть одно из движений этого класса
*i = Ф1 (О
*2 = ф2 (О
фЛО
(17.9)
принято за невозмущенное движение.
Пусть в некоторой я-мерной области Gb которая содержит
внутри себя фазовую траекторию невозмущенного движения
(17.9), все функции Qj{t, zu z2,..., zn) /=1, 2,..., n имеют
непрерывные частные производные второго порядка всех комбинаций
по переменным zu z2,..., zn.
Как в § 9, напишем систему возмущений для класса (17.8)
относительно невозмущенного движения (17.9):
xj = Hj(tyxlix2f...ixn) /=l,2,...,n. (17.10)
Согласно замечанию 1 § 9 возмущения (17.10) могут быть
стационарными или нестационарными. Впрочем, для
нелинейной системы (17.8), которую мы сейчас рассматриваем,
возмущения (17.10), как правило, нестационарны, т. е. обычно в пра-
2 04
вую часть хотя бы одного уравнения системы (17.10) время tl
входит непосредственно.
Итак, в некоторой n-мерной области D, содержащей начало
координат фазового пространства х\9 #2,..., хп> система
возмущений (17.10) описывает, вообще говоря, нестационарное
движение. При движении системы координат Х(х\, #2, ..., хп)
область D должна все время находиться внутри области G\.
В силу условий, которым удовлетворяет система (17.8),
в соответствии с формулами (9.10) и (9.13) § 9 получаем
следующее: система возмущений (17.10) нелинейная; для правых
частей уравнений (17.10) выполняются тождества
Я,(*,0,0,...,0)а0 / = 1,2 я; (17.11)
в области D функции Hj(t, хи х2у ..., хп) У=1, 2,..., п имеют
непрерывные частные производные второго порядка всех
комбинаций по переменным х\, х2,..., хп.
В звездообразной области Do, которая содержится в
области D или совпадает с ней, представим правые части системы
возмущений (17.10) по формуле Маклорена (17.7) при т=1
только по переменным х\у х2у..., хПу несмотря на то, что эти
правые части зависят и от t. При этом напишем в развернутом виде
линейные члены, т. е. члены с первыми степенями x\t х2, ..., хп-
Hi(t9xl9x%9...9xn)=Hi(t909Q9...90) +
L \ dxi /'.о \ дх2 )t,o " л \ дхп До j
+
+ ^(^^ун^9хХ9х%9...9хп^ / = 1.2 я. (17.12)
/=i
Здесь индекс ty 0 означает, что частные производные взяты
dxk
при переменном t и в начале координат О пространства х1У х2, ...,
хПУ а индекс t9 Si указывает, что частные производные
dxk dxi
взяты при переменном t и в некоторой промежуточной точке
Sj(QjXlt 9,-*а,. . ., ByjtJ отрезка, соединяющего точки О и
г (Xi, Х2,..., Хп).
Введем краткие обозначения:
/dHJ\ /А / = 1,2, ...,л
п
~n(^lXi~hf Hj V'Хъx*'" •' x^,si=Rii V' *u x*'---' *J
j = l,2,...,n,
205
причем здесь индекс /1 написан потому, что им обмечен
остаточный член формулы Маклорена первого порядка для
функции Ну Используя эти обозначения и учитывая тождества
(17.11), перепишем равенства (17.12) так:
#; (<, хи **..., хп) = (ajXxx + aj2x2 + ... + fl*A) +
+ Rji(t,Xi,*i, ....*я) /== 1.2, ...,n. (17.13)
Подставим эти выражения в правые части уравнений
системы (17.10):
±, = (апхг + aj2x2 + ... +ajnxn) + Rjl(t9xl, x29...,xn)
/ = 1,2, ...,л.
Из равенств (17.13) ясно, что система уравнений (17.14)
представляет собой лишь другую запись системы возмущений
(17.10). В записи (17.14), как и в равенствах (17.13),
существенно то, что в них выделена линейная относительно
*ь х2, ..., хп часть функций Hj(t, x\, х2, ..., хп) и нелинейная
часть, заключенная в остаточных членах.
Теперь напишем новую систему дифференциальных
уравнений, которая получается из системы (17.14) путем отбрасывания
остаточных членов Rji(t, xu #2, -,хп) и изменения обозначений
искомых функций (| вместо х):
I,- = %£i + (*sJU + • • • + *3Лп / = 1, 2, ..., /г. (17.15)
Очевидно, система (17.15)—это система линейных
однородных дифференциальных уравнений.
Переход от нелинейной системы (17.10) к линейной системе
(17.15) называется линеаризацией системы возмущений (17.10).
Искомые функции в системах (17.10) и (17.15) обозначены
по-разному, потому что эти системы различны, неравносильны.
Это значит, что даже при одних и тех же начальных
возмущениях, которые здесь играют роль начальных условий
UO) = *i(0)=*io
1г(0) = х2(0) = х20
(17.16)
Ы0)=хп(0)=хп0 ]
соответствующие частные решения этих систем не совпадают,
Пусть начальным условиям (17.16) соответствует частное
решение системы (17.10):
*i = хх (t)
х2 = х2 (*)
(17.17)
206
и частное решение системы (17.15):
(17.18) j
При этом столбцы функций (17.17) и (17.18) не совпадают.
! Здесь функции (17.17) называются истинными возмущения- '
ми или возмущениями в целом, а функции (17.18) называ-'
i ются первым приближением к истинным возмущениям (17.17)
. или просто первым приближением.
Термин «приближение» здесь применяется потому, что в не- |
которых случаях, о которых кратко будет сказано ниже, функ- :
ции (17.18) действительно приближенно выражают функции ,
i (17.17). Термин «первое приближение» объясняется тем, что
при переходе от системы возмущений (17.10) к системе (17.15)
в правых частях оставлены только линейные части функций :
Hj(t, хи х2, ...,агп), т. е. только члены первой степени
относительно хи *2, •♦., хп. Ввиду этого сама система (17.15) называет- t
i ся системой первых приближений, так как каждое «
, ее частное решение является первым приближением к соответ- '
ствующим истинным возмущениям. '
I Если в л-мерной окрестности начала координат пространства ;
хи х2,...,хп (которая содержится в области Do или совпадает с^
ней) функции Hj(ty X\y х2, ..., хп) являются аналитическими, то,
| разлагая их в ряды Маклорена и затем отбрасывая все члены
; выше первой степени или выше второй степени, мы также полу-,
* чаем системы первых или вторых приближений. j
Невозмущенное движение (17.9) называется устойчивым'
(асимптотически или неасимптотически) в целом, если оно
устойчиво (соответственно асимптотически или неасимптотиче- *
j ски) по Ляпунову, т. е. если его устойчивость определяется пс '
/ общему решению системы возмущений (17.10), которое
выражает истинные возмущения.
Невозмущенное движение (17.9) называется неустойчи-
I вым в целом, если оно неустойчиво по Ляпунову, т. е. если
j его неустойчивость определяется по общему решению системы
возмущений (17.10), которое выражает возмущения в целом.
Невозмущенное движение (17.9) называется устойчивым!
i (асимптотически или неасимптотически) по первым при-(
I ближениям, если эта устойчивость определяется не по;
истинным возмущениям, а по общему решению системы пер- •
I вых приближений (17.15).
j Невозмущенное движение (17.9) называется
неустойчивым по первым приближениям, если эта неустойчи-
207
Х&Ы1ЖЯХ*Я.*7Ьг1Ь{!Ж~К-г/- I >Пе > -.^jfcj«m->r.--*-4JR3**ib-jLT ^M-.*rt5fc.5-^r
t.=lAt-)
вость определяется не по возмущениям в целом, а по общему
решению системы первых приближений (17.15).
Иначе говоря, определения устойчивости и неустойчивости
по первым приближениям получаются путем замены в
определениях устойчивости и неустойчивости по Ляпунову общего
решения системы возмущений общим решением системы первых
приближений.
Совершенно аналогично можно было бы составить определения
устойчивости и неустойчивости по вторым приближениям.
Возмущения называются стационарными в первом
приближении, если все коэффициенты
ОТм =а /= 1.2 л.
дхк До зк й = 1,2, ...,я
системы первых приближений не зависят от времени.
Возмущения называются нестационарными в
первом приближении, если хотя бы один из коэффициентов
системы первых приближений зависит от t.
Очевидно, если возмущения стационарны в целом, то они
стационарны и в первом приближении. Но если возмущения
нестационарны в целом, что как раз типично для нелинейной
системы (17.8), то возмущения в первом приближении могут
быть либо стационарными, либо нестационарными.
Линеаризацию системы возмущений полезно проводить по
следующим соображениям:
1) найти общее решение нелинейной системы возмущений,
как правило, не удается, а общее решение линейной системы
первых приближений либо легко находится (если возмущения
стационарны в первом приближении), либо поддается
некоторым методам анализа, которые мы здесь не излагаем;
2) в некоторых случаях по общему решению системы первых
приближений можно судить о поведении возмущений в целом
и, следовательно, об устойчивости или неустойчивости
невозмущенного движения.
Однако в некоторых случаях линеаризация может привести
к ошибочным или неполным выводам о характере
невозмущенного движения в целом (см. пример § 20). Поэтому для
практических приложений очень важно знать, при каких условиях по
поведению общего решения системы первых приближений
можно правильно судить об устойчивости или неустойчивости
невозмущенного движения в целом. Ответ на этот вопрос дают
результаты исследований, проведенных в основном А. М.
Ляпуновым [5].
Мы приведем без доказательства краткие формулировки тех
результатов, в которых содержатся критерии устойчивости и
неустойчивости невозмущенного движения в целом по
характеру первых приближений лишь для случая, когда возмущения
208
стационарны в первом приближении, т. е. когда в результате
линеаризации получается система линейных уравнений с п о-
стоянными коэффициентами:
1) если невозмущенное движение асимптотически устойчиво
по первым приближениям, то оно асимптотически устойчиво в
целом;
2) если невозмущенное движение неустойчиво по первым
приближениям вследствие того, что хотя бы один из корней
характеристического уравнения системы первых приближений
имеет положительную действительную часть, то оно
неустойчиво в целом;
3) если характеристическое уравнение системы первых
приближений имеет хотя бы один корень с нулевой действительной
частью (т. е. нулевой корень, либо чисто мнимые корни, либо и
нулевой и чисто мнимые корни) и не имеет корней с
положительной действительной частью, то по первым приближениям
нельзя правильно судить о характере невозмущенного движения
в целом.
В этом случае нужно пользоваться системой вторых приближений. Но
исследование ее решений даже в случае возмущений, стационарных во
втором приближении, проводится с помощью теории квадратичных форм,
которой мы не будем касаться в нашем курсе.
§ 18. ВТОРОЙ МЕТОД ЛЯПУНОВА.
ФУНКЦИИ ЛЯПУНОВА
Метод выяснения устойчивости или неустойчивости движения, в котором
требуется знать общее решение системы возмущений, называется первым
методом Ляпунова. Впрочем, мы знаем, что для анализа характера
движения, которое описывается системой линейных дифференциальных
уравнений с постоянными коэффициентами, достаточно знать не общее решение
системы возмущений, а лишь знаки действительных частей корней ее
характеристического уравнения (см. § 13—16).
Во втором методе Ляпунова, который будет кратко рассмотрен
в § 18—20, не требуется знать ни самого общего решения системы
возмущений, ни какой-либо характеристики этого решения. Это г метод основан на
так называемых функциях Ляпунова, которые строятся для каждой
исследуемой системы возмущений.
В этом параграфе мы составим само понятие функций Ляпунова и
выясним некоторые их свойства.
Мы будем рассматривать действительные функции в л-мерных областях
пространства Хи х2,...,хп, роль которого в дальнейшем будет выполнять
фазовое пространство возмущений.
1) Функция называется знакоопределенной в области, если ни
в одной точке этой области она не имеет значения нуль и во всей области
имеет значения только одного знака. Следовательно, функции, знакоопреде-
ленные в области, бывают положительно определенными и отрицательно
определенными.
2) Функция называется знакопостоянной в области, если в
некоторых точках этой области она имеет значение нуль, а в остальных точках
209
области имеет значения только одного знака. Функции, знакопостоянные в ,v
области, бывают неотрицательными и неположительными.
3) Функция называется знакопеременной в области, если в этой
области она имеет и положительные и отрицательные значения. -ч?
Эти общие определения относятся ко всем действительным функциям,
т. е. каждая действительная функция, взятая в некоторой области, является *
либо знакоопределенной, либо знакопостоянной, либо знакопеременной в этой •
области. Но при составлении понятий функций Ляпунова и особенно при их '
дальнейшем применении удобно пользоваться не этими общими
определениями, а несколько видоизмененными. i
Ввиду этого мы будем рассматривать только такие функции, которые
непрерывны в некоторых областях, содержащих начало координат
пространства *i, #2,..., хп, и имеют значение нуль в начале
координат. Тогда нужные нам видоизмененные определения выглядят так:
1°. Функция называется знакоопределенной в области, если она
имеет значение нуль только в начале координат, а в остальной области имеет
значения только одного знака. Функции, знакоопределенные в области,
бывают положительно определенными и отрицательно определенными.
2°. Функция называется знакопостоянной в области, если она
имеет значение нуль не только в начале координат, но и в некоторых других ^
точках области, а в остальной области имеет значения только одного знака. I
Функции, знакопостоянные в области, бывают неотрицательными и неполо- I
жительными. |
3°. Функция называется знакопеременной в области, если она |
имеет значение нуль в начале координат, а в остальной области имеет и по- \
ложительные и отрицательные значения. Очевидно, непрерывные
знакопеременные функции имеют значение нуль не только в начале координат, но и ;
на некоторых линиях или поверхностях, проходящих или не проходящих *
через начало. ";
Итак, всюду в дальнейшем мы будем пользоваться не определениями
1, 2, 3, а определениями Г, 2°, 3°.
Теперь мы дадим общее определение функций Ляпунова. %
Функциями Ляпунова называются функции переменных х\, *
хъ...»хПУ каждая из которых в некоторой я-мерной области, содержащей
начало координат пространства х\, Х2,...,хп, является знакоопределенной,
знакопостоянной или знакопеременной в смысле определений 1°, 2°, 3° и в ;
этой области имеет непрерывные частные производные первого порядка по
переменным xi, x2,..., хп. Функции Ляпунова принято обозначать через
У(хи х2 хп).
Отметим важнейшие свойства функций Ляпунова, вытекающие лишь из
непрерывности частных производных:
1) Каждая функция Ляпунова дифференцируема в рассматриваемой
области, т. е. в каждой точке этой области имеет полный дифференциал.
2) Обозначая через ei, e2,..., ert единичные векторы (орты) осей
Х\, х2'...,хп, можем написать:
'dV dV dV
grad У to, *„,..., xn)= -г—е!+-т—e2+ - + "ТГ"ея-
OXi OX2 OXn
Во всей рассматриваемой области градиент функции Ляпунова есть
непрерывная векторная функция. Напомним, что векторы градиента функции
направлены по нормалям к линиям или поверхностям уровня этой функции в г
сторону ее возрастания.
Заметим, что в некоторых вопросах приходится рассматривать
знакоопределенные, знакопостоянные и знакопеременные функции и функции Ля- *
пунова, зависящие не только от Хь х2,..., хп, но и непосредственно от време- |
ни t. Однако ниже мы почти не будем касаться вопросов, в которых исполь- 4
зуются функции Ляпунова, непосредственно зависящие от t. i
210 I
r-rv^»-<r>4j-'i?T-J>^-i> .jnp;vai гслЕйгднажкня
§ 19. ТЕОРЕМЫ ЛЯПУНОВА И ЧЕТАЕВА
ОБ УСТОЙЧИВОСТИ И НЕУСТОЙЧИВОСТИ ДВИЖЕНИЯ
1. Производная функции Ляпунова,
вычисленная в силу системы возмущений
Пусть в /г-мерной области G фазового пространства zit гъ .... zn задан
класс движений, который описывается нормальной системой
дифференциальных уравнений:
Zj = Qj(t, zlt z2l ...,zrt) /= 1, 2,...,/г, (19.1)
и пусть при всех t>0 в области G для системы (19.1) выполнены все
условия^ теоремы существования и единственности частного решения.
" Пусть одно из движений этого класса
*i = Ф1 (О
22=ф2(0
2/1 = фл(0 )
(19.2)
принято за невозмущенное движение.
. Напишем систему возмущений для класса (19.1) относительно невозму-
щеиного движения (19.2):
Xj = Hj(tt xltx2t ...,хп) /=1, 2 л.
(19.3)
Система возмущений (19.3) рассматривается в некоторой /г-мерной
области D, которая содержит начало координат пространства Х\, х&..., хп и при
движении координатной системы Х(хъ Х2,...,хп) все время находится внутри
области G.
В силу условий, которым удовлетворяет система (19.1), в соответствии
с формулами (9.10) и (9,13) § 9 при всех t> 0 в области D правые части
уравнений (19.3) обладают следующими свойствами: функции
Hj(t, Хи #2, ..., хп) /=1, 2, ..., п не только непрерывны, но и имеют
непрерывные частные производные первого порядка по Хи #2, ...» хп\ для этих
функций выполняются тождества:
Hj(t,0,0 0) = 0 /=1,2,...,п.
(19.4)
В области D система возмущений (19.3) также определяет класс
движений и, следовательно, определяет семейство траекторий этих движений, т. е.
семейство фазовых траекторий возмущений. Вместе с тем согласно § 7 при
t >0 в области D левые части, а значит и правые части уравнений системы
(19.3) определяют поле скоростей, направленное по касательным к фазовым
траекториям системы (19.3).
Возьмем какое-нибудь частное решение системы возмущений (19.3), т. е.
систему параметрических уравнений соответствующей фазовой траектории:
*i = *i(0 1
*2=*2(0
хп=хп (/)
(19.5)
211
т-т *жтзвяяяг&г *w«w*™iB-«i*:. ■■.
Обозначая, как выше, через еь е2,..., еп единичные векторы осей хи х2у...,хп
напишем выражения радиуса-вектора и вектора скорости точки K(t), движу-'
щейся по фазовой траектории (19.5):
г = *i (0 ех + х2 (0 е2 + ... + xn(t) ея,
г = xt (t) ei + i2 (/) е2 + ... + xn(t) e„. (19.6)
Чтобы выразить все поле скоростей системы (19.3) как векторную
функцию, определенную при *> 0 в области D, нужно в выражение (19.6) «место
Xi(t), x2(t), ...,xn(t) подставить правые части уравнений системы (19.3).
Тогда, обозначая эту векторную функцию через H(t, хь х2,...,хп)у выразим
поле скоростей системы (19.3) так:
п
H(t,xltx2t...,xn) = ^ Hi(ttxlix2 xn)tj. (19.7)
/=l
Пусть в области D задана какая-нибудь функция Ляпунова
V(xlt х2,...,хп).
Рассмотрим эту функцию на фазовой траектории (19.5) системы
возмущений (19.3), т. е. подставим в функцию V(xi, x2,...,xn) координаты точек
фазовой траектории, выраженные через t. При этом получится сложная
функция от t с промежуточными переменными х{, х2,...,хп:
V(t) = V[Xl(t)t хлф,~.,хпЦ)].
Найдем производную этой функции по t, пользуясь правилом
дифференцирования сложной функции, справедливым, как известно, для
дифференцируемой функции V(x\, x2,...,xn):
dV ( dV \ . / дП . f dV \
dt \ dxx ) K{t) \ dx, JKit) \ dxn J K(t)
Здесь индекс К(t) означает, что частные производные берутся в подвижной
точке K(t) траектории (19.5).
Выражение (19.8) называется производной функции Ляпунова
V(xu х2,...,хп) вдоль фазовой траектории (19.5) системы возмущений (19.3).
Теперь вместо X\(t), x2(t),..., xn(t), т. е. вместо проекций вектора
скорости на фазовые траектории (19.5), подставим в выражение (19.8) проекции
скоростей на всем семействе фазовых траекторий системы (19.3), т. е. проек-
3V
ции поля скоростей (19.7). Кроме того,—— /=1, 2, ..., п теперь возьмем не
OXj
в точках какой-то одной траектории, а в точке, как угодно перемещающейся
по области D. В результате этого из выражения (19.8) мы получим
Ш*вЁ-&гя'('-х1'* Хп)- (199)
7=1
Выражение (19.9) называется производной функции Ляпунова
V(xi, x2,...,xn) вдоль семейства фазовых траекторий системы возмущений
(19.3). Выражение (19.9) называется также производной функции Ляпунова
V(xi, х2,...,хп), вычисленной в силу системы возмущений (19.3).
( dV Л
В символе < > фигурные скобки и индекс D означают, что производ-
V dt ) d
ная функции Ляпунова берется не вдоль какой-то одной траектории, а вдоль
всего семейства траекторий, заполняющего область D.
212
Отметим важнейшие свойства функции < —— У . Из непрерывности фун-
I at )d
кций —— /=1,2, ... , п в области D и функций Hj(t, хх, х2, ... , хп)
OX j
( dV \
при t > О в области D следует, что функция \ —— > непрерывна при t >0
в области D,
Г аУ Л
В силу тождеств (19.4) функция \——V при всех t > О имеет значение
I at )d
нуль в начале координат пространства xlt х2 хп. Поэтому при / > 0 в
( dV Л
области D функция <——.— > является знакоопределенной, знакопостоянной
К dt ) d
или знакопеременной в смысле определений 1°, 2°, 3° § 18.
Г dV Л
Однако функция < —— > может не быть функцией Ляпунова в области D
( dt ) о
или в более узкой области. Если в некоторой области Dlt которая содержится в
области D или совпадает с ней и содержит начало координат, непрерывны
функции
d*V /=1. 2, ... , п
dx>dxk k=i9 2, ... , п,
( dV )
то можно проверить, что функция { \ является функцией Ляпунова в об-
\ dt }d
ласти Dv
Заметим, что если в функцию (19.9) вместо Х\, Х2,..., х п подставить
координаты (19.5) точки K{t), то получится функция (19.8). Поэтому свойства
функции (19.8) вытекают из свойств функции (19.9).
Ниже мы будем рассматривать функции Ляпунова V(xi, X2, ...,хп) и их
Л dt ]d
производные \ \ в областях специального вида, которые называются
{ dt )d
квадратными и кубическими е-окрестностями начала координат.
При п=2 рассматривается квадратная е-окрестность -начала координат,
т. е. квадрат, который вырезается на плоскости х\, х2 прямыми *i=±e и
*2=^:е. Квадратную е-окрестность начала мы будем обозначать краткой
записью \х12 К е.
При л=3 рассматривается кубическая е-окрестность начала, т. е. куб,
готорый вырезается в пространстве х\, х2, хг плоскостями xj — ±e j—h 2, 3.
Кубическая е-окрестность начала кратко обозначается так:
1*1,2,3 К8 или l*jl<e /=lt 2,3.
При п>3 кубическая е-окрестность начала — это л-мерный куб, конечно
не имеющий геометрической наглядности, который обозначается краткой
записью | xj\< e/=l, 2,..., п.
В дальнейшем, если в качестве области D будет взята квадратная или
кубическая е-окрестность начала координат, будем пользоваться обозначением
I dV \ ( dV\
{ ) вместо { }
\ dt je \ dt h
213
<n'-v»«?»-w.iMH--*:3^i
В следующем пункте мы увидим, что в определенных случаях сопостав-
( dV )
ление некоторых функций Ляпунова V(xb х2,...,хп) и их производных]-— >
позволяет выяснить характер невозмущенного движения (19.2), т. е.
характер равновесия точки в начале координат пространства х\, Х2,...,хпш
2. Теоремы Ляпунова и Четаева
Мы сформулируем теоремы Ляпунова и одну теорему Четаева, но в
несколько измененном и упрощенном виде по сравнению с тем, как они
изложены в самих работах Ляпунова [5] и Четаева [11]. Доказательства этих
теорем довольно сложны, и мы не будем их касаться.
Теоремы Ляпунова и Четаева относятся к классу движений (19.1),
невозмущенному движению (19.2) из этого класса и соответствующей системе
возмущений (19.3) при условиях, изложенных в п. 1 этого параграфа.
Первая теорема Ляпунова (об асимптотической устойчивости). Если для
некоторого положительного числа е (а значит и для всех меньших
положительных значений г) существует функция Ляпунова V= V(xu x2,..., хп), знако-
определенная в области \ Хг |<[е /=1, 2, ..,п, такая, что ее производная
[ dV )
{—— > , вычисленная в силу системы возмущений (19.3), является также
знакоопределенной в той же области и имеет знак, противоположный знаку
V, то невозмущенное движение (19.2) асимптотически устойчиво по Ляпунову.
Вторая теорема Ляпунова (о неустойчивости). Если для некоторого
положительного числа г (а значит и для всех меньших положительных
значений е) существует функция Ляпунова V=V(xi, X2,...,xn)t знакоопределенная
вычис-
( dV )
в области | Xj\ <е/=1, 2,...,/г, такая, что ее производная {~~"}7~| >
ленная в силу системы возмущений (19.3), является также
знакоопределенной в той же области и имеет знак, совпадающий со знаком V, то
невозмущенное движение (19.2) обязательно неустойчиво.
Третья теорема Ляпунова (об устойчивости). Пусть для некоторого
положительного числа е (а значит и для всех меньших положительных значений
г) существует функция Ляпунова ]/=У(*ь дг2>..., хп), удовлетворяющая
условиям:
1) в области 0<|*;- |<е /=1,2, ... , п gradV=£ 0:
2) в области \xj |< е /=1,2,... , п функция V знакоопределенная;
[ dV }
3) в области \Xj |< е /=1,2 п< —— > ,
т. е. производная функции V, вычисленная в силу системы возмущений
(19.3), либо знакопостоянная и имеет знак, противоположный знаку V, либо
hr}.s0-
Тогда невозмущенное движение (19.2) устойчиво по Ляпунову, причем в
(dV)
случае {—[ =£ 0 устойчиво, вообще говоря, неасимптотически, а в случае
( dt )е
m
/8
= 0 — обязательно неасимптотически.
Замечание. Эта теорема остается справедливой, если заменить
условие 1 одним из многих вариантов менее жестких условий, которых мы не
формулируем ввиду их сложности.
21^
г -«л? ••■•"* ■."'.' ч. - * /=t,-t-' B4 „?«£".№?, > ii^>wc*JK.^u. *
Теорема Четаева (о неустойчивости). Если для некоторого
положительного числа ei и для всех положительных чисел e<ei существует функция
Ляпунова V=V(xi, Х2,...,>п)> знакопеременная в области |*/|<е /=1, 2,..., п,
такая, что ее производная \ — \ , вычисленная в силу системы возмущений
\ dt )е
(19.3), является знакоопределенной в той же области, то невозмущенное
движение (19.2), вообще говоря, неустойчиво.
Замечание. Теоремы Ляпунова и Четаева содержат
достаточные условия соответственно устойчивости или неустойчивости
невозмущенного движения (19.2). С помощью этих достаточных условий во многих
случаях удается выяснить характер невозмущенного движения (19.2), не зная
общего решения соответствующей системы возмущений (19.3). Однако для
решения задач об устойчивости или неустойчивости движения с помощью
теорем Ляпунова и Четаева необходимо знать, существуют ли
соответствующие функции Ляпунова, нужные для применения этих теорем, и уметь строить
такие функции. Но сами теоремы Ляпунова и Четаева не отвечают на эти
вопросы. В этом состоит основная трудность применения второго метода
Ляпунова. Непосредственный подбор подходящих функции Ляпунова удается
сделать лишь в некоторых простых случаях. Впрочем, для многих задач об
устойчивости и неустойчивости движения по Ляпунову и в других смыслах
разработаны методы построения соответствующих функций Ляпунова.
Некоторые из этих методов изложены, например, в книге Красовского [4].
§ 20. ПРИМЕР ПРИМЕНЕНИЯ ТЕОРЕМ ЛЯПУНОВА
Пример.
Пусть класс движений описывается системой нелинейных уравнений:
2i = —Zf + Ozf|
i2 = Zl+azl J
(20.1)
Здесь а — параметр, не зависящий от времени.
Пусть в качестве невозмущенного движения взято состояние равновесия
точки, находящейся в начале координат:
^°Л - (20.2)
z2 = 0 J
Выяснить, устойчиво или неустойчиво это равновесие.
Решение. Применяя формулу (9.10) § 9 при <pi(t)= 0 и ^(t) = 0,
пишем систему возмущений, соответствующую невозмущеиному движению, т. е.
равновесию (20.2):
*1 = — *2 + аА )
з ' (20-3>
*2 = Х1 + аХ2 J
Очевидно, эта система также нелинейная, так как она отличается от системы
(20.1) лишь буквой х вместо г.
Мы не можем найти общее решение системы (20.3), по поведению
которого можно было бы выяснить характер равновесия (20.2).
Сначала проведем линеаризацию системы (20.3) и посмотрим, что это
даст для решения задачи. Заметим, что правые части уравнений системы
215
1 gi = *i0cos/ — #20sin/ |
J li = x10sint+ x20cost J"
(20.5)
(20.6)
(20.3) уже разложены в ряды Маклорена, только в каждом из этих рядов
лишь по два коэффициента отличны от нуля при а=£0. Линеаризация
сводится к отбрасыванию нелинейных членов ах\ и ах\, так что система
первых приближений выглядит так:
(20.4)
It = ii J
Найдем общее решение этой системы, что проще всего сделать, сведя ее
к одному уравнению второго порядка. Для этого продифференцируем,
например, первое из уравнений (20.4): |i = —Ъ и подставим g2=ei из второго
уравнения, после чего получим уравнение |i + ii = 0. Его характеристическое
уравнение г2+1=0 имеет корни rx^ 2 = ±I- Следовательно,
£i = Ci cos t + C2 sin / |
g2 = Ci sin / — C2 cos t J'
Это и есть общее решение системы первых приближений (20.4).
Начальным возмущениям #ю, #го соответствуют
Ci = #ю ) Si = #ю cos / — #20 sin t
C2 = #20
Очевидно, справедливы оценки
I 111 < l#lol +1*20 I
I It 1 < I #io I +1 #20 1
Поэтому если, задавая любое число е>0, подчинить начальные возмущения
8 8
условию |#ю |<-Г, |#2о1 < "Г у то при всех fe 0 будет | gi | < е, | g2|<e.
Это значит, что равновесие (20.2) устойчиво по первым приближениям,
причем обязательно неасимптотически, поскольку функции '(20,5) или (20.6) не
стремятся к нулю при t—>oo.
То же обнаруживается и по виду фазовых траекторий системы первых
приближений (20.4). Уравнение этого семейства получается путем возведения
в квадрат каждого из уравнений (20.5) и сложения результатов:
S?+El = c? + c|=c«.
Конечно, это же уравнение получается прямо из системы (20.4), если
разделить одно уравнение этой системы на другое:
dli — ?2
_ ^ отделить переменные:
^2 Si
li dli + £2 d>U = 0 и проинтегрировать: l\ + \\ = С2.
Покажем, что уравнение г2Н-1 = 0 является характеристическим не только
для уравнения ii + £i=0, но и для системы (20.4). Для этого действуем так
же, как в § 12 или в § 14, 15.
Ищем решение системы (20.4) в виде
216
После подстановки этих функций в систему (20.4) и сокращения на е1
лучаем
//
— гВх — В2 = 0 |
0 Г
Вх - гВ2
Эта система имеет ненулевое решение В\, В2 лишь при условии
-г -1
1 — г
-0, т. е. г2+ 1 = 0.
Получилось характеристическое уравнение системы первых приближений
(20.4), имеющее чисто мнимые корни rX2 = ±L Но в конце § 17 было сказа-
но, что именно в этом случае по первым приближениям нельзя правильно
судить о характере невозмущенного движения в целом.
Теперь для выяснения характера истинных возмущений, описываемых
системой '(20.3), воспользуемся вторым методом Ляпунова. Возьмем функцию
Ляпунова
v(*i. *■) = \(А+4)- <20-7)
Производная функции (20.7), вычисленная в силу системы возмущений
(20.3), выглядит так:
I — 1 = хх (— х2 + сиф + х2 (*! + ах\) = > (х\ + х\).
Ясно, что при а фд эта функция является знакоопределенной на всей
плоскости Хи Х2.
Поэтому поведение истинных возмущений, а значит и характер
равновесия (20.2) выявляются отдельно в каждом из трех случаев: а<0, а>0, а=0.
( dV )
1) а<0, V(x\, х2) положительно определенная, а \——\ отрицательно
» ( at )D
х\, X2. В силу перво
[ устойчиво по Ляпунс
2) а>0, V(xif x2) и J-——!- являются положительно определенными на
всей плоскости х\, х2. В силу второй теоремы Ляпунова равновесие (20.2)
обязательно неустойчиво.
f dV )
3) а=0, V(xu х2) положительно определенная, а<——> =0 на всей пло-
l at )d
скости х\у х2. В силу второго варианта третьей теоремы Ляпунова равновесие
(20.2) обязательно устойчиво неасимптотически.
Итак, мы видим, что только в третьем случае, т. е. при а=0, истинный
характер равновесия (20.2) совпадает с тем, что было обнаружено по первым
приближениям, а в двух других случаях, т. е. при а<0 и а>0, истинный
характер равновесия (20.2) коренным образом отличается от того, что было
получено с помощью линеаризации.
Мы рассмотрели один из так называемых примеров неправильного
применения линеаризации, т. е. примеров, в которых линеаризация приводит к
неполным и ошибочным выводам об истинном характере невозмущенного
движения. В то же время полные и правильные выводы мы получили с
помощью второго метода Ляпунова.
На этом мы заканчиваем изложение второго метода Ляпунова.
Заметим, что материал § 18—20 не входит в обязательную программу и
может быть изучен читателем добровольно.
217
определенная на всей плоскости х\, х2. В силу первой теоремы Ляпунова
равновесие (20.2) асимптотически устойчиво по Ляпунову.
Программа материала, после изучения которого
студент должен выполнить контрольное задание № 16
Тема «Системы дифференциальных уравнений и устойчивость движения
по Ляпунову»
1. О значении автоматического управления. Предварительное
представление об устойчивости и неустойчивости движения. Задача теории
устойчивости движения.
2. Определение системы дифференциальных уравнений. Система
дифференциальных уравнений в общем виде и в виде, разрешенном относительно
старших производных. Суммарный порядок системы. Нормальная форма
системы дифференциальных уравнений. Приведение системы к нормальной
форме. Система линейных дифференциальных уравнений.
3. Понятие решения системы дифференциальных уравнений. Решения
системы дифференциальных уравнений первого порядка: начальные условия,
частные решения; формулировка теоремы существования и единственности
частного решения; общее решение. Краткое изложение этих понятий для
систем высших порядков. Решение нормальной системы дифференциальных
уравнений путем приведения ее к одному уравнению более высокого
порядка.
4. Запись движения материальной точки в виде одного
дифференциального уравнения или системы дифференциальных уравнений второго или
первого порядка. Класс движений. Движение груза, подвешенного на пружине
при условии, что сила сопротивления и активная сила пропорциональны
скорости (рассмотреть случаи: сила сопротивления уравновешивается активной
силой, сила сопротивления превосходит активную силу и наоборот). Закон
радиоактивного распада. Электрический ток в простом LRCE контуре.
Химические реакции, скорости которых пропорциональны концентрациям
реагирующих веществ. Движение материальной системы как любой физический
пространственно-временной процесс (а не только механическое движение). Запись
движения материальной системы в виде системы дифференциальных
уравнений второго и первого порядков.
5. В примере движения груза на пружине рассмотреть понятия: реальные
движения и соответствующие им фиктивные движения изображающей точки,
фазовые траектории, интегральные кривые, фазовый портрет и фазовая
плоскость системы дифференциальных уравнений. То же в примере о химических
реакциях.
6. Рассмотреть в общем виде понятия: приведение системы
дифференциальных уравнений второго и первого порядков, описывающей класс движений
материальной системы к системе дифференциальных уравнений первого
порядка; реальные движения и соответствующие им фиктивные движения
изображающей точки, фазовые траектории, интегральные кривые, фазовый
портрет и фазовое пространство системы дифференциальных уравнений.
7. Поле скоростей, определяемое нормальной системой
дифференциальных уравнений. Стационарное (т. е. установившееся) и нестационарное
(т. е. неустановившееся) движение. Характер расположения интегральных
кривых и фазовых траекторий стационарного и нестационарного движения
в условиях теоремы существования и единственности частного решения.
Примеры.
8. Определения устойчивости и неустойчивости равновесия; пример:
твердое тело с одной неподвижной точкой выше или ниже центра тяжести.
Невозмущенное движение (реальное и фиктивное); начальные возмущения;
возмущенные движения и возмущения в последующее время как следствие
только начальных возмущений. Определения устойчивости, асимптотической
устойчивости и неустойчивости движения по Ляпунову. Пример устойчивого
и неустойчивого движения: движение груза на пружине из п. 4. Внешние
возмущающие воздействия, которые могут иметься при t>Q и изменять урав-
218
? ч1?* -. ?■«■„ -^ 1...П* „- КЧТЖТ«ЧМ J( -^ ™»WjrewW^E*J*Earen«i»MM!
нения движения; начальные возмущения, возмущения движения, возмущения
уравнений. Простейший вариант определений технической устойчивости и тех- ;
нической неустойчивости движения. ]
9. Преобразование системы, описывающей класс движений, в систему
возмущений; кинематическое толкование этого преобразования в фазовом
пространстве. Преобразование линейной системы движений в систему
возмущений. Пример. Стационарные и нестационарные возмущения. Определения :
устойчивости и неустойчивости движения по Ляпунову в терминах решения \
системы возмущений.
10. Правило раскрытия определителя любого порядка. Линейная
комбинация, линейная зависимость, линейная независимость столбцов; то же для
строк. Формулировки основных свойств столбцов и строк определителя и
квадратной таблицы.
11. Основные свойства решений нормальной системы линейных
однородных дифференциальных уравнений: теорема существования фундаментальной
системы решений и о форме общего решения, теорема о комплексном
решении (доказательства).
12. Нахождение общего решения нормальной системы линейных однород- \
ных дифференциальных уравнений с постоянными коэффициентами: состав- ;
ление фундаментальной системы решений (в случае простых корней
характеристического уравнения с доказательством; в случае кратных корней вид
ее дается без доказательства; в случае комплексных корней — переход кдей- ,
ствительным решениям), построение общего решения.
13. Критерии устойчивости и неустойчивости по Ляпунову движений,
описываемых нормальной системой линейных дифференциальных уравнений с
постоянными коэффициентами. (Критерии выражены через корни характери- \
стического уравнения системы возмущений.) Рассмотреть случаи: все корни
характеристического уравнения имеют отрицательные действительные части, '
хотя бы один корень имеет положительную действительную часть, имеется
простой нулевой и простые чисто мнимые корни, имеется кратный нулевой и !
кратные чисто мнимые корни, для которых п—«^=т^ и п—п#<.Щ
(доказательства). Обязательная устойчивость (асимптотическая и
неасимптотическая), обязательная неустойчивость движения; движение, вообще говоря,
неустойчивое (практически неустойчивое); движение, вообще говоря,
неасимптотически устойчивое; условная устойчивость (асимптотическая и
неасимптотическая). Критерии устойчивости и неустойчивости с учетом условной устой- -
чивости.
14. Критерии устойчивости и неустойчивости движений, описываемых
нормальной системой двух линейных дифференциальных уравнений с
постоянными коэффициентами (критерии выражены через коэффициенты
характеристического уравнения системы возмущений) — доказательства.
15. Примеры решения задач с помощью критериев п. 14. После разбора
этих задач студент может выполнять контрольное задание № 16
«Устойчивость движения по Ляпунову».
16. Необходимый признак асимптотической устойчивости движений,
описываемых нормальной системой линейных дифференциальных уравнений с ч
действительными постоянными коэффициентами (доказательство).
Формулировка критерия Рауса—Гурвица для многочлена. Необходимый и
достаточный признак асимптотической устойчивости движений, описываемых
нормальной системой линейных дифференциальных уравнений. Пример.
17. Формула Тейлора—Маклорена для функции двух переменных
(доказательство). Формулировка теоремы о разложимости функции двух
переменных в ряд Тейлора—Маклорена. Сокращенная символика для операторов .
частного дифференцирования. О формуле Тейлора—Маклорена и ряде Тей- ,
лора—Маклорена для функций нескольких переменных. Линеаризация
системы возмущений. Истинные возмущения или возмущения в целом и первые
приближения; система первых приближений. Определения устойчивости и
неустойчивости движения по первым приближениям. Формулировки Крите- ;
219 j
риев устойчивости и неустойчивости движения в целом по первым
приближениям для случая, когда в результате линеаризации получается линейная
система с постоянными коэффициентами.
Примечание. В программу включен материал, обязательный для
изучения. Этот материал изложен в § 1—17 предлагаемого пособия. При этом
материал, перечисленный в пунктах программы, содержится в параграфах
пособия с теми же номерами. В программу не включен материал § 18—20, а
также мелкий шрифт из § 2, 3, 5, 11, 17. Имеющиеся в тексте ссылки на
литературу (за исключением учебника И. И. Привалова [9]) принимать во
внимание необязательно.
Задачи для контрольного задания № 16.
«Устойчивость движения по Ляпунову»
Из приведенной ниже серии задач студент должен решить
одну задачу, причем последняя цифра номера этой задачи
должна совпадать с последней цифрой учебного шифра студента.
Каждая задача этой серии ставится так:
Постановка задачи
Пусть класс движений описывается системой уравнений вида
z1-a11(a,p)z1 + a12(a,P)z2 + /1(0 J
z2=a2l(a1$)z1+a22(a,$)z2 + f2(t) J
причем аир — параметры, не зависящие от времени.
а) При всех значениях аир выяснить характер движений
заданного класса, т. е. их устойчивость (обязательную,
условную, асимптотическую, неасимптотическую) или неустойчивость
(обязательную и вообще говоря).
б) Выяснить, при каких значениях аир возмущения имеют
колебательный характер.
в) При заданных фиксированных значениях аир выяснить
характер движений данного класса; если при этом возможна
условная устойчивость, то найти соотношение между
начальными возмущениями, при котором она получается. При
заданных начальных возмущениях хю, Хгэ найти возмущения как
функции времени.
Задачи
1) z1 = az1'+$z2 + f1(t)
z2 = — *\ + «z2 + /2 (t)
2) i1 = az1 + fa + f1(f)
z2 = azx + z2 + f2 (t)
a = — 3;
2
a = -l;
4
P = 4
1
*20- 5
P = 5;
2
220
3) 2i=«l + P2« + /i(0
i, = (2-P)«!+«,+/, (О
a = -i-; p = l;
*io —
^20
4) il = «K1 + {te, + A(0
2*a"=(p-2)z1-2az2 + /2(0
5) ii = «r1 + (te1 + /1(0
22 = (p-2)2l + aZi + /2(0
6) «! = «! +§z,+/!(*)
22 = (4-2p)z1-2az2 + /2(0
7) i1 = az1 + p22 + /1(0
22 = p21 + (4-2a)22 + /2(<>
8) «1 = cb1 + Pz, + /i(0
«=f; P = i;
4.0
*20
a = -4; P
•^10 — ^> ^
20
5
4
— f: P-4;
•£<>.n —
a =12; p = — 12;
1 __ 1
4 4
1 a = 8; p = —2,
22 = 9 (P -j- 4) 2l + 4 (a - 6) 22 + /2 (0 J *10=0,02; *20=0,03.
9)21 = a21 + p22 + /1(0 ) a = 3; P = -3;
2« = (P + 6)z1 + 3(o-4)214-/,(0J *io=l; *» = — !•
10)z1 = oz1 + Pz1 + /1(0
22 = (P + 6)2X+ А(а_4)22+/2(0
«=f; P = -3;
«^10 — ^> ^s
20
1.
Примечание. Образцы оформления работы даны при разборе
примеров в § 15. Однако объяснения по ходу решения должны быть значительно
короче, чем в § 15.
Принципиально правильный, достаточно крупный и четкий чертеж
следует сделать на странице 288X203 мм или 203X144 мм. При этом области
асимптотической устойчивости можно отмечать вертикальной зеленой
штриховкой, области обязательной неустойчивости — горизонтальной красной
штриховкой, области неасимптотической устойчивости — наклонной штриховкой
любого другого цвета.
221
Список литературы,
на которую имеются ссылки в тексте
{1] Г. Н. Берма н. Сборник задач по курсу математического анализа.
ГИТТЛ, 1956 г. и позже.
[2] А. Ф. Б ер мант. Курс математического анализа, ч. II. ГИТТЛ,
1955 г. и позже.
[3] Р. С. Г у т е р и А. Р. Я н п о л ь с к и й. Дифференциальные
уравнения. ГИФМЛ, 1962 г.
[4] Н. Н. К р а с о в с к и й. Некоторые задачи теории устойчивости
движения. ГИФМЛ, 1959 г.
[5] А. М. Ляпунов. Общая задача об устойчивости движения. ГИТТЛ,
1950 г.
[6] И. Г. Малки н. Теория устойчивости движения. ГИТТЛ, 1952 г.
[7] Н. С. П и с к у н о в. Дифференциальное и интегральное исчисления
для втузов. ГИФМЛ, 1961 г.
[8] Л. С. Понтрягин, В. Г. Болтянский, Р. В. Гамкрелид-
з е, Е. Ф. Мищенко. Математическая теория оптимальных процессов.
ГИФМЛ, 1961 г.
(9] И. И. Привалов. Аналитическая геометрия. ГИТТЛ, 1952 г. и
позже.
[10] В. В. Степанов. Курс дифференциальных уравнений. ГИТТЛ,
1950 г. и позже.
[11] Н. Г. Чет а ев. Устойчивость движения. Изд. 2. ГИТТЛ, 1956 г.
[12] Л. Э. Эльсгольц. Обыкновенные дифференциальные уравнения.
ГИТТЛ, 1950 г.
[13] К. А. К а р а ч а р о в, А. Г. П и л ю т и к. Введение в техническую
теорию устойчивости движения. ГИФМЛ, 1962 г.
г-"-*-ж<чЛ*К1№ у^а^я
СОДЕРЖАНИЕ
Предисловие ....■..■■.-••<••• jj
§ 1. Введение » 5
§ 2. Системы обыкновенных дифференциальных уравнений
(основные понятия) » 7
§ 3. О решениях системы дифференциальных уравнений ... 13
§ 4. Описание движений с помощью дифференциальных
уравнений - 23
1. Механическое движение материальной точки (23). 2.
Примеры движений, отличных от механического движения (31).
3. Движения материальной системы (37).
§ 5. Фазовые траектории и интегральные кривые (примеры) . . 39
§ 6. Фазовое пространство (общие определения) * 52
1. Случаи, когда п=2 и я=3 (52). 2. Обобщение на любое п
(60).
§ 7. Стационарное и нестационарное движения . 67
§ 8. Устойчивость и неустойчивость равновесия. Устойчивость и
неустойчивость движения 76
1. Устойчивость и неустойчивость равновесия (76). 2.
Устойчивость и неустойчивость движения по Ляпунову (80). 3.
Техническая устойчивость и неустойчивость движения (91).
§ 9. Преобразование системы, описывающей класс движений,
в систему возмущений . 95
§ 10. Об определителе любого порядка Ю8
§ 11. Основные свойства решений нормальной системы линейных
дифференциальных уравнений ....<-... ИЗ
§ 12. Нахождение общего решения нормальной системы
линейных однородных дифференциальных уравнений с
постоянными коэффициентами 120 *
§ 13. Критерии устойчивости и неустойчивости движений,
описываемых нормальной системой линейных дифференциальных
уравнений с постоянными коэффициентами (критерии
выражены через корни характеристического уравнения системы '
возмущений) 133 •
1. Критерии устойчивости и неустойчивости по Ляпунову (133).
2. Критерии устойчивости и неустойчивости с учетом условной
устойчивости (145). ;
§ 14. Критерии устойчивости и неустойчивости движений,
описываемых нормальной системой двух линейных
дифференциальных уравнений с постоянными коэффициентами
(критерии выражены через коэффициенты характеристического
уравнения системы возмущений) 149
§ 15. Примеры решения задач с помощью критериев,
полученных в § 14 , , 158
§ 16. Необходимый признак асимптотической устойчивости и
критерий Рауса — Гурвица т . > . 191
1. Необходимый признак асимптотической устойчивости
движений, описываемых нормальной системой линейных диффе-
223
ренциальных уравнений с действительными постоянными
коэффициентами (191). 2. Критерий Рауса — Гурвица для
многочлена. Необходимый и достаточный признак асимптотической
устойчивости движений (194).
§ 17. Линеаризация системы возмущений 198
1. О формуле Тейлора — Маклорена и ряде Тейлора — Макло-
рена для функций двух и нескольких переменных (198). 2.
Линеаризация системы возмущений. Критерии устойчивости и
неустойчивости по первым приближениям (204).
§ 18. Второй метод Ляпунова. Функции Ляпунова .... 209
§ 19. Теоремы Ляпунова и Четаева об устойчивости и
неустойчивости движения 211
1. Производная функции Ляпунова, вычисленная в силу
системы возмущений (211). 2. Теоремы Ляпунова и Четаева (214).
§ 20. Пример применения теорем Ляпунова 215
Программа материала, после изучения которого студент должен
выполнить контрольное задание № 16 ^ 218
Задачи для контрольного задания № 16. «Устойчивость движения
по Ляпунову» 220
Список литературы, на которую имеются ссылки в тексте . ! . 222
Анатолий Григорьевич Младов
СИСТЕМЫ
ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
И УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
ПО ЛЯПУНОВУ
Редактор М. Я. Зеликин
Редактор издательства А. #. Селиверстова
Технический редактор С. С. Горохова
Корректор Л. П. Тарасова
Переплет Б. А. Школьника
Т-00344 Сдано в набор 2/IX-65 г. Подп. к печати 5/II-66 г.
Формат 60x90l/ie« Объем 14 печ. л. Уч.-изд. л. 11,66 Изд. № ФМ-241
Тираж 28000 экз. Цена 51 коп. Зак. 849.
Тематический план издательства «Высшая школа»
(вузы и техникумы) на 1966 г. Позиция № 54.
Москва, И-51. Неглинная ул., д. 29/14,
Издательство «Высшая школа»
Типография Издательства МГУ. Москва, Ленинские горы