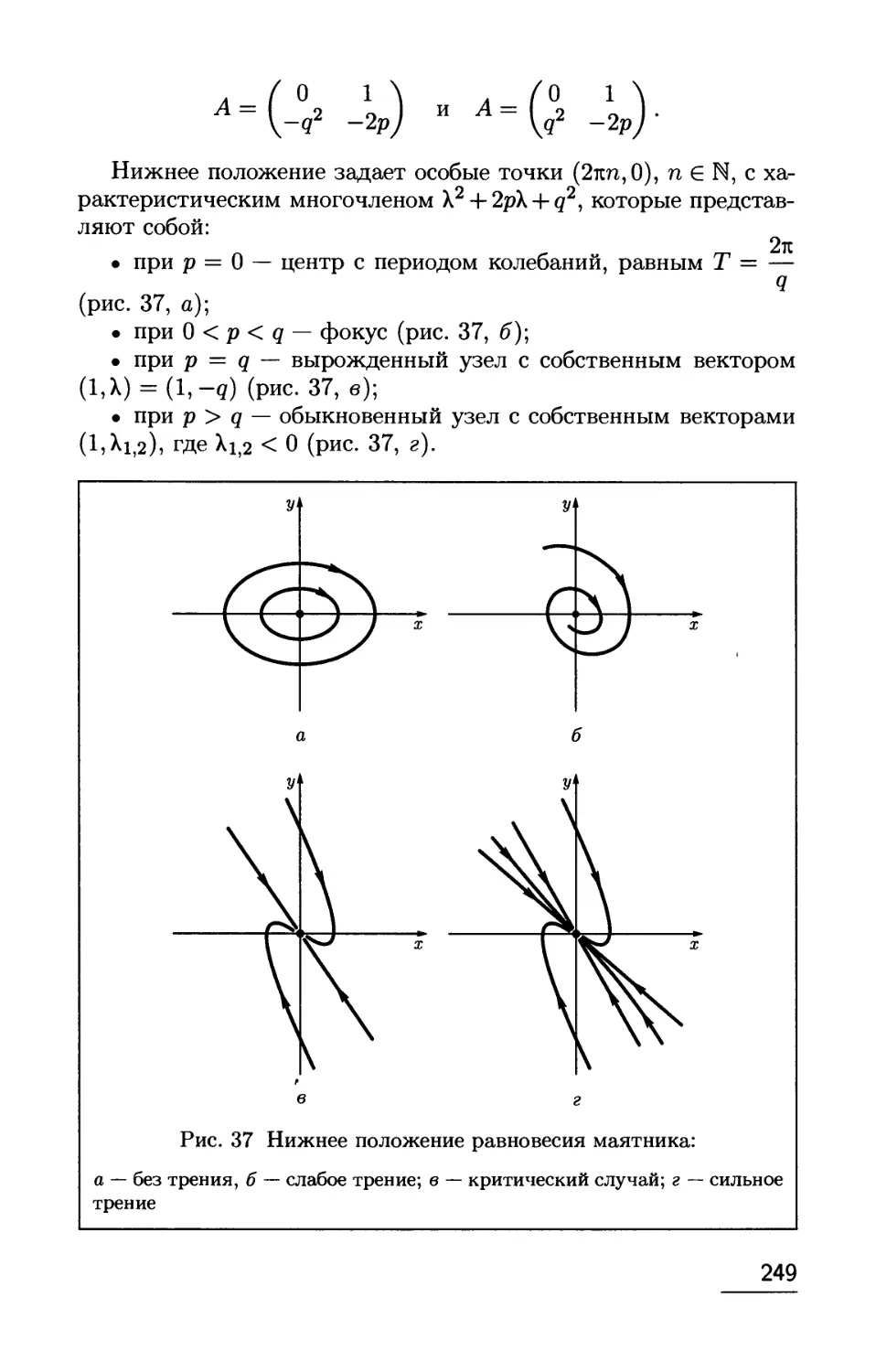
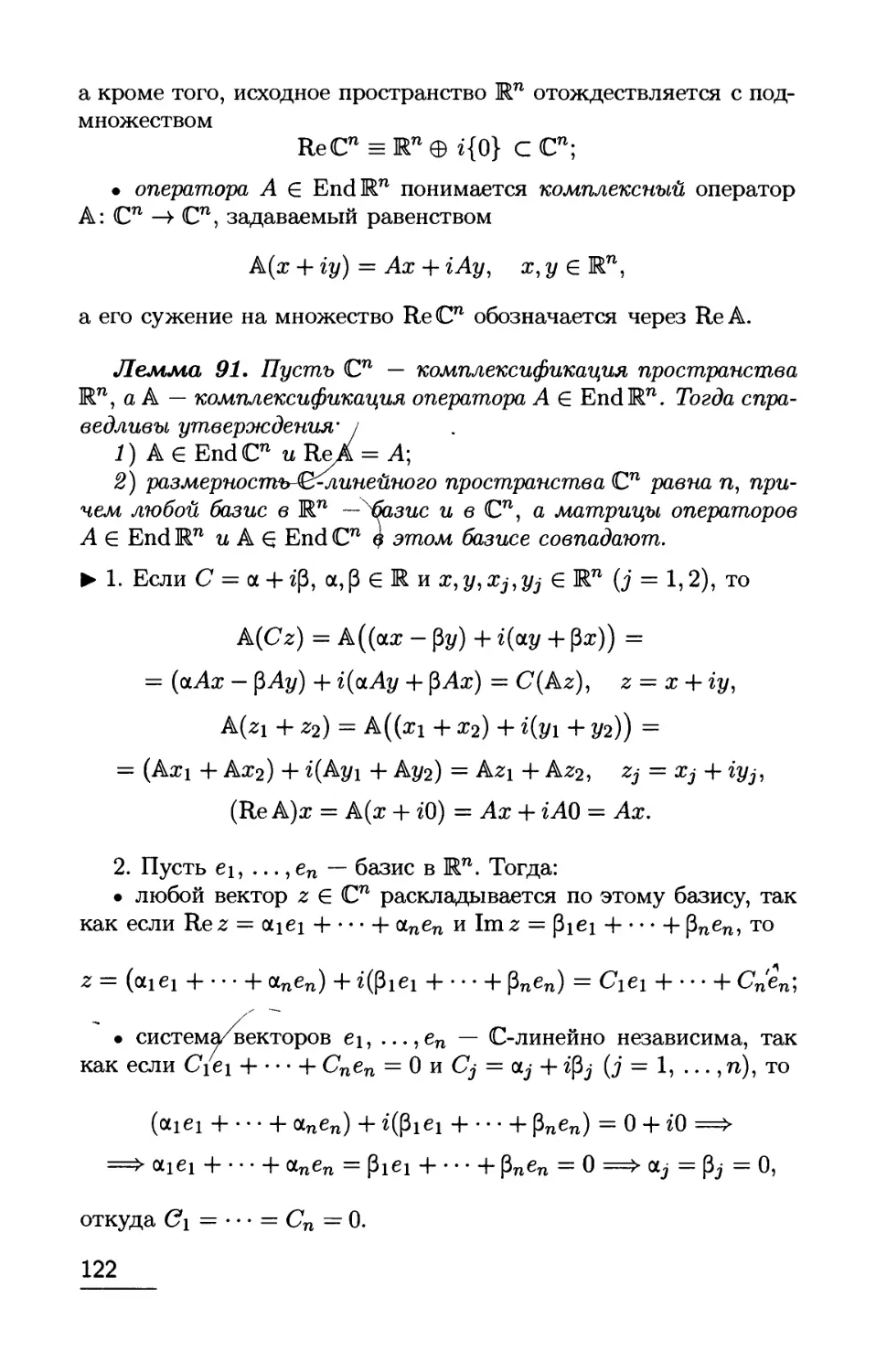Автор: Сергеев И.Н.
Теги: дифференциальные, интегральные и другие функциональные уравнения конечные разности вариационное исчисление функциональный анализ математический анализ математика информатика дифференциальные уравнения
ISBN: 978-5-7695-9606-3
Год: 2013
Университетский учебник
И. Н. Сергеев
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
Прикладная математика
и информатика
УДК 517.9(075.8)
ББК 22.161.6я73
С322
Рецензенты
д-р физ -мат наук, проф ГА Чечкин (кафедра дифференциальных уравнений
механико-математического факультета МГУ им Μ В Ломоносова),
д-р физ -мат наук, проф , акад РАН В А Ильин (зав кафедрой обшей математики
факультета вычислительной математики и кибернетики МГУ им Μ В Ломоносова)
Сергеев И. Н.
С322 Дифференциальные уравнения · учебник для студ.
учреждений высш проф. образования / И. Н. Сергеев. — М.:
Издательский центр «Академия», 2013 — 288 с. — (Университетский
учебник. Сер. Прикладная математика и информатика).
ISBN 978-5-7695-9606-3
Учебник создан в соответствии с Федеральным государственным
образовательным стандартом по направлениям подготовки «Математика»,
«Математика и компьютерные науки», «Механика и математическое моделирование»,
«Прикладная математика и информатика», «Фундаментальная информатика
и информационные технологии» (квалификация «бакалавр»)
Материал учебника знакомит с геометрической интерпретацией
уравнения первого порядка, с первыми интегралами, особыми точками и
предельными циклами автономных систем, с теорией линейных уравнений и систем,
в том числе с постоянными и периодическими коэффициентами, с
вопросами существования, единственности и продолжаемости решений, их
непрерывности и дифференцируемости по параметру, устойчивости по Ляпунову, а
также с вопросами существования и единственности решения задачи Коши
для уравнения с частными производными первого порядка Даны точные
определения, аккуратно сформулированы и доказаны утверждения, строго
обоснованы наиболее важные методы решения задач Приведены все
необходимые теоретические сведения, сопутствующие понятия и факты из смежных
разделов математики Предложены задачи для самостоятельного решения,
позволяющие глубже проникнуть в прочитанный материал
Для студентов учреждений высшего профессионального образования
УДК 517.9(075.8)
ББК22.161.6я73
Оригинал-макет данного издания является собственностью Издательского
центра «Академия», и его воспроизведение любым способом без согласия
правообладателя запрещается
© Сергеев И Η , 2013
© Образовательно-издательский центр «Академия», 2013
ISBN 978-5-7695-9606-3 © Оформление Издательский центр «Академия», 2013
ВВЕДЕНИЕ
в настоящий курс не может обойти стороной основное его
понятие — обыкновенное дифференциальное уравнение, т. е запись
вида
F(*,y,y',...,y<n>)=0. (1)
Не уточняя пока, откуда и куда действует функция F,
отметим лишь, что
• порядком уравнения (1) называется участвующее в его
записи значение η £ N (при условии, что последний аргумент
функции F не является фиктивным);
• переменная χ в уравнении (1), служащая первым
аргументом функции F, — скалярная1, а все остальные аргументы этой
функции могут быть и векторными, принимающими значения в
пространстве Ш.т (с одним и тем же значением т £ N).
I. Решение дифференциального уравнения. Запись (1)
приобретает смысл уравнения только после того, как
разъяснено, какой объект в нем является искомым.
Решением уравнения (1) назовем любую функцию
у: /->Rm,
определенную на каком-либо интервале2
I = (α,β) С R (α,β <Ξ Ш = {-оо} URU {+оо})
и удовлетворяющую тождеству
F (ζ, у (ζ ),/(*), ...,y(n)(*))=0, xel.
Интегральными кривыми уравнения (1) будем называть
графики его решений.
Именно поэтому уравнение (1) называется обыкновенным (в отличие от
уравнения в частных производных)
2Т е на открытом связном подмножестве / числовой прямой №. (в
дальнейшем буква /, как правило, будет обозначать интервал) Таким образом,
в настоящем курсе рассматриваются только классические решения
3
II. Общее решение. Обыкновенное дифференциальное
уравнение порядка η считается полностью решенным, если
найдено его общее решение, т. е множество всех решений, заданное
неявно уравнением
Ф(х,у,Сь ...,СП) = 0 (2)
или, что более предпочтительно, явной формулой
у = φ(χ,(7ι, . ..,СП).
При этом подразумевается, что.
• если запись (2) для какого-либо набора констант С\, ..., Сп
явно или неявно задает какую-либо функцию у = у (а;),
определенную на каком-либо интервале, то эта функция — обязательно
решение уравнения (1);
• и наоборот, любое решение уравнения (1) задается
уравнением (2) при некоторых значениях констант Ci, ... ,СП.
III. Обозначения и особенности нумерации. Здесь и
ниже одной и той же буквой, но разного начертания, обозначены и
переменные, и подставляемые вместо них функции, что
оправдано сходством самих объектов1. Так, переменным у,у',χ,χ,ζ,η...
в дальнейшем соответствуют функции у, у', х, х, z, u ...
Отметим, кстати, что производная функции по £, как
правило, обозначается точкой, а по а; или по какой-либо другой
переменной — штрихом.
Нумерация всех утверждений (лемм, теорем и следствий) —
сплошная, равно как и формул, а нумерация определений —
двойная, с номером главы впереди.
Значками ► и ■ всюду отмечены, соответственно, начало и
конец доказательства.
Некоторые разделы помечены звездочкой — это означает, что
при недостатке времени их позволительно изучать менее глубоко
(например, ознакомившись только с формулировками
утверждений, которые, возможно, подробно разбираются в других
математических курсах) или даже опустить совсем.
Кстати, в практических выкладках их обычно не различают вовсе
Глава 1
ПОЛЯ НАПРАВЛЕНИЙ
НА ПЛОСКОСТИ
1.1. Уравнение в дифференциалах
имеет вид
М(х, у) dx + N{x, у) dy = О, (χ, y)eGcR2, (3)
где функции Μ,Ν: G —> 1R нигде в области G не обнуляются
одновременно:
(М(х, у), N(x,у)) φ (0,0), (я,у) G G. (4)
Забегая вперед, поясним, что дифференциальное уравнение
более привычного вида
2 =/(*,»), (i,»)6C, (5)
является частным случаем уравнения в дифференциалах (3), в
котором коэффициент при dy отличен от нуля.
I. Поле направлений. С каждой точкой (х, у) Ε G свяжем
касательную плоскость1 Т(х,у) с координатами (dx,dy) (рис. 1):
ее начало координат совместим с точкой (х, у), а оси координат
будем считать параллельными соответствующим осям
координат области G.
Определение 1.1. В области G С R2 можно задать:
• векторное поле ν, т.е. отображение, которое каждой
точке (х,у) G G ставит в соответствие выходящий из нее вектор
v(x,y) еТ(Х)У);
1 Имеющую структуру векторного пространства
ν
У
,
/ \
Ν/φ(·
^s^ , ^4*ν^^
V dy
'ф(я.У)\
v(x,y)\
·>
Цъу)
! G
t,y)=o |
r\
\. £ Χ
Рис 1 Направление, нормаль и градиент в точке
• поле направлений11,те отображение, которое каждой
точке (х,у) Ε G ставит в соответствие проходящую через нее
прямую/(ж, у) ст(1)У).
Уравнение (3) естественным образом определяет в области
G следующее поле направлений /: для каждой фиксированной
точки (х, у) £ G само равенство (3), при условии (4), задает в
координатах (dx, dy) не что иное, как прямую, проходящую через
начало координат (т.е. графически через точку (х,у); рис. 1), —
ее и принимаем за прямую 1(х,у) поля направлений.
С уравнением в дифференциалах свяжем также еще и
векторное поле ν = (Μ,Ν), которое назовем полем нормалей,
поскольку для каждой точки (х, у) £ G вектор \(х, у) служит нормалью
к прямой 1(х,у).
II. Интегральная кривая. С геометрической точки зрения
решение представляет собой интегральную кривую, называемую
так именно по той причине, что само уравнение является
дифференциальным
Определение 1.2. Кривую Г С G назовем интегральной
кривой поля направлений / (или уравнения, задающего это
поле), если она в каждой своей точке (х,у) Ε Г касается прямой
1(х,у).
Правильнее было бы его назвать полем прямых, так как направления-то
на них как раз не указываются
6
В этом определении мы уже предполагаем, что кривая Г
имеет в каждой своей точке касательную. Более того, сузим
множество возможных интегральных кривых еще сильнее, а именно:
ограничимся только такими кривыми, которые задаются одним
уравнением1,
Г = {(х,у)еС'\ ср(*,у) = 0}, (6)
где скалярная функция φ £ С1 (С), определенная в некоторой
подобласти G' С G, имеет на Г ненулевой градиент
Vcp(z,у) = (φ'χ(α:, у), у'у{х,у)) φ 0, (ж,у) G Г.
Из курса математического анализа известно (в частности, в
силу теоремы о неявной функции), что*
• при указанных условиях множество точек (6) есть
действительно кривая2, которая локально, τ е. в достаточно малой
окрестности U С G любой своей точки (хц,уо), задается
уравнением у = у(х) или χ = х(у) в зависимости от того, какая из
производных (р'у(хо,уо) или φ^χη,ΐ/ο) отлична от нуля;
• касательная к этой кривой в каждой точке (х, у) £ Г
существует и задается в плоскости Т(х у) уравнением
dy{x, у) = φ'χ(ζ, у) dx + у'у(х, у) dy = 0;
• вектор V(?(x,y) Ε Т^ху^ являясь нормалью к последней
прямой, перпендикулярен к касательной (или, что по
определению то же, к самой кривой).
Лемма 1. Кривая (6) является интегральной для
уравнения (3) тогда и только тогда, когда в каждой ее точке (х,у)
векторы V(?(x,y) и v(x,y) параллельны, т.е. справедлива
пропорция^
ν'χ{χ,ν) - ν'υ{χ,ν) = М{х,у) : N(x,y). (7)
► Кривая Г (см. рис 1), задаваемая уравнением (6), касается
поля направлений / уравнения (3) тогда и только тогда, когда
в каждой точке (х,у) £ Г касательная к Г совпадает с прямой
1(х,у) или когда их нормали V(?(x,y) и v(x,y) параллельны. ■
1 Локально (вблизи любой точки (х, у) G Г) оно может быть получено,
например, исключением параметра t из системы χ = χ(ί), у = y(i)
2Возможно, не связная — и тогда речь идет о любой ее компоненте
связности
33аметим, что в этой пропорции допустимы и нулевые члены
7
III. Обыкновенное дифференциальное уравнение.
Если уравнение (3) удовлетворяет, например, дополнительному
условию1
N{x,y)^0, (i,i/)eG,
то с помощью операций деления2 оно преобразуется к виду (5),
где / ξ -Μ/Ν.
• С одной точки зрения, уравнение (5) по-прежнему остается
уравнением в дифференциалах, но теперь уже вида
f(x,y)dx-dy = 0,
и задает поле направлений, которое каждой точке (х, у) Ε G
ставит в соответствие заведомо невертикальную (т. е. не
параллельную оси ординат) прямую с угловым коэффициентом3, равным
dy/dx = f(x,y). Это поле задает свои интегральные кривые.
• С другой точки зрения, левую часть уравнения (5) можно
воспринимать и как самую настоящую производную4 у'
искомого решения — и тогда уравнение (5) превращается в
обыкновенное дифференциальное уравнение 1-го порядка, разрешенное
относительно производной.
Его решениями, по определению, служат всякие функции
у: / —> R, удовлетворяющие равенству
/(χ) = /(χ,γ(χ)), χ el. (8)
Это уравнение также задает поле направлений, ставя в
соответствие каждой точке (х,у) Ε G касательную к проходящему
через нее графику Гу решения у, причем угловой коэффициент
у'(х) этой касательной, согласно равенству (8), совпадает с тем
же числом f(x,y).
Итак, рассмотренные два взгляда на уравнение (5) приводят
к одинаковым полям направлений и различаются лишь способом
задания интегральных кривых, что фактически и подтверждает
Случай М(х,у) φ 0 рассматривается аналогично
2Если dx = 0, то, в силу уравнения (3), также и dy = 0, однако точку
(dx,dy) = (0,0) можно смело считать удовлетворяющей уравнению (5)
(воспринимаемому как пропорция; впрочем, потеря этой точки была бы здесь
не существенной)
Совпадающим, по определению, с тангенсом ориентированного (против
часовой стрелки) угла наклона к положительному направлению оси абсцисс.
4Хотя, по своему происхождению, она представляет собой просто дробь
8
Лемма 2. Если f Ε C(G), то кривая Г (6) является
интегральной для уравнения в дифференциалах (5) тогда и только
тогда, когда она служит графиком Гу некоторого решения у
дифференциального уравнения (5).
► В силу вышеизложенного остается только доказать, что
способы задания интегральных кривых при рассмотренных выше
двух точках зрения на уравнение (5) эквивалентны.
1. Пусть кривая Г (6) — интегральная для уравнения (5) в
дифференциалах. Тогда она служит графиком некоторой
функции у. Действительно:
• в силу пропорции
Ух(х,У) : Уу&У) = f{x,y) ■ (-1), fay) е Г,
имеем
фу(^2/)т^0, (ж,у)€Г;
• следовательно, по теореме о неявной функции уравнение
Ф,У)=0 (9)
в достаточно малой окрестности каждой точки (хо,уо) Ε Г
задает функцию у = у (ж), т.е. кривая Г локально (вблизи каждой
своей точки) служит графиком такой функции;
• но тогда и вся кривая Г в целом обязательно служит
графиком некоторой функции у, однозначно1 определенной на полной
проекции кривой на ось абсцисс.
2. Обратно, если функция у: / —>■ R — решение
дифференциального уравнения (5), то ее график Гу задается уравнением2
ф,у) = у-у{х)=0 (Vcp = (-y',l)^0),
т.е. записывается в форме (6). ■
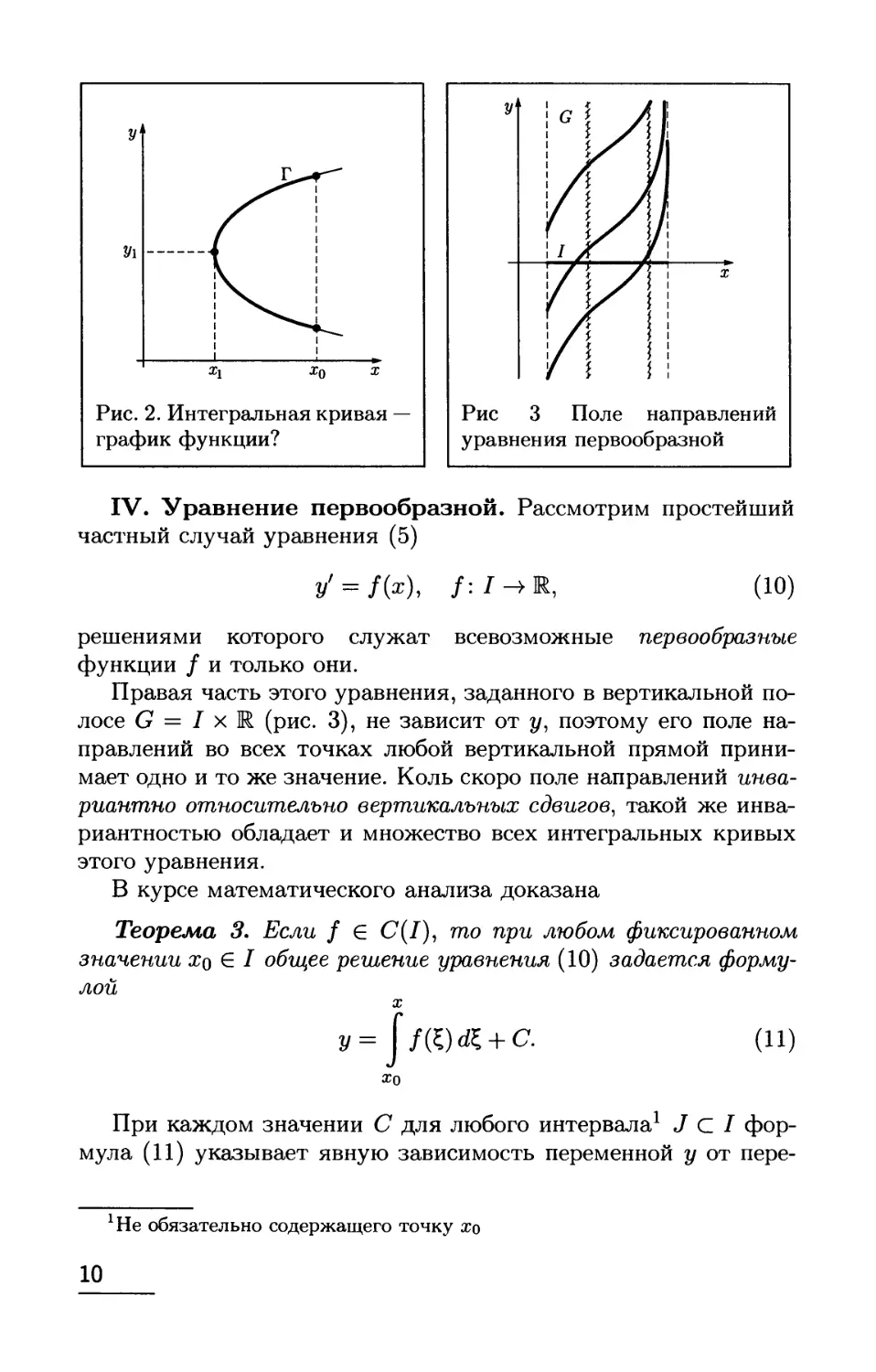
1 Действительно (рис. 2), если бы какие-то две точки кривой Г имели
одинаковую абсциссу хо, то на дуге кривой Г, соединяющей эти две точки,
нашлась бы внутренняя точка (xi,yi) с наименьшей или наибольшей
абсциссой х\ φ хо (например, самая левая на рис 2), а тогда уравнение (9)
не задавало бы функцию у = у(х) ни в какой полной окрестности точки х\
ввиду отсутствия точек дуги с одной стороны от нее
2В качестве области определения G' функции φ можно взять ту
компоненту связности открытого множества G(1(I x Ж), которая содержит график
Гу, а требование φ 6 С1 (С) выполнено, так как функция у' (8) непрерывна.
9
2/t
2/1
Рис. 2. Интегральная кривая
график функции?
у
Рис 3 Поле направлений
уравнения первообразной
IV. Уравнение первообразной. Рассмотрим простейший
частный случай уравнения (5)
j/ = /(x), /:/-HR,
(10)
решениями которого служат всевозможные первообразные
функции / и только они.
Правая часть этого уравнения, заданного в вертикальной
полосе G = I х R (рис. 3), не зависит от у, поэтому его поле
направлений во всех точках любой вертикальной прямой
принимает одно и то же значение. Коль скоро поле направлений
инвариантно относительно вертикальных сдвигов, такой же
инвариантностью обладает и множество всех интегральных кривых
этого уравнения.
В курсе математического анализа доказана
Теорема 3. Если f E С (I), то при любом фиксированном
значении х$ Ε / общее решение уравнения (10) задается
формулой
X
У =
J/го
άζ + C.
(И)
хо
При каждом значении С для любого интервала1 J С I
формула (11) указывает явную зависимость переменной у от
переде обязательно содержащего точку хо
10
менной χ £ J, определяющую решение уравнения (10), причем
никаких других решений это уравнение не имеет.
Таким образом, любая интегральная кривая уравнения (10)
совпадает с графиком функции (11), где χ £ /, или с его частью.
1.2. Общее решение
уравнения в дифференциалах ищется в виде линий уровня его
интеграла
I. Интеграл уравнения в дифференциалах. Ключевую
роль в решении уравнения (3) призвана сыграть скалярная
функция, принимающая постоянное значение вдоль каждой его
интегральной кривой (а не только вдоль одной, как в
формуле (6))
Определение 1.3. Функция φ £ C!(G) с ненулевым
градиентом называется интегралом1 уравнения (3), если в каждой точке
(х, у) £ G она удовлетворяет условию (7)
Любой интеграл φ уравнения (3) обладает следующими
свойствами:
• при каждом фиксированном значении С £ £(ср) любая
компонента связности2 множества φ-1 (С) точек (х,у) £ G,
удовлетворяющих уравнению
<Р(*,У) = С, (12)
есть именно кривая — так называемая линия уровня функции φ;
• любая линия уровня функции φ, согласно лемме 1, является
интегральной кривой уравнения (3);
• если две линии уровня функции φ соответствуют разным
значениям С, то они не имеют общих (и даже общих
предельных) точек в области G;
• через любую точку (хо,уо) £ G проходит ровно одна
линия уровня функции φ — а именно, та, которая соответствует
значению С = у(хо,уо).
II. Формула общего решения. Из теоремы 3 вытекает, что
интегралом уравнения первообразной (10), эквивалентного
уравнению в дифференциалах
1 Ср с первым интегралом автономной системы (см π 7 5)
2Которых, вообще говоря, несколько, причем разные компоненты
связности, по определению, не имеют в G общих предельных точек
11
dy = f(x) dx, (я, y) G G = I x R,
служит, например, функция
χ
ф,у) = у- jf(l)dl, (13)
χο
а интегральными кривыми этого уравнения служат линии
уровня этого интеграла (или их части) и только они.
Оказывается, последним свойством обладают все интегралы
любого уравнения в дифференциалах. Именно это и утверждает
Теорема 4· Если φ — интеграл уравнения (3), то его общее
решение задается уравнением (12).
► Исходя из свойств интеграла φ, для доказательства теоремы
остается лишь установить, что любая интегральная кривая Г
уравнения (3) совпадает с какой-либо линией уровня функции φ
или с ее частью. В самом деле:
• уравнение (3), в силу условия (7), переписывается в виде
ц'х(х, у) dx + ср'у(χ, у) dy = 0, (χ, у) G G;
• пусть (xo,yo) G Г, тогда без ограничения общности можно
считать выполненным, скажем, условие1
фу(^о,2/о) т^О,
а в силу непрерывности функции φ^ для достаточно малой
окрестности U точки (хо,уо) получаем неравенство
фу(я,2/) т^О, {х,у) G U;
• согласно лемме 2, уравнение (3) в окрестности U
записывается в виде
у' = -Шу {х'у)еи> (14)
и дуга Г(хо,уо) интегральной кривой Г, расположенная в
окрестности U, служит графиком Гу некоторого решения у = у(х);
• но тогда дуга Г(хо,уо) лежит на линии уровня функции φ,
т. е. для некоторой константы С имеем
ф|гу = С,
Случай ц>'х(хо,уо) φ 0 рассматривается аналогично
12
так как с учетом уравнения (14)
получаем
—(р(ж,у(ж)) = ([4(ж,у(ж)) +
+ φί(χ,γ(ι))/(χ) = 0, xeD{y)·
• наконец, из того факта, что
кривая Г локально (вблизи
каждой своей точки) совпадает с
какой-либо линией уровня
функции φ, следует, что она и в
целом содержится в некоторой
линии уровня1. ■
III. Уравнение в полных
дифференциалах. Важнейший частный случай уравнения в
дифференциалах и его интеграла описывает
Определение 1.4. Уравнение (3) называется уравнением в
полных дифференциалах, если существует его потенциал, т.е.
функция φ Ε CX(G), удовлетворяющая равенству
Vcp(s,у) = (М(х,у), N{x,у)), (ж,у) е G.
Например, уравнение первообразной (10) является
уравнением в полных дифференциалах, так как его интеграл (13) служит
одновременно и его потенциалом. Заметим, что:
• всякий потенциал уравнения (3) является его интегралом,
поскольку равенство в определении 1.4 влечет за собой
пропорцию (7);
• по большому счету, верно и обратное, т. е. всякий интеграл
φ уравнения (3) служит потенциалом другого уравнения,
получаемого из исходного уравнения (3) домножением обоих его
коэффициентов Μ и N на некоторый положительный
множитель2 μ: G —> IR, удовлетворяющий равенству
Действительно (рис 4), любая замкнутая дуга кривой Г с
концами (хо,уо) и [х\,у{) локально вблизи каждой своей точки принадлежит
какой-либо линии уровня, поэтому, в силу компактности этой дуги (по
лемме Гейне —Бореля), покрывается конечной цепочкой открытых дужек
Γι, . .,Γλγ некоторых линий уровня функции φ, последовательно
цепляющихся друг за друга, а значит, лежащих на одной линии уровня
Называемый, по понятным причинам, интегрирующим (см также
раздел III из п. 8.1 и раздел III из π 8.3)
Рис. 4. Вся интегральная
кривая
13
Vcp(s,у) = μ{χ,у) ■ (Μ{χ,у), Ν(χ, у)), {χ,у) e G;
• уравнение в полных дифференциалах с известным
потенциалом решается в соответствии с теоремой 4,
• левая часть уравнения в полных дифференциалах попросту
совпадает с полным дифференциалом его потенциала
dy(x, у) = Μ (ж, у) dx + Ν (χ, у) dy;
• для того чтобы уравнение в дифференциалах (3) с
коэффициентами Μ, Ν £ С1 (G) было уравнением в полных
дифференциалах, необходимо1 выполнение равенства
Му(х,у) = Nx(x,y), (x,y)GG, (15)
поскольку
M,Ne&(G) => ср'^еСЧС) => cpeC2(G)=>
=> Myix,У) = <?xyix,У) = φ£ζ(ζ,У) = Ν'χ(χ,у), (χ,у) e G.
IV*. Случай ветвления потенциала. Уравнение
-уах , xdy п ,_ _Л _ „_ш2
+ -TtS=°. (x,y)eG = R2\{(0,0)},
χ"2 4- 2/ ж + 2/
является уравнением в полных дифференциалах с потенциалом
φ, значение которого в точке (х,у) определяется как
ориентированный угол, образуемый радиус-вектором (х,у), например, с
положительным направлением оси абсцисс.
Действительно, левая часть уравнения в правой, верхней,
левой и нижней координатных полуплоскостях может быть
представлена, соответственно, в виде
I У Л Х , / У \ , / Х
d arctg -, α arcctg -, α ( arctg —h π , α arcctg —Ι- π
χ у \ χ ) \ у
И несмотря на то, что единой непрерывной ветви этого
потенциала во всей плоскости с выколотой точкой2 (0,0) не
существует, любые два потенциала данного уравнения локально вблизи
1А в случае односвязной области G — и достаточно, что доказано в курсе
математического анализа Более того, зачастую равенство (15) сразу
принимают за определение уравнения в полных дифференциалах
2Из-за чего плоскость перестает быть односвязной
14
любой точки проколотой плоскости отличаются друг от друга
на константу (аддитивную).
Поэтому множества линий уровня всех этих потенциалов по
существу одинаковы — они состоят из всех лучей, начинающихся
в выколотой точке. А значит, общее решение этого уравнения все
равно задается уравнением (12)
1.3. Автономное уравнение
имеет вид
У' = /(у), /:/->R, (16)
и задано в горизонтальной полосе G = Ш χ I.
I. Общее решение при отсутствии особых точек.
Уравнение (16) эквивалентно уравнению в дифференциалах
dy = f(y)dx.
Его поле направлений не зависит от х, а значит,
инвариантно относительно горизонтальных сдвигов, как и множество его
интегральных кривых (рис. 5).
Пусть на некотором интервале J С I нет особых точек1, т.е.
точек, в которых функция / обнуляется Тогда уравнение (16)
приводится к уравнению в полных дифференциалах
dx = -jt-t dy, {x,у) gG'eRxJ,
f(y)
и, в случае / £ С (J), имеет потенциал
у
ф,у) =х- I --г- {уо е J),
уо
задающий в области G' общее решение
у
χ
уо
=1т+в- <">
Векторного поля /
15
Заметим, что формула (17) действительно задает неявно
функцию у = у{х), поскольку на интервале J непрерывная
функция / не обнуляется, а значит, имеет на нем
фиксированный знак, следовательно, задаваемая формулой (17) функция
χ = х(у) монотонна и потому обратима.
II. Единственность при наличии особой точки. Пусть
некоторая точка a Ε I является особой, т.е. удовлетворяет
равенству
/(e) = 0.
Тогда прямая у — а заведомо служит интегральной кривой
уравнения (16).
Определение 1.5. Точка (хо,уо) £ G для уравнения (3)
называется:
• точкой существования, если через нее проходит хотя бы
одна его интегральная кривая;
• точкой единственности, если любые две его
интегральные кривые, проходящие через точку (хо,уо), локально (вблизи
(хо,Уо)) совпадают.
Если уравнение (3) имеет интеграл, то, в силу теоремы 4, все
точки области G — точки существования и единственности.
В рассматриваемом же здесь случае все точки прямой у = а
являются точками существования, а на вопрос, будут ли они еще
и точками единственности, дает ответ
Лемма 5. Если f E С(7), то для уравнения (16) любая точка
(х,у) G G — точка существования, причем:
• если у — неособая точка, то (х, у) — точка
единственности;
16
• если у = а — изолированная особая точка, то (х, у) —
точка единственности тогда и только тогда, когда расходятся оба
интеграла1
а±0
I
rfT1 (18)
т
► В силу вышесказанного для доказательства теоремы
остается лишь установить справедливость ее заключительного
утверждения. Пусть а — изолированная особая точка, для которой
выполнено, скажем, неравенство2
f{y) > 0, у0<У<а. (19)
Изучим поведение интегральных кривых вблизи произвольной
точки (xq, а) при у —> а — 0.
1. Пусть несобственный интеграл конечен (см. сплошную
интегральную кривую на рис. 5)
Jm - - «
УО
• Для некоторой функции х, задаваемой формулой (17),
имеем
а-0
х(а-0) = lim х(у) = —-\ + С\ = х\ 4- С\ = х0,
у-х*-о J /(η)
УО
как только С\ = xq — x\. А тогда для обратной функции у
получаем у(х) —> а — 0 при χ —> xq — 0. Поэтому через точку (xq, a)
проходит составная интегральная кривая, которая слева от этой
точки совпадает с графиком возрастающей функции у, а справа
идет по прямой у — а.
• Интегральная кривая, доопределенная по непрерывности
в точку (χο,α), имеет в ней горизонтальную касательную (т.е.
касается поля направлений): действительно, левосторонняя про-
1 Нижний предел интегрирования не указан, поскольку его значение, с
точки зрения сходимости интеграла, здесь не существенно (важно лишь, с
какой стороны от верхнего предела происходит интегрирование)
2Другие случаи исследуются аналогично.
17
изводная полученной функции у в точке xq равна следующему
пределу1
lim у'{х) = lim /(y(*)) = lim Ну) = /(а) = О,
х—>хо—0 х-»хо—0 у-»а—О
равному, как видим, нулю, а правосторонняя производная также
равна нулю, как производная от константы.
2. Пусть интеграл (20) бесконечен (см. штриховую часть
интегральной кривой на рис. 5). Тогда абсолютно все интегральные
кривые, идущие снизу от прямой у = а, приближаются к ней
лишь асимптотически при χ —> со, не имея с ней общих
предельных точек. Поэтому в точке (χο,α), точнее с нижней стороны от
нее, единственность не нарушается. ■
III. Дифференциальный признак единственности.
Одним из простейших, но, как оказывается2, перспективных
способов обеспечения локальной единственности решений уравнения
(16) является предположение самой обыкновенной дифференци-
руемости его правой части в особых точках, как показывает
Следствие 6. Если f E С(7) и в изолированной особой
точке a Ε / существует производная f'{a), то для уравнения (16)
все точки прямой у = а — точки единственности.
► При указанных в этом следствии условиях интегралы (18)
расходятся. Например3, в случае (19) из равенства
f(a + h) = /(α) + f(a)h + o(h) = f(a)h + o(h), h -> 0,
обозначив Le |/'(o)| + 1, для некоторого ho > 0 получаем
0 < /(α - h) < \f'{a){-h)\ + \o{-h)\ < Lh, 0 < h< /i0,
откуда имеем
α—0 ho ho
dh
= CO,
f _ώ)_= С dh Г
J /(η) J /(α - fc) - J Lh
a-ho 0 0
и остается только воспользоваться теоремой 5.
αΒ силу факта его существования (теорема из курса математического
анализа)
См теорему 9 далее.
3Остальные случаи рассматриваются аналогично.
18
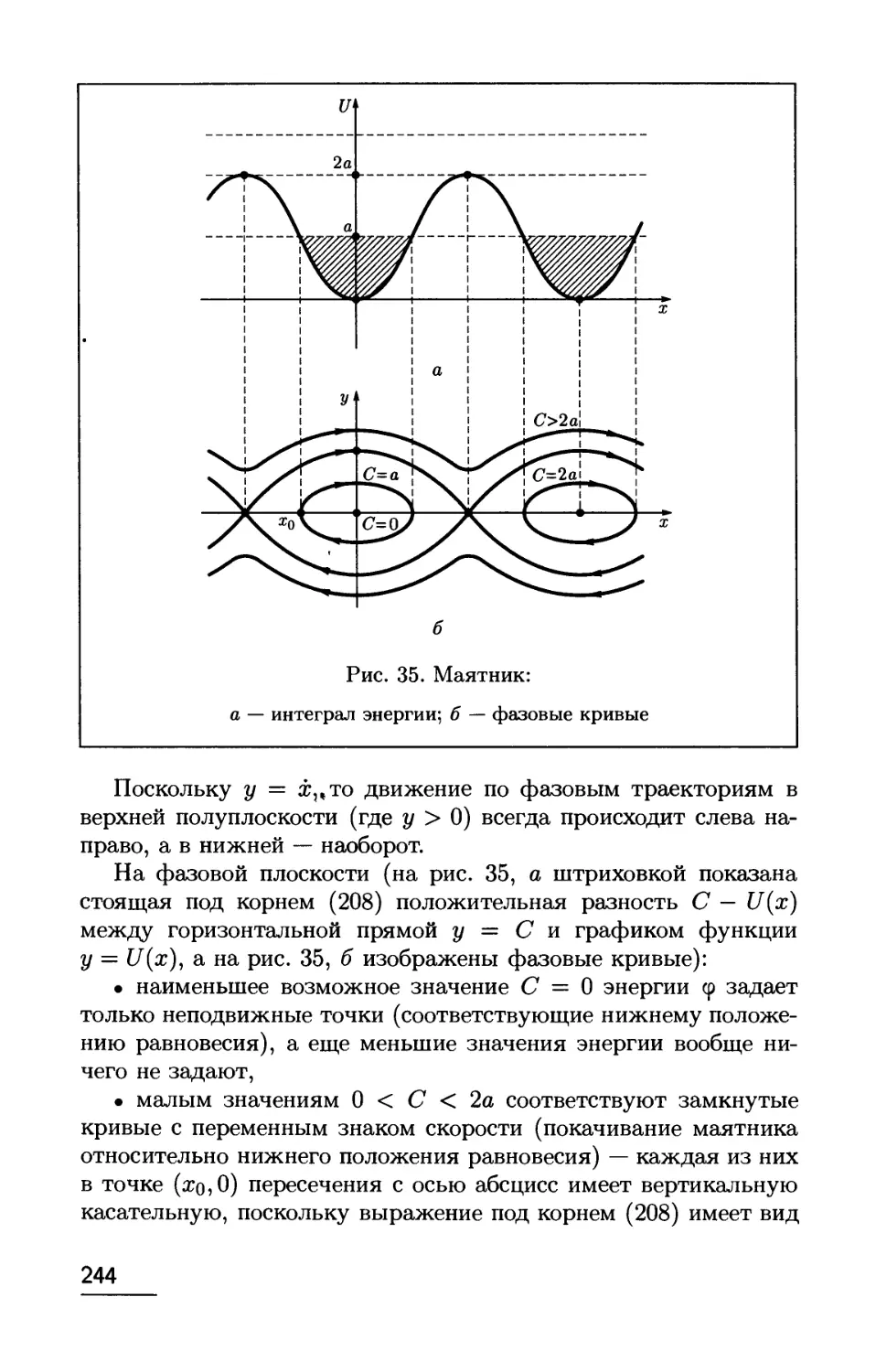
У'
у,
Уо1
^^^«. X
а
\\..
Xq X
б
Рис. 6. Убывание решения к нулю.
α — экспоненциальное; б — квадратичное
IV. Характерные примеры. Для разных эволюционных1
уравнений вопросы единственности решаются по-разному.
• Уравнение остывания тела
у' = -ку (*>0), (x,y)eG = R2,
в окружающей среде, температура которой поддерживается
равной нулю, задает температуру у = у(х) тела в момент χ при
начальном условии у(0) = Уо> 0 следующим равенством
_1<Ь\-}пУ ^ . -кх
ί
уо
кх = —- = In — <=> у = уое~
Уо
Здесь точки существования и единственности заполняют всю
плоскость, так как интегралы (18) расходятся: это означает, что
тело никогда не остынет до температуры окружающей среды
(рис. 6, а).
• В уравнении вытекания жидкости
y' = -ky/y (fc>0), (x,2/)gGeRx[0;oo),
исследуется, как функция от времени х, высота у = у(х) уровня
жидкости, вытекающей из сосуда через отверстие в его дне. Это
уравнение при условии у(0) = уо > 0 имеет решение,
определяемое формулой
*В которых (в частности, автономных) скорость изменения изучаемой
величины есть функция от самой этой величины, а также, возможно, от ее
производных по каким-то другим, не временным, переменным
19
У 2
Ι (ΊΎ\ ί ΚΎ\ η Τ*
-kx = Ι -д = 2(y/y - y/yS) <=*у= ( л/5о- γ ) > γ < л/δθ-
У0
Из нее видно, что вода полностью вытекает из сосуда за
конечное время (интеграл (18) здесь сходится), поэтому точки
интегральной кривой у = 0 не являются точками единственности:
указанное решение, обратившись в нуль в тот момент xq, когда
кхо = 2у/уо, далее уже совпадает с нулевым (рис. 6, б).
1.4. Уравнение с разделяющимися переменными
имеет вид
P{x)Q(y)dx = R{x)S(y)dy, P,R: /-► R, Q,S: J ^ R,
(21)
и задано в любой области
G с {(х,у) е / х J | (P(x)Q(y),R(x)S(y)) φ (0,0)}, (22)
а в случае обыкновенного дифференциального уравнения —
записывается в виде
y' = f{x)9(y), /:/->R, g:J^R.
I. Разделение переменных. Область G (22) по
определению не содержит ни одной точки (хо,уо), удовлетворяющей
сразу двум равенствам
R{x0) = 0, <2Ы = 0.
Тем не менее каждое значение х$ или у о, удовлетворяющее в
отдельности первому или второму из этих равенств, порождает
интегральную кривую χ = xq или у = yQ.
Рассмотренные ранее уравнение первообразной (10) и
автономное уравнение (16) служат примерами уравнения с
разделяющимися переменными. А оно, в свою очередь, разделением
переменных (см. доказательство теоремы 7 ниже) сводится к
уравнению в полных дифференциалах.
Из теоремы 4 вытекает
Теорема 7. Если P,Re C(I) и Q,S e C(J), а функции Q, R
не имеют нулей, то для уравнения (21) в области G (22):
20
• при любой фиксированной точке {хо,уо) Ε G общее
решение задается уравнением
хо уо
• все точки области G — точки существования и
единственности.
► Действительно, в области G уравнение с разделенными
переменными
М(х) dx + N(y) dy = О,
имеющее коэффициенты
равносильно исходному (так как их поля направлений
одинаковы) и является уравнением в полных дифференциалах с
потенциалом
χ у
^{x1y) = JM{l)dJi + JN{ii)d!i.
ХО УО
Поэтому к нему непосредственно применима теорема 4. ■
II. Однородное уравнение. Так называется уравнение,
которое имеет вид
У' = f (УΜ (24)
и задается в какой-либо из областей (секторов плоскости)
G = {(x,y) |ж>0, y/xel}
или
G = {(x,y) \x<0, у/х el}.
Правая часть этого уравнения зависит только от отношения
у/х, а потому его поле направлений во всех точках одного луча,
выходящего из начала координат, принимает одно и то же
значение, т. е. оно инвариантно относительно гомотетий с центром
(0,0) (рис. 7, а). Этим же свойством обладает и множество
интегральных кривых уравнения (24).
С помощью замены переменной у на
ζ = у/х (25)
21
У
*
4г Ж
4Г Ж
'Ж Ж и
у Ж Ж***^
У ,
У J
/ Ж*
-h
"У φ»
' χ
-^ G
а
Рис. 7. Замена переменных
а — сектор; б -
Zk
I
.-LL—D.x
6
в однородном уравнении
- полуполоса
(которая при подстановке у = у(х) и ζ = ζ(χ) задает зависимость
между функциями у и ζ) уравнение (24) сводится к уравнению
с разделяющимися переменными в том смысле, какой
подразумевает
Лемма 8. При переходе от переменных х,у к переменным
χ, ζ, связанным соотношением (25), все решения уравнения (24)
переходят в решения уравнения
*' = ^, g(z) = f(z)-z, z el, (26)
Ju
и наоборот.
► Действительно, замена (25) связывает старую функцию у и
новую функцию ζ (с общей областью определения J)
соотношением
у(х) = χζ(χ), χ Ε J,
поэтому верна цепочка эквивалентных утверждений
/(х) = / (уМ) <=* {хф))' =
= / (^) <=► xz'(x) = g(z(x)),
первое и последнее из которых означают, что функции у и ζ
являются решениями уравнений (24) и (26) соответственно. ■
III*. Геометрический смысл замены переменных.
Соотношение (25) можно интерпретировать и как формулу,
задающую отображение (рис. 7, а, б)
22
φ: G-> DeK+ χ I (ИГ х /),
которое каждой точке (х, у) Ε G ставит в соответствие точку
(χ,ζ) = у(х,у) = {х, у/х) е D.
При этом отображении каждая кривая сектора G переходит в
кривую полуполосы D, а интегральная кривая уравнения (24) —
в интегральную кривую уравнения (26), о чем и свидетельствует
лемма 8.
Задачи для самостоятельного решения
1. Могут ли два разных уравнения вида (3) задавать одинаковые
поля*
• нормалей,
• направлений7
2. Верно ли, что если функция φ € С1 (G) с ненулевым градиентом
постоянна вдоль каждой интегральной кривой уравнения (3), то она
есть интеграл этого уравнения?
3. Задает ли формула
X
у= j f(l)dl + C2
общее решение уравнения (10) первообразной? Каким недостатком
обладает эта формула?
4. Докажите или опровергните следующее утверждение
(аналогичное фактически установленному в процессе доказательства леммы 2).
если поверхность Г С (Ш2 χ R1) локально в окрестности каждой
своей точки (хо,уо) € Г служит графиком функции у = у(я), то опа и в
целом служит графиком некоторой такой функции.
5. Какое наибольшее количество не равных локально друг другу
интегральных кривых можно провести через точку прямой у = α в
формулировке теоремы 5, если:
• сходится ровно один из двух интегралов (18),
• сходятся оба интеграла (18)?
6. Получите явную (выражающую решение через коэффициенты
уравнения) формулу для общего решения уравнения (3) в полных
дифференциалах в области G = I x J при выполнении условия (15).
7. Есть предположение, что переживаемое человеком время Δί
вблизи настоящего момента t воспринимается им не как абсолютное, а
как его отношение ко всему времени x(t), прожитому этим человеком
23
к моменту t. Исходя из этого предположения составьте
дифференциальное уравнение для функции x{t) и решите его.
8. Может ли линия уровня (12) потенциала уравнения (3) в полных
дифференциалах быть несвязной, т. е. представлять собой не одну, а
объединение нескольких интегральных кривых7 Может ли число
таких кривых не быть одинаковым для всех С?
9. Докажите, что любые два потенциала уравнения (3) в полных
дифференциалах локально вблизи любой точки области G отличаются
друг от друга на константу (аддитивную).
10. Верно ли, что любая точка единственности какого-либо
уравнения, по определению, есть и точка существования?
11. Для уравнения
у' = \у\а (или у' = \у\а ■ sgny)
в зависимости от значения α € Μ исследуйте на существование и
единственность каждую точку (х, у) € R2 (доопределив при а < 0 по
непрерывности обобщенное поле направлений в точки, где у = 0).
12. В зависимости от значений α,β > 0 определите, сколько
проходит через начало координат локально различных интегральных
кривых уравнения (16) с правой частью:
'fiv) = \(-yf, У<0; '^ = {-{-yf, у<0.
13. Докажите, что если если Р, R € С(7) и Q, S € С(</), а функция
R имеет изолированный нуль α G /, то для уравнения (21) в области
(22) любой интервал прямой χ = α — интегральная кривая, причем ее
точка (α,β), удовлетворяющая условию
5(β) φ 0, (27)
есть точка единственности тогда и только тогда, когда расходятся оба
интеграла
а±0
J Щ)
Существенно ли в этом утверждении условие (27)?
14. Докажите, что если / € С(7) и функция д (26) обнуляется на
интервале / ровно в одной точке а € /, то для уравнения (24) любая
точка (х, у) € G — точка существования, причем.
• если у φ αχ, то (х, у) — точка единственности,
• если у = ах, то (х,у) — точка единственности тогда и только
тогда, когда расходятся оба интеграла
а±0
Глава 2
СУЩЕСТВОВАНИЕ
И ЕДИНСТВЕННОСТЬ РЕШЕНИЙ
2.1. Локальная теорема существования
и единственности
решения задачи Коши для нормальной системы
дифференциальных уравнений играет важнейшую роль в теории
дифференциальных уравнений, поскольку делает разговор об их решениях
содержательным.
I. Постановка задачи Коши. Пусть задано уравнение
x = f(t,x), (t,x)eGcRxRn = R1+n, f:G^Rn. (28)
Определение 2.1. Задача Коши получается добавлением к
уравнению (28) начального условия
x{to) = xo {to el), (29)
причем принята следующая теминология:
• функция / называется правой частью уравнения (28);
• начальная точка (to, xq) Ε G состоит из начального
момента to и начального значения1 хо',
• решение задачи Коши — это функция χ: / —> Rn,
удовлетворяющая условиям (28), (29), если совершить в них подстановку2
χ = х(£), т.е. удовлетворяющая равенствам
x(t) = f(t,x(t)), tel, *(t0) = xo; (30)
• переменная # Ε Rn называется фазовой, a t Ε 1R — временем.
Образующего вместе с правой частью уравнения (28) пару правых
частей задачи Коши
2С этой точки зрения начальное условие корректнее было бы записывать
в виде x\t=tQ = хо-
25
Рис 8. Вопросы об
интегральных кривых
Если в Ш71 фиксирован базис,
то одно уравнение (28)
записывается покоординатно в виде
системы
•L· I I I/ л «Z/ * · · · ■ *L· ι
ζ,η _ fnfj. ~Л n\
(более того, само n-мерное
уравнение (28) часто называют
нормальной1 системой из η
дифференциальных уравнений п-го
порядка), а начальное условие
(29) — в виде
хпЦ0) = х%.
II. Формулировка локальной теоремы. В дальнейшем, в
том числе и в настоящей главе, мы попытаемся выяснить, какие
свойства правых частей задачи Коши гарантируют ее решениям
(рис. 8):
• существование, хотя бы локальное;
• единственность, хотя бы локальную;
• неограниченную продолжаемость вправо или влево по оси
времени;
• продолжаемость до границы области G,
• единственность продолжения (глобальную);
• непрерывную зависимость от правых частей задачи Коши;
• дифференцируемость по начальным значениям.
Последние два вопроса будут изучаться в главе 5, а на
некоторые из первых вопросов при η = 1 в частных случаях мы уже
получали ответы ранее в главе 1 (теоремы 3, 4, 5 и 7). Более
общий, а потому и менее сильный ответ на них дает следующая
локальная теорема существования и единственности.
*Т е разрешенной относительно производной χ = (χ1, ,χη)
26
Теорема 9. Если f, f'x Ε C(G), то для любой точки (to, хо) Ε
Ε G в некоторой окрестности С/(ίο) точки to существует
единственное решение
х: U{t0)^Rn
задачи Коти (28), (29).
Доказательство теоремы предварим рядом вспомогательных
понятий и фактов
III. Сведение задачи к интегральному уравнению.
Любая задача Коши, состоящая по определению из двух условий,
сводится к эквивалентному ей интегральному уравнению,
причем всего одному
Лемма 10. Если f Ε C(G), то функция χ Ε С(/) —
решение задачи Коши1 (28), (29) тогда и только тогда, когда она
удовлетворяет интегральному уравнению
t
χ(ί) = *ο+[/(τ,χ(τ))<*τ, tel. (31)
ίο
► 1. С одной стороны, если χ — решение задачи Коши, то,
заменив t на τ в тождестве (30) и проинтегрировав его по τ от to до
произвольного t Ε Ι, получаем
ί
χ(ί)-χ(*0) = |/(τ,χ(τ))</τ,
ίο
а с учетом начального условия (30) имеем равенство (31).
2. С другой стороны, если функция χ удовлетворяет
равенству (31), то, продифференцировав его2 по t или,
соответственно, положив в нем t = to, получим для нее оба условия (30). ■
Проанализировав тождество (30), можно вывести
Следствие 11. Если f E C(G), то любое решение уравнения
(28) есть непрерывно дифференцируемая функция.
Для того чтобы, функцию χ молено было подставлять в
дифференциальное уравнение (28), ей необходима дифференцируемость, а чтобы быть
подставленной в интегральное уравнение (31), достаточно лишь
непрерывности.
2Что возможно, так как подынтегральная функция /(τ,χ(τ)) непрерывна
по τ (в силу непрерывности функций /их), следовательно, правая часть
равенства (31) дифференцируема по £, а значит, и левая — тоже
27
2.2. Нормы в конечномерных пространствах
обладают целым рядом полезных свойств, применяемых, в
частности, и в теории дифференциальных уравнений.
I. Инвариантность понятия производной. Производная
x(t) вектор-функции х: / —> Rn в точке t Ε / может пониматься
двояко:
• либо в Ш.п как абстрактном линейном векторном
пространстве
Щ = lim »(« + h\ - *(') ;
/ι->0 h
• либо в Rn как координатном линейном пространстве
χι ω
Χη(0
Перечисленные подходы к пониманию производной приводят к
одинаковому результату
из-за существования естественного изоморфизма1 между
указанными двумя линейными топологическими
пространствами — изоморфизма, сохраняющего:
• все сопутствующие взятию производной линейные
операции, которые, тем самым, арифметически соответствуют друг
другу;
• операцию предельного перехода, которая также приводит
к соответствующим друг другу предельным значениям.
В данном случае в обоих рассматриваемых линейных
пространствах топология задается с помощью нормы2: открытым
считается любое множество, в котором каждая точка
содержится вместе с шариком достаточно малого радиуса с центром в
Определяемого базисом в Rn.
2Существуют и другие способы задания топологии
ад =
28
этой точке (все такие шарики образуют базу топологии). И
хотя саму норму изоморфизм линейных пространств может и не
сохранять, но топологию сохраняет обязательно.
II*. Эквивалентность норм. Причина указанного выше
сохранения топологии кроется в том, что в конечномерном
линейном пространстве любые две нормы эквивалентны, что и
утверждает
Лемма 12. Для любых двух норм || · ||ι и || · ||2 в Ш.п
существует константа С, удовлетворяющая оценке
1№<С|И|2, хешп.
► Действительно, пусть в пространстве Rn, на время
доказательства — еще и евклидовом (т. е. наделенном скалярным
произведением), фиксирован некоторый ортонормированный базис
βι, ..., еп и евклидова норма
Ι^ιβι Η l· хпеп\ = \/Х\ Η \-x%,
тогда при х φ 0 (при χ = 0 доказываемая оценка верна) имеем
Mli ||*/М11
I<C=sup^<oo,
1Mb Ik/Nib" ~ ι,ι-ι llvlb
так как функция, стоящая здесь под знаком точной верхней
грани, непрерывна на компакте
Sn~l = {у | Μ = 1} С Ш."
в смысле топологии, задаваемой евклидовой нормой | · |,
поскольку любая норма || · || непрерывна в том же смысле в силу оценки
х\\ = Fiei Η Η^ηβη < \xi\ \\ei\\ -\ l· \xn\ \\en\\ < φ,
где c= \\ei\\ Η l· |en| . ■
III*. Определение топологии. Напомним, что предельный
переход в пространстве W1 возможен именно благодаря
имеющейся в нем системе открытых множеств (образующих, по
определению, окрестности содержащихся в них точек). Такая
система Τ определена в любом топологическом пространстве X
29
и называется его топологией, если только обладает следующими
свойствами.
1) 0,хеТ,
2) если Ui,U2e Τ, то U\ П U2 G Τ;
3) если Ua ЕТ при каждом α G Д то (J C/a G Т.
Например, с помощью топологии определяется предел
последовательности
lim хп, хп G X,
п—>оо
как такая точка a G X, что для любой ее окрестности Ϊ7(α) G Τ
существует число1 ЛГ, удовлетворяющее импликации
η > AT =* хп G С/(α).
Далее, с помощью топологии определяются также предельные,
внутренние и граничные точки множества, его открытость,
замкнутость, компактность и τ π
IV*. Операторная норма. Считая пространство W1
нормированным (с нормой | · |), определим в пространстве ЕпсШп
линейных операторов, действующих из Шп в Шп, операторную
норму || · ||, задаваемую формулой
||Л|| = sup Yf- = sup \Ах\, A G EndlRn.
\х\^0 \Х\ \χ\ = ι
При этом имеют место утверждения.
• величина \\А\\ — конечна, поскольку для фиксированного
единичного базиса βχ, ..., еп C.W1 имеем
\Ах\ < \Ах\е\\-\ h|Arnen| = \х\\ \Ае\\-\ \-\хп\ \Аеп\ < С\х\,
где С = \Ае\\ Η l· \Аеп\ и χ = х\е\ Л l· хпеп;
• справедлива оценка
\Ах\ < \\А\\ · |х|,
поскольку при χ = 0 она верна, а при χ φ 0 имеем
Которое, кстати, также задает окрестность в N — а именно, окрестность
{п € N | η > Ν} точки оо
30
\Ax\ = Mil . |ж| < ||Л|| · |ж|;
\х\
операторная норма — банахова, т. е.
\АВ\\ < ||Л|| · ||В||, А,ВеЕпаШп,
(32)
в силу цепочки
|/1D|. \АВх\ ^ \\Α\\·\Βχ\
\АВ\\ < sup ' ' < sup [
\х\^о \х\ \х\^о \х\
= \\А\\ · \\В
V*. Оценка конечных приращений. В формулировке
теоремы 9 участвует производная д' (в точке х, с параметром t)
конечномерной функции д: Жп —> Rn по конечномерной
переменной х, которая определяется как линейный оператор д'(х) Ε
Ε EndRn, удовлетворяющий условию
д(х + К) - д{х) = g'(x)h + o{\h\), h -► 0.
Следующее утверждение обобщает формулу конечных
приращений Лагранжа на случай такой функции.
Лемма 13. Если д Ε С1 (В), где В С W1 — выпуклое
множество, то
\g{y)-g{x)\ <sup||0'K)|| -\у-х\, х,у е В.
1ев
► Действительно, если x£Bny = x + h£B, то, благодаря
выпуклости множества В, имеем
(х + ЩеВ, θ Ε [0;1],
и, обозначив φ(θ) = g(x + θ/ι), получаем
\g(x + h) - g(x)\ = \ψ{1) - ψ(0)\ =
ι
/φ'(θ)
d»
1 1
J \g'{x + Qh)h\ dQ < J \\g'(x + ΘΛ)|| · \h\ dQ < sup ||</(ξ)|| · |Λ|,
о о
откуда и вытекает доказываемая оценка.
31
2.3. Равномерная метрика
позволяет говорить о сходимости функций сразу на целом
промежутке, а не только в каждой его точке отдельно.
I. Пространство непрерывных функций. Для начала
напомним, что если X — метрическое пространство с метрикой
р(·,·), то:
• последовательность точек хп Ε Χ (η Ε Ν) называется
фундаментальной, если выполнено условие
lim р(хт,хп) =0;
m>n—> оо
• пространство X называется полным, если в нем всякая
фундаментальная последовательность сходится;
• если пространство X полно, то любое его замкнутое
подпространство также полно.
Из курса математического анализа известно, что если для
заданного отрезка К С Μ множество всех непрерывных функций
х: К —> Rn наделить равномерной нормой (метрикой)
||х|| =sup|x(£)| (р(х,у) = ||х-у||),
teK
то полученное нормированное (метрическое) пространство,
обозначаемое через С(К), будет полным. Сходящиеся в этом
пространстве последовательности функций называются равномерно
сходящимися на отрезке К.
II*. Принцип сжимающих отображений. Так
называется один из наиболее популярных признаков существования
неподвижной точки отображения.
Определение 2.2. Пусть X — метрическое пространство,
тогда:
• отображение А: X —> X называется сжимающим, если
существует число q < 1, для которого справедлива оценка1
р(Ау, Ах) <q- р(у, х), х, у Ε Χ;
• любая точка χ Ε X, удовлетворяющая равенству Ах = х,
называется неподвижной точкой отображения А.
*Из которой сразу следует, что отображение А непрерывно и даже лип-
шицево (с константой L = q)
32
Лемма 14» Любое сжимающее отображение полного
метрического пространства в себя имеет единственную
неподвижную точку.
► 1. Единственность неподвижной точки докажем от
противного· если бы существовали две разные неподвижные точки х, у G
G X, то для них было бы выполнено неравенство р(х,у) > О,
приводящее к противоречию
р(х,у) = р(Ах, Ay) < qр(х, у) < р(ж, у).
2 Для нахождения неподвижной точки возьмем
произвольную точку xq G X и образуем последовательность хп = AnXQ,
η G N. Она фундаментальна, так как
p(xn,xn+i) < qp(xn-i,xn) < < qnp{xo,xi) =>
^р(Хп,Хт) < p(x ) + ρ(χη+ι,χη+2) Η Η p(xm-i,xm) <
< ρ(χ0,χ,)(," + qn+l + ■ ■ ■ + q™-1) < qn ^^ < ε
при достаточно больших значениях η <т.
Поэтому в полном пространстве X существует предел χ этой
последовательности, который и является неподвижной точкой
отображения А. Для доказательства этого утверждения
достаточно перейти в равенстве Ахп = χη+ι к пределу при η —У оо,
получив равенство Ах = χ (в силу непрерывности сжимающего
отображения А). ■
III*. Приближения Пикара. С задачей Коши (28), (29)
можно связать последовательность определенных на отрезке
KT = [to-T;t0 + T}, Г>0, (33)
функций
x0(t)=x0, teKT, xn = Axn-i, neN, (34)
где обозначено
t
{Ax){t)=x0-l· Γ/(τ,χ(τ))<ίτ, t G KT. (35)
ίο
33
Далее с помощью принципа сжимающих отображений будет
доказано, что в условиях теоремы 9 приближения Пикара (34)
на некотором отрезке Кт'.
• все одновременно определены;
• равномерно сходятся (при η —> оо) к решению
соответствующего интегрального уравнения (31).
2.4. Доказательство локальной теоремы
существования и единственности (см. теорему 9) будет
состоять в том, что по заданной области G, функции / и точке (to, хо)
будет построен упомянутый в формулировке теоремы интервал
U(to), на котором существует единственное решение задачи Ко-
ши.
1. Доказательство теоремы. Решение будет искаться как
единственная неподвижная точка оператора1 А (35),
действующего в некотором полном метрическом пространстве Χχ
непрерывных функций, определенных в замкнутой окрестности Кт
точки to- Уменьшая размеры этой окрестности (задаваемые
числом Т), мы добьемся того, чтобы оператор А:
• переводил указанное пространство в себя (для чего
понадобится локальная ограниченность функции /);
• был сжимающим (для этого будет использована локальная
ограниченность производной f'x).
► 1. Выберем целиком лежащий в области G замкнутый шар
B = {(t,x)\\(t,x)-(t0,xo)\<R} (36)
(что возможно, так как точка (to,xo) лежит в этой области
вместе с открытой шаровой окрестностью, содержащей меньшую,
но уже замкнутую; рис. 9) и обозначим
М= sup \f(t,x)\ < оо, L= sup \\f'x(t,x)\\<oc (37)
(t,x)eB (t,x)eB
(конечность этих величин вытекает из непрерывности на
компакте В С Rn+1 обеих функций под знаком верхней грани).
2. Поставим в соответствие каждому числу Τ > 0 отрезок Κχ
(33).
Нелинейного, вообще говоря.
34
χ,
ho
^^-^"
У^у^^ в ^\
\ / i
χ
\ /
\ /
\ / J
\ / Ж
\ / Ж
\ /Ж7
/
/
/
/
/
/
/
\ ι
\
\
\
\
\
\
\
■ W
с
-Χι
-^^ Ι
ι
ι
\ L-^-^—»—'
Ν. Τχ ί0 Τ0
^—iL
t
Рис. 9. Последовательное
уменьшение размера отрезка
• Выберем такие Ro, Tq > О, чтобы выполнялось включение1
С = {(£, x)\te КТо, \х - хо\ < Ro} с В.
Тогда получим, что при любом Τ < То множество функций
хт = {* е С(кт) \ \\х - χο\\τ < Ro}
есть замкнутый шар с центром хо(·) = хо и радиусом Ro в полном
пространстве С(Кт) с равномерной нормой, обозначаемой здесь
через || · \\т, а значит, и то же подмножество Χχ С С(Кт),
рассматриваемое как самостоятельное метрическое пространство, —
также полное.
• Выберем такое Τι < Tq, чтобы при любом Τ <Т\ формула
(35) задавала оператор
Αχ: Χχ —ϊ Χχ.
Это возможно, поскольку если
хеХт,
(38)
(39)
*Если взять, скажем, То = Ro = R/2, то для любой точки (t,x) € С будет
выполнено условие (t,x) G В, так как цилиндр С с осью χ = хо, радиусом
До и высотой 2То (рис. 9) целиком помещается внутри шара В радиусом R
|(ί,χ) - (io,xo)| = y/\t - ίο|2 + \x - xo\2 < iJtJ+Щ = R/V2 < R
35
το Αχ* G C(Kt) и для любого t G Κχ имеем
\ATx{t) -xq\ =
t t
/(τ,χ(τ))ί/τ < sup |/(s,a?)|dx
J J (s,x)eB
to to
<TM,
откуда при Τ <Τ\ < Rq/(M + 1) получаем1
ΙΙΛγχ-χοΙΙτ < #о,
(40)
а значит, Αχ* G Хт-
• Выберем такое Т2 < Γχ, чтобы при любом Τ < Т2 оператор
Лт (38) был сжимающим, например, с коэффициентом q = 1/2.
Это возможно, поскольку если х, у G Хт, то, применяя при
каждом фиксированном τ G Κχ лемму 13 к функции2 д(х) = /(τ, χ),
получаем для любого t G Кт оценку
\ATx{t) - ATy{t)\ =
t
||/(τ,χ(τ))-/(τ,γ(τ))|Λ
ίο
<
<
τ
ί sup \\ί'(8,χ)\\\χ(τ)-ν(τ)\άτ
J (s.x)GB
to
<TL||x-y||T<#c-y||T
при Τ < Τ<ι < q/(L + 1), откуда3
\\ΑΤχ - Ату\\т < g||x - у||т-
(41)
3. По принципу сжимающих отображений (лемма 14), при
любом Τ < Т<2 существует единственная неподвижная точка
χ G Хт оператора Ат (38). Отсюда следует и существование,
и единственность решения задачи Коши (28), (29) на интервале
U{t0) = I = {t0-T2;t0+T2).
(42)
1 Графики всех функций вида Ах оказываются лежащими даже не в
цилиндре С, а в конусе («воронке», рис 9) с центром (ίο,^ο), осью χ = хо и
угловым коэффициентом М, из-за чего и возникает возможность уложить
их все в цилиндр С исключительно за счет уменьшения высоты 2ΤΊ конуса
Определенной на выпуклом сечении шара В плоскостью τ = const.
3Если функции χ и у мало отличаются друг от друга, то функции Ат* и
Ату, совпадая в точке t = ίο, медленно (из-за липшицевости по χ функции
/) расходятся при отходе аргумента t от to, поэтому можно контролировать
величину их отклонения друг от друга числом Тг
36
Действительно
• сужение х|/ функции χ с отрезка Кт2 н& интервал /
представляет собой решение интегрального уравнения (31), а значит
(по лемме 10), и задачи Коши;
• всякое решение у: I —^ Ш.п задачи Коши совпадает с ее
решением х|/, так как функция у, будучи (по лемме 10) также и
решением уравнения (31), удовлетворяет неравенству1
sup|y(i) -х0\ < Яо,
tei
а значит, ее сужение у\кт на любой отрезок Κχ С /
принадлежит пространству Χχ и совпадает с единственной неподвижной
точкой х\кт оператора Αχ (38). ■
II. Усиление и ослабление гладкости. В формулировке
теоремы 9 условие /, fx Ε C(G), равносильное условию
df
можно заменить:
• более сильным, но легче проверяемым условием / Ε C^G),
слегка ослабив тем самым теорему;
• более слабым2, хотя и более трудным для проверки
требованием — непрерывностью функции / вместе с ее липшицево-
стъю по х, обозначаемой / Ε Lipx(G) и подразумевающей, что
некоторая константа L осуществляет оценку
\f(t, у) - f{t, х)\ < Цу - х\, {t, χ), {t, у) Ε G,
В противном случае, в силу начального условия (29), непрерывности
функции у и вытекающей из нее непрерывности по Τ функции ||у — хо||т,
для некоторого числа Τ <Т2 <Т\ имели бы место равенства
Яо = ||у - χο||τ = ||-Ату - хо||т,
противоречащие импликации (39) =Ф- (40)
2Формально, утверждение / G Lipx(G) из условия f'x 6 C(G) не вытекает,
так как единой для всей области G константы L может и не найтись. Однако
локальная, вблизи любой точки (to,xo) € ^*» липшицевость из этого условия
все же вытекает заменив область G какой-либо ограниченной замкнутой
выпуклой окрестностью В С G точки (ίο,^ο) € G, можно обеспечить
липшицевость по χ сужения /|в с константой L (37) Именно это рассуждение
и использовалось в доказательстве теоремы 9
37
(если / Ε Lipx(G), то оценка (41) в доказательстве теоремы
выводится прямо из условия Липшица, без применения леммы 13).
III*. Гарантированный интервал существования. В
теореме 9 непосредственно утверждается, что любая точка
области G (задания уравнения) есть точка существования в смысле
определения 1.5.
Более того, проанализировав доказательство этой теоремы,
можно даже явно указать размер интервала U(to) (42), на
котором заведомо существует решение. Его длина 2Т^ зависит только
от радиуса R содержащегося в области G замкнутого шара В с
центром в точке (to,xo) и величин M,L, заданных равенствами
(37), а в качестве Т^ заведомо годится, например, число
Т^ВДМ.цЛ-^щ}. (43)
2.5. Единственность решения
задачи Коши, утверждаемая в локальной теореме
существования и единственности, на деле оказывается гораздо более полной
и содержательной.
I. Локальная единственность. Из теоремы 9 вытекает1,
что любая точка области G является точкой единственности в
смысле определения 1.5, а именно, справедливо
Следствие 15. В условиях теоремы 9 любые два решения
задачи Коши (28), (29) локально (вблизи to) совпадают.
Чтобы доказать это утверждение, достаточно слегка
уточнить конец доказательства теоремы, но мы, однако, выведем его
как прямое следствие сформулированной теоремы.
► Пусть даны два решения задачи Коши
х': i/'-^R, x": U" -► R,
каждое из которых определено в своей окрестности точки to-
Тогда, уменьшив область G так, чтобы выполнялись условия
(«о, ж0) eGcUxW1, U = Ufn U",
Хотя явно это в ней и не утверждается.
38
и применив теорему 9, мы получим, что сужения обоих решений
х' и х" на некоторый интервал
U{t0) С U С U\ U"
совпадают с тем решением х, существование и единственность
которого утверждается в теореме 9. ■
II. Глобальная единственность. Из локальной
единственности решения (см. определение 1.5 и следствие 15) выводится
его глобальная единственность, т. е. совпадение любых двух
решений задачи Коши на их общей области определения.
Теорема 16. Если каждая точка области G — точка
единственности1 для уравнения (28), то любые два решения χ и у
задачи Коши (28), (29) удовлетворяют равенству
х|/ = у|/, I = D{x)nD{y).
► Пусть, напротив, решения χ и у задачи Коши различаются
хотя бы в одной точке Τ Ε /. Если, к примеру2, Τ > to, то для
числа
ii=inf{i>i0|x(0^y(<)}e[io;i1 (44)
выполнены равенства
x(t)=y(t), t0<t<tu
поэтому решения χ и у совпадают в точке t\, а значит (см.
следствие 15), и в целой ее окрестности, что противоречит
определению (44) числа t\. ■
2.6. Теорема существования
отличается от локальной теоремы существования и
единственности предположением меньшей гладкости правой части системы.
I. Существование при условии непрерывности. Для
существования3 решения задачи Коши не нужно ничего, кроме
непрерывности правой части системы. Это и утверждает
следующая (доказанная далее в п. 2.6) теорема Пеано.
*Для этого достаточно предположить, например, что /, f'x € C(G).
2 Случай Τ < to рассматривается аналогично
3В отличие от единственности, см пример в разделе IV из π 1 3.
39
Рис. 10. Не существование
или не продолжаемость
решений до границы
Теорема 17. Если f e C(G),
то для любой точки (ίο,χο) Ε G
существует решение задачи
Коти (28), (29).
В формулировке этой
теоремы условие непрерывности
правой части уравнения является не
только естественным, но и
весьма существенным: без него
существование решения задачи Коши
гарантировать нельзя.
Например, ни одна
интегральная кривая уравнения
х = f(t,x) =
1, χ > 0,
1, х<0,
{t,x)e
не проходит через начало координат.
Действительно, из вида соответствующего поля направлений
(рис. 10) следует, что если бы график какого-либо решения
содержал (внутри себя) точку (0,0), то ни при каком t < 0 это
решение не могло бы принимать ни положительного, ни
неположительного значения, что невозможно1.
II*. Ломаная Эйлера. С задачей Коши (28), (29) можно
связать непрерывную кусочно линейную функцию
cp:tf->Rn, ί0 Э /С= [α;β],
удовлетворяющую условию φ (ίο) = ^0 и Для некоторого
разбиения
σ = {s0, si, ..., sn<J, α = s0 < «ι < · · · < sUa ξ β,
(45)
отрезка К при каждом г Ε J ξ {1, ...,ησ} и некотором,
зависящем от г, значении s £ [si_i;sj] задаваемую равенством
Ф(0 = /(5>ф(5))> te [si-i;si].
График Γφ любой такой функции2 называется ломаной Эйлера,
а величина
1 Невозможно для решения не только данного уравнения, но даже и
соответствующего ему, более слабого, интегрального уравнения (31)
2Или, в зависимости от контекста, сама эта функция
40
|σ| = max (si — Si-i)
г€{1, ,ησ}
называется нормой разбиения σ.
Построим простейшую ломаную Эйлера:
• выберем в качестве одной из точек разбиения точку to и
будем двигаться от нее вправо, сначала положив1 s = to и выбрав
точку разбиения t\ > to, затем положив s = t\ и выбрав точку
разбиения t<i > ti, и так далее до тех пор, пока (s,cp(s)) Ε G;
• аналогично будем двигаться от to влево, сначала положив
s = to и выбрав точку разбиения t-\ < to, затем положив s = t-\
и выбрав точку разбиения t-2 < ί-ι, и т.д.;
• перенумеровав выбранные числа to, t±i,t±2, · .. подряд в
порядке возрастания, получим окончательное разбиение σ (45).
Значение s, фигурирующее в определении ломаной Эйлера,
следует считать функцией s = sa(t) по меньшей мере от
переменной t и разбиения σ, которая тогда удовлетворяет условиям
sa{t) G [si_i;sj], t e [si-ι;Si], i e J,=>
=> \sa(t) -t\ < |σ|, t e K,
а для кусочно дифференцируемой функции φ справедливо
равенство
φ(ί) = f{sa{t),φ(βσ(ί))), teK\ {so, ...,snJ. (46)
III*. Лемма Арцела — Асколи. Сначала дадим
Определение 2.3. Семейство Φ функций φ: К —> Ш.п с
равномерной на отрезке К С Μ нормой || · || называется:
1) равномерно ограниченным, если
sup||cp|| < оо;
2) равностепенно непрерывным, если для любого ε > 0
существует такое2 5 > 0, что для любых φ G Φ и i, s £ К имеет место
импликация
\t - s\ < δ => |φ(ί) — φ(β)| < ε;
Тем самым определив значение f(s,y(s)), задающее направление
соответствующего звена ломаной
2Не зависящее ни от встречающихся ниже чисел t,s 6 К (что означало
бы равномерную непрерывность каждой функции), ни от функции φ 6 Φ
41
3) предкомпактным, если из любой его последовательности
φη G Φ (η G N) можно выбрать фундаментальную
подпоследовательность.
Лемма 18. Всякое равномерно ограниченное и
равностепенно непрерывное семейство Φ С С(К) предкомпактно.
► По заданной последовательности φη G Φ (η G N) из
ограниченного и равностепенно непрерывного семейства Φ С С(К) мы,
согласно п. 1) определения 2.3, должны построить ее
фундаментальную подпоследовательность, чем и займемся.
1. Пусть задано ε > 0.
• В соответствии с п. 2) определения 2.3 выберем число δ > 0.
Кроме того, выберем разбиение σ (45) отрезка К с нормой |σ| < δ,
а в ограниченном, согласно п. 1) определения 2.3, множестве
X С Мп всех значений всех функций семейства Φ выберем
конечную ε-сеть {х{}, т.е. такое множество центров шаров
радиуса ε, что объединение этих шаров содержит множество X.
Рассмотрим конечное множество всех функций ψ/t G С(К), графики
которых являются ломаными1 с узлами в точках вида (sj,Xi).
• Каждой функции φη поставим в соответствие какую-либо
функцию ψ/fc, для которой
l<Pn(sj) - tyk{sj)\ < ε, j G J U {0}.
Тогда хотя бы одна из функций ψ& будет поставлена в
соответствие бесконечному числу членов последовательности φη,
образующих подпоследовательность, причем любые два члена φηι,
φη2 этой подпоследовательности при t G [sj-i;sj], j G J, будут
удовлетворять неравенству
|<Pm(i) - <Pna(*)l < l<Pm(*) - <Pm(sj)| + |<Pm(sj) ~ Ы8з)\ +
+ l<Pna(<) - <Pna(ej)l + l<Pna(*j) ~ Ы8з)\ < 4ε>
откуда будем иметь
ΙΙψηι -<pn2|| < 4ε·
• Из найденной подпоследовательности исключим первую
функцию, предварительно обозначив ее через cpj.
2. Уменьшим вдвое значение ε и проделаем с оставшейся
подпоследовательностью все операции, описанные в предыдущем
*Не ломаными Эйлера'
42
пункте построения. В результате получим функцию φ*,, затем
аналогично функцию cpj и т. д.
3. Полученная в итоге подпоследовательность φ* будет
фундаментальной, так как
П1>П2—>00
Таким образом, семейство Φ предкомпактно в смысле п. 3)
определения 2.3. ■
IV*. Доказательство теоремы Пеано. Оно основано на
том, что в смысле равномерной нормы на достаточно малом
отрезке:
• семейство ломаных Эйлера предкомпактно;
• некоторая их последовательность со стремящейся к нулю
нормой разбиения сходится;
• предельная функция служит решением задачи Коши.
► 1. Возьмем целиком лежащий в области G замкнутый шар В
(36) и константу Μ (37).
2. Обозначим через Φ множество всех ломаных Эйлера,
определенных на отрезке К = Κχ = [α; β] (33) и лежащих в шаре В,
а через Φσ С Φ — подмножество тех из них, которые
соответствуют разбиению σ отрезка К.
При этом число Τ > 0 выберем столь малым, чтобы любое из
множеств Φσ было не пусто. Это возможно, поскольку,
например, уже простейшая ломаная φ Ε Φσ может быть по индукции
достроена вправо (аналогично, влево) на весь отрезок К:
• во-первых, имеем
(*ο,φ(*ο)) = (to,xo) е в-,
• во-вторых, если уже
feip(ii))6B, г = 0, ...,fc-l,
то и (ifc,(p(ifc)) G В, так как в силу равенства (46) имеем
I ф(т)Л
|φ(**)-φ(*ο)Ι =
ίο
J /(βσ(Ό,φ(βσ(τ)))<ίτ
ίο
<
< sup |/(s, cp(s))| · (tk - t0) <MT=>
s£[io;ifc-i]
* |(tfc,cp(i)) - (to,*o)| < у/Т2 + (MTf < T(M + 1) < R,
43
как только Г < R/(M + 1).
3. Семейство Φ ломаных Эйлера:
• равномерно ограничено, поскольку
sup ||φ|| < \xq\ + sup |φ(ί) - xq\ < \xq\ + R < oo;
φ6Φ φ€Φ
• равностепенно непрерывно (даже равностепенно липшице-
во с константой М), поскольку в силу равенства (46) имеем
1<р(0-<р(*)1 =
Ι /(«σ(τ),φ(5σ(τ)))ί/τ
<
< M\t- s\ < ε, φ G Φ,
если только числа t,s Ε К таковы, что \t — s\ < δ = ε/Μ.
4. Выберем такую последовательность φη Ε Φ (η Ε Ν)
ломаных Эйлера, что соответствующие им разбиения ση отрезка
К удовлетворяют условию |ση| —> 0 при η —> оо. По лемме 18
из этой последовательности можно выбрать фундаментальную
подпоследовательность (сохраним для нее прежнее обозначение
φη), которая, в силу полноты пространства С(К), равномерно
сходится к некоторой непрерывной функции φο·
5. Докажем, что функция φ = φο|/, где / = (α; β) есть решение
задачи Коши.
A. Начальное условие выполнено, поскольку
φ(ί0) = Ит φη(ίο) = lim χο = ^ο·
η—юо η—>·οο
B. Для каждого t Ε I проверим равенство
ф(«) = /(«,ср(«))<=*
<=ϊ φ(ί + h) - φ(ί) - /(£, φ(£))/ι = ο(/ι), /ι -> 0.
• Действительно, пусть задано ε > 0. Тогда в силу
непрерывности функции / в точке (ί,φ(ί)) для некоторого δ > 0 имеем
1~-1(β)\<* =*Μ'>ν)-Κ·Μ»\<'-
Далее, с учетом равенства (46) имеем
44
|φ(ί + h) - φ(ί) - f(t, φ(ί))Λ| < |φ(ί + h) - φη(ί + h)\ +
+|φη(ί)-φ(*)Ι +
J (φη(τ)-/(ί,φ(ί)))Λ
<
< ε|/ι| + ε|/ι| +
J Ι/(βση(τ),φη(βσ„(τ)))-/(ί,φ(ί))|Λ
< 3ε|/ι|,
если только число h φ 0 достаточно мало и число η достаточно
велико, а именно, если только выполнены условия
ft ft
О < \h\ < min U - α, β - t, -,
iin < t — α,
2' 2Μ + ε
Μ
|ση| < \h\
||φη-φ||κ <ε|/ι|,
так как тогда
|βσ„(τ) - t\ < |βσ„(τ) - τ| + |τ - ί| < |σ„| + \h\ < 2\h\ < δ
* |φη(βσ„(τ)) - φ(ί)| < |φη(βσ„(τ)) - φη(ί)| + ΙΙφη - φ||κ <
< Μ|βση(τ)-ί| + ε|Λ| < (2Μ + ε)|/ι| < δ =*
* Ι/(βσ„(τ),φη(βσ„(τ))) - /(ί,φ(ί))| < ε.
Теорема 17 доказана. ■
В процессе доказательства теоремы 17 фактически было
дополнительно установлено
Следствие 19. Если f Ε C(G), mo для любой точки (to, хо)€
Ε G существует такой отрезок К, содержащий точку to, что:
• для любого его разбиения определена хотя бы одна ломаная
Эйлера;
• любая сходящаяся, в смысле равномерной на К нормы,
последовательность таких ломаных со стремящейся к нулю
нормой разбиения сходится к решению задачи Коти (28), (29).
2.7. Продолжаемость решений
до непродолжаемых является их естественным свойством.
I. Максимальное продолжение решения. Обычно
дифференциальное уравнение и даже задача Коши для него имеет
45
много решений, поэтому непраздным является вопрос об их
взаимосвязи.
Определение 2.4. Будем говорить, что решение χ·
• является продолжением решения у, если выполнено
равенство1
у = х1я(у);
• непродолжаемо (или максимально продолжено), если оно
не имеет продолжений, отличных от самого себя.
Существование непродолжаемого решения задачи Коши
обеспечивается наличием хотя бы одного ее решения2, как
показывает следующая
Лемма 20. Любое решение любого уравнения (28) можно
продолжить до непродолжаемого.
► 1. По заданному решению хо на интервале /о построим
последовательность решений х$ (г Ε N), определенных на
расширяющихся интервалах 1{ и замечательных тем, что каждое
следующее решение продолжает предыдущее.
Для этого занумеруем множество Q = {</ъ925 ...} всех
рациональных чисел (счетное и всюду плотное на прямой R) и
последовательно для каждого г Ε 1,2, ... определим, существует
или нет продолжение предыдущего решения х^—ι на больший
интервал, получающийся из предыдущего интервала U-ι заменой
одного из его концов точкой qf.
• если оно существует, то возьмем само это продолжение и
его область определения в качестве следующих х^ и Ц
соответственно;
• если же его нет3, то положим х^ = Xj_i и Ιι = 1%-\.
2. Закончив построение, определим новую функцию χ
следующим образом:
Дх) = (J h = 7' χΙ'* = х*' * G Ν·
геп
Молчаливо предполагающее включение D(x) D D(y).
Этот факт, при отсутствии каких-либо дополнительных предположений,
казалось бы, должен опираться на лемму Цорна Однако он не зависит от
нее (что видно из леммы 20), равно как и от других утверждений,
эквивалентных аксиоме выбора и признаваемых не всеми математическими
теориями
3В частности, если qi € 1%-\.
46
Полученная функция χ:
• определена корректно, так как она, совпадая на каком-либо
интервале 1{ с решением Х{, автоматически совпадает на этом
интервале и со всеми его продолжениями;
• является решением, так как любая точка ее области
определения / является внутренней для некоторого интервала U, на
котором функция χ совпадает с решением Xf,
• служит продолжением решения хо (совпадая с ним на
интервале /о);
• является непродолжаемым решением, поскольку если бы
существовало его продолжение на больший интервал V Э I, то
на некотором шаге, скажем, с номером г, описанного выше
построения нашлась бы внутренняя точка qi множества I'\I,
которая позволила бы продолжить решение х%-\ с интервала Ii-\ С /
на интервал U <£ I (имеющий точку qi одним из концов), что
противоречило бы определению интервала /. ■
Из доказанной леммы сразу же вытекает
Следствие 21. Если задача Коши имеет единственное не-
продолжаемое решение, то оно служит продолжением любого
ее решения.
II. Единственность непродолжаемого решения. Из
теоремы 16 и леммы 20 вытекает, что при изучении уравнения, во
всей области задания которого выполнены условия
существования и единственности, можно ограничиться одними лишь
максимально продолженными решениями, однозначно
задаваемыми своими начальными условиями, как показывает
Теорема 22. Если для уравнения (28) все точки области
G — точки существования и единственности, то для любой
точки (to,xo) Ε G существует единственное непродолжаемое
решение задачи Коши (28), (29).
► 1. Существование непродолжаемого решения задачи (28), (29)
обеспечивается наличием хотя бы одного ее решения и
леммой 20.
2. Пусть χ и у — непродолжаемые решения задачи (28), (29),
определенные на интервалах I и J соответственно, тогда χ = у.
Действительно:
• если / = J, то в силу теоремы 16 имеем χ = у;
• если же / φ J, то новое решение той же задачи
47
ίχ(ί), tei\j,
ζ(ί) = < χ(ί) = y(i), t e I n j Φ 0,
[y(0, *eJ\/,
что противоречит непродолжаемости решения х или у
соответственно. ■
III. Продолжаемость до границы области.
Нижеследующая теорема продолжаемости гласит, что любая
интегральная кривая уравнения (28) с непрерывной правой частью
асимптотически продолжается до границы области определения G
этого уравнения. Это означает, что график максимально
продолженного решения задачи Коши (существующего в силу
леммы 20) обязательно выходит, причем с какого-то момента вправо,
а с какого-то — влево, за пределы любого компакта, лежащего
в области задания уравнения1 (рис. 11).
Теорема 23. Если f Ε C(G), а х — непродолжаемое решение
уравнения (28), то для любого компакта С С G существует
отрезок К С D(x), удовлетворяющий условию
{t,x(t))(£C, t£K.
Последнее условие означает, что некоторые дужки
интегральной кривой решения х, примыкающие к ее левому и правому
концам, целиком лежат в окрестности границы области G,
образуемой внешностью компакта С:
rx|DMXKC(G\C).
Доказательство этого факта основано на том, что если бы, к
примеру, никакая левая концевая дужка данной интегральной
кривой не покидала полностью данный компакт, то указанная
непродолжаемая кривая имела бы (см. рис. 11):
• на своем левом конце предельную точку;
Или, что то же, входит в любую окрестность ее границы ведь
окрестностью границы области G как раз и следует признать дополнение любого
компакта С С G до G (аналогично, под окрестностью границы
интервала / естественно понимать дополнение любого отрезка К С / до /, ср с
окрестностями «граничных» точек ±оо числовой прямой) При таком
понятии окрестности границы заключение теоремы 23 можно сформулировать
совсем просто
(ί,χ(ί))-*0<7, t->dD(x)
48
Рис 11 Выход интегральной
кривой за пределы компакта
• в этой точке даже предел (в силу локальной липшицево-
сти решения вблизи этой точки, из-за локальной
ограниченности правой части уравнения);
• слева от этой точки продолжение (прямо по графику
решения задачи Коши с этой начальной точкой).
► Пусть непродолжаемое решение χ определено на интервале
/ = (α;β), но вопреки утверждению настоящей теоремы график
его сужения, например, на любой интервал вида1 (a; t) С I
имеет с некоторым фиксированным компактом С С G хотя бы одну
обитую точку.
1. Тогда для некоторой монотонно сходящейся к α
последовательности чисел ti Ε (α; β) выполнено условие
(и,х(и)) е С, ieN.
Поскольку С — компакт, то без ограничения общности
последовательность (U,x(ti)) можно считать сходящейся2 к некоторой
точке (а;а?о) G С С G.
2. Установим справедливость равенства
lim x(t) = xq.
ί->α+0
Зададим произвольное ε > 0, подчиненное условию
Сг = {(t,χ) Ι α < t < α + ε, \χ — xq\ < ε} С G,
(47)
интервалы вида (ί,β) рассматриваются аналогично
2Для этого сразу заменим ее нужной подпоследовательностью Кстати,
отсюда получим, что α — конечное число, а не символ — оо
49
и обозначим
М= sup \f(t,x)\ <oo, Ь=—^—.
• Тогда справедливо утверждение1
{t,x(t))eCe, te (α;α + δ),
которое, в силу произвольности ε, и обеспечивает равенство (47).
Действительно, выбрав момент U Ε (α; α + δ),
удовлетворяющий оценке
\x(ti) - Хо\ < δ,
для всех2 t Ε (а; а + δ) получаем
|x(t)-x(ti)| =
t t
|χ(τ)<*τ < ||/(τ,χ(τ))|
άτ
< Μδ < ε - 2δ,
\x(t) — χο\ < \x(t) — x(U)\ + \x{U) — xo\ < δ + ε — 2δ = ε — δ.
3. Теперь доопределим решение χ в точку α по непрерывности.
Тогда оно имеет в ней правостороннюю производную
х(а + 0)= lim x{t)= lim f(t,x(t)) = f(oL,x0).
1 Означающее, что весь соответствующий левый конец интегральной
кривой не выходит за пределы цилиндра С&. Для доказательства этого факта
нужна оценка скорости x(t) < Μ, но она справедлива только в те моменты £,
в которые интегральная кривая еще не вышла из цилиндра Се, —
получается логически порочный круг. Преодолеть его удается с помощью априорных
оценок, не позволяющих кривой даже приблизиться к границе дСе, а тем
более перейти через нее.
2Точнее, не для всех, а лишь для не превосходящих первого момента
(при движении от точки U вправо или влево) выхода интегральной кривой
на боковую поверхность цилиндра Се К счастью, такой момент никогда не
наступит, поскольку если, например, существует число
Τ = inf{i I t e (tt\α -(- δ), |χ(ί) - xo| = ε} > tt,
то для него имеем
(t,x(t))eCe, U<t<T, (48)
а значит, по доказанному, в силу непрерывности функции х, получаем
|х(Т) - хо| < ε - δ, (49)
что противоречит определению числа Т.
50
Следовательно, оно может быть продолжено влево за точку α
тем решением задачи Коши для уравнения (28) с начальной
точкой (а, хо), которое, согласно теореме 17, существует в
некоторой окрестности точки а. Это противоречит непродолжаемости
решения χ и, тем самым, доказывает настоящую теорему. ■
IV. Пример не продолжаемости на всю ось. Уравнение
взрыва
χ = х2
задано в области G = R2, все точки которой, согласно теореме 9,
являются точками существования и единственности. Однако ни
одно ненулевое непродолжаемое решение
этого уравнения не определено на всей прямой (рис. 12).
Причиной невозможности продолжить, скажем,
положительные решения вправо здесь является тот факт, что их графики
покидают любой наперед заданный компакт на плоскости,
уходя за конечное время именно вверх (в бесконечность), а не за
бесконечное время вправо.
Этот пример показывает, что никакая гладкость правой части
уравнения, даже заданного на всей плоскости, не может
обеспечить неограниченную продолжаемость его решений ни вправо,
ни влево.
V*. Существенность условия непрерывности. С одной
стороны, в формулировке теоремы 23 условие непрерывности
правой части уравнения является всего лишь достаточным.
Рис. 12. Решения, не
определенные на всей прямой
51
С другой стороны, совсем без этого условия попытка
гарантировать продолжаемость интегральных кривых до границы
области задания уравнения, даже в предположении, что эта
область сплошь заполнена точками существования и
единственности, оказывается несостоятельной
Например, для уравнения
II, х>0,
О, χ = О, (t,x) е IR2,
-1, х<0,
имеем (см. рис. 10):
• через любую точку (to,xo) Ε Ш2 на оси абсцисс проходит
ровно одно решение χ = 0, выше оси — ровно одно решение вида
χ = t + С, а ниже оси — вида χ = — t + С;
• график любого решения с положительным начальным
значением при убывании времени доходит до оси абсцисс и
обрывается, а потому при движении влево не достигает границы
никакого компакта С сШ2, содержащего точку обрыва внутри себя.
2.8. Непродолжаемые решения линейной системы
χ = A{t)x + F(t), (t,x) eG = IxRn, (50)
называемой линейной неоднородной, а в случае F = 0 —
линейной однородной, замечательны тем, что все они определены на
всем интервале непрерывности коэффициентов
А: /->ЕпсШп, F: I -+ Rn.
Доказательству этого факта предпошлем леммы об
интегральном и дифференциальном неравенствах, полезные и сами
по себе, поскольку позволяют получать априорные2 оценки
решений интегрального и дифференциального уравнений
соответственно.
I. Лемма Гронуолла — Беллмана. Простейший вариант
леммы об интегральном неравенстве представляет следующая
*Или хотя бы какого-то другого, более слабого
2Т е не предполагающие знания самих решений; метод априорных
оценок уже использовался ранее при доказательстве импликаций (39) =Ф- (40))
и (48) =► (49)
52
Лемма 24- Если функция и G C(J), где J = [ίο; β),
удовлетворяет для некоторых чисел а, Ь > О условию
t
О < u(t) < а + b \ и(т) άτ, t G J,
(51)
ίο
mo it оценке
и
(t) < aeb^-t0\ t G J.
► 1. Пусть а > О, тогда:
• поделим неравенство (51) на ее правую часть
(положительную) и умножим на Ь > О, заменив t на s:
— In I a + b \ и(т) άτ
bu(s)
ίο
a + 6 и(т)
<Ь;
ατ
• проинтегрировав последнее неравенство по s от to до £ G J,
получим оценку
α + 6 и(т) e/τ
ίο
In
а + Ь η(τ)
e/τ Ι — In α ξ In
ίο
< b{t -10);
ίο
• из полученной оценки, применяя еще раз неравенство (51),
имеем требуемое
и
t
(t) < α + 6 \и(т)ат < aeb{t~to\ t G J.
ίο
2. Пусть теперь а = 0, тогда условие (51) настоящей
леммы, справедливое при а = 0, тем более выполнено и при любом
а > 0. Следовательно, по доказанному в предыдущем пункте, и
заключительная оценка настоящей леммы также выполнена при
любом а > 0, а значит, и при а = 0. ■
Следствие 25. Если функция и G C(J), где J = (α; β), для
некоторых чисел а,Ь>0 и to € J удовлетворяет условию
t
0<u(t) <α + 6
J«(
τ)α4
ίο
, *G J,
53
то и оценке
u{t) <ae6|i_io1, teJ.
► Сформулированное утверждение:
• в случае t > to просто совпадает с доказанным в лемме 24;
• в случае t < to сводится к предыдущему сменой знака
времени, т.е. подстановкой t = — s и to = —so, а именно: из оценок
0< u(-s) <а + Ъ
выполненных для функции v(s) = u(—s), по лемме 24 вытекает
оценка
u(t) = u(-s) < aeb{s~So) = ое6'*-*01, t = -s < -s0 = t0,
совпадающая с требуемой. ■
II. Лемма о дифференциальном неравенстве. Исходя
из леммы Гронуолла — Беллмана можно сделать следующий
вывод: если правая часть уравнения (28) оценивается по норме
линейной функцией от \х\, то его решение оценивается по норме
некоторой экспонентой от t (правда, еще и с линейным по t
множителем).
Лемма 26. Если функция χ Ε С1 (J), где J = (α, β), для
некоторых чисел a,b>Outo£j удовлетворяет условию
|х(*)| <a + b\x{t)\, teJ,
то и оценке
Ht)\<(Hto)\ + a\t-to\)eb^-^, teJ.
► Действительно, для каждого фиксированного t Ε J сразу при
всех s Ε [to; t] или s E [t; to] (если t > to или t < to соответственно)
из цепочки неравенств
|x(s)-x(£0)| =
для функции и = |х| > 0 имеем
54
-so
—s s
и(т)ат = α + b \ и(—т)ат, s > sq,
so
s
ϊχ(τ)άτ
ίο
<
s
J"l*MI*
ίο
<
S
ί(α + 6|χ(τ)|)Λ
ίο
u(s) < \x(t0)\ + |x(s) - x(i0)| < (|x(«o)| + a\t - t0\) + b
откуда в силу следствия 25 получаем требуемое. ■
III. Теорема продолжаемости для линейной системы.
Все решения линейной системы продолжаются на весь интервал
непрерывности ее коэффициентов, что, в частности, и
утверждает
Теорема 27. Если A,F Ε С(/), то для любой задачи Коши
(50), (29) существует единственное непродолжаемое решение,
причем оно определено на всем интервале I.
Доказательство заключительного утверждения этой теоремы
опирается на априорную оценку решения, согласно которой ни
на каком отрезке, содержащемся в интервале /, решение по
норме не может уйти в бесконечность, а значит, непременно
продолжается за пределы этого отрезка1 (рис. 13).
► 1. Правая часть
f(t,x) = A(t)x + F{t)
линейной системы (50) удовлетворяет условиям теоремы 9 (а
также 22 и 23), так как A,F e С(1) и f'x{t,x) = A(t).
Поэтому непродолжаемое решение χ задачи Коши существует и
единственно.
2. Докажем, что максимально продолженное решение χ
определено на всем интервале / = (α; β). Действительно,
предположим, что, например, справа (аналогично слева) оно определено
только на промежутке J = [to; Τ), где Те (ίο; β)· Тогда:
• при всех t G J имеем
\x(t)\ < а + b\x(t)\, а = sup|F(s)| < оо, b = sup ||;4(s)|| < oo;
seJ seJ
• согласно лемме 26, при всех t G J получаем
KOI < (Ы + a\T - i0|)eb|T"io1 = R < oo;
Что обусловлено теоремой 23 о выходе интегральных кривых из любого
компакта.
s
S
ίο
и(т) άτ
55
• в силу полученной оценки
график непродолжаемого решения х,
выходя (по теореме 23) при t > to за
пределы цилиндра
С = {(t,x) |ie J, \χ\ < К] с
С G = Ι χ Rn,
обязан пересечь его правый торец,
что противоречит непродолжаемости
решения за точку Т. ■
В процессе доказательства
теоремы 27 фактически было установлено
Следствие 28. Если правая часть уравнения (28),
заданного в области G = I хК™, удовлетворяет условиям
\f(t,x)\<a(t) + b(t)\x\, (t,x)eG, /GC(G), a,6eC(J),
то любое его непродолжаемое решение χ определено на всем
интервале I.
X,
1
ι Xq
а\
Рис.
^
'о
X ^У
13.
J Τ
С
►Я
h
β ϊ
Продолжае-
мость решений на весь
интервал
2.9. Каноническая замена переменных
сводит любое уравнение η-го порядка
y{n)=f(t,y,y,...,y{n-l)), /:G->R, GcRl+n, (52)
разрешенное относительно старшей производной, к нормальной
системе из η уравнений специального вида.
I. Система, соответствующая уравнению. Обозначим
через Sf множество всех решений уравнения (52), а через
Sf(t0ly0l ...,yn-i) = Sf(t0,y0)
— его подмножество, состоящее из всех решений задачи Кошщ
определяемой набором начальных условий
'y{to) = 2/o
il{to) = У\
{y{n-l)(to) = yn-v
(53)
56
Аналогично обозначим через Sj и Sj(to,yQ) множества
решений следующей нормальной системы и, соответственно, задачи
Коши для нее
( ·12 \
x = f{t,x) = χη , x{t0) = y0 =
\/(i,a?i, ...,a:n)/
II. Простейшие свойства канонической замены. Для
заданного η Ε Ν обозначим через Фп-1 множество всех η — 1 раз
дифференцируемых скалярных функций (определенных на
всяких интервалах), а через Φ — множество всех функций,
принимающих значения в Ш.п.
Определение 2.5. Канонической заменой назовем
формальную операцию ψ, переводящую скалярную переменную у в
следующую векторную*
/ у \
В случае у Ε φη_1 функция фу называется (π — 1)-струей1
функции у, а ее график Гфу — [п — 1)-графиком функции у
Отображение
ψ:Φη_1^Φ (54)
замечательно тем, что оно:
• корректно определено, поскольку п—\ раз
дифференцируемую скалярную функцию переводит в векторную;
• сохраняет область определения функции, т. е.
£>(фу) = £>(у), уеФ"-1;
• сохраняет операцию перехода к сужению, т. е.
Ф(ук) = (Фу)1/, уеФ""1, /с£>(у);
*Для фиксированной точки ίο G D(y) отображение ψί0γ = (ψγ)(ίο)
принимает одно и то же значение на целом классе эквивалентных (с одним и тем
же рядом Тейлора степени η — 1 в точке ίο) функций — этот класс
называется (п — 1)-струей в точке ίο функции у, а определенное на таких классах
эквивалентности отображение ψί0 уже является биекцией
57
• есть инъекция, поскольку если совпадают вектор-функции
ψγι = фу2, то совпадают и их первые координаты у ι = У2-
III. Связь между уравнением и системой. Уравнение
нередко просто отождествляют с соответствующей ему
системой, чему обосновалием служит
Лемма 29. Каноническая замена осуществляет
изоморфизмы множеств
SfXSj и Sf{t0,y0) Л Sj(t0,y0),
а обратные к ним отображения задаются формулой
ф-1х = х\.
Свойства канонической замены схематически можно
изобразить так:
фп-1 _1> φ
U U
и
< V
°1
и
Sf(to,yo) <—> Sj(t0,y0).
► 1. Проверим, что отображение
<Hs/: sf -»· §7
(55)
корректно определено. Действительно, если у Ε Sf, то при всех
t Ε D(y) имеем
/
(ФУ) (*) =
\
fin-2)
Vy(n-Dy
/
(*) =
т
\
y("-l)(t)
\f(t,y(t),...,/n-l)(t)))
= /(*,Фу(*)),
поэтому фу Ε Sj.
2. Докажем, что отображение (55) — биекция, причем
k-i
Это вытекает из следующих двух утверждений:
• отображение (55) (и даже (54)) — инъекция;
58
• отображение (55) — сюръекция, поскольку если χ Ε Sj, то
для функции у = χι при всех t Ε D(x) имеем
<
y(t)=*l(*)=X2(i)
y(n-1)(«)=*n-i(*) = xn(i)
[y(n)W = *»(*) = /(*,χ(*)) = /(*,y(*), ··· .y^W),
откуда у Ε Sf и фу = χ.
3. Поскольку
Гу(*о) = 2/0
У(*о) = 2/1
[y(n-1)(^o) = 2/n-i
^(Ь)Ы=Уо,
то отображение (55) осуществляет также изоморфизм
подмножеств Sf(t0,y0) С Sf и Sj(to,y0) С Sj. ш
2.10. Теоремы существования, единственности
и продолжаемости для уравнения
произвольного порядка выводятся из соответствуюпщх теорем
для нормальной системы с помощью леммы 29, которая
фактически означает, что указанные две задачи с точки зрения
существования, единственности и продолжаемости их решений
устроены абсолютно одинаково.
I. Основные теоремы для уравнения. Исходя из
перечисленных выше свойств отображения (54) получаем, что
указанные в формулировке леммы 29 изоморфизмы (равно как и
обратные к ним) сохраняют:
• локальное совпадение решений (как равенство их сужений
на некоторую окрестность данной точки);
• глобальное совпадение решений (как равенство их сужений
на общую область определения);
• свойство одного решения быть продолжением другого (как
равенство сужения первого на область определения второго);
• непродолжаемость решения (как равенство его самого
любому его продолжению).
59
Таким образом, уже не нуждаются в доказательстве
следующие аналоги теорем 9, 16, 17, 22 и 23 для уравнений
произвольного порядка.
Теорема 30. Если f,fy, ..., /'(n_i) Ε C(G), то для любого
набора
(ίο,2/о, ...,2/η-ι) € G (56)
в некоторой окрестности U(to) точки to существует
единственное решение
у: U(to)->R
задачи Коти (52), (53).
Теорема 31. Если каждая точка области G — точка
единственности для уравнения (52), то любые два решения у и ζ
задачи Коти (52), (53) удовлетворяют равенству
y|/ = z|/, / = D(y) Π D(z).
Георел*а 52. ffc/ш / Ε C(G), mo для любого набора (56) су-
ществует решение задачи Коти (52), (53).
Теорема 33. Если все точки области G — точки
существования и единственности для уравнения (52), то для любого
набора (56) существует единственное непродолжаемое решение
задачи Коти (52), (53).
Теорема 34* Если f Ε C(G), а у — непродолжаемое решение
уравнения (52), то для любого компакта С С G существует
такой отрезок К С D(y), что имеет место условие1
(*,у(*) у(та_1)(*)) ^ С Η к.
II. Продолжаемость решений линейного уравнения.
Чтобы вывести теорему продолжаемости для линейного
уравнения из соответствующей теоремы для линейной системы, дадим
Определение 2.6. Уравнение
2/(η)+αι(%(п_1) + · · ·+αη(% = /(«), аи ... ,αη, /: / -> R, (57)
Означающее, что и левый, и правый концы (п — 1)-графика решения у
лежат в окрестности границы области G, дополняющей компакт С
Г(у, .у^-^Ьмчк С(С\С)
60
назовем линейным неоднородным уравнением1 п-го порядка, а в
случае / = 0 — линейным однородным. Матричную функцию А
и вектор-функцию F, определенные по формулам
А =
/О 1 ··· 0 \
О "·. *·. О
О · · 0 1
\—ап ··· -02 -αϊ/
f= η' . (58)
назовем матрицей уравнения и его векторной
неоднородностью соответственно.
Обозначим через «Saj/ и Sa,f множества решений уравнения
(57) и, соответственно, системы (50) с матрицей уравнения и
векторной неоднородностью (58). В добавление к лемме 29 верна
Лемма 35. Каноническая замена осуществляет
изоморфизм множеств
Sa,f ->· Sa,f-
► Действительно, каноническая замена приводит линейное
уравнение к линейной системе
( Х2 \
х=\ Хп \ = A(t)x + F(t), tel,
\-an(t)xi ai(t)xn + f(t)J
и, согласно лемме 29, осуществляет изоморфизм множеств их
решений. ■
Таким образом, справедлив следующий аналог теоремы 27
для линейных уравнений.
Теорема 36. Если сц, ...,on,/ G С(7), то для любой
задачи Коти (57), (53) существует единственное непродолоюаемое
решение, причем оно определено на всем интервале I.
III. Колебания математического маятника. Уравнение
колебаний точечного маятника массой ш, подвешенного на
невесомом стержне длиной / и вращающегося вокруг точки опоры
*И даже приведенным, тес коэффициентом ао = 1 при старшей
производной
2Постоянная матрица такого вида называется клеткой Фробениуса
61
ί !
> ®
\ 1
* ·ν
N.
\
\
\
\
1
1
/
Ч /'
0Г т
У
Рис 14. Математический
маятник
(на шарнире, рис. 14) в
фиксированной вертикальной плоскости,
записывается в виде
У +РУ + qsmy = f(t), t е R,
где у = y(t) — угол отклонения
маятника от направления силы
тяжести в момент t, q = g/l > 0 —
коэффициент (возможно зависящий от
времени1, т.е. q = q(t)), ρ > 0 —
коэффициент трения (обычно
постоянный; в случае ρ = 0 маятник — без
трения), mlf(t) — действующая на маятник в момент t внешняя
сила.
• Если внешняя сила отсутствует (/(£) = 0), то маятник
заведомо имеет решения y(t) = πη (η Ε Z), называемые
положениями равновесия: нижним при четных η и верхним при нечетных.
Согласно теореме 36, если функция q непрерывна, то движение
маятника полностью задается начальными значениями у(0) и
у(0). Следовательно, при отсутствии внешней силы сойти с
положения равновесия2, имея нулевую начальную скорость,
невозможно, так как одно решение (постоянное) с такими начальными
значениями уже есть.
• При малых (по модулю) значениях у представляется
естественной замена siny на у, дающая линейное уравнение3 малых
колебаний
y+w + qy = f{t), teR,
которые в случае / = 0 называются свободными, в противном
случае — вынужденными.
• Каноническая замена приводит уравнение колебаний
маятника к нелинейной системе
Х\ = Х2
х2 = -q sin χι - рх2 + f(t),
Например, при переменной длине маятника, каковая наблюдается, когда
стоящий на качелях человек раскачивается путем присядания.
Т. е раскачаться на качелях
3Тесно связанное с исходным (см раздел V из п. 5.7)
62
а в случае малых колебаний — к линейной
Х\ = Х2
Х2 = -qx\ -px2 + f(t).
• Если все коэффициенты в уравнении колебаний маятника
непрерывны, то все его решения продолжаются неограниченно
на всю числовую ось: в линейном случае это вытекает прямо из
теоремы 36, а в нелинейном — из следствия 28 (примененного к
соответствующей системе с учетом оценки | sinori| < \χι\).
Следовательно, как ни раскачивай маятник, ни одна из его фазовых
координат х\ = у или Х2 = У асимптотически при t —> Τ не уйдет
по норме в бесконечность1 ни при каком конечном значении Т.
2.11. Уравнение, не разрешенное относительно
производной
имеет общий вид
F(t,y,y)=0, (t,y,y)e Н CR3. (59)
I. Расширение задачи Коши. В каждой точке (£о,2/о) это
уравнение может задавать несколько2 значений поля
направлений в зависимости от количества корней уравнения
^ο,2/ο,2/ι) = 0 (60)
относительно переменной у\, так что поле направлений, вообще
говоря, многозначно. Поэтому для каждого из корней у\ этого
уравнения, и только для них, задаются свои начальные условия
2/(*о)=2/о, 2/(*о) = 2/1, (61)
определяющие расширенную задачу Коти (в случае
однозначности поля направлений последнее равенство выполняется для
любого решения уравнения автоматически и потому излишне).
iY\o крайней мере, теоретически. Практически же дело обстоит иначе,
слишком большие колебания попросту разрушают маятник.
2Одно или более, допустимо даже, что и бесконечно много, но, возможно,
и ни одного.
63
II*. Теорема существования и единственности.
Справедлив следующий аналог локальной теоремы существования и
единственности для уравнения, не разрешенного относительно
производной
Теорема 37. Если F,Fy,F^ Ε С(Н), то для любой тройки
(^от 2/0ί 2/1) £ Η, удовлетворяющей условию (60) и неравенству
*S(*o,Wb2Ji)^0, (62)
в некоторой окрестности U(to) точки to существует
единственное решение
у: U(to) ->R
расширенной задачи Коши (59), (61).
Доказательство этой теоремы сводится к тому, чтобы на
основании теоремы о неявной функции выразить явно
производную у из данного уравнения в окрестности точки (ίο»2/ο»2/ι)> а
затем и решить полученное дифференциальное уравнение для
найденной ветви его правой части.
Но это еще не все: чтобы доказать единственность решения,
нужно убедиться в том, что вблизи точки (^0ι 2/θί 2/ι) решение не
сможет перескочить с заданной ветви правой части на какие-
либо другие ее ветви — для этого достаточно изолировать
указанную ветвь от остальных и воспользоваться теоремой Дарбу
о промежуточном значении производной1.
► 1. По теореме о неявной функции, в силу неравенства (62), в
некоторой прямоугольной окрестности G х V точки (ίο»2/ο»2/ι)>
где
GEG(i0)yo)cR2, V = V(yi)cR\
уравнение (59) задает единственную функцию (рис. 15)
y = f(t,y), (t,y)eG, (63)
Утверждающей, что производная дифференцируемой числовой
функции на промежутке принимает вместе с любыми двумя своими значениями
также и любое промежуточное значение Впрочем, если в формулировке
теоремы 37 с самого начала повысить гладкость исходной функции,
предположив, что F G С1 (Я), то тот же факт будет вытекать еще и из теоремы
о промежуточном значении непрерывной функции
64
У = Р"
w<
У\
:?4--.
'k- ! .P
ι ^L_* г
/ 1
/ 1
/ 1
- — |
y=f(t,y)
Рис. 15 Выделение одной ветви уравнения
удовлетворяющую к тому же условиям
f(to,yo) = yu f'.G^V, /,/;GC(G).
2. Тогда по теореме 9 в некоторой окрестности U(to) = I
точки to существует функция у, удовлетворяющая:
• уравнению (63), а с ним и уравнению (59);
• первому из равенств (61), а значит, и второму
У(*о) = f{to,y(to)) = f{to,y0) = 2/ι·
Итак, на интервале / существует решение у задачи (59), (61).
3. Для доказательства единственности найденного решения у
предположим, что нашлось еще одно решение ζ той же задачи,
определенное на том же интервале и отличающееся от у хотя бы
в одной точке Τ Ε /. Пусть, например1, Τ > to, тогда:
• для числа
U = mf{t > t0 I z(t) φ y(t)} < Τ
(64)
имеем
ζ(«) = У(«), to < t < tu Zl = z(ti) = y(*i) G ^ (*L *0 G Φ
1 Случай Τ < to рассматривается аналогично.
65
• выберем окрестность J С I точки ίχ, в которой
выполняются два условия1
(t,z(t))eG, z{t)ev, teJ,
тогда на всем интервале J функция ζ, как решение уравнения
(59), будет удовлетворять именно его ветви (63);
• начальные значения решений ζ и у уравнения (63) в точке
t\ одинаковы, поэтому (согласно теореме 9) они совпадают друг
с другом в целой ее окрестности, что противоречит определению
(64) числа t\.
Таким образом, на интервале / решение задачи (59), (61)
единственно. ■
III. Особые решения. Чтобы выяснить, является ли данная
точка точкой существования и единственности для уравнения,
не разрешенного относительно производной, требуется
расширить набор (£(ь2/о) начальных значений еще и значением
производной у\, от которого может зависеть результат. Поэтому
определение 1.5 нуждается в следующем уточнении и дополнении.
Определение 2.7. Для уравнения (59):
• тройка (to,yo,yi) называется точкой неединственности,
если некоторые два решения, удовлетворяющие условиям (61),
локально вблизи to различны2;
• решение у называется особым (равно как и
соответствующая ему интегральная кривая), если при каждом t Ε D(y)
тройка (£,у(£),у(£)) является точкой неединственности;
• множество пар (£(ь2/о)> каждая из которых хотя бы при
одном значении у\ удовлетворяет сразу двум условиям
Первое достигается за счет непрерывности функции ζ в точке t\, а для
выполнения второго достаточно взять какую-либо окрестность W <ё V
точки z\ и, пользуясь непрерывностью функции / в точке (ίχ,ζι), уменьшить
(если потребуется) интервал J так, чтобы на нем выполнялось еще и условие
/(ί,ζ(ί)) € W, обеспечивающее импликацию
z(t)€V=>z(0 = /(t,z(0)€W
и тем самым (в силу соотношений
z(ti) = ziGW, z(t)#V\W, teJ,
и теоремы Дарбу) делающее невозможным событие ζ(ί) ^ V при t G J
Τ е не являются локально совпадающими.
66
F{to,yo,yi) = 0, i*(to,W),yi) = О, (65)
называется дискриминантной кривой1.
Согласно данному определению, решение является особым
тогда и только тогда, когда через каждую точку его
графика проходит, причем касаясь его, другая, локально отличная от
него, интегральная кривая2 Из теоремы 37 вытекает наличие
тесной связи между особым решением и дискриминантной
кривой.
Следствие 38.Если F,Fy,F^ Ε С(Я), то любая особая
интегральная кривая уравнения (59) содержится в его
дискриминантной кривой.
► Действительно, если точка (£(ь2/о) принадлежит интегральной
кривой, то для некоторого у\ выполнено первое из равенств (65),
а если эта кривая к тому же еще и особая, то (to, уо,у\) —
точка неединственности, а значит, в силу теоремы 37 выполнено и
второе равенство ■
Разрешенное относительно производной уравнение (63) не
имеет дискриминантной кривой, поскольку для него второе из
равенств (65), имеющее вид 1=0, невыполнимо в принципе.
Поэтому, согласно следствию 38, особое решение может возникнуть
у такого уравнения исключительно по причине недостаточной
гладкости его правой части.
IV. Сравнение свойств уравнений. Для заданной
функции / Ε C^R2) рассмотрим три уравнения
У = /(*> 2/)> У = /(*> 2/)> У = /(*> У)
и выясним, у какого из них две интегральные кривые в какой-
либо точке (£(ь?/о) £ ^2 (не будучи вблизи нее локально
совпадающими) могут:
• пересекаться друг с другом,
• касаться друг друга.
1. Первое уравнение имеет порядок 1 и удовлетворяет
теореме 9. Поэтому'если две его различные интегральные кривые
Для ее нахождения обычно из системы (65) исключают параметр у\
2Если «забыть» о существовании дифференциального уравнения (59),
то его особая интегральная кривая называется огибающей семейства всех
остальных его интегральных кривых
67
проходят через общую точку (£(ь2/о)> то соответствующие им
решения удовлетворяют одной и той же задаче Коши
i/ = f{t,y), y{k) = 2/0,
а значит, вблизи этой точки просто совпадают Так что они не
могут ни пересекаться, ни касаться.
2. Для второго уравнения, имеющего порядок 2 и
подпадающего под теорему 30, задача Коши ставится по-другому:
y = f(t,y), у(к) = Уо, y{to)=yi-
Следовательно, касаться ни в какой точке графики двух его
решений не могут (иначе решения будут удовлетворять общей
задаче Коши), а вот пересекаться могут. Более того, через любую
точку (to, yo) проходят, пересекаясь, не только две, а даже
бесконечно много интегральных кривых — столько, сколько
различных значений можно придать числу у\.
3. Что же касается третьего уравнения, то его решения могут:
• пересекаться — в точке (to,yo), для которой значение у ι из
уравнения (60) определяется неоднозначно;
• касаться — в точке (to,yo), принадлежащей дискриминант-
ной кривой.
Действительно, рассмотрим для примера сглаженное
уравнение вытекания жидкости1
У2 = У,
которое распадается на две ветви
У = ±у/У,
а потому в каждой точке (to, yo) при уо > 0 задает два
направления, соответствующие двум значениям у\ = ±у/у0> Каждого из
этих направлений касается своя интегральная кривая, а значит,
они в этой точке пересекаются.
Дискриминантная кривая этого уравнения получается из
системы
\2jr = 0 У
*См. соответствующий пример в разделе IV из π 1 3, где мы для
простоты взяли к = 1, а для достижения большей гладкости коэффициентов
возвели обе части уравнения в квадрат, распространив его и на положительные
значения у, соответствующие «втеканию» жидкости
68
и через каждую ее точку (to,0) проходят по меньшей мере две
локально различные, но касающиеся друг друга интегральные
кривые
у = О, y={t- t0)2β.
2.12. Метод введения параметра
позволяет свести уравнение, не разрешенное относительно
производной, к разрешенному, правда, при некотором ограничении.
I. Уравнение, разрешенное относительно функции.
Пусть уравнение (59) приведено к виду
y = f(t,y), fe&iG). (66)
С каждым искомым решением у уравнения (66) свяжем
дополнительную функцию ρ с помощью тождества
P(t) = y(t), te£>(y), (67)
приписав которое к исходному уравнению, получим
ί у(«) = /(*. у(*)) /y(t) = f(t, pW)
\ρ(ί) = y(i) \ρ(ί) = fl{t, p(t)) + fyt, ρ(ί))ρ(ί)
(второе тождество последней системы получается путем
дифференцирования первого по ί и применением тождества (67),
которое, в свою очередь, само выводится из последней системы тем
же дифференцированием ее первого тождества и сравнением
полученного результата со вторым тождеством).
Последнее уравнение системы, записанное для функции p(t)
в виде
Ρ = Л'(*,Р)+ /;(*, Р)Р, (68)
является дифференциальным и, кстати, разрешенным
относительно производной1. Найдя множество его решений ρ = p(t) и
подставив каждое из них в первое уравнение системы, получим
множество решений исходного уравнения.
Если же в качестве решения полученного
дифференциального уравнения будет найдена только зависимость t от р, то и она
При условии, что в рассматриваемой области выполнено неравенство
f'y{t>y) Φ 0> согласующееся с неравенством из формулировки теоремы 37
69
в системе с первым равенством также задаст искомую функцию
у(£), хотя и параметрически1
У = /№),Р)
t = t(p).
Этим и объясняется название данного метода, при
использовании которого тождество (67) обычно сразу истолковывается
как введение параметра, даже если его впоследствии и удастся
исключить.
II*. Уравнение Клеро. Рассмотрим один замечательный
частный случай уравнения (66), а именно, уравнение Клеро,
которое, по определению, имеет вид
y = tp-y(p), р = у.
Пусть функция φ Ε С1{1) вблизи любой точки ρ Ε / локально
нелинейна, т.е. ее производная φ' не есть константа2. Разобьем
область определения функции φ на промежутки монотонности
ее производной и будем, для простоты, сразу считать, что
интервал / и есть один из них.
Тогда уравнение (68) записывается в виде
p = p + tp- у'(р)р <=> (t - φ'(ρ))ρ = 0
и дает два типа решений:
1) семейство прямых
у = Ct — ср(С) (так как ρ = 0 4=> ρ = С);
2) параметрически заданную кривую
ί* = φ'(ρ)
]y = pt- φ(ρ) = ру'(р) - φ(ρ),
вдоль которой изменение параметра ρ влечет обязательное
монотонное изменение переменной t.
Последняя кривая — единственная особая интегральная
кривая уравнения Клеро. Действительно:
Причем параметром будет служить не что иное, как ее производная
2Если φ G С2(7), то достаточно предположить φ"(ρ) φ 0 при всех ρ 6 /.
70
• через любую точку (£(ь2/о) данной кривой, задаваемую
некоторым значением ро, проходит соответствующая прямая из
семейства, задаваемая константой С = ро;
• поскольку и кривая, и прямая имеют в этой точке
одинаковое значение производной у = ро (в силу самого смысла
параметра р), они касаются друг друга,
• данная кривая не совпадает ни с какой прямой, даже
локально вблизи (i(h2/o)i так как при изменении переменной t не
может оказаться постоянным параметр ρ = у, а значит,
зависимость переменной у от переменной t нелинейна,
• данная кривая в точности совпадает с дискриминантной
кривой уравнения Клеро, так что других особых решений оно
не имеет
Уравнение Клеро можно использовать для решения обратной
задачи, а именно для нахождения огибающей к данному
семейству прямых.
III*. Геометрическая интерпретация. Наиболее
естественно уравнение (59) изображается в пространстве
переменных (t,y,p) Ε Η, где ρ = у, которое называется
пространством 1-струй функций. В нем исходное уравнение задает
поверхность1 (см. рис. 15)
F(t,y,p)=0.
Лоле направлений (см. определение 1.1), которое раньше в
каждой точке (t, у) задавало прямую с угловым коэффициентом
ρ на горизонтальной плоскости, теперь, в связи с выходом из
плоскости в трехмерное пространство, превращается в поле
контактных плоскостей. А именно, в каждой точке (t,y,p) теперь
задается такая вертикальная (т.е. перпендикулярная
горизонтальной) плоскость, что ее проекция на горизонтальную
плоскость есть прямая с угловым коэффициентом р.
Таким образом, можно искать кривые на заданной
поверхности, т. е. 1-графики решений, которые в каждой своей точке
касаются соответствующей контактной плоскости2, а тогда их
проекции будут касаться поля направлений, т. е. окажутся
интегральными кривыми.
1 Заведомо — вблизи тех точек, где выполнено неравенство (62)
2Но по невертикальному направлению, что как раз и обеспечивается
неравенством (62), τ е невертикальностью касательной плоскости к
поверхности в этой точке
71
Ρ'
2p=t-c
p = 0-
Рис. 16. Склейка двух ветвей
Так, уравнение вида (66) задает в пространстве поверхность
y = f(t,p),
содержащую 1-графики решений. Их проекции на плоскость с
координатами (£,р), получаемые путем исключения переменной
у, интерпретируются как интегральные кривые уравнения (68).
Находя их аналитически и возвращая им снова координату у,
мы восстанавливаем 1-графики решений. Исключая из них
параметр1 р, окончательно проектируем их на горизонтальную
плоскость и получаем искомые интегральные кривые уравнения (66).
IV*. Сглаженное уравнение вытекания жидкости.
Уравнение (см. раздел IV из п. 2.11)
У = Р2, Р = У,
в пространстве (t,y,p) задает поверхность, состоящую из двух
ветвей, которые смыкаются вдоль оси t (рис. 16).
Перейдя к координатам плоскости (t,p), получим проекции
1-графиков на эту плоскость
ρ = 2рр <=>
Р = 0,
2p=l(<=>2p = t-C).
Далее, добавив координату у и исключив параметр р,
получим проекции 1-графиков на плоскость (ί, у)
хИли переставая его изображать, τ е принимая его именно за параметр
72
' y = o,
_ Ay = (ί - C)\
т. е. уже настоящие решения (здесь смысл константы С —
момент полного вытекания жидкости из сосуда).
Первая из полученных кривых совпадает с дискриминант-
ной кривой уравнения и является особой: вдоль нее контактные
плоскости не задают однозначного направления, поскольку
просто совпадают с касательными плоскостями к поверхности в
соответствующих точках. Все же остальные кривые попарно
пересекаются.
Задачи для самостоятельного решения
1. Докажите, что если / € С (G) (к € N U {0}), то любое решение
уравнения (28) есть к+\ раз непрерывно дифференцируемая функция.
2. Докажите, что теорема 9 останется в силе, если в ней условие
/, f'x € C(G) заменить следующим: / — непрерывна по t (а не по паре
(ί, χ)) и липшицева по χ в области G.
3. Сформулируйте и докажите аналоги теорем 9 и 16 для уравнения
(200) в дифференциалах.
4. Докажите, что если функция / липшицева по χ и непрерывна в
области G, содержащей множество
С = {(ί, χ) Ι α < t < β, \χ - χ0\ < R},
причем1
-^->Μ= sup |/(ί,*)|,
Ρ - α (t,x)ec
то для любой точки (ίο, xq) € С последовательность хп (34)
приближений Пикара сходится равномерно на отрезке [α, β] к решению
уравнения (31).
5. Постройте (графически) простейшую ломаную Эйлера для
задачи Кош и
χ = —х, х(0) = 1,
на отрезке [0,3] в случае разбиения σ, равного:
• (0, 1, 2, 3),
. (0, 1/2, 1, 3/2, 2, 5/2, 3).
Здесь допустимо также и значение Μ = оо, при котором R = оо
73
6. Для заданного уравнения (28) и компакта С С G оцените снизу
с помощью числа (43) время пребывания вне этого компакта графика
любого непродолжаемого решения, начинающегося в этом компакте,
при движении по оси времени, например, вправо.
7. Основываясь на определении 2 4, дайте определение непродол-
жаемой интегральной кривой уравнения в дифференциалах (3).
Докажите, что если все точки области G — точки единственности (см.
определение 1 5), то любые две непродолжаемые интегральные
кривые уравнения (3), имеющие общую точку, совпадают.
8. Какие из следующих утверждений для уравнения (28) верны
• если f E С1 (К2), то область определения D(x) любого
непродолжаемого решения χ есть вся числовая ось R,
• если / € СХ(М2) и область определения D(x) некоторого
непродолжаемого решения χ есть луч R+ ξ (0;οο), то существует
бесконечный (т.е. равный +оо или — оо) предел
lim χ(ί), (69)
• если / € C^R* xl) и область определения D(x) некоторого
непродолжаемого решения χ есть луч R+, то существует предел (69),
возможно, бесконечный?
9. Какая оценка для решения линейной системы (50) получится,
если в доказательстве теоремы 27 вместо леммы 26 о
дифференциальном неравенстве применить непосредственно лемму 24 об
интегральном неравенстве к соответствующему интегральному уравнению7
10. Известно, что функция у = tg 2ί служит одним из решений
задачи, состоящей из уравнения
у'" + a(t)y" + b{t)y' + c(t)y = 0, а,Ь,се C(t/(0)),
и двух условий у(0) = 0 и у'(0) = 2. Сколько решений имеет эта
задача7 На какой наибольшей окрестности U(0) точки t = 0 может быть
задано это уравнение7
11. Какой наименьший порядок может иметь уравнение
у{п) = f(t,y,y, .,ιΛ"1*), feCl(Rn+l),
с частными решениями yi(£) = t и уг(0 = sini?
12. Докажите, что все решения уравнения колебаний маятника
y + P{t)y + q{t)smy = f{t), i € R, p,g,/€C(R),
продолжаются всю числовую ось.
13. Продолжается ли на всю числовую ось любое решение
уравнения
y = (t3 + y*)smey?
74
14. Докажите, что любая огибающая к семейству решений
дифференциального уравнения (59) является его особым решением.
15. Обязательно ли является особым решением дискриминантная
кривая уравнения (59)? А если дополнительно известно, что она
является его решением7
16. Как приспособить метод введения параметра к уравнению (59),
разрешенному относительно независмой переменной
* = /(у,у), /ее1 (С)?
17. Решите методом введения параметра не разрешенное
относительно производной уравнение Лагранжа1
у = <р(у)« + ф(у), ф.фбСЧ/).
Более общее, чем уравнение Клеро
Глава 3
ОБЩАЯ ТЕОРИЯ ЛИНЕЙНЫХ
УРАВНЕНИЙ И СИСТЕМ
3.1. Общее решение однородной системы
x = A(t)x, xeRn, tel, (70)
имеет линейную структуру.
I. Линейное пространство вектор-функций. Пусть
фиксировано число η Ε N.
Для заданного интервала / С Μ обозначим через Ф(/)
линейное векторное пространство всех функций /:/—>· Rn с
естественными линейными операциями
(Ci/i + C2/2)(i) = Ci/i(i) + C2/2(i), tel, Ci,2eR.
Нулевым вектором в пространстве Ф(/) является нулевая
функция
0(0 = оеRn, tel.
Определение 3.1. Функции /ι,..., Λ Ε Ф(^) называются
линейно зависимыми, если некоторая их нетривиальная1
линейная комбинация равна нулю
<?ι/ι + ··· + <?*Λ = 0,
и линейно независимыми — в противном случае.
Согласно теореме 27 множества Sa,f и Sa = Sa,o всех непро-
должаемых решений линейной неоднородной системы
x = A{t)x + F(t), xeRn, tel, (71)
Т. е с набором констант С\, ,Ck, состоящим не из одних нулей
76
(при условии A, F Ε С(7), которое будем считать выполненным
в дальнейшем1) и соответствующей однородной системы
являются подмножествами пространства Φ(/).
II. Теорема об изоморфизме. Множество всех решений
линейной однородной системы образует линейное пространство,
изоморфное пространству их начальных значений, что и
утверждает следующая
Теорема 39. Множество Sa — линейное пространство,
причем для любого to Ε I отображение
φί0:<£4->Κη, где φίοχ = χ(ί0), (72)
есть изоморфизм линейных пространств.
► 1. Отображение (72) — биекция, так как согласно теореме 27
для любого начального значения а Е Rn существует
единственная функция χ Ε Sa, удовлетворяющая начальному условию
φίο(χ) Ξ*(*ο) = α·
2. Для любых χι, Χ2 Ε Sa и С\, C2 Ε Μ:
• имеем
(Cixi + C2x2) = Ci*i + C2x2 =
= CiAxi + C2Ax2 = A(CiXi + C2x2),
откуда (CiXi + C2x2) Ε «5м, а значит, подмножество Sa С Ф(/)
есть линейное подпространство;
• имеем
φί0(^ιχι + С2Х2) = Cixi(io) 4- C2x2(i0) = <?ιφίο(χι) 4- Ο2φίο(χ2),
поэтому отображение (72) — гомоморфизм линейных
пространств (а раз биекция, то и изоморфизм). ■
III. Фундаментальные системы решений. В силу
существования изоморфизма, описанного в теореме 39, любые
свойства и характеристики решений, определяемые только
линейными операциями2, оказываются такими же, как и для их
начальных значений.
На протяжении всей гл 3
2Как то размерность пространства или подпространства решений,
линейная зависимость или независимость данной системы решений,
принадлежность какого-либо решения ее линейной оболочке и τ π
77
Следствие 40. Размерность пространства решений
линейной однородной системы из η уравнений первого порядка
равна п.
Определение 3.2. Любой базис χι, ... ,хп в пространстве Sa
решений линейной однородной системы (70) называется
фундаментальной системой ее решений.
Существование фундаментальных систем решений линейной
однородной системы (70) вытекает из существования базисов в
Rn. Более того, для построения какой-либо фундаментальной
системы решений достаточно взять любой базис е\, ..., еп в Rn
и, выбрав какой-либо начальный момент to £ /, определить
решения
χ1 = Φίο ei' * *' ,Хп = Φίο βη#
Следствие J^l. Если χι, ...,xn — фундаментальная
система решений системы (70), то общее решение этой системы
имеет вид
χ = CiXi(i) Η h Cnxn(t).
3.2. Фундаментальная матрица и оператор Коши
тесно связаны друг с другом и решениями линейной однородной
системы.
I. Фундаментальная матрица. Пусть в пространстве Rn
фиксирован базис и задана система (70) Под решением, далее,
будем понимать функцию χ £ Sa, а под матрицей — (η χ п)-
матрицу.
Определение 3.3. Матрицу
Χ(ί) = (χι(ί), ...,x„(t)), tel, (73)
назовем:
• матрицей решений, если ее столбцы χι, ..., χη являются
решениями,
• фундаментальной матрицей, если ее столбцы Χι, ..., χη
образуют фундаментальную систему решений.
Из теоремы 39 вытекает
Следствие 4%· Для любого to Ε Ι матрица решений X:
78
• однозначно определяется начальным условием X(to) = Xq
при каждой начальной матрице Хо;
• фундаментальна тогда и только тогда, когда
detX(t0) т^О.
► Действительно, решения Χι, ... ,хп, они же — столбцы
матрицы X, однозначно определяются своими начальными
значениями
XI(ίθ) = ф*охЬ •••,Χη(ίθ) = Ьохп,
линейная независимость которых равносильна
фундаментальности системы этих решений. ■
Из следствия 41 получаем
Следствие J^S. Если X — фундаментальная матрица
системы (70), то общее решение последней имеет вид
χ = X{t)c, с е Жп. (74)
► Действительно, имеем
(сЛ
в силу равенства (73). ■
II. Оператор Коши. Определяемый ниже оператор Коши
замечателен своим естественным геометрическим смыслом,
который позволяет формулировать и доказывать утверждения с
его участием, не прибегая к координатной записи
пространства Rn.
Определение 3.4. Для заданной пары чисел t,s Ε / назовем
оператором Коши системы (70) (или оператором сдвига из s в
t) оператор
X(t,s):Rn ->Rn,
удовлетворяющий требованию
X(t,s)x(s)=x(t), xeSA. (75)
Таким образом, под оператором Коши понимается двухпара-
метрическое семейство операторов, задаваемых начальным s и
конечным t моментами времени и переводящих значение
любого решения в момент s в значение того же решения в момент t
(рис. 17).
79
Рис. 17. Геометрический
смысл оператора Коши
Лемма 44' Требование (75)
однозначно задает линейный
невырожденный оператор, причем для
любых t,s,r G I справедливы
следующие свойства:
• X(t, t) = X — тождественный
оператор;
X(t,s)X(s,r) = X{t,r);
X-1(t,s) = X(s,t).
► 1. Проверим корректность
определения: для любого а G Rn
однозначно определено решение х, для которого x(s) = α, поэтому
значение
X{t,s)a = X{t,s)x{s) = x(t)
также определено однозначно.
2. Проверим линейность оператора X(t,s): пусть Xi,X2 G Sa
и Ci, C2 G R, тогда (CiXi + C2X2) G Sa и
*(M)(CiXi(s) + C2X2(s)) =
= X(t, s)(CiXi + C2x2)(s) = (Cixi + C2x2) (i) =
= Cixi(i) + C2x2(i) = C1X(t,s)xl(s) + C2X(t,s)x2(s).
3. Проверим свойства оператора Коши:
• для всякого χ G Sa имеем
X(t,t)x{t) =χ(ί) = Jx(i),
откуда A*(i, ί) = Χ;
• для всякого χ G «Я4 имеем
#(ί, s)^(s, r)x{r) = X{t, s)x(s) = x{t) = X(t, r)x(r),
откуда X(t, s)X(s,r) = X(t,r);
• теперь из равенства
X(t,s)X(s,t)=X{t,t)= 1
получаем равенство X_1(t, s) = X(s,t), а заодно и
невырожденность оператора Коши. ■
III. Матрица Коши. Если в Rn фиксирован какой-либо
базис, то в нем матрица оператора Коши X(t,to) есть не что иное,
80
как фундаментальная матрица X{t), нормированная в
начальный момент to, т. е. удовлетворяющая условию
X(t0) = Ε.
Это, в частности, и утверждает следующая
Лемма 4&· При любых i,s 6 / матрица Коти X(t,s)
системы (70):
• для любой фундаментальной матрицы Х(-)
представляется в виде
X(t,s)=X(t)X-l(s);
• совпадает с матрицей решений X(t), нормированной в
момент s.
► 1. Если X — фундаментальная матрица, то для любого
решения χ существует такой вектор с G R™, что χ = Хс (см.
следствие 43) и
(X{t)X-l{s)) x(s) = X{t)X-l{s)X{s)c = X(t)c = χ(ί),
поэтому оператор X(t)X~l(s) удовлетворяет равенству (75), а
значит, согласно лемме 44, совпадает с оператором X(t,s).
2. Возьмем матрицу решений X, удовлетворяющую условию
X(s) = Ε (см. следствие 42), тогда X — фундаментальная
матрица, с которой, в силу равенства
X(t,s) = X{t)X-l{s) = Χ(ί),
совпадает матрица Коши X(t,s). ■
IV. Матричное дифференциальное уравнение.
Производную (п х п)-матричной функции1 X: I —у Л4пхп, по
определению, вычисляют покоординатно, а производную оператор-
функции X: / —> End Ш.п — по формуле
л-ю h
(предельный оператор, если он существует, обязательно
линейный в силу полноты пространства ЕгкШп).
*Как и вектор-функции; далее через А4пХп обозначено пространство всех
(η χ п)-матриц
81
Результаты этих вычислений соответствуют друг другу из-за
естественного изоморфизма1 между п2-мерными линейными
топологическими (даже нормированными, см. лемму 12)
пространствами ЕгкШп и Д4пхп: если матричная функция X служит
записью оператор-функции X в некотором базисе, то ее
производная X служит записью оператора X в том же базисе. Кроме
того, для таких функций будут верны все обычные правила для
взятия производных или пределов2.
Лемма 46· Решениями матричного дифференциального
уравнения
X = A(t)X, t е /, (76)
служат матрицы решений системы (70) и только они, а для
любого фиксированного to Ε Ι решением операторной задачи Ко-
ши
X = A(t)X, tel, X\t=t0=Z, (77)
служит оператор Коши X(t, to) системы (70) и только он.
► Во-первых, матричное уравнение (76) в обозначениях (73)
равносильно следующему:
\Χ\ι . . . , Хп) = \A\t)Xi 5 · · · 5 A\t)Xn) \ V Χΐ = A[t)Xi·) I = I, . . . , 7Ϊ,
и означает, что столбцы матрицы X являются решениями.
Во-вторых, операторная задача (77) в фиксированном базисе
в Ш.п задает нормированную в начальный момент ίο матрицу
решений, т. е. матрицу Коши (см. второе утверждение леммы 45). ■
3.3. Определитель Вронского
и формула Лиувилля — Остроградского
для вектор-функций отражают их специфические свойства,
связанные с линейной независимостью и объемом натянутого на них
параллелепипеда.
I. Определитель Вронского и линейная зависимость.
Пусть Ш.п — координатное пространство.
Определяемого базисом в Шп
2Такие как производная или предел суммы, произведения (композиции
операторов), вынос за знак производной постоянного множителя (вектора,
матрицы, оператора) и т. π
82
Определение 3.5. Назовем определителем Вронского
вектор-функций /i,...,/nG Ф(/) функцию
W/i, ,/„(«) = det(/i(i),...,/„(i)), ί€/.
В евклидовом пространстве Rn определителю Вронского
можно придать и инвариантный1 геометрический смысл, а именно,
W/1} ,fn(t) — это ориентированный объем параллелепипеда,
натянутого на репер /ι(ί), ..., /η(ί)·
Лемма 47> Если функции /χ, ..., fn Ε Ф(/) линейно
зависимы, то
Щи ,/.(0 = 0, tei.
► Если вектор-функции /ι, ...,/п линейно зависимы, то при
каждом t Ε I линейно зависимы и векторы /ι(ί), ••·,/η(0> а
значит, Wfu ,/η(ί) = 0. ■
Лемма 48. Утверждение, обратное к сформулированному
в лемме 47, неверно.
► В качестве контрпримера к обратному утверждению
рассмотрим функции
/i(*)=(j). Λ(0=β). *eK. (78)
Их определитель Вронского тождественно равен 0 (так как
соответствующая матрица имеет нулевую строку), хотя они и
линейно независимы: действительно, тождество
Ci · 1 + С2 · ί = 0, t Ε R,
возможно только, если Ci = С2 = 0. ■
Однако для решений линейной однородной системы
справедливо и обратное к лемме 47 утверждение2. Более точно, имеет
место
Теорема 4&· Если χχ, ..., χη Ε Sa, то следующие
утверждения эквивалентны:
1Не зависящий от выбора в Шп ортогонального базиса положительной
ориентации
2
Откуда следует, в частности, что функции (78) не являются
одновременно решениями никакой системы (70) при η = 2
83
функции Χι, ... ,χη — линейно зависимы;
Wxi, ,χη(0 — 0 для всех t G /;
WXlj ,Χη(ίο) = О для некоторого to G I.
► Из первого утверждения вытекает второе по лемме 47, из
второго — третье автоматически, а из третьего — первое в силу
следствия 42. ■
II. Формула Лиувилля — Остроградского. Так
называется равенство, утверждаемое в следующей теореме и
связывающее определитель Вронского решений линейной системы со
следом матрицы этой системы.
Теорема 50. Для любых решений χ ι, ..., χη G Sa имеет
место равенство t
ίτΑ(τ)άτ
Wxi, ,хп(0 = ^хь ,χη(*ο)·^° , to,tei.
► 1. Докажем, что определитель Вронского W = WXu >Xn
удовлетворяет дифференциальному уравнению
W = trA(t)-W, tel, (79)
из которого и будет вытекать требуемое
ίτΑ(τ)άζ
= СеК
W(t) = CeJto , С =
2. Производную определителя матричной функции Х(-)
можно считать по правилу1
= det | I +-.- + det ln_!
,хп/ \ xn
где хг — г-я строка матрицы X.
*Этот факт вытекает, например, из представления определителя в виде
знакопеременной суммы всевозможных произведений элементов матрицы,
взятых по одному из каждой строки и каждого столбца
(detX) = (]Γ(-1)σχί(ΐ)
χσ(η)
= Σ(-1)σ*ί(ΐ) .χ?(η)+ +Σ(-1)°Μΐ)
Χσ(η)
84
3. Если а1 = (а\, ... ,агп) — г-я строка матрицы А, то из
равенства X = АХ (см. лемму 46) имеем хг = агХ и
W =
X1
χη
=
X1
χη
+ ·
· +
X1
χη
=
ахХ
уП
+ ·
•4-
X1
OLnX
а\х1 4-
+ а1пхп
,п
-| +
tfx1 +
4- <ж
η
α\χλ
...
χη
4-··
•4-
X1
<χη
= (α} 4- · · · 4- О
χ
,η
= trA -W,
т.е. уравнение (79) выведено. ■
Следствие 51. Если tr A = О, то определитель Вронского
любых решений Χχ, ..., xn Ε Sa есть константа.
Таким образом, если след матрицы системы тождественно
равен нулю, то объем параллелепипеда, натянутого на любой
репер решений χι(ί), ... ,Хп(0> взятых в момент t, не меняется со
временем. Более того, в этом случае1 под действием оператора
Коши не меняется объем любого измеримого подмножества
фазового пространства Rn.
III*. Определитель и след оператора. Из формулы Ли-
увилля — Остроградского выведем формулу для определителя
оператора Коши.
Определение 3.6. Определитель aetX и след Χ,τΧ
оператора X Ε EndlRn — это определитель и след его матрицы X,
записанной в каком-либо базисе в Ш.п.
Инвариантность этих численных характеристик оператора
относительно выбора базиса или, что то же, относительно
матрицы L перехода к новому базису вытекает, например, из такой
же инвариантности его характеристического многочлена
det(X£ -L~lXL) = det L~l · det(X£ - X) · det L =
= det(KE -Χ)=λη-ίτΧ· λη_1 + · · · 4- (-l)n det X,
1 Аналогичное утверждение верно и в случае нелинейной системы, см
теорему Лиувилля 134 далее.
85
первый коэффициент и свободный член которого равны — tr X
и (—l)ndetX соответственно.
Следствие 52. Если X(t,s) — оператор Коти системы
(70), то
tr Α(τ) άτ
detX(t,s)=eJs
► Если в Rn задан базис, то по лемме 45 для любого
фиксированного s Ε / матрица X(-,s) оператора X(-,s) есть матрица
решений, причем X(s, s) = Ε, поэтому
det X(t, s) = det X(s, s) · eJ* = eJ* ,
согласно теореме 50. ■
3.4. Общее решение неоднородной системы
есть общее решение соответствующей однородной системы
плюс частное решение неоднородной.
I. Вид общего решения. Справедливость только что
сформулированного правила нахождения общего решения
неоднородной системы устанавливает следующая
Теорема 53. Для всякого хо Ε Sa,f справедливо равенство
Sa,f = хо 4- Sa = {хо 4- χ Ι χ е Sa}·
► Если у = х0 4- х, где х0 Ε Sa,-f,^o
у = Ау + F 4=Ф х0 + χ = AxqU- Ах + F <=> χ = Ах,
поэтому
у е SA,F <=> χ ε Sa,
откуда и вытекает доказываемое равенство множеств. ■
Следствие 54* Если Хо — частное решение линейной
неоднородной системы (71), а х1} ... ,хп — фундаментальная
система решений соответствующей однородной системы (70), то
общее решение системы (71) имеет вид
х = хо(0 4- Cixi(i) 4- · · · 4- Cnxn(t).
86
II. Аффинное пространство. Заметим, что любое
линейное векторное пространство Φ естественным образом
превращается в ассоциированное (обозначение: ~) с ним линейное
аффинное пространство Ф, представляющее собой множество точек1,
наделенное другой структурой.
А именно, в пространстве Φ определена лишь операция
сложения точки с вектором из исходного векторного
пространства Ф. Результатом этой операции является точка (а
результатом соответствующей обратной операции вычитания точек
служит вектор):
p + f = q {q-p = f), ρ,^φ, /еФ.
При этом для ассоциированных друг с другом аффинного Φ
и векторного Φ пространств, имеющих по определению
одинаковые размерности, оказывается верным равенство
φ = р + Ф, ρ е Ф,
не зависящее от выбора точки2 р.
Таким образом, в новой терминологии теорема 53
иллюстрируется диаграммой
Ф(7) ~ Ф(7)
U U
и утверждает, что множество Sa,f представляет собой п-мерное
аффинное подпространство Хо+^М С Ф(-0, ассоциированное с
векторным подпространством Sa С Ф(/)
III. Метод вариации постоянных. Согласно этому методу,
носящему имя Лагранжа, предлагается для нахождения
частного решения линейной неоднородной системы воспринимать
формулу (74) общего решения соответствующей однородной
системы так, как будто в ней неизвестной величиной является сам
В случае рассматриваемого превращения — тех же самых, прежде
называвшихся векторами. Векторы присутствуют и в аффинном пространстве,
но в нем они уже прикрепляются к различным точкам, а не свободны, как
раньше.
2Если одну из них выделить, объявив нулевой, то аффинное
пространство Φ снова станет векторным пространством Φ (главное отличие их друг
от друга как раз и состоит в отсутствии или наличии этой самой нулевой
точки).
87
векторный множитель с — прежде постоянный, а теперь
зависящий от t.
Обоснование методу вариации постоянных дает
Теорема 55. Для любой фундаментальной матрицы X
линейной однородной системы (70) верно следующее: если функция
с: I —> Шп удовлетворяет уравнению
X(t)c(t) = F{t), t е I, (80)
то функция Хс — решение неоднородной системы (71), т. е.
Хс е Sa,f. (81)
► В силу равенства X = АХ (см. лемму 46) имеем
Хс = F => (Хс)' = Хс + Хс = А(Хс) + F => Хсе SA,F,
т.е. справедлива импликация (80) =$>■ (81). ■
Согласно следствию 42, при каждом t Ε / матрица X(t)
невырождена, а значит, уравнение (81) однозначно разрешимо
относительно неизвестной с:
t
c(t) = X-x(i)F(i) «=Ф c(t) = c{tQ) + f X-^-OFMcft.
ίο
Положив в последней формуле c(to) = 0, по теореме 55
находим частное решение Хо линейной неоднородной системы (71) с
нулевым начальным условием x(to) = 0:
t t
x0{t) = X(t) [х^МОДЛе ix(i,-c)F(-c)cft (82)
ίο ίο
(см. лемму 45).
Прибавив к решению (82V общее решение соответствующей
однородной системы (70)т^юлучаем формулу1 вариации
постоянной для решения задачи Коши.
Следствие 56. Решение задачи Коши (71), (29) задается
формулой
x(t) = X{t,t0)x0+ | Χ{ί,τ)Ρ{τ)άτ,
ίο
где Χ — оператор Коши системы (70).
1Не зависящую ни от выбора фундаментальной матрицы X, ни от выбора
базиса в Ш.п
88
3.5. Линейные периодические системы
вида (71), о которых пойдет речь далее, будут молчаливо
предполагаться определенными на всей прямой / = 1R и
удовлетворяющими естественным требованиям A, F Ε С(7).
1. Матрица монодромии и мультипликаторы.
Фиксируем число Τ > 0.
Определение 3.7. Пусть коэффициенты А и F линейной
системы (71) — Т-периодические функции, тогда:
• сама система (71) называется Τ-периодической;
• при любом ί G R матрица Коши X(t + Τ, t)
соответствующей линейной однородной системы (70) называется матрицей
монодромии;
• каждое собственное значение μ матрицы монодромии
называется мультипликатором.
Из последнего утверждения следующей леммы вытекает, в
частности, что, несмотря на явную зависимость матрицы
монодромии от выбора момента t, ее жорданова форма и собственные
значения (мультипликаторы системы) задаются корректно1.
Основной причиной этого служит инвариантность множества
решений, а с ним и матриц Коши периодической системы
относительно временных сдвигов на целый период.
Лемма 57. Если χ — решение Τ-периодической линейной2
системы (71), то решением этой системы является и функция
xT(t) =χ(ί + Γ), t GR,
а если линейная однородная система (70) Τ-периодична, то.
• X(t + T,s + T) = X(t, s) при любых s, i G R;
• все ее матрицы монодромии подобны друг другу.
► 1. Если x(t) = A(t)x(t) + F(t), то
*т(*) = d^ + T) = A(t + T)x(t + T) + F(t + T) = A(t)xT(t) + F(t).
2. Далее:
*Их независимость от выбора базиса в Rn вытекает уже из факта
существования соответствующего линейного оператора монодромии X{t + T,t)
2Впрочем, не только линейной (71), но и любой другой системы (28) с
Т-периодической по t (при каждом х) правой частью f(t,x)
89
• при любых s, t Ε Μ для каждого решения χ имеем
X(t, s)x{s + Τ) = X(t, s)xT(s) = χτ(ί) = x(i + Τ),
а значит, по определению 3.4, X(t, s) = X(t + T,s + T);
• из предыдущего утверждения и леммы 44 при любом t Ε R
имеем
Χ(ί + Γ, ί) = Α"(ί + Τ, Г)Х(Г, 0)Х(0, i) = X{t, 0)Х{Т, О)*-1 (ί, 0),
поэтому каждая из матриц монодромии X(t + T,t) подобна
матрице Х{Т,0). ш
II*. Задача о периодическом решении. Постановка
задачи о нахождении Т- пери одического решения Т-периодической
системы (71) включает в себя, помимо самой этой системы,
всего лишь одно краевое условие
х(Т) = ж(0). (83)
Это условие, благодаря лемме 57, не только необходимо для
Т-периодичности решения х, но и достаточно: действительно, из
него вытекает совпадение решений хих^в начальный момент
to = 0, а значит, и полное их совпадение
χ(ί) = χτ(ί) = x(t 4- Τ), te R.
Определение 3.8. Назовем краевую задачу (71), (83) с
фиксированной Т-периодической матричной функцией А:
• невырожденной, если для\ любой Т-периодической
неоднородности F она имеет единственное решение1;
• вырожденной, еслц_^дя каждой Т-периодической
неоднородности F в отдельности она либо не имеет решений, либо
имеет их сразу бесконечно много.
Заметим, что логически возможна ситуация, когда при
одной неоднородности задача имеет единственное решение, а при
другой — нет2, т.е. она в смысле данного определения ни
вырождена, ни невырождена.
Которое может оказаться еще и непрерывно зависящим (в определенном
смысле) от неоднородности задачи — тогда задача называется корректной.
2Да и не факт, что если оно не единственно, то их сразу бесконечно много
90
III*. Критерий невырожденности задачи. Оказывается,
краевая задача для нахождения периодического решения
линейной системы бывает не иначе как либо вырожденной, либо
невырожденной — и это полностью определяется мультипликаторами
соответствующей однородной системы.
Теорема 58. Краевая задача (71), (83) с Τ-периодической
функцией А:
• невырождена тогда и только тогда, когда все
мультипликаторы однородной системы (70) отличны от единицы;
• вырождена тогда и только тогда, когда хотя бы один из
мультипликаторов однородной системы (70) равен единице.
► Условие (83) для решения χ неоднородной системы (71)
принимает вид (см. следствие 56)
х(0) = х(Г) = Х(Г,0)х(0)+х0(Г) «=> (Х(Т,0)-Е)х(0) = -хо(Г),
где хо — частное решение (82) системы (71) с начальным
условием хо(0) = 0. Поэтому все зависит от матрицы (Х(Т, 0) — 1·Ε):
• если она невырождена (т.е. число 1 не является
собственным значением матрицы монодромии Х(Т, 0), или
мультипликатором системы), то искомое решение χ определено однозначно;
• если же она вырождена, то искомых решений χ либо нет
вообще, либо бесконечно много. ■
Из доказанной теоремы вытекает
Следствие 59. Для Τ-периодических линейных систем
верны утверждения'.
• неоднородная система (71) имеет единственное Т-перио-
дическое решение тогда и только тогда, когда все ее
мультипликаторы отличны от единицы (или, что то же, когда у
однородной системы (70) нет ненулевых Τ-периодических
решений);
• однородная система (70) имеет хотя бы одно (а тогда их
сразу бесконечно много) ненулевое Τ-периодическое решение
тогда и только тогда, когда хотя бы один из ее
мультипликаторов равен единице.
IV. Одномерное периодическое уравнение. Если η = 1,
то периодическая система (70) записывается в виде одного
уравнения
x = a{t)x + f{t), xeR, teR,
с числовыми Т-периодическими коэффициентами а и /.
91
В этом случае любая из (1 х 1)-матриц монодромии
представляет собой просто положительное число, совпадающее с
единственным мультипликатором
τ
\a{t)dt
μ = ео
Действительно, всякое решение χ этого уравнения удовлетворяет
равенству х(Т) = μ·*(0), а если т = [t/T] Ε Ζ, то еще и равенству
x(i) = X{t, t - Τ) ·... · Χ(τ + Τ, τ)χ(τ) = μ™χ(τ),
где τ = t-mT e [О,Г).
Поэтому, учитывая следствия 54 и 59, получаем:
• при μ < 1 или μ > 1 любое ненулевое решение χ (фиксируем
одно из них) однородного уравнения асимптотически при t —> оо
или t —> — оо соответсвенно приближается к нулю, а
неоднородное уравнение имеет ровно одно Т-периодическое решение хо, к
которому, соответственно также асимптотически,
приближаются все остальные решения, задаваемые формулой
х = хоМ + Cx(t);
• при μ = 1 все решения однородного уравнения Т-перио-
дичны, а решения неоднородного уравнения в зависимости от
неоднородности / либо Т-периодичны (причем тогда уж все
сразу, например, при / = 0), либо непериодичны (например, при
/>0).
3.6. Общее решение] линейного уравнения
заданного на фиксированном интервале / и имеющего порядок
η G Ν, тесно связано с линейным векторным пространством
Фп_1(/) всех (п — 1) раз дифференцируемых функций f:I—¥ R
(ср. с пространством Ф(/) из п. 3.1).
I. Линейность канонической замены. Утверждения о
структуре множества решений линейного уравнения (57) могут
быть доказаны непосредственно, но мы сведем их к ранее
доказанным утверждениям для систем, вспомнив про каноническую
замену ψ (см. определение 2.5). Для этого определим
отображение
Фп_1(/) -^ Ф(/), Ф(/) = ψ (ФП_1(Л) С Ф(/). (84)
92
Лемма 60. Каноническая замена осуществляет
изоморфизм (84) линейных пространств Фп_1(7) и Ф(/)·
► Отображение
Фп-1{1)\ф{1)
есть:
• инъекция1;
• гомоморфизм линейных пространств, поскольку для
любых /ь/2 е ФП-1(Л и СиС2 е Ш имеем
Ф(С1/1 + С2/2) =
/ Ci/i + С2/2 \
Ci/i + Q2/2
= С1(ф/1) + С2(ф/2).
Поэтому образ Ф(/) линейного пространства Фп_1(/) при
этом отображении — тоже линейное пространство, а тогда
отображение (84) есть:
• еще и сюръекция, а значит, биекция;
• изоморфизм линейных пространств. ■
Исходя из леммы 60 можно сделать вывод, что каноническая
замена, отождествляя векторные пространства Фп-1(/) и Ф(/),
сохраняет как в одну, так и в другую сторону.
• свойство их подмножеств быть векторными
подпространствами данной размерности;
• операцию их превращения в аффинные пространства (см.
раздел II из п. 3.4), после которой каноническая замена
превращается еще и в изоморфизм полученных аффинных
пространств;
• свойство их подмножеств быть аффинными
подпространствами данной размерности, ассоциированными с данными
векторными подпространствами.
II. Сведение линейного уравнения к системе. Пусть
подмножества Sa,f,Sa С Фп_1(/) состоят из всех непродолжа-
емых решений линейного неоднородного уравнения
yin) + a1(t)y(n-V + -.-+an{t)y = f{t), yeR, t€/, (85)
Лаковой является даже более общее отображение (54).
93
и соответствующего однородного уравнения
y(n)+oi(i)y(n-1) + ... + o„(i)y = 0, yGR, tel, (86)
где α = (αϊ, ...,αη) и α, / G С(7) (см. теорему 36).
Тогда если А и F — матрица уравнения (85) и его векторная
неоднородность (см. определение 2.6), то множества1
Sa = ψ(5α), SA,F = ψ(5α,/)
являются линейным векторным подпространством пространства
Ф(/) и, соответственно, ассоциированным с ним аффинным
подпространством пространства Ф(/). Теперь лемма 60 позволяет
свести воедино две диаграммы
Ф(7) ~ Ф(7) ф-1 Φη~ι(Ι) ~ Φη~ι(Ι)
и и ^ и и
Sa ~ Sa,f ψ «5α ~ 5α>/
и тем самым вывести
Следствие 61. Прообразы
являются линейным векторным пространством и
ассоциированным с ним аффинным пространством соответственно, а
отображения
Sa ->■ Sa, Sa,f ->■ «S^,f
осуществляют их изоморфизмы.
III. Общее решение. В силу следствия 61 для уравнений
(85), (86) не нуждается в доказательстве следующий
объединенный аналог теорем 39 и 53, из^которого вытекают и аналоги
следствий 40, 41, 54.
Теорема 62. Множество Sa — линейное пространство,
причем:
• для любого to £ I отображение
ψίο : £а->-Rn, где ψίογ = φίο ο ψ = (фу)(£0),
есть изоморфизм линейных пространств',
См лемму 35 и теоремы 39, 53
94
• для всякого решения уо Ε Saj справедливо равенство
Sa,f = УО + Sa-
Таким образом, для линейных уравнений, как и для систем,
справедливо утверждение: общее решение линейного
неоднородного уравнения есть общее решение соответствующего
однородного уравнения плюс частное решение неоднородного.
Следствие 63. Размерность пространства решений
линейного однородного уравнения п-го порядка равна п.
Определение 3.9. Любой базис yi, ..., уп в пространстве Sa
решений линейного однородного уравнения (86) называется
фундаментальной системой его решений.
Фундаментальные системы решений линейного однородного
уравнения (86) существуют. Такую систему образуют,
например, решения
У1 =Ψί^6ΐ, ...,Уп = фГ01еп,
если только to Ε / и е\, ..., еп — базис в Rn.
Следствие 64- Если yi, ... ,уп — фундаментальная
система решений однородного уравнения (86), ауо — частное решение
неоднородного уравнения (85), то общие решения этих
уравнений имеют, соответственно, вид
y = Ciyi{t) + .-.+Cnyn{t)
и
У = уо(*) + Ciyi{t) + · · · + C„y„(t).
3.7. Определитель Вронского скалярных функций
/ι, ..., fn Ε Фп_1(7) это функция
/ι(*) ··· Ш
Λ ω ··· Ш teI
• · ♦ '
ήη~%) ... An-l\t)
I. Свойства определителя Вронского. Изоморфизм ψ
векторных пространств Фп_1(/) и Ф(/), а также пространств Sa
Щи ,Ш = Щ/и ,Ф/„(*) =
95
и Sa (см. лемму 60 и следствие 61) сохраняет еще и
определитель Вронского, что вытекает прямо из его определения.
Следующие утверждения об определителе Вронского
скалярных функций в основном (за исключением леммы 66) вытекают
из соответствующих утверждений для вектор-функций, а
именно, из леммы 47 и теорем 49, 50.
Лемма 65. Если функции /ι, ... ,/n G Фп_1(7) линейно
зависимы, то
Щи ,/„(*) = о, tel.
Лемма 66. Утверждение, обратное к сформулированному
в лемме 65, неверно.
Контрпример к обратному утверждению, приведенный по
аналогичному поводу в доказательстве леммы 48, здесь не
годится, поскольку функции (78) не принадлежат пространству Ф(/).
► Рассмотрим следующую пару функций1
fi{t) = t3, f2{t) = \t\3, teR.
• Их определитель Вронского тождественно равен нулю:
whth(t) =
• Однако они линейно независимы на всей прямой ί 6 1,
поскольку при любом t φ 0 имеем
Cit3 + C2t3sgnt = 0 <=> Ci = -C2sgnt,
хотя отдельно на каждом из лучей t θ Ш+ и t G Ш~ эти функции
все же линейно зависимы. ■
Теорема 67. Если yi, ..., yn G Sa, то следующие
утверждения эквивалентны:
• функции yi, ... ,уп — линейно зависимы;
• Wyu ,yn{t) = 0 для всех t G /;
• Wyi, ,Уп(^о) = 0 для некоторого to G /.
Чтобы перенести формулу Лиувилля — Остроградского на
случай уравнения (86), заметим, что для матрицы А этого
уравнения (см. определение 2.6) выполнено равенство tr А = —αι.
Заметим, что они, в отличие от функций (78), не аналитические, и этот
дефект настоящего контрпримера уже не устраним
t3 t3 Sgn t
3t2 3t2Sgnt
= 0.
96
Теорема 68. Для любых решений yi, ..., yn Ε Sa имеет
место равенство
Щи ,yn(*) = Wyi, ,yn(io)-e"iai(T)dT.
ίο,*
till*. Восстановление линейного уравнения. Для того
чтобы данные η функций образовывали фундаментальную
систему некоторого линейного однородного уравнения (86) η-го
порядка с непрерывными коэффициентами, необходимо, чтобы:
• они были η раз непрерывно дифференцируемыми1;
• их определитель Вронского нигде не обнулялся
(теорема 67).
Этого и достаточно, как показывает
Теорема 69. Если скалярные функции f\.
удовлетворяют условию
Щи ,/»(*) ^ о, tei,
fn е cn(/)
(87)
то они образуют фундаментальную систему решений
следующего линейного однородного уравнения п-го порядка:
Wfu ,/„(<)
/ι(ί)
/ι("_1)(ί)
пп)т
S(n\t)
У
У
(n-1)
У
(η)
= 0.
(88)
Сформулированная теорема позволяет восстанавливать (или
даже составлять) линейное однородное уравнение η-го порядка
по фундаментальной системе его решений.
► 1. Если определитель (88) разложить по последнему столбцу
и, разделив на коэффициент (87) при старшей производной у^п\
приравнять к нулю, то получится линейное однородное
дифференциальное уравнение η-го порядка относительно у.
2. Каждая из функций /$ удовлетворяет полученному
уравнению, так как при подстановке у = fi(t) определитель (88)
обнуляется. А все вместе они, согласно теореме 67, образуют
фундаментальную систему решений. ■
Непрерывность n-й производной решения следует из самого уравнения,
разрешимого относительно этой производной
97
III*. Признаки линейной зависимости. Достаточное
условие линейной зависимости функций, причем исключительно
в терминах определителя Вронского, дает
Следствие 70. Если скалярные функции /ι, ..., /п £
G Сп-1(/) удовлетворяют условиям
И7., ,/„(*) = о, w>„ ,/„-,(*) * о, <е/,
mo омм линейно зависимы.
► Из данных условий и теоремы 69 вытекает, что функция fn —
частное решение линейного однородного уравнения (п — 1)-го
порядка с фундаментальной системой решений /ι, ..., fn-\.
Поэтому линейная оболочка последних содержит функцию /п. ■
Ослабленный вариант обращения1 леммы 65 представляет
Следствие 71. Если определитель Вронского скалярных
функций /ι, ..., fn G Cn-1(J) тождественно равен нулю, то их
сужения на некоторый интервал J С I линейно зависимы.
► 1. Если
wfl{t) = Ш = о, tei,
то уже подсистема из одной функции /ι линейно зависима,
причем сразу на всем интервале /.
2. В противном случае найдется такое k G {2, ...,п}, для
которого хотя бы в одной точке, а с ней и в целой ее окрестности2
J С /, выполнены условия
W/l ,/*(*) = О, W>„ Λ.,(ί)?4 0, t€J.
Тогда, в силу следствия 70, уже подсистема функций /ι, ..., Д
линейно зависима на интервале J. ш
Если линейное однородное уравнение имеет порядок η > 1, то
определитель Вронского к < η линейно независимых его
решений (в частности, одного ненулевого) вполне может в отдельных
точках и обнуляться в отличие от случая к = п. Тем не менее
справедливо
Локального, вблизи хотя бы одной точки.
2В силу непрерывности самих функций и их производных до (к — 2)-го
порядка, а с ними и определителя Вронскогр.
98
Следствие 72. Если определитель Вронского к < η
решений yi, ..., у/ь Ε Sa тождественно равен нулю, то они линейно
зависимы.
► При сделанном предположении, в силу следствия 71,
указанные решения линейно зависимы на некотором интервале J,
поэтому по теореме 62 для некоторого to Ε J линейно зависимы
векторы ψί0γι, ·.. ,ψίοΥ/Ь а значит, и решения yi, ... ,у/ь на всей
своей области определения. ■
3.8. Метод вариации постоянных
для линейного неоднородного уравнения (85) η-го порядка имеет
естественные отличия от аналогичного метода для системы.
I. Обоснование метода. В качестве отправной точки
используется формула
(Cl
y = yi(t)Ci+...+yn(t)Cn = Y{t)c, Y = (yi, ...,yn), c= ···
\Cn
общего решения соответствующего однородного уравнения (86)
через фундаментальную систему его решений yi, ...,уп (см.
следствие 64). В этой формуле постоянные Ci, ..., Сп
принимаются за функции от t и в целях нахождения частного решения
неоднородного уравнения для их производных записывается
система специального вида.
Теорема 73. Для любой фундаментальной системы
решений yi, ..., уп линейного однородного уравнения (86) верно
следующее: если вектор-функция с: I —> Rn удовлетворяет системе
fY(t)c(t) =0
Y(t)c(t) = 0
4 · · · tel, (89)
' Y(n-2\t)c(t) = О
Yt»-i)mt) = №,
то функция Υ с — решение неоднородного уравнения (85), т. е.
Υ с е 5а,/. (90)
99
► Если А и F — матрица уравнения (85) и его векторная
неоднородность соответственно (см. определение 2.6), то, введя
фундаментальную матрицу
Х = фУ = (фу1, ...,фу„), (91)
согласно теореме 55 и лемме 35, получаем
Хс = (фУ)с = F =» Хс е SAyF =>Yc = ф_1(*с) G SaJ,
т.е. справедлива импликация (89) =$>■ (90). ■
Заметим, что система (89) разрешима относительно
неизвестной вектор-функции с, так как при каждом t Ε / матрица
(фУ)(£) (91), состоящая из коэффициентов этой системы,
невырождена.
При η = 1 эта система превращается в одно уравнение
yi(t)Ci = /(«),
а при η > 1 — имеет вид
(Vl(t)C1+--- + yn(t)Cn = 0
Υΐ(ί)6ι + ···+Υη(ί)(7„ = 0
y(r2)WC1 + ... + yr2)WCn = o
II*. Функция Грина задачи Коши. Найдем решение уо
неоднородного уравнения (85) с однородными (нулевыми)
начальными условиями
у(«о) = --- = У(п"1)(*о)=0. (92)
Применив формулу (82) для решения хо соответствующей
системы (70) с начальным условием x(to) = 0, получим
\ t t
Уо(«) = Ф_1хоМ JjV^,-Ο^τ)) άτ = |γτ(ί)/(τ)Λ,
ίο to
где ут — первая координата последнего столбца матрицы Коши
Χ(ί,τ), представляющая собой (см. лемму 45) решение
однородного уравнения, удовлетворяющее условиям
ντ(τ) = ··· = νί"-2)Μ = 0, у("-1»(т) = 1. (93)
100
Полученное в итоге равенство задает оператор, ставящий в
соответствие каждой неоднородности / Ε С(7) решение уо
задачи Коши1 (85), (92) (с фиксированными функцией a Ε С(7)
и начальным моментом to £ I) и записываемый в следующем
виде.
Уо(0 = f £τ(Μο)/(τ)</τ, teJ= [ί0; β)· (94)
ίο
Определение 3.10. Ядро GT(t,to): J —> R интегрального
оператора (94), зависящее от параметра τ G J и определяемое
формулой
Г !t , ν _ /θ, ίθ < t < Τ,
στ{ί,ί0) = \*(ί). τ<<<β,
называется функцией Грина задачи Коши.
III*. Физический смысл функции Грина. Ее можно
интерпретировать как функцию влияния точечной единичной
неоднородности2 в момент τ > ίο на решение однородной задачи.
1 Однородность начальных условий (92) не сильно ограничивает
общность задачи Коши Действительно, в случае неоднородных условий (53)
достаточно подобрать какую-нибудь удовлетворяющую им функцию yi
(например, многочлен) и перейти к новой переменной ζ = у — yi(t), для которой
начальные условия превратятся в однородные, а в уравнении (85)
изменится только неоднородность — но и ее с равным успехом будет обслуживать
та же формула (94).
2Так называемой Ь-функции (обобщенной), сдвинутой в точку τ и
призванной «удовлетворять» следующему интегральному равенству (свертки)'
β
|δ(ί-τ)./(τ)Λ = /(ί).
to
Вообще, функция Грина задачи, определяемой линейным
дифференциальным оператором L, — это зависящее от параметра τ решение (называемое
фундаментальным) уравнения
Ly = b(t - τ)
Так, для рассматриваемой задачи Коши оператор L определен на
множестве функций, заданных на промежутке J и удовлетворяющих однородным
начальным условиям (92), а его действие на у задается левой частью
уравнения (85) Аналогично, в случае изучаемой ниже краевой задачи оператор L
определен на функциях с однородными (φι = φ2 = 0) краевыми условиями
(96) и задается левой частью уравнения (95)
101
Заметим, что если аргумент t функции GT(t, to) растет,
начиная с ίο5 то, пока он не достиг значения τ, она совпадает с
нулевым решением, а с момента τ она перескакивает на
некоторое новое решение ут(£) однородного уравнения, получаемое
специальным образом, а именно1:
• ее (п — 1)-я производная терпит единичный скачок
G(n-1'(T + 0,to)-G("-1»(T-0,i0) = l;
• все остальные ее производные от 0-го до (п — 2)-го порядка
включительно просто непрерывны.
Для получения же итогового решения уо, согласно формуле
(94), остается каждую из функций (2τ(ί,ίο) умножить на
соответствующую величину точечной неоднородности /(τ) и
проинтегрировать2 полученное семейство по τ G J.
3.9. Краевая задача
для линейного уравнения второго порядка
Ly = y+p{t)y + q{t)y = f{t), i€ J = [ii;i2], p,qeC(J), (95)
имеет два краевых условия
1гУ = СЦу{Ь) + M(U) = фг, («г, Рг) Φ (0, 0), % = 1, 2, (96)
которые с помощью дополнительных обозначений записываются
еще более компактно
где вектор-функция / линейна.
I. Теорема об альтернативе. Пусть по заданным неодно-
родноотям задачи, т. е. по скалярной функции / Ε C(J) и
числам срьЧР2 £ Л&5 требуется найти функцию у, удовлетворяющую
уравнению3 (95) и условиям4 (96).
^удя по начальным условиям (93) для решения ут(£) однородной
системы.
2Ср с леммой 115
3Непродолжаемые решения этого уравнения определены, вместе со
своими производными до 2-го порядка включительно, на всем отрезке J,
поскольку коэффициенты уравнения, с сохранением непрерывности, можно
доопределить на больший интервал I D J, ά затем применить теорему 36 о
продолжаемости решений на /
4В которых первые производные понимаются как односторонние
102
Понятия вырожденности и невырожденности краевой
задачи, данные в определении 3.8, без труда распространяются и на
краевую задачу (95), (96). условие периодичности
коэффициентов в ней, разумеется, снято, а роль неоднородности F теперь
играет тройка неоднородностей /, (pi,(p2·
Ситуация, когда при одних неоднородностях краевая задача
имеет единственное решение, а при других — нет, не возможна
и здесь (ср. с теоремой 58), как показывает-следующая теорема,
называемая теоремой об альтернативе.
Теорема 74- Краевая задача (95), (96) либо вырождена, либо
невырождена.
► Согласно следствию 64, общее решение неоднородного
уравнения (95) имеет вид
y = yo(t) + Y{t)c, y = (yi,y2), с =
где уо — его частное решение, a yi, у2 — два линейно независимых
решения соответствующего однородного уравнения.
Краевые условия (96) накладывают на вектор с следующие
ограничения
/(у0 + Yc) = y <=> (lY)c = φ - /у0,
где матрица ΙΥ = (/уь/уг):
• либо всегда1 невырождена — тогда полученная система
разрешима однозначно;
• либо всегда вырождена — и тогда полученная система или
не разрешима, или разрешима неоднозначно (причем тогда
имеет сразу бесконечно много решений) ■
Если все неоднородности задачи обнулить, то получится
соответствующая однородная задача, состоящая из:
• однородного уравнения (95) (в котором / = 0);
• однородных краевых условий (96) (в которых φι = ф2 = 0).
Учитывая, что любая однородная краевая задача имеет хотя
бы одно решение (нулевое), из теоремы 74 получаем
Следствие 75. Краевая задача (95), (96) имеет
единственное решение тогда и только тогда, когда соответствующая
однородная задача имеет только нулевое решение.
*Т е. сразу для всех неоднородностей /,φι,ψ2, от которых матрица ΙΥ не
зависит, поскольку полностью определяется видом левых частей краевых
условий (96) и двумя решениями yi, уг однородного уравнения (95)
а·
103
II*. Функция Грина краевой задачи. Исходя из
физического смысла функции Грина (как функции влияния точечной
единичной неоднородности в момент τ на решение однородной
задачи; см. раздел III из п. 3.8), можно дать
Определение 3.11. Функция Грина краевой задачи (95), (96)
это семейство функций
ΥΪ(ί), «ι<ί<τ,
У?(«), τ<ί<ί2,
GM = {yZ[' ^/JV' те J,
где функции у*, у^ удовлетворяют:
• однородному уравнению (95) при каждом фиксированном
τ е J:
(Lyj)(i) = y*(i) + p(t)y\(t) + q(t)y\(t) = 0, t G J;
• каждая своему однородному краевому условию (96): у* — в
точке ti, а у^ — в точке Ьч, т. е.
ity\ = ту\(и) + Ptyi(it) = о, i = i,2, τ е J;
• двум-уеловиям склейки в точке τ:
у?(х)-у'(т) = 0, у?(т)-#(т) = 1, t€J;
• условию непрерывности по паре переменных τ,ί G J,
причем вместе с первыми производными1 (по t).
Возможности применения функции Грина раскрывает
Теорема 76. Если Gz — функция Грина краевой задачи (95),
(96), то для любой функции f Ε С (J) формула
y(i) = ^6?τ(ί)/(τ)βίτ, teJ, (97)
ίι
задает решение соответствующей задачи с однородными
краевыми условиями.
1 Такая непрерывность функций y\{t),y\(t) обеспечит (в силу самого
однородного уравнения (95)) такую же непрерывность и вторых производных
y\(t), благодаря чему интегралы по τ от функций у*(£) можно будет
дважды дифференцировать по переменной t, как по параметру, путем прямого
дифференцирования подынтегральных функций
104
► Функция (97):
• в силу определений 3.10 и 3.11 представима в виде
*2 t2
y(t) = J (yi(i) + GT(i,ti)) /(т) с/т = JyiW/M с/т + y0(t)
ίι
(где уо — решение (94) уравнения (95) с нулевыми начальными
значениями yo(^i) = Ϋο(^ι) = 0 в начальной точке ίι), поэтому
служит решением неоднородного уравнения, так как
t2
(Ly)(t) = j(Ly])(t)f(r) с/т + (Ly0)(t) = 0 + /(ί), ί G J;
• удовлетворяет равенствам
ί2 *2
ky = |&<7τ(·))/(τ) с/т = JW)/(t) с/т = 0, г = 1,2,
ίι ίι
т. е. обоим однородным краевым условиям. ■
III*. Существование и единственность функции
Грина. Явную конструкцию для ее построения предлагает
Теорема 77. Любая невырожденная краевая задача (95), (96)
имеет единственную функцию Грина.
► Пусть краевая задача невырождена.
1. Фиксируем ненулевые частные решения ζ1, ζ2 однородного
уравнения, удовлетворяющие первому и второму краевым
условиям. Например, годятся решения задач Коши со следующими
начальными значениями1
г%) = &, г%) = -оц, г = 1,2.
Тогда функции z1, z2 G C2(J).
• удовлетворяют каждая, соответственно, только одному
однородному краевому условию, но не другому (если бы она,
удовлетворяя однородному уравнению, удовлетворяла бы еще и
обоим однородным краевым условиям, то вышло бы противоречие
с невырожденностью краевой задачи; см. следствие 75);
Ненулевыми, так как (αί,βί) φ (0,0)
105
• линейно независимы (следовательно, образуют
фундаментальную систему решений однородного уравнения), так как если
бы для некоторой константы с выполнялось, например,
равенство z1 = cz2, то функция ζ1 удовлетворяла бы обоим
однородным краевым условиям.
2. При любом значении τ G J искомые решения yj,y?,
фигурирующие в определении (3.11), являются линейными
комбинациями решений ζ1, ζ2, причем именно следующего вида:
yj=a(x)z1, y?=b«z2 (98)
(если, например,
yl = α^ζ1 + c(t)z2,
то с(т) = 0, так как функция ζ2, в отличие от у1 иг1, не
удовлетворяет однородному краевому условию в точке t\)
3. Условия склейки функций у1, у2 из определения 3.11
равносильны системе ,
'α(τ)ζ1(τ)-6(τ)ζ2(τ) = 0
α(τ)ζ1(τ)-6(τ)ζ2(τ) = -1,
которая однозначно задает функции α(τ),6(τ) G С1 (J)
(поскольку коэффициенты последней системы непрерывно
дифференцируемы по τ G J, а ее определитель, совпадающий с
определителем Вронского для решений ζ1, —ζ2, отличен от нуля), откуда, с
учетом условий z1,z2 G C2(J), сразу следует, что у1,у2 G Cl(J2).
Таким образом, функции (98), фигурирующие в определении
3.11 функции Грина, существуют и однозначно определены. ■
IV*. Уравнение равновесия струны. Интегральные
кривые у = y(t) уравнения
S = /(ί), ί€[0;1],
изображают установившуюся форму струны как функцию от
координаты t точки струны, к которой в поперечном1 направлении
приложена внешняя сила плотностью f(t).
Функции
zl(t) = t, z2(t) = l (99)
параллельном оси у
106
образуют фундаментальную систему решений однородного
уравнения.
1. В случае, когда на оба конца струны действуют постоянные
силы (в случае нулевых сил — концы свободны), имеем краевые
условия
2/(0)= φι, 2/(1) = Φ2·
При этом решением однородной задачи служит, например,
ненулевая функция ζ2, так что эта краевая задача вырождена (см.
следствие 75).
2. Если же, например, левый конец струны закреплен1, а на
правый действует постоянная сила, то краевые условия таковы:
2/(0) = φι, £(1) = φ2·
Эта задача невырождена, поскольку решением однородной
задачи служит только нулевая константа. Построим к ней функцию
Грина, следуя доказательству теоремы 77.
• Выбранные ранее решения ζ1, ζ2 (99) удовлетворяют,
соответственно, первому и второму однородным краевым условиям.
• Для коэффициентов a, b из равенств (98) имеем систему
α(τ).τ-6(τ).1 = 0
α(τ)· 1-6(τ)·0 = -1
• В соответствии с определением 3.11 получаем функцию
Грина
'α(τ)ζχ(ί) = -t, 0 < t <τ,
6(τ)ζ2(ί) = -τ, τ < t < 1.
GxW = ι ι,.^Μ _
3.10. Нули решений уравнения второго порядка
линейного однородного, имеющего вид
y + 2p(t)y + q(t)y = 0, у eR, tel, p,qeC(I), (100)
будут интересовать нас далее, а именно: будет изучаться вопрос
о количестве или частоте нулей всякого ненулевого2 решения.
обычно отклонение конца считают не просто постоянным, а равным
нулю.
2Точнее, не являющегося тождественно нулевым, всюду далее — по
умолчанию.
107
1. Конечность числа нулей на отрезке. Возможность для
любого решения определять нули, соседние с любым наперед
заданным его нулем, обосновывает, в частности, следующая
Лемма 78. Всякое решение уравнения (100) на любом
отрезке К С I имеет лишь конечное число нулей.
► Пусть, напротив, некоторое ненулевое решение у имеет на
отрезке К бесконечно много различных нулей. Тогда:
• некоторая их последовательность t\,t2, ..·, скажем строго
возрастающая, сходится к некоторому числу to £ К;
• по теореме Ролля на каждом интервале (£fc;£fc+i), k Ε Ν,
существует точка s/t, для которой y(s/fc) = 0;
• поэтому решение у удовлетворяет начальным условиям
y(i0) = lim y(ifc) = 0, y(i0) = Hm y{sk) = 0,
к—>оо к—>оо
а значит, согласно теореме 30 существования и единственности,
совпадет с нулевым решением, имеющим в точке to те же
начальные условия. Получили противоречие. ■
II. Перемежаемость нулей. Будем говорить, что нули двух
решений перемежаются, если выполнены следующие два
условия:
• нули обоих решений попарно различны;
• строго1 между любыми двумя соседними нулями любого из
этих двух решений есть хотя бы один нуль другого решения2.
Теорема 79. Нули любых двух линейно зависимых
решений уравнения (100) полностью совпадают, а линейно
независимых — перемежаются.
► 1. Если решения у и ζ линейно зависимы, то для некоторой
константы с φ 0 выполняется равенство у = cz и нули решений
у и ζ совпадают.
2. Пусть теперь решения у и ζ линейно независимы.
Предположим, что, вопреки утверждению настоящей теоремы, имеет
С учетом предыдущего условия, это слово здесь можно и опустить, а
если каждое решение имеет более одного нуля, то можно, наоборот, опустить
предыдущее условие
2А тогда уже ровно один, поскольку если бы нашелся еще один, то между
найденными двумя нулями второго решения не было бы ни одного нуля
первого решения
108
У
7*
А
У
■ ;—
\
\
^
t
Рис. 18. Противоречивая
ситуация
место хотя бы один из следующих двух случаев (каждый из
которых приводит к одному и тому же противоречию).
• Эти решения имеют общий нуль to, и тогда
W{to) = Wy,z(t0) =
О О
у(*о) ±(*о)
= 0.
• Строго между некоторыми двумя соседними нулями t\ <t2,
например, решения у нет ни одного нуля решения ζ. Тогда оба
решения у и ζ, в силу их непрерывности, имеют на интервале
(ίι;ί2) фиксированный знак, скажем для определенности,
положительный: если для какого-то из них это не так, поменяем его
знак на противоположный. Поэтому (рис. 18) имеем
y(t),z(t)>0, tl<t<t2, z{U) > 0 = y(ti), i = 1,2, (101)
y(ii) > 0 > y(i2), (102)
(неравенства (102) — строгие1, иначе y(t{) = y(U) = 0 при
некотором г Ε {1,2} и тогда по теореме 30 у = 0), откуда получаем
W{U) =
0 z(U)
= —y(*i)z(t»),
W{h) = -y(ii)z(ii) < 0 < -y(i2)z(i2) = W(t2).
(103)
Таким образом, в обоих случаях определитель Вронского
решений у и ζ обнуляется хотя бы в одной точке (в последнем
случае — в силу его непрерывности на отрезке [ίι;ί2])5 что
противоречит их линейной независимости. ■
III. Теорема сравнения. Разбираемая ниже теорема
Штурма позволяет для уравнений вида
*Хотя это здесь и несущественно
109
ji + r(t)y = 0, (104)
i + R{t)z = 0 (105)
судить о взаимном расположении нулей их решений по
коэффициенту при неизвестной функции, грубо говоря, по следующему
правилу: чем коэффициент больше, тем чаще колеблются ре-
тения. Более точно, верна
Теорема 80. Если коэффициенты уравнений (104), (105)
удовлетворяют неравенству
r(t) < R(t), t е I, (106)
то между {нестрого) любыми нулями всякого решения у есть
хотя бы один нуль всякого решения ζ.
► Пусть строго между двумя соседними нулями t\ < t^ решения
у нет ни одного нуля решения ζ. Тогда, рассуждая, как в
доказательстве теоремы 79 (см. последний случай в п. 2), имеем:
• Сходной стороны, справедливы неравенства (101) —(103);
• с другой стороны, на отрезке [ίχ; Лг] функция W = Wy)Z
нестрого/ убывает, поскольку
W = (yz — yz) = yz — yz = (г — R)yz < 0;
• такая ситуация возможна только при условиях
W{U) = -y(U)z(ti) = 0 = W(t), t = 1,2, h < t < t2,
откуда (в силу неравенств (102)) получаем
ζ(ίι)=ζ(ί2) = 0, r(t) = R(t), ti<t<t2. (107)
что и требовалось доказать ■
Фактически в процессе доказательства теоремы 80 получено
более сильное
Следствие 81. Если коэффициенты уравнений (104), (105)
удовлетворяют неравенству (106) и строго между соседними
нулями t\ < t<i решения у нет ни одного нуля решения ζ, то
выполнены равенства (107).
IV. Устранение первой производной в уравнении.
Теорема Штурма сильно выигрывает из-за того факта, что при
исследовании нулей решений уравнения (100) коэффициент р,
110
практически без ограничения общности, можно считать равным
нулю, как показывает следующая
Лемма 82. Уравнение (100), при условии ρ Ε С1^), с
помощью некоторой замены
у = a(t)z, a(t) > 0, t e I,
приводится к виду
ζ + r(t)z = 0, r = q-p2-pe C(I).
► Из равенств
у = az, у = άζ + az, у = άζ + 2άζ 4- az
получаем, что в левой части уравнения, равной
у 4- 2ру + qy = az + 2(ά + ρά)ζ + (α 4- 2ρά 4- qa)z,
коэффициент при ζ равен нулю, если
а 4- ра = 0 <(=> a(t) = Се Jto , t e I,
где С > 0 и to G / фиксированы, причем тогда
о · α4-2ρά4-<?α 2
α = — pa, a = pa — pa ==> г = = q — ρ —ρ,
α
что и требовалось доказать. ■
3.11. Оценки колеблемости
решений линейного однородного уравнения второго порядка
делаются с помощью теоремы сравнения 80.
I. Оценки расстояний между нулями. Прежде всего,
сравнивая коэффициент уравнения (104) с различными
константами, можно узнавать, насколько часто нули его решений
располагаются на числовой оси.
Следствие 83. Если выполнено неравенство
r{t) < о, tei,
111
то на интервале I всякое решение уравнения (104) имеет не
более одного нуля.
► Если неравенство выполнено, но какое-то решение у
уравнения (104) имеет на интервале / два нуля, то по теореме 80 между
ними имеет нуль и всякое решение уравнения ζ = 0, в частности
решение ζ = 1, что неверно. ■
Следствие 84- Если для некоторого ω > 0 выполнено
неравенство
r(t) < ω2, t G I, или, наоборот, r(t) > ω2, t G /,
то на интервале I любые соседние нули t\ < t^ всякого решения
уравнения (104) удовлетворяют, соответственно, оценке
t>2 — t\ > π/ω или, наоборот, t2 — t\ < π/ω.
► Расстояние между любыми соседними нулями всякого
решения уравнения1
ζ 4- ω^= 0 4=Ф z = Ci cosut + С\ βίηωί, С\,С2 G Ш, <=>
4=Ф ζ = Acos(<o£ + φ), A,cpGM,
равно π/ω, причем, подбирая параметр φ, можно располагать
эти нули в любом наперед заданном месте интервала /.
1. Если выполнено первое из данных в условии неравенств,
то соседние нули всякого решения у удовлетворяют первой из
утверждаемых оценок, так как иначе
t\ < Ϊ2 < t\ 4-π/ω
и обе точки t\ и Ϊ2 лежат внутри некоторого интервала {t'i,t2)
длины π/ω (рис. 19, а), поэтому решение ζ с нулями в концах
t'\,t'2 этого интервала не имеет нулей на отрезке [ίι,^]? что
противоречит теореме 80.
2. Если выполнено второе из данных в условии неравенств,
то соседние нули всякого решения у удовлетворяют второй из
утверждаемых оценок, так как иначе
t\ < t\ -f π/ω < ti
С постоянными коэффициентами (см п 4.6, 4 7)
112
Рис. 19. Расположение интервала стандартной длины:
α — внешнее; б — внутреннее
и решение с соседними нулями t\ и t^ не имеет нулей на
некотором отрезке [ί'ι,ί^] длины π/ω (рис. 19, б), концы ίΊ,ί^ которого
лежат внутри интервала (ίι; *г) и являются нулями некоторого
решения ζ, что противоречит теореме 80. ■
II*. Теорема Кнезера. Как было показано (следствие 84),
свойство решений1 уравнения (104) быть колеблющимися, т.е.
иметь на положительной полуоси бесконечно много нулей,
обеспечивается уже отделенностью от нуля положительного
коэффициента г. Следующая теорема Кнезера устанавливает, с
какой скоростью2 этот коэффициент может все же приближаться
к нулю при t —¥ оо, не нарушая указанного свойства.
Теорема 85. Если для данного луча I = (to,oo), to > 0,
выполнено неравенство
r(t)<
1/4
t2 '
t Ε I, или, наоборот, r(t) >
ω2 + 1/4
t2
tel,
для некоторого ω > 0, то на луче I всякое решение уравнения
(104) имеет не более одного нуля или, соответственно
наоборот, бесконечно много нулей.
► Обозначим τ = In t и для каждого ω > 0 рассмотрим уравнение
ζ +
ω2 + 1/4
t2
z = 0^=^
d2z dz
z = 0<=
ζ =
еъ/2(С\ cos ωτ + С2 sin ωτ), ω > 0,
eT/2(Ci + C2T), ω = 0,
Ci,C2G
1 Сразу всех, согласно теореме 79
2Измеренной в некоторой специальной шкале
113
имеющее частное решение1
-ω
(t) = Vtcos((o\nt), tel.
1. Если выполнено первое из данных в условии неравенств,
но какое-то решение у уравнения (104) имеет на луче / два нуля,
то по теореме 80 между ними имеет нуль и решение zo(t) = y/t,
что неверно.
2. Если выполнено второе из данных в условии неравенств, то
по теореме 80 всякое решение у уравнения (104) имеет нуль
между любыми нулями решения ζω, которых бесконечно много. ■
III. Колеблемость маятника. Если уравнение свободных
малых колебаний маятника
y + 2py + q{t)y = 0, teR,
(переменной длины, но с постоянным трением) привести к виду
(104) в соответствии с леммой 82, то коэффициент
r(t) = q(t)-p2(t)-p(t) = q(t)-P2
будет-1хропорционален дискриминанту2 квадратного трехчлена
Ζ,(λ) = λ2 + 2ρλ + q(t).
Применяя следствия 83, 84 или, соответственно, теорему Кне-
зера, получаем, что при условии малости трения
о о о ч ω2 +1/4 _
Ρ < ЯкЧ—м или даже ρ < q(t) ^ > * — ^0 (ω > 0),
решения этого уравнения еще являются колеблющимися (т.е.
маятник бесконечно много раз проходит положение равновесия),
а при условии его немалости
р2 > q(t) или даже р2 > q(t) ^ ί > *о»
α4το проверятся обыкновенной подстановкой Хотя нелишне заметить,
что данное уравнение есть уравнение Эйлера, которое экспоненциальной
заменой времени сводится к уравнению с постоянными коэффициентами (см.
раздел III из п. 4.6)* корни характеристического многочлена для данного
уравнения равны λι,2 = - ± го.
23ависящему от параметра £, с множителем —1/4
114
— уже не являются (при этом маятник либо вообще не доходит
за конечное время до положения равновесия, либо проходит его
ровно один раз).
IV*. Характеристические частоты. Если линейное
уравнение (86) задано на полупрямой / = (0;оо), то можно
определить частоту любого его ненулевого решения у формулой
v(y)=!im£v(y,t), (108)
где v(y,£) — число нулей функции у на промежутке (0;ί]. Из
теоремы 126 вытекает
Следствие 86. Все ненулевые решения фиксированного
уравнения (86) порядка η = 2 имеют одинаковую частоту.
► Нули любых двух решений у и ζ уравнения (100) либо
полностью совпадают, и тогда совпадают их частоты
v(y) = v(z), (109)
либо перемежаются, откуда для тех же частот имеем оценку
v(y) = Urn jv(y,i) > lim £(v(z,t) - 1) = v(z)
и аналогичную оценку v(y) < v(z), а с ними и равенство (109). ■
Задачи для самостоятельного решения
1. Какое наименьшее количество решений уравнения (85) нужно
знать, чтобы по ним можно было восстановить все остальные его
решения (не зная самого уравнения)?
2. Докажите, что в методе вариации постоянной для системы (71)
импликация, обратная к (80) =Ф· (81), верна, а для уравнения (85) в
случае η > 1:
• импликация, обратная,к (89) ==> (90), неверна;
• при выполнении первых (п— 1) условий в системе (89) последнее
равенство этой системы равносильно условию (90).
3. Проверьте' справедливость явной формулы
Ι α(τ) άτ
X{t,s) = eJ» , s,tel,
для матрицы Коши линейного однородного уравнения 1-го порядка
115
χ = a(t)x, χ Ε Μ, t e I.
С помощью этой формулы и формулы вариации постоянной
(следствие 56) выразите в случае η = 1 общее решение линейного
неоднородного уравнения 1-го порядка через его коэффициенты.
4. Какой операторной задаче Коши, подобной задаче (77),
удовлетворяет при каждом фиксированном значении to £ I оператор Коши
Л!(to, ) системы (70) как функция второго аргумента?
5. Верно ли, что определитель Вронского любых (к — 1) раз
дифференцируемых функций /ι, ..., fk: I —> К либо тождественно равен
нулю на интервале /, либо нигде на нем не обнуляется? Верно ли это
утверждение для решений yi, ..., у к € Sa уравнения (86) η-го порядка,
где:
• η = к;
. η>№
6. Докажите, что коэффициенты уравнения (86)
восстанавливаются по фундаментальной системе его решений однозначно.
7. Докажите, что если определитель Вронского скалярных
функций /ι, ...,/η_ι € Сп(1) не обнуляется ни в одной точке интервала
/, тохсуществует такая скалярная функция /п € Сп(7), что
определитель Вронского Wfu jn также не обнуляется ни в одной точке этого
интервала.
£к Докажите, что если определитель Вронского скалярных
функций /ι, . ,/п € Сп-1(/) тождественно равен нулю, то объединение
всех интервалов, на каждом из которых они линейно зависимы, всюду
плотно в /.
9. Докажите, что если к скалярных функций на интервале /
являются аналитическими, то тождественное равенство нулю их
определителя Вронского на каком-либо интервале J С. I необходимо и
достаточно для их линейной зависимости. Верен ли аналогичный факт
для бесконечно дифференцируемых (не обязательно аналитических)
функций?
10. Может ли у какого-либо уравнения (86) с непрерывными
коэффициентами найтись ненулевое решение:
• имеющее при η > 2 на данном отрезке бесконечно много нулей;
• имеющее при η = 2 на данном отрезке производную с
бесконечным числом нулей?
11. Перемежаются ли нули двух решений уравнения (100), для
одного из которых ίο — точка максимума, а для другого — точка
минимума?
12. Выведите непосредственно из теоремы 80 справедливость
теоремы 79 для уравнения (104).
13. Какие из функций
yi(i) = sin(2i - 1), y2{t) = sin2i - 1
116
не могут быть решениями уравнения
У + P(t)i/ + q{t)y = 0, p,qeC{R),
одним из решений которого служит функция yo(t) = cost?
14. Является ли колеблющимся всякое решение уравнения
У + ^У = 0, ί>0?
15. Верна ли теорема 74 для краевой задачи в точности с теми
же краевыми условиями, но с линейным неоднородным уравнением не
второго, а:
• первого порядка,
• третьего порядка?
16. Сколько решений имеет уравнение
y + y = f(t)
с краевыми условиями:
• 2/(0) = φι, 2/(π) = φ2;
• у(0) = φι, £(π) = φ2?
Найдите для этой задачи функцию Грина в том случае, когда она
существует.
Глава 4
ЛИНЕЙНЫЕ УРАВНЕНИЯ
И СИСТЕМЫ С ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ
4.1. Экспонента и логарифм оператора
имеют непосредственное отношение к линейным системам с
постоянными или периодическими коэффициентами.
I. Определение экспоненты и логарифма. Далее будем
рассматривать как действительные операторы A Ε EndRn, так
и комплексные A Ε EndCn.
Определение 4.1. Экспонента оператора А определяется
как сумма ряда
Α2 Α3 Ά Ak
еЛ=1 + А + — + — + ... =]Tefc(A), ek(A) = —, А0 = Ζ,
fc=0
а логарифмом In А этого оператора называется любой из
операторов В, удовлетворяющий равенству1
ев = А.
II. Свойства числовых рядов. Рассмотрим случай η = 1,
когда оператор А есть просто умножение на число а:
• как для действительных, так и для комплексных чисел
справедливы разложения в абсолютно сходящиеся ряды
а2 а3 °°
еа = 1+а+у + — + ... =Y^ efc(a),
fc=0
а2 а3 °° (~а)к
1п(1 + а) = а-у + — ξ]Γ 9fc(o), эк(а) = ~^-^-?
fc=l
Запись В = In Л, имеющая оттенок некорректности, означает всего
лишь, что оператор В служит одним из значений In A
118
(первый — при всех а, а последний — при \а\ < 1), откуда
вытекают разложения в абсолютно сходящиеся ряды произведения
экспонент и экспоненты от логарифма соответственно:
оо оо оо
Σ emW · Σ ek(b) = ea-eb = ea+b = £ *к{а + Ь), (ПО)
m=0 fc=0 fc=0
oo
оо / оо \ ^2эк(а)
Σ em Σ9^α) = efc=1 = eln(1+a) = X + a' (U1)
m=0 \fc=l /
• кроме того, для комплексного числа
а = a + гр = p(cos φ 4- г sin φ)
справедливы, соответственно, формулы
еа = ea(cosp + zsinp), 1ηα = 1ηρ + κρ (р > 0), (112)
первая из которых называется формулой Эйлера, как и
следующие два следствия из нее
еФ л. е~Ф еФ - е~Ф
cosp = , sinp = , (113)
а вторая показывает, что комплексный логарифм определен
неоднозначно, поскольку значение1
φ = Arg a = arg a + 2π&, fceZ,
определено с точностью до слагаемого 2кк.
III. Сходимость ряда для экспоненты. Корректность
определения 4.1, в частности, доказывает следующая
Лемма 87. Ряд для экспоненты любого оператора А
сходится абсолютно, причем для любого ограниченного
подмножества Μ С EndlR^ — равномерно по A Ε М.
► Свойство ограниченности множества, а также факт
абсолютной и равномерной сходимости ряда, как и значение его суммы,
не зависят от нормы в пространстве операторов
(конечномерном, см. лемму 12). Поэтому достаточно доказать утверждение,
*В качестве главного значения arg о аргумента комплексного числа а
обычно выбирают ближайшее к нулю (положительное, если их два)
119
например, для операторной нормы (банаховой, см неравенство
(32)).
В самом деле, если
sup \\А\\ = а < оо,
Аем
то ряд для экспоненты оператора мажорируется абсолютно
сходящимся числовым рядом:
ЫЛ)\\ =
к\
,к
оо
- ~й = efc^' пРичем Σε^(α)= е<1'
fc=0
откуда, по признаку Вейерштрасса, получаем утверждение
теоремы. ■
IV. Экспонента и оператор Коши. Связь между экспо-
нентой оператора А и соотЁетстЁующей линейной однородной
системой с постоянными коэффициентами
х = Ах, хежп, teR, (Ш)
раскрывает
Теорема 88. Оператор Коти X системы (114)
удовлетворяет равенству
X{t,s) = eA{t-s\ teR.
► Согласно лемме 46, доказываемое утверждение вытекает из
двух фактов:
. еА(*-^ = X,
• справедлива цепочка равенств1
ι ОО ОО
±е«*-) = ^(ek(A(t - s))) =ΑΣ *k№ - s)) = Ae**-),
fc=0 fc=0
т. е функция еЛ^~8^ удовлетворяет уравнению (76). ■
1 Алгебраически выкладки верны, так как совпадают с выкладками для
числовых рядов, а почленное дифференцирование исходного (сходящегося)
ряда здесь законно, так как ряд из производных его членов, согласно
лемме 87, сходится равномерно в любой ограниченной окрестности точки t.
120
Из теоремы 88 (с помощью следствия 52) получаем
Следствие 89. Если X — оператор Коши системы (114),
то справедливы равенства1
еА = *(1,0), deteA = etrA.
Следствия 90. Экспонента любого оператора
невырождена, а логарифм вырожденного оператора не существует.
4.2. Комплексификация оператора и системы
позволят впоследствии применить метод жордановых форм для
нахождения общего решения линейной однородной системы.
I*. Комплексификация оператора. Пространство Rn
естественным образом вкладывается в Сп, а действительный
оператор A G EndRn распространяется до комплексного A G EndCn.
Определение 4.2. Под комплексификацией
(действительного, или R-линейного):
• пространства Шп понимается С-линейное пространство2
Сп = Rn Θ Жп,
представляющее собой множество векторов
ζ = х + iy, х, у G Шп,
с компонентами х = Re z и у = Im z, в котором, помимо
покомпонентного равенства, сложения и умножения на
действительные числа, заданы также умножение на комплексные числа,
основанное на правиле3
г(х + гу) = -у + гх, х,уеШп,
и комплексное сопряжение
χ + iy — χ — гу, х, у еШп,
Первое из которых можно считать определением экспоненты оператора
А и даже использовать для ее вычисления
2 Ил и переход к нему, в зависимости от контекста
3И доопределяемое с помощью аксиом линейного пространства на все
остальные комплексные числа
121
а кроме того, исходное пространство Rn отождествляется с
подмножеством
ReCnEERn0 г{0} С Сп;
• оператора А Ε EndRn понимается комплексный оператор
А: Сп —>■ Сп, задаваемый равенством
А(х 4- гу) = Ах 4- iAy, x,yeRn,
а его сужение на множество Re Cn обозначается через Re А.
Лемма 91. Пусть Сп — комплексификация пространства
Rn, α А — комплексификация оператора А Ε EndRn. Тогда
справедливы утверждения- ι
1) А Е EndCn uReA = A;
2) размерность-билинейного пространства Сп равна п,
причем любой базис в Rn —^базис и в Сп, а матрицы операторов
А Е End Rn и А Е End Cn β этом базисе совпадают.
► 1. Если С = α 4- гр, α,β Ε R и χ,у, Xj,yj E Rn (j = 1,2), то
A(Cz) = A((olx - py) 4- г(оц/ 4- pa:)) =
= (aAx - β Ay) 4- i(ctAy 4- pAr) = C(Az), ζ = x + iy,
M*i + г2) = A((si 4- ж2) 4- i(yi 4- 2/2)) =
= (Ax\ 4- Ажг) 4- i(Ayi 4- Ауг) = Αζι 4- A22, г, = Zj 4- iyj,
(Re A)z = A(z 4- гО) = Αχ 4- гЛО = Aa\
2. Пусть ei, ..., еп — базис в Rn. Тогда:
• любой вектор 2бСп раскладывается по этому базису, так
как если Re2 = и.\е\ Η 4- о-п^п и1т2 = piei Η 4-рпбти то
ζ = (aiei Η 4- anen) 4- ί(βιβι Η 4- pnen) = C'lei Η 4- Cnen;
• система/векторов ei, . ..,en — С-линейно независима, так
как если С\е\Л 4- Спеп = 0 и Cj = olj 4- ipj (j = 1, ..., π), то
(aiei Η h anen) 4- ί(βιβι Η h pnen) = 0 4- гО =>
=> aiei Η h anen = p^i Η h pnen = 0 =* aj = pj = 0,
откуда 6Ί = · · · = Cn = 0.
122
Поэтому ei, ..., en — базис в Сп, причем
Aej = (Re A)ej = Aej, j = 1, ..., η,
значит, матрицы операторов А и А одинаковы. ■
II*. Комплексификация системы. Действительную
линейную систему (114) можно комплексифицироватъ, получив ее
комплексификацию, т. е. комплексную линейную однородную
систему
z = Az, zeCn, teR, (115)
где Сп и А — комплексификации пространства Rn и оператора
A G EndRn соответственно (см. определение 4.2), а производная
комплексной вектор-функции1 ζ = χ + гу вычисляется по
формуле
x(t + fe)-x(t) . y(t + h) - y(t) v.v , ..,.χ
В принципе ничто не мешает таким же образом комплексифи-
цировать и неавтономную линейную однородную систему (70).
Доказательства многих сформулированных ранее теорем о
действительных линейных системах практически дословно
переносятся на комплексный случай. В частности, все решения
комплексной линейной системы (115) с постоянными
коэффициентами определены на всей прямой и образуют n-мерное С-ли-
нейное пространство *Sa, а ее оператор Коши также совпадает с
соответствующей экспонентой (см. теорему 88).
III. Действительные и комплексные решения. Для
множеств Sa и §л = «Sa всех решений действительной системы (114)
и ее комплексификации (115) соответственно, а также для
множеств всех действительных и, соответственно, мнимых частей
комплексных решений
ReSA = {Rez(·) | ζ е §л}, 1т§л = {Imz(·) | z G SA}
справедлива
Лемма 92.' Если А е EndRn, то:
• §А =SA + iSA;
• Re Sa = Im §>a = $α·
1 Правда, от действительного аргумента, благодаря чему производная
определяется лишь М-линейной структурой пространства Сп.
123
► Из логической цепочки
(х + гу) G §л <=> (х + *у) = А(х + гу) <=*
{х =^ Ах
4=> χ, у е Sa
у = Ау
вытекает первое равенство леммы, а из него — все остальные. ■
Следствие 93. Если вектор-функции χχ, ...,χη
действительны и образуют фундаментальную систему решений для
комплексифицированной линейной однородной системы, то и
для исходной — тоже.
► Если решения χι, ... ,xn Ε оа С-линейно независимы, то тем
более и R-линейно независимы, поэтому образуют базис в Sa- ■
4.3. Метод жордановых форм
пр^меняетсякакдля вычисления экспоненты и логарифма
матрицы, так и для решения линейной однородной системы с
постоянной матрицей коэффициентов.
I. Жорданова матрица. Из курса алгебры известно, что
каждому оператору можно подобрать его жорданов базис
(вообще говоря, комплексный), в котором этот оператор
записывается в виде жордановой матрицы, состоящей из жордановых
клеток и определяемой, с точностью до их перестановки,
однозначно. Устройство этой матрицы описывает
Теорема 94- Матрица комплексификации A Ε EndCn
любого действительного оператора А Ε EndRn в некотором
специальном базисе имеет клеточно-диагональный вид, причем:
• каждая клетка
/λ 1 ··. 0\
О λ '■· :
J\,m —
1
\о о ··· λ/
порядка т отвечает некоторому собственному значению λ
оператора А и порождается своей подсистемой h\, ...,hm
векторов базиса1;
1Т е. образуется как (m x т)-матрица сужения оператора А на линейную
оболочку этих векторов (инвариантную относительно оператора А)
124
• если Jx,mi ■>···■> A,m/ ~ все клетки, отвечающие
собственному значению λ кратности к, то
mi Η 4- гщ = к;
• если λ Ε R, то каждая клетка J\^m и все векторы
порождающей ее подсистемы hi, ..., hm действительны; _
• если λ φ R, то все клетки, отвечающие значениям λ и λ,
разбиваются на пары комплексно сопряженных клеток Jx>m и
J^m ξ J\,m, порождаемых комплексно сопряженными
подсистемами векторов h\, ..., hm и hi, ..., /im.
II. Вычисление экспоненты и логарифма. Приведем
матрицу А к жордановой форме J и, взяв от каждой ее жор-
дановой клетки J^m экспоненту или логарифм, вернемся к
исходному базису:
А -^ J —у {Л,т}
И L-1 eJ
{еЛ,т Ϊ
InA InJ
Обоснование этого способа оформим в виде лемм 95 — 98.
Лемма 95. Если матрица
/Ах · · · О
А = I : ' ■
\0 ··· Л>
клеточно-диагоналъна, то справедливы равенства1
гм ··· 0\ /ln^i ··· О
О ... ел7 \ 0 ... 1пЛь
► Действительно, имеем
1 Последнее из них предполагает существование матриц 1η Αι, ,\ηΑι
125
oo
eA = Σ е*И) =
fc=0
'Σε^) ... О
fc=0
ex»
0
\
fc=0
0
0
/
и, обозначив правую часть последнего из доказываемых
равенств через В, получаем
ев =
,ΐη^ι
О
,А+В _ еА . еВ
т.е. В = \пА.
Лемма 96, Если АВ = В А, то е1
► Доказываемое равенство для матричных рядов проверяется
непосредственно — так же, как и равенство (110) для числовых
рядов1. ■
Лемма 97. При каждом t Ε Μ справедливо равенство
>J\,m* — ρλί
= е
/1 t
0 1
\0 0
em-i(*)\
t
1
, €m_i(t) =
t
m—1
(m-l)!'
/
аРяды для экспонент еА и ев сходятся абсолютно, поэтому, переставляя
при необходимости местами множители Ач В в произведении е -ев, можно
получить ряд для экспоненты еА+в (так, равенство
(А + В)2 = А2 + АВ + ВА + В2 = А2 &
2 2 2 2
существенно опирается на возможность переставлять местами, как числа,
множители А и В в произведении В А)
126
а если λ φ О, то еще и равенство1
/In λ 1/λ ··· эт_х(1/Х)\
, 7 Ο Ιηλ '·.
1η Л,т =
• ♦ ·
V ο ο ···
ΙΑ ,
Ιηλ /
, 9m_i(a = -±—'——
m — 1
► Обозначив N = J^m — λΕ, где Ε — единичная πι χ т-матрица,
получаем2
к нулей
Nk =
/ О
О
\о
о\
о
о
о У
, Nm = 0
(116)
• Учитывая, что единичная матрица коммутирует с любой
другой, имеем
eJx,mt = eUE+tN = eUE . etN = βλί(Ε + ίΑΓ + ... + е^^^ДГ^"1).
• Аналогично, получаем3
Л,т = λΕ + ЛГ = λ£ · {Ε + ΑΓ/λ) =
оо
= einX£.efc=1
= β1ηλ β+1/λ ЛГ+ +9m_i(l/X) ЛГ™"1 = gB
где В — правая часть второго из доказываемых равенств.
Лемма 98. Если А = LJL-1, то
еА = L · eJ · L"1, In A = L · In J · L"1.
► Действительно, имеем
1 Здесь значения всех логарифмов на диагонали матрицы одинаковы.
Действительно, если ег — г-й столбец (нулевой при г φ 1, ..., m)
матрицы Ε, то ЛГег = e,-i, iVfcei = ег-* и Nk = (ei_*, ,ет-*)
Пользуясь равенством (111), справедливым для абсолютно сходящегося
числового ряда, а значит, и для конечного матричного
127
fc=0 fc=0 ' \fc=0 /
откуда, обозначив правую часть последнего из доказываемых
равенств через В, получаем
еВ = eLln JL-i = Le\nJL-l = LJL-1 = д
т. е. В = In А. ш
III. Фундаментальная система решений. Один из
способов решения линейной однородной системы с постоянными
коэффициентами состоит^нахождении ее жордановой матрицы и
жорданова базиса с последующим построением по ним
фундаментальной системы решений.
Теорема 99. Фундаментальная система:
• комплексных решений комплексификации (115)
действительной системы (114) получается в результате слияния в
одну систему всех функций, которые строятся по жордановой
матрице оператора А и соответствующему жорданову базису
следующим образом: каждой оюордановой клетке J\,m,
порожденной подсистемой векторов h\, ..., hm жорданова базиса,
отвечает подсистема функций
ζι(ί) = eXthx, z2{t) = eu{h2 + thx), ...,
zm{t) = eu{hm + thm-x + · · · + em-i{t)h{) (t G R);
• действительных решений действительной системы (114)
строится аналогично предыдущему пункту теоремы, но со
следующим изменением: в случае λ ^ R каждые две подсистемы
по т комплексных функций
^lj · · · ■> Z-m IL Ζι, ...,Ζ
mi
отвечающие паре комплексно сопряженных клеток J\^m и J\,m,
заменяются одной подсистемой из 2га действительных
функций
xi=Rezi, yi=Imzi, ..., xm = Rezm, ym = Imz
m·
► 1. Согласно теореме 88, eAt — оператор Коши линейной
системы (115), поэтому решения
Zj(t) = eMhj = еи (hj + thj-i Η 1- €j-i(t)hi), j = 1, ..., πι,
128
построенные1 по каждой жордановой клетке и взятые все
вместе, образуют фундаментальную систему решений.
2. В построенной в π 1 фундаментальной системе
решений каждую пару решений Zj,Zj (j = 1, ...,m)
можно заменить парой действительных решений (см. лемму 92)
Xj = Rezj, yj = Imzj, имеющих ту же С-линейную оболочку,
так как
' Zj = Xj + iyj, zj = xj-iyj.
В итоге получится снова базис в §^, а значит, и в Sa
(поскольку он состоит только из действительных функций;
следствие 93). ■
4.4. Теория Флоке — Ляпунова
относится к линейным периодическим (см. определение 3.7)
системам, решения которых, как выясняется, сильно похожи на
решения систем с постоянными коэффициентами.
I*. Комплексный и действительный логарифм.
Комплексный логарифм невырожденной матрицы2 строится по ее
жордановой форме в соответствии со сформулированными в
п. 4.3 леммами.
По лемме 95, при переходе от клеточно диагональной
матрицы как к ее экспоненте, так и к ее логарифму клетки матрицы
не сливаются, а значит, и не делятся (иначе при обратном
переходе они слились бы), т.е. жорданова структура матрицы не
меняется3. Поэтому справедливо
Следствие 100. Если оператор А Ε EndCn невырожден,
то существует такой его логарифм In Л Ε EndCn, что
между жордановыми клетками матриц этих операторов
имеется взаимно однозначное соответствие, при котором каждой
клетке J\iTn оператора А соответствует клетка Jinx,m
оператора In А.
Задаваемые соответствующими столбцами жордановой матрицы
оператора eAt (см леммы 95 и 97)
2 Необходимость ее невырожденности отмечалась ранее в следствии 90
о
В частности, жорданова форма матрицы In J\yTn в лемме 97 состоит
ровно из одной клетки J\n\,m
129
Достаточное условие существования действительного
логарифма матрицы дает
Следствие 101. Для любой действительной
невырожденной матрицы А существует действительный логарифм In (А2)
ее квадрата.
► Для нахождения действительного логарифма матрицы А2
дополнительно заметим следующее:
• в результате возведения в квадрат действительной жорда-
новой клетки матрицы А ее собственное значение становится
положительным, и у нее появляется действительный логарифм
(см. лемму 97);
• если слить две комплексно-сопряженные жордановы
клетки матрицы А в одну сдвоенную клетку, порождаемую жордано-
вым базисам hi, ..., hm, h\, ..., hm, то после возведения в
квадрат эта клетка и ее комплексный логарифм примут вид
(в силу равенств β1ηβ = β1ηβ = Β);
• в действительном базисе Reh\, ..., Re hm, Im hi, ..., Im hm
(имеющем прежнюю С-линейную оболочку) матрица In J будет
уже действительной, так как все векторы
lnJ.Re^^lnJ.^±^^lnJ-^+lnJ'^
3 2 2
, т т , , т hj — hj \nj-hj — \nj-hj
In J · Im hj = In J · 0. = ~r. -, j = 1, ..., τη,
действительны. ■
II*. Ляпуновские преобразования. Конкретный
механизм приведения действительной (комплексной) системы
χ = A(t)x, хеШп {хе Cn), t e R, (117)
к системе
y = B(t)y, yeRn (yeCn), teR, (118)
линейным невырожденным преобразованием координат
предлагает
130
Лемма 102. Если преобразование L: R —>· AutRn(AutC,mn)
связывает операторы Коти X и У систем (117) и (118)
равенством
y{t, 0) = L{t)X(t, 0), t e R, (119)
то оно переводит решения системы (117) в решения системы
(118).
► Пользуясь равенством (119), для решений χ и у систем (117) и
(118) с одинаковыми начальными значениями х(0) = у(0) имеем
y(i) = y(t, 0)y(0) = L(t)X(t, 0)x(0) = L(t)x(t), t e R,
т. е. у = Lx. ■
Определение 4.3. Преобразование L Ε C(R) называется ля-
пуновским, если оператор-функции L и L-1 ограничены1 на R.
Ляпуновские преобразования сохраняют такие важные
свойства решений, как ограниченность (неограниченность),
стремление к нулю при t —> оо и др.
III*. Теорема Флоке — Ляпунова. Следующая теорема
говорит о приводимости любой периодической линейной
однородной системы периодическим (а значит, ляпуновским)
преобразованием координат к системе с постоянными коэффициентами.
Теорема 103. Любая комплексная Τ-периодическая
система (117) некоторым линейным Τ-периодическим
преобразованием приводится к комплексной системе (118) с постоянной
оператор-функцией
B(t) = В = ψ\ηХ(Т,0), t е R.
► Примем равенство (119) за определение преобразования L,
которое тогда:
• приводит систему (117) к системе2 (118) (по лемме 102);
• сохраняет оператор монодромии
У(Т,0) = евт = Х{Т,0)
Функция L при каждом ί 6 К задает оператор L (t), обратный к
L(t) Кстати, обычно функцию L считают, по определению, еще и
непрерывно дифференцируемой, а производную L — также ограниченной (для
автоматического сохранения ограниченности коэффициентов системы)
2С постоянной функцией β(·) — ее можно считать и Т-периодической.
131
(см. теорему 88 и определение оператора В в формулировке
настоящей теоремы);
• является Т-периодическим, поскольку по лемме 57 при
любом t Ε Μ верна цепочка равенств
L(t + Τ) = y(t + Τ, 0)*(0, t + Τ) =
= 3>(ί + Τ, Γ)3>(Τ, 0)*(0, Γ)^(Γ, ί + Γ) = 3>(ί, 0)*(0, t) = L(t).
Таким образом, преобразование L удовлетворяет всем
требованиям доказываемой теоремы ■
Вспоминая (следствие 101), что для действительного
оператора Коши действительной системы (117) существует
действительный логарифм
ln#(2T,0) =ln^2(T,0),
получаем
Следствие 104- Любая действительная Τ-периодическая
система (117) некоторым линейным 2Т-периодическим преоб-
pa3QeanueM приводится к действительной системе (118) с
постоянной оператор-функцией.
4.5. Метод неопределенных коэффициентов
позволяет найти решение линейной однородной системы с
постоянными коэффициентами, далее не прибегая к выяснению ее
жордановой структуры.
I. Квазимногочлены. Согласно этому методу, в систему
(114) в качестве решений подставляются выражения
определенного вида — так называемые векторные квазимногочлены.
Определение 4.4. Введем следующие функции и
множества:
• любую функцию q вида
q(t) = eupk(t),
где pk — многочлен степени к над полем R (С), назовем
действительным (комплексным) квазимногочленом степени degg = к
с показателем λ Ε Μ (λ Ε С);
• множество всех действительных (комплексных)
квазимногочленов степени, меньшей к, с показателем λ обозначим через
Q\,k (Qx,fc);
132
• при α, р G Μ определим еще и множество
Qa±i&,k = {qi(t)co&pt + q2(t)sm$t | gi,g2 G Q*,k}
действительных квазимногочленов степени
max{deggbdegg2} < к
с парой показателей α ± гр;
• будем обозначать через1 Q™+ (Q* *) множество всех
векторных квазимногочленов — все их координаты хотя бы в одном2
базисе пространства Rn (Cn) принадлежат множеству Q*,* (Q*,*)·
Лемма 105. Каждое из мнооюеств QjJfc или φχ*., Φα±ΐβ fc
есть С-линейное или, соответственно, Ж-линейное
пространство, причем
dim Qx,fc, dim Q^k < k, dim Qa±ip,fc < 2k, (120)
ReQa+iP)fc С Q*±ip,k С Qa+ip,fc + Qa-iP,fc (Ρ φ 0). (121)
► Чтобы установить справедливость неравенств (120),
достаточно заметить, что участвующие в них множества — это линейные
оболочки следующих систем функций3:
еи, eut, ...,eutk~1', (122)
eaicospi, ...,eaiifc_1cospi, eaisinpi, ... ,eaiifc_1 sin pi. (123)
Включения же (121) вытекают из формул Эйлера (112), (ПЗ).и
II. Вид общего решения. Обоснованию метода
неопределенных коэффициентов для решения систем с постоянными
коэффициентами посвящена
Теорема 106. Если \\, ... ,λι — все попарно различные
собственные значения оператора A G EndRn, α га ι, ... ,пц —
наибольшие порядки4 отвечающих им оюордановых клеток, то
1 Звездочками обозначены некоторые фиксированные индексы.
2 А значит, в любом.
3Линейно независимых (последняя — при β φ 0): см следствие 112 далее.
4Впрочем, их можно заменить любыми большими значениями — проще
всего, кратностями fci, . ., hi тех же собственных значений
133
Если же, кроме того, первые г чисел \j действительны, а
остальные 2р = I — г чисел разбиваются на ρ пар комплексно
сопряженных, т. е. если
XjGR, j = l,...,r, (124)
xj = аз + *Pi = \?'+р (Pi ^ °)> i = г + 1, ..., г 4- ρ, (125)
то
г г+р
$Л С /_^Я\у,т3 + 2-^ QvLj±i$3,m3'
► 1. Добавим к набору из I жордановых клеток наибольших
порядков, соответствующих собственным значениям оператора А,
все остальные клетки с номерами j = 1 + 1, ..., V. Тогда получим
разложение пространства решений §л в прямую сумму
подпространств
§А = Ζλ Θ---Θ2*/,
где каждое из подпространств Zj размерности nrij есть С-линей-
ная оболочка своей подсистемы функций zi, ...,zmj Ε QjJ. m ,
определяемой жордановой клеткой J\ m. и включаемой в
фундаментальную систему решений в соответствии с теоремой 99.
Поэтому с учетом включений Zj С Q™. т получаем цепочку
3=1 j=l
(в конце цепочки каждое из подпространств QJJ т. при j > I
отброшено, так как оно содержится в одном из первых Ζ
подпространств, соответствующем тому же собственному значению).
2. Из предыдущего пункта с учетом лемм 92 и 105 имеем
г г+р
SA = ReS^ с 5>QSU + Σ Re (<«U +%,mj) c
j=l j'=r+l
r r+p
j=l j=r+l
откуда и следует последнее из доказываемых включений. ■
134
4.6. Характеристический многочлен
линейного уравнения
У
(п)
+ αι?/(η-1) + ··· + αη2/ = 0, y,teR, аь .... ,ап G R, (126)
с постоянными коэффициентами — это многочлен
L{\) = Xn + al\n-l + ---+an.
I. Совпадение характеристических многочленов.
Между линейным уравнением (126) и его матрицей А (см.
определение 2.6) имеется естественная связь, которую и раскрывает
Лемма 107. Характеристический многочлен линейного
уравнения с постоянными коэффициентами совпадает с
характеристическим многочленом det(\E — А) матрицы этого урав-
нения.
► Доказательство проведем индукцией по степени η Ε N
характеристического многочлена:
1) при η = 1 имеем
det(\E - А) = λ + αϊ = Ζ,(λ);
2) если утверждение уже доказано для многочленов (π— 1)-й
степени, то, разложив определитель по первому столбцу,
получим требуемое
= λ
det(X£ - А) =
λ
-1 ··· С
) 0
0 λ '·. 0 0
0 0 '·. -1 0
0 0 ··· λ -1
«η ο,η-ι ··· α2 \ + α\
λ '·. 0 0
0 '·. -1 0
0 ··· λ - -1
CLn-l '·' «2 λ-Ь
■αϊ
+ {-l)n-lan
-1 ··· 0
λ '·. 0
ο *·. -ι
0 ···
λ
0
0
0
-1
η-1
η-2
νη-1
= \{\η~ι + αλ\η~ζ + · · · + αη_ι) + (-Ι)""1 · (-1)
чем и завершим индуктивный переход.
п-\
ап = L(X),
135
II*. Оператор дифференцирования. Пусть Ф°° —
линейное пространство скалярных бесконечно дифференцируемых
функций на всей прямой1 R. Если оператор дифференцирования
· ф°° _). ф°°
at'
обозначить через Т>, а тождественный оператор Т>° — через X,
то тот же характеристический многочлен L, взятый не от λ, а
οτί), и имеющий вид
L(V) = Vn-l· axVn~l + · · · + an-XVl + αηΧ,
будет также линейным оператором L(D): Ф°° —> Ф°°, а
уравнение (126) запишется в виде L(D)y = 0.
Произведение многочленов, взятое от оператора V,
совпадает с композицией2 соответствующих сомножителей-операторов,
что и утверждает
Лемма 108. Если L(\) = Μ(λ) · Ν(λ)> mo
L(V) = M(V) · N(V).
► Достаточно проверить свойства:
. (Μι + M2){V) · N(V) = Mi{V) · N(V) + M2{V) · N{V),
. aVl · (Ni + N2)(V) = aVl · Nx(V) + aVl - N2{V), г > 0,
. aV{ · VD> = abVi+i, i,j > 0,
последовательным применением которых и получается
требуемое равенство. ■
III*. Уравнение Эйлера. Так называется уравнение вида3
zVn) + а^-У"-1) + · · · + α,η-ixy' + апу = 0, у G R, (127)
которое вырождается в точке х = 0и потому рассматривается
отдельно при ж>0и при х < 0.
Или на каком-либо ее интервале /СК.
2Которую можно обозначать как обычно точкой, поскольку она не
зависит от порядка сомножителей-многочленов (что верно, к сожалению, только
для многочленов с постоянными коэффициентами: см. последнее свойство
из доказательства леммы 108).
3Переменная у в этом уравнении зависит от переменной х,
производная по которой обозначена через у' (оператор дифференцирования по t по-
прежнему обозначаем через ТУ).
136
Теорема 109. Уравнение (127) заменой переменной χ на
t = In \х\
приводится к линейному уравнению L(D)y = 0 с постоянными
коэффициентами и характеристическим многочленом
Щ) = /η(λ) 4- αιΖη-ι(λ) Η 4- αη_ι/ι(λ) 4- αη10(λ),
где
ifc(X) = λ(λ — 1) -... - (λ - (Λ — 1)) , Α; ΕΝ (Ζ0(λ) = 1).
► Доказательство проведем индукцией по k > 0:
1) при k = 0 имеем lo(D)y = у, поэтому 1о(Т>) = X;
2) далее, при любом к > 0 из цепочки
получаем равенство Ζ&+ι(Ζ>) = /&(!>) · (2? — кТ). ■
4.7. Решение однородного уравнения
(126) с постоянными коэффициентами основывается
исключительно на информации о корнях его характеристического
многочлена.
I. Общее решение. Множество решений комплексификации
уравнения (126)
2(η) + αι2(η-1) + ···+αη2 = 0, zeC, t е R, (128)
будем обозначать через §α· Для такого уравнения также
справедливы теоремы, которые были доказаны ранее лишь в
действительном случае: в частности, все его решения определены
на всей прямой и образуют С-линейное пространство, причем
ψ(§α) = Sa, где А — матрица уравнения (126) (см.
определение 2.6).
137
Теорема 110. Если λι, ... , λ^ — все попарно различные
корни характеристического многочлена линейного уравнения (126),
имеющие кратности к\, ... ,ki соответственно, то
ι
3 = 1
Если же, кроме того, первые г чисел \j действительны, а
остальные 2р = I — г чисел разбиваются на ρ пар комплексно-
сопряженных (см. условия (124) и (125)), то
г г+р
Sa = 22Q\3,k3 + Σ Q«i±«Pj.fej·
j=i j=r+l
► Пусть га ι, ... , га/ — наибольшие порядки жордановых клеток
матрицы А уравнения (126), соответствующих числам λι, ... ,λ/.
Тогда в силу теоремы 106 имеют место два включения
ι
3=1
г г+р
$а = ψ-1(£4) С 2j^XJ'mJ + Σ Q*j±i&3im3·
j=l j=r+l
• Из первого включения получаем цепочку
ι ι ι
η = dim§a < ^dimQxj)mj < ^mi - Σ*^ = η'
3 = 1 3 = 1 3=1
в которой все неравенства, а с ними и исходное включение,
обращаются в равенства, откуда dim Qx ?m = rrij = kj при каждом
• Аналогично, с аналогичными же последствиями, из второго
включения получаем цепочку
г г+р
η = dimSa < ^dimQxj)mj 4- Σ Φ^ϋβ,,™,· <
3=1 j=r+l
r r+p I I
<Σ^+ Σ 2^ = Σ^'-Σ^ = η'
3=1 j=r+l j=l j=l
откуда и следует последнее из доказываемых равенств. ■
138
II. Стандартная фундаментальная система. Из
доказанной теоремы выводится целый ряд следствий. Так, с учетом
леммы 105, получаем
Следствие 111. Фундаментальная система:
• комплексных решений комплексификации (128)
действительного уравнения (126) получается в результате слияния в
одну систему всех функций, которые строятся по корням
характеристического многочлена следующим образом: каждому
корню λ кратности к отвечает подсистема из к функций (122);
• действительных решений действительного уравнения
(126) строится аналогично предыдущему пункту следствия, но
со следующим изменением: в случае λ = α+гр φ R две
подсистемы по к функций, отвечающих паре комплексно-сопряженных
корней α ± гр, заменяются одной подсистемой из 2к
действительных функций (123).
Следствие 112. Все неравенства (120) обращаются в
равенства, причем суммы пространств квазимногочленов,
фигурирующие в формулировке теоремы 110, как и сумма (121) при
η = 1, прямые.
► Действительно:
• каждое из пространств квазимногочленов, фигурирующих
в формулировке леммы 105, реализуется как подпространство
решений некоторого уравнения (126) или (128);
• размерность каждой из перечисленных сумм равна сумме
размерностей ее слагаемых. ■
Следствие 113. Каждому собственному значению
матрицы уравнения (126) отвечает ровно одна жорданова клетка1.
III. Решение уравнения малых колебаний.
Характеристический многочлен
L(X) = λ2 + 2р\ + q2
уравнения свободных малых колебаний маятника
y + 2py + q2y = 0, ρ > 0, q > 0,
имеет корни
Порядок которой равен кратности этого значения.
139
λι,2 = -Ρ ± Vp2 ~ Q2 = <
±iq, P = 0,
—p±id, О < ρ < q,
-ρ < Ο, ρ = q,
-p±d<0, p>q,
где обозначено d = y/\p2 — q2\, поэтому общее решение
дифференциального уравнения задается формулой
У=<
Cicosqt+ C2 sin qt, ρ = О,
e~pt(C\ cos dt + C2 sindt), 0 < ρ < q,
e-*(Ci + C2t), p = q,
e-vt{Cledt + C2e-dt), ρ > q.
Следовательно, если трения нет (при ρ = 0), то все решения
периодичны, а если есть (при ρ > 0) — экспоненциально
затухают при t —> оо, причем все ненулевые решения в случае
малости трения (при р < q) колеблются, а в противном случае (при
ρ > q) — не колеблются1.
IV*. Частоты решений уравнения второго порядка.
Все ненулевые решения линейного однородного уравнения (86)
второго порядка имеют одинаковые частоты (108) (см.
следствие 86), которые в автономном случае полностью
определяются корнями его характеристического многочлена, а как именно —
разъясняет следующее следствие, вытекающее из теоремы 110,
Следствие 114- Частоты всех ненулевых решений
уравнения (126) порядка η = 2 равны модулю мнимой части корней
его характеристического многочлена.
► Корни λι52 характеристического многочлена,
соответствующего уравнению (126) второго порядка:
• либо оба действительны, и тогда, скажем, решение у = βλιί
не имеет корней, откуда v(y) = 0;
• либо имеют вид \\^ = α ± гр (β > 0), и тогда, например,
решение у = eai sin βί имеет частоту
π
v(y) = lim
t—юо ь
βί
π
= lim - · lim
t—юо t 7t t—Юо
i{?}
= β·
Таким образом, в обоих случаях получаем v(y) = | ImXi^l
*И даже имеют не более одного нуля (см. раздел III из п 3 11)
140
4.8. Уравнение с квазимногочленом в правой части
также можно комплексифицировать, получив уравнение
2(η)+αι2(η-1) + ···+αη2 = /(£), zeC, t e R. (129)
Множество всех его комплексных решений обозначим через §а,/·
I. Разложение неоднородности. Первое утверждение
следующей леммы служит одним из проявлений так называемого
принципа суперпозиции, а второе — обосновывает метод
комплексных амплитуд.
Лемма 115. Для уравнения (129) с действительными
коэффициентами αχ, ... ,αη справедливы следующие утверждения:
• если Zj Ε §α,/ Щ>и 3 — 1> · · · ■> h mo
ζι+···+ζ性α,/1+ +//;
• если ζ Ε §а,Я то
Re ζ Ε «Sa,Re/, Im z E «Sa,im /·
► Доказательства получаются, соответственно, из цепочек
равенств
L(2>)(zi + . · · + ζί) = L(V)zi + · · · + L{V)zi = /ι + · · · + Д,
L(V) Rez + гХ(£>) Im ζ = L(£>)z = / = Re / + г Im /
(последняя влечет L(D)Rez = Re/ и L(X>)Imz = Im/). ■
II. Определение резонанса. Для каждого линейного
пространства Q*,*(Q*,*) действительных (комплексных)
квазимногочленов (см. определение 4.4) обозначим
Q*,*,k = {tkq{t) I q Ε Q*,*} (Q*,*,fc = {tkq{t) \ q Ε Q*,*})
и заметим, что каждое из новых множеств также является
линейным пространством.
Определение 4.5. Пусть неоднородность / линейного
уравнения (129) есть квазимногочлен с показателем μ (или с парой
показателей α ± гр φ R). Тогда будем говорить, что:
• имеет место резонанс кратности к, если число μ (или,
соответственно, каждое из чисел a ± гр) является /г-кратным кор-
141
нем характеристического многочлена соответствующего
однородного уравнения1;
• резонанса нет или, что то же, его кратность равна 0 — в
противном случае.
III. Комплексное частное решение. Для уравнения (129)
с квазимногочленом в правой части такое решение находится
однозначно в специальном виде, который описывает
Теорема 116. Пусть к — кратность резонанса в уравнении
(129), тогда если
f e ®μ,ηι,
то в множестве (Q^,m,fc существует единственное частное
решение zo Ε §α,/·
► 1. Характеристический многочлен соответствующего
однородного уравнения представляется в виде
Щ) = (λ - μ)* · Μ(λ), где Μ (μ) φ 0.
2. Докажем, что линейный оператор2
L(V) = M(V) · (V - [il)k
осуществляет следующую (сквозную) биекцию:
_ {V-\>X)k _ M{V) _
пространства Ομ)Τη,Α; в пространство (Q^,m. Действительно:
• матрица оператора
в базисе βχ, ..., em+fc, где
ej{t) = εμ1εό-ι{ί), €j_i(i) ξ , j = 1, ...,m + fc,
есть жорданова клетка J^,m+fc = μ-Ε" + JV, поскольку
V (e^ej_iW) = μ (e^-iW) + e*V2(t) (ε_χ = 0);
*Для уравнения с действительными коэффициентами кратности
комплексно-сопряженных корней оказываются равными автоматически.
2Точнее, его сужение, и ниже — тоже
142
• матрица оператора
,m+k
в том же базисе имеет вид (116), поэтому оператор
есть биекция, так как переводит базис βχ+&, ..., em+k
пространства ΐ^μ,ηι^ в базис ei, ..., em пространства Ομ,™;
• аналогично, матрица оператора
в базисе βχ, ..., ет есть также жорданова клетка J^m, а значит,
матрица оператора М{Т>) в том же базисе — треугольная с
числами Μ (μ) φ 0 на диагонали1. Поэтому оператор
M(V): %,m -> Q^m
есть тоже биекция. ■
IV*. Действительное частное решение. Такое решение
имеет смысл искать только в том случае, когда неоднородность и
все коэффициенты левой части уравнения (129) действительны.
И это позволяет сделать
Следствие 117. Пусть а\, ..., ап G R, а к — кратность
резонанса в уравнении (129), тогда если
f е Qv,m, μ е Μ, или f е фа±*р,ш, Ρ Φ θ,
то в множестве Q^m,k или Qa±i&,m,k соответственно
существует единственное частное решение уо G Sa,f-
Теорему 116 и следствие 117 можно объединить так:
Re 7K f ^ 4μ,τη * 2/0 £ Q\i,m,k
Z0 G Q^m,fc <— / G Ομ,πι — (
/ £ Qa±ip,m >· 2/0 £ Qa±ip,m,fc·
► 1. Если μ G R'H / G <5μ,τη С Ομ,τη5 то по теореме 116 существует
частное решение zq G <Q^,m,fc5 поэтому (см. лемму 115)
1 При сложении или перемножении верхнетреугольных матриц их
диагонали почленно складываются или, соответственно, перемножаются — чисто
алгебраический факт
143
уо = Rez0 G Sa,f Π Q^m,k С Sa>/ Π Q^m^k,
а такое решение уо, согласно теореме 116, единственно.
2. Если >κ6μΞα + ζβ^Μπ
θΟμ,π»
(см. лемму 105 и следствие 112), то по теореме 116 существует
частное решение z0 G Ομ,τη,Α; θ %,m,fc, поэтому
уо ξ Rez0 G Sa,/ П Qa±ip,m,fc С §a,/ Π (Q^m,fc θ %,m,fc),
а такое решение уо единственно, поскольку оператор
есть биекция, так как по той же теореме 116 он
осуществляет взаимно-однозначное соответствие между каждым слагаемым
первой прямой суммы и соответствующим слагаемым второй. ■
4.9. Явление резонанса
связано с влиянием частоты неоднородности линейного
уравнения на амплитуду его решений.
I. Неограниченные колебания маятника. Общее
решение уравнения вынужденных малых колебаний маятника без
трения
у + а2у = Asin((ut 4- φ), α, Л, ω>0,
имеет вид
У = Уо(0 4- С\ cos at + Ci sinat,
причем, согласно следствию 117, частное решение1
\ С0sin((ut+ <]>), ω/ο,
Ί tCosin((ut + ψ), ω = a,
ограничено, если резонанса нет (т. е. при ω φ α), и неограничено,
если он есть (т.е. при ω = α). Таким образом, при плавном
изменении параметра ω (или а) свойство ограниченности решений
может меняться скачкообразно.
Как и любое другое
144
II*. Колебательный контур. Пусть в электрической цепи,
называемой колебательным контуром, последовательно
расположены, источник тока напряжением Vsm((ot + y),
сопротивление R, конденсатор емкостью С и катушка индуктивностью L.
Тогда заряд конденсатора χ = x(t) и сила тока у = y(t) в момент
t удовлетворяют уравнениям
х = у
Ly + Ry+ —x = V sm((ut + φ)
где
R 1 V
αϊ = — > 0, α2 = γητ > 0, f(t) = —<ocos(<o£ + φ), ω > 0.
Если корни λι)2 характеристического многочлена
Ζ,(λ) = λ2 + αχλ + α2
действительны, то по теореме 110 общее решение однородного
уравнения имеет вид
_ iCieXli + Ci2eX2i, λχ < λ2 < 0,
y"\exi*(Ci+tC2), λ! = λ2<0,
а если λχ)2 = α ± ф ^ R, то
у = eat (Ci cos βί + C2 sin βί), α < 0.
Поэтому в любом случае все решения соответствующего
однородного уравнения экспоненциально стремятся к нулю при
t —> оо.
Так как правая часть / есть квазимногочлен нулевой степени
с парой показателей ±ш φ λχ)2, то резонанса в смысле
определения 4.5 нет и в силу следствия 117 существует единственное
периодическое частное решение уо неоднородного уравнения,
являющееся квазимногочленом той же степени с той же парой по-,
казателей и называемое установившимся режимом1.
*К нему при t —> оо будет асимптотически приближаться любое другое
решение неоднородного уравнения (поскольку Sa,f = уо 4- Sa).
145
III*. Параметрический резонанс. Найдем амплитуду
установившегося режима в колебательном контуре. Так как.
/(«) = Λω(κ>8(ωί+φ) = Re (Αωβί{ωί+(*Α = Re (Βωείωί) , |Β| = А,
то частное решение уо можно искать как действительную часть1
решения
zo(i) = 0>eieteQuM, Сое С,
комплексного уравнения с комплексной неоднородностью
Ви>еш*. Подставляя в него решение zo, получаем
С0еш(-и2 + αιΐω + α2) = Βωβίωί =» С0 = В
—ω 4- a-ii + α2/ω'
откуда находим
ζο(ί) = С0еш = |0>|βί(ωί+φ) => y0(i) = Rezo(t) = |С70| со8(со«+ф),
где амплитуда
yaf + (ω - α2/ω)^
при фиксированных значениях параметров αχ и Л имеет
максимум в случае равенства
ω2 = <Ζ2,
называемом также резонансом2, но уже в широком смысле.
Задачи для самостоятельного решения
1. Пусть А € EndCn — комплексификация действительного
оператора, который в некотором базисе ei, ..., еп € Еп записывался
матрицей А. Если овеществить пространство Сп, рассмотрев его как R-
линейное пространство3 размерности 2п, то каким в этом пространстве
*В этом состоит метод комплексных амплитуд (см лемму 115).
2Это явление используется при настройке радиоприемника путем изме-
нения параметра аг. Частота ω резонансных колебаний совпадает с частотой
l/y/CL свободных колебаний контура, возникающих при условиях / = 0 и
αϊ = 0 (т. е. R = 0)
3Т. е. сохранив в нем умножение лишь на действительные числа, но не на
комплексные
146
должен быть естественный базис? Если после этого овеществить
оператор А, рассмотрев его как R-линейный оператор в
овеществленном пространстве Сп, то какова матрица этого оператора в
естественном базисе?
2. Докажите, что если вектор-функции χι, ..., χη действительны и
образуют фундаментальную систему решений действительной
линейной однородной системы (114), то ее комплексификации (115) — тоже1.
3. Докажите, что для двумерной матрицы А с собственными
значениями2
λι,2 = α±β (2a = trA, β = у/а.2 - det A)
справедлива следующая формула, представляющая экспоненту
матрицы А в виде линейной комбинации матриц А и Ε с коэффициентами,
зависящими только от чисел α и β:
еА = е« (рф)Е + дф)(А - «Я)),
где
p(p) = chp, Q®) = S-y (9(0) = 1)
sin ύ
(в частности, если β = г-χ ^ R, то ρ(β) = cosy и дф) = ).
4. Найдите еА, где а, 6 € Μ и:
(а 6 У
U -а
. А
. А
. А
5
'а -Ь\
'а Ь\
Ь а Г'
Ь а ,
. А-
5. Приведите пример операторов А и В, для которых
еА+в φ еА ■ ев.
Обратимо ли утверждение леммы 96?
*Ср следствие 93
2Которые обычно получаются как раз в таком виде (кстати, проф
А. Ф. Филиппов указанным способом вычислял в уме не только
собственные значения матрицы, но и ее экспоненту).
147
6. Справедлива ли явная формула
X(t,s) = el
для оператора Коши линейной однородной системы (70)?
7. Зная семейство матриц Коши X(t,s), t,s € R, системы (114),
найдите матрицу А.
8. Найдите все значения In А, где
А=(; °), aeR\{0}.
9. Проверьте, что подстановка:
• у = eXi в линейное уравнение (126) с постоянными
коэффициентами дает равенство L(X)eXi = 0, где L(k) —- характеристический
многочлен данного уравнения;
• у = χλ в уравнение Эйлера (127) дает равенство L(X)xx = 0, где
L(k) — характеристический многочлен соответствующего уравнения с
постоянными коэффициентами.
10. Докажите, что любая система функций, получаемая
объединением подсистем (122) для различных значений
λ = λι, .. , λΓ € R
с соответствующими им значениями к = к\, ... ,кг и подсистем (123)
для различных пар
α ± ζβ = ar+i ± ΐβΓ+ι, ..., ctr+p ± грг+р £ R
с соответствующими им значениями /г = /гг+ь · · · ■> кг+р, линейно
независима.
11. Для какого наименьшего N € N уравнение
yiN) + aiy(N-l) + -' + aNy = 0, αϊ, ...,адг € R,
(с постоянными коэффициентами) может иметь решения
ife, t1, imeai, ineaicospi (130)
при
к = 3, / = 2, m = 1, η = 4, a = -1, β = 2?
12. В каком виде (с неопределенными коэффициентами) следует
искать первообразные функций
y(t) = tneat, y(t) = tneatcos^ n€NU{0}, a,p€R?
13. Найдите все наборы чисел /г, /, га, η € N и α, β € R, при которых
система функций (130) линейно зависима.
14. Опишите множество частот всех ненулевых решений линейного
однородного уравнения третьего (четвертого) порядка с постоянными
148
коэффициентами в зависимости от корней его характеристического
многочлена.
15. Верно ли, что если dj € Ш (j = 1, .. , η), μ € Ш и
неоднородность / есть квазимногочлен степени т с показателем μ, то
существует частное решение уо € Sa,f, являющееся квазимногочленом (с тем
же показателем) степени именно т + к, где к — кратность резонанса7
Верно ли аналогичное утверждение для квазимногочлена / с парой
показателей α ± φ £ R?
16. Для системы с постоянными действительными
коэффициентами и неоднородностью в виде векторного квазимногочлена докажите
следующий аналог теоремы 116 и следствия 117: система
x = Ax + F(t), F€Q£m (F€gj,m, μ = α±ΐβ),
имеет частное решение в пространстве Qum+fc (соответственно
Φμ,τη+fc)' гДе ^ — кратность корня μ характеристического
многочлена матрицы А.
Глава 5
ЗАВИСИМОСТЬ РЕШЕНИЙ
ОТ ПАРАМЕТРОВ
5.1. Непрерывная зависимость от правых частей
решения задачи Коши
x = f(t,x), x{t0) = x0, (t,x),(t0,x0)eGcR1+n, (131)
предполагает, что фиксированы некоторая задача (131) и ее
решение х, которые принимаются в дальнейшем за исходные и по
отношению к которым остальные задачи Коши вида
У = 9(t, У), y(to) = 2/о, (t, у) е G,
с соответствующими решениями у считаются возмущенными.
I. Формулировка основной теоремы. И исходное, и все
возмущенные решения заранее считаются максимально
продолженными, а вопрос ставится так: можно ли гарантировать, что
при малых отклонениях правых частей возмущенной задачи от
правых частей исходной задачи возмущенное решение:
• определено в области, в каком-то смысле близкой к
исходной, т. е. к области определения исходного решения;
• на этой, близкой к исходной, области в каком-то смысле
мало отличается от исходного решения?
Ответ оказывается положительным уже при весьма слабых
ограничениях на правую часть уравнения1, в чем и состоит
основная теорема (рис. 20).
Теорема 118. Пусть f,f'x Ε C(G), a x — исходное решение.
Тогда для любого компакта К С D(x) и любого ε > 0
существует такое δ > 0, что если g, д' Ε C(G) и выполнены неравенства
Таких же, как в теореме существования и единственности (см гл 2).
150
ж,
ϊ/ο
Xq
^0i0^~-~~'
\ ! ! К
\ k
Ιε/
|·ε
Gy
t
Рис. 20. Гарантия близости
решений на компакте
\\f-g\\G= sup \f(t,x)-g(t,x)\<b, \х0-у0\<Ъ, (132)
(t,x)eG
то возмущенное решение у заведомо определено на компакте К
и удовлетворяет оценке
x-y|k = sup|x(£)-y(£)| <ε·
teK
(133)
II*. Расстояние между множествами. Прежде чем
доказывать теорему, напомним, что расстоянием между
подмножествами Χ,Υ заданного метрического пространства Μ
называется величина
ι
p(X,Y) = inf р(х,у),
xex,yeY
и докажем, что справедлива
Лемма 119, Если Χ,Υ С Μ, Χ Π Υ = 0, Χ — компакт, а
Υ замкнуто, то ρ(Χ, Υ) > 0.
► Пусть, напротив, ρ{Χ, Υ) = 0. Тогда для некоторых двух
последовательностей хп G X и уп G Υ (η G Ν), первую из которых,
в силу компактности множества X, сразу можно считать
сходящейся к некоторому xq G X, имеет место равенство
Q = p(X,Y)= lim р{хп,Уп),
, η—юо
а значит, и цепочка
0 < р(яо, Уп) < р(яо, Хп) + р(хп, Уп) -► 0 + 0 = 0, η -юо,
1 Равная по определению оо, если хотя бы одно из этих подмножеств
пусто
151
из которой, в силу замкнутости множества Y, получаем условие
уп —ν хо Ε Υ, а с ним и противоречие: х$ Ε Χ Π Υ = 0. ■
III*. Полная поверхность трубки. Для заданной
непрерывной вектор-функции х, числа ε > 0 и отрезка К С D(x) С R
назовем множество
Ge>*(x) = {(«, ж) Ε R1+n | t Ε К, \х- χ(ί)| < ε} (134)
ε-трубкой графика функции χ на отрезке К (см. рис. 20).
Граница трубки (134) состоит только из:
• ее боковой поверхности, на которой выполнено равенство
\х — x(t)\ = ε;
• двух торцов, на которых переменная t принимает крайние
для отрезка К значения.
Все остальные точки трубки являются для нее внутренними1.
IV. Доказательство основной теоремы. Теперь докажем
теорему 118, для чего (см. рис. 20):
• возьмем такую трубку графика исходного решения,
которая помещается вместе с замыканием в области задания
исходного уравнения (известно, что за переделы этой трубки выйдет
график любого возмущенного решения);
• зададим достаточную малость возмущения правых частей,
обеспечив такую априорную малость отклонения возмущенного
решения от исходного, чтобы график возмущенного решения в
принципе не мог дойти до боковой поверхности трубки (поэтому
будет вынужден дойти до ее торцов).
Действительно, если точка (£, х) € Gt,K удовлетворяет условиям
telntK, |a:-x(i)| =α<ε = α + 2β,
то в силу непрерывности функции χ в точке t при достаточно малом
положительном δ < β для любой точки (s,y), удовлетворяющей оценкам
|5-ί|<δ, |у-*|<а,
будут выполнены соотношения
зек, |χ(*)-χ(«)|<β,
\у-χ(β)| <\у-х\ + \х-χ(01 + КО -Φ)Ι <δ + α + β<ε,
откуда (s, у) G Gs,k
152
► 1. Без ограничения общности1 считаем, что-
• данный компакт — это отрезок
K = [ol^]cD(x),
содержащий внутри себя точку to',
• данное число ε > 0 удовлетворяет оценке
г<г0 = р(ГхЫЛ1+п\С)
(условие εο Ε (0; оо] выполнено в силу леммы 119, так как
дополнение R1+n\G к области G замкнуто, а график Гх|к непрерывной
функции χ на отрезке К — компакт).
Тогда замыкание2
C = Ge,K(x) = {(t,x) еШ1+п \teK, |ж —χ(ί)| < ε}, (135)
содержится в области G, а в силу его ограниченности — является
компактом. Следовательно, существует константа3
L=||/£||c<oo.
2. Если для числа
8 Ξ 2(1+βΛ)β«Ρ-> (136)
правые части возмущенного уравнения удовлетворяют оценкам
№-/Ι|σ<δ, \уо-хо\<Ь<г (137)
(последнее неравенство выполняется автоматически), то
справедливо утверждение
&y(*))e<w(x), teK.
Действительно, согласно теореме 23, график непродолжаемо-
го возмущенного решения у непременно покинет компакт С,
например, при достаточно больших t > to. Поэтому для функции
и = у — χ
Заметим, что компакт К, не в ущерб доказательству теоремы, можно
увеличивать, а число ε уменьшать
2См. раздел III настоящего пункта.
3См лемму 13 (требуемая в ней выпуклость области С по переменной χ
здесь, конечно, имеет место)
153
имеем неравенство Щ£о)| — ^ и ПРИ BCexl i G [ίο? β] —
соотношения
\Ш = |у(<) - χ(*)Ι = \g(t,y(t)) - /(t,x(t))| <
< |p(t,y(t)) - /(*,у(0)1 + l/(«.yW) - /(ί,χ(ί))| < δ + L|«(i)|,
из которых по лемме 26 о дифференциальном неравенстве
получаем
|y(i) - x(t)| = \u(t)\ < (\u(t0)\ + b\t - ioDe^-'ol <
< 5(1 + β - a.)eL®~^ < ε/2.
Таким образом, при выполнении условий (137) решение у
определено до самого конца2 отрезка К и удовлетворяет
требуемой оценке (133). ■
5.2. Компактно-открытая топология
наиболее адекватно отражает близость решений
дифференциальных систем.
I. Естественные топологии. Теорема 118 фактически
утверждает3, что решение χ задачи Коши непрерывно зависит
от ее правых частей, т. е. от правой части / самого уравнения и
от начального значения xq.
Для уточнения этой формулировки, введем следующие
обозначения:
1 Точнее, только до первого (при движении вправо от ίο) момента
• Τ = inf{i 1ί G J, |y(i) - x(t)| = ε}
выхода интегральной кривой Гу на боковую поверхность трубки Gs,k
(согласно разделу III настоящего пункта других граничных точек при ί 6 [ίο, β)
эта трубка не имеет), однако этот момент так никогда и не наступит,
поскольку для него, в силу неравенства (138), получилось бы противоречие с
его же определением
(*,У(0) е С?е,к, ίο < t < Τ, |у(Г) -х(Г)| < ε/2 < ε.
гПравого и аналогично левого
3Оправдывая, тем самым, название предыдущего подраздела.
154
• C0,1(G) — множество функций, определенных на области
G и непрерывных вместе с производной по х, наделенное
равномерной топологией, которая задается всякими δ-окрестностями1
Щ(Л = {деС°'1{С)\\\/-д\\а<Ь}
всяких функций / Ε C0,1(G);
• Gt0 С Rn — сечение2 области G гиперплоскостью t = to с
топологией, индуцированной топологией пространства Шп, т. е.
задаваемой всякими δ-окрестностями
Щ{х0) = {уо Ε Gto | \уо - х0\ < Ъ}
всяких точек xq Ε Gt0\
• S(G) — множество всех непродолжаемых3 решений всех
уравнений с правыми частями из пространства C0,1(G),
наделенное компактно-открытой топологией, т. е. равномерной, но
не на полных областях определения решений, а лишь на любых
их компактных4 подмножествах. Эта топология задается
всякими ε-трубками5
Ι/ε,κΜ = {у е S(G) | D(y) D К, ||у - х||к < ε}
всяких функций χ G S(G) на всяких компактах К С D(x) С R.
В новой терминологии теорема 118 звучит как
Следствие 120. Отображение
C°>l(G)xGt0^S(G), (139)
которое каждой паре f Ε C0,1(G) и xq Ε Gt0 правых частей
задачи Коти ставит в соответствие ее непродолжаемое
решение χ Ε S(G), непрерывно.
II. Топологическое усиление теоремы. В множестве
C0,1(G) правых частей системы можно задавать не только
равномерную, но и компактно-открытую топологию с помощью δ-
трубок
Щ,с(Л = {я еС^ЧС) |||з- /||с < δ}
1 Образующими базу топологии
2Точнее, его проекция на пространство М.п (координата t опущена).
3Асимптотически доходящих до границы области G (см теорему 23).
4Кстати, не обязательно содержащих точку ίο
5Так же назывались ранее и множества Се,к(х) С G (134), т. е ε-трубки в
геометрическом, а не в функциональном смысле
155
всяких функций / Ε C0,1(G) на всяких компактах С С G. Из
доказательства теоремы 118 можно извлечь несколько более
тонкий1, чем вынесенный в ее формулировку, результат,
составляющий
Следствие 121. Если равномерную топологию в C0,1(G)
заменить компактно-открытой, то отображение (139)
останется непрерывным.
► Действительно, по данным компакту К С D(x) и числу ε > О
в процессе доказательства теоремы 118 были построены такие
компакт С С G (135) и число δ > 0 (136), что оказалась
справедливой импликация
9 е С/5,с(/), уо е иь{х0) => у е υε,κ(χ)
(см. неравенства (137) и (133)). ■
III*. Варианты непрерывности по двум переменным.
Непрерывность функции по паре переменных является:
• более сильным требованием, чем одновременная ее
непрерывность по каждой переменной в отдельности;
• менее сильным требованием, чем ее непрерывность по
одной переменной вместе с равномерной по ней (как по параметру)
непрерывностью по другой переменной;
• равносильна ее непрерывности по одной переменной вместе
с равномерной на компактах2 по ней непрерывностью по другой
переменной — именно это и утверждает
Лемма 122. Для любых областей3 X сШк и Υ С Ш™
функция
F:XxY^Rn
непрерывна тогда и только тогда, когда каждому у G У
соответствует непрерывная функция F(>,y) Ε С(Х), причем
задаваемое таким образом отображение
Υ -> С(Х)
непрерывно в смысле компактно-открытой топологии в С(Х).
Поскольку любое множество, открытое в компактно-открытой
топологии, открыто и в равномерной, но не наоборот.
2 В предположении локальной компактности пространств этих
переменных.
3Возможно, замкнутых.
156
► 1. Пусть функция F непрерывна по совокупности своих
переменных. Тогда она тем более непрерывна по одной переменной χ
при каждом у Ε Υ. Докажем, что для любого компакта К С X
функция F(-,y) непрерывна по у равномерно по χ Ε К, т. е по
заданным у* Ε Υ и ε > 0 укажем δ > 0, для которого будет
справедлива импликация
\у-у*\<Ь => \\F{',y)-F(.rf)\\K<z.
Действительно:
• выберем такое δ > 0, что точка у* лежит в области Υ вместе
с замыканием В ее δ-окрестности;
• используя равномерную непрерывность функции F на
компакте К χ В, уменьшим, если потребуется, число δ, обеспечив
для всех Х\,Х2 Ε К и у Ε В справедливость импликации
\х\-Х2\<*, \V-V*\<* => \F(xuy)-F(x2,y*)\<z;
• полученная импликация превращается в требуемую, если
в ней положить χ ι = χ2 = x и взять в последнем неравенстве
максимум по χ Ε Κ
2. Пусть теперь функция F непрерывна по а: и равномерно на
компактах по χ непрерывна по у. Докажем, что она непрерывна
по совокупности переменных, т. е. по заданным χ* Ε X, у* Ε Υ и,
ε > 0 укажем δ > 0, для которого будет справедлива импликация
\х-х*\<Ь, \у-у*\<Ъ =» \F(x,y)-F(x\y*)\<z.
Действительно:
• выберем такое δ > 0, что точка х* лежит в области X вместе
с замыканием К ее δ-окрестности;
• уменьшим, если потребуется, число δ, обеспечив
справедливость импликации
\у-у'\<Ъ =* \\F(.,y)-F(.,y')\\K<z/2
(это возможно, поскольку функция F непрерывна по у
равномерно на компакте К с. Х)\
• при необходимости, еще уменьшим число δ (пользуясь
непрерывностью по χ функции F в точке (х*,у*)), обеспечив
справедливость импликации
\х-х*\<Ь => \F{x,y*)-F{x*,y*)\<z/2;
157
• доказываемая импликация будет верна, поскольку при
выполнении ее предпосылки имеем
\F(x,y)-F(x*,y*)\ < \F(x,y)-F(x,y*)\+\F(x,y*)-F(x*,y*)\ < ε,
т. е. выполнено и заключение. ■
5.3. Непрерывность по параметру
предполагает, что для некоторой области Μ С Шт значений
параметра μ задано семейство задач Коши
χ = /{ί,χ,μ), χ{ί0) = χ0(μ), {t,x) G G С R1+n, μ G Μ,
(140)
в котором начальное значение также зависит от параметра
x0:M^Gto. (141)
I. Зависимость от параметра. Непрерывность по
параметру μ решения задачи (140), обозначаемого здесь через1 χ(ί,μ),
понимается как малость его изменения при малых изменениях
параметра, т. е. как непрерывность отображения
Μ -> 5(G),
которое каждому значению μ G Μ ставит в соответствие
максимально продолженное решение χ(·,μ) G S(G). Она имеет место
уже при совершенно естественных предположениях, как
показывает
Теорема 123. Пусть f,f'x G C(G χ Μ) и χ0 G С(М). Тогда
для любого μ* G Μ, любого компакта К С Ζ)(χ(·,μ*)) и любого
ε > 0 существует такое δ > 0, что если
|μ-μ*|<δ,
то решение χ(·, μ) задачи (140) заведомо определено на компакте
К и удовлетворяет оценке
||χ(·,μ)-χ(·,μ*)||* <ε.
Во избежание путаницы здесь начальное условие тем более правильнее
было бы записывать в виде x\t=t0 = #ο(μ)
158
► Утверждение данной теоремы означает непрерывность в точке
μ* композиции отображений
М-^С0'1^) xGt0 ->S(G),
первое из которых по каждому μ G Μ определяет правые части
/(·, ·,μ) G C0,1(G) и Χο{μ) G Gt0 задачи Коши, а второе — ставит
им в соответствие непродолжаемое решение χ(·,μ) G S(G) этой
задачи.
Докажем, что если в пространстве C0,1(G) из двух
упомянутых выше возможных вариантов топологий1 выбрать
компактно-открытую, то каждое из этих отображений (а с ними и
сквозное) будет непрерывным:
• первое из этих отображений непрерывно, так как функции
#ο(μ) и /(·, ·, μ) непрерывны по μ (последняя — в силу леммы 122,
поскольку функция / непрерывна по совокупности всех своих
переменных);
• второе отображение непрерывно согласно следствию 121. ■
II. Решение семейства задач Коши. Рассмотрим
описанную выше функцию χ как решение сразу всего семейства задач
Коши (140), т.е. как функцию пары переменных ί и μ. Для
такого решения справедливо
Следствие 124- В условиях теоремы 123 область
определения D(x) решения χ есть область в R1+m, на которой функция
χ вместе с производной χ (по t) непрерывна по паре (£,μ).
► 1. Множество D(x) (рис. 21) есть область, так как оно:
• связно, поскольку связными являются его сечение как
плоскостью t = to (область Μ), так и любой прямой вида μ = μ*
(интервал £)(χ(·,μ*)));
• открыто, так как если (ί*,μ*) G D(x), то решение χ(·,μ*)
заведомо определено на замыкании К некоторого интервала /,
содержащего точку £*, — на нем, по теореме 123, определены и
все решения χ(·,μ), для которых параметр μ принадлежит
некоторой окрестности ΙΙ(μ*), следовательно, множество D(x) вместе
с любой точкой (£?, μ*) содержит целую ее окрестность / χ ΙΙ(μ*).
2. Непрерывность функции χ в точке (ί*,μ*) вытекает,
согласно лемме 122, из непрерывности указанных выше решений
Равномерная или компактно-открытая; в остальных двух пространствах
Μ и S(G) топология однозначна.
159
no t G / и их непрерывности по μ G Ιϊ(μ*) в смысле компактно-
открытой в С(/) топологии (см. теорему 123).
3. Если в уравнение (140) подставить непрерывную (по
совокупности переменных t и μ) функцию χ = χ(ί,μ), то получится
тождество
χ(ί,μ) = /(ί,χ(ί,μ),μ), (ί,μ) G D(x), (142)
правая часть которого также непрерывна, каковой тогда
является и левая часть, совпадающая с функцией х. ■
Если условие (141), выполненное для семейства задач (140),
заменить более слабым условием
х0: M->Rn,
считая область определения решения χ(·,μ) пустой всякий раз,
когда χο{μ) ^ Gt0, TO утверждение последнего следствия
останется верным во всех деталях, кроме одной: не гарантируется
связность множества D(x).
III. Зависимость от начального значения.
Непрерывность решения задачи Коши (131) по начальному значению хо
при фиксированном начальном моменте to означает
непрерывность отображения
Gt0 -> 5(G),
которое каждому начальному значению хо из области1 Gt0
ставит в соответствие максимально продолженное решение,
обозначаемое здесь через x(-,xq).
1 Открытое сечение Gt0 С Шп области G плоскостью t = to здесь
предполагается еще и связным.
160
Для так определенного решения справедливо следствие,
вытекающее, по большому счету, уже из теоремы 118 (где взято
9 = Л·
Следствие 125. Пусть /, f'x Ε C(G). Тогда для любого
Xq Ε Gt0, любого компакта К С D (х(·, х$)) и любого ε > 0
существует такое δ > 0, что если
\хо - Xq\ < δ,
то решение х(·, а?о) задачи (131) заведомо определено на
компакте К и удовлетворяет оценке
\\χ(',χο)-χ{·,χ%)\\κ < ε.
► Чтобы доказать это утверждение, достаточно, например,
объявить параметром μ само начальное значение Xq и, положив
M = Gto, /(έ,ζ,μ) = f(t,x), χ0(μ) = μ,
применить теорему 123. ■
Если же функцию χ рассмотреть как решение семейства
задач Коши (131), т. е. как функцию пары переменных t и хо, то к
такому решению можно применить следствие 124, получив
Следствие 126. В условиях следствия 125 область
определения D(x) решения χ есть область в R1+n, на которой функция
χ вместе с производной χ непрерывна по паре (t,xo).
IV*. Контрпример к непрерывности на интервале.
Рассмотрим задачу Коши
ж = -у, x(l) = x0, (i,i)6G = (0,2)xR,
Is
имеющую при xq — 0 нулевое решение. Согласно следствию 125,
семейство решений
х(«,*о) = у, * 6(0,2),
этой задачи при любом α Ε (0; 1) непрерывно зависит от xq в
точке 0 равномерно по ί Ε [α, 1]. Это означает, что на любом
заранее выбранном отрезке такого вида можно добиться наперед
161
заданной равномерной близости
решения к нулю, уменьшая величину
\хо\ (рис. 22).
Однако на объединении
(0,1]= (J [α,Ι]
α€(0;1)
этого обеспечить нельзя, так как
все ненулевые решения стремятся
по модулю к бесконечности при
t —У 0. Отсюда вытекает, что в
следствии1 125 упоминание компакта2 К
является оправданным и, вообще
говоря, нельзя брать К = D(x(-,Xq)).
5.4. Дифференцируемость по параметру
решения задачи Коши (140) обеспечивается гладкостью ее
правых частей.
I. Формулировка теоремы. Согласно следствию 124,
решение χ всего параметрического семейства задач Коши (140),
рассматриваемое как функция времени t и параметра μ, при
естественных условиях определено и непрерывно в некоторой
области D(x) с R1+m.
Оказывается, при разумных дополнительных
предположениях оно к тому же и непрерывно дифференцируемо, что с
избытком утверждает
Теорема 127. Пусть /,/£,/£ G C(G χ Μ) и х0 е С1 (Μ).
Тогда решение χ семейства задач (140) имеет во всей области
D(x) непрерывные по паре (t, μ) производные3
Χμ U (Χμ) =Χμ·
Основную идею доказательства существования производной
решения по параметру можно изобразить в виде диаграммы
*А стало быть, и в более общем утверждении — теореме 118.
2А не интервала
3Точкой, как обычно, обозначена производная по ί, а выражение х£
понимается, естественно, как (χ)μ.
162
Рис. 22. Близость
решений на отрезке, но не на
интервале
!(.>ΜΞΧ(.,ν)-Χ(·,μ) ^ ζ(.)μ,μ)=χ,(.,μ)
V μ
; t
ζ = G(t, ζ, μ, ν) v-ш ί ζ = G(t, ζ, μ, μ)
z(to) = *ο(μ, ν) \z(to) = ζ0(μ, μ)
и выразить следующими словами.
• представим искомую производную решения по параметру
(точнее, по одной из его координат) в фиксированной точке μ
как предел отношения приращения функции (решения) к
приращению аргумента ν — μ при ν —> μ;
• тогда само это отношение при ν φ μ будет удовлетворять
некоей допредельной задаче Коши, зависящей от параметра ν,
причем непрерывно;
• предельная же задача Коши, получаемая при ν —> μ, также
будет иметь решение, которое, в силу непрерывности решения
по параметру ν, и будет совпадать с пределом отношения, т. е. с
искомой производной.
II*. Лемма Адамара. Доказательству теоремы 127
предпошлем лемму Адамара, которая выражает приращение функции
/(·,·): i/->Rn, C/cR1+fc,
от t G Ш и и G Шк через приращение переменной и, по которой
область U предполагается выпуклой (при каждом
фиксированном £), причем предлагаемое в лемме выражение (143) весьма
напоминает линейное1 и к тому же с непрерывными
коэффициентами.
Лемма 128. Если f,f'u G С(С/), то справедливо
представление
/(«, υ) - /(ί, и) = φ(ί, и, ν){ν - и), (t, и), (t, v) G С/, (143)
где φ — непрерывная оператор- функция2.
► Обозначив ν =,u + h, в силу выпуклости по и области U имеем
а3десь не утверждается, что приращение функции f(t, v)—f(t, и) и
вправду линейно по приращению аргумента ν — и ведь действующий на него
оператор φ(£, и, ν) сам зависит от переменных и и ν
2Принимающая значения в пространстве Hom(IRfc,IRn).
163
1
/(*,t;) - /ft,и) = f(t, и 4- Щ\\= J df{t'Ud + Щ dQ = cpft,ц,v)h,
о
где функция
ι
φ(ί,Μ,ν) = J/i(i,ti + e(v-ti))d8,
о
непрерывная по совокупности всех своих переменных (как
интеграл от функции, непрерывной по той же совокупности),
принимает свои значения в пространстве Hom(Rfc,Rn), так же как
и подынтегральная функция f'u. ■
III*. Доказательство теоремы. Теперь докажем
теорему 127.
► 1. Для произвольной точки (£*,μ*) Ε D(x):
• возьмем интервал / d Ζ)(χ(·,μ*)), содержащий точки t*, to;
• найдем такое число ε > 0, что выпуклая по χ область
Gt,i = {(t, x)\tel, \х- χ(ί, μ*)| < ε}
содержится в области G (см. п. 4 доказательства теоремы 118);
• выберем с помощью теоремы 123 такую выпуклую
окрестность υ(μ*) С М, что при любом μ Ε υ(μ*) решение χ(·,μ)
принадлежит ε-трубке функции χ(·,μ*) на компакте1 /.
2. Согласно лемме 128, для функции f(t,u) = /(ί,χ,μ),
определенной на выпуклой по и = (χ, μ) области
U = GtJ χ £/(μ*) С R1+fc, A; = η 4- m,
при любых μ, ν Ε U(μ*) существует непрерывная
оператор-функция cp(£,w, v), удовлетворяющая равенству
/(«, χ(ί, ν), ν) - /(«,χ(ί, μ), μ) ξ /(«, ν) - /(«, μ) =
= φ(ί, w, ν) (ν - w) = ψ(ί, μ, ν) ((χ(ί, ν) - χ(ί, μ), 0) 4- (0, ν - μ)) ξ
= #(*, μ, ν) (χ(ί, ν) - χ(ί, μ)) 4- Λ(ί, μ, ν)(ν - μ),
1 Поэтому оно определено на отрезке /, а график его сужения на / лежит
в области Gej.
164
где функции и = (x(t, μ),μ) и ν = (x(t, v), ν) непрерывны по
совокупности переменных t и μ, ν G ΙΙ(μ*), равно как и оператор-
функция ψ(£, μ, ν) = φ(£, и, ν), а также ее компоненты1 g(t, μ, ν) и
Λ(ί,μ,ν).
3. Фиксировав базис ei, ...,em в пространстве Rm,
представим точки множества Μ С Rm как наборы координат в этом
базисе. Обозначив для заданных μ G υ(μ*) и г G {1, ...,m}
функцию
_ / .. vx _ Χ(·,ν)~χ(·,μ)
Ζΐ(·,μ, vj = ,
ν—μ*
зависящую от параметра
ν = μ + (vi - μί)βί ^ μ, (144)
из задачи Коши (140) получаем
, Λ_χ(*,ν)-χ(*,μ) _ /(^χ(^ν),ν)-/(^,χ(^,μ),μ) _
где, μ, ν j — — —
Vi - μ* Vj - μ«
= #(£, μ, ν)ζί(ί, μ, ν) 4- fci(i, И> ν)> ^г = Ле<,
/. λ χ(*ο, ν) - χ(ί0, μ) ^ο(ν) - χ0(μ)
Ζί(ίο5μ5ν] = = ,
Vi - μί Vj - μι
т.е. функция Ζί(·,μ,ν) удовлетворяет задаче Коши
ζ = g(t, μ, \)ζ 4- Ы(Ь, μ, ν), 2(ί0) = —·
νί μ%
4. Предельная, при ν —>■ μ, задача Коши2
ζ = ρ{ί,μ,μ)ζ + ^(ί,μ,μ), z{t0) = (χο)'μί(μ), (145)
также имеет решение, обозначаемое через Ζΐ(·,μ) и определенное
на всем интервале / (так как уравнение в этой задаче линейно,
с непрерывными по t G / коэффициентами; теорема 27).
Более того, согласно следствию 124, решение ζ%(·,μ)
предельной задачи Коши удовлетворяет первому из равенств цепочки
*(i,H) = lim*(i,M= ΗιηΧ(^ν)~Χ(^μ)=:χ^(^,μ), t G /,
1 Которые получаются, как сужения оператора ψ(ί,μ,ν) на
подпространства Шп χ {0} и {0} х Шт, отождествляемые с пространствами Шп и М.т
соответственно.
2 Начальное значение в ней определено по условию
165
в которой первый, а значит, и второй из пределов, взятые при
условии (144), существуют.
5. Функция χ имеет в окрестности / х £/(μ*) точки (£*,μ*)
непрерывную производную по μ, а также обе смешанные
производные по t и μ — непрерывные и потому равные друг другу1.
Действительно:
• каждая компонента Ζ{ = х' (г = 1, ..., га) функции
ζ(*, μ) = х|Л*> μ), (*, μ) ^ / χ ί/(μ*),
равно как и ее производная Ъ{ = (х' ) , непрерывна по
совокупности своих переменных (поскольку следствие 124 применимо к
задаче Коши (145)), следовательно, этим же свойством обладает
и функция х^;
• если в уравнение (140) подставить его решение χ = χ(ί,μ),
то получится равенство (142), правая часть которого имеет
непрерывную по совокупности переменных t и μ частную
производную по μ (так как, по уже доказанному, ее имеет функция
χ(ί,μ)), а значит, и левая часть, совпадающая с функцией х, —
тоже. ■
IV. Дифференцируемость по начальному значению.
Решение χ всего семейства задач Коши (131) с фиксированным
начальным моментом to, рассматриваемое как функция времени
t и начального значения xq = μ, определено в области D(x) (см.
следствие 126) итюдпадает под действие теоремы 127, частным
случаем которой и является
Следствие 129. Пусть f,fx G C(G). Тогда решение χ
семейства задач (131) имеет во всей области D(x) непрерывные
по паре (t,xo) производные
ххо и (хх0) = Ххо'
V*. Выпрямление интегральных кривых. Пусть задана
точка (to,xo) e G С R1+n и диффеоморфизм
φ: U(t0,x0) -¥ V
Теорема из математического анализа.
166
(т. е взаимно-однозначное отображение, непрерывно
дифференцируемое1 вместе со своим обратным) некоторой ее окрестности
U(to,xo) С G в некоторую область V С R1+r\
При отображении φ график Гх С U(to,xo) любого решения
х(·) системы
x = f(t,x), (t,x)€G,
переходит в кривую с координатами
(s,y) = cp(t,x(t)), teD(x),
которая также может служить графиком какой-либо функции
y(s). Если же все интегральные кривые переходят в
интегральные кривые системы
6 = 0, {s,y)eV,
то диффеоморфизм φ называется выпрямляющим.
Теорема 130. Если /, f'x Ε C(G), то для любой точки
(to, хо) G G существует выпрямляющий диффеоморфизм
некоторой ее окрестности С/(£о,#о) С G, оставляющий все точки
вида (to,x) на месте и сохраняющий первые координаты всех
точек (t,x) E U(to,xo).
► 1. Для каждого χ Ε Gt0 обозначим через х(-,х) непродолжае-
мое решение, удовлетворяющее начальному условию
x(to,x) = χ.
Согласно следствию 126 (без ограничения общности считаем
множество Gt0 С Rn областью2), функция х(·,·) определена в
некоторой области D(x) С 11+п.
2. Отображение
χ:ΐ>(χ)-»σ,
ставящее в соответствие каждой точке (t, χ) Ε D(x) точку
X(t,x) = (t,x(t,x)) (146)
Определение диффеоморфизма допускает и другие варианты
дифференцируемое™ от простой до бесконечной.
2В этих целях, если нужно, область G можно и уменьшить
167
области G, непрерывно дифференцируемо (см. следствия 126
и 129), причем верны равенства
χ{ί0,χ) = (t0,x(t0,x)) = {t0,χ), χ eGt0,
xx(t0,x0) = {x(to,x))fx\x=Xo = xfx\x=x0 =le End(Rn).
3. Матрица производной (в Rn выберем какой-либо базис)
Х(*,х)(*0'а:о)=(х(«0,а:0) ε)
невырождена, а значит, отображение χ осуществляет
диффеоморфизм достаточно малой окрестности точки (to,xo), которую
можно выбрать прямоугольной, т. е. представимой в виде
произведения
V=IxV(x0), /Cl, V(x0)cGto,
в окрестность U(to, Xo) той же точки. Следовательно, и обратное
к нему отображение φ — также диффеоморфизм.
4. Наконец, для каждой точки χ Ε V(xq) отображение φ
переводит график решения х(-,х) в график решения у(·) = χ новой
системы
φ(ί,χ(ί,χ)) = χ-^ί,χί*,*)) = (t,x), t e I
(в соответствии с равенством (146)). ■
5.5. Система в вариациях
это дифференциальная система для производной решения
задачи Коши (131) по параметру.
I. Вариации по параметру. Для того чтобы явно найти
коэффициенты задачи Коши для (η χ т)-матричной функции1
Ζ('>Η· ) — ΧμΙμ=μ* = (Χμι j · · · )Χμτη)|μ=μ*5
можно, например, детально проанализировать доказательство
теоремы 127, обеспечивающей существование самой этой
функции.
Предполагается, что в пространствах Ш.п и Шт фиксированы базисы и
поэтому для каждой координаты функции ζ можно записать задачу (145).
168
Однако достаточно воспользоваться лишь окончательным
результатом (этой же теоремы, гарантирующей правомерность
следующих выкладок) — а именно, последовательно выполнить
следующее:
• совершить подстановку χ = χ(ί,μ) в задаче Коши (140);
• продифференцировать по μ все полученные равенства
(χμ) Л μ) =*[ι(<,μ) = /χ(^χ(^μ),μ)χμ(^μ) + /μ(^χ(^μ)>μ)>
χμ(*ο,μ) = ζο'(μ);
• положить всюду в них μ = μ*.
Получаемая в результате линейная неоднородная система
называется системой в вариациях по параметру (вдоль решения
χ(·,μ*)) и записывается в виде
z = A(t)z + F(t), ί€ΐ>(χ(.,μ*)),
где функция
Α(ί)=^(ί,χ(ί,μ*),μ*)
принимает (η χ п)-матричные значения, а неоднородность
^)ΞΕ/μ(ί,χ(ί,μ*),μ*)
— (η х га)-матричные, так же как и сама искомая функция1 ζ с
начальным условием
z{t0) = Ζ(/(μ*)·
II. Вариации по начальному значению. Если роль
параметра μ в задаче Коши (140) играет начальное значение xq
в момент to, то правая часть /(ί,χ,μ) = f(t,x) уравнения этой
задачи уже не зависит от своего третьего аргумента. Поэтому
система в вариациях по такому параметру
z = A(t)z, A(t) = f'x(t,x(t,x*)), (147)
является линейной однородной и называется системой в
вариациях по начальному значению (вдоль решения x(-,Xq)).
Обе функции приобретают привычный векторный вид, когда т = 1, т. е.
когда параметр μ скаля рен.
169
Любопытно, что эта система оказывается одинаковой как для
полной (п х п)-матричной функции
так и для каждого ее столбца, т. е. вектор-функции ζ^, равной
производной решения χ по г-й координате начального значения.
Правая же часть начального условия в исходной задаче Коши
(140) равна просто xq, так что начальное значение z(to):
• в случае матричной функции ζ — совпадает с единичной
матрицей
z(t0) = Ыхо(х'0) = Е,
а значит, сама функция z(t) — с матрицей Коши1 Z(t,to,XQ)
системы (147), т.е. справедливо равенство
x'xo(t, х*0) = Z(t, t0, x*0), t e £>(χ(·,*5)); (148)
• в случае вектор-функции Ζ{ — совпадает с г-м столбцом
единичной матрицы, а функция Zi(t) — с г-м столбцом матрицы
(148).
5.6. Разложение решений по параметру
в ряд тесно связано с их непрерывностью или дифференцируе-
мостью по параметру и оказывается равномерным на отрезках.
I. Нулевое приближение. Непрерывность решений задачи
Коши (140) по параметру в фиксированной точке μ (см.
теорему 123) можно интерпретировать как сходимость
χ(·>μ + η) ->χ(·>μ)> η->ο,
в смысле компактно-открытой топологии в S(G), т.е. как
возможность для любого компакта К С D(x(·, μ)) и всех достаточно
малых по модулю значений η Ε Rm представить решение в виде
χ(ί, μ 4- η) = x(i, μ) 4- α(ί, η), t e Κ,
где функция α удовлетворяет условию
Μ·,η)||*=ο(1), η->0. (149)
Зависящей еще и от третьего аргумента — начального значения х^ того
решения, вдоль которого берется производная
170
II. Первое приближение. Дифференцируемость же
решений по параметру в точке μ дает более тонкое разложение:
также равномерное по t Ε К, но с дополнительным, линейным по η
членом и с остаточным членом уже вида ο(η) при η —> 0.
Следствие 131. В условиях теоремы 127 для любого
значения μ £ Μ и компакта К С Ζ)(χ(·,μ)) существует такая
окрестность U(0) С Шт точки 0, что при всех η Ε U(0)
справедливо представление
χ(ί, μ 4- η) = x(i, μ) 4- χ^ί, μ)η 4- α(ί, η) |η|, te Κ,
где функция α удовлетворяет условию (149).
► 1. Выбрав выпуклую окрестность
U{μ) = μ 4- С/(0) С Μ
точки μ, для которой (см. следствие 124 и лемму 119)
К х U(μ) <е £>(х),
обозначим (см. теорему 127)
2. Функция
а: /Гх С/(0) -► Мп,
задаваемая формулой1
_ χ(^μ + η)-χ(^μ)-χμ(^μ)η
α(ί,η) =
η ^ 0,
0, η = 0,
имеет производную по t (см. теорему 127), причем равномерно
ограниченную, так как ά(ί, 0) = 0 и (см лемму 13)
|«(«,η)|<!^'>1+.?),"^'μ)Ι + Ι^',μ)ηΙ<2£, η^Ο.
3. Поэтому функция α(ί,η):
1При η = 0 она доопределена своим нулевым (в силу существования
производной χ^,(ί,μ) при каждом t G К) предельным значением
171
• не только непрерывна по η, но и липшицева по t, а значит,
непрерывна по t G К равномерно по η G С/(0);
• следовательно (лемма 122), непрерывна по совокупности
переменных t и η;
• значит, непрерывна по η равномерно по t G К;
• стремится κα(ί,Ο) =0 равномерно по t G К при η —> 0. ■
III*. Равномерность по параметру. Полученное в
следствии 131 представление решения оказывается равномерным не
только по t на любом наперед заданном компакте К, но и по μ
на любом наперед заданном компакте С.
Следствие 132. В условиях теоремы 127 для любых
компактов
С СМ, КС Ρ|£>(χ(·,μ))
существует равномерное по паре (ί,μ) G К χ С представление1
χ(ί, μ 4- η) = χ(ί, μ) 4- χ^ί, μ)η 4- ο(η), η -► 0.
► Чтобы доказать это утверждение, достаточно
усовершенствовать доказательство следствия 131, заменив в нем окрестность
U (μ) множеством
U(C)= U^4-C/(0))CM,
μ£θ
а функцию α(ί,η) — функцией α: КхСх С/(0) —>■ Rn, задаваемой
прежней формулой (непрерывной по паре (μ, η) и равномерно по
ней непрерывной по t, а значит, непрерывной по η равномерно
по паре (ί,μ)). ■
IV*. Теорема Лиувилля о фазовом объеме. В случае,
когда параметр μ есть начальное значение хо, следствие 132
превращается в
Следствие 133» В условиях следствия 129 для любых
компактов
CcGt0, Kef] £>(χ(·,*ο))
хоес
Определенное при всех достаточно малых по модулю значениях η.
172
справедливо равномерное по паре (t,xo) Ε К χ С представление
x(t, хо + h) = x(t, xo) + Z(t, to, xo)h + o(h), h ->· 0,
где Z(t,to,xo) ~ оператор Коти системы в вариациях по
начальному значению вдоль решения x(-,xq).
Пусть в следствии 133 компакт С С Gt0 представляет собой
замыкание некоторой области.
• Тогда равенство
X(t, s)x(s,xo) = x(t,xo), t,s е К, хо Ε С,
корректно определяет отображение Коши1 X(t,s) задачи (131).
• Обозначим через V(C(t)) фазовый2 объем множества
C{t) = X{t,t0)CcRn.
• Разбивая множество С = С (to) в сумму большого числа
δ-мелких (т.е. помещающихся каждая в шарик диаметром, не
превосходящим δ > 0) частей С\,Сч, ... с отмеченными в них
точками χ\,χι, ..., получаем с помощью следствия 133 цепочку
равенств
V(C(t)) = YimTV(X(t,t0)Ci) =
δ-»·ο
г
= lim ]Г ν (*(*. *о)С* - X(t, t0)xi) =
i
= lim Σ V ((Z(t, to, Xi)(d - Xi)) · (1 + o(l))) =
δ-ю
г
= lim SZ (^et ^(*» ^o? xi) · V(Ci)) = det Z(t, to, x) dx.
с
С учетом следствия 52 и равенств (147) имеем
d_
at
А С
■V(C{t)) = — det Z(t, t0, x) dx =
\ —detZ(t\to,χ)dx = (tr f'x(t,x(t,x)) · aetZ(t,to,x))dx,
C(t0)
1 Вообще говоря, нелинейное в отличие от аналогичного отображения из
определения 3 4
2Т. е взятый в фазовом пространстве (а не в расширенном).
173
причем дифференцирование интеграла по параметру t
правомерно, так как последняя подынтегральная функция
непрерывна по паре (t, χ) £ К χ С.
• Положив в последней цепочке t = to и опустив в итоговом
равенстве индекс 0, получаем формулу
V(C(t))= f dwx f(t,x)dx,
d_
di
C(t)
где
Xr
из которой вытекает следующая теорема, носящая имя Лиувил-
ля
Теорема 134- Если /, fx G C(G) и d\vxf = 0, то
отображение Коти задачи (131) сохраняет фазовый объем.
V*. Гамильтонов инвариант. Отображение Коши так
называемой гамильтоновой системы
*-5ЙГ"\ {t,x,y)€GcU1+n+n, tf€C2(G),
У — Η-Χ\ι, χ, у),
всегда сохраняет фазовый объем, поскольку
<ϋν(*,„)(/ς, -К) = Ьг(Н'у)'х + tr(-H'x)y = 0.
5.7. Зависимость решений уравнений от параметра
определяется зависимостью от того же параметра решений
нормальных систем, в которые переходят уравнения под действием
канонической замены
I. Каноническое преобразование топологии. Пусть
семейство задач Коши для уравнения η-го порядка
У(п) = Ж</,</, ...,2/(n-V),
y{to) = 2/ο(μ)
y(t0) = 2/1 (μ)
(150)
174
где
(ί, у, у, ..., у(п_1)) е С с R1+n, μ е Μ с IRm,
под действием канонической замены (см определение 2 5)
χι
χ = '
= ψ0Ξ
/ У \
У
,х
п,
\у
(п-1)
/
переходит в семейство задач Коши для системы
Х2
ж = /(ί,ζ,μ) ξ
а;
η
ν/\ί? ^ι? · · · 5 «^η? μ)>
/ г/о (μ)
χ(ίο) = ίο(μ)= Λ(μ)
\2/η-ι(μ)>
Обратное отображение ψ-1 осуществляет изоморфизм (см
лемму 29) множества Sf всех непродолжаемых решений χ(·,μ)
задач последнего семейства в множество Sf всех
непродолжаемых решений γ(·,μ) задач семейства (150).
Более того, отображение ψ-1 переводит компактно-открытую
топологию первого пространства1 в компактно-открытую же
топологию второго пространства, задаваемую ε-трубками
U^\y) = {z€Sf\ D(z) D К, ||z - у||Г' < ε}
функций у £ Sf на компактах К С D(y), но уже по норме
пространства (п — 1)-струй Сп~1(К), имеющей вид2
0<г<п
(151)
индуцированную топологией объемлющего пространства Sf
формально она зависит еще и от нормы в Rn, но, как видно из леммы 12, фактически
не зависит
23десь и ниже производные г-го порядка берутся по t
175
Теорема 135. Пусть f,f'(t) e C(G χ Μ) и yi e C(M) при
с/
каждом г = О, ... ,п — 1. Тогда для любого μ* £ М, любого
отрезка К С Ζ)(γ(·,μ*)) и любого ε > О существует такое δ > О,
что если
|μ-μ*|<δ,
то решение γ(·,μ) задачи (150) заведомо определено на отрезке
К и удовлетворяет оценкам
ΙΙν(ί)(·,μ)-γ(ί)(·.μ*)ΙΙκ<ε, < = ο,...,η-ι.
► Утверждение вытекает из непрерывности композиции
отображений
Μ -> Sj Ψ-^ Sf,
первое из которых, ставящее в соответствие каждому μ Ε Μ
решение χ(·,μ) Ε Sf, непрерывно в силу теоремы 123, а второе —
просто изоморфизм топологических пространств. ■
II. Колебания, близкие к резонансным. Рассмотрим
семейство задач Коши, зависящих от параметра ω, для уравнения
вынужденных малых колебаний маятника без трения
у + а2у = cos ωί (α,ω>0), y(0) = y(0) = 0.
Так как правая часть уравнения имеет вид
cos<o£ = Re(eiwi),
то специальное (см. теорему 116) его частное решение уо,
согласно лемме 115, можно искать как действительную часть решения
/ Ае™\ ω φ α,
Zo{t) = \Ate^, ω = «, ЛеС'
комплексного уравнения
ζ + α ζ = е .
В первом, нерезонансном, случае имеем
Αβίωί(-ω2 + α2) = еш =» z0(t) = 9 * 0еш,
αζ — ωζ
а во втором, резонансном,
176
Аеш{2ш - ίω2 + ίο2) = еш =» z0(t) = Jr-eiat,
2га
поэтому
y0{t) = Rez0{t) =
α2 — ω2
οοβωί, ω/α,
(152)
2α
sin αί,
ω = α.
Учитывая, что общее решение соответствующего линейного
однородного уравнения имеет вид
у = С\ cos at + С2 sin at, C\$ Ε R,
получаем решение задачи Коши
α2 — ω2
(cos ωί — cos at) =
sin^^i
а — ω
Υ(*,ω)= <
(α + ω)
sin —-—t,
ω/ο,
2α
sinai, ω = α.
Таким образом, в полном согласии с теоремой 135, при
плавном изменении параметра ω решение у(·, ω) вместе со своей
производной меняется также плавно, причем равномерно на любом
отрезке временной оси.
Даже на очень большом отрезке вида [0;Т] при достаточно
близком к α значении параметра ω нерезонансное решение
оказывается весьма похожим на резонансное (рис. 23, а): правда, со
У
у У
^KJ \ / 1 *
г ^v
ιι=— / 1 sin(a-to)i
Чл/ 1 / I / \r\ 'ι
^ч. if i# **г
"■^Ч*. If \ /-X^
\
\
\
N
а б
Рис. 23. Сближение внешней частоты с внутренней:
a — предельное; б — допредельное
177
временем амплитуда нерезонансного решения все же неизбежно
падает до нуля, затем снова растет и снова падает... —
происходит так называемое биение (рис. 23, б).
III. Дифференцируемость по параметру.
Непрерывность по паре (£,μ) функций χ ξ фу и χ ξ ψγ влечет за собой
такую же непрерывность функции у со всеми ее производными
у, ...,y(n_1) и у(п). Поэтому следствие 124, отнесенное к
решению у(·, ·) всего семейства задач Коши (150) для уравнения п-го
порядка, звучит как
Следствие 136. В условиях теоремы 135 область
определения D(y) решения у есть область в R1+m, на которой функция
у вместе с ее производными у, ..., y(n) no t непрерывна по паре
(*,μ)·
Если после перехода к системе оказываются выполненными
условия теоремы 127, то непрерывны функции
Φ(/μ)=к., (фу;) = ю = (*& = (фу&.
так что справедлива
Теорема 137. Пусть /,/'(ί),/μ € C(G χ Μ) и у{ е С1 (Μ)
при каждом г = 0, ..., гг — 1. Тогда решение у семейства задач
(135) имеет во всей области D(y) непрерывные по паре (£,μ)
производные1
№)(<) = (УЧ. < = 0,...,п.
IV*. Уравнение в вариациях. Если в семейство (150) задач
Коши подставить у = y(t, μ) и формально продифференцировать
его по μ, а затем положить всюду μ = μ* (благодаря теореме 137
эти выкладки оправданы), то для производной
* = 2/μΙμ=μ*
получится снова задача Коши
'*(*.) = ΐά(μ·)
2<n> = ao(t)z + ■■■ + αη-^ήζ^-» + g(t), <
*(*») = ν1(μ*)
2(«-ι)(ίο) = ^_1(μ«),
1 Здесь г-я производная берется по t
178
с линейным уравнением в вариациях по параметру (вдоль
решения у(·, μ*)), где1
аг — fv(i) μ=μ* > г — О, . . . , П — 1, 9 ~ ίμ
μ=μ
Фу=Фу( ,μ*) Фу=Фу( ,μ*)
V*. Разложение в ряд. Производная по параметру
решения задачи Коши для уравнения п-го порядка дает разложение
этого решения в такой же ряд, как и в следствии 131, но с более
сильным остаточным членом.
Следствие 138. В условиях теоремы 137 для любого
значения μ* G Μ, отрезка К С /}(γ(·,μ*)) и всех значений μ из
некоторой окрестности U(μ*) С Μ справедливо представление
γ(ί,μ) = γ(ί,μ*) + /μ(ί,μ*)(μ - μ*) + α(ί,μ)|μ - μ*|, t G Κ,
где функция α удовлетворяет условию
Ы-,Жкх = т? 11»(<)(·.μ)11κ = °т> μ -> μ*· (ΐ»)
0<г<тг
VI*. Переход к уравнению малых колебаний. С
помощью последнего утверждения сравним две задачи Коши.
• для уравнения свободных колебаний маятника без трения
с нулевой начальной скоростью
y + siny = 0, у(0) = у0, у(0)=У1=0, (154)
• для уравнения малых колебаний с теми же начальными
условиями
$ + У = 0, у(0)=у0, 5(0) = 0. (155)
Примем начальное отклонение уо за параметр (т. е. μ = уо) и
будем считать его близким к нулю (т.е. μ* ξ 0). При уо = 0 обе
задачи имеют нулевое решение
у(-,0)=у(.,0)=0,
а последняя з*адача при каждом уо имеет решение
y(t,y0) =y0cost.
1 Подстановка μ = μ* осуществляется не только в последнем аргументе
функций /'(t) и /μ, но и в других, косвенно зависящих от μ
179
Дифференцируя все равенства задачи (154) по уо и кладя
Уо = О, получаем, соответственно, уравнение в вариациях вдоль
ее решения у(-,0) и начальные условия
ζ + ζ = 0, *(0) = 1, i(0)=0.
Полученная линейная задача Коши имеет решение z(t) = cost,
совпадающее с производной y'yo(t,Q).
Поэтому, в силу следствия 137, на любом отрезке К числовой
оси при достаточно близких к нулю значениях уо справедливо
разложение
у(*»2/о) = 0 + cos£ · г/о+ <*(*> 2Λ)) -Уо = 2/o(cosi 4- а(*,г/0)), t G К,
где
||а(-,2/о)||к -► 0, ||ά(·,Μ))ΙΙ* ~> 0, г/о -► 0.
Таким образом, решение задачи (154) оказывается близким1
к решению y(t, г/о) задачи (155). Указанная близость как раз и
оправдывает замену исходного нелинейного уравнения
линейным уравнением малых колебаний.
Благодаря этой близости гарантируется, например, что на
отрезке
Α-=[0;π]
решение у(-,г/о) задачи (154) имеет единственный нуль t\,
который при уо —> 0 сходится к нулю2 π/2 решения у(-,г/о) задачи
(155):
• существование нуля t\ и его сходимость к π/2
обеспечивается противоположностью знаков функции у(£,г/о) по разные
стороны от сколь угодно малой окрестности точки π/2
ί/ε(π/2) = (π/2 - ε, π/2 + ε), ε > 0
(т.е. ее положительностью слева и отрицательностью справа,
что достигается малостью величины ||α(·,2/ο)||ΑΓ при малых \уо\)',
• единственность же нуля обеспечивается монотонностью той
же функции у(£, г/о) внутри той же окрестности (т. е.
отрицательностью ее производной
У(*> Уо) = Уо(~ sin t + ά(ί, уо)), te ί/ε(π/2),
что достигается малостью величины ||ά(·,2/ο)||κ при малых \уо\).
вместе с первой производной равномерно на любом компакте К
А разность £2 — t\ между соседними нулями этого решения сходится к
полупериоду малых колебаний, равному π.
180
Задачи для самостоятельного решения
1. Останется ли справедливым утверждение теоремы 118, если в
нем:
• условие f'x € C(G) заменить условием / € Lipx(G) или убрать
вообще,
• условие д' € C(G) заменить условием д € Lipy(G) или убрать
вообще7
Аналогичный вопрос для теоремы 123 и следствий из нее.
2. Останется ли справедливым утверждение леммы 119, если в нем
условие компактности множества X заменить условием его
замкнутости?
3. Останется ли справедливым утверждение раздела III из п. 5.1,
если в нем снять условие непрерывности с функции χΊ
4. Можно ли усилить теорему 118, утверждая, что при надлежащем
выборе δ > 0 оценка (133) будет выполнена не только для компакта
К С / ξ .D(x), но и сразу для всего интервала J, если обеспечены
какие-либо из следующих условий:
• 9 = f\
• интервал / ограничен на прямой R;
• все возмущенные решения у определены на интервале /;
• исходное решение χ доопределяется на замыкание К = /;
• исходное и все возмущенные решения доопределяются на
замыкание К = Π
5. Если X и Υ — пространства функций с равномерной или
компактно-открытой топологией каждое, то утверждение о
непрерывности функции /: X —> Υ можно понимать в четырех разных
смыслах. В каком смысле оно получается логически самым сильным, а в
каком — самым слабым?
6. Докажите (используя следствия 124 и 136), что в условиях
теоремы 123 можно распространить утверждаемую в ней оценку для
разности решений х( ,μ) и х( ,μ*) также и на разность их производных
по ί, а в условиях теоремы 135 — оценки для разности производных
решений у(·, μ) и у(·, μ*) до (п — 1)-го порядка также и на разность их
производных η-го порядка.
7. Сформулируйте и докажите следующие теоремы, аналогичные
утверждениям 125, 129 и 135 соответственно.
• о непрерывности по начальной точке (ίο,^ο) € G решения
χ(ί,ίο,^ο) семейства задач Коши (131);
• о дифференцируемости по начальному моменту to решения
χ(ί,ίο) семейства задач Коши (131) с фиксированным начальным
значением xq. Нужно ли для нее существование производной //?
Запишите систему в вариациях по начальному моменту и начальное условие
для производной у = x't ,
181
• о непрерывности по начальным значеньям уо, ..., уп-\ решения
y(t,yo, .. · ,2/η-ι) семейства задач Коши (52), (53) для уравнения п-го
порядка с фиксированным начальным моментом to.
8. При каждом к € N докажите справедливость следующего
утверждения для решения х:
• задачи (131): если / € Cfe(G), то χ € Cfe+1(£>(x)),
. задачи (140): если /((*>μ) € C(G х Μ), то χμ*° € С(Л(х))
9. Найдите систему в вариациях по начальному значению для
решений системы
χ = A{t)x + F(t), A,FeC(I)
10. Для произвольного вектора zq € W1 выясните, что за
производная ζ = χ' решения χ семейства задач Коши (131) удовлетворяет
начальному условию z(to) = zq и системе (147) в вариациях по
начальному значению.
11. Является ли семейство решений (152) равномерно на
компактах по t непрерывным по параметру ω (нет ли здесь противоречия с
теоремой 135)?
12. Найдите разложение решения задачи (154) по параметру у\ при
t/o = 0c остаточным членом вида о(у\) при у\ —> 0.
13. Верно ли, что отображение χ (146), заданное на всей своей
области определения D(x), является диффеоморфизмом?
Глава б
УСТОЙЧИВОСТЬ ПО ЛЯПУНОВУ
6.1. Определение устойчивости
предполагает, что фиксирована система
х = f(t, χ), (t, x)eGc R1+n, (156)
с исходным решением xq(·), а кроме того, фиксирован начальный
момент to Ε Μ, причем область определения D(xo) исходного
решения содержит луч
R+ = [t0;oo).
I. Устойчивость решения системы. Любое решение χ
системы (156) будем называть возмущенным (по отношению к
исходному) и по умолчанию считать непродолжаемым.
Определение 6.1. Решение хо системы (156) называется:
• устойчивым (по Ляпунову), если для любого ε > 0
существует такое δ > 0, что любое решение χ удовлетворяет
импликации1 (рис. 24)
|х(*о) - хо(*о)| < δ => |χ(ί) - χο(ί)| < ε, t e R+ С D(x); (157)
• асимптотически устойчивым, если решение Хо устойчиво
по Ляпунову и, сверх того, для некоторого δο > 0 любое решение
χ удовлетворяет импликации
|х(*о) - хо(*о)1 < δο ==► Иш |χ(ί) - χο(ί)| = 0; (158)
ί—юо
• неустойчивым, если оно не является устойчивым.
Из которой, в частности, следует, что δ < ε
183
Χ;
яо(*о)
,
^^|}ε
y^^^^^^^^Z^^^/k
^^^^Ш^^^Щщк
ψ-^Л^^^^^ш^
1 . ^
ί0 ί
Рис. 24. Устойчивость по Ляпунову
Заключительное неравенство импликации (157) эквивалентно
тому, что возмущенное решение лежит в ε-трубке
и,л+Ы) = {х I D(x) D R+, ||χ(·) - xo(-)IIr+ < ε}
исходного решения, но не как обычно — не на компакте , а на
целом луче2 R+.
Пусть отображение
Gt0 -> Sf (159)
каждому начальному значению χ Ε Gt0 ставит в соответствие
максимально продолженное решение х(-,х) Ε Sf задачи Коши с
начальным условием x(to,x) = χ. Тогда трубки С/ед+(хо)
образуют в множестве Sf такую базу топологии в точке"* хо, которая
позволяет говорить о непрерывности этого отображения,
причем:
• исключительно в одной точке хо = хо(£о)>
• равномерной по t Ε R+.
Эта непрерывность и означает устойчивость по Ляпунову
решения Хо
II. Устойчивость решения уравнения. Пусть для
заданного уравнения
у = /(«, у, у, ..., г/"-1)), (t, у, у, ..., у^) Ε G С R1+n, (160)
Для которого импликация имеет место и так (см. следствие 125).
2Это требование нарушается, например, если возмущенное (непродолжа-
емое) решение определено не на всем луче
Или фильтра, т. е системы всех множеств, каждое из которых содержит
хоть какой-нибудь элемент базы
184
фиксированы начальный момент to Ε Μ и исходное решение уо,
удовлетворяющее условию D(yo) Э И&+
Определение 6.2. Решение уо уравнения (160)
называется устойчивым, асимптотически устойчивым или
неустойчивым, если таковым, соответственно, является решение хо = фу о
системы (156), в которую переходит это уравнение при
канонической замене (см. определение 2.5).
Устойчивость решения уо уравнения (160) равносильна такой
же, как и для систем (равномерной по t Ε И+), непрерывности
в точке 2/0 = фуо(^о) £ ^п отображения, которое каждому
начальному значению у = (yo,yi, ...,yn-i) ставит в соответствие
максимально продолженное решение у(-,у) Ε S/ задачи Коши
(см. п. 5 7).
Подчеркнем, что базу топологии в точке уо в последнем
множестве образуют такие же ε-трубки
И.Д+(У0) = {У I D(y) D E+, ||y(.) -yftOIIS;1 < ε},
но по норме пространства Cn_1(R+), которая определяется
формулой, аналогичной (151), с заменой К на R+.
Асимптотическая же устойчивость дополнительно
предполагает, что для некоторого δο > 0 выполнена импликация
\У ~Уо\ < δο => Ит |фу(£,г/) - ψγ(ί,2/0)Ι = °>
t—юо
заключение которой, в частности, дает равенство
lim \y(t,y) - y{t,y0)\ = 0.
ί—юо
III. Существенные упрощения. Задача об исследовании
на устойчивость состоит в следующем: зная лишь правую часть
дифференциальной системы (156) или уравнения (160), а также
исходное решение, выяснить, является ли последнее
устойчивым, асимптотически устойчивым или неустойчивым.
При этом предпочтение отдается таким методам
исследования, которые не требуют нахождения возмущенных решений в
явном виде. Рщутимую пользу могут порой принести
следующие простые наблюдения:
• важно лишь то, как ведут себя решения, начинающиеся
достаточно близко к исходному;
• не играет никакой роли выбор конкретной нормы в фазовом
пространстве (конечномерном);
185
• не имеет значения выбор конкретного начального момента
(при естественной гладкости правой части системы);
• исходное решение без ограничения общности можно
считать нулевым
Именно об этом и говорит
Лемма 139. Факт устойчивости, асимптотической
устойчивости или неустойчивости решения Хо системы (156)
не нарушится, если:
1) ограничить множество возмущенных решений лишь
теми из них, что начинаются в какой-нибудь наперед заданной
окрестности Ur(xo) С Rn начального значения х$ = Хо(^о);
2) изменить норму в Rn — в частности, фиксировать
какой-либо базис в Жп и выбрать норму, выражающуюся через
координаты векторов в этом базисе,
3) поменять начальный момент to Ε -D(xo) в
предположении непрерывной зависимости решений от начальных
значений1;
4) сдвинуть начало координат пространства Rn в
какую-либо новую точку а, возможно даже непрерывно
дифференцируемо зависящую от времени t — например, пустить его вдоль
исходного решения (которое в новых координатах окажется
нулевым) .
► 1. Определение 6.1 действительно не пострадает, если
фигурирующие в нем числа δ, δο > 0 считать меньшими наперед
заданного числа г > 0.
2. Ни топология в пространстве Rn, ни определяемая ею
топология в точке хо Ε Sf, не зависят от нормы в Rn (см. лемму 12),
поэтому от нее не зависят ни факт непрерывности в точке х$
отображения (159), ни факт равенства нулю предела (158).
3. Пусть К — отрезок с концами to,t'0 Ε D(xq), а решение хо
устойчиво (асимптотически) с начальным моментом t$. Тогда в
силу равномерной по t E R+ непрерывности решения от
значения в начальный момент to и равномерной по t Ε К
непрерывности решения от значения в начальный момент t0 имеем: для
любого ε > 0 существуют такие числа δ > 0 (а в случае
асимптотической устойчивости еще и δο > δ соответственно) и δ' > 0,
что верны две импликации
См следствие 125
186
|κ(ίθ) - Χθ(*θ)| < δ => ||χ(ί) - Xo(i)llR+ < ε>
|χ(*ό) - χο(*ό)Ι < δ' => ||χ(ί) - xoWk < δ < ε,
откуда получаем требуемую для устойчивости с начальным
моментом t'0 импликацию (157)
|х(*о) - χο(*ό)Ι < δ' => ||х(«) - xoWIIr+u* < ε
(и, соответственно, предпосылку, а с ней заключение
импликации (158) для асимптотической устойчивости).
4. При замене у = χ — a(t), где а Е C1(R+), имеем
x = f(t,x) 4=Ф y = f{t,y + a(t))-a(t)=g(t,y),
а факт устойчивости, асимптотической устойчивости или
неустойчивости сохраняется и для нового исходного решения
Уо(*) = хо(0-<*(<), teD(x),
так как он полностью определяется совпадающими друг с
другом при такой замене выражениями
У(<) - Уо(*) = (х(*) " <*(*)) - (хо(*) - a(t)) = χ(ί) - χο(ί), t G R+.
В частности, положив а = xq, получим равенство уо = 0. ■
6.2. Устойчивость решений линейной системы
x = A{t)x + F{t) (161)
или линейного уравнения
уЫ + ахСОу*"-1* + · · · + ап(% = /(«) (162)
будем рассматривать при стандартных условиях
A,F,au ...,an,/eC(/), R+ С/.
Множества всех непродолжаемых1 решений линейной
неоднородной системы (161) и соответствующей ей однородной
системы, как и прежде, обозначаем через Sa,f и $а соответственно.
При этом, наряду с действительными линейными системами,
для которых x,F(t) Ε Rn и A(t) Ε EndRn, будем рассматривать
и комплексные.
А значит, определенных на всем интервале /
187
I. Устойчивость линейной системы. Согласно п. 1
нижеследующей леммы 140, устойчивость (в том числе и
асимптотическая) либо имеет место сразу для всех решений данной
линейной системы, либо не имеет места ни для одного из них.
По этой причине зачастую устойчивой {асимптотически)
называют, пользуясь вольностью речи, прямо саму линейную
систему с устойчивыми (асимптотически) решениями.
Лемма 140. Любая линейная система (161) обладает
следующими свойствами.
1. Устойчивость {асимптотическая) решения Xq Ε Sa,f
'неоднородной системы равносильна устойчивости
{асимптотической) нулевого решения 0 Ε Sa соответствующей однородной
системы.
2. Следующие утверждения об однородной системе
эквивалентны'
• система устойчива {асимптотически);
• все решения системы ограничены {стремятся к нулю при
t —¥ оо);
• существует фундаментальная система ограниченных
{стремящихся к нулю при t —> оо) решений.
3. Действительная система устойчива {асимптотически)
тогда и только тогда, когда устойчива {асимптотически) ее
комплексификация.
► 1. Если пустить начало координат вдоль решения xo{t) (см.
п. 4 леммы 139), то множество Sa,f всех решений неоднородной
системы перейдет (см. теорему 53) в множество
Sa, f — хо = Sa
всех решений однородной системы, а решение хо Ε Sa,f перейдет
в нулевое 0 Ε Sa, причем факт его устойчивости,
асимптотической устойчивости или неустойчивости не претерпит изменений.
2. Пусть задана однородная система.
• Из ее устойчивости (асимптотической) вытекает
ограниченность (и соответственно стремление к нулю при t —> оо) всех ее
решений, начинающихся в некоторой окрестности нуля С/(0), а
значит, и всех решений вообще, так как каждое из них после
умножения на достаточно малое число будет начинаться в С/(0).
• Далее, если ограничены (стремятся к нулю при t —> оо)
все решения системы, то таковыми тем более являются и все
решения из некоторой фундаментальной системы.
188
• Наконец, пусть решения χι, ..., χη образуют
фундаментальную систему и ограничены. Докажем, что система
устойчива.
Действительно, набор начальных значений χι(£ο)? --чХп^о)
образует базис в Rn, а сумма модулей координат векторов в этом
базисе служит новой нормой | · | в Rn (см. п. 2 леммы 139),
причем, обозначив
max ||хг(011м+ = Μ < оо,
г=1, ,тг
имеем для любого решения χ = С\Х\ + · · · + Спхп импликацию
δ > |χ(ί0)| = |Cixi(i0) + · · · + CnMto)\ = \Ci\ + · · · + \Cn\ =*
=^ Hx(*)IIr+ < |βΊΙΙ|χιΙΙκ+ + ··· + Ι^η|||χ»ι||κ+ <Μδ<ε
при достаточно малом δ < ε/Μ. Таким образом, система
устойчива.
Если, сверх того, все решения χι(ί), ... ,xn(£) стремятся к
нулю при t —> оо, то и любая их линейная комбинация — тоже, а
значит, система асимптотически устойчива.
3. Для множеств решений Sa и §д действительной и
комплексной системы с оператор-функцией А и А соответственно,
согласно лемме 92 (распространенной на неавтономные
линейные системы), справедливо равенство
§л = Sa + iSa,
из которого следует, что ограниченность (стремление к нулю при
t —>■ оо) всех решений из множества Sa равносильна
ограниченности (стремлению к нулю при t —>■ оо) всех решений из
множества Sa· ■
II*. Необходимое условие устойчивости. Из следующей
леммы можно выудить коэффициентный признак отсутствия
устойчивости или асимптотической устойчивости для линейных
систем и уравнений.
Лемма 1^1. Для устойчивости (асимптотической)
линейной системы (161) или линейного уравнения (162) необходимо
выполнение соотношения
lim ίτΑ(τ)άτ = —оо
189
или, соответственно, соотношения
inf
i€R+
ίο
t I
α\{τ)άτ > —oo I lim α\(τ)άτ = oo
► Из ограниченности (стремления к нулю при t —¥ оо) любых
решений χχ, ... ,хп устойчивой (асимптотически) системы
вытекает ограниченность (стремление к — оо при t —> оо)
показателя экспоненты в формуле Лиувилля — Остроградского для их
определителя Вронского
tr Α(τ) άτ
Jt0
|wxi, ,Χη(ίο)Ι·βΛ° =Ι^χι, ,χ»(*)Ι<|χι(*)Ι·····Μ0Ι
(см. теорему 50). Остальные утверждения леммы вытекают из
уже доказанных благодаря теореме 68. ■
Из леммы, в частности, следует, что положение равновесия
уравнения свободных малых колебаний маятника, даже
переменной длины, но без трения
# + а(% = 0, t е /DR+,
не может оказаться асимптотически устойчивым (т. е. все его
решения сразу вместе со своими производными первого порядка не
могут стремиться к нулю при t —>■ оо), так как в этом уравнении
коэффициент при у равен нулю.
III. Система с постоянными коэффициентами. Из
утверждений 2 и 3 леммы 140 с помощью теоремы 99 выводится
Теорема 142. Линейная система с постоянным
оператором:
• асимптотически устойчива тогда и только тогда, когда
действительные части всех его собственных значений
отрицательны,
• устойчива тогда и только тогда, когда действительные
части всех его собственных значений отрицательны или равны
нулю, причем последним отвечают жордановы клетки только
первого порядка.
► Без ограничения общности считаем систему комплексной: при
необходимости ее можно комплексифицировать, от чего факт ее
190
устойчивости (асимптотической) не претерпит изменений (см.
п. 3 леммы 140).
Воспользуемся свойствами фундаментальной системы
комплексных решений, складываемой из подсистем, каждая из
которых строится по своей жордановой клетке, порожденной
собственным значением λ = α + гр и имеющей порядок га. Такой
клетке ставим в соответствие подсистему из га решений
zj W = eCti ' β*βί (fy + thj-ι Η 1- tj(t)hi), j = 1, ..., m,
причем |ег^| = 1 и deg£j(t) = j — 1. Эти решения ограничены
все сразу тогда и только тогда, когда:
• или α < 0, и тогда все они даже стремятся к нулю при
t —> оо;
• или а = 0ига=1,и тогда подсистема состоит всего из
одного решения — не стремящегося к нулю при t —> оо. ■
IV. Малые колебания маятника. Матрица линейного
уравнения свободных малых колебаний маятника постоянной
длины с постоянным трением
y + 2py + qy = 0 (p>0, <7>0), t G / Э R+,
согласно лемме 107, имеет тот же характеристический
многочлен, что и само уравнение.
Поэтому по теореме 142 и определению 6.2 получаем, что
положение равновесия этого уравнения:
• при наличии трения (т. е. при ρ > 0) асимптотически
устойчиво, так как корни его характеристического многочлена имеют
отрицательные действительные части (см. раздел III из п. 4.7),
• при отсутствии трения устойчиво, но не асимптотически,
так как корни его характеристического многочлена чисто
мнимые, но некратные.
V*. Периодическая система. Исследуя на устойчивость
линейную Т-периодическую систему (161), можно ее:
• сделать однородной (отбросив неоднородность F),
• комплексифйцировать1 (см. п. 4.2),
• привести Т-периодическим (а значит, ляпуновским;
определение 4.3) преобразованием координат к системе с некоторой
постоянной матрицей В (см. теорему 103).
Если, конечно, она с самого начала не была комплексной
191
При всех этих ее изменениях факты устойчивости,
асимптотической устойчивости или неустойчивости не нарушатся1.
Кроме того (см. определение 3.7), в силу следствия 100 между жор-
дановыми клетками матрицы монодромии
Х(Г,0) =етв
комплексифицированной системы и жордановыми клетками
матрицы В можно будет установить соответствие, сохраняющее
их порядки и связывающее соответствующие собственные
значения μ (мультипликаторы) и λ соотношением
μ^β7^ =^ |μ| =e^ReX.
Благодаря этим наблюдениям теорема 142 может быть
перенесена на случай периодических систем и сформулирована как
Следствие 143. Линейная периодическая система (161):
• асимптотически устойчива тогда и только тогда, когда
модули всех ее мультипликаторов меньше 1;
• устойчива тогда и только тогда, когда модули всех ее
мультипликаторов меньше или равны 1, причем последним
отвечают жордановы клетки только первого порядка.
6.3. Функция Ляпунова
привязана к системе
x = f(t,x), /,/£eC(G), (i,x)6(?DR+xi/(0), (163)
имеющей нулевое решение, благодаря равенству /(-,0) = 0.
I. Определение функции Ляпунова. Эта функция
υ: 17(0) ->· R,
определенная в какой-либо окрестности С/(0) С Rn точки 0 и
призванная подтвердить факт устойчивости, асимптотической
устойчивости или неустойчивости нулевого решения, составляет
основу второго метода Ляпунова2.
Например, в силу утверждений 1, 2 и 3 леммы 140.
2 По поводу его первого метода см теорему 150.
192
Определение 6.3. Производной в силу системы (163)
функции ν в точке χ в момент t называется выражение1
vt{x) = v'{x)f{t,x) = v'Xl{x)fi{t,x) + --- + v'Xn{x)fn{t,x)
(последнее равенство предполагает наличие базиса в Rn).
Функцией Ляпунова для системы (163) называется любая функция2
удовлетворяющая условию
0) v(0) = 0,
а также условиям 1) и 2) на знак функции ν и ее производной в
силу системы соответственно, описанным конкретно в каждой из
нижеследующих лемм Ляпунова 145, 147 и 148 (об устойчивости,
асимптотической устойчивости и неустойчивости).
II. Смысл производной в силу системы. Некоторый свет
на понятие функции Ляпунова проливает
Лемма 144- Для любой функции Ляпунова ν системы (163),
ненулевого решения χ и промежутка
J=[to;ti)cD(x)
справедливы утверждения'.
• если χ — x(t) G С/(0) при некотором t G -D(x), то
. dv(x(t))
vt{x) = -щ-;
• если x(t) G С/(0) при всех t G J, то
ν(χ(ίι))-ν(χ(ίο))= U(x(t))df;
ίο
• если x(t) G V С U(0) при всех t G J и выполнено
соотношение
vt(x) < 0 (vt(x) < 0, vt(x) = 0, vt(x) > 0), χ G У, t G J,
13ύά «производная» берется по t. Однако индекс t у нее обозначает вовсе
не переменную, по которой происходит дифференцирование, а параметр, от
которого эта производная, вообще говоря, зависит (правда, в автономном
случае этот индекс можно и опустить)
2Окрестность ί/(0) проколота, т. е. не содержит точку 0.
193
то функция v(x(t)) на промежутке J убывает
(соответственно нестрого убывает, постоянна, возрастает).
► В условиях первого утверждения леммы имеем равенство
^&®1 = v'(x(tm) = v'(x(t))f(t,x(t)) = *(x(t)),
проинтегрировав которое по t от to до ίχ, получаем второе
утверждение, из которого вытекает и третье. ■
Таким образом, если в качестве функции Ляпунова ν (χ)
взять, к примеру, самое обычное расстояние (или его квадрат)
от точки χ до точки 0, то знакопостоянство ее производной в
силу системы непосредственно влияет на характер изменения
этого расстояния при движении точки χ вдоль фазовой кривой с
увеличением времени t: отрицательность производной означает
ее приближение точки к началу координат, положительность —
удаление и т. д.
III*. Равномерные оценки производной. В условии 2)
леммы 147 и теоремы 149 встретится непрерывная (в проколотой
окрестности U(0)) функция w, осуществляющая равномерную
по t Ε М+ оценку производной
щ(х) > w(x) (щ(х) < w(x)).
Однако если система (163) автономна, то, нисколько не
ослабляя соответствующих утверждений, можно сразу
положить
w = v = vff е C(i/(0)),
от чего всякое упоминание о функции w становится излишним
и формулировки упомянутых условий упрощаются.
6.4. Леммы Ляпунова и теорема Четаева
позволяют устанавливать устойчивость, асимптотическую
устойчивость или неустойчивость нулевого решения с помощью
функций Ляпунова (Четаева).
I. Лемма об устойчивости. Первая лемма представляет
собой признак устойчивости нулевого решения системы,
состоящий в наличии положительно определенной функции Ляпунова
с неположительной производной в силу системы.
194
Лемма 145. Пусть для
системы (163) существует функция
Ляпунова ν, удовлетворяющая при всех
х Ε U(0) ut G R+ условиям:
1) v(x) >0;
2) vt{x) < 0.
Тогда нулевое решение этой
системы устойчиво по Ляпунову.
Идея доказательства этой леммы
такова (рис. 25):
• внутри заданной малой
окрестности1 начала координат выберем
достаточно малый шарик, в котором все значения функции
Ляпунова строго меньше, чем на границе окрестности;
• тогда любая фазовая кривая, начинающаяся в выбранном
шарике, не сможет выйти за пределы заданной окрестности, так
как не дойдет до ее границы (ведь значения функции Ляпунова
вдоль фазовой кривой не увеличиваются).
► Пусть задано число ε > 0, удовлетворяющее (без ограничения
общности) условию
С/е(0) = {х е Жп | \х\ < ε} (ε С/(0). (164)
1. Функция ν непрерывна и:
• положительна в проколотой окрестности Щ0), поэтому
верны соотношения
inf v(x) = min v(x) = α > 0;
хедие(о) хедие(0)
• равна нулю в точке χ = 0, а значит, для указанного α
найдется положительное δ < ε, удовлетворяющее условию
sup v(x) < α.
x€Ub(0)
2. Любое непродолжаемое решение χ с начальным значением
х(«о) G £>δ(0) С £/ε(0) (165)
*В фазовом пространстве Шп Проекции интегральных кривых
(графиков решений) на фазовое пространство называются фазовыми кривыми (см.
также π 7 1).
Рис 25. Лемма об
устойчивости
195
(предполагается включение1 Е(х(·)) С U(0)):
• согласно лемме 144, удовлетворяет неравенству
v(x(t)) < v(x(t0)) < α, t > t0, te D(x);
• удовлетворяет условию
x{t) i dUs(0), t>t0, te D(x)
(иначе, вопреки предыдущему, v(x(t)) > α), а значит, и условию2
x(t) е £/ε(0), t е R+, (166)
чем и завершается доказательство леммы 145. ■
II. Признак не асимптотической устойчивости. Если в
лемме об устойчивости производная функции Ляпунова в силу
системы окажется в точности равной нулю (а не только меньше
или равной), то нулевое решение будет не просто устойчивым,
а устойчивым не асимптотически, и даже более того, ни одно
возмущенное решение не будет стремиться к нулю при t —> оо.
Следствие 146. Если в формулировке леммы 145 выполнено
еще более сильное условие3
2) vt(x) = О,
то устойчивость нулевого решения системы (163) не является
асимптотической.
► Действительно, если бы какое-то решение x(t) с ненулевым
начальным значением х(£о) стремилось к нулю при t —> оо, то, в
силу условия v(x(t)) = const, оказалась бы справедливой
противоречивая цепочка
О < v(x(t0)) = lim v(x(t)) = ν (lim x(t)) = v(0) = 0
(в силу непрерывности функции ν в нуле). ■
1Но не предполагается (по крайней мере, пока) включение D(x) D М+.
2Решение χ определено при всех t G М+, поскольку его график выходит
на границу (в силу теоремы 23) любого компакта
[ίο;ίι] Χί7ε(0)
в некоторый момент Τ > ίο, а именно Τ = ti, откуда [ίο; *ι] С D(x).
3Взамен прежнего условия 2).
196
III. Устойчивость маятника без трения. Уравнение
колебаний нелинейного маятника без трения
у + a sin у = О, а > О,
записывается в виде системы
х = f(x) =( χ2 λ х=( ХЛ = ( У
J v ' у -asinxi J ' у Х2 ) \y
Функция Ляпунова1
v(x\,X2) = α(1 — cos χι) + -x\
в окрестности начала координат удовлетворяет соотношениям
Г=о, х = 0,
V(afbaf2)\>0, χφ^ Ν<2π,
v(a:i, а?2) = α sin #ι · #2 + #2 * (—β sin a?i) = О,
т.е. всем условиям не только леммы 145, но и следствия 146,
подтверждая тем самым факт устойчивости, но не
асимптотической, нижнего положения равновесия маятника при отсутствии
трения.
IV. Лемма об асимптотической устойчивости.
Следующая лемма Ляпунова гарантирует асимптотическую
устойчивость нулевого решения системы при наличии положительно
определенной функции Ляпунова, имеющей отрицательно
определенную (равномерно по t) производную в силу системы.
Лемма 147. Пусть для системы (163) существует
функция ν Ляпунова, удовлетворяющая при всех χ Ε U(0) и t Ε M+
условиям:
1) v{x) >0;
2) щ(х) < w(x) < 0 для некоторой функции w Ε С(£/(0)).
Тогда нулевое решение этой системы асимптотически
устойчиво.
1 Интеграл энергии (см. раздел II из п 7 9).
197
Рис. 26. Лемма об
асимптотической устойчивости
Доказательство леммы
происходит по следующему плану (рис. 26):
• если некоторая фазовая
кривая не приближается
асимптотически к началу координат, то вдоль
нее значения функции Ляпунова
(убывающие) отделены от нуля
снизу, а значит, фазовая кривая все
время лежит вне некоторой
окрестности нуля;
• вне последней окрестности
отделена от нуля, правда, уже сверху,
отрицательная производная в силу
системы функции Ляпунова, а с ней
и скорость убывания этой функции вдоль фазовой кривой, что
противоречит положительности самой функции.
<
► В условиях 1) и 2) настоящей леммы применима предыдущая
лемма 145, гарантирующая устойчивость нулевого решения и
существование таких окрестностей ί/ε(0),ί/δ(0), для которых:
• выполнено включение (164);
• любое возмущенное решение χ с начальным значением (165)
удовлетворяет условию (166).
1. Предположим, что хотя бы одно из указанных
возмущенных решений χ не удовлетворяет условию
lim |χ(ί)| =0.
t—юо
Тогда для этого решения:
• при некотором γ < ε справедлива оценка
(167)
lim |χ(ί)| >γ>0;
t—юо
• в силу непрерывности функции ν и ее положительности в
проколотой окрестности U(0) имеем неравенство
limv(x(i)) > _min υ (χ) = α > 0;
*->°° хеие(о)\иг(о)
• вследствие убывания функции v(x(t)) (см. лемму 144)
последний верхний предел является точным и
v(x{t)) > lim ν(χ(τ)) > α, te
τ—юо
198
поэтому
χ(ί) G Vх = {χ G Ζ7ε(0) Ι υ{χ) > α}, te R+.
2. Множество Vх: _
• есть компакт, как пересечение компакта ί/ε(0) с замкнутым
(вследствие непрерывности функции ν) прообразом г>_1([а;оо));
• не содержит точку χ = 0, так как г>(0) = 0 < а. Поэтому
vt(x(t)) < max w(x) = -β < 0, ί G R+,
x6Va
откуда по лемме 144 при достаточно большом t получаем
t
v(x(t)) < v{x{t0)) - ϊϋ)(χ{τ))άτ < v{x{t0)) - β(ί - t0) < О,
ίο
что невозможно, как и сделанное выше предположение о
невыполнении условия (167) (стало быть, это условие выполнено). ■
V*. Лемма о неустойчивости. В следующей лемме
Ляпунова, как и в двух предыдущих его леммах 145 и 147, функция
Ляпунова имеет знакопостоянную (здесь даже знакоопределен-
ную) производную в силу системы.
Сформулируем лемму о неустойчивости без доказательства,
поскольку вместо нее в доказательстве теормы 150 будет
использоваться теорема 149 (Четаева).
Лемма 148. Пусть для системы (163) существует
функция Ляпунова ν, удовлетворяющая условиям:
1) v(xj) > 0 для некоторой последовательности xj,
стремящейся к нулю при j —> оо;
2) щ{х) > w(x) > 0 при всехх G U(0) ut G Ш+ для некоторой
функции w G С(С/(0)).
Тогда нулевое решение этой системы неустойчиво.
VI*. Теорема Четаева. В отличие от функции Ляпунова из
леммы 148 функция, используемая в предлагаемой ниже
теореме, может быть определена не в полной окрестности нуля, а
лишь в замыкании некоторой области1 с нулем на границе.
Вне которой функция Четаева не обязана иметь положительную
производную в силу системы — и в этом главное ее преимущество перед функцией
Ляпунова.
199
Георема 149. Пусть для системы (163) существует
область1 V С Ш.п и функция Четаева
veCivOnc^V),
удовлетворяющие условию
0) 0 е dV, v{x)\xedvnu(0) = О,
а при всех χ Ε V Π ί/(0) it £ Ε R+ — условиям:
1) v(s) > 0;
2) щ{х) > w;(a;) > 0 длл некоторой функции w G C(V Π C/(0)).
Тогда нулевое решение этой системы неустойчиво.
Здесь неустойчивость нулевого решения вытекает из того
факта, что любая фазовая траектория, начинающаяся в области
V, удаляется от начала координат на почтительное расстояние.
Действительно, в противном случае:
• траектория не смогла бы покинуть некоторую компактную
часть этой области, отделенную от ее границы (так как в силу
возрастания функции Четаева вдоль этой траектории не смогла
бы выйти на ее границу и далее сильно приблизиться к ней);
• значит, скорость возрастания функции Четаева вдоль этой
траектории была бы отделена от нуля (положительной
константой), что противоречило бы ограниченности самой функции в
указанной области.
► Возьмем произвольное ε > 0, для которого выполнено
включение (164).
1. Предположим, что некоторое решение χ с начальным
значением
χ(*ο) е V (168)
удовлетворяет условию
x(t)€t/e(0), teR+. (169)
Тогда:
• множество
Г = {t e R+ | χ(ί) е dV}
На самом деле от множества V не требуется связности — достаточно
лишь его открытости (ведь тогда в нем можно выбрать компоненту
связности, примыкающую к точке 0, и объявить ее новой областью V).
200
пусто, так как иначе для числа t\ = inf T > to выполнялись бы
соотношения
me\dV, t = tlt
а в силу леммы 144 — и соотношения
, т, /> ν(χ(*ο)) ξ α > 0, ίο < ί < ίι,
υ(χ(ί))(=ο, * = *lf
противоречащие непрерывности последней функции;
• выполнены условия
x(to) G ^, χ(ί) 0 dV, te
из которых имеем
χ(ί) € V, ί G
• более того, с учетом условия (169) получаем
x(i) G Κα = {ζ G 7 П !7ε(0) | v(s) > α}, ί €
2. Компакт Κα не содержит точек χ G dV (в них v(a;) = 0 < α),
поэтому
vt{x(t)) > min ю(ж) = β > 0, t G R+,
откуда по лемме 144 получаем
v(x(t)) > v(x(to)) + β(ί - ίο), * € M+,
а значит, непрерывная на компакте Κα функция ν неограничена,
что неверно, как, следовательно, и предположение (169).
3. Таким образом, любое непродолжаемое решение с
начальным значением (168), среди которых можно выбирать сколь
угодно близкие к точке 0 (граничной для области V), не
удовлетворяет условию (169). Следовательно, нулевое решение
неустойчиво. ■
6.5. Система первого приближения
получается из исходной системы
x = Ax + F(t,x), F,F^GC(G), GdR+xU(0), (170)
201
при условиих
\\F(;x)\\R+=o(x), х^О, (171)
путем ее линеаризации, в результате которой остается система
χ = Ах, te R+. (172)
I. Линеаризация системы. Для приведения системы (163)
общего вида с нулевым решением к виду (170) с условием (171)
в качестве оператора A Ε EndRn при каждом фиксированном
t Ε Ш+ необходимо взять производную fx(t,0) ее правой части
f(t,x), а потому линеаризованная система (172) просто обязана
совпадать с системой (147) в вариациях по начальному значению
вдоль нулевого решения.
Оператор А в упомянутой системе в вариациях, как и
остаточный член F(t,x), могут оказаться зависящими от времени.
И здесь существенную роль играют два дополнительных
предположения:
• автономность2 системы первого приближения (заведомо
имеющая место в случае автономности исходной системы (163));
• равномерная малость остаточного члена на всей полуоси
времени.
JB случае ненулевого положения равновесия хо(·) = xq
линеаризацию системы (163) в точке хо можно совершить,
предварительно сдвинув в нее начало координат или сразу взяв
производную ее правой части в этой точке.
II. Формулировка теоремы Ляпунова. Следующая
теорема об исследовании устойчивости по первому приближению
кладет начало первому методу Ляпунова, позволяющему
делать заключение об асимптотической устойчивости или
неустойчивости нулевого решения системы по наличию того же3
свойства у соответствующей ей системы первого приближения.
Теорема 150. Если действительные части всех
собственных значений оператора А отрицательны, то нулевое решение
1 Обеспечивающем наличие нулевого решения и обычно обозначаемом
так F(t, χ) = о(х) при χ —> 0.
2А. М. Ляпунов рассматривал и неавтономные системы первого
приближения, правда, не любые, а лишь правильные, при этом роль собственных
значений играли так называемые показатели Ляпунова (см. π 6.7)
Но, так сказать, ярко выраженного (в случае вырожденной ситуации
теорема не дает ответа на вопрос об устойчивости)
202
системы (170) с условием (171) асимптотически устойчиво, а
если хотя бы одна из них положительна — то неустойчиво.
Доказательство сформулированной теоремы будет проведено
в п. 6.6.
III. Положения равновесия маятника. Исследуем на
устойчивость по первому приближению все положения
равновесия нелинейного уравнения свободных колебаний маятника
у 4- 2ру 4- q sin у = 0, ρ > 0, q > 0.
Каноническая замена приводит это уравнение к нелинейной
системе
Х2
J v ' \ — gsin^i — 2px2j '
линеаризация которой в точке хо = (πη, 0) (η G Ζ) дает систему
первого приближения
χ = f'(xo)x = ί _
с характеристическим многочленом1
L(X) = λ2 4- 2ρλ 4- q cos πη.
Для нижнего положения равновесия маятника, когда η четно
и cosnn = 1, теорема Ляпунова при наличии трения (р > 0)
гарантирует асимптотическую устойчивость, а при его отсутствии
(р = 0) — оставляет вопрос открытым (напомним, что в этом
последнем случае вопрос уже был решен ранее с помощью
функции Ляпунова; см. раздел III из п. 6.4).
Верхнее же положение равновесия, согласно теореме
Ляпунова, неустойчиво, причем независимо от трения2, так как здесь
η нечетно и cosnn = — 1, а значит, корни характеристического
многочлена заведомо действительны и имеют разные знаки.
1Который, впрочем, ищется и прямой линеаризацией исходного
уравнения, без перехода к системе.
2И даже от его знака. Таким образом, никакое трение, даже очень
сильное, не может обеспечить устойчивость верхнего положения равновесия.
203
6.6. Доказательство теоремы Ляпунова
разобьем на две части в полном соответствии с ее
формулировкой.
I. Признак устойчивости. Доказательство первой части
теоремы 150, дающей признак асимптотической устойчивости по
первому приближению, проведем путем комплексификации
исходной системы и перехода к такому базису, в котором система
линейного приближения близка к диагональной с собственными
числами на диагонали. В этом базисе в качестве функции
Ляпунова (из леммы 147) возьмем квадрат нормы вектора.
► Предположим, что действительные части всех собственных
значений λχ, ... ,λη оператора А отрицательны, и обозначим
а= min (-ReXi) = 3δ > 0.
ι=1, ,η
1. Комплексифицируем систему (170) с условием (171),
перейдя к системе
z = Az + F(t,z),
где A Ε EndCn — комплексификация оператора A Ε EndRn (см.
определение 4.2), а функция
F(i, ζ) = f (i, Re ζ) = o(Re ζ) = ο(ζ), ζ -> 0, (173)
определена в области
G = {(t,x + iy) I {t,x)eG, yeRn}DR+ xU(0),
U(0) = Щ0) + Шп С Cn,
причем ее сужение на область G совпадает с функцией F.
2. Выберем такой базис ei, ...,en в Сп, в котором матрица
оператора А имеет вид
А =
Αϊ δ2 ·
0 λ2 '
* ·
\0 0 ·
• 0\
·. о
■· к
·· К/
δ2, -.·,δη е {о,δ}.
204
Этот базис получается из жорданова базиса hi, ..., hn для
оператора А с помощью специального преобразования,
производимого по формулам1
е\ = δΛ-ι, β2 = δ /i2, ..., еп — bnhn.
(174)
3. Объявим базис ei, ...,en ортонормированным, задав тем
самым в Сп новую норму
= νζ*ζ, ζ =
от чего условие (173) не пострадает (см. лемму 12).
4. Для матриц
'2ReXi О
О 2ReX2
О
О
Л= Ι Ι, Δ =
О 0 ··· 2ReXn,
справедливы соотношения
Α + Α* = Λ + Δ, |Δ*| <
/о δ2
δ2 ο
\о ···
δ2^2
νηΖη
0
+
0
δη^η—Ι
< 2δ|ζ|
5. Возьмем действительнозначную функцию
= 0, 2 = 0,
> 0, 2^0,
υ(ζ) = \ζ\2 = ζ*ζ { "' ~ "' г G U(0),
0\
'η
··. δ
δη 0/
1Действительно, рели в жордановом базисе в матрице оператора А над
главной диагональю стояли числа Ъъ, .. ,δη € {0,1}, то при переходе к
новому базису они умножатся на δ, остальное в этой матрице сохранится:
Аег = АЪгкг = Ъг(Кгкг + btht-i) = Xiet +
(индукция по г, где ео = ho = 0, δο =0).
6i-l), Ι = 1,
,η
205
тогда при (t, ζ) Ε G и \z\ < г для ее производной1 имеем
vt(z) = {z*z)t = z*(Az+F{t,z)) + (Az + F{t,z))*z <
< z*Az + \z*Az + z*F(t,z) + F*(t, z)z\ <
η
<^2KeXi\zi\2 + \z*bz\ + \z*F{t,z)+F*{t,z)z\ <
i=l
< (-2α + 2δ + o(l)) \z\2 < -ol\z\2 = w(z),
как только о(1) < δ = a/3, что достигается малостью2 параметра
г >0.
6. Если теперь к исходной системе (170) с функцией
Ляпунова, равной сужению функции ν на область С/г(0), применить
лемму 147 (см. также п. 4 леммы 139), то получится, что нулевое
решение асимптотически устойчиво. ■
II*. Признак неустойчивости. В доказательстве той части
теоремы 150, которая дает признак неустойчивости по первому
приближению, будет использована функция Четаева, а не
Ляпунова.
► Пусть действительная часть хотя бы одного из собственных
значений λχ, ..., λη оператора А положительна. Без ограничения
общности считаем, что
ReXi > · · · > ReXm = 2a > 0 > ReXm+i > · · · > ReXn, δ ξ α/3.
»,
1. Комплексифицируем систему (170), затем выберем в Сп
базис ei, ..., еп и норму в соответствии с пп. 1 — 3 доказательства
признака устойчивости настоящей теоремы (см. раздел I
настоящего п. 6.6).
2. К матрицам Λ и Δ, введенным в п. 4 доказательства
признака устойчивости, добавим матрицы Е' и Δ;, для которых
Е' = (Е™ _£° V ΕΆ + А*Е' = |А| + Δ;, ||Δ'|| < 2δ,
αΒ силу системы, причем производная bt(z) также действительнозначна
(как и сама функция v(z)), чем мы молчаливо пользуемся в приведенной
ниже цепочке оценок, считая некоторые слагаемые (например, z*Az) или их
суммы (например, z*Az + z*W(t, z) + F*(i, z)z) действительными.
Без ограничения общности считаем также, что имеет место включение
С/г(0) С С/(0)
206
где Ет — единичная матрица порядка га, а |Л| — матрица,
составленная из модулей элементов матрицы Л.
3. Возьмем действительнозначную функцию и,
соответственно, область
т η
v(z) = ^2\Zi\2- Σ \zi\2 = z*E'z, V={zeCn\v(z)>0},
i=l i=m+l
тогда
mm η
2ΣΝ2>Σ№+ Σ № = №> zeY>
г=1 г=1 г=т+1
поэтому при (£, z) EG, z Ε V и \z\ < г имеем
vt{z) = (z*E'z)t = z*E'(Az + F(t,z)) + (Az+ F{t,z))*E'z =
= z*\A\z + (z*A'z + 2*£'F(*,z) + F*(t,г)£';г) >
η
> ^2|ReXi| |^|2 - \z*A'z\ - \z*E'F(t,z)+F*(t,z)E'z\ >
i=l
m
> 4α Σ Ы2 ~ ЩА2 ~ o(\z\2) >
> (2a - 2δ - o(l)) \z\2 > ol\z\2 = w(z),
как только о(1) < δ = a/3, что достигается малостью1 числа
г >0.
4. Сечение исходным действительным пространством Rn
области V открыто и не пусто, так как она содержит, например,
векторы βι,βι, а с ними и действительный вектор е\ 4-ei, а
также натянутый на него луч. Содержащая этот луч компонента
связности сечения имеет точку 0 на границе.
Пересечение этой компоненты с окрестностью £/г(0) примем
за область V, а оужение функции ν на эту область — за функцию
Четаева. После этого применим к исходной системе (170)
теорему 149 (и п. 1 леммы 139), согласно которой нулевое решение
окажется неустойчивым. ■
1 Считаем также, что С/г(0) С С/(0)
207
6.7. Показатели Ляпунова
служат вспомогательным инструментом при исследовании
устойчивости первым методом Ляпунова.
Определение 6.4. Показатель Ляпунова вектор-функции
χ: Ш+ —¥ Ш.п определяется формулой
χ(χ) = lim -1η|χ(ί)| (In0 = -оо).
t—too t
I*. Свойства показателей. Если показатель Ляпунова
функции χ конечен, то он совпадает с точной нижней гранью
значений λ, осуществляющих оценку
|χ(ί)Ι < eXi> * ^ τ· (175)
Лемма 151. Для любых вектор-функций х, у справедливы
утверждения:
1) для каждого λ > χ (χ) при некотором Τ Ε R+ выполнена
оценка1 (175), которая, наоборот, не выполнена ни для какого
λ < χ (χ) ни при каком Т;
2) если у = Lx, где L e AutRn, mo x(y) = χ(χ);
3) х(Сх) = χ(χ), С φ 0;
4) Х(* + У) < шах{х(х),х(у)}.
► 1. Первое утверждение настоящей леммы — это
непосредственная расшифровка определения показателя Ляпунова χ(χ)
вектор-функции х.
2. Докажем второе утверждение: если L Ε AutRn и у = Lx,
то
X(y)=Thn"iln|Lx(i)|<
ί—юо Τ
< lim-ln||L||+lim-ln|x(i)|=X(x)
t—>oot t—Hxt
и, аналогично, χ(χ) = x(L_1y) < x(y), откуда х(у) = χ(χ).
3. Третье утверждение вытекает из второго при L = СХ.
4. Чтобы доказать последнее утверждение настоящей леммы,
установим (и этого будет достаточно), что для любых λ < μ
справедлива импликация
аКоторую обычно записывают в форме |x(i)| < Cext, t G М+, для
некоторой константы С.
208
λ > max{X(x), x(y)} =» μ > χ(χ + у). (176)
самом деле, с помощью первого утверждения настоящей
леммы получаем: если предпосылка импликации (176) верна, то при
достаточно больших t выполнены оценки
|х(<)| < е", |у(«)| < еи,
а при еще больших t — оценка
|x(i) +у(*)| < |x(i)l + |у(*)| < 2ext = -^щ ■ ё* < е"1,
а с ней — и заключение импликации (176). ■
II*. Показатели линейной системы. Рассмотрим
линейную однородную систему с непрерывными ограниченными
коэффициентами
x = A(t)x, zeRn, teR+, AeC(R+), \\А\\Л+ < a. (177)
Лемма 152. Показатель Ляпунова любого ненулевого
решения χ G Sa системы (177) по модулю не превосходит числа а.
► Используя выполненную для любого t Ε Ш+ оценку
|χ(τ)| = |Λ(τ)χ(τ)| < ο · |χ(τ)|, ί0 < τ < ί,
по лемме 26 о дифференциальном неравенстве имеем
|х(«)| < |χ(ίο)|βα(ί-ίο), |χ(ί0)| < Ht)\ea{t~t0\
откуда получаем оценку
1ηχ(ίο)|+ο(ί-ί0)
ν(χ) = lim - In |x(£)| < lim — = a
t—юо t i—юо t
и, аналогично, χ(χ) > —α. ■
Благодаря следующей теореме1 можно определить набор
показателей Ляпунова системы (177)
1 Опирающейся на два последних утверждения леммы 151, которые
вместе с утверждением
χ(χ) = оо ■«=*> χ = О, χ Ε Sa,
означают, что показатель χ (точнее, —χ) на линейном пространстве Sa
задает так называемое неархимедово (логарифмическое) нормирование
209
λι(Α)<...<λη(Α), (178);'
состоящий ровно из η чисел. '
Теорема 153. Для системы (177) существует такой набор
чисел (178), а в пространстве Sa ее решений — такой флаг
подпространств
Lo С L\ С · · · С Ln, dim Li = г, г = 0,1, ..., η,
-что выполнены равенства
χ(χ) = λΐ(Α), χ е Li\Li-u г = 1, ...,п.
► Каждому значению aGRU{-oo} функции
χ: £л ->MU{-oo} (χ(χ) = -οο <ί=Φ χ = 0) (179)
поставим в соответствие прообраз замкнутого луча [—оо, оф
• множество Х_1[—оо, а] есть подпространство линейного
пространства Sa, поскольку для любых С\,Съ Ε Μ и х,у Ε Sa по
лемме 151 имеем: если х(*)»х(у) < а> то
X(Cix + C2y) < max{x(Cix),x(C2y)} < max{x(x),x(y)} < а;
• если αχ < ot2, то
dim (χ-1 [-οο, αϊ]) < dim (χ-Χ[—οο, ot2]) ,
поэтому функция (179) принимает не более η различных
конечных значений;
• прообразы всех различных значений функции (179)
составляют систему вложенных подпространств, которая
произвольным образом дополняется до искомого флага. ■
С помощью описанной в теореме 153 общей структуры
отображения (179) можно вывести
Следствие 154- Показатели Ляпунова (178) системы (177)
задаются формулами1
λί(Α) = inf supx(x), г = 1, ...,η,
где Q\ — мнооюество всех г-мерных подпространств
пространства Sa-
В. М. Миллионщикова (сам Α. Μ Ляпунов определял показатели
системы описательно, через нормальные фундаментальные системы ее решений)
210
ι Следствие 155. Показатели Ляпунова (178) линейной
автономной системы (172) совпадают с действительными
частями собственных значений ее оператора А, упорядоченными
по нестрогому возрастанию.
► Для доказательства достаточно заметить, что по теореме 99
(с учетом определения 4.4) существует базис1 в Rn, в котором:
• каждому действительному собственному значению λ
оператора А кратности к соответствует fc-мерное подпространство
решений со своим набором только к возможных ненулевых
координат, каждая из которых есть квазимногочлен q Ε Qx,fc> причем
если q φ 0, то для некоторого ненулевого многочлена ρ имеем
χ(,) = ~ш\ In |extp(i)| = λ + -Έ^Ά = χ.
ί—»οο t t—юо ι
• каждой паре комплексно-сопряженных собственных
значений α ± гр оператора А суммарной кратности 2к соответствует
2/г-мерное подпространство действительных решений со своим
набором только 2к возможных ненулевых координат, каждая из
которых есть квазимногочлен q Ε Qa±ip,fc5 причем если q φ 0, то
для некоторой ненулевой пары многочленов ρι,ρ2 имеем
X(q) = lim - In |eai (pi(t) cos fit + p2{t) sinfit) \ = a;
• пространство Sa раскладывается по указанным
подпространствам в прямую сумму, причем если в соответствии с
этим разложением какое-то решение представлено в виде суммы
функций, то его показатель равен наибольшему из их
показателей (в силу третьего утверждения леммы 151 и того факта, что
показатель вектор-функции не может быть меньше показателя
какой-либо ее координаты). и
III*. Связь показателей Ляпунова с устойчивостью.
Если наибольший из показателей (178) линейной системы
отличен от нуля, то ее устойчивость эквивалентна его
отрицательности, как показывает
Теорема 156. Система (177):
• в случае λη(Α) < 0 — асимптотически устойчива',
• в случае λη(Α) > 0 — не устойчива,
От выбора которого, по лемме 151, показатели Ляпунова не зависят.
211
• в случае λη(Α) = О — может оказаться как устойчивой
(даже асимптотически), так и неустойчивой.
► 1. В первом случае выберем отрицательное λ, осуществляющее
для любого χ С Sa оценку
λ > λη(Α) > χ(χ),
а с ней, согласно лемме 151, — и оценку (175), из которой по
лемме 140 вытекает асимптотическая устойчивость системы (177).
2. Во втором случае выберем положительное λ,
осуществляющее для некоторого χ с Sa оценку
λ < λη(Α) = χ(χ),
из которой по лемме 151 вытекает неограниченность решения х,
а по лемме 140 — неустойчивость системы (177).
3. В третьем случае уже при η = 1 возможны разные
ситуации: так, единственный показатель Ляпунова линейного
уравнения (
х = - · χ <=^ χ = Ct°, С еШ,
Is
при любом σ Ε R равен
χ(ί°) = σ lim — = 0,
AV ; ί-юо t
тогда как при σ = — 1 уравнение асимптотически устойчиво, при
σ = 0 — устойчиво, но не асимптотически, а при σ = 1 —
неустойчиво. ■
IV*. Условная устойчивость. С ней наиболее тесно
связаны показатели системы, отличные от старшего.
Определение 6.5. Скажем, что для заданного г Ε {1, ..., п}
линейная система (177) условно устойчива по г координатам,
если для любого ε > 0 существует такое δ > 0 и такое г-мерное
подпространство1 L С Sa, что любое решение χ G L
удовлетворяет импликации (157), где хо = 0.
Из данного определения и теорем 153, 156 вытекает
Следствие 157, Для любого г Ε {Ι, ...,η} система (177)
в случае \{(А) < 0 условно устойчива по г координатам, а в
случае Хг(Л) > 0 — не является таковой.
В нелинейном случае — многообразие, содержащее точку хо
212
Задачи для самостоятельного решения
1. Докажите, что если G D Ш+ х С/(0) и /, f'x € C(G), то в
определении 6.1 устойчивости по Ляпунову решения системы (156) можно
опустить требование определенности на R+ непродолжаемого
возмущенного решения, заменив условие t € Ш+ С -D(x) в импликации (157)
более слабым условием t G Ш+ Π D(x).
2. Может ли случиться, что разные решения одной и той же
системы (156) ведут себя при t —> оо по-разному:
• одни — устойчивы (не асимптотически) по Ляпунову,
• другие — асимптотически устойчивы,
• третьи — неустойчивы?
3. Пусть системы (156) с правой частью / € CX(G) имеет нулевое
решение. Верно ли, что:
• если все ее решения стремятся к нулю при t —> оо, то нулевое
решение устойчиво по Ляпунову (асимптотически устойчиво);
• если все ее решения возрастают по модулю при t > to, то нулевое
решение неустойчиво?
Рассмотрите отдельно случай η = 1.
4. Найдите аналогичное сформулированному в теореме 142
необходимое и достаточное условие устойчивости (асимптотической) для
линейного уравнения с постоянными коэффициентами.
5. Докажите, что линейное уравнение
у + ay + by = 0
второго порядка с постоянными коэффициентами асимптотически
устойчиво тогда и только тогда, когда a, b > 0.
6. Докажите, что для устойчивости уравнения
У + г(«)у = 0, i€R+,
с непрерывным ограниченным коэффициентом г достаточно, чтобы
все его решения (лишь сами решения, без производных) были
ограничены на R+.
7. Докажите лемму 148 (лемму Ляпунова о неустойчивости).
8. Останется ли справедливым утверждение леммы 147 или,
соответственно, теоремы 149, если условие 2) заменить более простым
(не содержащим функции w) условием щ(х) < 0 или, соответственно,
щ{х) > 0 в случае/когда система (163):
• автономна,
• неавтономна?
9. Можно ли, постоянно увеличивая (уменьшая) длину
маятника без трения, обеспечить асимптотическую устойчивость
(неустойчивость) его нижнего положения равновесия?
213
10. Докажите, что если все диагонали матрицы некоторого
оператора, параллельные главной диагонали (их всего 2п + 1), в некотором
базисе h\, ..., hn занумерованы подряд снизу вверх целыми числами
г = —п, ..., 0, . ., η (например, главная диагональ имеет номер 0), то
при переходе к новому базису ei, .. , еп (174) каждый элемент г-й
диагонали этой матрицы умножается на δ*.
11. Докажите, что факт устойчивости, асимптотической
устойчивости или неустойчивости нулевого решения системы (156) не
нарушится, если перейти к новому базису в Шп ляпуновским
преобразованием координат у = L(t)x (определение 4.3).
12. Существует ли какая-либо логическая связь между
асимптотической устойчивостью линейной однородной системы (177) и
отрицательностью действительных частей всех собственных значений ее
матрицы A(t) при всех t € R+?
13. Докажите, что для любого решения х. £ Sa системы (177)
справедливо неравенство Важевского
Г λ(τ)ίίτ Γ Λ(τ)ίίτ
|χ(ίο)|βΛ° ^ |χ(01 < |x(io)|eJ*o , t0,t e ш+.
где Λ(τ),λ(τ) — наибольшее и наименьшее собственные значения
оператора 2 им+А* м)·
14. Докажите, что показатели Ляпунова вектор-функций обладают
следующим свойством, если χ(χ) < х(у), то χ(χ + у) = х(у).
15. Докажите, что показатели Ляпунова (178) любой системы (177)
удовлетворяют неравенству Ляпунова
t
λι (А) + ... + λη(Α) > lim - tr Α(τ) άτ.
t-*oc t J
to
Глава 7
АВТОНОМНЫЕ СИСТЕМЫ
7.1. Фазовое пространство
автономной1 системы
χ = f(x), xeGcRn, (180)
есть область G. Множество всех непродолжаемых решений этой
системы будем обозначать через S/(G)
I*. Превращение системы в автономную. Из любой
неавтономной системы
х = f(t,x)
можно стандартным образом получить автономную, расширив
ее фазовое пространство за счет временной переменной:
(если последнее дополнительное ограничение на переменную xq
убрать, то исходное время из новой автономной системы
будет восстанавливаться лишь с точностью до аддитивной
постоянной и добавятся лишние решения, получаемые из прежних
времнными сдвигами).
II. Интегральные и фазовые кривые. Фазовая
траектория решения χ — это параметрически заданное множество2
Е(х) = {χ(ί) | t e D(x)} С G.
1Τ е. с we зависящей от времени правой частью
2Так называемый годограф решения, который, пользуясь вольностью
речи, можно даже отождествлять с самим решением.
215
Рис. 27. Фазовая
кривая
Оно получается проектированием
интегральной кривой (графика решения)
Гх = {(ί,χ(ί)) | t G D(x)} С R х G
на фазовое пространство.
Собственно множество значений Е(х)
решения х, отвлеченное от его временной
параметризации, называется фазовой
кривой этого решения, а совокупность всех фазовых траекторий или
кривых системы — ее фазовым портретом.
III. Фазовая скорость и ее направление. Задать
автономную систему (180) — это то же самое, что задать на ее
фазовом пространстве векторное поле
/:G->Rn, (181)
т. е. каждой точке χ Ε G поставить в соответствие вектор
/(*) =7(x(t)) = χ(<) = ^
геометрический смысл которого, по определению решения, есть
мгновенная фазовая скорость x(t) некоторого1 решения х(·),
взятая в тот момент t, когда x(t) = χ (рис. 27).
Таким образом, для любой фазовой кривой Г системы (180)
в каждой точке χ Ε Г вектор f(x) является касательным к этой
кривой. Этот факт обычно выражают словами: фазовая кривая
Г касается векторного поля /.
Возможен и менее информативный вариант2 изображения
зависимости переменной χ от параметра t вдоль фазовой
траектории — в виде одной лишь стрелки на ней, показывающей
направление движения по траектории с ростом времени.
7.2. Фазовый поток
рассматривается при дополнительном предположении
(действующем в пп.3 7.2 и 7.3), что каждое решение χ G Sf(G) системы
(180) определено на всей числовой оси.
:На самом деле, любого, что как раз и доказывает приведенная выкладка.
По сравнению с вектором фазовой скорости
3Впрочем, леммы 158, 159 и теорема 162 (вместе с определением 7 2)
допускают формулировки и без этого предположения.
216
I. Сдвиги фазовых траекторий. Так как фазовая скорость
решения автономной системы зависит только от значения χ его
фазы (но не от момента t прохождения траектории через точку
ж), то временная параметризация фазовой траектории задается,
по меньшей мере, с точностью до аддитивной постоянной, что и
утверждает
Лемма 158. Для любого решения χ системы (180) и для
любой константы С Ε Μ функция
xc{t) = x{t + С), t e R,
есть таксисе решение этой системы.
► Если χ G Sf(G), то
а значит, хс £ Sf(G). ■
II. Непересекаемость фазовых кривых. При
непрерывности правой части автономной системы через каждую точку ее
фазового пространства проходит1 хотя бы одна фазовая кривая,
а при непрерывной дифференцируемое™ — даже ровно одна,
как показывает следующая
Лемма 159. Если f Ε CX(G) и фазовые кривые решений
х, у Ε Sf(G) имеют общую точку
х(*о) = у(*о), (182)
то эти фазовые траектории с точностью до сдвига времени
совпадают:
x(£ + £0)=y(£ + So), teR. (183)
► Если х,у — решения, то по лемме 158 функции х^0 и ySo —
тоже решения, а из совпадения (182) их начальных значений в
момент t = 0 и теоремы 16 следует их полное совпадение (183).■
III. Динамическая система и фазовый поток. С
системой (180) можно связать отображение Коши J7, зависящее от
переменных t, x и определяемое формулой2
J*(x(0))=x(t), xeSf(G), teR. (184)
Причем в любой момент времени (см теорему 17).
2Ср. с формулой (75) для оператора Коши.
217
Однако можно на некоторое время забыть о происхождении
отображения (184), что собственно и делает
Определение 7.1. Пусть на топологическом пространстве G
задано семейство отображений
P.G^G, teR. (185)
Назовем семейство Т\
• динамической системой1, если выполнены три условия:
1) 7го = 1 — тождественность на G начального отображения;
2) ^+1" = J71 о .р8, t, s Ε Μ, — аддитивность по времени;
3) Τ Ε C(R x G) — непрерывность функции Т по паре (t,x);
• фазовым потоком, если динамическая система Τ
удовлетворяет, сверх того, условиям2
Р,{Р) eC\G), teR, и GcRn; (186)
• каскадом, если параметр t в семействе (185) с самого начала
ограничен лишь целыми значениями3.
Орбитой точки χ Ε G называется траектория или кривая
Т{х) = {Т\х) 11 e R (Z)}.
Заметим, что в определении 7.1 каждое из отображений Т*".
• обратимо, так как в силу условий 1) и 2) имеем
J* о Т~1 = Т1~1 = 7ю = X;
• в случае фазового потока — есть диффеоморфизм
пространства G, так как оба отображения Т1 и (^Γί)_1 = Τ~ι непрерывно
дифференцируемы по х.
IV*. Генератор фазового потока. Как видно из
следующей леммы, автономная система (или ее векторное поле)
порождает фазовый поток, т. е. является его генератором.
Лемма 160.Если f G C^G), то отображение Коти (184)
задает на множестве G фазовый поток Τ.
Непрерывным действием однопараметрической группы преобразований.
2Требования гладкости в определении фазового потока могут
варьироваться, но всегда G есть топологическое подпространство пространства Шп
с евклидовой топологией
3Возможно даже только натуральными — в этом случае отображения JF*
могут оказаться и необратимыми
218
■Λ*ι)=(^)'(*ό)Λ*ΰ)
Рис 28. Касательное отображение
► Формула (184) действительно задает отображение G —ν G, так
как через каждую точку χ Ε G в момент to = О проходит ровно
одно решение χ Ε Sf(G) (см. теорему 9).
Проверим выполнение всех условий определения 7.1:
1) для каждого решения χ имеем 7го (х(0)) = х(0);
2) для любых £, s Ε Μ и любого решения χ имеем (см.
лемму 159)
(J* сГ)(х(0)) = J*(x(s)) = ^(xs(0)) = xs(t) =
= x(i + s) = J-i+s(x(0));
3) отображение J-^ix) совпадает с отображением х(£,ж) из
следствий 126 и 129 (с начальным моментом to = 0), а значит,
оно не только непрерывно по паре своих переменных, но и
удовлетворяет условиям (186). ■
Оказывается, фазовый поток можно смело отождествлять с
его генератором, что, в частности, и подтверждает
Лемма 161. У любого фазового потока Τ (185) существует
единственный генератор
/ = (Т')и=0еС\С), (187)
который к тому же удовлетворяет равенству1
(J*)'of = foJ*, teR. (188)
► 1. Единственность и существование генератора вытекает,
соответственно, из следующих двух фактов.
аТ. е. как бы коммутирует с потоком. Здесь диффеоморфизм IF* . G -* G
отображает окрестность точки хо в окрестность точки ^(хо) = χι, а его
производная {JF*)' (по фазовой переменной) отображает касательное (к G)
пространство ТХо в касательное же пространство Тх, (рис. 28).
219
• Векторное поле /, порождающее фазовый поток Т,
определяется им однозначно как поле фазовых скоростей:
/(*) = (J*(x)) |ί=0 = (7*) |(=0(х), χ € G.
• Векторное поле /, задаваемое по фазовому потоку Τ
формулой (187), реально служит его генератором. Действительно,
для любой фиксированной точки χ G G функция J^ix)
совпадает с решением1 x(t,x) G S/(G), поскольку фазовая скорость
потока Τ в любой точке J^ix) совпадает со значением поля / в
той же точке:
2. Если же предыдущую строку дополнить цепочкой
ds
s=0
s-0 ds
то получится равенство (188). ■
V*. Генератор экспоненты. Генератором фазового потока
Т\х) = eAtx, xeRn, t G R,
где A G EndRn, служит векторное поле
№ = (^) |м(*) = (А) 1*=о = Ах.
7.3. Три типа фазовых кривых
а именно, незамкнутая кривая, цикл и неподвижная точка —
только они выделяются в качестве возможных типов фазовых
кривых автономной системы.
I. Точные определения. Пусть фиксировано решение
χ G Sf(G) автономной системы (180).
Определение 7.2. Фазовую кривую (траекторию) Е(х)
назовем (рис. 29):
• незамкнутой, если
x(* + s)^x(i), £gR, s>0;
αΒ силу его единственности.
220
• замкнутой, или циклом, если
для некоторого числа Τ > О,
называемого периодом цикла,
выполнено условие
x(i + s)
= x{t), ί G R, s = Τ;
φ x(t), teR, 0 < s < Τ;
• неподвижной точкой, или
точкой покоя, если
χ(ί) = so, * G
Незамкнутая
кривая
Рис. 29. Различные типы
фазовых кривых
Согласно этому определению, свойство незамкнутости
фазовой траектории, пусть даже и не являющейся точкой покоя, не
совпадает с формальным логическим отрицанием свойства ее
замкнутости.
II. Отсутствие других типов. Несмотря на то что можно
представить себе какие-либо еще типы фазовых кривых,
отличные от перечисленных в определении 7.2, в действительности же
их нет1, о чем и говорит
Теорема 162. Если f Ε C^G), то фазовая траектория
любого решения χ G Sf(G) может быть только одного из трех
типов, перечисленных в определении 7.2.
► 1. Пусть фазовая траектория Е(х) не является незамкнутой.
Тогда множество <S таких чисел s > О, каждое из которых хотя
бы для одного t G R удовлетворяет равенству x(t + s) = x(t), не
пусто.
2. Обозначим через Τ множество всех периодов (всех вообще,
включая отрицательные и нулевой) функции χ и заметим, что:
• Τ D S, так как если Τ Ε <S, то для некоторого t G Μ
выполнено условие x(t 4- Τ) = x(t), откуда по лемме 159 имеем
χ((τ + t) + Τ) = χ(τ + (t + Τ)) = χ(τ + t), τ G R,
а значит, Τ — период функции х;
• Τ D (J mS, поскольку если Τ G Τ, то πιΤ G Τ при πι G Ζ;
1Πο крайней мере, при условии непрерывной дифференцируемое™
векторного поля.
221
• Τ D Τ, т.е. если множество Τ содержит сходящуюся
последовательность Т^ —>· Τ (к —> оо), то Τ G Τ, так как
х(£ 4- Г) = lim x{t 4- Tfc) = lim χ(ί) = χ(ί), ί G R.
fc—юо fc—юо
3. Возможны два варианта:
• либо
inf<S = T>0,
тогда траектория Е(х) замкнута, поскольку Τ G Τ и для любого
s G (0; Т) имеет место условие s ^ «S;
• либо, наоборот,
inf<S = 0,
тогда множество Τ всюду плотно на прямой R (действительно,
для любых t G Μ и ε > 0 существуют такие s G (0; ε) C\S и m G Ζ,
что |ί — ms\ < ε и ms G T), поэтому
Г = Г = R ==> χ(ί) = χ(0), ί G R,
следовательно, траектория J5(x) — неподвижная точка. ■
III. Точки покоя. Особой точкой векторного поля f (181)
называется любая точка х$ G G, в которой f(xo) = 0.
Точка покоя xq G G:
• геометрически всегда совпадает с особой точкой векторного
поля, так как для соответствующего этой траектории решения
χ имеем
χ(ί) = χ0, iGR,4=>0 = /Or0);
• в случае непрерывной дифференцируемости векторного
поля служит единственной проходящей через нее фазовой кривой
(лемма 159);
• является, по определению, устойчивой (асимптотически),
если устойчиво (асимптотически) соответствующее ей решение,
называемое положением равновесия.
IV*. Период цикла. По определению 7.2 цикл есть Т-пе-
риодичная несамопересекающаяся фазовая траектория. Однако
если ту же траекторию рассматривать, например, как 2Т-пери-
одичную (каковой она также является), то она уже перестанет
быть несамопересекающейся.
Корректность определения 7.2 в части понятия периода
цикла подтверждает
222
Следствие 163. Период фиксированного цикла Г = Е(х)
поля f G C*(G) является наименьшим положительным периодом
задающего его решения χ Ε Sf(G) и не зависит от выбора
последнего.
► Действительно, если цикл Г имеет период Т, то:
• в силу теоремы 162, функция χ — Т-периодична, причем
в точности (т.е. положительного периода, меньшего Т, у нее
нет);
• если цикл Г есть еще и фазовая кривая Е(у) другого
решения у, то функция у отличается от χ временным сдвигом, а
значит, тоже в точности Т-периодична. ■
7.4. Выпрямление фазовых траекторий
оказывается осуществимым вблизи любой неособой точки
векторного поля.
I. Выпрямляющий диффеоморфизм. Пусть
фиксирована неособая точка xq ε G С Мп векторного поля (181). Тогда
локальное (вблизи хо) выпрямление фазовых траекторий
автономной системы (180) или, что то же, выпрямление самого
векторного поля (181) происходит под действием диффеоморфизма
y:U(x0)->V, (189)
переводящего некоторую окрестность U{xq) С G этой точки в
некоторую область КсЕп.
При отображении φ (189) фазовая траектория Е(х) С U(xq)
любого решения χ переходит в траекторию
Е(у) = {y(i) = φ(χ(ί)) I t e D(x)}.
Определение 7.З. Если диффеоморфизм φ (189) переводит
все фазовые траектории векторного поля (181), суженного на
окрестность U(xo), в фазовые траектории системы
/0\
У = еп =
0
\1/
(190)
то он называется выпрямляющим (вблизи хо, рис. 30).
223
χ1, ,η-1
U{x0)
Ы)п
2/1, ,η-ι
φ
ку У
§η
у, ·
(Vo)n
Рис. 30. Выпрямляющий диффеоморфизм
уп
Заметим, что вблизи особой точки выпрямление поля
невозможно в принципе, так как при любом диффеоморфизме
неподвижная точка переходит в неподвижную.
II. Локальное выпрямление векторного поля. Все
векторные поля (равно как и соответствующие им фазовые
портреты) в окрестности своих неособых точек выглядят с точностью
до диффеоморфизма одинаково, как показывает следующая1
Теорема 164.. Если xq £ G — неособая точка векторного
поля f £ C^G), то существует выпрямляющий диффеоморфизм
некоторой ее окрестности U{xq) С G, оставляющий на месте
эту точку, а при условии fn(xo) Φ 0 — еще и все точки
гиперплощадки S С U(xo), задаваемой равенством2 хп = (хо)п.
и
Выпрямляющий диффеоморфизм получается как
отображение, обратное к получающемуся в результате последовательного
выполнения следующих двух действий (см. рис. 30):
• ортогональное проектирование π точки у на площадку S,
при котором точка у смещается на некоторое расстояние;
• применение к полученной проекции ку отображения Коши
за время, равное упомянутому расстоянию.
► На время доказательства, для простоты, сдвинем и
перенумеруем координаты3 точек χ так, чтобы выполнялись
дополнительные условия:
1 Подобная теореме 130.
23десь хп — п-я координата точки х, а под гиперплощадкой мы понимаем
область из некоторой гиперплоскости (размерности η — 1, с топологией,
индуцированной пространством Мп).
3Сохранив для всех объектов теоремы прежние обозначения.
224
. xq = 0 и S = {χ Ε U{0) I xn = 0};
• /n(0) φ 0 (напомним, что f(xo) Φ 0).
1. Обозначив
?/о = 0, т:у = (yi, ...,2/n_i,0),
рассмотрим отображение (где J7 — отображение Коши (184),
определяемое полем /)
хЫ = -Я/тг(7ч/) = х(?/п,7и/)
(см. следствие 126 при начальном моменте to = 0), определенное
на множестве всех точек у Ε Rn, удовлетворяющих условию1
ку, χ (у) Ε G. Заметим, что функция χ:
• оставляет все точки у Ε 5 и, в частности, точку уо == #о на
месте, так как
Х(У)=^°(У) = У (Уп = 0);
• непрерывно дифференцируема (см. следствие 129), причем
ее производная2 χ'(0) невырождена, так как имеет компоненты3
x*u i(^(o));jyn=o=/(o).
г = п,
причем /η(0) φ 0.
2. По теореме об обратной функции отображение χ можно
сузить (сохранив для него прежнее обозначение) на достаточно
малую окрестность V точки 0, получив диффеоморфизм
χ·.ν->υ(ο).
Более того, окрестность V можно считать прямоугольной, т.е.
представимой для некоторых окрестностей 5(0) С 5 и /(0) С R
точек 0 Ε 5 и 0 Ε Μ соответственно в виде
V = {у Ε Rn I Tty E 5(0), 2ME/(0)}.
1 Обеспечивающему, кстати, открытость этого множества
2См. доказательство леммы 161, правомерное и без предположения о
продолженное™ решений на всю числовую ось
3Столбцы матрицы оператора χ'(0) в стандартном базисе.
225
3. Диффеоморфизм χ для каждой точки у G 5(0) переводит
проходящую1 через нее фазовую траекторию решения системы
(190)
y(t)=y + ten, ί€/(0),
в фазовую траекторию решения исходной системы (180)
x(i) = Х(уй) = Ρ (π(</ + ten)) = Р(у), t G /(0),
проходящую через ту же точку у, а значит, обратный
диффеоморфизм φ = χ-1 — наоборот. ■
Следствие 165. В условиях теоремы 164 образ V
окрестности U(xq) при выпрямляющем диффеоморфизме (189) можно
считать прямоугольным.
7.5. Первый интеграл автономной системы
(180) (или векторного поля (181)) — это такая скалярная
функция2 φ G Cl(G), что ее сужение на любую фазовую кривую этой
системы есть константа3, т.е. для любого решения χ G S/(G)
выполнено равенство
φ ίχ(ί) J = const, t e D(x).
I. Дифференциальный критерий. Чтобы выяснить,
является ли данная функция φ первым интегралом данного
векторного поля (181), вовсе не требуется решать систему (180) —
достаточно лишь уметь вычислять производную в силу этой
системы4
ф(я) = y'(x)f(x), xeG,
что и подтверждает
Лемма 166. Функция φ G Ol(G) является первым
интегралом векторного поля f G C(G) тогда и только тогда, когда
φ{χ) =0, χ G G. (191)
Равномерно и прямолинейно
2 Не зависящая от t
Вполне возможно (и далее как правило) для каждой кривой — своя.
43десь далее не зависящую от времени; ср с определениями 6.3 и 1 3
226
► Постоянство сложной функции φ ο χ для каждого решения
х G Sf(G) равносильно равенству (см. лемму 144)
о = |φ(χ(<)) = φ'(χ(ί))/(χ(ί)) = Φ(χ(ί)), 1e D(x), χ e Sf(G),
что, в свою очередь, равносильно равенству (191) (поскольку все
возможные значения χ = x(t) заполняют всю область G). ■
II. Автономная гамильтонова система. Одним из первых
интегралов гамильтоновой системы
заведомо является ее гамильтониан, т. е. сама скалярная
функция Η G C2(G). В самом деле, здесь применима лемма 166,
поскольку
Н(х,у) = Н'х(х, у)Н'у(х, у) + Н'у(х,у){-Н'х{х,у)) = 0, (ж, у) G G
(в обоих произведениях первые сомножители — вектор-строки,
а вторые — вектор-столбцы).
III*. Инвариантные множества. Пусть задана подобласть
G' С G. Определенную на ней функцию φ: G' —> R будем также
называть первым интегралом векторного поля /, если эта
функция является первым интегралом сужения /|g'·
Определение 7.4. Подмножество Ρ С G' называется
инвариантным (относительно векторного поля / в подобласти
G' С G), если вместе с каждой точкой χ G Ρ оно содержит всю
проходящую через нее фазовую кривую решения х(·, х) G Sf(G').
Простейшим примером инвариантного множества служит
сама фазовая кривая.
Лемма 167. Любое множество уровня любого первого
интеграла φ G Cl(G') инвариантно.
► Действительно, для любой константы С G Μ и любого первого
интеграла φ G С1 (С) множество уровня
P={xeG'\ φ) = С}
227
замечательно тем, что если жбРи x(-,#) G Sf(G'), то
φ(χ(ί, χ)) = φ(χ(0, χ)) = φ(ζ) = С, ί G D(x),
откуда Е(х(',х)) С Р. ■
IV. Первые интегралы в разных областях. Фазовыми
кривыми векторного поля
f(x) = x, xe R2,
служат лучи, выходящие (асимптотически) из начала координат
(рис. 31):
• в качестве первого интеграла этого векторного поля в
любой подобласти G С Ш2 заведомо годится любая функция
φ Ε CJ(G), принимающая вдоль каждого такого луча
постоянное значение;
• если такой луч пересекает подобласть С С Ш2
(невыпуклую) не по одному, а по нескольким интервалам, то на них
первый интеграл, вообще говоря, может принимать разные
значения и, тем самым, не быть константой на всем луче;
• если же подобласть G" С R2 выпукла и содержит точку О,
то для каждого такого луча Г должно быть выполнено равенство
Ф) = Ит срЫ = φ(0), хеГ,
ГЭу->0
J
поэтому любой первый интеграл φ в такой подобласти G" обязан
быть просто константой.
228
7.6. Независимые первые интегралы
в случае, когда их набирается достаточное количество, образуют
в множестве всех первых интегралов базис, но не в обычном, а
в функциональном смысле и к тому же лишь локально.
I. Независимость в точке и зависимость в области.
Речь пойдет о функциональной зависимости1 первых
интегралов.
Определение 7.5. Пусть первые интегралы φι, ..., φ&
системы (180) определены в некоторой подобласти G' С G:
• назовем их независимыми в точке хеС, если векторы
φί(*)> • ••,φίΟ*)
линейно независимы;
• скажем, что скалярная функция ψ зависит от них в
области G', если существует функция F e Cl(D), определенная в
некоторой области D С Шк и удовлетворяющая равенству2
ψ(χ) = ^(φι(χ), ...,cpfc0r)), xeG'. (192)
Лемма 168. Любая функция, зависящая в некоторой
области от первых интегралов системы (180), есть первый
интеграл этой системы.
► Для любых первых интегралов φι, ..., φ&: G' —> R, любого
решения χ G Sf(G') системы (180) и некоторых констант С\, ..., Ck
имеем
q>i(x(·)) =Ci, г = 1, ...,fc,
поэтому для любой функции FgC1 (D) получаем
^(φι(χ(·))> •••»<PfcM·))) =F(Ci, ...,Cfc) = const,
т.е. функция (192) — тоже первый интеграл (по определению).·
II. Универсальная система первых интегралов. В
достаточно малой окрестности любой неособой точки векторного
поля в множестве первых интегралов автономной системы
всегда можно выбрать набор из η — 1 независимых первых
интегралов. И это позволяет сделать
Линейная зависимость — ее частный случай.
2 Осмысленному при надлежащем выборе области D.
229
Теорема 169. Если xq G G — неособая точка поля f G
G C^G), то в некоторой ее окрестности U(xo) С G
существуют независимые в этой точке первые интегралы φι, ... , φη-ι
этого поля, от которых в подобласти U{xq) зависит любой
первый интеграл того же поля.
В качестве искомой полной системы первых интегралов
годятся, например, первые η — 1 координата выпрямляющего
диффеоморфизма (189), переводящего кривые системы (180) в
кривые системы (190).
► 1. Пусть функция φ — выпрямляющий диффеоморфизм,
существование которого утверждается в теореме 164 (с учетом
следствия 165). Тогда:
• координаты φι, ..., φη_ι вектор-функции φ G Cl{U{x$))
являются первыми интегралами системы (180), так как для любого
решения χ G Sf(U(xo)) функции
фг(х('))> г = 1, ...,п- 1,
постоянны, поскольку
(<РМ<))) = У(<) = е«, te D(x);
• эти первые интегралы независимы в точке хо, поскольку
векторы
φΊ(*ο), ...,φ'„_ι(*ο)
служат строками невырожденной матрицы q/(a;o).
2. Если ψ: U(xq) —> R — первый интеграл системы (180), то:
• функция _
ψ ξ ψ ο φ
есть первый интеграл системы (190), так как для любого ее
решения у ξ φ(χ) имеем
Ф(У(<)) = (Ψ ° Ф"1) (<РМ<))) = Ф(х(*)) = const, t G £>(y);
• для ортогональной проекции
^у = (г/ъ -чУп-ьМп)
точки у на гиперплоскость, задаваемую равенством уп = (яо)ти
имеем
ФЫ = Ж*У) = Ψ (2/1, ...,2/n-i,(^o)n), ye V;
230
• имеет место представление (192)
ф(я) =ψ(φ(ζ)) = ψ(φι(χ), ...,φη_ι(χ),(χ0)η), a: G £/(ζ0),
из которого хорошо видно, как именно функция ψ выражается
через функции φι, ..., φη-ι· ■
III*. Произвольная локально полная система. Любой
первый интеграл автономной системы локально, вблизи
неособой точки векторного поля, зависит от любого1 набора из η — 1
независимых первых интегралов, что и утверждает
Лемма 170. Если первые интегралы φι, ..., φη_ι
векторного поля f G C^G) независимы в его неособой точке хо, то
любой первый интеграл этого поля зависит от них в достаточно
малой окрестности точки xq.
► 1. Пусть ψ — первый интеграл поля /, тогда для вектор-строк
составляющих матрицу J(x), имеем:
• первые п— 1 векторов — при χ = xq линейно независимы (по
определению 7.5 независимости в точке xq первых интегралов
φι, ...,φη_ι);
• все η векторов вместе — при каждом значении χ G G' С G,
при котором f(x) φ 0 (эти значения заполняют целую
окрестность G' точки xq, так как f(xo) φ 0) линейно зависимы,
поскольку
J(x)f(x) =
Ι φί(*) \
, φή-iW
V Ψ'(ζ) /
№ =
ο
W
xeG',
в силу леммы 166.
2. Применяя достаточное условие зависимости функций2,
получаем, что в некоторой окрестности U(xo) С G' точки xq
функция ψ зависит от функций φι, ..., φη-ι· ■
*Не обязательно универсального, построенного в теореме 169
2Теорема из курса математического анализа
231
IV. Первые интегралы малых колебаний маятника.
Одним из первых интегралов гамильтоновой системы
описывающей малые колебания маятника без трения
(коэффициент перед χ нормирован линейным преобразованием времени),
служит ее гамильтониан Η Ε C^R2).
Согласно лемме 170, любой другой первый интеграл локально
вблизи любой ненулевой1 точки задается формулой ψ = F о Η
npHFeC^R2).
V*. Локальное задание фазовых кривых. Любая
отличная от точки покоя фазовая кривая локально получается как
линия уровня, общая для η — 1 независимых первых интегралов.
Теорема 171. Если первые интегралы φι, ... ,φη_ι
векторного поля f Ε C*(G) независимы в его неособой точке Xq, то в
некоторой ее окрестности U(xo) С G проходящая через нее
фазовая кривая этого поля задается системой
Ιφι(ζ) = φι(ζο)
(193)
<pn-i(s) = <pn-i(so)·
г
► 1. Выберем окрестность U(xq) точки хо, в которой2 система
(193) однозначно задает кривую Г:
• проходящую через точку хо;
• доходящую до границы окрестности U(xo) (при движении
по кривой как в одну, так и в другую сторону).
Этот выбор возможен по теореме о неявной функции,
согласно которой кривая Г является графиком зависимости от какой-
то одной координаты вектора χ всех остальных его координат
(поскольку ранг матрицы из производных у[(хо), ... ,(^'п_1(хо)
равен η — 1; определение 7.5) — конкретно по этой координате
и ограничим окрестность U(xo) так, чтобы кривая дошла до ее
границы.
Конкретно здесь это ограничение можно и снять
2 А в любой меньшей окрестности — и подавно.
232
2. Фазовая кривая Е(х) решения χ Ε Sf(U(xo)), проходящая
через точку хо, также удовлетворяет системе (193) (лемма 167).
Поэтому справедливо включение Е(х) С Г.
3. В соответствии с теоремой 164 уменьшим (если
потребуется) окрестность U{xq) так, чтобы существовал
выпрямляющий диффеоморфизм (189) (см. рис. 30). Так как образ φ(£'(χ))
кривой Е(х) в выпрямленных координатах доходит до
границы области V, то и сама кривая Е(х), как и кривая Г, доходит
до границы окрестности U(xo). Поэтому справедливо равенство
Е(х) = Г. ■
7.7. Одномерное фазовое пространство
автономного уравнения уже изучалось ранее в п. 1.31.
I. Критерий устойчивости на прямой. Автономная
система (180) в одномерном (п = 1, т. е. G С Щ случае имеет свою
специфику:
• никакая ее фазовая кривая не может оказаться циклом;
• непрерывное поле / между любыми своими соседними
особыми точками имеет фиксированный знак.
Теорема 172. Пусть f Ε C(G) и задан интервал I С G,
тогда:
1) если на I нет особых точек поля /, то фазовая кривая
любого решения χ Ε Sf(I) содержит весь интервал I;
2) если а — единственная на I особая точка поля /, в
которой существует производная f'(a), то следующие
утверждения эквивалентны:
• точка а устойчива по Ляпунову;
• точка а асимптотически устойчива;
... > 0, а> χ е I,
• fix) \
w | < 0, а < χ Ε I.
<
► 1. Предположив, что
f(x) ^ о, χ ε /, χ е Sf(l),
хГде были получены формулы общего решения и описаны точки
существования и единственности
233
У
У
α\. χ
1
^ч^ h=f(x)
а х
y=f(x)
a 6
Рис. 32. Особая точка на прямой:
α — устойчивая; б — неустойчивая
докажем включение Е(х) D I. Действительно, если, напротив,
существуют точки, удовлетворяющие, например1, соотношениям
х0 = x(t0) el, χι е Ι \ Ε(χ), χι > хо, f(x0) > 0,
то:
• [ίο;οο) С D(x), поскольку функция χ возрастает, но не
принимает значение х\, а ее график, тем не менее, достигает
границы любого компакта [to;ti] χ [ζοί^ι] (см. теорему 23);
• в силу связности фазовой кривой имеем
inf x(t) = inf /(x(t)) > min /(*) = β > 0;
t>to t>to xe[xo;xi\
• при достаточно больших t получаем противоречие
χ(ί)>χ(ίο)+β(*-*ο)>*ι·
2. Согласно предыдущему пункту, фазовая траектория
любого решения χ Ε Sf(I) есть либо неподвижная точка а, либо один
из интервалов Ι Π {х \ χ > а} или I Г\{х \ χ < а}. Поэтому:
• если условие (из формулировки теоремы) на знаки
функции / выполнено, то точки фазовых траекторий монотонно
движутся по этим интервалам, стремясь при t —> оо к точке а (т. е.
точка а асимптотически устойчива; рис. 32, а);
• если же упомянутое условие не выполнено, то точки
фазовых траекторий хотя бы с одной стороны от точки а
монотонно удаляются от нее на почтительное расстояние (т.е. точка а
неустойчива; рис. 32, б). ■
Случаи, когда х\ < xq или f(xo) < 0, рассматриваются аналогично.
234
II. Колебания маятника и поворот окружности. Пусть
задано уравнение малых колебаний маятника
у + ь>2у = 0 (ω>0).
С каждым его ненулевым решением
у(£) = Acos(<o£ + cp0), teR (Α,φ0€ΐ),
можно связать функцию, получающуюся из полной фазовой
переменной фу = (у, у) путем ее специального нормирования:
x(t) = — ( y(t), y(t) J = (cos((ut 4- φο), βίη(ωί 4- φο))·
Она задает поворот начальной точки (coscpo,sincpo) единичной
окружности S на угол ωί, который для ее угловой координаты
φ записывается одним уравнением
φ = ω, cpE«S~R (πιοά2π).
Последнее уравнение порождает на единичной окружности
каскад, определяемый с помощью формулы
J*(φ) = φ 4- ω£ (πιοά2π), φ G <S, A; G Ν, (194)
и называемый поворотом окружности — рациональным
(иррациональным), если рационально (иррационально) число
ω
α = ^~·
2π
Лемма 173. Любая орбита рационального поворота
окружности (194) замкнута, а иррационального — незамкнута.
► Действительно, для любого φ G S замкнутость орбиты ^(φ)
равносильна выполнению при некотором k G N условия
7* (φ) - φ = 2πα& = 0 (πιοά2π) -$=» otfc G Ν,
что равносильно требованию α G
III. Фазовое и временное средние. Следующее
определение без труда распространяется на любую динамическую
систему, заданную в области конечной меры. Мы же рассмотрим
здесь только каскад Τ на окружности S.
235
Определение 7.6. По заданной функции χ: S —> R
определим:
• ее фазовое среднее как интеграл (если он существует)
2π
1
х =
^Jx(q>)^p>
2π
о
• ее временное среднее вдоль орбиты ·7·"(φ) как предел (если
он существует)
χ(φ) = „Jto, ^ (χ(^(φ)) + · · · + χ(^"(φ))) · (ΐ«)
Если χ есть характеристическая функция множества Μ С S
ίΐ, φ Ε Μ,
то ее фазовое среднее хм называется относительной мерой1
множества М, а временное среднее Хм(ф) ~~ частотой
попадания орбиты Τ (у) в множество М.
IV*. Иррациональный поворот окружности. Любая
орбита иррационального поворота окружности (194) всюду
плотна в окружности ц даже, более того, равномерно распределена
по ней. Именно это и утверждает
Теорема 174- Для любой дуги Μ окружности S временное
среднее ее характеристической функции χΜ вдоль любой
орбиты иррационального поворота окружности существует и
равно фазовому среднему этой функции
ΧΜ (φ) = ΧΜ, φ G «S. (196)
Доказательство опирается на теорему Вейерштрасса о
равномерном приближении непрерывной функции на отрезке
тригонометрическими рядами, для которых временное и фазовое
средние совпадают, а также на возможность приближать в
интегральном смысле ступенчатые функции непрерывными.
1 Относительно всей окружности, мера которой принимается за единицу
236
► 1. Сначала докажем, что равенство (196) будет справедливым,
если в него вместо функции χ^ подставить произвольный
конечный тригонометрический ряд
к
θ(φ) = Σ W*^ ск е С> К е N>
k=-K
представляющий собой 2к-периодическую функцию, т.е.
функцию на единичной окружности.
Действительно, для функции θ имеем:
• фазовое среднее равно
2π
К " ckeik* 2π
θ=Σ||^,φ = ί, + Σ
k=-K Χ кфО
О
• временное среднее равно
1 т К 1 т
θ(φ)= lim — νθϋω + φ)= Υ ck lim — \^ β^'ω+φ) =
j=l k=-K j=l
ι (Jb\m ι
= со + у Cfce*(»+4>) ит -Li£_J i = ^
*—* т—юо ГП егК<л — 1
поскольку последний предел равен нулю ввиду ограниченности
выражения
ipiktu\m _ -ι
gifcca _ ι
— Igifcca _ ]|
(знаменатель дроби отличен от нуля из-за несоизмеримости
чисел к(о и 2π).
2. Теперь по функции χ^ и заданной числовой
последовательности гт > 0 (га Ε N), стремящейся к нулю при га —> оо,
подберем две последовательности тригонометрических рядов 0т
и Gm, обладающие следующими свойствами:
θηι(φ) < ΧΜ(φ) < вт(ф), φ G 5, (197)
ХМ ~ £т < К < Хм < вт < хм 4- ет. (198)
Чтобы подобрать, скажем, последовательность 0т
(аналогично, вт), достаточно для каждого га Ε N:
237
• найти непрерывную кусочно-линейную функцию фт,
удовлетворяющую оценкам
2π
<Μφ) < хм (φ), φ е S1, (хм (φ) - <Μφ)) ^φ < ε™π
о
(например, за счет малости параметра δ > 0 на рис. 33);
• найти (с помощью теоремы Вейерштрасса; рис. 33)
тригонометрический ряд 0т, удовлетворяющий недостающим оценкам
ψ™(φ) - -у < θ™(φ) < фт(ф), φ е «S,
О < хм - 9т = (хм - фт) + (фт - 9т) < -^ + -^ = ε
т·
3. Наконец, из оценок (198) получаем соотношения
Вт(ф) = Вт -)- хм <- вт = вт(ф), т -)- сю, φ G «S,
откуда и из оценок (197) вытекает и существование предела1
(195) в определении временного среднего Хм(ф)> и ег° равенство
фазовому среднему.хм· ■
7.8. Двумерное фазовое пространство
можно истолковать, в частности, и как расширенное (за счет
времени) одномерное фазовое пространство, изученное ранее в
пп. 1.1, 1.2.
По теореме о «двух милиционерах» из естественных оценок для
допредельных выражений
238
1. Уравнение фазовых кривых на плоскости. В
двумерном случае (п = 2) автономная система (180) записывается в
виде
i = f(x,y) {x,y)eGcR2. (199)
У = 9{х,У),
Она тесно связана с уравнением в дифференциалах (3)
д{х, у) dx = f(x, у) dy, (x, y)eGcG, (200)
которое задает поле направлений в открытом множестве
G = {(х,у) е G | (f(x,y),g(x,y)) Φ (0,0)},
не содержащем особых точек векторного поля (/,#).
Теорема 175. Если f,g e CX(G), то всякая отличная от
точки покоя фазовая кривая системы (199) является
интегральной кривой уравнения (200) и наоборот.
► 1. Если отличная от точки покоя1 фазовая траектория Г
решения
* = X5J! i€D(x,y), (201)
У = У(*)>
системы (199) проходит в какой-либо момент to через какую-
либо точку (хо,уо) е G и, например, f{xo,yo) φ 0, то x(to) φ 0 и
система (201) параметрически задает функцию y(t(x)) = Y(x),
определенную в некоторой окрестности точки х$ и
удовлетворяющую равенству
dY ιχ \ = У(^о) = 9(хо,Уо)
dx ° χ(ί0) 1(хо,УоУ
Таким образом, фазовая траектория Г касается в любой
своей точке (хо,уо) поля направлений уравнения (200) и потому
является интегральной кривой γ для этого уравнения.
2. С другой стороны, любая интегральная кривая γ
уравнения (200), проходящая через какую-либо точку (хо,уо) Ε G,
локально вблизи нее совпадает (теорема 9) с любой другой
интегральной кривой и, в частности, с фазовой кривой Г,
проходящей через ту же точку. Из доказанного локального совпадения
*А значит, не проходящая через особые точки векторного поля
239
следует1 и полное включение γ С Г, означающее, что
интегральная кривая γ уравнения (200) является фазовой кривой системы
(199). ■
II. Пара маятников. Рассмотрим систему из двух
уравнений малых колебаний маятника
2/1 + (ofyi = 0
2/2 4- ω^2 = 0,
2 _ п ωι,ω2 > 0.
Фазовое пространство этой системы четырехмерно: оно
задается координатами 2/i, yi, 2/2» 2/2- Однако существуют естественные
способы понижения его размерности.
• На неполной фазовой плоскости с координатами (2/1,2/2)
система задает так называемые фигуры Лиссажу:
yiW = Aicos(<oi£ + cpi) 04ι,Α2,φι,φ2 е -,
y2(0 = 42cos(<o2£ + cp2), teR.
• Та же система после нормирования2 полной фазовой
переменной задает для угловых координат φι,φ2 G S двух
единичных окружностей систему
φι =ωι
ф2 = ω2·
Она порождает на двумерном торе Τ = S x S фазовый поток,
определяемый формулой
J*(cpi, φ2) = (φι + ωχί, φ2 + ω2ί), (φι, φ2) € Τ, ί G R, (203)
и называемый обмоткой тора — рациональной
(иррациональной), если рационально (иррационально) число3
ω2
α = —.
ωχ
*В самом деле (см. рис 4), любая замкнутая дуга кривой γ с концами
(хо,Уо) и (xi,yi) локально вблизи каждой своей точки совпадает с какой-
либо фазовой кривой системы, поэтому по лемме Гейне—Бореля найдется
конечная цепочка (непродолжаемых) фазовых кривых Γι, . ,Τν,
совпадающих с кривой γ на последовательно пересекающихся друг с другом
открытых дужках и потому совпадающих как друг с другом (см. лемму 159), так
и с кривой Г.
2Описанного в разделе II из п. 7 7.
3Равное угловому коэффициенту наклонных прямых на рис 34.
240
• Наконец, если на торе
фиксировать нулевую окружность
S0 = {0}xS = {(φι,φ2) е Τ I φι = 0},
то следы обмотки тора на ней
образуют естественный каскад Пуанкаре1
(рис. 34)
Vk:S0^S0, keN,
(204)
Лемма 176. Каскад (204) представляет собой поворот
окружности So — рациональный (иррациональный), если
обмотка тора (203) рациональна (иррациональна).
► Действительно, этот каскад задается формулой
^fc(0?92) = (2π&, ф2 +ω&) = (0, φ2 + ω&) (πιοά2π), ω = 2πω2/ωχ,
а его рациональность эквивалентна рациональности числа
ω 6ύ2
2π ωι
т. е. рациональности обмотки тора. ■
III. Обмотка тора. Из леммы 173 и теоремы 174 вытекает
Следствие 177. Любая фазовая траектория рациональной
обмотки тора (203) замкнута, а иррациональной —
незамкнута и к тому же всюду плотна на торе.
► Фиксировав произвольную точку φ = (срьфг) Ε Τ и
выходящую из нее орбиту ^"(φ), обозначим s = φι/ωχ и заметим, что:
• для того чтобы орбита ^(φ) прошла через точку φ снова
ТТ(у) = ^°(φ) е Τ, Г>0,
необходимо и достаточно, чтобы совпали проекции2
TT-S(<?) = J-S(cp) = (0, φ2 - ω28) G <S0
*Ср. с определением 7.7 отображения Пуанкаре.
2Вдоль линии обмотки.
241
на нулевую окружность, принадлежащие одной и той же орбите
каскада Пуанкаре (204) — а это возможно (и даже непременно
происходит; см. лемму 173) тогда и только тогда, когда обмотка
тора рациональна;
• если обмотка тора иррациональна, то следы орбиты ·7·"(φ)
Гк(Т~3(^)) = (0, φ2 - ω25 + ω*:) G <S0, к G Ν, ω = 2πω2/ωι,
на нулевой окружности всюду плотны (в ней), равно как ее же
следы
Vk (^""(φ)) = (ωιί, φ2 + ω2(ί - s) + ω*), к G Ν,
на любой другой окружности, получаемые при надлежащем
выборе значения t G К. ■
7.9. Интеграл энергии для уравнения Ньютона
в одномерном случае
x + f(x) = 0, xelcR, feCl(I),
или, что то же, для получающейся из него1 нормальной
автономной системы
по определению, совпадает с потенциалом φ (χ, у)
соответствующего уравнения в полных дифференциалах (см. определение 1.4)
f(x)dx + ydy = Q. (206)
I. Закон сохранения энергии. Интеграл энергии системы2
(205) вычисляется по формуле
χ
φ(χ)2/) = |/(ξ)<*ξ+1,Α
Xq
1С помощью канонической замены в данном случае — добавлением ско-
:и у = х.
Или соответствующего уравнения Ньютона
рости у = χ
2
242
в которой первое слагаемое называется потенциальной энергией
(относительно некоторой точки xq Ε /), а второе —
кинетической. Он действительно служит потенциалом уравнения (206):
dy(x, у) = f(x) dx + y dy.
Закон сохранения энергии, τ е. утверждение о ее
постоянстве вдоль любого решения, в данной терминологии
формулируется, как вытекающее1:
• из определения первого интеграла (см. п. 7.5);
• из теоремы 175, согласно которой последнее уравнение
(206) задает фазовые кривые системы (205);
• из теоремы 4 (о выражении φ = С общего решения
уравнения (206) через его потенциал φ).
Следствие 178. Потенциал уравнения (206) является
первым интегралом системы (205).
II. Энергия колебаний маятника. Интеграл энергии
(относительно точки xq = 0) для уравнения колебаний маятника
x + asinx = Q, α>0, (207)
имеет вид
у(х,у) = U(x) + -у2, U(x) = а(1 - cos χ) > 0.
Именно он и был ранее (см. раздел III из п. 6.4) принят за
функцию Ляпунова, успешно подтвердившую факт не
асимптотической устойчивости нижнего положения равновесия
маятника при отсутствии трения.
III*. Исследование фазового портрета маятника.
Фазовые кривые системы, соответствующей уравнению колебаний
маятника (207), лежат на линиях уровня его интеграла энергии
ф, у) = U(x) + \у2 = С «=Ф у = ±y/2{C-U(x)), (208)
которые симметричны относительно оси абсцисс и определены
только при условии С > 0 (так как U > 0).
*А также проверяемое непосредственно с помощью леммы 166
Ф(я,у) = f{x)y + y(-f{x)) = О
243
Uk
χ
Рис. 35. Маятник:
α — интеграл энергии; б — фазовые кривые
Поскольку у = ж,»то движение по фазовым траекториям в
верхней полуплоскости (где у > 0) всегда происходит слева
направо, а в нижней — наоборот.
На фазовой плоскости (на рис. 35, а штриховкой показана
стоящая под корнем (208) положительная разность С — U(x)
между горизонтальной прямой у = С и графиком функции
у = U(x), а на рис. 35, б изображены фазовые кривые):
• наименьшее возможное значение С = 0 энергии φ задает
только неподвижные точки (соответствующие нижнему
положению равновесия), а еще меньшие значения энергии вообще
ничего не задают,
• малым значениям 0 < С < 2а соответствуют замкнутые
кривые с переменным знаком скорости (покачивание маятника
относительно нижнего положения равновесия) — каждая из них
в точке (ж(ь0) пересечения с осью абсцисс имеет вертикальную
касательную, поскольку выражение под корнем (208) имеет вид
244
ol(x - x0) + р(ж - xq)2 + o(x - xo)2, χ ->· xo, (209)
где α^Ο;
• большим значениям С > 2а соответствуют незамкнутые
кривые с постоянным знаком скорости (полное обращение
маятника вокруг точки подвеса);
• наконец, при С = 2а линия уровня энергии состоит как из
неподвижных точек (а?о50), хо = ±π,±3π, ... (соответствующих
верхнему положению равновесия), так и асимптотически
приближающихся к ним фазовых кривых1 — причем под
наклонным направлением, поскольку в окрестности каждой такой
точки выражение под корнем (208) имеет тот же вид (209), но уже
при условиях α = 0 < β.
7.10. Особые точки на плоскости
в отличие от неособых (см. теорему 164) имеют в своей
окрестности более или менее индивидуальные фазовые портреты.
Разбираемая здесь классификация Пуанкаре таких точек применяется
к линейной системе
z = Az, ze R2, (210)
в случае, когда ее нулевая особая точка изолирована:
ΑζφΟ, ζ φ 0, <=> detA/0 <=* λι,λ2/0,
где λι,2 — собственные значения оператора А.
Для жордановой формы матрицы А могут представиться три
возможности: либо она диагональна и действительна, либо не
диагональна, либо не действительна2. Рассмотрим их
последовательно, решая каждый раз эту систему в специальном базисе,
(х
в котором будем обозначать ζ = I
I. Диагональный действительный случай. Пусть
матрица оператора А в некотором базисе в Ш2 имеет диагональный вид
с числами λι52 Ε Η на диагонали: ищем общее решение системы
χ = CieXli
2/ = C2eX2i, СьС2еМ,
1 Называемых сепаратрисами.
2Случай, когда она ни диагональна, ни действительна, отпадает из-за
малости порядка матрицы.
245
а ее фазовые кривые, при (х,у) Φ (0,0), находим из уравнения
\2ydx = \\xdy <=>
ау_ = ..2/
dx
х = 0
dx χ 4=Ф
у = С\х\*
х = 0, С е R,
где μ = λ2/λι·
1. Если μ < 0, то особая точка называется седлом (рис. 36, а).
Нетривиальные (т.е. отличные от собственных лучей и непо-
\\£
Ж
в
д е
Рис. 36. Особые точки в каноническом базисе:
α — седло; б — обыкновенный узел; в — дикритический узел; г
денный узел; д — центр; е — фокус
вырож-
246
движной точки) фазовые кривые седла напоминают ветви
гиперболы. Кроме того, седло всегда неустойчиво по Ляпунову,
так как его собственные значения имеют разные знаки и потому
одно из них положительно (теорема 142).
2. Если μ > 0, то особая точка называется узлом (рис 36, б, в
и, забегая вперед, г). Асимптотическая устойчивость узла
равносильна отрицательности его собственных значений (всегда
имеющих общий знак), а неустойчивость — положительности. При
этом возможны варианты:
• в случае μ > 1 (к которому перестановкой переменных χ и
у местами сводится и случай μ < 1), особая точка —
обыкновенный узел (см. рис. 36, б), все нетривиальные фазовые
траектории которого при t —> оо или при t —> — оо стремятся к началу
координат, касаясь оси абсцисс, и похожи на ветви параболы;
• в случае μ = 1 особая точка — дикритический узел (см.
рис. 36, в), все фазовые кривые которого тривиальны:
неподвижная точка и собственные лучи.
II. Недиагональный случай. Пусть λι,2 = λ Ε R и матрица
оператора А в некотором базисе1 имеет недиагональный вид:
ищем общее решение системы
χ = λχ \ χ = С\еи
у = \х + \у ^ \у = dteu + С2еи, СиС2еШ,
а ее фазовые кривые, при (х, у) φ (0,0), находим из уравнения
dy у + х
\{у + х) dx = λχ dy <=
dx x
x = 0
y= (С + 1п|ж|):г
χ = 0, С е R.
• Эта точка — вырожденный узел2 (см. рис. 36, г). Все его
нетривиальные фазовые кривые при t —> оо или при t —> — оо
стремятся к началу координат, касаясь собственных лучей, и
имеют специальный вид. Устойчивость (сразу асимптотическая)
этой разновидности узла, как и всех других, равносильна
отрицательности его собственных значений (в данном случае —
совпадающих).
1 Полу чающемся из жорданова с помощью специального преобразования
из п. 2 доказательства признака устойчивости (см. раздел 1 из π 6 6).
2Тоже узел, поскольку собственные значения — одного знака
247
III. Недействительный случай. Пусть оператор А имеет
комплексные собственные значения λ = α -f ζβ (β φ 0) и λ, тогда
матрица его комплексификации А в жордановом (комплексном)
базисе h = hi -\- %h2 и h диагональна.
Комплексифицированная система имеет, в частности,
решения вида
ζ = w(t)h, w{t) = Сеи = u(t) + iv{t), C G С,
действительные части которых являются решениями исходной
действительной системы (см. лемму 92). Значит, решением
последней заведомо служит любая функция, задаваемая
уравнением
ζ = Re((u(t) + iv(t))(hi + ih2)) = u(t)hi + v(t){-h2).
Если принять координаты χ и у вектора ζ в базисе hi, — h2 за
действительную и мнимую части комплексного числа ζ = χ -f iy
соответственно1, то все найденные действительные фазовые
траектории запишутся на комплексной плоскости уравнением
ζ = u(t) + iv(t) = w(t) = Ceai(cos βί + г sin βί), Се С,
причем эти кривые заполнят всю комплексную плоскость,
поэтому других фазовых кривых на действительной фазовой
плоскости нет.
3. Если a = 0, то фазовые траектории замкнуты, а особая
точка называется центром (рис. 36, д). Он всегда устойчив по
Ляпунову и всегда не асимптотически.
4. Если же a < 0 или a > 0, то фазовые траектории
закручиваются или, соответственно, раскручиваются по спирали и
стремятся при t —> оо или, соответственно, при t —> —оо к началу
координат, а особая точка называется фокусом (рис. 36, е) —
асимптотически устойчивым или неустойчивым соответственно.
IV. Положения равновесия маятника. Исследуем особые
точки уравнения свободных колебаний маятника с трением
x + 2px + q2sinx = 0, ρ > 0, q > 0. (211)
Линеаризованная система2 (см. раздел III из п. 6.5) в нижнем и,
соответственно, верхнем положении равновесия записывается с
помощью матрицы
1 Векторы /ii,/i2 (как и h,h) — линейно независимы.
2Она же — система в вариациях по начальному значению, фазовый
портрет которой вблизи особой точки сильно напоминает истинный, что
вытекает из следствия 131
248
A =
О 1
V -2p,
И Л = ( о
,9
■2Р.
Нижнее положение задает особые точки (2πη,0), η Ε Ν, с
характеристическим многочленом λ2 + 2ρλ + #2, которые
представляют собой:
гт, 27t
• при ρ = 0 — центр с периодом колебаний, равным Τ = —
(рис. 37, α);
• при 0 < ρ < q — фокус (рис. 37, б);
• при ρ = q — вырожденный узел с собственным вектором
(1Д) = (1,-д) (рис. 37, в);
• при ρ > q — обыкновенный узел с собственным векторами
(1,λι)2), где λι|2 < 0 (рис. 37, г).
—»-
χ
а
в г
Рис. 37 Нижнее положение равновесия маятника:
а — без трения, б — слабое трение; в — критический случай; г — сильное
трение
249
Рис. 38. Верхнее
положение равновесия маятника
Заметим, что при плавном
возрастании параметра ρ > 0
(отвечающего за трение) дважды
происходят скачкообразные изменения
фазового портрета (так называемые
бифуркации1) вблизи нижнего
положения равновесия маятника,
например:
• при отходе параметра ρ от
значения 0 фазовые кривые в
окрестности особой точки теряют
цикличность;
• при прохождении параметром
ρ значения q у особой точки
появляется собственное направление, которое сразу же раздваивается.
Верхнее же положение задает особые точки (π + 2πη, 0) с
характеристическим многочленом λ2 + 2р\ — q2, которые при
любом ρ > 0 представляют собой седло с собственным векторами
(1Λι,2)> где числа λχ^ — разного знака (рис. 38). Так что его
фазовый портрет не терпит бифуркаций.
V. Экологическая модель Лотки — Вольтерра.
Система «хищник — жертва» связывает друг с другом количество
χ = x(t) жертв и количество у = y(t) хищников (например,
карасей и щук в пруду) в зависимости от времени t. В простейшей
модели Лотки — Вольтерра эта взаимосвязь описывается
автономной системой
χ = ах — fixy
х,у>0 (α,β,γ,δ>0).
(212)
у = -уу + Ьху,
Система (212) имеет единственную точку покоя (рис. 39)
а в остальных точках ее фазовые кривые задаются уравнением2
Ъх — γ 3?/ — ot
(Ъху - уу) dx + фху - ах) dy = 0 <=> dx + — dy = 0.
χ
У
αΤ е раздвоения.
2С разделяющимися переменными; см п. 1.4
250
Первый интеграл системы
(212)
у(х,у) = (δζ-γΐηζ) +
+ фу-*\пу) = f{x)+g(y)
обладает следующими
свойствами:
• функции / и д в точках xq и
уо соответственно имеют строгий
минимум, поскольку их
производные
Рис. 39. Фазовый портрет
экологической модели
χ
У
меняют в этих точках знак с минуса на плюс;
• сумма ср(ж, у) функций f(x) и д(у) имеет в точке покоя
(хо,Уо) строгий минимум, поэтому функция
v(x,y) = φ(ζ,2/)-φ(ζο,2/ο)
ι
в окрестности этой точки служит функцией Ляпунова для
системы (212) и доказывает ее устойчивость, причем не
асимптотическую (см. следствие 146);
• если точка (ж, у) движется из точки (хо,уо) по какому-либо
лучу1, то значения функции у(х,у) неограниченно растут, так
как то же делают и значения каждой из функций f(x) и д(у)
(или только одной из них, если другая — константа);
• любая отличная от точки покоя фазовая траектория
системы (212), будучи линией уровня первого интеграла у(х,у),
пересекает любой такой луч ровно в одной точке, а значит, окружив
точку (хо,уо), зацикливается: на ней происходят периодические
колебания численностей хищников и жертв относительно
положения равновесия.
Для вычисления периода малых колебаний системы Лотки —
Вольтерра в особой точке найдем матрицу линеаризованной
системы '
оуо
-β^ο
-γ + Ьх0
αΒ пределах положительного квадранта.
251
Поскольку ее характеристический многочлен λ +αγ имеет корни
iz^/αγ, линеаризованная особая точка — центр1, период
колебала 2π
ний которого равен Τ = ——.
ч/άγ
7.11. Свойства циклов
определяются поведением соседних с ними фазовых кривых.
I. Мультипликаторы системы в вариациях. Пусть цикл
Г С G периода Τ > 0, представляющий собой (согласно
определению 7.2) замкнутую несамопересекающуюся фазовую
кривую векторного поля / Ε CX(G) (или задаваемого им фазового
потока Т), соответствует периодическому решению автономной
системы (180) с наименьшим положительным периодом Т.
Система в вариациях (147) по начальному значению вдоль
цикла Г = ^(^о), задающая производную ζ = x'x(t,xo) решения
x(t,x) по начальному* значению χ в точке χ = xq, имеет вид
z = A(t)z, A(t) = fx(x(t,x0)) = fx(P(x0)), teR. (213)
Лемма 179. Система в вариациях (213) вдоль цикла
периода Τ — таксисе Τ-периодична, а одним из ее мультипликаторов
заведомо служит число μο = 1.
► Действительно:
• при любом t Ε Μ. имеем
A(t + Τ) = f'x (Ρ+Τ(χ0)) = i'x (РЫ) = A(t);
• оператор монодромии системы в вариациях (см. равенство
(148))
Ζ(Τ,0,χ0) = χχ(Τ,χ0) = (Ττ)'(χ0)
удовлетворяет равенству (см. лемму 161)
(ТТ)Г (хо) · /Ы = / (ГТЫ) = 1 · /(хо),
поэтому вектор f(xo) для оператора монодромии — собственный
и соответствует собственному значению μο = 1. ■
Все остальные мультипликаторы системы в вариациях вдоль
цикла называются мультипликаторами цикла, или
орбитальными мультипликаторами2 системы (213).
*Что естественно, так как нелинеаризованная особая точка — тоже центр
2Их количество равно η — 1, и среди них также могут найтись единичные
252
II. Отсутствие асимптотической устойчивости.
Наличие у любой системы в вариациях вдоль цикла единичного
мультипликатора — не орбитального — отражает тот факт, что
исходная автономная система (180) имеет решения, начинающиеся
непосредственно в точках цикла и не меняющиеся под действием
отображения фазового потока за период.
Благодаря таким решениям цикл не может задаваться
асимптотически устойчивым решением, т. е. верна
Лемма 180. Решение автономной системы, фазовая
кривая которого есть цикл, не является асимптотически
устойчивым.
► Пусть фазовая кривая решения x(-,xq) с начальным
значением Xq = χ(Ο,^ο) есть цикл Г периода Т. Тогда среди решений
х(-,х) с начальными значениями хбГ, отличными от xq:
• найдутся начинающиеся сколь угодно близко к точке х$\
• абсолютно все — Т-периодические, так как каждое из них
отличается от решения х(-,х$) только временным сдвигом;
• ни одно не приближается асимптотически с ростом времени
к решению χ(·,χο), поскольку
p(x(kT,x),x(kT,x0)) = p(x(Q,x),x(Q,x0)) = p(x,x0) > 0, k e N.
Значит, решение x(-,Xq) — никак не асимптотически устойчиво.·
III*. Отображение Пуанкаре. Пусть через некоторую
точку Xq цикла Г С G векторного поля / проходит гиперплощадка
5, пересекающая цикл ровно в одной точке.
Фазовые траектории того же потока, начинающиеся
достаточно близко к точке х$, на протяжении всего периода [0; Т] цик-
253
л а Г не уходят далеко от него и также пересекают площадку S.
На этом основано
Определение 7.7. Отображение последования (Пуанкаре) V
строим так (рис. 40):
• из произвольной точки χ Ε S выпускаем орбиту Т(х)\
• ищем первую (в некоторый момент t = Τ (χ) > 0) точку
J^ix) ее пересечения с площадкой 5;
• если такая точка найдется, то принимаем ее за образ V(x)
точки χ при отображении последования.
И хотя логически возможен вариант, что описанная в
определении точка пересечения не найдется вовсе, все же данное
определение корректно, что и обосновывает
Теорема 181. Если f Ε CX(G) и гиперплощадка S в
точке xq трансверсальна1 к циклу Г = Т{хо), то для достаточно
малой окрестности U{xq) этой точки определение 7.7 задает
непрерывно дифференцируемое отображение последования
V: S' ->5, S' = SnU(x0).
► 1 Отображение
фазового потока за период Τ цикла Г является
диффеоморфизмом и переводит.
• точку xq — в себя;
• окрестность точки Xq — в некоторую окрестность (ее же);
• площадку S — в некоторую гиперповерхность.
2. Пусть φ — выпрямляющий диффеоморфизм (189), который
оставляет на месте все точки множества 5, лежащие в -Ο(φ) (см.
теорему 164 и следствие 165; рис.40). Тогда диффеоморфизм
^Ξφο7τοφ-1 {G{xo) = Xo)
определен на некоторой прямоугольной окрестности V точки xq.
3. Выберем меньшую, но также прямоугольную, окрестность
V С V точки Xq, удовлетворяющую условию Q{V) С V, и по
окрестности
определим упомянутую в формулировке леммы площадку S'.
Или, что то же, не касается вектора f(xo)
254
4. Далее, обозначив через π ортогональный проектор на
площадку S, имеем включение
k(G(V')) CVHS.
Таким образом, отображение последования1
-ρ = (φ"1 ο π о Q о φ)|5, = π о Q\s,: Sf -> S
определено и непрерывно дифференцируемо. ■
Уменьшив еще, если потребуется, в приведенном
доказательстве окрестность V' С V точки xq, можно обеспечить, сверх того,
и любую близость точек Тт{х) и V(x) ξ jWx\x) (см.
определение 7.7), что и констатирует
Следствие 182. Для любого наперед заданного ε > 0
построенное в теореме 181 отображение последования V можно
подчинить дополнительному требованию, что время Т(х)
движения по фазовой траектории от точки χ Ε S' до ее образа
V(x) отличается от периода Τ цикла Г менее чем на ε.
IV*. Орбитальные мультипликаторы. Зная производную
отображения последования для цикла, можно найти все его
мультипликаторы или, что то же, набор из всех η — 1
орбитальных мультипликаторов системы в вариациях (213) вдоль этого
цикла.
Для того чтобы сам цикл Г пересекал площадку S ровно в одной точке,
а отображение последования задавало именно первое пересечение
траектории с площадкой S, возможно, придется еще уменьшить окрестность U(xo)
так, чтобы в ней не было ни одной точки некоторой достаточно малой (не
содержащей точки хо) окрестности всей дуги
Tltl't2](xo) = {7*(хо) I t G [ίι;ί2] С [0;Г]},
где ti,t2 — моменты первого выхода траектории Т(хо) из области φ-1 (V)
и, соответственно, последнего входа в нее в течение периода [0;Т] Тогда
для любой точки χ € U(xo) никакая точка 1^{х) при t G [ίι; 4г] также не
будет лежать в окрестности U{xo), что достигается дополнительным
уменьшением этой окрестности, благодаря непрерывности решений по начальным
значениям (см следствие 125)
sup р(У(х),7"[*1;*2](х0)) < sup р(Т*{х),Т\х0)) ^0, χ -► х0
te[ti,t2] ч ' *e[ti,t2l
2Расстояние между их образами в области V равно \Т — Т(х)\
255
Следствие 183. В условиях теоремы 181 набор всех
мультипликаторов1 цикла Г = F(xo) совпадает с набором всех
собственных значений производной V{xo) отображения
наследования в точке xq.
► 1. Матрицы операторов (см. доказательство теоремы 181)
А = (ТТ)' Ы, В = д'(х0) = ср'Ы о (Тт)' (х0) о (q/Ы)"1
подобны, а значит, имеют одинаковую жорданову форму,
причем собственный вектор f(xo) (с собственным значением μο = 1)
оператора А соответствует собственному вектору еп оператора
В, перпендикулярному площадке 5.
2. Если система ho = еп, h\, ..., hn-\ образует жорданов
базис2 оператора В с собственными значениями μο,μι, • •чЦп-ь
то построенные по ней две системы3 векторов
ho,nhi, · · · 5πΛ-η_ι, Tihi, ... ,nhn-i (214)
служат жордановыми базисами для двух операторов
С ξ π о G'(x0), D = V'(x0) = (π о G(x0)\s)' = π о G'(x0)\s
с собственными значениями 0,μι, ...,μη_χ и μι, ...,μη_χ
соответственно, поскольку
Cho = nBho = Tiho = 0 · ho
и для любых векторов
k = izh = h + α/ίο Φ ho (α Ε С), к' = π/ι' φ ho
из списка (214) имеем
(μπ/i = μk, Bh = μh,
π(μ/ι + h') = μk + к', Bh = )±h + h',
nfaoh + ho) = μok, Bh = μoh + ho,
причем Dk = Ck. ■
С учетом кратности
23десь мы вышли в комплексное пространство Сп (см. определение 4 2).
Линейно независимые, в силу линейной независимости исходной
системы.
256
7.12. Предельные множества
фазового потока Τ (или автономной системы (180)) состоят из
предельных точек его траекторий при t —> оо или t —> — оо.
I. Предельные точки и множества. Фиксируем
произвольную точку хо Ε G.
Определение 7.8. Для данной орбиты Τ(χο):
• точка χ Ε G называется ω-предельной точкой, если она
является частичным пределом функции ^(xq) при t —> оо, т.е.
для некоторой неограниченной последовательности t\ < t^ < . ·.
имеет место равенство
lim ТЬк(хо) = х;
к—юо
• множество Ω всех ω-предельных точек называется
ω-предельным множеством;
• ^-предельные точки и множества определяются
аналогично, с заменой символа оо на — оо.
Заметим, что если фазовая траектория есть точка покоя или
цикл, то ее ω-предельное множество просто совпадает с самой
этой траекторией.
Кроме того, ω-предельное множество фазовой траектории
Т(х{)) состоит ровно из одной точки тогда и только тогда,
когда существует обычный предел функции ^(xq) при t —> оо,
т. е. когда эта траектория:
• либо сама является точкой покоя;
• либо асимптотически (при t —> оо) приближается к
некоторой точке, которая тогда непременно есть точка покоя (в силу ее
инвариантности, утверждаемой в нижеследующей теореме 184).
II*. Свойства предельных множеств. Целый ряд
содержательных утверждений самого общего характера предлагает
Теорема 184» Для любого фазового потока Τ ω-предельное
множество его фазовой траектории:
• всегда замкнуто и инвариантно1;
• пусто тогда и только тогда, когда эта траектория
асимптотически {ripu t —У оо) приближается к границе2
области G;
В смысле определения 7.4.
2См разъяснение в доказательстве настоящей теоремы, а также в π 2.7.
257
• непусто, ограничено и связно, если эта траектория,
начиная с некоторого момента, ни разу не покидает некоторый
компакт, лежащий в области G.
► 1. Если задана орбита ^(xq), to ее ω-предельное множество Ω:
• замкнуто, _поскольку внутри любой окрестности U(x)
любой точки χ G Ω найдется ω-предельная точка х' G Ω, но коль
скоро U(x) — окрестность также и для точки х', то для любого
Τ найдется такое t > Т, что ^(^о) G U(х), а значит, χ G Ω;
• инвариантно, так как для любых χ Ε Ω и t G M имеем
J*(x) = P\\\m J*k{x0)) = lim P+tk(xQ) G Ω.
\k—юо J k—юо
2. Напомним, что по определению, траектория
асимптотически (при t —> оо) приближается к границе области G, когда
она покидает любой наперед заданный компакт К С G при всех
достаточно больших<t > Т(К):
• с одной стороны, если из любого компакта К С G
траектория с какого-то момента безвозвратно выходит, то она не имеет
ω-предельных точек внутри любого компакта, а значит, и внутри
области G (представимой в виде объединения таких компактов);
• с другой стороны, если траектория ни с какого момента не
покидает безвозвратно некоторый компакт К С G, то в нем (а
значит, и внутри области G) она имеет ω-предельную точку.
3. Если все точки J^ix^) при t > Τ лежат в некотором
компакте К С G, то ω-предельное множество Ω:
• ограничено, поскольку все предельные точки множества
Р(х{)) С К содержатся в множестве К;
• связно, так как в противном случае множество Ω можно
было бы представить в виде объединения двух непересекающихся
замкнутых множеств Ωχ и Ω2, расстояние между которыми (см.
лемму 119) было бы положительным
ρ(Ωι,Ω2) = 3ί/>0,
а значит, нашлась бы неограниченная последовательность
Si < t\ < Г\ < $2 < ^2 < Г2 < S3 < · · . ,
для которой при каждом k G N выполнялись бы неравенства
ρ(^θ*(χ0),Ωι) < d, 9(Гк(хо),П2) < d, ρ(7**(χο),ΩιυΩ2) > d,
258
а тогда любая предельная точка χ (которая в компакте К
обязательно есть) последовательности Jrtk(xo) была бы ω-предельной
для траектории Т(хо), но тем не менее удовлетворяла бы
неравенству
р(х, Ω) = р(х, Ωι U Ω2) > d,
т. е. не принадлежала бы множеству Ω. ■
7.13. Предельный цикл на плоскости
обладает определенной спецификой по сравнению с его аналогом
в многомерном фазовом пространстве.
I. Разновидности плоских циклов. Пусть в плоской
области G С R2 задан цикл Г. Тогда он разбивает область G на две
части1: внешнюю и внутреннюю.
Определение 7.9. Цикл называется:
• изолированным, если в достаточно малой его окрестности
нет других циклов;
• предельным, если он служит ω-предельным или
α-предельным множеством для некоторой незамкнутой траектории;
• устойчивым снаружи (изнутри), если он служит
ω-предельным множеством для любой траектории, начинающейся во
внешней (внутренней) части достаточно малой его окрестности;
• неустойчивым снаружи (изнутри), если он служит
α-предельным множеством для любой траектории, начинающейся во
внешней (внутренней) части достаточно малой его окрестности;
• устойчивым2 (неустойчивым), если он устойчив
(неустойчив) одновременно и снаружи, и изнутри;
• полуустойчивым, если он устойчив снаружи и неустойчив
изнутри, или наоборот.
II. Функция последования для плоского цикла. Так как
в случае π = 2 трансверсальная к циклу гиперплощадка S
одномерна, на ней можно ввести одну координату s, отобразив в эту
площадку диффеоморфно интервал
σ: / ->S,
Это утверждение называется леммой Жордана.
2Не по Ляпунову.
259
Рис. 41. Мешок Бендиксона
после чего каждая точка χ Ε S получит свой прообраз в виде
числа s = ο_1(χ) Ε / (рис. 41).
Пусть, для определенности, точка хо площадки 5, лежащая
на цикле Г, соответствует значению s — О (т. е. σ(0) = хо),
внешние точки площадки соответствуют положительным значениям
s, а внутренние — отрицательным. Тогда отображение последо-
вания V: S' —>■ S можно отождествить с числовой функцией
р = о~1 oVoa: ΐ ^Ι, Γ = G~\Sf).
Введенная функция обладает следующими свойствами:
• р(0) = 0? так как Р(яо) = #о;
• знак числа p(s) совпадает со знаком числа s, поскольку
любая фазовая траектория расположена целиком либо во внешней,
либо во внутренней части;
• изолированность цикла Г означает, что функция последо-
вания не имеет неподвижных точек в некоторой проколотой
окрестности точки 0 — в этом случае в каждой из двух
полуокрестностей нуля знак разности p(s) — s фиксирован, в силу
непрерывности функции последования.
III. Предельный цикл. Согласно следующей теореме,
любой изолированный цикл на плоскости — предельный1.
Теорема 185. Пусть функция последования ρ·, построенная
по данному циклу Г на плоскости, имеет единственную
неподвижную точку 0. Тогда:
Благодаря чему цикл на плоскости иногда с самого начала, по
определению, называют предельным, если он просто изолированный.
260
• если хотя бы для одного s > О верно неравенство p(s) < s
(p(s) > s), то цикл Г устойчив (неустойчив) снаружи-,
• если хотя бы для одного s < О верно неравенство p(s) > s
(p(s) < s), то цикл Г устойчив (неустойчив) изнутри.
► 1. Рассмотрим, например1, случай, когда для некоторого2
s > О выполнено неравенство p(s) < s. Тогда последовательность
«ι = s,s2= p(si), s3 = p(s2), · · ·
итераций функции последования р, примененная к начальной
точке s, в силу свойств этой функции (см. рис. 41):
• ограничена снизу числом 0;
• убывает;
• сходится к некоторому числу so ^ 0·
Переходя в равенстве
sk+i=p(sk), keN,
к пределу при к —> оо, получаем so = p(so), откуда, в силу
единственности неподвижной точки 0, имеем so = 0.
2. Таким образом, имеет место сходимость
хк = a(sfc) =^к(х\) -)· хо = σ(0), к ->· оо,
причем, согласно следствию 182, при всех достаточно больших
к > К выполнены оценки
Т/2 < tk+l -tk< 2Г,
а значит, последовательность tk неограничена.
Поэтому ω-предельное множество Ω для траектории ^(^ι)
(см. теорему 184):
• содержит точку xq;
• в силу инвариантности, содержит все точки цикла Г;
• более не содержит никаких точек, поскольку орбита ^(^ι)
целиком лежит в мешке Бендиксона (ограниченном первым
витком этой орбиты, кончающимся в точке х2 = V(x\) G 5, и
отрезком [£i,a?2] площадки S; см. заштрихованную часть на рис. 41)
и асимптотически (при t —> оо) приближается к циклу Г, т.е.
Остальные случаи рассматриваются аналогично.
2А значит, в силу вышесказанного, и для любого.
261
лежит в любой наперед заданной его окрестности при всех
достаточно больших t, так как в силу непрерывности решений от
начальных значений (следствие 125) при к —> оо имеем
sup р(1*(хк)),Р{хо)) < ||x(-,zfc),x(-,zo)||[ibifc+2r] -► О,
где через х(-,я) обозначено решение системы (180),
удовлетворяющее начальному условию х(0, х) = х.
Следовательно, Ω = Г, что и требовалось доказать. ■
IV. Исследование устойчивости цикла. Рассмотрим
систему на плоскости
χ = у 4- а(х2 4- у2 - \)х ίχ\
у = -х + а{х2 -{-у2- 1)у, \у) Ψ
У нее заведомо имеется цикл Г, задаваемый уравнением
х2 + у2 = 1
и представляющий собой единичную окружность с центром в
начале координат: действительно, в каждой точке (х, у) этой
окружности проекция вектора фазовой скорости
у + а(х2 + у2 - 1)х \ = ( у
-х 4- а(х2 -f у2 — \)у) \—χ,
на радиус-вектор этой точки равна нулю.
Кроме того, при а = 0 таким же свойством обладает любая
окружность с тем же центром, а значит, упомянутый цикл не
изолирован.
Далее, при а ф 0 аналогичная проекция в каждой точке
внутри единичного круга имеет один знак, а снаружи — другой.
Поэтому найденный цикл изолирован, и если по нему построить
функцию последования р(-), то будет иметь место одна из
следующих двух ситуаций:
./<s, s>0, /\/>s> s>0> /oir;\
pis) < или p(s) < Λ (215)
ИУ ' \>s, s<0, ИК } |<s, s<0, v }
а именно:
• при а < 0 — первая, с устойчивым предельным циклом
(рис. 42, а);
262
5
5
а б
Рис. 42. Предельный цикл:
α — устойчивый; б — неустойчивый
• при а > О — вторая, с неустойчивым предельным циклом
(рис. 42, 5).
V*. Мультипликатор плоского цикла. Зная производную
функции последования ρ для цикла на плоскости, можно найти
его единственный мультипликатор μίΐ, а если он отличен от
1 — то и исследовать цикл на устойчивость.
Теорема 186. Если ρ — функция последования,
построенная по данному циклу Г на плоскости, то его мультипликатор
равен
μ = Р'(0) > О,
при этом в случае μ < 1 цикл устойчив, а в случае μ > 1 —
неустойчив.
► 1. Равенство μ = р'(0) вытекает из следствия 183.
2. Из свойств функции последования ρ получаем нестрогое
неравенство р'(0) > 0, а с учетом невырожденности оператора
монодромии (^гГ) (хо) — даже строгое р'(0) > 0.
3. Наконец, если р'(0) < 1 или р'(0) > 1, то при всех
достаточно близких к 0 значениях s выполнены неравенства (215), что
означает, в силу теоремы 185 устойчивость или, соответственно,
неустойчивость предельного цикла Г. ■
Формулу для' вычисления мультипликатора в случае η = 2
дает
Теорема 187. Мультипликатор цикла Г = Т(хо) периода
Τ > 0 автономной системы (180) на плоскости вычисляется
по формуле
263
[Tdiv/(^(x0))di , ,
μ = eJo , div/ = (/ι )Χ1 + (/2)Χ2.
► Пользуясь формулой Лиувилля — Остроградского (см.
теорему 50), получаем
μ = μ0 · μ = det Z(T, 0, x0) =
f tr A(t)dt Γ tr f'( 7* (x0))dt [ div/(7*(xo))dt
= e-Ό = e-Ό = eJo ,
где μο = 1 — не орбитальный мультипликатор системы (213)
(лемма 179). ■
Задачи для самостоятельного решения
1. Могут ли две различные фазовые (соответствующие им
интегральные) кривые векторного поля / € C(G), G С 1", содержащие
точку хо G G (соответственно точку {to,xo) 6lx G):
• пересекаться в этой точке;
• касаться друг друга в этой точке;
• различаться локально вблизи этой точки, если f(xo) = 0 и
существует производная f'(xo)?
Одинаковы ли ответы на эти вопросы:
• при η = 1 и при η > 1;
• для фазовых и интегральных кривых?
2. Чем отличается понятие замкнутости фазовой траектории Е(х)
от понятия периодичности функции х? Является ли понятие
замкнутости траектории формальным отрицанием понятия ее несамопересе-
каемости?
3. Докажите, что если кривая инвариантна для системы (180) в
смысле определения 7.4 и не содержит особых точек ее векторного
поля, то она — фазовая кривая этой системы.
4. Найдите формулу для фазового потока JF1 (t G Μ), задаваемого
линейной системой
х = Ах, xeG = Rn, AeEndR".
5. При каких условиях на параметры ωι, g>2 фигуры Лиссажу (202)
являются:
• замкнутыми,
• всюду плотными в прямоугольнике [—Αι, Α\] χ [—Лг,^]?
6. Можно ли утверждать, что отображение χ в доказательстве
теоремы 164 осуществляет диффеоморфизм области V для интервала
/(0) = R?
264
7. Всегда ли один первый интеграл автономной системы (180)
независим в каждой точке своей области определения? Существует ли
первый интеграл, зависящий от пустого набора первых интегралов в
области?
8. Найдите все первые интегралы:
• одномерного уравнения Ньютона;
• гамильтоновой системы при η = 1.
9. Рассмотрим два решения уравнения (211) колебаний маятника
с трением ρ > 0: одно — входящее (асимптотически) в верхнее
положение равновесия χ = π, другое — исходящее из него. Какое из этих
решений за меньшее время проходит данный фиксированный
отрезок χ € [π + δ; π + ε] для положительных и близких к нулю чисел
ε>δ?
10. Каков биологический смысл правой части системы в модели
Лотки — Вольтерра? Каков биологический механизм периодического
изменения численности хищников и жертв? Можно ли, регулярно
отлавливая карасей, сохранять, тем не менее, в среднем их количество в
пруду?
11. Докажите, что если в некоторой окрестности особой точки
системы (180) существует первый интеграл, принимающий
положительные значения во всех точках, кроме особой (где он равен нулю), то
последняя — устойчива, но не асимптотически.
12. Первый интеграл неавтономной системы (156) — это такая
скалярная функция φ € CX(G) (здесь уже, возможно, зависящая и от
£), что ее сужение на любую интегральную кривую этой системы есть
константа. Сформулируйте и докажите аналоги теорем 169 и 171 для
таких первых интегралов.
13. Как связаны между собой поле направлений уравнения (200)
и векторное поле системы (199)? Докажите, что любой первый
интеграл системы (199) является интегралом уравнения (200) (см.
определение 1.3), и наоборот.
14. Для каждой тройки (а, Ь, с) € М3 определите тип особой точки
системы:
χ = ах + Ьу
У= су,
а, с φ 0;
ас + Ь2 φ 0.
χ = ах — by
у = Ъх + су,
15. Какие типы особых точек на фазовой плоскости для системы
(210):
• допускают первый интеграл, отличный от константы, когда
оператор А невырожден;
• и с какими фазовыми портретами могут получиться, когда
оператор А вырожден?
265
16. Можно ли однозначно определить, устойчива ли данная особая
точка — седло или узел (не дикритический) — линейной системы на
плоскости, на которой нарисованы все ее собственные прямые (в
случае вырожденного узла только одна прямая) и вектор фазовой
скорости в некоторой точке, не лежащей на собственной прямой?
17. Какие типы особых точек может иметь двумерная линейная
система (210), получаемая в результате овеществления одномерного
комплексного линейного уравнения
ζ = λζ (ХеС), СеС1?
18. Две автономные системы, заданные в области G = Мп,
назовем топологически эквивалентными, если существует гомеоморфизм
(т. е. взаимно-однозначное отображение, непрерывное вместе со своим
обратным) φ Rn —> Rn, переводящий все фазовые траектории одной
системы в фазовые траектории другой Докажите, что все линейные
автономные системы на плоскости с особой точкой какого-либо одного
из трех типов:
• седло;
• центр;
• устойчивый фокус или узел (обыкновенный, дикритический или
вырожденный);
• неустойчивый фокус или узел
— топологически эквивалентны, а разных типов — нет.
19. Запишите в полярных координатах систему, рассмотренную в
разделе IV из п. 7.13. Найдите функцию последования и
мультипликатор ее цикла
20. Проследите за бифуркацией цикла (его рождением и
раздвоением) и его устойчивостью при возрастании параметра α € Μ в системе:
г = (г — I)2 — а
φ = 1.
21. Может ли устойчивый цикл на плоскости быть:
• устойчивым по Ляпунову;
• асимптотически устойчивым (по Ляпунову);
• неустойчивым (по Ляпунову)?
Глава 8
УРАВНЕНИЯ В ЧАСТНЫХ
ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА
8.1. Линейное уравнение
в частных производных первого порядка имеет вид1
/ι(χΚ1+... + /η(χΚη=ο, xeGcW1, (216)
в предположении
/Л(*)\
f(x)=[ : Uo, xeG.
\fn(x)J
I. Характеристики линейного уравнения. Решением
уравнения (216) в подобласти G' С G называется такая
функция2 u: G' —> R, что подстановка
и = и(х), χ е G', (217)
превращает это уравнение в тождество
u'(x)f(x) = 0, хе G'.
График любого решения (217) уравнения (216) называется его
интегральной поверхностью.
Для линейного уравнения (216) векторное поле / и
задаваемая им автономная система (180) называются
характеристическими, а их фазовые кривые — характеристиками.
Более точно, это уравнение называется линейным однородным. Если
вместо нуля в правой части уравнения (216) поставить функцию д(х) или
даже д(х,и), то уравнение будет называться линейным неоднородным или,
соответственно, полулинейным
2Дифференцируемая, судя по определению
267
Так как левая часть последнего тождества совпадает с
производной (ι(χ) в силу системы (180), то из определения первого
интеграла с помощью леммы 166 выводится
Следствие 188. Если f Ε CJ(G), то для любой функции
u Ε C^G') следующие утверждения эквивалентны:
• поверхность (217) — интегральная для уравнения (216);
• функция и — решение уравнения (216);
• функция и — первый интеграл системы (180);
• сужение функции и на любую характеристику уравнения
(216) — есть константа.
II. Общее решение. Благодаря теореме 169, уравнение
(216) локально полностью решается нахождением полной
системы независимых первых интегралов его характеристической
системы.
Следствие 18р. Если f Ε C*(G), то для любой точки
хо Ε G существует ее окрестность U(xo) С G и набор из η — 1
решений уравнения (216), от которых в области U(xo)
зависят1 все решения u Ε С1(С/(жо)) этого уравнения и только они.
Более того, согласно лемме 170, любое решение уравнения
(216) локально вблизи любой точки области G зависит и от
произвольного набора из η — 1 независимых (в той же точке) его
решений.
III*. Общий эдщ интегрирующего множителя. Пусть в
односвязной области G С R2 задано уравнение в
дифференциалах
M(x,y)dx + N(x,y)dy = 0, (х, у) е G, M,N e Cl(G).
1. Напомним, что положительная функция μ Ε CJ(G)
называется интегрирующим множителем для этого уравнения, если
эквивалентное ему уравнение
μ(χ, у)М(х, у) dx + μ(ζ, y)N(x, у) dy = 0, (χ, у) G G, (218)
есть уравнение в полных дифференциалах (определение 1.4).
2. Функция μ — интегрирующий множитель тогда и только
тогда, когда она удовлетворяет уравнению
(μ{χ,ν)Μ(χ1ν)),υ = fa(x,y)N(x,y)yx,
Функционально, в смысле определения 7 5
268
или
Ν(χ, ν)μ'χ - Μ (χ, υ)μ'ν = μ (Му(х, у) - Ν'χ(χ, у)). (219)
3. Уравнение (219) переписывается в виде линейного
неоднородного уравнения
Ν(χ, у)и'х - М(х, у)и'у = М'у(х, у) - Ν'χ{χ, у)
для функции и = 1η μ:
• общее решение соответствующего однородного уравнения
N(x,y)u'x-M(x,y)uy=0,
в силу следствия 189, локально (вблизи любой точки (хо,уо) £
£ G) получается взятием произвольной непрерывно
дифференцируемой функции F от некоторого одного его решения (ро,
которое, кстати, является интегралом1 исходного уравнения в
дифференциалах (определение 1.3);
• далее, общее решение неоднородного уравнения
выражается через его частное решение uo = In μο как сумма2
и = u0(x,y) + F(yo(x,y)).
4. Итак, общий интегрирующий множитель уравнения в
дифференциалах локально выражается через его частный
интегрирующий множитель μο и частный интеграл φο как произведение
8.2. Задача Коши
для уравнения в частных производных первого порядка
состоит в нахождении решения уравнения (216), удовлетворяющего
начальному условию
u\s = wo, (220)
с заданной (рис. 43) начальной функцией
щ: S -¥ R
на начальной гиперповерхности S С G.
1 Условие Vcpo(xo,yo) Φ 0 вытекает из независимости в точке (жо,уо)
системы, состоящей всего лишь из одного первого интеграла φο.
2Правило аналогично сформулированному перед теоремой 53.
269
I. Пояснения к начальному условию. По определению,
функция и, заданная в подобласти G' С G, удовлетворяет
начальному условию (220), если подстановка (217) превращает его
в тождество
и(х) = щ(х), xeS' = SnG'.
Будем предполагать, что поверхность S С Мп является
образом некоторой области D С Rn_1 при непрерывно
дифференцируемом отображении
σ: £>-> 5,
задающем на S координаты
ΰ= (ϊ/1, ...,2/η-ι) е D
и имеющем нигде не вырожденную1 производную σ'.
Требование tto G С1 (5), по определению, будем
отождествлять с требованием
(u0oG)eC1{D).
II. Существование и единственность решения.
Справедлива следующая локальная теорема существования и
единственности решения задачи Коши.
Теорема 190. Если f e CX(G), xq = о(уо) Ε S и векторы
σ^0/ο), ••·>σ/?/η_1(?/ο),/(ζο)
(221)
1Последнее означает, например, что векторы а'У1(у), ... ,оУп1(у) при
каждом у € D линейно независимы.
270
*n
У
/ ~г^/г \
f—f-^/ JK °' \ Уо
L—1/ \
*1,
ν{Ψώ
1» φ -
/ ffwoWe,,
ZJ
. ζη-ΐ
S'
ι
D'
е*
А о уп о
Рис. 44. Выпрямление гиперповерхности и характеристик
zn
линейно независимы1, то в некоторой окрестности U(xo) С G
точки xq для любой функции щ Ε С1 (5) существует
единственное решение и задачи Коти (216), (220).
Идея доказательства состоит в последовательном локальном
(вблизи данной точки; рис. 44) выпрямлении:
• начальной гиперповерхности;
• характеристик уравнения,
в результате чего утверждение доказываемой теоремы резко
упрощается.
► 1. Добавим к каждому вектору у Ε D еще одну (n-ю)
координату уп, обозначив
У = (у,Уп) е D С D χ R, S ξ D х {0}, у0 = (у0,0),
и зададим формулой
х = Х(У) = °(У) + 2/п/(я0), У € А
отображение2 χ: D —> Rn, которое:
• удовлетворяет равенству
Х(у,0) = а(у), yeD,
откуда
x(s) = s, хЫ = о(уо) = χο;
1 Иными словами (с учетом линейной независимости первых η — 1
векторов системы (221)), гиперповерхность S в точке хо не касается вектора
/(хо), т.е. трансверсалъна к характеристикам уравнения (216) в точке хо (а
значит, и в целой ее окрестности).
2Для начала можно считать D = D χ №..
271
• непрерывно дифференцируемо, а его производная
Х'Ш = (<>'У1Ы, · · · Чп-! W,/(zo)) (222)
невырождена (в силу линейной независимости системы (221)),
поэтому сужение отображения χ на достаточно малую
окрестность точки 2/о представляет собой диффеоморфизм — сохраним
для него прежнее обозначение
уменьшив для этого, если потребуется, прежние области D и G
(что повлечет за собой и соответствующее уменьшение
поверхностей S и S).
2. Обратное отображение χ-1: G —> D:
• переводит фазовые траектории исходного векторного поля
/ в фазовые траектории нового векторного поля /,
определяемого равенством1 '
f(x) = x'(y)'f(y), z = x(2/)> г/еД
• выпрямляет_гиперповерхность 5, переводя ее в
гиперплощадку χ-1 (5) = 5, задаваемую условием уп = (уо)п = 0> причем
имеет место равенство
/(г/о) = (χ'(г/о))-1 · /(*о) = еп
(из вида последнего» столбца матрицы (222) оператора х'(уо)),
откуда
Urn) Φ ο.
3. Согласно теореме 164, для векторного поля / Ε CX(D)
существует выпрямляющий диффеоморфизм ζ = φ (J/), который:
• переводит некоторую окрестность V(2/o) С Ό точки щ в
прямоугольную окрестность и той же точки, т. е. представимую
для некоторых окрестностей D' С D и /(0) С Ш точек уо и 0,
соответственно, в виде
Ф(У(2/о)) = ТУ х /(0) = D';
1Это — стандартный факт для его доказательства достаточно заметить,
что если фазовая траектория Е(у) поля / переходит в фазовую траекторию
Х(Я(У)) = Щ*) поля /, где х(0) = х, у(0) = у и х = χ(£), то
f{x) = х(0) = (x(y(t))) |*=о = x'(S(0)) · ϋ(Ό) = χ'(у) f(y).
272
• оставляет на месте все точки гиперплоскости
S' = D' χ {0},
включая точку уо = φ (г/о)·
Поэтому сквозной выпрямляющий диффеоморфизм ζ = ψ (χ)
векторного поля /, где обозначено
ψΞΕφοχ-1:^)-^', U(x0) = χ (У (г/о)),
переводит гиперплоскость S' = S Π U(xo) в гиперплоскость S ,
ортогональную к вектору еп нового (постоянного) векторного
поля.
4. В новых (выпрямленных) координатах задача Коши
выглядит так:
u'Zn=0, zeD', и(у,0) = щ(<]>-1(у,0)) = ио(о(у)), у e D''.
Функция и = й(г) — есть решение этой задачи Коши тогда и
только тогда, когда она не зависит от координаты zn и
удовлетворяет равенству
ΰ(ζ) =ΰ(ζι, ...,2η_ι,0) =Μο(σ(2ι, ...,2η_ι)), ζ G ϋ',
однозначно задающему функцию П Ε CX(D ). Поэтому искомая
функция
и(х) = Π(ψ(ζ)), χ G U(xo),
существует и единственна. ■
III. О единственности решений. Глобальная
единственность для решений задачи Коши (216), (220), вообще говоря, не
имеет места. Тем не менее справедливо
Следствие 191. В условиях теоремы 190 любые два
решения задачи Коти локально {вблизи х$) совпадают друг с другом.
► Если ui: U\{xq) —> R и U2: £/2(^0) —>· Η — два решения задачи
Коши, то, уменьшив область G так, чтобы выполнялись условия
' хо eGcUi(x0)nU2(xo),
и применив теорему 190, мы получим, что сужения решений Ui
и U2 на некоторую окрестность точки хо совпадают с тем
решением, существование и единственность которого утверждает
теорема. ■
273
Следом множества Ρ С G на поверхности S назовем
множество p = PC\S.
Следствие 192. В условиях теоремы 190 любое
инвариантное1 для системы (180) в области U(xo) множество Ρ
однозначно задается своим следом на гиперповерхности S.
► В доказательстве теоремы 190 область U{xq) выбрана так, что
каждая характеристика Е(х), χ Ε Sf(U(xo)) пересекает
гиперповерхность S, поэтому вся она либо содержится в инвариантном
множестве Р, либо не содержится, в зависимости от того, имеет
или не имеет она общую точку с множеством р, а значит,
множество Ρ полностью определяется множеством р. Ш
8.3. Квазилинейное уравнение
в частных производных первого порядка имеет вид
/ι(ж, 10*4 + ··· -Η/η(ζ,ιφ4η = g(x,u), (χ,и) е н с Rn+1,
(223)
в предположении
(fi{x,u)\
: I/O, (x,u)€H.
fn(x,u)/
I. Характеристики квазилинейного уравнения.
Решением уравнения (2£3) называется такая скалярная функция и,
определенная в некоторой области GcRn, что подстановка
и = и(х), xeG, (224)
превращает это уравнение в тождество2
u'(x)f(x, u(x)) = g(x, u(x)), xeG. (225)
График любого решения (224) уравнения (223) называется его
интегральной поверхностью.
Характеристиками квазилинейного уравнения (223)
называются фазовые кривые его характеристической системы
* = Л*'М> (х,и)еН. (226)
и = д(х,и),
*См. определение 7.4.
2Из которого видно, что график функции υ должен лежать в области Н.
274
II*. Поверхности уровня первых интегралов.
Следующая лемма утверждает, что в качестве интегральных
поверхностей уравнения (223) заведомо можно брать поверхности уровня
первых интегралов системы (226). Для этой системы все такие
поверхности оказываются инвариантными, а значит,
сотканными из характеристик.
Лемма 193. Если f,g Ε С1 (Я), α φ — первый интеграл
системы (226), определенный в некоторой окрестности Я'сЯ
некоторой точки (хо,щ) и удовлетворяющий условиям
φ(ζ0, щ) = 0, у'и(хо, щ) φ 0, (227)
то для некоторой окрестности U(xo,uo) С Н' точки (х$,щ)
равенство
φ(ζ, и) = 0, (х, и) G U(x0, щ), (228)
задает неявно решение (224) уравнения (223).
► 1. По теореме о неявной функции, в силу условий (227),
равенство (228) в достаточно малой окрестности U(xo,uo) однозначно
задает непрерывно дифференцируемую функцию (224),
удовлетворяющую, без ограничения общности, соотношениям
ф(ж,и(ж))=0, у'и(х,и(х)) /0, x,x0eG. (229)
2. Если φ — первый интеграл системы (226), то в силу леммы
166 и, соответственно, равенства (229) при χ Ε G имеем
О = ф(ж, и) = ψ'χ(χ, и) f(x, и) + cp'Jz, и) д(х, и), и = и(х),
о = -^Ф> и(х)) = Φχ(ζ> Φ)) + <ρύ(*> и(х)) и'(χ),
откуда
а с учетом неравенства (229) получаем тождество (225),
следовательно, и — решение уравнения (223). 'З
III*. Существование интегрирующего множителя.
Характеристики уравнения (219) (задающего интегрирующий
множитель для уравнения в дифференциалах (3)) являются
фазовыми кривыми характеристической системы
χ = N(x, у)
у = -М{х, у) (х, у, μ) G G+ = Gx (0; оо).
μ = μ(Μ^χ,υ)-Κ(χ,υ)),
275
В достаточно малой окрестности любой точки (#ο,2/ο5μο) £ G+
эта система имеет первый интеграл φ, удовлетворяющий
условию
φμ(^ο,2/ο,μο) т^О.
Действительно, если, скажем, N(xo,yo) φ 0, то в силу
теоремы1 190 существует первый интеграл, удовлетворяющий,
например, начальному условию
φ(ζο,2/,μ) = 2/ +μ, (χο,υ,μ) е G+,
поскольку тогда начальная гиперповерхность задается
отображением σ(?/,μ) = (χο,ι/,μ), причем векторы2
о'у = (0,1,0), σ^ = (0,0,1), f = {N,-M,y.{M'y-N'x))
линейно независимы в точке (£ο>2/ο?μο) (так как N(xo,yo) φ 0).
Таким образом, по лемме 193, интегрирующий множитель
локально существует.
<
IV*. Инвариантные поверхности. Утверждение
леммы 193 обратимо в том смысле, что любая интегральная
поверхность уравнения (223) непременно соткана из характеристик.
Лемма 194- Если f,g£ СХ(Я) иие CX(G) — решение
уравнения (223), то поверхность (224) инвариантна для системы
(226) в любой подобласти Я'с(СхМ)ПЯ.
► Действительно, если точка (хо,щ) лежит на поверхности
(224), то на ней заведомо целиком лежит и любая кривая вида
£(x,v) = {(х,и) = (χ(ί),ν(ί)) I t e D(x,v)} С Я',
удовлетворяющая при всех t Ε D(x, v) следующей системе
^χ(ί) = /(χ(ί),υ(χ(ί))), х(«о)=*о,
' ν(ί) = u(x(i)),
ν
равносильной системе
χ(ί) = /(χ(ί),ν(ί)), x(to) = *o,
v(t) = u'(x(t))/(x(t),v(t)) = ^(χ(ί),ν(ί)), v(i0) = u(x(io)) = щ,
*B ней, правда, утверждается существование решения соответствующего
линейного однородного уравнения в частных производных, но это, согласно
следствию 188, то же самое
2Последний образован правой частью рассматриваемой системы.
276
и, стало быть, являющаяся характеристикой уравнения (223),
проходящей через точку (хо,щ). Ш
8.4. Решение задачи Коши
для квазилинейного уравнения (223) с начальным условием
(220) ищется при естественных предположениях:
• график начальной функции tto лежит в области Η;
• как и прежде, начальная поверхность S = o(D) задана
координатами у G D С Rn_1.
I*. Существование и единственность решения.
Справедлива следующая локальная теорема существования и
единственности решения задачи Коши для квазилинейного
уравнения.
Теорема 195. Если f,g е СХ(Я), щ € Сх(5), х0 = о(у0) е 5,
щ = щ(хо) u векторы
σ'νι (ϊ/ο)> · · · > σ/?/η_1 {уо), f(x0, щ) (230)
линейно независимы, то в некоторой окрестности U(xo)
точки хо существует единственное решение и задачи Коши (223),
(220).
► 1. Для линейного однородного уравнения в частных
производных1 с характеристиками, задаваемыми системой (226) с правой
частью / = (/, д), поставим задачу Коши:
• с начальной гиперповерхностью 5, содержащей точку
(хо,щ) и задаваемой отображением
д(у, и) = (а(у), и), (у, u)eDc Rn,
где D — такая окрестность точки (уо,исо), что o(D) С Η (ее
существование обеспечено условием д(уо,щ) = (хо,щ) Ε Н);
• с начальной функцией
йо(х, и) = и - щ(х), (х, и) е S С (S х R) Π Я;
• с линейно независимыми векторами
£'Уг(г/о,ио) = (о'Уг(уо),0), г = 1, ...,п- 1,
о'и(у0, щ) = (0,1) и /(я0, ио) = (/(ж0, г*о), д(х0, щ)),
хСамо уравнение не выписано (см. задачу 2 на с. 281)
277
так как первые η векторов этой системы линейно независимы в
силу условия (230), а последний вектор не может быть их
линейной комбинацией (иначе их линейной комбинацией был бы и
вектор
(/(so, mo), 0) = /fa), uo) - д(хо, г*о)(0,1),
что неверно).
2. В силу теоремы 190 и следствия 188 в некоторой
окрестности U(xo,uo) С Η точки (хо,щ) существует первый интеграл φ
системы (226), удовлетворяющий начальному условию
ср(ж, и) = щ(х, и), (х, и) Ε 5,
и задающий искомое решение и:
• в силу неравенства
у'и(х0,и0) = 1^0,
равенство *
φ(ζ, it) = 0, (χ, и) е U(xo, tto),
согласно лемме1 193, действительно, неявно задает решение и
уравнения (223), определенное в некоторой окрестности U(xq)
точки хо, так как
φ(ζο,ΐίο) =Щ- щ(х0) = 0;
• функция и удовлетворяет начальному условию (220),
поскольку
0 = ср(ж, и(х)) = йо(х, и(х)) = и(х) — щ(х), χ е S Π U(xo).
3. Найденное решение единственно. В самом деле, след
инвариантной (по лемме 167) для системы (226) поверхности и = и(х)
на гиперповерхности S задается равенством
и = щ(х),
а значит, любое решение v: U(xo) —> R задачи Коши, задающее
также инвариантную (по лемме 194) поверхность и = v(x) с тем
Окрестность U(xo,uo), если нужно, уменьшим, но так, чтобы осталось
применимо следствие 192
278
же следом на гиперповерхности 5, в силу следствия 192
совпадает с решением1 и. ■
Из теоремы 195 вытекает2
Следствие 196. В условиях теоремы 195 любые два
решения задачи Коти локально (вблизи хо) совпадают друг с другом.
II. Одномерное поле скоростей свободных частиц.
Решением квазилинейного уравнения Хопфа
и'х + ии'у = О, (х,у,и) GR3, (231)
служит функция двух переменных
и = и(х,у),
совпадающая в каждой точке (ж, у) со скоростью той частицы
из данного потока, которая в момент χ имеет на прямой как раз
координату у. При этом предполагается, что в данном потоке
частицы друг с другом не взаимодействуют, т. е. каждая из них
движется просто по инерции.
1. Для вывода уравнения (231) достаточно рассмотреть
функцию
задающую зависимость координаты произвольной частицы от
времени, заметив, что:
• по определению функции и, скорость этой частицы равна
у'{х) = и{х,у{х));
• тогда ее ускорение равно
у"(х) = их(хМх)) + и'у(х,У(х))у'(х) = и'х{х,у) + и{х,у)иу(х,у);
• тот факт, что все частицы сразу движутся по инерции,
означает, что у каждой такой частицы ускорение равно нулю
и'х(х,у) + и{х,у)и'{х,у) = 0, (ж,у) G М2.
Точнее, та часть графика функции ν, которая находится в
окрестности U(xo,uo), совпадает с графиком решения и, откуда вытекает и полное
совпадение этих графиков, поскольку тем самым функция ν оказывается
однозначно определенной во всех точках χ G U(xo) = £*(v)
2Абсолютно так же, как и следствие 191 — из теоремы 190.
279
2. Характеристики уравнения Хопфа задаются автономной
системой
(х=1
у = и
й = 0,
имеющей следующие два независимых первых интеграла
φι (я, у, it) =u, у2{х,У,и)=у-их.
Поэтому любой ее первый интеграл представляется в виде
у(х,у,и) = F(u,y-ux),
где F — произвольная непрерывно дифференцируемая функция.
3. Задача Коши для уравнения (231), включающая в себя еще
и начальное распределение скоростей частиц
>и(0,у)=и0(у), yeD, (232)
на гиперповерхности а{у) = (0, у) локально вблизи любой точки
(хо,Уо,щ) (где хо = О, щ = щ(уо)) имеет решение, поскольку
векторы о'(уо) = (0,1) и /(хо,уо,щ) = (1,^о) линейно
независимы.
Приведя уравнение для поверхности уровня произвольного
первого интеграла к специальному виду1 у = их + f(u) и
подставив в него начальное условие (при χ = 0)
У = НМу)) <=> f(u) = ио\и),
получим неявное уравнение для искомой функции и = и(х,у):
у = их + Uq (и).
Возможная неразрешимость последнего уравнения
относительно переменной и при достаточно больших значениях χ
связана с тем, что отдельные частицы потока, летя с разными
скоростями, могут догонять друг друга и даже сталкиваться2,
придавая одному и тому же значению у несколько значений и.
Пригодному лишь тогда, когда начальная функция ио обратима (см
полученную ниже формулу для /).
2 Создавая так называемые ударные волны.
280
Задачи для самостоятельного решения
1. Как изменятся характеристики линейного однородного
уравнения (216), если заменить их характеристиками того же уравнения,
рассмотренного как частный случай квазилинейного уравнения (223)?
2. Как выглядит линейное однородное уравнение в частных
производных, характеристики которого задаются системой (226)?
3. Докажите, что к линейному уравнению вида (216) сводится и
линейное уравнение наиболее общего вида
fi(x)u'Xl + · · · + fn{x)u'Xn = g(x)u.
4. Обратимо ли утверждение леммы 193 в прямом смысле, т. е.
задается ли график любого решения квазилинейного уравнения (223)
локально как поверхность уровня некоторого первого интеграла
системы (226)?
5. Сформулируйте и докажите аналогичное следствию 189
утверждение об общем решении уравнения (223).
6. Каков геометрический смысл условия (230) линейной
независимости векторов в формулировке теоремы 195 в терминах
характеристик уравнения (223)?
7. Сохранится ли верной теорема 195, если в ней (как и в
теореме 190) дополнительно утверждать, что окрестность U{xq) можно
выбрать единой для всех начальных функций ΐίο?
8. Можно ли в условиях теоремы 190 или 195 утверждать
дополнительно, что:
• любые два решения задачи Коши совпадают на общей области
определения;
• в любой подобласти U'{xq) С U{xq) решение задачи Коши
единственно?
9. Для уравнения хи'х — уи'у = 0, х, у > 0, найдите все решения
задачи Коши и определите их количество:
• и = χ при у = х\
• и = χ при у = \/х\
• и = 1 при у = 1/х.
10. Найдите решение задачи (231), (232) с каждой из следующих
начальных функций:
• и0{у) = -у; · «о(у) = -у3',
• и0{у) = -arctgy; · u0(y) = -ffi.
Верно ли, что решение и (я, у) определено:
• в целом, т.е. сразу для всех у € R, но хотя бы при достаточно
малых значениях χ > 0 (если да, то найдите их верхнюю грань);
• локально вблизи любой точки (0,уо, щ{уо)) (если нет, то
укажите все начальные точки, ни в какой окрестности которых решение не
определено)?
СПИСОК ЛИТЕРАТУРЫ
Учебники1
1 Айне Э JI. Обыкновенные дифференциальные уравнения. —
Харьков ОНТИ, 1939
2. Арнольд В. И. Обыкновенные дифференциальные уравнения. —
М. Наука, 1984.
3. Бибиков Ю. Н. Общий курс обыкновенных дифференциальных
уравнений — М. · Высшая школа, 1991.
4 Боровских А. В. Лекции по обыкновенным дифференциальным
уравнениям / А. В. Боровских, А. И. Перов. — Ижевск : НИЦ РХД,
2004.
5. Голубев В. В. Лекции по аналитической теории
дифференциальных уравнений. - М.-Л. : ГТТИ, 1950.
6. Еругин Н. П. Книга для чтения по общему курсу
дифференциальных уравнений. — Минск : Наука и техника, 1979.
7. Есипов А. А. Практикум по обыкновенным дифференциальным
уравнениям / А А Есипов, Л. И. Сазонов, В. И. Юдович. — М. :
Вузовская книга, 2001.
8. Зайцев В. Ф. Справочник по обыкновенным дифференциальным
уравнениям / В. Ф. Зайцев, А. Д. Полянин. — М. . Физматлит, 1995.
9. Камке Э. Справочник по обыкновенным дифференциальным
уравнениям. — М. : Наука, 1971.
10. Коддингтон Э. А. Теория обыкновенных дифференциальных
уравнений / Э. А. Коддингтон, Н. Левинсон. — М. : ИЛ, 1958.
11. Краснов М. Л. Сборник задач по обыновенным
дифференциальным уравнениям / М. Л. Краснов, А. И. Киселев, Г. И. Макаренко. —
М. . Высшая школа, 1978.
12. Матвеев Η. Μ. Обыновенные дифференциальные уравнения. —
СПб . Специальная литература, 1996.
13. Матвеев Η. Μ. Сборник задач и упражнений по обыновенным
дифференциальным уравнениям. — Минск : Вышэйшая школа, 1987.
14. Петровский И. Г. Лекции по теории обыкновенных
дифференциальных уравнений / Под ред. А. Д. Мышкиса, О. А. Олейник. — М. :
Изд-во Моек ун-та, 1984.
При составлении этого списка мы ограничились только учебной
литературой по обыкновенным дифференциальным уравнениям, включая
справочники и задачники
282
15. Понтрягин Л. С. Обыкновенные дифференциальные
уравнения. — М. : Наука, 1974.
16. Самойленко А. М. Дифференциальные уравнения: примеры и
задачи / А. М. Самойленко, С. А. Кривошея, Н. А. Перестюк. — М. :
Высшая школа, 1989
17. Сансоне Дою. Обыкновенные дифференциальные уравнения: в
2 т. - Μ .ИЛ, 1953-1954.
18. Степанов В. В. Курс дифференциальных уравнений. — М. :
Физматгиз, 1959.
19. Тихонов А. Н. Дифференциальные уравнения / А.Н.Тихонов,
А.Б.Васильева, А.Г.Свешникова. — М. : Наука, 1998.
20. Трикоми Ф. Дифференциальные уравнения. — М. : ИЛ, 1962.
21 Филиппов А. Ф. Введение в теорию дифференциальных
уравнений. — М. : КомКнига, 2007.
22. Филиппов А. Ф. Сборник задач по дифференциальным
уравнениям. - Ижевск . НИЦ РХД, 2000.
23. Хартман Ф. Обыкновенные дифференциальные уравнения —
М. : Мир, 1970.
Дополнительная литература1
1. Амелъкин В. В. Дифференциальные уравнения в
приложениях. — М. : Наука, 1987.
2. Андрианова Л. Я. Введение в теорию линейных систем
дифференциальных уравнений. — СПб. : СПГУ, 1992.
3. Андронов А. А. Теория колебаний / А.А.Андронов, А. А. Витт,
С. Э. Хайкин. — М. : Физматгиз, 1959.
4. Андронов А. А. Качественная теория динамических систем
второго порядка / А. А. Андронов, Е. В. Леонтович, И. И. Гордон,
A. Г. Майер. — М. : Наука, 1966.
5. Арнольд В. И. Дополнительные главы теории обыкновенных
дифференциальных уравнений. — М. : Наука, 1978.
6. Арнольд В. И. Математические методы классической
механики. — М. : Наука, 1989.
7. Барбашин Е. А. Введение в теорию устойчивости. — М. : Наука,
1967.
8. Беллман Р. Теория устойчивости решений дифференциальных
уравнений. — М. . ИЛ, 1954.
9. Былое Б. Ф. Теория показателей Ляпунова и ее приложения к
вопросам устойчивости / Б.Ф. Былов, Р. Э. Виноград, Д. М. Гробман,
B. В. Немыцкий. — М. : Наука, 1966.
В этом, далеко не полном, списке собраны монографии по различным
областям дифференциальных уравнений и смежным разделам математики,
в том числе и прикладным.
283
10. Васильев Η. И. Основы теории краевых задач обыкновенных
дифференциальных уравнений / Н. И Васильев, Ю. А Клоков. —
Рига : Зинатне, 1978.
11. Васильева А. Б. Асимптотические методы в теории
сингулярных возмущений / А. Б. Васильева, В. Ф. Бутузов, — М. : Высшая
школа, 1990.
12. Гайшун И. В. Введение в теорию нестационарных линейных
систем. — Минск : НАН Беларуси, 1999.
13. Гантмахер Ф. Р. Теория матриц. — М. : Наука, 1989.
14 Гюнтер Η. М. Интегрирование уравнений первого порядка в
частных производных. — М. — Л. : ГИТТЛ, 1934.
15. Далецкий Ю. Л. Устойчивость решений дифференциальных
уравнений в банаховом пространстве / Ю. Л. Далецкий, М. Г. Крейн. —
М. : Наука, 1970.
16. Демидович Б. П. Лекции по математической теории
устойчивости. — М. : Наука, 1967.
17. Еругин Н. П. Линейные системы обыкновенных
дифференциальных уравнений с периодическими и квазипериодическими
коэффициентами. — Минск j АН БССР, 1963.
18. Ибрагимов Н.ХХ. Опыт группового анализа обыкновенных
дифференциальных уравнений. — М. : Знание, 1991.
19. Изобов И. А. Введение в теорию показателей Ляпунова. —
Минск : БГУ, 2006
20. Илъяшенко Ю. С. Нелокальные бифуркации / Ю. С. Ильяшен-
ко, В. Ли. - М. : МЦНМО, 2009.
21. Картан Э. Внешние дифференциальные системы и их
геометрические приложения. — М. : МГУ, 1962.
22. Карташев А. П. Обыкновенные дифференциальные уравнения
и основы вариационного исчисления / А. П. Карташев, Б. Л.
Рождественский. — М. : Наука, 1979.
23. Каток А. Б. Введение в современную теорию динамических
систем / А. Б. Каток, Б. Хасселблат. — М. : МЦНМО, 2005.
24. Кигурадзе И. Т. Некоторые сингулярные краевые задачи для
обыкновенных дифференциальных уравнений. — Тбилиси : ТГУ, 1975.
25. Красносельский М. А. Оператор сдвига по траекториям
дифференциальных уравнений. — М. : Наука, 1966.
26 Козлов В. В. Методы качественного анализа в динамике
твердого тела. — Ижевск : НИЦ РХД, 2000.
27. Левитан Б. В. Почти-периодические функции и
дифференциальные уравнения // Б. В. Левитан, В. В. Жиков. — М. : Изд-во Моск.
ун-та, 1978.
28. Ляпунов A.M. Общая задача об устойчивости движения. —
М.-Л : ГИТТЛ, 1950.
29. Малкин И. Г. Теория устойчивости движения. — М. : Наука,
1966.
284
30. Мищенко Ε. Φ. Дифференциальные уравнения с малым
параметром при старшей производной / Е. Ф. Мищенко, Н. X. Розов. — М. :
Наука, 1975
31. Мищенко Ε. Φ. Периодические движения и
бифуркационные процессы в сингулярно возмущенных системах / Ε Φ. Мищенко,
Ю. С. Колесов, А.Ю. Колесов, Н.Х.Розов. — М. : Физматлит, 1995.
32. Мышкис А. Д. Линейные дифференциальные уравнения с
запаздывающим аргументом. — М. : Наука, 1972.
33. Немыцкий В. В. Качественная теория дифференциальных
уравнений / В. В.Немыцкий, В.В.Степанов. - М.-Л. : ГТТИ, 1949.
34. Овсянников JI. В. Групповой анализ дифференциальных
уравнений. — М. : Наука, 1978.
35. Олвер П. Приложения групп Ли к дифференциальным
уравнениям. — М. : Мир, 1989.
36. Плисе В. А. Интегральные множества периодических систем
дифференциальных уравнений. — М. : Наука, 1977.
37. Пуанкаре А. О кривых, определяемых дифференциальными
уравнениями. - М.-Л. : ГИТТЛ, 1947
38. Румянцев В. В. Устойчивость и стабилизация движения по
отношению к части переменных / В. В. Румянцев, А. С. Озиранер. — М. :
Наука, 1987.
39. Сибирский К. С. Введение в топологическую динамику. —
Кишинев : АН МССР, 1970.
40. Филиппов А. Ф. Дифференциальные уравнения с разрывной
правой частью. — М. · Наука, 1985.
41. Чезаре Л. Асимптотическое поведение и устойчивость
обыкновенных дифференциальных уравнений. — М. : Мир, 1964.
42. Четаев Н. Г. Устойчивость движения. — М. : Наука, 1965.
43. Элъсголъц Л. Э. Дифференциальные уравнения и вариационное
исчисление. — М. : Эдиториал УРСС, 2000.
44. Якубович В. А. Линейные дифференциальные уравнения с
периодическими коэффициентами / В. А. Якубович, В. М. Старжин-
ский. — М. : Наука, 1972.