Η.Α.ΓΛΑΓΟΛΕΒ
ЭЛЕМЕНТАРНАЯ
ГЕОМЕТРИЯ
СТЕРЕОМЕТРИЯ
УЧПЕДГИЗ -МОСКВА-1948

Η. Α. ГЛАГОЛЕВ
ЭЛЕМЕНТАРНАЯ
ГЕОМЕТРИЯ
ЧАСТЬ II
Стереометрия
ДЛЯ IX—X КЛАССОВ
СРЕДНЕЙ ШКОЛЫ
Издание второе
ПОД РЕДАКЦИЕЙ Д. И. ПЕРЕПЁЛКИНА
ГОСУДАРСТВЕННОЕ
УЧЕБНО-ПЕДАГОГИЧЕСКОЕ ИЗДАТЕЛЬСТВО
МИНИСТЕРСТВА ПРОСВЕЩЕНИЯ РСФСР
МОСКВА 1948

Утверждено
Министром просвещения РСФСР
к переизданию 1 октября 1947 г., протокол Μ 321
Редактор А. В. Зансохов. Техн. редактор-В. В. Соколовская.
Подписано к печати 24/Ш 1948г. А 01970. Печатных листов 9%.
Учетно-изд. л. 9,28. Заказ №7710.
Отпечатано в тип. Н-23 с матриц 1-й Образцовой тип. треста
«Полиграфкнига» Огиза при Совете Министров СССР.
Москва, Валовая, 28.

ВВЕДЕНИЕ.
ИЗОБРАЖЕНИЕ ПРОСТРАНСТВЕННЫХ ФИГУР
НА ПЛОСКОСТИ.
§ 1. Общие замечания.
В стереометрии изучаются свойства таких геометрических
фигур, не все точки которых лежат на одной плоскости. Они
называются пространственными фигурами. Примерами их
служат геометрические тела. Чтобы облегчить себе представление
действительного вида пространственной фигуры, обычно
пользуются рисунками, изготовленными так, чтобы они производили
на глаз приблизительно такое же впечатление, как и сама фигура.
Но так как пространственная фигура не может полностью быть
помещена на плоскости, то этот рисунок содержит неизбежные
искажения формы и размеров отдельных частей фигуры. Так, две
точки, в действительности весьма далёкие одна от другой, на
рисунке могут оказаться очень близкими. Учащиеся сами могут
легко заметить это на различных картинах, фотоснимках и т. д.
Такие рисунки вполне пригодны длх общего созерцания фигуры,
но замечать на них геометрические свойства фигур весьма трудно.
Поэтому рисунки, которыми пользуются при изучении
пространственных фигур, выполняются по указанному ниже способу.
§ 2. Параллельное проектирование пространственных фигур.
Предположим, что мы имеем проволочный каркас куба.
Поместив его перед доской, освещенной солнцем, мы заметим,
что каркас даёт на доске тень. Эта тень может служить
изображением куба на плоскости. Лучи солнца, ввиду дальности
их источника, можно считать параллельными. А потому эта тень
называется параллельной проекцией куба, а самый способ её
получения — параллельным проектированием. Рассматривая
полученное таким образом изображение, легко подметить
следующее;
3

1. Параллельные и равные отрезки, например параллельные
рёбра куба, изображаются параллельными и равными отрезками.
2. Если какой-либо отрезок, например ребро куба, разделить
на две части в отношении т:п, то они изобразятся отрезками,
также находящимися в отношении т:п.
Эти правила и соблюдают обычно при изображении
пространственных фигур на плоскости. Полученные таким путём
изображения соответствуют действительному виду фигуры, если смотреть
на неё с очеиь большого расстояния.
ГЛАВА ПЕРВАЯ.
ПРЯМЫЕ И ПЛОСКОСТИ.
I. ОБЩИЕ ПОЛОЖЕНИЯ О ВЗАИМНОМ РАСПОЛОЖЕНИИ
ПРЯМЫХ И ПЛОСКОСТЕЙ.
§ 3. Изображение плоскости на чертеже.
Многие предметы, поверхность которых близка к
геометрической плоскости, имеют форму прямоугольника. Таковы,
например, оконное стекло,
поверхность письменного
стола и т. п. При
параллельном проектировании
прямоугольника по способу,
описанному выше (§ 2), на
чертеже получается парал-
лелограм. Поэтому обычно
плоскость на чертеже
изображают в виде паралле-
лограма. Этот параллелограм обычно обозначается одной
буквой, например „плоскость Ми (черт. 1). Иногда для большей
наглядности одну из сторон параллелограма (или даже две)
заменяют кривой линией.
§ 4. Основные свойства плоскости.
Аксиомы: 1. Через всякие три тонки, не лежащие
на одной прямой, можно провести плоскость, и
притом только одну.
2. Если две плоскости имеют общую точку, то они
пересекаются по прямой, проходящей через эту точку.
4

3. Если две тонки прямой линии лежат на
плоскости, то и все точки этой прямой лежат на той
же плоскости (короче, вся прямая лежит на той же
плоскости).
Следствие 1. Через прямую и точку вне её можно
провести плоскость, и притом только одну.
В самом деле, какие-либо две точки данной прямой вместе
с данной точкой составляют три точки, не лежащие на одной
прямой. В силу аксиомы 1 через них проходит единственная
плоскость, а в силу аксиомы 3 данная прямая лежит в этой плоскости.
Следствие 2. Через две пересекающиеся прямые можно
провести плоскость, и притом только одну.
В самом деле, если взять на каждой из прямых по одной
точке, отличной от точки пересечения прямых, то они вместе
с этой точкой пересечения составят три точки, не лежащие на
одной прямой. Через них проходит единственная плоскость
(акс. 1·), на которой лежат обе данные прямые (акс. 3).
Следствие 3. Через две параллельные прямые можно
провести плоскость (и только одну).
Действительно, параллельные прямые, по определению, лежат
в одной плоскости; эта плоскость единственная, так как через
одну из параллельных и какую-нибудь точку другой можно
провести только одну плоскость (след. 1).
§ 5. Вращение плоскости вокруг прямой.
Через каждую прямую можно провести бесчисленное
множество плоскостей. В самом деле, пусть дана прямая а (черт. 2).
Возьмём какую-нибудь точку А вне её. Через
точку А и прямую а проходит единственная
плоскость (§ 4). Назовём её плоскостью М.
Возьмём новую точку В вне плоскости М. Через
точку В и прямую а в свою очередь проходит
плоскость. Назовём её плоскостью N. Она не
может совпадать с Ж, так как в ней лежит точка
Ву которая не принадлежит плоскости Ж. Мы
можем далее взять ещё новую точку С вне
плоскостей Μ и N. Через точку С и прямую а
проходит новая плоскость. Назовём её Р. Она
не совпадает ни с Ж, ни с Л/, так как в ней
находится точка С, не принадлежащая ни
плоскости /И, ни плоскости N. Продолжая брать всё
новые точки, мы будем таким путём получать всё новые
плоскости, проходящие через данную прямую а. Таких плоскостей,
5

очевидно, можно получить бесчисленное множество.
Их можно рассматривать как различные положения одной и той
же плоскости, которая вращается вокруг прямой а.
Мы можем, таким образом, отметить ещё одно свойство
плоскости: плоскость может вращаться вокруг всякой прямой,
лежащей на этой плоскости.
§ 6. Возможные взаимные положения прямых и плоскостей.
Из предыдущего следует, что две прямые линии могут:
1. Пересекаться, тогда они лежат в одной плоскости.
2. Быть параллельными, тогда они также лежат в одной
плоскости.
3. Не пересекаться и не быть параллельными. Таковы,
например, два неограниченно продолженные не параллельные ребра
куба, лежащие в разных гранях (ЛВ
и ЕН, черт. 3).
Такие прямые называются
скрещивающимися.
Прямая и плоскость могут иметь
одну общую точку, тогда прямая
пресекается с плоскостью. Прямая,
не лежащая в плоскости, может
пересекаться с нею не более чем в
одной точке. Точка пересечения
прямой с плоскостью называется следом
этой прямой на плоскости.
Если прямая и плоскость не имеют
ни одной общей точки, то они называются параллельными.
Возможность такого положения прямой и плоскости будет далее
доказана (§ 11). Две плоскости могут пересекаться по прямой,
и тогда они не имеют других общих точек вне этой прямой
(§ 4, акс. 1).
Если две плоскости вовсе не имеют общих точек, то они
называются параллельными. Возможность такого положения двух
плоскостей будет далее доказана (§ 14).
Черт. 3.
II. ЗАДАЧИ НА ПОСТРОЕНИЕ ПРОСТРАНСТВЕННЫХ
ФИГУР.
§ 7. Постановка задач на построение.
Все построения, которые делались в планиметрии, выполнялись
в одной плоскости при помощи чертёжных инструментов.
6

Для построения пространственных фигур чертёжных
инструментов становится уже недостаточно, так как вычерчивать
пространственные фигуры на одной плоскости невозможно. Кроме
того, при построениях пространственных фигур появляется ещё
новый элемент — плоскость, построение которой нельзя выполнять
столь простыми средствами.
Поэтому при построении пространственных фигур необходимо
точно определить, что значит выполнить то или иное
построение и, в частности, что значит построить плоскость.
Во всём дальнейшем мы будем считать, что:
1) плоскость построена, если найдены элементы,
определяющие её положение (§ 4), т. е. что мы умеем построить
плоскость, проходящую через три данные точки, через прямую и
точку вне её, через две пересекающиеся или две параллельные
прямые;
2) если даны две пересекающиеся плоскости, то дана и
линия их пересечения;
3) если дана плоскость, то мы можем выполнять на ней все
построения, которые делались в планиметрии.
В дальнейшем мы будем считать, что выполнить
построение в пространстве — значит свести его к конечному числу трёх
основных построений:
1) проведение плоскости через три данные точки;
2) нахождение линии пересечения двух плоскостей;
3) выполнение с помощью циркуля и линейки построений в
данной или построенной плоскости.
Рассмотрим несколько примеров.
§8.
Задача 1. Построить точку пересечения данной прямой
а с данной плоскостью Ρ (черт. 4).
Решение. Возьмём на плоскости Ρ какую-либо точку Л.
Через точку А и прямую а
проводим плоскость Q. Она
пересекает плоскость Ρ по
некоторой прямой Ь. В
плоскости Q находим точку С
пересечения прямых а и Ь. Эта
точка и будет искомой. Если
прямые а и b окажутся
параллельными, то задача не
будет иметь решения. Черт. 4.

§9.
Задача 2. Через данную точку А вне данной прямой
а провести прямую, параллельную прямой а.
Решение. Через прямую а и точку А проводим плоскость
Жив этой плоскости через точку А проводим прямую,
параллельную прямой а.
Задача имеет только одно решение. В самом деле, по
определению параллельных прямых (Планиметрия, § 36) прямая,
параллельная а, должна лежать с нею в одной плоскости. В этой
же плоскости должна лежать и точка Л, через которую
проходит искомая прямая. Но через прямую а и точку А проходит
лишь одна плоскость, — это плоскость Ж. Значит, искомая
прямая должна лежать в плоскости Ж. А в силу аксиомы о
параллельных прямых, в плоскости Ж через точку А проходит только
одна прямая, параллельная данной прямой а.
§ Ю.
Задача 3. Через данную точку А провести прямую,
пересекающую две данные скрещивающиеся прямые а и Ь>
не проходящие через А.
Решение. Так как искомая прямая должна проходить
через точку А (черт. 5) и пересекать прямую а, то она лежит
в плоскости Ж, проходящей через прямую а и точку А (так как
две её точки: точка А и точка пересечения с прямой а, должны
лежать в плоскости Ж). Она лежит также и в плоскости Ny
проходящей через точку А и прямую Ь. Значит, она служит линией
пересечения плоскостей Ж
и N. Отсюда такое
построение: через точку А
и прямую а проводим
плоскость Ж, через точку А
и прямую b проводим
плоскость N. Прямая
пересечения плоскостей Ж
и N будет искомой,
если только она не
окажется параллельной
прямой а или прямой Ь.
В этом последнем
случае задача не имеет
Черт. 5. решения.
8

III. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ И ПЛОСКОСТИ.
§11. Условие параллельности прямой и плоскости.
Черт. 6.
Теорема. Если прямая параллельна какой-либо
линии на плоскости, то она пареллельна и самой
плоскости.
Дано: прямая а на плоскости Μ и прямая Ь || а. Требуется
доказать, что Ь\\М (черт. 6). Прямые а и Ьу как параллельные,
лежат в одной плоскости N.
Плоскости Μ и N
пересекаются по прямой а. Если
бы прямая b пересекла
плоскость /И, то она пересекла
бы и прямую а, что
невозможно, так как а || Ь.
Следовательно, b || Μ.
Теорема обратная.
Если прямая и
плоскость параллельны, то всякая плоскость, проходящая
через данную прямую и не параллельная данной
плоскости, пересекает эту плоскость по прямой,
параллельной данной.
Дана прямая Ьу параллельная плоскости Μ (черт. 6), и
плоскость /V, проходящая через b и пересекающая Μ по прямой а.
Требуется доказать, что а || Ь. Если бы α и b не были
параллельны, то они пересеклись бы, так как они лежат в одной
плоскости N. Если бы b пересекла а, то
в этой точке b пересеклась бы с
плоскостью Му в которой лежит а, что
невозможно, так как Ь\\М. Следовательно,
а\\Ь.
§ 12. Плоскости, проходящие через
параллельные прямые.
Теорема. Две непараллельные
плоскости, проходящие через две
параллельные прямые,
пересекаются по прямой, параллельной
этим прямым.
Дано: а\\Ь (черт. 7); Μ и N непарал-
проходящие через а и Ь; с — линия их
Черт. 7.
лельные плоскости,
пересечения.
Требуется доказать, что с\\а и с\\Ь

Так как a\\b> а Улежит на N, то a\\N, но если a||iV, то
плоскость Му проходящая "через а, пересекает N по линии,
параллельной а (§ 11). Следовательно, с\\а. Так же докажем, что с\\'Ь,
§ 13. Две прямые, параллельные третьей.
Теорема. Две прямые, параллельные третьей,
параллельны между собою.
Дано: а\\Ь и а\\с. Требуется доказать, что Ь\\с (черт. 8).
Возьмём на с произвольную точку Ρ и проведём две
плоскости: плоскость Μ через а и Ρ и плоскость Л/ через Ъ и Р.
Эти плоскости проходят через параллельные прямые а и b и по-
Черт. 8. Черт. 9.
тому пересекаются по прямой, параллельной обеим этим прямым.
Но через точку Ρ проходит единственная прямая, параллельная
а; это — прямая с. Значит, она и будет линией пересечения
плоскостей Μ и N и потому будет параллельна как прямой а,
так и прямой Ь.
§ 14. Параллельные плоскости.
Теорема. Плоскость, проходящая через две
пересекающиеся прямые, параллельные данной плоскости,
параллельна той же плоскости.
Дано: а\\М и Ь\\М. N проходит через а и Ь.
Требуется доказать, что Ν\\Μ (черт. 9).
Если бы плоскость N пересекла плоскость Ж, то линия их
пересечения была бы параллельна и прямой а и прямой Ъ (§ 11).
Следовательно, прямые а и Ъ были бы параллельны между собою
(§ 13), что противоречит условию. Значит, Ν\\Μ.
Примечание. Эта теорема доказывает существование
параллельных плоскостей.
10

Следствие. Если две пересекающиеся прямые, лежащие
на одной плоскости, соответственно параллельны двум
прямым, лежащим на другой плоскости, то данные плоскости
параллельны (§ И).
Теорема. Две параллельные плоскости
пересекаются третьей плоскостью по линиям
параллельным.
Даны две параллельные плоскости Μ и Л/, пересечённые
третьей плоскостью Р, соответственно, по прямым тип (черт. 10).
Требуется доказать, что т\\п.
•Прямые тип лежат в одной плоскости Ρ и не
пересекаются. В самом деле, если бы они пересекались, то точка их
встречи была бы и точкой встречи плоскостей Μ и Л/, что
невозможно, так как Λί\\Ν. Следовательно, т\\п.
§ 15. Отрезки прямых между параллельными плоскостями.
Теорема. Отрезки параллельных прямых,
заключённые между параллельными плоскостями,
равны.
Черт. 10. Черт. 11.
Даны параллельные плоскости Μ и N и параллельные
прямые АВ и CD (черт. 11). Требуется доказать, что АВ =
=CD.
Через параллельные прямые АВ и CD проведём плоскость Р.
Она пересечёт Μ и Л/ по параллельным прямым АС и BD
(§ 14). Отрезки АВ и CD составляют противоположные стороны
параллелограма ACDB, а потому AB = CD.
И

Теорема. Отрезки двух произвольных прямых,
заключённые между тремя параллельными плоскостями,
пропорциональны.
Даны три
параллельные плоскости Μ, Ν и Р,
пересекающие две прямые
АС и DF соответственно
в точках Л, Ву С и D, Е,
F (черт. 12).
Требуется доказать,
АВ DE
ЧТ0 BC = ~EF'
Проведём прямую
AH\\DF.
Тогда DE = AG и
EF=GH (по
предыдущей теореме).
Проведя плоскость
через прямые АС и АН,
получим треугольник АСНУ
в котором BG\\CH (§ 14).
Следовательно,
АВ_ AG
BC~GH'
Черт. 12.
А так как AG = DE и GH = EF, то
A8_DE
§ 16. Углы с параллельными сторонами.
Теорема. Два
угла с параллель-
ными и
одинаково направленными
сторонами равны.
Даны углы ABC и
DEF (черт. 13),
лежащие соответственно в
плоскостях Μ и Ν,
причём лучи ВА и ED
параллельны и
направлены в одну сторону,
лучи ВС и EF
параллельны и также
направлены в одну сторону.
12
Черт. 13.

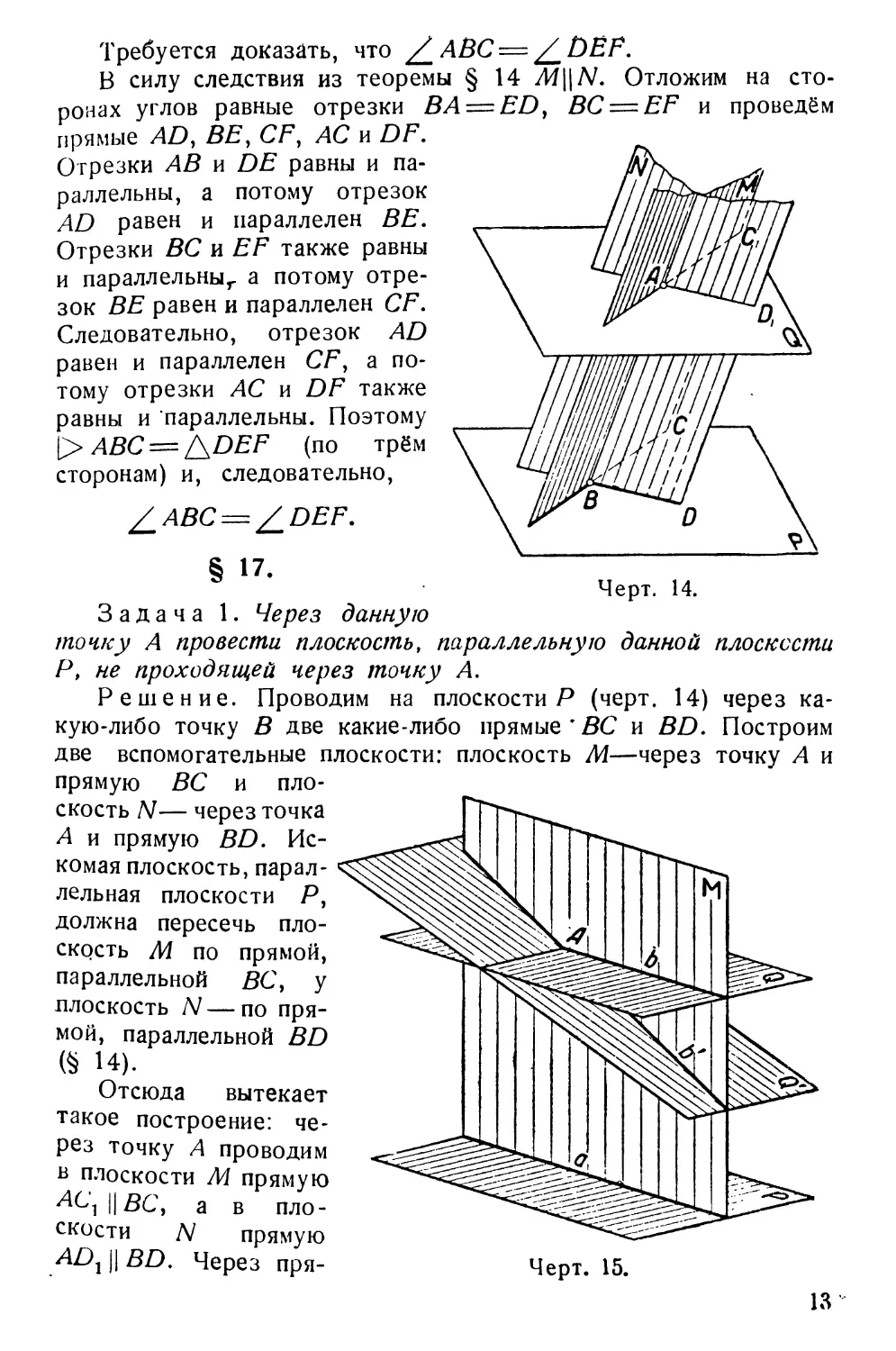
Требуется доказать, что / ЛВС== / DEF.
В силу следствия из теоремы § 14 M\\N. Отложим на
сторонах углов равные отрезки BA = ED, BC = EF и проведём
прямые AD, BE, CF, АС и DF.
Отрезки АВ и DE равны и
параллельны, а потому отрезок
AD равен и параллелен BE,
Отрезки ВС и EF также равны
и параллельны,, а потому
отрезок BE равен и параллелен CF.
Следовательно, отрезок AD
равен и параллелен CF, а
потому отрезки АС и DF также
равны и параллельны. Поэтому
[> ЛЯС = ДЛ^/7 (по трём
сторонам) и, следовательно,
/_ABC = ^DEF.
§ 17.
Черт. 14.
Задача 1. Через данную
точку А провести плоскость, параллельную данной плоскости
Р, не проходящей через точку А.
Решение. Проводим на плоскости Ρ (черт. 14) через
какую-либо точку В две какие-либо прямые ВС и BD. Построим
две вспомогательные плоскости: плоскость Μ—через точку А и
прямую ВС и
плоскость N— через точка
А и прямую BD.
Искомая плоскость,
параллельная плоскости Р,
должна пересечь
плоскость Μ по прямой,
параллельной ВС, у
плоскость N—по
прямой, параллельной BD
(§ И).
Отсюда вытекает
такое построение:
через точку А проводим
ь плоскости Μ прямую
^! || ВС, а в
плоскости Λ/ прямую
ЛОг || BD. Через пря- Черт. 15.
13

мые АСХ и ADX проводим плоскость Q. Она и будет
искомой.
Задача имеет только одно решение. В самом деле,
предположим, что через точку А проходят две плоскости Q и Q\ обе
параллельные плоскости Ρ
(черт. 15). Проведём тогда
через А какую-либо
плоскость Ж, пересекающую Ρ по
какой-либо прямой а. Эта
плоскость пересечёт
плоскости Q и Q'
соответственно по прямым b и Ь\
Черт. 1G. которые обе должны быть
параллельны прямой а (§ 14),
что невозможно, так как через точку А в плоскости Μ проходит
лишь одна прямая, параллельная прямой а.
Задача 2. Через данную прямую а (черт. 16) провести
плоскость, параллельную другой данной прямой Ь.
Решение. Если прямые а и Ь скрещиваются, то через какую-,
нибудь точку А прямой а проводим прямую Ъ', параллельную Ь\
через прямые а и Ь' проводим плоскость. Она и будет искомой
(§ 11). Задача имеет в этом случае единственное решение.
Если прямые aw Ъ параллельны, то задача будет
неопределённой: всякая плоскость, проходящая через прямую а, будет
параллельна Ъ (конечно, кроме той, которая проходит через а и Ь).
Наконец, если прямые а и Ъ пересекаются, то задача не
имеет решения.
IV. ПАРАЛЛЕЛЬНОЕ СМЕЩЕНИЕ.
§ 18. Смещение точек.
Если взять какие-либо две точки А и А' (черт. 17), то их
можно рассматривать как два различных положения одной точки,
переместившейся из одного места в другое, например, из А,
в А'. Такое смещение можно представить
себе совершённым по прямой АА'. Длина
отрезка АА' называется величиною
смещения точки Л, а направление прямой
АА* от точки А к точке А' называется
направлением смещения. Для указания
направления смещения при конце отрезка Черт. 17.
АА' ставится стрелка. Отрезок,
определяющий величину и направление смещения точки,
называется вектором смещения этой точки. Он обозначается двумя
14

буквами со стрелкой над ними, например А4\ Чтобы указать,
какому смещению подвергается точка, достаточно задать вектор
этого смещения; этот вектор можно задать в стороне от самой
точки. Так, чтобы подвергнуть точку С смещению, указанному
вектором АВ, достаточно провести через С прямую,
параллельную АВ, и отложить на ней отрезок СС, равный АВ и
одинаково с ним направленный (черт. 18).
Если вектор смещения точки С задан в стороне от этой
точки, то принято говорить, что точка С смещается, следуя
вектору АВ.
Теорема. Если две точки сместить, следуя одному
и тому owe вектору, то расстояние между ними не
изменится.
Даны: вектор смещения MN (черт. 19), две точки А и В и
их положения А' и В' после смещения. Требуется доказать, что
А'В' = АВ.
Черт. 18.
Черт. 19.
Так как MN — вектор смещения точки А, то AA'\\MN,
AA=MN. А так как MN есть вектор смещения точки В, то
BB'\\MN, и BB'=MN. Следовательно, АА'\\ВВ' и АА' = ВВ'.
Прямые АА' и ВВ', как параллельные прямые, лежат в одной
плоскости и так как АА и ВВ' равны и параллельны, то
четырёхугольник ААВВ* — параллелограм, а потому А'В' = АВ.
§19. Параллельное смещение пространственных фигур.
Если все точки какой-либо пространственной фигуры сместить,
следуя одному и тому же век.ору, то все полученные таким
образом точки образуют новую фигуру, в которой расстояние
между двумя любыми её точками равно расстоянию между двумя
соответствующими точками старой фигуры. Поэтому смещение
всех точек данной фигуры, следуя одному и тому же вектору,
можно рассматривать как смещение всей фигуры как одного
целого, следуя тому же вектору.
15

При таком смещении пространственной фигуры все её точки
описывают равные и параллельные отрезки. А потому такое
смещение называется параллельным смещением данной фигуры.
Параллельное смещение есть простейший вид перемещения
пространственных фигур, его можно
постоянно наблюдать в обыденной
жизни. На черт. 20 представлено
параллельное смещение треугольной
пластинки ЛВС.
Примечание. Так как вектор
параллельного смещения тела можно
задавать в стороне от этого тела, то
все векторы, определяющие различные
параллельные смещения, можно
представлять себе исходящими из одной
точки, т. е. имеющими общее
начало.
§ 20. Сложение параллельных смещений.
Допустим, что нам дано какое-либо тело F и два вектора
смещения АВ и АС.
Сместим параллельно тело F, сначала следуя первому
вектору АВ. Оно займёт новое положение F'. После этого сместим
его вновь параллельно, следуя второму вектору АС. Оно
займёт новое положение F". Нетрудно убедиться, что такое
последовательное выполнение двух параллельных смещений одно за
другим равносильно одному параллельному смещению тела из
положения F в F". В самом деле, построим параллелограм ABDC,
двумя сторонами которого служили бы данные векторы АВ и
АС. (Построить чертёж.) Возьмём теперь какую-либо точку Μ
тела F. После первого смещения (следуя вектору АВ) она
займёт положение М\ а после второго — точка М' переместится
в М". Соединим Μ с Ж", А с /И, В с М\ D с М".
Так как АВ\\ММ и АВ = ММ\ то AM || ВМ! и АМ=ВМ\
Так как BD \\ М'М" и BD=MM\ то ВМ \\ DM" и
BM' = DM".
А потому AM || DM" и AM = DM", следовательно, AD || MM"
и AD = MM". Значит, точка Μ перемещается в Μ", следуя
вектору AD. То же самое справедливо и для всех других точек
тела. Но смещение всех точек тела, следуя одному и тому же
вектору, составит параллельное смещение всего тела. Значит,
последовательное выполнение двух параллельных смещений гела
F, сначала следуя вектору АВ, затем следуя вектору АС, рав-
16

посильно одному параллельному смещению этого тела, следуя
вектору AD. Последовательное выполнение двух данных
параллельных смещений называется сложением двух смещений, а
получаемое в результате параллельное смещение называется суммой
двух смещений.
Вектор смещения AD называется суммой векторов АВ и
АС. Он служит диагональю параллелограмма ABDC со сторонами
АВ и АС. Отсюда следует, что векторы параллельных смещений
тела складываются по тому же правилу, как силы и скорости в
физике. Из предыдущих построений вытекает теорема:
Сумма двух параллельных смещений есть третье
параллельное смещение, вектор которого есть сумма
векторов данных смещений.
V. ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ И ПЛОСКОСТИ.
§ 21.
Теорема. Если прямая перпендикулярна к двум
прямым на плоскости, проведённым через её след, то
она перпендикулярна ко всякой прямой, лежащей на
этой плоскости и
проходящей через её след.
Дана прямая АВ,
перпендикулярная к прямым
ВС и BD, лежащим на
плоскости М. Требуется
доказать, что АВ
перпендикулярна ко всякой
прямой BE, лежащей на
плоскости Μ и
проходящей через след В
прямой АВ (черт. 21).
Отложим на прямой АВ по обе стороны от точки В равные
отрезки AB = BF, а на прямых ВС и BD какие-либо отрезки
ВС и BD. Проведём прямую CD, пересекающую BE в какой-
либо точке Е. Далее, соединим точки С, D и Ε с точками А и
F. Рассмотрим полученные треугольники.
Д ACD = £sFCD,
так как DC их общая сторона, AC = FCy как наклонные
к прямой AFy равноудалённые от основания В перпендикуляра
ВС, и также AD = FD.
17

Следовательно,
/mACD = /mFCD.
Далее,
Δ АСЕ = Д FCE
по двум сторонам и углу между ними; следовательно,
AE=FE.
Наконец,
/\ABE = /\FBE
по трём сторонам; следовательно,
/_АВЕ = /ЕВЕ\
а так как эти углы смежные, то они прямые.
§ 22. Прямая, перпендикулярная к плоскости.
Прямая называется перпендикулярной к плоскости, если она
перпендикулярна к каждой прямой, лежащей на этой плоскости и
проходящей через её след. Из предыдущего следует, что
прямая будет перпендикулярна к плоскости, если она
перпендикулярна двум пересекающимся прямым, лежащим на этой
плоскости.
Если через точку А вне плоскости Μ провести прямую ЛВУ
перпендикулярную к Ж, то её след В называется проекцией
точки А на плоскость Ж, а длина отрезка АВ — длиной
перпендикуляра, проведённого из точки А к плоскости М. Прямая АС,
не параллельная и не перпендикулярная к плоскости, называется
наклонной. Её след С на плоскости Μ называется основанием
наклонной. Отрезок ВС прямой, соединяющей основание
перпендикуляра с основанием наклонной, называется проекцией
наклонной.
§ 23. Перпендикуляр и наклонные к плоскости.
Теорема. Если из тонки вне плоскости провести
к ней перпендикуляр и наклонные, то:
/. Перпендикуляр короне всякой наклонной.
2. Те из наклонных равны, которые имеют равные
проекции.
3. Из двух неравных наклонных больше та,
которая имеет большую проекцию.
18

Черт. 22.
1. Дана точка А вне плоскости Ж, АВ— перпендикуляр
к Μ (черт. 22). АС—наклонная, ВС—проекция наклонной.
Так как АВ ±_МУ то
Д ABC— прямоугольный,
причём АС—его
гипотенуза, АВ — катет, а
потому АС^>АВ.
2. Дано BC=BD.
Прямоугольные
треугольники ABC и ABD равны
(по двум катетам), след о-с—
вательно, AC = AD.
3. Дано BC^>BD.
Требуется доказать, что AC^>AD. Отложим на ВС отрезок
BE — DB и соединим точки А и Е. По только что
доказанному AE = AD. В треугольнике АЕС угол АЕС тупой (так как
угол АЕВ острый) и^потому АС^> АЕ. Следовательно, АС^> AD.
Теорема обратная. Если из тонки вне плоскости
провести к ней перпендикуляр и наклонные, то:
/. Равные наклонные имеют равные проекции.
2. Большая наклонная имеет и большую проекцию.
Доказательство (от противного) учащиеся проведут сами.
§ 24. Теорема о трёх перпендикулярах.
Теорема. Прямая, проведённая ни плоскости через
основание наклонной и перпендикулярная к её
проекции, перпендикулярна к
самой наклонной.
Дано: плоскость Αί,
наклонная АС, её проекция
ВС и прямая DE±BC
(чёрт. 23). Требуется
доказать, что DE _]_ АС.
На прямой DE отложим
по обе стороны от точки С
равные отрезки CD = СЕ и
соединим точки D и Ε с
точками А и В. Тогда BD=
= BE, как наклонные к
прямой DE, имеющие равные
проекции CD и СЕ. Далее, AD = AEy как наклонные к плоскости
М, имеющие равные проекции BD и ВЕУ а потому Д ACD = Д АСЕ
(по трём сторонам). Следовательно, ^/ ACD = /_ АСЕ, а так
как эти углы смежные, то они прямые.
19
Черт. 23.

Теорема обратная. Прямая, проведённая на
плоскости через основание наклонной и перпендикулярная
к ней, перпендикулярна и к её проекции.
Дано: DE ^_АС. Требуется доказать, что DE _\_ВС.
Отложив, как и раньше, равные отрезки CD = CE и
соединив точки D и Ε с точками А и В, найдём AD = AE, как
наклонные к прямой DE в плоскости ADEy имеющие равные
проекции CD и СЕ. Далее BD = BE, как проекции равных
наклонных (AD и АЕ). А потому
Д BCD = Д ВСЕ;
по трём сторонам. Следовательно,
£ BCD =2. ВСЕ,
а так как эти углы смежные, то они прямые.
VI. ЗАВИСИМОСТЬ МЕЖДУ ПАРАЛЛЕЛЬНОСТЬЮ И
ПЕРПЕНДИКУЛЯРНОСТЬЮ ПРЯМЫХ И ПЛОСКОСТЕЙ.
§ 25. Предварительные замечания.
Параллельность прямых и плоскостей и перпендикулярность
прямой к плоскости находятся в некоторой зависимости. Именно,
наличие параллельности одних элементов влечёт за собой
перпендикулярность других, и обратно: из перпендикулярности одних
элементов можно сделать заключение о параллельности других.
Эта связь между параллельностью и перпендикулярностью
прямых и плоскостей выражается следующими теоремами.
§ 26. Плоскость, перпендикулярная к двум прямым.
Теорема. Если одна из двух параллельных
прямых перпендикулярна
к плоскости, то и
другая
перпендикулярна к той же
плоскости.
Дано: АВ±Р и
АВ || CD.
Требуется доказать,
что CD±P (черт. 24).
Проведём через точку
В на плоскости Ρ две
какие-нибудь прямые BE
и BF, а через точку D проведём прямые DG и DHy
соответственно параллельные прямым BE и BF. Тогда будем иметь
20
Черт. 24.

Черт. 25.
/ABE = £CDG и /^ABF = ^CDH, как углы с
параллельными сторонами. Но углы ABE и ABF — прямые, так как
АВ \_ Р, значит, углы
CDG и CD Η—также
прямые. Следовательно,
CD\_P (§ 21).
Теорема
обратная. Если две прямые
перпендикулярны к
одной плоскости, то
они параллельны.
J\zho:AB±M,CD±M
(черт. 25).
Требуется доказать,
что АВ || CD.
Предположим, что прямые АВ и CD не параллельны. Проведём
через точку D прямую DCV параллельную АВ, и через прямые
CD и CXD — плоскость Q. Обозначим через DE линию
пересечения плоскостей Μ и Q. В силу прямой теоремы CXD J_ M,
а так как по условию CD J_M, то в плоскости Q к прямой
DE из одной её точки D будут восставлены два перпендикуляра
DC и DCX, что невозможно.
§ 27. Прямая перпендикулярная к двум плоскостям.
Теорема. $сли одна из двух параллельных
плоскостей перпендикулярна к прямой, то и другая
перпендикулярна к той же
прямой.
Дано: Ρ || Q, АВ JL Я.
Требуется доказать, что
АВ \_ Q (черт. 26).
Проведём через прямую АВ
какие-либо две плоскости Μ и
N. Каждая из них пересекается
с Ρ и Q по параллельным
прямым: первая — по ВС и BXCV
вторая —по BD и BXDV Так
как прямая АВ по условию
перпендикулярна к плоскости Р,
то она перпендикулярна к
прямым ВС и BD. Следовательно,
она перпендикулярна и к парал-
Черт. 26.
лельным им прямым ВгСг и BXDV а потому она перпендикулярна
И к пдоскости Q, на которой лежат прямые ВгСг и BXDV

Теорема обратная. Если две плоскости
перпендикулярны к одной прямой, то они параллельны.
Даны плоскости Ρ и Q и прямая АВ (черт. 26), причём
АВ _]_Р и АВ J_ Q. Требуется доказать, что плоскости Ρ и Q
параллельны.
Проведём через Л£ какую-либо плоскость Ж, пересекающую
плоскости Ρ ύ Q соответственно по прямым ВС и BXCV Так
как плоскости Я и Q перпендикулярны к АВ, то
^/ ЛЯС = ^/ ВВ1С1 = </.
Следовательно, Z^CH^C^ а потому £С || Q. Проведя через
АВ другую плоскость N, пересекающую Ρ и Q по прямым £D
и ^Dp таким же образом найдём, что BD || Q. А потому (§ 14)
плоскость Ρ параллельна плоскости Q.
§ 28.
Задача 1. Через данную точку провести плоскость,
перпендикулярную к данной прямой а.
Решение. Возможны два случая — когда данная точка
лежит и когда она не лежит на данной прямой.
. Первый случай. Данная
точка С лежит на прямой а
(черт. 27).
Проведём через прямую а
какие-нибудь две плоскости Ρ
и Q. Искомая плоскость должна
пересекать эти плоскости по
прямым, перпендикулярным к
прямой а (§ 22).
Отсюда вы ι екает такое
построение: через а проводим
две произвольные плоскости Ρ
и Q. В каждой из этих
плоскостей восставляем
перпендикуляр к прямой а в точке С
(в плоскости Ρ перпендикуляр CD, в плоскости Q
перпендикуляр СЕ). Плоскость, проходящая через прямые CD и СЕ> есть
искомая.
Второй случай. Данная точка D не лежит на прямой а
(черт. 28). Через точку D и прямую а проводим плоскость Ρ
и в этой плоскости строим прямую DC,
перпендикулярную к а.
Через прямую а проводим прозвольно вторую плоскость Q
и в этой плоскости строим прямую СЕУ перпендикулярную к а.
|Р|||| 1II ΜΙ |]]К.
1 Щ н|
и' 1 1 1 1,1 1 1 Ι ι 1Ь
ι Ш1Щ||||
Черт. 27.

Черт. 28.
Искомая плоскость должна пересечь плоскости Ρ и Q но
прямым, перпендикулярным к а.
Отсюда вытекает такое построение: через точку D
проводим в плоскости Ρ
прямую DCу перпендикуляр- ^ηΤίΤΡΙ
ную к а. Прямая DC
встретит прямую а в
некоторой точке С. Через
точку С проводим в
плоскости Q прямую СЕ,
перпендикулярную к а.
Плоскость /?, проходящая
через прямые CD и СЕ,—
искомая.
Так как в каждой из
плоскостей Ρ и Q через
данную точку можно
провести лишь одну прямую,
перпендикулярную к
данной, то задача в обоих
случаях имеет одно решение, т. е.
через каждую точку можно провести лишь одну плоскость,
перпендикулярную к данной прямой.
§ 29.
Задача 2. Через данную точку О провести прямую,
перпендикулярную к данной плоскости Р.
Решение. Возможны
два случая — когда данная
точка лежит и когда она не
лежит на данной плоскости.
Первый случай:
точка О лежит на плоскости Ρ
(черт. 29).
Проведём на плоскости
Ρ через точку О две какие-
либо взаимно
перпендикулярные прямые ОА и ОВ.
Через прямую ОА проведём
какую-либо новую плоскость
Q и на ней построим пря-
ерт' * мую ОС _]_ ОА. Через
прямые ОВ и ОС проведём новую плоскость R и построим в ней
прямую ОМ _[_ О В, Прямая ОМ и будет искомым перпендикуляром
23

к плоскости Р. Действительно, так как ОА^ОВ и О А _]_ ОС,
то CMJ_/? и, следовательно, ОА^_ОМ. Итак, ОМ_[_ОА и
OAiJLOB, а потому ОЖ _]_ Р.
Второй случай: точка О не лежит на плоскости Р.
Возьмём на плоскости Ρ какую-нибудь точку А (черт. 30)
и выполним для неё предыдущее построение. Мы получим тогда
прямую АВУ перпендикулярную
к плоскости Р. После этого
через точку О проводим
прямую OD, параллельную АВ.
Эта прямая и будет искомой
■Д / (§ 26).
Задача в обоих случаях
имеет одно решение. В самом
Черт. 30. деле, так как два
перпендикуляра к одной и той же
плоскости параллельны, то через одну и ту же точку О нельзя
провести двух перпендикуляров к плоскости Р. Следовательно,
через каждую точку можно провести одну и только одну
прямую у перпендикулярную к данной плоскости.
§ 30.
Задача 3. Даны две скрещивающиеся прямые а и Ь.
Построить прямую, пересекающую обе данные прямые и
перпендикулярную к ним обеим.
Решение. Проведём через прямую а плоскость Μ (черт.31),
параллельную прямой Ъ (§ 17). Из двух каких-нибудь точек
Черт. 31.
А и Упрямой Ь опустим перпендикуляры ААА и ВВг на плоскость М.
Соединим точки Ах и Вх прямой линией и найдём точку Сх
пересечения прямых \ВЛ и а. Через точку СА проведём
прямую, перпендикулярную к плоскости Λί. Предоставляем самим
24

учащимся доказать, что эта прямая: 1) пересечётся с прямой Ь
в некоторой точке С и 2) будет перпендикулярна как к прямой
я, так и к прямой Ь.
Прямая ССЛ будет, следовательно, искомой прямой.
Заметим, что отрезок ССХ меньше всех других отрезков,
которые можно получить, соединяя точки прямой а с точками
прямой Ь. В самом деле, возьмём на прямой а какую-нибудь точку
£ и на прямой Ъ какую нибудь точку F, соединим эти точки
прямою и докажем, что EF^>CCA. Опустим из точки F
перпендикуляр FFX на плоскость М. Тогда будем иметь EF^>FFX
(§ 23). Но FFX=CCV следовательно, EF^>CCi. На этом
основании длина отрезка СС1 называется кратчайшим
расстоянием между скрещивающимися прямыми а и Ь.
VII. УГЛЫ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ И
МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ.
§ 31. Угол между двумя скрещивающимися прямыми.
Если даны две скрещивающиеся прямые а и Ъ, то они не
образуют угла в обычном смысле, так как они не имеют общей
точки. Тем не менее для них
также можно определить наклон
одной к другой. Для этой цели
поступают так.
Через какую-либо точку С
(черт. 32) проводят прямые СЛ
и СВ, соответственно
параллельные прямым аи b (С А \\ а иСВ \\ Ь).
Прямые СЛ и СВ лежат в одной
плоскости и образуют в этой
плоскости некоторый угол ВСА.
Величина этого угла не зависит
от того, где взята точка С.
Действительно, если вместо точки С
взять другую точку С1 и провести
прямые С А1 || а и С В1 \\ Ь, то
будем иметь СЛ || СЛ' и СВ\\С'В' (§ 13). Следовательно,
Z.ACB^/iA'CB'.
В частности, можно взять точку на одной из данных прямых,
например, точку С" на прямой а. Тогда через неё достаточно
провести лишь прямую с, параллельную Ь. Угол между прямыми
а и с будет равен углу АСВ. Величина угла АСВ и принимается
за меру угла между прямыми а и Ь. Таким образом, мы приходим
к следующему определению.
35
Черт. 32.

Углом между двумя скрещивающимися прямыми
называется угол между параллельными им прямыми, проходящими
через одну точку.
В частности, если этот угол окажется прямым, то данные
скрещивающиеся прямые называются взаимно
перпендикулярными. Таковы, например, рёбра АВ и НЕ куба, изображённого
на чертеже 3.
Пользуясь понятием угла между скрещивающимися прямыми,
можно многим теоремам придавать более общую форму. Так, из
теоремы § 21 легко вывести следующее, более общее заключение:
Прямая, пересекающая плоскость и перпендикулярная
к двум каким-либо пересекающимся прямым на плоскости
(хотя бы и не
проходящими через след
данной прямой),
перпендикулярна и ко
всякой прямой,
лежащей на той же
плоскости.
Даны прямые CD,
EF и KL, лежащие в
плоскости Ρ (черт. 33),
и прямая АВ,
встречающая плоскость Ρ в
точке θ, причём АВ ±_CD и АВ ±_EF. Требуется доказать,
что АВ\_KL
Проведём через точку В в плоскости Ρ прямые BG || CD,
BH\\EF и BS\\KL Так как АВ _L CD, то это значит, что
АВ \_BG\ и так как АВ \_EF, то, значит, АВ ±_ВНУ а потому,
в силу теоремы § 21, ABJ_BS. А это значит, что АВ ±_KL
Черт. 33.
§ 32. Угол между прямой и плоскостью.
Пусть даны плоскость Ρ и прямая АВ,
в точке В (черт. 34).
Различные прямые, лежащие
на плоскости Ρ и проходящие
через Ву образуют с прямой
АВ углы различной величины.
Найдём наименьший из этих
углов. Докажем теорему.
Теорема. Острый угол
между прямой и её
проекте*
пересекающая её
А
Черт

цией на плоскость меньше угла между этой прямой
а всякой другой прямой, лежащей на той оке плоскости.
Дана плоскость Ρ (черт. 34), прямая АВУ её проекция ВС
на плоскость Ρ и произвольная прямая BD на плоскости Р.
Требуется доказать, что
£ABC<C/_ABD.
Из какой-либо точки Ε прямой АВ опустим на плоскость Ρ
перпендикуляр EF. Так как ВС есть проекция прямой АВ, то
точка F упадёт на прямую ВС. Отложим на BD отрезок BG,
равный BF, и соединим точки G и Е. Тогда EG^>EF (§ 23).
В треугольниках BEG и BEF сторона BE — общая, BF = BG
и EG^>EFy следовательно,
/^GBEy^FBE.
Углом между прямой и плоскостью называется острый угол
между прямой и её проекцией на эту плоскость.
VIII. ВРАЩЕНИЕ И ПЕРЕМЕЩЕНИЕ ПРОСТРАНСТВЕННЫХ
ФИГУР.
§ 33. Вращение точки.
Пусть дана точка Л и не проходящая через неё прямая а.
Проведём через А плоскость Р, перпендикулярную к прямой а,
и обозначим через В точку её пересечения с прямой а (черт. 35).
Соединим А с В w i
проведём через В на о\
плоскости Ρ
произвольную прямую BAV
на которой отложим
отрезок BAV равный ВА.
Так как BA = BAV
то точки А и Αχ лежат
в плоскости Ρ на
окружности с центром
в точке В и радиусом,
равным ВА. Точку Αχ
можно рассматривать
как новое положение
точки Л, переместившейся по дуге окружности ΑΑχ. Такое
перемещение точки А на плоскости Ρ называется вращением
точки А вокруг оси а. Угол ABAV называется углом
вращения точки А вокруг оси а,
27

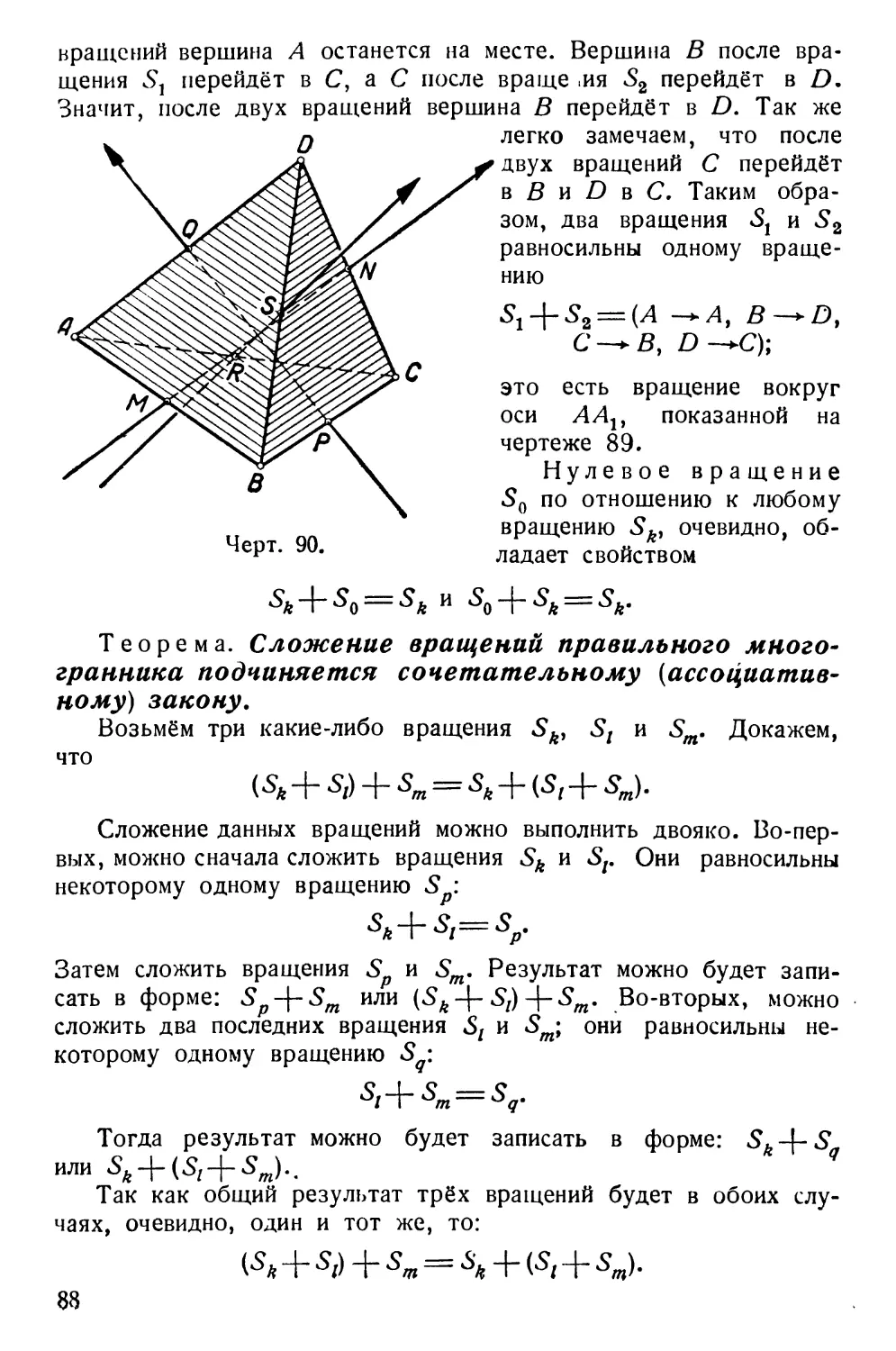
Теорема. Если две тонки повернуть вокруг какой-
либо оси в одну и ту же сторону на один и тот же
угол, то расстояние между этими точками не
изменится.
Даны: ось а и две точки А и В. Точка А повёрнута вокруг оси
а на угол АСА' в положение Л'; точка В — в ту же сторону на
угол BDB' в положение £', причём ^/ АСА' =/_BDB' (черт. 36).
Требуется доказать, что
| А'В' = АВ.
Точки А и А' лежат
на плоскости Р,
перпендикулярной к оси а и
пересекающей её в
точке С .Точки В и В' лежат
на плоскости Q,
перпендикулярной к α и
пересекающей её в точке D.
Следовательно, Ρ \\ Q
(§ 27). Через точки А
и А' проведём прямые,
параллельные оси а, до
встречи в точках F и F'
с плоскостью Q и
соединим точки F и F' с точ-
Черт. 36. кой D. Так как Ρ \\ Q,
T0AF=A'F = CD(§ 15)
и, следовательно, AC = FD, A'C = FD и ЛС || ГО, Л'С || FD,
следовательно (§ 16), ^АСА'= ^FDF; а так как, по
условию, 2.ACA' = 2.BDB'> T0 ZFDF = Z.BDB'.
Отсюда следует, что /_BDF= £B'DF. Соединим теперь точку
В с точкой Z7 и точку Б' с точкой F и рассмотрим
треугольники BDF и £'DF. В них BD = B'Dy FD = FD (так как
ЛС = Л'С) и /_BDF =/_B'DF. Следовательно, /\BDF=
— l^B'DF, а потому BF=B'F.
Рассмотрим теперь треугольники ABF и A'B'F'. Эти
треугольники прямоугольные. В самом деле, AF \\ a, a_LQ,
следовательно, /^XQ и, значит, AFJ_FB. Совершенно так же
убедимся, что A'F' ± FB\ Так как BF=B'F и AF=A'F,
то [\ABF= /\A'B'F. Следовательно, АВ = А'В'.
Доказанная теорема допускает две обратные теоремы.
Теорема обратная 1. Если после вращения двух
точек вокруг данной оси в одну и ту же сторону
расстояние между ними не изменится, то углы
вращения обеих точек одинаковы,
23

Даны: ось а и две точки А и В. Точка А после вращения
вокруг оси а на угол АСА заняла положение А' и точка В
после вращения вокруг той же оси на угол BDB' —
положение В', причём АВ = АВ'.
Требуется доказать, что ^/mACA=J/mBDB' (черт. 36).
Точки А и А' лежат на плоскости Р, перпендикулярной
к оси а и пересекающей её в некоторой точке С, причём
АС = А'С. Точки В и В' лежат на плоскости Q,
перпендикулярной к α и пересекающей её в некоторой точке D, причём
BD = B'D. Плоскости Ρ и Q параллельны. Так же, как и при
доказательстве прямой теоремы, проведём через точки А и А'
прямые AF и AF'y параллельные оси а.
Так как Ρ || Q, то AF = AFf = CD и AC = FD, A'C = F'D;
значит, FD = F'D и AC\\FD, A'C\\F'D. Отсюда /_АСА' =
В треугольниках ABF и AB'Ff по условию АВ=А'В\ по
доказанному Л/^^Л'/7'; кроме того, ^/mAFB = 4i/mA,F,B,=
= 90°; следовательно, /\ABF=/\AB'F\ откуда BF=B'F'.
Далее, /\BDF=AB'DF'
(по трём сторонам), откуда
/^BDF^^B'DF'.
Прибавляя к обеим
частям по углу B'DFy получим:
Ζ_ΒΏΒ'= /_FDF\ Ho
/_ FDF' = /_ АСА,
следовательно,^/ АСА = /_BDB'.
Теорема обратная 2.
£сли да/ш два
равных непараллельных
отрезка, то концы
первого молено совместить
с концами второго
вращением вокруг одной оси в одну и ту оке сторону на
один и тот же угол.
Дано АВ = А'В\ Возможны два случая.
Первый случай. Прямые АВ и А В' пересекаются
(черт. £7). Тогда отрезки АВ и А'В' лежат в одной плоскости Ж,
и в 5Той плоскости точки А и В могут быть совмещены
соответственно с точками А и В' вращением вокруг
некоторого центра О на один и тот же угол (см. Планиметрия,
стр. 134, упр. 23). Такое вращение вокруг центра О является в то
же время вращением вокруг оси а, перпендикулярной к Ж и
проходящей через точку О. Значит, точки А и В совмещаются с А
и В' вращением вокруг оси а на /_АОА (равный ^/ ВОВ').
29
Черт. 37.

Черт. 38.
Второй случай. Прямые АВ и А'В'— скрещивающиеся
прямые (черт. 38). Тогда и прямые АА' и ВВ' будут
скрещивающимися, и, следовательно, через прямую АА' можно провести
плоскость Ρ || ВВ', а через прямую ВВ' плоскость Q || АА'.
Проведём на плоскости
Ρ через середину Μ
отрезка АА' прямую
а\_АА\ а на плоскости Q
через середину N отрезка
ВВ' — прямую Ь\_ВВ'.
Построим далее общий
перпендикуляр CD к
прямым а и Ъ. Очевидно,
CD±P и CD±Q(§ 30).
Так как С лежит на
перпендикуляре из
середины отрезка АА', то
СА=СА'. Следовательно,
точка А после вращения
вокруг оси CD на угол
АСА' совместится с А'.
Точно так же DB — DB'
и, значит, точка В, после вращения вокруг оси CD на угол
BDB\ совместится с В'. По условию АВ — А'В\ а потому, по
предыдущей теореме, /_ АСА' — /^BDB'. Значит, точки А и В
совмещаются с А' и В' вращением вокруг оси CD на один
и тот же угол, равный ^/ АСА'.
§ 34. Вращение пространственных фигур.
Если все точки какой-либо пространственной фигуры или
геометрического тела повернуть вокруг произвольной оси в
одну и ту же сторону и на один и тот же угол, то все
полученные таким образом точки образуют новую фигуру, в
которой расстояние между любыми двумя её точками равно
расстоянию между двумя точками старой фигуры.
Такое вращение на один и тот же угол всех точек данной
фигуры вокруг данной оси называется вращением этой
фигуры вокруг данной оси. Таким образом каждая
геометрическая фигура может вращаться вокруг оси без изменения
расстояния между её точками.
При вращении пространственной фигуры вокруг оси каждая
её точка описывает дугу окружности в плоскости,
перпендикулярной к оси вращения, с центром на этой оси.
30

Вращение тел вокруг оси можно постоянно наблюдать в
обыдённой жизни; так, переплёт книги вращается вокруг
корешка, дверь и оконные рамы вращаются вокруг оси,
проходящей через дверные или оконные навески. Колёса экипажа,
винт корабля, пропеллер самолёта вращаются каждый вокруг
своей оси.
Вращение вокруг оси является наиболее распространённым
видом движения отдельных частей различных механизмов
(колесики часового механизма и т. п.).
§ 35. Понятие о перемещении геометрических тел и о их
равенстве.
В § 20 было рассмотрено последовательное выполнение двух
параллельных смещений геометрического тела. Аналогично можно
выполнить последовательно любое число параллельных смещений
и вращений данного тела. Результат последовательного
выполнения нескольких параллельных смещений и вращений (в частности —
одно параллельное смещение или вращение) геометрического тела
называется его перемещением. При всяком перемещении
геометрического тела расстояние между его точками, очевидно,
не изменяется. Если после какого-либо перемещения данное
геометрическое тело совмещается с другим данным геометрическим
телом, то оба геометрические тела называются равными между
собой.
§ 36. Теоремы о перемещении твёрдого тела.
Если в каком-либо физическом теле расстояние между его
частицами остаётся неизменным, то это тело называется твёрдым телом.
Как следует из
доказанных выше теорем, М'
твёрдое тело может
перемещаться из
одного положения в
другое, как
геометрическое тело.
Возможные виды
перемещений твёрдого
тела определяются
следующими
теоремами.
Теорема 1.
Если три, не ле- Черт. 39.
жащие на одной
прямой, точки твёрдого тела остаются неподвижными, то
и все его точки также остаются неподвижными.
Дано какое-либо тело F и три его точки Л, В и С, не лежащие
"а одной прямой (черт. 39). Тогда через них проходит одна пло-
31

скость Р. Возьмём какую-либо точку Μ тела F и предположим, что
она переместилась в некоторое новое положение Μ', а точки Л, В, С
остались неподвижными. Так как при перемещении твёрдого тела
расстояния между его точками не изменяются, то АМ = АМ',
ВМ = ВМ', СМ —СМ', следовательно, £\АМВ = £\АМ'В. Проведя
в этих треугольниках высоты MD и ΜΌ', замечаем, что /\AMD=z
= /\AM'D' и, следовательпо, AD = AD', т. е. точки D
и D' совпадают в одну. Так как MDJ_AB и M'D' J__ AB,
то AIM' A-AB. Так же точно докажем, что ММ' _[_ ВС.
Значит MM' J_P. Продолжим прямую ММ' до встречи в
точке N с плоскостью Р. Тогда £MNA = 9Q° и, следо-
С'\
В
Черт. 40.
вательно, /\ANM=/\ANM' (так как AM = AM' и AN—
общий катет), откуда NM = NM'. Значит М' совпадает
с М, т. е. точка Μ остаётся неподвижной.
Теорема 2. Если при данном перемещении
две точки тела остаются неподвижными, то это
перемещение тела есть вращение вокруг оси,
проходящей через неподвижные точки.
Дано какое-либо твёрдое тело F и две его
неподвижные точки А и В.
Возьмём сначала какую-либо точку С на прямой
АВ (черт. 40). Допустим, что точка С переместилась в
новое положение С. Тогда АС = АС и ВС=ВС, и так
как АС-\-СВ — АВ, то и АС + СВ = АВ. Значит, точка С лежит
на прямой АВ, и так как АС = АС, то С совпадает с С. Значит, вес
точки прямой АВ остаются неподвижными.
Возьмём теперь точку Μ вне прямой
АВ (черт. 41). Допустим, что она
переместилась в новое положение М'. Тогда AM—
=АМ' и ВМ = ВМ', следовательно, £\АМВ—
= /\АМ'В. Проведя в этих треугольниках
высоты MN и M'N', замечаем, что /\AMN-
= /\AM'N', откуда AN = AN'. Значит, точки
N и N' совпадают. Далее, MN = M'N и
MN _[_ АВ, M'N _[_ АВ. Следовательно, точка Μ
перемещается в М' вращением вокруг
прямой АВ на угол ΜΝΜ'. Возьмём теперь
какую-либо другую точку Ρ тела F. Допустим,
что она переместилась в новое положение Р*.
Так же точно докажем, что это
перемещение есть вращение вокруг прямой АВ на
некоторый угол PQP'. Так как тело F твёрдое,
то МР—М'Р' и, значит, Ζ. ΜΝΜ' = £ PQP'
(§ 33).
Таким образом, все точки тела F при
данном перемещении вращаются вокруг A3
на один и тот же угол. Значит, данное перемещение есть вращение
тела F вокруг оси АВ.
Теорема 3 (теорема Даламбера). Если при данном
перемещении одна точка тела остаётся неподвижной, то это
перемещение можно осуществить одним поворотом вокруг
оси, проходящей через неподвижную точку.
Дано какое-либо тело F. После некоторого перемещения оно
заняло положение F', причём одна его точка О осталась
неподвижной. Возьмём на F какие-либо две точки А и В, не лежащие на од-
Черт. 41.
32

ной прямой с точкою
Черт,
неподвижные
потому вовсе
перемещение
точки А', В' и О, не
не может переме-
точек А и В в А'
вращением вокруг некоторой оси
О (черт. 42 и 43). После перемещения тела F они
займут некоторые положения А' и В', причём АВ = А'В' и точки А\
R' и О не будут лежать на одной прямой. В самом деле, для точек
А В О имеем АО + ОВ>АВ, а так как АО = А'0, ОВ = ОВ
ъАВ = А'В\ то ΑΌ +
+ ОВ* > А'В'. Значит,
Л', В' и О не лежат на
одной прямой.
Легко заметить, что
переместив точки А и
β в А' и 5' и оставив
неподвижной точку О,
мы тем самым
осуществим и всё данное
перемещение всего тела F.
Действительно, после
перемещения точек А и
В в А' и В' они должны
остаться неподвижными,
так как их перемещение
уже осуществилось. Но
тогда тело F будет иметь уже 3
лежащие на одной прямой, и
щаться. Так как АВ = А'В'У то
и В' можно осуществить одним
а. Чтобы найти эту ось, рассмотрим два возможных случая.
Первый случай.
Прямые АВ и А'В' лежат в
одной плоскости Μ (черт.42).
Проведём через точку
О прямую ΟΟλ_]_Μ. Тогда,
так как ОА = ОА' и OB=z
= ОВ', то ОхА = ОхА' и
Оф—Оф'. Следовательно,
перемещение точек А и
В есть вращение их на
плоскости Μ вокруг центра
Οχ на один и тот же угол
ΑΟιΑ', равный углу ΒΟχΒ'',
а перемещение тела F есть
вращение его вокруг оси
ΟΟχ на тот же угол.
Второй случай.
Прямые АВ и А В'
скрещивающиеся. Тогда и прямые
АА' и ВВ' также будут
скрещивающимися (черт.43).
Проведём через прямую
АА' плоскость Ρ \\ ВВ\ через
ВВ' — плоскость Q||/L4', a
значит, Οχ02 J_ <?· Так как
Следовательно,
Черт. 43.
через точку О прямую OiO>_LP
ОА — ОА' и ОВ = ОВ', то ОхА = ОхА' и 02В=02В'.
перемещение точек А и В есть вращение их вокруг оси ΟχΟ^
проходящей через точку О. Значит, всё перемещение тела F
осуществляется вращением его вокруг оси Οχ02.
33

Теорема 4. Всякое перемещение твёрдого тела можно
выполнить при помощи одного параллельного смещения и
одного вращения вокруг некоторой оси.
Допустим, что твёрдое тело F после нескольких параллельных
смещений и вращений около различных осей приняло новое
положение F'. Требуется доказать, что всю совокупность параллельных
смещений и вращений, которая переводит тело F в новое
положение F', можно заменить одним параллельным смещением и одним
вращением.
Возьмём какую-либо точку Μ тела и π усть NV новое положение,
которое заняла точка Μ после указанного перемещения тела F в
новое положение F'. Подвергнем тело F параллельному смещению,
следуя вектору ММ'. Оно примет некоторое новое положение F",
причём точка Μ займёт положение М'. Чтобы перевести после этого
данное тело в положение F\ нужно подвергнуть его новому
перемещению, причём точка М' должна остаться неподвижной. А такое
перемещение, в силу теоремы Даламбера, можно осуществить одним,
вращением вокруг оси, проходящей через точку М'.
IX. УПРАЖНЕНИЯ К ГЛАВЕ ПЕРВОЙ.
А. Доказать теоремы:
1. Две плоскости, параллельные третьей, параллельны между
собой.
2. Все прямые, параллельные данной плоскости и проходящие
через одну точку, лежат в одной плоскости, параллельной данной.
3. Дана плоскость Ρ и параллельная ей прямая /. Доказать, что
все точки прямой / находятся на одинаковом расстоянии от
плоскости Р.
4. Доказать, что все точки одной из двух параллельных
плоскостей находятся на одинаковом расстоянии от другой плоскости.
5. Если прямая параллельна одной из двух параллельных
плоскостей, то она параллельна и другой.
6. Если одна из двух параллельных прямых параллельна данной
плоскости, то и другая прямая параллельна той же плоскости.
7. Если прямая / параллельна плоскости М, то всякая прямая,
проходящая через точку, лежащую на плоскости Μ и параллельная
прямой /, лежит на плоскости М.
8. Прямая, параллельная каждой из двух пересекающихся
плоскостей, параллельна и линии их пересечения.
9. Прямые, проходящие через одну точку и перпендикулярные
к данной прямой /, лежат в одной плоскости, перпендикулярной к /.
10. Если плоскость и прямая перпендикулярны к одной прямой,
то они параллельны.
11. Даны прямые а и Ь и плоскость М. Если а\\М и Ь_[_Λί,
то а\_Ь
12. Если через каждую из двух скрещивающихся прямых
провести плоскость, параллельную другой, то эти плоскости будут
параллельны между собою.
13. Если две плоскости перпендикулярны каждая к одной из двух
скрещивающихся прямых а и Ь, то линия пересечения этих
плоскостей параллельна общему перпендикуляру к прямым а и Ь.
34

14. На плоскости Μ построен параллелограм ABCD, диагонали
которого пересекаются в точке О. Если G— точка вне плоскости Μ
и AG = CG, BG = DG, то GO±M.
15. Дан треугольник ЛВС. Через середину каждой его стороны
проведена плоскость, перпендикулярная к этой стороне. Доказать,
что эти три плоскости проходят через одну прямую, и определить
положение этой прямой относительно треугольника ЛВС.
Отв. Прямая перпендикулярна к плоскости треугольника ЛВС
и проходит через центр описанной около него окружности.
16. Проекции двух параллельных прямых параллельны между
собою.
17. Отношение проекций двух параллельных отрезков равно
отношению самих отрезков.
18. Даны две пересекающиеся плоскости Μ и Ν, две прямые а
и Ь\ аь Ь^ — проекции данных прямых на плоскость М\ а2,
Ь2—проекции тех же прямых на плоскость N. Доказать, что если «ill^
и а2\\Ь^ то а\\Ь. Какое исключение допускает эта теорема?
19. Две параллельные прямые, пересекающие данную плоскость,
одинаково наклонены к этой плоскости.
20. Если проекции двух равных наклонных равны между собою,
то углы обеих наклонных с плоскостью одинаковы.
21. Острый угол, образуемый прямой с её проекцией на какую-
либо плоскость Λί, меньше угла, образуемого этой прямой с любой
другой прямой, лежащей на плоскости М.
22. Если прямая одинаково наклонена к двум пересекающимся
плоскостям, то её следы на этих плоскостях одинаково удалены от
линии пересечения плоскостей.
23. Если стороны одною треугольника параллельны сторонам
другого, то прямые, соединяющие вершины равных углов,
пересекаются в одной точке или параллельны.
24. Если плоскости двух треугольников ЛВС и i41fi1C1 не
параллельны и прямые ЛАЪ ЬВг и ССг проходят через одну точку, то
прямые АВ и АгВь ВС и ВгСъ АС и ΑλΟλ попарно пересекаются,
и 3 точки пересечения этих прямых лежат на одной прямой. Какое
исключение допускает эта теорема? Обратно: если' прямые АВ
и Афъ ВС и JBjCj, AC и i41C1 попарно пересекаются, то точки их
пересечения лежат на одной прямой, а прямые ААЪ ВВг и ССг
проходят через одну точку или параллельны.
25. Замкнутая линия, звенья которой не лежат в одной плоскости,
называется пространственным многоугольником. Доказать, что
противоположные стороны всякого плоского четырёхугольника,
вписанного в пространственный четырёхугольник, пересекаются на
диагоналях последнего. Какие исключения допускает эта теорема?
26. Середины сторон пространственного четырёхугольника
образуют вершины параллелограма.
27. Если дано η прямых, из которых каждые две пересекаются,
то или все они проходят через одну точку, или все лежат в одной
плоскости.
Б. Геометрические места.
28. Найти геометрическое место точек, находящихся на данном
расстоянии от данной плоскости. Отв. Две плоскости, параллельные
яаииой.
35

29. Найти геометрическое место точек, равноудалённых от двух
данных параллельных плоскостей. Отв. Плоскость, параллельная
данным.
30. Найти геометрическое место точек, отношение расстояний
которых от двух данных параллельных плоскостей имеет данную
величину. Отв. Две плоскости, параллельные данным, если данное
отношение не равно единице, и одна плоскость, параллельная данным,
если отношение равно единице.
31. Определить геометрическое место середин отрезков прямых,
пересекающих две данные параллельные плоскости и заключённых
между этими плоскостями. Отв. Плоскость, параллельная данным и
равноотстоящая от них.
32. Определить геометрическое место точек, делящих
(внутренним образом) в данном отношении отрезки прямых, пересекающих
две данные параллельные плоскости, заключённые между этими
плоскостями. Отв. Плоскость, параллельная данным.
33. Найти геометрическое место центров тяжести
треугольников, основания которых лежат на данной плоскости Λί, а вершины
на плоскости Ν, параллельной Λί. Отв. Плоскость, параллельная
данной.
34. Найти геометрическое место вершин треугольников,
основания которых лежат на данной плоскости Λί, а центры тяжести
находятся на плоскости N \\ М. Отв. Плоскость, параллельная М.
35. Найти геометрическое место центров окружностей,
описанных около прямоугольных треугольников, у которых вершина
прямого угла лежит в данной плоскости, а вершины острых углов —
в двух других данных плоскостях, параллельных первой. Отв.
Плоскость, параллельная данным.
36. Даны отрезок АВ и плоскость Λί, параллельная'прямой АВ.
Отрезок CD данной длины перемещается на плоскости М, оставаясь
параллельным АВ. Определить геометрическое место точек
пересечения прямых АС и BD, а также AD и ВС. Отв. Оба
геометрических места — плоскости, параллельные данной.
37. Отрезок АВ постоянной длины скользит своими концами по
двум параллельным плоскостям Μ и N. Через точку А проведена
плоскость Р_}_АВ, а через точку В — прямая /_[_Λί, пересекающая Ρ
в точке С. Найти геометрическое Л место точек С. Отв. Плоскость,
параллельная М.
38. Найти геометрическое место середин отрезков лучей,
проведённых из данной точки вне данной плоскости, ко всем точкам
этой плоскости. Отв. Плоскость, параллельная данной.
39. Отрезки лучей, проведённых из данной точки вне плоскости
ко всем точкам этой плоскости, разделены (внутренним образом)
в данном отношении т:п. Найти геометрическое место делящих
точек. Отв. Плоскость, параллельная данной.
40. Найти геометрическое место точек, делящих (внутренним
образом) в данном отношении отрезки параллельных прямых,
заключённых между двумя пересекающимися плоскостями. Отв.
Плоскость, проходящая через линию пересечения данных плоскостей.
41. Найти геометрическое место точек, равноудалённых от двух
данных точек. Отв. Плоскость, проходящая через середину отрезка
прямой, соединяющей данные точки, и перпендикулярная к этой
прямой.
42. Найти геометрическое место точек, равноудалённых от
вершин данного треугольника. Отв. Прямая, перпендикулярная к пло-
36

скости этого треугольника и проходящая через центр описанной около
него окружности.
43. Найти геометрическое место оснований равных наклонных,
проведённых из одной и той же точки вне данной плоскости. Отв.
Окружность, лежащая на данной плоскости.
44. Определить геометрическое место концов равных отрезков,
имеющих общее начало на данной плоскости и наклонённых к этой
плоскости под одинаковыми углами. Отв. Две окружности, лежащие
в плоскостях, параллельных данной.
45. Дана прямая АВ. Через точку А этой прямой проведены
прямые, наклонённые к АВ под данным углом. На этих прямых, по
обе стороны от точки Л, отложены отрезки данной длины. Найти
геометрическое место концов этих отрезков. Отв. Две окружности,
лежащие в плоскостях, перпендикулярных прямой АВ.
46. Найти геометрическое место точек, находящихся на данном
расстоянии а от данной плоскости Μ и на данном расстоянии b от
прямой I \_М. Отв. Две окружности, лежащие на плоскостях,
параллельных М.
47. Найти геометрическое место точек, находящихся на данном
расстоянии а от данной плоскости Μ и на данном расстоянии Ь от
данной точки Л, не лежащей на плоскости М. Отв. Две окружности,
лежащие на плоскостях, параллельных М> или одна такая окружность,
или геометрическое место вовсе не существует (одна из
окружностей может обращаться и в точку).
48. Найти геометрическое место оснований перпендикуляров,
опущенных из данной точки вне данной прямой, на все плоскости,
проходящие через эту прямую. Отв. Окружность, лежащая в
плоскости, перпендикулярной к данной прямой.
49. Найти геометрическое место центров окружностей данного
радиуса, лежащих в плоскостях, проходящих через данную прямую
и касающихся этой прямой в одной и той -же точке. Отв.
Окружность с центром на данной прямой, лежащая в плоскости,
перпендикулярной к этой прямой.
В. Задачи на построение.
50. Через данную точку провести плоскость, параллельную двум
данным прямым а и Ь.
51. Через данную точку провести прямую, параллельную данной
плоскости и пересекающую данную прямую.
52. Построить прямую, пересекающую две данные прямые и
параллельную третьей данной прямой.
53. Построить какую-либо прямую, пересекающую две данные
прямые и параллельную данной плоскости (задача неопределённая).
54. Построить какую-либо прямую, пересекающую три данные
прямые (задача неопределённая).
55. Через данную точку провести прямую, перпендикулярную
к двум данным скрещивающимся прямым.
56. Через данную точку А на плоскости Μ провести на этой
плоскости прямую, перпендикулярную данной прямой а, не лежащей
на плоскости М.
57. На данной плоскости найти точку, находящуюся на данных
расстояниях от двух данных плоскостей.
58. На данной прямой найти точку, находящуюся на данном
расстоянии от данной плоскости.
37

59. Йерез данную точку вне плоскости провести к этой
плоскости наклонную, имеющую данную длину и параллельную данной
плоскости.
60. Через данную точку А провести прямую, пересекающую
данную прямую / так, чтобы её отрезок, заключённый между прямою /
и параллельной ей плоскостью Λί, имел данную длину.
61. На данной прямой найти точку, равноудалённую от двух
данных точек. В каком случае задача становится неопределённой?
62. На данной плоскости провести прямую так, чтобы
расстояния её точек от двух данных вне плоскости точек были равны между
собою.
63. На данной плоскости найти точку, равноудалённую от
вершин данного треугольника, не лежащего на данной плоскости.
64. Построить точку, равноудалённую от четырёх данных точек,
не лежащих на одной плоскости.
65. Дана плоскость Μ и две точки А и В по одну сторону от
неё. Найти на плоскости Μ такую точку X, чтобы сумма АХ-\-ХВ
была наименьшей.
66. На данной прямой найти точку, сумма расстояний которой
от двух данных точек вне прямой была бы наименьшей.
67. Даны три параллельные прямые, не лежащие в одной
плоскости. Построить прямую, параллельную данным и равноудалённую
от всех трёх данных прямых.
68. Через данную прямую провести плоскость, находящуюся
на данном расстоянии от данной точки.
69. Через данную точку на плоскости провести на этой
плоскости прямую, находящуюся на данном расстоянии от данной точки
вне плоскости.
70. На данной плоскости Μ через данную точку А провести
прямую, образующую с данной прямой / (не лежащей на М) данный
угол.
Указание. Сначала провести прямую, параллельную искомой,
через след прямой / на плоскости М.
71. Через данную точку провести плоскость, параллельную
данной прямой и находящуюся от неё на данном расстоянии.
72. Через данную точку провести плоскость, пересекающую
данную прямую / в данной точке А и образующую с / данный
угол.
73. Через данную точку провести плоскость, параллельную
данной прямой / и образующую с другой данной прямой т
данный угол.
74. Три данные скрещивающиеся прямые пересечь прямой так,
чтобы её отрезки, заключённые между данными прямыми, находились
в данном отношении.
75. Построить прямоугольный треугольник, катеты которого даны,
так, чтобы вершина его прямого угла находилась в данной точке,
вершина одного острого угла лежала на данной прямой, вершина
другого — на данной плоскости.
76. Данную треугольную пластинку поместить в пространстве
так, чтобы одна её вершина совпала с данной точкой, другая легла
на данную прямую, третья легла на данную плоскость. Сколько
таких положений может иметь пластинка? Отв. Самое большее — 24.
77. Построить равносторонний треугольник, одна вершина
которого находилась бы в данной точке, другая на данной прямой, третья
на данной плоскости (задача неопределённая).
3S

78. Дана плоскость Μ и три точки Л, В и С вне её. Найти на
плоскости Μ такую точку Х> чтобы прямые АХ> ВХ, СХ были
наклонены к плоскости Μ под равными углами.
Указание: Если Ль Въ Q — проекции точек Л, В, С на
плоскость Λί, то A1X:BiX:C1X=A1A:BiB:ClC.
Г. Задачи на вычисление.
79. Из точки А, отстоящей на расстоянии 8 см от плоскости Λί,
проведена к ней наклонная АВ. Длина этой наклонной на 4 см
больше длины её проекции. Определить длину наклонной. Отв. 10 см.
80. Определить длину наклонной, если длина её проекции
равна я, а угол наклонной с плоскостью равен 45° или 60°. Отв. аУ 2
или 2а.
81. Даны проекции Ръ Ръ Рь некоторого отрезка на три взаим-
ноперпендикулярные прямые. Определить длину этого отрезка.
Отв. Кя^+^+^з-
Указание. Через конец искомого отрезка провести прямые,
параллельные данным.
82. На плоскости Μ дан отрезок АВ=\2 см. В точках А и В
восставлены к плоскости Μ перпендикуляры ЛС=9 см и BD = 4 см.
Определить расстояние между концами этих перпендикуляров.
Отв. 13 см или У313 см.
83. В двух точках на плоскости Μ восставлены к ней
перпендикуляры, длины которых а и Ь. Отрезок прямой, соединяющей их
концы, разделён в отношении т:п. Определить расстояние делящей
.. ^ ап-\-Ът
точки от плоскости М. Отв. L. .
т-\-п
84. Точка А отстоит от плоскости Μ на расстоянии 5 см.
Прямая /, лежащая на плоскости М, отстоит от проекции точки А на
расстоянии 12 см. Определить расстояние прямой / от точки А.
Отв. 13 см.
85. Металлический стержень, поставленный параллельно
плоскости освещенного экрана, отбрасывает на экран тень длиною 1 м.
Определить длину этого стержня, если известно, что расстояние
стержня от экрана равно 3 м> а расстояние экрана от источника
света равно 5 м. Отв. 40 см.
86. Даны три параллельные прямые а> Ьу с и параллельная им
плоскость М. Расстояние между прямыми а и Ь равно 4 му между
прямыми а и с—5 м и между Ь и с — 3 м. Расстояние прямых а
и Ь от плоскости Μ равно 7 м. Определить расстояние плоскости Μ
от прямой с. Отв. 10 м или 4 м.
87. Две параллельные плоскости, расстояние между которыми
равно 2 м, пересечены прямой, образующей с ними угол 60°.
Определить длину отрезка этой прямой, заключённого между этими пло-
скостями. Отв. -Цг-^ м.
и
88. Отрезки двух прямых, заключённые между двумя
параллельными горизонтальными плоскостями, равны 12 м и 18 м. Расстояние
между плоскостями равно 10 м. На каком расстоянии от одной из
39

этих плоскостей должна быть проведена между ними параллельная
им плоскость так, чтобы отсекаемый этой плоскостью верхний
отрезок одной прямой был равен нижнему отрезку другой. Отв. 4 м
или 6 м.
89. Найти геометрическое место точек, находящихся на данных
расстояниях а и Ь от двух данных точек А и В, если АВ = с.
У4а2с2— (β2_ &2 _|_ ^2)2
2с
лежащая в пло-
Отв. Окружность радиуса
скости, перпендикулярой к АВ и отстоящей от конца А на расстоя-
fl2— Ь* + С*
2с
НИИ
ГЛАВА ВТОРАЯ.
СИММЕТРИЯ ПРОСТРАНСТВЕННЫХ ФИГУР.
I СИММЕТРИЯ ОТНОСИТЕЛЬНО ПЛОСКОСТИ.
§ 37. Симметричные точки.
Две точки называются симметричными относительно
плоскости, если они лежат по разные стороны от этой плоскости
на прямой, перпендикулярной к ней, и
на одинаковом от неё расстоянии. Так,
точки А и А будут симметричны
относительно плоскости Μ (черт. 44),
если АА' ±М и ОА = ОА\ где О —
точка встречи прямой АА' с плоскостью
М. Плоскость Μ называется плоскостью
симметрии точек А и А'.
Из этого определения следует:
1. Две тонки имеют лишь одну
плоскость симметрии, так как
через середину отрезка прямой,
соединяющей эти точки, можно провести
лишь одну плоскость,
перпендикулярную к этой прямой.
2. Каждая тонка плоскости симметрии сама себе
симметрична, так как если точка А лежит на
плоскости М, то она совпадает с точкой О, а следовательно,
и с А\
3. Каждая тонка, лежащая на плоскости
симметрии двух данных точек, одинаково удалена от этих
точек.
Черт. 44.
40

Дано: Μ — плоскость симметрии точек Л и Л', С — какая-
либо точка плоскости Μ (черт. 45). Требуется доказать, что
АС = А'С.
Проведём прямую ЛЛ\ пересекающую Μ в некоторой точке О.
В силу симметрии точек Л и Л' имеем: АО = ОА' и
^ЛОС = ^/Л'ОС = 90°.
А потому ДАОС = ДЛ'ОС. Следовательно,
АС = А'С
Имеет место и обратное предложение:
4. Если тонка одинаково удалена от двух данных
точек, то она лежит на плоскости симметрии этих
точек.
Черт. 45. Черт. 46.
Даны три точки Л, Л', С, причём АС = А'С. Требуется
доказать, что точка С лежит в плоскости симметрии точек Л
и Л'.
Соединим точки Л и Л' и проведём через С плоскость Ж,
перпендикулярную к прямой А А, пересекающую А'А в точке О.
В треугольниках АОС и А'ОС имеем:
^/ЛОС = ^/Л'ОС = 90° и АС = А'С,
а потому
/\АОС = &А'ОС.
Следовательно, АО = А'0. Значит, точки Л и Л' симметричны
относительно М.
41

§ 38. Симметричные прямые.
Теорема. Если две какие-либо точки одной прямой
симметричны двум точкам другой прямой
относительно данной плоскости, то и все точки одной
прямой симметричны точкам другой.
Даны прямые АВ и А'В' (черт. 46), причём точки А и В
симметричны соответственно точкам А' и В' относительно
плоскости М. Требуется доказать, что для каждой точки прямой АВ
есть симметричная ей точка на прямой А'В'.
Пусть Oj и 02 точки пересечения прямых АА' и ВВ'
с плоскостью Ж.
Проведём через параллельные прямые АА' и ВВ' плоскость N.
Она пересечётся с Ж по прямой Ох02У причём АА' _[_Ολ02,
ВВ' ±_Ох02, Α0λ=ΑΌι и В02 — В'02. Следовательно, в
плоскости N прямые АВ и А'В' симметричны относительно оси
Ог02. Возьмём на АВ произвольную точку С; в плоскости N
,есть симметричная ей относительно оси Ολ02 точка С,
лежащая на прямой А'В' (Планиметрия, § 45). Точки С и С,
очевидно, симметричны относительно плоскости Ж. В самом деле,
прямые СС и АА' параллельны, так как в плоскости N они
обе перпендикулярны прямой 0}02. А так как АА' _]_ Ж, то
и СС \_М (§ 26). Из симметрии точек С и С относительно
оси OjOo в плоскости N следует, кроме того, что 0BC = OzC'.
Значит, точки С и С симметричны относительно плоскости Ж.
Если точки одной прямой симметричны точкам другой прямой
относительно данной плоскости, то прямые называются
симметричными относительно плоскости.
Из доказанной теоремы следует, что если две точки одной
прямой симметричны двум точкам другой относительно
данной плоскости, то эти две прямые симметричны
относительно той же плоскости.
§ 39. Симметричные плоскости.
Теорема. Если три какие-либо не лежащие на
одной прямой точки одной плоскости симметричны,
трём точкам другой относительно некоторой третьей
плоскости, то и все точки первой плоскости
симметричны точкам второй плоскости.
Даны плоскости Ж, Ж' и Ρ и точки Л, В и С в
плоскости Ж, симметричные соответственно точкам А'у В', С
плоскости Ж' относительно плоскости Ρ (черт. 47)., Требуется.
42

доказать, что для каждой точки на плоскости Μ есть
симметричная ей точка на плоскости М'.
Построим на плоскости Μ треугольник ABC, а на
плоскости Μ—треугольник А'В'С. Соответственные стороны этих
треугольников, очевидно, будут симметричны относительно Ρ
(§ 38).
Проведём на плоскости Μ через произвольную точку D
какую-либо прямую, пересекающую прямые АВ и АС
соответственно в точках Ε и F. Точкам Ε и F найдутся симметрич-
Черт. 47.
ные им точки Е' и F' на прямых А'В' и А'С на
плоскости Μ. Соединив точки Е' и F' прямой линией, получим
прямую E'F', симметричную EF. На E'F' найдётся точка D'
симметричная D.
Так как прямая E'F' лежит на плоскости Ж', то и точка D'
также лежит на плоскости Μ'. Таким же способом и для
всякой другой точки плоскости Μ можно найти симметричную ей
точку на плоскости Μ'.
Если все точки одной плоскости симметричны точкам другой
относительно некоторой третьей плоскости, то две данные
плоскости называются симметричными относительно этой
плоскости.
Из предыдущего следует, что если три, не лежащие на
одной прямой, точки одной плоскости симметричны трём
мочкам другой плоскости относительно какой-либо третьей
плоскости, то данные плоскости симметричны относительно
этой плоскости.
43

§ 40. Пространственные фигуры, симметричные
относительно плоскости.
Если для каждой точки данной фигуры построить точку, ей
симметричную относительно данной плоскости, то все полученные
талим образом точки образуют новую фигуру, которая
называется симметричной данной относительно данной
плоскости.
Простейшим примером симметричных фигур являются любой
предмет и его отражение в плоском зеркале: они симметричны
относительно плоскости зеркала.
Из предыдущего следует, что соответственные
(симметричные) отрезки, входящие в состав двух симметричных фигур,
равны между собою. Тем не менее, порядок расположения
частей одной фигуры обратен тому, который имеется в фигуре,
ей симметричной. Поэтому совместить произвольную фигуру
с фигурой, ей симметричной, так, чтобы совпали их
соответственные части, невозможно. Это особенно ясно видно на
примере зеркального отражения.
Отражение правой руки человека, стоящего перед зеркалом,
является левой рукой для его отражения. Но кисть правой руки
нельзя совместить с кистью левой, что видно хотя бы из того,
что одна и та же
перчатка не может подходить
и к правой и к левой
руке.
§ 41.
Задача. Построить
фигуру, симметричную
данной треугольной
пластинке ABC
относительно данной плоскости Р.
Решение. Из точек Лу
В и С (черт. 48) опускаем
перпендикуляры АОХУВО^
СОъ на плоскость Ρ и
продолжаем их за плоскость Ρ на такое же расстояние:
ОхА9 = ОхА, 02В' = О^Ву ОгС = OzC.
Тогда Д А*В'С будет симметричен Д ABC относительно
плоскости Р.
Черт. 48.
44

§ 42. Пространственные фигуры, имеющие плоскость
симметрии.
Если какую-либо пространственную фигуру можно разбить
на две части, симметричные относительно некоторой плоскости,
то эта плоскость называется
Г"
I
-ΐν
fc
1
"4i—:
плоскостью симметрии данной
фигуры.
Геометрические тела,
имеющие плоскость симметрии,
весьма распространены в
природе и в обыденной жизни.
Так, тело человека и
животного имеет плоскость
симметрии, разделяющую его на
правую и левую части. Большое
число предметов домашнего
обихода имеет плоскость
симметрии: обеденный стол, стул,
книжный шкаф и пр.
Некоторые, как, например,стол, имеют
даже не одну, а две плоскости симметрии (черт. 49). Обычно,
рассматривая предмет, имеющий плоскость симметрии, мы
стараемся придать ему или самим занять такое положение, при
котором его плоскость симметрии совпадает с плоскостью
симметрии нашей головы. При таком положении предмета его
симметричная форма становится особенно заметной.
Черт. 49.
II. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ ПРОСТРАНСТВЕННЫХ
ФИГУР.
§ 43. Симметричные точки.
Точки А и А' называются симметричными относительно
Центра О, если точка О есть середина отрезка АА' (черт. 50).
д Из этого определения следует:
1. Две точки, А и А' имеют
лишь один центр симметрии
(так как отрезок АА' имеет лишь
одну середину).
2. Точка, симметричная
центру симметрии, совпадает с
Черт. 50. ним самим.
45

§ 44. Симметричные прямые.
Теорема. Если две точки одной прямой
симметричны двум точкам другой относительно некоторого
центра, то и все точки этой прямой
симметричны точкам другой относительно того же центра.
Даны две прямые АВ и
Л'В'у причём точки А и В
симметричны соответственно
точкам А' и В' относительно
некоторого центра О (черт. 51)
Требуется доказать, что
для любой точки С прямой АВ
есть симметричная ей точка С
на прямой А'В'.
Проведём через
пересекающиеся прямые АА' и ВВ'
плоскость Ж, тогда прямые АВ и
А'В' окажутся лежащими в этой
Черт. 51. плоскости, для прямых же,
лежащих в одной плоскости, теорема была доказана в планиметрии
(Планиметрия, § 105).
Две прямые, точки которых симметричны относительно
какого-либо центра, называются симметричными относительно
этого центра.
Две симметричные прямые, как только что показано, лежат
в одной плоскости. А потому для них верны теоремы,
доказанные в планиметрии (Планиметрия, § 105):
1. Две прямые, симметричные относительно какого-
либо центра, параллельны между собою.
2. Соответственные отрезки двух симметричных
прямых равны.
§ 45. Симметричные плоскости.
Теорема. Если три, не лежащие на одной прямой,;
точки одной плоскости симметричны трём точкал^
другой плоскости относительно некоторого центра,,
то и все точки этой плоскости симметричны точкам^
другой относительно того же центра.
Даны плоскости Μ и Μ, причём точки Л, В и С плоскости!
Μ симметричны соответственно точкам А*, В', С плоскости А}'*
относительно центра О (черт. 52). Требуется доказать, что для!
произвольной точки на плоскости Μ есть симметричная ей точкаа
на плоскости Ж'.
46

Построим на плоскости /И треугольник ЛВС, а на
плоскости М' — треугольник А'В'С. Соответственные стороны этих
треугольников, очевидно, будут симметричны относительно
центра О (§ 44). Проведём через произвольную точку D
на плоскости Μ какую-
либо прямую, пересекающую
прямые АВ и АС
соответственно в точках Ε и F.
Точкам Ε и F найдутся
симметричные им точки Е' и V\ 1 //
F' на прямых А'В[ и А'С. \\[/
Соединив точки Ё' и F'
прямой линией, получим
прямую E'F', симметричную EF.
На E'F' найдется точка D',
симметричная D.
Так как прямая E'F'
лежит на плоскости Ж', то и
точка D' также лежит на плос- Черт. 52.
кости Μ. Таким же способом
и для всякой другой точки плоскости Μ можно найти
симметричную ей точку на плоскости М\
Если все точки одной плоскости симметричны точкам другой
относительно некоторого центра, то две данные плоскости
называются симметричными относительно этого центра.
Из предыдущего следует, что если три не лежащие на
одной прямой точки одной плоскости симметричны трём
точкам другой плоскости относительно некоторого центра,
то данные плоскости симметричны относительно этого
центра.
Теорема. Две плоскости, симметричные
относительно какого-либо центра, параллельны между собою.
Даны плоскости Μ и М\ симметричные относительно центра
О (черт. 52). Возьмём в плоскости Μ какой-либо Д ABC и
построим симметричный ему Д А'В'С на плоскости М'. Прямые
АВ и АС симметричны соответственно прямым А'В' и А'С\ а
потому (§ 44) АВ\\А'В' и АС\\А'С. Следовательно (§ 14),
плоскости Μ и М' параллельны.
§ 46. Пространственные фигуры, симметричные
относительно какого-либо центра.
Если для каждой точки какой-либо фигуры построить ей
симметричную относительно данного центра, то все полученные
таким образом точки образуют новую фигуру, которая назы-
47

вается симметричной данной фигуре относительно данного
центра.
Все соответственные отрезки в двух таких фигурах равны
между собой (§ 44).
Задача. Построить фигуру, симметричную данной
треугольной пластинке ABC относительно данного центра О.
Решение. Точки Л, В и С
(черт. 53) соединим с точкой О
и продолжим прямые АО, ВО и
СО за точку О на такое же
расстояние, так что О A =.АО,
ОВ' = ВОу ОС = СО.
Тогда /\А'В'С будет
симметричен Д ABC относительно
центра О.
При решении этой задачи мы
получили треугольник А'В'С,
симметричный треугольнику ABC и
в то же время ему равный (по трём сторонам). Однако,
как общее правило, как и в случае симметрии относительно
плоскости, две фигуры, симметричные относительно центра,
совместить одну с другой так, чтобы совпали все их соответственные
части, — невозможно, так как порядок расположения этих частей
в одной фигуре обратен тому, который имеется в другой.
III. ОСЕВАЯ СИММЕТРИЯ ПРОСТРАНСТВЕННЫХ ФИГУР.
§ 47. Осевая симметрия точек.
Две точки называются симметричными относительно оси,
если при повороте одной из них вокруг этой оси на 180° она
совмещается с другой.
Из этого определения
следует:
1. Две точки,
симметричные
относительно какой-
либо оси, лежат
на прямой,
перпендикулярной к этой
оси и пересекающей
её в точке,
служащей серединою отрезка прямой, соединяющей данные
точки.
48

Действительно, пусть дана точка А. Чтобы построить точку А',
симметричную А относительно оси а (черт. 54), проведём через
точку А плоскость Му перпендикулярную к оси а и обозначим
через О точку её пересечения с этой осью. Соединим О с А.
Тогда, очевидно, О А _]_ а. После поворота точки А вокруг оси а
на 180° точка А займёт положение А' на прямой О А, причём
ОА = ОА'.
2. Каждая тонка оси симметрии симметрична сама
себе.
3. Каждые две тонки имеют бесчисленное
множество осей симметрии.
Именно, осью симметрии двух точек служит всякая прямая,
проходящая через середину отрезка прямой, соединяющей эти
точки и перпендикулярная к этой прямой. Все эти оси,
очевидно, лежат в одной плоскости, перпендикулярной к прямой,
соединяющей данные точки.
4. Две тонки, симметричные относительно какой-
либо оси, одинаково удалены от любой тонки этой оси.
Действительно, пусть С—какая-либо
точка оси симметрии а точек А и А'
(черт. 55). Прямоугольные треугольники
АОС и А'ОС равны (по двум катетам),
а потому АС = А'С.
Имеет место и обратное предложение:
5. Если какая-либо тонка
одинаково удалена от двух данных
тонек, то она лежит на одной из
осей симметрии этих тонек.
Действительно, пусть дано, что ЛС =
= А'С. В таком случае треугольник АСА' —
равнобедренный. Его высота СО, очевидно,
служит осью симметрии точек А и А'. Черт. 55.
§ 48. Осевая симметрия прямых.
Теорема. Если две тонки одной прямой
симметричны двум точкам другой прямой относительно
некоторой оси, то и все точки первой прямой
симметричны точкам второй прямой относительно той
же оси.
Дано, что точки А и В симметричны соответственно
точкам А' и В' относительно оси а. Требуется доказать, что для
каждой точки прямой АВ есть симметричная ей точка на
прямой А'В' (черт. 56).
49

Возьмём на прямой АВ какую-либо точку С (например, между
точками А и В), построим точку С, симметричную С
относительно а, и докажем, что С лежит на прямой А'В'.
Точки А\ В' и С
получаются поворотом точек Л, В
и С вокруг оси а на угол 180°.
При таком повороте расстояния
между этими точками не
меняются, т. е. АВ = А'В\
ВС=В'С и АС=:А'С
(§ 33). Но так как точки
Л, В и С лежат на одной
прямой, то
Черт. 56. АВ + ВС = АС,
а потому, в силу написанных равенств, имеем:
A'B' + ffC = A'C.
Из этого равенства следует, что точки А1, В' и С также
лежат на одной прямой, т. е. точка С лежит на прямой А'В'.
Две прямые называются симметричными относительно
оси, если все точки одной прямой симметричны всем точкам
другой относительно этой оси.
§ 49. Осевая симметрия плоскостей.
Теорема. Если три, не лежащие на одной прямой,
тонка одной плоскости симметричны трём точкам
другой относительно какой-либо оси, то и все точки
этой плоскости симметричны точкам другой
плоскости относительно той лее оси.
Эта теорема доказывается совершенно так же, как теорема
о плоскостях, симметричных относительно плоскости (§ 39), и
теорема о плоскостях, симметричных относительно центра (§ 45).
Доказательство учащиеся легко проведут сами по образцу
доказательств §§ 39 и 45.
Если все точки одной плоскостл симметричны точкам другой
относительно какой-либо оси, то эти плоскости называются
симметричными относительно этой оси.
Из предыдущего следует, что
если три, не лежащие на одной прямой, точки одной
50

плоскости симметричны трём точкам другой плоскости
относительно какой-либо оси, то данные плоскости
симметричны относительно этой оси.
§ 50. Осевая симметрия пространственных фигур.
Если для каждой точки данной фигуры построить точку, ей
симметричную относительно какой-либо оси, то все построенные
таким образом точки образуют новую фигуру, которая
называется фигурой, симметричной
данной относительно этой оси.
Фигура, симметричная данной
относительно какой-либо оси, при
повороте на 180° вокруг этой
оси совмещается с данной фигурой.
Следовательно,
всякие две фигуры, сим- &4
метричные относительно какой-
либо оси, равны между собою.
Задача. Построить фигуру,
симметричную данной треугольной
пластинке ABC относительно
данной оси а.
Решение. Из точек Л, В и С „ -_
(черт. 57) опускаем перпендикуляры ерт*
AOv В02, СОь на ось а и продолжаем их за точки Ог,
09, 03 на такое же расстояние: ОгА' = AOv 02B' = В02У
Of.
■■со,.
Тогда Д А'В'С будет симметричен Д ABC относительно
оси а.
§ 51. Фигуры, имеющие ось симметрии.
Если для каждой точки данной пространственной фигуры
есть симметричная ей относительно некоторой оси тс^чка той же
самой фигуры, то говорят, что данная фигура имеет ось
симметрии второго порядка.
При повороте вокруг этой оси на 180° данная фигура
совмещается сама с собою.
Название „ось симметрии второго порядка* объясняется тем,
что при полном обороте вокруг этой оси фигура в процессе
вращения будет дважды принимать положение, совпадающее
с исходным (считая и исходное).
51

Примером фигуры, имеющей ось симметрии второго порядка,
может служить, например, параллелограм: осью его симметрии
второго порядка служит
прямая, проходящая
через его центр и
перпендикулярная к его
плоскости (черт. 58).
Пространственные
фигуры, имеющие ось
симметрии второго
порядка, весьма часто
встречаются в природе
и в обыдённой жизни.
Так, стволы деревьев
и стебли многих
растений имеют ось симметрии второго порядка (ось * ствола или
стебля).
§ 52. Оси симметрии высших порядков.
Возможны случаи, когда фигура приходит в совмещение
с исходным положением после поворота вокруг некоторой оси
на угол, меньший
180°.
Таким образом,
когда фигура
сделает полный оборот
вокруг этой оси, то
в процессе вращения
она несколько раз
совместится со
своим исходным
положением. Такая ось
вращения
называется осью симметрии
высшего порядка.
Порядком оси сим- Черт. 59.
метрии называется
число положений фигуры, совпадающих с исходным (считая и
исходное). Например, правильный треугольних имеет ось
симметрии третьего порядка: этой осью служит прямая,
перпендикулярная к плоскости этого треугольника и проходящая через
его центр (черт. 59).
52

§ 53. Зависимость между различными видами симметрии
пространственных фигур.
Между различными видами симметрии пространственных фигур:
осевой, плоскостной и центральной — существует зависимость,
выражаемая следующей теоремой.
Теорема. Если тонка А симметрична точке А'
относительно плоскости Ρ и в то же время симметрична
точке А" относительно точки О, лежащей в плоскости Р, то
точки А' и А' симметричны
относительно оси, проходящей
через точку О и
перпендикулярной к плоскости Р.
Пусть В точка пересечения
отрезка АА' с плоскостью Ρ (черт.60).
Проведём плоскость через точки
Л, А* и О. Эта плоскость будет
перпендикулярна к плоскости Р, так
как проходит через прямую АА\
перпендикулярную к этой
плоскости. На плоскости АА'О
проведём прямую ОН, перпендикулярную
к ОВ. Эта прямая ОН будет
перпендикулярна и к плоскости Р.
Пусть далее С—точка пересечения
прямых А'А" и ОН.
В треугольнике АА'А" отрезок
ВО соединяет середины сторон АА
и АА"\ следовательно, ВО || А'А". Но ВО±ОН, значит, А'А"\_ОН.
Далее, так как О— середина стороны АА1 и СО || АА', то А'С— А"С.
Отсюда заключаем, что точки А' и А" симметричны относительно
оси ОН.
Следствие. Если все точки какой-либо фигуры F
симметричны точкам фигуры F' относительно плоскости Ρ и в то же
время симметричны точкам другой фигуры F" относительно
точки О, лежащей β плоскости Р, то фигуры F и F" симметричны
относительно оси, проходящей через точку О и перпендикулярной
к плоскости Р.
ГУ. УПРАЖНЕНИЯ К ГЛАВЕ ВТОРОЙ.
1. Доказать, что всякая прямая, лежащая в плоскости симметрии
двух данных пересекающихся прямых а и Ь, составляет с этими прямыми
равные углы.
2. Доказать, что две плоскости Μ и М'', симметричные одна другой
относительно третьей плоскости Р, или пересекаются по прямой,
лежащей на плоскости Р, или параллельны между собою.
3. Доказать, что угол между двумя прямыми равен углу между
прямыми, им симметричными относительно данной плоскости (или
данной оси, или данной точки).
4. Даны: плоскость Μ и прямая а, пересекающая Μ в точке А.
Доказать, что прямая а', симметричная а относительно Λί, проходит
через-Л.
5. Даны: плоскость Λί и прямая а \\ Λί. Доказать, что прямая а',
симметричная а относительно М, параллельна Λί.
Черт. 60.

6. Доказать,что две прямые, симметричные относительно какой-либо
плоскости, лежат в одной плоскости (т. е. или пересекаются, или
параллельны).
7. Доказать, что две прямые, симметричные относительно данной
плоскости, одинаково наклонены к этой плоскости, а симметричные
отрезки этих прямых равны между собою.
8. Доказать,что если фигура имеет ось симметрии порядка п=.п\пъ
гцеп1ип2—целые числа, то она имеет также оси симметрии порядка /ιΑ
и порядка п2.
9. Найти геометрическое место точек, симметричных данной
точке А относительно всех точек данной прямой а. Отв. Прямая,
параллельная а.
10. Найти геометрическое место точек, симметричных данной
точке А относительно всех точек данной плоскости Λί, не
проходящей через Л, а также относительно всех прямых, лежащих на
плоскости М. Отв. Плоскость, параллельная М.
11. Найти геометрическое место точек, симметричных данной
точке А относительно всех точек, лежащих на данной плоскости Μ
и одинаково удалённых от А. Отв. Окружность, лежащая в плоскости,
параллельной М.
12. Найти геометрическое место точек, симметричных данной
точке А относительно всех плоскостей, проходящих через данную
прямую а. Отв. Окружность, лежащая в плоскости,
перпендикулярной к а.
13. Найти геометрическое место точек, симметричных данной
точке А относительно всех прямых, параллельных данной прямой а.
Отв. Плоскость, перпендикулярная к а.
14. Найти геометрическое место осей симметрии двух данных
точек А и В. Отв. Плоскость, перпендикулярная прямой АВ,
проходящая через середину отрезка АВ.
15. Построить центр и плоскость симметрии двух данных точек.
16. На данной прямой а найти точку, симметричную данной
точке А относительно точки, лежащей на данной плоскости М.
17. Построить плоскость симметрии двух данных плоскостей
в случае, когда они пересекаются и когда они параллельны.
18. Построить плоскости симметрии двух пересекающихся прямых.
19. Для двух данных точек построить ось симметрии, которая
пересекала бы данную прямую:
20. Построить ось симметрии двух данных скрещивающихся
прямых.
21. Сколько плоскостей симметрии имеет правильный л-угольник?
Отв. /f-f-1.
22. Сколько и какого порядка осей симметрии имеет правильный
восьмиугольник?
ГЛАВА ТРЕТЬЯ.
ДВУГРАННЫЕ И МНОГОГРАННЫЕ УГЛЫ.
I. ДВУГРАННЫЕ УГЛЫ.
§ 54. Определение двугранного угла.
Каждая прямая, лежащая на плоскости, разделяет её на две
части. Все точки одной части лежат по одну сторону прямой,
все точки другой части — по другую сторону прямой.
54

Каждая из этих частей называется полуплоскостью, а
прямая, разделяющая плоскость на две полуплоскости, называется
граничной прямой, или границей полуплоскости. Две полу-
Черт. 61. Черт. 62.
плоскости, имеющие общую граничную прямую, образуют
фигуру, которая называется двугранным углом. Полуплоскости,
образующие двугранный угол, называются его гранями, а их
общая граничная прямая — его ребром.
Двугранный угол с гранями Ρ и Q и ребром а (или АВ)
обозначается PaQ (или PABQ) (черт. 61).
§ 55. Смежные и вертикальные двугранные углы.
Два двугранных угла с общим ребром и общей гранью, две
другие грани которых лежат по разные стороны от общей грани,
Черт. 63. Черт. 64.
называются прилежащими. Таковы углы PaQ и QaR (черт. 62).
Угол PaRt образуемый не совпадающими гранями углов PaQ
и QaR, называется их суммой: PaR = PaQ-\-QaR. Два дву-
55

гранных угла называются смежными; если они имеют одну общую
грань, а две другие их грани составляют две полуплоскости
одной и той же плоскости. Таковы углы PaQ и Р'aQ (черт. 63).
Два двугранных угла называются вертикальными, если они
имеют общее ребро, и грани одного дополняют грани другого
до полных плоскостей. Таковы углы PaQ и P'aQ! (черт. 64).
§ 56. Линейный угол двугранного угла.
Проводя через различные точки ребра двугранного угла
плоскости, перпендикулярные к этому ребру, будем получать
в сечении с гранями углы, стороны которых перпендикулярны
к ребру (§ 22). Каждый из них
называется линейным углом данного
двугранного угла (черт. 65).
Все линейные углы одного
двугранного угла между собою равны.
Действительно, стороны АВ и А В'
двух линейных углов ABC и А'В'С
двугранного угла PaQ (черт. 65)
параллельны, так как они лежат в
одной плоскости и перпендикулярны
к ребру. Стороны ВС и В'С тех
же углов также параллельны.
Следовательно (§ 16),
Черт. 65.
/_АВС = /_А'В,С.
§ 57. Равенство двугранных углов.
Два двугранных угла называются равными, если их можно
совместить один с другим.
Теорема. Если двугранные углы равны, то равны
и их линейные углы.
Дано: PaQ = P,a,Q' (черт. 66); Z.ABC и /_А'В'С —
линейные углы двугранных углов PaQ и Р'a'Q'. Требуется
доказать, что
^ ABC =^ А'В'С'.
Совместив прямую а' с прямой а так, чтобы точка В'
совпала с В, будем вращать второй двугранный угол вокруг ребра
а' до тех пор, пока полуплоскости Р' и Q' не совместятся
с Ρ и Q (это совмещение возможно, так как двугранные углы
равны). Стороны угла А'В'С совпадут при этом со сторонами
угла ABC, так как в полуплоскостях Ρ и Q через точку В
56

можно провести только по одной прямой, перпендикулярной
к прямой а. Следовательно, угол А В'С совместится с углом
ABC. Значит,
£АВС = /_ А'В'С'.
а с
Черт. 66.
Теорема обратная. Если линейные углы
двугранных углов равны, то и двугранные углы равны.
Дано: /_ АВС = /^ А'В'С; Μ и Μ — плоскости этих углов;
/_АВС и /^ А'В'С— линейные углы двугранных углов PaQ
и P'a'Q'. Требуется доказать, что
PaQ = P'a'Q'.
Совместим углы ABC и А'В'С; тогда плоскость М'
совместится с Ж, а прямая а' с прямой я, так как через
точку В можно провести только одну прямую, перпендикулярную
к плоскости М. Так как а' совпадёт с α и А'В' совпадёт с АВ,
то плоскость Р' совпадёт с Я. И так как В'С совпадёт с ВС,
то плоскость Q' совпадёт с Q. Следовательно, двугранные углы
PaQ и P'a'Q' совместятся; значит, они равны.
§ 58. Измерение двугранных углов.
Двугранный угол, линейный угол которого содержит 1°, на-
зывается двугранным углом в 1°; ^ часть двугранного угла
в 1° называется двугранным углом в Г; ^ этого угла
называется двугранным углом в 1". Двугранному углу в Г,
очевидно, соответствует линейный угол в Г и двугранному углу
в 1" — линейный угол в 1". Очевидно, что каждый двугранный
угол содержит столько градусов, минут и секунд, сколько
градусов, минут и секунд содержит его линейный угол.
Следовательно, мерою двугранного угла служит его
линейный угол.
57

§ 59. Прямой двугранный угол.
Если два смежных двугранных угла равны между собою, то
каждый из них называется прямым двугранным углом.
В силу теорем § 57 прямому двугранному углу
соответствует прямой линейный угол, и обратно, прямому
линейному углу — прямой двугранный. Плоскости, образующие
прямой двугранный угол, называются взаимно, перпендикулярными.
§ 60. Перпендикулярные плоскости.
Теорема. Плоскость, проходящая через прямую,
перпендикулярную к данной плоскости,
перпендикулярна к этой плоскости.
Дано: BD±P.
Требуется доказать, что
плоскость Q, проходящая через BD,
перпендикулярна к плоскости Ρ
(черт. 67).
Проведём через точку В на
плоскости Ρ прямую GF_\_AC.
Так как BD±P, то BD±GF,
следовательно, /^DBG=/^DBF.
Но эти углы служат
линейными углами смежных двугранных
углов, образованных плоскостями
Черт. 67. ρ и Q, следовательно, эти
двугранные углы равны, а потому
плоскость Ρ перпендикулярна к плоскости Q.
Теорема. Если две плоскости взаимно
перпендикулярны, то всякая прямая, лежащая в одной из них
и перпендикулярная к линии их пересечения,
перпендикулярна к другой плоскости.
Даны две перпендикулярные плоскости Ρ и Q,
пересекающиеся по прямой АС, и прямая BF, лежащая на плоскости Ρ
и перпендикулярная к АС (черт. 67). Требуется доказать, что
BF±Q.
Проведём на плоскости Q прямую BD J_ AC. Тогда /DBF
будет линейным углом двугранного угла PACQ (так как по условию
BF \_АС и по построению BDJ^AC), но по условию PJ_Q,
следовательно,/_DBF = 90°, т. е. и BF_\_BD.
А так как, кроме того, BF ]_ АС, то BF J_ Q.
Следствие 1. Если две плоскости взаимно
перпендикулярны, то перпендикуляр, опущенный на одну плоскость
из какой-либо точки другой, весь лежит в этой плоскости.
58

В самом деле, этот перпендикуляр должен совпасть с
перпендикуляром, опущенным из той же точки на линию
пересечения обеих плоскостей.
Следствие 2. Если две пересекающиеся плоскости
перпендикулярны к третьей
плоскости, то и линия
их пересечения
перпендикулярна к той
же плоскости.
В самом деле, если
Ρ ± Μ и Q_]_ M
(черт.68), то, взяв на
линии пересечения
плоскостей Ρ и Q какую-либо Черт. 68.
точку Л и опустив из неё перпендикуляр на плоскость М,
заметим, что он должен будет лежать и в плоскости Ρ и в
плоскости Q, т. е. будет служить линией их пересечения.
II. ТРЁХГРАННЫЕ УГЛЫ.
§ 61. Определение трёхгранного угла.
Три луча, выходящие из одной точки и не лежащие в одной
плоскости, и внутренние области трёх углов, сторонами которых
служат эти лучи, образуют пространственную фигуру,
называемую трёхгранным углом.
Точка, из которой выходят лучи, называется вершиной,
самые лучи — рёбрами.
Через каждые два ребра трёхгранного угла проведём
плоскость. Части этих плоскостей, ограниченные рёбрами,
называются гранями трёхгранного угла.
Двугранные углы, образованные каждыми двумя гранями
трёхгранного угла, называются его двугранными углами, а углы,
образованные каждыми двумя его рёбрами, — его плоскими
углами.
Трёхгранный угол, очевидно, имеет три грани, три ребра,
три двугранных угла и три плоских угла. Трёхгранный угол
обозначается четырьмя буквами: на первом месте ставится буква,
указывающая его вершину, а затем три буквы, поставленные
У трёх его рёбер, например SABC (черт. 69).
59

§ 62. Свойства плоских углов трёхгранного угла.
Теорема. Всякий плоский угол трёхгранного угла
меньше суммы двух других его плоских углов.
Черт. 69. Черт. 70.
Дан трёхгранный угол SABC (черт. 70). Допустим, что
/ ASC— его наибольший плоский угол, т. е. что
^ASCy/^ASB и /^ASCy/^BSC.
Чтобы доказать теорему, мы должны доказать, что
^ asc <C/_asb-\-/_ BSC-
Проведём в грани ASC прямую SD, образующую с SC угол,
равный углу BSC, и отложим на этой прямой отрезок SD,
равный SB. Через точки В и D проведём какую-либо плоскость,
пересекающую рёбра SA и SC в точках Л и С, и рассмотрим
образовавшиеся треугольники.
/\CSD = /\CSBy
так как ^BSC = ^D$C, BS = DSy SC —общая сторона.
Следовательно,
BC = CD.
В треугольнике ABC имеем:
ЛС<Л£+- ВС,
или
AD-\-DC<AB-\-BC,
а так как DC = BC, то
AD<AB.
60

В треугольниках ASD и A SB имеем: AS — общая сторона,
SD = SB и AD<^AB. Следовательно,
Прибавляя к левой части этого неравенства /^DSC, а к
правой— равный ему /_BSC, получим:
/_ASD-\- Z.DSC<CZ.ASB-\-Z.BSC,
или £ Л£С< /_ASB + /_BSC.
Следствие. Всякий плоский угол трёхгранного угла
больше разности двух других его плоских углов.
§ 63. Симметричные трёхгранные углы.
Если продолжить рёбра трёхгранного угла SABC за его
вершину, то продолжения этих рёбер образуют рёбра нового
трёхгранного угла SA'B'C (черт. 71),
симметричного данному относительно
вершины S (§ 46). Все плоские и
двугранные углы этого нового трёхгранного угла
равны соответствующим плоским и
двугранным углам данного. Но порядок
расположения этих плоских и двугранных углов
в новом трёхгранном угле обратен порядку
расположения соответствующих углов
данного, а потому эти два симметричных
трёхгранных угла нельзя совместить один
с другим так, чтобы ребро SA совпало
с JSA\ ребро SB —с SB' и ребро SC —
с SO (см. § 46). Следовательно, два
симметричных трёхгранных
угла нельзя назвать рав-
н ы м и. Черт. 71.
§ 64. Теоремы о равенстве трёхгранных углов.
Согласно определению равных фигур (§ 35), два
трёхгранных угла называются равными между собой, если с помощью
какого-либо перемещения один из них можно совместить с другим.
Простым совмещением трёхгранных углов легко убедиться
в справедливости следующих теорем:
1. Два трёхгранных угла равны, если они имеют
по равному двугранному углу, заключённому между
двумя соответственно равными и одинаково
расположенными плоскими углами.
61

2. Два трёхгранных угла равны, если она имеют
по равному плоскому углу, заключённому между двумя
соответственно равными и одинаково
расположенными двугранными углами.
III. МНОГОГРАННЫЕ УГЛЫ.
§ 65. Определение многогранного угла.
Пусть дана плоскость Μ и лежащий на ней какой-нибудь
простой многоугольник, например ABCDE (черт. 72). Возьмём
какую-либо точку S вне
плоскости Ж, соединим её с
вершинами данного многоугольника
лучами SAy SB, SCy SDy SE
и продолжим эти лучи
неограниченно за точки А, В, С, D, Ξ.
Через каждые два луча,
проходящие через соседние
вершины данного
многоугольника, проведём плоскость.
Фигура, образованная частями
этих плоскостей,
ограниченными проведёнными лучами,
называется многогранным углом.
Точка S называется верши-
лучи SA, SB и т. д.
называются рёбрами многогранного угла, а части плоскостей,
ограниченные лучами,— его гранями. Углы, образованные лучами,
ограничивающими каждую грань, называются плоскими углами
многогранного угла. Каждый многогранный угол содержит
равное число рёбер и граней, а следовательно, и плоских углов.
Многогранный угол называется выпуклым, если все его грани
лежат по одну сторону от каждой из остальных граней,
неограниченно продолженной. Очевидно, выпуклому многоугольнику
ABCDE соответствует выпуклый многогранный угол.
Черт. 72.
ной многогранного угла,
§ 66. Свойство плоских углов многогранного угла.
Теорема. Сумма плоских углов выпуклого много-
гранного угла меньше 4d.
Дан выпуклый многогранный угол SABCDE (черт. 72). Пере*
секая его грани какой-либо плоскостью, получаем в сечении
выпуклый многоугольник ABCDE.
62

При каждой вершине этого многоугольника мы получаем
трёхгранный угол, образованный двумя гранями данного многогранного
угла и секущей плоскостью. Для каждого из этих трёхгранных
углов имеем (§ 62):
£ А ВС < ^ ABS + Ζ SBC;
Z_ bcd </_вс$ Л-/-$£&>
Z_ CDE < ^/ CDS -f Ζ SDE>
Ζ DEA < Ζ DES -j- Ζ SEA;
/_EAB<^AEAS-Y/-SAB.
Складывая почленно эти неравенства, мы в левой части
получим сумму углов многоугольника ABCDE, т. е. величину
2dn— Ыу где η — число сторон многоугольника; в правой части
мы, очевидно, получим сумму углов всех треугольников: ASB,
BSC и т. д., без суммы тех их углов, которые имеют вершину
в точке S, т. е. без суммы плоских углов многогранника.
Обозначая эту последнюю сумму буквой 5, мы после сложения всех
правых частей неравенств получим 2dn — S. Таким образом, после
сложения наших неравенств мы получим следующее неравенство
2dn — 4d<2dn — S.
Отсюда следует, что S<^4d.
IV. УПРАЖНЕНИЯ К ГЛАВЕ ТРЕТЬЕЙ.
А. Доказать теоремы.
1. Вертикальные двугранные углы равны между собой.
2. Сумма двух смежных двугранных углов равна двум прямым
двугранным углам.
3. Плоскости, делящие пополам два смежных двугранных угла,
взаимно перпендикулярны.
4. Двугранные углы с параллельными гранями или равны, или
составляют в сумме два прямых двугранных угла.
5. Если грани одного двугранного угла перпендикулярны граням
другого, а рёбра их параллельны, то эти углы или равны, или
составляют в сумме два прямых двугранных угла.
6. Две плоскости Μ и М', пересекающиеся по прямой а и
симметричные одна другой относительно третьей плоскости Р, образую!
с плоскостью Ρ равные двугранные углы.
Указание. Взять на плоскости Μ произвольную точку А и
построить симметричную ей точку А' на плоскости Μ. Прямая АА' _[_я.
Через АА* провести плоскость QJ_a. В сечении плоскости Q с
плоскостями 7И, М' и Ρ образуются линейные углы двугранных углов.
Легко заметить равенство этих линейных углов.
7. Плоскость, перпендикулярная к одной из двух параллельных
плоскостей, перпендикулярна и к другой.
8. Прямая и плоскость, перпендикулярные к одной плоскости,
параллельны.
63

9. Сумма трёх двугранных углов, образованных тремя
плоскостями, пересекающимися по параллельным прямым, равна двум прямым
двугранным углам.
10. Прямая, соединяющая проекции какой-либо точки на грани
двугранного угла, перпендикулярна к его ребру.
11. Прямая, соединяющая точки, симметричные данной
относительно граней двугранного угла, перпендикулярна к его ребру.
12. Если в трёхгранном угле два плоских угла прямые, той
противоположные им двугранные углы также прямые.
13. Если в трёхгранном угле все плоские углы прямые, то и все
двугранные углы прямые.
14. Трёхгранный угол, плоские углы которого прямые,
пересечён плоскостью. Доказать, что ортоцентр треугольника сечения
служит проекцией вершины трёхгранного угла на секущую плоскость.
Указание. Доказательство основывается на теореме о трёх
перпендикулярах.
15. Прямой трёхгранный угол SABC (т. е. такой, у которого все
плоские углы прямые) пересечён плоскостью Р, встречающей его
рёбра в точках Л, В и С.
Доказать, что: 1) площадь каждого из треугольников SBC, SCA,
SAB есть средняя пропорциональная между площадью проекции этого
треугольника на плоскость Ρ и площадью треугольника ЛВС;
2) сумма квадратов площадей треугольнков SBC,SCA, SAB равна
квадрату площади треугольника ЛВС.
16. Плоскости, делящие пополам двугранные углы трёхгранного
угла, проходят через одну прямую.
Указание. Точки, принадлежащие прямой пересечения двух
таких плоскостей, одинаково, удалены от всех трёх граней.
17. Плоскости, перпендикулярные к граням трёхгранного угла и
проходящие через равноделящие этих граней, проходят через одну
прямую.
Указание. Точки, принадлежащие прямой пересечения двух
таких плоскостей, одинаково удалены от их трёх рёбер.
18. Три плоскости, проходящие через каждое ребро и равноделя-
щую противолежащего ему плоского угла, проходят через одну
прямую.
Указание. На рёбрах данного угла от его вершины отложить
равные отрезки и через их концы провести плоскость. Она
пересечёт три проведённые плоскости по медианам треугольника сечения.
19. Плоскости, проходящие через рёбра трёхгранного угла
перпендикулярно к противоположным граням, проходят через одну
прямую.
Указание. Провести плоскость, перпендикулярную к линии
пересечения двух таких плоскостей. Рассмотреть треугольник
сечения и применить теорему о трёх перпендикулярах.
Б. Геометрические места.
20. Найти геометрическое место точек, равноудалённых от граней
двугранного угла. Отв. Полуплоскость, делящая двугранный угол
пополам.
21. Найти геометрическое место точек, отношение расстояний
которых от граней двугранного угла равно данной величине. Отв.
Полуплоскость, имеющая своей границей ребро двугранного угла.
64

22. Наьти геометрическое место точек, сумма или разность
расстояний которых от двух данных пересекающихся плоскостей равна
данной величине. Отв. Две пары плоскостей, параллельных
плоскостям, делящим пополам двугранные углы между данными плоскостями.
23. Найти геометрическое место точек, находящихся на данных
расстояниях от граней двугранного угла. Отв. Прямая,
параллельная ребру двугранного угла.
24. Найти геометрическое место точек, равноудалённых от граней
двугранного угла и находящихся на данном расстоянии от данной
плоскости. Отв. Прямая линия или две прямые линии, или
геометрическое место не существует.
25. Найти геометрическое место прямых, проходящих через
данную точку и одинаково наклонённых к граням данного двугранного
угла. Отв. Плоскость.
26. Найти геометрическое место ортоцентров треугольников,
получаемых в сечении трёхгранного угла параллельными плоскостями.
Отв. Прямая, проходящая через вершину угла.
27. Найти геометрическое место центров тяжести треугольников,
получаемых в сечении трёхгранного угла параллельными плоскостями.
Отв. Прямая, проходящая через вершину угла.
28. Найти геометрическое место центров окружностей,
описанных около треугольников, получаемых в сечении трёхгранного угла
параллельными плоскостями. Отв. Прямая, проходящая через
вершину -угла.
29. Найти геометрическое место точек, равноудалённых от граней
трёхгранного угла. Отв. Прямая, проходящая через вершину угла.
30. Найти геометрическое место точек, равноудалённых от рёбер
трёхгранного угла. Отв. Прямая, проходящая через вершину угла.
31. Найти геометрическое место точек, расстояния которых от
трёх граней данного трёхгранною угла пропорциональны трём данным
числам. Отв. Прямая, проходящая через вершину угла.
В. Задачи на построение.
32. Построить двугранный угол, линейный угол которого дан.
33. Построить линейный угол данного двугранного угла.
34. Данный двугранный угол разделить пополам.
35. Через точку пересечения «двух данных прямых провести
плоскость, одинаково наклонённую к этим прямым.
36. Через данную точку провести плоскость, параллельную ребру
двугранного угла и одинаково наклонённую к его граням.
37. Через данную прямую провести плоскость, одинаково
наклонённую к граням данного двугранного угла.
33. На гранях двугранного угла даны две точки А и В. Найти на
ребре угла точку, равноудалённую от А и В. Рассмотреть случаи:
1. Точки А и В лежат на одной грани.
2. Точки А и В лежат на разных гранях.
39. На каждой грани двугранного угла взято по одной точке.
Найти на ребре угла такую точку, чтобы прямые, соединяющие её
со взятыми точками на гранях, были взаимно перпендикулярны.
40. Построить трёхгранный угол, симметричный данному
относительно одного из его рёбер.
41. Построить трёхгранный угол, если даны один из его
двугранных углов и плоские углы, лежащие в гранях, образующих этот
двугранный угол.
42. Построить трёхгранный угол, если даны два его двугранных
угла и плоский угол, принадлежащий их общей грани.
65

43. Построить трёхгранный угол, если даны три его плоских угла.
44. Построить трёхгранный угол, если даны три его двугранных
угла.
45. Через вершину трёхгранного угла провести плоскость,
одинаково наклонённую ко всем трём его рёбрам.
46. Через вершину трёхгранного угла провести плоскость,
одинаково наклонённую ко всем его граням.
47. Пересечь грани данного выпуклого четырёхгранного угла
плоскостью так, чтобы в сечении получился параллелограм.
Отв. Искомая плоскость параллельна прямым пересечения
противоположных граней данного четырёхгранного угла.
Г. Задачи на вычисление.
48. Определить величину двугранного угла, зная, что прямая,
соединяющая точ*ки, симметричные данной относительно его граней,
пересекает его ребро. Отв. Двугранный угол—прямой.
49. На грани двугранного угла взяты две точки, расстояния
которых от второй грани равны 5 см и 8 см. Расстояние второй точки
от ребра двугранного угла равно 16 см. Определить расстояние
первой точки от того же ребра. Отв. 10 см.
50. Линейный угол двугранного угла равен 30°. На каком
расстоянии от ребра угла находится точка, лежащая на одной его грани
и отстоящая от другой грани на расстоянии 7 см? Отв. \\см.
51. Концы отрезка Л£ = 15 см находятся на двух гранях
прямого двугранного угла и отстоят от его ребра на расстоянии АА\ = 10 см
и ΒΒι = \\ см. Определить величину проекции отрезка АВ на ребро
двугранного угла (т. е. длину отрезка Аф^). Отв. 2 см.
52. Линейный угол двугранного угла равен 60°. В одной его грани
взята точка Л, в другой—точка В. Проекция Ах точки А на вторую
грань отстоит от ребра на а см, а проекция Вг точки В на первую
грань отстоит от ребра на b см. Вычислить длину отрезка АВ, зная,
что длина его проекции на ребро равна 2d см. Отв. 2Vaz—ab -\-b2 -f-rf2.
53. Сколько граней может содержать выпуклый многогранный
угол, если каждый его плоский, угол содержит 1) 45°? 2) 60°?
Отв. 1) 3, 4, 5, 6, 7. 2) 3, 4, 5.
ГЛАВА ЧЕТВЁРТАЯ.
МНОГОГРАННИКИ,
I. ОБЩИЕ СВОЙСТВА МНОГОГРАННИКОВ.
§ 67. Определения.
Геометрическое тело, поверхность которого состоит из частей
плоскостей, ограниченных простыми многоугольниками, называется
многогранником. Таков, например, куб.
Части плоскостей, ограничивающие многогранник, называются
его гранями.
65

Для краткости обычно говорят: „гранями многогранника
служат многоугольники". Стороны этих многоугольников называются
рёбрами многогранника. Каждое из них служит общею стороною
двух многоугольников, принадлежащих двум соседним граням. Грани
многогранников, проходящие через одну его вершину, образуют
многогранный угол. Вершины этих многогранных углов
называются вершинами многогранника, их двугранные углы —
двугранными углами многогранника, их плоские углы — плоскими
углами многогранника.
Отрезок прямой, соединяющий две вершины многогранника,
не принадлежащих одной грани, называется диагональю
многогранника. Плоскость, проходящая через три вершины многогранника,
не принадлежащих одной грани, называется диагональной
плоскостью, а сечение её с поверхностью многогранника —
диагональным сечением.
§ 68. Выпуклые многогранники.
Многогранник называется выпуклым, если все его грани лежат
по одну сторону от каждой из его граней, неограниченно
продолженной. Если пересечь выпуклый
многогранник плоскостью, то в сечении всегда
получится выпуклый многоугольник,
стороны которого лежат на поверхности
многогранника. Наименьшее число граней
многогранника равно четырём.
Действительно, в вершине многогранника сходится
не меньше трёх граней, — они образуют
трёхгранный угол. Чтобы получить
многогранник, необходимо провести ещё одну
плоскость, пересекающую все три грани Черт. 73.
трёхгранного угла. Эти четыре плоскости
будут ограничивать многогранник с наименьшим числом граней
(черт. 73). Он имеет четыре грани, четыре вершины и шесть
рёбер и носит название тетраэдра, или треугольной пирамиды.
§ 69. Соотношение между числом плоских углов
многогранника и числом его рёбер.
Теорема. Число плоских углов многогранника вдвое
больше числа его рёбер.
На каждой грани многогранника число его плоских углов
равно числу углов многоугольника, ограничивающего эту грань.
Но каждое ребро многогранника служит общей стороной двух
многоугольников, ограничивающих соседние грани. А потому число
67
4

рёбер многогранника вдвое меньше числа сторон
многоугольников, ограничивающих каждую грань в отдельности. Если число
рёбер многогранника равно k, то число сторон всех отдельно
взятых многоугольников равно 2k. Но число сторон каждого
многоугольника равно числу его углов. А эти углы и составляют
плоские углы многогранника.
Следовательно, число плоских углов многогранника равно 2k.
Следствия. 1. Число плоских углов многогранника всегда
чётное.
2. Если в каждой вершине многогранника сходится по
одинаковому числу ρ рёбер и если е — число его вершин, то
ep = 2k.
Действительно, число плоских углов при каждой вершине
многогранника равно числу сходящихся в ней рёбер.
Следовательно, число всех плоских углов многогранника этого вида равно ер.
3. Если все грани многогранника образованы
многоугольниками с одинаковым числом η сторон и f—число граней,
то fn = 2k.
Действительно, число плоских углов, лежащих в одной грани,
равно числу η сторон многоугольника, образующих эту грань.
Следовательно, число всех плоских углов многогранника этого
вида равно fn.
§ 70. Соотношение между суммой плоских углов
многогранника и числом его рёбер и граней.
Теорема. Сумма плоских углов многогранника с
числом рёбер k и числом граней f равна 4d(k—f).
Дан многогранник, имеющий / граней и k рёбер, причём
гранями многогранника служат многоугольники с числом сторон:
в одной грани nv в другой я2, в третьей я3, и т. д.
По теореме § 69:
ni+n2 + ns + - - = 2*.
Сумма углов первого многоугольника равна 2dnx — 4d,
второго 2dn(1 — 4dy третьего 2dn2 — Ы и т. д. Сумма всех этих
углов равна:
2d{nx -f /i2 + я3 + · · ·) — 4rf — Ы — \d — .. . — 4rf =
= 2d-2k — 4df = 4d(k—f).
§71. Теорема Эйлера о выпуклых многогранниках.
Теорема. Если f—число граней выпуклого
многогранника, е—число его вершин, k — число его рёбер,
то е —k-\-f=2.
68

Возьмём вне данного многогранника какую-либо точку S, не
лежащую ни на одной из плоскостей его граней и ни на одной
из его диагональных плоскостей, и проведём из неё лучи ко
всем вершинам и ко всем точкам рёбер данного . многогранника.
Пересекая всю совокупность этих лучей плоскостью Λί, не
проходящей через s, мы получим в сечении многоугольную фигуру,
которая называется центральной проекцией многогранника.
Эта фигура ограничена выпуклым многоугольником Ρ (с
некоторым числом η сторон). Стороны его являются проекциями
некоторых η рёбер многогранника, а вершины — проекциями
некоторых η его вершин. Остальные е—η вершин многогранника
и k— η его рёбер проектируются на плоскость Μ внутрь
многоугольника Ρ η образуют вершины и стороны выпуклых
многоугольников, лежащих внутри многоугольника Р.
Подсчитаем сумму плоских углов данного многогранника. По
теореме § 70 она равна \d(k —/). С другой стороны, ту же сумму
можно выразить через углы той многоугольной фигуры, которая
получена в плоскости М.
Сумма углов многоугольника определяется лишь числом его
сторон и поэтому, при проектировании многоугольника на другую
плоскость, эта сумма не меняется. Поэтому сумма всех плоских
углов данною многогранника равна сумме проекций этих углов
на плоскость М. Эту последнюю сумму можно подсчитать так:
внутри многоугольника Ρ имеется е — η проекций вершин
многогранника, сумма углов при каждой из них равна Ы, а
следовательно, сумма всех углов с вершинами внутри многоугольника
Ρ равна 4d (е— п).
Сумма углов многоугольника Я равна 2dn— 4д?, но так как
при каждой вершине многоугольника Ρ проектируются плоские
углы с двух сторон многогранника (верхний и нижний), то сумма
проекций всех этих углов равна (2dn— 4d)· 2. А поэтому сумма
проекций всех плоских углов многогранника равна
\d (* — /i) + (2rf/i — Щ2 = Ые — Sd = 4d(e — 2).
Этой же величине равна сумма всех плоских углов
многогранника. Сравнивая эту формулу с найденной ранее, будем иметь:
4d(e — 2) = 4d(k—f).
Отсюда,
e—2 = k—f
или
e — k+f=2.
69

II. ПРИЗМА.
§ 72. Общие свойства призмы.
Призмой называется многогранник, две грани которого
параллельны, а остальные грани пересекаются по параллельным
прямым. Построить такой многогранник можно следующим образом:
возьмём какой-либо многоугольник ABCDE
и через все его вершины проведём прямые,
.g параллельные между собою и не лежащие
в плоскости многоугольника. Через каждые
две прямые, проходящие через две соседние
вершины многоугольника, проводим
плоскость и всю совокупность построенных
плоскостей пересечём плоскостью,
параллельной плоскости многоугольника.
Геометрическое тело, ограниченное всеми
построенными плоскостями, и будет призмой. Такова
С призма ABCDE Αβ^β^ (черт. 74).
Коротко обозначим её ADV
Многоугольники ABCDE и AiB^ClDiE1,
лежащие в параллельных плоскостях,
называются основаниями призмы, остальные
грани призмы называются боковыми гранями, а рёбра, по которым
они пересекаются, называются боковыми рёбрами. Отрезок
прямой, перпендикулярной к плоскостям оснований призмы,
заключённый между этими плоскостями, называется высотой призмы.
Из способа построения призмы легко усмотреть следующие её
свойства.
1. Основаниями призмы служат два равные
многоугольника, соответственные стороны которых
параллельны.
2. Боковыми гранями призмы служат параллело-
г рамы.
§ 73. Виды призм.
Призма называется треугольной, четырёхугольной и т. д.,
когда в основании её лежит треугольник, четырёхугольник и т. д.
Призма называется прямой, если её боковые рёбра
перпендикулярны к плоскостям её оснований. Боковыми гранями прямой
призмы служат прямоугольники. Призма называется правильной,
если она прямая и если её основаниями служат правильные
многоугольники. В правильной призме все боковые грани — равные
прямоугольники. Все трёхгранные углы при вершинах оснований
правильной призмы равны чмежду собою.
70

Прямая, соединяющая центры оснований правильной призмы,
перпендикулярна к плоскостям оснований призмы и служит
осью её симметрии порядка, равного числу боковых граней призмы.
Так, правильная треугольная призма имеет ось симметрии третьего
порядка, правильная я-угольная призма имеет ось симметрии /2-го
порядка.
§ 74. Сечения призмы.
Плоскость, проходящая через два боковых ребра
призмы, не лежащие в одной грани, называется
диагональной плоскостью, или плоскостью диагонального сечения.
Диагональные плоскости пересекают поверхность призмы по парал-
лелограмам, называемым диагональными сечениями призмы.
Таково, например, сечение ACCiAl (черт. 74).
Диагонали этих параллелограмов называются диагоналями
призмы.
Если пересечь призму плоскостью, параллельной плоскостям
сё оснований, то в сечении призмы получится многоугольник,
равный многоугольникам, служащим основаниями призмы.
Если пересечь призму плоскостью, перпендикулярной к её
боковому реору, то в пересечении с плоскостями боковых граней
получится многоугольник, называемый прямым или
перпендикулярным сечением призмы.
Легко заметить, что в сечении призмы
двумя какими-либо параллельными плоскостями,
пересекающими все боковые рёбра призмы,
получаются равные многоугольники.
§ 75. Поверхность призмы.
Поверхностью призмы называется сумма
площадей всех её граней. Боковой
поверхностью призмы называется сумма площадей
всех её боковых граней.
Теорема. Боковая поверхность
призмы равна произведению
периметра перпендикулярного сечения призмы
на её боковое ребро.
Дана призма AD} (черт. 75). Если
провести плоскость перпендикулярного сечения,
то в сечении получится многоугольник
MNPQRy стороны которого перпендикулярны к боковым рёбрам
призмы. В каждой боковой гр*ани сторону этого многоугольника
можно принять за высоту параллелограма, образующего эту грань.
Тогда основанием этого параллелограма будет служить боковое
71

ребро призмы. Если обозначить длину бокового ребра через /,
то площади боковых граней будут /-МЛ/, l*NPy l-PQ и т. д.,
а сумма их равна:
l.MN-\-l.NP-\-...-\-l-RM = l(MN-\-...-\-RM)=lP,
где Ρ — периметр перпендикулярного сечения.
Следствие. Боковая поверхность прямой призмы равна
произведению периметра её основания на боковое ребро.
§ 76. Параллелепипед.
Четырёхугольная призма, основанием которой служит параллело-
грам, называется параллелепипедом.
Теорема. Противоположные грани
параллелепипеда равны между собой, а плоскости их параллельны.
Черт. 76. Черт. 76а.
Дан параллелепипед ABCDEFGH, или AG (черт. 76). Возьмём
его грани ABFE и DCGH. В этих гранях:
AB = DQEF = HG,
как противоположные стороны параллелограмов, служащих
основаниями параллелепипеда;
BF=CG,AE = DHy
как противоположные стороны параллелограмов, составляющих
боковые грани параллелепипеда;
£ABF = £DCQ,
как углы с параллельными сторонами. Следовательно, параллело-
грам ABFE равен параллелограму DCGH и плоскости этих
параллелограмов параллельны.
72

Следствие. Каждую пару противоположных граней
параллелепипеда можно принять га его основания.
Теорема. Все диагонали параллелепипеда
пересекаются в одной точке и делятся при пересечении
пополам.
Диагонали AG и ЕС служат диагоналями параллелограма
EGCA и в точке О делятся пополам. Диагонали AG и ИВ
служат диагоналями параллелограма ABGH, и потому диагональ
ИВ проходит через точку О — середину диагонали AG.
Наконец, диагонали DF и ИВ служат диагоналями параллелограма
DHFB и потому диагональ DF проходит через середину О
диагонали ИВ.
§ 77. Прямой и прямоугольный параллелепипед.
Параллелепипед, рёбра которого перпендикулярны к
плоскостям оснований, называется прямым.
Прямой параллелепипед, основания которого прямоугольники,
называется прямоугольным.
В прямоугольном параллелепипеде все грани — прямоугольники,
все диагонали равны.
Три ребра прямоугольного параллелепипеда, сходящиеся
в одной вершине, называются его измерениями.
Теорема. Квадрат диагонали прямоугольного
параллелепипеда равен сумме квадратов трёх его
измерений.
Пусть ABCDEFGH — прямоугольный параллелепипед
(черт. 76 а). Из треугольника AGC имеем:
AG2 = AC2-\-CG2,
но
АС2 = АВ2-\-ВС2 и CG = BFy
2l ПОТОМУ
AG2 = AB2 -f- ВС2 -f- BF2.
Прямоугольный параллелепипед, три ребра которого,
сходящиеся в одной вершине, равны, называется кубом. Все грани
куба—равные квадраты.
III. ПИРАМИДА.
§ 78. Определения.
Если пересечь все грани многогранного угла какою-либо
плоскостью, то секущая плоскость вместе с гранями
-многогранного угла будет ограничивать многогранник, называемый пира-
73

мидой. Такова пирамида SABCDE (черт. 77). Многоугольник,
получаемый в секущей плоскости, называется основанием
пирамиды.
Если основанием пирамиды служит треугольник,
четырёхугольник, ... , многоугольник, то пирамида называется соответственно
треугольной, четырёхугольной,...,
вообще многоугольной.
Треугольная пирамида является
в то же время тетраэдром (§ 68.)
Остальными гранями пирамиды
служат треугольники с общей
вершиной, называемой вершиной
пирамиды. Эти треугольники называются
боковыми гранями пирамиды.
Рёбра, по которым пересекаются
боковые грани пирамиды, называются её
боковыми рёбрами. Длина
перпендикуляра, опущенного из вершины
пирамиды на плоскость её основания,
называется высотой пирамиды. Пирамида называется
правильной, если основанием её служит правильный многоугольник и
перпендикуляр из вершины пирамиды
на её основание проходит через центр
этого многоугольника.
Все боковые рёбра, а также все
плоские углы при вершине правильной
пирамиды, равны между собой.
Боковыми гранями правильной
пирамиды служат равнобедренные
треугольники, равные между собою. Высота
каждого из них называется апофемою
пирамиды. Такова, например, высота SG
в треугольнике ABS (черт. 78).
§ 79. Сечения пирамиды.
Черт. 78.
Плоскость, проходящая через два несмежных боковых ребра
пирамиды, называется диагональной плоскостью, а сечение её
с поверхностью пирамиды называется диагональным сечением
пирамиды. Таково, например, сечение ACS (черт. 77).
Диагональными сечениями пирамиды служат треугольники
с общей вершиной в вершине пирамиды. Основаниями этих
треугольников служат диагонали основания пирамиды. Таковы
треугольники ASC и ASD (черт. 77).
74

Теорема. Если пересень пирамиду плоскостью,
параллельной её основанию, то:
1) боковые рёбра и высота пирамиды разделятся
на пропорциональные между собою
части;
2) сечение есть многоугольник,
подобный основанию;
3) отношение площадей сечения
и основания равно отношению
квадратов их расстояний от вершины
пирамиды.
1. Дана пирамида SABCDE (черт. 79),
пересечённая плоскостью AlBlCxDlEv
Проведём высоту пирамиды SP,
встречающую плоскость сечения в точке Pv
и соединим точки Ρ и Рг соответственно *
с точками А и АГ
Из подобных треугольников ASP и Черт. 79.
AXSPX имеем:
SPi_SAit
SP — SA '
и так же найдём:
S£i_5£i. SJ\_SCi. SPi_S£h.
SP ~SB ' SP ~SC ' SP~SD ''"
Следовательно,
SP1_SA1 _SBj _Sd _
SP ~~~ SA — SB ~ SC
2. Так как секущая плоскость параллельна плоскости
основания пирамиды, то (§ 14)
ΑΒ\\ΑχΒύ ЯСПад...
Следовательно (§ 16),
Так как
Д Л^Зс/эД ABS,
то
AiBi_AiS_ P\S
АВ ~~ AS -— PS '
Так же найдём:
Bid f\S_. C1D1_P1S .
ВС ~~~ PS ' CZ) — PS '
следовательно,
A\Bi_Bid d£\__
АВ "ВС CD"'"
75

А потому
О AXBXCXDXEX со О ABCDE.
3. По теореме о площадях подобных многоугольников
(Планиметрия, § 254) имеем:
2
ϊΐΛοιιχ.ΑιΒιΟχΡιΠι А\В\
нлощ. ABCDE ~ АВ* '
а так как
AlBl_AlS _PXS
АВ — AS "" AS '
то
площ. i4tД^Д/?! ___ Ρ^2
площ. ABCDE ~~ PS* *
§ 80. Поверхность пирамиды.
Сумма площадей боковых граней пирамиды называется её
боковою поверхностью. Сумма боковой поверхности пирамиды
и площади её основания называется полной поверхностью
пирамиды. Чтобы найти боковую поверхность пирамиды, нужно
определить площадь каждой её боковой грани и взять сумму
всех полученных таким образом площадей. Если же пирамида
правильная, то её боковая поверхность может быть вычислена
проще на основании следующей теоремы.
Теорема. Боковая поверхность правильной
пирамиды равна произведению периметра её основания
на половину апофемы.
Если а (черт. 78) — сторона основания правильной пирамиды
(АВ = а), а / — её апофема (SG = /), то площадь боковой грани
равна -7J· al, а сумма S площадей всех её боковых граней равна
-Tytial. Но па — Ру где Ρ—периметр основания, а потому
§ 81. Усечённая пирамида.
Часть пирамиды, заключённая между её основанием и секущей
плоскостью, параллельной основанию, называется усечённой
пирамидой (черт. 80).
Параллельные грани усечённой пирамиды называются её
основаниями. Отрезок прямой, перпендикулярной к плоскостям
оснований усечённой пирамиды, заключённый между этими
плоскостями, называется высотой усечённой пирамиды. Основаниями
76

усечённой пирамиды служат подобные многоугольники (как
параллельные сечения пирамиды).
Усечённая пирамида называется правильной, если основаниями
её служат правильные многоугольники и прямая, соединяющая
центры оснований, перпендикулярна
к плоскостям этих оснований.
Боковыми гранями правильной
усечённой пирамиды служат равные
между собой равнобедренные
трапеции; высота каждой из них
называется апофем эй усечённой
пирамиды .
Боковой поверхностью
усечённой пирамиды называется сумма
площадей её боковых граней. Полной
поверхностью усечённой пирамиды
называется сумма её боковой поверхности и площадей основания.
Теорема. Боковая поверхность правильной
усечённой пирамиды равна произведению полусуммы
периметров её оснований на апофему.
Если а — сторона нижнего основания, Ь — сторона верхнего
основания, / — апофема данной усечённой пирамиды, то площадь
а + b ι о
—^—/, а сумма 6 площадей всех боко-
её боковой грани равна
вых граней равна
а + Ь , na-X-nb .
где η — число боковых граней, но аш = Р, где Ρ — периметр
нижнего основания, a nb=Q, где Q — периметр верхнего
основания, а потому
IV. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ.
§ 82. Общие свойства правильных многогранников.
Многогранник называется правильным, если все его грани —
равные правильные многоугольники и все его двугранные углы
равны между собой. Отсюда следует, что все плоские углы
многогранника, а также все его многогранные углы и все его рёбра
равны между собой.
Если обозначить через е — число вершин правильного
многогранника, /—число его граней, k — число всех рёбер, ρ — число
77

рёбер, сходящихся водной вершине, и η — число сторон
многоугольника в каждой грани, то между числами еу f, k, η и ρ
должны иметь место следующие соотношения:
Теорема. Число рёбер, сходящихся в каждой
вершине правильного многогранника, не может быть
более пяти.
Сумма плоских углов многогранного угла меньше 360° (§ 66),
а потому, если бы в какой-либо вершине правильного
многогранника сходилось 6 рёбер, то и число плоских углов при этой
вершине правильного многогранника было бы равно 6, и,
следовательно, каждый угол должен быть меньше 60°, что невозможно.
В самом деле: гранями правильного многогранника служат
правильные многоугольники, но правильного многоугольника, угол
которого был бы меньше 60°, не существует.
Теорема. Число сторон правильных
многоугольников, образующих грани правильного многогранника,
не может быть более пяти.
В каждой вершине многогранника сходится не меньше трёх
плоских углов, сумма которых должна быть меньше 360°, и
следовательно, каждый из них должен быть меньше 120°.
Так как угол правильного шестиугольника равен 120°, а угол
многоугольника с большим числом сторон больше 120°, то
правильные многоугольники с числом сторон шесть или больше
не могут служить гранями правильного многогранника.
Так как в правильных многогранниках во всех е вершинах
сходится по одинаковому числу ρ рёбер и многоугольники всех
его / граней содержат по одинаковому числу η сторон, то для
всех правильных многогранников должны иметь
место равенства (§ 69, ел. 2 и 3):
ep = 2k и fn = 2k.
§ 83. Возможные виды правильных
многогранников.
1. Если гранями правильного
многогранника служат треугольники, то при вершинах
могут сходиться три, четыре или пять рёбер.
Ниже будет показано, что все эти три случая действительно
могут иметь место.
В первом случае многогранник называется правильным
тетраэдром; он имеет 4 грани, 4 вершины и 6 рёбер (см. черт. 73),
во втором — октаэдром, имеющим 8 граней, 6 вершин и 12
р'гб^р (черт. 81), в третьем — икосаэдром. Икосаэдр имеет 20
граней, 12 вершин и 30 рёбер (черт. 82).
78

2. Если гранями правильного многогранника служат квадраты,
то многогранник может быть только один (так как в каждой
вершине в этом случае не может сходиться более трёх рёбер).
Такой многогранник действительно существует, это — куб; он
имеет 6 граней, 8 вершин и 12 рёбер (черт. 83).
Черт. 82. Черт. 83. Черт. 84.
3. Если грани многогранника — пятиугольники, то многогранник
также может быть только один; он действительно существует и
носит название додекаэдра; он имеет 12 граней, 20 вершин и
30 рёбер (черт. 84).
§ 84. Существование правильных многогранников.
. Изложенные выше теоремы доказывают, что могут
существовать не более пяти видов правильных многогранников.
Но из этих теорем ещё не следует, что все эти пять видов
правильных многогранников действительно существуют, т. е. что
можно проведением плоскостей в пространстве осуществить
построение каждого из этих пяти возможных правильных
многогранников. Чтобы убедиться в существовании всех указанных выше
правильных многогранников, достаточно указать способ
построения каждого из них.
§ 85. Построение куба.
Для построения куба берём произвольную плоскость Ρ и в
ней какой-либо квадрат; через стороны этого квадрата проводим
плоскости, перпендикулярные к плоскости Р. Таких плоскостей
будет четыре. Далее проводим плоскость Q, параллельную Ρ и
отстоящую от неё на расстоянии, равном стороне квадрата.
Шесть полученных плоскостей образуют грани куба; двенадцать
прямых пересечения каждой пары пересекающихся плоскостей
являются рёбрами куба, а восемь точек пересечения каждой
тройки пересекающихся плоскостей служат вершинами куба.
В этом легко убедиться непосредственно, рассматривая получен-
79

ную совокупность точек, прямых и плоскостей. Умея построить
куб, легко найти способ построения всех других правильных
многогранников.
§ 86. Построение правильного тетраэдра.
Пусть дан куб (черт. 85). Возьмём какую-либо его вершину,
например А. В ней сходятся три грани куба, имеющие форму
квадратов. В каждом из этих
квадратов берём вершину,
противоположную точке А. Пусть
это будут вершины куба В, С
и D. Точки А, В, С и D
служат вершинами правильного
тетраэдра. Действительно,
каждый из отрезков АВ, ВС, CD,
AD, BD и АС, очевидно,
служит диагональю одной из гра-
о ней куба, а потому все эти
отрезки равны между собою.
Отсюда следует, что в
треугольной пирамиде с вершиной
А и основанием BCD все
грани— правильные треугольники, следовательно, эта пирамида —
правильный тетраэдр. Этот тетраэдр вписан в данный куб.
Полезно заметить, что оставшиеся четыре вершины куба
служат вершинами второго правильного тетраэдра, равного
первому и также вписанному в данный
куб.
§ 87. Построение октаэдра.
Если в данном кубе построить
центры всех его граней, то шесть
полученных точек служат вершинами
октаэдра. В этом легко убедиться,
рассматривая чертёж 86.
§ 88. Построение додекаэдра.
Если через каждое из двенадцати Черт. 86.
рёбер куба провести плоскость, ые
имеющую с поверхностью куба других общих точек, кроме точек
этого ребра, то полученные 12 плоскостей образуют грани
некоторого 12-гранника. Более подробное изучение формы этого
80

многогранника показывает, что можно так подобрать наклон этих
плоскостей к граням куба, что грани этого 12-гранника будут
правильными пятиугольниками, а сам 12-гранник будет
додекаэдром (черт. 87).
§ 89. Построение икосаэдра.
Если мы умеем построить додекаэдр, то построение икосаэдра
не представляет затруднений .-центры граней додекаэдра служат
вершинами икосаэдра (черт. 88.)
Черт. 87. Черт. 88.
§ 89а. Центр правильного многогранника.
Все диагонали куба между собой равны (§ 77), пересекаются
в одной точке и делятся в ней пополам (§ 76). Следовательно,
точка пересечения диагоналей куба равноудалена от всех его
вершин. Эта точка называется центром куба. Легко видеть, что
других точек, равноудалённых от всех вершин, куб не имеет.
В правильном тетраэдре также существует единственная
точка, равноудалённая от всех вершин. Такой точкой будет
центр того куба, с помощью которого мы строили правильный
тетраэдр (черт. 85). То же имеет место и для октаэдра (черт. 86).
Более подробное проведение рассуждений, относящихся к
додекаэдру и к икосаэдру (§ 88 и § 89), показывает, что как
в додекаэдре, так и в икосаэдре также существует единственная
точка, равноудалённая от всех вершин. В додекаэдре такой
точкой будет центр того куба, с помощью которого строится
додекаэдр (черт. 87), в икосаэдре — центр соответствующего
додекаэдра (черт. 88).
Итак, во всяком правильном многограннике существует
единственная точка, равноудалённая от всех его вершин.
Точка, равноудалённая от всех вершин правильного
многоугольника, называется центром правильного многогранника.
81

§ 90. Самосовмещения правильных многогранников.
Благодаря тому, что в правильном многограннике все грани —
равные между собою правильные многоугольники, все плоские, а
также все двугранные углы равны, — его можно переместить
так, что одни его вершины займут место других, а весь
многогранник в целом сохранит прежнее положение. Если взять,
например, деревянный кубик и перенумеровать его грани, написав
на каждой грани её номер, а затем начертить на столе на листе
бумаги квадрат, равный грани кубика, то кубик можно будет
поставить на стол так, что одна его грань, например грань №5,
совместится с начерченным квадратом. Эта грань может занять
при этом 4 различных положения <^£ю· То
же справедливо и для каждой из других граней. Так как куб
имеет 6 граней, то всего можно поставить кубик на данный
квадрат на столе 24 различными способами. Если заменять одно
из этих положений другим, то кубик будет принимать одно и
то же положение на столе, или, как говорят, будет совмещаться
сам с собой. Каждое положение многогранника, при котором он
совмещается сам с собой, называется его самосовмещением.
Получать такие самосовмещения можно различными способами,
заставляя одну вершину многогранника занимать место то одной,
то другой из остальных вершин. Полное число всех самосовмег
щений правильного многогранника, считая и исходное его
положение, определяется следующей теоремой.
Теорема. Полное число всех самосовмещений
правильного многогранника в два раза более числа его
рёбер.
Действительно, при всех возможных самосовмещениях
многогранника любой его плоский угол может совместиться с каждым
из других его плоских углов и с самим собою и притом только
одним способом. Следовательно, полное число всех
самосовмещений многогранника равно числу его плоских углов, а это
число, как было показано выше, в два раза больше числа его
рёбер (§ 69).
Таким образом, правильный тетраэдр имеет 12
самосовмещений, куб — 24, октаэдр — 24, додекаэдр — 60, икосаэдр — 60.
§ 91. Оси симметрии правильных многогранников.
При каждом самосовмещении правильного многогранника его,
центр не меняет своего положения, т. е. остаётся неподвижным.;
А потому, в силу теоремы Даламбера, каждое такое самосовмеще-ί
82

ние можно осуществить вращением вокруг некоторой оси,
проходящей через центр многогранника (§ 36).
Если тело совмещается само с собой вращением вокруг оси,
то эта ось называется, как мы знаем (§ 51), его осью симметрии.
Найдём все оси симметрии правильных многогранников.
Первую группу осей симметрии найдём, рассматривая
вершины многогранника. Концы всех рёбер, выходящих из одной
вершины, лежат в одной плоскости. Это очевидно в случае
тетраэдра, куба, октаэдра и додекаэдра; в случае икосаэдра это
свойство можно доказать. Эта плоскость отсекает от
многогранника правильную р-угольную пирамиду. Высота / этой пирамиды
служит её осью симметрии порядка р. Но при вращении
пирамиды вокруг этой оси вместе с нею будет вращаться и весь
многогранник, и когда пирамида совместится сама с собой, и весь
многогранник придёт в самосовмещение. Отсюда следует, что
прямая / служит и для многогранника осью симметрии порядка р.
Найдём число таких осей. Если для каждой вершины много
гранника есть ей противолежащая (куб, октаэдр, додекаэдр и
икосаэдр), то прямая / проходит не только через взятую вер-.
шину, но и через вершину противолежащую.
В самом деле, вершина, противолежащая взятой, при
совмещении многогранника должна совместиться сама с собой, т. е.
остаться неподвижной. Значит, эта вершина лежит на прямой /.
Следовательно, прямая / соединяет противолежащие вершины.
^>
Число найденных осей многогранника равно -^ .
Таким образом, куб имеет 4 оси симметрии этого типа,
октаэдр— 6, додекаэдр — 10, икосаэдр — 6. Для куба и додекаэдра
это будут оси 3-го порядка, для октаэдра — 4-го и для
икосаэдра— 5-го порядка.
В тетраэдре вершины не имеют себе противоположных, и
потому для тетраэдра число осей симметрии этого типа равно
полному числу его вершин, т. е. 4. Все они будут осями 3-го
порядка.
Вторую группу осей симметрии многогранника получим,
рассматривая его грани. Возьмём какую-либо его грань. Прямая
/', проходящая через центр этой грани и перпендикулярная к её
плоскости, очевидно, служит осью симметрии η -го порядка для
многоугольника, образующего эту грань. Но при вращении этого
многоугольника вокруг оси /' вместе с ним будет вращаться и
весь многогранник и, когда многоугольник совместится сам с
собой, и весь многогранник придёт в самосовмещение. Отсюда
следует, что прямая /' служит для многогранника осью симметрии
порядка я. Определим число таких осей. Если для каждой грани
83

многогранника есть ей противолежащая (куб, октаэдр, додекаэдр,
икосаэдр), то прямая /' проходит через центр противолежащей
грани. В этом убедиться так же легко, как и для осей первой
группы. Следовательно, число осей этой второй группы равно у.
Таким образом, куб имеет 3 таких оси, октаэдр — 4,
додекаэдр— 6, икосаэдр—10. Для октаэдра и икосаэдра это будут
оси третьего порядка, для куба — четвёртого, для додекаэдра —
пятого. Для всех четырёх многогранников—куба, октаэдра,
додекаэдра, икосаэдра—оси второй группы, очевидно, отличны от
осей первой группы. Иначе будет обстоять дело для тетраэдра.
В тетраэдре грани не будут иметь себе противолежащих, и
потому для него число осей симметрии равно полному числу его
граней, т. е. 4.
Очевидно, эю те же самые оси 3-го порядка, которые были
найдены выше. Таким образом, для тетраэдра оси второй группы
совпадают с осями первой группы.
Наконец, третью группу осей симметрии многогранника
получим, рассматривая его рёбра. Прямая /", проходящая через
середину ребра, перпендикулярная к нему и одинаково
наклонённая к обеим прилежащим граням, очевидно, служит для
многогранника осью симметрии 2-го порядка. Чтобы найти число осей
этой группы, заметим, что во всех правильных многогранниках
для каждого ребра есть ему противолежащее, и так же, как и раньше,
легко убеждаемся, что прямая Г проходит не только через
середину взятого ребра, но и через середину ребра противолежащего.
Отсюда следует, что число осей этой группы равно -^ · Таким
образом, тетраэдр имеет 3 оси этой группы, куб— б, октаэдр — б,
додекаэдр—15, икосаэдр—15. Для всех многогранников это
будут оси 2-го порядка. Для всех 5 многогранников оси
третьей группы, очевидно, отличны от осей первой и второй
групп. Все самосовмещения, получаемые вращением многогранника
вокруг найденных осей, очевидно, различны, так как они
получаются вращением или вокруг разных осей, или вокруг одной оси
на разные углы.
Легко убедиться, что никаких других осей симметрии,
кроме найденных выше, правильные многогранники не имеют.
Действительно, рассмотрим вначале тетраэдр. Для него мы нашли!
4 оси симметрии 3-го порядка и 3 оси симметрии 2-го порядка.)
Вращение около каждой оси симметрии 2-го порядка даёт одно!
самосовмещение тетраэдра, отличное от исходного положения.,!
Вращение около оси симметрии 3-го порядка даёт два таких само-|
совмещения. Таким образом, вращением около найденных осеЙ|
84

можно получить всего 3· 1 —{— 4·2 == 11 самосовмещений тетраэдра,
отличных от исходного положения. Вместе с исходным
положением они составляют 12 самосовмещений тетраэдра, т. е.
исчерпывают собой полное число его самосовмещений. А потому
никаких других осей симметрии тетраэдр не имеет.
Возьмём теперь какой-либо другой правильный многогранник.
Вращение около его осей симметрии первой группы даёт (р—1)
самосовмещений многогранника, отличных от исходного. Число
таких осей равно -~ , а потому вращения около них дают всего
(ρ— 1) различных самосовмещений, отличных от исходного.
Точно так же вращения около осей симметрии второй группы
дают ---(# — 1) различных самосовмещений.
Наконец, вращение вокруг каждой из осей третьей группы
даёт лишь одно самосовмещение многогранника, отличное от ис-
ь
ходного. Следовательно, число таких самосовмещений равно -^.
в f k
Таким образом получаем N=~(p — \)-\-~(п—1)_|_ ~
различных самосовмещений, отличных от исходного.
Преобразуя это выражение, найдём:
к]—е2_ е \fn ./ \.*—eP + fn e+f\b
iV— 2 2~» 2 2 ■ 2 ~~ 2 2 "^ 2 '
Ho (§ 69 и § 71):
а потому
fn = ep = 2k и e-\-f=k-\-2,
Столько различных самосовмещений, отличных от исходного,
можно получить вращением около всех найденных осей. Вместе
с исходным положением они составляют 2k самосовмещений, т. е.
исчерпывают собой полное число возможных самосовмещений
правильного многогранника. Отсюда следует, что никакик других
осей симметрии правильный многогранник не имеет. Исходное
положение многогранника можно также рассматривать как
самосовмещение, полученное вращением вокруг какой-либо оси симметрии
на угол 0. Это вращение называется нулевым, или
тождественным.
85

Число и порядок осей симметрии и число самосовмещеннй
правильных многогранников представлены следующей таблицей.
Вид
многогранника
тетраэдр ....
куб
октаэдр
додекаэдр ....
икосаэдр ....
2-го
порядка ι
3
б
б
15
15
Число осей симметрии
3-го
порядка
4
4
4
10
10
4-го
порядка
3
3
—
—
5-го
порядка
—
—
б
б
всего
осей
7
13
13
31
31
Полное
' ЧИСЛО
ι
самосовмещений
12
24
24
60
60
§ 92. Свойства вращений правильных многогранников.
Рассмотрим все найденные выше вращения правильных
многогранников вокруг их осей симметрии. Два такие вращения
считаются различными, если они дают различные самосовмещения
многогранника. Два вращения считаются равносильными, если
они дают одно и то же самосовмещение. Таковы будут,
например, вращения вокруг одной оси, углы вращения которых
разнятся на угол, кратный 360°. Значит, нулевое вращение
равносильно вращению на 360°.
Таким образом, чтобы указать, какому вращению
подвергается многогранник, достаточно указать, какие положения
должны занимать его вершины после вращения. Так, после
вращения тетраэдра ABCD вокруг оси DDX (черт. 89) на 120°
вершина А займёт место вершины В, вершина В—место
вершины С, вершина С—место вершины Л, а вершина D останется,
на месте. Это коротко записывают так:
А-+В, В -*С, С —Л, D—+D.
Нулевое вращение запишется так:
А-.А, В-+В, С-+С, D-+D.
Каждое вращение обозначают какою-либо одной буквой,
например,
Si=(A-+B, Я —С, С—* Λ, D-+D).
Сложение вращений. Последовательное выполнение
двух вращений Sx и S2 называется сложением этих вращений;
и изображается обычно в виде суммы Sj-f-Sg.
86

Теорема. Сумма всяких двух вращений
правильного многогранника равносильна некоторому одному
вращению.
В самом деле, при всех вращениях многогранника его центр
остаётся неподвижным. А потому положение многогранника,
занятое им после двух вращений Sk и S(i приводящих его в
самосовмещение, может быть получено одним вращением вокруг оси,
Черт. о9.
проходящей через центр (теорема Даламбера), также
приводящим его в самосовмещение, т. е. некоторым вращением Sm
вокруг одной из осей симметрии.
Рассмотрим, например, два вращения тетраэдра ABCD:
5, = (Л —5, В-+С, С—+А, D—+D)
—> вращение вокруг оси DDX (черт. 89) и
S2 = (A-+B, B-+A, C-+D, D—+Q
— вращение вокруг оси MNt проходящей через середины рёбер
АВ и CD (черт. 90). Выполним их последовательно одно за
другим.
После первого вращения вершина А перейдёт в В, а после
второго — вершина В перейдёт в А. Значит, в результате двух
87

вращений вершина Л останется на месте. Вершина В после
вращения vSj перейдёт в С, а С после враще ,ия S2 перейдёт в D.
Значит, после двух вращений вершина В перейдёт в D. Так же
легко замечаем, что после
двух вращений С перейдёт
в В и D в С. Таким
образом, два вращения St и S2
равносильны одному
вращению
51 + 5а = (Л — Л, В-+ D,
С—* В, D-+C);
это есть вращение вокруг
оси ЛЛг, показанной на
чертеже 89.
Нулевое вращение
50 по отношению к любому
вращению Sk, очевидно,
обтерт. »и. ладает свойством
5л + 50 = 5Аи S0 + Sk = Sk.
Теорема. Сложение вращений правильного много-
гранника подчиняется сочетательному
{ассоциативному) закону.
Возьмём три какие-либо вращения Sk, Sz и Sm. Докажем,
что
{Sk+S} + Sm = Sk + (St+SJ.
Сложение данных вращений можно выполнить двояко.
Во-первых, можно сначала сложить вращения Sk и Sr Они равносильны
некоторому одному вращению S :
Затем сложить вращения S и Sm. Результат можно будет
записать в форме: S -\-Sm или (5^-f-^/) ~t~^w· .Во-вторых, можно
сложить два последних вращения St и Sm; они равносильны
некоторому одному вращению S :
Тогда результат можно будет записать в форме: S.4-S
или 5, + (5,+5J.. "
Так как общий результат трёх вращений будет в обоих
случаях, очевидно, один и тот же, то:
(^ + 5,) + ^ = 6,-f-(S, + ^).
88

Пример. Возьмём три вращения тетраэдра ABCD:
51 = (A~^B, Я —>С, С-+А, D-+D)
— вращение вокруг оси DDX (черт. 89);
£2 —(Л—*Л, B-+C, C—+D, D—+B)
— вращение вокруг оси ААг;
53 = (Л-^С, B-+Bt С—D, D-+A)
— вращение вокруг оси BBV
Составим сначала (Sr -f- S2) -f- S3, затем 5, -f- (S2 -j- SB) и
сравним оба результата между собой.
Имеем:
51+5а = (Л-*С| B-+D, С—^Л, D—*Я)
— вращение вокруг оси RS (черт. 90);
(S1 + S2)-\-Sfl = (A-^Di B-+A, C~+Ct D-+B)
— вращение вокруг оси СС1. Далее:
S2-{-Sz = (A-+C, B-+D, С—+А, D-+B)
— вращение вокруг оси RS;
S1 + {Si-}-Sb) = (A-+D9 Я —Л, С-+С, D-+B)
— вращение вокруг оси CCV Сравнивая оба результата,
замечаем, что
(•Si + 5i) + 5, = S1 + (5i + 5i).
Важно ещё отметить, что переместительный закон для
сложения вращений правильного многогранника не имеет места.
В этом можно убедиться на примере вращений тетраэдра. Возьмём
два вращения:
SX=(A —Я, В-+С, С -+А, D ~^D)
— вращение вокруг DDX\
52 = (A-+At Я— С, C-+D, D—+B)
— вращение вокруг ΑΑχ.
Тогда
Si+S2 = (A-^C9 В — D, C-+A, D-+B)
— вращение вокруг оси RS (черт. 90);
5а + 51=(Л-*Я| В-+Ау C-+D, D-+C)
— вращение вокруг оси MN (черт. 90),
89

Следовательно,
Вращение, обратное данному. Вращение, которое
при сложении с данным вращением Sk даёт нулевое вращение,
называется обратным данному и обозначается через — Sk, так
что
Для каждого вращения существует ему обратное, именно:
вращение вокруг той же оси на тот же угол в обратную
сторону или в ту же сторону на угол, дополнительный до 360°.
Так, для вращения
51 = (Л—5, В—*С, С-+А, D—+D)
обратное будет
— St = (A—>С, В —>Л, С—*ВУ D—+D).
Нулевое вращение обратно самому себе:
S0 = S0.
§ 93. Группы вращений правильных многогранников.
Из всего изложенного выше следует, что совокупность
вращений правильного многогранника обладает такими свойствами:
1. Два любые вращения из этой совокупности
можно складывать, причём сумма двух вращений
равносильна одному вращению, принадлежащему к этой
же совокупности:
Sk + St*=Sm.
2. Сложение вращений многогранников подчиняется
сочетательному (ассоциативному) закону:
(Sk+Sl)-\-Sm = Sk + (Sl^-SJ.
3. В числе вращений многогранника есть нулевое,
или тождественное S0:
3* + ^о —^*; ^оЧ"^*—^*·
4. Для каждого вращения Sk есть ему обратное
— S*:
Sk + (-Sk)=S0.
Совокупность вращений, обладающих указанными четырьмя
свойствами, называется группой вращений, а вращения,
составляющие группу, называются элементами этой группы.
90

Таким образом, каждый правильный многогранник имеет свою
группу вращений. Группа вращений правильного тетраэдра
содержит 12 элементов, группа вращений куба—24 элемента,
группа октаэдра — 24, группа додекаэдра — 60 и группа
икосаэдра — 60 элементов.
Изоморфизм групп вращений октаэдра и куба,
а также икосаэдра и додекаэдра. Группы вращений
куба и октаэдра находятся между собой в некоторой
зависимости. Именно, выше было показано (§ 87), что вершины
октаэдра служат центром граней куба. При вращении куба вместе
с ним вращается и вписанный в него октаэдр. Так как при
самосовмещении куба центр каждой его грани совмещается с
центром другой грани, то каждая вершина вписанного октаэдра
совмещается с другой его вершиной, и весь октаэдр приходит в
самосовмещение. Отсюда следует, что каждому вращению куба
соответствует своё вращение октаэдра и сумме двух
вращений куба соответствует сумма двух вращений октаэдра.
Группы вращений, связанные между собой таким образом,
называются изоморфными. Таким образом, группа вращений
октаэдра изоморфна группе вращений куба. В такой же
зависимости находятся и группы додекаэдра и икосаэдра. Эти группы
изоморфны между собой.
Понятие „группа" встречается не только при вращении
многогранников, но и при многих других операциях. Так, например, все
параллельные смещения данного тела (§ 20) образуют группу, так
как для них выполняются все четыре условия. Можно также
привести примеры групп, заимствованные из арифметики и алгебры.
Так, например, рассматривая сложение целых чисел, легко
заметить, что совокупность всех чётных чисел образует при этом
группу: самые чётные числа будут элементами группы. Напротив,
нечётные числа группы не образуют, так как сумма двух нечётных
чисел есть число чётное. Понятие группы является одним из
основных понятий современной математики.
V. ПОДОБНОЕ ПРЕОБРАЗОВАНИЕ МНОГОГРАННИКОВ.
§ 94. Определение подобного преобразования
пространственных фигур.
Пространственные фигуры, так же как и плоские, можно
подвергать преобразованию подобия, которое будет, изменять
размеры фигур, не меняя их формы. Для выполнения этого
преобразования поступают следующим образом: выбирают где-
либо точку (центр подобия), которую соединяют со всеми
точками данной фигуры, и все полученные таким образом отрезки
изменяют в одном и том же отношении. Концы всех изменённых
9\

таким образом отрезков образуют новую фигуру, которая
является результатом преобразования данной фигуры. Это
преобразование называется преобразованием подобия. Точка S
называется центром подобия.
Отношение, в котором
изменяются все отрезки,
соединяющие центр подобия с
точками данной фигуры,
называется коэфициентом
подобия. На чертеже 91
показано подобное
преобразование тетраэдра. Фигуры,
получаемые одна из другой
преобразованием подобия,
С0 называются перспективно-
подобными.
§ 95. Подобие
многогранников.
Черт. 91. Если преобразование
подобия применить к какому-
либо многограннику, то в результате получим новый
многогранник, перспективно-подобный данному, с тем же числом вершин,
рёбер и граней, что и данный.
Из способа выполнения преобразования подобия легко
заметить следующие свойства двух перспективно-подобных
многогранников:
1. Соответственные рёбра перспективно-подобных
многогранников параллельны между собой, а их длины
находятся в одном и том же отношении, равном
коэфищиенту подобия.
Действительно, если через каждое ребро данного многогранника,
например АВ (черт. 91), и через центр подобия 5 провести
плоскость,' то преобразование подобия ребра А В будет происходить
в этой плоскости по тем правилам, которые были изложены в
планиметрии (Планиметрия, гл. VI). Именно, отрезок АВ
преобразуется в отрезок АВ\ причём
А'В'\\АВ
А В* _SA__h
АВ~ SA — *'
где k — коэфициент подобия.
92

Таким же способом найдём, что
В'С'\\ВС; C'D'WCD; ...
и
ВС CD ~~ *"
2. Соответственные плоские углы перспективно-
подобных многогранников равны между собой.
Именно:
£ А'В'С = Z. A&C\ Z B'C D' = /_ BCD;
как углы с параллельными сторонами.
3. Соответственные грани двух
перспективно-подобных многогранников представляют собой подобные
многоугольники, а плоскости этих граней параллельны
между собой (как плоскости углов с параллельными сторонами).
4. Поверхности двух перспективно-подобных
многогранников пропорциональны квадратам их
сходственных ребер, или: отношение поверхности
преобразованного многогранника к поверхности данного равно
квадрату коэфициента подобия.
Действительно, отношение площадей подобных
многоугольников равно отношению квадратов их сходственных сторон,
а поэтому, если Sv S2, Sv . .. площади граней данного
многогранника, 5', S'2j S!oy ... — площади граней преобразованного,
/j и Γχ—длины двух каких-либо сходственных рёбер, входящих
в состав первой пары сходственных граней, то
_ -JL £2
5,- l\~k'
где k — коэфициент подобия.
Точно так же >f ,
s2 .« ss
следовательно:
отсюда
— — k2 — — £2
S = — = — =... = k2;
6'j S2 «S3
s\+s'2 + s'3 + ..._ ι?
5. Соответственные двугранные и многогранные
углы двух перспективно-подобных многогранников
равны между собою.
93

§ 96. Подобные многогранники.
Если как-либо переместить один из двух
перспективно-подобных многогранников так, чтобы нарушилась параллельность
соответственных граней, то многогранники нельзя будет уже
назвать перспективно-подобными, но соотношения между их
углами, гранями и рёбрами останутся теми же, что и были до
перемещения, именно: их соответственные рёбра будут
пропорциональными; соответственные грани будут подобны
и расположены в одинаковом порядке в обоих
многогранниках; их соответственные двугранные и многогранные углы
будут равны.
Такие многогранники называются подобными. Подобным
преобразованием каждого из них можно получить многогранник,
равный другому.
ГЛАВА ПЯТАЯ.
ОБЪЁМЫ МНОГОГРАННИКОВ.
I. СРАВНЕНИЕ ОБЪЁМОВ МНОГОГРАННИКОВ.
§ 97. Равносоставленные многогранники.
Совокупность всех точек, лежащих внутри многогранника,
называется его внутренней областью.
Пересекая многогранник различными плоскостями, можно
разбивать его на
отдельные части,
представляющие собой более мелкие
многогранники.
Перекладывая эти
части по-другому, можно
)8 иногда составить из них
новый многогранник. Так,
например, если дана
треугольная пирамида SABC
(черт. 92), в основании
которой лежит
равнобедренный треугольник ABC
(АВ = ВС)> то, проведя
плоскость через ребро SB и высоту BD треугольника ABC, мы
разобьём пирамиду SABC на две пирамиды SABD и SCBD.
Эти две пирамиды можно приложить одну к другой, совместив
94

их грани ABD и CBD, и получить, таким образом, новый
многогранник ASXBDS (черт. 93). Этот многогранник имеет
другую форму, но составлен из тех же частей, что и данная
пирамида. Два многогранника называются равносоставленными,
если один из них можно разбить на части, из которых можно
составить другой многогранник. Таким образом, многогранник
ASXBDS и пирамида SABC — равносоставлены.
§ 98. Равносоставленные призмы.
Теорема. Каждая призма равносоставлена с
прямой призмой, основанием которой служит
перпендикулярное сечение данной призмы, а
высотой — её боковое ребро.
Дана призма ABCDEAlBlCxDxEl
(черт. 94) или, коротко, ADV Возьмём
на ребре ААХ какую-либо точку Ρ и
проведём через неё перпендикулярное
сечение призмы PQRST. Продолжим
боковые рёбра и боковые грани призмы за
плоскость A1B1CiDlE1 и возьмём на
продолжении ребра ААХ точку Ρχ так, чтобы
ΑλΡλ было равно АР, Проведя через точку
Рг плоскость, перпендикулярную ребру AAV
получим в сечении с продолженными
боковыми гранями многоугольник P1QiR1S1T^y
равный многоугольнику PQRST. Эти два
многоугольника служат основаниями прямой
призмы PSV боковые рёбра которой PPV
QQV ... равны боковым рёбрам ААг, BBV ...
данной призмы.
Сечение PQRST разбивает данную
призму на два многогранника:
многогранник AS и многогранник PDV Прямая
призма PSX сечением /Ij^Cj-Djft также
разделяется на два многогранника PD+ и
A\sv
Теперь легко заметить, что
многогранники AS и A1Sl равны между собой. В самом деле,
многоугольник PQRST равен многоугольнику /^Q^S,?,. Боковые
рёбра призмы перпендикулярны к плоскостям эгих
многоугольников. Далее, но построению,
АР-.
Afv
95

и так как BBl = QQv то
BQ=B1Q1;
так же найдём, что
CR=C1RV 03=0^1 и ΕΤ = ΕλΤν
А потому, если сдвинуть многогранник AXSX в направлении
ребра ΑΑλ так, чтобы многоугольник P\Q\R\SXTY совместился
с многоугольником PQRST, то вершины Аг, Bv Cv Dv Εχ
совместятся с вершинами Л, В, С, D, Ε и весь многогранник
A{SX совместится с многогранником AS.
Таким образом, обе призмы ADX и PSX составляются из
равных многогранников: общего им многогранника PSX и равных
между собой многогранников AS и АгЗг.
§ 99. Равносоставленные прямоугольные
параллелепипеды.
Теорема. Если произведение трёх измерений одного
прямоугольного параллелепипеда равно произведению
трёх измерений другого, то эти параллелепипеды
равносоставлены.
Даны два параллелепипеда AG и AXGX (черт. 95), причём
Н, в,
Η G
F
В
Черт. 95.
AB-AD.AE = AiB1-AlDrA1Ev
Требуется доказать, что эти параллелепипеды равносоставлены.
Возможны два случая.
1. Параллелепипеды имеют по одному равному измерению,
например, АЕ = АгЕг.
В этом случае обе части данного равенства можно разделить
на АЕ. В результате будем иметь:
AB-AD = AiBrA1Dv
96

Отсюда следует (Планиметрия, § 250), что прямоугольник
ABCD равносоставлен с прямоугольником AJBlClDi. Значит,
прямоугольник AlBiCiDl можно разбить секущими прямыми на
такие части, из которых составится прямоугольник ABCD.
Произведя это разбиение, мы через все секущие прямые проведём
плоскости, перпендикулярные к плоскости прямоугольника
ε
А
/\
νί.
*V~
/
Г
/
/>
д
Черт. 96.
A^BiC1Di. Этими плоскостями параллелепипед Αλϋλ разобьётся
на прямые призмы. При перекладывании частей прямоугольника
AlBiCiDl эти призмы будут переставляться и, когда из частей
прямоугольника ΑιΒιΟχί)λ составится прямоугольник ABCD, из
полученных призм составится параллелепипед AG. В этом случае
теорема доказана.
2. Параллелепипеды не имеют равных измерений.
Построим вспомогательный параллелепипед
в котрром
А2В2 = А}В,
A2G2 (черт.
96),
/ЛпСп /\ίΖ ,
и А<р2 определяется из равенства
Значит,
Λ252·νν
Л9£2 = Л£.
AD-AE.
A,D2-.
AB-AD-AE
А^В2*А2Е2
ADAB
А2В.
2^2
откуда:
A2D2
AD '
_АВ_
ZA&
(так как Α2Β2 = ΑλΒλ), τ. е. отрезок
четвёртый пропорциональный к трём данным
V>2
определяется
отрезкам ADy
AXBV
как
АВУ
По предыдущему, параллелепипед A2G2 равносоставлен и с
параллелепипедом AG и с
с каждым из них по одному равному измерению
параллелепипедом AxGXi так как имеет
97

Отсюда следует, что параллелепипеды AXGX и AG равно-
составлены. Действительно, чтобы из параллелепипеда A^GX
получить параллелепипед AG, мы сначала разобьём его на такие
части, из которых составим параллелепипед A2G2, а затем этот
последний разобьём на такие части, из которых составим
параллелепипед AG.
II. ИЗМЕРЕНИЕ ОБЪЕМОВ МНОГОГРАННИКОВ.
§ 100. Общие принципы измерения объёмов.
Объёмом многогранника называется число, характеризующее
размер его внутренней области.
При измерении объёмов многогранников придерживаются
двух следующих принципов:
1) Объёмы двух равных многогранников считаются
равными.
2) Если многогранник разбит на части, представляющие
более мелкие многогранники, то объём всего многогранника
считается равным сумме объёмов всех этих частей.
В силу этих принципов объёмы двух равносоставленных
многогранников должны считаться одинаковыми. Многогранники,
имеющие равные объёмы, называются равновеликими. Всякие
два равносоставленные многогранника — равновелики.
§ 101. Объём прямоугольного параллелепипеда.
Для простейшего случая, когда измерения прямоугольного
параллелепипеда выражаются целыми числами, способ
вычисления объёма известен из арифметики: объём параллелепипеда равен
произведению всех трёх его измерений. Это число показывает,
сколько кубов с ребром, равным единице, можно поместить
внутри данного параллелепипеда, целиком'заполнив его
внутреннюю область. Так, если рёбра параллелепипеда равны 5 см, 7 см и
10 см,то объём параллелепипеда равен 350куб. см; это значит, что
внутри данного параллелепипеда, целиком его заполняя,
умещаются 350 кубиков с ребром в один сантиметр, т. е. внутреннюю
область параллелепипеда можно разбить на 350 кубиков с
ребром в один сантиметр.
Если все измерения прямоугольного параллелепипеда
выражаются дробными числами, то объём параллелепипеда также
равен произведению трёх его измерений (ср. Планиметрия, § 252).
Если одно или несколько измерений параллелепипеда
иррациональны, то, очевидно, внутреннюю область параллелепипеда
98

нельзя разбить на кубики с ребром, равным какой-либо
рациональной доле единицы длины. Тем не менее и в этом случае
произведение трёх измерений параллелепипеда принимается за
меру его объёма.
Теорема § 99 показывает, что если два прямоугольных
параллелепипеда имеют одинаковый объём, то каждый из них
можно рассечь плоскостями на такие части, из которых
можно сложить второй параллелепипед.
Заметим, что произведение двух измерений прямоугольного
параллелепипеда равно площади одной его грани. Примем эту
грань за основание прямоугольного параллелепипеда, Тогда третье
измерение прямоугольного параллелепипеда будет служить его
высотой. А потому
объём прямоугольного параллелепипеда равен
произведению площади его основания на высоту.
В частности, объём куба, ребро которого а, равен а3.
§ 102. Объём прямого параллелепипеда.
Дан прямой параллелепипед AG (черт. 97), основанием
которого служит параллелограм ABCD. Проведя через рёбра АЕ
и BF плоскости, перпендикулярные к
АВУ получим прямоугольный паралле- ζ__ Л__ 0 _β
лепипед AQ. Примем за основания
данного параллелепипеда AG грани AEHD Ef
и BFGC, тогда его боковые рёбра
будут EF, АВ, CDy GH.
В силу теоремы § 98 о равносо-
ставленных призмах, параллелепипеды
AG и AQ будут равносоставлены и,
значит, равновелики. Но объём
параллелепипеда AQ будет равен AB*AS»AE.4U
Заметим теперь, что, так как
AS^AB, то произведение AB*AS
равно площади параллелограма ABCD. Ребро же АЕ служит
высотой параллелепипеда AG. Следовательно, объём прямого
параллелепипеда равен произведению площади его
основания на высоту.
§ 103. Объём наклонного параллелепипеда.
Дан наклонный параллелепипед АСХ (черт. 98). Проведя через
какую-либо точку Μ ребра ВС плоскость, перпендикулярную
к этому ребру, получим перпендикулярное сечение MNPQ. При-
99

лелепипеда АСХ равен объёму
& С
мем за основание параллелепипеда АСХ грань АВВХАХ. Тогда его
боковые рёбра будут ВС, ВХСХ, AD, AXDV
В силу теоремы о равносоставленных призмах, объём парал-
прямого параллелепипеда,
основанием которого служит параллело-
грам MNPQ, а высотой — ребро
ВС, т. е. произведению площади
параллелограма MNPQ на ВС. Но
площадь MNPQ равна QM*SR,
где SR—высота параллелограма
MNPQ, опущенная на сторону
MQ, т. е. SR±MQ.
А потому,
объём ACX = BC-QM.SR.
Теперь заметим, что QM^BC
(так как ВС _]_ плоскости MNPQ).
Следовательно, произведение
BC'MQ есть площадь параллелограма ABCD.
Рассмотрим теперь отрезок SR. По построению SR J^MQ.
Кроме того, SR лежит в плоскости MNPQ, перпендикулярной
к ребру ВС, а потому SR _\_ ВС.
Отсюда следует, что SR _]_ пл. ABCD. Значит, отрезок SR
служит высотой данного параллелепипеда АСХ. А потому
объём наклонного
параллелепипеда равен про- 0* Ρ
изведению площади его
основания на высоту.
§ 104. Объём треугольной
призмы.
Дана треугольная призма
АВСАХВХСХ (черт. 99).
Проведя через ребро ΑΑχ
плоскость, параллельную грани ВСХ,
а через ребро ССХ—плоскость,
параллельную грани ВАХ, и
продолжив плоскости
оснований, получим параллелепипед
ACV в котором грань данной призмы АСХ служит
диагональным сечением, разбивающим параллелепипед на две треугольные
призмы.
100

Легко заметить, чти эти призмы равновелики. В самом деле,
проведём перпендикулярное сечение MNPQ. Тогда первая
призма равновелика прямой призме, основанием которой служит
треугольник MNP, а высотой ребро ААХ. Вторая призма
равновелика прямой призме, основанием которой служит треугольник
MQPy а высотой ребро ААХ. Эти две прямые призмы равны между
собою, так как вследствие равенства треугольников MNP и
MQP и перпендикулярности их боковых рёбер к плоскости
основания эти призмы, очевидно, можно совместить одну с
другой. Но сумма объёмов этих прямых призм составляет объём
прямого параллелепипеда с основанием MNPQ и высотой AAV
равновеликого параллелепипеду АСХ. Отсюда следует, что объём
данной призмы равен половине объёма параллелепипеда ACV
т. е. половине произведения площади ABCD на высоту призмы.
Но половина площади ABCD есть площадь треугольника АВС>
следовательно,
объём треугольной призмы равен произведению
площади её основания на высоту.
§ 105. Объём многоугольной призмы.
Дана многоугольная призма АСХ (черт. 100). Проведя через
ребро ААХ диагональные плоскости ААХСХСУ AAADXD, мы
разобьём данную призму на треугольные. Объ- ρ
ём каждой из них будет" равен произве- Ει, "^
дению площади её основания на высоту. /\^
Но все эти треугольные призмы имеют
одну и ту же высоту, равную высоте "ч
данной призмы АСХ. Площади же
оснований в сумме составляют площадь
основания ABCDE данной призмы.
Называя эти площади через bv b2,
Ьъ, а высоту призмы через Λ, получим:
объём Л С, = bxh -\-b2h-\-b3h=h.(b}-{-
-j- b2 -\- Ьг) = h · пл. ABCDE,
Следовательно,
объём всякой призмы равен
произведению её основания на высоту.
Следствие 1. Призмы, имеющие равновеликие основания
и равные высоты, равновелики.
Следствие 2. Объём всякой призмы равняется
произведению площади перпендикулярного сечения на боковое
ребро (§ 98).
101
Черт. 100.

§ 106. Объём пирамиды.
Объём пирамиды не удаётся получить так же просто, как
объём призмы. Поэтому для определения объёма пирамиды
приходится прибегать к значительно более сложным приёмам,
которые могут даже показаться искусственными.
Дана треугольная пирамида SABC (черт. 101). Проведём её
высоту SD и разобьём её на η равных частей. Через точки
деления проведём плоскости, параллельные основанию ABC.
В сечении получим η треугольников. Площади этих
треугольников легко вычислить, зная площадь треугольника ABC·
Обозначая эту последнюю буквой &, а площади
треугольников сечений
S
через Ьх
"ч* "з» · * ·»
пирамиды,
иметь:
Un-V
по
считая
теореме
1
от вершины
§ 79 будем
or ,
SD* — п*'
к
ь
точно так же
b л* ' " '
отсюда:
(W
SD*
2!.
1 /Z2;
*,=·?-·
2^
(/? — 1)«6
-1 /г2
Для каждого полученного в сечении треугольника построим
треугольную призму, приняв этот треугольник за верхнее
основание призмы, а отрезок одного из рёбер пирамиды, например
ребра SA, заключённый между соседними параллельными
сечениями, за боковое ребро призмы.
Мы получим, таким образом, η—1 треугольных призм,
заключённых* внутри пирамиды SABC, с рёбрами, параллельными ребру
SD
η
площади соответ-
SD
ствующего треугольного сечения на высоту, т· е. на — .
SA; высота каждой из этих призм, очевидно, равна
каждой из этих призм равен произведению
Объём
Совокупность всех этих призм образует некоторый
многогранник Рп. Плоскость одной из его граней совпадает с ило-
102

скостью ЛВС. Плоскости двух других совпадают с плоскостями
SAB и SAC· Остальные грани образуют ступенчатую
поверхность, примыкающую к грани SBC данной пирамиды.
Вычислим объём многогранника Рп. Этот объём, очевидно,
равен сумме объёмов всех построенных призм. Обозначив его
через Vn, будем иметь:
Vn=br\sDJrb,.lsD+...Jrbn_l.±SD =
Внося сюда вместо bXi £2,..., bn_x найденные для них
выражения, получим:
'.->·ο+ιη-...+^·;
или
Vn— b-SD ^-^ .
Из алгебры известно, что
12 + 22 4- З2 + ... 4- (п — 1)« =^—1^—Л
а потому
V=b.SD.^-{){2n-l)
6/z2
Будем теперь увеличивать число п, т. е. делить высоту SD
ipa всё более и более мелкие части. При этом число получаемых
[призм будет становиться все большим, высоты их будут делаться
^сё меньше, а ступенчатая поверхность многогранника Рп будет
|рсё плотнее прилегать к боковой грани SBC данной пирамиды.
За объём пирамиды SABC мы примем предел объёма
многогранника Рп при неограниченном увеличении п. Чтобы вычислить
« * н ·♦ (л—1)(2л — 1)
(Этот объём, найдем сначала предел величины —% ' .
Выполняя действия, получим:
(п — 1) (2/г — 1) _ 2пА — Ъп + Г_ 2 ___ 3_ ι J_
л5 л2 л "1" /г2 '
о 3 1
При неограниченном возрастании η величины — и —%, оче-
in — 1 WO» — 1 ^
Видно, стремятся к нулю, а потому пределом дроби ~
103

служит число 2. Следовательно,
1
предел I/ = b-SD^-2 = ^ b-SD,
т. е.
объём треугольной пирамиды равен -~ части
произведения площади её основания на высоту:
где V — объём, b — площадь основания, h — высота пирамиды.
§ 107. Объём многоугольной пирамиды.
Дана многоугольная пирамида SABCDE (черт. 102). Для
получения её объёма разбиваем её диагональными плоскостями
SAC и SAD на треугольные пирамиды и сумму их объёмов
принимаем за объём V данной многоугольной пирамиды.
Обозначая высоту пирамиды через Л, будем иметь:
V — 4 · площ. Л£С-[-4 · площ. ACD +
или
V =
-\- площ.
т. е.
-J- -^ · площ. ADE,
(площ. ABC -j-площ. ACD-\-
ADE) = I · площ. ABCDE,
s
^--
\\
\\
\ \
\ \
\ \
\ \
£//--— ---
объём многоугольной пирамиды равен ^
произведения площади её основания на высоту.
§ 108. Объём усечённой пирамиды.
Дана усечённая пирамида ADX (черт. 103). Продолжив её
грани за верхнее основание AiB1CiDiEif дополним её до
полной пирамиды SABCDE. В таком случае объём V усечённой
пирамиды ADX будет равен разности объёмов двух полных
пирамид SABCDE и SA1B1CiDiEv
104

Обозначим площади оснований ABCDE и AXBXCXDXEX
соответственно через b и bv высоту усечённой пирамиды ADX че-
рзе Л, а высоту пирамиды SAXBXCXDXEX через х.
Тогда высота пирамиды SABCDE будет равна h-\-x, а
потому объём усечённой пирамиды /4Dj
у=£.*±£_b^=±[bh+(b-bx)x\.
Определим теперь величину х.
По теореме § 79 имеем:
Ь _(лг-И)2
откуда
V&7 л: "*"■*'
отсюда последовательно получим:
А = О _ ι — ^ —^
или
Vh
Vb -Vbx '
Подставляя это в выражение для объёма пирамиды ADU
получим:
з L ~ Vb —Уьг 1'
но
ь-ьх = (К* + К*!) (К ft — Vbx),
а потому дробь ( 7^-—т^"* можно сократить на J^ft —j/^ ,
и тогда
l/ = i [** + (/* + Vbx) hVbx\ =1 [ftA + AKWj + ^Л],
или
K=5-(* + *1+|/w"1).
105

Эту формулу можно прочитать так:
объём усечённой пирамиды равен сумме объёмов
трёх пирамид, у которых общая высота равна высоте
усечённой пирамиды, а площади оснований равны: у
первой пирамиды — площади нижнего, у второй
пирамиды— верхнего основания усечённой пирамиды, у
третьей — среднему пропорциональному между ними.
§ 109. Изменение объёма многогранника при подобном
преобразовании.
Теорема. Объёмы двух подобных многогранников от-
носятся как кубы их сходственных рёбер.
Даны два подобных многогранника, у которых объёмы равны V и
Vv длины двух каких-либо сходственных рёбер / и 1г. Требуется
доказать, что
Yl—A
V — β'
1. Рассмотрим сначала случай двух подобных тетраэдров.
Пусть 5 и· 52—площади двух каких-либо их сходственных
граней, h и Л1 — длины высот, опущенных на эти грани.
Тогда
т/_1 яи ι/ =!.<:./». и Yl — ^lh
~ Sh ·
а
Но, как было
потому
Следовательно
3 "
) И , V
показано
У
Si
S ~
ι— з 11
■ (§ 95),
Ρ ' h
Si*i l\
Sh — β -
Vi l\
V ~ β ·
n
h
I
2. Рассмотрим теперь два выпуклых подобных
многогранника. Сохраним те же обозначения. Возьмём две какие-либо
сходственные вершины этих многогранников и соединим каждую
из них прямыми линиями со всеми остальными вершинами того же
многогранника. Проводя плоскости через пары этих прямых,
можно оба многогранника разбить на попарно подобные
тетраэдры.
106

Обозначим их объёма соответственно через:
V\ V\ V"
у) ι/" у»
ν ν ν ν ν ι » · ■ ·
Тогда
V = V"+K+rV""-f...
По доказанному:
Υδ-ΥΪ-ΥΙ- -Δ.
у у у* * * /з '
отсюда:
V + V + V" +...— V ~ β '
3. Так же легко доказать теорему для любых подобных
многогранников.
///. УПРАЖНЕНИЯ К ГЛАВАМ ЧЕТВЁРТОЙ И ПЯТОЙ.
А. Доказать теоремы.
1. Число вершин многогранника, из которых выходит нечётное
число рёбер, всегда чётное. Указание. См. § 69, след. 1.
2. Число многоугольников с нечётным числом сторон, входящих
в состав граней многогранника, всегда чётное. Указание. См.
§ 69, след. 1.
3. Если две диагональные плоскости параллелепипеда
перпендикулярны к его основаниям, то параллелепипед прямой.
4. Если диагональные плоскости четырёхугольной призмы
проходят через одну точку, то эта призма есть параллелепипед.
5. В трёхгранной призме большая боковая грань лежит против
большего трёхгранного угла.
6. В треугольной призме, усечённой плоскостью, не
параллельной ни одной из сторон основания, три точки пересечения
продолженных соответственных сторон треугольников, лежащих в
основаниях призмы, лежат на одной прямой.
7. Если через каждую вершину верхнего основания треугольной
призмы и через противолежащее ей ребро нижнего основания
провести плоскости, то эти плоскости пересекутся в точке, лежащей
на линии, соединяющей центры тяжести обоих оснований.
8. Плоскости, проходящие через боковые рёбра треугольной
призмы и перпендикулярные противолежащим боковым граням,
пересекаются по одной прямой.
9. Плоскости, делящие пополам углы между боковыми гранями
треугольной призмы, пересекаются по одной прямой.
107

10. Если два диагональных сечения параллелепипеда, не
проходящих через одну и ту же вершину, — прямоугольники, то
параллелепипед— прямой.
11. Если наклонная призма имеет основанием трапецию, то объём,
этой призмы равен произведению полусуммы площадей
параллельных боковых граней на расстояние между ними.
12. Секущая плоскость, параллельная двум противоположным
рёбрам тетраэдра, пересекает остальные его рёбра в точках,
образующих вершины параллелограма.
13. Если в тетраэдре ABCD имеем: АВ \_CD и AC \_BDy то
AD±BC и АВ* + CD* =АС* + BD* = AD* + ВС\
14. Отрезки прямых, соединяющих середины противоположных
рёбер тетраэдра, проходят через одну точку и делятся в ней
пополам.
15. Четыре прямые, соединяющие каждую вершину тетраэдра
с центром тяжести противолежащей ей грани, проходят через одну
точку.
16. Прямые, соединяющие три вершины правильного тетраэдра
с серединой высоты, проведённой через четвёртую вершину,
образуют рёбра прямого трёхгранного угла.
17. Плоскости, проходящие через боковые рёбра трёхгранной
пирамиды и через медианы противоположных граней, пересекаются
по одной прямой.
18. Шесть плоскостей, проходящих каждая через одно из рёбер
и середину противоположного ребра тетраэдра, пересекаются в
одной точке.
19. Плоскости, перпендикулярные к рёбрам тетраэдра и
проходящие через середины этих рёбер, пересекаются в одной точке.
20. Центры тяжести граней данного тетраэдра служат
вершинами тетраэдра, перспективно-подобного данному.
21. Через каждую вершину тетраэдра проведена плоскость,
параллельная противоположной грани. Доказать, что четыре
полученных таким образом плоскости образуют тетраэдр, перспективно-
подобный данному. Найти центр подобия и величину коэфициента
подобия.
22. Точки пересечения сторон основания пирамиды с
соответствующими сторонами сечения пирамиды плоскостью, не
параллельной ни одной из сторон основания, лежат на одной прямой.
23. Плоскости, проходящие через боковые рёбра пирамиды и
перпендикулярные к плоскости её основания, пересекаются по одной
прямой.
24. Правильная «-угольная пирамида имеет ось симметрии л-го
порядка.
Б. Задачи на построение.
25. Построить прямую четырёхугольную призму, если даны её
основание и одна из диагоналей.
26. Построить треугольную пирамиду, если даны её основание,
два боковых ребра и проекция третьего ребра на плоскость основания.
27. Построить треугольную пирамиду, если даны её основание,
проекции на плоскость основания двух боковых рёбер и третье
боковое ребро.
28. Построить треугольную пирамиду, если даны её основание,
высота и два боковых ребра.
108

29. Построить треугольную пирамиду, если даны её основание,
вмсота и углы наклона двух боковых рёбер к плоскости основания.
30. Построить треугольную пирамиду, если даны её основание,
два боковых ребра и угол наклона одного из них к плоскости
основания.
31. Построить треугольную пирамиду, если дано её основание
и три боковых ребра.
32. Построить треугольную пирамиду, если даны её высота, три
боковых ребра, одно из рёбер основания и прилежащий к нему угол
основания.
33. Построить треугольную пирамиду, если даны три её боковых
ребра, два ребра основания и двугранный угол, имеющий ребром
одно из данных рёбер основания.
34. Построить треугольную пирамиду, если даны длины её
боковых рёбер и плоские углы при вершине.
35. Построить тетраэдр, если даны шесть его рёбер.
36. Построить треугольную пирамиду, если даны её высота, три
боковых ребра и два ребра основания.
37. Построить треугольную пирамиду, если даны три её
боковых ребра, двугранный угол при одном из боковых рёбер и два
ребра основания, лежащих в гранях данного двугранного угла.
38. Построить треугольную пирамиду, если дана боковая грань
и двугранные углы при основании пирамиды.
39. Построить треугольную пирамиду, если даны отношение трёх
рёбер её основания, двугранные углы при основании и высота
пирамиды.
40. Построить треугольную пирамиду, если даны две её
боковых грани и двугранный угол между ними.
41. Построить треугольную пирамиду, если даны отношения
трёх её боковых рёбер, плоские углы при вершине и одно из рёбер
основания.
42. Построить треугольную пирамиду, если даны отношения
трёх рёбер её основания, двугранные углы при основании и одно
из боковых рёбер.
4 43. Построить четырёхугольную пирамиду, если даны её
основание, высота и два двугранных угла при основании.
44. На плоскости дано изображение в параллельной проекции
четырёхугольной призмы. Построить изображение сечения этой
призмы плоскостью, проходящей: 1) через три данные точки на
рёбрах призмы; 2) через три данные точки на гранях призмы; 3;
через три данные точки, из которых две лежат на соседних боковых
рёбрах призмы, а третья на Соковой грани, не содержащей этих
рёбер.
45. На плоскости дано изображение в параллельной проекции
шестиугольной пирамиды. Построить изображение сечения этой
пирамиды плоскостью, проходящей через три какие-либо точки, взятые
на её рёбрах или гранях.
46. Найти точку, расстояния которой от вершин данного
тетраэдра пропорциональны четырём данным числам. Сколько решений
имеет задача?
47. Какая фигура получается в сечении куба плоскостью,
проходящей через его центр и перпендикулярной к его диагонали?
48. Дан тетраэдр, противоположные рёбра которого
перпендикулярны. Пересечь его плоскостью так, чтобы в сечении получился
квадрат.
109

В. Задачи на вычисление.
49. Прямоугольный параллелепипед с квадратным основанием
пересечён плоскостью, проходящей через ребро основания.
Определить площадь сечения, если секущая плоскость встречает ось
параллелепипеда в точке, отстоящей от его основания на расстоянии
1,5 м, а сторона основания параллелепипеда равна 4м. Отв. 20 кв. м.
50. Определить площадь диагонального сечения, проходящего
через противоположные рёбра оснований прямоугольного
параллелепипеда, основанием которого служит квадрат, если даны ребро
основания а и объём параллелепипеда V. Отв. — VΦ + V2.
51. В прямоугольном параллелепипеде дано отношение трёх его
измерений 1:2:3. Полная поверхность параллелепипеда равна 88 кв. м.
Определить его измерения. Отв. 2, 4, 6 м.
52. Найти объём правильной треугольной призмы, ребро
основания которой равно высоте призмы и равно 2 м. Отв. чУъ куб. м.
53. В основании прямой треугольной призмы лежит треугольник,
стороны которого равны 2, 3 и 4 м. Через одну из его вершин
проведена плоскость, пересекающая боковые грани призмы по
правильному треугольнику. Вычислить его стороны. Отв. 4,07 м.
54. Определить площадь сечения куба плоскостью, проходящей
через концы трёх его рёбер, выходящих из одной вершины,если ребро куба
равно а. Отв. —г}—.
55. Вычислить объём наклонной треугольной призмы, каждое
ребро основания которой равно боковому ребру и равно 2 м, а
боковые рёбра наклонены к плоскости оснований под углом в 60°.
Отв. 3 куб. м.
56. Через две точки, взятые на ребре правильной треугольной
призмы на расстоянии а одна от другой, проведены две
параллельные плоскости. Определить боковую поверхность, образовавшуюся
между этими плоскостями наклонной призмы» если ребро основания
данной призмы равно Ь. Отв. ЪаЪ.
57. Сторона основания правильной треугольной пирамиды равна ау
а её высота 2а. Вычислить поверхность пирамиды. Отв. 2 cflV Ъ.
58. Вычислить объём треугольной пирамиды, боковые рёбра ко-
. r\ abc
торой взаимно перпендикулярны и равны я, о и с. Отв. -^-.
59. От куба отсечены его углы плоскостями, проходящими через
середины рёбер, выходящих из отсекаемых вершин. Вычислить объём
оставшегося тела. Отв. -сЗ, где а — ребро куба.
60. От октаэдра, ребро которого а = 2, отсечены его углы
плоскостями, проходящими через середины рёбер отсекаемых углов.
Вычислить объём оставшегося тела. Отв. -~Y2.
о
61. На каком расстоянии от вершины пирамиды следует провести
плоскость, параллельную её основанию, чтобы она разделила объём
пирамиды в отношении 1:4? Отв. 6/ — , где h—высота пирамиды.
110

62. Площади основания усечённой пирамиды равны 64 м2 и 100 м2.
Определить площадь сечения пирамиды плоскостью, параллельной её
основанию и проходящей через середину её высоты. Отв. 81 м2.
63. Определить высоту правильной усечённой четырёхугольной
пирамиды, если рёбра её оснований равны а и Ь, а боковая
поверхность равна сумме площадей оснований. Отв. .
ГЛАВА ШЕСТАЯ.
КРУГЛЫЕ ТЕЛА.
I. ЦИЛИНДР.
§ ПО. Цилиндрическая поверхность.
Поверхность, образованная движением прямой линии,
которая во всех своих положениях остаётся параллельной самой себе,
называется цилиндрической
поверхностью.
Закон движения прямой можно
установить, заставив движущуюся прямую
постоянно пересекать некоторую
заданную линию (черт. 104).
Движущаяся прямая называется
образующей цилиндрической поверхности, а
линия, которую при своём движении
постоянно пересекает образующая (и
которая, таким образом, устанавливает
закон движения образующей),
называется направляющей этой поверхности.
Если за направляющую
цилиндрической поверхности принять
окружность, плоскость которой
перпендикулярна образующей цилиндра, то по- ц
лучаемая при этом цилиндрическая ерт*
поверхность называется круглой цилиндрической поверхностью.
§ 111. Круглый цилиндр.
Если пересечь круглую цилиндрическую поверхность двумя
плоскостями, перпендикулярными к её образующим, то обе
секущие плоскости вместе с цилиндрической поверхностью будут
ограничивать цилиндрическое тело, называемое прямым круглым
цилиндром или просто цилиндром (черт. 105).
111

Это геометрическое тело может быть получено вращением
прямоугольника ABCD вокруг одной из его сторон, например,
вокруг стороны АВ (черт. 106), при этом его стороны ВС
и AD опишут круги, называемые основаниями цилиндра. Пря-
DV
Черт. 105.
Черт. 106.
мая АВ называется осью цилиндра, а длина отрезка АВ —
высотою цилиндра. Вращающаяся сторона CD называется
образующей цилиндра.
Цилиндр обладает, очевидно, следующими свойствами:
1. В пересечении цилиндра плоскостями,
перпендикулярными к его оси, получаются равные окружности.
2. Сечение цилиндра плоскостью, проходящей через его
ось (осевое сечение), даёт прямоугольник, две стороны
которого служат образующими цилиндра, а две другие
служат диаметрами окружностей, лежащих в основаниях
цилиндра.
3. Сечение цилиндра плоскостью, параллельной его оси,
даёт прямоугольник, две стороны которого служат
образующими цилиндра, а две другие являются равными между
собой хордами окружностей оснований (черт. 107).
§ 112. Касательная плоскость к цилиндру.
Плоскость, параллельная оси цилиндра и отстоящая от неё
«а расстоянии, равном радиусу окружности основания, содержит
в себе целиком одну образующую цилиндра и не имеет с
поверхностью цилиндра других общих точек (черт. 107).
Эта плоскость называется касательной плоскостью к
цилиндру. Касательная плоскость к цилиндру обладает
следующими очевидными свойствами:
J12

1. Плоскость у проходящая через ось цилиндра и
образующую, по которой касательная плоскость касается цилиндра,
перпендикулярна к касательной
плоскости.
2. Прямая, по которой
касательная плоскость к цилиндру пересекает
плоскость основания цилиндра,
служит касательной к окружности
этого основания.
3. Прямая, лежащая в
касательной плоскости и не параллельная
образующей, по которой плоскость
касается цилиндра, имеет с
поверхностью цилиндра лишь одну общую
точку, именно точку пересечения с Черт. 107.
образующей цилиндра, лежащей в касательной плоскости.
Такая прямая называется касательной к цилиндру.
§ 113. Поверхность цилиндра.
Правильная призма, основанием которой служит правильный
многоугольник, вписанный в основание цилиндра, а высотой —
высота цилиндра, называется вписанной призмой.
Боковая поверхность вписанной призмы принимается за
приближённую величину поверхности самого цилиндра. При
увеличении числа боковых граней правильной вписанной призмы её
.боковая поверхность, как легко заметить, стремится к
некоторому определённому пределу, и этот предел принимается за
величину боковой поверхности цилиндра.
Боковая поверхность правильной призмы равна Ph, где Ρ —
/периметр основания правильной призмы, вписанного в основание
^цилиндра, a h—.её высота.
При неограниченном увеличении числа боковых граней
правильной призмы периметр Ρ стремится к определённому
пределу— именно к длине окружности основания, т. е. к 2ттг; где
г—радиус основания цилиндра. А потому боковая поверхность
вписанной призмы, при неограниченном увеличении числа её
боковых граней, имеет пределом величину 2nrh. Следовательно,
Доковая поверхность цилиндра равна произведению
длины окружности его основания на высоту.
Полной поверхностью цилиндра служит его боковая поверхность,
сложенная С площадями его оснований; она, следовательно, равна
2nrh -f 2тгг2 = 2тгг (h -f г)э
113

§114. Объём цилиндра.
За объём цилиндра принимают предел объёма правильной
вписанной в него призмы при неограниченном увеличении числа
её граней.
Объём правильной
призмы равен bh, где b—
площадь её основания,
h— высота. При
неограниченном увеличении
числа боковых граней
призмы величина b имеет
пределом площадь
круга основания,
т. е. величину иг2.
А потому пределом для
объёма призмы, служит
величина ur2h.
Следовательно,
объем цилиндра
равен произведению
площади его основа-
ния на высоту.
II. КОНУС.
Черт. 108.
§ 115. Коническая поверхность.
Поверхность, образованная движением прямой линии, которая
во всех своих положениях проходит через одну и ту же точку,
называется конической поверхностью. Точка, через которую
проходит прямая, называется вершиной конической поверхности,
а движущаяся прямая— её образующей.
Чтобы установить закон движения образующей конической
поверхности, достаточно указать какую-либо линию, которую
образующая при своём движении должна постоянно пересекать
(черт. 108). Эта линия называется направляющей конической
поверхности.
§ 116. Круглый конус.
Если за направляющую конической поверхности принять
окружность, а за вершину — точку, лежащую на прямой, проходящей
через центр окружности и перпендикулярной к её плоскости, то
коническая поверхность называется круглой конической
поверхностью, а прямая, соединяющая её вершину с центром направ-
114

ляющей окружности, называется осью круглой конической
поверхности. Секущая плоскость, перпендикулярная к оси, вместе с
самой конической поверхностью ограничивает геометрическое тело,
называемое круглым конусом, или просто конусом (черт. 109).
Круглый конус может быть образован вращением
прямоугольного треугольника ЛВС вокруг одного из его катетов, например,
Черт. 109, Черт. 110.
вокруг катета АВ (черт. 110). Прямая АВ служит осью круглого
конуса, а длина катета АВ называется высотой конуса. Круг,
описанный катетом С А, называется основанием конуса.
§ 117. Сечения конуса.
Конус обладает, очевидно, следующими свойствами:
1. В сечении конуса плоскостью, перпендикулярной к его
оси, получается окружность.
2. В сечении конуса плоскостью, проходящей через ось
(осевое сечение), получается равнобедренный треугольник,
боковыми сторонами которого служат образующие конуса, а
основанием — диаметр основания конуса.
3. В сечении конуса плоскостью, проходящей через его
вершину и пересекающей его поверхность, получается
равнобедренный треугольник, боковыми сторонами которого служат
образующие конуса, а основанием — хорда окружности основания.
§ 118. Касательная плоскость к конусу.
Плоскость, проходящая через образующую конуса и
перпендикулярная к плоскости осевого сечения, проходящей через ту
же образующую, не имеет с поверхностью конуса других общих
точек, кроме точек этой образующей. Эта плоскость называется
касательной плоскостью к конусу (черт. 111).
115

Касательная плоскость обладает следующими свойствами:
1. Прямая пересечения касательной плоскости с плоско-
стью основания касается окружности основания,
2. Все касательные плоскости к конусу одинаково
наклонены к плоскости его основания.
Черт. 111. Черт. 112.
3. Все прямые, лежащие в касательной плоскости и
пересекающие образующую, по которой плоскость касается
конуса,— касаются поверхности конуса (т. е. имеют с нею лишь
одну общую точку).
Такие прямые называются касательными к конусу.
§ 119. Поверхность конуса.
Правильная пирамида с вершиной в вершине конуса,
основанием которой служит правильный многоугольник, вписанный
в окружность основания, называется правильной вписанной
пирамидой (черт. 112).
Поверхность этой пирамиды принимается за приближённую
величину поверхности конуса.
При неограниченном увеличении числа боковых граней
вписанной пирамиды её боковая поверхность стремится к
некоторому пределу, который принимается за боковую поверхность
Ра
конуса. Боковая поверхность правильной пирамиды равна -^-, где
Ρ — периметр основания пирамиды и а—её апофема.
При неограниченном увеличении числа сторон основания его
периметр Ρ возрастает и стремится к пределу, равному длине
окружности основания, т. е. к 2тгг, где г— радиус основания
конуса. Апофема а вписанной пирамиды будет иметь пределом
образующую конуса /.
116

Действительно (черт. 112),
SA — SK<TAK,
или
SA-SK<™;
АВ
но —, как сторона правильного вписанного многоугольника,
стремится к нулю, следовательно, SA служит пределом для SK.
Отсюда следует, что боковая поверхность конуса равна
S=i-.27T/7:
-nrl.
Итак,
боковая поверхность конуса равна половине
произведения длины окружности его основания на образующую.
Полная поверхность конуса равна тгг (г -[-/).
§ 120. Вторая формула для боковой поверхности конуса.
При вычислении боковой поверхности конуса иногда бывает
удобно заменять конус цилиндром с той же высотой и таким
радиусом основания, чтобы боковые
поверхности цилиндра и конуса были
одинаковы. Докажем следующую теорему.
Теорема. Боковая
поверхность конуса равна боковой по-
верхности цилиндра с тою же
высотой и радиусом основания,
равным высоте равнобедренного
треугольника, основанием
которого служит образующая, а
вершина лежит на оси конуса.
Пусть ABC (черт. ИЗ) — осевое
сечение конуса; АСО — равнобедренный
треугольник с вершиной О на оси
конуса; ОМ—его высота. Требуется доказать, что боковая
поверхность 5 конуса может быть представлена в виде
S = 2n. MO-CD.
Черт. ИЗ.
По формуле § 119 имеем:
S
АС
u-AD-AC = 2n-AD~==2u-AD.MC.
Прямоугольные треугольники ACD и ОМС подобны,
следовательно, А£_МО
DC~MC
117

откуда
AD-MC = MO-DC.
Произведя подстановку в выражение для S, получим:
5 = 2ττ· MO-CD.
§ 121. Объём конуса.
Объём /z-угольной вписанной в. конус правильной пирамиды
при увеличении η стремится к некоторому пределу, коюрый
принимается за объём конуса.
Объём пирамиды равен γ, где Ь — площадь основания
пирамиды и Л — её высота. Пределом для Ь служит площадь круга
основания, т. е. величина тгг2. А потому объём конуса V равен
з *
Следовательно,
объём конуса равен одной трети произведения
площади его основания на высоту.
§ 122. Усечённый конус.
Часть конуса, заключённая между его основанием и секущей
плоскостью, параллельной основанию, называется усечённым
конусом (черт. 114).
Усечённый конус может быть
образован вращением прямоугольной
трапеции вокруг её боковой
стороны, перпендикулярной к основанию.
Вторая боковая сторона этой
Черт. 114. трапеции служит образующей
конуса. Две параллельные стороны
трапеции описывают круги, называемые основаниями усечённого
конуса.
Если вписать в основания усечённого конуса правильные
многоугольники с одинаковым числом сторон и с соответственно
параллельными сторонами и через каждую пару этих параллельных
сторон провести плоскость, то все эти плоскости вместе с
плоскостями оснований будут ограничивать правильную усечённую
пирамиду, вписанную в данный усечённый конус. При
неограниченном увеличении числа боковых граней правильной вписанной
пирамиды её поверхность и объём стремятся к определённым
пределам, которые принимаются соответственно за поверхность
и объём усечённого конуса.
118

,-τ Ρ-\-ρ
Поверхность правильной усечённой пирамиды равна —-—а,
где Ρ и ρ — периметры оснований и а — апофема.
При увеличении числа боковых граней пирамиды периметры
Ρ и ρ стремятся соответственно к длинам окружностей оснований,
т. е. к 2nR и 2ттг, где R и г — радиусы оснований конуса.
Апофема а пирамиды, очевидно, имеет пределом длину /
образующей усечённого конуса. А потому боковая поверхность S
усечённого конуса равна
или
S = rd(R + r).
Следовательно,
боковая поверхность усечённого конуса равна про-
изведению полусуммы длин окружностей его оснований
на образующую.
Заметим, что J~ = MN (черт. 115) есть радиус среднего
сечения усечённого конуса. Обозначая его через гр получим:
S = 2ulrv
Так же, как и в случае простого конуса, при вычислении
боковой поверхности можно заменить усечённый конус цилиндром
с той же высотой и таким радиусом
основания, чтобы его боковая поверх- Bf fe^ ^
ность была равна боковой поверхности
данного усечённого конуса. ^
Докажем следующую теорему: '
Теорема. Боковая поверх- L
ность усечённого конуса равна ^r-lk k Л
боковой поверхности цилиндра с ^iL_ ^S
той owe высотой и радиусом ос-
нования, равным высоте равно- Черт. 115.
бедренного треугольника,
основанием которого служит образующая конуса, а
вершина лежит на его оси.
Дано: ЛВ020^ — половина осевого сечения данного усечённого
конуса (черт. 115), АВО — равнобедренный треугольник с
вершиной О на оси конуса, МО— его высота, ВС — высота
усечённого конуса, S—его боковая поверхность. Требуется
доказать, что
S = 2it.МО-ВС.
119

Как показано выше,
S=2iz-AB-MN.
Так как
Z.ABC = Z.OMN и Z.ACB=zZMNO = 90°y
то
Δ ABC -ν- Δ ΟΜΝ;
следовательно,
ΑΒ__ΜΟ
BC~~~MN'
откуда
AB-MN = MO-BC.
Подставляя это выражение для S, получим:
S = 2n-MO-BC.
§ 123. Общее выражение для боковой поверхности
цилиндра, конуса и усечённого конуса.
Для круглого цилиндра высота равнобедренного треугольника,
основанием которого служит образующая, а вершина лежит на
оси, очевидно, равна радиусу основания цилиндра. А потому
выведенные в §§ 120 и 122 формулы для боковой поверхности
применимы и к цилиндру.
Таким образом, для боковых поверхностей цилиндра, конуса
и усечённого конуса можно дать одно общее выражение:
боковая поверхность каждого из трёх тел:
цилиндра, конуса и усечённого конуса, равна боковой
поверхности цилиндра с той owe высотой и радиусом
основания, равным высо пе равнобедренного
треугольника, основанием которого служит образующая, а
вершина лежит на оси тела.
§ 124. Объём усечённого конуса.
Объём усечённой пирамиды равен
где Ь и Ьх— площади её основания и h — высота.
При неограниченном увеличении числа боковых граней
площади её оснований Ь и Ьх стремятся соответственно к пределам
тг/?3 и иг2. А потому объём усечённого конуса равен:
120

Следовательно,
объём усечённого конуса равен сумме объёмов трёх
конусов, у которых общая высота равна высоте
усечённого конуса, а площади оснований равны: у первого
конуса—площади нижнего, у второго конуса —
площади верхнего основания усечённого конуса, у треть-
его — среднему пропорциональному между ними.
III. ТЕЛА ВРАЩЕНИЯ.
§ 125.
Плоская ломаная называется правильной, если все её звенья
равны и все углы между её звеньями также равны. Правильная
ломаная имеет центр, т. е. точку, равноудалённую от всех
вершин и от всех звеньев.
Теорема. Поверхность, образованная вращением
правильной ломаной вокруг оси, лежащей в плоскости
ломаной,
проходящей через её центр
и не пересекающей
ломаной, равна
боковой поверхности
цилиндра, радиус
основания
которого равен апофеме
ломаной, а
высота—проекции
ломаной на ось
вращения.
Дана поверхность
(черт. 116),
образованная вращением
правильной ломаной линии
ABCDE (черт. 117)
вокруг оси хуу
проходящей через центр О ломаной; обозначим через а = ОМ =
= ON=OP = OQ апофему ломаной, через Ьу с, d и е —
проекции точек В, С, D и Ξ на ось ху, через S — величину
поверхности, образованной вращением ломаной. Требуется
доказать, что
3='2π·α·Αβ.
При вращении ломаной каждое её звено будет описывать или
конус, или цилиндр, или усечённый конус. Так, звено АВ опишет
121
fy
f-
L_
/А
\^
--r-/£-
A
_j
Черт. 116.
Черт. 117.

конус с высотой ЛЬУ звено ВС— усечённый конус с высотой Ьсу
звено CD — цилиндр с высотой cd и звено DE— усечённый
конус с высотой de. Каждую из этих поверхностей можно
вычислить по общей формуле, данной в § 123. При этом «высота
равнобедренного треугольника с вершиной на оси, основанием
которого служит образующая, будет для всех звеньев ломаной
одинакова и равна апофеме ломаной {МО = NO = PO—QO = а).
А потому поверхности, образованные вращением звеньев АВ,
ВС, CD и DE ломаной, соответственно равны 2πα·ΑΙϊ, 2na-bc,
2Tia»cd и 2na»de. Складывая эти выражения, получим:
5 = 2πα · (АЬ + be -f- cd -f- de) = 2m · Ae.
§ 126. Объём тела вращения.
Теорема. Объём тела, образованного вращением
треугольника вокруг оси, лежащей в его плоскости,
проходящей через его вершину и не пересекающей
самого треугольника, равен произведению поверхности,
образованной вращением основания треугольника, на
одну треть его высоты.
Могут представиться три случая:
1. Ось вращения ху совпадает с одной из
сторон, например, со стороной АВ (черт. 118).
Тогда сторона ВС при вращении описывает
поверхность конуса, радиус основания которого
равен СЕ (C£_L АВ), а высота равна BE. Объём
этого конуса равен -^ъ-ЕС2,-BE. Точно так же
сторона АС опишет конус, объём которого равен
^ и-ЕС2- АЕ. А потому объём всего тела
вращения равен
±ъ.ЕС2-ВЕ-\-±ъ.ЕС*-АЕ= -π-Εσχ
X (АЕ-\-ЕВ) = ~п-ЕС2 - АВ=\ъ-ЕС - ЕС - АВ.
Но ЕС-АВ = AC-BD (как удвоенная площадь
ника ABC); а потому объём тела вращения равен
±it.EC'AC.BD = K*EC-AC·^.
о о
треуголь-
Здесь π·ΕΟ·АС есть боковая поверхность конуса,
образованного вращением основания АС треугольника ABC.
122

2. Ось вращения ху проходит через одну из вершин, но не
совпадает ни со стороной АС, ни со стороной ВС и не
параллельна стороне АВ (черт. 119).
Продолжим сторону АВ до пересечения в точке Ε с осью ху.
Тогда объём тела, образованного вращением треугольника ABC,
Черт. 119.
Черт. 120.
будет равен разности объёмов тел, образованных вращением
треугольников АСЕ и ВСЕ. Первый объём равен произведению
поверхности, образованной вращением отрезка АЕ, на -~- высо-
о
ты CD .Второй объём равен произведению поверхности,
образованной вращением отрезка BE, на -^ высоты CD. А потому разность
этих объёмов равна произведению поверхности, образованной
вращением отрезка АВ, на -^ высоты CD.
3. Ось вращения ху параллельна основанию АВ
треугольника ABC (черт. 120).
В этом случае опустим из точек А и В перпендикуляры АЕ
и BF на ось вращения. Объём тела, образованного вращением
треугольника ABC, равен разности между объёмом цилиндра,
образованного вращением прямоугольника ABFE, и суммой
объёмов двух конусов, образованных вращением треугольников
АСЕ и ВСЕ.
Объём цилиндра равен k>CD2-AB.
Объём первого конуса равен
k-C£}'-AD
123

Объём второго конуса равен
π-CD''-BD
Сумма объёмов этих конусов равна
*.CD2.AD , k-CD2.BD %-CD2/Ar. . ОГк, 7t.CD2AB
3 + 3 =-r-{AD + BD) = з ■
А потому объём искомого тела вращения равен
uCD2.AB — 4 тт.CD2·Л# =
2n-CDAB-CD
I
2kCD.AB-CD.
Но 2u-CD-AB равно поверхности, описанной основанием АВ.
Назовём правильным многоугольным сектором фигуру,
образованную правильной ломаной и двумя отрезками, которые
соединяют центр ломаной с её концами.
Теорема. Объём тела, образованного вращением
правильного многоугольного сектора вокруг оси, лежа-
х щей в его плоскости, проходящей
через его центр и не пересекающей сек-
тор, равен произведению поверхности,
образованной вращением ломаной
линии, на о- её апофемы.
Дан многоугольный сектор ABCDEO
(черт. 121), ограниченный правильной
ломаной линией ABCDE и радиусами АО и ЕО
окружности, описанной около этой ломаной.
Объём тела, образованного вращением
этой ломаной вокруг оси ху, очевидно,
равен сумме объёмов тел, образованных
вращением треугольников АОВ, ВОС, COD и
DOE.
Но объём тела, образованного вращением
треугольника АОВ, равен произведению поверхности,
образованной вращением отрезка АВУ на одну треть апофемы OF
данной ломаной. Точно так же объёмы тел, образованных
вращением треугольников ВОС, COD и DOE, соответственно
равны произведениям поверхностей, образованных вращением
отрезков ВС, CD и DE, на одну треть апофемы.
А потому искомый объём всего тела вращения равен
произведению поверхности, образованной вращением ломаной ABCDE,
на одну треть апофемы.
124
Черт. 121.

IV. СФЕРА.
§ 127. Определение.
Геометрическое место точек, равноудалённых от одной и той
же точки (центра), образует поверхность, называемую сферой,
или шаровою поверхностью. Тело, ограниченное шаровою
поверхностью, называется шаром.
Отрезки прямых, соединяющих центр с точками сферы,
называются её радиусами. Отрезок прямой, соединяющей какие-
либо две точки сферы, называется хордой сферы. Хорда,
проходящая через центр, называется диаметром сферы. Диаметр сферы
равен двум её радиусам. Сфера может быть образована
вращением полуокружности вокруг диаметра. Центр вращающейся
полуокружности служит центром сферы, а её радиус — радиусом
сферы.
§ 128. Сечения сферы.
Теорема. Сечение сферы плоскостью есть
окружность.
Для плоскости, проходящей через центр сферы, это
очевидно. Поэтому будем предполагать, что секущая плоскость Μ
не проходит через центр (черт. 122). Опустим из центра О сферы
на плоскость сечения Μ
перпендикуляр ОР и
докажем, что все точки
линии пересечения сферы
с плоскостью Μ
одинаково удалены от точки Р.
Возьмём произвольные
точки сечения: А, В, С, ...
Соединим их с точкой Ρ
и с центром сферы О. Черт. 122.
Отрезки РА, РВ, PC, ...
служат проекциями равных наклонных (радиусов сферы) АО, ВО,
СО,..., а потому АР = ВР = СР=... Следовательно, сечение
сферы плоскостью есть окружность с центром Р.
Следствие 1. Если секущая плоскость не проходит
через центр сферы, то радиус окружности сечения меньше
радиуса сферы, так как АР<^АО.
Следствие 2. Сечение имеет наибольший радиус, когда
плоскость сечения проходит через центр сферы.
Такое сечение называется большим кругом сферы.
125

Следствие 3. Плоскость большого круга есть плоскость
симметрии сферы.
Следствие 4. Радиусы сечений, плоскости которых
равноудалены от центра сферы, равны.
Задача. Через две данные тонки сферы, не служащие
концами одного диаметра, провести окружность большого
круга.
Пусть А и В — две точки сферы, О — её центр. По условию,
точки Л, В и О не лежат на одной прямой, и, следовательно,
через них проходит единственная плоскость. Сечение её
поверхностью сферы даёт искомую окружность большого круга,
проходящую через точки А и В.
Задача имеет только одно решение.
§ 129. Касательная плоскость к сфере.
Плоскость, имеющая с поверхностью сферы лишь одну общую
точку, называется касательной плоскостью к сфере.
Теорема. Плоскость,
проходящая через конец
радиуса сферы и
перпендикулярная к нему,
служит касательной
плоскостью.
Проведём через конец А
радиуса ОА данной
сферы плоскость Μ J_ О А
(черт. 123) и докажем, что все
Черт. 123. точки этой плоскости, кроме
точки Л, лежат вне сферы.
Пусть В — произвольная точка плоскости М. Соединим её с
центром сферы О. Тогда ОА<^ОВ (так как перпендикуляр
короче наклонной). Следовательно, точка В лежит вне сферы.
§ 130. Касательная прямая к сфере.
Прямая, лежащая в касательной плоскости к сфере и
проходящая через точку прикосновения, называется касательной
прямой к сфере. Касательная прямая, очевидно, имеет лишь
одну общую точку со сферой и перпендикулярна к радиусу
сферы, проведённому в точку прикосновения.
Теорема. Все касательные к сфере, проведённые
из одной внешней тонки, равны между собой.
Проведём из внешней точки S касательные к сфере SA, SB,
SC (черт. 124). Точки их прикосновения Л, В> С соединим
126

с центром сферы О. Прямоугольные треугольники AOS, BOS,
COS имеют общую гипотенузу SO и
равные катеты
О А = О В = ОС,
а потому они равны между собой.
Следовательно,
SA = SB = SC.
Черт. 124.
всех образующих
лежат на одной
§ 131. Коническая поверхность,
описанная около сферы.
Проведя из какой-либо внешней точки
все касательные прямые к сфере, получим
коническую поверхность, касающуюся
сферы и называемую описанной
конической поверхностью.
Теорема. Точки прикосновения
описанной конической поверхности
окружности (окружность прикосновения).
Действительно, построив в равных треугольниках AOS, BOS,
COS у . . . высоты из вершин А, В, С, ... на общую сторону SO
(черт. 124), найдём, что
все они пересекают
прямую SO в одной и той
же точке Р. Так как
AP±SO, BP±SO,
СР J_ SO, ..., то прямые
АР, ВР, СР, ... лежат
в одной плоскости М,
перпендикулярной к SO.
А так как
АР = ВР= СР = . . .,
то точки А, В, С, . ..
лежат на одной
окружности с центром в точ-
Черт. 125. ке Р.
§ 132. Пересечение двух сфер.
Теорема. Линия пересечения двух пересекающихся
сфер есть окружность, лежащая в плоскости,
перпендикулярной к линии центров сфер.
Даны две пересекающиеся сферы (черт. 125). Соединим их
центры О и Ох и возьмём на линии их пересечения произволь-
127

ные точки Лу В и С. Соединив их с центрами сфер, получим
равные треугольники:
Δ оло, = д овог = δ осог
(по трём сторонам). Опустив из их вершин Л, В, С
перпендикуляры на общую сторону ΟΟλ, заметим, что все они встретят
общую сторону ООг в одной и той же точке Р, и,
следовательно, все они будут лежать на одной плоскости MJL_001.
Так как
АР = ВР = СР,
то точки /1, В, С, ... лежат на одной окружности с центром
в точке Р.
§ 133. Части шара.
Тело, отсекаемое от шара какою-либо плоскостью,
называется шаровым сегментом. Сферическая поверхность сегмента
называется шаровым сводом. Тело, отсекаемое от шара двумя
параллельными секущими плоскостями, называется шаровым
слоем. Сферическая поверхность шарового слоя называется
шаровым поясом. Расстояние между обеими параллельными
секущими плоскостями называется высотой шарового пояса.
Если одна из секущих плоскостей становится касательной
плоскостью, то шаровой слой обращается в шаровой сегмент,
шаровой пояс — в шаровой свод, а высота пояса — в высоту
шарового свода.
Геометрическое тело, образованное вращением кругового
сектора вокруг оси, лежащей в его плоскости, проходящей через
его центр и не пересекающей сектора, называется шаровым
сектором. Шаровой сектор может быть двух родов:
1) простой шаровой сектор, когда ось вращения совпадает
с одним из радиусов, ограничивающих круговой сектор;
2) полый шаровой сектор, когда ось вращения не
совпадает с радиусом, ограничивающим круговой сектор.
Шаровой поверхностью простого сектора служит шаровой
свод; шаровой поверхностью полого сектора служит шаровой
пояс.
§ 134. Поверхность шара и его частей.
1. Поверхность шарового пояса. Шаровой пояс
может быть образован вращением дуги окружности вокруг не
пересекающего её диаметра (черт. 126). Впишем в дугу окруж-
128

Черт. 126.
ности ЛВ правильную ломаную линию. Тогда поверхность,
образованная вращением этой ломаной, но теореме § 125,
равна 2иа · GH, где а — апофема
ломаной, GH—высота пояса.
При неограниченном
увеличении числа звеньев
вписанной ломаной её апофема
а стремится к радиусу
ОМ=г дуги АВ, а потому
предел поверхности,
описанной этой ломаной, равен
2ur-GH. Этот предел и
принимается за величину
поверхности шарового пояса.
Итак: поверхность
шарового пояса равна произведению длины окружности
большого круга на высоту пояса.
2. Поверхность шарового свода. Если плоскость
одного из оснований шарового . слоя обращается в касательную
плоскость, то шаровой слой обращается
в шаровой сегмент, а ограничивающий
его шаровой пояс в шаровой свод.
Поэтому поверхность шарового
выражается той же формулой,
шарового пояса, т. е.
поверхность шарового свода
равна произведению длины
окружности большого круга на
высоту свода.
3. Поверхность шара. Если
плоскости обоих оснований шарового
слоя сделаются касательными
плоскостями, то шаровой пояс обращается
в полную сферу, а его высота
становится равной диаметру шара, т. е. 2/?.
А потому поверхность шара равна
свода
что и
Черт.
2тг/?.2/?:=4тг/?2.
Следовательно,
поверхность шара равна боковой поверхности
цилиндра,радиус основания которого равен радиусу шара,
а высота — его диаметру (черт. 127).
129

§ 134. Объём шара и его частей.
1. Объём шарового сектора. Шаровой сектор
образуется вращением кругового сектора около оси, проходящей
через его центр. Впишем в круговой сектор ОАВ (черт. 126)
правильную ломаную линию. Тогда объём тела, образованного
вращением этой ломаной, равен произведению поверхности,
образованной вращением ломаной, на -~- её апофемы. При
неограниченном увеличении числа звеньев ломаной поверхность, ею
описываемая, стремится к поверхности шарового пояса (для полого
сектора) или свода (для простого сектора). Апофема ломаной
стремится к радиусу сферы. А потому предел объёма тела,
описанного вращением многоугольного сектора, равен
1 '*
2шИ · — г = γΤΓΓ2/?,
где h — высота шарового пояса (или свода).
Этот предел и принимается за объём шарового сектора.
Следовательно,
объём шарового сектора равен произведению
поверхности соответствующего шарового пояса (или свода)
на одну треть радиуса шара.
2. Объём шара. Если h = 2/?, то шаровой сектор
становится полным шаром. А потому объём шара ранен
Следовательно,
объём шара равен двум третям объёма цилиндра,
радиус основания которого равен радиусу шара, а
высота— его диаметру (черт. 127).
3. Объём шарового сегмента. Объём шарового
сегмента может быть найден как разность объёмов простого
шарового сектора и конуса.
V. УПРАЖНЕНИЯ К ГЛАВЕ ШЕСТОЙ.
А. Доказать теоремы:
1. Касательная плоскость к цилиндру перпендикулярна к
плоскости, проходящей через образующую прикосновения и через ось
цилиндра.
2. Две непараллельные плоскости, касающиеся цилиндра,
пересекаются но прямой, параллельной оси цилиндра.
3. Если одна из трёх граней треугольной призмы, вписанной
в цилиндр, проходит через его ось, то две другие её боковые грани
взаимно перпендикулярны.
130

4. Двугранный угол, ребром которого служит образующая
цилиндра и грани которого проходят через две образующие цилиндра,
равен половине двугранного угла, ребром которого служит ось
цилиндра и грани которого проходят через те же образующие.
5. Угол между двумя образующими, принадлежащими осевому
сечению конуса, больше угла между образующими, не
принадлежащими осевому сечению.
6. Плоскость, касательная к конусу, перпендикулярна к
плоскости, проходящей через образующую прикосновения и через ось
конуса.
7. Касательная к окружности основания конуса перпендикулярна
к образующей, проходящей через точку прикосновения.
8. Все плоскости, пересекающие данную сферу по окружности
Данного радиуса, касаются сферы, концентрической с данной.
9. Если через данную точку,не лежащую на поверхности сферы,
провести к ней различные секущие, то произведение отрезков
каждой секущей, считая от данной точки до точек встречи со сферой,
есть величина постоянная для всех секущих.
Указание. Провести плоскость через взятую секущую и центр
сферы,— тогда утверждение сведётся к теореме §222 Планиметрии.
10. Если через данную точку провести к данной сфере различные
секущие плоскости, то степень данной точки относительно всех
окружностей, получаемых в сечении, будет одинакова. Она
называется степенью данной точки относительно данной сферы.
11. Доказать, что подобным преобразованием с коэфициентом
подобия k сфера радиуса R преобразуется в сферу радиуса kR.
12. Всякие две сферы перспективно-подобны и имеют два центра
подобия: один внешний, другой внутренний.
13. Цилиндр (или конус), ось которого проходит через центр
сферы, пересекает эту сферу по окружности.
14. Плоскость, касающаяся двух данных сфер, проходит через
их центр подобия.
15. Внутренние и внешние центры подобия трёх сфер, взятых
попарно, расположены по три на четырёх прямых.
16. Около каждой правильной пирамиды можно описать сферу и
во всякую правильную пирамиду можно вписать сферу.
17. Объём многогранника, описанного около сферы, равен
произведению его поверхности на -^- радиуса сферы.
18. В цилиндр можно вписать сферу, если осевое сечение
цилиндра — квадрат.
19. Если в усечённый конус можно вписать сферу, то его
образующая равна сумме радиусов обоих оснований.
Б. Геометрические места.
20. Найти геометрическое место точек, находящихся на данном
расстоянии от данной прямой. Отв. Цилиндрическая поверхность,
осью которой служит данная прямая.
21 .Найти геометрическое место осей цилиндров данного радиуса,
касающихся данного цилиндра вдоль его образующих (говорят, что
два цилиндра или цилиндр и конус или два конуса касаются вдоль
образующей, если они имеют общую образующую и в точках этой
131

общей образующей — общие касательные плоскости). Отв. Два
цилиндра, оси которых совпадают с осью данного цилиндра.
22. Найти геометрическое место рёбер двугранных углов данной
величины, грани которых проходят через две данные параллельные
прямые а и Ь. Отв. Искомое геометрическое место состоит из
частей двух цилиндров, к образующим которых принадлежат
прямые а и Ь\ если данный двугранный угол — прямой, то получается
один цилиндр.
23. Найти геометрическое место центров сфер данного радиуса,
касающихся боковой поверхности данного цилиндра. Отв. Два
цилиндра, имеющие ту же ось, что и данный.
24. Найти геометрическое место центров сфер данного радиуса,
пересекающих данную плоскость по окружности данного радиуса.
Отв. Две плоскости, параллельные данной. /
25. Найти геометрическое место центров сфер данного радиуса,
касающихся данной плоскости. Отв. Две плоскости, параллельные
данной.
26. Найти геометрическое место прямых, наклонённых под
данным углом к данной прямой и проходящих через данную на ней
точку. Отв. Поверхность конуса, осью которого служит данная
прямая.
27. Найти геометрическое место осей цилиндров данного
радиуса, касающихся данного конуса вдоль его образующих
(см. упр. 21). Отв. Два конуса, имеющих ту же ось, что и данный.
28. Найти геометрическое место осей конусов с данным углом
в осевом сечении, касающихся данного конуса вдоль его
образующих (см. упр. 21) и имеющих с ним общую вершину. Отв. Два
конуса с той же осью и той же вершиной, что и данный.
29. Найти геометрическое место центров сфер, проходящих
через вершины данного треугольника. Отв. Прямая линия,
перпендикулярная к плоскости этого треугольника и проходящая через центр
окружности, описанной около него.
30. Найти геометрическое место центров сфер данного радиуса,
касающихся граней данного двугранного угла. Отв. Прямая,
параллельная ребру.
31. Найти геометрическое место центров сфер, касающихся
граней данного трёхгранного угла. Отв. Луч, выходящий из вершины угла.
32. Найти геометрическое место центров сфер, касающихся
рёбер данного трёхгранного угла. Отв. Луч, выходящий из вершины
угла.
33. Найти геометрическое место центров сфер данного радиуса,
проходящих через две данные точки. Отв. Окружность, лежащая
в плоскости, перпендикулярной к прямой, соединяющей эти точки,
или одна точка, или геометрическое место не существует.
34. Найти геометрическое место центров сфер данного радиуса,
проходящих через данную точку и касающихся данной плоскости.
Отв. Окружность, лежащая в плоскости, параллельной данной, или
точка, или две точки, или геометрическое место не существует.
35. Найти геометрическое место точек, из которых три
последовательных отрезка прямой линии АВ, ВС, CD видны под равными
углами. Отв. Окружность или геометрическое место не существует.
36. Найти геометрическое место середин параллельных хорд·
сферы. Отв. Точки круга, лежащего в диаметральной плоскости,
перпендикулярной данным хордам.
132

37. Найти геометрическое место вершин прямых углов, стороны
которых проходят через две данные точки. Отв. Сфера, для которой
отрезок, соединяющий данные точки, служит диаметром.
38. Найти геометрическое место центров сфер данного радиуса,
касающихся данной сферы. Отв. Две сферы, концентрические с данной
39. Найти геометрическое место точек, из которых данный
отрезок виден под данным углом. Отв. Поверхность, образованная
вращением дуги окружности вокруг некоторой оси; если данный
угол прямой, — сфера.
40. Найти геометрическое место точек, из которых данная сфера
видна под данным углом, т. е. найти геометрическое место вершин
конусов, описанных около сферы и имеющих данный угол в осевом
сечении. Отв. Сфера, концентрическая с данной.
В. Задачи на построение.
41. Построить линии пересечения поверхности цилиндра с
плоскостью, параллельной его оси.
42. Построить точки пересечения поверхности цилиндра с
данной прямой.
43. Через данную образующую цилиндра провести плоскость,
касающуюся этого цилиндра.
44. Через данную точку вне цилиндра провести плоскость,
касающуюся цилиндра.
45. В данный цилиндр вписать правильную шестиугольную
призму.
46. В данный цилиндр вписать треугольную призму с данными
двугранными углами между боковыми гранями.
47. Даны три точки на окружности основания цилиндра.
Построить его ось.
48. Построить общую касательную* плоскость к двум цилиндрам
с параллельными осями.
49. Построить точки пересечения данного конуса с прямой
линией.
50. Через данную точку вне конуса провести плоскость,
касающуюся конуса.
51. Дана ось конуса и две точки, лежащие на поверхности
конуса. Построить вершину конуса.
52. Построить точки пересечения данной прямой с поверхностью
сферы.
Указание. Через данную прямую провести диаметральную
плоскость и в ней выполнить построение.
53. Построить окружность, по которой данная плоскость
пересекает сферу, для которой даны центр и радиус.
Указание. Основание перпендикуляра, опущенного из центра
сферы на данную плоскость, служит центром искомой окружности.
Её радиусом служит катет прямоугольного треугольника, гипотенуза
которого равна радиусу сферы, а другой катет равен расстоянию
центра от плоскости.
54. Построить линию пересечения двух данных сфер.
55. Построить точку пересечения трёх данных сфер.
133

56. Через данную точку провести прямую, касающуюся данной
сферы и параллельную данной плоскости.
57. Построить окружность прикосновения к данной сфере
описанного конуса, имеющего вершину в данной точке.
58. Через две данные точки провести плоскость, касательную
к данной сфере.
59. Построить плоскость, касающуюся трёх данных сфер. Сколько
решений имеет задача? Отв. Самое большее 8 решений.
Указание. См. упр. 14.
60. Найти точку, из которой три данные сферы видны под
данными углами.
61. Найти точку, из которой четыре данные сферы видны под
равными углами.
62. На данной прямой найти точку, из которой данный отрезок
был бы виден под прямым углом.
63. Построить центр сферы данного радиуса, проходящей через
вершины данного треугольника.
64. В данный тетраэдр вписать сферу.
65. Около данного тетраэдра описать сферу (найти ее центр и
радиус).
Г. Задачи на вычисление.
66. Вычислить площадь сечения круглого цилиндра, радиус
основания которого равен 8 см, а высота— 50 см, плоскостью, параллельной
его оси и отстоящей от неё на расстоянии 4 см. Отв. 692,8 кв. см.
67. Круглый цилиндр с радиусом R и высотой Η пересечён
плоскостью, параллельной оси цилиндра, так, что хорда сечения на
основании цилиндра равна его радиусу. Определить объём части
п HR2(k V"S\
цилиндра, отсекаемой плоскостью. Отв. —пг~(-т у~)·
68. Радиус основания конуса равен 22,35 м и высота 29,8 м.
Определить боковую поверхность конуса. Отв. 2615 кв. м.
69. Определить образующую конуса, если его боковая
поверхность равна 106,76 кв. м, а высота 7,5 м. Отв. 8,5 м.
70. Боковая поверхность конуса, развёрнутая на плоскость,
представляет собой кругог.ой сектор, радиус которого равен 32,867 му
а дуга содержит 90°. Вычислить объём конуса. Отв. V =2250 куб. м.
71. Вычислить объём V и поверхность S конуса, осевое сечение
которого представляет собой равносторонний треугольник со
стороной, равной 2 м. Отв. V=l,8 куб. м\ 5 = 9,4 кв. м.
72. Определить объём конуса с площадью основания S и боко-
вой поверхностью М. Отв. — у —-—
73. Даны образующая конуса / и боковая поверхность М. Опре-
»*2 /-
делить объём конуса. Отв. τς-zToVя2/4 — М2.
74. Дан конус, радиус основания которого г и высота Н. На каком
расстоянии от плоскости основания нужно провести плоскость, ей
134

параллельную, чтобы этой плоскостью конус разделился на две
равновеликие части. Каков радиус такого сечения? Отв. — (2 — у 4); L· у 4.
75. На каком расстоянии от основания отстоят две
плоскости, параллельные плоскости основания и делящие боковую по-
верхнссть конуса на 3 равные части, если высота конуса равна Ю
76. Высота конуса разделена на 3 равные части и через эти
точки деления проведены плоскости параллельно плоскости
основания конуса. В каком отношении делится объём конуса этими
плоскостями? Отв. 1:7: 19.
77. Дан конус, радиус основания которого г и образующая 2п
Плоскость, параллельная основанию, делит его на два тела, полные
поверхности которых одинаковы. Чему равна образующая конуса,
отсечённого этой плоскостью? Отв. rV'o.
78. Определить, в каком отношении делится боковая поверхность
конуса плоскостью, проведённой через его вершину и хорду
основания, равную по длине радиусу основания. Отв. 5:1.
79. Определить высоту усечённого конуса, радиусы оснований
которого 18 и 10 м, а образующая 28 м. Отв. 26,83 м.
80. Определить радиусы оснований усечённого конуса R и г и
образующую /, если известно их отношение R:r:l = 2:1:0, а боковая
поверхность этого конуса равна 452,16 /св. м. Отв. R =8 м,г = 4 м,
/=12 м.
81. Определить высоту усечённого конуса, радиусы основании
которого R и г и боковая поверхность которого равна сумме пло-
о η 2Rr
щадеи его основании. Отв.---,— .
R +г
82. Дан усечённый конус с высотой Η и радиусами оснований R
и г. На каком расстоянии от плоскости нижнего основания его
следует провести плоскость, параллельную основанию, чтобы площадь
сечения была средней пропорциональной между площадями основа-
а, η hVW
ний? Отв. /-т_. _/-— ■ .
VR+V г
83. Усечённый конус, радиусы оснований которого равны R и г,
высота h и образующая /, разделён на две части плоскостью,
параллельной основанию.
Определить радиус сечения, если плоскость делит:
1) Объём усечённого конуса на две равные части. Отв. л/ уг .
2) Объём усечённого конуса на две части, находящиеся в
отношении p'.q. Отв. л/ g_°, Л~ГГ
У Ρ λ-Q
Ъ) Боковую поверхность усеченного конуса на две равные части.
Oms. уГ«1±£
135

4) Боковую поверхность усечённого конуса на две части, нахо-
дящиеся в отношении р'.а.Отв. л/ ^_—L_c— .
У p + q
84. Высота усечённого конуса //, радиусы оснований R и г.
Плоскость, параллельная основанию, делит объём конуса на две равные
части. Определить расстояние этой плоскости от нижнего
основания
конуса. Отв. -^ZT} I R~ у 2 /'
85. Полная поверхность усечённого конуса равна т2, а
образующая наклонена к плоскости основания под углом в 60° и равна а.
~ ш / За'2 , rrfi Ъа
Вычислить радиусы основании этого конуса. Отв. Ι/ "ΤζΉ~ <J7 ~λ\
ν
Ъа* ,т'2 а
86. Определить высоту шарового слоя, сферическая поверхность
которого равна 22,609 кв. м, а радиус шара, которому принадлежит
слой, равен 2,4 м. Отв. 1,5 м.
87. Радиус шара равен 2 л/, радиус сечения шара плоскостью
равен 1 м. Определить объём сектора, соответствующего сегменту,
отсекаемому плоскостью. Отв. 2,26 куб. м.

ДОПОЛНЕНИЕ.
ОБ АКСИОМАХ ГЕОМЕТРИИ.
1. Геометрия среди других областей математики (алгебра,
арифметика) выделяется одной только ей присущей особенностью.
Эта особенность состоит в том, что те теоремы и свойства
фигур, которые изучаются в геометрии, не только устанавливаются
путём ряда рассуждений, но во многих случаях могут
служить объектом непосредственного созерцания; справедливость
этих свойств не только доказывается, но и подтверждается
непосредственным зрительным впечатлением. Так, равенство углов
при основании равнобедренного треугольника или равенство двух
треугольников, имеющих одинаковые длины сторон, и многие
другие свойства фигур можно непосредственно созерцать.
Наглядность геометрических объектов помогает обнаруживать
и угадывать многие геометрические факты прежде, чем они
будут точно доказаны. Непосредственное созерцание геометрических
фигур у древних египтян (за 2000 лет до нашей эры) служило
главным способом доказательства наличия тех или иных их свойств.
Но такой способ мог быть пригоден лишь для установления
простейших геометрических фактов. С такими именно фактами и
имели дело египтяне, которые пользовались геометрией для узко-
практических целей. Уже простое расширение и усложнение
практических задач привело к необходимости изучать свойства всё более
сложных геометрических фигур, а для этого уже недостаточно
было простого созерцания чертежа; появилась необходимость
применять всё более сложные формы рассуждений.
Кроме того, сама наглядность чертежа в применении к более
сложным геометрическим фигурам часто весьма обманчива и при-
137

водит иногда прямо к неверным заключениям. Можно привести
много примеров, когда общий вид чертежа подсказывает
неверное заключение о взаимном расположении и свойствах
изображённых на нём фигур. На этом основано много геометрических
парадоксов, приводить которые мы-здесь не будем.
Древние греки, воспринявшие геометрическую науку от
египтян, обобщили отдельные факты, известные египтянам, и
выработали определённые формы рассуждений, при помощи которых они
обнаруживали новые геометрические факты. Приблизительно за
300 лет до начала нашей эры греческий геометр Евклид-в ряде
своих книг, носивших общее название „Начала", дал первое
научное обоснование геометрии. Он постарался в достаточно
отчётливых терминах в форме определений выразить словами те
общие представления о простейших геометрических образах —
точках, линиях, поверхностях — и о взаимоотношениях между
ними, которые считались до того времени само собой понятными.
Базируясь на этих определениях, он дал полное логически
строгое построение геометрии, по форме в высшей степени
совершенное и с точки зрения современной науки.
Евклид прежде всего попытался дать точные определения
основных геометрических понятий: точки, линии, поверхности и
геометрического тела. Приведём данные им определения:
1. Точка есть то, что не имеет частей.
2. Линия есть длина без ширины.
3. Границы линии суть точки.
4. Прямая линия есть та, которая одинаково
расположена относительно всех своих точек.
5. Поверхность есть то, что имеет только длину и
ширину.
6. Границы поверхности суть линии.
7. Плоскость есть поверхность, которая одинаково
расположена относительно всех своих прямых.
8. Телом называется то, что имеет длину, ширину а
глубину.
9. Границы тела суть поверхности.
Целью этих определений было достигнуть того, чтобы
термины „точка", „прямая" и т. д. не только вызывали
определённое зрительное представление, но, одновременно с тем,
определяли некоторое понятие, опираясь на которое, можно было бы
делать дальнейшие логические выводы. И хотя эти определения
несовершенны с точки зрения современной науки, но они вполне
соответствовали тогдашнему состоянию научной мысли и являлись
первым шагом к переходу от образов к понятиям. Они послужили
отправным пунктом всех последующих работ по геометрии и
138

определили собой пути её дальнейшего развития.
Все истины, которые устанавливаются в геометрии, Евклид
разделил на три вида: постулаты, аксиомы и теоремы. К
первым двум видам1 были отнесены простейшие истины, которые
не возбуждали никаких сомнений, были непосредственно очевидны
и могли поэтому служить исходными предложениями, из
которых логически выводились другие истины.
Третий вид предложений — теоремы — истины, которые
должны доказываться, т. е. путём рассуждений выводиться из
двух первых видов истин.
Приведём постулаты и аксиомы Евклида:
а) Постулаты. Требуется, чтобы:
1) от каждой точки до каждой другой точки можно
было провести одну прямую линию;
2) ограниченную прямую можно было неограниченно
продолжать;
3) из любого центра можно было описать окружность
любым радиусом;
4) все прямые углы были равны между собой;
5) две прямые, которые при пересечении с третьей обра-
зуют с ней по одну сторону внутренние углы, в сумме
меньшие двух прямых, при продолжении в ту же сторону
пересекались.
б) Аксиом ы.
1) рлвные одному и тому же равны между собой;
2) если к равным прибавить поровну, то суммы будут
равны;
3) если от равных отнять поровну, то остатки будут
равны;
4) совмещающиеся друг с другом равны;
5) целое больше своей части.
Эти аксиомы и постулаты Евклида в течение долгого ряда
последующих столетий служили базой, на которой строилась вся
геометрия.
2. Уже ближайшие последователи Евклида обратили особое
внимание на пятый из данных Евклидом постулатов. Он
привлекал к себе внимание сложностью своей формулировки и далеко
не полной очевидностью. Эта неочевидность вызывала стремление
так или иначе доказать справедливость постулата, т. е. вывести
его из остальных, не возбуждающих сомнений истин. Попытки
1 Принципиальгой разницы между теми и другими Евклид не
указывает, но с постулатами он обычно связывает утверждение
возможности выполнить то или иное построение.
139

дать доказательство пятого постулата продолжались в течение 2000
лет, но не привели и, как оказалось впоследствии, не могли
привести к положительному результату. Удавалось лишь заменить
постулат другим предложением, ему равносильным, но столь же
неочевидным и не вытекавшим из остальных геометрических
аксиом и постулатов.
3. В первой половине XIX в. великий русский матаматик,
профессор Казанскою университета, Николай Иванович
Лобачевский высказал смелую мысль, что пятый постулат Евклида не
является логическим следствием остальных аксиом геометрии и
потому не может быть доказан и что принятие этого постулата
не является необходимым для построения геометрии.
В подтверждение своей мысли он построил новую геометрию,
в которой пятый постулат Евклида был заменён другим
предложением, а именно, что через данную точку в данной плоскости
можно провести бесчисленное множество прямых, не
пресекающих данной.
Предложения $той геометрии существенно отличались от те-
ирем геометрии Евклида. Так, сумма углов треугольника
оказывалась меньше двух прямых углов, к теоремам о равенстве
треугольников присоединялась новая: треугольники равны, когда
гри угла одного равны трём углам другого. В этой геометрии,
следовательно, не существует треугольников, подобных и в то же
время неравных между собой.
Несмотря на всю непривычность таких предложений новой
геометрии, она имела такую же стройную и -законченную форму,
как геометрия Евклида. Впоследствии ей было дано название
неевклидовой геометрии. Одновременно с её открытием возник
вопрос, какая же геометрия имеет место в действительном
материальном мире и какой геометрией следует пользоваться при
решении различных вопросов физики, астрономии и др.
Лобачевский пытался решить этот вопрос опытным путём —
астрономическими наблюдениями. Но решить этот вопрос столь простыми
средствами оказалось невозможным. Дело в том, что наши
пространственные восприятия лишь приблизительно отражают
пространственные отношения материального мира.
Геометрия Евклида выросла из наблюдений над материальным
миром и потому с большою точностью отражает существующие
в нём взаимоотношения, по крайней мере в их простейших
проявлениях. Поэтому опыты Лобачевского не дали исчерпывающего
ответа на поставленный вопрос: они не обнаружили заметных
отклонений от того, что давала геометрия Евклида, но и не
установили абсолютного совпадения предложений этой геометрии
с пространственными взаимоотношениями материального мира.
140

Открытие неевклидовой геометрии произвело глубокие изме
нения в сознании геометров. Самый факт существования
стройной и непротиворечивой неевклидовой геометрии подрывал вековое
доверие к „наглядности" и „очевидности", руководившими
мыслью древних геометров. Многовековой анализ пятого постулата
расшатал устои первичных геометрических представлений, на
которых покоилась геометрия Евклида. Он вскрыл глубокие
зависимости между отдельными, казавшимися далёкими одни от
других, геометрическими фактами и представил в новом свете
пространственные взаимоотношения материального мира. Поэтому
система аксиом и определений Евклида как база для построения
геометрии стала уже недостаточной. В свете новых идей его
определения и аксиомы обнаружили недостаточную полноту и
не могли уже отвечать возросшим требованиям научной
строгости.
Такое, например, определение, как „линия есть длина без
ширины", не могло уже удовлетворить геометров, так как в их
сознании сами понятия длины и ширины уже утратили ту
абсолютную ясность, которую они имели во времена Евклида. Для
геометров нового времени стало ясно, что многие определения
Евклида требовали некоторых дополнительных предположений,
которые явно не высказывались, но незаметно принимались сознанием
древних геометров. Иначе трудно объяснить, почему, например,
определение 4 нельза применить к окружности и определение 7
к поверхности круглого цилиндра или сферы.
Требование большей полноты геометрических определений и
аксиом привело к тому, что в конце XIX в. перед учёными
встала задача общего пересмотра и уточнения всей
аксиоматической базы геометрии. Это привело к созданию новой
аксиоматики геометрии, вполне отвечающей современным требованиям
математической строгости.
Ниже мы даём краткое изложение современного состояния
этого вопроса.
4. Прежде всего поставим вопрос об определении основных
геометрических образов: точка, прямая линия и плоскость.
Заметим, что определить какое-нибудь понятие, значит выразить
его через понятия, ранее уже установленные. Если же искать
определение простейших понятий, то дело неизбежно сведётся
лишь к замене одного термина другим, в свою очередь
требующим определения. Так и было у Евклида, который понятие
„линии" определил через понятие „длины" или „границы", а эти
последние не определил.
Поэтому можно с самого начала не искать определения
простейших геометрических понятий, а принять их за исходные,
141

которые нельзя уже выразить через понятия более простые.
„Точка", „прямая" и „плоскость" и принимаются за такие
первичные, неопределимые геометрические понятия. По отношению к ним
устанавливается целая система основных положений—„аксиом44,
принимаемых за исходные недоказуемые положения. По существу
эти аксиомы представляют собой лишь
целесообразные абстракции пространственных
взаимоотношений материального мира.
Мы приведём здесь (с несущественными изменениями) ту
систему аксиом, которая была дана немецким математиком
Гильбертом. В этой системе все аксиомы геометрии разделяются
на 5 групп.
Первая группа аксиом — „аксиомы соединения". Аксиомы
этой группы имеют целью установить те взаимоотношения между
понятиями точка, прямая и плоскость, которые обычно
характеризуются словами: „прямая проходит через точку",
„точка лежит на прямой или на плоскости" и т. п. Эта группа
состоит из следующих аксиом:
1. Через две точки проходит единственная прямая.
2. На каждой прямой лежит не менее двух точек;
существуют, по крайней мере, три точки, не лежащие на
одной прямой.
3. Через три точки, не лежащие на одной прямой,
проходит единственная плоскость'. В каждой плоскости лежит,
по крайней мере, одна точка.
4. Если две точки прямой линии лежат в данной плоскости,
то и все точки этой прямой лежат в той же плоскости,
5. Если две плоскости имеют одну общую точку, то они
имеют и ещё, по крайней мере, одну общую точку.
6. Существуют, по крайней мере, четыре точки, не
лежащие в одной плоскости.
При первом взгляде на эти аксиомы некоторые из них могут
показаться или недостаточными, или вообще ненужными. Так,
аксиома 2 как бы противоречит обычному представлению о прямой,
на которой мы мыслим бесчисленное множество точек. Но не
следует забывать, что точки и прямые введены у нас как
первичные, не зависящие одно от другого понятия. Они могут
существовать раздельно. Поэтому, когда мы говорим, что точка
лежит на прямой или что прямая проходит через точку, мы
приписываем точке и прямой способность находиться между
собой в некотором взаимоотношении. Чтобы яснее представить
себе такое раздельное существование точек, прямых и плоскостей
и взаимоотношения между ними, будем их представлять себе
в виде конкретных, физических предметов. Точки будем пред-
142

ставлять себе в виде горошин какой-нибудь определённой
величины. Эти горошины будем предполагать шарообразной формы
и достаточно мягкими (например, разбухшими в воде), чтобы их
можно было прокалывать тонкими иглами и резать на части.
Прямые линии будем представлять в виде очень тонких стальных
иголок, а плоскости в виде столь же тонких пластинок. Сначала
эти пластинки, иглы и горошины представляем себе ничем не
связанными и даже находящимися в разных местах: в одном
месте кучка гороха, в другом — груда стальных игл, в третьем —
пачка сложенных пластинок. Начнём теперь подчинять их тем
условиям, которые содержатся в наших аксиомах. Мы будем
считать, что точка лежит на прямой, если игла прокалывает
горошину, или хотя бы частично входит в неё. Будем считать,
что точка лежит на плоскости, если тонкая пластинка режет
горошину пополам, или лишь надрезает горошину. Что означают
при этих условиях аксиомы? Они требуют, чтобы наши горошины,
иглы и пластинки приняли такое расположение в пространстве,
при котором бы: каждые две горошины были проколоты по
крайней мере одной иглой или нанизаны на одну иглу (акс. 1);
каждая игла прокалывала не менее двух горошин (акс. 2); каждые
три горошины были разрезаны (или надрезаны) одной пластинкой
и чтобы каждая пластинка надрезала по крайней мере одну
горошину (акс. 3); если две горошины, нанизанные на одну иглу,
надрезать некоторой пластинкой, то и все другие горошины,
которые могут оказаться нанизанными на ту же иглу,
надрезывались бы той же пластинкой (акс. 4); если две пластинки
надрезывают одну и ту же горошину, то они надрезывали бы, но
крайней мере, ещё одну горошину (акс. 5); имеются по крайней
мере четыре горошины, не разрезанные (и не надрезанные) одной
и той же пластинкой (акс. 6). Таким условиям должны
удовлетворять наши горошины, иглы и пластинки. И такую комбинацию
горошин, игл и пластинок нетрудно построить. Действительно,
отделим от пачки пластинок четыре пластинки. Обрежем их по
краям так, чтобы каждая из них приняла форму равностороннего
треугольника определённого размера. Из груды игл возьмём
6 штук и обломаем их концы так, чтобы все иглы стали одной
длины, равной стороне треугольной пластинки. Возьмём, далее,
4 горошины и составим следующую фигуру: из 4 пластинок
составим правильный тетраэдр; в пазы между прилегающими
краями пластинок вложим иглы, а на вершинах тетраэдров
поместим горошины так, чтобы пластинки их надрезали, а иглы
прокалывали. Для этой совокупности горошин, игл и пластинок
удовлетворяются все поставленные выше требования, т. е. все
наши аксиомы.
143

Из этого примера видно, что множество точек, прямых и
плоскостей, удовлетворяющих аксиомам 1-й группы, может быть
конечным. В нашем примере мы имеем всего 4 точки, 6 прямых
и 4 плоскости.
Вторая группа аксиом — „аксиомы порядка" — имеет целью
в отчётливой форме высказать те положения, на которые мы
опираемся, когда говорим о том или ином порядке
расположения точек на прямой и на плоскости. Главным понятием здесь
является расположение на прямой одной точки между двумя
другими. Логическое содержание этого понятия и устанавливается
жсиомами этой группы. Она состоит из следующих аксиом:
1. Если В лежит между А и С, то А, В и С —
различные точки прямой, и В лежит также между С и А.
2. При данных двух точках А и В на прямой линии на
ней существует по крайней мере одна точка С, такая, что
В лежит между А и С.
3. Из трёх данных точек на прямой не более чем одна
лежит между двумя другими.
4. Если в данной плоскости даны треугольник ABC и
какая-либо прямая а, не проходящая ни через одну из его
вершин и пересекающая отрезок АВ, то она непременно
пересечёт или отрезок ВС или отрезок АС.
Эти аксиомы предъявляют к нашим точкам, прямым и
плоскостям требования, которым они должны удовлетворять. Та
совокупность граней, рёбер и вершин тетраэдра, которая
удовлетворяла аксиомам 1-й группы, уже не удовлетворяет аксиомам
2-й группы. В самом деле, на каждой нашей игле были нанизаны
лишь 2 горошины, между тем как вторая аксиома 1-й группы
требует, чтобы на прямой было не менее трёх точек. А более
подробный анализ показывает, что аксиомам 2-й и 1-й групп,
вместе взятым, может удовлетворять лишь бесконечное множество
точек, прямых и плоскостей.
Третья группа аксиом — „аксиомы конгруентности" — имеет
целью установить основные предложения о равенстве отрезков
и углов. Она содержит следующие аксиомы:
1. На любой прямой от любой её точки можно
отложить отрезок, равный данному.
2. Два отрезка, равные третьему, равны между собой.
3. Пусть А, В, С — точки одной прямой и Ах, Вх, Сх —
также точки одной прямой и ΑΒ = ΑλΒν BC = BlCl; если
отрезки АВ и ВС, а также ΑχΒχ и ВХСХ не имеют общих
точек, то АС = АгСг.
4. В данной плоскости от любой точки данной прямой
по данную её сторону можно построить один и только
144

один угол, равный данному; каждый угол равен самому себе.
5. Если в двух треугольниках ABC и ЛгВ]С1 стороны
ΑΒ = ΑχΒν АС = АгСг и 2.BAC = Z.B\A\C\> mo Z.ABC =
Следует обратить внимание на последнюю аксиому.
В учебниках геометрии эта аксиома есть следствие первого
признака равенства треугольников. Но само это равенство
треугольников доказывается путём наложения и, следовательно,
предполагает возможность перемещения фигур; возможность же
такого перемещения сама составляет некоторую новую аксиому
и притом не включённую в нашу систему. Поэтому
предложение 5 и приходится принимать как новую аксиому. Пользование
ею заменяет применение в геометрии метода перемещения фигур.
Четвёртую группу аксиом составляет одна „аксиома о
параллельных прямых". При этом возможность
существования параллельных доказывается без помощи новых аксиом.
А потому аксиома требует лишь единственности параллельной
прямой: через данную точку β данной плоскости можно
провести не более одной прямой, не пересекающей данной. Об
этой аксиоме мы уже говорили выше.
Наконец, пятую и последнюю группу аксиом составляют
„аксиомы непрерывности". Эта группа состоит из двух аксиом:
1. Аксиома Архимеда. Если АВ и CD два
произвольных отрезка, то на прямой АВ существует ряд точек
Αχ, Αν Αν . . ., Ап таких, что ΑΑχ = АгА2 = A2AS = . . . =
= A~t_xAn = CD и что В будет лежать между Лп_г и Аа.
2. Аксиома линейной полноты. Точки прямой
линии образуют систему точек, которую нельзя дополнить
новыми точками, которые можно было бы считать
принадлежащими той же прямой без нарушения ранее устан.
елейных аксиом1.
Содержание первой из этих аксиом — аксиомы Архимеда —
достаточно ясно: аксиома требует, чтобы каждой точки прямой,
как бы далеко она ни была намечена, можно было достигать с
помощью конечного числа равных шагов и, следовательно, чтобы
можно было измерить расстояние от данной точки до любой точки
прямой. Поэтому эту аксиому и называют иногда „аксиомой
измерения".
Посмотрим, в чём сущность аксиомы линейной полноты.
Учащиеся знают из курса алгебры, что если на числовой
оси построить все точки с рациональными абсциссами, то этим
1 Точнее: без нарушения первых двух аксиом соединения, аксиом
порядка, первой аксиомы конгруентности и аксиомы Архимеда.
145

не исчерпаются все точки прямой: прямая не будет сплошь
заполнена этими точками. Так, точки с иррациональными
абсциссами ещё не будут построены. Когда вводятся алгебраические
иррациональные числа в виде корней всевозможных степеней из
рациональных чисел и корней алгебраических уравнений с
рациональными коэфициентами и строятся соответствующие им
точки на числовой оси, то числовая ось обогащается новыми
точками с иррациональными абсциссами. Но на числовой оси всё
ещё остаются пустые места, где ещё могут быть вставлены
новые точки. Так, точки с абсциссами π, -£■, ~ , Υπ и т. п. не
будут нанесены на числовой оси. Ось заполнится вся лишь после
того, как будут введены все действительные числа. После этого
на ней нельзя будет вставить новую точку. На ней уже не
останется пустых мест. Аксиомча полноты требует, чтобы именно
этим свойством обладала геометрическая прямая: чтобы на ней
не оставалось ни одного пустого места, куда можно было бы
вставить новую точку.
Принятие этой аксиомы позволяет считать, что каждому
действительному числу соответствует определённая точка на прямой
при выбранном начале отсчёта абсцисс, и обратно — каждой
точке прямой соответствует определённое действительное число.
Таков перечень всех аксиом, на которых базируется в
настоящее время евклидова геометрия.

ОГЛАВЛЕНИЕ
Стр.
Введение.
Изображение
пространственных фигур на плоскости . . 3
Глава первая.
ПРЯМЫЕ И ПЛОСКОСТИ.
I. Общие положения о
взаимном расположении
прямых и плоскостей 4
II. Задачи на построение
пространственных фигур.. . 6
III. Параллельные прямые и
плоскости 9
IV. Параллельное смещение 14
V. Перпендикулярные
прямые и плоскости 17
VI. Зависимость между
параллельностью и
перпендикулярностью прямых и
плоскостей 20
VII. Углы между
скрещивающимися прямыми и между
прямой и плоскостью ... 25
VIII. Вращение
пространственных фигур вокруг оси . 27
IX. Упражнения к главе
первой 34
Глава вторая.
СИММЕТРИЯ
ПРОСТРАНСТВЕННЫХ ФИГУР.
I. Симметрия относительно
плоскости 40
II. Центральная симметрия
пространственных фигур . 45
III. Осевая симметрия
пространственных фигур ... 48
IV. Упражнения к главе
второй 53
Стр.
Глава третья.
ДВУГРАННЫЕ И
МНОГОГРАННЫЕ УГЛЫ.
I. Двугранные углы .... 54
И. Трёхгранные углы .... 59
III. Многогранные углы ... 62
IV. Упражнения к главетретьей 63
Глава четвёртая.
МНОГОГРАННИКИ.
I. Общие свойства
многогранников 66
II. Призма 70
III. Пирамида 73
IV. Правильные
многогранники 77
V. Подобное преобразование
многогранников 91
Глава пятая.
ОБЪЁМЫ
МНОГОГРАННИКОВ.
1. Сравнение объёмов
многогранников 94
II. Измерение объёмов
многогранников 98
III. Упражнения к главам
четвёртой и пятой 107
Глава шестая.
КРУГЛЫЕ ТЕЛА.
I. Цилиндр 111
II. Конус 114
III. Тела вращения 121
IV. Сфера 125
V. Упражнения к главе
шестой . 130
Дополнение. Об аксиомах
геометрии 137