Автор: Винс Р.
Теги: менеджмент управление предприятием управление капиталом активны инвестиционные инструменты
Год: 2003
Текст
THE NEW MONEY
MENEGEMENT
A Framework for Asset Allocation
Ralph Vince
JOHN WILEY & SONS, INC.
New York • Chichester • Brisbane • Toronto • Singapore
новый подход
К УПРАВДЕНИЮ КАПИТААОМ
Структура распределения активов между
различными инвестиционными
инструментами
Ральф Винс
МОСКВА 2003
Перевод с английского
канд. техн, наук К. Г. Гэршкова
Выражение благодарности
Есть несколько человек, помощь или влияние которых способ-
ствовали тому, что мои размышления вылились в эту книгу.
К сожалению, многие из них работают в финансовых компани-
ях, поэтому я не могу упомянуть их имен. Впрочем, они знают,
о ком идет речь, ведь их влиянием пронизана вся книга. Им
я чрезвычайно благодарен. Настоящая книга — результат гораздо
больших усилий, нежели мои собственные. Но таков уж наш
мир, что воздать должное этим людям можно, лишь одновремен-
но причинив им вред. А этого мне совсем бы не хотелось.
Я должен также поблагодарить тех замечательных сотрудни-
ков издательства «Wiley & Sons», особенно Карла Вебера и Май-
лса Томпсона, которым, несмотря на мое франко-итальянское
происхождение, никак не облегчавшее сотрудничество, удалось
подготовить к публикации и эту, третью по счету, книгу. Руко-
пись с изложением моей исходной идеи была в конце 1989 г.
отвергнута всеми издателями, кроме Уайли, который опублико-
вал ее на следующий год под названием «Формулы управления
портфелем». Мне всегда казалось забавным, что самый предпоч-
тительный для меня издатель оказался также и единственным,
кто был готов рискнуть и опубликовать мои соображения в той
6
первой маленькой книжке, тогда как издатели менее крупного
калибра уклонились от этого. Мне чрезвычайно повезло, что
у «Wiley & Sons» работают столь дальновидные и терпеливые люди,
и еще более оттого, что именно им, в какой-то мере к собствен-
ному их несчастью, было поручено заниматься мной.
Должен поблагодарить моих друзей Дикси Джердона и
Гордона Николса, которые в известном смысле, и прямо или
косвенно подвигли меня к написанию книги и повлияли на ее
содержание. Не повстречай я Гордона, будучи еще клерком, то
наверняка не пошел бы этой дорогой.
За материалы, вошедшие в книгу, я благодарен сотрудни-
кам «First October Trading Company» Фреду Хоули, Дейву Стас-
ко, Грегу Кингу, Хенку Джилетгу и Крису Флинору. Они из-
менили мои воззрения на рынки и на жизнь. Должен также
упомянуть моих собеседников за обедом по пятницам Джорджа
Соммера, Девида Ланге и Гарри Рёгнера.
Не посмею не поблагодарить Ральфа Винса I — «Буббу» —
моего прадеда, который в 1906 г. шестилетним Рафаэлем да Винчи
прибыл в Америку и позже играл за Национальную Футбольную
Лигу против таких игроков, как Джим Торп. Я уважаю его
гораздо глубже, чем когда-либо смогу выразить это. Хотя мы
постоянно расходились во мнениях, в самые тяжелые моменты он
всегда оказывался рядом и приходил мне на выручку.
Моему отцу, Ларри Винсу, эта книга пришлась бы по
вкусу. Он заслуживает не меньше благодарности, чем все другие,
за то, что в юности пробудил во мне интерес к оптимальным
математическим решениям, рассказывая о транспортных потоках
и об управлении светофорами на Карнеги Авеню в Кливленде.
Я должен также поблагодарить и свою мать, Реджину,
вероятно, самого разумного человека, которого я знаю. Во многих
отношениях я не очень практичный человек. Называю ее наиболее
разумной из всех, ибо она куда практичнее меня. Когда мне по-
настоящему нужно чье-либо мнение, ее совет всегда оказывается
самым действенным. Хотел бы и я быть так же полезен для нее.
С большим опозданием благодарю здесь Ларри Вилльямса,
которому многим обязана и эта, и предыдущие мои книги. Всем,
что я сделал в данной области, я обязан ему и его редкостному,
по-детски любознательному уму. Благодаря Ларри я начал рабо-
7
тать в этом направлении, но ничего бы из этого не получилось,
если бы мне не посчастливилось сотрудничать с ним. Все полу-
ченные мной результаты в равной мере принадлежат и ему.
Я также весьма обязан Ричарду Уилки не только за те
прекрасные возможности, которые он создал для меня в «First
October Trading Company», но и за его решительную поддержку
в тяжелые времена. Я очень это ценю.
Последние двенадцать месяцев, или около того, были осо-
бенно трудными для меня лично. Поэтому под конец, но, разу-
меется, ничуть не меньше, я должен поблагодарить Вики ДеВитг,
не только за ее терпение ко мне во время написания книги, но
и за ее помощь в этом и во всех других делах в то действительно
трудное время. Ее замечательный характер оказал благотворное
влияние на меня лично, на мою жизнь и мышление, что, как
я надеюсь, отразилось на этой книге.
Я бесконечно благодарен всем вам.
Оглавление
Выражение благодарности .................................... 5
Предисловие.................................................. 13
Введение................................................... 17
Убирайся вон и не смей возвращаться назад.................. 17
Все беды - от незнания ...................................... 20
Структура, терминология и обозначения........................ 21
1
Новая методология............................................ 25
Преимущества новой методологии............................... 27
Общее представление о новой методологии...................... 32
Несколько одновременных игр.................................. 37
Сравнение со старыми подходами............................... 40
На пути к анализу нового типа................................ 43
Статистическая независимость................................. 45
История параметра f.......................................... 45
10
Оценочное среднее геометрическое (или как дисперсия
исходов влияет на геометрический рост).................... 54
Фундаментальное уравнение торговли........................ 59
Существует ли оптимальное /?.............................. 60
Ответ критикам............................................ 63
Введение в портфели с оптимальным f....................... 65
Заблуждения относительно текущих потерь
и диверсификации.......................................... 67
Следующий шаг.............................................. 69
Сценарное планирование .................................... 71
Сценарные спектры.......................................... 85
Дополнение первое.......................................... 88
Сокращение дефицита за счет увеличенной дисперсии
Валового Внутреннего Продукта.......................... 88
Дополнение второе.......................................... 90
Обманчивая суть наращивания оплаты менеджмента
и временного взвешивания............................... 90
2
Законы роста, полезность и конечные потоки................. 95
Рост человеческой популяции............................... 97
Минимизация ожидаемого среднего общего роста............... 101
Теория полезности ....................................... 112
Теорема ожидаемой полезности............................... ИЗ
Свойства функций полезности................................ 114
Иные взгляды на классическую теорию полезности............. 117
Как найти свою кривую полезности........................ 119
Полезность и новая методология............................. 124
3
Условные вероятности и корреляция.......................... 131
Количество реализаций (частота) и вероятность............ 134
Теория условной вероятности................................ 155
Совместные вероятности двух непрерывных распределений .... 164
Оценка совместных вероятностей ............................ 165
4
Новая модель............................................... 171
Математическая оптимизация................................. 172
Целевая функция ........................................... 174
Математическая оптимизация или отыскание корней............ 183
и
Методы оптимизации ....................................... 183
Естественный отбор........................................ 189
Генетический алгоритм..................................... 190
Важные замечания.......................................... 196
5
Управление капиталом для профессионалов................... 199
Реализация новой модели................................... 201
Активный и неактивный капитал............................. 201
Перераспределение......................................... 215
Страхование портфеля и оптимальное f...................... 220
Верхняя граница активного капитала и ограничение
по марже.................................................. 227
Торговля акциями.......................................... 231
Смещение f и построение устойчивого портфеля.............. 231
Настройка торговой программы с помощью
перераспределения......................................... 232
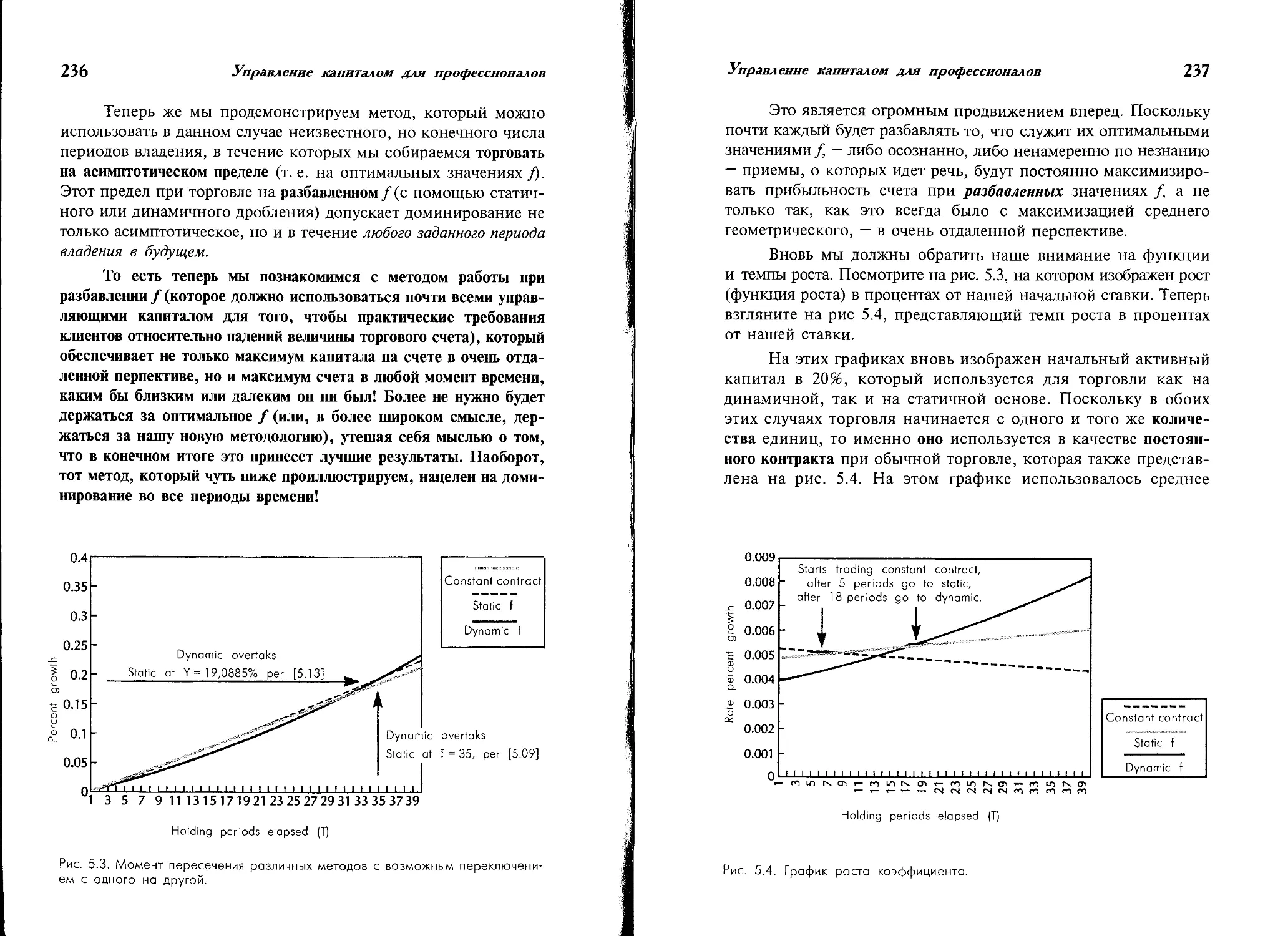
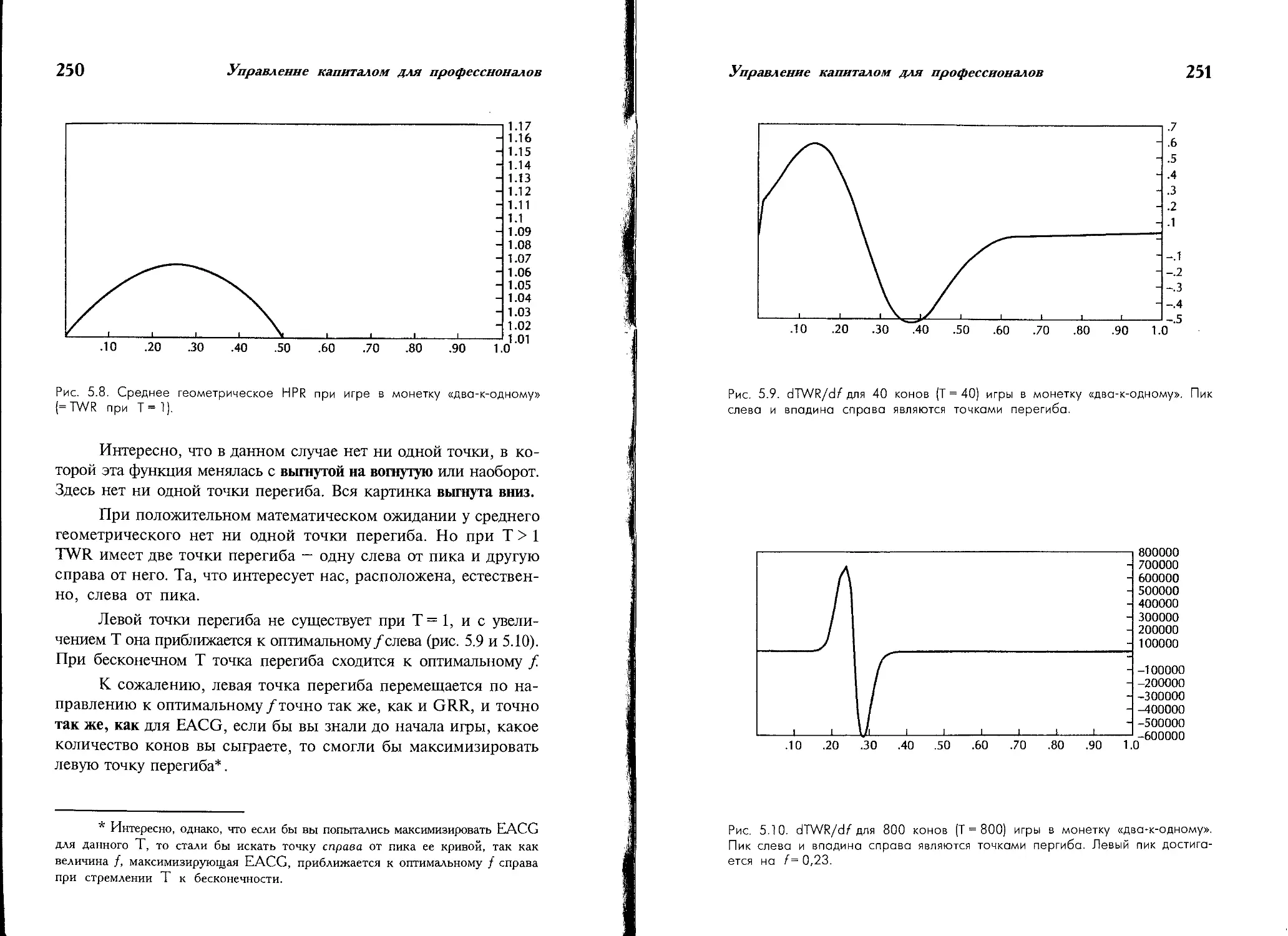
Градиентная торговля и непрерывное доминирование.......... 235
Важные точки слева от пика на (и + 1)-мерной
поверхности............................................... 244
Управление текущими потерями и новая методология.......... 253
Новая роль инвестиционного аналитика...................... 260
Список использованной литературы.......................... 263
Предисловие
Эта книга — третья из серии книг, посвященных понятию оп-
тимального f Для меня она, по сути, является, скорее, третьим
томом одной книги. С течением времени картина все более про-
ясняется, и теперь у меня есть твердое ощущение, что это —
наиболее полная книга о том, во что выливается идея оптималь-
ного f Некоторые могут меня не одобрить: «Вы написали об этом
уже две книги. Стоит ли так нещадно эксплуатировать эту тему?»
Я же считаю, что ничего более важного просто нет.
Данная книга увязывает воедино все, когда-либо сделанное
мной. Все, что я написал на эту тему прежде, лишь заложило
теоретический фундамент того, что я называю новой методоло-
гией инвестирования. Я полагаю, что она настолько значима, что
может применяться не только фьючерсными и опционными
трейдерами, но и вообще при любом инвестировании.
Вскоре после опубликования в 1990 г. книги «Формулы уп-
равления портфелем» появилось множество критических замеча-
ний по поводу того, что торговля на уровнях оптимального f
приводит к столь глубоким текущим потерям, которые не по
силам большинству людей, и, следовательно, ущербна по своему
замыслу.
14
В этом меня огорчило не только невежество моих критиков,
но, в не меньшей степени, и мое собственное неумение излагать
материал. «Я знаю об этих текущих потерях! — возражал я. — Я не
предлагал ни торговой системы, ни способа управления вашими
деньгами при торговле!» Складывалось впечатление, что люди,
прочитавшие мою книгу, полагали, будто бы я пытаюсь отстоять
некий способ, если угодно, систему, в рамках которой можно
управлять величиной своей позиции таким образом, который
я называю оптимальным, но который слишком агрессивен для
99,99% всех трейдеров.
Найти контраргументы мне удалось лишь с помощью ин-
тенсивных дополнительных исследований предмета, занявших у
меня около пяти лет. Ведь, по сути, в своих «Формулах управления
портфелем» я пытался объяснить, что вне зависимости от нашей
воли мы находимся где-то на кривой f и, учтя преимущества и
недостатки этого, можем осознанно принимать решение о своих
действиях при открытии позиции. Другими словами, я пытался
изложить методологию — так это было бы правильнее называть.
Методология — это не только точка зрения, или ракурс
видения окружающего в перспективе, но и многое другое. Это
способ количественного восприятия и осмысления, часто визу-
ального, следствий и результатов наших действий на основе
анализа информации об этих действиях с определенных позиций.
Методология — это способ оценки позитивных и негатив-
ных последствий наших действий, охватывающий торговлю каж-
дого из нас, независимо от того, осознаем мы это или нет. Новая
методология дает нам новый подход к построению инвестицион-
ных моделей с позиций принятых в ней критериев оценки ка-
чества.
Хотя основным предметом этой книги является новая иде-
ология построения портфеля, она также дает и модель, или
способ, претворения ее на практике. Старая идеология, бытующая
в разных формах в течение последних сорока лет или около того,
трактует риск и доход как противоборствующие сущности. Наш
подход опирается на иную диспозицию. Точнее, он сосредоточи-
вается на отыскании пика некоей поверхности в пространстве
финансовых рычагов (левереджей — leverages) размерности п + 1,
где п — количество составляющих портфеля. (Этими составляю-
15
щими могут быть не только рыночные системы, но и различные
сценарии, что важно, ибо делает книгу столь же полезной и для
трейдеров, торгующих без четкой математической системы.)
Портфель, соответствующий этому пику, оптимален по крите-
рию геометрического роста. В книге описывается новая методоло-
гическая модель (способ) оптимального построения портфеля —
я называю ее моделью в пространстве рычагов.
Во-вторых, все, что я написал ранее, относилось к асим-
птотическому доминированию. То есть, все методы, описанные
мною в прошлом, давали наибольший доход в очень отдаленной
перспективе. Данная книга важна тем, что показывает, как до-
стичь постоянного доминирования. Другими словами, книга по-
казывает, как управлять деньгами торгового счета так, чтобы
результаты обычно были бы наилучшими в любой данный мо-
мент времени, а не только в очень отдаленной перспективе. Это
— огромный скачок вперед, имея в виду тех, кто использует
наши подходы в повседневной практике. Теперь управляющий
капиталом может методически достигать наибольшей вероятности
того, что в любой данный момент доля собственных средств на
торговом счете будет максимальной!
Я считаю, что это своевременная книга. Старая парадигма
построения портфеля рассматривала кредитование, или рычаг,
лишь в качестве второстепенного фактора. У нас он выступает на
первый план. В современном мире, где все более превалируют
производные/кредитные торговые инструменты, уже нельзя по-
прежнему недооценивать фактор рычага.
Кроме того, из новой модели, представленной в книге,
вытекает несколько очень интересных следствий относительно
самой сути анализа рынка. Так, вопреки принятому ранее, из нее
следует, что ключевым моментом анализа является вовсе не
выбор актива и тайминг рынка. Напротив, задачей анализа дол-
жна быть оценка вероятности будущих возможностей. В рамках
новой модели анализ рынка может принести более значительные
выгоды, нежели при прежнем упрощенном подходе к нему как
к выбору актива и таймингу. Новая модель, опираясь на веро-
ятности, получаемые из анализа рынка, впервые придает мате-
матическую строгость выбору актива и таймингу.
Введение
Убирайся вон и не смей
возвращаться назад
В конечном счете всякая книга автобиографична. Боюсь, что и эта
книга не составляет исключения. Будучи в девятом классе, я по-
лучил уведомление из своей средней школы, по сути, гласящее
«убирайся вон и не смей возвращаться назад». Это было поистине
сумасшедшее местечко — сугубо мужская школа, которой заправ-
ляли иезуитские священники, по горло сытые такими умниками,
как я.
На этом мое систематическое образование закончилось. Не
подумайте, что я против систематического образования. Я, воз-
можно, преуспел бы куда больше, будь оно у меня побогаче, но
иезуитские священники не одобряли меня и не разделяли моих
устремлений.
Как оказалось, мне повезло. Все, что я знаю из математи-
ки, изучено мной самостоятельно. Я обнаружил, что между зна-
2 - 9727
18
ниями, полученными в рамках официальной системы образова-
ния и теми, что добыты ввиду крайней необходимости, имеется
фундаментальное различие. Неудача в первом случае исчерпыва-
ется огорчением от плохой отметки. Во втором случае — это конец
света, если вы понимаете, о чем идет речь. Такие знания при-
стают намертво.
Вскоре после этого я получил место залогового клерка
в отделе брокерской фирмы, занимающемся ведением счетов
и оформлением операций. Эту работу я поначалу презирал. Я дол-
жен был отслеживать счета, которые были «одобрены для тор-
говли» короткими опционами. Другими словами, в мои обязан-
ности входило отслеживать те счета, которые использовались во
всяческих опционных стратегиях, а не в сделках аутрайт. По-
скольку отслеживание маржинальных требований тогда еще не
было автоматизировано, нам приходилось рассчитывать все со-
ставляющие проводимых опционных сделок по счетам, чтобы
обеспечивать минимальные маржинальные требования.
Эта работа заставила меня задуматься. Со временем я все
более увлекался как атмосферой рынка, так и используемой
математикой. В итоге я полюбил эту работу, полюбил повсе-
дневную жизнь рынка. Я проникся мыслью о том, что рынок
— это самая беспристрастная игровая площадка на свете: там
ничто не важно, ни кто вы такой, ни каков ваш образователь-
ный уровень, цвет кожи, пол, возраст — ничего! Он олицет-
воряет возможности. Это — огромное рыкающее чудище из иного
мира, его ничем не купишь, он не знает ничего и никого. Он
ничуть не помедлит ни обанкротить вас, ни наградить за при-
нятый риск.
Я обнаружил, что с нетерпением жду начала каждого ра-
бочего дня.
Вскоре должны были появиться микрокомпьютеры. Финан-
совые фьючерсы еще только входили в практику, и вот-вот
должны были появиться опционы на фьючерсы и множество
других производных инструментов. Естественно, у меня возникла
тяга и к компьютерам, и к новым рынкам, рождение которых
так счастливо для меня совпало по времени.
В 1986 г. мне крупно повезло ответить на телефонный
звонок от человека по имени Ларри Уильямс, прозвучавший
19
в 4 часа утра. Я знал, что он дедушка почти всех механических
торговых систем. Это были восьмидесятые годы, когда жизнь
действительно кипела повсюду. Ларри Уильямс — одна из круп-
нейших фигур в сфере управления фьючерсными контракта-
ми — интересовал меня больше всех остальных. Он оставил на
моем автоответчике едва слышимое сообщение о каких-то сооб-
ражениях по части торговых систем, которые ему нужно было
запрограммировать.
Программирование для него вскоре стало моим основным
занятием.
О Ларри Уильямсе нужно сказать, что имей он хоть сотню
постоянных программистов, ему бы этого не хватило. Не считая
северного полюса, офис Ларри был одним из самых интересных
мест в мире. В его голове как будто был цирк с тридцатью
аренами, где он одновременно вел всевозможные представле-
ния — от обычных до эксцентрических, от торговли на рынках
до поисков места пересечения Моисеем Красного моря. Ларри
постоянно звонили люди со всего мира, которые работали над
этими его проектами. Брокеры, наемники, ученые и сумасброды.
Это было настолько хаотично, что едва не доводило меня до
нервного срыва. Только в области рынка Ларри постоянно вел
больше проектов, чем исследовательские подразделения большин-
ства брокерских фирм.
На моей памяти Ларри выиграл (и проиграл) на рынках
огромные для меня деньги. Он был одним из немногих, кто
действительно мог торговать полностью оптимальными количе-
ствами и преодолевать сопутствующие текущие потери.
Одним из направлений исследований Ларри было управле-
ние капиталом. В них я и погрузился с головой. Это позволило
мне соединить воедино то, что я узнавал о рынках и о торговле
Ларри в контексте его системных исследований и математических
премудростей. Получившаяся восхитительная смесь притягивала
меня как ничто ранее.
Меня так захватила идея управления капиталом и его
оптимального инвестирования, что я уже не мог больше зани-
маться только программированием торговых систем. Наступило
время, чтобы целиком посвятить всю свою энергию этой области.
Это было то, что считал важным именно я.
2*
20
Все беды - от незнания
Один очень дорогой для меня человек недавно умер от
неизлечимой болезни. Я считаю несправедливым и противоесте-
ственным, что в огромной вселенной, где материю нельзя ни
создать, ни уничтожить, самое драгоценное на свете, человечес-
кая жизнь, может остановиться. В этом есть логическое противо-
речие. Для меня же лично это было большой утратой.
Не могу отделаться от мысли, что дело было не в том, что
болезнь дорогого мне человека была неизлечимой. Беда была
в том, что я не умел излечивать ее, как не знал и никого, кто
бы умел это.
Выходит так, что причиной большинства, если не всех,
моих бед обычно является незнание. На самом деле проблемы
возникают не из-за слабого здоровья, недостатка капитала, бед-
ности, предубеждений, наших собственных физических ограниче-
ний или чего-то еще.
Не исключено, что невежество, или недостаток знаний,
вредит и вам. Вам невдомек, что благодаря вращению земли
вокруг солнца вы в данный момент рассекаете пространство со
скоростью около тридцати километров в секунду! Вы не скажете,
в какую сторону вращается земля вокруг солнца, если смотреть
на нее из точки над северным полюсом. Вы не знаете, непрерыв-
но или дискретно само время, то есть развивается ли все сущее,
как череда кинокадров, только неразличимо малых, или течет
непрерывно?
Вы не станете читать эту книгу сверху вниз, хотя это не
менее логично, чем читать ее, что называется, слева направо
и сверху вниз. Вы и не подумаете поступить так для того, чтобы
просто увидеть предмет в новом свете, хотя это всего лишь дело
привычки.
Не все, что кем-то утверждается, является истиной. Если
кто-то придерживается определенных правил поведения, еще на
значит, что и нам нужно поступать так же, или что мы преус-
пеем, приняв эти правила. Принято считать, что, занимаясь
таймингом входа в рынок и выхода из него, можно стать хоро-
шим трейдером. Поэтому и вы так думаете — вас к этому
21
приучили. Вы полагаете, что инвестирование капитала представ-
ляет собой задачу простой максимизации дохода и минимизации
риска, просто потому, что так принято считать.
Говорю об этом для того, чтобы вы не воспринимали все
написанное в этой книге на веру. Засядьте за компьютер или
проработайте математические выкладки на бумаге и лично убе-
дитесь в правоте ее концепций. Поступать иначе — значит уве-
ковечивать свое невежество.
Эта книга посвящена тому, как преодолеть невежество
в вопросах принятия решений при неизвестных исходах, а точ-
нее, тому, как выстраивать оптимальный портфель для торговли
на рынках. За исключением совсем немногих, большинство трей-
деров не осведомлено о том, что для них это имеет решающее
значение. Столь же радикальное, как разница между жизнью
и смертью.
Что же касается тайминга рынка, то, в итоге, он здесь
почти совсем не причем.
Структура, терминология
и обозначения
Как и в двух предыдущих книгах, мне хотелось обратиться
к возможно более широкой аудитории. Именно поэтому я решил
представить материал в книжной форме. Книги обходятся потре-
бителям информации дешевле всего, они значительно доступнее
и, как правило, привлекательнее других носителей.
Есть пара терминов, известных читателям первых двух моих
книг, которые стоит пояснить для тех, кто еще не знаком с этим
материалом. Во-первых, это понятие рыночной системы. Попросту
говоря, оно означает заданный метод торговли на заданном рынке.
Например, если у меня есть два метода торговли А и В, которые
я собираюсь использовать для торговли на рынках J и К, то это
значит, что у меня есть четыре рыночных системы: метод А на
22
рынке J, метод А на рынке К, метод В на рынке J и метод В
на рынке К.
Во-вторых, это понятие единицы. Оно означает минималь-
ное количество актива, которое вы готовы использовать при
торговле на данном рынке. Выбор величины единицы — за вами,
пользователем. Например, вы можете решить, что единицей будет
одна акция, или принять в качестве таковой полный лот в сто
акций. Вы можете выбрать за единицу один фьючерсный кон-
тракт, или принять за нее один мини-контракт. В целом, чем
меньше удастся выбрать единицу, тем успешнее вы сможете
применять нашу новую методологию.
Книга изобилует математикой — в большей степени, чем
мне бы того хотелось, ибо я ориентируюсь на непрофессионала.
Однако она необходима для адекватного изложения материала.
Чтобы скомпенсировать это, я постарался сделать текстовую часть
максимально легкой, дружелюбной и привлекательной. Как будто
бы мы с вами беседуем о чем-то таком, что не стоило бы
принимать всерьез, не будь это в контексте книги. Надеюсь, что
это не принижает серьезности материала по сути. Лично я считаю,
что раз уж жизнь так переполнена похоронами и поминками, то
мы сами должны находить причины для веселья, с неба они не
свалятся.
Нет такой математики, которую вы не смогли бы освоить.
Скорее всего, вы ушли дальше меня в систематическом образо-
вании. Не бойтесь формул — если вы, подобно мне, захотите
в них разобраться, то сможете, неважно, насколько сложными
они могут казаться.
Раньше кое-кто критиковал меня за выбор некоторых
математических обозначений. Я всегда старался избегать того, что
считаю двусмысленными математическими символами. Примером
служит использование некоторых символов не только в своей
функции, но и для группировки переменных. Обычно в таком
качестве выступает знак радикала (предполагающий, что симво-
лы, находящиеся под ним, заключены в скобки) и горизонталь-
ная черта в качестве знака деления (где символы под чертой, или
делитель, считаются заключенными в скобки). Ладно, они побе-
дили. В этом тексте я допускаю использование таких неоднознач-
ных символов, но не мирюсь с ними. Если это хоть как-то
23
облегчает жизнь читателя, я иду на это. Более того, я воздержи-
ваюсь от использования знака (Л) для обозначения возведения в
степень и возвращаюсь к традиционному обозначению. Однако я
настаиваю на использовании звездочки (*) для обозначения
умножения вместо множества других традиционно применяемых
для этого символов, что привело бы к неразберихе. Моя цель —
избежать путаницы. Иначе, почему бы всюду в тексте не исполь-
зовать римские цифры!
Предполагается, что вы знакомы хотя бы с основными
идеями из двух первых книг или из статей на данную тему
других авторов. Кроме того, я надеюсь, что вы хорошо владеете
математикой на уровне колледжа. Учитывая, что это может быть
не так, настоятельно рекомендую вам не огорчаться по поводу
математики — пусть ей займутся компьютеры — и вместо этого
сосредоточиться на освоении концепций.
Я постарался включить в книгу больше примеров. Мне
хотелось бы, чтобы книга была ясной, четкой и свободной от
неуместных отклонений от сути дела. Как смог, избегал после-
днего, хотя это свойственно мне по натуре.
Будем надеяться, что эта книга станет полезным напутстви-
ем для тех, кто займется собственными исследованиями в этой
и других областях рыночной торговли.
1
Новая методология
Я не намеревался писать всего этого. В своей прошлой книге
«Математика управления капиталом»* я заявил, что она будет
последней, которую я когда-либо напишу.
Но случаются и не такие курьезы.
Мне стали бы звонить и писать читатели. Те, что просто
пожирают идеи. Такие люди есть повсюду и происходят из самой
разной среды - это доктора, недоучки, инженеры, заключенные,
судьи, трейдеры, дезертиры, жулики, мошенники и фантазеры.
Они — знатоки не только в своем деле, но как минимум и еще
в одном. Обычно в этой дополнительной области они являются
абсолютными самоучками, как зачастую и в сфере своей основ-
ной деятельности. Эти люди искренне верят, что нет ничего
такого, чего они не смогли бы разгадать или понять. Они так же
нуждаются в обдумывании идей и познании нового, как боль-
* Vince, Ralph .The Matematics of Money Management, New York: John
Wiley & Sons, 1992.
26
Новая методология
шинство людей — в кислороде. Меня влечет к этим людям. Из
переписки с ними я почерпнул массу нового как для своей
прежней работы, так и для этой книги. Хотя ничего особенно
сложного не было, кое-что из их вопросов просто сводило меня
с ума. Я обыскал буквально все закоулки в поиске ответов или
подходов к некоторым внешне простым задачам. Я давно бы все
бросил и больше не возвращался ко всему этому, если бы не
постоянные подстрекательства таких вот людей. Они подогревали
мой интерес.
С 1950-х годов, когда была выдвинута концепция формаль-
но-логического построения портфеля, начались поиски оптималь-
ных портфелей как функции двух конкурирующих сущностей:
риска и дохода. Цель этих усилий состояла в том, чтобы макси-
мизировать доход и минимизировать риск. Такова старая парадиг-
ма, и именно так нас приучили думать.
«Овладение системой понятий и наиболее тонкими методами
исследования, которые она предоставляет, является признаком
зрелости в развитии любой научной отрасли», — писал Кун*.
Именно так и происходило. Построение портфеля после
Второй мировой войны обрело математическую строгость, кото-
рой ему не хватало ранее. До этого, как бывало во многих других
областях, проходил этап накопления фактов, когда одинаково
уместной кажется любая частичка информации. Впрочем, в рам-
ках концепции, предложенной так называемой Современной Те-
орией Портфеля (иначе ее называют: E-V-теорией, или средне-
дисперсионной моделью), были развиты уже более тонкие методы
исследования.
Основные затруднения в этой ранней системе взглядов
возникали из-за того, что в ней так и не удалось дать адекват-
ного определения негативной сущности, или риска. Сначала ут-
верждалось, что риск — это дисперсия дохода. Позднее под
воздействием аргументов о том, что дисперсия дохода может быть
бесконечной или неопределенной и что он, в отличие от риска
катастрофической потери, не является настоящим риском, опре-
деления риска стали еще более туманными.
* Thomas S. Kuhn, The Structure of Scienti/ic Revolution, The University
of Chicago Press, 1962.
Новая методология 27
В поисках истины часто нужно взглянуть на вещи как-то
иначе, по-новому. Новая методология нацелена на поиск опти-
мальных портфелей, но не в контексте противостояния риска
и дохода.
Преимущества новой
методологии
В течение почти сорока лет построение портфеля изобража-
лось на двумерной плоскости, где доход измерялся по вертикаль-
ной оси, риск же, а фактически некий его суррогат (ибо кто
знает, что в действительности есть риск), измерялся по горизон-
тальной оси. Основная идея состояла в том, чтобы добиться
^возможно большего дохода при данном уровне риска или наи-
меньшего возможного риска при заданном уровне дохода, что
укладывалось в возможности такого двумерного представления
(см. рис. 1.1). Этот подход долгое время считался столь же безуп-
речным, как жена Цезаря.
Рис. 1.1. Концептуальная картина старой (слева) и новой {справа) методоло-
гии построения портфеля.
28
Новая методология
Новая методология, которая будет изложена далее, — это
совершенно новый взгляд на построение портфеля, отличный от
двумерного представления в контексте противоборства между
доходом и риском. Имеется несколько причин, по которым новый
подход предпочтительнее старого.
Новый подход лучше, так как исходные данные теперь уже
не располагаются вдоль линий ожидаемых доходов и (достаточно
расплывчатой) дисперсии ожидаемых доходов или какой-то другой
эрзац-меры риска. Аргументами новой модели являются различ-
ные сценарии возможных исходов инвестирования (более точная
аппроксимация реального распределения дохода). Теперь, в отли-
чие от оценок таких величин, как ожидаемые доходы и их
дисперсии, исходная информация гораздо ближе к тому, чем
может мысленно оперировать менеджер по инвестициям, напри-
мер, 5%-ная вероятность выигрыша или потери в х%, и т. д.
Теперь за аргументы новой модели менеджер по инвестициям
может принимать даже неестественно маловероятные сценарии.
То, что менеджер по инвестициям использует в качестве
аргументов новой модели, представляет собой спектры сценариев
для каждого рынка или рыночной системы (заданный метод
торговли на данном рынке). Новая модель определяет оптимальное
инвестирование для каждого сценарного спектра при торговле по
многим сценарным спектрам одновременно.
Более того, и это, возможно, гораздо важнее, новая модель
пригодна для любого распределения дохода! Ранние модели пор-
тфелей чаще всего предполагали нормальное распределение при
оценке различных исходов, к которым могут привести инвес-
тиции. При этом хвосты распределения — самые благоприятные
и неблагоприятные исходы — оказывались много тоньше, чем
должны были быть в случае реального, отличающегося от нор-
мального, распределения. Следовательно, самые хорошие и са-
мые плохие возможные исходы инвестиций этими ранними
моделями обычно недоучитывались. В новой модели различные
сценарии входят в хвосты распределения исходов, и вы можете
назначить им любые вероятности по своему усмотрению. Даже
непостижимо устойчивое распределение доходов Парето можно
описать с помощью различных сценариев, на основании чего
построить оптимальный портфель. Любое распределение можно
смоделировать в виде сценарного спектра; кривая плотности
Новая методология
29
вероятности сценарных спектров может принимать любую жела-
емую форму, и сделать это совсем несложно. Вместо вопроса
«Какова вероятность оказаться на расстоянии х от моды распре-
деления?», нужно задавать другой: «Какова вероятность реали-
зации наших сценариев?»
Таким образом, новый подход можно применить к любому
распределению дохода, а не только к нормальному. Поэтому
можно использовать реальные распределения с тяжелыми хвоста-
ми, ведь сценарный спектр — это просто другой способ задания
распределения.
Но важнее всего то, что новая методология, в отличие от
ее предшественников, в большей мере нацелена не на структуру
портфеля, а на его динамику. Это относится к использованию
рычага и к тому, как вы меняете размер позиции со временем
по мере изменения собственных средств на счете.
Примечательно, что все это — различные проявления од-
ного и того же. А именно рычаг и то, как вы со временем
увеличиваете размер позиции, по сути, представляют собой одно
и то же.
Обычно кредитование трактуется следующим образом:
«Сколько нужно занять для того, чтобы располагать определен-
ным количеством инвестиционного актива?» Например, если я хочу
иметь 100 акций корпорации АВС, стоимостью по 50 долл., то
это обойдется мне в 5000 долл. Так, если на моем счете имеется
менее 5000 долл., то сколько мне нужно занять? Таково тра-
диционное понимание финансового рычага.
Но понятие рычага применимо и к заимствованию своих
собственных денег. Предположим, что на моем счете имеется
1 миллион долл. Я покупаю 100 долей акции АВС. Предположим
далее, что эта акция поднимается и мои 100 акций приносят
прибыль. Теперь я хочу иметь 200 акций, хотя прибыль на мои
100 акций еще не достигла 5000 долл. (т. е. акция АВС еще не
выросла до 100 долл.). Однако я все равно покупаю еще 100 ак-
ций. План моих будущих покупок (продаж) по АВС (или по
любой другой акции, пока я владею акциями АВС) основыва-
ется на кредитовании — займу ли я чужие деньги для выполне-
ния этих операций или использую собственные. Именно этот
план, это продвижение вперед является тем, что называется
30
Новая методология
рычагом в данном смысле. Если вам понятны эти соображения, то
вы вполне разберетесь и с новой методологией инвестирования.
Итак, мы видим, что финансовый рычаг — это термин,
обозначающий либо уровень, до которого мы заимствуем средства
для того, чтобы занять позиции по некоторому активу, или план,
согласно которому мы открываем последующие позиции при
инвестировании (занимаем мы для этого или нет).
Из сказанного ясно, что поскольку новая методология
сфокусирована на финансовом рычаге, она ориентирована на спе-
кулятивные операции в том же смысле, в каком рычаг означает
уровень заимствования для открытия позиции по какому-либо
(спекулятивному) активу. Впрочем, новый подход, акцентируя
использование рычага, пригоден для всех активов, включая са-
мые консервативные, в том смысле, в каком рычаг означает
продвижение вперед, или план, согласно которому мы открываем
(закрываем) последующие позиции по активу. В конечном счете
финансовый рычаг в обоих смыслах ничуть не менее важен, чем
тайминг сделок. То есть продвижение вперед в накоплении актива
или освобождении от него даже для самого консервативного
облигационного фонда столь же важно, как тайминг рынка
облигаций или процесс их выбора.
Следовательно, понятие оптимального/во всей своей пол-
ноте касается не только фьючерсных и опционных трейдеров, но
и любых инвестиционных схем, не ограничиваясь распределением
средств между типами инвестиционных инструментов.
В результате произошедшего в последнее время резкого
увеличения торговли производными инструментами биржевой мир
сегодня очень сильно изменился по сравнению с тем, что было
всего несколько десятилетий назад. Как правило, основной чертой
многих производных инструментов является привнесение рычага,
который негативно влияет на торговый счет. Старая методоло-
гия — двумерная E-V-модель — плохо приспособлена для разре-
шения связанных с этим проблем. Современная среда требует
новой методологии инвестирования, сфокусированной на резуль-
татах применения рычага. Именно на это и ориентирован изла-
гаемый далее подход.
Такое акцентирование рычага лучше всего другого говорит
о том, почему новая методология лучше своих предшественников.
Новая методология
31
Подобно им, новая методология указывает оптимальное распреде-
ление средств между активами. Но, кроме того, она дает и многое
другое. Она динамична, ибо описывает непрерывную череду
проигрышей и выигрышей от вложения и изъятия средств соглас-
но принятому плану, реализующемуся во времени. Она задает
рамки, или карту, указывающую, каких убытков и прибылей мы
можем ожидать, действуя по тому или другому плану. Опреде-
ленные точки на этой карте могут иметь не одинаковую привле-
кательность для разных людей, нужды и интересы которых раз-
личаются. Оптимальное для одного может быть не оптимальным
для другого. Тем не менее, эта карта позволяет увидеть, что мы
получаем и теряем, действуя по определенному плану — такого
старые методологии не давали. Данное свойство, а именно карта
пространства рычагов (не забудьте, что рычаг понимается здесь
двояко), отличает новую методологию от прежних, что, само по
себе, определяет ее предпочтительность.
Наконец, новая методология лучше старых еще и тем, что
применяющий ее может легко представить себе последствия своих
действий. Вместо того, чтобы как раньше гадать, что будет, если
немного увеличить V при данном Е, теперь вы можете точно
видеть ту высоту, на которую вас вынесет движение изображения,
то есть на какой именно коэффициент прирастет ваш начальный
торговый счет (относительно вершины изображения) при опера-
циях с различным уровнем кредитования (не забывайте, что в
книге это понимается двояко), или, что то же самое, вы будете
точно знать, каких минимальных потерь следует ожидать при
операциях с различными уровнями кредитования. Следуя новой
методологии, вы сразу же поймете, насколько тесно связана
функция инвестирования с результатами вашей торговли и ва-
шим болевым порогом.
Подытоживая, повторим, что новая методология лучше ста-
рой, основанной на двумерном противопоставлении риска и дохода,
в первую очередь потому, что она фокусируется на динамике
кредитования. Она предпочтительнее еще и потому, что ее аргу-
менты — сценарии — первичны в информационном плане и
позволяют работать с любым распределением дохода. И, наконец,
последователи нового подхода смогут отчетливее осознавать по-
зитивные и негативные последствия своих действий.
32
Новая методология
Общее представление о новой
методологии
Предположим, что я предложил сыграть в монетку так, что
если выпадет орел, то вы платите мне один доллар, иначе я плачу
вам два доллара.
Получив такое предложение, вы сможете определить (ариф-
метическое) математическое ожидание результата игры (в этой
книге эта величина также часто называется просто ожидаемым
значением), взяв сумму произведений каждого исхода на его
вероятность:
(Арифметическое) Математическое ожидание = Z />(«,) * «,• [1-01],
;=1
где:
п = количество возможных исходов;
а! = i-й исход;
р(а.) = вероятность /-го исхода.
Поскольку в нашей игре «два-к-одному» п = 2, получаем:
(Арифметическое) Математическое ожидание = 0,5 * 2 + 0,5 * (—1) = 0,5.
Таким образом, вы можете рассчитывать в среднем за кон
выигрывать по 50 центов (но только в том случае, если будете
ставить по 1 доллару на каждый кон игры без пропусков).
В данном случае, то есть при таких условиях игры, вы,
вероятно, приняли бы мое предложение. Но оно бы вас насто-
рожило, ведь когда что-то выглядит слишком хорошо, то это
обычно оборачивается неправдой. Именно так и получается в этой
равновероятной игре с выплатой два-к-одному в вашу пользу,
а равно в любой такой же игре, включая использование выиг-
рышной торговой системы.
Большинство людей сочтет такой расклад благоприятным,
ибо он дает преимущество. Однако это лишь половина правды.
Новая методология
33
Независимо ни от величины преимущества, ни от размера вашего
начального капитала, вы все равно можете проиграться вчистую,
если будете ставить на кон ненадлежащую сумму.
Допустим, трое людей отправляются в казино, где предла-
гается описанный вариант орлянки. Поскольку это вымышленный
пример, мы можем предложить игру с положительным матема-
тическим ожиданием. Реально же казино могут предложить игру
с нулевым математическим ожиданием. Так как количество денег
у каждого игрока конечно, это создает низкую поглощающую
границу, которая рано или поздно будет достигнута, и казино все
равно окажется в выигрыше.
Итак, трое наших гипотетических игроков, Ларри, Керли
и Мо, отправляются в казино. У каждого из них свой характер
и различное отношение к риску. Они независимо друг от друга
решают1 на каждом коне рисковать некоторой постоянной долей
своих денег. Но доля эта у каждого своя: Мо решает ставить на
каждый кон 10% (0,10) своих денег, Ларри останавливается на
25% (0,25), а Керли выбирает 40% (0,40).
График, приведенный на рис. 1.2, иллюстрирует положение
в этой игре после сорока конов. На нем показано, каким мог
быть выигрыш, измеряемый коэффициентом увеличения исход-
ного капитала (откладывается по вертикальной оси), в зависимо-
сти от его доли, которая ставится на каждый кон (откладывается
по горизонтальной оси). Заметьте, что если, подобно Ларри, вы
ставите на каждый кон по 25% вашего капитала, то увеличите
свой начальный капитал в 10,55 раза. Это — оптимальная доля
(оптимальное f) для ставки в данной конкретной игре. Заметьте
далее, что если вы отступите от оптимума только на 15%, то
есть, ставя на каждый кон по 10% или 40%, как сделали Мо
и Керли, то увеличите свой исходный капитал только в 4,66 раза.
Отступив всего лишь на 15%, вы не получите и половины того,
что могла бы дать эта игра. Очевидно, чрезмерно высокая ставка
не оправдывает себя.
В том же казино наши игроки встретили Шемпа, который
ставил 51% (0,51) своего капитала на каждый кон без пропусков.
Он ошибочно полагал, что простая агрессивность в игре с пре-
имуществом на его стороне позволит ему быстрее увеличить свой
капитал.
3 - 9727
34
Новая методология
Заметьте, что на графике для ставок величиной 50% и бо-
лее итоговый коэффициент прибыли меньше единицы. Так, если
вы ставите 50% или более вашего капитала, то разоритесь с ве-
роятностью, приближающейся к достоверной по мере продолже-
ния этой весьма благоприятной игры!
Рис. 1.2. Игра в манетку «два-к-одному»; 40 конов. Итоговый коэффициент
увеличения начального капитала при различной доле счета, которая ставится
на каждый кон.
Любая игра, всякая прибыльная торговая система имеет
именно такую кривую, как изображенная на рис. 1.2. Точки, где
эти кривые достигают пиков, как и те, где они опускаются ниже
единицы, меняются от одной системы к другой. Но у всех систем
кривые имеют только по одному пику. Для того чтобы действи-
тельно реализовать это преимущество, нужно на каждый кон
ставить надлежащую сумму. Тот же принцип действует и в тор-
говле, вне зависимости от того, осознаем мы это, или нет.
Долю капитала, которая ставится на кон, мы обозначаем
просто буквой f. Каждый трейдер имеет свое место в спектре
значений f определяемое как:
(количество контрактов
максимальная возможная
потеря на один контракт)
[1-02]
величина счета
Новая методология 35
Эту величину можно рассчитать, поскольку известны все
три входных переменных:
1) количество контрактов, которым трейдер торгует в насто-
ящее время;
2) максимальная возможная потеря на один контракт;
3) величина счета.
Таким образом, в каждый момент времени всякому трей-
деру с любой торговой системой можно сопоставить некоторое
значение / определяющее его положение на рельефе (двумерном,
так как разыгрывается всего одна игра).
Признает это трейдер или нет, это никак не влияет на
то, что есть некое значение / сопоставленное ему и его по-
зиции в данной рыночной системе и в данное время. Даже если
трейдер постоянно торгует одним контрактом, скажем по со-
евым бобам, то у него всегда есть некое значение f Предпо-
ложим, что его система прибыльна и его торговый счет растет.
Тогда это значение f с ростом счета будет смещаться влево (т. е.
уменьшаться), если только он не увеличит количество кон-
трактов, которыми торгует. Каждый трейдер, как бы он ни
действовал, всегда имеет отдельное значение f для каждой
отдельной своей позиции на каждом отдельном рынке, осоз-
нает он это или нет.
Почему это так важно? Потому что каждой прибыльной
системе соответствует некоторая кривая от / имеющая един-
ственную вершину. Расположение величины / сопоставленной
трейдеру, относительно этой вершины диктует, какие его ожи-
дают прибыли, текущие потери и прочее. Например, если трей-
дер находится слева от вершины, то есть его /меньше оптимума
(другими словами, количество контрактов у него меньше опти-
мального), как было у Мо, то он сократит потери арифмети-
чески, в то время как его прибыль сократится геометрически. Но
если он сместится вправо от вершины, то есть в направлении
значений / больших оптимального (другими словами, количе-
ство контрактов у трейдера будет больше оптимального), как
было с Керли, то его прибыль по-прежнему сократится геомет-
рически, как если бы он торговал слишком малым числом
3*
36
Новая методология
контрактов, а потери увеличатся арифметически. Обратите вни-
мание, что и Керли и Мо после сорока конов игры увеличили
свой капитал в 4,66 раза, но минимальный ожидаемый проиг-
рыш у Керли был в четыре раза больше, чем у Мо! Очевидно,
что лучше съехать влево от вершины и иметь позицию меньше
оптимальной, чем оказаться справа от нее с позицией, которая
больше оптимальной.
Где-то правее вершины, в точке, координаты которой за-
висят от системы, кривая опускается ниже отметки 1,0. Это
значит, что, торгуя на этом уровне, подобно Шемпу, трейдер со
временем наверняка разорится. Такая точка есть у каждой систе-
мы, какой бы хорошей она ни казалась.
Все сказанное не означает, что я заклинаю вас непременно
попасть на вершину кривой от f. Скорее, я имею в виду, что,
оказавшись там, вы сможете получить по максимуму. Выбор
остается за вами.
Отсюда, как вы, должно быть, уже поняли, начинает вы-
страиваться методология.
Двинемся дальше, заметив, что положение на кривой от
f не менее значимо, чем то, насколько хороши используемая
система, или торговый метод, наши трейдерские качества и тай-
минг рынка. Слабая, приносящая минимальную прибыль сис-
тема может показать прекрасные результаты, если она действу-
ет на вершине кривой от f И, наоборот, прекрасная система
может быть неэффективной при неверном f Действуя в ненад-
лежащей точке кривой /, она, фактически, будет транжирить
деньги трейдера и в конце концов разорит его. Можно лишь
удивляться тому количеству усилий и времени, которые зат-
рачиваются трейдерами на изучение рынков и выбор позиции,
когда это не важнее, чем выбор размера позиции. Далее, если
от трейдеров, по большому счету, не зависит, будет ли сле-
дующая сделка прибыльной или убыточной, то они полностью
ответственны за размер позиции в этой сделке, что не менее
значимо.
По логике, уклоняться от вершины кривой нет никакого
резона. Вспомним Мо, который оказался слева от вершины. Оче-
видно, ему нужна была более пологая кривая роста капитала, чем
у других игроков, ради чего он готов был пожертвовать геомет-
Новая методология
37
рическим ростом прибыли. Если вы, как Мо, согласны на по-
логий рост капитала, то лучше купите 90-дневные государствен-
ные облигации, вместо того, чтобы торговать разжиженным спе-
кулятивным счетом (много левее вершины кривой от f).
Несколько одновременных игр
Теперь предположим, что вы собираетесь вести две точно
такие же игры одновременно. В каждой из них монета будет
использоваться независимо и так же, как в рассмотренной ранее
игре. Сколько теперь нужно ставить на кон? Ответ зависит от
того, каким образом связаны между собой эти игры. Если игры
некореллированы друг с другом, то оптимальной ставкой будет
23% в каждой из них (рис. 1.3). Но если имеется абсолютная
положительная корелляция, то на кон в каждой игре следует
ставить по 12,5%. Ставя в каждой игре на кон 25% или более,
вы разоритесь с вероятностью, приближающейся к единице по
мере продолжения игры.
Начиная использовать в торговле более одной рыночной
системы, вы более не остаетесь на кривой с одной вершиной.
Теперь вы располагаетесь на некоторой поверхности размерности
п + 1 (где п — число используемых рыночных торговых систем),
также имеющей единственную вершину! В нашем примере с
метанием одной монеты вершина кривой соответствовала 25%.
Тогда у нас была одна игра (л = 1) и, следовательно, двумерный
(т. е. п + 1) рельеф (плоская кривая) с единственной вершиной.
Когда мы ведем две таких игры одновременно, у нас получается
трехмерный (т. е. п + 1) рельеф (поверхность) в пространстве
рычагов, имеющий единственную вершину. Если коэффициент
корелляции между играми равен нулю, то пик будет соответство-
вать 23% как у первой, так и у второй игры. Заметьте, что здесь
по-прежнему всего одна вершина, хотя размерность рельефа
увеличилась!
38
Новая методология
mean HPR
Рис. 1.3. Две игры
в монетку «два-к-одному».
Если мы одновременно ведем две игры, то имеем дело
с трехмерной поверхностью, на которой нужно найти наивыс-
шую точку. Если бы мы одновременно вели три игры, то искали
бы вершину четырехмерной поверхности. Размерность поверхно-
сти, вершину которой мы должны отыскать, равна количеству
игр (рынков и систем) плюс один.
Заметьте, что с увеличением числа одновременно разыгры-
ваемых конов вершина становится все выше и выше, а разница
между вершиной и любой другой точкой поверхности — все
больше и больше (см. рис. 1.3, 1.4 и 1.5). То есть, чем больше
разыгрывается конов, тем больше разница между положением на
вершине и в любой другой точке. Это верно безотносительно
к тому, как много рынков или систем используется, даже в слу-
чае одного рынка и системы.
Не попасть на вершину — значит платить завышенную
цену. Вспомните, к чему приводит отклонение от вершины при
Новая методология
39
Geomean HPR
Рис. 1.4. Десять игр в монетку «два-к-одному».
одной игре в монетку. Последствия этого не менее серьезны
и в случае нескольких одновременных игр. Фактически, если вы
упустили вершину (л + 1)-мерного рельефа, то разоритесь быст-
рее, чем в случае одной игры!
Наше согласие или несогласие с этими закономерностями
никак не отражается на том факте, что они властвуют над нами.
Вспомните, что в любое время мы можем сопоставить некое f
любому трейдеру с любой системой и на любом рынке. Когда вы
применяете одну торговую систему и не попадаете на вершину
кривой от f для этой системы, вы можете, если повезет, полу-
чить некую часть должной прибыли, но при этом почти навер-
няка подвергнетесь большим текущим потерям, чем следовало бы.
Если же не повезет, то вы непременно разоритесь даже с исклю-
чительно прибыльной системой!
Когда мы торгуем портфелем рынков и/или систем, мы
просто усиливаем эффект отклонения от вершины кривой
в (п + 1)-мерном пространстве.
40
Новая методология
Рис. 1.5. Сорок конов двух игр в монетку «дво-к-одному».
Сравнение со старыми
подходами
Давайте проведем простое сравнение результатов, которые
дает новая и старая (E-V) методологии.
Предположим для простоты, что мы собираемся одновре-
менно вести две игры. Каждая из них — это уже известная нам
игра в монетку «два-к-одному». Предположим далее, что попарная
корреляция исходов отсутствует. Согласно новой методологии
оптимальная точка, или вершина четырехмерного (и + 1) релье-
фа, будет соответствовать 23% для обеих игр.
Новая методология
41
В тех же условиях (т. е. в отсутствии попарной корреляции)
старая методология дает среднее значение Е = 0,5 и дисперсию
V = 2,25. Отсюда, согласно старой методологии, получается 50%
для обеих игр.
Это значит, что половину вашего счета следует вложить в
каждую игру. Но что это значит в смысле рычага? Во что
обходится игра? При ставке в один доллар (т. е. максимальной
потере за кон) средние потери в 0,5 долл, будут много больше
оптимума в 0,23 долл, на кон. Как мне увеличивать ставку по ходу
игры? Корректный, математически оптимальный ответ на этот
вопрос с учетом рычага (включая увеличение ставки по ходу
игры) был бы таков: 0,5 от 0,46 суммы на счете. Но из старых
моделей средней дисперсии этого не следует. Они не присоблены
для использования рычага (в обоих значениях). Они ничего не
говорят о моем положении на (л + 1)-мерной поверхности. Кроме
вершины на (л + 1)-мерной поверхности есть и другие важные
точки. Например, как мы узнаем из последней главы, весьма
важны и точки перегиба поверхности. Старые E-V-модели ничего
не говорят нам ни о том, ни о другом.
Фактически, старые модели утверждают лишь, что инвес-
тирование половины капитала в каждую из этих игр будет оп-
тимальным в том смысле, что вы получите максимум дохода для
заданного уровня дисперсии, или минимальную дисперсию для
заданного уровня дохода. В какой мере вы хотите применить
рычаг, зависит от вас, от вашего личного предпочтения.
На самом деле, однако, есть некая оптимальная величина
рычага — оптимальная точка на (л + 1)-мерной поверхности. Есть
на ней и другие важные точки. Торгуя, вы автоматически ока-
зываетесь где-то на этой поверхности (повторим, что не призна-
вая этого факта, вы никоим образом его не устраняете). Старые
модели это игнорируют. Новый подход, напротив, учитывает
данное обстоятельство, в результате чего его последователи сразу
же вооружаются пониманием того, что такое правильное и не-
правильное использование рычага в рамках оптимального порт-
феля. Короче говоря, новая методология просто дает гораздо
больше полезной информации, чем ее предшественники.
Напомним, что для трейдера, одновременно использую-
щего две торговые системы, все определяется его положением
42
Новая методология
на трехмерном изображении. Оно не менее важно, чем его
торговые системы, тайминг или его трейдерские способности.
От положения трейдера на (л + 1)-мерном изображении зави-
сит, как минимум на 50%, насколько велики будут его тор-
говые успехи.
Дело осложняется тем, что безотносительно к размерности
изображения его вершина плавает. Я с готовностью это признаю.
То есть системы нестационарны. Конечно, мне это тоже не нра-
вится. Однако это не отрицает того факта, что на (л + 1)-мерном
изображении, где мы находимся, имеется вершина, преимуще-
ства попадания на которую, как и потери от промаха, по-
прежнему остаются в силе.
Неосведомленные люди — я так называю их, поскольку
они, очевидно, не накопили ни достаточного опыта работы
с реальными торговыми системами, ни достаточного опыта ком-
пьютерного моделирования виртуальных торговых систем, —
часто ошибочно утверждают, что «все системы в конце концов
лопаются». В большинстве случаев, когда люди говорили так о
своей системе, оказывалось, что в долгосрочном плане она вовсе
не перестала приносить прибыль. Время от времени система
может приносить убытки (т. е. текущие потери). Но если она не
совсем никчемна и имеет приличный запас прочности, то она
вновь станет прибыльной. Возможно, прибыль будет не столь
велика, как когда-то раньше, но система вновь примется ковать
доход, хотя бы на минимальном уровне. Дело не в том, что
в долгосрочном плане система стала неприбыльной, просто вер-
шина кривой от / сместилась влево от своего прежнего положе-
ния. Поэтому, продолжая использовать ту же систему, трейдер
теперь оказывается справа от вершины, даже если на первых
порах он был слева от нее!
Отсюда немедленно возникают два вопроса. Во-первых, как
найти вершину кривой в (п + 1)-мерном пространстве в любой
данный момент времени. И во-вторых, как предсказать, в каком
направлении она будет сдвигаться. В этой книге мы попытаемся
ответить только на первый из этих вопросов.
Новая методология
43
На пути к анализу нового типа
В давние времена технический анализ был предметом насме-
шек со стороны тех, кто, по сути, и не понимал его. Сегодня
едва ли не каждый прибыльный участник торговли использует
технический анализ. Хотя фундаментальные аналитики все еще
остаются у дел, общественное внимание теперь, несомненно,
переключилось на технических аналитиков.
Какой бы хорошей ни была система, она все равно будет
приносить меньше прибыли, чем могла бы, если не расположить
ее на вершине (л + 1)-мерного изображения. Минимально эффек-
тивные трейдеры и торговые системы могут заработать значитель-
но больше денег, чем выдающиеся трейдеры или системы, если
будут полнее учитывать рельеф этой поверхности. Степень эф-
фективности мало зависит от трейдера, используемых систем или
концепций, чего не скажешь о местоположении на (л + 1)-мерном
пространстве.
И все же люди не прекращают поисков лучших систем
и методов анализа. Ситуация сходна с той, когда некто, уже
играя в монетку на условиях «два-к-одному», не оставляет по-
исков игры с лучшим соотношением вероятностей. Он не ведает
того, что даже если и найдется такая игра, то ему все равно
нужно найти вершину ее кривой. Кроме того, на этой кривой
будет и такая точка, где он спустит все свои деньги. Полагая,
что нужно лишь найти игру с лучшим раскладом, он упускает
из виду, что мир не «плоский». Он «изогнут», поэтому вне
зависимости от того, в какую игру играет трейдер и каков в ней
расклад, осознавая это или нет, он заплатит завышенную цену,
если отклонится от вершины кривой. Хуже того, уплачиваемый им
штраф будет расти с течением времени.
В дополнение ко всему, средства, применяемые для оценки
эффективности систем, абсолютно ничего не говорят нам о той
неустойчивой поверхности, где мы находимся. Фактически, они,
возможно, вводят в заблуждение в большей степени, чем все
прочее. Дело в том, что эффективность систем оценивается по
средней сделке. Хотя, по сути, мы нуждаемся в оценке средне-
44
Новая методология
геометрической сделки — в оценке того, сколько мы зарабатываем
на контракт по сделке, что всегда меньше, чем в средней сделке.
В стремлении к знанию часто приходится как-то иначе, по-
новому, посмотреть на известные вещи, научиться воспринимать
их по-детски непосредственно, безо всяких предубеждений.
Как только торговое сообщество воспримет эти новые идеи,
как только его члены выйдут за рамки своего плоскостного
восприятия мира, с техническим анализом случится то же самое,
что сейчас происходит с анализом фундаментальным. Те, кто
хочет преуспеть на рынке, еще ближе подойдут к пониманию
того, что действительно влияет на их эффективность, то есть они
достигнут той же цели, которую преследовали ранее, переориен-
тировавшись с фундаментального анализа на технический.
Когда методологией овладеют инвесторы, они поймут, что
построение портфеля — это не поиск компромисса между риском
и прибылью и что оптимальный портфель — это не точка дву-
мерного E-V-пространства. Напротив, они увидят его как карту
полиморфной* поверхности в пространстве рычагов, где дисперсия
дохода (риск) интересна лишь постольку, поскольку она снижает
среднегеометрический доход и влияет на оптимальное использо-
вание рычага**. То есть дисперсия дохода лишь снижает относи-
тельные высоты этого изображения***. Хитрость состоит в том,
чтобы найти именно вершину изображения, а не какой-то удов-
летворительный компромисс между доходом и его дисперсией,
как это обычно делается при инвестировании.
* Допускающего возможность реконфигурации. — Прим. пер.
** Далее в этой главе будет показано, что среднегеометрическое доходов
за период владения активом может быть достаточно точно аппроксимировано
с помощью теоремы Пифагора для среднеарифметического и стандартного
отклонения доходов за период владения. То есть среднеарифметическое и
стандартное отклонение (дисперсия) доходов за период владения позволяют
оценить среднегеометрическое доходов за период владения, или высоту в (п + 1)-
мерном пространстве.
*** Из всего этого не следует, что риск и доход не связаны между собой
сложным образом — наоборот. Если вам нужен высокий доход, то следует
мириться с высоким риском. Говорю это, поскольку из-за незнания топографии
(п + 1)-мерной поверхности своего местопребывания кто-то, вероятно, окажется
не на вершине и, следовательно, будет получать совсем не такой доход, как
следовало бы, учитывая тот уровень риска, которому он себя реально подвергает.
Новая методология
45
Статистическая независимость
На протяжении всей книги мы будем считать, что для
фиксированного метода торговли последовательность доходов за
периоды владения (holding period returns - HPR) на одном
участке временной оси независима от HPR в любое другое время
и что все они независимо распределены по одному и тому же
закону распределения.
Существует множество способов проверки статистической
независимости и принадлежности двух случайных величин к одному
и тому же распределению. Мы не будем здесь их приводить.
Читателей, которые заинтересованы в более подробном рассмот-
рении этого вопроса, отсылаем к двум предыдущим книгам
Portfolio Management Formulas и The Mathematics of Money
Management.
Если, однако, какая-то статистическая завсимость все же
имеется, то поначалу наш метод торговли будет субоптимальным
(т. е. не оптимальным) Позже трейдер сможет встроить в него
данные о зависимости и таким образом повысить его эффектив-
ность. Только при статистической независимости трейдер, воз-
можно, будет вправе утверждать, что улучшить свой метод тор-
говли он уже не сможет.
История параметра f
Где-то в конце Второй мировой войны немецко-американ-
ский математик венгерского происхождения Джон фон Нейман
и экономист Оскар Моргенстерн явили миру концепцию теории
игр, которую они подробно изложили в своем классическом
трактате «Теория Игр и Экономического поведения». Эта теория,
изначально разработанная для решения экономических задач,
положила начало новой прикладной дисциплине, называемой
46
Новая методология
исследованием операций, и впоследствии, благодаря своим при-
ложениям к военной стратегии, социологии и политике, стала
одной из великих «золотых жил» двадцатого столетия. Возможно-
сти, которые дает нам эта теория, столь же неисчерпаемы, сколь
и мало исследованы.
Во время Второй мировой войны серьезные трудности воз-
никали при обеспечении связи на дальние расстояния. Теория
передачи данных на ранних этапах своего развития изобиловала
проблемами, не последней из которых были ложные сигналы,
порождаемые, казалось бы, неустранимым электронным шумом,
накладывавшимся на сообщения.
В 1948 г. Клод Шеннон опубликовал в «Bell System Tehnical
Journal» статью «Математическая теория информации», которая
положила начало тому, что сейчас называется теорией информа-
ции. По сути, Шеннон утверждал, что при надлежащем кодиро-
вании двоичные символы могут передаваться по зашумленному
каналу с произвольно малой вероятностью ошибки.
К 1956 г. Дж. Л. Келли Мл. объединил некоторые идеи те-
ории игр и теории информации в ставшей теперь знаменитой
статье «Новая интерпретация скорости передачи информации»*.
Хотя в статье речь шла о теории информации, из нее вытекало,
что игроку следует стремиться максимизировать ожидаемую ве-
личину логарифма своего капитала**. Это было прямой противо-
положностью методологии, принятой еще во времена Паскаля,
утверждавшей, что игрок должен максимизировать ожидаемую
величину самого капитала.
Начиная с 1962 г., когда вышла классическая книга Эдвар-
да О. Торпа «Как победить дилера», критерий Келли начал при-
обретать известность среди технических аналитиков, главным об-
разом, благодаря усилиям Эдварда О. Торпа***. Он показал порядок
применения данного критерия на практике и предложил такие
рабочие формулы, которые были приняты на вооружение сооб-
* J. L. Kelly, Jr., A New Interpretation of Information .Rafe,«Bell System
Technical Journal», July 1956, pp. 917—926.
** Впоследствии это положение стало известно как критерий Келли.
*** Edward О. Thorp, Beat the Dealer, New York: Vintage Books, Random
House, Inc., 1966.
Новая методология
47
ществом так называемых профессиональных игроков. Биржевое
сообщество в целом, однако, отнюдь не торопилось принять
критерий, несмотря на то, что в его полезности Торпу удалось
убедить профессиональных игроков. Оно, следовавшее за корифе-
ями управления риском из бизнесс-школ, осталось, в основном,
равнодушным к этому.
В 1980 г. Торп опубликовал в «Gambling Times» статью,
посвященную формулам Келли*.
Позже эти формулы были вновь рассмотрены в ныне зна-
менитой книге Фреда Гема «Управление капиталом на товарных
рынках», благодаря которой критерий Келли стал понемногу вос-
приниматься всем торговым сообществом, включая трейдеров-
спекулянтов и трейдеров товарных рынков, а не только горсткой
математически подготовленных трейдеров, которые приняли его
еще раньше.
Так продолжалось до 1986 г., когда достоинства формул
Келли начал пропагандировать видный трейдер Ларри Вильямс.
Вскоре после этого стало уже трудно найти опытного спекуля-
тивного трейдера, который бы не знал о формулах Келли.
Формулы Келли, говоря кратко, удовлетворяют критерию
Келли, то есть они дают ответ на вопрос, какую долю средств
следует инвестировать в каждую игру, чтобы максимизировать
ожидаемую величину логарифма капитала. Эту долю мы, вслед за
Торпом, обозначаем буквой f
Первая из этих формул такова:
/=2*р—1 [1.03а]
или
f=P~q [1.03b],
где:
р — вероятность выигрыша в игре;
q — вероятность проигрыша в игре (поскольку она допол-
няет р, она равна 1 -р).
* Е. О. Thorp, The Kelly Money Management System, «Gambling Times»,
Dec. 1980, pp. 91-92.
48
Новая методология
Эту формулу можно применять, однако, только когда
возможный выигрыш равен проигрышу. Например, если с веро-
ятностью 60% вы выигрываете один доллар и проигрываете один
доллар с вероятностью 40%, получаем:
/= 0,6 - 0,4 = 0,2.
То есть для того, чтобы удовлетворить критерий Келли,
нужно было бы на каждую игру ставить по 0,2, или 20%, нашего
капитала.
Когда выигрываемые и проигрываемые величины не оди-
наковы (и даже если равны), можно использовать следующую
формулу:
/= в .g-Ll) [1.04а],
где:
р — вероятность выигрыша в игре;
b — отношение величины выигрыша по выигрышной сделке
к величине проигрыша по проигрышной сделке.
Так, для игры вроде нашей орлянки «два-к-одному», упо-
минавшейся ранее, получаем:
/= + [1.04а]
(3 * 0,5 - 1)
2
= 0^5
- 2
= 0,25.
То есть оптимальная ставка на каждый кон игры составляла
бы 25% от величины счета.
Новая методология
49
Обратите внимание, что числитель в формуле [1.04а] равен
(арифметическому) математическому ожиданию [1.01а]. Поэтому
можно сказать, что:
the edge
b
[1.04b]
Исходя из этого, формулу Келли также часто представляют
в виде:
P~Q
b
[1.04с]
Любая из формул [1.04] будет удовлетворять критерию
Келли, или, как я говорю, рассчитывают оптимальное / неза-
висимо от того, равны или нет величины выигрыша и проигры-
ша. В формуле [1.03] величины выигрыша и проигрыша должны
быть равны.
Однако я считаю, что все эти формулы применимы только
к распределению Бернулли, имеющему лишь два различных исхода.
Поскольку многие азартные игры имеют только два различных
исхода (выигрышный исход и проигрышный исход), проблемы
не возникает. В торговле же сделка может иметь много исходов.
Поэтому я вывел формулу, дающую оптимальную долю при
наличии более двух возможных исходов.
Для начала мы должны усвоить понятие дохода за период
владения (HPR). Оно обозначает просто процент чистого дохода
от данной сделки плюс единица. Следовательно, чистый доход
в 10% эквивалентен HPR, равному 1,10, а убыток в 25% — HPR
в 0,75.
Но процент дохода, который мы используем, является
функцией величины, которая используется в формуле для / То
есть мы можем утверждать, что математически HPR представляет
собой:
HPR = 1 +/* ( к ) [1.05]
J v biggest loss ' L
4 - 9727
50
Новая методология
Предположим теперь, что у нас имеется Т сделок. Мы
можем перемножить HPR всех этих сделок и получить коэффи-
циент прироста нашего исходного капитала, который будем на-
зывать относительным конечным капиталом (TWR):
TWR=f]HPR [1.06]
/=1
или
TWR =П 1+Л (.. ггаАе>
Н J v biggest loss
Наконец, если извлечь корень степени Т из [1.06], то
получим средний общий прирост за игру, называемый также
средним геометрическим HPR, важность которого прояснится
далее:
G = TWR1/r
[1-07]
или
о = (П (i+/* (h~ г/.е‘ ))]
\ 11 \ J V biggest loss ''I
Но как из этих формул получить значение /? Оно макси-
мизирует выражения [1.06] или [1.07] и отыскивается с помощью
одномерного перебора. Другими словами, оптимальное f — это
такое f которое максимизирует либо TWR, либо G (среднее
геометрическое HPR).
Предположим, например, что мы провели две сделки (т. е.
Т= 2), в которых, как в орлянке «два-к-одному», было потеряно
1 доллар и выиграно 2 доллара, соответственно. В качестве метода
поиска оптимального f воспользуемся довольно грубым перебо-
ром значений/с шагом 0,01, начиная с 0,01 и кончая 1,0. То
есть, взяв / равное 0,01, вычислим величины HPR. Поскольку
7=2, нашим двум сделкам будут соответствовать только два
HPR:
Новая методология
51
Trade________________________HPR________________________
-1000 1 + 0,01 * (—10001 -1000) = 1 + 0,01 * -1 = 0,99
2000 1 + 0,01 * (-2000 / -1000) = 1 + 0,01 * 2 = 1,02
Перемножив HPR, получим TWR = 0,99*1,02 = 1,0098. Оно
соответствует значению f= 0,01. Далее попробуем значения 0,02,
0,03 и так далее до тех пор, пока получаемое значение TWR
станет меньше предыдущего. Это произойдет на значении/= 0,26,
что дает оптимальное /= 0,25, на котором достигается максимум
кривой.
Но что следует из того, что оптимальное /имеет такое-то
значение? Как мы знаем, это значит, что на каждый кон нужно
ставить долю торгового счета, равную / А торгуя, скажем, фью-
черсами, сколько нужно задействовать контрактов, чтобы это
было эквивалентно ставке в х% счета?
Решение этой задачи, которое было дано в моей книге
1990 г., получается делением абсолютной величины самого боль-
шего проигрыша на оптимальное / Результатом будет долларовая
величина, обозначаемая через /$:
abs(biggest losing trade)
optimal / [L08]
Так, если наше оптимальное /равно 0,25, а наибольший
проигрыш равен —1000, то получим:
_ abs(-lOOO)
0,25
1000
0,25
= 4000
Далее, разделив /$ на величину счета, получим количество
контрактов (или долей акции), которым нужно торговать. Так, если
мы торгуем одним контрактом на каждые 4000 долларов счета,
как в нашем примере, то мы в каждой игре рискуем 25% счета.
4*
52
Новая методология
Эта величина — наш счет, деленный на/$, — далее округ-
ляется, ибо можно делать только целые ставки. Причем округля-
ется в меньшую, а не в большую сторону, поскольку в случае
ошибки выгоднее оказаться левее вершины кривой от f (имея
меньшее количество контрактов), нежели правее (имея большее
количество контрактов):
_ т п . / account equity \
Number of units to trade = int( -----------), [1.09],
J J5
где
Number of units to trade — количество контрактов;
account equity — свободные средства на счету.
Итак, если на счете имеется 25000 долларов, то:
хт , с . , . / 25000 х
Number of units to trade = int( ^qqq )
= int(6,25)
= 6
Значит, торговать нужно было бы шестью контрактами.
Какой смысл единицы? Такой, который вы в нее вклады-
ваете. Это может быть один товарный контракт, опционный
контракт, одна или 100 долей акции. Вы должны решить, какой
будет единица актива, которым вы торгуете. И лишь потом
определять ваш HPR в расчете на торговлю одной единицей. То
есть долларовая величина выигрыша или проигрыша по сделкам
привязана к торговле тем, что вы приняли за единицу. Рассчитав
величины HPR и воспользовавшись формулой [1.08], задающей
величину/$, вы узнаете, что торгуете 1 единицей на каждые /$
вашего счета.
Иногда задать единицу нелегко. Например, некто, торгую-
щий валютой на межбанковском рынке, сталкивается с допол-
нительной проблемой, когда размер позиции является функцией
цены. Так, межбанковскому трейдеру для определения, каким
Новая методология
53
количеством единиц следует торговать, нужно выполнить свои
расчеты по управлению капиталом на основе обратной операции
подобно тому, как это делается на фьючерсном рынке, и только
после этого вернуться к форексу.
Поскольку, чем точнее выражается размер позиции в тор-
говых единицах, тем лучше — вы больше получаете от макси-
мизации ожидаемой величины логарифма счета — нужно ста-
раться брать единицы как можно меньшей величины. Например,
вместо единицы в 100 долей акции, возможно, стоит взять
единицу величиной в одну долю и перейти к торговле непол-
ными лотами. Вместо использования полных фьючерсных кон-
трактов, возможно, стоит перейти к единице, основанной на
мини-контракте. Так, если один котракт идет за два мини-
контракта, то при расчетном оптимуме в одиннадцать мини-
контрактов вы можете задействовать пять полных и один мини-
контракт. Действуя таким образом, вы больше получите от
максимизации ожидаемого логарифма счета, чем при торговле
крупными единицами.
Геометрическое математическое ожидание — это то, что вы
получили на единицу по сделке. Оно гораздо важнее арифмети-
ческого математического ожидания, которое часто называют сред-
ней сделкой. В действительности же, настоящая средняя сделка —
это геометрическое математическое ожидание — настоящая, ибо
это именно то, что вы получили на контракт по сделке. Оно
рассчитывается следующим образом:
(Геометрическое) Математическое ожидание =
=/$ * (среднее геометрическое HPR — 1).
Так, если для нашей орлянки «два-к-одному» арифметичес-
кое математическое ожидание равно 0,50, то геометрическое
математическое ожидание на уровне 0,25 f будет:
(Геометрическое) Математическое ожидание =
= 4 *(1,060660172- 1)
= 4 * 0,060660172
= 0,242640688.
54
Новая методология
Это то, что вы действительно получили бы на единицу по
сделке (а не 0,50), если на каждый кон орлянки «два-к-одному»
ставили бы по одному доллару из каждых четырех долларов своих
денег.
Встречая термин ожидание в других источниках, его сле-
дует понимать, как среднее арифметическое, а не среднее гео-
метрическое математическое ожидание.
Оценочное среднее
геометрическое
(или как дисперсия исходов
влияет на геометрический рост)
В дальнейшем для простоты будем использовать примеры из
азартных игр. Рассмотрим две системы: систему А, которая вы-
игрывает 10% сделок с выплатой «двадцать восемь-к-одному»,
и систему В, выигрывающую 70% сделок с выплатой «один-к-
одному». Наше математическое ожидание на единицу ставки для
системы А равно 1,9 и для системы В — 0,4. Следовательно, мы
можем сказать, что на каждую единицу ставки система А будет
приносить в среднем в 4,75 раза больше, чем система В. Но
давайте взглянем на это с позиций торговли фиксированной
долей счета. Мы можем найти наши оптимальные /, деля мате-
матические ожидания на отношения цен выигрыша и проигрыша
(по формуле [1.04b]). Это дает оптимальное f для А — 0,0678
и для В — 0,4. Средние геометрические для каждой из систем при
их оптимальных f будут равны:
для А - 1,044176755;
для В - 1,0857629.
Новая методология
55
System % Wins Win: Loss ME f Geomean
А 0Д 28U 0,0678 1,0441768
В 0,7 1:1 0,4 0,4 1,0857629
Как вы видите, система В, имея математическое ожидание
менее четверти математического ожидания системы А, дает почти
в два раза больше на сделку (в среднем 8,57629% всего торго-
вого счета на сделку при реинвестировании на оптимальных
уровнях У), чем система А (в среднем 4,4176755% всего торго-
вого счета на сделку при реинвестировании на оптимальных
уровнях У).
Теперь, исходя из того, что для покрытия потери в 50%
нужно отыграть 100% счета, проведем дальнейшие расчеты. По-
скольку
1,044177 в степени х будет равно 2,0 при х, равном при-
мерно 16,5, это означает, что для системы А потребуется
более 16 сделок для восстановления после 50% потери счета.
В отличие от этого, системе В, где 1,0857629 в степени х
равно 2,0 при х, равном примерно 9, для восстановления
50% потери понадобится 9 сделок.
Что же происходит? Не потому ли так получается, что в
системе В более высок процент выигрышных сделок? Причина,
по которой система В превосходит систему А, заключается в
дисперсии исходов и ее воздействия на функцию геометрического
роста. Большинство людей ошибочно полагает, что функция роста,
или TWR, есть:
TWR = (1 + RY,
где:
R — процентный прирост за период, например 7% = 0,07;
Т — количество периодов.
56
Новая методология
Хотя (1 + 7?) есть то же самое, что HPR, мы можем
сказать, что большинство ошибается, считая, что функция ро-
ста* , или TWR, задается формулой:
TWR = HPR7
А это верно лишь тогда, когда доход (т. е. HPR) постоянен,
чего в торговле не бывает.
Настоящая функция роста в торговле (или в любой другой
сфере с переменным HPR) есть произведение значений HPR.
Предположим, что мы торгуем кофе и наш оптимальный f— это
один контракт на каждые 21000 долларов торгового счета. Пусть
проведено две сделки, первая из которых принесла убыток в
210 долл., а вторая — доход в 210 долл, (соответствующие зна-
чения HPR равны 0,99 и 1,01). В таком случае TWR был бы равен:
TWR= 1,01 *0,99 = 0,9999.
Для лучшего понимания этого можно использовать оценоч-
ное среднее геометрическое (EGM), которое довольно точно
аппроксимирует среднее геометрическое из выражения [1.07]:
G = Vx2-№
или
G=V/42- V
[1.10а]
[1.10b],
где:
G — среднее геометрическое HPR;
* Многие ошибочно используют среднее арифметическое HPR в
формуле для HPR7. Как здесь показано, это не даст истинного TWR за Т
игр. В формуле для HPRT нужно использовать среднее геометрическое от
значений HPR, а не среднее арифметическое. Это даст истинную величину
TWR. Если же стандартное отклонение значений HPR равно 0, то среднее
арифметическое и среднее геометрическое HPR эквивалентны, и можно исполь-
зовать любое из них.
Новая методология
57
А — среднее арифметическое HPR;
S — стандартное отклонение значений HPR;
V — дисперсия значений HPR.
Теперь для для получения оценки TWR возведем уравнения
[1.07] и [1.10а,Ь] в степень Т. Эта оценка будет весьма точно
аппроксимировать мультипликативную функцию роста, или на-
стоящее TWR, из формулы [1.06]:
TWR = “ S2)7 [1.11],
где:
Т — количество периодов;
А — среднее арифметическое HPR;
S — стандартное отклонение совокупности значений HPR.
Суть полученного результата заключается в том, что теперь
мы можем математически представить зависимость между ростом
средней арифметической сделки (HPR) и дисперсией значений
HPR, то есть причину, по которой система В (70%, «один-к-
одному») более эффективна, чем система А (10%, «двадцать
восемь-к-одному»).
Мы должны стремиться к максимальному приросту функ-
ции, заданной формулами [1.10а,Ь], или, говоря буквально,
к максимизации квадратного корня из квадрата среднего арифме-
тического HPR за вычетом дисперсии значений HPR.
Показатель степени Т в оценочном TWR позаботится о себе
сам. Другими словами, увеличение Т не составляет проблемы, ибо
мы всегда можем увеличить количество рынков, на которых
торгуем, использовать более краткосрочные торговые системы
и так далее.
Формулу [1.10а] можно переписать в виде:
А2 =(? + S2 [1.12]
Это позволяет понять существо зависимости. Обратите вни-
мание, что по форме — это знакомая теорема Пифагора, глася-
58
Новая методология
щая, что квадрат гипотенузы прямоугольного треугольника равен
сумме квадратов его сторон (рис. 1.6)! Здесь гипотенуза равна А,
а максимизировать нам нужно одну из сторон — G.
Трейдеры должны
максимизировать
этот катет
S
Большинство
трейдеров ошибочно
максимизируют
гипотенузу
Рис. 1.6. Теорема Пифагора в управлении капиталом.
При максимизации G любое увеличение S нужно компен-
сировать увеличением А. Если S равно нулю, то А равно G, что
приводит к неверному толкованию функции роста TWR как
(1 + R)r.
Отсюда, характеризуя относительное влияние А и S на G,
мы можем утверждать, что приращение А эквивалентно соответ-
ствующему уменьшению S, и наоборот. То есть любое уменьше-
ние величины дисперсии по сделкам (в смысле уменьшения
стандартного отклонения) эквивалентно увеличению среднего
арифметического HPR. Это верно вне зависимости от того, тор-
гуем мы на оптимальном f или нет.
Если трейдер торгует на основе фиксированной доли счета,
то ему нужно максимизировать G, но не обязательно А. Макси-
мизируя G, трейдер должен понимать, что, согласно теореме
Пифагора, стандартное отклонение S влияет на G точно в той
же пропорции, как и А! То есть, если трейдер уменьшает стан-
дартное отклонение (5) для своих сделок, то это эквивалентно
соответсвующему увеличению среднего арифметического HPR (А),
и наоборот!
Новая методология
59
Фундаментальное уравнение
торговли
Мы можем пойти гораздо дальше, не ограничиваясь лишь
пониманием того, что сокращение потерь, или дисперсии в
сделках, улучшает конечные результаты торговли. Вновь обратим-
ся к формуле [1.11], аппроксимирующей величину TWR. По-
скольку (XY)Z = X(Y’Z), мы можем далее упростить показатели
степени в [1.11], приведя его к виду:
т = [1.13]
Это последнее выражение, упрощающее формулу аппрокси-
мации TWR, мы будем называть фундаментальным уравнением
торговли, поскольку оно описывает, каким образом различные
факторы A, S и Т влияют на конечные результаты торговли.
Отметим несколько вполне очевидных моментов. Во-пер-
вых, если А меньше или равно единице, то вне зависимости от
двух других переменных, S и Т, наш результат не может быть
больше единицы. Если А меньше единицы, то при стремлении Т
к бесконечности, А стремится к нулю. Это означает, что если А
меньше или равно единице (математическое ожидание меньше
или равно нулю, ибо оно равно А~ 1), то у нас нет ни шанса
на получение прибыли. По сути, если А меньше единицы, то
наше разорение — это лишь вопрос времени.
Если А больше единицы, то с ростом Т увеличивается и
наша общая прибыль. Ведь каждая следующая сделка умножает
коэффициент прибыли на квадратный корень из него.
Каждый раз, увеличивая Т на единицу, мы наращиваем
TWR кратно квадратному корню из среднего геометрического. То
есть каждый раз, когда происходит сделка, или истекает HPR,
Т увеличивается на единицу и коэффициент прибыли умножается
на среднее геометрическое.
Значимость фундаментального уравнения торговли заклю-
чается в том, что из него следует, что, уменьшая стандартное
отклонение в большей степени, чем среднее арифметическое HPR,
60
Новая методология
мы улучшаем наш конечный результат. Поэтому имеет смысл по
возможности ограничивать убытки — это приносит пользу. Вместе
с тем уравнение показывает, что в некоторой точке ограничение
потерь станет уже неблагоприятным. В этой точке вы будете с
небольшими потерями выходить из слишком большого количе-
ства сделок, которые позже окажутся прибыльными, тем самым
снижая А больше, чем S.
Аналогичным образом, уменьшение числа крупных выиг-
рышных сделок будет способствовать итоговому успеху, если это
сокращает А больше, чем S. Во многих случаях этого можно
добиться, включив в свою торговую программу опционы. Небес-
полезной может оказаться опционная позиция, направленная против
вашей позиции по основному активу (покупка или продажа
соответствующего опциона).
Как видите, фундаментальным уравнением торговли можно
воспользоваться для решительного и многогранного изменения
нашей торговли. Этого можно добиться путем приближения или
удаления стоп-приказов, задания ценовых ориентиров и т. д.
Необходимость изменений диктуется неэффективностью нашего
способа ведения торговли, а также неэффективностью наших
торговых программ или методологии.
Существует ли оптимальное f ?
Оптимальность f в смысле максимизации капитала видна из
того, что:
since G = (П HPR.)' 7 [1.14]
/=1
и
(П HPR,)1/r= exp Г?! ln(HPR,)\ [1.15]
м ' Т
Новая методология
61
Отсюда, согласно закону больших чисел в слабой форме
или Центральной предельной теоремы теории вероятностей при-
менительно к сумме независимых переменных (т. е. к числителю
правой части выражения [1.15]), если максимизировать среднее
геометрическое по всем периодам владения на достаточно боль-
шой выборке данных, то почти наверняка получим больший
конечный капитал, чем с помощью любого другого решающего
правила.
Кроме того, для доказательства оптимальности f мы можем
также воспользоваться теоремой Ролля. Вспомните, что под оп-
тимальностью мы понимаем то, что дает наибольший геометри-
ческий рост с увеличением количества испытаний. Поскольку
показателем среднего геометрического роста является TWR, нам
нужно доказать, что существует такое значение f при котором
достигается максимум TWR.
Теорема Ролля утверждает, что если некая функция пере-
секает линию, параллельную оси х в двух точках а и Ь, и
функция непрерывна на интервале [а, Ь], то на этом интервале
существует по крайней мере одна точка, в которой первая про-
изводная этой функции обращается в нуль (т. е. имеется по
крайней мере один относительный экстремум).
Поскольку все функции с положительным арифметическим
математическим ожиданием пересекают ось х дважды* (в качестве
оси х выступает ось f), при f = 0 и в той точке справа, где f
дает такие расчетные HPR, что их дисперсия превосходит среднее
арифметическое HPR минус один. Эти две точки будут опреде-
лять наш интервал [а, Ь] на оси х. Далее, первая производная
фундаментального уравнения торговли (т. е. оценочного TWR)
будет непрерывна при всех f внутри данного интервала, посколь-
ку f дает такие значения AHPR и дисперсии HPR внутри интер-
вала, которые дифференцируемы на нем. Следовательно, оценоч-
ное TWR как функция от f непрерывна внутри интервала. Значит,
согласно теореме Ролля, на этом интервале должен быть по
* В действительности при /=0 и TWR = 0. Поэтому мы не можем
сказать, что TWR пересекает 0 снизу вверх. Вместо этого мы можем утвер-
ждать, что при значении /, которое бесконечно близко к нулю, TWR пересекает
линию, расположенную над осью х и бесконечно близкую к ней. Аналогичным
образом характеризуется и правая точка пересечения.
62
Новая методология
крайней мере один относительный экстремум. Поскольку на этом
интервале оценочное TWR положительно, то есть расположено
над осью х, на нем должен содержаться, по меньшей мере, один
максимум.
Фактически, на этом интервале может быть лишь один
максимум, так как изменение среднего геометрического HPR
(среднее геометрическое HPR является корнем степени Т из
TWR), согласно теореме Пифагора, впрямую зависит от AHPR
и дисперсии, когда оба они при изменении f изменяются в про-
тивоположных направлениях. Этим гарантируется единственность
вершины. Таким образом, на данном интервале должен быть
максимум, и он может быть только один.
Теперь вернемся к уравнению [1.06] и вновь рассмотрим
игру в монетку с выплатой «два-к-одному». У нас имеется две
сделки, или два возможных сценария. Взяв первую производную
от [1.06] по /, получим:
aTWR
df
— trade,
biggest loss
— trade,
----- 4
biggest loss
(( ~trade; (1 + Л ( ~trade2 ))
" biggest loss ' \ d \ biggest loss [1-16]
При количестве сделок большем двух можно использовать
эту же формулу, но она сразу же сильно разрастается. Поэтому
для простоты мы остановимся лишь на двух сделках. В этих
условиях для серии исходов +2, —1 при /= 0,25 будем иметь:
<TTWR _ /I / -2\\ /—1U , //—2\ I—1\\\
—-J7— ~ 111 + 0,25 * [ —- II * [—- I + и—.1*11 + 0,25 * |—— )))
df ' -1" ' -1 " "-Г ' '-1
d 1WR
—— = ((1 + 0,25 * 2) * -1) + (2 * (1 + 0,25 * -1))
df
rfFWR
- = ((1 + 0,5) * -1) + (2 * (1 - 0,25))
df
Новая методология
63
dTWR = (1,5 * -1) + (2 * 0,75))
df
= —1,5 +1,5 = 0
df
Как видим, функция достигает вершины при /= 0,25, где
наклон касательной равен нулю, то есть точно при оптимальном
f и никакого другого локального экстремума существовать не
может из-за ограничений, накладываемых теоремой Пифагора.
Наконец, покажем, что оптимальное f не зависит от Т. Взяв
первую производную от оценочного TWR в форме [1.13] по
переменной Т, получим:
6frWR= (А2 - Х2)^2 * In (А2 - S2) [1.17]
dT
Поскольку In (1) = 0, то при том значении f когда А2—
S2 = 1, функция достигает вершины — максимума TWR, завися-
щего лишь от f Отметим также, что и А (среднее арифметическое
HPR) и 5 (стандартное отклонение этих HPR) не являтся фун-
кциями от Т — они не зависят от него. Поэтому [1.13] не зависит
от Т при оптимальном f. То f которое оптимально в смысле
максимизации оценочного TWR, всегда будет иметь одно и то же
значение, независимо от Т.
Ответ критикам
Вскоре после того, как в 1990 г. были опубликованы эти
формулы, некоторые загорелись идеей поиска оптимального f
с помощью моделирования по методу Монте Карло. Одно из наи-
более серьезных замечаний относительно этих формул состояло
в том, что они игнорируют необходимость торговли целочислен-
64
Новая методология
ними количествами контрактов, например, что нельзя торговать
0,37 контракта на золото. Тогда как метод Монте Карло позволяет
определить оптимальное f с учетом реальных ограничений, допус-
кающих торговлю только целыми количествами контрактов.
Способ моделирования по Монте Карло в данном случае
мог бы выглядеть следующим образом. Предположим, у вас имеется
начальный капитал величиной, скажем, в 50000 долл. Возьмите
все сделки и бросьте их в мешок, а затем вытаскивайте их
обратно по одной. Каждый раз, вытащив одну сделку, рассчитай-
те новую величину вашей ставки на основе значения f которое
вы сейчас тестируете. Повторяя это вновь и вновь, вы сможете
взять за оптимальное f то, которое фактически дало вам наиболь-
ший выигрыш.
Все это прекрасно. Однако метод, впервые предложенный
в 1990 г., даст вам оптимальное f для всех возможных значений
начального капитала. То есть он дает оптимальное/ учитывая все
возможные начальные условия. Во-вторых, с ростом начального
капитала оба метода: и формулы 1990 г., и метод Монте Карло —
дают все более близкие значения оптимального f В-третьих, чем
меньше целочисленный размер ставки, тем ближе сходятся оба
подхода. То есть чем меньшей единицей вы пользуетесь в торговле
(т. е. чем точнее приближаетесь к дробным ставкам), тем ближе
сходятся оба подхода и лучше становятся результаты обоих. Сле-
довательно, чем чаще вы уточняете целочисленное число торгу-
емых контрактов при изменении вашего торгового счета, тем
больше получите от максимизации ожидаемого значения лога-
рифма капитала. Благодаря этому торговля овсом может оказаться
прибыльней торговли индексом S&P.
Наконец, вам вовсе не нужно использовать при расчете
значений HPR долларовые величины. Выразив исходы за периоды
владения в процентах, при расчете значений HPR возьмите
наибольший процент проигрыша и найдите значение оптималь-
ного /по процентным исходам. Далее, переходя к формуле [1.08],
возьмите наибольший процент проигрыша, умножьте на текущую
цену актива и примите результат за наибольший проигрыш на
сделку, как это показано ниже.
_ abs(biggest losing percentage * current price)
optimal /
[1-18]
Новая методология
65
Введение в портфели
с оптимальным f
Помимо прочего в книге 1990 г. был дан способ определе-
ния оптимальных величин f для компонентов портфеля.
Начнем с того, что, когда мы работаем с компонентами
портфеля, нужно использовать одинаковые периоды владения. То
есть период владения нельзя более отождествлять с продолжитель-
ностью сделки. Теперь это должен быть какой-то единый период
времени - день, неделя, месяц, квартал или год. Я предпочитаю
использовать день, но от вас этого не требуется. Нужно лишь,
чтобы вы использовали стандартный период времени при опре-
делении всех HPR, и его продолжительность должна быть неиз-
менной от одного рынка к другому, от одного метода торговли
к другому. Поэтому, если длительность вашего периода владения
равна, скажем, одному дню, значит, вы определяете значения
HPR, исходя из изменений счета от торговли единицей актива
за день.
Для применения формул 1990 г. к портфелю нужно изме-
нить только выражение [1.05], чтобы учитывать более одного
компонента:
in / —trade., \\
HPR,= 1+ (E/,4bigge7tl'—))
[1.19],
где:
HPRa = HPR за к-й период владения;
сделка;Ч= изменение капитала от торговли одной единицей
1-го компонента за к-й период;
максимальный проигрыш = самое большое отрицательное
изменение капитала по этой компоненте на единицу актива за все
периоды владения;
п = количество компонент в портфеле;
/ = f ассоциированное с i-й компонентой.
5 - 9727
66
Новая методология
Таким образом, вам нужно найти п оптимальных значений
f по одному на каждый компонент. Заметьте также, что хотя
значения f не могут быть меньше нуля, каждое из них может
быть больше единицы. Причина этого в том, что если между
двумя компонентами имеется достаточно высокая отрицательная
корреляция, то соответствующие им значения f будут стремиться
к бесконечности.
Чтобы продемонстрировать это, рассмотрим два потока
исходов. Первый из них приносит два доллара в первом исходе
и теряет один доллар во втором исходе. Второй поток теряет
1,10 доллара в первом исходе, но приносит один доллар во
втором. То есть:
Holding Period# Stream 1 Stream 2
1 2 -1,1
2 -1 1
Обратите внимание, что вы можете назначить оптимальное
/для этих двух потоков, равным бесконечности (тогда /$ будет
бесконечно мало, и у вас будет бесконечное количество единиц),
ибо суммарно нет ни одного убыточного периода владения. За-
метьте также, что торговля этим портфелем много агрессивнее
торговли первого потока с оптимальным / равным 0,25. Наконец,
отметьте, что хотя поток 2 имеет отрицательное математическое
ожидание, благодаря отрицательной корреляции с потоком 1,
торгуя ими одновременно, вам следовало бы задействовать бес-
конечное количество единиц актива! То есть иногда подключение
компонента с отрицательным математическим ожиданием повы-
шает общую эффективность портфеля.
Приемы работы, описанные в книге 1990 г., имели эмпи-
рический характер. То есть при определении портфеля они опи-
рались на реальные данные. В книге 1992 г. было показано, как
можно работать с оптимальными / для компонентов портфеля
в рамках E-V-модели. Оба эти подхода, эмпирические методы
1990 г. и E-V-модель 1992 г., имеют свои недостатки. Они на-
столько серьезны, что заставили меня взяться за эту книгу.
Новая методология
67
Прежде чем продолжить, следует упомянуть еще одно об-
стоятельство, касающееся портфелей. Предположим, что у нас
есть счет в 50000 долларов и портфель, состоящий из двух
компонентов. Оптимальное инвестирование в эти компоненты,
или оптимальные /$ для компонентов, - это 5000 и 10000 дол-
ларов, соответственно. Спрашивается, как нам поделить 50000 дол-
ларов между двумя этими компонентами, исходя из их /$?
Ответ очень прост. Во-первых, разделите все 50000 долл, на
первую компоненту /$. Это даст 50000/5000 = 10. Это означает,
что нужно торговать десятью единицами первой компоненты. Во-
вторых, возьмите ту же сумму, 50000 долл., и разделите ее на /$
второй компоненты. Это даст 50000/10000 = 5. То есть, нам нужно
было бы торговать пятью единицами второй компоненты. Другими
словами, в случае портфеля все компонентные /$ делят один и тот
же счет, что отражает элемент пересечения инвестиций, объектив-
но свойственный процедуре определения количества контрактов
(формула [1.09]) при формировании портфелей*.
Заблуждения относительно
текущих потерь
и диверсификации
Нетрудно понять, что при торговле одной единицей метод
торговли будет выглядеть тем лучше, чем больше оптимальное f
Поэтому, чем меньше /$, тем больше будут задействованные
позиции. В этом заключается некий парадокс. Заметьте, что при
каком бы f мы ни торговали (а у нас всегда есть какое-то f),
максимальные текущие потери означают сокращение торгового
счета на/%. Так, например, в орлянке «два-к-одному» оптималь-
* Подробнее см. «One Combined Bankroll Versus Separate Bankroll»
книги Ральфа Винса The Mathematics of Money Management, New York: Wiley,
1992, pp. 68-70.
5*
68
Новая методология
ное f равно 0,25, что эквивалентно одной ставке на каждые
четыре долл, счета (/"$). Значит, как только происходит макси-
мальный проигрыш (в данном случае —1 долл.), наш счет сокра-
щается на/%. То есть каждый проигрыш сокращает наш счет на
/%•
Это верно не только для оптимального, но и для любого
другого значения f Вновь вернемся к нашей игре в монетку,
предположив теперь, что мы торгуем при f равном 0,1, что
эквивалентно одной ставке на каждые десять долл, счета. При
максимальном проигрыше наш счет сократится на 10%. В этом
проявляется великий парадокс: чем лучше система, тем больше
сокращение счета при проигрыше, ибо обычно ее используют на
более высоких значениях /!
Казалось бы, в нашей орлянке «два-к-одному» мало что
зависит от того, играем ли мы при /= 0,1, или при оптимальном
f — 0,25: после 40 конов в первом случае мы получим 366%
дохода при проигрыше, как минимум, в 10%, а во втором —
955% дохода при проигрыше, как минимум, в 25%. Это пример-
но одно и то же. Но если продлить игру до 100 конов, то
ожидаемый минимум потерь останется тем же, а ожидаемый
доход вырастет до 4590% при / = 0,1, против 36009% при / =
0,25. Ясно, что разница между коэффициентами ожидаемого
прироста дохода и ожидаемого сокращения счета при оптималь-
ном f будет больше, чем при любом другом f и будет расти с
увеличением числа разыгранных конов, или реализованных пери-
одов владения.
Заметьте, что в зависимости от f ожидаемый минимум
сокращения счета меняется арифметически, а доход меняется
экспоненциально. То есть, мы можем утверждать, что, разжижая
f (ш. е. торгуя меньшим количеством, чем оптимальное), вы со-
кращаете потери арифметически и одновременно экспоненциаль-
но сокращаете прибыль. Смещение вправо от вершины сокращает
лишь прибыль (опять экспоненциально), но арифметически уве-
личивает минимальные ожидаемые потери (в процентах сокраще-
ния счета).
Теперь обратимся к некоторым заблуждениям, касающимся
диверсификации. Реальная польза диверсификации состоит не в
том, что она обеспечивает безопасность, как ошибочно (и под-
Новая методология
69
сознательно) полагают некоторые. В математической форме эф-
фект от диверсификации выражает фундаментальное уравнение
торговли. Диверсификация позволяет увеличивать Тза данный период
времени. То есть она предусматривает больший рост за данный
период времени, но не дает дополнительной безопасности.
Более того, с помощью диверсифицикации вы увеличи-
ваете размерность поверхности, делая ее еще более хрупкой
и склонной к разрушению. Безотносительно к тому, сколько
компонентов содержит портфель, когда-то наступит такой пе-
риод, который будет плохим для всех них одновременно. Поэто-
му добавление новых компонентов может сгладить кривую из-
менения счета (тем самым создавая обманчивое ощущение
безопасности), но зачастую одновременно увеличит потери наи-
худшего исхода!
Другое расхожее заблуждение состоит в том, что будто бы
увеличение числа компонентов портфеля снижает его эффектив-
ность, или что в пределе выгода от увеличения числа компонен-
тов убывает, то есть достигает некоторой асимптоты. Это не так:
кривая зависимости между этими факторами отличается от лога-
рифмической и, скорее всего, представляет собой прямую ли-
нию, поднимающуюся снизу вверх и слева направо, ибо с по-
мощью диверсификации мы достигаем только увеличения Т.
Всякий прирост Т соответствующим образом увеличивает прирост
счета, который не имеет асимптот.
Следующий шаг
Основной недостаток формул [1.05—1.07] заключается в
том, что они предполагают одинаковую вероятность реализации
всех HPR. Поэтому нужна новая формула, которая допускала
бы, чтобы с разными HPR ассоциировались различные вероят-
ности. Такая формула позволила бы находить оптимальное/при
условии, что дано описание распределение вероятностей HPR.
70
Новая методология
В 1992 г. я опубликовал набор формул, которые именно это и
обеспечивали:
HPR =
[1.20],
где:
А — исход сценария;
Р — вероятность сценария;
W — худший исход всех п сценариев;
f — тестируемое значение f
Откуда получаем относительный конечный капитал, или
TWR*:
т
TWR=[[HPR [1.21]
/=1
или
Наконец, если взять корень степени ^Р, из уравнения [1.21],
то получим средний прирост на игру, или среднее геометрическое
HPR (оно будет играть важную роль в дальнейшем):
G = TWR1/&' [1.22]
или
* В этой формулировке, в отличие от формулировок 1990 г., TWR не
имеет самостоятельного значения. В данном случае это просто промежуточная
величина, которая используется для отыскания G и не представляет собой
коэффициент увеличения начального капитала.
Новая методология
71
где:
Т — количество различных сценариев;
TWR — относительный конечный капитал;
HPRдоход от периода владения z-ro сценария;
А. — исход z-ro сценария;
Р — вероятность z-ro сценария;
W — худший исход всех п сценариев;
f— тестируемое значение f
Точно так же, как вы могли пользоваться выражениями
[1.04] для решения уравнений [1.03], уравнение [1.22] можно
использовать для решения любых проблем с оптимальным f Вместо
формул [1.03—1.07] вы можете взять [1.22]. Для данных с рас-
пределением Бернулли это уравнение дает те же результаты, что
и формулы Келли. Вы получите те же результаты, как и по
формулам 1990 г., если подставите это распределение сделок (где
вероятность каждой сделки равна 1/7) в [1.22]. Эту формулу
можно использовать для максимизации ожидаемого значения
логарифма любого начального количества чего угодно в условиях
экспоненциального роста. Теперь посмотрим, как использовать
эту формулу в контексте сценарного планирования.
Сценарное планирование
Все, кто зарабатывает прогнозированием, будь то экономи-
сты, аналитики рынка акций, метеорологи, госслужащие и т. д.,
неизбежно когда-то ошибаются. Но от этого никуда не уйти, ибо
большинство решений, которые должны приниматься человеком
в жизни, обычно требуют от него прогноза будущего.
Наше прогнозирование страдает как минимум двумя оче-
видными недостатками. Начнем с того, что человеку свойственно
делать более оптимистичные предположения о будущих событиях,
72
Новая методология
чем их реальные вероятности. Большинство людей считает, что
у них есть куда больше шансов выиграть в лотерею в этом месяце,
чем погибнуть в автокатастрофе, хотя вероятность последнего выше.
Это справедливо не только в отношении отдельных лиц, но еще
более выражено на групповом уровне. Работая вместе, люди склон-
ны считать благоприятные исходы более вероятными.
Второй, и еще более пагубный недостаток, состоит в том,
что люди прогнозируют будущее прямолинейно. Они предсказы-
вают, какой будет цена галлона бензина двумя годами позже, что
будет с их работой, кто будет следующим президентом, какими
будут моды и так далее, и так далее. Задумываясь о будущем, мы
склонны рассматривать его как единственный наиболее вероят-
ный исход. В результате, как только нужно принять решение и на
индивидуальном, и на групповом уровне, мы склонны опираться
на то, что, по нашему мнению, будет единственным наиболее
вероятным исходом в будущем. Вследствие этого, мы становимся
беззащитными перед неприятными сюрпризами.
Сценарное планирование дает частичное решение этих про-
блем. Сценарий представляет собой один из возможных прогно-
зов, описание одного из путей, которым могут пойти события
в будущем. Сценарное планирование нацелено на составление
набора сценариев, покрывающего определенный спектр возмож-
ностей. Разумеется, охватить весь спектр возможностей нереально,
поэтому планировщик сценариев желает учесть их по максимуму.
Действуя таким образом, в отличие от линейного прогнозирова-
ния наиболее вероятного исхода, планировщик сценария может
приспосабливаться к будущим событиям, куда бы они ни повер-
нули. Более того, сценарное планирование позволяет планировщи-
ку подготовиться к тому, что в ином случае стало бы неожидан-
ностью. Сценарное планирование согласуется с реальной жизнью,
ибо оно исходит из иллюзорности нашего детерминизма.
Предположим, что в ваши обязанности входит участие в дол-
госрочном планировании для вашей компании, которая произво-
дит какой-то конкретный продукт. Вместо того чтобы положиться
на единственный наиболее вероятный линейный прогноз, вы ре-
шаете заняться сценарным планированием. Вы усаживаетесь вместе
с другими планировщиками и методом «мозговой атаки» прини-
маетесь вырабатывать возможные сценарии. Что, если у вас не
Новая методология
73
хватит сырья для производства вашего продукта? Что, если одного
из ваших конкурентов постигнет неудача? Что, если появится
новый конкурент? Что, если вы серьезно недооцените спрос на
ваш продукт? Что, если на каком-либо континенте разгорится
война? И что, если она будет ядерной?
Поскольку каждый сценарий представляет лишь одну из
возможностей, его можно основательно проработать. Но что де-
лать после того, как вы проделали это для всех своих сценариев?
Для начала вы должны определить, какую цель вы хотели
бы достичь в каждом из сценариев. Эта цель зависит от сценария
и не обязана быть прогрессивной. Например, при негативном
сценарии ваша цель может состоять просто в поддержании жи-
вучести компании. Определившись с целью по каждому сцена-
рию, вы должны будуте выработать планы достижения вашей
цели в случае реализации данного сценария. Например, на случай
маловероятного негативного сценария, когда ваша цель — остать-
ся на плаву, нужно иметь планы, позволяющие минимизировать
ущерб. Главное преимущество сценарного планирования состоит
в том, что оно вооружает вас конкретным образом действий на
случай определенного развития событий. Оно принуждает вас
к составлению планов до того, как произойдут те или иные
события, заставляет подготовиться к неожиданностям.
Впрочем, сценарное планирование позволяет добиться мно-
го большего. Оно тесно взаимосвязано с оптимальным f что дает
возможность оптимально распределять инвестиции между компо-
нентами сценарного набора. Хотя мы и закладываемся на много-
вариантное развитие событий в будущем, жизнь всегда выбирает
какой-то один сценарий. Поэтому при сценарном планировании
нам нередко приходится согласовывать текущее инвестирование
с возможными сценариями завтрашнего дня. В этом проявляется
подлинная суть сценарного планирования — его нацеленность на
количественное осмысление будущего.
Прежде всего, мы должны описать каждый сценарий по
отдельности. Затем мы должны сопоставить ему вероятность его
реализации. Вероятность - это число между 0 и 1. Нам не нужно
рассматривать такие сценарии, вероятность реализации которых
равна 0. Кроме того, сопоставляемые вероятности не носят ин-
тегрального характера. Другими словами, каждому сценарию от-
74
Новая методология
вечает своя вероятность. Предположим, что мы планируем дея-
тельность некоторой промышленной компании. При этом согласно
одному из множества отслеживаемых сценариев наша компания
с вероятностью 0,15 будет привлечена к суду за банкротство,
а согласно другому — с верояностью 0,07 разорится в результате
острой иностранной конкуренции. Теперь мы должны задаться
вопросом, не является ли первый сценарий (привлечение к суду
за банкротство) следствием второго сценария (банкротство в
результате острой иностранной конкуренции). Если это так, тогда
из вероятности первого сценария нужно исключить вероятность
второго сценария, то есть понизить вероятность первого сценария
до 0,08 (0,15-0,07).
Не менее важным, чем уникальность вероятностей сцена-
риев, является другое требование: сумма вероятностей всех рас-
сматриваемых сценариев должна быть строго равна 1. То есть она
не может быть равна ни 1,01, или 0,99, а только 1.
Теперь, когда каждому сценарию сопоставлена вероятность
реализации, нам нужно сопоставить ему его исход. Это — чис-
ленная величина. Она может выражать заработанные или потерян-
ные деньги в результате реализации сценария, количество единиц
какого-то средства, лекарства или еще чего-то. Требуется лишь,
чтобы исход измерялся в тех же единицах, в которых выражаются
наши инвестиции.
Для использования данного метода нужно, чтобы хотя бы
у одного сценария был отрицательный исход. Это — обязательное
требование.
Последним требованием данного метода является положи-
тельность математического ожидания, т. е. суммы произведений
исходов на их вероятности (формула [1.01]). Если математическое
ожидание равно нулю или отрицательно, то излагаемый ниже
метод применять нельзя*. Это не значит, что нельзя использо-
вать сценарное планирование как таковое. Его можно и нужно
использовать. Но оптимальное f может работать в рамках сценар-
ного планирования только при положительном математическом
ожидании.
* Далее по тексту мы будем применять сценарное планирование к
портфелям, где допускается отрицательное математическое ожидание, которое
может способствовать эффективности портфеля в целом.
Новая методология
75
Кроме перечисленного, нужно стараться охватить как мож-
но большую часть спектра возможных исходов. Другими словами,
очень желательно, чтобы было учтено 99% возможных исходов.
Это может показаться почти нереальным, но поскольку многие
сценарии можно расширить, то для покрытия 99% спектра вам
не понадобятся 10000 сценариев.
Расширяя сценарии, следует избегать типичной ошибки
планирования трех вариантов: одного оптимистического сценария,
другого пессимистического и третьего, сохраняющего положение
неизменным. Это — слишком просто, и вытекающие отсюда реше-
ния часто слишком грубы для того, чтобы хоть чем-то помочь.
Ведь вы же не станете ограничиваться только тремя сделками при
определении оптимального f своей торговой системы?
Итак, даже если для охвата всего спектра исходов нужно
запредельное количество сценариев, то 99% спектра покрыть
вполне реально. Когда количество сценариев превосходит наши
операционные возможности, можно расширять сценарии, тем
самым уменьшая их количество. Однако, действуя подобным
образом, мы теряем некое количество информации. Если мы
сокращаем количество сценариев (расширяя их) только до трех
(типичная ошибка), то безвозвратно теряем так много информа-
ции, что это серьезно снижает эффективность данного метода.
Спрашивается, какое количество сценариев будет достаточ-
ным? Оно должно быть как можно больше, но не превосходить
ваших операционных возможностей. При необходимости их можно
расширить с помощью компьютера.
Представим нашу орлянку «два-к-одному» в виде спектра
из двух сценариев. Один из них предусматривает выпадение орла,
а другой - решки. Они равновероятны (по 0,5) и имеют исходы
+2 и —1, соответственно. То есть:
Сценарий Вероятность Исход
Орел 0,5 2
Решка 0,5 —1
Предположим, что мы вновь планируем деятельность про-
мышленной компании на основе продаж какого-то своего про-
дукта в отдаленной и слаборазвитой карликовой стране. Предпо-
76
Новая методология
ложим далее, что мы отслеживаем всего пять возможных сцена-
риев (в реальности их было бы гораздо больше, но для простоты
мы ограничимся пятью). Эти пять сценариев отражают наше
видение возможного будущего данной страны, вероятности их
реализации, а также прибыли и потери от инвестирования:
Сценарий Вероятность Результат
Война ОД $-500 000
Кризис 0,2 $-200 000
Застой 0,2 0
Мир 0,45 $500 000
Процветание 0.05 $1 000 000
Итого: 1,00
Сумма наших вероятностей равна 1. По крайней мере исход
одного сценария отрицателен, а математическое ожидание поло-
жительно:
(0,1 * -500 000)+(0,2 * -200 000) + ... = 185 000
Следовательно, к этому сценарному набору можно приме-
нить наш метод.
Заметим для начала, что если бы мы заложились на един-
ственный наиболее вероятный исход, то пришли бы к выводу,
что мир — это и есть будущее данной страны, и стали бы
действовать так, как если бы мир уже воцарился (как непрелож-
ный факт), и лишь смутно осознавая прочие возможности.
Следуя нашему методу, мы должны определить оптималь-
ное f Оно представляет собой такое значение f (между нулем
и единицей), которое максимизирует среднее геометрическое
в выражениях [1.20-1.22]. Далее, используя формулу [1.21], по-
лучаем значение относительного конечного капитала, или TWR*.
Наконец, взяв корень степени от [1.21], получим средний
* В этой формулировке, в отличие от формулировок 1990 г., TWR не
означает ничего, кроме некоторой промежуточной величины, которая использу-
ется для отыскания G, и не является коэффициентом увеличения начального
капитала.
Новая методология
77
общий прирост на игру, или среднее геометрическое HPR. Для
этого воспользуемся формулой [1.22].
Такова последовательность применения наших формул. Но
для начала нужно выбрать схему оптимизации, или способ пе-
ребора значений f который приводит к такому / которое мак-
симизирует выражения [1.20—1.22]. Для этого мы можем, как и
раньше, воспользоваться прямым перебором значений f от 0,01
до 1, или прибегнуть к параболической интерполяции.
Затем мы должны определить наихудший возможный ре-
зультат по сценарию среди всех отслеживаемых нами сценариев,
какой бы малой ни была вероятность его реализации. В примере
с промышленной компанией наихудшим результатом будет —
500000 долл.
Теперь для каждого возможного сценария нужно разделить
наихудший возможный результат на значение f с минусом. В на-
шем примере с промышленной компанией мы будем предолагать,
что эта процедура выполняется в ходе перебора значений f от 0,01
до 1. Поэтому мы начинаем со значения f равного 0,01. То есть
мы делим наихудший возможный исход отслеживаемых сценариев
на значение f с минусом и получаем:
$-500 000
-0,01
= 50 000 000
Заметьте, что деление отрицательной величины на отрица-
тельную величину дает положительный результат, и наоборот. По-
этому в данном случае наш результат положителен. Теперь, переходя
от сценария к сценарию, мы будем делить его исход на только что
полученную величину. Поскольку исход первого сценария является
также и самым худшим (потеря 500000 долл.), для него получаем:
$-500 000
50 000 000 ” -0’01
На следующем шаге прибавляем эту величину к 1. Это дает
нам:
1 + (-0,01) = 0,99
78
Новая методология
Наконец, возводим полученный результат в степень, рав-
ную вероятности реализации сценария, которая в нашем примере
равна 0,1:
(0,99)°-’ = 0,9989954713.
Далее переходим к следующему сценарию, названному
Кризисом, который, реализуясь с вероятностью 0,2, приносит
потерю 200000 долл. Наш результат худшего случая остается
прежним: -500000 долл. Раз мы используем для f прежнее зна-
чение 0,01, то и величина, на которую нужно делить результат
данного сценария, будет по-прежнему равна 50 миллионам:
-200 000
50 000 ООО “ ~°’°4'
Проделав оставшиеся шаги, получим наше HPR:
1+(—0,004) = 0,996,
(0,996)°-2 = 0,9991987169.
Продолжив перебор сценариев при тестируемом значении
/=0,01, получим значения HPR, соответствующих трем после-
дним сценариям:
Застой 1,0;
Мир 1,004487689;
Процветание 1,000990622.
Преобразовав каждый сценарий в его HPR для данного
значения / перемножим эти HPR между собой и получим:
0,9989954713
*0,9991987169
*1,0
*1,004487689
*1,000990622
1,003667853
Новая методология
79
Эта дает нам промежуточное значение TWR, которое в
данном случае равно 1,003667853. Нашим следующим шагом будет
возведение этого числа в степень, равную единице, деленной на
сумму вероятностей сценариев. Поскольку эта сумма всегда равна
1, можно утверждать, что, возведя TWR в степень 1, мы должны
получить среднее геометрическое. Так как возведение любого
числа в степень 1 равняется ему самому, можно сказать, что в
данном случае наше среднее геометрическое равно TWR. То есть
оно равно 1,003667853.
Если снять требование, что каждому сценарию соответству-
ет своя, уникальная вероятность, то мы можем допустить, что
сумма вероятностей больше 1. В таком случае для получения
среднего геометрического нам пришлось бы возвести наше TWR
в степень, равную 1, деленной на эту сумму вероятностей.
Мы только что получили среднее геометрическое, которое
соответствует/ = 0,01. Теперь перейдем к/ = 0,02, и повторим
весь процесс вплоть до получения соответствующего среднего
геометрического. Будем действовать таким образом, пока не най-
дем такое / которое дает самое большое среднее геометрическое.
В нашем примере оказывается, что максимум среднего гео-
метрического, равный 1,1106, достигается при /=0,57. Разделив
худший исход по сценариям (—500000) на оптимальное / с
минусом, получим 877192,35 долл. Другими словами, если наша
компания захочет инвестировать в маркетинг своего нового про-
дукта в этой отдаленной стране, то в текущий момент оптималь-
ным вложением будет указанная сумма. По мере развития собы-
тий в стране сценарии, их исходы и вероятности, скорее всего,
будут меняться. Тогда велична /тоже изменится. Чем пристальнее
мы будем отслеживать изменение сценариев, чем точнее будут
сами эти сценарии, которые мы используем в качестве исходных
данных, тем точнее будут наши планы. Заметьте, что если ком-
пания не сможет своевременно вложить в маркетинг своего про-
дукта все 877192,35 долл., то она окажется слишком далеко от
вершины кривой от / То же самое можно сказать о трейдере,
имеющем слишком много товарных контрактов по сравнению с
тем, что диктуется оптимальным / Если инвестиции пройдут
своевременно, но превысят указанную сумму, то это будет ана-
логично ситуации с товарным трейдером, у которого слишком
мало контрактов.
80
Новая методология
Обращаю ваше внимание на ряд важных обстоятельств,
касающихся сценариев и торговли. При формировании сценариев
можно использовать массу самых различных факторов:
1. Подобно тому, как это было сделано в предыдущем при-
мере, сценарии можно ассоциировать с исходами данной
сделки. Это дает эффект, когда вы торгуете только одним
активом. Но если вы торгуете портфелем активов, то вы,
скорее всего, нарушаете правило, согласно которому все
периоды владения должны иметь одинаковую длину.
2. Если вы знаете, каким будет распределение ценовых исхо-
дов, то это можно использовать в сценариях. Предположим,
что у вас есть основание полагать, что завтрашнее распре-
деление цен на данный актив будет нормальным. Следова-
тельно, вы можете описывать ваши сценарии на основе
нормального распределения. Так, при нормальном распреде-
лении в 97,7% случаев прирост цены не превысит двух,
а в 99,86% случаев — трех стандартных отклонений. Поэто-
му один из сценариев может состоять в том, что прирост
цены остановится где-то между двумя и тремя стандартны-
ми отклонениями (какой бы ни была долларовая величина
вашей торговой единицы в течение завтрашнего дня, при-
нимаемого за период владения). Вероятность такого сцена-
рия равнялась бы 0,9986 — 0,9772 = 0,0214, или 2,14%.
3. Вы можете использовать распределения возможных ценовых
исходов при торговле одной единицей актива по данной
методе в следующем периоде владения. Это мой излюблен-
ный прием, который хорошо согласуется с формированием
портфеля по новой методологии.
Хотя я настоятельно рекомендую использовать третий пункт
вышеприведенного перечня, какому бы методу вы ни следовали,
не забывайте, что по мере изменения условий вам нужно посто-
янно модернизировать свои сценарии, их исходы и вероятности
реализации. Кроме того, следующий период владения нужно откры-
вать, непременно исходя из того, что по формулам является
оптимальным в текущий момент. Это аналогично ситуации, в ко-
торой находится игрок в очко. С вытягиванием каждой следующей
карты комбинация в оставшейся колоде изменяется, как и шансы
Новая методология
81
игрока. Тем не менее, он всегда должен основываться только на
текущем раскладе вероятностей.
Хотя обсуждавшиеся выше количественные величины вы-
ражались в деньгах, они могут выражаться и в чем-либо дру-
гом, — методика остается в силе.
Если вы создаете различные сценарии для рынка акций, то
оптимальное f полученное по этому методу, укажет вам точную
долю средств, которую следует вложить на рынке акций в дан-
ный момент. Например, если полученное f равно 0,65, это значит,
что 65% средств следует вложить в акции, а оставшиеся 35%
оставить в наличности. В долгосрочном плане такой подход обес-
печит вас наибольшим геометрическим ростом вашего капитала.
Разумеется, результат будет не точнее исходных данных, кото-
рыми вы снабжаете систему (сценарии, вероятности их реализа-
ции, итоговых выплаты и издержки).
Тот же самый процесс можно использовать в качестве
альтернативного параметрического метода определения оптималь-
ного f для данной сделки. Предположим, что вы основываете свои
торговые решения на фундаментальных факторах. При желании
вы можете расписать различные сценарии возможных исходов
сделки. Чем больше сценариев, чем они точнее, тем лучше будут
ваши результаты. Скажем, вы решили заработать на покупке
муниципальных облигаций, но не планируете держать их до
погашения. Тогда вы можете рассмотреть множество различных
сценариев развертывания ситуации в будущем, а затем исполь-
зовать их при определении того, сколько следует инвестировать
в данный конкретный заем.
Предположим, что некий трейдер вынашивает решение о
покупке соевых бобов. Он может прибегнуть и к волнам Эллиота,
и опереться на прогнозы погоды, но в любом случае он в состо-
янии определить следующие сценарии этой потенциальной сделки:
Сценарий Вероятность Результат
Лучший 0,05 150 центов/бушель (прибыль)
Желательный 0,4 10 центов/бушель (прибыль)
Типичный 0,45 —5 центов/бушель (убыток)
Плохой 0,05 —30 центов/бушель (убыток)
Катастрофический 0,05 — 150 центов/бушель (убыток)
6 - 9727
82
Новая методология
Когда наш соевый последователь Эллиота (или трейдер-
метеоролог) распишет этот набор сценариев (множество возмож-
ных исходов данной сделки) и, стремясь оптимизировать рост
своего торгового счета в долгосрочной перспективе, придет к не-
обходимости принятия одного и того же торгового решения
в будущем бесконечно много раз, он обнаружит с помощью
сценарного планирования, что оптимальным размером позиции в
данной сделке будет 0,02 (2%) счета. Это означает открытие
одного контракта по соевым бобам на каждые 375000 доллара
счета: наибольшая потеря на сценарий, —150 центов за /бушель,
деленная на оптимальное/= 0,02 для данного набора сценариев,
дает 7500/0,02 = 375000 доллара. То есть с одним контрактом на
каждые 375000 долл, счета в следующей сделке трейдер будет
рисковать 2% своей позиции.
Параметры сценария всякой сделки, безотносительно к
тому, чем ее обосновывает трейдер (т. е. волнами Эллиота,
погодой и т. д.), могут меняться. Тем не менее, при максими-
зации геометрического роста своего счета в долгосрочной пер-
спективе трейдер должен исходить из того, что одни и те же
параметры сценария будут бесконечно повторяться. Иначе, как
мы выяснили на примере рис. 1.2, ему придется серьезно по-
платиться. Обратите внимание, что отклонись наш соевый трей-
дер вправо от вершины f-кривой (взяв немного больше контрак-
тов), он ничего на этом не выиграет. Другими словами, если бы
наш соевый трейдер открывал по одному контракту на каждые
300000 долл, счета, то на поверку в долгосрочной перспективе
он заработал бы меньше, чем с одним контрактом на каждые
375000 долл.
Если мы имеем дело с принятием решения, каждому ас-
пекту которого соответствует свой набор сценариев, то, выбирая
сценарий с наибольшим средним геометрическим при оптималь-
ном f мы улучшаем наши решения в ассимптотическом смысле.
Предположим, что нам нужно принять решение, которое
включает два возможных выбора. Их могло бы быть гораздо
больше, но для простоты мы ограничимся двумя альтернативами,
которые будем называть «белой» и «черной». Если мы выбираем
белую альтернативу, то останавливаемся на следующем сценарном
раскладе:
Новая методология
83
Сценарий____________Вероятность_________Результат
А й —20
В 0,4 0
С 0,3 30
Математическое ожидание = 3,00 долл.;
Оптимальное / = 0,17;
Среднее геометрическое = 1,0123.
Что это за сценарии — неважно. Они могут означать все,
что угодно. В дальнейшем обсуждении они будут именоваться по
сопоставленным им буквам А, В и С. Неважно также, в чем
выражается результат, — это может быть почти все, что угодно.
Пусть, далее, черная альтернатива задается следующим
сценарным раскладом:
Сценарий Вероятность Результат
А 0,3 -10
В 0,4 5
С 0,15 6
D 0,15 20
Математическое ожидание = 2,90 долл.;
Оптимальное /= 0,31;
Среднее геометрическое = 1,0453.
Многие люди предпочли бы белую альтернативу, посколь-
ку у нее большее математическое ожидание. Выбрав белую аль-
тернативу, вы можете ожидать 3,00 долл, среднего выигрыша на
сделку против 2,900 долл, для черной. Однако правильным выбо-
ром в действительности является черная альтернатива, поскольку
она дает большее среднее геометрическое. Выбрав черную альтер-
нативу, вы можете ожидать 4,53% прибыли (1,0453 — 1) в среднем
против 1,23% прибыли для белой. Если учесть эффект реинвес-
тирования, то получим, что черная альтернатива в среднем дает
в три с лишним раза больше, чем белая!
е*
84
Новая методология
Тут читатель может возразить, что «мы не собираемся без
конца повторять эту сделку, мы проводим ее лишь однажды. Мы
не реинвестируем вновь в одни и те же сценарии. Разве не лучше
всегда выбирать сценарий с наибольшим математическим ожида-
нием для каждого набора решений, с которым мы сталкиваемся?»
Ориентироваться на максимальное арифметическое матема-
тическое ожидание нужно лишь тогда, когда вы намерены сделать
последнюю ставку и прекратить игру. Однако почти всегда мы
продолжаем ее, и деньги, которыми мы рискуем сегодня, завтра
же снова будут поставлены на кон. При этом предыдущие выиг-
рыши и проигрыши влияют на то, чем мы в состоянии рискнуть
сегодня. В этой ситуации мы заинтересованы в максимальном
росте нашего капитала в долгосрочной перспективе и нам следует
ориентироваться на большее среднее геометрическое. Даже если
сценарии, которые появятся завтра, будут отличаться от сегод-
няшних, мы все равно максимизируем эффективность наших
решений, если всегда будем отдавать предпочтение большему
среднему геометрическому. То же самое происходит при выборке
без замещения или при игре в очко. От сдачи к сдаче вероятности
меняются, как меняется и оптимальная доля счета, которую
следует ставить на кон. Однако, постоянно ставя на следующий
кон оптимальную долю для текущей сдачи, мы максимизируем
наш долгосрочный рост. Помните, что для максимизации долго-
срочного роста мы должны исходить из того, что текущий рас-
клад будет бесконечно повторяться в будущем. Другими словами,
мы должны рассматривать каждое отдельное событие, как если
бы мы ставили на него бесконечное количество раз, если хотим
максимизировать рост за много розыгрышей с различными рас-
кладами.
Обобщая, можно утверждать, что если исход события вли-
яет на исход(-ы) следующего события(-ий), то нам лучше пред-
почесть решение с наибольшим геометрическим ожиданием. В ред-
ких случаях, когда исход события не влияет на последующие
события, лучше ориентироваться на наибольшее арифметическое
ожидание.
Математическое ожидание (арифметическое) не учитывает
дисперсии исходов различных сценариев и поэтому может при-
вести к неверным решениям в контексте реинвестирования.
Новая методология
85
Использование данного подхода к сценарному планирова-
нию позволяет выбирать размер позиции, исходя из возможных
сценариев, их исходов и вероятностей реализации. Этот подход
внутренне более консервативен, чем ориентация на наибольшее
математическое ожидание. Среднее геометрическое набора чисел
не превосходит их среднего арифметического. Поэтому наш под-
ход никогда не перегрузит (в смысле размера позиции) вас так,
как это бывает при ориетации на максимальное математическое
ожидание. В ассимптотическом смысле (в долгосрочной перспек-
тиве) превосходство данного метода проявляется не только в том,
что он позволяет вам достичь наибольшего геометрического
роста, но также и в большей его консервативности по сравне-
нию с ориентацией на критерий наибольшего математического
ожидания.
Поскольку реинвестирование стало чуть ли не каждоднев-
ным (за исключением дня, предшествующего уходу от дел),
текущие решения нужно принимать, исходя из того, что они
будут задействоваться тысячи раз, и таким образом максимизи-
ровать их совокупную эффективность. Мы должны принимать
свои решения и инвестировать так, чтобы максимизировать гео-
метрическое ожидание. Далее, поскольку исходы большинства
событий действительно влияют на исходы последующих событий,
мы должны действовать, ориентируясь на максимум геометричес-
кого ожидания, что может привести к инвестициям, которые не
всегда очевидны.
Сценарные спектры
Теперь мы должны подробнее остановиться на понятии
сценарного спектра. Сценарный спектр — это набор сценариев
с вероятностями от 0 до 1, упорядоченных от наихудшего исхода
к наилучшему. К примеру, сценарный спектр простой игры в мо-
нетку, где мы с равной вероятностью проигрываем на орлах
86
Новая методология
и выигрываем на решках, состоит из двух сценариев, каждый из
которых реализуется с вероятностью 0,5 (рис. 1.7).
Сценарный спектр может содержать более двух сценариев —
столько, сколько вам угодно (рис. 1.8).
Рис. 1.7.
Probabilities
Worst
case
Scenarios
Рис. 1.8.
Этот сценарный спектр соответствуют сценариям из преды-
дущего раздела, касающимся инвестиций промышленной компа-
нии в маркетинг нового продукта в отдаленной стране:
Сценарий Вероятность Результат Вер. * Рез.
Война од -$500 000 —$50 000
Кризис 0,2 -$200 000 —$40 000
Застой 0,2 $0 $0
Мир 0,45 $500 000 $225 000
Процветание 0.05 $1 000 000 $50 000
Итого: 1,00 Ожидание $185 000
Новая методология
87
Заметьте, что это эффективный сценарный спектр, ибо:
А Имеется, по крайней мере, один сценарий с отрицатель-
ным исходом.
В. Сумма вероятностей равна 1,00.
С. Сценарии внутри спектра не пересекаются.
Сценарий застоя, например, предполагает мир. Но сценарий
застоя предполагает мир с нулевым экономическим ростом. Сце-
нарий мира с ним не пересекается, так как предполагает мир при
наличии хоть какого-то экономического роста. Другими словами,
сценарий застоя не является частью сценария мира, также как
и все другие сценарии по отношению друг к другу.
Все сценарии внутри данного спектра должны относиться
к исходам одного и того же периода владения. Как уже отмеча-
лось, длительность периода владения может быть любой по ва-
шему усмотрению — это может быть день, неделя, десять дней,
месяц, год — все, что угодно, но ее нужно выбрать заранее. Как
только это сделано, всем сценариям данного спектра следует
сопоставить их возможные исходы в следующем периоде владе-
ния, и все сценарные спектры должны соответствовать периодам
владения одинаковой длительности. Это имеет решающее значение.
Так, если вы остановитесь на одном дне, то все сценарии всех
сценарных спектров должны соответствовать возможным исходам
следующего дня.
Далее мы покажем, как определить оптимальное размещение
средств в случае нескольких сценарных спектров, которые одновре-
менно используются в торговле. Данный результат является раз-
витием моей ранней работы об оптимальном f и опционах. Для
этого нам потребуется ознакомиться с условными вероятностями.
Но сначала мы приведем некоторые подготовительные сведения.
88 Новая методология
Дополнение первое
Сокращение дефицита за счет
увеличенной дисперсии Валового
Внутреннего Продукта
В номере «Wall Street Journal» за 25 марта 1993 г. опублико-
вана весьма интересная редакционная статья У. Курта Хаузера. По
сути, в ней утверждалось, что, несмотря на изменения налоговых
ставок и налогового законодательства в послевоенный период,
доля ВВП, приходящаяся на собранные налоги (в США), стаби-
лизировалась на среднем значении 19,5%. Кроме того, разброс
около этого среднего был относительно невелик и составлял на
максимуме в 21,1% (1981г.) и на минимуме — 17,9% (1964—
65 гг.). Автор представил весьма убедительные доводы в пользу
необходимости более высоких темпов прироста ВВП по сравне-
нию с увеличением правительственных расходов. Отсюда следует,
что клинтоновское налоговое послание 1993 г. было некорректно
в том смысле, что более стимулирующим для ВВП является вовсе
не повышение налогов, как утверждалось, а их понижение.
Согласно утверждению м-ра Хаузера, к сокращению дефи-
цита ведет не повышение налоговых ставок, а увеличение ВВП.
Похоже, что эта идея имеет широкую поддержку. Однако сокра-
щения дефицита можно достичь, увеличивая дисперсию ВВП,
причем столь же эффективно, как за счет увеличения самого
ВВП! Эта идея бросает вызов не только обыденному, но и по-
литическому мышлению.
Общий дефицит представляет собой экспоненциально рас-
тущую функцию. Чем больше становится дефицит, тем больше
проценты по нему. Покрывая определенную часть процентов по
дефициту, то есть капитализируя некоторую часть этих процентов
обратно в дефицит, мы создаем (точнее, позволяем нашему
правительству создавать) экспоненциально растущую функцию
общего дефицита.
У всех функций с экспоненциальным ростом имеется не-
которое значение f которое можно им сопоставить. Но как нам
изменять это значение /, с которым мы (т. е. правительство)
Новая методология
89
действуем? Федеральное правительство неосознанно вырабатывает
определенное значение для f Тем не менее, имеется определенное
значение / которое воздействует на него (на всех нас), признаем
мы это или нет. Где бы ни находилось федеральное правительство
(т. е. мы) на кривой / мы можем видеть, что сможем извлечь
пользу из такого значения / которому не соответствует вершина
кривой. На определенном значении вне вершины, где TWR опус-
I кается ниже 1, мы можем получить огромный выигрыш, ибо на
этом значении мы имеем гарантию того, что функция роста будет
сломана. То есть на значении f где TWR становится меньше 1,
мы достоверно знаем, что разорились бы, будь мы игроками
с таким значением f.
Поэтому, если никто не знает, какое значение f мы ис-
пользуем, и при условии, что какое бы значение f ни исполь-
зовалось де-факто, мы можем выгадать, смещая значение/ближе
к 1 (если мы действительно находимся не на вершине кривой).
I Как можно этого добиться?
! Мы концентрировались на А, общих государственных дохо-
дах. То есть мы акцентировали на увеличении доходов (или
сокращении расходов). Однако при этом очень мало внимания
было уделено дисперсии этих доходов. Если, согласно идее м-ра
Хаузера (а я верю в его правоту), доходы прямо связаны с ВВП
(более, чем налоговое законодательство), то можно утверждать
кое-что весьма существенное относительно дисперсии ВВП.
В конечном счете то, что мы должны сократить, — это G,
или коэффициент прироста за период значений HPR федерально-
I го дефицита. По теореме Пифагора противостоящие компоненты
1 формулы для оценки среднего геометрического, этого можно
достичь не только увеличением А, средних доходов (или среднего
ВВП), но также и путем увеличения S, стандартного отклонения
;i или дисперсии доходов (стандартного отклонения или дисперсии
ВВП, согласно данным из статьи Хаузера)! Так, увеличение
дисперсии ВВП уменьшает скорость роста федерального дефицита
на величину, которая больше эквивалентного увеличения в ариф-
метическом среднем ВВП!
При увеличении / от 0 до 1 изменяются и стандартное
>1 отклонение, и арифметическое среднее значений HPR. При ну-
I левом / стандартное отклонение (или его квадрат — дисперсия)
90
Новая методология
равно нулю. При увеличении дисперсии величина f приближается
к 1. Так, увеличивая дисперсию ВВП, мы подталкиваем значение
f к работе на нас на правой части кривой f Но ни сама кривая,
ни ее вершина не изменяются. Меняется лишь наше положение
на кривой. То есть чем больше мы можем увеличить дисперсию
в ВВП, тем лучше это для сдерживания роста общего федераль-
ного дефицита.
Тем не менее, наша политика диаметрально противополож-
на всему вышесказанному. Во времена экономических спадов мы
прибегали к стимулированию понижением налоговых ставок и
государственного субсидирования. Во времена подъемов обычно
акцентировалась борьба с инфляцией и общее повышение ставок.
Такая политика только способствовала увеличению темпа роста
федерального дефицита. С математической точки зрения, прави-
тельству не следует стремиться к сдерживанию поквартальных
или погодовых колебаний ВВП. Мы платим завышенную, хотя
и скрытую, цену в смысле более высокого, чем необходимо,
темпа роста общего дефицита, проводя правительственную и фе-
деральную политику, направленную на противодействие эконо-
мическим циклам. Это именно то, что не следовало бы делать,
пожелай мы минимизировать темп роста федерального дефицита.
Дополнение второе
Обманчивая суть наращивания оплаты
менеджмента и временного
взвешивания
Когда счета управляются другими лицами (менеджерами),
начисление оплаты менеджерам часто производится не помесячно
(обычно оплата начисляется поквартально). Регулирующие агент-
ства (в США, например) настаивают на том, чтобы эта оплата
документально проводилась в помесячном начислении. Когда
Новая методология
91
реально оплата производится поквартально, отчетные ведомости
для таких менеджеров должны подгоняться с помощью бухгал-
терской процедуры, называемой начислением без выплаты.
Упрощенный пример поможет показать ошибочную суть
начисления без выплаты. Пусть у нас есть гипотетический счет
с 10000 долл., который использутся в торговле гипотетическим
менеджером в течение гипотетического 3-месячного периода.
Предположим, далее, что единственной оплатой, получаемой
менеджером, является 20-процентное поощрение. То есть только
20% прироста капитала, получаемых менеджером, подлежат оп-
лате. Каждый квартал, который заканчивается приростом капита-
ла, менеджер получает в качестве поощрения 20% разницы между
новым и старым максимумами капитала. Это вовсе не является
нетипичным для управляемых счетов на фьючерсных рынках.
Месяц Начальная сумма Изменение за месяц Реальная выплата Конечная сумма Процент прироста
Янв. $10 000 $10 000 0,00%
Февр. $10 000 $20 000 $30 000 200,00%
Март. $30 000 ($15 000) $1000 $14 000 -53,33%
Счет вырастает с 10000 долл, до 14000 долл, кварталом
позже после выплаты 1000 долл, поощрения в конце марта. Это
согласуется с TWR, который мы получаем прибавлением 1 к
величинам из колонки Процент прироста и перемножением по-
лученных результатов:
1 * 3 * 0,4667 = 1,4.
Но если мы начисляем оплату помесячно без выплаты, то
получим следующее:
Месяц Начальная Изменение Реальная Конечная Процент сумма за месяц выплата сумма прироста
Янв. Февр. Март. $10 000 $10 000 0,00% $10 000 $20 000 $4000 $26 000 160,00% $30 000 ($15 000) $3000 $18 000 -40,00%
92
Новая методология
Заметьте, что чистая выплата в конце квартала по-прежне-
му равна 1000 долл. Однако, вычисляя TWR, преобразовав про-
центы прироста в HPR прибавлением 1, получаем 1 * 2,6 * 0,6 =
1,56. Откуда следует, что квартал должен закончиться при счете
15600 долл.
Это различие возникает из-за того, что по своей сути
начисление без выплаты будет вызывать сокращение стандартного
отклонения для месячных итогов без компенсирующего сокраще-
ния арифметического среднего месячного итога. То есть оно со-
кращает основание прямоугольного треугольника без сокращения
гипотенузы. Вертикальная сторона (средний геометрический итог)
может скомпенсировать это только увеличением.
Несомненно, взяв итоговый баланс обеих таблиц, 14000 долл.,
и разделив его на начальный баланс обеих таблиц, 10000 долл.,
мы придем к одинаковому выводу — в итоге заработано 40%. Ведь
кто же станет преобразовывать месячные процентные итоги в
HPR, перемножать их, получая TWR, а затем вычитать из про-
изведения 1, чтобы узнать средний геометрический итог?
Но это именно то, что происходит! Существует такая по-
пулярная мера эффективности, называемая VAMI. Она оценивает
итог от начального инвестирования 1000 долл. То есть VAMI —
это просто TWR за любой данный месяц, умноженный на 1000.
Для таблицы с реальной выплатой имеем:
Месяц Начал, сумма Измен. за мес. Реальная выплата Конечная сумма Процент прироста VAMI
Янв. $10 000 $10 000 0,00% 1000
Фев. $10 000 $20 000 $30 000 200,00% 3000
Мар. $30 000 ($15 000) $1000 $14 000 -53,33% 1400
С добавлением VAMI в таблицу с накоплением без выплаты
получаем:
Месяц Начал, сумма Измен. за мес. Реальная выплата Конечная сумма Процент прироста VAMI
Янв. $10 000 $10 000 0,00% 1000
Фев. $10 000 $20 000 $4000 $26 000 160,00% 2600
Мар. $30 000 ($15 000) $3000 $18 000 -40,00% 1560
Новая методология
93
Многие потенциальные инвесторы видят в показателе VAMI
способ очистки отчетов от бухгалтерской ерунды и получения
осмысленной статистики. Кроме того, на него весьма полагаются
многие службы, отслеживающие работу управляющих счетами. То
есть эта коварная суть разлагает универсум потенциальных инве-
сторов многими различными способами.
А именно начисление без выплаты вводит в заблуждение
потенциальных инвесторов, так как при этом нередко завышается
оценка эффективности. Рассмотренный пример, пусть и предель-
ный, нельзя назвать нетипичным. При начислении без выплаты
он дает 56% дохода за квартал, тогда как фактически было
заработано только 40%. То есть регулирующие учреждения, требу-
ющие использовать в отчетах начисление без выплаты, способ-
ствуют распространению ошибочной практики и оказывают мед-
вежью услугу потенциальный инвесторам. По иронии судьбы, это
прямо противоположно тому, к чему должны стремиться регули-
рующие инстанции.
Другая вредоносная идея — это временное взвешивание
дополнения средств на счете и частичного их изъятия. Временное
взвешивание широко практикуется в сфере управления капита-
лами, несмотря на то, что из-за свойственной ему недооценки
фактических итогов, оно действует против менеджеров. Обычно
при временном взвешивании требуется, чтобы итоги вычислялись
как функция от количества дней за период (как правило, за
месяц), в течение которых деньги были доступны. То есть если
некто открывает счет на шестнадцатый день 30-дневного месяца,
то деньги будут доступны для менеджера половину (0,5) этого
месяца. Итоги по данному счету за весь месяц будут далее ум-
ножены на 2. Так, если в том месяце по данному счету был
получен доход в 10%, то в качестве итога будет показано 20%.
Аналогично, при потере 10% будет показана итоговая потеря 20%.
Пусть прямолинейная экстраполяция и довольно надуманна, она
должна применяться здесь не в аддитивном, а в мультипликатив-
ном смысле. Другими словами, доход в 10% нашего примера,
будучи экстраполирован на оставшуюся часть месяца, должен бы
составить 1,1*1,1 = 1,21, или 21% дохода. Аналогичным образом,
потеря в 10% в данном случае должна бы представляться, как
0,9 * 0,9 = 0,81, или потерю в 19% за месяц.
94
Новая методология
Когда средства доступны только в течение одного или
нескольких дней, отчетные итоги становятся все более неверными.
Советник, от которого требуется использование временного взве-
шивания изъятий со счета и дополнений его, при потере 3!/з%
за день доступа к счету должен будет заявить о месячной потере
по этому счету, превышающей 100%. (Мультипликативный ме-
тод, продемонстрированный выше, также не адекватен, хоть
и в меньшей степени — вы не получите итогов, больших 100%,
и он не всегда направлен против менеджера. Однако это тоже
экстраполяция, которая предполагает, что итоги по другим сег-
ментам месяца не будут отличаться от тех, что получены за время
доступности средств.)
Эти вводящие в заблуждение требования: начисление воз-
награждения без выплаты и временное взвешивание изъятий со
счета и дополнений его — привносят огромную долю фикции.
Они обманывают публику. Это сродни тому, чтобы согласиться
с равенством 2 + 2 = 5 только потому, что какой-то ворчливый
маленький маньяк утверждает это. Управляющим капиталами
и инвестиционной общественности жилось бы гораздо лучше
в таком мире, где регулирующие учреждения не настаивают на
столь вредных математических заблуждениях.
2
Законы роста, полезность
и конечные потоки
Поскольку в данной книге используется математический аппарат,
описывающий процессы роста, мы не можем пройти мимо самих
законов роста. Подходя к ним с математических позиций, мы
можем обсуждать их в терминах функций роста или соответству-
ющих темпов роста.
Функции роста можно разделить на три отдельные катего-
рии, каждой из которых соответствует свой темп роста. На
рис. 2.1 эти три категории представлены линиями В, С и D,
а их темпы роста — линиями А, В и С, соответственно. Непо-
средственно слева от каждой функции роста расположен ее темп
роста.
Так, для функции роста В, или линейной функции роста,
темпом роста служит линия А. Хотя В сама является функцией
роста, она одновременно служит темпом роста для функции С,
которая называется экспоненциальной.
96
Законы роста, полезность и конечные потоки
Обратите внимание, что существует три функции роста:
линейная, экспоненциальная и гиперболическая. То есть гиперболи-
ческая функция роста имеет экспоненциальный темп роста, экс-
поненциальная функция роста имеет линейный темп роста, а ли-
нейная функция роста имеет горизонтальную функцию роста.
Здесь важную роль играют оси X и Y. При обсуждении
функций роста (В, С или D) ось Y представляет количество,
а ось X — время. При обсуждении темпов роста ось Y представ-
ляет изменение количества в зависимости от времени, а ось X
представляет количество.
Рис. 2.1.
Когда мы говорим о темпах и функциях роста в общем
плане, мы часто имеем в виду рост некоторой популяции. Первая
из трех основных функций роста — это линейная функция роста
(линия В), а ее темп роста — линия А. Члены популяции,
характеризующейся линейным ростом, склонны легко находить
уровень сосуществования.
Следующей идет экспоненциальная функция роста (ли-
ния С) со своим линейным темпом роста (линия В). Члены
этой популяции конкурируют между собой, и в действие всту-
пает принцип выживания сильнейшего. При экспоненциальной
функции роста возможно возникновение мутации, которая дает
селективное преимущество и закрепляется в потомках.
Наконец, в случае функции гиперболического роста
(линия D) и ее экспоненциального темпа роста (линия С) си-
Законы роста, полезность и конечные потоки 97
туация меняется. В отличие от экспоненциальной функции роста,
имеющей линейный темп роста, этот темп роста сам экспонен-
циальный. То есть, чем больше количество, тем быстрее темп
роста! Гиперболическая функция роста, в отличие от экспонен-
циальной функции, обладает свойством, которое мы называем
сингулярностью', в некоторой точке функция становится бесконеч-
но большой вертикальной асимптотой. Этого не происходит с фун-
кцией экспоненциального роста, которая просто все увеличива-
ется и увеличивается. При гиперболической функции роста мы
также обнаруживаем конкуренцию между членами популяции по
принципу выживания сильнейшего. Однако в некоторой точке
роста гиперболической популяции селективные преимущества
мутаций уже практически не могут закрепляться в следующем
поколении из-за очень быстрого увеличения остальной части
популяции.
Если при экспоненциальной или гиперболической функци-
ях роста между конкурирующими членами популяции имеются
функциональные связи, то это может закончиться любой из
следующих альтернатив:
1. Усиленной конкуренцией между партнерами;
2. Взаимным упрочением партнеров;
3. Вымиранием всей популяции.
Поскольку обсуждение математики роста почти невозможно
без привлечения понятия популяции, мы будем время от времени
обращаться к ней и далее. Математика роста является связующим
звеном между ростом популяций и нашей новой методологией.
Рост человеческой популяции
По прошествии первых двух миллионов лет нашей эволю-
ции на Земле было, самое большее, десять миллионов человек.
Далее, примерно десять тысяч лет тому назад, в неолите, чело-
7 - 9727
98
Законы роста, полезность и конечные потоки
веческая популяция начала увеличиваться в возрастающем темпе.
Несмотря на приблизительность данных, можно оценить размеры
населения Земли за последние две тысячи лет (рис. 2.2):
Год
Оценка величины населения, млрд.
0 0,25
1650 0,5
1850 1
1930 2
1990 5,3
С помощью элементарной экстраполяции легко убедиться,
что этим данным удовлетворяет гиперболическая функция роста
с сингулярностью. Асимптота, по которой наша популяция взле-
тит в бесконечность, располагается где-то в середине следующего
столетия!
Причина, по которой данная функция является гипербо-
лической, кроется в продолжающемся росте средней продолжи-
тельности жизни. Все больше женщин достигают детородного
возраста. Это приводит к сокращению времени, необходимого для
удвоения популяции, которое и так уже меньше средней продол-
жительности жизни!
Имейте в виду, что этот график и эти показатели роста
популяции получены после таких катастроф, как эпидемия «чер-
ной смерти»* четырнадцатого века, которая истребила почти две
трети населения Европы, после двух мировых войн (последняя
уничтожила около пятидесяти миллионов человек, из которых
двадцать семь миллионов приходится только на одну Россию!)
и всего остального, чем природа наказывала нас между делом. То
есть даже нечто столь катастрофическое, что стерло бы с лица
Земли две трети Европы, сегодня привело бы лишь к небольшо-
му временному сдвигу этой асимптоты вперед.
Прогнозы о будущем популяции разнятся. Согласно наибо-
лее оптимистичному из них, к 2075 году на Земле будет жить
от восьми до девяти миллиардов человек. Этот прогноз основы-
* Эпидемия чумы в Европе в 1348—1349 гг. — Прим. пер.
Законы роста, полезность и конечные потоки
99
Рис. 2.2. Рост человеческой популяции.
вается на темпах рождаемости и смертности, усредненных по всем
континентам. Отчет ООН 1990 г. не столь оптимистичен и назы-
вает цифру в 13 миллиардов человек к концу следующего сто-
летия при условии хоть какой-то формы регулирования роста
населения в мировом масштабе. В противном случае численность
населения Земли может легко достичь четырнадцати миллиардов.
Беда в том, и это наглядно показано на рис. 2.2, что рост
популяции является гиперболической функцией, которая очень
хорошо аппроксимирует как сами исторические данные, так и их
экстраполяцию в будущее.
Поскольку мы физически не можем превратиться в беско-
нечную популяцию, то чего же нам ждать? Взглянув на рис. 2.2,
вы можете обнаружить, что при теперешнем темпе роста числен-
ность населения станет превращаться в нашу основную проблему
много раньше середины следующего века.
Нетрудно себе представить целый ряд катастрофических
сценариев развития ситуации в будущем. Они прекрасно уклады-
ваются в два широких сценария, в первом из которых человек
поднимается против человека, и мы получаем какой-либо вари-
ант 3-й мировой войны. Не приходится сомневаться, что эта
отчетливая возможность способна основательно сократить наши
шеренги.
т
100 Законы роста, полезность и конечные потоки
Если сценарий военного противостояния в ближайшее вре-
мя не реализуется, то это увеличит вероятность другого широкого
сценария — противостояния природы и человека, который может
осуществиться благодаря всемирному заражению быстро распро-
страняющимися вирусами и стойкими бактериями. Кроме СПИДа
существуют и другие более заразные, но столь же смертельные
вирусы, передающиеся воздушно-капельным или другим путем,
которые атакуют нас уже сегодня. К ним относятся такие, как
вирус Эбола и человеческий парвовирус, угрожающие нам пол-
ным уничтожением.
Нельзя исключать, что в отдаленном будущем реализуется
другой сценарий полуоптимистического характера. Я называю его
сценарием космической станции, с которой в следующем столе-
тии мы начинаем распространяться за пределы нашей планеты,
обеспечивая благодаря этому свое выживание как вида. В долго-
срочном плане данный сценарий способен обеспечить большую
численность популяции, чем это возможно на одной лишь Земле.
Но он не предполагает, что проблема перенаселенности Земли
будет смягчена. Он просто допускает большую численность попу-
ляции в целом.
Описывая эти сценарии, нельзя не заметить их общей
доминанты. Так или иначе, но нам придется прибегнуть к поли-
тике регулирования численности населения в мировом масштабе,
или же она будет навязана нам естественным ходом событий.
Только жесткое ограничение прироста численности популяции
линейной функцией роста (как это делается в Китайской Народ-
ной Республике), оказывающей весьма щадящее воздействие на
земные ресурсы, может гарантировать нам длительное мирное
существование.
Все контраргументы свидетельствуют лишь о непонимании
математических свойств гиперболической функции роста! Это
прекрасно иллюстрирует так называемое зеленое движение. Я не
подвергаю критике принципы этого движения. В конечном итоге
то, к чему призывают зеленые, безусловно, необходимо. Но все
это вторично по сравнению с проблемой популяции, которая по
самой своей природе растет гиперболически. Если этот рост про-
должится, то мы столкнемся с экологической катастрофой из-за
истощения озонового слоя, вызванного избытком метана, когда
все пересядут на лошадей, либо с разрушительными для эколо-
Законы роста, полезность и конечные потоки
101
гии последствиями чрезмерного использования электрической энер-
гии, когда все пересядут на электромобили.
Автомобилист, попавший в дорожный затор, может ви-
нить в этом неэффективность современного технократического
устройства мира, но автомобильная пробка, узником которой он
стал, — это результат роста популяции. Она никуда не денется,
неважно, ездим ли мы на современных автомобилях или на
конных повозках.
То обстоятельство, что наша популяция генетически склон-
на к гиперболическому росту, представляет собой самую крупную
и первостепенную проблему современности. Поэтому было бы
неразумно обсуждать темпы роста в каком-либо ином контексте,
не рассмотрев их прежде в связи с ростом популяции.
Но хватит об этом. Вернемся к росту вообще и в торговле,
в частности.
Торговля экспоненциальна, а не гиперболична. Впрочем,
если некто с практически неограниченными средствами снабжал
бы вас деньгами для торговли при условии, что ваша результа-
тивность будет не ниже обещанной, то тогда торговля станет
гиперболичной. Это похоже на управление капиталом. Основная
проблема управляющих капиталом состоит именно в том, чтобы
выполнить это условие — обеспечить результативность не ниже
обещанной. В последней главе этой книги мы обсудим методы
решения этой проблемы.
Минимизация ожидаемого
среднего общего роста
До сих пор в этой книге, как и в двух ее предшествен-
ницах, мы занимались поиском значения /, которое приводило
бы к асимптотическому доминированию. То есть для данной
рыночной системы мы искали единственное значение/ которое
при реальной независимости между сделками с достоверностью
102
Законы роста, полезность и конечные потоки
приводило бы к максимальному геометрическому росту при стрем-
лении количества сделок (или периодов владения) к бесконеч-
ности. Это значит, что в весьма отдаленной перспективе с веро-
ятностью, приближающейся к достоверной, мы выиграли бы
больше, чем с помощью любой другой стратегии управления
капиталом.
Напомню, что если у нас есть только одна игра, то мы
максимизируем рост, прибегая к максимизации среднего ариф-
метического дохода за период владения (т. е. f= 1). Если у нас
бесконечное количество игр, то мы максимизируем рост путем
максимизации среднего геометрического итога периодов владения
(т. е. используем оптимальное f). Однако действительно оптималь-
ное f является функцией планируемой нами продолжительности
торговли — количества следующих друг за другом итогов конечных
периодов владения (HPR).
Для одного HPR игры с положительным математическим
ожиданием оптимальное /всегда будет равно 1,0. Если мы сыг-
раем при любом / отличном от 1,0, и остановимся после одного
периода владения, то мы не максимизируем наш ожидаемый
средний геометрический рост. То, что считается оптимальным /
будет таковым, если бы мы сыграли бесконечное количество
периодов владения. Для игры с положительным математическим
ожиданием действительно оптимальное /начинается с единицы
и стремится к оптимальному значению, при стремлении количе-
ства периодов владения к бесконечности.
Чтобы убедиться в этом, вновь рассмотрим нашу игру
в монетку «два-к-одному», для которой определенное нами оп-
тимальное / равно 0,25. Если в этой игре результат очередного
выбрасывания не зависит от предыдущих, то, ставя на каждый
кон без пропусков 25% счета, мы наверняка максимизируем наш
геометрический рост при стремлении продолжительности игры,
или количества подбрасываний (т. е. количества периодов владе-
ния), к бесконечности. Это значит, что наш ожидаемый средний
геометрический рост, то есть то, чем мы могли бы рассчитывать
закончить, — ожидаемая величина по всем возможным комбина-
циям исходов — будет самым большим, если ставить на кон по
25% счета.
Рассмотрим первое подбрасывание. С вероятностью 50% мы
выигрываем два долл, и с вероятностью 50% проигрываем один
Законы роста, полезность и конечные потоки 103
доллар. Перед вторым выбрасыванием мы имеем следующие шан-
сы: 25% на выигрыш двух долларов при первом выбрасывании
и 25% на выигрыш двух долларов при втором; 25% на выигрыш
двух долларов при первом выбрасывании и 25% на проигрыш
одного доллара при втором; 25% на проигрыш одного доллара
при первом выбрасывании и 25% на выигрыш двух долларов при
втором; 25% на проигрыш одного доллара при первом выбрасы-
вании и 25% на проигрыш одного доллара при втором (мы
считаем эти вероятности истинными, ибо исходим из предпосыл-
ки о независимости этих событий — см. раздел «Стохастическая
независимость» следующей главы). В ходе игры комбинации об-
разуют древовидную структуру. Поскольку в нашем сценарном
спектре только два сценария (орел и решка), из каждого узла
игрового дерева отходят только две ветви. Если бы в нашем
сценарном спектре было больше сценариев, то и ветвей было бы
больше:
№ выбрасывания
{1}{2}{3}
орел
орел решка
орел решка орел
решка орел
орел решка
решка решка орел
решка
Если мы поставим 25% наших денег на первое выбрасыва-
ние и выйдем из игры, то мы не максимизируем наш ожидаемый
средний общий рост (EACG).
104
Законы роста, полезность н конечные потоки
А что будет, если выйти из игры после второго выбрасы-
вания? Какой тогда должна быть оптимальная ставка, максими-
зирующая наш ожидаемый средний общий итог, когда в одном
случае мы играем при /= 1, и выходим из игры после первого
кона, а в другом — играем при оптимальном /и продолжаем игру
бесконечно долго?
Если мы вернемся назад и найдем оптимальное / которое
давало бы максимум среднего геометрического HPR за два пер-
вых кона в предположении, что при первом и втором выбра-
сываниях использовались различные значения / то получим
следующее. Во-первых, оптимальное/для выхода из этой игры
после двух конов приближается к асимптотически оптимально-
му, меняя свое значение с 1,0 (выход после первого кона) на
0,5 для первого и второго кона. То есть если бы мы собирались
выйти из игры после второго кона, то для максимизации роста
нам следовало бы на оба кона, первый и второй, ставить по 0,5
счета. Напоминаю, что мы имеем право для первого и второго
кона брать разные значения / Но в данном случае они оказы-
ваются одинаковыми: 0,5. Дело в том, что максимум роста для
конечных и бесконечных потоков достигается на одном и том
же оптимальном /
Мы можем убедиться в этом, если рассмотрим две первых
возможных комбинации выбрасываний монеты:
№ выбрасывания
{1}{2}
орел
орел
решка
орел
решка
решка
Откуда, перейдя к исходам, получаем:
Законы роста, полезность и конечные потоки 105
______№ выбрасывания______
{1}{2}
2
2
-1
2
-1
-1
Эти исходы можно преобразовать в итоги периодов владения
для различных значений f Ниже это сделано для /= 0,5, как при
первом, так и при втором выбрасывании монеты:
№ выбрасывания_
{1}_______________________{2}
2
2
0,5
2
0,5
0,5
Теперь мы можем выразить все выбрасывания, следующие
за первым, в виде значений TWR с помощью умножения на
последующие выбрасывания согласно дереву игры. Число в скоб-
ках, стоящее рядом с последней ветвью дерева — это корень
степени п из последнего значения TWR (п равно количеству
HPR, или выбрасываний, в данном случае — 2), который явля-
ется средним геометрическим HPR для конечного узла дерева:
______№ выбрасывания______
{1} {2}
4(2.0)
2
1(1,0)
1(1,0)
0,5
0,25 (0,5)
106
Законы роста, полезность н конечные потоки
Если теперь сложить средние геометрические значения HPR
и взять арифметическое среднее, то получим ожидаемый средний
общий доход. В данном случае он будет равен:
2,0
1,0
1,0
0,5
4,5/4 = 1,125
Следовательно, если бы мы прекращали игру после двух
конов, но делали бы это бесконечное количество раз (т. е. оста-
навливались после двух конов), ставя на каждый кон без про-
пусков оптимальные 50% счета, то максимизировали бы тем
самым наше EACG.
Обратите внимание, что ставка первого кона не соответ-
ствовала / = 1,0, хотя это оптимизировало бы ожидаемый сред-
ний общий рост, остановись мы после этого. Вместо этого,
планируя остановиться после двух конов, мы максимизируем
EACG, ставя на оба кона по 0,5 счета.
Заметьте, что оптимальное / доставляющее максимум ро-
ста, одинаково для всех конов игры, хотя и является функцией
того, как долго вы будете играть. Если вы собираетесь остано-
виться после первого кона, то оптимальное f максимизирует
среднее арифметическое HPR (для игры с положительным мате-
матическим ожиданием это /всегда равно 1,0, а игры с отри-
цательным математическим ожиданием - 0,0). Для игры с поло-
жительным математическим ожиданием оптимальное /убывает по
мере увеличения времени до остановки (асимптотически убывает
для бесконечной игры) и максимизирует среднее геометрическое
HPR. Для игры с отрицательным математическим ожиданием
оптимальное / всегда остается нулевым.
Однако в течение всей игры значение / которое вы ис-
пользуете для максимизации роста, остается постоянным, и эта
постоянная величина зависит (функционально) от того, где вы
собираетесь прекратить игру. Если вы играете в орлянку «два-к-
одному» и собираетесь остановиться после первого кона, то
получите максимальный рост при /= 1,0. Если вы собираетесь
Законы роста, полезность и конечные потоки
107
остановиться, сыграв два кона, то получите максимальный рост
при f = 0,5, как при первом, так и при втором выбрасывании.
Заметьте, что, желая максимизировать EACG для остановки
после второго кона, вы не ставите все свои деньги (1,0 счета)
на первый кон. Аналогичным образом, планируя играть бесконеч-
но долго, вы и на первый, и на все следующие выбрасывания
будете ставить по 0,25 счета.
Обращаю ваше внимание на радикальное отличие понятий
бесконечно и неограниченно. Все потоки конечны, всем нам суж-
дено в конце концов умереть. Поэтому, когда мы говорим, что
оптимальное /максимизирует ожидаемый средний общий итог,
то имеем в виду такое / которое максимизирует его при беско-
нечной игре. На деле, оно слегка отличается от оптимального, ибо
никто из нас не сможет играть бесконечно долго. То / которое
даст максимум EACG, будет немного больше того, что мы
называем оптимальным / а наши позиции — немного крупнее.
А что получится, если мы остановимся, сыграв три кона?
Должно ли тогда / которое максимизирует ожидаемый средний
общий рост, быть меньше 0,5 (остановка после двух конов), но
все же больше оптимального / = 0,25 для бесконечной игры?
В этом случае наше дерево комбинаций будет следующим:
№ выбрасывания
{1}{2}{3}
орел
орел решка
орел решка орел
решка орел
орел решка
решка орел
решка
решка
108 Законы роста, полезность н конечные потоки
Преобразуя это дерево в исходы, получим:
№ выбрасывания
{1} {2} {3}
2
2 -1
2 -1 2
-1
2
2 -1
-1 -1 2
-1
Если мы обратимся к компьютеру и путем перебора найдем
значение f которое максимизирует средний общий рост при
остановке после трех розыгрышей, то получим f = 0,37868.
Преобразуя исходы в HPR при данном значении /, получим:
№ выбрасывания
{1} {2} {3}
1,757369
1,757369 0,621316
1,757369 0,621316 1,757369
0,621316 1,757369
1,757369 0,621316
0,621316 1,757369
0,621316
0,621316
Законы роста, полезность и конечные потоки
109
Теперь мы можем выразить все выбрасывания, следующие
за первым, в виде значений TWR с помощью умножения на
последующие выбрасывания согласно дереву игры. Число в скоб-
ках, стоящее рядом с последним выбрасыванием дерева, — это
корень степени п из последнего значения TWR (л равно коли-
честву HPR, или выбрасываний, в данном случае - 2), который
является средним геометрическим HPR для конечного узла дерева:
№ выбрасывания______________
{1}____________________________________________________{3}
5,427324 (1,757369)
3,088329
1,918831 (1,242641)
1,757369
1,918848 (1,242644)
1,09188
0,678409 (0,87868)
1,918824 (1,242639)
1,091875
0,678401 (0,878676)
0,621316
0,678406 (0,878678)
0,386036
0,239851 (0,621318)
..8,742641 =1,09283 = EACG
8
Если вы хоть чуть сомневаетесь в полученных результатах,
то я рекомендую вам перепроверить несколько последних вык-
ладок с карандашом и бумагой или на компьютере и найти
значения / которые дадут EACG, больше представленного. До-
пустите возможность использования разных f то есть, что f
может меняться при каждом выбрасывании. Вы обнаружите, что
ваши результаты совпадают с нашими и что величина /посто-
янна, хотя и зависит от длины игры.
Подводя итоги, приходим к следующим выводам:
1. Максимизируя ожидаемый средний общий рост (EACG),
мы всегда приходим к постоянной величине / То есть
величина / не меняется от кона к кону.
110
Законы роста, полезность и конечные потоки
2. То /, которое оптимально в смысле максимизации EACG,
является функцией от длины игры. Для игр с положитель-
ным математическим ожиданием оно изменяется от 1,0,
максимизирующего среднее арифметическое HPR, немного
уменьшаясь с каждым коном, и асимптотически приближа-
ется к такому значению, которое максимизирует среднее
геометрическое HPR (это значение мы будем далее назы-
вать оптимальным f).
3. Поскольку длина всякого потока конечна, то наша торгов-
ля на основе оптимального f всегда будет слегка субопти-
мальной, независимо от того, как долго мы торгуем. Од-
нако различие с каждым периодом владения будет
уменьшаться. В итоге мы окажемся слева от вершины,
положение на которой действительно оптимально. Это ни в
коей мере не отрицает всего сказанного об (л + 1)-мерного
изображения в пространстве рычагов (недостатки и преиму-
щества положения рыночной системы относительно своего
оптимального f). Но само это изображение зависит от ко-
личества периодов владения, на котором мы останавлива-
емся. По мере удлинения игры она асимптотически прибли-
жается к действительно оптимальной поверхности, которую
мы выстраиваем с помощью приемов, излагаемых в книге.
1
0.9
0.8
0.7
0.6
0Л
0.4
0.3
0.21-
0.1 -
О'-------1------1-------i------1------1-------1------
1 2 3 4 5 6 7 8
Number of HPRs
Optimal f
—— f which maximizes
EACG
Рис.
2.3.
Оптимальное f в качестве горизонтальной асимптоты.
Законы роста, полезность и конечные потоки
111
Чтобы убедиться в сказанном, продолжим нашу орлянку
«два-к-одному». На графике (рис. 2.3) показаны значения /,
которые максимизируют наш ожидаемый средний общий рост
при остановке после 1—8 конов. Обратите внимание, что они
приближается к оптимальному значению 0,25, которое асимпто-
тически максимизирует рост при стремлении количества периодов
владения к бесконечности.
Орлянка «два-к-одному»
Остановка после HPR № Значение/, максимизирующее EACG
1 1,0
2 0,5
3 0,37868
4 0,33626
5 6 0,3148 0,3019
7 0,2932
8 0,2871
бесконечность
0,25 (оптимальное значение f)
В реальности, если мы торгуем при значении /, которое
в этой книге называется оптимальным, тем не менее, мы оста-
немся немного субоптимальны, и степень этой субоптимальности
будет уменьшаться по мере того, как будет проходить все больше
и больше периодов владения. Если бы мы точно знали, сколько
периодов владения будем торговать, то могли бы использовать то
значение /, которое максимизирует EACG и действительно оп-
тимально для этого количества владений (оно было бы несколько
больше оптимального J). К сожалению, мы редко с определенно-
стью можем сказать, сколько периодов владения будем торго-
вать, поэтому остается утешаться тем фактом, что оптимальное
f приближается к оптимальному значению для максимизации
EACG по мере истечения все большего количества периодов
112 Законы роста, полезность и конечные потоки
владения. В заключительной главе этой книги мы познакомимся
с методами постоянного доминирования, которые позволят нам
подойти к идее максимизации EACG в условиях разделения
счета на активную и пассивную части (т. е. когда торговля ведется
менее агрессивно, чем это рекомендуется оптимальным У).
Обратите внимание, что ни одна из этих идей не рассмат-
ривается или даже не упоминается в старых среднедисперсионных
моделях по типу «риск-прибыль». Старые модели почти полностью
игнорируют фактор финансового рычага и последствия его при-
менения, что еще раз указывает на предпочтительность нашего
нового подхода.
Теория полезности
Вопрос о теории полезности поднимается в книге из-за того,
что сторонников максимизации среднего геометрического часто
критикуют за то, что они способны максимизировать лишь случай
логарифмической (In х) полезности. То есть они стремятся мак-
симизировать только богатство, а не удовлетворенность инвесто-
ра. В этой книге мы попытаемся показать, что максимизацию
среднего геометрического можно применять при любой функции
полезности. Поэтому теперь нам придется обсудить теорию по-
лезности в общем плане, на уровне основных понятий.
Теорию полезности часто критикуют за то, что она трак-
тует поведение инвестора в отрыве от практики. К сожалению,
большинство этих нападок исходит от людей, принявших априор-
ное предположение, что все функции полезности инвестора явля-
ются логарифмическими, то есть что они нацелены на максими-
зацию капитала. Не являясь большим сторонником теории
полезности, я принимаю ее из-за отсутствия лучшего объяснения
предпочтений инвестора. Вместе с тем, я твердо убежден, что
если функция полезности инвестора отличается от In х, то на
рынках и в инвестировании в целом ему не место — ваше поло-
Законы роста, полезность и конечные потоки
ИЗ
жение на (п + 1)-мерного изображения, которую мы обсудили в
главе 1, не зависит от вашей кривой предпочтения, и когда оно
неудачно, вы расплачиваетесь за это реальными деньгами. Короче
говоря, рынки — это не подходящее место для тех, кто не
стремится максимизировать свой капитал. Возможно, куда ком-
фортнее им было бы на приеме у психиатра.
Теорема ожидаемой полезности
Некто в аэропорте имеет 500 долл., но ему нужно 600 долл.,
чтобы купить билет, который ему необходим. Ему предлагается
пари, где он с вероятностью 50% выигрывает 100 долл, и с
вероятностью 50% проигрывает 500 долл. Благоприятен ли такой
расклад? В данном случае, когда иметь билет жизненно необхо-
димо, этот расклад является хорошим.
В данном случае математическое ожидание полезности зна-
чительно отличается от математического ожидания прибыли.
Когда мы следуем теории полезности, мы определяем благо-
приятность пари на основе математического ожидания полезно-
сти, а не прибыли. Значит, в данном случае математическое
ожидание полезности положительно, хотя, с точки зрения
прибыли, это не так. В рамках дальнейшего обсуждения мы
будем трактовать понятия полезности и удовлетворенности
одинаковым образом.
Итак, у нас есть теорема ожидаемой полезности, которая
гласит, что инвесторы располагают функцией полезности капита-
ла U(x), где х — капитал, который они стремятся максимизиро-
вать. То есть инвесторы предпочитают такие инвестиционные
решения, которые максимизируют их функцию полезности капита-
ла. Лишь тогда, когда функция полезности U(x) = In х, то есть
когда полезность, или удовлетворение, капитала совпадает с са-
мим капиталом, теорема ожидаемой полезности приведет к тому
же выбору, что и максимизация капитала.
8 - 9727
114
Законы роста, полезность и конечные потоки
Свойства функций полезности
Функции полезности имеют пять основных свойств:
1. Функции полезности инвариантны относительно положи-
тельных линейных преобразований. Так, функция предпоч-
тения полезности In х, приведет к выбору тех же инве-
стиций, что и функции полезности 25 + In х, 7 * In х или
(In х)/1,453456. То есть функция полезности, подвергнутая
воздействию положительной константы (прибавлением, вы-
читанием, умножением или делением), приведет к выбору
тех же самых инвестиций. Другими словами, она приведет
к тому же набору инвестиций, максимизирующих полез-
ность, что и до воздействия на нее положительной кон-
стантой.
2. Большее предпочтительнее меньшего. В экономической ли-
тературе это часто называется ненасыщением. Другими сло-
вами, функция полезности никогда не приведет к предпоч-
тению меньшего капитала большему при достоверных исходах
или равенстве их вероятностей. Поскольку при росте капи-
тала должна расти и полезность, то первая производная от
полезности как функции капитала должна быть положи-
тельной. То есть:
U’(x) >= 0 [2.01]
Если полезность измерять по вертикальной оси, а капитал
— по горизонтальной, то у кривой полезности никогда не будет
отрицательного наклона.
Первой производной функции полезности In х будет х-1.
3. Предполагается три возможных типа отношения инвестора
к риску, называемых также нерасположенностью к риску.
Он может либо уклоняться от риска, либо быть нейтраль-
ным к нему, либо жаждать риска. Все эти категории могут
быть описаны в терминах справедливой азартной игры. Если
взять справедливую игру, такую, как подкидывание моне-
ты, с выигрышем одного доллара на орлах и проигрышем
Законы роста, полезность и конечные потоки
115
одного доллара на решках, то мы обнаружим, что матема-
тическое ожидание капитала равно нулю. Уклоняющийся от
риска индивидуум отверг бы такое пари, тогда как жаж-
дущий риска его бы принял. Инвестор, который нейтрален
к риску, был бы индифферентен к этому пари.
Неприятие риска характеризуется второй производной фун-
кции предпочтения полезности U"(x). У индивидуума, уклоняю-
щегося от риска, вторая производная отрицательна, у склонного
к риску — положительна, а у нейтрального к риску — вторая
производная функции предпочтения риска нулевая.
На рис. 2.4 изображены три основных типа функций пред-
почтения полезности в зависимости от U''(x), или степени непри-
ятия риска инвестора. Функция предпочтения полезности, равная
In х, демонстрирует нейтральное отношение к риску. Инвестор
индифферентен к справедливой азартной игре*. Для логарифми-
ческой функции предпочтения полезности вторая производная
будет равна —х~2.
4. Четвертое свойство функций предпочтения полезности ка-
сается того, как изменяется степень неприятия риска ин-
вестора при изменении капитала. При этом говорят об
абсолютной величине нерасположенности к риску. Здесь вновь
имеются три категории. К первой относятся индивидуумы,
которые проявляют возрастающее абсолютное неприятие
риска. По мере роста капитала они держат все меньше
средств в рискованных активах. Следующими идут индиви-
дуумы с постоянным абсолютным неприятием риска. С ростом
капитала они сохраняют те же денежные вложения в рис-
кованные активы. Последними идут те, кому свойственно
понижение абсолютного неприятия риска. С ростом капитала
они готовы держать больше денег в рискованных активах.
* Фактически, инвесторы должны отвергать справедливую азартную игру.
Поскольку количество денег, с которыми может работать инвестор, конечно, это
дает более низкая поглощающая граница. Можно показать, что если инвестор
периодически принимает справедливую азартную игру, то это лишь вопрос
времени, когда будет достигнута эта граница. То есть если вы не прекращаете
участвовать в справедливых азартных играх, то в итоге вы разоритесь с
вероятностью, приближающейся к достоверной.
8*
116
Законы роста, полезность и конечные потоки
Рис. 2.4. Три основных типа функций полезности.
Математически абсолютное неприятие риска А(х) выражает-
ся следующим образом:
= £Г(х) t2'02!
Если нам нужно узнать, как изменяется абсолютное непри-
ятие риска с изменением капитала, то мы берем первую произ-
водную от А(х) по х (капитал) — А '(х). При этом у индивидуума
с возрастающим абсолютным неприятием риска было бы А'(х) >0,
при постоянном абсолютном неприятии риска было бы А'(х) = 0,
а при понижающемся абсолютном неприятии риска было бы
А'(х) < 0.
В случае логарифмической функции предпочтения полезно-
сти имеет место понижающееся абсолютное неприятие риска. Для
In х имеем:
А(х) = —~5'2) = х-1 и А'(х) = -х~2<в
5. Пятое свойство функций предпочтения полезности касается
того, как изменяется доля средств, инвестированных в
Законы роста, полезность и конечные потоки 117
рискованные активы, с изменением капитала. При этом
говорят об относительной величине нерасположенности к риску.
Другими словами, это касается того, как изменяется доля,
а не денежная величина средств, инвестированных в рис-
кованные активы, в зависимости от изменения капитала.
Здесь вновь имеются три возможные категории: возраста-
ющее, постоянное и убывающее относительное неприятие
риска, где доля инвестиций в рискованные активы возра-
стает, постоянна или убывает, соответственно.
Математически относительное неприятие риска R(x) выра-
жается следующим образом:
*(х) = (~Х^)(Х)) = [2-03]
Отсюда R ’ (х), первая производная относительного избега-
ния риска, будет характеризовать, как изменяется относительное
неприятие риска в зависимости от изменений капитала. Поэтому
индивидуумам, которым свойственно возрастание, постоянство
и понижение относительного неприятия риска, будут отвечать
положительная, нулевая и отрицательная R ' (х), соответственно.
В случае логарифмической функции предпочтения полезно-
сти имеет место постоянное относительное неприятие риска. Для
In х имеем:
(~х * (—х-2))
R(x) = -----= 1 и R’(x) = 0
Иные взгляды на классическую
теорию полезности
Читателям следует иметь в виду, что, хотя теория полез-
ности получила широкую поддержку, она не является единствен-
ным объяснением поведения инвестора. Например, Р. К. Вентуорт
118
Законы роста, полезность и конечные потоки
утверждает, что использование среднего значения в теореме
ожидаемой полезности является неоправданным и искусственным.
Он исходит из того, что игроки большее значение придают моде
распределения, нежели среднему, и действуют в направлении ее
максимизации.
Лично я нахожу работы Вентуорта в этой области весьма
интересными*. В них содержится ряд довольно любопытных по-
ложений. В первую очередь они напрямую атакуют классическую
теорию полезности, что автоматически ожесточает против них
всех профессионалов из исследовательских подразделений в обла-
сти методов управления. Нелинейность функции полезности ка-
питала, лежащая в основе классической теории, для этих людей
священна. Вентуорт же проводит параллель между максимизацией
моды и эволюцией. На этом он основывает свою гипотезу выжи-
вания. Краткий сравнительный обзор этих двух подходов выгля-
дит следующим образом:
Теория полезности
Одноразовое, Нелинейная Наблюдаемое
рискованное + функция => поведение
принятие решений полезности капитала
Гипотеза выживания
Одноразовое, Выстраивание
рискованное + эквивалентных
принятие решений временных рядов
Идентичное
=> наблюдаемое
поведение
Кроме того, существуют несколько интересных биологичес-
ких экспериментов, говорящих в пользу идей Вентуорта. В час-
тности, подвергаются сомнению контрольные эксперименты со
шмелями, отыскивающими нектар по канонам классической те-
ории полезности.
Так зачем же вообще упоминать классическую теорию
полезности? В рамках данной книги мы избегаем каких-либо
* См. «Utility, Survival and Time: Desision Strategies Under Favorable
Uncertainty» и «А Theory of Risk Management Under Favorable Uncertainty».
8072 Broadway Terrace, Oakland, CA 94611.
Законы роста, полезность и конечные потоки
119
предпосылок из области теории полезности. Вместе с тем, суще-
ствует определенная взаимосвязь между полезностью и нашей
новой методологией инвестирования. Те, кто следует теории
полезности, увидит, как она применяется. Эта часть книги адре-
сована тем читателям, которые не знакомы с кривыми предпоч-
тения полезности, но никоим образом не отстаивает адекватность
теории полезности, как таковой. Читатель должен учитывать
существование и других, основанных не на полезности, подхо-
дов, которые могут объяснять поведение инвесторов.
Как найти свою кривую
полезности
Будем исходить из того, что себя лучше знать, чем наобо-
рот, и безотносительно к классической теории полезности под-
робно рассмотрим методы определения нашей собственной фун-
кции полезности. Далее следует пересказ материала из книги
Тьюлса, Харлоу и Стоуна «Игра с товарными фьчерсами. Кто
выигрывавет ? Кто проигрывает ? И почему ?»21
Для начала следует задаться двумя предельными величина-
ми, одной положительной, другой отрицательной, которые дол-
жны играть роль экстремальных исходов торговли. Обычно в
качестве таких величин следует выбирать 3-5-кратный макси-
мальный выигрыш или проигрыш, которые вам привычно ожи-
дать от следующей сделки.
Давайте предположим, что в лучшем случае вы рассчиты-
ваете выиграть 5000 долл, или проиграть 3000 долл. Следователь-
но, за верхний экстремум можно принять 20000 долл., а за
нижний — минус 10000 долл.
Далее сформируем таблицу, как показано ниже, самый
левый столбец которой называется Вероятность наилучшего ис-
хода и имеет десять строк, заполненные убывающими величина-
ми от 1,0 до 0 с шагом 0,1. Наш следующий столбец следует
120
Законы роста, полезность и конечные потоки
назвать Вероятность наихудшего исхода, значения в котором
будут просто равны 1 минус вероятность наилучшего исхода из
этой строки первого столбца. Третий столбец будет назван Цена
достоверности. В первой строке вы поставите стоимость наилуч-
шего исхода, а в последней — стоимость наихудшего исхода.
В результате вся таблица будет выглядеть следующим образом:
р (Наилучший исход) Р (Наихудший исход)
1,0 0
0,9 0,1
0,8 0,2
0,7 0,3
0,6 0,4
0,5 0,5
0,4 0,6
0,3 0,7
0,2 0,8
0,1 0,9
0 1,0
Цена
уверенности
Расчетная
полезность
$20000
-$10000
Объясним смысл термина цена уверенности. Он обозначает
ту плату, на которую мы наверняка согласились бы вместо
возможности проведения сделки, или цену, которую мы бы сами
заплатили, чтобы избежать проведения сделки.
Теперь нужно заполнить третий столбец ценами уверенности.
Значение в первой строке, куда мы занесли 20000 долларов,
означает просто, что мы бы лучше сразу приняли 20000 долларов
наличными, нежели совершить сделку со 100% вероятностью
выиграть 20000 долларов. Аналогичным образом -10000 долларов,
занесенные в последнюю строку, означают просто, что вы готовы
сразу заплатить 10000 долларов, чтобы уйти от сделки со 100%
шансами проиграть 10000 долларов.
Затем во вторую строку нужно занести цену уверенности
для сделки с 90% шансами выигрыша 20000 долларов и 10%
Законы роста, полезность и конечные потоки
121
шансами проигрыша 10000 долларов. Какую сумму наличными вы
готовы были бы принять вместо проведения этой сделки? Напо-
минаю, что это — реальные деньги с реальной покупательной
способностью, а доход или убыток от проведения сделки будет
немедленным и в наличных. Давайте предположим, что для вас
это стоит 15000 долларов. То есть за 15000 долларов, врученных
вам немедленно, вы откажетесь от возможности с вероятностью
90% выиграть 20000 долларов и с вероятностью 10% проиграть
10000 долларов.
Таким же образом нужно заполнить и остальные ячейки
этого столбца таблицы. Например, заполняя предпоследнюю ячей-
ку, нужно задаться вопросом, сколько вы готовы заплатить,
чтобы отказаться от 10 шансов (10%) выиграть 20000 долл,
против 90 шансов (90%) проиграть 10000 долл. Поскольку за-
платить придется вам, эту цену уверенности нужно писать со
знаком минус.
После третьего столбца нужно заполнить четвертый столбец
таблицы под названием Расчетная полезность. Формула расчетной
полезности проста:
Computed Utility = U* /’(best outcome) + V* P(worst outcome) [2.04],
где:
U = заданная константа, равная 1,0 в данном случае;
К= заданная константа, в давном случае равная —1,0.
Отсюда для второй строки таблицы получим:
Расчетная полезность = 1 * 0,9 — 1 * 0,1
= 0,9-0,1
= 0,8
Когда вы закончите заполнение столбца расчетной полезно-
сти, ваша таблица примет следующий вид:
122 Р (Наилучший исход) Законы роста, полезность н конечные потоки
Р (Наихудший исход) Цена уверенности Расчетная полезность
1,0 0 " $20000 1,0
0,9 0,1 $15000 0,8
0,8 0,2 $10000 0,6
0,7 0,3 $7500 0,4
0,6 0,4 $5000 0,2
0,5 0,5 $2500 0
0,4 0,6 $800 -0,2
0,3 0,7 -$1500 -0,4
0,2 0,8 -$3000 -0,6
0,1 0,9 -$4000 -0,8
0 1,0 -$10000 -1,0
Computed utility
Рис. 2.5. Пример функции полезности.
Законы роста, полезность и конечные потоки
123
Далее, расположив расчетную полезность по оси у, а цену
уверенности по оси х, вычертите соответствующий график. В ре-
зультате ваша функция полезности будет выглядеть так, как это
показано на рис. 2.5.
Теперь нужно повторить расчеты, но только с другими
наилучшим и наихудшим исходами. В качестве таковых выберите
из предыдущей таблицы по одной цене уверенности для наилуч-
шего и для наихудшего исходов. Предположим, мы выбрали
10000 долларов и —4000 долларов. Заметьте, что расчетные полез-
ности, ассоциированные с этими ценами уверенности, равны 0,6
(10000 долларов) и —0,8 (и —4000 долларов). Поэтому значения
U и V при определении расчетных полезностей в этой второй
таблице будут равны 0,6 и -0,8, соответственно. Вновь назначьте
цены уверенности и рассчитайте соответствующие расчетные по-
лезности:
р (Наилучший исход) Р (Наихудший исход) Эквивалент достоверности Расчетная полезность
1,0 0 $10000 0,6
0,9 0,1 $8000 0,46
0,8 0,2 $6000 0,32
0,7 0,3 $5000 0,18
0,6 0,4 $4000 0,04
0,5 0,5 $2500 -0,10
0,4 0,6 $500 -0,24
0,3 0,7 -$1000 -0,38
0,2 0,8 -$2000 -0,52
0,1 0,9 -$3000 -0,66
0 1,0 -$4000 -0,80
А затем снова вычертите их на графике. Этот процесс
нужно повторить несколько раз, продолжая вычерчивать все
величины на одном и том же графике. При этом перед вами,
124 Законы роста, полезность и конечные потоки
возможно, начнет открываться некоторая разбросанность вели-
чин, то есть не все они будут четко тяготеть к одной и той же
линии. Такой разброс свидетельствует о непоследовательности
ваших решений. Разброс обычно более выражен около экстрему-
мов графика (слева и справа). Это естественно и лишь указывает
те области, где вы, по-видимому, не обладаете большим опытом
выигрышей и проигрышей.
Большое значение имеет форма кривой, которую нужно
рассматривать с позиций предыдущего раздела {Свойства фун-
кций предпочтения полезности). Довольно часто эта форма ока-
зывается не такой идеальной, как приводимые в учебниках
вогнутые вверх, вогнутые вниз или прямолинейные разновид-
ности. Это вновь как-то характеризует вас и заслуживает тща-
тельного изучения.
В конечном итоге наиболее продуктивной формой функ-
ции предпочтения полезности в смысле максимизации капитала
является прямая, устремленная вверх с понижающейся абсо-
лютной величиной и постоянной относительной величиной
неприятия риска и почти индифферентная к справедливой
азартной игре. То есть мы индифферентны к азартной игре, не
имеющей хотя бы самого минимального положительного мате-
матического ожидания. Если ваша кривая хоть в чем-то хуже
этого, то, возможно, пришло время подумать над тем, к чему
и зачем вы стремитесь, и, быть может, провести некоторую
самокоррекцию.
Полезность и новая
методология
У этой книги нет никакой иной позиции относительно
теории полезности, кроме следующей: независимо от вашей
кривой предпочтения полезности, вы располагаетесь где-то на
плоскости рычагов для одной игры (рис. 1.2) и где-то в
Законы роста, полезность и конечные потоки 125
(п + 1)-мерном пространстве рычагов для многих одновремен-
ных игр, пользуясь преимуществами и оплачивая издержки
этого, вне всякой связи с тем, каково ваше предпочтение
полезности.
Зачастую критерий среднего геометрического критикуют за
его нацеленность исключительно на максимизацию капитала и за
то, что он максимизирует полезность только для логарифмичес-
кой функции.
На деле же, тот, кто не придерживается логарифмической
функции предпочтения полезности, всегда может максимизиро-
вать полезность во многом подобно тому, как мы максимизируем
капитал с помощью оптимального f за тем исключением, что
для каждого периода владения будет свое значение оптимального
f То есть если чья-то функция предпочтения полезности отлича-
ется от In х (максимизация капитала), то его оптимальное f для
максимизации (асимптотической) полезности будет переменным,
в то время как его оптимальное f для максимизации капитала
будет постоянным. Другими словами, если, зарабатывая больше
денег, вы следуете такой полезности, что готовы рисковать все
меньше, то ваше оптимальное /будет уменьшаться с завершени-
ем каждого периода владения.
Не смешивайте это с ранее высказаным положением, со-
гласно которому оптимальное / для максимизации ожидаемого
среднего общего роста является функцией количества периодов
владения, после которого вы останавливаетесь. Это по-прежнему
так. Здесь же обсуждается другое положение, согласно которому
оптимальное для максимизации полезности / меняется со време-
нем. Например, мы убедились при рассмотрении игры в монетку
«два-к-одному», что если мы планируем остановиться после трех
игр, или трех периодов владения, то максимизировали бы рост,
ставя на каждый кон по 0,37868 счета. То есть мы постоянно
ставили бы по 0,37868 счета на все три кона.
Если теперь нам нужно максимизировать иную полезность,
чем при максимизации капитала, то у нас не будет единого зна-
чения /для всех и для каждого розыгрыша. Напротив, для каждого
кона мы получили бы свое, отличное от других, значение /
Таким образом, с помощью данного подхода можно мак-
симизировать полезность, не сводящуюся к логарифмической
126 Законы роста, полезность и конечные потоки
функции предпочтения полезности, использовать разные значения
f при переходе от одного периода владения к другому. Если
предпочтение полезности логарифмическое, то есть как при
максимизации капитала, то оптимальное f всегда постоянно.
Другими словами, оптимальное f не изменяется от одного кона
к другому. Если предпочтение полезности отличается от In х
(максимизация капитала), то нужны различные оптимальные f
при переходе от одного периода владения к другому.
Максимизировать полезность можно тем же самым спосо-
бом, который используется при максимизации капитала. Для
этого исходам каждого сценария вместо долларовых величин
нужно сопоставлять величины, выраженные в ютилах (может
быть, просто в «единицах полезности» ?). Под ютилом понимается
некая единица удовлетворенности. Набор сценариев должен со-
держать сценарии с отрицательными ютилами точно так же, как
при максимизации капитала нужно иметь сценарии, соответ-
ствующие потере денег. Кроме того, (арифметическое) матема-
тическое ожидание набора сценариев в ютилах должно быть
положительным или отрицательным, когда это улучшает общую
смесь компонентов.
Но как определять переменное значение f по мере увели-
чения количества периодов владения, если наша кривая пред-
почтения полезности отличается от In х? Когда при изменении
счета вы обновляете стоимость исходов (в ютилах) перед нача-
лом нового периода владения, вы получаете новое значение
оптимального f Деля его на исход самого проигрышного сцена-
рия (в ютилах), вы получаете оптимальную величину/$ (также
в ютилах) и определяете, сколькими контрактами торговать.
Это совсем несложно: вы просто заменяете доллары на ютилы.
Единственное, что еще необходимо, — это отслеживать общую
величину счета в ютилах (вместо долларов). Заметьте, что если
вы действуете таким образом и ваша функция предпочтения
полезности отличается от In х, то в итоге вы действительно
получаете изменяющиеся оптимальные f от одного периода
владения к другому в долларовом выражении.
Например, если вновь обратиться к игре в монетку, кото-
рая предлагает нам два доллара за выпадение орла и отбирает
один доллар за выпадение решки, то сколько нам следует ставить
Законы роста, полезность и конечные потоки
127
на кон? Мы знаем, что если мы хотим максимизировать капитал
в непрерывном режиме, в каждом следущем розыгрыше распо-
лагая теми же деньгами, что и в начале игры, то на каждый кон
мы должны ставить 25% того, что можем. Это максимизировало
бы не только капитал, но и полезность, если мы определим, что
выигрыш двух долларов для нас в два раза ценнее, чем проигрыш
одного доллара.
А что, если выигрыш двух долларов был бы для нас лишь
в полтора раза ценнее проигрыша одного доллара? Для максими-
зации такой полезности мы сопоставляем проигрышному сцена-
рию, то есть решкам, значение —1 (в ютилах), а выигрышному
сценарию, то есть орлам, — значение 1,5 (в ютилах). Определив
оптимальное f применительно к измерению в ютилах, а не
в долларах, получим, что оно равно 0,166666. Это означает, что
для максимизации нашей средней геометрической полезности на
каждый кон следует ставить по 162/з %. То есть, чтобы определить
количество контрактов, нужно общую величину счета в ютилах
разделить на 0,166666.
Далее мы можем преобразовать это значение в количество
контрактов на долларовую величину счета и отсюда рассчитать то
значение f (между нулем и единицей), которое мы действительно
используем (в долларах, а не в ютилах).
Проделав это, мы сможем применить к этой задаче все ту
же кривую оптимизации капитала для игры в монетку «два-к-
одному», имеющей вершину при /= 0,25 (рис. 1.2), но в данном
случае абсцисса ее пика будет равна 0,166666. В долларовом вы-
ражении негативные последствия субоптимальности нашей пози-
ции будут по-прежнему зависеть от f— 0,25. Однако кривая
полезности достигает вершины при /= 0,166666, где мы и нахо-
димся. Заметьте, что если бы мы расположились на этой кривой
в точке с абсциссой 0,25, то оказались бы много правее ее
вершины и оплачивали бы соответствующие издержки в единицах
полезности.
Предположим теперь, что в данном периоде владения нам
повезло и мы собираемся продолжить игру, обновляя исходы
сценариев в ютилах. На этот раз у нас больше денег, поэтому
полезность выигрышного сценария в следующем периоде владе-
ния понизится до 1,4 ютила. Мы вновь рассчитываем наше оп-
128 Законы роста, полезность и конечные потоки
тимальное f в ютилах и, определилив, сколькими единицами
торговать в следующем периоде владения (исходя из величины
счета в ютилах), можем получить долларовую величину f (от нуля
до единицы). Проделав это, мы обнаружим, что она иная, чем
в предыдущем периоде владения.
В рассмотренном примере мы предполагали, что участвуем
в двух и более последовательных розыгрышах, в каждом из
которых мы повторно используем те деньги, с которых начали.
Если бы мы участвовали лишь в одном розыгрыше, то есть в
одном периоде владения, или получали бы дополнительные день-
ги для игры в каждом следующем периоде владения, то опти-
мальной стратегией была бы максимизация арифметической
ожидаемой полезности. Однако в большинстве случаев нам при-
ходится в следующем розыгрыше (периоде владения) вновь ис-
пользовать те деньги, которыми мы располагали в предыдущем
розыгрыше. Поэтому мы должны стремиться максимизировать
геометрический средний рост. Для одних это может означать
максимизацию геометрического ожидаемого роста капитала, для
других — максимизацию геометрического ожидаемого роста по-
лезности. Математика в обоих случаях одна и та же. И там, и там
мы имеем две поверхности в (n + 1)-мерном пространстве: повер-
хность максимизации капитала и поверхность максимизации
полезности. Для тех, кто максимизирует ожидаемый рост капи-
тала, эти кривые совпадают.
В этом месте я повторю сказанное в начале данной главы
относительно того, интересует ли вас что-то еще, кроме денег.
Рынок — это не место ни для забавы, ни для того, чтобы что-
то доказать себе или кому-нибудь еще. Если вы инвестируете
с какой-то иной целью, кроме максимизации капитала, то бу-
дете склонны к таким инвестиционным решениям, которые вам
дорого обойдутся.
В последующем мы будем предполагать, что читатель стре-
мится к максимизации капитала. Однако если кривая предпочте-
ния полезности читателя отличается от In х, то он может восполь-
зоваться изложенными здесь приемами при условии, что денежная
стоимость исходов сценариев будет выражена в ютилах. Это при-
ведет к непостоянству значений оптимального f (они будут ме-
няться от одного периода владения к другому).
Законы роста, полезность и конечные потоки 129
Впрочем, мы предупредили этих читателей, что им все
равно придется оплатить (деньгами) издержки своего субопти-
мального положения в (и + 1)-мерном пространстве рычагов
максимизации капитала. Вновь повторю, что это так потому,
что безотносительно к вашей кривой предпочтения полезности,
вы находитесь где-то на плоскости (см. рис. 1.2) для одной
игры и где-то в (и + 1)-мерном пространстве рычагов для
нескольких одновременных игр. Вы пользуетесь преимущества-
ми, точно так же, как оплачиваете издержки этого вне всякой
связи с вашей функцией предпочтения полезности. В идеале,
ваша функция предпочтения полезности должна быть логариф-
мической.
3
Условные вероятности
и корреляция
Наша новая методология инвестирования требует использования
условных вероятностей. Они являются краеугольным камнем нашего
подхода. Не умея оценивать условные вероятности, мы не сможем
определить оптимальное инвестирование. Итак, что же такое
условная вероятность?
Условная вероятность — это вероятность реализации одного
события при условии предварительной реализации другого собы-
тия или одновременной реализации двух событий. То есть это
вероятность наступления события В при условии, что уже насту-
пило событие А. Это записывается как р(А|В), что буквально
означает «Вероятность события А при условии наступления собы-
тия В».
Условные вероятности нередко называют также совместны-
ми вероятностями. С точки зрения математики, эти вероятности
означают одно и то же. Но обычно термин условные вероятности
9*
132
Условные вероятности и корреляция
используют для обозначения вероятностей, когда одно из собы-
тий уже заведомо наступило (т. е. предполагается, что события
происходят по очереди), а термин совместные вероятности ис-
пользуют, когда события происходят одновременно. На протяже-
нии данной главы эти термины будут пониматься одинаково
(поскольку одинакова их математика*); поэтому термины услов-
ные вероятности и совместные вероятности будут использоваться
попеременно.
Вероятность наступления хотя бы одного из двух событий
А или В равна сумме их индивидуальных вероятностей минус их
условные вероятности:
р(А или В) = р(А) + р(В) — р(А | В).
Отсюда для случая двух монет получаем:
р(орел на монете 1 или орел на монете 2) = р(орел на монете 1)
+ р(орел монеты 2) — р(орел на обеих монетах).
То есть в численном выражении,
р(орел монеты 1 или орел монеты 2) = 0,5 + 0,5 — 0,25 = 0,75.
Если мы подбрасываем две монеты одновременно (или одну
монету два раза подряд), то могли бы ожидать появления, по
крайней мере, одного орла с вероятностью 0,75.
Если события взаимоисключающие, то есть оба наступить
не могут в том смысле, что если наступает одно событие, то
другое наступить не может — тогда условная вероятность р(А | В)
равна нулю, и формула принимает вид:
р(А или В) = р(А) + р(В).
* Данное утверждение автора, мягко говоря, неточно. В действительности
соотношение между совместными и условными вероятностми определяется
формулой: р(В | А) = Р(АВ)/Р(А). — Прим. пер.
Условные вероятности и корреляция
133
Например, если мы бросаем монету, которая с вероятно-
стью 0,5 выпадает орлом и с вероятностью 0,5 - решкой, то
вероятность выпадения орла или решки равна 0,5 + 0,5 = 1.
А вот пример того, какое отношение имеют условные ве-
роятности к нашей новой методологии. Предположим, что мы
рассматриваем вопрос распределения инвестиций между двумя
акциями, акцией АВС и акцией XYZ. Мы можем поинтересоваться,
какова вероятность, скажем, 2%-ного или более роста цены XYZ
при условии, что по АВС также имеется рост в 2% или более:
p(XYZ >= 2% | АВС >= 2%).
Или же нам понадобится узнать, какова вероятность роста
по XYZ на 2% или более при условии падения по АВС на 1%
или более:
p(XYZ >= 2% | АВС <= -1%).
При поверхностном рассмотрении это может выглядеть
достаточно просто, как и считается в традиционной статистике,
но для очень ограниченного типа случаев. В отношении условных
вероятностей традиционная статистика может решить эту пробле-
му лишь в частном случае, когда коэффициент корреляции между
АВС и XYZ равен нулю.
Продолжим бросать монету. Исход индивидуального случай-
ного события (случайного в том смысле, что мы не знаем исхода
события до того, как оно произойдет, как при бросании монеты)
называется случайной величиной. Так, в процессе бросания монеты
исход бросания является случайной величиной, которая в данном
случае может принимать два значения: орел или решка.
Предположим на время, что мы бросаем две монеты. Веро-
ятность выпадения орла при бросании одной из двух монет равна
0,5. (Мы предполагаем, что имеем дело с идеальными монетами,
у которых вероятности выпадения орла и решки равна по 0,5.)
Следовательно, вероятность выпадения орла на обеих монетах
равна 0,25, что получается умножением вероятности выпадения
орла на первой монете 0,5 на вероятность выпадения орла на
второй монете 0,5.
134
Условные вероятности и корреляция
Эта совместная вероятность 0,25 выпадения орлов на обеих
монетах может быть получена из того, что всего имеется четыре
равновероятных возможных исхода при бросании двух монет (00,
OP, РО, РР), образующих выборочное пространство. Следова-
тельно, шансы 00 равны 1 из 4, или 0,25.
Количество реализаций
(частота) и вероятность
Чаще всего совместные вероятности для двух случайных
переменных представляются в табличной форме. Например, для
нашего потока исходов одновременного бросания двух монет
(00, ОР, РО, РР) мы можем составить таблицу, демонстриру-
ющую эти четыре одновременных события:
Количество реализаций (частота)
Монета 1
Орел Решка
Орел 1 1
Монета 2
Решка 1 1
Часто с помощью таблиц представляют и вероятности:
_____________Вероятности_____________
Монета 1
Орел Решка
Орел 0,25 0,25
Монета 2
Решка 0,25 0,25
Условные вероятности и корреляция 135
Мы предполагаем, и вполне правомерно, что между двумя
монетами нет никакой корреляции. То есть исходы бросаний двух
монет не зависят друг от друга. Если бы это было не так, то
каждый из четырех возможных исходов (00, ОР, РО, РР) не
имел бы одну и ту же вероятность реализации.
Теперь введем понятие стохастической независимости. Если
совместная вероятность двух событий равна произведению их
индивидуальных вероятностей (как в нашем примере с бросанием
монеты), то говорят, что налицо стохастическая независимость.
То есть, когда верно выражение
р(В | А) = р(А) * р(В) [3.01],
тогда имеет место стохастическая независимость. Часто через
это уравнение определяют совместную вероятность независимых
случайных переменных.
Стохастическая независимость, следовательно, синонимич-
на в используемом нами смысле нулевому коэффициенту корре-
ляции между двумя потоками исходов.
Поэтому при наличии стохастической независимости мы
можем говорить, что коэффициент корреляции равен нулю.
Обратное, однако, неверно. Мы вскоре увидим, что бывает и так,
когда коэффициент корреляции равен нулю, а стохастической
независимости нет.
Когда мы говорим о таблице исходов одной случайной
переменной, мы имеем в виду безусловное распределение этой
переменной. Например:
Монета 1
Орел Решка
0,5 0,5
Когда речь идет о таблице исходов большего количества
переменных, мы имеем в виду то, что называется совместным
распределением переменных. Например:
136
Условные вероятности и корреляция
Монета 1
____________Орел____Решка
Орел 0,25 0,25
Монета 2
Решка 0,25 0,25
Обычно условные вероятности рассматриваются в предпо-
ложении стохастической независимости. Во многих случаях, вроде
бросания двух монет, это предположение оправданно. Но есть
масса реальных ситуаций, например, при оценке вероятности
того, что в определенный день одновременно вырастут две акции
(акции обычно положительно коррелированны друг с другом, т. е.
коэффициент корреляции > 0), это традиционное предположение
теряет силу. Совместные вероятности нельзя рассчитать простым
перемножением индивидуальных вероятностей.
Эта проблема изводила меня в течение трех лет. Я пытался
найти решение на пути обобщения теории условных вероятностей.
То есть такое, которое бы давало условные вероятности для
любых значений коэффициента корреляции, а не только для
удобных значений, вроде 0, 1 или —1. Мне нужна была теория,
которая давала бы условные вероятности для всех значений ко-
эффициента корреляции между двумя случайными переменными.
Я докучал университетам, докторам математики, свихнув-
шимся профессорам, южноамериканским знахарям, статистикам
из страховых обществ и всем прочим, кто, по моему мнению,
мог бы иметь ключ к этой проблеме. Часами я просеивал горы
скучных технических журналов.
Я лично непрестанно искал решение этой проблемы. Я без-
результатно возился с идеей суперпозиции двух распределений ис-
ходов под углом между ними, согласно коэффициенту корреляции,
вычисляя интегралы по образуемым ими поверхностям. Долгое вре-
мя я думал, что смогу воспользоваться направляющими (частью
очевидных на желаемых вероятностях и туманных в остальном). Я хотел
выстроить их под углами, согласно их корреляции, пустить вектора,
которые пройдут через очевидные части. Пересекаемые ими области
будут разделены параллелограммом, образованным возможными зона-
ми пересечения событий, откуда будут получены совместные вероят-
ности. Я вывел все необходимые формулы и запрограммировал их
в виде огромных электронных таблиц для анализа результатов этой
Условные вероятности и корреляция
137
концептуальной эквилибристики. На это ушла масса блокнотных
страниц, салфеток и этикеток спичечных коробков.
Чем больше я работал над этой проблемой, тем более важ-
ным казалось мне ее решение. Почему же никто не мог решить
проблему совместных вероятностей, столь важной для практичес-
ких нужд? Почему же условные вероятности проработаны лишь
для самых удобных значений коэффициента корреляции? Это было
единственное, чего не хватало нашей новой методологии инвести-
рования. Я вывел целевую функцию, но в ней в качестве аргу-
ментов использовались именно эти условные вероятности.
Как вы увидите в следующей главе, для реализации более
совершенного подхода к инвестированию имелось все, кроме
способа расчета совместных вероятностей по любым значениям
коэффициента корреляции между двумя потоками случайных
переменных.
Подлинное страдание причиняла мне известная теорема об
условных вероятностях, утверждавшая, что совместную плотность
вероятности нельзя получить из безусловных плотностей вероятно-
сти компонент. Согласно традиционной точке зрения считалось,
что в отсутствие стохастической независимости функция совмес-
тной плотности вероятности является уникальной, вполне самосто-
ятельной, которая возникает как бы ниоткуда! То есть она не
выражается через функции безусловных плотностей составляющих,
а есть новая, самостоятельная функция плотности вероятности,
которая не может быть восстановлена из функций безусловных
плотностей составляющих. Чтобы убедиться в этом, рассмотрим
следующую таблицу, позаимствованную у Феллера*, которую мы
графически проиллюстрировали на рис. 3.1.
X
0 12 3 Безусл. плотностьУ
1 2 0 0 1 3
Y 2 6 6 6 0 18
3 0 6 0 0 6
Безусл. плотность X 8 12 6 1 27
* William Feller, An Introduction to Probability Theory and Its Applications,
Vol. II, New York: John Wiley & Sons, 1966.
138
Условные вероятности и корреляция
Рис. 3.1. Распределение совместной вероятности.
Коэффициент корреляции между потоками исходов собы-
тия X и события Y равен нулю. Поэтому, если бы имела место
стохастическая независимость, то можно было бы ожидать, что
вероятность Х = 0 и Y = 3 будет равна (6/27) * (8/27) =
0,222 * 0,0658 = 0,0658. Вместо этого, эта вероятность равняется
нулю, подтверждая тем самым принятую теорему условных ве-
роятностей о том, что совместные плотности не могут быть
получены из безусловных плотностей компонентов.
Было известно, как определять коэффициент корреляции
при наличии только совместной плотности и безусловных плот-
ностей* , но долгое время считалось, что нельзя определить со-
вместную плотность, располагая лишь безусловными плотностями
и коэффициентом корреляции потоков. А именно это мне и было
нужно.
Я не мог принять традиционную точку зрения и стал еще
более одержим поисками такого решения этой проблемы, которое
* Fred Gehm, Commodity Market Money Management, New York: Wiley,
1983, p. 3.
Условные вероятности и корреляция
139
было бы четким и легко применимым на практике. То есть мне
нужно было такое решение, посредством которого при наличии
коэффициента корреляции и вероятностей, ассоциированных с
двумя сценарными спектрами (например к двум монетам, име-
ющими два равновероятных сценария О и Р), представленными
двумя безусловными плотностями вероятности, можно было бы
рассчитать плотность совместной вероятности.
В конце концов я понял механизм формирования совмес-
тной плотности вероятности из безусловных плотностей вероят-
ности. Однако, как вы увидите, этот механизм оказался не столь
четким и простым, как мне бы хотелось.
Природа вновь не идет на сотрудничество.
Рассмотрим два одновременных сценарных спектра с нену-
левым коэффициентом корреляции и оценим вероятность совме-
стной реализации двух заданных сценариев, по одному из каж-
дого спектра.
Вспомним, что, когда мы бросаем две монеты и исходы
стохастически независимы (т. е. коэффициент линейной корреля-
ции г равен 0), вероятность выпадения двух орлов равна произ-
ведению индивидуальных вероятностей (см. формулу [3.01]):
р(Н1|Н2) = р(Н,)*р(Н2),
или в более краткой форме:
Р(ц2) = Pi*P2.
Теперь давайте представим себе, что две наши монеты
могут телепатически общаться между собой так, что, когда пер-
вая монета выпадает орлом, вторая также выпадает орлом. Это
ситуация соответствует коэффициенту линейной корреляции г,
равному 1. Вероятность выпадения двух орлов равна 0,5 — веро-
ятности выпадения орла на первой монете.
Если бы коэффициент корреляции был равен —1 (то есть
если первая монета выпадает орлом, то вторая обязательно —
решкой), то при бросании двух монет вероятность выпадения
140
Условные вероятности и корреляция
двух орлов была бы равна нулю. Однако вероятность выпадения
на первой монете орла, а на второй монете — решки равна 0,5,
что равно вероятности выпадения на первой монете орла (так как
г = —1, вторая монета всегда выпадает решкой, если первая
выпала орлом).
Введем теперь понятие, которое за неимением лучшего
термина будем называть интерантисечением. Для этого вновь
обратимся к случаю г = 1, то есть, когда при выпадении одной
монеты орлом, другая монета также выпадает орлом. Мы гово-
рим, что вероятность этого (0,5) равна вероятности выпадения
одной из монет орлом, поскольку используются идеальные мо-
неты с вероятностью выпадения орла, равной 0,5.
Предположим далее, что одна из монет не идеальна и ве-
роятность выпадения на ней орла равна не 0,5, а 0,4. Теперь
вероятность выпадения двух орлов будет равна 0,4 — меньшая из
вероятностей перекрывает большую.
Если бы вероятность выпадения решки была равна 0,4 (и,
следовательно, вероятность выпадения орлов была бы равна 0,6),
то вероятность выпадения двух орлов была бы равна 0,5 —
меньшей из двух вероятностей (так как вероятность орла на
одной монете равна 0,6, а на другой равна 0,5).
Условные вероятности и корреляция
141
Монета 1 Решка
Монета 2 Решка ~
О 0,5
При этом у какой из монет, первой или второй, вероят-
ность меньше, роли не играет:
Монета 1
Монета 2
Интерантисечение при r = 1 и есть описанное перекрытие,
то есть меньшая из двух вероятностей. На предыдущем рисунке
интерантисечением выпадения обеих монет решкой будет 0,4.
Другими словами, при положительном г интерантисечение есть
пересечение двух вероятностей.
Когда коэффициент корреляции отрицателен, второй сце-
нарный спектр (в данном случае монета 2) переворачивается на
180 градусов.
0 0,6 1,0
Рошк. I
1,0 0,5 0
0 0,5
Заметьте, что на предыдущем рисунке вторая монета пере-
ворачивается на 180 градусов, давая тем самым совместную ве-
роятность 0,5 выпадения орла на первой монете (с вероятностью
142
Условные вероятности и корреляция
0,6) и решки (с вероятностью 0,5) — на второй, если коэффи-
циент корреляции между двумя монетами равен — 1.
Если бы мы захотели найти интерантисечение выпадения
двух орлов, то, как явствует из следующего рисунка, получили
бы вероятность 0,1.
1,0
Монета 1
Монета 2
Interantisection
Вспомните теперь, что при бросании двух монет в условиях
стохастической независимости между ними (т. е. коэффициент
линейной корреляции г = 0), вероятность выпадения двух орлов
равнялась произведению индивидуальных вероятностей (см. урав-
нение [3.01]):
р(Н1|Н2) = р(Н1)*р(Н2),
или в более краткой форме:
Р(1|2) = Pi * Р2 •
Следовательно, для идеальных монет (т. е. у каждой веро-
ятность выпадения орла равна 0,5) при нулевом коэффициенте
вероятность выпадения двух орлов будет равна:
р(Н1|Н2) = р(Н1)*р(Н2)
= 0,5 *0,5
= 0,25.
Но когда коэффициент корреляции равен 1, совместная
вероятность представляет собой пересечение индивидуальных ве-
роятностей, или 0,5 в данном случае. Когда коэффициент кор-
Условные вероятности и корреляция
143
реляции равен —1, это будет пересечение после поворота на 180
градусов (антисечение) одного из сценарных спектров, что в
данном случае даст нулевую вероятность выпадения двух орлов.
Итак, мы научились находить совместные вероятности, когда
коэффициент корреляции между двумя сценарными спектрами
равен ~1 или 1. Как же нам аппроксимировать совместные ве-
роятности, когда коэффициент корреляции имеет не столь удоб-
ные значения?
Обратите внимание на два фактора, которые влияют на
совместные вероятности. Первый из них — это произведение
индивидуальных вероятностей (при г = 0):
Pi*Pr
Вторым из них является интерантисечение двух вероятно-
стей (при |r| = 1):
/(Pi * р2)-
Нижним пределом совместных вероятностей является нуль,
получающийся, когда интерантисечение равно 0, а также, когда
хотя бы одна из вероятностей р, или р2 равна 0. Тогда и первый
фактор, произведение двух вероятностей, и второй фактор, их
интерантисечение, будут нулевыми.
Верхний предел величины совместной вероятности может
быть меньше меньшего из р, или р2. В этом легко убедиться, ибо
фактор интерантисечения никогда не может быть больше, чем
минимум из р, и р2. Поскольку вероятность не может быть
больше 1, то произведение р, *р2 не может быть больше мень-
шего из р, и р2. То есть мы можем утверждать, что верхний
предел величины совместной вероятности равен меньшей из
вероятностей.
Исходя из нулевой нижней границы и верхней границы,
равной минимуму из р, и р2, будем искать условную вероятность
в виде линейно взвешенной суммы двух этих факторов:
Р[ * р2 * Wl + Z(Pj * р2) * W2.
144
Условные вероятности и корреляция
Но что мы будем использовать в качестве весов W1 и W2?
Как оказывается, W1 равен 1 минус абсолютная величина ко-
эффициента корреляции:
wi = (1 - И)-
A W2 есть просто абсолютная величина коэффициента
корреляции:
W2 = |ф
Эта весовая схема гарантирует нам, что мы останемся в
пределах верхних и нижних границ. Так, когда г = 0, наше
уравнение целиком склоняется в пользу произведения двух ве-
роятностей, а когда |r| = 1, перевес будет целиком в пользу
интерантисечения. Полностью уравнение для аппроксимации со-
вместных вероятностей имеет вид:
p(Pj I р2)=р, * р2 * (1 - И) + /(Pj * р2) * И-
Мы называем функцию линейно взвешенной (т. е. ни один
из ее аргументов не имеет степени большей единицы), так как
ее графиком служит прямая линия. Мы можем убедиться в ли-
нейности соотношений между р, * р2 и Яр, * р2), наблюдая за сле-
дующими двумя потоками исходов бросания монеты:
Поток! ОООООРРРРР
Поток2 ООООРОРРРР
ВРЕМЯ
Если приглядеться к этим двум потокам, то мы увидим,
что в каждом из них вероятность исхода О и исхода Р равна 0,5.
Подсчитав коэффициент корреляции между этими потоками,
получим 0,6.
Далее, для г = 0 получаем р, * р2 = 0,5 * 0,5 = 0,25. Если нас
интересует выпадение орлов в обоих потоках одновременно, то
получаем интерантисечение /(pj * р2), равное 0,5:
Условные вероятности и корреляция
145
Если коэффициент корреляции больше 0, то мы не разво-
рачиваем сценарный спектр на 180 градусов. Заметьте, что, когда
нас интересует интерантисечение обоих потоков, одновременно
дающих решку, получим, что его величина также равна 0,5.
При г = 0 имеем, что совместная вероятность выпадения
обоих орлов равна р, * р2 (или, как в данном случае, и для обеих
решек). При г = 1 имеем совместную вероятность, равную ин-
терантисечению 0,5. При г = — 1 интерантисечение было бы
равно 0, а, значит, и совместная вероятность равна 0, как
явствует из следующего рисунка.
Таким образом, получаем следующие три точки, в которых
мы уверены:
Г Вероятность
-1 0 1 0 0,25 0,5
Изобразим эти три точки на графике (см. рис. 3.2.).
Мы видим, что эти три точки можно соединить прямой
линией. Впрочем, их можно соединить и какой-нибудь кривой
10 - 9727
146
Условные вероятности и корреляция
Рис. 3.2.
(т. е. функция не будет линейно взвешенной), например сигмо-
идой (т. е. растянутой S-образной кривой, проходящей через наши
три точки).
Итак, в обоих потоках орел выпал четыре раза из десяти
(аналогично, решка выпала в обоих потоках четыре раза из
десяти), что дает вероятность 0,4. Обратите внимание, что если
функция линейна, то есть изображается на графике прямой
линией, то эта прямая проходит через точку, соответствующую
коэффициенту корреляции 0,6 и вероятности 0,4. Если бы график
функции отличался от прямой, то коэффициенту корреляции 0,6
соответствовало бы все, что угодно, кроме 0,4! (см. рис. 3.3).
Теперь рассмотрим нашу функцию применительно к этим
двух потокам исходов:
Р(ц2) =Pj *Р2 * (1 - И) + Др, * Р2) * И
= 0,5 * 0,5 * (1 - |0,6|) + 0,5 * |0,6|
= 0,25*0,4 + 0,5*0,6
= 0,1 + 0,3
= 0,4
То есть мы видим, что наша формула дает такой результат,
который подтверждается самим потоком исходов. Мы можем
ожидать появления орлов в обоих потоках одновременно с веро-
ятностью 0,4, при бросании двух идеальных монет с коэффици-
ентом корреляции г = 0,6.
Условные
вероятности и корреляция
147
Рис. 3.3. Совместные вероятности линейно взвешены с помощью коэффици-
ента корреляции.
Эта аппроксимация проходит только в случае биномиаль-
ного распределения (т. е. при двух сценариях в спектре). Чем более
уклоняются вероятности от 0,5 на сценарий, тем менее точной
она становится. Другими словами, это решение является точным,
когда вы дихотомизируете два сценарных спектра; в противном
случае она превращается в аппроксимацию убывающей точности.
Впрочем, любые сценарные спектры можно свести к бино-
миальным распределениям (наборам только из двух сценариев),
путем дихотомизации около их центров. Вновь обратимся к сце-
нарному спектру нашей промышленной компании. Он содержит
восемь различных сценариев. Мы можем дихотомизировать их,
объединив воедино сценарии Войны, Кризиса и Стагнации в
один сценарий нового сценарного спектра, который мы будем
называть сценарием Плохой половины исходов. Аналогичным обра-
зом, мы можем объединить воедино сценарии мира и процвета-
ния в сценарий Хорошей половины исходов нового спектра. Теперь
мы можем обращаться с преобразованным спектром так же, как
и с другими спектрами, содержащими по два сценария, и ап-
проксимировать совместные вероятности четырех возможных со-
вместных исходов (рис. 3.4).
Дихотомизация сценарных спектров для аппроксимации
совместных вероятностей эффективна лишь до тех пор, пока вы
разделяете их примерно на равновероятном уровне (0,5). Чем
дальше от него проводится дихотомизация, тем менее точной
становится аппроксимация.
10*
148
Условные вероятности и корреляция
0,1 0,3 0,5 0,95 1,0
War Trouble Stgntn Peace Pty
I I
0 0,5 1,0
Bad Half of Outcomes Good Half of Outcomes
Рис. 3.4.
Вновь обратимся к примеру из Феллера, приведенного в
начале этой главы:
X Безусл. плотность Y
0 1 2 3
1 2 0 0 1 3
Y 2 6 6 6 0 18
3 0 6 0 0 6
Безусл. плотность X 8 12 6 1 27
Если дихотомизировать сценарный спектр X, объединив
исходы 0 и 1 в сценарий А спектра X, а исходы 2 и 3 в сценарий
В спектра X, то мы удалимся от равновероятного уровня. Уровень,
который мы получим при такой дихотомизации, будет равен
0,74074, поскольку, судя по безусловным плотностям в X, двад-
цать из двадцати семи исходов (74,074%) приходятся на 0 или
1, и только семь из двадцати семи исходов (25,92%) приходятся
на 2 или 3 (см. рис. 3.5).
Если то же самое проделать со сценарным спектром Y,
объединяя исходы 1 и 2 в сценарий А спектра Y, а исход 3
переименовывая в сценарий В спектра Y, то преобразованный
спектр Y станет таким, как показано на рис. 3.6.
Заметьте, что спектр Y также дихотомизирован не равно-
вероятно, а поблизости к 0,777.
Приступим к формированию таблицы совместных вероятно-
стей в следующем виде:
Условные вероятности и корреляция
149
X
А В Безусл. плотность Y
А ? ? 0,777
Y В ? ? 0,222
Безусл. плотность X 0,74074 0,2592 1,0
О 0,296 0,74074 0,9629 1,0
"0" "Г "3"
0 0,74074 1,0
"А" "В"
Рис. 3.5. Дихотомизация безусловной плотности X.
Рис. 3.6. Дихотомизация безусловной плотности Y.
Теперь, исходя из того, что коэффициент корреляции г
между этими двумя сценарными спектрами равен 0, определим
четыре совместные вероятности нашей таблицы:
р(А | А) = 0,74074 * 0,777 * (1 - 0) + 0,74074 * 0 = 0,5761;
р(А | В) = 0,74074 * 0,222 * (1 - 0) + 0 * 0 = 0,16461;
150
Условные вероятности и корреляция
р(51 Л) = 0,2592 * 0,777 * (1 - 0) + 0,0362 * 0 = 0,2016461;
р(В | В) = 0,2592 * 0,222 * (1 - 0) + 0,222 * 0 = 0,05761316873.
(Обратите внимание на величины интерантисечений в пре-
дыдущих уравнениях.)
Теперь мы можем завершить таблицу:
А В
А 0,5761 0,2016461
В 0,16461 0,05761
Поскольку в исходной таблице мы использовали не веро-
ятности, а фактические замеры по двадцати семи реализациям,
мы можем умножить полученные вероятности на двадцать семь
и получить таблицу ожидаемых частот:
X
А В
А 15,56 5,44
В 4,44 1,56
Мы видим, что можно ожидать 15,56 реализаций (из двад-
цати семи) по сценарию А из спектра X и по сценарию А из
спектра Y. Вспомните, что это соответствует реализации 0 или 1
исходного спектра X и 1 или 2 исходного спектра Y. Переходя
к исходному спектру, обнаруживаем, что на самом деле таких
реализаций было четырнадцать (из двадцати семи):
X Безусл. плотность Y
0 1 2 3
1 2 0 0 1 3
Y 2 6 6 6 0 18
3 0 6 0 0 6
Безусл. плотность X 8 12 6 1 27
Условные вероятности и корреляция
151
Сходные ошибки можно найти и в других трех квадрантах.
Такой неточностью мы обязаны тому, что дихотомизировали
исходное распределение слишком далеко от действительно равно-
вероятного уровня (мы дихотомизировали на уровнях 0,74074 и
0,777). Поэтому наши аппроксимации совместных распределений
оказались менее точными.
Давайте вернемся назад и дихотомизируем эту таблицу на
уровнях 0,5. Для этого попытаемся ответить на вопрос: «Где на
оси X находится уровень 0,5?»
Сначала просуммируем произведения каждого исхода X на
его частоту:
8*2 =
12* 1 =
6*2 =
0;
12;
12;
1*3 = 3.
Итого = 27.
Теперь разделим полученную сумму на общее количество
реализаций (27) и найдем взвешенное по вероятности среднее:
27/27 = 1
Это значит, что если бы это было непрерывное распреде-
ление, то мы могли бы ожидать 50% реализаций меньше 1 и 50%
— больше.
1*3 = 3;
2* 18 = 36;
3*6= 18;
Итого = 57.
Теперь разделим полученную сумму на общее количество
реализаций (27) и найдем взвешенное по вероятности среднее:
57/27 = 2,111
152
Условные вероятности и корреляция
То есть если бы это было непрерывное распределение, то
мы могли бы ожидать 50% его реализаций меньше 2,111 и 50%
— больше.
Теперь рассчитаем вероятности для четырех квадрантов:
р(< 0,5 | < 0,5) = 0,5 * 0,5 * (1 - 10 |) + 0,5 * 101
= 0,25 * 1 + 0,5 * 0
= 0,25.
«Подождите, — скажете вы, — поскольку имеет место
стохастическая независимость, нет нужды все это проделывать;
мы можем просто перемножить вероятности для каждого из четырех
квадрантов и определить вероятности, ассоциированные с каж-
дым квадрантом. Это даст совместную вероятность 0,25 для каж-
дого квадранта» Все это совершенно верно. Квадранты разделены
точно значением 1 по X и значением 2,111 по Y. То есть в каждом
квадранте мы можем ожидать 25% всех реализаций, или 6,75
реализаций из 27 (27 * 0,25).
Глядя на таблицу, может оказаться сложновато выделить в
каждом квадранте 6,75 исходов: ведь в ней представлены диск-
ретные исходы, а мы для удобства дихотомизации таблицы на
равновероятных уровнях обращались с ними, как с непрерывны-
ми. Например, если взять строку реализаций Y для исхода «2»,
то сколько их будет ниже, а сколько выше уровня 2,111?
Разумеется, в случае более удобных распределений меха-
низм образования совместных вероятностей из составляющих
безусловных вероятностей более нагляден.
А сейчас рассмотрим другую ситуацию с двумя потоками
исходов двенадцати конов:
ПотокХ 2 1-1-221-1 2 1-1-2
HotokY 2 2 2 1 1 1 -1 -1 -2 -2 -2
ВРЕМЯ
Мы можем определить, что коэффициент корреляции этих
двух потоков равен 0,33333. Если мы теперь примемся составлять
Условные вероятности и корреляция
153
таблицу совместных вероятностей, то определим также и безус-
ловные плотности (каждый из четырех сценариев каждого сценар-
ного спектра имеет вероятность реализации 0,25).
X Безусл. плотность Y
-2 -1 1 2
-2 1 1 1 0 3 (р = 0,25)
Y -1 1 1 0 1 3 (р = 0,25)
1 1 0 1 1 3 (р = 0,25)
2 0 1 1 1 3 (р = 0,25)
Безусл. плотность X 3 3 3 3 12
вероятность 0,25 0,25 0,25 0,25 р = 1,0
Если мы теперь проведем дихотомизацию точно на уровне
0,5 для обоих сценарных спектров, то в каждом спектре получим
по два сценария, которые будем называть «+» и «». Вероятность
реализации каждого сценария в спектре равна 0,5. Сценарий «+»
включает те исходы, которые больше 0, а сценарий «—» содержит
исходы, меньшие 0. Таблица будет выглядеть следующим образом:
X
- +
- 4 2
2 4
Вернемся теперь к нашему уравнению для определения
совместных вероятностей и посмотрим, насколько близки эти
данные к расчетным:
р(-|-) = 0,5 * 0,5 * (1 -10,3333 |) + 0,5 * 10,3333 |
= 0,25 * 0,6666 + 0,5 * 0,3333
= 1,66666 + 0,166666
= 0,33333
154
Условные вероятности и корреляция
р(-|+) = 0,5 * 0,5 * (1 -1 0,3333 |) + 0 * 10,3333 |
= 0,25 * 0,6666 + О
= 1,66666 + О
= 1,66666
р(+|+) = 0,5 * 0,5 * (1 -1 0,3333 I) + 0,5 * I 0,3333 |
= 0,25 * 0,6666 + 0,5 * 0,3333
= 1,66666 + 0,166666
= 0,33333
р(+|-) = 0,5 * 0,5 * (1 - 10,3333 |) + 0 * I 0,3333 |
= 0,25 * 0,6666 + О
= 1,66666 + О
= 1,66666
Таким образом, наша формула дает следующие оценки
совместных вероятностей:
X
- +
— 0,333333 0,1666666
Y + 0,1666666 0,3333333
Если умножить их на количество исходов (12), то получим
следующую таблицу частот ожидаемых исходов:
Условные вероятности и корреляция
155
Это точно совпадает с эмпирическими данными потока
исходов. Заметьте, что такая точность объясняется тем, что мы
провели дихотомизацию на уровне 0,5.
Судя по таблице, мы, например, можем ожидать отрица-
тельного числа в потоке X и отрицательного числа в потоке Y
в четырех из двенадцати случаев и так далее (для трех других
квадрантов.
«Подождите, — скажете вы, — разве нельзя взять один из
этих квадрантов и дихотомизировать его для получения более
детальных вероятностей, не ограничиваясь достигнутым?» Други-
ми словами, в этом примере вы хотите знать не только, какова
вероятность, скажем, положительного числа в обоих потоках, но
и какова вероятность —2 в потоке X и —1 в потоке Y. То, чему
мы пока что научились, даст вам точное совместное распределе-
ние, если у вас есть два бинарных безусловных распределения —
то есть, когда у вас есть два безусловных распределения, каждое
из которых имеет только два возможных исхода, два возможных
сценария (как в большинстве азартных игр, где вы выигрываете
М с вероятностью Хи проигрываете Nс вероятностью Y). Однако
хотелось бы получать совместные распределения для любых бе-
зусловных распределений, а не только для бинарных.
Тут-то мы и подходим к сути дела.
Теория условной вероятности
Мы можем дихотомизировать таблицу совместных вероят-
ностей любых двух сценарных спектров при условии, что изве-
стны сами эти сценарные спектры (т. е. вероятности, ассоцииро-
ванные с каждым сценарием) и коэффициент корреляции между
ними. То есть мы можем определить величины в каждом из
четырех квадрантов таблицы совместных вероятностей.
Мы можем продолжить дихотомизацию таблицы для полу-
чения более детальных вероятностей, не ограничиваясь уровнем
156
Условные вероятности и корреляция
четырех квадрантов таблицы. Так, мы можем взять, скажем,
верхний левый квадрант и использовать его в качестве исходной
таблицы. Проделав это со всеми четырьмя квадрантами, мы получим
по четыре квадранта для каждого квадранта из четырех исходных.
То есть мы получим совместные вероятности для каждой из
шестнадцати частей таблицы. Мы можем продолжить эту проце-
дуру, если требуется еще больший уровень детализации.
Здесь, однако, мы сталкиваемся с затруднением, в котором
отражается вся суть взаимосвязи условных вероятностей и кор-
реляции. А именно у каждого квадранта есть свой собственный
коэффициент корреляции. Чтобы убедиться в этом, вернемся к
нашему предыдущему примеру. Мы начали со следующих двух
потоков исходов:
ПотокХ 2 1-1-221-1 2 1-1-2
Потоку 2 2 2 1 1 1 —1 —1 —2 —2 -2.
ВРЕМЯ —►
Исходя из этих потоков, мы можем построить следующую
таблицу:
X
-2 -1 1 2 Безусл. плотность У
-2 1 1 1 0 3 (р = 0,25)
У -1 1 1 0 1 3 (р = 0,25)
1 1 0 1 1 3 (р = 0,25)
2 0 1 1 1 3 (р = 0,25)
Безусл. плотность X 3 3 3 3 12
Мы знаем, что коэффициент корреляции г между этими
двумя потоками равен 0,33333. Но этот коэффициент корреляции
касается только первого квадранта, представляющего собой всю
таблицу.
Теперь, применяя нашу формулу для определения совмес-
тных вероятностей, в которую входит коэффициент корреляции
потоков, для дихотомизированных сценарных спектров, найдем
совместные вероятности для всех квадрантов таблицы:
Условные вероятности и корреляция
157
- +
— 0,333333 0,1666666
У + 0,1666666 0,3333333
Если умножить эти вероятности на количество исходов
(12), то получим следующую таблицу частот ожидаемых исходов:
X
- +
4 1
2 4
Теперь мы можем утверждать, что квадрант «—»«—», то есть
верхний левый квадрант, является таблицей, которую мы хотели
бы дихотомизировать, например, для того, чтобы узнать совме-
стные вероятности, ассоциированные с X и Y, когда они оба
отрицательны:
Но теория условных вероятностей, опирающаяся на корре-
ляцию, говорит нам, что здесь мы не можем пользоваться ко-
эффициентом корреляции всего потока (он, как мы знаем, равен
0,333). Вместо этого мы должны использовать коэффициент кор-
реляции только тех исходов, где и X, и Y отрицательны. Поэто-
му, беря только те отрезки потоков исходов, где они оба отри-
цательны, получаем:
Поток X —1 —2 —1 —2
ПотокУ -1 -1 —2 —2.
ВРЕМЯ
158
Условные вероятности и корреляция
Определяя коэффициент корреляции этих двух потоков,
получаем, что он равен 0. Заметьте также, что вероятности по-
явления —1 и —2 в каждом из двух потоков равны 0,5, и мы
должны использовать 0,5 в качестве индивидуальных вероятнос-
тей. Отсюда мы получаем следующие совместные вероятности:
р(—2|—2) = 0,5 * 0,5 * (1 - 101) + 0,5 * 101
= 0,25 * 1 + 0,5 * 0
= 0,25
Следовательно, 0,25 верхнего левого квадранта должны при-
ходиться на (-2,-2), и, поскольку 0,3333 всего распределения
сосредоточено в верхнем левом квадранте, мы могли бы ожидать,
что 0,25 * 0,3333, или 0,08333 всего распределения, придется на
-2,-2.
р(—2|—1) = 0,5 * 0,5 * (1 -101) + 0,5 * 101
= 0,25 * 1 + 0,5 * 0
= 0,25
Следовательно, 0,25 верхнего левого квадранта должны
приходиться на -2,-1, и, поскольку 0,3333 всего распределения
сосредоточено в верхнем левом квадранте, мы могли бы ожидать,
что 0,25 * 0,3333, или 0,08333 всего распределения, придется на
-2,-1.
р(—1|—2) = 0,5 * 0,5 * (1 -101) + 0,5 * 101
= 0,25 * 1 + 0,5 *0
= 0,25
Следовательно, 0,25 верхнего левого квадранта должны
приходиться на —1,-2, и, поскольку 0,3333 всего распределения
сосредоточено в верхнем левом квадранте, мы могли бы ожидать,
что 0,25 * 0,3333, или 0,08333 всего распределения, придется на
-1,-2.
Условные вероятности и корреляция
159
р(—1|—1) = 0,5 * 0,5 * (1 -101) + 0,5 * 101
= 0,25 * 1 + 0,5 * О
= 0,25
Следовательно, 0,25 верхнего левого квадранта должны
приходиться на -1,-1, и, поскольку 0,3333 всего распределения
сосредоточено в верхнем левом квадранте, мы могли бы ожидать,
что 0,25 * 0,3333, или 0,08333 всего распределения, придется на
-1, -1).
X -2 -1
-2 -1 0,0833 0,0833 0,0833 0,0833
Вспомните, что исходные потоки дали 12 исходов, пред-
ставленных в таблице. Умножая найденные вероятности (0,08333)
на 12, получаем 1. То есть мы будем иметь следующую таблицу
ожидаемых частот исходов:
Заметьте, что это абсолютно совпадает с левым верхним
квадрантом таблицы для полных потоков.
Нижний правый квадрант может быть получен аналогич-
ным образом. Поэтому займемся нижним левым квадрантом (а,
значит, и верхним правым квадратом, который можно получить
аналогично тому, как мы собираемся действовать с нижним
левым).
Поток X —1 —2
Поток Y 2 1.
ВРЕМЯ —>
160
Условные вероятности и корреляция
Коэффициент корреляции равен 1. Вероятность получения
— 1 или —2 в потоке X равна 0,5, как и вероятность, ассоции-
рованная с получением 1 или 2 в потоке Y. Отсюда мы имеем
следующие совместные вероятности:
р(—2|1) = 0,5 * 0,5 * (1 -1 11) + 0,5 * 1
= 0,25*0 + 0,5* 1
= 0,5
Следовательно, 0,5 нижнего левого квадранта должны при-
ходиться на —2,1, и, поскольку 0,16666 всего распределения
сосредоточено в нижнем левом квадранте, мы могли бы ожидать,
что 0,5 * 0,16666, или 0,08333 всего распределения, придется на
-2,1.
р(—2|2) = 0,5 * 0,5 * (1 - | 11) + 0,5 * 1
= 0,25 *0 + 0*1
= 0
Следовательно, 0 нижнего левого квадранта должен прихо-
диться на —2,2, и, поскольку 0,16666 всего распределения сосре-
доточено в нижнем левом квадранте, мы могли бы ожидать, что
0*0,16666, или 0 всего распределения, придется на —2,2.
р(-1|1) = 0,5 * 0,5 * (1 - |1|) + 0 * 1
= 0,25 *0 + 0*1
= 0
Следовательно, 0 нижнего левого квадранта должен прихо-
диться на —1,1, и, поскольку 0,16666 всего распределения сосре-
доточено в нижнем левом квадранте, мы могли бы ожидать, что
0*0,16666, или 0 всего распределения, придется на —1,1.
Условные вероятности и корреляция
161
р(—1|2) = 0,5 * 0,5 * (1 - 111) + 0,5 * 1
= 0,25 * 0 + 0,5 * 1
= 0,5
Следовательно, 0,5 нижнего левого квадранта должны при-
ходиться на -1,2, и, поскольку 0,16666 всего распределения
сосредоточено в нижнем левом квадранте, мы могли бы ожидать,
что 0,5 *0,16666, или 0,08333 всего распределения, придется на
-1,2. Таким образом, нижний левый квадрант может быть дихо-
томизирован к виду:
X
-2 -1
-2
-1
0,0833 0
0 0,0833
Отсюда, умножая найденные вероятности на общее число
исходов в исходных потоках (12), получаем следующие ожидае-
мые частоты:
X
-2 -1
-2
-1
1 0
0 1
Заметьте, что это абсолютно совпадает с таблицей для
исходных потоков.
Таким образом, вы можете дихотомизировать сценарные
спектры и, применяя формулу, получить условные вероятности,
учитывающие корреляцию. Трудность состоит лишь в том, что
вместо использования одного коэффициента корреляции для
всей таблицы вы должны использовать коэффициенты корреля-
ции только тех исходов, которые составляют обрабатываемую
подтаблицу.
11 - 9727
162
Условные вероятности и корреляция
Давайте рассмотрим еще один пример. Предположим, что
мы бросаем три монетки по 10 центов и три монетки по 25 цен-
тов. Пусть в сценарный спектр А входят общее количество орлов
на всех шести монетах, а в сценарный спектр В — общее коли-
чество орлов только на 25-центовиках. Таблица совместных веро-
ятностей будет иметь вид:
0 1 2 А 3 4 5 6 Безусл. плотн. В
0 1 3 3 1 0 0 0 8
1 0 3 9 9 3 0 0 24
В 2 0 0 3 9 9 3 0 24
3 0 0 0 1 3 3 1 8
Безусл. плотн. А 1 6 15 20 15 6 13 64
Всего здесь имеется 26 (64) различных исходов, а коэффи-
циент корреляции составляет 0,707 (рис. 3.7). Поэтому, если мы
Рис. 3.7. Пример совместного распределения исходов бросания трех 10-
центовиков и трех 25-центовиков.
Условные вероятности н корреляция
163
хотим определить совместные вероятности, ассоциированные с
А = 2 и В — 1 (т. е. вероятность при бросании всех шести монет
получить два или менее орлов среди всех шести монет и не более
одного орла среди 25-центовиков), то:
р(<=2|<=1) = ((15 + 6 + 1)/64) * ((8 + 24)/64) *
* (1 - | 0,707 |) + ((15 + 6 + 1)/64) * | 0,707 |
=(22/64) * (32/64) * 0,293 + (22/64) * 0,707
=0,34375 * 0,5 * 0,293 + 0,37375 * 0,707
=0,050359375 + 0,26424125
=0,314600625.
Что при умножении на 64 (общее число исходов) дает в
данном квадранте ожидание, равное 20,1344 исходам. Мы же
знаем, что в этом квадранте имеется 19 исходов.
Обратите внимание, что, хотя мы и дихотомизировали В на
уровне 0,5, мы не дихотомизировали А. Отсюда расхождения
наших результатов с эмпирическимим данными. Если бы мы и
А дихотомизировали на уровне 0,5, то получили бы совершенно
точный результат.
После дихотомизация таблицы мы можем взять одну из ее
новых частей и дихотомизировать ее при условии, что известен
коэффициент корреляции этой новой таблицы.
Поэтому, если бы мы захотели дихотомизировать верхний
левый квадрант этой таблицы, то не смогли бы использовать
0,707 в качестве коэффициента корреляции. Нам пришлось бы
определить (или оценить) коэффициент корреляции только для
такого набора данных, где при бросании наших шести монет
выпадают не более двух орлов на всех монетах и не более одного
орла на 25-центовиках.
Таким образом, при наличии двух сценарных спектров и
коэффициента (ов) корреляции между ними мы можем опреде-
лить совместные вероятности реализации двух сценариев, по одному
из каждого спектра.
и*
164
Условные вероятности н корреляция
Тот, кто следует среднедисперсионному подходу, или ста-
рой методологии, опирается в основном на совместные распре-
деления, у которых только четыре квадранта, — так уж они
используют коэффициент корреляции в качестве меры взаимо-
зависимости компонентов. Это плохо приближает реальные со-
вместные распределения, что еще раз подчеркивает предпочти-
тельность нашей новой методологии по сравнению со старыми
подходами.
Совместные вероятности двух
непрерывных распределений
i
Сценарные спектры можно представлять себе как дискрет-
ные распределения. Такой же подход можно использовать и для |
определения вероятностей для непрерывного распределения, если i
рассматривать его как дискретное распределение с бесконечно '
малым шагом квантования (т. е. с бесконечным множеством сце-
нариев).
Например, мы знаем, что центрированная нормально рас- j
пределенная случайная величина с вероятностью 0,9772 не пре-
вышает двух стандартных отклонений, а с вероятностью 0,9986 :
— трех стандартных отклонений. Если один из сценариев спектра !
состоит в том, что нормально распределенная случайная величина
попадает в пределы от +2 до +3 стандартных отклонений, то мы |
знаем, что вероятность этого сценария равна 0,0214 (0,9986 — j
0,9772). Значит, мы можем определять совместные вероятности ;|
для непрерывных распределений. Кроме того, мы можем сделать s
сценарий таким маленьким, как нам нужно. В упомянутом ранее
примере мы можем использовать сценарий, который состоит в
том, что нормально распределенная случайная величина попадает ;
в пределы от +2 до +2,1 стандартных отклонений, или между +2
и +2,000001 стандартных отклонений.
Условные вероятности и корреляция
165
Оценка совместных
вероятностей
Изложенный метод поквадрантной оценки совместных рас-
пределений вероятности при известных безусловных плотностях
и коэффициенте корреляции между ними весьма привлекателен.
Он точно описывает механизм формирования совместного распре-
деления из компонентных безусловных распределений. Когда мы
используем распределение Бернулли (распределение, у которого
только два возможных исхода, т. е. сценарные спектры состоят
только из двух сценариев), можно получить очень хорошую
и простую оценку совместных вероятностей. Но чтобы сделать ее
еще точнее, т. е. найти более детальные совместные вероятности,
не ограничиваясь на квадрантах, требуется наперед знать коэф-
фициенты корреляции составляющих квадрантов (или наперед
знать совместные вероятности, чтобы, обратив формулу, полу-
чить коэффициенты корреляции).
При наличии зависимости совместные распределения будут
изменяться под влиянием непосредственно предшествующих ис-
ходов.
Нередко нам будут известны не все коэффициенты корре-
ляции между двумя сценарными спектрами, и поэтому мы будем
вынуждены получить недостающие данные либо эмпирическим
путем, либо с помощью оценки.
Если у вас имеются необходимые эмпирические данные, то
рассчитать совместные вероятности совсем не сложно. Предполо-
жим, например, что вас интересуют совместные вероятности для
двух акций — корпораций XYZ и АВС. У вас есть масса различ-
ных сценариев ожидаемого поведения цены каждой из них на
следующий период владения (а период владения может быть
любой единой длины по нашему выбору — это может быть день,
два дня, неделя, месяц, год — что угодно). Один из сценариев
спектра АВС соответствует подъему цены ее акций на два пункта.
У вас также есть сценарий из спектра XYZ, соответствующий
падению цены ее акций на подпункта. (Вместо абсолютных ве-
личин можно использовать изменения цены в процентах.) С по-
мощью компьютера можно просчитать ценовые данные по обеим
166
Условные вероятности и корреляция
этим акциям и подсчитать, в скольких периодах владения акции
АВС поднимались на два пункта, а акции XYZ — опускались на
подпункта, и поделить полученную величину на общее количе-
ство периодов владения анализируемого массива данных. Затем
мы можем проделать то же самое для каждой комбинации двух
сценариев из наших сценарных спектров. То есть мы бы получили
таблицу совместных вероятностей двух сценарных спектров эмпи-
рическим путем.
Разумеется, располагая эмпирическими данными, можно
сначала рассчитать требуемые коэффициенты корреляции, а затем
на их основе построить таблицу совместных вероятностей.
Мы можем также оценить величины входящих в таблицу
совместных вероятностей двух сценарных спектров. Делая это,
нужно помнить о верхних и нижних границах каждой совместной
вероятности, чтобы наши оценки не вышли за их пределы. Нижняя
граница совместной вероятности, как вы помните, равна 0. Вер-
хняя граница равна минимуму из двух индивидуальных вероят-
ностей.
Кроме того, нужно, чтобы сумма всех совместных вероят-
ностей в таблице строго равнялась 1,0.
Вспомните также, что каждая строка и каждый столбец
таблицы совместных вероятностей двух сценарных спектров дол-
жны в сумме давать безусловную вероятность этой строки или
столбца. Например, рассмотрим два различных сценарных спектра:
Спектр Y
Сценарий Вероятность
Хорошие исходы 0,4
Плохие исходы 0,6
Спектр X
Сценарий Вероятность
Война 0,1
Кризис 0,2
Стагнация 0,2
Мир 0,45
Процветание 0,05
Условные вероятности и корреляция
167
Исходя из этого, строим таблицу:
Хорошие Исходы Плохие Исходы Безусловная Плотность X
Война 0,1
Кризис 0,2
Стагнация 0,2
Мир 0,45
Процветание 0,05
Безусловная Плотность Y 0,4 0,6 1,0
Из этого примера видно, что сумма вероятностей в первом
столбце должна равняться безусловной плотности, ассоциирован-
ной со столбцом «Хорошие исходы» (0,4). То есть сумма совме-
стных вероятностей «Войны», «Кризиса», «Стагнации», «Мира»
и «Процветания», с одной стороны, и «Хороших исходов», с дру-
гой — должна быть строго равна 0,4.
Аналогично, сумма вероятностей в первой строке, то есть
совместная вероятность «Хороших исходов» и «Войны» плюс
совместная вероятность «Плохих исходов» и «Войны», должна
равняться величине, ассоциированной с этой строкой, то есть
с «Войной» (0,1). Если взять последнюю строку «Процветание»,
то суммарно «Хорошие исходы» с «Процветанием» и «Плохие
исходы» с «Процветанием» должны давать 0,5.
Заметьте, что если потребовать, чтобы совместные веро-
ятности в каждой строке и в каждом столбце суммарно равня-
лись безусловной плотности, ассоциированной с каждой стро-
кой и каждым столбцом (как и должно быть), то уже не нужно
будет беспокоиться о том, чтобы ни одна совместная вероят-
ность не превысила бы верхней границы (и, пока все ваши
совместные вероятности больше или равны 0, как это и поло-
жено, не нужно беспокоиться о пересечении ими нижней гра-
ницы). Кроме того, если совместные вероятности в каждой
строке и в каждом столбце равны безусловным плотностям,
ассоциированным с каждой строкой и каждым столбцом, то
168
Условные вероятности и корреляция
сумма всех совместных вероятностей в таблице будет строго
равна 1,0 (в предположении, что сумма вероятностей в каждом
сценарном спектре строго равна 1,0).
При возможности вам хорошо бы почаще сочетать оба
метода определения совместных вероятностей*. Конечно, если вам
удастся раздобыть необходимые коэффициенты корреляции, то
вы сможете получить совместные вероятности по формуле.
Наконец, когда вы группируете эмпирические данные,
в качестве исходов групп используйте их медианы. Например,
если в данных по доходам выделена группа 0—100 долл., в ко-
торую попадают три значения 10, 20 и 90 долл., то в качестве
исхода этого сценария используйте медиану 20 долл.
Новая модель, представленная в следующей главе этой
книги, отличается математической строгостью. Единственными
исходными данными, которых она требует, являются сценарии,
то есть вероятности всевозможных исходов. Они играют первосте-
пенную роль при оценке совместных (условных) вероятностей.
Если вероятности неточны, то и отдача от новой модели будет
невелика. Проблема заключается в том, чтобы точно назначать
совместные вероятности возможным исходам многих одновремен-
ных сценарных спектров. Достижение вершины (п + 1)-мерного
изображения столь же важно, как и усилия по таймингу и выбору
сделки. Эту вершину (как и любую другую точку, в которой мы
* При оценке совместных вероятностей вы, возможно, захотите смоде-
лировать кривые, образуемые значениями строк и столбцов таблицы, с помощью
какого-нибудь математического процесса. Возможно, что при оценке совместных
вероятностей или коэффициентов корреляции, введенных совместными распре-
делениями изложенной здесь Теории Условной Вероятности, пригодится
какая-нибудь разновидность регрессионного анализа, нейронных сетей или дру-
гого аппарата. Это поистине широко открытая область приложений. В главе
4 Математики управления капиталом рассказано о моделировании распре-
деления одной случайной величины с помощью критерия Колмогорова-Смир-
нова. Этот метод можно также использовать для моделирования строк и
столбцов таблицы совместных вероятностей. Тем, кто заинтересован в развитии
сходных методов, следует изучить кривые Пирсона, а также Байесову стати-
стику. Для этого рекомендую прочитать Прикладную теорию статистичес-
ких решений Говарда Райффы и Роберта Шлайфера (изд-во Гарвардского
университета, Бостон, 1961 г.) и Адаптивные процессы управления Ричарда
Беллмана (изд-во Принстонского университета, Принстон, 1961 г.).
Условные вероятности н корреляция 169
хотели бы находиться) дает нам новая модель столь же точно,
сколь точно мы оценили совместные вероятности. Поэтому мы
можем утверждать, что оценка совместных вероятностей, безус-
ловно, так же важна, как и усилия по таймингу и выбору сделки.
А, возможно, и более важна, ибо мы сами контролируем наши
оценки, а решать, будет ли следующая сделка прибыльной или
нет, мы не можем.
4
Новая модель
Освоив условные вероятности, а также материал глав 1 и 2, мы
располагаем базой для создания новой модели. Новая модель ин-
вестирования, которая будет представлена далее, позволит нам
посмотреть на вещи в контексте новой методологии, подробно
рассмотренной в начале книги.
Эта новая модель алгоритмична в плане практического
применения. То есть она не предполагает использования архивных
исходных данных. В главе 1 была описана эмпирическая модель (та,
что, напротив, использует архивные исходные данные), позволяю-
щая вам, при желании, работать с топографией (п + 1)-мерного
изображения. Но алгоритмическое решение, вроде того, что будет
представлено ниже, более желательно, особенно если в будущем
будут достигнуты успехи в отслеживании смещения вершины в
(п + 1)-мерного изображения. Вообще говоря, эмпирическое реше-
ние бывает не только весьма времяемким, но и не облегчает
имитационного моделирования методом проб и ошибок. Кроме
того, в алгоритмической модели вы, при желании, всегда можете
172
Новая модель
использовать архивные исходные данные (т. е. создавать сценар-
ные спектры, точно соответствующие прошлым событиям). Об-
ратное, однако, неверно.
Математическая оптимизация
Математическая оптимизация представляет собой задачу
отыскания максимального или минимального значения некоторой
целевой функции по заданному параметру (s). Целевая функция
есть, таким образом, нечто такое, что может быть оптимизиро-
вано только с помощью итеративной процедуры.
Например, отыскание оптимального f для одной рыночной
системы или одного сценарного спектра является задачей мате-
матической оптимизации. В этих случаях методы математической
оптимизации могут быть достаточно грубыми, вроде перебора
всех значений f от 0 до 1,0 с шагом 0,01. В качестве целевой
функции для отыскания среднего геометрического HPR при
различных условиях и заданном значении f может выступать одна
из функций, представленных в главе 1. Роль варьируемого пара-
метра здесь играет то значение f которое тестируется в интервале
от 0 до 1.
Значение целевой функции вместе с подставляемыми в нее
значениями аргументов дают координаты нашего положения в
(л + 1)-мерном пространстве. Отыскивая f для одной рыночной
системы или одного сценарного спектра, когда п равно 1, мы
получаем координаты в двухмерном пространстве. Одной из ко-
ординат является значение/ подставляемое в целевую функцию,
а другой координатой — значение целевой функции от этого f
Поскольку не всем достаточно легко представить себе
более трех координат, мы будем считать, что п равно 2 (то есть
оперировать с трехмерной, (л + 1)-мерной картины). В условиях
такого упрощения значение целевой функции дает нам высоту
трехмерного изображения. Значения / связанные с одним из
Новая модель
М3
сценарных спектров, мы можем представить себе в виде коор-
динат север-юг, а значения /, связанные с другим спектром,
— с координатами восток-запад. Каждый сценарный спектр
соответствует возможным исходам данной рыночной системы.
Поэтому мы, например, можем сказать, что координаты север-
юг соответствуют определенному значению f для данного рын-
ка и для данной системы, а координаты восток-запад — зна-
чению /, относящемуся либо к торговле на другом рынке или
к другой системе, когда торговля по обеим системам идет
одновременно.
Целевая функция дает нам высоту для данного набора
значений f Другими словами, целевая функция дает нам высоту,
которая соответствует единственной координате восток-запад и
единственной координате север-юг. То есть координаты каждой
точки задаются следующим образом: широта и долгота — парой
значений f а высота — значением целевой функции от этих
значений f
Теперь, когда у нас есть координаты для отдельной точки
(ее широта, долгота и высота), нам нужна некая процедура
поиска, метод математической оптимизации, для изменения зна-
чений /, подставляемых в целевую функцию таким образом,
чтобы возможно скорее и проще добраться до вершины повер-
хности.
То, что мы делаем, направлено на составление карты оп-
ределенной области в (и + 1)-мерного изображения, ибо коорди-
наты его вершины дают нам оптимальные значения f для исполь-
зования в каждой рыночной системе.
В прошлом было разработано множество методов математи-
ческой оптимизации, многие из которых весьма продуманны и
эффективны. У нас есть из чего выбирать. Ключевым вопросом
является: «К какой целевой функции мы будем применять эти
методы математической оптимизации в нашей новой методологии
инвестирования капитала?» Целевая функция является ее сердце-
виной. Далее мы обсудим этот вопрос и проиллюстрируем на
примерах, как работать с целевыми функциями. После этого мы
займемся методами оптимизации целевых функций.
174
Новая модель
Целевая функция
Целевая функция, которую мы хотим максимизировать,
представляет собой среднее геометрическое от HPR, которое
обозначается просто G:
пт
G(/j../„) = (ft hprJ(1 -'Pr°V [4-01],
<1=7
где:
п — количество сценарных спектров (рыночных систем или
компонентов портфеля);
т = возможное количество комбинаций исходов между
различными сценарными спектрами (рыночными системами)
в зависимости от количества сценариев в каждом наборе; т =
число сценариев в первом спектре * число сценариев во втором
спектре число сценариев в л-том спектре;
Probk = сумма вероятностей всех т HPR для данного мно-
жества значений f. Probk обозначает сумму величин в фигурных
скобках из выражения [4.02] для всех значений т данного набора
значений f,
HPRk = итог А>го периода владения. Эта величина равна:
HPRjt= (1 + (Z (4 *(-PWBL)))) w Л(+1 [4.02],
7=1
где:
п = количество компонент (сценарных спектров, т. е. ры-
ночных систем) в портфеле;
= значение f используемое для г-ой компоненты; j\
должно быть > 0 и может быть не ограничено большим (т. е.
может быть больше 1,0);
РЦ. = прибыль или потеря, приносимая исходом i-ой
компоненты (т. е. сценарного спектра или рыночной системы),
ассоциированная с k-ой комбинацией сценариев;
Новая модель 175
BLz = худший исход i-oro сценарного спектра (рыночной
системы).
То есть Probk в предыдущем выражении для G имеет вид:
Рп*. = (П(П 14 031
<=1 j=i+l
Величина P(jk\jk) ~ это просто совместная вероятность (пред-
мет обсуждения предыдущей главы) сценариев i-ro и j-ro спек-
тров, которые входят в к-ую комбинацию сценариев. Например,
если у нас есть три монеты, то каждой из них соответствует
сценарный спектр из двух сценариев: орел и решка. Количество
сценарных спектров (2) выражается переменной п. Откуда полу-
чаем восемь (2*2*2) возможных комбинаций исходов, которые
обозначаются переменной т.
В выражении [4.01] переменная к изменяется от 1 до m в
одометрическом {лексикографическом) порядке:
Монета 1 Монета 2 Монета 3 к
решка решка решка 1
решка решка орел 2
решка орел решка 3
решка орел орел 4
орел решка решка 5
орел решка орел 6
орел орел решка 7
орел орел орел 8
То есть изначально все спектры установлены на свои худ-
шие (крайне левые) значения. Затем крайне правый спектр цик-
лически проходит через все свои значения, после чего второй
справа спектр переходит к следующему (справа) сценарию. Про-
должаем таким образом дальше: циклически меняем все сценарии
крайне правого спектра, когда второй справа сценарный спектр
176
Новая модель
циклически прошел все свои значения, третий переходит к сво-
ему следующему сценарию. Данный процесс абсолютно аналоги-
чен тому, как работает одометр в автомобиле, откуда и взялось
название одометрический.
Таким образом, если бы к было больше 3 (т. е. к = 3), i
равно 1, a j равно 3, то величина P(ik|jk) обозначала бы совме-
стную вероятность выпадения монеты 1 решкой и выпадения
монеты 3 решкой. Наконец, подставив выражения [4.02] и [4.03]
в [4.01], мы можем создать одну полную целевую функцию. То
есть мы сможем максимизировать G в виде:
т п
((1 + (s
k=l /=1
п-1 п \/т л-1 п
и*(-рц,/вь.))) " )) [4-041
Данная целевая функция, которую нам нужно максимизи-
ровать, выражает суть нашей новой методологии инвестирования
капитала. Она дает нам высоту, среднее геометрическое HPR,
в (п + 1)-мерном пространстве используемых значений f Это точ-
ное значение, безотносительно к тому, как много сценарных
спектров используется в качестве аргументов. Это — целевая
функция модели в пространстве рычагов.
Хотя выражение [4.04] может показаться несколько устра-
шающим, нет никаких причин пугаться его. Как можно заметить,
это выражение представляет собой компактную форму выражения
[4.01], с которой работать много удобнее.
Возвращаясь к нашему примеру с тремя монетами, пред-
положим, что мы выигрываем два доллара на выпадении орла
и проигрываем один доллар на выпадении решки. У нас имеется
три сценарных спектра, три рыночных системы, называемые
Монета 1, Монета 2 и Монета 3. Два сценария, орел и решка,
представляют каждую монету, каждый сценарный спектр. Для
простоты будем предполагать, что взаимные коэффициенты кор-
реляции всех трех сценарных спектров (монет) равны 0.
Новая модель
177
Следовательно, мы должны найти три различных значения
f Мы отыскиваем оптимальное значение /для Монеты 1, Монеты
2 и Монеты 3, обозначаемые через /, / и / соответственно,
которые дают наибольший рост, то есть комбинацию трех зна-
чений / которые приводят к наибольшему среднему геометричес-
кому HPR (выражение [4.01] или [4.04]).
В данный момент мы не обращаем никакого внимания на
избранный метод оптимизации. Сейчас наша цель заключается в
том, чтобы показать, как вычисляется целевая функция. По-
скольку методы оптимизации обычно назначают переменным
некоторые начальные значения, мы произвольно выбираем 0,1
в качестве начального значения для всех трех величин /
Для простоты вместо формулы [4.04] мы будем исполь-
зовать выражение [4.01]. Исходя из него, мы начнем переби-
рать все комбинации сценарных наборов по возрастанию ин-
декса к от 1 до ш, вычисляя HPR комбинаций сценарных
наборов по формуле [4.02] и перемножая все эти HPR вместе.
Каждый раз, вычисляя выражение [4.02], нужно отслеживать
показатели степени в фигурных скобках, ибо далее нам пона-
добится их сумма.
Итак, мы начинаем с k = 1, где сценарный спектр 1 (Мо-
нета 1) поворачивается решкой, как и два других сценарных
спектра (монеты).
Формулу [4.02] можно переписать в виде:
hpra= (1 + ох
С = Г (4*(-рц ./вь,.))
/=1
[4.05]
Заметьте, что помещенный в скобки показатель степени
в формуле [4.02], который мы должны отслеживать, в формуле
[4.05] обозначен переменной х. Его же представляет и [4.03].
Таким образом, для получения С мы действуем следующим
образом. Проходя через каждый сценарный спектр, берем исход
12-9727
178
Новая модель
текущего сценария согласно значению индекса к и делим его
отрицательное значение на величину наихудшего исхода в данном
спектре. Полученное частное умножаем на значение /, которое
используется с данным сценарным спектром. По мере продвиже-
ния от одного сценарного спектра к другому эти величины
суммируются.
Индекс i обозначает тот сценарный спектр, который мы
рассматриваем в текущий момент. Наибольшая потеря в сценар-
ном спектре 1, происходящая при выпадении решки, составляет
один доллар (т. е. —1). Следовательно, ВЦ равен —1 (каковыми
будут и ВЦ, и ВЦ, поскольку наибольшая потеря в каждом из
двух других сценарных спектров, или на двух других монетах,
равна —1). Ассоциированная величина PL, то есть исход того
сценария в i-ом спектре, который соответствует тому сценарию
этого спектра, на который указывает к, равна —1 в сценарном
спектре 1 (так же, как и в двух других спектрах). В данный
момент значение f равно 0,1 (как это сейчас и в двух других
спектрах). Итак:
с=Е (4 *(-рц,/вц))
/=1
С = (0,1 * (—1/-1)) + (0,1 * (—1/-1)) + (0,1 * (—1/-1))
С = (0,1 * -1) + (0,1 * -1) + (0,1 * -1)
С = -0,1+ -0,1+ -о,1 = -о,з
Обратите внимание, что значения PL отрицательны, поэто-
му выражения во внутренних скобках положительны.
Теперь берем значение для С из формулы [4.05], прибав-
ляем к нему 1 и получаем 0,7 (так как 1 + (—0,3) = 0,7). Теперь
мы должны определить показатель степени, или переменную х из
формулы [4.05].
Величина P(ik| jk) обозначает просто совместную вероят-
ность к-го сценария из i-ro спектра и k-го сценария из j-ro
спектра. Поскольку индекс к в данный момент равен 1, то он
указывает на выпадение решки во всех трех сценарных спектрах.
Значение х находим следующим образом. Берем произведение
Новая модель
179
совместных вероятностей сценариев из спектров 1 и 2, умножаем
его на совместную вероятность сценариев из спектров 1 и 3 и на
совместную вероятность сценариев 2 и 3. Иначе это можно вы-
разить так:
1
2
3
2
3
3
Если бы имелось четыре спектра, то мы бы взяли произ-
ведение всех совместных вероятностей согласно схеме:
1
1
1
2
2
3
2
3
4
3
4
4
Поскольку все наши совместные вероятности равны 0,25,
для х получаем:
х = (0,25 *0,25)
(l/(3-D)
х = (0,015625)
1/2
х = (0,015625)
х = 0,125
12*
180
Новая модель
Таким образом, х, равное 0,125, составляет совместную
вероятность k-й комбинации сценариев. (Отметьте, что мы соби-
раемся определить совместную вероятность трех случайных пере-
менных с использованием совместных вероятностей двух случай-
ных переменных!)
Отсюда HPRk = 0,70125 = 0,9563949076, когда k= 1. С по-
мощью формул [4.02] или [4.05] мы должны вычислить эту
величину для всех значений к от 1 до m (в данном случае m равно
8). Проделав это, получим:
к HPR, Probk
1 0,956395 0,125
2 1 0,125
3 1 0,125
4 1,033339 0,125
5 1 0,125
6 1,033339 0,125
7 1,033339 0,125
8 1,060511 0,125
Суммирование по формуле [4.04] всех Probk, получаемых из
[4.03], дает 1. Далее, перемножив все HPR, согласно [4.01] или
[4.04], получим 1,119131. Откуда следует, что величина G из
[4.01], равная 1,119131, отвечает значениям 0,1, 0,1, 0,1 величин
/, f2 и f3 соответственно.
т
< ?(о,1, од, 0,1) = ([[ hprJ(1 «РгоЬ/;)
к=1
< 7(0,1, 0,1, 0,1) = (0,956395 * 1 * 0,1 * 1,033339 * 1 * 1,033339 *
* 1,033339 * 1,0605011)(1/(0’125 + °-125 + °>125+ 0Д25-1- 0,125 + 0,125 + 0,125+ 0,125))
(7(0,1, 0,1, 0,1) = (1,119131)(1/1)
Новая модель
181
<7(0,1, 0,1, 0,1) =--1,119131
Далее, руководствуясь используемым методом математичес-
кой оптимизации, мы стали бы изменять наши значения f. В итоге
мы нашли бы оптимальные значения 0,21, 0,21, 0,21 для f2
и fv соответственно. Это дало бы нам:
к HPRk Probk
1 0,883131 0,125
2 1 0,125
3 1 0,125
4 1,062976 0,125
5 1 0,125
6 1,062976 0,125
7 1,062976 0,125
8 1,107296 0,125
Эти данные получаются по формуле [4.01] следующим
образом:
т
< 7(0,21, 0,21, 0,21) = ([[ HPRk)(1 «Рг°Ь/;)
< 7(0,21, 0,21, 0,21) = (0,883131 * 1 * 0,1 * 1,062976 * 1 * 1,062976 *
* 1 062976 * 1 1О7296)(1/(ОЛ25 + 0Л25 + 0,125 + 0,125 + 0,125+ 0,125+ 0,125+ 0,125»
< 7(0,21, 0,21, 0,21) = (1,174516)(1/1)
(7(0,21, 0,21, 0,21) = 1,174516
Данная комбинация значений f дает наибольшее G для
заданных сценарных спектров. Поскольку это очень упрощен-
182
Новая модель
ный случай, то есть все сценарные спектры одинаковы и
корреляция между ними нулевая, мы получили одинаковые
значения (0,21) для всех сценарных спектров. Обычно так не
бывает, и вы получите свое значение f для каждого сценарного
спектра.
Теперь, когда мы знаем оптимальные значения для всех
сценарных спектров, мы можем определить, насколько велики
эти десятичные величины в денежном выражении. Для этого
разделим наихудший исход (потерю) сценариев каждого спектра
на отрицательное значение оптимального f этого спектра. Напри-
мер, для первого сценарного спектра, Монеты 1, максимальная
потеря была равна —1. Деля —1 на отрицательное оптимальное
f —0,21, получаем 4,761904762 в качестве значения /$ для
Монеты 1.
Подведя итоги, укажем:
1. Начните с некоторого набора значений f Knn.fv..fn , где п —
количество компонент в портфеле, т. е. рыночных систем
или сценарных спектров. Начальный набор значений f за-
дается используемым методом оптимизации.
2. Переберите комбинации сценарных наборов в одометричес-
ком порядке по индексу к от 1 до т, для каждого к
вычислите HPR и перемножьте их вместе. Попутно ведите
текущую сумму показателей степени, в которые возводятся
эти HPR.
3. Вычислите последнее HPR при к= т. Возведите последнее
произведение в степень, обратную сумме показателей (ве-
роятностей) всех HPR, и получите G — среднее геометри-
ческое HPR.
4. Это среднее геометрическое HPR дает нам высоту в (п + 1)-
мерном пространстве. Нам нужно найти вершину в этом
пространстве, поэтому далее нам следует выбрать и опро-
бовать новый набор значений f, который помог бы нам
найти эту вершину. Этот процесс и называется математи-
ческой оптимизацией.
Новая модель
183
Математическая оптимизация
или отыскание корней
Уравнения имеют левую и правую части. Вычитая одну из
другой, получаем уравнение, одна из частей которого равна нулю.
Отыскивая корни уравнения, вы хотите узнать, какие значения
независимой переменной (-ных) разрешают это уравнение (это —
корни). Найти корни можно с помощью традиционных методов,
например методом Ньютона (метод касательных).
Можно сказать, что отыскание корней имеет отношение
к математической оптимизации, так как первая производная
в точке оптимума функции (т. е. на экстремуме) будет равна 0.
Следовательно, вы могли бы заключить, что традиционные методы
отыскания корней, например метод Ньютона, можно использо-
вать для решения оптимизационных задач (применение собствен-
но методов оптимизации для отыскания корней уравнения, на-
против, чревато обилием трудностей).
Наша дискуссия, однако, будет касаться лишь методов
оптимизации, а не методов отыскания корней, как таковых.
Сведения о последних можно почерпнуть в таком уникальном
источнике, как «Численные методы»*.
Методы оптимизации
Математическую оптимизацию можно вкратце описать сле-
дующим образом. У вас есть некая целевая функция (обозначим
ее G), зависящая от одного или большего количества независи-
* William Н. Press, Brian Р. Flannery, Saul A. Teukolsky, and William
T. Vetterling, Numerical Recipes: The Art of Scientific Computing, New York:
Cambridge University Press, 1986.
184
Новая модель
мых переменных (которые мы обозначим ..., fn). Вы хотите
найти значение (-ния) независимой переменной (-ных), достав-
ляющее минимум (или иногда, как в нашем случае, максимум)
целевой функции. Максимизация и минимизация, по сути, яв-
ляются одним и тем же (то, что для одного равно G, для другого
будет — G).
В самом примитивном случае вы можете оптимизировать
следующим образом: перебирая все комбинации значений пере-
менных и подставляя их в целевую функцию, искать такую
комбинацию, которая дает наилучший результат. Предположим,
например, что мы хотим найти оптимальное f для одновремен-
ного бросания двух монет с точностью до 0,01. Тогда мы могли
бы неизменно проводить расчеты для монеты 1 на значении 0,0,
в то время как для монеты 2 переходить от 0,0 к 0,01 к 0,02
и так далее, пока не дойдем до 1,0. После этого мы могли бы
вернуться к монете 1 и, просчитывая ее на значении 0,01,
опробовать все возможные значения для монеты 2. Действуя
таким образом и далее, мы придем к тому, что значения обеих
переменных окажутся на их максимумах, то есть станут равны 1,0.
Поскольку у каждой переменной в данном случае имеется по 101
возможному значению (от 0 до 1,0 включительно с шагом 0,01),
то мы должны опробовать 101 * 101 комбинаций, то есть целевая
функция должна быть рассчитана 10201 раз.
При желании, мы могли бы потребовать большей точно-
сти, чем 0,01. Тогда у нас стало бы 1001 * 1001 комбинаций,
подлежащих опробованию, то есть целевую функцию пришлось
бы рассчитать 1002001 раз. Если бы мы собрались взять три
переменных вместо двух и потребовали бы точности 0,001, то
нам пришлось бы вычислить целевую функцию 1001 * 1001 * 1001
раз, что равно 1003003001, то есть нам пришлось бы вычислить
целевую функцию более одного миллиарда раз. А ведь мы ис-
пользуем всего лишь три переменных и требуем лишь 0,001
точности!
Хотя рассмотренный примитивный случай оптимизации
наиболее понятен по сравнению с использованием всех других
методов оптимизации, он же обладает сомнительным достоин-
ством быть слишком медленным, для применения к большин-
ству задач.
Новая модель
185
Почему не перебрать все значения первой переменной и найти
оптимум для нее, потом, зафиксировав первую переменную на
оптимуме, перебрать все значения второй переменной и, найдя
ее оптимум, получить таким образом оптимумы для первых двух
переменных, после чего искать оптимум для третьей переменной
при фиксированных первых двух на их оптимумах и так далее,
пока задача не будет решена?
Недостатком этого второго подхода является то, что часто
таким способом невозможно найти оптимальный набор значений
переменных. Отметьте, что, когда мы добираемся до третьей
переменной, значения первых двух равны своим максимумам,
как будто других переменных нет. Поэтому, при оптимизации по
третьей переменной первые две, зафиксированные на своих оп-
тимумах, мешают нахождению ее оптимума. То, на чем это может
закончиться, представляет собой не оптимальный набор значе-
ний, а, скорее, оптимальное значение для первой переменной,
оптимум для второй, когда первая зафиксирована на своем оп-
тимуме, оптимум для третьей, когда первая зафиксирована на
своем оптимуме, а вторая установлена на некоем субоптимуме,
который оптимален при условии помех со стороны первой пере-
менной, и так далее. Иногда удается провести такой перебор по
всем переменным и в итоге получить-таки оптимальный набор
значений переменных, но когда переменных больше трех, он
становится все более и более длительным, если вообще осуще-
ствимым, учитывая влияние других переменных.
Кроме двух описанных грубых методов математической
оптимизации существуют и более совершенные. Это — замечатель-
ная ветвь современной математики, и я настоятельно призываю
вас познакомиться с ней, просто в надежде, что вы извлечете
из этого какую-то долю того удовлетворения, которую получил
я от ее изучения.
Экстремум, максимум это или минимум, может быть либо
глобальным (действительно наибольшее или наименьшее значе-
ние), либо локальным (наибольшее или наименьшее значение
в непосредственной окрестности). Наверняка знать глобальный
экстремум почти невозможно, так как вы не представляете себе
область значений независимых переменных. Но если область
значений вам известна, то вы просто нашли локальный экст-
ремум. Поэтому зачастую, когда люди говорят о глобальном
186
Новая модель
экстремуме, они в действительности имеют в виду локальный
экстремум на очень широкой области значений независимых
переменных.
Для отыскания максимумов или минимумов в таких слу-
чаях существует масса методов. Любой из них, как правило,
накладывает на переменные некие ограничения, которые должны
удовлетворяться применительно к экстремуму. К примеру, в нашем
случае эти ограничения заключаются в том, чтобы все незави-
симые переменные (значения f) были бы большими или равными
нулю. Нередко требуется выполнение ограничивающих функций
(т. е. чтобы значения других функций от используемых перемен-
ных были бы болыие/меньше или равны некоторым величинам).
Линейное программирование с его симплекс-методом — эта весь-
ма хорошо разработанная область такой оптимизации в условиях
ограничений — применима лишь, когда и оптимизируемая, и ог-
раничивающие функции являются линейными (многочленами
первой степени).
В целом, различные методы математической оптимизации
могут быть классифицированы по принципу используемого ап-
парата следующим образом:
1. По размерности целевых функций: с одной переменной
(двумерных) или многомерных (с размерностью три и более).
2. По тому, линейный метод или нелинейный. Если, как
отмечалось ранее, и функция, подлежащая оптимизации, и
ограничивающие функции являются линейными (т. е. не
содержат ни одного из своих аргументов в степени, боль-
шей 1), имеется масса очень хорошо разработанных методов
решения задачи отыскания экстремума.
3. По использованию производных. Некоторые методы требу-
ют вычисления первой производной целевой функции.
В многомерном случае первая производная представляет со-
бой векторную величину, называемую градиентом.
4. По эффективности вычислений. То есть такие методы,
которые применяются, когда вам нужно найти экстремум
возможно быстрее (т. е. с меньшим количеством вычисле-
ний) и возможно проще (нечто, сочетающееся с методами,
требующими вычисления производных) и с использовани-
ем возможно меньшей компьютерной памяти.
Новая модель
187
5. По устойчивости. Помните, вы хотели найти локальный
экстремум на очень широкой области значений независи-
мых переменных и использовать его вместо глобального
экстремума. Поэтому, если в этой области имеется более
одного экстремума, вы не захотите попасть в объятия та-
кого из них, который менее экстремален.
В нашей дискуссии мы будем рассматривать лишь много-
мерный случай. То есть мы займемся лишь теми алгоритмами
оптимизации, которые относятся к двум и более переменным
(т. е. с числом сценарных наборов, большим двух). Как это
подробно показано в «Формулах управления портфелем», при
отыскании единственного значения f, то есть /для одной рыноч-
ной системы или одного сценарного набора, как правило, наи-
более эффективным и быстродействующим методом будет пара-
болическая интерполяция.
Несмотря на обилие хороших алгоритмов для многомер-
ного случая, идеального все же нет. Какие-то методы эффек-
тивнее других применительно к определенным типам задач.
Как правило, основным критерием отбора среди методов мно-
гомерной оптимизации являются личные предпочтения (при
наличии компьютерных мощностей, необходимых для выбран-
ного метода).
Многомерные методы можно классифицировать по пяти
широким категориям.
Во-первых, это симплекс-методы скорейшего подъема. Они,
вероятно, становятся наименее эффективными из всех, если
вычислительная нагрузка немного увеличивается. Вместе с тем,
они обычно легко применимы и не требуют вычисления частных
производных первого порядка. К сожалению, им свойственна
медлительность, а требуемый объем используемой памяти имеет
порядок п2.
Второе семейство образуют direction set methods, известные
также как line minimization methods или (методы сопряженных
направляющих) conjugate direction methods. Наиболее примеча-
тельными среди них являются различные методы Пауэла. В смысле
скорости они эффективнее симплекс-методов скорейшего подъе-
ма (не путайте с симплекс-алгоритмом для линейных функций,
188
Новая модель
упоминавшимся ранее), не требуют вычисления частных произ-
водных первого порядка, но требования по памяти по-прежнему
имеют порядок п2.
Третье семейство образуют метод сопряженных градиентов
conjugate gradient methods. Среди них выделяются методы Флет-
чера-Ривза и тесно примыкающие к ним методы Полака-Рибьера.
Они тяготеют к группе наиболее эффективных методов в смысле
скорости и памяти (порядка п), но требуют вычисления частных
производных первого порядка.
Четвертое семейство методов многомерной оптимизации об-
разуют квази-ньтоновы, или методы с переменной метрикой
variable metric methods. Туда входят алгоритмы Дэвидсона-Флет-
чера-Пауэла (DTP) и Бройдена-Флетчера-Голдфарба-Шанно (BJGS).
Подобно conjugate gradient methods, они требуют вычисления
частных производных первого порядка, обычно быстро приводят
к экстремуму, однако эти алгоритмы требуют большей памяти
(порядка л2). Вместе с тем они уравновешивают достоинства conjugate
gradient methods тем, что дольше известны, шире используются
и лучше документально обеспечены.
Пятое семейство — это имитационные методы многомерной
оптимизации. Они гораздо более примечательны, поскольку дви-
жутся к экстремуму при помощи процессов моделирования, по-
заимствованных в природе. В их число входят метод генетического
алгоритма (genetic algorithm) и имитируемого отжига (simulated
annealing), моделирующего процесс кристаллизации, в ходе ко-
торого система находит свое минимальное энергетическое состо-
яние. Среди прочих эти методы отличаются наибольшей устойчи-
востью, почти иммунитетом по отношению к локальным
экстремумам, и могут решать задачи огромной сложности. Но они
не всегда самые быстрые и стать такими в большинстве случаев
не смогут. Вместе с тем, они так новы, что про них еще мало
что известно.
Хотя вы можете использовать любой упомянутый алгоритм
многомерной оптимизации, я предпочел генетический алгоритм
потому, что он является, возможно, единственным наиболее
устойчивым методом математической оптимизации, за исключе-
нием весьма грубых приемов перебора всех возможных комбина-
ций значений переменных.
Новая модель
189
Это метод общей оптимизации и поиска, который был
применен к решению многих задач. Нередко его применяли в
нейронных сетях, ибо он хорошо сокращает помехи и размерность
крупных нелинейных задач. Поскольку этот метод не требует
информации о градиенте, его можно применять и к разрывным,
и к эмпирическим функциям точно так же, как он применяется
к аналитическим функциям.
Применимость данного алгоритма, хотя он часто исполь-
зуется в нейронных сетях, не ограничивается исключительно
ими. В наших условиях мы можем использовать его в качестве
метода отыскания оптимальной точки на (л + 1)-мерном изобра-
жении.
Естественный отбор
Считается, что генетический алгоритм реализует принцип
естественного отбора в природе. Так оно и происходит, но не
совсем так, как в природе. Ведь в действительности мы многого
не знаем о том, как природа осуществляет этот принцип.
Прежде всего, если в природе взять какую-нибудь популя-
цию одинаковых индивидов, то один всегда выйдет в победите-
ли, то есть он будет считаться самым приспособленным. Это
верно, даже если все кандидаты одинаковы!
Например, если я бросаю на стол пригоршню монет и еще
одну монету использую для подбрасывания, то могу сыграть в
следующую игру. Монеты на столе разделены поровну на орлов
и решек. Я бросаю переворачивающуюся монету, и если она
выпадает орлом, то я убираю монету, лежащую вверх орлом. Если
выпадает решкой, то я убираю монету, лежащую вверх решкой.
Игра заканчивается, когда остаются только одни орлы или одни
решки.
Это — глупая игра, но она доказывает то, что не будучи
ни орлом, ни решкой, получаешь в этой игре селективное пре-
190
Новая модель
имущество (у орла и решки вероятность стать победителем оди-
накова), которое выдвигает одного из них в победители, то есть
в самые приспособленные.
Поэтому, когда мы спрашиваем «Какой из кандидатов
наиболее приспособлен?», мы сталкиваемся с парадоксальным
ответом «Тот, который является победителем».
Кроме того, создается впечатление, что у природы имеется
много различных целевых функций. Если бы это было не так,
то мир, в конце концов, заселили бы амфибии, умеющие
летать, причем, быстро! Как, например, вы можете объяснить
существование колибри? У нее ужасающая, безотлагательная
зависимость от сахаров, по сравнению с людьми она неразумна,
и все же выживает на планете вместе со столь многими другими
видами. Очевидно, колибри нашла некую нишу в естественном
устройстве планеты — предложенную природой целевую функ-
цию, которая так удовлетворяется нашей колибри, чтобы не
вымереть.
По сравнению с этим генетический алгоритм много проще.
Здесь у нас имеется одна целевая функция, которую мы пы-
таемся удовлетворить. Поэтому, хотя мы и говорим, что гене-
тический алгоритм скопирован в природе, он настолько проще
происходящего в природе, что вряд ли заслуживает своего на-
звания.
Генетический алгоритм
В двух словах, данный алгоритм действует путем перебора
множества возможных вариантов решений и упорядочивания их
согласно тому, насколько хороши их результаты, какими бы
целевыми функциями они ни определялись. Далее, по аналогии
с теорией естественного отбора, выживают наиболее приспособ-
ленные и репродуцируются в следующем поколении вариантов
решений, которое наследует как свойства родительских решений,
Новая модель
191
так и свойства предшествующих поколений. Средняя приспособ-
ленность популяции за многие' поколения будет возрастать и
приближаться к оптимуму.
Основной недостаток алгоритма — это большой объем
накладных расходов на обработку данных, требуемых для рас-
чета и хранения вариантов решений. Тем не менее, благодаря
своей конструктивной устойчивости и эффективности прило-
жений в области оптимизационных проблем, будь то крупные,
нелинейные или зашумленные, по убеждению автора, он ста-
нет фактически предпочтительным методом оптимизации в бу-
дущем (не считая появления лучших алгоритмов, обладающих
теми же желательными свойствами). По мере того, как компь-
ютеры становятся все более мощными и дешевыми, проблема
вычислительных издержек утрачивает свою остроту. Воистину,
если бы скорость обработки была нулевой, если бы скорость
не играла роли, то генетический алгоритм стал бы предпочти-
тельным методом решения для почти всех задач математической
оптимизации.
Алгоритм содержит следующие основные шаги:
Длина гена. Вы должны задать длину гена. Ген — это дво-
ичное представление члена популяции вариантов решений. Каж-
дый член этой популяции характеризуется значением каждой
переменной (т. е. значением /для каждого сценарного спектра).
Так, если мы принимаем длину гена в двенадцать раз больше
количества сценарных спектров, то каждой переменной (т. е. зна-
чению J) у нас будет соответствовать по двенадцать бит. Двенад-
цати битов достаточно для представления величины в интервале
от 0 до 4095. Последнее число представляется в виде:
2° + 21 + 22 + ... + 2й = 4095
Возводим 2 в степень 0 и прибавляем 2 в следующей
степени, пока не дойдем до степени, равной количеству битов
минус 1 (т. е. 11, в данном случае). Если имеется, скажем, три
сценарных спектра и на каждый из них мы используем длину
в двенадцать битов, то длина гена каждого варианта решения есть
12 * 3 = 36 бит. То есть ген в данном случае — это строка из
36 двоичных битов.
192
Новая модель
Обратите внимание, что данный способ кодирования дво-
ичных строк подходит только для целых величин. Но мы можем
приспособить его и для чисел с плавающей запятой с помощью
некоторого постоянного делителя. Так, если мы выберем посто-
янный делитель равным, скажем, 1000, то сможем представлять
числа от 0/1000 до 4095/1000, или от 0 до 4,095, с точностью
до 0,001.
Теперь нам понадобится процедура преобразования вариан-
тов решений в кодовые двоичные строки и обратно.
Инициализация. Требуется исходная популяция — популяция
вариантов решений. Битовые строки этого первого поколения
закодированы случайным образом. Более высокая численность
популяции повышает вероятность того, что мы найдем хорошее
решение, но при более высокой численности требуется большее
время обработки.
Задание целевой функции. Битовые строки декодируются в
свои десятичные эквиваленты, которые используются для зада-
ния целевой функции. (Например, при наличии двух сценарных
спектров целевая функция дает нам величину координаты Z, или
высоту трехмерного изображения, в предположении, что величи-
ны f соответствующих сценарных спектров — это координаты X
и Y.) Это проделывается для всех вариантов решений, и значе-
ния целевой функции для них сохраняются. (Важно: значения
целевой функции должны быть неотрицательными!)
Репродуцирование
Ранжирование по приспособленности. Теперь ранжируются
значения целевой функции. Для этого сначала выявляется наи-
меньшая целевая функция всех вариантов решений, и эта ве-
личина вычитается из всех вариантов решений. Полученные ре-
зультаты суммируются. Разделив на эту сумму результаты
вычитания из каждой целевой функции наименьшей, получают
коэффициенты приспособленности, содержащиеся в интервале
от 0 до 1. Отсюда сумма всех коэффициентов приспособленности
будет равна 1,0.
Случайный отбор по приспособленности. Теперь ранжирован-
ные целевые функции упорядочиваются следующим образом. Если,
скажем, у первой целевой функции коэффициент приспособлен-
ности равен 0,05, у второй — 0,1, а у третьей — 0,08, то они
Новая модель
193
следующим образом включаются в схему отбора (образуются
интервалы):
первый вариант 0 — 0,05;
второй вариант 0,05 — 0,15;
третий вариант 0,15 — 0,23.
И так продолжают далее, пока верхняя граница последнего
варианта не окажется на 1,0.
Далее генерируются два случайных числа в интервале от
0 до 1, нужные для определения на основе предыдущей схемы
отбора, какими будут два родителя. Теперь для каждого варианта
решения следующего поколения нужно выбрать двух родителей.
Кроссовер*. Последовательно формируется каждый бит ре-
бенка — нового варианта решения популяции. Начинают с копи-
рования первого бита первого родителя в первый бит ребенка.
Одновременно с этим вы должны генерировать случайное число.
Если это случайное число оказывается меньше или равно веро-
ятности кроссовера, деленной на длину гена, то переключаемся
на копирование битов от другого родителя. Так, если у нас три
сценарных спектра с двенадцатью битами для каждой перемен-
ной, то длина гена равна тридцати шести. Если используемая
нами вероятность кроссовера равна 0,6, то для переключения на
копирование кода другого родителя в последующих битах, гене-
рируемое при каждом бите случайное число должно быть меньше
0,6/36, или 0,01667. Это продолжается до тех пор, пока все биты
не будут скопированы в коде ребенка. Данную операцию нужно
проделать для всех новых членов популяции.
Обычно вероятности кроссовера находятся в интервале от
0,6 до 0,9. Так, вероятность кроссовера 0,9 означает, что шансы
возникновения кроссовера у ребенка будут равны 90% , в сред-
нем; то есть 10% шансов будет за то, что ребенок будет точной
копией одного из родителей.
Мутация. Попутно с копированием каждого бита родителя
в бит ребенка генерируется второе случайное число. Если это
* Принятый в биологии термин, обозначающий генотип, образующийся
в результате перекрестной рекомбинации. — Прим. пер.
13-9727
194
Новая модель
случайное число оказывается меньше или равно вероятности
мутации, то данный бит инвертируется. То есть, бит, бывший
О у родителя, становится 1 у ребенка, и наоборот. Мутация
помогает сохранить разнообразие в популяции. Вероятность му-
тации обычно должна быть невелика (= 0,001), иначе алгоритм
вырождается в случайный поиск. Однако по мере приближения
алгоритма к оптимальному варианту, мутация приобретает все
большее значение, ибо кроссовер не может сохранить генетичес-
кое разнообразие в столь локализованном объеме (п + 1)-мерного
пространства.
Теперь вы можете вернуться к заданию целевой функции
и выполнить процесс для следующего поколения. Попутно вы
должны отслеживать наибольшую текущую целевую функцию
и соответствующий ей ген. Повторяйте этот процесс до тех
пор, пока не получите X неулучшившихся поколений, то есть
X поколений, для которых наилучшее значение целевой фун-
кции не было превзойдено. При выполнении этого условия
остановитесь и используйте ген, соответствующий наилучшему
значению целевой функции, в качестве искомого множества
решений.
Для примера рассмотрим реализацию генетического алго-
ритма с целевой функцией вида:
Y = 1500- (X- 15)2
Для простоты в этом примере у нас будет только одна
переменная, то есть каждый член популяции будет нести двоич-
ный код только для этой одной переменной.
Присмотревшись к целевой функции, легко заметить, что
оптимальная величина X равна 15, что приводит к значению Y,
равному 1500. Какими бы редкими ни были случаи, когда до-
ведется узнать оптимальные значения переменных, в этом про-
стом примере нам будет полезно знать оптимум, чтобы можно
было проследить, как к нему нас приведет алгоритм.
Пусть у нас есть начальная популяция из трех членов,
каждый со значениями переменной, закодированными пятибито-
выми строчками, которые вначале случайны:
Новая модель
195
Первое поколение
Индив. № X Двоичн. X Y Коэфф. Приспос.
1 10 01010 1475 0,4751
2 0 00000 1275 0
3 13 01101 1496 0,5249
Теперь путем случайного отбора по приспособленности
определяются Родители 1 и 3 первого поколения для Индиви-
дуума 1 второго поколения (заметьте, что Родитель 2 с приспо-
собленностью 0 погиб и не передаст далее своих генетических
свойств). Предположим, что случайный кроссовер происходит
после четвертого бита. Поэтому, наследуя первые четыре бита от
Индивидуума 1 и последний бит от Индивидуума 3 первого
поколения, Индивидуум 1 во втором поколении принимает вид
01011.
Предположим, что Индивидууму 2 второго поколения
выпадают те же родители; кроссовер происходит только после
первого и третьего битов. То есть он наследует бит 0 от Инди-
видуума 1 первого поколения, биты 11 в качестве второго и
третьего битов от третьего индивидуума первого поколения и два
последних бита от первого индивидуума первого поколения. В ре-
зультате этого генетический код второго индивидуума второго
поколения оказывается равным 01110.
Предположим далее, что в оба родителя третьего индиви-
дуума второго поколения попадает Индивидуум 1. То есть третий
индивидуум во втором поколении получает точно такой же ге-
нетический материал, как у первого индивидуума первого поко-
ления, а именно 01010.
Второе Поколение
Индивидуум № X Двоичный X
1 11 01011
2 14 ОШО
3 10 01010
13*
196
Новая модель
Пусть далее путем случайной мутации изменился третий
бит первого индивидуума. В результате для задания целевой фун-
кции имеем следующие данные:
Второе Поколение
Индив. № X Двоичн. X Y Коэфф. Приспос.
1 15 01110 1500 0,5102
2 14 ОШО 1499 0,4898
3 10 01010 1475 0
Обратите внимание, насколько во втором поколении под-
нялось, или эволюционировало, среднее значение Y.
Важные замечания
Нередко бывает полезно целиком перенести в следующее
поколение генетический код самого сильного индивидуума. Вы-
полнение этого условия наверняка сохранит хорошие множества
решений и благоприятно скажется на ускорении алгоритма. Кроме
того, вы можете следовать агрессивной тактике поддержания
генетического разнообразия путем увеличения параметров, ис-
пользуемых в качестве вероятностей кроссовера и мутации.
Я пришел к выводу, что, приняв за вероятность кроссовера
0,2, а за вероятность мутации — 0,05, можно ускорить полу-
чение решения, при условии, что код наиболее приспособлен-
ного индивидуума сохраняется при переходе от одного поко-
ления к другому — это удерживает алгоритм от вырождения
в случайный поиск.
По мере стремления размера популяции к бесконечности,
то есть, когда вы используете все большие величины для размера
популяции, повышается точность получаемого решения. То же
происходит и тогда, когда к бесконечности устремляется пока-
Новая модель
197
затель неулучшившихся популяций, то есть если вы используете
все больший порог количества неулучшившихся популяций. Вме-
сте с тем, прирост по каждому из этих показателей приводит
к увеличению затрат машинного времени.
Данный алгоритм может становиться времяемким. По мере
роста числа сценарных множеств и количества входящих в них
сценариев время обработки увеличивается в геометрической про-
грессии. В зависимости от ваших временных ограничений вам было
бы желательно придерживать количество сценарных наборов и
сценариев на управляемом уровне. Весьма благоприятным факто-
ром здесь является скорость компьютера (то есть использование
самого быстрого из доступных вам компьютеров).
Как только вы нашли оптимальный портфель, то есть
нашли значения для / разделите эти значения на наибольший
проигрыш по соответствующим сценарным спектрам и определите
/$ для этого конкретного сценарного спектра. Это именно то, что
мы делали в первой главе для того, чтобы определить, сколь-
кими контрактами торговать в оптимальном портфеле.
5
Управление капиталом для
п рофессионалов
Распределение активов является основной задачей тех, кто управ-
ляет капиталом. Результаты недавних исследований 82 крупных
пенсионных планов* за десятилетний период, полученные Бринсо-
ном, Сингером и Бибовером, свидетельствуют, что 91,5% прибыли
было получено благодаря политике распределения капитала. Актив-
ные инвестиционные решения, принимаемые спонсорами и менедже-
рами пенсионных планов как по избирательности, так и таймингу
внесли очень малый вклад в эффективность, в то время как
политика распределения капитала оказала на нее абсолютно до-
минирующее влияние.
Почему же тогда инвестиционной политике столь многих
инвестиционных программ свойственна произвольность, а не мате-
* Схема инвестирования, при которой работодатель делает регулярные
взносы в пенсионный фонд. — Прим. пер.
200
Управление капиталом для профессионалов
матическая выверенность? Мы, без сомнения, окружены невеже-
ством. Хуже того, с распространением торговли производными
инструментами и использования финансового рычага загадка рас-
пределения капитала становится еще более облачной, а тенденция
к произвольному размещению усиливается. Управляющим инвести-
циями нужна новая методология для анализа их политики распре-
деления, которая обоснована математически и учитывает влияние
финансового рычага в обоих его смыслах.
Мы можем отыскать вершину (п+1)-мерного изображения
в пространстве рычагов с помощью новой модели, представленной
в предыдущей главе. К сожалению, управляющие капиталом долж-
ны жить в рамках заданного множества ограничений, которые
в большинстве случаев не позволили бы им находиться на вершине
этого изображения. Текущие потери почти всегда будут больше
того, что позволят им их инвесторы. Однако эта неспособность
к пребыванию на вершине не означает, что они не могут восполь-
зоваться этой новой методологией для осуществления выгодного
выбора.
Поэтому в данной главе с позиций новой методологии мы
попытаемся отыскать жизнеспособные альтернативы нахождению
на вершине (п + 1)-мерного изображения. Вместо этого наша новая
методология предлагает другие прибыльные способы передвижения
по нему. Поскольку, в итоге, все управляющие инвестициями рас-
полагаются где-то на этом изображении, им следует понять, что
в этих условиях им может быть выгоднее вести себя несколько
иначе, чем они это делают, даже если им не по плечу временные
потери, связанные с нахождением на вершине. Эти иные благопри-
ятные альтернативы являются предметом данной главы, как
и многие другие реальные препятствия, такие, как требования по
марже, с которыми сталкиваются управляющие капиталами при
реализации этой новой методологии.
Управление капиталом для профессионалов
201
Реализация новой модели
Обычно, входя в новый период владения, вы знаете, в ка-
кие рынки и системы (т. е. сценарии) вы будете инвестировать,
равно, какие из уже имеющихся позиций, установленных в пре-
дыдущих периодах владения, вы перенесете в этот новый период
владения. Кроме того, вы, скорее всего, будете корректировать
сценарии различных сценарных спектров для того, чтобы отразить
в них больше текущей информации (их вероятностей или исхо-
дов, или и то, и другое) или создавать новые и исключать
старые сценарии из различных сценарных спектров.
Эти аспекты не составляют проблемы. То, что нужно сде-
лать, — это на основе новой информации определить оптимальный
портфель по всем позициям, которые вы переносите в новый
период владения. Эти позиции нужно подогнать к количественным
показателям, рекомендуемым моделью, так, чтобы вы всегда имели
то, что считается оптимальным размещением. Когда бы вы ни
собирались открыть новую позицию, вам следует заново опреде-
лить оптимальный портфель по новой модели и вновь изменить
ваши позиции так, чтобы вы имели позиции, которые на данный
момент считаются оптимальным распределением.
Короче говоря, всегда вновь пересматриваете модель, входя
в каждый новый период владения, чтобы учесть все изменения,
произошедшие с входной информацией, всегда имеете то, что
в настоящий момент выглядит оптимальным.
Активный и неактивный
капитал
Когда мы торгуем оптимальным портфелем по всему капи-
талу, мы можем ожидать ужасных текущих потерь по всему
портфелю в смысле сокращения собственных средств на счете.
202
Управление капиталом для профессионалов
Наша единственная защита от этого — каким-то образом разба-
вить портфель. Степень риска и безопасности любой инвестиции,
следовательно, не есть функция самой этой инвестиции, а, скорее,
функция уровня такой разбавленности.
Даже портфель из акций голубых фишек, когда они тор-
гуются на их оптимальных геометрических уровнях, продемонст-
рирует ужасные текущие потери. Тем не менее, эти голубые
фишки должны торговаться на этих уровнях, ибо они максими-
зируют потенциальную геометрическую прибыль по отношению
к дисперсии (риску), а также обеспечивают достижение цели
в наикратчайшее время. С этой точки зрения, торговля голубыми
фишками не более рискованна, чем торговля свиной грудинкой,
которая ничуть не менее консервативна, чем торговля акциями
голубых фишек. То же самое можно сказать о торговых системах,
работающих с товарным портфелем и портфелем облигаций.
Обычно инвесторы практикуют разжижение либо намерен-
но, либо нет. То есть если в оптимальном варианте нужно
торговать некоторым компонентом портфеля на уровне /$, ска-
жем, 2500, то они могут намеренно торговать им на уровне /$,
скажем, 5000, сознательно пытаясь сгладить кривую торгового
капитала и сдемпфировать текущие потери, или бессознательно,
на таких полуоптимальных уровнях /, значения которых могут
быть определены для любой позиции, как это подробно описано
в Главе 1.
Другой способ, который можно использовать при распре-
делении капитала, — это разделение торгового капитала на два
субсчета: активный субсчет и неактивный субсчет. Они не явля-
ются двумя отдельными счетами; напротив, теоретически, они
олицетворяют способ разделения единственного счета.
Данный метод используется следующим образом. Прежде
всего, вы должны выбрать начальное соотношение долей разде-
ления. Давайте предположим, что изначально вы хотите имити-
ровать счет на уровне половины от f. Поэтому уровень вашего
начального сечения равен 0,5 (начальный уровень дробления должен
быть больше 0 и меньше 1). Это значит, что вы будете делить
свой счет так, что 0,5 капитала пойдет на пассивный субсчет,
а 0,5 — на активный субсчет. Давайте предположим, что мы
начинаем со счетом в 100 000 долл. То есть изначально 50 000 долл.
Управление капиталом для профессионалов
203
будут на пассивном субсчете и 50 000 долл. — на активном
субсчете. Именно средства на активном счете используются при
определении того, сколькими единицами торговать. Эти субсчета
в действительности не существуют; они являются гипотетической
конструкцией, созданной вами для того, чтобы управлять своими
деньгами более эффективно. В данном методе вы всегда исполь-
зуете полностью оптимальное f Всякое изменение капитала отра-
жается только на активной части счета. Поэтому вы должны
ежедневно из общей величины счета (закрытые и открытые
позиции в пересчете по текущим рыночным ценам) вычитать
величину пассивных средств (она будет неизменной изо дня
в день). Эта разность является вашими активными средствами,
и по ней вы будете определять количество единиц для торговли
на уровне f
Предположим, что оптимальный уровень f торговли для
рыночной системы А составляет один контракт на каждые 2500 долл,
счета. В первый день вы начали с 50 000 долл, активных средств
и, следовательно, будете торговать двадцатью единицами. Если бы
вы следовали простой тактике половинной /, то в перый день вы
торговали бы тем же количеством единиц. При половинном f вы
торговали бы одним контрактом на каждые 5000 долл, средств на
счете (2500 долл./0,5) и исходили бы из всех 100 000 долл, счета
при определении того, сколькими единицами торговать. Поэтому,
следуя тактике половинного f вы в этот день также торговали
бы двадцатью единицами.
Однако как только величина счета изменяется, количество
единиц, которым вы будете торговать, также изменяется. Пред-
положим, что в этот день вы заработали 5000 долл., увеличив
таким образом общую величину вашего счета до 105 000 долл. При
тактике половинного /вы теперь будете торговать двадцать одной
единицей. А по методу дробления счета вы должны вычесть
неизменные 5000 долл, пассивной доли из всего капитала
в 105 000 долл. Это даст 55 000 долл, активной доли, исходя из
которой вы определите, что размер вашей позиции на оптималь-
ном по /уровне даст один контракт на каждые 2500 долл, счета.
Следовательно, по методу дробления счета вы теперь будете
торговать двадцатью двумя единицами.
Данная процедура действует аналогичным образом и при
понижении кривой капитала, то есть метод дробления счета
204
Управление капиталом для профессионалов
быстрее сокращает количество торгуемых единиц, чем при так-
тике дробления f Допустим, мы потеряли 5000 долл, в первый
день торговли, сократив таким образом общую величину счета до
95 000 долл. Согласно тактике дробления f мы теперь стали бы
торговать девятнадцатью единицами (95 000 долл./5000 долл.). В то
же время по методу дробления счета вы, имея 45 000 долл,
активных средств, будете торговать восемнадцатью единицами
(45 000 долл./2500 долл.).
Обратите внимание, что при следовании методу дробления
счета точная доля оптимального / которую мы используем,
меняется с изменением капитала. Мы определяем ту долю, с ко-
торой хотим начать. В нашем примере мы использовали начальное
дробление пополам. Когда капитал увеличивается, эта доля оп-
тимального f также растет, приближаясь в пределе к 1 при
стремлении величины счета к бесконечности. Когда величина
счета уменьшается, эта доля приближается к 0 в пределе на том
уровне, где общий торговый капитал равняется своей пассивной
части. Это обстоятельство, а именно наличие встроенного меха-
низма страхования портфеля при дроблении счета, являющееся
громадным преимуществом, мы подробно обсудим в данной главе
далее.
Поскольку методу дробления счета отвечает изменяющаяся
доля f мы будем называть его методом динамического дробления
f в отличие от тактики простого дробления f (которую будем
называть статическим дроблением f).
Использование метода динамического дробления f анало-
гично торговле на оптимальном уровне/при начальной величине
счета, равной активной доле капитала.
Таким образом, мы видим, что существует два способа
разбить счет относительно по-настоящему геометрически опти-
мального портфеля. Мы можем торговать статически дробным или
динамически дробным / Хотя оба этих метода взаимосвязаны,
они также и различаются. Какой из них лучший?
Для начала нам нужно уметь определять арифметическое
среднее HPR для одновременной торговли п данными сценарны-
ми спектрами, а равно дисперсию этих же HPR для данных
значений/.../, сопоставленных этим сценарным спектрам. Те-
перь они задаются в виде:
Управление капиталом для профессионалов
205
AHPR(4.../„) =
m n n-l п (1/(л—1))
X [(1 + (X(4*(-PL /ВЬ.)))*{(П(П P(/Jyj)) }] [5.01],
*=1 /—1 i=l ;=/+;
m
Е Prob*
где:
п = количество сценарных спектров (рыночных систем или
компонентов портфеля);
m = возможное количество комбинаций исходов различ-
ных сценарных спектров (рыночных систем) в зависимости от
количества сценариев в каждом наборе, m = количество сцена-
риев в первом спектре * количество сценариев во втором
спектре * ... * количество сценариев в л-том спектре;
Prob = сумма вероятностей всех m значений HPR для
данного набора значений f. Probk — это сумма величин в фигур-
ных скобках числителя для всех m значений данного набора
значений /;
f= значение f, используемое для i-й компоненты (^ должно
быть >0 и может быть бесконечно большим, т. е. может превос-
ходить 1,0);
PLk j = прибыль или потери исхода i-й компоненты (т. е.
сценарного спектра или рыночной системы), ассоциированной с
k-й комбинацией сценариев;
BL. = наихудший исход i-ro сценарного спектра (рыночной
системы).
То есть Probk в данной формуле то же, что и в формуле
[4.03].
Формула [5.01] просто суммирует значения HPR с коэф-
фициентами, равными их вероятностям, и делит все это на сумму
вероятностей.
Для определения дисперсии значений HPR данного набора
нескольких одновременных сценарных спектров, торгуемых при
данных значениях f возьмем сначала грубый коэффициент от
HPR:
206
Управление капиталом для профессионалов
rawcoef, = 1 + (£ (f. * (-PL, ./BL.)) [5.02]
Затем эти грубые коэффициенты усредняются по всем
значениям к между 1 и m и получается их среднее арифмети-
ческое:
(У rawcoef.)
Л=1 к
arimeanrawcoef ------------------
m
Теперь можно определить дисперсию V:
m
Е (rawcoef,. - arimeanrawcoef)Е 2* Prob,
[5.03]
[5.04]
Е Prob,
Здесь снова Probk определяется по формуле [4.03].
Зачем нам все это нужно? Если припомнить фундаменталь-
ное уравнение из Главы 1, то знание среднего арифметического
HPR и дисперсии этих HPR может быть весьма полезным, что
мы сейчас и продемонстрируем.
Если мы знаем, каковы значения AHPR и дисперсии на
данном уровне f (скажем, для определенности, на уровне опти-
мального f), то мы можем использовать эти значения в торговле
на уровне разбавления, который мы будем называть FRAC. И,
поскольку мы можем вычислить эти две стороны прямоугольного
треугольника, то мы можем также определить и среднее гео-
метрическое HPR на этом разбавленном уровне. Далее приводятся
формулы для разбавленного AHPR, называемого FAH PR, разбав-
ленного стандартного отклонения (являющегося просто квадрат-
ным корнем из дисперсии), называемого FSD, разбавленного
среднего геометрического HPR, называемого K3HPR.
FAHPR = (AHPR - 1) * FRAC + 1 [5.05]
FSD = SD * FRAC
[5.06]
Управление капиталом для профессионалов
207
FGHPR = VFAHPR2 - FSD2
[5-07],
где:
FRAC = доля оптимального f которую мы определяем;
AHPR = среднее арифметическое HPR при оптимальном/;
SD = стандартное отклонение HPR при оптимальном /;
FAHPR = среднее арифметическое HPR при дробном /;
FSD = стандартное отклонение HPR при дробном /;
FGHPR = среднее геометрическое HPR при дробном f
Предположим, что у нас имеется система, где AHPR равен
1,0265. Стандартное отклонение при этих HPR равно 0,1211 (т. е.
— это квадратный корень из дисперсии, получаемой по формуле
[5.04]); откуда расчетное среднее геометрическое равно 1,019. Теперь
посмотрим, какими будут эти характеристики для статического
дробления /на уровнях 0,2 и 0,1. Они таковы:
Полное / 0,2/ 0,1/
AHPR 1,0265 1,0053 1,00265
SD 0,1211 0,02422 0,01211
FGHPR 1,01933 1,005 1,002577
Вот еще одна формула, которая также окажется полезной,
для определения ожидаемого времени достижения конкретной
цели:
In(goal)
ln(geometric mean)
[5.08а],
где:
Т = ожидаемое количество периодов владения до достиже-
ния конкретной цели;
цель = цель, выраженная в виде множителя к нашему
начальному капиталу, или TWR;
1п( ) = функция натурального алгоритма.
208
Управление капиталом для профессионалов
Теперь мы сравним торговлю согласно тактике статичного
дробления f на уровне 0,2 и со средним геометрическим 1,005
с методом динамического дробления f на уровне 0,2 (при 20%
начального активного капитала) и с дневным средним геомет-
рическим 1,01933. Время (в количестве дней, поскольку исполь-
зуется дневное среднее геометрическое), потребное для удвоения
статичного дробного / согласно формуле [5.08а] равно:
1п<2>
taOOlSr = 138,9751
Для удвоения динамического дробного / потребуется уста-
новить цель на 6. Это так, поскольку, если изначально в работе
задействуются 20% капитала, составлявшего вначале 100 000 долл.,
то сначала в работе у вас будет 20 000 долл. Цель состоит в том,
чтобы довести активный капитал до 120 000 долл. Поскольку
пассивный капитал остается равным 80 000 долл., тогда всего на
вашем счете, где изначально было 100 000 долл., будет 200 000 долл.
Следовательно, для увеличения счета с 20 000 до 120 000 долл,
вам нужно достичь TWR, равного 6. Если для удвоения динами-
ческого дробления / на уровне 0,2 цель равняется 6, то:
1п(6)
1п(1,01933)
= 93,58634
Обратите внимание, что при динамическом дроблении /
потребуется 93 дня в отличие от 138 дней, потребных при
статическом дроблении /
Теперь займемся уровнем дробления 0,1. Ожидаемое ко-
личество дней для удвоения счета при статичном дроблении
составит:
1п(2)
1п(1,002577) “ 269’3404
По сравнению с этим для удвоения при динамическом
дроблении с начальной активной долей 0,1 потребуется достичь
Управление капиталом для профессионалов
209
TWR, равного 11. Следовательно, потребное количество дней для
сравнимого результата при динамическом дроблении составит:
1п(11)
1п(1,01933) - 125’2458
Таким образом, для удвоения капитала при уровне дроб-
ления /0,1 в нашем статичном примере понадобится 269 дней
против 125 дней, потребных при динамическом дроблении. Чем
меньше доля / тем быстрее динамический метод станет лучше
статичного.
Рассмотрим утроение при дроблении/на уровне 0,2. Ожи-
даемое количество дней для утроения при статичном методе
равно:
1п(3)
---------- =220,2704
1п(1,005)
По сравнению с этим динамический аналог требует:
1п(11)
1п(1,01933) 125-2458
Для получения 400% прибыли (т. е. когда цель, или TWR,
равно 5) при статическом методе на уровне 0,2 потребуется:
1п(5)
^(йоозГ =322’6902
По сравнению с чем в динамическом варианте имеем:
1п(21)
1п(1,01933) = 159’0201
В этом примере для достижения цели в 400% динамический
метод не занимает и половины того времени, которое нужно при
14-9727
210
Управление капиталом для профессионалов
статическом методе. Кроме того, если поинтересоваться, какое
TWR будет через 322,6902 дня, нужных для четырехкратного
роста при статичном методе, то получим:
= 0,8 + (1,01933 Л 322,6902) * 0,2
= 0,8 + 482,0659576 * 0,2
= 97,21319
Это означает получение 9600% за то время, которое уходит
на получение 400% при статичном методе.
Теперь можно изменить формулу [5.08а], чтобы приспосо-
бить оба метода дробления /для определения ожидаемой длитель-
ности, требуемой для достижения конкретной цели в терминах
TWR. Начнем с выражения [5.086] для статичного дробления /
In(goal)
In(FGHPR)
[5.08b],
где:
Т = ожидаемое количество периодов владения, нужных для
достижения конкретной цели;
goal = цель в терминах множителя к начальному капиталу,
TWR;
FGHPR = скорректированное среднее геометрическое. Оно
получено из выражения [5.07], определяющего среднее геометри-
ческое для заданного статичного дробного /
1п( ) = функция натурального алгоритма.
Для динамического дробления /имеем выражение [5.08с]:
ln(((goal - 1)/FRAC) + 1)
ln(geometric mean)
.[5.08c],
где:
Управление капиталом для профессионалов
211
Т — ожидаемое количество периодов владения, нужных для
достижения конкретной цели;
goal = цель в терминах множителя к начальному капиталу,
TWR;
FRAC = начальная доля активного капитала;
среднее геометрическое = грубое среднее геометрическое
HPR при оптимальном f (здесь не используется корректировка,
подобная той, что в выражении [5.086]);
1п( ) = функция натурального алгоритма.
Итак, для иллюстрации использования формулы [5.08с]
предположим, что мы хотим определить, сколько времени уйдет
на удвоение счета (т. е. для получения TWR = 2) при активной
доле капитала 0,1 и среднем геометрическом 1,01933:
ln(((goal - 1)/FRAC) + 1)
Т = ---------------------------
ln(geometric mean)
ln(((2- 1)/0,1) + 1)
ln(l,01933)
ln(((l)/0,l) + 1)
ln(l,01933)
ln(10 + 1)
ln(l,01933)
ln(ll)
ln(l,01933)
2,397895273
~ 0,01914554872
= 125,2455758
14*
212
Управление капиталом для профессионалов
То есть если наши средние геометрические определены для
сценариев, периоды владения которых исчисляются в днях, то
мы можем ожидать удвоения примерно через 125’/4 дней. Если
наши сценарии используют периоды владения, исчисляемые
в днях, то мы ожидали бы удвоения через 125'/4 месяцев.
Пока вы имеете дело с такими Т, которые достаточно
велики для того, чтобы значение [5.08с] превышало значение
[5.086], вы выгадаете от использования в торговле метода ди-
намического дробления f Это можно также выразить в виде
[5.09]:
FGHPRr<= geometric mean7* FRAC + 1 — FRAC [5.09]
To есть вы должны итеративно перебирать значения Т,
пока правая часть этого выражения не станет больше ее левой
части, это и будет то значение Т (количество периодов владе-
ния), которое следовало бы подождать до перераспределения
портфеля. До этого будет лучше торговать на основе статичного
дробления f
На рис. 5.1 это иллюстрируется графически. Стрелкой отме-
чено то значение Т, при котором правая сторона [5.09] равна
левой стороне.
Таким образом, если используемая нами активная доля
капитала равна 20%, то есть FRAC = 0,2, то FGHPR следует
рассчитывать на основе 0,2 f Поэтому для случая, когда наше
среднее геометрическое при полном оптимуме /равно 1,01933
и 0,2/ (FGHPR) равно 1,005, нам нужно значение Т, удовлет-
воряющее следующему условию:
1,005г<= 1,01933г* 0,2+ 1-0,2
Мы определили наше среднее геометрическое для оптималь-
ного / а значит, и наше среднее геометрическое для дробного
/(FGHPR), применительно к периодам владения, измеряемых
в днях. Желательно было бы знать, хватит ли нам квартала.
Поскольку в квартале содержится около шестидесяти трех торго-
вых дней, нам нужно определить, будет ли Т, равное шестиде-
сяти трем, достаточным временем для того, чтобы выгадать от
Управление капиталом для профессионалов 213
использования динамического дробления f Поэтому проверим,
что дает выражение [5.09] при подстановке в качестве Т вели-
чины шестьдесят три:
1,005г <= 1,01933 г * 0,2 + 1-0,2
1,369184237 <= 3,340663933 * 0,2 + 1 - 0,2
1,369184237 <= 0,6681327866 + 1 -0,2
1,369184237 <= 1,6681327866 - 0,2
1,369184237 <= 1,4681327866
Поскольку в данном случае левая часть меньше правой, то
условие [5.09] выполнено. Следовательно, при заданных парамет-
Percent growth
Constant contract
Dynamic f
overtaks
T = 35, per [5.09]
Рис. 5.1. Процентное соотношение между торговлей но основе методов
стотичного и динамического дробления fa зависимости от истекшего времени.
Static f
214
Управление капиталом для профессионалов
рах мы можем перераспределить портфель через квартал и вос-
пользоваться преимуществами динамического дробления f
На рис. 5.1 показано соотношение между торговлей на
основе методов статичного и динамического дробления /в зави-
симости от истекшего времени.
Данный график иллюстрирует торговлю с начальной актив-
ной долей капитала в 20% как на статичной, так и на динамич-
ной основе. Оба варианта начинаются с одинакового количества
единиц, поэтому именно это количество единиц, как постоян-
ный контракт, торгуется все периоды владения. Среднее геомет-
рическое HPR при полном / используемом в этом примере,
было равно 1,01933, а среднее арифметическое HPR было равно
1,0265. Отсюда среднее геометрическое при статичном дробном f
на уровне 0,2 было равно 1,005.
Из всего этого следуют два важных момента: динамичное
дробление f опережает статичное дробление f тем быстрее, чем
меньше активная доля и чем больше среднее геометрическое. То
есть при использовании начальной активной доли капитала ве-
личиной 0,1 (для статичного и динамичного методов) динамич-
ный метод быстрее превзойдет статичный метод, чем при ис-
пользовании доли величиной 0,5. Поэтому обычно метод
динамичного дробления /тем скорее превзойдет статичный ва-
риант, чем меньше начальная доля активного капитала. Другими
словами, портфель с начальной активной долей капитала вели-
чиной 0,1 скорее станет лучше своего статичного варианта, чем
портфель с начальной долей в 0,2 станет лучше своего статич-
ного варианта. При начальной активной доле капитала в 100%
(1,0) динамичный метод никогда не превзойдет статичного (ско-
рее, они будут давать одинаковый прирост). Кроме того, на
скорость, с которой динамичный метод становится лучше ста-
тичного, влияет среднее геометрическое самого портфеля. Чем
больше среднее геометрическое, тем скорее метод динамичного
дробления превзойдет статичный вариант. При среднем геомет-
рическом 1,0 динамичный вариант никогда не станет лучше
статичного.
Чем больше истекшего времени, тем больше разница между
методами статичного и динамичного дробления / Асимптотически
метод динамичного дробления / приносит значительно больший
капитал, чем метод статичного дробления.
Управление капиталом для профессионалов
215
Наконец, еще один важный момент, касающийся рис. 5.1.
Линия постоянного контракта пересекает две других линии рань-
ше, чем они пересекутся друг с другом.
В конечном итоге большую выгоду приносит распределение
капитала с использованием метода динамичного дробления f То
есть вы определяете начальный уровень — процент — для разме-
щения в качестве активного капитала. Остаток — это пассивный
капитал. Ежедневные изменения капитала отражаются только на
его активной доле. Пассивная долларовая величина остается не-
изменной. Поэтому вы ежедневно вычитаете из вашего общего
капитала на счете его пассивную часть. Получаемая разница со-
ставляет активную часть капитала, по которой вы будете опре-
делять объемы вашей торговли с использованием оптимальных
уровней f
Теперь, когда рассчитывается требование по доходности
позиций, оно не будет точно таким же, как ваш активный
капитал. Оно может быть больше или меньше - роли это не
играет. То есть если только ваше требование по доходности не
составляет 100% капитала на счете, то в каждом данном пе-
риоде владения у вас на счете будет определенная неисполь-
зуемая наличность. Следовательно, вы почти всегда ненамерен-
но размещаете что-то в наличности (или в эквиваленте
наличности). Очевидно, что при этом нет никакой нужды в
сценарном спектре, предусматривающем переход в наличность
или ее эквиваленты, — в наличность уже делается должное
вложение, когда вы выделяете активную и пассивную части
капитала.
Перераспределение
Обратите внимание, что при торговле на основе динамич-
ного дробления/пассивная часть вашего капитала станет в конце
концов казаться малой, и вы столкнетесь с портфелем, который
слишком агрессивен для вашего темперамента. То есть повторится
216
Управление капиталом для профессионалов
та же ситуация, которая имела место вначале, когда вы собира-
лись торговать портфелем на полном объеме оптимального f
Следовательно, в какой-то момент времени в будущем вы захо-
тите переразместить капитал обратно до некоторого уровня на-
чального активного капитала.
Например, вы начинаете с 10% начального активного ка-
питала от счета величиной в 100 000 долл. Следовательно, у вас
есть 10 000 долл, активного капитала — капитал, которым вы
торгуете полностью на уровне оптимального f Каждый день вы
будете вычитать 90 000 долл, от капитала на счете. Разница соста-
вит активный капитал — тот капитал, которым вы торгуете
полностью на уровнях оптимального f
Теперь предположим, что капитал на этом счете вырос до
1 000 000 долл. То есть вычитание постоянного пассивного долла-
рового объема в 90 000 долл, оставляет вам 910 000 долл, активного
капитала, что означает, что ваш активный капитал теперь состав-
ляет 91% всех средств. То есть вам снова грозят те ужасные
текущие потери, которых вы старались избежать вначале, когда
вы разбавили f и начали торговать начальным активным капи-
талом в 10% всего.
Рассмотрим случай, когда перераспределение производится
после каждой сделки или ежедневно. Таковым является случай
торговли на основе статичного дробления f Вновь припомните
выражение [5.08а] для времени, потребного для достижения
конкретной цели.
Вернемся к нашей системе, в которой мы торговали 0,2 ак-
тивной долей и средним геометрическим 1,01933. Мы сравним
это с торговлей при статичном дроблении f на уровне 0,2
и итоговым средним геометрическим 1,005. Теперь, если мы
начинаем с 100 000 долл, на счете и хотели бы произвести пе-
рераспределение при общем капитале в 110 000 долл., то коли-
чество дней (ибо наше среднее геометрическое здесь рассчиты-
вается на дневной основе), требуемое статичной долей 0,2/ будет
равно:
1п(1,1)
= 19,10956
1п(1,005)
Управление капиталом для профессионалов
217
Сравним этот результат с тем, что дает использование
20 000 долл, из общего капитала в 100 000 долл, при полном
значении / для увеличения всего счета до 110 000 долл. Это
означает, что целью является увеличение 20 000 долл, в полтора
раза:
1п(1,5)
—(1,01933) =21’17807
При меньших целях тактика статичного дробления /дает
больший рост, чем соответствующий вариант динамичного дробле-
ния / С течением времени динамичный вариант превосходит
статичный и в конце концов бесконечно его опережает. На рис.
5.1 графически изображено соотношение между статичным и
динамичным дроблением /
Если вы переразмещаете капитал слишком часто, то вы
лишь ухудшаете положение, так как данный метод будет хуже по
сравнению с соответствующим статичным дроблением / Поэтому,
раз в итоге вам выгоднее использовать метод динамичного дроб-
ления /при распределении капитала, вам также будет выгоднее
прибегать к перераспределению средств между активным и пас-
сивным субсчетами как можно реже. В идеале, вы будете произ-
водить такое деление между активным и пассивным капиталом
лишь один раз в самом начале программы.
Слишком частое перераспределение невыгодно. В идеале, вы
никогда не станете перераспределять капитал и дадите доле оп-
тимального / которую вы используете, возможность приближать-
ся к 1 с ростом капитала на вашем счете. В действительности,
однако, в какой-то момент вы, скорее всего, произведете пере-
распределение. Будем надеяться, что вы не станете перераспреде-
лять капитал так часто, что это превратится в проблему.
Похоже, что перераспределение дает прямо противополож-
ное тому, что мы хотим, так как оно урезает активный капитал
после его роста или пополняет активную часть капитала после
периода, за который он понизился.
Перераспределение — это компромисс. Компромисс между
теоретически идеальной и реальной практической реализацией.
Обсужденные нами методы позволяют нам извлекать максимум
218
Управление капиталом для профессионалов
из этого компромисса. В идеале, вы никогда не стали бы
перераспределять капитал. Ваш скромный счет из всего-то
10 000 долл., вырастая до 10 000 000 долл., ни разу не подвергся
бы перераспределению. В идеале, вы перетерпели бы текущие
потери, которые понизили ваш счет до 50 000 долл, с отметки
в 10 млн. долл., после чего он подскочил до 20 млн. долл.
В идеале, если ваш активный капитал сократился бы до одного
доллара, то вы все равно могли бы торговать дробным контрак-
том (микроконтрактом?). В сдельном мире все это было возмож-
ным. В реальной жизни вы соберетесь перераспределять капитал
где-то вверху или внизу. При условии, что вы собираетесь это
делать, вы могли бы к тому же делать это систематическим,
прибыльным способом.
При перераспределении, или разрешении компромисса, вы
возвращаетесь обратно в то состояние, в котором вы бы начи-
нали программу заново, только на другом уровне капитала.
Следовательно, между перераспределениями вы позволяете ре-
зультатам торговли диктовать, куда смещать долю /при исполь-
зовании динамичного дробления / С помощью рычага можно
чрезвычайно быстро увеличить капитал, даже если вы начинаете
с выделения в активную долю только 5% капитала. Напоминаю,
что если вы используете все оптимальное / на этих 5% и если
ваша программа достаточно эффективна, то вы в скором вре-
мени будете торговать значительными объемами, сопоставимыми
со всем капиталом на счете.
В Математике Управления Капиталом подробно рассматри-
ваются четыре метода такого выполнения перераспределения,
которые могут быть выгодны трейдеру. Здесь мы не будем их
повторять. Вместо этого следует сформулировать несколько важ-
ных замечаний, относящихся к перераспределению вне зависимо-
сти от метода.
Первое и, возможно, наиболее важное, что нужно понять
о перераспределении сейчас, можно увидеть на рис. 5.1. Посмот-
рите на стрелку на рисунке, которая определяется как Т, которое
уравнивает части выражения [5.09]. Данное значение времени, Т,
является переломным. Если вы перераспределяете капитал раньше
Т, то вы наносите себе ущерб торговлей на динамичном дроб-
лении /вместо статичного.
Управление капиталом для профессионалов
219
Следующий важный момент перераспределения, который
нужно усвоить, состоит в том, что вы обладаете определенным
контролем над максимальными текущими потерями, выраженны-
ми в виде процента коррекции капитала. Отметьте, что вы тор-
гуете активной долей счета, как если бы это был счет точно
этого размера на полностью оптимальных уровнях. Раз вы дол-
жны быть готовы к почти 100% текущим потерям, когда торгуете
на полностью оптимальных уровнях /, то вы должны ожидать,
что когда-то произойдет и почти 100% ликвидация активной
части капитала.
Далее, многие трейдеры, которые пару последних лет ис-
пользовали метод динамичного дробления /, упоминают эмпири-
ческое правило, представляющееся очень хорошим: Выберите
величину своего начального активного капитала равной половине
максимальных текущих потерь, которые вы сможете перенести.
Так, если вы можете принять 20% текущую потерю, то остано-
витесь на 10% вашего начального капитала (однако, когда на счет
поступает прибыль и ваш активный капитал начинает превышать
20%, вы будете весьма подвержены текущим потерям, которые
больше 20%).
Существует и более точная реализация той же самой идеи.
Отметьте, что для определения потенциального риска портфеля
вы должны использовать сумму всех f То есть вы должны про-
суммировать значения f по всем компонентам. Это важно по
следующей причине. Пусть у нас есть портфель из трех компо-
нент, значения f для которых получены по методу, который
подробно описан в Главе 4. Пусть эти значения равны 0,5, 0,7
и 0,69, соответственно. Их сумма равна 1,89 — то есть тому /,
которым вы оперируете на портфеле в целом. Если теперь по
каждой компоненте реализуется самый худший сценарий, то счет
подвергнется текущим потерям в 189% от активного капитала!
Работая с портфелями, вы должны неизменно быть весьма бди-
тельны на такой случай и иметь это в виду, когда выделяете
начальный активный капитал.
Третий важный аспект перераспределения касается концеп-
ции портфельного страхования и его связи с оптимальным f
220
Управление капиталом для профессионалов
Страхование портфеля
и оптимальное f
Предположим на время, что вы управляете инвестицион-
ным фондом. На рис. 5.2 демонстрируется типичная тактика стра-
хования портфеля, известная также как динамичное хеджирова-
ние. В этом примере точкой отсчета является текущая стоимость
портфеля 100 долл, за акцию. Обычный портфель будет точно
следовать за рынком акций. Этот случай отображается непрерыв-
ной линией. Застрахованный портфель отражается прерывистой
линией. Вы видите, что прерывистая линия расположена под
непрерывной, когда портфель находится на своей начальной ве-
личине 100 или больше долларов. Разница между ними отображает
стоимость проведения портфельного страхования. В ином случае,
когда величина портфеля падает, страхование портфеля поддер-
живает его минимальную величину на желаемом уровне (в дан-
ном случае — это текущая стоимость 100 долларов за акцию)
минус стоимость реализации данной тактики.
Undering portfolio value
Рис. 5.2. Страхование портфеля.
BEL
Управление капиталом для профессионалов
221
По сути, страхование портфеля сродни покупке пут-опци-
она на этот портфель. Предположим, что фонд, которым вы
управляете, состоит лишь из одной акции, текущая стоимость
которой равна 100 долл. Покупка пут-опциона на эту акцию
с ценой исполнения 100 долл, и стоимостью 10 долл, скопиро-
вала бы прерывистую линию на рис. 5.2. Худшее, что может
случиться с вашим портфелем из этой акции и пут-опциона на
него, состоит в том, что вы исполните пут, в результате чего
продадите акцию за 100 долл, и потеряете на этом стоимость
пута - 10 долл. То есть самая меньшая стоимость портфеля
составит 90 долл., независимо от того, как бы низко ни упала
базовая акция.
При высоких ценах акции ваш застрахованный портфель
теряет часть прибыли от того, что его стоимость всегда сокраща-
ется на цену пута.
Теперь примем во внимание, что покупка колл-опциона
даст тот же результат, что и покупка базового актива вместе с
покупкой пут-опциона с такими же ценой и датой исполнения,
как у колл-опциона. Когда мы говорим об одинаковом резуль-
тате, мы имеем в виду эквивалентность позиции в смысле
показателей риск/прибыль при различной стоимости базового
актива. Поэтому прерывистая линия на рис. 5.2 может также
представлять портфель, который может быть составлен из длин-
ной позиции по колл-опциону ценой в 100 долл, при его ис-
течении.
Вот как действует динамичное хеджирование при обеспече-
нии портфельного страхования. Предположим, что вы покупаете
для своего фонда 100 долей этой единственной акции по цене
100 долл, за штуку. Теперь вы реплицируете (воспроизводите)
колл-опцион с использованием данной базовой акции. Вы сделаете
это путем задания начального минимума для акции. Пусть этот
определенный вами минимум равен 100. Вы также зададите дату
истечения этого гипотетического опциона, который вы собира-
етесь создать. Пусть назначенная вами дата истечения падает на
конец текущего квартала.
Теперь вы определите дельту (текущую скорость изменения
цены колл-опциона при изменении цены базового инструмента)
для этого 100-долларового колл-опциона с выбранной датой
истечения. Предположим, что эта дельта равна 0,5. Это значит,
222
Управление капиталом для профессионалов
что вы должны инвестировать 50% вашего капитала в данную
акцию. То есть у вас было бы только 50 этих акций вместо
100 штук, которые вы бы имели, не используй вы страхование
портфеля. С ростом цены акции то же происходит и с дельтой,
а равно и с количеством акций в вашем распоряжении. Верхним
пределом дельты является 1, где вы были бы инвестированы на
100%. В нашем примере при дельте, равной 1, у вас было бы
100 акций.
При понижении акции то же происходит и с дельтой.
Аналогичным образом сокращается и величина позиции по дан-
ной акции. Нижним пределом дельты является 0, где у вас не
было бы позиции по данной акции.
На практике управляющие фондами применяют неагрессив-
ные методы динамичного хеджирования. Они не предусматривают
необходимости торговли портфелем из наличных акций. Вместо
этого портфель, в целом, подстраивается к тому, какой должна
быть текущая дельта, величина которой диктуется моделью ис-
пользования фьючерсов на индексы акций и иногда пут-опци-
онов. Одно из преимуществ метода использования фьючерсов
состоит в том, что они имеют низкие операционные издержки.
Короткая продажа фьючерсов против портфеля эквивален-
тна продаже части портфеля и обращения ее в наличность. При
снижении стоимости портфеля продается больше фьючерсов, а при
росте его стоимости эти короткие позиции покрываются. Ущерб
портфелю, когда он растет, а короткие фьючерсные позиции
покрываются, составляет цена страхования портфеля, или цена
реплицированных пут-опционов. Достоинством динамичного хед-
жирования является то, что оно позволяет нам довольно точно
оценивать эту цену в самом начале. Менеджерам, которые опро-
бывают эту тактику, она позволяет сохранять портфель в непри-
косновенности, в то время как необходимые изменения в рас-
пределении средств осуществляются за счет сделок с фьючерсами.
Данная неагрессивная методика использования фьючерсов позво-
ляет отделить размещение капитала от активного управления
портфелем.
Те, кто использует страхование портфеля, должны посто-
янно корректировать портфель в соответствии с дельтой. Это
означает, что для определения дельты пут-опциона, который вы
Управление капиталом для профессионалов 223
стараетесь симитировать, вам нужно ежедневно подставлять в це-
новую модель опциона текущую стоимость портфеля, время,
оставшееся до истечения, уровни процентных ставок и волатиль-
ность портфеля. Прибавление этой дельты (представляющей собой
число между 0 и —1) к 1 даст вам дельту соответствующего кола.
Она представляет собой степень хеджирования, или процент,
который вам следует инвестировать в данный фонд.
Предположим, что ваша степень хеджирования в настоящий
момент составляет 0,46. Пусть объем фонда, которым вы управ-
ляете, эквивалентен пятидесяти фьючерсным единицам на ин-
декс S&P. Поскольку вы хотите инвестировать только на 46%,
значит, 54% вы оставляете незахеджированными. Пятьдесят четы-
ре процента от пятидесяти единиц составляют двадцать семь
единиц. Следовательно, на теперешнем ценовом уровне при дан-
ных уровнях процентных ставок и волатильности в настоящий
момент фонд должен наряду с длинной позицией в акциях
включать и короткую позицию из двадцати семи фьючерсных
единиц на индекс S&P.
Поскольку нужно все время отслеживать соответствие пор-
тфеля и дельты, требующей постоянного пересчета, эта тактика
хеджирования называется динамичной.
Использование фьючерсов в рамках данной тактики ослож-
няется тем, что рынок фьючерсов не следует точно за наличным
рынком. Далее, портфель, против которого вы продаете фьючер-
сы, может не вполне точно отслеживать сам индекс, лежащий
в основе фьючерса. Такой дисбаланс может внести свой вклад
в неустойчивость страхования портфеля. Более того, когда имити-
руемый опцион очень близко подходит к сроку своего истечения
и стоимость портфеля приближается к цене исполнения, гамма
этого опциона астрономически вырастает. Гамма — это текущая
скорость изменения дельты, или степени хеджирования. Другими
словами, гамма — это дельта дельты. Когда дельта изменяется
очень быстро (т. е. если имитируемый опцион имеет высокую
гамму), проведение страхования портфеля все больше осложня-
ется. Есть множество способов справиться с этой проблемой,
некоторые из которых весьма изощренные. Один из простейших
опирается на концепцию бессрочного опциона. Вы, например,
всегда можете предположить, что опцион, который вы имитиру-
224
Управление капиталом для профессионалов
ете, истекает, скажем, через три месяца. Каждый день вы станете
сдвигать дату истечения опциона на один день вперед. Повторю,
что эта высокая гамма обычно только тогда становится пробле-
мой, когда приближается дата истечения и при этом очень близ-
ки цена портфеля и цена исполнения опциона.
Имеется очень интересная взаимосвязь между оптимальным
f и страхованием портфеля. Когда вы открываете позицию, вы
можете утверждать, что инвестированы f процентов ваших средств.
Например, рассмотрим азартную игру, в которой ваше оптималь-
ное /равно 0,5, наибольший проигрыш равен —1, а ресурсы —
10 000 долл. В данном случае вы стали бы ставить по одному
доллару на каждые два доллара вашего счета, ибо — 1, или наи-
больший проигрыш, деленный на —0,5, или на отрицательное
оптимальное / дает 2. Деля 10 000 долл, на 2, получаем 5000 долл.
Следовательно, вы поставили бы на следующий кон 5000 долл.,
которые составляют /процентов (50%) вашего капитала. Если бы
вы умножили величину своего капитала на/(0,5), то в результате
пришли бы к тем же 5000 долл. Поэтому вы поставили на кон
/процентов своего капитала.
Аналогичным образом, если бы наш наибольший прогрыш
был равен 250 долл., а все остальное не изменялось, то мы бы
делали одну ставку на каждые 500 долл, своего счета, ибо —
250 долл./—5 = 500 долл. Деление 10 000 долл, на 500 долл,
показывает, что мы сделали бы двадцать ставок. Поскольку самое
большее, что мы можем потерять на одной ставке, равно 250 долл.,
то тогда мы рисковали бы / процентами (50%) своего счета,
играя 5000 долл. (250 долл. * 20).
Поэтому мы можем утверждать, что /равно тому проценту
нашего капитала, которым рискуем, или что /равно коэффици-
енту хеджирования. Вспомните, что, обсуждая портфели, мы рас-
сматривали сумму значений / его компонент. Поскольку при
использовании метода динамичного дробления / мы применяем
его только к активной части нашего портфеля, мы можем утвер-
ждать, что коэффициент хеджирования портфеля Н равен:
И- ас“те$---- (510а],
' 1 total equity
Управление капиталом для профессионалов 225
где:
Н = степень хеджирования портфеля;
f. = значение f для i-й компоненты портфеля;
active $ = активная часть средств на счете.
Выражение [5.10а] дает нам степень хеджирования портфе-
ля, который торгуется на основе тактики динамичного дробления
f Страхование портфеля действует и при статичном дроблении f
только частное activeS/общий капитал равно 1, а значение для f
(оптимальное f) умножается на ту величину, которую мы ис-
пользуем в качестве доли f Таким образом, при использовании
статичного дробления f степень хеджирования равна:
н= (E/)*frac [510b]
/=1
Мы можем утверждать, что, торгуя счетом на основе ди-
намичного дробления/ мы проводим страхование портфеля. В этом
случае минимум известен заранее и равен начальному пассивному
капиталу плюс цена проведения страхования. Чаще, однако, за
минимум при тактике динамичного дробления f проще принять
начальные пассивные средства счета.
Мы можем утверждать, что выражения [5.10а или Ь] дают
величину дельты колл-опциона, как ее понимают в портфель-
ном страховании. Более того, мы обнаруживаем, что эта дельта
во многом изменяется так же, как колл-опцион с глубоко «без
денег» (deep out-o/— the-money) и с очень отдаленным сроком
истечения. Таким образом, благодаря использованию постоянной
пассивной долларовой суммы торговля счетом согласно тактике
динамичного дробления f эквивалентна обладанию пут-опционом
с глубоко «в деньгах» (deep in-the-money) и с очень отдален-
ным сроком истечения. Аналогичным образом, мы можем утвер-
ждать, что торговля согласно тактике динамичного дробления f
представляет собой то же самое, что владение колл-опционом на
портфель с глубоко «без денег», и который очень долго не
истекает.
15-9727
226
Управление капиталом для профессионалов
Однако страхование портфеля можно также использовать и
как метод перераспределения средств для управления их эффек-
тивностью. Это управление возможно аналогично попытке управ-
лять танкером с помощью весла гребной лодки, но оно является
ценным методом перераспределения. Данный метод предполагает,
что сначала задаются параметры для программы. Во-первых, вы
должны определить величину минимума. Выбрав ее, вы должны
принять решения относительно даты истечения, уровня волатиль-
ности и других исходных параметров конкретной опционной
модели, которую вы намереваетесь использовать. Эти параметры
будут давать вам дельту опциона в любой данный момент вре-
мени. Как только дельта известна, вы можете определить, каким
должен быть ваш активный капитал. Поскольку дельта для счета,
или переменная Н в формуле [5.10а], должна равняться дельте
имитируемого колл-опциона:
я= (h). -.actlve$
total equity
Поэтому:
active $
total equity
if H<
i=l
[5.П]
иначе:
active $
H=---------------- = 1
total equity
Поскольку дробь асйуе$/общий капитал равна проценту
активного капитала, мы можем утверждать, что доля средств,
которую нам следует иметь в активной части капитала, равна
Управление капиталом для профессионалов
227
дельте колл-опциона, деленной на сумму величин f компонентов
портфеля. Однако вы заметите, что если Н больше суммы этих
f , то это указывает на то, что вы определили в качестве
активной части больше 100% капитала на вашем счете. Посколь-
ку это невозможно, то существует верхний предел в 100%
капитала на счете, который может быть использован в качестве
активного.
Страхование портфеля прекрасно в теории, но слабо на
практике. Как показал крах рынка акций 1987 г., беда порт-
фельного страхования состоит в том, что когда цены падают
в бездну, то ликвидности нет ни при какой цене. Однако здесь
нас это не заботит, поскольку мы интересуемся соотношением
между активным и пассивным капиталом и тем, насколько ма-
тематически это похоже на страхование портфеля.
Проблема практического использования страхования порт-
феля в качестве метода перераспределения капитала, как было
подробно показано выше, состоит в том, что перераспределение
происходит постоянно. Это принижает тот факт, что тактика
динамичного дробления асимптотически превзойдет тактику ста-
тичного дробления f. В результате попытки управлять эффектив-
ностью путем страхования портфеля как метода динамичного
перераспределения /, вероятно, не является такой уж хорошей
идеей. Однако всякий раз, когда вы используете дробление f
статичное или динамичное, вы пользуетесь некоей формой стра-
хования портфеля.
Верхняя граница активного
капитала и ограничение по
марже
Есть одна проблема, которая постоянно возникает, когда
мы берем любой метод торговли с постоянной долей из его
теоретического контекста и применяем его в условиях реального
15*
228
Управление капиталом для профессионалов
мира. В Математике Управления Капиталом показано, что всякий
раз, как к портфелю добавляется дополнительная рыночная си-
стема, то пока линейный коэффициент корреляции дневных
изменений капитала этой системы и другой системы в портфеле
меньше +1, портфель улучшается. То есть среднее геометрическое
дневных значений HPR выросло. Не лишено смысла, что вы
захотели бы иметь в портфеле как можно больше рыночных
систем. Естественно, в какой-то момент препятствием станут
соображения достаточности маржи для претворения в жизнь всего
задуманного.
Даже если вы торгуете только с одной рыночной систе-
мой, маржевые требования нередко могут быть проблемой. Уч-
тите, что оптимальное f в долларах очень часто меньше, чем
начальное требование по марже для данного рынка. Тогда в за-
висимости от того, какую долю f вы используете в настоящий
момент, используете ли вы тактику статичного или динамично-
го дробления, вы столкнетесь с требованием о внесении допол-
нительной маржи («маржи поддержки»), если эта доля слишком
велика.
Когда вы торгуете портфелем рыночных систем, сложности
с маржей поддержки становятся еще более вероятными.
То, что нужно, — это способ согласования того, как со-
здать оптимальный портфель с учетом депозитных требований
к компонентам портфеля. Он может быть очень легко найден.
Сделать это можно, найдя ту долю f которую вы можете исполь-
зовать в качестве верхней границы. Эта верхняя граница L дается
выражением [5.12]:
[5.12],
Е ((мег (/;$)//$)* marginj
fc=l /=1
где:
L = верхняя доля f. При этой конкретной доле/вы торгуете
оптимальным портфелем так агрессивно, как это только возмож-
но без получения маржевого требования;
/$ = оптимальное /в долларах для k-й рыночной системы;
Управление капиталом для профессионалов
229
margin к$ = начальное маржевое требование к-й рыночной
системы;
п = общее количество рыночных систем в портфеле.
Формула [5.12] в действительности много проще, чем она
выглядит. Для начинающих поясню, что выражение
МАХ _
,=1 в числителе и знаменателе означает просто наиболь-
шее /$ по всем компонентам портфеля.
Предположим, что у нас есть 2-компонентный портфель,
компоненты которого мы назовем спектрами А и В. Мы можем
представить информацию, необходимую для определения верхней
границы активного капитала в виде следующей таблицы:
Компонент/$Депозит Наибольшее /$//
Спектр А 2500 долл. 11 000 долл. 2500/2500 = 1
Спектр В 1500 долл. 2000 долл. 2500/1500 = 1,67
Теперь можно подставить эти величины в формулу [5.12].
Обратите внимание, что
п
МАХ равно 2500 долл., тогда как только второе /$ равно
1500, что меньше. Таким образом:
2500
1 * 11000+ 1,67*2000
2500 _ 2500
11 000 + 3340 14,340
= 17,43375174%
Это говорит нам, что нашим максимальным верхним про-
центом должно быть 17,434%.
Предположим теперь, что у нас был счет в 100 000 долл.
Если бы мы остановились на 17,434% активного капитала, то
230
Управление капиталом для профессионалов
у нас в активе было бы 17434 долл. Поэтому, предположив на
время, что можно торговать дробными единицами, мы купили
бы 6,9736 (17434/2500) спектра А и 11,623 (17434/1500) спек-
тра В. Маржевые требования при этом были бы следующими:
6,9726 * 11 000 = 76698,60
11,623 *2000 = 23245,33
Общее маржевое требование = 99943,93 долл.
Если, однако, вы все еще используете тактику статичного
дробления /(несмотря на возражения автора), то максимальная
доля, которую вы должны установить, равна 17,434%. Это при-
ведет к такому же маржевому требованию, как выше.
Заметьте, что использование формулы [5.12] дает выс-
шую долю / без начального маржевого требования, которое дает
одинаковые отношения различных рыночных систем друг к
другу.
В Главе 2 Математики Управления Капиталом объясняется,
что добавление все больше и больше рыночных систем (сценар-
ных спектров) приводит к все более высоким средним геомет-
рическим для портфеля в целом. Однако здесь имеет место сво-
еобразный баланс, так как каждая рыночная система чуть меньше
улучшает среднее геометрическое и чуть больше ухудшает эффек-
тивность за счет одновременных, а не последовательных исходов.
Поэтому ясно, что вы не захотите торговать бесконечно большим
количеством сценарных спектров. Более того, теоретически опти-
мальные портфели сталкиваются с проблемой маржевых требова-
ний при внедрении на практике. Другими словами, как следует
из формулы [5.12] вам обычно выгоднее торговать тремя сценар-
ными спектрами на полностью оптимальных уровнях / чем 10
при резко сокращенных уровнях. Как правило, вы сочтете, что
оптимальное количество сценарных спектров для торговли, осо-
бенно когда вам нужно отдавать много приказов и у вас большой
потенциал ошибок, никак не будет велико.
Управление капиталом для профессионалов
231
Торговля акциями
Методы, которые описаны в данной книге, касаются не
только фьючерсных трейдеров, но и трейдеров на любых рын-
ках. Даже тот, кто торгует портфелем только из акций, отно-
сящихся к числу голубых фишек, не имеет иммунитета от
принципов и выводов, рассмотренных в данной книге. Вы ви-
дели, что такой портфель из голубых фишек имеет оптимальный
уровень использования рычага (в обоих своих смыслах), где
максимизируется отношение потенциальных прибылей к потен-
циальным убыткам капитала на счете. На данном уровне ожи-
даемые текущие потери также весьма серьезны, поэтому порт-
фель должен быть разбавлен преимущественно за счет тактики
динамичного дробления f.
При операциях с акциями маржинальные требования могут
быть либо собственно маржинальными требованиями (в случае
маржинального счета), либо реальной ценой акций, когда они
применяются к наличному счету. То есть если акция идет по
40 долл, за долю, то маржинальные требования для 100 акций
при наличном счете составляют 4000 долл.
Смещение f и построение
устойчивого портфеля
Ранее по тексту упоминалось о полиморфной природе (л + 1)-
мерного изображения, то есть, что это изображение волнообразно
изменяется — его вершина обычно перемещается при изменении
свойств рынков и средств, используемых нами для торговли.
Такие изменения f безусловно являются проблемой для всех
трейдеров. Зачастую, если сдвиг /для многих осей направлен
к нулю, то есть при ослаблении сценарных спектров он может
привести к тому, что выигрышный в иных условиях метод
232
Управление капиталом для профессионалов
торговли на базе постоянной единицы станет проигрышной про-
граммой, поскольку трейдер находится не на пике кривой f
(правее пика), что эквивалентно тому, что трейдер находится
в проигрышной позиции.
Смещение/присуще всем рынкам и всем методам торговли.
Часто оно доходит до такой точки, где многие сценарные спек-
тры реализуются в инвестициях за один период в виде оптималь-
ной конструкции портфеля, а в непосредственно следующем
периоде не имеют рекомендаций вообще. Это говорит нам о том,
что эффективность, вне выборки, имеет тенденцию к значительно-
му ухудшению. Верно и обратное. Рынки, кажущиеся плохими
кандидатами для одного периода, где определен оптимальный
портфель, далее усиливаются в каждый следующий период, ибо
прошлые сценарии уже не оправдываются.
Конструируя сценарии и сценарные наборы, следует обра-
щать особое внимание на это свойство: рынки, которые прежде
вели себя хорошо, в следующий период обычно будут ухудшать-
ся, и наоборот. Понимание этого при выработке сценариев и
сценарных спектров поможет вам создать более устойчивые пор-
тфели и смягчить последствия сдвигов /
Настройка торговой программы
с помощью перераспределения
Нередко управляющие капиталом могут предпочесть дина-
мичное /статичному, даже если количество периодов владения
меньше того, что определено формулой [5.09], просто потому,
что оно дает лучшее страхование портфеля.
В таких случаях важно, чтобы управляющие капиталом не
проводили перераспределения портфеля ранее, чем будет удовлет-
ворено выражение [5.09], — то есть пока не пройдет достаточно
периодов владения, чтобы динамичный метод смог превосходить
статичный вариант.
Управление капиталом для профессионалов
233
Ключевым моментом настройки торговых программ в соот-
ветствии с целями тех, кто управляет капиталом, в данных
условиях является перераспределение инвестиций при росте счета.
То есть при достижении размером активного капитала некоторой
верхней точки следует произвести его перераспределение, чтобы
достичь определенную цель, хотя эта точка и не превосходит
некой минимальной временной грани (т. е. количества истекших
периодов владения).
Формула [5.09] дает нам величину Т, или горизонтальную
координату пересечения линий f при статичном и динамичном
дроблении (см. рис. 5.1). Эта та точка, измеренная в количестве
истекших периодов владения, где нам выгоднее торговать при
динамичном / чем при статичном f. Но если мы знаем Т (из
формулы [5.09]), то можем определить вертикальную координату
точки пересечения Y:
Y= FRAC * geometric mean7- — FRAC [5.13],
где:
T = величина переменной Т, полученная из формулы [5.09];
FRAC = начальная активная часть средств на счете;
geometric mean = необработанное среднее геометрическое
HPR (без такой подгонки, как в формуле [5.08b]).
Пример: начальная доля активного капитала = 5% (т. е.
0,05), среднее геометрическое за период = 1,004171, Т = 316.
Из [5.09] получаем, что, в среднем, после 316 периодов
динамичный метод начнет превосходить статичный вариант для
одного и того же значения f Это то же, что и сказать, что если
начать с исходных 5% активного капитала, то после того, как
счет увеличится на 13,63% (0,05 * 1,004171316 — 0,05), для одина-
ковых значений/динамичный метод начнет превосходить статич-
ный метод.
Итак, мы видим, что должно пройти некое минимальное
количество периодов владения, чтобы динамичное дробление /
стало лучше статичного (ранее этого не имеет смысла произво-
234 Управление капиталом для профессионалов
dumb перераспределение при использовании динамичного дробления f
а после этого лучше не использовать статичное дробление f).
Кроме того, эта величина на горизонтальной оси может быть
преобразована в вертикальную координату. То есть вместо мини-
мального количества периодов владения можно использовать ори-
ентир минимальной прибыли.
Перераспределение инвестиций, когда активный капитал
равен этому ориентиру или больше него, обычно приводит к
более гладкой кривой изменения торгового капитала, нежели при
перераспределении инвестиций на основе Т — горизонтальной
координаты. То есть большинство управляющих капиталом со-
чтут, что производить перераспределение инвестиций, исходя из
продвижения вверх, лучше, чем ориентируясь на количество
истекших периодов владения.
Самое интересное в этом то, что заданному уровню началь-
ного активного капитала всегда отвечает один и тот же верти-
кальный ориентир, каким бы ни были используемые величины сред-
него геометрического HPR или Т! Так, при начальном уровне
активного капитала в 5% динамичный метод всегда станет лучше
статичного после того, как будет получена прибыль в 13,6% к
исходному капиталу!
Поскольку у нас имеется оптимальный вертикальный ори-
ентир, мы можем утверждать, что существует также оптимальная
вертикальная дельта для портфеля. Но какова же формула для
этой оптимальной вертикальной дельты? Ее можно вывести из
выражений [5.10а, Ь], полагая FRAC равным той доле активного
капитала, которая удовлетворяет уравнению [5.13]. Это выглядит
следующим образом:
FRAC = Active Equity + Upside Target)
(1 + Upside Target)
To есть если начинать с исходных 5% активного капитала,
то на вертикальном ориентире в 13,6% динамичный метод стал
бы лучше статичного, что было бы использовано для FRAC
в [5.10а, Ь] при определении коэффициента хеджирования в вер-
хней точке Y, удовлетворяющей уравнению [5.13]:
Управление капиталом для профессионалов
235
еоло — (0,05 + 0,1363)
FRAC~ (1 + 0,1363)
= = 0,1639531814
1,1363
Иными словами, если начать с исходной активной доли
в 5%, то, когда весь капитал вырастет на 13,6%, мы будем
знать, что его активная доля составляет 16,39531814%.
Г радиентная торговля
и непрерывное
доминирование
В этой книге, как и в двух предыдущих, мы продемонст-
рировали, что при заданной рыночной системе или сценарном
спектре торговля на оптимальном f (или на наборе оптимальных
/для нескольких одновременно действующих сценарных спектров
или рыночных систем) даст асимптотически самый большой рост,
то есть в итоге, по мере того, как количество периодов владения,
в которые мы торговали, становится все больше и больше. Од-
нако из Главы 2 мы узнали, что если у нас было конечное
количество периодов владения и мы знаем, сколько периодов мы
собираемся торговать, то действительно оптимальными будут такие
величины, которые даже несколько агрессивнее, чем оптималь-
ные / То есть это те значения / которые максимизируют ожи-
даемый средний общий рост (EACG).
В конце концов, каждый из нас может проторговать только
конечное число периодов владения - никто не будет жить вечно.
Однако кроме редчайших случаев мы не знаем точной продол-
жительности этого конечного числа периодов владения. Поэтому
в качестве следующего наилучшего приближения мы используем
асимптотический предел.
236
Управление капиталом для профессионалов
Теперь же мы продемонстрируем метод, который можно
использовать в данном случае неизвестного, но конечного числа
периодов владения, в течение которых мы собираемся торговать
на асимптотическом пределе (т. е. на оптимальных значениях f).
Этот предел при торговле на разбавленном f (с помощью статич-
ного или динамичного дробления) допускает доминирование не
только асимптотическое, но и в течение любого заданного периода
владения в будущем.
То есть теперь мы познакомимся с методом работы при
разбавлении f (которое должно использоваться почти всеми управ-
ляющими капиталом для того, чтобы практические требования
клиентов относительно падений величины торгового счета), который
обеспечивает не только максимум капитала на счете в очень отда-
ленной перпективе, но и максимум счета в любой момент времени,
каким бы близким или далеким он ни был! Более не нужно будет
держаться за оптимальное f (или, в более широком смысле, дер-
жаться за нашу новую методологию), утешая себя мыслью о том,
что в конечном итоге это принесет лучшие результаты. Наоборот,
тот метод, который чуть ниже проиллюстрируем, нацелен на доми-
нирование во все периоды времени!
Percent growth
Рис. 5.3. Момент пересечения различных методов с возможным переключени-
ем с одного на другой.
Управление капиталом для профессионалов
237
Это является огромным продвижением вперед. Поскольку
почти каждый будет разбавлять то, что служит их оптимальными
значениями f — либо осознанно, либо ненамеренно по незнанию
— приемы, о которых идет речь, будут постоянно максимизиро-
вать прибыльность счета при разбавленных значениях /, а не
только так, как это всегда было с максимизацией среднего
геометрического, — в очень отдаленной перспективе.
Вновь мы должны обратить наше внимание на функции
и темпы роста. Посмотрите на рис. 5.3, на котором изображен рост
(функция роста) в процентах от нашей начальной ставки. Теперь
взгляните на рис 5.4, представляющий темп роста в процентах
от нашей ставки.
На этих графиках вновь изображен начальный активный
капитал в 20%, который используется для торговли как на
динамичной, так и на статичной основе. Поскольку в обоих
этих случаях торговля начинается с одного и того же количе-
ства единиц, то именно оно используется в качестве постоян-
ного контракта при обычной торговле, которая также представ-
лена на рис. 5.4. На этом графике использовалось среднее
Constant contract
Static f
Dynamic f
Рис. 5.4. График роста коэффициента.
238
Управление капиталом для профессионалов
геометрическое HPR (на полном f), равное 1,01933, и, следо-
вательно, среднее геометрическое при статичном дроблении f
в 0,2 было равно 1,005, а среднее арифметическое HPR на
полном /было — 1,0265.
Обратите внимание, что если постоянно использовать в
торговле тот метод, который в данный момент имеет больший
градиент, то с наибольшей вероятностью счет в любой момент
времени будет в своей наибольшей части доступного капитала.
Так, мы начинаем торговать на базе фиксированного контракта
с числом единиц, равным тому, которым бы мы начинали
торговлю при дробном /
Далее, в тот момент (по времени или по приросту капи-
тала), когда доминирует статичный градиент / мы переключаем-
ся на торговлю со статичным / Наконец, когда доминирует
динамичный градиент, мы переходим на торговлю на основе
динамичного / Обратите внимание, что, постоянно используя тот
метод, у которого в данный момент наибольший градиент, вы
всегда будете находиться на самой высокой кривой из трех,
изображенных на рис. 5.3.
Функция роста Y для метода постоянного контракта теперь
дается в виде*:
Y= 1 + (AHPR - 1) * FRAC * Т [5.15]
* Точно так же, как формула [5.09] дает нам ту точку по горизон-
тальной оси Т, в которой динамичный подход становится лучше статичного, мы
можем из формул [5.15] и [5.16], где статичный подход станет лучше
торговли постоянным контрактом: это будет то значение Т, при котором [5.15]
равно [5.16]. А именно:
1 + (AHPR - 1) * FRAC * Т => FGHPR7
Сходным образом это же можно выразить через координату У, откуда
узнаем, при достижении какого процента дохода от начального капитала на
счете следует перейти с торговли постоянным контрактом на торговлю со
статичным /:
Y = FGHPRT - 1
Значение Т, использованное в предыдущем уравнении, получено из
уравнения выше.
Управление капиталом для профессионалов
239
Функции роста берутся из формулы [5.09]. Таким образом,
функция роста для статичного /является левой частью [5.09],
а для динамичного / — правой. То есть функция роста для ста-
тичного / имеет вид:
Y = FGHPR7 [5.16]
И для динамичного /
Y = среднее геометрическое7-* FRAC + 1 — FRAC [5.17]
Формулы [5.15—17] дают нам функции роста в виде про-
изведения нашей начальной ставки на заданное количество пе-
риодов владения Т. Поэтому, вычитая из [5.15-17] единицу,
получаем процентный рост, который изображен на рис. 5.3.
Градиенты, изображенные на рис. 5.4., являются просто
первыми производными по Т функций Y, заданных формулами
[5.15—17]. То есть градиенты определяются следующим образом:
Для торговли постоянным контрактом:
dY = ((AHPR-1)* FRAC) ig]
dT (1 + AHPR- 1) * FRAC* T
Для статичного дробного /
dY
= FGHPR7 * In(FGHPR) [5.19]
И наконец для динамичного дробного /
dY
dT..= geometric mean7- * ln(geometric mean) * FRAC [5.20],
где
T = количество периодов владения;
FRAC= начальный процент активного капитала;
среднее геометрическое = грубое среднее геометрическое
при оптимальном /;
240
Управление капиталом для профессионалов
AHPR= арифметическое среднее HPR, задаваемое [5.07];
1п( )= функция натурального логарифма.
Применяются эти формулы, особенно если ваши сценарии
(сценарные спектры) и совместные вероятности изменяются от
одного периода владения к другому, следующим образом. Вспом-
ним, что перед каждым периодом владения мы должны опреде-
лить оптимальные инвестирования. Для того чтобы сделать это,
мы собираем всю необходимую информацию для получения
значений переменных, перечисленных выше (FRAC, среднего
геометрического, AHPR и аргументов функции [5.07] для опре-
деления FGHPR). Затем мы подставляем эти значения в формулы
[5.18], [5.CAPut!’] и [5.20]. Та формула, которая дает больший
результат, определяет наш метод торговли.
Чтобы проиллюстрировать это на примере, обратимся к
знакомой нам игре в монетку «два-к-одному». Предположим, что
это наш единственный набор сценариев, содержащий два сцена-
рия для орлов и решек. Предположим далее, что мы собираемся
играть с долей 0,2 (т. е. одной пятой оптимального f). Таким
образом, FRAC равно 0,2, среднее геометрическое равно 1,06066,
и AHPR равно 1,125. Для определения FGHPR по формуле [5.07]
у нас уже есть FRAC и AHPR, и нужно только SD — стандартное
отклонение значений HPR, которое равно 0,375. Таким образом,
FGHPR равно
1,022252415 = (V((l, 125 -1) * 0,2 + I)2 - (0,375 * 0,2)2)
Подстановка этих величин в три градиентные функции,
задаваемые формулами [5.18—120], дает нам следующую таблицу:
Eq. [5.18] Eq. [5.19] Eq. [5.20]
Т Constant Contract Static f Dynamic f
1 0,024390244 2 0,023809524 3 0,023255814 4 0,022727273 0,022498184 0,012492741 0,022998823 0,013250551 0,023510602 0,014054329 0,02403377 0,014906865
Управление капиталом для профессионалов
241
5 0,022222222 0,024568579 0,015811115
6 0,02173913 0,025115289 0,016770217
7 0.021276596 0,025674165 0,017787499
8 0,020833333 0,026245477 0,018866489
9 0,020408163 0,026829503 0,02001093
10 0,02 0,027426524 0,021224793
11 0,019607843 0,02803683 0,022512289
12 0,019230769 0,028660717 0,023877884
13 0,018867925 0,029298488 0,025326317
14 0,018518519 0,02995045 0,026862611
15 0,018181818 0,030616919 0,028492097
16 0,017857143 0,03129822 0,030220427
17 0,01754386 0,031994681 0,032053599
18 0,017241379 0,03270664 0,03399797
19 0,016949153 0,033434441 0,036060287
20 0,016666667 0,034178439 0,038247704
Мы видим, что наибольший градиент для двух первых
периодов владения дает игра на основе постоянной ставки, а на
третий период нам следует переключиться на статичное f На
семнадцатом периоде нам нужно переключиться на динамичное f
Если бы мы поступили таким образом, то, как это видно на рис.
5.5, за первые двадцать конов преуспели бы в среднем гораздо
больше, чем при простом использовании метода динамичного f.
Обратите внимание, что в каждом периоде при описанном
подходе ставка в игре имеет большее ожидаемое значение, чем
даже при игре с динамичным дроблением f Далее, начиная
с семнадцатого периода, где мы переключились со статичного на
динамичный метод, обе линии впредь имеют одинаковый гради-
ент. То есть динамичная линия никогда не сможет «догнать»
линию постоянного доминирования. Таким образом, принцип
постоянной торговли с наибольшим градиентом для достижения
постоянного доминирования помогает управляющему капиталом
максимизировать величину счета в любой момент в будущем,
а не только в асимптотическом смысле.
16-9727
242
Управление капиталом для профессионалов
Continuous dominance
Рис. 5.5. Постоянное доминирование динамического f.
Dynamic f
Продолжим пояснение на примере, предположив, что мы
играем в монетку с начальным счетом в 200 долл. Наше опти-
мальное /равно 0,25, а 0,2/равно одной пятой этой величины,
что означает, что мы играем со значением /, равным 0,5, или
ставим один доллар на каждые двадцать долларов счета. Следо-
вательно, на первый кон мы ставим десять долларов. Поскольку
мы играем с постоянной ставкой, то независимо от состояния
счета мы будем ставить столько же на каждый следующий кон,
пока не перейдем на статичное / Это происходит на третьем
кону. Поэтому на третьем кону мы оцениваем наш счет и ставим
один доллар на каждые двадцать долларов капитала. Пройдя
таким образом до 16-го кона включительно, перед семнадцатым
переключимся на динамичный метод. Таким образом, играя с 3-го
по 16-й кон, мы каждый раз делим наш капитал на части по
двадцать долларов и ставим на кон столько долларов, сколько
получилось таких частей, то есть действуем по методу статич-
ного дробления /
Итак, предположим, что после второго кона на нашем
счете имеется 210 долл. На следующий кон мы поставили бы
десять долларов (так как 210/20 = 10,5, а ближайшее целое —
10). Так же мы будем действовать каждый следующий кон до
шестнадцатого включительно.
Управление капиталом для профессионалов
243
На семнадцатом кону мы можем видеть, что градиент
динамичного /выше других. Поэтому мы должны переключиться
на игру на основе динамичного / И вот как именно. Когда мы
начинали, мы решили играть активным капиталом в 20% счета
(так как мы решили играть одной пятой всего оптимального f).
Поскольку наш исходный счет составлял 200 долларов, мы на-
чали первый кон с 40 долларов активной части счета. Значит,
пассивная часть счета составляла бы 160 долларов.
Таким образом, перед началом 17-го кона, на котором мы
хотим переключиться на динамический метод, мы вычитаем
160 долларов из всего того, что есть на нашем счете. Полученную
разность мы далее делим на части по 4 доллара, или на опти-
мальное /$, и получаем в итоге величину ставки, которую можно
сделать в 17-м коне. Продолжаем действовать таким образом перед
каждым коном до бесконечности.
Предположим, что на нашем счете после 16-го кона име-
ется 292 доллара. Вычитая из этого 160 долларов, получаем 132,
деля которые на 4 доллара, приходим к величине 33. То есть в
17-м коне мы можем сделать 33 ставки по 1 доллару (или одну
ставку в 33 доллара).
Если хотите, то вы также можете представить эти точки
перелома при постоянном доминировании в виде прироста про-
цента выигрыша, который необходимо иметь до перехода на
следующий уровень. Поскольку формула [5.13] дает нам вер-
тикальную координату, или Y, соответствующую горизонталь-
ной координате из формулы [5.09], то мы можем определить
вертикальные координаты, соответствующие формулам [5.18—
20]. Так как вы переключаетесь с постоянной ставки на ста-
тичное /при таком значении Т, на котором [5.19] больше, чем
[5.16], то вы можете подставить это Т в [5.16] и вычесть из
результата 1. Это будет процентный прирост на ваш начальный
капитал, который нужен для перехода с постоянной ставки на
статичное /
Так как вы переключаетесь на динамичное / при таком
значении Т, на котором [5.20] больше, чем [5.CAPut!’], то вы,
следовательно, можете подставить это Т в [5.16] и вычесть из
результата 1, что и и будет процентом прибыли на начальный
капитал для перехода к игре на основе динамичного /
16*
244
Управление капиталом для профессионалов
Важные точки слева от пика на
(п + 1)-мерной поверхности
Мы продолжим эту дискуссию, адресованную к большин-
ству управляющих капиталом, которые будут торговать на мно-
жестве с рабавленным /; то есть они будут торговать на менее
агрессивных уровнях, чем оптимальный, для различных сценар-
ных спектров или рыночных систем, которые они используют.
Мы называем это смещением влево - термином, который следует
из идеи о том, что, если мы посмотрим на торговлю на одном
сценарном спектре, у нас была бы одна кривая, начерченная в 2-
мерном пространстве, где смещение влево от пика соответствует
задействованию в торговле меньшего количества единиц, чем
оптимальное. Если мы торгуем двумя сценарными спектрами, то
у нас топологическая карта в 3-мерном пространстве, где такие
управляющие капиталом ограничивали бы себя областью влево от
пика, если смотреть на изображение с юга на север. Мы могли
бы продолжить эту мысль на большее количество измерений, но
термин влево безотносителен к размерности; он просто означает
смещение к меньшим, чем полностью оптимальная, величинам
по каждой из осей (сценарных спектров).
Управляющие капиталом не максимизируют благосостояние.
То есть их функция полезности или, скорее, функция полезно-
сти, возложенная на них их клиентами и их сферой деятельности,
или их U"(x), меньше нуля. Поэтому они действуют левее пика
их оптимальных f
Тогда в условиях ограничений реальной жизни, требующих
более гладких кривых изменений капитала, чем те, что предпо-
лагаются при полной оптимизации, а также понимание того, что
не совсем типичные падения капитала на оптимальном уровне
наверняка приведут к оттоку клиентов, мы сталкиваемся с пер-
спективой, когда смещение влево будет уместно (для того, чтобы
удовлетворить их U"(x))? Как только такое благоприятное смеще-
ние будет найдено, мы можем последовать методе постоянного
доминирования. Действуя таким образом, мы гарантируем себе то,
что, торгуя при таком левом смещении, мы будем иметь макси-
мальную ожидаемую величину счета в любой момент в последующем.
Управление капиталом для профессионалов
245
Впрочем, это не означает, что он превысит счет, которым торгуют
при наборе с полностью оптимальным f Так не получится.
Теперь мы действительно начинаем работать с этой новой
методологией. С этих пор цель данного раздела становится двоя-
кой: во-первых, показать, что существуют возможные благопри-
ятные точки слева, и, во-вторых, показать на примерах, как
можно использовать эту новую методологию.
Существует множество благоприятных точек левее пика,
и следующее далее обсуждение их всех не исчерпывает. Скорее,
это лишь стартовая площадка для вас.
Первая интересная точка слева касается торговли постоян-
ным контрактом, то есть такой, при которой всегда используется
одно и то же количество единиц безотносительно к тому, как
вырастет или упадет торговый капитал. Кандидаты в управляю-
щие капиталом не должны отбрасывать ее как чрезмерно простую
по следующим причинам: Постоянная торговля одним и тем же
неизменным количеством безотносительно к капиталу на счете
максимизирует вероятность того, что прибыльная система будет
прибыльной и в будущем. Варьирование торгуемым количеством
в зависимости от капитала на счете — это попытка максими-
зировать данную вероятность (хотя и не максимизирует вероят-
ность самой прибыльности).
Недостаток торговли постоянным количеством контрактов
состоит в том, что он не только помещает вас левее пика, но
и в том, что по мере роста капитала на счете вы по существу
сдвигаетесь к нулю по различным осям f
Например, пусть мы играем в нашу монетку «два-к-одному».
Пик находится при f = 0,25, что означает выставление на кон
одного доллара на каждый четвертый доллар капитала на счете.
Пусть у нас есть счет в двадцать долларов и мы планируем всегда
делать по две ставки, то есть всегда ставить два доллара на кон
безотносительно к тому, как изменяется счет. Тогда мы начинаем
(к счастью, это 2-мерный случай, ибо мы рассматриваем только
один сценарный спектр) торговать долей /$ из десяти долл.,
которая равна f от 0,1, ибо /$ = — BL// откуда следует, что f =
-BL//$. Предположим теперь, что продолжаем постоянно ставить
по два доллара; тогда, если бы весь капитал увеличился до трид-
цати долларов при условии, что мы по-прежнему ставим только
246
Управление капиталом для профессионалов
по два доллара, то наше f соответстветствующее /$ в пятнадцать
долларов, сместился бы к 0, 067. Пока деньги на счете продолжат
прибывать, используемое нами /продолжит сдвиг налево. Впрочем,
это также действует и в обратном направлении: если мы теряем
деньги, то используемое /смещается направо и в какой-то момент
может действительно оказаться на пике кривой. Таким образом,
пик представляет собой то место, где трейдер, торгующий посто-
янным контрактом, должен прекратить это при сокращении счета.
То есть перемещающееся/проходит через другие точки плоскости,
некоторые из которых еще нужно будет обсудить.
При другом подходе нужно определить наихудший случай
максимального сокращения счета, на которое может пойти управ-
ляющий капиталом, выразив его в процентном уменьшении
капитала, и использовать эту величину вместо оптимального /
при определении /$.
abs(biggest loss scenario)
f$= . , , [5.21a]
maximum drawdown percent
Таким образом, если приемлемое для управляющего капи-
талом сокращение счета составляет 20%, а наихудший сценарий
предполагает потерю 1000 долл., то:
$1000
/$ = —= $5000
То есть он должен использовать в качестве /$ 5000 долл.
Поступая таким образом, он по-прежнему не ограничит макси-
мальные потери 20% от всего капитала. Скорее, он достигнет
того, что сокращение счета при реализации одного катастрофи-
ческого события будет определено заранее.
Заметьте, что, используя данный подход, управляющий
капиталом должен следить за тем, чтобы максимальный процент
сокращения счета не превысил бы оптимального / Иначе данный
метод сместит его правее пика. Например, когда действительное
значение / равно 0,1, а управляющий капиталом использует
данный метод со значением 0,2 для максимального процентного
сокращения, то он будет торговать с /$, равным 5000 долл.,
Управление капиталом для профессионалов
247
вместоравного 10 000 долл., соответствующего оптимальному
уровню! Его наверняка постигнет беда.
Учтите и то, что приведенный пример иллюстрирует только
торговлю на одном сценарном спектре. Если вы торгуете на
большем количестве сценарных спектров, то вы должны соответ-
ственно изменить знаменатель, поделив максимальное процентное
сокращение на количество сценарных спектров — т.е. на число п.
abs(biggest loss scenario)
/$ ; - . [5.21b],
/maximum drawdown percent^
' n 7
где n = число составляющих (сценарных спектров или
рыночных систем) портфеля.
Обратите внимание, что в результате у вас, как и раньше,
будет определено максимальное процентное снижение стоимости
всего портфеля, даже если все сценарные спектры одновременно
реализуют свои наихудшие сценарии.
Теперь переходим к другой важной точке слева от пика,
которая может заинтересовать некоторых управляющих капита-
лом: коэффициент роста риска, или GRR (рис. 5.6). Если мы
возьме в качестве роста TWR (числитель), а используемый /(или
сумму значений / для портфеля) - в качестве риска, ибо он
представляет собой долю вашей ставки, которую вы потеряли бы
в случае реализации наихудшего сценария (сценариев), то коэф-
фициент роста риска можно записать в виде:
TWRr [5.22]
GRR, = --------
1 n
ZZ
1=1
Этот коэффициет точно соответствует своему названию,
а именно выражает прирост (TWRT, или ожидаемый прирост на-
шего счета после Т конов игры) риска (как суммы значений /
представляющей собой общий процент ставки в игре, которым мы
рискуем). Если TWR является функцией от Т, то такова же и GRR.
То есть когда Т возрастает, GRR перемещается от той точки, где
248
Управление капиталом для профессионалов
/бесконечно мало, к оптимальному/(см. рис. 5.7). При бесконечном
Т GRR равно оптимальному/ Это очень похоже на работу с EAGG:
вы можете торговать на / максимизируя GRR, если априори
знаете, на каком значении Т вы хотите получить максимум.
Изменение от бесконечно малого значения / при Т=1 до
оптимального/при Т= 8 происходит по всем осям, но на рис. 5.6
и 5.7 это демонстрируется на примере торговли с одним сценарным
спектром. Если бы вы торговали одновременно с двумя спектрами,
то при увеличении Т пик GRR переместился бы по трехмерной
плоскости почти от 0,0 по обоим значениям / до оптимальных
значений /(при 0,23 и 0,23 для игры монетку «два-к-одному»).
Определить GRR для случая одновременной торговли с
большим количеством сценарных спектров нетрудно с помощью
формулы [5.22] безотносительно к тому, сколько многокомпо-
нентных сценарных спектров одновременно отслеживается.
Следующей и последней точкой слева от пика, подлежащей
рассмотрению, которая может быть весьма благоприятной для
многих управляющих капиталом, является точка перегиба фун-
кции TWR от /
Вновь обратимся к рис. 1.2. Обратите внимание, что, когда
мы приближаемся к пику при оптимальном / слева, начиная от
Рис. 5.6. Игра в монетку «два-к-одному», GRR при Т=1.
Управление капиталом для профессионалов 249
О, происходит все ускоряющийся по вертикали рост TWR. То есть
так мы достигаем все большей и большей выгоды при линейном
росте риска. Но рост кривой TWR продолжается только до оп-
ределенной точки, все в более медленном темпе для каждого
увеличения f Эта точка перелома, называемая точкой перегиба,
ибо она представляет то место, где функция переходит от вы-
гнутости к вогнутости, является еще одной точкой слева, которая
представляет интерес для управляющего капиталом. Точка пере-
гиба представляет собой ту точку, в которой малейший рост
прибылей фактически прекращается и начинает уменьшаться при
всяком малейшем увеличении риска. Таким образом, эта точка
может оказаться исключительно важной для управляющего капи-
талом и может даже оказаться в некоторых случаях оптимальной
с точки зрения управляющего капиталом как точка, где дости-
гается действительный максимум.
Напомню, однако, что рис. 1.2 представляет TWR после
сорока конов игры. Давайте рассмотрим TWR после одного кона
игры в монетку «два-к-одному» (см. рис. 5.8), который также
называется попросту средним геометрическим HPR.
Рис. 5.7. Игра в монетку «два-к-одному», GRR при Т = 30.
250
Управление капиталом для профессионалов
Рис. 5.8. Среднее геометрическое HPR при игре в монетку «дво-к-одному»
(=TWR при Т = 1).
Интересно, что в данном случае нет ни одной точки, в ко-
торой эта функция менялась с выгнутой на вогнутую или наоборот.
Здесь нет ни одной точки перегиба. Вся картинка выгнута вниз.
При положительном математическом ожидании у среднего
геометрического нет ни одной точки перегиба. Но при Т > 1
TWR имеет две точки перегиба — одну слева от пика и другую
справа от него. Та, что интересует нас, расположена, естествен-
но, слева от пика.
Левой точки перегиба не существует при Т = 1, и с увели-
чением Т она приближается к оптимальному f слева (рис. 5.9 и 5.10).
При бесконечном Т точка перегиба сходится к оптимальному f
К сожалению, левая точка перегиба перемещается по на-
правлению к оптимальному/точно так же, как и GRR, и точно
так же, как для EACG, если бы вы знали до начала игры, какое
количество конов вы сыграете, то смогли бы максимизировать
левую точку перегиба*.
* Интересно, однако, что если бы вы попытались максимизировать EACG
для данного Т, то стали бы искать точку справа от пика ее кривой, так как
величина /, максимизирующая EACG, приближается к оптимальному / справа
при стремлении Т к бесконечности.
Управление капиталом для профессионалов
251
Рис. 5.9. dTWR/df для 40 конов (Т = 40) игры в монетку «два-к-одному». Пик
слева и впадина справа являются точками перегиба.
-1 800000
- 700000
- 600000
- 500000
- 400000
- 300000
- 200000
- 100000
- -100000
- -200000
- -300000
- -400000
- -500000
J -600000
.10 .20 .30 .40 .50 .60 .70 .80 .90 1.0
Рис. 5.10. dTWR/dfflna 800 конов (Т = 800) игры в монетку «два-к-одному».
Пик слева и впадина справа являются точками пергиба. Левый пик достига-
ется на f= 0,23.
252
Управление капиталом для профессионалов
Резюмируя, покажем, как происходит перемещение точки
перегиба к оптимальному f с помощью таблицы по количеству
сыгранных конов:
Игра в монетку «два-к-одному»
К-во конов игры Лев. точка перегиба
1 0
30 0,12
40 0,13
80 0,17
800 0,23
То есть мы вновь видим, что с течением времени, или
с увеличением Т, отступление от оптимального /влечет за собой
серьезное наказание. Асимптотически почти все максимизировано,
будь то EACG, GRR или левая точка перегиба. С увеличением
Т все они сходятся к оптимальному / Поэтому с увеличением Т
расстояние между этими благоприятными точками и оптималь-
ным /сокращается.
Предположим, что управляющий капиталом использует днев-
ные HPR и намерен действовать оптимальным образом (в смысле
точки перегиба GRR) в течение текущего квартала (63 дня). Тогда
он использовал бы величину 63 для Т и позиционировался бы
в тех координатах, которые оптимальны для каждого квартала.
Когда мы начинаем работать больше чем с двумя измере-
ниями, то есть когда у нас имеется более одного сценарного
спектра, мы одновременно сталкиваемся с более сложной задачей.
Ее решение может быть выражено математически, как та
точка слева от пика (по всем осям), в которой вторые частные
производные TWR (формула [4.04], при Т — количество пери-
одов владения, для которого отыскивается точка перегиба) по
каждому/в отдельности равны нулю. Это усложняется еще и тем,
что такая точка, в которой вторые частные производные по всем
/равны нулю, зависит от параметров самих сценарных спектров
и величины Т и может не существовать вовсе. Если Т= 1, то
TWR равна среднему геометрическому HPR, кривая которого
является перевернутой параболой и не имеет ни одной точки
перегиба! Но когда Т стремится к бесконечности, точка (точки)
Управление капиталом для профессионалов
253
перегиба приближаются к оптимальному (оптимальным) /! В от-
сутствие бесконечного Т в большинстве случаев такой удобной
общей для всех осей точки пергиба может не быть*.
Все сказанное возвращает нас к началу данной книги. Суть
понятия (л + 1)-мерного изображения в пространстве рычагов, или,
если угодно, осей, соответствующих значениям /различных сце-
нарных наборов, состоит в том, чтобы служить методологией
анализа состава портфеля и определения его объема с течением
времени. Для выработки этой новой методологии нужно еще очень
многое сделать. Эта книга далеко не исчерпывает данного предмета.
Скорее, она является введением в новый и одновременно, как
я полагаю, лучший способ решения проблемы распределения ин-
вестиций. Она почти наверняка дает портфельным стратегам, при-
кладным математикам, практикам в области распределения инве-
стиций и программистам много новой плодородной почвы для
работы. Честно говоря, нужно еще очень много сделать в области
анализа, практического использования и развития этой новой
методологии, плоды чего нельзя даже и определить.
Управление текущими
потерями и новая методология
Большие текущие потери происходят по трем причинам.
Первая и наиболее распространенная из них — это катастрофи-
ческий проигрыш на одной сделке. Я пришел в этот бизнес
* Вспомните, что единственное, что достигается с помощью диверсифи-
кации, т. е. при использовании в торговле более одного сценарного спектра, или
при работе с более чем с двумя измерениями, — это увеличение Т, или
количества периодов владения за данный период времени. Вы не сокращаете
риск. В свете этого всякий, кто стремится максимизировать минимальный доход
при минимальном риске, вполне может предпочесть торговать только с одним
сценарным спектром.
254
Управление капиталом для профессионалов
в качестве маржевого клерка, задачей которого было отслеживать
состояние сотен счетов. Я поработал программистом и консуль-
тантом на многих крупнейших трейдеров мира. Я торговал и
прорабатывал проблемы в области торговли всю мою взрослую
жизнь, зачастую наблюдая с птичьего полета за тем, как люди
действуют на рынках и в смежных сферах. Я был свидетелем
того, как множество людей были уничтожены в течение одной
сделки. Кроме того, у меня есть большой собственный опыт
поражения на единственной сделке.
Общим знаменателем во всех случаях, когда такое происхо-
дит, является недостаточная ликвидность рынка. Важность лик-
видности нельзя переоценить. Ликвидность не есть что-то такое,
что мне удалось оценить количественно. Это не просто некая
функция открытого интереса и объема. К тому же, ликвидность
вовсе не должна испаряться надолго, чтобы нанести огромный
вред. Фьючерсы на казначейские облигации США были самыми
ликвидными контрактами в мире в 1987 г. Однако и они оказались
совершенно неликвидными на несколько дней в октябре 1987 г.
В отношении ликвидности вы должны быть постоянно на чеку.
Второй путь, который ведет людей к крупным потерям,
даже более трагичен, но не менее распространен. На него приво-
дит незнание своей позиции на рынке до того, как он бесжа-
лостно двинется против нее. Это трагично потому, что этого
всегда можно избежать. Однако это распространенное явление. Вы
всегда должны знать свои позиции на каждом рынке.
Третьей причины потерь боятся больше всего, хотя она при-
водит к тем же последствиям, что и первые две причины. Потеря
этого типа характеризуется затяжной полосой проигрышей, между
которыми иногда могут вклиниваться несколько выигрышных сде-
лок. Это тот тип потерь, перед которыми большинство трейдеров
живут в постоянном страхе. Потери этого типа заставляют системных
трейдеров задаваться вопросом, работают ли все еще их системы. Но
именно этот тип потерь поддается управлению и значительному
сокращению с помощью нашей новой методологии.
Новая методология в распределении активов сосредоточива-
ется на оптимальности роста. Однако для сообщества управляю-
щих капиталом вопросы оптимальности роста стоят, как правило,
на втором месте. Основная забота — сохранение капитала.
Управление капиталом для профессионалов
255
Это верно не только для управляющих капиталом, но
также и для большинства инвесторов. Сохранение капитала осно-
вывается на сокращении потерь. Предложенная нами новая мето-
дология впервые позволяет свести деятельность по минимизации
потерь к математической задаче. Как ни парадоксально, это одно
из многих неожиданных следствий новой методологии.
Все написанное мной и ранее, и в этой книге касается
оптимальности роста. Впрочем, разрабатывая методологию под
углом зрения оптимальности роста, в ее же рамках мы можем
взглянуть на вещи и с позиций оптимизации потерь. Выводы,
которые следуют из новой методологии, нельзя было бы полу-
чить на иной основе.
Идея оптимального /, которая вылилась в эту новую ме-
тодологию распределения активов, теперь может выйти за рамки
теоретических формулировок и концепций в область практичес-
кого применения с прицелом на достижение целей управляющих
капиталом, а равно и инвесторов.
Старые среднедисперсионные модели были плохо приспо-
соблены для реализации идеи управления потерями. Первой при-
чиной этого является то, что риск сводился к упрощенному
представлению в виде дисперсии доходов. Причем возможно,
и в действительности довольно часто, сократить дисперсию дохо-
да, однако не сократить сами потери.
Представьте себе два компонента, отрицательно скоррелирован-
ных друг с другом. Компонент 1 растет по понедельникам и средам,
но падает по вторникам и четвергам. Компонент 2 ведет себя точно
противоположным образом и падает по понедельникам и средам, но
растет по вторникам и четвергам. По пятницам обе компоненты
падают. Торговля обеими компонентами вместе сокращает диспер-
сию дохода, однако в пятницу понесенные потери могут быть на
деле больше, чем при торговле только одним из двух компонентов.
В конце концов, все корреляции сводятся к одной. Модель средней
дисперсии не ориентирована на потери и просто минимизирует
дисперсию дохода. Хотя она может отсечь многие потери, она все
же оставляет вас беззащитными перед серьезными потерями.
Рассмотрение потерь с позиций новой методологии все же
даст нам некоторую очень полезную информацию. Задумайтесь на
минуту о том, что потери минимизируются путем отказа от
256
Управление капиталом для профессионалов
торговли (т. е. при /= 0). То есть если мы обратимся к случаю двух
одновременных игр в монетку «два-к-одному», то рост максими-
зируется при f равном 0,23 для каждой игры, в то время как
потери минимизируются при f равном 0 для обеих игр.
Первым важным моментом в понимании оптимальности потерь
(т. е. минимизации потерь) является то, что к ней можно прибли-
зиться в торговле. Оптимальная точка, в отличие от точки опти-
мального роста, не может быть достигнута никак иначе, чем путем
отказа от торговли. Но к ней можно приблизиться. Таким образом,
для минимизации потерь, то есть для приближения к оптималь-
ности потерь, требуется использовать для каждой компоненты
минимально возможные значения f Другими словами, для того
чтобы приблизиться к оптимальности потерь, вы должны присесть
в том углу поверхности, где значения всех f близки к 0.
На рис. 5.11, изображающем нечто похожее на игру в
монетку «два-к-одному», пик никуда не перемещается. Это тео-
ретически идеальный случай, и, как таковой, он может исполь-
зоваться в качестве модели совершенного портфеля для сравнения
с обычными моделями.
Рис. 5.11. К оптимальным потерям приближаются в иной точке изображения,
нежели точка оптимального росто.
Управление капиталом для профессионалов
257
Впрочем, как упоминалось ранее, в реальном мире торгов-
ли рынки не согласуются столь четко с теоретическим идеалом.
Дело в том, что в отличие от рассмотренных игр в монетку «два-
к-одному» распределение доходов со временем меняется при
изменении условий на рынке. Поверхность обладает способностью
к реконфигурации и перемещается в разных направлениях при
изменении условий на рынке. Чем ближе вы находитесь к пику,
тем драматичнее это скажется на потерях при ее перемещении уже
просто потому, что поверхность имеет наибольшую крутизну
ближе всего к пику. Если бы мы вычертили карту поверхности
вроде той, что изображена на рис. 5.11, но только по данным за
период, когда обе системы приносили убытки, то поверхность
(высота, или TWR) была бы на отметке 1,0 в /-координатах (0;
0), а далее параболически соскальзывала бы оттуда.
Мы приближаемся к оптимальности потерь по тем/ которые
близки к 0 по всем компонентам. В случае поверхности, изображен-
ной на рис. 5.11, нам было бы лучше переместиться в левый
верхний угол поблизости от 0 по значениям всех / Причина этого
в том, что когда плоскость изгибается и пик смещается в стороны,
негативный эффект от этого в данном углу будет самым минималь-
ным. Другими словами, при изменении ситуации на рынке отрица-
тельные последствия для трейдера в этом углу минимизированы.
Может создаться обманчивое впечатление, что при этом в
жертву приносится рост, который уменьшается по экспоненте. Раз-
веять эти опасения можно с помощью фундаментального уравнения
торговли. Поскольку рост, или TWR, представляет из себя среднее
геометрическое доходов за периоды владения, возведенное в степень
Т, то количество конов игры можно получить из формулы:
TWR=C' [5.23]
В вышеуказанном углу значение G гораздо меньше. Но с
увеличением Т мы сталкиваемся с экспоненциальным уменьшени-
ем роста, представляющего собой экспоненциальную функцию.
Короче говоря, если трейдеру нужно минимизировать по-
тери, то ему выгоднее торговать при очень малых значениях /
и задействовании много большего количества периодов владения
на одном том же отрезке времени.
17-9727
258
Управление капиталом для профессионалов
Рассмотрим, например, разыгрывание только одной игры
в монетку «два-к-одному». После 40 периодов владения при / =
0,25 среднее геометрическое HPR равно 1,060660172, a TWR
равно 10,55. Если бы мы играли в ту же самую игру при значении
f 0,01, то наше среднее геометрическое HPR было бы равно
1,004888053, что превысило бы 10,55 при возведении в степень
484. Таким образом, если можно сыграть 484 кона (периода
владения) за то же время, которое ушло бы на 40 конов, то это
дало бы эквивалентный рост при резком сокращении в потерях.
К тому же вы значительно оградили бы себя от изменений
поверхности. То есть вы одновременно весьма защитились бы и от
изменений ситуации на рынке.
Может показаться, что вам понадобится торговать более
чем одним компонетом (т. е. сценарным спектром) одновременно.
То есть что для увеличения Т нужно торговать много большим
количеством компонентов одновременно. Это противоречит мыс-
ли, высказанной ранее при обсуждении точек перегиба, что
может оказаться выгоднее торговать только одним компонентом.
Но, увеличивая количество компонентов, торгуемых одновремен-
но, вы увеличиваете составное /портфеля. Например, если бы вы
одновременно торговали по 20 сценарным спектрам с/ = 0,005
для каждого, то ваше составное /для всего портфеля было бы
равно 0,1. На данном уровне одновременная реализация наихуд-
ших сценариев привела бы к потере 10% капитала. И напротив,
вы преуспели бы больше, торгуя только по одному сценарному
спектру, если бы могли задействовать эквивалент 20 периодов
владения за тот же самый отрезок времени. Это может оказаться
невозможным, но это — направление, в котором вы стали бы
действовать для минимизации потерь.
Наконец, когда трейдер старается приблизиться к мини-
мизации потерь, он может при этом использовать идею посто-
янного доминирования. Постоянное доминирование прекрасно
для теоретически идеальной модели. Однако оно весьма чувстви-
тельно к изменениям поверхности. То есть при изменении ис-
ходных сценариев для подстройки к изменяющимся характери-
стикам рынка постоянное доминирование начинает сбоить.
В азартной игре, где условия не изменяются от одного периода
к другому, постоянное доминирование идеально. В реальном
мире торговли вы должны защитить себя от колебаний повер-
Управление капиталом для профессионалов
259
хности. Поэтому минимизация потерь в рамках новой методоло-
гии очень хорошо приспосабливается к внедрению постоянного
доминирования.
Итак, теперь мы завершили полный цикл от рассмотрения
поверхности в пространстве рычагов и отыскания точки оптималь-
ного роста на ней до отступления от этой точки во имя удовлет-
ворения реальных основополагающих ограничений по части мини-
мизации потерь и сохранения капитала. Просто увеличив показатель
степени тем или иным доступным образом, мы достигаем роста.
Мы, возможно, достигнем эквивалентного роста, если сможем
добиться достаточно большого Т, или достаточно высокого пока-
зателя степени. Поскольку показатель степени равен количеству
периодов владения за данный отрезок времени, мы постараемся
задействовать максимально возможное количество периодов владе-
ния за данный отрезок времени. Но при этом вовсе не обязательно
торговать по максимально возможному количеству сценариев. Все
корреляции приводят к одной. К тому же мы должны постоянно
допускать случай, когда наихудшие сценарии реализуются одно-
временно для всех торгуемых компонент. Мы должны учитывать,
что составное f или сумма значений f для всех одновременно
торгуемых компонентов, представляет собой потери, которые нам
предстоит перенести. Отсюда вытекает, что, стараясь приблизиться
к оптимальности потерь, но и стремясь получить такой же рост,
как и в оптимальной точке роста, следует торговать по минималь-
но возможному количеству компонент и при минимально возмож-
ных значениях f для каждого компонента, а также добиваться
задействования максимально возможного количества периодов
владения за данный отрезок времени.
Точка оптимального роста — опасное место локализации. Но
точно определив ее, то есть если мы располагаемся на том месте,
где будет пик, то мы можем получить колоссальный рост. Даже
в этом случае нам предстоит пережить серьезные потери. Впрочем,
методология пространства рычагов позволяет нам выбрать такое
место на карте в пространстве рычагов, где будет достигнута
минимизация потерь. Это далее откроет нам альтернативный путь
к достижению роста с помощью увеличения Т, или показателя
степени, любыми доступными способами. Математически данная
стратегия не столь очевидна с методологических позиций, изве-
стных прежде.
17*
260
Управление капиталом для профессионалов
Новая роль инвестиционного
аналитика
В конечном итоге инвестиционное решение опирается исклю-
чительно на точность вероятностей, сопоставленных сценариям.
Поскольку мы интересуемся тем, какой процент инвестировать
в ту или иную благоприятную возможность, мы не рассматри-
ваем ситуацию в булевском смысле. То есть нас не интересует
вопрос «Следует инвестировать в это или нет?». Вспомните при-
мер нашей игры в монетку «два-к-одному» из первой части этой
книги. Согласно обыденному здравому смыслу нам следут вос-
пользоваться этой благоприятной возможностью, то есть сделать
ставку, ибо имеет место положительное математическое ожидание.
Но, инвестируя, мы заработаем на этой возможности с вероят-
ностью не больше 25%. С вероятностью 50% или более мы
наверняка проиграем. Нам не следует рассматривать возможности
в простом булевском смысле, инвестировать или нет, покупать
или не покупать данную акцию. Скорее, мы должны рассматри-
вать ситуацию в оттенках черно-белого, спрашивая себя «Сколько
я инвестирую в эту благоприятную возможность?» (может 0%
или 100%, или, наиболее вероятно, что-то между двумя этими
булевскими экстремумами). То есть когда мы рассматриваем ин-
вестирование в рынок акций, перед нами стоит не вопрос «Сле-
дует ли?», а, скорее, «Сколько следует инвестрировать?»
Новая методология, представленная в данной книге, требу-
ет от вас отказаться от булевского мышления. Булевский подход
состоит в том, чтобы либо инвестировать во что-то (т.е. значение
«единица»), либо нет (т. е. значение «нуль»). Новая методология
требует не-булевского мышления, когда вместо вопроса «Инве-
стировали ли вы в этот рынок (имеете ли на нем длинную
позицию)?» задают вопрос «Сколько процентов вы инвестирова-
ли в этот рынок (в длинную позицию)?», ожидая получить такие
ответы, как 0% или 100%, или, чаще, математически точный
ответ (с учетом возможных сценариев для данного рынка) —
точное значение между нулем и единицей.
Теперь мы знаем, что для данного набора сценариев или
множества набора сценариев мы можем математически определить
Управление капиталом для профессионалов
261
оптимальную величину инвестирования. В книге это поставлено на
первое место. Данная величина будет точной при условии, что
сценарии, их исходы и вероятности реализации верны. Результаты
точны лишь до той степени, до которой точны исходные данные.
Поскольку при сопоставлении сценариев с тем, чем может обер-
нуться благоприятная возможность, все сценарии допустимы,
единственные предположения, которые необходимо сделать — это
сопоставляемые сценариям вероятности. Таким образом, в конечном
итоге инвестиционное решение опирается исключительно на точ-
ность сопоставленных вероятностей. Это не так легко сделать,
поскольку мы не можем проверить сопоставляемые вероятности
постфактум. Когда в конце некоторого периода владения реализо-
вался один из сценариев, вы не можете знать, точна ли вероят-
ность, которую вы сопоставили ему до его реализации, что вполне
согласуется со строками Стейнбека, процитированными в начале
книги. Поэтому анализ рынка не должен выдвигать на первый
план вопрос о том, инвестировать или нет. Напротив, основной
целью анализа рынка должно быть получение ответов на гораздо
более важные вопросы, такие как «Какова вероятность того, что
на рынке произойдет нечто определенное?» Решение таких вопро-
сов в долгосрочном плане принесет инвестору или управляющему
капиталом гораздо больше, чем любые предсказания рынка.
Вот мы и вернулись к нашей исходной посылке о том, что
анализ рынка, технический или иной, столь же важен, как
решение о том, какую сумму инвестировать. Представляется,
однако, что такое количественное решение может быть получено
лишь при условии, что мы используем анализ рынка для сопо-
ставления точных вероятностей возможностям того, как могут
повести себя данные рынки, в противоположность тому, что мы
думаем о том, как они себя поведут.
Список используемой
литературы
Bellman, Richard, Adaptive Control Processes, Princeton: Princeton
University Press, 1961.
Brinson, Gary P.; Singer, Brian D.; and Beebower, Gilbert L.,
«Determinants of Portfolio Performance II: an update,» Financial
Analysts Journal 47, May—June, 1991, pp. 40-49.
Feller, William, An Introduction to Probability Theory and Its
Application, Vol. II, New York: John Wiley & Sons, 1966.
Gehm, Fred, Commodity Market Money Management. New York:
Ronald Press, John Wiley & Sons, 1983.
Kelly, J. L., Jr.; «А New Interpretation of Information Rate,» Bell
System Technical Journal, July, 1956, pp. 917—926.
Kuhn, Thomas S.; The Structure of Scientific Revolutions, The
University of Chicago Press, 1962.
Press, William H.; Flannery, Brian P.; Teukolsky, Saul A.; and
Vetterling, William T, Numerical Recipes: The Art of Scientific
Computing, New York: Cambridge University Press, 1986.
264
Raiffa, Howard, and Schlaifer, Robert, Applied Statistical Decision
Theory, Boston: Harvard University, 1961.
Samuelson, Paul A., «The “Fallacy” of Maximizing the Geometric
Mean in Long Sequences of Investing or Gambling,» Proc. Nat.
Acad. Sci. USA, Vol. 68, No. 10, October, 1971, pp. 2493-
2496.
Shannon, С. E., «А Mathematical Theory of Communication,» Bell
System Technical Journal, October, 1948, pp. 379—423, 623—
656.
Tewles, Richard J.; Harlow, Charles V.; and Stone, Herbert L., The
Commodity Futures Game, Who Wins? Who Losses? Why?, New
York: McGraw-Hill Book Company, 1977.
Thorp, Edward O, Beat the Dealer, New York: Vintage Books,
Random House, Inc., 1966.
Thorp, Edward O, «The Kelly Money Management System,» Gambling
Times, Dec. 1980, pp. 91—92.
Thorp, Edward O, «The Mathematics of Gambling,» Gambling Times,
Hollywood, California, 1984.
Vince, Ralph, The Mathematics of Money Management, New York:
John Wiley & Sons, 1992.
Vince, Ralph, Portfolio Management Formulas, New York: John
Wiley & Sons, 1990. von Neumann, John, and Morgenstern,
Osker, Theory of Games and Economic Behavior, Princeton:
Princeton University Press, 1944.
Wentworth, R. С., «А Theory of Risk Management Under Favorable
Uncertainty,» unpublished. 8072 Broadway Terrace, Oakland,
CA 94611.
Wentworth, R. C., «Utility, Survival, and Time: Decision Strategies
Under favorable Uncertainty,» unpublished. 8072 Broadway
Terrace, Oakland, CA 94611.
Ральф Винс
НОВЫЙ ПОДХОД
К УПРАВЛЕНИЮ КАПИТАЛОМ
Структура распределения активов между различными
инвестиционными инструментами
Тираж 1000 экз.