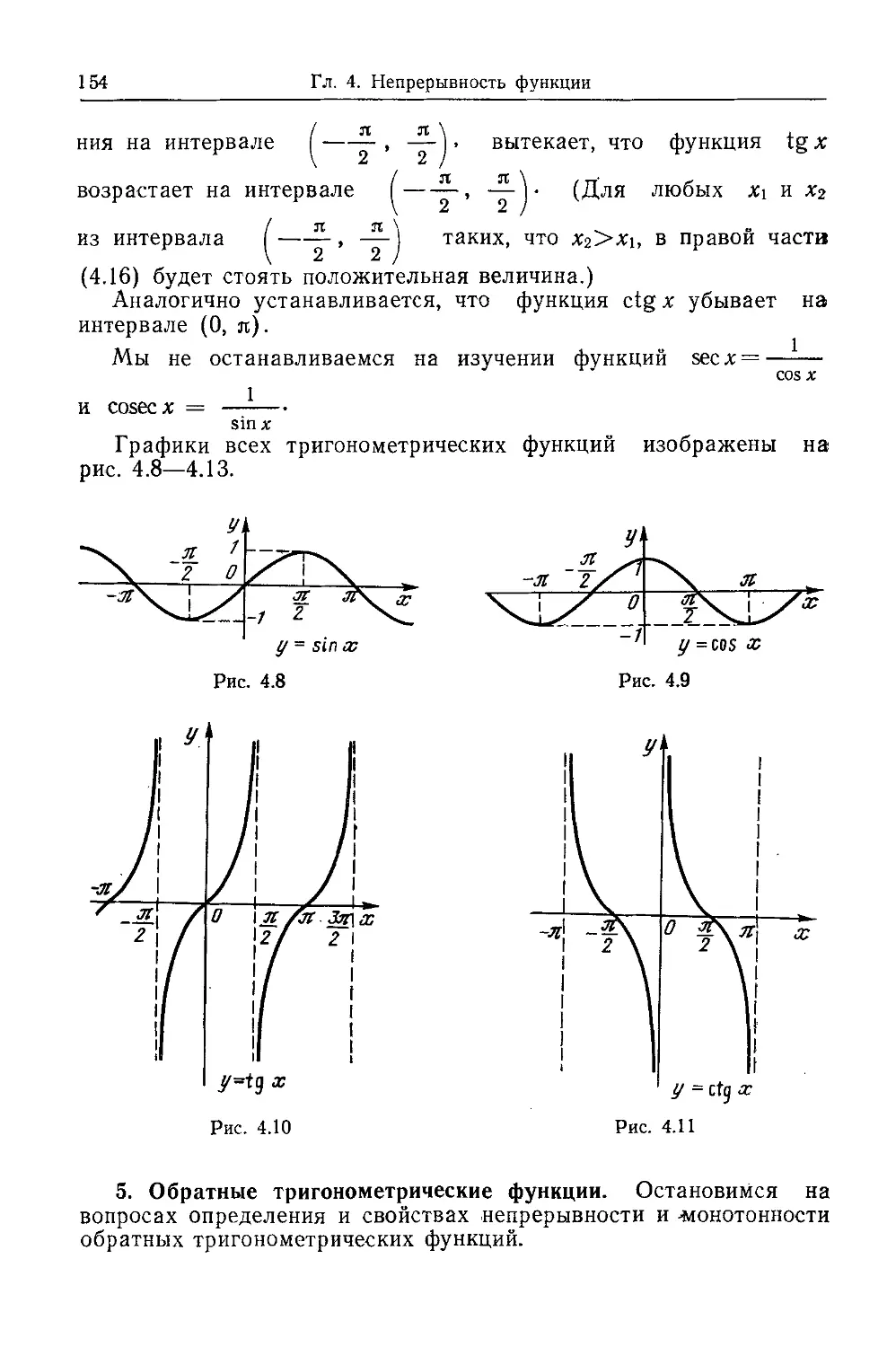
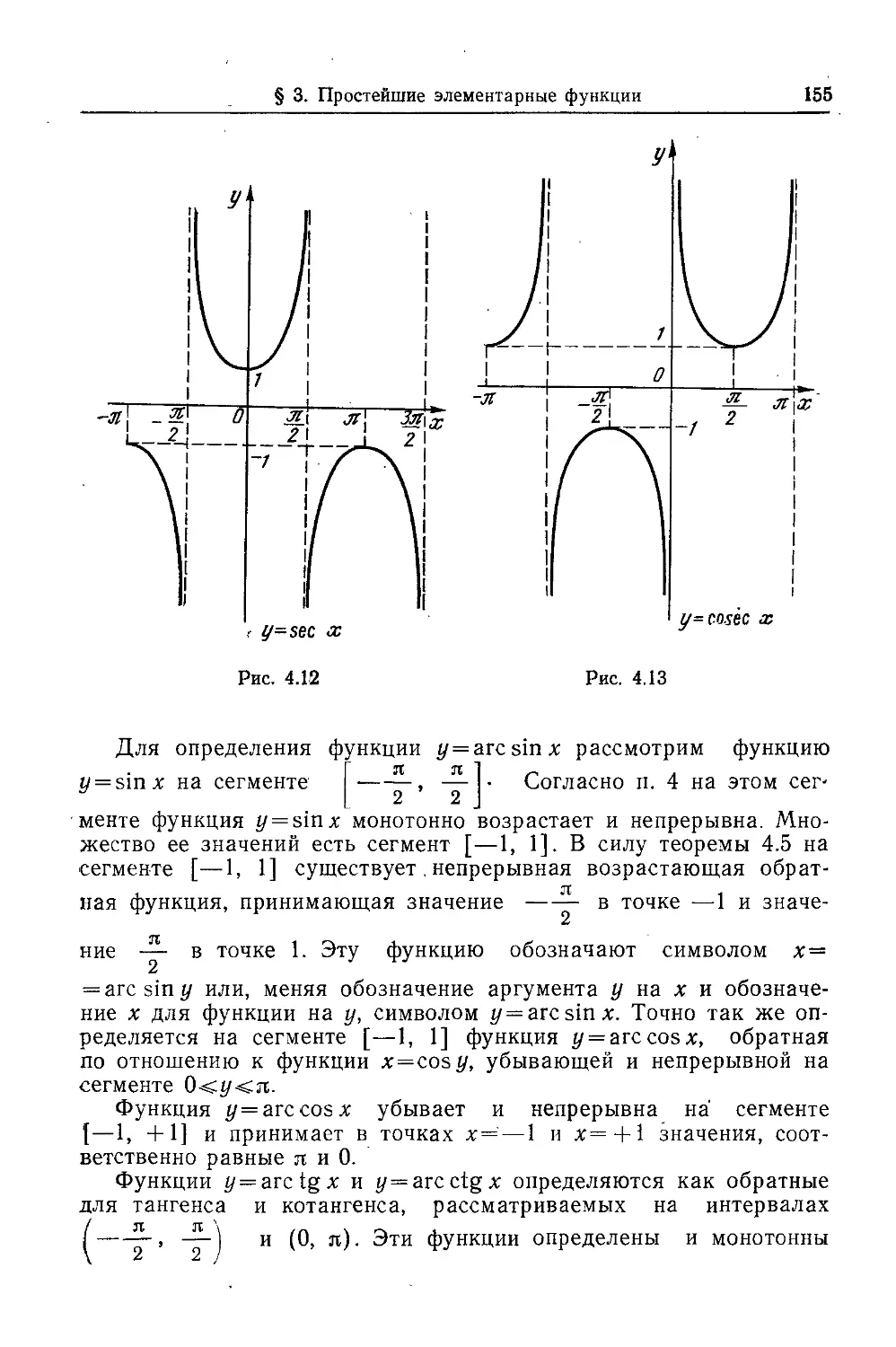
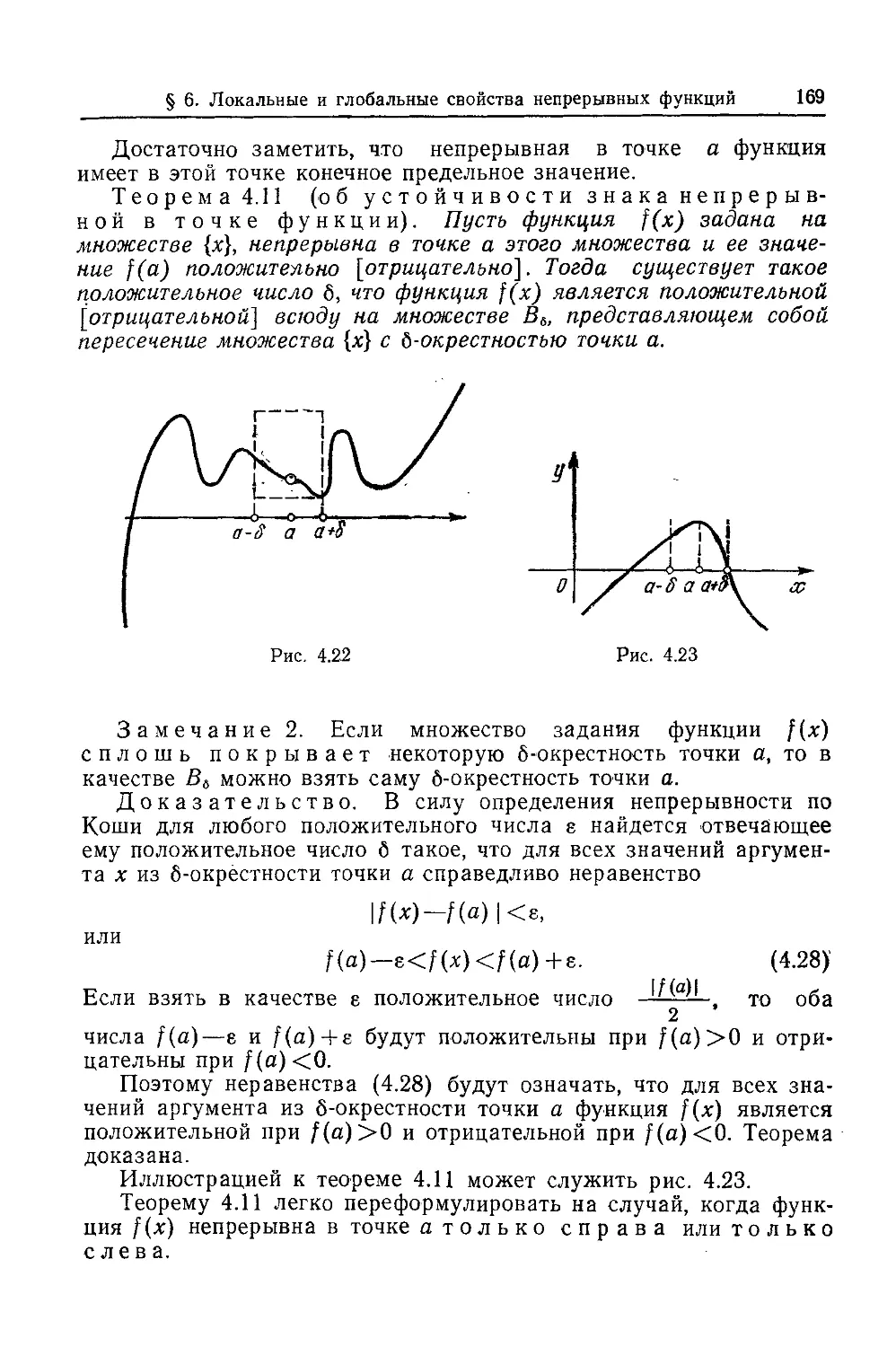
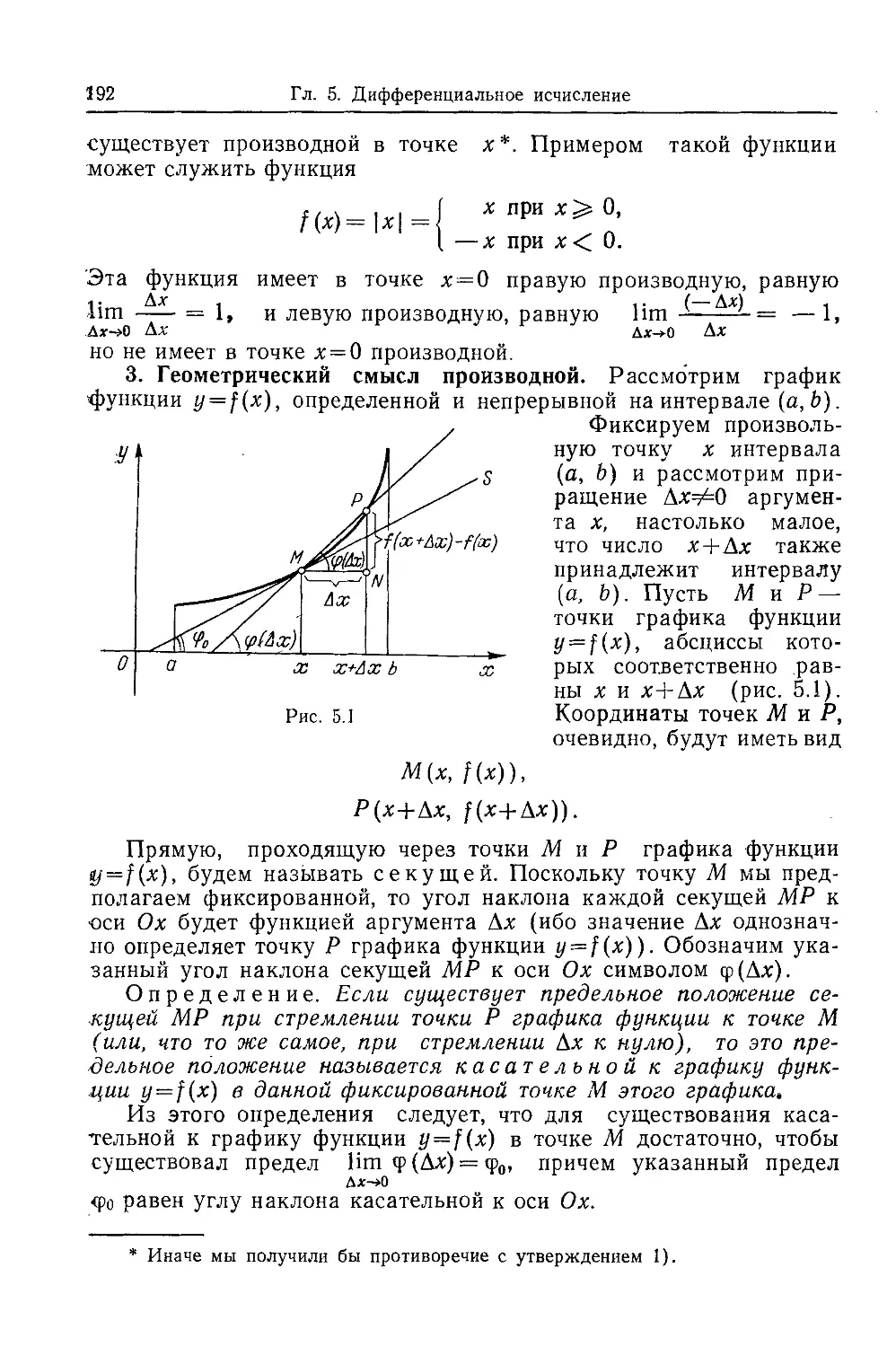
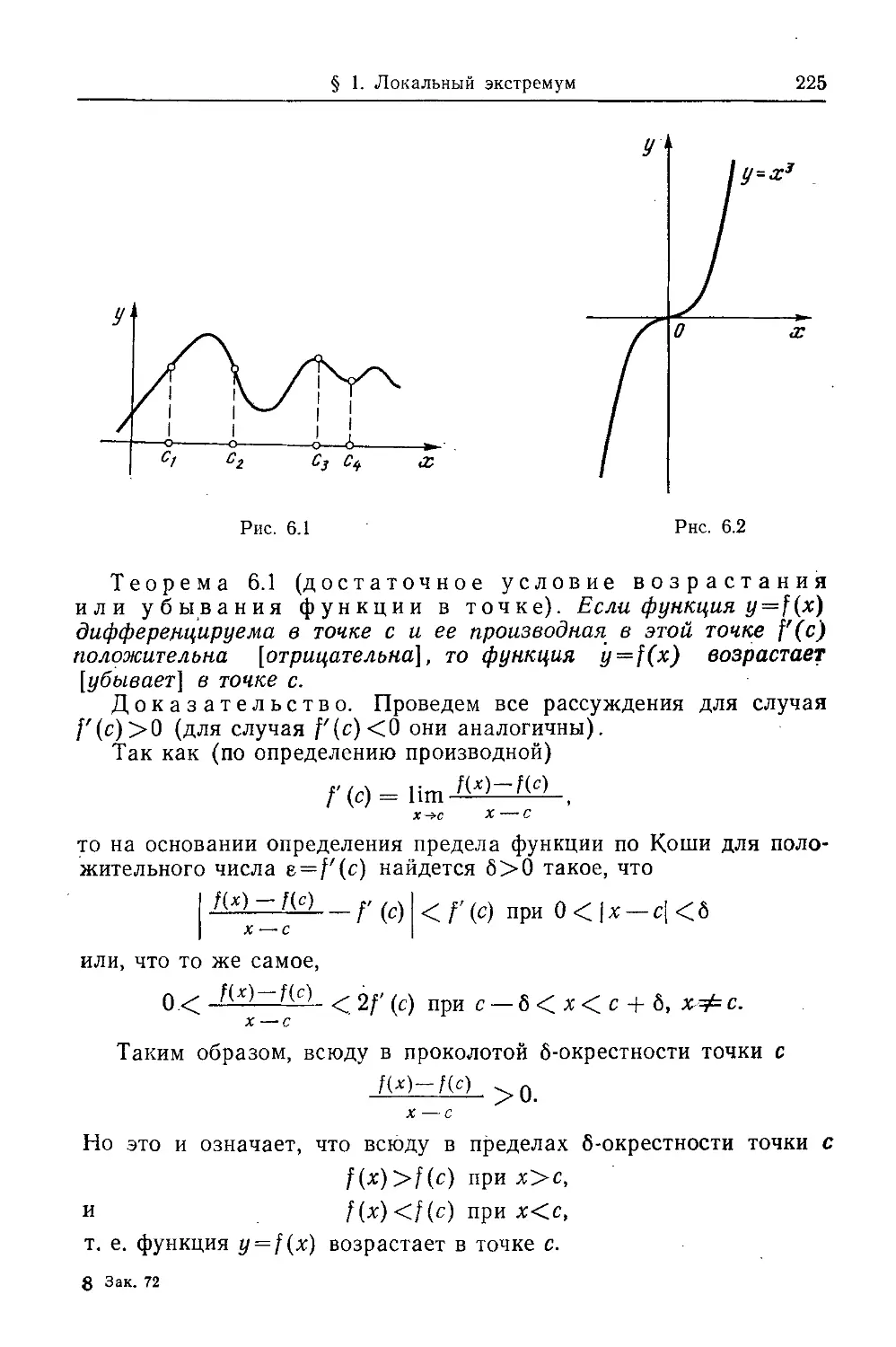
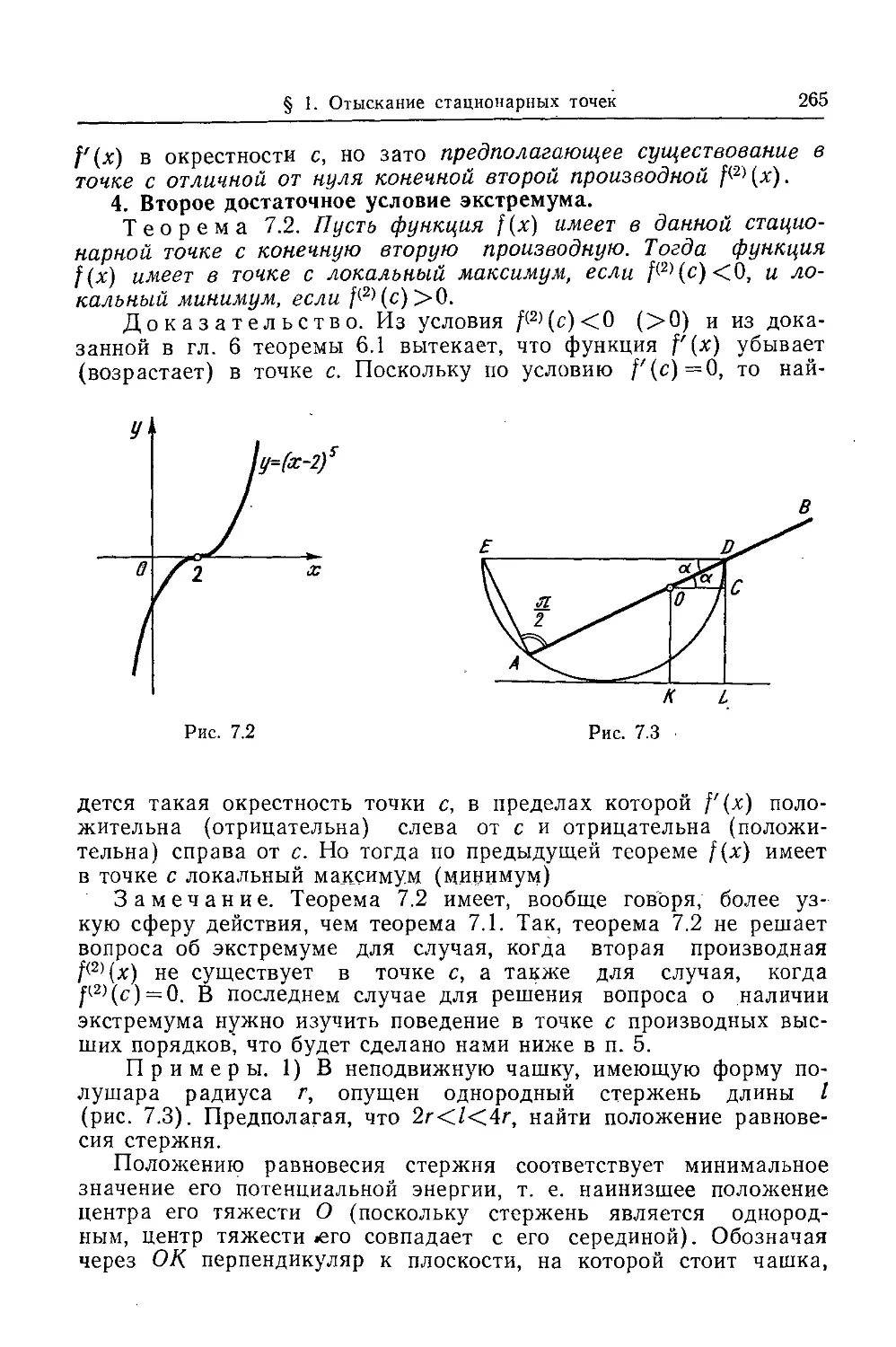
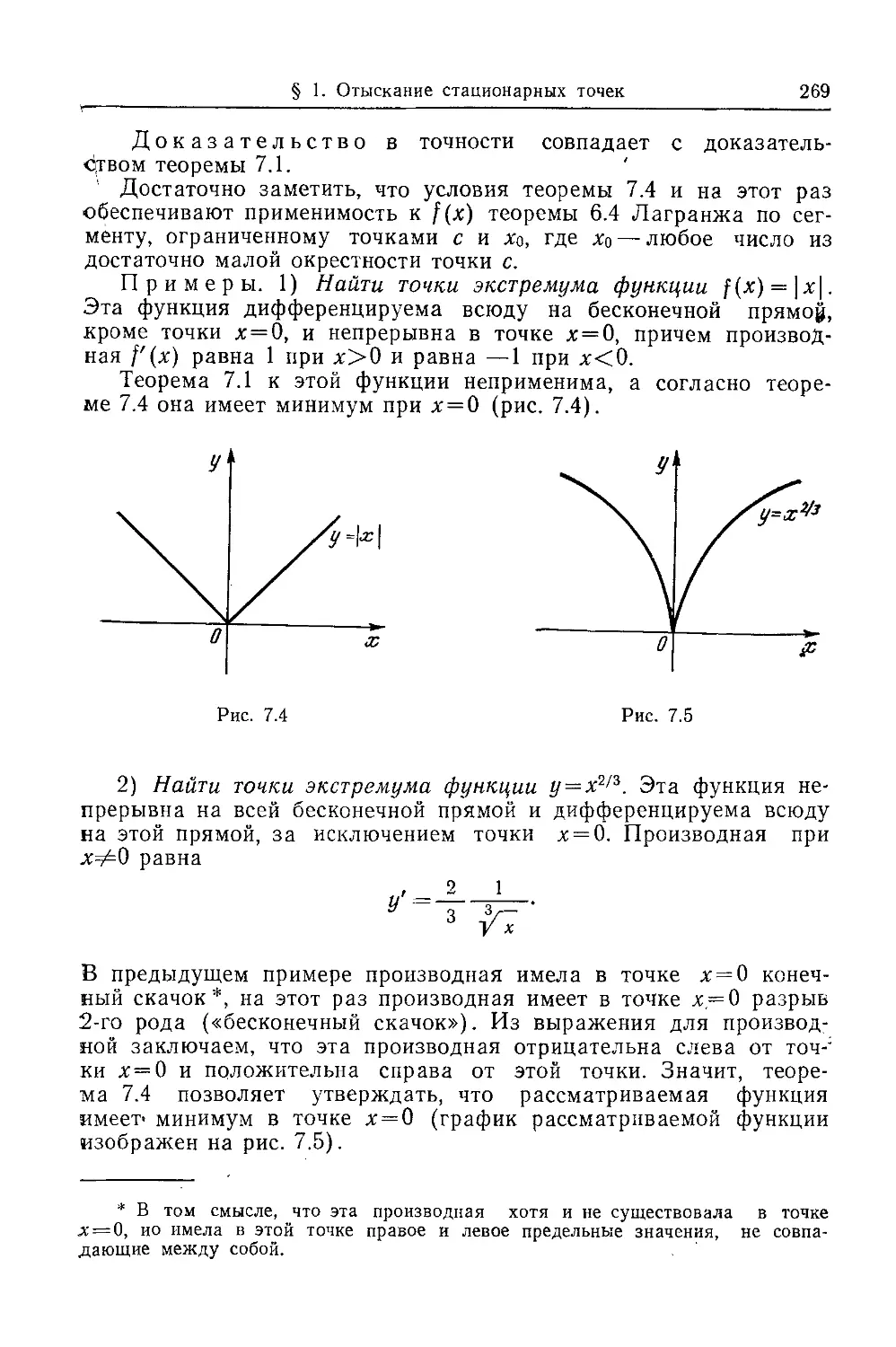
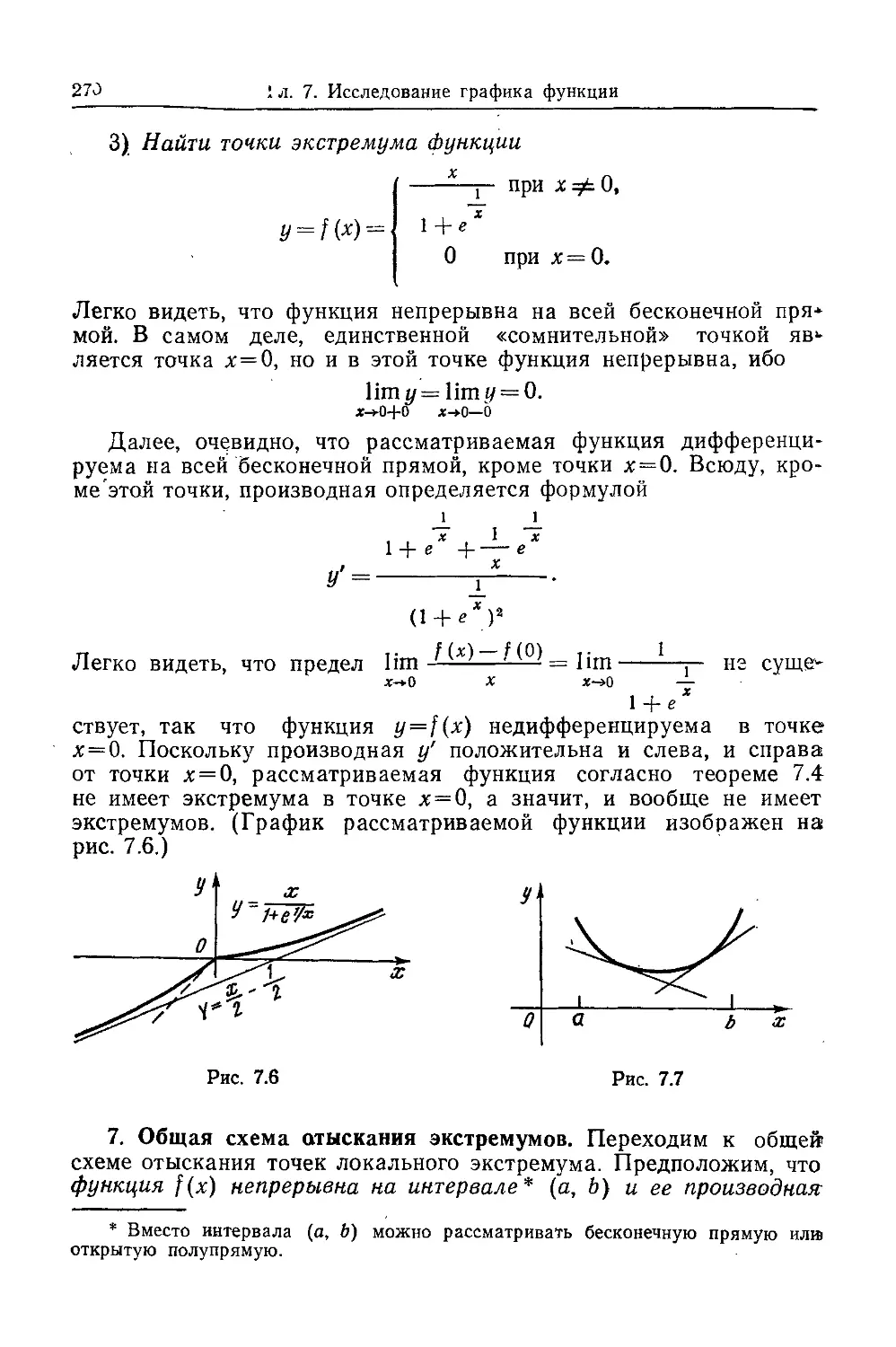
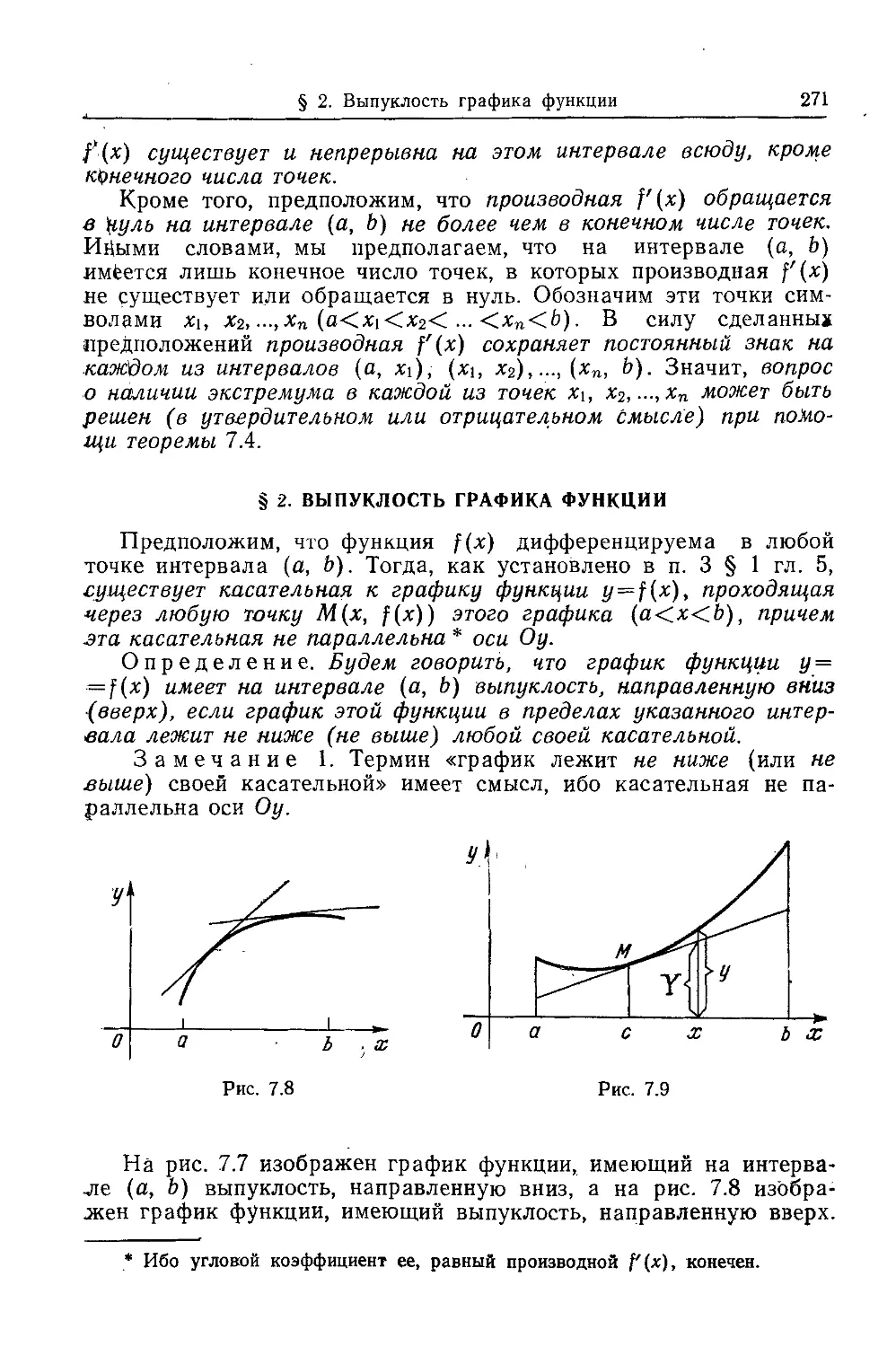
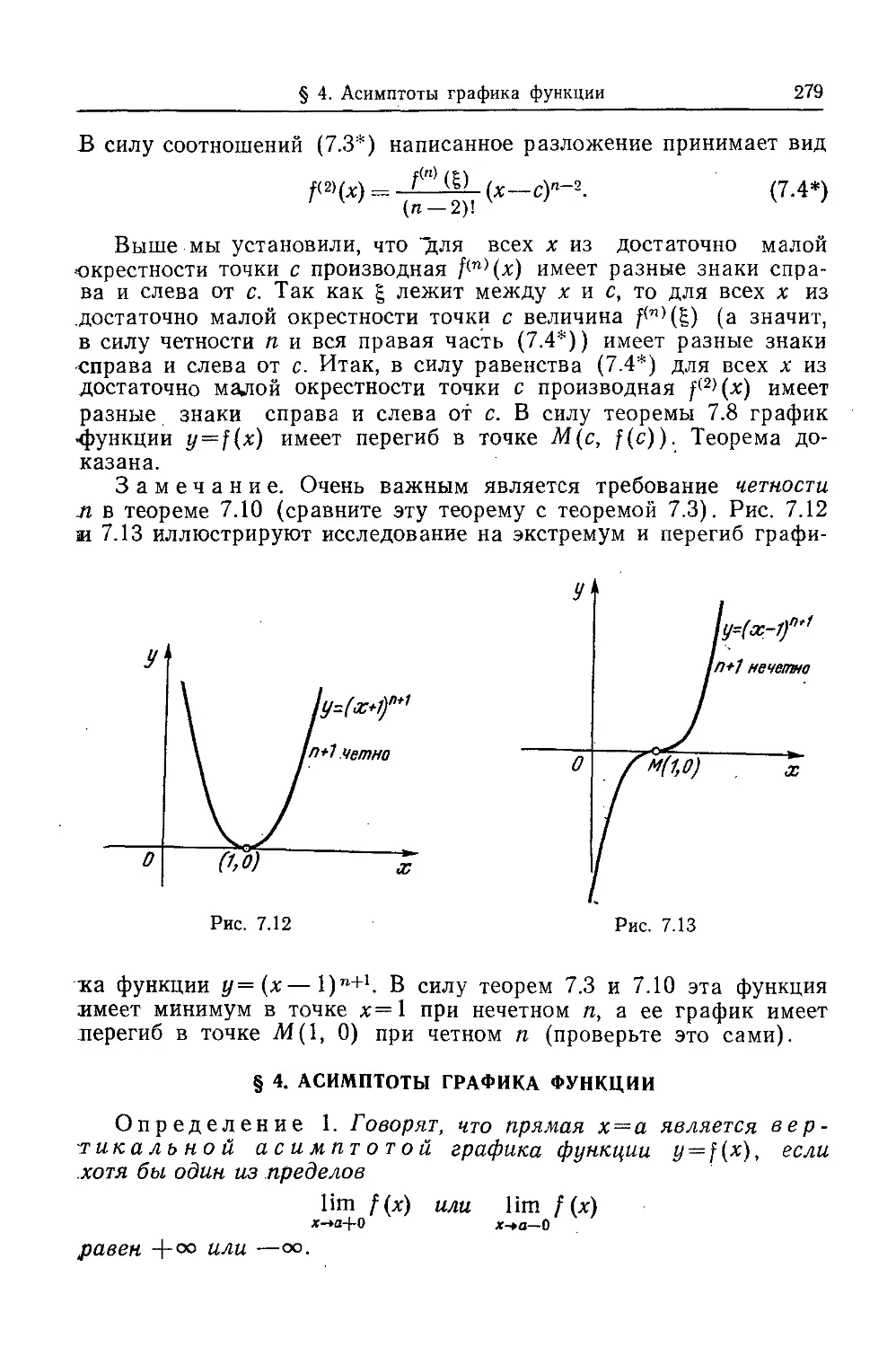
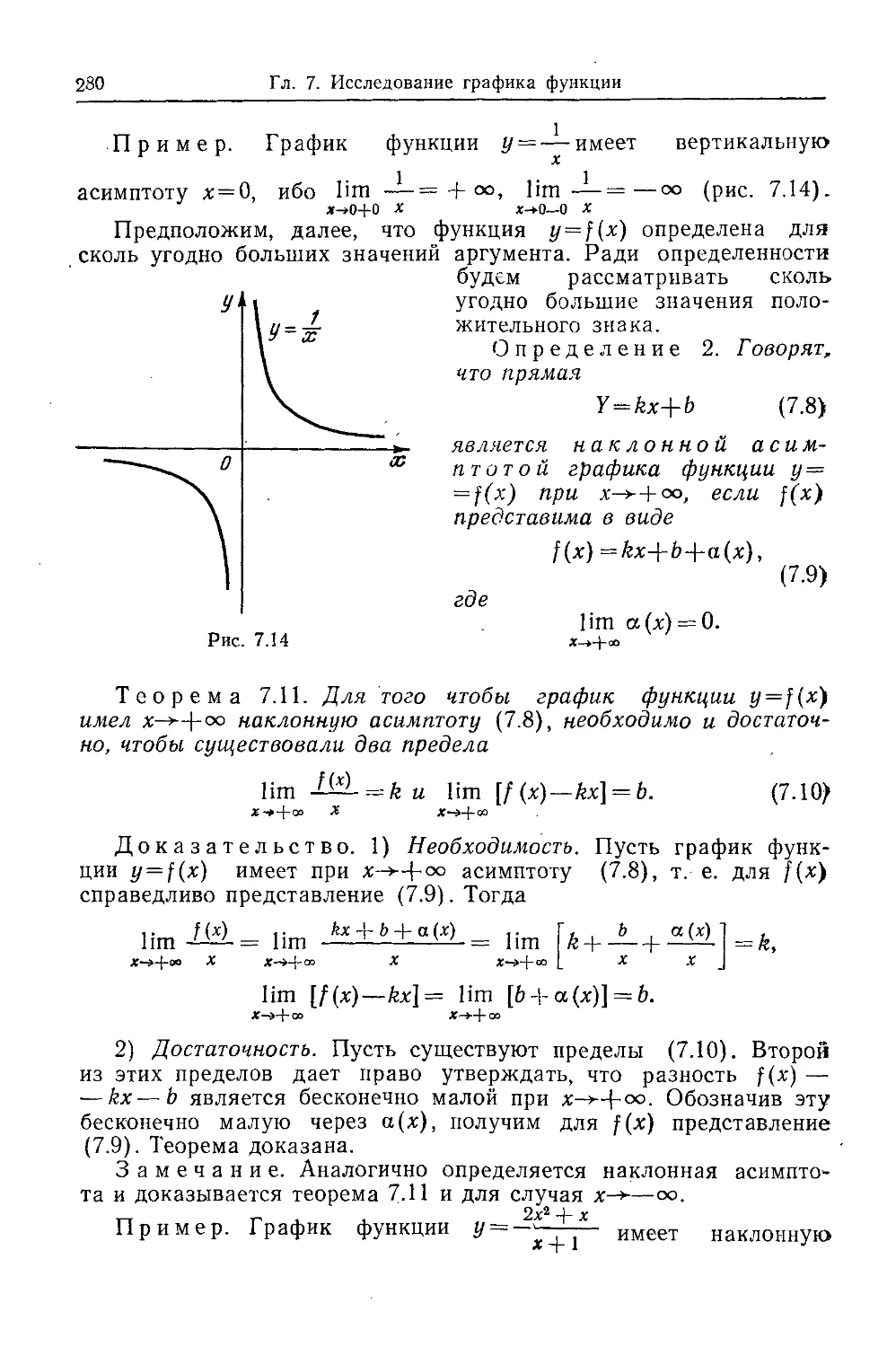
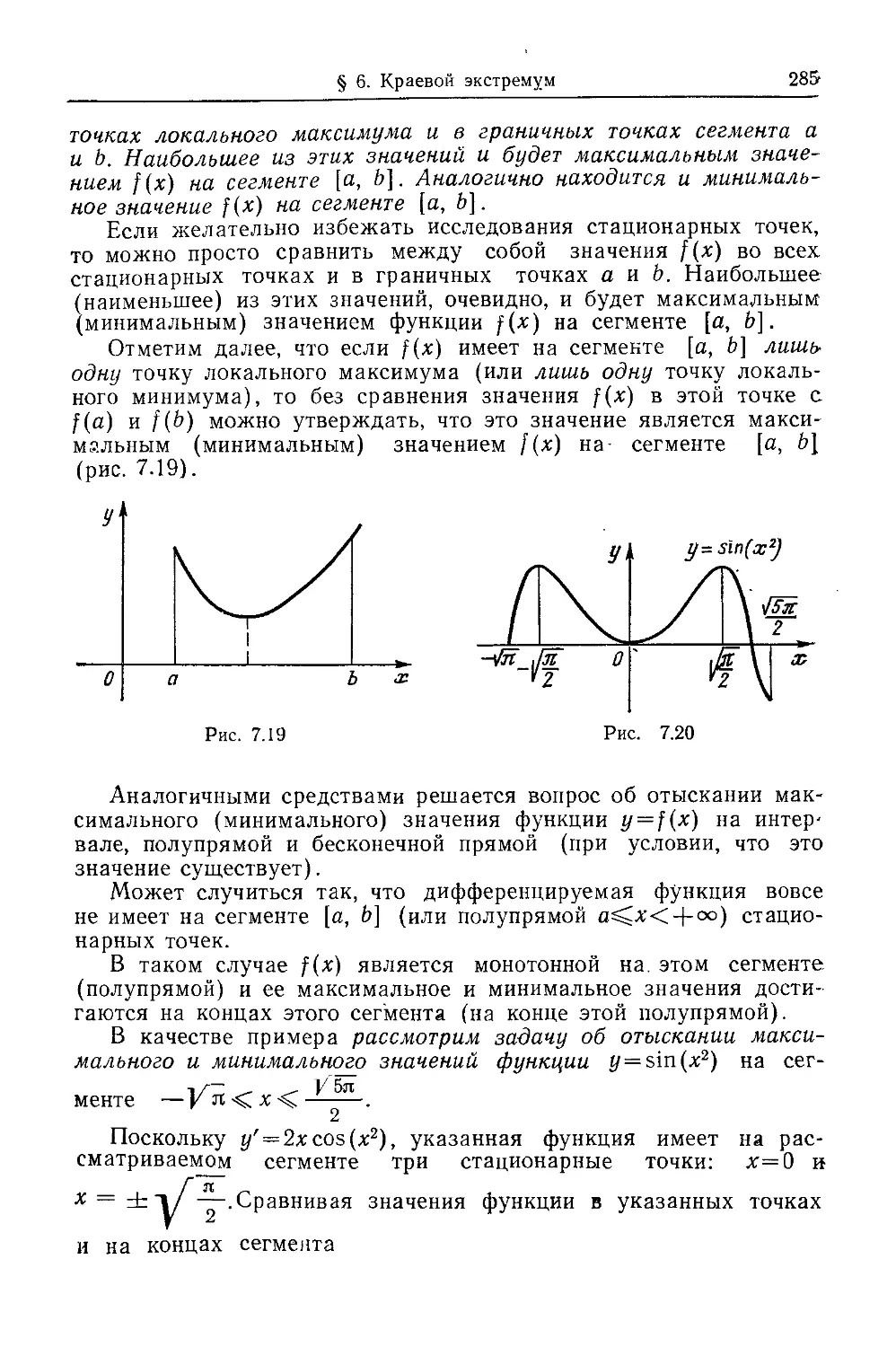
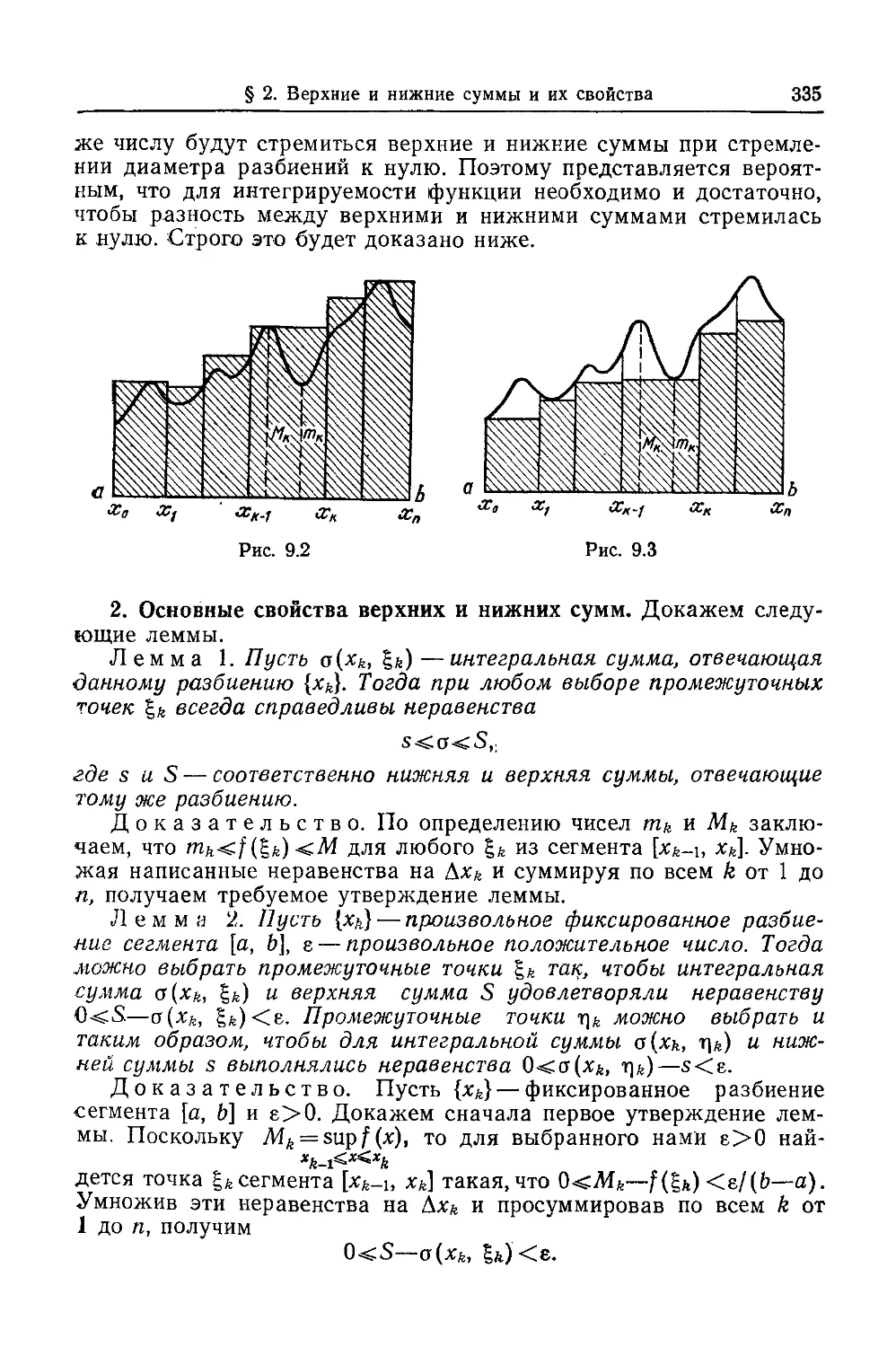
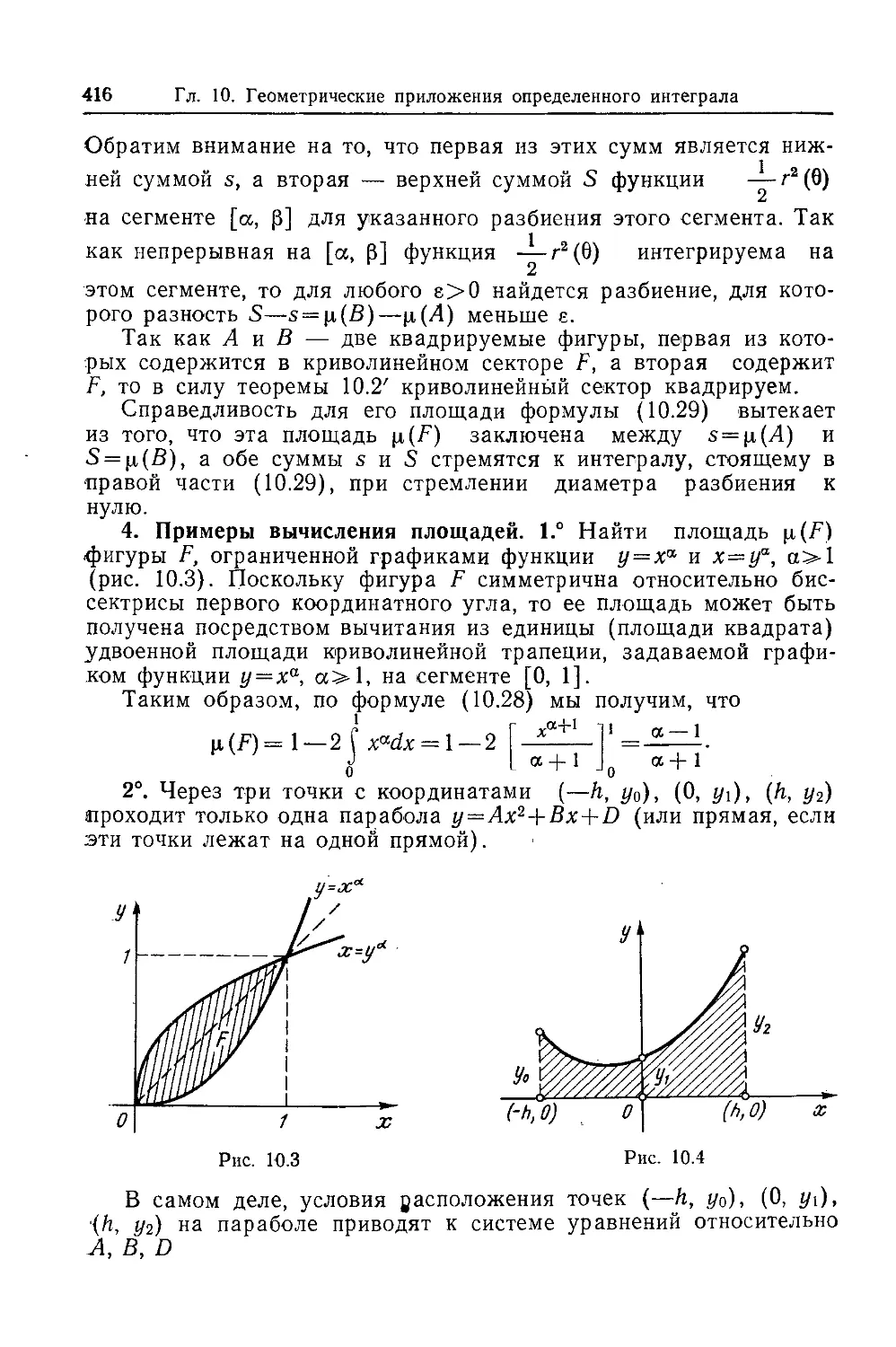
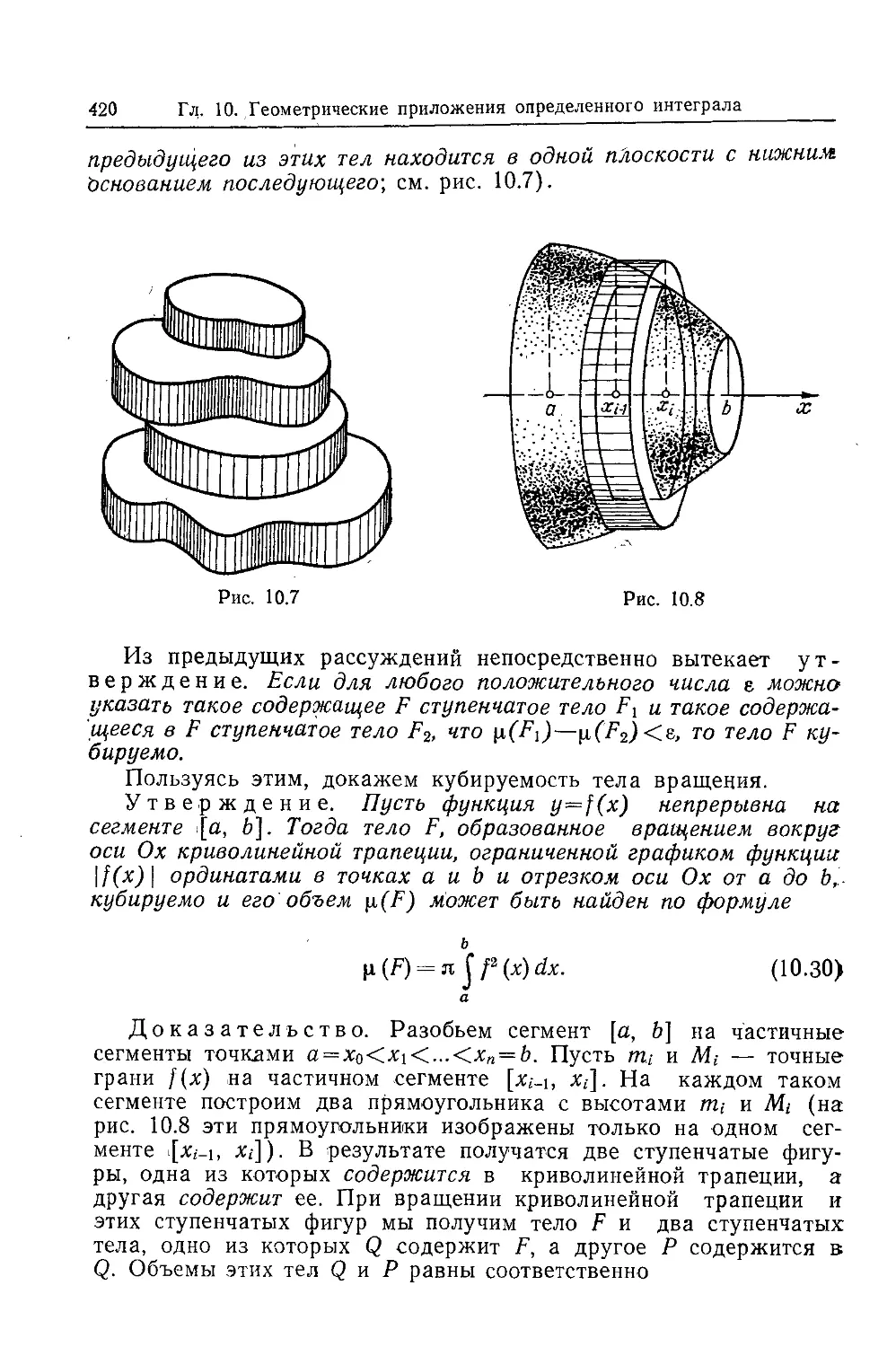
Текст
B.A. Ильин, B.A. Садовничий,
Бл.Х. Сендов
МАТЕМАТИЧЕСКИЙ
АНАЛИЗ
НАЧАЛЬНЫЙ КУРС
Под редакцией академика А.Н. Тихонова
ИЗДАНИЕ ВТОРОЕ,
ПЕРЕРАБОТАННОЕ
Допущено Министерством высшего
и среднего специального образования СССР
в качестве учебника для студентов вузов,
обучающихся по специальностям „Математика",
„Прикладная математика"
ИЗДАТЕЛЬСТВО
МОСКОВСКОГО УНИВЕРСИТЕТА
1985
iiiiiiiiiii
СОВМЕСТНОЕ ИЗДАНИЕ
МОСКОВСКОГО
ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА
ИМЕНИ М.В. ЛОМОНОСОВА
И СОФИЙСКОГО УНИВЕРСИТЕТА
ИМЕНИ КЛИМЕНТА ОХРИДСКОГО,
НАПИСАННОЕ В СООТВЕТСТВИИ
С ЕДИНОЙ ПРОГРАММОЙ
ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
УДК 517
Ильин В. А. и др. Математический анализ. Начальный курс/В. А. Иль-
Ильин, В. А. Садовничий, Бл. X. Сендов. Под ред. А. Н. Тихонова.— 2-е изд.,
пёрераб.— М.: Изд-во МГУ, 1985.— 662 с.
Учебник представляет собой первую часть трехтомного курса матема-
математического анализа для высших учебных заведений СССР, Болгарии и
Венгрии, написанного в соответствии с соглашением о сотрудничестве
между Московским, Софийским и Будапештским университетами. Книга
включает в себя теорию вещественных чисел, теорию пределов, теорию не-
непрерывности функций, дифференциальное и иитегральное исчисления функ-
функций одной переменной и их приложения, дифференциальное исчисление
функций многих переменных и теорию неявных функций.
Рецензент:
Кафедра математики МИФИ
(зав. кафедрой проф. А. И. Прилепко)
Издательство
9585 @
077@2)—S5 Московского университета, 1985 г.
ПРЕДИСЛОВИЕ ТИТУЛЬНОГО РЕДАКТОРА
В настоящее время прогресс в математике в большой степени
связан с развитием электронно-вычислительных средств. Матема-
Математические методы исследования проникают во все области челове-
человеческой деятельности. Все это повышает интерес к математике со
стороны смежных наук, использующих различный объем матема-
математических знаний, и ставит новые задачи в изучении самой мате-
математики. В связи с этим возникает потребность в написании учеб-
учебника по математическому анализу, учитывающего указанные за-
закономерности.
То обстоятельство, что решение математических задач реали-
реализуется на ЭВМ с помощью вычислительных алгоритмов, предъ-
предъявляет повышенные требования к четкости алгоритмического
уровня изложения математических дисциплин. Однако такое из-
изложение должно базироваться на классических концепциях ма-
математики и не должно их затемнять.
Эти общие принципы вместе с задачей четкого, ясного и до-
доступного изложения и положены в основу написания предлагае-
предлагаемой читателю книги. Книга написана с учетом согласованней
между Московским и Софийским университетами программы пре-
преподавания первой части математического анализа.
В предлагаемом учебнике уделено большое внимание вопро-
вопросам оптимизации, играющим в математике и ее приложениях
большую роль. В частности, в книге впервые в учебной литерату-
литературе в законченном виде излагается алгоритм отыскания как вну-
внутреннего, так и краевого экстремума функции. В учебнике уделе-
уделено значительное внимание изучению вопроса об исходной инфор-
информации, доступной при решении задачи. Так, например, для отыс-
отыскания экстремума функции одной переменной авторы предлагают
алгоритм, базирующийся на информации только о значениях
функции в точках области ее задания. Предлагаемое решение не
опирается на знание значений производной в точках области за-
задания и пригодно для отыскания экстремума недифференцируе-
мых функций.- Такая постановка типична при решении задач об
оптимизации производственных процессов.
При выборе метода изложения авторы отправляются от того,
что выбор алгоритма решения задачи зависит от того, какая ин-
информация из постановки этой задачи может быть использована.
Так, например, при введении понятия определенного интеграла
Предисловие титульного редактора
Римана авторы отправляются от концепции изложения, базирую-
базирующейся на использовании значений функции в точках сегмента.
Эта концепция, несомненно, является более предпочтительной
по сравнению с концепцией введения определенного интеграла
Римана с помощью первообразной, ибо она отвечает идее числен-
численных методов вычисления определенного интеграла, используемых
на ЭВМ.
В заключение хочу высказать уверенность, что предлагаемая
книга будет способствовать повышению математической культуры
читателей с различными запросами к объему математических
знаний.
А. Тихонов
Москва,
сентябрь 1978 г.
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Во втором издании книга подверглась существенной перера-
переработке и сокращению в целях максимального приближения ее ма-
материала к тому курсу, который реально может быть прочитан
студентам первого года обучения.
Особенно существенной переработке были подвергнуты разде-
разделы, посвященные теории вещественных чисел, теории множеств и
теории метрических, топологических и нормированных про-
пространств.
В книге сохранены три уровня изложения (облегченный, ос-
основной и повышенный).
Так.же, как и в первом издании, текст повышенного уровня
выделен в книге двумя вертикальными чертами, текст основного
уровня — одной вертикальной чертой, а остальной текст книги
относится к облегченному уровню изложения.
Проведенные во втором издании переработки улучшили воз-
возможности использования книги на указанных трех различных
уровнях изложения.
Авторы выражают благодарность сотрудникам кафедры ма-
математического анализа механико-математического факультета
МГУ и сотрудникам кафедры общей математики факультета вы-
вычислительной математики и кибернетики МГУ за критические за-
замечания по первому изданию этой книги. Авторы благодарят так-
также В. М. Говорова, В. Н. Денисова, И. С. Ломова и В. В. Тихо-
Тихомирова за помощь при подготовке второго издания этой книги.
Особую благодарность авторы приносят А. И. Прилепко, прочи-
прочитавшему рукопись второго издания и сделавшему критические за-
замечания, способствующие ее улучшению.
Москва,
февраль 1985 г.
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Настоящая книга является учебником по математическому
анализу по согласованной между Московским и Софийским уни-
университетами единой программе первого года обучения. Она пол-
полностью охватывает материал первого года обучения, предусмот-
предусмотренный программой для студентов университетов СССР и НРБ,
обучающихся по специальностям «математика», «механика» и
«прикладная математика».
Особенностью этой книги является то, что она содержит три
четко отделяемых друг от друга уровня изложения: облегченный,
основной и повышенный, причем для понимания материала об-
облегченного уровня не требуется чтения материалов основного и
повышенного уровней, а для понимания материала основного
уровня не требуется чтения материала повышенного уровня.
Облегченный уровень отвечает программе технических вузов
СССР с углубленным изучением математического анализа; основ-
основной уровень изложения отвечает программе специальностей «при-
«прикладная математика» и «физика» университетов СССР; материал
повышенного уровня дополняет материал основного уровня раз-
разделами, обычно излагаемыми на механико-математических фа-
факультетах университетов.
Текст, выделенный в книге двумя вертикальными чертами, от-
относится к повышенному уровню изложения; текст, выделенный
одной вертикальной чертой, — к основному уровню изложения;
остальной текст книги составляет содержание облегченного уров-
уровня изложения.
Книга содержит вводную главу, разъясняющую возникновение
основных понятий математического анализа и облегчающую вос-
восприятие последующего материала.
В книге нашла отражение возросшая роль вычислительных
методов и содержится ряд примеров применения аппарата мате-
математического анализа для вычисления элементарных функций, ин-
интегралов и отыскания корней уравнений и точек экстремума.
В настоящее время в СССР и НРБ имеется целый ряд учеб-
учебников по математическому анализу, среди которых особенно
удачными, по нашему мнению, являются учебники, написанные
Л. Д. Кудрявцевым и С. М. Никольским в СССР и Я. Тагамлиц-
ким в НРБ.
Предисловие к первому изданию
Авторы настоящей книги, несомненно, испытали влияние этих
прекрасных учебников.
При написании этой книги авторы использовали часть мате-
материала книги В. А. Ильина и Э. Г. Позняка «Основы математиче-
математического анализа», а также опыт преподавания математического ана-
анализа в университетах.
Авторы выражают глубокую благодарность титульному редак-
редактору этой книги академику 'А. Н. Тихонову за большое количест-
количество ценных советов и замечаний.
Авторы благодарят также Л. Д. Кудрявцева, И. И. Ляшко,
В. Л. Макарова, Д. Б. Дойчинова и Т. Боянова, критические за-
замечания которых способствовали улучшению этой книги.
Особой благодарностью авторы отмечают труд В. М. Говорова
и Г. Христова, который намного превзошел рамки обычного ре-
редактирования.
София,
март 1978 г.
Глава 1
ОСНОВНЫЕ ПОНЯТИЯ
МАТЕМАТИЧЕСКОГО АНАЛИЗА
В настоящей главе, не претендуя на точность формулировок и
отправляясь от простейших задач механики, мы постараемся об-
обрисовать основной круг понятий и проблем математического ана-
анализа.
1. Начнем наше рассмотрение с выяснения тех математиче-
математических понятий, которые неизбежно возникают при описании само-
самого простейшего вида движения — движения материальной точки
вдоль прямой линии.
Если материальная точка движется вдоль оси Оу, а х обозна-
обозначает время, отсчитываемое от некоторого начального момента, то
для описания указанного движения необходимо знать правило,
посредством которого каждому значению времени х ставится в
соответствие координата у движущейся точки в момент вре-
времени х.
В механике такое правило называют законом движе-
движения. Абстрагируясь от конкретного механического смысла пере-
переменных х и у и рассматривая в качестве х и у две совершенно
произвольные переменные величины, мы придем к понятию функ-
функции, являющемуся одним из важнейших понятий математиче-
математического анализа.
Если известно правило, посредством которого каждому значе-
значению одной переменной х ставится в соответствие определенное
значение другой переменной у, то говорят, что переменная у яв-
является функцией переменной х, и пишут у=у(х) или y=f(x).
При этом переменную х называют аргументом или не-
независимой переменной, а переменную у — функцией
аргумента х.
Букву f в записи y = f(x) обычно называют характери-
характеристикой рассматриваемой функции, а значение #=f(*) назы-
называют частным значением функции в точке х. Сово-
Совокупность всех частных значений функции принято называть о б -
ластью изменения этой функции.
Отметим сразу же, что приведенная формулировка понятия
функции требует уточнения, ибо в этой формулировке ничего не
говорится о том, из какого множества берутся значения незави-
независимой переменной х.
Множество, состоящее из тех и только тех чисел, которые яв-
являются значениями независимой переменной х, обычно называют
11
областью задания функции. Описание областей задания
функции требует развития теории числовых множеств.
Отметим еще, что понятие функции (так же, как и понятие
числа, множества и переменной величины) естественно считать
начальным понятием (т. е. таким понятием, которое мож-
можно описать, но нельзя строго определить, ибо любая попытка
дать строгое определение указанного понятия неизбежно сведется
к замене определяемого понятия ему эквивалентным). Таким об-
образом, вместо термина «определение функции» естественнее упр-
треблять термин «понятие функции».
Отметим, наконец, что для обозначения аргумента функции и
ее характеристики могут употребляться различные буквы. Так,
например, запись x=y(t) обозначает, что переменная х является
функцией аргумента t, причем характеристика этой функции .обо-
.обозначена через ф. При одновременном рассмотрении нескольких
функций одного аргумента t для обозначения характеристик этих
функций необходимо употреблять различные символы.
2. Часто приходится рассматривать такую функцию y = f(x);
аргумент х которой сам является функцией вида x=q>{t) некото-
некоторой новой переменной t. В таком случае говорят, что переменная
у представляет собой сложную функцию аргумента t, а
переменную х называют промежуточным аргументом. Ука-
Указанную сложную функцию называют также суперпозицией
функций f и ф. Для обозначения указанной сложной функции
естественно использовать символ y = f[y(t)]-
Рассмотрим простой пример, иллюстрирующий
вение понятия сложной функции. Предположим, что
ная точка М равномерно с постоян-
постоянной угловой скоростью со враща-
вращается по окружности радиуса R.
Найдем закон движения проекции
М' точки М на некоторую ось Оу,
проходящую через центр О окруж-
окружности и лежащую в ее плоскости
(рис. 1.1). При этом естественно
предположить, что в начальный мо-
момент времени /=0 движущаяся точ-
точка М находилась в точке Мо пере-
пересечения окружности с осью Оу.
Обозначим через у координату про-
проекции М' точки М на ось Оу, а через х угол М0ОМ, на который по-
повернется точка М за время t. Очевидно, что y=R cos x, x = at, и мы
получим, что координата у проекции М' представляет собой
сложную функцию времени t вида y=Rcosx, где x=at. Эту
сложную функцию можно записать в виде y=R cos u>t. Отметим,
что движение по закону y=R cos со/ в механике принято называть
гармоническим колебанием.
возникно-
материаль-
материальРис. 1.1
12 Гл. 1. Основные понятия математического анализа
3. Из курса физики известно, что важной характеристикой
движения материальной точки является ее мгновенная скорость
в каждый момент времени х. Если материальная точка движется
вдоль оси Оу по закону y = f(x), то, фиксировав произвольный
момент времени х и какое угодно приращение времени Ах, мы
можем утверждать, что в момент времени х движущаяся точка
имеет координату f(x), а в момент времени х+Ах— координату
Н
)
Таким образом, число Ay = f(x-\-Ax)—f(x) представляет собой
путь, пройденный движущейся точкой за промежуток времени от
х до х+Ах.
Отсюда вытекает, что отношение
Ах Ах
/1 1ч
обычно называемое разностным отношением, представ-
представляет собой среднюю скорость движущейся точки за про-
промежуток времени от х до х-\-Ах.
Мгновенной скоростью (или просто скоростью)
движущейся точки называется предел, к которому стремится сред-
средняя скорость A.1) при стремлении к нулю промежутка време-
времени Ах.
Если использовать известный из курса средней школы символ
предела, то можно записать следующее соотношение для мгно-
мгновенной скорости v(x) в момент времени х:
lm lm
дх-i-o Ах дж-»о Ах
Физическое понятие мгновенной скорости приводит к фунда-
фундаментальному математическому понятию производной. Абстраги-
Абстрагируясь от механического смысла рассмотренной выше функции у=
==f(x), мы назовем производной произвольной функции у=
= f(x) в данной фиксированной точке х предел, стоящий в пра-
правой части A.2) (при условии, конечно, что этот предел сущест-
существует) .
Используя для обозначения производной функции y = f{x) в
точке х символ f'(x) или у'(х), мы можем по определению за-
записать следующее равенство:
/' (х) = lim -^ = lim
до Ах a
lm lim .
д*-»о Ах ax-j-o Ax
Операцию нахождения производной договоримся называть диф-
дифференцированием.
Наше рассмотрение показывает, что при вычислении произ-
производной фундаментальную роль играет понятие предела функции.
'13
Предварительное представление о понятии предела функции
(да и о^самом понятии производной) дается в курсе средней шко-
школы. Однако строгое и последовательное изучение понятия преде-
предела возможно лишь на базе строгой теории вещественных чисел.
Так, например, без строгой теории вещественных чисел невоз-
невозможно установить существование двух следующих важных пре-
пределов:
iHiи ИтA+ ,)»/',
неизбежно возникающих, как мы увидим ниже, при вычислении
производных функций г/= sin л: и y=\ogax.
Итак, проведенное нами рассмотрение показывает, что вопрос
о существовании и вычислении производной упирается в необхо-
необходимость развития строгой теории вещественных чисел и на ее
базе теории пределов.
4. Займемся теперь вычислением производных двух конкрет-
конкретных элементарных функций y=sinx и y = \ogax и выясним, какие
математические проблемы неизбежно возникают при этом.
Сначала вычислим производную функцию y=smx в любой
фиксированной точке х. Для этой функции разностное отношение
A.1), очевидно, имеет вид
• .AL
Д</ _ sin(*+A*)— sins _„_„/„, Аж \ 2
Ax Ax \ 2
Таким образом, производная функции y = sinx в точке х по опре-
определению равна пределу
Ах
lim •
д*-»о
cos [х +
sin —
Аде \ 2
A.3)
Ах
2
(при условии, что этот предел существует).
Можно ожидать, что
lim cos (x + —) = cosx. A.4)
д*-*о \ 2 /
Заметим, однако, что не для всякой фуйкции f(x) справедливо
равенство
nmf(x + ^f)=f(x). A.5)
д*->о V 2 /
Функция f(x), для которой в данной точке х справедливо ра-
равенство (\ .5) , называется непрерывной (в точке х). Поня-
14 Гл. 1. Основные понятия математического анализа
тие непрерывности функции является одним из важйейших мате-
математических понятий и будет основательно изучаться в системати-
систематическом курсе математического анализа. В частности, в система-
систематическом курсе будет доказано, что функция y — cosx является
непрерывной в каждой точке х, т. е. в каждой точке х справед-
справедливо равенство A.4).
Заметим теперь, что для вычисления предела A.3) недоста-
недостаточно доказать справедливость соотношения A.4). Для этого не-
необходимо еще вычислить следующий предел:
sin —
1 • 2 , • sin t I. Ax \ /л ел
Urn = lim \t — \ (l.b)
A t \ 2 /
В систематическом курсе анализа будет строго доказано, что
предел A.6), часто называемый первым замечательным
пределом, существует и равен единице.
Только после того, как будет установлена непрерывность
функции i/ = cos;t (т. е. равенство A.4)) и вычислен первый за-
замечательный предел A.6), мы сможем, опираясь еще на то, что
предел произведения равен произведению пределов сомножите-
сомножителей, строго утверждать, что предел A.3) существует и равен
cos л: или, что то же самое, производная функции y = sinx суще-
существует и равна cos x.
Перейдем теперь к вычислению производной функции у =
= log0jc, считая, что 0<а=И=1, и фиксировав произвольную точку
х>0. Для этой функции разностное отношение A.1) имеет вид
Ay _ logq(x+-Ax)—l
Ах Ах
( и выбирается так, что х+Дх>0). Таким образом, произ-
производная функции y=\ogax в любой точке *>0 по определению
равна пределу
lim logq(х + А*) — '°ga* п j\
д*-*о Ах
(при условии, что этот предел существует). Преобразуем дробь,
стоящую в A.7), проделав следующие операции: 1) заменим раз-
разность логарифмов логарифмом частного; 2) произведем умноже-
умножение и деление на одну и ту же величину х>0\ 3) внесем множи-
множитель, стоящий перед логарифмом, под знак логарифма, сделав
его показателем степени. В результате получим, что предел A.7)
равен
Д*-+0
15
i
_,In, {-Llog.[(l+,)<]) (<--?-<>). A.8)
Рассмотрим отдельно предел при f->0 выражения, заключен-
заключенного в правой части последнего равенства в квадратные скобки:
Шп[A+ *)']• A.9)
Этот предел часто называют вторым замечательным
пределом. В систематическом курсе анализа будет установле-
установлено, что этот предел равен иррациональному числу е, которое с
точностью до пятнадцати знаков после запятой имеет вид е=
= 2,718281828459045...
Кроме того, в систематическом курсе будет доказана непре-
непрерывность функции у=logo х в каждой точке х>0 и, в частности,
в точке х—е. Но тогда из существования равного е предела
A.9) будет следовать, что
lim 1о& [A + t)~\ = loga e.
Последнее соотношение и соотношение A.8) позволяют утвер-
утверждать, что предел A.7) равен
х
lm
Дх->о Ах
Таким образом, после того как будет вычислен второй заме-
замечательный предел и установлена -непрерывность функции у=
= logo* в точке е, мы сможем строго утверждать, что логариф-
логарифмическая функция имеет производную, причем
(lq&, х)' - — logo е при 0 < а ф 1, х > 0.
X
5. В курсе средней школы кроме двух рассмотренных нами
функций #=sin* и y=\ogax изучались еще следующие функции:
y=cosx, y = tgx, y = ctgx, y = xa (a — вещественное число), у=
— ах @<a=?l), i/ = arcsinx, i/=arccosx, z/=arctgA::, i/ = arcctgx.
Все перечисленные функции принято называть простей-
простейшими элементарными.
Замечательным является тот факт, что при вычислении произ-
производных всех простейших элементарных функций не возникает ни-
никаких новых трудностей, кроме тех, с которыми мы встретились
при вычислении производных функций у=sin x и y=\ogax. He-
16 Гл. 1. Основные понятия математического анализа
трудно проверить, что для вычисления производных всех простей-
простейших элементарных функций требуются лишь арифметические
свойства операции предельного перехода, два замечательных пре-
предела и факт непрерывности каждой из этих функций в точках
областей их задания.
Отмеченное обстоятельство дает нам право без дальнейших
разъяснений привести таблицу производных всех простейших эле-
элементарных функций.
1°. (ха)' = аха~1 (х>0, а— вещественное число).
2°. (log,, х)' = -i- logoг .@<аф1, х> 0).
В частности, при а = е
3°. (а*)'=а* log,а @<аФ1).
В частности, при а = е
(ех)'=ех.
4°. (sin;t)' = cos;t.
5°. (cos*)'=— sin*.
6°. (tg*)' = —L_ (Хф±. + пя, где я = 0, ±1,±2, ..Л.
cos2 л: \ 2 /
7°. (ctgx)'= ^— (хфпя, где л = 0, ±1, ±2,...).
8°. (avCsmxy = -^=^ (|>|< 1).
9°. (агссо5л:):=1 (U|<1)
10°. (aretg*)^-^.
11°. (arcctg*)'=—-|—.
Строгое обоснование приведенной таблицы является одной из
важных задач той части математического анализа, которую при-
принято называть дифференциальным исчислением.
Традиционной задачей классического дифференциального ис-
исчисления является и несколько более общая задача — вычисление
производной любой функции f(x), которая получается из перечис-
перечисленных выше простейших элементарных функций путем конечного
числа суперпозиций и конечного числа четырех арифметических
действий (сложения, умножения, вычитания и деления). Такую
функцию f(x) принято называть просто элементарной.
Итак, элементарной называется функция, которая по-
получается из простейших элементарных функций путем конечного
числа суперпозиций и четырех арифметических действий.
17
Примером элементарной функции может служить функция
Для вычисления производной любой элементарной функции-
следует присоединить к выписанной нами таблице производных
простейших элементарных функций два правила: 1) правило-
дифференцирования сложной функции, 2) правило дифференци-
дифференцирования суммы, разности, произведения и частного функций.
Правило дифференцирования сложной функции y=f(u), где
u=(f(x), имеет следующий вид: если функция и=<р(х) имеет
производную в данной точке хо, а функция y=f(u) имеет
производную в соответствующей точке мо=<р(*о), то сложная
функция y = f[<f(x)] имеет производную в точке хо, причем эта
производная (обозначим ее через у') равна
/=Пф(*о)]<р'(*о). A-10>
т. е. равна произведению производной функции y = f(u) в точке
«о=ф(*о) на производную функции и=«р(х) в точке хо.
Справедливость для производной сложной функции формулы
A.10) легко оправдать с помощью наводящих соображений, но
строгий вывод формулы A.10) не является простым и будет при-
приведен в систематическом курсе математического анализа.
Гораздо проще устанавливаются правила дифференцирования
суммы, разности, произведения и частного двух функций, которые
имеют вид
[u(x)±v(x)]' = u'(x)±vr(x),
[u{x)v(x)Y=u'{x)v{x)+u(x)v'(x)t
и(х) 'I' __ и' (х) v (х) — и (х) v' (х)
v(x) J ^(х)
(в последней формуле требуется необращение в нуль функции
v(x) в рассматриваемой точке х).
Подводя итог, мы можем заключить, что одной из важных за-
задач части математического анализа, называемой дифференциаль-
дифференциальным исчислением, является строгое обоснование таблицы произ-
производных простейших элементарных функций и правил дифферен-
дифференцирования сложной функции, а также суммы, разности, произве-
произведения и частного функций.
Это обоснование позволит вычислить производную любой эле-
элементарной функции f{x), т. е. любой функции fix), получаю-
получающейся из простейших элементарных путем конечного числа супер-
суперпозиций и четырех арифметических действий. При этом оказы-
оказывается, что производная любой элементарной функции представ-
представляет собой также элементарную функцию, т. е. операция диффе-
дифференцирования не выводит нас из класса элементарных функций.
18 Гл. 1. Основные понятия математического анализа
Отмеченное обстоятельство оправдывает введение класса элемен-
элементарных функций как традиционного объекта классического ана-
анализа.
6. Еще раз обратимся к рассмотрению механической задачи о
движении материальной точки вдоль прямой линии — оси Оу, но
на этот раз предположим, что для любого момента времени х
нам задана мгновенная скорость f(x) движущейся точки и тре-
требуется найти закон движения этой точки.
Поскольку мгновенная скорость f(x) является производной
¦функции y=F(x), определяющей закон движения, то задача сво-
сводится к разысканию по данной функции f(x) такой функции F(x),
производная F'(х) которой равна f(x). Отвлекаясь от механиче-
механического смысла функций f(x) и F(x), мы придем к математическим
понятиям первообразной и неопределенного интеграла.
Первообразной функции f(x) называется такая функция
F(x), производная которой F' (х) равна f(x). .
Это определение требует уточнения: следует четко оговорить,
«а каком множестве должно быть справедливо равенство F'(x) =
= f(x). Отмеченное обстоятельство еще раз подчеркивает необхо-
необходимость развития теории множеств. Уточнение понятия первооб-
первообразной будет дано в систематическом курсе.
Заметим, что если функция F(x) является первообразной
¦функции f(x), то и функция F(x)-\-C, где С — произвольная по-
-стоянная, также является первообразной функции f(x) (в силу
того, что производная постоянной С равна нулю).
Более трудным является обратное утверждение: любые две
первообразные одной и той же функции f(x) на интервале (а, Ь)
могут отличаться лишь постоянным слагаемым. Доказательство
этого утверждения требует развитого аппарата математического
¦анализа и будет проведено в систематическом курсе анализа.
Опираясь на указанное утверждение, мы можем констатиро-
констатировать следующий факт: если функция F(x) является одной из пер-
первообразных функции f(x), то любая первообразная функции f(x)
имеет вид F(x)-\-C, где С — постоянная.
Совокупность всех первообразных данной функции f(x) назы-
называется неопределенным интегралом от функции f(x)
и обозначается символом
U(x)dx.
Только что отмеченный нами факт позволяет утверждать, что
если F(x)—одна из первообразных функции f{x), то неопреде-
неопределенный интеграл от функции f(x) равен
где С — любая постоянная.
Возвратимся к поставленной нами задаче об отыскании зако-
закона движения материальной точки вдоль оси Оу по известной
19
мгновенной скорости f(x) этой точки. Мы теперь можем утвер-
утверждать, что искомый закон движения определяется функцией # =
() С —
д, р фу
= F(x) + C, где F(х) —любая первообразная функция f(x)> а
постоянная. Как мы видим, без дополнительных условий закоа
движения по мгновенной скорости определяется неоднозначно: с
точностью до постоянного слагаемого С. Для определения посто-
постоянной С должно быть привлечено дополнительное условие, обыч-
обычно заключающееся в задании координаты уо движущейся точки
в некоторый момент времени Хо- Используя это условие, мы п?>-
лучим соотношение yo = F(хо)-\-С, из которого С=уо — F(x0), так
что окончательно искомый закон движения имеет вид
7. Рассмотрим вопрос об отыскании первообразных и неопре-
неопределенных интегралов от некоторых элементарных функций. Так
как функция f(x)=cosx является производной функции F(x) =
= sin*, то функция F(x)=sinx является одной из первообразных
функции f(Ar)=cosx, и потому любая первообразная функции
f(x)=cosx имеет вид sinx+C, где С — постоянная. Таким об-
образом,
Г cos xdx = sin x + С.
Только что проведенное рассуждение имеет общий характер..
Можно утверждать, что любая формула дифференциального ис-
исчисления F'(x)=f(x), утверждающая, что функция f(x) является:
производной функции F(x), порождает эквивалентную ей форму-
формулу интегрального исчисления jf(x)dx = F(x)-\-C, утверждающую*
что неопределенный интеграл от функции f(x) равен Р(х)-{-С,„
где С — любая постоянная.
Таким образом, выписанная выше таблица производных про-
простейших элементарных функций порождает эквивалентную ей
таблицу важных неопределенных интегралов, которую мы приво-
приводим ниже.
1°.
[xx
2о. fJl = log,*H
3°. [axdx = -^
J l
+
loge а
В частности, при а = е
f exdx = i
4°. f sin xdx = —cosx+ С.
5°. $cosxdx = sin х+С.
f—^—= tgx + C ( — ¦—+пп<х<^- + пп, где п = 0, ±1,
J cos2* \ 2 2
20 Гл. 1. Основные понятия математического анализа
6°.
70. Г dx =—ctgx+C (лп<*<л+лге, гдеп = 0, ±1, ±2, ...)•
J sin2 л:
8°. Г .*^_ =arcsinx+C (|*|<1).
Приведенная таблица в систематическом курсе анализа будет
дополнена двумя важнейшими правилами интегрирования (инте-
(интегрированием посредством замены переменной и интегрированием
ло частям).
Здесь мы не будем приводить формулировку этих правил, а
лишь отметим, что написанная таблица вместе с этими правила-
правилами составляет важный вычислительный аппарат той части мате-
математического анализа, которую принято называть интеграль-
иым исчислением.
Следует, однако, сразу же подчеркнуть, что для вычисления
многих важных неопределенных интегралов этого аппарата ока-
оказывается недостаточно. Например, этого аппарата недостаточно
для вычисления неопределенного интеграла
Т
dx, A.11)
играющего важную роль в теории вероятностей и в других разде-
разделах точных наук.
Интеграл A.11) служит примером интеграла от элементарной
функции, не являющегося элементарной функцией. Таким обра-
образом, в отличие от операции дифференцирования, операция инте-
интегрирования выводит нас из класса элементарных функций. Это об-
обстоятельство подчеркивает условность самого понятия элементар-
элементарной функции как традиционного объекта классического анализа.
Недостаточность описанного нами аппарата ставит на повест-
повестку дня задачу о существовании и о вычислении первообразной и
неопределенного интеграла от любой функции f(x), только не-
непрерывной в каждой точке х области своего задания.
Оказывается, такую задачу можно решить при помощи друго-
то подхода к проблеме интегрирования функции, к выяснению ко-
которого мы сейчас и перейдем.
8. Снова предположим, что функция f(x) представляет собой
мгновенную скорость движущейся вдоль оси Оу материальной
точки. Поставим цель — вычислить путь, пройденный этой точкой
за промежуток времени от х=а до х = Ь.
21
Для облегчения рассуждений будем считать, что скорость f(x)
неотрицательна для всех значений времени х.
Для решения поставленной задачи разобьем промежуток вре-
времени на малые промежутки, ограниченные моментами времени
а = хо<Х\<х2< ... <хп-1<хп = Ь.
Естественно считать, что на каждом малом промежутке вре-
времени от Xh-\ до хи (?/=1, 2,..., п) скорость f(x) меняется мало
(что заведомо будет иметь место всякий раз, когда f(x) является
непрерывной в каждой точке х). Но тогда приближенно можно
считать скорость f{x) постоянной на каждом промежутке [xh^u
Xh] и равной значению f(lu), где |& — некоторое значение време-
времени из промежутка [Xk-u Xk] ¦
Таким образом, путь S[xk-i, Хь), пройденный движущейся
точкой за промежуток времени от хп-\ до хъ., приближенно мож-
можно считать равным произведению f(lu) на длину Axu — Xk — Хь-i
промежутка [xu-i, Xh] ¦ Итак,
S[xk-i, xk] ~f{lk)bxk.
В таком случае путь' S [а, Ь], пройденный материальной точ-
точкой за весь промежуток времени от х=а до х—Ь, будет прибли-
приближенно равен сумме
S[a, b]~f(h)/±xl+{(b)bx2+...+f(tn)/±xn. A.12)
Сумму, стоящую в правой части A.12), принято называть ин-
интегральной суммой.
Естественно ожидать, что точное значение пути S [а, Ь) мы
получим, переходя в интегральной сумме, стоящей в правой части
A.12), к пределу при стремлении к нулю наибольшей из длин
bkXk (при этом, конечно, общее число п частичных промежутков
будет неограниченно возрастать).
Используя символ предела и обозначая через d наибольшее
из чисел Ал:], Ахг,..., Дх„, получим, что
SM] = lim{/(g1)Ax1 + /(yAx2+... + /(yA*J. A.13)
Разумеется, требует уточнения вопрос о том, что мы пони-
понимаем под пределом интегральной суммы, стоящим в правой ча-
части A.13). На этот раз операция предельного перехода встре-
встречается в новой и более сложной форме, чем при вычислении
обычного предела функции ttmf(x).
Строгое определение и изучение свойств предела вида A.13)
будет дано в систематическом курсе анализа. Здесь же мы ука-
укажем,; что в математике предел, стоящий в правой части A.13),
22
Гл. 1. Основные понятия математического анализа
называется определенным интегралом от функции f(x)
в пределах от а до Ь и обозначается символом
ь
dx. (
Итак, определенный интеграл A.14) равен пути S[a, b], прой-
пройденному движущейся со скоростью f(x) материальной точкой за?
промежуток времени от х = а до х — Ь.
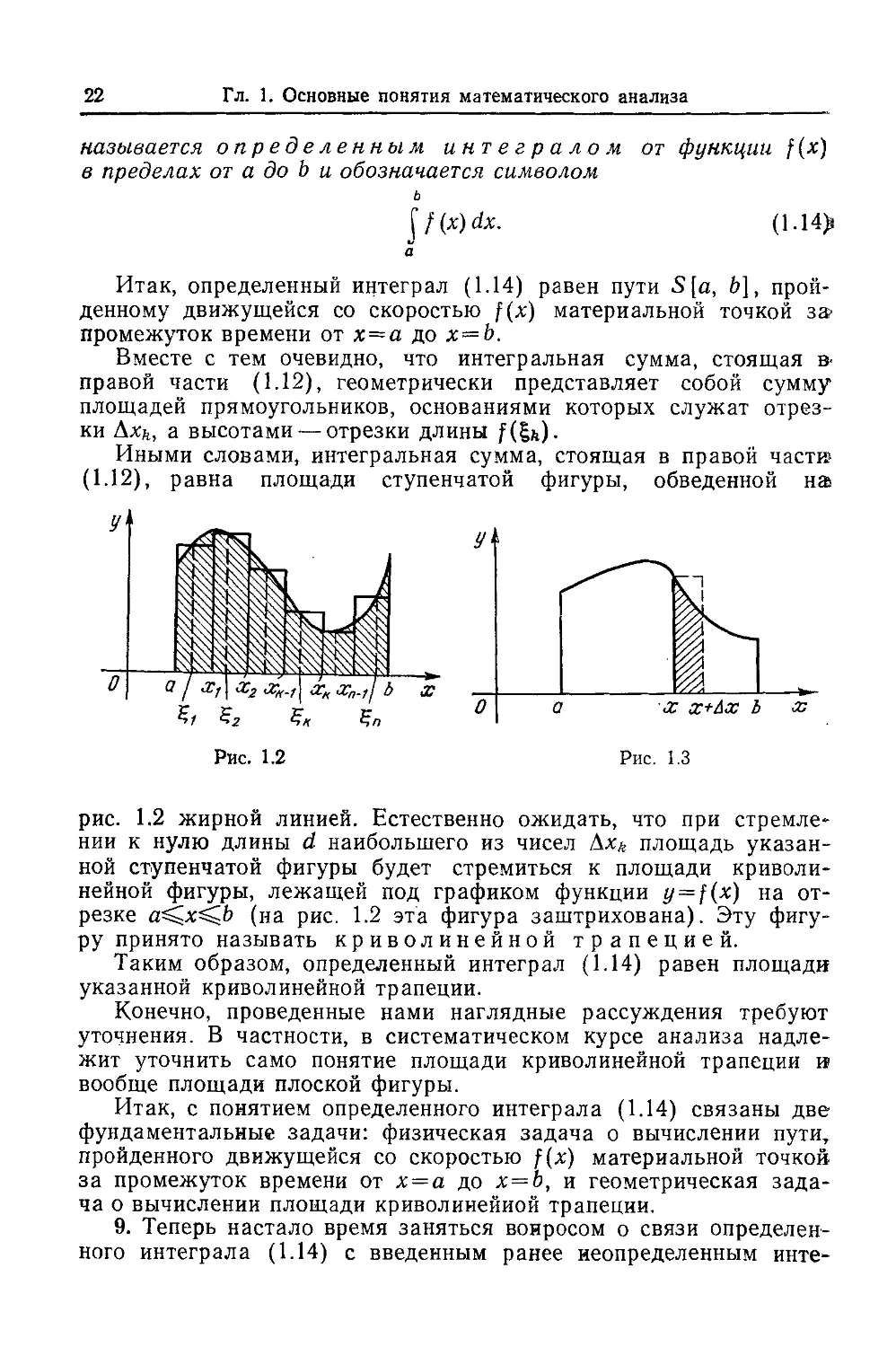
Вместе с тем очевидно, что интегральная сумма, стоящая в-
правой части A.12), геометрически представляет собой сумму
площадей прямоугольников, основаниями которых служат отрез-
отрезки Axjj, а высотами — отрезки длины f(ih).
Иными словами, интегральная сумма, стоящая в правой част»
A.12), равна площади ступенчатой фигуры, обведенной на
У'
О
0
И
П
• х+Дх 1
ее
Рис. 1.2
Рис. 1.3
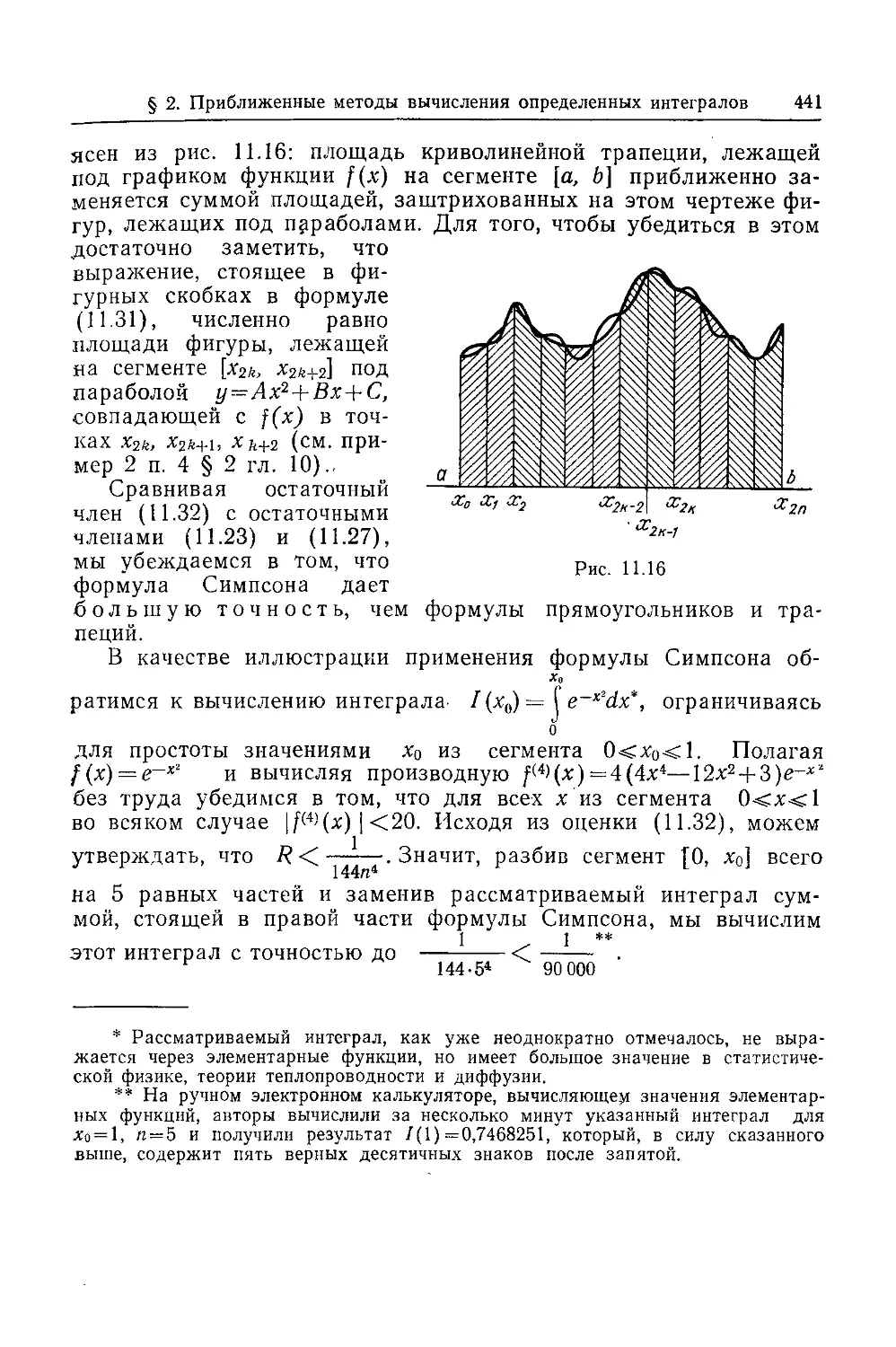
рис. 1.2 жирной линией. Естественно ожидать, что при стремле-
стремлении к нулю длины d наибольшего из чисел Axk площадь указан-
указанной ступенчатой фигуры будет стремиться к площади криволи-
криволинейной фигуры, лежащей под графиком функции y = f(x) на от-
отрезке а^х^Ь (на рис. 1.2 эта фигура заштрихована). Эту фигу-
фигуру принято называть криволинейной трапецией.
Таким образом, определенный интеграл A.14) равен площади
указанной криволинейной трапеции.
Конечно, проведенные нами наглядные рассуждения требуют
уточнения. В частности, в систематическом курсе анализа надле-
надлежит уточнить само понятие площади криволинейной трапеции и
вообще площади плоской фигуры.
Итак, с понятием определенного интеграла A.14) связаны две
фундаментальные задачи: физическая задача о вычислении пути,
пройденного движущейся со скоростью f(x) материальной точкой
за промежуток времени от х = а до х=Ь, и геометрическая зада-
задача о вычислении площади криволинейной трапеции.
9. Теперь настало время заняться вонросом о связи определен-
определенного интеграла A.14) с введенным ранее неопределенным инте-
23
гралом (или с первообразной), а также вопросом о способах вы-
вычисления определенного интеграла.
Обозначим через F(x) определенный интеграл от функции f{x)
в пределах от а до х, где а — некоторое фиксированное значение
аргумента, а х — переменное значение. Иными словами, поло-
F(x)= f f{t)dt. A.Д5)
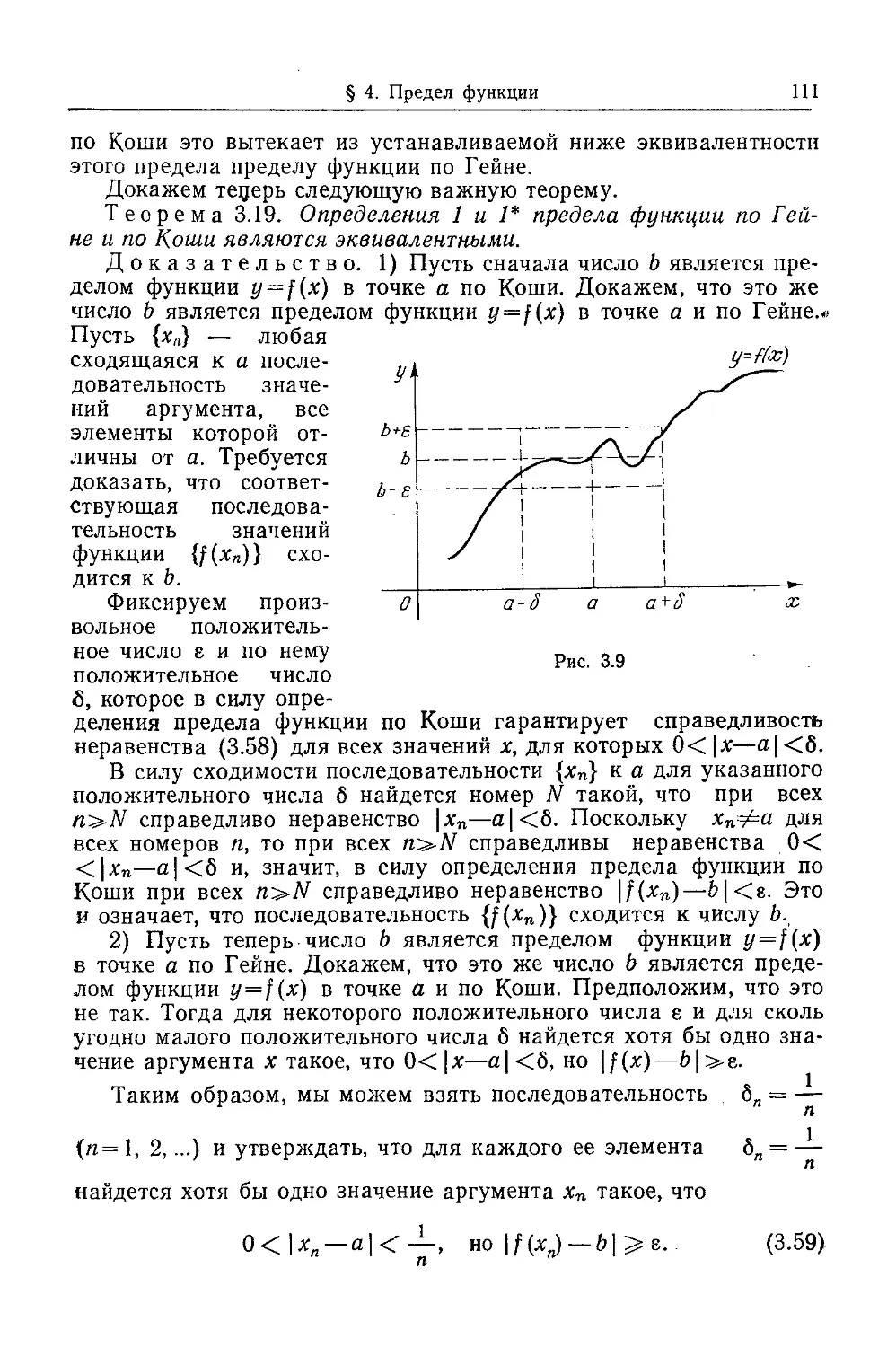
С геометрической точки зрения этот интеграл, как это пока-
показывает проведенное выше рассмотрение, равен площади криволи-
криволинейной трапеции, лежащей под графиком функции y = f(x) на
сегменте [а, х]. На рис. 1.3 эта криволинейная трапеция обве-
обведена жирной линией.
Используя наглядные геометрические соображения, убедимся
в том, что введенная нами функция A.15) является одной из
первообразных функции f(x), т. е. убедимся в том, что F'(x) =
= f(x).
Пусть Ал; — некоторое достаточно малое приращение аргумен-
аргумента х. Очевидно, разность F{x-\-Ax)—F(x) представляет собой
площадь «узкой» криволинейной трапеции, заштрихованной на
рис. 1.3. С другой стороны, если функция f(x) непрерывна в
каждой точке х, т. е. если значение этой функции при малом из-
изменении аргумента меняется мало, то указанная площадь «узкой»
криволинейной трапеции мало отличается от площади f(x) Ax
прямоугольника с основанием Ах и высотой f(x).
Отсюда следует, что при малом Ах разностное отношение
F(x + bx)-F(x) A 16)
Ах
мало отличается от высоты f(x) указанного прямоугольника, т. е.
предел при Ах-+0 разностного отношения A.16) обязан быть ра-
равен f(x). Вместе с тем, по определению, указанный предел ра-
равен производной F'(x).
Итак, мы убедились в том, что F'(x)==f{x), т. е. функция
A.15) является одной из первообразных функции f(x). Но тогда
любая первообразная функции f(x) равна
<D(*) = J/(*)#+С, A.17)
а
где С — постоянная.
Проведенные нами рассуждения имеют предварительный ха-
характер, но при наличии развитого аппарата математического ана-
* Переменную под знаком определенного интеграла мы обозначаем через
t, чтобы не путать ее с верхним пределом интегрирования х.
24 Гл. 1. Основные понятия математического анализа
лиза им легко придать строгий характер и строго доказать, что
у любой функции f(x), только непрерывной в каждой точке х, су-
существует первообразная (а значит, и неопределенный интеграл),
причем любая первообразная этой функции определяется равен-
равенством A.17).
Равенство A.17), в свою очередь, позволяет установить связь
ь
между определенным интегралом \f(x)dx и любой первообраз-
а
ной Ф(х) функции f(x).
Для установления такой связи возьмем в равенстве A.17) в
качестве верхнего предела интегрирования сначала число b, a
затем число а. При этом получим
, A.18)
<D(a)=[f(t)dt + C = C A.19)
(ибо интеграл {f(t)dt, очевидно, равен нулю).
а
Вычитая из равенства A.18) равенство A.19), мы получим,
знаменитую формулу Ньютона — Лейбница
сводящую вопрос о вычислении • определенного интеграла
ъ
Г / (х)Лх к вычислению разности значений любой первообразной
а
Ф(х) функции f(x) в точках Ъ и а.
Строгое обоснование формулы Ньютона — Лейбница является
одной из важных задач математического анализа.
10. Заметим, однако, что точное аналитическое выражение
для первообразной можно получить лишь для узкого класса
функций. Поэтому наличие формулы Ньютона — Лейбница не
снимает вопроса о приближенных способах вычисления опреде-
определенного интеграла.
Простейший способ приближенного вычисления определенного
интеграла (так называемый метод прямоугольников)
ь
основан на замене вычисляемого интеграла \f{x\dx интеграль-
а
ной суммой, стоящей в правой части A.12), у которой все точки
25
5ft являются серединами соответствующих сегментов [ ]
длины всех указанных сегментов, т. е. все числа k
равны друг другу.
В систематическом курсе анализа будет доказано, что при
определенных требованиях на функцию f{x) ошибка, совершае-
ъ
мая при замене интеграла {f(x)dx указанной специальной инте-
а
тральной суммой, имеет порядок п~ъ, где п — число частичных
сегментов.
Замечательным является то обстоятельство, что метод прямо-
прямоугольников (как и многие другие методы приближенного вычис-
вычисления определенного интеграла) допускает удобную реализацию
на ЭВМ. Это обстоятельство и равенство A.17) делают эти ме-
методы эффективным средством вычисления первообразных и не-
неопределенных интегралов.
Ниже мы приводим результат вычисления на ЭВМ по методу
прямоугольников так называемого интеграла Пуассона
i 2 dt
для значения х из сегмента
Результаты вычислений собраны нами в табл. 1, в которой в
первой колонке стоит аргумент х интеграла Пуассона, во второй
колонке указана длина h частичного сегмента (или шага), в
третьей колонке приведен результат вычисления, а в четвертой
колонке указано число п частичных сегментов *.
Таким образом, для интеграла Пуассона, не являющегося, как
указано выше, элементарной функцией, с помощью ЭВМ и про-
простейших приближенных методов без труда могут быть составле-
составлены таблицы его значений, делающие использование этого инте-
интеграла столь же доступным, как и использование любой элемен-
элементарной функции.
11. Наряду с приближенными методами вычисления интегра-
интегралов важную роль в современной математике играют приближен-
приближенные методы отыскания корней различных уравнений.
Рассмотрим простейшее уравнение
/(*)=0. A.20)
В систематическом курсе анализа будет доказано, что при опре-
* При этом следует учитывать ошибки округления, возникающие при пере-
переводе чисел, взятых в десятичной системе счисления, в двоичную систему ЭВМ
и обратном переводе чисел, полученных в двоичной системе счисления, в деся-
десятичную. Вследствие указанных ошибок округления из десяти выписанных после
запятой десятичных знаков можно гарантировать правильность первых шести
знаков (остальные четыре знака в табл. 1 взяты в скобки).
26
Гл. 1. Основные понятия математического анализа
Таблица 1
X
0,0999999642
0,1999999285
0,2999998927
0,3999998569
0,4999998212
0,5999997854
0,6999997497
0,7999997139
0,8999996781
0,9999996424
0,0999999642
0,1999999285
0,2999998927
0,3999998569
0,4999998212
0,5999997854
0,6999997497
0,7999997139
0,8999996781
0,9999996424
А
0,0099999964
0,0099999964
0,0099999964
0,0099999964.
0,0099999964
0,0099999964
0,0099999964
0,0099999964
0,0099999964
0,0099999964
0,0009999996
0,0009999996
0,0009999996
0,0009999996
0,0009999996
0,0009999996
0,0009999996
0,0009999996
0,0009999996
0,0009999996
F[x)
0,039827 (9885)
0,079260 @074)
0,117911 (8581)
0,155422 C028)
0,191463 A319)
0,225747 F439)
0,258037 A805)
0,288145 D843)
0,315940 G870)
0,341345 F679)
0,039827 (8248)
0,079259 F848)
0,117911 C861)
0,155421 F952)
0,191462 D058)
0,225746 (8192)
0,258036 B789)
0,288144 E284)
0,315939 G992)
0,341344 F698)
п
10
20
30
40
50
60
70
80'
90
100
100
20О
300
400
500
600
700
800
900
1000
деленных требованиях, налагаемых на функцию f{x), корень х—
= с уравнения A.20) может быть найден как предел последова-
последовательности итераций хп («=1, 2, 3,...), первая из которых х\ бе-
берется из некоторого достаточно широкого диапазона, а все по-
последующие шаг за шагом определяются по формуле
/ (хп) /„ 19 4 ^ Л 211
Г (хп)
Указанный метод приближенного вычисления корня уравнения
A.20) называется методом Ньютона (или методом ка-
касательных). Этот метод допускает очень удобную реализа-
реализацию на ЭВМ.
В качестве конкретного примера рассмотрим уравнение A.20)
с функцией f(x) вида f(x)=xk — а, где а — положительное веще-
вещественное число, а 1С^2 — целое положительное число. Для такой,
функции f(x) положительным корнем уравнения A.20) будет яв-
являться число Уга (т. е. корень степени k из положительного ве-
вещественного числа а).
Формула A.21), определяющая последовательные приближе-
приближения метода Ньютона, на этот раз принимает вид
— 1 9 ч 1 Л 221
kx
.ft—1
(Чтобы убедиться в этом, достаточно учесть, что f'(x)=kxk~l.)
27
Формула A.22) представляет собой эффективный легко реали-
реализуемый на ЭВМ алгоритм вычисления корня степени k из поло-
положительного числа а.
Приведем пример вычислений, проведенных на ЭВМ по этой
формуле.
Всякое положительное вещественное число а представимо
(и притом единственным способом) в виде а = 21х, где / — целое
число, а х удовлетворяет неравенствам 1/2^х<1. Будем каждой
раз выбирать за первое приближение х\ число %\ = 2Wh\ где k —
степень извлекаемого корня, а символ [l/k] обозначает целую
часть числа l/k.
Результаты вычислений собраны нами в приводимую ниже
табл. 2, в которой в первой колонке стоят числа а, из которых из-
извлекается корень, во второй колонке указаны степени k извле-
извлекаемых корней, в третьей колонке приведен результат вычисле-
вычислений, а в четвертой колонке указано число сделанных итераций.
Таблица 2
а
2
3
4
2
3
4
2
3
4
k
2
2
2
5
5
5
10
10
10
к г —
У "
1,41423181
1,732049942
1,999999046
1,148697853
1,245730400
1,319507599
1,071773529
1,116123199
1,148697853
п
4
5
5
5
5
6
5
6
6
12. Мы рассмотрели постановку важнейших задач математи-
математического анализа, отправляясь от простейшей механической моде-
модели— движения материальной точки вдоль прямой линии. Такая
модель естественно привела нас к необходимости построения диф-
дифференциального и интегрального исчисления функции f(x) од-
одной независимой переменной.
При описании более сложных задач естествознания возникает
понятие функции нескольких независимых переменных Х[,
Х2,—,хт. Так, например, температура и нагреваемого тела пред-
представляет собой функцию четырех независимых переменных: трех
координат xi, X2, хз точки этого тела и времени t. Эту функцию
естественно обозначить символом u = f(x\, x2, #з, t) ¦
Для функции нескольких независимых переменных естествен-
естественно ввести понятие производной по каждой из переменных (такую
производную называют частной производной по данной
переменной).
28 Гл. 1. Основные понятия математического анализа
Важной задачей для последующего развития математического
анализа является построение дифференциального и интегрально-
интегрального исчислений функций нескольких переменных.
Наконец, математический анализ, понимаемый в совсем ши-
широком смысле, включает в себя теорию так называемых диффе-
дифференциальных уравнений (т. е. уравнений, содержащих искомые
функции под знаками производных).
В последние десятилетия широкое развитие получили теории,
исходящие из обобщенной трактовки самого понятия функции,
понятия производной и понятия решения дифференциального
уравнения, связывающего производные функции.
Создание математического анализа является одним из вели-
величайших достижений человеческого разума. Оно позволило от рас-
рассмотрения отдельных разрозненных физических и геометрических
задач (таких, как падение тела под действием силы тяжести, вы-
вычисление площади, лежащей под параболой) перейти к развитию
общих методов решения больших классов задач. Развитие мате-
математического анализа, в свою очередь, оказало огромное влияние
на прогресс науки и техники.
Классический математический анализ представляет собой
очень удобную идеализированную модель, основанную на том, что
мы располагаем точными значениями всех исходных величин и
можем найти точные значения всех вычисляемых величин.
Заметим вместе с тем, что, отправляясь от этой модели, мы,
как правило, можем оценить погрешность, возникающую вслед-
вследствие того, что исходные величины заданы нам с некоторой
ошибкой и все вычисления могут быть проведены лишь с опреде-
определенной точностью.
Таким образом, аппарат математического анализа может быть
использован для построения численных методов и оценки погреш-
погрешностей.
Подводя итог, систематизируем первоочередные и наиболее
важные проблемы, выявившиеся в результате проведенного нами
предварительного рассмотрения.
1. Уточнение понятий вещественного числа, множества и
функции.
2. Развитие теории пределов и связанного с этой теорией по-
понятия непрерывности функции.
3. Построение аппарата дифференциального и интегрального
исчислений.
4. Построение теории определенного интеграла как предела
сумм специального вида.
5. Развитие приближенных методов вычисления определенных
интегралов и приближенных методов решения уравнений.
6. Выяснение некоторых геометрических понятий (таких, как
площадь плоской фигуры, длина дуги).
Глава 2
ВЕЩЕСТВЕННЫЕ ЧИСЛА
В предыдущей главе мы убедились в том, что развитие тео-
теории вещественных * чисел необходимо для строгого и последова-
последовательного изучения понятия предела, являющегося одним из важ-
важнейших понятий математического анализа.
Необходимая нам теория вещественных чисел, излагаемая в
этой главе, включает в себя определение операций упорядочения
сложения и умножения этих чисел и установление основных
свойств указанных операций, а также доказательство существо-
существования точных граней у множеств чисел, ограниченных сверху ил го
снизу.
В конце главы дается представление о дополнительных вопро-
вопросах теории вещественных чисел, не являющихся необходимыми1
для построения теории пределов и вообще курса математического
анализа (полнота множества вещественных чисел в смысле Гиль-
Гильберта, аксиоматическое построение теории вещественных чисел,
связь между различными способами введения вещественных:
чисел).
Самый последний параграф главы посвящен элементарным
вопросам теории множеств, близко примыкающих к теории веще-
вещественных чисел.
§ 1. МНОЖЕСТВО ЧИСЕЛ, ПРЕДСТАВИМЫХ
БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ,
И ЕГО УПОРЯДОЧЕНИЕ
1. Свойства рациональных чисел. Понятие рационального чис-
числа и основные свойства рациональных чисел известны из курса
средней школы. В настоящем пункте мы даем систематизацию*
хорошо известных из курса средней школы вопросов теории ра-
рациональных чисел.
Рациональным называется число, представимое (хотя
бы одним способом) в виде отношения двух целых чисел, т. е.
виде дроби tn/n, где тип — целые числа и 0
* Вместо термина «вещественное число» часто употребляют термин «дей-
«действительное число».
30 Гл. 2. Вещественные числа
Рациональные числа обладают следующими 16 основными
свойствами *. (При формулировке этих свойств мы вместо терми-
термина «рациональное число» употребляем более краткий термин
•«число».)
1°. Любые два числа а и Ь связаны одним и только одним из
трех знаков >, < или =, причем если а>Ь, то &<а. Иными
-словами, существует правило, позволяющее установить, каким из
указанных трех знаков связаны два данных числа. Это правило
называется правилом упорядочения**.
2°. Существует правило, посредством которого любым числам
€i и b ставится в соответствие третье число с, называемое их
суммой и обозначаемое символом с = а+Ь***. Операция на-
нахождения суммы называется сложением.
3°. Существует правило, посредством которого любым числам
а и Ъ ставится в соответствие третье число с, называемое их
произведением и обозначаемое символом с=а•&****. Опе-
Операция нахождения произведения называется умножением.
Правило упорядочения обладает следующим свойством:
4°. Из а>Ь и 6>с вытекает, что а>с (свойство транзитивно-
транзитивности знака >); из а = Ь и Ъ = с вытекает, что а = с (свойство тран-
транзитивности знака =).
Операция сложения обладает следующими четырьмя свойст-
свойствами:
5°. а-\-Ь = Ъ-\-а (коммутативность или перестановочное свой-
свойство) .
6°. (а-\-Ъ)-\-с = а-\-{Ъ-\-с) (ассоциативность или сочетательное
свойство).
7°. Существует число 0 такое, что а+0=а для любого числа а
(особая роль нуля).
8°. Для каждого числа а существует противоположное ему чи-
число а' такое, что а+я' = 0.
Аналогичными четырьмя свойствами обладает операция умно-
умножения :
* Все приводимые нами свойства рациональных чисел могут быть получены
из свойств целых чисел.
** Правило упорядочения рациональных чисел формулируется так: два не-
неотрицательных числа a=ml/nl и Ь=/п2/«2. у которых /ii>0 и Лг>0, связаны
тем же знаком, что и два целых числа т\-п2 и m2-«i; два неположительных
числа а и b связаны тем же знаком, что и два неотрицательных числа |Ь| и
\а\; если а неотрицательно, а Ь отрицательно, то с>6.
*** Правило образования суммы двух рациональных чисел а=т.\\п\ и
m-L /щ m1-n2-\-nh-n1
J> = m2iri2 определяется равенством -\ = , которое
пх п2 щ-щ,
получается с помощью известного приема приведения к общему знаменателю.
**** Правило образования произведения двух рациональных чисел а =
= т-[1п\ и Ь = т2/л2 определяется равенством ¦ = "".
Пх «2 Пх-«2
§ 1. Множество чисел, представимых бесконечными дробями 31
9°. а-Ъ = Ъ-а (коммутативность).
10°. (а-b) -с = а- (Ь-с) (ассоциативность).
11°. Существует число 1 такое, что а-1=а для любого чис-
числа а (особая роль единицы).
12°. Для каждого числа аф& существует обратное ему число-
а' такое, что а-а'=\.
Операции сложения и умножения связаны следующим свой-
свойством:
13°. (a-\-b) -c = a-c-\-b-c (дистрибутивность или распредели-
распределительное свойство умножения относительно суммы).
Следующие два свойства связывают операцию упорядочения
с операцией сложения или соответственно умножения:
14°. Из а>Ь вытекает, что а-\-С>Ь-\-с.
15°. Из а>Ь и с>0 вытекает, что а-с>Ъ-с.
Особая роль принадлежит последнему свойству.
16°. Каково бы ни было число а, можно число 1 повторить
слагаемым столь раз, что сумма превзойдет а *.
Перечисленные 16 свойств называют основными потому,
что все другие алгебраические свойства, относящиеся к опера-
операциям сложения и умножения и к сочетанию равенств и нера-
неравенств, могут быть извлечены как логические следствия из ука-
указанных 16 свойств.
Так, например, из основных свойств вытекает следующее часто
используемое в дальнейшем свойство, позволяющее почленно
складывать неравенства одного знака:
если а>Ъ и c>d, то a-\-c>b-\-d.
В самом деле, из неравенств а>Ь и c>d и из свойств 14° и
5° вытекает, что а-\-с>Ъ-\-с и b-\-c~>b-\-d, а из двух последних
неравенств и свойства 4° вытекает, что a+Ob-f-d
2. Недостаточность рациональных чисел для измерения отрез-
отрезков числовой оси. Договоримся называть числовой осью прямую»
на которой выбраны определенная тонка О (начало отсчета),
масштабный отрезок ОЕ, длину которого мы принимаем равной
единице, и положительное направление (обычно от О к Е). Оче-
Очевидно, каждому рациональному числу соответствует на числовой
оси определенная точка. В самом деле, из курса средней школы
известно, как построить отрезок, длина которого составляет 1/я
часть длины масштабного отрезка ОЕ (п — любое целое положи-
положительное число). Следовательно, мы можем построить и отрезок,
длина которого относится к длине масштабного отрезка как
m/л, где m и п — любые целые положительные числа. Отложив
такой отрезок вправо (влево) от точки О, мы получим точку
М\(М2), соответствующую рациональному числу пг/п (—пг/п)
(рис. 2.1).
* Это свойство часто называют аксиомой Архимеда.
32
Гл. 2. Вещественные числа
Заметим теперь, что не каждой точке М числовой оси соответ-
соответствует рациональное число. Так, например, если точка М выбра-
выбрана так, что длина отрезка ОМ равна диагонали квадрата, сторо-
стороной которого служит масштабный отрезок ОЕ, то поскольку дли-
длина масштабного отрезка ОЕ равна единице, по теореме Пифаго-
Пифагора длина х отрезка ОМ является корнем уравнения х2 = 2 и, как
показано в курсах средней школы, не является рациональным
числом. Но это и означает, что указанной точке М не соответ-
соответствует рациональное число.
0
м2{-%-)
о ' ' ' о ' ¦ о
о
-о 1 I I 1 1 1 > I 1 о
о ' '
и
а,
рм,
Рис. 2.1
Рис. 2.2
Естественно, возникает потребность расширить множество ра-
рациональных чисел и ввести в рассмотрение более широкое множе-
множество чисел так, чтобы каждой точке числовой оси соответствовало
некоторое число из этого более широкого множества (или, что
то же самое, чтобы с помощью этого более широкого множества
чисел можно было выразить длину любого отрезка ОМ числовой
оси).
Убедимся в том, что посредством измерения отрезка ОМ каж-
каждой точке М числовой оси можно поставить в соответствие впол-
вполне определенную бесконечную десятичную дробь.
Пусть М — любая точка числовой оси. Ради определенности
'Предположим, что точка М лежит направо от О. Проведем про-
¦цесс измерения отрезка ОМ при помощи масштабного отрез-
отрезка ОЕ.
Сначала выясним, сколько раз целый масштабный отрезок
уложится в отрезке ОМ*. Могут представиться два случая:
1) Отрезок ОЕ укладывается в отрезке ОМ целое число а0 раз
•с некоторым остатком NM, меньшим ОЕ (рис. 2.2). В этом слу-
случае целое число ао представляет собой результат измерения по
недостатку с точностью до числа 1.
2) Отрезок ОЕ укладывается в отрезке ОМ целое число а0
раз без остатка. В этом случае процесс измерения можно
считать законченным и целое рациональное число ао считать дли-
длиной отрезка ОМ. Формально мы можем утверждать, что в этом
•случае точке М соответствует бесконечная десятичная дробь
.ао.ООО..., которая отождествляется с целым рациональным чис-
числом ао-
* В силу аксиомы Архимеда для отрезка, каковы бы ни были два отрезка
АВ и CD, повторив один из этих отрезков слагаемым достаточно большое
число раз, мы получим отрезок, длина которого превосходит длину второго
«отрезка.
§ 1. Множество чисел, представимых бесконечными дробями 33
В первом случае процесс измерения следует продолжить и вы-
выяснить, сколько раз 1/10 часть масштабного отрезка ОЕ уклады-
укладывается в отрезке NM (являющемся остатком измерения с по-
помощью целого отрезка ОЕ). Снова могут представиться два
случая:
1) 1/10 часть ОЕ укладывается в отрезке NM а\ раз с некото-
некоторым остатком РМ, меньшим 1/10 части ОЕ (см. рис. 2.2). В этой
случае рациональное число ао, а\ представляет собой результат
измерения ОМ по недостатку с точностью до числа 1/10.
2) 1/10 часть ОЕ укладывается в отрезке NM целое число а,\
раз без остатка. В этом случае процесс измерения можно
считать законченным и рациональное число ао, а\ считать длиной
отрезка ОМ. Формально мы можем утверждать, что в этом слу-
случае точке М соответствует бесконечная десятичная дробь
ao,aiOOO..., отождествляемая с рациональным число ао.сц.
Продолжая указанные рассуждения далее, мы придем к двум
возможностям:
1) либо описанный процесс измерения оборвется на га-м шаге
вследствие того, что точке М соответствует рациональное число
ao,aia2.-.an (в этом случае точке М соответствует бесконечная
десятичная дробь ao,aiu2... ап000..., которую мы отождествляем с
рациональным числом ao,aia2 ... ап);
2) либо описанный процесс измерения никогда не оборвется и
мы получим бесконечную последовательность рациональных чисел
а0; ao,'ai; ...; ao,aia2...an; ..., B.1)
представляющих собой результат измерения по недостатку отрез-
отрезка ОМ с точностью до 1, , ... , ——, ....
Каждое из чисел последовательности B.1) может быть полу-
получено обрыванием на соответствующем знаке бесконечной десятич-
десятичной дроби
ао, а\а2...ап.... B.2)
Таким образом, в случае 2) точке М числовой оси отвечает
вполне определенная бесконечная десятичная дробь B.2). Можно
сказать, что и в случае 1) точке М отвечает бесконечная десятич-
десятичная дробь B.2), но в этом случае у этой дроби все- десятичные
знаки с номером, большим п, равны нулю, т. е. указанная дробь
в случае 1) имеет вид а0, а\а%... а„000 ....
Приведенные нами рассуждения применимы и для случая, ко-
когда точка М лежит левее точки О, только в этом случае естест-
естественно считать, что все элементы последовательности B.1) и бес-
бесконечная дробь имеют отрицательный знак.
Итак, мы убедились, что описанный нами процесс измерения
позволяет поставить в соответствие каждой точке М числовой оси
вполне определенную бесконечную десятичную дробь. Это об-
2 Зак. 72
34 Гл. 2. Вещественные числа
стоятельство естественно приводит нас к необходимости рассмот-
рассмотрения чисел, представимых бесконечными десятичными дробями.
Замечание. Конечно, описанный нами процесс измерения
отрезка ОМ можно видоизменить так, что он будет приводить к
рассмотрению не бесконечных десятичных, а, например, бесконеч-
бесконечных двоичных или бесконечных троичных дробей. Жела-
Желание рассматривать бесконечные десятичные дроби вызвано лишь
той особой ролью, которую традиционно играет десятичная систе-
система счисления. Развитие электронной вычислительной техники по-
повысило роль двоичной и троичной систем счисления, ибо (в"силу
конструктивных особенностей ЭВМ) эти системы счисления более
удобны в практике использования ЭВМ.
3. Упорядочение множества бесконечных десятичных дробей.
Во вводной главе мы уже отмечали, что понятие числа относится
к так называемым начальным понятиям (т. е. к понятиям,
которые могут быть разъяснены, но не могут быть строго опре-
определены, ибо всякая попытка дать строгое определение такого по-
понятия неизбежно сведется к замене определяемого понятия ему
эквивалентным). Мы введем понятие вещественных чисел, отправ-
отправляясь от множества бесконечных десятичных дробей.
Рассмотрим множество всевозможных бесконечных десятичных
дробей (как положительных, т. е. взятых со знаком +, так и от-
отрицательных, т. е. взятых со знаком —).
Мы будем придерживаться следующего плана.
Для множества всех чисел, представимых бесконечными деся-
десятичными дробями, мы введем операцию упорядочения. После это-
этого мы убедимся, что для введенной нами операции упорядочения
остается справедливым то же самое свойство 4°, которое сформу-
сформулировано в п. 1 для рациональных чисел (т. е. свойство транзи-
транзитивности знаков > и =).
Наличие только одного этого свойства позволит нам доказать
замечательную теорему о том, что у множества чисел, представи-
представимых бесконечными десятичными дробями и ограниченных сверху
(или соответственно снизу), существует число, представимое бес-
бесконечной десятичной дробью и являющееся точной верхней (или
соответственно точной нижней) гранью указанного множества
чисел.
После этого вводятся операции сложения и умножения чисел,
представимых бесконечными десятичными дробями. Это дает нам
возможность ввести вещественные числа как такие числа, которые
представимы бесконечными десятичными дробями и для которых
указанным нами способом определены операции упорядочения,
сложения и умножения. Доказанная нами теорема о существова-
существовании точных граней позволит доказать существование суммы и
произведения двух любых вещественных чисел, а также справед-
справедливость для этих чисел тех же самых 16 основных свойств, кото-
которые сформулированы в п. 1 для рациональных чисел.
§ 1. Множество чисел, представимых бесконечными дробями 35
Приступим к реализации указанного плана.
В этом пункте мы введем для чисел, представимых бесконеч-
бесконечными десятичными дробями, операцию упорядочения и установим,
что эта операция обладает свойством 4°, сформулированном в
п. 1 для рациональных чисел (т. е. свойством транзитивности зна-
знаков > и =).
Рассмотрим произвольное число, представимое бесконечной
десятичной дробью, отличной от 0,000.... Это число мы будем на-
называть положительным, если оно представимо бесконечной
десятичной дробью, взятой со знаком +, и отрицательным,
¦если оно представимо бесконечной десятичной дробью, взятой со
знаком —.
Числа, не являющиеся положительными, мы будем называть
неположительными, а числа, не являющиеся отрицательны-
отрицательными,— неотрицательными.
Сразу же отметим, что все рациональные числа относятся к
множеству чисел, представимых бесконечными десятичными дро-
дробями. Представление данного рационального числа бесконечной
десятичной дробью можно получить двумя способами:
1) взяв точку М, отвечающую данному рациональному числу
на числовой оси, и произведя измерение отрезка ОМ с помощью
масштабного отрезка способом, указанным в п. 2;
2) взяв обыкновенную дробь mfn, представляющую данное ра-
рациональное число, и поделив числитель пг на знаменатель п
«столбиком» *.
Мы представляем читателю убедиться в том, что оба эти спо-
способа эквивалентны друг другу. Так, при любом из указанных
способов рациональному числу 1/2 ставится в соответствие бес-
бесконечная десятичная дробь 0,5000..., рациональному числу 4/3 —
¦бесконечная десятичная дробь 1,333....
Прежде чем перейти к формулировке правила упорядочения
чисел, представимых бесконечными десятичными дробями, рас-
рассмотрим вопрос о представлении в виде бесконечных десятичных
дробей тех рациональных чисел, которые представимы в виде ко-
конечной десятичной дроби.
Заметим, что такие рациональные числа допускают два
представления в виде бесконечных десятичных дробей. На-
Например, рациональное число 1/2 = 0,5 можно представить в виде
двух бесконечных десятичных дробей:
1) 1/2 = 0,5000..., 2) 1/2 = 0,4999....
Вообще, рациональное число а = ао,а\аг...ап, где ап?=0, мож-
можно записать в виде двух бесконечных десятичных дробей:
1) а = а0,aia2...an000..., 2) а = а0, aia2... an-i(an —1)999....
* В курсе средней школы доказывается, что при таком делении получается
обязательно периодическая бесконечная десятичная дробь.
2*
36 Гл. 2. Вещественные числа
Естественно, мы должны отождествить указанные две беско-
бесконечные десятичные дроби (т. е. считать, что они представляют
одно и то же вещественное число).
Рассмотрим теперь два произвольных вещественных числа а
и Ъ и предположим, что эти числа представляются бесконечными
десятичными дробями
... а„ ..., b = ±bQ, Ьф2 ... Ьп ..., B.3)
где из двух знаков + и — в каждом представлении берется ка-
какой-то один.
Исключим уже рассмотренный выше случай, когда обе беско-
бесконечные десятичные дроби в B.3) имеют одинаковые знаки и слу-
служат двумя различными представлениями одного и того же рацио-
рационального числа, представимого конечной десятичной дробью. По-
После исключения этого случая договоримся называть два числа а
и Ь равными, если их представления в виде бесконечных десятич-
десятичных дробей B.3) имеют одинаковые знаки и если справедлива
бесконечная цепочка равенств
ao = bo, a1 = bu a2 = b2,...,an = bn,.... B.4)
Итак, мы называем два числа а и b равными, если их
представления в виде бесконечных десятичных дробей B.3) имеют
одинаковые знаки и если либо справедлива цепочка равенств
B.4), либо бесконечные десятичные дроби в B.3) служат двумя
представлениями одного и того же рационального числа, предста-
представимого конечной десятичной дробью.
Пусть даны два неравных числа а и Ь, представимых беско-
бесконечными десятичными дробями. Установим правило, позволяю-
позволяющее заключить, каким из двух знаков, > или <, связаны эти
числа.
Договоримся называть модулем числа а, представимого
бесконечной десятичной дробью, число, представимое той же са-
самой бесконечной десятичной дробью, что и число а, но всегда взя-
взятой со знаком +•
Модуль числа а будем обозначать символом \а\. Число \а\
всегда является неотрицательным.
Рассмотрим отдельно три возможных случая: 1) случай, когда
а и b оба неотрицательны; 2) случай, когда оба числа а и b от-
отрицательны; 3) случай, когда одно из чисел а и Ъ неотрицательно,
а другое отрицательно.
1) Пусть сначала аи 6 оба неотрицательны и имеют
представления а = а0,a\a2...; b = bo,blb2.... Так как числа а и b не
являются равными, то нарушается хотя бы одно из равенств B.4).
Обозначим через & наименьший из номеров я, для которого
нарушается равенство ап = Ьп, т. е. предположим, что
§ 1. Множество чисел, представимых бесконечными дробями 37
Тогда мы будем считать, что а>Ь, если ah>bh, и будем счи-
считать, что а<Ь, если ak<bh.
2) Пусть теперь оба числа а и Ъ отрицательны. Тогда
мы будем считать, что а>Ь, если |Ь|>|а|, и а<Ь, если \Ь\<
<|а|*.
3) Пусть, наконец, одно число (например, а) неотрицательно,
а другое число (Ь) отрицательно. Тогда, естественно, мы будем
считать, что а>Ь.
Итак, мы полностью сформулировали правило упорядо-
упорядочения чисел, представимых бесконечными десятичными дро-
дробями.
Чтобы сделать, сформулированное правило безупречным с ло-
логической точки зрения (или, как говорят в математике, коррект-
корректным), докажем следующую лемму.
Лемма. Если а = а0, а\п2 ¦¦¦.ап ...— произвольное неотрица-
неотрицательное число, a b/ = b0,bib2....bn^ibn000... и b" = bo,bib2...
...bn-i(bn—1)999... при Ь«>0 — два различных представления
одного и того же рационального числа bo,b\b2...bn, то условие
а<Ь' эквивалентно условию а<Ь", а условие а>Ь' эквивалентно
условию а>Ь".
Эта лемма позволяет при упорядочении двух неравных чисел
не заботиться о том, какое из двух возможных представлений в
виде бесконечной десятичной дроби взято для числа, представи-
мого конечной десятичной дробью.
Доказательство. Для полного доказательства леммы сле-
следует доказать четыре утверждения: 1) из а<У вытекает а<Ъ"\
2) из а<Ь" вытекает а<Ь'; 3) из а>Ь' вытекает а>Ь"; 4) из
а~>Ь" вытекает а>Ь'.
Мы ограничимся доказательством утверждений 1) и 2), ибо
утверждения 3) и 4) доказываются аналогично.
Пусть а<.Ь'. Тогда по правилу упорядочения найдется номер
k такой, что
ao = bo, ai = 6i,..., afc_i = bft_i, ah<bh B.5)
(в этих соотношениях следует считать все bn+\, bn+2,... равными
нулю).
Сразу же заметим, что ?</г, ибо при k>n неравенство ak<bk
не может выполняться, так как 0^а^<9, a bh = Q.
Если при этом &</г, то, поскольку при k<.n все десятичные
знаки до порядка k у Ь' и Ь" совпадают, условия а<Ь' и а<Ь",
очевидно, эквивалентны.
Остается рассмотреть случай k = n. В этом случае соотношения
B.5) принимают вид ao = bo, a\ — bu..., a-n_i = 6n_i, an<bn- Самое
последнее неравенство эквивалентно неравенству ап^Ьп—1.
Если при этом ап<.Ьп—1, то по правилу упорядочения а<Ь".
* При этом мы учитываем, что для неотрицательных а и Ь прави-
правило упорядочения уже определено (см. случай 1)).
38 Гл. 2. Вещественные числа
Если же в указанном последнем неравенстве а„ = Ьп—1, то
все десятичные знаки у чисел а и Ь" до порядка п совпадают.
Поскольку у числа Ъ" все десятичные знаки порядка, большего п,
равны девяти, то и в этом случае а<о", ибо у числа а все деся-
десятичные знаки порядка, большего п, не могут быть равны девяти
(в силу того, что а не равно о').
Итак, утверждение 1) доказано.
Перейдем к доказательству утверждения 2). Предположим,
что а<Ь". Договоримся о следующих обозначениях бесконечных
десятичных дробей, представляющих числа о' и Ь".
и/ U г и 'U I U ' h" U " U "U " h I"
0 = 0О ,01 02 ... 0П ..., О — 00 , О\ 02 ... 0„ ... .
В этих представлениях
Ь0' = Ь0" = Ь0, Ь1'=Ь1" = Ьи...,Ь'п-1 = Ь"п-1 =^-1, &„' = &., bn" = bn—1.
Иными словами, справедлива цепочка соотношений
С другой стороны, поскольку а<Ь", найдется номер k такой,
что справедлива цепочка соотношений
ао = Ьо", а\ = Ьх",..., ah-i = b"h-i, ah<bk"-
Обозначим через т. наименьший из двух номеров п и k
и сопоставим между собой две последние цепочки соотношений.
Используя свойства транзитивности знаков > и = для целых чи-
чисел, мы получим при этом следующую цепочку соотношений:
ао=Ь0', а.\ = Ъ\',...,ат-\ = Ь'т-\, ат<Ъ'т.
Полученные соотношения на основании правила упорядочения
вещественных чисел устанавливают справедливость неравенства
а<Ь'. Тем самым утверждение 2) также доказано.
Еще раз подчеркнем, что доказанная лемма позволяет при
упорядочении двух чисел, представимых бесконечными десятич-
десятичными дробями, пользоваться любым из двух представлений в
виде бесконечной десятичной дроби для рациональных чисел,
представимых конечной десятичной дробью.
Легко убедиться в том, что сформулированное правило упо-
упорядочения в применении к двум рациональным числам, пред-
представленным в виде бесконечных десятичных дробей, приводит
к тому же результату, что и прежнее правило упорядочения
рациональных чисел, представленных в виде отношения двух
целых чисел.
В самом деле, достаточно рассмотреть случай двух неот-
неотрицательных рациональных чисел а и о. Пусть а~>Ъ со-
согласно прежнему правилу упорядочения рациональных чисел,
и пусть а — ао,а\а2.--ап...; b = b0, b\b2... 0ft .... Отложив рацио-
рациональные числа а и Ъ на числовой оси, мы получим отвечающие
§ 1. Множество чисел, представимых бесконечными дробями 39
им точки Mi и М2, причем, поскольку а>Ь, отрезок ОМ\ боль-
больше отрезка ОМ2. Из описанного в п. 2 процесса измерения от-
отрезка числовой оси вытекает, что целое число а^ахйч... а-и пока-
показывает, сколько раз 10~ft часть масштабного отрезка ОЕ укла-
укладывается в отрезке ОМ\, а целое число babib2...bn показывает,
сколько раз 10~ft часть ОЕ укладывается в отрезке ОМ2. По-
Поскольку отрезок ОМ\ больше отрезка ОМ2, то найдется номер
k такой, что aoai ...a,k-\ — bobi ...bh-i, a аой\ ...au>bobi... bh, но
это и означает, что а>Ь согласно правилу упорядочения чи-
чисел, представимых бесконечными десятичными дробями.
Докажем теперь, что для сформулированного нами правила
упорядочения чисел, представимых бесконечными десятичными
дробями, остается справедливым свойство 4°, приведенное в п. 1
для рациональных чисел, т. е. докажем, что для любых трех чи-
чисел a, b и с, представимых бесконечными десятичными дробями,
из справедливости неравенств а>Ь и Ь>с вытекает справедли-
справедливость неравенства а>с (свойство транзитивности знака >), а из
справедливости равенств а = Ь и Ь = с вытекает справедливость
равенства а —с (свойство транзитивности знака =).
Свойство транзитивности знака = сразу же вытекает из спра-
справедливости соответствующего свойства для целых чисел.
Докажем свойство транзитивности знака >. Пусть a>b, b>c.
Требуется доказать, что а>с.
Рассмотрим три возможных случая: 1) с неотрицательно; 2) с
отрицательно, а неотрицательно; 3) с отрицательно и а отрица-
отрицательно.
1) Пусть сначала с неотрицательно. Тогда b также неотрица-
неотрицательно, ибо если бы b было отрицательно, то в силу правила упо-
упорядочения мы получили бы, что с>Ь, и это противоречило бы ус-
условию &>с. Далее, повторяя те же рассуждения, мы получим,
что и а неотрицательно (ибо в противном случае мы получили
бы, что b>a, и это противоречило бы условию а>Ь).
Итак, в рассматриваемом случае все три числа а, Ь и с неот-
неотрицательны. Записав представления этих чисел бесконечными де-
десятичными дробями
а = ао, а\а2...; b = bG,bibi..:, c=co,C\c2..., мы получим, что в силу
условия а>Ь найдется номер k такой, что
B.6)
Аналогично в силу условия Ь>с найдется номер р такой, что
&о = со, bi = ci,..., bp_i = Cp_i, bp>cp. B.7)
Обозначим через пг наименьший из двух номеров k и р. Тогда,
очевидно, из соотношений B.6) и B.7) и из справедливости
свойства транзитивности знаков > и = для целых чисел выте-
вытекает, что Оо=с0, ai = ci, ..., am_i = cm_i, am>cm, а это и означает (по
правилу упорядочения), что а>с.
40 Гл. 2. Вещественные числа
2) Пусть теперь с отрицательно, а неотрицательно. Тогда (не-
(независимое от знака числа Ь) неравенство а>с справедливо в
силу правила упорядочения.
3) Рассмотрим, наконец, случай, когда оба числа а и с отри-
отрицательны. Заметим, что в этом случае и Ь отрицательно (ибо в
противном случае мы получили бы из правила упорядочения, что
Ь>а, и это противоречило бы условию а>Ь).
Итак, в рассматриваемом случае все три числа а, Ь и с отри-
отрицательны. Но в таком случае (в силу правила упорядочения) не-
неравенства a>b, b>c эквивалентны неравенствам |Ь|>|а| и
|с|>|Ь|. Hi последних двух неравенств (в силу свойства тран-
транзитивности знака >, уже доказанного нами в случае 1) для не-
неотрицательных чисел) вытекает, что |с|>|а|, а это и означает
(в силу правила упорядочения отрицательных чисел а и с), что
а>с. Тем самым доказательство свойства транзитивности знака
> полностью завершено.
§ 2. ОГРАНИЧЕННЫЕ СВЕРХУ (ИЛИ СНИЗУ)
МНОЖЕСТВА ЧИСЕЛ, ПРЕДСТАВИМЫХ
БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ
1. Основные понятия. Рассмотрим совершенно произвольное
множество {х} чисел, представимых бесконечными десятичными
дробями.
Отдельные числа, входящие в состав множества {х}, мы будем
называть элементами этого множества.
Всюду в этом параграфе мы будем требовать, чтобы рассмат-
рассматриваемое множество {л:} содержало хотя бы один элемент (такое
множество принято называть непустым).
Введем важное понятие ограниченности множества сверху
(или соответственно снизу).
Определение 1. Множество {х} чисел, представимых беско-
бесконечными десятичными дробями, называется ограниченным
сверху' (соответственно ограниченным с низ у), если су-
существует такое представимое бесконечной десятичной дробью чи-
число М (соответственно такое представимое бесконечной десятич-
десятичной дробью число ш), что каждый элемент х множества {х} удов-
удовлетворяет неравенству
х^-М (соответственно x^tri). B.8)
При этом число М (число гп) называется верхней гранью
(нижней гранью) множества {х}.
Конечно, любое ограниченное сверху множество {х} имеет бес-
бесконечно много верхних граней. В самом деле, если число М — од-
одна из верхних граней множества {х}, то любое число М', большее
числа М, также является верхней гранью множества {х} (ибо из
§ 2. Ограниченные множества 4!
справедливости неравенства B.8) будет следовать, что
Аналогичное замечание можно сделать в отношении нижних гра-
граней ограниченного снизу множества {х}.
Так, например, множество всех представимых бесконечными
десятичными дробями отрицательных чисел ограничено сверху.
В качестве верхней грани М такого множества можно взять лю-
любое неотрицательное число. Множество всех целых положитель-
положительных чисел 1, 2, 3,... ограничено снизу. В качестве нижней грани"
этого множества можно взять любое число т, удовлетворяющее
неравенству m=sCl.
Естественно, возникает вопрос о существовании наименьшей
из верхних граней ограниченного сверху множества и наибольшей
из нижних граней ограниченного снизу множества.
Определение 2. Наименьшая из всех верхних граней
ограниченного сверху множества {х) называется г очной верх-
верхней гранью этого множества и обозначается символом х=
= sup {л:} *.
Наибольшая из всех нижних граней ограниченного снизу мно-
множества {х} называется точной нижней гранью этого мно-
множества и обозначается символом x=inl{x} **.
Определение 2 можно сформулировать н по-другому, а именно:
Число х (число х) называется точной верхней (точной
нижней) гранью ограниченного сверху (снизу) множества {х},
если выполнены следующие два требования: 1) каждый элемент
х множества {х} удовлетворяет неравенству х^х (х^х); 2) како-
каково бы ни было число х', меньшее х (большее х), найдется хотя бы
один элемент х множества {х}, удовлетворяющий неравенству х>
(
В этом определении требование 1) утверждает, что число х
(число х) является одной из верхних (нижних) граней, а требо-
требование 2) говорит о том, что эта грань является наименьшей (наи-
(наибольшей) и уменьшена (увеличена) быть не может.
2. Существование точных граней. Существование у любого
ограниченного сверху (снизу) множества точной верхней (точной
нижней) грани не является очевидным и требует доказательства.
Докажем следующую основную теорему. *
Основная теорема 2.1. Если Множество {х} чисел,
представимых бесконечными десятичными дробями, ограничено
сверху (соответственно снизу) и содержит хотя бы один элемент,
то у этого множества существует точная верхняя (соответственно
точная нижняя) грань.
* sup — первые три буквы латинского слова supremum («супремум»),
которое переводится как «наивысшее».
** inf — первые три буквы латинского слова infimum («инфимум»), кото-
которое переводится как «наинизшее».
42 Гл. 2. Вещественные числа
Доказательство. Мы остановимся лишь на доказатель-
доказательстве существования точной верхней грани у любого ограниченно-
ограниченного сверху множества, ибо существование точной нижней грани у
любого ограниченного снизу множества доказывается совершенно
аналогично.
Итак, пусть множество {х} ограничено сверху, т. е. существует
такое число М, что каждый элемент х множества {х} удовлетво-
удовлетворяет неравенству х^М.
Могут представиться два случая:
1°. Среди элементов множества {х} есть хотя бы одно не-
неотрицательное число. 2°. Все элементы множества {х} явля-
являются отрицательными числами. Эти случаи мы рассмотрим от-
отдельно.
1°. Рассмотрим лишь неотрицательные числа, входящие в со-
состав множества {х}. Каждое из этих чисел представим в виде бес-
бесконечной десятичной дроби и рассмотрим целые части этих деся-
десятичных дробей. В силу неравенства х^М все целые части не пре-
превосходят числа М, а поэтому найдется наибольшая из целых
частей, которую мы обозначим через х0. Сохраним среди неотри-
неотрицательных чисел множества {х} те, у которых целая часть равна
х0, и отбросим все остальные числа. У сохраненных чисел рассмот-
рассмотрим первые десятичные знаки после запятой. Наибольший из этих
знаков обозначим через х\. Сохраним среди неотрицательных чи-
чисел множества {х} те, у которых целая часть равна х0, а первый
десятичный знак равен х\, и отбросим все остальные числа. У со-
сохраненных чисел рассмотрим вторые десятичные знаки после за-
запятой. Наибольший из этих знаков обозначим через х2. Продол-
Продолжая аналогичные рассуждения далее, мы последовательно опре-
определим десятичные знаки некоторого числа х:
х = х0, хххъ ... хп .... B.б)
Докажем, что это число х и является точной верхней гранью
множества {х}. Для этого достаточно доказать два утвер-
утверждения: 1) каждый элемент х множества {х} удовлетворяет не-
неравенству хк^х; 2) каково бы ни было число х', меньшее х, най-
найдется хотя бы один элемент х множества {х}, удовлетворяющий
неравенству х>х'.
Докажем сначала утверждение 1). Так как х по построению
является неотрицательным числом, то любой отрицательный эле-
элемент х множества {х} заведомо удовлетворяет неравенству х<х.
Поэтому нам достаточно доказать, что любой неотрицатель-
неотрицательный элемент х множества {х} удовлетворяет неравенству x<jc.
Предположим, что некоторый неотрицательный элемент х=
=х0, x\Xi ...Xn ••• не удовлетворяет неравенству х<х. Тогда х>х и
по правилу упорядочения найдется номер k такой, что хо = хо,
xi = хк •¦¦ ,Xk—\—Xk~i, xft >xk. Но последние соотношения про-
§ 2. Ограниченные множества 43
тиворечат тому, что в качестве Xk берется наибольший из
десятичных знаков хн тех элементов х, у которых целая часть и
первые k—1 знаков после запятой соответственно равны хо,х\,...
...,Хк-\.
Полученное противоречие доказывает утверждение 1).
Докажем теперь утверждение 2). Пусть х' — любое число,
удовлетворяющее условию х'<х. Требуется доказать, что сущест-
существует хотя бы один элемент х множества {х}, удовлетворяющий
неравенству х>х'.
Если число х' является отрицательным, то неравенству х>х'
заведомо удовлетворяет неотрицательный элемент х множества
{х} (по предположению хотя бы один такой элемент существует).
Остается рассмотреть случай, когда число х', удовлетворяю-
удовлетворяющее условию х'<х, является неотрицательным. Пусть х'=х0', х/...
...хп'--- Из условия х'<х и из правила упорядочения вытекает,
что найдется номер т такой, что
/о = Хо, х[=Х1г ... , ХА~\ = Хт-и х'т < Хт. B.10)
С другой стороны, из построения числа B.9) вытекает, что для
любого номера т найдется неотрицательный элемент x=xo,xix2...
...хп— множества {х} такой, у которого целая часть и все первые
т знаков после запятой те же, что у числа х. Иными словами,
для номера т найдется элемент х такой, для которого
Xq = Xq, Х1=Х1, ... , Хт—\ = Хт—\, Хт = Хт. (z.ll)
Сопоставляя B.10) и B.11), мы получим, что
Xq — Xq, Xj = Х\, . • • , Хт—1 — Хт—Ь Хт _^> Х/н,
а это и означает (в силу правила упорядочения), что х>х'.
Утверждение 2), а с ним и вся теорема для случая 1° доказаны.
2°. Аналогично доказывается существование точной верхней
грани и во втором случае, когда все элементы х множества {х}
являются отрицательными числами.
В этом случае мы представим все элементы х отрицательными
бесконечными десятичными дробями и обозначим через х0 наи-
наименьшую из целых частей этих дробей, через х\ — наименьший из
первых десятичных знаков тех дробей, целая часть которых рав-
равна xq, через х2 — наименьший из вторых десятичных знаков тех
дробей, целая часть и первый десятичный знак которых соответ-
соответственно равны Xq и х,\ и т. д.
_ Таким образом^ мы определим неположительное число
X = Xq , Xj X2 • • • Хп ....
В полной аналогии со случаем 1° доказывается, что это число
х является точной верхней гранью множества {х}, т. е. доказы-
доказывается справедливость утверждений 1) и 2), сформулированных
при рассмотрении случая 1°. Теорема доказана.
44 Гл. 2. Вещественные числа
§ 3. ПРИБЛИЖЕНИЕ ЧИСЕЛ, ПРЕДСТАВИМЫХ
БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ,
РАЦИОНАЛЬНЫМИ ЧИСЛАМИ
Докажем три леммы о приближении чисел, представимых бес-
бесконечными десятичными дробями, рациональными числами.
Сначала убедимся в том, что произвольное число а, предста-
вимое бесконечной десятичной дробью, можно с наперед задан-
заданной точностью приблизить рациональными числами.
Ради определенности будем считать а неотрицательным и
представим его дробью а=а0, а\а2... ап ¦¦¦.
Обрывая указанную дробь на п-м знаке после запятой, мы
получим рациональное число а0, а\а2...ап, причем из правила упо-
упорядочения чисел, представимых бесконечными десятичными дро-
дробями, сразу же вытекает, что
Увеличив указанное рациональное число на-10~", мы получим
другое рациональное число а0, а\а2...an+10~", которое (в силу
правила упорядочения) обязано удовлетворять неравенству
Итак, для любого номера п мы нашли два рациональных чис-
числа ai = a0, aia2...an и а2=а0, a\a2...an+\Qrn такие, что ai«sa<a2
и a?—«i = 10~n.
Убедимся в том, что для любого наперед взятого положитель-
положительного рационального числа г, начиная с некоторого номера п, спра-
справедливо неравенство 10~п<е.
В самом деле, в силу аксиомы Архимеда найдется лишь конеч-
конечное число натуральных чисел, не превосходящих чисел 1/е. Зна-
Значит, лишь для конечного числа номеров п справедливо неравенст-
неравенство 10"<1/е, или 10~п>е. Для всех остальных номеров п справед-
справедливо противоположное неравенство 10~л<е, что и требовалось
доказать.
Мы приходим к следующему утверждению.
Лемма 1. Для любого пред ставимого бесконечной десятичной
дробью числа а и любого наперед взятого положительного рацио-
рационального числа е найдутся два рациональных числа ai и а2 такие,
что ai<a<a2 и a2—ai<e.
Докажем еще две леммы, характеризующие густоту распреде-
распределения рациональных чисел среди произвольных чисел, представи-
представимых бесконечными десятичными дробями.
Лемма 2. Каковы бы ни были два представимых бесконечны-
бесконечными десятичными дробями числа а и b такие, что а>Ь, найдется
рациональное число а, заключенное между ними, т. е. такое, что
a>a>b (а следовательно, найдется и бесконечное множество раз-
различных рациональных чисел, заключенных между а и Ь).
§ 3. Приближение чисел 45
Доказательство. Достаточно рассмотреть случай, когда
оба числа а и Ь неотрицательны, ибо случай, когда а и b
неположительны, сводится к указанному случаю посредст-
посредством перехода к модулям, а случай, когда Ъ отрицательно, а а по-
положительно, тривиален (в качестве а можно взять нуль).
Итак, пусть а>Ь и оба числа а и Ъ неотрицательны. Предполо-
Предположим, что а = ао, а\п2...ап ...; b = bo, Ьф2 ...Ьп ..., причем в случае,
если а является рациональным числом, представимым конечной
десятичной дробью, договоримся брать представление а десятич-
десятичной дробью, заканчивающейся бесконечным числом девяток.
Так как а>Ь, то найдется номер k такой, что ao = bo, a\ = b\, ...,
ak-i = bk-i, ak>bk.
В силу принятой нами договоренности все десятичные знаки ап
при n>k не могут быть равны нулю.
Обозначим через р наименьший из номеров /г, больших к, для
которых пп'ФО. Тогда число а можно записать в виде
. 0ap... (
С помощью правила упорядочения легко проверить, что рацио-
рациональное число
a = a0, aia2...uft00...0(ap—1)999 ...
удовлетворяет неравенствам а>а>Ь. Лемма доказана.
Лемма 3. Пусть Х\ и х2 — два заданных числа, пред ставимых
бесконечными десятичными дробями.
Пусть далее для любого положительного рационального числа
« найдутся два рациональных числа уг и у2 такие, что
Тогда числа х\ и х2 равны.
Доказательство. Допустим противное, т. е. предположим,
что Х\Ф%2. Не ограничивая общности, будем считать, что х\<х2.
В силу леммы 2 найдутся два рациональных числа си и ссг такие,
что
Пусть теперь yi и 72 — какие угодно рациональные числа,
удовлетворяющие неравенствам Yi<*i<Y2, yi<^'2<'Y2-
Из написанных выше неравенств и свойства транзитивности зна-
знаков > и = получим Yi<ai<a2<Y2- Но тогда Y2—Yi>a2—«ь что
противоречит тому, что разность у2—yi может быть сделана мень-
меньше любого наперед взятого положительного рационального числа
€. Лемма доказана.
4 6 Гл. 2. Вещественные числа
§ 4. ОПЕРАЦИИ СЛОЖЕНИЯ И УМНОЖЕНИЯ.
ОПИСАНИЕ МНОЖЕСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ
1. Определение операций сложения и умножения. Описание по-
понятия вещественных чисел. Хорошо известно, как складывают два
числа, представимых бесконечными десятичными дробями, когда
требуется вычислить их сумму на практике.
Для того чтобы сложить два таких числа а и Ь, заменяют их с
требуемой точностью рациональными числами и за приближенное
значение суммы чисел а и b берут сумму указанных рациональных
чисел. При этом совершенно не заботятся о том, с какой стороны;
(по недостатку или по избытку) взятые рациональные числа при-
приближают а и Ъ.
Фактически указанный практический способ сложения чисел,,
представимых бесконечными десятичными дробями, предполагает,,
что чем точнее рациональные числа аир приближают (с любой;
стороны) числа а и b соответственно, тем точнее сумма а+р при-
приближает то представимое бесконечной десятичной дробью число,.
которое должно являться суммой чисел а и Ь.
Желание оправдать указанный практический способ сложения
естественно приводит к следующему определению.
Определение 1. Суммой двух представимых бесконечны-
бесконечными десятичными дробями чисел а и Ъ называется такое представи-
представимое бесконечной десятичной дробью число х, которое для любых
рациональных чисел <ц, аг, Рь $2, удовлетворяющих соотношениям
2, Pi<b<p2, удовлетворяет неравенствам
Это число х обозначают символом а+Ь.
В п. 2 будет доказано, что такое число х существует и притом
только одно. Там же будет установлено, что таким числом явля-
является точная верхняя грань множества {ai + Pi} сумм всех рацио-
рациональных чисел cEi и Рь удовлетворяющих неравенствам ai<ay
pi<b, или точная нижняя грань множества {(Z2 + P2} сумм всех ра-
рациональных чисел «2 и р2, удовлетворяющих неравенствам
р
В п. 2 будет доказано также, что в применении к двум рацио-
рациональным числам данное нами определение приводит к тому же
результату, что и старое определение суммы рациональных чисел..
Перейдем теперь к определению произведения двух чисел, пред-
представимых бесконечными десятичными дробями. Сначала опреде-
определим произведение двух положительных чисел а и Ь.
Определение 2. Произведением двух представимых
положительными бесконечными десятичными дробями чисел а и Ь
называется такое представимое бесконечной десятичной дробью'
число х, которое для любых рациональных чисел аь аг, Рь Рг*
§ 4. Операции сложения и умножения 47
удовлетворяющих соотношениям 0<<xi<a<a2, 0<Pi<b<p2, удов-
удовлетворяет неравенствам ai-Pi<x<a2-P2-
Это число х обозначают символом а-Ъ.
В п. 2 будет установлено, что такое число х существует и при-
притом только одно. Таким числом х является точная верхняя грань
множества {ap pi} произведений всех рациональных чисел ai и Рь
удовлетворяющих неравенствам 0<at<.a, 0<Pi«:b, или точная
нижняя грань множества {а2-Рг} произведений всех рациональных
чисел сс2 и р2, удовлетворяющих неравенствам а<аг, Ь<р2.
Произведение чисел любого знака определяется по следующе-
следующему правилу:
1) для любого представимого бесконечной десятичной дробью
числа а полагают, что
2) для произвольных отличных от нуля и представимых беско-
бесконечными десятичными дробями чисел а и Ъ полагают
, [ \a\-\b\, если а и Ь одного знака,
a-b — I
{ —\а\ • |Ь|, если а и Ъ разных знаков.
В п. 2 будет установлено, что в применении к двум рациональ-
рациональным числам данное нами определение произведения приводит к
гому же результату, что и прежнее определение произведения ра-
рациональных чисел.
Теперь мы располагаем всем тем, что необходимо для описа-
описания понятия вещественных чисел.
Договоримся называть вещественными числа, представив
мые бесконечными десятичными дробями, при условии, что для этих
чисел указанным выше способом определены три операции: упоря-
упорядочения, сложения и умножения.
Так как все изложенное в § 2 и 3 (и, в частности, основная
теорема 2.1 и леммы 1—3) справедливо для произвольных чисел,
представимых бесконечными дробями, для которых определена
только одна операция упорядочения, то все изложенное в этих
параграфах справедливо и для произвольных вещественных чисел.
В дальнейшем будут рассматриваться числа, представимые
¦бесконечными десятичными дробями, для которых кроме опера-
операции упорядочения определены также и операции сложения и ум-
умножения.
Такие числа в соответствии со сформулированным нами поня-
понятием мы в дальнейшем будем называть вещественными.
2. Существование и единственность суммы и произведения ве-
вещественных чисел.
Теорема о существовании суммы веществен-
вещественных чисел. Для любых вещественных чисел а и b существует
вещественное число х, являющееся их суммой.
48 Гл. 2. Вещественные числа
Доказательство. Фиксируем произвольные рациональные
числа а2 и рг, удовлетворяющие неравенствам а<аг, Ь<рг, и рас-
рассмотрим всевозможные рациональные числа ai и рь удовлет-
удовлетворяющие неравенствам си<а, pi<b.
Убедимся в том, что множество {ai + pi} всех сумм ai + Pi, от-
отвечающих указанным выше всевозможным рациональным ai и рь
ограничено сверху.
В силу свойства транзитивности знаков > и = из неравенств
а^а.2 и ai<a вытекает, что ai<a2, а из неравенств Ь<р2 и $\<Ь
вытекает, что р1<Рг.
Но два неравенства ai«X2 и Pi<<P2 одного знака, связывающие
рациональные числа, можно складывать почленно (см. конец п. 1
§ 1). Значит, справедливо неравенство
которое и доказывает ограниченность множества {ai + pj сверху и
тот факт, что число аг+Рг является одной из верхних граней это-
этого множества.
По основной теореме 2.1 (см. § 2) у множества {ai + pi} суще-
существует точная верхняя грань, которую мы обозначим через х.
Остается убедиться в том, что это вещественное число х и являет-
является суммой чисел а и Ь, т. е. удовлетворяет неравенствам ai + Pi<
<x<ct2+p2- Справедливость левого неравенства ai-f Pi<x вытека-
вытекает из того, что х является верхней гранью множества {ai + Pi}, а
справедливость правого неравенства х<аг + Рг вытекает из того,
что число а2 + р2 является одной из верхних граней множества
{ai + Pi}, а число х является точной, т. е. наименьшей, верхней
гранью этого множества. Теорема доказана.
Аналогично можно было бы доказать, что в качестве х можно
взять точную нижнюю грань множества {а2+Рг} сумм а2+Рг все-
всевозможных рациональных чисел аг и Рг, удовлетворяющих нера-
неравенствам a<a2) Ь<Рг-
Теорема единственности суммы двух вещест-
вещественных чисел. Может существовать только одно вещественное
число х, являющееся суммой двух данных вещественных чисел а
и Ь.
Доказательство. Предположим, что существуют два ве-
вещественных числа Х\ и х% удовлетворяющие неравенствам
Рг- B.12)
ai + Рг < Х2 < а2 + Рг
для всевозможных рациональных чисел ai, a2, рь рг. удовлетворя-
удовлетворяющих неравенствам
ai<a<a2, Pi<b<p2. B.13)
Фиксируем произвольное положительное рациональное число е.
В силу леммы 1 из § 3 для положительного рационального числа
§ 4. Операции сложения и умножения 49
е/2 и для данного вещественного числа а найдутся такие рацио-
рациональные числа cci и СЕ2, что ai<a<a2, причем а2—ai<e/2.
Аналогично для указанного е/2 и для данного вещественного^
числа b найдутся такие рациональные числа pi и р2, что Pi<fr<gp2,,
причем р2—Pi <е/2.
Если взять в неравенствах B.13) указанные сц, a2, pi и р2, то
мы получим, что оба числа х\ и х2 удовлетворяют неравенствам.
B.12), которые можно переписать в виде
положив Yi =
Учитывая, что
мы получим, что оба числа х\ и х2 заключены между рациональ-
рациональными числами Yi и у2, разность между которыми меньше наперед,
взятого положительного рационального е.
В силу леммы 3 из § 3 мы получим, что Х\=х2.
Теорема доказана.
Следствие. В применении к двум рациональным числам а
и b данное нами определение суммы вещественных чисел приводит
к тому же результату, что и прежнее определение суммы рацио-
рациональных чисел.
В самом деле, пусть а и Ъ — два рациональных числа, а+Ь —
их сумма согласно прежнему определению, ai, аг, Pi и р2 — какие
угодно рациональные числа, удовлетворяющие неравенствам;
B.13). Тогда, очевидно, справедливы неравенства*
B.14)
причем, согласно теореме единственности число а + Ь является
единственным вещественным числом, удовлетворяющим неравен-
неравенствам B.14).
Совершенно аналогично доказывается существование и един-
единственность произведения двух данных вещественных чисел.
Ясно, что достаточно доказать существование и единственность,
произведения двух положительных чисел а и Ъ.
Для доказательства существования произведения фиксируем
произвольные рациональные числа а2 и р2, удовлетворяющие не-
неравенствам а<.а.2, Ь<р2, и рассмотрим всевозможные рациональ-
рациональные числа си и рь удовлетворяющие неравенствам 0<ai<a,
0<pi«:b. Легко убедиться в том, что множество {ai-Pi} всех про-
произведений cti-Pi ограничено сверху, причем число а2-р2 является
одной из верхних граней этого множества.
* Ибо для рациональных чисел неравенства одного знака можно склады-
складывать почленно (см. конец п. 1 § 1).
350 Гл. 2. Вещественные числа
По основной теореме 2.1 существует точная верхняя грань это-
этого множества х, которая, как легко проверить, удовлетворяет не-
неравенствам <xrPi-<:*<a2'f$2, т. е. является произведением чисел
•а и Ь.
Аналогично можно было бы доказать, что произведением по-
положительных чисел а и b является точная нижняя грань множест-
множества {ссг-рг} произведений а2-р2 всевозможных рациональных чисел
«2 " рг, удовлетворяющих неравенствам а<а2, Ь<р2.
Для доказательства единственности* произведения двух
положительных вещественных чисел а и Ь предположим, что суще-
существуют два вещественных чиола х\ и х2, удовлетворяющие нера-
шенствам
B.15)
для всевозможных рациональных <ц, аг, Pi и р2 таких, что *
B.16)
Фиксировав любое положительное рациональное число е, мы
-с помощью леммы 1 найдем для данных вещественных чисел а и
b такие рациональные числа <ц, аг, Pi и р2, удовлетворяющие нера-
неравенствам B.16), для которых а?—ai<e/2M и р2—Pi<e/2M.
Но тогда в силу B.15) оба числа х\ и Xi будут заключены меж-
между рациональными числами а2-р2 и arPi, разность между кото-
которыми
«2-Р2 — «г Pi = a2 (Ря—Pi) + Pi («2—«i) < 2M • -^ = e.
В силу леммы 3 из § 3 получаем, что Xi = x2-
С помощью теоремы единственности так же, как и для суммы,
.доказывается, что в применении к двум рациональным числам
¦.данное нами определение произведения вещественных чисел при-
приводит к тому же самому результату, что и прежнее определение
произведения рациональных чисел.
§ 5. СВОЙСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ
1. Свойства вещественных чисел. В этом пункте мы убедимся
в справедливости для произвольных вещественных чи-
чисел всех основных свойств, перечисленных в п. 1 § 1 для рацио-
рациональных чисел. Справедливость для вещественных чисел свойств
1°—4° уже установлена выше. Таким образом, нужно выяснить
лишь вопрос о справедливости для вещественных чисел свойств
5°—16°. Легко убедиться в справедливости для вещественных чи-
чисел свойств 5°—8° и 14°, связанных с понятием суммы. Справедли-
Справедливость свойств 5°—8° непосредственно вытекает из определения
В качестве М можно взять, например, число Af=2 (a+6).
§ 5. Свойства вещественных чисел 51
суммы вещественных чисел и из справедливости указанных
свойств для рациональных чисел.
Остановимся на доказательстве свойств 14°, т. е. докажем, что
если a, b и с— любые три вещественных числа и а>Ь, то а+с>
>Ь + с.
Так как а>Ь, то в силу леммы 2 из § 3 найдутся рациональные
числа си и р2 такие, что a>ai>[32>b. Для вещественного числа с
и для положительного рационального числа е = си—р2 найдутся-
рациональные числа yi и Y2 такие, что "Yi^c<Y2> причем Y2—Yi<e==
= а\~—р2 (см. лемму 1 § 3). Пусть, далее, а2 и Pi— любые рацио-
рациональные числа, удовлетворяющие неравенствам a2>a, b>Pi. Тогда
по определению суммы вещественных чисел
Для доказательства того, что а+с~>Ь + с, в силу транзитивности
знака > достаточно доказать, что ai+Yi>P2 + Y2> но это непосред-
непосредственно вытекает из неравенства у2—у\<о,\—fb-
Заметим, что вопрос о вычитании вещественных чисел как о
действии, обратном сложению, полностью исчерпывается на осно-
основании свойств 5°—8°. Назовем разностью вещественных чисел
а и b вещественное число с такое, что с + Ь=а.
Убедимся в том, что таковой разностью является число с =
= а + Ь', где Ь' — число, противоположное Ь.
В самом деле, используя свойства 5°—8°, можем записать
Убедимся в том, что существует только одно вещественное чис-
число, являющееся разностью двух данных вещественных чисел.
Предположим, что кроме указанного выше числа с = а + Ь'~
существует еще одно число d такое, что d+b — a. Тогда, с одной
стороны, (d + b) +b/ = a+b' — c, с другой стороны, (d + b)+b' =
= d+(b + b')=d+O=d, т. е. c = d.
Из определения разности и из свойства 8° вытекает, что число
а', противоположное а, равно разности 0—а. Это число обычно за-
записывают в виде —а. Не вызывает затруднения перенесение на
случай вещественных чисел свойств 9°, 10°, 11°, 12°, 13° и 15°, свя-
связанных с понятием произведения. Отметим лишь в отношении
свойства 12°, что если а — положительное вещественное число, а
ai и а2 — какие угодно рациональные числа, удовлетворяющие
неравенствам 0<ai<a<a2, то число а', обратное для а, определя-
определяется как единственное вещественное число, удовлетворяющее не-
неравенствам <С а! <^
а2 аг
* В качестве числа а' может быть взята точная верхняя грань множества
всех рациональных чисел {1/аг}.
:52 Гл. 2. Вещественные числа
Свойства 9°—12° позволяют заключить, что для любых двух ве-
вещественных чисел а и Ъ (ЬфО) существует и притом только одно
вещественное число с, удовлетворяющее условию с-Ь = а. Это чис-
число с называется частным чисел а и Ъ. Из определения частного
и из свойства 12° вытекает, что число а', обратное числу а, равно
частному 1/а.
Заметим, наконец, что на случай вещественных чисел перено-
переносится и последнее, 16-е, свойство рациональных чисел, а именно:
Каково бы ни было вещественное число а*, можно число 1 по-
повторить слагаемым столько раз, что полученная сумма превзой-
превзойдет а *.
Докажем это свойство. В случае а<0 доказательства не тре-
требуется, ибо \>а. Пусть й>0, а = ао, а\а2 — - В силу того, что опре-
,деление суммы вещественных чисел в применении к сумме рацио-
анальных чисел совпадает с определением суммы рациональных
чисел, повторив число 1 слагаемым п раз, получим целое число п.
"Таким образом, достаточно доказать, что для числа а найдется
целое число п такое, что п>а. Но это очевидно: достаточно взять
Таким образом, на случай вещественных чисел переносятся все
основные свойства, сформулированные для рациональных чисел в
п. 1 настоящего параграфа. Следовательно, для вещественных
чисел сохраняют силу все правила алгебры, относящиеся к ариф-
арифметическим действиям и к сочетанию равенств и неравенств.
2. Некоторые часто употребляемые соотношения. Докажем
справедливость для любых вещественных чисел а и Ъ следующих
двух соотношений:
|а-Ь| = |а|-|Ь|, B.17)
|а| + |Ь|. B.18)
Соотношение B.17) непосредственно вытекает из-определения про-
произведения двух вещественных чисел. Докажем соотношение B.18).
На основании определения модуля и правила упорядочения для
любых вещественных чисел а и Ь справедливы неравенства
В силу справедливости основных свойств для вещественных чисел
можно почленно складывать неравенства одного знака (это дока-
доказано в конце п. 1 § 1). Поэтому
Используя в случае а + Ь>0 правое, а в случае а + Ь«:О левое из
последних неравенств, мы получим неравенство B.18).
3. Некоторые конкретные множества вещественных чисел.
В дальнейшем нам часто придется иметь дело с различными мно-
* Заметим, что это свойство называют аксиомой Архимеда.
§ 5. Свойства вещественных чисел 53
жествами вещественных чисел. Будем обозначать произвольное
множество вещественных чисел символом {х}, а числа, входящие в
состав этого множества, будем называть элементами или
точками этого множества. Мы будем говорить, что точка Х\
множества {х} отлична от точки х2 этого множе-
множества, если вещественные числа Х\ и х2 не равны друг другу. Если
при этом справедливо неравенство Xi>x2 {x\<x2), то мы будем
говорить, что точка Х\ лежит правее (левее) точки х2.
Рассмотрим некоторые наиболее употребляемые частные виды
множеств вещественных чисел.
1°. Множество вещественных чисел х, удовлетворяющих нера-
неравенствам скх^сЬ, где а<Ь, будем называть сегментом и обо-
обозначать символом [а, Ь]. При этом числа а и Ъ мы будем называть
граничными точками или концами сегмента [а, Ь],
а любое число х, удовлетворяющее неравенствам а<х<Ь, будем
называть внутренней точкой сегмента [а, Ь].
2°. Множество всех вещественных чисел х, удовлетворяющих
неравенствам а<х<Ь, будем называть интервалом и обозна-
обозначать символом (а, Ь).
3°. Интервал (а—г, а+е), где е>0, будем называть е-окре-
е-окрестностью точки а.
4°. Любой интервал, содержащий точку а, будем называть
окрестностью точки а.
5°. Множество всех вещественных чисел х, удовлетворяющих
неравенствам а<сх<Ь (или а<х<Ь), будем называть полусег-
полусегментом и обозначать символом [а, Ь) (или (а, Ъ\).
6°. Множество всех вещественных чисел будем называть чис-
числовой (бесконечной) прямой и обозначать символом
(— оо, +оо).
7°. Множество вещественных чисел х, удовлетворяющих нера-
неравенству х>а (или х<&), будем называть полупрямой и обо-
обозначать символом [а, +оо) (или (¦—оо, Ь]).
8°. Множество всех вещественных чисел х, удовлетворяющих
неравенству х>а (или х<Ь), будем называть открытой полу-
полупрямой и обозначать символом (а, +оо) (или (—оо, а)).
Произвольное множество {х} будем называть плотным в
себе, если в любой окрестности каждой точки х этого множества
содержится хотя бы одна точка множества, отличная от х.
Примером плотного в себе множества может служить любое
из определенных выше множеств Г—8°. Другим примером плотного
множества может служить множество всех рациональных чисел,
входящих в состав любого из множеств 1°—8°.
В изложенном нами материале содержатся сведения, необходи-
необходимые для построения аппарата математического анализа. В следу-
следующих параграфах этой главы будут рассмотрены некоторые до-
дополнительные вопросы теории вещественных чисел и элементы
теории множеств.
54 Гл. 2. Вещественные числа
§ 6. ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ ТЕОРИИ
ВЕЩЕСТВЕННЫХ ЧИСЕЛ
Выше, для того чтобы ввести вещественные числа, были ис-
использованы бесконечные десятичные дроби. Для множества бес-
бесконечных десятичных дробей были определены правила упорядо-
упорядочения, сложения и умножения и было установлено, что эти пра-
правила удовлетворяют 16 основным свойствам (перечисленным в-
п. 1 § 1 для рациональных чисел). Описанный метод введения'
вещественных чисел, хотя и обладает несомненными эвристиче-
эвристическими и методическими достоинствами, не является единствен-
единственно возможным. Вещественные числа можно было бы ввести с
помощью бесконечных двоичных дробей, с помощью так назы-
называемых дедекиндовых сечений в области рациональных чисел*,
с помощью последовательностей рациональных чисел ** и дру-
другими способами.
Чтобы выяснить взаимосвязь между различными методам»
введения вещественных чисел, привлечем некоторые новые по-
понятия и установим еще одно важное свойство множества изу-
изученных выше вещественных чисел.
1. Полнота множества вещественных чисел. Пусть А и В —
два произвольных множества. Будем говорить, что между мно-
множествами А и В установлено взаимно однозначное со-
соответствие, если каждому элементу множества А отвечает
единственный элемент множества В, каждый элемент множе-
множества В сопоставлен некоторому элементу множества А и разным
элементам множества А отвечают разные элементы множест-
множества В.
Назовем два множества, для элементов каждого из которых
определены правила упорядочения, сложения и умножения,
изоморфными друг другу относительно этих правил, если
между элементами этих множеств можно установить взаимно-
взаимнооднозначное соответствие так, что если элементам а и b перво-
первого множества соответствуют элементы а' и Ь' второго множест-
множества, то 1) элементы а' и Ь' связаны тем же знаком (>, < ил»
= ), что и элементы а и Ь; 2) элементу а + b соответствует эле-
элемент а'+Ь'; 3) элементу а-Ъ соответствует элемент а'-Ь'.
Аналогично можно было бы говорить не о правилах упоря-
упорядочения, сложения и умножения, а о каких-либо других прави-
правилах, характеризующих соотношения между элементами, и вве-
* Введение вещественных чисел с помощью дедекиндовых сечений изложе-
изложено, например, в гл. 1 книги Ф. Франклина «Математический анализ» или в гл. 1
книги Г. М. Фихтенгольца «Основы математического анализа».
** Этот способ введения вещественнмх чисел принадлежит Кантору. Его
изложение можно, например, найти в книге В. В. Немыцкого, М. И. Слудской
и А. Н. Черкасова «Курс математического анализа», т. I, гл. II, а также в кни-
книге Я. Тагамлицкого «Дифференсиално смятане» (София, 1971).
§ 6. Дополнительные вопросы 55
сти понятие множеств, изоморфных друг другу относительно
указанных правил.
Примером двух множеств, изоморфных друг другу относи-
относительно правил упорядочения, сложения и умножения, служит
множество рациональных чисел, введенных в виде отношения
целых чисел, с соответствующими (см. п. 1 § 1) правилами
упорядочения, сложения и умножения и множество рациональных
чисел, записанных в виде бесконечных дробей с обычными прави-
правилами упорядочения, сложения и умножения вещественных чисел.
Рассмотрим более внимательно два множества: множество
всех рациональных чисел и множество всех вещественных чи-
чисел. Для каждого из этих множеств определены правила упо-
упорядочения, сложения и умножения и справедливы остальные из
16 основных свойств. Вместе с тем ясно, что множество всех
вещественных чисел является более «широким», чем множество
всех рациональных чисел, ибо в целом множество всех вещест-
вещественных чисел не изоморфно относительно правил упорядочения,
сложения и умножения множеству всех рациональных чисел *,
но в множестве вещественных чисел можно выделить часть,
изоморфную относительно указанных правил множеству рацио-
рациональных чисел.
Естественно, возникает вопрос, нельзя ли и для множества
всех вещественных чисел построить более «широкое» множе-
множество объектов, обладающее такими свойствами: 1) в этом более
«широком» множестве определены правила упорядочения, сло-
сложения и умножения и справедливы остальные из 16 основных
свойств; 2) в целом более «широкое» множество не изоморфно
относительно указанных правил множеству всех вещественных
чисел; 3) в более «широком» множестве можно выделить часть,
изоморфную относительно указанных правил множеству всех
вещественных чисел. Мы докажем, что такого более «широко-
«широкого» множества не существует, т. е. множество всех веществен-
вещественных чисел является полным относительно правил упорядочения,
сложения и умножения и остальных 16 основных свойств.
Вообще, произвольное множество объектов, для которого
определены некоторые правила и справедливы некоторые свой-
свойства, называется полным относительно этих правил и свойств,
если нельзя построить более «широкое» множество объектов
такое, чтобы 1) в этом более «широком» множестве были опре-
определены те же правила и справедливы те же свойства; 2) в це-
целом это более «широкое» множество не было изоморфно данно-
данному относительно указанных правил; 3) в этом более «широком»
* Это вытекает из того, что между множеством всех рациональных чисел
-и всех вещественных чисел нельзя установить взаимно однозначное соответ-
соответствие. В п. 3 § 7 будет доказано, что такого соответствия нет между рацио-
рациональными числами и вещественными числами сегмента [0, 1]. Отсюда и выте-
вытекает требуемое утверждение.
56 Гл. 2. Вещественные числа
множестве существовала часть, изоморфная данному множеству
относительно указанных правил.
Можно утверждать, что множество всех рациональных чисел
не является полным относительно правил упорядочения, сложе-
сложения и умножения и остальных 16 основных свойств, ибо суще-
существует более «широкое» множество (множество вещественных;
чисел), удовлетворяющее требованиям 1), 2) 3) из только что
сформулированного определения.
Докажем теперь, что множество всех вещественных чисел
является полным относительно правил упорядочения, сложения
и умножения и остальных 16 основных свойств.
Предположим противное, т. е. предположим, что существу-
существует более «широкое» множество объектов {х'} такое, что выпол-
выполнены требования 1), 2), 3) из сформулированного выше опреде-
определения, и обозначим через {х'} ту часть множества {х'}, которая:
изморфна относительно правил упорядочения, сложения и ум-
умножения множеству {х} всех вещественных чисел.
Заметим прежде всего, что у множества {х'} существует един-
единственная пара элементов 0' и Г, играющих особую роль нуля
и единицы*. Далее можно утверждать, что элементы 0' и V
входят в состав множества \х'} и находятся во взаимно одно-
однозначном соответствии с вещественными числами 0 и 1 **. Пусть.
а' — какой-либо элемент множества {х'}, не принадлежащий
множеству {xf}.
В силу правила упорядочения мы можем разбить все эле-
элементы множества {х'} на два класса — верхний и нижний, отне-
отнеся к верхнему классу все элементы х', удовлетворяющие нера-
неравенству х'~>а, а к нижнему классу все элементы х', удовлетво-
удовлетворяющие неравенству х'<а'. Оба эти класса не являются пусты-
пустыми. В самом деле, докажем, например, что верхний класс не
пуст. Повторив элемент Г слагаемым достаточное число раз, мы,
в силу свойства 16°, получим элемент п' множества {х'}, удов-
удовлетворяющий неравенству и'>а', т. е. принадлежащий верхне-
верхнему классу. Из свойства 4° вытекает, что каждый элемент ниж-
нижнего класса меньше любого элемента верхнего класса.
* Если бы нашлись два элемента O'i и 02', играющие особую роль нуля, то
в силу свойства суммы мы получили бы Oi'=Oi'-t-Oa'=О2Ч-О1'=О2', т. е..
02' = 02'. Аналогично доказывается единственность элемента 1', играющего осо-
особую роль единицы.
** Докажем, например, что нулевой элемент 0' множества {х'} принадле-
принадлежит множеству {*'} и находится в соответствии с вещественным числом 0.
Обозначим через 0 тот элемент множества {xf}, который находится в соответ-
соответствии с вещественным числом 0, и заметим, что сумма 9+9 отвечает вещест-
вещественному числу 0+0=0, и потому 9+9 = 9. С другой стороны, 0'+9 = 9 (па
определению нулевого элемента (У). Из двух последних равенств заключаем, что
6+9 = 0' + 9. Прибавляя к обеим частям полученного равенства элемент W.
противоположный 9, и учитывая, что 9+9' = 0', получим 9+0'=0'+0\ или (в
силу свойства нулевого элемента) 9=0/. Аналогично проводятся рассуждения
для единичного элемента.
§ 6. Дополнительные вопросы 57
В силу изоморфизма множества {х'} и множества {х} всех
вещественных чисел можно утверждать, что множество всех
вещественных чисел разбивается на два класса, причем каж-
каждое число из нижнего класса меньше любого числа из верхнего
класса. Но это означает, что нижний класс вещественных чисел
ограничен сверху и имеет (в силу теоремы 2.1) точную верх-
верхнюю грань М, а верхний класс имеет точную нижнюю грань
т. Из определения точных граней вытекает, что обе грани рг
и М заключены между вещественными числами, как угодно
близкими между собой, а поэтому т=М. Так как число т=М
является одним из вещественных чисел, то оно принадлежит
одному из классов, т. е. существует либо наименьший элемент
в верхнем классе, либо наибольший элемент в нижнем классе.
Докажем, что оба зти утверждения абсурдны. Пусть, например,
существует наименьший элемент в верхнем классе веществен-
вещественных чисел. Тогда существует наименьший элемент чп' и в верх-
верхнем классе, отвечающем разбиению множества {х'}. По опреде-
определению верхнего класса т'~>а'. Согласно свойствам суммы су-
существует разность т'—а', причем согласно этим свойствам
т'—а'ХУ. Но тогда в силу свойства 12° для элемента т'-—а'
существует обратный, который в силу свойств произведения ра-
равен частному \'1{т'—а'). Согласно свойству 16° элемент V мож-
можно повторить слагаемым столько раз, что полученный при этом
«целый» элемент п' будет принадлежать {х'} и удовлетворять
неравенству п'~>\'1{т'—а). Из последнего неравенства в силу
свойств произведения и суммы получим*
т' — >а'. B.19)
п'
Так как элементы т', 1' и п' принадлежат множеству {х'}, то
/ , г \
и элемент т также принадлежит этому множеству и,
V п 1
у
очевидно, удовлетворяет неравенству т' ¦ < т'. Но тогда
п'
неравенство B.19) означает, что в верхнем классе имеется эле-
элемент,- меньший т', т. е. т не является наименьшим элементом.
Полученное противоречие доказывает полноту множества веще-
вещественных чисел **.
2. Аксиоматическое введение множества вещественных чисел.
Для введения вещественных чисел мы использовали множество
бесконечных десятичных дробей. Определив для множества
этих дробей правило упорядочения и операции сложения и ум-
* Эти свойства обеспечивают применимость всех правил алгебры.
** При доказательстве этой теоремы использовалась идея так называемого
дедекиндова сечения. Дедекиндовым сечением в области рациональных чисел
называется разбиение множества всех рациональных чисел на два непустых
подмножества А и В таких, что любой элемент А меньше любого элемента В.
58 Гл. 2. Вещественные числа
ножения, мы установили, что элементы этого множества обла-
обладают 16 основными свойствами и, кроме того, свойством полно-
полноты относительно 16 основных свойств.
Описанный способ введения вещественных чисел, хотя и об-
обладает несомненными эвристическими и методическими достоин-
достоинствами, не является единственно возможным и целесообразным
с научной точки зрения. Для окончательного оформления и
полного логического завершения наших представлений о веще-
вещественных числах более предпочтительным является аксиомати-
аксиоматический метод введения этих чисел.
Этот метод заключается в следующем.
Множество вещественных чисел вводится как совокупность
объектов*, удовлетворяющих 17 аксиомам, в качестве которых
берутся 16 основных свойств и аксиома о полноте относительно
16 указанных свойств. Впредь мы будем называть упомянутые
17 аксиом аксиомами вещественного числа. Конк-
Конкретной реализацией совокупности объектов, удовлетворяющих
17 аксиомам вещественного числа, и является изученное нами
выше множество бесконечных десятичных дробей. Возможны и
другие реализации указанной совокупности объектов.
Имеет место следующее замечательное утверждение:
Любая реализация совокупности объектов {х'}, удовлетворя-
удовлетворяющих 17 аксиомам вещественного числа, изоморфна изученно-
изученному выше множеству {х} бесконечных десятичных дробей.
Доказательство этого утверждения можно найти в книге
В. А. Ильина и Э. Г. Позняка: «Основы математического ана-
анализа», ч. 1 (М., Наука, 1982, с. 608—612), а также в книге
В. А. Ильина, В. А. Садовничего и Бл. X. Сендова «Математи-
«Математический анализ» (М., Наука, 1979, с. 65—69).
Подчеркнем, что аксиоматический метод и понятие изоморф-
изоморфных (в различных смыслах) совокупностей объектов широко,
используются в разнообразных разделах современной матема-
математики и физики (при построении геометрии, теории вероятностей,
классической механики, статистической физики, квантовой ме-
механики** и др. разделов).
В заключение заметим, что в геометрии множество точек
прямой вводится как совокупность объектов, удовлетворяющих
некоторым аксиомам, среди которых фундаментальную роль
играет аксиома о полноте этой совокупности относительно ос-
остальных аксиом. Упомянутые аксиомы позволяют установить
* При этом ничего не предполагается о природе этих объектов.
** Так, квантовая механика первоначально возникла в виде двух внешне
различных теорий: «матричной механики» Гейзенберга и «волновой механики»
Шредингера. Позже было доказано, что эти две теории используют две изо-
изоморфные друг другу конкретные реализации одной общей совокупности объек-
объектов, вводимой аксиоматически и называемой абстрактным гильбертовым прост-
пространством.
§ 7. Элементы теории множеств 59
взаимно однозначное соответствие между множеством точек
прямой и множеством всех вещественных чисел *. Это соот-
соответствие позволяет изображать вещественные числа точками на
прямой (числовой оси), чем мы будем широко пользоваться в
иллюстративных целях.
§ 7. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
1. Понятие множества. В предыдущих параграфах при изуче-
изучении теории вещественных чисел важным понятием являлось поня-
понятие множества. Подчеркнем, что множество мы рассматривали
как начальное понятие, неопределяемое через другие. В этом па-
параграфе мы будем изучать множества произвольной природы, или,
как говорят, абстрактные множества. Это означает, что объекты,
составляющие данное множество, или, как говорят, элементы дан-
данного множества, уже не обязаны быть вещественными числами.
Элементами абстрактного множества могут быть, например, функ-
функции, буквы алфавита, фигуры на плоскости и т. д.
В математике обычно вводят множество как совокупность объ-
объектов любой природы, обладающих определенным свойством.
Множества мы будем обозначать прописными буквами А, В, ...
или X, У, ... и т. п., их элементы — малыми буквами а, Ь, ... или
х, у,... и т. п. Утверждение «элемента принадлежит множеству
А» будем записывать в виде а^А, если же элемент а н е при-
принадлежит множеству А, то будем писать, что сеА или а^А.
Если рассматриваются два произвольных множества А и В и из-
известно, что все элементы множества В содержатся в множестве А,
то В называется подмножеством множества А и обозначает-
обозначается этот факт так: Вс=А. При этом говорят, что множество В вклю-
включается в множество А. (Заметим, что при этом возможен случай
В = А, т. е. случай, когда каждый элемент множества В принад-
принадлежит множеству А и, наоборот, каждый элемент множества А
принадлежит множеству В.)
В дальнейшем удобно будет рассматривать множества, являю-
являющиеся подмножествами некоторого фиксированного множества Е.
Если множество вводится как совокупность объектов, облада-
обладающих некоторым свойством, причем оказывается, что объектов,
обладающих указанным свойством, не существует, то множество
называется пустым и обозначается символом 0.
Таким образом, пустое множество — это множество, не содер-
содержащее ни одного элемента. Пустое множество является подмноже-
подмножеством любого множества.
Заметим, что когда речь идет о некотором выборе элементов,
для которых ранее было введено обозначение, скажем, о наборе
* См. книгу В. А. Ильина и Э. Г. Позняка «Аналитическая геометрия»
(М., Наука, 1981; приложение в конце книги).
60 Гл. 2. Вещественные числа
элементов х, то данная совокупность или данное множество может
обозначаться и так {х} (говорят —«множество элементов «икс»).
Далее, если X — какое-то множество, а Р — определенное свойство,
то запись {х^Х:Р(х)} или {х^Х\Р(х)} обозначает множество
элементов х, обладающих свойством Р. Например, если обозна-
обозначить через N = {x) множество натуральных чисел: 1, 2, 3, ..., то за-
запись {x^N : х2—4=0} означает множество корней уравнения
х2—4 = 0, являющихся натуральными числами. В данном случае
это множество состоит из одного элемента: 2. Таким образом,
{x&V:x2—4=0} = 2.
Множество всех тех вещественных чисел {х}, которые одновре-
одновременно удовлетворяют двум условиям: х<1 и 2<х, является пус-
пустым. Пустым является и множество {хе?: хфх).
2. Операции над множествами. С ум мой (или объединен и-
е м) двух множеств А и В называется третье множество С, состоя-
состоящее из элементов, принадлежащих хотя бы одному из множеств
А и В. Сумма двух множеств обозначается так: C^=A[jB. Анало-
Аналогично определяется сумма А любого числа множеств Аа. В этом
случае пишут A = \jAa, что и означает, что множество А состоит из
CS
элементов, принадлежащих хотя бы одному Аа:
Заметим, что не следует путать понятие суммы двух множеств
с понятием суммы двух вещественных чисел. Например, если мы
рассматриваем множества Л = {1}, В = {2}, т. е. множества, состоя-
состоящие всего из одного элемента: в первом случае из единицы, во
втором из числа два, то C=A\JB = {1\ 2} есть множество, состоя-
состоящее из двух элементов — чисел 1 и 2. Ясно, что при этом 1+2 = 3
не является даже элементом множества С.
Пересечением двух множеств А и В называется третье
¦ множество С, состоящее из элементов, принадлежащих как мно-
множеству А, так и множеству В, т. е. из элементов, общих для мно-
множеств А и В. Пересечение С двух множеств А и В обозначается
так: С=А(]В. Аналогично определяется пересечение С произволь-
произвольного числа множеств Aa:C=f\Aa, т. е. множество С, состоящее из
а
элементов, принадлежащих, каждому множеству Аа.
Разностью С—А\В двух множеств А и В называется мно-
множество, состоящее из элементов А, не принадлежащих В. Заметим,
что если рассматриваемые множества являются подмножествами
некоторого фиксированного множества Ё, то разность А' = Е\А на-
называется дополнением множества А или дополнением до
Е множества А.
Подчеркнем также, что понятие разности двух множеств так-
также не следует путать с понятием разности двух вещественных
чисел.
Дополнительные сведения о свойствах операций над множест-
множествами и понятие отображения множеств будут даны в п. 4 в конце
настоящего параграфа.
§ 7. Элементы теории множеств 6F
3. Счетные и несчетные множества. Несчетность сегмента [0, 1].
Мощность множества. Важным вопросом при изучении множеств»
является вопрос о том, как сравнивать между собой два множе-
множества, имея в виду «количество» элементов, в них содержащихся.
Если мы имеем два множества, каждое из которых содержит ко-
конечное число элементов, то элементы в этих множествах мы мо-
можем просто каким-нибудь способом занумеровать. При этом может-
оказаться, что в первом и втором множествах содержится одина*
ковое число элементов. Назовем такие два множества, содержа-
содержащие конечное и одинаковое число элементов, эквивалентны-
м и. Если в одном из рассматриваемых множеств элементов ока-
окажется больше, то мы будем говорить, что оно имеет большую»
мощность, чем другое из рассматриваемых множеств.
Обратимся теперь к множествам, состоящим из, вообще гово-
говоря, бесконечного числа элементов. Примерами таких множеств
являются множество рациональных чисел или множество вещест-
вещественных чисел, лежащих на сегменте [0, 1].
Назовем два множества А и В эквивалентными, если меж-
между ними существует взаимно однозначное соответствие, т. е. каж-
каждому элементу а^.А отвечает единственный элемент Ь^В, каждый,
элемент ЬеВ сопоставлен некоторому элементу аеЛ и разным
элементам множества А отвечают разные элементы множества В.
Взаимно однозначное соответствие называют иногда биектив-
биективным соответствием.
В частности, множества, содержащие конечное число элемен-
элементов, эквивалентны тогда и только тогда, когда они содержат оди-
одинаковое число элементов. Эквивалентность множеств А и В обо-
обозначается так: А~В.
Покажем, например, что множество R = {r} рациональных чисел
и множество N={n] натуральных чисел эквивалентны. Заметим
сначала, что для любого целого кфО два рациональных числа
пг/п и mkjnk являются одинаковыми (здесь п=?=0). Поэтому всякое-
рациональное число г можно записать в виде г= — (q > 0)?
q
и дробь считать несократимой. Число 0 будем считать записанным
одним способом: 0 = —.
Назовем число h=\p\+q высотой рационального числа plq.*
Ясно, что рациональных чисел г, имеющих данную высоту, конеч-
конечное число. Будем нумеровать натуральными числами 1, 2, 3, ...-
рациональные числа по возрастанию высоты, т. е. сперва зануме-
занумеруем все рациональные числа высоты h—\. Такое число только-
одно: 0. Этому рациональному числу припишем индекс 1, т. е..
поставим ему в соответствие натуральное число 1. Затем зануме-
занумеруем рациональные числа высоты 1г = 2. Таких чисел два: 1 =
2 Гл. 2. Вещественные числа
-и 1 = . Первому из них поставим в соответствие натураль-
натуральное число 2 (т. е. занумеруем его индексом 2), второму — число 3.
После этого занумеруем рациональные числа высоты 3 и т. д.
Ясно, что при этом мы установим взаимно однозначное соответст-
соответствие между всеми рациональными числами и всеми натуральными
числами, т. е. R~N.
Введем понятие счетного множества.
Определение 1. Множество называется счетным, если
¦оно эквивалентно множеству натуральных чисел.
Согласно этому определению и рассуждениям, проведенным
гвыше, мы получаем, что множество рациональных чисел является
•счетным множеством.
Докажем следующие два простых утверждения о счетных мно-
множествах.
Утверждение 1. Всякое непустое подмножество счетного
множества является или множеством, состоящим из конечного
числа элементов, или множеством счетным.
Доказательство. Пусть А — исходное счетное множество,
т. е. A~N—множеству натуральных чисел. Это означает, что эле-
элементы множества А можно занумеровать каким-нибудь способом.
'Расположим элементы множества А в виде последовательности:
«ь а2, ..., ап, .... Пусть В — непустое подмножество множества А.
Рассмотрим последовательно элементы аи а% а3,... множества А.
"Если а^В, то этот элемент мы обозначим через Ъ\\ если at^B,
мы переходим к рассмотрению элемента а2. При рассмотрении
•элемента а2 могут представиться две возможности: а) элемент
щ^.В; если при этом было выполнено, что и а\^В, то элемент а2
Лш обозначим через Ь2; если же Щ^В, то элемент а^ обозначается
через Ъ\\ б) элемент a2efi, тогда переходим к рассмотрению эле-
элемента а3 и т. д. Ясно, что при этом может случиться, что все эле-
элементы множества В будут расположены в виде конечной последо-
последовательности: Ь\, Ь% >.., Ьм (М<оо). В этом случае множество В
^состоит из конечного числа элементов. Если этого не случится, то
мы выпишем все элементы множества В в виде бесконечной по-
последовательности элементов Ъ\, Ь2, ..., Ьп, ..., откуда следует, что
множество В счетное. Утверждение доказано.
Утверждение 2. Сумма любой конечной или счетной сово-
совокупности счетных множеств есть множество счетное.
Доказательство. Рассмотрим, например, случай, когда
«имеется счетная совокупность счетных множеств. Пусть А\, А2,
А3, ... —совокупность множеств, каждое из которых счетно. Рас-
лоложим элементы множеств А\, А2, А3, ... в виде последователь-
«юстей:
§ 7. Элементы теории множеств 6S
At = {а„ , а,2 , %, . ••),
Пусть Л= у Л„. Произведем нумерацию элементов а множе-
л=1
ства Л = {а} следующим образом*:
a,i = an, a2=a2u as=ct\2, сц=ази 05=^22, ав=сцз и т. д.
У некоторых множеств Л, и Л/ могут оказаться общие элементы
(при ?=/=/). В этом случае мы их учитываем только один раз.
Таким образом, элементы множества Л можно занумеровать*
т. е. поставить во взаимно однозначное соответствие с множест-
множеством натуральных чисел N, т. е. Л счетно. Утверждение доказано.
Возникает вопрос: существуют ли бесконечные несчетные мно-.
жества, т. е. такие бесконечные множества, которые нельзя поста-
поставить во взаимно однозначное соответствие с множеством натураль-
натуральных чисел? Ответ содержится в доказываемой ниже теореме.
Теорема 2.2. Множество всех точек сегмента [0, 1] несчетно.
Доказательство. Рассмотрим интервал @, 1). Очевидно,,
что если мы докажем, что интервал @,1) несчетен, то и сегмент-
[0, 1] будет несчетен, так как множество точек сегмента [0, 1] отли-
отличается от множества точек интервала @,1) всего двумя точками:
0 и 1. Итак, докажем, что множество точек интервала @, 1) не-
несчетно. Допустим противное, т. е. предположим, что все вещест-
вещественные числа интервала @, 1) можно занумеровать.
Записывая все числа интервала • @, 1) в виде бесконечных:
десятичных дробей, получим, что
Х\ = 0, п\\С1\2 ... й\п ... ,
хп — 0, ап\аП2... апп...,
Рассмотрим на интервале @,1) вещественное число х=0,Ьф2 ...
... Ьп..., где Ь\ — любая цифра, отличная от аи, 0 и 9; Ь2 — любая»
цифра, отличная от а22, 0 и 9; и т. д.; Ъп — любая цифра, отличная
от а„п, 0 и 9. Достаточно доказать, что число х не совпадает ни
с одним из чисел Х\, Xi, ..., хп, .... Число х не содержит после за-
запятой нулей и девяток, т. е. это число не принадлежит классу ра-
* В записи всех элементов множеств А\, А% приведенной выше, стрелки?
указывают порядок, в котором мы производим нумерацию.
«64 Гл. 2. Вещественные числа
циональных чисел, представимых двумя способами в виде беско-
бесконечных десятичных дробей. В таком случае число х допускает
единственное представление в виде бесконечной десятичной дроби
и оно отлично от всех чисел х\, х% ¦¦¦, хп, ..., ибо совпадение чис-
числа х с каким-либо числом хп означало бы совпадение Ь„ и аПп-
Таким образом, интервал @, 1), а вместе с тем и сегмент [0, 1]
несчетен. Теорема доказана.
Определение 2. Множество, эквивалентное' множеству то-
точек сегмента [О, 1], называется множеством мощности конти-
континуум а.
Из доказанной теоремы 2.2 следует, что множества мощности
континуума и счетные множества не являются эквивалентными
между собой множествами. В частности, из теоремы 2.2 следует,
что существуют иррациональные числа, так как уже на сегменте
[О, 1] не все числа рациональны: в противном случае их можно
было бы перенумеровать. Из теоремы 2.2 также следует, что ирра-
иррациональных чисел несчетное множество, так как если бы их было
счетное множество или конечное число, то по утверждению 2 и
всех чисел — рациональных и иррациональных — было бы счетное
множество.
Рассмотрим два произвольных множества А и В. Если эти
множества являются эквивалентными, то мы будем говорить,
что они имеют одинаковую мощность или являются
равно мощными.
Для обозначения равномощности множеств А и В использу-
используют следующую символику:
m(A)=m(B) *.
Если множество А эквивалентно некоторому подмножеству
множества В и при этом множество А не содержит подмножест'
ва, эквивалентного множеству В, то будем говорить, что мощ-
мощность множества А меньше мощности множе-
с т в а В.
Для обозначения того, что мощность множества А меньше
мощности В, используют следующую символику:
m{A)<m(B).
Например, из данного выше определения множества мощности
континуума, из теоремы 2.2 и из утверждения 1 о счетных мно-
множествах следует, что мощность счетного множества меньше мощ-
мощности множества сегмента [0, 1], т. е. мощности континуума.
Итак, нами введено сравнение мощностей двух множеств.
Л.огически возможны еще два случая:
* Величину m(А), представляющую собой общую характеристику класса
всех эквивалентных множеству А множеств, принято называть кардиналь-
кардинальным числом. В частности, если А состоит из конечного числа элементов, то
т(А) равно количеству элементов этого множества.
§ 7. Элементы теории множеств 65
а) Множество А содержит подмножество, эквивалентное
множеству В, а множество В содержит подмножество, эквива-
эквивалентное Л.
б) Множества Л и В не эквивалентны, и ни одно из них не
содержит подмножества, эквивалентного другому множеству.
Нетрудно доказать, что в случае а) множества А и В будут эк-
эквивалентны. Случай же б) на самом деле невозможен.
Заметим еще, что трудной проблемой оказался вопрос о
существовании множества промежуточной мощности между
мощностью счетных множеств и мощностью континуума. Ока-
Оказалось, что утверждение как о существовании, так и об отсутст-
отсутствии множества промежуточной мощности не противоречит ак-
аксиомам теории множеств и не может быть выведено из них. Тем
самым это утверждение является одной из аксиом аксиомати-
аксиоматической теории множеств.
В заключение докажем, что сегмент [0, 1] и интервал @, 1) —
эквивалентные или, что то же, равномощные множества. Для
этого установим взаимно однозначное соответствие между их
элементами. Выберем на сегменте [0, 1] и интервале @, 1) по-
последовательность точек 1 —, —, ... , —, ... I.
I 2 3 п J
Точке 0 сегмента [0, 1] поставим в соответствие точку
— интервала @, 1), точке 1 сегмента [0, 1] поставим в соот-
соответствие точку — интервала @, 1), далее точке— сегмента
о Z
[О, 1] поставим в соответствие точку — интервала @, 1)
4
и т. д., точке — сегмента [0, 1] поставим в соответствие точку
п
¦ интервала @, 1), и>2. Всем остальным точкам сегмента
п+2
(т. е. точкам, отличным от 0,1 и не принадлежащим-выбранной
последовательности) ставятся в соответствие те же точки инт
тервала, т. е. точки, имеющие те же абсциссы. Таким образом,
взаимно однозначное соответствие между сегментом [0, 1] и ин-
интервалом @, 1) установлено.
4. Свойства операций над множествами. Отображение мно-
множеств. Отметим ряд свойств, введенных выше операций над
множествами. Отношение включения двух множеств облада-
обладает следующими свойствами:
1°) АаА;
2°) если AczB и BczA, то А = В;
3°) если ВаА и AczC, то BczC;
4°) 0czA для любого множества А.
3 Зак. 72
66 Гл. 2. Вещественные числа
Операции суммы (объединения) и пересечения мно-
множеств обладают следующими, непосредственно проверяемыми
свойствами:
5°) (\jAa)f\B = \j(Aaf\B) (дистрибутивность пересечения);
а а
6°) (r\Aa)\jB — Q(Aa\JB) (дистрибутивность объединения);
а а,
7°) Лс=В эквивалентно условиям A\jB = B или Af\B=A.
Напомним, что для подмножеств {А} некоторого фиксирован-
фиксированного множества Е мы ввели операцию дополнения Л' =
=Е\А. Очевидно эта операция удовлетворяет следующим свой-
свойствам:
8°) А\)А' = Е, АГ\А' = 0;
9°) 0' = Е, Е' = 0;
10°) ШЛ
11°)
а а.
Последние два свойства суть правила де Моргана *.
Симметрической разностью двух множеств Л и В
назовем множество C(A\JB)\(A(]B). Симметрическая разность
множеств А и В обозначается символом ААВ. Легко видеть,
что ААВ= (А\В)[)(В\А).
Важнейшим понятием в анализе является понятие отобра-
отображения одного множества в другое. Пусть X и У—какие-то
множества. Если в силу некоторого закона f каждому элементу
х^Х соответствует элемент y = f(x)^Y, то говорят, что задано
отображение f множества X в множество У. Записывают этот
факт в виде
f:X-*Y или X-+Y.
В этом случае элемент y=f{x) называют образом элемента
х или значением f на элементе х, а элемент х — про-
прообразом или одним из прообразов элемента у. Часто элемент
х^Х называют переменным или аргументом отобра-
отображения /.
Образом множества AczX при отображении f: X^-Y назы-
называют множество всех таких элементов из У, которые являются
образами элементов хеЛ. Это множество обозначается симво-
символом /(Л). Если BczY, то прообразом (или полным прообра-
прообразом) множества В называют совокупность всех элементов j;el
таких, что f(x)^B. Прообраз множества В обозначается сим-
символом f~l(B).
Отображение f:X^>-Y иногда удобно называть функцией
с областью определения X и областью (или множеством) зна-
значений f{X)aY. В некоторых разделах математики в зависимо-
зависимости от природы множеств X и У и свойств / отображение f на-
называется оператором, функционалом и т. д.
А. де Морган — шотландский математик A806—1871).
§ 7. Элементы теории множеств 67
Про отображение f:X-*-Y говорят, что оно сюръективно
(или является отображением X на У), если f(X)=Y; инъек-
тивно (или является вложением), если для любых эле-
элементов Х\, %2 множества X из условия f(xi)=/(x2) вытекает, что
Xi = x2, т. е. различные элементы имеют различные образы;
биективно (или взаимно однозначно), если оно
сюръективно и инъективно одновременно. Если отображение
f:X->-Y биективно, то, как мы отмечали в п. 3, множества X и
Y называются эквивалентными (или равномощными). В случае
биекции f : X-*-Y можно определить обратное отображе-
отображение /~' : Y-*-X по правилу: если при отображении f элементу
х^Х соответствует элемент je7, то /"'(</) полагается равным
элементу х. Для любого г/еУ в силу сюръективности отображе-
отображения f элемент f~x(y) всегда существует, а ввиду инъективности
отображения / этот элемент/-1 (у) единственен.
3*
Глава 3
ТЕОРИЯ ПРЕДЕЛОВ
В гл. 1 уже указывалось, что одной из основных операций ма-
математического анализа является операция предельного перехода
и что эта операция встречается в курсе анализа в различных фор-
формах.
В настоящей главе изучаются простейшие формы операции пре-
предельного перехода. Мы начинаем с изучения самой простейшей
формы операции предельного перехода, основанной на понятии
предела так называемой числовой последовательности.
Понятие предела числовой последовательности облегчит нам
введение и другой весьма важной формы операции предельного
перехода, основанной на понятии предельного значения (или, ко-
короче, предела) функции.
В конце главы дается общее определение предела функции
по базе.
§ 1. ПОСЛЕДОВАТЕЛЬНОСТЬ И ЕЕ ПРЕДЕЛ
1. Понятие последовательности. Арифметические операции над
последовательностями. Понятие числовой последовательности из-
известно из курса средней щколы. Примерами числовых последова-
последовательностей могут служить: 1) последовательность всех элементов
арифметической или геометрической прогрессии; 2) последова-
последовательность периметров правильных л-угольников, вписанных в дан-
данную окружность; 3) последовательность рациональных чисел
Xi = 0,3, X2=0,33, х3 = 0,333, ..., приближающих число 1/3.
Если каждому значению п из натурального ряда чисел 1, 2, ...
..., п, ... ставится в соответствие по определенному закону некото-
некоторое вещественное число х„, то множество занумерованных вещест-
вещественных чисел
Х\, Х2, ... , Хп, ... C.1)
мы и будем называть числовой последовательностью
или просто последовательностью.
Отдельные числа хп мы будем называть элементами или члена-
членами последовательности C.1). Для сокращенной записи последова-
последовательности C.1) будем использовать символ {хп}.
Так, например, символ |—— J обозначает последовательность
1, 1/22, 1/32, ..., 1/п2, ..., а символ {1 + (—1)"} обозначает после-
последовательность 0, 2, 0, 2, ....
§ 1. Последовательность и ее предел 69
Рассмотрим наряду с последовательностью C.1) еще одну
последовательность
Уи Уг, .- , Уп C.2)
Назовем последовательность X\ + yi, Х2+У2, •••, хп+Уп, ...
суммой последовательностей C.1) и C.2), последовательность
Х\—У\, х2—г/г, ..., хп—Уп, ... — разностью последовательностей
C.1) и C.2), последовательность Х\-уи х2-у2, —, хп-уп, ... — про-
произведением последовательностей C.1) и C.2) и, наконец, по-
последовательность -^-, -^-, ... I—^Ц ... — частным последо-
У\ Уг Уп
вательностей C.1) и C.2).
Конечно, при определении частного последовательностей C.1)
и C.2) необходимо требовать, чтобы все элементы последователь-
последовательности C.2) были отличны от нуля. Заметим, однако, что если у
последовательности {уп} обращается в нуль лишь конечное число
элементов, то частное I—2-} можно определить с того номера,
I Уп J
начиная с которого все элементы уп отличны от нуля.
2. Ограниченные, неограниченные, бесконечно малые и беско-
бесконечно большие последовательности. Совокупность всех элементов
произвольной последовательности {хп} образует некоторое числовое
множество. Отправляясь от понятий ограниченного сверху, снизу
или с обеих сторон множества, мы приходим к следующим опре-
определениям.
Определение 1. Последовательность {хп} называется ог-
раниченно й сверху (с низ у), если существует веществен-
вещественное число М (вещественное число пг) такое, что каждый элемент
этой последовательности хп удовлетворяет неравенству
При этом число М (число ш) называется верхней гранью
(нижней гранью) последовательности {хп}, а неравенство
хп<сМ (х„»т) называется условием ограниченности
этой последовательности сверху (снизу).
Отметим, что любая ограниченная сверху последовательность
имеет бесконечное множество верхних граней * и что в условии
ограниченности последовательности сверху хп<М в качестве М
может браться любая из верхних граней. Аналогичное замечание
относится и к нижним граням ограниченной снизу последователь-
последовательности.
Определение 2. Последовательность {хп} называется огра-
ограниченной с обеих сторон (или просто ограниченной),
если она ограничена и сверху, и снизу, т. е. если существуют два
* В самом деле, если число М — одна из верхних граней, то в силу свой-
свойства транзитивности знаков >и = и любое.яисло М*, большее М, является
верхней гранью.
70 Гл. 3. Теория пределов
вещественных числа Mum такие, что каждый элемент этой после-
последовательности хп удовлетворяет неравенствам
т<.хп<.М. C.3)
При этом числа т и М называются соответственно нижней и
верхней гранями последовательности {хп}, а неравенства C.3) на-
называются условием ограниченности последовательности
w.
Подчеркнем, что в условии ограниченности C.3) могут фигу-
фигурировать любая нижняя и любая верхняя грани последовательно-
последовательности. Определение ограниченности последовательности требует су-
существования хотя бы одной пары вещественных чисел т и М та-
таких, что для любого элемента последовательности хп справедливы
неравенства C.3).
Заметим, что условие ограниченности последовательности мож-
можно записать не только в форме удовлетворения неравенствам C.3),
но и в другой эквивалентной форме: последовательность {хп} явля-
является ограниченной тогда и только тогда, когда существует поло-
положительное вещественное число А такое, что каждый элемент по-
последовательности хп удовлетворяет неравенству
\хя\<А. C.4)
В самом деле, если каждый элемент хп удовлетворяет нера-
неравенству C.4), то, положив пг=—А, А(=+Л, мы получим, что хп
удовлетворяет неравенствам C.3). Если, наоборот, каждый эле-
элемент хп удовлетворяет неравенствам C.3), то, обозначив через
А наибольшее из двух чисел \гп\ и \М\, мы можем утверждать,
что Хп удовлетворяет неравенству C.4).
В соответствии с определением 2 ограниченной последователь-
последовательности и условием ограниченности, взятым в форме C.4), мы мо-
можем определить понятие неограниченной последовательности.
Последовательность {хп} называется неограниченной, если
для любого положительного вещественного числа А * найдется
хотя бы один элемент последовательности хп, удовлетворяющий
неравенству
\хп\>А. C.5)
С точки зрения этого определения всякая последовательность,
которая ограничена только сверху или только снизу, является не-
неограниченной.
Так, например, последовательность 1, 2, 1, 4, ..., 1, 2/г, ... огра-
ограничена только снизу и является неограниченной: какое бы положи-
положительное вещественное число А мы ни взяли, найдется элемент этой
последовательности с четным номером, удовлетворяющий нера-
неравенству C.5).
* Сколь бы болышщ мы ни взяли это число.
§ 1. Последовательность и ее предел 71
Последовательность I —!, очевидно, является ограниченной:
I л J
каждый элемент этой последовательности удовлетворяет неравен-
неравенствам C.3) при любых т<0 и Л1>1.
Введем теперь понятия бесконечно большой и бесконечно ма-
малой последовательностей.
Определение 3. Последовательность {хп} называется бес-
бесконечно большой, если для любого положительного веще-
вещественного числа А* найдется номер N такой**, что при всех
n>N элементы хп этой последовательности удовлетворяют нера-
неравенству C.5).
Очевидно, что всякая бесконечно большая последовательность
является неограниченной, ибо определение бесконечно большой
последовательности требует, чтобы для любого Л>0 неравенству
C.5) удовлетворяли все элементы последовательности, начиная с
некоторого номера N, а определение неограниченной последова-
последовательности требует, чтобы для любого Л>0 неравенству C.5) удов-
удовлетворял хотя бы один элемент последовательности.
Вместе с тем не всякая неограниченная последовательность
является бесконечно большой. Так, например, рассмотренная выше
последовательность 1, 2, 1, 4, ..., 1, In, ..., будучи неограниченной,
не является бесконечно большой, ибо для любого Л>1 неравенст-
неравенство C.5) не имеет места для элементов хп со сколь угодно больши-
большими нечетными номерами п.
Определение 4. Последовательность {а„} *** называется
бесконечно малой, если для любого положительного веще-
вещественного числа г **** найдется номер N такой*****, что при всех
n>>N элементы а„ этой последовательности удовлетворяют нера-
неравенству
|ая|<е. C.6):
Докажем, что последовательность q, q2, ..., qn, ... является бес-
бесконечно большой при |<?|>1 и бесконечно малой при
\я\<\.
Пусть сначала |<7|>1. Тогда |^| = 1+б, где б>0. Используя
формулу бинома Ньютона, можем записать
191^= A + 6)^=1 +N8+ (положительные члены).
Отсюда следует неравенство
\q\N>8N. C.7)
* Сколь бы большим мы ни взяли это число.
** Так как этот номер JV, вообще говоря, зависит от А, то иногда пишут:
N=N(A).
*** Элементы бесконечно малых последовательностей мы будем стремиться
обозначать греческими буквами.
**** Сколь бы малым мы ни взяли это число.
***** Так как этот номер N, вообще говоря, зависит от 8, то иногда пишут:
N=N(e).
72 Гл. 3. Теория пределов
Фиксируем произвольное положительное число А и выберем по
нему номер N такой, чтобы было справедливо неравенство
8N>A. C.8)
Убедимся в том, что по любому Л>0 можно выбрать номер N,
удовлетворяющий неравенству C.8). Договоримся обозначать сим-
символом [х] целую часть положительного вещественного числа х.
Поскольку неравенство C.8) эквивалентно неравенству N > —,
то этому неравенству заведомо будет удовлетворять номер N, вы-
[Л "I Г Л "I
—- + 1 = + 1.
6 J , L \Я\— 1 J
Заметим теперь, что поскольку |<7|>1. то из свойств произве-
произведения вещественных чисел мы получим, что при всех n>-N
\q\n>\q\N. C.9)
Сопоставляя неравенства C.7), C.8) и C.9), мы получим, что для
любого Л>0 найдется номер N = + 1 такой, что при
L 191-1 J
всех n>JV
Это и доказывает, что при |<7|>1 последовательность {qn} явля-
является бесконечно большой.
Рассмотрим теперь случай |<7|<1. Мы должны доказать, что в
этом случае последовательность {qn} является бесконечно малой.
Исключая тривиальный случай <7 = 0, положим =1 + 6, где
\я\
6>0. Используя, как и выше, бином Ньютона, мы вместо C.7)
получим неравенство
^ 1 C.7')
Фиксируем произвольное положительное число е и выберем по
нему номер N такой, чтобы было справедливо неравенство
< е. C.8')
6N
В силу того, что неравенство C.8') эквивалентно неравенству
N > ——-, для выбора указанного номера достаточно положить
во
N = —— + 1 = — +1- Далее, поскольку, в силу
L еб J [ еA —|<7|) J
свойств произведения вещественных чисел, при |<7|<1 Для всех
справедливо неравенство
\q\n<\q\N, C.9')
§ 1. Последовательность и ее предел 73
то из сопоставления неравенств C.7'). C-8') и C.9') мы полу-
получим, что для любого е>0 найдется номер N = — —— Ч- 1
L е A — \Я\) л
такой, что при всех n~>N справедливо неравенство
Это и доказывает, что при |<7|<1 последовательность является
бесконечно малой.
3. Основные свойства бесконечно малых последовательностей.
Теорема 3.1. Сумма {ап + Рп} двух бесконечно малых последо-
последовательностей {ап} и {prt} представляет собой бесконечно малую по-
последовательность.
Доказательство. Фиксируем произвольное положительное
число е. Так как последовательность {ап} является бесконечно
малой, то для положительного числа е/2 найдется номер Ni такой,
что при n>iVi справедливо неравенство
|оп|<в/2. C.10)
Аналогично, так как последовательность {рп} является беско-
бесконечно малой, то для положительного числа е/2 найдется номер N2
такой, что при п>Лт2 справедливо неравенство
C.11)
Обозначим через N наибольший из двух номеров Ni и N2.
Тогда при «>jV будут справедливы оба неравенства C.10) и
C.11).
Учитывая, что модуль суммы двух чисел не превосходит сум-
суммы их модулей, мы получим, что для всех номеров n>-N
|а» + р„|<|а»| + |ря|. C.12)
Из соотношений C.12)., C.10) и C.11) вытекает, что при
N справедливо неравенство
Это и означает, что последовательность {<zn + prt} является беско-
бесконечно малой. Теорема доказана.
Теорема 3.2. Разность {ап—Рп} двух бесконечно малых по-
последовательностей {ап} и {р„} представляет собой бесконечно ма-
малую последовательность.
Доказательство этой теоремы отличается от доказательства
теоремы'3.1 только тем, что вместо неравенства C.12) следует
взять неравенство
|оп—р»|<|оп|Ч-|Р»|.
Следствие. Алгебраическая сумма любого конечного числа
бесконечно малых последовательностей представляет собой беско-
бесконечно малую последовательность.
74 Гл. 3. Теория пределов
Теорема 3.3. Произведение ограниченной последовательно-
последовательности на бесконечно малую последовательность представляет собой
бесконечно малую последовательность.
Доказательство. Пусть {хп} — ограниченная и {а„} — бес-
бесконечно малая последовательности. По определению ограниченной
последовательности найдется вещественное число Л>0 такое, что
для всех элементов хп справедливо неравенство
\хп\<А. C.13)
Фиксируем произвольное положительное число е. Так как по-
последовательность {ап} является бесконечно малой, то для положи-
положительного числа г/А найдется номер N такой, что при n>jV спра-
справедливо неравенство
C.14)
Учитывая, что модуль произведения двух чисел равен произве-
произведению модулей этих чисел, мы получим с помощью неравенств
C.13) и C.14), что для всех п>Л/>
|| [|||^ =е.
Это и означает, что последовательность {хп-ап} является беско-
бесконечно малой. Теорема доказана.
Теорема 3.4. Всякая бесконечно малая последовательность
является ограниченной-.
Доказательство. Пусть {ап} — бесконечно малая последо-
последовательность. Фиксируем некоторое положительное число е. По оп-
определению бесконечно малой последовательности найдется отве-
отвечающий этому е номер N такой, что |ая|<е для всех номеров
n>jV. Обозначим через А наибольшее из следующих № чисел:
в, \щ\, [ct21, .... |ctw-i|. Тогда очевидно, что |а„|<Л для всех но-
номеров п, а это и означает ограниченность последовательности
{ап}. Теорема доказана.
Следствие из теорем 3.3 и 3.4. Произведение двух (и лю-
любого конечного числа) бесконечно малых последовательностей
представляет собой бесконечно малую последовательность.
Теорема 3.5. Если все элементы бесконечно малой последо-
последовательности {ап} равны одному и тому же числу с, то с = 0.
Доказательство. Допустим, что сфО. Обозначим через е
положительное число е=|с|. По определению бесконечно малой
последовательности для указанного е=|с| найдется номер N та-
такой, что |art|<|c| при всех n>-N. Но неравенство |art|<|c|
(в силу того, что все ап равны с) превращается в заведомо аб-
абсурдное неравенство |с|<|с|. Следовательно, наше допущение
сФО не имеет места, и теорема доказана.
Теорема 3.6. Если {хп} — бесконечно большая последова-
последовательность, то, начиная с некоторого номера п, определено частное
§ 1. Последовательность и ее предел 75
{—— 1 двух последовательностей {1}* и {хп}, которое представля-
{ хп J
ет собой бесконечно малую последовательность. Если все элемен-
элементы бесконечно малой последовательности {ап} отличны от нуля, то
частное I 1 двух последовательностей {1} и {ап} представляет
I а„ J
собой бесконечно большую последовательность.
Доказательство. Докажем сначала первую часть теоремы.
Заметим, что у бесконечно большой последовательности {хп} лиш»
конечное число элементов может быть равно нулю. В самом деле,
по определению- бесконечно большой последовательности для
числа А = \ найдется номер N* такой, что |л:п|>Л = 1 для всех
n>N*. Значит, при п^Л/1* все элементы хп не обращаются в нуль,
и мы можем, начиная с номера N*, рассматривать частное | \
[ хп )
последовательностей {1} и {хп}. Докажем, что это частное являет-
является бесконечно малой последовательностью. Фиксируем произволь-
произвольное положительное число е. По определению бесконечно большой
последовательности для положительного числа — найдется но-
8
мер N (этот номер мы возьмем таким, чтобы он превосходил N*)
такой, что \хп\ >— при n>iV или, что то же самое,
8
1
Хп
< е при n^N. Это и означает, что последовательность
м
— 1 является бесконечно малой.
Для доказательства второй части теоремы предположим, что
все элементы бесконечно малой последовательности {ап} отличны
от нуля. Фиксируем произвольное положительное число А. Так
как \ап} является бесконечно малой последовательностью, то для
положительного числа — найдется номер N такой, что |а„| < —
А А
при n^s>N или, что то же самое,
1
1«„|
при
Это и означает, что последовательность I — 1 является бесконечно
UnJ
большой. Теорема доказана.
4. Сходящиеся последовательности и их свойства. Введем фун-
фундаментальное понятие сходящейся последовательности и ее пре-
предела.
Определение 1. Последовательность {хп} называется схо-
сходящейся, если существует такое вещественное число а, что по-
последовательность {хп—а} является бесконечно малой. При этом ее-
* .Символ {1} обозначает последовательность, все элементы которой рав-
равны 1.
76 Гл. 3. Теория пределов
щественное число а называется пределом последовательности
{Хп}*.
Если последовательность {хп} является сходящейся и имеет
своим пределом число а, то символически это записывают так:
Игл хп = а или хп-*-а при n-voo.
п-
Используя определение бесконечно малой последовательности,
мы приходим к другому определению сходящейся последовательно-
последовательности, эквивалентному определению 1.
Определение 2. Последовательность {хп} называется схо-
сходящейся, если существует такое вещественное число а, что для
любого положительного вещественного числа г найдется номер N
такой **, что при всех n>>N элементы хп этой последовательности
удовлетворяют неравенству
\хп-а\<е. C.15)
При этом число а называется пределом последовательности
{Xnl
Неравенство C.15) можно записать в эквивалентной форме
—г<хп—а< + г
или, что то же самое,
а—е<хп<а+е. C.15')
На геометрическом языке неравенства C.15') означают, что
элементы хп при n^N лежат в интервале (а—е, а+е), который
мы договорились называть е-окрестностью точки а.
Это позволяет сформулировать еще одно определение сходящей-
сходящейся последовательности, эквивалентное определениям 1 и 2.
Определение 3. Последовательность {хп} называется схо-
сходящейся, если существует такое число а, что в любой г-окрест-
ности точки а находятся все элементы последовательности {хп},
начиная с некоторого номера (зависящего, конечно, от е).
Установим специальное представление для элементов любой
сходящейся последовательности {х„}. В силу определения 1 раз-
разность хп—а — ап является элементом бесконечно малой последова-
последовательности. Следовательно, элемент хп сходящейся последователь-
последовательности, имеющей своим пределом вещественное число а, может быть
представлен в следующем специальном виде:
х„=а+ап, C.16)
где ап — элемент некоторой бесконечно малой последовательно-
последовательности {ап}.
* В соответствии с этим определением всякая бесконечно малая последова-
последовательность является сходящейся и имеет своим пределом число о=0.
** Так как этот номер N, вообще говоря, зависит от е, то иногда пишут:
N=N(e).
§ 1. Последовательность и ее предел 77
Замечание 1. Из определения сходящейся последовательно-
последовательности и ее предела сразу же вытекает, что удаление любого конеч-
конечного числа элементов последовательности не влияет на сходимость
этой последовательности и величину ее предела.
Замечание 2. Последовательности, не являющиеся сходя-
сходящимися, принято называть расходящимися.
Замечание 3. Иногда формально договариваются тракто-
трактовать бесконечно большие последовательности как последователь-
последовательности, сходящиеся к пределу оо. Такая формализация позволяет^
использовать для бесконечно большой последовательности {хп)
следующую символику
Игл хп = оо.
Л-»ОО
Если при этом элементы бесконечно большой последователь-
последовательности, начиная с некоторого номера, имеют положительный [отри-
[отрицательный] знак, то используют следующую символику*:
lim хп = + °° [Пт хп = —оо].
л-»а> я-»оо
В качестве примера докажем, что последовательность {хп} с
элементами
*„=0,33...3
п раз
сходится к пределу а = 1/3. Фиксируем произвольное положитель-
положительное число е и докажем возможность выбора по этому е такого но-
номера N, что
< е при всех n>N. Так как число 1/3
3
представимо бесконечной десятичной дробью 0,333..., то из прави-
правила упорядочения вещественных чисел вытекают следующие нера-
неравенства:
0,33 ...3 < — <0,33 ...3+
3 ~ 10" '
л раз л раз
справедливые для любого номера п.
Из последних неравенств мы получим для числа хп = 0,33 ... 3
л раз
следующее соотношение:
3 ^ 10" *
Так как <—тг для всех п>М то для нахождения по дан-
10" 10™
ному е>0 номера N такого, что хп <'8 при всех n>-N,
О |
достаточно выбрать этот номер N. из условия —^- < 8-
* Иными словами, limxn = -f-oo[=—оо], если для любого Л>0 найдется
отвечающий этому А номер N такой, что хп>А[хп<—А] для всех
78 Гл. 3. Теория пределов
Напомним, что в п. й мы установили возможность выбора но-
номера N из условия |<7|^<е для любого |^| <1. Там доказано, что
такой номер N можно взять равным
(-1.
В нашем случае |<7|=0> 1, так что
Перейдем к установлению свойств произвольных сходящихся
последовательностей.
Теорема 3.7. Сходящаяся последовательность имеет только
один предел.
Доказательство. Предположим, что два вещественных
числа а и Ь являются пределами сходящейся последовательности
{хп}. Тогда в силу специального представления элементов сходя-
сходящейся последовательности C.16) мы получим, что хп=а + ап и
Хп=Ь + $п, где {ап} и {рп} — некоторые бесконечно малые последо-
последовательности. Из последних двух равенств получим, что ап—рп =
= Ъ—а. В силу теоремы 3.2 последовательность {«„—рп} является
бесконечно малой, а в силу равенства аи—Р«.=Ь—а все элементы
этой бесконечно малой последовательности равны одному и тому
же вещественному числу ?>¦—а. На основании теоремы 3.5 это чис-
число b—а равно нулю, т. е. Ь = а. Теорема доказана.
Теорема 3.8. Всякая сходящаяся последовательность являет-
является ограниченной.
Доказательство. Пусть {хп} — сходящаяся последова-
последовательность на — ее предел. Фиксируем некоторое положительное
число е и по нему номер N такой, что \хп—а\ <enpnn>iVили,что
то же самое, а—г<хп<.а + г при n^N. Обозначим через А наи-
наибольшее из следующих (N+1) чисел: \а— е|, |а + е|, |*i|, \x2\,...
..., |jcjv_i|. Тогда, очевидно, |я„|«:Л для всех номеров п, а это и
доказывает ограниченность последовательности {хп}. Теорема до-
доказана.
Замечание 4. Не всякая ограниченная последовательность
является сходящейся. Так, например, последовательность 0, 1, О,
1, ..., 0, 1, ... является ограниченной, но не является сходящейся.
В самом деле, обозначим п-й член этой последовательности симво-
символом хп и предположим, что эта последовательность сходится к не-
некоторому пределу а. Но тогда каждая из последовательностей
{Хп+\—а) и {хп—а} являлась бы бесконечно малой. Стало быть,
являлась бы бесконечно малой и разность этих последовательно-
последовательностей {хп+\—Хп}, а этого быть не может в силу того, что \xn+i—хп\ =
= 1 для всех номеров п.
§ 1. Последовательность и ее предел 79
Следующие четыре теоремы показывают, что четыре арифме-
арифметические операции над элементами сходящихся последовательно-
последовательностей приводят к аналогичным операциям над их пределами.
Теорема 3.9. Сумма сходящихся последовательностей {хп}
и {уп} представляет собой сходящуюся последовательность, предел
которой равен сумме пределов последовательностей {хп} и {уп}-
Доказательство. Предположим, что последовательности
{хп} и {уп} сходятся к пределам а и b соответственно. Тогда в силу
специального представления элементов сходящейся последователь-
последовательности C.16) будут справедливы соотношения
хп=а+ап, #n = fc + Pn, C.17)
в которых ап и ря представляют собой элементы некоторых беско-
бесконечно малых последовательностей {ап} и {р„}. Из соотношений
C.17) вытекает, что
C.18)
Так как сумма {art+pn} Двух бесконечно малых последовательно-
последовательностей {ап} и {рп} представляет собой бесконечно малую последова-.
тельность (теорема 3.1), то из соотношения C.18) вытекает в силу
определения 1, что последовательность {хп+уп} сходится и веще-
вещественное число а + Ь является ее пределом. Теорема доказана.
Теорема 3.10. Разность сходящихся последовательностей
{хп} и {уп} представляет собой сходящуюся последовательность,
предел которой равен разности пределов последовательностей {хп}
и {Уп}.
Доказательство этой теоремы аналогично доказательству
теоремы 3.9, только вместо соотношения C.18) мы получим соот-
ношение
(хп—Уп) — (а—Ь) = а„—р„.
Теорема 3.11. Произведение сходящихся последовательно-
последовательностей {хп} и {уп} представляет собой сходящуюся последователь-
последовательность,, предел которой равен произведению пределов последова-
последовательностей {хп} и {«/„}.
Доказательство. Предположим, что последовательности
{хп} и {уп} сходятся к пределам а и b соответственно. Тогда для
элементов этих последовательностей справедливы специальные
представления C.17), перемножая которые, мы получим
хп • уп = а • b + а ¦ р„ + b ¦ ап+ап ¦ рп
или, что то же самое,
хпуп—a-b = a$n + ban+<in-$n. C.19)
Для доказательства теоремы в силу определения 1 остается убе-
убедиться в том, что в правой части C.19) стоит элемент бесконечно
малой последовательности, но это сразу же вытекает из теоремы
80 Гл. 3. Теория пределов
3.3 (согласно этой теореме последовательности {а-$п} и {Ь-ап}
являются бесконечно малыми), из следствия из теорем 3.3 и 3.4
(согласно этому следствию последовательность {ап-$п} является
бесконечно малой) и из теоремы 3.1 (согласно этой теореме сум-
сумма трех бесконечно малых последовательностей {а-ря}, {Ь-ап} и
{an-PrJ является бесконечно малой последовательностью). Теоре-
Теорема доказана.
Теореме о частном двух сходящихся последовательностей пред-
предпошлем следующую лемму.
Лемма 1. Если последовательность {уп} сходится к отлично-
отличному от нуля пределу Ь, то, начиная с некоторого номера, определе-
определено частное | — \ последовательностей {1} и {уп}, которое пред-
\ Уп )
ставляет собой ограниченную последовательность.
Доказательство. Учитывая, что ЬфО, обозначим через е
положительное число е =-"—-. Для этого е найдется номер N
такой, что при п>Лг справедливо неравенство \уп—Ь\<Сг или, что
то же самое,
\Уп-Ь\<-^-. C.20)
Итак, для всех номеров п, начиная с номера N, выполняется
неравенство C.20). Убедимся в том, что из неравенства C.20) вы-
вытекает следующее неравенство:
\Уп\>-^-> C-21)
которое тем самым оказывается ¦ справедливым также для всех
номеров п, начиная с номера N. В самом деле, так как модуль
суммы двух чисел не превосходит суммы модулей этих чисел, то,
исходя из тождества bs=(b—уп)+уп и используя неравенство
C.20), мы получим
Из последнего неравенства сразу же вытекает неравенство C.21),
справедливость которого, начиная с номера N, установлена.
Неравенство C.21) позволяет утверждать, что при n^>N эле-
элементы уп не обращаются в нуль и, начиная с номера N, можно
рассматривать частное I —}.
I Уп)
Из C.21), в свою очередь, вытекает, что для всех и>Я спра-
справедливо неравенство
1 <_2_
Уп ¦ I Ь\ '
§ 1. Последовательность и ее предел 81
Это последнее неравенство и доказывает, что последователь-
последовательность {—1, если ее рассматривать, начиная с номера N, явля-
I Уп)
ется ограниченной. Лемма доказана.
Теорема 3.12. Частное двух сходящихся последовательнос-
последовательностей {хп} и {уп}, предел второй из которых отличен от нуля, опре-
определено, начиная с некоторого номера, и представляет собой сходя-
сходящуюся последовательность, предел которой равен частному преде*-
лов последовательностей {хп} и {«/„}.
Доказательство. Предположим, что последовательности
{хп} и {уп} сходятся к пределам а и ЬфО соответственно. В силу
леммы 1 найдется номер N такой, что при n>N элементы уп не-
необращаются в' нуль, определена последовательность <—} и эта
I Уп }
последовательность является ограниченной. Начиная с указанного»
номера N, мы и будем рассматривать частное I—2-}. В силу опре-
I Уп )
деления 1 достаточно доказать, что последовательность
|— — I является бесконечно малой. Будем исходить из тож-
I Уп Ь )
дества
Уп Ь Уп-Ь
Так как для элементов хп и уп справедливы специальные представ-
представления C.17), то
х-п-Ь—уп-а= (а+ап) -Ь—(fe + pn) -a = anb—рп-а. C.23)
Подставляя C.23) в C.22), получим
хп а 1
тт , "fp« • C-24)
Уп о уп \ о 1
Остается доказать, что в правой части C.24) стоит элемент
бесконечно малой последовательности, но это сразу вытекает из
теоремы 3.3 и из того, что последовательность I — I (в силу
I Уп )
леммы 1) является ограниченной, а последовательность
Ып — р„ I (как разность двух бесконечно малых) является
бесконечно малой последовательностью. Теорема доказана.
Убедимся теперь в том, что неравенства, которым удовлетво-
удовлетворяют элементы сходящихся последовательностей, приводят к ана-
аналогичным неравенствам для пределов этих последовательностей.
Теорема 3-13. Если все элементы сходящейся последова-
последовательности {хп}, по крайней мере начиная с некоторого номера,
удовлетворяют неравенству xn>-b[xn<b], то и предел х этой по-
последовательности удовлетворяет неравенству x>-b[x-<b].
<82 Гл. 3. Теория пределов
Доказательство. Предположим, что все элементы хп, по
крайней мере начиная с некоторого номера N*, удовлетворяют не-
неравенству хп>-Ь. Докажем, что и предел х этой последователь-
последовательности удовлетворяет неравенству х>-Ь. Допустим, что это не так,
т. е. справедливо неравенство х<Ъ.
Тогда по определению сходящейся последовательности для по-
положительного числа г = Ь—х найдется такой номер N (этот номер
•мы возьмем еще и таким, чтобы он превосходил N*), что при n>N
•будет справедливо неравенство \хп—#|<е или \хп—х\<.Ь—х.
Последнее неравенство эквивалентно неравенствам — (Ь—х) <
<хп—х<Ь—х, правое из которых означает, что хп<Ь при всех
n>N, а это противоречит условию теоремы. Полученное противо-
противоречие означает, что наше предположение о том, что х<Ь, неверно,
т. е. х>&.
Случай хп<Ь рассматривается аналогично. Теорема доказана.
Замечание 5. Если все элементы сходящейся последова-
¦гельности {хп} удовлетворяют строгому неравенству хп>Ь, то
отсюда, вообще говоря, не вытекает, что и предел х этой последо-
&ательности удовлетворяет строгому неравенству х>Ь. (Можно
лишь утверждать, что #>Ь.)
Например, если хп = —, то для всех номеров хп>0, однако
п
шредел lim — = х = 0 не удовлетворяет неравенству х>0.
Следствие 1. Если все элементы двух сходящихся после-
последовательностей {хп} и {уп}, по крайней мере начиная с некоторого
номера, удовлетворяют неравенствам хп*суп, то и пределы этих
последовательностей удовлетворяют такому же неравенству
limxrt<lim у„. C.25)
Л-»-00 Л->00
В самом деле, начиная с указанного номера, все элементы по-
последовательности {уп—хп} неотрицательны. В силу теоремы 3.13
и предел указанной последовательности Jim(уп — хп) неотрицате-
лен. В силу теоремы 3.10 tim(yn — хп) = lim уп — lim xn и мы по-
rt-»0O rt-»oo Л-»-00
лучим, что lim уп—limxn^0. Из последнего неравенства выте-
Л-» 00 П-ЮО
кает C.25).
Следствие 2. Если все элементы сходящейся последова-
последовательности {хп} находятся на сегменте [а, Ь], то и предел х этой
последовательности лежит на сегменте [а, Ъ].
В самом деле, так как а*?хп<Ь для всех номеров п, то (в силу
теоремы 3.13) а<л:<6.
Доследнюю теорему, к доказательству которой мы сейчас пере-
-ходим, можно назвать принципом двустороннего огра-
шичения.
§ 2. Монотонные последовательности 8Э
Теорема 3.14. Пусть {хп} и {уп} — две сходящиеся последо-
последовательности, имеющие общий предел а. Пусть, кроме того, все-
элементы третьей последовательности {zn}, no крайней мере начи-
начиная с некоторого номера, удовлетворяют неравенствам
xn<zn*cyn. C.26)'
Тогда последовательность {zn} сходится к тому же самому пре-
пределу а.
Доказательство. Предположим, что неравенства C.2В)
справедливы, начиная с номера N*. Тогда, начиная с того же само-
самого номера N*, справедливы и неравенства
хп—a<zn—а<уп—а. C.27)
Из неравенств C.27) вытекает, что для каждого номера п, пре-
превосходящего N*,
\zn—a|<max{|*n—a\, \yn—а\}. C.28)
(Эта запись означает, что \zn—а\ не превосходит наибольшего из-,
двух чисел \хп—а\ и \уп—а\.)
Фиксируем произвольное положительное число е. Тогда в силу-
сходимости последовательностей {хп} и {уп} к пределу а найдутся»
номера Ni и N2 такие, что
\хп — а\<г при n^Nlt „ 2g.
\У„ — а\<е при « > jV2.
Если мы теперь обозначим через N наибольший из трех номеров-
N*, Ni и Л/2, то при n>N будут справедливы оба неравенства в-
C.29) и мы получим в силу C.28), что при n>iV справедливо не-
неравенство
\zn—а\<г.
Это и доказывает сходимость последовательности {zn} к преде-
пределу а. Теорема доказана.
§ 2. МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
1. Понятие монотонной последовательности.
Определение 1. Последовательность {хп} называется неубы-
неубывающей [невозрастающей], если каждый элемент этот
последовательности, начиная со второго, не меньше [не больше]
предыдущего ее элемента, т. е. если для всех номеров п (я=1,2, ...)•
справедливо неравенство
¦^n<#n+i [хп^-Хп+\]. C.30);
Определение 2. Последовательность {хп} называется-
монотонной, если она является либо неубывающей, либо невоз-
невозрастающей.
84 Гл. 3. Теория пределов
Если элементы неубывающей последовательности для всех но-
номеров п удовлетворяют строгому неравенству xn<xn+i, то эту по-
последовательность называют возрастающей.
Аналогично, если элементы невозрастающей последовательнос-
последовательности для всех номеров п удовлетворяют строгому неравенству
Хп>хп+и то эту последовательность называют убывающей.
Заметим, что всякая монотонная последовательность заведомо
ограничена с одной стороны (либо сверху, либо снизу). В самом
деле, всякая неубывающая последовательность ограничена снизу
(в качестве нижней грани можно взять величину ее первого эле-
элемента), а всякая невозрастающая последовательность ограничена
сверху (в качестве верхней грани также можно взять величину ее
первого элемента).
Отсюда следует, что неубывающая последовательность будет
ограниченной с обеих сторон, или просто ограниченной, тогда и
только тогда, когда она ограничена сверху, а невозрастающая по-
последовательность будет ограниченной тогда и только тогда, когда
она ограничена снизу.
Рассмотрим примеры монотонных последовательностей.
1. Последовательность 1, 1, 2, 2,... является неубывающей. Она
ограничена снизу величиной своего первого элемента, а сверху не
ограничена.
о гт 2 3 4 п+\
2. Последовательность —, —, —, ... , , ... является
1 2, о ft
убывающей. Она ограничена с обеих сторон: сверху величиной
своего первого элемента 2, а снизу, например, числом 1.
2. Теорема о сходимости монотонной ограниченной последова-
последовательности. Справедливо следующее фундаментальное утверждение.
Основная теорема 3.15. Если неубывающая (невозрас-
(невозрастающая) последовательность {хп} ограничена сверху (снизу), то
она сходится.
Доказательство. Рассмотрим случай неубывающей и огра-
ограниченной сверху последовательности {хп}. Множество всех элемен-
элементов такой последовательности ограничено сверху, а потому по ос-
основной теореме 2.1 гл.2 у этого множества существует точная верх-
верхняя грань, которую мы обозначим символом х. Докажем, что это
число х и является пределом последовательности {хп}. Во-первых,
заметим, что по определению верхней грани любой элемент хЛ
последовательности {хп} удовлетворяет неравенству
Хп*?Х. C.31)
Далее фиксируем произвольное положительное число е и заме-
заметим, что по определению точной верхней грани найдется хотя бы
один элемент последовательности Xn, удовлетворяющий нера-
неравенству
х—e<xN. C.32)
§ 2. Монотонные последовательности 85
Учтем теперь, что последовательность {хп} является неубываю-
неубывающей и вследствие этого Xn^xu для всех номеров п, удовлетворяю-
удовлетворяющих неравенству n>.N. Сопоставляя неравенство Хх<хп с нера-
неравенством C.32), мы получим, что для всех n>N
х—е<хп. C.33)
Объединяя неравенства C.31) и C.33), мы получим, что для
всех n^>N справедливы неравенства х—е<хп<х.
Следовательно, для всех n^>N справедливо неравенство
\хп—*|<е, которое и доказывает, что последовательность {хп}
сходится к пределу * = sup{xn}-
Если последовательность {хп} является невозрастающей и
ограничена снизу, то совершенно аналогично доказывается, что она
сходится к пределу х=Ш{хп}- Теорема доказана.
Замечание 1. Теорему 3.15 можно сформулировать в дру-
другом виде. Во-первых, заметим, что в силу сказанного в п. 1 после-
последовательность {хп}, удовлетворяющая условию теоремы 3.15, яв-
является ограниченной с обеих сторон, или просто ограниченной.
Поэтому теорему 3.15 можно переформулировать так: для того
чтобы монотонная последовательность {хп} сходилась, достаточно,
чтобы она была ограничена.
Легко убедиться в том, что эта формулировка может быть заме-
заменена более «сильной»: для того чтобы монотонная последователь-
последовательность {хп} сходилась, необходимо и достаточно, чтобы она была
ограничена (необходимость вытекает из теоремы 3.8).
Замечание 2. Конечно, не всякая сходящаяся последова-
последовательность является монотонной. Например, заведомо сходящаяся
к нулю последовательность , —, , ... , —, , ...
Л 2> о о ft tl
не является монотонной, так как знаки ее элементов чередуются.
Замечание 3. Из приведенного выше доказательства тео-
теоремы 3.15 вытекает, что все элементы неубывающей, ограниченной
сверху последовательности {хп} не больше ее предела х (хп<х).
Аналогично легко убедиться в том, что все элементы невозрастаю-
невозрастающей, ограниченной снизу последовательности не меньше ее пре-
предела ?_
Извлечем важное следствие из теоремы 3.15.
Договоримся называть бесконечную последовательность сегмен-
сегментов [аи bi], [a2, bz],...,[an, bn],-.. стягивающейся систе-
системой сегментов, если выполнены два требования: 1) каждый
следующий сегмент содержится в предыдущем, т. е. ап<ап+и
bn+l*?bn для любого я=1, 2,...; 2) длина n-го сегмента [ап, Ьп],
т. е. разность Ьп—ап, стремится к нулю при п->-оо.
Следствие из теоремы 3.15. У всякой стягивающейся
системы сегментов {[ап, &„]} существует и притом единственная
точка с, принадлежащая всем сегментам этой системы.
86 Гл. 3. Теория пределов
Доказательство. Прежде всего заметим, что точка с,
принадлежащая всем сегментам, может быть только одна. В самом
деле, если бы нашлась еще одна точка d, отличная от с и принад-
принадлежащая всем сегментам, то, предположив ради определенности,
что d>c, мы получили бы, что сегмент [с, d] принадлежит всем
сегментам [ап, Ьп]. Но тогда для любого номера п выполнялись
бы неравенства Ьп—an>d—с>0, что невозможно в силу того, что
Ьп—an-v0 при п-*-оо.
Докажем теперь, что существует точка с, принадлежащая
всем сегментам. Так как система сегментов является стягиваю-
стягивающейся, то последовательность левых концов {ап} не убывает, а по-
последовательность правых концов {Ьп} не возрастает. Поскольку
обе эти последовательности ограничены (все их элементы нахо-
находятся на сегменте [ab &i]), то обе они сходятся (в силу теоре-
теоремы 3.15). Из того, что разность Ъп—ап является бесконечно ма-
малой, вытекает, что эти две последовательности {ап} и {&„} сходят-
сходятся к общему пределу, который мы обозначим через с. В силу заме-
замечания 3 для любого номера п справедливы неравенства ап<с<Ьп,
т. е. с принадлежит всем сегментам [ап, Ьп]. Следствие доказано.
3. Число е. Применим теорему 3.15 для доказательства сходи-
сходимости последовательности {хп}, элемент хп которой определяется
равенством
В силу теоремы 3.15 достаточно доказать, что эта последова-
последовательность 1) является возрастающей; 2) ограничена сверху.
Применяя формулу бинома Ньютона, получим для хп следую-
следующее выражение:
г - 1 -1-я 1 д. "("-1) 1 | я(п-1)(я-2) 1
" я 2! л2 3! п*
+ я(я-1)(л-2) ...[я-(п-1I 1
. +
Это выражение перепишем в следующем виде:
Для следующего элемента последовательности {хп} в полной
аналогии с C.34) получится следующее выражение:
§ 2. Монотонные последовательности 87
|
(( (
п\\ п + 1 А п+1 ) ' \ п + 1
) C.35)
+
(я + 1)!
Для того чтобы убедиться в том, что последовательность {хп}
является возрастающей, сравним между собой выражения C.34)
и C.35). Во-первых, заметим, что правая часть C.34) состоит
из п слагаемых, а правая часть C.35) — из я+1 слагаемых, при-
причем последнее (и+1)-е слагаемое в правой части C.35) является
«трого положительным.
Сопоставим теперь между собой любое из остальных п слагае-
!мых в правой части C.35) с соответствующим слагаемым в пра-
правой части C.34). Легко видеть, что для любого номера k, равного
2, 3,..., п, справедливо неравенство
AI V п+1 )\ я+1 У \ я+1
Это последнее неравенство означает, что k-e слагаемое в правой
части C.34) меньше соответствующего fe-ro слагаемого в правой
части C.35).
Итак, мы доказали, что хп<хп+1, т. е. последовательность {хп}
является возрастающей.
Докажем теперь, что эта последовательность ограничена свер-
ху. Заметим, что если каждую круглую скобку в правой части
C.34) заменить единицей, то указанная правая часть возрастет.
Поэтому
Заметим далее, что для любого номера fe>2 справедливо нера-
неравенство &! = 2-3...fe>2ft.
Поэтому неравенство C.36) дает право утверждать, что
хп< 2 + — + — +... Н — ^з — < 3. C.37)
" 2 22 2" 2"
(Мы воспользовались формулой для суммы членов геометрической
прогрессии.) Неравенство C.37) доказывает ограниченность после-
последовательности {хп}.
По основной теореме 3.15 последовательность {хп} имеет пре-
предел, который, следуя Л. Эйлеру *, мы обозначим через е.
* Леонард Эйлер A707—1783) — великий математик, член Петербургской
Академии наук, большую часть жизни провел в России, по происхождению
швейцарец.
88 Гл. 3. Теория пределов
Убедимся в том, что число е удовлетворяет неравенствам
2<е<3. Для этого (в силу следствия 2 из теоремы 3.13) достаточ-
достаточно доказать, что каждый элемент хп последовательности {хп}
удовлетворяет неравенствам 2<е<3.
Неравенство *„<3 вытекает из C.37), а неравенство 2^.хп
вытекает из C.34), если отбросить в C.34) все члены, кроме пер-
первого.
В дальнейшем выяснится, что число е играет важную роль
в математике, и будет указан способ вычисления этого числа с
любой степенью точности.
4. Примеры сходящихся монотонных последовательностей. Нач-
нем с рассмотрения последовательности, которая широко исполь-
используется в современной вычислительной математике для приближен-
приближенного нахождения корня квадратного из положительного вещест-
вещественного числа а. Эта последовательность определяется следующей
рекуррентной формулой *:
хп+1 = -L (хп + -?-) (п = 1, 2, ... ), C.38)
где в качестве первого приближения xi берется любое положитель-
положительное число.
Прежде всего докажем, что такая последовательность {хп}
сходится, для чего в силу теоремы 3.15 достаточно доказать, что
она ограничена снизу и, начиная со второго номера, является не-
возрастающей.
Начнем с доказательства огр а ниче нности снизу. По ус-
условию #i>0. Но тогда из рекуррентной формулы C.38), взятой
при я=1, вытекает, что х2>0, далее из той же формулы C.38),.
взятой при п = 2, вытекает, что #з>0,.... Продолжая эти рассужде-
рассуждения далее, мы последовательно докажем, что все хп>0. Итак, рас-
рассматриваемая последовательность ограничена снизу.
Докажем теперь, что при п>2 все элементы хп удовлетворяют
неравенству #n>"|/a. Переписав формулу C.38) в виде
C.39)
воспользуемся тривиальным неравенством t -\ > 2, справед-
справедливым для всех />0 **.
* Рекуррентная формула (от латинского recurrens — возвращающийся) —¦
формула, выражающая (я+1)-й элемент последовательности через значения ее
первых п элементов.
** Это неравенство для всех <>0 эквивалентно неравенству t2+l>2t, выте-
вытекающему из того, что (t—1J0
§ 2. Монотонные последовательности 89
?Х X
Взяв в этом неравенстве t =^-й=>0, мы получим, что—т= +
У а V а
-f ^ 2, и поэтому соотношение C.39) дает xn+i>ya при п=\,
хп
2,.... Это и означает, что хп>>^а при п = 2, 3,....
Докажем, наконец;, что последовательность {хп}, если ее рас-
рассматривать с номера п=2, является невозрастающей. Из рекур-
рекуррентной формулы C.38) вытекает, что *
-i2±L —J-
xn 2 \~ +
Из последнего соотношения, учитывая, что хп~^Уа при п>2, по-
получим, что -Хп+1 <1 при п>2 или xn+i<.xn при п>2. Итак, при
хп
п>2 последовательность {#п} является невозрастающей.
По теореме ЗЛ5 последовательность {хп} сходится к некоторо-
некоторому пределу х. Остается найти этот предел. Учитывая, что хп^а
при п>2, мы получим (в силу теоремы 3.13), что х>~\/а>0.
Принимая во внимание, что *>0, перейдем к пределу при
я-мэо в рекуррентном соотношении C.38). Мы получим в пределе
при п-*-оо из C.38) следующее равенство:
2
Это равенство представляет собой уравнение для определения
предела х. Единственный положительный корень этого уравнения
есть х = Ya ¦
Итак, мы окончательно доказали, что последовательность {хп},
определяемая рекуррентной формулой C.38) при любом выборе
JCi>0, сходится к пределу У^а . ¦
В качестве другого применения теоремы 3.15 рассмотрим во-
вопрос о вычислении предела последовательности {хп}, элементы ко-
которой имеют вид
*„ = -^-. C.40)
л!
где t — любое фиксированное вещественное число. Для любого
фиксированного t найдется номер N такой, что |?|<и+1 при всех
Но тогда, поскольку -*n+1 = , мы получим, что
х я+1
]+||
тельность {
при всех n>iV, т. е., начиная с номера N, последова-
последовахп\} является убывающей. Так как, кроме того, эта
( )
{ \} у р
последовательность ограничена снизу (например, числом нуль), то
90 Гл. 3. Теория пределов
по теореме 3.15 она сходится к некоторому пределу х. Для нахож-
нахождения х запишем соотношение C.40) для номера п+1:
__ *n+i _ Vх t _¦ \t
Xn+1 ~ (л+1)! ~~ ~~п~\ ' я+1 ~Х"' п+1 '
Таким образом, IXn+J = |хп 1 • , и, перейдя в последнем равен-
п+1
стве к пределу при л-voo, мы получим соотношение
1x1 = Ы-lim —^— = 0.
it it «ii
п-+<х> Я + 1
Итак, последовательность \хп\, а вместе с ней и последователь-
последовательность C.40), сходится к пределу х = 0.
В обоих рассмотренных примерах мы применили часто употреб-
употребляемый прием: сначала с помощью теоремы 3.15 доказали сущест-
существование предела последовательности, а затем нашли этот предел,
устремив номер п к бесконечности в рекуррентном соотношении,
выражающем (л + 1)-й элемент последовательности через ее
л-й элемент.
В качестве третьего примера изучим вопрос о сходимости после-
последовательности {хп}, элемент хп которой имеет вид
= V
C.41)
при условии, что а>0 и общее число извлекаемых корней рав-
равно п.
Указанную последовательность {хп} можно задать рекуррент-
рекуррентным соотношением
Va + xn (л=1,2, ...) C.42)
при условии, что
xx = Va. C.43)
.Для доказательства сходимости рассматриваемой последова-
последовательности достаточно (в силу теоремы 3.15) доказать, что она воз-
возрастает и ограничена.
Сначала докажем возрастание последовательности C.41), т. е.
докажем, что для любого номера
*„<*„+!. C.44)
Доказательство этого неравенства проведем по индукции До-
Достаточно доказать два утверждения: 1) неравенство C.44) спра-
справедливо для номера п=\, т. е. справедливо неравенство
Xi<xz; C.45)
2) из справедливости неравенства C.44) для данного номера п
§ 2. Монотонные последовательности 91
вытекает справедливость этого неравенства и для номера л+1,
т. е. вытекает справедливость неравенства
Xn+l<Xn+Z. C.46)
Справедливость неравенства C.45) сразу вытекает из равенст-
равенства C.43) и из соотношения x2=V a + У а ~>У а •
Докажем, что из справедливости неравенства C.44) вытекаеу
справедливость неравенства C.46). Из неравенства C.44) и рекур-
рекуррентной формулы C.42) вытекает, что
хп+1 = Va + xn < У a + xn+1. C.47)
С другой стороны, записывая рекуррентное соотношение C.42)
для номера п+\, мы получим равенство
C.48)
Из сопоставления равенства C.48) с неравенством C.47) и выте-
вытекает неравенство C.46). Тем самым индукция завершена и воз-
возрастание последовательности C.41) доказано.
Докажем теперь, что эта последовательность ограничена свер-
сверху. Снова пользуясь методом математической индукции, мы дока-
докажем, что для всех номеров п
хп<М, C.49)
где М — наибольшее из двух чисел а и 2.
Сначала проверим, что неравенство C.49) справедливо для
номера п=\. Пользуясь равенством C.43) и рассматривая от-
отдельно случаи 0<а<2 и а>2, мы получим
х1=Уа'<]^2<2 при 0<а<2,
C.50)
хх = ~\Га < а при а > 2.
Из C.50) вытекает, что Х\<.М, где М = тах{а, 2}.
Пусть теперь неравенство C.49) справедливо для данного но-
номера п. Пользуясь рекуррентным соотношением C.42) и рассмат-
рассматривая отдельно случаи 0<а<2 и а>2, мы получим, что
хп+1 = Va + хп < Vi + 2 = 2 приО<а<2,
__ C-51)
хп+1 = У а + хп < У а + а = У 2а < а при а > 2.
Из C.51) вытекает справедливость неравенства xn+i<.M, где
М = тах{с, 2}.
Таким образом, индукция завершена, и ограниченность последо-
последовательности C.41) доказана.
92 Гл. 3. Теория пределов
По теореме 3.15 последовательность C.41) сходится к некото-
некоторому пределу х.
Остается найти этот предел.
Из соотношения C.41) очевидно, что все элементы рассматри-
рассматриваемой последовательности неотрицательны. Следовательно, в си-
силу теоремы 3.13 и искомый предел х этой последовательности не-
неотрицателен.
Возводя в квадрат рекуррентное соотношение C.42), мы полу-
получим равенство
C.52)
Так как последовательность {хп} сходится к пределу х, то,
переходя в равенстве C.52) к пределу при я-voo и пользуясь тео-
теоремой о пределе суммы и произведения двух сходящихся последо-
последовательностей, мы получим следующее соотношение для определе-
определения искомого предела х:
х2=а + х
или, что то же самое,
х*—х—а = 0. C 53)
Соотношение C.53) представляет собой квадратное уравнение
для определения искомого предела х. Это уравнение имеет два
корня:
i + Ki+4a Оих= 1-/T+S
2 2 ^
Так как искомый предел, как уже указано выше, является не-
неотрицательным числом, то мы окончательно получим, что он сов-
совпадает с положительным корнем уравнения C.53), т. е. равен
X :==:
§ 3. ПРОИЗВОЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
1. Предельные точки, верхний и нижний пределы последова-
последовательности. Рассмотрим некоторую последовательность Х\, х2,..., хп, ...
и произвольную возрастающую последовательность целых по-
положительных чисел ki, kz,..., kn Выберем из последовательности
{хп} элементы с номерами k\, k2, ..., kn,— и расположим их в по-
порядке возрастания указанных номеров. Мы получим при этом но-
новую последовательность .
которую принято называть подпоследовательностью ис-
исходной последовательности {хп}.
В частности, и сама последовательность {хп} может рассмат-
рассматриваться как подпоследовательность с номерами kn = n.
§ 3. Произвольные последовательности 93
, Заметим сразу же, что всегда kn^>n, ибо любая подпоследова-
подпоследовательность, не совпадающая со всей последовательностью, получает-
получается путем некоторого прорежения элементов последовательности.
Справедливы два тривиальных утверждения:
1°. Если последовательность {хп} сходится к пределу а, то и
любая ее подпоследовательность сходится к тому же самому пре-
пределу а.
2°. Если все подпоследовательности некоторой последователь*
ности {хп} сходятся, то все они сходятся к одному и тому же пре-
пределу а (к этому же пределу а сходится и вся последовательность).
Докажем сначала утверждение 1°.
Фиксируем произвольное положительное число е и, пользуясь
сходимостью последовательности {хп} к пределу а, выберем по
этому е номер N такой, что \хп—а|<е при всех n>-N. Пусть
{xkn} — произвольная подпоследовательность последовательности
'{#„}. Так как kN>-N,To для всех номеров n^N элементы подпосле-
подпоследовательности {Xkn} удовлетворяют неравенству \xkn — а|<е, а эта
и означает, что подпоследовательность {Xkn} сходится к пределу а.
Для доказательства утверждения 2° достаточно учесть, что так
как сама последовательность {хп} (как частный случай подпосле-
подпоследовательности) сходится к некоторому пределу а, то и любая ее.
подпоследовательность сходится к тому же пределу а (в силу
утверждения 1°).
В полной аналогии с утверждением Iе доказывается, что любая
подпоследовательность бесконечно большой последовательности
представляет собой также бесконечно большую последовательность.
Введем фундаментальное понятие предельной точки последо-
последовательности.
Определение 1. Точка х бесконечной прямой (—оо, +оо)
называется предельной точкой последовательности {хп},
если в любой г-окрестности точки х содержится бесконечно много-
элементов этой последовательности.
Определение 2. Точка х бесконечной прямой (—оо, +оо)
называется предельной точкой последовательности {хп}у
если из этой последовательности можно выделить подпоследова-
подпоследовательность, сходящуюся к пределу х.
Убедимся в том, что определения 1 и 2 эквивалентны.
1) Пусть в любой е-окрестности х содержится бесконечно много
элементов последовательности {хп}. Рассмотрим совокупность е-ок-
рестностей точки х, для которых е последовательно равно
1 J_ _L _L
1 2 ' 3' ••¦" n
В первой из этих окрестностей выберем элемент последователь-
последовательности xhl с некоторым номером ku во второй из указанных окрест-
окрестностей выберем элемент последовательности Хиг с номером кг,
удовлетворяющим условию kz>ki, в третьей из указанных окрест-
Гл. 3. Теория пределов
ностей выберем элемент последовательности хиг с номером k3,
удовлетворяющим условию k3>k2.... Этот процесс можно продол-
продолжать неограниченно, так как в любой е-окрестности точки х со-
содержится бесконечно много элементов последовательности {хп}.
В результате мы получим подпоследовательность **,,.**,,**,, ....
jCkn, ... последовательности {хп}, которая сходится к пределу х,
ибо \xkn — x\<—.
2) Предположим, что из последовательности {хп} можно выде-
выделить подпоследовательность, сходящуюся к пределу х. Тогда в лю-
любой е-окрестности точки х лежит бесконечно много элементов под-
подпоследовательности (все, начиная с некоторого номера). Так как
каждый элемент подпоследовательности является элементом и всей
последовательности, то в любой е-окрестности х лежит бесконечно
много элементов последовательности.
Эквивалентность определений 1 и 2 доказана.
Выясним вопрос о наличии предельных точек у сходящейся
последовательности.
Лемма 1. Каждая сходящаяся последовательность имеет
только одну предельную точку, совпадающую с пределом этой по-
последовательности.
Доказательство. Пусть последовательность {хп} сходится
•к пределу х. Тогда в любой е-окрестности х лежит бесконечно
много элементов последовательности {хп} (все, начиная с некоторо-
некоторого номера), а поэтому х является предельной точкой последова-
последовательности {хп}.
Остается доказать, что ни одно число х', отличное от х, не яв-
является предельной точкой последовательности {хп}, но это непо-
непосредственно вытекает из доказанного выше утверждения 1, соглас-
согласно которому из сходимости всей последовательности к пределу х
вытекает сходимость любой ее подпоследовательности к тому же
пределу х.
Приведем пример ограниченной последовательности {хп}, имею-
имеющей две предельные точки. Докажем, что последовательность
—, 1 , —, 1 —, 1 , ... имеет только две
2 2 3 3 it ti
предельные точки х=0 и х—1. Тот факт, что эти две точки д;=0 и
х=1 являются предельными, вытекает из того, что подпоследова-
подпоследовательность всех нечетных элементов рассматриваемой последова-
последовательности сходится к пределу х = 0, а подпоследовательность всех
четных элементов рассматриваемой последовательности сходится
к пределу х=\. Остается доказать, что ни одно число Хо, отличное
ют 0 и 1, не является предельной точкой нашей последовательности.
Так как хо=т^О и х<ф\, то заведомо можно указать столь малое по-
положительное число е, что е-окрестности трех точек 0, 1 и Хо не
будут иметь общих точек (рис. 3.1).
§ 3. Произвольные последовательности 95
Но все нечетные элементы нашей последовательности, начиная с
некоторого номера, находятся в е-окрестности числа 0, а все чет-
четные элементы нашей последовательности, начиная с некоторого ног
мера, находятся в е-окрестности числа 1. Поэтому за пределами
е-окрестностей чисел 0 и 1 (и, в частности, в е-окрестности числа*
Хо) может лежать лишь конечное число элементов нашей последо-
последовательности. Это и означает, что х0 не является предельной точкой
последовательности.
Приведем теперь пример ограниченной последовательности
{хп}, имеющей бесконечно много предельных точек. Выше (в п. 3
§ 7 гл. 2) мы установили, что множество всех рациональных чисел
из сегмента [0, 1] можно занумеровать в последовательность {хп}-
Докажем, что любое вещественное число х из сегмента [0, 1] яв-
является предельной точкой указанной последовательности {хп}-
Заметим, что, каково бы ни было число х из сегмента [0, 1] для-
любого 0<е<1/2 хотя бы одно из двух чисел х—е и х + е также
принадлежит сегменту [0,1].
Предположим ради определенности, что число х + е принад-
принадлежит сегменту [0, 1]. Между двумя не равными друг другу ве-
вещественными числами х и х+е, в силу леммы 2 § 3 гл. 2, лежит
бесконечно много различных рациональных чисел. Это означает,
что при любом 0<е<1/2 в е-окрестности точки х лежит бесконеч*
но много элементов последовательности {хп}, т. е. х является пре-
предельной точкой этой последовательности.
Естественно, возникает идея рассмотрения наибольшей и наи-
наименьшей предельных точек последовательности.
Определение 3. Наибольшая предельная точка последова-
последовательности {Хп} называется верхним пределом этой последо-
последовательности и обозначается символом
х= lim xn.
Определение 4. Наименьшая предельная точка последова-
последовательности {хп} называется нижним пределом этой последо-
последовательности и обозначается символом
х = lim xn.
Возникает вопрос о существовании хотя бы одной предельной
точки и верхнего и нижнего пределов у любой ограниченной по-
последовательности.
Гл. 3. Теория пределов
Справедлива следующая замечательная теорема.
Основная теорема 3.16. У всякой ограниченной последо-
еательности существуют верхний и нижний пределы и, в. частно-
частности, существует хотя бы одна предельная точка.
Доказательство. Остановимся на доказательстве сущест-
существования у любой ограниченной последовательности хотя бы одной
предельной точки и верхнего предела. (Существование нижнего
предела доказывается аналогично.)
Пусть {хп} — произвольная ограниченная последовательность.
По условию ограниченности найдутся два вещественных числа m
и М такие, что любой элемент хп последовательности {хп} удов-
удовлетворяет неравенствам т<схп<М.
Рассмотрим множество {х} всех вещественных чисел х таких,
что правее * каждого из этих чисел либо вовсе нет элементов по-
последовательности {хп}> либо таких элементов лишь конечное число.
Иными словами, вещественное число х принадлежит множест-
множеству {х}, если правее х лежит не более чем конечное число элемен-
элементов последовательности {хп}, и не принадлежит множеству {х},
•если правее этого числа х лежит бесконечно много элементов по-
последовательности {Хп}-
Заметим, что множество {х} заведомо не является пустым: ему
принадлежит любое вещественное число х, удовлетворяющее нера-
неравенству x>Af (ибо правее такого х нет элементов последователь-
последовательности {хп}). Кроме того, очевидно, что множество {х} ограничено
снизу и в качестве его нижней грани может быть взято любое
число, меньшее т (правее такого числа лежат все элементы после-
последовательности {хп}, а их бесконечно много).
По основной теореме 2.1 гл. 2 у множества {х} существует
точная нижняя грань, которую мы обозначим символом х. Дока-
Докажем, что это число x=inf{x} и является верхним пределом после-
последовательности {хп}.
Достаточно доказать два утверждения:
1°. Число х является предельной точкой последовательности
\хп} (т. е. в любой е-окрестности х лежит бесконечно много эле-
элементов последовательности {хп})-
2°. Ни одно число х, большее х, уже не является предельной
точкой последовательности {хп} (это и будет означать, что х яв-
является наибольшей предельной точкой, т. е. верхним пределом
{*„}).
Для доказательства утверждения 1° фиксируем произвольное
положительное число е. По определению нижней грани любое
число, меньшее х (и, в частности, число х—е), не принадлежит
введенному нами множеству {х}. Значит, правее х—е лежит беско-
бесконечно много элементов последовательности {хп}.
* Напомним, что термин «г/ лежит правее хъ означает, что числа х и у
связаны неравенством у>х.
§ 3. Произвольные последовательности 97
Далее, из того, что число х является точной нижней гранью {х},
и из неравенства х<х+г вытекает, что найдется хотя бы один
элемент х' множества {х}, удовлетворяющий неравенствам х<х'<.
<х + е, т. е. лежащий левее х + г (рис. 3.2). В силу определения
множества {х} правее этого числа х' лежит не более чем конечное
число элементов последовательности {хп}.
На рис. 3.2 условно указано, что правее числа х—е лежит бес-
бесконечно много элементов последовательности {хп}, а правее чис-
числа х' лежит не более чем конечное число элементов этой последо-
последовательности.
Бесконечное число элементов
Конечное_чиспо*'
злементод~*~ _ _ _ = =
ос-е х сс+е=х-е х
Так как правее х—е лежит бесконечно много, а правее х' —
лишь конечное число элементов последовательности {хп}, то мы
приходим к выводу, что на полусегменте (х—е, х'] (а значит, и
на интервале (х—е, х+г)) лежит бесконечно много элементов по-
последовательности {хп}-
Итак, мы доказали, что для любого е>0 в е-окрестности точ-
точки х лежит бесконечно много элементов последовательности
{хп}- Это и означает, что х является предельной точкой последо-
последовательности {хп}. Утверждение 1° доказано.
Подчеркнем, что попутно мы доказали, что для любого е>0
правее числа х+г лежит не более чем конечное число элементов
последовательности {хп}.
Это последнее утверждение используем для доказательства
утверждения 2° о том, что х является наибольшей предельной
точкой. _
Пусть х — любое число, большее х. Обозначим через е поло-
положительное число г=_(х—хI2. При таком выборе е_интервалы
(х—е, х+г) и (х—е, х+г), т. ек е-окрестности точек х и х, не будут
иметь общих точек, а точнее, вся е-окрестность точки х будет
лежать правее числа х+г, т. е. правой границы е-окрестности точ-
точки х (рис. 3.3).
Выше мы установили, что для любого е>0 правее х+г лежит
не более чем конечное число элементов последовательности {хп}.
Значит, в рассматриваемой нами е-окрестности точки х лежит не
более чем конечное число элементов последовательности {хп}, а это
и означает, что х не является предельной точкой последователь-
ности {х„}. Утверждение 2° доказано.
4 Зак. 72
98 Гл. 3. Теория пределов
Мы доказали существование у ограниченной последовательнос-
последовательности {хп} верхнего предела (т. е. наибольшей предельной точки). Со-
Совершенно аналогично доказывается, что у такой последователь-
последовательности существует нижний предел, являющийся точной верхней
гранью того множества вещественных чисел {х}, левее каждого из
которых лежит не более чем конечное число элементов последова-
последовательности {хп}. Теорема 3.16 доказана.
Следствие 1 из теоремы 3.16. Если {хп} — ограничен-
ограниченная последовательность, х и х — ее нижний и верхний пределы,
е — любое положительное число, то на интервале (х—е, х + г)
лежат все элементы этой последовательности] начиная с некоторо-
некоторого номера (зависящего, конечно, от е).
Достаточно доказать, что для любого е>0 вне интервала
(х—е, х+е) лежит не более чем конечное число элементов после-
последовательности {Хп}- Тем более достаточно доказать, что правее
— . е е ^
х-\ и левее х лежит не более чем конечное число элемен-
элементов последовательности {хп}. Тот факт, что для любого е>0 правее
х -\ лежит не более чем конечное число элементов {хп}, уже
установлен в процессе доказательства теоремы 3.16. Совершенно
аналогично доказывается, что для любого е>0 левеех — лежит
не более чем конечное число элементов последовательности {хта|}.
Следствие 2 из теоремы 3.16. Пусть {хп} — ограничен-
ограниченная последовательность, х и х — ее нижний и верхний пределы,
(а, Ъ) — интервал, вне которого лежит не более чем конечное чис-
число элементов последовательности {хп}. Тогда интервал (х, х) со-
содержится в интервале (а, Ь) и, в частности, х—х-<Ь—а.
Доказательство. Достаточно доказать два неравенства
х<.Ь и а<х. Первое из этих неравенств вытекает из того, что точ-
точка Ь, правее которой лежит не более чем конечное число элемен-
элементов последовательности {хп}, принадлежит множеству {я}, рас-
рассмотренному при доказательстве теоремы 3.16, а х является точной
нижней гранью этого множества. Второе неравенство а<х уста-
устанавливается аналогично.
Следствие 3 из теоремы 3.16 (теорема Больца-
но — Вейерштрасса*). Из всякой ограниченной' последо-
последовательности можно выделить сходящуюся подпоследовательность.
Эта теорема является непосредственным следствием теоремы
3.16 и определения 2 предельной точки.
Теорема 3.16 проливает свет на то, как устроено множество
всех предельных точек любой ограниченной последовательности.
* Бернгард Больцано — чешский философ и математик A781—1848), Карл
Вейерштрасс — немецкий математик A815—1897).
§ 3. Произвольные последовательности 99
Если, как и выше, обозначить через х и х нижний и верхний пре-
пределы этой последовательности, то можно утверждать, что все ее
предельные точки лежат на сегменте [х, 5с], причем если указан-
указанная последовательность не является сходящейся, то она имеет по
крайней мере две предельные точки х и х. Рассмотренная нами
1,11,1 1 ,
выше последовательность —, 1 , —, 1 , ... , —, 1 —
2 2 3 3 п
, ... представляет собой пример последовательности, имею-
п
щей только две предельные точки х=0 и х= 1.
Другая рассмотренная выше последовательность {хп}, содер-
содержащая все рациональные числа из сегмента [0, 1], представляет
собой пример последовательности, предельные точки которой по-
покрывают весь сегмент [х, х], у которого ?=0, х=1.
Легко построить пример последовательности, предельными точ-
точками которой служат; 1) наперед заданное конечное множество
точек «1, а2, ••¦, аи; 2) наперед взятая бесконечная последователь-
последовательность точек аь а2, •••. #п> ••• * (во втором случае каждая предельная
точка последовательности предельных точек {ап} будет являться
предельной точкой исходной последовательности {*п})-
2. Расширение понятий предельной точки и верхнего и нижнего
пределов. Аналогом теоремы Больцано — Вейерштрасса для не-
неограниченной последовательности является следующее утверж-
утверждение.
Лемма 2. Из всякой неограниченной последовательности
можно выделить бесконечно большую подпоследовательность (и,
в частности, бесконечно, большую подпоследовательность, все эле-
элементы которой имеют определенный знак).
Доказательство. Прежде всего заметим, что если у не-
неограниченной последовательности отбросить любое конечное число
первых ее элементов, то после такого отбрасывания получится
снова неограниченная последовательность**. Пусть {xn}i — произ-
произвольная неограниченная последовательность. Тогда найдется эле-
элемент Xkx этой последовательности, удовлетворяющий неравенству
1*4, |>1. Учитывая, что последовательность {хп}, рассматривае-
рассматриваемая с номера ki+l, также является неограниченной, мы получим,
что найдется элемент этой последовательности х^, удовлетворяю-
удовлетворяющий неравенству \х/,,\ >2 при kz>ki. Продолжая эти рассуждения
далее, мы получим, что для любого номера п найдется элемент
Xkn, удовлетворяющий неравенству \xkn\>n при kn>kn-i.
* Таковой является последовательность
<h, ai, <h> <h< <h, <h, ... •
** Ибо предположение о том, что это не так, приводит к противоречию с
требованием неограниченности исходной последовательности.
100 Гл. 3. Теория пределов
Очевидно, что построенная нами подпоследовательность Xkt*
Xk,, ... >Xkn> ••• является бесконечно большой. Замечая, что эта
подпоследовательность заведомо содержит бесконечно много либо
положительных, либо отрицательных членов, мы может выделить
из нее бесконечно большую подпоследовательность, все элементы
которой имеют определенный знак. Лемма доказана.
Из леммы 2 и из теоремы Больцано — Вейерштрасса вытекает
следующее утверждение.
Лемма 3. Из совершенно произвольной последовательности
можно выделить либо сходящуюся подпоследовательность, либо
бесконечно большую подпоследовательность, все элементы которой
имеют определенный знак.
Лемма 3 естественно приводит к идее расширения понятия пре-
предельной точки последовательности. Договоримся формально до-
дополнить введенные выше конечные предельные точки последова-
последовательности еще двумя возможными предельными точками +оо и
— се.
Будем говорить, что + се [—се] является предельной точкой
последовательности {хп}, если из этой последовательности можно
выделить бесконечно большую подпоследовательность, все элемен-
элементы которой положительны [отрицательны].
При таком расширении понятия предельной точки из леммы 3
вытекает следующее утверждение: у совершенно произвольной по-
последовательности1 существует хотя бы одна предельная точка *.
Естественно, считая, что + се и — сю связаны с любым конеч-
конечным вещественным числом х соотношением -^-ce<x< + ce, убе-
убедимся в том, что у совершенно произвольной последовательности
{хп} существуют верхний и нижний пределы (т. е. существуют наи-
наибольшая и наименьшая предельные точки).
Ради определенности остановимся на доказательстве существо-
существования верхнего предела.
В силу теоремы 3.16 достаточно рассмотреть лишь случай, ког-
когда последовательность {хп} не является ограниченной.
Если при этом последовательность {хп} не является ограничен-
ограниченной сверху, то из нее можно выделить бесконечно большую после-
последовательность, все элементы которой положительны, и поэтому
+ се является предельной точкой, а значит, и верхним пределом
последовательности {хп}.
Остается рассмотреть случай, когда неограниченная последова-
последовательность {хп} является ограниченной сверху, т. е. когда сущест-
существует вещественное число М такое, что все элементы хп последова-
последовательности удовлетворяют неравенству хп^.М. Так как при этом
последовательность \хп} не является ограниченной снизу, то из
нее можно выделить бесконечно большую подпоследовательность,
* Либо конечная, либо равная +<х> или —оо.
§ 3. Произвольные последовательности 101
все элементы которой отрицательны, т. е. — оо является предель-
предельной точкой такой последовательности.
Если при этом указанная последовательность {хп} не имеет ни
одной конечной предельной точки, то единственная предельная точ-
точка — оо и является верхним пределом этой последовательности.
Если же при этом у указанной последовательности есть хотя бы
одна конечная предельная точка Хо, то, фиксировав некоторое е>0»
мы выделим из этой последовательности подпоследовательность тех
ее элементов хп, которые удовлетворяют неравенствам *
М
Хд
Выделенная подпоследовательность ограничена, и по теоре-
теореме 3.16 у нее существует наибольшая предельная точка, которая
является наибольшей предельной точкой (т. е. верхним пределом)
и всей последовательности {#„}. Существование у совершенно
произвольной последовательности верхнего предела доказано. Ана-
Аналогично доказывается, что у совершенно произвольной последова-
последовательности существует нижний предел.
В заключение заметим, что почти все понятия и утверждения,
установленные нами в этом и в предыдущем пунктах, переносятся
на случай произвольного числового множества {х}, имеющего
бесконечное число элементов.
Точку а бесконечной прямой (—оо, + оо) назовем предель-
предельной точкой такого множества, если в любой е-бкрестности точ-
ки а содержится бесконечно много элементов этого множества.
Наибольшую и наименьшую предельные точки множества {х}
назовем соответственно верхней и нижней предельными
точками этого множества.
Повторяя рассуждения теоремы 3.16 с заменой термина «по-
«последовательность {хп}» термином «множество {х}, содержащее бес-
бесконечное число элементов», мы придем к следующему утвержде-
утверждению: у всякого ограниченного множества {х}, имеющего бесконеч-
бесконечное число элементов, существуют верхняя и нижняя предельные
точки (и, в частности, существует хотя бы одна предельная точка).
Из этого утверждения вытекает следующее обобщение теоремы
Больцано — Вейерштрасса: из элементов всякого ограниченного
множества {х}, имеющего бесконечное число элементов, можно
выделить сходящуюся подпоследовательность **.
Как и для случая последовательности, удобно расширить поня-
понятие предельной точки и считать, что + оо [—оо] является пре-
предельной точкой множества {х}, если из элементов этого мно-
* Заметим, что Хо^М, ибо все элементы хп последовательности {хп}
удовлетворяют неравенству хп^.М. Далее заметим, что в силу того, что хо —
предельная точка, существует бесконечно много элементов хп последователь-
последовательности {хп}, удовлетворяющих неравенству хо—е^хп^.М.
** Любые два элемента которой являются различными элементами мно-
множества {х}.
102 Гл. 3. Теория пределов
жества можно выделить бесконечно большую последовательность,
состоящую из положительных [отрицательных] чисел.
Эта формализация позволяет нам утверждать, что у совер-
совершенно произвольного числового множества {х}, имеющего
бесконечное число элементов, существуют хотя бы одна
предельная точка, а также верхняя и нижняя предельные точки.
3. Критерий Коши * сходимости последовательности. При изу-
изучении вопроса о сходимости последовательности {хп} с помощью
определения сходящейся последовательности приходится оценивать
разность хп—а элементов последовательности и ее предполагаемо-
предполагаемого предела а.
Иными словами, приходится предугадывать величину предела а
этой последовательности.
В этом пункте мы установим «внутренний» критерий сходимости
последовательности, позволяющий сделать заключение о ее сходи-
сходимости лишь по величине ее элементов и не использующий величи-
величины предполагаемого предела этой последовательности. Для уста-
установления такого критерия введем понятие фундаментальной по-
последовательности.
Определение. Последовательность {хп} называется фун-
фундаментальной, если для любого положительного числа в най-
найдется номер N такой, что для всех номеров п, удовлетворяющих
условию n>-N, и для любого натурального р (р=1, 2,...) справед-
справедливо неравенство
\хп+р—Хп\<е.
Установим два важных свойства л ю б о й фундаменталь-
фундаментальной последовательности.
Свойство 1. Для любого положительного числа г найдется
элемент фундаментальной последовательности х^ такой, что в
е-окрестности этого элемента xN находятся все элементы хп этой
последовательности с номерами п, удовлетворяющими условию
N
Другими словами, для любого е>0 найдется элемент фундамен-
фундаментальной последовательности Xn, вне е-окрестности которого лежит
не более чем конечное число элементов этой последовательности.
Для доказательства этого свойства следует фиксировать произ-
произвольное положительное число е и взять в определении фундамен-
фундаментальной последовательности номер п равным N. Мы получим при
этом, что для любого натурального р (р=1, 2,...) элементы фун-
фундаментальной последовательности удовлетворяют неравенству
\xN+P—xN[\<e
или, что то же самое, неравенству
Xn—е < xN+p <xN + e.
* Огюстен Луи Коши — французский математик A789—1857).
§ 3. Произвольные последовательности 103
Так как р — любое натуральное число, то последние неравенства и
означают, что все элементы фундаментальной последовательности,
номер которых не меньше N, находятся в интервале
(хк—е, Xjv + e), т. е. в е-окрестности Xn- Свойство 1 доказано.
Свойство 2. Фундаментальная последовательность является
ограниченной.
Доказательство. Фиксируем некоторое е>0. Так как по-
последовательность {хп} является фундаментальной, то для этого g.
(в силу свойства 1) найдется элемент х$ такой, что все элементы
хп с номерами n>iV удовлетворяют неравенству
Обозначим теперь через А наибольшее из следующих (N+1)
чисел: \xi\, \х2\,..., \xN-i\, \xn—е|, |*лг + в|. Тогда, очевидно, для
всех номеров п будет справедливо неравенство |хте|<Л, которое и
означает ограниченность последовательности {.*„}. Свойство 2 до-
доказано.
Докажем теперь следующую вспомогательную теорему.
Теорема 3.17. Для того чтобы последовательность {хп}
была сходящейся, необходимо и достаточно, чтобы она была огра-
ограниченной и ее верхний и нижний пределы х и х совпадали между
собой.
Доказательство. 1) Необходимость. Пусть последова-
последовательность {хп} сходится. Тогда она ограничена (в силу теоре-
теоремы 3.8) и имеет единственную предельную точку (в силу леммы 1
из п. 1 этого параграфа). Это и означает, что ее верхний и нижний
пределы х и х совпадают между собой.
2) Достаточность. Пусть последовательность {хп} ограничена
(при этом она в силу теоремы 3.16 имеет верхний предел х и
¦'нижний предел х), и пусть х~х. Положим х—х=х. В силу следст-
следствия 1 из теоремы 3.16 для любого е>0 в интервале (х—г, х+&)
лежат элементы последовательности {хп}, начиная с некоторого
номера. В силу определения 3 сходящейся последовательности (см.
п. 4 § 1) это и означает, что последовательность {хп} сходится к
пределу х. Теорема 3.17 доказана.
Докажем теперь следующую важнейшую теорему.
Основная теорема 3.18 (критерий Коши сходи-
сходимости последовательности). Для того чтобы последова-
последовательность {хп} была сходящейся, необходимо и достаточно, чтобы
она была фундаментальной.
Доказательство. 1) Необходимость. Пусть последова-
последовательность {хп} сходится к некоторому пределу х. Докажем, что эта
последовательность является фундаментальной. Фиксируем произ-
произвольное положительное число г. Так как последовательность {хп}
сходится к пределу х, то для положительного числа в/2 найдется
номер N такой, что при всех iV
104 Гл. 3. Теория пределов
\хп—х\<г/2. C.54)
Если р — любое натуральное число, то при всех n>-N и подавно
будет справедливо неравенство
\хп+р—х\<е/2 C.55)
(ибо при n^N заведомо будет справедливо неравенство n+p>N).
Так как модуль суммы двух чисел не превосходит суммы их мо-
модулей, то из неравенств C.54) и C.55) мы получим, что при всех
n>N и для любого натурального р
\Хп+р—Хп\ = | [Хп+р~X] + [X—Хп] | < \Хп+р—Х\ + \ХП—Х\ <В,
а это и означает фундаментальность, последовательности {хп}.
2) Достаточность. Пусть последовательность {хп} является
фундаментальной. Требуется доказать, что эта последовательность
является сходящейся. В силу теоремы 3.17 достаточно доказать,
что последовательность {хп} ограничена и что ее верхний и нижний
пределы х и х_совпадают между собой.
Ограниченность любой фундаментальной последовательности
уже установлена нами выше (см. свойство 2). Остается доказать,
что для любой фундаментальной последовательности {хп} верхний
предел х и нижний предел х совпадают. Фиксируем произвольное
положительное число в. В силу свойства 1 фундаментальной после-
последовательности найдется элемент этой последовательности xN такой,
что вне е-окрестности этого элемента, т. е. вне интервала
(xN—e, xN+s) лежит не более чем конечное число элементов по-
последовательности {хп}- Но тогда в силу следствия 2 из теоре-
теоремы 3.16 интервал (х, х) обязан содержаться в интервале
(xN—e, Xzv + e) и, в частности, должно быть справедливо неравенст-
неравенство х—#< (xN + e) — (xN—в) =2е.
Так как, кроме того, х>?, то для любого е>0 будут справедли-
справедливы неравенства 0<х—л:<2в. В силу произвольности е из этих не-
неравенств вытекает, что х—?=0*, т. е. х=х. Критерий Коши пол-
полностью доказан.
Применим критерий Коши для установления расходимости
последовательности {хп} с элементами хп= 1 -J Ь ••• + —.
2 п
Заметим, что если для любого номера п натуральное число р
взять равным п, то мы получим, что для всех номеров п
*„|=
2n
* В самом деле, если бы разность х~х равнялась положительному числу
а, то,_взяв в качестве е число а/3, мы бы получили противоречие с неравен-
неравенством х—х
§ 4. Предел функции • 105
1
я+1
1 _
2я ~~
¦+¦
1
2
1
я+2
1
1
2я
ибо подчеркнутая сумма содержит п слагаемых, наименьшее из
которых равно .
Таким образом, для положительного числа е = — не сущест-
существует номера N такого, что при всех n>-N и для любого натураль-
натурального р справедливо неравенство \хп+Р—хп\<е. Это означает, что
рассматриваемая последовательность не является фундаменталь-
фундаментальной и (в силу критерия Коши) расходится.
В качестве второго примера применим критерий Коши для уста-
установления сходимости последовательности {хп} с элементами хп=*
— \ + q + ... +qn, где q — любое число из интервала 0<д<1.
Для любого номера п и любого натурального числа р (р =
= 1, 2,...) справедливо неравенство
\хп+р-хп\ = A + q + .. • + qn+P) -(I + q+....+ <7n)>
^^ !li C.56)
^ <
1—^ 1—
Фиксируем произвольное положительное .число е. Так как при
0<<7<1 последовательность {qn} является бесконечно малой, то
для положительного числа еA—q) найдется номер N такой, что
прк всех n>N справедливо неравенство
q). C.57)
Из неравенств C.56) и C.57) вытекает, что при всех tf>N и
для любого натурального р
а это означает, что рассматриваемая последовательность является
фундаментальной и (в силу критерия Коши) сходится.
§ 4. ПРЕДЕЛ (ИЛИ ПРЕДЕЛЬНОЕ ЗНАЧЕНИЕ)
ФУНКЦИИ
Перейдем теперь к изучению другой более сложной формы
операции предельного перехода, основанной на понятии предела
(или предельного значения) функции. Но прежде всего мы должны
уточнить сами понятия переменной величины и функции.
1. Понятия переменной величины и функции. Как мы уже ви-
видели в гл. 1, к понятию функции приводит изучение двух перемен*
106 Гл. 3. Теория пределов
ных величин, изменение которых взаимообусловлено. Поэтому есте-
естественно начать с уточнения понятия переменной величины.
Рассмотрение реальных физических переменных величин при-
приводит нас к выводу, что эти величины не всегда могут принимать
произвольные значения. Так, скорость материальной точки не
может быть больше 3-1010 см/с (т. е. скорости света в пустоте),
температура тела не может быть меньше —273°, смещение мате-
материальной точки, совершающей гармонические колебания по закону
у=Асо$(о)?+6), может принимать значения только из сегмента
[-А, +А]. .
Отвлекаясь от конкретных физических свойств наблюдаемых
в природе переменных величин, мы приходим к понятию матема-
математической переменной величины, характеризуемой толь-
только численными значениями, которые она может принимать *.
Множество {х} всех значений, которые может принимать дан-
данная переменная величина х, называется областью измене-
изменения данной пер ем е иной в ел и ч и н ы. Переменная вели-
величина считается заданной, если задана область ее изменения.
В дальнейшем мы, как правило, будем обозначать переменные
величины малыми латинскими буквами х, у, t,..., а области изме-
изменения этих переменных величин соответственно символами {х},
{у}, {/},....
Перейдем теперь к уточнению понятия функции.
Пусть задана переменная величина х, имеющая областью изме-
изменения некоторое множество {х}.
Если каждому значению переменной х из множества {х} ста-
ставится в соответствие по известному закону некоторое число у, то
говорят, что на множестве {х} задана функция у = у{х) или
y=f(x).
При этом переменная х называется аргументом или неза-
независимой переменной, множество {х} называется об-
областью задания функции, а то число у, которое соответ-
соответствует данному значению х, называется частным значением
функции в точке х. Совокупность всех частных значений об-
образует вполне определенное множество {у}, которое называют
либо областью изменения функции, либо множест-
множеством всех значений функции.
В обозначении y=f(x) букву / часто называют характерис-
характеристикой фун кци.и.
Для обозначения аргумента, функции и ее характеристики
могут употребляться различные символы.
Остановимся на примерах функций.
I9. г/ = К4—х2. Эта функция задана на сегменте — 2<л:«:2
(при этом выражение под знаком корня является неотрицатель-
* Понятие переменной величины также относится к числу начальных мате-
математических понятий.
§ 4. Предел функции
107
ным), а множеством всех ее значений является сегмент 0<су<2
(рис. 3.4).
2°. Так называемая функция Дирихле*, которая опреде-
определяется так:
, _., . @, если х — иррациональное число,
У=Р(х)=\л
{1, если х — рациональное число.
Эта функция задана на бесконечной прямой — оо<лг< +
жество всех ее значений состоит из двух точек 0 и 1.
3°.
у = sgn х =
+ 1, если х >0,
0, если х = 0,
— 1, если х < 0.
а мно-
мно(Термин «sgn» происходит от латинского слова signum —, знак.)
Читается: «г/ равно сигнум х». Эта функция задана на всей беско-
бесконечной прямой — оо<х< + оо, а множество всех ее значений со-
состоит из трех точек у=—1, г/ = 0 и г/=1 (рис. 3.5).
2 х
У
1
0
X
-1
Рис. 3.4
Рис. 3.5
4°. у=[х], или у=Е(х), где символ [х] или Е(х) обозначает
целую часть числа х или, точнее, наибольшее целое число, не пре-
превосходящее х. Читается: «г/ равно антье я» (от французского слова
entier — целый). Эта функция задана на всей бесконечной пря-
прямой— oo<#< + oo, а множеством всех ее значений является мно-
множество всех целых чисел (рис. 3.6).
5°. у = п\. Эта функция задана на множестве всех натуральных
чисел я=1, 2, 3 Множеством всех значений этой функции яв-
является множество натуральных чисел вида л! = Ь2-3- ... -п, где
л=1, 2, 3,... (рис. 3.7).
Часто закон, устанавливающий соответствие между множеством
всех значений аргумента и множеством всех значений функции, за-
задается посредством формул. Такой способ задания функции назы-
называется аналитическим.
* Петер Густав Л ежен-Дирихле — немецкий математик A805—1859).
108
Гл. 3. Теория пределов
При этом следует подчеркнуть, что функция может задаваться
разными формулами на разных участках области своего задания.
Например, функция
— х при х<С О,
х2 при х > О
задана аналитическим способом
э (рис. 3.8).
на всей бесконечной прямой
I — — _
х
х.
Рис. 3.8
Рис. 3.7
Весьма распространенным способом задания функции является
так называемый табличный способ, заключающийся в задании
таблицы отдельных значений аргумента и соответствующих им
значений функции. При таком способе задания можно приближен-
приближенно вычислить не содержащиеся в таблице значения функции, отве-
отвечающие промежуточным значениям аргумента. Для этого приме-
применяется метод интерполяции, заключающийся в замене функ-
функции между ее соседними табличными значениями какой-либо
функцией простой природы (например, линейной или квадратич-
квадратичной). Примером табличного способа задания функции может слу-
служить расписание движения поезда, которое определяет местополо-
§ 4. Предел функции 109
жение поезда в отдельные моменты времени. Интерполяция позво-
позволяет приближенно определить местоположение поезда в любой
промежуточный момент времени.
В практике физических измерений весьма распространенным
является и еще один способ задания функции — так называемый
графический способ, при котором соответствие между ар-
аргументом и функцией задается посредством графика (снимаемого,
например, на осциллографе).
2. Предел функции по Гейне и по Коши. Пусть функция
y—f(x) определена на некотором бесконечном множестве {х}, и
пусть а — точка бесконечной прямой (—оо, +оо), быть может и
не принадлежащая множеству {х}, но обладающая тем свойством,
что в любой б-окрестности этой точки а имеются точки множества
{х}, отличные от а *.
Например, множеством {х} может служить интервал (а, Ь); в
этом случае точка а, являясь граничной точкой интервала, ему не
принадлежит, но в любой б-окрестности а содержатся точки ука-
указанного интервала.
Другим примером множества {х}, на котором задана функция
f{x), может служить множество всех рациональных чисел, принад-
принадлежащих интервалу (а—б, а+6) с выкинутой точкой а.
Заметим, кстати, что при любом б>0 интервал (а—б, а+б),
из которого выкинута точка а, принято называть проколотой
6-окрестностью точки а.
Определение 1 (предел функции по Гейне**).
Число b называется пределом (или предельным значе-
значением) функции z/=/(x) в точке а {или при х-*-а), если для любой
последовательности значений аргумента Х\, Xz,..., хп, —, сходящейся
к а и состоящей из чисел хп, отличных от а, соответствующая по-
последовательность значений функции f(Xi), f(X2),...,f(xn) ...сходит-
...сходится к числу Ь.
Определение 1* (предел функции по Коши).
Число b называется пред ело м (или предельным значе-
значением) функции y—f(x) в точке а (или при x-xz), если для
любого положительного числа в найдется отвечающее ему поло-
положительное число б такое***, что для всех значений аргумента х,
удовлетворяющих условию 0<|х—а|<б, справедливо неравенство
\f(x)-b\<e. C.58)
Для обозначения предельного значения функции y=f(x) в точ-
точке а используют следующую символику:
lim/(#) = & или f(x)-+b при х-*¦ а.
* Это означает, что # является предельной точкой множества {*}.
** Генрих Эдуард Гейне — немецкий математик A821—1881).
*** Так как б зависит от е, то иногда пишут: б=6(е).
ПО Гл. 3. Теория пределов
Прежде чем доказывать эквивалентность определений 1 и 1 *,
сделаем несколько замечаний, разъясняющих смысл этих опреде-
определений.
Замечание 1. Подчеркнем важность фигурирующего в оп-
определении 1 требования, обязывающего элементы последователь-
последовательности значений аргумента хп быть отличными от а, и аналогичного
требования в определении 1*, обязывающего брать значения ар-
аргумента х, удовлетворяющие условию 0<|л:—а\, т. е. отличные от
а. Это требование вызвано уже тем, что функция y=f(x) может
быть не определена в точке а. Отсутствие этого требования сдела-
сделало бы невозможным использование предела функции для опреде-
определения производной функции. В самом деле, из гл. 1 нам известно,
что производная f (а) функции f(x) в точке а представляет собой
предел при x-mz следующей функции:
х — а
Очевидно, что эта функция F(x) не определена в точке а и это
вызвано существом дела.
Замечание 2. Особо подчеркнем, что множество {х}, на
котором задана функция f{x), вовсе не обязано сплошь покрывать
некоторую проколотую б-окрестность точки а. От этого множест-
множества {х} требуется только, чтобы оно имело хотя бы один элемент
в любой проколотой б-окрестности точки а. Примером множества
{х} может служить множество всех элементов последовательности
лежащих в фиксированной б-окрестности точки а = 0.
Замечание 3. Заметим, что фигурирующее в определе-
определении 1* условие 0<|л:—а\<6 эквивалентно соотношениям а—б<
<х<а+8, хфа, т. е. означает, что х принадлежит проколотой
б-окрестности точки а. Аналогично, фигурирующее в определе-
определении 1* неравенство C.58) эквивалентно неравенствам Ъ—в<
<f(x)<b + e, т. е. означает, что f(x) принадлежит е-окрестности Ь.
Замечание 4. Привлекая идею приближения функции f(x)
в окрестности точки а с наперед заданной точностью в, мы можем
следующим образом перефразировать определение 1* предела
функции по Коши: число Ъ называется предельным значе-
значением функции f(x) в точке а, если для любой наперед за-
заданной точности е>0 можно указать такую д-окрестность точ-
точки а, что для всех значений аргумента х, отличных от а и принад-
принадлежащих указанной Ь-окрестности точки а, число Ь приближает
значение функции f(x) с точностью в (рис. 3.9).
Замечание 5. Отметим, что функция f(x) может иметь в
точке а только один предел. В самом деле, для определения
предела функции по Гейне это вытекает из единственности предела
последовательности {f(xn)}, а для определения предела функции
§ 4. Предел функции
111
„¦
по Коши это вытекает из устанавливаемой ниже эквивалентности
этого предела пределу функции по Гейне.
Докажем теперь следующую важную теорему.
Теорема 3.19. Определения 1 и 1* предела функции по Гей-
Гейне и по Коши являются эквивалентными.
Доказательство. 1) Пусть сначала число b является пре-
пределом функции y~f(x) в точке а по Коши. Докажем, что это же
число Ъ является пределом функции y = f(x) в точке а и по Гейне.»
Пусть {хп} — любая
сходящаяся к а после-
последовательность значе-
значений аргумента, все
элементы которой от-
отличны от а. Требуется
доказать, что соответ-
соответствующая последова- / i
тельность значений
функции {f{xn)} схо-
сходится к Ъ.
Фиксируем произ-
произвольное положитель-
положительное число в и по нему
положительное число
8, которое в силу опре-
определения предела функции по Коши гарантирует справедливость
неравенства C.58) для всех значений х, для которых 0< \х—а|<б.
В силу сходимости последовательности {хп} к а для указанного
положительного числа б найдется номер N такой, что при всех
n>-N справедливо неравенство \хп—а|<б. Поскольку хпфа для
всех номеров п, то при всех n>>N справедливы неравенства 0<
<\хп—а|<б и, значит, в силу определения предела функции по
Коши при всех n^N справедливо неравенство \f(xn)—b\<e. Это
и означает, что последовательность {f{xn)} сходится к числу Ь.
2) Пусть теперь число b является пределом функции y=f{x)
в точке а по Гейне. Докажем, что это же число Ь является преде-
пределом функции y=f(x) в точке а и по Коши. Предположим, что это
не так. Тогда для некоторого положительного числа е и для сколь
угодно малого положительного числа б найдется хотя бы одно зна-
значение аргумента х такое, что 0<|л:—а|<б, но \f{x)—й|>е.
Таким образом, мы можем взять последовательность
Рис. 3.9
(я=1, 2,...) и утверждать, что для каждого ее элемента
найдется хотя бы одно значение аргумента хп такое, что
п
1
0<\xn-a\<j-,
но
C.59)
112 Гл. 3. Теория пределов
Левое из неравенств C.59) означает, что последовательность {хп}
сходится к а и состоит из чисел, отличных от а. Но в таком случае
согласно определению предела по Гейне соответствующая последо-
последовательность значений функции {f(xn)} обязана сходиться к чис-
числу Ь, а этому противоречит правое из неравенств C.59), справед-
справедливое для всех номеров п. Полученное противоречие доказывает
теорему.
Приведем примеры функций, как обладающих, так и не обла-
обладающих в данной точке а предельным значением.
Г. Функция f(x) =c = const имеет равный с предел в каждой
точке а бесконечной прямой. В самом деле, для любого значения
аргумента х разность f(x)—с равна нулю, и поэтому \f(x)—с|<е
для любого е>0 и для всех значений аргумента (в данном случае
для любого в>0 в определении предела по Коши можно брать в
качестве б любое положительное число).
2°. Функция f(x) =x в любой точке а бесконечной прямой имеет
предел, равный а. В самом деле, для этой функции последователь-
последовательности значений аргумента и соответствующих значений функции
тождественны, и поэтому, если последовательность {хп} сходится
к а, то и последовательность {f{xn)} также сходится к а.
3°. Функция Дирихле D(x), значения которой в рациональных
точках равны единице, а в иррациональных точках — нулю, не
имеет предела ни в одной точке а бесконечной прямой. Это выте-
вытекает из того, что для сходящейся к а последовательности рацио-
рациональных значений аргумента предел последовательности соответ-
соответствующих значений функции равен единице, в то время как для
сходящейся к а последовательности иррациональных значений ар-
аргумента предел последовательности соответствующих значений
функции равен нулю.
Введем теперь понятие одностороннего (т. е. правого
или левого) предела функции в данной точке а. Для этого нам
прежде всего следует уточнить характер того множества {х}, на
котором задана функция f(x). Мы теперь потребуем, чтобы это
множество {х} для любого б>0 имело хотя бы один элемент, при-
принадлежащий интервалу (а, а+б) [интервалу (а—б, а)].
Определение 2 (правый [левый] предел функ-
функции по Гейне). Число b называется правым пределом
[левым пределом} функции y = f(x) в точке а, если
для любой последовательности значений аргумента {хп}, сходя-
сходящейся к а и состоящей из чисел, больших а [меньших а], соответ-
соответствующая последовательность значений функции {f(xn)} сходится
к числу Ь.
Определение 2* (правый [левый] предел функ-
функции по Коши). Число b называется правым пределом
[ле в ым п р е д е ло м] функции y = f(x) в точке а, если
для любого положительного числа в найдется отвечающее ему по-
положительное число б такое, что для всех значений аргумента х.
§ 4. Предел функции ¦ ИЗ-
удовлетворяющих условию а<х<а-\-8 [условию а—6<х<а]„
справедливо неравенство C.58).
Для обозначения правого [левого] предела функции f (x) в точ-
точке а используют следующую символику:
lim f(x) = b [ lim f{x) = b]
*->-a+0 x-+a—0
или более краткую символику
f(a+O)=fr [f {a—0)=&].
В полной аналогии с теоремой 3.19 доказывается эквивалент-
эквивалентность определений 2 и 2*: следует лишь во всех проведенных при;
доказательстве этой теоремы рассуждениях брать значения аргу-
аргумента х и элементы последовательности {хп} большими числа №
[меньшими числа а].
В качестве примера рассмотрим функцию
+ 1, если х > О,
f(x)=sgnx= ¦
О, если х = О,
— 1, если- х < 0.
Эта функция имеет в точке а — О как правый, так и левый преде-
пределы, причем sgn@+0) = + 1, sgn@—0) =—1. В самом деле, для-
любой сходящейся к а=0 последовательности {хп}, состоящей и»
чисел, больших нуля, соответствующая последовательность-
{sgnxn} сходится к +1, а для любой сходящейся к а—О последо-
последовательности {хп}, состоящей из чисел, меньших нуля, соответству-
соответствующая последовательность {sgnxn} сходится к —1.
Из проведенных рассуждений вытекает, что у рассматриваемо»
функции z/ = sgnx не существует в точке а = 0 предела.
Итак, функция y = sgnx не имеет в точке а=0 предела, но-
имеет в этой точке правый предел, равный +1, и левый предел,
равный —1. Тот факт, что правый и левый пределы этой функции
не равны друг другу, не является случайным, ибо справедливо'
следующее утверждение: если функция f(x) имеет в точке а как
правый, так и левый пределы и если эти односторонние пределы-,
равны одному и тому же числу Ь, то эта функция имеет в точке а-
предел, равный Ь*.
Для доказательства этого утверждения достаточно воспользо-
воспользоваться определениями 1* и 2* и учесть, что если неравенство»
C.58) справедливо для значений аргумента х, удовлетворяющих,
условиям а<д;<а+б и а—6<#<a, то неравенство C.58) справед-
справедливо и для всех значений аргумента х, удовлетворяющих условию*
0<|лг—a|6
* Очевидно, справедливо и обратное утверждение: если функция f(x) име-
имеет в точке а равный Ь предел, то как правый, так и левый пределы f(x) в»
точке а существуют и оба равны Ь.
Щ4 Гл. 3. Теория пределов
Сформулируем теперь понятие предела функции при л;->с».
Для введения этого понятия следует потребовать, чтобы множест-
'ео {х}, на котором задана функция y=f(x), для любого б>0 име-
имело хотя бы один элемент, лежащий вне сегмента [—б, +б].
Определение 3 (предел функции при х-^-оо по
Гейне). Число Ъ называется пределом (или предельным
значением) функции y=f(x) при #->-оо, если для любой
^бесконечно большой последовательности значений аргумента
{хп} соответствующая последовательность значений функции
lf(Xn)} сходится к числу Ь.
Определение 3* (предел функции при #->-оо по
!Коши). Число b называется пределом (или предельным
значением) функции y=f(x) при х-^оо, если для любого
¦положительного числа е найдется отвечающее ему положительное
•число б такое, что для всех значений аргумента х, удовлетворяю-
удовлетворяющих условию |х|>6, справедливо неравенство C.58).
Для обозначения предела функции y=f{x) при л:->-оо исполь-
используют следующий символ:
lim/(») = &.
В полной аналогии с теоремой 3.19 доказывается эквивалент-
эквивалентность определений 3 и 3*. Следует лишь в рассуждениях, исполь-
использованных при доказательстве этой теоремы, всюду заменить схо-
сходящуюся последовательность значений аргумента {хп} бесконечно
большой последовательностью значений аргумента {хп}, а нера-
неравенство 0<|х—а|<б заменить неравенством |#|>б.
Примером функции, имеющей предел при #->-оо, может слу-
служить функция f(x) — — (хфО), В самом деле, для любой беско-
X
¦иечно большой последовательности значений аргумента {хп} соот-
соответствующая последовательность значений функции f{xn) = 1/хп
(в силу теоремы 3.6) является бесконечно малой, т. е. имеет
«своим пределом число Ь=0. Значит, в силу определения 3
lim — = 0.
Сформулируем, наконец, понятие предела функции при стрем-
стремлении х к бесконечности определенного знака. Для введения тако-
такого понятия потребуем, чтобы функция y=f(x) была задана на та-
талом множестве {х}, которое для любого б>0 имеет хотя бы один
элемент, лежащий правее б [левее — б].
Определение 4 (предел функции при л;->- + оо
[х-^>—оо] по Гейне). Число Ъ называется пределом
¦¦(или предельным значением) функции y = f(x) при
jc-^+ оо [при х-+—оо], если для любой бесконечно большой пос-
последовательности значений аргумента {хп}, все элементы которой
§ 4. Предел функции 115
положительны {отрицательны], соответствующая последователь-
последовательность значений функции {f(xn)} сходится к числу Ь.
Определение 4* (предел функции при х-^ + оо
[х-*—оо] по Коши). Число b называется пределом
(или предельным значением) функции y = f(x) при*
х->- + оо [при х->—<х>]1 если для любого положительного числа в
найдется отвечающее ему положительное число б такое, что для\
всех значений аргумента х, удовлетворяющих условию х>8 [х<
<—:б], справедливо неравенство C.58).
Для обозначения введенных понятий используется следующая
символика:
lim f(x) = b [ lim f(x) = b].
дс-Н-оо ж-»—оо
Эквивалентность определений 4 и 4* доказывается по схеме до-
доказательства теоремы 3.19: следует только во всех рассуждениях,
заменить сходящуюся последовательность значений аргумента1
{Хп} на бесконечно большую последовательность значений аргу-
аргумента {х„}, состоящую из положительных [отрицательных] чисел,.,
а неравенство 0<|х—а|<б заменить неравенством х>8 [х<—б].
Замечание 6. Отметим, что изученное нами в § 1—3 поня-
тие предела числовой последовательности {хп} можно рассматри-
рассматривать как частный случай предела функции при #->-+оо. В самом-
деле, если взять в качестве {х} множество всех натуральных чисел,
1, 2, ..., п, ..., а в качестве функции f(x), заданной на этом множе-
множестве, ту функцию, которая каждому значению аргумента п ставит
в соответствие л-й член последовательности хп, то определение 4*"
предела такой функции при л:->+оо в точности совпадет с опре~
делением предела числовой последовательности {хп}.
Замечание 7. Естественно, возникает идея связать воеди-
воедино все введенные нами понятия пределов функции и предел
числовой последовательности. В § 5 настоящей главы вводите»
понятие общего предела функции по базе, включающее в себя»
как частный случай все введенные нами понятия пределов;
функции и понятие предела числовой последовательности.
3. Критерий Коши существования предела функции. Ради опре-
определенности рассмотрим подробно случай предела функции z/=f(x)*
в точке а, введенного определениями 1 и 1*.
Определение. Будем говорить, что функция y=f(x) удов-
удовлетворяет в точке а условию Коши, если для любого поло-
жительного числа г найдется отвечающее ему положительное чис-
число б такое, что для любых двух значений аргумента х' и х"'„
удовлетворяющих условиям
0<|x'—а|<б, 0<|лг"—а|<б, C.60>
справедливо неравенство
116 Гл. 3. Теория пределов
Теорема 3.20 (критерий Коши существования
предела функции в то'чке а). Для того чтобы, функция
y^f(x) имела в точке а конечный предел, необходимо и достаточ-
достаточно, чтобы функция y=f(x) удовлетворяла в точке а условию
JKouiu.
Доказательство. 1) Необходимость. Пусть существует
конечный предел lim/(x) = 6. Фиксируем произвольное положи-
х-ю
тельное число е. В силу определения 1* предела функции по Коши
для положительного числа в/2 найдется положительное число б
такое, что, каковы бы ни были два значения аргумента х' и х",
удовлетворяющие условиям 0<\х'—а|<06, 0<|х"—а|<б, для со-
соответствующих значений функции справедливы неравенства
\f(x')-b\<-±-, \f(x")~b\<-^ C.62)
Так как модуль суммы двух величин не превосходит суммы
дах модулей, то в силу неравенств C.62) мы получим, что
\f(x')-f (х") | = | [f{x')-b] + [b-f
& это и означает, что функция */=/(*) удовлетворяет в точке а
условию Коши.
2) Достаточность. Пусть функция f(x) удовлетворяет в точке
<t условию Коши. Требуется доказать, что функция f(x) имеет
ъ точке а предел. Пусть {хп} — произвольная последовательность
значений аргумента;- сходящаяся к а и состоящая из чисел, отлич-
отличных от а. В силу определения 1 предела по Гейне достаточно до-
доказать, что соответствующая последовательность значений функ-
функции {f(xn)} сходится к некоторому числу b и что это число b одно
и то же для всех сходящихся к а последовательностей {хп}, состо-
состоящих из чисел, отличных от а.
Докажем сначала, что для каждой сходящейся к а последо-
последовательности {хп} значений аргумента, отличных от а, соответству-
соответствующая последовательность значений функции {f(xn)} сходится
к некоторому пределу. Фиксируем произвольное положительное
число в и по нему отвечающее ему, согласно условию Коши, по-
положительное число б. В силу сходимости последовательности {хп}
к а и в силу условия хпфа для этого б>0 найдется номер N та-
такой, что 0<|хп—а|<б при n>>N. Если теперь р — любое нату-
натуральное число (р=1, 2, 3, ...), то тем более 0<\хп+р—а\ <б при
n>N *
Таким образом, при ri^N и для любого натурального р спра-
справедливы два неравенства:
0<\хп+р—а\<8, 0<\хп—а\<8.
* Ибо если ri^N, то и подавно
§ 4. Предел функции 117
Из этих двух неравенств и из условия Коши вытекает, что при
N и для любого натурального р
а это означает фундаментальность последовательности {f(xn)}-
В силу критерия Коши. сходимости числовой последовательности
(см. теорему 3.18) последовательность {/(#«)} сходится к некото-
некоторому числу Ь.
Остается доказать, что для любых двух сходящихся к а после-
последовательностей значений аргумента {хп} и {х/}, все элементы кото-
которых отличны от а, соответствующие последовательности значений
функции {/(#„)} и {/(а/)} сходятся к одному и тому же пределу.
Предположим, что последовательности {/{#„)} и {f(xn')} сходятся
к пределам Ь и Ъ' соответственно. Рассмотрим новую последова-
последовательность значений аргумента х\, Х\, х2, х2, #з,1 #з', .... хп, хн', ...,
также сходящуюся к а и состоящую из чисел, отличных от а.
В силу доказанного выше соответствующая последовательность
значений функции /(*,), /(*/), f(x2), f(x2'), .... f(xM), f(x/),... обя-
'зана сходиться к некоторому пределу Ь". Но тогда в силу утверж-
утверждения, доказанного в начале п. 1 § 3, и любая подпоследователь-
подпоследовательность этой последовательности обязана сходиться к тому же са-
самому пределу Ь". Значит, как подпоследовательность нечетных
элементов f(xi), f(x2), ..., f(xn), —, так и подпоследовательность
четных элементов f(xi'), f(x2), ..., f(xn'), ... обе сходятся к Ь".
Отсюда вытекает, что Ъ — Ъ'=Ъ". Теорема полностью доказана.
Аналогично формулируется условие Коши и доказывается кри-
критерий Коши и для случаев правого [левого] предела в точке а,
предела при лс->-оо и предела при лг->+оо[д;->-—оо].
При формулировке условия Коши достаточно в приведенном
выше определении заменить условия C.60) для случая правого
[левого] предела в точке а условиями
а<х"<а+8 [а—8<х'<а, а—61<х"<а],
для случая предела при #->oo условиями
И>6, |*"|>6
и, наконец, для случая предела при #-»-+ оо [#-»—-оо] условиями
Соответствующие критерии Коши доказываются по схеме дока-
доказательства теоремы 3.20: следует только во всех рассуждениях
понимать под последовательностями значений аргумента {хп'} и
{хп"} в случае правого [левого] предела в точке а последователь-
последовательности, сходящиеся к а и состоящие из чисел, больших а [меньших
л], в случае предела при х->оо бесконечно большие последова-
последовательности и, наконеп, ; случае предела при х-> + оо[х->—оо] бес-
1 18 Гл. 3. Теория пределов
конечно большие последовательности, состоящие из положитель-
положительных [отрицательных] чисел.
4. Арифметические операции над функциями, имеющими пре-
предел. Справедлива следующая фундаментальная теорема.
Основная теорема 3.21. Пусть две функции f(x) и g(x)
заданы на одном и том же множестве {х} и имеют в точке а пре-
пределы, соответственно равные b и с. Тогда функции f(x)+g(x)f
f(x)—g(x), f(x)-g(x) u f(x)/g(x) имеют в точке а пределы, соот-
соответственно равные b + c, b—с, Ь-с, b/с (в случае частного нужно-
дополнительно требовать, чтобы с было отлично от нуля).
Доказательство. Пусть {хп} — произвольная сходящаяся
к а последовательность значений аргумента, все элементы которой
отличны от а. В силу определения 1 предела по Гейне соответст-
соответствующие последовательности значений функции {f{xn)} и {g(хп)}
сходятся к пределам бис соответственно. Но тогда в силу теорем
3.9—3.12 последовательности {/(*„) +g(xn)}, {f(xn)—g(xn)},
{f(xn) -g(Xn)} и 1 '(Xn>А сходятся к пределам b + c, b—с, b-c и
bjc соответственно. Это последнее в силу произвольности последо-
последовательности значений аргумента {хп}, сходящейся к а, и в силу
определения 1 предела по Гейне означает, что функции f(x) +
+ §(х), Hx)-g(x), f(x)-g(x) и f{x)/g(x) имеют в точке а преде-
пределы, соответственно равные b + c, b—с, Ь-с и Ь/с. Теорема доказана.
Доказательство соответствующей теоремы для случаев правого
[левого] предела в точке а, предела при л:->-оо и предела при
х-*- + оо[х-+—оо] проводится по той же схеме. Все отличие состо-
состоит в том, что в качестве последовательности значений аргумента
{хп} следует взять в случае правого [левого] предела в точке а
последовательность, сходящуюся к а и состоящую из чисел, боль-
больших а [меньших а], в случае предела при х->оо — бесконечно
большую последовательность и, наконец, в случае предела при
¦х-у-+ оо [х-*—оо] бесконечно большую последовательность, состо-
состоящую из положительных' [отрицательных] чисел.
Рассмотрим примеры применения теоремы 3.21. Выше в п. 2
мы убедились в том, что для любой точки а бесконечной прямой
limx = a. Используя теорему 3.21, мы можем утверждать, что
х-*а
limx2 = Шплг-Итл: = аа = а?
х-м дс-ш х-»а
и, вообще, для любого номера п
Нт Xя — ап.
х-+а
Пусть теперь Лг(*) =bo+blx+b2x2+... + bnxn, где b0, bu ..., &„_,,
Ьп?=0 — некоторые постоянные числа. Такая функция Рп(х) на-
называется многочленом степени п. В силу той же теоремы
3.21
§ 4. Предел функции 119
lim Pn(x) = lim [b0 + Ъхх + ... + bnxn\ = Ь0+Ьха + ... + bnan = Р„(а)
для любой точки а бесконечной прямой.
Итак, многочлен Рп(х) имеет предел в любой точке а бесконеч-
бесконечной прямой, и этот предел равен частному значению этого много-
многочлена в точке а.
Пусть, наконец, Рп(х) и Qm(x) — два произвольных многочле-
многочлена степеней пят соответственно. Частное R(x)~——— принято*
Qm{x)
называть рациональной дробью. В силу теоремы 3.21 для случая
частного
lim Pn(x)
UmR(x) = lim M^J^l = MEl = R{a)
x+a Qm(x) HmQm(x) Qm(a)
x-»a
в любой точке а, не являющейся корнем многочлена Qm(x). Таким
образом, рациональная дробь имеет предел в каждой точке а бес-
бесконечной прямой, не являющейся корнем ее знаменателя, и этот
предел равен частному значению этой дроби в указанной точке а.
5. Бесконечно малые и бесконечно большие функции. Ради оп-
определенности будем рассматривать предел функции в точке а.
Функция а(х) называется бесконечно малой в точке а,
если предел этой функции в точке а равен нулю.
Примером бесконечно малой в точке а функции может служить
функция а(х) = (х—а)п, где п — любое целое положительное
число.
В самом деле, в конце предыдущего пункта мы установили, что
многочлен (х—а)п имеет предел в каждой точке а, причем этот
предел равен частному значению этого многочлена в точке х=а,
т. е. равен нулю.
Заметим, что если функция f(x) имеет предел в точке а, рав-
равный числу Ь, то функция a(x)=f(x)—b является бесконечно ма-
малой в точке а.
Это вытекает из того, что пределы каждой из функций f(x) и
g(x)==b в точке а равны числу Ь, и из теоремы 3.21 для случая
разности f(x)—g(x).
Сформулированное утверждение приводит нас к следующему
специальному представлению для функции f(x), имею-
имеющей равный b предел в точке а:
f(x)=b + a(x), C.63)
где a(x) — некоторая бесконечно малая в точке а функция. Пред-
Представление C.63) весьма удобно в различных приложениях теории
пределов.
Введем теперь понятие бесконечно большой в данной точке а
справа [или слева] функции.
120 Гл. 3. Теория пределов
Функция А(х) называется бесконечно большой в точ-
точке а справа [слева] функцией, если для любой сходя-
сходящейся к а последовательности {хп} значений аргумента, все эле-
элементы которой больше а [меньше а], соответствующая последова-
последовательность значений функции {А(хп)} является бесконечно большой
последовательностью, все элементы которой, начиная с некоторого
номера, либо положительны, либо отрицательны.
Для бесконечно больших в точке а справа [слева] функций
используется следующая символика:
ИЛИ
lim А(х) = +оо [ lim А(х> = + оо]
x-ta+0 х-*а—0
lim А(х) = —оо [ lim А(х) = — оо].
-»а+0 х-*а—0
Иногда употребляют более лаконичную символику:
А (а+0)'= + оо [Л (а—0) = +оо]
или
А (а+0) =—оо [Л (а—0) =—оо].
Остановимся на методике сравнения двух бесконечно малых
в данной точке а функций. Пусть а(х) и $(х) — две функции, за-
заданные для одних и тех же значений аргумента и обе являющиеся
бесконечно малыми в точке а.
1°. Говорят, что а(х) является в точке а бесконечно
малой более высокого порядка, чем $(х) (имеет
в точке а более высокий порядок малости, чем
$(х)), если
lim-^- = 0. C.64)
х-*а
2°. Говорят, что a(х) и р(х) являются в точке а беско-
бесконечно малыми одного порядка (имеют в точке а
одинаковый порядок малости), если предел, стоящий
в левой части C.64), равен конечному числу, отличному от нуля.
3°. Говорят, что а(х) и р(х) являются в точке а эквива-
эквивалентными бесконечно малыми, если предел, стоящий в левой
части C.64), равен единице.
Для обозначения того, что а(х) является в данной точке беско-
бесконечно малой более высокого порядка, чем р(#), используют сле-
следующую запись:
а=о(р)
(читается: «а равно о малому от р»).
Итак, символ о(р) обозначает любую бесконечно малую в дан-
данной точке а функцию, имеющую в этой точке более высокий по-
порядок малости, чем бесконечно малая в той же точке функция
§ 4. Предел функции 121
). Из этого определения символа «о малое» вытекают следую-
следующие его свойства:
1) o(p)+o(p)=o(j3), o(P)-o(p)=o(p);
2) если7 = о(Р), то о(р) +о{у) = о(р);
3) если а и р— любые две бесконечно малые в данной точке
функции, то а-р = о(а) и а-р=о(Р).
Аналогично сравниваются две бесконечно большие в данной
точке а справа (или слева) функции.
Пусть А(х) и В(х) определены для одних и тех же значений»
аргумента и для определенности
lim А(х) = + о°, ()
x-ta+Q х-ю+0
1°. Говорят, что А (х) имеет в точке а справа б о лее вы-
со кий порядок роста, чем В (х), если функция
В(х)
является бесконечно большой в точке а справа.
2°. Говорят, что А(х) и В(х) имеют в точке а справа оди-
А(х)
наковый порядок роста, если предел функции —^-^- при
х->а+О равен конечному числу, отличному от нуля.
Приведем примеры сравнения бесконечно малых и бесконечно
больших функций.
1. Функции а(х) = х'6—х5 и $(х) = 5х3+х* являются в точке
дг = О бесконечно мальп/и одного порядка, ибо
,. а(х^ ,. д;3~д* .. 1 х* 1
lim—i— lim = lim
x-+Q p(x x-*o 53 + *
2. Функции a(x) = (x—2J- (x— 1) и p(a;) = (x—2J являются
в точке х=2 эквивалентными бесконечно малыми, ибо
(ЛГ-2)
О I v 1
3. Функции А (х) = и В(х) = — являются бесконечно
большими одинакового порядка роста в точке я = 0 как справа,
так и слева, ибо
lim -4гг = Нт B + х) = 2.
х»0 в(х) х0
х-»0
Аналогично определяются и сравниваются функции, бесконеч-
бесконечно малые или бесконечно большие при х-^оо, а также при х-^+оо
(соответственно при х—г—с»).
122 Гл. 3. Теория пределов
§ 5. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ
ПО БАЗЕ
Анализируя определения различных видов предела функции
f (х) по Коши, мы легко можем заметить, что во всех этих опре-
определениях требуется, чтобы для любого е>0 все значения этой
функции, отвечающие значениям аргумента х, принадлежащим
некоторому множеству С6, удовлетворяли неравенству C.58),
т. е. принадлежали е-окрестности Ь.
При этом множество С5, определенное для всех 6>0, имеет
разный вид при определении различных видов предела. При оп-
определении предела в точке а множество С6 представляет собой
проколотую б-окрестность точки а, при определении правого
[левого] предела в точке а множество С6 представляет собой
интервал (а, а + б) [соответственно (а—б, а)], при определении
предела при х->=оо множество Св представляет собой внешнюю
часть сегмента [—6, +6] и, наконец, при определении предела
при х->оо [при х-*—оо] множество Св представляет собой отк-
открытую полупрямую (б, +оо) [соответственно (—оо, —б)].
Если функция f(x) задана на множестве {х}, то во всех оп-
определениях пределов по Коши требуется, чтобы неравенство
C.58) было справедливо для тех элементов множества {х\, ко-
которые принадлежат соответствующему множеству Сб. Догово-
Договоримся обозначать символом Вв подмножество тех элементов {х},
которые принадлежат С5, т. е. положим
Естественно, возникает вопрос, какими общими свойствами
обладает совокупность всех подмножеств Вь множества {х}.
Анализ условий, при которых формулируются определения
1*—4* пределов функции по Коши, приводит нас к выводу, что
множество {х} задания функции f(x) всякий раз имеет хотя бы
один элемент, принадлежащий Сб, т. е. множество В5 всегда
не является пустым.
Далее легко убедиться в том, что для всех видов пределов
пересечение двух любых множеств совокупности {В6} представ-
представляет собой некоторое множество той же совокупности.
Так, например, пересечение двух множеств В6 и В/, первое
из которых состоит из значений аргумента, принадлежащих
проколотой б-окрестности точки а, а второе — из значений
аргумента, принадлежащих проколотой б'-окрестности точки а,
представляет собой совокупность значений аргумента, принад-
принадлежащих проколотой б"-окрестности точки а, где б" — наимень-
наименьшее из двух положительных чисел б и б', т. е. представляет
собой множество Вь" той же совокупности {В6}.
В более общей ситуации, которая может встретиться, напри-
например, при изучении функции нескольких переменных, пересече-
§ 5. Общее определение предела функции по базе 123
ние двух любых множеств совокупности {В&} само может не яв-
являться элементом этой совокупности, но обязательно содержит
элемент этой совокупности.
Проведенное рассмотрение, естественно, приводит нас к фун-
фундаментальному понятию базы множества {х} задания функции.
Определение 1. Будем говорить, что бесконечная со-
совокупность B = {B6} подмножеств В6 множества {х} образует
базу (или базис фильтра) множества {х}, если для
элементов этой совокупности выполнены два требования:
1) каждый элемент В6 является непустым подмножеством мно-
множества {х}; 2) в пересечении любых двух элементов совокуп-
совокупности {В6} обязательно содержится некоторый элемент этой же
совокупности.
Приведем примеры наиболее употребительных баз (базисов
фильтра).
1°. Пусть функция f(x) задана на множестве {х}, имеющем
хотя бы один элемент в любой проколотой б-окрестности точки
а. Указанную проколотую б-окрестность точки а обозначим
символом С(, и положим Bt = {x}[\Cb. Очевидно, совокупность
В = {В«} множеств Вь при всех б>0 образует базу множества
{л:}, ибо каждое множество В6 при любом б>0 не является пус-
пустым и пересечение любых двух множеств совокупности {BJ, как
уже отмечалось выше, представляет собой множество из той
же совокупности.
Рассмотренную базу {В6} принято обозначать символом
х->а.
2°. Пусть функция /(х) задана на множестве {х}, имеющем
при любом б>0 хотя бы один элемент, принадлежащий интер-
интервалу (a, a+ 6) [соответственно (а—б, а)]. Обозначив указан-
указанный интервал символом С6, положим Bi = {x}plCs. Тривиально
проверяется, что совокупность В = {В6} множеств Bs, отвечаю-
отвечающих всевозможным б>0, образует базу множества {х}.
Указанную базу принято обозначать символом х-^а + 0 [со-
[соответственно х->а—0].
3°. Пусть функция f(x) задана на множестве {х}, имеющем
хотя бы один элемент вне сегмента [—б, +б] при любом б>0.
Положим Сб=(—оо, +оо)\[—б, +'б], B6={x}f\CB. Легко прове-
проверить, что совокупность В = {В6} образует базу множества {х}.
Эту базу принято обозначать символом jc-voo.
4°. Пусть функция f(x) задана на множестве {х}, имеющем
при любом б>0 хотя бы один элемент на полупрямой
( + б, +оо) [соответственно (—с», —б)]. Обозначим указанную
полупрямую символом С„ и положим В& = {х}(\С6. Легко убедить-
убедиться в том, что совокупность В—{В6} образует базу множест-
множества {х}.
Эту базу обозначают символом л:->+оо [соответственно
JC-»-—оо].
124 Гл. 3. Теория пределов
5°. Пусть, наконец, множество {х} представляет собой мно-
множество всех натуральных чисел 1, 2, 3 п Положив Вв=
= {¦*}(")( + 6. +°°)-Для любого 6>0, мы легко убедимся и в том,
что совокупность В={5«} образует базу множества {х}.
Эту базу принято обозначать символом я->оо.
Сформулируем теперь фундаментальное определение преде-
предела функции f(x) по базе В множества ее задания, содержащее
в себе как все рассмотренные выше виды предела функции, так
и предел числовой последовательности.
Предположим, что функция f(x) задала на множестве {х} и
что совокупность В = {В6} подмножеств Вь множества {х} обра-
образует базу множества {х}.
Множество всех значений, которые принимает функция f(x),
когда ее аргумент х пробегает множество В6, договоримся на-
называть образом множества В6 и обозначать символом.
f(B)
Определение 2. Число Ь называется пределом
функции f(x) no базе В множества ее задания,
если для любого е>0 существует такой элемент В6 базы В,
образ f(Bt) которого принадлежит е-окрестности точки Ъ, т. е.
принадлежит интервалу (Ь—е, Ь + е).
Для обозначения предела функции f(x) по базе В множест-
множества ее задания будем использовать симв )л
lim f(x) = b.
в
Читатель без труда проверит, что это общее определение
предела по базе содержит в себе как часовые случаи изученные
выше виды пределов, отвечающие базам »->а, я->а+0, х->а—0,
я-^°°, д;-^-+оо, х->—оо И «->оо.
Легко проверить также, что для общего определения преде-
предела по базе остаются справедливыми основные свойства преде-
предела, отвечающего простейшей базе х-*~а.
Мы ограничимся тем, что докажем критерий Коши сущест-
существования общего предела функции f(x) по базе В множества ее
задания.
Теорема 3.22. Для существования предела функции f(x)
по базе В = {В6} множества ее задания необходимо и достаточно,
чтобы для любого е>0 нашелся элемент Вь базы В, образ f(Bt)
которого содержится в некотором интервале длины 2е.
Доказательство. 1) Необходимость очевидна: если су-
существует предел b функции {(х) по базе В, то для любого
е>0 найдется элемент этой базы 58, образ которого /(fi5) со-
содержится в интервале (Ь—е, Ь + е), имен щем длину 2е.
2) Достаточность. Пусть для любого е>0 существует эле-
элемент Вц базы В, образ которого f(B6) содержится в некотором
интервале длины 2е. Рассмотрим бесконечно малую последова-
§ 5. Общее определение предела функции по базе 12S
тельность положительных чисел е„ = — («=1, 2, 3, ...)• Для:'
п
каждого 8п найдется элемент базы В&п, образ которого /(?sra)
содержится в некотором интервале длины 2е«.
По определению базы в пересечении элементов 5а, и B6i,
обязательно лежит некоторый элемент базы, который мы обоз-
обозначим символом.^. Образ этого элемента /!Ве2) лежит как
в некотором интервале Д длины 2ei, так и в некотором интер-
интервале /2' длины 2е2. Пересечение интервалов 1Х и 1% представляет-
собой интервал h длины, не большей 2ег, содержащийся в ин-
интервале 1\. Далее, по определению базы в пересечении элемен-
элементов Вег и Бб3 обязательно лежит некоторый элемент базы, ко-
который мы обозначим символом В(,3. Образ этого элемента
/B?63) лежит как в интервале h длины, не большей 2г% так н
в некотором интервале h' Длины 2ез. Пересечение интервалов-
h и h' представляет собой интервал h длины, не большей 2ез,-
содержащийся в интервале /г.
Продолжая эти рассуждения далее, мы построим последо-
последовательность элементов базы В&г, В&„...,Ъ&, ... таких, чт&
образ f(B(,n) каждого элемента В&п содержится в некотором
интервале /„ длины, не большей 2е„, причем в последовательнос-
последовательности интервалов h, h, ¦¦-, In, ... каждый следующий интервал со-
содержится в предыдущем. Обозначим символом 1„ сегмент, по-
получающийся добавлением к интервалу 1п его концов. Так как
последовательность 72, h, ..., Тп, ... представляет собой стяги-
стягивающуюся систему сегментов (см. п. 2 § 2), то в силу следствия;
из теоремы 3.15 существует, и притом единственная, точка Ъ,
принадлежащая всем сегментам.
Остается доказать, что Ь является пределом функции f(x)
по базе В, т. е. убедиться в том, что для любого е>0 найдется
элемент базы В, образ которого содержится в интервале-
(Ь—г, Ъ + г).
В силу того, что система сегментов {/«} является стягиваю-
стягивающейся и Ъ является общей точкой всех сегментов, мы можем
утверждать, что для любого е>0 найдется сегмент 7« с доста-
достаточно большим номером п, содержащийся в интервале
(Ь—е, Ь + е). Это означает, что при соответствующем номере п
элемент базы Ё&п имеет образ f{B$ ), содержащийся в интер-
интервале (Ь—е, b + г). Теорема доказана.
Подчеркнем, что доказанная теорема содержит в качестве-
частных случаев как критерий Коши сходимости числовой пос-
последовательности, так и критерии Коши существования всех
рассмотренных выше видов предела функции.
J26 Гл. 3. Теория пределов
В качестве возможных обобщений изложенной теории мож-
можно рассматривать функции, заданные на подмножествах произ-
произвольного метрического пространства (см. по этому поводу до-
дополнение 2 к гл. 12).
Замечание. Базы В и D множества {х} называются экви-
эквивалентными, если для любого элемента B&t базы В най-
найдется такой элемент D^ базы D, что D^CZB^, и для любого
элемента D^ базы D найдется такой элемент 5в2 базы В,
что Be.CZDe,. Совокупность всевозможных эквивалентных
между собой баз В множества {а'} называется фильтром мно-
множества {х}.
Нетрудно убедиться, что утверждения о пределах функции
по эквивалентным базам В и D справедливы одновременно.
Глава 4
НЕПРЕРЫВНОСТЬ ФУНКЦИИ
В настоящей главе будет всесторонне изучаться важнейшее по-
понятие математического анализа — понятие непрерывности»
функции.
В дополнении 2 к гл. 12 понятие непрерывности будет введено
в общей ситуации, когда задано отображение одного метрического»
пространства в другое.
§ 1. ПОНЯТИЕ НЕПРЕРЫВНОСТИ ФУНКЦИИ
1. Определение непрерывности функции. Пусть точка а при-
принадлежит области задания функции f{x}* и любая е-окрестность
точки а содержит отличные от а точки области задания функции*
Формальное определение непрерывности в.
точке а. Функция f{x} называется непрерывной в точке
а, если функция f(x) имеет в точке а предел и этот предел равен
частному значению f(a) функции f(x) в точке а.
Используя определения предела функции y=f(x) в точке а по.
Гейне и по Коши, мы приходим к определению непрерывности
функции в данной точке а по Гейне и по Коши.
Определение 1 (непрерывность в точке а по?
Гейне). Функция y=f(x) называется непрерывной в точке
а, если для любой сходящейся к а последовательности значений
аргумента хи х%, ..., хп, соответствующая последовательность зна-
значений функции f(xi), /(x2), ..., f(xn), ... сходится к числу f(a).
Замечание 1. По сравнению с определением 1 предела
функции по Гейне (см. п. 2 § 4, гл. 3) в определении непрерывнос-
непрерывности по Гейне мы опустили требование, обязывающее все элементы
последовательности {хп} быть отличными от а. Это можно сделать
в силу того, что добавление к элементам последовательности
{f(xn)}, сходящейся к числу f(a), любого числа новых элементов,
равных f(a), не нарушит сходимости этой последовательности,
к /(а).
* Заметим, что этого не требовалось, когда мы рассматривали предел1
функции {(х) .в точке а.
** Т. е. точка а является предельной точкой множества {х}, на котором
задана функция f(x).
fl28 Гл. 4. Непрерывность функции
Определение 1* (непрерывность в точке а по
Кош и). Функция f(x) называется непрерывной в точке
•а, если для любого положительного числа е найдется отвечающее
«ему положительное число б такое, что для всех значений аргумен-
аргумента х, удовлетворяющих условию \х—а|<б, справедливо неравен-
ство |/(*)-/(а)|<е.
Замечание 2. По сравнению с определением 1* предела
-функции по Коши (см. п. 2 § 4, гл. 3) в определении непрерывнос-
непрерывности по Коши мы опустили требование, обязывающее все значения
аргумента х удовлетворять неравенству \х—а|>0, т. е. быть от-
отличными от а. Это можно сделать в силу того, что для значений
jc=a разность f(x)—/(а) равна нулю и удовлетворяет неравенству
\f(x)— /(°0 I <е при любом s>0.
Условие непрерывности функции f(x) в точке а символически
можно выразить следующим равенством:
limf(je) = /(a).
Так как а = \\тах, то этому равенству можно придать следую-
х-+а
щую форму:
lim f(x) = f{\\mx).
Следовательно, для непрерывной в точке а функции символ lim
х-*а
лредельного перехода и символ / характеристики функции можно
менять местами.
Из теоремы об эквивалентности определений предельного зна-
значения по Гейне и по Коши (см. теорему 3.19 из п. 2 § 4 гл. 3)
«следует, что определения непрерывности функции по Гейне и по
Коши (определения 1 и 1*) эквивалентны.
Сформулируем теперь определение односторонней непрерыв-
непрерывности функции f(x) в точке а, т. е. непрерывности в точке а либо
только справа, либо только слева.
От множества {х} задания функции f(x) мы на этот раз долж-
должны потребовать, чтобы это множество включало точку а и для
любого б>0 имело хотя бы один элемент, лежащий на интервале
[а, a+б) Соответственно (а—б, а)].
Формальное определение непрерывности в
точке а справа [слева]. Функция f(x) называется непре-
непрерывной в точке а справа [с л е в а], если правый [левый]
предел этой функции в точке а существует и равен частному зна-
значению f(a) функции f(x) в точке а.
Используя определения правого [левого] предела функции
f(x) в точке о по Гейне и по Коши, мы придем к определениям
непрерывности функции f(x) в точке а справа [слева] по Гейне и
яо Коши.
§ 1. Понятие непрерывности функции 129
Определение 2 (непрерывность функции в точ-
точке а справа [слева] по Гейне). Функция f(x) называется
непрерывной в точке а справа [слева], если для
любой сходящейся к а последовательности значений аргумента
{Хп}, все элементы которой удовлетворяют условию хп>а[хп<а],
соответствующая последовательность значений функции {/(*«)}
сходится к числу f(a).
Заметим, что в этом определении условие хп>а [хп<а] можно
заменить менее жестким условием хп^а [хп^а], ибо добавление
к последовательности {/(#«)}> сходящейся к f(a), какого угодно
числа новых элементов, равных f(a), не нарушит сходимости этой
последовательности к f(a).
В применениях более эффективно условие хп>а[хп<а].
Определение 2* (непрерывность функции.в точ-
точке а справа [слева] по Кош и). Функция f(x) называется
непрерывной в точке а справа [слева], если для лю-
любого положительного числа е найдется отвечающее ему положи-
положительное число б такое, что для всех значений аргумента х, удов-
удовлетворяющих условию a<x<a+6 [а—8<х<.а], справедливо не-
неравенство
Заметим, что и в этом определении условие а<х<а + 6
[а—б<х<а] можно было бы заменить менее жестким условием
а^х<а + 8 [а—8<х^а].
Эквивалентность определений 2 и 2* вытекает из эквивалент-
эквивалентности соответствующих определений предела функции.
Тот факт, что функция f(x) непрерывна в точке а справа
[слева], записывают так:
lim/(х) = f (а) или f(a + O) = f (a)
х-нг+О
[ lim/(%) = /(а) или/(а-0) = /(а)].
х-*а—О
Замечание 3. Если функция j(x) непрерывна в точке а и
слева, и справа, то она непрерывна в этой точке. Действительно,
в силу утверждения, доказанного в п. 2 § 4 гл. 3, в этом случае
существует предел функции в точке а, равный f(a).
Точки, в которых функция не обладает свойством непрерывнос-
непрерывности, называются точками разрыва этой функции.
Рассмотрим примеры.
1) Степенная функция f(x)=xn, где п — натуральное число,
непрерывна в каждой точке а бесконечной прямой (—оо, +оо).
Действительно, в гл. 3 было установлено, что предельное зна-
значение этой функции в любой точке а бесконечной прямой равно
частному значению а".
5 Зак. 72
130 Гл. 4. Непрерывность функции
2) Многочлены и рациональные дроби имеют в каждой точке
области задания предельное значение, равное частному значению
(см. п. 3 § 4 гл. 3). Поэтому они являются непрерывными функ-
функциями в каждой точке области задания.
3) Функция f(x)=sgnx имеет разрыв в точке х = 0 и непрерыв-
непрерывна во всех остальных точках числовой оси. Действительно, в точке
х=0, как было показано в гл. 3, существуют правый (равный +1)
и левый (равный —1) пределы функции sgn;c. Поскольку эти од-
односторонние пределы не равны друг другу, функция sgnx в точ-
точке 0 разрывна (не является непрерывной). В остальных точках
оси она обладает предельным значением, равным частному значе-
значению, и непрерывна.
4) Функция Дирихле D(x) (см. § 4 гл. 3) разрывна в каждой
точке числовой оси, поскольку она не имеет предельного значения
ни в одной точке.
Заметим, однако, что функция f(x)=x-D(x), где D(x) — функ-
функция Дирихле, является непрерывной в точке д; = 0 и разрывной во
всех остальных точках бесконечной прямой. Разрывность f(x)
в любой точке Хот^О устанавливается точно -так же, как для функ-
функции D(x) (для любой сходящейся к Хо последовательности {хп}
рациональных точек соответствующая последовательность {f(xn)}
сходится к числу Хо=т^О, а для любой сходящейся к х0 последова-
последовательности {хп} иррациональных точек соответствующая последова-
последовательность {f(xn)} сходится к нулю).
Убедимся в том, что функция f(x) = x-D(x) непрерывна в точке
х=0. Для любой бесконечно малой последовательности значений
аргумента {хп} последовательность {D(xn)} ограничена, а потому
(в силу теоремы 3.3 из гл. 3) последовательность f(xn)=xn-D(xn)
является бесконечно малой, т. е. имеет предел нуль, равный част-
частному значению /@).
Мы будем говорить, что функция непрерывна на множе-
с т в е {х}, если она непрерывна в каждой точке этого множества.
Например, функция, непрерывная в каждой точке интервала,
называется непрерывной на интервале.
Особо договоримся называть функцию f(x) непрерывной
на сегменте [а, Ь], если она непрерывна в каждой внутренней
точке этого сегмента и, кроме того, непрерывна справа в точке а
и непрерывна слева в точке Ь.
Выше, давая определение непрерывности функции f(x) в точке
а, мы предположили, что точка а обладает тем свойством, что
в любой ее е-окрестности содержатся точки области задания, от-
отличные от а. Формально этого предположения можно бы было и
не делать и допустить, что точка а обладает е-окрестностью, сво-
свободной от точек области задания функции, а в самой точке а
функция определена. В этом случае формально .функцию .[(х)
можно считать непрерывной в точке а. Однако вся содержатель-
содержательная часть понятия непрерывности функции относится как раз
§ 1. Понятие непрерывности функции 131
к случаю, когда а —• предельная точка области определения
функции.
Определение непрерывности функции можно дать и в следу-
следующей, эквивалентной форме.
Определение 1**. Функция f(x) называется непре-
непрерывной в точке а, если для любой окрестности точки f(a)
найдется такая окрестность точки а, что образ всех точек мно-
множества задания функции, лежащих в этой окрестности точки а?
при отображении, осуществляемом функцией f(x), целиком ле-
лежит в указанной окрестности точки f(a).
В дополнении 2 к гл. 12 будет показано (даже в более об-
общей ситуации), что последнее определение непрерывности экви-
эквивалентно предыдущим. Предлагается в качестве упражнения
проверить это.
Используя введенное в § 5 гл. 3 общее определение предела
функции f(x) по базе В множества ее задания, мы можем объ-
объединить в одной формулировке понятие непрерывности в точке
а, в точке а справа и в точке а слева.
Пусть функция f{x) задана на множестве {х}, которое вклю-
включает точку а и допускает базу В одного из видов х-^-а, х->а+0,
х-уа—0*.
Функция f(x) называется непрерывной в точке а, если ее
предел по базе В множества ее задания существует и равен
На).
2. Арифметические операции над непрерывными функциями.
Убедимся в том, что арифметические операции над непрерыв-
непрерывными функциями приводят снова к непрерывным функциям.
Справедлива следующая теорема.
Основная теорема 4.1. Пусть на одном и том же Мно-
Множестве заданы функции f(x) и g(x), непрерывные в точке а. Тогда
функции f(x) + g(x), f(x)—g(x), f(x)-g(x) и -^-L непрерывны.
g{x)
в точке а (в случае частного нижно дополнительно требовать
8{а)Ф0).
Доказательство. Так как непрерывные в точке а функции
f(x) и g(x) имеют в точке а пределы, соответственно равны f(a)
и g(a), то в силу теоремы 3.21 из гл. 3 пределы функций f(x) +
+ 8{х), }(x)—g(x), f(x)-g(x) и ' (х' существуют и равны соот-
соответственно f(a)+g(a), f(a)—g(a), f{a)-g{a) и -Ю-. Но как раз
эти величины равны частным значениям перечисленных функций
в точке а. По определению эти функции непрерывны в точке а,
что и требовалось доказать.
* См. § 5 гл. 3.
132 Гл. 4. Непрерывность функции
3. Сложная функция и ее непрерывность. Функции, полученные
в результате суперпозиции двух или нескольких функций, мы бу-
будем называть сложными. Под суперпозицией двух функций
мы понимаем функцию, полученную в результате наложения или
последовательного применения указанных двух функций в опреде-
определенном порядке. Ясно, что достаточно определить сложную функ-
функцию, полученную в результате суперпозиции только двух функций.
Указанный алгоритм можно будет применять, беря суперпозицию
трех и большего конечного числа функций.
Пусть функция x = q>(t) задана на множестве {/}, и пусть {х} —
множество ее значений. Допустим, что на множестве {х} задана
функция y=f(x). Тогда говорят, что на множестве {}} задана
сложная функция y=f[<f(t)]=F(t) или y=f(x), где х = ф(?).
Справедлива следующая теорема.
Теорема 4.2. Пусть функция x=<p(t) непрерывна в точке а,
а функция y=f{x) непрерывна в точке Ь = у(а), Тогда сложная
функция y=f[<p(t)] —F(t) непрерывна в точке а.
Доказательство. Пусть {tn} — произвольная последова-
последовательность значений аргумента сложной функции, сходящаяся к а.
Так как функция x = q>(t) непрерывна в точке а, то (в силу опре-
определения 1 непрерывности по Гейне) соответствующая последова-
последовательность значений функции xn = q>{tn) сходится к числу Ь = ф(а).
Далее, поскольку функция y=f(x) непрерывна в точке Ь=ф(а)
и для нее указанная выше последовательность {хп}, сходящаяся
к Ь=ф(а), является последовательностью значений аргумента,
то (в силу того же определения 1 непрерывности по Гейне) соот-
соответствующая последовательность значений функции f(xn) =
=f[4(tn)]=F(tn) сходится к числу /(Ь)=/[ф(а)] =F(a).
Итак, для любой последовательности {tn} значений аргумента
сложной функции, сходящейся к а, соответствующая последова-
последовательность значений самой сложной функции {F(tn)} = J[q>(tn)]
сходится к числу F(a) =/[ф(а)]. В силу определения 1 непрерыв-
непрерывности по Гейне сложная функция непрерывна в точке а. Теорема
доказана.
§ 2. СВОЙСТВА МОНОТОННЫХ ФУНКЦИЙ
1. Монотонные функции. Введем понятие монотонной функции.
Определение I.-Функция f(x) называется неубываю-
неубывающей [невозрастающей] на множестве {х}, если для любых
Х\ и х2 из этого множества таких, что Х\<.х2, справедливо неравен-
неравенство f(xO^f(x2) U(xO>f(x2)].
Неубывающие и невозрастающие функции называют моно-
монотонными функциями.
Определение 2. Функция называется возрастающей
[убывающей] на множестве {х}, если для любых Х\ и х2 из
§ 2. Свойства монотонных функций 133
этого множества таких, что Xi<.x2, справедливо неравенство
f(xi)<f(x2) [Д*1)>/Ы].
Возрастающие и убывающие функции называются строго
монотонными.
Приведем примеры монотонных функций.
1. Функция f(x) =xz — строго монотонна, а именно возрастает
на всей числовой оси.
2. Функция у — х2 — возрастает на полуоси х^О и убывает на»
полуоси х<0.
3. Функция y=sgnx — неубывающая на всей числовой оси.
4. Функция f(x) = убывает на множествах х<0 и х>0.
2. Понятие обратной функции. Пусть функция y = f{x) задана
на сегменте [а, Ь], и пусть сегмент [a, р] является множеством
значений этой функции. Пусть, кроме того, каждому у из сегмента
[а, р] соответствует только одно значение х из сегмента [а, Ь],
для которого f(x)=y. Тогда на сегменте [а, р] определена функ-
функция, которая каждому у из [а, р] ставит в соответствие то значе-
значение х из [а, Ь], для которого f(x)=y. Эта функция обозначается
символом x=f~1(y) и -называется обратной для функций
В проведенных выше рассуждениях вместо сегментов [а, Ь\
и [а, р] можно было бы рассматривать интервалы (а, Ь) и (а, р)
или, например, случай, когда один или оба из этих интервалов
превращаются в бесконечную прямую или открытую полупрямую.
Можно рассматривать и самый общий случай, когда задано
отображение / одного множества {х} на другое множество {у},
причем отображение / устанавливает взаимно однозначное соот-
соответствие между элементами этих множеств. Тогда можно опреде-
определить обратное отображение /"' множества {у} на множество {х}.
В этом случае уравнение y=f{x) можно разрешить относительно
х, т. е. можно однозначно определить х, зная элемент у, и мы име-
имеем x = f~l(y).
Отметим, что если x—f~l(y) — обратная функция для y=f(x),
то, очевидно, функция y=f{x) является обратной для функции
x=f~1(y). Поэтому функции y=f{x) и x=f~l(y) называются вза-
взаимно обратными. Очевидно, что f[f~l{y)]=y, f~l[f{x)]=x.
Приведем примеры взаимно обратных функций.
1. Пусть на сегменте [а, Ь] задана функция у = 2х. Множест-
Множеством значений этой функции будет сегмент [2а, 2Ъ]. Функция
x = f~x{y) = — ' определенная на [2а, 2Ь], будет обратной к за-
заданной функции у — 2х.
2. Рассмотрим на сегменте [0, 2] функцию у=х2. Множество
значений этой функции есть сегмент [0, 4]. На этом сегменте оп-
определена обратная к заданной функции функция х=Уу .
134 Гл. 4. Непрерывность функции
3. Рассмотрим на сегменте [0, 1] функцию
х, если х—рациональное число,
1-х, если х—иррациональное число.
Нетрудно убедиться, что заданная на сегменте [0, 1] функция
( у, если у—рациональное число,
{ 1—у, если у—иррациональное число,
будет обратной к заданной функции.
Докажем несколько утверждений о монотонных функциях.
Начнем с доказательства леммы, справедливой для любой мо-
монотонной (не обязательно строго монотонной) функции.
Лемма. Если функция f(x) является монотонной на сегменте
[а, Ь], то у нее существуют правый и левый пределы в любой
внутренней точке сегмента [а, Ь] и, кроме того, существуют пра-
правый предел в точке а и левый предел в точке Ь.
Доказательство. Для полного доказательства леммы дос-
достаточно доказать два факта: 1) существование правого предела
в любой точке с, удовлетворяющей неравенствам a^.c<cb; 2) су-
существование левого предела в любой точке с, удовлетворяющей
неравенствам a<c*cb.
Мы установим только первый из указанных двух фактов, ибо
второй устанавливается аналогично.
При этом мы проведем все рассуждения для функции f{x),
неубывающей на сегменте [а, Ь] (ибо для невозрастающей функ-
функции они проводятся аналогично).
Итак, пусть функция f(x) не убывает на [а, Ь], с — любая
точка, удовлетворяющая неравенствам а^.с<Ь. Рассмотрим мно-
множество {/(л)} всех значений функции f(x) для значений аргумента
х, удовлетворяющих неравенствам с<х^Ь. Это множество {/(*)}
непусто (в силу того, что с<Ь) и ограничено снизу (в силу неубы-
неубывания функции f(x) для всех х из полусегмента с<.х^Ь справед-
справедливо неравенство f(c)^.f(x), которое означает, что f(c) является
нижней гранью рассматриваемого множества). По основной тео-
теореме 2.1 гл. 2 у рассматриваемого множества существует точная
нижняя грань, которую мы обозначим символом у. Докажем, что
это число у и является правым пределом функции f(x) в точке с,
т. е. докажем, что y=f(c + O).
Фиксируем произвольное е>0. По определению точной нижней
грани найдется положительное число б, не превосходящее Ъ—с
и такое, что значение функции /(с+6) удовлетворяет неравенству
Но тогда в силу неубывания функции f(x) для всех х из ин-
интервала с<х<с + б и подавно 'будет справедливо неравенство
f(x)<y + e. Так как, кроме того, для всех х из указанного интер-
интервала справедливо неравенство y^.f(x), то мы получим, что для
всех х из интервала c<x<c + 6 справедливы неравенства
§ 2. Свойства монотонных функций 135
или |у—/(*)|<е,
а это и означает (в силу определения правого предела по Коши)',
что число 7 является правым пределом f(x) в точке с. Лемма до-
доказана.
Замечание к лемме. В предположениях леммы при ус-
условии неубывания f(x) для любых сих, удовлетворяющих соот-
соотношениям а<с<л:<Ь, будут справедливы неравенства
D.1)
а для любых с я х, удовлетворяющих соотношениям а^.х<с^.Ь,
будут справедливы неравенства
D.2)
При условии невозрастания f(x) все знаки в неравенствах D.1) и
D.2) следует заменить на противоположные.
Пусть, например, f(x) не убывает на [а, Ь] и а^.с<х^Ь. Тог-
Тогда /(flX/(c)</(jc)</fb). Из последних неравенств сразу же вы-
вытекает, что /(аХ/(сХ/(с + 0Х/(Ь). Для завершения доказа-
доказательства неравенств D.1) следует убедиться в том, что /(с+0)^
^f(x)^.f(b) для любого х из полуинтервала с<х^.Ь, но это сразу
вытекает из того, что число y = f(c+O) является, как доказано
в лемме, точной нижней гранью множества значений f(x) на полу?
интервале с<х^Ь. Справедливость неравенств D.2) проверяется
аналогично.
' Докажем теперь три. теоремы о строго монотонных функциях.
Теорема 4.3. Пусть функция y=f{x) возрастает (убывает)
на сегменте [а, Ь], и пусть a=f(a), р = /(Ь). Тогда, если множе-
множеством всех значений функции y — f(x) является сегмент [а, р]
(соответственно сегмент [р, а]), то на этом последнем сегменте
определена обратная для y=f(x) функция x=f~l(y), которая так-
также возрастает (убывает) на указанном сегменте.
Доказательство. Проведем все рассуждения в предполо-
предположении, что f(x) возрастает на сегменте [а, р] (для убывающей
функции рассуждения аналогичны).
Убедимся в том, что функция y = f{x) устанавливает взаимно
однозначное соответствие между сегментами а^.х^.Ь и а^г/^р.
Действительно, то, что каждому х из [а, Ь] соответствует только
одно значение у из [a, р], следует из самого понятия функции
y=f(x), а то, что каждому у из [а, р] соответствует только одно
х из [а, Ь], вытекает из возрастания функции y=f(x).
Убедимся теперь, что если y=f(x) возрастает на [а, Ь], то и
x=f~l(y) также возрастает на [а, р]. Пусть У\<у%, где уi и уч —
любые два числа из [а, р]. Тогда лсх =/~I(f/i) <X2=zf~1(y2), ибо из
неравенства х\^х2 и из возрастания функции y—f(x) следовало
бы, что уи^уъ, что противоречит неравенству у\<у2- Теорема до-
доказана.
136 Гл. 4. Непрерывность функции
Замечание 1. Совершенно аналогично доказывается более
общее утверждение: пусть y = f(x) задана и возрастает (убывает)^
на некотором множестве {х}, а {у} — множество всех значений
этой функции. Тогда на множестве {у} определена обратная для
y=f(x) функция x = f~1(y), которая также возрастает (убывает)
на указанном множестве {у}.
Теорема 4.4. Пусть функция y = f(x) возрастает (или убы-
убывает) на сегменте [а, Ь], и пусть a=f(a), $=f(b). Тогда для того,
чтобы функция y=f(x) являлась непрерывной на сегменте
[а, Ь], необходимо и достаточно, чтобы любое число у, заключен-
заключенное между а и р, было значением этой функции.
Доказательство. Все рассуждения проведем для возрас-
возрастающей на сегменте [а, Ь] функции, ибо для убывающей функции
они аналогичны.
1) Необходимость. Пусть функция y = f(x) возрастает и непре-
непрерывна на сегменте [а, Ь]. Требуется доказать, что любое число у,
удовлетворяющее условиям а<-у<Р, является значением функции
в некоторой точке с сегмента [а, Ь].
Пусть {*} — множество всех значений х из сегмента [а, Ь],
для которых f(x)^y. Это множество {х} непусто (ему принадле-
принадлежит, например, точка а, ибо f(a)=a<y) и ограничено сверху (на-
(например, числом Ь). По основной теореме 2.1 гл. 2 у множества
{х} существует точная верхняя грань, которую мы обозначим через
с: c = sup{;t}. Остается доказать, что f{c)=y.
Сначала убедимся в том, что f(x)^.y для всех х из [а, Ь], ле-
лежащих левее с, и f(x)>y для всех х из [а, Ь], лежащих правее с.
В самом деле, если х<с, то по определению точной верхней
грани найдется х' из полуинтервала х<х'^.с, принадлежащее
множеству {х}, т. е. такое, что f(x')^.y. Но тогда из возрастания
f(x) будет вытекать, что и f{x)^.y (ибо f(x) <f(x')).
Далее, любое х, лежащее правее с, не принадлежит множеству
{х}, а потому для такого х справедливо неравенство f{x)>y.
Теперь убедимся в том, что с является внутренней точкой
сегмента [а, Ь]. Докажем, что с<Ь. Предположим, что это не так,
т. е. допустим, что с = Ь. Возьмем любую сходящуюся к с=Ь воз-
возрастающую последовательность {хп} точек сегмента [а, Ь]. Так
как все ее элементы хп лежат левее с, то f(xn)^y для всех номе-
номеров п, а поэтому (в силу теоремы 3.13 гл. 3) и Нт/(хй)<у- Но
так как функция f(x) непрерывна в точке с—Ъ, то \\mf{xn)=f(b).
Тем самым мы получаем неравенство P=/(bXv. которое проти-
противоречит условию y<P- Полученное противоречие доказывает, что
с<Ь.
Совершенно аналогично доказывается, что а<с.
Итак, доказано, что с — внутренняя точка сегмднта [а, Ь].
Теперь для того, чтобы доказать, что f(c)=y, рассмотрим две
§ 2. Свойства монотонных функций 137
сходящиеся к с с разных сторон последовательности точек сегмен-
сегмента [а, Ь] — возрастающую последовательность {хп'} и убывающую
последовательность {хп}. В силу того, что функция f(x) непре-
непрерывна в точке с,
lim / {х'п) = lim / (х"п) = / (с).
С другой стороны, поскольку Хп <с<хп" для любого номера п,
то f(Xn)^y, f(Xn")>y (для любого номера п). Но тогда в силу
теоремы 3.13
т. е. /(c)=v
Необходимость доказана.
2) Достаточность. Пусть функция f{x) возрастает на сегменте
[а, Ь], и пусть любое число у из сегмента [а, р] является значе-
значением этой функции. Докажем, что функция f(x) непрерывна на
сегменте [а, Ь]. Достаточно доказать, что f(x) непрерывна справа
в любой точке с, удовлетворяющей условиям а^с<Ь, и непрерыв-
непрерывна слева в любой точке с, удовлетворяющей условиям а<с^Ь.
Мы ограничимся доказательством непрерывности справа
в любой точке с, удовлетворяющей условиям а^с<Ь, ибо вторая
часть утверждения доказывается аналогично.
Предположим, что функция f(x) не является непрерывной
справа в некоторой точке с, удовлетворяющей условиям а^.с<.Ь.
Тогда ее правый предел /(с + 0), который существует согласно
доказанной выше лемме, будет отличен от значения f(c), и по-
поэтому справедливые в силу замечания к указанной лемме неравен-
неравенства D.1) примут вид
a=/(a)<f(c)<f(c + O)<f(xKf(b)=f5 D.2')
(для всех х из полуинтервала с<х^Ь).
Неравенства D.2') означают, что содержащийся в [а, |3] ин-
интервал (f{c), /(с+0)) не содержит значений функции f(x)*, а это
противоречит тому, что любое число у из сегмента [а, р] является
значением этой функции. Теорема 4.4 полностью доказана.
Теорема 4.5. Пусть функция y=f(x) возрастает (убывает)
и непрерывна на сегменте [а, Ь), и пусть a=f(a), fi=f(b). Тогда
на сегменте [а, р] (соответственно на сегменте [р, а]) определе-
определена обратная для y=f(x) функция x=f~x(y), которая возрастает
(убывает) и непрерывна на указанном сегменте.
Кратко можно сказать, что из строгой монотонности и непре-
непрерывности на сегменте [a, b] данной функции вытекают существо-
* В самом деле, для х^с значение f(x) удовлетворяет неравенству {()^
f(c) (в силу возрастания функции), а для х~>с значение f(x) удовлетворяет
неравенству /(с+0)</(х) (в силу D.2')).
138 Гл. 4. Непрерывность функции
вание, строгая монотонность и непрерывность на соответствующем
сегменте обратной функции.
Доказательство. Проведем все рассуждения для возрас-
возрастающей функции, ибо для убывающей функции они проводятся
аналогично.
Так как f(x) возрастает и непрерывна на сегменте [а, Ь], то
в силу необходимости теоремы 4.4 множеством всех значений этой
функции является сегмент [а, р]. Но тогда теорема 4.3 обеспечи-
обеспечивает существование на этом сегменте возрастающей обратной
функции x—f^l(y). Остается доказать непрерывность указанной
обратной функции на сегменте [а, р]. Для этого достаточно
учесть, что множеством всех значений обратной функции x=f~l(y)
служит сегмент [а, Ь], где а=/~1(а), 6=f~'(P). и использовать
для этой обратной функции достаточность теоремы 4.4. Доказа-
Доказательство теоремы 4.5 завершено.
Замечание 2. Можно показать, что из существования об-
обратной функции для функции f(x), непрерывной на сегменте
[а, Ь], следует, что f(x) строго монотонна на этом сегменте
(см. п. 2 § 6 настоящей главы).
§ 3. ПРОСТЕЙШИЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Простейшими элементарными функциями, как уже отмечалось,
обычно называют следующие функции: у=ха, у = ах, y = \ogax,
y=sinx, y=cosx, y — tgx, y=ctgx, #=arcsin*, «/ = arccosx, y =
= arctg*, i/ = arcctg;e. ¦
Нашей основной целью является изучение вопроса об опреде-
определении и непрерывности простейших элементарных функций. Сле-
Следует заметить, что вопрос об определении простейших элемен<
тарных функций далеко не прост. Так, например, показательная
функция у = ах легко может быть определена для рациональных
значений аргумента х, вместе с тем эту функцию следует опреде-
определить для произвольных вещественных значений х, т. е. следует оп-
определить возведение вещественного числа в любую вещественную
степень х. Далее, определение тригонометрических функций sin*
и cos х с помощью наглядных геометрических соображений имеет
логический пробел. Возможность определить эти функции для
всех вещественных значений аргумента х сводится к возможности
установления взаимно однозначного соответствия между точками
единичной окружности и всеми вещественными числами полусег-
полусегмента [0, 2я).
Всеми этими вопросами мы и будем заниматься в настоящем
параграфе.
1. Показательная функция. Начнем наше рассмотрение с опре-
определения рациональных степеней положительных чисел. Для того
чтобы возвести любое вещественное число х в целую положитель-
положительную степень п, следует умножить это число х само на себя п раз.
§ 3. Простейшие элементарные функции 139
Следовательно, при целом п мы можем считать определенной
степенную функцию у=хп для всех вещественных значений х.
Установим некоторые простейшие свойства этой функции.
Утверждение 1. Степенная функция у = х" при х^О и це-
целом положительном п возрастает и непрерывна.
Доказательст.во. Покажем, что функция у = хп возраста-
возрастает. Пусть 0<jci<jc2. Тогда x2n—xin= (x2—x{) {x2n-l + x2n'2-Xi + ...
... + JE1"). Оба сомножителя в правой части, в соответствии с вы-
выбором значений х2 и х\, положительны. Поэтому положительна и
левая часть равенства, т. е. x2n~>x\n, а это означает возрастание
функции у = хп при х^О.
Непрерывность функции у = хп в любой' точке а бесконечной
прямой (—оо, +оо) была установлена в примере 1 п. 1 § 1 нас-
настоящей главы. Утверждение 1 доказано.
Рассмотрим степенную функцию у=хл на сегменте [О, N], где
N — любое положительное число. Так как эта функция непрерывна
и возрастает на указанном сегменте, то в силу теоремы 4.5 она
имеет на сегменте [О, N"] возрастающую и непрерывную обратную
функцию, которую мы обозначим через х=у1/п. Поскольку Л' мож-
можно выбрать как угодно большим, то и Nn также можно сделать
сколь угодно большим. Следовательно, функция х = у1/п определе-
определена для всех неотрицательных значений у. Меняя для этой функ-
функции обозначение аргумента у на х, а обозначение функции х на у,
мы получим степенную функцию у = х1/п, определенную для всех
вещественных х^О.
Теперь мы в. состоянии определить любую рациональную сте-
степень г положительного числа а. Определим, прежде всего, а1/п дак
вещественное число Ь, равное значению функции х11" в точке а.
Далее, если г = —. где тип — целые положительные числа,
п
то мы положим
т
ar = an = (al'n)m.
Кроме того, положим по определению
а°=1, сгг= {—) при г>0.
\ а I
Тем самым, мы определили любую рациональную степень положи-
положительного вещественного числа а.
Выполняются следующие свойства рациональной степени по-
положительных вещественных чисел:
(ar)s = ars, ar-br=(a-b)r, ar-as = ar+s. (*)
I Докажем сначала справедливость первого свойства (*).
т
Заметим, что при целом положительном р равенство (а"I =
140 Гл. 4. Непрерывность функции
=а , в котором под тип понимаются любые целые поло-
положительные числа, заведомо справедливо, ибо как левая, так и
правая части этого равенства равны произведению числа а11*
самого на себя т-р раз.
Полагая г = -^-, s = -^-> докажем равенство (ar)s~ars
пг щ.
в ситуации любых положительных рациональных г и s. Поло-
mi m2 mt-m2
жим сг — (а "')"*, с2 = ап'. Если бы с\ было отлично от Сг,
то из возрастания степенной функции у = хПг следовало бы, что
и С\п'Фс2Пг, а последнее соотношение, в силу уже доказанной
m m-p
справедливости равенства (ая)р = ап при целом р, означало
бы, что (ап')т'^=а "* . Полученное соотношение противоречит
уже доказанному нами для целых положительных ть п\ и тг
равенству (ani)m' = a "' . Тем самым С\ = с2, и первое равенство
(*) доказано для любых положительных рациональных г и 5.
Распространение этого равенства на неположительные г и s
не представляет труда в силу нашей договоренности о том, что
а0 = 1, а~г = — при г > 0.
аг
Второе равенство (*) также достаточно доказать для поло-
положительного рационального г. Полагая это г равным
пг/п, где тип — целые положительные числа, заметим, что
нам достаточно доказать равенство axln-bl^n~{a-b)l/n, ибо пе-
перемножением т таких равенств будет доказано общее соотно-
соотношение ar-br= (a-b)r.
Для доказательства равенства d[ln-bl'n={a-b)l/n заметим,
что в силу свойств взаимно обратных функций у = х1/п и х=уп
мы можем утверждать, что (bx/n)n=b, (d[ln)n—a, {{ab)l'n)n —
= ab. Поэтому, положив ci = ai/n-b1'n, c2=(ab)l/n и предполагая,
что С\ФС2, мы получили бы, что С\пФс2п, что противоречит ра-
равенству a-b = ab.
Докажем теперь последнее свойство (*), учитывая, что
первые два уже доказаны. Пусть r = -^-, s=-^-. тогда г=;
пх п2
Л%1 * tl% 171л • П.л
= ' s= , и мы приходим к следующему равенству:
1 1 1
дг ,qs _ /?»t ¦ п*\«»• «2 ia«1 ¦ плгщ ¦ л, __ , в, л,ч/Л1 • га2+т2 • п,
(Последнее равенство справедливо, так как т^-Яг и m2-«i —
целые числа.)
§ 3. Простейшие элементарные функции 141
Таким образом,
f g Hi-fis /-»"* f t g
что и требовалось.
Яры а>\ и рациональном г>0 справедливо неравенство
аг>\.
В самом деле, пусть г = — и аг = ат/"<1. Перемножая пот
п
членно п указанных неравенств, получим ат^1. Но это неравенст-
неравенство противоречит неравенству ат>\, полученному почленным пере-
перемножением т неравенств вида а>1.
Отметим также, i что если рациональная дробь г = —имеет
нечетный знаменатель п, то определение рациональной степени
можно распространить и на отрицательные числа, полагая при
«>0, что
(—а)г = аг, если т четное,
(—а)г=—аг, если т нечетное.
Убедимся в том, что функция у = а" при а>1, определенная
нами на множестве рациональных чисел, монотонно возрастает
на этом множестве.
Действительно, пусть rt и г2 — два рациональных числа таких,
что г2>г\. Тогда
ан—ап = агг (a'2-<-i — 1). D.3)
Поскольку r-i—/"i>0 и а>1, то (в силу установленного выше)'
ar*-r'>l. Таким образом, правая часть равенства D.3) поло-
положительна. Следовательно,
ап—ап > о, т. е. аг* > аг',
что и требовалось.
Определим, наконец, функцию у—ах не только для рациональ-
рациональных значений х, но и для любых вещественных значе-
значений. Пусть х — произвольное вещественное число. Рассмотрим
всевозможные рациональные числа аир, удовлетворяющие нера-
неравенствам
D.4)
Определим а" при а> 1 как вещественное число у, удовлетворяю-
удовлетворяющее неравенствам
D.5)
при всевозможных рациональных аир, удовлетворяющих нера-
неравенствам D.4).
142 Гл. 4. Непрерывность, функции
Оказывается, что такое число у существует и притом только
одно. Следовательно, таким путем функция у = а" будет определе-
определена на множестве всех вещественных х.
Мы покажем, что эта функция возрастает и непрерывна на
всей вещественной прямой. Эти результаты содержатся в доказы-
доказываемых ниже утверждениях.
Утверждение 2. Для любых фиксированных вещественных
чисел х и а>\ и всевозможных рациональных чисел а и $, удов-
удовлетворяющих неравенствам D.4), существует и притом единствен-
единственное вещественное число у, удовлетворяющее неравенствам D.5).
Доказательство. Докажем сначала существование такого
числа у. Фиксируем произвольное рациональное число р, удовлет-
удовлетворяющее правому неравенству D.4), и рассмотрим всевозможные
рациональные числа а, удовлетворяющие левому неравенству
D.4). Так как а<р и показательная функция, определенная на
множестве рациональных чисел, возрастает, то аа<аР. Таким об-
образом, множество {аа} ограничено сверху, и число ав является
одной из верхних граней этого множества. Из основной
теоремы 2.1 следует, что множество {аа} имеет точную верхнюю
грань, которую мы обозначим через у. Покажем, что у удовлетво-
удовлетворяет неравенствам D.5). Из определения верхней грани вытекает
справедливость левого неравенства D.5), а справедливость пра-
правого неравенства D.5) вытекает из того, что а9 — одна из верх-
верхних граней, а у — точная верхняя грань множества {аа}.
Докажем теперь, что такое число у только одно. Достаточно
доказать, что для любого е>0 найдутся такие рациональные
числа аир, удовлетворяющие неравенствам D.4), для которых
ар—аа<е. Тогда любые два числа у\ и у2, удовлетворяющие нера-
неравенствам D.5), обязаны совпасть, так как разность между ними
по модулю меньше любого наперед заданного числа е>0.
Фиксируем произвольное положительное число е и некоторое
рациональное число Ро, удовлетворяющее правому неравенству
D.4). Тогда так как аа<а$\ то
а»—аа=аа(ар-а— 1)<аР° (а»-а— 1).
Неравенство а9—аа<е будет доказано, если мы установим воз-
возможность выбора в неравенствах D.4) таких рациональных а и р,
что а$~а — 1 < —в- •
В гл. 2 было доказано, что для любого натурального п можно
выбрать рациональные числа аир, удовлетворяющие неравенст-
неравенствам D.4), так, что разность р—а будет меньше 1/л. Таким обра-
образом, достаточно доказать, что существует такое натуральное п,
что
а>!« - 1 < -4-.
§ 3. Простейшие элементарные функции 143
Пусть а1/п==1 + бл. Так как al/n>\, то бп положительно. Используя
первые два члена бинома Ньютона, мы получим, что
Отсюда а—1>п-8п, т. е. 0<6„<^—L Значит а>1п — 1 <^^•
п п
Выберем теперь натуральное п удовлетворяющим неравенству
— <4" или п> ^-')-flP° . тогда a^-l<^i<-4-..
n aPo е п а9"
и доказательство однозначной определенности числа у, удовлетво-
удовлетворяющего неравенствам D.5), завершено. Утверждение 2 дока-
доказано.
Заметим, что если х — рациональное число и ах — значение
в точке х показательной функции, первоначально определенной
лишь на множестве рациональных чисел, то ах и является тем
единственным числом у, которое удовлетворяет неравенствам
D.5).
Утверждение 3. Показательная функция у=ах при а>1
возрастает на всей бесконечной прямой.
Доказательство. Пусть х\ и х^ — любые два веществен-
вещественных числа такие, что x\<.x%. Всегда существуют рациональные
числа аир такие, что Xi<a<p<X2 (см. лемму 2 § 3 гл. 2). Так
как xi<a и Р<#2> то по определению показательной функции вы-
выполнены неравенства а*1 •< аа, аР *С а?'- С другой стороны, так
как а<р, то из возрастания показательной функции на множестве
рациональных чисел вытекает аа<а9. Сопоставляя неравенства
cx'-<aa, aa<iaP и а®<СаХг и используя свойство транзитивнос-
транзитивности знаков > и =, получим, что ax^<iax\ а это и доказывает воз-
возрастание функции ах. Утверждение доказано.
Утверждение 4. Показательная функция у — ах при а>1 яв-
является непрерывной функцией в любой точке бесконечной прямой.
Доказательство. Пусть х — произвольное вещественное
число, а {хп} — любая сходящаяся к х последовательность. В силу
определения непрерывности по Гейне достаточно доказать, что
для любого е>0 существует такой номер N, что \а"п—а*|<е
при всех ri^N. Фиксируем произвольное е>0 и по нему рацио-
рациональные числа аир такие, что а<х<р и а?—аа<е. Возможность
фиксировать по любому е>0 такие рациональные числа аир
была установлена в утверждении 2. Поскольку последователь-
последовательность {хп} сходится к х и а<х<р, то существует такой номер N,
что при всех ri^-N справедливы неравенства а<х„<р. Так как по-
показательная функция монотонно возрастает, то a < ах < аР, аа <
< а*п < ар при всех ri^-N.
Таким образом, оба числа а*п и ах при ri^N заключены меж-
между двумя числами аа и а?, разность между которыми а"—аа мень-
меньше е. Отсюда следует, что при ri^N справедливо неравенство
144 Гл. 4. Непрерывность функции
\а"п—ах|<е, которое и доказывает непрерывность показатель-
показательной функции в произвольной точке х. Утверждение 4 доказано.
Получим теперь некоторые следствия из доказанных свойств
показательной функции. Прежде всего заметим, что если 0<а<1,
то а = —. где Ь>\. Поэтому функцию г/=аЛ при 0<а<1 можно
Ь
определить как функцию у—Ь~х при Ь = — > 1.
Следствие 1. Показательная функция у — ах при а>1 поло-
положительна (при всех значениях х).
Если х — произвольная точка числовой оси, а г — рациональ-
рациональное число такое, что г<х, то по определению показательной функ-
функции на множестве рациональных чисел ar>0, a по утверждению 3
ах>аг при а>\. Следовательно, ах>0.
Следствие 2. Показательная функция у = ах при а>\ удов-
удовлетворяет условиям: limax = 0, lima*=+oo.
В самом деле, так как а>1, то a=l-f6, где б>0 и а" =
= A+6)">л6. Следовательно, lima"=+°°- В силу монотон-
П—
ности функции у = ак получаем, что и lim ax= +оо. Так как
агп ——, то lima~" = 0, и поэтому lima* = 0.
йп Я-юо Х-»-—оо
Следствие 3. Значения функции у=ах при а>\ заполняют
всю положительную полупрямую у>0.
Действительно, по следствию 1 функция у=ах принимает
только положительные значения, а по следствию 2 она принимает
как сколь угодно малые, так и сколь угодно большие положитель-
положительные значения. Из непрерывности и строгой монотонности а* и из
теоремы 4.4 вытекает, что любое положительное число является
значением функции у = ах.
Следствие 4. Для любых вещественных чисел х\ и Хг
справедливы соотношения
В самом деле, эти соотношения уже были установлены нами
для рациональных показателей. Отсюда вытекает справедливость
их и для произвольных вещественных показателей. Убедимся, на-
например, в справедливости первого соотношения. Пусть {/¦'„} и
{/•„"} — последовательности рациональных чисел, сходящиеся со-
i ir /и
ответственно к х\ и х2. Тогда (ап)п = ап ". Переходя к пределу
при п-^-оо и используя непрерывность показательной функции,
получим (a*i)x2=aXi*2. Аналогично устанавливаются и остальные
равенства.
Заметим теперь, что мы фактически изучили и сврйства пока-
показательной функции у — ах при 0<а<1. Действительно, ее непре-
§ 3. Простейшие элементарные функции
145
рывность следует из самого определения. Из определения следует
также, что эта функция монотонно убывает на бесконечной пря-
прямой. Следствия 1, 3, 4 верны и для функции у = ах при 0<а.<1, а
следствие 2, очевидно, будет выглядеть так:
lima*=+oo, lima* = 0.
На рис. 4.1 и 4.2 изображены графики показательной функции
у —а" для случаев а>\ и 0<а<1.
СС
Рис. 4.2
Замечание. Показательную функцию можно было бы опре-
определить как решение некоторого функционального уравнения, удов-
удовлетворяющее определенным условиям. Можно доказать, что суще-
существует, и притом единственная, функция }(х), определенная на
всей бесконечной прямой и удовлетворяющая трем требованиям:
1) для любых вещественных х\ и х% выполнено соотношение
f(xl+x2)=f(xl)-f(x2);
2) /@) = 1*ЛA)=апр.иа>1;
3) функция f(x) непрерывна при х=0.
Такой функцией и является построенная выше функция f(x)=ax
при а>1.
2. Логарифмическая функция. Логарифмическую функцию мы
определим как обратную к показательной. Пусть [с, к] — произ-
произвольный сегмент бесконечной прямой. На этом сегменте функция
у=ах при а>1 возрастает и непрерывна. Поэтому в силу теоремы
4.5 функция y=f(x)=ax имеет на сегменте [ас, ad\ возрастающую
и непрерывную обратную функцию x = f~1(y), которая и называ-
называется лога ри ф мической и обозначается так:
Заменяя обозначение аргумента у на х, а обозначение функции х
на у, запишем ее в более привычном нам виде:
* Можно доказать, что требование f@)=l является следствием остальных,
требований (и потому может быть опущено).
146
Гл. 4. Непрерывность функции
Случай 0<а<1 рассматривается аналогично. Отметим следу-
следующие свойства логарифмической функции, вытекающие из ее
¦определения:
1) Логарифмическая функция определена для всех положи-
положительных значений х. В самом деле, аргумент логарифмической
«функции представляет собой значения показательной функции,
которые, как мы знаем, только положительны и заполняют всю
полупрямую х>0.
2) Логарифмическая функция непрерывна и возрастает на
зсей полупрямой х>0 при а>\ и непрерывна и убывает на всей
полупрямой х>0 при 0<а<1, причем
Нт1о§^л:= —оо, limlogajc = + <х> при а > 1,
Х->-0+0 Х-*+а>
limlogaje = -foo, limlogax =—оо при 0<а<1.
Х-»0+0 +
'Справедливость этих свойств вытекает из свойств показательной
¦•функции.
3) Для любых положительных х\ и Х2
\0ga (Xi • X2) = loga X\ + logo X2.
Это свойство также вытекает из свойств показательной функции.
Замечание. Следует особо выделить логарифмическую
функцию y = \ogex, где e = lim(l 4-—) ¦ Для этой функции
л-><ю \ П j
используется обозначение у = \пх. Логарифмы по основанию е на-
называются натуральными.
У
х
х
Рис. 4.3
Рис. 4.4
На рис. 4.3 и 4.4 изображены графики логарифмической функ-
функции y = \ogax для случаев а>1 и 0<а<1.
3. Степенная функция. Определим теперь степенную функцию
с любым вещественным показателем а через суперпозицию лога-
логарифмической функции и показательной. Пусть х>0г Тогда общая
степенная функция определяется так:
§ 3. Простейшие элементарные функции 147
где а — любое фиксированное число, ради определенности
большее единицы:
Из этого определения и из того, что при а>1 логарифмиче-
логарифмическая функция возрастает на всей полупрямой х>0, а показатель-
показательная функция возрастает на всей бесконечной прямой, вытекает,
что степенная функция у = ха = ааЛоеах возрастает при а>0 и
убывает при а<0 на полупрямой х>0.
Справедливы следующие свойства:
1) Для степенной функции выполнены соотношения:
ПтлЯ = 0 при a > 0, limxa = +°o при сс<0.
*-»0+0 х-*0+0
В самом деле, пусть {хп} ¦— любая сходящаяся к нулю справа
последовательность значений аргумента хп. Так как limlogaxn =
п-
= — оо, то из свойств показательной функции вытекает, что
1с8<»х" = 0 при а>0 и Птаа1°8Л= +оо при а<0. По-
ПО П
определению положим 0а=0 при а>0 и будет считать это выраже-
выражение неопределенным при а<0.
2) Степенная функция у~ха = аа']0°аХ непрерывна в каждой
точке х открытой полупрямой х>0.
Это сразу же вытекает из теоремы 4.2 непрерывности слож-
сложной функции с учетом того, что функция u = a-\ogax непрерыв-
непрерывна в любой точке х>0, а функция у=аи непрерывна в любой,
точке и бесконечной прямой.
Замечание. Если показатель а степенной функции пред-
представляет собой рациональное число пг/п, где п — нечетное целое
число, то степенную функцию у = ха можно определить на всей
числовой оси, полагая при х<0:
у = | х \а, если а — — и пг четное,
п
у= — | х \а, если a = — и пг нечетное.
На рис. 4.5—4.7 изображены графики степенной функции у—х^
для различных значений а.
4. Тригонометрические функции. Мы уже имеем представление
о тригонометрических функциях y=sinx и y=cosx и функциях,
s in х cos y
которые через них выражаются, y~\gx = , y = ctgx =
cos a: sin a;
, t/ = cosecx =
i
cos x sin x
Во введении к этому параграфу мы уже говорили о логических
пробелах, возникающих при определении функций # = sinx к
48
Гл. 4. Непрерывность функции
X
Рис. 4.5
Рис 4.6
а.70
Рис. 4.7
г/ = соэл; с помощью наглядных геометрических соображений. Ло-
Логически безупречно эти функции можно определить как решение
некоторой системы функциональных уравнений. Точнее, можно до-
доказать следующее утверждение: существует и притом единственная
пара функций f(x) и g(x), определенных для всех вещественных
значений аргумента х и удовлетворяющих условиям:
1) f(xi + x2)=f(xl)g(x2)+f(x2)-g(x1),
g(xi+x2)=g(xl)-g(x2)—f(xl)-g(x2), f(
[2)
3)
-0, g@) = \, f
—1>
f]=0;
Справедливость неравенства
f(x)
g(x)
8 (¦*•)
D.6)
для 0 < х < —— следует из ос-
тальных сформулированных здесь условий (см. по этому поВоду указываемое
ниже дополнение к книге В. А. Ильина и Э. Г. Позняка).
§ 3. Простейшие элементарные функции 149
Первую из этих функций назовем синусом и обозначим
символом f(x) = sinх, вторую назовем косинусом и обозначим
символом g(x) = cos х.
Доказательство приведенного утверждения можно найти в до-
дополнении к гл. 4 книги В. А. Ильина и Э. Г. Позняка «Основы
математического анализа», 1 (М., Наука, 1982).
Нетрудно доказать, что из свойств 1), 2) и 3) можно извлечь
в виде следствий все другие свойства функций y = s'mx $
y—zosx, известные читателю из школьных учебников и устанав-
устанавливаемые в средней школе из наглядных геометрических сообра-
соображений. Впрочем, этот факт сразу вытекает из того, что свойства
1), 2) и 3) определяют единственную пару функций
f(x) и g(x) и что введенные в средней школе из наглядных гео-
геометрических соображений функции f(x)=sinx и g(x)=cosx
этими тремя свойствами обладают.
В качестве примера установим с помощью свойств 1), 2), 3)
некоторые свойства функций y = sinx и y=cosx, которые понадо-
понадобятся нам при доказательстве непрерывности этих функций и для
отыскания участков их монотонности.
а) Из третьего соотношения 1), имеющего вид sin2x+cos2x=l,
сразу же вытекает, что sin2x<l и cos2^<l, т. е.
<:l. D.7)
б) Далее, с помощью первых двух соотношений 1) и первых
двух равенств 2) мы получим, что
sin 0=sin[x+ (—х)] =sin*-cos(—х) +cos^-sin(—х) =0,
cosO=cos[x+ (—х)] =cos;C'COs(—x)—sin x- sin (—x) = 1.
Полученные два равенства представляют собой систему двух
уравнений относительно двух неизвестных cos(—х) и sin(—х). Ре-
Решая эту систему и учитывая, что sin2x+cos2x=l, мы получим,
что
cos (—х) = cos х, sin (—х) = —sin x, D.8)'
т. е. cos* представляет собой четную функцию, a sinx — нечет-
нечетную функцию *.
в) Из соотношений 1), в свою очередь, вытекают равенства
sin (xi— х2) = sin [xi + (—х2) ] = sin xx ¦ cos (—х2) +
+ cos x\ ¦ sin (—х2) = sin x{ • cos x2—cos x\ ¦ sin x%,
D.9)
COS (X1—X2) =COS [Xi + (—X2) ] = COS Xi • COS (—*2) —
—sinxi -sin(—x2) =
* Функция <f(x), определенная для всех вещественных значений х, назы-
называется четной, если <р(—дг)=ф(д:) (для любого значения х), и нечетной, если
<р(—х)=—ц>(х) (также для любого значения х).
150 Гл. 4. Непрерывность функции
г) Из первого соотношения 1) и первого соотношения D.9)
мы получим, что
/ хг + xi i
sinх2 = sin 2^ 1 +
2 \ 2
+
\ 2 2
. cos -^=^- + sin ?—& ¦ cos
Складывая и вычитая полученные два равенства, мы придем к
соотношениям
sinx2+ sinx1 = 2sin-^C^i-.Cos-^—ii-,
* -* DЛ0>
sin x» ¦— sin x, = 2cos *2 * ¦ sin ——— ¦
21 2 2
д) Далее, из первого соотношения D.9) и из последних двух
равенств 2) получим, что
sin (— х) = sin—-cosх—cos — • sinx = cosx,
V 2 ) 2 2
т. e.
cosx=sin( ——x\- D.11)
e) Убедимся, наконец, в периодичности функций /(x)=sinx и
g(x)=cosx с периодом 2л. Из первых двух соотношений 1) при
x=xi = x2 получим, что
sin2x=2sinx-cosx, cos2x=cos2x—sin2x. D.12>
Учитывая, что в силу равенств 2) sin—=1, cos— = 0, мы-по-
лучим из соотношений D.12) при х — — , что sinn = 0, соэя=
= —1, а из последних двух равенств и из соотношений D.12) при
х=тт получим, что sin2n = 0, соэ2я=1.
Используя последние два равенства, мы получим из первых
двух соотношений 1), что
sin(x+2jt) =sinx-cos2it + sin 2it-cos x = si
cos(x + 2n) =cos x-cos 2я—sin х- sin 2sx = cos x,
§ 3. Простейшие элементарные функции 151
а это и означает периодичность функций sin x и cos x с перио-
периодом 2я*.
ж) В заключение несколько усилим неравенства, содержащие-
содержащиеся в свойстве 3). Мы установим, что для всех вещественных х
справедливо следующее несколько общее неравенство:
|sin*|<:|*|. D.13)
При 0<#<— соотношение D.13) следует из неравенств,
содержащихся в свойстве 3).
При <#<0, в силу соотношения sin(—х) = —sinx,
неравенство D.13) следует из следующих неравенств:
О < sin (—х) < — х при —— < х < О,
а эти последние неравенства справедливы вследствие того, что
{—х) лежит в интервале @, —) • При *=0 sin;t=.*;.
При — <|*| имеем f sltiл:| < 1< — < \х\, т. е. |sin*[«s.
<г|*|.
Перейдем к установлению двух основных свойств функций
) =sin х и g(x) =cos x.
1°. Функции sin х и cos x непрерывны в каждой точке х беско-
бесконечной прямой.
Доказательство. Достаточно установить непрерывность
в каждой точке х только функции f(x) = smx, ибо непрерывность в
каждой точке х функции g(;t)=cos;t будет при этом вытекать из
•соотношения D.11) и теоремы 4.2.
Сначала докажем, что функция sin x непрерывна в точке
х—0. Так как в силу первого равенства 2) sin 0 = 0, то в силу
•определения непрерывности по Гейне достаточно доказать, что
для любой бесконечно малой последовательности {хп} последова-
последовательность значений функции {sin*,,} также является бесконечно
малой.
Из неравенства D.13) и из условия |sinx|>0 вытекает, что
для всех х
0<:|sinx|<|x|. D.13')
¦Следовательно,
0< | sinХя| < \Xn\-
Последние неравенства в силу принципа двустороннего ограни-
ограничения (см. теорему 3.14 гл. 3) означают, что последовательность
* Функция ф(х), определенная для всех вещественных х, называется перио-
периодической с периодом Т, если <р(х+Т) =q>(#) для всех х.
152 Гл. 4. Непрерывность функции
{|sinдг«j}, а значит, и последовательность {sin*,,} является беско-
бесконечно малой. Непрерывность функции sin* в точке х=0 доказана.
Докажем теперь, что функция sin x непрерывна в любой точке
х бесконечной прямой. Пусть {хп} — произвольная последова-
последовательность, сходящаяся к х. Достаточно доказать, что соответству-
соответствующая последовательность {sin xn} сходится к sin x.
Воспользуемся вторым соотношением D.10), положив в нем
Х2 = хп, Х[ = х. Получим
+ -sin Xn~x • D.14)
2
Достаточно доказать, что в правой части D.14) стоит элемент
бесконечно малой последовательности, но это сразу вытекает из.
sin—- , в силу уже доказан-
доказанной непрерывности синуса в нуле, является бесконечно малой, а
последовательность ]2соз Хп х 1. в силу второго неравенства
D.7) является ограниченной.
2°. Функция sin х возрастает на каждом из сегментов 2Ы—
—, 2kn + — \ и убывает на каждом из сегментов Bk + 1) я—
—, Bk+l)n + — ; функция cos x убывает на каждом из
2 2 J
сегментов \2kn, 2йя+я] и возрастает на каждом из сегментов
[2kn—п, 2kn] (здесь всюду k — любое целое число, т. е. k = 0,
±1, ±2,...).
Доказательство. Все рассуждения достаточно провеет»
для функции sin х, ибо после нахождения всех участков монотон-
монотонности функции sin х участки монотонности функции cos x могут
быть получены, исходя из равенства D.11).
Далее, поскольку sin x — периодическая функция с периодом
2я, то достаточно найти участки ее монотонности, лежащие в
пределах одного периода, т. е., например, для значений аргумента
—, 2я — — •
Докажет сначала, что функция sin x возрастает на сегменте
0, — • Пусть х\ и дг2 — любые два числа из этого сегмента
такие, что'*2>*1- Тогда, очевидно, числа *» + ¦** и *«~*i..
принадлежат интервалу @, —), причем в силу второго равен-
равенства D.10)
sins,—зШ*^2cos Xt + Xl -Bin Xt~Xl ¦ D.15>
§ 3. Простейшие элементарные функции 153
Достаточно доказать, что в правой части D.15) стоит положи-
положительное число, а для этого достаточно убедиться в том, что для
всех значений аргумента из интервала 10, —) функции sin x
и cos х принимают только положительные значения. Для функции
/(*)=sin* это вытекает из свойства 3), а для функции cos x
следует из равенства D.11).
Итак, доказано, что функция sin* возрастает на сегменте
0, — • Из нечетности функции sin x, т. е. из второго соотно-
соотношения D.8), в таком случае следует, что функция sin x возрастает
и на сегменте , 0 •
Тем самым доказано, что функция sin x возрастает на сегменте
—, —- • Остается исследовать поведение функции sin*
на сегменте -—, я + — • В пункте е) мы убедились в том,
что sinn = 0, cosjt= —1, а из этих равенств и из первого соотно-
соотношения 1) вытекает, что
эт(*+я) =sin *-cos я+cos *-sin я= •—sin x.
Полученное соотношение позволяет заключить, что из установлен-
. . Г я я 1
ного нами возрастания функции sin х на сегменте , —
вытекает убывание этой функции на сегменте —, я -\ •
L 2 2 J
Изучение участков монотонности функций sin x и cos x пол-
полностью завершено.
т-. , sin* , cos*
В силу представлении tg* = , ctgx= и в силу
cos* sin*
теоремы 4.1 для случая частного функция tg* непрерывна в любой
точке х Ф \-Ы, а функция ctg л: непрерывна в любой точке
хфкл. Пользуясь соотношениями sin(*+rc) =—sin*, cos (x+n) =
= —cos *, мы получим, что tg (* + я) = S1 = tg * и аналогично
COSX
ctg (*+я) = ctgл:. Это означает, что tg* и ctg* являются периоди-
периодическими функциями с периодом я. Значит, достаточно произвести
исследование участков монотонности этих функций только в пре-
пределах интервала длины п. Из равенства
D.16)
g2g1
cos xz cos x1 cos x2 ¦ cos хг
и из того, что sin x принимает только положительные значения на
интервале @, я), a cos* принимает только положительные значе-
154
Гл. 4. Непрерывность функции
ния на интервале ( — , —) • вытекает, что функция tg х
возрастает на интервале
— , — )• (ДЛЯ ЛЮбых
И Х2
из интервала ( —, —) таких, что х{>х\, в правой части
V 2 2 /
D.16) будет стоять положительная величина.)
Аналогично устанавливается, что функция ctg x убывает на
интервале @, п).
Мы не останавливаемся на изучении функций secx: = -
COS X
и cosecjc =
l
sin*
Графики всех тригонометрических функций изображены на
рис. 4.8—4.13.
-я
л
2/
У
У>
/1
и
-1
я
и = cos х
Рис. 4.9
-п\
у = ctg х
Рис. 4.11
5. Обратные тригонометрические функции. Остановимся на
вопросах определения и свойствах непрерывности и -монотонности
обратных тригонометрических функций.
§ 3. Простейшие элементарные функции
155
y=cosec х
Рис. 4.13
Для определения функции «/ = arcsinx рассмотрим функцию
г я я 1 „ .
V = sinx на сегменте , — • Согласно п. 4 на этом сег-
L 2 2 J
менте функция y = sinx монотонно возрастает и непрерывна. Мно-
Множество ее значений есть сегмент [—1, 1]. В силу теоремы 4.5 на
сегменте [—1, 1] существует. непрерывная возрастающая обрат-
обратная функция, принимающая значение в точке —1 и значе-
значение — в точке 1. Эту функцию обозначают символом х=
= arcsin«/ или, меняя обозначение аргумента у на х и обозначе-
обозначение х для функции на у, символом z/ = arcsin;t. Точно так же оп-
определяется на сегменте [—1, 1] функция у = arc cos x, обратная
по отношению к функции x=cosy, убывающей и непрерывной на
сегменте 0<г/<я.
Функция «/ = arccosx убывает и непрерывна на сегменте
f—1, +1] и принимает в точках х= — 1 и лг= + 1 значения, соот-
соответственно равные л и 0.
Функции i/ = arctgx и (/ = arcctgx определяются как обратные
для тангенса и котангенса, рассматриваемых на интервалах
(-——, — \ и @, п). Эти функции определены и монотонны
156
Гл. 4. Непрерывность функции
У
Я
2
. 2
y-arcsinse
Рис. 4.14
y~
ж
2
У
л
2
's*—
0
у = arctfl х
X
У'
0
л
2
у=тй^ *
Рис. 4.16
Рис. 4.17
на всей бесконечной прямой. На рис. 4.14—4.17 изображены гра-
графики обратных тригонометрических функций.
x *
6. Гиперболические функции. Функции
gX I g"
——
gX g
называются соответственно гиперболическим косинусом
и гиперболическим синусом и обозначаются символа-
символами chx и sh*:
Гиперболический тангенс и гиперболический котангенс определя-
определяются соответственно формулами
sh х ех — ё~х
chx
ех+ех
sh x
Из определения гиперболических функций следует, "что гипербо-
гиперболический косинус, гиперболический синус и гиперболический тан-
§ 3. Простейшие элементарные функции
157
гене заданы на всей числовой оси, а гиперболический котангенс
определен всюду на числовой оси, за исключением точки х=0.
На рис. 4.18—4.21 изображены графики этих функций.
У
У
+1
0
-/1
y=thcc
У'
+1
0
y = cthx
Рис. 4.20
Рис. 4.21
Гиперболические функции непрерывны в каждой точке облас-
области их задания (это следует из непрерывности показательной
функции и теоремы 4.1).
Гиперболические функции обладают рядом свойств, аналогич-
аналогичных свойствам тригонометрических функций. Например, для ги-
гиперболических функций имеют место теоремы сложения, анало-
аналогичные теоремам сложения для тригонометрических функций:
sh(x+y) =sh дг-ch y+ch лг-.sh у,
ch(x+y) =ch *-ch y+sh дг-sh y.
Непосредственно также проверяются формулы sh 2jc = 2 sh^-ch x,
158 Гл. 4. Непрерывность функции
ch2 х—sh2;t=l-. Эпитет же «гиперболический» связан с тем обстоя-
обстоятельством, что равенства x=a-cht, y=a-sht задают гиперболу,
подобно тому, как равенства x=a-cost, y = a-smt задают. ок-
окружность. Действительно, в первом случае мы, очевидно, имеем
Х2—у2=а2^ т е уравнение гиперболы, а во втором х2+у2=а2 —
уравнение окружности.
§ 4. ДВА ЗАМЕЧАТЕЛЬНЫХ ПРЕДЕЛА
1. Первый замечательный предел. Прежде всего докажем сле-
следующую теорему, представляющую собой функциональный аналог
теоремы 3.14.
Теорема 4.6 (функциональный аналог принци-
принципа двустороннего ограничения). Пусть в некоторой
проколотой д-окрестности точки а* заданы три функции f{x), h(x)
и g(x), две из которых f(x) и g(x) имеют в точке а общий пре-
предел, равный Ъ. Тогда если всюду в указанной проколотой Ь-ок-
рестности точки а справедливы неравенства
f(x)<h(x)<g(x), D.17)
го и функция h(x) имеет в точке а предел, равный Ъ.
Доказательство. Пусть {хп} — произвольная, сходящаяся
к а последовательность значений аргумента, все элементы которой
отличны от а. Тогда, с одной стороны, в силу определения пре-
предела по Гейне, обе последовательности соответствующих значений
функций {/(*„)} и {g(xn)} сходятся к Ь, а с другой стороны, в си-
силу D.17), для всех номеров п справедливы неравенства
f{Xn)<h(Xn)<g(Xn).
В силу теоремы 3.14 мы можем утверждать, что последователь-
последовательность h(xn) также сходится к Ь, а это и означает, что число Ъ
является пределом функции h(x) в точке а.
Теорема доказана.
Теорема 4.7. Предел функции h{x) — в точке
jc = O существует и равен единице, т. е.
*-»о х
Доказательство. Будем отправляться от неравенств
О/ oifi v .x*"" v jS' \ct v I гтгмл1 C\ ^~ v -^* ^___ \ (A. 1 Q\
* Напомним, что проколотой 6-окрестностью точки а назувается интервал
{а—б, а+б), из которого выкинута точка а.
§ 4. Два замечательных предела 1591
указанных в п. 4 § 3. Посредством деления на sin;t>0 мы по-
получим из D.18) следующие неравенства:
1 < х < 1
sin* cos л; \ 2
Для обратных величин, очевидно, справедливы обратные нера-
неравенства
I (при 0<х<— )• D.19)
л V 2 /
Заметим, что из того, что неравенства D.19) справедливы при
0<jc<—. вытекает, что эти неравенства справедливы и при
< х < 0, ибо при замене х на —х все три функции cos xr
и 1 не меняют своих значений*.
х
Таким образом, неравенства D.19) справедливы для всех зна-
значений х из интервала—^- < х < -^ За исключением точки х=0,
т. е. справедливы всюду в проколотой окрестности точки
x = 0. Так как, кроме того, обе функции /(;t)=cos;t и g{x) = l
имеют в точке jc=O равный единице предел, то в силу теоремы 4.6
, t / \ sin* „
и функция п(х) = имеет в точке х=0 предел, равный еди-
единице. Теорема доказана.
2. Второй замечательный предел.
Теорема 4.8. Предел функции f{x) = A+хI/х в точке х=О
существует и равен числу е **.
Доказательство. Достаточно доказать, что как правый,
так и левый пределы функции f(x) = A+*I/JC в точке х=0 суще-
существуют и оба равны е.
1) Сначала докажем, что правый предел указанной функ-
функции в точке х=0 существует и равен е.
В силу определения правого предела по Коши достаточно до-
доказать, что для любого е>0 найдется отвечающее ему б>0 такое,
* В самом деле в п. 4 § 3 мы установили, что cos(—x)=cosj:, sin(—х) =
sin (—х) sin*
= — sin* и, значит, —; =
(—х) х
** Число е введено в п. 3 § 2 гл. 3 как предел последовательности | I 1 +
160 Гл. 4. Непрерывность функции
что для любого х из интервала 0<jc<6 справедливо неравен-
неравенство
х—е|<е. D.20)
Фиксируем произвольное е>0 и рассмотрим две последова-
последовательности {ап} и {Ьп} с элементами ага= A -i ) , bn= (l +
\ и + 1 / \
Н ] • Убедимся в том, что обе эти последовательности схо-
п )
дятся ке. В самом деле, поскольку в силу п. 3§2гл. 3 lim A +
1 \п
4-— = е, то на основании теорем о пределе частного и произ-
п 1
ведения двух сходящихся последовательностей мы получим, что
lim a. = lim ч -"¦¦*¦'
Л->со
l+-
п+1 -,
1 +
1
Я+1
lim 1 +
lim 1 +
П-кв
"+1/ _ e -„
¦— ~ к,
1 \ 1
п+\
n
Так как обе последовательности {ап} и {Ьп} сходятся к е, то
для фиксированного выше е>0 найдутся номера N\ и N2 такие,
что \ап—е|<е при n^Nu \bn—е|<е при n>>N2. Пусть N — это
наибольший из двух номеров N\ и Af2. Тогда, очевидно, при tC^N
будут справедливы оба неравенства:
\ап—е\<г и \Ьп—е\<е. D.21)
Теперь для завершения доказательства существования равно-
равного е правого предела функции f(x) = A+хI/х в точке jc = O убе-
убедимся в том, что если взять б = —, то для любого х из интер-
интервала 0<л:<6 = — будет справедливо неравенство D.20).
В самом деле, пусть х — любое число из интервала 0 < х <
< 6=—. Тогда—> ^.Обозначив через п целую часть числа
N х
—, т. е. положив п = — , мы, во-первых, с помощью нера-
х I х \
венства —>N можем утверждать, что n>-N, а во-вторых, мо-
х
жем утверждать, что справедливы неравенства
§ 4. Два замечательных предела 161
«< — О+1. D.22)
х
Из D.22) вытекают неравенства
1 <Ки1 + <1 + д:<1 +
п+1 п п-\-\ п
D.23)
Из сопоставления неравенства D.22) со вторым неравенством
D.23) и из свойства возрастания показательной функции с осно-
основанием, большим единицы, вытекает, что
, 1
\A<(\+y<( +) или
n+l 1 \
Итак, мы доказали, что для любого х из интервала
<6= — при некотором tf>N, зависящем, конечно, от х, будут
справедливы неравенства an<.(l + xI/x<bn, а значит, и неравен-
неравенства
ап—е<{\ + хУ'х—е<Ьп—е. D.24)
Из сопоставления D.24) с неравенствами D.21), справедливыми
для любого n>-N, мы окончательно убедимся в том, что для лю-
любого х из интервала 0<д:<б = — будут справедливы нера-
неравенства D.20).
2) Докажем теперь, что и левый предел функции f(x) =
= A + хI/х в точке х=Ь существует и равен е.
В силу определения левого предела по Гейне достаточно дока-
доказать, что для любой бесконечно малой последовательности отри-
отрицательных чисел {хп} соответствующая последовательность значе-
значений функции /(*„) = A + хп) 1/хп сходится к е.
Пусть {хп} — произвольная бесконечно малая последователь-
последовательность отрицательных чисел. Эту последовательность мы будем
рассматривать, начиная с того номера N, с которого все элементы
хп по модулю меньше единицы.
Положим уп= —, так что хп = —. Тогда, оче-
1 + Хп 1 +Уп
видно, {уп} будет являться бесконечно малой последовательностью,
состоящей из положительных чисел, причем
1+Уп
1+Уп
6 Зак. 72
162 Гл. 4. Непрерывность функции
Таким образом,
f + yn) D.25>
при условии, что существуют пределы в правой части D.25). Но
поскольку {уп} сходится к нулю и состоит из положительных чи-
чисел, то lim A + уУ" — е (в силу уже доказанного существовав
ния равного е правого предела), a lim A+ «/„)= 1. Тем самым
Л-»оо
доказано, что последовательность {/(#„)} сходится к числу е.
Теорема 4.8 полностью доказана.
Следствие. Предел функции f(t)=(l + — } при ^->-оо>
существует и равен е.
В силу определения предела при t-+<x> по Гейне требуется до-
доказать, что для любой бесконечно большой последовательности
{/„} соответствующая последовательность значений функции
f(tn)=ll-j ) " сходится к числу е. Мы будем рассматри-
V n I
вать бесконечно большую последовательность {tn}, начиная с того
номера N, с которого все ее элементы tn по модулю превосходят
единицу. Положим хп=—, так что tn= . В силу теоре-
мы 3.6 из гл. 3 последовательность {хп} является бесконечно ма-
малой, причем /(у= (l +±Y» = (
Остается заметить, что в силу теоремы 4.8
§ 5. ТОЧКИ РАЗРЫВА ФУНКЦИИ И ИХ
КЛАССИФИКАЦИЯ
1. Классификация точек разрыва функции. В § 1 мы договори-
договорились называть точками разрыва функции f(x) те точки, в которых
эта функция не обладает свойством непрерывности. При этом
подразумевается, что функция f(x) определена в той точке, кото-
которую мы апробируем на предмет наличия или отсутствия в ней
свойства непрерывности-.
Расширяя наше рассмотрение, мы можем подвергнуть изуче-
изучению и те точки, в которых функция f(x) не определена (при усло-
условии, конечно, что эти точки являются предельными для множест-
множества задания функции).
Выясним возможные типы точек разрыва.
§ 5. Точки разрыва функции и их классификация 163
1°. Устранимый разрыв. Точка а называется точкой устра-
устранимого разрыва функции y=f{x), если предел функции f(x)
в точке а существует, но в точке а функция f(x) либо не опреде-
определена, либо имеет частное значение f(a), отличное от предела f(x)
в этой точке.
Например, функция
sin*
0,5 при х = 0
имеет в точке х=0 устранимый разрыв.
Действительно, предельное значение этой функции в точке
д;=0, как мы доказали в п. 1 § 4, равно 1. Частное же значение
051
Если функция f(x) имеет в точке а устранимый разрыв, то
этот разрыв можно устранить, не изменяя при этом значений
функции в точках, отличных от а. Для этого достаточно поло-
положить значение функции в точке а равным ее предельному значе-
значению в этой точке. Так, в рассмотренном выше примере достаточ-
достаточно положить /@) = 1 и тогда lim = /@) = 1, т. е. функция
*-»-о х
f(x) станет непрерывной в точке jc = O.
В физических процессах точки устранимого разрыва встреча-
встречаются при сосредоточенных распределениях физических величин.
2°. Разрыв первого рода. Точка а называется точкой раз-
разрыва, первого рода, если в этой точке функция f(x) имеет
конечные, но не равные друг другу правый и левый пределы
lim !(х)Ф lim
х-+а+0 х->а—0
Образно выражаясь, разрыв первого рода можно назвать конеч-
конечным скачком. Приведем некоторые примеры.
1) Функция
1 при х > 0,
/ (х) = sgn х = | 0 при х = 0,
—1 при х<С 0
в точке х = 0 имеет разрыв первого рода*. Действительно,
Функция f(x)=sgnx, очевидно, может быть записана так:
х
при *=^=0,
О при х = 0.
1 64 Гл. 4. Непрерывность функции
lim sgnдс = 1, lim sgnx=—1, и, таким образом, эти пределы
Х-+0+О дс-»О—О
не равны между собой.
2) Другой пример дает функция /(*) = при хфО. Для
этой функции lim smx = 1, lim smx . — —\t так что точка
х~М)+0 \х\ х-»0— 0 \х\
х=0 является точкой разрыва первого рода.
3) Функция /(*) = , определенная всюду, кроме точ-
точки х=1, имеет в точке х=1 разрыв первого рода.
В самом деле, если {хп} сходится к 1 и состоит из элементов
л;га>1, то I 1 является бесконечно большой последователь-
I хп — 1 )
ностью с положительными членами. Поэтому {1 + 2*п—1} —
бесконечно большая последовательность и, значит, последователь-
последовательность / (хп) = является бесконечно малой, т. е.
Если же {хп} сходится к 1 и состоит из элементов хп<1, то
1 1 является бесконечно большой последовательностью с
I хп — 1 J
отрицательными членами. Поэтому {2х" } сходится к нулю и,
значит, последовательность f (хп) ~ ¦ сходится к еди-
1 + 2
нице, т. е. lim /(*) = 1.
дс->-1—О
3°. Разрыв второго рода. Точка а называется точкой раз-
разрыва второго рода, если в этой точке функция f(x) не
имеет по крайней мере одного из односторонних пределов или ес-
если хотя бы один из односторонних пределов бесконечен.
Примеры. 1) Функция
¦ x-cos— при jc< О,
X
/(*) = { 0 при х = О,
cos — при х > О
"I х
обладает левым пределом в точке х=0, равным нулю: lim f{x) —
х-*й—О
= 0. В самом деле, если {хп} — последовательность, сходящаяся
§ 5. Точки разрыва функции и их классификация 165
к нулю и состоящая из чисел хп<0, то
0<
cos-
<\хп\.
х„
Поскольку |дсп]-»-0 при «->-оо, то lim f(x,) = Q.
rt-»oo
Убедимся теперь в том, что рассматриваемая функция не имеет
в точке х=0 правого предела. Для этого рассмотрим две сходя-
сходящиеся к нулю и состоящие из положительных чисел последовав
тельности х„ = и х'п— . Если бы функция обладала
+ 1Ш
2
в точке х=0 правым пределом, то обе последовательности {f(xn)}
и {f{x'n)} сходились бы к одному и тому же числу. Однако
(л \
Ь ял =
2 I
= 0 сходится к нулю.
Итак, рассматриваемая функция имеет в точке *=0 разрыв вто-
второго рода.
2) Функция /(jc) = tg лг, очевидно, имеет разрыв второго рода в
каждой из точек xft = \-nk, где k = 0, ±1, ±2,..., ибо в каж-
каждой такой точке Xk
lim /(*)= +оо, lim f(x)=—oo.
x->-xh— 0
Можно образно сказать, что в каждой точке хи функция tgjc
имеет бесконечный скачок.
3) Функция
sin — при х ф 0,
/(*) =
X
1 при х = О
имеет разрыв второго рода в точке *=(), ибо в этой точке у нее
не существует ни правого, ни левого пределов. В самом деле, по-
поскольку sin = —sin—, достаточно удостовериться в отсут-
—х х
ствии в точке #=0 только правого предела, а для этого достаточ-
достаточно заметить, что двум последовательностям значений аргумента
хп= — и хп = отвечают последовательности значе-
ний функции f(xn) = sin nn=0 и / (х'п) = sin f — + 2пп I = 1,
сходящиеся первая к нулю, а вторая — к единице.
Введем понятие кусочно непрерывной функции, часто встре-
встречающееся в математике и в ее приложениях.
166 Гл. 4. Непрерывность функции
Функция f(x) называется кусочно непрерывной на
сегменте [а, Ь], если эта функция определена всюду на сег-
сегменте [а, Ь], непрерывна во всех внутренних точках этого сегмен-
сегмента, за исключением, быть может, конечного числа точек, в кото-
которых она имеет разрыв первого рода и, кроме того, имеет правый
предел в точке а и левый предел в точке Ъ.
Функция f(x) называется кусочно непрерывной на
инт е р в але (или на бесконечной прямой), если](х)
кусочно непрерывна на любом принадлежащем этому интервалу
(или бесконечной прямой) сегменте.
Например, функция у=[х] кусочно непрерывна как на любом
сегменте, так и на бесконечной прямой.
2. О точках разрыва монотонной функции. Следующее ут-
утверждение проливает свет на природу точек разрыва монотон-
монотонной функции.
Теорема 4.9. Если функция f(x) определена на сегменте
[а, Ь] и является монотонной * на этом сегменте, то она может
иметь на этом сегменте только точки разрыва первого рода,
причем множество всех ее точек разрыва не более чем счетно.
Доказательство. В силу леммы, доказанной в п. 1
§ 2, монотонная функция имеет конечные правый и левый пре-
пределы в любой внутренней точке сегмента [а, Ь] и, кроме того,
конечный правый предел в точке а и конечный левый предел в
точке Ъ. Отсюда и вытекает, что точками разрыва монотонной
функции могут быть только точки разрыва первого рода.
Чтобы доказать вторую часть теоремы о том, что множество
всех точек разрыва не более чем счетно, будем ради опреде-
определенности считать, что f{x) является неубывающей на сегменте
[а, Ь]. Достаточно доказать не более чем счетность множества
точек разрыва, расположенных на интервале (а, Ь), т. е. точек
разрыва, являющихся внутренними точками сегмента [а, Ь].
Заметим, что в каждой такой точке разрыва х справедливо не-
неравенство для правого и левого пределов f(x+O)>f(x—0) (см.
замечание к указанной выше лемме). В силу леммы 2 гл. 2,
каковы бы ни были два вещественных числа, не равных друг
другу, всегда найдется рациональное число, заключенное меж-
между ними.
Так как в каждой точке разрыва х справедливо неравен-
неравенство f(x + O)>f(x—0), то каждой точке разрыва х можно по-
поставить в соответствие некоторое рациональное число г(х),
удовлетворяющее неравенствам /(л:4-0)>г(л:)>/(л:—0).
Заметим, что при этом разным точкам разрыва будут постав-
поставлены в соответствие разные рациональные числа. В самом деле,
если х\ и *2 — две точки разрыва такие, что xi<x2, то из не-
Т. е. либо неубывающей, либо невозрастающей.
§ 6. Локальные и глобальные свойства непрерывных функций 167
убывания функции следует, что /(*i + 0) </(jc2—0), а поэтому
r(xi)<r(x2).
Таким образом, множество всех точек разрыва функции f(x),
расположенных внутри сегмента [а, Ь] эквивалентно подмноже-
подмножеству множества рациональных чисел, которое, как доказано в
§ 7 гл. 2, является не более чем счетным.
Теорема доказана.
§ 6. ЛОКАЛЬНЫЕ И ГЛОБАЛЬНЫЕ СВОЙСТВА
НЕПРЕРЫВНЫХ ФУНКЦИИ
К локальным свойствам относятся те свойства функции,
которые справедливы в сколь угодно малой окрестности фиксиро-
фиксированной точки области определения функции. Эти свойства харак-
характеризуют поведение функции при стремлении аргумента к иссле-
исследуемой точке. Например, непрерывность функции в некоторой точ-
точке области ее определения является локальным свойством этой
функции.
Глобальные свойства — это свойства, связанные со всей
областью определения функции. Например, монотонность функции
на сегменте [а, Ь] является ее глобальным свойством.
1. Локальные свойства непрерывных функций. Введем новые
понятия. Предположим, что функция f(x) задана на множестве
М-
Определение 1. Функция f(x) называется о г р а н и ч е н-
ной сверху (снизу) на множестве {х}, если существует
такое вещественное число М (вещественное число пг), что для
всех значений аргумента х из множества {х} справедливо нера-
неравенство f(x)<^M (f(x)^>m). При этом число М (число пг) называ-
называется верхней (нижней) гранью функции f(x) на мно-
множестве {х}.
Определение 2. Функция f(x) называется ограничен-
ограниченной с обеих сторон (или просто ограниченной) на
множестве {х}, если она ограничена на этом множестве и сверху,
и снизу, т. е. если найдутся такие вещественные числа пг и М, что
для всех значений аргумента х из множества {х} справедливы не-
неравенства m<:f(x)<M.
Таким образом, ограниченность функции f(x) на множестве
{х} фактически означает ограниченность множества всех значений
этой функции (отвечающих значениям аргумента из множества
to)-
Примеры. 1) Функция /(лг) = tgлг, рассматриваемая на ин-
интервале @,—), ограничена на этом интервале снизу (в ка-
качестве нижней грани можно взять число т<0), а сверху не огра-
ограничена.
168 Гл. 4. Непрерывность функции
2) Функция Дирихле D(x), равная нулю в иррациональных
точках и единице в рациональных точках, ограничена (с обеих
сторон) на любом множестве {х}.
Справедлива следующая теорема о локальной ограниченности
функции, имеющей конечное предельное значение.
Теорема 4.10 (о локальной ограниченности
функции, имеющей конечный предел). Пусть функ-
функция f(x) задана на множестве {х} и имеет конечное предельное
значение в точке а. Тогда существует такое положительное число
6, что функция f(x) ограничена на множестве Вь, представляющем
собой пересечение множества {х} с интервалом (а—б, а + б), т. е. с
8-окрестностью точки а.
Замечание 1. Если множество задания функции f(x)
сплошь покрывает некоторую б-окрестность точки а, то в
качестве Вь можно взять сам интервал (а—б, а + б).
Доказательство. Пусть предел f(x) в точке а равен Ь.
В силу определения предела по Коши для некоторого положи-
положительного числа е найдется отвечающее ему положительное число
б такое, что для всех значений аргумента х из проколотой 6-ок-
рестности точки а* справедливо неравенство \f(x)—Ь[<е или
b—z<f(x)<b + e. D.26)
Если множество {х} задания функции не содержит точку а,
то теорема доказана, ибо в этом случае неравенства D.26) озна-
означают, что для всех точек множества В6 = {х}{](а—б, а + б) значе-
значения функции f(x) заключены между числами m = b—е и М = Ь + е.
Если же множество {х} задания функции f(x) содержит точку
а и этой точке отвечает некоторое значение функции f(a), то,
обозначив через m наименьшее из двух чисел Ъ—е и f(a), а через
М наибольшее из двух чисел b + е и f{a), мы получим, что для
всех точек множества В6 = {х}(](а—б, а + б) будут справедливы
неравенства**
m<f(x)<M, D.27)
которые и означают ограниченность f{x) на множестве В6. Теорема
доказана.
Иллюстрацией к доказанной теореме может служить рис. 4.22.
Следствие из теоремы 4.10. Если функция f(x) непре-
непрерывна в точке а, то эта функция ограничена на множестве всех
значений ее аргумента, принадлежащих некоторой 8-окрестности
точки а.
* Напомним, что проколотой б-окрестностью точки а называется интервал
(а—б, а+б) без точки а.
** В самом деле, для всех точек множества В6={х}(](а—б, а+6), за
исключением точки а, будут справедливы неравенства D.26), а потому и нера-
неравенства D.27). Для точки х=а неравенства D.27) справедливы вследствие
выбора чисел m и М.
§ 6. Локальные и глобальные свойства непрерывных функций
169
Достаточно заметить, что непрерывная в точке а функция
имеет в этой точке конечное предельное значение.
Теорема 4.11 (об устойчивости знака непрерыв-
непрерывной в точке функции). Пусть функция f(x) задана на
множестве {х}, непрерывна в точке а этого множества и ее значе-
значение f(a) положительно [отрицательно]. Тогда существует такое
положительное число б, что функция f(x) является положительной
[отрицательной] всюду на множестве В6, представляющем собой
пересечение множества {х} с 8-окрестностью точки а.
Рис. 4.22
Замечание 2. Если множество задания функции f(x)
сплошь покрывает некоторую б-окрестность точки а, то в
качестве В6 можно взять саму б-окрестность точки а.
Доказательство. В силу определения непрерывности по
Коши для любого положительного числа е найдется отвечающее
ему положительное число б такое, что для всех значений аргумен-
аргумента х из б-окрестности точки а справедливо неравенство
или
то
D.28)
оба
f(a)-E<f(x)<f(a)+s.
Если взять в качестве е положительное число
2
числа f(a)—е и f(a) + s будут положительны при f(a)>0 и отри-
отрицательны при f(a)<Q.
Поэтому неравенства D.28) будут означать, что для всех зна-
значений аргумента из б-окрестности точки а функция f(x) является
положительной при /(а)>0 и отрицательной при /(а)<0. Теорема
доказана.
Иллюстрацией к теореме 4.11 может служить рис. 4.23.
Теорему 4.11 легко переформулировать на случай, когда функ-
функция /(х) непрерывна в точке йтолько справа или только
слева.
170 Гл. 4. Непрерывность функции
Договоримся называть полусегмент [а, а+б) правой Ь-полу-
окрестностью точки а, а полусегмент (а—6, а] — левой Ь-полу-
окрестностью точки а.
Теорема 4.11*. Пусть функция f(x) задана на множестве
{х}, непрерывна в точке а этого множества справа [слева] и ее
значение f(a) не равно нулю. Тогда найдется такое положительное
число б, что функция f(x) не обращается в нуль и имеет тот же
знак, что и в точке а, для всех значений х из множества {х}, при-
принадлежащих правой [левой] 6-полуокрестности точки а.
Для доказательства этой теоремы следует дословно повторить
доказательство теоремы 4.11 с заменой термина «б-окрестность
точки а» термином «правая [левая] б-полуокрестность точки а».
Замечание 3. К числу локальных свойств непрерывных в
данной точке функций следует отнести доказанные выше теоремы
4.1 и 4.2 о непрерывности суммы, разности, произведения и част-
частного двух непрерывных в данной точке функций и о непрерыв-
непрерывности сложной функции.
2. Глобальные свойства непрерывных функций.
Теорема4.12 (прохождение непрерывной функ-
функции через нуль при смене знаков). Пусть функция
f(x) непрерывна на сегменте [а, Ь], и пусть значения этой функ-
функции на концах сегмента f(a) и f(b) суть числа разных знаков.
Тогда внутри сегмента [а, Ь] найдется такая точка ?, значение
функции в которой равно нулю.
Доказательство. Не ограничивая общности, можно счи-
считать, что /(а)<0, /F)>0. Пусть {х} — множество всех значений х
из сегмента [а, Ь], для которых /(д;)<0. Это множество непусто
(ему, например, принадлежит точка х=а) и ограничено сверху
(например, числом Ь).
Согласно теореме 2.1 у множества {х} существует точная
верхняя грань, которую мы обозначим через |.
Заметим, что точка % — внутренняя точка сегмента [а,
Ь], так как из непрерывности функции f(x) на [а, Ь] и из условий
f(a)<0, f(b)>0, в силу теоремы 4.11*, вытекает, что найдется
правая 6-полуокрестность точки а, в пределах которой f(x)<0, и
левая б-полуокрестность точки Ъ, в пределах которой f(x)>0.
Убедимся в том, что /(?)=0. Если бы это было не так, то по
теореме 4.11 нашлась бы б-окрестность \—б<л:<? + б точки |,
в пределах которой функция f(x) имела бы определенный знак.
Но это невозможно, так как по определению точной верхней гра-
грани найдется хотя бы одно значение х из полусегмента %—б<дг<|
такое, что /(*)<0, а для любого значения х из интервала
?<лг<|+б справедливо неравенство /(л:)»0. Полученное противо-
противоречие доказывает, что /(|)=0. Теорема доказана. Иллюстрацией
к теореме 4.12 может служить рис. 4.24.
Теорема 4.13 (прохождение непрерывной функ-
функции через любое промежуточное значение).
§ 6. Локальные и глобальные свойства непрерывных функций
171
1.
V
0
А
/ |
>- -У л
I "/Т
Рис. 4.24
Рис. 4.25
Пусть функция f(x) непрерывна на сегменте [а, Ь], причем
/(а)=а, /(&)={5. Пусть, далее, у — любое число, заключенное
между а м р. Тогда на сегменте [а, Ь] найдется точка | такая,
что f{l)=y.
Доказательство. В доказательстве нуждается, очевид-
очевидно, лишь случай аф$ (в противном случае \ = <х = р и можно
взять %=а). По этой же причине отпадает случай, когда у совпа-
совпадает с одним из чисел а или р.
Не ограничивая общности, будем считать, что а<р, a<v<P-
Рассмотрим функцию q>(x)=f(x)—у. Эта функция непрерывна
на сегменте [a, b] (как разность непрерывных функций) и при-
принимает на концах этого сегмента значения разных знаков:
Ф(а) =f (а)-у = а-у<0, ч(Ь) =/F)_Y = p_Y>0.
По теореме 4.12 внутри сегмента [a, b] найдется точка | такая,
что ф(|) =/(?)—y = 0, т. е. f(l) =y. Теорема доказана.
Используя только что доказанную теорему, мы убедимся
в справедливости замечания 2, высказанного в п. 2 § 2.
Пусть функция f(x) непрерывна на сегменте [а, Ь] й су-
существует функция, обратная для f(x), рассматриваемой на
этом сегменте. Тогда f(x) строго монотонна на указанной
сегменте [а, Ь].
Доказательство. Из существования обратной функ-
функции для f(x) следует, что f(a)^f(b). Пусть f(a)<f(b)
[f(a)>f(b)]. Покажем, что f(x) строго монотонно возрастает
[убывает] на сегменте [a, b]. Рассмотрим случай f(a)<f(b).
(Если f(a)>f(b), то рассуждения аналогичны.) Предвари-
Предварительно установим справедливость неравенства f(x)<f(b) для
всех х из (a, b). Действительно, пусть существует такое
iie(a, b), что f(xi) >f(b). (Равенство f(x\)=f(b) невозможно
ввиду, существования обратной функции для функции f(x).)
Применяя теорему 4.13 для сегментов [a, Xi] и [хи Ь] и ис-
используя вытекающие из f (a) <f (b) <f (xi) неравенства
f{a)<m±m<Hxih
172 Гл. 4. Непрерывность функции
убедимся в существовании двух таких чисел gie(a, х\) и
fee (ж,, Ь), что f(g1)-f(i2)=/faH+f(&). Итак, ЬФ\ъ но
f(li)=/(|2), что противоречит существованию обратной функ-
функции для функции f(x) на сегменте [a, b].
Установим теперь строго монотонное возрастание f(x) на
сегменте [а, Ь]. Пусть существуют два числа Xi<x2, принадле-
принадлежащие полусегменту [а, &), такие, что f(xi)>f(x2). Покажем,
что это предположение приводит нас к противоречию. Приме-
Применяя теорему 4.13 для сегментов [х\, х2] и [дг2, Ь] и используя
вытекающие из f(xi)>/(x2), /(*i)<f(b) неравенства
убедимся в существовании двух таких чисел |з^ (х\, х2) и
g4e(*2,b), что /(|з) = /(У = ^М±1М. Итак, ЬФЬ, но
/Aз)=/(§4), что также противоречит существованию обратной
функции для функции f(x) на сегменте [a, b]. Замечая, что
условие f(xi) = /(я2) для Xi<x2 также невозможно, мы прихо-
приходим к выводу, что f(xi)<f(x2) для любых х\<х2 из сегмента
[a, b]. Замечание доказано.
Теорема 4.14 (первая теорема В ейер штр а ее а).
Если функция f(x) непрерывна на сегменте [а, Ь], то она ограни-
ограничена на этом сегменте.
Доказательство. Докажем, что функция f(x) ограни-
ограничена на сегменте [a, b] сверху (ограниченность снизу доказыва-
доказывается аналогично).
Доказательство проведем от противного, т. е. предположим,
что f(x) не является ограниченной сверху на сегменте [a, b].
Тогда для любого натурального п (я=1, 2,...) найдется хотя бы
одна точка хп из [a, b] такая, что f(xn)>n. (В противном случае
f(x) была бы ограничена сверху на сегменте [а, &].)
Таким образом, мы указали последовательность значений {хп}
из сегмента [a, b] такую, что соответствующая последователь-
последовательность значений функции {f(xn)} является бесконечно большой.
В силу теоремы Больцано—Вейерштрасса (см. следствие 3 из
теоремы 3.16 п. 1 § 3 гл. 3) из последовательности {хп} можно
выделить подпоследовательность {**„}, я=1,2,..., сходящуюся
к некоторой точке |. Так как все элементы подпоследовательности
{Xk } лежат на сегменте [a, ft], то и точка | принадлежит сег-
§ 6- Локальные и глобальные свойства непрерывных функций 173
менту [а, Ь] (в силу следствия 2 из теоремы 3.13). В силу непре-
непрерывности функции f(x) в точке | соответствующая подпоследова-
подпоследовательность значений функции {/(**„)} обязана сходиться к
/(?). Но это противоречит тому, что подпоследовательность
{/(*&„)}, будучи выделена из бесконечно большой последова-
последовательности {f(xn)}t сама является 0есконечно большой. Получен-
Полученное противоречие доказывает теорему.
Замечание 1. Для интервала (или полусегмента) утверж-
утверждение, высказанное в теореме 4.14, уже несправедливо, т. е. из
непрерывности функции на интервале (или полусегменте) не вы-
вытекает ее ограниченность на этом множестве. Рассмотрим, напри-
например, функцию f(x) = — на интервале @,1) (или на полу-
полусегменте @,1]). Эта функция непрерывна на указанном множе-
множестве, но неограниченна на нем. В самом деле, последовательность
х =— (л = 2,3,...) принадлежит указанному множеству, а
п
последовательность значений функции {f(xn)}={n} является бес-
бесконечно большой.
Рассмотрим функцию f(x)> ограниченную на данном множест-
множестве {х} сверху (снизу).
Определение. Число М (число т) называется точной
верхней (точной нижней) гранью функции f(x) на
множестве {х}, если выполнены два требования: 1) для каждого
значения х из множества {х} справедливо неравенство f(x)*cM
(f(x)>-m); 2) для любого числа е>0 существует такое значение х
из множества {х}, что для соответствующего значения функции
f(x) справедливо неравенство
f(x)>M—e (f(x)<m+e).
Заметим, что в данном определении условие 1) означает, чго
число М (число пг) является одной из верхних (нижних) граней
функции f(x) на множестве {х}, а условие 2) означает, что эта
грань является наименьшей (наибольшей) и уменьшена (увели-
(увеличена) быть не может.
Точная верхняя грань М функции f(x) на множестве {х} обыч-
обычно обозначается символом
М = sup {f{x)}]= sup f{x).
{*) {*}
Аналогично точная нижняя грань m функции f(x) на множестве
{х} обозначается символом.
m = ini{f(x)}= inff(x).
W {*}
В частности, точная верхняя грань функции f(x) на сегменте
{а, Ь] может обозначаться любым из следующих четырех симво-
символов:
174 Гл. 4. Непрерывность функции
sup /(*) = sup {f(x)}= sup f(x)= sup {f(x}}.
^^b <«b x?[a,b] x?[a,b]
Аналогичные четыре символа для точной нижней г,рани имеют
вид
inf f(x)= infj {/(*)} = inf f(x)= inf/t/ (x)>.
<<b ^cb x?[a,b] *Е[ДО]
Справедливы следующие утверждения:
1) если функция f(x) ограничена на множестве \х} сверху
[снизу], то у нее существует на этом множестве точная верхняя
грань [точная нижняя грань];
2) если функция f(x) ограничена на множестве {х} (с обеих
'сторон), то у нее существуют на атом множестве как точная верх-
верхняя, так и точная нижняя грани.
Эти утверждения являются прямым следствием теоремы 2.1
гл. 2, ибо ограниченность функции f(x) на множестве {х} сверху
[снизу] означает, что множество всех значений этой функции
ограничено сверху [снизу].
Возникает вопрос о том, является ли точная верхняя [точная
нижняя] грань ограниченной на множестве {х} функции f{x)
достижимой, т. е. существует ли среди точек множества {х}
такая точка х0, значение функции в которой f(xo) равно точной
верхней [соответственно точной нижней] грани f(x) на множест-
множестве {х}.
Следующий пример показывает, что точные грани ограничен-
ограниченной на данном множестве функции, вообще говоря, не являются
достижимыми.
Рассмотрим на сегменте [0, 1] функцию f(x) следующего вида
(рис. 4.25):
х2 при 0 < х < 1,
1/2 при х = 0 и х — 1.
Эта функция ограничена на сегменте [0, 1] и имеет на нем
точную верхнюю грань М=1 и точную нижнюю грань т=0. Од-
Однако эти грани недостижимы: среди точек сегмента [0, 1] не су-
существует точек, значения функции в которых были бы равны нулю
или единице.
Заметим, что рассматриваемая функция f(x) не является не-
непрерывной на сегменте [0, 1] (она имеет разрывы в точках х=0
и x=l). Оказывается, это обстоятельство не является случайным,
ибо справедливо следующее утверждение.
Теорема 4.15 (вторая теорема Вейерштр а ее а).
Если функция f(x) непрерывна на сегменте [а, Ь], то она дости-
достигает на этом сегменте своих точных верхней и нижней граней,
т. е. среди точек сегмента [а, Ь] найдутся такие точки Х\ и Хг,
что значение \{х\) равно точной верхней грани f(x) на сегменте
§ 6. Локальные и глобальные свойства непрерывных функций 175
[а, Ь], а Значение f(x2) равно точной нижней грани f(x) на сег-
сегменте [а, Щ.
Доказательство. В силу первой теоремы Вейерштрасса
4.14 функция f{x) ограничена на сегменте [a, b], a поэтому у нее
существует на этом сегменте точная верхняя грань М и точная
нижняя грань т.
Остановимся на доказательстве достижимости точной верхней
грани М, ибо достижимость точной нижней грани т доказывается
аналогично.
Предположим, что точная верхняя грань М не является дости-
достижимой, т. е. предположим, что во всех точках сегмента [а, Ь]
функция f{x) принимает значения, строго меньшие М. Тогда мы
можем рассмотреть функцию
F(x) = -
M-f(x)
Знаменатель М—f(x) представляет собой функцию, непрерыв-
непрерывную и строго положительную на сегменте [а, Ь]. Поэтому по тео-
теореме 4.1 (для случая частногр) функция F(x) будет являться не-
непрерывной на сегменте [а, Ь]. Значит, по первой теореме Вейер-
Вейерштрасса 4.14 функция F(x) ограничена на сегменте {а, Ь], т. е.
найдется положительное число А такое, что F (х) = <"
M—f(x)
-<Л для всех х из сегмента [а, Ь]. Так как функция М—f(x)
строго положительна на [а, Ь], то последнее неравенство экви-
эквивалентно неравенству f(x)^.M- для всех х из сегмента
[а, Ь], а это противоречит тому, что число М является точной
верхней гранью, т. е. наименьшей из всех верхних граней функции
f(x) на сегменте [а, Ь].
Полученное противоречие доказывает, что наше предположе-
предположение о недостижимости точной верхней грани является неверным.
Теорема доказана.
Замечание 2. После того как доказана достижимость не-
непрерывной на сегменте [а, Ь] функцией своих точных верхней и
нижней граней, мы можем назвать точную верхнюю грань М
максимальным значением, а точную нижнюю грань т
минимальным значением функции \{х) на сегменте
[а, Ь]. Теорему 4.15 можно переформулировать в виде: непрерыв-
непрерывная на сегменте [а, Ь] функция f(x) имеет на этом сегменте мак-
максимальное и минимальное значения.
Максимальное значение функции f(x) на сегменте [а, Ь]
обозначается одним из следующих символов:
max /(x)= max {f(x)}— max f(x)= max {f (x)}.
<<6 <*;& x&[a,b] 6[&]
176 Гл. 4. Непрерывность функции
Аналогичные символы для минимального значения f(x) на
сегменте [а, Ь] имеют вид
min /(x)= min {/(*)}= min f(x) — min {/(*)}•
а<х<Ь as^xfb х6[аЬ] *6[&]
Замечание З. Заметим, что и функции, не являющиеся
непрерывными на данном сегменте, могут достигать на этом сег-
сегменте своих точной верхней и точной нижней граней. Примером
может служить функция Дирихле D{x), равная нулю для всех
иррациональных х и равная единице для всех рациональных х.
Эта функция разрывна в каждой точке сегмента [0, 1], но, оче-
очевидно, достигает на этом сегменте своей точной верхней грани,
равной единице, и своей точной нижней грани, равной нулю.
Замечание 4. Утверждение теоремы 4.15 окажется невер-
неверным, если в ее формулировке термин «сегмент» заменить терми-
термином «интервал» или «полусегмент».
Так, функция f(x)=x является непрерывной на интервале
(О, 1) или на полусегменте [0, 1), однако точная верхняя грань
этой функции на указанном интервале или полусегменте М—1
хотя и существует, но не достигается.
К этому следует добавить, что у функции, являющейся непре-
непрерывной на интервале или полусегменте, точные грани могут даже
не существовать, ибо такая функция может не являться ограни-
ограниченной на указанном интервале или полусегменте (см. замеча-
замечание 1).
3. Понятие равномерной непрерывности функции. Предполо-
Предположим, что функция y=f(x) задана на таком множестве {х}, каж-
каждая точка которого является предельной точкой этого множества.
Примером такого множества могут служить сегмент, интервал,
полусегмент, полупрямая, бесконечная прямая, множество всех
рациональных точек, принадлежащих любому из перечисленных
множеств.
Определение. Функция y—f(x) называется равномер-
равномерно непрерывной на множестве {х}, если для любого поло-
положительного числа е найдется отвечающее ему положительное чис-
число б такое, что для любых двух точек х' и х" множества {х}, удов-
удовлетворяющих условию \х'—x"|<6, справедливо неравенство
\f(x')-f(x")\<z. D.29)
Замечание 1. Сразу же подчеркнем, что если функция
f(x) равномерно непрерывна на множестве {х}, то она непрерывна
в каждой точке х множества {х}. В самом деле, взяв в сформу-
сформулированном определении в качестве х" данную фиксированную
точку хо множества {х}, а в качестве х' — любую точку этого
множества, мы придем к определению непрерывности функции
f(x) в точке хо по Коши.
Замечание 2. Основным в сформулированном определе-
определении равномерной непрерывности является требовайие, гаранти-
§ 6. Локальные и глобальные свойства непрерывных функций
177
рующее существование по любому е>0 такого универсального
5>0, которое обеспечивает справедливость неравенства D.29)
сразу для всех точек х' и х" множества {х}, удовлетворяющих
условию \х/—х"\ <б.
Если потребовать непрерывности функции f(x) в каждой точ-
точке хо множества {х}, то для любого е>0 и любой точки х0 мно-
множества {х} можро гарантировать существование «своего» положи-
положительного числа б = б(е, Хо), зависящего не только от е, но и or
Хо и обеспечивающего справедливость неравенства- |/(д;)—f(xo)\<
<е для всех х из множества {х}, удовлетворяющих условию
\х—Яо|<6(е, Хо). При этом, вообще говоря, может не существо-
существовать положительной точной нижней грани указанных
б(е, х0) по всем точкам хо множества {х}, т. е. равномерная не-
непрерывность функции на множестве {х} не вытекает, вообще го-
говоря, из непрерывности этой функции в каждой точке хо мно-
множества {х}.
Замечание 3. Из данного нами определения равномерной
непрерывности непосредственно вытекает, что если функция f{x}
равномерно непрерывна на множестве {х}, то эта функция равно-
равномерно непрерывна и на любом подмножестве множества {х}.
Рассмотрим примеры функций, как обладающих, так и не об-
обладающих на данном множестве {х} свойством равномерной не-
непрерывности.
1. Убедимся в том, что функция /(*) = — равномерно не-
непрерывна на полупрямой х>1. В самом деле, для любых двух
х' и х" из указанной полупрямой справедливо неравен-
точек
ство
(*')-/(*•)!= -V
1 1
х' х"
X" — X'
X' ¦ X"
\х" —х'\
х' ¦ х"
I y" y' I
I х —х \
Поэтому, взяв для любого е>0 положительное число б рав-
равным е, мы получим, что для любых двух точек х' и х" полупря-
полупрямой [1, +°о), удовлетворяющих условию \х"—х'|<8, справед-
справедливо неравенство \\{х')—/(л;")|<6=е.
2. Функция /(x) = sin— не является равномерно непрерыв-
непрерывной на интервале @, 1)*. Чтобы убедиться в этом, достаточно
доказать, что для некоторого е>0 и для любого как
угодно малого 6>0 найдется хотя бы одна пара точек х' и-
х" интервала @, 1) таких, что
\х'—х"\<Ь, но [fix')—
* Хотя эта функция и является непрерывной в каждой точке интервала-
@,1).
178 Гл. 4. Непрерывность функции
Рассмотрим две последовательности точек, принадлежащих
интервалу @, 1), {х'п} и {х"п} с элементами
х' и х"п = , п=1, 2
п-п " п
—
Обе эти последовательности, а значит, и их разность являются
бесконечно малыми. Поэтому для любого как угодно малого
5>0 найдется номер п такой, что \х'п—х"п\ < б. Вместе с тем
для любого номера п
sin я/г—sin (— + 2я/г) | = 1.
Поэтому для е= — >0 и для как угодно малого б>0 най-
найдется пара точек х' и х" из интервала @, 1) таких, что \хп'—
—Хп"\<6, в то время как \f{xn')—f(xn") |>e, это и означает, что
рассматриваемая функция не является равномерно непрерывной
на интервале @, 1).
Заметим, что если бы мы рассмотрели ту же самую функцию
f(x) — sm— не на интервале @, 1), а на интервале (у, 1), где
у — любое число из интервала 0<y<1, to приведенные выше рас-
рассуждения уже не имели бы места. Этот факт не является случай-
случайным, ибо ниже мы покажем, что указанная функция является
равномерно непрерывной на интервале (y, 1) при 0<y<1.
3. Докажем, что функция f(x)=x2 не является равномерно не-
непрерывной на полупрямой я>1. Заметим, что для любых двух то-
точек х' и х" полупрямой л;> 1 справедливо неравенство
(Т1
D.30);
= \х/+х"\ • \х'—х"\>х'- \х'—х"\.
Убедимся теперь в том, что не только для некоторого
s>0, а даже для любого е>0 и для любого как угодно мало-
малого 6>0 найдется пара точек х' и х" из' полупрямой х>-\ таких,
что
\х'-х"\<8, но
(Это и будет означать отсутствие свойства равномерной непре-
непрерывности у функции f(x)=x2 на рассматриваемой полупрямой.)
Фиксировав произвольные е>0 и 6>0, возьмем в качестве х'
произвольное число, превосходящее единицу и такое, что хг>—^~,
о
и положим х" = х'-\ . Для таких х' и х" будет справедливо
§ 6. Локальные и глобальные свойства непрерывных функций 179
неравенство \х'—х"\ — — < б. С другой стороны, в силу
D.30) для этих же х' и х" будет справедливо неравенство
Заметим, что если бы мы рассмотрели ту же самую функцик>
f(x)=x2 не на полупрямой *>1, а на любом сегменте [1, Ь], где
b — любое число, то проведенные нами рассуждения уже не име-
имели бы места.
Этот факт становится понятным в силу следующей фундамен-
фундаментальной теоремы.
Основная теорема 4.16. Если функция f(x) непре-
непрерывна на сегменте [а, Ь], то она и равномерно непрерывна на
этом сегменте.
Доказательство. Предположим, что функция f(x) не-
непрерывна на сегменте [а, Ь], но не является равномерно непре-
непрерывной на этом сегменте.
Тогда для некоторого е>0 и для любого как угодно малого
б>0 найдутся две точки х' и х" сегмента [а, Ь] такие, что
\х'—х"\<Ь, но |/(л:')— /(*")!>е.
Выберем бесконечно малую последовательность положительных
чисел б„=— (я=1,2,...). Можно утверждать, что для ука-
п
занного е>0 и для любого номера п найдутся две точки хп' и
хп" сегмента [а, Ь] такие, что
К-К1 <т- но 1/«)-/Ю1>«- D-3D
Так как последовательность {х„'} состоит из точек сегмента [а>
Ь], то она ограничена и по теореме Больцано—Вейерштрасса
(см. следствие 3 из теоремы 3.16 гл. 3) из нее можно выделить
сходящуюся подпоследовательность {х'ь}, я=1, 2 Предел
| указанной подпоследовательности (в силу следствия 2 из тео-
теоремы 3.13 гл. 3) будет также принадлежать сегменту [а, Ь].
В силу левого неравенства D.31) соответствующая подпоследо-
подпоследовательность {x"k } будет сходиться к той же самой точке |.
Поскольку функция f(x) непрерывна в каждой точке сегмента
[а, Ь], она непрерывна и в точке ?*. Но тогда, в силу определе-
определения непрерывности по Гейне, обе подпоследовательности соответ-
соответствующих значений функции {f(x'k )} и {f(x"k )} обязаны схо-
сходиться к f(S), т. е. разность указанных подпоследовательностей
* В случае, если | совпадает с одним из концов сегмента [а, Ь], под не-
непрерывностью следует понимать одностороннюю непрерывность.
380 Гл. 4. Непрерывность функции
if ix'k )—f(xl)} обязана быть бесконечно малой. Это противо-
противоречит правому неравенству D.31), справедливому для всех номе-
номеров п и потому для всех номеров kn.
Полученное противоречие доказывает, что наше предположе-
предположение о том, что непрерывная на сегменте [а, Ь] функция не явля-
является равномерно непрерывной на этом сегменте, является невер-
неверным. Теорема доказана.
Возвратимся теперь к рассмотренному выше примеру 2 и по-
покажем, что функция f(x) = sin— является равномерно непре-
X
рывной на интервале (у, 1) при любом у из интервала 0<y<1.
В самом деле, при любом таком у функция f(x) = sin— непре-
непрерывна на сегменте [у, 1]. Значит, по теореме 4.16 функция f(x) =
= sin равномерно непрерывн • на сегменте [у, 1]. В силу заме-
X
чания 3 к определению равномерной непрерывности функция
f(x) = sin—. тем более является равномерно непрерывной на
интервале (у, 1), представляющем собой подмножество сегмента
[Y, !]•
Теорему 4.16 удобно переформулировать в терминах колеба-
колебания функции на данном сегменте.
Пусть функция f(x) ограничена на данном сегменте [с, d].
Назовем колебанием функции f(x) на сегменте [с, d] раз-
разность (и = М—m между точной верхней и точной нижней гранями
функции f(x) на этом сегменте.
Для непрерывной на сегменте [с, d] функции f(x) колебание
равно разности между максимальным и минимальным значения-
значениями этой функции на указанном сегменте.
Из теоремы 4.16 непосредственно вытекает следующее утверж-
утверждение.
Следствие из теоремы 4.16. Если функция f(x) не-
непрерывна на сегменте [а, Ь], то для любого положительного чис-
числа е найдется отвечающее ему положительное число б такое, что
колебание функции f(x) на любом содержащемся в сегменте
[а, Ь] сегменте длины, меньшей б, будет меньше числа г.
Замечание 4. Анализируя доказательства теорем 4.14 и
¦4.15 Вейерштрасса и теоремы 4.16, нетрудно заметить, что в этих
трех теоремах вместо сегмента [а, Ь] можно взять произвольное
множество {х}, для которого выполнены два требования: 1) это
множество {х} является ограниченным; 2) это множество {х} со-
содержит любую свою предельную точку (такое множество догово-
договоримся называть замкнутым).
Множество {х}, удовлетворяющее указанным двум требова-
требованиям, договоримся называть компактным множеством
§ 6. Локальные и глобальные свойства непрерывных функций 181
или компактом. Таким образом, указанные три теоремы
(т. е. две теоремы Вейерштрасса и теорема 4.16) справедливы не
только для функции, непрерывной на сегменте, но и для функции,
непрерывной на любом компакте.
В § 7 настоящей главы будут сформулированы более точные оп-
определения замкнутого и компактного множеств. Впрочем, для
случая числовых множеств эти более точные определения оказы-
оказываются эквивалентными приведенным нами выше определениям^
4. Понятие модуля непрерывности функции. Предположим,
что функция f(x) определена и непрерывна на некотором мно-
множестве {х}, каждая точка которого является предельной точкой
этого множества.
Определение. Для каждого б>0 назовем модулем
непрерывности функции f(x) на множестве {х} точную
верхнюю грань модуля разности \f{x')—f{x")\ no всем точкам
%'. и х", принадлежащим множеству {х} и удовлетворяющим
неравенству | х'—х" | < б.
Для обозначения указанной точной верхней грани обычно
употребляют следующий символ:
sup{| f (x')-/{х") | : \х'-х"| <: б; х', х"^{х}}.
Сам же модуль непрерывности функции f(x) на множестве
{х} принято обозначать символом со(/, б).
Таким образом, по определению
со (/, б) = sup{ | f (x') -f (х") | : | х'-х" | <: б; х', /е{4
D.32)
Замечание. При определении' модуля непрерывности
o)(f, 6) в правой части D.32) вместо \f(x')—f(x") | можно
было бы писать разность [f(x')—f(x")] без знака модуля. Это
вытекает из того, что точки х' и х" можно поменять местами
(при этом разность [f{x')—f{x")] изменит знак на противопо-
противоположный, в то время как величина \х'—х"\ не изменится).
Отметим два свойства модуля непрерывности со(/, 6).
Г. Модуль непрерывности со(/, б) всегда неотрицателен:
со(/, б)>0.
Это свойство непосредственно вытекает из определения мо-
модуля непрерывности D.32).
2°. Модуль непрерывности со(/, б) представляет собой не-
неубывающую функцию б всюду на полупрямой б>0.
В самом деле, при уменьшении б множество, по которому
берется супремум D.32), сужается, а супремум на части мно-
множества не превосходит супремума на всем множестве.
Вычислим модули непрерывности некоторых функций.
1. Вычислим модуль непрерывности функции f(x)=x2 на
сегменте [0, 1].
Пусть х' и х" — любые две точки сегмента [0, 1] такие, что
х" = х'—б, где 0<б<1. Тогда, очевидно,
182 Гл. 4. Непрерывность функции
Из последнего неравенства, учитывая замечание к определению
модуля непрерывности, мы получим, что
С другой стороны, взяв х'=1, х"=\—б, так что \х'—*"|=6,
мы получим, что
Значит, ы(/, 6)=а(х2, б) =26—б2 (если б<1).
2. Вычислим далее модуль непрерывности функции / (х) —
= sin— на интервале @, 1).
х
Так как
—^—sin—г ^ sin-^ + sin-^ < 2,
sin
1
sin
1
x"
I/(*')-/(*")! =
то (o(/, 6) «2.
С другой стороны, взяв две бесконечно малые после-
последовательности {хп'} и {хп"} точек интервала @, 1) вида
х' = . х" = . где п = 1, 2, ..., мы для любо-
" я я
2 ^ 2
го б>0 сможем указать номер «такой, что 0<х„'<6 и 0<хп"<
<б, так что |дгп'—хп"\<б, причем
1 1
х'п хп
Отсюда следует, что ю(/, б) = « (sin—, S j = 2.
3. Вычислим, наконец, модуль непрерывности функции
f(x) = — на интервале @, 1). Убедимся в том, что этот
модуль непрерывности равен +оо.
Фиксировав произвольное 6>0, рассмотрим только такие
точки х' и х", которые удовлетворяют соотношениям 0<*'<6\
х" = 8, так что \х'—*"|<:6. Очевидно, что*
В заключение докажем теорему, устанавливающую связь
между свойством равномерной непрерывности функции f(x) на
* Мы учитываем, что при сужении множества значений xf t и х", по кото-
которым берется супремум, этот супремум может только уменьшаться.
§ 6. Локальные и глобальные свойства непрерывных функций 183
множестве {х} и величиной модуля непрерывности этой функ-
функции на указанном множестве.
Теорема 4.17. Для того чтобы функция f(x) являлась
равномерно непрерывной на множестве {х}, необходимо и дос-
достаточно, чтобы модуль непрерывности со(/, б) этой функции на
указанном множестве удовлетворял соотношению
Ига ю(/,б) = 0. D.33)
6-s-O+O
Доказательство. 1) Необходимость. Пусть функция
}(х) равномерно непрерывна на множестве {х}. Требуется дока-
доказать, что справедливо соотношение D.33), т. е. требуется дока-
доказать, что для любого е>0 найдется отвечающее ему 6е>0 та-
такое, что для всех б, удовлетворяющих условию 0<6<6е, спра-
справедливо неравенство at(f, 6)<е*.
По определению равномерной непрерывности для любого
е>0 найдется отвечающее ему бЕ>0 такое, что для всех х1 и
х" из множества {х}, удовлетворяющих условию \х'—х"\<Ь„
справедливо неравенство \f(x')—/(#")|<-—. Но это и оз-
начает, что для любого 6 из интервала 0<6<б„ справедливо
неравенство
e>(f,6) = suv{\f(x')-f(x")\:\x'-x"\<6; х', х» е= {*}}< -j- < г.
2-) Достаточность. Пусть выполнено соотношение D.33), т.е.
для любого е>0 существует отвечающее ему бе>0 такое, что
для всех 6, удовлетворяющих условию 0<6<6„, справедливо
неравенство ©(/, б)<е.
Из определения модуля непрерывности ¦ следует, что для
всех х' и х" из множества {х}, удовлетворяющих условию
\х'—дс//|-<б<бе, справедливо неравенство \f{x')—/(д;")|<е, а
это и означает, что функция f{x) равномерно непрерывна на
множестве {х}. Теорема доказана.
Выше мы вычислили модули непрерывностей трех функций:
функции х2 на сегменте [0, 1] и функций sin— и — на
X X
интервале @, 1).
Так как со (х2,6) = 26—б2, «(sin—, б) =2, «of—, б) = +оо,
V х ) \ х )
то из теоремы 4.17 сразу же вытекает, что функция х2
равномерно непрерывна на сегменте [0, 1], а функции sin —
и — не являются равномерно непрерывными на интервале
(О,*)-
• Мы учитываем при этом, что ш(/, б)>0.
184 Гл. 4. Непрерывность функции
§ 7. ПОНЯТИЕ КОМПАКТНОСТИ МНОЖЕСТВА
1. Открытые и замкнутые множества. Рассмотрим произ-
произвольное множество вещественных чисел {х}.
Определение 1. Точка х множества {х} называется
внутренней точкой этого множества, если существует поло-
положительное число б такое, что ^-окрестность точки х также при-
принадлежит множеству {х}.
Определение 2. Множество {х} называется от к р ы-
т ы м, если любая точка этого множества является внутренней:
его точкой.
Примерами открытых множеств могут служить интервал,,
открытая полупрямая, бесконечная прямая, объединение не-
нескольких непересекающихся интервалов.
Определение 3. Множество {х} называется замкну-
замкнутым, если дополнение этого множества (т. е. разность (—<х>>,
+ оо)\{д:}) является открытым множеством.
В замечании 4 в конце п. 3 § 6 было дано другое опреде-
определение замкнутого множества. Напомним его формулировку.
Определение 3*. Множество {х} называется з амкну-
т ы м, если это множество содержит все свои предельные-
точки.
Убедимся в том, что для случая произвольных числовых
множеств определения 3 и 3* эквивалентны.
1) Пусть сначала множество {х} является дополнением от-
открытого множества. Докажем, что в таком случае любая пре-
предельная точка х этого множества {х} обязательно ему принад*
лежит.
В самом целе, предположив, что предельная точка х не при-
принадлежит множеству {х}, мы бы получили, что х принадлежит
дополнению множества {х}, которое является открытым мно-
множеством. Но тогда х принадлежала бы этому открытому мно-
множеству вместе с некоторой своей 6-окрестностью, т. е. некото-
некоторая б-окрестность точки х не содержала бы точек множества
{х}, а это противоречило бы тому, что х является предельной,
точкой множества {х}.
2) Пусть любая предельная точка множества {х} принадле-
принадлежит этому множеству. Докажем, что множество {х} является до-
дополнением открытого множества. Пусть х — любая точка до-
дополнения множества {х}. Требуется доказать, что это дополне-
дополнение содержит и некоторую б-окрестность точки х.
Если бы это было не так, то любая б-окрестность точки х
содержала бы точки множества {х}, т. е. точка х являлась бы
предельной точкой множества {х} и по условию ему принадле-
принадлежала, а это противоречило бы тому, что х — точка дополнения
множества {х}.
2. О покрытиях множества системой открыты* множеств.
§ 7. Понятие компактности множества 185
Определение1. Будем говорить, что система {Еа} от-
открытых множеств Бо образует покрытие множества
{х}, если любая точка х множества {х} принадлежит хотя бы
одному из множеств системы {2а}-
Докажем две замечательные леммы о покрытиях множест-
множества системой открытых множеств.
Лемма Гейне—Бор ел я для сегмента. Из лю-
любой системы {2а} открытых множеств 2а, образующей покры-
покрытие сегмента [а, Ь], можно выделить конечную подсистему,
также образующую покрытие этого сегмента.
Доказательство. Пусть бесконечная система {2а}
открытых множеств 2а образует покрытие сегмента [а, Ь]*.
Допустим, что сегмент /= [а, Ь] нельзя покрыть конечным
набором открытых множеств из системы {Ба}. Тогда, разделив
этот сегмент / пополам, мы получим, что хотя бы одну из по-
половин сегмента / нельзя покрыть конечным набором открытых
множеств из системы {Ба}. Обозначим эту половину, через 1\.
Поделив /i пополам, мы получим, что хотя бы одну из поло-
половин h (обозначим ее через /2) нельзя покрыть конечным набо-
набором множеств из системы {2а}.
Продолжая далее эти рассуждения, мы получим систему
вложенных сегментов {/«}, каждый из которых нельзя покрыть
конечным набором множеств из системы {2а}. Длина я-го сег-
сегмента 1п составляет 1/2п часть длины основного сегмента
I=[a, b] и стремится к нулю при п-+оо.
В силу следствия из теоремы 3.15 (см. п. 2 § 2 гл. 3) су-
существует единственная точка с, принадлежащая всем сегмен-
сегментам {In}- Так как эта точка с принадлежит основному сегмен-
сегменту I=[a, b], то в системе {Ба} найдется открытое множество
2а, которому принадлежит точка с. В силу того, что множество
2а является открытым, найдется б>0 такое, что б-окрестность
точки с, т. е. интервал (с—б, с + 6) также принадлежит мно-
множеству 2а.
В силу того, что все сегменты /„ содержат точку с и длины
этих интервалов стремятся к нулю при я-э-оо, можно утверж-
утверждать, что найдется номер п0 такой, что при п>яо все сегменты
/„ содержатся в интервале (с—6, с+б).
Но это означает, что все сегменты 1п при п>Ло могут быть
покрыты одним множеством Ба системы {?«}. Тем самым мы
получили противоречие с утверждением о том, что ни один
сегмент 1п нельзя покрыть конечным набором множеств из
системы {2«}. Полученное противоречие завершает доказатель-
доказательство леммы.
Докажем теперь более общее утверждение.
* Если бы система {So}, образующая покрытие сегмента [а, Ь], не явля-
являлась бесконечной, то лемма была бы доказана.
186 Гл. 4. Непрерывность функции
Лемма Гейн е— Б ореля для замкнутого огра-
ограниченного множества. Из любой системы {S«} откры-
открытых множеств 2а, образующей покрытие замкнутого ограни-
ограниченного множества {х}, можно выделить конечную подсистему,
также образующую покрытие множества {х}.
Доказательство. Пусть {х} — замкнутое ограниченное
множество, {2а} — система открытых множеств, образующая
покрытие множества {х}.
Так как множество {х} ограничено, то найдется сегмент
[а, Ь], содержащий это множество. Обозначим через Ер от-
открытое множество, являющееся дополнением к замкнутому
множеству {х} и заметим, что объединение системы {Еа} с от-
открытым множеством 2р образует покрытие сегмента [а, Ь].
В силу леммы Гейне—Бореля для сегмента из этого покрытия
можно выделить конечную подсистему, также образующую
покрытие сегмента [а, Ь].
Если множество 2Р входит в эту конечную подсистему, то,
удалив его из нее, мы получим конечную подсистему системы
{2а}, образующую покрытие множества {х}*.
Если же множество 2Р не входит в конечную подсистему,
образующую покрытие сегмента [а, Ь], то эта конечная под-
подсистема состоит исключительно из множеств 2а системы {2„}
и образует покрытие множества {х}, содержащегося в сегмен-
сегменте [а, Ь]. Лемма доказана.
3. Понятие компактности множества. Пусть {х} — произ-
произвольное множество вещественных чисел.
Определение 1. Множество {х} называется компакт-
компактным множеством (или компактом), если из любой
системы {Б«} открытых множеств, образующей покрытие мно-
множества {х} можно выделить конечную подсистему, также обра-
образующую покрытие множества {х}.
В замечании 4 в конце п. 3 § 6 было дано другое опреде-
определение компактного множества. Напомним его формулировку.
Определение 1*. Множество {х} называется компакт-
компактным, если оно является замкнутым и ограниченным**.
Докажем, что для произвольных числовых множеств опре-
определения 1 и 1* эквивалентны.
1) Пусть сначала множество {х} является замкнутым и огра-
ограниченным. Тогда тот факт, что из любой системы открытых
множеств {2а}, образующей покрытие {х}, можно выделить ко-
конечную подсистему, также образующую покрытие {х}, сразу
вытекает из леммы Гейне—Бореля (см. п. 2).
* Мы учитываем, что множество 2j, являясь дополнением к множеству
{*}, не содержит ни одной точки множества {х}.
** Относительно термина «компактность» см. п. 2 § 3 гл. 12. -
§ 7. Понятие компактности множества 187
2) Пусть множество {х} таково, что из любой системы от-
открытых множеств {Бо}, образующей покрытие {х}, можно выде-
выделить конечную подсистему, также образующую покрытие {х}.
Докажем, что множество {х} является замкнутым и ограни-
ограниченным.
Сначала докажем замкнутость множества {х}.
Достаточно доказать, что дополнение D множества {х} яв-
является открытым множеством.
Фиксируем произвольную точку у дополнения D. Требуется
доказать, что существует некоторая б-окрестность точки у, так-
также принадлежащая дополнению D.
Пусть х — любая точка множества {х}. Так как хфу, то
число б (х) = является положительным, причем
6(х) — окрестности точек х и у
), Wx=(y~8(x), y+6(x))
не пересекаются.
Поскольку система открытых множеств {2*}, отвечающих
всевозможным точкам х множества {х} образует покрытие мно-
множества {х}, то из этой системы можно выделить конечную под-
подсистему 2Xl, S*2, ... ,Ихп, также образующую покрытие мно-
множества {х}.
Обозначим через WXi, Ч*"^, ... ,ХРХ соответствующую ко-
конечную подсистему б-окрестностей точки у. Наименьшая
из этих б-окрестностей будет содержаться во всех множествах
Ч"*,. ^х2. ¦••,Ч?хп и потому не будет иметь общих точек ни с
одним из множеств 2*,, S*,,... ,2Жп. Но тогда, поскольку под-
подсистема 2Х,, 2^,. .., S*n образует покрытие множества {х},
указанная наименьшая б-окрестность точки у не будет содер-
содержать точек множества {х}, т. е. будет целиком принадлежать
дополнению D множества {х).
Тем самым доказано, что множество D является открытым
и потому множество {х} является замкнутым.
Докажем теперь, что множество {х} является ограничен-
ограниченным. Если бы это было не так, то нашлась бы последователь-
последовательность {хп} не совпадающих друг с другом точек множества
{х}, удовлетворяющая условию
(л=1, 2,...).
Так как эта последовательность не имеет конечных пре-
предельных точек, то каждая точка хп имеет б-окрестность 2*п ,
свободную от других точек последовательности {хп}.
Очевидно, что из бесконечной системы открытых множеств
{2* }, образующих покрытие множества точек {#„}, нельзя
188 Гл. 4. Непрерывность функции
выбрать конечной подсистемы, образующей покрытие всех то-
точек {Хп}-
Так как множество {хп} является подмножеством {х}, то
тем более нельзя из всякой системы открытых множеств, обра-
образующих покрытие {х}, выделить конечную подсистему, также
образующую покрытие {х}. Но это противоречит нашему пред-
предположению о множестве \х). Полученное противоречие доказы-
доказывает ограниченность множества {х}.
Заметим в заключение, что все введенные в этом параграфе
понятия в более общей ситуации изучаются в дополнении 2 к
гл. 12.
Глава 5
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
В настоящей главе будут введены фундаментальные понятия
производной и дифференциала функции. Мы установим основные
правила дифференцирования и вычислим производные всех прос-
простейших элементарных функций, уже приведенные нами в гл. 1 а
известные из школьного курса. В конце главы будут рассмотре-
рассмотрены производные и дифференциалы высших порядков и вопрос о^
дифференцировании функции, заданной параметрически.
§ 1. ПОНЯТИЕ ПРОИЗВОДНОЙ
1. Приращение функции. Разностная форма условия непрерыв-
непрерывности. Рассмотрим функцию y = f(x), заданную на интервале (а,
Ь)*. Пусть х — любая фиксированная точка интервала (a, b), a
Ал; — произвольное число, настолько малое, что значение х+Ах
также находится на интервале (а, Ь). Это число Ал; обычно на-
называют приращением аргумента.
Приращением функции y = f(x) в точке х, отвечающим
приращению аргумента Ах, будем называть число
Ay = f(x+Ax)-f(x). E.1)
Так, для функции у = sin х приращение в точке х, отвечающее
приращению аргумента Ал;, имеет вид
Ay = sin(x+ Ах) — sinA; = 2cos (х Н — j sin——. E.2)
Справедливо следующее утверждение:
Для того чтобы функция y = f(x) являлась непрерывной в точ-
точке х, необходимо и достаточно, чтобы приращение Ау этой функ-
функции в точке х, отвечающее приращению аргумента Ах, являлось
бесконечно малым при Дх-»-0.
В самом деле, по определению функция y = f{x) непрерывна
в точке х, если существует предел
Urn f(x+Ax) = f(x). E.3)
Дж->0
В силу п. 4 § 4 гл. 3 существование предельного значения E.3)
* В качестве множества задания функции вместо интервала (а, Ь) можна
взять любое плотное в себе множество {х} (см. гл. 2, § 5, п. 3).
t90 Гл. 5. Дифференциальное исчисление
эквивалентно тому, что функция [f(x + Ax)—f{x)] аргумента А*
является бесконечно малой при Ддс-^О.
Доказанное утверждение позволяет выразить условие непре-
непрерывности функции y = f{x) в точке х в следующей форме: функ-
функция y=f(x) непрерывна в точке х, если приращение Ау- этой
функции в точке х, отвечающее приращению аргумента Ах, явля-
является бесконечно малым при Д*-^0, т. е. если
lim by = lim [f(x + Ax)—f(x)] = 0. E.4)
Д*-»0 Дх-»0
Условие E.4) мы будем называть разностной формой
условия непрерывности функции y=f(x) в точке х. Это
условие мы будем неоднократно использовать в дальнейшем.
С помощью условия E.4) еще раз убедимся в том, что функ-
функция y = sinx непрерывна в любой точке х бесконечной прямой.
В самом деле, из формулы E.2), из условия cos (ян —
Ах
1 и из равенства lim sin = 0 непосредственно вытекает^
что lim Дг/ = О.
д*-»о
2. Определение производной. Пусть, как и в п. 1, функция
if^=f(x) определена на интервале (а, Ь), х — фиксированная точ-
точка этого интервала, Ах — любое приращение аргумента, настоль-
настолько малое, что число х+Ах также принадлежит интервалу (а, Ь).
Считая, что Д#=#=0, рассмотрим в данной фиксированной
точке х отношение приращения Ау функции y = f(x) в этой точке
к соответствующему приращению аргумента Ах:
hy __ f{x + Ax)-f(x) E5)
Дх Ах
Отношение E.5) будем называть разностным отноше-
отношением (в данной точке х). Так как х фиксировано, разностное
отношение E.5) представляет собой функцию аргумента Ах. Эта
функция определена для всех значений аргумента Ах, принадле-
принадлежащих некоторой достаточно малой б-окрестности точки Дя=0,
за исключением самой точки Дл;=0, т. е. определена всюду в дос-
достаточно малой проколотой б-окрестности точки Дл;=0. Это дает
нам право рассматривать вопрос о существовании предела ука-
указанной функции при Дх->-0.
Определение 1. Производной функции y=f(x) в
данной фиксированной точке х называется предел при Дя->0 раз-
разностного отношения E.5) (при условии, что этот предел сущест-
существует) .
Производную функции y = f(x) в данной фиксированной точке
х будем обозначать символом f'(x) или у'(х) или кратким симво-
символом у'.
§ 1. Понятие производной 191
Итак, по определению
и i \ 1 • Л У 1 ¦ f(x + Ах) — / (х)
р (х) — lim —— = lim 'v —'w .
Дж-,о Ax д*-+о Ax
Если функция имеет производную для всех точек х интервала
(а, Ь), то эта производная будет представлять собой некоторую-
функцию аргумента х, определенную на интервале (а, Ь).
Приведем два тривиальных примера вычисления производных*
1°. f(x) = С = const. Совершенно очевидно,, что производная
Р(х) этой функции тождественно равна нулю, ибо приращение
этой функции Ay=f{x+Ax)—f(x) равно нулю для всех х и всех:
Ах.
2°. f(x)=x. Для этой функции разностное отношение E.5)
равно
Ду __ (х + Ах) — х Аде _ .
Ах Ах Ах
Отсюда следует, что и производная указанной функции равна еди-
единице в любой точке х бесконечной прямой.
В полной аналогии с понятиями правого и левого пределов
функции в данной точке вводятся понятия правой и левой
производных функции y — f(x) в данной фиксированной точке х.
Определение 2. Правой [левой] производной функции
У=!(х) в данной фиксированной точке х называется правый
[левый] предел разностного отношения E.5) в точке Ах = 0 (при
условии, что этот предел существует).
Для обозначения правой [левой] производной функции в точке
х используют символ Р(х+0) [f'(x—0)].
Из сопоставления определений 1 и 2 и из свойства правого к
левого пределов функции, установленного в п. 2 § 4 гл. 3 *, выте-
вытекают следующие утверждения:
1) если функция f(x) имеет в точке х производную f'(x), то-
эта функция имеет в точке х как правую, так и левую производ-
производные, причем f'(x+O)=f'(x—Q)=f'(x);
2) если функция f{x) имеет в точке х как правую, так и ле-
левую производные, причем эти производные равны друг другу, та
функция f(x) имеет в точке х производную f'(x), причем
В дополнение к утверждению 2) следует отметить, что если у
функции f(x) существуют правая и левая производные в точке х»
но эти производные не равны друг другу, то у этой функции не
* Если функция f(x) имеет в точке х и правый, и левый пределы, оба
равные одному н тому же числу Ь, то функция f(x) имеет в этой точке предел,
равный числу Ь.
192
Гл. 5. Дифференциальное исчисление
существует производной в точке х*. Примером такой функции
может служить функция
(—Аде) _ ,
— * i
— х при х<С 0.
'Эта функция имеет в точке х = 0 правую производную, равную
lim = 1» и левую производную, равную Игл
Ах-чЛ Ах Д*->-0 Ах
но не имеет в точке х = 0 производной.
3. Геометрический смысл производной. Рассмотрим график
функции y = f(x), определенной и непрерывной на интервале (а, Ь).
Фиксируем произволь-
произвольную точку х интервала
{а, Ь) и рассмотрим при-
Pj/\ ^ ращение Ахф§ аргумен-
аргумента х, настолько малое,
что число х+Ах также
принадлежит интервалу
{а, Ъ). Пусть М и Р —
точки графика функции
y = f(x), абсциссы кото-
которых соответственно рав-
равны х и х+Ах (рис. 5.1).
Координаты точек М и Р,
очевидно, будут иметь вид
Рис. 5.1
М(х,
Р(х+Ах, f(x+Ax)).
Прямую, проходящую через точки М и Р графика функции
y=f(x), будем называть секущей. Поскольку точку М мы пред-
предполагаем фиксированной, то угол наклона каждой секущей МР к
¦оси Ох будет функцией аргумента Ах (ибо значение Ах однознач-
однозначно определяет точку Р графика функции y = f(x)). Обозначим ука-
указанный угол наклона секущей МР к оси Ох символом ф(Дл:).
Определение. Если существует предельное положение се-
секущей МР при стремлении точки Р графика функции к точке М
(или, что то же самое, при стремлении Ах к нулю), то это пре-
предельное положение называется касательной к графику функ-
функции y — f{x) в данной фиксированной точке М этого графика,
Из этого определения следует, что для существования каса-
касательной к графику функции y=f{x) в точке М достаточно, чтобы
существовал предел Игл ф(Ал;) = ср0, причем указанный предел
д*->о
<ро равен углу наклона касательной к оси Ох.
* Иначе мы получили бы противоречие с утверждением 1).
§ 2. Понятие дифференцируемости функции 193
Докажем следующее утверждение:
Если функция y = f(x) имеет в данной фиксированной точке х
производную, то существует касательная к графику функции
y—f(x) в точке М(х, f(x)), причем угловой коэффициент этой ка-
касательной (т. е. тангенс угла наклона ее к оси Ох) равен произ-
производной f'{x).
Опустим из точек М и Р перпендикуляры на ось абсцисс (см.
рис. 5.1). Проведем через точку М прямую, параллельную оси абс-
абсцисс, и обозначим через N точку пересечения этой прямой с пер-
перпендикуляром, опущенным из Р на ось абсцисс. Из треугольника
MNP очевидно, что
Таким образом,
Ф(Дх) = arctg ^. E-6)
Ах
Убедимся в том, что существует предел правой (а значит, и левой)"
части E.6) при Дл;->-0. В самом деле, в силу существования про-
производной f'(x) существует предел lim —— = f'(x). Отсюда и из
дх-»о Ддг
непрерывности функции arctg и для всех значений и следует, что
существует предел правой части E.6), равный arctg f(x).
Итак, мы доказали, что существует предел
lim ф (Ах) = arctg/' (х).
Лх-»0
Но это и оаначает, что существует предельное положение секу-
секущей, т. е. существует касательная к графику функции в точке
М(х, f(x)), причем угол наклона фо этой касательной к оси Ох
равен фо = arctg f'(x).
Значит, угловой коэффициент указанной касательной tgфo ра-
равен f'{x).
Сформулированное утверждение доказано.
§ 2. ПОНЯТИЕ ДИФФЕРЕНЦИРУЕМОСТИ ФУНКЦИИ
1. Определение дифференцируемое™ функции. Пусть, как и в
предыдущем параграфе, функция y — f(x) определена на интерва-
интервале (а, Ь), х — любое фиксированное число из этого интервала,
Ах — произвольное приращение аргумента, настолько малое, что
значение аргумента х+Ах также принадлежит интервалу (а, Ь),
&y=f(,x+Ax)—f(x) —приращение функции в точке х, отвечающее
приращению аргумента А*.
Определение. Функция y — f(x) называется дифференцируе-
дифференцируемой в точке х, если приращение Ау этой функции в точке х, отве-
7 Зак. 72
194 Гл. 5, Дифференциальное исчисление
чающее приращению аргумента Ах, может быть представлена
в виде
(Дл:)Дл:, E.7)
где А — некоторое число, не зависящее от Ах, а а (Ах) — функция
аргумента Ах, бесконечно малая в точке Дх = 0.
В самой точке Дх=0 эта функция а (Ах), вообще говоря, не
определена, и ей можно приписать в этой точке любое значение.
Для дальнейшего удобно считать это значение а@) равным нулю.
При такой договоренности функция а (Ля) будет непрерывна в
точке Дх=0 и равенство E.7) можно распространить и на значе-
значение Дх=0.
Замечание. Второе слагаемое в правой части E.7) а (Ах) Ах
можно переписать в виде о (Ах) *. В самом деле, так как обе функ-
функции а(Дх) и Ах являются бесконечно малыми в точке Ах=0, то
произведение этих функций а (Ах) Ах представляет собой бесконеч-
бесконечно малую в точке Дх=0 функцию более высокого порядка, чем
Ах (см. п. 5 § 4 гл. 3). Таким образом, представление E.7) можно
переписать в виде
Ау = ААх + о(Ах).
Докажем следующее утверждение.
Теорема 5.1. Для того чтобы функция y = f(x) была диффе-
дифференцируемой в точке х, необходимо и достаточно, чтобы она имела
в этой точке конечную производную f (x).
Доказательство. 1) Необходимость. Пусть функция у =
=f(x) дифференцируема в точке х, т. е. ее приращение Ау в этой
точке, отвечающее приращению аргумента Ах, представимо в виде
E.7). Считая Ах отличным от нуля и поделив E.7) на Ах, получим
+(Ах). E.8)
Ах
Правая (а поэтому и левая) часть E.8) имеет равный А предел в
точке Дх=0**. Остается заметить, что предел при Дх->-0 левойчас-
ти E.8) (в случае, если он существует) по определению равен
производной f'(x).
Итак, мы доказали, что если для функции f(x) справедливо
представление E.7), то эта функция имеет в точке х производную
f'(x), причем f'(x)=A.
2) Достаточность. Пусть существует конечная производная
f'(x), т. е. существует конечный предел
^ = П*). E-9)
д*->о Ах
* Напомним, что символ о (Ах) обозначает бесконечно малую в точке
А*=0 функцию более высокого порядка, чем Ах,
** Ибо lirn A = A, lim a = 0.
Ддг-*О
§ 2. Понятие дифференцируемое™ функции 195
Обозначим символом а (Ах) разность —-—/' (х), т. е. по-
положим
а(Дл;) = ^—/'(*)¦ EЛ°)
Ах
Из существования предела E.9) вытекает, что функция а (Ах), оп-
определяемая соотношением E.10), имеет предел при Алг->-0, равный
нулю.
Умножая соотношение E.10) на Ах, мы придем к представ-
представлению
Ay = f (х) Ах+а (Ах) Ах,
совпадающему с представлением E.7) при A=f'(x).
Тем самым доказано, что из существования конечной произ-
производной I'(х) вытекает дифференцируемость функции y = f(x) в
точке х, причем в условии дифференцируемости E.7) число А
совпадает с f'(x). Теорема доказана.
Доказанная теорема позволяет нам в дальнейшем отождест-
отождествлять понятие дифференцируемости функции в данной точке с по-
понятием существования у этой функции в данной точке конечной
производной.
Операцию нахождения производной в дальнейшем договоримся
называть дифференцированием.
2. Дифференцируемость и непрерывность. Легко доказывается
следующее утверждение.
Теорема 5.2. Если функция y = f{x) дифференцируема в
данной точке х, то она и непрерывна в этой точке.
Доказательство. Так как функция f(x) дифференцируе-
дифференцируема в точке х, то для ее приращения Ау в этой точке справедливо
представление E.7), из которого следует, что lira Дг/ = О, а это
A.v-»0
и означает непрерывность функции y=f(x) в данной точке (в силу
разностной формы условия непрерывности E.4), введенной в
п. 1 § 1). Теорема доказана.
Заметим, что утверждение, обратное к теореме 5.2, несправед-
несправедливо, т. е. из непрерывности функции y=f(x) в данной точке х,
вообще говоря, не вытекает дифференцируемость функции f(x)
в этой точке.
Примером может служить функция г/=|х|, которая, очевидно,
непрерывна в точке х=0, но (как мы уже видели в конце п. 2
§ 1) не имеет в этой точке производной.
Отметим, что существуют функции, непрерывные в каждой точ-
точке некоторого интервала, но не имеющие производной ни в одной
точке этого интервала. (Первый пример такой функции был по-
построен Вейерштрассом. Один из примеров такой функции строится
в дополнении к гл. 10.)
196
Гл. 5. Дифференциальное исчисление
3. Понятие дифференциала функции. Рассмотрим функцию
y=f(x), дифференцируемую в данной точке х. Приращение Ау та-
такой функции в точке х может быть представлено в виде E.7).
Заметим, что приращение E.7) представляет собой сумму двух
слагаемых, первое из которых ААх линейно относитель-
относительно Ах, а второе а(Дх)Дл; является в точке Ax=0 бесконечно
малой функцией более высокого порядка, чем Ах.
Если число А, равное согласно теореме 5.1 производной f'(x),
отлично от нуля, то указанное первое слагаемое AAx=f {х)Ах
представляет собой главную часть приращения Ау дифферен-
дифференцируемой функции y = f(x). Эта главная часть приращения явля-
является линейной однородной функцией аргумента
Ах* я называется дифференциалом функции y = f(x).
В случае, если A = f(x)=0, дифференциал функции по опреде-
определению считается равным нулю.
Итак, дифференциалом функции y=f(x) в данной
фиксированной точке х, отвечающим приращению аргумента Ах,
называется число, обозначаемое символом dy и равное
dy=f(x)Ax. E.11)
В случае f'(x)=^=O это число представляет собой главную часть
приращения Ау функции y=f(x), линейную и однородную относи-
относительно приращения аргумента Ах.
Сразу же отметим, что дифференциал dy и приращение Ау
функции y = f(x) в данной точке х, оба отвечающие одному и тому
же приращению аргумента Ах, вообще говоря, не равны друг
другу.
Это легко уяснить из рассмотрения графика функции у = \(х)
(рис. 5.2). Пусть М и Р — точки графика функции y = f(x), отвеча-
отвечающие значениям аргумента, соответственно равным х и х+Ах,
MS — касательная к графику в точке М, MN\\Ox, NP\\Oy, Q —точ-
—точка пересечения касательной
й P
зс+йх
х
Рис. 5.2
р
с прямой PN. Тогда при-
приращение Ау функции y=f(x)
в точке х, отвечающее прира-
приращению аргумента Ах, очевид-
очевидно, равно величине отрезка
NP, в то время как диффе-
дифференциал dy этой функции в
точке х, отвечающий тому же
самому Ах, равен величине
отрезка NQ. (Это сразу выте-
вытекает из формулы E.11) и из
того, что в прямоугольном
* Напомним, что линейной функцией аргумента, t называется функ-
функция вида y=At+B, где А и В — некоторые постоянные. В случае В=0 ли-
линейная функция называется однородной.
§ 3. Дифференцирование сложной и обратной функций 197
треугольнике MQN величина отрезка MN равна Ах, а тангенс угла
QMN равен f'(x).) Ясно, что величины отрезков NP и NQ явля-
являются, вообще говоря, различными.
Весьма удобно ввести в рассмотрение понятие дифферен-
дифференциала аргумента х. При этом следует различать два случая:
1) случай, когда указанный аргумент х представляет собой неза-
независимую переменную; 2) случай, когда аргумент х сам является
дифференцируемой функцией вида x=<p(t) некоторой новой пере*
менной t, которую мы можем считать независимой.
Договоримся.для случая, когда аргумент х является независи-
независимой переменной, отождествлять дифференциал этого аргумента
с его приращением Ах*, т. е. считать, что dx=Ax.
В силу этой договоренности равенство E.11) принимает вид
dy = f'(x)dx. E.12)
Таким образом, для случая, когда аргумент х является независи-
независимой переменной, для дифференциала функции y=f(x) справедли-
справедливо представление E.12).
Ниже в п. 3 § 3 мы докажем, что представление E.12) носит
универсальный характер и справедливо также и в случае, когда
аргумент х не является независимой переменной, а является диф-
дифференцируемой функцией вида x=y(t) некоторой независимой пе-
переменной t. (В этом случае в формуле E.12) величину dx нельзя
считать равной Ах, ибо в силу сказанного выше она равна dx—
= q>'(t)dt.)
§ 3. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ И
ОБРАТНОЙ ФУНКЦИИ
1. Дифференцирование сложной функции. Установим правило,
позволяющее найти производную сложной функции y=f[y(t)] в
точке t при условии, что известны производные составляющих ее
функций x=y(t) и y=f(x) в точках t и х=ц>A) соответственно.
Теорема 5.3. Пусть функция x=(f(t) дифференцируема в
точке t, а функция y=f(x) дифференцируема в соответствующей
точке x = y(t). Тогда сложная функция y=f[y(t)] дифференцируе-
дифференцируема в указанной точке t, причем для ее производной в этой точке
справедлива формула
Доказательство. Придадим аргументу функции x=y(t)
в данной точке t произвольное отличное от нуля приращение At.
Этому приращению отвечает приращение Ax=y{t+At)—<р@
* Эта договоренность согласуется с рассмотрением независимой перемен-
переменной х как функции вида y=f(x) =х, для которой dy=f'(x)Ax—Ax, т. е.
dx=Ax.
J98 Гл. 5. Дифференциальное исчисление
функции x=y{t), причем указанное приращение Ах может обра-
обращаться в нуль.
Приращению Ах, в свою очередь, отвечает приращение Дг/ =
= /(x+Ax)—f(x) функции y = f(x) в соответствующей точке
x=(f(t). Поскольку функция y — f{x) по условию дифференцируе-
дифференцируема в указанной точке x=y{t), то ее приращение Аг/ в этой точке
может быть представлено в виде *
Ay = f'{x)Ax+a(Ax)Ax, E.14)
где а (Ах) имеет при Ax->0 предел, равный нулю.
Подчеркнем, что, как указано в п. 1 § 2, представление E.14)
остается справедливым и при Дх=0.
Поделив E.14) на Д^О, будем иметь
М.-Г<ЛМ. + ат± E.15)
Докажем, что правая (а значит, и левая) часть E.15) имеет
предел при А/-*-0, причем этот предел равен величине, стоящей в
правой части E.13). Этим будет доказана дифференцируемость
сложной функции и формула E.13) для ее производной.
Из дифференцируемое™ функции x = q>(t) в точке t вытекает,
что отношение ~~гг имеет предел при Af-*-O, равный ср'(О- Оста-
Остается доказать, что функция а (Ах) имеет предел при At->-0, равный
нулю, но это сразу вытекает из того, что а(Дх)->-0 при Дх->-0 и
что Дл:->-0 при Д?->-0 на основании разностной формы условия не-
непрерывности дифференцируемой в точке t функции x=y(t) **.
Итак, вся правая часть E.15) имеет предел при At->-Q, и этот пре-
предел равен величине, стоящей в правой части E.13).
Теорема доказана.
Замечание 1. Теорема 5.3 и содержащееся в ее формули-
формулировке правило вычисления производной сложной функции после-
последовательно переносится на сложную функцию, являющуюся супер-
суперпозицией трех и большего числа функций. Так, для сложной функ-
функции, являющейся суперпозицией трех функций y = F[f(y(f))], пра-
правило дифференцирования имеет вид
{/г[/(ф@)]}/=П/(ф@)]/'(ф@)ф'@. E.16)
причем формула E.16) справедлива при условии, что функция
x = (p(t) дифференцируема в данной точке t, функция u = f{x) диф-
¦ ференцируема в соответствующей точке x = y(t), а функция у —
= F(u) дифференцируема в соответствующей точке u = f(x) =
/[@]
* См. п. 1 § 2 определение дифференцируемое™ и Феорему 5.1.
** В силу теоремы 5.2 дифференцируемая в точке t функция x—q>(t) явля-
является непрерывной в этой точке.
§ 3. Дифференцирование сложной и обратной функций 199
Замечание 2. При доказательстве теоремы 5.3 мы рассмат-
рассматривали сложную функцию вида y=f(x), где x = y(t), т. е. обозна-
обозначили символом х промежуточный аргумент. Эта символика,
конечно, может быть изменена. Чаще удобнее бывает обозначать
символом х окончательный аргумент, т. е. рассматривать сложную
функцию вида y=f[y(x)]. В этих обозначениях правило дифферен-
дифференцирования сложной функции E.13) принимает вид
]-ф'(*)- E-13*)
Примеры применения правила дифференцирования сложной
функции будут приведены в следующем параграфе.
2. Дифференцирование обратной функции.
Теорема 5.4. Пусть функция y = f(x) возрастает (или убыва-
убывает) и непрерывна в некоторой окрестности точки х. Пусть, кроме
того, эта функция дифференцируема в указанной точке х и ее про-
производная в этой точке f (х) отлична от нуля. Тогда в некоторой
окрестности соответствующей точки y = f{x) определена обратная
для y = f(x) функция x=f~1(y), причем указанная обратная функ-
функция дифференцируема в соответствующей точке y = f(x) и для ее
производной в этой точке у справедлива формула
_!_ E.17);
Доказательство. Так как функция y=f(x) строго моно-
монотонна и непрерывна в некоторой окрестности данной точки х, то
в силу теоремы 4.5 (см. § 2 гл. 4) обратная функция x—f~l(y\
определена, строго монотонна и непрерывна в некоторой окрест-
окрестности соответствующей точки y = f(x).
Придадим аргументу этой обратной функции в указанной точ-
точке произвольное достаточно малое и отличное от нуля при-
приращение А г/. Этому приращению Дг/ отвечает приращение Ах =
= f~l(y + Ay)—f~l{y) обратной функции в соответствующей точке
y = f(x), причем в силу строгой монотонности обратной функции
указанное приращение Ах от л ичн о от нуля.
Это дает нам право написать следующее тождество *:
^L E.18)
Ay Ах
~д7
Пусть теперь в тождестве E.18) приращение Ау стремится к
нулю. Тогда в силу разностной формы условия непрерывности об-
обратной функции x=f~1(y) в соответствующей точке' y = f(x) при-
приращение этой функции Ах также стремится к нулю. Убедимся в
том, что в таком случае существует предел правой части E.18),
* Указанное тождество можно написать для любых двух чисел Ау и Д*,
отличных от нуля.
200 Гл. 5. Дифференциальное исчисление
равный величине, стоящей в правой части E.17). Этим будет до-
доказано, что. тот же самый предел имеет и левая часть E.18), т. е.
будет доказано, что обратная функция имеет производную в соот-
соответствующей точке y=f(x) и для этой производной справедливо
равенство E.17).
Итак, для завершения доказательства теоремы остается убе-
убедиться в том, что правая часть E.18) имеет предел при Дх->-0
равный l/f'(x), где х— данная точка.
Так как л; =/"'(г/), дх = /-1(г/+Дг/)— f~l(y),TO x + Ax = f~l(y + Ay),
т. е. y+Ay=f(x+Ax) и Ay = f{x+Ax)—f{x).
Отсюда следует, что правая часть E.18) может быть перепи-
переписана в виде
1 1
Ay ~ f(x+Ax)-f(x) ¦
Ах Ах
Из последнего равенства в силу определения производной f'(x)
и предположения {'(х)Ф0 сразу же вытекает, что предел при
&х-+0 правой части E.18) существует и равен l/f'(x).
Теорема доказана.
Примеры применения доказанной
теоремы будут даны в следующем пара-
параграфе.
Доказанная теорема имеет простой
геометрический смысл. Пусть М — точ-
точка графика функции y~f(x), отвечаю-
щая данному значению аргумента х
(рис. 5.3). Тогда, очевидно, производная
f (х) равна тангенсу угла наклона а
касательной, проходящей через точку
М, к оси Ох, а производная обратной
функции {f~l{y)Y в соответствующей
точке y=f(x) равна тангенсу угла наклона р той же самой каса-
касательной к оси Оу. Поскольку углы наклона аи р в сумме состав-
составляют я/2, то формула E.17) выражает очевидный факт:
приа+р = л/2.
tga
3. Инвариантность формы первого дифференциала. В п. 3 § 2
мы убедились в том, что для случая, когда аргумент х дифферен-
дифференцируемой функции y=f(x) представляет собой независимую
переменную, для дифференциала dy этой функции справед-
справедливо представление
dy=f'(x)dx. E.12)
Сейчас мы докажем, что представление E.12) является универ-
универсальным и справедливо также и в случае, кЬгда аргумент х сам
является дифференцируемой функцией вида x=y(t) некоторой
§ 3. Дифференцирование сложной и обратной функций 201
независимой переменной t. Это свойство дифференциала функции
принято называть инвариантностью его формы*.
Итак, пусть аргумент х дифференцируемой функции y=f(x)
сам является дифференцируемой функцией вида x=q>(t) некоторой
независимой переменной t. В таком случае у можно рассматривать
как сложную функцию вида y=f[q>{t)] аргумента t. Поскольку
этот аргумент t является независимой переменной, то
для указанной функции y = f[<p(O] и Для функции x=q>(t) диф-
дифференциалы представимы в форме E.12), т. е. в виде
dy={f[v(t)]}'dt, dx=tf(t)dt. E.19)
По правилу дифференцирования сложной функции
0. E.13)
Подставляя E.13) в первую из формул E.19), придадим этой
формуле вид
dy = f'(x)(f'(t)dt. E.20)'
Сопоставляя полученное равенство E.20) со вторым из равенств
E.19), окончательно получим для dy выражение
dy=f'(x)dx,
совпадающее с представлением E.12).
Инвариантность формы E.12) первого дифференциала функ-
функции dy установлена.
Замечание. Можно дать и другую эквивалентную формули-
формулировку свойства инвариантности формы первого дифференциала,
сразу же вытекающую из универсальности представления EЛ2):
производная дифференцируемой функции y = f(x) равна отноше-
отношению дифференциала этой функции dy к дифференциалу ее аргу-
аргумента dx, т. е. определяется равенством
/'(*) = -?-. E-21>
как в случае, когда аргумент х является независимой переменной,
так и в случае, когда аргумент х сам является дифференцируемой
функцией вида x=(p(t) некоторой независимой переменной t.
Универсальность представления для производной E.21) позво-
позволяет использовать отношение —— для обозначения производной
dx
функции y — f(x) по аргументу х.
4. Применение дифференциала для установления приближенных
формул. Пусть ради простоты аргумент х функции y = f{x) явля-
является независимой переменной. В п. 3 § 2 мы показали, что диф-
* Ниже мы введем понятия второго и последующих дифференциалов функ-
функции y=f(x) и обнаружим, что эти дифференциалы уже не обладают инва-
инвариантностью формы. Вследствие этого доказываемое свойство называют инва-
инвариантностью формы первого дифференциала.
202 Гл. 5. Дифференциальное исчисление
ференциал dy функции y = f{x), вообще говоря, не равен прира-
приращению Ау этой функции. Тем не менее с точностью до бесконечно
малой функции более высокого порядка малости, чем Ад;, справед-
справедливо приближенное равенство
Ayzzdy. E.22)
Отношение — естественно назвать относительной
Дл:
погрешностью равенства E.22). Так как Ay—dy = o(Ax) *, то
относительная погрешность равенства E.22) становится как угод-
угодно малой при уменьшении |Дд;|.
Соотношение E.22) позволяет приближенно заменять прираще-
приращение Ау дифференцируемой функции y = f{x) дифференциалом dy
этой функции. Целесообразность такой замены оправдывается тем,
что дифференциал dy является линейной функцией Дл:, в то время
как приращение Ау, вообще говоря, представляет собой более
сложную функцию аргумента Ах.
Учитывая, что Ay = f(x+Ax)—f(x), dy = /' (х) Ах, мы можем пе-
переписать приближенное равенство E.22) в виде f(x+Ax)—f{x)&
»/' (х)Ах или, что то же самое, в виде
f(x+Ax)ttf(x)+f'(x)Ax. E.23)
Приближенное равенство E.23), так же как и E.22), справедливо
для любой дифференцируемой в данной точке х функции f(x) с
точностью до величины о (Ад;) более высокого порядка малости,
чем Ах.
Это приближенное равенство позволяет с ошибкой о (Ад;) за-
заменить функцию f(x) в малой окрестности точки х (т. е. для ма-
малых значений Дл:) линейной функцией аргумента Ад;, стоящей в
правой части E.23).
Приближенная формула E.23) часто применяется для различ-
различных конкретных видов функции f{x).
§ 4. ДИФФЕРЕНЦИРОВАНИЕ СУММЫ, РАЗНОСТИ,
ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ФУНКЦИИ
Теорема 5.5. Если каждая из функций и(х) и v(x) диффе-
дифференцируема в данной точке х, то сумма, разность, произведение и
частное этих функций (частное при условии, что значение v (х) Ф0)
также дифференцируемы в этой точке, причем имеют место фор-
формулы
[u(x)±v(x)]'^u'(x)±v'(x),
[u{x)-v{x)]' = u'(x)-v(x) + u(x)-v'(x), E 24)
и(х) V __ и'(х)-у(х) — и(х).у'(х)
o(x)
* См. п. 3 § 2.
§ 4. Диф. суммы, разности, произведения и частного функций 203
Доказательство. Рассмотрим отдельно случаи суммы
(разности), произведения и частного.
1°. Пусть y(x) = u(x)±v(x). Обозначим символами Аи, Av и
Ау приращения функций и(х), v(x) и у(х) в данной точке х, от-
отвечающие приращению аргумента Ах. Тогда, очевидно,
Ay = y{x+Ax)—y{x)=[u(x+Ax)±v{x+Ax)]—[u(x)±v(x)]=
= [и(х+Ах)—и(х)] ±[v(x+Ax)—v(x)]=Au±Av.
Таким образом,
Ах Ах Ах
Пусть теперь Дя'-^О. Тогда в силу существования производных
функций и(х) и v(x) в точке х существует предел правой части
E.25), равный и (x)±v'(x). Значит, существует предел (при
Алг-э-О) и левой части E.25). По определению производной ука-
указанный предел равен у {х), и мы приходим к требуемому равенст-
равенству У' ix) = и' (х) ± v' (x).
2°. Пусть, далее, у(х) =u(x)v(x). Сохраняя за Аи, Av и Ау тот
же смысл, что и выше, будем иметь
Ау=у(х+Ах)—у(х) —u(x+Ax)v(x+Ax)—u(x)v(x) =
= [u(x+Ax)v(x+Ax)—u(x+Ax)v{x)]+ [u(x+Ax)v(x)—u(x)v(x)].
(Мы прибавили и вычли слагаемое u(x+Ax)v(x).)
Далее можем записать
Ay=u(x+Ax)[u(x+Ax)—v(x))+v(x)[u(x+Ax)—u(x)] =
= u(x+Ax)Av + v(x)Au.
Таким образом,
E.26)
u(+Ax) + {x).
Ах Ах Ах
Пусть теперь Ах-^-0. Тогда в силу дифференцируемости функ-
функций и(х) и v(x) в точке х существуют пределы отношений
Аи Av г, \ г, •. т-г ¦
и , соответственно равные и (х) и v (х). Далее, из диф-
Ах Ах
ференцируемости функции и(х) в точке х в силу теоремы 5.2 сле-
следует непрерывность и(х) в этой точке. Значит, существует предел
lim u(x-j-Ax), равный и(х).
Л0
Таким образом, существует предел правой части E.26) при
Ля-'-О, равный u(x)v'(x)+u(x)vf(x).
Значит, существует предел (при Дх-*-0) и левой части E.26).
По определению производной указанный предел равен у (х), и
мы приходим к требуемой формуле y'(x)—u'(x)v(x)+u(x)v'(x).
204 Гл. 5. Дифференциальное исчисление
3°. Пусть, наконец, у(х)= и^х' . Тогда, поскольку и(х)Ф0, по
у(х)
теореме 4.11 об устойчивости знака непрерывной в данной точке х
функции ь(х+Ах)Ф0 для всех достаточно малых Ад;, и мы можем
записать, что
и (х -)- А*) у{х) — у (х + A*) v (х)
у (х) v(x+ Ах)
Добавляя и вычитая в числителе слагаемое u(x)v(x), будем
иметь
Л [и(х + Ах)у(х)-и(х)у(х)]-[у(х + Ах)и(х)-и(х)у(х)] _
у(х)у(х + Ах)
v (x)v(x
Таким образом,
Ах у (х) у {х + Ах)
E.27)
Пусть теперь Ддс-э-О. В силу дифференцируемости (и вытекаю-
вытекающей из нее непрерывности) функций и(х) и v(x) в точке х суще-
существуют пределы
lim — = и'(х), Игл — = v' (х), lim v(x+ Ax) = v{x).
А0 Ах дх^о Ах Дх-»0
Таким образом, поскольку v(x)=?0, существует предел при
Дд;->-0 правой части E.27), равный
у(х)и'(х)-и(х)у'(х)
у*(х)
Значит, существует предел при Дл:-»-0 и левой части E.27).
По определению производной указанный предел равен у'{х), и
мы получим требуемую формулу
у' (Х) = Ц'(*М*)— v'(x)u{x)
у* (х)
Теорема 5.5 полностью доказана.
Следствие из теоремы 5.5. Если для функций и(х) и
v(x) выполнены в данной точке х те же предположения, что и в
теореме 5.5, то в этой точке х справедливы следующие соотношения
для дифференциалов:
§ 5. Производные простейших элементарных функций
205
d (и ± v) = du ± dv,
d(u ¦ v) = vdu 4- udv,
vdu — udv
E.28)
Для установления соотношений E.28) достаточно умножить
равенство E.24) на dx и воспользоваться универсальным пред-
представлением E.12) дифференциала произвольной функции y=f(x).#
§ 5. ПРОИЗВОДНЫЕ ПРОСТЕЙШИХ ЭЛЕМЕНТАРНЫХ
ФУНКЦИЙ
Из вводной главы и из гл. 4 нам уже извество, что простей-
простейшими элементарными функциями принято называть
следующие функции: показательную функцию у — ах и логариф-
логарифмическую функцию y = \ogax, рассматриваемые для любого фикси-
фиксированного значения а такого, что 0<а=5^1, степенную функцию
у=ха, где а — фиксированное вещественное число, четыре триго-
тригонометрические функции y = sinA;, y=cosx, y=tgx и y=ctgx и четы-
четыре обратные тригонометрические функции i/ = arcsin д:, t/=arccos;e,
«/ = arctg* и y=arcctgx.
В настоящем параграфе мы вычислим и систематизируем в
таблицу производные всех простейших элементарных функций, уже
выписанные нами в гл. 1.
1. Производные тригонометрических функций.
1°. Производная функции y = sinx. Так как для этой
функции
Ау=в1п(х+Ах)~ — - " — /- ' Л*
то при любом
\
разностное отношение имеет вид
Ах
Ay I Ax\ Si" —
— = COS JC + *
Д* V 2
Ах
2
По определению производной
(sin~*)'= li
Лх->0 Ах Дя:-»О
cos х +
Ах
sin
Ах \ 2
Ах
2
E.29)
В силу непрерывности функции #=cosa: в любой точке х беско-
бесконечной прямой
lim cos (x + —) =cos x. E.30)
V 2 /
206 Гл. 5. Дифференциальное исчисление
Далее, в силу первого замечательного предела и элементарной
„ . Ах *
замены переменной t=,
Ах
lim ?_ = ijm—=1. E.31)
Д.К-И) Ах <->о t
Из существования пределов E.30) и E.31) и из теоремы о пре-
пределе произведения двух функций вытекает существование предела
в правой части E.29) и равенство
Да:
sin ¦
(sinx)'= lim
Длг-М)
cos ( х -\—^- ) } — cos x.
2
Итак,
(sinx)' = cosA; E.32)
(для любой точки х бесконечной прямой).
2°. Производная функции z/ = cos x. Так как для любой
точки х бесконечной прямой
cosx = sin (— х),
то по правилу дифференцирования сложной функции ** и по фор*
муле E.32)
= cos (— х\ (— 1) = — sinх.
Итак,
(cosx)'=—sinx E.33)
(для любой точки х бесконечной прямой).
3°. Производная функции y = tgx. Так как tg*=sinx
cos х
то в силу правила дифференцирования частного*** и соотношений
E.32) и E.33) в любой точке х, в которой cos
Ах
* Очевидно, что t — »-0 при Дд-->0.
**\См. п. 1 § 3, формулу E.13).
*** См. § 4, третью формулу E.24).
§ 5. Производные простейших элементарных функций 207
., ,, / sin х \ ' __ (sin x)' cos х — (cos x)' sin х
(gx) ~ [1^7) 7^~х
cos2 х + sin2 x 1
COS2 X COS2 X
Итак,
E.34)
(в любой точке х Ф — + tin, где п = 0, ± 1, ± 2, ... J.
4°. Производная функции y = ctgx Так как ctgx = —: ,
Sill X
то в силу правила дифференцирования частного и соотношений
E.32) и E.33) в любой точке х, в которой sin хфО,
, , ,, / cos л; \ ' _ (cos x)' sin л: — (sin x)' cos jc
(ctg х) — —; — ¦
\ sin л: / sin8*
—sin2* — cos2 л: 1
sin'' x sin x
Итак,
(ctgx)' = 7- = -A + ctg2 x) E.35)
sm2 x
(в любой точке хфпп, где /г = 0, ±1, ±2, ±3, ...).
2. Производная логарифмической функции. Пусть y = \ogax,
где 0<аф\, х>0 — фиксированная точка. Тогда для любого до-
достаточно малого АхфО
Ay 1oga (а: + Да:) — loga* I
^7 = ^ =z-J
По определению производной
х
Aо&ад;)' = Пт 4^- = —lim loga 171 + -^-)А* 1. E.36)
д*-*о Ах х дх-»о L \ х / i
В силу второго замечательного предела и элементарной замены
переменной t =
х
X I
lim f(l +-^L\A*|=lim[(l + 0'] = e. 'E-37)
Дх
* Так как д:>0 фиксировано, то /= »-0 при
208 Гл. 5. Дифференциальное исчисление
Из существования предела E.37) и из непрерывности функции
y=\ogaX в точке х = е* вытекает, что предел в правой части
E.36) существует и равен —log^e.
X
Итак,
(logax)'=—logae E.38)
X
(для любых 0<аф1 и
В частности, при а = е
(lnjc)' =— (для любого х > 0).
3. Производные показательной и обратных тригонометрических
функций. Для вычисления производных указанных функций ис-
используем теорему 5.4 о дифференцировании обратной функции,
доказанную нами в п. 2 § 3 настоящей главы.
1°. Производная функции у = ах @<аФ1). Так как
функция у = ах, определенная на всей бесконечной прямой
—оо<д:< + оо, является обратной для функции x = \ogay, опреде-
определенной на полупрямой 0<у< + °о, и для функции x=\ogay в ок-
окрестности л'юбой точки у полупрямой 0<«/< + оо выполнены все
условия теоремы 5.4, то в силу этой теоремы функция у = ах диф-
дифференцируема в любой точке x=\ogay и для ее производной в
этой точке справедлива формула
(logo У)' 1 , logae
(Мы использовали выражение E.38) для производной логариф-
логарифмической функции.)
Из полученного равенства в силу элементарного соотношения
= 1па и соотношения ц—ах окончательно получим
logae
(a*)' = a*lna E.39)
(для любой точки х бесконечной прямой).
В частности, при а — е
2°. Производная функции t/=arcsiriA:. Так как функция
t/=arcsinA;, определенная на интервале —1<д;<1, является обрат-
обратной для функции x=s'my, определенной на интервале < у <С
* В п. 2 § 3 гл. 4 доказано, что функция y=\ogax непрерывна в любой
точке х>0.
§ 5. Производные простейших элементарных функций 209
< + —, и для функции x = siny в окрестности любой точки у
интервала — — < у< Н выполнены все условия теоремы
5.4, то по этой теореме функция y = arcsin;e дифференцируема в
любой точке x=siny и для ее производной в этой точке справед-
справедлива формула
(arcsin;t)' = —-— = —1—= * E.40)
(sinу)' cosy у 1-sina у
Мы использовали равенство E.32) и взяли перед корнем знак +
в силу того, что cosy положителен всюду на интервале <
Учитывая, что siny=x, мы окончательно получим из E.40)
(arcsin х)' — , '
(для всех х из интервала —1<д;< + 1).
3°. Производная функции y=arccos.*:. Так как функция1
y = arccos*, определенная на интервале —1<*< + 1, является
обратной для функции x = cosy, определенной на интервале
0<y<ji, и для функции x=cosy в окрестности любой точки у ин-
интервала 0<у<я выполнены все условия теоремы 5.4, то по этой
теореме функция y = arccos;e дифференцируема в любой точке
x=cosy и для ее производной в этой точке справедлива формула
(arccosx)'= = — г E.
(cosy)' (— sint/) — у 1 — cos* i/
Мы использовали равенство E.33) и взяли перед корнем знак —
в силу того, что sin у положителен всюду на интервале 0<у<тс.
Учитывая, что cosy=;e, мы окончательно получим из E.41)
(arccos х)' = ,
/I-*2
(для всех х из интервала —1<*< + 1).
4°. Производная функции y=arctg*. Так как функция
y = arctgj;, определенная на бесконечной прямой —оо<д:< + оо,
является обратной для функции x=tgy, определенной на интерва-
интервале — < у < —, и для функции *=tgy в окрестности каждой
Jt 2,
точки у интервала —— < У < — выполнены все условия теоремы
5.4, то по.этой теореме функция y — bxzigx дифференцируема в
каждой точке ;t=tgy и для ее производной в этой точке справед-
справедлива формула
210 Гл. 5. Дифференциальное исчисление
(arctg*)' =
(tgjf)'
(Мы использовали соотношение E.34).)
Итак,
(arctgx)' = 1
1 -f- ¦*
(для любой точки х бесконечной прямой).
5°. Производная функции y = arcctg;e. Так как функция
J/ = arcctgx, определенная на бесконечной прямой —оо<л'< + оо
является обратной для функции x = ctgy, определенной на интерва-
интервале 0<«/<jt, и для функции x=ctgy в окрестности каждой точки
интервала 0<у<л выполнены все условия теоремы 5.4, то по этой
теореме функция z/=arcctgx дифференцируема в каждой точке
x=ctgy и для ее производной в этой точке справедлива формула
(arcctg x)' =
(ctgy)' _(i+ctg»y) 1+*»
(Мы использовали соотношение E.35).)
Итак,
(arcctg ,)'=_!
(для любой точки х бесконечной прямой).
4. Производная степенной функции. Пусть у = хос, где а — любое
вещественное число, х — любая точка полупрямой 0<л:< + оо.
В гл. 4 мы уже рассматривали степенную функцию у = ха как су-
суперпозицию логарифмической и показательной функций
(где а — любое фиксированное число 0<а=тЧ).
По правилу дифференцирования сложной функции у = аи, где
u = a\ogax, получим
У' = (о")' • (а l°ga х)' = а" • In a ¦ а-— loga e =
-а-
X X
Итак, окончательно
(для любого )
5. Таблица производных простейших элементарных функций.
Соберем теперь в таблицу все вычисленные нами производные
простейших элементарных функций.
Г. (xa)' = i @)
§ 5. Производные простейших элементарных функций 211
В частности, (—У = \-, К V
\ х j х2
У =\, (К*) = о V- •
х j х2 2у х
2°- (logax)'= ^logae @<a^l, x>0).
В частности, Aпд;)' = —.
х
3°. (a*)' = aMna @<а=тЧ).
В частности, (ех)' = ех.
4°. (sinx)' = cos х.
5°. (cosx)' = —sinx.
6°. (tgx)'=_J—=l + tg2x (х^-^ + ля; л = 0, ±1,...).
cos2x \ 2 /
7°. (ctgx)'=—4— --(l + ctg2x) (х^=/гп;п = 0, ±1, ...)>
8°. (arcsinx)f=i/]/l— x2 (—1<х< + 1).
9°. (arccos д:)' =¦— l/]/l — x2 {— 1 < x < + 1).
10°. (arctgx)' = —-!—.
1 + хг
11°. (arcctgx)'=—i
В гл. 4 мы ввели в рассмотрение четыре гиперболические функ-
функции y = shx, y — ohx, y=thx и y = cthx, являющиеся простыми ком-
комбинациями показательных функций. Из представления этих функ-
функций через показательные функции элементарно вытекают следую-
следующие выражения для их производных:
12°. (shx)' = chx.
13°. (chx)' = shx.
14°.
x) .
ch2 x
.. 15°. (cthx)'=—-^ {хфО).
Установленная нами таблица производных вместе с правилом
дифференцирования сложной функции (установленным в п. 1 § 3)
и правилами дифференцирования суммы, разности, произведения
и частного (установленными в § 4) составляет вычислительный
аппарат той части математического анализа, которую принято на-
называть дифференциальным исчислением.
В гл. 1 и 4 мы уже ввели понятие элементарной функции, как
такой функции, которая выражается через простейшие элементар-
элементарные функции посредством четырех арифметических действий и
суперпозиций, последовательно применяемых конечное число раз.
Из установленной нами таблицы производных и правил диффе-
дифференцирования суммы, разности, произведения, частного и сложной
функции вытекает следующий важный вывод: производная любой
элементарной функции представляет собой также элементарную!
212 Гл. 5. Дифференциальное исчисление
функцию, т. е. операция дифференцирования не выводит нас из
класса элементарных функций.
6. Таблица дифференциалов простейших элементарных функций.
В п. 3 § 3 мы установили, что дифференциал dy функции y = f(x)
всегда равен производной этой функции f (х), умноженной на диф-
дифференциал аргумента dx. Поэтому установленная нами таблица
производных сразу же приводит нас к соответствующей таблице
дифференциалов простейших элементарных функций.
Г d(a) a4
В частности, d | —) = dx, d (\fx) =—y=dx.
\ X J X JL у X
2°. d(loga x) =— loga edx @ < а ф 1, x >0).
В частности, d(lnx) = .
3°. d(a*)=a*\nadx
В частности, d(ex) =exdx.
4°. d(sinx) —cosxdx.
5°.d{cosx)=—sinxdx.
COS2 X
Ф — +лп;п = О, ±1, ±2, ...
8". d (arcsin x) = dx/Vl —x2 (— 1 < x < + 1).
9°. d (arccosx) = — dx/VT^x2 (— 1< x < + 1).
10°. d(arctgx)= dx
1+*2
11°. d(arctgx) = — y~-
7. Логарифмическая производная. Производная степенно-пока-
степенно-показательной функции. Пусть функция y=f(x) положительна
¦и дифференцируема в данной точке х. Тогда и сложная функция ар-
аргумента х вида w=\r\.y, где y = f(x), в силу теоремы 5.3 будет
также дифференцируема в указанной точке х, причем для произ-
производной этой сложной функции по аргументу х будет справедлива
формула
1\п!(х)]' = (\пу)'у'=У~ = Ш-. E.42)
Величину E.42) принято называть логарифмической
"производной функции y = f(x) в данной точке х.
Логарифмическая производная может быть использована для
вычисления производных некоторых функций, не являющихся про-
простейшими элементарными.
§ 6. Производные и дифференциалы высших порядков 213
В качестве примера вычислим производную так называемой
степенно-показательной функции, т. е. функции вида у = и (х) v(-x\
где и(х) и v(x) —две функции, дифференцируемые в данной точ-
точке х, первая из которых и(х) строго положительна в этой точке.
При таких ограничениях функция w — \ny = v(x) lnu(x) будет
дифференцируема в данной точке х. В самом деле, в силу теоремы
5.3 функция \пи(х) дифференцируема в точке х. Значит, на осно-
основании теоремы о дифференцируемое™ произведения двух диффе-
дифференцируемых функций можно утверждать дифференцируемость в
данной точке х и функции w=\ny = v(x) Лпи(х), причем в силу
второй формулы E.24)
(lny)' = v' {х) In и {х) + v (х) [In и {х)\ =
= v' (x) In u(x) + v {x) -??L. E.43)
Из E.42) и E.43) получим, что
-? =о'(х)lnu(x) + v{x) ?Q
У
и(х)
Учитывая, что y = u(x)v<x\ окончательно получим следующее вы-
выражение для производной степенно-показательной функции:
{и (*)«*»}' = и (я)**» Го' (*) In и (х) + v (х) -^-1. E.44)
Формула E.44) справедлива в предположении, что и(х) и v(x)
дифференцируемы в данной точке х и и(д;)>0 в этой точке.
§ 6. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ
ПОРЯДКОВ
1. Понятие производной n-го порядка. Как уже отмечалось в
о. 2 § 1, производная f'(x) функции y=f{x), определенной и диф-
дифференцируемой на интервале (а, Ь), представляет собой функцию,
также определенную на интервале {а, Ь). Может случиться, что
функция f (х) сама является дифференцируемой в некоторой точке
х интервала (а, Ь), т. е. имеет в этой точке производную. Тогда
указанную производную называют второй производной
(или производной второго порядка) функции y = f(x)
в точке х и обозначают символом fB)(*) или г/B>*.
После того .как введено понятие второй производной, можно
последовательно ввести понятие третьей производной, затем чет-
четвертой производной и т. д. Если предположить, что нами уже
введено понятие (п—1)-й производной и что (п—1)-я производная
дифференцируема в некоторой точке х интервала (а, Ь), т. е.
* Для обозначения второй производной используют также символы f"
или у".
214 Гл. 5. Дифференциальное исчисление
имеет в этой точке производную, то указанную производную на-
называют п-й производной (или производной /z-ro порядка) функции
y=f{x) в точке х и обозначают символом fw(x) или г/(га).
Таким образом, мы вводим понятие п-й производной индук-
индуктивно, переходя от первой производной к последующим. Соотно-
Соотношение, определяющее /г-ю производную, имеет вид
у(«> =[y<*-i>]'. E.45)
Функцию, имеющую на данном множестве {х} конечную про-
производную порядка п, обычно называют п раз дифференцируемой
на данном множестве.
Понятие производных высших порядков находит многочислен-
многочисленные применения. Здесь мы ограничимся тем, что укажем механи-
механический смысл второй производной. Если функция y=/(x) описы-
описывает закон движения материальной точки вдоль оси Оу, то, как
мы уже знаем из гл. 1, первая производная f'(x) дает мгновенную
скорость движущейся точки в момент времени х. В таком случае
вторая производная /B)(*) равна скорости изменения скорости,
т. е. равна ускорению движущейся точки в момент времени х.
Методика вычисления производных высшего порядка предпо-
предполагает умение вычислять только производные первого
порядка, ибо последовательное применение формулы E.45)
есть не что иное, как многократное вычисление первых производ-
производных. В качестве примеров вычислим производные /г-го порядка
некоторых простейших элементарных функций.
2. n-ые производные некоторых функций.
1°. Вычислим п-ю производную степенной функции у—ха
0, а — любое вещественное число). Последовательно диффе-
дифференцируя, будем иметь
у' = аха'\ yW = a{a—\)x«-2, у& = а(а— 1) (а—2
Отсюда легко уяснить общий закон
"> = а (а— 1) ... (а—п+1)ха~
Строгое доказательство этого закона легко проводится методом
математической индукции.
В частном Случае а=/и, где т — натуральное число, получим
) = О при n>tn.
Таким образом, п-я производная многочлена m-го порядка при
п>т равна нулю*.
* Прн этом мы используем следующую очевидную формулу: [Аи(х)-
+Bv(x)]n=Au!-ni(x)+BvW{x), где А и В — постоянные.
§ 6. Производные и дифференциалы высших порядков
215
2°. Далее вычислим /г-ю производную показательной функции
у=ах. Последовательно дифференцируя, будем иметь
Общая формула, легко устанавливаемая по методу индукции,
имеет вид
= ax In" a.
В частности,
= ех.
3°. Вычислим п-ю производную функции y = smx.
Первую производную этой функции можно записать в виде
у'= cosx = sin (х +—). Таким образом, дифференцирование
функции y = sinx прибавляет к аргументу этой функции величину
—. Отсюда получаем формулу
«2
(sin х)<п) = sin (х + п — \.
4°. Совершенно аналогично устанавливается формула
(cos*)<">= cos (x+n —
5°. Вычислим /г-ю производную функции y = arctg.*:. Докажем
с помощью метода математической индукции, что справедлива
следующая формула:
(arctg *)<"> = ¦
sin [n (arctgA;+ j-
1
1
Учитывая, что y = avctgx, x = tgy,
можем переписать устанавливаемую формулу в виде
E.46)
= cos2?/, мы
С) = {п —1I cos" у sin \п (у +—)j.
E.46*)
Убедимся методом индукции в справедливости формулы E.46*).
При п=1, в силу п. 3 § 5, y' = (aTcigx)' = —
¦ = cos2 у. То же
самое выражение получается при л=1 из E.46*) (достаточно
учесть, что sin ( у + — ) =cosy).
Таким образом, при /г=1 формула E.46*) справедлива.
216 Гл. 5. Дифференциальное исчисление
Предположим теперь, что формула E.46*) справедлива для
некоторого п, и убедимся, что в таком случае эта формула спра-
справедлива и для следующего номера п+1.
В самом деле, производя дифференцирование E.46*), получим
(n—\)l—lcosnysm\n (у + — \ 11 =
Учитывая, что у' = cos2 у, (cos" у) = п cos"-1 у (—sin у), мы по-
лучим, что
у |—sin у sin л (у + — J + cos у cos /г (г/ + —) 1 =
У L V 2 /J LV 2 /JJ
= п\cos^1 г/cos [(n+ 1)у + тг —1 =n!cos"+i г/sin [(тг+ \)(у + — \ 1.
L 2J 1_ \2/J
Мы получаем для у(п+1' формулу вида E.46*), взятую для но-
номера п+1. Тем самым индукция завершена и формула E.46) до-
доказана.
6°. В заключение вычислим /г-ю производную так называемой
дробно-линейной функции у= , где а, Ь, с и* d —
cx-\-d
некоторые постоянные.
Последовательно дифференцируя эту функцию, будем иметь
у.= °«* + <В-«Р* + Ь) ={ad-bc)(cx+d)-*.
(сх + dJ
yw=(ad—bc) (—2) (cx+d)-%
yW=(ad—bc) (—2) (—3) (cx+d)~*c2
Легко усмотреть и общий закон
ax + b )(n) = (ad—be) (— 1)"-' fi! (ex + d)-<n+»> c»-«,
cx + d J
который доказывается по методу индукции.
3. Формула Лейбница для п-й производной произведения двух
функций. В то время как установленное выше правило вычисления
§ 6. Производные и дифференциалы высших порядков 21 7
первой производной от суммы или разности двух функций
(u±v)'=u'±vr легко переносится (например, по методу индук-
индукции) на случай /г-й производной (u±v)(n) = u<-n)±v<-n\ возникают
затруднения при вычислении /г-й производной от произведения
двух функций и v.
Соответствующее правило носит название формулы Лейбница
и имеет следующий вид:
E.47)
Легко подметить закон, по которому построена правая часть
формулы Лейбница E.47): она совпадает с формулой разложения
¦бинома (u + v)n, лишь вместо степеней и и v стоят про-
производные соответствующих порядков.
Это сходство становится еще более полным, если вместо самих
функций и и v писать соответственно и@) и v<0> (т. е. если рассмат-
рассматривать саму функцию как производную нулевого порядка).
Докажем формулу Лейбница по методу индукции. При п—1
эта формула принимает вид (uv)' = u'v + uvf, что совпадает с ус-
установленным выше (в § 4) правилом дифференцирования произ-
произведения двух функций. Поэтому достаточно, предположив спра-
справедливость формулы E.47) для некоторого номера п, доказать
ее справедливость для следующего номера /г+1.
Итак, пусть для некоторого номера п формула E.47) верна.
Продифференцируем эту формулу и объединим слагаемые, стоя-
стоящие в правой части, так, как это указано ниже:
Clnu{n)v'] + [С^нС
E.48)
(При этом мы воспользовались тем, что 1 = СП°.)
Легко проверить, что для любого номера k, не превосходящего
л, справедлива формула
С* + С*-' = С*+1. E.49)
Для того чтобы убедиться в справедливости формулы E.49),
достаточно заметить, что
rk_ п(п — 1) ... (д — fe-f 1) ^fc-i _ n(n — 1) ...(n— fe + 2)
rk _ (n+\)n...(n-k + 2)
Cn+h .
Из написанных соотношений вытекает, что
...(n—k+\) , n(n —1)...(я—
218 Гл. 5. Дифференциальное исчисление
_^ п(п — \)...(Л — k + 2)(n — k + iy+n {n— 1) ..,(" —
_ п (п - 1) ... (п - к + 2) [(в - k + 1) + k] __
k\
n — \)...(n—k-\-1)_nk
Используя формулу E.49), мы можем следующим образом
переписать соотношение E.48):
Тем самым мы убедились в справедливости формулы E.47)'
для номера /г+1. Индукция проведена, и вывод формулы Лейбни-
Лейбница E.47) завершен.
Пример. Вычислим я-ю производную функции у=х2ех. По-
Полагая в формуле Лейбница E.47) и — ех, v=x2 и учитывая, что
и(Ю = ех (для любого номера k), v' = 2x, tK2) = 2, uC) = uD>=...=0,
мы получим, что
Подчеркнем, что формула Лейбница особенно эффективна
в том случае, когда одна из перемножаемых функций имеет лишь
конечное число отличных от нуля производных
и не представляет затруднения вычисление всех производных
другой из перемножаемых функций.
4. Дифференциалы высших порядков. Выше для обозначения
дифференциала аргумента и соответствующего ему дифференциа-
дифференциала функции мы использовали символы dx и соответственно dy.
В рассуждениях настоящего пункта нам придется использовать
для обозначения дифференциала аргумента и соответствующего
ему дифференциала функции и другие символы. В частности, мы
будем обозначать дифференциал аргумента и соответствующий
ему дифференциал функции символами 6л: и 8у соответственно.
В этих обозначениях инвариантное по форме выражение для
первого дифференциала функции у—Цх) будет иметь вид 8у =
=f'(x)8x. »
Рассмотрим выражение для первого дифференциала диффе-
дифференцируемой в данной точке х функции у—Цх):
dy = f'(x)dx. E.50)
Предположим, что величина, стоящая в правой части E.50),
представляет собой функцию аргумента х, дифференцируемую
в данной точке х. Для этого достаточно потребовать, чтобы функ-
функция y = f(x) была два раза дифференцируема в данной точке х, а
аргумент либо являлся независимой переменной, либо представ-
§ 6. Производные и дифференциалы высших порядков 219
лял собой дважды дифференцируемую функцию некоторой неза-
независимой переменной L
При этих предположениях мы можем рассмотреть дифферен-
дифференциал
8(dy)=8[f'(x)dx]
от величины E.50).
Определение 1. Значение 8(dy) дифференциала от первого
дифференциала E.50), взятое при 8x = dx, называется ¦ вторым
дифференциалом функции y—f(x) (в данной точке х) и обознача-
обозначается символом d2y.
Итак, по определению*
<Ру = 6 (dy) | &x=dx = {б [/' (х) dx]} 16x=dx-
Дифференциал dny любого порядка п вводится по индукции.
Предположим, что уже введен дифференциал dn~xy порядка
я—1 и что функция y=f(x) n раз дифференцируема в данной
точке х, а ее аргумент х либо является независимой переменной,
либо представляет собой п раз дифференцируемую функцию не-
некоторой независимой переменной i.
Определение 2. Значение 8(dtl~1y) дифференциала от
(п—\)-го дифференциала dn~ly, взятое при 8x—dx, называется
л-м дифференциалом функции y = f(x) (в данной точке х)
и обозначается символом d"y.
Итак, по определению dny = б (dn~ly) \§x=dx.
При вычислении второго и последующих дифференциалов при-
приходится существенно различать два случая: 1) случай, когда ар-
аргумент х является независимой переменной; 2) случай, когда аргу-
аргумент х представляет собой соответствующее число раз диффе-
дифференцируемую функцию некоторой независимой переменной t.
В первом случае, когда х является независимой переменной,
мы имеем право считать, что dx не зависит от х и равен од-
одному и тому же приращению аргумента Ах (для всех точек х).
При этом мы получим, что 8(dx) = (dx)f8x = 0.
Последнее соотношение и второе соотношение E.28) позволяют
нам записать следующую цепочку равенств:
d2y = б (du) 16x=dx = {б [f (x) dx}} 16x=dx =
= {S If (xftdx + f (x) 6 (dx)} 15x==dx = {6 [f (x)} dx} | &x=dx =
=(fc = P (x) (dxJ. E.51)
Итак, в случае, когда аргумент х является независимой пере-
переменной, для второго дифференциала функции y=f(x) справедливо
представление
(dxJ. E.52)
* Символ {...} |ах = <*х означает, что в выражении, заключенном в фигурные
скобки, следует положить (jx=dx.
220 Гл. 5. Дифференциальное исчисление
Совершенно аналогично, по индукции легко убедиться в том,
что в случае, когда аргумент х является независимой переменной,
для /г-го дифференциала п раз дифференцируемой функции у =
=f(x) справедливо представление
Таким образом, в случае, когда аргумент х является независи-
независимой переменной, производная порядка п функции y=f(x) равна
отношению n-го дифференциала этой функции dny к /г-й степени
дифференциала аргумента dx.
Совсем другой вид имеют представления для второго и после-
последующих дифференциалов в случае, когда аргумент х является
соответствующее число раз дифференцируемой функцией некото-
некоторой независимой переменной t.
Установим выражение для второго дифференциала, считая,
что функция y=f(x) два раза дифференцируема в данной точке
х, а ее аргумент х является два раза дифференцируемой функци-
функцией некоторой независимой переменной t.
Повторяя рассуждения из цепочки E.51), мы на этот раз
получим
d2y = б (dy) 16x=dx = {б [/' (х) dx]} 16x=dx =
= {б [/' (*)] dx + f (x) б (dx)} | t^dx =
= {/<2> (x) bxdx} 16x=dx + {/' (x) б (dx)} 16X=dx.
Заметим, что в силу определения второго дифференциала
функции у = х
Учитывая это соотношение, мы приходим к следующему пред-
представлению:
d2y=fW(x)(dx)*+f'(x)d2x. E.53)
Сравнивая полученное представление E.53) с представлением
E.52), мы убедимся в том, что (в отличие от первого дифферен-
дифференциала) второй дифференциал уже не обладает свойством инва-
инвариантности формы.
Тем более не обладают свойством инвариантности формы пос-
последующие дифференциалы.
§ 7. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ, ЗАДАННОЙ
ПАРАМЕТРИЧЕСКИ
Мы будем говорить, что переменная у как функция аргумента
х задана нам параметрически, если обе переменные х
и у заданы как функции некоторой третьей переменной t: x=q>(t),
§ 7. Дифференцирование функции, заданной параметрически 22t
При этом указанную переменную t обычно называют пара-
параметром.
Мы, естественно, будем предполагать, что функции ф(?) и ty(ty
имеют нужное число производных по параметру / в рассматривае-
рассматриваемой области изменения этого параметра.
Кроме того, мы всегда будем считать, что функция x = q>(t)
в окрестности рассматриваемой точки t=U имеет обратную функ-
функцию t=q>-l(x)*, ибо это позволяет рассматривать у как функ-
функцию х.
Рассмотрим вопрос о вычислении производных функции у =
=у(х) по аргументу х.
В силу свойства инвариантности формы первого дифференциа-
дифференциала (см. п. 3 § 3) мы можем записать равенства:
, dytf(t), d y{) E.54>
Из этих равенств сразу же вытекает, что
у1 (Х) = *Ж . E.55).
Для вычисления второй производной уB){х) достаточно заме-
заметить, что в силу свойства инвариантности формы первого диффе-
дифференциала
yW(x)= dly'(x)] E.56)-
y() .
Используя в правой части E.56) соотношение E.55) и третье
равенство E.54), получим
„B)
<?{t)dt [Ф'(/)]2
По такому же принципу вычисляются производные третьего и»
последующих порядков. Так, для вычисления третьей производной-
г/C) (х) достаточно представить эту производную в виде
у {х)
и воспользоваться "соотношением E.57) и третьим равенством!
E.54).
В качестве примера вычислим первую и вторую производные-
следующей функции, заданной параметрически:
x = a(t — sin t),
к ' — эо< t< + оо.
у = аA — cost),
* В гл. 14 будет доказано, что для существования у функции x=<f(t) в.
окрестности точки t=U обратной функции достаточно, чтобы производив ж.
<р'@ была непрерывна и отлична от нуля в точке to.
222
Гл. 5. Дифференциальное исчисление
Кривая, являющаяся графиком этой функции, называется цик-
циклоидой. Эта кривая представляет собой траекторию некоторой
фиксированной точки окружности радиуса а, которая катится без
скольжения по прямой линии (параметр t равен углу поворота
радиуса этой окружности).
Пользуясь формулами E.55) и E.57), получим
У'(х) =
у{2) W =
a sin t
o(l-
t
B 2
a{\ —
, t
= ctg —,
2
4a sin4 —
§ 8. ПРОИЗВОДНАЯ ВЕКТОРНОЙ ФУНКЦИИ
В приложениях математики часто встречаются понятия вектор-
векторной функции и ее производной.
Если каждому значению переменной t из некоторого множест-
множества {t} ставится в соответствие по известному закону определенный
вектор а, то говорят, что на множестве {t} задана векторная
функция a = a(t).
Так как каждый вектор а в заданной декартовой прямоуголь-
«ой системе координат однозначно определяется тремя координа-
координатами х, у и z, то задание век-
М торной функции а = а (t) экви-
эквивалентно заданию трех ска-
скалярных функций x = x(t), у =
Понятие векторной функ-
функции приобретает особую на-
наглядность при обращении к
так называемому годогра-
ф у этой функции (т. е. гео-
геометрическому месту концов
*х всех векторов а = а(^), прило-
Рис 54 женных к началу координат
О). На рис. 5.4 кривая L
представляет собой годограф
векторной функции а = а(^).
Понятие годографа векторной функции является естественным
¦обобщением понятия графика скалярной функции.
Введем понятие производной векторной функции а = а(/)
в данной фиксированной точке t.
Зададим аргументу в точке t произвольное приращение ЫфО
и рассмотрим соответствующий вектор приращения Да =
-а(/). (На рис. 5.4 указанный вектор совпадает с МР.)
§ 8. Производная векторной функции 223
Умножив указанный вектор на число , мы получим новый
вектор
J±- = -L.[a(t + M)-z(t)], E.58)
коллинеарный прежнему. Этот вектор E.58) является аналогом
разностного отношения E.5).
Вектор E.58), очевидно, представляет собой среднюю скорость
изменения векторной функции на сегменте [t, t+At].
Производной векторной функции a. = a.(t) в данной фик-
фиксированной точке t называется предел при Д?->-0 вектора E.58)
(при условии, что этот предел существует).
Для обозначения производной векторной функции а —а(^) ис-
.... da
пользуются символы а (г) или .
dt
Из геометрических соображений очевидно, что производная
векторной функции а = а(?) представляет собой вектор, касатель-
касательный к годографу этой функции.
Так как координаты разностного отношения E.58) соответст-
соответственно равны
x(t+At)-x(t) y(t + M)-y{t) z(< + AQ-z(Q
At At At
то ясно, что координаты производной а'@ равны производным
функций x'(t), y'(t), z'(t). Таким образом, вычисление производ-
производной векторной функции сводится к вычислению производных ее
координат.
Замечание 1. Так как векторная функция а = а(?) опреде-
определяет закон движения материальной точки по кривой L, представ-
представляющей собой годограф этой функции, то производная а.'(I) равна
скорости движения по указанной кривой.
Замечание 2. Из курса аналитической геометрии известны
различные типы произведений векторов (скалярное произведение,
векторное произведение и смешанное произведение). Выражение
всех этих произведений в координатах дает возможность указать
правила, по которым вычисляются производные соответствующих
произведений векторных функций. В качестве примера приведем
правило вычисления производной скалярного произведения двух
векторных функций a(/) = (ai(/), a2{t), a3(t)) и b(t) = (bi(t),
bs(t), MO) : {а(О-Ь@}'=а'@-Ь@+а@-Ь'@ ={al'{t)-bi(t) +
+ a2'(t)-b2(t) + a8'@-M0} + {ai(t)-bi'(t) + a2(t)-b2'(t) +
+ a.i(t) -bz (t)}. Аналогичное правило справедливо и для вектор-
векторного произведения двух векторных функций:
Г л ава 6
ОСНОВНЫЕ ТЕОРЕМЫ
О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
В настоящей главе будет установлен ряд важных теорем, от-
относящихся к произвольным дифференцируемым функциям. Эти
теоремы чрезвычайно эффективны при исследовании поведения
функции (как в окрестности отдельных точек области ее задания,
так и на целых участках области ее задания).
§ 1. ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИИ В ТОЧКЕ.
ЛОКАЛЬНЫЙ ЭКСТРЕМУМ
Рассмотрим функцию y=f{x), определенную всюду в некото-
некоторой окрестности фиксированной точки с.
Определение 1. Будем говорить, что функция y=f(x)
¦возрастает в точке с, если найдется такая 8-окрестность
точки с, в пределах которой
f(x)<f(c) при х<с
и
f(x)>f(c) при х>с.
Определение 2. Будем говорить, что функция y=f(x)
убывает в точке с, если найдется такая Ь-окрестность точки
с, в пределах которой
f(x)>f(c) при х<с
и
f(x)<f(c) при х>с.
Определение 3. Будем говорить, что функция y=f(x)
имеет в точке с локальный максимум [локальный
минимум], если найдется такая Ь-окрестность точки с, в преде-
пределах которой значение f(c) является наибольшим [наименьшим]
среди всех значений f(x) этой функции.
Определение 4. Будем говорить, что функция y=f(x)
имеет в точке с локальный экстремум, если эта функция
имеет, в указанной точке либо локальный максимум, либо локаль-
локальный минимум.
На рис. 6.1 изображена функция, возрастающая в точке С\,
убывающая в точке с2, имеющая локальный максимум в точке Сз
.и локальный минимум в точке с4.
Докажем следующие две теоремы.
§ 1. Локальный экстремум
225
С, С*.
Рис. 6.1
Рнс. 6.2
Теорема 6.1 (достаточное условие возрастания
или убывания функции в точке). Если функция у — ] {х)
дифференцируема в точке с и ее производная в этой точке f'(c)
положительна [отрицательна], то функция y = f(x) возрастает
[убывает] в точке с.
Доказательство. Проведем все рассуждения для случая
}'(с)>0 (для случая /'(с)<0 они аналогичны).
Так как (по определению производной)
то на основании определения предела функции по Коши для поло-
положительного числа е = /'(с) найдется б>0 такое, что
f (с) </'(с) при
— с|<6
X —С
или, что то же самое,
О <- Kx)-f(c) ^ щ, ^ при с _ g < ^ < с + 6j ^_^ с_
X —С
Таким образом, всюду в проколотой б-окрестности точки с
К*)-/(с) >0_
X —С
Но это и означает, что всюду в пределах б-окрестности точки с
f(x)>f(c) при х>с,
и f(x)<f(c) при я<с,
т. е. функция y = f(x) возрастает в точке с.
8 Зак. 72
226
Гл. 6. Основные теоремы о дифференцируемых функциях
Случай /'(с)<0 рассматривается аналогично. Теорема дока-
доказана.
Замечание 1. Подчеркнем, что положительность [отрица-
[отрицательность] производной f'(c) не является необходимым условием
возрастания [убывания] дифференцируемой в точке с функции
Так, функция у = х3 возрастает в точке с = 0, в то время как
производная этой функции f'(x)=3x2 обращается в нуль в точке
с = 0 (график функции — на рис. 6.2).
Теорема 6.2 (необходимое условие локального
экстремума дифференцируемой в данной точке
функции). Если функция y = f(x) дифференцируема в точке с
и имеет в этой точке локальный экстремум, то f'(c) = O.
Доказательство. По условию теоремы существует конеч-
конечная производная /'(с). Так как функция у=}(х) имеет в точке с
локальный экстремум, то она не может в этой точке с ни возрас-
возрастать, ни убывать. Значит, в силу теоремы 6.1 производная /'(с)
не может быть ни положительной, ни отрицательной. Тем самым
доказано, что /'(с) =0.
Теорема 6.2 имеет очень простой геометрический смысл: она
утверждает, что если в той точке кривой y=f(x), в которой дос-
достигается локальный экстремум, существует касательная к этой
кривой, то эта касательная обязательно параллельна оси Ох
(рис. 6.3).
У>
Касательная
с
Рис. 6.3
Касательная
Рис. 6.4
Замечание 2. Пример той же самой функции у=хг (см.
рис. 6.2) показывает, что обращение в нуль производной является
лишь необходимым и не является достаточным условием локаль-
локального экстремума. (Производная f'(x)=3x2 этой функции обраща-
обращается в нуль в точке с = 0, но никакого экстремума в этой точке
нет.)
§ 2. ТЕОРЕМА О НУЛЕ ПРОИЗВОДНОЙ
Теорема 6.3 (теорема Рол л я*). Пусть функция f(x)
непрерывна на сегменте [а, Ь] и дифференцируема во всех внут-
Мишель Ролль — французский математик A652—1719).,
§ 3. Формула конечных приращений 227
_i . _ .
ренних точках этого сегмента. Пусть, кроме того, f(a)=f(b). Тог-
Тогда внутри сегмента [а, Ь] найдется точка | такая, что значение
производной в этой точке /'(?) равно нулю.
Кратко можно сказать, что между двумя равными значениями
дифференцируемой функции обязательно лежит нуль производной
этой функции.
Доказательство. Так как функция f(x) непрерывна на
сегменте [а, Ь], то согласно теореме 4.15 эта функция достигает
на этом сегменте максимального значения М и своего минималь-
минимального значения пг. Могут представиться два случая: 1) М — пг;
2) М>т. В случае 1) f(x)=M = m = const. Поэтому производная
f (х) равна нулю в любой внутренней точке сегмента [а, Ь].
В случае М>т, поскольку f(a)—f(b), можно утверждать, что
хотя бы одно из двух значений М или т достигается функцией
в некоторой внутренней точке | сегмента [а, Ь]. Но тогда функ-
функция f(x) имеет в этой точке | локальный экстремум. Поскольку
функция f(x) дифференцируема в точке |, то по теореме 6.2
f (|)=0. Теорема полностью доказана.
Теорема Ролля имеет простой геометрический смысл: если
крайние ординаты кривой y—f(x) равны, то согласно теореме
Ролля на кривой y=f(x) найдется точка, в которой касательная
к кривой параллельна оси Ох (рис. 6.4).
Как мы увидим ниже, теорема Ролля лежит в основе многих
формул и теорем математического анализа.
Замечание. В теореме Ролля требуется, чтобы функция
y = f(x) была непрерывна на сегменте [а, Ь] и дифференцируема
во всех внутренних точках этого сегмента. Так как из дифферен-
дифференцируемое™ f(x) во всех внутренних точках вытекает непрерыв-
непрерывность }(х) во всех внутренних точках, то по существу вместо
непрерывности f(x) на сегменте [а, Ь] можно было бы потребо-
потребовать непрерывность f(x) в точке а справа и в точке Ъ слева.
§ 3. ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ
(ФОРМУЛА ЛАГРАНЖА)
Большое значение в анализе и его приложениях имеет следую-
следующая теорема, принадлежащая Лагранжу*.
Теорема 6.4 (теорема Лагранжа). Если функция
}(х) непрерывна на сегменте [а, Ь] и дифференцируема во всех
внутренних точках этого сегмента, то внутри сегмента [а, Ъ] най-
найдется точка | такая, что справедлива формула
/(Ь)-/(а)=/'(|)(й-а). F.1)
Формулу F.1) называют формулой Лагранжа или формулой
конечных приращений.
Жозеф Лун Лагранж — великий французский математик и механик
228 Гл. 6. Основные теоремы о дифференцируемых функциях
Доказательство. Рассмотрим на сегменте [а, Ь] следу-
следующую вспомогательную функцию
ММ х_а). F.2)
о — а
Проверим, что для функции F(x) выполнены все условия тео-
теоремы Ролля. В самом деле, F(x) непрерывна на сегменте [а, Ь]
(как разность функции f(x) и линейной функции) и во всех
внутренних точках сегмента [а, Ь] имеет производную, равную
F (х) = П*) -
о — а
Из формулы F.2) очевидно, что F(a) =F(b) =0.
Согласно теореме Ролля внутри сегмента [а, Ь] найдется точ-
точка Ъ, такая, что
тт =0. F.3)
Из равенства F.3) вытекает формула Лагранжа F.1). Подчерк-
Подчеркнем, что в формуле F.1) вовсе не обязательно считать, что Ь~>а,
эта формула верна и при Ь<а.
Замечание. Мы получили теорему Лагранжа как следствие
теоремы Ролля. Заметим вместе с тем, что сама теорема Ролля
является частным случаем теоремы Лагранжа (при f(a)=f(b)).
Для выяснения геометрического смысла теоремы Лагранжа
заметим, что величина ——-—-—— есть угловой коэффициент се-
Ъ — а
кущей, проходящей через точки А(а, f(a)) и B(b, f(b)) кривой
y=f(x), a /'(I) есть угловой коэффициент касательной к кривой
y = f(x), проходящей через точку
С(%, f(t)). Формула Лагранжа
F.1) означает, что на кривой у —
= f(x) между точками А и В най-
найдется такая точка С, касательная
в которой параллельна секущей
АВ (рис. 6.5).
_^ Часто бывает удобно записы-
х вать формулу Лагранжа в виде,
несколько отличном от F.1). Пусть
Рис. 6.5 f(x) удовлетворяет условиям тео-
теоремы 6.4. Зафиксируем любое ха
из сегмента [а, Ь] и зададим
ему приращение Ах произвольное, но такое, чтобы значение хо+
+Ах также лежало на сегменте [а, Ь]. Тогда, записывая формулу
Лагранжа для сегмента, ограниченного точками х0 и #0+Дл:, будем
иметь
f(Xo+Ax)—f(Xo)=Axf(l), F.4)
§ 4. Некоторые следствия из формулы Лагранжа 229
где | — некоторая точка, лежащая между х0 и хо+Ах. Можно ут-
утверждать, что найдется такое (зависящее от Ах) число 8 из ин-
интервала 0<6<1, что
Таким образом, формуле F.4) можно придать вид
f(xo+Ax)—f(xo) =Axf'(xo+QAx), F.5)
где 8 — некоторое число из интервала О<0<1. Формула Лагран-
жа в виде F.5) дает точное выражение для приращения функции
через вызвавшее его произвольное конечное приращение Ах аргу-
аргумента. Этот вид формулы Лагранжа оправдывает термин «форму-
«формула конечных приращений».
§ 4. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ФОРМУЛЫ
ЛАГРАНЖА
1. Постоянство функции, имеющей на интервале равную нулю
производную.
Теорема 6.5. Если функция f(x) дифференцируема всюду
на интервале (а, Ь) и если всюду на этом интервале f'(x)=0, то
функция f(x) является постоянной на интервале (а, Ь).
Доказательство. Пусть х$ — некоторая фиксированная
точка интервала (a, b), a x — любая точка этого интервала.
Сегмент [х0, х] или соответственно [х, хо] целиком принадле-
принадлежит интервалу (а, Ь). Поэтому функция f(x) дифференцируема
(а значит, и непрерывна) всюду на этом сегменте. Это дает право
применить к функции f(x) на этом сегменте теорему Лагранжа.
Согласно этой теореме внутри указанного сегмента найдется точка
? такая, что
/(*)-/(*<>) = (*-*<>)/'F). F.6)
По условию производная функции f(x) равна нулю всюду в ин-
интервале (а, Ь). Значит, /'(|)=0 и из формулы F.6) мы получим
f(x)=f(xo). F.7)
Равенство F.7) утверждает, что значение функции f(x) в любой
точке х интервала (а, Ь) равно ее значению в фиксированной тол-
толке #о- Это и означает, что функция f(x) постоянна всюду на интер-
интервале (а, Ь). Теорема доказана.
Теорема 6.5 имеет простой геометрический смысл: если каса-
касательная в каждой точке некоторого участка кривой y = f(x) парал-
параллельна оси Ох, то указанный участок кривой y=f(x) представля-
представляет собой отрезок прямой, параллельной оси Ох.
Замечание. Теорема 6.5 будет использована нами в гл. 8
«Первообразная функция и неопределенный интеграл». Во всем
остальном гл. 8 является независимой от гл. 6 и 7 и может чи-
читаться сразу после гл. 5.
230 Гл. 6. Основные теоремы о дифференцируемых функциях
2. Условия монотонности функции на интервале. В качестве
второго следствия формулы Лагранжа рассмотрим вопрос об ус-
условиях, обеспечивающих неубывание (невозрастание) функции на
данном интервале.
Прежде всего напомним определения неубывания, невозраста-
невозрастания, возрастания и убывания функции на данном интервале.
1°. Говорят, что функция f(x) не убывает (не возрас-
возрастает) на интервале (а, Ь), если для любых точек х\ и х2 из интер-
интервала (а, Ь), удовлетворяющих условию Х\<х2, справедливо нера-
неравенство
2°. Говорят, что функция f(x) возрастает (убывает) на
интервале (а, Ь), если для любых точек Х\, х2 из интервала (а, Ь),
связанных условием хх<х2, справедливо неравенство
f(Xl)<f(x2) (f(Xl)>f(x2)).
Теорема 6.6. Для того чтобы дифференцируемая на интерва-
интервале (а, Ь) функция \(х) не убывала (не возрастала) на этом интер-
интервале, необходимо и достаточно, чтобы производная этой функции
была неотрицательной (неположительной) всюду на этом интер-
интервале.
Доказательство. 1) Достаточность. Пусть fr(x)^O (^0)
всюду на интервале (а, Ь). Требуется доказать, что f(x) не убыва-
убывает (не возрастает) на интервале (а, Ь). Пусть Х\ и х2 —¦ любые
две точки из интервала (а, Ь), удовлетворяющие условию Xi<x2.
Функция f(x) дифференцируема (а значит, и непрерывна) всюду
на сегменте [х\, х2]. Поэтому к f(x) можно применить на сегмен-
сегменте [х\, х2] теорему Лагранжа, в результате чего получим
№)-/(*,) = (*2-*1)/'Ш, F.8)
где х\<1<х2.'
По условию f'(|)=^0 (^0), Х2—*i>0. Поэтому правая, а зна-
значит, и левая части F.8) неотрицательны (неположительны), что
и доказывает неубывание (невозрастание) f(x) на (а, Ь).
2) Необходимость. Пусть функция f(x) дифференциру-
дифференцируема на интервале (а, Ь) и не убывает (не возрастает) на этом ин-
интервале. Требуется доказать, что f'(x)^0 (^0) всюду на этом
интервале. Так как f(x) не убывает (не возрастает) на интервале
(а, Ь), то эта функция не может убывать (возрастать) ни в одной
точке интервала (а, Ь). Значит, в силу теоремы 6.1 производная
1'{х) йи в одной точке интервала (а, Ь) не может быть отрица-
отрицательной (положительной), что и требовалось доказать.
Теорема 6.7. Для того, чтобы функция f(x) возрастала (убы-
(убывала) на интервале (а, Ъ), достаточно, чтобы производная f'(x)
была положительной (отрицательной) всюду на этом интервале.
Доказательство проводится по той же схеме, что и дока-
доказательство достаточности в теореме 6.6. Пусть хи х2 — любые
§ 4. Некоторые следствия из формулы Лагранжа 231
две точки из интервала (а, Ь), удовлетворяющие условию Xi<x2.
Записывая для сегмента [хи х2] формулу Лагранжа, получим ра-
равенство F.8), но на этот раз в этом равенстве /'E)>0 (<0).
Вследствие этого левая часть F.8) положительна (отрицатель-
(отрицательна), что и доказывает возрастание (убывание) f(x) на интервале
(а, Ь).
Замечание. Подчеркнем, что положительность (отрицатель-
(отрицательность) производной f'(x) на интервале (а, Ь) не является не об-
обход и м ым условием возрастания (убывания) функции f(x) на
интервале (а, Ь). Так, функция у = х3 возрастает на интервале
(—1, +1), но производная этой функции f'(x) = 3x2 не является
всюду положительной на этом интервале (она обращается в нуль
в точке х = 0). Вообще, легко доказать, что функция f(x) возрас-
возрастает (убывает) на интервале (а, Ь), если производная этой функ-
функции f'(x) положительна (отрицательна) всюду на этом интервале,
за исключением конечного числа точек, в которых эта производ-
производная равна нулю. (Для доказательства достаточно применить тео-
теорему 6.7 к каждому из конечного числа интервалов, на которых
f'(x) строго положительна (отрицательна), и учесть непрерыв-
непрерывность f(x) в тех точках, в которых производная равна нулю.)
Установленную теоремой 6.7 связь между знаком производной
я направлением изменения функции легко понять из геометричес-
геометрических соображений. Поскольку про-
производная равна угловому коэф-
коэффициенту касательной к графику
функции y = f(x), знак производ-
производной указывает, острый или тупой
угол с положительным направле-
направлением оси Ох составляет луч каса-
касательной, лежащей в Еерхней по-
полуплоскости. Если f'(x)>0 всюду
на интервале (а, Ь), то всюду на
этом интервале луч касательной, Рис. 6.6
лежащей в верхней полуплоско-
полуплоскости, составляет с положительным
направлением оси Ох острый угол, значит, и кривая y = f(x) идет
вверх всюду на этом интервале (рис. 6.6).
3. Отсутствие разрывов первого рода и устранимых разрывов
у производной. Теорема Лагранжа позволяет установить одно
замечательное свойство производной. Начнем с доказательства
следующей леммы.
Лемма. Пусть функция y = f(x) имеет конечную производную
f'(x) всюду на интервале (с, с + 8) [на интервале (с—б, с)}, где
б — некоторое положительное число и, кроме того, имеет правую
производную /'(с + 0) [левую производную /'(с—0)]. Тогда, если
производная f'(x) имеет в точке с правый предел [левый предел],
а:
232 Гл., 6. Основные теоремы о дифференцируемых функциях
то этот предел совпадает с правой производной f'(c+O) [с левой
производной f'(c—0)].
Доказательство. Из существования правой производной
f'(c+O) [левой производной /'(с—0)] вытекает существование ко-
конечного предела
Пт -ШМ. Г lim П*)-Пс)
х-ю+0 Х—С [х->-с-0 Х — С
Но это означает, что существует равный нулю предел
lim {/(*)-/(с)) = 0 [ Игл {/(*)-/(с)} = 0],
x-w+0 x-*c—0
т. е. функция y = f(x) является непрерывной в точке с справа
[слева].
Фиксируем любое х из интервала (с, с+б) [(с—б, с)]. Так
как функция y=f(x) дифференцируема (а значит, и непрерывна)
всюду на указанном интервале и, кроме того, непрерывна в точке
с справа [слева], то для этой функции выполнены на сегменте
[с, х] [на сегменте [х, с] ] все условия теоремы Лагранжа 6.4.
В силу этой теоремы между х и с найдется точка | такая, что
справедливо равенство
п*)-пс) =П6Ь F.9)
X С
Перейдем теперь в равенстве F.9) к пределу при х->-с + 0 [при
х-*-с—0]. Если производная f'(x) имеет в точке с конечный пра'-
вый предел lim /' (x) [конечный левый предел lim f'(%)], то
Х-+С+0 х-*с—0
правая часть F.9) обязана стремиться к этому пределу (ибо
?->с + 0 [?->с—0] при *-к:+0 [х->-с—0]).
Тот же самый предел при х-»-с+0 [х->с—0} обязана иметь
и левая часть F.9). Но предел левой части F.9) при х^-с + 0
[х-*-с—0] по определению равен правой производной /'(с + 0)
[левой производной f'(c—0)]. Лемма доказана.
Применяя только что доказанную лемму в каждой точке с
некоторого интервала (а, Ь), мы придем к следующему утвержде-
утверждению: если функция f(x) имеет конечную производную всюду на
интервале (а, Ь), то эта производная f'(x) не может иметь на этом
интервале ни точек устранимого разрыва, ни точек разрыва пер-
первого рода.
В самом деле, если в некоторой точке с интервала (а, Ь) су-
существуют конечные правый и левый пределы функции /'(*)> то
f'(x) непрерывна в точке с (в силу доказанной нами леммы*).
* В силу этой леммы lim f (x)= f'(c+ 0), lim f'(x)= f'(c—0),
а поскольку f(c+0)=/'(c—0)=/'(c), то lim f(x)= lim f{x) = f'{c).
*-+c-fO *0
Это и означает, что f'(x) непрерывна в точке с.
§ 4. Некоторые слеаствия из формулы Лагранжа 233
Если же не существует хотя бы одного из пределов lim /' (х)
х->с-{-0
и limp(х), то функция f(x) по определению имеет в точке с
х-ю—О
разрыв второго рода. Итак, производная f'(x) в каждой точке с
интервала (а, Ь) либо непрерывна, либо имеет разрыв второго
рода. Сформулированное нами утверждение доказано.
Приведем пример функции f{x), производная f'{x) которой
существует и конечна всюду на некотором интервале и имеет*
в некоторой точке этого интервала разрыв второго рода.
Рассмотрим на интервале (—1, +1) функцию
1х2 cos— при хфО,
О при х — 0.
Очевидно, что для любого хфО производная f'(x) этой функции
существует и равна /'(х) = 2хcos (-sin—. Существование
X X
производной f (х) в точке х = 0 непосредственно вытекает из су-
существования предела
lim
Производная f'(x) не имеет в точке х=0 ни правого, ни левого
пределов, ибо первое слагаемое 2xcos— имеет в точке х = 0
X
равный нулю предел, а второе слагаемое sin — не имеет в точке
X
х = 0 ни правого, ни левого пределов. (Это было доказано в при-
примере, рассмотренном в п. 3 § 5 гл. 4.)
4. Вывод некоторых неравенств. В заключение покажем, как
с помощью теоремы Лагранжа могут быть получены некоторые
весьма полезные неравенства. В качестве примера установим сле-
следующие два неравенства:
| sin xi—sin х2 К [xi—x2\, F.10)
| arctg xi—arctg x21< | Xi-~x2 j. F.11)
(Здесь под х\ и х2 можно понимать любые значения аргумента.)
Для установления неравенства F.10) применим теорему Лагран-
Лагранжа к функции f(x) =sin x по сегменту [хи х2]. Получим
sin*!—sin 2= (Xi—x2)}'{%). F.12)
Учитывая, что f'(g)=cos| и что |cos||^l для любого |, по-
получим, переходя в F.12) к модулям, неравенство F.10).
234 Гл. 6. Основные теоремы о дифференцируемых функциях
Для установления неравенства F.11) следует применить теоре-
теорему Лагранжа по сегменту [х\, Хг] к функции /(x)=arctgx и
учесть, что /' (I) = < 1 •
§ 5. ОБОБЩЕННАЯ ФОРМУЛА КОНЕЧНЫХ
ПРИРАЩЕНИИ (ФОРМУЛА КОШИ)
В этом параграфе мы докажем теорему, принадлежащую Коши
и обобщающую установленную выше теорему Лагранжа.
Теорема 6.8 (теорема Коши). Если каждая из двух
функций f(x) и g(x) непрерывна на сегменте [а, Ь] и дифференци-
дифференцируема во всех внутренних точках этого сегмента и если, кроме
того, производная g'(x) отлична от нуля всюду внутри Сегмента
[а, Ь], то внутри этого сегмента найдется точка | такая, что спра-
справедлива формула
( )
g(b)-g(a) g'd) '
Формулу F.13) называют обобщенной формулой ко-
конечных приращений или формулой Коши.
Доказательство. Прежде всего докажем, что g(a) =H=g(b).
В самом деле, если бы это было не так, то для функции g(x)
были бы выполнены на сегменте [а, Ь] все условия теоремы 6.3
(Ролля) и по этой теореме внутри сегмента [а, Ь] нашлась бы
точка % такая, что g'(?)=0. Последнее противоречит условию
теоремы. Итак, g(a)=?g(b), и мы имеем право рассмотреть следу-
следующую вспомогательную функцию:
F (х) = f (х) - f (a) - ^Z^l) ^ W -S («)!• F-14>
В силу требований, наложенных на функции f(x) и g{x), функций
F(x) непрерывна на сегменте [а, Ь] и дифференцируема во всех
внутренних точках этого сегмента. Кроме того, очевидно, что
F(a)=F(b). Таким образом, для F(x) выполнены все условия
теоремы 6.3 (Ролля). Согласно этой теореме внутри сегмента
[а, Ь] найдется точка | такая, что
/г'A)=0. F.15)
Имея в виду, что F' (х) = /' (х) — ^ >~1Ка> ^'до|И используя
g(b)—g{a)
равенство F.15), будем иметь
Учитывая, что g'(%)?=$, из равенства F.16) получим формулу
Коши F.13). Теорема доказана.
§ 6. Раскрытие неопределенностей 235
Замечание 1. Формула Лагранжа F.1) является частным
случаем формулы Коши F.13) при g(x)=x.
Замечание 2. В формуле F.13) вовсе не обязательно счи-
считать, что Ь>а. Эта формула верна и при Ь<а.
§ 6. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ
(ПРАВИЛО ЛОПИТАЛЯ)
1. Раскрытие неопределенности вида —. Будем говорить, что
отношение двух функций представляет собой при х-+а
-. , О
неопределенность вида —¦, если
Umf(x) = hmg(x) = 0.
х-ю х-ю
Раскрыть эту неопределенность — это значит вычислить предел
fix)
lim -!±-L- (при условии, что этот предел существует).
х^а g(x)
Аналогично вводится понятие неопределенности вида — при
[х->а—0], при х-*-оо, а также при #->-+oo [х-*-—оо],
Следующая теорема дает правило раскрытия неопределенности
вида —¦ для предела в точке а.
Теорема 6.9 (первое правило Л опит а л я*). Пусть
множество Сй представляет собой проколотую ^-окрестность точки
а**, функции f(x) и g(x) определены и дифференцируемы на Са
и, кроме того, производная g'(x) не обращается на Сб в нуль.
Пусть, далее,
(x) = O. F.17)
Тогда если существует (конечный или бесконечный) предел
то существует и предел
причем справедливо соотношение
lim i^fEL, F.18)
х-а g'(x)
lim -М-, F.19)
х^а g(x)
lim J^L = lim ?(fL. F.20)
x-,a g(x) x->a g'(x)
* Гильом Франсуа де Лопиталь — французский математик A661—1704).
** Напомним, что проколотой 6-окрестностью точки а называется интер-
интервал (а—б, а+б) с выкинутой точкой а (при условии, конечно, что б>0).
236 Гл. 6. Основные теоремы о дифференцируемых функциях
Теорема 6.9 дает правило раскрытия неопределенности вида
О
—, сводящее вычисление предела в точке а отношения двух
функций к вычислению предела в этой точке отношения производ-
производных этих функций.
Доказательство. Пусть {хп} — произвольная последова-
последовательность значений аргумента, сходящаяся к а и состоящая из чи-
чисел отличных от а. Доопределим функции f(x) и g(x) в точке а,
положив их равными нулю в этой точке. При таком доопределе-
доопределении функции f(x) и g(x) окажутся непрерывными всюду на мно-
множестве С5, дополненном точкой а, т. е. всюду в 6-окрестности точ-
точки а. В самом деле, непрерывность f(x) и g(x) во всех точках
6-окрестности точки а, за исключением самой точки а, вытекает
из их дифференцируемости в этих точках, а непрерывность f(x)
и g(x) в точке а вытекает из того, что в силу нашего доопределе-
доопределения этих функцих их пределы в точке а равны частным значениям
в этой точке.
Учитывая, что все элементы последовательности {хп} принад-
принадлежат множеству Сц, рассмотрим произвольный сегмент, ограни-
ограниченный точками а и хп.
В силу сказанного выше обе функции f(x) и g(x) будут непре-
непрерывными на таком сегменте. Кроме того, функции f(x) и g(x)
дифференцируемы во всех внутренних точках указанного сегмен-
сегмента, и производная g'{x) не обращается в этих внутренних точках
в нуль.
Это дает нам право применить к функциям f(x) и g(x) по
указанному сегменту, ограниченному точками а и хп, теорему
Коши 6.8.
В силу этой теоремы между точками а и хп найдется точка |„
такая, что справедливо равенство
f(Xn)-f(a) _ f (in)
g(*n)-g(a) g'(\n)
К ' '
Учитывая, что по нашему доопределению функций f(x) и g(x)
справедливы равенства f(a)=g(a)=0, мы можем переписать со-
соотношение F.21) в виде
«> НЬ) (б22)
Пусть теперь в соотношении F.22) номер п стремится к бес-
бесконечности, тогда хп-*~а. Поскольку |„ заключено между а и хп, то
и %п-+а при п->оо. В силу существования предела F.18) и опре-
определения предела функции по Гейне правая часть F.22) имеет
предел при n-^оо, равный пределу F.18). Значит, тот же самый
предел при «->оо имеет и левая часть F.22). В силу произволь-
произвольности последовательности значений аргумента {х„}, сходящейся
к а, и в силу определения предела функции по Гейне существо-
§ 6. Раскрытие неопределенностей 237
вание равного F.18) предела при п-^-оо левой части F.22) озна-
означает существование предела функции F.19), также равного F.18).
Итак, в пределе из F.22) при я->-оо мы получаем соотношение
F.20). Теорема доказана.
Замечание 1. Правило Лопиталя «действует» не всегда,
т. е. предел отношения функций F.19) может существовать и
в случае, когда предела отношения производных F.18) не суще-
существует.
Например, при а = 0, /(*) = ;c2cos—,g(x)=smx существует
х2 cos —
flJCi XX 1
предел lim — lim = lim lim#cos — = 0, в то
x-*a g(x) x-tQ Sin.»: x-,-0 Sin л: *^>0 Х
1x cos — + sin —
время как предел Hm = lim не сущест-
существо g'(x) x->o cos л;
вует ( в силу того, что не существует предел lim sin—, а предел
lim Bxcos — | существует и равен нулю).
Д-ч-0 \ X I
Замечание 2. Если к условиям теоремы 6.9 добавить тре-
требование непрерывности производных f'{x) и g'{x) в точке а, то
при условии g'{a)^0 соотношение F.20) можно переписать
в виде
g(x) g'(a)
Замечание 3. Если производные f'{x) и g'(x) удовлетво-
удовлетворяют тем же требованиям, что и сами функции f(x) и g(x), то
правило Лопиталя можно применять повторно, т. е. предел отно-
отношения первых производных функций f{x) и g(x) можно заменить
пределом отношения вторых производных этих функций. Мы по-
получим при этом, что
x-*a g(x) x->a g'(x) x-*a g" (x)
Примеры. 1)
2х
2) Следующий предел вычисляется двукратным применением
правила Лопиталя:
,. х — sin х ,. 1 —cos х ,. sin x 1
hm = lim :— = lim —¦— — —.
я 32
238 Гл. 6. Основные теоремы о дифференцируемых функциях
3) Трехкратным применением правила Лопиталя вычисляется
предел
х* ,. 4х3 ,. 12а-2
lim = hm
х*о л:2+ 2 cos*— 2 х^о 2х— 2 sin л: *-»о 2 — 2 cos x
Мы рассмотрели вопрос о раскрытии неопределенности вида
— для случая предела в точке а. Совершенно аналогичные
результаты справделивы и для случаев предела в точке а спра-
справа [слева], предела при х-*-оо, а также предела при х-»-+оо
[при х-^>—оо].
Мы сейчас убедимся в том, что теорема 6.9 остается спра-
справедливой в каждом из следующих трех случаев:
1) в случае, если в этой теореме в качестве множества С»
взять интервал (а, с+б) [соответственно (а—б, а)], а все пре-
пределы F.17) — F.20) взять при х-+а+0 [соответственно при
х-+а-0];
2) в случае, если в теореме 6.9 в качестве Сб взять множест-
множество всех точек, лежащих вне сегмента [—б, б], а все пределы
F.17) —F.20) взять при л^оо;
3) в случае, если в теореме 6.9 в качестве множества Сь
взять полупрямую (б, +оо) [соответственно (—оо, —б)], а все
пределы F.17) — F.20) взять при х-> + оо [соответственно при
JC—> оо] .
Случай 1. В этом случае остается справедливой вся схема
доказательства теоремы 6.9, только вместо последовательности
,{хп}, сходящейся к а и состоящей из чисел хп, отличных от а,
следует взять последовательность {хп} точек интервала
(а, а + 6) [соответственно (а—б, а)], сходящуюся к а. Детали
рассуждений предоставляем читателю.
Случай 2. Пусть функции f(x) и g(x) определены и диф-
дифференцируемы всюду вне сегмента [—б, б] при некотором
б>0 и производная g'(x) не обращается в нуль вне указанного
сегмента. Путь, кроме того, существует предел
lim ?i?L. FЛ8')
д:-»о° g'(x)
Сделаем замену переменной t ==,— и положим G(t) =g (—\ =
X \ I /
= g(x), F(t) = f( — J = f(x). Тогда, очевидно, функции
/•"(/) и G(t) будут определены и дифференцируемы в проколо-
§ 6. Раскрытие неопределенностей 239
той окрестности точки t = 0* и производная
о
G'@ = ^ (-7) (--^) =*'(*)(-*•)
не будет обращаться в нуль в указанной проколотой — -ок-
-окрестности.
Кроме того, в силу существования предела F.18') сущест-
существует предел
F.23)
Но тогда в силу теоремы 6.9 существует и предел
/ 1 \
lim -Ж- = lim )f/=limJ(jO_ F24)
причем справедливо соотношение F.20), принимающее (в силу
F.23) и F.24)) вид
.. fix) ,. F(t) ,. F'(t) ,. f'(*)
lim fV ' = hm —^- =hm —^- = lim ' v .
() G@ G'@ '()
Рассмотрение случая 2 завершено.
Случай 3. В этом случае действует та же замена t, = —,
X
что и в случае 2, однако на этот раз эта замена сводит
рассмотрение предела при х-»-+оо[л;-э—оо] к пределу при
t->-0+0[t-+-0—0], рассмотренному в случае 1. Детали рассуж-
рассуждений предоставляем читателю.
X6
Примеры. 1) Вычислить lim (для любого
х-»о+о !пA -\-х)
6>1). Этот пример относится к случаю 1. Применяя правило
Лопиталя, получим
„б RY6—1
lim — = lim ~—-= lim бх6-1 A+*) = 0.
*-»0+0 ln(l-j-*) *-*0-f0 ( ' \ 0+0
1+х
* Т. е. всюду в интервале —— <.t<:—, за исключением точки t =
о о
240 Гл. 6. Основные теоремы о дифференцируемых функциях
— — arctg A — — j
2) Вычислить lim : — (этот пример отно-
х-*°° sin ¦
X
сится к случаю 2).
Применяя правило Лопиталя, получим
я / 1
— — arctg I 1— —
*f
sin — * cos —
X \ X
1 -f
—1
/.
. 1 —
\
1 ¦
X
/
1 \
X2 J
1 \ 2
2
2. Раскрытие неопределенности вида . Будем говорить, что
оо
отношение двух определенных в окрестности точки а функций f(x)
и g(x) представляет собой при х-+а неопределенность вида -^-,
оо
если
lim / (х) = оо, lim g (x) = оо*. F.25)
х-ых х-ю
Для раскрытия этой неопределенности, т. е. для вычисления
предела lim , справедливо утверждение, полностью анало-
дс-.в g(x)
гичное теореме 6.9.
Теорема 6.9* (второе правило Лопиталя). Пусть
множество Св представляет собой проколотую 6-окрестность точки
а, функции f(x) и g(x) определены и дифференцируемы на Св ы,
кроме того, производная g'(x) не обращается на d в нуль. Пусть,
далее,
Пт/(л:) = oo, limg(x) = oo. F.17'V
x-*a x~>a
Тогда, если существует (конечный или бесконечный) предел
х^а g'(x) '
то существует и предел
(x)
* Вместо оо в F.25) может стоять +оо или —оо.
§ 6. Раскрытие неопределенностей 241
причем справедливо соотношение
lim 2-. F.20-)
х-^а g(x) x-+a g'(x)
Доказательство. 1) Предположим чсначала, что су-
существует конечный предел F.18*), равный числу Ь. Докажем,
что в этом случае существует предел F.19*), также равный
числу Ь.
Пусть {хп} — произвольная последовательность значений
аргумента, сходящаяся к а либо справа, либо слева *. Так как
все элементы этой последовательности принадлежат множеству
С6) то, каковы бы ни были два элемента этой последовательнос-
последовательности хт и хп, для функций f(x) и g (x) выполнены на сегменте
[Хщ, хп] все условия теоремы Коши 6.8. По этой теореме между
хт и хп найдется точка %тп такая, что справедливо равенство
_ П*т)
f(xn)—f{xm) _ /(*„) f(xn)
g(xn)-g(xn) [g(xn) t _ 8(*m)
Из этого равенства заключаем, что
1
f(Xn) _ f'dmn) g(xn)
§(*n) »)
Фиксируем теперь произвольное положительное число е. Так
как по условию lim -L^—— = b, а последовательность \хп\ схо-
х-*а g'{x) l
дится к а, то для положительного числа — можно фиксировать
такой номер т, что для любого номера п, превосходящего т,
будет выполняться условие **
-^Ь = Ъ + атп, где |omj< -|-. F.27>
g )
Далее заметим, что в силу условий F.17*) lim f(xn) = oo,
П-»сзо
lim g(xn) = оо, а поэтому, поскольку номер т фиксирован,
существует равный единице предел
l_g(xm)
lim^
. l\
/(*!,)
* Т. е. {хп} — такая сходящаяся к о последовательность, у которой либо
все х„>а, либо все хп<.а.
** Мы учитываем, что %тп заключено между хт и х„.
242 Гл. 6. Основные теоремы о дифференцируемых функциях
8/2
Это означает, что для положительного числа и для
I Ь I + е/2
фиксированного нами номера т найдется превосходящий его
номер п0 такой, что при всех л>п0
t _ g(xm)
—gf = 1 -f (W где |Pmn| < ^. F.28)
Из соотнвшений F.26), F.27) и F.28) вытекает, что
Щ^ атп) A + p\J = 6> (ft + атп) ртл + ат„
Значит, справедливо неравенство
g(xn)
Учитывая неравенства, стоящие в условиях F.27) и F.28),
мы получим, что при всех
(
V
Итак, для произвольного фиксированного нами е>0 мы
нашли номер по^т такой, что при всех я>я0
Это и означает, что предел F.19*) равен числу Ь и справед-
справедливо соотношение F.20*). Таким образом, для случая конечно-
конечного предела F.18*) теорема доказана.
2) Пусть теперь предел F.18*) равен оо. Тогда, очевидно,
предел обратного отношения lim ¦ будет равен нулю и по
только что рассмотренному нами случаю конечного предела
F.18*) мы получим, что*
0.
f(x)
Последнее соотношение с учетом F.17*) эквивалентно тому,
что
х->а g(x)
Теорема 6.9* полностью доказана.
* Мы учитываем, что для обратного отношения выполнены все условия
теоремы 6.9*. В частности, производная f'(x) не обращается в нуль в доста-
достаточно малой проколотой б-окрестности точки а. (Это вытекает из существова-
существования равного оо предела F.28*) и из необращения в указанной проколотой
^-окрестности производной g'(x)-)
§ 6. Раскрытие неопределенностей 243.
Так же как и теорема 6.9, теорема 6.9* остается справедливой
в каждом из следующих трех случаев:
1) в случае, если в этой теореме в качестве множества С« взять
интервал (а, а + д) [соответственно (а—б, а)], а все пределы
F.17*)-—F.20*) взять при х-^а + 0 [соответственно при х^-а—0];
2) в случае, если в качестве множества Св взять совокупность
всех х, лежащих вне сегмента [—б, б], а все пределы F.17*) —
F.20*) взять при х->-оо;
3) в случае, если в качестве множества С6 взять полупрямую»
(б, + оо) [соответственно (—оо, ¦—б)], а все пределы F.17*) —
F.20*) взять при х-> + оо [соответственно при х->—оо].
Обоснование справедливости теоремы 6.9* в этих трех случаях
может быть заимствовано из предыдущего пункта.
Примеры. 1)
lim Ух lnx = lim "* =
Х-.-0+0 х-»0+0 Х^ '
1
= Пт -, т^- = —2\\гаУх =0.
,.—3/2 x-s.O-1-O
2) я-кратным применением правила Лопиталя вычисляется',
предел
Пт ^1= lim -^1= lim ««-№' = .. .= ИтЛ = р.
х-++а> ех х-»+оо ех х-*+<*> ех *-»+«> ех
3. Раскрытие неопределенностей других видов. Кроме изучен-
0 оо
ных выше неопределенностей видов — и , часто встречают-
0 оо
ся неопределенности следующих видов: 0-оо, оо—оо, 1°°, 0°°, оо°.
Все эти неопределенности сводятся к изученным выше двум не-
неопределенностям путем алгебраических преобразований. Покажем
это, например, по отношению к последним трем из указанных
выше неопределенностей. Каждая из этих неопределенностей име-
имеет вид
y = f(x)z(x\ F.29 >
где при х-иг функция f(x) стремится соответственно к 1, 0 или
оо, a g(x) стремится соответственно к оо или 0. Логарифмируя вы-
выражение F.29), получим (считая, что f(x)>0)
\ny=g{x) lnf(x). F.30>
Для нахождения предела выражения F.29) достаточно найти пре-
предел выражения F.30).
Заметим, что в любом из трех рассматриваемых случаев вы-
выражение F.30) представляет собой при х-^а неопределенность
244 Гл. 6. Основные теоремы о дифференцируемых функциях
вида О-оо. Значит, достаточно научиться сводить неопределен-
неопределенность вида О-оо к неопределенности вида — или . Покажем,
О сю
как это делается. Итак, пусть
2=ф(х) ф(*), F.31)
причем
Птф(х)=0, lim \J)(x) = оо.
Перепишем F.31) в виде
z = <p(x)i|>(x)=-J&>_. F.32)
Очевидно, выражение F.32) представляет собой при х->а неопре-
неопределенность вида —. Наша цель достигнута.
Примеры. 1) Вычислить lim хх. Обозначим у=хх. Тогда
*->0-)-0
1пу=х\пх = пх . Применяя правило Лопиталя, будем иметь
() lim "* = lim —-г
х->0+0 *-»0+0 _L х-»0+0 _i
Отсюда ясно, что
lim у = 1.
0+
1
2) lim A + хг) *х-1-*. Пусть у = A +
дг-»О
Тогда ,
\A +
ех — 1 — х
Пользуясь правилом Лопиталя, получим
2х
Нш (Щ у) = lim lnA+^> = lim
«->о х->о ех — 1 — х лг-»о ех — 1
—1J*
Отсюда ясно, что lim у — ег.
х-+0
§ 7. Формула Тейлора 245
§ 7. ФОРМУЛА ТЕЙЛОРА
В этом параграфе мы установим одну из важнейших формул
математического анализа, имеющую многочисленные приложения
как в математике, так и в смежных дисциплинах.
Теорема 6.10 (теорема Тейлора*). Пусть функция
f(x) имеет в некоторой окрестности точки а производную поряд-
порядка** п-\-\ (п — любой фиксированный номер). Пусть, далее, х —
любое значение аргумента из указанной окрестности, р — произ-
произвольное положительное число. Тогда между точками а и х найдет-
найдется точка ? такая, что справедлива следующая формула:
+ fi){a) (x - а)" + Rn+l (x), F.33)
где
Замечание. Так как точка ? лежит между х и а, то дробь
——^- всегда положительна, а поэтому для любого р>0 опреде-
лена степень
х—1
Формула F.33) называется формулой Тейлора (с цент-
центром в точке а), а выражение Rn+i(x) называется остаточным
членом. Как мы увидим ниже, остаточный член может быть
записан не только в виде F.34), но и в других видах. Принято на-
называть остаточный член, записанный в виде F.34), остаточным
членом в общей форме***.
Доказательство. Обозначим символом ср(х, а) многочлен
относительно х порядка п, фигурирующий в правой части F.33),
т. е. положим
— а)п. F.35)
+
«I
Далее обозначим символом Rn+i(x) разность
/?n+i(*) =/(*)—Ф(*. а). F.36)
* Брук Тейлор — английский математик A685—1731).
** Отсюда вытекает, что сама функция f(x) и ее производные до порядка
« непрерывны в указанной окрестности точки а.
*** эТу форму остаточного члена называют также формой Шлемильха—¦
Р о ш а.
246 Гл. 6. Основные теоремы о дифференцируемых функциях
Теорема будет доказана, если мы установим, что Rn+i(x) опре-
определяется формулой F.34).
Фиксируем любое значение х из окрестности, указанной в фор-
формулировке теоремы. Ради определенности будем считать, что
х>а. Обозначим через t переменную величину, имеющую областью
своего изменения сегмент [а, х], и рассмотрим вспомогательную
функцию \p(t) следующего вида:
Ч>(')=/(*)-ф(*. n-(*-t)pQM. F-37)
где
Q (х) = -fo+l(*) . F.38)
(х — а)Р
Подробнее ty(t) можно записать так:
п\
И ч
(x — tr — (x-t)pQ(x). F.39)
Наша цель — выразить Q(x), исходя из свойств введенной нами
функции г|)(/).
Покажем, что функция \p{t) удовлетворяет на сегменте [а, х]
всем условиям теоремы 6.3 (Ролля).
Из формулы F.39) и из условий, наложенных на функцию
f(x), очевидно, что функция ty(t) непрерывна на сегменте [а, х] и
дифференцируема во всех внутренних точках этого сегмента *.
Убедимся в том, что ty(a) =\${х)=0. Полагая в F.37) t=a и при-
принимая во внимание равенство F.38), будем иметь
y(a)=f(x)— <р(х, a)— Rn+i(x).
Отсюда на основании F.36) получим яр (а) =0. Равенство
г|)(х)=0 сразу вытекает из формулы F.39).
HjaK, для функции ty(t) на сегменте [а, х] выполнены все
условия теоремы 6.3 (Ролля). На основании этой теоремы внутри
сегмента [а, х] найдется точка | такая, что
Ч>'A) = 0. F.40)
Подсчитаем производную г|/@- Дифференцируя равенство F.39),
будем иметь
* Это вытекает из того, что из условия существования у функции /(/) в
окрестности точки а производной порядка п +1 вытекает непрерывность самой
функции f(t) и всех ее производных до порядка п в указанной окрестности
точки а, а потому и на сегменте [а, х]. Далее можно утверждать, что сама
функция f(t) и все ее производные до порядка п один раз дифференцируемы
всюду в указанной окрестности точки а, а потому и всюду внутри сегмента
[а, х].
§ 7. Формула Тейлора 247
... + fW{t) п(х — ty-1 — /(+)@ (х — t)n + р (х — О" Q (х) ¦
л! я!
F.41)
Легко видеть, что все члены в правой части F.41), за исключе-
исключением последних двух, взаимно уничтожаются. Таким образом,
!>'(О = - ; ,() (x — t)n + p-(x-ty-'-Q(x). F.42)
ft!
Полагая в формуле F.42) f=rg и используя равенство F.40),
ПОЛУЧИМ , гч«-р+1
Q {х) = А±^П /(*+!) (|) . F.43)
rt!/7
Сопоставляя F.43) и F.38), окончательно будем иметь
= (х- a)" Q (х) =
f ), (
Случай, когда х<а, рассматривается совершенно аналогично.
Теорема доказана.
Найдем разложение по формуле Тейлора простейшей функ-
функции — алгебраического многочлена п-го порядка. Пусть
Тогда, поскольку f<"+1)(х) ^0, остаточный член 7?„+1(х)=0 и фор-
формула Тейлора F.33) принимает вид
(Здесь в качестве а можно взять любую точку бесконечной пря-
прямой.) Таким образом, формула Тейлора позволяет представить
любой многочлен f(x) в виде многочлена по степеням (х—а), где
а — любое вещественное число.
Пусть теперь f(x) — произвольная функция, удовлетворяющая_
условиям теоремы 6.10. Постараемся выяснить, какими свойства-*
ми обладает многочлен F.35), фигурирующий в формуле Тейлора
для этой функции. Как и выше, будем обозначать этот многочлен
символом ф(х, а). Символом ф(">(х, а) обозначим л-ю производ-
производную ф(х, а) по х. Дифференцируя формулу F.35) по х и затем
полагая х=а, мы получим следующие равенства:
у (a, a) =f(a),
<р'(а,а)=Г(а),
F.44)
q>B>(a)p>()
Ф<п) (а,а) = /("> (а).
248 Гл. 6. Основные теоремы о дифференцируемых функциях
Таким образом, фигурирующий в формуле Тейлора для произ-
произвольной функции f(x) многочлен ф(х, а) обладает следующим
свойством: он сам и его производные до порядка п включительно
равны в точке х=а соответственно f(x) и ее производным до по-
порядка п. .
§ 8. РАЗЛИЧНЫЕ ФОРМЫ ОСТАТОЧНОГО ЧЛЕНА.
ФОРМУЛА МАКЛОРЕНА
1. Остаточный член в форме Лагранжа, Коши и Пеано. Выше
мы установили формулу Тейлора с остаточным членом в общей
форме. Здесь мы установим другие возможные представления
для остаточного члена. Два из них могут быть получены в качест-
качестве частных случаев из общей формы.
Прежде всего несколько преобразуем формулу для остаточ-
остаточного члена F.34). Поскольку точка "?, лежит между точками а и
х, найдется такое число Q * из интервала 0<б<1; что |—а =
= Q(x—а). При этом ?,—а + в(х—а), х—\—{х—а) A—9). Таким
образом, формула F.34) может быть переписана в виде
()П+1^9)"Р+1 + 8 (* - а)]. F.45)
Рассмотрим теперь два важных частных случая формулы F.45):
1) р = «+1; 2) р=1 .(напомним, что в формулах F.34) и F.45) в
качестве р может быть взято любое положительное число). Пер-
Первый из этих частных случаев (р = п+1) приводит нас к остаточ-
остаточному члену в форме Лагранжа:
К+1 (х) = (Х{~^ f<n+1) [а + 6 <* - а)]. F.46)
Эта форма остаточного члена наиболее употребительна в прило-
приложениях. Остаточный член в форме Лагранжа напоминает сле-
следующий, очередной член формулы Тейлора, лишь только
(п + 1)-я производная функции f(t) вычисляется не в точке а,
а в некоторой промежуточной между а и х точке ?, = a + Q(x—а).
Второй из указанных выше частных случаев (р=1) приводит
нас к ост аточн ом у члену в форме Коши:
Rn+1 (*) = (*-й)^;A-9)" /<"+1> [а. + 6 (х - а)]. F.47)
Так как формы Лагранжа и Коши отвечают разным значе-
значениям р, а 0 зависит от р, то значения 6 в формулах F.46) и
F.47) являются, вообще говоря, различными. Для оценки некото-
некоторых функций форма Коши является более предпочтительной, чем
форма Лагранжа. Обе формы остаточного члена (Лагранжа и
* Следует подчеркнуть, что %, а значит, и 0 зависит от р.
§ 8. Формула Маклорена 249
Коши) обычно используются в тех случаях, когда требуется при
тех или иных фиксированных значениях х, отличных от а, при-
приближенно вычислить функцию f(x).
Естественно приближенно заменить f(x) многочленом ф(х, а)
и численно оценить сделанную при этом ошибку. Наряду с этим
встречаются задачи, в которых нас интересует не численная вели-
величина указанной ошибки, а лишь порядок ее относительно малой
величины (х—а). Для этой цели удобна другая форма записи
остаточного члена (так называемая форма Пеано*), к уста-
установлению которой мы и переходим.
Предположим, что функция f(x) имеет производную порядка
п—1 в некоторой окрестности точки а и производную порядка п
в самой точке а '**.
При этих предположениях мы можем рассмотреть многочлен
<р(х, а), определяемый соотношением F.35). Разность между f(x)
и этим многочленом, как и при доказательстве теоремы 6.10, обо-
обозначим символом Rn+i(x), т. е. положим
Rn+i(x)=f(x)— <Р(*> а)-
Докажем, что при сделанных нами предположениях для оста-
остаточного члена Rn+i(x) справедливо следующее представление***:
/?„+!.(*) =о[(*-а)»]. F.48)
Представление F.48) принято называть остаточным чле-
членом в форме Пеано.
Используя установленное в конце предыдущего параграфа
свойство многочлена <р(х, а), выражающееся соотношениями
F.44), мы получим следующие равенства:
Rn+1 (а) = 0, R'n+l (а) = О, Я$, (а) = 0, .... /ОД>, (а) = 0. F^49)
Нам остается доказать, что из равенств F.49) вытекает представ-
представление F.48). Доказательство того, что из равенств F.49) выте-
вытекает представление F.48), проведем методом математической ин-
индукции.
Сначала убедимся в том, что равенства F.49) влекут представ-
, ление F.48) при л=1.
При л=1 F.49) превращаются в два равенства:
R2(a)=0, R'2(a)=0,
из которых сразу же вытекает, что
МП **(*)-*i«0 = R- {а) = 0>
х — а х~>а х — а
* Джузеппе.Пеано — итальянский математик A858—1932).
** Таким образом, мы подчиняем функцию f(x) требованиям более слабым,
чем в теореме 6.10.
*** Напомним, что символ о[(х—а)п] обозначает бесконечно малую при
х-*а функцию более высокого порядка малости, чем (х—а)п (см. п. 5 § 4
гл. 3).
250 Гл. 6. Основные теоремы о дифференцируемых функциях
а это и означает, что Rz{x)=o(x—а), т. е. при п=\ представле-
представление F.48) вытекает из F.49).
Теперь для завершения индукции предположим, что представ-
представление F.48) вытекает из F.49) для некоторого номера п>1, и
убедимся, что в таком случае представление F.48) вытекает из
F.49) и для следующего номера п+1. Для номера п+ 1 равенст-
равенства F.49) имеют вид
Rn+2 (а) = 0, R'n+2 (а) = 0, R%2 (а) = 0 /?<$ч (а) = 0. F.49*)
Поскольку мы предположили, что для номера п равенства
вида F.49) влекут представление вида F.48), то, отбросив первое
из равенств F.49*), мы можем утверждать, что остальные ра-
равенства
К+2 (а) = 0, R%2 (а) = 0 ОД» (а) = 0
влекут представление
К+2(х)=о[(х-аГ]. F.50)
С другой стороны, применяя к функции Rn+2{x) по сегменту
[а, х] теорему 6.4 Лагранжа * и учитывая первое равенство
F.49*), мы получаем, что между а и х найдется точка ? такая,
что
Rn+2 (*) = К+2 (*) - Rn+2 (a) = R'n+2 (I) (x-a). F.51)
Сопоставляя соотношения F.50) и F.51) и учитывая, что
o[(h,—а)п]=о[(х—а)"] (в силу того, что g заключено между а
и х), мы окончательно получим, что 7?п+2(х) =о[(х—а)п], а это
совпадает с представлением F.48), взятым для номера п+1.
Тем самым индукция проведена и вывод представления F.48)
остаточного члена в форме Пеано завершен.
В заключение запишем полностью формулу Тейлора с остаточ-
остаточным -членом в форме Пеано:
f(a)+(xa)+ ... + . (хаГ+оЦха)].
1! П\
F.52)
2. Другая запись формулы Тейлора. Часто записывают формулу
Тейлора F.33) в несколько ином виде. Положим в F.33) а=х0,
х—а = Ах и возьмем остаточный член в форме Лагранжа F.46).
При этом х = ХоЧ-Дя, и мы получим
* При любом п>1 для Rn+2(x) выполнены все условия применимости тео-
теоремы 6.4 Лагранжа.
§ 9. Оценка остаточного члена. Разложение элементарных функций 251
... + ?)Ш {Ах)п + /">(*.+ ед*) {Ах)п+1 _ (б53)
п\ (п -f- 1)!
(Здесь 0 — некоторое число из интервала 0<6<1.) Формула Тей-
Тейлора F.53) является естественным обобщением формулы Лагран-
жа F.5) (см. § 3). Формула Лагранжа F.5) получается из фор-
формулы F.53) в частном случае п = 0.
3. Формула Маклорена. Принято называть формулой Макло-
Маклорена * формулу Тейлора F.33) с центром в точке а=0. Таким об-
образом, формула Маклорена дает представление функции в окрест-
окрестности точки х=0. Запишем формулу Маклорена для произвольной
функции с остаточным членом в форме Лагранжа, Коши и Пеано**:
F.54)
где остаточный член имеет вид:
1) в форме Лагранжа
^+l(x)=T^+T)T/(n+1)(ex) @<0<1); F>55)
2) в форме Коши
W*)= *"+1(^6)"' Р+'Чб*); F.56)
3) в форме Пеано
Rn+i{x)=o(xn). F.57)
(Мы использовали формулы F.46), F.47) и F.48).)
Перейдем к оценке остаточного члена в формуле Тейлора —
Маклорена, к отысканию разложения по формуле Маклорена важ-
важнейших элементарных функций и к рассмотрению различных при-
приложений этой формулы.
§ 9. ОЦЕНКА ОСТАТОЧНОГО ЧЛЕНА. РАЗЛОЖЕНИЕ
НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
1. Оценка остаточного члена для произвольной функции. Оце-
Оценим для произвольной функции f(x) остаточный член в формула
Маклорена F.54), взятый в форме Лагранжа F.55).
Предположим, что рассматриваемая нами функция f(x) обла-
обладает следующим свойством: существует такое вещественное число
М, что для всех номеров п и для всех значений аргумента х из рас-
* Колин Маклореи — английский математик A698—1746).
** При этом предполагается, что f(x) имеет (п+1)-ю производную в ок-
окрестности точки х = 0, а для остаточного члена в форме Пеано (п—1)-ю про-
производную в окрестности точки х = 0 и и-ю производную в самой точке х = 0.
252 Гл. 6. Основные теоремы о дифференцируемых функциях
сматриваемой окрестности точки х=0 справедливо неравенство
F.58)
Функцию, обладающую указанным свойством, будем называть
функцией, совокупность всех производных кото-
которой ограничена в окрестности точки х = 0.
Из неравенства F.58) и из того, что 0<6<1 вытекает, что
F.59)'
и поэтому из формулы F.55) получим
Итак, мы получаем следующую универсальную оценку остаточного
члена для функции, совокупность всех производных которой огра-
ограничена числом М в окрестности точки х=0:
^|. F.60)
Напомним, что при любом фиксированном х
Нш 1х]П+1 =0
п-»оо (П+ I)!
(см. пример из п. 4 § 2 гл. 3). Отсюда вытекает, что, выбирая
достаточно большой номер п, мы можем сделать правую часть
F.60) как угодно малой. Это дает нам возможность применять
формулу Маклорена для приближенного вычисления функций, об-
обладающих указанным свойством, с любой наперед заданной точ-
точностью. Приведем примеры функций, совокупность всех производ-
производных которых ограничена в окрестности точки х = 0.
1) f(x)=ex, f(-n)(x)=ex. Совокупность всех производных этой
функции ограничена на любом сегменте [—г, г] (г>0) числом
Af = er.
2) f(x)=cosx или /(jc)=sinjc. Совокупность всех производных
каждой из этих функций ограничена всюду на бесконечной пря-
прямой числом М=1.
2. Разложение по формуле Маклорена некоторых элементар-
элементарных функций. A. f(x) = ex. Поскольку }(пЦх)—ех, /<п>@) = 1 для
любого п, формула Маклорена F.54) имеет вид
где остаточный член в форме Лагранжа равен
= {^\у е** @< в< 1). F.62)
§ 9. Оценка остаточного члена. Разложение элементарных функций 253
На любом сегменте [—г, г] (г>0) в силу того, что \евх\<ег, по-
получим следующую оценку для остаточного члена:
vrV- (б-б2>>
Б. f (x) = sin х. Поскольку /<"> (х) = sin (x + п —),
О при четном п,
п—1
п~ при нечетном п>
формула Маклорена F.54) имеет вид
? + 44 +• + (L + ^iw.
о! О! /! /7!
где п —• нечетное число, а остаточный член в форме Лагранжа
равен
Очевидно, что на любом сегменте [—г, г] (г>0) для остаточного
члена справедлива следующая оценка:
- F'64)
В. f (x) =cosx. Поскольку /<п) (х) = cos (х + и— \,
п
О при нечетном п,
2
К-1)
формула Маклорена F.54) имеет вид
Y при четном п,
У2 v4 „8 — уП
2! 4! 6! n! "
где « — четное число, а остаточный член в форме Лагранжа ра-
равен
На любом сегменте [—г, г] (г>0) получаем для остаточного члена
оценку F.64).
Г. f(x)=ln(l+x). Поскольку
' /<»>¦(*) = (_ l)"-i l«~W , /@) = 0, /(«) @) = (- 1)"-' (/»-!)!,
254 Гл. 6. Основные теоремы о дифференцируемых функциях
формула Маклорена F.54) имеет вид
1пA+*) = *—? + -?-т-+ -.. + (- I)"-1 — +Rn+i(x). F.66)
2 о ^ П
Остаточный член на этот раз запишем и оценим и в форме Лаг-
ранжа, и в форме Коши:
Rn+1{x) = (яЧ_.1)(]+9;е)я+1 (в Ф°Рме Лагранжа). F.67)
Rn+i (*) = (- l)"*"+1A(|~)*+t '(в Форме Коши). F.68>
Для оценки функции ln(l+Jt) для значений х, принадлежащих
сегменту 0<х<1, удобнее исходить из остаточного члена в форме
Лагранжа F.67). Переходя в формуле F.67) к модулям, получим
для всех х из сегмента 0<х<1
x)\<1^-T. F.69)
Из оценки F.69) очевидно, что для всех х из сегмента
¦Rn+i(x)-*~0 при n-voo.
Оценим теперь функцию 1пA+х) для отрицательных значе-
значений х из сегмента —г<х<0, где 0</"<1. Для этого будем исхо-
исходить из остаточного члена в форме Коши F.68).
Перепишем этот остаточный член в виде
Принимая во внимание, что для рассматриваемых значений х вы-
J Q
ражение < 1, и переходя в формуле F.70) к модулям,
1 + 0*
будем иметь
^. F.71)
Так как г<1, то оценка F.71) позволяет утверждать, что
WmRn+1--=0.
Д. }(х) = A+я)а, где а — вещественное число. Поскольку
/<»)(*) =а(а— 1) ... (а—n+l)(H-jc)a-«,
f«»)@) = a(a—1) ... (а—л+1),
* Еще раз отметим, что в формулах F.67) и F.68) значения 9 являются,
вообще говоря, различными.
§ 9. Оценка остаточного члена. Разложение элементарных функций 255
формула Маклорена F.54) имеет вид
,+
+ х + Rn+i {x)y
п\
где остаточный член в форме Лагранжа равен
Rn+1 (х) = а(а~1} •••("-") A + Qx)a-(n+i) xn+i @ < 6 < 1). F.73)
В частном случае, когда а = п ¦— натуральное число, Rn+i(x) =0,
и мы получим известную из элементарного курса формулу бинома
Ньютона
A +х)п= 1 + -^-* + "("у1* хг+ ... +хп. F.74>
Если нужно получить разложение не двучлена (\+х)п, а двучле-
двучлена (а+х)и, то можно вынести ап за скобку и воспользоваться
формулой F.74). При этом получим
2!
Таким образом, общий случай бинома Ньютона является частным
случаем формулы Маклорена.
Е. /(х) =arctgx. Поскольку
fin) {х)= {n~l)-^ -sin [я (arcigx + -
(см. пример 5 из п. 2 § 6 гл. 5), то
0 при четном п,
/<»> @) = „_,
(—1) 2 (п — 1)! при нечетном п,
и формула Маклорена F.54) принимает вид
arctgx = х -^ + 4-4 +¦•¦+(- I)"" — + К+* W. F-75)
0 0/ П
где п — нечетное число, а остаточный член в форме Лагранжа
равен
256 Гл. 6. Основные теоремы о дифференцируемых функциях
@<<i)
(я+ 2) 1±2 V
¦ п+@*J] 2
Для остаточного члена на любом сегменте [—г, г] (где
0) справделива оценка
^- F-76)
Из оценки F.76) очевидно, что при любом г<=: 1 остаточный
член Rn+2(x) стремится к нулю при я-voo.
§ 10. ПРИМЕРЫ ПРИЛОЖЕНИИ ФОРМУЛЫ
МАКЛОРЕНА
1. Вычисление числа е на ЭВМ. В п. 3 §2 гл. 3 мы ввели число е
как предел последовательности i ( 1 —f j I и получили для е
(\ п I i
грубую оценку вида 2<е<3.
В этом пункте мы укажем, как вычислить число е с любой ин-
интересующей нас точностью.
Воспользуемся формулой Маклорена F.61) и оценкой остаточ-
остаточного члена F.62*), положив в этих формулах х=г=\. Мы получим
при этом, что
е=1 +^Т + -^+ ¦¦¦ + \ + Rn+i(V- F-77)
1! 21 fl \ -
где
-u^<idw F-78)
Выбирая номер п в F.77) и F.78) достаточно большим, мы
можем оценить с помощью этих формул число е с любой наперед
заданной интересующей нас точностью.
Алгоритм вычисления числа е, основанный на формулах F.77)
и F.78), легко реализуется на электронно-вычислительных маши-
машинах.
Мы приведем пример вычисления числа е по этим формулам при
п = 400. Вычисления велись в МГУ на электронно-вычислительной
машине БЭСМ-6 с 600 знаками после запятой. Учитывая возмож-
возможные ошибки округления, мы отбросили последние 10 знаков и при-
приводим результат вычисления с 590 знаками после запятой*:
2,718281 828459 045235 360287 471352 662497 757247 093699 959574 966967
627724 076630 353547 594571 382178 525166 427427 466391 932003 059921
* Для читателей, знакомых со стандартным алгоритмическим языком
АЛГОЛ, нас. 261 приведена записанная на этом языке программа вычис-
вычислений.
§ 10. Примеры приложений формулы Маклореиа 257
817413 596629 043572 900334 295260 595630 738132 328627 943490 763233
829880 753195 251019 011573 834187 930702 154089 149934 884167 509244
761460 668082 264800 168477 411853 742345 442437 107539 077744 992069
551702 761838 606261 331384 583000 752044 933826 560297 606737 113200
709328 709127 443747 047230 696977 209310 141692 836819 025515 108657
463772 111252 389784 425056 953696 770785 449969 967946 864454 905987
931636 889230 098793 127736 178215 424999 229576 351482 208269 895193
668033 182528 869398 496465 105820 939239 829488 793320 36...
Таким образом, использование формулы Маклорена дает воз-
возможность вычислить е с любой интересующей нас точностью.
2. Доказательство иррациональности числа е. Докажем теперь
с помощью той же формулы Маклорена F.77), что число е являет-
является иррациональным.
Используем для ^n+i(l) формулу F.62), положив в ней х=\.
Мы получим, что.
Ян-'^Т^Т).- F'79)
где 0 — некоторое число, удовлетворяющее неравенствам 0<6<1.
Из этих неравенств и из F.79) вытекает, что Rn+i(l) удовлетво-
удовлетворяет неравенствам
тгтттг<л"+1A)<тгтттг- <6-ад
Итак, для е справедливо представление F.77) с неравенствами
дляЯп+1A) вида F.80).
Предполжим теперь, что число е является рациональным, т. е.
его можно представить в виде е = ^' где т и п — некоторые целые
положительные числа, второе из которых (п), мы, не ограничивая
общности, можем считать не меньшим двух*.
Выбирая в формуле Маклорена F.77) номер п равным знаме-
- m
нателю рациональной дроби е = —. мы получим, умножая фор-
п
мулу Маклорена F.77) на п\, что каждое из чисел п\е и и! | 1 +
4- Ь ... Л ) является целым, в то время как число п\ Rn+i в
1! п\ ]
силу неравенств F.80) удовлетворяет условиям—-— < n! Rn+l A) <
п+ 1
Если бы в представлении е = — число п оказалось равным единице, то
, i2m
мы взяли бы эквивалентное ему представление е = i в знаменателе кото-
2я
рого стоит число 2п=2.
9 Зак. 72
258 Гл. 6. Основные теоремы о дифференцируемых функциях
о
<; и заведомо не является целым *. Таким образом, при
п +1
умножении формулы Маклорена F.77) на число п\ мы получаем
соотношение
2! n\
в левой части которого стоит целое число, а в правой части — чис-
число, не являющееся целым. .
Мы получаем противоречие, которое доказывает, что наше пред-
предположение о том, что е — рациональное число, является ошибоч-
ошибочным.
Иррациональность е доказана.
3. Вычисление значений тригонометрических функций. Легко
убедиться в том, что значения тригонометрических функций sin x и
cosx для х, принадлежащих сегменту 0, — > полностью опреде-
I 4 J
ляют значения этих функций для всех х. Поэтому мы можем огра-
ограничиться вычислением sinjc и cosjc для значений х из указанного
сегмента. Желая обеспечить точность 10~4, положим в формуле
F.63) и в оценке F.64) п = Ъ, г — Тогда
4
/ л V
[-
\Rn+2(x)\ = |Я7(х)|<-Ц
и поэтому для любого х, удовлетворяющего условию |х|<—>
4
С ТОЧНОСТЬЮ ДО 10
Xs X5
6 120 '
Аналогично, полагая в формуле F.65) и в оценке F.64) п = 6,
т ——, получим
4
/ Я \8
| Rn+2 (х) | = | R81< -Lii- < 10-5,
01
* Достаточно учесть, что в представлении е = как уже сказано выше,
1 3
можно считать гС^2, а при п>2 из неравенств < п\ Rn+1 A) <
п+1 ' л+1
вытекает, что 0<п!/?п+1<1, т. е. п!/?„+1A) не является целым.
§ 10. Примеры приложений формулы Маклорена 259
и поэтому для любого х, удовлетворяющего условию |х|< —.
с точностью до 10~5
, X2 X* Xя
COSX = 1
2 24 720
4. Асимптотическая оценка элементарных функций и вычисле-
вычисление пределов. Формула Тейлора — Маклорена является мощным
средством для вычисления тонких пределов.
Из установленного нами в п.2§9 разложения ряда элементар-
элементарных функций вытекают асимптотические * оценки этих функций,
характеризующие их поведение в окрестности точки х = 0, т. е. при
малых значениях |х| с точностью до членов любой степени п ма-
малой величины х.
Беря в формулах Маклорена для функций ех, sin*, cosx,
in(H-jc), A+jc)° и arctgjc остаточный член в форме Пеано, мы
получим, что для любого номера п справедливы следующие оцен-
оценки:
V Y2 Хп
, F.8D
—
Tt
l+-jy-JC
jyJC +
Приведем примеры использования асимптотических оценок
F.81).
1°. Привлекая вторую из оценок F.81), взятую при /1=1, вы-
вычислим предел
,. sin* — х ,. Х~ 31 ~>~0(х > ~х г 1 -г 1
1ш — = hm = lim —-—holx) = -.
»-o x» x^0 д» ж-^о L 31 J 3!
* Формулу или оценку, характеризующую поведение функции f(x) при
х-+а (в данном случае при х-*0), называют асимптотической.
9*
260 Гл. 6. Основные теоремы о дифференцируемых функциях
— —
2
2 о г 1 • б OOS л
. /=hm ¦
х->о х3 sin х
Исходя из вида знаменателя, можно заключить, что опреде-
определяющую роль должны играть члены четвертого порядка относи-
относительно х (ибо sinx=x+o(x)). Пользуясь F.81), можно записать:
cosx=l— — + — + о(хъ), F.82)
sinx = x + o(x), F.83)
e*=l+z+ —+ oB2). F.84)
2
д.2
Значит, при z— получим
е 2 = 1 —— + — + о(х*). F.85)
Из формул F.82), F.83) и F.85) следует, что
/ = hm = lim
^ + D) l
(Здесь символом а(х) мы обозначили величину ——-. являю-
являющуюся бесконечно малой при х-+0.)
I х3 \*(sin х~х)
3°. /=lim cos^+ -:— . Обозначим через г/ величину
дг-.о \ 2 /
1
/ хг \ ж (sin х— х)
у= cosx-f . Тогда /=Птг/. Прологарифмируем у
\ 2 / О
\ 2 /
(так как при малых х это выражение положительно):
1 / л:2 \
In у = In cos х -f .
ж (sin x — %) \ 2 /
In
Вычислим lim In у = lim
(sin x — x)
§ 10. Примеры приложений формулы Маклореиа 261
Х2 xt хз
Поскольку cosx=l \-—— + о{хъ), sinx = x Ьо(*4),
2 24 6
24
получим
Учтем теперь, что \n(\-\-z) =z+o(z). Из этой формулы
lnfl Н (- о (л:5)^ = + о(х4). Таким образом,
\ 24 /24
Hm In у = lim = lim ¦
Отсюда
Программа вычисления числа е
Система Алгол—БЭСМ6, вариант 10—12—69
begin integer /, с, р, п, m; integer array a, b, e [0 : 601];
от:=400; marg C9, 50, 39, 10, 0, 0);
е[0]: = 1; *[0]:-1;
for /:=1 step I until 601 do
a \i\: =b [i] : =e[j]:=O;
for n : = 1 step 1 until m do
begin for /: =0 step 1 until 600 do
аЩ:=ЬЩ; с:=а[0];
for i =0 step 1 until 600 do
begin b [i]: =c+n;
с : = (c—nxb [i]) X 10+a [i+1] end
p: =0
for i: = 600 step—1 until 0 do
begin c: =e \i]+b[i]+p;
p:=0
if c<10 then e[i]: =c else
begin e [i]: =c—10; p : =1 end
end
end
for л: = 1 step 1 until 6 do
begin output ('10/', 'zd.', e[0]);
for i: = 1 step 1 until 590 do
output ('zd', e\i\)
end
end
Глава 7
ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ
И ОТЫСКАНИЕ ЭКСТРЕМАЛЬНЫХ
ЗНАЧЕНИЙ
В настоящей главе мы применим разработанный в предыду-
предыдущих двух главах аппарат дифференциального исчисления для ис-
исследования графика функции и для отыскания как локальных,
так и глобальных экстремумов функции.
§ 1. ОТЫСКАНИЕ СТАЦИОНАРНЫХ ТОЧЕК
1. Признаки монотонности функции. Из предыдущей главы
мы уже знаем, что изучение вопроса об участках монотонности
дифференцируемой функции f(x) сводится к исследованию знака
первой производной этой функции.
Для удобства сформулируем еще раз найденные нами в
предыдущей главе условия монотонности функции.
1°. Для того чтобы дифференцируемая на интервале (а, Ь)
функция f(x) не убывала (не возрастала) на этом интервале, не-
необходимо и достаточно, чтобы производная f'(x) этой функции
была неотрицательна (неположительна) всюду на этом интер-
интервале*
2°. Для того чтобы дифференцируемая на интервале (а, Ь)
функция f{x) возрастала (убывала) на интервале (а, Ъ), доста-
достаточно, чтобы производная f'(x) была положительна (отрицатель-
(отрицательна) всюду на этом интервале.
Найдем участки монотонности функции f(x)=x3 — Зх2 — 4.
Производная f'(x)=3x(x — 2) этой -функции положительна при
—оо<х<0, отрицательна при 0<я<2 и положительна при 2<
<я<+°о. Поэтому, согласно сказанному, данная функция f(x)
возрастает на полупрямой (—оо, 0) убывает на интервале @, 2)
и возрастает на полупрямой B, +°°)-
График этой функции изображен на рис. 7.1.
2. Отыскание стационарных точек. Напомним- определения
локального максимума и локального минимума функции.
Пусть функция f(x) определена всюду в некоторой окрестно-
окрестности точки с. Тогда эта функция имеет в точке с локальный мак-
максимум [или соответственно локальный минимум], если сущест-
существует такая окрестность точки с, что для всех точек этой окрест-
окрестности значение f(c) является наибольшим [или соответственно
наименьшим] среди всех значений f(x) этой функции.
§ 1. Отыскание стационарных точек
263
У
0
4
1 '
1 Z ,
_
-
Рис. 7.1
Локальный максимум и" локальный минимум объединяются
общим названием л о к а л ь н ы и экстремум.
В § 1 предыдущей главы нами было установлено необходимое
условие экстремума дифференцируемой в данной точке функции.
Это условие имеет следую-
следующий вид: если функция у =
= f(x) дифференцируема в
данной точке с и имеет в этой
точке локальный экстремум,
то f'(c)=O.
Вместе с тем в § 1 гл. 6
было указано, что обращение
в нуль производной является
только необходимым и не
является достаточным
условием локального экс-
экстремума дифференцируемой в
данной точке функции.
Так, функция f(x)=x3
имеет производную }'(х) =
= 3х2, обращающуюся в нуль
в точке х = 0, но никакого
экстремума в этой точке х=0 функция f(x)=x3 не имеет (графи-к.
этой функции см. на рис. 6.2).
Точки, в которых производная f'(x) функции f(x) обращается
в нуль, будем называть стационарными точками функ-
функции f(x).
Каждая стационарная точка — это точка возможного экстре-
экстремума функции.
Однако сделать заключение о том, что в данной стационар-
стационарной точке на самом деле имеется экстремум, можно лишь на ос-
основании дополнительного исследования, для проведения которого
мы должны установить достаточные условия экстре-
экстремума.
Такие условия будут установлены в ближайших трех пунктах.
3. Первое достаточное условие экстремума.
Теорема 7.1. Пусть функция f(x) дифференцируема всюду
в некоторой окрестности точки с, и пусть точка с является ста-
стационарной точкой функции f(x). Тогда если в пределах указан-
указанной окрестности производная f'(x) положительна (отрицательна)
слева от точки с и отрицательна (положительна) справа от точки
с, то функция f(x) имеет в точке с локальный максимум (мини-
(минимум). Если же в пределах указанной окрестности точки с произ-
производная f'(x) имеет один и тот же знак слева и справа от точки
с, то экстремума в точке с нет.
Доказательство. 1) Пусть сначала производная f'{x) в
пределах рассматриваемой окрестности положительна (отрица-
264 Гл. 7. Исследование графика функции
тельна) слева от с и отрицательна (положительна) справа от с.
Требуется доказать, что значение f\c) является наибольшим (наи-
(наименьшим) среди всех значений f(x) в рассматриваемой окрестно-
окрестности. Обозначим через jco любое значение аргумента из рассматри-
рассматриваемой окрестности, отличное от с. Достаточно доказать, что
f(c)-f(xo)>O «О).
Так как функция f{x) дифференцируема всюду в рассматри-
рассматриваемой окрестности точки с, то на сегменте, ограниченном точка-
точками с и jco, для функции f(x) выполнены все условия теоремы 6.4
Лагранжа. В силу этой теоремы
/(с)-/(*») =ПБ)(с-*о), G-1)
где ?•—некоторое значение аргумента между с и хо. Поскольку
производная /'(?) положительна (отрицательна) при хо<с и от-
отрицательна (положительна) при хо>с, правая часть G.1) поло-
положительна (отрицательна).
2) Пусть теперь производная f'(x) имеет один и тот же знак
слева и справа от с. Обозначая, как и выше, через хо любое зна-
значение аргумента, отличное от с, и повторяя проведенные выше
рассуждения, мы теперь докажем, что правая часть G.1) имеет
разные знаки при Хо<с и при хо>с. Это доказывает отсутствие
экстремума в точке с.
Вытекающее из теоремы 7.1 правило можно кратко сформули-
сформулировать так: 1) если при переходе через данную стационарную
точку с производная f'(x) меняет знак с плюса на минус (с ми-
минуса на плюс), то функция f(x) имеет в точке с локальный мак-
максимум (минимум); 2) если же при переходе через данную стацио-
стационарную точку с производная f'(x) не меняет знака, то экстрему-
ма в точке с нет.
Примеры. 1) Найти точки экстремума функции f{x) =
=х3— Зх2— 4. Поскольку f'(x) = 3х{х— 2), то функция f(x)
имеет две стационарные точки: х = 0 и х = 2. При переходе через
точку х = 0 производная меняет знак с плюса' на минус, а при пе-
переходе через точку х = 2—-с минуса на плюс. Следовательно, х =
= 0 —точка локального максимума, а х—2— точка локального
минимума (см. рис. 7.1).
2) Найти точки экстремума функции f(x) = (x — 2M. Произ-
Производная f'(x)=5(x — 2L обращается в нуль в единственной точке
х = 2. Так как f'(x) положительна как слева, так и справа от
этой точки, то функция f(x) = (x — 2M не имеет точек экстрему-
экстремума. График функции f(x) = (x — 2M изображен на рис. 7.2.
Иногда вызывает затруднение исследование знака первой про-
производной f'(x) слева и справа от стационарной точки. На этот
случай мы укажем другое достаточное условие экстремума в дан-
данной стационарной точке с, не требующее исследования знака
§ 1. Отыскание стационарных точек
265
f'{x) в окрестности с, но зато предполагающее существование в
точке с отличной от нуля конечной второй производной fB){x).
4. Второе достаточное условие экстремума.
Теорема 7.2. Пусть функция f{x) имеет в данной стацио-
стационарной точке с конечную вторую производную. Тогда функция
f(x) имеет в точке с локальный максимум, если /B)(с)<0, и ло-
локальный минимум, если Р'(с)>0.
Доказательство. Из условия /<2>(с)<0 (>0) и из дока-
доказанной в гл. 6 теоремы 6.1 вытекает, что функция f'{x) убывает
(возрастает) в точке с. Поскольку по условию /'(с)=0, то най-
х
Рис. 7.2
дется такая окрестность точки с, в пределах которой /' (х) поло-
положительна (отрицательна) слева от с и отрицательна (положи-
(положительна) справа от с. Но тогда по предыдущей теореме f{x) имеет
в точке с локальный максимум (минимум)
Замечание. Теорема 7.2 имеет, вообще говоря, более уз-
узкую сферу действия, чем теорема 7.1. Так, теорема 7.2 не решает
вопроса об экстремуме для случая, когда вторая производная
/B)(х) не существует в точке с, а также для случая, когда
р)(с) = 0. В последнем случае для решения вопроса о наличии
экстремума нужно изучить поведение в точке с производных выс-
высших порядков', что будет сделано нами ниже в п. 5.
Примеры. 1) В неподвижную чашку, имеющую форму по-
полушара радиуса г, опущен однородный стержень длины /
(рис. 7.3). Предполагая, что 2г</<4г, найти положение равнове-
равновесия стержня.
Положению равновесия стержня соответствует минимальное
значение его потенциальной энергии, т. е. наинизшее положение
центра его тяжести О (поскольку стержень является однород-
однородным, центр тяжести »его совпадает с его серединой). Обозначая
через ОК перпендикуляр к плоскости, на которой стоит чашка,
266 Гл. 7. Исследование графика функции
мы сведем задачу к отысканию того положения стержня АВ, при
котором отрезок ОК имеет минимальную длину. Прежде всего
вычислим длину отрезка О К как функцию угла а наклона стерж-
стержня к плоскости, на которой стоит чашка. Пусть прямая DL па-
параллельна прямой ОК, а прямая ОС перпендикулярна OK (D —
точка, в которой стержень опирается на край чашки).
Из рассмотрения прямоугольного треугольника EAD следует,
нто AD=ED cos a = 2r cos а. По условию АО=—. Таким образом,
1
OD=AD—АО = 2r cosa —•
2
С другой стороны, DC = DL—ОК—г— ОК. Поэтому из рассмот-
рассмотрения прямоугольного треугольника ODC следует, что
DC r — OK
sma = =
0D I
2r cos a— —
Таким образом, длина отрезка О К, которую мы обозначим /(а),
равна
f(a) = г -\ sin a—г sin 2a.
Переходим к отысканию того значения угла а, которое доставляет
минимум /(а). (Понятно, что мы можем ограничиться значениями
угла а из первой четверти.) Так как
f (а) == — cosa—2rcos2a = — cosa-f- 2r—4rcos2a,
то стационарные точки находятся как решения квадратного урав-
уравнения
4rcos2a cosa—2r = 0.
2
Поскольку cos a в первой четверти положителен, то нам приго-
пригоден только положительный корень этого уравнения
16г
G.2)
Хотя по смыслу задачи и ясно, что единственная стационарная
точка ао является точкой минимума функции Да), мы установим
это строго при помощи теоремы 7.2. Достаточно убедиться в том,
что Р)(а0)>0. Поскольку
а) = sina+ 4r sin2a = 8rsina« (cosa
§ 1. Отыскание стационарных точек 267
ТО в силу G.2)
р(а) = 8г sin а0 (cos а0 -) = -^- Vl2 + 128г2 > 0.
\ 16г / ¦ 2
Тем самым установлено, что положению равновесия стержня от-
отвечает угол наклона его к плоскости, на которой стоит чашка,
определяемый формулой G.2).
2) Еще раз найдем точки эксртемума функции f(x) =
= хъ—Зх2—4. Стационарными точками этой функции, как мы уже
видели выше, являются точки х = 0 и х=2. Так как
P(*)=6jc — 6, /<2)@)=— 6<0, РB)=6>0,
то в силу теоремы 7.2 функция f(x) имеет максимум в точке 0 и
минимум в точке 2. Экстремальные значения этой функции равны
= /@)=-4, /rain = fB)=-8.
5. Третье достаточное условие, экстремума. Установим еще
одно достаточное условие локального экстремума, пригодное в
случае, когда вторая производная функции в данной стационар-
стационарной точке обращается в нуль.
Теорема 7.3. Пусть и> 1 — некоторое нечетное число, и
пусть функция y = f(x) имеет производную порядка п в некоторой
окрестности точки с и производную порядка и+1 в самой точке с.
Тогда, если выполнены соотношения
f'(c) =р)(с) = ... =/<»>.(с) =0, р"+1Цс)Ф0, G.3)
то функция y = f(x) имеет в точке с локальный экстремум, точнее,
локальный максимум при f<n+1>(c)<0 и локальный минимум при
f(n+D(c)>0.
Доказательство. При п=\ теорема 7.3 совпадает с уже
доказанной выше теоремой 7.2, так что нужно вести доказатель-
доказательство лишь при нечетном и>3.
Пусть нечетное число п удовлетворяет условию л>3, и пусть
ради определенности f(n+1)(c)>0. Докажем, что функция y = f(x)
имеет в точке с локальный минимум.
Так как /<п+1)(с)>0, то, в силу теоремы 6.1 о достаточном ус-
условии возрастания функции в точке, функция f<!l)(jc) возрас-
возрастает в точке с. Но тогда, поскольку /<п)(с)=0, можно утвер-
утверждать, что всюду в достаточно малой окрестности точки с функ-
функция f(n)(x) отрицательна слева от с и положительна справа от с.
Заметив это, разложим функцию f'(x) в окрестности точки с
по формуле Тейлора, записав остаточный член в форме Лагранжа
(см. § 7 и 8 гл. 6). Мы получим, что для всех х из достаточно ма-
малой окрестности точки с между х и с найдется точка | такая, что
268 Гл. 7. Исследование графика функции
(n-l)l V
В силу соотношений G.3) написанное разложение принимает вид
Выше мы установили, что для всех х из достаточно малой
окрестности точки с производная /<т)(х) отрицательна слева от с
и положительна справа от с. Так как § лежит между х и с, то
для всех jc из достаточно малой окрестности точки с величина
f(n)(|) (а значит, в силу нечетности п и вся правая часть G.4))
отрицательна слева от с и положительна справа от с.
Итак, с помощью равенства G.4) мы доказали, что производ-
производная {'(х) для всех х из достаточно малой окрестности точки с от-
отрицательна слева от с и положительна справа от с.
В этой ситуации, в силу первого достаточного условия экстре-
экстремума (т. е. теоремы 7.1), функция y — f{x) имеет в точке с ло-
локальный минимум.
Случай /<п+1)(с)<0 рассматривается совершенно аналогично.
Те же рассуждения и формула G.4) в этом случае дают возмож-
возможность заключить, что функция y — f(x) имеет в точке с локальный
максимум. Теорема полностью доказана.
Замечание. Очень важным является требование нечет-
нечетности числа п в теореме 7.3. При четном «и при сохране-
сохранении всех остальных условий теоремы 7.3 никакого экстремума у
функции y = f(x) в точке с не будет (см. по этому поводу теоре-
теорему 7.10 из п. 5 § 3 этой главы).
6. Экстремум функции, недифференцируемой в данной точке.
Выше мы рассмотрели вопрос о наличии у функции f(x) экстре-
экстремума в такой точке с, в которой функция f(x) дифференцируема.
В этом пункте мы изучим вопрос о наличии экстремума в точке с
у такой функции, которая недифференцируема в точке с, но диф-
дифференцируема всюду в некоторой окрестности справа и слева от
с и, кроме того, непрерывна в точке с.
Оказывается, теорема 7.1 может быть обобщена на случай та-
такой функции. Именно, имеет место следующее утверждение.
Теорема 7.4. Пусть функция f (х) дифференцируема всюду
в некоторой окрестности точки с, за исключением, быть может,
самой точки с, и непрерывна в точке с.
Тогда, если в пределах указанной окрестности производная
Y (х) положительна (отрицательна) слева от точки с и отрица-
отрицательна (положительна) справа от точки с, то функция f(x) имеет
в точке с локальный максимум (минимум). Если же производная
f'(x) имеет один и тот же знак слева и справа от точки с, то экс-
экстремума в точке с нет.
§ 1. Отыскание стационарных точек
269
Доказательство в точности совпадает с доказатель-
доказательством теоремы 7.1.
Достаточно заметить, что условия теоремы 7.4 и на этот раз
обеспечивают применимость к f(x) теоремы 6.4 Лагранжа по сег-
сегменту, ограниченному точками с и хо, где хо — любое число из
достаточно малой окрестности точки с.
Примеры. 1) Найти точки экстремума функции f(Jt) = |x|.
Эта функция дифференцируема всюду на бесконечной прямой,
кроме точки х = 0, и непрерывна в точке х = 0, причем производ-
производная f'(x) равна 1 при х>0 и равна —1 при х<0.
Теорема 7.1 к этой функции неприменима, а согласно теоре-
теореме 7.4 она имеет минимум при х = 0 (рис. 7.4).
Рис. 7.4
Рис. 7.5
2) Найти точки экстремума функции у = х2/3. Эта функция не-
непрерывна на всей бесконечной прямой и дифференцируема всюду
на этой прямой, за исключением точки х = 6. Производная при
хф§ равна
, 2 1
3 У х
В предыдущем примере производная имела в точке х = 0 конеч-
конечный скачок*, на этот раз производная имеет в точке х — 0 разрыв
2-го рода («бесконечный скачок»). Из выражения для производ-
производной заключаем, что эта производная отрицательна слева от точ-*
ки х=0 и положительна справа от этой точки. Значит, теоре-
теорема 7.4 позволяет утверждать, что рассматриваемая функция
имеет- минимум в точке х = 0 (график рассматриваемой функции
изображен на рис. 7.5).
* В том смысле, что эта производная хотя и не существовала в точке
л = 0, ио имела в этой точке правое и левое предельные значения, не совпа-
совпадающие между собой.
270
1 л. 7. Исследование графика функции
3) Найти точки экстремума функции
— при х ф 0,
О при х=0.
Легко видеть, что функция непрерывна на всей бесконечной пря*
мой. В самом деле, единственной «сомнительной» точкой яв>-
ляется точка х=0, но и в этой точке функция непрерывна, ибо
y y
х-4-0+0 х-*0—О
Далее, очевидно, что рассматриваемая функция дифференци-
дифференцируема на всей бесконечной прямой, кроме точки х = 0. Всюду, кро-
ме'этой точки, производная определяется формулой
Легко видеть, что предел lim —;-^=
-j— не суще-
ствует, так что функция у = {(х) недифференцируема в точке
jc = O. Поскольку производная у' положительна и слева, и справа
от точки jc = O, рассматриваемая функция согласно теореме 7.4
не имеет экстремума в точке х = 0, а значит, и вообще не имеет
экстремумов. (График рассматриваемой функции изображен на
рис. 7.6.)
х
if'
0
^^
1
а
<
ь
X
Рис. 7.6
Рис. 7.7
7. Общая схема отыскания экстремумов. Переходим к общей
схеме отыскания точек локального экстремума. Предположим, что
функция f(x) непрерывна на интервале* (а, Ь) и ее производная
* Вместо интервала (а, Ь) можно рассматривать бесконечную прямую или
открытую полупрямую.
§ 2. Выпуклость графика функции
271
f(x) существует и непрерывна на этом интервале всюду, кроме
конечного числа точек.
Кроме того, предположим, что производная f'(x) обращается
в Цуль на интервале (а, Ь) не более чем в конечном числе точек.
Щыми словами, мы предполагаем, что на интервале (а, Ь)
имеется лишь конечное число точек, в которых производная f (х)
не существует или обращается в нуль. Обозначим эти точки сим-
символами х\, X2,.-.,xn(a<xi<x2<-..<Xn<b). В силу сделанных
предположений производная f'(x) сохраняет постоянный знак на
каждом из интервалов (а, х\), {х\, х2),..., {хп, Ь). Значит, вопрос
о наличии экстремума в каждой из точек х\, х2,...,хп может быть
решен (в утвердительном или отрицательном смысле) при помо-
помощи теоремы 7.4.
§ 2. ВЫПУКЛОСТЬ ГРАФИКА ФУНКЦИИ
Предположим, что функция f(x) дифференцируема в любой
точке интервала (а, Ь). Тогда, как установлено в п. 3 § 1 гл. 5,
существует касательная к графику функции y=f{x), проходящая
через любую точку М(х, f{x)) этого графика (а<х<Ь), причем
эта касательная не параллельна * оси Оу.
Определение. Будем говорить, что график функции у =
= f(x) имеет на интервале (а, Ь) выпуклость, направленную вниз
{вверх), если график этой функции в пределах указанного интер-
еала лежит не ниже (не выше) любой своей касательной.
Замечание 1. Термин «график лежит не ниже (или не
выше) своей касательной» имеет смысл, ибо касательная не па-
параллельна оси Оу.
. X
О а
с х
ъ х
Рис. 7.8
Рис. 7.9
На рис. 7.7 изображен график функции, имеющий на интерва-
интервале (а, Ь) выпуклость, направленную вниз, а на рис. 7.8 изобра-
изображен график функции, имеющий выпуклость, направленную вверх.
* Ибо угловой коэффициент ее, равный производной f(x), конечен.
27 2 Гл. 7. Исследование графика функции
Теорема 7.5. Если функция y = f(x) имеет на интервале
(а, Ь) конечную вторую производную и если эта производная не-
неотрицательна (неположительна) всюду на этом интервале, то
график функции y = f(x) имеет на интервале (а, Ь) выпуклость,
напрЬвленную вниз (вверх).
Доказательство. Ради определенности рассмотрим сщу-
чай, когда вторая производная р2)(х)^0 всюду на (а, Ь). Обозна-
Обозначим через с любую точку интервала (а, Ь) (рис. 7.9). Требуется
доказать, что график функции y = f(x) в пределах интервала
(а, Ь) лежит не ниже касательной, проходящей через точку
М(с, f(c)). Запишем уравнение указанной касательной, обозна-
обозначая ее текущую ординату через Y. Поскольку угловой коэффици-
коэффициент указанной касательной равен f'(c), то ее уравнение имеет
вид*
Y-f(c)=f{c)(x-c). G.5)
Разложим функцию f(x) в окрестности точки с по формуле Тей-
Тейлора, беря в этой формуле п=\. Получим
y = f(x) = f (с) + ?jp- (х-с) + fi2)^] (х-с)*, G.6)
где остаточный член взят в форме Лагранжа, | заключено между
сих. (Поскольку по условию f(x) имеет вторую производную на
интервале (а, Ь), формула G.6) справедлива для любого х из ин-
интервала (а, Ь)\ см. §§ 7 и 8 гл. 6.)
Сопоставляя G.6) и G.5), будем иметь
y — Y= f<2)(?) {x—cf. G.7)
Поскольку вторая производная по условию ^0 всюду на (а, Ь),
то правая часть G.7) неотрицательна, т. е. для всех х из (а, Ь)
справедливо у— У>0, или y>-Y.
Последнее неравенство доказывает, что график функции у —
— ]{х) всюду в пределах интервала {а, Ь) лежит не ниже каса-
касательной G.5).
Аналогично доказывается теорема для случая р2Цх)^.О.
Замечание 2. Если /B>(д;.)=0 всюду на интервале (а, Ь),
то, как легко убедиться, y — f(x) —линейная функция, т. е. график
ее есть прямая линия. В этом случае направление выпуклости
\можно считать произвольным.
Теорема 7.6. Пусть вторая производная функции y = f(x)
непрерывна и положительна (отрицательна) в точке с. Тогда су-
существует такая окрестность ** точки с, в пределах которой график
.* Уравнение прямой, проходящей через точку М(а, Ь) и имеющей угловой
коэффициент k, имеет вид Y—b=k(x—а) (см. курс аналитической геометрии).
** Напомним, что окрестностью точки с называется интервал, содержащий
точку с.
§ 3. Точки перегиба
273.
функции y — f{x) имеет выпуклость, направленную вниз (вверх).
Доказательство. По теореме об устойчивости знака не-
непрерывной функции найдется такая окрестность точки с, в преде-
пределах', которой вторая производная fi2)(x) положительна (отрица-
(отрицательна). По предыдущей теореме график функции y = f{x) имеет
в пределах этой окрестности выпуклость, направленную вниз
(вверх).
Таким образом, направление выпуклости графика функции,
полностью характеризуется знаком второй производной этой-
функЦии.
Пример. Исследовать направление выпуклости графика
функции у = х3 — Зх2— 4. Из вида второй производной f&(x) =
= 6(х—1) вытекает, что эта производная отрицательна при х<1
и положительна при х>1. Таким образом, выпуклость графика
функции у—хь— Зх2 — 4 направлена вверх на участке (—оо, 1),
и вниз на участке A, °°) (см. рис. 7.1).
§ 3. ТОЧКИ ПЕРЕГИБА
1. Определение точки перегиба. Необходимое условие перегиба.
Пусть a, b и с — некоторые три числа, связанные неравенствам»
а<с<Ь. Предположим, что функция у = }(х) дифференцируема]
на интервале (а, Ь), т. е. существует касательная к графику этой
функции во всех точках, абсциссы которых принадлежат интер-
интервалу (а, Ь). Предположим, кроме того, что график функции у =
= f(x) имеет определенное направление выпуклости на каждом:
из интервалов (а, с) и (с, Ь).
Определение. Точка М(с, f(c)) графика функции y=f(x)
называется точкой перегиба этого графика, если сущест-
существует такая окрестность точки с
оси абсцисс, в пределах которой
график функции y = f(x) слева
и справа от с имеет разные на-
направления выпуклости.
На рис. 7.10 изображен гра-
график функции, имеющий перегиб
в точке М(с, f(c)).
Иногда при определении точ-
точки перегиба графика функции
y = f(x) дополнительно требуют,
чтобы указанный график веюду
в пределах достаточно малой
окрестности точки с оси абсцисс слева, и справа от с лежал по-
разные стороны ют касательной к этому графику в точке М(с„
f(c)). Ниже мы докажем, что это свойство будет вытекать из дан-
данного нами определения в предположении, что производная f'{x),
является непрерывной в с.
х
Рис. 7.10
274 Гл. 7. Исследование графика функции
Докажем следующие две леммы.
Лемма 1. Пусть функция y = f{x) имеет производную f (х)
всюду в Ь-окрестности точки с, причем эта производная непрерыв-
непрерывна в точке с. Тогда, если график функции y = f(x) имеет на интер-
интервале (с, с+б) выпуклость, направленную вниз [вверх], то всюду
в пределах интервала (с, с+б) этот график лежит не ниже [не
.выше] касательной к графику, проведенной в точке М(с, f(c)).
Доказательство. Рассмотрим последовательность {хп}
точек интервала (с, с+б), сходящуюся к точке с. Через каждую
точку Мп(хп, f(xn)) графика функции' y=f(x) проведем [каса-
[касательную к этому графику, т. е. прямую *
У» = /(*»)+f (*»)(*"*»)•
Так как по условию график функции y = f(x) имеет на интервале
(с, с+б) выпуклость, направленную вниз [вверх], то для любого
жшера п и любой фиксированной точки х интервала (с, с+б)
f(x)-Yn = f(x)-f(xn)-f'(xn)(x-xn)>0 [<O]. (*)
Из условия непрерывности f'(x) (и тем более f(x)) в точке с
и из определения непрерывности по Гейне вытекает, что сущест-
существует предел
= f(x)-f(c)-f'(c)(x-c).
Из существования последнего предела в силу неравенства (*) и
теоремы 3.13 из § 1 гл. 3 мы получим, что
f(x)-f(c)-f'\c){x-c)>O
Если обозначить через У текущую ординату касательной G.5),
проходящей через точку М(с, /(с)), то последнее неравенство
можно переписать в виде
Итак, переходя в (*) к пределу при /г-»-оо и используя теоре-
теорему 3.13, мы получим, что f(x) — У^О [^0] для любой фиксиро-
фиксированной точки х из интервала (с, с+б), причем У обозначает те-
текущую ординату касательной, проведенной через точку М(с, f(c)).
Лемма доказана.
Замечание. Аналогично формулируется и доказывается
лемма 1 и для случая, когда график функции имеет определенное
направление выпуклости не на интервале (с, с+б), а на интерва-
интервале (с — б, с).
* Мы используем уравнение прямой, проходящей через данную точку
Мп{хп, f{Xn)) и имеющей угловой коэффициент, равный f'(xn). Текущую
•ординату этой прямой обозначаем через Yn.
§ 3. Точки перегиба 27S
Лемма 2. Пусть функция y=f(x) имеет производную f'(x) в
некоторой окрестности точки с, причем эта производная непре-
непрерывна в точке с. Тогда, если график функции y=f(x) имеет пере^
гиб, в точке М(с, f(c)), то в пределах достаточно малой Ь-окрест-
ноОти точки с этот график слева и справа от с лежит по разные-
стороны от касательной, проведенной через точку М(с, f(c)).
Для доказательства этой леммы следует выбрать б>0-
настолько малым, чтобы на каждом из интервалов (с — б, с) и.
(с, с+б) график функции y = f(x) имел определенное направле-
направление выпуклости (это направление будет различным на интерва-
интервалах (с — б, с) и (с, с+б). После этого для доказательства лем-
леммы 2 остается применить лемму 1 к функции y = f(x) по каждому
из интервалов (с — б, с) и (с, с+6).
Лемма 2 позволяет нам установить необходимое условие пере-
перегиба графика дважды дифференцируемой в данной точке функции
y=f(x).
Теорема 7.7 (необходимое условие перегиба
графика дважды дифференцируемой функции).
Если функция y = f(x) имеет в точке с вторую производную и
график этой функции имеет перегиб в точке М(с, /(с)), то
р(с)=0.
Доказательство. Пусть, как выше, У — текущая ордина-
ордината касательной Y=f(c)-\-f(c)(x — с), проходящей через точку-
графика М(с, f(c)).
Рассмотрим функцию
F(xL(x)-Y=f(x)-f(c)-f'(c)(x-c),
равную разности f(x) и линейной функции f (c)-j-f'(c) (x — с).
Эта функция F(x), как и функция f(x), имеет в точке с вто-
вторую производную (а потому имеет первую производную в некото-
некоторой окрестности с, причем эта первая производная непрерывна в.
точке с). В силу леммы 2 в малой окрестности точки с график
функции y = f(x) лежит слева и справа от с по разные стороны:
от касательной, проходящей через точку М(с, f(c)), а потому
функция F(x) в малой окрестности точки с имеет слева и справа;
от с разные знаки.
Значит, функция F' (х) не может иметь в точке с локального
экстремума.
Предположим теперь, что fB)(c)^=0. Тогда, поскольку F'(x) —
= ?(х)—Г(с), FW(x)=fB>(x), выполняются условия F'(c)=0,.
Я2' (с) =5^=0 и функция F(x) в силу теоремы 7.2 имеет в точке с ло-
локальный экстремум. Полученное противоречие доказывает, что-
предположение ft2)(c)^Q является неверным, т. е. f<2)(c)=O. Тео-
Теорема доказана.
Тот факт, что обращение в нуль второй производной является
лишь необходимым условием перегиба графика дважды диффе-
дифференцируемой функции, вытекает, например, из рассмотрения:
276 Гл. 7. Исследование графика функции
графика функции у = х4. Для этой функции вторая производная
у"=\2х2 обращается в нуль в точке х = 0, но ее график не имеет
перегиба в точке М@, 0).
В силу теоремы 7.7 для отыскания всех точек перегиба графи-
графика дважды дифференцируемой функции y = f(x) нужно рассмот-
рассмотреть все корни уравнения fB>(*) =0-
Поскольку равенство нулю второй производной является лишь
необходимым условием перегиба, то нужно дополнительно иссле-
исследовать вопрос о наличии перегиба в каждой точке, для которой
f2)(x)=Q. Для проведения такого исследования следует устано-
установить достаточные условия перегиба, к чему мы и переходим.
2. Первое достаточное условие перегиба.
Теорема 7.8. Пусть функция y = f(x) имеет вторую произ-
производную в некоторой окрестности точки с и f<2)(c)=O. Тогда, если
& пределах указанной окрестности вторая производная f{2){x)
имеет разные знаки слева и справа от с, то график этой функции
имеет перегиб в точке М (с, f{c)).
Доказательство. Заметим, во-первых, что график функ-
функции y = f(x) имеет касательную в точке М(с, f{c)), ибо из усло-
условий теоремы вытекает существование конечной производной /'(с).
Далее, из того, что f2){x) слева и справа от с имеет разные зна-
знаки, и из теоремы 7.5 заключаем, что направление выпуклости сле-
слева и справа от с является различным. Теорема доказана.
Пример. Найти точки перегиба графика функции f(x) —
= хъ — Зх2— 4. Эту функцию мы неоднократно рассматривали
выше (график ее изображен на рис. 7.1). Поскольку fB)(x) =
— 6х — 6 = 6(д;—1), то единственное значение аргумента, для ко-
которого возможен'перегиб, есть х—\. Этому значению аргумента
•соответствует точка графика МA, —6). Так как f{2){x) имеет раз-
разные знаки при х>1 и при х<1, то точка М(\, —6) является точ-
точкой перегиба графика рассматриваемой функции.
3. Некоторые обобщения первого достаточного условия пере-
перегиба. Прежде всего заметим, что в условиях теоремы 7.8 можно
отказаться от требования двукратной дифференцируемости функ-
функции y = f(x) в самой точке с, сохраняя это требование лишь
для точек, лежащих в некоторой окрестности слева и справа от
с. При этом следует дополнительно предположить существование
конечной производной {'(с).
Доказательство теоремы 7.8 с указанными изменениями
дословно совпадает с доказательством, приведенным выше.
Далее можно договориться при определении. точки перегиба
не исключать случая, когда касательная к графику в рассматри-
рассматриваемой точке параллельна оси Оу *. При такой договоренности в
теореме 7.8 можно отказаться даже от требования однократной
* В этом случае первая производная f'yX) в точке с принимает бесконеч-
бесконечное значение.
§ 3. Точки перегиба
277
дифференцируемости функции f(x) в самой точке с и сформули-
сформулировать эту теорему следующим образом:
Пусть функция y = f(x) имеет конечную вторую производную
всюду в некоторой окрестности точки с, за исключешем, быть мо-
может, самой точки с. Пусть, далее, функция y=f(x) непрерывна в
точке с и график этой функции имеет касательную * в точке
М{с, f(c)). Тогда, если в пределах указанной окрестности вторая
производная fB)(X) имеет разные
знаки слева и справа от точки с,
то график функции y=f(x) имеет
перегиб в точке М(с, f(c)).
Доказательство сформу-
сформулированного утверждения пол- _
ностью аналогично доказательству
теоремы 7.8.
Пример. Найти точки пере-
перегиба графика функции у—х1/3. Эта
функция имеет вторую производ-
производную всюду на бесконечной прямой,
за исключением точки х=0. В точ-
точке х = 0 рассматриваемая функция
непрерывна, но уже первая производная обращается в бесконеч-
бесконечность. Однако график функции у = х1/3 имеет в точке @, 0) каса-
касательную, параллельную оси Оу** (рис. 7.11).
2 1
Так как вторая производная г/B) = -щ- имеет слева и
Рис. 7.11
справа от точки х=О разные знаки, то график функции г/ = ;
имеет перегиб в точке @,0).
4. Второе достаточное условие перегиба. На случай, когда
нежелательно исследование знака второй производной в окрест-
окрестности точки с, мы сформулируем второе достаточное условие пе-
перегиба, предполагающее существование у функции y = f(x) в точ-
точке с конечной третьей производной.
Теорема 7.9. Если функция y = f(x) имеет в точке с конеч-
конечную третью производную и удовлетворяет в этой точке условиям
f&(c) — O, ^C)(с)=й0, то график этой функции имеет перегиб в точ-
точке M(c,f(c)).
Доказательство. Из условия fC)(c)#=0 и из теоремы 6.1
вытекает, что функция fB){x) либо возрастает, либо убывает в
точке с. Так как f2)(c) =0, то и в том, и в другом случае найдется
такая окрестность точки с, в пределах которой р7Цх) имеет раз-
разные знаки слева и справа от с. Но тогда по предыдущей теореме
график функции y = f(x) имеет перегиб в точке М(с, /(с)).
* Быть может, параллельную оси Оу.
** Эте вытекает, например, из того, что график обратной функции х=у3
имеет в этой точке касательную х = 0.
278 Гл. 7. Исследование графика функции
Замечание. Конечно, теорема 7.9 имеет более узкую- сферу
действия, чем теорема 7.8. Так, теорема 7.9 не решает вопроса о
наличии перегиба для случая, когда у функции y = f(x) не суще-
существует конечной третьей производной, а также для случая, когда
f<3)(c)=0'. В последнем случае для решения вопроса о наличии,
перегиба нужно изучить поведение в точке с производных высших,
порядков, что будет сделано нами ниже (см. п. 5). ,
Возвратимся к примеру, рассмотренному в п. 2, и покажем,,
что вопрос о наличии перегиба у графика функции у=х3— Зх2 — 4
может быть решен и при помощи теоремы 7.9. В самом деле,,
f&{x) =6=?М), значит, точка МA, —6) является точкой перегиба
согласно теореме 7.9.
5. Третье достаточное условие перегиба. Установим еще одно
достаточное условие перегиба, пригодное для случая, когда в дан-
данной точке с обращаются в нуль как вторая, так и третья произ-
производные рассматриваемой функции.
Аналогом теоремы 7.3 является следующее утверждение.
Теорема 7.10. Пусть п^2 некоторое четное число, и пусть-
функция y — f(x) имеет производную порядка п в некоторой
окрестности точки с и производную порядка п-\-\ в самой точке-
с. Тогда, если выполнены соотношения
f)(c) =p>(c) = ... =р)(с) =0, f(n+»(c)^0, G.3*),
то график функции y = f(x) имеет перегиб в точке М(с, f(c)).
Доказательство. При я=2 теорема 7.10 совпадает с уже
доказанной выше теоремой 7.9, так что нужно вести доказатель-
доказательство лишь для четного п^4.
Пусть четное число п удовлетворяет условию я>4, и пусть
/(и+1)(с)=?^0. Тогда, в силу теоремы 6.1 о достаточном условии
возрастания или убывания функции в точке, функция f<n)(x) либо*
убывает в1 лючке с (при /(п+1)(с)<0), либо возрастает в этой точ-
точке (при f<n+1)(c)>0). Поскольку, кроме того, /<п)(с)=0, то и в,
том, и в другом случае всюду в достаточно малой окрестности)
точки с функция f(n)(x) имеет разные знаки справа и слева от с
Заметив это, разложим функцию fB>(*) B окрестности точки с
по формуле Тейлора, записав остаточный член в форме Лагран-
жа (см. § 7 и 8 гл. 6). Мы получим, что для всех х из достаточ-
достаточно малой окрестности точки с между х и с найдется точка | тас-
таская, что
(х-с)
(хс) + ... + fff
I! (я — 3I
(л-2)! V '
§ 4. Асимптоты графика функции
279
В силу соотношений G.3*) написанное разложение принимает вид
-с)"-2. G.4*)
(п — 2)!
Выше мы установили, что "для всех х из достаточно малой
«окрестности точки с производная /<п)(х) имеет разные знаки спра-
справа и слева от с. Так как | лежит между х и с, то для всех х из
достаточно малой окрестности точки с величина fn)(l) (а значит,
в силу четности п и вся правая часть G.4*)) имеет разные знаки
справа и слева от с. Итак, в силу равенства G.4*) для всех х из
достаточно малой окрестности точки с производная fB){x) имеет
разные знаки справа и слева от с. В силу теоремы 7.8 график
функции y = f(x) имеет перегиб в точке М(с, f(c)). Теорема до-
доказана.
Замечание. Очень важным является требование четности
л в теореме 7.10 (сравните эту теорему с теоремой 7.3). Рис. 7.12
и 7.13 иллюстрируют исследование на экстремум и перегиб графи-
A,0)
Рис. 7.12
х
\П*1
п+1 нечетно
X
Рис. 7.13
на функции у=(х—l)n+1. В силу теорем 7.3 и 7.10 эта функция
имеет минимум в точке х=1 при нечетном п, а ее график имеет
лерегиб в точке М{\, 0) при четном п (проверьте это сами).
§ 4. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
Определение 1. Говорят, что прямая х = а является вер-
вертикальной асимптотой графика функции y = f{x), если
хотя бы один из пределов
равен +оо или —оо.
lim f(x)
ж-»а+0
или
lim f(x)
x-*a—0
280
Гл. 7. Исследование графика функции
Пример. График функции у =— имеет вертикальную
асимптоту х=0, ибо Пт —= + оо, Пт—= —оо (рис. 7.14).
*->0+0 X Х-+0—0 X
Предположим, далее, что функция y = f{x) определена для
сколь угодно больших значений аргумента. Ради определенности
будем рассматривать сколь
угодно большие значения поло-
положительного знака.
Определение 2. Говорят,
что прямая
G.8)
О
(С
Рис. 7.14
является наклонной асим-
асимптотой графика функции у =
= f(x) при х->-+оо, если f(x)
представима в виде
f(x)=kx+b+a(x),
G.9)
где
lim a(x) = 0.
Теорема 7.11. Для того чтобы график функции y=f(x)
имел х—>-+°° наклонную асимптоту G.8), необходимо и достаточ-
достаточно, чтобы существовали два предела
lim
lim [f(x)—kx] =
+
G.10)
Доказательство. 1) Необходимость. Пусть график функ-
функции y = f(x) имеет при x-^-+°° асимптоту G.8), т. е. для f{x)
справедливо представление G.9). Тогда
lim [f(x)—kx]= Hm [b + a(x)] =
t+ +
2) Достаточность. Пусть существуют пределы G.10). Второй
из этих пределов дает право утверждать, что разность f(x) —
— kx—b является бесконечно малой при х—>-+°°- Обозначив эту
бесконечно малую через а(х), получим для f(x) представление
G.9). Теорема доказана.
Замечание. Аналогично определяется наклонная асимпто-
асимптота и доказывается теорема 7.И и для случая х->—с».
Пример. График функции у = —
имеет наклонную
§ 5. Построение графика функции
281
асимптоту Y = 2x—1 и при *->- + оо, и при х->—оо и, кроме того,
имеет вертикальную асимптоту х = — 1 (рис. 7.15). В самом деле,
X л;->+ао X (X ¦
lim [f(x) — 2x]= lim f— 1
=—-l,
lim /(*)=+<»,
х-»—1+0 x^-
Наряду с линейной асимптотой
G.8) рассматривают также и асим-
асимптоты более сложного вида.
Говорят, что парабола п-го по-
порядка, определяемая многочленом
f{x)=—oo.
G.8* >
является асимптотой графика
функции y = f(x) при х-у + оо, если
функция f(x) представима в виде
f{x)=anxn+an-lXn-l+...
-\-aiX+ao+a(x),
lim a(x) = 0.
Легко доказать следующее ут-
тверждение.
Для того чтобы график функ-
функции У = }(х) имел при x-v+oo Рис. 7.15
асимптоту G.8*), необходимо и до-
достаточно, чтобы существовали следующие п+\ пределов:
{х)~апхП =а„_ь...,
1 im
lim
«-»+«> f
lim [/
(x) - {
+ a^
IT
+ ...
= alt
(x) — {anxn + an^
... + axx)\ = a0.
§ 5. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ
В этом параграфе мы изложим схему, по которой целесообраз-
целесообразно проводить исследование графика функции, и приведем пример,
иллюстрирующий эту схему.
282 Гл. 7. Исследование графика функции
Для исследования графика функции y=f(x) целесообразно
прежде всего провести следующие исследования:
Iе. Уточнить область задания функции.
2°. Выяснить вопрос о существовании асимптот (вертикальных
и наклонных).
3°. Найти области возрастания и убывания функции и точки
экстремума.
4°. Найти области сохранения направления выпуклости и точ-
точки перегиба.
5°. Найти точки пересечения графика функции с осью Ох.
По полученным данным легко строится эскиз графика функ-
ции. В качестве примера построим график функции
Будем следовать изложенной выше схеме.
1°. Поскольку функция G.11) представляет собой рациональ-
рациональную дробь, то она определена и непрерывна всюду на бесконеч-
бесконечной прямой, кроме точки х=0, в которой обращается в нуль зна-
знаменатель.
2°. Выясним вопрос о существовании асимптот. Очевидно, что
lim *3-5*2 + ^~ '5=_оо,
*-»о±о х2
поэтому график функции имеет вертикальную асимптоту х—0.
Далее, из существования пределов
х
lim [Пх)-х]= li
х-*±а> х-+
вытекает, что при х-»-+оо и при х-*—°о график функции имеет
наклонную асимптоту Y=x — 5.
3°. Для нахождения областей возрастания и убывания вычис-
вычислим первую производную функции G.11):
_ (х-\-5)(х — 2)(х — 3)
Имея в виду, кроме того, что сама функция и первая производная
не, существуют при х = 0, мы получим следующие области сохра-
сохранения знака у:
§ 5. Построение графика функции
283
Область значения х
Знак у'
Поведение функции
— оо < х < —5
+
возрастает
—5 < х < 0
—
убывает
0 < х<2
+
возрастает
2<*<3
—
убывает
3<Ж<+оо
+
возрастает
Из приведенной таблицы очевидно, что функция имеет следую-
следующие точки экстремума:
1) максимум при х = —5, причем f(—5) = —14, 4;
2) максимум при х=2, причем /B) =2,75; .
3) минимум при х = 3, причем f C) =2,666....
4°. Для нахождения областей сохранения направления вы-
выпуклости вычислим вторую производную
У
B) =
38*— 90
38
19
Имея в виду, что сама функция и ее производные не существуют в
точке х=0, мы получим следующие области сохранения 'зна-
'знака г/B):
Область значений х
Знак г/B)
Направление выпукло-
выпуклости графика
— оо < х< 0
—
вверх
19
—
вверх
^-<х< + ~
19
+
ВНИЗ
Из приведенной таблицы очевидно, что график функции имеет
. / 45 , / 45 \\ „
перегиб в точке , / I. Легко подсчитать, что
\ 1У \ 1У / /
6968 _
' V 19 / 2565
5°. Остается найти точки пересечения графика с осью Ох. Эти
точки соответствуют вещественным корням уравнения
х3 — 5лг2+19х— 15 = 0.
Легко видеть, что
xz — 5x2+\9x— 15= (х— 1) {х2 — 4х+15).
Поскольку квадратный трехчлен х2 — 4х+15 не имеет веществен-
вещественных корней, то рассматриваемое уравнение имеет только один ве-
284
Гл. 7. Исследование графика функции
щественный корень х=1, так
что график функции пересека-
пересекает ось Ох в точке A,0). По по-
полученным данным строим эс-
эскиз графика рассматриваемой
функции (рис. 7.16).
§ 6. ГЛОБАЛЬНЫЕ
МАКСИМУМ И МИНИМУМ
ФУНКЦИИ НА СЕГМЕНТЕ.
КРАЕВОЙ ЭКСТРЕМУМ
1. Отыскание максималь-
максимального и минимального значе-
значений функции, определенной на
сегменте. Рассмотрим функ-
функцию y = f(x), определенную
на сегменте [а, Ь] и непрерыв-
непрерывную на нем. До сих пор мы
занимались лишь отысканием
локальных максимумов и
минимумов функции. Теперь поставим задачу об отыскании гло-
глобальных максимумов и минимумов или, по-другому, об отыскании
максимального и минимального значений f(x) на сегменте [а, Ь].
Подчеркнем, что в силу теоремы Вейерштрасса (см. теорему 4.15
из гл. 4) непрерывная функция f(x) обязательно достигает в не-
некоторой точке сегмента [а, Ь] своего максимального (минималь-
(минимального) значения. Ради определенности остановимся на отыскании
максимального значения f (х) на сегменте [а, Ь].
Максимальное значение функции f(x) может достигаться либо
во внутренней точке хо сегмента [а, Ь] (тогда оно совпадает с
Рис. 7.16
Рис. 7.17
а
Рис. 7.18
Ъ X
одним из локальных максимумов функции f(x)) (рис. 7.17), либо
на одном из концов сегмента \а, Ь] (рис. 7.18). Отсюда ясно, что
для нахождения максимального значения функции f(x) на сег-
сегменте [а, Ь] нужно сравнить между собой значения f(x) во всех
§ 6. Краевой экстремум
285
точках локального максимума и в граничных точках сегмента а
и Ъ. Наибольшее из этих значений и будет максимальным значе-
значением }(х) на сегменте [а, Ь]. Аналогично находится и минималь-
минимальное значение f(x) на сегменте [а, Ь].
Если желательно избежать исследования стационарных точек,
то можно просто сравнить между собой значения f(x) во всех
стационарных точках и в граничных точках а и Ь. Наибольшее
(наименьшее) из этих значений, очевидно, и будет максимальным
(минимальным) значением функции f(x) на сегменте [а, Ь].
Отметим далее, что если f(x) имеет на сегменте [а, Ь] лишь
одну точку локального максимума (или лишь одну точку локаль-
локального минимума), то без сравнения значения f(x) в этой точке с
f(a) и f(b) можно утверждать, что это значение является макси-
максимальным (минимальным) значением f(х) на- сегменте [а, Ь\
(рис. 7.19).
b x
Рис. 7.19
Рис. 7.20
Аналогичными средствами решается вопрос об отыскании мак-
максимального (минимального) значения функции y = f(x) на интер'
вале, полупрямой и бесконечной прямой (при условии, что это
значение существует).
Может случиться так, что дифференцируемая функция вовсе
не имеет на сегменте [а, Ь] (или полупрямой а^х< + °°) стацио-
стационарных точек.
В таком случае f(x) является монотонной на.этом сегменте
(полупрямой) и ее максимальное и минимальное значения дости-
достигаются на концах этого сегмента (на конце этой полупрямой).
В качестве примера рассмотрим задачу об отыскании макси-
максимального и минимального значений функции y = sin(x2) на сег-
сегменте —Уп ¦< х •< .
2
Поскольку y' = 2xcos(x2), указанная функция имеет на рас-
рассматриваемом сегменте три стационарные точки: х=0 и
р р
X = ± л/ —.Сравнивая значения функции в указанных
точках
и на концах сегмента
286 Гл. 7. Исследование графика функции
1 [ 2 j 4 2
убедимся в том, что максимальное значение рассматриваемой
¦функции равно +1 и достигается в двух внутренних точках сег-
сегмента: хл = —1/ — Hxa=i/—, а минимальное значение
/я /я
И Х„ = 1 / ,
2 * у 2
фун
/5я
- л, /2
рассматриваемой функции равно и достигается на правом
.конце сегмента
График рассматриваемой функции изображен на рис. 7.20.
2. Краевой экстремум. Пусть функция y = f(x) определена на
некотором сегменте [а, Ь]. Будем говорить, что эта функция
.имеет в граничной точке Ь этого сегмента краевой макси-
максимум (краевой минимум), если найдется левая полуокрест-
полуокрестность точки Ь, в пределах которой значение f(b) является наи-
наибольшим (наименьшим) среди всех других ¦ значений этой
функции.
Аналогично определяются краевой максимум и краевой мини-
минимум в граничной точке а сегмента [а, Ь].
Краевой максимум и краевой минимум объединяются общим
названием: краевойэкстремум.
Имеет место следующее достаточное условие крае-
краевого экстремума: для того чтобы, функция y~f{x) имела в
точке b сегмента [а, Ь] краевой максимум (краевой минимум),
достаточно, чтобы эта функция имела в точке Ь положительную
(отрицательную) левую производную*. (Доказательство
совершенно аналогично доказательству теоремы 7.1.) Из указан-
указанного достаточного условия краевого экстремума непосредственно
вытекает следующее необходимое условие краевого
экстремума функции, имеющей в точке Ъ левую производ-
производную: для того чтобы функция y = f(x), обладающая в точке Ь ле-
левой производной, имела в этой точке краевой максимум (краевой
минимум), необходимо, чтобы указанная производная была неот-
неотрицательной (неположительной).
Аналогично, для того чтобы функция y = f(x), обладающая в
точке а правой производной, имела в этой точке краевой макси-
* Для граничной точки а достаточным условием краевого максимума (крае-
(краевого минимума) является отрицательность (положительность) правой производ-
производной в точке а.
§ 6. Краевой экстремум 287
мум (краевой минимум), необходимо, чтобы указанная производ-
производная была неположительной (неотрицательной).
3. Теорема Дарбу*.
Определение. Будем говорить, что функция f(х) имеет
производную на сегменте {а, Ь\ если f(x) имеет конечную про~
изводную в каждой внутренней точке [а, Ъ] и, кроме того,
имеет конечные односторонние производные f'(a~\-0) it
6 —0).
Очевидно, функция, имеющая производную на сегменте, бу-
будет непрерывной на этом сегменте **.
Докажем теперь следующую теорему.
Теорема 7.12 (теорема Дарбу). Пусть функция
f(x) имеет производную на сегменте [а, Ь]. Тогда, каково бы
ни было число С, заключенное между A = f (а+0) и В =
— f{b — 0), на этом сегменте найдется точка | такая, что
т)=с.
Итак, производная при одном только условии существова-
существования на сегменте [а, Ь] принимает любое промежуточное зна-
значение.
Доказательство. Сначала докажем следующее ут-
утверждение: если F(x) имеет конечную производную на [а, Ь]
и если F'(a+0) и F'(b-O) — числа разных знаков, то на сег-
сегменте [а, Ь] найдется точка | такая, что F'(?)=0.
Пусть ради определенности F'(a + Q)<0, F'(b—0)>0. Тогда,
функция Р(х) имеет краевой максимум на обоих концах сег-
сегмента [а, Ь]. Но это, означает, что минимальное значение F{x)
на сегменте [а, Ь] достигается в некоторой внутренней точке g
этого сегмента (функция F(x) имеет производную, а значит,.,
и непрерывна на сегменте [а, Ь] и поэтому достигает на этом
сегменте своего минимального значения). В указанной точке |
функция F(x) имеет локальный минимум, и поэтому F'(E,)=0.
Для доказательства теоремы 7.12 остается положить F(x) =
= f(x)—Сх*** и применить к F(x) только что доказанное-
утверждение.
Заметим, что непрерывность производной f (х) мы не пред-
предполагали.
Из теоремы Дарбу сразу же следует доказанное в п. 3 § 4
гл. 6 утверждение об отсутствии у прозводной точек разрыва
первого рода.
* Гастон Дарбу — французский математик A842—1917).
** В самом деле, из существования производной f {х) во внутренних..
точках [а, Ь], вытекает непрерывность f(x) во внутренних точках fa, b], а из;
существования односторонних производных f'(a+O) и f (b—0) вытекает непре-
непрерывность справа в точке а и слева в точке Ь.
*** При этом мы, не ограничивая общности, предполагаем, что f'(a+O) =
=A<C<B=f'(b—0).
288 Гл. 7. Исследование графика функции
ДОПОЛНЕНИЕ
Алгоритм отыскания экстремальных значений
функции, использующий только значения этой
функции
Предположим, что функция f(x) задана на сегменте [а, Ь],
мы располагаем значениями этой функции в узлах сетки, полу-
получающейся при делении сегмента [а, Ь] на 2" равных частей
¦(«=1,2,3,...).
Ради определенности остановимся на отыскании точки мини-
минимума функции f(x).
При этом мы будем предполагать, что выполнены следующие
два условия: 1) функция f(x) имеет на сегменте [а, Ь] единствен-
единственную точку минимума с; 2) при а<с функция f(x) убывает на сег-
сегменте [а, о] (т. е. убывает слева от точки минимума), а при
>с<Ь функция f(x) возрастает на сегменте [с, Ь] (т. е. возрастает
справа от точки минимума).
Эти условия будут выполнены, например, в случае, если функ-
функция f(x) два раза дифференцируема на сегменте fa, b], причем
/'(с)=0, а }"(х) строго положительна на [а, Ь]. Однако для вы-
выполнения указанных двух условий дифференцируемость f(x), во-
вообще говоря, не требуется.
Мы сейчас укажем алгоритм построения стягивающейся сис-
системы сегментов*, содержащих точку с минимума функции f(x).
Остановимся на построении первого сегмента стягивающейся
системы, имея в виду, что все последующие сегменты этой систе-
системы строятся по тому же принципу, что и первый ее сегмент.
Разделим сегмент [а, Ь] при помощи точек а = хо, х\, x2, х$ и
х4 = Ь на четыре равных частичных сегмента [xi-i, xi\ (i=l,
•2,3,4).
Данный частичный сегмент [x»-i, x[\ договоримся называть
сегментом убывания, если /(*<-i) >f(xi), т. е. если значе-
значение функции f(x) на левом его конце строго больше, чем на пра-
правом, и соответственно сегментом возрастания, если
!(xi-\)<.f(xi), т. е. если значение функции f(x) на левом конце
строго меньше, чем на правом.
Так как функция f(x) имеет на сегменте [а, Ь] единственную
точку минимума с, то указанная точка минимума с принадлежит
одному из четырех частичных сегментов [х,_ь х{\.
Тот частичный сегмент [ям, х{\, которому принадлежит
точка минимума с, можем являться либо сегментом
возрастания, либо сегментом убывания, либо, наконец, сегментом,
на концах которого функция f(x) имеет равные значения.
* Определение и свойства стягивающейся системы сегментов см. в п. 2
<§ 2 гл. 3.
Дополнение 289
Кроме того, из того, что по условию функция f(x) убывает
слева от точки минимума с и возрастает справа от этой точки,
вытекает, что если данный частичный сегмент содержит точку
минимума с, то любой частичный сегмент, лежащий налево от
данного, является сегментом убывания, а любой частичный сег-
сегмент, лежащий направо от данного, является сегментом возраста-
возрастания.
Но тогда можно утверждать, что тот частичный сегмент, ко
торый содержит точку минимума с, является либо самым правым
сегментом убывания, либо самым левым сегментом возрастания,
либо, наконец, частичным сегментом, на концах которого f(x)
имеет равные значения.
Сформулированное утверждение позволяет указать алгоритм
построения первого сегмента [аь Ь{\ стягивающейся системы сег-
сегментов [ап, Ьп], каждый из которых содержит точку минимума с.
Рассмотрим четыре возможных случая.
1) Среди частичных сегментов [xi-i, xi\ есть сегмент, на кон-
концах которого f(x) имеет равные значения. В этом случае этот
сегмент содержит точку минимума с*, и мы примем его за пер-
первый сегмент [alt b\] стягивающейся системы.
2) Все частичные сегменты \xi-i, х{\ (t=l, 2, 3, 4) являются
сегментами убывания. В этом случае точка минимума с лежит на
самом правом из частичных сегментов, т. е. на сегменте [х3> xi],
и мы примем этот сегмент за [а\, Ы\.
3) Все частичные сегменты [xi-i, Xi\ (t=l, 2, 3, 4) являются
сегментами возрастания. В этом случае точка минимума лежит
на самом левом из частичных сегментов, т. е. на сегменте [xq, xi],
и мы примем этот сегмент за [аи Ь\\.
4) Среди частичных сегментов имеются как сегменты убыва-
убывания, так и лежащие правее их сегменты возрастания. В этом
случае можно утверждать, что точка минимума с лежит на объ-
объединении самого правого сегмента убывания и самого левого сег-
сегмента возрастания. Указанное объединение двух частичных сег-
сегментов мы и примем за <[аи Ь\\.
Тем самым мы указали однозначный алгоритм построения
первого сегмента [аи ЬЛ из стягивающейся системы сегментов
\[ап, bn]}.
Второй сегмент этой системы [а2, Ь2] строится, отправляясь от
[аи Ь\\, точно так же, как сегмент [ai, Ь\\ строился, отправляясь
от [а, Ь]. По такому же принципу, отправляясь от я-го сегмента
[#л, bn], строится (я+1)-й сегмент стягивающейся системы.
* Точка минимума с не может лежать налево от частичного сегмента
[Xi-u x'i], на концах которого f(x) имеет равные значения, ибо при этом
указанный сегмент является сегментом возрастания. Аналогично предположе-
предположение о том, что с лежит направо от частичного сегмента, на концах которого
f(x) имеет равные значения, привело бы к тому, что этот частичный сегмент
является сегментом убывания.
10 Зак. 72
290 Гл. 7. Исследование графика функции
Ясно, что построенная система сегментов {[ап, Ьп]} является
стягивающейся и, поскольку все эти сегменты содержат точку
минимума с, обе последовательности правых концов {Ьп} этих
сегментов и левых их концов {ап} сходятся к точке минимума с.
Аналогично строится алгоритм отыскания точки максимума
функции f(x), имеющей на сегменте [а, Ь] единственную точку
максимума с при условии, что эта функция возрастает слева от
с при с>а и убывает справа от с при с<Ь.
Глава 8
ПЕРВООБРАЗНАЯ ФУНКЦИЯ
И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
В этой главе мы изучим операцию, обратную по отношению к
операции дифференцирования, т. е. займемся вопросом о восста-
восстановлении функции по известной производной этой функции.
Изучение этого вопроса естественно приведет нас к понятиям
первообразной и неопределенного интеграла (уже упоминавшимся
в гл. 1).
Откладывая до гл. 9 вопрос о существовании первообразной, и
неопределенного интеграла, мы изучим в настоящей главе важ-
важнейшие методы интегрирования и выделим классы функций, не-
неопределенные интегралы от которых выражаются через элемен-
элементарные функции.
§ 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ И
НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
1. Понятие первообразной функции. К числу важных задач ме-
механики относятся задача об определении закона движения мате-
материальной точки по заданной ее скорости, а также задача об оп-
определении закона движения и скорости материальной точки по
заданному ее ускорению *.
Эти задачи приводят к математической проблеме отыскания
функции по заданной производной этой функции.
Переходим к рассмотрению этой проблемы.
Определение. Функция F(x) называется первообраз-
первообразной функцией (или просто первообразной) для функ-
функции f(x) на интервале (а, Ь), если в любой точке х интервала
(а, 6) функция F(x) дифференцируема и имеет производную
F'.(x), равную f(x).
Замечание. Аналогично определяется первообразная для
функции f(x) на бесконечной прямой и на полупрямой **.
* Вместо ускорения материальной точки можно задать действующую на
эту точку силу (ибо согласно второму закону Ньютона сила определяет уско-
ускорение этой точки).
** Можно ввести первообразную для функции f(x) и на сегменте [а, Ь],
понимая под такой первообразной функцию F(x), имеющую производную F'(x)
в любой внутренней точке сегмента [а, Ь], равную f(x), и, кроме того,
имеющую правую производную F'(a+0), равную f(а+0), и левую производ-
производную F'(b-O), равную f F—0).
1-0*
292 Гл. 8. Первообразная функция и неопределенный интеграл
Примеры. 1) Функция F(x) = ]^l—х2 является перво-
первообразной для функции f(x)= -т== на интервале (—1,
у 1 —хг
+ 1), ибо в любой точке х этого интервала (у\—х2)' =
2) Функция F(x)=sinx является первообразной для функции
f(x)=cosx на бесконечной прямой (—с», +оо), ибо в каждой
точке х бесконечной прямой (sinx)' = cos^.
3) Функция F(x)=\nx является первообразной для функции
f(x)~— на открытой полупрямой х~>0, ибо в каждой точке
л этой полупрямой Aпх)' = —.
X
Если F(x) является первообразной для функции f(x) на интер-
интервале (а, Ь), то, очевидно, и функция F(x)+C, где С — любая
постоянная, является первообразной для функции f(x) на интер-
интервале {а, Ь).
Естественно, возникает вопрос, как связаны между собой раз-
различные первообразные для одной и той же функции f(x).
Справедлива следующая основная теорема.
Теорема 8.1. Если Fx(x) и Fi(x) — любые первообразные
для функции f(x) на интервале (а, Ь), то всюду на этом интер-
интервале Fi (х) —Fi (х) = С, где С — некоторая постоянная.
Другими словами, две любые первообразные для одной и той
же функции могут отличаться лишь на постоянную.
Доказательство. Положим <&(x)=F\lx)—F2(x). Так
как каждая из функций F\{x) и F2(x) дифференцируема на ин-
интервале (а, Ь), то в силу теоремы 5.5 и функция Ф(л;) дифферен-
дифференцируема на интервале (а, Ь), причем всюду на этом интервале
Ф' (х) = /Y (х) -7Y (х) = / (х) -f (х) = 0.
В п. 1 § 4 гл. 6 была доказана теорема 6.5 следующего со-
содержания: если функция Ф(л;) дифференцируема всюду на интер-
интервале (а, 6) и если всюду на этом интервале Ф'(л;)=0, то функ-
функция Ф(л;) является постоянной на интервале (а, Ь).
Из этой теоремы-получим, что C?>(x)=F1 (х)—F2 {х) = С = const,
что и требовалось доказать.
Следствие. Если F(x) — одна из первообразных функ-
функций для функции f(x) на интервале (а, Ь), то любая первообраз-
первообразная Ф(я) для функции f(x) на интервале (а, Ь) имеет вид
Ф(х) =F(x) +C, где С — некоторая постоянная.
2. Неопределенный интеграл.
Определение. Совокупность всех первообразных функ-
функций для данной функции f(x) на интервале (а, Ь) называется
неопределенным интегралом от функции f(x) (на
этом интервале) и обозначается символом
\f(x)dx. (8.1)
§ 1. Понятие первообразной и неопределенного интеграла 2 93
В этом обозначении знак J называется знаком интеграла,
выражение f{x)dx — подынтегральным выражением
а сама функция f(x) — подынтегральной функцией.
Если F(x) — одна из первообразных функций для функции
f(x) на интервале (а, 6), то в силу следствия из теоремы 8.1
(x)dx = F(x) + C, (8.2)
где С — любая постоянная *.
Подчеркнем, что если первообразная (а значит, и неопреде-
неопределенный интеграл) для функции f(x) на интервале (а, Ь) сущест-
существует, то подынтегральное выражение в формуле (8.1) представ-
представляет собой дифференциал любой из этих первообразных.
В самом деле, пусть F(x) — любая из первообразных для
функции f(x) на интервале (а, Ь), т. е. для всех х из интервала
(а, Ь) F'(x)=f(x). Тогда f(x)dx=*F'(x)dx^dF.
Примеры. 1) Г . ~х dr = y\ — г2 + Г на интервале
J у 1 — х*
— 1<л;<1, ибо функция F{x) = Y^—х* является одной из пер-
первообразных для функции f(r)= ~х на указанном интер-
V 1 —хг
вале.
2) j соя х dx = sin x + С на всей бесконечной прямой
—<х><х< + оо, ибо функция F(x)=sinx является одной из перво-
первообразных для функции /(a;)=cosa; на бесконечной прямой.
В этой главе мы не будем заниматься вопросом о существо-
существовании первообразных (или неопределенных интегралов) для ши-
широких классов функций. Здесь мы лишь отметим, что в § 4 гл. 9
будет доказано, что для всякой функции f(x), непрерывной на
интервале (а, Ь), существует на этом интервале первообразная
функция (и неопределенный интеграл).
3. Основные свойства неопределенного интеграла. Прежде
всего отметим два свойства, непосредственно вытекающие из оп-
определения неопределенного интеграла:
Г. \
2". \
Свойство 1° означает, что знаки d и j взаимно сокращаются в
случае, если знак дифференциала стоит перед знаком интеграла.
Свойство 2° означает, что знаки j и d взаимно сокращаются и
в случае, если знак интеграла стоит перед знаком дифферен-
дифференциала, но в этом случае к F(x) следует добавить произвольную
постоянную С.
Равенство (8.2) следует понимать как равенство двух множеств.
294 Гл. 8. Первообразная функция и неопределенный интеграл
Для установления свойства 1° достаточно взять дифферен-
дифференциал от обоих частей формулы (8.2) и учесть, что dF(x) =
=F{x)dx=f(x)dx.
Для установления свойства 2° достаточно в левой части (8.2)
воспользоваться равенством dF(x) =f(x)dx.
Следующие два свойства обычно называют линейными свой-
свойствами интеграла:
3°. \[f{x)±g{x)}dx=\f{x)dx±\g{x)dx.
4°. ][Af(x)]dx=Afi{x)dx D=const).
Подчеркнем, что равенство в формулах 3° и 4° имеет услов-
условный характер: его следует понимать как равенство правой и ле-
левой частей с точностью до произвольного постоянного слагаемого
(это понятно, поскольку каждый из интегралов, фигурирующих
в формулах 3° и 4°, определен с точностью до произвольного
постоянного слагаемого).
Поскольку две первообразные для одной и той же функции
могут отличаться лишь на постоянную, то для доказательства
свойства 3° достаточно доказать, что если F(x) — первообразная
для f(x), a G(x) — первообразная для g{x), то функция
F(x)±G(x) является первообразной для функции f(x)±g(x).
Это последнее непосредственно вытекает из того, что произволь-
произвольная (алгебраической) суммы функций равна сумме производных
этих функций, т. е.
[F(x)±G(x)]' = F'{x)±G'(x)=f{x)±g{x).
Аналогично доказывается свойство 4°. В этом случае использу-
используется равенство [AF(x)]'=AF'(x) =Af(x).
4. Таблица основных неопределенных интегралов. В гл. 5 мы
получили таблицу производных простейших элементарных функ-
функций (см. § 5 гл. 5), представляющую собой вычислительный ап-
аппарат дифференциального исчисления. Каждая формула этой
таблицы, устанавливающая, что та или иная функция F(x) име-
имеет производную, равную f(x), приводит нас, в силу определения
неопределенного интеграла, к соответствующей формуле интег-
интегрального исчисления
lf(x)dx=F(x)+C.
Таким путем мы приходим к следующей таблице основных
неопределенных интегралов:
Г. $0-dx=C.
2°. l\-dx=x+C.
3°.
f
J.
J x
a+1
4°. Г*1
5°. ^axdx = ax/\na-\-C @<аф\),
§ 1. Понятие первообразной и неопределенного интеграла 295
6°. §siaxdx=— cosx + C.
7°.
cos2*
(x=?^-+nn, n = 0, ±1, ¦•.).
9°. Г =1A+ ctg2x)dx = —ctgх+С{хФпп, где
J sin2* J
n = 0, ±1, ...)•
-^n f dx f arc sinx-\-C, . . . ^ ..
10. I— ={ (—1<*<1).
J /i -x2 I—arccosAr+C
jjs С dx farcctgx+C,
J1+*2 \—arctgAr+C.
12°. Г —==- = 1п|л:+ Vx*±\\ + С (в случае знака «минус» либо
х > 1, либо д;< — 1).
13°. i^±_ = _Lln
1 — л;2 2
1-х
+C
К этим формулам можно присоединить и соответствующие
формулы для гиперболических функций:
14°. §
15°. ]chxdx = shx+C.
16°. f_*L_
J eh2 л;
17°. J
Сделаем замечания в отношении формул 4°, 12° и 13°. Форму-
Формула 4° справедлива для любого интервала, не содержащего значе-
значения х=0. В самом деле, если д:>0, то из формулы (lnx)'= —
С dx
заключаем, что = 1пл:+С, , а если л:<0, то из формулы
[1п(—х)]'=— заключаем, что I = 1п(—х) + С. Тем самым
X J ,Х
формула 4° оправдана для любого хфО.
Формулы 12° и 13° занимают исключительное положение в на-
нашей таблице, ибо эти формулы не имеют аналогов среди фор-
формул таблицы производных.
Однако для проверки формул 12° и 13° достаточно убедиться
в том, что производные выражений, стоящих в правых частях
этих формул, совпадают с соответствующими подынтегральными
функциями.
296 Гл. 8. Первообразная функция и неопределенный интеграл
Наша ближайшая цель — дополнить таблицу неопределен-
неопределенных интегралов основными приемами и методами интегрирова-
интегрирования. Но прежде чем приступить к реализации этой цели, сделаем
одно важное замечание.
В гл. 1 и 4 мы ввели понятие элементарной функции, а в п. 5
§ 5 гл. 5 установили, что производная любой элементарной функ-
функции представляет собой также элементарную функцию. Иными
словами, мы установили, что операция дифференцирования не вы-
выводит нас из класса элементарных функций.
Отметим сразу же, что с операцией интегрирования дело
обстоит иначе. Можно доказать, что интегралы от некоторых эле-
элементарных функций уже не являются элементарными функциями.
Примерами таких интегралов могут служить следующие:
1°. ]e-*dx.
'2°. J cos (x2) dx.
3°. J R\n{x2)dx.
J lnx
5°. f-^-^dx (хфО).
] %
б».
Каждый из указанных интегралов представляет собой функ-
функцию, не являющуюся элементарной. Указанные функции не толь-
только реально существуют *, но и играют большую роль в различ-
различных вопросах физики. Так, например, интеграл 1°, называемый
интегралом Пуассона или интегралом ошибок, широко использу-
используется в статистической физике, в теории теплопроводности и диф-
диффузии, интегралы 2° и 3°, называемые интегралами Френеля,
широко применяются в оптике. Часто встречаются в приложениях
и интегралы 4°—6°, первый из которых называется интегральным
логарифмом, а последние два — интегральными косинусом и си-
синусом.
Для всех перечисленных новых функций (интеграла Пуассо-
Пуассона, интегралов Френеля, интегрального логарифма, синуса и ко-
косинуса) составлены таблицы и графики.
Ввиду важности для приложений эти функции изучены с та-
такой же полнотой, как и простейшие элементарные функции. Во-
Вообще, следует подчеркнуть условность понятия простейшей эле-
элементарной функции.
* Мы уже отмечали, что в § 4 гл. 9 будет доказано существование неоп-
неопределенного интеграла от любой непрерывной функции. Существование интегра-
интегралов 1°—6° обеспечивается непрерывностью подынтегральных функций.
§ 2. Основные методы интегрирования 297
§ 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
1. Интегрирование заменой переменной (подстановкой). За-
Замена переменной — один из самых эффективных приемов интег-
интегрирования. Этот прием базируется на следующем элементарном
утверждении.
Пусть функция t=q>(x) определена и дифференцируема на
множестве {х}, представляющем собой либо интервал, либо от-
открытую полупрямую, либо бесконечную прямую, и пусть символ
{t} обозначает множество всех значений этой функции. Пусть,
далее, для функции g(t) существует на множестве {t} первообраз-
первообразная функция G(t), т. е.
§ C. (8.3)
Тогда всюду на множестве {х} для функции ?[<р(лО]ф'М су-
существует первообразная функция, равная (?[ф(л:)], т. е.
J g [q. (*)] Ф' (х) dx = G [<p (х)\ + С. (8.4)
Для доказательства этого утверждения достаточно вос-
воспользоваться правилом дифференцирования сложной функции *
и учесть, что по определению первообразной G'(t)=g(t). Пред-
Предположим теперь, что нам требуется вычислить интеграл
\f{x)dx. (8.5)
В ряде случаев удается выбрать в качестве новой переменной
такую дифференцируемую функцию /=ф(лг), что имеет место ра-
равенство
f(x)=g[4(x)W(x), (8.6)
причем функция g(t) легко интегрируется, т. е. интеграл
просто вычисляется. Доказанное выше утверждение позволяет
нам написать следующую формулу для интеграла (8.5):
Этот прием вычисления интеграла (8.5) и называется интегри-
интегрированием путем замены переменной.
Конечно, такой прием применим не ко всякому интегралу.
Кроме того, следует подчеркнуть, что выбор правильной подста-
См. п. 1 § 3 гл. 5.
298 Гл. 8. Первообразная функция и неопределенный интеграл
новки в значительной мере определяется искусством вычисли-
вычислителя. Приведем ряд примеров, иллюстрирующих только что изло-
изложенный метод.
1°. Вычислить §sm3xdx. Для вычисления этого интеграла сле-
следует сделать простейшую подстановку t=3x, dt=3dx. В резуль-
результате этой замены получим
= Г— sintdt= —cos* + C = —соаЗх+С.
J 3 3 3
С dx
2°. •Вычислить I . Этот интеграл вычисляется посред-
J х + а
ством замены t=x+a, dt=dx.
При этом получим
\+C (хФ-а).
3°. Вычислить j ecos* sin x dx. Легко видеть, что этот интег-
интеграл вычисляется путем замены t=cosx.
В самом деле, при этом dt= —sinxdx и
slnxdx=—
С (зге tg яI00
4°. Вычислить — =-i— dx. Для вычисления этого интег-
рала удобна замена ^=arctgx. В самом деле, при такой замене
v Г dctg
J 1 +
+С
dtv ^(>^+
\+х* J 1 + х* J 101 101
5°. Вычислить интеграл /=J Ea;—6I984dx. Конечно, раскрывая
подынтегральную функцию по формуле бинома Ньютона, мы мо-
можем свести этот интеграл к сумме тысячи девятисот восьмидесяти
пяти табличных интегралов. Но гораздо проще сделать замену
переменной t=5x—6, dt=5dx, в результате которой мы получим,
что
5 J
/=-L [ртЛ = .??-+с =
5 J 9925
+с
9925 9925
6°. Вычислить Г . Чтобы усмотреть ту замену, посред-
J cos л;
ством которой может быть взят этот интеграл, перепишем его в
виде
С dx Г cos * dx С cosxdx
J cos x J cos2 x J 1 — sin2 x'
После этого понятно, что следует положить t=sinx> dt=cos x dx.
§ 2. Основные методы интегрирования 299
\—t
+ C=ln
tg(f + -5-Ц + С.
В результате получим
J cos* J 1— t2 2
Г я5 dx
7°. Вычислить интеграл . Для вычисления этого
J w*) *
интеграла удобна замена t=CxN, dt=4374x5dx. В результате
указанной замены получим
fi
Г <й ^arctg/ c== arctgC*)»
J 2
c== arctgC*)
4374
; + 1 4374 J t2 +1 4374 4374
С dx
8°. Вычислить I — J3/T- Для вычисления этого интегра-
ла оказывается удобной тригонометрическая подстановка й=
= arctg—, x = aigt, dx = a-
dt
cos2t
В результате этой подстановки интеграл принимает вид
Г
J
(х2 + a2N'2 a2 J a2
_ tgt , г__ х
а2 /1 + tg2 * а2 Ух2 + о2
9°. Вычислить ?то~- Здесь оказывается удобной под-
J (а2 — х2у'л
становка ^ = arcsin—, x = asint, dx = acostdt. При этом
а
Г ^ :. '[
J (ОТ JC'J ' 'О' J
a2 /1— Sin2*
cos21 a2
¦+c=-—4==+c.
10. Вычислить i "I/ ^-dx. Для вычисления этого интег-
J у ах
х
рала оказывается удобной замена 2^ = arccos—, x=acos2t
а '
dx= —2а sin 2t dt. Мы получим
Г ^/'^±^dx= -4а [coa2tdt= -4а Г f-L + J-cos 2t) dt =
J V a—x J J\2 2 /
==— 2at — 2a?cos2tdt= —2at—asia2t + C =
= — a farccos — + "l/l — (-Y 1 + C.
L a V \ a / J
300
Гл. 8. Первообразная функция и неопределенный интеграл
2. Интегрирование по частям. К числу весьма эффективных
методов интегрирования относится метод интегрирования по час-
частям. Этот метод основывается на следующем утверждении.
Пусть каждая из функций и(х) и v(x) дифференцируема на
множестве {х} и, кроме того,, на этом множестве существует пер-
первообразная для функции v(x)u'(x). Тогда на ' множестве {х} су-
существует первообразная и для функции u(x)v'(x), причем спра-
справедлива формула
J и (х) v' (x) dx = u (x) v (х) — j v (x) и' (х) dx. (8.8)
Замечание. Определение дифференциала и свойство инва-
инвариантности его формы позволяют записать формулу (8.8) в виде
(8.9)
\udv — u(x)v(x) — j vdu.
Для доказательства сформулированного утверждения запишем
формулу для производной произведения функций и(х) и v(x)
[u(x)v(x)]' = u(x)v'(x)+u'(x)v(x). (8.10)
Умножим равенство (8.10) на dx и возьмем интеграл от обеих
частей полученного таким путем равенства. Так как по условию
для всех х из множества {х} существует $v(x)u'(x)dx и
\ [u(x)v(x)]rdx=u(x)v(x)+C (см. свойство 2° из п. 3 § 1), то
для всех х из множества {х} существует и интеграл $u(x)v'(x)dx,
причем справедлива формула (8.8) (или (8.9)).
Формула (8.9) сводит вопрос о вычислении интеграла ]udv к
вычислению интеграла \vdu. В ряде конкретных случаев этот
последний интеграл без труда вычисляется.
Вычисление интеграла \udv посредством применения формулы
(8.9) и называют интегрированием по частям. Заметим, что при
конкретном применении формулы интегрирования по частям (8.9)
очень удобно пользоваться таблицей дифференциалов, выписан-
выписанной нами в п. 6 § 4 гл. 5.
Переходим к рассмотрению примеров.
1°. Вычислим интеграл I=\xn\n.xdx (пФ—1). Полагая
u = lnx, dv = xndx и используя формулу (8.9), получим du=—^-t
V — -
л+1
/ —
п + 1
— Г x"dx = —— flnx —
я+1 J л+1 V л+1
e.
2°. Вычислим, далее, интеграл I=$x arctg xdx. Полагая и =
= arctgx, dv^xdx и используя формулу (8.9), будем иметь
§ 2. Основные методы интегрирования 301
, dx хъ
du =v
1 + х2 2
/ = — arc tg x dx = — arc tg x -—!—- '¦—
2 S 2J1+X2 2 2 J 1 + *a
x2 , 1 Г . , 1 Г
= — arctgx \ dx-\ 1
2 2 J 2J
ж3 -f 1 ,
= —^— arctgx
2 &
arctgx
1+*2 2 & 2
3°. Вычислим интеграл I=$x2cosxdx. Сначала применим фор-
формулу (8.9), полагая и = х2, dv=cosxdx. Получим du = 2xdx,
y = sinx, / = A:2sin;t—2^x a'mxdx. Для вычисления последнего
интеграла еще раз применим формулу (8.9), полагая на этот раз
и = х, dv = sinxdx. Получим du—dx, v=—cos x, /=A:2sinA: +
+ 2х cos x—2jcos xdx= (x2—2) sin x+2xcos x+C.
Таким образом, интеграл lx2cosxdx вычислен нами посред-
посредством двукратного интегрирования по частям. Легко понять, что
интеграл jxn cos x dx (где п — любое целое положительное чис-
число) может быть вычислен по аналогичной схеме посредством
л-кратного интегрирования по частям.
4°. Вычислим теперь интеграл / = $ea*cos bxdx (a=const,
6=const). Сначала применим формулу (8.9), полагая и=еах,
dv = cos bxdx. Получим du=aeaxdx, v= m x ^
, eaxsinbx a {* _ . , .
/ = \ eax sin bx dx.
b 6 J
Для вычисления последнего интеграла еще раз применим форму-
формулу (8.9), полагая на этот раз и—еах, dv = sinbxdx. Получим
du = aeaxdx, v=— -
Таким образом, посредством двукратного интегрирования / по
частям мы получим для интеграла / уравнение первого порядка
(8.11). Из этого уравнения «аходим '
a cos bx -f- b sin bx .x
1 —
a2 + b2
Практика показывает, что большая часть интегралов, берущихся
посредством интегрирования по частям, может быть разбита на
следующие три группы:
1) К первой группе относятся интегралы, подынтегральная
функция которых содержит в качестве множителя одну из сле-
следующих функций: \пх, arc sin x, arc cos x, arctgx, (arctgxJ,
(arc cos xJ, 1пф(л;),... — при условии, что оставшаяся часть по-
302 Гл. 8. Первообразная функция и неопределенный интеграл
дынтегральной функции представляет собой производную извест-
ной функции (см. рассмотренные выше примеры 1° и 2°). Для
вычисления интегралов первой группы следует применить форму-
формулу (8.9), полагая в ней и(х) равной одной из указанных више
функций *.
' 2) Ко второй группе относятся интегралы вида J {ах+Ь)пХ
Xcos(cx)dx, $(ax+b)nsin(cx)dx, ]{ax+b)"ecxdx, где a, b, с — не-
некоторые постоянные, п —• любое целое положительное число (см.
рассмотренный выше пример 3°). Интегралы второй группы бе-
берутся путем я-кратного применения формулы интегрирования по
частям (8.9), причем в качестве и(х) всякий раз следует брать
(ах+b) в соответствующей степени. После каждого интегрирова-
интегрирования по частям эта степень будет понижаться на единицу.
3) К третьей группе относятся интегралы вида §еах sinbxdx,
$eaxsinbxdx, $ sin (Inx)dx, ]cos(\nx)dx, ... (см. рассмотренный
выше пример 4°). Обозначая любой из интегралов этой группы че-
через / и производя двукратное интегрирование по частям, мы соста-
составим для / уравнение первого порядка.
Конечно, указанные три группы не исчерпывают всех без ис-
исключения интегралов, берущихся посредством интегрирования по
частям. Приведем примеры интегралов, не входящих ни в одну
из перечисленных трех групп, но вычисляемых при помощи фор-
формулы (8.9).
5°. Вычислим интеграл /= \ -4-^—• Этот интеграл не входит
ни в одну из упомянутых трех групп. Тем не менее, применяя
формулу (8.9) и полагая в ней и=х, dv = — , получим
du=dx, v—
Г А С
J J sin л;
• d /sin x)
и. ^aiii л.) __ c\& X ~X~ 1 П I Sill X I -4- С
! sin x
(в проведенных рассуждениях хфпп, где п=0, ±1...).
Аналогично вычисляется интеграл 1 —-—.
6°. Вычислим, наконец, весьма важный для дальнейшего ин-
интеграл К}, = Г ш х , где а = const, Я= 1, 2, ... **. Этот интег-
интеграл также не входит ни в одну из упомянутых выше трех групп.
* В случае, если подынтегральная функция содержит в качестве множите-
множителя (arctgA;J, (arccos xJ,.... формулу интегрирования по частям (8.9) придется-
применить дважды.
** Для обозначения переменной под знаком этого интеграла нам удобнее
писать букву t.
§ 3. Классы функций, интегрируемых в элементарных функциях 303
Для вычисления этого интеграла установим для него рекуррент-
рекуррентную формулу, сводящую вопрос о вычислении Кк к вычислению
Дх_1. Можно записать (при ~Кф\):
а
dt If. ltdt
2aa J (*2+а2)я а2 l 2а2 J (*2 + а2)я"
Для вычисления последнего интеграла применим формулу интег-
d (fi 4- а2)
рирования по частям (8.9), полагая в ней u=t, dv= K г%-
Получим du = dt, v— г-.,
Из последнего равенства получим рекуррентную формулу
t 2X 3 /о о\
2а2 (X — 1) (t2 + a?)x~l a2 BX — 2)
Убедимся в том, что рекуррентная формула (8.12) позволяет
вычислить интеграл Кх для любого Х=2, 3,.... В самом деле,
интеграл Ki вычисляется элементарно:
dt 1
- +1
a J
После того как вычислен интеграл Къ полагая в формуле (8.12)
Я=2, мы без труда вычислим К.2- В свою очередь, зная /С2 и по-
полагая в формуле (8.12) Х = 3, мы без труда вычислим Кг- Продол-
Продолжая действовать таким образом дальше, мы вычислим интеграл
Кх для любого натурального X, выразив его через элементарные
функции.
§ 3. КЛАССЫ ФУНКЦИЙ, ИНТЕГРИРУЕМЫХ В
ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
Хотя, как уже отмечалось выше, неопределенный интеграл от
элементарной функции может не выражаться через элементарные
функции, все же существуют широкие классы функций, неопре-
неопределенные интегралы от которых выражаются через элементарные
функции. Изучению таких классов функций и будет посвящен
настоящий параграф.
Наиболее важным среди указанных классов функций является
класс рациональных дробей, представляющих собой, от-
304 Гл. 8..Первообразная функция и неопределенный интеграл
ношение двух алгебраических многочленов. Изучению класса ра^
циональных дробей, мы предпошлем краткие сведения о -комплекс-
-комплексных числах и об алгебраических многочленах.
1. Краткие сведения о комплексных числах. Два вещественных:
числа х и у мы будем называть упорядоченной napQU,
если указано, какое из этих чисел является первым, какое $то-
рым. Упорядоченную пару вещественных чисел х и у будем обоз-
обозначать символом (х, у), записывая на первом месте первый эле-
элемент этой пары.
Комплексным числом называется упорядоченная пара
(х, у) вещественных чисел, первое из которых х называется дей-
действительной частью, а второе у — мнимой частью
этого комплексного числа,
В случае, когда мнимая часть у равна нулю, соответствующую
пару (х, 0) договариваются отождествлять . с вещественным чис-
числом х. Это позволяет рассматривать множество всех веществен-
вещественных чисел как подмножество комплексных чисел.
Два комплексных числа Z\=(xu У\) u.z2=(x2, у2) называются
равными, если хх — х2, У\ — у2. Говорят, что комплексное число
z=(x,y) равно нулю, если х=0 и у = 0.
Определим операции сложения и умножения комплексных чи-
чисел. Поскольку вещественные числа являются подмножеством
комплексных чисел, эти операции должны быть , определены так,
чтобы в применении к двум вещественным числам они приводили
к уже известным нам из § 4 гл. 2 определениям суммы и произ-
произведения вещественных чисел.
Суммой двух комплексных чисел z\= (x\, у\) и 22 = (Х2, у2)
назовем комплексное число z вида
yi+y2). (8.13)
Произведением двух комплексных чисел Zi= (х\, г/j) и
= (х2, г/г) назовем комплексное число z вида
2= {х{х2—у{у2, x^y2+x2yi). (8.14)
Легко проверить, что сумма и произведение комплексных чисел
обладают теми же самыми свойствами, что и сумма и произве-
произведение вещественных чисел. Именно справедливы следующие свой-
свойства:
1°. z\ + z2 = z2-\-Z\ (переместительное свойство суммы).
2°. (zi+z2) +23 = Zi+ (z2+z3) (сочетательное свойство суммы).
3°. 2+@,0) =z (особая роль числа @, 0)).
4°. Для каждого числа z= {x, у) существует противоположное
ему число г'= (—х, —у) такое, что z+z'= @, 0).
5°. z\-Zi = z2-Zi (переместительное свойство произведения).
6°. (zi-z2) •z%=Z\" (z2-z3) (сочетательное свойство произведе-
произведения).
7°. 2-A,0) =2 (особая роль числа A,0)).
§ 3. Классы функций, интегрируемых в элементарных функциях 305»
8°. Для любого комплексного числа z=(x, у), не равного ну-
нулю1, существует обратное ему число г'= (— -, -1 та-
такое, что z-z''= A,0).
9°. (zi+Z2)-Z3 = zi-Z3 + Z2-z3 (распределительное свойство про-
произведения относительно суммы).
Свойства 1°—9° позволяют утверждать, что для комплексных
чисел полностью сохраняются все правила элементарной алгебры,,
относящиеся к арифметическим действиям и к сочетанию ра-
равенств.
Кроме того, эти свойства полностью решают вопрос о вычита-
вычитании комплексных чисел как о действии, обратном сложению, и о-
делении комплексных чисел как о действии, обратном умноже-
умножению.
Разностью двух комплексных чисел Zi=(x\, у\) и z2 =
= (*2, У2) называется такое комплексное число z, которое в сум-
сумме с z2 дает Z\. С помощью свойств Г—4° элементарно устанав-
устанавливается существование и единственность разности двух любых,
комплексных чисел *.
Легко проверить, что разностью двух комплексных чисел
Z\=(x\, у\) и 22= (х2, Ц2) является комплексное число z вида
z=(xi—x2; У1—У2). (8.15)
Частным двух комплексных чисел z\ = [xi, у\) и z%= (X2, Уг),
второе из которых не равно нулю, называется такое комплексное-
число z, которое при умножении на z2 дает Z\. С помощью»
свойств 5°—8° легко установить, что единственным частным двух
указанных комплексных чисел является комплексное число z:
вида
/ *i*2 + У\Уг хъУ\ — Х\Уг
\ 4+у22 ' 4+У2
В операциях с комплексными числами особую роль играет
число, представимое парой @, 1) и обозначаемое буквой i. Умно-
Умножая эту пару самое на себя (т. е. возводя ее в квадрат), полу-
получим в силу определения произведения комплексных чисел
@, 1) • @, 1) = (-1,0) = -1, т. е. Р= -1.
Заметив это, мы можем любое комплексное число z= (x, у),
представить в виде
2= {х, у) = (х,0) + @, у) = (*, 0) + (у, 0) ¦ @, 1) =x+iy.
В дальнейшем мы будем широко использовать для комплекс-
комплексного числа z= (x, у) представление z=x+iy. Это представление--
* Для этого следует дословно повторить рассуждения, проведенные в гл. 2:
для случая разности двух вещественных чисел (см. п. 1 § 5 гл. 2).
306 Гл. 8. Первообразная функция и неопределенный интеграл
и рассмотрение i в качестве множителя, квадрат которого равен
— 1, позволяет производить операции с комплексными числами
так же, как они производятся с алгебраическими многочленами.
Комплексное число z = {x, —у)—х—iy принято называть соп-
сопряженным по отношению к комплексному числу z = (х, у) =
y
Очевидно, что комплексное число равно нулю тогда и только
тогда, когда равно нулю сопряженное ему число *.
Для геометрического изображения комплексных чисел удобно
пользоваться декартовой прямоугольной системой координат.
При этом комплексное число z= (х, у) изображается или точкой
—*•
М с координатами (х, у), или вектором ОМ, идущим из начала
координат в точку М.
При таком способе изображения сложение и вычитание ком-
комплексных чисел сводится к сложению и вычитанию соответствую-
соответствующих им векторов (это понятно из формул (8.13) и (8.15)).
Непосредственно из определения (8.14) произведения двух
комплексных чисел вытекает следующее утверждение: про-
произведение двух (а значит, и нескольких) комплексных чисел рав-
равно нулю тогда и только тогда, когда обращается в нуль хотя бы
¦один из сомножителей.
В самом деле, если хотя бы одно из чисел Zi=(xu y{) и
•22= (хг, г/2) равно @,0), то из (8.14) очевидно, что z=ZiZ2 =
= @,0).
Если, наоборот, z=Z\Z2 равно @,0), то из (8.14) следует,
что
0, (8.14')
1 угх2 + хгу2 = 0,
и если 21=7^@, 0), т. е. х\-\-у\ФО, то (8.14') представляет собой
однородную систему двух уравнений относительно двух неизвест-
неизвестных х2 и г/2 с определителем x^+yf, отличным от нуля. Такая
система имеет только тривиальное решение, т. е. Z2=(^2, г/г) =
= @,0).
Непосредственно из определения (8.14) произведения двух
комплексных чисел вытекает и еще одно утверждение: ком-
комплексное число, сопряженное к произведению двух (а значит, и
нескольких) комплексных чисел, равно произведению комплекс-
комплексных чисел, являющихся сопряженными к каждому из сомножите-
сомножителей, т. е.
(8.14")
— y = 0.
§ 3. Классы функций, интегрируемых в элементарных функциях 307
С помощью правила перемножения комплексных чисел (8.14)
легко проверяется, что как правая, так и левая часть (8.14")
равна одному и тому же комплексному числу (х\Х%—у\Уч.>,
)
уУ)
2. Краткие сведения о корнях алгебраических многочленов.
1°. Алгебраическим многочленом я-й степени на-
называется выражение вида
f(z) =C0Zn + CiZ«-l + ... + Cn-iZ + Cn, (8.16}
где z= (x, y)=x+iy ¦— переменное комплексное число, а СоУ
С\,..., сп — некоторые постоянные комплексные числа, первое из
которых отлично от нуля. Как известно, любой алгебраический
многочлен степени я можно поделить «столбиком» на другой ал-
алгебраический многочлен степени не выше чем п. Таким путем мы
приходим к следующему утверждению: каковы бы ни были два
многочлена f(z) и cp(z) такие, что степень q(z) не выше, чем сте-
степень f(z), справедливо равенство
f(z)=<f(z)-q(z)+r(z), (8.17)
в котором q(z) и r(z) — некоторые многочлены, причем степень
q(z) равна разности степеней многочленов f(z) и q>(z), а степень
r(z) ниже степени q>(z).
По отношению к фигурирующим в равенстве (8.17) много-
многочленам f{z), q>(z), q(z) и r(z) обычно применяют вполне понят-
понятные термины «делимое», «делитель», «частное» и «остаток».
Говорят, что многочлен f(z) делится на многочлен <p(z), если;
в полученной посредством деления столбиком формуле (8.17)
остаток г (г) =0.
Договоримся называть многочленом нулевой сте-
степени любую комплексную постоянную. Тогда совершенно ясно,
что любой многочлен делится на отличный от нуля многочлея
нулевой степени. Изучим вопрос о делимости многочлена f(z) на
многочлен первой степени.
Определение. Назовем комплексное число Ъ корнем
многочлена f(z), если f(b) равно нулю.
Теорема 8.2. Многочлен ненулевой степени f(z) делится
на двучлен (z—b) тогда и только тогда, когда Ь является корнем
многочлена.
Доказательство. Запишем для многочленов /(z) и
<p(z) = (z—b) формулу (8.17). Поскольку степень остатка r(z) в
этой формуле обязана быть ниже степени делителя (p(z)=z—b,
то r(z) — многочлен нулевой степени, т. е. r(z) =c=const. Таким
образом, формула (8.17) принимает вид
f(z) = (z-b)q(z)+c.
Полагая в формуле (8.18) z=b,. найдем, что c — f(b). По опре-
определению f{z) делится на (z—b) тогда и только тогда, когда ос-
308 Гл. 8. Первообразная функция и неопределенный интеграл
таток в формуле (8.18) c — f{b) равен нулю, т. е. тогда и только
тогда, когда Ь является корнем f(z). Теорема доказана.
2°. Естественно, возникает вопрос, всякий ли алгебраичесдшй
многочлен имеет корни? Ответ на этот вопрос дает основная
теорема алгебры*: всякий многочлен ненулевой степени
имеет хотя бы один корень.
Опираясь на эту теорему, докажем, что алгебраический мно-
многочлен п-й степени имеет точно п корней**. В самом деле, пусть
f(z) — многочлен п-й степени. Согласно основной теореме алгеб-
алгебры /(z) имеет хотя бы один корень Ь\, т. е. для /(г) справедливо
представление
в котором через /1B) обозначен некоторый многочлен степени
(п—1). Если пф\, то, согласно основной теореме алгебры, fi(z)
имеет хотя бы один корень Ь2, т. е. для ft (z) справедливо пред-
представление
h(z) = (z-b2)h(z), (8.192)
ъ котором через f2(z) обозначен некоторый многочлен степени
{п—2). Повторяя указанные рассуждения далее, мы получим
"представления
f2(z) = (z-b3)f3(z), (8.193)
fn_,(z) = (z-6l,)/-(z). (8.19")
В последнем из этих представлений через fn(z) обозначен некото-
некоторый многочлен нулевой степени, т. е. fn(z) =c = const. Сопостав-
Сопоставляя между собой равенства (8.191) — (8.19") и учитывая, что
/„(z)=c, будем иметь
f (z) = (z-6,) (z-b2)... (z-bn) с (8.20)
Отметим, что комплексная постоянная с не равна нулю, ибо в
противном случае многочлен f(z) был бы тождественно равен
нулю и не являлся бы многочленом п-й степени ***.
Из равенства (8.20) очевидно, что f(bi)=f(b2)=...=f(bn)=0,
т. е. каждое из чисел Ьи Ь2,.... Ьп является корнем многочлена
f(z). Кроме того, из (8.20) очевидно, что, каково бы ни было
комплексное число Ь, отличное от Ьи Ь2,...,Ьп, комплексное число
* Доказательство основной теоремы алгебры обычно приводится в курсах
алгебры и в курсе теории функций комплексной переменной.
** При этом, конечно, предполагается, что п>0.
*** Здесь мы используем следующее утверждение: если многочлен /(г) =
=aozn+alzn-i + ...-i-an_lz+dn тождественно равен нулю, то все его коэффи-
коэффициенты равны нулю. В самом деле, если f(z)s=0, то при z=0 получим ап=0.
Нотогда f (z) =z[ao2n~I + aiz7I-2+---+an-i] =0. Так как гФО, то выражение в
квадратных скобках тождественно равно нулю, откуда при 2 = 0 получим
a,i_i=0. Продолжая аналогичные рассуждения далее, докажем, что все коэф-
коэффициенты равны нулю.
§ 3. Классы функций, интегрируемых в элементарных функциях 309
f(b) не равно нулю *. Таким образом, многочлен f(z) имеет
ровно п корней: Ьи Ь2 Ьп.
Равенство (8.20) дает разложение многочлена f(z) на множи-
множители. Если известен вид многочлена /(г) (8.16), то мы можем
определить постоянную с в равенстве (8.20). Сравнивая в равен-
равенствах (8.20) и (8.16) коэффициенты при г™, получим с — с0**.
Многочлен (8.16), у которого со=1, называется при вед еч-
н ы м. Для приведенного многочлена формула разложения (8.20J*
принимает вид
/B) = B-Ь,)(г-Ь2)...(г-Ьп). (8.21)
В Дальнейшем, если не оговорено противное, мы будем рассмат-
рассматривать приведенные многочлены.
Среди корней многочлена f(z) могут быть совпадающие кор-
корни. Пусть а, Ь,...,с — различные корни приведенного много-
многочлена f(z).
Тогда для этого многочлена представление вида (8.21) прини-
принимает форму следующего равенства:
f(z) = (z—a)«B—Ъ)К.{г—ф. (8.22)
В этом разложении а, р,..., у — некоторые целые числа, каждое
из которых не меньше единицы, причем a+fi + ... + y = n, где п —
степень многочлена f{z).
Если для многочлена f(z) справедливо разложение (8.22), то
говорят, что комплексное число а является корнем f(z) крат-
кратности а, комплексное число Ь является корнем f(z) крат-
кратности р,..., комплексное число с является корнем f(z) крат-
кратности у.
Корень, кратность которого равна единице, принято называть
однократным, а корень, кратность которого больше едини-
единицы, принято называть кратным.
Можно дать и другое эквивалентное определение корня дан-
данной кратности: комплексное число а называется корнем много-
многочлена f(z) кратности а, если для f(z) справедливо представ-
представление
, где <р(а)^=О. (8.23)
Пусть теперь
f(z) =zra + c1zn-1 + C2Zra-2+...+cn (8.24)
приведенный алгебраический многочлен с вещественными
коэффициентами сь с2,..., сп.
* Ибо произведение нескольких комплексных чисел равно нулю лишь в
том случае, когда равен нулю хотя бы один из сомножителей (см. п. 1).
** Здесь мы используем утверждение: если два многочлена aozn+uizn~l+...
~..+ап и bozn + bjZn-1 + ...-{-bn тождественно равны друг другу, то ао=6о.
Я\ — Ь\,..., ап — Ьп. Для доказательства достаточно к разности указанных много-
многочленов применить утверждение, отмеченное в сноске *** на с. 308.
310 Гл. 8. Первообразная функция и неопределенный интеграл
Докажем, что этот многочлен обладает следующим важным
свойством.
Теорема 8.3. Если комплексное число а является корнем
многочлена с вещественными коэффициентами (8.24) кратности
Я, то и сопряженное ему комплексное число а также является,
корнем этого многочлена той же самой кратности Я.
Доказательство. Начнем с того, что докажем следую-
следующий вспомогательный факт: если f(z) — многочлен с вещест-
веществе нн ым и коэффициентами, то комплексная величина f(z}
является сопряженной по отношению к величине f(z).
Так как коэффициенты многочлена (8.24) являются вещест-
вещественными числами, то для доказательства указанного факта дос-
достаточно убедиться в том, что для любого номера п комплексная:
величина (г)" является сопряженной по отношению гп. Но это-
последнее сразу вытекает из утверждения, доказанного в самом
конце п. 1, точнее, из соотношения (8.14^)_. Положив в этом соот-
соотношении zl = z2 = z, мы получим, что (г2) = BJ. Далее, поло-
положив в том же соотношении (8.14"), Z\~z2, z2=z, мы получим;
(?) = (?) г = GK.
Продолжая аналогичные рассуждения, мы убедимся в том, чтсь
(zn) = (z)n для любого номера п.
Итак, доказано, что величина f(z) является сопряженной no-
отношению к величине /(г), т. е.
или, что то же самое,
fS (8.25)
Пусть теперь комплексное число а является корнем много*
члена с вещественными коэффициентами f(z) кратности К, т. е„
справедливо представление
f(z) = (z-o)\p(z), (8.26>
в котором
<р(а)Ф0. (8.27>
Из сопоставления (8.26) и (8.25) вытекает, что
f(z) = (z~a)\(z),
а последнее равенство в силу (8.14") можно переписать в виде
/B) = (г—a)*q>B). (8.28>
Заметим теперь, что в силу установленного выше соотноше-
соотношения (zn) = (г") справедливо равенство
{z-af = {Г—a? = (z—a)\ (8.29)
§ 3. Классы функций, интегрируемых в элементарных функциях 311
Подставляя (8.29) и (8.28), мы получим представление
/(z) = (z-a)N|>(z), (8.30)
в котором через г|)(г) обозначена величина
Ф^Г (8-31)
Для завершения доказательства теоремы 8.3 остается убе-
убедиться в том, что г|)(а)=/=0*, но это сразу вытекает из того, что «в
>силу того, что согласно (8.27) ср(а) не обращается нуль**. Теоре-
Теорема 8.3 доказана.
3. Разложение алгебраического многочлена с вещественными
коэффициентами на произведение неприводимых множителей.
В дальнейшем нам придется иметь дело с многочленами от пере-
переменной, принимающей лишь вещественные значения. По-
Поэтому эту переменную мы будем обозначать буквой х, а не z.
Пользуясь теоремой 8.3, найдем разложение многочлена с ве-
вещественными коэффициентами f{x) на произведение неприводи-
неприводимых вещественных множителей. Пусть многочлен f(x) имеет ве-
вещественные корни Ь\, Ь2,..., Ьт кратности рь C2,..., рт соответствен-
соответственно и комплексно сопряженные пары корней а,\ и й\, а2 и аг,..-, ап
и ап кратности Х\, Яг, ...Д« каждая пара соответственно.
Тогда, согласно результатам п. 2, многочлен f(x) может быть
представлен в виде
/(х) = (х-Ь/' (x-b2f\ . .{x-bjrn х
X (x-a/'(*-«/'(*-a/2(*-a/2- • .(x-an)K"(x-a/n. (8.32)
Обозначим вещественную и мнимую части корня ctk (k=\,2,..., ri)
соответственно через uk и vk, т. е. пусть ak = uk + ivk. Тогда
йк = ик—ivk. Преобразуем для любого ? = 1,2,..., п выражение
(x-ak)h (x-~akfb = Цх-ак) (х-?
= [(x—uk—ivk) (x-uk + ivk)f
Pkx + qk)\ (8.33)
где pfc= — 2uk, qk =
Используя (8.33) в (8.32), окончательно получим следующее
разложение многочлена f(x) на произведение вещественных не-
неприводимых множителей:
* Ибо представление (8.30) при условии \р(а)фО и означает по определе-
определению, что комплексное число а является корнем многочлена }(z) кратности %.
** Мы учитываем, что комплексное число равно нулю тогда и только тогда,
жогда равно нулю сопряженное ему комплексное число (см. п. 1 настоящего
параграфа).
312 Гл. 8. Первообразная функция и неопределенный интеграл
/ \x> — \x ul) \x иг) • • ¦ \x um) л
X (x2 + Plx + 9l)fcl (x2 + p2x + q2)K ...(x2 + pnx + qn)\ (8.34)
Мы приходим к выводу, что многочлен f(x) с вещественными
коэффициентами распадается на произведение (8.34) неприводи-
неприводимых вещественных множителей, причем множители, соответствую-
соответствующие вещественным корням, имеют вид двучленов в степенях, рав-
равных кратности корней, а множители, соответствующие комплекс-
комплексным парам корней, имеют вид квадратных трехчленов в степе-
степенях, равных кратности этих пар корней.
4. Разложение правильной рациональной дроби на сумму прос-
простейших дробей. Рациональной дробью называется отно-
отношение двух алгебраических многочленов.
Всюду в дальнейшем мы будем рассматривать рациональную
дробь, являющуюся отношением двух алгебраических многочле-
многочленов с вещественными коэффициентами (такую дробь при-
принято называть рациональной дробью с веществен-
вещественными коэффициентами).
Р (х)
Рациональная дробь —— называется правильной, если
степень многочлена Р(х), стоящего в числителе, меньше степени
многочлена Q(x), стоящего в знаменателе.
В противном случае рациональная дробь называется непра-
неправильной.
Докажем две вспомогательные теоремы.
Р (х)
Лемма 1. Пусть —— правильная рациональная дробь
с вещественными коэффициентами, знаменатель Q(x) которой
имеет вещественное число а корнем кратности а, т. е.
Q(x) = (x—a)aq{x), где ц>(а)фО. (8.35)
Тогда для этой дроби справедливо следующее представление:
Р(х) А , ¦ $(х) .
Q(x) {х-of- (x-a)a~k<f(x)'
В этом представлении А — вещественная постоянная, равная:
Л = ——, k — целое число, удовлетворяющее условию &>1,
<р(а)
•§(х) — некоторый многочлен с вещественными коэффициентами
такой, что последняя дробь в правой части (8.36) является пра~
вильной.
Доказательство. Обозначив через А. — вещественное
число А = —— , рассмотрим разность
Ф(а)
* Число А всегда определено, ибо у(а)фО в силу (8.35).
§ 3. Классы функций, интегрируемых в элементарных функциях 313
Р(х) А
Q(x) (x-af
Приводя эту разность к общему знаменателю, будем иметь
Р(х) А _ Р(х)-Ац>(х) _ Ф(х)
Q(x) (x-af (х-а)а<?(х) (* - а)а q> (*) '
где через Ф(х) обозначен многочлен с вещественными коэффи-
коэффициентами вида Ф(х)=Р{х)—Ац>(х).
Так как Ф (а) = Р (а) —Ац> (а) = Р (а) —^- «р (а) = 0, вещест-
ф(а)
венное число а является корнем многочлена Ф(к) некоторой ^крат-
^кратности &>1.
Это означает, что справедливо представление
Ф{х) = (х—а)ку(х), где $(а)фО, (8.38)
а 1|)(лг) — некоторый многочлен с вещественными коэффициен-
коэффициентами.
Вставляя представление (8.38) в равенство (8.37), окончатель-
окончательно будем иметь
Р(Х) А _ !(>(*) .
Q(x) (x-a)a (x-af-k<?(x)'
Тем самым представление (8.36) доказано. Остается только
убедиться в том, что дробь, стоящая в правой части (8.39), явля-
является правильной, но это сразу вытекает из того, что разность двух
правильных рациональных дробей является правильной рацио-
рациональной дробью (чтобы убедиться в этом, достаточно привести
разность правильных рациональных дробей к общему знаменате-
знаменателю). Лемма 1 доказана.
Р (х)
Лемма 2. Пусть —— правильная рациональная дробь
с вещественными коэффициентами, знаменатель которой Q(x.)
имеет комплексные числа a = u+iv и а —и—iv корнями кратности
Я, т. е.
(x), где <?(а)фО, <р)
(8.40)
р=—2и, q = u2+v2.
Тогда для этой дроби справедливо следующее представление:
Р(х) _ Mx + N тК*) (84П
QOc) (х* + рх + qf- ^ (х* + рх + qt~kф(к) ' У' '
В этом представлении М и N — некоторые вещественные посто-
постоянные, k — целое число >1, а ty(x) — некоторый многочлен с
вещественными коэффициентами такой, что последняя дробь в
правой части (8.41) является правильной.
314 Гл. 8. Первообразная функция и неопределенный интеграл
Доказательство. Договоримся обозначать вещественную
часть комплексной величины А символом Re [Л], мнимую часть
комплексной величины А символом 1т[Л]. Положим*
м, 1 т Г Р(а) 1 », т, Г Р(а) I и г Г Р(а)
М = — Im —— , N = Re —*-?- Im ' ——
v I ф(а) J I <t(a) } v [ ф(а)
Нетрудно проверить, что указанные М и jV являются решением
следующего уравнения:
Р{а)~ (Ma+N)q>{a)=0. (8.42)
В самом деле, поделив это уравнение на ср(а) и приравняв нулю
действительные и мнимые части, мы получим два равенства
Р(а)
ф(а)
Р(о)
ф(а)
из которых определяются написанные выше М и N. Рассмотрим
теперь разность
Р(х) Mx + N
Q(x) (x* + px + qt "
Приводя указанную разность к общему знаменателю, будем иметь
Р(х) Mx + N = Р (х) - (Мх + N) Ф (х) = Ф(х)
Здесь через Ф (х) обозначен многочлен с вещественными коэффи-
коэффициентами вида Ф(х)=Р(х)—(Mx+N)q(x). Равенство (8.42) позво-
позволяет утверждать, что комплексное число а, а значит, в силу теоре-
теоремы 8.3 и сопряженное ему число а являются корнями многочлена
Ф(х) некоторой кратности fe>l. В таком случае для многочлена
Ф(х) справедливо представление
Ф{х) = (х2+рх+д)^(х), (8.44)
'где i|j(#) — некоторый многочлен с вещественными коэффициента-
коэффициентами, не имеющий в качестве корней числа а и а. Вставляя пред-
представление (8.44) в формулу (8.43), пслучим представление (8.41).
Тот факт, что последняя дробь, стоящая в правой части (8.41), яв-
является правильной, вытекает из того, что эта дробь равна разно-
разности двух правильных дробей.
Лемма 2 доказана.
Р (х)
Последовательное применение лемм 1 и 2 к дроби —— по
-> Q \х)
Р(а)
* В силу (8.40) <р(а)?=0, так что отношение — рассматривать
ф(а)
можно.
§ 3. Классы функций, интегрируемых в элементарных функциях 315
всем корням знаменателя приводит нас к следующему замечатель-
замечательному утверждению.
Р (х\
Теорема 8.4. Пусть —— правильная рациональная дробь
с вещественными коэффициентами, знаменатель которой имеет вид
(8.45)
Тогда для этой дроби справедливо следующее разложение на сум-
сумму простейших дробей:
р(х) Bi" 41' 4"
A) {by '" (b^
Q(x)
(x-bm)
+ Pix + ftJ + + (*» + PlX +
+ ,.. ... ¦ '+,..._¦¦ , „ + •••+—" -ГГ- (8-46)
В этом разложении B\l\ В$\ ..., fig, М?, М'\ • ¦ ¦, М№п, NQ —
некоторые вещественные постоянные, часть из которых может быть
равна нулю.
Замечание. Для конкретного определения только что ука-
указанных постоянных следует привести равенство (8.46) к общему
знаменателю и после этого сравнивать коэффициенты при одина-
одинаковых степенях х в числителе.
Примеры и разъяснения.
1°. Разложить на сумму простейших правильную дробь
Убедившись в том, что квадратный трехчлен х2+х+1 имеет комп-
комплексные корни, ищем, согласно теореме 8.4, разложение дроби
(8.47) в виде
2*3 + 4*2 + * + 2 = ^ + -^- + "* + N 48)
(v __ П2/Л L v t П /v 1 \ / *. 142 v2 _L_ v _L 1
Л I J ^Л —p Л -р I ^ ^А 1) уХ I J X ~~у~ X —р 1
Приводя равенство (8.48) к общему знаменателю, получим
2х3 + 4х2-\-х-\-2 _ В1(х3 — 1) + В2(х2 + х + I) + (Мх + N) (х2 — 2х + 1)
316
Гл. 8. Первообразная функция и неопределенный интеграл
Сравнивая в числителях коэффициенты при хР, х1, х2 и х3, придем
к системе уравнений *
Вх + М = 2,
B.2+N—2M = 4,
Решая эту систему, найдем #i = 2, 5г=3, УИ=О, N=\. Окончатель-
Окончательно получим
2х3 + 4л:2 + х + 2 _ 2.3, 1
¦ 1' (х ¦
IJ
(8.49)
Только что проиллюстрированный метод отыскания разложения
правильной рациональной дроби называется методом неопре-
неопределенных коэффициентов. Этот метод приводит к цели
всегда; доказывать разрешимость полученной в результате приме-
применения этого метода системы уравнений не нужно — разрешимость
вытекает из теоремы 8.4.
2°. Проиллюстрируем метод неопределенных коэффициентов
еще одним примером. Требуется найти разложение правильной
дроби
Так как квадратный трехчлен х2+1 имеет комплексные корни,
ищем, согласно теореме 8.4, разложение в виде
3xi + 2х3 -f Зх2 — 1 _ В Mxx + Ni MjX + Nj
Последнее равенство приводим к общему знаменателю и после
этого сопоставляем числители. Получим
= В(х*+2х2+\) + (Afjjc+tfi) (х3—2х2 + х~2) + (M2x+N2) (х—2).
Сравнивая коэффициенты при х°, х\. х2, х3 и л:4, придем к системе
уравнений
+ Мх =3,
1 — 2M1 =2,
B + M1 — 2N1 + Mi =3,
=— 1.
11
[B—2N1—2N2
* При этом мы используем утверждение, сформулированное в сноске ***
на с. 308.
§ 3. Классы функций, интегрируемых в элементарных функциях 317
Решая эту систему, найдем В = 3, М^ = 0, Ni=2, M2~l, N2=0~
Окончательно получим
»i 3l * (8.50>
2+1)а*
(х —2)(л-2+1J х— 2 х2+1 (х2+1)а*
3°. Метод неопределенных коэффициентов, как видно из рас-
рассмотренных примеров, является довольно громоздким. Естествен-
Естественно поэтому в тех случаях, когда это возможно, найти другой, более
простой метод отыскания коэффициентов в разложении правиль-
правильной рациональной дроби на сумму простейших. Пусть знамена-
Р (х)
тель Q(x) правильной рациональной дроби —-— имеет вещест-
венное число а корнем кратности а. Тогда.среди простейших дро-
дробей, на сумму которых раскладывается дробь ——, будет фигу-
фигурировать дробь
^ а . (8.51)
Укажем совсем простой метод вычисления коэффициента А при
этой простейшей дроби. Привлекая лемму 1 и формулу (8.36), мы
убедимся в том, что коэффициент А равен
А = —J—, где ф (х) = —•L-^-L—.
Q(a) {x—df
Мы приходим к следующему правилу: для вычисления коэффици-
коэффициента А при простейшей дроби (8.51), соответствующей веществен-
вещественному корню а многочлена Q (х) кратности а, следует вычеркнуть в
Р (х)
знаменателе дроби —-— скобку (х—а)" и в оставшемся выраже-
выражении положить х = а.
Указанный прием нахождения коэффициента А обычно назы-
называют методом вычеркивания. Отметим, что этот прием при-
применим лишь для вычисления коэффициентов при старших степенях
простейших дробей, соответствующих вещественным корням Q (х).
Метод вычеркивания особенно эффективен в случае, когда зна-
знаменатель Q (х) имеет лишь однократные вещественные корни, т. е.
когда Q(x) = (x—ai) (x—a2)...(x—а„). Тогда, как мы знаем, спра-
справедливо разложение
р(х) _ Ai | Ла' | | Ak j | Ап
Q(x) х—аг х—а2 "' x—ak '" х—ап'
все коэффициенты которого могут быть вычислены по методу
вычеркивания. Для вычисления коэффициента Ак следует вычерк-
Р (х}
нуть в знаменателе дроби —— скобку {х—ак) и в оставшемся
выражении положить х~ак.
318 Гл. 8. Первообразная функция и неопределенный интеграл
Пример. Найти разложение дроби
?±i . (8.52)
(х-\)х(Х-2)
"Согласно теореме 8.4 пишем:
,11 Я Л Л
(х— \)х(х — 2) ж —1 х х — 2
Для отыскания А\ вычеркиваем в выражении (8.52) скобку (л;—Г)
и в оставшемся выражении берем х—1. Получим А\ ——2. Анало-
Аналогично находим А2 = —, Л3 = 3/2.
Окончательно получим
—*±1 = _=i2_+_L+—з— (853)
{х — \)х(х — 2) х — \ 2х 2(х—2)
5. Интегрируемость рациональной дроби в элементарных функ-
функциях. Теперь мы подготовлены к тому, чтобы в общем виде ре-
решить проблему об интегрировании рациональной дроби с вещест-
вещественными коэффициентами.
Прежде всего отметим, что эта проблема сводится к проблеме
интегрирования только правильной рациональной дроби, ибо вся-
всякую неправильную рациональную дробь можно (посредством деле-
деления числителя на знаменатель «столбиком») представить в виде
-суммы алгебраического многочлена и правильной рациональной
дроби.
Пример. —— = (лг—2х)-\ — , ибо
х*—
х3+\ | х2 + х + 2
3 + 22
. О уЗ ___ Q j»2 I 1
~— 2л;3 — 2х2—4л;
остаток 1 + 4л;
Интегрировать многочлен мы умеем (напомним, что неопреде-
неопределенный интеграл от многочлена представляет собой некоторый
многочлен степени, на единицу более высокой). Остается научить-
научиться интегрировать правильную рациональную дробь. В силу теоре-
теоремы 8.4 проблема интегрирования правильной рациональной дроби
сводится к интегрированию простейших дробей следующих четы-
четырех типов:
I. -J-; П. —Ё-^; Ш. W + N ^ Mx + N
х—Ь (x — bf x2-+ px + q (х2 + рх + q)*- v
Здесь р = 2, 3, ... ; Л,=2, 3 ,... ; В, М, N, Ь, р, q — некоторые веще-
§ 3. Классы функций, интегрируемых в элементарных функциях 319
ственные числа, причем трехчлен x2+px+q не имеет веществен-
вещественных корней, т. е. q > 0.
4
Докажем, что каждая из четырех указанных дробей интегри-
интегрируема в элементарных функциях.
Дроби вида I и II элементарно интегрируются при помощи под-
подстановки t—x—b. Мы получим
В dx B{^ B\n\t\+C B\n\xb\+C (8.55>
J
x—b • J t
dt В 1 , „ —В
(8.56>
Для вычисления интеграла от дроби вида III представим квадрат-
квадратный трехчлен в виде х2 + рх + q= Iх + — ) +lq—^-) и, учиты-
учитывая, что q—— > 0, введем в рассмотрение вещественную по-
4
стоянную а = ,+ |/ q——. Сделав подстановку t = x+~?>
будем иметь
/ Мр
Mt+\N — —f-
2
2a
arctg——L= + C. (8.57>
Остается вычислить интеграл от дроби вида IV. Используя вве-
введенные выше обозначения t = x-\-—, a—t/q ——, будеш
иметь
320 Гл. 8. Первообразная функция и неопределенный интеграл
ь
^ «+(»q,
f J fc
М rd(^ + Q2) tN__'Mp_\ Г
V 2 ) J
= N
2 J (Я + «2)^ V 2 ) J (/» + а2)*' "
Введем обозначения
Интересующий нас интеграл будет вычислен, если будут вычисле-
вычислены интегралы / и Кх. Интеграл / берется элементарно:
/= 1 1 , С^ 1 ' , с
(А,-1) (/2 + с2)^1 (l-l) (x* + + )x~x
Интеграл Кх вычислен нами в примере 6 в конце § 2 настоящей
главы. Там мы получили для этого интеграла рекуррентную форму-
формулу C.12), позволяющую последовательно вычислить Кх для любо-
то Я=2, 3, ..., опираясь на то, что
Г dt 1 , t
= 1ГГ^ = — arctg—
с.
Итак, нами вычислены интегралы от всех четырех простейших
дробей (8.54) и доказано, что каждый из этих интегралов пред-
представляет собой элементарную функцию *. Тем самым мы приходим
к следующей теореме, исчерпывающей проблему интегрирования
рациональной дроби.
Теорема 8.5. Всякая рациональная дробь с вещественными
коэффициентами интегрируема в элементарных функциях.
В заключение этого параграфа мы остановимся на примерах
вычисления неопределенных интегралов от рациональных дробей.
Вычислим неопределенные интегралы от трех дробей, рассмотрен-
рассмотренных в предыдущем параграфе, (8.49), (8.50) и (8.53)-. Пользуясь
указанными тремя формулами, а также формулами (8.55) —
(8.57), будем иметь:
•*+b?
г» 2*»
• J (Х_
Jt-1
* Точнее, выражается через логарифм, арктангенс и рациональную функ-
функцию.
§ 3. Классы функций, интегрируемых в элементарных функциях 321
xdx
, Г- 3_rf +f
3d*
У(х-1)х(х-2) J x—1 J 2x J 2(*-2)
1 ч
nl_ I v I I _1_ J In I v\ _L In I v 9 I -L С
6. Интегрируемость в элементарных функциях некоторых три-
тригонометрических и иррациональных выражений. В рассуждениях
настоящего пункта важную роль будет играть рациональная
функция от двух аргументов. С определения такой
функции и выяснения некоторых ее свойств и начнем наше изло-
изложение.
Многочленом степени п от двух аргументов х и у назы-
называется выражение вида
Рп(х, у) =аоо+а1оХ+ао1у + а2оХ2 + ацху-{ ао2У2+ ... +аОпуп,
в котором через аОо, аю, ..., аы обозначены некоторые постоянные
вещественные числа такие, что среди чисел ano, a(n-i)i, й(п-2>2, ...
..., аОп есть хотя бы одно число, отличное от нуля.
Рациональной функцией от двух аргументов
х и у называется выражение вида
в котором через Рп{х, у) обозначен произвольный многочлен от
двух аргументов х и у степени п, а через Qm(x, у) обозначен про-
произвольный многочлен от двух аргументов х и у степени т.
Справедливо следующее тривиальное утверждение: если
R (х, у) — рациональная функция от двух аргументов х и у, а
-#i@> -#2@ и ЯзЩ—три произвольных рациональных функции
от одной переменной t *, то выражение вида
R[Ri(t), Ra(t)]Rs(t) (8.58)
представляет собой рациональную функцию от одной переменной.
Для доказательства этого утверждения достаточно заметить,
что в результате применения к рациональным функциям одной пе-
* Под термином «рациональная функция от одной переменной t* мы пони-
л рациональную дробь с вещественными коэффициентами от аргумента t.
маем рациональную дроб
11 Зак. 72
322 Гл. 8. Первообразная функция и неопределенный интеграл
ременной t операций сложения, вычитания, умножения и деления?
мы снова получим рациональные функции одной переменной t.
В дальнейшем для доказательства интегрируемости в элемен-
элементарных функциях некоторых выражений мы будем посредством
специально подобранной подстановки сводить интеграл от рассмат-
рассматриваемых выражений к интегралу от рациональной дроби *. При
этом мы будем говорить, что интеграл от рассматриваемого выра-
выражения рационализируется указанной специальной под-
подстановкой.
1°. Интегрирование некоторых тригонометриче-
тригонометрических выражений. Договоримся всюду в дальнейшем символом!
R(x, у) обозначать любую рациональную функцию от двух аргу-
аргументов х и у.
В этом пункте мы докажем интегрируемость в элементарных
функциях любой функции вида
R{s\nx, cos*). (8.59)
Докажем, что интеграл от этой функции рационализируется под-
подстановкой f = tg—. Действительно,
2
х , . х
2tg —¦ 1 — tg2 —
к 2 2t 2 * — <2
sin* = - = ——т, cos* = —- =
ЧМ
Х~ 1-й2'
так что
f
(8.6О>
О \ i-t-f" i -t- i-1 i -t-r-
о/ 1 . /э о
Если положить Ri(t) — , R»(t) — , ^э@ = . то-
в правой части (8.60) мы получим интеграл от выражения вида
(8.58), который представляет .собой интеграл от рациональной
функции аргумента t.
С dx
Пример. Вычислить интеграл L— \ , где а>0„
J 1 + a cos х
аф\. Применяя универсальную тригонометрическую подстановку
f=tg—, получим
х — 2arc tg t, dx — , cos x = -
* Интегрируемость в элементарных функциях рациональной дроби установ
лена в теореме 8.5.
§ 3. Классы функций, интегрируемых в элементарных функциях 323
dt 2 С dt
/i=:
\-а
Далее нужно отдельно рассмотреть два случая: 1) 0<а<1,
2) а>1.
В случае 0<а<1
2
В случае а> 1
4 =
/а2—1
In
1
V
''V
а —
а +
а +
1
1
—
Лп
fa — 1 дг
V a+l S 2
2°. Интегрирование дробно-линейных иррацио-
юальностей. В этом пункте мы докажем интегрируемость в
элементарных функциях любой функции вида
R х,
У
ах±Ь
(8.61)
.где а, Ь, с и d — некоторые постоянные, п — любое целое положи-
положительное число. Функцию такого вида мы будем называть дробно-
линейной иррациональностью.
Докажем, что интеграл от функции (8>61) при ad—ЬсФ§ рацио-
п
иализируется подстановкой t — л
cx-\-d
'-, Жс = -
В самом деле,
¦dt,
(a—
так что
f
dx
= f « fE1=
{ad-bc)nt'
(a —rf"J
dt. (8.62)
dl*
324 Гл. 8. Первообразная функция и неопределенный интеграл
Если положить /?!@ = —t Ri(t)r=t, Rs{t) = -±-,
а — га™ (а — сг™)а
то в правой части (8.62) мы получим интеграл от выражения вида
(8.58), который представляет собой интеграл от рациональной
функции аргумента t. Тем самым доказано, что интеграл от дроб-
дробно-линейной иррациональности (8.61) рационализируется подста-
подста= i/ax
новкой
cx + d
С f \ 1 ~х dx
Пример. Вычислить интеграл /= \ т/ — . Сделав
J у 1-х 1—х
подстановку
, ГТ+х ,2 1+х /а—1 . Atdt
у \—х' 1_х' /а + 1 (Р+\)
и учитывая, что 1—х=2/(/2+1), получим
1 = 2 Г_?!*- = 2 [dt—2 f-*- = 2f—
3°. Интегрирование квадратичных иррацио-
нальностей. В этом пункте мы докажем интегрируемость в
элементарных функциях любой функции вида
R{x, Vax2 + bx + c), (8.63)
где а, Ь и с — некоторые постоянные. Функцию такого вида будем
называть квадратичной иррациональностью. При этом
мы, конечно, считаем, что квадратичный трехчлен ах2+Ьх+с не
имеет равных корней (иначе корень из этого трехчлена может быть
заменен рациональным выражением).
Мы докажем, что интеграл от функции (8.63) всегда рациона-
рационализируется одной из так называемых подстановок Эйлера.
Сначала рассмотрим случай, когда квадратичный трехчлен
ах2+Ьх + с имеет комплексные корни. В этом случае знак
квадратного трехчлена совпадает со знаком а, и поскольку по
смыслу квадратный трехчлен (из которого извлекается квадрат-
квадратный корень) положителен, то а>0.
Таким образом, мы имеем право сделать следующую подста-
подстановку:
t = У ах* + Ьх 4- с + х\/а . (8.64)
Подстановку (8.64) обычно называют первой подстановкой
Эйлера. Докажем, что эта подстановка рационализирует интег-
интеграл от функции (8.63) для рассматриваемого случая. Возводя в
§ 3. Классы функций, интегрируемых в элементарных функциях 325
квадрат обе части равенства Vax2jt-bx+c = t — xVo., получим
Vtx, так что
VaX + bx + c=
2Vat+b * VaX+bX+C ¦ 2/Jt+b
Таким образом,
f R (x,
Г 2_
2/at + b ' 2Vat+b ) B-fat+b)%
Под знаком интеграла в правой части (8.65) стоит выражение
вида (8.58) при Rxif) = ^-+& , R,@ =
/?8(f) =2—-—j=—+СУ а. Таким образом, в правой части (8.65)
мы получаем интеграл от рациональной дроби.
Рассмотрим теперь случай, когда квадратный трехчлен
ах2+Ъх+с имеет несовпадающие вещественные корни х\ и х2.
В таком случае ах2 + Ьх+с=а(х—xi)(x—х?). Докажем, что в
этом случае интеграл от функции (8.63) рационализируется по-
посредством подстановки
(g66)
называемой обычно второй подстановкой Эйлера. В са-
самом деле, возводя в квадрат равенство Vах* + Ьх + с = t (х—хх)
и сокращая полученное равенство на х-—х\, получим а(х—хч) =
= t2(x—Х\), так что
t2—а
Таким образом,
-и
а (% — х2) t \ 2a (Xj—xt) t ,.
326 Гл. 8. Первообразная функция и неопределенный интеграл
В правой части (8.67) под знаком интеграла стоит выр'ажение
вида (8.58) при /?x(Q= "*? + **, /?,(*)= а(л^~*ж)* , Я3@ =
_—Li—flL. Таким образом, в правой части (8.67) мы получаем
(t —аJ
интеграл от рациональной дроби.
С dx
р р р
Примеры. 1) Вычислить интеграл /= \
J х
J + у + +
Поскольку квадратный трехчлен х2+х+1 имеет комплексные кор-
корни, сделаем первую подстановку Эйлера
Возвышая в квадрат обе части равенства Vx* + x+\ =t—х,
получим х2+x+\ = t2^2tx+х2, или x-\-\ = t2—2tx, так что
xldx2 +l dt.
l+2t A2/J
Таким образом,
^2f
J
D
+
1+2/ (l+2/)
Неопределенные коэффициенты А, В и D легко вычисляются:
Л=2, В = —3, D = —3. Окончательно получим
-ln\l + 2t\ +
2 ' 2A+»)
+ х | —-ln|l
2(l + 2+2/2++l)
2) Вычислить интеграл /= 1 , —— • Поскольку
квадратный трехчлен 1—2х—х2 имеет вещественные корни
*!= —1 + ^2 и х2 — —1 — V% сделаем вторую подстановку Эйле-
Эйлера (8.66)
t_ У 1 — 2х — х2
Х+1+У2* '
Возвышая в квадрат обе части равенства
У\ — 2х—х2 = t {х + 1 + V2~), будем иметь (—1)(* + 1— V2~) =
§ 4. Эллиптические интегралы 327
так что
_/2AЛ2+1)+/2"-1 т/1 о„ „2 _ 2У*" /.
Л ¦— ¦
Таким образом,
Ш
2/2+1)
Получаем интеграл от рациональной дроби, вычисление которого
предоставляем читателю.
§ 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
К интегралам от квадратичных иррациональностей естест-
естественно примыкают следующие интегралы:
J R (
х, Vaxa + bx2 + cx + d ) dx, (8.68)
)dx, (8.69)
подынтегральные функции которых содержат корень квадратный
из многочленов третьей или четвертой степени (с вещественны-
вещественными коэффициентами).
Эти интегралы весьма часто встречаются в приложениях. От-
Отметим сразу же, что интегралы (8.68) и (8.69), вообще говоря,
не являются элементарными функциями.
Оба эти интеграла принято называть эллиптическими
в тех случаях, когда они не выражаются через элементарные
функции, и псевдоэллиптическими в тех случаях, когда
они выражаются через элементарные функции *.
Ввиду важности для приложений интегралов (8.68) и (8.69)
возникла необходимость составления таблиц и графиков функ-
функций, определяемых этими интегралами. При произвольных ко-
коэффициентах а, Ь, с, d и е такие таблицы и графики составить
очень трудно. Поэтому возникла задача о сведении всех инте-
интегралов вида (8.68) и (8.69) к нескольким типам интегралов, со-
содержащих по возможности меньше произвольных коэффициен-
коэффициентов (или, как говорят, о приведении интегралов (8.68) и (8.69)
кканонической форме).
Прежде всего заметим, что интеграл (8.68) сводится к ин-
интегралу (8.69). В самом деле, кубичный трехчлен заведомо име-
* Эти названия происходят оттого, что впервые с этими интегралами встре-
встретились при решении задачи о спрямлении эллипса (см. пример 4° п. 6 § 1
гл. 10).
328 Гл. 8. Первообразная функция и неопределенный интеграл
ет хотя бы один вещественный корень хо, а поэтому его можно
представить в виде ax3+bx2+cx+d=a(x—хо) (x2+px+q).
Сделав подстановку х—xo=±t2, мы, как легко видеть, пре-
преобразуем интеграл (8.68) в (8.69).
Таким образом, нам достаточно рассмотреть лишь интеграл
(8.69).
В силу п. 3 § 3 многочлен четвертой степени можно разло-
разложить на произведение двух квадратных трехчленов с веществен-
вещественными коэффициентами
axi+bx3+cx2+dx+e=a(x2+px+q)(x2+p*x+q').
Всегда найдется некоторая линейная или дробно-линейная под-
подстановка, уничтожающая у обоих квадратных трехчленов ли-
линейные члены. Сделав такую подстановку, мы с точностью до
слагаемого, представляющего собой элементарную функцию,
преобразуем интеграл (8.69) к виду
-*С>* (8.70)
где R — некоторая рациональная функция. Далее можно пока-
показать, что при любых комбинациях абсолютных значений и зна-
знаков постоянных А, т и т' может быть найдена замена, сводя-
сводящая интеграл (8.70) к так называемому каноническому ин-
интегралу
R^z2)dz (8.71)
1 — Z2)(l — ?2Z2)
в котором через k обозначена постоянная, удовлетворяющая
условию 0<&<1.
Любой канонический интеграл (8.71) с точностью до слагае-
слагаемого, представляющего собой элементарную функцию, может
быть приведен к следующим трем стандартным интегралам:
С dz Г z4z
и (8.72)
Интегралы (8.72) принято называть эллиптическими ин-
интегралами соответственно 1-го, 2-го и 3-го рода. Каждый из
этих интегралов, как показано Лиувиллем *, представляет собой
неэлементарную функцию. Эллиптические интегралы 1-го и
2-го рода содержат только один параметр, принимающий веще-
вещественные значения из интервала 0<&<1, а эллиптический инте-
Жозеф Лиувилль — французский математик A809—1882).
§ 4. Эллиптические интегралы 329
грал 3-го рода, кроме того, содержит параметр h, который мо-
может принимать и комплексные значения.
ЛежанДр * подверг интегралы (8.72) дальнейшему упроще-
упрощению, сделав замену z = slntp @<ф< — )• G помощью этой
замены первый из интегралов (8.72) преобразуется к виду
dlf (8.73)
С
J
/l —
При этой же замене второй из интегралов (8.73) с точностью
до постоянного множителя равен разности интеграла (8.73) и
следующего интеграла:
JVl
1— k?sin2y dtp. (8.74)
Третий из интегралов (8.72) преобразуется к виду
d* (8.75)
A + Asinaq>) у \ —Aasinaф
Интегралы (8.73), (8.74) и (8.75) принято называть эллипти-
эллиптическими интегралами соответственно 1 -го, 2-го и 3-го
рода в форме Лежандра.
Особенно важную роль в приложениях играют интегралы
(8.73) и (8.74). Если считать, что оба эти интеграла обращают-
обращаются в нуль при ф = 0, то получатся две вполне определенные функ-
функции, которые обычно обозначают символами F(k, ф) и E(k, ф).
Для этих функций составлены обширные таблицы и графики.
Лежандром и другими математиками изучены свойства этих
функций, для них установлен ряд формул.
Наряду с элементарными функциями функции Е и F прочно
вошли в семейство функций, часто используемых в анализе.
Здесь еще раз стоит отметить условность понятия элементар-
элементарной функции. Вместе с тем следует подчеркнуть, что задачи ин-
интегрального исчисления вовсе не ограничиваются изучением
функций, интегрируемых в элементарных функциях.
* Андриан Мари Лежандр — французский математик A752—1833).
Глава 9
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА
Во вводной главе было показано, что к понятию определенного
интеграла приводят такие важные задачи естествознания, как за-
задача о вычислении площади криволинейной трапеции и задача об
определении пути, пройденного материальной точкой, двигающейся
со скоростью f(x) за промежуток времени от х=а до х=Ь. Целью
данной главы является построение строгой теории определенного
интеграла Римана.
§ 1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА.
ИНТЕГРИРУЕМОСТЬ
Рассмотрим функцию f(x), определенную в каждой точке сег-
сегмента [а, Ъ]. Введем понятия разбиения сегмента [а, Ь], из-
мельчения этого разбиения и объединения двух разбиений.
Определение 1. Будем говорить, что задано разбиение
сегмента [а, Ь], если заданы точки Хо, Хи ..., хп такие, что а =
=xo<*i< ...<хп-1<хп = Ь. Разбиение сегмента [а, Ь] будем в даль-
дальнейшем обозначать символом {хи}.
Определение 2. Разбиение {xk'} сегмента {а, Ь] называется
измельчением разбиения {х^ того же сегмента, если каждая
точка хр разбиения {хь} совпадает с одной из точек xq' разбиения
Определение 3. Разбиение {xk} сегмента [а, Ь] называется
объединением разбиений {xk'} и {xk"} того же сегмента, если
все точки разбиений {Xk} и {xk"} являются точками разбиения {Xk}
и других точек разбиение {xk} не содержит.
Заметим, что объединение двух-разбиений является измельче-
измельчением каждого из них.
Рассмотрим на сегменте [а, Ь] функцию f(x), принимающую в
каждой точке сегмента конечные значения. По данному разбиению
{xk} построим число, так называемую «интегральную сумм у»,
п
а (Ч> ?*) = ]?] f(lk){xk—xb-i)' где Ь —некоторая точка сегмента
k=i
\xk-u xk]. Подчеркнем, что интегральная сумма o{Xk, %,h) зависит
как от разбиения {xk}, так и от выбора точек \k на сегментах
fXk-u Xk]. Если обозначить через Axk разность Xh—xk~i, то инте-
§ 1. Определение интеграла. Интегрируемость 331
тральную сумму, в дальнейшем часто обозначаемую просто через
ст, можно записать и так:
о = ? / (Ik) Л**> Ik e= [**-!. **].
Сегменты [Xk-\, Xh] иногда называют частичными сегмен-
сегментами, а точки |fe — промежуточными точками.
Число d = maxhxl* договоримся называть диаметром раз-»
1&
биения {xk}- Введем фундаментальные понятия предела инте-
интегральных сумм и интегрируемости функции по Риману.
Определение 4. Число I называется пределом инте-
интегральных сумм а (xk, Is) при стремлении диаметра d разбие-
разбиений {xk} к нулю, если для всякого е>0 существует такое число
б = б(е) >0, что из условия d<& при любом выборе промежуточных
точек gft следует неравенство \1—сг|<е.
Легко убедиться в том, что может существовать только один
предел интегральных сумм а при d->0.
Для обозначения предела интегральных сумм употребляют
символ
Определение 5. Функция f(x) называется интегрируе-
интегрируемой по Риману на с е г мент е [а, Ь], если для этой функции
на указанном сегменте существует предел I ее интегральных сумм
а при стремлении диаметра d разбиений {хь} к нулю.
Число / называется определенным интегралом Р и-
м ан а от функции f(x) в пределах от а до 6 и обозначается сим-
ь
волом Г f (x) dx.
ь
Таким образом, по определению Г f(x)dx— lima(xk, |A). Отме-
J d—>0
а
тим, что число а называют нижнимпределом интегрирования,
а число Ь — верхним пределом интегрирования. Перемен-
Переменную х под знаком определенного интеграла можно заменить на
любую другую переменную, т. е. справедливы равенства
j f (х) dx = ft (у) dy = J / (t)dt и т. д.
a a a
Выясним геометрический смысл интегральной суммы. Рассмот-
Рассмотрим криволинейную трапецию, т. е. фигуру, ограниченную графи-
Т. е. длину наибольшего частичного сегмента.
332
Гл. 9. Определенный интеграл Римана
ком непрерывной неотрицательной функции «/ = /(%), заданной на
сегменте [а, Ь], двумя прямыми х=а и х=Ь, перпендикулярными к
оси абсцисс, и сегментом [а, Ъ] оси абсцисс (рис. 9.1). Очевидно,
интегральная сумма
<з(хи, 5ft), отвечающая
выбранному разбиению
{xk} и данному обозна-
обозначенному на рисунке вы-
выбору точек Ik, представ-
представляет собой площадь сту-
ступенчатой фигуры, заштри-
заштрихованной на этом ри-
рисунке.
В следующей главе
будет сформулировано
понятие площади про-
произвольной плоской фигу-
фигуРис. 9.1
ры и установлено, что предел при d-*-0 площади указанной
пенчатой фигуры равен площади криволинейной трапеции.
Приведем простейший пример интегрируемой по Риману функ-
функции. Покажем, что функция f (x) =c=const интегрируема на любом
ь
сегменте [а, Ь], причем (cdx = c(b—а). Действительно, при любом
а
разбиении {хь} и любом выборе точек |& на сегментах [**-ь х&\
справедливо равенство /(|*)=с. Следовательно,
a(Xk, %k) =cAxi + cAx2+ ... +сАхп =
... +Ахп) =с{Ь—а)
для любого разбиения {хк} и любого выбора точек %h^[xk-u Xk].
Поэтому
ь
f cdx = l\ma(xk, ?*.) = limc(&—a) — c{b—a).
a
Докажем следующее
Утверждение. Если функция f(x) не является ограниченной
на сегменте [а, Ь], то эта функция не интегрируема на этом сегмен-
сегменте. Пусть f(x) не ограничена на [а, Ь]. Покажем, что для любого
разбиения {xk} интегральную сумму a{xk, Ы можно сделать сколь
угодно большой по абсолютной величине только за счет выбора
промежуточных точек |ft. В самом деле, если функция f(x) не огра-
ограничена на сегменте [a, b], a сегмент [а, Ь] разбит на конечное число
сегментов [xk~n Xk], то функция f(x) будет неограниченной хотя бы
на одном частичном сегменте разбиения. Не нарушая общности,
будем считать, что f(x) не ограничена на сегменте [х0, х{\. На
§ 1. Определение интеграла. Интегрируемость 333
остальных сегментах [xh х2], [х2, х3], ..., [хп-\, хп] промежуточные
точки |2, |з, •••, In выберем произвольными и фиксируем. Обозна-
Обозначим через oi(xh, \к) величину
ai = ai (xh, lk)=f(b)&x2+f(b)Ax3+ ... +f{%n)Axn.
Рассмотрим теперь функцию f(x) только на сегменте [х0, х{\. По-
Поскольку фунцкия f(x) не ограничена на этом сегменте, то для лю-
любого наперед заданного положительного числа М найдется точка
gi из этого сегмента такая, что
Отсюда следует, что |/(Si) |A*i> |ai| +M, и поэтому
1 a (xk, W | = ? f (&) Axk\ = | / (У A*j + аг (xk,
Теперь уже совсем просто убедиться в неинтегрируемости функ-
функции f(x) на сегменте [а, Ь]. В самом деле, предположим, что f(x)
интегрируема на [а, Ь], т; е. для нее существует предел / интеграль-
интегральных сумм при стремлении диаметра разбиения d к нулю. В силу
доказанного выше для разбиения с как угодно малым диаметром
d и для положительного числа Л1=|/| + 1 найдется интегральная
сумма 0, удовлетворяющая условию (о|>|/| + 1, из которого в
силу неравенства \а—/|>|0| —1/| вытекает, что \а—/|>1 (для
разбиения с как угодно малым диаметром d). Это противоречит
определению 4 предела интегральных сумм. ¦
Итак, мы доказали, что интегрируемыми на сегменте [а, Ь] мо-
могут являться только ограниченные на этом сегменте функции.
Естественно возникает вопрос: всякая ли ограниченная на сегмен-
сегменте [а, Ь] функция является интегрируемой на этом сегменте?
Докажем, что функция Дирихле D(x), равная нулю в ирра-
иррациональных и единице в рациональных точках сегмента [а, Ь], пред-
представляет собой пример ограниченной и неинтегрируемой на этом
сегменте функции.
Для разбиения [а, Ь] с как угодно малым диаметром d, взяв в
качестве всех промежуточных точек иррациональные точки, мы
получим интегральную сумму ел, равную нулю, а взяв в качестве
всех промежуточных точек рациональные точки, мы получим ин-
интегральную сумму 02, равную b—а. Если бы существовал предел
/ интегральных сумм при стремлении d к нулю, то для положи-
положительного числа е = и для достаточно малого d мы получи-
получили бы \ох—/|<—~а , |02—/|< ~а-, откуда |о2—0i| =
= 1@2—I) + (/—0i)|«|02—Л + 1а1—Ц<Ь—а, а это противоречит
тому, что 02—а\ = Ь—а.
334 Гл. 9. Определенный интеграл Римана
§ 2. ВЕРХНИЕ И НИЖНИЕ СУММЫ И ИХ СВОЙСТВА
1. Определение верхней и нижней сумм. Утверждение, доказан-
доказанное в § 1, дает нам основание рассматривать всюду в дальнейшем
только ограниченные на данном сегменте функции (ибо неограни-
неограниченные функции заведомо не являются интегрируемыми по Ри-
ману).
Пусть f(x) —ограниченная на сегменте [а, Ь] функция и {xk}—
произвольное разбиение этого сегмента. Так как f(x) ограничена
на сегменте [а, Ь], то она ограничена и на любом частичном сегмен-
сегменте [xk-u Xh], а поэтому у функции f(x) существуют точная нижняя
грань т/г и точная верхняя грань Mk на частичном сегменте
[Xk-l, Xk].
Итак, пусть mk = inf / (х), Mk = sup / (х).
Введем фундаментальные понятия верхней и нижней
сумм.
Определение 1. Суммы
п
S = MxAxx + М2Ах2 + ...+ МпАхп = ? MkAxk
s = т1Ах1 + тг Ах2 + ...+ тпАхп = ? mkAxk
будем называть соответственно верхней и нижней сумма-
м и функции f (х) для данного разбиения {хк} сегмента [а, Ь].
Выясним геометрический смысл верхней и нижней сумм.
Рассмотрим снова криволинейную трапецию, т. е. фигуру, ограни-
ограниченную отрезком [а, Ь] оси Ох, графиком неотрицательной непре-
непрерывной функции г/=/(х)>0 и прямыми х = а, х=Ь, перпендикуляр-
перпендикулярными к оси Ох (рис. 9.2). Пусть дано любое разбиение {xk} сег-
сегмента [а, Ъ]. Число Mk в случае непрерывной функции y = f(x) яв-
является ее максимальным значением на частичном сегменте [xk-u
Xk]. Поэтому верхняя сумма равна площади элементарной ступен-
ступенчатой фигуры, содержащей криволинейную трапецию. Эта пло-
площадь заштрихована на рис. 9.2.
Аналогично нижняя сумма равна площади элементарной сту-
ступенчатой фигуры, которая содержится в криволинейной трапеций
(рис.-9.3). Отметим, что число т& в этом случае является мини-
минимальным значением функции y = f(x) на частичном сегменте
[Xk-u xk].
Анализируя геометрический смысл интегральной суммы, можно
ожидать, что интеграл от интегрируемой по сегменту [а, Ь] функ-
функции y = f(x) должен равняться числу, которое следует принять за
площадь соответствующей криволинейной трапеции. Но к этому
§ 2. Верхние и нижние суммы и их свойства
335
же числу будут стремиться верхние и нижние суммы при стремле-
стремлении диаметра разбиений к нулю. Поэтому представляется вероят-
вероятным, что для интегрируемости функции необходимо и достаточно,
чтобы разность между верхними и нижними суммами стремилась
к нулю. Строго это будет доказано ниже.
2. Основные свойства верхних и нижних сумм. Докажем следу-
следующие леммы.
Лемма 1. Пусть a(xk, ?&) — интегральная сумма, отвечающая
данному разбиению {xk}. Тогда при любом выборе промежуточных
точек %k всегда справедливы неравенства
где s и S — соответственно нижняя и верхняя суммы, отвечающие
тому же разбиению.
Доказательство. По определению чисел т& и Mk заклю-
заключаем, что mh<.f(%k)<M для любого |* из сегмента [xk-\, xk]. Умно-
Умножая написанные неравенства на Axk и суммируя по всем k от 1 до
п, получаем требуемое утверждение леммы.
Лемма 2. Пусть {Xk} — произвольное фиксированное разбие-
разбиение сегмента [а, Ь], г — произвольное положительное число. Тогда
можно выбрать промежуточные точки |& так, чтобы интегральная
сумма a(Xk, ?&) и верхняя сумма S удовлетворяли неравенству
0<S—a(xk, |fe)<e. Промежуточные точки r\k можно выбрать и
таким образом, чтобы для интегральной суммы a(xk, t\k) и ниж-
нижней суммы s выполнялись неравенства 0<га(х*, т^)—s<e.
Доказательство. Пусть {л^} — фиксированное разбиение
сегмента [а, Ь] и е>0. Докажем сначала первое утверждение лем-
леммы. Поскольку Mk = su.pf(x), то для выбранного нами е>0 най-
дется точка |йсегмента [xk-u Xk] такая,что 0*cMk—f(|ft)<e/(&—a).
Умножив эти неравенства на Ах& и просуммировав по всем k от
1 до п, получим
0«S—a{xk, Ъь)<е.
336 Гл. 9. Определенный интеграл Римана
Аналогично в силу того, что mk = in[f(x), существует -такая
xk-i<x<xk
точка г] ?<=[%?_!, хк], что
]k) —mk<e/(b—a).
Последние неравенства после умножения на Ахн и суммирования
приводят к оценкам
0<а{хк, T)fe)— s<e.
Лемма доказана.
Следствие. Для любого фиксированного разбиения {хь}
справедливы следующие соотношения:
S = supa(xk, gft), s = Mo(xk, t]k),
- h "ft
где точные верхняя и нижняя грани берутся по всевозможным
промежуточным точкам.
Лемма 3. При измельчении данного разбиения верхняя сум-
сумма может только уменьшиться, а нижняя сумма — только увели-
увеличиться.
Доказательство. Пусть {xk}—данное разбиение, а разбие-
разбиение {xh'} получается из него добавлением только одной новой точ-
точки х. Легко видеть, что общий случай сводится к данному. Пред-
Предположим, что х лежит внутри [Xk-u Xk]- Тогда в выражении для S
слагаемое MkAxk заменится на Mk(x—xA_j) -f- Mk(Xk—x), где
Mk = sup /_(x), Ml == sup f (x).
Точная верхняя грань функции на части сегмента не превосхо-
превосходит точной верхней грани функции на всем сегменте. Поэтому
M'M M"Mk и
Ml (xk—x) < Mk \{x—xk-i) + (xk—x)] = MkAxk.
Так как все другие слагаемые в выражении для верхней суммы
сохранятся, то мы доказали, что при добавлении точки х верхняя
сумма может только уменьшиться. Случай, когда к данному раз-
разбиению добавляется несколько новых точек, сводится, очевидно,
к рассмотренному. Точно так же устанавливается, что при измель-
измельчении данного разбиения нижняя сумма может только увеличить-
увеличиться. Лемма доказана.
Лемма 4. Для двух произвольных и, вообще говоря, различ-
различных разбиений сегмента [а, Ь] нижняя сумма одного из этих раз-
разбиений не превосходит верхней суммы другого разбиения.
Доказательство. Пусть {xk'} и {хь"} — два произвольных
разбиения сегмента [а, Ь), а 5', s', S", s" — верхние и нижние
суммы этих разбиений соответственно. Обозначим через {хь} объ-
объединение разбиений {х/} и {xk"}, а через 5 и s верхнюю и нижнюю-
суммы разбиения {xk}. Заметим, что {xk} является измельчением
§ 2. Верхние и нижние суммы и их свойства 337
как разбиения {%/}, так и разбиения {хь"}. Согласно утверждению»
леммы 3 справедливы неравенства
, S" > S, s' < s, s"<s.
Кроме того, в силу леммы 1 получим, что s <<5. Пользуясь свой-
свойством транзитивности для числовых неравенств и используя три
подчеркнутых выше неравенства, заключаем, что s"^5'. Анало-*
гично устанавливается, что s'^5". Лемма доказана.
Следствие. Множество верхних сумм данной функции f(x),.
отвечающих всевозможным разбиениям сегмента [а, Ь], ограниче-
ограничено снизу. Множество нижних сумм ограничено сверху.
Действительно, любая верхняя сумма не меньше некоторой
фиксированной нижней суммы, следовательно, множество верхних
сумм ограничено снизу. Аналогично проводятся рассуждения для:
нижних сумм. В силу основной теоремы 2.1 из гл. 2 существуют
точная нижняя грань множества {&} и точная верхняя грань мно-
множества {s}.
Определение 2. Верхним интегралом Дарбу от
функции f(x) называется число /*, равное точной нижней грани-
множества верхних сумм {S} данной функции f(x) для всевозмож-
всевозможных разбиений сегмента [а, Ь). Нижним интегралом Дар-
Дарбу от функции f(x) называется число /*, равное точной верхней
грани множества нижних сумм {s} данной функции f(x) для все-
всевозможных разбиений сегмента [а, Ь].
Лемма 5. Нижний интеграл Дарбу всегда не превосходит
верхнего интеграла Дарбу, т. е. 1*^1*.
Доказательство. Допустим противное, т. е. предположим,,
что /*>/*. Тогда /*—/* = е>0.
Для указанного е, согласно определению числа /*, найдется та-
такое разбиение {xkf} сегмента [а, Ь], что для соответствующей верх-
верхней суммы 5' будет выполнено неравенство 5'</* + е/2. Точна
так же можно указать такое разбиение {Xk") сегмента [а, Ь], чта
для соответствующей нижней суммы s" будет выполнено неравен-
неравенство s">/*—е/2. Вычтем второе неравенство из первого. Полу-
Получим S'—s"<I*—h + e. Но /*—/*=¦—е, поэтому 5'—s"<0, т. е.
s">S'. Получившееся неравенство противоречит утверждению-
леммы 4. Таким образом, доказываемое утверждение справедливо,,
т. е. /,</*.
Пусть M = supf(x), m = inf/(x), a {xk} — произволь-
x?[a,b] *6[o,6]
ное разбиение сегмента [a, b], d — диаметр этого разбиения. Обо-
Обозначим через {хи} разбиение, полученное из разбиения {xk} путем
добавления к нему / произвольных новых точек. Пусть S a s —
верхняя и нижняя суммы разбиения {хк}, а 5' и s' — верхняя и
нижняя суммы разбиения {xk}. Справедливо следующее утверж-
утверждение.
338 Гл. 9. Определенный интеграл Римана
Лемма 6. Для разностей S—S' и s'—s выполняются следу-
следующие неравенства: S—S'^(M—m)ld, s'—s^.(M—m)ld.
Доказательство. Не ограничивая общности, мы можем
провести рассуждения лишь для случая, когда к точкам разбиения
{xk} добавляется только одна новая точка х, и доказать, что
ш этом случае справедливы неравенства 5—5'<(М—m)d, sf—s<:
<(М—m)d.
Пусть вновь добавляемая точка х лежит внутри сегмента
\Xk-u xk]. Тогда верхняя сумма 5 будет отличаться от верхней
суммы 5' только тем, что одно слагаемое MkAxk у суммы S заме-
мится двумя слагаемыми Mk'(x—Xk-\)+Mk" {xk—х) у суммы S'
(здесь через Mk, Mk' и Мк" обозначены точные верхние грани
$(х) на сегментах [xh-U xh], [xh-i, x] и [a, xh] соответственно).
Все остальные слагаемые у верхних сумм 5 и 5' будут общи-
общими. Отсюда следует, что
5—S'=MkAxk- [М„'(х—хм) +Mk"(xk—x) ].
Из последнего соотношения, учитывая, что в силу свойств точных
«граней * МА<М, m^.Mh', m^.M^', получим, что
S—S'^MAXk—m [ (x—xk-i) + (хл—х)) = (M—m) Axft< (M—m) d.
Доказательство оценки для нижних сумм аналогично.
Лемма доказана.
Определение 3. Число А называется пределом верх-
<них сумм S при стремлении к нулю диаметра разбиений d,
если для любого положительного числа е можно указать положи-
положительное число б такое, что при условии d<8 выполняется неравен-
неравенство \S—А\ <е.
Для обозначения указанного предела естественно употреблять
•символ Л = Нт5.
d-»0
Аналогично определяется пр еде л В нижних сумме при
•стремлении d к нулю.
Основная лемма Дарбу. Верхний интеграл Дарбу I*
является пределом верхних сумм S при стремлении диаметра d
.разбиений к нулю, т. е. /* = limS. Аналогично / =lims.
Доказательство. Проведем доказательство первого ут-
шерждения леммы. Заметим, что если функция f (x) =c = const, то
S = c(b—а)=1* для любого разбиения. Поэтому HmS = /*. Если
d-tO
функция f(x) непостоянна, то M = sup/(x)> m= inf f (x). Фиксиру-
*6[а,Ь] х?[а,Ь]
>ем произвольное положительное число е. По определению числа
1* существует такое разбиение {хи*}, что верхняя сумма S* этого
* Если mh' и тк" — точные нижние грани f(x) на сегментах [xh-u x\ и
'{х, xh] соответственно, то, поскольку тн'^Мк', тн"^Мъ" н m<mh\
>m<mh', мы получили, что т<.М/, М"
§ 3. Классы интегрируемых функций 339»
разбиения будет удовлетворять условию S*—/*<е/2. Обозначим»
через / число точек разбиения {*&*}, не совпадающих с концамк-
сегмента [а, Ь].
Пусть \хк) — произвольное разбиение сегмента [а, Ь], диаметр
которого удовлетворяет неравенству d<8 = e/[2l(M—т)\, и пусть-
5 — верхняя сумма этого разбиения. Произведем измельчение
разбиения {xk}, добавив к нему отмеченные выше / точек разбие-
разбиения {Xk*}. Полученное при этом разбиение обозначим символом
{xk}. По лемме 6 верхняя сумма S' этого последнего разбиения)
удовлетворяет условию
0<5—5'< (М—т) W<e/2.
Но разбиение {%/} можно рассматривать как измельчение разбие-
разбиения {xk*}, к которому добавляются точки разбиения {х^}, не совпа-
совпадающие с концами сегмента [а, Ь]. Поэтому в силу определения!
/* и леммы 3
*, т. е. 0<5'—I*<S*—I*.
Выше было показано, что 5*—/*<е/2, поэтому 0^5'—/*<е/2..
Объединяя эти неравенства с установленными выше неравенства-
неравенствами 0<5—S'<e/2, получаем, что 0^5—/*<е, если только d мень-
меньше указанного выше б. Следовательно, /* = Нгп5. Для нижних.
d->0
сумм доказательство аналогично. Основная лемма Дарбу дока-
доказана.
§ 3. ТЕОРЕМЫ О НЕОБХОДИМЫХ И ДОСТАТОЧНЫХ
УСЛОВИЯХ ИНТЕГРИРУЕМОСТИ ФУНКЦИЙ.
КЛАССЫ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ
Доказанные выше утверждения о свойствах верхних и нижних:
сумм позволяют нам установить необходимые и достаточные ус-
условия интегрируемости по Риману произвольной ограниченной;
функции.
1. Необходимые и достаточные условия интегрируемости.
Вспомогательная теорема. Для того чтобы, ограничен-
ограниченная на сегменте [а, Ь] функция f(x) была интегрируема на этом
сегменте, необходимо и достаточно, чтобы выполнялось paвeнcтвo^
/. = /*.
Доказательство. Необходимость. Пусть функция f(x)
интегрируема по Риману на сегменте [а, Ь]. Тогда существует
предел / ее_ интегральных сумм а при стремлении диаметра d раз-
разбиений к нулю.
По определению предела интегральных сумм для любого е>0*
существует такое б>0, что для любого выбора промежуточных
точек gfe разбиения {Xk} с диаметром d<8 выполняется неравен-
неравенство
\I-a(xk,
340 Гл. 9. Определенный интеграл Римана
•Согласно лемме 2 для данного разбиения {Xk} можно так выбрать
промежуточные точки ?&' и \и' в каждом частичном сегменте
[xk-\, Xk], что будут справедливы неравенства
S—a{xk, |/)<е/4, a(xk, ?*")
Подчеркнем, что, кроме того, для данного разбиения {x/g} одно-
одновременно выполнены неравенства
\I-a(xk, |*')|<е/4, \I-e(xk, Ь") |<е/4.
Заметим теперь, что
S-S= [S-a(xk, ift')] + [а(хк, g*')-/] + [1—а(хк, Ь")] +
+ [о(хк, Ь")— s].
Отсюда, учитывая, что модуль суммы четырех величин не
превосходит суммы их модулей, получаем, что S—s<e. Итак, для
любого 8>0 существует такое 6>0, что для любого разбиения
х диаметром <i<6 справедливо неравенство S—s<e. Поскольку
для любого разбиения выполнены неравенства
то из неравенства S—s<e вытекает, что 0^/*—/*<е, а отсюда
.в силу произвольности е>0 вытекает, что /*=/*.
Достаточность. Пусть /* = /*=А. Согласно основной лем-
лемме Дарбу /* = limS, /„--iims, т. е. верхний интеграл является
'пределом верхних сумм, а нижний интеграл — пределом нижних
сумм при стремлении диаметра d разбиений к нулю. Поэтому для
любого е>0 можно указать такое число б>0, что для любого
разбиения с диаметром d<6 одновременно выполняются неравен-
неравенства /*—s=A—s<e, 5—I*=S—Л<е. При любом, указанном раз-
- биении любая интегральная сумма o(Xk, i&) удовлетворяет нера-
неравенствам s^a(xk, ?,k)^S, а значит, и неравенствам
A—e
Отсюда \А—e{xk, |ft)|<e (для любого разбиения с диаметром
.d, меньшим б).
Таким образом, A = lima(xk, |fe), т. е. функция f(x) интегри-
•руема.
Докажем следующую теорему, имеющую важное значение
в теории интеграла Римана.
Основная теорема. Для того чтобы ограниченная на
^сегменте [а, Ь] функция f(x) была интегрируемой на этом сегмен-
сегменте, необходимо и достаточно, чтобы для любого е>0 нашлось та-
такое разбиение {Xk} сегмента [а, Ь], для которого S—s<e.
Доказательство. Необходимость. Пусть функция /(х) ин-
интегрируема на сегменте [а, Ь]. При доказательстве необходимости
§ 3. Классы интегрируемых функций 341
вспомогательной теоремы установлено, что для любого е>0 су-
существует такое 8>0, что для любого разбиения сегмента [а, Ь]
с диаметром d, меньшим 6, справедливо неравенство S—s<e. Не-
Необходимость доказана.
Достаточность. Дано, что для любого е>0 существует
такое разбиние {хк} сегмента [а, Ь], что для соответствующих
верхней и нижней сумм выполнено соотношение S—s<e. Тогда
поскольку
то /*—/»<е. Из этого неравенства и из произвольности е заклю-
заключаем, что /* = /*, а по вспомогательной теореме получаем, что
функция f(x) интегрируема. Теорема доказана.
2. Классы интегрируемых функций. Выше в § 1 настоящей гла-
главы мы видели, что функция f(x), постоянная на сегменте [а, 6],
интегрируема по Риману на этом сегменте, а также что интегриру-
интегрируемые на данном сегменте функции обязаны быть ограниченными
на этом сегменте. Естественно, возникает вопрос об описании
классов функций, интегрируемых по Риману на сегменте [а, Ь).
Среди этих классов важную роль играет класс непрерывных на сег-
сегменте [а, Ь] функций. Докажем следующую фундаментальную
теорему.
Теорема 9.1. Непрерывные на сегменте [а, Ь] функции ин-
интегрируемы на этом сегменте по Риману.
Доказательство. Пусть f(x) непрерывна на сегменте
[а, Ъ]. Выберем произвольное число е>0. Поскольку функция
f{x), будучи непрерывной на сегменте, является равномерно не-
непрерывной на нем, то для любого данного е>0 существует такое
число б>0, что если ?' и |" — любые две точки сегмента [а, Ь],
для которых |6'—€"|<б, то |f(g')_f(g")|<e/(&—а). Отсюда сле-
следует, что разность между точными верхней и нижней гранями
f(x) на любом сегменте, имеющем длину, меньшую б, будет мень-
меньше числа е/(Ь—а). Выберем теперь разбиение {xk} сегмента [а, Ь]
с диаметром d, меньшим указанного числа б: d<8. Пусть
M f() mk=mif(x).
6ll
kvk) ferfe
По определению верхней и нижней сумм
Используя в этом соотношении установленное для выбранного
нами разбиения неравенство Мь,—/rt/j<&/(b—а), утверждающее,
что разность между точными гранями на любом частичном сег-
сегменте меньше е/(&—а), мы получим, что для выбранного раз-
вбиения
3 42 Гл. 9. Определенный интеграл Римана
S-s<-L-?Axk=e.
' — a _
По основной теореме заключаем, что функция f(x) интегрируема
на [а, Ь]. Теорема доказана.
Следующая теорема дает достаточное условие интегрируемости
некоторого класса разрывных функций.
Условимся говорить, что точка х покрыта интервалом,
если она содержится в указанном интервале.
Докажем следующую теорему.
Теорема 9.2. Пусть функция f(x) определена и ограничена
на сегменте [а, Ь]. Если для любого числа е>0 можно указать
конечное число интервалов, покрывающих все точки разрыва этой
функции и имеющих общую сумму длин, меньшую е, то функция
f(x) интегрируема по Риману на сегменте [а, Ь].
Доказательство. Пусть Mum — точные верхняя и ниж-
нижняя грани функции f(x) на сегменте [а, Ь]. Заметим, что если
М = пг, т. е. функция f(x) постоянна, то, как мы уже доказали
в § 1, она интегрируема. Поэтому будем считать, что М>пг. Пусть
е>0 — произвольное число. Покроем точки разрыва функции
f(x) конечным числом интервалов, сумма длин которых не пре-
превосходит числа ei = e/2-(Af—m). Точки сегмента [а, 6], не принад-
принадлежащие указанным интервалам, очевидно, образуют множество,
состоящее из конечного числа непересекающихся сегментов. Назо-
Назовем эти сегменты-дополнительными. На каждом из таких сегмен-
сегментов функция непрерывна, а следовательно, и равномерно непре-
непрерывна. Значит, существуют такие числа б;>0, что если ||'—|"[<'
<б/, то |/(Ю—/(?") |<е/B(Ь—а)) для всех |' и |", принадлежа-
принадлежащих i-му дополнительному сегменту.
Пусть 6 = min6?. Тогда если взять разбиения дополнительных
i
сегментов на частичные сегменты так, чтобы диаметр каждого из
частичных сегментов не превосходил б, то разность между точны-
точными верхней гранью Ми и нижней гранью mk функции f(x) на k-м
частичном сегменте будет не больше е/B(Ь—а)). Объединяя все
разбиения дополнительных сегментов и указанные выше интерва-
интервалы с присоединенными к ним концами, мы получим разбиение
{хк} всего сегмента [а, Ь]. Для так построенного общего разбие-
разбиения [а, Ь]
S-s = ? (Mk—mk) Axk = 2' (Mk-mk) Axk + 2" (Mk—mk) Axk,
где в сумму с одним штрихом отнесены слагаемые, отвечающие
частичным сегментам, образованным из интервалов, покрывающих
точки разрыва, а в сумму с двумя штрихами — все остальные.
Рассмотрим первое слагаемое правой части записанного выше
§ 3. Классы интегрируемых функций 343
равенства. Поскольку Мк—тк^.М—т для любого k, то
2' (Мк—тк) Axk^ (М—т) Ъ'Ахк < е/2.
Далее, в силу сказанного выше, из свойства равномерной не-
непрерывности функции f(x) на дополнительных сегментах получа-
получаем, что
2" (Mk—mk) Ах < - 2"Axk < ф—а) = — •
V k и \ 2F —а) 2F—аL 2
Таким образом, нами указано разбиение {хк}, для которого
S—s<e. По основной теореме получаем, что функция f{x) интег-
интегрируема. Теорема доказана.
Следствие. Ограниченная на сегменте [а, Ь] функция
f(x), имеющая лишь конечное число точек разрыва, интегрируема
на этом сегменте. В частности, кусочно непрерывная на данном
сегменте функция интегрируема на этом сегменте.
Действительно, в условии предыдущей теоремы достаточно вы-
выбрать интервалы, покрывающие точки разрыва, одинаковой дли-
длины, меньшей чем е/Bр), где р — число точек разрыва функции
Замечание. Пусть функция f(x) интегрируема на сегменте
fa, b], а функция g(x) совпадает с функцией f(x) во всех точках
сегмента [a, b], кроме, быть* может, конечного числа точек. Тогда
функция g(x) интегрируема на сегменте [а, Ь] и
Указание. Использовать схему доказательства следствия.
Теорема 9.3. Монотонная на сегменте [а, Ь] функция f(x)
интегрируема по Риману на этом сегменте.
Доказательство. Случай, когда функция f(x) постоянна
на сегменте [a, b], можно исключить. Рассмотрим, например, не-
неубывающую на сегменте [с, Ь] функцию f(x). Пусть е>0 — про-
произвольное число. Выберем разбиение {хк} сегмента [а, Ь] с диа-
диаметром d<e/(f(b)—f(a)). Заметим, что поскольку f(x) не посто-
постоянна, то f(b)>f(а). Оценим разность 5—s= ? (Mk~tnk) Axk,
fc=i
Mk и mk — верхняя и нижняя грани f(x) на [xk-i, xk]. Получим
П
(Mk—mk)l{f(b)— f (a)). Но для неубывающей
fc=l
n
функции ? (Mk—mk) = f(b)~ f (а)*. Поэтому S—s<b и функция
Ибо Mft==f(jck)=mft+i при ft = l, 2 n—l, Mn=f(b), mi=/(a).
344 Гл. 9. Определенный интеграл Римана
f(x) интегрируема. Для невозрастающей функции рассуждения
аналогичны. Теорема доказана.
Докажем сейчас теорему об интегрируемости суперпозиции
двух функций.
Теорема 9.4. Пусть функция f(x) интегрируема по Риману
на сегменте [a, b], M и m — ее точные верхняя и нижняя грани
на [а, Ь]. Пусть, далее, функция у(х) определена на сегменте
[гп, М] и удовлетворяет условию*: существует неотрицательное-
число С такое, что для любых х\ и х2 из сегмента [m, M] выпол-
выполняется неравенство
'тогда сложная функция h(x)—^(f(x)) интегрируема по Риману на
сегменте [а, Ь].
Доказательство. Пусть е — произвольное положительное
число. В силу интегрируемости функции f(x) на сегменте [а, Ь]
найдется такое разбиение {xk} этого сегмента, что S—s<&jC, где
S и s — верхняя и нижняя суммы функции f(x) соответственно,
С — постоянная из условий теоремы. Пусть Mk и mk — точные
грани функции f(x) на частичном сегменте [Xk-u Хь] разбиения
{xk}, a Mk* и ntk* — соответствующие величины для функции
h(x). Тогда в силу условия на функцию ф(л;) для любых точек х
и у, принадлежащих частичному сегменту [xk-\, Xk] разбиения
{xk}, справедливо неравенство
<C\f(x)-f(y)\<C(Mk-mk).
Поскольку неравенство h(x)—h(y)^C(Mk—mk) справедливо
для любых точек х и у, принадлежащих сегменту [Xk-i, Xk], то
тем более Mk*—mk*^C(Mk—mk), ибо найдутся две последова-
последовательности {хп} и {уп} точек сегмента [xk-\, Xk] такие, что h(xn)-*-
-+Mk*, h(yn)-+mk* при n-^oo.
Пусть, далее, S* и s* — соответственно верхняя и нижняя сум-
суммы функции h(x) для выбранного разбиения {xk} сегмента [а, 6].
Тогда
S'-s' = ? (Ml—ml) &xk < С J] (Mk—mk) Axk < e.
Поскольку e — произвольное положительное число, то в силу ос-
основной теоремы функция h(x) интегрируема на сегменте [а, Ь].
Теорема доказана.
Докажем теперь следующую несколько более общую тео-
теорему.
* Данное условие называется условием Липшица. Ясно, что функ-
функция, удовлетворяющая на сегменте условию Липшица, непрерывна на нем.
§ 3. Классы интегрируемых функций . 345
Теорема 9.4'. Пусть f(x) — интегрируемая по Риману на
Сегменте [а, Ь] функция, Миш — ее точные верхняя и нижняя
грани на [а, Ь]. Пусть, далее, функция ф(х) непрерывна на
сегменте [пг, М].
Тогда сложная функция h(x)=<p[f(x)] интегрируема по Ри-
Риману на сегменте [а, Ь].
Доказательство. Пусть С= max |ф(*)| и е — про-
извольное положительное число. Положим гх = г1(Ь—а+2С)„
Ввиду того, что ф равномерно непрерывна на [пг, M], сущест-
существует такое 6>0, что |ф(^)—<р(^)|<8ь если \ti—^|<б и
t\, t2^[m, M]. Выберем б еще и таким, что 6<еь В силу ин-
интегрируемости функции f(x) на [а, Ь] существует такое разби-
разбиение {xk} сегмента [а, Ь], для которого S—!s<62.
Положим
Mk= sup f(x), mk = inf f(x),
M*k= sup h(x), ml= inf h(x).
Разобьем целые числа 1, ..., n на два множества А и В: число
&еЛ, если Mh—mh<&, число реВ, если Мр—тр>б. Если ин-
индекс &еЛ, то Mk—tnk<8, следовательно, в силу равномерной
непрерывности функции ф(?) на сегменте [m, M] получим, что
Mk*—mft*^ei. Действительно, если рассматривается индекс
&еЛ, то мы получим, что Mh—mh= =sup f(x)— inf f(x)<. 6,
т. е. при x, y^[Xk-i, Xk] разность f(x) — f(y)=ti—h по абсо-
абсолютной величине не превосходит б: \t\—^|<б, где ^=/(лг),
t% = f(y). Следовательно, в силу равномерной непрерывности
функции ф на всем сегменте [пг, М] мы получим, что
Гак как последнее неравенство справедливо для любых х и у,
принадлежащих сегменту [Xk-i, Xk], то и
sup Ф (/(*))— inf <p(f(x))<s1.
t-xk-vxtJ txk-i-xkl
Далее, если teB, то, очевидно, что Mk*—mk*^.2C. Запишем
теперь разность (S* и s* — соответственно верхняя и нижняя
суммы функции h(x) для рассматриваемого разбиения {})
Xb-JZ (Ml-ml)Axk
(Ml—ml) Axk < 6l (b—a) + 2C ? Axk.
346 Гл. 9. Определенный интеграл Римана
Осталось произвести оценку для величины V Axk. Имеем
k€B
п
б ? Axk<C ? (Mk—/пй)Ал;й<? (Mk—mk) Axk
k€B k?B k—\
(здесь мы пользуемся тем, что все слагаемые (Мк—/)
являются неотрицательными). Учитывая, что при выбранном
п
разбиении V (Mk—mk) Axk = S—s< б2, получаем, что
fc=i
б ? Axk < ? (Mk~mk) Axk < б2, т. е. ? Axk < б.
fees k=i
Окончательно получим, что
S'—s" <ех(Ь—а) + 1С ? Axk<
fees
<е1 (b—a) + 2СЬ< ехF—а+ 2С) = е.
(Выше мы воспользовались тем, что 6<еь) Таким образом,
функция h(x) интегрируема, и теорема доказана.
Следствие. Если функция f(x) интегрируема на сегменте
[a, ft], то для любого положительного числа а функция \f(x)\a
интегрируема на этом же сегменте.
Действительно, достаточно рассмотреть непрерывную функ-
функцию <р(?) = |?|а и применить предыдущую теорему.
Приведем несколько примеров.
Примеры. 1) Пример интегрируемой функции, имеющей бес-
бесконечное число точек разрыва. Пусть на сегменте [0, 2/я] задана
1 *
функция f (х) = sgn sin — (рис. 9.4). Указанная функция имеет
разрывы 1-го рода во всех точках Xk^lfnk, k=l, 2, 3, ..., а также
разрыв 2-го рода в точке 0. Фиксируем произвольное число е>0.
Покроем точку я = 0 интервалом (—е/4, е/4). Вне этого интервала
находится лишь конечное число р точек разрыва функции. Число
р зависит от заданного е. Покроем каждую из этих точек интер-
интервалом длины меньше е/2р. Тогда все точки разрыва функции
/(я) = sgn sin— будут покрыты конечным числом интервалов,
общая сумма длин которых не превосходит \-р = 8. По
теореме 9.2 функция f(x) интегрируема на сегменте [0,2/я].
* В точке *=0 эту функцию доопределяем произвольно, например, пола-
полагаем /@)=0.
§ 4. Свойства определенного интеграла
347
п п
1
2) Из интегрируемости
функции | f (х) | не следует,
вообще говоря, интегрируе-
интегрируемость f(x). Действительно,
рассмотрим функцию D\(x),
равную единице для х ра-
рациональных и минус единице
для х иррациональных. Тогда
| Di (х) | = 1 интегрируема.
Точно также, как и для функ-
функции Дирихле D(x), показыва-
показывается, что функция D\(x) не-
интегрируема (см. пример из
§1).
§ 4. СВОЙСТВА
ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА. ОЦЕНКИ
ИНТЕГРАЛОВ.
ТЕОРЕМЫ О СРЕДНЕМ
ЗНАЧЕНИИ
1. Свойства интеграла. Вы-
Выясним основные свойства ин-
интеграла Римана.
а) Пусть функции f(x) и
g(x) интегрируемы на сегмен-
сегменте [а, Ь]. Тогда функции f(x)±
±g(x) также интегрируемы на этом сегменте, причем
ь ьь
/ (*) ±g(x)) dx = ^f (x)dx ±
-1
2_
X
Рис. 9.4
Действительно, при любом разбиении сегмента [с, Ь] и
любом выборе промежуточных точек ?*. справедливы следующие
равенства:
Axk ±
k=i
Axk
Поэтому, если существует предел правой части при стремлении
диаметра разбиений к нулю, то существует предел и левой части.
Из линейных свойств этого предела, которые устанавливаются
точно так же, как и для предела последовательностей, вытекает
доказываемое свойство.
348 Гл. 9. Определенный интеграл Римана
б) Если функция f(x) интегрируема на сегменте [а, ft], то
функция cf(x), где с=const, также интегрируема на этом сегмен-
сегменте, причем
ъ ь
(x)dx = c^ f(x)dx.
В самом деле, для любого разбиения сегмента [а, Ь] и
любого выбора промежуточных точек gft выполнено соотношение
откуда, так же как и выше, получаем доказательство утвержде-
утверждения б).
Следствие. Линейная комбинация ? с,Д(х) интегрируе-
1=1
мых функций fi(x) является интегрируемой функцией.
в) Пусть функции f(x) и g(x) интегрируема на сегменте
[а, Ь]. Тогда f(x)g(x) также интегрируема на этом сегменте.
Запишем очевидное тождество:
Заметим, далее, что в силу теоремы 9.4 из интегрируемости какой-
либо функции и(х) следует интегрируемость ее квадрата*. По-
Поскольку функции f(x)+g(x) и f(x)—g(x) по свойству а) интегри-
интегрируемы, то по сказанному интегрируемы и их квадраты, а следова-
следовательно, в силу указанного, функция f(x)g(x) интегрируема.
г) Пусть функция f(x) интегрируема на сегменте [а, ft]. Тогда
эта функция интегрируема на любом сегменте [с, d], содержа-
содержащемся в сегменте [а, Ь].
Выберем произвольное число е>0 и такое разбиение {xk} сег-
сегмента [а, 6], что S—s<e. Добавим к точкам разбиения {xk} точки
cud. Для верхних сумм S' и нижних s' вновь полученного раз-
разбиения {*//} в силу леммы 3 § 2 тоже будет справедлива оценка
S'—s'<e. Рассмотрим разбиение {xk} сегмента [с, d], образован-
образованное точками разбиения {xk'} всего сегмента [a, ft]. Для верхних
и нижних сумм S и s разбиения {Xk} выполнено, очевидно, соотно-
соотношение S—s^S'—s', поскольку каждое неотрицательное слагаемое
(Mk—mk)Axk в выражении S—s будет слагаемым и в выражении
S'—s'. Таким образом, S—s<e, и функция f(x) интегрируема на
сегменте [с, d]. Свойство г) доказано.
* Так как u2(x) = q>[u(x)] при ф(?) = '2 и функция q>(t) удовлетворяет усло-
условию Липшица на любом сегменте [т, М], ибо для любых ti и h из сегмента
\т, М] справедливо неравенство |<p(?i)—ф(У = U2i—^22| = |^i—h'
"'' -h\, где С — наибольшее из двух чисел 2 т\ и 2|Af|.
§ 4. Свойства определенного интеграла 349*
Будем по определению всегда считать, что интеграл Римана
от функции*, взятый в пределах от точки а до точки а, равен
а
нулю, т. е. [f (х) dx = 0. Это свойство следует рассматривать как
а
соглашение. Условимся также о том, что при а<Ь по определе-
а Ь
нию [f(x)dx= — [$(х)с1хдля любой интегрируемой функции^
Ь а
Эту формулу следует также рассматривать как соглашение.
*' д) Если функция f(x) интегрируема на сегментах [а, с] и
[с, Ь], то функция f(x) интегрируема и на сегменте [а, Ь], причем-
При а = Ь это свойство справедливо в силу принятых выше согла-
соглашений.
Предположим сначала, что а<с<Ь. Выберем произвольное
число е>0. Пусть {xk} и {xk") — такие разбиения сегментов-
[а, с] и [с, d], что на каждом из этих сегментов S—s<e/2. Пусть
{xk} — разбиение сегмента [а, Ь], состоящее из точек разбиений
{xk'} и {Xk"}. Очевидно, что разность между верхней и нижней
суммами разбиения {л:*} не будет превосходить е. Интегрируе-
Интегрируемость функции f(x) на сегменте [а, Ь] доказана. Пусть теперь
{xk} — произвольное разбиение сегмента [а, Ь], содержащее с.
Тогда
f (У Axk = 2' / (Ь) Axk + 2" / (У Ахк,
где 2' берется по частичным сегментам, принадлежащим [а, с]г
a 2" — по частичным сегментам, принадлежащим [с, d]. Посколь-
Поскольку это верно для любого разбиения, то, перейдя к пределу при
стремлении диаметра разбиений к нулю, получим, что
Если с не принадлежит [а, Ь], то сегмент [а, Ь] принадлежит
либо [с, Ь], либо [а, с]. Пусть, например, с<а<Ь. В силу свой-
свойства г) функция f(x) интегрируема на [а, Ь]. Действительно,
функция f(x) интегрируема на [с, Ь] по условию, а [а, Ь) а [с, Ь\.
Далее, поскольку с<а<.Ь,
abb
J /(*)dx + J /(х) dx= J /(x)dx.
* Функция в точке а определена и принимает конечное значение.
-350 Гл. 9. Определенный интеграл Римана
а с
fio по принятому соглашению ? f(x)dx= — f / (х) dx. Таким об-
с а
,разом, свойство д) установлено нами и для случая, когда с лежит
вне сегмента [с, ft]. Заметим, что формулу этого свойства можно
записать так:
§ f(x)dx+ § f(x)dx+ $ f{x)dx = O.
а с Ь
2. Оценки интегралов.
а) Если функция f(x) интегрируема на сегменте [а, ft] и
<f(X)^O для всех х из [a, ft], то интеграл, от функции f(x) no
этому сегменту неотрицателен.
Доказательство следует из того, что для любого разби-
разбиения {xk} и любого выбора \и. интегральная сумма
В этом случае предел интегральных сумм тоже будет неотрицате-
неотрицателен. Действительно, допустим, что предел А этих сумм отрицате-
отрицателен. Пусть е=|Л|. Выберем разбиение {л:*} такое, что |ст—Л|<
<|Л|. Но последнее неравенство может выполняться, только если
ь
-о<0, что противоречит условию о^О. Значит, f / (x) dx ^ 0.
а
б) Интегрирование неравенства. Если функции f(x) и g(x)
интегрируемы на сегменте [a, ft] и f(x)^g(x) для всех х из
[a, ft], то $f(x)dx<^g(x)dx.
а а
Действительно, функция g(x)—f(x) интегрируема и неотрица-
неотрицательна на [a, ft], так что
l(g(x)-f(x))dx>0.
а
Ь Ь
Но тогда в силу свойства а) из п. 1 {g(x)dx—f f(x)dx^0,
а а
¦что и требовалось установить.
в) Пусть функция f(x) непрерывна и неотрицательна на сег-
сегменте [a, ft]. Если существует хотя бы одна точка Хо сегмента
{a, ft], в которой f(xo)>Q, то найдется положительное число а
•лакое, что
§ 4. Свойства определенного интеграла 351
Действительно, пусть /(*0)=р>0. Тогда в силу непре-
непрерывности функции f(x) в точке х0 найдется такая окрестность
точки Хо, что для любого сегмента [с, d], c=?d, _ лежащего цели-
целиком в этой окрестности, будет выполнено неравенство f)l2
Но тогда в силу оценки из п. б)
и
Следовательно, f / (x) dx > a > 0.
г) Если функция f(x) интегрируема по Риману на сегменте
[а, Ь], то функция \f(x)\ интегрируема на этом сегменте и
Рассмотрим функцию <р@ = И1- Согласно теореме 9.4 из интег-
интегрируемости f(x) следует интегрируемость ср (/(*)) = \f(x) \ (так
как функция ф(/) = п| на любом сегменте удовлетворяет условию
Липшица*). Выберем теперь число а=±1 так, чтобы a
а
>0. Очевидно, что af(x)^\af(x) | = \f {x) \. Тогда в силу свойст-
свойства б)
\$f(x)dx\ = a$f{x)dx = $af(x)dx< \\f{x)\dx,
а а а а
что и требовалось.
д) Первая формула среднего значения. Пусть каждая из функ-
функций f(x) и g(x) интегрируема на сегменте [а, Ь] и функция g(x),.
кроме того, неотрицательна (или неположительна) на этом сег-
сегменте.
Обозначим через Mum точные грани f(x) на сегменте
[а, Ь]**. Тогда найдется число ц, удовлетворяющее неравенствам
^^М и такое, что справедлива следующая формула:
При дополнительном предположении о непрерывности f(x) на сег-
Функция <р@ = 1'|> очевидно, удовлетворяет условию Липшица на лю-
люб |(f)(й) I IU| UIKUk\
бом сегменте, ибо |<p(*i)—<Р(*г) I =IUi|—U2IKU1—к\.'
** Интегрируемая на [а, Ь\ функция ограничена на fa, k\ и потому у нее
существуют на fa, 6] точные грани. ч.*
¦352 Гл. 9. Определенный интеграл Римана
менте [а, Ь] можно утверждать, что на этом сегменте найдется
точка I такая, что справедлива формула
{x)dx. (**)
'Формулу (**) принято называть первой формулой сред-
среднего значения. Формулу (*) иногда также называют первой
формулой среднего значения.
Заметим сразу же, что формула (* *) сразу вытекает из фор-
формулы (*) и из того, что непрерывная на сегменте [а, Ь] функция
достигает на этом сегменте как своих точных граней М. и пг, так
и любого промежуточного значения ц,(т^Сц^С.М).
Таким образом, нужно доказать только формулу (*). Для дока-
доказательства формулы (*) заметим, что по определению точных
траней для -любого значения х из [а, Ь] справедливы неравенства
Предполагая ради определенности g{x) неотрицательной на
'fa, Ь],-мы получим, умножая последние неравенства на g(x), что
для любого х из [a, b]
mg(x)^f(x)g(x)^Mg(x). («*«)
Так как, кроме того, в силу свойств б) и в) из п. 1 каждая из
•функций mg(x), Mg(x) и f(x)g(x) интегрируема на [a, b], то
«оценка (***) позволяет утверждать справедливость следующих
неравенств:
ь ь ь
§mg(x)dx<jf(x)g(x)dx< \Mg{x)dx
а а а
или, что то же самое (в силу свойства б) из п. 1),
ь ь ь
m \g(x)dx < f / (х) g (x) dx < М \g (x) dx. (****)
о а а
Ь Ь
Могут представиться два случая: 1) Г g (x) dx = 0 и 2) Г g (x) dx > 0.
а а
В первом случае из неравенств (****) вытекает, что
ь
\f(x)g(x)dx = 0, и потому формула (*) справедлива при любом ц.
а
Во втором случае, поделив неравенства (****) на число
ъ
[g(x)dx, мы получим, что
§ 4. Свойства определенного интеграла 353
т<
\ fix) &(*)**
—ь
\g(x)dx
а
Для завершения доказательства формулы (*) остается обозна-
обозначить символом ц. число
$f(x)g{x)dx
$g(x)dx
а
Следствие. Сформулируем отдельно доказанную нами тео-
теорему для частного случая g(*) = l.
Пусть функция f(x) интегрируема на сегменте [а, Ь], а симво~
лы Миш обозначают точные грани f(x) на указанном сегменте.
Тогда найдется число ц, удовлетворяющее неравенствам
и такое, что справедлива формула
ь
При дополнительном предположении о непрерывности f(x) на
[а, Ь] можно утверждать, что на этом сегменте найдется точка I
такая, что справедлива формула
Последнюю формулу обычно также называют формулой
среднего значения.
е) Вторая формула среднего значения. Пусть
функция f(x) интегрируема, а функция g(x) монотонна на сег-
сегменте \а, Ь]. Тогда на этом сегменте найдется число | такое, что'
ъ \ ь
\ f (x) g (x) dx = g{a)\f (x) dx + g(b)\f (x) dx.
a a |
Установим сначала следующий факт, которым мы восполь-
воспользуемся ниже
Лемма Абеля*. Пусть числа pi удовлетворяют уело-
i
виям p^Pj^O при i^j, а числа Si = V qk (i= 1,2, ... ,п) —
* Нильс Генрих Абель — норвежский математик A802—1829).
12 Зак. 72
354 Гл. 9. Определенный интеграл Римана
неравенствам m^iS^M, где qh, m, M также некоторые числа.
п
Тогда пгрг < ]? pkqk < Мрх.
fe=i
Доказательство. Легко проверить, что
где положено So=O, pn+i=0. Так как рь^О, pk — pfc+i>0, то
заменив в последнем равенстве каждое Si сначала на т, а за-
затем на М, получим
ft=l
но
(Pk—Pk+I) = Pi —Pn+l = Pi-
Таким образом, лемма доказана.
Установим теперь вторую формулу средне-
среднего значения. Допустим, что функция g{x) не возрастает на
[а, Ь] и неотрицательна. Функция f(x)g(x) интегрируема как
произведение двух интегрируемых функций. Пусть Mk и т4 —
точные грани f(x) на частичных сегментах [*&_!, хь\-
Тогда очевидно, что
ft-l) Ахк <
В силу монотонности g (x) справедлива оценка
п п
? (Mk—mk) g (Xk-i) Axk< g (а)? (Mk—mk)Axk.
k=i k=\
В силу интегрируемости f(x) сумма в правой, а значит, и в ле-
левой части последнего неравенства стремится к нулю при стрем-
стремлении диаметра d разбиений к нулю. Следовательно, при лю-
любых числах цн таких, что mk^.\ih^.Mk, все суммы
п п п
k=\ ft=l ft=l
Ь
стремятся при d-И) к интегралу f f(x)g(x)dx. Это следует из
§ 4. Свойства определенного интеграла 355
двусторонней оценки для интегральной суммы функции
f(x)g(x)\
По свойству д) настоящего пункта числа ц*, где
x
к
<Mk, можно выбрать так, чтобы Г / (х) dx = \xk Axk.
х
Заметим теперь, что функция F (х) = / (t) dt непрерывна
а
на сегменте [а, Ь], так как
х+Ах
AF = F(x+Ax)—F(x)= J f{t)dt =
X
inf /@<p< sup f(t).
и, следовательно, Д^-^-О при Длг-^-О.
i
Рассмотрим следующие числа S{ = \ \ikAxk = Г f{t) dt.
k=\ a
Ясно, что m^.Si^M, где т и М—точные грани функции F(x)
на сегменте [а, Ь]. Введем следующие обозначения:
pk=g(xh-i),, qh=V-kAxh, k=l,2,...,n.
В силу монотонности и неотрицательности функции g(x) вы-
выполнимо pi>P;^0 при ?</. Числа ph, Sk, qh удовлетворяют ус-
условиям леммы Абеля. Поэтому
п
e)< ? g (**-i) VkAxk < Mg (a).
Сумма J] g(xk-i)PzAXk заключена между mg{a) и Mg(a).
ft=i
Устремим теперь диаметр d разбиений к нулю. Тогда и предел
этой суммы будет заключен между mg(a) и Mg(a), т. е. будут
справедливы - неравенства
ь
mg (a)< j / (x) g (x) dx < Л1^ (а).
а
* Т. е. из неравенств
п п п
?, mkS(.xk-i) &xk < ?, f (-^ft-i)§ (xk-i) &xk ^ Z-t Mfcg (x^ Axfe.
fe=l ft=l fe=l
12*
356 Гл. 9. Определенный интеграл Римана
х
Непрерывная функция F{x)=[f{t)dt принимает любое
а
значение, заключенное между ее точными гранями т и М. Так
как
ь
ff(x)g(x)dx
т < — < М,
gifl)
то существует точка | такая, что
ь
\ ] f (х) g W ^х
F (I) = "
Следовательно, в случае, когда g(x) не возрастает и неотрица-
неотрицательна, доказана формула
ь
Рассмотрим теперь общий случай невозрастающей функции
g(x). В этом случае функция h(x)=g{x)—g(b) не возрастает
и неотрицательна. Подставив ее вместо g(x) в формулу, дока-
доказанную выше, получим, что
J / (х) [g (х) -g (b)) dx = [g (a) -g (b)] f f (x) dx.
a a
Окончательно получаем равенство
J / (x) g (x) dx = g (a) |/ (x) dx + g (b) J f (x) dx-
а а
I Ь
что и требовалось доказать*.
Рассмотрим примеры на применение оценок для интегралов.
Примеры. 1) Рассмотрим функцию
f(x,\x*, xe@,l],
ПХ)-\1. х = 0.
Эта функция f(x) непрерывна на сегменте [0,1]. Легко убедиться
* Если g(x) не убывает, то заменой gi(x)= —g(x) сводим этот случай к
уже рассмотренному.
§ 5. Первообразная непрерывной функции 357
с помощью вычисления производной, что эта функция достигает
локального минимума при хо=\/е. При этом f(l/e)=e-1/e, и это
значение является ее наименьшим значением на сегменте [0,1].
Используя свойство б) настоящего пункта, получим, что е1/
< для числа е~1/е легко получить, что е-'/е=0,692....
о
Заметим, что в этом случае значение интеграла нельзя определить
через значения элементарных функций.
2) Если функция f(x) не является непрерывной, то формула
среднего значения (**) может быть несправедливой. Рассмотрим
функцию
Г1/2,0<*<1/2.
1 3/4, 1/2<*<1.
1
Тогда f f(x)dx = 5/8. Значение 5/8 не принимается функцией /(*)'
о
ни в одной точке ? сегмента [0,1]. Следовательно, не существует
числа ge [0, 1], для которого {f(x)dx = f(%).
§ 5. ПЕРВООБРАЗНАЯ НЕПРЕРЫВНОЙ ФУНКЦИИ.
ПРАВИЛА ИНТЕГРИРОВАНИЯ ФУНКЦИЙ
В предыдущих параграфах уже достаточно полно изучены
свойства интеграла Римана. В частности, было показано, что,
пользуясь определением интеграла, можно вычислить интеграл
от некоторых простейших функций. Однако такое вычисление ин-
интеграла с помощью предельного перехода в интегральных суммах
обладает рядом неудобств и приводит к значительным трудно-
трудностям. Поэтому на повестку дня встает вопрос о простых правилах
вычисления определенного интеграла Римана. Ниже нами будет
дано одно из таких правил вычисления определенного интеграла,
а именно будет доказана основная формула интегрального исчис-
исчисления (формула Ньютона — Лейбница).
1. Первообразная. Рассмотрим интегрируемую на сегменте
[а, Ь] функцию f(x). Пусть р принадлежит [а, Ь). Тогда для лю-
любого х из [а, Ь] функция f(x) интегрируема на [р, х], и поэтому
на сегменте [а, Ь] определена функция F(x)= i f(t)dt, которая
р
называется интегралом с переменным верх-
верхним пределом. Аналогично определяется функция F(x) на
интервале (а, Ь) при условии, что f(x) определена на интервале
(а, Ь) и интегрируема на любом сегменте, принадлежащем этому
интервалу.
358 Гл. 9. Определенный интеграл Римана
Теорема 9.5. Если функция f(x) интегрируема на сегменте
{a, b], p — любая точка этого сегмента, то производная функции
X
F {х) = \ f (t) dt существует в каждой точке х0 непрерывно-
р
сти подынтегральной функции, причем F'(xQ)=f{x0) *.
Доказательство. В силу непрерывности функции f(x) в
точке хо для любого е>0 найдется такое 6>0, что f(x0)—е<
<f(x)<f(xo)+e, если \х — *0|<6. Для всех t из [х0, х] выпол-
выполняется неравенство |^ — *o|^|* — *о|<6. Поэтому для всех та-
таких t
f(xQ)-e<f(t)<f(xQ)+e.
Согласно свойству д) п. 2 § 4 (независимо от знака разности
х — хо) получим из последних неравенств
X
/(*о)-«*<— f/@#</(*о) + в при |*-*6|<5.
X — Хо J
х„
X
1 Г
{Значение Ц = \ / @ dt не меняется при перестановке чи-
Хо
сел х и хо, так как при этом одновременно меняется знак у вели-
х *
чины х — хо и у интеграла ^f{t)dt.\ Но ———Г f(i)dt =
х° ха
= —— —, следовательно, при \х — л
х — х0
т. е. F'(x) существует и равна f(x0). Теорема доказана.
Следствие. Любая непрерывная на сегменте [а, Ь] функ-
функция f(x) имеет на этом сегменте первообразную. Одной из перво-
первообразных является функция F(x) = \ f (t) dt.
а
Замечание 1. Теорема остается справедливой, если f(x)
непрерывна на интервале (а, Ь). В этом случае в качестве ниж-
нижнего предела надлежит взять любую точку р этого интервала.
Все рассуждения сохраняются.
* Если точка дг0 совпадает с одним из концов сегмента [а, Ь], то под
производной в точке х0 функции F(x) понимается левая или правая производ-
производная соответственно. Доказательство теоремы при этом не меняется.
§ 5. Первообразная непрерывной функции 359 .
Замечание 2. Можно рассматривать и функцию нижнего
я
предела интеграла от f(x), т. е. функцию Ф(*) = J" f(t)dt. Для
X
такой функции
Ф'(*) =—/(*)•
Замечание 3. Если функция f(x) интегрируема на любом
сегменте, содержащемся в интервале (а, Ъ), то интеграл с пере-
переменным верхним пределом есть непрерывная на {а, Ь) функция
верхнего предела.
Действительно, пусть F (х) = J / (t) dt, p e (a, b). Тогда
р
х+Д*
где
inf. /(%)O< sup f(x)
xS[x,x+Ax] Sl+&]
по первой формуле среднего значения. Если функция f(x) инте-
интегрируема, то она ограничена, а поэтому для всех достаточно ма-
малых Д# ограничена и величина ц, зависящая от х и Д#. Более
точно, inf /(х)<ц< sup f{x)*. Поэтому А/7->0 при Ах->-0.
x?ld] eld]
Замечание 4. Интегралы с переменным верхним (или
нижним) пределом можно использовать для определения новых
функций, не выражающихся через элементарные функции.
х
Так, например, интеграл \e~t2dt, как уже отмечалось, назы-
о
X
вается интегралом Пуассона, интеграл I , 0<
о
<&<1 называется эллиптическим интегралом, интеграл
Г sini ,, г costdt
\~~p~ интегральным синусом, \ интегральным
о 1
косинусом и т. д.
2. Основная формула интегрального исчисления. Мы уже
знаем из предыдущих рассмотрений, что любые две первообраз-
первообразные функции f(x), заданной на сегменте [а, Ь], отличаются на
X
постоянную. Поэтому eauiF(x)=[f(t)dt, а Ф(х)~любая дру-
Здесь [с, d] — какой-либо фиксированный сегмент, принадлежащий ин-
интервалу (а, Ь) и такой, что х&[с, d], x + Axe=\c, d].
360 Гл. 9. Определенный интеграл Римана
гая первообразная непрерывной функции f(x), то Ф(х)—F(x) =
= С = const, т. е. Ф(х)= [f(t)dt + C (см. теорему 9.5). Положим
а
в последней формуле сначала х—а, а затем х=Ь. Как мы усло-
а
вились (см. п. 1 предыдущего параграфа), ff (t)dt = O для любой
а
функции, принимающей конечное значение в точке а, поэтому
ь
Ф(а) = С, <$(b) = $f(x)dx+C. Отсюда
a
Ь
и нами получена основная формула интегрального исчисления.
Сформулируем ее в виде теоремы.
Теорема (основная теорема интегрального
исчисления). Для того чтобы вычислить определенный инте-
интеграл по сегменту [а, Ь] от непрерывной функции f(x), следует
вычислить значение произвольной ее первообразной в точке b и в
точке а и вычесть из первого значения второе.
Теперь мы имеем правило вычисления определенного интегра-
интеграла от широкого класса интегрируемых функций. Задача вычисле-
вычисления определенного интеграла свелась к задаче нахождения пер-
первообразной непрерывной функции. Естественно, что не для вся-
всякой функции найти первообразную просто. Мы уже неоднократ-
неоднократно указывали функции, первообразные которых не выражаются
через элементарные функции (см. например, п. 1 этого парагра-
параграфа) . В этом случае, естественно, возникает вопрос о приближен-
приближенном вычислении определенных интегралов, о чем пойдет речь
ниже.
Основную формулу интегрального исчисления часто записы-
ъ
вают в форме f / (x) dx — Ф (х) | *, где введено обозначение
3. Важные правила, позволяющие вычислять определенные
интегралы. При вычислении определенных интегралов очень ча-
часто используется правило замены переменной под знаком опреде-
определенного интеграла.
Пусть функция x=g{t) имеет непрерывную производную на
§ 5. Первообразная непрерывной функции 361
сегменте [m, M] * и min g(/) = a, max g{t) = b, причем
tG[m,M] t?lmM)
b M
g(m)=a, g(M)=b. Тогда \f{x)dx = ^f[g{t)\g'{t)dt (при уело-
a m
вии, что функция f(x) непрерывна на сегменте [а, Ь]).
Указанная формула называется формулой замены пере-
переменной под знаком определенного интеграла.
Доказательство. Пусть Ф(х) — некоторая первообразная
функции f(x). функции Ф(х) и x=g(t) дифференцируемы на сег-
сегментах [а, Ь] и [ш, М] соответственно. Поэтому, согласно прави-
правилу вычисления производной сложной функции, для всех t из
[т,М]
-^-<s(g(t)) = <s'(g(t))g'(t).
Заметим, что производная Ф' в выражении справа вычислена по
аргументу x:<I>'{g(t))=<?'(x), x=g(t).
Заметим также, что Ф'(х)=[(х). Подставив в правую часть
формулы для ——- Ф {g{t)) это равенство, получаем
Таким образом, функция Ф(§@) является на сегменте
<Af первообразной для функции f(g{t))g'(t), т. е.
м
j / (g (*)) g' V) dt = O(g (M)) - Ф (g (m)) = Ф(Ь)-Ф (а)
m
b
согласно условию. Следовательно, с одной стороны, [f(x)dx —
а
М
= Ф(Ь)—Ф(а), а с другой стороны, Ф(Ь)—Ф(а)=\ f{g(t))g'(t)dt,
т
что и требовалось.
Сформулируем и установим теперь правило интегри-
интегрирования по частям.
Пусть функции f(x) и g(x) имеют непрерывные производные
на сегменте [а, Ь], тогда
/ (х) g' (х) dx = f(x)g (х) |»_ j g(x) Г {x) dx.
* Будем говорить, что g(t) имеет непрерывную производную на сегменте
[ш, М], если производная g'(t) существует и непрерывна в любой внутренней
точке [т, М] и существуют конечные пределы t->m+o t-*M—Q
362 Гл. 9. Определенный интеграл Римана
Действительно, — [/ (х) g {х)) = f (x) g' (х) + /' (х) g (x). Поэтому
функция f(x)g(x) является первообразной функции [f(x)g'(x) +
Hf (*) • S \x) ]. Следовательно,
и наше утверждение доказано. Последнюю формулу удобно запи-
записывать в виде
4. Остаточиыи член формулы Тейлора в интегральной фор-
форме. Целью этого пункта является получение формулы Тейлора
для функции f(x) в окрестности произвольной точки а с оста-
остаточным членом в так называемой интегральной
форме.
Пусть функция f(x) имеет в некоторой е-окрестности точки
а непрерывную производную (п+1)-го порядка. Пусть х при-
принадлежит указанной окрестности. Рассмотрим равенство
Полагая u(t)=f'(t), v(t)=—(x — t), применим к интегралу
X X
\f'(t)dt= [u{t)dv{t) формулу интегрирования по частям. По-
в
лучим
= /'(*) (*-<*)+J ПО (*-<
а
Таким образом, последовательно интегрируя по частям,, по-
получим
* х
f"{t)(x~t)dt =
а а
х
= /' (а) (х-а) + -i-Г (а) (x-af + ± \'Г @ {x-tfdt = ...
§ 5. Первообразная непрерывной функции 36$
dt
X
Л" f{n) (а) (*—а)п + -т f f{n+l) @ (х—*)п
га! п'. J
где
га!
a
Мы видим, что i?n+i {x) является остаточным членом разло^
жения Тейлора для функции f(x) в окрестности точки а. Эта
форма остаточного члена и называется интегральной
формой.
Если применить первую формулу среднего значения (см.
свойство д) п. 2 § 4), то
! (х) = — \ /("+«@ (x-~t)ndt = i iSZ. I (X—t)ndt =
и! J n! J
a
Г 16/ \* v
га! и+ 1
A+1I
где | — некоторая точка сегмента [а, х]. Следовательно, при
тех же предположениях мы получим остаточный член в форме
Лагранжа. На самом деле, легко заключить (используя теоре-
теорему Дарбу о прохождении производной через все промежуточ-
(х_в)+/(+)(|)
ные значения), что Rn+i\x) = — ¦—i2—лишь при усло-
(п + 1)!
1
вии существования и интегрируемости
Рассмотрим теперь примеры, иллюстрирующие изложенный в
этом параграфе материал.
Примеры. 1) Вычислить интегралы, применяя основную
формулу интегрального исчисления:
ь
xndx--
n+l
га+1
^
^
а
Ь
б) <\smxdx=—cosx|* = cosa—cos b,
ь
[cosxdx = s'mb—sin a.
364
Гл. 9. Определенный интеграл Римана
в)
а
J * + # dx = -±-ln(a»
Я/4 it/4
\ С sin* x , С
cosax
=1/5>
2) Вычислить интегралы, применяя правило замены пере-
переменной:
Я/4
а:
о
где t =
1
б)
о
где t =
3) Вычислить интеграл, применяя правило интегрирования по
частям:
Я/2 Я/2
1т = [ sinm *d;c = — f sin-1 xd (cos *) =
= tt2dt = —
1
Я/2
f
о
Отсюда: Im =
/
= — sin" x cos x |jf/2 + (m — 1) f cos2 x sinm~2 xdx =
о
Я/2
= (m—1) j A—sin2^)
/n
/m_2 при т. > 2.
Легко видеть, что /о=л/2, /i = l. По индукции получаем, что
2
для
2w—1 2/га — 3
2т+1
2т 2т—2 "¦
2т 2т — 2
2т+1 2т —1
3 1 я _ Bт—1I1 п
4 2 2 ~ Bт)!! 2 '
4 2 , Bт)Н
' 3 ~ Bт+1)!!'
4) Доказать, что для функции f{x)=(l+x)a остаточный
член Rn+i в интегральной форме стремится к нулю, если |*|<
<1. Заметим, что
§ 6. Неравенства для сумм и интегралов 365
Rn+l
о
Из очевидных неравенств tfx^O, 1—х>0 следует, что
^= — A— х)>0 или JLzL=i L< i_
Далее, поскольку я и х — / — числа одного знака, то
х — t
x I x
Следовательно,
= 1 i_<i_f=|i_f| или
X — t
\—t
<\Х\.
о о
где С(х, а) не зависит от п. Иными словами,
|#n+i|<C(*, а)-|а(а—1) ... (а—п)\\х\п1п\=рп.
Рассмотрим какое-либо число q, удовлетворяющее' условию
|я|<<7<1. Так как
Рп+1 \а— п— 1| \х\
—— = — 4*1 (п-^оо),
Рп Я+ 1
то найдется такой номер N, что < Ц при n^N. Отсюда
Рп
вытекает, что pn^pNqn~N при ri^N'. Устремляя в этом нера-
неравенстве п к оо, убеждаемся в том, что рп, а следовательно, и
Rn+i стремится к нулю.
§ 6. НЕРАВЕНСТВА ДЛЯ СУММ И ИНТЕГРАЛОВ
В этом параграфе мы получим некоторые важные неравен-
неравенства для сумм и интегралов.
1. Неравенство Юнга *. Рассмотрим два неотрицательных
числа а и b и два числа р и q, превосходящие единицу и та-
такие, что 1/р+1/<7=1. Докажем следующее неравенство
Юнга:
аЬ < — а" + —Ь".
Р Я
Доказательство. Рассмотрим функцию
xfp при х>0. Поскольку f (x) = '±-(x-1"i— 1), то f'(x\>0
* Вилиам Юнг — английский математик A882—1946).
366 Гл. 9. Определенный интеграл Римана
при 0<*<1 и f'(x)<0 при х>\. В точке х=1 функция f(x)
принимает наибольшее значение, причем /A) = 1 =—.
р я
Следовательно, х1'"—х/р < l/q при всех я>0. В последнем не-
неравенстве полагаем х=пр/Ьр, ЬфО. Неравенство Юнга при
ЬФО, таким образом, установлено. При Ь = 0 оно очевидно.
2. Неравенство Гельдера * для сумм. Пусть аи а2,.... а„ и
Ъ\, Ь2,...,Ьп — какие угодно неотрицательные числа. Тогда
где 1/р+1/<7=1, р>1, q^\. Это неравенство называется не-
неравенством Гельдера для сумм.
Доказательство. Заметим, что указанное неравенство
однородно в том смысле, что если оно выполнено для чисел аи
bt, то оно справедливо и для чисел taiy kbi. Поэтому доста-
п п Щп
точно установить, что ? atbi < 1 при условии ? аР= 1, V Ы =
;=i i=i i=i
= 1, так как мы всегда можем разделить числа а\ и Ьг- соот-
п п
ветственно на величины (V аРЛ р и (V bf\ **. Записав не-
i=i i=i
равенство Юнга для таких чисел а* и Ьг и просуммировав эти
неравенства по i, получим
It
V4 1 1
Поэтому у,a<Pi "^ 1 = * • чт0 и требовалось.
Замечание. В случае р=2, q—2 неравенство Гельдера
превращается в неравенство
называемое неравенством Коши — Буняковско-
го *** для сумм.
* О. Гёльдер — немецкий математик A859—1937).
** Мы предполагаем, что хотя би одно из чисел at и хотя бы одно из
чисел bi отлично от нуля. В противном случае неравенство очевидно.
*** Виктор Яковлевич Буняковский — русский математик A804—1889).
§ 6. Неравенства для сумм и интегралов 367
3. Неравенство Минковского* для сумм. Пусть щ, а2,...
...,ап и Ь\, Ь2 Ьп — произвольные неотрицательные числа, чи-
число р> 1. Тогда справедливо следующее неравенство
Минковского для сумм:
(? )()(
?=.1 1=1 1=1
Доказательство. Запишем равенство
(а,- + bty = ? а, (а, + Ь^4- ? Ь{ (а,
К каждой из сумм, стоящих в правой части, применимо нера-
неравенство Гёльдера. Если 1/р+1/<7=1, р>\, <7>1, то (р—1)<7 =
=р, —=.- . Поэтому
q p
(at + bt)p
Р
n
Поделив обе части последнего неравенства на [V
t=i
1—
+ be)" p , получим доказываемое неравенство.
4. Неравенство Гёльдера для интегралов. Пусть f(x) и
g(x) —две произвольные интегрируемые на сегменте [а, Ь]
функции, пусть р и q — два числа, превосходящие единицу, и
1/р+1/<7 = 1. Тогда справедливо неравенство 'Гёльдера
для интегралов
(все написанные интегралы существуют в силу следствия из
теоремы 9.4').
Герман Минковский — немецкий математик и физик A864—1909).
368 Гл. 9. Определенный интеграл Римана
Заметим, что, как и в п. 2, достаточно рассмотреть случай,
ь ь
когда [ \f(x)\pdx< 1 и [\g(x)\qdx<C i, и доказать неравен-
а
Ъ
ство I f f (x) g (x) dx < 1. Запишем неравенство Юнга в любой
а
точке х для функций \f(x)\ и \g{x) |. Получим
\f(x)\\g(x)\<±-\f(x)\»+-±-\g(x)\<>.
Интегрируя это неравенство, получим
[\f(x)\ \g(x)\dX<l,
а
но, согласно свойству д) п. 2 § 4
\$f{x)g(x)dx\<$\f(x)\\g(x)\dx.
а а
Поэтому доказательство завершено.
Как и при выводе неравенства Гёльдера для сумм, мы
ь ъ
предполагали, что Uf(x)\dx gtO и Ug(x)\dx^0. В противном
а а
случае неравенство очевидно.
Замечание. В случае р — 2, q = 2 неравенство Гёльдера
превращается в неравенство
которое называется неравенством Коши — Буняков-
ского для интегралов.
5. Неравенство Минковского для интегралов. Пусть f(x) и
g(x)—любые две неотрицательные и интегрируемые на сег-
сегменте [а, Ь] функции и число р>1. Тогда справедливо не-
неравенство Минковского для интегралов
{f (f W + в (x))pdxI/p < j( f (х) dXyp + (jgp (x) dxf».
а
а а а
Заметим, что согласно следствию из теоремы 9.4' все подынте-
подынтегральные функции интегрируемы.
Доказательство. Точно так же, как и при доказатель-
доказательстве неравенства Минковского для сумм, запишем равенство
§ 7. Дополнительные сведения об интеграле Римана 369
J (/(*) +Я (*))"<&
= J / (x) (f (x) + g (я))'-1 dx + j g (x) (f (x) + g (%))"-' dx.
a a
Далее применяем к интегралам, стоящим справа, неравенство
Гёльдера и, как и в п. 3, получаем доказательство.
По индукции можно доказать и более общее неравенство
для функций fi(x), f2(x),...,fn(x), неотрицательных и интегри-
интегрируемых на сегменте [а, Ь]:
ь
\h \x) t/iWt •••'Tin W) axi "C
)
a
< (J ft {x)dxfp+ (\ft(x)dxfl'+ ... + tjfn(x)dxI/p.
§ 7. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ
ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ РИМАНА
1. Предел интегральных сумм по базису фильтра. Рассмот-
Рассмотрим множество всех разбиений {Xh} сегмента [а, Ь]. Обозначим
это множество* всевозможных разбиений символом Р*. Каж-
Каждому фиксированному разбиению {%}еР* отвечает некоторая
интегральная сумма а. Таким образом, получается отображе-
отображение множества разбиений в множество интегральных сумм. Вы-
Выберем в Р* базис фильтра (базу) В* = {Ва*} с элементами
Эта запись означает: элемент Вй* есть разбиение {Xh} с диамет-
диаметром d, меньшим б. Вспоминая общее определение предела по
базе (базису фильтра), мы можем записать, что
ь
f(x)dx = li
d
где предел означает предел числовой функции а (интегральной
суммы функции f(x)) по базису фильтра (d-+0). В силу
свойств предела по базе такой предел является единственным.
Ясно, что все теоремы предыдущих параграфов, где использо-
использовался предел сумм при стремлении диаметра разбиений к нулю,.
* Предполагается, что каждому разбиению отвечает и некоторый выбор,
промежуточных точек.
370 Гл. 9. Определенный интеграл Римана
можно сформулировать, используя понятие предела по базису
фильтра.
2. Критерий интегрируемости Лебега. Будем говорить, что
множество Л точек сегмента [а, Ь] имеет меру нуль, если
для любого s>0 можно указать не более чем счетную систему
интервалов, покрывающую все точки множества А и имеющую
сумму длин, не большую чем 8. Заметим, что число интервалов
может быть и бесконечным, однако они имеют длины а„ такие,
что если
то limSn = /< 8.
В теории, изучающей меру множеств, доказывается следую-
следующий критерий интегрируемости функции f(x) на сегменте [а,
Ь] по Риману.
Теорема 9.6 (критерий Лебега). Для того чтобы
ограниченная на сегменте [а, Ь] функция f(x) была интегри-
интегрируемой по Риману на этом сегменте, необходимо и достаточно,
чтобы множество точек разрыва этой функции имело меру
нуль.
Доказательство этой теоремы можно найти в книге
В. А. Ильина, Э. Г. Позняка «Основы математического анали-
анализа», II, с. 265—266.
ДОПОЛНЕНИЕ 1
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Изученное в гл. 9 понятие определенного интеграла Римана
•существенно использовало два обстоятельства: 1) тот факт, что
^промежуток [а, Ъ], по которому требуется произвести интегриро-
интегрирование, является конечным; 2) тот факт, что подынтегральная
¦функция f(x) является на рассматриваемом промежутке огра-
ограниченной.
, В настоящем дополнении будет дано обобщение понятия опре-
определенного интеграла Римана на два случая: 1) на случай, когда
промежуток, по которому требуется произвести интегрирование,
является бесконечным*; 2) на случай, когда подынтеграль-
подынтегральная функция f(x) является неограниченной в окрестности
некоторых точек области интегрирования.
Возникающее при таком обобщении понятие интеграла приня-
принято называть несобственным интегралом соответственно первого
или второго рода.
Т. е. представляет собой полупрямую или всю бесконечную прямую.
Дополнение 1. § 1 37L
§ 1. Несобственные интегралы первого рода
1. Понятие несобственного интеграла первого рода. Перенесем;
понятие определенного интеграла на случай, когда область, по ко-
которой производится интегрирование, является бесконечной. На
прямой —oo<x<-foo существует три типа бесконечных связных,
замкнутых множеств: 1) полупрямая а^х< + °°; 2) полупрямая
—оо<х^й; 3) вся бесконечная прямая —оо<х< + о°-
Ради определенности рассмотрим подробно первое из указан-
указанных множеств, т. е. полупрямую а^х< +оо.
Предположим, что функция f(x) определена на полупрямой
а^х< + °° и что для любого числа А, удовлетворяющего неравен-
А
ству А^а, существует определенный интеграл Римана \ f(x)dx.
а
Этот определенный интеграл мы обозначим символом
jdx. (9.1.1>
Естественно, возникает вопрос о существовании предела функ-
функции .F (А) при А-*--\-оо
[f(x)d
x. (9.1.2).
Определение. Предел (9.1.2) в случае, если он существует,
называется несобственным интегралом первого*
рода от функции f(x) no полупрямой [a, -f-oo) и обозначается
символом
\dx. (9.1.3),
J/W.
При этом говорят, что несобственный интеграл (9.1.3) схо-
сходится, и пишут равенство
+о> А
[f(x)dx= Um [f(x)dx.
Впрочем, символ (9.1.3) употребляют и в случае, если указан-
указанного выше предела (9.1.2) не существует, но в этом случае гово-
говорят, что несобственный интеграл (9.1.3) расходится.
Совершенно аналогично определяются несобственные интегра-
интегралы по полупрямой —оо<д^& и по всей бесконечной прямой;
372 Гл. 9. Определенный интеграл Римана
Первый из этих интегралов определяется как предел
b b
lim $f(x)dx и обозначается символом f f(x)dx.
Л-i—00 J J
A —оо
GO
Что же касается интеграла \f(x)dx, то он определяется как
— СО
предел
А"
lim f f(x)dx
Л'-»—со •
при независимом друг от друга стремлении А' к —оо и А"
к -f-°°-
Из этих определений следует, что если для некоторого вещест-
вещественного числа а сходится каждый из несобственных интегралов
п -f-ao
\f(x)dx и \f{x)dx, то сходится и несобственный интеграл
— со а
$f(x)dx, причем справедливо равенство
— <й
-f-oo а] -{-ос
Г / (х) dx=^ if (x) dx+ f / (х) dx.
— оо —со а
Заметим еще, что если сходится несобственный интеграл
•+00
f(x)dx и Ь — любое число, превосходящее а, то сходится и
несобственный интеграл \f(x)dx, причем {f{x)dx— \f(x)dx +
Ь а а
+ f / (х) dx. Это утверждение непосредственно вытекает из опре-
ъ
деления сходимости несобственного интеграла.
Примеры. 1) Изучим вопрос о сходимости несобственного
интеграла
Поскольку функция f(x) = при любом Л>0 интегри-
\ -\- х
руема на сегменте [О, А], причем для нее
Дополнение 1. § 1 373
ТО
limF (i4) = limarctg,4 = я/2.
Л+ Л+
Поэтому несобственный интеграл \ — сходится и для
. I 1 + х2
о
+ 00
С dx я
него справедливо равенство I = —
J 1+х1 2
о
2) Изучим вопрос о сходимости несобственного интеграла
+ 00
С dx ,
\ —?-¦ где аил — произвольные вещественные числа, первое
а
из которых положительно (с>0).
Так как функция f(x) = l/xK при любом Л>0 интегрируема
на сегменте [а, А], причем
при Я, Ф 1,
1-Х
то при л>1 предел F(A) при Л->-+оо существует и равен — , •
а при л<1 указанный предел не существует.
Таким образом, при Я>1 несобственный интеграл ( —?-
а
сходится и равен , а при л<1 несобственный интеграл
А — 1
dx
~Т" расходится.
2. Критерий Коши сходимости несобственного интеграла пер-
первого рода. Достаточные признаки сходимости. Вопрос о сходи-
сходимости несобственного интеграла 1-го рода эквивалентен вопросу о
А
существовании предельного значения функции F (Л) = f / (x) dx
о
при А-*-+оо. Как известно*, для существования предель-
предельного значения функции F(A) при Л-э—^оо необходимо и дос-
достаточно, чтобы она удовлетворяла следующему условию Коши:
для любого е>0 можно указать такое В>а, что для любых
А\ и Л2, превосходящих В, выполняется неравенство
* Гл. 3, § 4, п. 3.
374 Гл. 9. Определенный интеграл Римана
A
<8.
A
=\jf(x)dx
Таким образом, справедливо следующее утверждение.
Утверждение 1 (критерий Коши сходимости
несобственного интеграла). Для сходимости несоб-
несобственного интеграла (9.1.3) необходимо и достаточно, чтобы для
любого 8>0 можно было указать такое В>а, что для любых А\
и Лг, превосходящих В,
A
Замечание. Отметим, что из сходимости несобственного
интеграла не вытекает даже ограниченность подынтегральной
функции. Например, интеграл Г f(x)dx, где функция f(x) рав-
Ъ
на нулю для всех нецелых х и равна п при х=п, где п — целое
число, очевидно, сходится, хотя подынтегральная функция не
ограничена.
Поскольку критерий Коши мало удобен для практических при-
применений, целесообразно указать различные достаточные признаки
сходимости несобственных интегралов.
В дальнейшем мы все время будем считать, что функция f(x)
задана на полупрямой а<х< + оо и для любого А>а существует
А
обычный интеграл f / (x) dx.
а
Докажем следующее утверждение.
Утверждение 2 (общий признак сравнения).
Пусть на полупрямой а<х< + °°
\f(x)\<g(x). (9.1.4)
Тогда из сходимости интеграла f g (x) dx вытекает сходимость
а
интеграла f / (x) dx.
а
Доказательство. Пусть f g(x)dx сходится. Тогда,
а
согласно критерию Коши, для любого е>0 найдется такое В>а,
что для любых А\>В и А2>В выполняется неравенство
А,
f g (x) dx
А
Дополнение 1. § 1 375
Согласно известным неравенствам для интегралов и неравенству
л2 л2 лг
(9.1.4) получим f/(x)d.x; < f| / (х) \ dx < f g (х) dx. Отсюда и из
л, А л,
неравенства (9.1.5) вытекает, что для любых А\~>В и А2>В спра-
А
ведливо неравенство
сходится.
f/(x)dx < е. Следовательно, интеграл
Утверждение 3 (частный признак сравнения).
Пусть на полупрямой 0<а<х< + <х> функция f(x) удовлетворяет
соотношению \f(x) |<c/xx, где с и К — постоянные, Х>1. Тогда
интеграл \ / (х) dx сходится. Если же существует такая посто-
а
яннпя с>0, что на полупрямой (9<а<:х< + оо справедливо со-
отношение f(x)>>c/xx, в котором К<1, то интеграл \f(x)dx
а
расходится.
Утверждение этой теоремы вытекает из утверждения 2 и при-
примера, рассмотренного в предыдущем пункте (достаточно поло-
положить g(x) =clxx).
Следствие (частный признак сравнения в
предельной форме). Если при Х> 1 существует конечный
+
предел lim|/(x)|^ = c, то интеграл [f(x)dx сходится. Если
же при Я<1 существует положительный предел \\mf(x)x% = c >
ДГ->+ов
> 0, то интеграл \ f (x) dx расходится.
а
Убедимся в справедливости первой части следствия. Для этого
заметим, что из существования предела при х-> +°° вытекает
ограниченность функции }f{x)\x%, т. е. с некоторой постоянной
Со>О выполняется неравенство \f(x) | <со/х\
После этого применяется первая часть утверждения 3. Спра-
Справедливость второй части следствия вытекает из следующих рас-
рассуждений. Так как с>0, то можно указать столь малое е>0, что
с—8>0. Этому е отвечает такое ?>0, что при х>В выполняется
неравенство с—e<f(x)xk (это неравенство следует из определе-
определения предела). Поэтому f(x)>(c—гIхх, и в этом случае дей-
действует вторая часть утверждения 3.
3. Абсолютная и условная сходимость несобственных интегра-
интегралов. Введем понятия абсолютной и условной сходимо-
376 Гл. 9. Определенный интеграл Римана
сти интегралов. Пусть f(x) интегрируема по любому сегменту
[а. А] *.
+00
Определение 1. Несобственный интеграл \f(x)dx на-
а
зывается абсолютно сходящимся, если сходится
j \f{x)\dx.
+
Определение 2. Несобственный интеграл \ f(x)dx на-
а
зывается условно сходящимся, если он сходится, а ин-
+ 00
теграл \ \f(x)\dx расходится.
а
Замечание. Положив в утверждении 2 g(x)=\f(x)\, мы
получим, что из абсолютной сходимости несобственного интеграла
вытекает его сходимость.
Отметим, что утверждения 2 и 3 позволяют установить лишь
абсолютную сходимость исследуемых несобственных интегралов.
Приведем еще один признак сходимости несобственного интег-
интеграла первого рода, пригодный для установления и условной схо-
сходимости этого интеграла.
Утверждение 4 (признак Дирихле — Абеля)..
Пусть выполнены следующие три условия:
1) функция f(x) непрерывна на полупрямой а<дс< + оо и име-
имеет на этой полупрямой ограниченную первообразную F(x) **;
2) функция g(x) определена и монотонно не возрастает на
полупрямой а<х< +оо и имеет равный нулю предел при
3) производная g'(x) функции g(x) существует и непрерывна
в каждой точке полупрямой а<х< +оо. При выполнении этих
трех условий несобственный интеграл
f
ff(x)g(x)dx (9.1.6)
а
сходится.
Доказательство. Воспользуемся критерием Коши схо-
сходимости несобственных интегралов. Предварительно проведем
* Тогда и функция \f(x)\ интегрируема по любому сегменту [а, А].
** Это означает, что первообразная F(x), которую можно определить как
f(t)dt, удовлетворяет для всех х^а неравенству |F(я) | ^.К, где К — по-
a
стоянная,
Дополнение I. § 1 377
интегрирование по частям интеграла \f(x)dx на произвольном
сегменте [Аи А2], А2>А\ полупрямой с<д;< + оо. Получим
p(x)g(x)dx=F(x)g(x)\AA'-^F(x)g'(x)dx. (9.1.7)
По условию теоремы F(x) ограничена: \F(x)\<.K. Так как
g(x) не возрастает и стремится к нулю при я-^ + оо, то g(je):>0,
а gr(x)<c0. Таким образом, оценивая (9.1.7), получим
Г/(х)g(x)dx <K[gD) + g(Л)] +K\(-g' (x))dx.
Так как интеграл в правой части этого неравенства равен
g(Ai)—g(A2), то, очевидно,
*f(x)g(x)dx\<2Kg(Al). (9.1.8)
Используя это неравенство, нетрудно завершить доказательство
теоремы. Пусть е — произвольное положительное число. Так
как g(x)-+0 при х->- + оо, то по данному е можно выбрать В так,
что при Ai^B выполняется неравенство g(Ai)<sJBK). Отсюда
и из неравенства (9.1.8) следует, что для любых Ai и Лг, больших
В, выполняется неравенство \[f(x)g(x)dx < e, которое, сог-
согласно критерию Коши, гарантирует сходимость интеграла (9.1.6).
Утверждение доказано.
Замечание. Требование 3) в утверждении 4 является
лишним и обусловлено лишь методом доказательства (жела-
(желанием применить формулу интегрирования по частям). Для того
чтобы доказать утверждение 4 без требования 3), достаточно
Л
применить для оценки интеграла \f(x)g(x)dx вторую форму-
i
лу среднего значения (см. свойство п. 2 § 4 гл. 9). Убедитесь в
этом сами.
Пример 1. Рассмотрим интеграл
smx-dx, a>0. (9.1.9)
ха
378 Гл. 9. Определенный интеграл Римана
Полагая f(x)=sinx, g(x) — \/xa, легко убедиться что для
этого интеграла выполнены все условия утверждения 4. Поэтому
интеграл (9.1.9) сходится*.
Пример 2. Рассмотрим интеграл Френеля \ slax2dx.
о
Согласно п. 1 этого дополнения его сходимость вытекает из схо-
+ 0О +00
димости интеграла Г sinx2dx = Г xsinx2—dx. Полагая Нх) —
= xs\nx2, g(x) = l/x, легко убедимся, что выполнены все условия
утверждения 4. Поэтому интеграл Френеля сходится.
4. Замена переменных под знаком несобственного интеграла »
формула интегрирования по частям. В этом пункте мы сформу-
сформулируем условия, при которых действуют формулы замены пере-
переменных и интегрирования по частям для несобственных интегра-
интегралов первого рода. Рассмотрим сначала вопрос о замене пере-
переменной под знаком несобственного интеграла.
Мы будем предполагать выполненными следующие условия:
1) функция f(x) непрерывна на полуоси а<х< + оо;
2) полуось а<х< + оо является множеством значений неко-
некоторой строго монотонной функции x—g(t), заданной на полуоси
а<?< + °° (или —оо<?<а) и имеющей на этой полуоси непре-
непрерывную производную;
3) g(a)=a.
При этих условиях из сходимости одного из следующих несоб-
несобственных интегралов
Jf(x)dx и +ff(g(t))g'(t)dt(mn -]f(g(t))g'(t)dt) (9.1.10)
а а —со
вытекает сходимость другого и равенство этих интегралов.
Сформулированное утверждение устанавливается с по-
помощью следующих рассуждений.
Рассмотрим произвольный сегмент [а, А]. Этому сегменту
'отвечает, согласно строгой монотонности функции g(t), сегмент
[а, р] (или [р, а]) оси t такой, что при изменении на сегменте
[а, р] значения функции x = g(t) заполняют сегмент {а, А], при-
причем g{p)—A. Таким образом, для указанных сегментов выполне-
1 1 "V" dx
* Так как | sin х | > sin2 х = -—- — -— cos 2х и интеграл \ —^
2t Л J Zx
С cos2x
расходится (см. пример 2 из п. 1 § 1), а интеграл I a dx сходится (в
силу утверждения 4 при /(x)=cos 2x, g(x) = \lBxa)), то при 0<а<1 интеграл
(9.1.9) сходится условно.
Дополнение 1. § 2 379
ны все условия п. 3 § 5 гл. 9, при которых действует формула
замены переменной под знаком определенного интеграла. Поэто-
Поэтому имеет место равенство
\f(x)dx=lf{g{t))g'{t)dt(*m =-]f{g{t))g'{t)dt). (9.1.11)
а а р
В силу строгой монотонности функции x=g(t), A-*-+oo при
р->- + оо и, обратно, р->- + °° при Л-> + оо (или А-*- + оо при
р->—оо и р->—сю при Л->- + оо). Поэтому из формулы (9.1.11)
вытекает справедливость сформулированного выше утверждения.
Перейдем теперь к вопросу об интегрировании по
частям несобственных интегралов первого ро-
рода.
Докажем следующее
Утверждение. Пусть функции и(х) и v(x) имеют непре-
непрерывные производные на полупрямой а<сх< + °о и, кроме того,
существует предельное значение lim[u(x)v(x)] = L. При этих
условиях из сходимости одного из интегралов
-4-00 4-°°
j и (х) v' (x) dx и f у (х) и' (х) dx (9.1.12)
а а
вытекает сходимость другого из этих интегралов и справедли-
справедливость формулы
(u(x)v'(x)dx = L—u(a)v{a)— Г v (x) и' (х) dx. (9.1.13)
а а
Для доказательства сформулированного утверждения рас-
рассмотрим произвольный сегмент [а, А]. На этом сегменте дей-
действует обычная формула интегрирования по частям. Поэтому
А А
j'u (х) v' (х) dx = [и (х) v (х)]а — Г v (х) и' (х) dx.
а а
Так как при Л->- + °° выражение [u(x)v(x)]aA стремится к
L—u(a)v(a), то из последнего равенства следует одновременная
сходимость или расходимость интегралов (9.1.12) и справедли-
справедливость формулы (9.1.13) в случае сходимости одного из интегра-
интегралов (9.1.12).
§ 2. Несобственные интегралы второго рода
В этом параграфе будет дано обобщение понятия определен-
определенного интеграла на случай неограниченных функций.
380 Гл. 9. Определенный интеграл Римана
Пусть на полусегменте [а, Ь) задана функция f(x). Точку Ь
мы будем называть особой, если функция не ограничена на
полусегменте [а, Ь), но ограничена на любом сегменте [а, Ь—а]
а>0, заключенном в полусегменте [а, Ь). Будем также предпола-
предполагать, что на любом таком сегменте функция f (x) интегрируема. При
наших предположениях на полусегменте @, Ъ—а) задана функ-
функция аргумента а
Ь—а
F(a)= j f(x)dx.
а
Исследуем вопрос о правом пределе функции F (ос) в точке а = 0:
Ь—а
lim (f(x)dx. (9.1.14)
а-Ч-0 J
Определение. Правый предел (9.1.14) в случае, если он
существует, называется несобственным интегралом вто-
второго рода от функции f(x) no сегменту [а, Ь] и обозначается
символом
§f(x)dx. (9.1.15)
а
При этом говорят, что несобственный интеграл (9.1.15) сходится
Ь Ь—а
и пишут равенство ff( x)dx = lim f / (х) dx.
J а-»-1-0 ^
а^+0
Символ (9.1.15) употребляют и в случае, если указанного вы-
выше предела (9.1.14) не существует, но в этом случае говорят, что
несобственный интеграл (9.1.15) расходится.
Замечание. Понятие несобственного интеграла второго
рода легко переносится на случай, когда функция f(x) имеет ко-
конечное число особых точек.
Пример. Рассмотрим на полусегменте [с, Ъ) функцию
f(x) = l/(b—x)k, Я>0. Ясно, что точка Ь является особой точкой
для этой функции. Кроме того, очевидно, что' функция интегри-
интегрируема на любом сегменте [а, Ь—а], а>0, причем
Ь-а
f dx
F -*)
'-*¦
Ь—а
(b-
при К ф 1,
— In F—х)|о~а = 1п(й—a) — In а при Я,= 1.
Ь—а
Очевидно, предел lim i х-существует и равен
а-ч-о J {Ь—ху
а
при Я<1 и не существует при А1>1. Следовательно, рассматривае-
рассматриваемый несобственный интеграл сходится при я<1 и расходится при
Х1
Дополнение 1. § 2 381
Сформулируем критерий Коши сходимости несобственного-
интеграла второго рода. При этом мы будем предполагать, что
функция f{x) задана на полусегменте [а, Ь) и b — особая точка
этой функции.
Утверждение 5 (критерий Коши). Для сходимо-
сходимости несобственного интеграла второго рода (9.1.15) необходимо и
достаточно, чтобы для любого е>0 можно было указать такое
6>0, что для любых а' и а", удовлетворяющих условию 0<ос"<
<а'<6, справедливо неравенство
Ь-а"
f f(x)dx
ь-V
Справедливость этой теоремы вытекает из того, что понятие
сходимости интеграла по определению эквивалентно понятию су-
существования предельного значения функции F(a), введенной в:
начале этого пункта. Мы не будем подробно развивать теорию не-
несобственных интегралов второго рода. Это объясняется тем, что-
основные выводы и теоремы предыдущего параграфа без труда
могут быть перенесены на случай интегралов второго рода. По-
Поэтому мы ограничимся некоторыми замечаниями.
1°. При некоторых ограничениях на подынтегральные функции-
интегралы второго рода сводятся к интегралам первого рода.
Именно: пусть функция f(x) непрерывна на полусегменте [а, Ь) и
b — особая точка этой функции. При этих условиях в интеграле
Ь—а
\ f(x)dx, a>0, мы можем произвести следующую замену пе-
а
ременных:
х Ьf , d* 4- l<t<
t t2 b—a a
В результате этой замены переменных мы получим равенство
Ь-а 1/ое
J/(*)<**= j f{b—j-'j±-dt. (9.1.16>
1)
а . 1/(Ь—а)
Ь
Пусть интеграл ^f{x)dx сходится. Это означает, что сущест-
а
b—а
вует предел lim Г f{x)dx. Обращаясь к равенству (9.1.16),..
а
мы видим, что существует также и предел при 1/а->- + оо выраже-
выражения в правой части (9.1.16). Тем самым доказана сходимость не-
несобственного интеграла первого рода
:382 Гл. 9. Определенный интеграл Римана
1
\Rb-a)
Ь
ж равенство этого интеграла интегралу [f{x)dx. Очевидно,
а
-сходимость только что указанного несобственного интеграла пер-
ь
:вого рода влечет сходимость интеграла [f(x)dx и равенство
\
этих интегралов. Итак, из сходимости одного из интегралов
'f(x)dxu yf[b—^\^dt
I/(fr-a)
•следует сходимость другого и равенство этих интегралов.
2°. Для несобственных интегралов второго рода легко доказы-
доказываются утверждения, аналогичные утверждениям п. 2 предыду-
предыдущего параграфа, которые можно объединить общим наименова-
наименованием «признаки сравнения». Отметим, что во всех фор-
формулировках функция f(x) рассматривается на полусегменте
[а, Ь), где b — особая точка функции.
Частный признак сравнения будет иметь следу-
лощий вид.
Если \f(x)\<.c(b—х)~\ где Я<1, то несобственный интеграл
(9.1.15) сходится. Если же f(x)>c(b—х)-%, где с>0 и к>1, то
..несобственный интеграл (9.1.15) расходится. Доказательство вы-
вытекает из общего признака сравнения и примера, рассмотренного
выше.
В полной аналогии с п. 4 предыдущего параграфа для несоб-
несобственных интегралов второго рода формулируются правила
интегрирования путем замены переменной и ин-
интегрирования по частям.
§ 3. Главное значение несобственного интеграла
Определение. Пусть функция f(x) определена на прямой
—оо<л;<+оо и интегрируема на каждом сегменте, принадлежа-
принадлежащем этой прямой. Будем говорить, что функция f(x) интегри-
А
руема по Кош и, если существует предел Игл [f(x)dx.
Этот предел мы будем называть главным значением
несобственного интеграла от функции f(x) (в смысле Коши) и
обозначать символом *
* V. р. — начальные буквы французских слов «Valeur principal», обозначаю-
обозначающих «главное значение». Подчеркнем, что, в отличие от понятия несобственного
Дополнение 1. § 3 383»
+ О5 А
V.p. f f(x)dx= lim Г f(x)dx
Пример 1. Найдем главное значение интеграла от функции?
х. Поскольку в силу нечетности х,
А +оо
f xdx = 0, то V. p. f xdx = 0.
—Л —оо
+ СО
Точно так же заключаем, что V.p. f sinxdx = O.
СО
Справедливо следующее
Утверждение. Пусть функция f(x) интегрируема на каж-
каждом сегменте прямой —оо<л;< + оо. Если эта функция f(x) не-
нечетна, то она интегрируема по Коши и главное значение интег-
интеграла от нее равняется нулю.
Если функция f(x) четна, то она интегрируема по Коши тогда,
и только тогда, когда сходится несобственный интеграл
j f(x)dx. (9.1.17).
о
Первая часть этого утверждения является очевидной. Для до-
доказательства второй части достаточно воспользоваться равенством
Л А
( f(x)dx = 2 [f(x)dx, справедливым для любой четной функ-
А О
ции, и определением сходимости несобственного интеграла-
(9.1.17).
Понятие интегрируемости по Коши можно ввести и для несоб-
несобственных интегралов второго рода в случае, когда особая точка!
является внутренней точкой сегмента, по которому производится:
интегрирование.
Определение. Пусть функция f(x) определена на сег-
сегменте [а, Ь], кроме, быть может, точки с, а<с<Ь, и интегрируе-
интегрируема на любом сегменте, принадлежащем либо \[а, с), либо (с, Ь].
Будем говорить, что функция f(x) интегрируема по Коши, если.
существует предел
со А"
интеграла I / (х) их, определяемого как предел lim I f(x)dx при
J А'-*— в>, Л"-»+со J,
00 ' ' А'
независимом стремлении А' к —оо, А" к +°о, интеграл по Коши определя-
определяется как предел при Л->+оо интеграла в симметричных пределах.
J f(x)dx.
—А
384 Гл. 9. Определенный интеграл Римана
lim f f f(x)dx+ f f{x)dx)=V.p. [f(x)dx, cc>0,
T a c+a a
называемый главным значением интеграла в смысле
Коши.
Пример 2. Функция 1/(х—с) не интегрируема на сегменте
fa, b], a<c<b, в несобственном смысле, однако она интегрируе-
интегрируема по Коши. При этом
Ь с—а Ь
,, С dx .. /Г dx , Г dx \ , Ь— с
V. р. \ = lim Ь = In .
J x — с a-i+o \ J л:—с J x — cj с — а
ДОПОЛНЕНИЕ 2
Интеграл Стилтьеса *
Понятие интеграла Стилтьеса является непосредственным
обобщением понятия интеграла Римана, построению которого
была посвящена гл. 9. В настоящем дополнении мы приведем
основные сведения об интеграле Стилтьеса.
1. Определение интеграла Стилтьеса и условия его сущест-
существования. Понятие интеграла Стилтьеса реализует идею интег-
интегрирования функции f(x) относительно другой функции и(х).
Пусть функции f(x) и и(х) определены и ограничены на
сегменте [а, Ь] и {хь} — разбиение этого сегмента **:
'Сумму вида
a = /(ii) [u(xi)—u(xo)]+...+f(b) [u{xi)—u(xi-i)]+...
(9.2.1)
¦¦¦ + f(ln)[u(Xn)—u(Xn-l)],
где Xi-i<.%i*iXi, t=l, 2,..., л, называют интегральной
суммой Стилтьеса.
Число / называют пределом интегральных сумм (9.2.1)
при max Ax(-», если для любого е>0 найдется б>0 такое,
1<«
что при max Ax< б справедливо неравенство \а—/|<е.
Определение. Функция f(x) называется интегри-
интегрируемой по функции и(х) на сегменте [а, Ь], если су-
существует конечный предел интегральных сумм (9.2.1) при
max Дл:?->-0. Указанный предел называется интегралом
Т. Стилтьес — голландский математик A856—1894).
* Мы предполагаем, что а<6. Случай а>Ъ сводится к рассматриваемому.
Дополнение 2 385
Стилтьеса (или интегралом Римана—Стилтьеса) от функ-
функции f(x) по функции и(х) на сегменте [а, Ь] и обозначается
символом
ь
. (9.2.2)
Функцию и(х) иногда называют интегрирующей
функцией.
Т. Стилтьес пришел к идее такого интеграла, рассматривая
положительное «распределение масс» на прямой, заданное воз-
возрастающей функцией и(х), точки разрыва которой соответ-
соответствуют массам, «сконцентрированным в одной точке».
Интеграл Римана представляет собой частный случай ин-
интеграла Стилтьеса, когда в качестве интегрирующей функции
взята функция х + с, где с = const.
Укажем ряд условий существования интеграла Стил-
Стилтьеса (т. е. условий, когда функция f(x) интегрируема по
функции и(х)).
Предположим, что интегрирующая функция и(х) является
возрастающей. Отсюда следует, что, поскольку а =
xo<Xi<...<Xi-i<Xi<...<xn=b, все Au(xt) = «(*,) — u(xt-i) >0.
Это позволяет, заменяя Axi на Au(xi), повторить почти все по-
построения, проводимые для интеграла Римана.
Аналогично суммам Дарбу для обычного интеграла Римана
вводятся верхняя и нижияя суммы Дарбу—Стилтьеса
S='?Ml[u(xl)—u(xt-l)], s = ^mt[u(xt) — u(**-i)]. (9-2.3)
где Mi и mi — точные верхняя и нижняя грани функции f(x)
на сегменте {xt-i, xi].
Суммы (9.2.3) называются соответственно верхней и
нижней суммами Дарбу—Стилтьеса.
Как и в случае сумм Дарбу (т. е. в простейшем случае
и(х)=х+с, с = const) при одном и том же разбиении выпол-
выполнены неравенства s<a<5, причем s и S служат точными
гранями для стилтьееовых сумм а, отвечающих всевозможным
выборам промежуточных точек |,- на частичных сегментах.
Суммы Дарбу—Стилтьеса обладают (как и в простейшем
случае) свойствами:
а) если к имеющимся точкам разбиения добавить новые
точки, то нижняя сумма Дарбу—Стилтьеса может от этого
лишь возрасти, а верхняя сумма — лишь уменьшиться;
б) каждая нижняя сумма Дарбу—Стилтьеса не превосхо-
превосходит любой верхней суммы, отвечающей тому же или другому
разбиению сегмента [а, Ь].
13 Зак. 72
386 Гл. 9. Определенный интеграл Римана
Аналогично тому, как это сделано при построении интегра-.
ла Римана, вводятся верхний и нижний интегралы Дарбу—-
Стилтьеса:
/* = inf{S}, /. = sup{s},
где нижняя и верхняя грани берутся по всевозможным разбие-
разбиениям сегмента [а, Ь].
Легко проверить, что справедливы соотношения
Точно так же, как и в случае обычного интеграла Римана,
в случае интеграла Стилтьеса доказывается, что верхний
интеграл Дарбу—Стилтьеса является пределом верхних сумм S
при стремлении диаметра разбиений к нулю. Аналогично ниж-
нижний интеграл Дарбу—Стилтьеса есть предел нижних сумм s
(см. п. 2, § 2, основную лемму Дарбу).
Сформулируем теперь теорему, которая является обобще-
обобщением основной теоремы п. 1 § 3 и справедлива в случае интег-
интеграла Римана—Стилтьеса.
Основная теорема. Для того чтобы ограниченная
на сегменте [a, b] (a<b) функция f(x) была интегрируемой на
этом сегменте по возрастающей функции и(х), необходимо м
достаточно, чтобы для ^любого е>0 нашлось такое разбиение
{xk} сегмента [а, Ь], для которого S—s<e.
Доказательство этой теоремы (как, впрочем, и других упо-
упомянутых выше фактов- и свойств) является дословным повто-
повторением рассуждений, проведенных для интеграла Римана.
Укажем теперь некоторые классы интегрируемых по Рима-
ну — Стилтьесу функций.
1. Если функция f(x) непрерывна, а и(х) возрастает на сег-
ъ
ъ
менте [а, 6], то интеграл Стилтьеса Г f(x)du(x) существует.
а
Доказательство этого факта полностью аналогично доказа-
доказательству теоремы 9.1 (см. п. 2 § 3).
Замечание. Указанный выше факт справедлив и в
том случае, когда функция и(х) является функцией ограни-
ограниченной вариации*. Так называются функции и(х), опре-
определенные на сегменте [a, b], a<b и обладающие тем свойством»
что для любого разбиения
п—\
числовое множество V[{xJ] = V \и(х,--н) — и(хг)\ ограниче-
но сверху.
* Или ограниченного изменения.
Дополнение 2 38'
Точная верхняя грань множества {V[{#a}]} называется пол-
полным изменением или полной, вариацией функ-
ъ
ции и(х) на сегменте [а, Ь] и обозначается символом Vu(x) =
а
= sup {V [{xk}]}. Для функций ограниченной вариации спра-
справедлив следующий основной критерий:
Для того чтобы функция и(х) имела на сегменте [а, Ь] ог-
ограниченную вариацию, необходимо и достаточно, чтобы онл
представлялась на этом сегменте в виде разности двух возрас-
возрастающих и ограниченных функций:
Таким образом, в случае, когда и(х) — функция ограни-
ограниченной вариации, сумму Стилтьеса, отвечающую функции
и(х), можно записать в виде
п п п
а = 2 f &) Аи (xt) = ? / (Ь) Ag (xt) — ? / (&)ДЛ (*<) = <fi — ot,
t=l i=\ 1=1
где Au(Xi)=u(xi)—u(xi-\), Ag(xi)=g(xi)—g(Xi-i), Ah(x{) =
Суммы ai и о2 стремятся к конечным пределам при стрем-
стремлении диаметра разбиений к нулю, так как g(x) и h(x) — воз-
возрастающие функции. Поэтому существует конечный предел и
сумм а при стремлении диаметра разбиений к нулю.
Следовательно, теорию интеграла Стилтьеса можно строить
и в случае, когда интегрирующая функция и(х) имеет ограни-
ограниченную вариацию, вполне аналогично случаю возрастающей
функции и(х).
Выделим еще один класс функций, для которых существует
интеграл Стилтьеса.
2. Интеграл Стилтьеса (9.2.2) существует при условии, что
функция f(x) интегрируема на сегменте [а, Ь] по Риману, а
функция и(х) удовлетворяет на этом сегменте условию Липши-
Липшица, т. е. условию
\иХх')—и(х")\<с\х'—х"\,
где c = const, для любых х' и х" из [а, Ь].
Так как функция, удовлетворяющая условию Липшица, яв-
является функцией с ограниченной вариацией, то для доказа-
доказательства этого критерия, очевидно, достаточно рассмот-
рассмотреть лишь случай возрастающей функции и(х), удовлетворяю-
удовлетворяющей условию Липшица, и заметить, что
П Л
S — s= ? (М? — m{) Аи [xt) < С J] (Mi — mL) Axt, (9.2.4)
аз*
388 Гл. 9. Определенный интеграл Римана
где M,- = supf(x), m, = inf/(x), xg [xw, xi\ ()
—u(xi-\), с — постоянная из условия Липшица. Выражение
п
V (Мс — т.;) Ахс в неравенстве (9.2.4) может быть сделано,
(=i
в силу интегрируемости по Риману функции f(x), сколь угодно
малой величиной за счет выбора разбиения сегмента [а, Ь].
Следовательно, величина 5—s также может быть сделана
меньше наперед заданного числа е>0, если выбрать диаметр
разбиения достаточно малым.
Согласно утверждению основной теоремы функция f{x)
интегрируема по Стилтьесу.
В общем случае функции и(х), удовлетворяющей условию
Липшица, также можно рассмотреть представление
и (х) = сх— [сх—и (х) ] = и\ (х) —и2 (х).
В этом представлении обе функции щ(х) и и2(х) удовлет-
удовлетворяют условию Липшица и возрастают *. В таком случае до-
доказательство завершается так же, как и выше.
Укажем, наконец, еще один класс интегрируемых по
Стилтьесу функций.
3. Если функция f(x) интегрируема на сегменте [а, Ь] по
Риману, а функция и(х) допускает представление в виде ин-
интеграла с переменным верхним пределом
X
и{х) =Л+
где <р(|) — интегрируемая на сегменте [а, Ь] по Риману функ-
функция, то интеграл (9.2.2) существует.
Действительно, так как ф(|) интегрируема по Риману, то
она ограничена: |ф(|) | </C=const. Следовательно,
Поэтому справедливость этого критерия вытекает из справед-
справедливости предыдущего.
Заметим, что в ряде случаев интеграл Стилтьеса
ь
/= ?f(x)du(x) сводится к интегралу Римана по формуле
dx. (9.2.5)
* Для функции иг(х) при х'>х", очевидно, можно записать соотношение
')и2(х")^с(х'—х") +[и(х')— и(х")]>0
Дополнение 2 389
В частности, равенство (9.2.5) имеет место в случае, если
и(х) имеет ограниченную и интегрируемую в смысле Римана
на сегменте [а, Ь] производную и'(х). В этом случае <р(х) =
= «'(*)•
2. Свойства интеграла Стилтьеса. Сформулируем ряд
свойств интеграла Стилтьеса, непосредственно вытекающих из
его определения.
а) Линейное свойство как относительно интегрируемой, так
и относительно интегрирующей функции (при условии сущест-
существования каждого из интегралов Стилтьеса в правой части):
ь ь ъ
j (a/i + Р/а) du = а j hdu + Р j /А>
a
b
j fd [аи, + рия] = a J /Л*! + P J /du
а а
здесь а, р — произвольные числа.
б) Если выполнено условие а<с<Ь, то
ь с ь
j/ (х) du (х) = J / (х) du (х) + \ f (х) du (х),
а а а
в предположении, что существуют все три интеграла.
Подчеркнем, что из существования обоих интегралов
с Ь
[f(x)du(x) и [f(x)du(x), вообще говоря, не вытекает су-
0 С
Ь
ществование интеграла f f(x)du(x). Вот соответствующий
а
пример:
О, если — 1 < х < О,
A, если 0 < х < 1, А Ф 0;
О, если — 1 < х < О,
B, если 0 < х < 1, В Ф 0.
о 1
Интегралы §f(x)du(x), \jf{x)du{x) оба существуют и рав-
равны нулю, так как соответствующие им суммы Стилтьеса все
равны нулю. Действительно, в первом интеграле f(x)=O,
Э, во втором Au(xi) — u(xi)—u(xi-\)=0 для любого
, р () ()()
разбиения сегмента [—1, 1]. Однако интеграл if(x)du(x)
—1
390 Гл. 9. Определенный интеграл Римана
не существует. В самом деле, пусть {xk} — разбиение сегмента
[—1, 1], не содержащее в качестве точки разбиения точку 0.
га
Тогда в сумме Стилтьеса сг=V /(?,) Ди(*г) остается лишь
одно слагаемое, а именно слагаемое
для которого точка нуль содержится в сегменте [x^-i, Xk].
В зависимости от того, будет ли |* удовлетворять условию
|а<0 или |fe>0, мы получим, что а=0 или а=А-ВфО, так что
а не имеет предела при стремлении диаметра разбиений к ну-
нулю.
Указанный факт связан с тем, что как у функции f(x), так
и у функции и(х) точка 0 является точкой разрыва.
в) Для интеграла Стилтьеса (9.2.2) справедлива формула
среднего значения.
Пусть функция f(x) ограничена на сегменте [а, Ь], так что
m<f(x)<M, а функция и(х) возрастает на этом сегменте. Тог-
Тогда найдется такое число ц., удовлетворяющее неравенствам
пг<\кМ, что для интеграла Стилтьеса справедлива формула
среднего значения
ь
В частности, если дополнительно предположить непрерыв-
непрерывность f(x) на сегменте ,[а, Ь], то найдется точка ge[a, b] та-
такая, что ц = /(|).
Доказательство этой формулы вполне аналогично доказа-
доказательству формулы среднего значения для интеграла Римана
(см. п. 2, § 4).
Глава 10
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
§ 1. ДЛИНА ДУГИ КРИВОЙ
1. Понятие простой кривой. Начнем наше рассмотрение с выяс-
выяснения понятия кривой. Пусть на сегменте [а, р] заданы две не-
непрерывные функции <p{t) и ty(t). Аргумент этих функций будет
в дальнейшем называться параметром. Рассмотрим плоскость
(х,у), т. е. совокупность всевозможных упорядоченных пар (х,у)
чисел хну. Каждая такая пара называется точкой плоскос-
плоскости, а числа х и у называются координатами этой точки. Точ-
Точка (х, у) может обозначаться также одной буквой М, при этом
запись М(х, у) означает, что точка М имеет координаты х и у.
Если рассматривать параметр t как время, то уравнения
*=<Р(О, У=Ф(О. «<*<Р (ЮЛ)
определяют закон движения точки М с координатами х и у на
плоскости. Множество {М} точек М, отвечающих всевозможным
значениям параметра t из [а, р] можно рассматривать как след
точки М, движущейся по закону A0.1).
В общем случае даже для непрерывных функций <р(?) и ij)(f)"
этот закон движения может быть очень сложным. Например, мож-
можно так подобрать непрерывные на сегменте а</<р функции
ср(О и ^(t), что при изменении параметра t на этом сегменте точки
{М(х, у)} заполняют целый квадрат*.
Введем понятие простой плоской кривой.
Определение. Множество {М} всех точек М, координаты
х и у которых определяются уравнениями x=y{t), y = ty(t) при t
из [а, р], называется простой плоской кривой L, если различ-
различным значениям параметра t из [а, р] отвечают разные точки мно-
множества {М}.
Каждую точку множества {М}, определяющего простую плос-
плоскую кривую, называют точкой этой кривой, причем точки,
отвечающие граничным значениям аир параметра /, называются
граничными точками простой кривой.
При этом говорят, что «уравнения A0.1) определяют простую
плоскую кривую L» или «простая плоская кривая L параметризо-
параметризована при помощи уравнений A0.1)».
* См. Бибербах. Дифференциальное и интегральное исчисление, ч. 1,
392 Гл. 10. Геометрические приложения определенного интеграла
Примером простой кривой является график полуокружности
радиуса г, лежащей в верхней полуплоскости с центром в начале
координат:
x=rcost, y = rsint, при 0<?<я.
Более общим примером простой кривой является график непре-
непрерывной на сегменте [а, р] функции y=f(x); параметризацию этой
кривой вводят по правилу
x = t, y—f(t) при t^[a, p].
Заметим, что простые кривые не исчерпывают всего множества
кривых, которые могут быть определены уравнениями A0.1).
В следующем пункте мы рассмотрим более общие кривые,
определяемые этими уравнениями.
В заключение этого пункта сделаем два замечания.
Замечание 1. Одна и та же простая кривая L может быть
параметризована различными способами. Целесообразно рассмат-
рассматривать только те параметризации, которые получаются из данной
путем представления параметра t в виде непрерывных строго мо-
монотонных функций другого параметра s. При таких преобразова-
преобразованиях параметра сохраняется порядок следования точек на кри-
кривой L.
Замечание 2. Пусть Ll и L2 —¦ две простые кривые, при-
причем граничные точки кривой Lt совпадают с граничными точками
кривой L2l а любые не граничные точки кривых Lj и L2 различны.
Кривая L, полученная объединением кривых Lt и L2, называется
простой замкнутой кривой.
2. Понятие параметризуемой кривой. В предыдущем пункте мы
рассматривали простые кривые. Следует заметить, что в матема-
математическом анализе часто приходится рассматривать кривые, не яв-
являющиеся простыми, например кривые, имеющие точки самопере-
самопересечения или целые участки самоналегания. В связи с этим воз-
возникает необходимость ввести в рассмотрение понятие так назы-
называемой параметризуемой кривой.
Будем считать, что множество {/} представляет собой либо сег-
сегмент, либо полусегмент, либо интервал, либо числовую прямую,
либо открытую или замкнутую полупрямую.
Введем понятие разбиения множества {/}. Будем говорить, что
конечная или бесконечная система сегментов {[U-u ti]} разби-
разбивает множество {t}, если, во-первых, объединение всех этих
сегментов представляет собой все множество {t} и, во-вторых, об-
общими точками любых двух сегментов системы могут быть лишь
их концы.
Рассмотрим примеры разбиений некоторых из указанных выше
множеств {t}.
1) Система сегментов [0, 1/2], [1/2, 1], очевидно, разбивает
сегмент [0, 1].
§ 1. Длина дуги кривой 393
2) Система сегментов [га—1, я], где я = 1, 2, ..., разбивает полу-
полупрямую [0, оо).
3) Система сегментов [я—1, я], где п — любое целое число,
очевидно, разбивает всю числовую прямую.
Пусть множество {t} представляет собой одно из указанных
выше множеств, а функции <p(f) и ty(t) непрерывны на этом мно-
множестве. Введем понятие параметризуемой кривой.
Определение. Будем говорить, что уравнения
*=Ф(О, У=Ч>@ (Ю.2)
задают параметризуемую кривую L, если существует такая
система сегментов {[^-i, ^t]}, разбивающих множество {t}, что
для значений t из каждого сегмента этой системы уравнения
A0.2) определяют простую кривую.
Между точками кривой L можно ввести некоторое отношение
порядка. Пусть точка Mt соответствует значению параметра ti,
а точка М% — значению 4-
Мы скажем, что точка М4 предшествует точке М2 (и за-
запишем Mi-^Mz) если ti<tz-
Заметим, что точки, отвечающие различным значениям пара-
параметра, всегда считаются различными.
Таким образом, параметризуемую кривую можно рассматри-
рассматривать как объединение простых кривых, причем эти простые кривые
последовательно пробегаются точкой М, координаты которой опре-
определяются уравнениями A0.2), когда параметр t, монотонно воз-
возрастая, пробегает множество {t}.
Замечание 1. Простую кривую можно рассматривать как
частный случай параметризуемой кривой. В этом случае система
сегментов, разбивающих сегмент [а, р], состоит из одного сегмен-
сегмента, а именно из самого сегмента [а, р].
Замечание 2. Про параметризуемую кривую, определяе-
определяемую уравнениями A0.2), говорят также, что эта кривая пара-
параметризована при помощи уравнений A0.2). Заметим,
что одна и та же кривая L может быть параметризована различ-
различными способами. Мы будем рассматривать всевозможные пара-
параметризации кривой L, получающиеся из любой данной параметри-
параметризации путем представления параметра t в виде непрерывных,
строго возрастающих функций другого параметра s. Только при
таких преобразованиях параметра сохраняется порядок следования
точек на кривой L.
Замечание 3. Понятие пространственной кривой вводится
в полной аналогии с понятием плоской кривой. Так же, как и для
плоской простой кривой, пространственная простая
кривая — это множество {М} точек пространства, координаты
х, у, z которых определяются уравнениями
(ю.З)
394 Гл. 10. Геометрические приложения определенного интеграла
при условии непрерывности функций (f(t), ty(t), х@ н& сегменте
[а, р] и при условии несовпадения точек множества {М}, отве-
отвечающих различным значениям параметра t.
Используя понятие простой пространственной кривой и понятие
разбиения множества {t} изменения параметра, так же как и в
плоском случае, дается определение параметризуемой
пространственной кривой (задаваемой уравнениями
A0.3)).
Приведем примеры параметризуемых кривых.
1) Пусть плоская кривая L задается уравнениями
x=cost, y=sint,
Очевидно, сегмент [0, Зя] можно разбить на сегменты [0,я],
[я, 2я], [2я, Зя] такие, что для значений t из каждого указанного
сегмента выписанные уравнения определяют простую кривую, а
именно полуокружность. В данном случае кривая L представляет
собой окружность, у которой полуокружность, лежащая в верхней
полуплоскости, проходится дважды.
2) Уравнения
x=cos/, y = smt, z—t, — о
задают простую пространственную кривую, называемую винтовой
линией.
3. Длина дуги кривой. Понятие спрямляемой кривой. В этом
пункте мы введем понятие длины дуги параметризуемой кри-
кривой и рассмотрим некоторые свойства кривых, имеющих длину
дуги (такие кривые принято называть спрямляемыми).
Условимся называть прямой линию, определяемую парамет<
рическими уравнениями x=at + b, y = ct+d. Всегда можно вы-
выбрать так постоянные а, Ь, с и d, чтобы прямая проходила через
две данные точки Mi(xi, y\) и М2(х2, г/г). Участок прямой между
точками Mi и М2 называется отрезком, соединяющим эти точ-
точки, а совокупность конечного числа примыкающих друг к другу
отрезков называется ломаной.
Пусть плоская кривая L параметризуется уравнениями
* = ф(9. «/ = Ф@, *е[а, р].
Пусть, далее, Т — произвольное разбиение сегмента [а, |3] точка-
точками a = to<ti<t2< ... <tn = $*- Обозначим через Mo, Mit...,Mn соот-
соответствующие точки кривой L, т. е. точки с координатами
Возникающую при этом ломаную 1{U) =МцМ\М2... Мп будем на-
* В гл. 9 разбиение сегмента мы обозначали символом {<*}.
§ 1. Длина дуги кривой 395
зывать ломаной, вписанной в кривую L и отвечающей
разбиению Т сегмента [а, р]. Длина \U\ звена U=Mi-\Mi этой
ломаной есть расстояние между точками M;_i(<p(^--i), ^{ti-\)) и
Mi(<p(ti),1p(*,)). Поэтому j/,-| = V[<!&) —Ф&-1)]2 + [Ч>(ti)
и длина |/| всей ломаной 1=М0М1М2... Мп будет равна
1=1 1=1
Введем понятие спрямляемой кривой.
Определение. Кривая L называется спрямляемой,
если множество {\1\} длин вписанных в кривую L ломаных 1 = 1 (/»),
отвечающих всевозможным разбиениям Т сегмента [а, р], ограни-
ограничено. При этом точная верхняя грань множества {\1\} называется
длиной дуги кривой L и обозначается символом \L\.
Из сформулированного определения нетрудно заключить, что
длина \L\ дуги L кривой всегда положительна.
Замечание 1. Существуют неспрямляемые кривые. Пример
неспрямляемой кривой можно найти в книге В. А. Ильина и
Э. Г. Позняка «Основы математического анализа», 1 (М., 1982,
с. 382—386).
Докажем следующее вспомогательное утверждение.
Лемма. Пусть |/0| — длина ломаной, вписанной в кривую L
и отвечающей разбиению То сегмента [ос, р], a \h\ — длина лома-
ломаной, вписанной в кривую L и отвечающей разбиению Th получен-
полученному из разбиения Го посредством добавления одной или несколь-
нескольких новых точек. Тогда \ 101 < | k |.
Доказательство. Достаточно рассмотреть случай, когда
к разбиению То добавляется одна точка у. В этом случае лома-
ломаная, отвечающая разбиению Го, отличается от ломаной, отвечаю-
отвечающей разбиению Т\, только тем, что одно звено MkMh+i ломаной,
отвечающей разбиению Го,"заменяется двумя звеньями MkN и
NMk+i * ломаной, отвечающей разбиению 7\ (все остальные звенья
у ломаных, отвечающих разбиениям То и Ти являются общими).
Так как длина одной стороны треугольника MkMk+iN не превос-
превосходит суммы длин двух других его сторон, то \MhMk+i\ «a
<\MhN\-\-\NMh+i\, а это и означает, что |/o|<|/i|. Лемма дока-
доказана.
Приведем некоторые свойства спрямляемых кривых:
1°. Если кривая L спрямляема, то длина \L\ ее дуги не за-
зависит от параметризации этой кривой.
Действительно, пусть имеются две параметризации кри-
кривой L, a t и s — параметры этих параметризаций, определенные
соответственно на сегментах [а, р] и [а, Ь]. Так как t представ-
представляет собой строго монотонную и непрерывную функцию от s, a
Мы обозначили через N точку, отвечающую значению параметра t—y.
396 Гл. 10. Геометрические приложения определенного интеграла
s — строго монотонную и непрерывную функцию от t, то каждому
разбиению Т сегмента [а, р] соответствует определенное разбие-
разбиение Р сегмента [а, Ь] и наоборот. Очевидно, что вписанные в L
ломаные, отвечающие соответствующим разбиениям сегментов
[а, р] и [а, Ь], тождественны, и поэтому их длины равны. Но
тогда и точные верхние грани двух тождественных числовых мно-
множеств равны, т. е. равны длины кривой L при двух различных
параметризациях.
2°. Если спрямляемая кривая L разбита при помощи конечного
числа точек Мо, Mi,..., Мп на конечное число кривых Li, причем
точки Mo, Mi,...,Mn соответствуют значениям to, U, —, tn параметра
t и a = to<ti< ... <tn — $, то каждая из кривых Lt спрямляема и
сумма длин |L,-| всех кривых Li равна длине \L\ кривой L.
Очевидно, это свойство достаточно доказать для слу-
случая, когда кривая L разбита точкой С на две кривые Lt и L2.
Обозначим через y значение параметра t, которому отвечает точ-
точка С. Тогда точки кривой Lt соответствуют значениям параметра t
из сегмента [а, у], а точки кривой L2 соответствуют значениям па-
параметра t из сегмента [у, р]. Пусть Г( и Тг — произвольные раз-
разбиения указанных сегментов, а Т ¦— разбиение сегмента [а, р],
полученное объединением разбиений Г4 и Т2. Если |^|, |/2|, |/| —
длины ломаных, вписанных в кривые Li, L2 и L и отвечающих раз-
разбиениям Ти Т2 и Т указанных выше сегментов, то, очевидно,
= |/|. (Ю.4)
Поскольку числа |/i|, |Z2| и |/| положительны, то из равенства
A0.4) и спрямляемости кривой L следует, что множества длин
вписанных в кривые Lt и L2 ломаных, отвечающих всевозможным
разбиениям сегментов [а, у] и [у, р], ограничены, т. е. кривые L\.
и L2 спрямляемы. Отметим, что из равенства A0.4) и из опреде-
определения длины дуги кривой следует, что длины |^i|, |?г| и 1^1 дуг
кривых Li, L2 и L удовлетворяют неравенству
|Li| + |L2|<|L|. A0.5)
Действительно, из равенства A0.4) вытекает, что для любых раз-
разбиений 7\ и Г2 сегментов [а, у] и [у, р] справедливо неравенство
'Wi| + |fe|<:|/|. Из этого неравенства и определения точной верх-
верхней грани получим неравенство A0.5).
Покажем, что в неравенстве A0.5) на самом деле знак нера-
неравенства можно заменить на знак равенства. Предположим против-
противное, т. е. предположим, что \L\ \ + \L2\ < \L\. Тогда число
|L|-(|L,H-|L2|)=e A0.6)
положительно. Из определения длины |L| дуги кривой L выте-
вытекает, что для положительного числа е можно указать такое раз-
разбиение Го сегмента [а, р], что длина |/о| ломаной 10, вписанной в
кривую L и отвечающей этому разбиению, удовлетворяет нера-
§ 1. Длина дуги кривой 397
венству \L\ — |/0|<е. Добавим к разбиению То точку у и обозна-
обозначим полученное при этом разбиение через Т. Тогда, в силу дока-
доказанной выше леммы, длина |/| ломаной, отвечающей разбиению Т,
тем более удовлетворяет неравенству \L\ — |/|<е- Так как раз-
разбиение Т сегмента [а, р] образовано объединением некоторых
разбиений Т\ и Т2 сегментов [а, у] и [у, р], то длины |/i| и |/а|
ломаных, отвечающих этим разбиениям, удовлетворяют соотноше-
соотношению A0.4). Поэтому справедливо неравенство \L\ — (|/i| + \k\) <«•
Так как |/i| + |/г| < |Li| + |L2|, то тем более справедливо нера-
неравенство \L\ — (|Li| +|jU|) <e. Но это неравенство противоречит
равенству A0.6). Полученное противоречие доказывает, что пред-
предположение о том, что |Li| + |^2| < \L\ является неверным, и, сле-
следовательно, |Li| + |L2| = \L\. Свойство 2° полностью установлено.
Замечание 2. Понятие длины дуги пространст-
пространственной кривой, заданной параметрическими уравнениями
A0.3), вводится точно так же, как и понятие длины дуги плоской
кривой. Точно так же, как и в плоском случае, рассматриваются
длины |/| ломаных, вписанных в кривую L, причем
Пространственная кривая L, определяемая уравнениями
A0.3), называется спрямляемой, если множество {\1\} длин
ломаных I, вписанных в эту кривую, ограничено. Точная верхняя
грань \L\ этого множества называется длиной дуги L.
Пространственные спрямляемые кривые обладают свойствами
1° и 2°, приведенными выше для плоских кривых. Доказательство
этих свойств аналогично доказательствам для плоских кривых.
4. Критерий спрямляемости кривой. Вычисление длины дуги
кривой. Приведем достаточное условие спрямляемости кривой и фор-
формулу для вычисления длины ее дуги.
Договоримся об употреблении следующей терминологии.
1°. Будем говорить, что функция f(t) имеет на сегмен-
сегменте [а, р] непрерывную первую производную, если
производная f'(t) существует и непрерывна в любой внутренней
точке этого сегмента и если, кроме того, существуют конечные
пределы lim /' (t) и lim /' (t).
f-кх+О f^p—0
При таком определении функция f(t) окажется непрерывной
на сегменте [а, {$], если значения этой функции на концах ука-
указанного сегмента положить равными пределам lim /' (t) и Пт/'(/)
/-мх+0 <-*р—0
соответственно *.
* Если в условиях определения 1° дополнительно потребовать существова-
существования односторонних производных /'(а+0) и Г (в—0), то в силу п. 3 S 4 гл. 6
iim f'(x) =/'(o + 0), НтПх)-ПР-0).
-х-нх+0
398 Гл. 10. Геометрические приложения определенного интеграла
2°. Будем говорить, что функция f(t) имеет на сегмен-
сегменте [а, р] ограниченную первую производную, если
f'(t) существует и удовлетворяет соотношению \f (t) \ -<М, где М —
некоторая постоянная, для всех внутренних точек сегмента
р
3°. Будем говорить, что производная функции f(t) ин-
интегрируема на сегменте [а, р], если f'(t) существует для
всех внутренних точек этого сегмента и после доопределения
произвольными конечными значениями на концах этого сегмента
представляет собой интегрируемую на этом сегменте функцию.
Теорема 10.1. Пусть функции x=<p(t) и y=$(t) непрерыв-
непрерывны и имеют непрерывные первые производные на сегменте [а, р].
Тогда кривая L, определяемая параметрическими уравнениями
x=(p(t), y=ty(t) при't из [а, р], спрямляема и длина \L\ ее дуги
может быть вычислена по формуле
\t) + V\t)dt. A0.7)
Доказательство. Сначала докажем, что кривая L спрям-
спрямляема. Рассмотрим формулу для длины |/| ломаной /, вписанной
в кривую L и отвечающей произвольному разбиению Т сегмента
[а. Р]:
Ш =
1=1
Для каждой из функций y(t) и ty(t) выполнены на каждом
частичном сегменте [U-i, Щ (при t=l, 2,...,n) все условия теоре-
теоремы 6.4 Лагранжа *. В силу этой теоремы между ^_t и U найдутся
точки ¦?{ и т}*, такие, что будут справедливы равенства
где Mi = ti—ti-i.
Следовательно,
(Ю.8)
4=1
По условию теоремы функции tp(i) Hifff) имеют на сегменте
[а, р] непрерывные, а потому и ограниченные первые производ-
производные, т. е. для всех t, лежащих внутри сегмента [а, р], справедли-
справедливы неравенства \<p'(t)\<M, \ty'(t)\<M. Поэтому из формульв
A0.8) следует, что
* Т. е. каждая из функций q>@ и а|)@ непрерывна на любом частичном сег-
сегменте [<j_i, tt] и дифференцируема во внутренних точках этого сегмента.
§ 1. Длина дуги кривой 399
О < 1 / К J) УМ* + М2 Mt = МУТ ? Af (= МУ2 (р—а).
i= 1 (=1
Таким образом, множество {|/|} длин вписанных в кривую L ло-
ломаных, отвечающих всевозможным разбиениям Т сегмента
[а, р], ограничено, и по определению кривая L спрямляема.
Докажем теперь, что длина \L\ кривой L может быть вычисл»-
«а по формуле A0.7).
Введем в рассмотрение следующую конкретную интегральную
сумму интегрируемой функции V <р'2@ +1|>'2@ :
отвечающую разбиению Т сегмента [а, р] и выбору промежуточ-
промежуточных точек igj, определенному в формуле A0.8). Пусть й — диа-
диаметр разбиения Т, т. е. d = raaxA^. Докажем, что для любого
положительного числа е можно указать такое 8>0, что при d<8
выполняется неравенство
предел при d-*~Q интегральных сумм o(U, ?,), т. е.
p' (/) + ч|/ (/) dt. Другими словами, мы покажем, что мож-
можно выбрать столь малым диаметр разбиения Т, что длина |/| ло-
ломаной /, вписанной в кривую L и отвечающей этому разбиению
Т, отличается от интеграла / на величину, меньшую, чем наперед
заданное число е/2. Заметим, что **
* Интегрируемость этой функции вытекает из ее непрерывности на сегменте
[а, р].
** Первое из этих неравенств вытекает нз следующих оценок, справедливых
для любых чисел a, b, bi\
а2 + b\ + JAj" +
Второе из этих неравенств очевидно, так как разность любых значений функции
«е больше разности ее точных граней.
400 Гл. 10. Геометрические приложения определенного интеграла
где Мг и rrii — точные грани функции $(t) на частичном сегменте
[ti-U U].
Поэтому
<
, —/n,)A^ = S—s, A0.10)
где 5 и s — соответственно верхняя и нижняя суммы функции
г|/(/) для разбиения Т сегмента [а,.р]-
Функции к ф'а @ + "Ф'2 (^) и Ф'@ непрерывны, а значит, и
интегрируемы на сегменте [а, р], поскольку по условию на [а, р],
непрерывны ф'(^) и я|/(/).
Из определения интегрируемости и из основной теоремы § 3
гл. 9 вытекает, что для любого е>0 можно указать такое 8>0,
что при диаметре разбиения d<8 выполняются неравенства
5s<f A0.11)
4 4
Поэтому при d<8 в силу A0.10) и A0.11) справедливы нера-
неравенства
\\l\-I\ = \\1\-в + а-1\<\ \l\-a\ + |<ж—/| <-|-+-| 1-,
и справедливость неравенства A0.9) доказана.
Докажем теперь, что среди всевозможных ломаных /, длины
|/| которых удовлетворяют неравенству A0.9), имеются ломаные,
длины которых отличаются от длины \L\ дуги кривой L меньше
чем на е/2.
Действительно, \L\ —¦ точная верхняя грань множества {|/|}
длин ломаных /, вписанных в кривую L и отвечающих всевозмож-
всевозможным разбиениям сегмента [а, р]. Поэтому найдется такое разбие-
разбиение Т*, что длина |/*| соответствующей этому разбиению лома-
ломаной /* удовлетворяет неравенству
0<Ш-|П<^- A0.12)
§ 1. Длина дуги кривой 401
Подвергаем теперь разбиение Т* измельчению, добавляя к нему
новые точки разбиения так, чтобы в результате добавления этих
точек получилось разбиение Т с диаметром d, меньшим б. При
этом, как мы показали, длина |/| ломаной /, отвечающей этому
разбиению Т, удовлетворяет неравенству A0.9). Так как все вер-
вершины ломаной, отвечающей разбиению Т*, являются также вер-
вершинами ломаной, отвечающей разбиению Т, то, согласно доказан-
доказанной в п. 3 лемме, 0< |/*| < |/| <|L|. Поэтому неравенства A0.12)
дают право утверждать, что
0<|Ц-|/|<-|-. A0.13)
Итак, мы доказали, что среди множества ломаных {/}, длины1
которых удовлетворяют неравенству A0.9), имеются ломаные, дли-
длины которых удовлетворяют и неравенству A0.13). Из неравенств
A0.9) и A0.13) получаем, что
Поскольку е — произвольное положительное число, то \L\=I к
теорема полностью доказана.
Замечание 1. Если функции ф(/) и ty(t) непрерывны и
имеют на сегменте [а, р], ограниченные первые производные, та-
кривая L, определяемая уравнениями x=<p(t), y = ty(t), спрям-
спрямляема.
Действительно, в ходе доказательства теоремы 10.1 мы устано-
установили, что если функции ф(^) и ty(t) непрерывны на [а, р], то при-
условии ограниченности на сегменте [а, E] первых производных
функций ф(^) и ф@ длины |/| ломаных, вписанных в кривую L
и отвечающих всевозможным разбиениям Т сегмента [а, р], огра-
ограничены.
Замечание 2. Формула A0.7) для вычисления длины ду-
дуги справедлива, если функции <p(t) и i\>(t) непрерывны, а произ-
производные ф'(t) и г|/@ только интегрируемы на сегменте [а, р].
В самом деле, из интегрируемости этих производных следует
их ограниченность, а поэтому, в силу замечания 1, и спрямляе-
спрямляемость кривой L. Для вывода неравенств A0.10), A0.11), а сле-
следовательно, и неравенства A0.9) достаточно лишь непрерывнос-
непрерывности ф(?) и ip(t) и интегрируемости <p'(t) и ty'(t) на сегменте
[а, р], так как отсюда, согласно теореме 9.4 (см. гл. 9), вытекает
интегрируемость на сегменте [а, р] функции V ф' (t) + i|/2@ *¦
Все остальные рассуждения такие же, как и при доказательстве
теоремы A0.1).
Замечание 3. Если кривая L является графиком функции
= f(x), непрерывной и имеющей на сегменте [а, Ь] непрерывную-
•402 Гл. 10. Геометрические приложения определенного интеграла
•производную f'(x), то кривая L спрямляема и ее длина \L\ может
чбыть найдена по формуле
\L\=\V\+f{x) dx. A0.14)
а
Действительно, график рассматриваемой функции представляет
»собой кривую, определяемую параметрическими уравнениями x = t,
_У = /@. o<t<b. При этом все условия теоремы 10.1 выполнены.
Полагая в формуле A0.7) <p(t)=t, i!p(t)=f(t) и заменяя перемен-
переменную интегрирования t на х, получим формулу A0.14).
Замечание 4. Если кривая L определяется так называе-
называемым полярным уравнением n=r(Q), 0i<0<02 и функция г@) не-
непрерывна и имеет на сегменте [0i, 02] непрерывную производную,
-то кривая L спрямляема и ее длина определяется равенством
1@)+r'2@)d0. A0.15)
Для доказательства надо воспользоваться формулами перехо-
перехода от полярных координат к декартовым x=r@)cos'0, z/ = r@)sin0.
Таким образом, кривая L определяется параметрическими уравне-
уравнениями (p = r(8)cos0, i|} = r(e)sine, 0e[0i, 02], причем выполнены все
условия теоремы 10.1. Простые вычисления приводят к форму-
формуле A0.15).
Замечание 5. Если рассматривается пространственная
параметризуемая кривая L, заданная уравнениями x=<p(t),
y = $i(t), z=%(t), и функции <р@. Ф@> х(*) непрерывны и имеюг
непрерывные первые производные на [а, р], то кривая спрямляе-
спрямляема и длина \L\ ее дуги может быть найдена по формуле
р .
IЦ = Jk ф'2@ + Ф'2@ + X'2@dt. A0.16)
Доказательство аналогично доказательству теоремы
10.1.
Замечание 6. Если функции <p(t), ty(t), %(t) непре-
непрерывны и имеют ограниченные на сегменте [а, р] первые произ-
производные, то кривая L, определяемая уравнениями A0.3), спрям-
спрямляема. Если при этом производные указанных функций, интег-
интегрируемы на сегменте [а, р], то длина \Ь\ дуги кривой L мо-
может быть также вычислена по формуле A0.16) (см. замеча-
замечания 1 и 2).
5. Дифференциал дуги. Пусть функции x=q>(t), y=ty(t) не-
непрерывны и имеют на сегменте [а, р] непрерывные первые про-
производные. В этом случае переменная длина дуги L(t), отвеча-
отвечающая значениям параметра из сегмента [a, t], как это следует
§ 1. Длина дуги кривой 40$
из теоремы 10.1, представляется в виде
VV2 dr.
Подынтегральная функция в правой части формулы A0.17)
непрерывна, поэтому функция L(t) дифференцируема и спра-
справедливо равенство
Возводя полученное равенство в квадрат и умножая на (diJt,
будем иметь
[L'(t)dt]*=W{t)dt]'+W(t)dt]*. A0.18)
Поскольку L'(t)dt=dL, q>'(t)dt=dx, ^'{t)dt=dy, из формулы
A0.18) получаем
(dL)*(dJ(d A0.19)
Если рассматривается пространственная кривая, определяемая*
уравнениями A0.3), то при условии непрерывности функций
q>(t), ty(t) и %(t) и их производных первого порядка на сег-
сегменте [a, t] для дифференциала dL пути пространственной
кривой справедлива формула
(dLJ = (dxJ + (dyJ + (dzJ. A0.20|
6. Примеры. 1) Найдем длину \L\ части дуги астроиды х=
= acos3t, у — a sin31, лежащей в первой четверти. Этой части, как
нетрудно видеть, соответствует изменение параметра t от 0 до-
доя/2. В рассматриваемом случае q>'(t) = —3acos2?sin?, i|/(?)=-
= За sin21 cos t. Поэтому по формуле A0.7) получим
Я/2 „ Я/2
\L\= ' V9а?cos4 sin21 +9a2sin*t cos21 dt = — f sln2tdt = — -
.! 2 J 2
о о
2) Вычислим длину \L\ дуги параболы у=ах2, 0<х<1. По-
Поскольку у' = 2ах, по формуле A0.14) получим
1
|L| = {.yi+4aVdx.
о
Неопределенный интеграл /= (Vl + 4a2x2dx вычислим..
следующим образом. Сначала проинтегрируем его по частям,
затем к числителю дроби, получившейся под знаком интеграла,,
прибавим и вычтем единицу, произведем деление и проинтегри-
проинтегрируем одну из получившихся дробей. Получим
404 Гл. 10. Геометрические приложения определенного интеграла
dx
-/+— In
2a
2ax + УI + 4a2*2
Нами получено уравнение относительно величины /. Решив
его, находим, что
2
Таким образом,
l
|L|=JV l+4a2x:
4uV +
j
2~
4a
У 1 + 4,
ax + Vl+iaW
22 H In |2a +
4a
3) Найдем длину дуги логарифмической спирали
r=aeb<f от точки (ф0, го) до точки (ср, г). По формуле A0.15)
имеем, что
<p
-J1
Фо
a
b
V a2e2b<? -
yi+b'
\-a2b2e2b<f dq> = a
(С С )
vi+ь2
b
ф
г
t
Фо
е*ф^ф =
"Го)-
4) Найдем переменную длину дуги эллипса -^- + -^-=
<=1, а>Ь, отсчитываемую от точки М0@,Ь). Рассмотрим парамет-
параметрическое уравнение эллипса x = a-smt, y = bcost, te[0, 2я]. По
^формуле A0.17) получим
t t
L(t)= Г У a2 cos2 т + Ъ2 sin2 т dx = a j" j/l — е2 sin2Tdx = a?(e, 0-
о 6
A0.21)
гт -Sat—b2
Число е = -1— называется эксцентриситетом
a
эллипса. '
Первообразная функции У\—z2sin2t, обращающаяся в нуль
при ? = 0, называется эллиптическим интегралом 2-го
рода (см. § 4 гл. 8). Этот интеграл обозначается символом
?(е, t) и не выражается через элементарные функции.
§ 2. Площадь плоской фигуры 405
§ 2. ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ
В этом параграфе мы изучим вопрос об определении и о су-
существовании площади так называемой плоской фигуры,
под которой мы фактически будем понимать произвольное огра-
ограниченное множество точек плоскости.
Мы начнем наше рассмотрение с уточнения понятия такой
фигуры и ее границы.
1. Понятия границы множества и плоской фигуры. Рассмотрим
множество всех точек плоскости и фиксируем одну из этих то-
точек А.
Договоримся называть е-окре'стностью точки А множество тех
точек плоскости, которые расположены внутри круга радиуса е
с центром в точке А.
Пусть теперь {М} — какое угодно множество точек плоскости.
Точку М множества {М} назовем внутренней точкой
этого множества, если найдется е>0 такое, что г-окрест-
ность точки М также принадлежит множеству {М}.
Точку М, не принадлежащую множеству {М}, назовем внеш-
внешней точкой множества {М}, если найдется е>0 такое,
что ъ-окрестность точки М также не принадлежит множест-
множеству {М}*.
Точку М назовем граничной точкой множества
{М}, если эта точка не является ни внутренней, ни внешней точ-
точкой этого множества **.
Совокупность всех граничных точек множества {М} назовем
границей этого множества.
Замечание. Для простейших типов множеств {М}, пред-
представляющих собой часть плоскости, ограниченную простым замк-
замкнутым контуром или несколькими такими контурами, введенное
нами понятие границы множества укладывается в наглядное
интуитивное представление о границе. Для множеств произволь-
произвольной природы граница в определенном нами смысле может иметь
весьма причудливый вид и не укладываться в интуитивное пред-
представление о граничном многообразии. Так, для множества {М}
тех точек круга, абсцисса и ордината которых являются рацио-
рациональными числами, границей в определенном нами смысле явля-
является весь указанный круг.
* Внешняя точка множества {М} является, очевидно, внутренней точкой
дополнения этого множества.
** Заметим, что точка М является граничной точкой множества {М} тогда
и только тогда, когда для любого е>0 в е-окрестности точки М содержатся как
точки, принадлежащие множеству {М}, так и точки, ему не принадлежащие.
В самом деле, если бы в некоторой е-окрестности точки М не нашлось
либо точек, принадлежащих множеству {М}, либо точек, ему не принадлежащих,
то точка М оказалась бы либо внешней, либо внутренней точкой множества {М}
и не являлась бы граничной точкой этого множества.
406 Гл. 10. Геометрические приложения определенного интеграла
Множество {М} точек плоскости будем называть ограничен-
ограниченным, если существует круг, содержащий все точки этого мно-
множества.
В дальнейшем мы будем рассматривать произвольное ограни-
ограниченное множество F точек плоскости и будем называть это мно-
множество плоской фигурой.
Границу плоской фигуры F будем обозначать символом dF.
2. Площадь плоской фигуры. Для введения понятия площади
плоской фигуры будем отправляться от специального частного
вида плоских фигур, так называемых многоугольных фи-
фигур.
Многоугольной фиг у р q й на плоскости мы, назовем
множество, составленное из конечного числа лежащих на этой
плоскости ограниченных многоугольников.
Из курса средней школы известно понятие площади много-
многоугольной фигуры.
В дальнейшем мы будем обозначать символом ц(Р) площадь
многоугольной фигуры Р.
Напомним, что площадь многоугольной фигуры является неот-
неотрицательным числом, обладающим следующими тремя свойства-
свойствами:
1° (Аддитивность). Если Р\ и Р2 — две многоугольные
фигуры без общих внутренних точек и символ Pi\]P2 означает
объединение этих фигур, то
li(P:{jP2)=ii(Pi)+ii(P2). A0.22)
2° (Инвариантность). Если многоугольные фигуры Р\
и Р2 равны между собой *, то
ii(P,)=lx(P2). A0.23)
3° (Монотонность). Если многоугольная фигура Pi со-
содержится^ многоугольной фигуре Р2, то (д,(Pi) <ц(Рг).
Заметим, что свойство монотонности является логическим
следствием свойства аддитивности и свойства неотрицательности
площади. В самом деле, если Pi содержится в Р2 то Р2 =
==Pi\j(P2\Pi)**, а потому в силу того, что Pi и Р2\Р\ не со-,
держат общих внутренних точек, и в силу свойства аддитивности
li(P2)=\x(P\)+\x(P2\Px). Остается заметить, что n(Pz\Pi)>0.
Замечание. Полезно подчеркнуть, что площадь много-
многоугольной фигуры естественно считать равной одному и тому же
числу независимо от того, с границей или без границы рассмат-
рассматривается эта многоугольная фигура. При рассмотрении разности-
двух многоугольных фигур Рг\р1 можно договориться считать
* Напомним, что две фигуры Fi и F2 называются равными, если сущест-
существует взаимно однозначное соответствие с сохранением расстояния между точка-
точками, при котором фигура /ч отображается на Рг-
** Причем разность P2\Pi двух многоугольных фигур представляет собой
также многоугольную фигуру.
§ 2. Площадь плоской фигуры 407
фигуру Рг взятой с границей, а фигуру Pi взятой без границы.
При такой договоренности разность P2\Pi будет представлять
собой некоторую многоугольную фигуру, взятую с границей.
Перейдем теперь к определению площади некоторой произ-
произвольной плоской фигуры F (т. е. некоторого произвольного огра-
ограниченного множества точек плоскости).
Рассмотрим всевозможные многоугольные фигуры Р, целиком
содержащиеся в F, и многоугольные фигуры Q, целиком содер-
содержащие F. Фигуры Р будем называть вписанными, а фигуры
Q — описанными. Числовое множество {ц(Р)} площадей всех
вписанных многоугольных фигур Р ограничено сверху (например,
площадью любой описанной многоугольной фигуры Q). Числовое
множество (n(Q)} площадей всех описанных вокруг фигуры Q
многоугольных фигур Q ограничено снизу (например, нулем). По-
Поэтому существуют точная верхняя грань.
^. M^ p
PCF
площадей всех многоугольных фигур, вписанных в фигуру F, и
и точная нижняя грань
(Ю.25)
площадей всех многоугольных фигур, описанных вокруг F.
Заметим, что если в фигуру F нельзя вписать ни одного мно-
многоугольника, то по определению полагается ^, = 0.
Величину ^» называют нижней площадью фигуры F,
а р.* — верхней площадью этой фигуры. Из того, что пло-
площадь любой вписанной фигуры не больше, чем площадь любой
описанной фигуры, следует, что
Определение 1. Плоская фигура F называется к в ад-
р up у е мой (или имеющей площадь), если верхняя
площадь ц* этой фигуры совпадает с ее нижней площадью ц*.
При этом число ц = [д,(F) = [д.* = (д,* называется площадью фи-
фигуры F.
Ясно, что всякая многоугольная фигура F является квадрируе-
мой в смысле данного нами определения и для нее площадь
;ц(F) = ц* (F) = {А^?), являющаяся точной нижней гранью площа-
площадей описанных многоугольных фигур и точной верхней гранью
площадей вписанных фигур, совпадает с исходной величиной
ллощади, заимствованной из элементарного курса.
Таким образом, мы распространили понятие площади много-
многоугольников на некоторый более широкий класс фигур.
Сохранение свойств аддитивности, инвариантности и монотон-
монотонности будет доказано ниже.
408 Гл. 10. Геометрические приложения определенного интеграла
Начнем с доказательства следующего критерия квадрируемости
плоской фигуры.
Теорема 10.2. Для квадрируемости плоской фигуры F не-
необходимо и достаточно, чтобы для любого е>0 нашлись такая
описанная вокруг F многоугольника фигура Q и такая вписан-
вписанная в F многоугольная фигура Р, для которых
|i(Q)—ц(Р)<е. A0.26)
Доказательства. Необходимость. Пусть фигура F квад-
рируема, т. е. |д,* = |д,,. По определению точных граней A0.24) и
A0.25) для любого фиксированного нами е>0 найдутся вписан-
вписанная многоугольная фигура Р и описанная многоугольная фигура
Q такие, что
I*.—|-<М^)<1*.. i*'<i*(QXi*' + -f-
Из этих неравенств и из равенств ц* = ц» заключаем, что
Q)—ц(Р)<е. Необходимость доказана.
Достаточность. Пусть для любого е>0 существуют много-
многоугольные фигуры Q и Р, указанные в формулировке теоремы. Тог-
Тогда из неравенства A0.26) и из соотношений
получаем, что
B— ц{Р)<г.
Поскольку е — произвольное положительное число, то из ус-
условия 0<ц*—(л*<8 вытекает, что ц* = ц*, т. е. доказано, что фи-
фигура F квадрируема. Теорема доказана.
Теорема 10.2 допускает простое, но важное обобщение: в ее
формулировке вместо описанной и вписанной многоугольных фи-
фигур Q и Р можно взять произвольные описанную и вписанную
квадрируемые плоские фигуры Q и Р. Именно справедлива тео-
теорема.
Теорема 10.2'. Для квадрируемости плоской фигуры F не-
необходимо и достаточно, чтобы для любого е>0 нашлись такие
содержащая F квадрируемая плоская фигура Q и такая содер-
содержащаяся в F квадрируемая плоская фигура Р, для которых
Необходимость доказательства не требует, ибо многоугольные
фигуры Q и Р являются квадрируемыми.
Докажем достаточность.
Фиксируем произвольное е>0 и построим по нему квадрируе-
квадрируемые плоские фигуры Q и Р, первая из которых содержит F, а
вторая содержится в F, такие, что
yL(Q)-\i(P)<~< A0.26')
§ 2. Площадь плоской фигуры 409
Так как Q и Р — квадрируемые плоские фигуры, то найдется
многоугольная фигура Q, содержащая Q, и многоугольная фигу-
фигура Р, содержащаяся в Р, такие, что
и-(Q)—и-CQ)<-f-. f
Из двух последних неравенств и из A0.26') вытекает, что
fi(Q)—\i{P)<s. Но тогда, поскольку многоугольная фигура &
содержит F, а многоугольная фигура Р содержится в F, фигура
F квадрируема в силу теоремы 10.2.
Установим теперь еще одну эквивалентную формулировку тео-
теоремы 10.2.
Пусть F — произвольная плоская фигура, Q — многоугольная
фигура, взятая вместе с границей и содержащая фигуру F, а
Р — многоугольная фигура, содержащаяся в фигуре F и взятая
без границы. Тогда разность Q\P представляет собой много-
многоугольную фигуру, взятую вместе с границей и содержащую все
точки OF фигуры F*.
В силу свойства аддитивности площади многоугольной фигуры
справедливо равенство ii(Q\P) =n(Q)—\х(Р), из которого сле-
следует, что неравенство A0.26) в формулировке теоремы 10.2 мо-
может быть переписано в виде
e. A0.26")
Договоримся о следующей терминологии.
Определение 2. Множество точек плоскости назовем
множеством площади ну ль, если оно содержится в мно-
многоугольной фигуре сколь угодно малой площади.
Неравенство A0.26") и тот факт, что многоугольная фигура
Q\f содержит все точки границы dF плоской фигуры F, дают
нам право следующим образом переформулировать теоре-
теорему 10.2.
Теорема 10.2". Плоская фигура F квадрируема тогда и
только тогда, когда ее граница dF имеет площадь нуль.
Необходимость условия теоремы очевидна.
Остановимся на доказательстве достаточности.
Впишем плоскую фигуру F в квадрат Е со сторонами, па-
параллельными координатным осям, и прямыми, параллельными
этим осям, разобьем квадрат ? на элементарные квад-
квадраты со стороной h. Это разбиение квадрата Е договоримся
называть с е т ко й с шагом h.
Докажем сначала, что если граница dF фигуры F содержит-
содержится в многоугольной фигуре площади, меньшей е, то при доста-
* Это следует из того, что любая внутренняя точка многоугольной фигуры
Р является внутренней точкой F, а любая внешняя точка многоугольной фигуры
Q является внешней точкой F. Достаточно учесть, что разность Q\P содержит
все точки плоскости, кроме внешних точек Q и внутренних точек Р.
410 Гл. 10. Геометрические приложения определенного интеграла
точно малом шаге h сетки граница dF фигуры F содержится в
объединении элементарных квадратов сетки, общая площадь
которых меньше 32 е.
В самом деле, достаточно заметить, что любая много-
многоугольная фигура, площади меньшей 8, представляет собой сум-
сумму конечного числа треугольников, не имеющих общих внутрен-
внутренних точек; каждый треугольник равен объединению двух пря-
прямоугольных треугольников (без общих внутренних точек); каж-
каждый прямоугольный треугольник содержится во вдвое большем
по площади прямоугольнике; каждый прямоугольник содержит-
содержится в объединении не более чем вдвое большей по площади сум-
сумме конечного числа квадратов; каждый квадрат содержится во
вдвое большем по площади квадрате со'сторонами, парал-
параллельными осям координат.
Итак, любая многоугольная фигура площади, меньшей е,
содержится в объединении конечного числа квадратов со сторо-
сторонами, параллельными координатным осям общей площади,
меньшей 8е.
Из указанного конечного числа квадратов выберем квадрат
с наименьшей стороной (если таких квадратов несколько, то
выберем один из них) и возьмем шаг h сетки равным полови-
половине длины стороны этого квадрата.
При таком выборе h каждый указанный квадрат (со сто-
сторонами, параллельными координатным осям) будет содержать-
содержаться в объединении элементарных квадратов сетки, общая пло-
площадь которых не больше учетверенной площади квадрата.
Поэтому вся многоугольная фигура, площади меньшей е, со-
содержится в объединении элементарных квадратов сетки, общая
площадь которых меньше 32 е.
Значит, если граница dF плоской фигуры F имеет площадь
нуль, то для любого 8>0 при указанном выше выборе шага
сетки h вся эта граница dF будет содержаться в объединении
элементарных квадратов сетки, общая площадь которых мень-
меньше 32 е.
Для завершения доказательства достаточности заметим, что
объединение всех элементарных квадратов, состоящих только
из внутренних точек фигуры F, представляет собой много-
многоугольную фигуру Р, содержащуюся в F, а объединение этой
фигуры Р со всеми элементарными квадратами сетки, содер-
содержащими точки границы dF фигуры F, представляет собой мно-
многоугольную фигуру Q, содержащую фигуру F, причем
|i(Q)-1*^X32 8.
Пользуясь этой теоремой, установим квадрируемость широ-
широкого класса плоских фигур.
Докажем следующую лемму.
Лемма. Всякая спрямляемая кривая имеет площадь
нуль.
§ 2. Площадь плоской фигуры 411
Доказательство. Пусть L — спрймляемая кривая, а
\L\ ее длина. Разобьем эту кривую с помощью я+1 точек на
части, длина каждой из которых равна \L\/n. (Возможность
такого разбиения не вызывает сомнений.) Примем каждую из
этих я+1 точек за центр квадрата со стороной 2\L\/n. Сумма
этих квадратов представляет собой многоугольную фигуру,
описанную вокруг кривой L, а площадь этой многоугольной
фигуры не превосходит суммы площадей составляющих ее
4 I LI2
квадратов, т. е. числа —¦—-(я+1). Так как |L| фиксирова-
фиксировано, а я можно выбирать произвольно большим, то число
4|L12 , л А
¦ (я + 1) может быть сделано меньшим любого наперед
заданного числа е>0. Следовательно, кривую L действительно
можно заключить внутрь многоугольной фигуры сколь угодно
малой площади.
Лемма доказана.
Из этой леммы и теоремы 10.2" вытекает следующая тео-
теорема.
Теорема 10.3. Всякая плоская фигура, граница которой
состоит из одной или нескольких спрямляемых кривых, квад-
рируема.
Покажем теперь, что введенное нами понятие площади плос-
плоской фигуры обладает свойствами аддитивности (см, A0.22)),
инвариантности (см. A0.23)) и монотонности. Убедимся сна-
сначала в а дд ит и в ноет и площади.
Пусть Fi и F2 — квадрируемые фигуры без общих внутрен-
внутренних точек и F ¦— их объединение. Тогда F квадрируема и
|i(F)=|i(Fi)+|i(Fs). (Ю.27)
Квадритируемость фигуры F следует из теоремы 10.2" и из того,
что ее граница dF составлена из множества площади нуль,
поскольку dF является частью объединения границ dFi и dF2
фигур Fi и F2. (Очевидно, что всякая часть множества площа-
площади нуль сама является множеством площади нуль.)
Докажем справедливость равенства A0.27). Рассмотрим мно-
многоугольные фигуры Pi и Р2, вписанные в Fi и Fa соответственно,
\и многоугольные фигуры Qi и Q2, описанные соответственно во-
вокруг Fi и F2. Фигуры Pi и Р2 составляют фигуру Р и не имеют
общих внутренних точек. Поэтому, согласно A0.22),
Многоугольные фигуры Qi и Q2, возможно, пересекающиеся,
в сумме составляют многоугольную фигуру Q, площадь которой
не превосходит (x(Qi) + |x(Q2). Поэтому
412 Гл. 10. Геометрические приложения определенного интеграла
С другой стороны, в силу определения квадрируемости, для
фигур Fx и F2 справедливы неравенства n(/:'i)^')Q
и [a(P2)<h(/;'2)<^(Q2), из которых следует, что
Таким образом, обе величины u(F) и ii{Fi)+^(F2) заклю-
заключены между двумя числами [^(Qi) +ц(<2г)] и [ц(Р0+ц(Р2I,
разность между которыми
может быть сделана как угодно малой.
Следовательно, указанные две величины равны, т. е. справед-
справедливо равенство A0.27).
Свойство инвариантности площади произвольной
плоской фигуры непосредственно вытекает из инвариантности
площади для многоугольных фигур (см. A0.23)) и из самого
способа определения площади квадрируемой фигуры через
площади многоугольных фигур.
Наконец, свойство монотонности площади непос-
непосредственно вытекает из определения квадрируемости плоской
фигуры.
Замечание. Пересечение двух квадрируемых фигур,
есть квадрируемая фигура.
Действительно, пусть F — F\[\F2, и Fi и F% квадри-
руемы. Каждая точка, граничная для F, является граничной
либо для Fi, либо для Р2. Поэтому наше утверждение следует
из теоремы 10.2" и того факта, что объединение двух мно-
множеств площади нуль само имеет площадь нуль.
Введенное в этом пункте понятие площади называют
понятием площади по Жордану* или мерой Жор-
дана.
Выше мы убедились, что площадь по Жордану обладает
свойством аддитивности, т. е. если F=F\\JF2, a Fi и F2 — квад-
рируемые фигуры без общих точек, то F квадрируема и
\i(F) =^(/7i) +ii(F2). Указанное свойство, очевидно, справедли-
справедливо и для объединения любого конечного числа F\,
F2,..., Fn квадрируемых фигур без общих внутренних точек.
Если
F=)JFt.
i
Камилл Жор дан — французский математик A838—1922).
§ 2. Площадь плоской фигуры 413
то F квадрируема и \i(F) = V[д.(Ff) (свойство конечной
аддитивности).
Однако площадь по Жордану (мера Жордана) не обладает
свойством счетной аддитивности, т. е. объединение
счетной совокупности квадрируемых фигур F\, F2,...
без общих внутренних точек не обязано быть квадрируемой фи-
фигурой.
Проиллюстрируем этот факт примером. Рассмотрим на
плоскости квадрат D: 0<х<1, 0<г/<1. Отметим в квадрате
D точки, у которых обе координаты рациональны. Нетрудно по-
показать, что таких точек счетное множество. Расположим их в
виде последовательности
2i= (Хь ух), 22= (*2, 1/2),-.. Zn=(Xn, у„)
Фиксируем число е>0 и построим круг Ох с центром в точке
Z\ радиуса Гх<г/2, целиком содержащийся в квадрате D.
Первую из точек z2, z3,..., не попавшую в круг Ох, обозна-
обозначим через Zn2 и построим круг О2 с центром в точке 1Пг
радиуса Гг<е/22, не пересекающийся с кругом Ох и целиком
лежащий в квадрате D.
Продолжая эти рассуждения далее, мы построим последо-
последовательность содержащихся в квадрате D непересекающихся
кругов Ох, О2,..., On,... радиусов гь г2, ....,г„,....
Каждый из этих кругов квадрируем и имеет площадь (меру
Жордана), равную я гп2 («=1, 2,...).
Убедимся в том, что объединение F счетного числа указан-
указанных кругов F—Ox\)Oz\J... представляет собой фигуру, не квад-
рируемую по Жордану. Пусть Q — любая много-
многоугольная фигура, содержащая фигуру F. Заметим, что в любой
е-окрестности каждой точки квадрата D есть точки последова-
последовательности {zn}, т. е. есть точки фигуры F. Но это означает, что
любая точка квадрата D является внутренней либо граничной
точкой фигуры F, т. е. многоугольная фигура Q содержи? весь
квадрат D и, значит,
Пусть, далее, Р —• любая многоугольная фигура, содержа-
содержащаяся в F. Тогда площадь \х(Р) не превосходит сумму площа-
площадей всех кругов Qx, Q2,---, т. е.
Итак, ц(<2)>1 и [д,(Р)<-^— для любой многоугольной
О
фигуры Q, содержащей F, и любой многоугольной фигуры Р,
-414
Гл. 10. Геометрические приложения определенного интеграла
содержащейся в F. Но это и означает, что при малом е раз-
2
ность (л (Q)—
больше 1
и не может быть сделана
как угодно малой, т. е. фигура F не квадрируема по Жордану.
Отметим, что можно ввести другое обобщение понятия пло-
площади, так называемую меру Лебега*, которая уже будет
обладать и свойством счетной аддитивности. Такое обобщение
понятия площади выходит за рамки приложений интеграла Ри-
мана и его естественно рассматривать при изучении так назы-
называемого интеграла Лебега.
3. Площадь криволинейной трапеции и криволинейного сектора.
криволинейной трапецией называется фигура, ограни-
ограниченная графиком заданной на сегменте [а, Ь] непрерывной и не-
неотрицательной функции f(x), перпендикулярными к оси Ох пря-
прямыми х=а и х=Ь и отрезком оси Ох между точками а и b
(рис. 10.1).
Справедливо следующее
Утверждение. Криволинейная трапеция представляет co-
Sou квадрируемую фигуру F, площадь которой \i(F) вычисляется
по формуле
A0.28)
Доказательство. Непрерывная на сегменте [а, Ь]
«функция f(x) интегрируема, поэтому для любого положительного
числа е можно указать такое разбиение сегмента [а, Ь], для ко-
которого разность между верхней суммой S и нижней суммой s
'будет меньше е. Но S и s равны соответственно [a(Q) и ц(Р),
где (i(Q) и \х(Р) — площади многоугольных фигур, первая из ко-
которых содержит криволинейную трапецию, а вторая содержится в
криволинейной трапеции (на рис. 10.1 изображены также и ука-
a
Ч
/
"i
\
i
i
i
i
л
ъ
Рис. 10.1
Рис. 10.2
Анри Лебег — французский математик A875—1941).
§ 2. Площадь плоской фигуры 415
занные многоугольные фигуры). Таким образом, n(Q)—ii(P)<e»
и в силу теоремы 10.2 криволинейная трапеция квадрируема. По-
Поскольку для любой интегрируемой функции предел при стремле-
стремлении диаметра разбиения к нулю как верхних S, так и нижних.
сумм s равен [f(x)dx и s<ja(F)<S, то площадь \i{F) криво-
а
линейной трапеции находится по формуле A0.28).
Замечание. Если функция f(x) непрерывна и неположи-
ь
тельна на сегменте [а, Ь], то значение интеграла ff(x)dx рав-
а
но взятой с отрицательным знаком площади криволинейной тра-
трапеции, ограниченной графиком функции |Д#)|, ординатами в
точках а и b и отрезком оси Ох между точками а и Ь. Поэтому
ъ
если f(x) меняет знак, то [f(x)dx равен сумме взятых с опре-
а
деленным знаком площадей криволинейных трапеций, располо-
расположенных выше и ниже оси Ох, причем площади первых берутся:
со знаком +, а вторых — со знаком —.
Перейдем теперь к рассмотрению площади так называемого
криволинейного сектора. Пусть кривая L задана в полярной сис-
системе координат уравнением г = г(8), а<0<р (рис. 10.2), причем
функция г (8) непрерывна и неотрицательна на сегменте [а, р].
Назовем криволинейным сектором плоскую фигу-
фигуру, ограниченную кривой L и двумя лучами, составляющими с
полярной осью углы аир.
Докажем следующее
Утверждение. Криволинейный сектор представляет со-
собой квадрируемую фигуру F, площадь \i(F) которой может быть-
вычислена по формуле
f A0-29>
Доказательство. Рассмотрим разбиение сегмента [а,.
Р] точками a=80<6i<...<8n=p и для каждого частичного сег-
сегмента i[6<_i, 0;] построим круговые секторы, радиусы которых,
равны минимальному г,- и максимальному Ri значениям функции
г F) на сегменте [6,--ь 6,-]. В результате получатся две квадри-
руемые фигуры, первая фигура А содержится в криволинейном
секторе, а вторая В содержит этот сектор (см. рис. 10.2).
Площади \х(А) и \i{B) указанных квадрируемых фигур А и;
п п
В соответственно равны —Vlr^Of—6,-^) и —V#?F,- — 6,_x)_
416
Гл. 10. Геометрические приложения определенного интеграла
Обратим внимание на то, что первая из этих сумм является ниж-
нижней суммой s, а вторая — верхней суммой 5 функции —г2 F)
на сегменте [а, р] для указанного разбиения этого сегмента. Так
как непрерывная на [а, р] функция —г2 F) интегрируема на
этом сегменте, то для любого е>0 найдется разбиение, для кото-
которого разность S—s = n(B)—ц(Л) меньше е.
Так как А и В — две квадрируемые фигуры, первая из кото-
которых содержится в криволинейном секторе F, а вторая содержит
F, то в силу теоремы 10.2' криволинейный сектор квадрируем.
Справедливость для его площади формулы A0.29) вытекает
из того, что эта площадь \n{F) заключена между s — \i{A) и
5 = (д,(В), а обе суммы s и S стремятся к интегралу, стоящему в
¦правой части A0.29), при стремлении диаметра разбиения к
нулю.
4. Примеры вычисления площадей. 1.° Найти площадь ^i(F)
фигуры F, ограниченной графиками функции у=ха и х=уа, а>1
(рис. 10.3). Поскольку фигура F симметрична относительно бис-
биссектрисы первого координатного угла, то ее площадь может быть
получена посредством вычитания из единицы (площади квадрата)
удвоенной площади криволинейной трапеции, задаваемой графи-
графиком функции у=ха, сс>1, на сегменте [0, 1].
Таким образом, по формуле A0.28) мы получим, что
J L « + i Jo
2°. Через три точки с координатами (—h, y0), @, r/i), (h, y2)
проходит только одна парабола y=Ax2+Bx+D (или прямая, если
эти точки лежат на одной прямой).
у=х"
У
1
0
ли'
/fflMw
г
1
1/
X
(h,0)
х
Рис. 10.3
Рис. 10.4
В самом деле, условия уасположения точек (—h, у0), @, r/i),
¦(h, y2) на параболе приводят к системе уравнений относительно
A,B,D
§ 3. Объем тела в пространстве
417
Ah2
=y0,
Ah2+Bh+D=y2.
Эта система имеет единственное решение
уу
Найдем площадь yi(F) криволинейной трапеции F, определяемой
указанной параболой, ординатами в точках (—h, 0) и (h, 0) от-
отрезком оси Ох между этими точками (рис. 10.4).
По формуле A0.28)
_ft
Рие. 10.5
Рис. 10.6
и
Подставляя найденные значения А и D через ординаты у0,
2 и величину h, получим [i(F) = — (г/0 + 4уг + yt).
О
3°. Найти площадь n(F) трилистника r=a cos 39 (рис.
10.5). Из рисунка можно заключить, что достаточно вычислить
площадь части трилистника, отвечающей изменению 8 от 0 до
л/6, и полученный результат умножить на шесть. Поэтому по фор-
формуле A0.29) получаем, что
я/6
It
12
sin 60
12
я/6
О
S4 Зак. 72
418 Гл. 10. Геометрические приложения определенного интеграла
§ 3. ОБЪЕМ ТЕЛА В ПРОСТРАНСТВЕ
Основные определения и утверждения настоящего параграфа
аналогичны соответствующим определениям и утверждениям § 2.
Это позволяет нам ограничиться основными формулировками.
1. Объем тела. Рассмотрим множество всех точек пространства
и фиксируем одну из этих точек А.
г-о к р е с т н ос т ь ю точки А будем называть множество
всех тех точек пространства, которые расположены внутри шара
радиуса 8 с центром в точке А.
Точку А будем называть внутренней [внешней] точ-
точкой произвольного множества точек пространства {М}, если най-
найдется 8>0 такое, что г-окрестность точки А целиком принадле-
принадлежит [целиком не принадлежит] множеству {М}.
Точки множества {М}, не являющиеся ни внутренними, ни
внешними, назовем граничными точками множества {М}, а
совокупность всех граничных точек назовем границей мно-
множества {М}.
Множество {М} точек пространства назовем ограничен-
ограниченным множеством или телом, если найдется шар, со-
содержащий все точки этого множества.
Среди всех тел выделим так называемые многогранные
тела, представляющие собой объединение конечного числа огра-
ограниченных многогранников. Объем многогранного тела заимствуем
из курса средней школы. Подчеркнем, что этот объем (как, и пло-
площадь многоугольной фигуры) обладает свойствами аддитивности,
инвариантности и монотонности.
Рассмотрим произвольное тело F, а также всевозможные мно-
многогранные тела Р, содержащиеся в F, и всевозможные много-
многогранные тела Q, содержащие F.
Назовем верхним объемом ' тела F точную нижнюю
грань числового множества {jj,(Q)} объемов всех многогранных
тел Q, содержащих F т. е. число
Аналогично назовем нижним объемом тела F точную
верхнюю грань числового множества (ц(Р)} объемов всех много-
многогранных тел Р, содержащихся в F, т. е. число
М-, = М-* (^") = sup [х (Р).
PF
Из этих определений очевидно, что |д,*ц
Определение 1. Тело F называется кубируемым (или
имеющим объем), если (д,* = (х*.
При этом число \x, = \l(F) =|д,* = ц* называется объемом
тела F.
В полной аналогии с теоремой 10.2 доказывается следующее
утверждение.
§ 3. Объем тела в пространстве 419
Теорема 10.4. Для кубируемости тела F необходимо и дос-
достаточно, чтобы для любого 8>0 нашлись такое содержащиеся в
F многогранное тело Р и такое содержащее F многогранное тело
Q, для которых n(Q)—ц(Р)<е.
Замечание. В формулировке теоремы 10.4 вместо много-
многогранных тел Р и Q могут быть взяты произвольные ку-
бируемые тела Р и Q, удовлетворяющие всем другим усло-
условиям этой теоремы.
Определение 2. Множество точек пространства назо-
назовем множеством объема нуль, если это множество содер-
содержится в многогранном теле сколь угодно малого объема.
Теорема 10.4 может быть переформулирована.
Теорема 10.4'. Тело F кубируемо тогда и только тогда,
когда его граница имеет объем нуль.
Введенное нами понятие объема тела обладает свойствами
аддитивности, инвариантности и монотонности.
2. Некоторые классы кубируемых тел. Цилиндрическим
телом будем называть тело, ограниченное цилиндрической по-
поверхностью с образующими, параллельными некоторой оси, и
двумя плоскостями, перпендикулярными этой оси.
Эти плоскости в пересечении с цилиндрической поверхностью
образуют плоские фигуры, называемые основаниями ци-
цилиндрического тела, а расстояние h между основаниями цилинд-
цилиндрического тела называется его высотой (рис. 10.6). •
Справедливо Следующее
Утверждение. Если основанием цилиндрического тела F
является плоская квадрируемая фигура G, то тело F кубируемо,
причем объем \i(F) этого тела равен \a(G)h, где \x(G) —• площадь
основания G, a h ¦—¦ высота.этого цилиндрического тела.
Доказательство. Поскольку плоская фигура G квад-
рируема, то для любого 8>0 можно указать такие описанную и
вписанную в эту фигуру многоугольные фигуры Q и Р, что
(Q(Р)А
)ц()
Объемы цилиндрических многогранных тел Fq и Fp, основа-
основанием которых служат многоугольные фигуры Q и Р, а высота
которых равна /г, равны соответственно n(Q)/i и ц(Р)А. Поэтому
Так как многогранное тело FQ содержит F, а многогранное тело
FP содержится в F, то в силу теоремы 10.4 тело F кубируемо.
Поскольку ii(P)h<.ii{G)h<.\x(Q)h, то объем цилиндрического те-
тела F равен (x(G)A.
Из свойства аддитивности объема и из доказанного утверж-
утверждения вытекает кубируемость ступенчатых тел (ступенча-
(ступенчатым телом называется объединение конечного числа цилиндриче-
цилиндрических тел, расположенных так, что верхнее основание каждого
14*
420
Гл. 10. Геометрические приложения определенного интеграла
предыдущего из этих тел находится в одной плоскости с нижним
Ьснованием последующего; см. рис. 10.7).
Рис. 10.7
Рис. 10.8
Из предыдущих рассуждений непосредственно вытекает ут-
утверждение. Если для любого положительного числа г можно
указать такое содержащее F ступенчатое тело Fx и такое содержа-
содержащееся в F ступенчатое тело F2, что \n(F^)—\i(F2)<z, то тело F ку-
бируемо.
Пользуясь этим, докажем кубируемость тела вращения.
Утверждение. Пусть функция y=f(x) непрерывна на
сегменте [а, Ь]. Тогда тело F, образованное вращением вокруг
оси Ох криволинейной трапеции, ограниченной графиком функции
\f(x)] ординатами в точках а и b и отрезком оси Ох от а до Ь,..
кубируемо и его объем \i(F) может быть найден по формуле
A0.30)
Доказательство. Разобьем сегмент [а, Ь] на частичные
сегменты точками a = xo<xi<...<xn=b. Пусть nit и М; — точные
грани f(x) на частичном сегменте [xi-u Xi]. На каждом таком
сегменте построим два прямоугольника с высотами /п,- и Mi (на
рис. 10.8 эти прямоугольники изображены только на одном сег-
сегменте [Xi-i, Xt]). В результате получатся две ступенчатые фигу-
фигуры, одна из которых содержится в криволинейной трапеции, а
другая содержит ее. При вращении криволинейной трапеции и
этих ступенчатых фигур мы получим тело F и два ступенчатых
тела, одно из которых Q содержит F, а другое Р содержится в
Q. Объемы этих тел Q и Р равны соответственно
§ 3. Объем тела в пространстве
421
ц (Q) = я? M2Axlt ]i (P) = я ? m?Ax,.
Легко видеть, что эти выражения представляют собой верхнюю и
нижнюю суммы для функции пР(х). Поскольку эта функция ин-
интегрируема, то разность указанных сумм для некоторого разбие-
разбиения сегмента [а, Ь] будет меньше наперед взятого положитель-
положительного числа е. Следовательно, тело кубируемо. Поскольку предел
указанных сумм при стремлении диаметра разбиения сегмента
ь
[а, Ь] к нулю равен я if{x)dx, то объем \x,{F) тела F вычйс-
а
ляется по формуле A0.30).
3. Примеры. 1) Найти объем \i(F) шара F радиуса г. Рас-
Рассмотрим этот шар как результат вращения полуокружности
у = угг2—х2 , —г*сх<сг, вокруг оси Ох (рис. 10.9). По формуле
A0.30) получим
ц (F) = п J (г2—х2) dx = пг2х
пх?
- з яг-.
2) Найдем объем \x(F) прямого кругового конуса с высотой,
равной h, и радиусом основания г. Рассматривая указанный ко-
конус как тело, полученное вращением треугольника с вершинами
в точках @,0), (h, 0) и (h, г) вокруг оси Ох (рис. 10.10), полу-
получим, согласно формуле A0.30),
яг2*3
3/г2
nr2h
(hr)
Рис. 10.9
Ж
2
Рис. 10.11
3) Найдем объем тела F, полученного вращением вокруг оси
Ох синусоиды y = sinx на сегменте [0, я]. Имеем (рис. 10.11):
n(F) = n [ sltf xdx=n [l~cos''lxdx^—.
Глава 11
ПРИБЛИЖЕННЫЕ МЕТОДЫ
ВЫЧИСЛЕНИЯ КОРНЕЙ УРАВНЕНИЙ
И ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
В этой главе рассматриваются приближенные методы нахож-
нахождения корней алгебраических и трансцендентных уравнений и
вычисления определенных интегралов.
§ 1. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ
КОРНЕЙ УРАВНЕНИЙ
В этом параграфе мы займемся приближенным вычислением
одного из корней уравнения f(x)=O, где y=--f{x) — некоторая,
во всяком случае, непрерывная функция. Мы будем считать, что
интересующий нас корень этого уравнения изолирован на некото-
некотором сегменте [а, Ь], т. е. будем считать, что этот корень являет-
является внутренней точкой сегмента [а, Ь], не содержащего других
корней рассматриваемого уравнения.
На практике обычно путем грубой прикидки определяют раз-
размеры указанного сегмента [а, Ь] *.
1. Метод «вилки». Мы начнем наше знакомство с метода, ко-
который часто используется для приближенного вычисления кор-
корней на современных быстродействующих математических маши-
машинах. Основой этого метода служит новое доказательство теоре-
теоремы 4.12 о прохождении непрерывной функции через нуль при
смене знака. Изложим это доказательство.
Требуется, доказать следующее
Утверждение. Если функция f(x) непрерывна на сегменте
[а, Ь] и если значения этой функции f(a) и f(b) на концах сег-
сегмента [а, Ь] суть числа разных знаков, то внутри сегмента
[а, Ь] найдется такая точка с, в которой значение функции f(c)
равно нулю, т. е. с является корнем уравнения f(x) =0.
Договоримся называть «вилкой» любой сегмент, на концах
которого функция f(x) имеет значения разных знаков. По усло-
условию сегмент [о, Ь] является «вилкой». Пусть ради определенно-
определенности f(a)<0, f(b)>0. Разделим сегмент [а, b] пополам. При этом
может представиться два случая: 1) значение функции в середи-
середине сегмента [а, Ь\ равно нулю (в этом случае теорема доказа-
доказана), 2) указанное значение не равно нулю. В этом случае одна
* При этом может быть использована вытекающая из физического содер-
содержания задачи дополнительная информация о расположении корня.
§ 1. Приближенные методы вычисления корней уравнений 423
из половин сегмента [а, Ь] является «вилкой». Эту половину мы
обозначим [аи Ь\]. Очевидно, что f(ai)<0, /F1) >0. С сегментом
[аи Ь\\ поступим точно так же, как с сегментом [а, Ь], т. е.
разделим сегмент [аи Ьу\ пополам.
Продолжая аналогичные рассуждения далее, мы будем иметь
две возможности: 1) либо описанный выше процесс оборвется
вследствие того, что значение функции в середине некоторого из
сегментов окажется' равным нулю (в этом случае теорема дока-
доказана), 2) либо описанный процесс можно продолжать неограни-
неограниченно, и мы получим стягивающуюся систему сегментов — «ви-
«вилок» [аи bi], [п2, Ь2], ..., [ап, Ь„], ..., причем для любого номе-
номера п f(an)<0, Дб„)>0. Согласно следствию из теоремы 3.15 ука-
указанная стягивающаяся система сегментов имеет одну общую
точку с, к которой сходятся каждая из последовательностей
{ап} и {Ьп}. Докажем, что f (с) = 0. Поскольку функция f(x) не-
непрерывна в точке с, то каждая из последовательностей f(an) и
f(bn) сходится к f(c). Но тогда из условий f(an)<0 и f(bn)>0
в силу теоремы 3.13 получим, что одновременно справедливы
неравенства f(c)<0 и /(с)>0, т. е. f(c)=O. Утверждение дока-
доказано.
Предположим теперь, что в условиях доказанного выше ут-
утверждения сегмент [а, Ь] содержит только один корень с урав-
уравнения f(x)—Q*. Тогда за приближенное значение этого корня
можно взять точку а" , т. е. середину сегмента [ап, Ьп).
Поскольку длина сегмента [ап, Ьп] равна , то число
-° " отличается от точного значения корня не более чем на
. Таким образом, описанный выше процесс последователь-
последовательного деления сегментов — «вилок» пополам позволяет вычислить
искомый корень с с любой наперед заданной степенью точности.
Так как описанный процесс приводит к многократному повторе-
повторению однотипных вычислительных операций, он особенно удобен
для проведения вычислений на быстродействующих математиче-
математических машинах.
2. Метод итераций**. Излагаемый в этом пункте метод лежит
в основе многих других приближенных методов. Этот метод при-
применяется для решения уравнения
x=F(x). A1.1)
* Т. е. предположим, что корень с является изолированным на сегменте
[а, Ь].
** Этот метод называют методом последовательных прибли-
приближений.
424 Гл. 11. Приближенные методы
Введем понятие итерационной последовательно-
последовательности.
Последовательность х0, х\, •••, хп, ... будем называть итера-
итерационной, если для любого п>>\ элемент хп выражается через
элемент хп-\ по рекуррентной формуле xn = F(xn-i), а в качестве
х0 взято любое число из области задания функции F(x).
Мы докажем, что при определенных условиях итерационная
последовательность сходится к корню уравнения A1.1) и, значит,
ее элементы могут быть взяты за приближенные значения этого
корня.
Справедливо следующее.
Утверждение 1. Пусть функция F(x) непрерывна на сег-
сегменте [а, Ь], и пусть все элементы итерационной последователь-
последовательности Хо, Хи ..., хп, ••• лежат на этом сегменте. Тогда, если эта
последовательность сходится к некоторому числу с, то указанное
число с является корнем уравнения A1.1).
Доказательство. Так как последовательность {хп} сходит-
сходится к с и все ее элементы принадлежат сегменту [а, &], то и пре-
предел с принадлежит сегменту [а, Ь] (см. следствие 2 из теоре-
теоремы 3.13). По условию функция F(x) непрерывна в точке с, и по-
поэтому последовательность {F(xn-i)} сходится к F(c). Таким об-
образом, равенство xn — F(xn-i) в пределе при п-*-оо переходит в
равенство c — F{c), т. е. с является корнем уравнения A1.1).
Доказанное утверждение будет существенно использовано нами
в п. 3 для обоснования метода хорд и касательных.
Докажем еще одно утверждение, часто используемое для при-
приближенного вычисления корня уравнения A1.1) с помощью ите-
итерационной последовательности.
Утверждение 2. Пусть с — корень уравнения A1.1), и
пусть в некотором симметричном относительно точки с сегменте
[с—е, c + ej производная функции F(x) удовлетворяет условию
\F'(x) | <а<1. Тогда итерационная последовательность х0, Х\, ...,
..., хп, ..., у которой в качестве х0 взято любое число из сегмента
[с—е, с + е], сходится к указанному корню с.
Доказательство. Прежде всего докажем, что все эле-
элементы итерационной последовательности {хп} принадлежат ука-
указанному сегменту [с—е, с+е]. В самом деле, х0 принадлежит
этому сегменту по условию. Поэтому достаточно, предположив,
что xn-i принадлежит этому сегменту, доказать, что ему принад-
принадлежит и хп. Для этого применим формулу Лагранжа к разности
F(xn-\)—F(c) и учтем, что F(c)=c. xn = F(xn-i). Получим
xn~c = F(xn-1)—F{c)=F'(l)(xn-i—с), A1.2)
где g — некоторая точка, лежащая между хп-\ и с и, значит,
принадлежащая сегменту [с—е, с + е]. Так как |F'(?) |«z<l,
то из равенства A1.2) получим
\хп—с|<а|хп_1—с\. (П.З)
§ 1. Приближенные методы вычисления корней уравнений 425
Из A1.3), поскольку 0<а<1, в свою очередь, получим
\хп—с\<\х„-1—с\. A1.4)
Неравенство A1.4) устанавливает,. что каждый последующий
элемент хп расположен к с ближе, чем предыдущий элемент
л'п-ь и, значит, так как хп-\ принадлежит сегменту [с—е, с+б]
и так как этот сегмент симметричен относительно точки с, то и
хп принадлежит этому сегменту. Остается доказать, что последо-
последовательность {хп} сходится к с. Поскольку неравенство A1.3)
справедливо для всех номеров п, то с помощью этого неравенст-
неравенства получим
\хп—с\<ап\х0—с\. (П-5)
Из последнего неравенства очевидно, что хп~+с, ибо а"-»-0.
Утверждение 2 доказано.
Сделаем практические замечания относительно только что до-
доказанного утверждения. Предположим, что путем предваритель-
предварительной прикидки мы установили, что интересующий нас корень
уравнения A1.1) изолирован на некотором сегменте [а, Ь], на
котором производная функции F(x) удовлетворяет условию
\F'(x) |<а<1. Так как сегмент [а, Ь], вообще говоря, не являет-
является симметричным относительно искомого корня, то, естественно,
возникает вопрос о том, как выбрать нулевое приближение Хо,
с тем, чтобы можно было применить доказанное выше утвержде-
утверждение 2.
Заметим, что где бы внутри сегмента [а, Ь] ни находился ис-
искомый корень с, хотя бы один из двух симметричных относитель-
относительно с сегментов [а, 2с—а], [2с—Ъ, Ь] (рис. 11.1) целиком принад-
принадлежит сегменту [а, Ь]. Поэтому хотя с 2с-а
бы одна из точек а или b принадле- ао " о о. 0&
щит симметричному относительно
корня с сегменту, всюду на котором ао с 0 сс а^
|F'(|l
|()|
Значит, по крайней мере одну из р ,, ,
точек а или b можно, согласно дока-
доказанному выше утверждению 2 вы-
выбрать за Хо. Конкретно за х0 следует выбрать ту из двух точек а
или Ь, для которой приближение xi = F(x0) не выходит за преде-
пределы сегмента [а, Ь].
На практике чаще всего встречается случай, когда производ-
производная F'(х) имеет на сегменте [а, Ь] определенный знак. Если этот
знак положителен, то из формулы A1.2) следует, что последова-
последовательность {хп} монотонна. Этот случай приводит к так называе-
называемой ступенчатой диаграмме, изображенной на рис. 11.2. Если же
производная F'(x) отрицательна на сегменте [а, Ь], то из той же
формулы A1.2) видно, что любые два последовательных элемея-
та xn-i и хп лежат по разные стороны от корня с.
426
Гл. 11. Приближенные методы
О
Рис. 11.2
а х0 хгсх3х,
Рис. 11.3
X
Этот случай приводит к так называемой спиралеобразной диа-
диаграмме, изображенной на рис. 11.3.
Замечание. Возникает вопрос об оценке погрешности мето-
метода итераций, т. е. об оценке отклонения n-го приближения х„ от
точного значения корня с. Из формулы A1.5) непосредственно
вытекает следующая оценка:
\хп—с\ <апF—а),
где а — точная верхняя грань функции |.Ру(л:)| на сегменте
[а, Ь], на котором изолирован рассматриваемый корень.
Если производная F'(х) отрицательна на сегменте [а, Ь], то,
как указано выше, х-Л-\ и хп лежат по разные стороны от кор-
корня с, и поэтому справедлива следующая оценка:
п С |
| Хп—Хп—\ |
Если же в рассматриваемом случае взять за приближенное зна-
значение корня полусумму двух последовательных приближений
то получим следующую оценку погрешности:
I V V 1
ХП Art.l
\х"п—с\<-
3. Методы хорд и касательных. К числу широко распростра-
распространенных приближенных методов решения уравнения /(л:)=0 от-'
носятся метод хорд и метод касательных, каждый из которых
является одним из конкретных вариантов метода итераций.
Прежде всего рассмотрим метод хорд. Пусть искомый ко-
корень уравнения
§ 1. Приближенные методы вычисления корней уравнений 427
/М-=о (п.6)
изолирован на некотором сегменте [а, Ь]. Предположим, что
функция y = f(x) имеет на сегменте [а, Ь] монотонную и непре-
непрерывную производную, сохраняющую определенный знак.
При этом возможны четыре случая: 1°. fix) не убывает и
положительна на [а, Ь]\ 2°. /'(х) не возрастает и отрицательна
на [а, Ь}\ 3°. У[х) не возрастает и положительна на [а, Ь]\
4°. f {х) не убывает и отрицательна на [а, Ь].
Ради определенности подробно рассмотрим случай 1°.
Рассмотрим вместо уравнения A1.6) уравнение вида
x = F(x), F(x) = x-(b~x)f(x)* . A1.7)
Легко видеть, что изолированные на сегменте [а, Ь] корни урав-
уравнений A1.6) и A1.7) совпадают, и поэтому на сегменте [а, Ь]
эти уравнения эквивалентны. Для решения уравнения (П.7)
применим к этому уравнению метод итераций, выбрав за нуле-
нулевое приближение Хо точку а. Как обычно, определим последова-
последовательность {х„} по рекуррентной формуле x»=-F(xn-i), n—\, 2
Докажем, что последовательность {хп} сходится к искомому кор-
корню с. Для этого, в силу утверждения 1 из п. 2, достаточно до-
доказать, что все хп лежат на сегменте [а, Ь] и что последователь-
последовательность {хп} сходится.
Применяя метод индукции, докажем, что все хп лежат на
сегменте [а, Ь], точнее, на сегменте [а, с], где с — искомый ко-
корень. Так как х0 лежит на сегменте [а, с], то для проведения
индукции достаточно, предположив, что хп лежит на указанном
сегменте, доказать, что xn+i также лежит на этом сегменте. По-
Поскольку
AL8)
то, учитывая, что f(c)=O, будем иметь **
_ (b~Xn)[f(c)-f(Xn)]
(n)
n+1 n f(b)-f(xn)
Применяя к выражениям в квадратных скобках формулу Ла-
гранжа, получим
* При этом мы считаем, что F(b)=b— . Тогда функция F(x)
ГКО)
"УДет непрерывна на всем сегменте [а, Ь].
** В дальнейшем мы предполагаем, что хп<с, ибо если хп — с, то f(xn) =
=/(с)=0 и, значит, хп-I=--х„^с, т. е. принадлежность xn+i сегменту [а, о\
Установлена.
428
Гл. 11. Приближенные методы
Г Aп)(с-хп)
(Н-9)
где хп<1п<с, c<ln*<b, т. е. |„<|„*.
В силу неубывания и положительности производной f'(x) мо-
можем записать 0<f'(t,n) <f'(ln*)- Отсюда, так как Ь—с>0 и
с—хп>0, получим
{b-c)f'(ln*) + (c-xn)f'{ln)>[(b-c) + {c-xn)]f'($n) =
= (Ь-хп)Г($п)-
Таким образом, из равенства A1.9) найдем xn+i—х„<с—хп,
или хп+1<-с, т. е. индукция проведена.
Докажем теперь, что последовательность {хп} является неубы-
неубывающей. Для этого достаточно доказать, что дробь, стоящая в
правой части равенства A1.8), является неположительной. Так
как производная f(x) положительна на сегменте [а, Ъ\, то функ-
функция f(x) возрастает на этом сегменте, и поэтому из
неравенств хп<с<Ь следует, что f(xn) <f(c) =0, f(b)—f(xn)>0.
Отсюда и вытекает неположительность указанной дроби.'
Итак, последовательность {хп} не убывает и ограничена свер-
сверху числом с. По теореме 3.15 эта последовательность сходится.
В силу утверждения 1 п. 2 пределом ее является искомый корень.
Дадим геометрическую иллю-
иллюстрацию рассмотренного выше
случая 1°. Из формулы A1.8)
вытекает, что хп+\ является абс-
абсциссой точки пересечения хор-
хорды, соединяющей точки Ап(хп,
f{xn)) и B(b, f(b)) графика
функции y = f(x) с осью Ох (на
рис. 11.4 изображены точки А\.
и А2).
Как уже указано выше, кро-
кроме рассмотренного выше случая
1° возможны еще следующие
три случая: 2° производная f'(x)
не возрастает и отрицательна на
сегменте [а, Ь], 3° производная }'{х) не возрастает и положительна
на сегменте [а, Ь], 4° производная не убывает и отрицательна на
сегменте [а, Ь]. Эти случаи изображены соответственно на рис. 11.5,
11.6, 11.7.
В случае 2° уравнение A1.6), так же как и выше, заменяется
уравнением A1.7) и в качестве нулевого приближения берется
точка хо = а (при этом последовательность {хп} также оказывает-
оказывается неубывающей). В случаях 3° и 4° уравнение A1.6) заменяется
,не уравнением A1.7), а следующим уравнением
Рис. 11.4
§ 1. Приближенные методы вычисления корней уравнений 429
X = F(x), F(x) = X—-
W W f
f(a)-f(x)
и в качестве нулевого приближения берется точка Хо = Ь (при
этом последовательность {хп} оказывается невозрастающей).
Рис. 11.5 Рис. 11.6
Приведенная выше геометрическая иллюстрация является ис-
источником наименования метода хорд.
Перейдем теперь к изложению метода касательных или
метода Ньютона.
Пусть, как и выше, искомый корень с уравнения A1.6) изо-
изолирован на сегменте [а, о], на котором f(x) имеет непрерывную
и монотонную первую производ-
производную, сохраняющую определенный ГЧ.
знак. При этом возможны те же —-J
самые четыре случая, которые от-
отмечены при изложении метода
Хор?- Рис 117
Ради определенности рассмот-
рассмотрим подробно случай 1°, т. е.
предположим, что производная /'(х) не убывает и положительна
на сегменте [а, Ь].
Заменим уравнение A1.6) эквивалентным ему на сегменте
[а, Ь] уравнением
x = F(x), где F(x) = x—f-j&-, A1.10)
и будем решать последнее уравнение методом итераций, приняв
за нулевое приближение Хо точку Ь и определив последователь-
последовательность {хп} рекуррентной формулой
A1.11)
Чтобы доказать, что последовательность {хп} сходится к искомо-
искомому корню с, достаточно в силу утверждения 1 п. 2, доказать, что
все хп лежат на сегменте [а, Ь] и что последовательность {хп}
сходится.
Применяя метод индукции, докажем, что все хп лежат на сег-
сегменте [а, Ь], точнее, на сегменте [с, Щ, где с — искомый корень.
Так как Хо=Ь лежит на сегменте. \с. Ь], то для проведения ин-
430 Гл. П. Приближенные методы
дукции достаточно, предположив, что х„ лежит на сегменте
[с, Ь], доказать, что и хп+\ также лежит на этом сегменте. Если
хп = с, то f(xn)—f{c)=O, и из формулы A1.11) следует, что
хп+\~хп = с, т. е. индукция проведена. Пусть теперь хп>с. Тогда
из формулы A1.11), учитывая, что /(с)=0, получим
Применяя к выражению, стоящему в числителе последней дроби,
формулу Лагранжа, найдем
/' (Ев)
хп—Хп+\ — \хп
Г (хп)
где с<1„<хп. В силу неубывания и положительности производ-
производной дробь положительна и не превосходит единицы, т. е.
V (хп)
хп—xn+i<xn—с или
Таким образом, индукция проведена. Из положительности
производной /' (х) следует возрастание функции f(x), а поэтому
из неравенства с<.хп следует, что 0=f(c)<cf(xn). Таким образом,
f{xn)lf'{xn)>-0. Отсюда в силу формулы A1.11) xn+i<*n, т. е. по-
последовательность {хп} не возрастает. Так как эта последователь-
последовательность, кроме того, ограничена снизу числом с, то по теореме 3.15
она сходится. В силу утверждения 1 из п. 2 пределом ее являет-
является искомый корень с.
Дадим геометрическую иллюстрацию рассмотренного нами
случая 1°. Из формулы A1.11) вытекает, что хп+\ является абс-
абсциссой точки пересечения с осью Ох касательной к графику
функции y — f(x) в точке Вп(хп, /(#„)) (на рис. 11.8 изображе-
изображены точки Во, В\ и Вп) ¦ Приведенная геометрическая иллюстра-
иллюстрация является источником наименования метода касательных.
Предлагаем читателю самостоятельно разобрать м'етод касатель-
касательных для случаев 2°, 3°, 4°, указанных при изложении метода
хорд.
Замечание 1. Возникает вопрос об оценке погрешности
метода хорд и касательных, т. е. об оценке отклонения и-го при-
приближения от точного значения корня с. Применяя к выражению
f(xn)—f(Xn)—f(c) формулу Лагранжа, будем иметь f{xn) =
= (хп—с)/'(|п). Отсюда получим следующую оценку:
1*„—сК 1/(%)| ¦ A1.12)
т
где т — минимальное значение |/' (х) | на сегменте [а, Ь]. Фор-
Формула A1.12) позволяет-оценить отклонение хп от точного значе-
значения корня с через значение модуля заданной функции y=f(x)
в точке хп.
§ 2. Приближенные методы вычисления определенных интегралов 431
Замечание 2. На практике часто используют комбиниро-
комбинированный метод, заключающийся в поочередном применении метода
хорд и метода касательных. Ради определенности остановимся
йа подробно рассмотренном выше случае Г, т. е. предположим,
Что f'(x) не убывает и положительна на сегменте [а, Ь]
(рис. 11.9). Определим Х\ по методу касательных, взяв за ну-
нулевое приближение точку Ь: После этого определим Хг, применяя
Ba=B
Рис. 11.8
Рис. 11.9
метод хорд, но не к сегменту [а, 6], а к сегменту [а, Х\\. Далее,
определим" Хг по методу касательных, исходя из уже найденного
Х\, а лг4 по. методу хорд, применяя его к сегменту [х2, х3]. Ука-
Указанный процесс иллюстрируется на рис. 11.9.
Преимущества комбинированного метода состоят в следую-
следующем: во-первых, он дает более быструю сходимость, чем метод
хорд, и, во-вторых, поскольку последовательные приближения хп
и хп+\ комбинированного метода с разных сторон приближается
к корню, то разность \хп+\—х„\ дает оценку погрешности это-
этого метода. Если за приближенное значение корня взять х„* =
= (xn + xn+i)/2, то для погрешности получим оценку \хп*—с\<
<\хп+1—х„\12.
§ 2. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
1. Вводные замечания. При решении ряда актуальных физи-
физических и технических задач встречаются определенные интегра-
интегралы от функций, первообразные которых не выражаются через
элементарные функции. Кроме того, в приложениях приходится
иметь дело с определенными интегралами, сами подынтегральные
функции которых не являются элементарными. Это приводит к
432
Гл. 11. Приближенные методы
необходимости разработки приближенных методов вычисления
определенных интегралов *.
В этом параграфе мы познакомимся с тремя наиболее употре-
употребительными приближенными методами вычисления определенных
интегралов: методом прямоугольников, методом
трапеций и методом парабол.
Основная идея этих методов заключается в замене подынтег-
подынтегральной функции f{x) функцией более простой природы — мно-
многочленом, совпадающим с f(x) в некоторых точках. Для уяснения
этой идеи рассмотрим при малых с интеграл у f(x)dx, пред-
представляющий собой площадь узкой криволинейной трапеции, ле-
лежащей под графиком функции y = f{x) на сегменте [—с, с]
(рис. 11.10).
Заменим функцию f(x) многочленом нулевого порядка, а
именно константой /@). При этом интеграл Iе f(x)dx, прибли-
приближенно заменится площадью прямоугольника, заштрихованного
на рис. 11.11. Ниже мы покажем, что при определенных требова-
требованиях на 1(х) ошибка, совершаемая при такой замене имеет по-
порядок с3.
Заменим, далее, функцию f(x) многочленом первого порядка,
а именно линейной функцией y = kx+b, совпадающей с f(x) в
точках —с и с. При этом интеграл fc f{x)dx приближенно за-
У
-с 0 с
Рис. 11.10
-с 0 с
Рис. 11.12
* Заметим, что приближенными методами часто пользуются и для вычис-
вычисления интегралов, выражающихся' через элементарные функции.
§ 2. Приближенные методы вычисления определенных интегралов 43&
менится площадью прямоугольной трапеции, заштрихованной
на рис. 11.12. Ниже мы покажем, что ошибка, совершаемая при,
такой замене, также имеет порядок с3.
Заменим, наконец, функцию f(x) многочленом второго поряд-
порядка, т. е. параболой у — Ах2 + Вх+С, совпадающей с /(х) в точ-
точках —с, 0 и с. При этом интеграл V f(x)dx приближенно за-
заменится площадью, лежащей под параболой фигуры, заштрихо-
заштрихованной на рис. 11.13. Ниже мы покажем, что
при определенных требованиях на функцию
f(x) ошибка, совершаемая при такой замене,
,у
имеет порядок са.
Если потребуется вычислить интеграл
[bf(x)dx по любому сегменту \а, Ь], есте-
J a
ственно разбить этот сегмент на достаточно
большое число малых сегментов и к каждо-
каждому из этих сегментов применить изложенные
выше рассуждения. При этом мы и придем
к методам прямоугольников, трапеций и па-
парабол в их общем виде. Для того чтобы оце-
оценить ошибку, возникающую при применении
методов прямоугольников, трапеций и пара-
парабол, мы подойдем к изложению этих методов
с другой точки зрения.
Прежде всего введем понятие усред-
нения ячисел.
Пусть A,i, Я,2, —, hn — какие угодно поло-
положительные числа. Любое число с вида
Ai • ; (#1) -f- %2i \хг) ~Ь • • • ~Ь "п/ \Хп)
назовем усреднением п чисел /(xi), f(x2), ..., f(xn).
Очевидно, что если все числа f(xi), f{xi), ..., f(xn) заключены
между числами m и М(пк.М), то и любое усреднение с этих чи-
чисел удовлетворяет неравенствам tn<.c<.M.
Предположим далее, что функция f(x) непрерывна на сегмен-
сегменте [а, Ь] и все значения х\, ~x<i, ..., хп лежат на этом сегменте.
Тогда, какое бы усреднение п чисел f(x\), f(xi), ..., f(xn) мы ни~
взяли, на сегменте [а, Ь\ найдется точка | такая, что это усред-
усреднение равно значению f(|) в точке |. В самом деле, так как функ-
функция f(x) непрерывна на сегменте [а, Ь], то все значения этой
функции на указанном сегменте заключены между ее наиболь-
наибольшим значением М и наименьшим значением пг. Значит, и любое-
усреднение с чисел f(xi), f(x2), ..., f(xn) заключено между пг и?
М. Но, каково бы ни было это промежуточное значение с, соглас-
согласно теореме 4.12 на сегменте [а, Ь] найдется точка ? такая, что»
434 Гл. 11. Приближенные методы
Таким образом, для непрерывной на сегменте [а, Ь] функции
формулу A1.13) можно переписать в виде
п) _ f (l) /11 14ч
^1 + А2 + •. ¦ + Ап
или в виде
W (*i) + W (*i) + ¦. ¦ + Kf (хп) (f,—g) = / (g) ф—а). A1.15)
Aj -\- Яг -(- ...-(- An
С другой стороны, для непрерывной на сегменте [а, Ь] функ-
функции, согласно п. 2 § 4 гл. 9, найдется точка |' из сегмента [а, Ь]
такая, что справедлива формула среднего значения
j7(*)dx = /(E')(&-a). (П. 16)
а
Сопоставление формул A1.15) и A1.16) позволяет сделать пред-
предположение о том, что при некотором разумном выборе чисел
b'
Аь А,2, -.., кп и точек Х\, Хг, ..., х„ вычисление интеграла \f(x)dx
а
можно с большой точностью заменить вычислением суммы, стоя-
стоящей в левой части формулы A1.15). Именно на этой идее разум-
разумного выбора чисел \it Х2, ¦¦¦, 'кп и точек х\, Х2, ..-, хп и основаны
лриближенные методы вычисления интеграла. Переходим'к изло-
изложению этих методов.
2. Метод прямоугольников. Будем считать, что функция f(x),
интеграл от которой нам требуется приближенно вычислить, име-
имеет на рассматриваемом сегменте непрерывную вторую производи
мую.
Начнем с рассмотрения .интеграла в симметричных пределах
с
[f(x)dx. Для вычисления этого интеграла будем исходить из
—с
формул A1.15) и A1.16), в которых положим л=1, а =—с, 6 =
= с, Xi = 0, Xi = l. Тогда, очевидно, | = 0 и правая часть A1.15)
равна f @) -2с. Таким образом,
A1.17)
где символом R обозначен остаточный член (т. е. отклонение чис-
числа f@)-2c от точного значения интеграла). Для того чтобы оце-
оценить величину остаточного члена R, обозначим через F(x) пер-
первообразную функции f(x). Поскольку в силу формулы Ньютона—
с
Лейбница f /(x)dx = F(с)—F(—с), то
R=F(c)—F{—c)—f@)-2c. A1.18)
§ 2. Приближенные методы вычисления определенных интегралов 435-
Разложим по формуле Маклорена функцию ty(x)=F(x)—
•—F(—х). Беря остаточный член в форме Лагранжа и обозначая
через |' возникающее при этом промежуточное значение аргумен-
аргумента из интервала @, с), будем иметь
^ m^(i). (ПЛ9)
Подсчитаем входящие в эту формулу значения ^@), я|/@), i|/'@),,
у'"A'). Имеем
ф (х) = F (х) -F (-х); ф @) = F @) -F @) = 0;
tf(x)=F'{x)+F'{-x)=f(x)+f{-x); -ф'@) = ДО) + ДО) =2f @);
Ц"(х) =f'(x) -f'(-x); 1>"@) =П0)-Г@) =0;
(В последнем равенстве мы воспользовались формулой A1.14)-
при и = 2, ?ц = А2=1, х-, = ?,', Хг =—|' и обозначили через | некото-
некоторую точку из интервала (—с, с) на котором по предположению-
непрерывна функция f"{x).)
Вставляя вычисленные значения в формулу A1.19), будем
иметь
Сопоставляя последнюю формулу с формулой A1.18), оконча-
окончательно получим
?2c Bс); c<g<c. A
Из полученной оценки остаточного члена видно, что формула
A1.17) тем точнее, чем меньше величина 2с. Поэтому для вы-
ь
числения интеграла [f(x)dx удобно разбить сегмент [а, Ь\ на*
а
достаточно большое число п частей и к каждой из этих частей
применить формулу приближенного интегрирования A1.17). Счи-
Считая, что функция f(x) имеет на сегменте [а, Ь] непрерывную вто-
вторую производную, разобьем этот сегмент на 2п равных частей,
при помощи точек а:=Хо<Х2< — <Х2П = Ь. Обозначим через x2k+i
среднюю точку сегмента [x2k, x2k+i]- Тогда
где
436
Гл. 11. Приближенные методы
A1.23)
(Здесь мы воспользовались для f" (х) формулой усреднения
A1.14) при А,1=А2 = ... = Яп = 1 и обозначили через | некоторое
.промежуточное значение аргумента из интервала (а, Ь).)
Формула A1.22) называется формулой прямоугольни-
прямоугольников. Ее геометрический смысл ясен из рис. 11.14: площадь кри-
Xo Xf
Рис. 11.14
Рис. 11.15
шолинейной трапеции, лежащей под графиком f(x) на сегменте
[а, Ь], приближенно заменяется суммой площадей, указанных на
¦этом чертеже прямоугольников.
3. Метод трапеций. Пусть, как и выше, функция f (x) имеет
:на рассматриваемом сегменте непрерывную вторую производную.
с
Снова начнем с вычисления интеграла f f(x)dx, но на этот
— с
фаз будем исходить из формул A1.15) и A1.16), считая, что
п = 2, а = —с, Ь = с,Х\ = —с, Х2 = с, A,i = ta— 1. Тогда
A1.24)
где R — остаточный член, подлежащий оценке.
Обозначая, как и в п. 2, через F(x) первообразную функции
с
J(x) и учитывая, что f /(х)dx = F(с)—F{—с), будем иметь
—с
2
Пусть, как и в методе прямоугольников, tp(x) =F(x)—F(—х). Раз-
Разлагая функции г|:(х) и ty'(х) по формуле Маклорена с остаточ-
остаточным членом в интегральной форме (см. п. 4 § 5 гл. 9) и полагая
.х = с, будем иметь
§ 2. Приближенные методы вычисления определенных интегралов 437
о
с
Подставляя в эти формулы значения ^@), я|/@), я1з"@), вычис-
вычисленные а п. 2, получим
/ (с) +f(-c) = 2f @) +1 Ч>"' (х) (с-х) dx.
о
Подставляя последние два выражения в A1.25), получим
Имея в виду, что функция с2—х2 неотрицательна на сегменте
{О, с], применим к последнему интегралу первую формулу сред-
среднего значения (см. п. 2 § 4 гл. 9). Учитывая, что ^'"(х) =
= f'(x)+f"(—х), и обозначая через %' некоторое значение аргу-
аргумента из сегмента [0, с], получим
р_ Г (?') + Г (-Г) Г (С2 Г2) dx_ Г Г(?) + /* (-?') 1 2Сз
о
Применяя к выражению в квадратных скобках формулу усред-
усреднения A1.14) при п — 2, Я,1 = Я,2=1 и обозначая через % некоторое
значение аргумента из сегмента [—с, с], окончательно получим
Я=-П9~=—^BсK.
о \Z
Ь
Для вычисления интеграла Jf(x)dx, как и в методе прямоуголь-
а
ников, разобьем сегмент [а, Ь] на п равных частей при помощи
точек a=Xo<Xi<...<xn = b и применим формулу A1.24) к каж-
каждому из частичных сегментов. Получим
438 Гл. 11. Приближенные методы
Ь га—1 xk+l
= ? ]f{x)dx =
k0
a k=0
k=0
n—1
Ь~а \f(a)+f(b)+2Yj(xk)\+R, A1.26)
где
- Г (So) + Г(Ь)+ •¦•+/" (?n-l) ,ft _«_
— — \p—a) —
~f^{b-af, a<l<b. A1.27)
(Мы воспользовались формулой усреднения A1.11).)
Формула A1.26) называется формулой трапеций. Гео-
Геометрический смысл этой формулы ясен из рис. 11.15: площадь
криволинейной трапеции, лежащей под графиком функции f(x)
на сегменте [а, Ь] приближенно заменяется суммой площадей,
указанных на этом чертеже прямолинейных трапеций. Сравнение
остаточного члена A1.27) с остаточным членом A1.23) показы-
показывает, что метод трапеций не дает увеличения точности по сравне-
сравнению с методом прямоугольников.
4. Метод парабол. На этот раз предположим, что функция
имеет на рассматриваемом сегменте непрерывную четвертую про-
с
изводную, и снова начнем с вычисления интеграла \ f (x) dx.
—с
Как и выше, будем исходить из формул A1.15) и A1.16), но
при этом положим в этих формулах и = 3, а=—с, b = c, A,i =
= Яз=1, Яг = Х (числом Я распорядимся в дальнейшем!), Х\=—с,
*2 = 0, *з = с. Тогда
(х) d,= iM±Ml 2c+ Л
—с
где R — подлежащий определению остаточный член. Для оценки
остаточного члена обозначим, как и выше, через F(x) первооб-
§ 2. Приближенные методы вычисления определенных интегралов 439
с
разную функции f(x) и учтем, что f /(х)dx = F(с)—F(—с). По-
—с
лучим, что
R = F(c)-Fi-c)-n-e) + XfW + nc) 2с. A1.28)
Пусть, как и выше, ty{x) — F(x)—F(—х). Разложим функции
\|з(х) и $'{х) по формуле Маклорена с остаточным членом в ин-
интегральной форме. Подставляя в эти разложения значения -ф@),
ij/@), г|/'@), вычисленные в п. 2, и учитывая, что ^4'@)=0, бу-
будем иметь
с
= 2/ @) с+ У-^- с3 + -1- Г а|M (х) (с—х)Чх, A1.29)
о
с
У (с) = f(c) + f(-c) = 2/ @) + 2-О^ с2 + -1- J f 5) (д) (с_х)з dx.
о
Из последней формулы вытекает, что
f (~с) + If @) + f (с)
2 + Я
с
= 2/ @) с + ilM 2с3 + — f ^<5> (х) (с-хK dx. A1.30)
' v 2+A. 2 + U!,l
о
Из формулы A1.28) видно, что остаточный член R равен разно-
разности выражений A1.29) и A1.30). Чтобы сделать этот остаточный
член более высоким по порядку малости, выберем значение к
так, чтобы вторые члены в правых частях формул A1.29) и
2' 2
A1.30) совпадали, т. е. положим -^г^^Цл' т" е' ^ = ^- При та-
таком значении разность формул A1.29) и A1.30) дает
с
Имея в виду, что функция (с—хK ( — +х\ неотрицательна
V 3 /
440 Гл. 11. Приближенные методы
на сегменте [0, с], применим к последнему интегралу первую»
формулу среднего значения. Учитывая, что ^(х) =f<4)(x) +
+ /D)(—х)у и обозначая через |' некоторое значение аргумента из
сегмента [0, -с], получим
J
о
D)D) BсM
2880
Применяя к выражению в квадратных скобках формулу усредне-
усреднения A1.14) при « = 2, ^! = я,2=1 и обозначая через | некоторое
значение аргумента из сегмента [—с, с], окончательно получим
2880
ь
Для вычисления интеграла [f(x)dx разделим сегмент [а, Ь] на
а
п равных частей точками а = Хо<х2<х^...<х2п = Ь и положим
+ * . Получим
1—1 *2fc+2
= ? j f(x)dx =
fe=0 д:,ь
n-1
n—1 n—1
^[ ^ ^]^^ A1.31)
где
n /D) (Ы + /D)(Si) + • • • + ^4)(?n-i) №_a\6 =
2880«*
(Здесь мы применим формулу усреднения A1.14).)
Формула A1.31) называется формулой Симпсона или
формулой парабол. Геометрический смысл этой формулы
§ 2. Приближенные методы вычисления определенных интегралов 441
ясен из рис. 11.16: площадь криволинейной трапеции, лежащей
под графиком функции f(x) на сегменте [а, Ь) приближенно за-
заменяется суммой площадей, заштрихованных на этом чертеже фи-
фигур, лежащих под параболами. Для того, чтобы убедиться в этом
достаточно заметить, что
выражение, стоящее в фи-
фигурных скобках в формуле
A1.31), численно равно
площади фигуры, лежащей
на сегменте [х2к, л^+г] под
параболой у—Ах2 + Вх+С,
совпадающей с f(x) в точ-
точках x2k, x2k+i, Хк+2 (см. при-
пример 2 п. 4 § 2 гл. 10).,
Сравнивая остаточный
член A1.32) с остаточными
членами A1.23) и A1.27),
мы убеждаемся в том, что
формула Симпсона дает
большую точность, чем формулы прямоугольников и тра-
трапеций.
В качестве иллюстрации применения формулы Симпсона об-
обратимся к вычислению интеграла /(л;0) = ( e~K'~dx*, ограничиваясь
о
для простоты значениями х0 из сегмента 0<л:0<1. Полагая
¦2к-1
Рис. 11.16
= e
и вычисляя производную /<4>(л:) = 4Dх4—
f() ру /() ( )
без труда убедимся в том, что для всех х из сегмента 0<л:<1
во всяком случае |fD)(*) | <20. Исходя из оценки A1.32), можем
утверждать, что R<C .Значит, разбив сегмент [0, х0] всего
144л4
на 5 равных частей и заменив рассматриваемый интеграл сум-
суммой, стоящей в правой части формулы Симпсона, мы вычислим
1 . 1 **
этот интеграл с точностью до <
144-54
90 000
* Рассматриваемый интеграл, как уже неоднократно отмечалось, не выра-
выражается через элементарные функции, но имеет большое значение в статистиче-
статистической физике, теории теплопроводности и диффузии.
** На ручном электронном калькуляторе, вычисляющем значения элементар-
элементарных функций, авторы вычислили за несколько минут указанный интеграл для
хо = \, я = 5 и получили результат 7A) =0,7468251, который, в силу сказанного
выше, содержит пять верных десятичных знаков после запятой.
Глава 12
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Многие вопросы естествознания приводят к рассмотрению та-
такой зависимости между несколькими переменными величинами,
при которой значения одной из переменных величин полностью
определяются значениями остальных переменных.
Так, например, при рассмотрении каких-либо физических ха-
характеристик тела (например, его плотности р или температуры
7") нам приходится учитывать изменение этих характеристик при
переходе от одной точки тела к другой. Поскольку каждая точ-
точка тела определяется тремя декартовыми координатами х, у и
z, то рассматриваемые характеристики (плотность р или темпе-
температура 7") определяются значениями трех переменных х, у и z.
При рассмотрении физических процессов, меняющихся во
времени, значения физических характеристик определяются зна-
значениями четырех переменных, трех координат точки х, у, z и вре-
времени t. Например, при изучении звуковых колебаний газа плот-
плотность р этого газа и его давление р определяются значениями
четырех переменных х, у, г и t.
Для изучения такого рода зависимостей в этой главе вводит-
вводится понятие функции нескольких переменных и развивается аппа-
аппарат для исследования таких функций.
Первая часть настоящей главы посвящена построению диф-
дифференциального исчисления функций нескольких переменных.
На случай функции нескольких переменных будут распрост-
распространены понятия и утверждения, установленные нами ,в гл. 3—7
для функции одной переменной.
В одном из дополнений к настоящей главе изучаются элементы
дифференциального исчисления для абстрактных функций, пред-
представляющих собой результат отображения одного нормированного
пространства в другое. Частным случаем такого отображения яв-
является довольно часто встречающееся отображение евклидова
пространства размерности т в другое евклидово пространство
размерности п.
§ 1. ПОНЯТИЕ ФУНКЦИИ m ПЕРЕМЕННЫХ
1. Понятие m-мерного координатного и m-мерного евклидова
пространств. При изложении теории функций т переменных удоб-
удобно использовать геометрическую терминологию, обобщающую и
§ 1. Понятие функции т переменных 443
формализующую наши представления о плоскости и о реальном
(трехмерном) геометрическом пространстве.
Назовем /n-мерным координатным пространством
множество всевозможных упорядоченных совокупностей (xi, x2, ...
..., Хт) вещественных чисел Xi, х2, ¦¦-, хт.
Будем обозначать /n-мерное координатное пространство симво-
символом Ат.
Каждую упорядоченную совокупность (xi, Xz, —, хт) мы будем
называть точкой /n-мерного координатного пространства и обо-
обозначать одной буквой М.
При этом числа Xi, хг,...,хт мы будем называть координа-
координатами точки М.
Запись M(xi, X2,...,xm) означает, что точка М имеет координа-
координаты хи хг,... хт.
Замечание 1. Если рассматривать координатное прост-
пространство Ат как множество всех векторов х с координатами
(Xi, xz,..., хт) и назвать суммой векторов х= (xi, xz, —, xm) и
У=(Уи У2, —, Ут) вектор с координатами (xi+yu х2+У2,-,хт+
+ ут), а произведением вектора х= (xi, Xz, —, хт) на ве-
вещественное число А — вектор с координатами (Ххи Хх2, ..., ХХт),
то координатное пространство Ат превращается в линейное про-
пространство *.
Из курса аналитической геометрии читатель хорошо знаком с
понятиями координатной плоскости и трехмерного координатного
пространства. Обобщением этих понятий и является /п-мерное
координатное пространство Ат. Понятия координатной плоскости
и трехмерного координатного пространства являются источниками
удобной геометрической терминологии, употребляемой при изуче-
изучении /n-мерного координатного пространства Ат.
Заметим теперь, что для наших целей оказывается недостаточ-
недостаточно понятия /n-мерного координатного пространства Ат. Мы не
обойдемся без измерения расстояний между точками этого прост-
пространства. Для введения понятия расстояния между точками коор-
координатного пространства Ат естественно отправляться от понятия
расстояния между двумя точками координатной плоскости и двумя
точками трехмерного координатного пространства (соответствую-
* Напомним, что линейным пространством называется совокупность векто-
векторов х, у, z, ... любой природы при условии, что для элементов этой совокупности
определены операция сложения векторов и операция умножения вектора на ве-
вещественное число, причем эти операции удовлетворяют восьми аксиомам: 1) х +
+У=У+Х; 2) (х+у) +z=x+ (y+z); 3)-существует нулевой вектор 0 такой, что
х+0=х для любого вектора х; 4) для любого вектора х существует противопо-
противоположный ему вектор х' такой, что х+х'=0; 5) Х(х+у) =Кх+Ху; 6) (Л+ц)х=
=Хх+цх; 7) Я(цх) = (Я(х)х; 8) 1-х = х.
Легко проверить, что координатное пространство Ат с определениями опе-
операции сложения векторов и операции умножения вектора на число, данными в
замечании 1, удовлетворяет восьми указанным аксиомам и, значит, является ли-
линейным пространством.
444 Гл. 12. Функции нескольких переменных
щие формулы хорошо известны читателю из курса аналитической
геометрии).
Определение. Координатное пространство Ат называется
m-мерным евклидовым пространством, если между
двумя ЛЮбЫМи ТОЧКама M'(Xi', Xz,...,Xm') И М"(х"и Xz",...,Xm")
пространства Ат определено расстояние, обозначаемое символом
р(ЛГ, М") и выражающееся соотношением
р(Мг, М") = V(x\-x\f + (x'2-x'tf + ...+ {х'т-х'т)\ A2.1)
Будем обозначать m-мерное евклидово пространство симво-
символом Ет.
Введенное нами понятие /n-мерного евклидова пространства Ет
является естественным обобщением понятий евклидовой плоскости
и трехмерного евклидова пространства, изученных в курсе анали-
аналитической геометрии.
Замечание 2. В курсе линейной алгебры дается общее
определение евклидова пространства как такого ли-
линейного пространства, для которого указано правило, ставящее
в соответствии любым двум элементам х и у этого пространст-
пространства вещественное число, называемое скалярным произве-
произведением этих элементов и обозначаемое символом (х, у),
при условии, что это правило удовлетворяет четырем аксиомам:
1) (х. У) = (У, х); 2) (х+у, z) = (x, z) + (у, z); 3) (А,х, у) =
= МХ, у); 4) (х, х) >0, причем (х, х) = 0 только для нулевого
элемента х=о.
Легко проверить, что если в пространстве Ат, элементы ко-
которого рассматриваются как векторы х с координатами {хи х2,...
...,хт), определить скалярное произведение двух элементов х=
= (xi, Xz, ¦¦; хт) и у= (г/ь г/г, •••, Ут) соотношением
(х, у) =Xiyi+x2yz+ - +хтут, A2.2)
то будут выполнены четыре указанные аксиомы и пространст-
пространство Ат превратится в евклидово пространство (сточки зрения
общего определения евклидова пространства).
Напомним, что линейное пространство называется норми-
нормированным, если указано правило, ставящее в соответствие
каждому элементу х вещественное число, называемое нормой
этого элемента и обозначаемое символом ||х||, причем указанное
правило удовлетворяет трем аксиомам:. 1) ||х+у||<||х|| + ||у||;
2) ||Ях||= \1\ -||х||; 3) ||х||>0, причем ||х|| = 0 только для нулево-
* В аксиоме 3) можно опустить требование ||х||>0. В самом деле, это тре-
требование является логическим следствием аксиом 1) и 2) и предположения о том,
что ||х|| = 0 только для нулевого элемента х (достаточно в аксиоме 1) положить
У=—х).
§ 1. Понятие функции т переменных 445
В курсе линейной алгебры доказывается, что всякое евкли-
евклидово пространство является нормированным: достаточно опре-
делить норму любого элемента х соотношением ||х|| = У (х, х)*.
Нормированное пространство всегда является так называе-
называемым метрическим пространством, т. е. таким прост-
пространством, в котором указано правило, ставящее в соответствие
любым двум элементам х' и х" вещественное число, называемое
расстоянием между этими элементами и обозначаемое сим-
символом р(х', х"), при условии, что это правило удовлетворяет
трем аксиомам: 1) р(х, у) =р(у, х); 2) р(х, у)<р(х, г) +p(z, x);
3) р(х, у)>0, причем р(х, у)=0, только когда х=у**.
Достаточно определить расстояние р(х', х") соотношением
р(х', х") = ||х'-х"|| = К(х'~х", х'-х").
Если учесть, что координатное пространство Ат является
евклидовым пространством со скалярным произведением, опре-
определяемым соотношением A2.2), то мы придем к следующему
выражению для расстояния р(х', х") между двумя элементами
\'=(х1', х'г, ...,х'п) и х"= (^", х{',..., хт") пространства^™-
р(х', х") = К(х'-х", х'-х") =
= У{х[-х'[У+ (х'2-х:У+ ... + {x'm-x"mf.
Полученное выражение в точности совпадает с величиной,,
стоящей в правой части A2.1).
2. Множества точек m-мерного евклидова пространства. Если
у функции y = f{x) одной независимой переменной х, областью
определения которой является некоторое множество {л:} точек од-
одномерного евклидова пространства Е1, заменить это множество {л:}
некоторым множеством {М} точек /n-мерного евклидова прост-
пространства Ет, то мы естественно придем к понятию функции т не-
независимых переменных.
Отсюда ясно, что введению функции т переменных должно
предшествовать описание важнейших типов множеств точек
m-мерного евклидова пространства Ет.
Перейдем к описанию таких множеств.
1°. Множество {М} всевозможных точек М пространства Ет
координаты xit X2,..., хт которых удовлетворяют неравенству
(Xi—Xi)z+{X2— °X2)Z+ ... +(хт— °XmJ<R2,
.называется открытым т-м е р н ы м шаром радиуса R с цент-
центром в точке М0(хи Х2, ..., хт).
* См., например: В. А. Ильин, Э. Г. Позняк. Линейная алгебра.
** В аксиоме 3) можно опустить требование р(х, у)>0. В самом деле, это«
требование является логическим следствием аксиом 1) и 2) и предположения с
446 Гл. 12. Функции нескольких переменных
Иными словами, открытый m-мерный шар радиуса R с цент-
центром в точке Мо — это множество всех точек М, для каждой из
которых расстояние от фиксированной точки Мо удовлетворяет не-
неравенству р(М, M0)<R.
2°. Множество {М} всевозможных точек М пространства Ет,
координаты xi, Xz, ••-, хт которых удовлетворяют неравенству
¦{х\—XiJ-[- .- + (хт—xmJ<.R2, называется замкнутым тп-м е р -
н ы м шаром радиуса R с центром в Мо.
3°. Множество {М} всевозможных точек М пространства Ет,
координаты xi, Xz, ¦¦¦, хт которых удовлетворяют равенству
(х{— °XiJ+ (хг—хгJ+ ... + (xm—xmJ = Rz, называется т-м е р н о й
•сферой радиуса Re центром в точке Мо.
Замечание 1. Отметим, что если к открытому /п-мерному
шару радиуса R с центром в точке Мо присоединить т-мерную
•сферу радиуса R с центром в точке Мо, то получится замкнутый
.тп-мерный шар радиуса R с центром в точке Мо.
4°. Открытый /n-мерный шар радиуса е>0 с центром в точке
Мо будем называть е-окрестностью точки Мо.
5°. Множество {М} всех точек М, координаты xi, Xz, ..., хт кото-
которых удовлетворяют неравенствам
\Xi.—Xi\<di, \хг—хг\ <d2,..., \xm—xm\<dm,
где dt, dz, ..., dm — некоторые положительные числа, называется
открытым /п-м ерным координатным параллелепи-
о о о
ледом с центром в точке М0{хи Xz,...,xm) или прямоуголь:
ной окрестностью точки Мо.
Справедливо следующее элементарное утверждение: любая
^.-окрестность точки Мо содержит некоторую прямоугольную ок-
окрестность этой точки; любая прямоугольная окрестность точки Мо,
•содержит некоторую е-окрестность точки Мо *.
6°. Точка М множества {М} точек пространства Ет называется
внутренней точкой этого множества, если существует неко-
некоторая е-окрестность точки М, все точки которой принадлежат мно-
множеству {М}.
7°. Точка М пространства Ет называется внешней точкой
множества {М}, если существует некоторая е-окрестность точки
М, все точки которой не принадлежат множеству {М}.
том, что р(х, у)=0, только когда х=у (достаточно в аксиоме 2) положить-
У=х).
*_В самом деле, если для фиксированного е>0 положить di=dz=-.=dm =
=.г/Ут, то прямоугольная окрестность точки Мо с указанными du dz, ..., dm бу-
будет содержаться в е-окрестности точки Мо. Если для фиксированных di>0,
-с/г>0, .... dm>0 положить e = min{di, d2, ..., dm}, то е-окрестность точки А1о бу-
будет содержаться в прямоугольной окрестности точки Мо с указанными dly dz, ...,
-.., dm.
§ 1. Понятие функции т переменных 447"
8°. Точка М пространства Ет называется граничной точкой
множества {М}, если эта точка не является ни внутренней, ни
внешней точкой указанного множества *.
Замечание 2. Граничная точка М множества {М} может
как принадлежать, так и не принадлежать этому множеству. Так
любая точка /n-мерной сферы радиуса R с центром в точке Мо яв-
является граничной как для открытого /n-мерного шара радиуса R
с центром в точке Мо, так и для замкнутого /n-мерного шара ра-
радиуса R с центром в точке Мо. Но любая точка указанной сферы
не принадлежит открытому шару радиуса R с центром в Мо и при-
принадлежит замкнутому шару радиуса R с центром в Мо.
9° Произвольное множество М точек пространства Ет назы-
называется открытым, если любая точка этого множества является
его внутренней точкой **.
10°. Произвольное открытое множество, содержащее данную»
точку Мо, принято называть окрестностью точки Мо.
11°. Произвольное множество {М} точек пространства Ет назы-
называется замкнутым, если это множество содержит все свои гра-
граничные точки.
Чтобы сформулировать другое эквивалентное определение
замкнутого множества, введем понятие предельной точки произ-
произвольного множества М в пространстве Ет.
12°. Точку А пространства Ет назовем предельной точ-
точкой множества {М}, если в любой е-окрестности точки А со-
содержится хотя бы одна точка этого множества, отличная от А.
Убедимся в том, что множество М замкнуто тогда и только-
тогда, когда оно содержит все свои предельные точки.
В самом деле, если множество М замкнуто, то оно со-
содержит все точки пространства Ет, кроме своих внешних то-
точек. Поскольку среди внешних точек множества М нет его пре-
предельных точек, то множество М содержит все свои предельные
точки. Если же множество {М} не содержит хотя бы одной сво-
своей граничной точки Мо, то эта точка Мо, очевидно, является пре-
предельной точкой множества {М}.
Доказанное утверждение позволяет дать другое эквивалент-
эквивалентное определение замкнутого множества: множество М называет-
называется замкнутым, если оно содержит все свои предельные точки***,
* Заметим, что точка М является граничной точкой множества {М} тогда к
только тогда, когда в любой е-окрестности точки М найдутся как точки, при-
принадлежащие множеству {М}, так и точки, ему не принадлежащие. В самом де-
деле, если в некоторой е-окрестности точки М не найдется точек, принадлежащих
{7W} [не принадлежащих {М}]> т0 точка М является внешней [внутренней] точ-
точкой М и не является граничной точкой этого множества.
** Т. е. если любая точка М множества {М} принадлежит этому множеству
вместе с некоторой своей е-окрестностью.
*** Еще одним эквивалентным определением замкнутого множества является
следующее определение: множество М пространства Ет называется замкнутым,
если его дополнение является открытым множеством.
Гл. 12. Функции нескольких переменных
13°. Множество {М} точек пространства Ет называется огра-
ограниченным, если найдется m-мерный шар, содержащий все точки
этого множества.
14°. Введем понятие непрерывной кривой в m-мерном евклидо-
евклидовом пространстве Ет.
Непрерывной кривой L в пространстве Ет мы будем
.называть множество {М} точек этого пространства, координаты
jet, Хг,..., Хщ которых представляют собой непрерывные функции
.лараметра t:
Xi=~cpi(t), X2,=(p2{t),..., xm = <pm(t), a<t<$. A2.3)
Мы будем говорить, что точки М' (хх\ х2', ..., хт') и М" (Xi", x2",...
,хт") пространства Ет мо жн о соединить непрерывной
кривой L, если существует такая непрерывная кривая L, опре-
определяемая параметрическими уравнениями A2.3), что
), -, xmr=i(fm(a),
Понятие непрерывной кривой в пространстве Ет позволяет нам
гввести понятие связного множества.
15°. Множество {М} точек пространства Ет называется связ-
н ы м, если любые две тонки этого множества можно соединить не-
лрерывной кривой, все точки которой принадлежат этому мно-
множеству.
Убедимся в том, что всякое связное множество {М} в прост-
пространстве Ет обладает следующим свойством: если множество
{М} связно, то не существует двух непустых непересекающихся
открытых множеств G' и G" таких, что пересечение каждого из
этих множеств с {М} не пусто и множество {М} содержится в
объединении G' и G".
Проведем доказательство этого свойства от противно-
противного. Предположим, что два указанных множества G' и G" су-
существуют. Так как пересечение каждого из этих множеств с
{М} не пусто, то найдутся две точки М' и М" множества {М},
первая из которых принадлежит G', а'вторая G".
Чтобы получить противоречие, завершающее наше доказа-
доказательство, нам достаточно установить, что точки М' и М" нельзя
соединить непрерывной кривой, все точки которой принадлежат
множеству {М}.
Пусть L — любая непрерывная кривая в пространстве Ет,
определяемая уравнениями A2.3) и соединяющая указанные
точки М' и М". Упорядочим все точки кривой L по возрастанию
параметра t, который изменяется в пределах сегмента a<f<p.
Обозначим через у точную верхнюю грань тех значений пара-
параметра t, для которых отвечающие им точки кривой L принадле-
§ 1. Понятие функции т переменных 449
жат множеству G', а через N точку кривой L, отвечающую зна-
значению параметра t=y.
Достаточно доказать, что указанная точка N не принадлежит
множеству {М}, а для этого достаточно убедиться, что эта точка
jV не принадлежит ни множеству G', ни множеству G".
Если бы точка N принадлежала G', то, поскольку множест-
множество G' является открытым, нашлась бы некоторая е-окрестность
точки N, также принадлежащая G', т. е. нашлись бы точки кри-
кривой L отвечающие значениям параметра t, превосходящим у,
принадлежащие G', а это противоречит тому, что у является
точной верхней гранью значений параметра t, для которых
соответствующие точки кривой L принадлежат G'.
Аналогично если бы точка N принадлежала G", то.она при-
принадлежала бы этому множеству вместе с некоторой своей е-ок-
рестностью, т. е. нашлись бы точки кривой L, отвечающие зна-
значениям параметра t, меньшим у, принадлежащие G" и потому
не принадлежащие G', а это противоречит тому, что у является
точной верхней гранью значений параметра t, для которых
соответствующие точки кривой L принадлежат множеству G'.
Итак, точка N не принадлежит ни G', ни G", и сформулиро-
сформулированное свойство доказано.
Мы не будем останавливаться на доказательстве обратного
утверждения о том, что если множество {М} в пространстве Ет
обладает указанным выше свойством, то оно является связным,
а лишь отметим, что установленное нами свойство может быть
положено в основу другого «топологического» определения по-
понятия связного множества.
16°. Всякое открытое и связное множество в пространстве Ет
принято называть областью.
17°. Если множество {М} представляет собой область, то мно-
множество {М}, полученное присоединением к множеству {М} всех
его граничных точек, называется замкнутой областью.
Открытый m-мерный шар и открытый /n-мерный координатный
параллелепипед являются ограниченными, связными и открытыми
множествами, т. е. дают примеры ограниченных областей в прост-
пространстве Ет.
/n-мерная сфера в пространстве Ет дает пример замкнутого и
ограниченного множества.
Замкнутый m-мерный шар представляет собой ограниченную
замкнутую область в Ет.
Дополнение к открытому /n-мерному шару представляет собой
неограниченное замкнутое множество.
Совокупность двух непересекающихся областей в пространст-
пространстве Ет дает пример несвязного множества.
3. Понятие функции m переменных. Теперь мы подготовлены
для того, чтобы ввести понятие функции т переменных. •
15 Зах. 72
450 . Гл. 12. Функции нескольких переменных
Если каждой точке М из множества {М} точек пг-мерного ев-
евклидова пространства Ет ставится в соответствие по известному
закону некоторое число и, то говорят, что на множестве {М} зада-
задана функция и = и(М) или u = f(M). При этом множество {М}
называется областью задания функции u = f(M).
Число и, соответствующее данной точке М из множества {М},
будем называть частным значением функции в точке
М. Совокупность всех частных значений функции u = f(M) назы-
называется множеством значений этой функции. Так как точ-
точка М определяется координатами х\, Х2, ..., хт, то для функции и =
=f(M) m переменных используется также обозначение u=f(xu
Х2, ..., Хт).
Рассмотрим примеры функций т переменных.
Начнем с примеров функций двух переменных.
1°. « = уг4—х2—у2. Областью задания этой функции является
круг радиуса 2 с центром в начале координат, а множество значе-
значений представляет собой сегмент 0<«<2.
2°. и—[угх2+ у2—4]~\ Областью задания этой функции яв-
является множество точек, лежащих вне круга радиуса 2 с центром
в начале координат, а множество значений представляет собой от-
открытую полупрямую м>0.
3°. u = yrcos (х2 + у2). Областью задания этой функции является
множество {УИ} точек, координаты которых удовлетворяют нера-
неравенству cos(xz+y2) >0. Это неравенство эквивалентно неравенст-
неравенствам 0 <; л:2 + у2 •<—, 2kn -< х2 + и2 <С 2&я -\ при k =
2 2 2
= 1, 2,.... Таким образом, {М} состоит из круга радиуса У л/2
с центром в точке О @,0) и кольцеобразных областей (рис. 12.1).
Приведем теперь примеры функций т переменных.
4°. Пусть u = yr\—x2i—х\— ...—х2т. Областью задания этой
функции служит, очевидно, m-мерный шар радиуса 1 с центром в
точке О @, 0,..., 0). Множеством значений рассматриваемой функ-
функции является сегмент [0, 1].
5. Пусть и = =г-. Областью зада-
V а\ а\ ¦••- а2т
ния этой функции является множество {М} всех точек М прост-
пространства Ет, координаты xi, Хг, •¦•, хт которых удовлетворяют нера-
неравенству
„2
L
2
r2 V2
Лп X
4- I J_ т
4 4
(при этом предполагается, что аи а2,..., От — некоторые положи-
положительные числа).
§ 2. Предел функции т переменных
451
Очевидно, указанное множество {М} будет представлять собой
область в пространстве Ет, все точки которой лежат внутри так
•называемого m-мерного эллипсоида, представляющего со-
*бой множество то-
точек, координаты ко- у>
торых удовлетворя-
удовлетворяют уравнению
Множеством всех
значений указан-
указанной функции являет--
ся полупрямая w>
Мы видим, что
область задания
функции т пере-
переменных представ-
представляет собой некото-
некоторое множество то-
точек m-мерного ев-
евклидова пространства ?"*, а множество всех значений этой функ-
функции представляет собой некоторое множество одномерного (евкли-
(евклидова пространства Е1.
Таким образом, введенную нами функцию т переменных можно
рассматривать как отображение некоторого множества в прост-
пространстве Ет в некоторое множество в пространстве Е1.
Рис. 12.1
§ 2. ПРЕДЕЛ ФУНКЦИИ m ПЕРЕМЕННЫХ
1. Последовательности точек пространства Ет. Введем понятие
последовательности точек m-мерного евклидова пространства Ет.
Пусть каждому числу п натурального ряда чисел 1, 2,... ставится
в соответствие точка Мп евклидова пространства Ет. Возникающий
при этом ряд точек Mi, Mz,..., Мп,..., рассматриваемый в указан-
указанном порядке, называется последовательностью точек ев-
евклидова пространства Ет. Мы будет кратко обозначать эту после-
последовательность символом {Мп}.
Введем, далее, понятие сходящейся последовательности точек
пространства Ет и ее предела.
Последовательность {Мп} точек евклидова пространства Ет
называется сходящейся, если существует точка А пространст-
15*
452 Гл. 12. Функции нескольких переменных
ва Ет такая, что для любого положительного числа е можно ука-
указать отвечающий ему номер N такой, что при n^>N выполняется
неравенство р(Мп, Л)<е. При этом точка А называется пределом
последовательности {Мп}.
Для обозначения предела А последовательности {Мп} исполь-
используется следующая символика:
•у Urn Мп = А, или Мп-+А при п-> оо.
Установим следующую лемму.
Лемма {.Последовательность {Мп} точек пг-мерного евкли-
евклидова пространства Ет сходится к точке А этого пространства тогда
и только тогда, когда числовые последовательности {х\п)}, {х^ },
..., {х?>} координат точек Мп сходятся соответственно к числам
аи а2,..., ат, представляющим собой координаты точки А.
Доказательство. Сначала докажем первую часть леммы.
Так как последовательность {Мп} сходится к точке А, то для лю-
любого е>0 можно указать номер N такой, что при n>JV выполняет-
выполняется неравенство р(Мп, А)<е. Пусть {х[п\ х?>, ..., х™}— коорди-
координаты точки Мп, а (аи а-г,.... о,т) — координаты точки А. Тогда не-
неравенство р(Мп, Л)<е можно записать следующим образом:
У (xfi-atf + (xf -a2J + ... + (x^-amf < e. A2.4)
Отсюда следует, что при n^N выполняются неравенства
Иными словами, последовательности {x',n)}, {xf]}, ...,. {х1^} коор-
координат точек Мп сходятся соответственно к числам аи аг,..., ат.
Первая часть леммы доказана.
Перейдем к доказательству второй части леммы. Предположим,
что указанные последовательности координат точек Мп сходятся
соответственно к числам аи а2,..., ат. Тогда для любого е>0 мож-
можно указать номера Nt, N2, ¦¦., Nm такие, что при n^>Ni,n^>N2, ...,«>
Л/ соответственно выполняются неравенства
Отсюда следует, что при n^>N = max{Nu N2,...,Nm} выполняется
неравенство A2.4). Иными словами, при n^N выполняется нера-
неравенство р(Мп, А)<е, где А — точка Ет с координатами аи а2,...
—,ат. Таким образом, последовательность {Мп} сходится к-точке
А. Лемма доказана.
Введем теперь понятие фундаментальной последовательности
точек пространства Ет. Последовательность {Мп} точек пг-мерног.
го евклидова пространства называется фундаментальной или
последовательностью Кош и, если для любого положи-
§ 2. Предел функции т переменных 453
тельного числа г можно указать отвечающий ему номер N такой,
что при n>-N и при любом целом р>0 выполняется неравенство
р(Мп+р, М„)<е.
В полной аналогии с леммой 1 может быть доказано следующее
утверждение.
Лемма 2. Последовательность {Мп} точек m-мерного евкли-
евклидова пространства Ет является фундаментальной тогда и только
тогда, когда является фундаментальной каждая из числовых после-
последовательностей {xf>}, {xBn)}, ..., {х№} соответствующих координат
точек Мп-
Доказательство. Для доказательства первой части леммы
предположим, что последовательность точек {Мп} является фунда-
фундаментальной, т. е. для любого е>0 найдется номер N такой, что
при n>-N и для любого целого р>-0 справедливо неравенство
р(Мп+р, iWn)<e или, что то же самое, неравенство
Из этого неравенства вытекает, что при n>iV и для любого це-
целого р»0 справедливы неравенства
l^-fn+p)—х'п'К 8> |х("+р) j(")|<(8, ..., |х("+р) х(п'К е,
которые и устанавливают фундаментальность каждой из числовых
последовательностей соответствующих координат точек Мп.
Для доказательства второй части леммы предположим фунда-
фундаментальность каждой из числовых последовательностей соответ-
соответствующих координат точек Мп.
Тогда для любого е>0 можно указать номера Nlt N2,..., Nm
ггакие, что соответственно при n>>Nu n>-N2 n>-Nm и для любых
целых р>0 будут справедливы неравенства
Отсюда следует, что при n^N=max{Nu N2 Nm} и для лю-
любого целого р>0 будет справедливо неравенство A2.4*), которое
и означает фундаментальность последовательности точек {Мп}.
Лемма 2 доказана.
С помощью лемм 1 и 2 легко доказывается критерий Кош и
сходимости последовательности точек прост^
р а н с т в а Ет: для того чтобы последовательность {Мп} точек
пространства Ет была сходящейся, необходимо и достаточно, что-'
бы она была фундаментальной.
В самом деле, если последовательность точек {Мп} яв-
является фундаментальной, то в силу леммы 2 является фундамен:
тальной и каждая из числовых последовательностей соответствую--
щих координат точек {Мп}. В силу критерия Коши сходимости
числовой последовательности указанные числовые последователь-
454 Гл. 12. Функции нескольких переменных
ности соответствующих координат сходятся к некоторым числам
fli, а2, •¦•, ат соответственно. Но тогда в силу леммы 1 последова-
последовательность точек {Мп} сходится к точке А (аи а%,..., ат).
Если, наоборот, последовательность точек {Мп} сходится к не-
некоторой точке А пространства Ет, то в силу леммы 1 каждая из
числовых последовательностей соответствующих координат точек
{Мп} сходится к соответствующей координате точки А. Но тогда
(в силу критерия Коши сходимости числовой последовательности)
каждая из числовых последовательностей соответствующих коор-
координат точек {Мп} является фундаментальной и, значит, в силу
леммы 2, является фундаментальной и последовательность
точек {Мп}.
2. Свойство ограниченной последовательности точек Ет. Введем
понятие ограниченной последовательности точек пространства Е™.
Последовательность {Мп} точек т-мерного евклидова простран-
пространства называется ограниченной, если существует такое число
а>0, что для всех п выполняется неравенство р(О, Мп)<а, где
О — точка, все координаты которой равны нулю.
Иными словами, ограниченность последовательности точек
{Мп} означает, что все точки этой последовательности принад-
принадлежат замкнутому шару достаточно большого радиуса с центром
в начале координат О.
Установим следующее важное свойство ограниченной последо-
последовательности точек пространства Ет.
Если щ, «2,..., nk,...— произвольная строго возрастающая
последовательность целых положительных чисел, то мы будем
называть последовательность точек
Мв,, МПг, •¦¦, Mnk, ...
подпоследовательностью последовательности точек Ми
М2,..., Мп,....
Теорема 12.1 (теорема Больцано — Вейерштрас-
с а). Из любой ограниченной последовательности {Мп} точек
m-мерного евклидова пространства можно выделить сходящуюся
подпоследовательность.
Доказательство. Убедимся, во-первых, что последова-
последовательности {4n)}> W^}» • ••> ixm) координат точек {Мп} являются
ограниченными. Действительно, так как последовательность {Мп}
ограничена, то для всех п выполняется неравенство р(О, Мп)<а.
Поскольку р(О, Мп) = Vlxff + [4П>]2 + • • • + [х{?]2> отсюда сле-
следует, что для всех п выполняются неравенства|л;(,п)К а, \хр\<Са,
•••> U(ml <а- Иными словами, последовательности {*\п)}, {хBп>}»
•••• i^m) координат точек Мп ограничены. В силу теоремы
Больцано — Вейерштрасса для числовых последовательностей (см.
п. 1 § 3 гл. 3) из последовательности {xf}} можно выделить под-
§ 2. Предел функции т переменных 455
последовательность {У/1*»'}, сходящуюся к некоторому числу а^.
Рассмотрим соответствующую подпоследовательность {x^kl)} по-
последовательности вторых координат точек Мп. В силу той же тео-
теоремы из подпоследовательности {x*?ki)} можно выделить подпосле-
подпоследовательность {х^1*2'}, сходящуюся к некоторому числу а2. Заме-
Заметим, что подпоследовательность {х\"к:>)} последовательности {x"kt>}
сходится к числу а\. Итак, подпоследовательности {xfk2} и /д^"*2' }
сходятся к числам а4 и а2 соответственно.
Очевидно, что если мы из подпоследовательности {х("к^} после-
последовательности третьих координат точек Мп выделим сходящуюся
к числу а3 подпоследовательность {х("кз)}, то подпоследовательнос-
подпоследовательности {Xj"*3'}, {х^кз)}, {xfkl)} сходятся соответственно к числам аи а2,
as. Продолжая эти рассуждения, мы, наконец, получим сходя-
сходящуюся к некоторому числу ат подпоследовательность {х^кт>} по-
последовательности т = х координат точек Мп, причем подпоследо-
вательности {х1 т), {х2 т), ..., {хт т\ сходятся к числам аи
а2,.-., ат соответственно.
Но тогда в силу леммы 1 подпоследовательность {Мп. } после-
довательности точек {Мп} сходится к точке А с координатами at,
а2,..., ат- Теорема доказана.
Замечание. Предел А последовательности {Мп} точек, при-
принадлежащих замкнутому множеству {М}, также принадлежит
этому множеству. Чтобы убедиться в этом, достаточно заметить,
что в любой е-окрестности точки А имеются точки {Мп}, т. е. точ-
точки множества {М}, и поэтому точка А является либо внутренней,
либо граничной точкой {М}, а следовательно, принадлежит {М}.
3. Предел функции m переменных. Рассмотрим функцию u = f(M),
определенную на множество {М} точек m-мерного евклидова про-
пространства Ет, и точку А пространства Ет, быть может и не при-
принадлежащую множеству {М}, но обладающую тем свойством, что
в любой е-окрестности этой точки А содержится хотя бы одна
точка множества {М}, отличная от А *.
Определение 1 (предел функции в точке А по
Гейне). Число Ъ называется пределом (или предельным
значением) функции u=f(M) в точке А (или при М->А), если
для любой сходящейся к А последовательности {Мп} точек мно-
множества {М} задания этой функции, все элементы Мп которой от-
отличны от А, соответствующая числовая последовательность значе-
значений функции {f(Mn)} сходится к числу Ъ.
* Это означает, что точка А является предельной точкой множества
{М} (см. п. 2 § 1 настоящей главы, определение 12°).
456 Гл. 12. Функции нескольких переменных
Определение 1* (предел функции в точке А до
Кош и). Число Ь называется пределом (или предельным значе-
значением) функции u=f(M) в точке А (или при М-+А), если для лю-
любого положительного числа е найдется отвечающее ему положи-
положительное число 8 такое, что для любой точки М из множества {М}
задания этой функции, удовлетворяющей условию 0<p(iW, Л)<6,
справедливо неравенство \f(M)—Ь|<е.
Для обозначения предела функции и=/(уИ) в точке А исполь-
используется следующая символика:
/() = 6 или lim f(xv x2, ..., xm) =b.
М-*А *i-*a,
(Здесь (ait a2,..., am) — координаты точки А.)
Доказательство эквивалентности определения 1 и 1* проводится
точно так же, как и для функции одной переменной. Следует лишь
в рассуждениях теоремы 3.19 (см. п. 2 § 4 гл. 3) заменить после-
последовательность {хп} последовательностью точек {Мп}, точку а —
точкой A(aiy a2,...,am), разности \х—а\ и \хп—а\ — расстояниями
р(М, Л) и р(Мп, А) соответственно, а числовую последователь-
последовательность {f(xn)} заменить числовой последовательностью {f(Mn)}-
Введем теперь понятие предела функции u = f(M) при Af->oo.
Для этого предположим, что множество {М}, на котором задана
функция u = f(M), для любого 6>0 имеет хотя бы один элементМ,,
лежащий вне шара радиуса б с центром в точке О@, 0 0).
Ограничимся определением соответствующего предела функции
по Крши.
Определение 2. Число Ь называется пределом функции
u = f(M) при уИ-^-оо, если для любого положительного числа г най-
найдется отвечающее ему положительное число б такое, что для всех
точек М из множества {М} задания функции, удовлетворяющих
условию р(О, М)>8, справедливо неравенство \f(M)—b\<e.
Для обозначения предела функции u = f(M) при М->оо исполь-
используется символ
lim f{M) = b.
М-кп
Так же, как и для функции одной переменной, легко убедиться
в том, что арифметические операции над функциями m перемен-
переменных, имеющими предел в данной точке А [или при уИ->оо], при-
приводят к функциям, также имеющим предел в точке А [соответст-.
венно при М->оо].
Сформулируем соответствующее утверждение для случая пре-
предела в точке А.
Пусть две функции f(M) и g(M) заданы на одном и том же
множестве {М} и имеют в точке А пределы, соответственно рае-
§ 2. Предел функции т переменных 457
ные Ь и с. Тогда функции f(M)+g{M), f(M)—g(M), f(M)-g(M)
и f(M)/g(M) имеют в точке А пределы, соответственно равные
Ь+с, Ь—с, Ь-с и Ь/с (в случае частного нужно дополнительно тре-
требовать, чтобы с было отлично от нуля).
Доказательство этого утверждения совершенно аналогично до-
доказательству теоремы 3.21 (см. п. 4 § 4 гл. 3), только вместо опре-
определения по Гейне предела функции одной переменной следует ис-
использовать определение по Гейне предела функции m переменных.
Установим теперь критерий Коши существования предела функ-
функции m переменных.
Определение 3. Будем говорить, что функция m перемен-
переменных f(M) удовлетворяет условию Коши в точке М = А
[соответственно при М->оо], если для любого положительного
числа е найдется отвечающее ему положительное число 8 такое,
что для любых двух точек М' и М" из множества {М} задания
функции, удовлетворяющих условиям . 0<p(Af', Л)<6, 0<
<р(М", Л)<6 [соответственно условиям р(М', О)>8, р(М", О)>
>б], справедливо неравенство \f(M')—f(M")\<e.
Теорема 12.2 (критерий Коши существования
предела функции m переменных). Для того чтобы
функция и = г(М) имела конечный предел в точке М=А [при,
М->оо], необходимо и достаточно, чтобы эта функция удовлетво-
удовлетворяла в точке М=А [при М^>~оо] условию Коши.
Доказательство этой теоремы полностью идентично доказатель-
доказательству теоремы 3.20 (см. п. 3 § 4 гл. 3) и может быть получено из
него формальной заменой букв хна буквами М и А и выражений
типа \х—а\ символом р(М, А).
Весьма полезно заметить, что определение предела функции
m переменных u=f(M) в точке А и при уИ-»-оо укладывается в
общее определение предела по базе, введенное в § 5 гл. 3.
Рассмотрим сначала предел функции u = f(M) в точке А.
Договоримся называть проколотой б-о к р е ст н о с ть к>
точки А открытый m-мерный шар радиуса б с центром в точ-
точке А, из которого удалена сама точка А.
Подчеркнем, что f(M) задана на таком множестве {М}, ко-
которое для любого 6>0 имеет хотя бы одну точку М, лежащую
в проколотой 6-окрестности точки А.
Обозначим символом Св проколотую б-окрестность точки А
и положим Bt,= {M}[)Ci. Очевидно, совокупность В={В,}
множеств В6 при всех б>0 образует базу множества {М},
ибо каждое множество В& (при любом б>0) не является пустым
и пересечение любых двух множеств совокупности {Вб} пред-
представляет собой множество той же совокупности *.
Эту базу естественно обозначить символом М-*-А, ибо, как
легко проверить, определение предела по такой базе совпадает
* Определения понятий базы и предела функции по базе см. в § 5 гл. 3.
458 Гл. 12. Функции нескольких переменных
с определением 1 * предела функции u — f (M) в точке А по
Крши.
Для случая предела функции u = f(M) при М^-оо эта функ-
функция должна быть задана на таком множестве {М}, которое для
любого 6>0 имеет хотя бы одну точку М, удовлетворяющую
условию р(М, О) >6, где О — точка с координатами @,0,..., 0).
Обозначим символом Сб множество всех точек М простран-
пространства Ет, удовлетворяющих условию р(М, О)>8, и положим
Ва={М}Г\С6. Легко проверить, что совокупность {В6} множеств
В6 при всех 6>0 образует базу множества {М}, ибо каждое
множество В6 не является пустым и пересечение любых двух
множеств совокупности {Вб} представляет собой множество той
же совокупности.
Эту базу естественно обозначить символом уИ->-оо, ибо, как
легко проверить, определение предела по такой базе совпадает
с определением 2 предела функции u=f(M) при Af-voo.
В заключение отметим, что теорема 12.2 (т. е. критерий Ко-
ши существования предела функции u=f(M) в точке А и при
М-^-оо) вытекает как частный случай из теоремы 3.22, устанав-
устанавливающей критерий Коши существования общего предела функ-
функции по базе.
4. Бесконечно малые функции т переменных. Функция u = f(M)
называется бесконечно малой в точке А (при М->~А), если
limf(Af) = 0.
М-+А
Легко убедиться, что функция f (М) = (^—aj11 + (хг—а2)"' +
+ ... + {хт—ат)Пт, где «1, пг пт — положительные числа, яв-
является бесконечно малой в точке А{аи а2, ..., ат) *.
Если функция u=f(M) имеет равное Ь предельное значение в
точке Л, то функция а(М) =f(M)—Ь является бесконечно малой в
точке А.
Имеем: lima(Af)= lim [f(M) — b]= Iim/(Af) — lim6 = 0. Ис-
M-+A M-+A M-+A M-+A
пользуя этот результат, мы получим специальное представ-
представление для функции, имеющей равный Ь предел в точке
A :f(M)=b + a(M), где Пта(М) = 0.
М-+А
Сравнение бесконечно малых функций нескольких переменных
производится точно так же, как это указано в п. 5 § 4 гл. 3
для бесконечно малых функций одной переменной. Отметим, что,
как и в случае одной переменной, под символом о(р) мы будем по-
понимать любую бесконечно малую в данной точке А функцию бблее
высокого порядка малости, чем бесконечно малая в данной точке
А функция р(М).
* Достаточно учесть, что каждая из функций одной переменной f{Xk) =
~(Xh—ан)пк является бесконечно малой в точке х*=ал.
§ 2. Предел функции т переменных 459
5. Повторные пределы. Для функции u=f(xi, X2,...,xm) не-
нескольких переменных можно определить понятие предела по одной
из переменных xh при фиксированных значениях остальных пере-
переменных. В связи с этим возникает понятие повторного предела.
Уясним это понятие на примере функции u=f(x, у) двух пере-
переменных х и у. Пусть функция u=f(x, у) задана в некоторой
прямоугольной окрестности \х—Xo\<du \у—yo\<d2 точки
Мо(хо, Уо), за исключением, быть может, самой точки Мо. Пусть
для каждого фиксированного у, удовлетворяющего условию
0<\у—yo\<d2, существует предел функции u = f(x, у) одной
переменной х в точке х=хо
lim f(x, y) =
х+х0
у—фикс
и пусть, кроме того, существует предел b функции ф(г/) в точке
У = Уо
lim ф (у) = Ь.
У-*У«
В этом случае говорят, что существует повторный предел Ь для
функции u=f(x, у) в точке Мо, который обозначается следую-
следующим образом:
lim lim/(x, y) = b.
У^-Уо Х-*Х0
Аналогично определяется повторный предел
lim lim/(x, у).
Установим достаточные условия равенства двух введенных
повторных пределов.
Теорема 12.3. Пусть функция u=f(x, у) определена в не-
некоторой прямоугольной окрестности \х—хо\ <dit \у—у0] <d2 точ-
точки Мо(хо, Уо) и имеет в этой точке предел, равный Ь. Пусть,
кроме того, для любого фиксированного х, 0<|х—xo|<di, су-
существует предел yp{x) = limf(x, у) и для любого фиксированно-
У-+Уо
го у, 0<\у—yo\<d2, существует предел <p(y) = limf(x, у). Тогда
повторные предела lim \imf(x, у) и lim lim f(x, у) существуют
Х-+Х„ у-+уа у-м/о Х-+Ха
и оба равны Ь.
Доказательство. Так как функция u=f(x, у) имеет
в точке Мо(хо, г/о) предел Ь, то для любого е>0 можно указать
такое 6>0, что при \х—хо\<8 и \у—Уо\<8 выполняется нера-
неравенство \f(x, у)—Ь\<е. Таким образом, в прямоугольной ок-
окрестности \х—хо|<б и \у—уо\<8 точки Мо значение функции
}(х, у) отличается от Ь не больше чем на е. Но тогда пределы
i|j(*) и ф(г/), указанные в формулировке теоремы при х и у,
460 Гл. 12. Функции нескольких переменных
удовлетворяющих неравенствам \х—хо\<8 и \у—г/о|<б, также
отличаются от b не больше чем на е. Следовательно, и пределы
этих функций в точках хо и у0 соответственно существуют и
равны Ь. Теорема доказана.
Можно определить понятие повторного предела для так на-
называемых двойных последовательностей {атп\, эле-
элементы атп которых определяются двумя индексами т и п.
Именно символ lim limamn означает, что сначала определяет-*
ся последовательность {bn}, bn=\\mamn, а затем находится
предел этой последовательности (bn).
Рассмотрим, например, двойную последовательность {атп},
где amn = cosm2jtnU, x — фиксированное число. Докажем, что
.. ,. п . П, если х—рациональное число,
lim urn cosm 2nn\x= {
n-*m г*+» [0, если х—иррациональное число.
В самом деле, если x = p/q, где р и q — целые числа, второе из
которых положительно, то при n>>q имеем сов2я«!х=1, и по-
поэтому lim cosm2jm!x= 1. Иными словами, если х — рацио-
нальное число, то limlimcosm2n«!A:=l. Если же х—ирра-
циональное число, то при любом п справедливо неравенст-
неравенство |сов2я«!х| <1, и поэтому
lim cosm 2яи!л; = 0, т.е. lim lim cosm2roz!x: = 0.
m-»oo m-»oo n-#oo
Замечание. Используя полученный результат, мы можем
аналитическим способом задать функцию Дирихле (см. п. 1 § 4
гл. 3) как повторный предел lim lim cosm 2nn\x.
§ 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ m ПЕРЕМЕННЫХ
1. Понятие непрерывности функции т переменных. Рассмотрим
функцию тпеременных u=f(M), заданную на некотором множест-
множестве {М} пространства Ет. Пусть А — некоторая точка Ет, принад-
принадлежащая множеству {М} и такая, что в любой б-окрестности точ-
точки А содержатся точки множества {М}, отличные от А. *
Формальное определение непрерывности функ-
функции в точке. Функция u=f(M) называется непрерывной в
точке А, если предел этой функции в точке А существует и равен
частному значению f(A).
Это означает, что А является предельной точкой множества {М}.
§ 3. Непрерывность функции т переменных 461
Заметим, что поскольку Л= lim M, то условие HenpepblBHOC-
Af-»^
ти функции f{M) в точке А можно символически записать в виде
/() /(
М-*А М-+А
- Таким образом, для непрерывной в данной точке А функции
символ lim предела и символ / характеристики функции можно
менять местами.
Точки пространства Ет, в которых функция u=f(M) не обла-
обладает свойством непрерывности, называются точками разрыва
этой функции.
Используя определение предела функции в точке А по Гейне и
по Коши, мы придем к определениям непрерывности функции в
данной точке по Гейне и по Коши.
Определение 1* (непрерывность функции в дан-
данной точке по Гейне). Функция u=f(M) называется непре-
непрерывной в точке А, если для любой сходящейся к А последова-
последовательности {Мп} точек множества {М} задания этой функции соот-
соответствующая числовая последовательность {f(Mn)} значений этой
функции сходится к числу f(A).
Определение 1* (непрерывность функции в дан-
данной точке по Коши). Функция u=f(M) называется непре-
непрерывной в точке А, если для любого положительного числа е
найдется отвечающее ему положительное число б такое, что для
любой точки М из множества {М} задания этой функции, удовле-
удовлетворяющей условию р(М, А)<8, справедливо неравенство
tf{M)-f(А) |<е.
Заме-чание. В отличие от определения предела по Гейне,
мы опускаем в определении 1 требование МпфА. Это можно сде-
сделать в силу того, что функция f(M) определена в точке А и добав-
добавление к последовательности {f(Mn)}, сходящейся к числу f(A),
любого количества новых элементов, равных f(A), не нарушит
сходимости этой последовательности к f(A).
Аналогично, в отличие от определения предела по Коши, мы
опускаем в определении 1* требование р(М, Л)>0 или, что то
же самое, МфА. Это можно сделать в силу того, что функция
}{М) определена в точке А и при М=А неравенство
\f(M)—f(A) |<e справедливо для любого е>0.
Можно сформулировать и еще одно эквивалентное определе-
определение непрерывности функции f(M) в данной точке А.
Определение 1**. Функция f(M) называется непре-
непрерывной в точке А, если для любой окрестности точки
f(A) пространства Е1 найдется такая окрестность точки А про-
пространства Ет, что образ всех точек множества задания функции,
лежащих в этой окрестности точки А, при отображении, осу-
осуществляемом функцией f, целиком лежит в указанной окрест-
окрестности точки f(A).
462 Гл. 12. Функции нескольких переменных
Пусть теперь {М} — множество точек пространства Е™, в лю-
любой б-окрестности каждой точки М которого содержатся другие
точки этого множества *. Такое множество {М} называется плот-
плотным в себе**.
Определение 2. Функция u=f(M), определенная на мно-
множестве {М}, называется непрерывной на этом множеств
в е, если она непрерывна в каждой точке М этого множества.
Назовем приращением или полным приращением
функции u = f(M) в точке А функцию Аи, определяемую формулой
Ди=/(АГ)-/(А), A2.5У
где М — любая точка из области задания функции. Пусть точки А
и М имеют соответственно координаты ait a2,..., ат и х%, х2,..., х1П-
Обозначим xi—ai = Axi, x2—а2—Ах2,..., хт—ат — Ахт. Используя эта
обозначения, получим для приращения функции Aw, соответствую-
соответствующего приращениям аргументов Axi, Дхг,..., Ахт, следующее выра-
выражение:
Au = f(a1 + Axl, a2+Ax2,...,am+Axm)—f(ai, a2,...,am). A2.6)г
Очевидно, для непрерывности функции u — f(M) в точке А не-
необходимо и достаточно, чтобы ее приращение Аи представляло*
собой бесконечно малую в точке А функцию, т. е. необходимо w
достаточно, чтобы
ИтАи= lim(f(M)—/(Л)) = 0, или Пт Ди = 0. A2.7)
М-+А М-+А Д^!->0,
Д*,—О,
Условие A2.7) естественно назвать разностной формой ус-
условия непрерывности функции u = f{M) в точке А.
2. Непрерывность функции m переменных по одной переменной.
Для функции u = f(xi, Xz,..., xm) нескольких переменных можно
определить понятие непрерывности по одной из переменных
при фиксированных значениях остальных переменных. Для введе-
введения этого понятия рассмотрим так называемые частные при-
приращения функции u = f(xu ..., Хщ) в точке М(х{, X2,...,xm), при-
надлежащей области определения функции. Зафиксируем все ар-
аргументы, кроме первого, а первому аргументу придадим произволь-
произвольное приращение А^ такое, чтобы точка с координатами Xi+Ax;,
X2,—,xm находилась в области задания функции. Соответствующее
* Это означает, что любая точка М множества {М} является предельной
точкой этого множества.
** Примером плотного в себе множества могут служить любое непустое"
открытое множество и любая замкнутая область, а также множество всех то-
точек, содержащихся в открытом множестве и таких, что все координаты этих
точек являются рациональными числами.
§ 3. Непрерывность функции т переменных 463
приращение функции называется частным приращением*
функции в точке M(Xi, x2. •••. хт), соответствующим приращению
AXi аргумента Хи и обозначается Ал:, и. Таким образом,
AXlu=*f(x1+ Axv х2, .... xm)—f(xlt x2, ..., хт). A2.8)
Аналогично определяются частные приращения функции, соответ-
соответствующие приращениям других аргументов:
A x2U = / (Xj, Х2 "Г А-?2> ^3> • • •' Хт) / (Xi, Х%, . . -, Хт),
A2.9)
A*m« = /(*i> x2, .... хт.ъ xm+Axm)—f(x1, x2, ..., хт).
Введем теперь понятие непрерывности функции u=f(xu x% ...
...,хт) по одной из переменных.
Функция u=f(xi, X2, ...,Хт) называется н е п р е р ы в но й в точ-
точке М{хи х2,...,хт) по переменной Xk, если частное прираще-
приращение &.хМ этой функции в точке М представляет собой бесконечно
малую функцию от Axh, т. е. если
lim А* и=0.
При фиксированных значениях всех переменных, кроме пере-
переменной xh, функция u — f(xu X2, ...,xm) представляет собой функцию
одной этой переменной. Отметим, что непрерывность функции по
переменной xft означает непрерывность указанной функции одной
переменной.
Очевидно, из условия непрерывности функции u = f(xi, x%,..., хт)
в данной точке М вытекает непрерывность этой функции в точке М
по каждой из переменных хи Хг,.., хт. Однако из непрерывности
^функции в точке М по каждой из переменных х\, хг, ...,хт не выте-
вытекает, вообще говоря, непрерывность функции в этой точке. Чтобы
убедиться в этом, рассмотрим следующие примеры.
1°. Мы будем говорить, что функция u = f(M)=f(x, у) непре-
непрерывна в точке М на прямой, проходящей через
эту точку, если для любой последовательности точек {Мп}
этой прямой, сходящейся к точке М, соответствующая последова-
последовательность {f(Mn)} значений функции имеет пределом частное зна-
значение f(M) функции в точке М. Так как на прямой функция и =
= /(х, у) представляет собой функцию одной переменной, то поня-
понятие непрерывности функции на прямой совпадает, очевидно, с по-
понятием непрерывности указанной функции одной переменной.
В частности, непрерывность функции в точке М по отдельным пе-
переменным х и у представляет собой непрерывность ее на прямых,
* Термин «частное приращение» употребляется для того, чтобы отличить
это приращение от полного приращения A2.6), соответствующего произвольным
приращениям Axiy Ax2, ..., Ахт всех аргументов хи Хг, ..., хт.
464 Гл. 12. Функции нескольких переменных
проходящих через точку М и параллельных координатным осям.
Докажем, что функция
A2Л0)
0 при
непрерывна в точке 0@, 0) по каждой из переменных х и у, т. е.
непрерывна на каждой из координатных осей, но не является не-
непрерывной на всех остальных прямых,, проходящих через эту точ-
точку, и поэтому" не является непрерывной в точке О'. Каждая пря-
прямая, отличная от координатных осей и проходящая через точку
0@, 0), может быть представлена уравнением y = kx, где 1гфО.
В каждой точке прямой y = kx при к^фО, за исключением точки
0@, 0) функция A2.10) принимает одно и то же постоянное зна-
Отсюда следует, что если последовательность {Мп} отличных
от О точек такой прямой сходится к точке О, то соответствующая
последовательность значений функции имеет предел -. Так
1 К"
как при ИфО этот предел отличен от нуля и не совпадает с част-
частным значением функции в точке О, то функция разрывна в этой
точке на рассматриваемой прямой. Непрерывность функции на ко-
координатных осях вытекает из того, что ее значения на этих осях
равны нулю.
Может сложиться впечатление, что если функция двух пе-
переменных непрерывна на любой прямой, проходящей через
данную точку, то эта функция непрерывна в указанной точке.
Следующий пример показывает, что это, вообще говоря, не так.
2°. Рассмотрим функцию
2 при хЧ-у2ф0,
0 при %*+г/2 = 0.
Докажем, что, хотя указанная функция непрерывна на любой
прямой, проходящей через точку О@, 0), она не является не-
непрерывной в этой точке. В самом деле, значения этой функции
kx
на прямой y — kx равны — -, и поэтому и-vO при х-*-0. Не-
Непрерывность этой функци на оси Оу вытекает из того, что ее
значения на этой оси равны нулю. С другой стороны, значения
функции на параболе у = рх2 постоянны и равны -, и по-
поэтому предельное значение функции при стремлении точки М к
точке О по указанной параболе также равно j. Так как
§ 3. Непрерывность функции т переменных 46S
|при рфО этот предел отличен от нуля и не совпадает с част-
частным значением функции в точке О, то функция разрывна в:
этой точке.
3. Основные свойства непрерывных функций нескольких пере-
переменных. В этом пункте мы перечислим основные свойства непре-
непрерывных функций нескольких переменных. Поскольку доказатель-
доказательства этих свойств в основном аналогичны доказательствам соот-
соответствующих свойств функций одной переменной, то, как прави-
правило, мы будем давать лишь краткие пояснения, предоставляя де-
детали доказательства читателю.
1°. Арифметические операции над непрерыв-
непрерывными функциями. Если функции f(M) и g(M) заданы на
одном и том же множестве {М} и непрерывны в некоторой точке-
А этого множества, то функции f(M)-\-g(M), f{M)—g(M),.
f(M) -g(M) и также непрерывны в точке А (в случае част-
частного нужно дополнительно потребовать, чтобы g(A)^O).
Это утверждение сразу же вытекает из соответствующего»
утверждения об арифметических операциях над функциями, имею-
имеющими предел (см. п. 3 § 2 настоящей главы).
2°. Непрерывность сложной функции. Введем по-
понятие сложной функции нескольких переменных. Пусть функции
•*l=<Pl('l» *2 4).
*2=Ф2^1> ^2> •••! **)» A2.11)
хт = Фт (^1- h> • • •» h)
заданы на множестве {N} евклидова пространства Eh(ti, ^2,—
..., tk — координаты точек в этом пространстве). Тогда каждой
точке N (t\, t2,...,th) множества {N} ставится в соответствие с по-
помощью формул A2.11) точка М (Х\, Х2,...,хт) евклидова про-
пространства Ет. Обозначим через {М} множество всех таких точек.
Пусть u = f(xi , хт)—функция гп переменных, заданная на ука-
указанном множестве {М}. В этом случае мы будем говорить, что на
множестве {iV} евклидова пространства Ек определена сложная
функция u = f(xi, Х2,—,хт), где х\, Х2,—,хт являются функциями
переменных U, t2,..., th, причем эти функции определяются соотно-
соотношениями A2.11). Справедливо следующее
Утверждение. Пусть функции Xi = (pi(tu...,th), x2 = <P2^i, ...
..., th),..., л;т=<рт(^,..., 4) непрерывны в точке А(аи аг,...,%), а
функция u=f(x\, X2,...,xm) непрерывна в точке B(bu b2,...,bm),
где bi = (fi(ai, a2,...,ah), i=l, 2,...,m. Тогда сложная функция и =
=f(xi, X2,...,xm), где xi, X2,—,xm представляют собой определен-
определенные выше функции аргументов tu t2,..., tk, непрерывна в точке
A(ah a2,...,ak).
¦466 Гл. 12. Функции нескольких переменных
Для доказательства этого утверждения рассмотрим произволь-
произвольную сходящуюся к А последовательность точек Nn=(t^n\ f2(n), —
..., 4(?г)) множества {Л/}. Обозначим через {Мп} соответствующую
лоследовательиость точек пространства Ет, координаты хг(п\
Х2(п), ...,Хт(п) КОТОрЫХ рЭВНЫ
Хг(п) = фг=(^„)='фг(^,(">, &»>,-» **<">), 1=1, 2 т.
Из непрерывности функций q>i(N) в точке А и из определения не-
непрерывности по Гейне вытекает сходимость последовательности
точек {Мп} к точке В (b\, b2, ...,bm).
Далее из непрерывности функции u=f(M) в точке В и из
•определения непрерывности по Гейне вытекает сходимость после-
.довательности {f(Mn)} к числу f{B). Но это и означает, что по-
последовательность f[<fi{Nn), (p2(Nn),..., фт(¦№„)] значений этой
•сложной функции сходится к частному значению этой
сложной функции f[<jpi(^), <рг(А), ...,ц>т(А)], т. е. непрерывность
сложной функции в точке А.
3°. Теорема об устойчивости знака непрерыв-
непрерывной функции.
Теорема 12.4. Если функция u = f(M) непрерывна в точке
А евклидова пространства Ет и если 1(А)фО, то существует та-
таская Ь-окрестность точки А, в пределах которой f(M) не обра-
обращается в нуль и имеет знак, совпадающий со знаком f(A).
Справедливость этой теоремы почти непосредственно
'вытекает из определения непрерывности функции f(M) в точке А
по Коши. В самом деле, из этого определения вытекает, что для
любого е>0 найдется отвечающее ему 6>0 такое, что f(A) —
e<f(M)<f(A) + E всюду в б-окрестности точки А. Если в этих
рассуждениях взять в качестве е положительное число |/(Л)|/2,
то мы получим, что все три числа f(A) —е, f(A) и f(Л) -J-e будут
•одного знака, и потому f(M) имеет тот же знак, что и f(A) всю-
всюду в б-окрестности точки А.
4°. Теорема о прохождении непрерывной функ-
функции через любое промежуточное значение.
Теорема 12.5. Пусть функция u — f(M) непрерывна во всех
точках связного множества {М} евклидова пространства Ет, при-
причем f(A) и f(B) —значения этой функции в точках А и В этого
множества. Пусть, далее, С ¦— любое число, заключенное между
f(A) и f(B). Тогда на любой непрерывной кривой L, соединяющей
точки А и В и целиком располагающейся в {М}, найдется точка
N такая, что f(N) =С.
Доказательство. Пусть xi=q>i(t), x2 = <p2(t), ...,xm=<fm{t),
а^^Р, — уравнения непрерывной кривой L, соединяющей точки
А и В множества {М} и целиком располагающейся в {Щ (См.
п. 2 § 1). На сегменте [а, р] определена сложная функция и =
f(* х2, ..., Хт), гдех(- = ф,-(*), i=l, 2, ..., т, /р
§ 3. Непрерывность функции т переменных 467
Очевидно, значения этой функции на сегменте [а, р] совпа-
совпадают со значениями функции u = f(M) на кривой L. Указанная-
сложная функция одной переменной t, в силу утверждения разде-
раздела 2° этого пункта, непрерывна на сегменте [а, р] и, согласно-
теореме 4.13, в некоторой точке ? сегмента [а, ($] принимает зна-
значение С. Поэтому в точке N кривой L с координатами <pi(?),-
Фг(|),..., фт(|) получим f(N)=C. Теорема доказана.
5°. Ограниченность функции, непрерывной на
замкнутом ограниченном множестве.
Теорема 12.6. (первая теорема Вейер шт р а ее а).
Если функция u=f(M) непрерывна на замкнутом ограниченном
множестве {М}, то она ограничена на этом множестве.
Для того чтобы убедиться в справедливости этой теоремы, вы-
выделим (как и в доказательстве аналогичной теоремы 4.14) после-
последовательность {Мп} точек множества {М}, для которых |/(Мп)|>
>л. В силу теоремы Больцано—Вейерштрасса (см. п. 2 § 2) из;
{Мп} можно выделить сходящуюся подпоследовательность {Мьп}*
предел М которой в силу замечания к теореме Больцано-Вейер-
штрасса принадлежит множеству {М}. Очевидно, последователь-
последовательность {f(Mkn)} бесконечно большая. С другой стороны, в силу не-
непрерывности функции в точке М эта последовательность {f (Mkn)}'
должна сходиться к f(M). Полученное противоречие доказывает
теорему.
6°. Достижение функцией, непрерывной на
замкнутом ограниченном множестве, своих точ-
точных граней. Точной верхней гранью функции f(M) на множе-
множестве {М} называется такое число п, которое удовлетворяет двум
требованиям: 1) f(M)^.u для всех точек М множества {М};
2) для любого е>0 найдется хотя бы одна точка М множест-
множества {М}, для которой {(М)>п — г.
Аналогично определяется точная нижняя грань и функции
f(M) на множестве {М}.
Для обозначения точных граней функции f(M) на множестве
используют следующую символику:
w = sup/(M), w = mf/(Af).
{м} - {«}
Теорема 12.7 (вторая теорема Вейерштрасса),
Если функция u = f(M) непрерывна на замкнутом ограниченном
множестве {М}, то она достигает на этом множестве своих точных
верхней и нижней граней.
Доказательство этой теоремы почти дословно повторяет дока-
доказательство теоремы 4.15 (т. е. второй теоремы Вейерштрасса для;
функции одной переменной).
Читатель без труда проведет это доказательство сам.
468 Гл. 12. Функции нескольких переменных
7Р. Понятие равномерной непрерывности
функции нескольких переменных. Функция u = f(M)
называется равномерно непрерывной на множестве
{М} * евклидова пространства Ет, если для любого положительно-
положительного числа е можно указать такое положительное б, зависящее
только от е, что для любых двух точек М' и М" множества, удов-
удовлетворяющих условию р(М', ЛГ')<6, выполняется неравенство
\f(M')-f(M")\<B.
Имеет место следующая теорема.
Теорема 12.8. (теорема о равномерной непре-
непрерывности). Непрерывная на замкнутом ограниченном множе-
множестве функция равномерно непрерывна на этом множестве.
Доказательство этой теоремы совершенно аналогично доказа-
доказательству теоремы 4.16 и получается из него путем замены терми-
термина «сегмент [а, Ь]» термином «множество {М}», замены буквы х
на букву М и замены выражений типа \х' — х"\ на символ
р (М', М").
Замечание. Назовем диаметром ограниченного
множества М точную верхнюю грань чисел р(М', М"), где М' и
М"—всевозможные точки множества {М}. Используя понятие
диаметра множества, отметим следующее свойство непрерывных
на замкнутых ограниченных множествах функций. Пусть функция
u = f(M) непрерывна на замкнутом ограниченном множестве {М}.
Тогда для любого положительного числа е можно указать такое
"8>0, что на каждом принадлежащем множеству {М} замкнутом
подмножестве {Л/}, диаметр которого меньше 8, колебание со **
функции f(M) меньше г.
Доказательство этого свойства совершенно аналогично дока-
доказательству следствия из теоремы 4.16.
Замечание. Множество {М} m-мерного евклидова про-
пространства называется компактом, если из любой системы
открытых множеств, покрывающих множество {М}, можно вы-
выделить конечную подсистему, также покрывающую это мно-
множество.
Точно так же, как и для пространства всех вещественных
чисел Е1 (см. п. 3 § 7 гл. 4), доказывается, что множество пг-
мерного евклидова пространства Ет является компактом, тогда
и только тогда, когда оно является замкнутым и ограниченным.
Таким образом, первая и вторая теоремы Вейерштрасса и
теорема о равномерной непрерывности справедливы АЩ функ-
функции, непрерывной на компакте.
* При этом предполагается, что множество {М} плотно в себе, т. е. в лю-
любой б-окрестности каждой точки М этого множества имеются отличные от М
точки множества {М}.
** Колебанием со функции f(M) на множестве {М} называется разность меж-
_ду точной верхней и точной нижней гранями функции f(M) на этом множестве.
§ 4. Производные и дифференциалы 469
§ 4. ПРОИЗВОДНЫЕ . И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
1. Частные производные функции нескольких переменных.
Пусть М (xi, X2,..., хт), — внутренняя точка области задания функ-
функции u = f(x\, X2 Хт). Рассмотрим в данной фиксированной точке
M(xi, X2 хт) отношение частного приращения Д*А« (см. п. 1
§ 3, формулы A2.8) и A2.9)) к соответствующему приращению
аргумента хк:
A2.12)
xkU _ f(*i, .... *t-i, xk + Axk, *fe+1, .... xm)—f{xlt x2, ... , xm)
Ajcfe Axk
Отношение A2.12) представляет собой функцию от Axh, опре-
определенную для всех отличных от нуля значений Ахи, для которых
точка M(xi, X2,...,Xk-\, Xh+Axk, Xh+\,—,xm) принадлежит области
задания функции u=f(xu X2,-,xm).
Определение. Если существует предел отношения A2.12)
частного приращения AXku функции в точке М{Х\, Х2,—,хт) к со-
соответствующему приращению Axk аргумента xh при Длг^г^-О, то этот
предел называется частной производной функции и =
=f(xu х2, ..., хт) в точке М по аргументу xk и обозначается одним
из следующих символов:
ди df ' ,.'
Таким образом,
дхь Дж,->.о А*4
Отметим, что частная производная функция u=f(xu x2,...,xm)
по аргументу Хн представляет собой обыкновенную производную
функции одной переменной хн при фиксированных значениях
остальных переменных. Поэтому вычисление частных производных
производится по обычным правилам вычисления производных
функций одной переменной.
Примеры
I) и = aictg<**¦). -^ У% dU ^
дх
ди
2) и = е г , =
дх г
1
2х
z
+ хгу* '
-е г ,
ди
ду
1 ~\-x2yi
„ х2+уг
—— = -JL.e г ^
ду г дг
Замечание 1. Из существования у функции в данной точ-
точке всех частных производных, вообще говоря, не вытекает непре-
470
Гл. 12. Функции нескольких переменных
рывность функции в этой точке. Мы уже убедились, что функциям
A2.10)
и =
0 при х2 + у2 = О
не является непрерывной в точке О@, 0) (см. пример Г п. 2 § 3)..
Однако в этой точке указанная функция имеет частные производ-
производные по х и у. Это следует из того, что f{x, 0)=0, f@, y)=0, и;
поэтому
дх
@.0)
= 0.
@,0)
Замечание 2. Подчеркнем, что данное нами определе-
определение понятия частных производных всегда пригодно для внут-
внутренних точек области задания функции, но для граничных то-
точек этой области, вообще говоря, непригодно.
Это связано, в частности,.
У\ с тем, что в граничных точках
области задания функции не-
невсегда можно вычислить част-
частные приращения функции
(так, например, обстоит дело-
с граничной точкой Mq обла-
области, изображенной на рис
12.2).
В связи со сказанным при-
принято определять частные про-
I ^. изводные в граничных точках.
хо & как пределы этих производ-
производных при стремлении точек к
Рис- 122 границе.
2. Дифференцируемость функции нескольких переменных. На-
Напомним, что приращением (или полным приращением) функции
u = f{x\, Х2,...,хт) в точке М (хи Х2,...,хт) соответствующим при-
приращениям Ахи Ах2,...,Ахт аргументов, называется выражение*
, Х2+Ах2,..., хт-\-Ахт) —f(xi, х2,...., хт).
О
Определение. Функция u=f(xu X2,...,xm) называется
дифференцируемой в данной точке М(х\, Х2,...,хт), если
ее полное приращение в этой точке может быть представлено в.
виде
A2.14)
* См. п. 1 § 3, формулы A2.5) и A2.6).
§ 4. Производные и дифференциалы 471
где А\, А%...,Ат — некоторые не зависящие от Ах\, Дх2,..., Дхт
числа, а а,\, а2, .... си — бесконечно малые при Axi-»-0, Дх2->0, .„
..., Дхто-И) функции, равные нулю при Д#1=Д#2 = •¦• Axm=Q.
Соотношение A2.14) называется условием дифферен-
цируемости функции в данной точке М. Условие A2.14)
дифференцируемое™ функции можно записать также в иной фор-
форме. Для этого рассмотрим бесконечно малую при Axi->-0, Дх2->-
->-0,..., &xm-+0 функцию р = V Ах\ + х\ + ... + Ахт * и отме-
тим, что эта функция обращается в нуль лишь при Дх1 = Дх2= ...
... = Ахт — 0. Убедимся теперь, что входящая в правую часть соот-
соотношения A2.14) сумма aiAxi-T-a2Ax2+ ••• +о-тАхт представляет
собой бесконечно малую более высокого порядка функцию по
сравнению с р. Иными словами, убедимся, что эта сумма пред-
представляет собой выражение о(р). В самом деле, при р#0 справед-
либо неравенство <1, и поэтому
Р
| Ах, I . . .1 Лх2
—- +1а1 J-f
I Р<
••• +|aj}p=o(p).
Таким образом, условие A2.14) дифференцируемости функции
может быть записано в следующей форме:
A2.15)
При этом величину о(р) мы считаем равной нулю при р = 0.
Чтобы доказать, что условие A2.15) эквивалентно условию
A2.14), нужно убедиться, что из представления A2.15), в свою
очередь, вытекает представление A2.14). Для этой цели, считая,
что не все Д*1, Дх2 Ахт равны нулю**, представим о(р) в виде
0( ч О(Р) Р2 ^_
Р Р
—^ I AX, ¦+- | —— | AX2 + . . . -+- | —^-^ - *"
L
Полагая — • —- —at и учитывая, что а; является бесконечно
Р Р
малой при р->-0 (а значит, и при Дх1-Н), Дх2^-0,..., Дхт->-0) функ-
функцией, мы придем к представлению A2.14).
* Геометрически эта функция представляет собой расстояние между точ-
жами М(хи Х2, ..., хт) и M'(xi+Axi, Хг+Ах2, ..., хт+Ахт).
** Если все Axi равны нулю, то все члены в первой части формул A2.14) и
iA2.15) равны нулю.
472 Гл. 12. Функции нескольких переменных
Итак, условие дифференцируемости функции можно записать
как в виде A2.14), так и в виде A2.15).
Если хотя бы одно из чисел А\, A<i,...,Am отлично от нуля, то
сумма А\Ах1-±-А2Ах2-}-...-{-АтАХт представляет собой главную,
линейную относительно приращений аргумен-
аргументов часть приращения дифференцируемой функции. Отметим,
что при определении понятия дифференцируемости функции мы
не исключали возможности обращения всех чисел А\, Az,...,Am в
нуль, и поэтому если приращение функции может быть представ-
представлено в влде A2.14) или A2.15) при /4i = 0, Л2 = 0, ...,Лт = 0, то
функция дифференцируема в данной точке.
Справедлива следующая теорема.
Теорема 12.9. Если функция u = f(xu x2,...,xm) дифферен-
дифференцируема в точке М(х\, Х2,...,хт), то в этой точке существуют
частные производные по всем аргументам, причем = А,, где
дх,-
Ai определяются из условия A2.14) или A2.15) дифференцируе-
дифференцируемости функции.
Доказательство. Из условия A2.14) дифференцируемо-
дифференцируемости функции в точке М(х\, Х2,...,хт) вытекает, что ее частное
приращение Ахи в этой точке равно Ах.и = AtAxt + atAxt. Отсю-
V
да вытекает, что —д^— = А{ + а,-,и поэтому, так как а,->0 при
^ Ах/ дх/
Следствие 1. Условие A2.15) дифференцируемости функ-
функции в данной точке М можно записать в следующей форме:
Au^^-AXl + ~Ax2+ ... + -^-Axm+o(p). A2.16)
дхг дхг dxm
Следствие 2. Если функция u = f(x\, X2,...,xm) дифферен-
дифференцируема в точке М(х\, Х2,...,хт), то представление ее приращения
Аи в форме A2.14) или A2.15) единственно.
В самом деле, коэффициенты Ai этих представлений равны
ди „ ,,
частным производным —— в данной точке М и поэтому опреде-
определяются единственным образом. ¦
Убедимся в справедливости следующего важного свойства
дифференцируемых функций.
Если функция u = f(xu x2,...,xm) дифференцируема в. точке
M(xi, X2, ...,xm), то она и непрерывна в этой точке.
В самом деле, из условия A2.14) дифференцируемости
функции в точке вытекает, что Пт Аи =0, а это озна-
§ 4. Производные и дифференциалы
473
Ту у
чает, что функция непрерывна в точке М (см. п. 1 § 3, формула
A2.7)).
3. Геометрический смысл условия дифференцируемости функ-
функции двух переменных. В случае функции u = f(x, у) двух пере-
переменных условие дифференцируемости может быть иллюстрирова-
иллюстрировано геометрически. Введем понятие касательной плоскости к по-
поверхности в точке.
Плоскость П, проходящая через точку No поверхности, назы-
называется касательной плоскостью в этой точке, если угол меж-
между этой плоскостью и секущей, проходящей через точку No и лю-
любую точку N\ по-
поверхности," стремит-
стремится к нулю, когда
точка Ni стремится
к No (рис. 12.3).
Если в точке Лго
существует каса-
касательная плоскость,
то очевидно, что ка-
касательная в точке
No к любой кривой
расположенной на
поверхности и про-
проходящей через No,
лежит в указанной
плоскости.
Убедимся, что из
условия дифферен-
дифференцируемости функ-
функции u = f(x, у) в
данной точке М0(х0,
Уо) вытекает существование касательной плоскости к графику S
этой функции в точке N0(x0, у о, «о). Положим Ах—х—х0, Аг/ =
= У — Уо, А« = « — "о, где Uo = f(xo, г/о). u=f(x, у). Очевидно, усло-
условие A2.14) дифференцируемости в рассматриваемом случае мож-
можно записать следующим образом:
и — ио=А(х — Хо) +В (у — г/о) +аД#+РЛ# = А (х — *0) +
+В(у-у0)+о(р),
л г, ди да
где А и В — постоянные, равные частным производным и •
ах ду
в точке Мо, а а и р — бесконечно малые при Дх-»-0 и Дг/-»-0 функ-
функции р= 1/Дл:2 + Дг/2 .
Рассмотрим следующее уравнение:
U — ио=А (х — Хо) +В (у — г/о).
Рис. !2.3
474 Гл. 12. Функции нескольких переменных
Из аналитической геометрии известно, что это уравнение опре-
определяет в декартовой системе координат (л;, у, U) некоторую плос-
плоскость П, проходящую через точку N0(x0, г/о, «о) и имеющую нор-
нормальный вектор п = {А, В, —1}*.
Докажем, что эта плоскость П является касательной плос-
плоскостью в точке Л/о поверхности S. Для этого достаточно убедиться,
что: 1) плоскость П проходит через точку No поверхности S и
2) угол ф между нормалью п этой плоскости и любой секущей
NcNi стремится к я/2, когда точка N\ поверхности S стремится к
точке Л'о. Утверждение 1) очевидно. Перейдем к доказательству
утверждения 2). Вычислим косинус угла ф, воспользовавшись из-
известной формулой для косинуса угла между двумя векторами.
Так как координаты вектора п равны А, В, —1, а координаты
вектора N0Ni секущей равны х — х0, у — г/о, «— «о (см. рис. 12.3),
то
cos А(х — хо)+В(у — г/о)—(и — щ)
Из условия дифференцируемое™ функции u = f(x, у) вытекает,
что
А(х — хоI+В(у — г/о) — (и — и0)=о(р).
Поэтому 1 cos ф | <: —^= |0(р)| =-= |о(р)| ->0, когда р^О,
У(х ЧJ+(У— УоJ Р
т. е. Нпкр= —. Утверждение 2) доказано.
Таким образом, дифференцируемость функции u — f(x, у) в
точке М0(хо, г/о) с геометрической точки зрения означает наличие
касательной плоскости к графику функции u = f(x, у) в точке
N0(x0, г/о, но).
Так как коэффициенты А и В равны соответственно частным
производным, вычисленным в точке Мо(хо, г/о), то уравнение ка-
касательной плоскости может быть записано в виде
тт ди , ч> ди , ч
0 =lir^x~Xo)' ~di^y~y°^
тт » ( ди ди ,}
Нормальный вектор n=i , ——, —I касательной плоско-
[ дх ду \
сти принято называть нормалью к поверхности u = f(x, у) в
точке N0(x0, уо, z0).
4. Достаточные условия дифференцируемости. Займемся выяс-
выяснением достаточных условий дифференцируемости функции т
переменных. Докажем следующую теорему.
Теорема 12.10. Если функция u = f(x\, х2,...,хт) имеет част-
частные производные по всем аргументам в некоторой окрестности
* Нормальным вектором плоскости называется любой ненулевой
вектор п, перпендикулярный к этой плоскости. .
§ 4. Производные и дифференциалы 475
точки ЛГо(*1°, Х2°, ...,х°т), причем все эти частные производные не-
непрерывны в самой точке Мо, то указанная функция дифференци-
дифференцируема в точке Мо.
Доказательство. Для сокращения записи проведем дока-
доказательство для функции двух переменных u = f(x, у). Итак, пусть
обе частные производные fx' и fy' существуют в окрестности точки
М0(хо, Уо) и непрерывны в этой точке. Дадим аргументам х и у
•столь малые приращения Ах и Дг/, чтобы точка М(хо-\-Ах, г/о+Аг/)
не выходила за пределы указанной окрестности точки Мо. Полное
приращение Аи — /(хо+А#, #о+Дг/о)—f(xo, уо) можно записать в
виде
Д« = [/(лго+Ах, уо+Ау) —f(x0, уо+Ау)] +
+ [f(xo, yo+Ay)—f(xo, уо)].
Выражение [/(xo+Axo, уо+Ауо) —f(xo, r/o+Ar/)] можно рассмат-
рассматривать как приращение функции f(x, r/o+Аг/) одной переменной
х на сегменте [х0, дго+Ах]. Поскольку функция u = f(x, у) имеет
частные производные, указанная функция f(x, г/о+Аг/) диффе-
дифференцируема и ее производная по х представляет собой частную
производную fx'. Применяя к указанному приращению формулу
¦Лагранжа, найдем такое 9i из интервала 0<9i<l, что
[/(хо+Дх, Уо+Ау) —f(x0, yo+Ay)] =fx (xo+QiAx, yo+Ay)Ax.
Рассуждая совершенно аналогично, получим
lf(xo, г/о+Аг/) —f{x0, г/о)] =fv'(xo, г/о+'Э2Аг/)Аг/, 0<92<1.
Так как производные fx' и fy' непрерывны в точке Мо, то
fx'(xo+QiAx, yo+Ay)=fx'(x0, г/0)+а,
где аир — бесконечно малые при Ал:->-0 и Аг/-»-0 функции. Отсю-
Отсюда, учитывая приведенные выражения для
{f(xa+Ax, уо+Ау) — f(x0, Уо+Ауо)] и [f(x0, Уо+Ау) —f(x0, Уо)]
и выражение для Аи, найдем
Au = fx'(xo, уо) Ax+fy' {хо, г/о)Дг/+аДх+рДг/.
Следовательно, функция u=f(x, у) дифференцируема в точке Мо.
Для функции т переменных u=f{xi, x2,..., хт) рассуждения
аналогичны, нужно только полное приращение Аи такой функции
представить в виде
Аи — / (х° + Axv х\ + Длг2, ... ,х°т + Ахт) — f (x°v х\ х°т) =
• • • xi—\ixi>xj+i + Ax{+V ¦ ¦ ¦ >xm+ Axm)].
476 Гл. 12. Функции нескольких переменных
Теорема доказана.
5. Дифференциал функции нескольких переменных.
Определение. Дифференциалом du дифференцируе-
дифференцируемой в точке М(х\, X2,-.,xm) функции u—f(xu X2,—,xm) назы-
называется главная линейная относительно приращений аргументов
часть приращения этой функции в точке М. Если все коэффициен-
коэффициенты Ai в представлении A2.14) приращения дифференцируемой
функции равны нулю, то дифференциал du функции в точке М
считается равным нулю.
Таким образом, дифференциалом du дифференцируемой в точ-
точке М функции u = f(x\, X2,—,xm) называется выражение
du = AyAxx+A2Ax2+ ....+AmAxm. A2.18)
Используя теорему 12.9, мы можем, очевидно, переписать выра-
выражение A2.18) для дифференциала du следующим образом:
du = ^-Ax1 + ^-Ax2 + ... + -^-Дхт. A2.19)
Введем понятие дифференциала dxt независимой
переменной Х{. Под дифференциалом dxi независимой пере-
переменной Xi можно понимать любое (не зависящее от Х\, Х2,...,хт)
число. Договоримся в дальнейшем брать это число равным при-
приращению Ахг независимой переменной Xi. Эта договоренность поз-
позволяет нам переписать формулу A2.19) в виде
du = ^.dr1+^-dxa+...+-^-dxn. A2.20)
дх дх дх
Подчеркнем, что формула A2.20) установлена нами лишь для
случая, когда аргументы xi, х2,..., хт являются независимыми пе-
переменными. Однако ниже, в п. 7 этого параграфа, мы докажем,
что формула A2.20) остается справедливой и для случая, когда
аргументы х\, Х2,—,хт не являются независимыми переменными,
а сами представляют собой дифференцируемые функции некото-
некоторых новых переменных.
6. Дифференцирование сложной функции. В этом пункте мы
рассмотрим вопрос о дифференцировании сложной функции вида
u=±f(xu X2,...,Xm), где
Х\ = <Pl (*i. t2, ... , tk),
хг = Фг(^1>^> • • • » **)> A2.21)
Мы докажем, что при определенных условиях эта сложная
функция является дифференцируемой функцией своих аргументов
t\, t2,...,th. При этом частные производные указанной сложной
функции по аргументам U, t2,...,th выражаются через частные
ди
ди
да
ди
дхг
_ ди
ди
ди
дхт
ди
дхт
ди
дхт
дхт
dt2
§ 4. Производные и дифференциалы 477
пр.оизводные функции u = f(x\, х2,...,хт) и через частные произ-
производные функций A2.21) по следующим формулам:
; . ди дх2 ,
dxt dtj.
i ди дх2
i дхг dt2
1 + J!LJ?*l+ ... + _^__^». A2.22)
dtk dxi dtk &X2 dtk dxm dt^
Докажем следующую основную теорему.
Теорема 12.11. Пусть функции A2.21) дифференцируемы в
некоторой точке M(t\°, t20 4°), а функция u = f(xu x2,...,xm)
дифференцируема в соответствующей точке N(xi°, х20,..., х°т), где
Xi°=q>i(ti°, 4°, ¦•-.4°), '=1, 2,..., т. Тогда сложная функция и =
= }{xi, Х2,...,хт), где Х\, х2,—,хт определяются соотношениями
A2.21), дифференцируема в точке М. При этом частные произ-
производные этой сложной функции в точке М определяются формула-
формулами A2.22), в которых все частные производные ——,——, ... *
дх1 дх2
—— берутся в точке N, а все частные производные —'-
ахт dtj
функций A2.21) по аргументам t\, t2,...,th берутся в точке М.
Доказательство. Придадим аргументам ^i, t2,...,th в точ-
точке M(ti°, t2°,...,tk°) произвольные приращения Д^, А12,..., Ath, не
равные одновременно нулю. Этим приращениям соответствуют
приращения Д-ti, Ах2,...,Ахт функций A2.21) в точке М. Прира-
Приращениям Ах\, Ах2,..., Ахт, в свою очередь, соответствует прираще-
приращение Аи функции u = f(x\, Х2,..-,Хт) в точке N. Поскольку функция
u = f(xi, x2,...,Xm) предполагается дифференцируемой в точке N,
указанное приращение Аи этой функции может быть записано в
виде
а ди . ди . , ди .
Аи -¦= —— Ахг + -— Дх2 + ... + —— Ахт
ох ох ох
A2.23)
ди ди ди .,
где частные производные ——, , ... , берутся в точке Nr
dxi дх2 дхт
a ai, a2,..., am — бесконечно малые при Д*1->-0, Ах2->-0,..., Ахт-+О
функции, равные нулю при Ддг1 = Дх2= ... =Дл:т = 0. Подчеркнем,,
что в соотношении A2.23) Длгь Ах2,...,Ахт представляют собой,
приращения функций A2.21), отвечающие выбранным прираще-
приращениям At}, At2,..., Ath аргументов этих функций. В силу дифферен-
цируемости функций A2.21) в точке M(tj°, t2°,..., tk°) указанные
приращения Axi можно записать в следующей форме:
478 Гл. 12. Функции нескольких переменных
Ах, = -^ At, + -g- Мг + ... + -f^- A^ + о (р), A2.24)
t=l, 2, .... т,
дх/
д*7 д*г дх/ , Л/Г
где частные производные , , ..., берутся в точке М,
OTt OT2 «ft
а р = Щ
Мы должны убедиться в том, что после подстановки в правую
часть A2.23) выражений A2.24) приращение Аы может быть при-
приведено к виду
to = AlAtl+A3Ata+...+Ah\th+o(p), A2.25)
ггде
А =_ди_^ + ^дх^+ _ _+_au_^!L> A226)
' dxi dte дхг dti ' дхт dti
Тем самым доказательство теоремы будет завершено, ибо форму-
_ла A2.25) устанавливает факт дифференцируемости сложной
функции, а выражение A2.26) представляет собой частную про-
производную указанной сложной функции по переменной tt (см. тео-
,рему 12.9).
При подстановке в правую часть A2.23) выражений A2.24)
:кроме группы слагаемых
AlAt1+A2At2+....+AkAtk
мы получим и другие группы слагаемых. Нам нужно убедиться в
том, что все другие группы слагаемых представляют собой вели-
величину о(р).
Действительно, подставляя выражения A2.24) в формулу
-A2.23), получим
ft
km
?=1
m
/=1 l=\ 1=1
Последние две суммы написанной выше формулы представ-
представляют собой величину о(р). В самом деле, величины -?- берутся
§ 4. Производные и дифференциалы 479»
в точке N и поэтому представляют собой постоянные не завися-
т
щие
от р числа. Следовательно, V~r~°(p) = °(р)- Далее, вели-
чины Axj для i=l, 2,...,m удовлетворяют в силу формулы A2.24)
неравенству |Ax,|<const-p, а величины а, = оA) для t = l, 2,..., /?i».
ибо все аг- являются бесконечно малыми при A#i-»-0, Дх2->-0,...
..., Ахт^-0, а из дифференцируемости и вытекающей из нее непре-
непрерывности в точке М функций A2.21) следует, что Axi, Ах2,..., Ахт
т
стремятся к нулю при р->0. Поэтому N atAxt = о(р). Теорема до--
i=i
казана.
Замечание. Рассмотрим важный частный случай, когда
функции A2.21) зависят от одного аргумента t. Тогда мы имеем,
сложную функцию одной переменной t: u=f(x\, X2,...,xm), где
Xt = q>i(t). Производная этой сложной функции определяется;
at
формулой
du _ ди dxx ди dx2 ди dxm _ П2 *>7>.
dt дхг dt дх2 dt '" дхт dt ^
Применим формулу A2.27) для доказательства теоремы Эйле-
Эйлера об однородных функциях.
Функция ы = /(хь Х2,...,хт) заданная на множестве {М}, назы-
называется однородной функцией степени р на этом мно-
множестве, если для каждой точки М (xi, xi,...,xm) множества {М} и
для каждого числа t, для которого точка N{tx\, tx2,..., txm) при-
принадлежит множеству М , выполняется равенство
f(txu txa,...,txm)=tPf(xi, xi%...,xm). A2.28)
Теорема 12.12 (теорема Эйлера об однородных
функциях). Если u=f(xi, X2,...,xm) является в некоторой об-
области {М} дифференцируемой однородной функцией степени р, то-
в каждбй точке М{х\, Х2,...,хт) области {М} справедливо равен-
равенство
^xx + ^x2+...+-f±-xm = pu. A2.29).
дх дх дх
Доказательство. Пусть Mo(xi°, X2°,...,x°m)—произволь-
X2°,...,x°m)—произвольная точка области {М}. Рассмотрим сложную функцию u = f(xu
x2,...,xm), где Xi = tXi° (i'=l, 2, ...,m), т. е. функцию u = f(txi°,
tx20,...,tx0m). Так как при ?=1 функции Xi = txi° дифференцируемы
и функция u = f(x\, X2,...,xm) дифференцируема в соответствую-
соответствующей точке Мо, то согласно теореме 12.11 и замечанию к этой тео~
du
реме мы можем вычислить производную указанной сложной!
dt
480 Гл. 12. Функции нескольких переменных
•функции в точке ?=1 по формуле A2.27). Так как —р-=я'9, то
-t"+^+-+-sr'p- A2'30)
dt
где производные берутся в точке Мо. С другой стороны, в
dxi
силу A2.28) рассматриваемая сложная функция может быть
лредставлена следующим образом:
u = f{txi°, tx2°,...,tx°m)=tPf(x10, x20,...,x°m). A2.31)
Из A2.31) вытекает, что — = рИ>-1 f (*°, х°2 х°т), т. е.
— -=р[(х°„х00, ... ,х°)=ри. A2.32)
dt t=\ ' 2 m
Сравнивая A2.30) и A2.32), мы и получим соотношение A2.29)
для точки Мо. Так как точка 'Мо — произвольная точка области
{М}, то теорема доказана.
7. Инвариантность формы первого дифференциала. В п. 5 мы
ввели понятие первого дифференциала du функции нескольких
переменных и установили, что когда аргументы х\, х2,...,хт явля-
являются независимыми переменными, то дифференциал
du можно представить в виде
du = dx1 -\ dx2 + ... Н dxm. A2.20)
дхх дх2 дхт
В этом пункте мы докажем, что формула A2.20) является
универсальной и справедлива и в том случае, когда аргументы
х\, x2,...,xm сами являются дифференцируемыми функциями неко-
некоторых новых переменных t\, t2,..., 4, которые мы можем считать
яезависимыми. Указанное свойство первого дифференциала обыч-
.но называют свойством инвариантности его формы.
Итак, пусть аргументы х\, х2,...,хт функции u — f(x\, x2,...,xm)
представляют собой дифференцируемые в точке Л(^°, t2Q,..., tk°)
функции Xi = q>i(ti, t2,...,th), а сама функция u = f(xu x2,...,xm)
дифференцируема в точке B(xi°, х20, ...,х°т), где л-г0 = фг(^10, i20,...
...,4°). В таком случае мы можем рассматривать и как сложную
функцию независимых переменных tlr t2,..., th, которая в силу тео-
теоремы 12.11 является дифференцируемой в точке А. Поэтому диф-
дифференциал du этой сложной функции можно представить в виде
du =^-dt1 + ~dt2 + . .. + -^~dtk, A2.33)
где —— определяются из соотношений A2.22). Подставляя ——
oti at/
§ 4. Производные и дифференциалы 481
из A2.22) в A2.33) и собирая коэффициенты при ди/дхи получим
Остается заметить, что в последнем соотношении коэффициент
при du/dxi равен дифференциалу dx{ функции лгг=фг(*ь h h)-
Мы получим для дифференциала du сложной функции формулу
A2.20), в которой дифференциалы dxi будут дифференциалами
функций Xi=<fi(t\, t2,...,th). Инвариантность формы первого диф-
дифференциала установлена.
Свойство инвариантности формы первого дифференциала поз-
позволяет установить следующие правила дифференцирования. Пусть
и и v — дифференцируемые функции каких-либо переменных.
Тогда
d(c-u) =c-du (c = const),
d(u±v) =du±dv,
d(uv) =udv-\-vdu,
Докажем, например, справедливость третьей из указанных фор-
формул. Рассмотрим функцию w = uv двух переменных и и v. Диф-
Дифференциал этой функции dw равен
. dw j dw ,
aw = аи 4 dv.
ди dv
Так как ——=v и ——==«, то dw = udv-\-vdu. В силу инвари-
ди dv ¦
антности формы первого дифференциала выражение udv-\-vdu
будет дифференциалом функции ко и в случае, когда и и v сами
являются дифференцируемыми функциями каких-либо пере-
переменных.
8. Производная по направлению. Градиент. Начнем с рассмо-
рассмотрения функции трех независимых переменных u = f{x, у, z).
Предположим, что эта функция определена в некоторой окрестно-
окрестности точки Мо(х°, у0, z°) пространства Е3 и дифференцируема в
точке Мо.
Рассмотрим всевозможные лучи, выходящие из точки Мо.
Каждый такой луч задается единичным вектором е с координата-
координатами (cosa, cosp, cosy) * и определяет некоторое направление.
* Из курса аналитической геометрии известно, что если единичный вектор
е составляет с осями координат углы, соответственно равные а, [3, ^ то коор-
16 Зак. 72
482 Гл. 12. Функции нескольких переменных
Фиксируем некоторый луч, выходящий из точки Мо и опреде-
определяемый единичным вектором е с координатами cos a, cos [3, cosy-
Взяв на прямой, содержащей этот луч, произвольную отлич-
отличную от Мо точку М, рассмотрим вектор или направленный отре-
отрезок MqM и обозначим через / величину этого направленного от-
отрезка на оси, определяемой единичным вектором e=(cosa, cosf$,
cosy) *•
Ясно, что вектор МоМ имеет координаты
(/cosa, /cosf$, /cosy)-
С другой стороны, если координаты точки М равны (х, у, z)r
то вектор М0М имеет координаты, равные (х— х°, у — у0, z— z°).
Сопоставляя два полученных нами соотношения для координат
вектора М0М, мы приходим к равенствам
x = x°+/cosa, у=y°+l cos $, z=2°+/cosy- A2.34)
Равенства A2.34) показывают, что на прямой, проходящей
через точку Мо и определяемой единичным вектором e=(cosa,
cosf$, cosy), функция u = f(x, у, z) представляет собой сложную
функцию одной независимой переменной / вида u = f(x°-\-l cos аг
r/°+/cosр, zo+/cosy).
Определение 1. Производную указанной сложной функции
по переменной I, взятую в точке 1 = 0, назовем производной
функции u = f(x, у, z) в точке Мо по направлению,
определяемому единичным вектором е, и будем обозначать сим-
символом ди/де.
Итак, по определению
— = — (Л!о) cos a + — (Мо) cos р + —- (Мо) cos у. A2.35)
де дх1 ay oz
Введем понятие градиента дифференцируемой в данной точке
Мо{хо, г/о, z0) функции u = f(x, у, z).
Определение 2. Градиентом функции u = f(x, у, z) в
данной точке М0(х°, у°, z°) называется вектор, координаты кото-
которого имеют вид
— (Мо), — (Мо), —(Мо).
Для обозначения градиента функции u = f(x, у, z) обычно ис-
используют символ
grad и.
динаты этого вектора равны ccs a, cos [3, cosy. Указанные три косинуса принято
называть направляющими косинусами вектора е.
* Величиной / направленного отрезка М0М оси, определяемой единичным
вектором е, называется число, равное длине отрезка МоМ, взятой со знаком
«плюс», если векторы МоМ и е направлены в одну сторону, и со знаком «ми-
«минус», если эти векторы направлены в разные стороны.
§ 4. Производные и дифференциалы 483
Итак, по определению
grad и (Мо) = (^j- (Mo), -g- (Mo), -g- (Л*о)). A2.36)
Так как скалярное произведение двух векторов равно сумме
произведений одноименных координат этих векторов, то выраже-
выражение A2.35) для производной по направлению, определяемому век-
вектором е, можно рассматривать как скалярное произведение век-
вектора A2.36) и e=(cosa, cos p, cos?)-
Итак, мы получаем, что
-^- = (e,grad«). A2.37)
де
С помощью равенства A2.37) убедимся, что градиент функции
u = f(x, у, г) в точке Мо характеризует направление и величину
максимального роста этой функции в точке Мо.
Точнее, докажем два утверждения:
1) производная функции u = f(x, у, г) в точке Мо по направ-
направлению, определяемому градиентом этой функции в указанной точ-
точке, имеет максимальное значение по сравнению с производной в
этой точке по любому другому направлению;
2) значение производной функции u = f(x, у, z) no направле-
направлению, определенному градиентом этой функции в данной точке,
равно | grad ы|, т. е. равно длине вектора grad и в данной точке.
Для доказательства указанных двух утверждений заметим, что
скалярное произведение двух векторов равно произведению длин
этих векторов на косинус угла между ними *. Поэтому выражение
A2.37) можно переписать в виде
—— =|е| |grad«| соэф,
де
где ф — угол между векторами е и grad и.
Учитывая, что |е| = 1, мы получим, что
— | grad и | cos ф.
де
Из последнего равенства вытекают оба утверждения 1) и 2).
Вди
самом деле, максимальное значение производной полу-
полуде
чится при cosq)=l, т. е. при совпадении направления е с направ-
направлением grad и, причем производная ди/де в этом направлении
равна j grad и |.
Доказанные два утверждения позволяют утверждать, что гра-
градиент не зависит от выбора системы координат (ибо и направле-
* Этот факт устанавливается в аналитической геометрии.
16*
484 Гл. 12. Функции нескольких переменных
ние, и длина вектора gradw в каждой данной точке инвариантны
относительно выбора системы координат).
Для выяснения геометрического смысла вектора grad и целе-
целесообразно ввести понятие поверхностей уровня функции
u=f(x, у, z), понимая под этим термином те поверхности, на ко-
которых функция u = f(x, у, z) сохраняет постоянное значение, т. е..
удовлетворяет соотношению f(x, у, z)=c = const.
Если в каждой точке М0{х°, у°, z°) поверхности уровня f(x, yr
z) = с построить касательную плоскость, то легко убедиться в
том, что нормальным вектором такой плоскости будет являться
вектор A2.36), т. е. gradw*. Отсюда следует, что вектор gradu
в каждой точке М поверхности уровня f(x, у, z)=c ортогонален к
этой поверхности.
Совершенно аналогично определяются производная по на-
направлению и градиент для дифференцируемой в данной точке
Mo(xi°, X2°, —,х°т) функции т переменных.
Для такой функции производная в данной точке
де
М0(х\°, Х2°,..., х°т) по направлению, определяемому единичным
вектором e=(cosai, соэаг, ...,cosaTO) **, вводится как обычная
производная по переменной / сложной функции u = f(xi°+
-Hcosai, Ar2°+/cosa2,...,x°m.+^cosaTO) взятая в точке /=0.
Для любой дифференцируемой в данной точке Мо(Х\°, х-?,...
...,х°т) функции u = f(xi, Xi,..., хт) производная в этой точке по
направлению, определяемому вектором e=(cosai, cosa2,...»
..., cosam), равна
-%- = -?- (Мо) cos ъ + -JL (Мо) cos a2 + ... + ^- (Мо) cos am.
де дхг дх2 дхт
A2.35*)
Градиентом дифференцируемой в данной точке М0(Х\°, Х2°,—
...,х°т) функции u=f(xi, X2,..., хт) называется вектор, обозна-
* Напомним, что нормальным вектором плоскости называется ненулевой
вектор, перпендикулярный к этой плоскости. В п. 3 настоящего параграфа была
установлено, что для поверхности, определяемой уравнением f(x, y)=z, нормаль-
нормальный вектор касательной плоскости в каждой точке этой поверхности имеет вид
I df df Л
• , —1 , Аналогично устанавливается, что для поверхности, опреде-
\ дх ду I
ляемой уравнением f(x, у, z)=c, нормальный вектор касательной плоскости в
/ df df df \
каждой точке этой поверхности равен • > —— = grad и.
\ dx dy dz I
** Так как все координаты единичного вектора по модулю не превосходят
единицы, то для каждой из этих координат найдется угол а, такой, что соответ-
соответствующая (=я координата равна cos ui (при этом можно считать, что Оёлх^я).
Таким образом, единичный вектор е можно записать в виде (cos cti, cos аг, ...,
..., cos-cim). Величины cos ai, cos аг, ..., cos am принято называть направляющими
косинусами.
§ 5. Производные и дифференциалы высших порядков 485
чаемый символом grad и имеющий координаты
ди , „. ¦. ди ... * ди ...
Так как скалярное произведение двух векторов простран-
пространства Ет равно сумме произведений одноименных координат этих
векторов, то равенство A2.35*) позволяет утверждать, что
-^- = (е, grad и).
де ¦
Из неравенства Коши—Буняковского, справедливого для
двух любых векторов пространства Ет *, вытекает, что
—— <|е| |gradы| = |gradы|,
де
причем знак ^ переходит в знак = только в случае, когда век-
векторы е и grad и коллинеарны.
Отсюда следует, что вектор grad и и в пространстве Ет обла-
обладает теми же двумя свойствами 1) и 2), что и в простран-
пространстве Ег.
Заметим, что в случае функции u=f{x, у) двух переменных
х и у единичный вектор е, определяющий направление в точке
Мо, имеет координаты cos а и sin а. Поэтому в указанном слу-
случае формула A2.35) принимает вид
ди ди ди ,
= cos a 4 sin а.
де дх ду
§ 5. ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
ВЫСШИХ ПОРЯДКОВ
1. Частные производные высших порядков. Пусть частная про-
ди , , .
изводная —— по аргументу х, функции u = f(X\, х2,...,хт), опре-
dxi
деленной в области {М}, существует в каждой точке области {М}.
В этом случае указанная частная производная представляет со-
* Для любых двух векторов а и b пространства Ет справедливо неравенство
Коши—Буняковского (а, ЬJ<(а, а) (Ь, Ь) или, что то же самое, | (а, Ь)|<3
<|а| |Ь|, причем в этом неравенстве знак < переходит в знак = только в слу-
случае, когда векторы а и b коллинеарны.
В самом деле, при любом вещественном X справедливо неравенство
(Яа—Ь, ка—Ь)=Я2(а, а)—2Ца, b) + (b, b)>0, причем в этом неравенстве знак
^ переходит в знак = только в случае, когда вектор Ка.—b является нулевым,
т. е. когда а и b коллинеарны. Исключая случай нулевого вектора а, когда до-
доказываемое неравенство заведомо справедливо со знаком =, мы можем утверж-
утверждать, что дискриминант квадратного трехчлена А,2 (а, а)—2Я,(а, b) + (b, b) удов-
удовлетворяет неравенству 4[(а, ЬJ—(a, a) (b, b)]^0, причем в этом неравенстве
знак ^ переходит в знак = только в случае, когда векторы а и b коллинеарны.
486 Гл. 12. Функции нескольких переменных
бой функцию переменных х\, Х2,-.,хт, также определенную в об-
области {М}.
да
Может случиться, что эта функция имеет частную про-
ОХ[
изводную по аргументу хи в некоторой точке М области {М}. То-
Тогда указанную частную, производную по аргументу хъ. называют
второй частной производной или частной производной второго по-
порядка функции u = f{x\, x2,...,xm) в точке М сначала по аргумен-
аргументу хи а затем по аргументу хи и обозначают одним из следующих
символом:
d*U гB) B)
При этом если 1фк, то частная производная назы-
вается смешанной частной производной второго порядка. По-
После того как введено понятие второй частной производной, можно
последовательно ввести понятие третьей частной производной, за-
затем четвертой и т. д.
Если предположить, что нами уже введено понятие (п—1)-й
частной производной функции u = f(xi, X2,...,xm) по аргументам
x(l, Xtt, ... , Xin i (отдельные или даже все номера которых мо-
могут совпадать) и что эта (я—-1)-я частная производная имеет в
точке М частную производную по аргументу х,п, то указанную
частную производную называют я-й частной производной
(или частной производной л-го порядка) функции и =
= {(х\, Х2,—,хт) в точке М по аргументам x(l, xiz, ... ,xin.
Таким образом, мы вводим понятие я-й частной производной
индуктивно, переходя от первой частной производной к последую-
последующим. Соотношение, определяющее я-ю частную производную по
аргументам xtlt Хсг, ...
дпи
дх, дх.
•ХЫ.гХ'п
dx{dxt
Если не все индексы iu
частная производная
дх,.
к, •
имеет вид
д
dxin
.., i
,.. дх, дх,
It t 1
i
п
\
дх{ ... dxi dxt I
совпадают между
называется с м е
собой,
ш анн
то
о и
частной производной n-го порядка.
Так как частная производная функции по аргументу х« опреде-
определяется как обыкновенная производная функции одной переменной
Xi при фиксированных значениях остальных переменных, то мето-
методика вычисления частных производных высших порядков предпо-
предполагает умение вычислять только обыкновенные производные перво-
первого порядка. В качестве примера вычислим частные производные
второго порядка функции u = arctg
у
§ 5. Производные и дифференциалы высших порядков
487
Имеем
ди
дх
дги
У
2ху
(х* + у2J
х2—у2
ди
ду
дги
дхду
д2и
X2
X2
(X2
-У2
±У*J
2ху
дудх
ду2
В рассмотренном примере смешанные частные производные
—— и —— равны друг другу. Вообще говоря, значения смешан-
дхду дудх
ных производных зависят от порядка, в котором производятся по-
последовательные дифференцирования. Убедимся, например, что
д2и д2и ,
смешанные частные производные и функции
дудх дхду
U =
О при х2+у2 = О
в точке @, 0) существуют, но не равны друг другу. Действительно,
ди
дх
при
при
Поэтому
д2и
дудх
ди
дх
х=0, у-ф.0
ди
дх
*=0, у=0
х=0, у=0
Проводя аналогичные вычисления, получим
д2и
дхду
= 1.
х=0, у=0
Таким образом, в точке @, 0) ф
н к ' дхду дудх
Выясним достаточные условия независимости значений смешан-
смешанных производных от порядка, в котором производятся последова-
последовательные дифференцирования.
Введем важное понятие функции т переменных, п раз диффе-
дифференцируемой в данной точке.
Определение. Функция u = f(xu Хг, ..., хт) называется п
раз дифференцируемой в точке M0(xi°, X20, ..., хт°), если все ее
частные производные порядка п—1 являются дифференцируемыми
в этой точке функциями.
Из этого определения вытекает, что если функция u = f (хь х2,...
) п раз дифференцируема в точке Мо, то при п> 1 любая ее
488 Гл. 12. Функции нескольких переменных
частная производная первого порядка п—1 раз дифференцируема
в точке Мо, при п>2 любая ее частная производная второго поряд-
порядка п—2 раз дифференцируема в точке Мо и т. д.
Укажем достаточное условие n-кратной дифференцируемости
функции в данной точке.
Для того чтобы функция u=f(xu х% ..., хт) была п раз диф-
дифференцируемой в точке M0(xi°, х20, ..., хт°), достаточно, чтобы все
ее частные производные п-го порядка были непрерывными
точке Мо.
Справедливость этого утверждения вытекает из опреде-
определения дифференцируемости функции и теоремы 12.10 о достаточ-
достаточных условиях дифференцируемости.
Теорема 12.13. Пусть функция u = f(x, у) дважды дифферен-
дифференцируема в точке М0(х0, г/о)- Тогда в этой точке частные производ-
производные fXJ/B) и fyxW равны.
Доказательство. Так как функция u = f(x, у) дважды диф-
дифференцируема в точке М0(х0, г/о), то частные производные )х' и fy'
определены в некоторой б-окрестности точки Мо и представляют
собой дифференцируемые функции в этой точке.
Рассмотрим выражение
Ф=/(хо+А, yo+h)—f{xo+h, yo)—f(xo, yo+h) +f(x0, г/о), A2.38)
где h — любое столь малое число, что точка M(xo+h, yo+h) на-
находится в указанной у-окрестности точки Мо. Выражение Ф мож-
можно рассматривать как приращение Лф = ф(хо + Л)—<р(#о) дифферен-
дифференцируемой на сегменте[лго, xo+h] функции <р(х) —f(x, yo+h)—f{x,y0)
одной переменной х. Поэтому по формуле Лагранжа, обозначая
через Э некоторое число из интервала 0<9<1, можно записать:
= {f/(xo+Qh, yo+h)—f{ )
A2.39)
= {[//(xo+e/i, yo+h)^f/{xo, г/о)]-[/*'(*о+e/i, yo)—f*'(*>, УоШ-
Так как частная производная // является дифференцируемой в
точке Мо функцией, то
[f/(xQ+Qh, yo+h)-fx'(xo, г/0)] =
= Р)хх(х0, yo)Qh+fWxy(xo, г/о)
[fx{xo+Qh, yo)—h'(xo,
где аь pi и а2 — бесконечно малые при Л->-0 функции. Подставляя
найденные выражения для \}х (xo+Qh, yo + h)—f/(xo, г/о)] и
[fx'(xo + Qh, г/о)—f/(xo, у0)] в формулу A2.39), получим
*о, yo)+aW, A2.40)
где a=ai0 + pi—аг9 — бесконечно малая при h->-0 функция. Сдру-
§ 5. Производные и дифференциалы высших порядков 489
гой стороны, выражение Ф, определяемое соотношением A2.38),
можно рассматривать как приращение Ai|; = i|)(r/o+/i)—я|;(г/о) диф-
дифференцируемой на сегменте [г/0, Уо+h] функции ^{y)=f{xo+h, у) —
Uxq, у)- Применяя формулу Лагранжа и учитывая дифференци-
руемость частной производной fy' в точке Мо, мы получим совер-
совершенно аналогично предыдущему следующее выражение для Ф:
A2.41)
где р— бесконечно малая при /i->0 функция. Приравнивая правые
части соотношений A2.40) и A2.41) и сокращая обе части полу-
полученного равенства на h2, найдем, что f-2)Xy(xo, уо)+а=
= f{2)yx(xo,Уй) +р. Так как аир — бесконечно малые при А->-0
функции, то из последнего равенства следует, что fi2)xy(xo, Уо) =
= р2)ух{хо, г/о). Теорема доказана.
Теорема 12.13 утверждает, что в данной точке Мо(хо, Уо) имеет
место равенство fB)*i/=/BV> если в этой точке дифференцируемы
fx и fy'. Из дифференцируемости f/ и fy' в точке Мо вытекает су-
существование в этой точке всех частных производных второго по-
порядка. Однако равенство fB)Xy и f^2)yx имеет место и при условии
существования лишь производных /B)жу и f<-2)yx, но при дополни-
дополнительном требовании непрерывности этих производных в рассмат-
рассматриваемой точке. Именно справедлива следующая теорема.
Теорема 12.13*. Пусть в некоторой окрестности точки
Мо(хо, г/о) функция u=f(x, у) имеет частные производные f/, fy,
f{2)xy, f{2)yx- Пусть, кроме того, производные ^2)ху и /B)Vx непрерыв-
непрерывны в точке Мо- Тогда в этой точке /<2)xV=/BV-
Для доказательства воспользуемся выражением Ф, определен-
определенным соотношением A2.38). Из A2.39) вытекает, что Ф представ-
представляет собой умноженную на h разность значений функции fx'(x, у)
в точках (xo+Qh, yo+h) и (xo + Qh, г/о)- Применяя к этой разности
формулу Лагранжа конечных приращений по переменной у на сег-
сегменте [г/о, г/0+/г], получим
Л, yo+Qih)h2, где
В силу непрерывности fWxy в точке М0(ха, г/0) из последнего ра-
равенства получаем
Ф = [р)*г/(^о, г/о)+а(А)]/г2,
где а(Л)->-0 при Л->-0.
С другой стороны, эта же величина Ф представляет собой умно-
умноженную на h разность значений функции fy'{x, у) в точках
{xo+h, уо+Qzh) и (дсо, г/о+бг^)..Применяя к этой разности формулу
Лагранжа конечных приращений по переменной х на сегменте
[*о, xo+h] и учитывая непрерывность fB)xv в точке М0(х0, уо), по-
получим
где р(А)->0 при h-*0.
490 Гл. 12. Функции нескольких переменных
Приравнивая последние два выражения для Ф и рассуждая так
же, как и в конце доказательства теоремы 12.13, мы убедимся в
справедливости нужного нам равенства
Докажем теперь теорему о независимости значения любой сме-
смешанной частной производной n-го порядка от порядка, в котором
производятся последовательные дифференцирования.
Теорема 12.14. Пусть функция u=f(x\, х2, ..., xm) п раз диф-
дифференцируема в точке M0(xi°, x2°,...,xm°). Тогда в этой точке зна-
значение любой смешанной частной производной п-го порядка не за-
зависит от порядка, в котором производятся последовательные диф-
дифференцирования.
Доказательство. Очевидно, достаточно доказать незави-
независимость значения любой n-й смешанной производной от порядка
проведения двух последовательных дифференцирований. Иными
словами, достаточно доказать равенство
дПи ¦ - д"и A2 42)
дх'п¦ ¦ ¦ dx'k+ldx'k¦ ¦ -д\ <Ч- • • dx'kdx<k+l¦ ¦ ¦ дХН
Рассмотрим функцию Эта функция представляет со-
dxik_v. .dxit
бой дважды дифференцируемую функцию переменных ж,- и Xt
Поэтому в силу теоремы 12.13
dx'k+idx'kdx'k-v --dxH dx'kdx'k+1dx'k-i- ¦ -д\
Отсюда и вытекает справедливость равенства A2.42). Теорема
доказана.
Отметим, что в случае п раз дифференцируемой в точке Мо
функции u = f(x\, X2 Хщ) любую ее частную производную п-го
порядка можно записать в виде
где аь аг, ..., ат — целые числа, удовлетворяющие условиям:
2. Дифференциалы высших порядков. Выше мы использовали
для обозначения дифференциалов аргументов функции ¦ и =
= f(x\, x2, ..., хт) и для обозначения дифференциала самой этой
функции символы dxu dx2 dxm и du соответственно.
Теперь нам придется использовать для обозначения дифферен-
дифференциалов аргументов указанной функции и дифференциала самой
этой функции и другие символы. В частности, мы будем обозна-
§ 5. Производные и дифференциалы высших порядков 491
чать дифференциалы аргументов функции u=f(xu х2, ..., хт) и диф-
дифференциал самой этой функции символами Ьх\, Ьх2, ..., 8хт и бы
соответственно. В этих обозначениях инвариантное по форме вы-
выражение для первого дифференциала этой функции A2.20) (см.
п. 7, § 3), будет иметь вид
бы = -— 6*! + -— 6х2+ ...+—— Ьхт.
дхг одг2 охт
Возвращаясь к прежним обозначениям, рассмотрим выражение
A2.20) для первого дифференциала дифференцируемой в данной
ТОЧКе М(Х\, Х2, ... , Хт) ФУНКЦИИ U — f(xU X2, ... , Хт):
du = -^-dx1 + -^-dx,+ ...+-^dxm. A2.20)
дх! дхг дхт
Предположим, что величина, стоящая в правой части A2.20),
представляет собой функцию аргументов х\, х2, ..., хт, дифферен-
дифференцируемую в данной точке М{х\, х2, ..., хт). Для этого достаточно
потребовать, чтобы функция u=f(x\, x2, ..., хт) была два раза
дифференцируема в данной точке М(х\, х2, ..., хт), а аргументы
Х\, х2, ..., хт являлись либо независимыми переменными, либо два
раза дифференцируемыми функциями некоторых независимых пе-
переменных t\, t2, ..., tk.
При этих предположениях мы можем рассмотреть дифферен-
дифференциал
*=i
от величины A2.20).
Определение 1. Значение 8{du) дифференциала от первого
дифференциала A2.20), взятое при 8xi = dxu 8x2 = dx2, ..., bxm=dxm,
называется вторым дифференциалом функции м =
— f(xu х2, ..., хт) (в данной точке М(хи х% ..., хт) и обозначается
символом d2u.
Итак, по определению *
Дифференциал dnu любого порядка п введем по индукции.
* Символ{ }
обозначает, что в выражении, заключенном в фи-
фигурные скобки, следует положить 6x1=dxi, 6x2=^x2 6xm=dxm.
492
Гл. 12. Функции нескольких переменных
Предположим, что уже введен дифференциал dn~lu порядка ¦
я—1 и что функция u = f(x\, х2 хт) п раз дифференцируема в
данной точке М(хи х2, ..., хт), а ее аргументы х\, х2, ..., хт явля-
являются либо независимыми переменными, либо п раз дифференци-
дифференцируемыми функциями некоторых независимых переменных t\, t2, ...
..., h.
Определение 2. Значение 8(dn~lu) дифференциала от
(п—\)-го дифференциала dn~xu, взятое при bx\ = dx\, bx2 = dx2, ...
..., 6xm = dxm, называется п-м дифференциалом функции «=
=*f(xu x2,...,xm) (в данной точке М(хи Х2,...,хт)) и обозначается
символом dnu.
Итак, по определению
При вычислении второго и последующих дифференциалов du
приходится существенно различать два случая: 1) случай, когда
аргументы х\, х2, ..., хт являются независимыми переменными,
2) случай, когда аргументы х\, х2, ..., хт являются соответствую-
соответствующее число раз дифференцируемыми функциями некоторых незави-
независимых переменных /ь t2, ..., tk.
Рассмотрим сначала первый случай. Если х\, х2, ..., хт явля-
являются независимыми переменными, то мы имеем право считать,
что dx\, dx2, ..., dxm не зависят от х\, х2, ..., хт.
Кал<дый дифференциал dxk мы можем взять равным одному и
тому же приращению Ая& для всех точек М(х\, х2, ..., хт). При
этом мы получим, что
Последнее соотношение и правила дифференцирования, уста-
установленные в конце п. 7 § 3, позволяют нам записать для два раза
дифференцируемой в данной точке М функции u=f(xi, x2, ..., хт),
следующую цепочку равенства:
dht = S(du)
[
§ 5. Производные и дифференциалы высших порядков 493
i-Ji». дх,
k=li=l
idxk J
m tn
A2.43)
(Мы воспользовались еще и тем, что для два раза дифференцируе-
дифференцируемой функции смешанные производные второго порядка не зависят
от того, в какой последовательности производится дифференци-
дифференцирование).
Итак, мы получаем, что в случае, когда аргументы х\, х2, ..., хт
являются независимыми переменными, для второго дифференциала
два раза дифференцируемой в данной точке функции и=
=f(x\, X2, ..., хт) справедливо представление
^-dxA*. A2.44)
Xdx
Замечание 1. Функция т переменных tu t% —, tk вида
m m
<Ф = К\ S\aJitkt где a,-ft — постоянные вещественные числа, на-
i=i k=i
зывается квадратичной формой от переменных t\, t% ..., tk,
.а числа а,& —• ее коэффициентами.
Квадратичная форма называется симметричной, если ее
-коэффициенты удовлетворяют условию Щн — пы (для всех i =
= 1, 2, ..., т; k=\, 2, ..., т).
Полученное нами выражение A2.44) позволяет утверждать, что
для случая, когда аргументы х\, х% ..., хт являются независимыми
переменными, второй дифференциал два раза дифференцируемой
:в данной точке М функции u = f(xi, x%, ¦¦¦, хт) представляет собой
-симметричную *, квадратичную форму от переменных dx\, dx-i, —
..., dxm, коэффициенты которой равны соответствующим частным
.производным второго порядка функции u — f(xi, х2, ..., хт), взятым
;В данной точке М.
Отметим, что полученное нами выражение для дифференциала
второго порядка A2.44) можно переписать и в другом виде, ис-
используя формальный символ
% ^-+ ... +dxm-?-. A2.45)
дхг дхт
* Симметричность этой квадратичной формы вытекает из равенства
д2и дЧ
Щ) Щ).
494
Гл. 12. Функции нескольких переменных
С помощью этого символа выражение A2.44) может быть пе-
переписано в виде
~ V- A2.46)
По индукции легко убедиться в том, что в случае, когда аргу-
аргументы х\, х2, ..., Хт п раз дифференцируемой в данной точке
М(хи х2, ..., хт) функции u=f(xu х2, •••, хт) являются независи-
мыми переменными, для л-го дифференциала этой функции спра-
справедливо представление
д"и
=i h
дх, дх, ... дх,
»„=1 *' н '«
Это представление с помощью формального символа A2.45)
может быть переписано в виде
дх2
dx2J-+...+dxm-?-Yu.
дхг
дхт)
A2.47)
Совершенно другой вид имеют представления для второго и
последующего дифференциалов в случае, когда аргументы
Х\, х2, ..., хт функции u=f(xi, x2, ..., хт) являются соответствую-
соответствующее число раз дифференцируемыми функциями некоторых незави-
независимых переменных t\, t2, ..., tk.
Обращаясь к этому случаю, установим выражение для второго
дифференциала два раза дифференцируемой в данной точке
М(хи х2, ..., хт) функции u = f(xu x2, ..., хт), аргументы х\, х2, ...
..., хт которой являются два раза дифференцируемыми функциями
некоторых независимых переменных t\, t2, ..., tk.
Повторяя рассуждения из цепочки A2.43), мы на этот раз
получим
fm
d*u = 6 (du)
6хт~ахт-
Заметим, что в силу определения второго дифференциала функ-
функции u—Xk (где k — любой из номеров 1, 2, ..., т)
= и лк.
§ 5. Производные и дифференциалы высших порядков 495
Учитывая это соотношение, мы приходим к следующему пред-
представлению для второго дифференциала:
или (с использованием символа A2.45))
d2u= fdx *+dx ,-?- + .. ^
\ дх дхг дхт]
%L ^L) A2.48)
Сравнивая полученное нами представление A2.48) с представ-
представлением A2.46), мы убедимся в том, что (в отличие от первого
дифференциала) второй дифференциал уже не обладает свойством
инвариантности формы.
Тем более не обладают свойством инвариантности формы все
последующие дифференциалы.
Замечание 2. Укажем важный частный случай, когда второй
и последующие дифференциалы функции т переменных и=
= /(*!, х2, ..., хт) все же обладают инвариантностью формы и оп-
определяются той самой формулой A2.47), что и для случая незави-
независимых переменных х\, х2, ..., хт.
Будем говорить, что переменные х\, х2, ..., хт являются линей-
линейными функциями независимых переменных t\, t2, ..., tk, если
они определяются равенствами
Xi = aio + anti+ai2t2+ ... +aiktk (t=l, 2, ..., m),
в которых через а-о, ац, —, сць. обозначены некоторые постоянные.
Заметим, что если функция u = f(xit x2, ..., хт) является п раз
дифференцируемой в данной точке М{х\, х2 хт), а ее аргумен-
аргументы Х\, Х2, ..., хт являются линейными функциями независимых пе-
переменных t\, t2, ..., tk, то п-й дифференциал функции u = f(xx, x2, ...
..., хт) определяется той же самой формулой A2.47), что и для
случая независимых переменных хи х2, ..., хт.
Для того чтобы убедиться в этом, заметим, что
поскольку t\, t2, ..., tk являются независимыми переменными, то
п-й дифференциал Xi как функции аргументов U, t2, ..., tk опреде-
определяется равенством типа A2.47), а точнее, равенством
d%= (dt°+dt*+... +dt*)nXi.
Но любая частная производная выше первого порядка от ли-
линейной функции xi равна нулю.
Значит, d2 d3
496 Гл. 12. Функции нескольких переменных
Равенство d2xi = 0 (при всех i—\, 2, .... т) и представление
A2.48) дают право заключить, что d2u определяется равенством
A2.46). Совершенно аналогично, используя соотношения dzxi = 0, ...
..., dnXi = 0, мы по индукции докажем, что d3u, d4u dnu опреде-
определяются равенством A2.47).
Замечание 3. При проведении вычислений иногда требу-
требуется расшифровать равенство A2.47) и, учитывая, что в этом
равенстве имеются совпадающие члены, выписать все различные
члены этого равенства со стоящими перед ними коэффициен-
коэффициентами.
Для этой цели может быть использована формула поли-
полинома Ньютона, имеющая вид
= У
(«г + «2+ >• • + «")'fl««fl«. ... fl«m. A2.49)
a±\ <x2l ... ccml m
(Суммирование в правой части этой формулы идет по всем це-
целочисленным индексам ссь ссг, ..., am, каждый из которых удов-
удовлетворяет неравенствам 0<:а;<:/г при условии, что сумма всех
этих индексов cci + a2+ ... +пт равна п.)
Формулу A2.49) нетрудно установить по индукции. В самом
деле, при т = 2 и любом целом п эта формула заведомо спра-
справедлива, ибо она переходит в известную формулу бинома Нью-
Ньютона.
Предположим, что эта формула справедлива для некоторого
номера т>2 и любого целого п, и проверим, что в таком слу-
случае она справедлива и для номера пг+1 и любого целого п.
Представив (ai+a2+ ... +ат + ат+1)п в виде
+ат+1]п,
подсчитаем с помощью бинома Ньютона коэффициент при
а^'а% . ¦ • аттат+11- В силу равенства a.i + a2+ ... +am+i=«, фор-
формулы бинома Ньютона и предположения о справедливости фор-
формулы A2.49) для номера т и любого целого п этот коэффици-
коэффициент равен *
i! a2! ... am!
Мы учитываем, что С„ = —— > и потому
«I (л — k)\
гат+1 рат и
§ 5. Производные и дифференциалы высших порядков 497
_ (Oil + «2+ ¦ • • + Pffi
ax!a2l...am!
ax! a2! ... am! am+1!
Полученное нами выражение для коэффициента прш
а%'а%\ . .a^"aam+l в точности совпадает с тем выражением, ко-
которое получится из формулы A2.49), если в этой формуле за-
заменить номер т на т+\.
Индукция завершена, и формула A2.49) доказана.
Формула A2.49). дает нам право переписать выражение
A2.47) для л-ro дифференциала в следующем виде:
3. Формула Тейлора с остаточным членом в форме Лагранжа ш
в интегральной форме. Договоримся обозначать k-й дифференциал
функции т переменных u=f(xi, х% ..., хт) в точке М пространства'
Ет символом с1ки\м-
Докажем следующую важную теорему.
Теорема 12.15. Пусть л>0 — целое число, функция и—
— f{x\, X2 Хщ) задана в некоторой г-окрестности* точки
М0(хи х2, ..., хт) и л+1 раз дифференцируема в указанной окре-
окрестности. Тогда полное приращение Au=f(M)—f{M0) этой функции!
в точке М может быть представлено в следующей форме:
м. 2!
— dnu
+
м0 (n+l)!
N
A2.50)
при этом N — некоторая точка указанной окрестности зависящая,
вообще говоря, от М(хи х%, ..., хт), а дифференциалы, dxi пере-
переменных Хи входящие в выражения dku\Mo и d"+1«|.jvi- равны Axi=
— xi—хр. Формула A2.50) называется формулой Тейлора
для функции u = f(M) с центром разложения в точке-
Мо, а последний член формулы A2.50) называется остаточ-
остаточным членом, записанным в форме Лагранжа.
Доказательство. Для сокращения записи проведем рас-
рассуждения для функции u—f(x, у) двух переменных х ну. Предва-
Предварительно запишем в специальной форме формулу Тейлора для?
л+1 раз дифференцируемой в некоторой окрестности точки to,-
функции u=F(t) одной переменной t. Напомним, что формула Тей-
* Вместо е-окрестности точки Мо можно взять любую звездную окре-
окрестность этой точки (т. е. любое открытое множество, содержащее точку Afo>
и обладающее следующим свойством: если точка М принадлежит этому множе~
ству, то и весь отрезок прямой МоМ ему принадлежит).
498 Гл. 12. Функции нескольких переменных
лора с центром разложения в to для функции u = F(t) одной пере-
переменной имеет следующий вид:
F(t) = F (t0) + F (g (f-Q + -i- Я2' (g (t-toy +...
(t-t0)) (t
(ttor + t ] ,
0 < 6< 1. A2.51)
Так как аргумент t является независимой переменной, то прира-
приращение At = t—t0 представляет собой дифференциал dt независимой
переменной t. Поэтому
Я« (д (/-/„)* = Я*>(/») Л* = dkF(t0) = d>u\u
« A2.52)
FC+D (/„ + 6(^-g) (t-tor+l =d«+>u\to+(Ht-to).
Если мы обозначим разность F(t)—F(t0) через Аи, то согласно
A2.52) формулу Тейлора A2.51) можно записать в следующей
специальной форме:
-f
и
1
2!
d2u
+
1
n\
dnu
(n+l)!
A2.53)
^Рассмотрим теперь в е-окрестности точки Мо(хо, г/о) произвольную
точку М(хо+Ах, уо+Ау) и соединим точки Мо и М прямой лини-
линией. Очевидно, координаты х и у точек указанной прямой представ-
представляют собой следующие линейные функции новой переменной t:
x=xo+tAx, y = yQ+tAy\ A2.54)
шри этом координаты точек отрезка М0М соответствуют значениям
переменной t из сегмента [0, 1]. Отметим, что значению t=0 отве-
отвечает точка Мо, а значению ^=1 — точка М. Так как по условию
«функция «=/(*, у) двух переменных хну п+1 раз дифференци-
дифференцируема в рассматриваемой окрестности точки Мо, то из формул
A2.54) вытекает, что на прямой М0М эта функция является слож-
сложной функцией переменной t из сегмента [0, 1]. Обозначим эту
•сложную функцию через F(t) и запишем для нее формулу Тейло-
Тейлора с центром разложения в точке ?0=0 в специальной форме
A2.53) при
Au=F(l)-F(O)=f(M)-f(Mo).
'Фигурирующие в формуле A2.53) дифференциалы различных по-
порядков представляют собой дифференциалы сложной функции и =
=f(x> У)> где хну являются линейными функциями A2.54). Сог-
-ласно замечанию 2 предыдущего пункта при этих условиях диф-
«ференциалы любого порядка функции u=f(x, у) могут быть запи-
записаны в форме A2.47). Поэтому
§ 5. Производные и дифференциалы высших порядков 499*
dku | <о=о = [dx -|- + dy -$-) и | Ma{x0,u0)dku | м„ A2.55)-
причем в формулах A2.55) dx и Л/ находятся из соотношений:
A2.54) при dt=At=l—O=l. Таким образом, в формулах A2.55)
dx=dtAx=Ax и dy = dtAy = Ay. A2.56>
Подставляя d*u|<, и ^п+хы | <0+в(г-<„) из A2.55) в формулу A2.53)
и учитывая соотношения A2.56), мы получим формулу Тейлор*
A2.50).
Приведем развернутое выражение формулы Тейлора A2.50)?
для функции u — f{x\, х2, ..., хт):
f (Xlt X2, . . ., Хт) = f (X°u
х/С,
«—хт) -—
+ 6 (х.-хЧ), 4+6(^-4), .. .,x°m+Q(xm-x°m)). A2.57>
Следствие. ?слм функция u = f(xh x2, ..., л:т) удовлетво-
удовлетворяет тем же условиям, что и в теореме 12.15, и, сверх того, все-
частные производные этой функции порядка п+ 1 непрерывны в-
рассматриваемой ^-окрестности точки Мо, то остаточный член^
т. е. последний член в формулах A2.50) и A2.57), может быть-
записан в виде
] х
х\), х\ + t(x2- х°2) x°m + t (xm~x°m)) dt.
Такую форму остаточного члена естественно назвать инте-
интегральной. Для получения формулы Тейлора с остаточным-
членом в интегральной форме следует записать в интегральной
форме остаточный член в формуле Тейлора для функции одной
переменной F{t), рассмотренной при доказательстве теоремы
12.15, т. е. воспользоваться результатами п. 4 § 4 гл. 9. В рас-
Гл. 12. Функции нескольких переменных
сматриваемом случае указанный остаточный член имеет вид
{Я"+» (/)(!_ tfdt.
о
—
Это и приводит нас к написанному выше выражению остаточно-
остаточного члена для функции u=f(x\, я2, ..., хт).
4. Формула Тейлора с остаточным членом в форме Пеано.
Теорема 12.15*. Пусть л>1 — целое число, функция и =
=f(M)=f(xi, х2 Хт) задана и п—1 раз дифференцируема в
«-окрестности точки M0(xi°, х20, ..., хт°) и п раз дифференцируе-
дифференцируема в самой точке Мо *.
Тогда для любой точки М из указанной г-окрестности справед-
справедлива следующая формула:
, 1
1!
м„
21
п\
Af,
A2.58)
ve которой через р обозначено расстояние р(Л10, М), а символ
>о(рп) обозначает бесконечно малую при р-*-0 (или при М-+Мо)
функцию более высокого порядка малости, чем рп.
Формула A2.58) называется формулой Тейлора (с цент-
центром в точке Мо) с остаточным членом в форме Пеано.
Замечание. В более подробной записи формула Тейлора
i( 12.58) имеет вид
f (Х1> Х2> • • • > xm) —f(Xl, Хч, ¦ . ¦ , Хт) +
X /(*?, х°2,
х°т) + о(рп).
A2.59)
Заметим, что в правой части A2.59) стоит сумма многочлена
«степени п от т переменных Х\, х%, ..., хт и остаточного члена о(р").
Обозначим через gn(M) разность между f{M) и указанным
.многочленом, т. е. положим
+ К-
A2-60)
Теорема 12.15* будет доказана, если мы установим, что при
выполнении условий этой теоремы gn{M) =o(p").
• При я=1 следует требовать, чтобы функция u=f(M) была только задана
ш е-окрестности точки Мо и дифференцируема в самой точке Мо.
§ 5. Производные и дифференциалы высших порядков 501
Доказательству теоремы 12.15* предпошлем две леммы.
Лемма 1. Если функция f(M)=f(xi, х% ..., хт) п раз диффе-
дифференцируема в точке M0(xi°, X20 Хт°), то как сама функция
gn(M), определяемая равенством A2.60), так и все ее частные
производные по любым переменным х\, х2, ..., хт до порядка п
включительно обращаются в нуль в точке Мо.
Доказательство. При л=1 функция A2.60) принимает вид
-(x1-xb -У- (Мо)- ... -(xm-x°m)f-{M0),
ОХ.-1 axm
и равенства gi{M0)—0, —— (yWo)=O при всех t=l, 2, ...,
m
веряются элементарно.
Для проведения индукции предположим, что лемма справедли-
справедлива для некоторого номера я>1, и докажем, что в таком случае
она справедлива и для номера я+1.
Пусть функция f{M) я+1 раз дифференцируема в точке Мо и
п+1
= f(M)-f(MD)-Yl±\(xl-x°l)-?-+ ... +(xm-x°m)JL\kf(M0).
A2.61)
Равенство gn+i(M)=0 проверяется элементарно (достаточно
учесть, что каждая круглая скобка (xi—хр) в A2.61) обращается
в нуль в точке Мо).
Нам остается доказать, что для любого t=l, 2, ..., m сама
функция g"+1 Щ) и все частные производные этой функции до
ОТ/
порядка я включительно обращаются в нуль в точке Мо, а для
этого в силу сделанного нами предположения о справедливости
леммы для номера п достаточно доказать, что функция
8n+
определяется равенством типа A2.60), а точнее, равенством
-Si [<*-9 -k + • • •+<**-<> ¦?]'¦&»*¦ A2-62)
Так как все переменные xi (t=l, 2, ..., т) равноправны и вхо-
входят в выражение для gn+i {Щ симметрично, то достаточно дока-
доказать равенство A2.62) для i=l, т. е. доказать равенство
502 Гл. 12. Функции нескольких переменных
дхг
i
Из A2.61) очевидно, что для доказательства A2.63) достаточ-
достаточно убедиться, что для каждого номера k=l, 2, ..., я+1 при фик-
фиксированных Х2, Хз, ... , Хт
*"' It (Л)°>-
A2.64)
Так как при дифференцировании по х\ переменные х% хз, ...
., хт фиксированы, то величину
5*2 т дхт
при дифференцировании по Xi можно рассматривать как постоян-
постоянную. К этому следует добавить, что поскольку символы——,——,
... , используются для образования частных производных
дхт
функции f в фиксированной точке Мо, то при дифферен-
дифференцировании по Х\ указанные символы нужно рассматривать как па-
стоянные величины.
В силу сказанного для доказательства равенства A2.64) доста-
достаточно убедиться в справедливости равенства
_i_ UXx — х$ -*_ + d]* = A—[(*!—*") — + d]*~!. A2.65)
(хг + х°) f- D\ no jti как
сложную и учитывая отмеченную выше независимость от х\ сим-
символов D и , мы получим равенство A2.65). Индукция завер-
завершена.
Лемма 1 доказана.
Лемма 2. Пусть g{M)=g(x\, х2, ..., Хщ)—произвольная
функция, удовлетворяющая двум требованиям:
1) g(M) п раз дифференцируема в точке M0{xi°, х20, ..., хт°);
2) сама функция g(M) и все ее частные производные по любым
переменным х\, х2, ..., хт до порядка п включительно обращаются
§ 5. Производные и дифференциалы высших порядков 50$
в нуль в указанной точке Мо. Тогда для функции g(M) справедли-
справедлива оценка
g(M)=o(p"), A2.66)
в которой через р обозначено расстояние р(Л1, Л1о) между точка-
точками М и Мо.
Доказательство. При я=1 утверждение леммы вытекает
из условия дифференцируемости * функции g(M) в точке Мо, ко-
торое имеет вид
Учитывая, что g{M0) = 0, —— (М0) = 0 для всех t=l, 2, ..., m мы
дх{
и получим, что g(M) =o(p).
Для проведения индукции предположим, что лемма 2 справед-
справедлива для некоторого номера я>1, и докажем, что в таком случае
она справедлива и для номера я+1.
Пусть функция g(M) удовлетворяет двум требованиям леммы
2 для номера п+\. Тогда, очевидно, любая частная производ-
производная этой функции первого порядка —— (М), t = l, 2, ..., m, будет
OXi
удовлетворять двум требованиям леммы 2 для номера я, а по-
потому (в силу сделанного нами предположения о справедливости
леммы 2 для номера я) будет справедлива оценка
Ji o(pn). A2.66*)
dxt
Заметим теперь, что поскольку я>1, то я+1>2 и функция
g(M), удовлетворяющая двум требованиям леммы 2 для номера
п+1, во всяком случае, один раз дифференцируема в окрестности
точки Мо. Поэтому для этой функции g(M) выполнены условия
теоремы 12.15 для номера я = 0. Согласно указанной теореме для
любой точки М из достаточно малой е-окрестности точки Мо на
отрезке ** М0М найдется точка N такая, что справедлива формула
т
g(M) = g {МЛ+ — У, {xt—x$ -^- (N). A2.67)
1! ^J bxi
Заметим теперь, что поскольку точка N лежит между точками
Мо и М, а р — это расстояние между точками Мо и М, то
p(N, уИ0)<:р, и потому из A2.66*) вытекает, что
дх{
* См. соотношение A2.16) из п. 2 § 4 настоящей главы.
** Т. е. на множестве точек вида M0 + t(M—Л10), где t — любое число из
сегмента
504 Гл. 12. Функции нескольких переменных
Подставляя последнюю оценку в A2.67) и учитывая, что g{M0)
= 0, мы получим
i=\
Так как \Xl—x\\< l/ fj (*<-х°)
то мы окончательно по
лучим, что g(M) = o(pn+l).
Индукция завершена. Лемма 2 доказана.
Доказательство теоремы 12.15* легко провидится с по-
помощью леммы 1 и 2.
В самом деле, выше уже отмечалось, что для доказательства
теоремы 12.15 достаточно установить, что при выполнении усло-
условий этой теоремы для функции A2.60) справедлива оценка
В силу леммы 1 сама функция A2.60) и все ее частные произ-
производные по любым переменным х\, х2, ..., хт до порядка я включи-
включительно обращаются в нуль в точке Мо. Но тогда в силу леммы 2
для функции A2.60) справедлива оценка gn(M) =o(pn). Теорема
12.15* доказана.
§ 6. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ m
ПЕРЕМЕННЫХ
1. Понятие экстремума функции m переменных. Необходимые
условия экстремума. Пусть функция т переменных u=f(M) =
= f(xi, x2, ..., хт) определена в некоторой окрестности точки
Мо(*1°, х20, ..., хт°) пространства Ет.
Определение 1. Будем говорить, что функция u=f(M}
имеет в точке Мо локальный максимум [локальный
минимум], если найдется такая 8-окрёстность точки Мо, в пре-
пределах которой значение f(M0) является наибольшим [наименьшим]
среди всех значений f{M) этой функции.
Определение 2. Будем говорить, что функция u=f(M}
имеет в точке Мо локальный экстремум, если она имеет в
этой точке либо локальный максимум, либо локальный минимум.
Установим необходимые условия локального экстремума функ-
функции u=f(M), обладающей в данной точке Мо частными,производ-
частными,производными первого порядка по всем переменным.
Докажем следующее
Утверждение. Если функция u=f(M)=f(xu х2, ..., хт}
обладает в точке M0(xi°, х2°, ..., хт°) частными производными пер-
первого порядка по всем переменным х\, х2, ...., хт и имеет в этой
§ 6. Локальный экстремум 505
точке локальный экстремум, то все частные производные первого
порядка обращаются в точке Мо в нуль, т. е.
¦Р-(МО) = О. -р-{М0) = 0, ... ,^-{М0) = 0. A2.68)
дхг oXi axm
Доказательство. Установим справедливость первого ра-
равенства A2.68). Фиксируем у функции u=f(xu х2 хт) аргу-
аргументы х2, хг, ..., хт, положив их равными соответствующим коор-
координатам точки Мо, т. е. положив х2 = х2°, Хз = х3°, ..., хт=хт°. При
этом мы получим функцию u = f(xi, х20, ..., хтп) одной переменной
Xi. Производная этой функции одной переменной в точке Xi = xi°
совпадает с частной производной (Мо).
Так как функция т переменных u=f(M) имеет локальный
экстремум в точке Мо, то указанная функция одной переменной
a — f(xu X20, ..., Хт°) имеет локальный экстремум в точке Xi = xi°,
и поэтому (в силу результатов п. 2 § 1 гл. 7) производная этой
функции одной переменной в точке х\ — х\°, совпадающая с част-
частной производной WQ), равна нулю.
дхг
Первое равенство A2.68) доказано. Остальные равенства
A2.68) доказываются аналогично.
Подчеркнем, что равенства A2.68) (т .е. обращение в нуль в
данной точке Мо всех частных производных первого порядка) яв-
являются лишь необходимыми и не являются достаточными усло-
условиями локального экстремума функции u=f{M) в точке Мо.
Например, у функции двух переменных и — ху обе частные
производные и обращаются в нуль в точке М0{0, 0), но
дх ду
никакого экстремума.в этой точке М0@, 0) указанная функция не
имеет, ибо эта функция и=ху равна нулю в самой точке уИо@, 0),
а в как угодно малой б-окрестности этой точки принимает как
положительные, так и отрицательные значения.
Точки, в которых обращаются в нуль все частные производные
первого порядка функции u—f(M), называются стационарны-
стационарными точками этой функции.
В каждой стационарной точке у функции u=f(M) возможен
локальный экстремум, однако наличие этого экстремума можно
установить лишь с помощью достаточных условий локального экс-
экстремума, выяснению которых посвящен следующий пункт.
Из доказанного выше утверждения вытекает и другая форма
необходимых условий локального экстремума: если функция и =
= f(M) дифференцируема в-точке Мо и имеет в этой точке локаль-
локальный экстремум, то дифференциал cLu\m° этой функции в точке
Мо равен нулю тождественно относительно дифференциалов неза-
независимых переменных dx\, dx2, ..., dxm.
506 Гл. 12. Функции нескольких переменных
В самом деле, поскольку
то из равенств A2.68) вытекает, что при любых йх\, dx2, ..., dxm
справедливо равенство ^ы|мо=О-
2. Достаточные условия локального экстремума функции m пе-
переменных. При формулировке достаточных условий локального
экстремума функции т переменных u—f(M) важную роль будет
играть второй дифференциал этой функции в обследуемой точ-
точке Мо.
В п. 2 § 5 настоящей главы мы убедились в том, что для слу-
случая, когда аргументы х\, х2 хт два раза дифференцируемой
функции u=f(x\, х2, ..., Хт) являются либо независимыми перемен-
переменными, либо линейными функциями некоторых независимых пере-
переменных, второй дифференциал этой функдии в данной точке Мо
представляет собой квадратичную форму относительно дифферен-
дифференциалов аргументов dxu dx2, ..., dxm следующего вида:
? d*t, A2-69)
i=i k=\
где
•atk=akl = -^-(M0). A2.70)
Для формулировки достаточных условий локального экстрему-
экстремума нам понадобятся некоторые сведения из теории квадратичных
форм, которые мы для удобства читателя приводим ниже *.
Квадратичная форма относительно переменных h\, h2, ..., hm
т т
Ф (Alf h2, ... , hm) = J] j; aikhthk A2.71)
называется положительно определенной [отрица-
[отрицательно определенной], если для любых значений hi, h2, ...
...,hm, одновременно не равных нулю, эта форма принимает стро-
строго положительные [строго отрицательные] значения.
Квадратичная форма A2.71) называется знакоопределен-
н о й, если она является либо положительно определенной, либо
отрицательно определенной.
Квадратичная форма A2.71) называется знакоперемен-
знакопеременной, если она принимает как строго положительные, так и строго
отрицательные значения.
* Все приводимые здесь определения и утверждения можно найти, например,
в книге В. А. Ильина и Э. Г. Позняка «Линейная алгебра», (М., Наука, 1974).
§ 6. Локальный экстремум 507
Квадратичная форма A2.71) называется к в а з и з н а к о о п р е-
деленной, если она принимает либо только неотрицательные,
либо только неположительные значения, но при этом обращается в
нуль для некоторых значений h\, h2, ..., hm, одновременно не рав-
равных нулю.
Сформулируем так называемый критерий Сильвестра
знакоопределенности квадратичной формы *.
Назовем матрицей квадратичной формы A2.71)
следующую матрицу:
(апа12 ... а1т
hm I- A2.72)
а11
ап
а
а12..
а221.
а
¦а1т
• &%т
-атт
Если все элементы матрицы А удовлетворяют условию aik~
= пы (t=l, 2, ..., т; k=\, 2 т), то указанная матрица назы-
называется симметричной.
Назовем главными минорами симметричной матрицы
A2.72) следующие определители:
апа12 д _ auai2ai3
t **ч — п п п
81 а31а32а33
Критерий Сильвестра формулируется в виде следующих двух
утверждений.
Г. Для того чтобы квадратичная форма A2.71) с симметричной
матрицей A2.72) являлась положительно определенной, необходи-
необходимо и достаточно, чтобы все главные миноры матрицы A2.72) были
положительны, т. е. чтобы были справедливы неравенства
Ai>0, A2>0, ..., Лт>0.
2°. Для того чтобы квадратичная форма A2.71) с симметрич-
симметричной матрицей A2.72) являлась отрицательно определенной, необ-
необходимо и достаточно, чтобы знаки главных миноров матрицы
A2.72) чередовались, причем знак А\ был отрицателен, т. е. чтобы
были справедливы неравенства
Л,<0, Л2>0, Л3<0, Л4>0, ....
Теперь мы подготовлены для того, чтобы сформулировать и
доказать теорему, устанавливающую достаточные условия локаль-
локального экстремума.
Теорема 12.16. Пусть функция т. переменных u=f(M) =
—f{xi, x% ..., хт) один раз дифференцируема в некоторой окрест-
окрестности точки М0{ху°, х20, ..., х,п°) и два раза дифференцируема в
самой точке Мо. Пусть, кроме того, точка Мо является стационар-
* Дж. Сильвестр — английский математик A814—1897).
508 Гл. 12. Функции нескольких переменных
ной точкой функции u=f(M), т. е. du\MQ=0. Тогда если второй
дифференциал A2.69), A2.70) представляет собой положительно
определенную [отрицательно определенную] квадратичную форму
от переменных dxu dxi, —, dxm, то функция u=f(M) имеет в точке
Мо локальный минимум [локальный максимум]. Если же второй
дифференциал A2.69), A2.70) представляет собой знакоперемен-
знакопеременную квадратичную форму, то функция u=f(M) не имеет локаль-
локального экстремума в точке Мо.
Доказательство. Докажем сначала первую часть теоре-
теоремы, предполагая ради определенности, что второй дифференциал
A2.69), A2.70) представляет собой положительно определенную
квадратичную форму от переменных dx\, dx% ..., dxm. Докажем,
что в этом случае функция u = f(M) имеет в точке Мо локальный
минимум.
Разложим функцию и—}(М) в окрестности точки Мо по фор-
формуле Тейлора с остаточным членом в форме Пеано, беря в этой
формуле л = 2*. Мы получим при этом, что
f{M)-f(M0) = du\M.+ -±-d*u\M»+o(p2), A2.73)
причем в равенстве A2.73) дифференциалы dxi переменных лг,-,
входящие в выражение для du\M0 и ^2ы|м0» равны соответствую-
соответствующим приращениям xi—хр эти переменных, а величина р равна
р = V{dXl)* + (dx2r +... + {dxmf =
-x°)*+(x2-xir+ ... + {xm~xlf. A2.74)
По условию теоремы точка Мо является стационарной. Поэтому
на основании результатов предыдущего пункта Лг|л{„=0. Учиты-
Учитывая это равенство и полагая в выражениях A2.69), A2.70) для
второго дифференциала dxi = xi—хр, мы придадим формуле Тейло-
Тейлора A2.73) следующий вид:
A2.75)
Достаточно доказать, что для всех достаточно малых р правая
часть A2.75) положительна. (Это и будет означать, что в доста-
достаточной малой окрестности точки Мо разность f(M)—f{M0) поло-
положительна, т. е. функция u=f(M) имеет в точке Мо локальный
минимум.)
* Для функции u=f(M) выполнены при я=2 все условия теоремы 12.15*
(см. п. 4 § 5 настоящей главы).
§ 6. Локальный экстремум 509*
Положим ht — , где ?=1, 2, .... Тогда из выражениям
A2.74) для р вытекают следующие соотношения:
\Ы\<1, hl2 + h22+ ... +ftm2=l. A2.76)*
С помощью введенных обозначений равенство A2.75) может быть-
переписано в виде
т т
-f (Мо) = ^- у V atththk + о (р2). A2.75*>
Отношение о(р2)/р2 представляет собой бесконечно малую при
р->0 (или при М-+Мо) функцию, которую мы обозначим через
а(р). Введение этой функции позволяет нам записать равенство
о(р2) =р2а(р), с помощью которого мы придадим соотношению'
A2.75*) вид
т т
|^? ?] A2.75**>
Теперь уже нетрудно доказать, что правая часть A2.75**) яв-
является положительной для всех достаточно малых р. Квадратич-
т т
ная форма Ф = Т] V ait}iihk представляет собой функцию, опре-
i=i *=i
деленную и непрерывную на поверхности единичной сферы A2.76),.
представляющей собой замкнутое и ограниченное множество. Па
второй-теореме Вейерштрасса (см. теорему 12.7 из п. 3 § 3) эта
функция достигает на указанном множестве своей точной нижней
грани [х, причем из положительной определенности квадратичной
формы A2.71) и из того, что h\, h2, ..., hm, удовлетворяющие соот-
соотношению A2.76), не равны одновременно нулю, вытекает, что ука-
указанная точная нижняя грань \х, строго положительна.
Так как бесконечно малая при р->0 функция а(р) при всех до-
достаточно малых р удовлетворяет неравенству |a(p)|<ji, то вся?
правая часть A2.75**) является положительной при всех достаточ-
достаточно малых р, т. е. при всех М, достаточно близких к .Мо-
Это и означает, что функция u=f(M) имеет в точке Мо локаль-
локальный минимум.
Совершенно аналогично доказывается, что в случае, когда вто-
второй дифференциал A2.69), A2.70) представляет собой отрица-
отрицательно определенную квадратичную форму, функция u = f(M) име-
имеет в точке Мо локальный максимум.
Докажем теперь вторую часть теоремы, т. е. докажем, что в;
случае, когда второй дифференциал A2.69), A2.70) представляет
;'51О Гл. 12. Функции нескольких переменных
собой знакопеременную квадратичную форму, функция u = f(M)
не имеет локального экстремума в точке Мо.
Прежде всего установим следующее свойство знакопеременной
квадратичной формы A2.71):
Если квадратичная форма Ф(^1, h2, ..., hm) знакопеременна,
:то найдутся две совокупности переменных (A/, h2, ..., hm') и
(hf, h2", ..., hm") такие, что
(h2"J+ ». + (Am"J= 1,
A2.77)
причем
Ф(А,'А2', .... hn')>0, Ф(А,", h2", ..., ftm")<0. A2.78)
В самом деле, в силу определения знакопеременной квад-
квадратичной формы найдутся две совокупности аргументов W, t2, ...
...., tm' и t\", t2", ..., tm", состоящие из чисел, одновременно не рав-
:ных нулю, и такие, что
Ф(*/, W, ..-, tm')>0, Ф{Ь", t2", ..., (m")<0. A2.79)
Положив
h'j= ' =-. А*= г ¦ ' ==• A2.80)
V{t[f + (ф2 + + (О2 V (t\? + DJ + • • • + D J
:и учитывая, что из определения A2.71) квадратичной формы сра-
сразу же вытекает, что
+...+(О2 (ь 2> ¦ ¦ ¦'nh
г, ... , h"m) = — ^ ^— Ф(Л, 4 • • • , С),
(/;J+DJ++(О2
¦мы получим (в силу A2.79)) неравенства A2.78), причем из соот-
соотношений A2.80) сразу же вытекают равенства A2.77).
Зафиксируем две совокупности переменных h\, h2, ..., hm' и
•h\", h2", ..., hm", удовлетворяющие соотношениям A2.77) и A2.78),
и докажем, что для любого р>0 найдутся две точки М'(х\, х2, ...
..., хт') и М"(х\", х2", ..., Хт") пространства Ет такие, что
(Af', Mo) =р(М", Мо) =р, причем
х\ хо
- = h'c, — - = h"i для всех i = l, 2, ..., т.
Р Р
A2.81)
В самом деле, положив для любого р>0 и для каждого но-
номера i
х{=х? + ф/, xi" = Xi°+phi",
§ 6. Локальный экстремум 5111
мы удовлетворим соотношениям A2.81), причем в силу равенств;
A2.77) будут справедливы равенства
', м0) = V(x[-xy + (<-*°J + • • • + K-xif =
м0) = Vixi-xir+(x;-xir +
Теперь уже нетрудно убедиться в том, что для случая, когда
второй дифференциал A2.69), A2.70) представляет собой знако-
знакопеременную квадратичную форму, функция u=f (M) не имеет экст-
экстремума в точке Мо.
Записывая для функции u=f(M) разложение в окрестности
точки Мо по формуле Тейлора с остаточным членом в форме Пеано
и беря это разложение в указанных выше точках М' и М", мы по-
получим вместо A2.75) следующие два разложения:
?'*(*;-*°)K-*2) + o(p2). A2.82)
)' A2-83>
справедливые для всех достаточно малых р>0.
Подставляя в эти разложения значения {х{—л:,0) и {х"—хр}
из равенств A2.81) и учитывая, что о(р2) =р2а(р), где а(р)-*-0
при р->0, мы придадим разложениям A2.82) и A2.83) следующий,
вид:
) -f (Mo) = p2 [ -L 2 ^ a"tih* + a (p) ] •
r=i k=i
Последние два соотношения можно также переписать в виде
o(p), A2.82*)
. A2.83*>
S12 Гл. 12. Функции нескольких переменных
Учитывая соотношения A2.78) и тот факт, что величины
•Ф (V, V hm') >0 и Ф (hi", Л2", - . hm") <0 не зависят от р, и
.вспоминая, что p==p(Af', М0)=р(М", Мо), мы получим из соотно-
соотношений A2.82*) и A2.83*), что для достаточно малого р>0 спра-
шедливы неравенства f(M')>f{M0) и f{M")<f(M0), которые и до-
доказывают отсутствие экстремума в точке Mq.
Теорема 12.16 полностью доказана.
Замечание. Если второй дифференциал два раза дифферен-
дифференцируемой в данной стационарной точке Мо функции u=f(M) пред-
представляет собой в этой точке квазизнакоопределенную квадратич-
шую форму, то нельзя сказать ничего определенного о наличии или
«отсутствии в этой точке локального экстремума.
Так, например, у каждой из двух функций щ—х3+у3 и и2=
=д:4+г/4 второй дифференциал в стационарной точке М0@, 0)
тождественно равен нулю (т. е. представляет собой квазизнакооп-
феделенную квадратичную форму), но только одна вторая из ука-
указанных двух функций имеет в этой точке локальный экстремум.
Для решения вопроса о локальном экстремуме для случая, ког-
Лй второй дифференциал представляет собой квазизнакоопределен-
квазизнакоопределенную квадратичную форму, следует привлечь дифференциалы более
.высоких порядков, но это выходит за рамки нашего курса.
Пример. Найти точки локального экстремума функции трех
переменных
u=%x2+y2+z2+2y+2z, A2.84)
где Я — вещественное число, отличное от нуля.
Так как — = 2%х, — = 2у+2, — = 2г+ 2, то единствен-
дх ду дг
той стационарной точкой является точка М0@, —1, .—1).
Далее очевидно, что второй дифференциал в этой точке имеет
«вид
&и | Мо = 21 (&)«•+ 2 (dyf + 2 (dzf.
При К>0 второй дифференциал в точке Мо представляет собой
•положительно определенную квадратичную форму*, и потому
«функция A2.84) имеет в точке М0@, —1, —1) локальный мини-
минимум.
При Я<0 указанный второй дифференциал представляет собой
знакопеременную квадратичную форму**, и потому функция
A2.84) не имеет локального экстремума в точке Мо .
3. Случай функции двух переменных. На практике часто встре-
встречается задача об экстремуме функции двух переменных u=f(x,y).
* Ибо этот второй дифференциал принимает строго положительные значе-
«гая при dx, dy и dz, одновременно не равных нулю.
** Ибо при Я<0 этот второй дифференциал положителен при dx=0, dy=l,
<dz=\ и отрицателен при dx=l,'dy=O, dz=0.
§ 6. Локальный экстремум 513
В этом пункте мы приведем результаты, относящиеся к этому слу-
случаю.
,.. дЧ дЧ дЧ
Пусть частные производные , , в некоторой точ-
дх* дхду ду2
ке М0(х0, уо) обозначены символами ац, а^, a2i соответственно.
Справедливо следующее
Утверждение. Пусть функция двух переменных u=f(x, у)
один раз дифференцируема в окрестности точки Мо и два раза
дифференцируема в самой точке Мо, и пусть Мо является стацио-
стационарной точкой. Тогда если в точке Мо выполнено условие
апйп—ai22>0, то функция u=f(x, у) имеет в точке Мо локальный
экстремум (максимум при аи<0 и минимум при ац>0).
Если же в точке Мо ацЯгг—ai22<0, то функция и=}(х, у) не
имеет в этой точке локального экстремума*.
Доказательство. Справедливость первой части утвержде-
утверждения непосредственно вытекает из теоремы 12.16 и критерия Силь-
Сильвестра знакоопределенности квадратичной формы, ибо
Докажем вторую часть утверждения. Итак, пусть в точке Мо
справедливо неравенство ацЯ22—аиг<0. Докажем, что в этом слу-
случае второй дифференциал d2u в точке Мо представляет собой зна-
знакопеременную форму. Рассмотрим сначала случай апф0. Исполь-
Используя введенные выше обозначения
получим следующее выражение для второго дифференциала:
2
d2u|м. = Р2 J] alkhthk = p2 (anh\ + 2a18ftA + aithb =
= — I(fliA + aiAJ + (anaa—ai2) h22].
an
Легко, проверить, что при fti = l, /гг = О и при Ах=
/г2 = —~а" дифференциал йги\м„- имеет разные знаки, т. е.
является знакопеременной формой, и поэтому согласно теореме
12.16 функция не имеет в точке Мо локального экстремума.
* Случай ацпы—a2i2=0 требует дополнительного исследования.
** При этом р может быть как угодно малой величиной. Условие fti2+/i22=l
выполнено.
17 Зак. 72
514 Гл. 12. Функции нескольких переменных
Рассмотрим теперь случай аи = 0. Тогда из условия ацЯг—fli22<
<0 вытекает, что а^фО. Следовательно, так же как и выше, имеем.
d2u\Mo = p2h2 BaxA + a22h2)- A2-85>
Пусть h\^0 и величина h2 столь мала (из условия hl2 + h22=l
следует, что такой выбор hi и h2 возможен), что выражение
Bai2hi + aiih-2) сохраняет знак величины 2a\2hx. Тогда из формулы
A2.85) вытекает, что йги\м0 имеет разные знаки при /*2>0 и
h2<0, т. е. функция u=f(x, у) не имеет локального экстремума в
точке Мо. Утверждение полностью доказано.
Замечание. Требование d2f(M0)>0 [соответственно d2f{M0)<
<0] является необходимым условием локального минимума [мак-
[максимума] в точке Мо дважды дифференцируемой в этой точке функ-
функции f(M).
В самом деле, пусть ради определенности f(M) имеет в
точке Мо локальный минимум, но условие d2f(M0)>>b не выполне-
выполнено. Тогда найдутся hu h2, ¦¦¦, hm такие, что
Рассмотрим функцию F(t) =f(xi° + thh ..., xm° + thm), заведомо оп-
определенную при всех t, достаточно малых по модулю. Функция
F(t) обязана иметь локальный минимум в точке ^=0, чему проти-
противоречит условие
F"@)=d2f(M0)<0.
ДОПОЛНЕНИЕ 1
Градиентный метод поиска экстремума сильно
выпуклой функции
В этом дополнении излагается теория широко применяемого
на практике градиентного метода поиска экстремума сильно
выпуклой функции.
Идея этого метода чрезвычайно проста. Для приближенного
отыскания точки минимума функции т переменных использу-
используется тот факт, что градиент этой функции имеет направление,
совпадающее' с направлением наибольшего возрастания этой
функции. Значит, вектор —grad/(x0) в каждой точке хо=
= (xi°, х20, ..., Хщ0) направлен в сторону наибольшего убывания
функции f(x). Это дает основание ожидать, что если, отправляясь
от некоторого нулевого приближения хо= (xi°, х20, ..., х°т) мы
построим &-е приближение xk=(xik, х2к, ..., хтк) по рекуррент-
рекуррентной формуле
i=xk~ agradfX**),
Дополнение 1 515
то при достаточно малом положительном а последовательность
точек {Xk} сойдется к точке минимума функции f{x).
Строгой реализации этой простой идеи и посвящено настоя-
настоящее дополнение.
1. Выпуклые множества и выпуклые функции. Пусть х\ =
= {х\1, х2\ ..., хтх) и x2={Xi2, x22, ..., хт2) — две точки /п-мер-
ного евклидова пространства Ет, которые мы можем рассматри-
рассматривать как векторы в Ет с соответствующими координатами.
Назовем отрезком или сегментом, соединяющим
точки х\ и х% множество точек пространства Еп вида
Xi + t(x2—Х\), где t — любое число из сегмента 0<^<1.
Будем обозначать отрезок, соединяющий точки х\ и х2, сим-
символом Х{Х2.
Определение 1. Множество Q точек пространства Ет
называется выпуклым, если оно обладает следующим свой-
свойством: каковы бы ни были две точки х\ и х2, принадлежащие
множеству Q, отрезок Х\х2, их соединяющий, также принадле-
принадлежит этому множеству.
Примером выпуклого множества в пространстве Ет может
служить m-мерный шар (безразлично, открытый или замкнутый)
или полупространство лгт>0 (т. е. множество всех точек {х\,
х2, ..., хт) пространства Ет, т-я координата которых удовлет-
удовлетворяет условию л."т>0).
Примером множества Q, не являющегося выпуклым, может
служить дополнение /n-мерного шара или /n-мерный открытый
шар, из которого удалена хотя бы одна точка.
Пусть Q — некоторое множество точек пространства Ет, а
х — любая фиксированная точка этого пространства.
Назовем расстоянием от точки х до множества
Q точную нижнюю грань расстояний от точки х до всевозмож-
всевозможных точек этого множества.
Будем обозначать расстояние от точки х до множества Q
символом р(х, Q). Итак, по определению
р(х, Q) = infp(x,y).
yeQ
Для любого множества Q пространства Ет и любой точки
х этого пространства существует расстояние р(х, Q) *. В част-
частности, если точка х принадлежит множеству Q, то р(х, Q)=0.
Однако у множества Q не всегда существует точка у такая,
что р(х, у)=р(х, Q).
Так, например, если множество Q представляет открытый
/n-мерный шар, ах — точка Ет, лежащая вне этого шара, то у
такого множества Q не существует точки у такой, что р (х, у) =
* Ибо множество р{х, у) для всевозможных у, принадлежащих Q, всегда
ограничено снизу (например, числом нуль).
17*
516 Гл. 12. Функции нескольких переменных
= р(*. Q) (ибо для всех точек у открытого шара справедлив»
неравенство р(х, у)>р(х, Q)).
Если все же у множества Q существует точка у такая, что
<р(х> У) = p(*> Q). т0 эта точка у называется проекцией точ-
точки х на множество Q.
Проекцию точки х на множество Q будем обозначать симво-
символом Pq(x).
Подчеркнем, что если точка х принадлежит множеству Q то
Pq{x)=x.
Итак, проекция Pq(x) точки х на множество Q определяется
соотношением
р (х, PQ (х)) = р (х, Q) = inf p (х, у).
я
Полезно отметить, что может существовать несколько проек-
проекций точки х на множество Q. Так, например, если Q—т-мерная
сфера с центром в точке х, то любая точка Q является проекци-
проекцией точки х на множество Q.
Справедлива, однако, следующая лемма:
Лемма 1. Если множество Q пространства Ет является
выпуклым и замкнутым, ах — любая точка Ет, то существует
и притом единственная проекция точки х на множество Q.
Доказательство. Сначала докажем существование
хотя бы одной проекции точки х на множество Q. Обозначим
через р(лг, Q) расстояние от точки х до множества Q. По опре-
определению р(х, Q) как точной нижней грани inf p(x, у) найдется
Q
последовательность {уп} точек множества Q такая, что р(х, уп)
( Q)
Р( )
По определению предела числовой последовательности для
любого е>0 все элементы уп, начиная с некоторого номера,
удовлетворяют соотношению
р{х, Q)— е<р(лг, уп)<р(х, Q)+e.
Отсюда следует, что последовательность [уп} точек пространства
Ет во всяком случае является ограниченной и потому в силу
теоремы Больцано — Вейерштрасса (см. п. 2 § 2 гл. 12) из этой
последовательности можно выделить сходящуюся подпоследова-
подпоследовательность укп, где я=1, 2, 3, .... Обозначим через у предел
подпоследовательности {#*„}• В силу замкнутости множества
Q точка у .принадлежит этому множеству. Остается доказать»
что ;
Р (х, у) = Р (х, Q) = Hm p (*, укп).
П-*со
Для доказательства этого заметим, что в силу неравенств тре-
треугольника
Дополнение 1 5П
Р (X, Укп) < р (X, у) + р (у, Укп) И р (х, у)< р (л;, ykn) + р (i/v у)
справедливо соотношение
IР (*. JfeJ — Р (х, у) | < р (У, </*„)•
Из этого соотношения и их сходимости подпоследовательности
{ykj кI/вытекает,что lim p(x, ^) = р(*. у), т. е. р(х, Q)=p(x, у).
П-*ОО
Тем самым доказательство существования хотя бы одной
проекции точки х на множество Q завершено.
Докажем теперь, что существует только одна проекция точ-
точки х на множество Q. Предположим, что существуют две раз-
различные проекции ух и у% точки х на множество Q. Так как мно-
множество Q является выпуклым, то весь отрезок у\у%, соединяю-
соединяющий точки i/i и г/2, принадлежит множеству Q. В частности, мно-
множеству Q принадлежит середина ¦У1 "*~Уг указанного отрезка.
Убедимся в том, что расстояние р (х, ) от точки х до
указанной середины отрезка у\уч строго меньше расстояния
р(х, yi)=p(x, у2).
Исключим из рассмотрения тривиальный случай, когда
+ = х. В этом случае р (х, Уг + н- \ =0, в то время
~ \ 2 /
х. В этом случае р (х,
2 ~ \ 2 /
как р(лг, yi)=p(x, У2)>0, ибо в противном случае обе точки ух
и у2 совпадали бы с х и не могли бы быть различными. Итак, в
тривиальном случае Ух 2 = х неравенство
( ^) Р(*'УЛ A2-1.1)
очевидно.
Докажем теперь неравенство A2.1.1) в случае, когда
^ х
Используя свойства скалярного произведения двух векторов
пространства Ет (см., например, замечание 2 из п. 1 § 1 гл. 12),
мы получим соотношение
/w t/л -i- На tit A- Uo
t Pi \ if* v У1 I У* « i
= — [(г/1—х, у1—х) + 2(у1 — х, у2—х) + (у2—х, yt — x)\. A2.1.2)
4
518 Гл. 12. Функции нескольких переменных
Убедимся теперь в справедливости строгого неравенства
—х, У2—х). A2.1.3)
В сноске на с. 485 доказано, что для любых векторов * а и
b пространства Ет, не коллинеарных друг другу (т. е. таких,
что аФХЬ ни для одного вещественного Я), справедливо строгое
неравенство Коши — Буняковского
\{а,Ь)\<У(а,а)(Ь,Ь).
Это означает, что для доказательства неравенства A2.1.3) нам
достаточно убедиться в том, что векторы у\—х и yt—х не кол-
Линеарны, т. е. убедиться в том, что ни для одного веществен-
вещественного Я не может быть справедливо равенство
У1~х=Х(У2-х). A2.1.4)
Если бы равенство A2.1.4) было справедливо для такого К,
для которого |Я|^=1, то было бы невозможно равенство
P(«/b *)=Р(#2, X).
Справедливость равенства A2.1.4) для Я=1 противоречила
бы тому, что точки г/i и г/г являются различными.
Наконец, справедливость равенства A2.1.4) для %= — 1 оз-
означала бы, что yi 2 = х, а этот случай мы исключили.
Итак, равенство A2.1.4) несправедливо ни для одного веще-
вещественного X, а потому доказательство неравенства A2.1.3) за-
вери1ено.
Сопоставляя равенство A2.1.2) с неравенством A2.1.3), по-
получим, что
+ 2У(у1—х, у!—х) V(y2—x, у2
= ¦— [У{У 1-х, Уг — х) + У(у2—х, y2—x)f =
= -J- [Р (х, уг) + р(х, у2)]2 = р2 (*, yj = р2 (х, у2).
Тем самым доказательство неравенства A2.1.1) завершено.
Но это неравенство означает, что у множества Q нашлась точ-
точка У1+ , более близкая к х, чем точки ух и у2, а это проти-
противоречит тому, что каждая из точек у\ и г/2 является проекцией
точки х на множество Q, т. е. является точной нижней гранью
расстояния р(х, у) для всевозможных у, принадлежащих Q.
* Векторы в данном дополнении не будем выделять жирным шрифтом.
Дополнение 1 519
Полученное противоречие показывает, что наше предположе-
предположение о том, что существуют две различные проекции у\ и г/2 точ-
точки х на множество Q, является ошибочным.
Доказательство леммы 1 полностью завершено.
Перейдем теперь к определению выпуклой функции.
Определение 2. Функция f(x), заданная на выпуклом
множестве Q пространства Ет, называется выпуклой вниз
или просто выпуклой на этом множестве, если для любых
двух точек Х{ и х2 множества Q и для любого вещественного
числа t из сегмента 0<t<l справедливо неравенство
fi.x1 + t(xa-x1)]<f{x1)+t[f(xt)—f(^)]. A2.1.5)
Определение 3. Функция f(x), заданная на выпуклом
множестве Q пространства Ет, называется строго выпу к-
ло й на этом множестве, если для любых двух точек Х\ и х2
множества Q и для любого вещественного числа t из интервала
0<^<1 справедливо строгое неравенство
f[xi + t(x,-xl)]<f(xl)+t[f(x2L(xi)l A2.1.6)
Ясно, что всякая строго выпуклая на множестве Q функция
f(x) является выпуклой на этом множестве.
Легко установить достаточное условие выпуклости [соответ-
[соответственно строгой выпуклости] дважды дифференцируемой на вы-
выпуклом множестве "Q функции f(x).
Лемма 2. Пусть функция f(x) задана и два раза диффе-
дифференцируема на выпуклом множестве Q. Тогда, для того чтобы
эта функция являлась выпуклой [строго выпуклой], на множест-
множестве Q достаточно, чтобы второй дифференциал d2f этой функции
во всех точках Q являлся квазиположительно определенной
[строго положительно определенной] квадратичной формой.
Доказательство. Пусть Х\ к Х2 — любые две фикси-
фиксированные точки множества Q. Рассмотрим на сегменте 0<^<1
следующую функцию одной независимой переменной t:
F(t) =f[xl + t(x2-x1)}-f(x1)-mxi)-f(xx)]. A2.1.7)
Напомним, что второй дифференциал d2f функции f(x) =
= f(xi, x2, ..., xm) независимых переменных (х\, х2, ..., хт) в
данной точке х= \х\, х% ..., хт) равен *
m m
^w-SSi&w^- A2Л-8)
Дифференцируя функцию A2.1.7) два раза по t по правилу
дифференцирования сложной функции, получим
* См. п. 2 § 5 гл. 12.
520 Гл. 12. Функции нескольких переменных
-*i). A2.1.9)
где (Xil, x2l, ..., xj) и (хг2, x22, .... xm2) — координаты точек хх и
x2 соответственно.
Сопоставляя соотношения A2.1.8) и A2.1.9), мы убедимся в
справедливости равенства
F"(t)=d*f[xi + t(x2-xl)], A2.1.10)
в котором в выражении для d2f приращения Ад:,- взяты равными
V2 г.1
Л; Л, .
Дальнейшие рассуждения ради определенности проведем для
случая, когда второй дифференциал d2f во всех точках Q явля-
является квазиположительно определенной квадратичной формой.
В этом случае для всех t из сегмента 0<^<1 правая (а зна-
значит, и левая) часть A2.1.10) неотрицательна, т. е. для всех t
из сегмента 0<?<:1
F"(/)>0. A2.1.11)
В силу определения 2 и соотношения A2.1.7) нам достаточно
доказать, что для всех t из сегмента 0<^<:1 справедливо не-
неравенство
F(f)<0. A2.1.12)
Для доказательства неравенства A2.1.12) используем соотно-
соотношение A2.1.11) и легко проверяемые равенства
F@)=0, f(l)=0. A2.1.13)
Предположим, что внутри сегмента 0<^<1 существует хотя
бы одна точка t, в которой F(t)>0. Тогда функция F(t) дости-
достигает своего максимального на сегменте 0<^<1 значения в неко-
некоторой внутренней точке to этого сегмента, причем F(to)>O.
В этой точке ^о функция F(t) имеет локальный максимум, а по-
потому F'(^0)=0. Но из неравенства A2.1.11) вытекает, что про-
производная F'(t) не убывает на всем сегменте 0<^<1, а потому
и на сегменте to<t<l. Отсюда и из условия F'(to)=Q следует,
что производная F' (t) неотрицательна всюду на сегменте
io^-t^cl, а поэтому функция F(t) не убывает на этом сегменте.
Это приводит нас к неравенству
противоречащему второму соотношению A2.1.13).
Полученное противоречие доказывает, что наше предположе-
предположение о том, что на сегменте 0</<1 существует хотя бы одна точ-
точка t, в которой F(t)>0, является ошибочным, т. е. доказывает
справедливость всюду на сегменте 0</<1 неравенства A2.1.12).
Дополнение 1 521
Тем самым первая часть леммы (о выпуклости f(x) при ус-
условии, что d2f является квазиположительно определенной квад-
квадратичной формой) доказана.
Вторая часть леммы (о строгой выпуклости f(x) при усло-
условии, что d2f является строго положительно определенной квад-
квадратичной формой) доказывается аналогично.. Исходя из нера-
неравенства A2.1.11), справедливого на этот раз со знаком >, и
из равенств A2.1.13) и предположив, что внутри сегмента
0<^<1 существует хотя бы одна точка t, в которой F(t)>-0, мы
придем к выводу, что F(t) имеет внутри сегмента 0<?<1 точку
локального максимума /о, причем F(to)>-0. Но тогда, поскольку
F'(to)=O, мы получим из A2.1.11), что F'(t)>0 всюду на по-
полуинтервале to<t<l, а это означает, что F(l)>F(t0)>>0.
Мы снова получаем противоречие со вторым соотношением
A2.1.13), которое доказывает, что F(t)<0 всюду на интервале
0</<1, т. е. доказывает строгую выпуклость f(x) на множе-
множестве Q.
Лемма 2 полностью доказана.
Доказанная лемма естественно наводит на мысль о рассмот-
рассмотрении следующего еще более узкого класса выпуклых на вы-
выпуклом множестве Q и два раза дифференцируемых на этом
множестве функций.
Определение 4. Два раза дифференцируемая на выпук-
выпуклом множестве Q функция f(x) называется сильно выпук-
выпукло й на этом множестве, если существуют такие две положи-
положительные постоянные k\ и k2, что второй дифференциал d2f этой
функции, определяемый соотношением A2.1.8), во всех точках
х множества Q удовлетворяет неравенствам
k1(AxJ<d2f^k2(AxJ. A2.1.14)
(В этих неравенствах через Ах обозначен вектор с координата-
координатами (Д*1, Ах2, •¦¦, Ахт), а символ (АхJ обозначает скалярный
квадрат этого вектора, т. е. скалярное произведение (Ах, Ах).)
Из левого неравенства A2.1.14) сразу же вытекает, что вто-
второй дифференциал сильно выпуклой функции представляет со-
собой строго положительно определенную во всех точках множе-
множества Q функцию, а потому (в силу леммы 2) сильно выпуклая
на множестве Q функция заведомо является строго выпуклой на
этом множестве.
Вместе с тем класс сильно выпуклых функций достаточно
широк и важен в прикладных задачах, и мы ограничимся этим
классом при изложении теории градиентного метода поиска ми-
минимума.
Начнем с выяснения вопроса о существовании и единственно-
единственности минимума.
2. Существование минимума у сильно выпуклой функции и
единственность минимума у строго выпуклой функции. Пусть
функция f(x) определена на выпуклом множестве Q.
522 Гл. 12. Функции нескольких переменных
Будем говорить, что эта функция имеет в точке Хо множества
(ЗлЪкальный минимум, если существует такая б-окрест-
ность этой точки Cs, что значение f (х0) не больше значений f(x)
этой функции во всех точках пересечения б-окрестности Св и
множества Q. При таком определении понятие локального ми-
минимума включает в себя и точки краевого минимума функции
f (х) на границе множества Q.
Таким образом, при данном нами определении можно под-
подразделить точки минимума на точки внутреннего ло-
локального минимума (для случая, когда эти точки явля-
являются внутренними точками Q) и точки краевого локаль-
локального минимума (для случая, когда эти точки являются
граничными точками Q).
Для изучения вопроса о существовании и единственности
точки локального минимума нам понадобится следующая вспо-
вспомогательная лемма.
Лемма 3. Пусть на выпуклом множестве Q задана диф-
дифференцируемая выпуклая функция f{x). Для того чтобы эта
функция имела локальный минимум в точке х0 множества Q,
необходимо и достаточно, чтобы для любого вектора Ах, для ко-
которого точка х+Ах принадлежит множеству Q, было справедли-
справедливо неравенство *
(gradf(xb), Д*)>0. A2.1.15)
Доказательство. Необходимость. В силу утверждения,
доказанного в п. 8 § 4 гл. 12, левая часть A2.1.15) равна произ-
произведению производной функции f(x) в точке Хо по направле-
направлению вектора Ах на длину \Ах\ этого вектора:
(grauf(x0), Ах) = -У-(х0) \Ах\, A2.1.16)
де
где е = Дд:/|Лл:| — единичный вектор в направлении Дл;.
Так как х0 является точкой локального минимума функции
f(x), то производная dffde(xo) по любому направлению е=
= Ах/\Ах\ неотрицательна (точнее, равна нулю в случае, если
Хо — точка внутреннего локального экстремума, и неотрицатель-
неотрицательна в случае, если х0 — точка краевого локального экстремума).
Итак, правая часть A2.1.16) (а потому и левая часть
A2.1.15)) неотрицательна. Необходимость доказана.
Достаточность. Пусть для любого вектора Ах, для которого
точка хо+Ах принадлежит Q, справедливо неравенство A2.1.15).
Докажем, что точка Хо является точкой локального минимума
функции f(x).
* В неравенстве A2.1.15) берется скалярное произведение векторов
gradf(Xo) и Д*. Определение grad/(x) см. в п. 8 § 4 гл. 12.
Дополнение 1 523
Так как функция f(x) по условию является выпуклой на
множестве Q, то для любых двух точек х\ и Хч этого множества
и любого числа t из сегмента 0<?«:1 справедливо неравенство
A2.1.5). Полагая в этом неравенстве Xi=x0, х2=Хо+Ах, мы мо-
можем переписать это неравенство в виде
/ (х0 + Ax)-f (x0) > ^ <*° + ***) -¦/ (*b) ^ A2.1.17)
Считая х0 и Ах фиксированными, перейдем в неравенстве
A2.1.17) к пределу при t-*-0 + 0. По определению производной
по направлению (см. п. 8 § 4 гл. 12) предел при ?->0 + 0 правой
части A2.1.17) в точности равен произведению, стоящему в пра-
правой части A2.1.16). Поэтому в силу соотношений A2.1.15) и
A2.1.16) этот предел неотрицателен. Учитывая, что левая часть
A2.1.17) не зависит от t, мы получим в пределе при f-»-0+0 из
неравенства A2.1.17), что
Последнее неравенство, справедливое для любого вектора Ах,
для которого точка Ха + Ах принадлежит Q, доказывает, что
функция f(x) имеет в точке х0 локальный минимум. Достаточ-
Достаточность доказана.
Лемма 3 полностью доказана.
Замечание 1. Из приведенного нами доказательства оче-
очевидно, что для случая, когда точка Хо является внутренней
точкой множества Q, т. е. когда речь идет о внутреннем локаль-
локальном минимуме, в формулировке леммы 3 знак з> в неравенстве
A2.1.15) можно заменить на знак =.
Замечание 2. При доказательстве необходимости леммы
3 мы не использовали требования выпуклости функции f{x).
Поэтому доказательство необходимости проходит без требова-
требования выпуклости функции f(x). Иными словами, справедливо
следующее
Утверждение. Если функция f(x) дифференцируема на
выпуклом множестве Q и имеет локальный минимум во внутрен-
внутренней [в граничной] точке х0 этого множества, то для любого век-
вектора Ах для которого точка хо+Ах принадлежит Q, справедли-
справедливо неравенство
(grad/(x0), Д*)=0 [(gradf(xo), Дх)>0].
Перейдем к вопросу об единственности и о существовании
точки локального минимума.
Теорема (об единственности локального ми-
минимума у строго выпуклой функции). Если функ-
функция f(x) дифференцируема и строго выпукла на выпуклом мно-
множестве Q, то она может иметь локальный минимум только в од-
одной точке этого множества.
524 Гл. 12. Функции нескольких переменных
Доказательство.. Предположим, что функция f(x)
имеет локальный минимум в двух различных точка Х\ и х%
множества Q. Тогда условие выпуклости A2.1.5) для точек xi*,
и Хя можно записать в виде
f (Х>) _; (Xl) >fl* + t (*i ~ *i)) ~ f Ы A2.1.18)
(здесь / — любое число из интервала )
Меняя в соотношении A2.1.8) точки х\ и х2 ролями, мы по-
получим неравенство
f (jCi) _; (xj >flx> + i(*i -*Я -/Ы ^ A2.1.19)
В пределе при /->0+0 правая часть A2.1.18) [соответствен-
[соответственно правая часть A2.1.19)] дает производную функции f(x) по
направлению вектора х2—х\ [соответственно вектора Х\—х&
взятую в точке Х\ [соответственно в точке х2], умноженную на
\х2—Xi\. Так как обе точки х\ и х2 являются точками локаль-
локального минимума, то обе указанные производные по направлению
неотрицательны, т. е. пределы правых частей A2.1.18) и
A2.1.19) при /-*0 + 0 оба неотрицательны.
Таким образом, из неравенств A2.1.18) и A2.1.19) в преде-
пределе при ?->0 + 0 мы получим
f(*2)>0.
Сопоставление двух последних неравенств приводит к заключе-
заключению о том, что ){х\) =f(x2).
Используя равенство f(x\) =f(*2), мы получим из условия
строгой выпуклости A2.1.6), что
Я*1 + *(*2—*i)]<f(*i) A2.1.20)
для всех t из интервала 0</<1.
Неравенство A2.1.20) противоречит тому, что функция f(x)
имеет локальный минимум в точке х\ (в точке X\ + t{x2—*i),
как угодно близкой пр'и малом t к точке хи функция f(x) име-
имеет значение, меньшее значения /(*0).
Полученное противоречие доказывает, что наше предположе-
предположение о том, что функция f(x) имеет локальный минимум в двух
различных точках множества Q, является ошибочным. Теорема
доказана.
Существование локального минимума докажем при более
сильных ограничениях, чем единственность.
Теорема (о существовании локального мини-
минимума у сильно выпуклой функции). Если функция
f(x) сильно выпукла на замкнутом выпуклом множестве Q, то
Дополнение 1 525
у этой функции существует на множестве Q точка х0 локально-
локального минимума *.
Доказательство. Сначала отметим, что теорема заве-
заведомо справедлива для случая, когда выпуклое замкнутое мно-
множество Q является, кроме того, ограниченным. В этом случае
по второй теореме Вейерштрасса (см. теорему 12.7) функция
[(ж), будучи во всяком случае непрерывной на множестве Q,
достигает в некоторой точке х0 этого множества своего мини-
минимального на Q значения. Указанная точка х0 и является точкой
локального минимума.
Остается доказать теорему в случае, когда выпуклое замкну-
замкнутое множество Q не является ограниченным. В этом случае мы
фиксируем некоторую внутреннюю точку Х\ множества Q и раз-
разложим функцию f(x) по формуле Тейлора с центром в.точке
Х\, взяв остаточный член к.%(х) в форме Лагранжа ** (см. п. 3
§ 5 гл. 12). Указанное разложение будет иметь вид
+Q(x-x1)], A2.1.21)
где Э — число из интервала Q<8<1, так что точка
)
принадлежит отрезку, соединяющему точки хг и х2 ***.
Если обозначить через Ах вектор х—хи то для df(xi) будет
справедливо равенство
d/(jc,) = (gradf(jc,), Дх).
Из этого равенства вытекает, что
|d/(x,)|<|gradf(jc,)||Ajc|. A2.1.22)
Далее, используя левое неравенство в определении сильной
выпуклости A2.1.14), мы придем к неравенству
d2f[xx+Q{x—*,)]>?, (А*J- A2.1.23)
Из соотношений A2.1.21) — A2.1.23) заключаем, что
— fgrad/(jcx)|
* Так как сильно выпуклая на выпуклом множестве Q функция f(x) явля-
является строго выпуклой на этом множестве, то по предыдущей теореме точка х0
будет единственной точкой локального минимума.
** Мы учитываем, что сильно выпуклая на множестве Q функция f(x) два
раза дифференцируема на этом множестве.
*** Какова бы ни была точка х множества Q, отрезок, соединяющий точки
Xi и х, принадлежит множеству Q в силу выпуклости этого множества. В сноске
к теореме Тейлора 12.15 отмечалось, что в качестве окрестности центра разло-
разложения можно брать любую звездную окрестность этого центра, т. е. можно брать
все множество Q.
525 Гл. 12. Функции нескольких переменных
так что
^j. A2.1.24)
Учитывая, что точка Xi фиксирована и величина | grad f (xi) [
представляет собой некоторое фиксированное число, мы заведо-
заведомо можем выбрать положительное число R настолько большим,
чтобы при |A*|>i? выражение в квадратных скобках в.
A2.1.24) было положительным.
Это означает, что при |Дл;|>/? справедливо неравенство
f(x)>f(x\), т. е. всюду вне замкнутого шара Сн радиуса R с
центром в точке хх значения f(x) превосходят значение f(x\),
(в центре указанного шара).
Обозначим через Qr пересечение множества Q с указанным
шаром Cr. Так как оба множества Q и Сл являются выпуклыми
и замкнутыми,- то и их пересечение Qn также является выпук-
выпуклым и замкнутым. Так как, кроме того, множество QR является:
ограниченным, то по доказанному выше функция f(x) имеет на
множестве QR единственную точку хо локального минимума.
Поскольку мы доказали, что во всех точках Q, лежащих за
пределами QH, значения f(x) превосходят f(xi), то эти значения
тем более превосходят f(x0), т. е. точка х0 является точкой ло-
локального минимума f(x) и на всем множестве Q.
Теорема полностью доказана.
3. Поиск минимума сильно выпуклой функции. Мы доказали^
что сильно выпуклая функция f(x), заданная на замкнутом вы-
выпуклом множестве Q, имеет на этом множестве единственную»
точку Хо локального минимума.
Обратимся к построению и обоснованию алгоритма, с по-
помощью которого отыскивается эта точка х0.
Фиксируем произвольную точку х\ множества Q и произ-
произвольное число а, удовлетворяющее неравенствам
0<a<-f, A2.1.25*
где k2 — постоянная из неравенства A2.1.14), определяющего
сильную выпуклость функции f(x).
Отправляясь от Х\ как от первого приближения, составим1
итерационную последовательность {хь} с помощью рекуррентно-
рекуррентного соотношения
= PQ(xk—agradf(xk)), ft= 1,2,3,.... A2.1.26)'
В настоящем пункте мы докажем следующее утверждение.
Основная теорема. Пусть функция f (x) является силь-
сильно выпуклой на замкнутом множестве Q, и пусть Х\ — произ-
произвольная точка множества Q. Тогда итерационная последователь-
последовательность {Xk}, определяемая рекуррентным соотношением A2.1.26)„
Дополнение 1 527
при любом а, удовлетворяющем неравенствам A2.1.25), сходит-
сходится к точке Хо локального минимума функции f(x).
Подчеркнем, что эта теорема дает алгорит отыскания любо-
любого (внутреннего или краевого) локального минимума функции
f(x), являющейся сильно выпуклой на произвольном (не обяза-
обязательно ограниченном) замкнутом выпуклом множестве.
Доказательству основной теоремы предпошлем четыре
леммы.
Лемма 4. Если Q — выпуклое замкнутое множество Е™,
х — произвольная фиксированная точка Ет, а у — произволь-
произвольная точка множества Q, то
(x-PQ (х), y~PQ (х)) <0. A2.1.27)
Доказательство. Предположим, что неравенство
A2.1.27) несправедливо. Тогда существует точка у множества
Q такая, что
(x-PQ (х) , y-PQ (х)) > 0. A2.1.28)
Из A2.1.28) сразу же вытекает, что точка у не совпадает с
Pq(x).
В силу выпуклости множества Q любая точка z = Pq(x) +
+ t(y—Pq{x)) отрезка, соединяющего точки Pq(x) и у, принад-
принадлежит множеству Q. Вычислим расстояние между любой такой
точкой z и точкой х:
рЦг, x) = {x-PQ(x)-t(y-PQ(x)), x-PQ{x)-t(y-PQ(x))) =
= рЦх, PQ(x))-2Hx-PQ{x), y-PQ(x))+tV{y, PQ(x)).
A2.1.29)
Так как х и у фиксированы, a t — любое число из сегмента
0</<1, то в силу неравенства A2.1.28) мы можем взять t
удовлетворяющим неравенству
2(x-PQ(x),y-PQ(x))
1< рЦу, PQ(X)) ¦
При таком выборе t
-2t(x-PQ(x), y-PQ(x))+ty(y, PQ(x))<0,
и мы получим из A2.1.29), что
р?(г,х)<р*{х,Ра(х)).
Последнее неравенство противоречит тому, что точка Pq(x) яв-
является проекцией точки х на множество Q: у множества Q наш-
нашлась точка z, удаленная от х меньше, чем Pq{x) от х. Получен-
Полученное противоречие завершает доказательство леммы.
Лемма 5. Пусть f (x) дифференцируема и выпукла на замк-
замкнутом выпуклом множестве Q. Если при некотором положитель-
положительном а проекция Pq{x0—agrad/(x0)) точки х0—agradf(*o) на
528 Гл. 12. Функции нескольких переменных
множество Q совпадает с точкой хо этого множества, то функ-
функция f(x) имеет в точке х0 локальный минимум.
Доказательст во. Используя лемму 4, запишем нера-
неравенство A2.1.27) для точек х=х0—agrad/(*0) и у=хо+Ах, где
Ах — любой вектор, для которого точка у — хо+Ах принадле-
принадлежит Q. В результате получим
(ха—a grad / {х0) — PQ (х0—а grad f (x0)),
Xo+Ax—Pq (хо—а grad /(х0))) <0.
Учитывая, что Pq(xq—a grad f (*о)) =хо, получим из последнего
неравенства следующее соотношение:
(grad / (*о), Ах)>0.
Это соотношение, справедливое для любого вектора Ах, для ко-
которого точка хо + Ах принадлежит Q, в силу леммы 3 устанав-
устанавливает, что функция f(x) име'ет в точке Хо локальный минимум.
Лемма 5 доказана.
Предположим, что функция f(x) является сильно выпуклой
на ограниченном замкнутом выпуклом множестве Q. Обозна-
Обозначим через m минимальное значение f(x) на множестве Q, а че-
через ц число, строго большее т, так что
\i >m = min fix).
Фиксируем число v, строго большее ц, и обозначим через
Q — подмножество тех точек х множества Q, для которых
|x<f(*)<v. A2.1.30)
Множество Q как подмножество ограниченного множества
Q само является ограниченным.
Убедимся в том, что множество Q является замкнутым. Пусть
{х/г} — произвольная сходящаяся последовательность точек мно-
множества Q. Требуется доказать, что предел х0* этой последова-
последовательности также принадлежит множеству Q. Так как каждая
точка хи принадлежит множеству Q, то для каждого номера к
y,<.f{xk)<v. A2.1.31)
Сильно выпуклая функция f(x) во всяком случае непрерыв-
непрерывна на Q, а поэтому из сходимости последовательности {х^} к
х0 в силу определения непрерывности функции по Гейне выте-
вытекает сходимость последовательности f(xk) к числу f{x0). Так
как все элементы сходящейся числовой последовательности f (Xk)
удовлетворяют неравенствам A2.1.31), то и предел f(xo) этой
последовательности удовлетворяет неравенствам \i^.f(xo) <v
* Так как исходное множество Q является замкнутым, то предел х0 во вся-
всяком случае принадлежит Q.
. Дополнение 1 529"
(см. гл. 3, следствие 2 из теоремы 3.13), а это и означает, что
точка х0 принадлежит множеству Q. Доказательство замкнуто-
замкнутости множества Q завершено.
Итак, множество Q всех точек х из множества Q, для кото-
которых справедливы неравенства A2.1.30), является замкнутым и
ограниченным.
Докажем теперь следующую лемму.
Лемма 6. Пусть функция f (x) сильно выпукла на выпук-
выпуклом замкнутом множестве Q, х — любая точка Q, а — любое-
положительное число, символ Ах обозначает разность
Ax=PQ(x—agradf(x))—x. A2.1.32).
Тогда справедливо неравенство
(gradf(x),Ax)< — |Ах|. A2.1.33)
а
Если же множества Q, кроме того, ограничено и точка х при-
принадлежит подмножеству Q тех точек Q, для которых справедли-
справедливы неравенства A2.1.30) при \а >min f(x), то найдется строго1
положительное число y такое, что справедливо неравенство
Доказательство. Докажем сначала неравенство
A2.1.33). Фиксируем произвольную точку х множества Q и,
привлекая лемму 4, запишем неравенство A2.1.27), взяв в нем
вместо х точку х—agrad/(ж), а вместо у точку х. При этом по-
получим неравенство
(х—аgrad f {x)—PQ(х—а grad f(x)), x—PQ(х—а grad/(
которое с учетом обозначения Ax = PQ(x—a grad f( x))—x пере-
перепишется в виде
(—a grad f{x)—Ax, —Длг)<0.
Из последнего неравенства и из свойств скалярного произ-
произведения вытекает, что
o(gradf(jc),
а это и приводит к неравенству A2.1.33).
Остается доказать, что при дополнительном предположении
о том, что Q ограничено и что х принадлежит подмножеству Q,
существует у>6 такое, что справедливо неравенство A2.1.34).
Рассмотрим неотрицательную функцию точки х вида
\Ax\ = \PQ(x—а grad/ (*))— х |. A2.1.35)
Убедимся в том, что эта функция является непрерывной на
множестве Q функцией точки х.
530 Гл. 12. Функции нескольких переменных
Докажем сначала, что векторная функция Pq(x) является
непрерывной функцией точки х. Для этого достаточно доказать
неравенство
Pq(x+Ax)—Pq{x)\<\Ax\, A2.1.36)
справедливое для любых векторов х и Ах.
В силу леммы 4 справедливы неравенства
(x—PQ{x), Pq(x + Ax)—Pq(x))<0,
(x + Ax—Pq{x + Ax), Pq{x)—Pq(x+Ax))<0.
Используя эти неравенства и неравенство Коши — Буняков-
ского получим цепочку соотношений
| PQ (х+Ах) —PQ (x)\2=(Pq(x+Ax) —Pq(x) ,
Pq{x+Ax)—Pq(x)) = {Pq(x+Ax) —x, PQ(x + Ax) —Pq(x)) +
+ (X—Pq (X) , PQ (X + AX) —Pq (x) ) <
<{PQ(x+Ax)— x, Pq(x+Ax)—Pq(x))=Pq(x+Ax)—x—Ax,
Pq(x+Ax)—Pq(x)) + (Ax, Pq(x+Ax)—Pq(x))*?
<.{Ax, Pq(x+Ax)—Pq(x))<z.\Ax\\Pq(x+Ax)—Pq(x)\,
из которой и вытекает неравенство A2.1.36).
Итак, доказано, что Pq(x) является непрерывной векторной
функцией точки х. Из сильной выпуклости f(x) на Q вытекает,
что функция agradf(x) также является непрерывной на Q век-
векторной функцией точки х. Но тогда из теоремы о непрерывно-
непрерывности сложной функции и непрерывности разности непрерывных
функций вытекает, что и функция
PQ(x—и gr ad f(x))—x
является непрерывной на множестве Q векторной функцией точ-
точки х.
Модуль указанной векторной функции, т. е. скалярная функ-
функция A2.1.35) тем более является непрерывной на множестве Q,
а потому и на его подмножестве Q.
Итак, функция A2.1.35) непрерывна и неотрицательна всюду
на замкнутом ограниченном множестве Q. В таком случае, по
второй теореме Вейерштрасса (см. теорему 12.7) эта функция
достигает на множестве Q своего неотрицательного минималь-
минимального значения у. Указанное минимальное значение y заведомо
строго положительно, ибо если бы у равнялась нулю, то на мно-
множестве Q нашлась бы точка х0 такая, что PQ(x0—agrad/(*0)) —
—*о=0, а это означало бы в силу леммы 5, что в этой точке х0
множества Q функция f(x) имеет единственный на множестве Q
локальный минимум (в то время как этот минимум по определе-
определению Q лежит вне Q). Итак, y>0, и неравенство A2.1.34) дока-
доказано.
Дополнение 1 53 Г
Лемма 6 полностью доказана.
Лемма 7. Пусть функция f(x) сильно выпукла на выпук-
выпуклом замкнутом множестве Q, х — любая точка Q, а — любое
число, удовлетворяющее неравенствам A2.1.25), Ах — разность
вида A2.1.32). Тогда при переходе из точки х в точку х* =
= PQ(x—agTadf(x)) значение функции f(x) не возрастает, при-
при*
A2.1.37)
Если же множество Q, кроме того, ограничено и точка х при-
принадлежит подмножеству Q тех точек Q, для которых справед-
справедливо неравенство A2.1.30) при ц. > min/(;c), то неравенство'
Q
A2.1.37) переходит в неравенство
f(x)-f (Л >(±--f) У2, A2.1.
где у>0 — постоянная из леммы 6.
Доказательство. Достаточно для любой точки х мно-
множества Q установить неравенство A2.1.37), ибо из этого нера-
неравенства и из неравенства A2.1.34) сразу вытекает и неравенст-
неравенство A2.1.38) (для точек х, принадлежащих Q, при условии, что-
Q ограничено).
Сначала докажем неравенство A2.1.37) для случая, когда.
точка х является внутренней точкой множества Q. Имея в виду,,
что точка x* = Pq(x—agrad/(*)) принадлежит множеству Q, на*
котором функция f(x) сильно выпукла, выразим значение f{x*)-
по формуле Тейлора с центром в точке х, взяв остаточный член
/?2(**) в форме Лагранжа. При этом получим
fix*) = f(x) + (gradf(x),AxX+ -jd*f(x + 6Ax), A2.1.39V
где Ах=х*—x=PQ(x—agrad/(*))—x,
Используя неравенство A2.1.33) и правое неравенств»-
A2.1.14), мы получим из формулы Тейлора A2.1.39)
так что для случая внутренней точки х неравенство A2.1.37)*
доказано.
* Из A3.1.25) вытекает, что —— -^Г
532 Гл. 12. Функции нескольких переменных
Пусть теперь х является граничной точкой множества Q.
По определению граничной точки * найдется последователь-
последовательность {хп} внутренних точек множества Q, сходящихся к х.
Для каждой точки хп по формуле Тейлора с центром в этой
точке мы получим
f(*•)=/(*»)+(grad/(*„), (*•-*„)) +
d2f[X+Qn(x*-xn)l A2.1.40)
где 0<е«<1.
Учитывая, что правое неравенство A2.1.14) справедливо для
d2f в любой точке множества Q и что grad/(*) является непре-
непрерывной векторной функцией точки х на множестве Q, мы полу-
получим, что в .пределе при п-^ + оо из соотношения A2.1.40) выте-
вытекает справедливость неравенства A2.1.37) для граничной точки
х множества Q.
Лемма 7 доказана.
Перейдем теперь непосредственно к доказательству
основной теоремы. Сначала докажем основную теорему
при дополнительном предположении о том, что замкнутое вы-
выпуклое множество Q является также ограниченным.
Возьмем произвольную точку хг множества Q и составим
итерационную последовательность {хь) точек, определяемых ре-
рекуррентным соотношением A2.1.26), при условии, что число а
удовлетворяет неравенствам A2.1.25).
Из леммы 7 (а точнее, из неравенства A2.1.37)) сразу же
вытекает, что
Таким образом, последовательность {f(xh)} является невозрас-
тающей. Так как, кроме того, эта последовательность ограниче-
ограничена снизу (минимальным значением т функции f(x) на множе-
множестве Q), то она является сходящейся (см. теорему 3.15 из гл. 3).
Обозначим предел последовательности {f{Xh)} через \i. Ясно, что
(х>т, где т — минимальное значение f(x) на множестве Q.
Кроме того, поскольку все члены невозрастающей сходящей-
сходящейся последовательности не меньше ее предела (см. замечание 3
к теореме 3.15, гл. 3), то для всех номеров k справедливо нера-
неравенство
f{Xk)^v. A2.1.41)
Докажем, что для предела ц справедливо равенство
[г = т = гшп/(л;).
JC6Q
* Так как множество Q выпукло, то оно не может иметь изолированных гра-
граничных точек.
Дополнение 1 533
Предположим, что это равенство несправедливо, т. е. пред-
предположим, что \i>m. Тогда если обозначить через v максималь-
максимальное значение f(x) на множестве Q, а через Q подмножество тех
точек Q, для которых справедливы неравенства A2.1.30), то в
силу леммы 7 найдется строго положительная постоянная у та-
такая, что справедливо неравенство A2.1.38), которое приводит к
следующему неравенству:
Dг~~1гЬ8>0> A2Л.42)
справедливому для любого номера.k.
Суммируя неравенства A2.1.42), записанное для номеров k,
равных 1, 2, ..., п—1, мы получим, что для любого номера п
l-l)\——f)r
или, что то же самое,
Неравенства A2.1.43), справедливые для любого номера п, про-
противоречат неравенству A2.1.41), ибо величина, стоящая в пра-
правой части A2.1.43), при достаточно большом номере п становит-
становится меньше числа \i.
Полученное противоречие доказывает ошибочность предполо-
предположения \i>m, т. е. доказывает что ц = т. Итак, доказано, что по-
последовательность f(xk) сходится к минимальному значению т
функции f(x) на множестве Q.
Остается доказать, что сама итерационная последователь-
последовательность {Xh} сходится к той точке хо, в которой это минимальное
значение достигается*.
Фиксируем произвольное положительное число е и обозна-
обозначим через Се открытый m-мерный шар радиуса е с центром в
точке Хо. Далее обозначим через Qe ту часть множества Q, ко-
которая не содержит точек шара Се. Ясно, что Qz — замкнутое
ограниченное множество, так что функция f(x) достигает (в си-
силу второй теоремы Вейерштрасса) своего минимального на этом
множестве значения, которое мы обозначим через тг.
Можно утверждать, что mz>m, ибо в противном случае на-
нарушалось бы условие существования у функции f(x) на множе-
множестве Q единственной точки локального минимума.
Далее, можно утверждать, что на множестве <58 имеется
лишь конечное число точек последовательности {хи} (ибо
последовательность {/{хь)}, у которой имеется бесконечное чис-
* Нами уже доказано, что минимальное значение функции f(x) на множе-
множестве Q достигается в единственной точке этого множества.
534 Гл. 12. Функции нескольких переменных
ло элементов, удовлетворяющих неравенству f(^)>me>/n, не
может сходиться к числу т).
Значит, мы доказали, что для любого е>0 найдется номер-
N, начиная с которого все элементы последовательности {хь}~
лежат в шаре СЕ радиуса е с центром в точке Хо. Это и означа-
означает, что последовательность {хк} сходится к точке х0.
Тем самым для случая ограниченного замкнутого вы-
выпуклого множества Q основная теорема доказана.
Пусть теперь Q — неограниченное замкнутое выпук-
выпуклое множество. Снова фиксируем произвольную точку Х\ этогс-
множества и составим итерационную последовательность
A2.1.26) при условии, что число а удовлетворяет неравенствам
A2.1.25).
При доказательстве теоремы о существовании локального'
минимума у сильно выпуклой функции (см. п. 2) мы установи-
установили, что точка Хо локального минимума сильно выпуклой функ-
функции f(х) на неограниченном замкнутом выпуклом мно-
множестве Q лежит в той части QR множества Q, которая содер-
содержится в шаре CR с центром в точке х\, радиус R которого вы-
выбран из условия
R
Там же установлено, что подмножество Qr множества Q ньля-
ется ограниченным выпуклым замкнутым множеством и что всю-
всюду вне QR значения f(x) превосходят f(xi).
Так как в силу леммы 7 (а точнее, в силу неравенства1
A2.1.37)) последовательность {f(xh)} является невозрастающей»
а за пределами QR все значения f(x) .превосходят 1{х\), то все
точки итерационной последовательности {xk} лежат в Qr, а по-
потому для любого номера k
Pq (xk — a grad / {xk)) = PQr {xk — a grad / (xk)).
Значит, итерационную последовательность A2.1.26) можно
заменить на
после чего все дальнейшие рассуждения сведутся к ограничен-
ограниченному замкнутому выпуклому множеству QR, т. е. к уже рассмот-
рассмотренному выше случаю.
Основная теорема полностью доказана.
Замечание 1. Особенно просто выглядит последователь-
последовательность A2.1.26) для случая, когда множество Q совпадает а>
всем пространством Ет. В этом случае для любой точки х
справедливо равенство Pq(x) =x, и потому рекуррентная форму-
формула A2.1.26) принимает вид
Дополнение 2 535
ДОПОЛНЕНИЕ 2
Метрические, нормированные пространства
В этом дополнении будут изложены важные понятия и факты
общей топологии, которые часто употребляются в различных
разделах математики. Читатель без труда обнаружит, что эти
понятия и факты являются естественным обобщением ряда опре-
определений и утверждений, содержащихся в предыдущих главах.
Метрические пространства
1. Определение метрического пространства. Примеры. Выше
мы уже подчеркивали, что фундаментальную роль в анализе
играет понятие предела. В основе этого понятия лежит опреде-
определение расстояния между числами, т. е. абсолютная величина
разности этих чисел. Поэтому представляется естественным
ввести понятие расстояния уже не между двумя числами, а меж-
между двумя произвольными элементами некоторого абстрактного
множества X. Ясно, что при этом это расстояние должно обоб-
обобщать свойства расстояния между числами числовой оси. В свя-
связи с вышесказанным дадим следующее определение.
Определение 1. На множестве X определена структу-
структура метрического пространства, если задана функция
р(х, у) двух произвольных элементов этого множества х и yt
удовлетворяющая аксиомам:
1) p(*i #)=0 тогда и только тогда, когда х=у\
2) р(х, у)=р(у, х) (аксиома симметрии);
3) р(х> У)<-р(У> z)+p(z> х) (неравенство треугольника).
Функция р(х, у) называется метрикой или функцией
расстояния, число р(х, у) называется расстоянием
между точками х и у множества X.
Таким образом, метрическое пространство образуют множе-
множество X и функция расстояния р. Поэтому обозначается метри-
метрическое пространство обычно так: (X, р) или просто X, если ясно,
о какой метрике идет речь.
Если в аксиоме 3) положить х=у, то, учитывая 1), получа-
получается, что 0<p(t/, г), т. е. функция расстояния — неотрицатель-
неотрицательная функция своих аргументов.
Приведем примеры наиболее часто встречающихся метриче-
метрических пространств.
Примеры.
1) Множество вещественных чисел превращается в метриче-
метрическое пространство, если для любых чисел х, у положить р(х, у) =
— \х—у|. Это метрическое пространство обычно обозначает-
обозначается ?>.
536 Гл. 12. Функции нескольких переменных
2) Координатное «-мерное пространство Х = Ап, точки кото-
которого (или элементы множества X) ¦— упорядоченные наборы п
чисел, х= (х\ хп), превращается в метрическое пространст-
п
во, если положить р(х, у) = (V \*i—&12I/2, где *=
= (х\„ ..., хп), у—(уи ..., Уп)\ обозначается оно* через Еп —
= (X, р). Аксиомы 1) и 2) определения метрического простран-
пространства, как легко видеть, выполняются. Справедливость аксиомы
3) вытекает из неравенства Коши — Буняковского для сумм
(см. § 5 гл. 9):
Р2(*,</) = ? 1*,-&|я=? К*,-**) + &-&)]¦ =
= ? (xt - г,.J + 2 ? & -
г,J + 2 ? | xt - z, 11 zt -
x(—2lJ+2(? ix,-Zi|2I()
i=l 1=1 ' t=l 1=1
= p2 (x, z) + 2p (x, z) p B, y) + p2 (г, г/) - [p (x, z) + p (г, г/)]2.
Таким образом, р(х, у)*ср(х, z)+p(z, у), и неравенство тре-
треугольника в этом случае установлено. Заметим, что выше мы
применили неравенство Коши —Буняковского к сумме
п п
V \Хс —zt | \Zi — ус | = V* afii, где положено
На множестве X, элементами которого являются упорядо-
упорядоченные наборы п чисел x=(xi, ..., хп), можно вводить и другие
функции расстояния, например положить, что:
, где функция р(х, у) введена выше, в примере 2); или положить
Pi(x,y) = max \Xi—yc\; б)
It t<n
* Этим же символом Еп мы обозначим и евклидово пространство, состоящее
из элементов произвольной природы и имеющее размерность п.
Дополнение 2 537
Pa(*.«/) = 5) \xt—yi\\ в)
1, если хфу, .
г)
О, если х = у;
1, если р(лг, у)>\,
где функция .р (х, у) определяется, как указано выше.
Естественно, что при этом одно и то же множество X превра-
превращается в разные метрические пространства (X, р,-), где i=0, 1,
2, 3, 4.
3) Пусть Y — множество непрерывных функций, заданных
на сегменте [а, Ь]. Введем метрику, полагая чтор(х,у) =
= max |*@— У @1 • Получившееся пространство ПреДСТаВЛЯ-
ет собой-метрическое пространство. Оно обозначается через
С[а, 6]=(У, р).
Точно так же множество Z п раз непрерывно дифференцируе-
дифференцируемых функций на сегменте [а, Ь], п>1, становится метрическим
пространством, если ввести метрику по правилу:
р (х, у) = max max | *<'> (t) — «/"> (t) |,
где xm(t)=x(t), y<°)(t)=y(t). Это пространство обозначается
обычно так:
С„[а, b]=(Z, p), л>1.
Пространство С[а, Ь] иногда обозначается символом С0[а, Ь].
4) Пусть V — множество всех ограниченных последователь-
последовательностей *=(*!, ..., хп, ...) действительных чисел. Положим
р(х>У) — sup|xt- — yd . Справедливость аксиом 1)—3) метри-
i
ческого пространства очевидна. Это пространство обозначается
через т= (V, р).
Заметим, -что каждое подмножество Хо метрического прост-
пространства (X, р), в свою очередь, является метрическим простран-
пространством с той же самой функцией расстояния р. Действительно,
если аксиомы, определяющие метрику р, выполнены для любых
х, у, ге1, то они выполнены и для х, у, z, принадлежащих Хо.
Таким образом, каждое подмножество Еп — метрическое прост-
п
ранство с функцией р(х, у) = (V \х( — у(|2I/2 . Точно так же
?= 1
любое подмножество Сп[а, Ь] — метрическое пространство, п —
= 0, 1, 2, ....
538 Гл. 12. Функции нескольких переменных
Пара (Хо, р) называется подпространством простран-
пространства (X, р).
Заметим также, что если р(х, у) — функция расстояния »
некотором метрическом пространстве, то по формулам а) или
(Ц) примера 2) мы можем получить новую функцию расстояния.
2. Открытые и замкнутые множества. Шаром О (а, г) &
Метрическом пространстве X (замкнутым шаром К (а, г))
с Центром в точке а и радиусом г называется совокупность всех
точек хеХ таких, что р(х, а)<г(р(х, а)<.г).
Определение 2. Множество ЕсХ называется о т к р ы-
т ым в пространстве Х= (X, р), если вместе с каждой своей точ-
точкой х оно содержит и некоторый шар О(х, г). 0 также назовем
открытым.
Определение 3. Окрестностью точки х^Х назы-
называется любое открытое множество, содержащее х. Окрестно-
Окрестностью некоторого подмножества X (быть может, са-
самого X) называется любое открытое множество, содержащее'
данное подмножество *. Окрестность точки х будем обозначать
через 2*.
Определение 4. Пусть множество YaX, тогда точка
хеА' называется предельной точкой множества Y, если
каждая окрестность точки х содержит по крайней мере одну
точку множества У, отличную от х.
Точка г/е У называется изолированной точкой мно-
множества У, если существует окрестность точки у, в которой нет
точек Y, отличных от у.
Определение 5. Точка у, принадлежащая множеству
У — подмножеству X, — называется внутренней, если она
содержится в У вместе с некоторой своей окрестностью. Точки,
внутренние для дополнения Y в X, называются внешними по»
отношению к Y. Если точка не является ни внутренней, ни внеш-
внешней по отношению к Y, то она называется граничной для Y.
Множество граничных точек для Y обозначается через dY.
Определение 6. Множество в метрическом пространстве-
называется замкнутым, если его дополнение открыто.
Справедливо следующее утверждение.
Лемма 1. Сумма любого числа открытых множеств, пере-
пересечение любого конечного числа открытых множеств есть мно-
* Шар О {а, г) в метрическом пространстве, очевидно, является открытым,
множеством, а поэтому его также можно считать окрестностью точки а. То, что<
шар О (а, г)—открытое множество, следует из того, что этот шар содержит
любую свою точку х вместе с некоторым шаром О(х, е), где 0<г<г—р(а, х).
Действительно, если у^О(х, е), то р(а, г/)<р(а, х)+р(х, у)<р(а, х)+г—
—р(а, х)=г, т. е. у^О(а, г), поэтому любая точка у^О(х, е) принадлежит так-
также шару О (а, г). Следовательно, шар О(х, е)сО(а, г), и поэтому исходный шар-
О (а, г) — открытое множество (см. также пример 3) в конце настоящего раз-
раздела).
Дополнение 2 539
жество открытое, 0 и все метрическое пространство X открыты.
Пересечение любого числа замкнутых множеств замкнуто,
сумма любого конечного числа замкнутых множеств замкнута,
0 и X замкнуты.
Доказательство. Пусть {2а} — семейство открытых в
X множеств. Если л: е U 2а, то существует а0 такое, что
а
л;е2ао следовательно, существует число г>0 такое, что
О(х, г)сИ,ао> т- е- 0(х, г) a U 2а. Следовательно, (J2a— от-
а а *
крытое множество.
п
Далее, если 2i, ..., 2„ открыты в X, то из того, что х <= (~| 2(-,
i=\
следует, что для любого t=l, ..., п xgS,-, т. е. для любого i =
= 1, ..., п существует такое г,->0, что О(л;, г()сг2/. Взяв
г = min rit получаем, что для любого i=l, ..., га
О (X, Г) С О (JC, Г,), О (X, Г)<= f) 2;,
т. е. пересечение множеств 2,-, t=l « — открытое множество.
Второе утверждение непосредственно следует из первого, ес-
^ли воспользоваться принципом двойственности для множеств.
Например, пусть {Ра} — семейство замкнутых в X множеств.
Для каждого а введем в рассмотрение открытое множество
За = Fa' *. Тогда (П Fa)' = U F'а = U 2И, т. е. (П Fa)' — открытое
а а а а
а а
;множество, следовательно, П ^а замкнуто. То, что 0 и X одно-
а
временно открыты и замкнуты, очевидно**.
Определение 7. Замыканием Y множества Y называет-
называется пересечение всех замкнутых множеств, содержащих Y.
Очевидно, что У содержится в каждом замкнутом множест-
множестве, содержащем Y. Следовательно, замыкание множества У есть
наименьшее из всех замкнутых множеств, содержащих У.
Справедлива следующая лемма.
Лемма 2. Операция замыкания в метрическом пространст-
пространстве удовлетворяет следующим свойствам:
3) Г=>У, 2) Т=Г, 3) Y[}Z = Y\}Z, 4) 0 = 0, Х = Х.
Доказательство. Свойство 1) очевидно: если леУ, то
х принадлежит любому замкнутому множеству, содержащему У,
¦следовательно, х принадлежит и пересечению этих замкнутых
множеств, т. е.
* Напомним, что А' обозначает дополнение множества А.
** Мы по определению полагаем 0 открытым. Так как X, очевидно, откры-
открыто, то 0=Х' будет являться по определению 6 и замкнутым множеством.
Аналогично Х=0' замкнуто.
540 Гл. 12. Функции нескольких переменных
Свойство 2) вытекает из того, что У, будучи пересечением
замкнутых множеств, является в силу леммы 1 замкнутым мно-
множеством.
Докажем свойство 3), так как YaY{JZ, то каждое замкнутое
множество, содержащее Y(jZ, содержит и У, следовательно, пе-
пересечение этих замкнутых множеств также содержит У, т. е.
YaY[)Z, но У принадлежит любому_замкнутому множеству, со-
содержащему У, следовательно, YaY\jZ. Аналогично ZaY\}Z.
Таким образом, Y\JZczY\JZ; обратно, F(JZ в силу леммы 1 замк-
замкнуто, следовательно, Y\JZzdY\JZ.
Утверждение 4) означает, что 0 и X — замкнутые множе-
множества.
Лемма полностью доказана.
Попутно мы показали, что если множество AczB, то ЛсЯ.
Дадим следующее определение.
Определение 8. Пространство (X, р) называется связ-
н ы м, если его нельзя представить в виде суммы двух непустых
открытых непересекающихся подмножеств.
Очевидно, что пространство связно тогда и только тогда,
когда его нельзя представить в виде суммы двух непустых
замкнутых непересекающихся множеств.
Множество У, принадлежащее метрическому пространству
X, связно, если У связно как подпространство в X.
3. Прямое произведение метрических пространств. Если
(Xi, pi), (Х2, рг) —два метрических пространства, то можно
определить прямое произведение этих метрических пространств.
Пусть Х = Х\ХХ2— прямое произведение множеств Xi и Х2>
т. е. множество всевозможных пар (х\, х2), где х^Хи х2^Х2.
Метрику на множестве X можно ввести, например, по следую-
следующему правилу:
р(х, у)=Лр12(хь yi)+P22(x2,y2))^,
где х={х\, х2), У=(уи «/г), х^Хи (/(еУ{, t=l, 2. Пара (X, р),
Х = Х\ХХ2, р — функция расстояния, введенная выше, является
метрическим пространством и, по определению, называется
прямым произведением метрических пространств (Xj,
pi) и (Х2, р2).
Если задана счетная последовательность метрических про-
пространств (Хи pi), (Х2, рг),... и через X обозначено прямое про-
оэ
изведение множеств Хи i=l, 2,..., X— П-^'» т- е- ^ состоит
из элементов х= (xi, x2,...), Xi^Xu то можно дать, например,
следующее определение.
Определение 9. Прямым произведением мет-
метрических пространств (Хи pi), (X2, p2),... называется пара
{X, р), где
Дополнение 2 541
. Ук)
х,у<=Х, xk,yk<=Xk, х = {хг,х2, ...), г/= г/i, г/2. •••)>
*= 1,2
со
Обозначается оно так: (X, р) = J~] (X,-, р,-).
i=i
4. Всюду плотные и совершенные множества.
Определение 10. Пусть А и В— два множества в мет-
метрическом пространстве (X, р). Множество А называется плот-
плотным в В, если AzdB. Множество А называется всюду плот-
плотным в пространстве X, если А = Х.
Пространства, н которых имеются счетные всюду плотные
множества, называются сепарабельными.
Рассмотренные выше примеры метрических пространств Е1,
Еп, Сп[а, Ь], п>-0, являются примерами сепарабельных метри-
метрических пространств. Так, в Еп счетным всюду плотным множе-
множеством является множество точек, у которых все координаты —
рациональные числа. В пространствах Сп[а, Ь], я>0, такими
множествами являются множества многочленов с рациональны-
рациональными коэффициентами.
Однако пространство in есть пример несепарабельного про-
пространства *. Если рассмотреть множество Ео последовательно'
стей, состоящих только из нулей и единиц, то мощность такого
множества есть континуум.
Убедимся в этом. Рассмотрим какое-либо число х^
е [0, 1]. Разобьем сегмент [Q, 1] пополам. Возьмем в качестве
первого элемента последовательности число 0, если х принад-
принадлежит левой половине, т. е. сегменту [0, 1/2], и число 1 — в
противном случае. Тот из двух рассматриваемых сегментов, ко-
которому принадлежит х, обозначим [а\, Ь\\. В качестве второго
элемента последовательности возьмем 0, если х принадлежит
левой половине сегмента [а\, Ь\], и 1—в противном случае.
Продолжая эти рассуждения далее, мы поставим в соответствие
рассматриваемому числу х вполне определенную последова-
последовательность из нулей и единиц. Если хфу, то в результате опи-
описанного процесса эти точки на некотором этапе станут принад-
принадлежать разным отрезкам, а поэтому и последовательности, им
отвечающие, будут разные. Следовательно, множество всевоз-
всевозможных последовательностей из нулей и единиц есть множе-
* См. пример 4 из п. 1.
42 Гл. 12. Функции нескольких переменных
ство мощности, не меньшей, чем континуум. Для наших целей1
этого и достаточно *.
Взаимные расстояния в пространстве m между двумя различ-j
ными элементами р и q множества Ео есть величина, равная^
единице. Следовательно, приблизить сколь угодно близко каж-4
дый из этих элементов элементами счетного множества нельзя,;,
так как множество шаров радиуса 1/3 с центрами в точках
множества Ео имеет мощность не менее континуума и эти шары1
не пересекаются.
Поскольку Е^ат, где m=(V, p), то и все пространство т
несепарабельно.
Множество А называется нигде не плотным в метри-
метрическом пространстве X, если любое открытое множество этого
пространства содержит другое открытое множество, целиком
свободное от точек множества А.
Например, в пространстве С [О, 1] множество А функций
вида у — пх2 (п — целые числа) нигде не плотно. Другой при-
пример нигде не плотного множества на сегменте [0, 1] (рассмат-
(рассматриваемом как метрическое пространство) дает так называемое
канторово совершенное множество.
Множество А точек метрического пространства называется
совершенным, если оно замкнуто и если каждая точка
множества А является его предельной точкой.
Канторово совершенное множество на сегменте /= [0, 1]
строится следующим образом. Из сегмента [0, 1] удаляется ин-
интервал A/3, 2/3) и оставшееся множество — объединение двух
сегментов [0, 1/3), [2/3, 1]—обозначается через 1\. Из этих
двух сегментов, в свою очередь, удаляются их трети — интерва-
интервалы A/9, 2/9), G/9, 8/9). Объединение оставшихся сегментов
обозначим через 1%. Продолжим этот процесс неограниченно.
Очевидно, /гэДгэ ... =>/„=> ... и /„ есть объединение 2™ сегмен-
сегментов, длина каждого из которых 3~п.
00
Множество К = Р) /„ и называется множеством
л=1
Кантора.
Покажем, что К совершенно. То, что оно замкнуто, следует
из построения и леммы 1; остается показать, что К не содер-
содержит изолированных точек. Пусть х^К, и пусть 2* — произ-
произвольная окрестность точки х, т. е. открытое множество. Тогда
по определению открытого множества найдется интервал ах
(шар с центром в точке *), содержащий точку х и принадле-
принадлежащий 2Ж. Пусть Ап-—тот сегмент множества 1„, который со-
содержит точку х. Если п достаточно большое, то Апавх. Обо-
Обозначим через ап тот конец сегмента Ап, который не совпадает
* На самом деле множество всевозможных последовательностей из нулей
и единиц есть множество мощности континуум.
Дополнение 2
с х. Очевидно, это следует из построения множества К, ап<=К.
Следовательно, произвольная окрестность точки х-—множество-
2Ж — содержит точку апфх : an<=AnczexczT,x, т. е. точка х —
предельная для множества К, и К совершенно.
Докажем теперь, что множество К нигде не плотно на сег-
сегменте [О, 1], рассматриваемом как метрическое пространство с
обычным евклидовым расстоянием. Поскольку любое открытое
множество на сегменте содержит внутри себя интервал, то до-
достаточно показать, что любой интервал (шар) содержит внутри
себя другой интервал, свободный от точек, принадлежащих К.
Пусть а — произвольный интервал сегмента [0, 1]. Если он не-
содержит точек К, то построение в этом случае закончено.
Если же имеется точка х^К и хеа, то мы можем выбрать,
столь большое пг, что хеЛтс/т и Атав, т — натуральное..
Найдем интервал длины 3~(П1+1) с центром в середине Ат. Этот-
интервал не содержит точек К и содержится в о.
Таким образом, нигде не плотность множества К на сегмен-
сегменте [0, 1] доказана.
5. Сходимость. Непрерывные отображения.
Определение 11. Последовательность {ап} точек метри-
метрического пространства называется сходящейся к то чк е а-
этого пространства, если любая окрестность точки а содержит
все элементы этой последовательности, за исключением конеч-
конечного их числа. Если последовательность {ап} сходится к а, то-
пишут ап->-а при п-^-оо или lim an = a.
Непосредственно из данного определения следует, что ап->"
->а, если р(ап, а)-Я), п-^-оо.
Лемма 3. Точка а метрического пространства X принад--
лежит замыканию А некоторого множества А тогда и только'
тогда, когда существует последовательность {ап} точек множе--
ства А, сходящаяся к а.
Доказательство. Пусть аеА, тогда а принадлежит'
каждому замкнутому множеству, содержащему А. Возьмем в
качестве окрестности точки а шар О (а, 1/л), п — натуральное.
В этом шаре имеется по крайней мере одна точка опеЛ. Если1'
бы это было не так, то оеЛ и существовала бы окрестность
точки а, свободная от точек множества А, Дополнение до этой.^
окрестности было бы замкнутым множеством, содержащим
множество А, и точка а не принадлежала бы этому замкнутому
множеству. Таким образом, получилось противоречие условию*
а^А, следовательно, мы построили последовательность точек
ап-+а при я->-оо, опеЛ. Заметим, что данная последователь-
последовательность {ап} может оказаться стационарной, т. е. такой, что все
Верно и обратное: если ап->-а и ап*^А, то
Для этого заметим, что если любая окрестность точки а пе—
544 Гл. 12. Функции нескольких переменных
ресекается с А, то ael. Действительно, если аеЛ, то
Если аеА, то, допустив, что oel, и взяв дополнение множест-
множества А, получим окрестность точки а — множество (А)', не пере-
пересекающееся с А, т. е. получим противоречие.
Доказательство леммы теперь завершается так. Нам дано,
что ап-^-а и ап^А. Следовательно, любая окрестность точкц а
содержит точки ап множества А. По сказанному аеД, что и
требовалось.
Одновременно нами доказано следующее утверждение.
Утверждение. Точка а принадлежит замыканию мно\
жества А в том и только том случае, если каждая окрестности
2а точки а пересекается с А.
В гл. 4 было подробно изучено понятие непрерывности
функции числового аргумента. Оказывается, что это понятие
допускает естественное обобщение на случай, когда задана
уже не обычная функция числового аргумента, а отображение
одного метрического пространства в другое. Введем понятие не-
непрерывного отображения.
Определение 12. Отображение g одного метрического
пространства (X, р) в другое (Хо, ро) называется непрерыв-
непрерывным в точке х, если для каждой окрестности ^g(X) точки
g(x) найдется такая окрестность Их точки х, что g(T,x)czT,g(x).
Если g непрерывно в каждой точке пространства X, то такое
отображение называется непрерывным на X.
Справедлива следующая лемма.
Лемма 4. Отображение g: Х-*-Хо одного метрического
пространства X в другое Хо непрерывно на X тогда и только
тогда, когда прообраз любого открытого множества открыт.
Доказательство. Необходимость. Пусть g : Х->- Хо — не-
непрерывное отображение X в Хо и 20 — открытое множество в
Хо. Если g~'Bo) ={x^X :g(x)^T,o} = 0, то открытость ?~'Bо)
очевидна, так как 0 открыто.
Пусть ?Г1Bо)=й:0 и xe2=g-IB0). Так как *eg-'Bo), то
g(;t)e2o, следовательно, 2о можно рассматривать как окрест-
окрестность точки g(x). Ввиду того, что g — непрерывное отображе-
отображение на X (а значит, и- в точке *), найдется окрестность 2Ж точ-
точки х такая, что ?Bж)сг2о, т. е. 2жсг^~1Bо). Итак, для любой
точки x^g~l(I.o) найдется окрестность 2Ж такая, что 2жсг
W.
Поскольку 2 == U 2Х, то множество 2 открыто как объеди-
JC62
нение открытых множеств 2Ж. Таким образом, прообраз любо-
любого открытого множества открыт.
Достаточность. Пусть дано, что при отображении g гХ->-Х0
прообраз любого открытого множества открыт. Возьмем любую
точку х^Х и произвольную окрестность 2г(Ж) ее образа в ^о-
Тогда •2ж = ^-1Bй(ж)) по условию — открытое множество в X,
Дополнение 2 545
т. е. является окрестностью точки х, причем образ 2Ж при отоб-
отображении g содержится в 28(Ж). Следовательно, отображение g
по определению непрерывно в точке х. Поскольку эти рассуж-
рассуждения применимы, для любой точна х^Х, то отображение g
непрерывно на X и лемма доказана.
Учитывая, что шар является открытым-множеством и вся-
всякое открытое множество содфжит любую свой? точку вместе с
некоторым шаром, можно определение 12 непрерывности отоб-
отображения g: Х-^-Хо в точке х^Х переформулировать следую-
следующим образом.
Определение 13. Отображение g одного метрического
пространства (X, р) в другое (Хо, ро) называется непрерыв-
непрерывным в точке х, если для любого числа ё>0 существует та-
такое число 6>0, что если точка у принадлежит открытому шару
О(х, 6) с центром в точке х радиуса б, то точка g(y) принад-
принадлежит открытому шару O(g(x), e) с центром в точке g(x) ра-
радиуса е, лежащему в пространстве (Хо, ро) •
Последнее определение можно переформулировать также
следующим образом: отображение g: А'->Х0 непрерывно в точ-
точке х, если limg(у) = g(х),
У-+Х
Из неравенства треугольника легко заключаем, что функ-
функция расстояния р{х, у) непрерывна в точке х при фиксирован-
фиксированном у. На самом деле она является непрерывной функцией и
по двум переменным*.
В случае, если метрическое пространство X есть числовая
ось с обычным расстоянием между числами, т. е. пространство
Е1, а отображение g — обычная скалярная функция на Ё1, дан-
данное определение 13 непрерывности, очевидно, совпадает с опре-
определениями гл. 4.
Введем понятие гомеоморфизма.
Определение 14. Отображение g:Х-*-Хо метрического
пространства X в метрическое пространство Хо называется го-
гомеоморфизмом, если g отображает X на Хо взаимно од-
однозначно и g непрерывно вместе с обратным отображе-
отображением g~l.
6. Компактность. Покрытием множества А в мет-
метрическом пространстве называется любое семейство открытых
множеств, объединение которых содержит А.
Определение 15. Метрическое пространство X назы-
называется компактным или компактом, если любое его по-
* Функция р(х, у) определена на произведении ХхК и отображает ХхХ в
•?'. Функция p(jc, у) непрерывна на произведении метрнческих пространств ХхХ.
Ее непрерывность следует из неравенства четырехугольника:
ip(*, г)— р(</, и)К|р(*, у)+р{г, и)\, которое получается из двух неравенств:
р(х, z)<p(*, y)+p(y, z)<p(x, y)+p(y, и)+р(и, г),
р(«/, ы)<р(«/, *)+р(к, *)<рОл х)+р(х, г)+р(г, и).
18 Зак. 72
546 Гл. 12. Функции нескольких переменных
крытие содержит конечное подпокрытие, т. е. из всякого покры-
покрытия пространства X открытыми множествами можно выделить
конечную систему, содержащую все пространство (подпокры-
(подпокрытие).
Сегмент [а, Ь] числовой оси является компактом, что выте-
вытекает из того факта, что из всякого покрытия этого сегмента
открытыми множествами можно • выделить конечное подпо-
подпокрытие.
Можно показать, что метрическое пространство компактно
тогда и только тогда, когда из всякой последовательности его
точек можно выделить подпоследовательность, сходящуюся к
некоторой точке из этого пространства.
Определение 16. Система подмножеств {Аа} множест-
множества называется центрированной, если любое конечное
подсемейство этой системы имеет непустое пересечение.
Справедливы следующие леммы.
Лемма 5. Для того чтобы метрическое пространство X
было компактным, необходимо и достаточно, чтобы каждая
центрированная система замкнутых его подмножеств имела не-
непустое пересечение.
Доказательство. Пусть X компактно, и пусть {Fa}—
центрированная система замкнутых подмножеств. Множества
Gn = X\Fa открыты, и никакая конечная система из этих мно-
множеств Gn, l^n^LN<oo не покрывает X. Значит, поскольку X
компактно, {Ga} не могут служить покрытием компактного про-
пространства X. В противном случае мы могли бы выбрать конеч-
конечное подпокрытие X из системы {Ga}. Но если {Ga} не покрывает
X, то (\Fa не пусто, так как i]Fa = [)(X\Ga) = Х\ \jGa.
а а а а
Обратно, пусть любая центрированная система замкнутых
подмножеств из X имеет непустое пересечение. Пусть {Ga} —
открытое покрытие X. Выберем из этого покрытия конечное
подпокрытие. Положим Fa=^X\Ga и заметим, что так как {Ga}
покрывает все X, то []Fa = 0. Следовательно, {Fa} не яв-
ляется центрированной, т. е. существуют такие Ft, F2,..., FM,
м
М<оо, что Р) Ft = 0, но тогда {G*}Mi=i = {X\Fi}Mf=i — конеч-
ное подпокрытие покрытия {Ga}, что и требовалось доказать.
Лемма 6. Замкнутое подмножество компактного метри-
метрического пространства компактно*.
Доказательство. Пусть F — замкнутое подмножество
компактного метрического пространства X и {2„}—некоторая
система открытых множеств — покрытие F. К системе {Ъа} при-
* Т. е. из всякого покрытия этого подмножества открытыми в данном пра-
странстве множествами можно выделить конечное подпокрытие.
Дополнение 2 547
соединим открытое множество G=X\F, и полученное покры-
покрытие всего пространства обозначим через {2a1}={2a}L)G. Выбе-
Выберем в силу компактности X из системы {2а1} конечное покрытие
всего пространства — систему {Si1}*^,. Выбрасывая, если это
необходимо, из системы {2г-'}^г=1 множество G, мы получим
конечное покрытие множества F, выбранное из системы {2в}-
Лемма доказана.
Лемма 7. Образ компактного пространства X при непре-
непрерывном отображении — компактное множество.
Доказательство. Пусть g— непрерывное отображение
X в Хо. Пусть {2а}—покрытие g(X)czX0 открытыми множест-
множествами, а ЧГа=^~1{2»}- Множества Wa открыты (см. лемму 4), и
{ЧУ — покрытие g(X). Выберем из этого покрытия в силу ком-
компактности X конечное подпокрытие: {1F,-}JVf«-=i; тогда {2*}м/=ь
М<оо — покрытие Хо, 2,= gDfJ)> *' = 1. •••» -М, что и требовалось
доказать.
Лемма 8. Компактное подмножество метрического про-
пространства X замкнуто*.
Доказательство. Пусть F — компактное подмножество,
и пусть a^X\F; для любого xef существуют окрестности 2«
и 2Ж точек а и х соответственно такие, что 2аГJж=0. В каче-
качестве таких окрестностей можно, например, взять шары О (а, г)
и О(х, г), г = —р(а,х). Множество G = [} 2Х— покрытие
3 x&F
множества F. В силу компактности F выберем из этого покры-
покрытия конечное подпокрытие: {2*,};Lr Рассмотрим соответствую-
соответствующие 2*/ окрестности 2аг', которые по построению не пересека-
N
ются с 2*-» и П 2а = 2 является окрестностью точки а.
Очевидно, что 2ГJ^. = 0, i=l,...,N, и поэтому 20-^=0. Сле-
Следовательно, 2crX\.F, т. е. множество X\F открыто, a F зам-
замкнуто.
Лемма 9. Пусть g :X->~El, где Е —действительная число-
числовая ось. Если g — непрерывное отображение, а X — компакт, то
g ограничено и достигает своих точных верхней и нижней
граней.
Доказательство. Пусть g(X) — непрерывный образ
компакта (компактного пространства). По лемме 7 подмноже-
подмножество g(X) метрического пространства ?' компактно, следова-
следовательно, ограниченно и замкнуто (см. гл. 4, § 7, п. 3). Осталось
заметить, что непустое ограниченное замкнутое множество чис-
* Заметим, что в отличие от множеств числовой осн (или Еп) в случае об-
общего метрического пространства ограниченность и замкнутость множества еще
недостаточна для его компактности (ср. с гл. 4, § 7, п. 3).
18*
5 48 Гл. 12. Функции нескольких переменных
ловой оси содержит точные верхнюю и нижнюю грани *.
доказана.
7. Базис пространства. Введем понятие базиса.
Определение 17. Система открытых множеств {Еа} мет-
метрического пространства X называется базисом этого про-
пространства, если всякое непустое открытое множество простран-
пространства X может быть получено как объединение некоторых 2а из
множеств системы.
Справедлива следующая лемма.
Лемма 10. Для того чтобы система {Ъа} открытых мно-
множеств была базисом пространства X, необходимо и достаточно,
чтобы для всякого открытого множества G и всякой точки а<=
eG нашлось бы такое множество 2ао из данной системы, что
ае 2а,,сг G.
Доказательство. Допустим, что система {2а}— базис
пространства. Тогда любое открытое множество G есть сумма
некоторых из множеств {2а}. Поэтому для всякой точки aeG
существует такое множество 2ао, что ae2aocG и 2а,, при-
принадлежит данной системе {2а}.
Обратно, пусть выполнены условия, сформулированные в
лемме. Тогда всякое открытое множество G представимо в виде
G = U
в
т. е. система {2а„}— базис пространства. Лемма доказана.
Определение 18. Метрическое пространство X назы-
называется пространством со счетным базисом, если
в нем существует хотя бы один базис, состоящий не более чем
из счетного числа множеств. Пространства со счетным базисом
называются также пространствами со второй ак-
аксиомой счетности.
Лемма 11. Метрическое пространство X является про-
пространством со счетным базисом тогда, когда в нем имеется
счетное, всюду плотное множество. Обратно, если в простран-
пространстве имеется счетный базис, то в нем есть и счетное всюду
плотное множество.
Доказательство. Пусть A = {an}°°n=i — счетное, всюду
плотное множество в X. Всевозможные шары О(ап, 1/ш), где
п, m — всевозможные натуральные числа, образуют базис про-
пространства, причем счетный.
Обратно, если в X имеется счетный базис {2n}°°n=i, то, вы-
выбрав по точке ane2n, мы получаем множество Л = {ап}°°п=ь
которое всюду плотно. Действительно, если бы АФХ, то откры-
открытое множество G = X\A было бы не пустым и не содержало бы
ни одной точки из А = {ап}°°п=и что невозможно, так как G —
См. также гл. 4, § 7, п. 3.
Дополнение 2 549
открытое множество и оно есть объединение некоторых из мно-
множеств системы {2„}, а о„еЕ„.
Примеры. 1) Легко построить метрическое пространство
{X, р) и замкнутые шары Ki(xu п) и К2\х2, г2) такие, что Kid
Действительно, пусть (X, р) — метрическое пространство,
состоящее из всех точек {*, у} замкнутого круга на плоскости
ху:Х=={х, у: х2-\-у2^9} с обычной евклидовой метрикой р.
Шар К2 определим так: Kz=(X, p). Пусть шар Ki=K2f){x, у:
: (лс—2 )»+#*< 16}. Тогда КхаК2, г, =4, г2=3, Г!>г2.
2) Множество А метрического пространства замкнуто тогда
и только_тогда, когда оно совпадает со своим замыканием А,
т. е. А = А.
Действительно, если А=А, то, так как замыкание любого
множества замкнуто (как пересечение замкнутых), А — зам-
замкнуто.
Обратно, А принадлежит любому замкнутому множеству, со-
содержащему А; одним из таких замкнутых множеств является
в данном случае само Л,_т. е. АаА. С другой стороны, по опре-
определению замыкания АаА, т. е. если А замкнуто, то А=А.
3) Шар О(хо, г), как уже говорилось выше, в метрическом
пространстве X — открытое множество. (Если х^О(х, г), т. е.
р(х, хо)<г, то шар О(х, е) при 0<е<г — р(*о, х) будет при-
принадлежать исходному множеству: О(х, е)аО(хо, г). Действи-
Действительно, если (/еО(х, е), т. е. р(х, у)<в, то
, у)<р(хо, х)+г — р(х0, х)=г.)
Аналогично замкнутый шар — множество К(х, г) ={у :р(х, у)^
^г} — замкнутое множество в X. Это следует из того, что его
дополнение есть множество открытое.
4) Замыкание А множества А метрического пространства
состоит из всех точек, которые являются либо предельными
точками множества А, либо элементами А *. Действительно,
всякое множество содержится в своем замыкании: АаА. До-
Докажем, что замыкание А содержит и предельные точки для А.
В самом деле, замыкание множества — множество замкнутое,
а если множество замкнуто, то оно содержит все свои предель-
предельные точки: если' точка не принадлежит замкнутому множеству,
то она принадлежит его дополнению, которое и является
окрестностью этой точки, свободной от точек замкнутого мно-
множества, т. е. точка не является предельной для замкнутого
множества. Иными словами, А содержит все свои предельные
* Это утверждение остается справедливым, а доказательство полностью со-
сохраняется и для топологических пространств, которые будут рас-
рассмотрены в следующем разделе. Заметим также, что предельная точка множества
А может оказаться элементом множества А.
550 Гл. 12. Функции нескольких переменных
точки; так как Лсгл, то А содержит и все предельные точки
множества Л. Таким образом, замыкание Л содержит точки мно-
множества Ли точки, предельные для Л. Обратно, пусть хеЖ,
покажем, что тогда либо* — предельная для Л, либо хеЛ.
Действительно, если х^.А и х^А, то все доказано. Если же
я&4, но х^А, то *—предельная для А. В самом деле, допу-
допустим противное, тогда существует окрестность точки х — 2Ж,
свободная от точек множества Л. Ее дополнение — замкнутое
множество, содержащее Л и не содержащее х, т. е. точка х^А,
что невозможно.
5) В метрическом пространстве (X, р) можно построить от-
открытый шар О(х, г)={у: р(х, у)<г} и замкнутый шар
К(х, г)={у :р(х, у)^г} с общим центром и равными радиуса-
радиусами такие, что О(х, г)ФК(х, г). Действительно, пусть X — мно-
множество, состоящее более чем из одной точки, и пусть
1, если хфу,
0, если х = у,
тогда К(х, 1)=Х, О(х, 1)=х, О(х, 1)=хФК(х, 1).
Свойства метрических пространств
В предыдущем разделе были изложены основные свойства
метрических пространств, базирующиеся на понятии открытого
и замкнутого множеств. Следует подчеркнуть, что фактически
все утверждения предыдущего раздела используют только свой-
свойства открытых множеств — то, что сумма любого числа и пере-
пересечение конечного числа открытых множеств есть множество от-
открытое, все пространство и пустое множество открыты, и не
используют такие понятия, как шар, расстояние. Все это наво-
наводит на мысль, что можно строить пространства, в которых от-
открытые (замкнутые) множества определяются аксиоматически
с сохранением свойств, сформулированных в лемме 1. Тогда
надобность в определениях 1 и 2 отпадает, а утверждение лем-
леммы 1 станет аксиомой. Именно так мы и поступим в следующем
разделе, когда будем изучать топологические пространства.
Ясно, что при этом будет достигнуто полное единообразие в
изучении основных свойств метрических и топологических про-
пространств.
Такой подход к изучению свойств метрических пространств
(формулировки и доказательства, использующие только свой-
свойства открытых (замкнутых) множеств) обладает, конечно, ря-
рядом преимуществ — например, допускает обобщения на классы
более общих пространств. Вместе с тем, поскольку в структуру
метрического пространства введена функция расстояния, эти
пространства должны обладать и своими, присущими" только
Дополнение 2 551
им свойствами. Более того, чаще всего именно эти свойства и
изучаются при рассмотрении метрических пространств.
В настоящем разделе мы и изложим эти фундаментальные
свойства метрических пространств. Все они используют понятие
полноты пространства.
Определение 1. Последовательность {хп} элементов
метрического пространства (X, р) называется фундамен-
фундаментальной, если для любого числа е>0 существует такое на-
натуральное число N, что для любых п, m~>N выполняется нера-
неравенство р(хп, хт)<г.
Определение 2. Метрическое пространство (X, р) назы-
называется полным, если в нем всякая фундаментальная после-
последовательность сходится к некоторому пределу, являющемуся
элементом этого пространства.
Заметим, что, как мы уже говорили, если последователь-
последовательность {хп} сходится к элементу х, то р(х, хп)^>-0 при л-»-оо *.
Теорема (принцип вложенных шаров). Для
того чтобы метрическое пространство было полным, необходи-
необходимо и достаточно, чтобы в нем всякая последовательность зам-
замкнутых вложенных друг в друга шаров, радиусы которых стре-
стремятся к нулю, имела непустое пересечение.
Доказательство. Необходимость. Пусть (X, р) — пол-
полное метрическое пространство, a Ki(x\, г^гэ/Сг^г, г2)=э...—
вложенные друг в друга замкнутые шары. Последовательность
их центров фундаментальна, так как р(хп, хт)<Гп, т~>п, а
гп-*0, л->оо.
Поскольку пространство X полное, то существует элемент х
00
пространства X такой, что х = lim хп. Очевидно, что #е f\ К,п.
Действительно, х — предельная точка для каждого Кп (см.
определение 4 п. 1) ввиду того, что при т>л xm^KmczKn, a
так как Кп— замкнутое множество, то х^Кп (см. пример 4
с. 549).
Достаточность. Пусть выполнены условия теоремы относи-
относительно шаров. Докажем, что пространство X полное. Мы дол-
должны показать, что если {хп} — фундаментальная последова-
последовательность, то она имеет предел х^Х. Выберем точку хП1 та-
такую, что р{хп,Хп,)< 1/2, л>пх. Примем хГл за центр замкну-
замкнутого шара радиуса 1, который обозначим через К(хп^ 1)- Выбе-
Выберем, далее, точку х„г из последовательности {хп}, удовлетво-
удовлетворяющую следующим условиям: р(л;П1,л:„2)< 1/2а для любого
п>П2, П2>п\. Примем точку хПг за центр шара К(хПг, 1/2) ра-
радиуса 1/2. Пусть хП1, хп„ •.' ,х„к (щ<П2,... <nh) уже выбраны,
* Очевидно, что любая сходящаяся последовательность является фундамен-
фундаментальной.
552 Гл. 12. Функции нескольких переменных
тогда Xnk+l выберем так, чтобы выполнялись условия:
p(xn'xnk+1)< l/2*+1 для любого n>nh+u nh+i>nh. Как и выше,
примем хп за центр замкнутого шара К(хп , 1/2*) ра-
радиуса l/2ft и т. д. Мы получили-последовательность вложенных
друг в друга замкнутых шаров, радиусы которых стремятся к
нулю. По предположению существует точка х, общая для всех
шаров. Ясно, что р(яП/г»х)->0,nk->-oo, т. е. фундаментальная
последовательность {хп} содержит последовательность {хпЛ,
сходящуюся к некоторой точке х пространства. Тогда и сама
последовательность сходится к этому же пределу. Действитель-
Действительно, применяя свойство треугольника для функции расстояния
(см. определение 1 п. 1), имеем
Р (*„» х) < Р (xnk, x) + p (*„, Xnk) ->- 0, nk, п ->- оо.
Таким образом, Нтхл = леХ. Теорема доказана.
Замечание. В условиях теоремы все условия являются
существенными: полнота пространства, замкнутость шаров, ус-
условие того, что они вложены, стремление их радиусов к нулю.
Наименее очевидным является необходимость последнего усло-
условия. Вот пример полного метрического пространства и последо-
последовательности вложенных друг в друга замкнутых шаров, имею-
имеющих пустое пересечение.
Пусть X=(N, р), где N — множество натуральных чисел, а
р {т, п) =
Пусть
11,1
II—1 , если пфт,
т-\-п
О, если п — т.
-^~) = {т : р (т, я)< 1 + 1/2п}, п = 1,2.
Тогда очевидно, что К (п, 1 -\ ) замкнуты и вложены друг
\ 2л /
в друга, а пространство полно, поскольку каждая фундамен-
фундаментальная последовательность сходится в пространстве (она яв-
является, как говорят, «стационарной»). Однако пересечение ука-
указанных шаров, очевидно, пусто.
Определение 3. Множество М, расположенное в метри-
метрическом пространстве X, называется множеством первой ка-
категории, если его можно представить в виде объединения
счетного числа нигде не плотных в X множеств.
Все остальные множества называются множествами вто-
второй категории.
Теорема (теорема о категориях). Пусть {X, р) —
непустое полное метрическое пространство, тогда X — множест'
Дополнение 2 553
во второй категории, т. е. X нельзя представить в виде объеди-
объединения счетного числа нигде не плотных множеств.
Доказательство. Предположим противное, что X —
00
= (J Ап и каждое из множеств Ап, п=1, 2,..., нигде не ПЛОТ-
ПЛОТЯМ
но в X. Пусть Ко — некоторый замкнутый шар радиуса едини-
единица. Поскольку множество А\ нигде не плотно, то существует
замкнутый шар К\ радиуса меньше 1/2 такой, что A'icr/C0 и
Ki(]Ai = 0. Поскольку множество А2 нигде не плотно, то точно
так же существует замкнутый шар К2 радиуса меньше 1/22*
принадлежащий Ki, для которого К2пА2=0 и т. д. В резуль-
результате мы получаем последовательность вложенных друг в друга
замкнутых шаров {Кп}е°п=и радиусы которых стремятся к
нулю. По предыдущей теореме существует д:е/(„_для любого
п, х^Х. Так как по построению КппАп = 0, то х^Ап для лю-
бого п. Следовательно, х е \J Ап = X. Это противоречит пред-
л= 1
со
положению: X = у Ап. Теорема доказана.
Определение 4. Отображение g метрического простран-
пространства X в это же пространство называется сжимающим,
если существует такое число 0<а<1, что
p(g(x),g(y)Xap(x,y).*
Теорема (принцип сжимающих отображе-
отображений. Всякое сжимающее отображение полного метрического
пространства (X, р) в это же пространство имеет и при том
только одну неподвижную точку х^Х, т. е. такую точку JteX,
что g(x) =х.
Доказательство. Пусть хо — некоторая точка из X.
Определим последовательность {jcn}con=i по правилу: Xi=g{x0),
g(),
Последовательность {хп} фундаментальна в X. Действитель-
Действительно, если пг>п, то
<...anp(*o, xm-n)<.an{p(x0> xl) + p(xu x2) +
+ ...+p(xm-n-u xm-n)}<anp(x0,
<anp(*0, jji)-A —a)-1,
где a<l.
* Отсюда следует, что сжимающее отображение g непрерывно, т. е.
g(y)=g(x).
554 Гл. 12. Функции нескольких переменных
Таким образом, р{хп, xm)-*-Q, m,n-*-oo. В силу полноты
пространства X существует Пт хп. Пусть х=\\тхп. Тогда
в силу непрерывности отображения g имеем
xn) = lim xn+1=x.
Итак, неподвижная точка существует. Докажем ее единствен-
единственность. Если g{x)=x и g(y)=y, то р(*. y)<ap(x, у), т. е.
р(дг, у)=0 и х = у.
Замечание. Если отображение g метрического простран-
пространства X в себя обладает лишь тем свойством, что p(g{x),
S(y))<p(x, у) при хфу, то неподвижной точки может и не
быть. Вот соответствующий пример: пусть Х= (Р, р), где Р =
= [1, оо), а р — обычная евклидова метрика. Пусть g{x) =
=*+ —. Тогда p(g(x),g(y)) =
<\х-у\.
х у
Однако неподвижной точки нет: g(x) = х+ — i=x ни для
какого лсеХ
Определение 5. Будем говорить, что два отображения g
и g\ метрического пространства (X, р) в это же пространство
коммутируют, если для любого х^Х справедливо равен-
равенство g(gi(x))=gl(g(x)).
Теорема (обобщение принципа сжатых
отображений). Пусть gi и gz — отображения полного мет-
метрического пространства (X, р) в это же пространство. Тогда,
если отображение gi сжимающее и отображения g и g\ комму-
коммутируют, то уравнение g(x) =x имеет решение х^Х.
Доказательство. По предыдущей теореме существует
и притом только одна точка jcel такая, что gi(x)=x. Приме-
Применим к обеим частям равенства отображение g. Воспользовав-
Воспользовавшись тем, что отображения коммутируют, получим
g(gi{x))=g{x)., gi{g{x))=g(x), gi{y)=y,
где y=g{x). Учитывая, что отображение g\ сжимающее и не-
неподвижная точка у этого отображения одна, получим, что х=
— y—g(x). Следовательно, и у отображения g существует не-
неподвижная точка, а именно найденная выше точка х.
Замечание. Степенью п отображения g называется отоб-
отображение gn, полученное в результате п последовательных при-
применений отображения g:
gn(x)=g(g(...g(x))...), jjeX.
Из предыдущей теоремы в силу того, что отображения g и gn
коммутируют, следует, что если отображение g таково, что не-
Дополнение 2 555
которая степень п его — сжимающее отображение, то уравне-
уравнение g(x)=x имеет единственное решение*.
Примеры. 1) Нахождение корней функции. Пусть <р@>-
a^t^b — действительная функция, удовлетворяющая условию
Липшица:
и отображающая сегмент [а, Ь] в себя. Если ввести метриче-
метрическое пространство (X, р), где Х= [a, b], a p — обычная евкли-
евклидова метрика на сегменте, то отображение <р в X сжимающее, и
потому числовая последовательность t0, ^1=ф(^о), ^2=<p(^i),...
сходится к единственному корню уравнения q>(t)=t для любо-
любого to^[a, b]. Отображение <р сжимающее, если, например,
|<р'(/)|<е<1, te=[a, b].
Пусть нам надо решить уравнение вида F(t)=O, причем
F(t) действительная, определенная на [а, Ь], функция, F(a)<
<0, F(b)>0, 0<Qi^F'(О<82 при t<=[a, b]. Тогда, если рас-
рассмотреть функцию q>(t)=t— kF(t), X^E1 и найти корень урав-
уравнения (p{t)=t, то мы решим исходную задачу. К этому послед-
последнему уравнению можно применить предыдущие рассуждения,,
если, например |ф'(/)|<0<1. Имеем 1 — Лбг^фЧО^1 — M)i-
Нетрудно подобрать действительное число Х>0, чтобы было
выполнено условие: 0^<р'(^)^6<1. Тогда, как нетрудно убе-
убедиться, функция >ф@ отображает сегмент [а, Ь] в себя. Дей-
Действительно, так как ф'(^)>0, то <f(t) не убывает, следователь-
следовательно, ф(а)^<р(?)^ф(Ь) для любого t из сегмента [а, Ь]. Но
<р(с)=а — KF(a)>a, <f(b)=b — KF(b)<b, т. е. a<<p(t)<b для:
любого te [а, Ь].
2) Нахождение решений систем уравнений вида у — Ах-\-Ь„
п
Пусть yi == ^ ацХ) + b, t=l,..., n — отображение n-мерного про-
странства в себя: набор {х\, Хъ,..., хп) переходит в набор (г/ь
Уч, —,уп)^Х, т. е. отображение g(x)=Ax+b переводит набор»
из п чисел в набор из п чисел. Здесь х, b, g{x)=y — векторы,,
А — матрица, А = {aa}ni, j=i.
Если отображение g(x) будет в некотором метрическом про-
пространстве и при некоторых условиях сжимающим, то векторное
уравнение ^(д:)=д: будет иметь по предыдущему одно и только*
одно решение. Найдем такие условия на отображении g и вве-
введем метрику на множестве X, т. е. образуем соответствующие
метрические пространства:
* Единственность решения следует из того факта, что всякая точка, непо-
неподвижная относительно отображения g, будет неподвижной и относительно отоб-
отображения gn.
556 Гл. 12. Функции нескольких переменных
А) Пусть рг(х, */) = max \xi—yt\ ax, yeX. Тогда
п
Pi (У', У") < т* ? I oti I Pi (xr, x"),
*', *", У1. /еХ, y' = Ax' + b, y" = Ax" + b,
и условие того, что отображение g сжимающее, будет выполне-
выполнено, если
|а,/|<а<1, i = \, 2, .... п.
Б) Если ввести метрику на X по правилу
1=1
то, как нетрудно вычислить, условие того, что отображение
сжимающее, будет иметь вид
п
|а</|<а< 1, /=1, 2, ..., /г.
В) Наконец, если метрика задана так:
то отображение g сжимающее, если
/
Выписанные условия достаточны, для того чтобы уравнение
g(x)=x имело и притом единственное решение или, что то же
п
самое, чтобы система xt — V а</ДС/ + &,-, i=l, 2,...,n, имела и
/=i
притом одно решение.
3) Существование и единственность решения обыкновенного
дифференциального уравнения первого порядка. Рассмотрим
так называемую задачу Коши. Надлежит найти такую диффе-
дифференцируемую функцию у(t), которая удовлетворяла бы уравне-
уравнению У —f(ty) и при t = t0 имела заданное значение y(to)=yo,
где уа — некоторое число; при этом надлежит доказать, йто при
определенных условиях такое решение у(t) только одно.
Дополнение 2 557
Предположим, что функция f(t, у) непрерывна на множест-
множестве: a^t^b, —оо<г/<оо и удовлетворяет с константой К усло-
условию Липшица по у, т. е. для всех точек te [a, b]
\f(t. yO-f(t, у2)\<К\у1-уа\,
и пусть to — внутренняя точка сегмента [а, Ь]. Легко убедиться,
что решение задачи Коши эквивалентно решению интегрально-
интегрального уравнения y(t) = yo + [f(b #(!))$;• Значит, задано отобра-
отобрало
жение множества функций {у} по правилу: ё{у) — у« +
+ [ f{%> y{l))d?,- Введем пространство С [а, Ь]. Тогда отобра-
i
жение g определено на этом пространстве и отображает его в
себя, а задача о нахождении решения интегрального уравне-
уравнения сводится к нахождению неподвижной точки отображения
g — нахождению функции у такой, что g(y)=y. Для того что-
чтобы такая точка существовала и была одна, достаточно, чтобы
отображение g было сжимающее.
Поскольку из условия Липшица следует, что
If a yi) —fit, у2)\<К\у1-у2\<Кр(Уи у2),
то
t
P(g(y)> #(*))< max fKp(J/. z)dI</CF—a)p(y, z).
Здесь p — метрика в С [a, b]. Следовательно, отображение сжи-
сжимающее, если сегмент [а, Ь] достаточно мал, так что
а)=8<1.
При этих условиях мы получаем теорему существования и
единственности решения задачи Коши на сегменте [а, Ь], со-
содержащем точку to-
4) Оператор Вольтерра, свойства его п-й степени. Покажем,
что некоторая степень отображения, задаваемого интеграль-
интегральным оператором Вольтерра, имеющим вид
t
где Я, —некоторое число, K(t, |), <p(t) —непрерывные функции
своих аргументов, представляет собой сжимающее отображе-
отображение в С [а, Ь], а</<Ь, о<^<6.
Пусть
М= max \K(t, l)\, p(Ji, /2)= max \f1(t)—f2(t)\.
558 Гл. 12. Функции нескольких переменных
Тогда
\g(h)-g(h)\ = Щ|\K{t, l){h{i)-
а
<\K\M(b-a)P(fu /2).
Отсюда
Всегда можно выбрать такое п, что1-1 * -< 1, и, следо-
п\
вательно, при этом п отображение gn будет сжимающим. Со-
Согласно замечанию после предыдущей теоремы интегральное
уравнение вида g(f)=f имеет при любом % решение, и притом
единственное.
Топологические пространства
В настоящем разделе будут рассмотрены основные свойства
топологических пространств. Материал данного раздела впол-
вполне аналогичен изложенному в разделе о метрических простран-
пространствах, и поэтому мы повторим лишь основные определения, а
доказательства некоторых теорем, поскольку они являются до-
дословным повторением соответствующих доказательств в разде-
разделе о метрических пространствах, опустим. Подробнее мы оста-
остановимся лишь на специфических особенностях топологических
пространств.
1. Определение топологического пространства. Хаусдорфово
топологическое пространство. Примеры.
Определение 1. Говорят, что на множестве X определе-
определена структура топологического пространства^
если задана система {2} его подмножеств, обладающая свой-
свойствами:
1) само множество X и пустое множество 0 принадле-
принадлежат {2};
2) сумма любого числа множеств системы {2} и пересечение
любого конечного числа множеств системы {2} принадле-
принадлежат {2}.
Система {2}, удовлетворяющая условиям 1)—2), называется
топологией на множестве X, а составляющие ее множест-
множества — открытыми в этой топологии *.
Таким образом, пара, состоящая из множества X и тополо-
топологии {2}, является топологическим пространством, которое ино-
иногда удобно обозначать через (X, 2).
* Множество, являющееся дополнением к открытому, называется замкну-
замкнутым в топологическом пространстве.
Дополнение 2 559
Определение 1 выделяет весьма общий класс пространств.
Обычно этот класс несколько сужают, добавляя к свойствам 1)
и 2) так называемые аксиомы отделимости. Из этих
аксиом мы рассмотрим наиболее часто используемые. ¦
Аксиома Т2 (Хаусдорфа): для любых различных то-
точек х и у, принадлежащих множеству X, существуют такое мно-
множество Ъх, содержащее точку х, и множество Ъу, содержащее
точку у, такие что они оба принадлежат системе {2} и не пере-
пересекаются, т. е. 2жП2!/=0.
Топологические пространства, удовлетворяющие аксиоме Т2
(аксиоме Хаусдорфа), называются х а у с д о р ф о в ы м и.
Аксиома Т\: для любых двух различных точек х и у,
принадлежащих множеству X, существует множество 2Ж, при-
принадлежащее системе {2}, содержащее точку х и не содержащее
точку у, а также существует множество 2^ из системы {2}, со-
содержащее точку у и не содержащее точку х.
Топологические пространства, удовлетворяющие аксиоме Т\,
называются 7Упр остр а нств а ми.
Ясно, что если выполнена аксиома Т2, то аксиома Т\ выпол-
выполнена, т. е. класс топологических пространств, удовлетворяющих
аксиомам 1), 2), 72, более узкий, чем класс топологических
пространств, удовлетворяющих аксиомам 1), 2), Т\.
Примером пространства, удовлетворяющего аксиомам
1), 2), Т\ и не удовлетворяющего аксиомам 1), 2), Т% является
следующее топологическое пространство. Множество X состоит
из точек отрезка [0, 1], а открытыми считаются следующие
множества: X, 0, 2ап = [0, 1]\{а„}, где {а„} — произвольное,
не более чем счетное множество отрезка [0, 1]. Очевидно, что
аксиомы 1), 2), Т\ выполнены. Однако аксиома Т2 не выпол-
выполняется.
Не всякое топологическое пространство удовлетворяет ак-
аксиоме Т\. Вот традиционный пример. Множество Х={а, Ь}
состоит из двух точек. Топологию зададим открытыми множе-
множествами, к которым отнесем все X, пустое множество 0 и точ-
точку Ь. Аксиомы 1) и 2) выполнены, а аксиома 7\ — нет.
Приведем наиболее часто встречающиеся примеры топологи-
топологических пространств.
Примеры.
1) Рассмотрим произвольное метрическое пространство
(X, р). Открытые множества в силу леммы 1 раздела о метри-
метрических пространствах удовлетворяют свойствам 1) и 2) опре-
определения 1 топологического пространства. Аксиома Т2 (Хаусдор-
(Хаусдорфа) также выполняется в метрическом пространстве: если
хфу, то р(х, у) = а>0 и шары О (х, -?-\, О (у, -—¦)— открытые
множества в (X, р), такие что О (х, —-) П О (у, -—1 = 0.
V о 1 \ ¦ d /
560 Гл. 12. Функции нескольких переменных
Таким образом, всякое метрическое пространство (X, р) яв-
является и хаудорфовым топологическим пространством (А*, I),
где {Б}— система открытых множеств в (X, р).
2) Рассмотрим множество X произвольной природы. Отне-
Отнесем к системе {5} только все множество X и пустое множество
0. Аксиомы 1), 2), очевидно, выполнены. Однако аксиомы 7\
и Гг не выполнены. Такая топология называется антидис-
антидискретной.
3) Пусть X — произвольное множество. Отнесем к системе
{Б} все подмножества множества X. Легко проверить, что
{Б}— хаусдорфова топология. Такая топология называется
дискретной.
Дадим следующее определение.
Определение 2. Окрестностью точки х, принадлежащей
топологическому пространству (X, Б), называется любое откры-
открытое множество, содержащее точку х. Окрестностью некоторого
подмножества X (быть может, самого X) называется любое от-
открытое множество, содержащее данное подмножество (или X),
Окрестность точки х будем обозначать Бх.
Предположим, что для каждой точки х, принадлежащей то-
топологическому пространству (X, Б) среди всех окрестностей
этой точки выделены некоторые, причем так, что какова бы ни
была точка х и ее произвольная окрестность Бх, существует
окрестность Б*1 точки х из выделенной системы, что '
Б
Определение 3. Система выделенных окрестностей {Б*1}
называется определяющей системой окрестно-
окрестностей данного топологического пространства *.
Справедлива следующая лемма, которая дает удобный спо-
способ задания топологии.
Лемма 1. Пусть X — произвольное множество. Для каж-
каждой точки х определим некоторые подмножества 2Х, называе-
называемые «окрестностями» точки х и удовлетворяющие ус-
условиям:
а) каждая точка имеет хотя бы одну свою «окрестность» и
принадлежит любой своей «окрестности»;
б) пересечение двух «окрестностей» точки содержит некото-
некоторую «окрестность» этой же точки;
в) какова бы ни была «окрестность» 5Ж точки хе.Х и точка
Бж, существует «окрестность» Ъу точки у такая, что Бус=Бж;
Тогда если отнести к системе {5} всевозможные «окрестно-
«окрестности» Б* точек х^Х, их всевозможные объединения и пустое
множество, то будет задана топология на множестве X и
(X, 2) — топологическое пространство, в котором система всех
* Если х фиксировано, то система {Е*1} называется определяющей,
системой окрестностей данной точки х.
Дополнение 2 56t
«окрестностей» является определяющей системой. Обратно, вся-
всякое топологическое пространство может быть получено таким,
способом.
Доказательство. Проверим выполнение аксиом 1)—2)
топологического пространства. То, что все X принадлежит {2},.
очевидно, 0 ртнесено к {2} по условию.
Аксиома 1) выполнена.
Для проверки аксиомы 2) надо убедиться лишь в том, что.
2in22^{2}, если 2ie{2}, 22е{2}. Следовательно, надо устано-
установить, что 2ifl22 может быть получено как объединение некото-
некоторых «окрестностей», т. е. надо убедиться, что для любой точки
xe2if]22 существует «окрестность» 2жсг21П22. Но 2i и 22 при-
принадлежат {2}, поэтому имеются «окрестности» 2a1c:2i и 2ж2сг
сг2г — их пересечение содержит по условию б) некоторую»
«окрестность» 2,; точки х, которая содержится, очевидно, в^
2,П22.
Обратно, если задано топологическое пространство (X, 2)„
то в качестве «окрестности» точки х, удовлетворяющей усло-
условиям а)—в), можно взять произвольное множество из системы.
{2}, содержащее точку х.
Используя эту лемму, приведем примеры еще двух хаусдор-
фовых топологических пространств.
Примеры.
1) В качестве X возьмем двумерную плоскость Е2. Окрест-
Окрестность любой точки iel получим, если из любого открытого-
круга с центром в х удалим все отличные от самой точки х
точки, лежащие на вертикальном диаметре этого круга. Полу-
Полученное топологическое пространство является хаусдорфовым.
2) Рассмотрим в качестве X отрезок [0, 1], окрестности всех
точек, кроме точки 0, определим обычным образом, а окрестно-
окрестностями точки 0 будем считать всевозможные полуинтервалы.
[О, а), а>0, из которых выкинуты точки —, где п — натураль-
натуральное число. Это, как легко видеть, пример хаусдорфова тополо-
топологического пространства.
Пусть (X, 2)—топологическое пространство, a Y — подмно-
подмножество X. Тогда на подмножестве X можно рассмотреть след.
системы {2}, т. е. множества вида {2у} = {ГП2а}, 2ае{2}. Легко
видеть, что тем самым на Y задана топология, поэтому Y само
превращается в топологическое пространство и (Y, 2у) назы-
называется подпространством пространства (X, 2). Тополо-
Топология, задаваемая системой {2г} = {ГП2а}, 2ае{2} называется:
индуцированной топологией.
Так же, как и в случае метрических пространств, простран-
пространство (X, 2) называется связным, если его нельзя предста-
представить в виде суммы двух непустых открытых непересекающихся,
•562 Гл. 12. Функции нескольких переменных
подмножеств. Множество Y в топологическом пространстве
(X, S) связно, если Y связно, как подпространство в (X, 2).
2. Замечание о топологических пространствах. После того
как введены открытые множества для топологических про-
пространств, можно ввести все понятия, введенные для метриче-
метрических пространств. Так, дословно сохраняются определения пре-
предельной точки множества (см. определение 4 раздела о метри-
метрических пространствах), определение внутренней точки* (см.
определение 5 раздела о метрических пространствах), опреде-
определение замкнутого множества (см. определение 6 раздела о ме-
метрических пространствах), определение замыкания множества
(см. определение 7 раздела о метрических пространствах),
определение плотного и всюду плотного множества (см. опре-
определение 10 раздела о метрических пространствах), полностью
сохраняется определение понятия нигде не плотного, совершен-
совершенного множества, данные для метрических пространств. Точно
так же, как и в случае метрических пространств, в случае то-
топологических пространств определяется важное понятие непре-
непрерывного отображения (определение 12 раздела о метрических
пространствах), понятие гомеоморфного отображения (опреде-
(определение 14 раздела о метрических пространствах), определение
компактного топологического пространства, или компакта (см.
определение 15 раздела о метрических пространствах). Так
же, как и для метрических пространств, для топологических
пространств вводится понятие центрированной системы (опре-
(определение 16 раздела о метрических пространствах), определение
базы топологии топологического пространства, топологического
пространства со счетной базой. Топологические пространства
со счетной базой называются топологическими пространствами
со второй аксиомой счетности.
Читатель без труда сформулирует эти определения для слу-
случая топологических пространств, для этого в соответствующих
определениях раздела о метрических пространствах выражение
«метрическое пространство» следует заменить на выражение
«топологическое пространство».
Согласно этим определениям в случае топологического про-
пространства остаются справедливыми основные утверждения, до-
доказанные для метрических пространств. Это вполне естествен-
естественно, поскольку доказательства этих утверждений в основном ис-
используют понятие открытого и замкнутого множества и непо-
непосредственно не зависят от введенной там метрики.
Так, лемма 1, утверждающая, что объединение произволь-
произвольного числа открытых множеств и пересечения конечного их чис-
* Совокупность всех внутренних точек множества У называется внутренно-
о о
<стью множества У и обозначается через У. Внутренность У, очевидно, есть объ-
объединение всех открытых множеств, принадлежащих У.
Дополнение 2 563»
ла является множеством открытым, есть соответствующая ак-
аксиома топологического пространства; утверждение леммы 2, в.
том числе и доказательства свойств операции замыкания, пол-
полностью сохраняется.
На топологические пространства переносится также и поня-
понятие сходящейся последовательности (определение 11 раздела
о метрических пространствах), а именно: последовательность-
{ап} точек топологического пространства называется сходя-
сходящейся к точке а этого пространства, если любая окрест-
окрестность точки а содержит все точки последовательности {ап} за,
исключением конечного числа. Если последовательность {ап}
сходится к точке а, то пишут, что ап-+а при я-»-оо или
liman = a.
п-*-<х>
Однако в топологических пространствах это понятие не иг-
играет столь большой роли, как в метрических пространствах.
В самом деле, лемма 3 утверждала, что в метрическом про-
пространстве точка а принадлежит замыканию А некоторого мно-
множества А тогда и только тогда, когда существует последова-
последовательность {ап} точек множества А, сходящаяся к а. В тополо-
топологическом пространстве этот факт может быть несправедлив.
(Вспомним, что при доказательстве этого утверждения в мет-
метрических пространствах мы строили последовательность шаров-
О [а, —), вложенных друг в друга для любого натурально-
\ п ;
го п.)
Можно выделить класс топологических пространств, обла-
обладающих аналогичным свойством.
Назовем топологическое пространство пространством с:
первой аксиомой счетности, если для любой его точ-
точки а существует счетная система ее окрестностей {2an} такая,,
что для любого открытого множества Ео, содержащего точку а,,
найдется окрестность^0, обладающая свойством: Е^»сБа..
Такая система окрестностей называется счетной опреде-
определяющей системой окрестностей точки а.
В метрическом пространстве первая аксиома счетности, оче-
очевидно, выполнена.
В топологическом пространстве (X, 2) с первой аксио-
аксиомой счетности справедливо утверждение: точка аеХ при-
принадлежит замыканию А некоторого множества А тогда и толь-
только тогда, когда существует последовательность {ап} точек мно-
множества А, сходящаяся к а.
Доказательство этого утверждения аналогично дока-
доказательству соответствующего утверждения для случая метри-
метрических пространств. Последовательность шаров О (а, —
следует заменить на последовательность окрестностей из систе-
S64 Гл. 12. Функции нескольких переменных
мы {2ап}, причем всегда можно считать, что 2</'+1сг2ап. В про-
п .
тивном случае 2ап надо заменить на П 2П.
Утверждение на с. 544 полностью сохраняется. Сохраняется
также и утверждение леммы 4 — критерий непрерывности ото-
отображения.
На случай топологических пространств полностью перено-
переносится критерий компактности в терминах центрированной си-
системы замкнутых подмножеств (лемма 5), утверждения лемм 6,
7, 8, 9 о свойствах компакта и непрерывных функций на нем.
Заметим, что топологическое пространство может не быть
пространством со счетной базой топологии даже тогда, когда
оно является пространством с первой аксиомой счетности и в
нем имеется счетное всюду плотное множество. Однако если в
топологическом пространстве есть счетная база топологии, то
топологическое пространство сепарабельно и удовлетворяет
первой аксиоме счетности (ср. с леммой 11). Точно так же, как
и в случае метрических пространств (см. определение 18), то-
топологическое пространство называется пространством со второй
аксиомой счетности, если в нем существует хотя бы одна база
топологии, состоящая не более чем из счетного числа множеств.
Линейные нормированные пространства,
линейные операторы
Понятие линейного пространства играет фундаментальную
роль в анализе. Линейное пространство и линейные операторы
в таких пространствах играют также важную роль во многих
других разделах математики.
1. Определение линейного пространства. Примеры.
Определение 1. Множество элементов L, содержащее
хотя бы один элемент, называется линейным или век-
векторным пространством, если выполнены следующие
аксиомы.
1. Для любых двух элементов х и у множества L однознач-
однозначно определен третий элемент z этого множества, называемый
их суммой и обозначаемый символом х-\-у, причем справед-
справедливы следующие свойства:
а) х+у=у+х (коммутативность);
б) (x+y),+z=x+{y+z) (ассоциативность);
в) существует такой элемент О, что х-\-О = х для любого
элемента х^Ь; элемент О называется нулевым или н у -
л е м пространства L;
г) для любого элемента xeL существует такой элемент х',
что х+х'=0; элемент х' называется противоположным
к элементу х и обозначается обычно так: —х.
Дополнение 2 565
2. Для любого числа а и любого элемента х пространства
L определен элемент у пространства L, называемый произ-
произведением а на х и обозначаемый символом ах, причем
справедливы следующие свойства;
а) а(рд:) = (сф)л: (для любых чисел а и E и любого элемен-
элемента х);
б) (а-\-$)х=ах-\-$х (для любых чисел а и Р и любого эле-
элемента х);
в) а(х-\-у) = ax-j-ay (для любого числа а и любых элемен-
элементов х и у);
г) \-х=х для любого элемента х.
Если в аксиоме 2 используются только действительные чис-
числа, пространство L называется действительным про-
пространством. Если же рассмотрения ведутся с использова-
использованием комплексных чисел, то и пространство L называется
комплексным.
Элементы линейного пространства называют также век-
векторами.
Рассмотрим некоторые примеры линейных пространств.
При изучении метрических пространств были рассмотрены сле-
следующие множества (см. раздел о метрических пространствах,
примеры): множество вещественных чисел, координатное я-мер-
ное пространство, множество непрерывных на сегменте функ-
функций и совокупность ограниченных последовательностей. Все эти
множества представляют собой и примеры линейных про-
пространств, если ввести операции сложения и умножения по сле-
следующим правилам.
1) В совокупности Л1 вещественных чисел — обычные ариф-
арифметические операции сложения и умножения.
2) В я-мерном координатном пространстве Ап — по формулам
2,-, Хп+Уп) ,
='a(*i, X2 хп) = (ajjb ax2,..., ахп).
3) В пространстве непрерывных функций на отрезке — обыч-
обычные операции сложения двух функций, т. е. f+g=/(*) +g(x),
и умножение функции на число, т. е. af=af(x).
В множестве ограниченных последовательностей введем опе-
операции сложения и умножения по формулам
(х+у) = (xi, х% ...).+ (уи «/2,...) = (xi+yi, Х2+У2, •••),
ax=a(jji, х2,.-) = (адсь ах2,...).
Нетрудно проверить во всех перечисленных выше примерах вы-
выполнимость аксиом, определяющих линейное пространство. За
этими линейными пространствами мы сохраним те же обозна-
обозначения, что и в случае, когда рассматривались метрические про-
пространства, т. е. соответственно в случае 1)—обозначение Е\ в
566 Гл. 12. Функции нескольких переменных
случае 2)—Еп, в случае 3)—обозначение С [а, Ь] и в случае
4) —обозначение т.
Определение 2. Линейные пространства L и L* назы-
называются изоморфными, если между их элементами можно
установить взаимно однозначное соответствие так, что если
элемент x^L соответствует элементу x*^L*, а элемент y^L
соответствует элементу y*^L*, то элемент х-\-у соответствует
элементу х*+у*, а элемент ах соответствует элементу ах*
(а — любое число).
Изоморфные пространства можно рассматривать как раз-
различные реализации одного и того же пространства, и такие
пространства можно не различать.
2. Нормированные пространства. Банаховы пространства.
Примеры.
Определение 3. Функция /(*) =11*11, ставящая каждому
элементу х линейного пространства L в соответствие вещест-
вещественное число \\x\\, называется нормой в линейном простран-
пространстве L, если она удовлетворяет следующим аксиомам-.
О /(*) = 11*11 = 0 тогда и только тогда, когда дг=О;
2) f(a*) = ||a*|| = |a| ||*|| = |a|f(*) для любого числа а;
3) f(*l.+*2) = IUl+*2lKII*l 11 + 11*211 для ЛюбЫХ *i U *2, при-
надлежащих L.
Определение 4. Линейное пространство L с введенной
функцией /(*) = 11*11 называется линейным нормиро-
нормированным пространством.
Чтобы подчеркнуть, что пространство L нормированное,
обозначают его обычно буквой N.
Значение нормы на элементе х пространства N называется
нормой вектора х или длиной или модулем этого,
вектора.
Норма вектора всегда неотрицательна и равна нулю только
для нулевого вектора. Действительно, полагая в аксио-
аксиоме 3) Х\ = —Хг с учетом 1) и 2), получаем, что
0=110|| = II*i-
В любом нормированном пространстве может быть введена!
естественная метрика по правилу р(*, у) = 11* — у\\. Из аксиом,,
задающих норму, вытекает, что функция р(*, у) действительно-
задает расстояние в пространстве, т. е. удовлетворяет аксиомам
расстояния.
Кроме того, поскольку N — линейное пространство, метрика
р(*, у) инвариантна относительно сдвигов, т. е„
Р(*1+*, *2+*) = Н(*1+*) — (*2+*) II = 11*1 — *2И = Р(*Ь *2).
и положительно однородна, т. е.
Дополнение 2 567
р(ад:, ay) = Wax — ay\\-\\a{x — y)\\=*\a\\\x — г/|| = |а|р(д:, у).
С появлением естественной метрики в нормированном про-
пространстве могут быть введены все те понятия, которые мы рас-
рассматривали в метрических пространствах, например полнота
и т. п.
Следующее определение выделяет из всех нормированных
пространств важнейший класс пространств, называемых бана-
банаховыми *.
Определение 5. Банаховым пространством
называется полное линейное нормированное пространство.
Приведем примеры банаховых пространств.
Примеры. 1) Пространство ?' — действительная число-
числовая ось с обычными арифметическими операциями, как мы
знаем, является линейным пространством. Оно превращается в
нормированное пространство, если норму числа х положить
равной его абсолютной величине: IUII = |jj|. Из свойств абсо-
абсолютной величины вытекает, что выполнены все свойства нор-
нормы. Это нормированное пространство Е1 является полным, т. е.
банаховым. Его полнота, т. е. полнота Е1 как метрического
пространства с обычным расстоянием между действительными
числами (р(х, у) = \\х — #11 = |*— у\), была установлена в гл. 3.
2) Линейное пространство Еп, рассмотренное нами выше,
также является нормированным пространством, если норму
вектора х= (xi, x% ...,хп) ввести по правилу
п
1/2
Аксиомы 1) и 2) нормы, очевидно, выполнены, а неравенство
треугольника превращается в неравенство
которое является частным случаем (при р = 2) неравенства
Минковского для сумм (см. § 5 гл. 9). Это пространство Еп яв-
является полным, так как сходимость хк к х в Еп означает, что
все координаты Xhl вектора хи сходятся к соответствующим ко-
координатам вектора х. Осталось применить утверждение приме-
примера 1).
* Стефан Банах — известный польский математик A892—1945).
568 Гл. 12. Функции нескольких переменных
3) Пространство С [а, Ь] непрерывных функций с обычными
операциями сложения функций и умножения функций на чис-
число, как мы уже говорили выше, является линейным простран-
пространством. Оно превращается в нормированное пространство, если
положить ||/||= max |/(л;)|,где f(x)—непрерывная на сегмен-
сегменте lab)
те [а, Ь] функция. Используя свойства абсолютной величины и
функции max, легко убедиться, что все аксиомы нормы здесь
выполнены *.
4) Пространство тп-ограниченных последовательностей так-
также можно сделать нормированным, положив |М| = sup \xk\ для
х= (xi, X2,...). Аксиомы нормы здесь также проверяются без
труда. Можно убедиться также, что оно является полным нор-
нормированным пространством, т. е. банаховым пространством.
3. Операторы в линейных и нормированных пространствах.
Пусть L\ и L2— два линейных пространства и А — отображение
пространства L\ в L2, т. е. А : Li-*-L2.
Определение 6. Отображение A: Li-*-L2 одного линей-
линейного пространства Li в другое L2 называется линейным
отображением или линейным оператором, если:
а) А(х\-\-х2) =Ах\-\-Ах2 для любых векторов Х\. и х2 про-
пространства Ьх;
б) Л(ад:)=аЛд; для любого вектора x^L\ и любого числа а.
Отображение A :LiXL2X ... XLn-+L прямого произведения
линейных пространств Lu L2,..., Ln** в линейное пространство
L называется полилинейным, если линейно каждое отоб-
отображение
Ai-.Li-^L, i=l, 2.....Л,
получаемое из А(х, y,...,z) фиксированием всех переменных,
кроме переменной, стоящей на i-м месте. Здесь L L
L
,
Если задано линейное отображение А : L\-+L2 линейного
пространства L\ в линейное пространство L2 и пространство
L2 является действительной числовой осью (или комплексной
плоскостью), то оператор А называют функционалом.
Рассмотрим некоторые примеры.
Примеры. 1) Пусть L — произвольное линейное простран-
пространство. Оператор Е ставит в соответствие каждому элементу х^
eL тот же элемент х этого же пространства, т. е. Е: L-+L и
Ех=х для любого x^L. Такой оператор называется единич-
единичным или единицей.
* Можно убедиться, что это пространство является и полным, т. е. бана-
банаховым.
** Линейные операции в LiXL2X...Xin определены равенствами
[*i, ..., xn] + [yi, .... yn] = [xi + yi, ..., *„ + (/„], ъ[хи ..., Xn] = [axt, .... axn\,
где [xi, .... xn], [Уи ..., (/n]eLiX-..Xln, xu уге=Ц, i=l, 2, .... n; а —число.
Дополнение 2 569
2) В трехмерном пространстве ?3 зададим оператор А как
линейное преобразование, состоящее в проектировании каждого
вектора на ось Ох (т. е. каждому вектору в соответствие ста-
ставится его координата на оси Ох). Оператор можно задать мат-
матрицей. Например, в базисе из единичных векторов ей е2, ез, на-
направленных по осям координат Ох, Оу, Ог соответственно, ука-
указанный оператор А можно задать так:
/1 0 0\/*Д
Ах = 0 0 0 )\х2 , *=--(*!, дс8, х3) е= Е3.
\0 0 О/ \х3/
3) В пространстве С[а, Ь] линейный оператор А задан по
ь
правилу: Af = f f (x) dx. Оператор А отображает С [а, Ь] в чис-
а
ловую ось и является функционалом.
4) Модуль непрерывности co(f, 6) (см. гл. 4) и дельта-
функция 6{х—а), т. е. оператор 6(лг—а), действующий по пра-
правилу б (а;—a)[f(x)]=f{a), также являются функционалами на
С [а, Ъ].
4. Пространство операторов. Пусть Lx и L2 — два линейных
пространства. Рассмотрим совокупность {А} всех линейных
операторов, отображающих L\ в L2. В множестве {А}, элемен-
элементами которого являются линейные операторы, отображающие
L\ в L2, можно ввести алгебраические операции. Пусть А\ и
Л2 — такие операторы. Определим сложение этих операто-
операторов посредством равенства
(Ai+A2)x=Aix+A2x, jceLi.
Умножение линейного оператора на число оп-
определим формулой
(аА)х-аАх.
Очевидно, что при таких определениях все необходимые ак-
аксиомы, задающие линейное пространство, будут выполнены и
рассматриваемое множество {А} линейных операторов будет
линейным пространством. Нулем этого пространства будет ну-
нулевой оператор О, т. е. оператор, переводящий любой вектор
х в нулевой вектор: Ох = 0. Пространство линейных операто-
операторов, которое мы ввели выше, обычно обозначается так: (Li->-
~+L2). Если пространства L\ и L2, кроме того, обладают неко-
некоторой топологией, например нормированы, то и пространство
операторов (L\->L2) будет обладать определенной топологией.
5. Норма оператора. Пусть jV'i и JV2 — два линейных норми-
нормированных пространства и оператор А отображает Л/'i в N2.
570 Гл. 12. Функции нескольких переменных
Определение 7. Линейный оператор A:h\-+N2, отобра*
жающий линейное нормированное пространство N\ в линейное
нормированное пространство Ni, называется ограничен*
ним, если существует такая постоянная М, что ||Ак||я2<
<ЛЯ|#||лгг для всех j;eA'i. Индекс внизу символа нормы озна-
означает то пространство, в котором вычисляется норма вектора.
Если это не будет вызывать недоразумений, эти индексы мы
будем опускать.
Справедливо следующее утверждение.
Теорема. Для того чтобы линейный оператор A:Ni-*-N2,
отображающий линейное нормированное пространство Ni в N2y
был непрерывен, необходимо и достаточно, чтобы он был огра-
ограничен.
(Заметим, что непрерывность оператора понимается как не-
непрерывность соответствующего отображения.)
Доказательство. Пусть А — непрерывный оператор.
Если бы он был неограничен, то нашлась бы последователь-
последовательность элементов {хп} такая, что
1Их„11>л||хп||.
Пусть уп = -~-. Тогда у„-^0, так как \\уп\\ =— -^Опри
я-voo. С другой стороны,
Заметим, что (в силу линейности оператора А) Л-0=0; дейст-
действительно, А-0=А(х—х) =Ах—Ах=0. Итак, Ауп не стремится
к А-0 = 0, т. е. оператор А не является непрерывным в нулевой
точке, что противоречит условию теоремы.
Обратно, если А ограничен, то |Их||<:.М||х||. Пусть хп-^х>
т. е. \\хп—jjjj->0 при «-voo. Тогда \\Ахп—Ах\\ = \\А(хп—х)\\<.
^М\\хп—#||->0 при /г-*-оо. Следовательно, Ахп-+Ах и опера-
оператор А непрерывен в точке х.
Определение 8. Пусть А — линейный ограниченный
оператор. Наименьшая из постоянных М, удовлетворяющих
условию
\\Ах\\<М\\х\\,
называется нормой оператора А и обозначается симво-
символом \\A\\.
Таким образом, согласно определению 8 норма оператора
обладает следующими свойствами:
а) для любого x^Ni справедливо неравенство
Дополнение 2 571
б) для любого числа е>0 найдется такой элемент хе, что
Покажем, что ||y4|| = sup ||Лл:|| или, что то же самое,
K1
= sup . Действительно, если ||х||«:1, то
M^o II* ||
|. Значит, и sup ||Лх||<||Л||. С другой стороны,
1WK1 ¦ -
для любого е>0 существует элемент хе такой, что
Пусть 6. = -^. Тогда №| = 1^1>11г(||Л||_е)||д?Е|| =
= 11Л||—е. Так как |,= 1, то
p
IWK1
Следовательно, sup ||Ак||>||Л||, и потому ||Л|| = sup ||Л*||.
WK1 1МК'
Замечание. Из проведенных рассуждений следует, что
Выше (см. п. 4) нами было введено пространство (Li-*-L2)
операторов, отображающих линейное пространство L\ в линей-
линейное пространство Ьг- Это пространство играет важную роль в
различных разделах анализа, и мы сейчас продолжим его изу-
изучение.
Предположим теперь, что указанные выше линейные прост-
пространства L\ и L2 являются нормированными. Переобозначим их
через AAi и Л'» соответственно, а соответствующее линейное
пространство, элементами которого являются линейные огра-
ограниченные операторы, через (Afi-j-A^). В пространстве {N\~*-N2)
можно ввести норму. Для этого норму элемента А пространст-
пространства (Ni-+N2) введем по правилу: ||Л|| = sup ||Л*||. Легко видеть,
что эта норма удовлетворяет аксиомам определения нормы.
Таким образом, линейное пространство (Ni*-*-N2), элементами
которого являются линейные ограниченные операторы, есть ли-
линейное нормированное пространство. Возникает естественный
вопрос: когда это пространство является полным, т. е. банахо-
банаховым?
Ответ на этот вопрос содержится в доказываемой ниже
теореме.
Теорема. Если линейное нормированное пространство
N2 = B2 банахово, то пространство. (Ni-yB2) линейных ограни-
ограниченных операторов также является банаховым.
572 Гл. 12. Функции нескольких переменных
Доказательство. Пусть {Л„} — фундаментальная по-
последовательность пространства операторов (N\-+B2), т. е.
11ЛП—Л mil-И), когда п, /п->оо. Для любого х получим, что
¦IIЛ „ли—Лтл;||<||Лта—Лт|||иИ->0 при п, т-+оо. Следовательно,
если xeA'i фиксировано, то последовательность элементов
{Апх} фундаментальна в В2, т. е. в силу полноты В2 эта после-
последовательность сходится. Обозначим у = ]\тАпх. Мы получи-
ли, таким образом, отображение Ni в В2. Оператор, осуществ-
осуществляющий это отображение, обозначим через Л. Из свойств пре-
предела следует, что он линеен. Докажем его ограниченность.
Из того, что ||Л„—Лт11-*0 при п, т-*-оо, следует, что |||ЛП||—
—ЦЛт|||-»-0 при п, т-*~оог т. е. числовая последовательность
{||Л„||} фундаментальна в Е1, а следовательно, и ограничена.
Существует такая постоянная Ж, что ||ЛП||<Л1 для любого
натурального п. Отсюда получаем, что ||Л„;е||<:||ЛгЛи||«:.М||л:|1,
т. е. в силу того, что функция, определяющая норму (расстоя-
(расстояние), непрерывна, имеем
\\Ах\\ = \ш\\Апх\\<М\\х\\.
Итак, оператор А — ограничен. Оператор А был нами опреде-
определен как оператор, отображающий N\ в В2 по указанному выше
правилу. Покажем, что Л является пределом последователь-
последовательности {Л„} в смысле сходимости по норме в пространстве
(iVi->B2). Зададим произвольное е>0 и выберем п0 так, что
ЦЛга+рДС—Лп*||<е для /г:>/г0 и любого х такого, что \\х\\<
<:1. Пусть р-*-оо. Тогда \\Ах—Апх\\<.г для п>-п0 и всех х с
нормой, не превосходящей единицы. Поэтому для п>>п0 uosiy-
чим ||ЛП—Л||= sup ||(ЛП—Л)х||< е. Следовательно, А=\\тАп
в смысле сходимости по норме в пространстве (N\-+-B2), т. е.
это пространство банахово, что и требовалось доказать.
6. Понятие гильбертова * пространства.
Определение 9. Гильбертовым пространст-
пространством называется множество Н элементов f, g, h, ..., обладаю-
обладающее следующими свойствами:
1) Н представляет собой линейное пространство, т. е. в Н
определены действия сложения и умножения на действитель-
действительные или комплексные числа {в зависимости от этого Н назы-
называется действительным или комплексным про-
пространством) .
2) Н является метрическим пространством, причем метрика
вводится с помощью скалярного произведения, т. е. числовой
функции (f, g) от пары аргументов fug, называемой их ска-
скалярным произведением и удовлетворяющей аксиомам:
Давид Гильберт — немецкий математик A862—1943).
Дополнение 2 57S
а) («f, g) =а(/, ^) для любого числа а;
б) (/+g, A)^(f, Л) + (Я.Л);
в) (f,g) = (g,f)*\
г) (/, /) >0 при f#0; (/, /) =0 при f = 0.
Норма 11/11 элемента f определяется равенством \\f\\ =
_ ^ ^ i/2) а расстояние между элементами fug полагается
равным
3) Я является полным пространством, как метрическое
пространство с введенным выше расстоянием. (Конечномер-
(Конечномерное пространство всегда полно.)
Возьмем произвольные элементы f, g^H, пусть % — дей-
действительное число. Тогда
0<(?+Mf. g)g. f+Hf, g)g) = (f, f)+2K\ (f, g) |2+
+ V\(f.g)\4g,g)
и, следовательно, такой многочлен относительно X не может
иметь различных действительных корней. Отсюда вытекает,
что
\(f,g)\i-(Lf)\(f,g)\4g>g)<o.
Таким образом (даже в случае (f, g)=0),
\(f.g)\2<(f,mg.g)K™ \(f,g)\<\\nw\g\\.
Мы получили неравенство Коши — Буняковского.
Знак равенства в нем, помимо тривиального случая f=0 или
g=0, достигается только тогда, когда /=—X{f, g)g при неко-
некотором значении %, т. е. когда векторы / и g коллинеарны.
Используя это неравенство, легко проверить, что норма
элемента ||f|| и расстояние р(/, g) = \\f—g\\ удовлетворяют всем
аксиомам, входящим в их определение.
Вместе с метрикой в гильбертовом пространстве появляют-
появляются понятия, связанные с предельным переходом в смысле вве-
введенного расстояния.
Наличие скалярного произведения позволяет ввести в Н
понятия угла между векторами (если Я вещественно).
Угол (f, g) между векторами f и g определяется равенством
T) = {f' e)
cos
11/1111*11
Это понятие, в свою очередь, позволяет назвать два вектора
ортогональными, если они образуют угол в 90°. Другими
словами, векторы fug называются ортогональными, если
(f,g)=O.
(g, f) означает комплексно сопряженное к числу (g, f).
574 Гл. 12. Функции нескольких переменных
Если вектор / ортогонален векторам gn ¦••> gn, то он орто-
п
гонален и их линейной комбинации V d(gt.
i=i
Если векторы g\, ..., gn, •¦• ортогональны вектору / и
g=\\mgn, то вектор g ортогонален вектору /.
n-t-oo
Из сказанного следует, что совокупность всех векторов, ор-
ортогональных векторам /ь .... /п, где п фиксировано, образует
замкнутое линейное многообразие, т. е. подпространство, назы-
называемое ортогональным дополнением к множеству
В гильбертовом пространстве Н можно ввести важное по-
понятие сопряженного оператора.
Определение 10. Оператор А* называется сопря-
сопряженным к линейному ограниченному оператору А, если для
любых элементов х, у^Н выполняется равенство (Ах, у) =
= (х,А*у).
Ограниченный линейный оператор А, действующий в гиль-
гильбертовом пространстве Н, называется самосопряженным,
если (Ах, у) = (х, Ау) для всех х и у из Я.
Примеры. 1) В «-мерном пространстве Еп, элементами
которого являются наборы чисел х= (х\, х2, ..., хп), можно вве-
п
сти скалярное произведение по формуле (х, у) = Х\ х^?. Учи-
i
тывая, что конечномерное пространство Еп полное, заключаем,
что Еп является гильбертовым пространством. Аксиомы ска-
скалярного произведения здесь, очевидно, выполнены.
2) Операторы Е (единичный), О (нулевой) являются при-
примерами самосопряженных операторов, действующих в гиль-
гильбертовом пространстве. Для них всегда выполнены соотноше-
соотношения
(Ех, у) = (х, у) = (х, Еу),
(Ох,у) = @,у)=0=(х,Оу).
ДОПОЛНЕНИЕ 3
Дифференциальное исчисление в линейных
нормированных пространствах
В гл. 5, 6, 7 были изучены вопросы дифференциального ис-
исчисления функции одной переменной, а также были исследова-
исследованы экстремальные свойства функции одной переменной. В пре-
предыдущих параграфах настоящей главы эти же вопросы изуча-
изучались уже для функций многих переменных.
Дополнение 3 575»
Подчеркнем, что всюду в гл. 5, 6, 7 под функцией мы по-
понимали соответствие между точками множества {М} числовой?
оси (или точками множества {М} m-мерного евклидова прост-
пространства) и подмножеством числовой оси. Другими словами,,
такие функции отображают множество {М\ числовой оси юнг
m-мерного евклидова пространства в подмножество числовой
оси. Такие функции могут быть названы числовыми (ска-
(скалярными) функциями, ибо множество значений таких
функций есть числа (скаляры) вещественной оси.
В дополнении 2 к этой главе мы вводили понятие функции,,
отображающей одно абстрактное множество в другое (напри-
(например, одно метрическое пространство в другое метрическое про-
пространство, одно нормированное пространство в другое норми-
нормированное пространство и т. д.). Такие функции называются-
операторами, отображениями, функциями множеств ю
т. д.
В частности, можно рассматривать функции, отображаю-
отображающие m-мерное евклидово пространство в га-мерное евклидово»
пространство. Такие функции называются уже векторными
функциями, поскольку значениями таких функций являют-
являются не числа, а векторы некоторого пространства. Например,,,
если отображение происходит в га-мерное евклидово простран-
пространство, то значениями функции, осуществляющей это отображе-
отображение, являются векторы га-мерного пространства.
Примером функции, осуществляющей отображение одного
метрического пространства X в то же пространство X может
быть тождественное отображение Е, ставящее в соответствие
каждой точке хеА' ту же точку хеХ. Отображение IUH, ста-
ставящее в соответствие точке х нормированного пространства ЛГ
число ||jc|| — норму элемента х, есть пример функции, задан-
заданной на нормированном пространстве N.
В этом параграфе будет построено дифференциальное ис-
исчисление функций, заданных на нормированном пространстве.
В качестве элементарного следствия наших построений могут
быть получены факты, относящиеся к функциям, осуществляю-
осуществляющим отображения m-мерного евклидова пространства в га-мер-
га-мерное евклидово пространство (при этом натуральное число «•
может как совпадать, так и не совпадать с натуральным чис-
числом пг).
1. Понятие дифференцируемости. Сильная и слабая диффе-
ренцируемость в линейных нормированных пространствах. Пусть.
Ni и Лг2 — два нормированных пространства и F — отобра-
отображение (функция), действующее из Ni в N2 (F:Ni-+N2) и опре-
определенное на некотором открытом множестве S пространства.1
Nb Напомним, что поскольку Ni — нормированное простран-
пространство, то оно, в частности, является и метрическим пространст-
пространством; следовательно, все понятия, введенные в метрических про-
376 Гл. 12. Функции нескольких переменных
странствах, такие, как открытое, замкнутое, ограниченное мно-
множество, расстояние между точками и т. д. имеют смысл. Под-
Подчеркнем, что в этом дополнении будут использоваться многие
понятия, введенные в дополнении 2. Введем понятие диффе-
дифференцируемого отображения.
Определение. Назовем отображение F:N1-+N2 диффе-
дифференцируемым* в данной точке х, принадлежащей откры-
открытому множеству ЕсгЛ'ь если существует такой ограниченный
линейный оператор Lx^(Nx-+N2) **, что для любого е>0 су-
существует 6>0 такое, что если /isiVi и \\h\\Nl <б, то
\\F(x+h)-F(x)-LM\Nt <e||ft||Wl
или, что то же самое,
\\F (x+h)—F (x)—Lxh\\N2 = o(h),
где o(h)l\\h\\-*0 при ||/iiLVl->0. Здесь x+h^'EczNi.
Индексы N2 или N\ у знака || ¦ || нормы означают, что нор-
норма берется соответственно в пространстве Л^г или Ni. Для про-
простоты записи договоримся в дальнейшем о том, что там, где
не будет возникать недоразумений, эти индексы опускать.
Выберем последовательность чисел ета->0. Согласно сфор-
сформулированному определению ей отвечает последовательность
чисел 6„ и для любой последовательности точек hn такой, что
l|fonll<6n, II/inII->0, мы получим, что
когда п~+оо (поскольку |А„||->0, еп->-0, a ||L*||<:C в силу огра-
ограниченности линейного оператора Lx).
Следовательно, UmF(x +hn) = F(x) при ||/inll->0, т. е. если
га->оо
обозначить x+hn через хп, то \imxn = x, YimF(xn) = F(x). Ta-
* Если, в частности, F(x) есть скалярная функция, определенная на некото-
некотором интервале (а, Р) (F (х) отображает подмножество числовой оси в подмно-
подмножество числовой оси F(x):(a, P)—>-?¦'), то в случае ее дифференцируемое™ в
точке Хо из интервала (а, E) можно записать:
F(x0+h)—F(xo)—Lh = o{h), o{h)[h-+Q, если ft^O,
тде h — некоторое число — приращение аргумента функции, L = L(x<>) — линей-
линейный оператор, являющийся производной отображения F(х) в точке хо, принад-
принадлежит в данном случае пространству операторов (Е'-кЕ1), т. е. является просто
оператором умножения на число. С другой стороны, если рассматривать F(x)
как обычную числовую функцию, то число L есть, очевидно, производная функ-
функции F(x) в точке хо, т. е. L=F'(x0).
** Через (Ni^-Nz) в дополнении 2 было обозначено пространство линейных
ограниченных операторов, отображающих одно линейное нормированное про-
пространство TVi в другое линейное нормированное пространство Nz-
Дополнение 3 577
ким образом, дифференцируемое в точке х отображение F(x)
непрерывно в этой точке.
Выражение Lxh при каждом h^Ni является элементом про-
пространства Л/*2 и называется сильным дифференциалом
(или дифференциалом Фреше) отображения F в
точке х (и иногда обозначается символом dF). Линейный опе-
оператор Lx называется производной или сильной произ-
производной отображения F в точке х. Будем обозначать эту про-
производную символом F'(x). Таким образом, можно записать,
что сильный дифференциал отображения F по определению
равен LxK т. е. dF = Lxh, а сильная производная F'(х) равна
Lx, т. е. F'(x) =LX.
Если отображение F дифференцируемо в точке х, то соот-
соответствующая производная определяется единственным об-
образом. В самом деле, пусть
F(x+h)— F(x)— L'xh=o(h)* и F(x+h)—F(x)—L2xh=o(h).
Тогда
Dxh—L2xh = o{h).
Следовательно, для любого е>0 найдется такое 6>0, что из
неравенства 1Ш1<6 следует неравенство
\\Dxh—L
Разделим обе части этого неравенства на И^Ц^О. Тогда полу-
получим, что выполнено неравенство
!fI h T2 я,
LА
\\h\\ \\h\\
е,
справедливое в силу свойства нормы и линейности операторов
Llx и /Л. Полагая —— = е, где ||е|| = 1, мы получим, что
II«II
для любого вектора е из единичной сферы (т. е. для любого
вектора, с нормой, равной единице).
В силу произвольности е отсюда следует совпадение опера-
операторов Llx и L2X всюду на единичной сфере. Поскольку опера-
операторы Llx и L2X линейные, то они, очевидно, совпадают и всю-
всюду, т. е.
* Написанное равенство следует понимать так:
\\F(x+h)-F(x)-Lxth\\=o(h).
В равенстве F(x+h)—F(x)—Lx4i=o(h), -^-|--^0, если Ш\->-°°, т. е. норма
величины о(я) является числовой величиной
19х/2 Зак. 72
578 Гл. 12. Функции нескольких переменных
Для того чтобы проиллюстрировать определение сильной
дифференцируемости отображения одного нормированного про-
пространства в другое на конкретном примере, рассмотрим случай
отображения F:Em-*-E1, т. е. отображения т-м,ерного евклидо-
евклидова пространства в числовую ось. В этом случае * отображение
F = F(xu х2, ..., хт) есть обычная числовая функция от т пе-
переменных. Если обозначить приращения аргумента Х\ через h\,
аргумента х2 через h2, ..., аргумента хт через hm, то, как это
следует из формулы A2.15), условие дифференцируемости
функции т переменных F{x\, x2, ..., хт) в точке х —
= (xi, x2, ..., хт), принадлежащей некоторому открытому мно-
множеству HczEm, записывается- в виде
, x2+h2, ..., xm + hm)—F(xb x2, ..., хт) =
U I , 1 ,1 , 1 \ Я dF(X)
1 ,л,ч_ л l ltp — V 1 ' 1* 2 ~ #t2* * " * » л/п *^ ^ftl/* I — -\ *
„ ^г Ул^ Л иг \Л* (U2 л_ U2- _1_ I U^ \*'^
2 — —; » • • • > лш — —X > Р — \п1 ~т Г12~г • • • "Г Mm) у
дх2 дхт
у I у y v* \
л \Л1» Л2' • • •» лт/'
Заметим, что справедливо равенство р=||/г||, где \\h\\
берется в пространстве Ет, как в нормированном пространстве.
Поэтому если функция т переменных дифференцируема, то
она, очевидно, и сильно дифференцируема, как отображение
нормированного пространства Ет в нормированное простран-
пространство Е1, причем сильная производная Lx определяется из уело-
т
вия Lxh=\ hit т. е. Lxh равно скалярному произведению
±J ди-
дивектора /7Г= ( , , ..., | на вектор h={h\,h2, ..., hm).
\ дхг дхг дхт I
Из курса линейной алгебры мы знаем, что всякий линейный
функционал из пространства (?"->?') имеет вид скалярного
произведения.
Таким образом, в случае отображения m-мерного евклидова
пространства в числовую ось понятие Сильной дифференцируе-
дифференцируемости функции F(xi,-x2, ..., xw), очевидно, в силу единственно-
единственности производной совпадает с понятием ее дифференцируемости.
Установим теперь некоторые элементарные факты, непо-
непосредственно вытекающие из определения производной.
* Выбрав базис в Ет, мы всегда, независимо от природы элементов
можем считать, что х является упорядоченной совокупностью т чисел.
Дополнение 3 579
Свойство 1. Если F(x)=F=const (оператор F от х не
зависит — является постоянным), то F'=O, где О — нуле-
нулевой оператор.
Доказательство этого свойства очевидно.
Свойство 2. Производная непрерывного (т. е. ограничен-
ограниченного) линейного отображения А есть само это отображение:
А'(х)=А.
Действительно,
A(x+h)—A(x) =A(x) +A(h)—A(x)=A{h).
Поэтому
А'(х)=А.
Свойство 3 (производная сложной функции).
Пусть Nu N2, N3 — три нормированных пространства, %Ха —
окрестность точки хоеЛ'ь F — отображение этой окрестности
в N2, Уо=Р(хо), 2Уо — окрестность точки г/0еЛ'2 и G — отоб-
отображение этой окрестности в Л'3. Тогда если отображение F
дифференцируемо в точке х0, a G дифференцируемо в точке yd,
то отображение H — GF (которое определено в некоторой ок-
окрестности точки Хо и отображает ее в Л'з) дифференцируемо в
точке хо и
H'(xo) = G'(yo)-F'(xo).
В самом деле, согласно условиям дифференцируемости
отображений F и G
где —величина, стремящаяся к нулю при стремлении
к нулю ЩИ; — величина, стремящаяся к нулю при
II i)ll
стремлении к нулю
Операторы F'(х0) и G'(y0) — постоянные операторы, огра-
ограниченные по норме. Поэтому o(F'(x0)?,) = o(l) и G(y0)o(l) =
= о(|). В самом деле, Цо^дсоШН^еЦ/^ХоШ, если
IIF'(*o)?ll<6, т. е. \\o(F'(x0m\\<e\\F'(x0)t\\<s\\F'(x0)\\\№\ =
= eil|?||, где ei = ?||.F(*o)ll, l|.F(*o)ll — норма ограниченного
оператора F'(xo) *. Таким образом, для всякого ei>0 сущест-
существует 6i>0 (а именно 6i = 6/||F(x0)II, ||F(jc0) 11=^0) такое, что
||o(F(xo)E)ll<e,||EH, если |||||<e, = e/||F(jco)||, т. е. если
11^'(^о)Н11ъ11<б (поскольку, если выполнено это неравенство,
то тем бол^е \\F'(xo)U<\\F/(xo) ||||6||<6.
* Мы воспользовались оценкой ||Лх|К1|Л||||л:[|, справедливой для любого ог-
ограниченного оператора (см. дополнение 2).
19Va*
580 Гл. 12. Функции нескольких переменных
Следовательно, o{F'(x0)?,) =о(?) *. Соотношение G(y0)o(l)
=о(|) доказывается еще проще.
Учитывая доказанные соотношения, получим
где т1 = /?'(дс0)|+О1(|). Далее,
Следовательно,
= G'(y0)F'(x0)l+o3(l),
и формула для производной сложной функции полностью до-
доказана.
Если F, G, Н — числовые функции, то это формула пре-
превращается в известное нам правило дифференцирования слож-
сложной функции.
Для отображений F, G, Н это правило называется еще пра-
правилом вычисления производной композиции отображений.
Свойство 4. Пусть F и G — два непрерывных отображе-
отображения, действующих из N\ в N2- Если F и G дифференцируемы
в точке Хо, то и отображения F+G и aF, где а — число, тоже
дифференцируемы в этой точке, причем
(F+G)'(xo)=F'(xo) +
В самом деле, из определения суммы операторов и произ-
произведения оператора на число *** получаем, что
(aF)(x0+h)=aF(xo)+aF'(xo)h+o2(h).
Из этих равенств и получаем требуемые соотношения.
Рассмотрим теперь еще одно понятие, связанное с диффе-
ренцируемостью отображения.
* Если F'(xo)=O, то ||.F'(*o)[|=0 и соотношение o(f(^o)i) =о(|) очевидно.
** Символам^ (F+G)'(xo) и (aF)'(xo) обозначены значения операторов
(F+G)' и (aF)' в точке х0.
*** Для нелинейных операторов эти определения такие же, как и в случае
линейных операторов (см. дополнение 1).
Дополнение 3 581
Определение. Слабым дифференциалом (или
дифференциалом Гато) отображения F:N\-+N2 назы-
называется предел
t->-o t dt
/=o
где сходимость понимается по норме в пространстве N2.
Слабый дифференциал называется еще первой вариа-
вариацией отображения F в точке х и обозначается символом
DF(x,h).
Слабый дифференциал DF(x, h) может и не быть линеен
по h. Если же оператор DF(x, h) оказывается линейным, т. е.
если
DF(x, h)=Fc'{x)h,
где Fc'{x) — ограниченный линейный оператор, то этот опера-
оператор называется слабой производной [или производ-
производной Г ат о).
2. Формула Лагранжа конечных приращений. При изучении
дифференцируемых числовых функций важную роль играла
формула Лагранжа конечных приращений. Выведем такую
формулу в случае дифференцируемого отображения F:Ni-^N2.
Пусть S — открытое множество в Ni, содержащее точку Хо, и
пусть множество точек xo+t(x—х0)* целиком содержится в 2,
Теорема. Пусть F:h\-+N2 — отображение, определенное
на открытом множестве SciiVi, непрерывное на [хо, х] и имею-
имеющее сильную производную F' в каждой точке интервала
(х0, х). Тогда
UF(x)-F(xo)\\< sup
= sup ||Г(хо
e<e<i
Доказательство. Рассмотрим сначала непрерывное
отображение f(t), заданное на сегменте [0, 1] и отображаю-
отображающее его в пространство N2, f-[0, 1]-WV2 и непрерывную функ-
функцию g(t), заданную на сегменте [0, 1], принимающую число-
числовые значения. Покажем, что если f(t) и g(t) сильно диффе-
дифференцируемы на интервале @, 1) (f(t) как отображение одного
нормированного пространства, а именно интервала @, 1), в
другое нормированное пространство N2, a g(t) дифференцируе-
* Множество точек вида xo+t(x—х0), где 0<f<l, называется отрезком
или сегментом н обозначается символом [хо, х] в Ni. При t=Q получаем
точку хо, а при ^=1 — точку х; если 0</<1, то множество точек xo+t(x—ХоУ
называется интервалом (хо, х).
19 Зак. 72
582 Гл. 12. Функции нескольких переменных
ма как числовая функция, определенная на интервале (О, I)),
и если
то
\\f(l)-f(O)\\<g(l)-g(O). (•>
Из этой формулы утверждение теоремы уже будет следовать
легко.
Докажем эту формулу. При каждом фиксированном
е>0 обозначим через Аг множество точек сегмента [О, I], в ко-
которых выполнено неравенство
11/@-/@) \\<g(t)—g(O) + *t+z. (**)
Покажем, что при любом е>0 число 1 принадлежит множест-
множеству Ав. Тогда при t=\ и е-^-0 получим доказываемую формулу.
В силу непрерывности отображения /(/) и функции g(t)
множество Ае замкнуто на сегменте [0, 1]. Действительно, ес-
если tn^.Ai и tn->-to, то в неравенстве
\\f(tn)-f(O)\\<g{tn)-g(O)
пользуясь непрерывностью функции нормы (или, что то же са-
самое, непрерывностью функции расстояния): 11л'Ц = р(д:, 0), не-
непрерывностью отображения f(t) и непрерывностью функции
g(t), можно перейти к пределу при tn-^t0 и заключить, что.
Ii/(M-/(O) \\<g(to)-g(O) +8^0+«,
'т. е. to^Ae, а следовательно, множество Ае замкнуто.
Множество Л, непусто, лоскольку (**), очевидно, выпол-
выполнено при достаточно малых t (левая часть неравенства (**)
при малых t в силу непрерывности f{t) мала, а правая имеет
положительный член е в качестве слагаемого, который не за-
зависит от I).
Пусть a = supAe. Поскольку множество Лес[0, 1] замкнуто»,
то а^Аг. Покажем, что а не может быть меньше числа 1. До-
Допустим противное, что а<1, т. е. 0<а<1. В силу дифферен-
цируемости f(t) и g(t) в точке а для достаточно малых поло-
положительных чисел h будем иметь
<\\f'{a)\\h + ±-h
(в данном случае \\h\\— \h\ =h, поскольку h — положительное
число, а норма элемента h сегмента [0, 1] совпадает с моду-
модулем числа h).
Далее,
g(a) = \g(a+h)—g(a)\, h>0,
Дополнение 3 583
поскольку функция g(t) на интервале @, 1) не убывает. Это
следует из того, что g'(t)>-0, 0<^<l, что, в свою очередь, сле-
следует из неравенства 0<i!/'(/) \\<.g'(t), 0<t<l.
Заметим теперь, что
для достаточно малых h. Поэтому
Поскольку
\\f(a)—f{0)\\<g{a)—g@)
то
)-f(O)\\ = l\f(a+h)-f(a)+f(a)-f(O)\U
\\f(a+h)-f(a)\\ + \\f(a)-f(O)\U
=g{a+h)—g@)+s{a+h) + &.
Мы видим, что а+h^As, а это противоречит выбору числа
а, т. е. число а не может быть меньшим единицы. Следователь-
Следовательно, а—\, и 1еЛв. Формула (*) доказана.
Завершим теперь доказательство теоремы. Положим
f(t)=F{xo+iAx), g(t)=M\\Ax\\t,
где
9*
Отображение f(t) и функция g(t) удовлетворяют, очевид-
очевидно, всем условиям вспомогательного утверждения, установлен-
установленного нами выше. Поэтому, подставляя эти выражения для f(t)
и g(t) в формулу (*), получаем формулу Лагранжа. Теорема
доказана.
Следствие. Если /4e(iVi->jV) — линейное непрерывное
отображение нормированного пространства N\ в нормирован-
нормированное пространство И?, не зависящее от х, a F(x) — отображе-
отображение открытого множества SciAfi в N2, удовлетворяющее усло-
условиям теоремы, то
\\F{x)-F(xo)-AAx\\< sup \\F'(t)-Al\\\Ax\\.
Действительно, применив теорему к отображению
F(x)—А Ах, Ах=х—х0,
584 Гл. 12. Функции нескольких переменных-
получим
\\F(x)-Abx-F(xo)\\< sup \\F' ®-А(х-хо)'\х=
5 6 (*>.*)
= sup \\F'(t)-A\\\\Ax\\,
что и требовалось доказать.
Можно показать, что теорема и следствие из нее верны,
если всюду вместо сильной производной F' (х) рассматривать
слабую производную Fc'(x).
3. Связь между слабой и сильной дифференцируемостью.
Сильная и слабая дифференцируемость представляет собой
различные понятия даже в случае m-мерного евклидова про-
пространства при т>2.
Действительно, рассмотрим, например, функцию двух пере-
переменных
1\
-^-р если *¦ + *•><>.
О, если х1 = 0 и х2 = 0,
х= (х\, х%) — точка плоскости.
Легко проверить, что эта функция непрерывна всюду на
плоскости, включая точку @, 0). В точке @, 0) имеем
— lim-
где h-= (hi, h2) — точка плоскости, представляющая собой не-
некоторое приращение аргумента х функции f(x) в точке @, 0).
Таким образом, мы видим, что в точке @, 0) слабый диф-
дифференциал f(x) существует и равен нулю.
С другой стороны, в начальной точке имеем f'x @, 0) =
=f^@, 0) = 0; это непосредственно вытекает из самого опре-
определения частных производных и из того, что f(*i, 0)=0,
/@, д:2)=0. Поэтому, записывая приращение функции в точке
@, 0) в виде
А1 + й1 + о(Л),
х дх2
где h=(hu h2) — приращение аргумента, ^ ^"->- 0 при
i\h\\ = (hi2+h22) 1'2-^0, получим, что
Дополнение 3 585
Выбирая h2 — h\2, имеем о (h) \ i — hJ2, что приводит к
П.2—ftj
противоречию. Действительно, величина \hi\J2, поделенная на
норму h, при hi=h\l стремится" к 1/2 при ||ft||->0, а величина
о (А), поделенная на [|А||, при любых /ц и h2 стремится к нулю
при ||/i||->-0, что следует из определения о(h).
Следовательно, функция f(x) не дифференцируема в точ-
точке @, 0) в сильном смысле.
Однако если отображение F имеет сильную производную,
то оно имеет и слабую производную, причем сильная и слабая
производные совпадают. Действительно, для сильно диф-
дифференцируемого отображения имеем
F(x + th) — F (jc) = F' (jc) (th) + o (th) = IF' (x)h + o {th),
lm\Fj) + UF{),
что и требовалось.
Выясним условия, при которых из слабой дифференцируе-
мости отображения F следует его сильная дифференцируе-
мость.
Докажем следующую теорему.
Теорема. Если слабая производная Fc'{x) отображения
F:N\—>-N2 существует в некоторой окрестности Б*о точки х0 и
представляет собой в этой окрестности функцию от х, непре-
непрерывную в точке х0*, то в точке х0 сильная производная F'(xq)
существует и совпадает со слабой.
Доказательство. По условию отображение F имеет
слабую производную Fc'(x0) в точке хо- Выбрав h так, что
je0 + A e Ех„, рассмотрим выражение
г(х0, h)=F(xo+h)—F(xo)—Fe'(xo) h.
Элемент г(х0, /г) принадлежит пространству N2. Пусть ср —
произвольный линейный ограниченный функционал на прост-
пространстве N2. Позже мы укажем некоторые условия на его вы-
выбор. Тогда из формулы для r(x0, h) получим
Рассмотрим функцию f(t)=q>(F(xo+th)—F(xo)) числового ар-
аргумента t, 0<^<l. Эта функция дифференцируема по t и для
нее
* Fc (x) отображает множество 2Жо пространства JVi в некоторое множе-
множество пространства операторов {Ni->-Nz), т. е. Fc'(x) — операторная функция.
Понятие непрерывной функции было нами определено даже для отображений
одного метрического пространства в другое (см. дополнение 2).
586 Гл. 12. Функции нескольких переменных
(Здесь мы воспользовались непрерывностью функционала ф,
поменяв местами символы lim и ф, а также слабой дифферен-
цируемостью F(x) в окрестности ЪХо.)
Применив к функции f(t) формулу конечных приращений
на сегменте {0, 1], получим
или
— F(xo))=<p{Fc'(xo+Qh)h),
Таким образом,
х0, h))=<v(F{xo+h)-F(xo))-<p(Fc'(xo)h) =
= q>(Fc'{xo+Qh)h)—<p(Fc/(xo)h) =
= Ф (F/ (xo+Qh) h—F/ (jc0) h).
Отметим теперь следующий факт: запись ^р(х), где
некоторому нормированному пространству, а гр — линейный
непрерывный функционал на N, можно рассматривать с двух
точек зрения. Во-первых, можно фиксировать функционал ф и
менять аргумент x^N. В этом случае, например, как мы от-
отмечали в дополнении 2, ||ф|| = sup |ф(я)|. Во-вторых, можно
им
им
фиксировать элемент x^N, а менять функционалы -ф. Линей-
Линейные непрерывные функционалы ф отображают пространство
N в пространство Р действительных (или комплексных) чисел
и принадлежат тоже нормированному (даже банаховому в си-
силу полноты Р, см. дополнение 2) пространству (N-+P). В этом
случае, например, .||д:|| = sup |ф(д:)|, где верхняя грань уже бе-
M=i
рется по всем функционалам \|зе(#-*-Р); ||ф|| = 1, т. е. по функ-
функционалам, имеющим нормы, равные единице. Поэтому, по опре-
определению верхней грани, существует такой функционал ф,
||ф|| = 1, что при фиксированном хеЛ' |ф(^)|> — ||д;||. Вое-
пользуемся этим фактом и выберем функционал ф, ||ф|| = 1,
таким, что
1ф(г(х0, A))|>-y||r(jc0, h)\\,
где h, а следовательно, r(xo, h) фиксированы.
Отсюда и из равенства для <р(г(х0, К)) получаем, что
||r(jc0, h)\\<2\\q>(Fc'(xo+Qh)h—Fcf(xo, h)\\<
<2\\Fc'(x0 + Qh)h—Fcf(x0)h\\\\<p\\<.
<2\\FC'(xo+Qh)— Fc'(xo)\\\\h\\. '
Дополнение 3 587
Но по условию Fc'(x) есть непрерывная в точке х0 функция от
х; поэтому
так что 1l(*o,7i)|| есть величина выше первого порядка мало-
малости относительно \\h\\, т. е. Fe'(x0)h, как это следует из фор-
формулы r(x0, h)=F(xo+h')—F{xo)—Fc'{xo)h есть главная, линей-
линейная по h, часть разности F(xo+h)—F(xa). Тем самым доказано
существование сильной производной F {х0) и ее совпадение со
слабой производной Fc'{x0).
4. Дифференцируемость функционалов. В предыдущих пунк-
пунктах нами было введено понятие дифференцируемого отображе-
отображения F:N\-*-N2, отображающего нормированное пространство
N\ в нормированное пространство N2. Мы уже отмечали, что
производная F'(x) такого отображения представляет собой
при каждом х линейный оператор, действующий из Ny в N2,
т. е. элемент пространства операторов (Ni->N2). В частности,
если N2—P, где Р — числовая прямая или комплексная плос-
плоскость, то отображение F принимает числовые значения на N\
и называется функционалом. При этом производная функцио-
функционала F в точке х0 есть линейный функционал, зависящий от х0.
Для примера найдем главную линейную часть приращения
функционала /"(л;) = ||л'Ц2, заданного в действительном гильбер-
гильбертовом пространстве Н. Имеем
F(x+h)—FM=]\x + h\\2-\\x\\2= (x+h, x+h) — {x, x) =
= (х, х)+2(х, h).— (x, x) + (h, Л)=2(х, h) + (h, h).
Можно убедиться, что F'(x)=2x. (Для этого следует заметить,
что всякий функционал в Н имеет вид скалярного произведе-
произведения.)
5. Интеграл от абстрактных функций. В этом пункте будет
изложен материал, являющийся, с одной стороны, .дополнени-
.дополнением к изложенному в гл. 9 материалу об определенном инте-
интеграле, а с другой стороны, являющийся необходимым в тео-
теории дифференцирования в банаховых пространствах.
Предположим, что отображение F действует из банахова
пространства В\ в другое банахово пространство В2, причем
пространство By есть числовая ось Е\ Таким образом, F:El^~
-+В2.
Отображение F, сопоставляющее числу х элемент банахова
пространства В2, назовем абстрактной функцией на
числовой оси. Производная F'(x) абстрактной функции при ус-
условии, что она существует, представляет собой при каждом х
элемент пространства В2 — касательный вектор к кри-
кривой F(x). Для абстрактной функции, представляющей собой
функцию числового аргумента х, очевидно, слабая дифферен-
588
Гл. 12. Функции нескольких переменных
цируемость совпадает с сильной. В этом случае, используя со-
соотношение
\\F(x+th)—F(x)—Fc'{x)ht\\=o(\t\), пфО, f->0,
вытекающее из слабой дифференцируемости, и полагая в нем
th=hi, получим, что
где число /tj-^O, т. е. F(x) сильно дифференцируемо и силь-
сильная производная совпадает со слабой.
Построим интеграл от абстрактной функции F(x), опреде-
определенной на сегменте [а, Ь]. Пусть {л:*} — разбиение сегмента
[а, Ь]. Введем интегральную сумму
, xk\.
Пусть d= max Axk— диаметр разбиения.
Абстрактную функцию F(x) назовем интегрируемой
на сегменте [а, Ь], если для этой функции на указанном сег-
сегменте существует предел I ее интегральных сумм при стремле-
стремлении диаметра d разбиений {xk} к нулю, причем этОт предел бе-
берется по норме пространства В2. Таким образом, абстрактна»
функция F(x) интегрируема, если
Игл
= 0.
Предел I называется интегралом от абстрактной функции
по сегменту [а, Ь] и обозначается символом
/=
dx.
Очевидно, что / является элементом В2, поскольку <т являете»
элементом В2 и пространство В2 полное, т. е. и предел а пр»
d->0 принадлежит В2.
Следует отметить, что построение теории интеграла от аб-
абстрактной функции мало чем отличается от построения теории
интеграла от числовой функции. Подчеркнем, что интеграл от
абстрактной функции не является уже числом, как обычный
интеграл, поэтому, например, всюду в доказательствах модуль
интеграла от числовой функции надо заменять на норму инте-
интеграла от абстрактной функции и т. п.
Дополнение 3 589*
Отметим следующие простые свойства интеграла от абст-
абстрактных функций. Их доказательства аналогичны доказатель-
доказательствам, приведенным в гл. 9 при построении интеграла Римана^
1. Интеграл от абстрактной непрерывной функции F(x) су-
существует, т. е. такая функция интегрируема.
2. Если С — линейное отображение пространства В2 в ба-
банахово пространство В3 (предполагается, что С также и не-
непрерывно), то
» ь
\CF(x)dx = C j F (jc) dx.
3. Справедливо неравенство
\§F(x)dx\<$\\F(x)\\dx,
a a
где справа стоит обычный интеграл Римана от числовой функ-
функции.
4. Если F(x) имеет вид f(x)y0, где f(x) — числовая функ-
функция, а уо — фиксированный элемент из В2, то
где справа также стоит интеграл Римана от функции f(x) na<
сегменту [а, Ь].
6. Формула Ньютона — Лейбница для абстрактных функций,.
В проведенных выше рассмотрениях через (JVi-k/V2) мы обо-
обозначали пространство всех линейных ограниченных (непрерыв-
(непрерывных) отображений из линейного нормированного пространства
Ni в линейное нормированное пространство N2. Топологию* в-
пространстве (N\-^N2) задает, например, норма в этом про-
пространстве. Заметим, что для задания топологии (системы»
окрестностей каждой точки) в линейном пространстве (Afi-*-
-*-N2) достаточно задать систему окрестностей начала коорди-
координат, в силу линейности пространства тем самым будут заданы?
окрестности каждой точки.
Рассмотрим теперь линейное пространство {Ni->N2) i всех,
непрерывных ограниченных, быть может, нелинейных, отобрав
жений пространства Ni в N2.
* Напомним, что для задания топологии на некотором множестве необходи-
необходимо указать систему множеств, удовлетворяющих аксиомам 1, 2 (см. дополне-
дополнение 2, раздел топологических пространств). Множества, удовлетворяющие этим»
аксиомам, называются открытыми. Открытые множества метрического или нор^
мнрованного пространства удовлетворяют упомянутым аксиомам.
590 Гл. 12. Функции нескольких переменных
Нелинейное отображение F:N\-*-Nz называется ограни-
ограниченным, если для всякого ограниченного множества AczN^
соответствующее множество F(A) ограничено в N2 (множест-
(множество в нормированном пространстве ограничено, если его можно
поместить внутрь некоторого шара с центром в начале коор-
координат) . Нелинейное непрерывное отображение не обязано
быть ограниченным.
Очевидно, что пространство (Ni->-N2) является подпростран-
подпространством (Ni-*-Ni)i. В линейном пространстве {Ni-+N2)i зададим
систему окрестностей нуля (для любого натурального п и про-
произвольного е>0):
. {p|
ИКп
и тем самым зададим топологию в пространстве (N\-*-N2)\.
Читателю предлагается проверить, что данной системой окре-
окрестностей в пространстве (Ni-*-N2)i задана топология. На под-
подпространстве (Ni-*~N2)cz(N\->-N2)i эта топология совпадает с
обычной топологией, задаваемой операторной нормой.
Рассмотрим сегмент [х0, хо + Ах] в Ni. Пусть задано непре-
непрерывное отображение F(x) этого сегмента в пространство
(Л/г1->Лг2)ь т. е. каждой точке х^[х0, хо+Ах] сопоставлено не-
некоторое отображение F(x)^(Ni-*-N2)\, непрерывно зависящее
от точки хеЛ'ь
Определим интеграл от F(x) no сегменту [х^, хо+
+ Ад:], по определению полагая
Здесь оператор F(xo+lAx) применяется к элементу
При каждом ?е[0, 1] величина F(xo + tAx] (Ля) представляет
собой элемент пространства N2 — образ элемента Ах при
отображении F(xo-rtAx).
Согласно построениям п. 5 интеграл, стоящий в правой ча-
части формулы, существует и является элементом пространст-
пространства JV2.
Используя эти замечания, докажем формулу Ньютона —
Лейбница для интеграла от абстрактной функции.
Рассмотрим отображение /•", которое действует из N\ в N2
и имеет на сегменте [л-0, *<H-Ax] сильную производную F'(x),
непрерывную по х.
Напомним, что отображение F(x) :Nl->-N2 непрерывно в точ-
точке хеЛ'ь если для любого шара с центром в точке F(x), ле-
лежащего в Л'г, найдется такой шар с центром в точке х, Лежа-
Лежащий в Nu образ которого при отображении ^(д:) целиком со-
содержится в указанном шаре с центром в точке F(x).
Дополнение 3 591
Отображение F(x) непрерывно на сегменте [х0, ]
(т. е. на множестве точек вида {xo+tAx}, где 0«^<1), если оно
непрерывно в любой внутренней точке сегмента (т. е. когда
точка отвечает параметру / такому, что 0</<1) и, кроме того,
непрерывно в точке Хо справа и в точке хо+Ах слева*.
Поскольку отображение Г'(х) непрерывно на сегменте
*о+Дх
[х0, хо+Ах], то существует интеграл Г F' (x)dx.
Докажем, что имеет место равенство
Хо
которое и называется формулой Ньютона — Лейбни-
Лейбница для абстрактных функций.
По определению интеграла можем записать
= limV F (х0 + tk Ax) Ax (tk+1-tk) = HraV F' (xk) (Axk),
d^° to . d-° to
где Xk = xo+tkAxk, AXk—(tk+i—tk)Ax, d — диаметр разбиения
сегмента [0, 1].
С другой стороны, легко заметить, что
га—1
[F(xo + tk+l Ax)~F (xo + tkAx)] =
n—\
Рассмотрим разность F(Xk+i)—F(xk)—F'(xk)Axk и применим к
ней формулу из следствия к теореме п. 2 Лагранжа. При Л =
= F'(Xk) получим
\\F{xk+l)-F{xk)-F'{xk)Axk\\K
< sup \\F' {xk + %Axk)~F' (xk)\\\\Axk\\.
* Говорят, что точка хе[хо, хо+Дл;] стремится к точке х0 справа, если
^{xo+tAx} и ^-^-0+0. Аналогично определяется стремление х к точке Яо
слева. Отображение F(x), определенное на сегменте [*о, Хо + &х], непрерывно в
точке Хо справа, если предельное значение F(x) при стремлении х к точке Хо
справа равно F(xo). Аналогично определяется непрерывность F(x) в точке
+ Д слева.
592 Гл. 12. Функции нескольких переменных
Просуммируем эти неравенства по всем k от 0 до п—1 и вме-
вместо ||Ах*|| поставим ИДяН |f*+i—tk\. Получим
п—1
| ? [F (**+,) - F (xk) -F1 (xk) Axk] | <
fc=i
(tk+l-tk) sup yf (xk+QkAxk)~Fr {xk)\\.
0<8<1
Так как производная /•"(*) непрерывна на сегменте [х0,
+ Ах], to она является и равномерно непрерывной* на этом
сегменте. Поэтому правая часть неравенства, написанного вы-
выше, стремится к нулю при неограниченном измельчении раз-
разбиения сегмента [xq, xo+Ax], откуда и вытекает, что
F(х0 + Ax)-F(х0) = ? [F(Xk+i)—F(x,)] =
4=0
= ? [F (Xk+d-F(xk)-Fr (xk) Axk] + ? F' (xk) Axk-*
'j F'(x)dx,
если d-^-0. Формула Ньютона — Лейбница доказана.
7. Производные второго порядка. Рассмотрим дифференци-
дифференцируемое отображение F:jVi->A/2. Мы уже отмечали, что произ-
производная F'(x) этого отображения при каждом фиксированном
x^Ni есть элемент пространства (iVi-^A^) — пространства ли-
линейных ограниченных операторов на N\, действующих в N2.
Допустим, что отображение F'(x), в свою очередь, дифферен-
дифференцируемо. Производная отображения F'(х) называется второй
производной отображения F и обозначается символом F".
При каждом фиксированном х отображение F"(х) является»
очевидно, элементом пространства (Ni-*-(Ni—>-N2)) — прост-
пространства линейных ограниченных операторов, действующих из
М{ в (JV!-WV2).
Элементы этого пространства допускают и другую интер-
интерпретацию в виде так называемых билинейных отображений.
* Абстрактная функция F{x) :Ni-+Nt называется равномерно непре-
непрерывной на множестве {x}=MczNi, если для всякого е>0 найдется такое б>0,
что ||.F(.»:i)—.F(*2)||<e для любых Xi и хг из множества М, если только
IUi—Х2\\<Ь. Доказательство того факта, что непрерывная абстрактная функция
на компакте в Ni является равномерно непрерывной, аналогично доказательству
этого факта для числовых функций на компакте (см. гл. 4, § 6, п. 3, теоре-
теорему 4.16).
Дополнение 3 593
Определение. Отображение В: (Ni-*-N2), отображающее
нормированное пространство N\ в нормированное пространст-
пространство N2, называется билинейным, если каждой упорядочен-
упорядоченной паре элементов (хи у у) *> из Nx поставлен в соответствие
элемент В(х\, у\) из N2 так, что выполнены следующие свой-
свойства:
1. Для любых х.и уи х2, г/г «з М{ и любых чисел аир име-
имеют место равенства
-2, ух)=аВ(хи у1)+^В{х2, у\),
В{хи ау1 + $уг)=оВ(хи у\)+$В(хи у2).
2. Существует такое положительное число М, что
\\В{х, у)\\<М\\х\\Ы
при всех х, у, из N\.
Первое из этих условий означает, что билинейное отображе-
отображение В линейно по каждому из двух своих аргументов. Второе
условие означает ограниченность билинейного отображения В.
Так же, как и в случае линейного отображения (см,, дополне-
дополнение 1), показывается, что ограниченное билинейное отображе-
отображение является непрерывным уже по совокупности своих аргу-
аргументов.
Определение. Наименьшая из постоянных М, удовлет-
удовлетворяющих условию \\В(х, у)\\<-М\\х\\\\у\\, называется нормой,
билинейного отображения В и обозначается симво-
символом \\B\\.
Точно так же, как и над линейными операциями (операто-
(операторами) (см. дополнение 1), над билинейными операциями мож-
можно определить операцию сложения двух билинейных отобра-
отображений, по определению положив (В\ + В2) (х, у)=В\(х, у) +
+ В2(х, у), а также операцию умножения отображения В
на число а: (аВ) (х, у)=аВ(х, у). Поскольку для билинейной
операции В определена и его норма, то билинейные отображе-
отображения пространства Ny в пространство N2 сами образуют линей-
линейное пространство. Обозначим его (jVi2—^ЛЛг) (здесь ин-
индекс 2 над символом N\ означает, что из пространства N\ бе-
берется два элемента (х, у), которые переводятся отображением
В в один элемент пространства N2).
Так же, как и в случае линейных отображений, показыва-
показывается (см. дополнение 1), что если пространство М2 банахово
(полное), то и пространство (N{2^>-N2) будет банаховым.
_ * Пара элементов хну называется упорядоченной, если указано, ка-
&ой из ее элементов является первым. Если элемент х является первым элемен-
элементом пары, а элемент у — вторым, то упорядоченную пару записывают так:
(х, У)-
594 Гл. 12. Функции нескольких переменных
Докажем следующее
Утверждение. Между элементами пространства
(Ni-»-(Ni-»-N2)) и пространства (Ni2^N2) можно установить
взаимно однозначное соответствие, сохраняющее линейные one-
рации (т. е. если элементу Л]^ (iVi—>-(Л']—^-YV^)), отвечает эле-
элемент 5ieGV12^-yv2), а элементу A2^(Ni-*-(Ni-*-N2)) отвечает
элемент 52e(iV12-^-iV2)! то элементу аА\ + $А2 отвечает элемент,
a/?i + p/?2, где аир — любые числа).
Действительно, каждому элементу Ле(Ni-*-(N\-*-N2))>
поставим в соответствие элемент В из (Ы^-^-Ыъ) по правилу
В(х,у) = (Ах)у.
Это соответствие, очевидно, линейно.
Покажем, что это соответствие сохраняет и нормы элемен-
элементов *, т. е. покажем, что ||Л|| = ||В||. Отсюда, в частности и бу-
будет следовать взаимная однозначность соответствия. Действи-
Действительно, если бы два различных элемента при изометричном
соответствии переходили бы в один элемент, то их разность
соответствовала бы нулевому элементу. Норма этой разности
равнялась бы норме нулевого элемента, т. е. нулю. Таким об-
образом, элементы совпадали бы, что противоречит их выбору.
Итак, докажем, что если элементу Ле(Л^—*-(Л^-»-Л^2)) отве-
отвечает элемент Be{Ni2-*-N2), то ||Л|| = ||?||, причем нормы эле-
элементов берутся в соответствующих пространствах.
Пусть z=B{x, у) = (Ах)у. Тогда
откуда
С другой стороны, если задано билинейное отображение В, тс
при фиксированном xe±Ny отображение у-+(Ах)у = В(х, у) яв-
является линейным отображением пространства N\ в N2.
Таким образом, каждому x^N\ ставится в соответствие эле-
элемент Ах пространства (Ni-+N2). Очевидно, что Ах линейно за-
зависит от х, т. е. билинейное отображение В определяет некото-
некоторый элемент Л пространства {N\-*-(Ni^*-N2)).
При этом отображение В восстанавливается по А при по-
помощи формулы
В(х, у) = (Ах)у.
Далее,
||Лх|| =sup \\{Ax) y\\ = sup \\B(x, у)\\<\\В\\ \\x\\.
I1K1 1М<1
* Соответствие между двумя упорядоченными пространствами, сохраняющее
нормы отвечающих друг другу элементов, называется изометричным. Подг
черкнем, что нормы берутся в соответствующих пространствах.
Дополнение 3 595»
Таким образом,
и\\<\\в\\.
Следовательно, из соотношений ||5||<||Л|| и |1Л||<||Б|| получа-
получаем, что
Нами, таким образом, доказано, что соответствие между про-
пространствами (Ni-+(Ni-+N2)) и (Ni2-+N2) линейно и изомет-
рично. При этом образ пространства (N~i-+(Ni-+N2)) при та-
таком соответствии есть все пространство (Ni2—*-N2). Утвержде-
Утверждение доказано.
Из доказанного утверждения следует, что если берется ка-
какой-нибудь элемент пространства (^i->(Ni-^N2)), то всегда =
можно указать его образ в пространстве (N\2-+N2).
Более того, норма элемента в исходном пространстве и нор-
норма его образа совпадают. Сохраняются также линейные опера-
операции при построенном соответствии в пространствах (Л^->-
—>- (tVi—*-yV2) ) и (iVi2—^iV2). Такие пространства можно не раз-
различать; называются они изоморфными. Эти пространства
отличаются только тем, что их элементы имеют различную
природу, а все остальные свойства пространств (Ni->(JVi->-
-+N2)) и (Ni2-^-N2) одинаковы.
В частности, мы выяснили, что вторая производная F"(x)
отображения F:Ni~*-N2 является элементом пространства
(Ni-+(Ni-+N2)). В соответствии с только что сказанным мы:
можем считать F"(х) элементом пространства (iVi2-*-^) •
8. Отображение m-мерного евклидова пространства в п-мер-
ное. Важным частным случаем введенных выше отображений
является случай отображения F(x) m-мерного евклидова про-
пространства в n-мерное. Напомним, что в евклидовом простран-
пространстве Ni = E"! норма элемента h= (hi, h2, ..., hm) записывается;,
в виде
т
1=1
а в пространстве N2 = E" норма элемента* F(x)=-~
= (Fl(x), F2(x) Fn{x)) записывается в виде
п
i р2 / ч"]1/2
1=1
* Мы, естественно, подразумеваем, что в пространствах Ет и Еп выбраныч
базисы, поэтому отображение F(x):Em-*-En можно рассматривать в координат-
координатной форме. Конкретная реализация элементов пространств Ет, Еп может быть»
любой.
596 Гл. 12. Функции нескольких переменных
где х — фиксированная точка из Ет; F\(x), F2(x), ..., Fn(x) —
координаты вектора F(x).
В случае отображения F(x) = (F\(x), F2(x), ..., Fn(x)), x =
= (х\, х2, ..., хт) m-мерного евклидова пространства Ет в
л-мерное евклидово пространство Еп естественно считать это
отображение или, что то же, эту вектор-функцию F(x) * диф-
дифференцируемой в точке х^Ет, если каждая компонента
Fi(xu х2, ..., х,„), F2(xu х2, ..., хт), -, Fn(xh x2, ..., хт) диффе-
ренцируема в точке х как функция т переменных Х\, х2, ..., хт.
Отображение F(x) можно рассматривать и с общей точки
зрения (а не как векторную функцию), т. е. как отображение
одного нормированного пространства N\ — Em в другое норми-
нормированное пространство А^2=?".
Определение дифференцируемого отображения F(x):Ni->
->-N2 в точке х в том случае будет таким же, как и в случае
общих нормированных пространств, только нормы, фигурирую-
фигурирующие в этом определении, будут определяться формулами для
норм в евклидовом пространстве. А именно мы назовем отоб-
отображение F(x):Em-+En, определенное на некотором открытом
подмножестве Scf, дифференцируемым в точке
хе2, если существует такой ограниченный линейный оператор
Lx^ (Em->-En), что для любого в>0 можно найти 6>0, при ко-
котором из неравенства \\h\\Em < 6 следует неравенство
\\F (x + h)-F (x)-Lxh\\En < e\\h\\Bm.
То же самое сокращенно можно записать так:
F (x+ h) — F (х) — Lxh = о (h),
где величина i|o(A)||/||A||-»-0 при ||/i||->0. Аналогично общему
случаю вводится и производная F'(x) отображения F(x).
Из курса линейной алгебры известно, что всякое линейное
отображение m-мерного евклидова пространства в л-мерное
(линейный оператор) можно задать некоторой матрицей поряд-
порядка (пгХп). Поскольку производная F'(x) отображения ^(д:),
действующегб из Ет в Еп, есть оператор из пространства Ет
в пространство Еп (элемент пространства (Ет-+Еп)), то F'(x)
есть зависящая от х матрица порядка (тХп). Найдем вид
матрицы.
Если в Ет и Еп выбраны базисы, а именно базис е\, е2, ...,
..., ет в Ет и базис fu f2, ..., fn в Еп, то всякий вектор х^Ет
запишется в виде x=x\el+x2e2 + ...+xmem, где хи х2, ..., хт —
координаты вектора х в базисе еи е2, ..., ет- Всякий вектор
у<=Еп можно записать в виде У=Уф+у2{2+ ... +ynfn, гдег/ь
У2, —, Уп — координаты вектора у в базисе fu f2, ..., fn.
* Мы учитываем, что при каждом х из Ет значение F(x) представляет со-
*бой вектор (Fi(x), Fi(x), ..., Fn(x)) из пространства Еп.
Дополнение 3
597
Отображение y~F(x) пространства Ет в пространство Еп
?, у^Еп) можно записать в виде
yi~Pl{Xl, Х2, ¦¦¦, Хт) ,
y2 = F2(xu х2 хт),
Уп — FniXl, Х2, ..., Хт).
Здесь Fx{xux2,...,xn), F2{xu x2, ..., хт), ..., Fn(xu x2, ..., хт) —
координаты вектора y = F(x) при фиксированном х= ¦
= (XU Х2, ..., Хт) ¦
Далее, отображение F'(x), как мы уже говорили, является
линейным оператором — элементом пространства (Ет-*-Еп).
Покажем, что если F(x) дифференцируема, как вектор-функ-
ция, то
I dyt дух дуг \
(***)
В самом деле, в этом случае F(x) = (Fx(x), F2(x), ...,
..., Fm(x)), F(x+h) = (Fy(x+h), F2{x+h), ..., Fm{x+h)), x =
~(xu x% ..., xm), x+h=(xi + hi, x2 + h2, ..., xm + hm), и если за-
записать вектор-функцию покомпонентно в виде столбца и вос-
воспользоваться тем, что каждая компонента является дифферен-
дифференцируемой функцией т переменных, то
F(x+h)-F(x) =
xm + hm)~F1
xm + hm)~F2
дуг
дхг
дуп
дхх
дх2
дх2
дуп
дхг •••
дхт
дуп
дхт.
К - .
Li дх<
2 \ 1» "^21 • • • »^т)
1=1
s
dxA
x2, .
dX;
xm)
598
Гл. 12. Функции нескольких переменных
dF2
dxx
dFn
dF1
dx2
dF2
dx2
dFn
dFt
dxm
dF2
dxm
dFn
•\ (
dx2
dxm
0(h)
0(h)
o[(h)
Здесь величины o(h)l\\h\\ *, принимающие вещественные'значе-
вещественные'значения, стремятся к нулю, если ||/i|| = (h2i + h22 +... + h2m) 1/2->-0. Эта
матричная запись допускает, как это легко видеть, такое, бо-
более простое представление
F(x+h)-F(x) = i
где
I dFx dFx dFj 1
дхг
dF2
dxx
dFn
dx2
dF2
dx2
dFn
dxm
dF2
dxm
dFn
h —
Cm J
(.
, o(A) =
0(h)
0(h)
причем величины o(/i)/||/i|i->-0, если \\h\\= (h
+ /i2mI/2-^-0. Поскольку координаты вектора o(h)/\\h\\ стремят-
стремятся к нулю, если |[/ii|->0, то и норма вектора o(h)/\\h\\ в про-
пространстве Еп (т. е. корень квадратный из суммы квадратов
его компонент) также стремится к нулю, если ||/i||-vO.
Поэтому можно заключить, что производная F (х) диффе-
дифференцируемого отображения F(x):Em-+En в точке х находится,
по формуле (***). Матрица, задаваемая формулой (***) на-
называется якобие.вой матрицей отображения
F:Em-+En, а в случае п — т ее определитель — якобианом
этого отображения в данной точке х.
9. Производные и дифференциалы высших порядков. Анало-
Аналогично тому, как это было сделано в п. 7 для второй производ-
производной отображения F(x) одного нормированного пространства
N\ в другое нормированное пространство N2, можно ввести
понятие третьей, четвертой и вообще n-й производной отобра-
отображения F (х), определив п-ю производную как производную от
производной (п—\)-го порядка. При этом, очевидно, п-я про-
производная представляет собой элемент пространства {N\^>-
-+(Ni-+...— (Ni-+N2))), Л*1 встречается п раз. Повторяя рас-
рассуждения, проведенные для второй производной, можно каждо-
каждому элементу этого пространства поставить в соответствие эле-
* В случае дифференцируемой функции m переменных величину о (h) мы
обозначали о(р) =о(ЦЛ||), где р=||ЛЦ.
Дополнение 3 599
мент пространства (iVin-K/V2) полилинейных (а именно га-ли-
га-линейных) отображений N\->-N2. При этом под полилиней-
полилинейным отображением (п-линейным) отображением одного нор-
нормированного пространства в другое понимается такое соответ-
соответствие у = А(х\, х2, ..., хп) между упорядоченными системами
(Х\, х2, ..., хп) элементов из Ni * и элементами пространства
N2, которое линейно по каждому из хи г=1, 2, ..., при фикси-
фиксированных остальных элементах и удовлетворяет при некотором
М>0 условию
\\А(хих2 *n)||<№illlU2||...||jcn||.
Таким образом, тг-ю производную F(n)(x) отображения F мож-
можно считать элементом пространства (Nin-+N2).
Рассмотрим теперь дифференциалы высших порядков. На-
Напомним, что мы определили сильный дифференциал dF отобра-
отображения F как результат применения к элементу h^Ni линейно-
линейного оператора F'(x), т. е. в виде dF = F'(x)h.
Дифференциал второго порядка определяется
как величина d2F=F"(x)(h, h), где F"(x)(h, h) является квад-
квадратичным выражением**, отвечающим отображению F"(x)^.
?e(jV,2-WV2).
Аналогично дифференциалом п-го порядка назы-
называется выражение dnF-F^n)(x) (h, h, ..., h), т. е. дифференциа-
дифференциалом п-го порядка называется элемент пространства N2, кото-
который получается в результате применения оператора F(n)(x) к
элементу (h, h, ..., h) пространства NlxNix...X^i=Nln.
п раз
10. Формула Тейлора для отображений одного нормирован-
нормированного пространства в другое. Согласно рассмотрениям п. 1 силь-
сильная дифференцируемость отображения F(x) означает, что раз-
разность F (x+h)—F(x) может быть представлена в виде линей-
линейного члена по h и слагаемого, имеющего порядок выше перво-
первого относительно \\h\\.
Этот факт обобщает, как мы знаем, соответствующее разло-
разложение для дифференцируемой функции F(x)—F(xi, х2, ¦¦¦, хт)
т переменных. Для функции F{x\, x2, ..., хт) справедлива, как
было показано в этой главе, формула Тейлора с остаточным
членом в форме Пеано. Поэтому, естественно, возникает во-
вопрос о получении формулы Тейлора с остаточным членом в
форме, аналогичной форме Пеано, и для отображений норми-
нормированных пространств. Справедлива следующая теорема.
Теорема. Пусть F — отображение нормированного про-
* Элемент (xt, хг, ..., хп) принадлежит пространству Nin~NiX...XNi (ср.
дополнение 2).
** Выражение В(х, х) называется квадратичным, если получено из би-
билинейного отображения В(х,у) при совпадающих аргументах, т. е. при х=у.
600 Гл. 12. Функции нескольких переменных
странства Ni в нормированное пространство Л^, определенное
на некотором открытом множестве SczA/'i и такое, что №>(*)
существует и представляет собой равномерно непрерывную-
функцию* от х в 2. Тогда имеет место равенство
F(x+h)—F(x)=F'(x)h+4iF"(x)(h, Л) + ...
h)
где ||г(х, й)|| =
Доказательство. Проведем доказательство этой тео-
теоремы по индукции. При п—\ равенство означает просто диф-
фе-ренцируемость отображения F(x), и тем самым это равен-
равенство по условию теоремы выполнено. Рассмотрим теперь про-
произвольное фиксированное целое число /г>2 и предположим,
что равенство, получающееся из D) заменой п на п—1, спра-
справедливо для всех отображений, удовлетворяющих условиям
теоремы, в которых п заменено на п—1. Докажем равенст-
равенство (****).
Рассмотрим отображение F'(x) и применим к нему формулу
Тейлора (****), в которой п заменено на га—1, а вместо прира-
приращения h рассмотрено приращение th, где / — число, принадле-
принадлежащее сегменту [0, 1]. Очевидно, что
F' (x+th)=F' (x) + tF" (x)h + ~
Ф.Щ
**;
'где \\п(х, й)Ц=о(^п-1||й||п-1), а форма (h, h,...,h) имеет п—\
аргумент©в. Проинтегрируем обе части формулы Тейлора для
F'(x+h)**** по сегменту [х, x+h] и воспользуемся формулой
* Отображение F:N 1-WV2 (или абстрактная функция F(x)) называется рав-
равномерно непрерывной функцией на множестве TWc/Vi, если для любо-
любого числа е>0 найдется такое число б>0, что ||f (а)—F(xz)\\<s для всех точек
Xi, Хъ из множества М одновременно, если только \\xi—*2||<в (см. также при-
примечание п. 6).
** Это равенство означает, что для любого числа е>0 найдется такое чис-
число 6>0, что \\г(х, Л)||<е||Л||в, если ||й||<6, т. е. Т „,' ^0, если п-Л).
*** Мы пользуемся тем, что формы (Л, К) (ft, ft, ..., Л) линейны по каж-
каждому из своих аргументов. Поэтому (th, th)—t2{h, A),
(th,th, ... ,th) = tn-i(h,h, ... , Л).
li—i гД
**** Т. е. формулу
F (х + /ft) = F (х) + tF" (x) ft +~ F" (x) (ft, ft) -f
+ ••¦+ J" iy FW(x)(h, ft, ... ,ft) + M*. h).