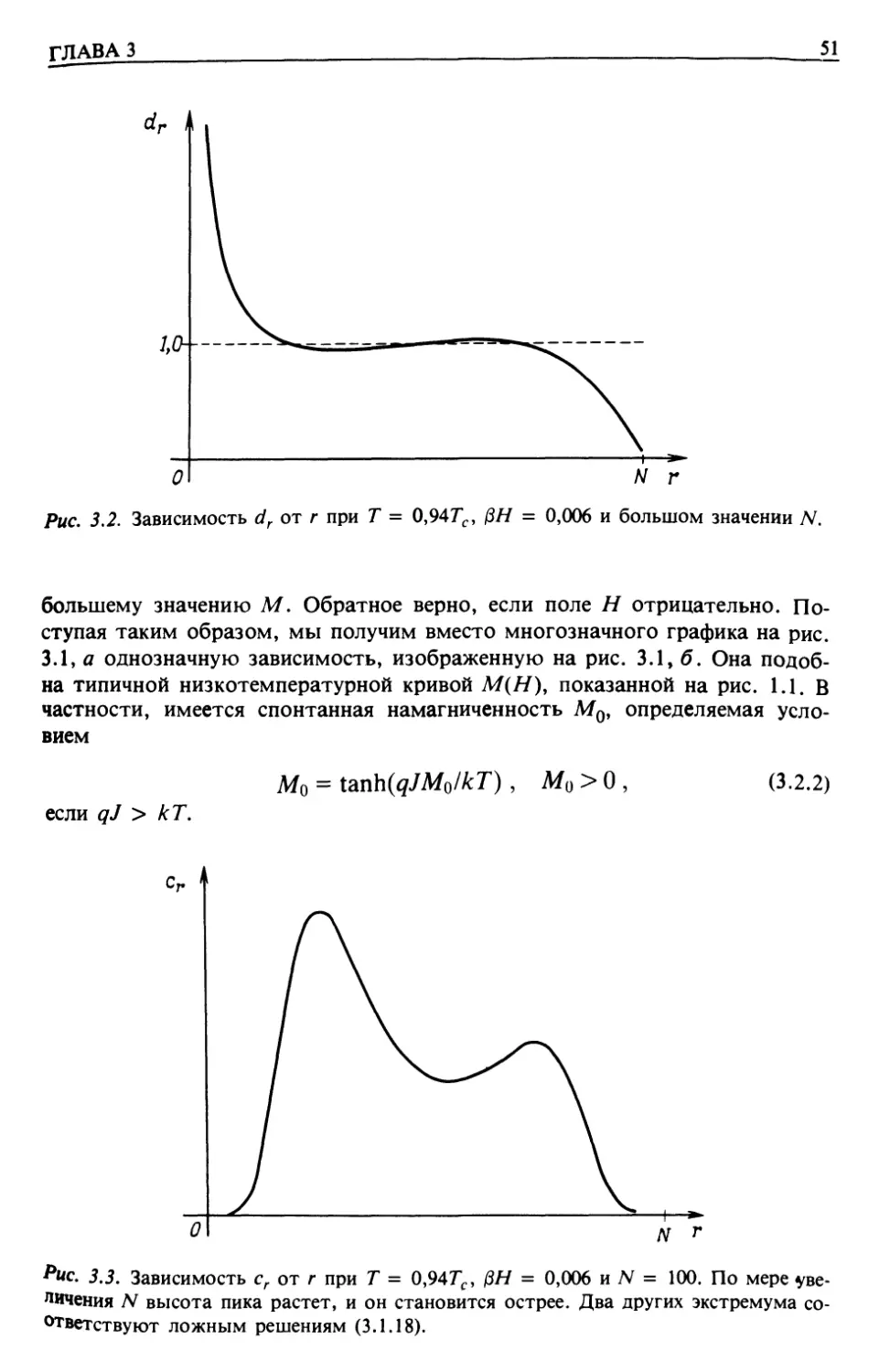
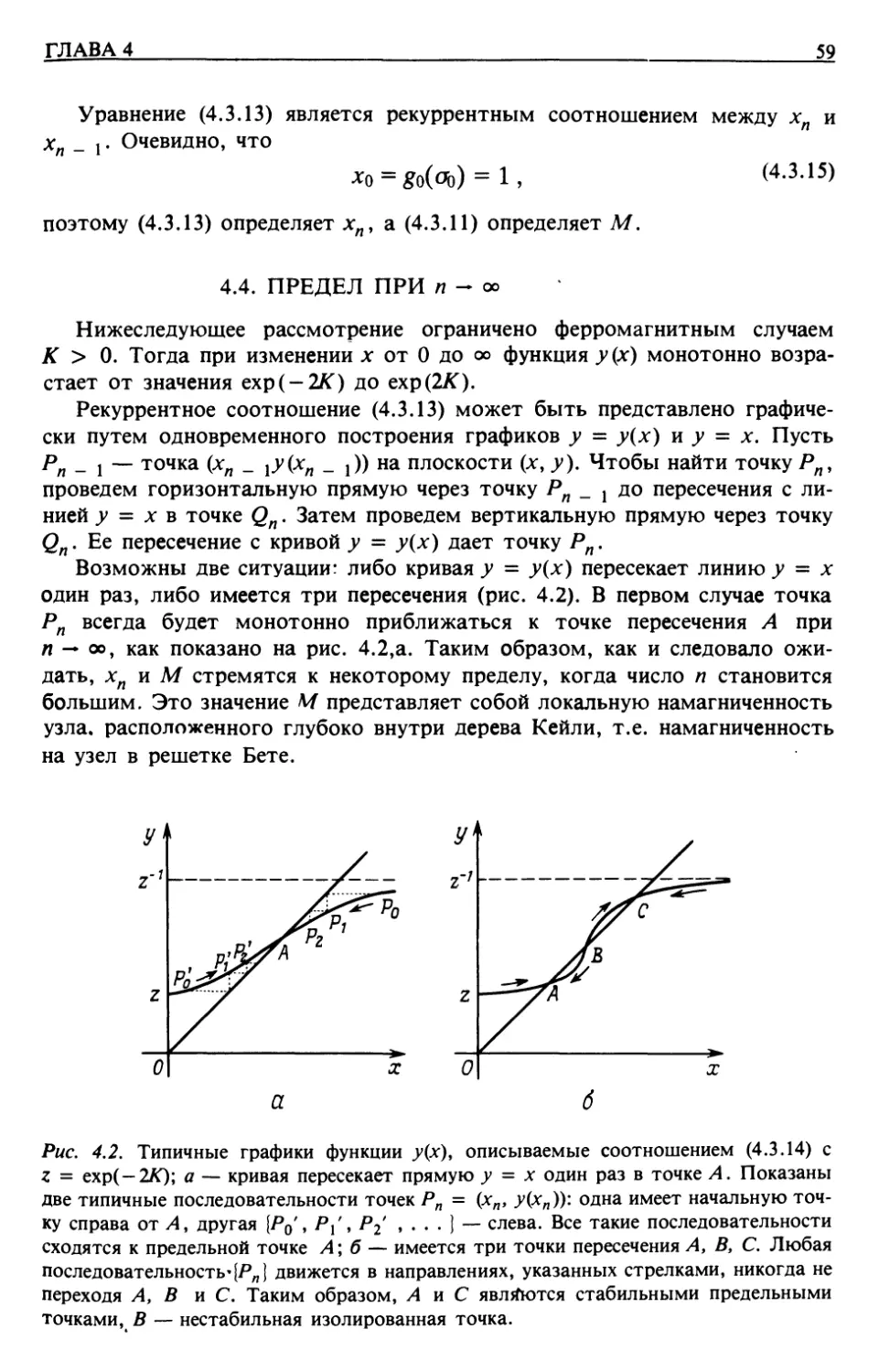
Точно решаемые модели в статистической механике - Бэкстер Р.

Автор: Бэкстер Р.
Теги: кинематика математическо-механическая геометрия движения физика механика статическая физика
Год: 1985
Похожие
Компьютерное моделирование физических систем
Фракталы в физике
Квантовая теория поля в физике конденсированного состояния
Устойчивые и фазовые переходы
Текст
                    Exactly Solved Models
in Statistical Mechanics
RODNEY J. BAXTER F. R. S.
Department of Theoretical Physics,
Research School of Physical Sciences,
The Australian National University,
Canberra, А. С. Т., Australia
ACADEMIC PRESS
A Subsidiary of Harcourt Brace Jovanovich, Publishers
London New York
Paris San Diego San Francisco Sao Paulo
Sydney Tokyo Toronto
1982

Р. Бэкстер
Точно решаемые
модели
в статистической
механике
Перевод с английского
д-ра физ.-мат. наук Е. П. Вольского
и канд. хим. наук Л. И. Дайхина
под редакцией
д-ра физ.-мат. наук А. М. Бродского
МОСКВА «МИР» 1985

ББК 22.317
Б97
УДК 531.19
Бэкстер Р.
Б97 Точно решаемые модели в статистической механике: Пер. с
англ. — М.: Мир, 1985. — 488 с, ил.
Книга крупного австралийского ученого — первая в мировой литературе монография, посвященная
результатам работ по исследованию двумерных моделей статистической физики, допускающих точное
аналитическое решение. Она представляет собой полный обзор двумерных моделей и методов их решения.
Анализ решений таких моделей сыграл чрезвычайно важтю роль в развитии теории фазовых переходов и в
исследовании критического поведения реальных систем.
Книгу можно рекомендовать научным работникам, занимающимся статистической физикой и математи-
математикой. Она может быть полезна также химикам.
Б 1704020000 — 020
54-85,ч. 1
041@1) - 85 ББК 22.317
530.1
Редакция литературы по физике
© 1982 by Academic Press, Inc.
© Перевод на русский язык,
«Мир», 1985

ПРЕДИСЛОВИЕ РЕДАКТОРА
ПЕРЕВОДА
Предлагаемая вниманию читателей книга является монографией,
посвященной описанию двумерных решеточных моделей в статистической
физике, допускающих аналитическое решение. Анализ свойств решений
таких моделей оказался чрезвычайно полезным для понимания поведения
сложных реальных систем. Прежде всего следует напомнить о той важней-
важнейшей роли, которую исторически сыграло решение Онсагером модели
Изинга. Эта модель, которая в пятидесятых годах рассматривалась как
некоторая модель ферромагнетизма и интересный объект для математичес-
математических упражнений, в шестидесятых годах после работ Янга и Ли стала
важнейшим источником информации о свойствах фазовых переходов.
Начиная с семидесятых годов представления и результаты теории модели
Изинга и других двумерных решеточных систем, такие, как скейлинг,
универсальность и т. д., стали плодотворно использоваться в теории поля.
В самое последнее время указанные представления стали активно использо-
использоваться в теории нелинейных динамических систем при описании хаоса.
Аналитическое решение двумерных моделей, более сложных, чем
модель Изинга, потребовало значительных усилий. Но эти усилия
оправдываются полученными результатами. В частности, было выяснено
на примере восьмивершинной модели, что гипотеза универсальности
может нарушаться, а на примере модели жестких гексагонов было
показано, что вошедшее в учебники утверждение об отсутствии линии
фазовых переходов второго рода при наличии оси симметрии третьего
порядка не всегда справедливо. Как восьмивершинная модель, так и
модель жестких гексагонов подробно рассмотрены в книге. К сказанному
можно добавить, что многие результаты, полученные для двумерных
решеточных моделей, могут быть непосредственно применены при
рассмотрении ряда реальных систем, например в теории адсорбции, и дру-
других двумерных и квазидвумерных систем.
Исходя из сказанного выше, следует весьма положительно оценить
появление рассматриваемой книги, в которой впервые собраны и
систематизированы как сравнительно известные, так и более новые
результаты, относящиеся к решеточным моделям. Значительный допол-
дополнительный интерес к книге вызывает то обстоятельство, что Р. Бэкстер
является одним из наиболее активно работающих в данной области авто-
авторов. В процессе изложения он (часто весьма эмоционально) описывает

ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
историю получения того или иного результата. Очень ценны и полезны
разбросанные по книге замечания автора о перспективах развития теории.
Книга Р. Бэкстера, несомненно, станет основным цитируемым источ-
источником во всех работах, посвященных как собственно статистической тео-
теории на решетках, так и ее приложениям. Она будет полезна не только фи-
физикам, но также математикам и химикам.
Предисловие и гл. 1 —9 и 12 переведены Е. П. Вольским, гл. 10, 11,
13 — 15 — Л. И. Дайхиным. При переводе исправлены замеченные опе-
опечатки.
А. М. Бродский

ПРЕДИСЛОВИЕ
Эта книга была задумана как небольшая монография, но она заметно
разрослась по сравнению с первоначальным замыслом, поскольку в ходе
работы над ней я попытался дать полный обзор двумерных моделей в
статистической механике и способов их решения. В процессе этой работы я
постоянно оказывался перед трудным выбором. С одной стороны, мне
вспоминался возглас аспиранта на одной из конференций: «Но вы же
опустили все выкладки — каким образом вы пришли от уравнения (81) к
уравнению (82)?» С другой стороны, я знал по собственному опыту, какое
количество бумаги отправляется в мусорную корзину после даже весьма
умеренных вычислений: было бы совершенно немыслимо опубликовать все
эти выкладки в полном объеме.
Я надеюсь, что достиг разумного компромисса, расставляя «ука-
«указательные знаки» вдоль всего маршрута вычислений, но не останавливаясь
на каждом отдельном шаге. При этом к каждому рассматриваемому
вопросу я старался подходить индивидуально. Например, в разд. 8.13, я
довольно детально обсуждаю функции к(а) и g(a), поскольку это дает
возможность особенно отчетливо показать, как именно используются
эллиптические функции в вычислениях. В противоположность этому я
просто привожу результат (8.10.9) для антисегнетоэлектрической
поляризации Ро в F-модели и отсылаю заинтересованного читателя к
оригинальной работе, поскольку вычисления в этом случае длинные и
довольно формальные и, по-видимому, рано или поздно будут заменены
более простыми, когда предположение A0.10.24) в теории восьмивершин-
ной модели будет проверено методами, подобными тем, которые были
использованы при выводе формулы A3.7.21) для намагниченности.
Существуют физики и химики, которые отрицают решеточные модели
как нереалистические. Их основной аргумент, выраженый в наиболее край-
крайней форме, состоит в том, что модель, которая может быть решена точно,
должна быть непременно патологической. Я считаю такие доводы пес-
пессимистической чепухой: трехмерная модель Изинга — весьма реалистичес-
реалистическая модель, по крайней мере для бинарных сплавов, таких, как латунь.
Если предсказания, основанные на принципе универсальности, правильны,
то мы должны получить точно такие же критические показатели.
Известно, что решение модели Изинга было получено только в случаях
одного и двух измерений, но ведь двумерные системы реально существуют

8 ПРЕДИСЛОВИЕ
(разд. 1.6) и могут быть весьма похожими на трехмерные. Справедливо
также, что решение двумерной модели Изинга получено только для нулево-
нулевого магнитного поля, и этот случай сильно отличается от случая ненулевого
магнитного поля; тем не менее с физической точки зрения Онсагер получил
решение в достаточно интересном и сложном случае. Его решение
чрезвычайно помогло нам представить себе полную картину поведения
модели Изинга в магнитном поле.
Аналогичным образом восьмивершинная модель помогла нам понять
более сложные системы и все разнообразие поведения, которое может
проявляться. Модель жестких гексагонов выглядит довольно экзотически,
но и она не нуждается в оправдании, поскольку идеально представляет
решеточный газ и может быть сопоставлена с мономолекулярным слоем
гелия, адсорбированного на поверхности графита [199].
Вероятно, существует также ощущение, что модели слишком услож-
усложнены математически. Это возражение также легко снимается: Рюэль [202]
правильно заметил в предисловии к своей книге, что если задача вообще
заслуживает рассмотрения , то никакой математический аппарат не может
считаться чрезмерно сложным.
Я полагаю, что основное оправдание изучения этих решеточных
моделей очень простое: они относятся к делу и могут быть решены. Поче-
Почему же тогда не сделать этого и не посмотреть, что это нам даст?
В заглавии книги слова «точно решаемые» выбраны с известной
осторожностью. Они не обязательно означают «строго решаемые».
Например, при выводе формулы A3.7.21) производится перемножение и
диагонализация бесконечномерных угловых трансфер-матриц. Следовало
бы показать, что матричные произведения сходятся. Я не сделал этого, но
полагаю, что они действительно сходятся (по крайней мере настолько,
чтобы обеспечить проведение вычислений) и, следовательно, формула
A3.7.21) совершенно правильна.
Разумеется, еще многое должно быть сделано. Б. Маккой и Ж. Перк
совершенно справедливо указали мне, что, хотя корреляции в модели
Изинга изучены довольно хорошо, почти ничего не известно о корреляциях
в восьмивершинной модели и в модели твердых гексагонов.
Я многим обязан тем людям, благодаря которым смог написать эту
книгу. Интерес к математике и теоретической физике привил мне мой отец
Т. Дж. Бэкстер, а также С. Адаме, Дж. С. Полкингхорн и К. Ж. Лекутер.
Э. Либ ввел меня в сложный мир моделей типа льда. Л. Николсон и
С. Торпи сделали чудо, превратив рукопись в безукоризненный маши-
машинописный текст. П. Пирс внимательно прочитал корректуру всей книги.
.Больше чем кто-либо другой, моя жена Элизабет воодушевляла меня в
процессе всей работы, особенно в течение последнего, самого напряжен-
напряженного года.
Канберра, Австралия р. дж. Бэкстер
Февраль 1982 г.

1
ОСНОВЫ СТАТИСТИЧЕСКОЙ
МЕХАНИКИ
1.1. ФАЗОВЫЕ ПЕРЕХОДЫ И КРИТИЧЕСКИЕ ТОЧКИ
Статистическая механика, как это следует из ее названия, имеет дело с ус-
усредненными характеристиками механической системы. Очевидными приме-
примерами являются атмосфера внутри комнаты, вода в чайнике и атомы в по-
постоянном магните. Такие системы составлены из огромного числа индиви-
индивидуальных компонент (обычно молекул). Наблюдатель в незначительной
степени и то не всегда способен контролировать состояние компонент си-
системы: он может лишь измерить небольшое число усредненных величин,
характеризующих систему, таких, как температура, плотность или намаг-
намагниченность. Задача статистической механики состоит в том, чтобы пред-
предсказывать соотношения между наблюдаемыми макроскопическими величи-
величинами, располагая лишь данными о микроскопических силах, действующих
между компонентами системы.
Допустим, например, что нам известны силы взаимодействия молекул
воды. Тогда мы, казалось бы, имеем возможность предсказать плотность
воды в чайнике при комнатной температуре и атмосферном давлении. Бо-
Более интересно то, что мы могли бы предсказать внезапное и драматическое
изменение плотности, когда температура поднимется от 99 до 101° С, а
именно уменьшение плотности в 1600 раз при превращении воды в пар.
Это явление называется фазовым переходом.
Могут происходить и более странные явления. Рассмотрим железный
стержень в сильном магнитном поле Я, параллельном его оси. Стержень
почти полностью намагничен; введя подходящие единицы, мы можем ска-
сказать, что его намагниченность М равна -I- 1. Снизим теперь поле Н до ну-
нуля: М уменьшится, но не до нуля. В нулевом поле стержень будет иметь
спонтанную намагниченность Мо.
С другой стороны, молекулярные силы должны быть инвариантны по
отношению к обращению времени. Из этого следует, что, изменяя направ-
направление поля на противоположное, мы обратим и намагниченость, так что
намагниченность М должна быть нечетной функцией Н. Таким образом,
график М(Н) должен иметь вид, показанный на рис. 1.1,а, с разрывом не-
непрерывности при Н = 0.
Этот скачок намагниченности очень похож на скачок плотности при фа-
фазовом переходе жидкость — газ. Действительно, в последнем разделе этой
главы будет показано, что между ними имеет место полная эквивалент-
эквивалентность. Можно считать, что железный стержень претерпевает фазовое прев-

10
ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
м
в
Рис. 1.1. Графики М(Н) при Т < Тс {а), Т = Тс (б), Т > Тс (в).
ращение при Н = 0, переходя скачком от отрицательной намагниченности
к положительной. В реальном эксперименте скачок размазывается и наб-
наблюдается явление гистерезиса; это связано с тем, что стержень не находит-
находится в истинном термодинамическом равновесии. Но если железо мягкое и
подвергается воздействию механического возмущения, то получается гра-
график, очень похожий на изображенный на рис. 1.1,а [62, 214].
Сказанное выше применимо к железному стержню при комнатной тем-
температуре. Предположим теперь, что температура Т немного увеличивается.
График М(Н) сохраняет прежний вид, но величина Мо уменьшается. На-
Наконец, если Т увеличивается до критического значения Тс (точка Кюри), то
Мо обращается в нуль и М(Н) становится непрерывной функцией с беско-
бесконечной производной (восприимчивостью) при Н = 0 (рис. 1.1,6). Если Т
увеличивается дальше, то М(Н) остается непрерывной функцией и стано-
становится аналитической при Н = 0 (рис. 1.1,в).
Эти наблюдения удобно суммировать с помощью диаграммы на пло-
плоскости (Г, Н) (рис. 1.2). На этой диаграмме имеется разрез вдоль оси Т от
0 до Тс. Намагниченность М является аналитической функцией Г и Я во
всех точках правой полуплоскости, за исключением точек на линии разре-
разреза. Она претерпевает разрыв при переходе через разрез.
Разрез представляет собой линию фазовых переходов. Ее конечная точ-
точка (Гс, 0) называется критической точкой. Ясно, что функция М(Н, Т) до-
должна быть сингулярной в этой точке; изучение этого сингулярного поведе-
поведения вблизи критической точки представляет собой одно из наиболее увлека-
увлекательных направлений статистической механики.

ГЛАВА 1
11
Рис. 1.2. Полуплоскость (Т, Я) с изо-
изображенным на ней разрезом, при переходе
через который М терпит разрыв.
В остальных точках полуплоскости М —
аналитическая функция Т и Н.
Спонтанная намагниченность как функция Т может быть определена
следующим образом:
М0(Т)= lim M(H,T),
н—> о
A.1.1)
где предельный переход осуществляется по положительным значениям Я.
Определенная таким образом величина положительна при Т < Тс и тож-
тождественно равна нулю при Т > Тс\ соответствующий график представлен
на рис. 1.3.
КРИТИЧЕСКИЕ ПОКАЗАТЕЛИ
Восприимчивость магнетика определяется как
A.1.2)
При рассмотрении критического поведения удобно ввести вместо Т новую
переменную
t=(T-Tc)/Tc. A.1.3)
Рис. 1.3. Зависимость спонтанной на-
намагниченности Мо от температуры.

12
ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
при
при
при
при
г->0-,
я^о,
A
A
A
A
.1.4)
.1.5)
.1.6)
.1.7)
Тогда сингулярности термодинамических функций должны иметь место
при Н = t — 0. Предполагается, что эти сингулярности имеют вид про-
простых степенных функций с дробными показателями; в частности, можно
положить
М0(Т) ~{-tY
М(Н,Тс)~НУд
Х@ , Т) ~ П
х(о,т) ~(-г)~у
Здесь X /^ Y означает, что X/ Y стремится к ненулевому пределу. Показа-
Показатели степени /3, б, у, у' — числа, не зависящие от Я и Т\ они называются
критическими показателями.
Для краткости в этой книге часто употребляется сочетание «вблизи Тс»
в смысле «вблизи критической точки»; при этом подразумевается, что поле
Н мало или равно нулю.
1.2. ГИПОТЕЗА ПОДОБИЯ (СКЕЙЛИНГА)
Естественно начинать с поисков какой-то упрощенной формы термоди-
термодинамических функций, которая описывала бы наблюдаемое поведение вбли-
вблизи Тс. Уидом [252] и Домб и Хантер [76] предположили, что некоторые
термодинамические функции могут быть однородными. В частности,
Гриффите [104] предположил, что поле Н может быть однородной функци-
функцией переменных М1/C и /. Поскольку Н — нечетная функция М, это означа-
означает, что вблизи Тс
где 0 и д — числа (пока не определенные), к — постоянная Больцмана и
hs(x) — безразмерная функция подобия. Типичный график hs(x) показан на
рис. 1Г4: hs(x) — положительная и монотонно возрастающая функция в ин-
интервале — х0 < х < оо, которая равна нулю при - а:0.
Рис. 1.4. Функция подобия hs{x) для модели
Изинга на квадратной решетке [97].

ГЛАВА 1 13
Заметим, что A.2.1) обеспечивает нечетный характер зависимости Н от
М, как и должно быть.
Гипотеза подобия предсказывает некоторые соотношения между крити-
критическими показателями. Чтобы увидеть это, рассмотрим сначала поведение
на линии разреза на рис. 1.2. Здесь Я=0, /<ОиМ= ± Мо. Из A.2.1)
следует, что функция hs(x) должна быть равна нулю, так что х — — хо>
т.е.
t=-xo\M\vfi. A.2.2)
Отсюда следует соотношение A.1.4), поэтому в A.2.1) C — критический по-
показатель, определенный в A.1.4).
Положим теперь t = 0 в A.2.1). Так как /*5@) не равно нулю, то вблизи
Тс имеем
Н-М6 A.2.3)
в согласии с A.1.5). Поэтому б в A.2.1) и в A.1.5) совпадают.
Продифференцируем A.2.1) по М при фиксированном t. Получим
I - p-lxh's(x)\, A.2.4)
где
x = t\M\~vP A 2^
Рассмотрим снова поведение на линии разреза на рис. 1.2. Здесь х имеет
фиксированное значение — хо> так что
-(-f)**". A.2.6)
Это согласуется с A.1.7) и показывает, что критический показатель у'
определяется выражением
У = Р(д-1). A.2.7)
Чтобы получить A.1.6) с помощью гипотезы подобия (скейлинга), необ-
необходимо знать поведение функций подобия hs(x) при больших значениях х.
Замечая, что при фиксированных положительных t должно быть
Н-М при М->0, A.2.8)
и сравнивая это с A.2.1), мы видим, что
hs(x) ~х^ ~ ' при х—> оо , A.2.9)
Из A.2.1) и A.2.9) следует, что для произвольно малых положительных
значений t
при М-»0, A.2.10)

И ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
так что из A.1.2) имеем
Х@,Т)~г№-1) при Г->0+. A.2.11)
Сравнивая с A.1.6) и используя A.2.7), мы видим, что гипотеза подобия
предсказывает следующее соотношение между показателями:
1). A2.12)
Другие показатели — a, i>, v\ rjy \k — определены в разд. 1.7, но для
полноты здесь приводится список различных предсказаний гипотезы подо-
подобия:
а+20+/ = 2, A.2.13)
v= v',B-y))v=y, A.2.14)
fi+v=2-oc, A.2.15)
dv = 2-a, A.2.16)
где d — размерность системы.
Частичный вывод соотношения A.2.14) дан в разд. 1.7, но обоснование
всех приведенных соотношений выходит за рамки этой книги. Заинтересо-
Заинтересованный читатель может обратиться к следующим источникам: [87, 108,
136, 212, 244, 252]. Для проверки соотношений между критическими показа-
показателями могут быть использованы точно решаемые модели. В самом деле,
мы увидим, что гипотеза подобия выдерживает любые проверки для всех
моделей, которые рассматриваются ниже.
Соотношения A.2.12)—A.2.15) находятся в хорошем согласии с имею-
имеющимися экспериментальными и теоретическими результатами, а функция
подобия hs(x) была получена в приближенном виде для многих систем (см.,
например, [97]).
Последнее соотношение A.2.16) включает в себя размерность d. Оно
выводится с помощью дополнительных предположений, известных под на-
названием «сильный скейлинг» или «гиперскейлинг». Можно ожидать,-что
оно выполняется для d < 4, но имеются некоторые сомнения относитель-
относительно того, что это соотношение согласуется с имеющимися численными ре-
результатами для трех- и четырехмерных моделей [11]. Полную систему
уравнений A.2.12)—A.2.16) иногда называют двухпоказательным скейлин-
гом, так как если два независимых показателя (например, 6 и /3) заданы, то
все остальные могут быть получены из этих уравнений.
1.3. УНИВЕРСАЛЬНОСТЬ
Рассмотрим систему с консервативными силами. Пусть s обозначает со-
состояние (или конфигурацию) системы. Тогда это состояние характеризует-
характеризуется энергией E(s)> где функция E(s) представляет собой гамильтониан си-
системы.

ГЛАВА 1 Ц
Термодинамические свойства, такие, как М(Н, Т) и Тс, конечно, зависят
от сил внутри системы, т.е. от E(s). Тем не менее предполагают [86, 105],
что критические показатели являются «универсальными», т.е. не зависят
от деталей гамильтониана E(s).
Они, конечно, зависят от размерности системы и от симметрии гамиль-
гамильтониана. Чтобы наглядно представить влияние этих факторов, допустим,
что E(s) можно записать в виде
E(s) = ?0E) + AEi(j) , A.3.1)
где E0(s) имеет некоторую симметрию (например, плоскость отражения), а
E{(s) ее не имеет. Тогда предполагается, что критические показатели зави-
зависят только от X и таким образом, что имеют одно значение для X = 0
(симметричный гамильтониан) и другое, фиксированное значение для всех
X Ф 0 (несимметричный гамильтониан). Например, существует два числа
C0 и /3j, таких, что
0 = А), еслиА = 0; ^
т.е. 0 как функция X имеет разрыв при X = 0.
С другой стороны, если E0(s) — какой-то простой гамильтониан, а
E{(s) — очень сложный, но имеющий ту же размерность и симметрию, то
показатель C должен оставаться постоянным при всех значениях X, вклю-
включая X = 0. Это имеет далеко идущие следствия. Можно взять реалистиче-
реалистический и сложный гамильтониан E(s), «обрезать» его до весьма идеализиро-
идеализированного гамильтониана Ео (s) и все еще получить точно такие же критиче-
критические показатели. Например, на основании этих соображений можно пред-
предположить, что диоксид углерода, ксенон и трехмерная модель Изинга име-
имеют одинаковые критические показатели. С точностью до погрешностей
эксперимента это действительно так [113].
Но имеются и трудности на этом пути, поскольку обычно существует
не один способ описания системы и в особенности идентификации ее состо-
состояний. При выборе одного из этих способов для некоторых значений пара-
параметров может возникать очевидная симметрия. В другой формулировке
проблемы эта симметрия может быть совсем не очевидна. Таким образом,
если используется вторая формулировка и эти особые значения параметров
выбраны случайно, то получаемые при этом критические показатели могут
неожиданно оказаться отличающимися от показателей, соответствующих
другим значениям параметров.
Еще одна проблема возникает в связи с рассматриваемой в данной книге
двумерной «восьмивершинной» моделью. Критические показатели в этой
модели изменяются непрерывно как функции параметров гамильтониана.
Это противоречит гипотезе универсальности, однако в настоящее время
предполагается, что подобные нарушения возможны лиши для некоторых
весьма специальных классов гамильтонианов.

\Ь ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
Следует заметить, что гипотезы скейлинга и универсальности представ-
представляют собой независимые предположения (хотя их часто объединяют). Одно'
из них может выполняться, а другое нет, например в указанном выше слу-
случае восьмивершинной модели, где универсальность нарушается, а принцип
подобия продолжает выполняться.
1.4. СТАТИСТИЧЕСКАЯ СУММА
Как вычислить термодинамические функции, такие, как М(Н, Г), исхо-
исходя из микроскопических сил, действующих между компонентами системы?
Ответ на этот вопрос дал Джон Виллард Гиббс в 1902 г. [99]. Рассмотрим
систему с набором состояний s и гамильтонианом E(s). Составим стати-
статистическую сумму:
2 A.4.1)
где к — постоянная Больцмана и суммирование выполняется по всем допу-
допустимым состояниям s системы. Тогда выражение для свободной энергии F
имеет вид
F=-kTlnZ, A.4.2)
а вероятность найти систему в состоянии s равна
Z~lexp[-E(s)/kT], A.4.3)
так что если X — некоторая измеряемая характеристика системы, такая,
как полная энергия или намагниченность, имеющая значение X(s) для со-
состояния 5, то ее измеренное среднее термодинамическое значение равно
(X) = Z12 X{s) exp[ - E(s)/kT]. A.4.4)
S
В частности, для внутренней энергии мы получаем формулу
U = (E)
, лг, A-4.5)
= Z~lZ, E(s) exp[- E(s)/kT]
и, используя приведенные выше определения A.4.1) и A.4.2), можем убе-
убедиться, что
U = kT2^-\nZ
дТ A.4.6)
= ..T2jL(F/Th
в согласии с обычной термодинамикой.

ГЛАВА 1 П
Таким образом, главная задача равновесной статистической механи-
механики — вычисление суммы по состояниям A.4.1) (для систем с непрерывным
спектром эта сумма превращается в интеграл, а для квантовомеханических
систем — в сумму диагональных элементов матрицы плотности). Резуль-
Результат такого вычисления дает Z и F как функции Т и любых других перемен-
переменных, входящих в E(s), например магнитного поля. Термодинамические ха-
характеристики можно получить затем посредством дифференцирования.
К сожалению, для любых реалистических систем макроскопического
размера со взаимодействием, включая рассмотренные выше примеры, вы-
вычисление Z представляет собой безнадежно трудную задачу. Мы вынужде-
вынуждены поэтому следовать по одному из следующих двух путей:
1. Заменить реальную систему некоторой простой идеализированной си-
системой, которая называется моделью. Математически это выражается в
указании состояний s и определении вида энергетической функции Гамиль-
Гамильтона E(s).
2. Сделать какое-то приближение, позволяющее вычислить сумму по со-
состояниям A.4.1).
1.5. ПРИБЛИЖЕННЫЕ МЕТОДЫ
Рассмотрим сначала второй путь. Перечислим некоторые,из наиболее
известных схем приближений.
I. Приближения ячеек или кластеров. В этом случае свойства системы в
целом получают в результате экстраполяции свойств небольшой совокуп-
совокупности ее компонент, заключенной внутри некоторой «ячейки». Приближен-
Приближенно оценивают взаимодействия ячейки с остальной частью системы. Приме-
Примерами могут ^служить приближения среднего поля [53, 63], квазихимическое
[107] и Кикучи [147]. Эти теории обладают преимуществом простоты; они
правильно предсказывают качественное поведение, показанное на рис.
1.1—1.3, и дают удовлетворительную точность, за исключением ближай-
ближайшей окрестности критической точки [65; 74].
И. Приближенные интегральные уравнения для корреляционных функ-
функций, в частности уравнения Кирквуда [149], гипер цепное [242] и Пер ку-
куса—Йевика [193, 194]. Они дают довольно хорошие численные значения для
термодинамических характеристик простых жидкостей.
III. Моделирование на ЭВМ, выполняемое для систем, достаточно боль-
больших в микроскопическом масштабе (т.е. содержащих несколько сотен ^то-
^томов), но все же не макроскопического размера. В этих вычислениях величи-
величина Z оценивается посредством статистической выборки членов в правой ча-
части A.4.1), так что статистические погрешности составляют обычно не-
несколько процентов. По этой причине эти методы представляют собой
именно аппроксимации, а не точные расчеты.
IV. Разложения в ряд по степеням подходящей переменной, такой, как
обратная температура или плотность. Для достаточно реалистических мо-
моделей может быть вычисленно только небольшое число членов ряда, но в
случае трехмерной модели Изинга было получено до 40 членов соответ-
соответствующего разложения [223, 225].

18 ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
Приближенные методы I—III могут давать весьма точные значения тер-
термодинамических величин, но не в непосредственной близости от крити-
критической точки. Причина состоит в том, что все эти методы в той или иной
форме пренебрегают корреляциями более высокого порядка, чем парные,
либо парными корреляциями на больших расстояних. Но вблизи Тс корре-
корреляционные длины становятся неограниченно большими, все части системы
оказываются скоррелированными и почти любое приближение становится
неприменимым. Это означает, что приближения типа I, II, и III едва ли
могут быть полезны для описания весьма интересного кооперативного по-
поведения термодинамической системы вблизи Тс.
Метод IV много лучше: если вычислить достаточное число членов раз-
разложения, то, проявив некоторую изобретательность, можно получить
правдоподобные заключения относительно характера сингулярностей тер-
термодинамических функций вблизи критической точки. В частности, наилуч-
наилучшие имеющиеся в настоящее время оценки критических показателей в трех-
трехмерном случае получены методом разложения в ряд. Но для вычисления
членов ряда должна быть выполнена колоссальная работа, и все же точ-
точность получаемых в результате показателей оказывается ниже желаемой.
V. Имеется еще один подход, связанный с именами Каданова [130] и
Вильсона [253] (см. также [90, 255]), — это так называемая ренормализаци-
ренормализационная группа. В этом методе вычисление суммы по состояниям в A.4.1)
выполняется последовательными ступенями, причем на каждой ступени
вычислений «ренормализационная» функция Гамильтона E(s) определяется
заново. Таким образом, вводится отображение в пространстве гамильтони-
гамильтониана. Если сделать довольно мягкие допущения относительно этого отобра-
отображения, в частности ввести предположение об его аналитичности, то удает-
удается установить, что термодинамические функции в критической точке имеют
особенность типа «точки ветвления» A.1.4), гипотеза подобия A.2.1) и со-
соотношения A.2.12)—A.2.16) выполняются и критические показатели до-
должны быть, как правило, универсальными [90].
В принципе ренормгрупповой подход может быть до конца проведен
точно. Но это сделать труднее, чем выполнить прямое вычисление стати-
статистической суммы. Поэтому для получения численных результатов во всех
случаях, кроме самых простейших моделей, необходимо использовать
какие-то приближенные методы. Этот подход привлекателен тем, что да-
даже весьма грубые аппроксимации ячеечного типа дают довольно точные
значения критических показателей [131]. Причины этого еще не вполне по-
понятны.
Итак, приближенные методы либо оказываются полностью непригод-
непригодными вблизи Гс, либо требуют принятия без доказательства некоторых
предположений.
1.6. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
Другой подход состоит в том, чтобы выбрать первый путь и идти по
нему до конца, т.е. попытаться найти модели, для которых E(s) достаточ-
достаточно простая функция, чтобы статистическая сумма A.4.1) могла быть вы-

ГЛАВА 1 19
числена точно. Возможно, что это не даст нам информации о значениях
термодинамических функций реальных систем, но мы получим качествен-
качественное представление о том, как могут вести себя системы, в особенности
вблизи Тс. В самом деле, если мы решили задачу для модели той же раз-
размерности и симметрии, что и реальная система, то, согласно принципу
универсальности, мы должны получить точные значения критических по-
показателей для реальной системы.
Имеется еще одно ограничение на применение принципа универсально-
универсальности, которое не упоминалось в разд. 1.3. В большинстве физических систем
межмолекулярные силы являются эффективно короткодействующими: в
инертных газах они убывают как г (г — расстояние между молекулами);
в кристаллах часто достаточно рассматривать только взаимодействие меж-
между ближайшими соседями. Корреляции неограниченного радиуса, возника-
возникающие в критической точке, обусловлены кооперативным поведением всей
системы, а не дальнодействующими взаимодействиями.
С другой стороны, если достаточно дальнодействуюшие взаимодейст-
взаимодействия включены в E(s), то они, очевидно, могут влиять на характер неогра-
неограниченного роста радиуса корреляций вблизи Гс, и мы не должны удивлять-
удивляться, если критические показатели при этом изменятся. Таким образом,
принцип универсальности применим только к системам с одинаковым ра-
радиусом взаимодействия. Чтобы получить правильное критическое поведе-
поведение, не следует вводить в модель реальной системы нефизические дально-
действующие взаимодействия.
К сожалению, еще не получено решение ни для одной по-настоящему
трехмерной модели с короткодействующими силами. Простейшей моделью
такого рода является трехмерная модель Изинга (которая кратко описана
ниже); эта модель интенсивно исследовалась методом разложения в ряд
[98], но точного решения не получено.
Модели систем со взаимодействием, для которых статистическая сумма
A.4.1) была вычислена точно (по крайней мере в термодинамическом пре-
пределе), могут быть, вообще говоря, сгруппированы в следующие четыре
класса.
Одномерные модели
Одномерные модели могут быть решены для взаимодействий конечного
радиуса, экспоненциально затухающих или кулоновских. Такие модели с ко-
короткодействующими парными взаимодействиями (включая экспоненциаль-
экспоненциально затухающие) имеют серьезный недостаток с точки зрения использова-
использования их для ориентации в мире критических явлений: они не имеют фазово-
фазового перехода при ненулевых температурах [160, 240]. Кулоновские системы
также не имеют фазового перехода [14—16, 156], хотя одномерный элек-
электронный газ имеет дальний порядок при всех температурах [154].
Из одномерных моделей в этой книге будет рассмотрена только модель
Изинга с взаимодействием между ближайшими соседями [117, 152]. Она
удобна в качестве простого введения в технику трансфер-матриц, которая
будет использоваться в более трудных двумерных моделях. Хотя эта мо-
модель и не имеет фазового перехода при ненулевых температурах, длина

20 ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
корреляции становится бесконечной при Н = Т = 0, так что в некотором
смысле это «критическая точка», и гипотеза подобия может быть провере-
проверена в ее окрестности.
Одномерная система может иметь фазовый переход, если во взаимо-
взаимодействии участвует неограниченное число частиц, как это имеет место в
модели взаимодействующих кластеров [89, 91]. Она также может иметь
фазовый переход, если радиус взаимодействия становится бесконечным, но
тогда система принадлежит уже, по существу, к следующему классу «бес-
«бесконечномерных» моделей.
«БЕСКОНЕЧНОМЕРНЫЕ» МОДЕЛИ
Чтобы уяснить себе смысл понятия «бесконечномерная система», необ-
необходимо дать рабочее определение эффективной размерности гамильтониа-
гамильтониана. Для систем с взаимодействием малого или ограниченного радиуса ника-
никакой трудности при этом не возникает: искомая размерность равна размер-
размерности рассматриваемого пространства.
Для других систем полезным приемом оценки размерности может слу-
служить подсчет числа узлов, в которых может побывать за п шагов частица,
совершающая случайное блуждание по решетке (начальная точка блужда-
блуждания выбирается произвольно). Для tf-черной регулярной решетки и для
больших значений п это число пропорционально объему ящика с ребром,
равным л, т.е. nd. Чем больше размерность, тем теснее располагаются со-
соседние узлы.
Если число соседей бесконечно велико, система становится эффективно
бесконечномерной. Примером может служить система, описываемая мо-
моделью среднего поля, которая обсуждается в гл. 3. В гл. 4 рассматривается
модель Изинга на решетке Бете. Эта «решетка» обладает тем свойством,
что число узлов, посещаемых за л шагов, растет экспоненциально с ростом
л. Это более быстрый рост, чем nd', независимо от значения d, поэтому та-
такая модель также бесконечномерна.
Результаты для этих двух моделей совпадают с результатами, получен-
полученными для регулярных решеток с помощью приближения среднего поля и
аппроксимации Бете соответственно (разд. 1.5). Таким образом, оба эти
приближения эквивалентны замене исходного гамильтониана гамильтониа-
гамильтонианом бесконечномерной модели.
В работе [129] рассмотрена решаемая одномерная модель газа со взаи-
взаимодействием, имеющим характерный радиус R. В такой модели «ближай-
«ближайшими соседями» можно считать все частицы, расположенные в пределах
радиуса R от данной частицы. В пределе R — оо (и только в этом пределе)
авторы работы показали существование фазового перехода. С современной
точки зрения это не удивительно, поскольку, устремляя R к бесконечности,
мы неограниченно увеличиваем число ближайших соседей; при этом одно-
одномерная система становится эффективно бесконечномерной. Замечательным
ее свойством оказывается то, что она описывается точно таким же уравне-
уравнением состояния, какое предложил, руководствуясь феноменологическими
соображениями, ван дер Ваальс в 1873 г. (уравнение A.10.1)). Все эти три

ГЛАВА 1 21
«бесконечномерные» модели согласуются с гипотезой подобия A.2.1) и
имеют классические показатели (разд. 1.10).
Сферическая модель
В первоначальной формулировке [51, 169] эта модель вводит ограниче-
ограничение, связывая в равной степени все компоненты системы независимо от то-
того, как далеко они расположены друг от друга. Таким образом, она «нефи-
«нефизическая» в том смысле, что включает взаимодействия неограниченного ра-
радиуса действия. Тем не менее Стенли [211] показал, что ее можно рассмат-
рассматривать как предельный случай системы с взаимодействием только между
ближайшими соседями. Эта модель обсуждается в гл. 5. Интересно то, что
ее критические показатели в трехмерном случае неклассические.
Двумерные решеточные модели
Имеется очень небольшое число двумерных моделей, которые были ре-
решены (т.е. вычислена их свободная энергия); в частности, это модели
Изинга, сегнетоэлектрическая, восьмивершинная и трехспиновая. Все они
«физические» в том смысле, что включают взаимодействия только ограни-
ограниченного радиуса, и все имеют критическую точку. Основное внимание в
этой книге будет уделено именно этим моделям.
Конечно, можно лишь пожалеть, что они только двумерные, но все же
они дают качественное представление о реальных системах. В самом деле,
имеются реальные кристаллы с сильными горизонтальными и слабыми
вертикальными взаимодействиями. Примерами являются K2NiF4 и Rb2MnF4
[4, 55]. Двумерные модели могут быть весьма полезными для описания та-
таких кристаллов.
Более неприятно, по-видимому, то, что для большинства двумерных
моделей решение было получено только в отсутствие внешнего поля
(Н = 0), так что имеется лишь ограниченная информация относительно их
критического поведения и функция скейлинга И(х) для них не вычислена.
Единственное исключение представляет собой сегнетоэлектрическая модель
в присутствии электрического поля, но она обнаруживает необычное, нети-
нетипичное поведение (разд. 7.10).
1.7. ОБОБЩЕННАЯ МОДЕЛЬ ИЗИНГА
Большинство моделей, обсуждаемых в этой книге, можно рассматри-
рассматривать как частные случаи обобщенной модели Изинга, которую в свою оче-
очередь можно считать моделью магнетика. Представим себе магнетик, со-
состоящий из молекул, расположенных в узлах регулярной решетки. Пред-
Предположим, что имеется N таких узлов, пронумерованных индексами
/ = 1, . . . , N.
Представим себе теперь каждую молекулу как микроскопическую маг-
магнитную стрелку, которая направлена всегда либо вдоль некоторой задан-
заданной оси, либо точно в противоположном * направлении. Таким образом,
каждая молекула / имеет две возможные конфигурации, которые можно

22 ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
• о о
7 8 9
4 *ч л ^ис' ^' конфигурация спинов на квадратной решетке с про-
пронумерованными узлами. Темные кружки обозначают спины,
# # # направленные вверх (положительные); светлые кружки — спины,
/ 2 3 направленные вниз (отрицательные).
описывать с помощью «спиновой» переменной а,, принимающей значения
+ 1 (параллельно оси) или — 1 (антипараллельно оси). Мы будем гово-
рить, что спин направлен «вверх», когда переменная <rt равна + 1» и
«вниз», когда она равна - 1. Часто эти значения будут кратко записывать-
записываться как + и —.
Пусть о = [а1э . . . , aN] обозначает набор значений всех N спинов, Име-
Имеется 2N различных наборов а, и каждый из них описывает некоторое состо*
яние системы. Например, на рис. 1.5 показана система из 9 спинов в состо-
состоянии
а= {+ , + , + 9 - , + , - , + , - , -}. A.7.1)
Гамильтониан представляет собой функцию Е (а[у . . . , a^)t или, более
кратко, Е(а). Эта функция состоит из двух частей:
+ вд, 0.7.2)
где Ео включает вклад межмолекулярных сил внутри магнетика, а
Ех(р) — вклад от взаимодействий каждого спина с внешним магнитным по-
полем. Поскольку ai представляет собой, по существу, магнитный момент
молекулы /, функцию Е{(а) можно записать в виде
Ei(a) = -#So/, 0.7.3)
i
где величина Н пропорциональна составляющей поля вдоль направления
выбранной оси системы. Ниже мы будем называть Н просто магнитным
полем. Сумма в A.7.3) берется по всем узлам решетки, т.е. / = 1 N.
В любой физической системе мы предполагаем все взаимодействия инва-
инвариантными по отношению к обращению времени, что означает инвариант*
ность Е при изменении знаков всех полей и намагниченностей, т,е, в дан»,
ном случае Н и о{, . . . , aN. Отсюда следует, что энергия должна быть
четной функцией а:
?oOi , • • • , Ы = ?o(-C7i,. . . , -oN). A.7,4)
Приведенные соотношения определяют весьма общую модель Изинга,
решение которой было получено только в некоторых частных случаях. С
точки зрения физика эта модель крайне упрощена; очевидное возражение
против нее состоит в том, что вектор магнитного момента молекулы мо-

ГЛАВА 1 23
жет быть направлен произвольным образом, а не только «вверх» или
«вниз». Можно учесть это возражение и прийти таким образом к класси-
классической модели Гейзенберга [213], но для этой модели решение не получено
даже в двумерном варианте.
В то же время имеется кристаллы с сильно анизотропными взаимо-
взаимодействиями, такими, что магнитные моменты молекул можно считать на-
направленными только «вверх» или «вниз», например FeCl2 [138] и FeCO3
[257]. Трехмерная модель Изинга должна хорошо описывать такие вещест-
вещества и, согласно принципу универсальности, давать правильные значения кри-
критических показателей.
Пробелы в разд. 1.1, 1.2 и 1.4, а именно статистикомеханическое опре-
определение М(Н, Т) и критических показателей a, v, rj, д, теперь могут быть
ликвидированы. Используя A.4.1), A.7.2) и A.7.3), мы можем напирать
статистическую сумму как функцию N, Я и Г в следующем виде:
ZN(H , Г) = S ехр{-[Ео(ст) - Я 2 о]1кТ). {ХЛ.5)
Свободная энергия и теплоемкость
По физическим соображениям свободная энергия большой системы до-
должна быть пропорциональна ее размеру; иначе говоря, мы предполагаем,
что существует термодинамический предел
/(#, Г) = -kT lim N~l InZN(H,T), A.7.6)
N-*oo
где / — свободная энергия на один узел решетки.
Мы предполагаем также, что этот предел не зависит от пути, по кото-
которому мы к нему приходим. Например, не имеет значения, одновременно
или поочередно длина, ширина и высота кристалла устремляются к беско-
бесконечности, лишь бы в конце концов все они становились бесконечно больши-
большими.
Из A.4.6) следует, что внутренняя энергия на один узел равна
и(Н,Т) = ~T2^-[f(H,T)/T]. A.7.7)
Теплоемкость на узел определяется как
С(Н,Т)=±и(Н,Т). A-7.8)
Критические показатели а и а' обычно определяют, утверждая, что
вблизи Тс теплоемкость при Н = О расходится по степенному закону, т.е.
С@,Г)~Г" при Г->0+,
A.7.9)
~(-f)~a при f-*0~,
где / определено в A.1.3).

24 ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
Трудность, связанная с таким определением, обусловлена тем, что С@,
Г), не будучи обязательно аналитической функцией при / - 0, может оста-
оставаться конечной величиной, когда / стремится к нулю со стороны положи-
положительных (или отрицательных) значений. Например, С@, Т) может иметь
конечный скачок в точке / = 0, как это имеет место в модели среднего по-
поля, рассматриваемой в гл. 3.
Чтобы получить критический показатель, характеризующий такое пове-
поведение, лучше действовать следующим образом. Пусть /+ (О, Г) и /_ (О,
7) — свооодные энергии при Н — 0 для 7 > i с и Т < Тс соответственно.
Аналитически продолжим эти функции на комплексную Г-плоскость и
определим «сингулярную часть» свободной энергии как
/,@,Г)=/+@,Л-/-@,Г). A.7.10а)
Обычно вблизи Тс она стремится к нулю по степенному закону, и а можно
определить следующим образом:
fs(O,T)-t2-a при Г-»0. A.7.106)
Это определение эквивалентно A.7.9) (с а' = а) в тех случаях, когда
м@, Т) — непрерывная функция, а С@, Г)расходится и выше, и ниже Тс.
Раньше обычно считали, что единственно возможной особенностью/@,
Т) является скачкообразный разрыв непрерывности некоторой ее произво-
производной. Если первые г — 1 производных были непрерывны, а r-я произво-
производная имела разрыв непрерывности, то говорили, что система имеет «фазо-
«фазовый переход r-го порядка». В частности, переход сопровождающийся скач-
скачком внутренней энергии и (т.е. со скрытой теплотой), был назван фазовым
переходом первого рода.
Хотя в настоящее время известно, что эта классификация не охватывает
все возможные случаи, тем не менее такое поведение содержится в A.7.10):
переход порядка г соответствует 2 — а = г. В частности, а = 1 для перехо-
перехода первого рода.
Определение A.7.10) с учетом A.7.7) требует, чтобы функция w@, T) со-
содержала член, пропорциональный tl~a. Так как обычно w@, T) — ограни-
ограниченная функция, отсюда следует, что
. A.7.11)
Показатель а может быть отрицательным.
Намагниченность
Намагниченность равна среднему значению магнитного момента систе-
системы в расчете на один узел решетки, т.е. с учетом A.4.4) имеем
M(H,T)=N-i(al + ...+aN) A.7.12)
+ . . . + oN) x

ГЛАВА 1 25
хехо(-[ЕпЫ-яЕа,кг1. О-7-13)
Дифференцируя A.7.5) по Я и используя A.7.6), получаем, что в термоди-
термодинамическом пределе (N — оо)
M(H,T) = -^-f(H,T). A.7.14)
G/7
Поскольку выражение под знаком суммы в A.7.5) не меняется при од-
одновременной перемене знака Я и а, то, следовательно, ZN и / — четные
функции Я, а М — нечетная функция, т.е.
М(-Н,Т) = -М(Н,Т). A.7.15)
Как видно из A.7.12), значения М заключены в интервале
Г)^1. A.7.16)
Дифференцируя A.7.13), получаем в соответствии с A.1.1) и A.4.4) вы-
выражение для восприимчивости
*=~ =(МкТУН(М2)-(МJ}, A-7.17)
art
где
М = У2а1. A.7.18)
i
Так как среднее от постоянной величины равно этой величине, то A.7.17)
можно переписать в виде
X=(NkT)-1<[M.-(M)Y). A.7.19)
Таким образом, восприимчивость х равна среднему значению неотрица-
неотрицательной величины, поэтому
Х = — ^0. A.7.20)
Следовательно, намагниченность М представляет собой нечеткую, моно-
монотонно возрастающую функцию Я, значения которой лежат в интервале
A.7.16), как это показано на рис. 1.1.
Заметим, что для конечных N величина Z представляет собой сумму по-
положительных аналитических функций Я, так что / и М также должны
быть аналитическими функциями. Разрыв непрерывности на рис. 1.1,я и
сингулярность на рис. 1.1,6 могут возникать только в термодинамическом
пределе.
Критические показатели /3, 6, у, у', связанные с намагниченностью,
определены в разд. 1.1. Соотношение A.2.13) можно получить интегриро-
интегрированием A.7.14), используя гипотезу подобия A.2.1).

26 ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
КОРРЕЛЯЦИИ
Корреляция спинов / и j равна
gq = (ор} - (оНоЦ • A.7.21)
Если функция Е0(а) трансляционно-инвариантна, как это обычно бывает,
то значение (о) одинаково для всех узлов /, так что из A.7.12) следует
(ог) = (о}) = М(Н,Т). A.7.22)
Кроме того, gy зависит только от вектора г^, соединяющего узлы / и у, т.е.
gij = g(rij), 0.7.23)
где g(r) — корреляционная функция.
Предполагается, что при удалении от Тс функция g(r) экспоненциально
затухает с ростом Г. Выражаясь точнее, мы ожидаем; что
g(jck) ~дГге~х/| прих-х», A.7.24)
где т — некоторое число, к — фиксированный единичный вектор, а
? — корреляционная длина в направлении к.
Корреляционная длина является функцией Я и Г, и предполагается, что
она стремится к бесконечности по мере приближения к Тс. По существу,
стремление корреляционной длины к бесконечности можно рассматривать
как отличительный признак критической точки. Математически это выра-
выражается следующим образом:
?(О,Г)~ГР при г-*0+;
' ' A.7.25)
~ (-tyv' при Г-»0~ ,
где v и v' — критические показатели корреляционной длины.
Немного неприятно, что ? зависит также от направления к. Но вблизи
TQ эта зависимость, по-видимому, исчезает, и дальнодействующие корреля-
корреляции становятся изотропными (см., например, [164], с. 306). Таким образом,
показатели v и v' не должны зависеть от направления, для которого опре-
определено ?.
В самой критической точке корреляционная функция g(r) все же сущест-
существует, но затухает с расстоянием не экспоненциально, а по степенному за-
закону:
g(r)~rd+2-\ d.7.26)
где г} — критический показатель. Все эти свойства представляют собой
естественные следствия гипотезы подобия для корреляционной функции,
согласно которой вблизи Тс и для г - ? имеем
A.7.27)

ГЛАВА 1 27
Восприимчивость х можно выразить через g(r). Чтобы сделать это,
просуммируем A.7.21) по всем / и j. Из A.7.17) немедленно следует
gij- A.7.28)
i j
Для трансляцдонно-инвариантной системы сумма
A.7.29)
/ j
нр завидит от /, так что A.7.28) переходит в
,Ь AЛ,ЗО)
]
где 0 — ^^ой-то фиксированный узел решетки.
Вблизи Тс функция g(f) представляет собой изотропную, ограниченную,
медленно меняющуюся функцию г, поэтому суммирование можно заменить
интегрированием:
A.7.31)
Производя подстановку г = х? и используя A.7.27), получаем, что
вблизи Тс
Х-?^- A.7.32)
Соотношения между показателями A.2.14) теперь следуют из определе-
определений 7» 7'» Y* v> ** равенства 7 = 7'.
Поверхностное ндтяжениц
Эта величина определена только на линии разреза, нз рис. J.2 , т.е, для
Ц = О И Т < Гс. Если мы приближаемся к линии разреза сверху, т*е. И
стремится ц нулю по положительном значениям, то ц равновесном состоя-
состоянии большинство спинор направлено вверх. Если МН приближаемся ъ раз-
разрезу снизу, то большинство спинов, направлено вниз.
При Н =5= 0 эти два рэдновеснцх состояния могут сосуществовать: кри-
кристалл мржет состоять из дву^ больших областей (доменов), одна из кото-
которых находится в ОДНОМ состоянии» Другая — в другом. Полная свободная
энергия тогда равна
A.7.33)
гд§ Nf — дрнчная объемная свободная энергия, a Ls — полная
н^я сво§рдн^я энергия, связ^н^ая с наличием поверхности раздела межДУ
доменами: Рели L — площадь этой поверхности, то s — поверхностное на-
натяжение на единицу площади.
В разд. 1.9 показано, что между рассматриваемой здесь моделью магне-

28 ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
тика и моделью фазового перехода жидкость — газ имеется соответствие.
По только что введенной терминологии s соответствует поверхностному
натяжению жидкости, находящейся в равновесии со своим паром, напри-
например вода и пар при 100 °С.
В теории критических явлений поверхностному натяжению обычно не
уделяют много внимания, тем не менее это одна из термодинамических ве-
величин, которая может быть вычислена для точно решаемых двумерных
моделей, так что в данной книге она представляет для нас интерес.
Поверхностное натяжение является функцией температуры. Когда Т
приближается к Тс снизу, два равновесных состояния сливаются в одно, и
величина s стремится к нулю. Ожидается, что вблизи Тс
s(T)~(-ty9 d.7.34)
где ft — еще один критический показатель, последний из вводимых в этой
книге.
Уидом [252], используя соображения подобия, предположил, что
вблизи Тс
s(T) ос §@ , Г) М2@ , ТIХ@ , Г) , A.7.35)
откуда следует соотношение A.2.15). Он получил также соотношение ги-
перскейлинга A.2.16).
1.8. МОДЕЛЬ ИЗИНГА С ВЗАИМОДЕЙСТВИЕМ
МЕЖДУ БЛИЖАЙШИМИ СОСЕДЯМИ
Все обсуждение в разд. 1.7 применимо к любому четному гамильтониа-
гамильтониану Е0(а) с некоторыми неявно выраженными ограничениями, такими, как
существование термодинамического предела A.7.6) и ферромагнитной кри-
критической точки.
Простейший гамильтониан такого типа, учитывающий взаимодействия
лишь между ближайшими соседями, имеет вид
-Jy2oioj, A.8.1)
(ч)
где суммирование выполняется по всем парам соседних узлов в решетке.
Это обычная модель Изинга, упоминавшаяся в разд. 1.6. Если
J — положительная величина, то в наинизшем энергетическом состоянии
все спины направлены в одну сторону, так что модель описывает ферро-
ферромагнетик.
Очень многое уже известно об этой модели. Даже для таких случаев,
когда нет точного решения, как, например, для тр^х измерений или для
двух измерений во внешнем поле, может быть получено разложение в ряд
в высокотемпературной или в низкотемпературной области.
Из (Г.7.5) следует, что статистическая сумма равна

ГЛАВА 129
N = S exp[К S OiOj + h E о;-] ,
A.8.2)
где
K = JlkT, h=H/kT, A.8.3)
так что ZN можно рассматривать как функцию И и К. Выражение для на-
намагниченности на один узел следует из A.7.6) и A.7.14):
М = ^- lim N~l In Zx(h , К). A.8.4)
Нетрудно представить правдоподобные, хотя и нестрогие аргументы в
пользу того, что намагниченность М ведет себя, как показано на рис. 1.1, и
что должна существовать критическая точка при Н = 0 и некотором поло-
положительном значении Т = Тс.
Для определенности рассмотрим квадратную решетку (хотя представля-
представляемые аргументы применимы к любой многомерной решетке). Правая часть
A.8.2) может быть разложена в ряд по степеням К:
ZN=Bcoshh)N{l +2NKt2
+ NK2[BN- 1) Г4 + 6Г2 + 1] + €(К3)}, A.8.5)
где
t = tanhh. A.8.6)
Подстановка этого ряда в A.8.4) дает
М = tanh h {I + 4 sech2/* [К + C - 7г2) К2 + €(К3)]}. A.8.7)
Все члены этого разложения представляют собой ограниченные анали-
аналитические нечетные функции И. Предполагая, что при достаточно малых А',
т.е. достаточно высоких температурах, ряд сходится, мы приходим к вы-
выводу, что для таких температур М(//, Т) описывается графиком, показан-
показанным на рис. 1.1,в. В частности, эта функция непрерывна при Н = 0 и
М0(Т) =Af(O,T) =0 О-8-8)
при достаточно высокой температуре Т.
С другой стороны, при низких температурах величина К большая,и пра-
правую часть A.8.2) можно разложить в ряд по степеням
и = ехр(-4?). A.8.9)
Ведущий член в этом разложении представляет собой вклад в Z состояния,
в котором все спины направлены вверх (или вниз). Следующий член проис-
происходит от N состояний с одним из спинов, направленным противоположно
всем остальным; следующий за ним — от 2N состояний, в которых два со-
соседних спина перевернуты. Затем идет член, происходящий от состояний, в

30 ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
которых перевернуты либо два не расположенных рядом спина, либо три
соседних, либо четыре спина, образующие квадрат, и т.д. Это дает
- 5) и4 е"
+ бЛГи'е* + М/е4 + Щи5)}
+ 2Nu3 е4Л + W(N - 5) и4 е4А
+ 6Nu* е6л + Nm4 e8A + Щи5)}. A.8.10)
Первый ряд в фигурных скобках представляет собой вклад состояний, в
которых почти все спины направлены вверх, второй ряд — вклад состоя-
состояний, в которых почти все спины направлены вниз. Равенство A.8.10) мож-
можно переписать в виде
iv ) + eW'"'*), A.8.11)
где
+ 2иъ е'4/2 + и\-2\ е'4/2 + 6 e~6/j + ъ~ш)
+ €(и5); A.8.12)
ф(И, К) не зависит от N во всех порядках w-разложения при условии, что N
достаточно велико.
Если И — положительная величина, то первый член в правой части
A.8.11) больше второго. В пределе больших N его вклад в ZN становится
доминирующим; поэтому из A.8.4) следует
= 1 - 2и2 e~2h -
-0(w5), A.8.13)
если И > 0, и спонтанная намагниченность равна
М0(Т) = lim M
= 1-2и2- 8и3 - 34м4 - Щи5). A.8.14)

ГЛАВА 1 !H
• •••ООООФФ
Рис. 1.6. Конфигурация спинов для одномерной модели
Изинга, дающая вклад в следующий за ведущим член
низкотемпературного разложения. Темные кружки обо-
обозначают спины, направленные вверх; светлые круж-
кружки — спины, направленные вниз.
Если эти разложения сходятся при достаточно малых значениях и (т.е.
при достаточно низких температурах), то опять-таки при достаточно ма-
малых и величина Мо будет положительной. Ьспоминая, что М(НУ
Т) — нечетная функция Н, мы заключаем, что при низких температурах
график функции М(Н, Т) имеет вид, показанный на рис. 1,1,о, с разрывом
непрерывности при Н = 0.
Итак, функция М0(Т) тождественно равна нулю для достаточно высо-
высоких температур Г, но строго положительна для достаточно малых Т. При
некоторой промежуточной температуре Тс она должна перейти от нулево-
нулевого к ненулевым значениям, как это показано на рис. 1.3, и в этой точке до-
должна быть неаналитической функцией Т. Таким образом, должна сущест-
существовать некоторая «критическая точка» Н = 0, Т = Гс, в которой термоди-
термодинамические функции становятся неаналитическими, что иллюстрирует
рис. 1.2.
Приведенное выше доказательство не исключает возможности сущест-
существования других сингулярностей внутри полуплоскости (Я, Г), но простей-
простейшая совместимая с ним картина именно та, которая представлена на рис.
1.1 — 1.3.
Некоторые части доказательства, или, точнее, их варианты, могут
быть проведены совершенно строго. Например, еще в 1936 г. Пайерлс [192]
показал, что для достаточно низких температур М0(Т) — положительная
величина (см. также [106], с. 59).
Аналогичное доказательство в случае одномерной модели Изинга не
может быть проведено. Это связано с тем, что следующий за ведущим
член низкотемпературного w-разложения обусловлен состояниями типа по-
показанного на рис. 1.6, где имеется целая цепочка, а не единичный перевер-
перевернутый спин. Число таких состояний равно l/iN(N — 1) вместо Л/, так что
даже до этого порядка ZN не имеет вида A.8.11). Конечно, это согласуется
с тем фактом, что одномерная модель не может иметь фазового перехода
при ненулевой температуре.
1.9. РЕШЕТОЧНЫЙ ГАЗ
Модель Изинга является не только моделью магнетика, но также мо-
моделью жидкости.
Чтобы уяснить себе этот довольно поразительный факт, рассмотрим
жидкость, состоящую из молекул, взаимодействие которых описывается
некоторым парным потенциалом ф(г). Как правило, этот потенциал имеет
твердую сердцевину (или по крайней мере очень сильное отталкивание на
малых расстояниях), потенциальную яму и довольно быстро затухающий

32
ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
-е -
Рис. 1.7. Потенциалы взаимодействия модельной жидкости: а — потенциал Ленард-
Джонса; б — потенциал с прямоугольной ямой.
хвост. Типичным примером является потенциал Ленард-Джонса
ф(г) =
У2 - (го/гN]
A.9Л)
график которого показан на рис. 1.7,а.
Вместо того, чтобы допустить произвольное расположение молекул в
пространстве, введем ограничение, согласно которому центры молекул мо-
могут находиться только в узлах некоторой сетки или решетки. Если сетка
достаточно мелкая, то такое ограничение представляет собой вполне ра-
разумный шаг: на самом деле оно даже необходимо для почти любого чис-
численного расчета.
Поскольку при г — О отталкивание бесконечно велико, центры каких-
либо двух молекул не могут находиться в одном узле. Каждому узлу / по-
поставим в соответствие переменную s,, равную нулю, если узел свободен, и
единице, если он занят. Если имеется N узлов, то любое пространственное
расположение молекул может быть задано набором чисел s = [s,, . . . ,

ПЛАВАЛ 33
Sjs/]. Число молекул в такой конфигурации составляет
п = 5i + . . . + sN, A.9.2)
а полная потенциальная энергия равна
где сумма берется по всем парам узлов решетки (не обязательно соседним),
а фу = Ф(гу) — энергия взаимодействия двух молекул с центрами в узлах /
и У-
Большая статистическая сумма тогда имеет вид
Z = 2 ехр[(л|И - ?)/?Г] , A.9.4)
где м — эффективный химический потенциал (для классических систем
вклад интегрирования по импульсному пространству можно включить в д).
В соответствующих единицах давление равно
P = N'lkT\nZ, A.9.5)
плотность выражается как среднее число молекул на узел, т.е.
р = (n)/N
_дР A -9-6)
v жимаемость — как
1 др
Все производные вычисляются при постоянной температуре.
Потенциал Ленард-Джонса A.9.1) является довольно реалистическим,
н0 качественные особенности фазового перехода жидкость —
газ не должны зависеть от деталей потенциала: достаточно, чтобы
он имел короткодействующее отталкивание и притяжение, описываемое
потенциальной ямой. Таким образом, функция фу должна быть большой и
положительной, когда узлы / и j расположены близко один к другому, от-
отрицательной при умеренных расстояниях и равной нулю, когда узлы распо-
расположены далеко друг от друга. Простейший потенциал, удовлетворяющий
этим условиям, имеет вид

34 ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
ф.. = + оо при i = j,
(\ 9 8)
= — ?, если / и / — ближайшие соседи,
= 0 в остальных случаях.
Это соответствует потенциалу с прямоугольной ямой, показанному на рис.
1.7,6, который, часто применяется в модельных вычислениях.
Условие фц = + оо эквивалентно запрещению двум молекулам одновре-
одновременно занимать один узел решетки. Это свойство потенциала уже было
включено в формулировку задачи, поэтому, если ф^ имеет вид A.9.8), из
A.9.3) следует, что энергия системы равна
Е= -e^LSiSj, A.9.9)
(ч)
где суммирование теперь выполняется только по парам ближайших соседей
в решетке.
Легко показать, что A.9.4) в данном случае сводится к статистической
сумме модели Изинга в поле с взаимодействием только между ближайши-
ближайшими соседями. Заменим переменную si спиновой переменной а; с помощью
соотношения
Oi = 2si-1. A.9.10)
Таким образом, о1¦ = — 1, если узел не заполнен, и oi = +1, если он запо-
заполнен. Если каждый узел имеет q соседей, то имеется ViNq пар ближайших
соседей. Учитывая это и исключая я, ?, sx, . . . , sN с помощью A.9.2),
A.9.4), A.9.9) и A.9.10), получаем
Z = 2 ехр| е 2 OtOj + Bд + eq) 2
19 П)
Сравнивая с A.8.2) и A.8.3), легко увидеть, что, за исключением несу-
несущественного множителя, полученное выражение для Z представляет собой
статистическую сумму для модели Изинга, если положить
/=?/4, Я = Bц + eq)/4. A.9.12)
Используя также A.9.5)—A.9.7), A.7.6), A.7.14) и A.7.18), можно выразить
характеристики решеточного газа через параметры модели Изинга:
?=4/, 0.9.13)
H = 2H-2qJ, d.9.14)
P=-iqJ+H-f, A.9.15)

ГЛАВА 1 35
p=i(l + M), A.9.16)
f?kT = ix. <L917>
Изученное общее поведение модели Изинга можно теперь использовать,
чтобы получить вид уравнения состояния решеточного газа. Чтобы сде-
сделать это, рассмотрим некоторое фиксированное значение Т. Тогда A.9.15)
и A.9.16) позволяют определить Р и р как функции Н. Используя также
A.7.14) и A.7.20), легко показать, что
Ц |g, d.9.18)
так что Р и р являются монотонными функциями Н. Когда значения Н ве-
велики (положительные или отрицательные), то в статистической сумме для
модели Изинга доминирующими являются члены, соответствующие парал-
параллельной ориентации всех спинов, так что
/-* -hqJ- \Щ при#-» ±оо. A.9.19)
Отсюда и из A.7.14), A.9.15) и A.9.16) следует, что
Р-*0, р-»0 при#-»-оо, A.9.20)
Р~2Н, р-»1 при#->+оо. A.9.21)
Так как Р и р — монотонно возрастающие функции Я, то, согласно
A.9.20), они должны быть всюду положительными.
Если Т > Тс, то/ и А/, а следовательно, Р и р являются непрерывными
функциями Н. Таким образом, Р есть монотонно возрастающая функция р
и монотонно убывающая функция объема, приходящегося на одну молеку-
молекулу:
у = р. A.9.22)
Когда v возрастает от 1 до оо, Р уменьшается от оо до 0.
Если Т < Тс, то М будет разрывной функцией Я, как показано на рис.
1.1,а. Поэтому р и v также имеют разрыв (но Р не имеет разрыва).
Замечая также, что коэффициент теплового расширения жидкости
v~l(dv/dT)p обычно положителен (исключение составляет вода между 0 и
4 °С), заключаем, что (Р, v )-изотермы решеточного газа (любой размерно-
размерности больше единицы) имеют общую структуру типа изображенной на рис.
1.8. Это типичные изотермы жидкости с межмолекулярным потенциалом,
имеющим твердую сердцевину.
Точка С на этом рисунке является критической точкой и соответствует
критической точке Н = 0, Т = Тс на рис. 1.2. Так как в этой точке М = 0,
мы получаем из A.9.14) и A.9.16), что критические значения д, о и v для ре-
решеточного газа равны

36
ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
Рис. 1.8. Типичные изотермы (Р, v) простой жидкости с межмолекулярным
потенциалом, включающим твердую сердцевину. Две верхние изотермы относятся к
температуре выше Тс, средняя изотерма критическая (Г = Тс), две нижние отно-
относятся к температурам ниже Тс.
jUc= -2qJ, pc= i, Vc= 2.
При Т = Тс на основании A.1.5) и A.9.16) мы ожидаем, что
vc — v ~ H
Уд
при #-»0.
A.9.23)
A.9.24)
Поскольку разность Р — Рс пропорциональна Н при малых значениях
Я, то, следовательно, вблизи точки С уравнение критической изотермы
имеет вид
P-Pc~{vc-v)*
A.9.25)
В области температур Т > Тс каждая изотерма состоит из трех частей.
Часть, что расположена левее ветви штриховой линии на рис. 1.8, соот-
соответствует довольно высоким плотностям и характеризует жидкое состоя-
состояние; область низких плотностей (правее правой ветви) соответствует газо-
газообразному состоянию; горизонтальные линии между ними соответствуют
двухфазной области, где жидкость может сосуществовать со своим паром.
Штриховая линия называется кривой сосуществования. Она соответствует
линии разреза на рис. 1.2, где Н - О и М - ± М0(Т). Из A.9.16) и A.9.23)
мы видим, что на этой кривой
\р- 0с\ = М0(Т). A.9.26)
Из A.1.3), A.1.4) и A.9.22) тогда следует, что вблизи Тс уравнение кривой
сосуществования на плоскости (v, T) имеет вид

ГЛАВА 1 37
V - VC\~(TC- ТУ. A.9.27)
В окрестности критической точки разность Р - Рс пропорциональна /,
так что, согласно A.9.27), уравнение кривой сосуществования на плоскости
(v, Р)У имеет вид
Pc-P~\v- vc\llfi. A.9.28)
Уравнения A.9.25) и A.9.28) устанавливают физический смысл показате-
показателей д и /3 при описании критической точки в системе жидкость — газ. Что-
Чтобы выяснить смысл показателей а, у и у' в этом случае, заметим сначала,
что М = 0 на полупрямой Н = О, Т > Тс на рис. 1.2. Согласно A.9.16),
эта полупрямая соответствует изохоре v = v с. Из A.7.7)—A.7.9) и A.9.15),
A.1.6), A.9.17) следует
д2Р/дТ2~Га, кт~Г\ A.9.29а)
когда мы приближаемся к точке С сверху вдоль критической изохоры
v = vc.
Отрезок прямой линии Н — О, Т < Тс на рис. 1.2 соответствует кривой
сосуществования на рис. 1.8; поэтому
д2Р/дТ2 ~ (-ty*, kT~ (-0~У, A.9.296)
когда мы приближаемся к точке С по кривой сосуществования и дифферен-
дифференцирование производится вдоль этой кривой.
Определения A.9.29) критических показателей а и а' аналогичны A.7.9)
и страдают тем же недостатком. Если производная дР/дТ не является не-
непрерывной функцией или если д2Р/д Т2 не расходится в точке С, то лучше
использовать аналог выражения A.7.10) и определить один показатель а с
помощью нижеследующей процедуры.
Пусть Р+(Т) — давление при v = vс и Т > То а Р_(Т) — давление при
Т > Тс, когда v определяется кривой сосуществования. Продолжим анали-
аналитически эти функции на комплексную Г-плоскость и определим PS(T) и а
посредством соотношения
Ps(T) = P+(T) -Р-{Т) -tl~\ (К9-30)
Резюмируем результаты этого раздела. Модель Изинга магнетика явля-
является одновременно и моделью решеточного газа; просто в одном случае
мы говорим на языке теории магнетизма (спины, направленные вверх или
вниз), а в другом — на языке молекулярной теории (узлы, занятые или пу-
пустые). Критические показатели X, /3, у, у', а во втором варианте определя-
определяются соотношениями A.9.25) и A.9.28) — A.9.30).
Язык теории магнетизма удобнее при теоретических выводах, так как
отчетливо выявляет симметрию гамильтониана и термодинамических
функций, в особенности соотношение М(-Я) = ~М{И).

38 ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
1.10. УРАВНЕНИЕ ВАН ДЕР ВААЛЬСА
И КЛАССИЧЕСКИЕ ПОКАЗАТЕЛИ
Известны феноменологические уравнения состояния, в частности урав-
уравнение, предложенное ван дер Ваальсом [239] для непрерывной системы
газ — жидкость:
Р = kT/(v - b) - a/v2, A.10.1)
где а и b — константы. Это уравнение справедливо только вне кривой со-
сосуществования, которая определяется с помощью построения Максвелла
([189], с. 376), обеспечивающего непрерывность Рид вдоль любой изотер-
изотермы. Как уже отмечалось в разд. 1.6, уравнение ван дер Ваальса является
точным уравнением состояния модели, решенной в работе [129].
Определения критических показателей A.9.25), A.9.28) — A.9.30) приме-
применимы к любой системе газ — жидкость, а не только к простому решеточ-
решеточному газу, рассмотренному в разд. 1.9. Уравнения типа уравнения ван дер
Ваальса предсказывают, что вблизи Тс критическая изотерма является ку-
кубической кривой, а кривая сосуществования — параболой. Из. A.9.25) и
A.9.28) тогда получаем
5=3, j8=i. A.10.2)
Кроме того, координаты критической точки, согласно уравнению ван
дер Ваальса A.10.1), равны
Tc = 8a/27bk, vc = 3b. A.10.3)
Легко убедиться, что вблизи этой точки кт ~ t~\ так что
у=/ = 1. A.10.4)
Из A.10.1) легко получить, что на критической изохоре
Р - Рс = AatlTlb2, A-Ю.5)
в то время как на кривой сосуществования более сложные вычисления по-
показывают, что
Р - Рс = Da/27b2) [t + 6r2/5 + С(г3)]. A.10.6)
Таким образом, производная д2Р/дТ2 ограничена в точке С, но имеет раз-
разрыв при переходе с критической изохоры на кривую сосуществования.
Определения а и а' с помощью A.9.29) в данном случае не пригодны, но
A.9.30) дает
ог=0. A.Ю.7)

ГЛАВА 1 39
Значения критических показателей A.10.2), A.10.4), A.10.7) называют
классическими. Они удовлетворяют соотношениям A.2.12) и A.2.13) и со-
совпадают со значениями, получаемыми для простой «бесконечномерной»
модели среднего поля и модели на решетке Бете (гл. 3 и 4). Они не соот-
соответствуют точным значениям для модели Изинга с взаимодействием меж-
между ближайшими соседями в случае двух и трех измерений, но, как сейчас
полагают ([90], с. 607), являются правильными для четырех и более изме-
измерений.

ОДНОМЕРНАЯ МОДЕЛЬ
ИЗИНГА
2.1. СВОБОДНАЯ ЭНЕРГИЯ И
НАМАГНИЧЕННОСТЬ
Изинг предложил свою модель в 1925 г. [117] и решил ее для одномерной
системы. Это решение приводится в данной главе частично потому, что
оно представляет собой по существу введение в технику трансфер-матриц,
которая будет использоваться ниже, но также вследствие того интереса,
который представляет любая простая, точно решаемая модель. Одномер-
Одномерная модель не имеет фазового перехода при какой-либо ненулевой темпера-
температуре, но, как будет показано ниже, она имеет критическую точку при
Н = Т = 0, в ней могут быть разумным путем введены критические пока-
показатели и выполняются гипотеза подобия и связанные с ней соотношения.
Рассмотрим модель Изинга, состоящую из N узлов, расположенных
вдоль одной линии и пронумерованных по порядку индексами у = 1,..., N
(рис. 2.1). Тогда энергия этой системы, согласно A.7.2), A.7.3) и A.8.1),
описывается выражением
N N
Е(а) = -jILojOj+x-hILoj. B.1.1)
Предполагается,что за узлом N опять следует узел 1, так что aN + { совпа-
совпадает с ffj в B.1.1). Это эквивалентно соединению двух концов линии так,
чтобы она образовывала круг, или наложению на систему периодических
граничных условий. Условия такого типа часто полезны хотя бы потому,
что обеспечивают эквивалентность узлов и трансляционную инвариант-
инвариантность системы. В частности,
= (а2) = . . . = (oN) , B.1.2)
так что, согласно A.7.12), намагниченность на один узел равна
B.1.3)
12 3 N
Рис. 2.1. Одномерная решетка из N узлов.

ГЛАВА 2 41
где 1 обозначает любой фиксированный узел решетки. Этот результат
справедлив для любой трансляционно-инвариантной системы.
(Из 1.8.2) получаем следующее выражение для статистической суммы:
N N
:2 OjGJ + l + А 2 o\i B.1.4)
7=1 /=1 J
где
K = J/kT, h = H/kT. B.1.5)
Заметим теперь очень существенное обстоятельство: экспонента в B.1.4)
может быть представлена в виде произведения сомножителей, каждый из
которых зависит только от одной пары соседних спинов:
ZN = 2 V(ox , о2) V(a2, оъ) У{оъ, а4). . .
B.1.6)
где
[ ( ] B.1.7)
Это не единственно возможный выбор V: можно было бы добавить
множитель ехр[я(а - о')] (с произвольным коэффициентом а), не изменяя
при этом B.1.6). Но сделанный выбор (при котором hoj делится поровну
между двумя V) обеспечивает выполнение равенства
V(o,&) = V(& ,о), B.1.8)
которое, как мы увидим, является полезным свойством симметрии.
Обратимся теперь к правой части B.1.6) и представим множители
У(о,о ) как элементы матрицы 2x2:
Тогда каждое суммирование по а2, or3,..., oN в B.1.6) можно рассматри-
рассматривать как последовательное умножение матриц, а суммирование по ох — как
операцию взятия следа, так что
ZN = Trace V". B.1.10)
На каждом шаге вычислительной процедуры умножение на матрицу V
соответствует суммированию по конфигурациям еще одного узла решетки.
Матрица V называется трансфер-матрицей. В последующих главах мы
увидим, что трансфер-матрицы могут быть определены для моделей в
двух и более измерениях. При этом уравнение B.1.10) все еще выполняется,
но, к сожалению, матрица V становится очень большой.

42 ОДНОМЕРНАЯ МОДЕЛЬ ИЗИНГА
Пусть Xj, х2 — два собственных вектора матрицы V, a Xj и Х2 — со-
соответствующие собственные значения. Тогда
\xj = kj\j,j = 1,2. B.1.11)
Если Р — матрица 2x2, столбцы которой составлены из компонент
векторов х1э х2, т. е.
Р= (xi,x2), B.1.12)
то из B.1.11) следует
VP = P . B.1.13)
\0 Я2/
Поскольку V — симметричная матрица, можно найти пару ортогональ-
ортогональных, линейно-независимых собственных векторов хр х2. Матрица Р, со-
составленная из компонент такой пары, не сингулярна, т. е. имеет обратную
матрицу Р. Умножение B.1.13) на Р справа дает
Mi о \ .
V = P P. B.1.14)
\0 А2/
После подстановки этого выражения для V в B.1.10) матрицы сокращают-
сокращаются и остается
Mi о \дг
ZN = Trace ( =а?ЧА^. B.1.15)
Пусть Xj — наибольшее из двух собственных значений; -Тогда перепи-
перепишем B.1.15) в виде
N~l In ZN = In kx + N~l In [1 + (kjky)»]. BJ.16)
Так как IX2/Xj I < 1, второй член справа стремится к нулю, когда N — оо.
Таким образом, согласно A.7.6), свободная энергия на один узел при
N — оо стремится к следующему пределу:
= -?F Hm iVMnZA/
N-*oo
= -kTlnk{ B.1.17)
= - kT\n [e^cosh /г + (e2/csinh2 h + e*)*] .
Дефференцируя этот результат по Л и используя A.7.14) и B.1.5), полу-
получаем
QKs'mhh
+ e-»il- BЛЛ8)

ГЛАВА 2 43
Свободная энергия является аналитической функцией И и Т для всех
действительных значений Н и положительных значений Т. Намагничен-
Намагниченность М(Я, Т) также является аналитической функцией Я, и эта зависи-
зависимость описывается графиком типа показанного на рис. 1.1, в. Таким обра-
образом, система не имеет фазового перехода при положительных температу-
температурах.
2.2. КОРРЕЛЯЦИИ
Согласно A.4.3), B.1.1), B.1.7), вероятность найти систему в состоянии
о s {<7j,...,<7N) равна
ZNX V{ox, ъ) V((h , cr3) V(a3, <j4) • • • V(oN, ox). B.2.1)
Таким образом, среднее значение, скажем величины а,^ равно
(охоъ) = Zu1 2 ox V{ox , o2) V(a2, а3) оъ V(o3 ,oA)...V(oN, o{). B.2.2)
а
Это равенство можно переписать в матричной форме. Пусть S обозначает
следующую диагональную матрицу:
/1 0 \
Но -J- B'23)
т. е. S имеет элементы
S{o,&) = od{o,&). B.2.4)
Тогда правая часть B.2.2) может быть представлена в виде
Z*1 Trace SVVSV . . . V , B.2.5)
так что
<Oi<t3> = Zul Trace SV^V^. B.2.6)
Аналогичным образом, если 0 ^ j — /"^ 7V, то
(OiOj) = ZNX Trace SV" S\N+i~j, B.2.7)
(од = ZNX Trace S\N. B.2.8)
Отметим, что трансляционная инвариантность системы ясно видна в
этих соотношениях: (а,) не зависит от /, а (о^р зависит от / и у только че-
через их разность j — i.
Определим число ф посредством равенства
h, 0<ф<-. B.2.9)

44 ОДНОМЕРНАЯ МОДЕЛЬ ИЗИНГА
Тогда путем прямого вычисления собственных векторов V с помощью
B.1.9) и B.1.11) с учетом B.1.12) обнаруживаем, что матрица Р может
быть выбрана ортогональной и представлена в виде
/cos ф - sin ф \
Р= ¦ ^ J- B-2Л0)
Vsin ф cos ф/
Выражения B.2.7), B.2.8) не изменятся, если преобразование B.1.14)
применить одновременно к V и к S, т. е. заменить V, S на
/Ai U
р 1VP =
Vo я2
B.2.11)
/ cos20 -sin20\
Р !SP = J
V-sin20 -cos2(p/
соответственно.
Подставляя эти выражения в B.2.7) и B.2.8) и переходя к пределу
N — оо (при фиксированной разности j — /), получаем
(ал) = cos2 2ф + sin2 2ф (-V 1, B.2.12)
(ai) =cos20. B.2.13)
Второе равенство вместе с B.1.3) дает альтернативный вывод выраже-
выражения для намагниченности М(Н, Т). Результат, разумеется, совпадает с по-
полученным выше результатом B.1.18).
С помощью A.7.21), B.2.12) и B.2.13) теперь можно вычислить корре-
корреляционную фуНКЦИЮ gjjl
gtj = (opj) - {о) (о) = sin2 2ф {l2lh)j~l, B.2.14)
где у ^ /.
Поскольку lX2/Xjl < 1, мы сразу видим, что gy экспоненциально стре-
стремится к нулю, когда разность У - / становится большой, и что корреляци-
корреляционная длина ? может быть представлена (в единицах межузельного рассто-
расстояния) в следующем виде:
§=[1п(А1/А2)]. B-2.15)
2.3. КРИТИЧЕСКОЕ ПОВЕДЕНИЕ ВБЛИЗИ Т = О
Для всех положительных температур Т и действительных полей Н име-
имеем IX2/X j I < 1, но если Н = 0, то
lim (A2/A1) = 1 .
г-»о+

ГЛАВА 2 45
Поэтому корреляционная длина ? становится бесконечной при Н = Т = 0.
Мы уже отмечали в разд. 1.7, что критическая точка может быть определена как
точка, в которой ? = оо, так что в этом смысле Н = 7=0 — действительно
критическая точка одномерной модели Изинга.
Это интересно, так как позволяет провести проверку гипотез подобия,
обсуждавшихся в разд. 1.2. и 1.7. Мы обнаружим при этом, что они под-
подтверждаются.
Гипотеза подобия A.2.1) сформулирована в терминах М, Н и
t = (Т — Тс)/Тс. Но если Тс = 0, то разумно перейти к переменным М,
h = Н/кТ и
t = exp(-2iO = Qxp(-2J/kT). B.3.1)
Тогда h и / определяют отклонения поля и температуры соответственно от
их критических значений.
Гипотеза подобия A.2.1) эквивалентна утверждению, что соотношение
между М,Л и / не изменится при замене их соответственно на Х^М, \^bh и
X/ при любом положительном числе X. Таким образом, A.2.1) можно вы-
выразить иначе (для малых Л и /):
M = h\h\y]-l(t>(t\h\-^d), B.3.2)
где ф(х) — другая функция подобия (скейлинга), связанная с И(х).
В случае одномерной модели Изинга из B.1.18) и B.3.1) следует, что ес-
если I h I < 1, то
М = h/(t2 + h2)k. B.3.3)
Ясно, что М зависит только от t/h\ поэтому гипотеза подобия B.3.2) дей-
действительно выполняется, если
Рд = 1 , д = оо , B.3.4)
ф(х) = (х2+ I)"*. B.3.5)
Соотношения A.2.12) и A.2.13) являются следствиями гипотезы подобия и
потому должны выполняться. Из них и B.3.4) следует
ос= 1,/?=0,у= 1. B-3.6)
Кроме того, если h = 0, мы видим из B.1.9), что собственные значения V
равны
Ai = 2 cosh К, А2 = 2 sinh К, B.3.7)
так что в соответствии с B.3.1)
Ax/A2 = A + Г)/A - 0; B.3.8)
поэтому равенство B.2.15) при / « 1 переходит в
S~Btyl, B.3.9)

46 ОДНОМЕРНАЯ МОДЕЛЬ ИЗИНГА
что имеет вид A.7.25) при
р=1. B.3.10)
В критической точке Xj = X2, так что, согласно B.2.14), корреляционная
функция gtj — константа. Это согласуется с A.7.26), если
Г)=1. B.3.11)
Мы можем теперь использовать эти значения критических показателей
для проверки соотношения A.2.16) и второго из равенств A.2.14). Они в са-
самом деле выполняются.
Другие соотношения *>=*>',/х + *> = 2 — а не могут быть проверены,
так как содержат функции, определяемые для упорядоченного состояния
0< Т < Тс и h = 0. Это состояние не существует в данной модели.
Определение / с помощью B.3.1) является несколько произвольным:
правая часть может быть заменена любой положительной степенью функ-
функции ехр( — 2 К). Результатом этого будет умножение величин 2 — а, у и v
на один и тот же множитель. Ввиду всего этого мы можем только сказать
по поводу критических показателей для одномерной модели Изинга, что
они удовлетворяют следующим соотношениям:
2 - <Х= у= v,
B.3.12)
0=0,6=оо,Ч=1.
Несмотря на то что Тс = 0, эти показатели представляют интерес, так
как их можно сравнивать с критическими показателями модели Изинга в
двух, трех и большем числе измерений.

3
МОДЕЛЬ СРЕДНЕГО ПОЛЯ
3.1 ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
В любой статистикомеханической системе каждая компонента взаимо-
взаимодействует с внешним полем и с соседними компонентами. В модели средне-
среднего поля второе взаимодействие заменяется величиной, усредненной по всем
компонентам.
Рассмотрим модель Изинга с взаимодействием между ближайшими со-
соседями, состоящую из /V спинов, с гамильтонианом, определяемым выра-
выражениями A.7.2), A.7.3) и A.8.1). Если каждый спин а, имеет q соседей, то
полное действующее на него поле равно
Я-ь/1^, C.1.1)
где сумма берется по q соседним узлам j. В модели среднего поля C.1.1)
заменяется на
причем сумма теперь берется по всем N - 1 узлам У, не совпадающим с /.
Это эквивалентно замене гамильтониана на
N
N - 1 (/,/) ' ; i = i
где первая сумма распространяется на все ViN(N — 1) пар (/, j).
Гамильтониан C.1.3), называемый гамильтонианом среднего поля, бу-
будет рассмотрен в этой главе. Как уже отмечалось в разд. 1.6, он в некото-
некотором смысле «бесконечномерный», поскольку каждый спин одинаково взаи-
взаимодействует со всеми остальными. К тому же он обладает нефизическим
свойством: зависимостью силы взаимодействия от числа частиц. Тем не
менее он позволяет получить достаточно разумные термодинамические
свойства.
Для данной конфигурации спинов полная намагниченность равна
N
Л1=2а,-, C.1.4)
и C.1.3) можно переписать (используя равенство oj = 1) в виде

48 МОДЕЛЬ СРЕДНЕГО ПОЛЯ
Е(а) = -\qJ{M2 - N)I{N -1)-HM. C.1.5)
Таким образом, в этой модели Е(о) зависит от о]у ...,<7уу только через
. /Л Это большое упрощение, так как суммирование по конфигурациям спи-
спинов в статистической сумме можно теперь заменить суммированием по
всем возможным значениям У/ с весом, равным числу спиновых конфигура-
конфигураций для каждого значения.
Если г спинов направлено вниз (-1), a TV - г спинов — вверх (+ 1), то,
согласно C.1.4),
M = N-2r. C.1.6)
/ N\
Поскольку имеются I J таких спиновых конфигураций, то из A.7.5)
получаем следующее выражение для статистической суммы:
N
Z=^Cr, C.1.7)
где
- 2гJ - N)/(N - 1) + pH(N - 2r)}, C.1.8)
P=llkT. C.1.9)
Кроме того, для намагниченности на один узел с помощью A.4.4) полу-
получаем
Л'
М = N~l(M) = A - 2rlN) = Z 2A- 2rlN) cr. C.1.10)
r = i)
Свойства функций cOj ^ c^ легче всего установить, рассматривая от-
отношения dr — cr + x/cr. Из C.1.8) имеем
dr = — =^Z^'exp{-2pqJ(N -2т- l)l(N - 1) - 2рН}. C.1.11)
Нас интересует случай больших N. Когда г увеличивается от 0 до
N — 1, правая часть C.1.11) убывает от больших значений (порядка N) до
весьма малых (порядка TV). При условии, что произведение 0qJ не слиш-
слишком велико, это убывание должно быть монотонным. Тогда должно су-
существовать единственное целое число л0, такое, что
dr > 1 при г = О,...,го-1,
dro^ly C-1.12)
dr < 1 при r = ro+l,...,N-l.

ГЛАВА 3 49
Поскольку cr + j = dfr, то сг возрастает при изменении л от 0 до г0,
уменьшается при изменении г от г0 + 1 до N, и, следовательно, сг являет-
является наибольшим значением сг
Когда N и г — большие числа, C.1.11) можно записать в виде
dr = cr + i/cr = 0A - 2rlN) , C.1.13)
где
ф(х) =j^exp[-2l3qJx - 2/SH] C.1.14)
в интервале — 1 < х < 1.
Пусть х0 — решение уравнения
1. C.1.15)
Тогда для больших значений N величина г0 определяется равенством
A;o. C.1.16)
Величина сг> рассматриваемая как функция г, имеет пик при г = г0, ши-
ширина которого пропорциональна Ny\ Хотя эта ширина велика по сравне-
сравнению с единицей, но она мала по сравнению с N. Таким образом, в пределах
ширины этого пика можно заменить 1 — 2r/N в C.1.10) на 1 — 2ro/N. По-
Поскольку значения г за пределами пика дают пренебрежимо малый вклад в
суммы C.1.7) и C.1.10), намагниченность на один узел равна
М = 1 - 2ro/N = х0. C.1.17)
Из C.1.14) и C.1.15) следует
М = tanh[(?/M + Н)/кТ]. C.1.18)
Это уравнение определяет М как функцию Н и Т. Его получили впервые
Брэгг и Вильяме в 1934 г. [63]. Свободную энергию можно теперь вычис-
вычислить либо интегрированием с использованием A.7.14), либо более прямым
способом, замечая, что для больших N в сумме C.1.7) существенны лишь
члены с л, близкими к г0; поэтому
-j3/= lim ATMnZ
N-+oo
C.1.19)
= lim ЛГЧпс*.
N-+ao °
Используя C.1.8), формулу Стирлинга
-ппп + ^ C.1.20)
а также C.1.17) и C.1.18), получаем
-flkT=\\n[4l(l-M2)]-\qJM2lkT. C.1.21)
Это соотношение определяет / как функцию М и Т.

50
МОДЕЛЬ СРЕДНЕГО ПОЛЯ
3.2. ФАЗОВЫЙ ПЕРЕХОД
Согласно C.1.18),
Н = -qJM + ATartanh(M).
C.2.1)
Это соотношение можно использовать для построения графика зависимо-
зависимости Я от М для — 1 < М < 1. Затем график, конечно, можно перевернуть,
чтобы получить зависимость М от Я. Если qJ < кТ, то результирующая
кривая подобна показанной на рис. 1.1, в, т. е. это типичный высокотемпе-
высокотемпературный график, указывающий на отсутствие спонтанной намагничен-
намагниченности.
Но если qJ > kTy то рассматриваемая зависимость выглядит так, как
это показано на рис. 3.1, а. Этот график противоречит физическому смыс-
смыслу, поскольку для достаточно малых значений Я он определяет три воз-
возможных значения М, в то время как, согласно A.7.12) или A.7.14), намаг-
намагниченность М должна быть однозначной функцией Я.
Источником этого противоречия является утверждение, предшествовав-
предшествовавшее C.1.12). Дело в том, что, когда qJ > кТ, правая часть C.1.11) не явля-
является монотонно убывающей функцией гу а ведет себя так, как это пред-
представлено на рис. 3.2.
Если поле Я достаточно мало, то уравнение dr = 1 имеет три решения,
как показано на рис. 3.2. Это означает, что функция сг имеет два максиму-
максимума (рис. 3.3). Вместе с разделяющим их минимумом они соответствуют
трем решениям уравнения C.1.18) для М. Если Н — положительная (отри-
(отрицательная) величина, то левый (правый) пик больше.
Сумма в C.1.7) по-прежнему определяется членами с л, близкими к л0,
где г0 соответствует теперь абсолютному максимуму сг как функции г. По-
Поэтому, если C.1.18) имеет три решения и поле Н положительно, мы дол-
должны выбрать решение, отвечающее наименьшему значению л0, т. е. наи-
МА
а
м
-/-¦
Рис. 3.1. Зависимость М от Я при Т = 0,94 Тс. а — все решения C.1.18);
б — правильная зависимость, полученная отбрасыванием ложных решений.

ГЛАВА 3
51
N г
Рис. 3.2. Зависимость dr от г при Т = 0,94Тс, (ЗН = 0,006 и большом значении N.
большему значению М. Обратное верно, если поле Н отрицательно. По-
Поступая таким образом, мы получим вместо многозначного графика на рис.
3.1, а однозначную зависимость, изображенную на рис. 3.1, б. Она подоб-
подобна типичной низкотемпературной кривой М(Я), показанной на рис. 1.1. В
частности, имеется спонтанная намагниченность Мо, определяемая усло-
условием
Мо = tanh(qJM0/kT) , Мо > 0 ,
C.2.2)
если qJ > kT.
0
N
^мс. 3.3. Зависимость сг от г при Т = 0,947С, (ЗН = 0,006 и N = 100. По мере уве-
увеличения N высота пика растет, и он становится острее. Два других экстремума со-
соответствуют ложным решениям C.1.18).

52 МОДЕЛЬ СРЕДНЕГО ПОЛЯ
Таким образом, модель среднего поля имеет фазовый переход для тем-
температур ниже температуры Кюри
Tc = qJ/k. C.2.3)
3.3. СВОЙСТВА ПРИ Н = О И КРИТИЧЕСКИЕ
ПОКАЗАТЕЛИ
Спонтанная намагниченность и /3
Положим
Г = (Г-ГС)/ГС; C.3.1)
тогда с помощью C.2.3) уравнение C.2.2) можно переписать в виде
Мо = A + t) artanh Мо. C.3.2)
Для значений Г, меньших, но близких к Гс, спонтанная намагничен-
намагниченность MQ мала, но не равна нулю, так что artanh Mo приблизительно равен
Мо + Mq/З. Решая результирующее уравнение для Мо, получаем
м„ = (-зо»{1 +0@}. (з.з.з)
Таким образом, величина Мо пропорциональна (— t)Vl. Поэтому, со-
согласно A.1.4), существует критический показатель
j8=J. C.3.4)
Свободная энергия и а
Пусть Н — 0. Если Т > Тс, то М — 0 и, согласно C.1.21), свободная
энергия имеет простой вид:
-f/kT =1п2. C.3.5)
Если Г < 7С, то М — Мо. Из C.1.21) для малых Мо следует
-//ЛГ = In 2 4- ?МоA - qJIkT)
C.3.6)
+ Mg/4 + O(Af§).
Используя C.2.3), C.3.1) и C.3.3), получаем для малых отрицательных
значений / следующее выражение для свободной энергии:
-f/kT = In 2 + 3r2/4 + 0(Г3). C.3.7)
Из A.7.7), A.7.8), C.3.5) и C.3.7) следует, что свободная энергия и внут-

ГЛАВА 3 53
ренняя энергия непрерывны при Т = Тс, а теплоемкость испытывает скач-
скачкообразный разрыв. Определение критических показателей а и а' с по-
помощью A.7.9) теряет смысл, но альтернативное определение A.7.10) дает
ог=0. C.3.8)
Восприимчивость и 7, у'
Фиксируем Т и дифференцируем C.2.1) по Н. Подставляя A.7.17), C.2.3)
и C.3.1), получаем выражение для восприимчивости
/ = A - M2)/[qJ(t + М2)]. C.3.9)
Пусть теперь Н — 0. Если Т > Тс, то М — 0, что дает
/=(?Л)- C.3.10а)
Если Т < Гс, то М - Мо. С помощью приближенного соотношения C.3.3)
получаем тогда, что вблизи Тс
X~{-2qJtyx. C.3.106)
Таким образом, при Тс восприимчивость в нулевом поле расходится как
f1. Тогда в соответствии с A.1.6) и A.1.7) критические показатели у и у'
равны
y=yf = 1. (З.з.п)
3.4. КРИТИЧЕСКОЕ УРАВНЕНИЕ СОСТОЯНИЯ
Используя C.2.3) и C.3.1), перепишем точное уравнение состояния в виде
Н1кТс = -М + A + г) artanhM. C.4.1)
Вблизи критической точки величина М мала. Разлагая гиперболический
арктангенс в ряд Тейлора и пренебрегая членами порядка /М3 или М5, при-
приведем C.4.1) к виду
Я//сГс-М3D + гМ). C.4.2)
Сравнивая этот результат с A.2.1), мы видим, что гипотеза подобия в
самом деле подтверждается для этой модели при
hs(x) = J + х , C.4.3)
/?=i 6=3. C.4.4)
Это согласуется с C.3.4), и легко убедиться, что соотношения A.2.12) и
A.2.13) выполняются. В самом деле, так и должно быть, поскольку они яв-
являются следствием гипотезы подобия.

54 МОДЕЛЬ СРЕДНЕГО ПОЛЯ
Значения критических показателей C.3.4), C.3.8), C.3.11) и C.4.4) такие
же, как для жидкости ван дер Ваальса, обсуждавшейся в разд. 1.10, т. е.
они имеют классические значения.
Так как каждый спин взаимодействует в равной степени со всеми
остальными, корреляции не зависят от расстояния; кроме того, две физиче-
физически оазделенные базы не могут сосуществовать в данной модели. Таким
образом, критические показатели v, ч\ и /х не могут быть определены.
3.5. МОДЕЛЬ СРЕДНЕГО ПОЛЯ ДЛЯ РЕШЕТОЧНОГО
ГАЗА
Рассматривая спин «вниз» как пустой узел, а спин «вверх» как узел, за-
заполненный частицей, мы сведем рассматриваемую модель к модели реше-
решеточного газа. Подставляя A.9.13) — A.9.16) в C.2.1) и C.1.21), получим
следующие выражения для химического потенциала /х и давления Р:
ц = -qep + kT\n[p/(l - р)], C.5.1)
Р = -кТ\пA - р) - iqep2. C.5.2)
Здесь р — плотность, т. е. среднее число частиц на узел. Она должна ле-
лежать в пределах 0 < р < 1.
Равенство C.5.2) представляет собой уравнение состояния решеточного
газа в модели среднего поля. Сравнивая его с A.9.31) и учитывая, что
v = р, мы видим, что оно очень похоже на уравнение ван дер Ваальса.
Оба уравнения приводятся к виду
Р = кТф(р)-ар2, C.5.3)
где а — константа, а функция ф(р) не зависит от температуры Т. В самом
деле, существуют решаемые модели, которые имеют уравнение состояния
в точности вандерваальсова типа [129].

МОДЕЛЬ ИЗИНГА
НА РЕШЕТКЕ БЕТЕ
4.1 РЕШЕТКА БЕТЕ
Еще одна простая модель, которая может быть решена точно, — это мо-
модель Изинга (или любая модель с взаимодействием между ближайшими со-
соседями) на решетке Бете. Так же как и модель среднего поля, она эквива-
эквивалентна приближенному рассмотрению некоторой модели, допустим, на
квадратной или кубической решетке [53]. Но она может быть определена
как точно решаемая модель, и это как раз то, что мы собираемся сделать.
Рассмотрим граф, который строится следующим образом: выбираем
произвольно центральную точку 0, добавляем еще q точек и каждую из них
соединяем с центральной точкой. Назовем эту совокупность q точек «пер-
«первой оболочкой». Последующие оболочки строим, беря точку на оболочке г
и соединяя ее с q — 1 новыми точками. Проделаем эту операцию со всеми
точками оболочки г и назовем всю совокупность новых точек оболочкой
г + 1.
Действуя указанным образом, построим оболочки 2, 3, ..., п. В резуль-
результате получим граф, подобный показанному на рис. 4.1. В оболочке г имеет-
имеется q(q — If ~ l точек, а общее число точек графа равно
q[(q - 1)" - \]l{q - 2).
D.1.1)
Точки на оболочке п будем называть граничными точками. Они исклю-
исключительны в том смысле, что каждая из них имеет только одного соседа, в
то время как все остальные точки (внутренние точки) имеют q соседей каж-
каждая.
Рис. 4.1. Дерево Кэйли (при q = 3 и п = 4),
разделенное в центральном узле 0 на три
подграфа. Они идентичны, но на данном
рисунке узлы верхнего подграфа обозна-
обозначены темными кружками. Точка 0 является
корневой точкой каждого подграфа. На
верхнем подграфе указан узел 1, примыкаю-
примыкающий к узлу 0. В точке 0 спин равен а0, а в
точке 1 спин равен sx.

56 МОДЕЛЬ ИЗИНГА НА РЕШЕТКЕ БЕТЕ
Такой граф не содержит замкнутых путей и известен под названием «де-
«дерево Кейли». Для наших целей его можно рассматривать как регулярную
«решетку» с координационным числом q (т.е. каждый узел имеет q сосе-
соседей) при условииу что можно не учитывать граничных узлов.
Здесь возникает проблема, поскольку обычно отношение числа гранич-
граничных узлов к числу внутренних узлов решетки становится малым в термоди-
термодинамическом пределе большой системы. В данном случае это не так, по-
поскольку оба числа растут экспоненциально как (q - \)п. Чтобы преодо-
преодолеть эту трудность, мы рассмотрим только локальные свойства узлов, рас-
расположенных глубоко внутри графа (т. е. бесконечно далеко от границы в
пределе п — оо). Такие узлы должны быть эквивалентны друг другу. Каж-
Каждый из них характеризуется координационным числом qy и все они в сово-
совокупности образуют решетку Бете. (Это различие между деревом Кейли и
решеткой Бете терминологически полезно, хотя и не всегда подчеркивает-
подчеркивается. Я благодарен профессору Нейглу за то, что он обратил мое внимание
на это обстоятельство и указал на соответствующую работу [67].)
Иначе говоря, если мы построим модель Изинга на полном дереве Кей-
Кейли, то статистическая сумма Z будет включать вклады как от внутренних
узлов, так и от узлов, расположенных на границе. Этот последний вклад
не является пренебрежимо малым даже в термодинамическом пределе.
Если рассматривать полную статистическую сумму, то мы приходим к
«модели Изинга на дереве Кейли». Эта задача была решена [77, 172, 203], и
оказалось, что она имеет весьма необычные свойства. Тем не менее мы не
будем рассматривать эту задачу. Вместо этого мы рассмотрим только
вклад в Z, происходящий от узлов, лежащих глубоко внутри графа, т. е. от
решетки Бете.
Как-то мотивировать сделанный выбор можно, рассматривая разложе-
разложения в ряд статистической суммы. Если произвести низкотемпературное
разложение для любой регулярной решетки подобно тому, как это сделано
в разд. 1.8, то для вычисления членов до второго порядка включительно
нужно знать только такие характеристики решетки, как число узлов и ко-
координационное число. В третьем порядке уже потребуется число треуголь-
треугольников на решетке, в четвертом — число тетраэдров (т. е. кластеров, состо-
состоящих из четырех связанных узлов) и других высокосвязных четырехточеч-
четырехточечных графов и т. д. Интересен простой случай, когда замкнутые цепочки
узлов отсутствуют и поэтому нет треугольников, тетраэдров и т. п. Тогда
мы получаем модель Изинга на решетке Бете, как мы ее здесь определили.
4.2. РАЗМЕРНОСТЬ
Рассмотрим произвольную регулярную решетку. Пусть тх = q — число
ближайших соседей на узел, т2 — число соседей, следующих за ближайши-
ближайшими, /г?з — число узлов в третьей координационной сфере и т. д. Тогда сум-
сумма сп = 1 + тх + т2 + ... + тп представляет собой число узлов, находя-
находящихся в пределах п шагов от заданного узла. Для гиперкубических решеток
легко показать, что

Р(а) = ехр К X G,G, + h ^ а{\. D.3.2)
ГЛАВА 4 57
lim (In с„)/1п n = d , D-2.1)
П-+ oo
где d — размерность решетки. Соотношение D.2.1) выполняется также для
всех регулярных двух- и трехмерных решеток и может рассматриваться как
определение размерности d.
Вернемся теперь к рассмотрению решетки Бете. В этом случае сп опре-
определяется выражением D.1.1). Подстановка его в D.2.1) дает d = оо, так
что в этом смысле решетка Бете является «бесконечномерной».
4.3. РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ
ДЛЯ НАМАГНИЧЕННОСТИ ЦЕНТРАЛЬНОЙ ТОЧКИ
Рассмотрим модель Изинга на полном дереве Кейли (ниже мы отбро-
отбросим члены, связанные с граничными узлами, и возвратимся к решетке
Бете). Статистическая сумма дается выражением A.8.2), т. е.
где
Первое суммирование в D.3.2) выполняется по всем линиям графа,
второе — по всем узлам. Функцию Р(а) можно рассматривать как ненорми-
ненормированное распределение вероятностей; в частности, если а0 — спин в цент-
центральном узле 0, то локальная намагниченность там равна
М = (G0> = 2 o0P(a)/Z. D.3.3)
о
На рис. 4.1. ясно видно, что если разрезать граф в точке 0, то он распа-
распадется на q идентичных, не связанных друг с другом частей (подграфов).
Каждая из них представляет собой дерево с корневой точкой (точка 0). В
результате выражение D.3.2) распадается на множители:
ч
Р(а) = ехр(йао) П Ш^оИ), D-3-4)
где 5^ обозначает все спины (кроме а0) на у~м подграфе и
Qn(oo\s) = explK^StSj + KsiOb + h 2sA D.3.5)
L ('"'/) ' J
(Sj — спин на узле / подграфа, не совпадающем с корневой точкой, которая
имеет спин а0). Узел 1 примыкает к 0, как это показано на верхнем подгра-
подграфе рис. 4.1. Первая сумма в D.3.5) берется по всем линиям подграфа, кро-
кроме линии @,1); вторая — по всем узлам, кроме 0. Индекс п отмечает тот

58 МОДЕЛЬ ИЗИНГА НА РЕШЕТКЕ БЕТЕ
факт, что подграф имеет п оболочек, т. е. путь от корневой до любой гра-
граничной точки состоит из п шагов.
Далее, если разрезать верхний подграф на рис. 4.1 в точке 1, примыка-
примыкающей к точке 0, то он также распадается на q частей, из которых
одна — «ствол» @, 1), а остальные — совершенно идентичные ветви. Каж-
Каждая из этих ветвей представляет собой подграф, аналогичный исходному,
но имеющий только п — 1 оболочек. Таким образом,
Qn(oo\s) = ехрС^сто*! + hsx) П Qn-iis^), D.3.6)
где № обозначает все спины (кроме s{) нау-й ветви подграфа.
Соотношения D.3.4) и D.3.6) позволяют легко вычислить М. Пусть
?*(<*) = 2 &.(c%|j). D.3.7)
5
Тогда из D.3.1) и D.3.4) следует
Z = 2 ехр(/ш0) [8пЫ]я • D.3.8)
Аналогичным образом из D.3.3) и D.3.4) получаем
М = Z-1 2 oQ ехр(/ш0) [gn(oo))q ¦ <4-3-9>
Пусть
D.3.10)
Тогда, согласно D.3.8) и D.3.9),
Таким образом, М известно, если известно хп. Чтобы получить хп, мы
просуммируем D.3.6) по всем спинам s, т. е. по s{ и fi\ что дает с учетом
D.3.7)
gn(ob) = 2 expiKooSi + hsi) [gn-i(si)]q~\ D.3.12)
Вспоминая, что а0 и s{ — единичные спиновые переменные со значения-
значениями -hi и - 1, мы выполняем суммирование в D.3.12) для а0 = + 1 или — 1,
делим одно на другое и, используя D.3.10), получаем
xn=y(xn-i), D.3.13)
где функция у(х) определяется следующим выражением:
е"*-^-1]. D.3.14)

ГЛАВА 4
59
Уравнение D.3.13) является рекуррентным соотношением между хп и
хп _ х- Очевидно, что
поэтому D.3.13) определяет хп, а D.3.11) определяет М.
4.4. ПРЕДЕЛ ПРИ п - оо
Нижеследующее рассмотрение ограничено ферромагнитным случаем
К > 0. Тогда при изменении х от 0 до оо функция у(х) монотонно возра-
возрастает от значения ехр( — 2К) до ехрBК).
Рекуррентное соотношение D.3.13) может быть представлено графиче-
графически путем одновременного построения графиков у = у(х) и у = х. Пусть
Рп _ j — точка (хп _ \У(хп _ j)) на плоскости (х, у). Чтобы найти точку Рп,
проведем горизонтальную прямую через точку Рп _ х до пересечения с ли-
линией у = х в точке Qn. Затем проведем вертикальную прямую через точку
Qn. Ее пересечение с кривой у = у(х) дает точку Рп.
Возможны две ситуации: либо кривая у = у(х) пересекает линию у = х
один раз, либо имеется три пересечения (рис. 4.2). В первом случае точка
Рп всегда будет монотонно приближаться к точке пересечения А при
п — оо, как показано на рис. 4.2,а. Таким образом, как и следовало ожи-
ожидать, хп и М стремятся к некоторому пределу, когда число п становится
большим. Это значение М представляет собой локальную намагниченность
узла, расположенного глубоко внутри дерева Кейли, т.е. намагниченность
на узел в решетке Бете.
а 6
Рис. 4.2. Типичные графики функции у(х), описываемые соотношением D.3.14) с
z = exp(-2tf); а — кривая пересекает прямую у = х один раз в точке Л. Показаны
две типичные последовательности точек Рп = (хп, у(хп)): одна имеет начальную точ-
точку справа от А, другая [Ро\ РХ\Р{ ,...)— слева. Все такие последовательности
сходятся к предельной точке А; б — имеется три точки пересечения А, В, С. Любая
последовательность*[PJ движется в направлениях, указанных стрелками, никогда не
переходя А, В и С. Таким образом, А и С являются стабильными предельными
точками, В — нестабильная изолированная точка.

60 МОДЕЛЬ ИЗИНГА НА РЕШЕТКЕ БЕТЕ
Если имеется три точки пересечения, то две внешние (А и С на. рис.
4.2,б)являются стабильными предельными точками соотношения D.3.13),
в то время как расположенная между ними точка В нестабильна. Если Ро
лежит слева (справа) от В, то Рп стремится к А(С). Таким образом, снова
Рп стремится к пределу, определяющему намагниченность М решетки Бете.
Нам необходимо какое-то достаточно простое правило выбора одной из
двух стабильных точек А и С. Граничная ситуация возникает, когда Ро сов-
совпадает с точкой В, т. е. когда х = 1 является решением уравнения
х = у(х). Согласно D.3.14), это имеет место в том и только в том случае,
когда /? = 0. Если h > 0, то Ро лежит слева от В и Рп стремится к А. На-
Наоборот, если И < 0, то Рп стремится к С.
Суммируя предшествующее обсуждение, мы заключаем, что при п — оо
намагниченность в соответствии с D.3.11) описывается выражением
D.4.1)
где переменная х является решением уравнения
х = у(х). D.4.2)
Если оно имеет три решения, то при h > 0 выбирается наименьшее из
них, а при h < 0 — наибольшее.
Эти уравнения можно переписать в более привычной форме, введя обо-
обозначения
z = e~2K, // = eA, ju^ju**. D.4.3)
Тогда с помощью D,3.14) уравнение D.4.2) приводится к виду
*='(z + /Xi)/(l + /XiZ). D.4.4)
Из D.4.3), D.4.4) и D.4.1) следует
\хх1\х = [(г + №)/A + fiiz)]q~l, D.4.5а)
М = A - 1л\)/A + ia\ + 2piz) . D.4.56)
Первое из выражений D.4.5) определяет д1э второе — намагниченность
М. Такие же выражения получаются в результате применения аппроксима-
аппроксимации Бете к решетке с координационным числом q (см. [74], с. 251 — 254).
4.5. НАМАГНИЧЕННОСТЬ КАК ФУНКЦИЯ Н
Предположим теперь, что Г, а следовательно, и К фиксированы, и рас-
рассмотрим зависимость х и М от h = Н/кТ. Используя D.3.14), можно запи-
записать уравнение D.4.2) в следующем виде:

ГЛАВА 4
61
Рис. 4.3. Типичный график зависи-
зависимости h от х при Г < Тс.
\\
Все хп положительны, поэтому положительно и их предельное значение
х. Чтобы правая часть D.5.1) была положительна, значение х должно ле-
лежать в интервале
е~2К < х < е2К. D.5.2)
Ясно, что D.5.1) определяет h как функцию х при фиксированном К.
(Эту функцию, конечно, не следует отождествлять с функцией скейлинга
hs(x) в разд. 1.2.) Логарифмически дифференцируя D.5.1), получаем
2sinh2A:
D.5.3)
В интервале D.5.2) правая часть D.5.3) имеет максимум при х = 1. Если
этот максимум отрицателен, т.е. если К < Кс, где
¦ 2)] , D.5.4)
то h монотонно убывает от оо до — оо, когда х возрастает от ехр(- 2К) до
ехрBА'). Поэтому для заданного действительного значения И выражение
D.5.1) имеет одно и только одно действительное и положительное решение
для ху и х является аналитической функцией h в интервале — оо < И < оо.
С другой стороны, если К > Кс, то производная dh/dx положительна
для значений дг, достаточно близких к единице. Из D.5.1) следует, что
h = О, когда х = 1, так что функция h(x) имеет график типа показанного
на рис. 4.3. Поэтому при достаточно малых И уравнение D.5.1) имеет три
решения для х. Как следует из обсуждения, проведенного в разд. 4.4, при
h > О предельная точка последовательности, определяемой D.3.13), соот-
соответствует наименьшему решению для х. Если h < 0, то она соответствует
наибольшему решению.
Рассматривая поведение х при уменьшении Л от оо через нуль до - оо,
мы убеждаемся с помощью рис. 4.3, что х является аналитической функци-
функцией h везде, за исключением точки И = 0, где имеет место скачок от наи-
наименьшего к наибольшему решению.

62 МОДЕЛЬ ИЗИНГА НА РЕШЕТКЕ БЕТЕ
Во всех случаях х — убывающая функция Л, удовлетворяющая соотно-
соотношению
x(-h) = l/x(h). D.5.5)
Из D.4.1) следует, что М является нечетной функцией Л, которая моно-
монотонно возрастает от — 1 до 1 при увеличении А от — оо до + оо. Эта функ-
функция аналитическая, если К < Кс. Если К > Кс, то она аналитическая везде,
кроме точки h = О, где испытывает скачкообразный разрыв.
Это типичное поведение ферромагнетика, описанное в разд. 1.1. Таким
образом, модель Изинга на решетке Бете соответствует ферромагнетику с
критической точкой Я = О, Т = Тс> причем
J/kTc = h\n[q/(q-2)]. D.5.6)
4.6. СВОБОДНАЯ ЭНЕРГИЯ
Полная свободная энергия дерева Кейли равна
F=-kT\nZ, D.6.1)
где Z определяется формулами D.3.1) и D.3.2). Дифференцирование этих
равенств по Я — ИКТ дает
-^=2М,, D.6.2)
где суммирование выполняется по всем узлам / и Mi = <a,> представляет
собой локальную намагниченность узла /. Каждое слагаемое Mt является
функцией Я и, следовательно. И при заданной температуре Г. Чтобы под-
подчеркнуть это, мы иногда будем писать А/,(Л).
Если поле Н велико и положительно, то доминирующий вклад в сумму
D.3.1) вносит состояние, в котором все спины направлены вверх, так что в
этом пределе
F/kT=-KNe-hN, D.6.3)
где Ne — число линий, а N — число узлов. Кроме того, в этом пределе
(о;) = 1 при / = 1, ..., N.
Мы можем теперь проинтегрировать D.6.2) по Я, используя при этом
D.6.3), чтобы определить константу интегрирования. В результате полу-
получим
FlkT = -KNe -hN+2j\ [Mt(hf) - 1] d/i'. <4-6-4)
i Jh
Если qt — число узлов, примыкающих к узлу /, то ? , <?, = 2Ne, и D.6.4)
можно выразить как F = V ,//, где
filkT = -iKq, -h+Г [M,(h') - 1] dft'. D.6.5)
Jh

ГЛАВА 4 63
Каждое значение fi можно рассматривать как свободную энергию узла /. В
случае однородной решетки все fi равны обычной свободной энергии /, и,
дифференцируя D.6.5), мы возвращаемся к обычному соотношению
A.7.14).
Как уже отмечалось выше, трудность, связанная с деревом кейли, со-
состоит в том, что оно неоднородно, т. е. имеет значительное число гранич-
граничных или соседних с границей узлов, свойства которых отличаются от
свойств внутренних узлов. Но все узлы, расположенные глубоко внутри
графа, имеют одинаковую локальную намагниченность М и потому одну и
ту же локальную свободную энергию/, определяемую выражением D.6.5).
Таким образом, эта свободная энергия является свободной энергией моде-
модели Изинга на решетке Бете. Она вычисляется путем приравнивания qt = q,
Mj = М в D.6.5) и использования равенств D.5.1), D.4.1), определяющих
зависимость х и М от И.
Замечая, что х — монотонная дифференцируемая функция h при И > О,
мы производим замену переменной интегрирования в D.6.5), переходя от
hf к *' = x(h'). Опуская индекс / и используя равенство z = ехр( — 2К), по-
получаем
flkT = -\Kq -h-\ [M{x') - 1] — dxf D.6.6)
при условии, что h > О (или К < Кс).
После подстановки выражения D.5.1) для ехрBЛ) в D.4.1) подынте-
подынтегральное выражение в D.6.6) в результате небольших преобразований и с
учетом D.5.3) приводится к виду
1 — 7Y1 1 + y'~ — 7x' 7
Это выражение легко интегрируется. Исключая И с помощью D.5.1), полу-
получаем
f/kT= -\
+ Щг2 + 1 - z(x + jT1)] + \{q - 2) 1ф +x~l- 2z). D'6'8)
Обращение знака h эквивалентно замене х на обратную величину, что не
меняет D.6.8). Так как свободная энергия / должна быть четной функцией
К отсюда следует, что формула D.6.8) верна при всех действительных зна-
значениях И. Вместе с уравнением D.5.1) для х она определяет свободную
энергию на один узел в модели Изинга на решетке Бете.
4.7. РЕЗУЛЬТАТЫ ДЛЯ НИЗКОТЕМПЕРАТУРНОЙ
ОБЛАСТИ В ОТСУТСТВИЕ ПОЛЯ
При рассмотрении любой ферромагнитной модели Изинга при Н = 0 и
Т < Тс возникает известная трудность. В этом случае преимущественное
направление спинов (вверх или вниз) неопределенно. Только если гранич-

64 МОДЕЛЬ ИЗИНГА НА РЕШЕТКЕ БЕТЕ
ные спины фиксированы в направлении вверх, то и все спины с большей ве-
вероятностью будут иметь направление вверх, чем вниз. В некотором смысле
«термодинамический предел» в этом случае не существует, поскольку объ-
объемные свойства зависят от граничных условий.
Сказанное особенно очевидно для рассматриваемой модели: если
Н = 0, то из D.3.13) — D.3.15) сразу следует, что хп = 1 для любого зна-
значения п. Если Г < Гс, то это означает, что все точки Рп = (хп, уп) совпа-
совпадают с точкой В на рис. 4.2, б. Но.это нестабильная изолированная точка
уравнения D.3.13): если х$ не равно единице, а лишь немного меньше, то
последовательность (Рп) будет сходиться не к В, а к стабильной предельной
точке А.
Имеются по крайней мере две возможности обхода этого затруднения:
одна из них состоит в том, чтобы положить Н = 0 и фиксировать все гра-
граничные спины в положении вверх; в другом варианте берем Н > О, перехо-
переходим к пределу п — оо и затем убираем поле: Н — 0+ . В обоих случаях пос-
последовательность ( Рп) будет сходиться к А, и предельное значение х в со-
соответствии с D.4.2) и D.3.14) будет равно наименьшему положительному
решению уравнения
Если Т < Тс, то это значение х меньше единицы. Тогда выражения для
спонтанной намагниченности М и свободной энергии/, согласно D.4.1) и
D.6.8), имеют вид
1 -xq
Интересно сравнить эти результаты с тем, что получается для двумер-
двумерной модели Изинга. Это будет сделано в разд. 11.8.
4.8. КРИТИЧЕСКОЕ ПОВЕДЕНИЕ
Положим х = ехр( —2s). Тогда D.5.1) преобразуется к виду
h = -(q- 1M + i ln[sinh(J: + s)/sinh(J: - s)], D.8.1)
откуда ясно, что h — нечетная функция s. Разлагая в ряд Тейлора, получаем
h = [coth K-q + l]s + i coth К cosech2 К s3 + D.8.2)
Критическое значение К определяется соотношением D.5.4), или иначе
coth Кс = q — 1. Полагая, как обычно,
t = (T-Tc)ITc D-8.3)

ГЛАВА 4 65
и учитывая, что К = J/kT, получаем для малых значений t
coth K-q+l = q(q- 2)Kct + G(t2). D.8.4)
Подстановка этого результата в D.8.2) вместе с h = Н/кТ дает (для ма-
малых / « s)
Н1кТс = q(q - 2) {Kcts + Jfo - l)s3 + O(ft, tt3,*5)}. D.8.5)
Выражение D.4.1) для намагниченности М приводится к виду
М = tanh(A + qs). D.8.6)
Из D.8.5) следует, что h значительно меньше 5, которая тоже мала, поэто-
поэтому М * qs, или
M3). D.8.7)
Подставляя этот результат в D.8.5) и пренебрегая членами порядка /2М,
гМъ или Л/5, получаем
Н1кТс = М%(Ш2), D.8.8)
где
ВД = J(9 - 2)х \n[q/(q - 2)] + (q-l)(q- 2)/Cq2). D.8.9)
Сравнивая A.2.1) с D.8.8), мы видим, что гипотеза подобия подтверж-
подтверждается для этой модели, если hs(x) считать функцией скейлинга. Эта функ-
функция линейна, а критические показатели /3 и д имеют значения
0=4, 6=3. D.8.10)
Таким образом, все критические показатели 0, 6, а, а', 7, 7' должны
иметь те же значения, что и в модели среднего поля, т. е. «классические»
(значения разд. 3.3).
Все полученные выше результаты весьма похожи на результаты для мо-
модели среднего поля, найденные в гл. 3. (На самом деле они совпадают в
пределе q — оо; qK — конечная величина.) Но в действительности модель
на решетке Бете в значительно большей степени заслуживает доверия, чем
модель среднего поля, поскольку в данном случае взаимодействия не зави-
зависят от размера системы, и каждый спин взаимодействует только со своими
ближайшими соседями.
4.9. АНИЗОТРОПНАЯ МОДЕЛЬ
Ключевые уравнения D.3.14), D.4.2), D.4.1), D.6.8) предшествующего
вывода можно суммировать (используя первые два уравнения для исключе-
исключения z из последнего) следующим образом:
z = ехр(-2*:) = (х - iixq-l)l{\ - yxq), D.9.1)
М = A - fJXq)/(l + fjxq) , D.9.2)
-flkT =h + hqK+ ln(l + рос*) + \q ln[(l - д2^~2)/A - fi2x2q)].
D.9.3)

66 МОДЕЛЬ ИЗИНГА НА РЕШЕТКЕ БЕТЕ
Линии решетки Бете можно сгруппировать в классы 1, ..., q так, чтобы
каждый узел лежал на одной линии каждого класса. Тогда разным классам
линий можно присвоить различные значения коэффициента взаимодействия
К. Пусть Кг — значение этого коэффициента для класса г (где г = 1, ..., q)\
тогда мы приходим к анизотропной модели, которая также может быть
решена описанными выше методами.
Уравнения D.9.1) — D.9.3) в этой более общей формулировке имеют
вид
zr = ехр(-2Яг) = (хг - tXrl)l(l - 0 , г = 1 ,. . . , q , D.9.4а)
fi = exp(-2/t) = t/(xi ...xq), D.9.46)
Af = A - f)/(l + 0 D-9-5)
-flkT =h + i(Kx + ... +Kq) + ln(l + t) + ? 2 In ——-f-. D.9.6)
r= 1 1 i
Эти уравнения определяют Ми/ как функции Кх, ..., Кд9 h\ параметры
лгр ...,хд, t вводятся с помощью D.9.4). В критической точке И = 0, а
*! ,...,л:^, t пренебрежимо мало отличаются от единицы. Из D.9.4) тогда
следует
exp(-2A'i) + • • • + ехр(-2^) = q - 2. D.9.7)
(Вывод этого результата см. в A1.8.37)— A1.8.42).)

5
СФЕРИЧЕСКАЯ МОДЕЛЬ
5.1. ФОРМУЛИРОВКА МОДЕЛИ
В 1952 г. Берлин и Кац [51] получили решение еще одной модели
ферромагнетика — так называемой сферической модели. Она сходна с мо-
моделью Изинга, описанной в разд. 1.8. Рассматривается пространственная
решетка -/(например, простая кубическая решетка), содержащая N узлов.
Каждому узлу j из ^f ставится в соответствие спин oj, который взаимо-
взаимодействует со своими соседями и с внешним полем. Но вместо того чтобы
иметь значения только +1 или — 1, каждый спин <jj может теперь прини-
принимать любые действительные значения с одним ограничением:
N
^aj = N. E.1.1)
7 = 1
В случае однородной системы это ограничение обеспечивает равенство еди-
единице среднего квадрата любого спина, как это имеет место в обычной мо-
модели Изинга.
Статистическая сумма также определяется выражением A.8.2), но сум-
суммирование по о заменяется интегрированием с учетом условия E.1.1):
ZN= I ... I doi. . . dovexp К 2 opi + h 2 о)\д\N - 2 of .
Первое суммирование в E.1.2) выполняется по всем связям (/, О между
соседними узлами ^ две другие суммы берутся по всем узлам. Как обыч-
обычно, К = J/kT, h = H/kT.
Берлин и Кац рассматривали такую формулировку как аппроксимацию
обычной модели Изинга. Они утверждали, что в модели Изинга а-
суммирование можно рассматривать как суммирование по всем углам TV-
мерного гиперкуба в ст-пространстве. В сферической модели это суммирова-
суммирование заменяется интегрированием по поверхности гиперсферы, проходящей
через все эти узлы.
Это соображение вполне разумно с математической точки зрения, но
все же условие E.1.1) противоречит физическому смыслу, так как устанав-
устанавливает одинаковую связь или взаимодействие между всеми спинами незави-
независимо от того, как далеко один от другого они расположены в решетке -/.
К счастью, Стэнли [211] показал, что сферическая модель являетсягчаст-
йым предельным случаем другой модели (п-векторной модели) с взаимо-

68 СФЕРИЧЕСКАЯ МОДЕЛЬ
действием только между ближайшими соседями. Эта эквивалентность
впоследствии была строго доказана [127, 190]. Тем самым высказанные вы-
выше возражения снимаются, и репутация сферической модели как физически
приемлемой модели, имеющей критическую точку, восстанавливается.
О сферической модели было написано много работ (см. [124] и приве-
приведенные там ссылки), отражающих различные ее аспекты. Дело в том, что
это одна из немногих (если не единственная) моделей ферромагнетика, для
которой можно получить точное решение в присутствии поля и которая ха-
характеризуется неклассическим критическим поведением.
В этой главе мы не будем пытаться рассмотреть все стороны этой мо-
модели, а наметим вывод уравнения состояния и обсудим критическое поведе-
поведение термодинамических функций.
5.2. СВОБОДНАЯ ЭНЕРГИЯ
Приступая к вычислению E.1.2), заметим, что результат не изменится,
если в подынтегральное выражение ввести дополнительный множитель
E.2.1)
поскольку дельта-функция обеспечивает его равенство единице. Воспользу-
Воспользуемся тождеством
Г00
д(х) = Bл:) exp(wjc) ds, E.2.2)
J — OO
чтобы получить
ZN = Bл) 1 I ... I dGi... daN I ds exp К
+ ft 2 a, + (a + is)N - (a + is) 2 <JJ\.
E.2.3)
Аргумент экспоненты в E.2.3) представляет собой сумму квадратичной
и линейной форм от переменных о1, ..., oN. Для удобства обращения с ни-
ними полезно ввести матричные обозначения.
Пусть а представляет собой TV-мерный вектор с компонентами
ctj, ..., oN, а V — симметричная матрица N х N, такая, что
crT\cr = 22 OjVjiOi = (a + is) 2 o] - К 2 o,ot. E.2.4)
i i i (/.О
Наконец, пусть Л является TV-мерным вектором, все компоненты которого
равны И. Тогда E.2.3) можно записать в виде
Гоо /*оо /*оо
ZN = Bл)-1 ... do- 6s exp[-o-rVo- + hT<r + (a + is)N].
J—oo J — oo J — oo
E.2.5)

ГЛАВА 5 6?
Выберем произвольную постоянную а достаточно большой, чтобы все
собственные значения V имели положительную действительную часть. После
этого (и только после этого) можно поменять порядок интегрирования по о
и 5. Интегрирование по о может быть выполнено с помощью замены пере-
переменных
t=o--iVh E.2.6)
и последующего вращения осей координат в пространстве (tx, ..., tN), приво-
приводящего V к диагональному виду. Это дает
ZN = \nw~l Г ds [det V]"*exp[(e + is)N + h^V'^M]. E.2.7)
J-00
Матрица V зависит от 5 и от структуры решетки, на которой располо-
расположены спины. Пусть -zf является ^/-мерной гиперкубической решеткой, зак-
заключенной в ящик, каждая сторона которого равна L периодам решетки.
Тогда
N = Ld. E.2.8)
Наложим периодические граничные условия. Тогда V — циклическая
матрица, и в соответствии с E.2.4) ее собственные значения могут быть
вычислены с помощью следующего выражения:
А(й>ь . . . , cod) = а + is - K(cos щ + . . . + cos (od), E.2.9)
где каждая переменная wy может принимать любое из значений 0, 2тг/Ь,
4*/L, ..., 2tt(L - 1)/L.
Детерминант матрицы равен произведению ее собственных значений, так
что
In det V = 2 ... 2 In k((ou ...,(od). ...
аз\ aid p.Z.lUj
В термодинамическом пределе L велико, и суммирование в E.2.10) перехо-
переходит в интегрирование. Используя E.2.8) и E.2.9), получаем
E.
E.
2.11)
.2.12)
-cos a)d].
E
.2.13)
где
z = {а + is - Kd)IK ,
... do>i. . . d(odln[z + d-
o Jo
Кроме того, поскольку V — циклическая матрица, h является ее соб-
собственным вектором, соответствующим минимальному собственному значе-
значению а + is - Kd = Kz. Таким образом,
h^h = (Kz)lhTh = Nh2/Kz . E.2.14)
Заменяя переменную интегрирования s на z и используя E.2.11) и

70 СФЕРИЧЕСКАЯ МОДЕЛЬ
E.2.14), приводим равенство E.2.7) к виду
ZN = (K/2m) (л/К)*" Г + " dz exp[N<p(z)], E.2.15)
Jc~i<x>
где
Kd- ig(z) + h2/4Kz E.2.16)
и с = (а - Kd)/K. Из E.2.9) очевидно, что все собственные значения V
имеют положительную действительную часть только в том случае, если
а > Kd; поэтому число с должно быть положительным. Функция ф(г) ана-
аналитическая при Re(z) > 0, так что правая часть E.2.15) одинакова для всех
положительных значений с.
В пределе больших значений N интеграл E.2.15) можно вычислить ме-
методом скорейшего спуска [68]. Рассмотрим сначала </>(z) в области действи-
действительных и положительных z. При условии что К > 0 и h Ф 0, имеем
ф(г) — +оо при z —• 0 или при z —• <». Таким образом, в этом интервале
функция </>(z) должна иметь минимум при некотором положительном зна-
значении z0 переменной z. Далее из E.2.16) и E.2.13) легко усмотреть, что
ф" (z) > 0, так что имеется только один такой минимум.
Выберем произвольную постоянную с равной z0. Тогда вдоль пути ин-
интегрирования в E.2.15) </>(z) имеет максимум при z = z0. В пределе боль-
больших значений N этот максимум дает доминирующий вклад в интеграл, так
что
-flkT = ^lim AT1 In ZN = \ \rv{nlK) + 0(zo). E.2.17)
Здесь/ — как обычно, свободная энергия на один узел. Параметр z0, конеч-
конечно, определяется условием ф'(z0) = 0, т. е. с учетом E.2.16)
К - h2/4Kz20 = hg'(zo). E.2.18)
Имеется одно и только одно положительное решение для z0, поэтому
E.2.16) — E.2.18) определяют / как функцию К и h при условии К > 0 и
И Ф 0.
5.3. УРАВНЕНИЕ СОСТОЯНИЯ И ВНУТРЕННЯЯ
ЭНЕРГИЯ
Между параметром z0 и намагниченностью существует простая связь.
Чтобы ее установить, фиксируем К и дифференцируем E.2.17) по Л, ис-
используя E.2.16). Учитывая, что переменная z0 сама по себе зависит от Л,
получаем
-.±A\=_2±_+ф>{2^ E.3.1)
dh \кТ) 2Kz0 9 К 0) dh
ием ф'(z0) = 0. Поэтому
7.14) и A.8.3) приводится
М = h/2Kz0 = H/2Jzo , E.3.2)
Но z0 определяется условием ф'(z0) = 0. Поэтому уравнение E.3.1) упро-
упрощается и с помощью A.7.14) и A.8.3) приводится к виду

ГЛАВА 5 71
где М — намагниченность на один узел. Мы можем теперь исключить z0 из
E.2.18) и E.3.2). Используя определения К и И A.8.3), получаем
2/A - М2) = kTg\HI2JM). E.3.3)
Это и есть точное уравнение состояния (т. е. соотношение между М, Н
и Г) для сферической модели.
Согласно A.7.7), внутренняя энергия на один узел вычисляется как
(f/T), E.3.4)
где дифференцирование выполняется при фиксированных значениях У и Я.
Из A.8.3), E.2.16) и E.2.17) тогда следует
и = \кТ - J(z0 + d)- H2/4Jz0 + кТ2ф'B0) (dzo/дТ). E.3.5)
Снова замечаем, что Ф'^о) = О- Используя E.3.2), чтобы исключить z0,
получаем
u = ikT-Jd-
Это точное соотношение между энергией и намагниченностью.
5.4. ФУНКЦИЯ g'(z)
Уравнение состояния E.3.3) содержит функцию gf(z). Ее можно полу-
получить дифференцированием E.2.13), но результат представляет собой до-
довольно громоздкий многомерный интеграл. Полезно упростить его следу-
следующим образом.
Дифференцируем E.2.13) и используем формулу
к'1= Гехр(-Аг)с1г, E.4.1)
Jo
чтобы записать результат в виде
Пл Пл Г *
g'(z) = Bn)~d I . . . I do>i. . . da>d I dt x
j° Jo j° E.4.2)
x exp{ - t[z + d - cos o)\ - . . . - cos a)d].
При условии Re(z) > 0 интеграл сходится, и порядок интегрирования
можно менять. Тогда интегрирование по coj, ..., wd можно выполнить, ис-
используя формулу
J0(it) = Bл)-1 | exp(r cos со) dco , E.4.3)
где У0(л:) — обычная функция Бесселя [68J. Это дает
g'(z) = Г ехр[ - t(z + d)] [Mit)]ddt. E.4.4)
JQ

72 СФЕРИЧЕСКАЯ МОДЕЛЬ
Выражение для g' (z) E.4.4) удобно при рассмотрении зависимости тер-
термодинамических функций от размерности d решетки Л. В действительности
теперь не обязательно ограничиваться только целыми значениями d: допу-
допустимы любые положительные значения.
Эта концепция непрерывно изменяющейся размерности весьма распро-
распространена в современной статистической механике [90, 254]. Она может
быть очень полезной при обсуждении зависимости критических показате-
показателей от d, как мы увидим в разд. 5.6.
Чтобы обсудить поведение g'(z), необходимо рассмотреть сходимость
интеграла в E.4.4). Для этого воспользуемся асимптотическим соотноше-
соотношением
h{it) = Bлг)'*е'[1 + ©(Г1)], E.4.5)
справедливым при больших t. С его помощью находим, что интеграл
E.4.4) сходится, если Re(z) > 0, так что g' (z) — аналитическая функция в
правой полуплоскости. В частности, она аналитична для действительных
положительных значений z и, монотонно убывая, стремится к нулю при
г — оо.
Ниже мы увидим, что критические свойства зависят от поведения g' (z)
при малых положительных значениях z. Если z = 0, то из E.4.5) следует,
что интеграл в E.4.4) сходится при d > 2, но расходится при d < 2:
g'@) = оо при 0 < d ^ 2 ,
E.4.6)
< оо при d>2.
При d > 2 нам понадобится главная часть разности g'@) — g'(z) в об-
области малых z. Чтобы найти ее, продифференцируем g'(z), а затем приме-
применим рассуждения, аналогичные предшествующим. Это дает
g"@) = оо
E.4.7)
< оо при d > 4.
Если d < 4, то главную часть g"(z) при малых z легко получить, отбра-
отбрасывая члены порядка t~x в E.4.5) и подставляя в E.4.4):
g
"{z) - - Bл)'ы I 1Х~Ы е~Г2 dr - - Bя)-*ГB - Ы) гы~2. E.4.8а)
При d = 4 несколько более тонкие вычисления приводят к следующему
результату:
g"(z)--Bл)-2 In z. E.4.86)
Определим (положительный) коэффициент Ad посредством соотноше-
соотношений
Ad = Bл)"w (id - I) ГB - W), 2 < d < 4,
d = 4, E.4.9)
d>4.

ГЛАВА 5
73
Тогда из E.4.7) и E.4.8) следует, что для малых z
E.4.10)
d>4.
5.5. СУЩЕСТВОВАНИЕ КРИТИЧЕСКОЙ ТОЧКИ ПРИ
d > 2
Предположим, что Г, а следовательно, и К фиксированы. С помощью
E.3.2) и A.8.3) функцию М(Н) можно получить, исходя из функции zo(h).
Чтобы понять поведение этих функций, построим зависимости обеих ча-
частей уравнения E.2.18) от z0 (или точнее от z) для неотрицательных z. Ти-
Типичные графики приведены на рис. 5.1.
Пусть Р — точка пересечения двух кривых на графике. Тогда ее z-
координата является решением z0 уравнения E.2.18). При условии что
h Ф 0, z0 тоже не равно нулю и плавно меняется при изменении Л; в действи-
действительности Zq — четная аналитическая функция Л. Поэтому М будет нечетной
аналитической функцией Я, если Н Ф 0.
Предположим теперь, что И2 уменьшается, стремясь к нулю. График ле-
левой части уравнения E.2.18) превращается в ступенчатую кривую ОКА на
рис. 5.1. Таким образом, точка Р движется влево, ее предельным положе-
положением будет точка пересечения ОКА с кривой l/ig'(z). Следует рассмотреть
два случая в зависимости от того, лежит ли предельная точка Р на гори-
горизонтальной линии КА (рис. 5.1, а) или на вертикальной линии ОК
(рис. 5.1, б).
а о
Рис. 5.1. Типичные зависимости левой A) и правой B) частей уравнения E.2.18) от z
(Zq заменено на z). Точка пересечения Р соответствует решению уравнения z = z0.

74 СФЕРИЧЕСКАЯ МОДЕЛЬ
Определим Кс, Тс посредством соотношения
E.5.1)
Тогда первый случай имеет место при Т > Тс, а второй — при Т < Тс.
Случай Т > Тс.
Допустим, что Т > Тс, т. е. К < Кс = Vig'@), как на рис. 5.1,а. Когда
И2 — О, Р — Л, так что в соответствии с E.2.18) z0 стремится к ненулевому
значению w, определяемому равенством
ig'(w)=K. E-5.2)
Для достаточно малых И член h2/4Kzl в E.2.18) можно рассматривать
как возмущение, и, решая уравнение итерациями, получаем z0 как ненуле-
ненулевую четную аналитическую функцию И. Поэтому М, согласно E.3.2) и
A.8.3), будет нечетной аналитической функцией Я при Я = 0, и ее график
должен быть подобен изображенному на рис. 1.1, в. Нет ни спонтанной на-
намагниченности, ни фазового перехода в точке И = 0.
Если d < 2, то g'@) и Кс бесконечно велики, поэтому К всегда меньше
Кс. Таким образом, сферическая модель не имеет фазового перехода при
d < 2.
Случай Т < Тс.
Допустим теперь, что d > 2, так что Кс — конечная величина и
К > Кс, т. е. Т < Тс. Тогда кривые E.2.18) принимают вид, изображен-
изображенный на рис. 5.1, б. Когда И2 — 0, точка Р стремится к точке @, Кс), а
z0 — к нулю. Более того, правая часть E.2.18) стремится к Кс, так что
лс)у. E.5.3)
Из E.3.2) и A.8.3) следует
lim М = sgn (Я) Мо , E.5.4)
где Мо определяется выражением
МО = A-77ГС)*. E.5.5)
Таким образом, в этом случае Л/(Я) испытывает скачкообразный раз-
разрыв при переходе через Я = 0, как на рис. 1.1, а. Имеется ненулевая спон-
спонтанная намагниченность Л/о, определяемая замечательно простой точной
формулой E.5.5).
Таким образом, при d > 2 сферическая модель проявляет типично фер-
ферромагнитное поведение, описанное в разд. 1.1. Имеется точка Кюри (т. е.
критическая точка) при Я = О, Т = Тс, где Тс определяется равенством
E.5.1).

ГЛАВА 5 75
5.6. СВОЙСТВА В ОТСУТСТВИЕ
ВНЕШНЕГО ПОЛЯ: ПОКАЗАТЕЛИ а, 0, 7, у'
ВНУТРЕННЯЯ ЭНЕРГИЯ И а
Пусть Н — 0 в E.3.6). Если Т < Тс, то М стремится к ненулевому зна-
значению Мо, так что
Jd при Т<ТС. E.6.1а)
Если Т > Гс, тоМ-Ои, согласно E.3.2), Н/М — 2/w, где w определяет-
определяется соотношением E.5.2). Таким образом,
u = u+ = hkT-Jd-Jw. E.6.16)
Ясно, что низкотемпературная функция и(Т) E.6.1а) является аналити-
аналитической в Тс, поэтому определение A.7.9) неприменимо, и мы должны ис-
использовать A.7.10), чтобы определить а. Пусть сингулярная часть внутрен-
внутренней энергии us. Пусть сингулярная часть внутренней энергии us определяет-
определяется выражением
и,(Г) = и+(Г) -и-(Т). E.6.2)
Как ив A.1.3), положим
t = (T- TC)ITC. E.6.3)
Тогда для малых / из A.7.10) следует
Us(T)~-t1-". E.6.4)
Это соотношение определяет а.
Подставим теперь E.6.1) в E.6.2) (принимая Т > Тс). Это дает
us(T) = -Jw. E.6.5)
Из E.4.10), E.5.1) и E.5.2) следует, что w обращается в нуль, когда / - 0,
по следующему асимптотическому закону:
w~t2/{d~2\ 2<d<4,
~t/\n(t~l), d = 4, E.6.6)
~t, d>4.
Таким образом, при d ± 4 соотношение E.6.4) выполняется для
a=-D-d)/(d-2), 2<d<4,
E.0./)
= 0, d > 4 .
Спонтанная намагниченность и C
Спонтанная намагниченность вычисляется по формуле E.5.5). Сравни-
Сравнивая этот точный результат с A.1.4), получаем
P=i. E.6.8)

76 СФЕРИЧЕСКАЯ МОДЕЛЬ
Восприимчивость И), )'
Восприимчивость х определяется с помощью A.1.2). Дифференцируя
E.3.3) по Я и подставляя E.3.2), получаем
X'1 = Uzo ~ 8JKM2/g"(z0). E.6.9)
Пусть Я стремится к нулю. Тогда если Г> Гс, тоМ стремится к ну-
нулю, a z0 к w, что дает
X~l = 2Jw. E.6.10)
Из E.6.6) следует, что х неограниченно растет, когда Т — Тс сверху.
При условии, что d Ф 4, асимптотическое поведение восприимчивости опи-
описывается степенным законом A.1.6), где
2), 2d4,
h E.6.11)
= 1, d>A.
С другой стороны, если Я — 0 при некотором (фиксированном) значе-
значении Г < Тс, то z0 — 0. Согласно E.4.7), величина g"@) неограниченна, ес-
если d < 4, так что из E.6.9) следует
Х->оо приЯ->0. E.6.12)
Этот результат качественно отличается от того, что дают классические
модели среднего поля и на решетке Бете. Когда d < 4, восприимчивость
при Н = 0 бесконечно велика при всех температурах ниже Тс. Обычное
определение A.1.7) критического показателя у' теряет смысл.
Если d > 4, то g"@) — конечная величина и E.6.9) дает
X-l=-8JKMl/gf@). E.6.13)
Поэтому для малых / восприимчивость х пропорциональна MJ, т. е., со-
согласно E.5.5), (—ГI- Таким образом, выполняется степенной закон A.1.7)
при
у' = 1, d>4. E.6.14)
5.7. КРИТИЧЕСКОЕ УРАВНЕНИЕ СОСТОЯНИЯ
С помощью E.5.1) и E.6.3) точное уравнение состояния можно написать
в виде
g'@) - g'(H/2JM) = 2Г(М2 + t)/kT. E.7.1)
Если Hut малы, то малы и обе части уравнения E.7.1). При этом Т в
правой части можно заменить на Гс, а левую часть аппроксимировать по-
посредством E.4.10). Разрешая результирующее уравнение относительно Я,
получаем

ГЛАВА_5 77
+ t)/Ad]2*d-2), 2<d<4,
~ DJKJA4)M(M2 + t)/ln[(M2 + tyl], d=A, E 7.2)
i) M(M2 + t), d>4.
Величины J, Kc, Ad являются константами, так что критическое уравне-
уравнение состояния имеет вид A.2.1), где Д = Vi (в согласии с E.6.8)) и
-2), 2<d<4,
= 3, d>4. '5Л-3)
Используя E.6.11) и пренебрегая постоянными множителями, получаем
функцию скейлинга ЛД*) в виде
при условии, что й Ф 4.
Таким образом, гипотеза подобия подтверждается, а следовательно,
справедливы также соотношения A.2.12) и A.2.13). Это действительно так,
что с очевидностью следует из E.7.3) и результатов предыдущего раздела,
но с оговоркой» что при d < 4 величина у' не существует.
Если d < 4, то критические показатели в большинстве своем зависят от
d, но для d > 4 все они принимают постоянные классические значения.
Возможно, это является наиболее интересным результатом рассмотрения
сферической модели, так как предполагается, что тот же самый вывод, но
с другими значениями критических показателей при d < 4 справедлив для
обычной модели Изинга с взаимодействием между ближайшими соседями
[90].

6
ДУАЛЬНОСТЬ И
ПРЕОБРАЗОВАНИЕ ЗВЕЗДА —
ТРЕУГОЛЬНИК ПЛОСКИХ
МОДЕЛЕЙ ИЗИНГА
6.1. ОБЩИЕ ЗАМЕЧАНИЯ ОТНОСИТЕЛЬНО
ДВУМЕРНЫХ МОДЕЛЕЙ
В этой и остальных главах книги рассматривается несколько моделей типа
Изинга, для которых были получены точные решения в двумерном случае.
Как было отмечено в разд. 1.6, заслуживает сожаления, что они только
двумерные и что решения получены лишь в отсутствие внешнего поля. Не-
Несмотря на это, они содержат существенные предпосылки, оправдывающие
использование их в качестве «физической» модели магнетика или жидко-
жидкости, а именно ненулевые короткодействующие взаимодействия и наличие
критической точки. Поэтому они могут быть использованы для исследова-
исследования физической природы (особенно в критической области) реальных си-
систем.
В частности, двумерные точно решаемые модели представляют боль-
большую ценность для проверки общих теорий и предположений, таких, как ги-
гипотезы подобия и универсальности. Например, первое доказательство уни-
универсальности было получено Онсагером в 1944 г. [184] в результате реше-
решения модели Изинга на квадратной решетке. Онсагер предположил, что кон-
константы взаимодействия У и У' в горизонтальном и вертикальном направле-
направлениях различны, но его решение показало, что для температур Г, близких к
Тс, теплоемкость расходится как In \T — Тс\ независимо от величины от-
отношения J' /J. Доказательства универсальности накапливались в течение
последующих 25 лет. Потребовалось еще одно точное решение, а именно
решение восьмивершинной модели [25], чтобы стало ясно, что имеются ис-
исключения из правила универсальности.
6.2. СООТНОШЕНИЕ ДУАЛЬНОСТИ
ДЛЯ МОДЕЛИ ИЗИНГА
НА КВАДРАТНОЙ РЕШЕТКЕ
За три года до того, как Онсагер получил решение для модели на квад-
рятной решетке, Крамере и Ванье [152] определили ее критическую темпе-
температуру. Их доказательство может быть сведено к следующим простым
рассуждениям.
Рассмотрим модель Изинга на квадратной решетке У, показанной на
рис. 6.1. В каждом узле имеется спин а, с двумя возможными значениями:
+ 1 или -1. Два соседних спина а, и oj дают член -JojOj гамильтониана,
если они являются соседями по горизонтали, и член — J'o{Oj, если они сосе-

ГЛАВА 6
79
Рис. 6.1. Квадратная решетка У (тем-
(темные кружки и сплошные линии) и ее
дуальная решетка Уо (светлые круж-
кружки и штриховые линии).
1
• > ,
• 1 '
л 1 ,
• 1 '
1
1
—<
1
>—
U
<
i '
1
-f-
1
ГГ",

—<
4
(
>--
-9—
i
—(
--C
—<
i ! -
—(
>
ди по вертикали (У и У — некоторые фиксированные значения энергии).
Если нет внешнего поля, то гамильтониан представляет собой просто сум-
сумму указанных членов, по одному от каждой пары ближайших соседей ре-
решетки У. Согласно A.4.1), для решетки из N узлов аналог выражения
A.8.2) для статистической суммы имеет вид
= Z exp
К 2 Ot
L ('"'/)
+ L 2 otok
О'.*)
J
F.2.1)
где первая сумма в скобках берется по всем горизонтальным связям (/, j), a
вторая — по всем вертикальным связям (/, к); внешнее суммирование вы-
выполняется по всем конфигурациям спинов, и
= JlkBT, L=J'lkBT
F.2.2)
(кв — постоянная Больцмана, / — температура).
Чтобы определить критическую температуру, замечаем, что ZN можно
представить графически двумя различными, но сходными по форме спосо-
способами.
«Низкотемпературное» графическое представление
Для заданного набора значений спинов (спиновой «конфигурации») пусть
г — число вертикальных пар соседних узлов, имеющих разные спины, а
s — число аналогично определяемых горизонтальных пар. Пусть
М — общее число вертикальных связей в У, и допустим, что J имеет оди-
одинаковое число вертикальных и горизонтальных рядов, так что М одновре-
одновременно и число горизонтальных связей. Тогда имеется М — г вертикальных
пар соседей с одинаковыми спинами и М — s таких же горизонтальных
пар; выражение под знаком суммы в F.2.1) принимает вид
exp[K(M - 25) 4- ЦМ - 2г)].
10.2.3)
В частности, оно зависит только от числа пар соседних узлов с разными
спинами.
В двумерных решеточных моделях полезно понятие дуальной решетки:
на базе любой плоской решетки У можно построить еще одну решетку, по-
помещая точки в центры ячеек У и соединяя между собой точки в примыкаю-

80
ДУАЛЬНОСТЬ И ПРЕОБРАЗОВАНИЕ ЗВЕЗДА — ТРЕУГОЛЬНИК
Рис. 6.2. Конфигурация спинов в ячейках
квадратной решетки. Показаны много-
многоугольники, разделяющие спины двух
типов.
щих (т.е. имеющих общую границу) ячейках. Эти точки и соединяющие
их линии являются узлами и связями дуальной решетки Уо.
Решетка SD, дуальная по отношению к квадратной решетке -4 тоже
квадратная; она также показана на рис. 6.1. Эта решетка сдвинута относи-
относительно ~/ на полупериод в обоих направлениях.
Вместо того чтобы считать спины расположенными в узлах решетки -^,
мы можем рассматривать их как находящиеся в центрах ячеек решетки ~/D.
Для заданной спиновой конфигурации мы можем поставить в соответствие
каждой паре соседних узлов с разными спинами линию решетки ,/D следу-
следующим образом: если два соседних спина различны, проводим линию ре-
решетки JD между ними, если же они одинаковы, то не делаем этого. Выпо-
Выполним эту операцию для всех пар ближайших соседей.
Это порождает совокупность г горизонтальных и s вертикальных линий
на^р. В каждом узле должно сходиться четное число линий, поскольку
число последовательных изменений спина при обходе узла по четырем
окружающим его ячейкам должно быть четным. Поэтому все линии соеди-
соединяются, образуя многоугольники, как показано на рис. 6.2.
Эти многоугольники делят плоскость на домены со спинами «вверх» и
домены со спинами «вниз», как это видно на рис. 6.2. Для любой такой
конфигурации многоугольников имеются только две соответствующие ей
спиновые конфигурации, переходящие одна в другую при изменении знаков
всех спинов.
С помощью F.2.3) выражение F.2.1) для ZN может быть представлено
в следующем эквивалентном виде:
ZN = 2 ехр[М(К + L)] S exp(-2Lr - 2Ks),
F.2.4)
где суммирование выполняется по всем конфигурациям многоугольников
на yD, т. е. по всем возможным комбинациям линий с четным числом ли-
линий, сходящихся в каждом узле. Число горизонтальных и вертикальных
линий равно г и s соответственно.
Выражение F.2.4) полезно при вычислении низкотемпературных разло-
разложений, поскольку тогда К и L велики и доминирует член ряда с г = s = 0,

ГЛАВА 6 81
т. е. соответствующий полному отсутствию линий. Поэтому такое пред-
представление удобно называть «низкотемпературным», имея, однако, в виду,
что оно является точным для всех температур.
«Высокотемпературное» графическое представление.
Другбе представление ZN можно получить, замечая, что так как произ-
произведение OjOj может иметь только два значения (+1 или — 1), то
exp[KoiOJ\ = cosh К + sinh К ор,. F.2.5)
Используя это тождество и его аналог, получаемый заменой К на L, равен-
равенство F.2.1) можно переписать в виде
ZN = (cosh A: cosh L)M 2 П A + vOiOj) Ц A + wa{ok), F.2.6)
° Р.Л (i,*)
где
v = tanh K, w = tanh L F.2.7)
и первое произведение берется по всем М горизонтальным связям решетки
-4 а второе — по всем М вертикальным связям.
Представим теперь все выражение под знаком суммы в F.2.6) также в
виде суммы. Поскольку имеется всего 2М множителей (по одному для каж-
каждой связи), каждый из которых включает два слагаемых, получается сумма
22М членов. Каждый член в этой сумме может быть представлен графиче-
графически следующим образом: проводим линию вдоль связи (/, у), если из соот-
соответствующего множителя выбирается слагаемое vojOj или wojOj', не прово-
проводим такой линии, если выбирается слагаемое 1; выполняем эту операцию
для всех связей решетки -/:
Таким образом, получаем соответствие один к одному между членами
суммы и конфигурациями линий решетки _^ Каждый член суммы имеет
вид
fof . . . , F.2.8)
где r{s) — общее число горизонтальных (вертикальных) линий в соответст-
соответствующей конфигурации, а пх — число линий, оканчивающихся в узле /.
Просуммируем теперь F.2.8) по ох, о2, ..., oN. Поскольку а, = ±1, ре-
результат не равен нулю в том случае, если все пх, п2 ,..., nN четные; в этом
случае он равен vrws2?.
Классифицируя такие слагаемые по соответствующим конфигурациям
линий, перепишем F.2.6) в виде
ZN = 2N(cosh К cosh L)M X v'w5, F.2.9)
p
где суммирование производится по всем конфигурациям на решетке с чет-
четным числом линий, сходящихся в каждом узле, т. е. по конфигурациям
многоугольников на ^f.

82 ДУАЛЬНОСТЬ И ПРЕОБРАЗОВАНИЕ ЗВЕЗДА — ТРЕУГОЛЬНИК
Дуальность
Пусть квТф — свободная энергия на один узел, т.е., согласно A.7.6),
-\р= lim N~l\nZN. F.2.10)
Как следует из F.2.1), функция ф зависит от К и L, так что мы можем за-
записать ее в виде ф(К, L).
Суммирование в F.2.4) и F.2.9) сходно, но не полностью идентично,
поскольку в первом случае производится по конфигурациям многоугольни-
многоугольников на ~/D, а во втором — по конфигурациям многоугольников на У. Для
квадратных решеток конечного размера <JD и -/различаются на границе.
Но в термодинамическом пределе это различие не влияет на свободную
энергию. Кроме того, в этом пределе M/N = 1, так что F.2.4), F.2.9) и
F.2.10) дают
- хр(К, L) = К + L + Ф (eL, e~2K) = F.2.11)
= ln[2cosh К cosh L] + Ф(у, н>), F.2.12)
где
Ф(у,н>)= lim N~lln\^vrws\. F.2.13)
ЛГ_юо I p J
Заменяя К, L в F.2.12) на A'*, L*, которые удовлетворяют соотношени-
соотношениям
tanh К* = e~2L , tanh L* = е*, F.2.14а)
и сравнивая с F.2.11), мы видим, что функция Ф исключается и
гр(К* ,L*) = K + L + \p(K,L)- ln[2coshК* coshL*]. F.2.146)
Если К и L велики, то К* и L* малы. Таким образом, соотношение
F.2.14) связывает свободные энергии при низкой и высокой температурах.
Оно называется соотношением дуальности и может быть записано в более
симметричной форме:
sinh 2K* sinh 2L = 1, sinh 2L* sinh 2АГ = 1 ,
F.2.15)
гр(К* ,L*) = tp(K,L)+i In(sinh2# sinh2L).
которая ясно показывает, что это соотношение взаимности.
Чтобы определить критическую точку, рассмотрим сначала изотропный
случай, когда J = У , так что К = L и К* = L*. В критической точке сво-
свободная энергия — неаналитическая функция, поэтому ф — также неанали-
неаналитическая функция Т и, следовательно, К. Допустим, что это происходит
при некотором значении Кс переменной К; тогда из F.2.15) следует, что,
когда К* = Кс, ф также должна быть неаналитической функцией. Вообще

ГЛАВА 6
83
Рис. 6.3. Дуальность квадратной решетки:
F.2.15) отображает область I в II и наобо-
наоборот, оставляя на месте все точки кривой
АВУ для которой sinh 2 К sinh 2 L = 1.
говоря, это должно соответствовать другому значению К, т. е. будет две
критические точки. Если мы предположим, что имеется только одна кри-
критическая точка, то она должна соответствовать К* = К, т. е. Кс определя-
определяется условием
sinh 2Kc = l,Kc = 0.44068679.... F.2.16)
i В анизотропном случае рассуждения аналогичны: отображение (А',
t) — (К*, L*) переводит область I на рис. 6.3 в область II и наоборот.
Оно оставляет ня месте все точки кривой АВ. Таким образом, если имеется
Линия критических точек внутри I, то должна быть другая такая линия в
Области II. Если же имеется только одна линия критических точек, то это
Должна быть граничная линия АВ, определяемая уравнением
sinh 2K sinh 2L = 1.
F.2
В следующей главе будет показано, что это действительно условие кри-
критичности для модели Изинга на квадратной решетке.
6.3. ВЗАИМНАЯ ДУАЛЬНОСТЬ ШЕСТИУГОЛЬНОЙ
И ТРЕУГОЛЬНОЙ РЕШЕТОК
Модели Изинга можно построить на любой решетке, в частности на
шестиугольной и треугольной решетках, показанных на рис. 6.4.
с. 6.4. Шестиугольная решетка (сплошные линии) и треугольная решетка (пунк-
линии), связанная с шестиугольной: а — дуальностью, б — преобразованием
звезда — треугольник.

84
ДУАЛЬНОСТЬ И ПРЕОБРАЗОВАНИЕ ЗВЕЗДА — ТРЕУГОЛЬНИК
Рис. 6.5. Звезда ijkl на шестиугольной решет-
решетке и связанный с ней треугольник (штриховые
линии). Указаны коэффициенты взаимодействия,
соответствующие различным линиям.
Рассмотрим сначала шестиугольную решетку, состоящую из N узлов.
Линии, связывающие узлы, можно разделить на три класса: параллельные
линиям Lx на рис. 6.5, параллельные линиям L2 и параллельные линиям L3.
Пусть энергия двух соседних спинов а, а' равна -kBTLroof, если линия
между ними принадлежит классу Lr. Тогда в отсутствие магнитного поля
аналог выражения A.8.2) для статистической суммы имеет вид
Z%{L) = 2 ехрГ^ 2 <ВД + L2 2 орх + L3 2 okoX
F.3.1)
Здесь L обозначает набор из трех «коэффициентов взаимодействия» Ll9 L2,
L3, а три суммирования в аргументе экспоненты выполняются по всем ли-
линиям классов Lj, L2, L3 соответственно. Например, последнее суммирова-
суммирование производится по всем вертикальным линиям (к, /) решетки.
Аналогичным образом можно получить выражение для статистической
суммы треугольной решетки, состоящей из N узлов:
ZUK} = 2 ехрГКх 2 орк + Кг 2 ака{ + К3 2 ojojl, F.3.2)
где первое суммирование в показателе экспоненты выполняется по всем
связям (/, ?), параллельным линии К{ на рис. 6.5, второе — по связям (к,
/), параллельным линии К2, и третье — по связям (/', у), параллельным /Г3.
Используя метод разд. 6.2, легко получить соотношение дуальности
между этими двумя статистическими суммами. Вначале применим «низко-
«низкотемпературную» процедуру разд. 6.2 к модели Изинга на шестиугольной
решетке. Как видно на рис. 6.4,а, треугольная решетка из N узлов является
дуальной по отношению к шестиугольной решетке из 2N узлов. Отсюда
следует, что аналогом F.2.4) является следующее выражение:
+ L2 + L3)] 2 exp[ - 2Lxrx - 2L2r2 - 2L3 r3], F.3.3)
где суммирование по Р выполняется по всем конфигурациям многоугольни-
многоугольников на треугольной решетке, п — число линий на связях типа у.
^Множитель 2 в F.2.4) отброшен и число связей каждого класса взято
равным N, что означает пренебрежение краевыми эффектами. Эти прибли-
приближения не влияют на свободную энергию в термодинамическом пределе.)

ГЛАВА 6
85
Применим далее «высокотемпературную» процедуру разд. 6.2 к треу-
треугольной решетке. Это дает
ZJAK) = B cosh K{ cosh K2 cosh K3)N 2 vrM2vr33, F.3.4)
где
Vj = tarihKJ9 / = 1,2,3, F.3.5)
и в термодинамическом пределе суммирования по Р имеет тот же смысл,
что и в F.3.3).
Сравнивая F.3.3) и F.3.4), мы видим, что если
tanh Kj = ехр( - 2Lj), /=1,2,3, F.3.6)
то
ZUQ = BslS2s3)m ZtiK}, F.3.7)
где
Sj = i expBL;) sech2 K, = sinh 2L, = 1/sinh 2Kj. F.3.8)
Если Kl9 K2, Кг велики и положительны, то Lj, L2, L3 малы, и наобо-
наоборот. Таким образом, соотношение дуальности F.3.7) отображает низко-
низкотемпературную (высокотемпературную) модель на треугольной решетке на
высокотемпературную (низкотемпературную) модель на шестиугольной ре-
решетке.
Этого недостаточно для определения критической температуры: необхо-
необходима некоторая дополнительная информация, чтобы можно было отобра-
отображать низкотемпературную модель на высокотемпературную на той же ре-
решетке. Эта информация дается в следующих двух разделах.
6.4. СООТНОШЕНИЕ ЗВЕЗДА — ТРЕУГОЛЬНИК
Помимо соотношения дуальности F.3.7), между статистическими сум-
суммами моделей Изинга на треугольной и шестиугольной решетках существу-
существует еще одно соотношение между ними, известное как соотношение
«звезда — треугольник». Онсагер [184] ссылается на него мимоходом во
введении к своей статье, посвященной решению модели Изинга для квад-
квадратной решетки. Ванье [246] выписал его в явном виде, и с тех пор оно бы-
было представлено во многих работах (см., например, [114]).
Чтобы вывести это соотношение, заметим вначале, что шестиугольная
решетка состоит как бы из двух частей, т. е. ее узлы можно разделить на
два класса А и В, такие, что все соседи узлов А являются узлами типа В и
наоборот, Это обстоятельство отражено на рис. 6.4, где узлы А изображе-
изображены темными кружками, а узлы В — светлыми.
Поэтому выражение под знаком суммы в F.3.1) можно записать в виде
где 1
,cT/,cT*h F.4.1)
W(oi\Oi, <jj, ok) = exp[oi(LiOi + L2cj; + L3ak)]; F.4.2)

86 ДУАЛЬНОСТЬ И ПРЕОБРАЗОВАНИЕ ЗВЕЗДА — ТРЕУГОЛЬНИК
произведение в F.4.1) распространяется на все узлы / типа В, а /, у,
/с — соседние с / узлы типа Л, расположенные, как показано на рис. 6.5.
Важной особенностью выражения F.4.1) является то, что Я-спин а, по-
появляется в одном и только в одном множителе. С помощью F.4.1) сумми-
суммирование в F.3.1) по Б-спинам может быть выполнено сразу и дает
ZHN{L) = 2 П *К<7(, Щ , ок), F.4.3)
О А (/,/,1)
где
w(Oi, Oj ,ак) = ^ W{oi\oi, о,, ак) = 2 cosh(Lio; + L1o] + L3ak), F.4.4)
а суммирование в F.4.3) производится по остальным А -спинам.
Поскольку w(oh Oj, ак) не меняется при перемене знака у всех а,, Оу, ак
и так как oi9 Oj, ок принимают только значения 4-1 или - 1, то должны су-
существовать параметры /?, К{, К2, Къ, такие, что
j F.4.5)
для всех значений a,, oJf ok. Подстановка этого выражения для w в F.4.3) дает
Ztt{L} = Rm 2 П exp(tfiq-a* + К2око{ + ^з^) • F.4.6)
оа (ijJ)
Суммирование выполняется по всем N/2 спинам на узлах типа А шести-
шестиугольной решетки. Как видно из рис. 6.4, б, эти узлы образуют треуголь-
треугольную решетку. Произведение в F.4.6) распространяется на все перевернутые
треугольники (/, у, к) этой треугольной решетки.
Поэтому сумма в F.4.6) является в точности статистической суммой
для модели Изинга на треугольной решетке, состоящей из N/2 спинов. За-
Заменяя N на 2N и сравнивая с F.3.2), получаем
Это соотношение между статистическими суммами шестиугольной и
треугольной решеток известно как соотношение звезда — треугольник, так
как оно выводится посредством суммирования по центральному спину звез-
звезды (рис. 6.5), а в результате получается треугольник.
Соотношения между коэффициентами взаимодействия
При заданных значениях L{, L2, L3 параметры /?, К{, К2, Кг определя-
определяются четырьмя уравнениями, которые получаются в результате приравни-
приравнивания F.4.4.) и F.4.5) при всех значениях ah aJf ak. Эти уравнения имеют
следующий вид:
2 cosh(L! + L2 + L3) =R exp^ + К2 + К3), F.4.8а)
i + L2 + L3) = R ехр(^ -К2- Къ), F.4.86)
-L2 + L3) =R ехр(-Кг + К2- К3), (б.4.8в)
2 cosh(L! + L2 - L3) = R exp(-*i -K2 + K3). F-4.8r)

ГЛАВА 6 87
Перемножая первые два уравнения и деля результат на произведение
остальных двух, получаем
ссхкгСъ = ехрD*0 , F.4.9)
где для всех перестановок /, у, к чисел 1, 2, 3 имеем
с = cosh(Li + L2 + L3), С/ = cosh(-L, + L, + Lk). F.4.10)
Из F.4.9) с учетом стандартных тождеств для гиперболических функций
следует
ехрD*0 - 1 = sinh 2L2 sinh 2L3/c2C3, F-4Л О
поэтому
^^ts • • ^ г sinh 2Li sinh 2L2 sinh 2L3
sinh 2ATi sinh 2Li = — — -j . F.4.12)
2(ccic2c3)*
Ясно, что исходная система уравнений F.4.8) инвариантна по отноше-
отношению к перестановке индексов 1, 2, 3, поэтому еще два уравнения можно по-
получить из F.4.12) с помощью такой перестановки. Но правая часть F.4.12)
является симметричной функцией Lj, L2, L3 и остается неизменной. Ее зна-
значение обозначим к; тогда
sinh 2Kj sinh 2Ц = к~\ j = 1,2,3 . F.4.13)
Это замечательное и очень важное свойство соотношений
звезда — треугольник: все произведения sinh IKjsinh 2Lj при j = 1, 2, 3
имеют одно и то же значение.
Перемножая все четыре уравнения F.4.8), используя F.4.12), чтобы ис-
исключить ccjC2c3, а затем F.4.13), получаем
R2 = 2к sinh 2Li sinh 2L2 sinh 2L3 -
F.4 14)
= 2/(fe2 sinh 2tfi sinh 2*2 sinh 2*3) •
Последние три уравнения определяют КХУ К2, #3,/с и R как функции L1?
L2, Ly С другой стороны, можно выразить Lv k и т.д. как функции К{, К2,
Кг. Например, исключая /?, L2 и L3 из уравнений F.4.8), после некоторых
преобразований приходим к равенству
sinh 2*i cosh 2*2 cosh 2*3 + cosh 2*i sinh 2*2 sinh 2*3=
F.4.15)
= sinh 2*i cosh 2Li.
Исключение Lx из этого равенства с помощью F.4.13) дает
k A - v\) A - vl) (I - vb
ViV2V3) (Vi
гДе i>j, v2, v3 определены посредством F.3.5).
F416)

88 ДУАЛЬНОСТЬ И ПРЕОБРАЗОВАНИЕ ЗВЕЗДА — ТРЕУГОЛЬНИК
Операторная форма
В задачах для двумерных решеток часто полезно рассматривать ряд
(строку) из спинов <7j, ..., oN и операторы, которые достраивают решетку,
добавляя узлы и (или) линии. Эти операторы представляют собой матри-
матрицы 2Nx2N, строки которых помечены индексами а{у ..., oN, a
столбцы — индексами а/, ..., oN Два важных набора операторов составля-
составляют Sj, ...,5nh q, ...,cN, где.
, o'N),
здесь а и о' обозначают соответственно (р{у ..., oN) и (aj , ..., aN ).
Таким образом, st — диагональная матрица с компонентами a,, a
с7 — оператор, который переворачивает спин в положении /. Обозначим
скобкой (л", у) коммутатор ху — ух двух операторов л", у и буквой / единич-
единичной оператор; очевидно, что
SJ = Cf = / , SiCi + С/5/ = 0 ,
F.4.18)
В модели Изинга базисные наборы операторов имеют вид
,. . . , Pn-i(K) , Gi(L),. . . , QN{L),
где
' = exp(KoiOi+t) д(о{, af). .. d(oN, o'N\
' = д(о{, сгО . . . dioi-г, a/_i) ехр(?акт/) F.4.19)
X 6((J/+i , O/Vi) . . . б(алг, Gлг) .
Оператор Pt(K) вводит связь между узлами / и / + 1с коэффициентом
взаимодействия Л\ Оператор Qi(L) создает новый узел в положении /, свя-
связанный со старым связью с коэффициентом взаимодействия L. Если рас-
рассматривать <7j, ..., oN как горизонтальный ряд спинов, то Р^К) добавляет
горизонтальную линию связи, а Qj(L) — вертикальную.
С помощью F.4.17) определения F.4.19) можно представить в более
компактном виде
F.4.20)
Qt(L) = exp(L) / + exp(-L) с,.
Поскольку cf = /, отсюда вытекает
exp(Lc/) = (cosh L)I + (sinh L)c, F.4.21)

ГЛАВА 6 89
для всех комплексных чисел L. Таким образом, оператор Qt{L) может
быть представлен как
Qt(L) = B sinh 2L)* exp(L*c,), F.4.22)
где число L" связано с L соотношением
tanh L* = exp(-2L). F.4.23)
(Оно совпадает с соотношением F.2.14а), которое возникает при дуальном
преобразовании.)
Полезно расставить операторы Pi9 Q/ в последовательности Ql9 Px, Q2%
P2,...,QN и определить соответствующий набор операторов Ulr
U2, ..., иж _ j, зависящих от двух коэффициентов взаимодействия К и L
следующим образом:
ЩК, L) = Р,(К) = ехр(/йА+1) при i = 2/,
F.4.24)
= B sinh 2L)-*<2y(L) = exp(L*cy) при i = 2/ - 1.
Этих операторов достаточно, чтобы построить модель Изинга на ква-
квадратной решетке с горизонтальным коэффициентом взаимодействия К и
вертикальным коэффициентом L.
Пусть A'j, K2, А'з, Lj, L2> L^ связаны соотношениями преобразования
«звезда — треугольник» F.4.8) — F.4.15). Тогда, используя F.4.19) для
прямого вычисления матричных произведений, а также F.4.13) и F.4.14),
находим, что из F.4.4), F.4.5) следует
(/1+1(^!, L,) ЩЬг, К2) Ui+l(K3,L3) =
F.4.25)
= ВД , ^з) Ui+i(L2, Кг) UAKx, L О
при / = 1, ..., 2N — 2. Очевидно также, что
U,(K, L) U,(K' ,L') = ЩК', L') UIK, L) F.4.26)
для любых комплексных чисел К, L, K\ L' при условии, что I/ - j\ > 2.
Так же как Р( и Qi9 операторы Ut(K, L) вводят новые линии в решетку.
Если / — четное число, то левая часть F.4.25) добавляет к решетке звезду
(Lj, L2, L3), в то время как правая часть добавляет треугольник (Кх> К2.
К^)\ если / нечетное, то наоборот. Таким образом, F.4.25) представляет со-
собой простую операторную форму соотношения звезда — треугольник.
Если мы обозначим Ut(K{y L{), U^L^ K2), Uf(K39 L3) просто как • Ui9
Vit Ui соответственно, то соотношение F.4.25) примет вид
iU,, F-4-27>
что несколько проясняет его структуру. Кроме того, из F.4.26) следует
UjUit |i-/|>2. F.4.28)

90 ДУАЛЬНОСТЬ И ПРЕОБРАЗОВАНИЕ ЗВЕЗДА — ТРЕУГОЛЬНИК
Важность соотношения звезда — tpevi ильник.
Соотношение звезда — треугольник имеет весьма важные следствия.
Рассмотрим две модели Изинга на квадратной решетке, аналогичные опи-
описанным в разд. 6.2, с разными значениями К и L, но с одинаковым значе-
значением sinh 2K sinh 2L. Онсагер [186] заметил, что из соотношения
звезда — треугольник следует коммутативность диагональ-диагональных
трансфер-матриц при условии, что наложены циклические граничные усло-
условия.
Строгий вывод этого утверждения дан в разд. 7.3, но частная иллюст-
иллюстрация его справедливости может быть легко получена из F.4.25). Рассмот-
Рассмотрим оператор
V{K, L) = Ui(K, L) U2(K, L). .. Un(K, L), F.4.29)
где n = 2N — 1. Этот оператор соответствует добавлению вертикальной
связи в столбце Ny затем горизонтальной между столбцами N - 1 и 7V, за-
затем вертикальной в столбце N — 1 и т. д. Вся процедура в целом добавля-
добавляет «лестницу» к обычной квадратной решетке. Поэтому V(K9 L) является
диагональ-диагональной трансфер-матрицей квадратной решетки, если не
принимать во внимание граничные условия (и тривиальный нормирующий
множитель).
Примем опять, что Kl9 К2, Кг> L,, L2> L3 удовлетворяют сотношениям
«звезда — треугольник» F.4.8) — F.4.15). Обозначим V(K{, Lj), K(L2,
К2) просто как К, V. Тогда
V = UiU2. . . Un , F.4.30а)
V' = U[U'2...U'H. F.4.306)
Применяя повторно только F.4.27) и F.4.28), легко убедиться, что
w (игп-1щип) = (Uiiriur1) vv. <6-4-31)
Множители, заключенные в скобки, являются «граничными членами» про-
произведения, включающими только операторы, действующие на крайние спи-
спины. Поэтому едва ли покажется удивительным, что эти члены исчезают,
когда обычным образом вводятся циклические граничные условия (как это
сделано в разд. 7.3), так что в результате остается
W' = V'V. F.4.32)
Таким образом, V(Kl9 Lj) и K(L2, K2) коммутируют при условии, что
Кг, L3 могут быть выбраны так, чтобы выполнялись соотношения
F.4.8) — F.4.15). Это справедливо, если sinh 2AT,sinh 2LX = sinh 2L2sinh 2K2.
В более общей формулировке, если мы имеем любую решеточную мо-
модель, трансфер-матрица V которой может быть представлена в виде
F.4.30а), и если мы можем построить операторы U\, ..., и'п = и\', ..., Un ,
удовлетворяющие соотношениям F.4.27) и F.4.28), то V и V' удовлетворя-
удовлетворяют правилу псевдокоммутации F.4.31). В гл. 9 и 10 показано, что это мо-
может быть сделано для шести- и восьмивершинных моделей. Соответствую-

ГЛАВА 6 91
щее коммутационное соотношение является необходимым первым шагом в
решении восьмивершинной модели.
Чтобы получить точные коммутационные соотношения, необходимо
использовать явное представление операторов для введения циклических
граничных условий. Кроме того, чтобы привести трансфер-матрицу к фор-
форме, аналогичной F.4.30а), необходимо вводить неудобный циклический
сдвиг спиновых индексов при переходе от одного ряда к следующему. По
этим причинам коммутационные соотношения для шести- и восьмивершин-
ных моделей Изинга будут получены непосредственно без использования
F.4.30), F.4.31). Но и в этом случае коммутационные соотношения всегда
являются, как будет подчеркнуто ниже, прямым следствием соответствую-
соответствующего соотношения звезда — треугольник.
В разд. 11.7 будет показано, что в случае модели Изинга можно полнос-
полностью избежать применения формализма трансфер-матрицы: свободная энер-
энергия получается с помощью одного лишь соотношения звезда — треуголь-
треугольник и его следствий!
6.5. САМОДУАЛЬНОСТЬ ТРЕУГОЛЬНОЙ РЕШЕТКИ
Если коэффициенты Lj, L2, ?3 в F.4.8) малы, то малы также и величи-
величины КХу К2> А'з- Поэтому соотношение звезда — треугольник F.4.7) отобра-
отображает высокотемпературную модель на треугольной решетке на высокотем-
высокотемпературную модель на шестиугольной решетке.
Применим теперь преобразование дуальности F.3.6) — F.3.8). Оно
отображает высокотемпературную модель на шестиугольной решетке на
низкотемпературную модель на треугольной решетке.
Взятые вместе в указанном смысле преобразования звезда — треугольник и
дуальности приводят к следующему соотношению самодуальности для модели
Изинга на треугольной решетке:
ZUK) = к~т ZUK*) , F.5.1)
где
sinh 2K* = k sinh 2К,, /=1,2,3, F.5.2)
а к выражается через К{, К2, Кг посредством F.4.16) и F.3.5). С другой сторо-
стороны, коэффициент к выражается через А',*, К\, К\ следующим обра-
образом:
ri= A-.Г2)A-.2*2)A-.3*2)
4[A + vtvM) (vt + v№) {v$ + vivX) И + *!)]*'
где
vf = tanh К*, /=1,2,3. F.5.4)
Ясно, что это отображение является взаимным, т. е. оно отображает точку
К = (К{УК2, Кг) в точку К* = (К\, К\, /ф, а точку К* обратно в точку К. )Лз
F.5.2) следует, что имеется поверхность самодуальных точек в пространстве

92 ДУАЛЬНОСТЬ И ПРЕОБРАЗОВАНИЕ ЗВЕЗДА — ТРЕУГОЛЬНИК
(ЛГР ЛГ2, ЛГ3), соответствующая к = 1. Поэтому мы можем утверждать, как и в
разд. 6.2, что если имеется только одна критическая поверхность в пространстве
(ЛГР К2у А'з), то это должна быть самодуальная поверхность, что приводит к
условию критичности
к = 1 . F.5.5)
Это действительно верно, как показано в гл. 11. Для изотропной треуголь-
треугольной модели с Кх = К2 = А'з = К критическая точка К = Кс определяется усло-
условием
sinh 2КС = 3~*, Ке = 0.27465307 ., . . F.5.6)
Поэтому, согласно F.3.6), изотропная шестиугольная модель имеет критиче-
критическую точку при L = L2 = L3 = ^с где
sinh 2LC = 3*, Lc = 0.6584789 F.5.7)

7
МОДЕЛЬ ИЗИНГА
НА КВАДРАТНОЙ РЕШЕТКЕ
7.1. ИСТОРИЧЕСКОЕ ВВЕДЕНИЕ
Свободная энергия двумерной модели Изинга в отсутствие внешнего поля
впервые была вычислена Онсагером [184] в 1944 г. Он диагонализировал
трансфер-матрицу, используя неприводимые представления соответствую-
соответствующей матричной группы. Его студентка Брурия Кауфман упростила этот
вывод в 1949 г. [143], показав, что трансфер-матрица принадлежит к группе
спинорных операторов.
С тех пор было предложено много альтернативных выводов. Метод
трансфер-матрицы использовался в ряде работ [25, 208, 215, 232].
Совершенно другой метод разработали Кац и Уорд [128], которые при-
применили комбинаторику, чтобы записать статистическую сумму в виде лег-
легко вычисляемого определителя. Этот метод был улучшен в работе [197].
Херст и Грин [116] и Кастелейн [140] также использовали комбинатори-
комбинаторику, но на этот раз, чтобы записать статистическую сумму в виде пфаффиа-
на. Еще одно комбинаторное решение, приведенное в курсе Ландау и Лиф-
шица [155], было получено Вдовиченко [243].
Совсем недавно [37, ПО] было показано, что плоская модель Изинга
может быть решена весьма прямым способом с помощью соотношения
звезда — треугольник разд. 6.4, используемого как рекуррентное соотноше-
соотношение.
Обсуждение всех этих подходов в деталях выходит далеко за пределы
данной книги. В этой главе будет представлен метод, который может быть
назван методом коммутирующих трансфер-матриц. Его преимуществом
является возможность обобщения для решения восьмивершинной модели,
как это показано в гл. 9.
Основная идея состоит в том, что диагональ-диагональная трансфер-
матрица рассматривается как функция двух коэффициентов взаимодействия
К и L. Нетрудно установить, что две такие матрицы коммутируют, если
они характеризуются одинаковыми значениями к = (sinh2ATsinh2L)~1, и
для любой такой матрицы может быть найдена другая, фактически обрат-
обратная ей матрица. Этих свойств в основном достаточно, чтобы получить
собственные значения трансфер-матрицы. С их помощью можно вычис-
вычислить свободную энергию, межфазное поверхностное натяжение и корреля-
корреляционную длину.
Результат для спонтанной намагниченности Мо также приведен ниже
(разд. 7.10), но без вывода, поскольку вычисления в этом случае довольно

94 МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
сложны: между первой работой Онсагера с выводом выражения для сво-
свободной энергии и его выступлением на конференции во Флоренции, где он
объявил результат для Мо [185, 186], прошло пять лет. Первый опублико-
опубликованный вывод принадлежит Янгу [262], а Монтролл и др. [170] получили
его более простым методом пфаффиана в 1963 г. Вывод, использующий
угловые трансфер-матрицы, приведен в разд. 13.7 для более общей восьми-
вершинной модели.
В разд. 7.7 — 7.12 обсуждаются по отдельности случаи к < 1. к = 1 и
к > 1. Как показано в разд. 7.12, они соответствуют низким температурам
Т < Тс, критической температуре Т = Тс и высоким температурам Т > Тс
соответственно.
7.2. ТРАНСФЕР-МАТРИЦЫ К, W
Рассмотрим модель Изинга на квадратной решетке в отсутствие внеш-
внешнего поля, как мы ее определили в разд. 6.2, но изобразим решетку по диа-
диагонали, как показано на рис. 7.1. Статистическая сумма по-прежнему опи-
описывается выражением F.2.1), но теперь первое суммирование внутри ско-
скобок выполняется по всем линиям, параллельным линиям, отмеченным на
рис. 7.1 буквой К, а второе — по линиям, параллельным линиям, отмечен-
отмеченным буквой L.
Сгруппируем узлы по горизонтальным рядам; например, узлы, изобра-
изображенные темными кружками на рис. 7Л, образуют один такой ряд. Как по-
показано на рис. 7.1, эти ряды можно разделить на два класса А и В (светлые
и темные кружки). Ряды А и В чередуются при перемещении вверх или
вниз по решетке.
Пусть m — число таких рядов в решетке. Пронумеруем их таким обра-
образом, чтобы ряд г был расположен ниже ряда г + 1, и наложим циклические
граничные условия, такие, что за рядом m следует ряд 1. Это означает, что
число m должно быть четным.
Пусть п — число узлов в каждом ряду; пронумеруем узлы слева напра-
направо. Наложим снова циклические граничные условия, но на этот раз такие,
что за узлом п следует узел 1. (В совокупности эти циклические граничные
условия эквивалентны изображению решетки на торе, поэтому их называ-
называют тороидальными.)
Пусть фг обозначает все спины ряда гу так что фг принимает 2п возмож-
возможных значений. Выражение под знаком суммы в F.2.1) можно рассматри-
рассматривать как функцию ф{9 . . . , фт. Поскольку каждый спин взаимодействует
W
Рис. 7.1. 1ри последовательных ряда
квадратной решетки (изображенной по
диагонали).

ГЛАВА 7 95
только со спинами примыкающих рядов, эта функция факторизуется, и
F.2.1) принимает вид
zN = 2 2... 2 vw w^ v*,,* ww... Wb,,* ¦ G.2.0
Ф\ Фг Фт
Здесь Уф.,ф j содержит все больцмановские весовые множители в каждом
слагаемом Усуммы, которые зависят только от спинов соседних рядов У и
y'+l, причем нижний ряду относится к типу А. То же самое верно по от-
отношению к 1Уф^ ф но в этом случае нижний ряд принадлежит к типу В.
Рассмотрим7 isa. типичных соседних ряда. Пусть ф = {о{, ... ,
адг) — спины нижнего ряда, а ф' = (а{, . . . , о'п\ — спины верхнего ряда.
Тогда из F.2.1) и рис. 7.1 ясно, что
п
]S (Kdj+i&j + barf) ,
п
2 (Ка)°} + L°i°j+i) >
Ф,ф' = ехр | ^
G.2.2)
W = exp [
™e °n + 1 S °l И °n + 1 S °\'
Все предшествующее аналогично соответствующим рассуждениям в
гл. 2 по поводу одномерной модели Изинга; К(ф, ф') можно снова рас-
рассматривать как элемент ф, ф'' матрицы К, то же верно и для W. Тогда
G.2.1) можно записать в виде
ZN = Trace VWVW. . . W = Trace (VW)^2. G.2.3)
Главное отличие от одномерного случая состоит в том, что как <р, так и
ф' имеют 2п значений, поэтому V и W являются матрицами 2п х 2", а не
2x2. Кроме того, теперь неверно, что VW — симметричная матрица; но
и в этом случае соотношения B.1.11) — B.1.15) можно обобщить таким
образом, чтобы из G.2.3) следовало
V ктп I ктп I I Л ф \/.Z.4)
где Лр х\, . . . — собственные значения VW.
Нас интересует в первую очередь термодинамический предел, когда т и
п — большие числа. Чтобы его получить, можно сначала положить т — оо
при фиксированном значении п. Тогда из G.2.4) немедленно следует
Z*~(Amaxy\ G.2.5)
где Л^ах — наибольшее по величине собственное значение матрицы VW.
Матрицы V и W известны как трансфер-матрицы. Задача состоит те-
теперь в том, чтобы найти максимальное собственное значение VW.

96 МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
7.3. ДВА ВАЖНЫХ СВОЙСТВА МАТРИЦ V И W
Коммутативность
Из G.2.2) следует, что матрицы V и W являются функциями коэффици-
коэффициентов взаимодействия К и L. Здесь удобно выразить это явным образом и
писать V и W как V(K, L) и W(K, L).
В настоящем разделе мы установим два свойства этих матричных функ-
функций, а в последующих разделах покажем, что такие свойства делают воз-
возможным вычисление Лтах. Принятый (хотя и непрямой) способ изложения
позволяет выявить тот факт, что, по существу, используются только ло-
локальные свойства решеточной модели.
Выражение G.2.3) включает произведение матриц V(K, L)W(K, L). Рас-
Рассмотрим более общее произведение
V{K,L)W(K\L')> G.3.1)
где К, L, К', L' временно считаются комплексными числами. Это матрич-
матричное произведение имеет смысл трансфер-матрицы перехода от нижнего ря-
ряда светлых кружков на рис. 7.1 к верхнему ряду при условии, что коэффи-
коэффициенты взаимодействия К, L, относящиеся к линиям над темными кружка-
кружками, заменены на К\ L' соответственно.
Поэтому каждый элемент такого произведения матриц является про-
просуммированным по всем спинам о'{, . . . , а„ промежуточных темных круж-
кружков произведением больцмановских весовых множителей всей совокупности
связей, изображенной на рис. 7.1. Пусть ф = {ov ... , оп) — спины ниж-
нижнего, а ф' = [о[у . . . , о'п] — спины верхнего рядов светлых кружков. Тог-
Тогда элемент ф, ф' матричного произведения G.3.1) имеет вид
п
2 2 П exp [a1; (KOj+i + Loj + К1 о) + L'o)+{j\. G-3.2)
Экспонента в G.3.2) представляет собой просто больцмановский весо-
весовой множитель четырех связей на рис. 7.1, исходящих из темного кружка j.
Поскольку oj входит только в этот множитель, суммирование по oj легко
выполняется. Проведя эту операцию для af, . . . , a^, получаем вместо
G.3.2) выражение
Jah oj+u oj.o',+i), G.3.3)
где для а, Ь, с, d = ±1 имеем
Х{а, b;c, d) = Et exp[/(Le + Kb+ K'c + L'd)]. G.3.4)
Поставим теперь следующий вопрос. Предположим, что мы поменяем
местами коэффициенты взаимодействия К и К' и коэффициенты L и L'.
Изменится ли при этом матричное произведение G.3.1)? Иначе говоря,

ГЛАВА 7
97
Рис. 7.2. Сегменты решетки, статистические веса которых (просуммированные по
спинам темных узлов) составляют левую и правую части урав-
уравнения G.3.7) (а), и те же сегменты после применения преобразования звез-
звезда — треугольник (б).
справедливо ли уравнение
V(K, L) W{K', V) = V{Kf, V) W(K, L).
G.3.5)
Это обобщенное коммутационное соотношение. Если оно верно, то, как
будет показано в следующем разделе, все трансфер-матрицы коммутиру-
коммутируют, и это свойство будет использовано для получения свободной энергии.
Но сначала ограничимся выяснением вопроса о том, может ли выполнять-
выполняться равенство G.3.5).
Ясно, что G.3.3) не изменится, если Х(ау Ь> с, d) заменить на
ъ-Mbd
G.3.6)
так как экспоненциальные множители соседних членов сокращаются. Та-
Таким образом, равенство G.3.5) будет определенно верным, если существует
такое число М, что
сШсX{a,b;c,d)= X\a ,b;c9d) tMbd,
G.3.7)
где Xf получается из X при перемене местами К с К' и L с L'.
Это уравнение можно интерпретировать графически (рис. 1.2>а). Оно эк-
эквивалентно требованию, чтобы больцмановские веса обеих фигур, просум-
просуммированные по центральному спину, были одинаковы для всех значений
(± 1) внешних спинов а, Ь> с, d.
Условие G.3.7) может быть исследовано прямым способом, но, чтобы
связать обсуждение с результатами разд. 6.4, лучше действовать следую-
следующим образом.
Обе фигуры содержат треугольник (L, К\ М). Введем обозначения Ки

98 МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
К2у К^у причем
KX = L, K2 = K', К3 = М, G.3.8а)
и превратим эти треугольники в звезды с помощью преобразования
звезда — треугольник F.4.4), F.4.5). Тогда Ll9 L2, ?3 определяются соот-
соотношениями F.4.8) — F,4.15), и мы видим, что с точностью до общего
множителя R больцмановские веса те же, что для фигур на рис. 7.2,6, если
просуммировать по двум внутренним спинам. Ясно, что эти веса равны,
если
L{ = К, L2 = L'. G.3.86)
Из F.4.14) следует, что К, L, К'9 L' должны удовлетворять равенству
sinh 2Ksinh 2L = sinh 2K' sinh 2L'. G.3.9)
Это условие можно получить и более прямым путем, подставляя G.3.8)
в F.4.8) и исключая /?, L3, M. Если равенство G.3.9) справедливо, то мы
всегда можем выбрать /?, L3, M таким образом, чтобы уравнения F.4.8)
удовлетворялись. Отсюда немедленно следуют соотношения G.3.7) и
G.3.5).
Итак, мы воспользовались преобразованием звезда — треугольник и по-
показали, что равенство G.3.9) является достаточным условием, для того
чтобы выполнялись точные коммутационные соотношения G.3.5). Это ра-
равенство является также и необходимым условием.
Обращение
Другое свойство, которое нам потребуется, можно рассматривать как
соотношение для матриц, обратных матрицам V или W. Полезно начать с
вопроса: можно ли при заданных К, L так выбрать К', L\ чтобы произве-
произведение G.3.1) было диагональной или «почти диагональной» матрицей?
Поскольку элементы G.3.1) имеют вид G.3.3), на этот вопрос можно
было бы ответить положительно, если бы величины Х(а, Ь\ с, d) обраща-
обращались в нуль при а Ф с (или b Ф d). Это требование является слишком
сильным, и в общем случае оно не может быть удовлетворено.
Может быть выполнено более слабое условие, а именно что Х(а, Ь\ с,
d) обращается в нуль, если а =? с и Ь = d. Согласно G.3.4), это эквива-
эквивалентно двум уравнениям
cosh(L + K-Kf + L') = 0,
G.3.10)
LA:A:'L') 0
Эти уравнения не имеют действительных решений, но имеют комплекс-
комплексное решение
K' = L + lm, L' = -K. G.3.11)

ГЛАВА 7 99
Что означает требование равенства нулю Х(а> Ь\ с, d) при а Ф с и
If = dl С учетом G.3.3) оно означает, что для ненулевых элементов матри-
матрицы VW, если оу, Оу неодинаковы, и о]¦, + 2, aj + 2 должны быть тоже неоди-
неодинаковыми. Поскольку у = 1, • • • , п с циклическими граничными условия-
условиями, отсюда следует, что либо во всех парах (ау, о-) спины одинаковы, либо
go всех неодинаковы.
Если они одинаковы, то нас интересует только Х(а, Ь\ с, d) для а = с и
j = с/. Из G.3.4) и G.3.11) следует, что такие значения X равны
Arlike = 2/sinh2L. G.3.12а)
Если же они неодинаковы, то а Ф с, Ь =? d и
Unlike = / ab sinh 2#. G.3.126)
После подстановки этих выражений в G.3.3) получаем, что G.3.3) мо-
цсет быть представлено в виде
B/ sinh 2L)n 8@,, а[) 8(а2 ,о'2)... 8(ап, о'п)+
G.3.13)
+ (-2/ sinh 2К)п 6{ах, -ai) 5(cj2 , -a*). . . 8(ап, -а;,).
Таким образом, ^(/Г, L)H/(Ar/, L') —матрица с элементами G.3.13).
Яусть / — единичная матрица размерности 2", a R — матрица с элемента-
элементами
Тогда очевидно, что мы установили матричное тождество
ЩК, L) W(L + Цл, -К) = Bi sinh 2LO + (-2* sinh2А:)ПЛ. G.3.15)
Поскольку
R2 = I, G.3.16)
Правую часть G.3.15) легко обратить; поэтому G.3.15) можно использо-
1№ть, чтобы получить матрицу, обратную матрице V(K, L). По этой при-
причине я иногда буду называть это соотношение инверсным тождеством.
7.4. СООТНОШЕНИЯ СИММЕТРИИ
Кроме установленных выше свойств коммутации и обращения, нам по-
потребуются также некоторые простые свойства симметрии трансфер-
матриц.
Меняя местами К и L и все ojy о- в G.2.2), мы меняем местами матрицы
* ъ W. Это означает, что
W(K,L) = VT(L,K), G.4.1)
V(K, L) W(K, L) = [V(L , tf) W(L , K))T. G.4.2)

ЮО МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
Изменение знаков К и L в G.2.2) эквивалентно изменению знака у всех
ои . . . , оп или о[, . . . , о'п. Отсюда следует
V(-K ,-L)=R V(K, L) = V(K, L) Л G.4.3)
и аналогичное соотношение для W.
Наконец, пусть г — число пар (а, + j, aj) с разными спинами, а
5 — число пар (ау, Оу) такого же типа. Тогда г + s — число изменений зна-
знака в последовательности о{, aj, a2, a^, . . . , o'n. Это означает, что число
г + 5 должно быть четным, и, согласно G.2.2),
Уф,ф. = ехр[(л - 2г) А: + (л - 2j) L]. G.4.4)
Нас интересует термодинамический предел, когда п — большое число.
Не важно, каким образом п становится большим; поэтому мы ограничимся
четными значениями п. Это несколько упрощает последующее обсуждение,
так что ниже в этой главе мы полагаем
п = 2р , G.4.5)
где р — целое число.
Равенство G.4.4) теперь можно записать в виде
Уф,ф. = cxp[±2r'K ± 2s'L], G-4.6)
где rf us' — неотрицательные целые числа в интервале @. р). Они либо
оба четные, либо оба нечетные; поэтому правая часть не изменится при од-
одновременном изменении знака expB/Q и expBL); следовательно, матрица
V(K, L) удовлетворяет условию
V(K±hm,L±hm) = V(K, L); <7.4.7)
аналогичное условие имеет место для матрицы W.
7.5. КОММУТАЦИОННЫЕ СООТНОШЕНИЯ
ДЛЯ ТРАНСФЕР-МАТРИЦ
Соотношение G.3.5) справедливо, если выполняется условие G.3.9). От-
Отсюда следует, как мы сейчас покажем, что все матрицы V(K, L), W(Ky L),
K(Ar/, L'), W(K', L') коммутируют. Определим С как матрицу 2" х 2" с
элементами
6(а{, oi) 6(а2, а'3). . . д(ап, о\). G.5.1)
Соответствующий оператор С сдвигает столбцы решетки влево или впра-
вправо; например, применение преобразования Л — С~ ХЛС к любой матрице Л
приводит к замене нумерации спинов 1, . . . , п на 2, . . . , л, 1. Из G.2.2) с
очевидностью следует, что матрицы V(K, L) и W(K, L) при этом не меня-
меняются:

ГЛАВА 7 101
/ , G52)
) = C-lW(K,L)C.
Кроме того, согласно G.2.2),
W(K,L) = V(K,L)C. G.5.3)
Таким образом, С, V(Ky L), W(Ky L) все коммутируют друг с другом.
Подставим теперь G.5.3) в G.3.5). Мы сразу получим
V(K,L)V(K\L')=V(K',L')V(K,L), G.5.4а)
;если выполняется условие G.3.9), т.е.
sinh 2К sinh 2L = sinh 2К' sinh 2V . G.5.46)
Поэтому, как мы и утверждали, V(K> L), V(K', L') и, следовательно,
fT(tf, L), Ж(АГ', L') коммутируют.
С помощью G.5.3) из тождества G.3.15) можно исключить матрицу W,
too дает
V(K,L)V(L+iin,-K)C = Bisinh2L)nI + (-2isinh2K)nR. G.5.5)
Наконец, согласно G.3.14), преобразование А — R~lAR эквивалентно пе-
перемене знака всех спинов ар . . . , а„, а[, . . . , о'п что не меняет G.2.2); поэ-
поэтому
V(K, L) = /Г1 V(K, L) R. G.5.6)
Таким образом, ^(/Г, L) коммутирует также и с R. То же справедливо и
для W(K, L).
7.6. ФУНКЦИОНАЛЬНОЕ СООТНОШЕНИЕ
ДЛЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ
Пусть
k = (sinh 2K sinhaL)'1. G.6.1)
Предположим, что к — заданное фиксированное действительное число, и
будем рассматривать К и L как комплексные переменные, подчиняющиеся
условию G.6.1). Тогда в зависимости от меняющихся таким образом К и L
можно получить бесчисленное число матриц V(Ky L).
Согласно G.5.4), все такие матрицы коммутируют. Из G.5.2) и G.5.6)
следует, что они коммутируют также с С и /?, а потому и с W(K, L). Сле-
Следовательно, все эти матрицы для всех значений К и L, удовлетворяющих
G.6.1), имеют общий набор собственных векторов.
Пусть л" — один из таких собственных векторов. Он не может зависеть

102 МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
от К или от L, пока выполняется условие G.6.1). Он может (и должен) за-
зависеть от к, так что его можно записать в виде х(к).
Пусть v(K, L)y с, г — собственные значения матриц V(K, L), С, R соот-
соответственно. Тогда для всех К, L, удовлетворяющих G.6.1), имеем
V(K,L)x(k) =v(K,L)x(k\ Cx(k)=cx(k), Rx(k)=rx(k).
G.6.2)
Поскольку Сп — R2 = /, собственные значения с, г являются равными
по модулю единице константами, удовлетворяющими условию
с" = г2 = 1. G.6.3)
Заметим, что если К, L удовлетворяют G.6.1), то же справедливо и для
К\ Z/, определенных равенствами G.3.11). Умножим теперь на х(к) спра-
справа обе части равенства G.5.5). Сразу получим
v(K,L) v(L 4- iin, -К) с = B/sinh2L)" 4- (-2/sinh2K)nг. G.6.4)
Квадраты Лу, введенные в разд. 7.2, являются собственными значения-
значениями матрицы К(ЛГ, L)W{K, L). Согласно G.5.3) и G.6.2), х(к) — собствен-
собственный вектор этой матрицы. Пусть А(К, L) — соответствующее Лу. Тогда
A2(K,L) = v\K,L)c. G.6.5)
Таким образом, Л(ЛГ, L) можно определить как
L) = v(K,L)c*. G-6.6)
Поскольку с и, следовательно, сл являются константами, соотношение
G.5.4) можно переписать в форме, не зависящей от с:
А(К, L) A(L 4- i in, -К) = B/ sinh 2L)n 4- (-2/ sinh 2K)n r. G.6.7)
7.7. СОБСТВЕННЫЕ ЗНАЧЕНИЯ Л ПРИ Т = Тс
Уравнение G.6.7) представляет собой функциональное соотношение для
функции А(К, L). Это соотношение весьма полезно: вместе с некоторыми
простыми аналитическими свойствами А(К, L) оно полностью определяет
А(К, L). Конечно, имеется много решений, соответствующих различным
собственным значениям.
Чтобы увидеть это, полезно вначале рассмотреть случай к = 1. Как
уже отмечалось в гл. 6 и будет подтверждено ниже, этот случай соответст-
соответствует температуре Г, равной ее критическому значению Тс.
Параметризация К, L
Если к = 1, то, вместо того чтобы работать с К и L, удобнее ввести
переменную м, определяемую соотношениями

ГЛАВА 7 103
sinh 2K = tan и , sinh2L = cotw. G.7.1)
Тогда условие G.6.1) выполняется автоматически. Если К и L принимают
действительные и положительные значения, то и лежит в интервале
@, тг/2).
Ясно, что \{К, L) можно теперь рассматривать как функцию и и запи-
записывать в виде А(и). Тогда G.6.7) принимает вид
А(и)А(и 4- ?л) = B/cot и)" 4- (-2/tanu)nr. G.7.2)
Использование переменной и дает то преимущество, что не только вы-
выполняется условие G.6.1), но и ехр(±2К) и exp(±2L) также являются
«простыми» функциями и. Действительно,
ехрBК) = A 4- sin w)/cos и ,
= A - sin w)/cos и ,
expBL) = A 4- cos w)/sin и ,
expf-2L) = A - cos w)/sin и.
Точнее эти функции (если рассматривать и как комплексную перемен-
переменную) имеют следующие свойства:
а) являются однозначными;
б) мероморфны, т.е имеют особенности только типа полюсов (в дейст-
действительности типа простых полюсов);
в) периодичны с периодом 27г.
Вид функции \(и).
После подстановки выражений G.7.3) для ехр(±2ДО и exp(±2L) в
G.4.6) становится ясным, что каждый матричный элемент К^ ф, имеет вид
Уф, Ф' = t(u)/(sin и cos и)р , G.7.4)
где t{u) — полином относительно sinw и cosw с суммарной степенью 2р.
Таким образом, для любого матричного элемента t(u) можно представить
в виде
t{u) = t~2ipu(c0 + cie'4... + c2n e4H . G.7.5)
Рассмотрим теперь первое векторное уравнение G.6.2). На самом деле
это 2п скалярных уравнений, каждое из которых выражает собственное
значение v(K, L) через линейную комбинацию элементов матрицы V(KL).
Коэффициентами являются отношения элементов х(к). Существенным мо-
моментом, о котором следует помнить, является то, что (по причинам, свя-
связанным с коммутативностью и обсуждавшимся в разд. 7.6) эти отношения
зависят только от к. Они не зависят от и.

104 МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
Таким образом, собственное значение v(Ky L) представляет собой ли-
линейную комбинацию функций вида G.7.4) с постоянными коэффициентами.
Ясно, что оно должно иметь тот же вид. Согласно G.6.6), функция А(К,
L), теперь Л(м), также должна быть такого вида.
Такую форму представления собственных значений можно упростить с
помощью соотношений симметрии. Предположим, что мы заменили и на
и + 7г. Согласно G.7.3), это эквивалентно замене К и L на — К ± Vnri и
— L± Ynri. Согласно G.4.3) и G.4.6), это эквивалентно умножению V на
R. Поэтому, записывая v (К, L) как и (и), мы можем представить первое из
уравнений G.6.2) в виде
V(K, L) R x(k) = v(u + л) x(k), G.7.6)
используя снова независимость х(к) о«т и.
С помощью первого и последнего из уравнений G.6.2) сразу получаем
v(u + л) = rv{u) , G.7.7)
поэтому, согласно G.6.6),
Л(м + л:) = гЛ(м). G.7.8)
Таким образом, А(и) имеет вид G.7.4) и удовлетворяет соотношениям
периодичности G.7.8). Поэтому у полинома в G.7.5) отличны от нуля
только четные коэффициенты, если г = +1, и только нечетные, если
г = — 1. Факторизуя этот полином, получаем следующее выражение для
А(и):
i
Л(м) = р (sin и cos и)~р 11 sin {и - му) , G.7.9а)
где р, i/j, . . . , Uj — постоянные (пока не известные) и
/ = 2р, г=+1,
G.7.96)
= 2р-1, г=-1.
Нули А(и)
Подставим теперь выписанное выше выражение для А(и) в соотноше-
соотношение G.7.2). С учетом G.4.5) это дает
/
р2 П sin(w - щ) cos(w - Uj) = 22p [cos4*7 и + r sin4*7 u]. G.7.10)
Написанное равенство должно выполняться тождественно для всех зна-
значений и. Это утверждение становится особенно очевидным, если перепи-
переписать G.7.10) в новых переменных:
z = ехрBш), Zj = ехрBш). G.7.11)

ГЛАВА 7 105
Тогда G.7.10) принимает вид
/
^(М/ П [(z2 - zj)/zj] = 2-V-2' [(z + IL" + r(z - iyp). G.7.12)
Согласно G.7.96), обе части последнего уравнения являются полинома-
полиномами степени / относительно z2, так что константы р, z{, ... , Z/ действи-
действительно могут быть выбраны таким образом, чтобы равенство G.7.12) вы-
выполнялось тождественно. Очевидно, что z\> ... , zj — I различных нулей
правой части равенства, которые легко получить в виде
zj = -tan2@y/2), G.7.13)
где для j = 1,...,/ имеем
у г=1,
G.7.14)
= njllp, г = -1 .
Все эти 6j лежат в интервале @, 7г). Определим <ДР . . . , ф1 посредством со-
соотношения
ф^Цптпф/!), у=1,...,/. G.7.15)
Тогда из G.7.11) и G.7.13) следует
Uj= + \jz-i<t>h 7=1,...,/. G.7.16)
Имеются другие решения, но они получаются прибавлением к и- числа
тг, умноженного на целочисленный множитель. Согласно G.7.9а), это
оставляет функцию А (и) неизменной (с точностью до несущественного зна-
знака), поэтому все действительно различные решения определяются G.7.16).
Поскольку знак в G.7.16) можно выбрать независимо для каждого зна-
значения У, мы имеем 21 возможных решений. Но не все они допустимы.
Пусть и -* ±/оо. Тогда в соответствии с G.7.3) ехрBАг) и
ехр( — 2L) — ±/. Однако, как следует из G.4.7), элементы трансфер-
матрицы не меняются при одновременной перемене знака у ехрBАг) и
expBL). Поэтому
Л(/оо) = Л(-/оо). G.7.17)
Согласно G.7.9), это условие выполняется автоматически, если г— — 1.
Если же г — +1, то необходимо, чтобы
(Mi + . . . + и2р)/л = целое число + \р , G.7.18)
так что в G.7.16) можно выбирать независимо лишь 2р — 1 знаков. Поэто-
Поэтому .в обоих случаях (когда г — + 1 или г — — 1) имеется 2^ ~ * собствен-
собственных значений Л, как и предполагалось.
После подстановки и- в форме G.7.16) равенство G.7.9а) принимает вид
Л(м) = р (sin и cos и)~р 11 sin(w + /0У + ?уу;г) , G.7.19)

106 МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
где 7р • • • , У/ имеют значения ± 1, и если г - +1, то
У\ + . . . . + у2р = 2р - 4 X целое число. G.7.20)
Ясно, что константу р можно теперь вычислить (с точностью до несу-
несущественного знака), подставляя выражение G.7.19) для А(и) в тождество
G.7.2). Мы не будем продолжать далее эти вычисления, поскольку рас-
рассматриваемый здесь случай является предельным по отношению к случаю,
рассматриваемому в следующем разделе. Главный результат уже получен:
собственные значения матрицы VW при к = 1 определяются коммутацион-
коммутационными соотношениями и тождеством G.6.7) и могут быть вычислены мето-
методами обычной алгебры.
7.8. СОБСТВЕННЫЕ ЗНАЧЕНИЯ Л ПРИ Т < Тс
Решение для случая к = 1 представлено так детально потому, что весь
вывод может быть проведен исключительно в элементарных функциях.
Главные этапы вывода следующие:
I. Для заданного значения к находим параметризацию G.6.1), такую,
что ехр(±2К) и exp(±2L) оказываются однозначными мероморфными
функциями переменной и.
II. Замечаем, что, согласно G.4.6), каждый элемент матрицы V также
является однозначной мероморфной функцией и. Из G.6.2) следует, что то
же справедливо для любого собственного значения v(и) и, следовательно,
для А(и).
III. Нули А(и) должны содержаться среди нулей правой части G.6.7),
являющейся известной функцией. Поэтому они могут быть вычислены.
Имеется много различных комбинаций нулей, соответствующих различным
собственным значениям. Нормировку А(и) можно затем определить (с точ-
точностью до знака) с помощью G.6.7).
Параметризация К, L
Можно ли использовать эту программу, когда Т Ф Тс, т.е. при к Ф 1?
Если исходить из G.6.1), то очевидным первым шагом было бы введение
промежуточной переменной х, такой, что
. G.8.1)
Решения этих уравнений относительно ехрBАг) и expBL) имеют вид
ехрBЯ) = х + A + х2)\ expBL) = (кх)'1 [1 + A + А:2*2)*]. G.8.2)
Мы получили параметризацию expBA") и expBL), согласующуюся с
G.6.1), но она не является однозначной и мероморфной вследствие наличия
квадратных корней из 1 + х2 и 1 + к2х2.
Когда к = 1, от корней можно избавиться, полагая х = tanw, как это
сделано в разд. 7.7. Тогда 1 + х2 становится полным квадратом, a expBJO

ГЛАВА 7 107
и expBL) — мероморфными функциями и. Для произвольных значений к
такой параметризации с помощью элементарных функций, которая одно-
одновременно превращала бы в полные квадраты 1 + х2 и 1 + к2х2, не сущест-
существует. Но такая параметризация может быть выполнена с помощью эллип-
эллиптических функций. В гл. 15 определены мероморфные функции snw, cnw,
dnw и показано, что они удовлетворяют соотношениям A5.4.4) и A5.4.5),
cn2w = l-sn2w, dn2M = l -k2sn2u. G.8.3)
Сравнивая G.8.2) и G.8.3), легко видеть, что если положить
х = -isn(iu) , G.8.4)
то
ехр(±2К) = сп ш + i sn ш ,
G.8.5)
exp(±2L) = ik~l (dn ш ± l)/sn ш .
В A5.1.6) функции sn, en, dn выражены через тэта-функции Я, Hv G,
Gj. Из G.8.5) и G.8.3) тогда следует
= [k'*Hx(iu)
G.8.6)
exp(±2L) = i[Jt'*e(/) в()]/[**()]
Тэта-функции являются целыми (т.е. всюду аналитическими), поэтому
G.8.6) дает явное представление ехр(±2Д0 и exp(±2L) в виде отношения
целых функций м, т.е. как мероморфных функций.
Эти эллиптические функции возникают также при решении шести- и
восьмивершинных моделей в последующих главах. При некотором зна-
знакомстве с элементарной теорией функций комплексного переменного ими
нетрудно пользоваться; более того, решение оказывается удивительно лег-
легким. На этом этапе я предлагаю читателю просмотреть гл. 15, обратив
особое внимание на три теоремы в разд. 15.3. После того как они будут
поняты, все последующие соотношения не вызовут затруднений.
В соответствии с G.8.1) и G.8.4) соотношение между коэффициентом
взаимодействия К и параметром и может быть записано в следующем
виде:
sniu = sin2iK. G.8.7)
Из A5.5.7) и A5.5.8), полагая а = ;/J, получаем
М, G.8.8)
-Г
так что если К и L — действительные и положительные числа, то
и — также действительная величина, причем 0 < и < Г.
Если к = 1, то интеграл G.8.8) вычисляется, давая первое из уравнений
G.7.3). Действительно, при к = 1 G.8.6) сводится к G.7.3), и большинство

Ю8 МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ PEUIETKF
соотношений этого раздела и разд. 7.7 совпадают. Производя такое сопо-
сопоставление, обнаружим, что если к — 1, то / = оо, /' = »/27г, sn/'w = /tanw
H(iu) ~ ism и и 0(ш) ~ cosw.
В гл. 15 эллиптические функции определены только для
0<к<1, G89)
поэтому для определенности в этом разделе будем предполагать, что к ле-
лежит в этом интервале, т.е. что Т < Тс. В следующем разделе это ограни-
ограничение будет снято.
Вид функции Л (С/)
Теперь нетрудно обобщить программу разд. 7.7, резюмированную в на-
начале этого раздела. Пункт I уже выполнен при помощи равенств G.8.6). Из
них и G.4.6) с очевидностью следует, что каждый элемент матрицы V име-
имеет вид
Уфф=ЩШ)У' G-8ло>
где
h(u) = Щи) в(и) G.8.11)
и многоточие в числителе G.8.10) обозначает целую функцию и.
Как видно из G.6.2) и G.6.6), каждое собственное значение Л представ-
представляет собой линейную комбинацию элементов V с коэффициентами, кото-
которые зависят от к, но не зависят от и. Записывая Л как Л(м), из G.8.10) по-
получаем
A{u)=JhQU)f' <7-812>
где многоточие снова означает целую функцию.
Рассмотрим теперь эффект добавления к и величин 21' и -2/7, где /,
/' — полупериоды эллиптических функций. (Такие нетрадиционные обозна-
обозначения вместо К и К' приняты, чтобы избежать смешивания с коэффициен-
коэффициентами взаимодействия.) Согласно A5.2.5), прибавление II' к и в G.8.5) экви-
эквивалентно замене #, L на —К ± Vi-niy —L ± Vnri. Как показано в разд. 7.7,
это приводит к замене Л на гЛ, где г(= ± 1) — собственное значение пере-
переворачивающей спин матрицы К. Таким образом,
Л(м + 2/') = гЛ(м). G.8.13)
Кроме того, из A5.2.5) следует, что прибавление -2/7 к и в G.8.5) экви-
эквивалентно замене A, L на К ± Vnri. L ± Vn^i. Поскольку сумма г' + s' в
G.4.6) является четным числом, такая замена оставляет матричные элемен-
элементы V без изменения, так что
Л(м - 2/7) = Л(м) . G.8.14)

ГЛАВА 7 109
Мы можем воспользоваться теперь важной теоремой 15 (в) из разд. 15.3.
В соответствии с G.8.13) и G.8.14) функция является двоякопериодической,
в то время как, согласно G.8.12), эта функция имеет 2р полюсов в преде-
пределах прямоугольника периодов. Следовательно,
Л(и) = р еЯи [h(iu)]-P П H(iu - Щ , G.8.15)
где i/j, ... , Uty — нули А (и) в пределах прямоугольника периодов, р и
X — константы, причем выбор X должен обеспечивать выполнение G.8.13)
и G.8.14).
Выражение G.8.15) представляет собой требуемое обобщение G.7.9).
Таким образом, пункт II выполнен.
Нули функции Л (и)
Следующим шагом должно быть определение нулей i/j, ... , и2 функ-
функции А(и) при помощи тождества G.6.7). Заменим сначала и на и + /' в
G.8.5). Используя A5.2.6), находим, что это эквивалентно замене К, L на
L + !/2 7г/, —К. Поэтому тождество G.6.7) после подстановки G.8.1) и
G.8.4) приводится к виду
Л(и) Л(и + /') = (к*.) + (-2 sn ш)яг. G.8.16)
Это соотношение является обобщением G.7.2). С помощью G.4.5),
G.8.11), G.8.15) и A5.1.6) оно приводится к виду
2р
р2 ехр[АBм + /')] ПH(iu - шЛ Щш - ш, 4- //')=
r rL v 'J/-i v ;/ v ; ' G.8.17)
= D/ЛУ[04"(ш) 4- rHAP{iu)],
что является обобщением G.7.10).
Правая часть G.8.17) обращается в нуль, когда
Выражение в левой части G.8.18) представляет собой двоякопериодическую
функцию iu с периодами 2/, 2/7'. Оно имеет один полюс кратности Ар в
прямоугольнике периодов, поэтому, согласно теореме 15F), оно имеет в
этом прямоугольнике Ар нулей. Чтобы определить их координаты, поло-
положим
и=-Н'-*ф G-8.19)
Тогда с помощью A5.4.12) уравнение G.8.18) приводится к виду
ехр[4фАш(ф)] 4- г = 0. G.8.20)

110
МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
-7
| X • X • X <
-1\ 0
1 X • X • X '
-f
X • X • X |
/|
X • X • X f
J
Рис. 7.3. Размещение Ар нулей правой части
G.8.17), а именно ш = 0y=F ViiV, на комплексн-
комплексной / — и -плоскости. Крестиками обозначены
нули для г — +1, кружками — для г = — 1.
Штриховая линия — периметр прямоугольника
периодов.
Определим 0у так же, как в G.7.14), Тогда равенство G.8.20) будет без-
безусловно выполняться, если ф = 0у, где
; = !,...,2р.
G.8.21)
Как показано в разд. 15.4, Ат@) — действительная функция, возраста-
возрастающая монотонно от — 7г/2 до 7г/2 при увеличении ф от — / до /. Поскольку
0 < 6j ^ 7г, уравнение G.8.21) имеет одно действительное решение, такое,
что — / < 0у ^ /. Решения с различными У не совпадают.
Из A5.2.6) следует, что если и является решением уравнения G.8.18), то
это справедливо также для и + Г. Таким образом, G.8.18) имеет Ар реше-
решений
«,= +*/'-!>/, ) = 1,...,2р. G-8.22)
Будучи определены с точностью до целого числа периодов И', 2/7, все они
различны, так что мы нашли Ар нулей правой части G.8.17). Их располо-
расположение на плоскости / — и показано на рис. 7.3.
Левая часть G.8.17) имеет Ар нулей, объединенных в пары Uj и Uj - Г.
Таким образом, общее решение уравнения G.8.17) имеет вид
где
Уу=±1, 7=1,..., 2р.
G.8.23)
G.8.24)
Мы получили обобщение решения G.7.16). (Значение j = 2/7, когда г = — 1,
опущено в разд. 7.7, так как при к — 1 / и 0^ стремятся к бесконечности.)
Как и в разд. 7.7, не все решения G.8.23) допустимы. Причину этого те-
теперь даже легче понять, чем в том случае, если учесть ограничение A5.3.7),
которое теорема 15(в) налагает на положение нулей двоякопериодической
функции. В применении к уравнениям G.8.12) — G.8.15) это ограничение
имеет следующий вид:

ГЛАВА 7 jl,
и, + . . . + «2р = (р + 21') Г + /[i(l - г) + 21] I, G.8.25)
где / и /' — целые числа.
Если г = +1, то фу распадаются на пары (ф, -ф). То же справедливо в
случае г = -1, за исключением фр = 0 и ф^ = /. Подставляя G.8.23) в
G.8.25), мы видим, что равенство мнимых частей всегда выполняется, в то
время как для равенства действительных частей необходимо, чтобы при
г = ±1
Yi + • • • + Yip = 2p - 4 X целое число, G.8.26)
как в G.7.20). Таким образом, г и все yj9 кроме одного, могут быть выбра-
выбраны независимо, что дает 2^ = 2" собственных значений. Этого можно бы-
было ожидать, поскольку V и W являются матрицами 2" х 2".
Подставляя эти результаты для wlf . . . , u^ в G.8.15) и выбирая X та-
таким образом, чтобы удовлетворялись G.8.13) и G.8.14), получаем
2р
А(и) = р[А(ш)Р Ц е"^и/4/Я(ш - ф7- + J/ у,-/'). G.8.27)
Этот результат можно несколько упростить путем возведения в квадрат
[Обеих частей равенства и использования соотношения A5.2.4) между
'0(ы + //') и 0(м), что дает
2P
Л2(") = p' П {Ш ~ Ф> + *' ?' > 0(ш - Ф/" Ь у>/ ) G 8 28)
W ^ М Я(ш) 0(ш)
где р' — еще одна константа.
С помощью A5.1.6) это равенство может быть записано в виде
\\и) = D П jfc* sn (ш - ф/ + J i 7}Г) , G.8.29)
где Z) не зависит от у{, . . . , у^ и определяется выражением
^, " ' ' Г/ЧЛ/" ^ -г'4 G.8.30)
Р М Я(ш) 0(ш)
Согласно A5.2.4) и A5.2.3), D является двоякопериодической функцией
ш с полюсами порядка 2/7 в точках ш = 0 и /' и имеет 4/7 простых нулей в
точках ш = фу ± '/г//', у = 1, . . . , 2/7. Как видно из G.8.18) — G.8.22),
одной из таких функций является
Поэтому отношение D к выражению G.8.31) является целой двоякопери-

112. МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
одической функцией ш. Согласно теореме 15(а), оно должно быть констан-
константой.
Таким образом, с точностью до постоянного нормирующего множите-
множителя D в G.8.29) можно заменить выражением G.8.31). Нормирующий мно-
множитель легко определить из G.8.16), после чего получаем
ip G.8.32)
X Д#8П(ш-фу+*|уу/'),
где
т= 4-1 при г = 4-1 , G.8.33)
= -I при г = -1.
7.9. ОБЩИЕ ВЫРАЖЕНИЯ
ДЛЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ
Использовав эллиптические функции и в особенности связанную с ними
теорему факторизации 15(в), чтобы вычислить собственные значения Л, мы
можем теперь эти функции исключить. Из G.8.21), A5.4.12), A5.4.4) и
A5.4.5) следует
ft*sn@y - ИГ) = -ехр(/0у), G.9.1)
сп(ф; -ИГ) с1п(фу - i i /') = -i ft* exp(/0y)cy, G.9.2)
где
с; = ft A + ft2 - 2ft cos20y)*. G.9.3)
Отсюда с помощью дополнительной формулы A5.4.21) получаем
ft*sn(Ju - ф + Jf /') = cn/udnm -iftcysnm
' exp(-«0y) - ft exp(/0y) sn2 (ш)'
Кроме того, из G.8.5) имеем
sinh 2К = -i sn ш, cosh 2А^ = en ш,
cosh 2L = i dn iul(k sn ш), sinh 2L = //(ft sn iu),
в то время как из A5.2.6) получаем
ft* sn(/u - фу - i i Г) = [ft* sn(iu — фу + 41 /')] -\ G.9.6)
С помощью этих соотношений перепишем G.&.J2) (опуская явную зави-
зависимость Л от и) в следующем виде:
ip
Л2 = r(~4y?[(sinh2LJ^ + r(sinh2/O2p] Пыу'. G-9-7)

ГЛАВА7 ИЗ
ГДС cosh IK cosh 2L + q
^ " exp(Wj) sinh 2АГ + exp (-i0y) sinh 2L * (?'9'8)
Аналитическое продолжение на область Т ^ Тс
Приведенный результат получен при условии к < 1, так как только в
этом случае можно пользоваться определениями для эллиптических функ-
функций из гл. 15. Но для конечных р каждое собственное значение должно
быть алгебраической функцией ехрBАг) и expBL), поэтому соотношение
G.9.7) может быть аналитически продолжено на область к ^ 1, т.е. на
т > т
Единственная возникающая при этом трудность связана со знаками ве-
величин Cj. Если 0 < 0у < 7г, то нет никакой проблемы: выражение G.9.3) по-
положительно при к < 1 и стремится к строго положительному пределу, ког-
когда к — 1, так что аналитическим продолжением G.9.3) является положи-
положительное значение квадратного корня.
С другой стороны, если г = -1 и j = 2р, то в}г = 7г и для к < 1 G.9.3)
дает
с2р = A - k)lk if г = — 1. G.9.9)
Эта функция стремится к нулю, когда к — 1, и ее аналитическое продолже-
продолжение, очевидно, отрицательно при к > 1.
Таким образом, формулы G.9.7), G.9.8) и G.9.3) применимы не только
при к < 1, но и при к ^ 1 при условии, что в G.9.3) выбирается положи-
положительный знак во всех случаях, кроме одного, когда г — — \,j=2p, k ^ \.
Подсчет числа собственных значений
Недостаток используемого здесь метода, как и любого метода, не свя-
связанного с явным представлением трансфер-матрицы, состоит в том, что с
его помощью мы можем лишь показать, что любые собственные значения
матрицы VW должны иметь вид G.9.7) при подходящем выборе ух, . . . ,
72р. Но этот метод не позволяет найти, сколько собственных значений
имеется при заданном выборе у{, ... , у^ и имеется ли вообще хотя бы
одно.
Существует два пути преодоления этой трудности: можно рассмотреть
предел низких или высоких температур, когда по крайней мере некоторые
собственные значения (в частности, максимальное) могут быть легко од-
однозначно идентифицированы, или можно провести сравнение с результата-
результатами прямого вычисления с помощью спинорных операторов [143]. Так или
иначе, выясняется, что для каждой комбинации значений г и yv . . . , у2р,
удовлетворяющей G.8.26), имеется одно и только одно собственное значе-
значение, определяемое выражением G.9.7).

114 МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
Максимальное собственное значение и свободная
энергия
В термодинамическом пределе статистическая сумма z определяется вы-
выражением G.2.5). Так как решетка имеет т рядов, состоящих из 2/7 узлов,
то общее число N узлов равно Imp. Поэтому из A.7.6) и G.2.5) получаем
следующее выражение для свободной энергии / на один узел:
-flkBT = BрУ1 In Amax , G.9.10)
где кв — постоянная Болыдмана, а Лтах — наибольшее по модулю соб-
собственное значение.
Из G.6.1), G.9.3) и G.9.8) следует, что для действительных значений
К и L
cosh 2K cosh 2L + с,
= G911)
причем для положительных К и L
0 ^ с/ ^ cosh 2К cosh 2L . G.9.12)
Следовательно, l/xyl ^ 1, так что правая часть G.9.7) максимизируется
выбором 7i = У г — • • • = Ч2р = + 1» который допускается условием
G.8.26). Произведение знаменателей ц{, ... , /х^, входящих в G.9.7) и
определяемых формулой G.9.8), тогда может быть вычислено с помощью
G.7.14). Оно сокращается множителем, стоящим впереди в G.9.7), остав-
оставляя только АР и приводя к равенству
Лтах = П 2(cosh 2K cosh 2L + cj), G.9.13)
которое справедливо как при г = + 1, так и при г = — 1. Однако, согласно
теореме Перрона — Фробениуса [94], максимальное собственное значение
матрицы, составленной из положительных элементов, соответствует соб-
собственному вектору, все компоненты которого положительны. Согласно
G.6.2), это может быть только в случае г = +1.
Определим
F@) = In {2 [cosh 2К cosh 2L + AT1 A + k2 - 2k cos 26)*]}. G.9.14)
Тогда из G.7.14), G.9.3) и G.9.13) при г = + 1 следует
In Лтах = i 2 F[n(j - i)/2p]. G.9.15)
/=i
Написанное выражение представляет собой сумму членов lAFFj), где 0Р
. . . , #2р распределены равномерно в интервале @, 7г). Поэтому в пределе
больших р оно сводится к интегралу от функции ViF(B), деленной на вели-
величину субынтервала ir/lp. Таким образом, G.9.10) принимает вид

ГЛАВА7 115
d<9. G.9.16)
Это главный результат данной главы — свободная энергия модели
Изинга на квадратной решетке в термодинамическом пределе.
7.10. СЛЕДУЮЩИЕ ЗА МАКСИМАЛЬНЫМ
СОБСТВЕННЫЕ ЗНАЧЕНИЯ;
ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ,
КОРРЕЛЯЦИОННАЯ ДЛИНА
И НАМАГНИЧЕННОСТЬ ПРИ Т < Тс
В этом разделе, как правило, предполагается, что 0 < к < 1.
Асимптотическое вырождение и поверхностное натя-
натяжение
Каково следующее за максимальным собственное значение трансфер-
матрицы? Ясно, что одним из кандидатов является Aj — собственное зна-
значение, которое получаем, полагая г = — 1, ^j = . . . = 7^7 = +1- Соглас-
Согласно G.9.13), G.9.14), G.9.3) и G.7.14), оно определяется выражением
In Ai = i 2 F{njl2p\ при к < 1. <7.10.1)
Две суммы в G.9.15) и G.10.1) различаются только членами, которые
экспоненциально малы, когда р велико. Чтобы это увидеть, представим
F{6) в виде ряда Фурье:
2 amcos2md. G.10.2)
m = 0
Подставим это выражение для FF) в G.9.15) и G.10.1) и поменяем поря-
Д®к суммирования по j и по т. Тогда суммирование по j легко выполняет-
выполняется и дает
In Amax = р(а0 -а2р + аЛр-а6р+...),
G.10.3)
In Ai = р(а0 + а2р + аАр + а^ + ...).
Это преобразование является частным случаем формулы суммирования
Пуассона [68]. Оно идеально подходит для оценки Лтах и Ах при больших
Р* так как ат обычно экспоненциально стремятся к нулю при увеличении
•flil. Чтобы увидеть это, положим
z = expB/0) G.10.4)

Ш> МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
и рассмотрим функцию F@), определяемую G.9.14), как функцию z. Она
имеет точки ветвления при z = О, к, к'1 и оо и является аналитической
функцией в области к < \z\ < k~{.
Фурье-разложение G.10.2) можно записать в виде
F@) - i 2 am(zm + z~m), G.10.5)
m = 0
что представляет собой ряд Лорана. Поскольку функция F аналитична на
окружности kl = 1, этот ряд сходится. Более сильное утверждение состо-
состоит в том, что, поскольку функция F аналитична в области к < \z\ < к~1
и сингулярна в точках z - к, к~\ ряд G.10.5) должен сходиться в области
к < \z\ < к'1 и расходиться, когда z = к или к~1. Из критерия сходимо-
сходимости по отношению величин последовательных членов ряда непосредственно
следует
ат~кт, т-+оо. G.10.6)
Поскольку Л, < Лтах, из G.10.3) теперь следует, что, когда р велико,
Л1/Лтах=1-0(^). G.10.7)
Поэтому при к < 1 два наибольших собственных значения Лтах и А{ яв-
являются асимптотически вырожденными в том смысле, что их отношение
отличается от единицы на величину, экспоненциально убывающую с рос-
ростом горизонтального размера решетки.
Скорость этого экспоненциального убывания служит мерой величины
поверхностного натяжения s, как можно показать с помощью следующих
аргументов [88].
Рассмотрим величину
ZN = Trace (VW)m/2R , G.10.8)
где К, W — трансфер-матрицы, связывающие ряды спинов, а
R — оператор обращения спина, определенный посредством G.3.14). Как и
G.2.3), это статистическая сумма решетки, состоящей из т рядов, но с ан-
антициклическим условием, требующим, чтобы спины верхнего ряда были
перевернуты по отношению к спинам нижнего ряда.
В упорядоченном ферромагнитном состоянии в пределах какой-то обла-
области решетки все спины направлены либо преимущественно вверх, либо пре-
преимущественно вниз. Допустим, что в нижней части решетки они направле-
направлены преимущественно вверх. Тогда в силу антициклического граничного ус-
условия в верхней части решетки они должны быть направлены преимущест-
преимущественно вниз, как это показано на рис. 7.4.
Где-то в промежуточной области должна существовать линия, пересека-
пересекающая решетку и разделяющая области с различной преимущественной ори-
ориентацией спинов. Так как в ряду имеется п узлов, эта линия вносит допол-
дополнительный вклад ns в величину свободной энергии, где s — поверхностное

jggABA_7 LIZ
J%c. 7.4. Две области, возникающие при низких — — — — 4- —
температурах в результате требования, чтобы спины _ ~>*;-~/>~ _ ~ _ ~ _
Лйрхнего ряда были направлены противоположно спинам -'+ + + ••., _ ,.-+ \
Нижнего ряда. Ниже разделительной линии (показанной + - + +'v'+ +
|цудактиром) имеется «море» спинов, направленных вверх, с _ "*" , ~ , +__"*" , "*"
||)стровками» спинов, направленных вниз. Обратная + + + + +
Ситуация имеет место выше разделительной линии. + + — + + +
цатяжение на единицу длины. Таким образом,
-kBTlnZ'N = Nf+ns, G.10.9)
fде / — обычная свободная энергия на один узел решетки, определяемая с
помощью A.7.6). Поэтому
ZJv/Z/v = cxp(-ns/kBT). G.10.10a)
Это соотношение не совсем верно: оно дает правильный вклад в стати-
статистическую сумму от одной линии раздела, но можно провести'много таких
щиний, как нетрудно увидеть, рассматривая предел нулевой температуры.
8 этом случае все спины выше линии раздела должны быть направлены
ШИиз, а спины ниже ее — вверх, и длина линии должна составлять 2/7 пери-
периодов решетки, что представляет собой минимально возможную длину.
Все такие конфигурации минимизируют энергию при заданных гранич-
Пых условиях и потому являются равновероятными. Если ячейка, в кото-
^й расположен певый конец линии, задана, то имеется Bп)\/(п\J таких
Йний: это число путей равной длины, по которым в городе с прямоуголь-
прямоугольной планировкой можно добраться от пересечения нулевой стрит и нулевой
|(веню до пересечения /7-й стрит и /7-й авеню. Поэтому правую часть
f7.10.10a) следует умножить на этот множитель, но поскольку при боль-
большом /7 этот множитель сводится к экспоненте, то его можно включить в
Определение s.
С другой стороны, имеется т рядов и, следовательно, т/2 ячеек, в ко-
которых может находиться левый конец линии раздела. Таким образом, пра-
правая часть G.10.10а) должна быть умножена и на этот множитель. Его
Нельзя включить в 5, и он, очевидно, сохраняется при ненулевых темпера-
температурах, так что G.10.10а) следует заменить на
Z'N/ZN = \m exp(-nslkBT). G.10.106)
Из G.2.3) и G.10.8) следует, что

JJ8 МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
Поскольку R коммутирует с V и W, этот результат в свою очередь можно
записать в виде
\т txp(-ns/kBT) = 2 r/Af/2 Af , G.10.12)
i ' i
где Л? — собственные значения VW, a r- — соответстующие собственные
значения R.
Когда т велико, вклад в суммы в G.10.12) вносят только два наиболь-
наибольших собственных значения Лтах иЛр Соответствующие собственные значе-
значения R равны +1 и — 1, так что
кт __ кт
km exp(-ns/kBT) = ^\Vm- G-10-13>
Положим
С=1-Л1/Лти, G.10.14)
тогда G.10.13) принимает вид
km txp(-ns/kBT) = | ~ || ~ ^. G.10.15)
Согласно G.10.7), е экспоненциально убывает с ростом п. Определением
с помощью G.10.9) имеет смысл только в том случае, если шип велики и
одного порядка величины, откуда следует малость е в G.10.15); поэтому
\m exp(-ns/kBT) = \me. G.10.16)
Отсюда и из G.10.14) следует
Ai/Amax =1-0 {exp(-ns/kBT)}. G.10.17)
Это общий результат, применимый к любой двумерной ферромагнит-
ферромагнитной системе при Т < Тс. Сравнивая его с G.10.7), мы видим, что для моде-
модели Изинга
5/ВД = *. G.10.18)
Таким образом, поверхностное натяжение 5 велико и положительно при
низких температурах (к < 1), убывает с ростом температуры (увеличением
к) и обращается в нуль при критической температуре (к = 1).
Корреляционная длина
Каково следующее по величине после Лтах и А1 собственное значение
матрицы (VW)Vll Согласно G.9.7) и G.8.26), его можно получить, полагая
отрицательными знаки двух ту» соответствующих наименьшим из I /xy I. По-
Поэтому для г = + 1 из G.9.11), G.9.3) и G.7.14) получаем, что следующее по
величине собственное значение Л2 соответствует значениям

ГЛАВА 7 П9
Y\ = Y2p = -l, У2= • • • = Y2p-i= +1 , G.10.19)
Л2/Лтах=±(^2р)-1. G.10.20)
Поскольку в^ = тг - 0Р из G.9.8) следует, что /х^ = -/х*, так что,
согласно G.9.11),
Л2 _ cosh 2K cosh 2L - с\
Л^ " cosh 2АГ cosh 2L + ci ' G.10.21)
где для удобства взят нижний знак в G.10.20).
В пределе больших р величина вх стремится к нулю, а сх стремится к
II — к I /к у так что
Л2/Лтах = Л , G.10.22)
где
cosh2# cosh2L-\l-k\/k 7 {Q
cosh 2К cosh 2L + |1 -fc|/fc"
Аналогичные аргументы применимы в случае г = — 1. Если теперь взять в
ткачестве Л2 следующее по величине собственное значение для г = — 1, то
при больших /7 мы снова получим результат G.10.22) с точностью до несу-
несущественного знака.
Таким образом, все собственные значения Лу, кроме Лтах и Лр удовлет-
удовлетворяют (при /7 — оо) неравенству
1М^ЛЛтах, G.10.24)
где 0 < А < 1, если к Ф 1. Этот результат оправдывает упрощение при
переходе от G.10.12) к G.10.13).
При условии что все собственные значения Лу являются действительны-
действительными числами, отношение Л2/Лтах оказывается связанным с корреляционной
длиной ?. Чтобы увидеть это, допустим, что Я, Q — два каких-то узла ре-
решетки, а ору oq — соответствующие им спины. Тогда в соответствии с
A.4.4) и A.8.1) среднее значение произведения opoQ равно
(oPoQ) = Zn1 2 opOq ехр К 2 OiOj + L 2 o{ok , G.10.
о L 0\» 0.*) J
.25)
где внешняя сумма берется по всем значениям всех спинов, а внутренние
суммы имеют тот же смысл, что и в F.2.1).
Используя те же соображения, которые привели к G.2.1), мы можем за-
записать G.10.25) в виде
(oPoQ) = ZNX 2 2 ... 2 oPoQ Кф1,Л,фз VW • • • ™Фт,Фг • G.Ю.26)
Ф\ Фг Фт
Пусть ф — набор из п спинов {о{, . . . , ап], a Sj — диагональная матри-

]20 МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
ца 2п х 2п со следующими элементами:
G.10.27)
= Oh ф' = ф .
Тогда, если Р и Q — первые узлы в рядах х и у соответственно, причем но-
номера х и у являются нечетными, то G.10.26) можно переписать в виде
{opoQ) = Zul Trace VW. . . VWsx VW. . .
G.10.28)
x VWsxVW. . .VW,
где s{ возникают перед матрицами К, стоящими на местах х и у в ряду со-
сомножителей. Таким образом,
= Z*1 Trace (VW)^-^Sl (VW)h(y'x) sl (VW)*(m-y+1). G.10.29)
Доказательство продолжается почти параллельно тому, которое было
проведено в разд. 2.2 для одномерной модели Изинга. Пусть U — матрица
собственных векторов матрицы VW, a D — соответствующая диагональ-
диагональная матрица с диагональными элементами D-- = Лу, j = 1, 2, 3, . . . . Тог-
Тогда для всех целых х имеем
(VW)xf2= UDxUl. G.10.30)
Используя этот результат, перепишем G.10.29) в виде
(aPaQ) = Z^^XtijAJ-'t^Ar^-^ G.10.31)
где f" '
^(IT^iI/V G.10.32)
Пусть теперь т — оо. В сумме по / в G.10.31) доминирующим оказыва-
оказывается член с Л, = Лтах. Присвоим ему индекс 0. Используя G.2.5), получаем
(opoQ) = 2 tOj (л/лтах;г * tj0. G.Ю.ЗЗ)
)
Из G.3.14) и G.10.27) следует
SlR = -Rsu G.10.34)
так что, в то время как трансфер-матрица VW коммутирует с матрицей /?,
спиновый оператор sx с ней антикоммутирует.
Поскольку R2 = /, имеется представление, в котором
R=(! °\ G.10.35)
Из упомянутых выше коммутационных и антикоммутационных свойств
следует, что в этом представлении матрицы К, W и U все являются

ГЛАВА 7 121
блочно-диагональными, т.е. имеют вид
в то время как slt а следовательно, и U lslU имеют вид
о\
О
Отсюда сразу следует, что
tij = О кроме случая г,- = -rh G.10.36)
где ri и-rj — собственные значения /?, соответствующие Л,- и Лу.
Так как собственное значение Ло = Лтах соответствует. г0 = + 1, то это
означает, что tQj и tjQ в G.10.33) не обращаются в нуль только в том случае,
когда гу- = — 1. Поэтому суммирование можно ограничить этими значения-
значениями индекса у, что дает
(opOq) = Го^1о(Л,/Лтаху -* + t02t20(A2/Amaxy -*+.... G.10.37)
В пределе п — оо имеем Л2 = Лтах. При условии что все Л2, Л3, . . . яв-
являются действительными, для больших разностей у — х получаем
(<JP<7q) = foi'lO + СКЛг/ЛтахУ*] . G.10.38)
Корреляционная функция gPQ определена соотношением A.7.21), кото-
которое в большинстве случаев можно представить в виде
gpQ = {oPoQ)- lim (<jP0q) , G.10.39)
у-Х-+°С
т.е. gpQ представляет собой разность между средним {opOQ> и его предель-
предельным значением для далеко расположенных узлов Р и Q
При таком определении корреляционной функции из G.10.38) следует,
что для больших разностей у — х
gP2 ~ (Л2/Лтах;Г \ G.10.40)
Так как у — х есть расстояние между узлами Р и Q, то из определения
A.7.24) корреляционной длины ? следует
Г1 = 1п(Лтах/Л2) . G.10.41)
Эта весьма общий результат, но его нельзя сразу же применить к рас-
рассматриваемой задаче. Чтобы увидеть это, заметим, что узел Q расположен
вертикально над узлом Р, так что gPQ представляет собой вертикальную

122 МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
корреляционную функцию на квадратной решетке, одна из диагоналей ко-
которой направлена по вертикали. Если поменять местами К и L, то она дол-
должна перейти в горизонтальную корреляционную функцию. Но если Р и Q
расположены в одном горизонтальном ряду в положениях 1 и у, то повто-
повторение вывода G.10.26) — G.10.33) дает
(OpOq) = (U~l Stfj U)oo . G.10.42)
Здесь U — матрица собственных векторов матрицы VW, которая, как мы
установили, зависит от К и L только через к. Таким образом, gPQ и ? так-
также должны зависеть только от к, в то время как из G.10.22), G.10.23) сле-
следует, что для Лтах/Л2 это неверно.
Это кажущееся противоречие возникает из-за того, что трансфер-
матрица VW не является, вообще говоря, симметричной матрицей; поэто-
поэтому не все ее собственные значения действительны. Собственное значение Л2
является просто наибольшим в целой полосе собственных значений, разли-
различающихся аргументами. В пределе больших п эта полоса становится непре-
непрерывной, и вклад от у = 2 в G.10.33) может быть компенсирован вкладами
от собственных значений, которые сколь угодно близки к Л2 по модулю,
но различаются своими аргументами. Было показано [120, 122], что подоб-
подобная ситуация имеет место в случае восьмивершинной модели, обсуждаемой
в гл. 10.
К счастью, в рассматриваемом случае легко исправить положение, по-
поскольку ? может зависеть только от к. Для заданного значения к рассмот-
рассмотрим изотропный случай К = L. Согласно G.4.2), трансфер-матрица тогда
будет симметричной, так что ее собственные значения будут действитель-
действительными, и формула G.10.41) окажется правильной. Используя G.6.1),
G.10.22) и G.10.23), для 0 < к < 1 получаем
Г1= "In А. G.10.43)
Сравнивая этот результат с G.10.18), мы видим, что поверхностное на-
натяжение s и корреляционная длина ? удовлетворяют простому точному со-
соотношению
s!==kBT. G.10.44)
Спонтанная намагниченность
Согласно A.7.22), намагниченность М определяется выражением
М = (оР). G.10.45)
При вычислении этого среднего для Т < Тс и Н = 0 следует соблюдать
осторожность. Для рассматриваемой в этой главе системы, размеры кото-
которой конечны, а внешнее поле отсутствует, среднее значение (ар) должно
быть равным нулю, так как каждому состоянию с ор = +1 соответствует
равновероятное состояние (получаемое переворотом всех спинов) с
ор = -1. Из рис. 1.1 ясно, что нужно сделать. При Н = 0 намагничен-
намагниченность может принимать любое значение между Мо и -Мо, где спонтанная

ГЛАВА 7 123
намагниченность Мо определяется выражением
Мо= lim+(aP>, G.10.46)
т.е. среднее (ар) должно быть вычислено для Н > 0 в термодинамическом
пределе, а затем следует устремить Н к нулю.
Но для Н > 0 корреляция gPQ, определяемая с помощью A.7.21), несо-
несомненно, стремится к нулю при удалении узлов Р и Q друг от друга. По-
Поскольку система трансляционно-инвариантна, то (ор) = <<Jq>, откуда сле-
следует
(оРJ= \\m^(opOQ). G.10.47)
Это соотношение можно принять в качестве определения (ар) для
Н > 0. При Н — 0 оно дает определение Мо, так что с помощью G.10.38),
G.10.46) и G.10.47) получаем
Мо = (foifio)*. G.10.48)
Вычисление этой величины является весьма сложной в техническом от-
отношении задачей, поэтому я отсылаю читателя к превосходной книге [164].
Впрочем, одно свойство можно легко вывести из вышеизложенного: соб-
собственные векторы матрицы VW и, следовательно, U зависят от К и L
только через к. Поэтому, как видно из G.10.32), то же справедливо для t^.
Тогда из G.10.48) следует
Мо = функция только от к. G.10.49)
На самом деле Онсагер [185] обнаружил, а Янг [262] строго показал,
что
Мо = A - к2)ш = к'щ. G.10.50)
Учитывая всю трудность вычисления, это изумительно простой резуль-
результат. Интересно, что какой-либо простой способ его получения так и не
найден. Вывод, использующий угловые трансфер-матрицы и применимый
к более общей восьмивершинной модели, дан в разд. 13.7.
7.11. СЛЕДУЮЩЕЕ ЗА МАКСИМАЛЬНЫМ
СОБСТВЕННОЕ ЗНАЧЕНИЕ
И КОРРЕЛЯЦИОННАЯ ДЛИНА ДЛЯ Т > Тс
Как и в предыдущем разделе, пусть Aj — максимальное собственное
значение для г = — 1, но теперь к > 1.
В соответствии с G.9.9) в рассматриваемом случае с^ — отрицательная
величина. Формула G.10.1) все еще верна, если F(%) определять с помощью
G.9.14) с отрицательным знаком перед корнем, однако более разумно со-
сохранить положительный знак у корня для всех В, но скорректировать член

J24 МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
j' = 2р в G.10.1), что дает
1пЛ, = ЛпЛ + i 2 F(jt//2/?) , G.11.1)
I 1
где величина Л определяется выражением G.10.23).
Можно снова использовать аргументацию, связанную с цепочкой ра-
равенств G.10.2) — G.10.6), чтобы показать, что для больших р суммы в
G.9.15) и G.11.1) отличаются экспоненциально малыми членами. Единст-
Единственное отличие от прежнего случая заключается в том, что область анали-
аналитичности функции F(B) теперь к~х < \z\ < к, так что ат ~ к~т.
Вычитая G.9.15) из G.11.1), получаем для больших р
Л,/Лтах = Л*. G.11.2)
Поскольку А < 1, асимптотического вырождения Aj и Лтах больше не
существует, и поверхностное натяжение в соответствии с G.10.13) отсутст-
отсутствует.
Все другие собственные значения по-прежнему удовлетворяют G.10.24),
так что они меньше, чем Aj. Если собственные значения VW все действи-
действительные, то формула G.10.33) при больших значениях у - х дает
(ОрО0)~А^-*). G.11.3)
Как и в предыдущем разделе, этот результат может быть правильным
только для К = L, поскольку {орОд) является функцией только к. Поэто-
Поэтому, согласно A.7.21) и A.7.24), корреляционная длина ? определяется выра-
выражением
?=2/lnJfc G.11.4)
для всех К, L, таких, что к > 1.
Эта величина мала при высоких температурах (больших /г), увеличива-
увеличивается с уменьшением температуры (уменьшением к) и становится бесконеч-
бесконечно большой при критической температуре (к = 1). Отметим, что высоко-
высокотемпературная формула G.11.4) отличается от низкотемпературной
G.10.43) множителем -2. Спонтанная намагниченность отсутствует.
7.12. КРИТИЧЕСКОЕ ПОВЕДЕНИЕ
Согласно G.6.1) и F.2.2),
к = [sinhBJ/kBT) sinhBJ'/kBT)]-1, G.12.1)
где У и У — энергии взаимодействия в модели Изинга в двух направлени-
направлениях. Обычно У и У считаются фиксированными, а температура Т изменяет-
изменяется.
При монотонном увеличении Т от 0 до оо величина к тоже монотонно
возрастает. Таким образом, величина к является мерой температуры.

ГЛАВА 7 125
Свободная энергия и показатель а
Свободная энергия определяется выражениями G.9.14) и G.9.16). Для
положительных к и действительных в функция FF) является аналитической
функцией не только 0, но также cosh IK cosh 2L и к всюду, кроме 0 = 0 и
к = 1. Таким образом, / является аналитической функцией К и L всюду,
кроме, может быть, случая, когда к = 1.
Поскольку квадратный корень в G.9.14) обращается в нуль при 0 = О и
к = 1, доминирующее сингулярное поведение / можно определить путем
разложения F(B) по степеням этого квадратного корня, рассматривая толь-
хо два первых члена разложения, т.е. полагая
F{6) = lnB cosh 2 A: cosh 2L)+
G.12.2)
+ AT1 sech 2K sech 2L A + k2 - 2k cos 20)*.
Подставляя это выражение в G.9.16), мы видим, что вклад в/первого чле-
члена всегда аналитический, даже при к = 1, так что доминирующая сингу-
сингулярная часть /, обозначаемая далее /5, определяется только вторым чле-
членом. Используя соотношение cos 20 = 2cos20 - 1 и заменяя переменную
интегрирования в на тг/2 - в, получаем
? > GЛ2'3)
як cosh 2K cosh 2L
где
kx = 2k{l{\ + Jfc) G.12.4)
и E(k) — полный эллиптический интеграл второго рода:
Е(к) = |Ли A - к2 sin20)* дв . G.12.5)
Jo
Вблизи значения к = 1 этот интеграл описывается приближенной фор-
формулой [101]
Е(к) ~ 1 + \ A - к1) 1п[16/A - к1)] , G.12.6)
так что из G.12.3), пренебрегая снова аналитической частью/, получаем
,_ (! + *)(!-*)' „^ GЛ2.7)
2пк cosh 2Л: cosh 2L
1-А
Ясно, что функция / действительно сингулярна при А: = 1.
Критическая температура может быть определена либо как такое значе-
значение Г, для которого / является сингулярной функцией, либо как такое, для
которого спонтанная намагниченность или поверхностное натяжение исче-
исчезает, либо как такое, для которого корреляционная длина ? становится бес-
бесконечной. Согласно любому из этих критериев, теперь очевидно, что мо-
модель Изинга на квадратной решетке имеет одну и только одну критическую

J26 МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
температуру Гс, определяемую условием к = 1, т.е.
квТс) sinhB/7Aerc) = 1. G.12.8)
Вблизи Т = Тс величина к — 1 пропорциональна Т - Тс. Таким обра-
образом, определение A.1.3) можно заменить следующим определением:
t = k-l, G.12.9)
а из G.12.7) можно получить
fs^flnlt]. G.12.10)
Этот результат можно записать в виде
1 - \t\~a
/,oc/Mim '' . G.12.11)
а-+0 ОС
Сравнивая это выражение с определениями A.7.7) — A.7.9) термодинами-
термодинамических величин w, С и критических показателей а и а', мы видим, что в
смысле указанного предельного соотношения
ос =а> = 0. G.12.12)
Другие показатели
Из G.10.18), G.10.50), G.10.43) и G.11.4) следует, что волизи Тс поверх-
поверхностное натяжение 5, спонтанная намагниченность Мо и корреляционная
длина ? ведут себя следующим образом:
s~-t, Мо~(-Ош, Г-+0-,
G.12.13)
Сравнивая эти результаты с A.7.34), A.1.4) и A.7.25), мы видим, что
соответствующие показатели /*, C, v, v' существуют и равны:
/*=1, /3=4, v=v' = l. G.12.14)
Таким образом, соотношения A.2.15) и A.2.16) выполняются.
Поскольку двумерная модель Изинга решена только при Н = 0, полная
проверка гипотезы подобия невозможна. Вместе с тем имеется большое
количество численных результатов [38, 75, 226] и математических теорем,
применимых к модели во внешнем поле. Например, Абрагам [1] строго по-
показал, что
7=7/4 G.12.15)
в согласии с A.2.14). Нет никаких оснований предполагать, что гипотеза
подобия не подтверждается. В частности, показатель 6, определяемый по-
посредством A.1.5), по-видимому, равен
6=15. G.12.16)

ГЛАВА 7 127
7.13. ПАРАМЕТРИЗОВАННОЕ СООТНОШЕНИЕ
ЗВЕЗДА — ТРЕУГОЛЬНИК
Во всем предшествующем изложении я воздерживался от введения эл-
эллиптических функций до тех пор, пока это было возможно, т.е. вплоть до
разд. 7.8. Там они были необходимы, чтобы выразить функции ехрBАг) и
expBL) как мероморфные функции некоторой переменной w, удовлетворя-
удовлетворяющие в то же время уравнению G.6.1) для к, не зависящего от и.
Это уравнение G.6.1) представляет собой «условие коммутации»: две
трансфер-матрицы, характеризуемые одним и тем же значением к, но раз-
разными значениями w, коммутируют. Это было установлено в первой части
разд. 7.3 с помощью соотношения звезда — треугольник F.4.4), F.4.5). По
существу, G.6.1) представляет собой просто новую интерпретацию F.4.13).
Таким образом, было бы совершенно естественно ввести эллиптические
функции еще в разд. 6.4, чтобы получить параметризацию соотношения
F.4.13), а на самом деле полной системы F.4.8) соотношений
звезда — треугольник.
Онсагер ([184], с. 135 и 144) отметил, что эта идея представляется до-
довольно очевидной, поскольку величины Кх, К2, К3, Lj, L2, L3 удовлетворя-
удовлетворяют соотношениям, подобным тем, которые характерны для гиперболичес-
гиперболической тригонометрии [69]. Хорошо известно, что эти последние могут быть
упрощены с помощью эллиптических функций [102]; Онсагер назвал это
«униформизующей подстановкой». Результирующие тождества очень про-
просты и имеют аналоги в других моделях, поэтому мы выпишем их прежде,
чем расстаться с моделью Изинга.
Пусть Kj, Lj из разд. 6.4 для У = 1, 2, 3 определяется соотношениями
G.8.5) с заменой К, L, и на Kj, Lj, Uj. Тогда F.4.13) выполняется автомати-
автоматически.
Подстановка этих выражений для Кх, ... , L3 в F.4.14) и F.4.15) дает
R2 = -2i/(k2sniui sn iu2 sn/w3), G.13.1)
ii СПШ3-СПШ1 sn/w2 sn/w3 = k~{dniui • G.13.2)
Согласно A5.2.5), все функции snw, cnw, dnw строго периодичны с пери-
периодами 4/ и 4/7'. Сравнивая G.13.2) с формулой A5.4.22), мы видим, что
один набор решений G.13.2) имеет вид
Mi = Dл + 1) /' - м2 - м3 + 4/т/ G.13.3а)
для всех целых т, п.
Из A5.2.5) следует, что G.13.2) не изменится, если одновременно изме-
изменить знаки и2 и w3 или заменить знак и2 и добавить 21' + 2/7 к иъ или по-
поменять местами иг и иъ. Поэтому, согласно G.13.3а), равенство G.13.2) вы-
выполняется также при
щ = Dп + 1) /' + и2 + иъ + 4iml =
= Dл - 1)/' + м2- м3 + Dт - 2)И= G.13.36)
= Dл - 1) /' + иъ - и2 + Dт - 2)//

МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
Разность правой и левой частей G.13.2) является периодической функци-
функцией шх с периодами 4/, 4/7'. В пределах каждого прямоугольника периодов
она имеет четыре полюса: при iux — ±U' и iux = ±U' + II. Поэтому, со-
согласно теореме 15F), она имеет .как раз четыре нуля в таком прямоуголь-
прямоугольнике периодов. Все они описываются соотношениями G.13.3); таким обра-
образом, это полный набор решений G.13.2).
В дополнение к F.4.15) имеется еще два соотношения, которые получа-
получаются перестановкой индексов 1, 2, 3, т.е. перестановкой их, и2, иъ в G.13.2).
Решение G.13.3а) при этом не изменяется, чего нельзя сказать о решениях
G.13.36). Поэтому правильно решение G.13.3а).
Согласно G.8.5), добавление 4/' или 4/7 к их оставляет Кх и Lx неизмен-
неизменными. Поэтому без потери общности можно принять, что решение G.13.2)
имеет следующий вид:
Mi + M2 + ^ = /'. G.13.4)
Соотношения F.4.8) при этом выполняются.
Операторная форма
Рассмотрим теперь операторную форму F.4.25) соотношения звез-
звезда— треугольник. Операторы Ui являются функциями A, L, и, согласно
F.4.13), каждый оператор характеризуется тем же значением k~l произве-
произведения sinh2Arsinh2/. Поэтому все они являются функциями одной перемен-
переменной и в G.8.5), если считать к постоянной.
Оператор, стоящий посередине, имеет аргументы L2, K2, а не К2, L2. Из
A5.2.6) и A5.2.5) следует, что обмен местами К и L эквивалентен замене и
на /' - и. Таким образом, переменную и2 следует заменить на /' - и2,
что равно их + иъ согласно G.13.4). Записывая \Ji как функции w, а не К и
L, приводим уравнение F.4.25) к следующему простому виду:
/,-(wi + из) ?/i + i(n3) = Щи3) f/l + i(wi + и3) Utiux). G.13.5)
Это операторное тождество, справедливое для / = 1, . . . , 2/V - 2 и
для всех комплексных значений Wj, Ыу В частности, оно справедливо, когда
t/j, иъ принимают свои «физические» значения 0 < их < /', 0 < иъ < /',
соответствующие действительным Кх, Lx, K3, L3.
7.14. ЗАДАЧА ДИМЕРА
Прежде чем перейти к следующей главе, следует упомянуть о плоской
задаче димера. Это полезно сделать, с одной стороны, потому, что ее ре-
решение [139, 230] было следующим большим достижением точной статисти-
статистической механики после решения модели Изинга Онсагером, а с дру-
другой — потому, что статистическая сумма модели Изинга в отсутствие
внешнего поля сама может быть выражена через решение задачи димера.
Димер — объект, занимающий два соседних узла решетки, т.е. молеку-
молекула, имеющая форму гантели. Задача димера состоит в том, чтобы опреде-

?ЛАВА7 129
дить число способов покрытия данной решетки димерами таким образом,
чтобы все узлы были заняты и не было наложения каких-либо двух диме-
ров. Если имеется N узлов, то число N должно быть четным и должно
быть Ш2 димеров.
Простой иллюстрацией является задача о нахождении числа способов
покрытия шахматной доски костяшками домино так, чтобы каждая кость
занимала два квадрата доски. Фишер [85] использовал свое решение, чтобы
цычислить это число: оно оказалось равным 12 988 816.
Для любой решетки число покрытий димерами, очевидно, равно
^p6). . .b(pN-upN), G.14.1)
ргде т = N/2, сумма берется по всем перестановкам Р = [pl9 . . . , pN] це-
рых чисел 1, ... , N и
b(i,/) = 1, если ij — соседние узлы,
G.14.2)
= 0 в остальных случаях.
рто выражение определяет число способов объединения N узлов в т пар
ближайших соседей, что эквивалентно покрытию их димерами. Множитель
%Jm\ учитывает тот факт, что между отдельными парами нет никакого
(щзличия, а множитель 2~т связан с отсутствием различия между парой (/,
|) и парой (/, /).
К сожалению, в общем случае не существует легкого способа вычисле-
вычисления суммы в G.14.1).
Но можно продвинуться вперед, используя выражение
(m\2my1^epa(pl,p2)a(p3,p,)...a(pN-upN), G.14.3)
НДе
a(i,j) = -a(j,i), G.14.4)
ш ер = +1 для четных перестановок и ер = -1 для нечетных.
Если А — матрица N х N с элементами я(/, j) (т.е. а^), то выражение
17.14.3) называется пфаффианом от А [171]. Он равен просто квадратному
корню из определителя А:
Pf(A) = (detA)k, G.14.5)
Ш определители вычисляются сравнительно просто, главным образом пото-
iiy, что определитель произведения матриц равен произведению их опреде-
Ьителей.
Поэтому в работах [139, 230] был поставлен вопрос: можно ли предста-
представить G.14.1) в виде G.14.3) посредством подходящего выбора знаков я(/,
1)? Вообще говоря, ответ должен быть отрицательным, но для любой
шлоской решетки (т.е. не имеющей пересекающихся линий) это оказывается

130 МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ
возможным. Кроме того, для регулярной решетки результирующая матри-
матрица А является циклической, так что ее определитель может быть вычислен.
Вслед за решением этой плоской задачи димера Кастелейн [140] пока-
показал, что вычисление статистической суммы модели Изинга на квадратной
решетке в отсутствие внешнего поля может быть представлено как задача
димера, и поэтому получил снова решение Онсагера. Как уже упоминалось
в разд. 7.1, метод пфаффиана оказался весьма полезным для вычисления
характеристик модели Изинга [164, 170, 233].

8
МОДЕЛИ ТИПА ЛЬДА
8.1. ВВЕДЕНИЕ
После модели Изинга следующим установленным классом статистикомеха-
ничсских моделей, поддающихся решению, стали модели типа льда, для
трех основных разновидностей которых решение было получено Либом
A57 — 159] и затем в более общем случае Сэзерлендом [219].
В природе существует множество кристаллов с водородными связями.
Наиболее широко известным примером является лед, в котором атомы
кислорода образуют решетку с координационным числом четыре, где меж-
между каждой парой соседних атомов расположен ион водорода. Каждый та-
кой ион находится ближе к одному из концов связи, на которой он разме-
размерен. Слэтер [209] предположил (основываясь на соображениях локальной
Нейтральности), что ионы должны подчиняться правилу льда:
из четырех ионов, окружающих каждый атом, два расположены близ-
§Ш, а два удалены вдоль линий соответствующих связей.
Это означает, что статистическая сумма определяется выражением вида
Ц.4.1), т.е.
*2), (8.1.1)
где суммирование теперь выполняется по всем конфигурациям водородных
Ионов, допускаемым правилом льда, a <f— энергия конфигурации.
Для самого льда величина ^одинакова для всех разрешенных конфигу-
конфигураций. Поэтому при подходящем выборе начала отсчета на энергетической
Шкале энергию 6'можно считать равной нулю. Тогда Z становится просто
Числом разрешенных конфигураций, и энтропия равна
S = kB\nZ. (8.1.2)
Эта величина не равна нулю, поскольку имеется много конфигураций,
Допускаемых правилом льда. Одна из них — для квадратной решет-
решетки — показана на рис. 8.1,а.
Конечно, реальный лед и другие кристаллы являются трехмерными, но,
* сожалению, единственные точные решения, которые мы имеем для трех-
Иерных моделей типа льда, относятся к весьма специальным «заморожен-
«замороженным» состояниям [176].
В этой главе будут рассмотрены только модели типа льда на квадрат-
Ф решетке. Они ведут себя аналогично трехмерным реальным объектам,
имеют то огромное преимущество, что могут быть решены. (В частно-

132
МОДЕЛИ ТИПА ЛЬДА
<
(
(
1
^
i
Рис. 8.1. Размещение ионов водорода на
квадратной решетке 3 х 3 (с циклическими
граничными условиями), удовлетворяющее
правилу льда; а — положение ионов
водорода на линиях связи; б — со-
соответствующие электрические диполи;
в — соответствующее представление линия-
линиями.
сти, модель типа льда на квадратной решетке является действительно весь-
весьма хорошей аппроксимацией реального льда, так как энтропия лишь в сла-
слабой степени чувствительна к структуре решетки.)
Связи между атомами через водородные ионы образуют электрические
диполи, так что их удобно представлять стрелками на линиях связи, на-
направленными к тому концу связи, который занят ионом, как это показано
на рис. 8.1,6. Тогда правило льда эквивалентно утверждению, что у каждо-
каждого узла (вершины) решетки имеются две стрелки, направленные к нему, и
две стрелки, направленные от него. Всего имеется шесть таких конфигура-
конфигураций стрелок (рис. 8.2). (Поэтому модели типа льда иногда называют «ше-
стивершинными» моделями в противоположность «восьмивершинной» мо-
модели гл. 10.)
Вообще говоря, каждая из этих шести локальных конфигураций может
характеризоваться своей энергией; обозначим их elt ... , е6 в последова-
последовательности, соответствующей рис. 8.2. Тогда статистическая сумма опреде-
определяется выражением (8.1.1), где
П2?2
П6?6
(8.1.3)
и rij — число вершин типа j в решетке.
Мы приходим к весьма общей модели, которая включает*в себя как
частные случаи следующие три важные модели.
ЛЕД
Как уже было отмечено, собственно модель льда можно получить, при-
приравнивая нулю все энергии, т.е.
е i = е2 = . . . = е 6 - 0 .
(8.1.4)
J
Г
Рис. 8.2. Шесть допустимых конфигураций
_| 1 I . J стрелок у вершины и соответствующие
конфигурации линий.

ГЛАВА 8
133
KDP
Дигидрофосфат калия КН2РО4 (называемый далее KDP) образует кри-
кристалл с водородными связями, характеризуемый координационным числом
Четыре и упорядочивающийся сегнетоэлектрически при низких температу-
температурах (т.е. все диполи выстраиваются в одном направлении). Слэтер [209] по-
|сазал, что он может быть представлен моделью типа льда при подходя-
подходящем выборе ?j, . . . , е6. Для квадратной решетки этот выбор следующий:
е 1 = е2 = 0, ?3 = ?4 = ?5 = в6 > 0 .
(8.1.5)
Основное состояние — это то состояние, в котором все стрелки направ-
направлены либо вверх и вправо, либо вниз и влево. Оба эти состояния типичны
для упорядоченного сегнетоэлектрика.
F-МОДЕЛЬ
Рис [205] предположил, что модель антисегнетоэлектрика можно полу-
полудить при следующем выборе:
в 1 = вг = ?з = вА > 0, е5 = е6 = 0 .
(8.1.6)
Основным состоянием тогда будет такое состояние, в котором имеются
Только вершинные конфигурации 5 и 6. Существует лишь два таких состоя-
состояния. Одно из них показано на рис. 8.3, а другое получается из него обраще-
обращением всех стрелок. Заметим, что направления стрелок чередуются, как и
должно быть в упорядоченном антисегнетоэлектрике [175].
Ограничения
В этой главе на е,,..., е6 налагаются следующие ограничения:
В\ = В2, ВЪ = В4, Е5=?6. (8.1.7)
Они обеспечивают инвариантность модели по отношению к обращению
Знаков всех диполей, что довольно естественно для модели в отсутствие
внешнего электрического поля. Таким образом, мы рассматриваем модель
<<без поля», которая включает лед, KDP и F-модель как частные случаи.
В действительности третье условие е5 = е6 вообще не является ограни-
ограничением. Из рис. 8.2 ясно, что вершинная конфигурация 5 является «стоком»
для горизонтальных стрелок, в то время как конфигурация 6 является для
Рис. 8.3. Одна из двух возможных конфигураций стрелок,
соответствующая основному состоянию антисегнето-
электрической модели типа льда. Присутствуют только
вершинные конфигурации типов 5 и 6.
1
\
i
1

134 МОДЕЛИ ТИПА ЛЬДА
них «истоком». Если наложены цилиндрические или тороидальные гранич-
граничные условия, то стоков должно быть столько же, сколько и истоков, так
что п5 = п6. Тогда из (8.1.3) следует, что е5 и е6 входят в статистическую
сумму только в комбинации е5 + е6, поэтому, не теряя общности, можно
положить е5 = е6.
Другие два условия (е, - е2 и е3 = ?4) приняты больше по соображени-
соображениям удобства, чем по необходимости, поскольку вычисления разд. 8.2 — 8.7
легко могут быть обобщены на случай, когда ограничения отсутствуют
(при условии что каждая из шести энергий, например ер одинакова для
всех узлов квадратной решетки). Эффект снятия этих ограничений (т.е. вве-
введения внешнего электрического поля) обсуждается в разд. 8.12.
8.2. ТРАНСФЕР-МАТРИЦА
Еще один способ представления диполей, образуемых водородными ио-
ионами, состоит в том, чтобы проводить линию вдоль связи, если соответст-
соответствующая стрелка направлена вниз или влево, и не проводить ее в остальных
случаях. Типичная конфигурация линий показана на рис. 8.1,в, а шесть воз-
возможных конфигураций линий в окрестности вершины — на рис. 8.2.
Предположим, что решетка имеет М рядов и N столбцов, и наложим
циклические (т.е. тороидальные) граничные условия. Рассмотрим ряд, со-
состоящий из N вертикальных линий (между двумя соседними рядами узлов).
Имеется М таких рядов; пронумеруем их последовательно снизу вверх:
г = 1,2, ... , М. Пусть <рг — «состояние» ряда г, т.е. размещение линий
на N вертикальных связях. Так как каждая связь может быть или не быть
занята линией, то <рг имеет 2^ возможных значений. Тогда, как обычно,
мы можем записать статистическую сумму в виде
Ф1 Ф2 ФМ
= Trace Vм, (8.2.1)
где К — трансфер-матрица 2N x 2N с элементами
V(<p, ф') = 2 ехр[ - (wifi + т2е2 + . .. + Шб?б)/ЛдГ]. (8.2.2)
В (8.2.2) <р обозначает размещение линий на одном ряду вертикальных свя-
связей, а <р' относится к следующему ряду, расположенному выше, как это по-
показано на рис. 8.4. Суммирование выполняется по всем допустимым разме-
У\ У г У1 У г
I I У' II
г-*— ' [ ' г— Рис. 8.4. Характерные размещения линий
' V ' ' на двух соседних рядах (при п = 2). Ко-
Х1 Х1 Х2 ординаты ух , . . . , уп должны чередо-
а 6 ватьсяс^1 ,*„.

ГЛАВА 8 135
тениям линий на промежуточных горизонтальных связях. Эти размещения
должны удовлетворять правилу льда на каждой вершине; если такого раз-
размещения не существует, то элемент Vdpy <p') равен нулю. Число допусти-
допустимых размещений всегда не более двух. Числа т{, . . . , т6 определяют ко-
количество промежуточных узлов, относящихся к типам 1, . . . , 6.
Пусть Л — собственное значение матрицы К, a g — соответствующий
собственный вектор. Тогда
Ag = Vg. (8.2.3)
Так же как в разд. 2.1 и 7.2, при больших М из (8.2.3) следует
Z - Ajfax , (8.2.4)
где Лтах — наибольшее из 2^ собственных значений матрицы V.
8.3. СОХРАНЕНИЕ ЛИНИЙ
На рис. 8.2 и 8.1,в четыре линии, образующие вершинную конфигура-
конфигурацию типа 2, разделены на две пары линий. При этом становится ясно, что
линии, соединяясь, образуют непрерывные непересекающиеся пути через
всю решетку. Если мы начинаем движение по одному из путей вверх или
вправо, то и далее будем смещаться по тому или другому из этих двух на-
направлений, но ни в коем случае не вниз и не влево. Циклические граничные
условия обеспечивают нескончаемость этого пути.
Допустим, что имеется п таких путей, идущих через всю решетку снизу
вверх. Каждый путь проходит через какой-то ряд вертикальных связей
один и только один раз. Отсюда следует, что если имеется п линий в ниж-
нижнем ряду вертикальных связей, то и в каждом ряду имеется п линий.
В частности, должно быть п линий во втором ряду, из чего следует,
что элемент V(<p, <pf) равен нулю, если р и <р' не содержат одинакового
числа линий.
Поэтому матрица V разбивается на N + 1 диагональных блоков, один
из которых соответствует переходам между состояниями с отсутствием
линий, другой содержит элементы переходов между состояниями с одной
линией и т.д. до состояния с N линиями. Таким образом, число линий в од-
одном ряду п представляет собой как бы «квантовое число» матрицы V. Мы
можем сосредоточить наше внимание на состояниях с заданным значени-
значением п.
Очевидным способом идентификации такого состояния является указа-
указание положений jcj, ... , хп линий, упорядоченных таким образом, что
(8.3.1)
Пусть А" = \xv . . . , хп) — такая идентификация, и пусть g(X) — соот-
соответствующий элемент собственного вектора g. Тогда (8.2.3) можно запи-
записать в виде
() ^ (8.3.2)

П6 МОДЕЛИ ТИПА ЛЬДА
где V(X, Y) — элемент матрицы V между состояниями X и У, по-
прежнему определяемый выражением (8.2.2). Учитывая (8.1.7), удобно вве-
ввести следующие обозначения:
ц= схр(-в/квТ1 /=1,...,6, <8-З.За)
а = a>i = ео2, Ь = 0)з= ео4, с=еу5=<Уб- (8.3.36)
(Таким образом, со,, ... , со6 — больцмановские веса вершинных конфигу-
конфигураций 1, . . . , 6.) Тогда (8.2.i) принимает вид
V(X,Y) = Xami+m2fcm3+m4cm5+m6, (8.3.4)
где А", У заменяют ^, v>'; суммирование снова выполняется по всем допу-
допустимым размещениям линий в промежуточном ряду горизонтальных свя-
связей; Wj, ... ,. m6 — количества промежуточных вершин типов 1, ... ,6.
Два типичных случая изображены на рис. 8.4 (при п = 2).
Задача теперь состоит в том, чтобы решить уравнение (8.3.2) при задан-
заданном значении п. Весьма полезно начать с рассмотрения простых случаев,
когда п = О, 1 и 2.
Случай п = О
Если п = О, то нет вертикальных линий на двух последовательных ря-
рядах. На промежуточном горизонтальном ряду имеется два возможных раз-
размещения линий: либо все связи остаются пустыми, либо все они покрыты
линией. В первом случае все вершины относятся к типу 1, во втором — к
типу 4. Таким образом, блок п = 0 матрицы V представляет собой следу-
следующую матрицу 1x1:
A=aN+bN. (8.3.5)
Случай п = 1
Если п = 1, то мы можем записать g(X) как g(x), где х — положение
вертикальной линии в ряду. Величина х может принимать значения 1, . . . ,
N, так что этот блок матрицы V представляет собой матрицу N х N с эле-
элементами К(х, у).
Если х меньше, чем у, то все горизонтальные связи между х и у должны
быть покрыты линиями, а все остальные должны быть пустыми (как на
первой половине рис. 8.4,я). Если х больше, чем у, то верно обратное ут-
утверждение. Если х = у, то либо все горизонтальные связи остаются пусты-
пустыми, либо все они покрыты линиями. Подсчитывая числа ml9 ... , m6 для
различных случаев, получаем вместо (8.3.2) следующее уравнение:
N
2
у = х+ 1
х-1 (8.3.6)

ГЛАВА 8 137
Мы ищем решение в виде
g(x) = z*, (8.3.7)
где z — комплексное число. Подставляя g(x) в такой форме в (8.3.6) и сум-
суммируя элементарные геометрические прогрессии, получаем
Azx = aNL{z) zx - ax~l bN~xс2 zN+ll{a - bz) +
v ' (8.3.8)
+ bNM(z) zx + ax~l bN~xc2z/(a - bz),
где
L(z) = [ab + (c2 - b2)z]/(a2 - abz),
(8.3.9)
M{z) = [a2 -c2- abz]/(ab - b2z).
Второй и четвертый члены в правой части (8.3.8) представляют собой
«граничные члены», происходящие от предельных значений у = N и у = 1
в суммах (8.3.6) соответственно. Они различаются только множителем
( — zN), поэтому их сумма может быть сделана равной нулю выбором
zN=l. (8.3.10)
Остающиеся первый и третий члены в правой части являются «жела-
«желательными членами» в том смысле, что имеют тот же вид, что и левая
часть равенства (константа х zx). Таким образом, уравнение (8.3.8) теперь
удовлетворяется, если
Л = aN L(z) + bNM(z). (8.3.11)
Имеется N решений (8.3.10) для комплексного числа z. Вместе с (8.3.7)
это определяет ожидаемое число N собственных векторов этого блока мат-
матрицы V. Соответствующие собственные значения определяются уравнени-
уравнением (8.3.11).
Уравнения (8.3.7) и (8.3.10) можно было бы предсказать из соображений
трансляционной инвариантности, но было бы ошибочно в этой задаче сли-
слишком рано вводить соответствующие, соображения, так как при п > 1 это
завуалировало бы структуру g(X).
Случай п = 2
Если п = 2, то g(X) принимает вид g(xlt х2), где хх и х2 — положения
двух линий. Суммирование в (8.3.2) распространяется на все разрешенные
положения ух и у2 в верхнем ряду вертикальных связей при заданных поло-
положениях хх и х2 линий в нижнем ряду.
Две основные ситуации показаны на рис. 8.4. Имеются также специаль-
специальные случаи, когда координата.^ или^2 равнахх илих2, ho^i и^2» согласно
правилу льда, должны удовлетворять одному из следующих двух условий:
Х\ ^ У\ ^ х2 ^ уг или у\ ^Х\ ^у2 ^х2.
Таким образом, ух и у2 должны чередоваться с хх и х2.
Подсчитывая тх, ... , т6 и учитывая специальные случаи, приводим

П8 МОДЕЛИ ТИПА ЛЬДА
(8.3.2) к виду
х2 N
X] Х2
*^1Ojc1) (8.3.12)
где
D(y , л:) = я/с, x = у
(8.3.13)
-\ y>x.
Звездочка (*) указывает, что любые члены с ух = у2 должны быть исклю-
исключены из суммы. В каждом случае имеется только один такой член:
уг = х2 = y-i в первой сумме и ух = хх = у2 во второй.
Первым шагом в решении (8.3.12) является очевидное обобщение реше-
решения (8.3.7); испробуем решение в виде
g(xX9x2) =Al2zflz?, (8.3.14)
где у412, zx, z2 — комплексные числа.
Суммирования в (8.3.12) выполняются теперь непосредственно, но тре-
требуют довольно утомительной процедуры. Наиболее легкий путь состоит в
том, чтобы игнорировать вначале знак *, а затем вычесть вклад лишних
членов. Первая двойная сумма в (8.3.12) тогда равна
z?) (L2aN-X2zx22 -
а вторая составляет
At&pi ax> + Mi bXl zf1) (L2a*'*1 & + M2b*-*1 zf) bN~*-
Здесь Lj ж L(Zj), Mj ж M(Zj) и
Pi a p(Zj) = c2z}'/(a2 - abzj). (8.3.16)
Перемножая скобки в (8.3.15а) или (8.3.156), получаем в общей сложно-
сложности пять членов. Они могут быть сгруппированы в три класса.
Желательные члены. Эти члены имеют тот же вид, что и сама функция

ГЛАВА 8 139
g(xx, x2), т.е. они пропорциональны z[lzx22. Имеется по одному такому чле-
члену в (8.3.15а) и (8.3.156), и их сумма равна
Л12 (aN UU + bNMlM2) zV zx22. (8-зл7)
Учитывая (8.3.14), их можно приравнять левой части (8.3.12), если
Л = aNLxL2 + bNMxM2. (8.3.18)
Нежелательные внутренние члены. Они имеют вид (z^z^f1 или (Z\Z2)X{ и
включают последние корректирующие члены в (8.3.15а) и (8.3.156). Их сум-
сумма в (8.3.15а) равна
Al2aN+x'-x>b»-4 (MlL2-l)(zlz2y\
а в (8.3.156)
(8.3
(8.3
(8.
(8.
.19a)
.196)
3.20)
3.21)
С помощью (8.3.9) можно убедиться, что
MXL2 - 1 = -c2snl[{a - bzx) {a - bz2)],
где если
д = (а2 + Ь2 - c2)/2ab ,
то
512= I -2Az2+ Ziz2. (8.3.22)
Граничные члены. Они происходят от предельных членов у2 = N или
у1 = 1 в суммах в (8.3.12), и их отличительным признаком в (8.3.15) явля-
является наличие множителя р2 или рх. Определим
Rj(x ,*') = Ljax'-Xzj + Mjbx'-Xzf. (8.3.23)
Тогда сумма граничных членов в (8.3.15а) равна
- AnaXxbN-X2Rx(xx, x2) fhzi , (8.3.24а)
а в (8.3.156)
Ai2flKlbN-X2R2(xi, jc2) Pi. (8.3.246)
Исключение нежелательных членов. Чтобы выполнялось равенство
(8.3.12), должны быть устранены нежелательные члены (8.3.19) и (8.3.24).
Как это может быть сделано? Совершенно очевидная идея состоит в том,
чтобы обобщить решение (8.3.14) и попробовать линейную комбинацию
членов такого типа, т.е.
bzb- (8'3-25)
Иначе говоря, мы пытаемся просуммировать по различным парам Z\ и
z2 с подходящими коэффициентами Ах2.
Равенство, по желательным членам будет, наверняка, соблюдено, если
оно выполняется для каждого г, т.е. если условие (8.3.18) выполняется для

140 МОДЕЛИ ТИПА ЛЬДА
каждой пары z{ и z2. Поскольку Л не зависит от г, правая часть (8.3.18)
должна быть одной и той же для любой пары zx и z2.
Кроме того, возможность сокращения нежелательных внутренних чле-
членов (8.3.19) должна сохраняться и в том случае, если для любой пары zx и
z2 существует другая пара z{ и z'2 с тем же значением zxz2. Вместе с пред-
предшествующим замечанием это означает, что z\ и z2 должны удовлетворять
условиям
z[z2 = zxz2 ,
aNL{z[) L{z'2) + bNM(z[) M(z'2)= • (8.3.26)
N
Исключая z2 и используя (8.3.9), получаем квадратное уравнение для z[.
Поэтому имеется только два решения для z[ и z2, и они, очевидно, имеют
вид
z[ = zx, z'2 = z2 и zi = z2, Z2 = Z!, (8.2.27)
поскольку перестановка z[ и z2 оставляет равенство (8.3.26) без изменения.
(Для более сложных задач, в частности для антиферроэлектрических
моделей типа льда с различными весами на двух подрешетках имеются до-
дополнительные решения для z[ и z2. Рассматривая (8.3.14) как пробную
функцию, имеющую форму «плоской волны», мы можем считать z[ и z2
«рассеянными волнами», причем два уравнения (8.3.26) играют роль усло-
условий сохранения полного импульса и полной энергии. Для п = 2 задачи та-
такого типа с использованием этих рассеянных волн могут быть решены, но,
к сожалению, вычисления нельзя обобщить каким-либо полезным спосо-
способом на случай п > 2.)
Из (8.3.27) следует, что к паре fej, z2) мы должны также присоединить
пару (z2, Z\). Таким образом, имеется всего два члена в (8.3.25), и результи-
результирующая подстановка для g(xu x2) может быть записана в виде
g(jci ,x2) = Al2zxilzx22 + ^2izfzf2. (8.3.28)
После суммирования (8.3.19) по этим двум вариантам решения (второй по-
получается из первого перестановкой индексов 1 и 2 везде кроме х{ и х2) ста-
становится очевидным, что нежелательные члены сокращаются, если
{MXL2 - \)Ап + (M2Li - 1)Л21 = 0. (8.з.29)
С помощью (8.3.20) это условие упрощается и принимает вид
= 0. (8.3.30)
Наконец, суммируя совместно граничные члены (8.3.24а) и (8.3.246), со-
соответствующие двум вариантам решения, получаем
i(*b*2) (Агх ~ z^An)+
+ plR2(xux2) (An-z?A2i)}.

ГЛАВА 8 141
Ясно, что это выражение обращается в нуль для всех хх и х2, если
Z\ — А\21А2\ , z2 = ^*2i'^i2 • (8.3.32)
Решая (8.3.30) относительно АХ2/А2Х и подставляя результат в (8.3.32),
получаем два уравнения для zx и z2. В принципе они могут быть решены
(имеется много решений, соответствующих различным собственным векто-
векторам матрицы V). С точностью до нормировочной постоянной компоненты
собственного вектора g определяются тогда выражением (8.3.28), а соб-
собственные значения Л — выражением (8.3.18).
8.4. СОБСТВЕННЫЕ ЗНАЧЕНИЯ
ДЛЯ ПРОИЗВОЛЬНОГО п
Решение задачи определения собственных значений для произвольного п
является прямым обобщением решения для случая п = 2. В этом разделе
кратко излагаются основные моменты этого обобщения. Более полное
описание (для модели льда) дано в работе [157].
Уравнение для собственных значений (8.3.12) принимает вид
uDaEnDn. ¦ ¦ EnncaN-?«g(yx ,...,у„)
XI *2 ХП (8.4.1)
2 2 ... Т b»-lDnEl2D22E2i...
У1 = 1У2=Х1 Уп=Хп-\
где 1 ^ хх < х2 < . . . < хп ^ N, звездочка (*) означает, что никакая пара
координат из ylt . . . , уп не может совпадать, и D^ = D(yit Xj), E^ = E(xh
Сначала испробуем решение в виде
,. . . ,хп) =i4i...nzi1. . . zj", (8.4.2)
х
где A j n — постоянный коэффициент.
Первое /7-кратное суммирование в правой части (8.4.1) дает
Ai.^ni^R^Xi ух2). . . Rn-i(xn-i >*л)
:8.4.3а)
х (LnaN~Xnzxnn - pnbN~XnZn) - поправочные члены,
а второе
— поправочные члены.

МОДЕЛИ ТИПА ЛЬДА
Здесь поправочные члены возникают в результате явного вычитания из-
излишних вкладов от членов с у1 = у2, У2 = Уг> • • • или Уп - \ ~ Уп-
Согласно (8.3.23), каждый множитель Rj(x, х') представляет собой сум-
сумму двух слагаемых. Поэтому, разлагая произведение п - 1 сомножителей
/?, получаем Т " * слагаемых. Только одно из них в каждом из выражений
(8.4.3а) и (8.4.36) является «желательным» (т.е. имеет тот же вид, что и
#(*!,..., хп)). Приравнивая эти желательные члены с обеих сторон урав-
уравнения (8.4.1), получаем
А = aNU . . . L, + bNMx ...Mr,. (8.4.4)
За исключением «граничных членов», содержащих множитель рп или р1?
все остальные содержат по крайней мере один множитель вида
1 или (ZjZj+iY'. (8.4.5)
Их можно сократить путем добавления в (8.4.2) членов с переставленными
Zj и zj + j. Делая это для всех у и для всех исходных наборов zv . . . , zn, ге-
генерируемых таким образом, мы получаем вместо (8.4.2) выражение
,.. .,xn) =^Apu...,Pnzxp\.. .zxpnn, (8.4.6)
где суммирование распространяется на все п\ перестановок Р = [plf . . . ,
рп) целых чисел 1, . . . , п.
Такую же пробную собственную функцию использовал Бете [52] для
диагонализации квантовомеханического гамильтониана одномерной модели
Гейзенберга, поэтому она известна как анзац Бете.
Вычисляя нежелательные внутренние члены, содержащие множители
(8.4.5) (к ним относятся и «поправочные члены»), мы обнаруживаем, что
они сокращаются, если для всех перестановок Риу=1,...,я-1 выпо-
выполняется следующее обобщение условия (8.3.30):
sPhPt+iApu...,pH + Sp,+i,p,Api,...,pJ+uPh...,pn =0. (8.4.7)
В результате остаются только граничные члены, содержащие множи-
множитель pj для некоторого значения у. После замены z^ . . . , zn в (8.4.3а) на
z2, • • • » zn, zx становится очевидно, что имеющиеся граничные члены со-
сокращаются с теми, которые содержатся в (8.4.36), если
-гРЛ2...„1+Л1...я = 0. (8.4.8)
Производя все возможные перестановки чисел Zj, ...
следующее условие сокращения всех граничных членов:
для всех перестановок Р.
Условия (8.4.4), (8.4.7) и (8.4.9) действительно обеспечивают выполне-
выполнение равенства (8.4.1) (см. [157], где проведено полное исследование доста-

ГЛАВА 8 143
точности этих условий для модели льда). Однако сразу не очевидно, что
все они могут быть одновременно удовлетворены, так как имеется много
больше уравнений, чем неизвестных. Тем не менее легко убедиться, что
(8.4.7) имеет решение (с точностью до нормирующего множителя)
где еР — сигнатура перестановки Р(еР = + 1 для четных перестановок,
?р = - 1 для нечетных). Подставляя это выражение в (8.4.9), получаем,
что для всех Р
п
Zv = {-)n~l\\sPhPJsPuPl. (8.4.11)
Правая часть этого уравнения симметрична по /?2> • • • » Рп> поэтому
имеется только п таких существенно различных уравнений, а именно
для у = 1, . . . , п.
Таким образом, мы имеем п уравнений для Zj, . . . , zn. В принципе они
могут быть решены, и коэффициенты Ар могут быть вычислены с по-
помощью (8.4.10). Собственные функции g определяются тогда выражением
(8.4.6), а собственное значение Л — выражением (8.4.4).
8.5. МАКСИМАЛЬНОЕ СОБСТВЕННОЕ ЗНАЧЕНИЕ;
ОПРЕДЕЛЕНИЕ *„...,*„
К сожалению, уравнения (8.4.12) не решены в общем случае для конеч-
конечных п и N. (В противоположность этому для модели Изинга все собствен-
собственные значения могут быть выражены в явном виде для конечных N.) Оказы-
Оказывается, что решение этих уравнений для максимального собственного зна-
значения в термодинамическом пределе (N велико) может быть получено, но
необходима разумная осторожность, чтобы обеспечить получение именно
максимального собственного значения.
Замечательной особенностью уравнений (8.4.2), (8.4.10), (8.4.12) и
(8.3.22) является то, что они не просто по форме совпадают с анзацем Бете
для модели Гейзенберга, но представляют собой в точности то же самое!
Таким образом, собственные векторы этой модели являются собственны-
собственными векторами нашей трансфер-матрицы V. Это означает, что Либ
[157 — 159] мог воспользоваться известными свойствами модели Гейзен-
Гейзенберга, в частности результатами работы [263], чтобы идентифицировать и
вычислить максимальное собственное значение в пределе N — оо. Указан-
Указанная работа является весьма строгой в математическом смысле, и заинтере-
заинтересованному читателю предлагается к ней обратиться. Здесь я просто приве-

144 МОДЕЛИ ТИПА ЛЬДА
ду некоторые правдоподобные соображения, позволяющие определить ре-
решение (8.4.12), соответствующее максимальному собственному значению, и
вычислить его для больших N.
Случай п = 2
Полезно снова начать с рассмотрения случая п = 2, когда (8.4.12) пре-
превращается в (8.3.32). Перемножая два уравнения (8.3.32), получаем
=l, (8.5.1)
откуда следует
*1*2 = т, (8.5.2)
где 7 — корень степени N из единицы.
Последнее соотношение является простым следствием трансляционной
инвариантности К, так как с учетом (8.3.28) оно приводит к следующему
равенству:
g{xx + 1 ,*2 + 1) = *g(*i ,x2) • (8.5.3)
Согласно теореме Перрона — Фробениуса [93J, собственный вектор, со-
соответствующий максимальному собственному значению, должен иметь все
положительные компоненты. Из (8.5.3) видно, что это возможно только в
том случае, когда т = 1; поэтому мы должны выбрать решение
Z\Z2 = 1 (8.5.4)
уравнения (8.5.1) (т.е. вектор $(*,, х2) сам трансляционно инвариантен, как
и можно было ожидать).
Кроме того, из (8.3.28) и (8.3.32) следует
g(xx , х2) = A2l(z?+Xi z? + z? zf) , (8.5.5)
так что, используя (8.5.4) и полагая
zx = exp(iik), r = Ш - 1, (8.5.6)
получаем
g(xi , х2) ос cos к(хг -х2 + Ш). (8.5.7)
Величина хх — х2 + N/2 может принимать все целые (или полуцелые)
значения от -г до г. Поэтому для обеспечения неотрицательности g(xl9 x2)
достаточно, чтобы к было либо действительным числом, лежащим в ин-
интервале (-тг/2/*, тг/2/*), либо чисто мнимым числом.
Далее, изменение знака к просто меняет местами zx и z2, оставляя соб-
собственный вектор g без изменения. Таким образом, мы можем с таким же
успехом ограничиться действительными значениями к в интервале @, тг/2/*)
или положительными чисто мнимыми значениями.
Используем теперь (8.3.22), (8.3.30) и (8.3.32), чтобы записать z1? в виде
рациональной фукнции zx иг2, и исключим z2 с помощью (8.5.4). Результи-
Результирующее уравнение для zx имеет вид

ГЛАВА 8 145
A(zf + Zi) = zf+ 1, (8.5.8)
или после подстановки (8.5.6)
А = cos(r+l)/:/cosrA:. (8.5.9)
Построив график правой части (8.5.9) в зависимости от к для действи-
действительных и для чисто мнимых к, мы легко установим следующее:
если Д < 1, то уравнение (8.5.9) имеет одно действительное решение в
интервале @, тг/2г) и не имеет ни одного мнимого решения;
если Д > 1, то уравнение (8.5.9) не имеет действительных решений в ин-
интервале @, тг/2г), но имеет единственное положительное мнимое решение.
В обоих случаях из (8.5.7) с очевидностью следует, что все значения
g(xly x2) строго положительны, поэтому, согласно теореме Перро-
Перрона — Фробениуса, мы нашли решение, соответствующее максимальному
собственному значению матрицы V в субблоке п = 2.
Если п = 1, то из (8.3.7) и (8.3.10) очевидно, что собственный вектор с
положительными составляющими соответствует z = 1.
Следует признать, что эти результаты для п = 2 и п = 1 дают лишь
весьма скудные сведения, но они действительно намечают правильное на-
направление: если Д < 1 (и я < N/2), то решение, которое максимизирует Л,
таково, что все Zp . . . , zn различны, лежат на единичном круге, распреде-
распределены симметрично относительно единицы и так плотно, как только воз-
возможно. Уравнение (8.4.12) допускает решения с двумя или более совпадаю-
совпадающими Zp . . . , zn, но они должны быть отброшены, поскольку, согласно
(8.4.6) и (8.4.10), все элементы g в этом случае тождественно равны нулю.
Результаты для п = 2 и п = 1 позволяют также предположить, что
при Д > 1 все Z\, . . . , zn — положительные действительные числа, но это
предположение нам не потребуется.
8.6. СЛУЧАЙ Д > 1
Случай Д > 1 тривиален. Пусть Ап — максимальное собственное значе-
значение для данного п. Тогда с помощью приведенных выше результатов мож-
можно убедиться, что для достаточно больших N
A0>Ai и Л0>Л2. (8.6.1)
В действительности можно показать [159], что
Л0^Л„, л = 0,... ,N. (8.6.2)
Таким образом, максимальное собственное значение — это просто Ло, т.е.,
согласно (8.3.5),
&m*x = aN+bN. (8.6.3)
Поэтому из A.7.6), (8.2.4) и (8.3.3) с учетом того, что решетка имеет
MN узлов, для свободной энергии при больших N получаем следующий ре-

146 МОДЕЛИ ТИПА ЛЬДА
зультат:
/= min^ , ?3) • (8.6.4)
Система является «замороженной» в том смысле, что если одна вертикаль-
вертикальная стрелка фиксирована в направлении вверх, то вероятность того, что
любая другая стрелка направлена вверх, равна единице, как бы далеко она
ни была расположена по отношению к первой. (Конечно, при условии, что
взят правильный термодинамический предел; обе стрелки должны распола-
располагаться глубоко внутри неограниченной решетки.) Это полный сегнетоэлект-
рический порядок.
Такие замороженные решения существуют и для трехмерных моделей
типа льда [176]; это один из немногочисленных точных результатов в трех-
трехмерной статистической механике.
8.7. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ ПРИ Д < 1
Если точки Zj, . . . , zn лежат на единичной окружности, то уравнения
(8.4.12) включают комплексные числа. Они могут быть приведены к систе-
системе действительных уравнений следующим образом.
Определим «волновые числа» кх, . . . , кп и функцию Sip, q) посредст-
посредством соотношений
Zj = ехр(/?у), SiJSjj = ехр[-/0(/:у, /;,)]. (8.7.1)
Из (8.3.22) следует
1 - ? A eip + etp + iq
е-*НР.*) = - (8.7.2)
l-2Aeiq + eip + lq
и, следовательно,
в(р , q) = 2 tan"l{A sin \(p - <?)/[cos J(p + q) - A cos J(p -?)]}, (8.7.3)
так что 0(р, q) — действительная функция.
Произведение в (8.4.12) не изменится, если добавить множитель с / = j;
поэтому (8.4.12) можно теперь записать в виде
п
ехр(йМ,-) = (-)"-' П ехр[|в(*у ,*,)]. (8.7.4)
Обе части этого уравнения унимодулярны, т.е. имеют вид ехр(/0); поэтому
естественно прологарифмировать их и поделить на /, что дает (для j = 1,
.... /1)
п
Nk, = 2лIj - 2 ®{kj, к!), (8.7.5)
где каждое /у — либо целое число, если п нечетное, либо полуцелое в слу-
случае четного п.
Уравнение (8.7.5) согласуется с предположением о том, что все кх, . . . ,

ГЛАВА 8 147
кп являются действительными числами, поскольку при этом обе части
(8.7.5) будут действительными.
Мы хотим, чтобы все кх, . . . , кп были различны и распределены сим-
симметрично относительно нуля, причем как можно плотнее. Это предполага-
предполагает следующий выбор:
/,- = ,/-*("+ 1), / = 1,... ,и. (8.7.6)
В работе [263] показано, что уравнение (8.7.5) тогда имеет единственное
действительное решение для кх, . . . кп.
Отношение n/N представляет собой долю стрелок, направленных вниз,
в каждом ряду решетки, так что эту величину можно считать вероятнос-
вероятностью того, что вертикальная стрелка направлена вниз. Если N велико, мы
ожидаем, что эта вероятность будет стремиться к некоторому термодина-
термодинамическому пределу. Последнее означает, что мы интересуемся решением
(8.7.5) в пределе больших Nun при фиксированном отношении n/N.
В этом пределе кх, . . . , кп оказываются плотно упакованными в неко-
некотором фиксированном интервале (-(?, б), так что фактически они образу-
образует непрерывное распределение. Пусть число значений kj9 лежащих в интер-
интервале между к и к + dk, равно Np(k)dk. Тогда в пределе больших N величи-
величина р(к) является функцией распределения. Поскольку полное число всех kj
|равно я, то р(к) должно удовлетворять условию
f p(k)dk = n/N. (8.7.7)
J-Q
Для заданного значения к-, равного к, величина /у + Уг{п + 1) представ-
Шяет собой количество различных к{ с / < j. Таким образом, (8.7.5) приво-
приводится к виду
f
J-
Nk = -jz{n+l) + 2nN \ p(k')dk' -N \Q <д{к,к')р{к')дк'.
(8.7.8)
Дифференцируя по к, деля на N и переставляя члены, получаем
2лр(к) = 1 + Г Эе(*,'*)р(*') dUk'. (8.7.9)
J-Q дк
Это линейное интегральное уравнение для р(к). Для заданного отно-
отношения n/N величину Q можно определить с помощью (8.7.7).
Собственное значение Л определяется выражением (8.4.4). В пределе,
больших N оба слагаемых в его правой части растут экспоненциально, при-
причем полностью доминирует то, которое больше. Поэтому из A.7.6), (8.2.4)
и (8.3.3) для свободной энергии / получаем выражение
п п
f = mini e, - квТ 2 [In L(zt)]/N, e3 - квТ 2 [In M(z,)]/n) . (8.7.10)
I /=1 ;=1 )

Ы8 МОДЕЛИ ТИПА ЛЬДА
В пределе больших Nun эти суммы превращаются в интегралы, что дает
/= mini б! - квТ \ [In Це1"*)] р(к) <\к ,
Q fQ , (8ЛЛ1)
8Ъ-квТ\ [\nM(elk)]p(k)dk .
Поскольку р(?) — четная функция, эти интегралы действительные.
8.8. СВОБОДНАЯ ЭНЕРГИЯ ПРИ - 1 < Л < 1
Задача теперь состоит в том, чтобы решить линейное интегральное
уравнение (8.7.9). Для случая Д = -1 в работе [115] было отмечено, что
путем подходящей замены переменной к это уравнение можно преобразо-
преобразовать в уравнение с разностным ядром. Этот результат был обобщен [245]
на область Д < — 1, а затем [263] на область Д < 1. Имеются и более
сложные модели, которые могут быть решены с помошью анзаца Бете [18,
20, 21, 27, 43, 144, 162J. о каждом случае такое преобразование к разност-
разностному ядру существует. (См. также замечания, сделанные после (8.13.77) и
A0.4.31), имея в виду, что тригонометрические функции являются частны-
частными случаями эллиптических функций.)
При -1 < Д < 1 подходящим преобразованием будет замена ^ на а,
где если
A = -cos<u, 0<<и<я, (8.8.1)
то
ехр(*А:) = [ехр(*>) - ехр(аг)]/[ехр(*> + а) - 1]. (8.8.2)
Логарифмическое дифференцирование дает
Ак sin \х
(8.8.3)
dor cosh oc- cos \i'
так что к — действительная монотонно возрастающая функция а, нечетная
и изменяющаяся от \к — тг до 7г - /а при возрастании а от -оо до <х.
Положим в (8.7.2) р = к(а) и q = k($). Тогда последнее равенство
упрощается и принимает вид
г .^/ м ехр(ог-0) - ехрBш)
ехр[-1<д(р , q)] = V) Н) КШ , (8.8.4)
exp(/J - а) - ехрB^)
так что 0(р, q) является функцией только разности а — /3 (и константы /х).
Пусть Bir)~lR(a) — преобразованная функция распределения, определя-
определяемая соотношением
R(a) dor = 2лр(к) dk. (8.8.5)
Подставляя (8.8.2), (8.8.4) и (8.8.5) в (8.7.8), дифференцируя по а и исполь-
используя (8.8.3), получаем интегральное уравнение

ГЛАВА 8 149
п/ ч sin<u 1 fQl sin2^ л/_ч ,_
«(or) = — - — —— 5^Г 7~ л(#) d^' (8.8.6)
cosh а - cos \х 2л J-Ql cosh(or - /J) - cos 2ц
где (-(?!, Qj) — интервал на оси а, соответствующий интервалу (-Q, (?)
на оси А:. Условие (8.7.7), определяющее границы интервала, принимает
вид
Bл)-1 f ' R(a)da=nlN. (8.8.7)
J-Qi
Свободная энергия определяется с помощью (8.7.11) и (8.3.9). При под-
подстановке (8.8.2) и (8.8.5) естественно ввести еще одну константу W:
alb = [ехр(!» - exp(iw)]/[exp(iju + iw) - 1], -ju < w < \i. (8.8.8)
Из (8.3.21) и (8.8.1) тогда следует
а: Ъ: с = sin \(\x - w): sin \(pt + w): sin /г, (8.8.9)
а из (8.8.2) имеем
ехр(аг) - exp(iiv) ' (8 8 Ш)
ехр(аг) - exp(ivv)
С учетом (8.8.5) формула (8.7.11) для свободной энергии теперь прини-
принимает следующий вид:
(8.8.11)
\ ' [\п L(eik)]R(a) da,
еъ-{квТ12л) \ l [\nM(eik)]R(a)da}.
J-Qy
Решение методом интегралов фурье
Поскольку уравнение (8.8.6) является линейным интегральным уравне-
уравнением с разностным ядром, оно может быть решено с помощью интегралов
Фурье, если Q{ = оо. Предположим, что это так. Пусть
— Г00
R(x) = Bл)-1 R(a) exp(aa) da. (8.8.12)
J-00
Умножая обе части (8.8.6) на ехр(т*) и интегрируя по а, получаем
sinhTrjc sinhTrjc v

150 МОДЕЛИ ТИПА ЛЬДА
Отсюда немедленно следует
Щх) =isech рос. (8.8.14)
Согласно (8.8.12), левая часть (8.8.7) равна просто #@), т.е., согласно
(8.8.14), равна Уг. Таким образом, если Qx = оо, то
n=%N. (8.8.15)
Мы хотим выбрать п так, чтобы максимизировать Л, или, что эквива-
эквивалентно, минимизировать выражение (8.8.11) для/. Представляется весьма
разумным предположение, что (8.8.15) и есть правильное значение я, по-
поскольку оно соответствует симметричной ситуации, когда в каждом ряду
решетки числа стрелок, направленных вверх и вниз, одинаковы. Дальней-
Дальнейшее обоснование этого предположения дано в работах [157 — 159].
Мы могли бы предсказать, что Q{ = оо, рассуждая следующим обра-
образом: пусть первый член в (8.4.4) доминирует, тогда величину Л можно мак-
максимизировать, выбирая п настолько большим, насколько это возможно,
чтобы все Lj, ... , Ln имели модуль больше единицы. Если доминирует
второй член, то это же самое относится к Л/р ... , Мп. Поэтому, если
имеется такое действительное значение к, для которого модуль L[exp(//:)]
или Л/[ехр(/?)] равен единице, то оно соответствует к = ±Q. При
- 1 < Д < 1 имеются два таких значения, которые, согласно (8.8.10), соот-
соответствуют а = ±оо, т.е. Qx = оо, Q = тг - /л.
Таким образом, нам повезло в том смысле, что мы можем вычислить
R(a) аналитически в том и, как правило, только в том случае, когда
п = 7V/2, а это как раз то значение, которое требуется, чтобы получить
Лтах. Природа может быть милостива!
Если w = О, то а = Ъ, е1 = е3 и 111 = 1Л/1, так что оба члена в
(8.8.11) равны. Если w < 0, то первый из них меньше; если w > 0, то
меньше второй.
Рассмотрим сначала случай w < 0. Поскольку функция R(a) четная,
функцию In(L[exp(ik)]) в (8.8.11) можно заменить ее четной частью, кото-
которая одновременно является ее действительной частью. Фурье-образ имеет
вид
B7Г) J exp(aor)ln|L(e/A:)|dar
sinh (|ц + w)x sinh (тг - ф (8*8Л6)
х sinh тех
Фурье-образы R(a) дают выражения (8.8.12) и (8.8.14). Используя все
эти результаты, приводим (8.8.11) для w < 0 к следующему виду:
(8.8.17)
J- a, 2x sinh nx cosh рос
С помощью (8.8.3), (8.8.9) и формулы

ГЛАВА 8 щ 151
sinh {pi + w)x = sinh {pi - w)x + 2 coshpix sinhwx (8.8.18)
это выражение для свободной энергии можно записать в виде
sinh {pi - w)x sinh (я - u)x /o o im
———— ~ dbc (o.o.l")
2x sinh ях cosh рос
Это в точности совпадает с соответствующим выражением, получен-
полученным для w > 0. Таким образом, обе формулы (8.8.17) и (8.8.19) справедли-
справедливы во всем интервале -д < w < д. Никакой особенности при и> = 0 нет.
В общем случае эти интегральные выражения для свободной энергии не
могут быть вычислены аналитически. Исключение составляет случай, ког-
когда (л является рациональной долей числа тг. Например, для модели льда
(8.1.4) а = Ъ - с - 1, w = 0 и /х = 2тг/3. Тогда интеграл в (8.8.17) может
быть вычислен путем суммирования по вычетам в верхней полуплоскости,
что дает
zi/mn = ехр( _^вГ) = D/3K/2, (8.8.20)
а это и есть результат Либа [157] для энтропии модели льда на квадратной
решетке.
8.9. СВОБОДНАЯ ЭНЕРГИЯ ПРИ Д < - 1
Если А < -1, то параметры /х, а, определяемые посредством (8.8.2),
являются чисто мнимыми, так что их можно заменить на -/X, -/а, где X
и новое а — действительные параметры. Тогда вместо (8.8.1) и (8.8.2) по-
получаем
А =-cosh А, А>0, (8.9.1)
е/* = (ея _ е-'")/(ея-'* - 1) . (8.9.2)
Если а увеличивается от - тг до тг, то и к возрастает от -тг до тг.
Интегральное уравнение (8.8.6) теперь принимает вид
sinh A I fQi sinh2A _ ,
(8.9.3)
*(g) = cosh Я - cos а Гя U ^2Х - cosfr - ft
а условие (8.8.7) остается без изменения.
В то время как (8.8.6) можно было решить с помощью интегралов
Фурье в случае Qx = оо, соответствующее ему уравнение (8.9.3) решается с
помощью рядов Фурье, если Q{ = тг. Для всех целых т положим
— (ж
Rm = BЯ) R(a) exp(ima) da. (8.9.4)
J-л
Умножая (8.9.31 на exp(/wa) и интегрируя, получаем
2A!m|)^m, (8.9.5)

\S2 МОДЕЛИ ТИПА ЛЬДА
так что
JRW = i sech Am . (8.9.6)
В соответствии с (8.9.4) левая часть (8.8.7) равна просто #0, поэтому
мы снова имеем п = N/2. Это такое значение я, при котором, как мы
ожидаем, Л принимает свое максимальное значение.
Свободная энергия все еше определяется посредством (8.8.10) и (8.8.11),
но теперь w (так же как /х и старое а) является чисто мнимой величиной,
поэтому мы заменим ее на —iv, где —\<v<\. Тогда (8.8.9) и (8.8.10)
принимают вид
а\Ъ\с = sinhi(A%— v) :sinhi(A + v) :sinhA, • (8.9.7)
exp(-ia) - exp(v)
У ' (8.9.8)
M (e*) = ехР(^ " я) ~ ехР(я ~ to)
exp(-«ar) - exp(v)
Если v < 0, то первый член в (8.8.11) меньше, и функцию L [exp(ik)] лег-
легко представить в виде ряда Тейлора по степеням ехр(/а). Делая это и ис-
используя затем (8.9.6), получаем
, гЛл, ч v ехр(-тк) sinhт(А + v)
= \ mcoshmA
Последнее выражение можно преобразовать к виду
J
m = 1 m cosh mA
что в точности совпадает с результатом для v > 0. Таким образом, обе
формулы (8.9.9) и (8.9.10) справедливы во всем интервале -X < v < X.
Уравнения для конечного п
Вместо того чтобы сначала переходить к пределу TV, /7 — 00, а затем
производить замену переменных (8.9.1), мы могли бы с не меньшим успе-
успехом выполнить замену переменных в первую очередь. Получающиеся при
этом промежуточные уравнения потребуются в следующих двух главах, по-
поэтому удобно представить их здесь.
Пусть olj — значение а при к = kj. Тогда из (8.7.1) и (8.9.2) следует
Zj = exp(tfry) = sinh i(A + /a))/sinh |(A - iaj) (8.9.11)
при у = 1, . . . , п. Используя это выражение, а также (8.7.1) и (8.7.2), пе-
перепишем исходные уравнения (8.4.12), (8.4.4) для конечного п в виде

ГЛАВА 8
153
Lsinh J(A - щ
- <xj) - A']
A']
NyTsinhi(v + i<Xj + 2k') Nyrsintihiv + iaj-lk')
}= i sinh \{v + щ) j = i sinh i(^ + Ц)
(8.9.12)
(8.9.13)
где
A'=A-i7T.
(8.9.14)
При n <— oo совокупность ofj, ... , otn стремится к непрерывному рас-
распределению на отрезке (-7Г, 7г). Количество ау в интервале (а, а + с/а)
тогда равно Bic)~lNR(a)da. В этом пределе уравнения (8.9.12) для al9 . . . ,
а„ сводятся к интегральному уравнению (8.9.3) для R(a).
8.10. КЛАССИФИКАЦИЯ ФАЗ
Мы видим, таким образом, что свободная энергия принимает различ-
различные аналитические формы в зависимости от того, будет ли Д > 1,
1 > Д > - 1 или - 1 > Д. В терминах больцмановских множителей я, Ь, с
в соответствии с (8.3.21) это означает, что следует рассмотреть четыре об-
области (фазы), показанные на рис. 8.5.
СЕГНЕТОЭЛЕКТРИЧЕСКАЯ ФАЗА: а > Ъ + С
В этом случае Д > 1 и, согласно (8.3.2) и (8.3.3), е{ < е3, е5. Поэтому
наинизшее энергетическое состояние системы — это то состояние, в кото-
котором либо все вершины принадлежат к типу 1, либо все принадлежат к
типу 2. Все стрелки направлены либо вверх или вправо, либо вниз или вле-
влево. Таким образом, при очень низких температурах система сегнетоэлект-
рически упорядочена (все параллельные стрелки направлены в одну сторо-
сторону) и свободная энергия/ равна ех.
Но в соответствии с результатами разд. 8.6 такое значение / характери-
характеризует всю фазу I. Это означает, что вклад возбужденных состояний в стати-
статистическую сумму пренебрежимо мал, и повсюду в пределах фазы I система
заморожена в том или другом из двух наинизших состояний. Как было
разъяснено в разд. 8.6, имеется полный сегнетоэлектрический порядок.
Рис. 8.5. Фазовая диаграмма модели типа льда
в отсутствие внешнего поля в координатах,
выраженных через отношения больцмановских
весовых множителей а, Ь, с. Состояния, со-
соответствующие точкам на проведенной пункти-
пунктиром четверти окружности, описываются
собственной функцией газа свободных фермио-
нов; при этом А = 0, и модель может быть
решена с помощью пфаффианов.
а/с j
и
а/с

154 МОДЕЛИ ТИПА ЛЬДА
II. СЕГНЕТОЭЛЕКТРИЧЕСКАЯ ФАЗА: Ь > а + С
Это, по существу, та же ситуация, что и в случае I, за исключением то-
того, что теперь доминирующими являются вершины типов 3 и 4. Имеется
полный сегнетоэлектрический порядок: фактически все стрелки либо на-
направлены вверх и влево, либо вниз и вправо.
III. Неупорядоченная фаза: а, Ъ, с < хЛ(а + Ъ + с)
В данном случае - 1 < Д < 1. К этому случаю относится и предел бес-
бесконечно высокой температуры а = Ъ = с = 1; поэтому можно ожидать,
что система будет разупорядочена. Это верно в том смысле, что все корре-
корреляции спадают до нуля при увеличении расстояния г.
Но если а2 + Ъ1 — с2 (при этом больцмановские весовые множители
должны лежать в области III), то из (8.3.21) и (8.3.22) следует, что Д = 0 и
Sjj = Sj{. Тогда уравнения (8.4.12) кардинально упрощаются, коэффициенты
Ар пропорциональны ер и собственная функция (8.4.6) становится просто
детерминантом.
В этом случае задача может быть решена методом пфаффиана, упоми-
упоминавшимся в конце предыдущей главы [83, 261], и корреляции вычисляются.
Было обнаружено [19], что они спадают пропорционально отрицательной
степени г, а не экспоненциально. Поэтому, согласно A.7.24), корреляцион-
корреляционная длина ? бесконечна, так что система не является неупорядоченной в
обычном смысле.
Как показано в гл. 10, модели типа льда представляют собой специаль-
специальный случай восьмивершинной модели, которая также может быть решена.
Модели типа льда в фазе III соответствуют восьмивершинной модели при
критической температуре. В этом случае имеется бесконечное число соб-
собственных значений трансфер-матрицы, вырожденных с максимальным зна-
значением. Спонтанный порядок и поверхностное натяжение отсутствуют, но
корреляционная длина бесконечно велика.
Поэтому модель типа льда обладает весьма необычным свойством: она
находится в критическом состоянии при всех я, Ь, с в области III.
IV. АНТИСЕГНЕТОЭЛЕКТРИЧЕСКАЯ ФАЗА: С > а + Ъ
В этом случае Д < - 1 и е5 < ер е3- Наинизшим энергетическим состоя-
состоянием является либо состояние, показанное на рис. 8.3, либо состояние, по-
получаемое из него обращением всех стрелок. В обоих случаях направления
стрелок. чередуются.
При достаточно низких температурах следует ожидать, что система
будет находиться в таком упорядоченном антисегнетоэлектрическом состо-
состоянии. Поскольку свободная энергия является аналитической функцией всю-
всюду в пределах области IV, мы полагаем, что это будет упорядоченная анти-
сегнетоэлектрическая фаза. Этот вывод подтверждается приведенными ни-
ниже результатами для Д < - 1, т.е. для с > а + Ъ.

ГЛАВА 8 155
ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ
При Д < - 1 имеем Q{ = Q = 7г, так что максимальному собственному
значению соответствует распределение zv ... , zn по всей единичной
окружности. Более тщательный анализ [28] показывает, что для четного N
в действительности имеется два таких решения в подпространстве
п = N/2. Наибольшее по величине из этих двух собственных значений (Ло)
соответствует собственному вектору, который симметричен по отношению
к изменению направлений всех стрелок; меньшее собственное значение (Aj)
отрицательно и соответствует антисимметричному собственному вектору.
Точки гр . . . , zn одного решения перемежаются с точками zv . . . , zn дру-
другого, и для большого N
А11А0= -1 + 0{exp(-Ns/kBT)}, (8.10.1)
где если
х = ехр(-А), (8.10.2)
то
X
П/ 1 + хАт \2
(Вывод этого результата дан в разд. 10.10 для более общей восьмивершин-
ной модели.)
Таким образом, Ло и Aj асимптотически вырождены. По соображениям,
сходным с приведенными в разд. 7.10, 5 — поверхностное натяжение меж-
между двумя упорядоченными антисегнетоэлектрическими фазами.
Спонтанная антисегнетоэлектрическая поляризация
Будем рассматривать основное состояние с расположением стрелок, по-
показанным на рис. 8.3, как «стандартную» конфигурацию. Для произволь-
произвольной конфигурации стрелок каждому значению / сопоставим параметр г- по
следующему правилу:
Т{ = +1, если стрелка на линии связи / имеет то же на-
направление, что и на рис. 8.3;
7, = -1, если стрелка направлена противоположно.
Тогда символ <т,> обозначает среднюю «поляризацию» электрического
диполя на линии /', нормированную так, что ее значение лежит в интервале
от - 1 до +1. Она определена по отношению к антипараллельной конфигу-
конфигурации стрелок на рис. 8.3, поэтому является антисегнетоэлектрической по-
поляризацией.
Здесь имеет место та же проблема, с которой мы уже сталкивались в
разд. 7.10 при определении спонтанной намагниченности для модели Изин-
га. Если мы определяем поляризацию с помощью A.4.4), то она должна
равняться нулю, поскольку каждому состоянию со стрелкой вверх (или
вправо) на линии / соответствует еще одно состояние (получаемое обра-

156 МОДЕЛИ ТИПА ЛЬДА
щением всех стрелок) с той же энергией и со стрелкой на линии /, направ-
направленной вниз (или влево).
Однако если использовать только те элементы симметрии, которые
оставляют стандартную конфигурацию на рис. 8.3 неизменной (обращение
стрелок плюс трансляция, зеркальное отражение плюс вращение плюс об-
обращение стрелок), то можно показать, что <rt> должно иметь одно и то же
значение для всех линий /, горизонтальных и вертикальных. Если Ро — это
значение, то по аналогии с G.10.47) мы можем определить его как
), (8.10.4).
где предел соответствует неограниченному удалению линий / и j друг от
друга. Эта величина Ро представляет собой спонтанную антисегнетоэлект-
рическую поляризацию. (Как А/о является предельным значением М при
Н -* 0+, так и Ро является предельным значением <г/>, получаемым путем
приложения антисегнетоэлектрического поля к модели типа льда и после-
последующего его выключения.)
Воспользуемся теперь соображениями, подобными тем, которые были
связаны с цепочкой равенств G.10.25) — G.10.37). Рассмотрим какой-то
определенный столбец С решетки. Пусть т/= +1, если вертикальная
стрелка в ряду / вдоль этого столбца направлена вверх, и т/ = - 1, если она
направлена вниз. Пусть 5 — диагональная матрицы 2^ х 2N с элементами
+ 1 (-1) для состояний вдоль столбца С со стрелками вверх (вниз). Тогда
для j > 1 имеем
(г/г/) = Joi'io^/Ao)' + Го2Г2о(Л2/ЛоУ"' + . . . , (8.10.5)
где если U — матрица собственных векторов трансфер-матрицы К, то
/01 — элемент @, 1) матрицы U~xsU, т.е.
Гш = (f/Jf/)oi, (8.10.6)
и аналогично для /10, /02 и т.д. Суммирование в (8.10.5) выполняется по
всем собственным значениям Лр Л2, . . . , соответствующим собственным
векторам, антисимметричным по отношению к обращению всех стрелок.
Таким образом, собственное значение Ло(= Лтах) не входит, а А{ входит в
сумму (8.10.5).
Сначала перейдем к пределу при N — оо в (8.10.5). Согласно (8.10.1),
Aj/Aq — — 1. Все другие собственные значения остаются строго меньше по
модулю, чем Ло. Таким образом, если мы теперь предположим, что раз-
разность j - i становится большой, то получим
Величины т/ определены относительно параллельной конфигурации (все
стрелки вверх), в то время как т{ определены относительно антипараллель-
антипараллельной конфигурации рис. 8.3. Следовательно, r'pr'j = (-1)' + ^-ту, поэтому из

ГЛАВА 8 157
(8.10.4) и (8.10.7) получаем
P2o = t0ltlo. (8ЛО.8)
Матричные элементы t0l и t{0 вычислены в работе [29] (вычисления оказа-
оказались весьма сложными и запутанными). Получен следующий результат:
,= П
P0=lliG-r^) . (8.10.9)
КОРРЕЛЯЦИОННАЯ ДЛИНА
Следующее по величине после Ло и \{ собственное значение Л2 является
максимальным собственным значением в подпространстве п = N/2 - 1
(или п = N/2 + 1) для четного N. Точки Z\, ... , zn снова распределены
по окружности единичного радиуса, но в этом распределении имеется дыр-
дырка при z = — 1. Такие неполные распределения поддаются исследованию
[95, 119, 229, 264]. Конкретизируя более общий результат для восьмивер-
шинной модели [120, 122], для бесконечного N получаем
= А + „ + 2
т=\ га cosh га А
Эта формула пригодна только для интервала -X < v < 0, поскольку
для v > 0 сумма расходится. Но если выражение под знаком суммы разло-
разложить в ряд по степеням ехр(-2Х), то последующее почленное суммирова-
суммирование дает
(8Л0Л1)
где z = exp(f). Это бесконечное произведение сходится во всем допусти-
допустимом интервале ~Х < v < X.
Корреляционную длину ? теперь можно получить с помощью рассужде-
рассуждений, аналогичных проведенным в разд. 7.10. Формула G.10.41) с необходи-
необходимостью выполняется только при условии, что трансфер-матрица V являет-
является симметричной, а это справедливо лишь при о = Ь и у = 0. В самом де-
деле, было показано [120, 122], что длина ? должна совпадать с длиной зату-
затухания корреляции между двумя вертикальными стрелками в том же ряду (а
не в том же столбце). Так же как (opoq) в G.10.42), эта корреляция зави-
зависит от больцмановских множителей а, В, с только через матрицу собствен-
собственных векторов U. Из (8.4.6), (8.4.10), (8.4.12) и (8.3.22) следует, что со-
собственные векторы зависят только от Д. Это означает в соответствии с
.(8.9.1) и (8.9.7), что U является функцией X, но не зависит от v. (Этот во-
вопрос рассмотрен в следующей главе.) Таким образом, длина ? также не до-
должна зависеть от i/, что противоречит G.10.41) и (8.10.11).
Так же как в случае модели Изинга, эти соображения разрушают одно

158 МОДЕЛИ ТИПА ЛЬДА
построение, но служат основой для другого. Дело в том, что соотношения
G.10.41) и (8.10.11) справедливы для v = 0, когда матрица К симметрична,
и ее собственные значения — действительные числа. Поскольку ? не зави-
зависит от i>, результирующее выражение для ? должно быть справедливо по-
повсюду в пределах допустимого интервала —\<v<\. Оно имеет вид
Эта формула была проверена [122] посредством прямого суммирования
(8.10.5) по всем входящим туда собственным значениям. Сравнивая
(8.10.12) и (8.10.3), мы видим, что поверхностное натяжением и корреляци-
корреляционная длина ? удовлетворяют точному соотношению
s§=*B7\ (8-10.13)
которое совпадаем с соответствующим соотношением G.10.44) для модели
Изинга.
8.11. КРИТИЧЕСКИЕ СИНГУЛЯРНОСТИ
Рассмотрим заданный набор значений энергий взаимодействия ер . . . ,
е6, удовлетворяющих условию (8.1.7). Больцмановские множители я, Ь, с
для некоторой температуры Т определяются с помощью (8.3.3); они соот-
соответствуют точке на плоскости (а/с, b/с) на рис. 8.5.
Когда температура Т растет от 0 до оо, эта точка описывает траекто-
траекторию на указанной плоскости, которая всегда оканчивается в точке A, 1) об-
области III. В зависимости от значений вр е3, е5 эта траектория переходит
или не переходит из одной области в другую.
Если две наименьшие из величин ер е3, ?5 Равны> то траектория всегда
будет проходить внутри области III. Свободная энергия является аналити-
аналитической функцией при всех температурах Т.
Если одна из энергий ер е3, ?5 меньше ДВУХ других, то при достаточно
низких температурах траектория оказывается в одной из областей I, II или
IV. При повышении температуры она переходит в область III при некото-
некоторой «температуре перехода» Тс. Может существовать только одна такая
температура перехода.
Свободная энергия имеет особенность при Т = Тс, так что в этом
смысле эта точка является критической. Но это весьма необычная критиче-
критическая точка, поскольку, как было отмечено в предыдущем разделе, корреля-
корреляционная длина бесконечна повсюду в пределах области III.
Следует рассмотреть три случая.
СЕГНЕТОЭЛЕКТРИК: ?j < ?3> ^5
В этом случае при достаточно низких температурах точка на рис. 8.5,
определяемая весовыми множителями я, Ь, с, лежит в области I. Модель

ГЛАВА 8 159
характеризуется тогда полным сегнетоэлектрическим порядком. Типичным
примером является модель KDP, обсуждавшаяся к разд. 8.1.
Температура перехода Тс определяется условием
а = Ь + с. (8.11.1)
При Т > Тс величина / определяется формулами (8.8.9) и (8.8.17); если
Т < Тс, то свободная энергия/ равна просто е{.
Если Т-* Г+, то из (8.3.21), (8.8.1) и (8.8.8) следует, что д - тг,
w — — 7г. Поэтому полезно ввести новые параметры 5, е:
[л = я-д, w=-jc+?. (8.11.2)
Тогда (8.8.9) принимает вид
a:b:c = sini(d+ e):sin?(e- 6): sin 6. (8.11.3)
Если Г— Г+, параметры 5 и е, оставаясь все время положительными,
стремятся к нулю; при этом их отношение будет конечной величиной, не
равной нулю. Разность температур Т - Тс пропорциональна величине
t = (b + c-a)/a (8.11.4)
при условии, что t — малая величина. Поэтому мы можем использовать
(8.11.4) в качестве меры отклонения Т от Тс вместо A.1.3). Согласно
(8.11.3), t связано с 5 и ? посредством соотношения
t = 2 sin id (cos id - cos?e)/sin JF 4- e), (8.11.5)
которое для малых дне приводится к виду
,Таким образом, дне стремятся к нулю как tV: при t — 0+.
Подставим теперь (8.11.2) в (8.8.17) и допустим, что t — малая величи-
величина. Используя (8.11.6), получим
/= ?1 - к.ТАе - 6) ?^
(o.l1. /)
Этот результат относится к области / > 0. При / < 0 свободная энер-
энергия/ равна просто е{. Ясно, что/ будет непрерывной функцией при t = 0;
ее первая производная (внутренняя энергия) испытывает конечный скачок, а
ее вторая производная (теплоемкость) расходится как / ~ 2 при / > 0. Из
определения A.7.10) критического показателя а следует (вследствие конеч-
конечного скачка), что
а=\ (8.11.8)
как для фазового перехода первого рода.
При Т < Тс система полностью упорядочена, так что спонтанная поля-

160 МОДЕЛИ ТИПА ЛЬДА
ризация
Ро=1. (8.11.9)
Точно так же, как мы определили с помощью A.1.4) критический пока-
показатель /3 для намагниченности Мо, мы определим показатель &е для элект-
электрической поляризации Ро. В рассматриваемом случае
& = 0. (8.11.10)
Выше Тс длина корреляции всегда бесконечна, в то время как ниже Тс
она равна нулю, а поверхностное натяжение бесконечно. Поэтому показа-
показатели и, v' и jit нельзя определить разумным образом. Несмотря на такое
ненормальное поведение, модель представляет интерес, так как это одна из
очень немногих моделей, которая может быть решена в присутствии поля,
нарушающего симметрию (в данном случае постоянного электрического
поля). В следующем разделе намечен ход соответствующих вычислений и
получено критическое уравнение состояния.
СЕГНЕТОЭЛЕКТРИК: ?3 < 6{, 65
Результаты для этого и предыдущего случаев совпадают, если поме-
поменять местами ех с ?3> а с Ь и область I с областью II. Действительно, такая
замена соответствует просто зеркальному отражению решетки или ее вра-
вращению на 90°.
АНТИСЕГНЕТОЭЛЕКТРИК: ?5 < ?l5 ?3
При достаточно низких температурах точка на рис. 8.5, определяемая
весовыми множителями, расположена в области IV. Переход из области IV
в область III происходит при критической температуре Тс, определяемой
условием
с = а + Ь. (8.11.11)
При Т > Тс свободная энергия / определяется с помощью (8.8.9) и (8.8.17);
при Т < Тс ее можно найти из (8.9.7) и (8.9.9).
Этот случай заметно отличается от двух предыдущих, так как упорядо-
упорядоченное состояние характеризуется микроскопическим антисегнетоэлектриче-
ским порядком, а не макроскопическим сегнетоэлектрическим порядком.
«Сингулярную часть» /sing свободной энергии можно определить с по-
помощью A.7.10а). Сравнивая (8.8.1) с (8.9.1) и (8.8.9) с (8.9.7), мы видим,
что аналитическим продолжением /х и w из области Т > Тс на область
Т < Тс являются —/X и —w соответственно. В обеих областях отношение
w//x — действительная величина, причем -1 < w/p < 1. Вблизи Тс
А » — 1, и параметр /х мал.
Таким образом, мы хотим получить аналитическое продолжение инте-
интеграла в (8.8.17) из области малых действительных положительных значе-
значений (л и /х + w на область малых мнимых отрицательных Значений. Чтобы
выполнить эту задачу, воспользуемся сначала четностью подынтегрально-
подынтегрального выражения, чтобы записать (8.8.17) в виде

ГЛАВА 8 J6\
f
J-o
2jtsinh;ct cosh
(8.11.12)
где ^— главное значение интеграла. Если д, w имеют отрицательные
мнимые части, то путь интегрирования можно замкнуть через верхнюю по-
полуплоскость комплексной переменной х. Полагая д = —/X и w = —iv и
суммируя по вычетам, получаем
f=ex-kBT -
exp(-mA)sinhm(A + и)
у)+ 2 . ,
m = i m cosh ml
(8.11.13)
. у (-)т ехр[-(т - j)^/A] cosh[(m - \)kvII\\
~ l m = i (m - i) sinh[(m - i)^/A]
(Этот результат для F-модели, когда v = 0, приведен в работе [100]
(уравнение А13).)
Очевидно, действительная часть (для действительных X, v) этого выра-
выражения совпадает с (8.9.9). Таким образом,/sing представляет собой мнимую
часть (8.11.13). Вблизи Тс величина X мала, поэтому
/sine ^ -ШВТС ехр(-я2/А) cosh(jry/2A). (8.11.14)
Аналогично (8.11.4) определим отклонение Т от Тс следующим образом:
t = (a + b-c)/c. (8.11.15)
Тогда из (8.9.7) следует, что отношение v/\ остается конечной и не равной
нулю величиной при t — 0, в то время как для малых X и v
t^-\{k2- v2). (8.11.16)
Таким образом, вблизи Тс как X, так и v пропорциональны (-t)Vl.
Отсюда следует, что свободная энергия имеет необычную сингуляр-
сингулярность при Т = Тс, а именно
/sing <* ехр [-constant^-r)*]. (8.11.17)
Это очень слабая сингулярность. Величина/sing и все ее производные стре-
стремятся к нулю при f — 0~. Действительно, все температурные производные
свободной энергии существуют и одинаковы по обе стороны от точки
перехода [100, 163]. Мы имеем дело с фазовым переходом бесконечного
порядка.
Ясно, что E.11.7) не имеет обычно постулируемого вида A.7.106), по-
поэтому показатель а в правильном смысле не существует. Если все же по-
потребовалось бы указать его значение, то единственно разумным выбором
был бы следующий:
аг=-оо. (8.11.18)

262 МОДЕЛИ ТИПА ЛЬДА
При Т < Тс длина корреляции ?, поверхностное натяжение 5 и спонтан-
спонтанная антисегнетоэлектрическая поляризация Ро определяются соотношения-
соотношениями (8.10.3), (8.10.9) и (8.10.12). Их критическое поведение легче всего полу-
получить, замечая, что эти соотношения, содержащие бесконечные произведе-
произведения, в точности совпадают с соотношениями между эллиптическими моду-
модулями и нтегралами, с одной стороны, и их параметром Якоби — с другой.
В самом деле, из A5.1.1) — A5.1.4) следует
(8.11.19)
Р0 = 2к'1/л,
где к, к\ I — модуль, сопряженный модуль и эллиптический интеграл, со-
соответствующие параметру Якоби
q=x2 = exp(-2A). (8.11.20)
Вблизи Тс величина X мала, поэтому х и к приближаются к единице.
Тогда /' — тг/2, так что, согласно A5.1.3),
q (8.11.21)
Кроме того, заменяя к и q в A5.1.4) сопряженными параметрами к' и q\
где q' = ехр( — тг///'), получаем
к' - 4q'* = 4 ехр(-я2/4А), (8.11.22)
In к =-8q' = -8ехр(-л:2/2А). (8.11.23)
Подстановка этих формул в (8.11.19) приводит к следующим выражени-
выражениям, справедливым вблизи Тг:
Г1 = slksT^A ехр(-я2/2А), Ро- Bя/А) ехр(-л:2/4А). (8.11.24)
Таким образом, ?~!, 5 и Ро быстро спадают к нулю, когда X — 0, т.е.
когда Т — Тс. Каждая из этих величин имеет существенную особенность,
подобную той, которая была установлена для/51п8, т.е. вида (8.11.17). Они
не стремятся к нулю по простому степенному закону. Поэтому определе-
определения A.7.9), A.7.34) и A.1.4) соответствующих им критических показателей
v, IX и 0е оказываются непригодными.
С другой стороны, из (8.11.14) и (8.11.24) следует, что соотношения
пропорциональности
(8.11.25)
выполняются. Если бы эти величины убывали по степенному закону, то
соответствующие степенные показатели должны были бы удовлетворять
соотношениям
v = \х = i + 2/3, = iB - а). (8.11.26)

ГЛАВА 8 ИЗ
В этом смысле мы можем поэтому утверждать, что эти соотношения
между показателями выполняются. В частности, соотношения A.2.15) и
A.2.16) удовлетворяются.
К сожалению, наложение постоянного электрического поля не снимает
вырождения антисегнетоэлектрического основного состояния. Для этого
необходимо было бы приложить электрическое поле, ориентация которого
вдоль двух соседних связей в решетке антипараллельна. Мы не располагаем
решением этой модели в присутствии такого поля, поэтому в данном слу-
случае не можем провести дальнейшую проверку гипотезы подобия.
8.12. СЕГНЕТОЭЛЕКТРИЧЕСКАЯ МОДЕЛЬ
В ПРИСУТСТВИИ ПОЛЯ
В отсутствие поля статистическая сумма z определяется выражениями
(8.1.1) и (8.1.3), а вершинные энергии е1э . . . , е6 удовлетворяют соотноше-
соотношениям симметрии (8.1.7) по отношению к одновременному обращению всех
стрелок.
Эта симметрия может быть нарушена путем наложения вертикального
и горизонтального полей Е и Е' соответственно. В результате этого каж-
каждая направленная вертикально вверх (вниз) стрелка приобретает дополни-
дополнительную энергию — Е( + Е), а направленная горизонтально вправо (влево)
стрелка — энергию —Е' ( + ?").
При желании эти энергии можно включить в вершинные энергии, деля
при этом энергию каждой стрелки между вершинами, которые она соеди-
соединяет. Если gj, ... , е6 — исходные энергии вершин в отсутствие поля,
удовлетворяющие условиям (8.1.7), то в соответствии с рис. 8.2 шесть ре-
результирующих вершинных энергий равны
Ei -Е-Е\ е2+Е+Е'9 ?3+Е-Е', ?4-Е + Е\ е5, е6.
(8.12.1)
Как уже отмечалось в разд. 8.1, мы не теряем общности, полагая е5 = с6;
поэтому в (8.12.1) можно подставить любые шесть энергий, используя
(8.1.7). Таким образом, мы имеем общую шестивершинную модель.
Она может быть решена [163, 265]; выкладки разд. 8.2 — 8.7 соответст-
соответственным образом обобщаются, приводя к линейному интегральному уравне-
уравнению вида (8.7.9). Вообще говоря, это уравнение теперь уже не может быть
решено аналитически, но его свойства могут быть исследованы и, конечно,
его можно решить численно.
Обобщение выполняется особенно просто, если Е' = О, т.е. когда при-
приложено только вертикальное электрическое поле Е; поэтому ниже мы рас-
рассмотрим этот случай. Вместо того чтобы включать вертикальное поле в
энергии вершин, сохраним эти названия за величинами е1э ... , е6, по-
прежнему удовлетворяющими (8.1.7). Тогда (8.1.3)-следует заменить на
- E(Nt - 2Nd), (8.12.2)

164 МОДЕЛИ ТИПА ЛЬДА
где Nt — общее число вертикальных связей, a Nd — число стрелок, направ-
направленных вниз. (Таким образом, Nt — 2Nd — число стрелок, направленных
вверх, минус число стрелок, направленных вниз.)
Вспомним теперь очень важный результат из разд. 8.3: в каждом ряду
имеется ровно п стрелок, направленных вниз. Поскольку в решетке М ря-
рядов и N столбцов, имеем
Nt-2Nd = M(N-2n). (8.12.3)
Заменяем (8.1.3) на (8.12.2) и вспоминаем, что трансфер-матрица V рас-
распадается на N + 1 диагональных блоков со своими значениями п. При
этом выражение (8.2.1) принимает следующий вид:
N
Z = 2 txp[EM(N - 2п)/квТ] Trace Vff, (8.12.4)
л = 0
где Vn — л-й диагональный блок исходной трансфер-матрицы V. Если
Ап — максимальное собственное значение в этом блоке, то для больших М
имеем
N
Z ~ 2 Л^ txp[EM(N - 2п)/квТ]. (8.12.5)
п — О
Для больших М в сумме (8.12.5) доминирует член со значением л, для ко-
которого выражение под знаком суммы максимально. Поэтому в соответст-
соответствии с A.7.6) выражение для свободной энергии на один узел имеет следую-
следующий вид:
f = fn-E(l-2n/N), (8.12.6)
где
U = -N~l квТ \пАп (8.12.7)
и значение п должно соответствовать минимуму правой части (8.12.6).
Поскольку V — исходная трансфер-матрица, fn для заданного значения
п совпадает со свободной энергией /, определяемой посредством (8.7.7),
(8.7.9) и (8.7.11). Единственное различие между вычислениями данного и
предшествовавших разделов состоит в том, что раньше мы выбирали п та-
таким образом, чтобы минимизировать величину fn саму по себе (подходя-
(подходящим значением оказалось п = N/2), теперь же мы должны найти минимум
выражения (8.12.6).
Более детально это означает, что для каждого значения п мы должны
решить (8.7.7) и (8.7.9) относительно Q и р(?), используя определение
(8.7.3) для 0. Затем мы должны вычислить fn с помощью (8.7.11) и, након-
наконец, выбрать п так, чтобы минимизировать (8.12.6).
Поляризация Р равна среднему от (Nt — 2Nd)/Nn и так как в сумме
(8.12.5) доминирует член с соответствующим л, то
Р= 1 -2nlN. (8.12.8)
Когда Е меняется, то п меняется тоже; но поскольку п выбирается так,

i ГЛАВА 8 165
чтобы обеспечить стационарность (8.12.6) по отношению к вариациям п
(при заданном Е), то из этого сразу следует
¦ -%= l~2n/N=P. (8.12.9)
дЕ
; Это равенство является очевидным аналогом A.7.14) для электрических
I систем.
КРИТИЧЕСКОЕ УРАВНЕНИЕ СОСТОЯНИЯ
f
\ Допустим, что е{ меньше, чем е3 и ?5; Тогда в отсутствие поля имеется
переход при температуре Тс, определяемой соотношением (8.11.1). В доста-
достаточно близкой окрестности этой температуры описанная выше программа
может быть выполнена в первом порядке по температурной переменной t,
которую мы определили с помощью (8.11.4).
Наиболее легкий способ сделать это состоит в том, чтобы вернуться к
соотношениям (8.4.12), (8.3.22) для Z\, ... , zn. Вводя kv ... , кп с по-
помощью (8.7.1) получаем
П1 _ О A eik, _l ei(k, + ki)
i ZAe ^e (8.12.10)
при j = 1, . . . , n.
Определим /, Ь так же, как в разд. 8.11. Тогда, согласно (8.8.1) и
(8.11.2),
А = cos <5, (8.12.11)
и t - 0, д - 0 при Т - Тс.
В разд. 8.8 было показано, что если п = N/2, то Q = ж - /л= 8. Таким
образом, к1% . . . , кп распределены в интервале (-5, 8). При п < N/2 мы
ожидаем, что числа к будут распределены по некоторому меньшему интер-
интервалу симметрично относительно начала отсчета.
Если 8 — малая величина, то kv . . . , кп должны быть порядка 8. Ло-
Логарифмируя (8.12.10), в первом порядке по 8 получаем
^( ji)(kj - ki). (8.12.12)
*j
Устремим теперь п и N к бесконечности, сохраняя постоянным значение
n/N. Как и в разд. 8.7, числа кх, ... , кп образуют в этом пределе факти-
фактически непрерывное распределение на некотором интервале ( —Q, Q). Пусть
Np(k)dk снова определяет количество kj в интервале между к и к + dk.
Тогда (8.12.12) превращается в интегральное уравнение
-»jr
- кк'
—~p(k')dk', (8.12.13)
— /С

266 МОДЕЛИ ТИПА ЛЬДА
где — Q < к < Q, а ^— главное значение интеграла. Величина Q снова
связана с n/N условием (8.7.7). Используя определение поляризации Р
(8.12.8), это условие можно представить в виде
) (8.12.14)
-q
Записывая кк' в (8.12.13) как к1 - к (к - к') и используя (8.12.14), при-
приводим интегральное уравнение к виду
Рк [ p()k
®L^ (8л2л5)
Это сингулярное интегральное уравнение с ядром типа Коши [173]. Оно
может быть решено точно. (Прямолинейный способ состоит в том, чтобы
перейти от переменных к, к' к а, а', где к = Q tanh а, и затем использо-
использовать интегралы Фурье.) При Q ^ 8 решение имеет вид
Подставляя его в (8.12.14) и используя формулу
CQ (Q2 _ ?2ч*
I
75 гг-<*к = Ф - A - Q ISry\ , (8.12.17)
-q dz-kz
находим следующее выражение для Q:
Q = 6A - Р2)*. (8.12.18)
Так как 0 ^ п ^ N, то Р лежит в интервале (—1, 1); поэтому Q всегда
меньше 5, и полученное решение верно для всех допустимых значений n/N.
Для данного значения п свободная энергия fn определяется выражением
(8.7.11). Поскольку ?j < ?3, первый член меньше второго, так что мы до-
должны произвести разложение L [ехр(/?)] в окрестности д = 0 и к = 0.
Используя (8.3.9) и (8.11.4) и замечая, что к - 5, t - б2, получаем
In L (е*) = Ъ + ik + (l - ^) к2 + ОE3). (8.12.19)
Подставляя это выражение в (8.7.11) и используя (8.12.16) и (8.12.18), при-
приходим к следующему результату:
fn = ?i- kBT\t{\ - Р) + A - -) д\1 - РJ/4 + €F3)] (8.12.20)
L V с/ J
Но из (8.11.3) и (8.11.6) в пределе малых <5 следует
Л --\д2= -It, (8.12.21)

ГЛАВА 8
167
поэтому, если пренебречь членами, малыми по сравнению с t, выражение
(8.12.20) упрощается и принимает вид
fn = el-lkBTct(l-P2). (8.12.22)
Выберем теперь п таким образом, чтобы минимизировать (8.12.6), по-
помня о том, что п лежит между 0 и N и связано с Р соотношением (8.12.8).
Это дает
P = EI{kBTct)f если \E\<kBTct, (8.12.23а)
= sign(?) в остальных случаях. (8.12.236)
Результирующее разбиение плоскости (г, Е) показано на рис. 8.6. В об-
области А система разупорядочена, и поляризация Р определяется выражени-
выражением (8.12.23а). В областях В и С система полностью упорядочена, иР = +1
и — 1 соответственно.
Гипотеза подобия (скейлинга)
Соотношение (8.12.23) представляет собой критическое уравнение состо-
состояния, справедливое для всех отрицательных и для малых положительных
значений t. Оно выглядит удивительно простым, если принять во внимание
сложность его получения.
Вспоминая, что Р является электрическим аналогом М, а Е — аналогом
//, мы можем сравнить (8.12.23) с предсказываемым гипотезой подобия
выражением A.2.1), а именно
Е/квТс = Р \Р\6~l hs(t\P\"vfi). (8.12.24)
После короткого размышления мы приходим к выводу, что если общий
характер зависимости hs(x) соответствует графику на рис. 1.4 и
lim x~lhs{x) = 1, 6=1 + /Г
(8.12.25)
то (8.12.24) приводится к виду (8.12.23) в пределе 0 - 0+. Таким образом,
гипотеза подобия подтверждается в смысле такого предела, и критические
Е к
Рис. 8.6. Фазовая диаграмма сегнето-
электрической модели вблизи ее критиче-
критической точки t = Е = 0. Границами неупо-
неупорядоченной фазы Л являются линии
Е = ±kBTct.

МОДЕЛИ ТИПА ЛЬДА
показатели равны
a=l,pe=0,Ye= l,6e= оо, (8.12.26)
где индекс е отмечает «электрические» показатели. Эти результаты, разу-
разумеется, согласуются с полученными выше результатами (8.11.8) и (8.11.10).
Если не считать ограничения, накладываемого условием (8.12.25), функ-
функция hs(x) остается неизвестной. Можно лишь пожалеть об этом, поскольку
из всей совокупности моделей, включающей двумерную модель Изинга,
модели типа льда и восьмивершинные модели, только эта сегнетоэлектри-
ческая модель решена в присутствии поля, нарушающего симметрию. Бы-
Было бы исключительно интересно получить точную двумерную функцию
скейлинга.
8.13. РАСКРАШИВАНИЕ КВАДРАТНОЙ РЕШЕТКИ
ТРЕМЯ КРАСКАМИ
Модель льда является таким частным случаем шестивершинной модели,
или модели типа льда, для которого все е1э ... , е6 равны нулю, как в
(8.1.4). Ленард [157] показал, что эта модель эквивалентна задаче о подсче-
подсчете числа способов раскрашивания ячеек квадратной решетки тремя краска-
красками так, чтобы никакие две соседние ячейки не были одного цвета.
Чтобы увидеть это, рассмотрим раскрашенную как-то по указанному
правилу решетку и введем для цветов обозначения 1, 2, 3. Нарисуем стрел-
стрелки на линиях, соединяющих узлы решетки, руководствуясь следующим пра-
правилом:
если наблюдатель, находясь на ячейке, имеющей цвет а, смотрит на со-
соседнюю ячейку, имеющую цвет а + 1 (цикл равен трем единицам), то на
пограничной линии между ячейками рисуем стрелку, направленную влево
по отношению к наблюдателю; если соседняя ячейка имеет цвет о — 1
(цикл равен трем единицам), то рисуем стрелку, направленную вправо.
Представим себе теперь, что наблюдатель совершает обход вокруг
какого-то узла. Пусть / — число его переходов в соседнюю ячейку, при ко-
которых номер краски увеличивается (стрелка направлена влево), а
D — число переходов с уменьшением номера краски (стрелка направлена
вправо). Поскольку он возвращается к исходному цвету, I — D = 0 (цикл
равен трем единицам). Поскольку вокруг каждого узла имеется четыре
ячейки, получаем также / + D = 4. Единственное неотрицательное реше-
решение этих уравнений имеет вид I = D = 2, так что имеются две стрелки, на-
направленные к этому узлу, и две стрелки, направленные от него. Поэтому
правило льда (разд. 8.1) выполняется для этого и для всех остальных узлов
решетки.
Таким образом, каждому трехцветному раскрашиванию решетки соот-
соответствует конфигурация стрелок на ее линиях, удовлетворяющая правилу
льда. И обратно, каждой такой конфигурации стрелок отвечают три допу-
допустимые раскраски решетки (один квадрат раскрашивается произвольно;

ГЛАВА 8 169
цвета остальных после этого определены однозначно). Таким образом, чис-
число способов раскраски решетки равно 3Zice, где Zice — статистическая сум-
сумма для модели льда. Это число равно также
HG(NltN2,N3), (8.13.1)
где G(fcv N2, N3) — число допустимых способов раскрашивания ячеек так,
что Nl из них имеют цвет 1, N2 — цвет 2 и N3 — цвет 3. Если общее число
ячеек равно Nt, то очевидно
ЛГ1 + ЛГ2 + Л/з = ЛГ,. (8.13.2)
Суммирование в (8.13.1) распространяется на все неотрицательные целые
числа Nj, N2, N3, удовлетворяющие условию (8.13.2).
Очевидное обобщение задачи раскрашивания состоит в том, чтобы вы-
вычислять G(N{, N2, N3) по отдельности, а не только в сумме. Это эквива-
эквивалентно тому, чтобы попытаться вычислить производящую функцию
Zc = Z zM2z? G{N,, N2, N3) (8.13.3)
для произвольных значений Z\9 z2, Zy
Другой подход к этой задаче (более явно статистикомеханический) со-
состоит в том, чтобы рассматривать цвета 1, 2, 3 как три сорта частиц.
Каждая ячейка решетки содержит только одну частицу; соседние частицы
должны быть другого сорта. Тогда ZG в (8.13.3) является большой стати-
статистической суммой этого плотноупакованного решеточного газа; zx, z2,
z3 — три активности.
Оказывается, что эта задача может быть решена [21, 24]. Выражаясь
точнее, можно вычислить предельную «статистическую сумму на один
узел»
к= lim Z%Nt, (8.13.4)
Nt-+*>
где, как обычно, Nt — 00 означает термодинамический предел, когда высо-
высота и ширина решетки становятся большими.
Методом решения является снова анзац Бете. Ниже даются требуемые
модификации разд. 8.2 — 8.8.
Еще одна задача, которая может быть решена, — это задача о раскра-
раскрашивании узлов треугольной решетки четырьмя красками [20]. Как указано
в разд. 12.1 и 12.2, обе эти задачи о раскрашивании (если активности равны
единице) являются частными случаями модели Поттса.
Трансфер-матрица
Пусть М — число рядов в решетке, а N — число столбцов. Наложим
циклические (т.е. тороидальные) граничные условия. Тогда
Nt = MN. (8.13.5)
Рассмотрим какой-то ряд решетки. Пусть о{, . . . , oN — цвета N ячеек,

170 МОДЕЛИ ТИПА ЛЬДА
Рис. 8.7. Ряд, состоящий из ячеек квадратной решетки, раскрашенных красками
ах , . . . , aN. На линиях, разделяющих ячейки, нарисованы стрелки, направления
которых выбраны в соответствии с правилом, приведенным в разд. 8.13.
Показанная здесь конфигурация соответствует а2 = ах + 1, а3 = а2 - 1 , . . . ,
ах = aN - 1.
как показано на рис. 8.7. Стрелки на линиях, разделяющих ячейки, направ-
направлены в соответствии с описанным выше правилом. На линии у стрелка на-
направлена вверх, если oj + { = а- + 1, и вниз, если <jj¦ + t = Oj — 1.
Пусть в ряду имеется п стрелок, направленных вниз, под номерами xlf
. . . , хп> где 1 < хх < х2 < . . . < хп < N. Тогда цвета alf . . . , oN одно-
однозначно определяются указанием ох и х1у . . . , хп. Ниже вместо ох будем пи-
писать просто о. Произведение активностей для такого ряда имеет вид
п
= zaizO2 ...zON= (Zlz2z3)m П Rxj + j + a), (8.13.6)
где
?(a) = zaza+1/(z1z2z3J/3. (8.13.7)
Здесь X обозначает набор [х1у . . . , xj, и мы используем следующие усло-
условия цикличности:
^a+3 = za, ?(a+3)= ?(ст). (8.13.8)
Отметим также, что для согласования раскраски с циклическим граничным
условием oN + j = at числа N и п должны быть такими, что
iV-2n = 0, modulo 3 (8.13.9)
с точностью до целого числа, кратного трем.
Теперь для указания состояния ряда требуются о и X. Пусть
ф — такая совокупность а и X. Тогда мы снова имеем (8.2.1), где Z = ZG и
V — трансфер-матрица. Элементы V теперь можно представить в виде
V(<p , ф') - Da{XO если ф, ф' согласуются,
= 0 в остальных случаях. (8.13.10)
Здесь ф = (а, X) определяет раскраску какого-то одного ряда ячеек, а
ф' = (a', Y) —раскраску соседнего ряда, расположенного над первым.
Таким образом, Da(X) — произведение активностей для нижнего ряда.
Индекс X обозначает совокупность номеров направленных вниз стрелок
для нижнего ряда, Y — то же самое для верхнего ряда. Правило льда (две

ГЛАВА 8 УП
стрелки направлены к узлу и две — от него) по-прежнему должно выпо-
выполняться, поэтому, так же как и выше, число направленных вниз стрелок
одинаково в каждом ряду, и мы можем рассматривать это число (п) как
фиксированное. Далее, если X = (л^, ...,х„],аУ= [уи . . . , уп], то ко-
координаты ylf ... , уп должны чередоваться с хх, . . . , хп. Из всего этого
следует, что фиф' будут согласованы, если
о* = о+ 2» l^Xi^yi^x2^ . . .^уп*^ N (8.13.10а)
или
о7 = сг-К 1, 1 ^)>i^ xi^ у2^ . . . ^хп^ N. (8.13.106)
Мы по-прежнему имеем равенства (8.2.3) и (8.2.4), где g — собственный
вектор трансфер-матрицы V. Пусть gn(X) — элемент g, соответствующий
состоянию ряда ф = (а, X]. Тогда уравнение (8.3.2), определяющее соб-
собственные значения, принимает вид
2} (8.13.11)
Здесь L обозначает суммирование по у{у . . . , уп> удовлетворяющим усло-
условию (8.13.10а), а/? — аналогичное суммирование для (8.13.106). Мы прини-
принимаем следующее условие цикличности:
ga+3(X) =go(X). (8 Л 3.12)
Анзац Бете
Как и в разд. 8.3, мы можем рассмотреть последовательно случаи
п = 0, 1, 2, . . . . Это приведет нас к модификации (8.4.6), представляю-
представляющей собой анзац типа Бете следующего вида:
ga(X) = Ъа'г П фрЦх! +/ + а). (8.13.13)
Здесь Р = (/?!,..., pN] — перестановка целых чисел A, . . . , п}, сумми-
суммирование распространяется на все п\ таких перестановок, коэффициенты Л'р
и функции Ф](х) находятся в нашем распоряжении.
Мы можем обеспечить выполнение условия (8.13.12), потребовав, чтобы
существовали золновые числа klf . . . , кп> такие, что
0/(jc + 3) = ф]{х) ехрC//с.) (8.13.14)
*1 + ... +кп = 0. (8.13.15)
Таким образом, Фj(x) можно рассматривать как плоскую волну, составлен-
составленную из блоков длиной в три единицы. Условие (8.13.15) означает, что мы
ищем трансляционно инвариантный собственный вектор трансфер-

Г72 МОДЕЛИ ТИПА ЛЬДА
матрицы. Это относится и к собственному вектору, соответствующему
максимальному собственному значению Лтах.
Если Zi = z2 = ^з = 1» мы возвращаемся к модели льда и ожидаем, что
<t>j(x) будет обычной плоской волной. Чтобы сохранить аналогию с
разд. 8.4, следует использовать не А'р> а другой, связанный с ними набор
коэффициентов
AP = A'Pexp[i(kpl + 2kP2 + ... +nkPn)]. (8.13.16)
Если Z\ = Zi = ^з» эти коэффициенты совпадают с коэффициентами Ар мо-
модели льда.
Подставляя выражение (8.13.13) для ga(X) в уравнение (8.13.11), мы на-
находим, так же как в разд. 8.4, что имеются «желательные члены», «неже-
«нежелательные внутренние члены» и «граничные члены». Приравнивание жела-
желательных членов (для четных п) дает
Л = 2 (ziZ2z3)M3 ft . . . у„ , (8.13.17)
где
М§|Ы)) ^+2) (8-13Л8)
?
при j = 1, . . . , п и всех целых х.
Равенства (8.13.14) и (8.13.18) дают кубическое уравнение для у как
функции кр решение которого можно записать как т, = y(kj), где
у{к) = i txpCik/2)/g(k) (8.13.19)
и функция g = g(k) (не смешивать с собственным вектором g\) определяет-
определяется уравнением
g3 - 3Bg + 2 sinC)t/2) = 0. (8.13.20)
Константа В задана выражением
- B;г, + гэг, + VPfJ0]
Из условия сокращения нежелательных внутренних членов мы все так
же получаем уравнения (8.4.7). На самом деле на первый взгляд создается
впечатление, что мы получаем три таких уравнения, каждое со своей функ-
функцией s^ Но более тщательное исследование показывает, что все они со-
совпадают. (Если бы этого не было, анзац Бете был бы непригоден для дан-
данной задачи.) Оказывается, что
Sji = g(kj) exp[/(/c/ + ikj)] + g(ki) expf-i(*y + ikt)]. (8.13.22)
Таким образом, коэффициенты Ар снова определяются формулой
(8.4.10). Далее (8.4.8) и (8.4.9) с заменой Zj на exp(/Ary-) по-прежнему явля-

ГЛАВА 8 173
ются условиями сокращения граничных членов. Поэтому мы снова прихо-
приходим к (8.4.12), т.е.
п
exp(fl№,) = П [s
(8.13.23)
при у = 1 п.
Эти уравнения (8.13.23) вместе с (8.13.20) и (8.13.22) определяют кх> . . .
. . . , кп; тогда ylf . . . , уп можно вычислить с помощью (8.13.19). Заме-
Заметим, что активности zx> Z2> Z$ входят в эти соотношения только через
единственный безразмерный параметр В. Почему это так, неясно.
Если zx = z2 = z3, то В = \, и уравнение (8.13.20) имеет решение
g(k) = 2sin(?/2). Подставляя его в написанные выше уравнения, мы снова
получаем результаты разд. 8.4 для модели льда.
Разумеется, уравнения (8.13.23) имеют много решений для кх> . . . , кп>
соответствующих различным собственным значениям матрицы V. Нас ин-
интересует решение, соответствующее максимальному собственному значе-
значению. Согласно (8.2.4) с Z = ZG, а также (8.13.4) и (8.13.5), мы имеем тогда
к^ lim Л^; (8.13.24)
или, используя (8.13.19) и (8.13.15) и записывая gj как g(kj)y получаем
*= (глгзI73 lim [(-rV . .gn]-yN. (8.13.25)
N
ПРЕДЕЛ N - оо
Я полагаю, что анализ, проведенный в разд. 8.7, применим также и к
задаче о трехцветном раскрашивании, т.е. в пределе больших п и N волно-
волновые числа кх> . . . , кп образуют непрерывное распределение на некотором
интервале ( —Q, Q) с функцией распределения р(к)> удовлетворяющей урав-
уравнениям
2лр(к) = 1+{ д@(к/к>} p(k')dk' , (8.13.26)
J-Q дк
си
p(k)dk = n/N, (8.13.27)
j-q
i:
где функция Q(k, kf) определена с помощью (8.7.1). Из (8.13.22) следует
txp[-i@(p ,
_ g(q) exp[/(p + jq)] + g(p)exp[-i(q + jp)] (8Л3.28)
g(p) Qxp[i(q + ip)] + g(q) exp[-/(p + iq)] '
Поскольку gp ... , gn появляются в виде пар одинаковых по величине и

174 МОДЕЛИ ТИПА ЛЬДА
противоположных по знаку функций, из (8.13.25) получаем
In * = iln(ziZ2Z3) ~ Г ln\g(k)\p(k)dk. (8.13.29)
J-Q
ПРЕОБРАЗОВАНИЕ К ИНТЕГРАЛЬНОМУ УРАВНЕНИЮ
С РАЗНОСТНЫМ ЯДРОМ
Важным этапом в решении моделей типа льда является преобразование
(8.8.2) от переменной к к новой переменной а. Используя это преобразова-
преобразование для перехода от переменных р, q к новым переменным а, /3, мы обна-
обнаружили в (8.8.4), что ехр[-/0(/7, q)] становится функцией только разности
а — C. Интегральное уравнение (8.13.26) имеет тогда разностное ядро, и
для требуемого значения Q может быть решено посредством преобразова-
преобразования Фурье.
Можно ли эту процедуру повторить в данном случае, т.е. существует ли
функция к (а), такая, что если
P = k(a),q=k(P)9 (8.13.30)
то
®(Р>Ч)- Функция только ос— /3? (8.13.31)
Если это так, то
йрдО(р,д) dqdO(p,q)
di dp +Тр dq ~°- (81332)
С помощью (8.13.20) и (8.13.28) мы можем убедиться, что
&(p,q)=p-q[l- g\p)IB] + €(q2) . (8.13.33)
Переходя к пределу при ^-0в (8.13.32) и выбирая а = 0 в качестве нуля
функции к (а), получаем
к'{ас) = fc'@) [1 - В~?(к)]. (8.13.34)
Подстановка этого результата обратно в (8.13.32) дает
С помощью (8.13.28) и (8.13.20) можно непосредственно убедиться, что это
необходимое в данном случае тождество действительно имеет место для
всех комплексных чисел р и q. Это означает в свою очередь, что утвержде-
утверждение (8.13.31) является правильным, и преобразование, сводящее (8.13.26) к
интегральному уравнению с разностным ядром, в самом деле существует.
Функцию в правой части (8.13.31) легко найти, полагая /3 = 0. Тогда

ГЛАВА 8 175
q = О, так что из (8.13.33) и (8.13.30) получаем
®(Р ,Я) =к(а-р). (8.13.36)
Перейдем в (8.13.26) от переменных к, к' к а, /3, где к = к(а) и
к' = к(C). Функцию R(a) определим так же, как в (8.8.5). Тогда получает-
получается интегральное уравнение
R(a) = k'(a) + Bjzyl \ ' к\ос- Д)Д(Д) ф, (8.13.37)
где Q = k(Qx). (Функция к (а) является монотонно возрастающей и нечет-
нечетной.)
Условие (8.13.27), определяющее пределы интегрирования, и равенство
(8.13.29) для к приобретает следующий вид:
Bл)-1 f ' R(a)da=n/N, (8.13.38)
J-Q,
fQi
1пк= 41n(ziz2z3) - Bл)-1 In|g(a)\R(a) dor (8.13.39)
J-Qi
(здесь g рассматривается как функция а, а не к).
ФУНКЦИЯ g (а), к (а)
Функции g(a) и к (а) определены посредством соотношений (8.13.20) и
(8.13.34). Нужно решить уравнение (8.13.37) для R(a) и затем вычислить к
из (8.13.39).
Исключая к из (8.13.20) и (8.13.34), приходим к уравнению
^= [2В/кЩ] {4 -g\3B -g2J}-* (8.13.40)
между а и g. Это уравнение можно проинтегрировать с помощью эллипти-
эллиптических интегралов [101]. Пусть иу v, w — три значения ху удовлетворяющие
кубическому уравнению
х(ЗВ - хJ = 4, (8.13.41)
и пусть Кт> т — следующие константы:
km = [(и - v)w/(u - w)v]^ (8.13.42)
г = [uw/(u - w)]*B/k'@). (8.13.43)
Согласно (8.13.21), В > 1. Отсюда следует, что и, v, и> являются дейст-
действительными положительными числами. Выберем их так, чтобы
u>v^w. (8.13.44)

Г76 МОДЕЛИ ТИПА ЛЬДА
Тогда кт — действительное число, удовлетворяющее условию
0<А:т^1. (8.13.45)
Введем теперь новую переменную 5, связанную с g следующим соотно-
соотношением:
g2 = uws2/(u - w + ws2). (8.13.46)
Подставим это выражение для g в (8.13.40). Дифференциальное уравнение
преобразуется к виду
^=т[A-*2)A-*^2)Г*. (8-13.47)
Интегрируя его с учетом того, что к = g = s = 0 при а = 0, получаем
(8.13.48)
а= г Г[A - 0A - к2т?)]-><\1.
Этот интеграл определяет а как функцию 5 (это действительно эллипти-
эллиптический интеграл). Нас интересует 5 как функция а. Сравнивая с A5.5.6), мы
видим, что
s = sn(r~la,km), (8.13.49)
где sn(M, к) — эллиптическая функция sn аргумента и и модуля ку которая
определена посредством A5.1.1) — A5.1.6).
В дальнейшем будем считать эллиптический модуль кт (не путать с вве-
введенными выше волновыми числами klf , . . , кп\) подразумевающимся и не
писать его явно. Кроме того, можно произвольно выбирать любой удоб-
удобный масштаб а; выберем его так, что
т=1. (8.13.50)
Тогда (8.13.43) определяет ?'(()), а переменная s равна просто sna.
Как показано в разд. 15.2, функция sna мероморфна, т.е. имеет сингу-
сингулярности только типа полюсов. Поскольку ut vy w — константы, из
(8.13.46) следует, что g2 также является мероморфной функцией а.
Пусть г) — один из полюсов g2(a). Тогда, согласно (8.13.46),
sn2r/= -(w- w)/w. (8.13.51)
ми
Как и в гл. 15, полные эллиптические интегралы первого рода с модуля-
кт> к'т = A - kfy/2 обозначим / и /' соответственно. Пусть символ q
далее обозначает параметр Якоби, определяемый соотношениями
A5.1.1) — A5.1.4), т.е.
? = ехр(-л/7/). (8.13.52)
Когда переменная а смещается вдоль мнимой оси комплексной плоско-

ГЛАВА 8 177
сти от 0 до //', функция sna также принимает чисто мнимые значения, из-
изменяющиеся от 0 до +/оо. Так как правая часть (8.13.51) отрицательна, мы
можем выбрать q в интервале (О, //') на мнимой оси.
Используя A5.4.4), A5.4.5), (8.13.42) и (8.13.51), имеем
cn Y] = (w/w)*, dn rj = (u/v)h, (8.13.53)
1 - k2m sn4 Y] = u(v + w - u)l{vw). (8.13.54)
Извлекая квадратный корень из обеих частей (8.13.41), получаем кубиче-
кубическое уравнение относительно х/г. Для суммы корней этого уравнения (с
учетом их знаков) получаем однородное соотношение
n* = i;*+w*. (8.13.55)
Возведение его в квадрат дает
v + w-u= -2(Vw)h. (8.13.56)
Умножая обе части уравнения на u/vw и используя (8.13.53), (8.13.54), по-
получаем
1 -k2msnAr}= -2cnrj dnr/. (8.13.57)
Отсюда, используя A5.4.21) при и = -v = 77, находим
sn2r/= -snr/, (8.13.58)
т.е., согласно A5.2.5),
sn2r) = snBU' -V). (8.13.59)
Это уравнение имеет только одно решение в интервале (О, /У'), а именно
г/= 2*773. (8.13.60)
Таким образом, ц составляет простую долю //'.
Используя (8.13.51) и помня о том, что g теперь рассматривается как
функция а у можно переписать (8.13.46) в виде
g2(a) = и sn2ar/(sn2ar - sn2rj). (8.13.61)
Константу и можно выразить через г). Произведение трех корней
(8.13.41) равно 4, т.е. uvw = 4. С учетом (8.13.53) отсюда следует
cn Y] dn Y] = \иш . (8.13.62)
Это равенство с помощью A5.1.6) и A5.4.30) можно переписать в виде
\иш = НЫ ei(ij) 02(О)/[Я!(О) 0!(О) ®\г\)\, (8.13.63)
где Н(и), Нх(и), в(и), 0j(h) — эллиптические тэта-функции, определяемые
посредством A5.1.5).

178 МОДЕЛИ ТИПА ЛЬДА
Из A5.2.36) (если и заменить на —ц) следует
Н{2г)) = q~mH(rj) , (8.13.64)
а из A5.4.17) (если и, v заменить на г?, —у) следует
2Н{г)) вМН^) Q^ri) = Щ2г}) в@)Я!@) в^О). (8.13.65)
Исключая НBг})/Н(г}) и Hl(r])Ql(rj) из трех последних уравнений, получа-
получаем
и = q~m в2@)/в2(г/). (8.13.66)
Подставляя это выражение в (8.13.61) вместе с A5.1.6) и A5.4.19), нахо-
находим
g(cc) = q-wH\a)l[H{a- rj)H{a+ t))]. (8.13.67)
Рассмотрим теперь функцию к(а). Из (8.13.34) и (8.13.43) при условии
7 = 1 следует
к'{а) = [uw/(u - w)]h[B -g\a)}. (8.13.68)
Правая часть этого уравнения является мероморфной функцией а; подобно
g2(a), она имеет простые полюса в точках, где знаменатель (8.13.61) равен
нулю, т.е. где
а= ±г)+ 2т1+ 2тГ (8.13.69)
для всех целых w, п. Значение вычета в таком полюсе можно получить об-
обычным путем, дифференцируя знаменатель. С учетом A5.5.1а) и A5.5.5)
это дает
Res[k'(a)] = - [uw/(u - w)}hu sn ос/B en or dn or), (8.13.70)
Подставляя значения переменной а из (8.13.69), используя соотношения
периодичности A5.2.5) совместно с (8.13.51) и (8.13.62), находим
Res[/c'(<*)] = +i, (8.13.71)
где верхний (нижний) знак соответствует верхнему (нижнему) знаку в
(8.13.69).
Точно такие же полюса и вычеты в них имеет следующая функция а:
Лща+г,) Н(а-г,I
Н(а-г,)
Поэтому разность между ней и к' (а) является мероморфной функцией без
полюсов, т.е. целой функцией. Кроме того, эта разность — двоякопериоди-
ческая функция с периодами 2/ и 2/7, так что она должна быть ограничен-
ограниченной функцией. Следовательно, в соответствии с теооемой Лиувилля она
равна константе. (Это пример использования теоремы 15(а) из разд. 15.3.)

ГЛАВА 8 179
Интегрируя (8.13.68) при условии, что к@) = 0, получаем
к(а) = Ca+i \n[H(r) + a)/H(rj - а)] , (8.13.73а)
где С — некоторая константа.
Поскольку функция g2(a) периодична с периодами 2/ и ИГ, то, согласно
(8.13.20), этим же свойством обладает функция sin2C?/2). Отсюда с при-
привлечением A5.2.3) определяем константу С:
С=-2я/C/). (8.13.736)
Этим завершается вывод выражений для g(a) и к (а). Нам понадобятся
еще фурье-разложение к (а) и интегралы Фурье
Gm = B/) f ехр(/тяог/7) \n[g\a)] da, (8.13.74)
j-i
где т — целое число. Из (8.13.60), (8.13.61), (8.13.73) и представления
A5.1.5) эллиптической тэта-функции Н(и) в виде бесконечного произведе-
произведения непосредственно следует
Go = - 4лг/7(97),
Gm = (r2m - \)/[т{\ + гт + г2т)Ъ тФО, (8.13.75)
Гу (8.13.76)
Здесь а — действительная величина и
г = qm = ехр(-2л/737). (8.13.77)
Эллиптические функции появляются весьма часто в точно решаемых
двумерных моделях статистической механики. Рассматриваемая модель ин-
интересна в том отношении, что эллиптические функции здесь нужны для
преобразования (8.13.26) в интегральное уравнение с разностным ядром.
Аналогичным образом они возникают также в предложенном автором ме-
методе решения трехспиновой модели [42, 43]. Как замечено в конце
разд. 10.4, я предполагаю, что это преобразование к разностному ядру тес-
тесно связано с параметризацией обобщенного соотношения звезда — тре-
треугольник с помощью эллиптических функций.
Решение интегрального уравнения
Мы можем решить интегральное уравнение (8.13.37) путем разложения
в ряды Фурье при условии, что величина интервала 2QX равна периоду эл-
эллиптических функций, т.е.
Gi = /. (8.13.78)

180 МОДЕЛИ ТИПА ЛЬДА
Подставляя выражение (8.13.76) для к (а) и полагая
00
R(a) = (л/1) Ь?о + 2 2 Rm со^тла/1)) , (8.13.79)
легко установить, что
^ = ^/A + r2m). (8.13.80)
Отсюда и из (8.13.38) следует
n = hN, (8.13.81)
и, таким образом, число стрелок, направленных вверх и вниз, одинаково.
Как и в разд. 8.8, мы полагаем, что этот случай соответствует максималь-
максимальному собственному значению трансфер-матрицы V.
Согласно (8.13.78) и (8.13.76), функция к(а) монотонно возрастает от
-тг/3 до тг/3 при изменении а от -Qx до Qv Таким образом, Q = тг/3 в
(8.13.26), и волновые числа кх, . . . , кп заполняют интервал (—тг/3, тг/3).
Это тот же самый интервал, что и для исходной модели льда, хотя рас-
распределение будет, вообще говоря, иным.
Подставляя фурье-разложение (8.13.79) для R(a) в (8.13.39), получаем
00
ln*=jln(ziz2z3)-i E GmRm (8.13.82)
т = - »
(считая R_m = Rm). С учетом (8.14.75) и (8.13.80) отсюда следует
In* =Hn(ziZ2z3) - ilnr + У _ (8.13.83)
Это соотношение определяет k/(zv z2, z-^a как функцию г. Можно счи-
считать, что г определено посредством (8.13.77) и (8.13.66). Из этих формул,
используя A5.1.5), получаем
\ = r-i/6 TT Vi-JI J_^ (8.13.84)
Резюмируем общую схему всего вывода. При заданных zx, z2, z$ опреде-
определим В посредством (8.13.21) и возьмем в качестве и наибольший из корней
уравнения (8.13.41). Определим г@ < г < 1) с помощью (8.13.84). Тогда
к — статистическая сумма на один узел для задачи о * трехцветном раскра-
раскрашивании со статистическими весами — дается выражением (8.13.83). Отме-
Отметим, что к/(г1г2г3I/з зависит от zl5 z2, zs только через В.
Такая форма представления результата удобна, когда величина В боль-
большая, что имеет место, если один из факторов zx, z2, z^ велик или мал по
сравнению с остальными. В этом случае г — малая величина, и соответст-

ГЛАВА 8 181
вующие ряд и бесконечное произведение быстро сходятся.
Критическое поведение
Рассматриваемая как функция действительных положительных перемен-
переменных Z\, z2, z$ статистическая сумма на один узел к является аналитической
всюду, за исключением, быть может, случая zx = z2 = z^ когда В = I,
и = 2 и г = 1.
Из этого следует, что величина г лишь немного меньше единицы, когда
z\> %2> ^3 почти равны. В этом случае выражения (8.13.83), (8.13.84) не явля-
являются уже удобными, так как входящие в них ряд и произведение сходятся
медленно. Тогда полезно применить формулу суммирования Пуассона
(разд. 15.8) к (8.13.83) и формулу A5.7.26) для сопряженного модуля к
(8.13.84). В результате указанные соотношения принимают следующий вид:
(8.13.86)
Здесь 5 = ехр( — Зтг//2/'), но мы можем рассматривать (8.13.86) как опреде-
определение этой переменной. Она мала, если величина В близка к единице. В
частности, если zx = z2 = z$ = 1, то В= 1, и = 2, 5 — 0, и мы снова полу-
получаем результат (8.8.20) для модели льда, а именно к = D/3K/2 [157].
Мы можем также исследовать характер приближения к предельному
случаю модели льда. Пусть zx, z2, z3 отличаются от единицы членами по-
порядка ?. Тогда В превосходит единицу на величину порядка е2. Выбирая
масштаб е подходящим образом, мы можем написать
5 = 1 + ^, (8.13.87)
где \е\ < 1. Отсюда и из (8.13.41) следует
м* = 2{1 + № + 0(е4)}, (8.13.88)
так что, согласно (8.13.86),
5- ~ |е/3|3/2 (8.13.89)
и, согласно (8.13.85).
к= D/3K/2 (Ziz223I/3{1 + 4|^3|3/2 + 0(?2)}. (8.13.90)
Таким образом, к имеет «сингулярную часть», пропорциональную е3/2. В
этом смысле мы можем утверждать, что в задаче о трехцветном раскра-
раскрашивании имеется критическая точка при zx = z2 = Zy Определяя критиче-
критический показатель а аналогично A.7.10), имеем
a=i. (8.13.91)

№ МОДЕЛИ ТИПА ЛЬДА
Можно явным образом исключить переменную г из (8.13.83) и (8.13.84)
[21], что дает
(8.13.92)
[(u-wKuY-[(v-wW
Отсюда ясно, что k/{zxz-^.^)a является алгебраической функцией В.

9
АЛЬТЕРНАТИВНЫЙ СПОСОБ
РЕШЕНИЯ МОДЕЛЕЙ
ТИПА ЛЬДА
9.1. ВВЕДЕНИЕ
В гл. 8 решение моделей типа льЯа было получено путем использования ан-
заца Бете для собственных векторов трансфер-матрицы. Этот метод су-
существенно зависит от того факта, что число «линий», или направленных
вниз стрелок, сохраняется при переходе от одного ряда к следующему. Не-
Неясно, как можно обобщить этот метод, чтобы он был применим к моде-
моделям, где такое сохранение линий отсутствует.
Цель данной главы состоит в том, чтобы исследовать результаты гл. 8
и показать, что они содержат указание на возможность другого способа их
вывода. Этот альтернативный способ может быть назван методом комму-
коммутирующих трансфер-матриц; он будет использован в гл. 10 для решения
восьмивершинной модели.
9.2. КОММУТИРУЮЩИЕ ТРАНСФЕР-МАТРИЦЫ
Пусть К—связывающая ряды трансфер-матрица для модели типа льда.
Согласно (8.3.3) и (8.3.4), она является функцией больцмановских весовых
множителей а, Ь, с.
Пусть g — собственный вектор матрицы К, как в (8.2.3). Тогда компо-
компоненты g определяются посредством (8.4.6), (8.4.10) и (8.3.22), где zx , . . .
• • • » zn — решения уравнений (8.4.12).
Но эти уравнения для g содержат а, Ь, с только в виде комбинации
д = (д2 + ъ1 - c2)/2ab . (9.2.1)
Таким образом, если мы рассмотрим две трансфер-матрицы с различными
а, Ь, с, но с одинаковым значением Д, то они будут иметь общие собствен-
собственные векторы.
Если все собственные векторы определены с помощью анзаца Бете и
порождают 2дг-мерное векторное пространство (что действительно имеет
место) и если Р — матрица, составленная из компонент собственных
векторов, то отсюда следует
V=PVdP'1, (9.2.2)
где Vd — диагональная матрица, и обе матрицы V и Vd являются функция-
функциями а, Ь, с; в то же время Р является функцией только Д.

284 АЛЬТЕРНАТИВНЫЙ СПОСОБ РЕШЕНИЯ МОДЕЛЕЙ ТИПА ЛЬДА
В гл. 8 мы уже получали параметризацию (8.9.7) (или (8.8.9)), а именно
a,b,c = р sinh i(A - v),p sinh J(A + v), p sinh Я , (9.2.3)
где p — нормирующий множитель.
Будем рассматривать р, X и v как переменные, причем не обязательно
действительные. Тогда (9.2.3) определяет а, Ь, с. Матрицы V и Vd являют-
являются теперь функциями р, X и v. Но, согласно (8.9.1),
А =-cosh Я. (9.2.4)
Таким образом, матрица Р является функцией только X; она не зависит ни
от v9 ни от р.
Мы можем рассматривать X и р как константы, a v как (комплексную)
переменную, выражая явно зависимость матрицы Кот у и записывая ее
как V(v). Тогда из (9.2.2) следует
V(v) V(u) = V(u) V(v) (9.2.5)
для всех комплексных чисел w, v, т. е. трансфер-матрицы V(u) и V(v) ком-
коммутируют.
9.3. УРАВНЕНИЯ ДЛЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ
Рассмотрим теперь уравнения (8.4.4) и (8.4.12), которые определяют
точные собственные значения Л матрицы V для конечных п и N. По ана-
аналогии с (8.7.1) и (8.9.1) (с заменой ау на ivj) произведем преобразование
переменных: от переменных zx , . . . , zn перейдем к переменным
Zj = (ek-ev')/(ek+v'-1). (9.3.1)
Тогда из (8.3.22), (8.3.9) и (9.2.3) получим
= sinh я sinh jBA + Vj - vk)
ik sinh i(A - Vj) sinh i(A - Vk)'
_ __ sinhj(i;-i;y-2A)
Для заданных значений р и vx , . . . , vn определим функции ф(у), q(v)
выражениями
(f>(v) = pNsinhN(v/2), (9.3.4)
n
q{v) = H sinh i(v - vi). (9.3.5)

ГЛАВА 9 185
Тогда (8.4.4) можно записать в виде
Л = [0(А - v) q(v + 2А') + ф(к + v) q(v - 2k')]lq{v), (9.3.6)
где
Я'=А-/я. (9.3.7)
В соответствии с (8.4.12), (9.3.1) и (9.3.2) переменные vx , . . . , vn
определяются системой из п уравнений
9.4. СООТНОШЕНИЕ МЕЖДУ МАТРИЧНЫМИ
ФУНКЦИЯМИ,
ОПРЕДЕЛЯЮЩЕЕ СОБСТВЕННЫЕ ЗНАЧЕНИЯ
Метод, связанный с использованием анзаца Бете, требует значитель-
значительного количества вычислительной работы, чтобы получить уравнения
(8.4.12), т. е. (9.3.8). Теперь покажем, что эти уравнения являются про-
простым следствием коммутационных соотношений и (9.3.6).
Для этого воспользуемся соображениями, сходными с теми, которые
приводились в разд. 7.7 для модели Изинга. Согласно (9.2.2), если Л
является собственным значением К, соответствующим столбцу г матрицы
Р, то
1. (9.4.1)
Будем рассматривать р и X как фиксированные величины, a v как
переменную. Правая часть (9.4.1) представляет собой сумму по элементам
матрицы V с коэффициентами из Р, которые от v не зависят. Согласно
(8.3.4) и (9.2.3), каждый элемент V является целой функцией v. Таким
образом,
Л = A(v) (9.4.2)
также является целой функцией.
Рассмотрим теперь (9.3.6). Правая часть данного равенства представляет
собой отношение двух целых функций, причем знаменатель q(v) равен нулю,
когда V = v} , . . . , vn. Поскольку это отношение должно быть целой
функцией, числитель также должен обращаться в нуль при тех же значениях
аргумента. Отсюда немедленно следуют уравнения (9.3.8).
Таким образом, равенство (9.3.6), рассматриваемое как соотношение
между функциями A(v) и q(p), определяет A(i;).
Каждое допустимое решение(9.3.8) определяет vx , . . . , vn и, следо-
следовательно, собственное значение A(v) и функцию q(v). Это справедливо для
каждого значения п. Всего должно быть 2N таких собственных значений A(v)
и связанных с ними функций q{v).
Обозначим их ЛДи), qr(v), г = 1 , . . . , 2N. Матрица Vd в (9.2.2)

186 АЛЬТЕРНАТИВНЫЙ СПОСОБ РЕШЕНИЯ МОДЕЛЕЙ ТИПА ЛЬДА
представляет собой диагональную матрицу с диагональными элементами
А{ , . . ., A2N. Аналогично пусть Qd будет диагональная матрица с элемента-
элементами д{ , . . . , q2N. Тогда полная система уравнений (9.3.6) (по одному для
каждого собственного значения) может быть записана как одно матричное
уравнение
Vd(v) Qd(v) = 0(А - v) Qd(v + 2А') + 0(А + v) Qd(v - 2А'). (9.4.3)
(Множители Ф(\ - v), Ф(\ + v) одинаковы для всех собственных значений,
поэтому они являются просто скалярными коэффициентами.)
Определим теперь недиагональную матричную функцию
Q(v) = Р Qlv) P-1. (9.4.4)
Трансфер-матрицу будем снова писать как V(v), чтобы явно выразить ее зави-
зависимость от v. Умножая равенство (9.4.3) слева на Р и справа на Р~ *, исполь-
используя (9.2.2), (9.4.4) и независимость Р от v, приводим (9.4.3) к следующему
виду:
V(v) Q(v) = 0(А - v) Q(v + 2А') + 0(А + v) Q(v - 2A'), (9.4.5)
что представляет собой соотношение между матричными функциями V(v),
Q(v).
Поскольку V^v), QJiv) диагональны для всех v, то Q(v) коммутирует с
V(u) и Q(u) для всех комплексных чисел и и v.
В разд. 8.3 показано, что матрица V(v) распадается на N + 1 диаго-
диагональных блоков, по одному для каждого значения п. Поэтому она
определенно распадается на два блока: один с четными значениями л, другой
с нечетными. Это утверждение является простым следствием коммутационн-
коммутационного соотношения
, (9.4.6)
где S — диагональный оператор с элементами 4-1 (—1) для состояний с
четным (нечетным) числом направленных вниз стрелок в ряду.
Поэтому матрица Р также может быть выбрана коммутирующей с 5.
В соответствии с (9.3.5) и поскольку п < N, все диагональные элементы
Qd(v) имеют вид
2/2), (9.4.7)
где для четных (нечетных) п сумма распространяется на все четные (не-
(нечетные) значения г в интервале —N < г < N. Коэффициенты dr не зависят от
v; некоторые из них могут быть равны нулю.
Согласно (9.4.4), каждый элемент матрицы Q(v) является суммой
выражений типа (9.4.7) либо только для четных /?, либо только для нечетных.
Таким образом, каждый элемент Q(v) сам имеет вид (9.4.7).

ГЛАВА 9 187
9.5. СВОДКА МАТРИЧНЫХ СВОЙСТВ
Резюмируя приведенный выше вывод, можно сказать, что мы исполь-
использовали результаты вычислений, выполненных в гл. 8 методом анзаца Бете,
чтобы установить следующие свойства:
I. Для каждой заданной трансфер-матрицы К, характеризуемой опре-
определенными значениями а, Ъ> с, существует бесчисленное множество других
трансфер-матриц (с разными а, Ь, с, но с одинаковым параметром Д), кото-
которые с ней коммутируют.
II. Если а, Ь, с определены через параметры р, X, v посредством (9.2.3) и
если р, X рассматриваются как константы, г, v — как комплексная перемен-
переменная, то матрицы K(w), V(v) коммутируют для всех значений ut v.
III. Все элементы матрицы V(v) являются целыми функциями v.
IV. Существует матричная функция Q(v)t такая, что матричное соот-
соотношение (9.4.5) выполняется для всех комплексных чисел v.
V. Определитель матрицы Q(v) не равен тождественно нулю. Матрицы
Q(w), Q(v), V(v) коммутируют для всех значений w, v.
VI. Матрицы Q(v), V(v) коммутируют с диагональным оператором 5,
состоящим из элементов + 1 (— 1) для состояний с четным (нечетным) числом
стрелок, направленных вниз. Поэтому эти матрицы распадаются на два
диагональных блока. В пределах каждого блока все элементы Q(v) имеют вид
(9.4.7), где -N < г < Nn r принимает только четные или только нечетные
значения.
Достаточность
Свойства I — VI оказываются действительно достаточными для опреде-
определения собственных значений матрицы V(v). Все, что нам нужно
сделать, — это провести рассуждения в обратном порядке, чтобы вернуться
к формулам (9.3.6) и (9.3.8).
Из свойств коммутации II и V следует, что существует матрица Р (не
зависящая от v), такая, что
p-lV{v)P = Vd{v), P~xQ{v)P=Qd{v), (9.5.1)
где Vd(v) и Qd(v) — диагональные матрицы. Согласно свойству IV, соотно-
соотношение (9.4,5) выполняется и поэтому может быть приведено к диаго-
диагональной форме (9.4.3). Пусть A(v) — некоторое собственное значение мат-
матрицы V(v), a g(v) — соответствующее собственное значение матрицы Q(v).
Тогда соответствующий элемент в (9.4.3) представляет собой функциональ-
функциональное соотношение (9.3.6),
Согласна (9.5.1), A(v) и g(v) представляют собой суммы по элементам
матриц V(v) и Q(v) соответственно с коэффициентами (из Р~{ и Р), кото-
которые не зависят от v. Из свойства III следует, что А(у) — целая функция. Из
свойства VI следует, что и q(v) является целой функцией и имеет вид
(9.4.7), где индекс г принимает либо только четные, либо только нечетные
значения.

№ АЛЬТЕРНАТИВНЫЙ СПОСОБ РЕШЕНИЯ МОДЕЛЕЙ ТИПА ЛЬДА
Если бы q(v) были тождественно равны нулю для всех v, тогда то же
самое можно было бы сказать о детерминанте Q(v). При условии, что
этого не происходит, должно быть возможно представить q(v) в виде
(9.3.5) (где 0 < п < N) с каким-то ненулевым множителем, который
сокращается в (9.3.6). Как показано в начале разд. 9.4, из соотношения
(9.3.6) с необходимостью следуют уравнения (9.3.8). Они в свою очередь
определяют vx , . . . , vn. После этого, согласно (9.3.5), функция q{v) стано-
становится известной, так что из (9.3.6) можно вычислить A(v).
Все эти равенства являются точными для конечных п и N. Разумеется,
еще остается решить уравнения (9.3.8). Вообще говоря, их аналитическое
решение может быть получено только в пределе п, N — оо с помощью
методов, описанных в разд. 8.6 — 8.9. Даже в этом случае уравнения
(9.3.8) представляют собой колоссальное упрощение исходной задачи
определения собственных значений: их можно, например, быстро решить с
помощью ЭВМ даже для довольно больших значений п и N. В этом
смысле они представляют собой «решение» задачи.
Отметим, что в свойствах I — VI число п не фигурирует. Поэтому
можно надеяться обобщить их на случай моделей, в которых условие
сохранения линий не выполняется. Это будет сделано в гл. 10.
9.6. ПРЯМОЙ ВЫВОД МАТРИЧНЫХ СВОЙСТВ:
КОММУТАЦИЯ
Можно ли получить свойства I — VI без использования анзаца Бете и
тем самым найти другой способ диагонализации V(v)l Как будет показано
в этом и в двух последующих разделах, это возможно.
Рассмотрим ряд узлов решетки, лежащих на одной горизонтальной
линии, и отходящие от этих узлов вертикальные линии связей. Каждой
линии связи / сопоставим «спин» /х; так, что /х; =4-1, если соответ-
соответствующая стрелка направлена вверх или вправо, и /х; = —1, если стрелка
направлена вниз или влево.
Пусть «J , . . . , aN — спины нижнего ряда вертикальных связей,
0j , . . . , 0N — спины такого же верхнего ряда, а символы /^ , ... , fxN
обозначают спины горизонтальных связей, как показано на рис. 9.1. Сово-
Совокупность символов [а{ , ... , aN] обозначим одним символом а и анало-
аналогично {0j , ... , 0N] — символом 0. Очевидно, что а @) задают спины
нижнего (верхнего) ряда. Таким образом, трансфер-матрица V имеет
элементы Ка/3, которые определяются выражением
(9.6.1)
Здесь w(n, a I /3, /х') — больцмановский статистический вес вершинной
конфигурации, задаваемой спинами /х, а, /3, ц'. Из рис. 8.2 и (8.3.3) следует

ГЛАВА 9
189
Pi
Mn+i
Рис. 9.1. Ряд квадратной решетки, на котором показаны «спины», сопоставленные
различным линиям, соединяющим узлы. Приняты циклические граничные условия
(9.6.2)
а для всех других сочетаний /х, а, /3, /х' величина и>(/х, a, I /3, /х') равна
нулю.
Пусть V — другая трансфер-матрица, определенная посредством (9.6.1)
и (9.6.2), но с заменой а, Ь, с на а', Ъ'', с'. Соответствующую вершинную
весовую функцию обозначим wf. Тогда в соответствии с (9.6.1) получаем
(9.6.3)
где
, ar|y ,
, I/).
(9.6.4)
Эта величина 5 представляет собой просто больцмановский весовой
множитель пары узлов, расположеных один над другим, как показано на
рис. 9.2, просуммированный по допустимым направлениям стрелки на
общей линии связи.
Рис. 9.2. Сегмент решетки, статистический вес которого
(просуммированный по спину 7 внутренней линии связи)
S(pt v I д', v' I a, C) определяется выражением (9.6.4).
W
¦и-'
а

j90 АЛЬТЕРНАТИВНЫЙ СПОСОБ РЕШЕНИЯ МОДЕЛЕЙ ТИПА ЛЬДА
Пусть S(a, 0) — матрица 4 х 4 с рядами, нумеруемыми парой индексов
(/х, *>), столбцами, нумеруемыми посредством (/х', vr), и элементами S(/x,
v I /х', v' I a, 0). Тогда (9.6.3) можно записать в более компактном виде:
(W')ag> = Tr S(a, , ft) 5(а2, /32). . . . S(aN, flv). (9.6.5)
Аналогично
(V'V)aP = TrS'(*i ,/3,) S'(*2 ,ft).... S'(*jv. Av), (9.6.6)
где S' определяется так же, как 5, но и> и w' меняются местами в (9.6.4).
Чтобы получить свойство I, нужно найти матрицу V, которая
коммутирует с К, т. е. правые части равенств (9.6.5) и (9.6.6) равны. Ясно,
что это требование будет выполнено, если существует несингулярная
матрица М размера 4x4, такая, что
(,P)(a,P)M-1 (9.6.7)
при а = ±1 и/3 = ± 1.
Соотношение звезда — треугольник
Матрица М имеет ряды, нумеруемые парой индексов (/*, v),
и столбцы, нумеруемые парой индексов (ji', vf). Будем писать ее
элементы как и>"(*>, ц I v\ /*')• Тогда, умножая (9.6.7) справа на М и
выписывая с помощью (9.6.4) матричные произведения в явном биде,
получим
(9.6.8)
\t w"{v, 1л\гУ , pif) w'(ju" , a\y, ju') и>(^', y|^, \l),
при a, 0, /x, у, /x', *>' = ±1.
Мы можем рассматривать и>"(*>, /x I v\ /x') как «больцмановскую вес-
весовую функцию» для вершины, окруженной спинами v, /x, v\ /x\ Тогда со-
соотношению (9.6.8) можно дать простую графическую интерп-
интерпретацию, представленную на рис. 9.3: комбинированный статистический
вес левой фигуры (просуммированный по спинам внутрен-
внутренних линий) должен быть равен аналогичной величине для правой
фигуры. Это должно быть справедливо для любых значений
шести внешних спинов.
Одна фигура может быть получена из другой путем смещения одной
линии за точку пересечения двух других. На обеих фигурах точка пересеч-
пересечения линий (/х, v') и (а, 0) определяет вершину с весовой функцией w. Анал-
Аналогичным образом пересечение линий (а, 0), (*>, /х') дает вершину с весом
w', а пересечение (у, /х'), (/х, v') — вершину с весом w".
Такое наглядное представление равенства (9.6.8) может быть исключ-
исключительно полезным, как это будет показано в гл. 11.

ГЛАВА 9
191
Р
р
w
Рис. 9.3. Сегменты решетки, статистические веса которых (просуммированные по
спинам 7> м"» v" внутренних линий связи) определяют левую и правую части
равенства (9.6.8), представляющего собой соотношение звезда — треугольник
вершинных моделей.
Равенство (9.6.8) можно записать также в операторной форме. Пусть
Ui — матрица с элементами
w(ai9 ai+i\pi ,pi
d(aN,pN).
(9.6.9)
Таким образом, оператор Ut действует на спины в положениях / и / + 1,
оставляя остальные без изменения. Его можно назвать вершинным опера-
оператором.
Аналогичным образом определим U\ и и] с помощью соотношения
(9.6.9), в котором фактор w заменен на w' и и>" соответственно.
Тогда из (9.6.8) с необходимостью следует
Ui+iU'ilfi+i = U"Ui+iUi, (9.6.10)
а из (9.6.9) очевидно, что
= ?/'?/;, (9.6.11)
если I/ - j\ >2.
Уравнение (9.6.10) совпадает с F.4.27). Таким образом, введенные
здесь операторы U. удовлетворяют тому же соотношению звезда —
треугольник, что и соответствующие операторы в разд. 6.4 для
модели Изинга. Поскольку (9.6.10) является прямым следствием (9.6.8), я
буду называть (9.6.8) соотношением звезда — треугольник для моделей
типа льда, хотя это и не совсем точное название.
Согласно (9.6.11), операторы U. удовлетворяют также соотношению
F.4.28). Кроме того, если в (9.6.9) заменить N на N 4- 1, то элемент

]92 АЛЬТЕРНАТИВНЫЙ СПОСОБ РЕШЕНИЯ МОДЕЛЕЙ ТИПА ЛЬДА
оператора UN будет представлять собой весовой ^множитель крайней
вершины справа на рис. 9.1. Таким образом, UN можно рассматривать как
оператор, добавляющий вершину при переходе от спинов 0N, nN + г к
спинам fiNi aN.
Аналогично произведение операторов Ux . . . UN добавляет ряд вершин,
осуществляя переход от 0{ , . . . , 0N, /xN + х к /хр ах , . . . , aN. Поэтому,
если не учитывать граничные условия и сдвиг спиновых индексов, это про-
произведение можно рассматривать как трансфер-матрицу, и оказывается
применимым частичное доказательство коммутативности F.4.30), F.4.31).
Таким образом, во всех указанных отношениях операторы Ui этой главы
соответствуют операторам разд. 6.4.
Резюмируем все сказанное выше следующим образом: трансфер-
матрица V коммутирует с другой трансфер-матрицей V, если можно по-
подобрать и>" так, чтобы выполнялось равенство (9.6.8). Это условие анало-
аналогично соотношению звезда — треугольник для модели Изинга.
Решение соотношения звезда — треугольник
Задавшись и\ мы хотим найти такие w', w", чтобы выполнялось усло-
условие (9.6.8). Тривиальное решение имеет вид w' ~ w, w"(v, д I /, /х').=
= 6(*>, ^'M(/х, /х'), но такое решение не представляет интереса, поскольку
оно означает лишь, что матрица V коммутирует сама с собой. Нам
нужны решения, в которых элементы w' не просто пропорциональны
элементам w.
Из рис. 9.3 очевидно, что и>" играет роль, сходную с w и w'. Поэтому
естественно предположить, что и>" также описывается соотношениями
(9.6.2), но с а", Ъ", с" вместо а, Ь, с.
Если числа а, Ь, с заданы, то а', Ь'', с' и а", Ь", с" находятся в нашем
распоряжении. Поскольку соотношение (9.6.8) однородно по w' и w",
остается четыре параметра, подлежащих определению.
С другой стороны, каждый из символов а, /3, /х, v, /x', v' в (9.6.8) может
независимо принимать значения ±1, так что (9.6.8) представляет собой
систему из 64 скалярных уравнений. На первый взгляд кажется, что задача
добиться одновременного выполнения всех этих уравнений невыполнима.
К счастью, возникает много упрощений. Из (9.6.2) следует, что и>(/х,
а I /3, v) = 0, если не выполняется условие /х + а = /З+у; то же
справедливо по отношению к и>', w". Отсюда следует, что обе части
(9.6.8) равны нулю, если не выполняется условие v + ix + a = f$+vf
+ ц'. В результате остается только 20 нетривиальных уравнений.
Поскольку обращение знаков всех спинов не меняет w, w', w" и (9.6.8),
эти 20 уравнений сводятся к 10 уравнениям.
Кроме того, перестановка пар символов (а, 0), (/х, О» 0*'» *0» 0*"» »")
просто меняет местами правую и левую части (9.6.8). Из этого следует,
что 4 из оставшихся 10 уравнений выполняются тождественно, в то время
как остальные образуют три пары эквивалентных уравнений. Таким обра-
образом, окончательно (9.6.8) сводится к трем уравнениям, а именно

ГЛАВА 9 193
ас'а" = Ъс'Ъ" + са'с",
аЬ'с" = Ьа'с" + сс'Ь" ,ш (9.6.12)
сЬ'а" = са'Ь" + Ьс'с» .
Исключая а", Ъ"', с"', получаем одно уравнение
(а2 + Ъ2- с2I{аЪ) = (а'2 + Ь'2 - с'2I{а'Ъ'). (9.6.13)
Определяя параметр Д так же, как в (8.3.21) и (9.2.1), приходим к вы-
выводу, что w" можно подобрать так, чтобы соотношение звезда — треу-
треугольник (9.6.8) выполнялось при условии
Д = Д' . (9.6.14)
Таким образом, если матрицы V и V характеризуются различными
значениями а, Ъ> с, но одинаковым значением Д, то они коммутируют.
Поэтому можно считать, что мы непосредственным образом (не используя
анзац Бете) установили свойство коммутации, обнаруженное в разд. 9.2.
Этим исчерпывается содержание пункта I разд. 9.5.
9.7.ПАРАМЕТРИЗАЦИЯ В ЦЕЛЫХ ФУНКЦИЯХ
Чтобы получить свойства II и III (разд. 9.5), нужно параметризовать а,
Ь, с в терминах трех других переменных, скажем р, ли v, причем так, что-
чтобы величины at b, с были целыми функциями v, но параметр Д не зависел
от v.
Очевидной является следующая параметризация: а, Д рассматриваются
как «константы» и вводится переменная х = b/а. Тогда в соответствии с
(9.2.1) имеем
а = а, Ь = ах, с = а{\ + х2 - 2Дх)*. (9.7.1)
Но с здесь не является целой функцией дг, а представляет собой квадратный
корень из многочлена от х.
Существует простой способ параметризации функции
F =[(х - х1 )(х - х2)]Vl, а именно определяется
Г2 - (х ~ хг)/{х - х2) , (9.7.2)
т. е. вводится
* = (*!- Ас2)/A " t2). (9.7.3)
Тогда знак t можно выбрать таким образом, что
F=(xl-x2)t/(l-t2), (9.7.4)
так что х и F оказываются рациональными функциями t.
В нашем случае хх и х2 являются нулями квадратного трехчлена

194 АЛЬТЕРНАТИВНЫЙ СПОСОБ РЕШЕНИЯ МОДЕЛЕЙ ТИПА ЛЬДА
1 + х2 - 2Ах. Таким образом,
b = h(Xl + x;1), je2 = Jef\ (9-7.5)
и (9.7.1) переходит в
а = а, Ь = о(дс1 - tW)l{\ ~ '2)>
Чтобы убрать знаменатели, мы можем «перенормировать» эти соотно-
соотношения, положив а = р'хх(\ — t2). Тогда
в = р'дс1A-/2), b = p'(x]-t2),
(9.7.7)
c = p'{x\-l)t.
При такой параметризации а, Ъ> с являются целыми функциями р', х1 и
/, но Д зависит только от х{. Варьируя /, мы влияем на а : Ъ : с, но
оставляем Д без изменения.
Этим завершается вывод свойств II и III, и мы можем использовать
далее эту параметризацию, рассматривая р', хх как константы, a t как
переменную величину. Но чтобы восстановить связь с прежними
результатами (и облегчить последующее обобщение на восьмивершинную
модель), полезно произвести завершающее преобразование от р', дгр t к р,
X, vt положив
хг = -ехр(-А), t = exp[h(v - к)], р' = \pt~W . (9-7.8)
В результате мы снова получим (9.2.4), (9.2.3) и свойства II и III (разд.
9.5).
Параметризованное операторное соотношение
звезда — треугольник
До сих пор мы использовали только следствие (9.6.14) соотношений
звезда — треугольник (9.6.12). Но поскольку соотношения (9;6.12) не
меняются при перестановке весовых множителей а, Ь, с с двумя штрихами
и без них, имеется еще одно очевидное следствие: А" = Д'. Таким обра-
образом, (a', b', cf) и (а", Ь", с") также могут быть параметризованы с по-
помощью соотношений (9.2.3), причем все наборы будут характеризоваться
одним и тем же значением X.
При этом значения v будут разными; обозначим их v' и v" со-
соответственно (и аналогично для р, но этот нормировочный множитель
тривиально сокращается в (9.6.12)). Подставляя результирующие
выражения (9.2.3) для а , . . . , с" в (9.6.12), получаем, что все эти
три уравнения удовлетворяются, если
sinh i(A + v - v' + v") = 0. (9.7.9)

ГЛАВА 9 195
Добавление слагаемого 4тг/ к v' оставляет а', Ь', с' без изменения,
поэтому, не теряя общности, можно принять, что решение уравнения
(9.7.9) имеет вид
у'=А + v+ v". (9.7.10)
Для некоторых целей удобно использовать в качестве переменной
u = i{k+v) (9.7.11)
вместо v. Тогда (9.2.3) принимает вид
(9.7.12)
и если и' = 1/2(X + v')y и" = 1/г(Х + v"), то (9.7.10) превращается в
и' = и + и". (9.7.13)
Вершинные операторы Ujy определяемые посредством (9.6.9) и (9.6.2),
являются функциями а, Ъ, с. Поэтому в соответствии с (9.7.12) они зависят
от р, X, и. Считая р, X константами, мы можем рассматривать оператор Ui
как функцию и и записывать его как Ц(м). Тогда (/• и U'- в (9.6.10) означа-
означают Ufa') и Ufa") соответственно. Используя (9.7.13), приводим опера-
операторное соотношение звезда — треугольник (9.6.10) к виду
Ui+l(u) U{u + и") Ui + l(u") = Ui(u") Ui + l(u +u") Ui(u). (9.7.14)
Это тождество, справедливое для / = 1 , . . . , N — 2 и для всех
комплексных чисел и и и". В частности, оно верно для 0 < и/к < 1,
0 <ы"/\ < 1. В случае Д < 1 в этих интервалах лежат имеющие физи-
физический смысл значения м, и", соответствующие положительным больцма-
новским весовым множителям а, Ь, с, а", Ь", с".
Сравнивая (9.7.14) с G.13.5), мы снова видим весьма близкую аналогию
между соотношениями звезда — треугольник для модели типа льда и
модели Изинга.
9.8. МАТРИЦА Q(v)
Векторы-столбцы у
Следующим шагом должно быть получение свойства IV, т. е. построе-
построение матрицы Q(v), удовлетворяющей уравнению (9.4.5).
Пусть у — некоторый столбец матрицы Q{v). Тогда из (9.4.5) следует
V(v)y=y'+y", (9.8.1)
где у' и у" пропорциональны у с заменой v на v + 2Х' и v — 2Х' со-
соответственно.
Попытаемся непосредственно построить векторы у, у', у". Пусть
y(av . . . , aN) — элемент (ар ... , aN) вектора у. Тогда произведение

196 АЛЬТЕРНАТИВНЫЙ СПОСОБ РЕШЕНИЯ МОДЕЛЕЙ ТИПА ЛЬДА
V(v)y упрощается, если у(а{ , . . . , aN) имеет вид
)>(<*!,.. ..,<**) =gi(ari)g2(ar2). •¦ -Ы^Ь (9.8.2)
т. е. >> представляет собой прямое произведение двумерных векторов
8\> • • • t gtf- Действительно, согласно (9.6.1), элемент (ар . . . , aN) про-
произведения V(v)y описывается выражением
[V(v)y]a = TrG,(ai) Gia2).... GN(aN), (9.8.3a)
где G,(+) и G{(—) — матрицы 2 x 2 со следующими элементами (ji, /л'):
a)U' = 2 w(n, a\P, (i')g,(P) ¦ (9.8.36)
Р
В явном виде с учетом (9.6.2) имеем
0
G'() l 0 agi(-)J
Нам нужно, чтобы правая часть (9.8.3а) распадалась на сумму двух
членов, каждый из которых имеет вид (9.8.2). Это так и будет, если суще-
существуют матрицы Рх , . . . , PN размера 2x2, такие, что
Gfa) = РЩа) РГ^и (9.8.5)
где каждая матрица ЯДа) является верхней треугольной и PN + j = Рх.
Чтобы доказать это, подставим в выражение (9.8.3а) С/Да) в виде
(9.8.5). Тогда Р( сокращаются, поэтому в результате происходит замена
каждой матрицы С/Да) на НЦа). Если //Да) имеет вид
««¦сг :«)•
то (9.8.3а) дает
[V(v)y]a = gi(an).... g'N(*N) +8'Ш ... g'iv(^). (9-8-7>
«Прохождение» пары векторов через вершину
Могут ли условия (9.8.5) и (9.8.6) быть выполнены, т. е. можно ли по-
подобрать такие Р{, чтобы нижний левый элемент Рг^Да)/^ + { был равен
нулю как для а = + 1, так и для а = - 1? Иначе говоря, должно быть
i =gi(a)Pi (9.8.8)

ГЛАВА 9 197
Pi
Рис. 9.4. Прохождение пары векторов через вершину:
графическое представление уравнения (9.8.9).
ft
'Phi
для а = ±1. Здесь С/,(+) и G,(-) — матрицы 2x2, р( обозначает
двумерный вектор, соответствующий первому столбцу Р/, #•(+) и
g'j(-) — скаляры.
Пусть элементы /?, будут /?Д+) и /?,(-). Используя (9.8.36), условие
(9.8.8) можно написать в явном виде как
для а, /х = ± 1.
Это равенство можно наглядно интерпретировать с помощью рис. 9.4.
Пусть /х, а, /3, /х' — спины на линиях связи вокруг одной вершины, как это
показано на рис. 9.4. Верхней и правой линиям поставим в соответствии
статистические веса #,(/3), р{,+ Д/х'). Просуммируем по всем /3, /х' с
вершинным весом w в качестве коэффициента. Эта операция даст
функцию /х и а. Условие (9.8.9) означает, что эта функция факторизуется в
произведение статистического веса gf (а) для нижней линии и веса p-fji) для
левой линии.
Таким образом, смысл соотношения (9.8.9) можно выразить сле-
следующими словами: функции (или векторы) gjf р{ + 1 «проходят» через
вершину, превращаясь в gjt pr И в самом деле, используя (9.6.9), можно
переписать (9.8.9) в довольно очевидных операторных обозначениях как
Ui{gi®Pi + \)—Pi®g'i- (9.8.10)
Поскольку /х, а = ±1, условие (9.8.9) представляет собой систему
четырех скалярных уравнений. Они имеют следующий явный вид:
(9.8.11)
Эти уравнения линейны и однородны по переменным #,( + ), g{ - ),
8,- ( + )t 8j( - )> поэтому последние можно исключить (вычисляя детер-
детерминант из коэффициентов), что дает
a2 + b2-c2 = rhl + Jj_ (9812)
ab г, г, +, '

298 АЛЬТЕРНАТИВНЫЙ СПОСОБ РЕШЕНИЯ МОДЕЛЕЙ ТИПА ЛЬДА
где
n=Pi(-)/pi( + \ / = 1 TV. (9.8.13)
Мы получили квадратное рекуррентное соотношение между ri и г, + {.
Оно имеет две интересные особенности: во-первых, включает ау Ь, с
только через параметр Д, определяемый формулой (9.2.1); во-вторых, с
учетом (9.2.4) факторизуется в простое выражение
П+i = ~Г/ехр(±А). (9.8.14)
ВЕКТОРЫ-СТОЛБЦЫ у [у) И МАТРИЦА QR(v)
Соотношение (9.8.14) должно выполняться для / = 1 , . . . , TV; но
выбор знака производится независимо для каждого /. Таким образом,
наиболее общее решение для г1 , . . . , rN + j имеет вид
П = (-Угехр[А((Т1 + • . . + c7,-i)] , (98.15)
где г — произвольный коэффициент и каждая переменная ot имеет значения
± 1. Циклические граничные условия выполняются, если
cti+ .. . + aN=0, (9.8.16)
откуда следует требование четности N.
(Если 1Д1 < 1, то параметр X является чисто мнимой величиной. Если
X принимает значения 2%im/n, где тип — целые числа, то достаточно,
чтобы сумма ох + . . . + oN была целым кратным от п. Такие случаи
часто представляют особый интерес; например, модель льда характери-
характеризуется величиной X = 2тг/УЗ.)
Мы можем положить все /?Д 4- ), g,( + ) равными единице, так что
/?Д - ) = г.. Тогда, решая (9.8.11) с помощью (9.8.15) и (9.2.3.), получаем
.•(-) = rf-exp[i(A + i7)oi],
(9.8.17)
/(-) = "^ exp[iCA + v)a^ .
Уравнение (9.8.8), где р. — первый столбец матрицы />,, теперь удо-
удовлетворяется. Из этого следует, что матрица Н((а) определенная пос-
посредством (9.8.5), должна иметь вид (9.8.6) при любом выборе второго
столбца Р{ (при условии что все Р. несингулярны). Элементы g; (а) мож-
можно получить, вычисляя определитель от обеих частей (9.8.5) и используя
(9.8.4) и (9.8.6). Это дает
При подстановке этого выражения в последнее слагаемое в (9.8.7)
определители Pi сокращаются, поэтому их можно не учитывать в (9.8.18)

ГЛАВА 9 199
(или потребовать их равенства единице). Тогда из (9.8.17) следует
" A)aJ . (9.8.19)
Для заданного / определим двумерную векторную функцию h;(v) как
шу. , ,)> (9.8.20)
r,exp[i(A + v)Oi]/
где г. определены выражением (9.8.15), и, следовательно, все гх , . . . , rN
не зависят от v. Пусть g. — следующий двумерный вектор:
Аналогично определены g{, gi .
Тогда уравнения (9.8.17), (9.8.19) можно представить в очень компакт-
компактной форме:
gi = hi(v), gi=ahi(v+2k'), g? = bht{v - 2A'), (9.8.22)
где X' = X + /тг, как в (9.3.7). Если мы определим также 2дг-мерную век-
векторную функцию y(v) выражением
y(v) = hi(v)®h2(v) ® . . . ® hj^v), (9.8.23)
то, используя (9.8.2), равенство (9.8.7) можно записать в виде
V(v)y(v) = aNy(v + 2А') + bNy(v - 2А'). (9.8.24)
Согласно (9.2.3) и (9.3.4), а" = Ф(\ - v), bN = Ф(\ + i;). Выбирая все-
всевозможные г, ох , . . . , (Тдг в (9.8.15) с единственным ограничением, налага-
налагаемым условием (9.8.16), мы получим много различных y(v). Пусть
QR(v) — матрица 2N x 2N, столбцы которой представляют собой линей-
линейные комбинации (с коэффициентами, не зависящими от v) таких векторов
y(v). Тогда из (9.8.24) немедленно следует равенство
V(v) QbHv) = ф(к - v) QR(v + 2А') + ф(к + v) QR(v - 2A'), (9.8.25)
которое, по существу, совпадает с (9.4.5). Таким образом, мы получили,
свойство IV (разд. 9.5).
Векторы-строки^- v) и матрица Ql(v)
Осталось еще получить свойства V и VI. С помощью (9.6.1) и (9.6.2)
(путем перестановки а/ и /3/ и обращения знака у всех /х^ мы убеждаемся,
что обмен местами а и b эквивалентен транспонированию трансфер-
матрицы V. Поэтому, согласно '9.2.3),
V(-v) = VT(v). (9.8.26)

200 АЛЬТЕРНАТИВНЫЙ СПОСОБ РЕШЕНИЯ МОДЕЛЕЙ ТИПА ЛЬДА
Если мы определим
Ql(v) = QTR(-v), (9.8.27)
то транспонирование (9.8.25) и перемена знака v дают
Ql(v) V(v) = 0(А - v) QL(v + 2А') + 0(А + v) QL(v - 2A'), (9.8.28)
так что QL(v) играет роль, подобную QR(v)y если не считать того, что она
умножается на трансфер-матрицу слева, а не справа.
Вектор^) определен формулами (9.8.23), (9.8.20) и (9.8.15), поэтому
он зависит от г, о{ , . . . , oN, а также от v. Это можно выразить, записы-
записывая его в виде y(v I r, а). Рассмотрим скалярное произведение
%
Ут(-и\г' ,&)y(v\r,o) (9.8.29)
двух таких векторов. Для него легко получить следующее выражение:
N
П{1 + rr' exp[A(Gi + . . . + a,_i + oi + . . . + &t-x)+
(9.8.30)
Оно зависит, в частности, от а{ , ... , oN, и и v, поэтому обозначим
его J(u, v I а, , . . . , oN) и рассмотрим отношение
J(u,v\. . . , cj + i, о}-,. . .)/7(и,у|. . . , сту, ау + ь. . .), (9.8.31)
в котором числитель отличается от знаменателя только перестановкой о^ и
(jy+1. Поскольку во все сомножители в (9.8.30), за исключением i=j
и / = j + 1, числа ay, ay + j входят симметрично, написанное выше отно-
отношение упрощается; в числителе и знаменателе остаются только указанные
несимметричные сомножители. Тогда путем прямого вычисления (ис-
(используя тот факт, что Gjf 0у+р о'р а] + \ пРинимают только значе-
значения ± 1) мы обнаруживаем, что отношение (9.8.31) является симметричной
функцией и и v.
Но из (9.8.30) очевидно, что функция J{u, v I ox , . . . , oN) симметрична
По отношению к переменным и и vf если а{ = о\ для / = 1 , . . . , N.
Поскольку все значения ох , ... , oN, допускаемые условием (9.8.16),
являются перестановками этого частного набора значений и все такие
перестановки можно получить последовательными перестановками пар ((Ту,
(Ту + j), отсюда следует, что (9.8.30) всегда является симметричной
функцией и и v. Таким образом,
ут(-и\г' ,&)у(и\г,о)=ут(-и\г',&)у(иУ, а). (9.8.32)
Рассмотрим теперь матричное произведение QL(u)QR(v). Так как любой
столбец QR(v) представляет собой линейную комбинацию векторов y(v I г,

ГЛАВА 9 201
о) и любая строка QL(u) является линейной комбинацией векторов
уТ(_ и | г>} о')у из (9.8.32) следует
Ql(u)Qr(v)=Ql(v)Qr(u) (9.8.33)
для всех комплексных чисел и, v.
Несингулярность матрицы Qr(v)
Рассмотрим теперь множество векторов y(v I г, а), где г — произволь-
ное комплексное число, а о = [ох , . . . , oN\ принимает все [ дут ) значе-
ний, допускаемых условием (9.8.16). Я хочу доказать, что имеются такие
значения vy для которых это множество векторов порождает все 2уУ-мерное
пространство, так что QR(v) и QL(- v) можно подобрать так, чтобы они
были несингулярными. К сожалению, я не знаю простого способа доказать
это утверждение полностью, но оно почти наверняка правильно, что
подтверждают следующие соображения.
Согласно (9.8.23), (9.8.20) и (9.8.15), элемент (ах , . . . , aN) вектора
y(v I г, о) содержит множитель
^-^-.....^ (9.8.34)
в то время как другие множители от г не зависят. Таким образом,
N
y(v\r,a)= ^rnyn(v\o), (9.8.35)
где каждый вектор yn(v I о) имеет ненулевые элементы только в том слу-
случае, если ах + ... + aN = N — 2/2,т.е. если имеется п стрелок, направ-
направленных вниз.
Пусть Уп — ( J -мерное пространство векторов, ненулевые элементы
которых удовлетворяют условию ах + . . . + aN = N — 2/2. Тогда
достаточно показать, что пространство Уп (для п = 0 , . . . , N порож-
порождается векторами уп(v I а), соответствующими всем возможным значениям
а.
Поскольку имеется ( ) таких значений а, допускаемых условием
/N \
( I
(9.8.16), количество векторов yn(v l о) по крайней мере не меньше раз-
размерности Уп. Наиболее деликатным является случай п = N/2, когда век-
векторов ровно столько, сколько необходимо.
Каждый элемент (ах , ... , aN) вектора yn(v I о) содержит множитель
N
o 2 о{\ - ai-)l, (9.8.36)

202 АЛЬТЕРНАТИВНЫЙ СПОСОБ РЕШЕНИЯ МОДЕЛЕЙ ТИПА ЛЬДА
другие множители от v не зависят и не равны нулю. С учетом (9.8.16) этот
множитель упрощается до
N
(9.8.37)
exp -iv 2 °i<Xi\ •
Если п = N/2, а параметр v имеет большое отрицательное значение, то
существует единственный доминирующий элемент yn(v I а), соответст-
соответствующий а{ , . . . , aN = ох , . . . , oN, который максимизирует (9.8.37)
и согласуется с (9.8.16). Таким образом, имеется ( ) векторов-столбцов
\п/
с доминирующим элементом в различных строках. Ясно, что эти векторы
образуют базис Уп.
Поэтому искомое утверждение определенно верно для п = N/2. По-
Поскольку это подпространство содержит максимальное собственное значе-
значение К, его можно получить рассматриваемыми методами. В более общем
случае, когда п Ф 7V/2, имеется больше векторов yn(v I сг), чем необходи-
необходимо, и нет оснований предполагать, что они (для произвольного значения v)
не порождают пространство Уп.
Матрица Q(v) и коммутационные соотношения
для нее
Учитывая вышесказанное, будем предполагать далее, что определители
QR(v) и, следовательно, QL(v) не равны тождественно нулю (они могут,
конечно, равняться нулю для ограниченного множества комплексных значе-
значений t;). Пусть v0 — такое значение этого параметра, для которого ука-
указанный определитель не равен нулю; определим
Q(v) = Qr(v) Qh\vo) . (9.8.38)
Полагая и = v0 в (9.8.33), получаем
Q(v) = Ql\vо) QL{v). (9.8-39)
Поэтому умножение (9.8.25) справа на QR~l(p^ и (9.8.28) слева на
sQL~\v^ дает
V(v) Q(v) = Q(v) ()
(9.8.40)
= ф(к - v) Q{v + 2A') + ф(К + v) Q(v - 2A').
Кроме того, из (9.8.39) и (9.8.38) следует
Q(u) Q(v) = Ql\vo) QL{u) QR(v) Qr\v0) . (9.8.41)
Согласно (9.8.33), правая часть этого равенства не меняется при

ГЛАВА 9 203
перестановке и и v, так что
Q(u)Q(v) = Q(v)Q(u). (9.8.42)
Таким образом, такая матричная функция Q(v) удовлетворяет соотно-
соотношению (9.4.5) и обладает свойствами IV и V (разд. 9.5).
КОММУТАЦИОННЫЕ СООТНОШЕНИЯ,
ВКЛЮЧАЮЩИЕ ОПЕРАТОР S
Наконец, диагональный оператор 5, упоминаемый в пункте VI, может
быть представлен в виде
и; >¦¦¦< -")¦
Из (9.8.20) и (9.8.23) следует
Sy(v) =y(v +2m), (9.8.44)
и, поскольку все столбцы QR(v) являются линейными комбинациями векто-
векторов у(р),
SQr(v) = Qr(v +2я1). (9.8.45)
Транспонирование, обращение знака v, использование (9.8.27) и того
факта, что QR(v + 4тг/) = QR(v), даю!
Умножая (9.8.45) справа на QR~\v0) и (9.8.46) слева на QL~l(v0) и
используя (9.8.38) и (9.8.39), получаем
5 Q(v) = Q(v) S = Q(v + 2т). (9.8.47а)
Кроме того, поскольку w((/x, a I 0, /*') не изменяется при умножении на ^,
а, 0, /а', из (9.6.1) следует
SV(v) = V(v)S. (9.8.476)
Согласно (9.8.20) и (9.8.23), при t; — ± оо любой элемент у(р) и, следо-
следовательно, Q(y) растет по меньшей мере так же быстро, как ехр(М;/2).
Свойство VI (разд. 9.5) теперь сразу следует из (9.8.47).
Как показано в разд. 9.5, из свойств I — VI с необходимостью следуют
уравнения (9.3.6), (9.3.8) для собственных значений Л матрицы К. Таким
образом, мы получили эти уравнения, не используя анзац Бете. Имеется
два ключевых момента в проделанных вычислениях — соотношение звез-
звезда — треугольник (9.6.8) и соотношение (9.8.9), описывающее прохождение
пары векторов через вершину. Следует подчеркнуть, что каждое из них
представляет собой локальное свойство: первое относится к* треу-
треугольнику из трех вершин, второе — к отдельной вершине.

204 АЛЬТЕРНАТИВНЫЙ СПОСОБ РЕШЕНИЯ МОДЕЛЕЙ ТИПА ЛЬДА
9.9. ЗНАЧЕНИЯ р, X, v
Все соотношения, полученные в этой главе, являются алгебраическими
тождествами, поэтому они справедливы для всех значений а, Ь, с и р, X, v,
действительных или комплексных. Нет необходимости указывать поло-
положение соответствующих точек на комплексной плоскости до тех пор, пока
мы не приступим к анализу решения уравнений (9.3.8). переходя к пределу
при N — оо и выбирая решение, отвечающее максимальному собственному
значению Л. (Такой анализ выполнен в разд. 8.5 — 8.9.)
Если энергии взаимодействия ех , ... , е6, характеризующие вершины,
являются действительными величинами (и удовлетворяют условию (8.1.7)),
то и больцмановские весовые множители af b, с, определяемые посредст-
посредством (8.3.3), — действительные положительные числа. При установлении
значений параметров р, X, v следует рассмотреть четыре случая, со-
соответствующих четырем фазам, показанным на рис. 8.5. Значения р, X, v
могут быть выбраны следующим образом:
I. Д > 1, а > b + с:
где р', X', v' —действительные и р' > 0, v' > X' > 0;
II. Д > 1, b > а + с:
где р', X',v' — действительные и р' > 0, vr > X' > 0;
III. -I < Д < 1, a -I- b > с > I а - Ь\:
где р\ /х, w — действительные ир'>0, 7r>^>lwl (это те же /*, w,
что и в разд. 8.8);
IV. Д < - 1, с > а + Ь:
Р, X, v — действительные,' р > О, X > \v\.

10
ВОСЬМИВЕРШИННАЯ МОДЕЛЬ
НА КВАДРАТНОЙ РЕШЕТКЕ
10.1. ВВЕДЕНИЕ
Наиболее значительным новым точным результатом после работы Бер-
Берлина и Каца [51] по сферической модели и пионерской работы Онсагера
[184], посвященной модели Изинга, было полученное Либом [157 — 159]
решение для модели типа льда (шестивершинной модели).
Модели типа льда как модели критических явлений обладают некото-
некоторыми необычными свойствами: сегнетоэлектрическое упорядоченное
состояние в них «заморожено» (т. е. имеется полное упорядочение даже
при ненулевой температуре); критическое поведение антисегнетоэлектриков
характеризуется более сложным законом, чем простая степенная зависи-
зависимость от разности температур Т— Тс (разд. 8.11).
Первое из этих необычных свойств, несомненно, связано со структурой
льда. Пусть в начальной конфигурации все вертикальные стрелки
направлены вверх, а все горизонтальные — вправо. Простейшая допусти-
допустимая деформация состоит в том. чтобы провести через решетку прямую (с
юга-запада на северо-восток) и обратить направления всех стрелок,
лежащих на этой прямой. В случае неограниченной решетки с сегне-
тоэлектрическим упорядочением для такой деформации потребуется беско-
бесконечно большая энергия. Поэтому указанная деформация дает бесконечно
малый вклад в статистическую сумму.
Сезерленд [220] и Фан и By [83] предложили в связи с этим следующее
обобщение моделей типа льда:
на каждом ребре квадратной решетки находится одна стрелка;
допустимы только такие конфигурации, когда в каждый узел входит (и
выходит) четное число стрелок;
существует восемь возможных конфигураций стрелок в узле (вершине),
как показано на рис. 10.1 (отсюда и название модели). Для образования j-й
«вершины» необходима энергия ^ (/' = 1 , . . . , 8). Для такой модели
статистическая сумма имеет вид
Z = 2 exp[-(ni?i + . . . + пъ?%IквТ], A0.1.1)
где сумма берется по всем допустимым конфигурациям С стрелок в решет-
решетке, п- — число вершин типа j в конфигурации С, кв — постоянная Больц-
мана, Т — температура.
На рис. 10.1, помимо первых шести вершин, которые совпадают с

206 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Т Т Т Т т Ж * г
1 2 3 4 5 6 7 8
Рис. 10.1. Восемь допустимых вершинных конфигураций.
моделью льда (рис. 8.2), имеются еще новые вершины, для которых все
стрелки входят в узел или все стрелки выходят из узла. Теперь для
локальной деформации (например, обращения всех стрелок, лежащих на
сторонах квадрата) состояния решетки, в котором все стрелки направлены
вверх или вправо, необходима лишь конечная энергия. Поэтому следует
ожидать, что сегнетоэлектрическое состояние не будет полностью упорядо-
упорядоченным; можно надеяться также, что и в других отношениях модель
окажется менее патологической.
Из A0.1.1) ясно, что Z является функцией восьми больцмановских весов
(Oj = txp(-EjlkBT)J = 1 ,. . . , 8 . A0.1.2)
На рис. 10.1, видно, что вершина 7 представляет собой сток стрелок, а
вершина 8 — источник. Если на решетку наложены тороидальные гранич-
граничные условия, то из них следует
Аналогично обращение всех вертикальных стрелок делает вершину 5
стоком, а вершину 6 источником; поэтому
Отсюда следует, что энергии е5 , . . . , е8 в A0.1.1) появляются только в
виде комбинаций е5 + е6, е7 + е8; поэтому без потери общности можно
взять
?5 = ?6, ?i = ?s- A0.1.5а)
Особенно интересная ситуация возникает, если выполняются также
равенства
?i = ?2, ?з = ?4- A0.1.56)
При условиях A0.1.5) состояния модели не изменяются при обращении всех
стрелок. Если считать, что стрелки представляют собой электрические
диполи, то последнее свойство означает, что внешнее электрическое поле
равно нулю. Такая специализированная модель известна как восьми-
вершинная модель без внешнего поля.
Полная восьмивершинная модель не решена, и ниже приводится
решение только для модели без внешнего поля. В отличие от восьми-
вершинной модели шестивершинная модель может быть решена даже
при ненулевом электрическом поле (разд. 8.12).

ГЛАВА 10
207
10.2. СИММЕТРИИ
Рассмотрим модель без внешнего поля и введем обозначения
а = щ = аJ, Ъ = щ = со4,
с = аM = со6, d = со-! = щ .
Тогда из A0.1.1) и A0.1.2) получаем
A0.2.1)
A0.2.2)
откуда ясно, что Z есть функция Z(a, о; с, d) от а, Ь, с, d.
Фан и By [83] показали, что функция Z(a, b; с, d) имеет некоторые сим-
симметрии. Пусть IX, a, v, C — «стрелки-спины», связанные с четырьмя
ребрами, образующими вершину, как показано на рис. 10.2. Они прини-
принимают значения + 1 (— 1), если соответствующая стрелка направлена вверх
или вправо (вниз или влево). Поэтому больцмановский вес вершины, пред-
представленной на рис. 10.2, равен w(/x, a I 0, v), где
A0.2.3)
и вес w(/x, a I 0, *>) равен нулю для всех других значений /*, а, C, v (это
обобщение условий (9.6.2)). Данное определение можно записать в более
компактном виде:
, а\р , v) = \{а'{\ + а
для всех /х, а, 0, *>, где
а' = J(<i + Ь + с + d), b' =i(a + b-c-d),
с' =$(a-b + c-d), d' =h(a-b-c + d).
A0.2.4)
A0.2.5)
Рис. 10.2. Четыре стрелки-спина /х, а, 0, р на ребрах,
примыкающих к вершине. Вес w(p., a \ 0, v) вершинной
конфигурации (jx, a, C, v) дается формулой A0.2.3).

208 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Допустим, что решетка имеет М рядов (обозначаемых индексами
/ = 1 , . . . ,М) и N столбцов (/ = 1 , . . . , N). В соответствии с
определением w статистическая сумма может быть записана в виде
Z = 2 И>цИ>12 • . . WM7V , A0.2.6)
а, ц
где
Wy = w(iMj, Oiyk + i,/, № ,у + l) • A0.2.7)
Суммирование в A0.2.6) может быть распространено на все значения (± 1)
стрелок-спинов ап , . . . , aMN, /*п , . . . , /*MiV.
С учетом выражения A0.2.4) для футт^ттии и> Формула A0.2.7) принимает
вид
Viy = w\P + . . . + nf}, (Ю.2.8)
где w\p соответствует А:-му слагаемому в правой части A0.2.4) и пред-
представляет собой произведение веса и стрелок-спинов, например wjp =
С учетом A0.2.8) выражение A0.2.6) может быть записано в виде
суммы SMN слагаемых вида
и>ц . . . wMN , uu.z.y;
где каждое ktj является целым числом, принимающим значения от 1 до 8.
Каждое такое слагаемое A0.2.9) может быть представлено с помощью
графа стрелок G на исходной решетке: на каждом узле (/, j) нужно нарисо-
нарисовать вершину типа к-^, изображенную на рис. 10.1. Таким образом, сущест-
существует две стрелки на каждом ребре, по одной на каждый узел, принадлежа-
принадлежащий данному ребру.
Рассмотрим какое-нибудь ребро, скажем вертикальное ребро между
узлами (/ — 1, j) и (/, j) со стрелкой-спином а^. Только два множителя в
A0.2.9) могут содержать с^-, а именно те, которые отвечают узлам (/ — 1,
j) и (/, j). Сравнивая A0.2.4) и рис. 10.1, мы находим, что а- не содержит-
содержится (содержится) в каждом из этих множителей, если соответствующая
стрелка в G направлена вверх (вниз).
Но выражение A0.2.9) следует просуммировать по всем ап , . . . , hMn>
в частности по а у. Если A0.2.9) содержит нечетную степень а-, то сумми-
суммирование по ctjj дает нулевой вклад в сумму. Поэтому нужно учитывать
только члены с четными степенями а-: степень может быть равной 0 (оба
множителя не содержат а^) или 2 (оба множителя содержат а у). В обоих
случаях соответствующие стрелки в G направлены в одну сторону.
Применяя данный результат ко всем ребрам, как вертикальным, так и
горизонтальным, получаем, что член A0.2.9) дает вклад в A0.2.6) только в
том случае, если все ребра в G содержат пары параллельных стрелок.
Заменим каждую, такую пару на одну стрелку, указывающую общее
направление. Суммирование A0.2.9) по а и /х дает тогда просто множитель

ГЛАВА 10 209
4MN9 который сокращается с множителем ХЛ в каждом из и>^. Таким об-
образом, A0.2.6) и A0.2.9) дают
Z = 2я'т1 + т2 Ь'т+т с>т5+тб d'm7+ms , A0.2.10)
где тк — число вершин в G типа к (к = 1 , . . . , 8) и суммирование прово-
проводится по всем стрелочным покрытиям G, таким , что каждая вершина
является одной из восьми вершин, показанных на рис. 10.1.
Но выражение A0.2.10) в точности совпадает с выражением A0.2.2), в
котором а, Ь, с, d заменены на а', Ъ', c't d'. Таким образом,
Z(a , Ь\ с , d) = Z(a' ,b';c',d'). A0.2.11)
Метод, использованный для получения этого результата, является, по
существу, методом слабого разложения графа [174, 177, 249]. Подобно со-
соотношению дуальности в модели Изинга (разд. 6.2), выражение A0.2.11)
связывает высокотемпературную модель (а, Ь, с, d почти дэавны) с низ-
низкотемпературной (а > bt с, d). Действительно, в следующем разделе
показано, что модель Изинга представляет собой частный случай
восьмивершинной модели: соотношение дуальности F.2.14) может быть
выведено из соотношения A0.2.11).
Некоторые другие простые симметрии, которые устанавливают связь
между различными высокотемпературными моделями и между различ-
различными низкотемпературными моделями, легко выводятся из выражений
A0.1.1) — A0.2-2). Из рис. 10.1 очевидно, что изменение направлений всех
горизонтальных стрелок на противоположные дает
Z(a , Ъ ; с , d) = Z(b , a ; d , с) , A0.2.12)
в то время как поворот на 90° приводит к
Z(a,b \c,d) =Z(b ,a ;c ,d). A0.2.13)
Предположим, что М и N четны. Тогда решетку можно разделить на
две подрешетки А и В, такие, что ближайшие соседи каждого узла в А
принадлежат В, а ближайшие соседи каждого узла в В принадлежат А.
Обратим все стрелки на горизонтальных (вертикальных) ребрах, у которых
на левом (верхнем) конце находится узел подрешетки А. Новая модель так-
также является восьмивершинной моделью без внешнего поля, в которой, од-
однако, а, Ь, с, d заменены на с, d, a, b. Отсюда следует равенство
Z(a,b;c,d)=Z(c,d;a,b). A0.2.14)
Из выражений A0.1.3) и A0.1.4) следует, что статистическая сумма
A0.2.2) содержит только четные степени с и flf, а из A0.2.14) следует, что Z
должна быть четной функцией а и Ь. Таким образом, имеют место
следующие соотношения:.
Z(a,b \c,d) =Z(±a, ±b ; ±c, ±d), A0.2.15)

210 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
где каждый знак можно выбирать независимо от других.
Все полученные выше соотношения симметрии A0.2.11) — A0.2.15)
можно описать, вводя величины
и>! = \{а + Ь), и>2 = \{а - Ь) ,
A0.2.16)
и понимая Z как функцию Z[w{ , . . . , w4] от величин w{ , . . . , w4, а не
величин а, Ь, с, d. После этого соотношения симметрии принимают
следующий вид:
и>2 , и>з, W4] =Z[±W/, ±Wj, ±Wk, ±^i] (Ю.2.17)
при произвольном выборе знаков и произвольной перестановке (/, у, к, I) из
A, 2, 3, 4). Таким образом, функция Z не изменяется при изменении знаков
и при перестановке любых величин из Wj , . . . , w4.
10.3. ФОРМУЛИРОВКА ВОСЬМИВЕРШИННОЙ
МОДЕЛИ КАК МОДЕЛИ ИЗИНГА
С ВЗАИМОДЕЙСТВИЕМ
МЕЖДУ ДВУМЯ И ЧЕТЫРЬМЯ СПИНАМИ
Рассматривая восьмивершинную модель как обобщение шестивершин-
ной, естественно описывать ее с помощью стрелок, находящихся на ребрах
решетки. Такая модель соответствует сегнетоэлектрику, если стрелки рас-
рассматривать как электрические диполи.
Но восьмивершинную модель можно» также сформулировать на языке
спинов и рассматривать ее как обобщение модели Изинга для магнетиков
[135, 258].
Для этого установим соответствие между спинами о^ и гранями решет-
решетки так, как показано на рис. 10.3. Каждый спин может принимать значения
-I- 1 или - 1. Будем учитывать взаимодействия между спинами пер-
первой и второй координационных сфер. Тогда наиболее общий трансляци-
онно инвариантный гамильтониан, удовлетворяющий A.7.4), имеет вид
м N
A0.3.1)
Таким образом, данная модель содержит взаимодействия между четырьмя
спинами. Статистическая сумма, которую мы обозначим через Z/5 опреде-
определяется выражением A.7.5), в котором Н = 0.
Для всех /, j введем величины
1, IMj = OijOi+hj • A0.3.2)

ГЛАВА 10
211
Рис. 10.3. Восьмивершинная модель
на квадратной решетке. Исходная
решетка показана пунктирными
линиями; узлы дуальной решетки
обозначены кружками.
Тогда A0.3.1) можно записать в виде
м N
= ~ 2 2
и для всех / и у выполняется равенство
= 1
^ + w} , A0.3.3)
A0.3.4)
Каждой конфигурации а-спинов соответствует одна конфигурация а,
/3-спинов, удовлетворяющих условию A0.3.4). Наоборот, каждой конфи-
конфигурации а, /х-спинов, удовлетворяющих A0.3.4), соответствуют две
конфигурации сг-спинов, удовлетворяющих A0.3.2). (Чтобы проверить
последнее утверждение, фиксируем произвольное значение одного спина,
скажем оп. Тогда соотношение A0.3.2) определяет значения соседних спи-
спинов. По этим значениям снова с помощью A0.3.2) определяются значения
следующих спинов и т. д.; условие A0.3.4) обеспечивает согласованность
полученных таким способом значений. Следовательно, существует именно
два решения A0.3.2), которые определяются выбором первого спина.)
Из установленного соответствия следует
/ = 22exp(-«/ifc*r),
а, ц
A0.3.5)
где сумма берется по всем значениям (+ 1, - 1) спинов аи , ... ,
удовлетворяющим условию A0.3.4). '
Поскольку w(pt, a I 0, v) в A0.2.3) отлично от нуля только при условии
ixafiv = 1, A0.2.6) не изменяется при наложении условия A0.3.4). Таким об-
образом, суммы в A0.2.6) и A0.3.5) совпадают при выполнении равенства
(для ца&1> = 1)
р) =
A0.3.6)
где через Jvatj обозначены энергии взаимодействия между узлами (/, J) и
(/ — 1, У); аналогично через J^n^ обозначены энергии взаимодействия

212
ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
между узлами (/, j) и (/, j - 1). Следовательно,
Z/ = 2Z%y,
A0.3.7)
где Zsv — определенная выше статистическая сумма восьмивершинной
модели, причем а^-, ру представляют собой стрелки-спины. Кроме того, с
учетом рис. 10.1 и формул A0.3.6), A0.1.2) имеем
= -Jh-Jv-J-J'-J\
= -Jh + Jv + / + /' + J\
f- Г,
A0.3.8)
?7 =?8= -/+/'+/".
Таким образом, общая модель Изинга и общая восьмивершинная
модель эквивалентны друг другу. В частности, восьмивершинная модель
при нулевом внешнем поле (со, = о>2, <*>3 = Ш4) соответствует модели
Изинга с Jh = Jv = 0, в которой учитываются только диагональные
взаимодействия и взаимодействия между четырьмя спинами. В последнем
случае из A0.1.2) и A0.2.1) следует
а = ехр[(/ + /' + Г)/квТ\, Ъ = ехр[(-/ - /' + J")lkBT]}
с = ехр[(-/ + /' - J")/kBT], d = exp[(/ - /' - Г)/квТ].
A0.3.9)
Если, кроме того, J" = 0, то остаются только диагональные
взаимодействия и а, Ь, с, d удовлетвоояют условию
ab = cd. A0.3.10)
На рис. 10.4 видно, что в последнем случае рассматриваемая модель
Изинга распадается на две невзаимодействующие друг с другом модели
Изинга на квадратных подрешетках, на каждой из которых взаимодей-
взаимодействуют только ближайшие соседи. Соответствующие подрешетки пока-
показаны на рис. 10.4 темными и светлыми кружками. Эти две модели
тождественны. Энергии взаимодействия между соседними узлами в них
равны J вдоль одного направления и J' вдоль другого. Отсюда следует,
Рис. 10.4. Изинговы спины, введенные
на рис. 10.3. Сплошные и штриховые
линии соединяют пары спинов, взаимо-
взаимодействие между которыми описывается
диагональными членами (с коэффициен-
коэффициентами J и /') в выражении A0.3.1).
Исходная решетка разбивается на две
подрешетки, показанные темными и
светлыми кружками.

ГЛАВА 10 213
что в термодинамическом пределе свободная энергия, приходящаяся на
один узел, для данной восьмивершинной модели (f$v) совпадает с со-
соответствующей величиной (/isjng) для обычной модели Изинга на квадрат-
квадратной решетке с взаимодействием между ближайшими соседями:
/8V=/lsing. О0'3'11)
Следовательно, восьмивершинная модель при нулевом внешнем поле
включает в себя как частные случаи и модель типа льда при нулевом
внешнем поле, изложенную в гл. 8 и 9, и модель Изинга, описанную в гл.
7. Вообще ее можно рассматривать как две тождественные модели Изинга,
расположенные по одной на каждой из подрешеток и связанные между со-
собой с помощью взаимодействия четырех спинов, окружающих каждый узел
исходной решетки.
10.4. СООТНОШЕНИЕ ЗВЕЗДА — ТРЕУГОЛЬНИК
В этом разделе я покажу, как можно решить восьмивершинную модель
с помощью обобщения метода, изложенного в разд. 9.6 — 9.8; данный спо-
способ был предложен в работах [22, 25].
Фактически можно также обобщить подходящим образом [27] метод
Бете (разд. 8.3 и 8.4), но это приводит к очень громоздким выражениям. И
хотя можно получить выражения для собственных значений и собственных
функций, извлечь из них пользу не удается.
Чтобы получить результаты в виде, аналогичном результатам, получен-
полученным в разд. 9.6 — 9.8, необходимо использовать эллиптические функции. Я
введу их на раннем этапе, хотя Кумар [153] показал, что данную процедуру
можно отложить по крайней мере до разд. 10.7.
Попытаемся снова удовлетворить соотношению «звезда — треуголь-
треугольник» (9.6.8), но теперь w(/a, a \ C, v) задается выражениями A0.2.3), а не
(9.6.2). В связи с этим вместо трех уравнений (9.6.12) нужно использовать
шесть уравнений
ас'а" + da'd" = Ъс'Ъ" + са'с\
ad'b" + db'c" = bd'a" + cb'd'\ A0A1)
aa'd" + dc'a" = bb'd" + cd'a",
da'a" + ac'd" = db'b" + ad'd'.
Эти уравнения однородны и линейны относительно а", Ь", с", d".
Детерминант, построенный из коэффициентов первого, третьего, четверто-
четвертого и шестого уравнений, имеет вид
{cda'b' - abc'd')[(a2 - Ь2)(с'2 - d'2) + (с2 - d2){a'2- b'1)]. A0.4.2)

214 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Чтобы существовало ненулевое решение а", Ь", с", d", детерминант
A0.4.2) должен быть равен нулю.
Цель состоит в том, чтобы построить класс трансфер-матриц (с весами
а', Ь'', с', d'), которые коммутируют с исходной матрицей V (с весами а,
Ь, с, d). Если матрица V сама принадлежит данному классу (это выглядит
желательным, но может оказаться несущественным), то мы хотим, чтобы
детерминант A0.4.2) обращался в нуль, когда а', Ь', с', d' равны со-
соответственно а, Ь, с, d. При этом первый множитель в выражении для
детерминанта обратится в нуль, но второй множитель не будет равен
нулю.
Поэтому и в общем случае мы потребуем, чтобы обращался в нуль
первый множитель в A0.4.2), т. е. чтобы выполнялось равенство
cd c'd'
Vb = -*b- A0A3)
Первое, третье, четвертое и шестое из уравнений A0.4.1) могут быть
разрешены относительно а": Ь": с": d". Используя A0.4.3), из указанных
уравнений с точностью до общего множителя получаем
а" = а{сс' - dd'){b2c'2 - с2а'2Iс,
b" = b{dc' - cd')(a2c'2 - d2at2)ld,
с" = c(bb' - аа'){а2с'2 - d2a'2)la,
d" = d(abf - ba'){b2c'2 - c2a>2)lb . <10A4)
Подставляя данные выражения во второе или в пятое из уравнений
A0.4.1) и используя A0.4.3), получаем
ab a'b'
Введем величины
д = {а2 + Ъ2 - с2 - d2)/2(ab + cd),
A0.4.6)
Г = {ab - cd)l{ab + cd);
величины Д' и Г' определяются аналогично с заменой в A0.4.6) а, Ь, с, d
на а', Ь', с', d'. Тогда равенства A0.4.3) и A0.4.5) эквивалентны равенст-
равенствам
А = А', Г = Г. A0.4.7)
Отсюда следует, что любые две трансфер-матрицы коммутируют
между собой, если им соответствуют одинаковые параметры Д и Г. Кроме
тривиального нормировочного множителя, приведенное условие оставляет

ГЛАВА 10 215
только одну степень свободы в выборе величин а, Ь, с, d. Таким образом,
можно построить нетривиальный класс коммутирующих между собой
трансфер-матриц.
Параметризация с помощью целых функций
Следующий шаг состоит в обобщении результатов разд. 9.7. Необхо-
Необходимо параметризовать а, Ь, с, d с помощью четырех других переменных р,
к, X, v так, чтобы веса at b, с, d были целыми функциями у, а величины Л
и Г не зависели от v (и от нормировочного множителя р).
Исключим сначала d из двух уравнений A0.4.6). При этом получим
2АA + у) аЪ = а2 + Ъ2 - с2 - a2b2y2c~2, A0.4.8)
где
(Ю.4.9)
Уравнение A0.4.8) представляет собой симметричное биквадратное
выражение относительно а/с и Ь/с. При заданном b/с оно является
квадратным уравнением для а/с, дискриминант которого равен
А2A + уJ(ЫсJ - [(ЫсJ - 1][1 - у\ЫсJ]. (Ю.4.Ш)
Квадратичную форму A0.4.10) относительно (b/сI можно записать в
виде
A - у 2Ъ21с2)(\ - к2у2Ъ21с2) , A0.4.11)
где А, у зависят только от Д и у и определяются уравнениями
к2у4 = у2
A0.4.12)
Мы хотим представить b/с как функцию некоторого переменного,
например w, так, чтобы квадратный корень из A0.4.11) был мероморфной
функцией. Как показано в разд. 15.4, это можно сделать, положив
b/с =y~lsniu , A0.4.13)
где sn и — эллиптическая функция Якоби аргумента и и модуля к, а мно-
множитель / в аргументе введен для удобства дальнейших выкладок. При та-
такой записи b/с квадратный корень из выражения A0.4.11) равен an/w dn/w,
так что решение A0.4.8) имеет вид
а ^ у[ДA + у) sn щ + у сп ш dn ш] A0.4.14)
с у2 - у2 sn2 ш
Правая часть A0.4.14) представляет собой мероморфную функцию; ее
можно упростить, если ввести параметр X, определяемый уравнением
/csn/A= - у/у . A0.4.15)

216 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Тогда из выражений A0.4.12) и A0.4.9) следует
y = sm'A, y= -A:sn2/A, A0.4.16)
T=(l + A:sn2/A)/A-A:sn2/A)>
А = - cn/Adn/A/(l - A:sn2/A). A0.4.17)
Используя теорему сложения A5.4.21) для эллиптических функций,
выражение A0.4.14) можно привести к виду
ale = sru(A- w)/sn/A, A0.4.18)
так что из A0.4.9) и A0.4.16) следует
die = -ksniu sni(k-u). A0.4.19)
Функция snw является обобщением тригонометрической функции sinw.
Из A5.1.4) — A5.1.6) следует, что при к = 0 функция snu совпадает с sinw.
Так же как в гл. 9 было удобно использовать гиперболический синус sinhw,
здесь удобно ввести функцию snhw, определяемую выражением
snh и = -i sn iu = i sn(-m). A0.4:20)
Это мероморфная функция w, действительная при действительных значе-
значениях и (и 0 < к < 1).
Из выражений A0.4.13), A0.4.16), A0.4.18), A0.4.19) имеем
а: Ъ :с : d = snh(A - и): snh и : snh A : к snh A snh и snh(A - ju) . A0.4.21)
Из формул A5.1.6) и A0.4.20) следует
snh и = -ik-*H(iu)/Q(iu), A0.4.22)
где тэта-функции Н(и), О(и) — целые функции и. Определим параметр v с
помощью соотношения
и = J(A + v) . A0.4.23)
Подстановка A0.4.22) в A0.4.21), при которой тэта-функции в знаменателях
сокращается, дает
а = -ipe(iA) Н[Ы{Х - v)] 0[i/(A + v)],
b = -ipG(iX) 0[ii(A - v)] ЩЦК + v)),
A0.4.24)
с = -ipH(ik) 0[i/(A - v)] 0[Ji(A + v)],
d - ipH{ik) Н[Ы{к -v)) H[U{k + v)],

ГЛАВА 10 217
где р — некоторый нормировочный множитель. При вещественных пара-
параметрах р, X, v вещественны также веса а, Ь, с, d.
Приведенные выражения завершают обобщение свойств I — III (разд.
9.5): с помощью выражений A0.4.24) веса а, Ь, с, d определяются через
параметры р, к, X, v; из A0.4.17) следует, что Г и Д зависят только.от к и
X.
Фиксируем величины р, к и X и будем рассматривать трансфер-матрицу
К, определенную выражениями (9.6.1) и A0.2.3), как функцию V(y). Тогда
для всех комплексных чисел v, v' получаем
V(v) V(v') = V(v') V(v) . A0.4.25)
Поскольку из A0.4.24) следует, что а, Ь, с, d. — целые функции у, все
элементы матрицы V(v) также являются целыми функциями v.
Если фиксировать X, м, а к устремить к нулю, то snhw — sinhw. Из
выражения A0.4.21) следует, что в этом случае d — 0 (по отношению к а,
Ь, с), и мы возвращаемся к шестивершинной модели, описанной в гл. 8 и 9
(параметры А, X, и, v имеют тот же смысл, что и в настоящей главе). В
частности, выражение A0.4.21) переходит в (9.7.12), а A0.4.17) дает
формулу (9.2.4).
СВЯЗЬ МЕЖДУ ПЕРЕМЕННЫМИ U, и', и"
Уравнения A0.4.1) не изменяются при перестановке переменных без
штрихов и с двумя штрихами. Таким образом, из выражения A0.4.7)
следует
Д = Д' = Д", Г = Г=Р. A0.4.26)
Поэтому веса а', Ь', с', d' и а", Ь", с", d" можно также представить
в виде A0.4.24) с теми же значениями параметров А: и X. Но переменные р,
w, v будут другими; мы обозначим их р', и'', и' и соответственно р", и",
v".
Первое из уравнений A0.4.1) можно представить в виде
с'(аа" - ЬЪ") = а'{ее" - dd"). A0.4.27)
Подставляя выражения A0.4.21) и используя тождество A5.4.23), приведем
уравнение A0.4.27) к виду
sn /(А -и- и") = sn i(A - и). A0.4.28а)
Действуя аналогично, но используя выражение A5.4.24), четвертое из
уравнений A0.4.1) также можно привести к виду A0.4.27). Второе и пятое
уравнения записываются в виде
sn i(uf ~u) = sn(/M") , A0.4.286)
а третье и шестое принимают вид
sn i(u' - и") = sn(/w). A0.4.28b)

218 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Общее решение уравнений A0.4.28) записывается в виде
2пГ , A0.4.29)
где /, /' — полные эллиптические интегралы, определенные в гл. 15, а »,,
п — произвольные целые числа. Но увеличение переменной и' на 4/7 или на
21' не влияет на A0.4.21); поэтому без потери общности можно принять
и' = и + и" . A0.4.30)
Выражение A0.4.30) в точности совпадает с выражением (9.7.13) для
шестивершинной модели, поэтому восьмивершинные операторы Uit опре-
определенные с помощью формул (9.6.9), A0.2.3) и A0.4.22), также удовлетво-
удовлетворяют соотношению звезда — треугольник (9.7.14). т. е.
Ui+l(u) Ui(u + и") Ui+X{u") = и(и") Ui + l(u + и") Ut(u). A0.4.31)
Заметим, что величина и" равна разности и' — и. Я думаю, что данное
обстоятельство тесно связано с преобразованием к разностному ядру,
которое проводится в уравнениях (8.8.2) — (8.8.4) и (8.13.30) — (8.13.38)
при использовании анзаца. Бете. Параметризация с помощью эллипти-
эллиптических функций введена здесь просто вследствие математического удобства.
Но если бы мы с самого начала потребовали, чтобы веса а, Ь, с, d были
некоторыми функциями переменной и (а веса а', Ь', с', d' и а", Ь", с",
d" — теми же функциями и' и и" соответственно), такими, чтобы величи-
величины Д и Г были постоянными, а переменная и" зависела только от разности
и' — w, то неизбежно пришли бы, учитывая соотношение A0.4.1)
звезда — треугольник, к параметризации с помощью эллиптических функ-
функций A0.4.21) точно таким же путем, как в разд. 8.13 мы пришли от выра-
выражений (8.13.31) к выражениям (8.13.67) и (8.13.73).
10.5. МАТРИЦА Q(v)
Прохождение пары векторов через вершину
Попытаемся теперь обобщить результаты разд. 9.8. Первые десять
уравнений обобщаются тривиально (мы считаем, что //Да) имеет треуголь-
треугольный вид, причем элементы, лежащие ниже диагонали, равны нулю). Усло-
Условия «прохождения пары векторов через вершину» (9.8.11) принимают вид
(индекс / заменен на j)
Эти уравнения линейны и однородны относительно величин #7( + ),
gj( — )> gj ( + )> gj¦ ( ~ )• Приравнивая нулю детерминант, составленный из

ГЛАВА 10 219
коэффициентов системы уравнений A0.5.1), и используя выражения A0.4.6)
и A0.4.9), получаем
2ДA + у) rjrj + l = rj + rj+l-y(l + rjrj+l), (Ю 5 2)
где величина г- определяется формулой (9.8.13).
Выражение A0.5.2) является симметричной биквадратной формой отно-
относительно величин г- иг]Ч1, Она содержит веса а, Ь, с, d только в виде
«постоянных» комбинаций А и Г. Биквадратная форма A0.5.2) в точности
совпадает с выражением A0.4.8), в котором веса а, Ь, с заменены на ry- + х,
г- и 7/2 соответственно.
Следовательно, мы можем использовать решение A0.4.21) уравнения
A0.4.8) в качестве решения уравнения A0.5.2). При фиксированному такое
решение, в котором и заменено на /, имеет вид
y"*r>+i = snh(A - t) /snh Я , y~*ry = snh t/snh Я , A0.5.3)
т. е.,используя выражения A0.4.16) и A0.4.20), получаем
ry = k^snht, ry+i = -fc*snh(f - Я). A0.5.4)
Из формул A5.2.5) и A0.4.20) следует, что замена / на 2/7—/ не
изменяет гу-, а г;- + j переходит в —kVl snh (/ -I- X). Таким образом, если
ry = jfc* snh Г, A0.5.5)
то два решения уравнения A0.5.2) имеют вид
ry+i = - ifc*snh(r± А). A0.5.6)
Поскольку A0.5.2) является квадратным уравнением относительно rj + {,
выражение A0.5.6) описывает все решения.
Рассмотрим теперь выражения A0.5.5) и A0.5.6) последовательно для
j = 1 , . . . , N, определяя / для каждого значения j. Поскольку выбор
знака в A0.5.6) можно производить независимо для каждого значения j,
наиболее общее решение для гх , . . . , rN + { имеет вид
rj= (- у к* snh Sj, A0.5.7)
где
. . . + cj/+i) ; A0.5.8)
5 — произвольная постоянная и каждая из величин а принимает значения
± 1. (Величины ох , ... , aN никак не связаны со спинами Изинга,
введенными в разд. 10.3.) Циклическое граничной условие rN + { = гх удов-
удовлетворяется, если N — четное число и выполняется соотношением
ОХ + . . . + oN= 0 A0.5.9)
(Так же как и для шестивершинной модели данное условие может' быть
ослаблено для специальных значений Dim/ + 2гГ)/п параметра X, где т,

220 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
г, п — целые числа. Для таких значений X достаточно, чтобы сумма
ох + . . . + oN была кратна п. Такие случаи часто представляют собой
интерес: например, в модели Изинга (К" = 0) параметр X равен Г /2.)
Очевидно, что решение для гх , ... , rN аналогично решению (9.8.15)
для шестивершинной модели. Если положить г = kVle^ и принять к — 0,
считая число г фиксированным, то выражение A0.5.7) сведется к (9.8.15).
Исключая g'j(+) из первого и третьего уравнений A0.5.1), получим
A0.5.10)
Используя выражения A0.4.21), A0.5.7), A0.5.8) и тождество A5.4.23), со-
соотношение A0.5.10) можно привести к виду
4хТ = (- У*' snh(*/ + aiu) ¦ A0.5.11)
4х
8j\ *)
Взяв отношение первого и второго из уравнений A0.5.1), используя сно-
снова A5.4.23), получим
?|^ = (- Г1к> snh[sj + ау(и + Я)]. (Ю.5.12)
Мы можем еще произвольным образом выбирать величины /?у( + ) и
gj( + ). В гл. 9 получено важное свойство, состоящее в том, что элементы
матрицы Q(v) являются целыми функциями v (или и). Как показано в разд.
9.8, указанное свойство обусловлено тем, что каждая функция gj( + ) и
gj( — ) является целой. Из выражений A0.5.11) и A0.4.22) видно, что рас-
рассматриваемое свойство может быть сохранено и в более общей ситуации
при выборе gj( -I- ) в виде
gj( + ) = e[i(Sj + OjU)] , A0.5.13а)
так как тогда
*/(") = (- У+Чтъ+ «М)\ ¦ (Ю.5.136)
Аналогично с учетом выражений A0.5.7) и A0.4.22) мы можем выбрать
Pj( -I- ) так, что
Pj{ + ) = в(иу), р,{ - ) = ( - У+11Я(Й;) . (Ю.5.14)
Используя формулы A0.4.24), A0.4.23) и A5.4.25), из первого уравнения
A0.5.1) имеем
g/( + ) = ph(X - и) &[is} + iOj(u + Я)], A0.5.15а)
так что из A0.5.12) получаем
gj(-) = p h{X - и)(- )HH[iSj + i<jj(u + Я)], (Ю.5.156)
где функция И(и) определяется формулой

ГЛАВА 10 22\
h(u) = - i 0@) H(iu) 0(ш). A0.5.16)
Теперь матрицы Gy( ± ) содержат ненулевые элементы ctgj( т ) вместо
нулей, как это было в (9.8.4). Детерминанты этих матриц вычисляются с
помощью формул A0.4.24), A0.5.13) и A5.4.25) или A5.4.26) и имеют вид
det Gj( + ) = p2h(u) h{X - и) @[isj + щ(и + Я)] Q[isj + i(jj(u - Я)],
det Gj(-) = - p2h(u)h{X - u)H[isj + ioj(u + Я)]H[is} + ioj(u - Я)].
A0.5.17)
Величины g'j (а), входящие в (9.8.6), вычисляются так же, как в гл. 9, с
помощью взятия детерминантов в (9.8.5). Детерминанты матриц Р, и
Pj + j можно снова не учитывать, поскольку их вклад в gj (а) сокращается в
выражении (9.8.7) (что эквивалентно требованию det Pi = 1). Используя
A0.5.15) и A0.5.17), для функций g'j'(+) и ?,-(-) получаем выражения
A0.5.18)
g]( -) = ph(u) (- yiH[isj + ioj(u - A)].
ВЕКТОРЫ-СТОЛБЦЫ y(v)
Элементы г^-мерного вектора у определены формулой (9.8.2), откуда
видно, что у представляет собой прямое произведение двумерных векторов
У =g\®g2® • • >®gN, A0.5.19)
где
8)=\gj(-))> A0-5-20)
т. е. из выражений A0.4.23) и A0.5.13) получаем
Как видно из сопоставления выражений (9.8.1) и (9.8.7), вектору {у")
также определяется формулой A0.5.19), в которой каждый вектор gj заме-
заменен на gj (g'j). Выражения A0.5.15) и A5.2.5) показывают, что gj можно
получить из величины gy, умножив последнюю на ph(\ - и) и увеличив и
на X', где
A'=A-2i7. A0.5.22)
Будем рассматривать вектор у как функцию y(v), считая величины к, X, 5
постоянными. Из формулы A0.4.23) следует,, что увеличение и на X'
эквивалентно увеличению v на 2Х', так что справедливо выражение
У' = [ph[\{X - v))}Ny(v + 2А'). A0.5.23а)

222 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Аналогично, используя A0.5.18), получаем
/ = {pA[i(A + v)]}Ny(v - 2А'). A0.5.236)
Удобно ввести функцию
<P(v) = [ph(v/2)]N; A0.5.24)
тогда уравнение (9.8.1) можно записать в виде
V(v) y(v) = ф(Я - v) y(v + 2А') + ф(Х + v) y(v - 2А') . A0.5.25)
Полученное уравнение представляет собой обобщение уравнения (9.8.24) на
случай восьмивершинной модели. Существует много способов выбора y(v),
соответствующих различным значениям величин s, ох , . . . , oN> входящих
в A0.5.8) и удовлетворяющих условию A0.5.9). Обозначим через QR(v)
матрицу 2N х 2N\ столбцы которой являются линейными комбинациями с
не зависящими от v коэффициентами таких векторов y(v). Тогда из выра-
выражения A0.5.25) следует
V(v) QR(v) = ф(к - v) QR(v + 2А') + 0(А + v) QR(v - 2к'). A0.5.26)
Векторы-ряды yT(-v) и матрица Ql(v)
Уравнения (9.8.26) — (9.8.29) непосредственно обобщаются на случай
восьмивершинной модели; единственная модификация состоит в том, что в
выражении (9.8.29) величину г необходимо заменить на "s. Пусть Sj
определяются формулой A0.5.8), в которой s, ох , . . . , oJ¦, _ х заменены на
5', а,' , . . . , o'j _ ,. Используя A0.5.19), A0.5.21) и тождество A5.4.27),
находим
N
yT{-u\s\ o')y(v\s, о) = П tF[Sj-s'j + U(oj- о)) + h(v<Jj+ uo'j)] х
7 = 1
х G[Sj + sj + Що, + о)) + \{voj - uo'})] , A0.5.27)
где
F(u) = - Н[Ы(Г + и)] Н[Ы(Г ~ и)] , A0.5.28)
Мы можем теперь, используя индуктивное рассуждение, аналогичное
тому, которое следует за формулой (9.8.31), показать, что правая часть
выражения A0.5.27) является симметричной функцией и и v. (Нужны
только выражения A0.5.27) и A0.5.8); определения A0.5.28) здесь не сущес-
существенны. Необходимо представить A0.5.27) в виде двух сомножителей, один
из которых содержит только функции F, а другой — только функции G.

ГЛАВА 10 223
Индукция применяется к каждому сомножителю; сначала удобно рассмот-
рассмотреть случай Gjs — Oj для F-множителя и ау = — о- для G-множителя.)
Таким образом, соотношение (9.8.33) также обобщается на
восьмивершинную модель, т. е. справедливо соотношение
Ql(u) Qr(v) = QL(v) Qdu) , A0.5.29)
где
Ql(v) = Qtr(-v). (Ю.5.30)
Несингулярная матрица Qr(v)
Каждый вектор y(v) определяется выражениями A0.5.19), A0.5.21),
A0.5.8) и A0.5.9). Существует много таких векторов, поскольку s может
быть любым комплексным числом, а ох , . . . , oN — любым набором
чисел ± 1, удовлетворяющим условию A0.5.9). Мы утверждаем, что набор
всех таких векторов покрывает все 2^-мерное пространство (возможно, за
исключением ситуаций, отвечающих некоторым особым значениям и).
Как и в гл. 9, я не могу дать полного доказательства данного'утверж-
данного'утверждения, хотя оно почти наверняка выполняется (оно справедливо для N - 2
и N = 4).
Приведенное утверждение не выполняется только в том случае, если
детерминанты всех возможных матриц QR(v) тождественно равны нулю
при всех к, X, v. Если эти детерминанты тождественно равны нулю, то они
равны нулю и при к — 0, что соответствует шестивершинной модели. Но
мы знаем, что в последнем случае собственные значения трансфер-
матрицы правильно определяются из предположения о несингулярности
QR(v) и что данное предположение может быть строго доказано.
С учетом сказанного выше предположим, что матрица QR(v) несин-
несингулярна при некотором значении vQ. Если определить матрицу Q(v) по фор-
формуле (9.8.38), т. е. положить
то отсюда следуют соотношения (9.8.39) — (9.8.42); в частности, при всех
комплексных числах v и и справедливы соотношения
V(v)Q(v) = Q(v)V(v)
= ф(к - v) Q(v + 2А') + ф{к + v) Q(v - 2А'), U '
Q(u)Q(v)=Q(v)Q(u), A0.5.33)
Коммутационные соотношения, включающие матрицы
S и R
Как следует из выражений A5.2.3а) и A5.2.4), тэта-функции 9(w) и Щи)
удовлетворяют соотношениям
@{и + 21) = 0(и), Щи + 21) = -Щи). A0.5.34)

224 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Таким образом, увеличение v в выражении A0.5.21) на 4/7 приводит к
изменению знака функции Н.
Определим диагональный оператор S по формуле (9.8.43). Диа-
Диагональные элементы такого оператора равны + 1 (—1) для ряда с четным
(нечетным) числом направленных вниз стрелок. Из выражений A0.5.19) и
A0.5.21) следует, что умножение вектора у слева на 5 эквивалентно
изменению знака у всех функций //, поэтому справедливо выражение
Sy(v) =y(v +4*7). A0.5.35)
Данное выражение является обобщением на случай восьмивершинной мо-
модели формулы (9.8.44). Мржно сразу написать обобщения уравнений
(9.8.45) — (9.8.47) (просто заменить тг на 21). В частности, получаем
S Q(v) = Q(v) S = Q(v+ Ail) , A0.5.36a)
SV(v) = V(v)S. A0.5.366)
Из выражений A5.2.36) и A5.2.4) следует, что тэта-функции Щи) и 9(м)
удовлетворяют соотношениям
0(ы + //') - iq'k exp(-hmull) Щи),
Щи + i/') - iqT* ехр(-«лм//) @(и). (Ю.5.37)
Определим 2N x 27У-матрицу R следующим образом:
/О 1\ /0 1\ /0 1\
R=[ ® ®...® . A0.5.38)
VI 0/ VI 0/ VI О/
(Умножение на /? приводит к обращению всех стрелок.) Из выражений
A0.5.19) и A0.5.21) следует
y(v + 2/') = 0-шехр(*л 2 M-+ i(A + u)]//]ftSy(i;). A0.5.39)
Из формул A0.5.8) и A0.5.9) поручаем
N
2 SjOj = Я 2 oi-ay- =
A0.5.40)
откуда следует
y(i; + 2Г) = q'm exp(Njzv/4I) RSy(v). A0.5,41)
Данное соотношение не зависит от 5 и ох , . . . , oN, поэтому оно удов-
удовлетворяется при подстановке любых столбцов матрицы QR(v). Используя
также формулу A0.5.30), легко проверить, что

ГЛАВА 10 225
QR(v + 2/') = q'm exp(Nxv/4I) RS QR(v),
A0.5.42)
QL(v + 2/') - ?-m ехр(Д^л-у/47) QL(v) RS ,
поэтому с учетом (9.8.38) и (9.8.39) получаем
RS Q(v) = Q(v) RS = qm exp(-Njw/4I) Q(v + 2/'). A0.5.43a)
Как видно из выражений A0.2.4), функция w(jn a \ C, v) не изменяется при
замене знаков величин /а, а, /3, v. Из формул (9.6.1) и A0.5.38) следует
RV(v) = 1/(у)Л. A0.5.436)
Таким образом, матрицы Q(f), Q(u), K(i>), К(м), /?, 5 коммутируют при
всех комплексных числах и и v.
Выражения (9.6.1), A0.2.3) и A0.4.24) показывают, что все элементы
матрицы V(v) являются целыми функциями. То же справедливо и для
элементов матрицы Q(v), как это следует из A0.5.19) и A0.5.21).
Этим завершается обобщение на восьмивершинную модель приведен-
приведенных в разд. 9.5 свойств I — VI шестивершинной модели. Изложенный
выше вывод проведен в тесной связи с выводом свойств шестивершин-
шестивершинной модели в разд. 9.6 — 9.8.
10.6. УРАВНЕНИЯ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
МАТРИЦЫ V(v)
Важнейшими результатами двух предыдущих разделов являются выра-
выражения A0.4.25), A0.5.24), A0.5.32), A0.5.33), A0.5.36) и A0.5.43), а также
выяснение того факта, что все элементы матриц V(v) и Q(v) —
целые функции.
Теперь мы обобщим условие «достаточности», приведенное в разд. 9.5.
Поскольку все матрицы коммутируют между собой, существует матрица Р
(не зависящая от v)> такая, что входящие в (9.5.1) матрицы V^(v) и Q^(v)
диагональны. Выражения A0.5.23) приводят к матричному уравнению
(9.4.3). Пусть A(v) — некоторое собственное значение матрицы V(v), a
q(v) — соответствующее собственное значение матрицы Q(v). (Функцию
q(v) не следует путать с параметром Якоби q эллиптических функций.)
Тогда соответствующий элемент матричного уравнения (9.4.3) представ-
представляет собой скалярное уравнение (9.3.6), т. е. имеет вид
A(v) q{v) = ф(к - v) q(v + 2А') + 0(А + v) q(v - 2A') , (Ю.6.1)
но теперь функция ф(и) определена выражением A0.5.24), а X' — формулой
A0.5.22).
Поскольку все элементы матриц V(v), Q(v) — целые функции, собст-
собственные значения A(v) и q(v) — также целые функции. Пусть г — (±1) —
собственное значение матрицы /?, соответствующее величинам A(v) и q(v),
а 5 = (± 1) — собственное значение оператора S. Тогда из A0.5.36а)

226 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
и A0.5.43а) следует
q(v + 4il) = s q(v) ,
A0.6.2)
q(v + 2/') = rsq'm ехр(Мш/4/) q(v).
Интегрируя q'(v)/q(v) по некоторому прямоугольнику периодичности с
шириной 71' и высотой 4/ и применяя интегральную формулу Коши
A5.3.4), легко найти, что функция q(v) имеет в таком прямоугольнике 7V/2
нулей. Положим
п = MI2 A0.6.3)
и обозначим через v{ , . . . , vn указанные выше нули. Рассмотрим функцию
A0.6.4)
где И(и) определено выражением A0.5.16). Из формул A0.6.2), A5.2.3) и
A5.2.4) получаем
f(v + 2/') = (-)-rs expMu, + . .. + vn)/2I]f(v). U°'6'5)
Как видно из определения A0.6.4), функция f(v) является целой и не
равной нулю функцией. Тогда из A0.6.5) следует, что /' (v)/f(v) — целая
двоякопериодическая функция; согласно теореме 15а, она равна постоян-
постоянной. Поэтому функция f(v) имеет вид
f(v) = constant x exp(ri;). A0.6.6)
Подставляя A0.6.6) в A0.6.5), находим
т= яE - 1 + 2п + 4/?')/8/, A0.6.7а)
vi + . . .+vn = h(s-l+2n)I' +i(rs-l+2n)I + 2pT + 4ipl, A0.6.76)
где р, р' — целые числа.
Комбинируя соотношения A0.6.4) и A0.6.6), с точностью до мно-
множителя, который сокращается в последующих вычислениях, получаем
следующее выражение для q(v):
(^) <10-6-8>
Полученное выражение является восьмивершинным обобщением форму-
формулы (9.3.5). Функция h(u) имеет простой нуль при и = 0; поэтому, по-
положив v — Vj9 получаем, что левая часть выражения A0.6.1) обращается в
нуль. Отсюда следует

ГЛАВА 10 _227
или, учитывая A0.5.24) и A0.6.8),
= "ехр(гА
при у = 1 , . . . , п.
Уравнение A0.6.10) является восьмивершинным обобщением уравнений
(8.4.12). Они определяют величины v{ , . . . , vn. После того как найдены
нули fj, ... ,vn> функция q(v) задается выражением A0.6.8), a A(v) —
выражением A0.6.1). Существует много решений уравнений A0.6.10),
соответствующих разным собственным значениям.
Если все нули v{ , . . . , vn различны, то из уравнений A0.6.10) видно,
что отношение правой части A0.6.1) к q(v) является целой функцией; по-
поэтому A(v) — целая функция, что и требовалось. Но если какие-нибудь две
величины из v{ , . . . , vn равны между собой, то выполнение A0.6.10) не
является достаточным условием того, чтобы функция A(v) была целой.
Уравнения A0.6.10) следует дополнить полученными дифференцированием
по v выражения A0.6.1) уравнениями, в которых v заменено значением vj,
соответствующим кратному нулю. Поэтому решения уравнений A0.6.10) в
общем случае при наличии кратных нулей не пригодны. (Заметим, что в гл.
8 мы также отбросили подобные решения, хотя там это было сделано из-
за того, что им соответствовал нулевой собственный вектор).
10.7. МАКСИМАЛЬНОЕ СОБСТВЕННОЕ ЗНАЧЕНИЕ:
ОПРЕДЕЛЕНИЕ ВЕЛИЧИН v{ , . . . , vn
Основная область
Рассмотрим случай, когда параметры к, \, v, p удовлетворяют усло-
условиям
0<fc<l, 0<А</\ |у|<А, р>0, A0.7.1а)
так что, согласно A0.4.23),
0<м<Я. A0.7.16)
Из выражений A0.4.21) и A0.4.24) следует, что все веса а, ЬУ с, d поло-
положительны. Поэтому ограничения A0.7.1а) физически допустимы.
Из выражений A0.4.17) и A5.4.4) следует
1 - А2 = A - кJ sn2 iA/(l - к sn2 /ЯJ , (Ю.7.2)
и, поскольку функция sn2 /X действительна и отрицательна, справедливо
неравенство д<^ (Ш 7 3)
Из приведенного неравенства с учетом формулы A0.4.6) получаем
(a + bJ<(c-dJ. A0.7.4)

228 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Определяемое выражением A0.4.21) отношение d/c равно
к snh и snh(X - и); данная функция имеет максимум при и = Х/2. Как сле-
следует из A5.4.24), этот максимум должен быть меньше единицы, по-
поэтому d < с. Извлекая положительный квадратный корень из A0.7.4) и за-
замечая, что правые части всех уравнений (ГО.4.24) положительны, получаем
c>a + b + d, a>0, b>0, d>0. A0.7.5)
Следовательно, ограничения A0.7.1) приводят к неравенствам A0.7.5).
Наоборот, если веса а, Ь, с, d удовлетворяют неравенствам A0.7.5), то
существуют действительные числа к, X, v, p, м, удовлетворяющие
уравнениям A0.4.21), A0.4.24) и A0.7.1).
Неравенства A0.7.5) определяют область в пространстве (а, Ь, с, d).
В случае восьмивершинной модели конфигурации, отвечающие данной
области, аналогичны конфигурациям шестивершинной модели, принад-
принадлежащим области с антисегнетоэлектрическим упорядочением (область
IV на рис. 8.5). Наибольшим больцмановским весом является вес с, по-
поэтому в основном состоянии стрелки на решетке могут располагаться в двух
возможных конфигурациях. Первая конфигурация показана на рис. 8.3,
вторая получается из первой обращением всех стрелок. Используя обоз-
обозначения шестивершинной модели, мы автоматически приходим к пони-
пониманию области, определяемой неравенствами A0.7.5), как архитипической
области для восьмивершинной модели.
Выделение данной области имеет некоторое неудобство, связанное с
рассмотрением восьмивершинной модели как обобщения модели Изинга
(разд. 10.3). В последнем случае при больших параметрах У и У
естественно сосредоточиться на области с ферромагнитным упорядоче-
упорядочением. В таком случае наибольшим больцмановским весом будет вес а, а не
с. К счастью, данный случай можно свести с помощью соотношений сим-
симметрии A0.2.14) к ситуации, описываемой неравенствами A0.7.5).
В действительности, как показано в разд. 10.11, любой набор весов а, Ь>
с, d можно отобразить в область A0.7.5), используя соотношения сим-
симметрии A0.2.11) — A0.2.17). Указанные величины можно отобразить в
другие области, например в такую, где а > b + с + d. Но ниже я
выделяю область A0.7.5) с положительными весами а, Ь, с, d и называю ее
основной областью.
Низкотемпературный предел
Уравнения A0.6.10) достаточно сложны и при конечных п в общем виде
не решены. Мне кажется полезным рассмотреть сначала простой пре-
предельный случай, который позволит получить представление о поведе-
поведении при больших п.
Пусть е5 < е,, e3f «7 и температура Т мала. Тогда из D0.1.2) и A0.2.1)
получаем неравенства
Oa,b,d, A0.7.6)

ГЛАВА 10 229
так что веса, несомненно, лежат в основной области. Отсюда следует, что
к < 1, а величины /', X, v велики и одинаковы по порядку величины. Из
A5.1.4) видно, что параметр q мал, поэтому из A5.1.5) получаем асимпто-
асимптотики
Э(ш) =* 1, #(ш) ~ iq{ ехр(лм/2/), A0.7.7)
если 0 < Re(w//') < 1. Следовательно, выражение A0.4.24) для веса с
принимает вид , .
c=*pq*x~l, A0.7.8)
где
q = ехр(-л/7/), х = ехр(-яА/2/). A0.7.9;
Предположим, что все величины v{ , . . . , vn порядка единицы (или
меньше). Тогда в рассматриваемом пределе выражение A0.6.10) с учетом
A0.6.3) приводится к виду
zf + (-)" ехр(-4гА') (Zl. . . zn)~l = 0 , A0.7.10)
j = 1 , • • . , п.
Левая часть уравнения A0.7.10) имеет вид полинома степени п отно-
относительно Zj, поэтому уравнение имеет п корней. Мы требуем, чтобы вели-
величины fj , ... , vn были различны, поэтому Z\ , ... , zn должны быть
разными корнями уравнения A0.7.10). Отсюда следует, что для всех
комплексных чисел z справедливо соотношение
zn + (-1)яехр(-4тА') (zb . . zn)~l - f[(z - zj). A0.7.12)
/=i
Положив z = 0 и извлекая квадратный корень, получаем
zi. ..zn = ±ехр(-2гЯ'), A0.7.13)
в то время как из выражений A0.6.76) и A0.7.11) находим
zi...zn = rs(-)n exp(-2r/'). A0.7.14)
Из формулы A0.6.7а) следует, что величина т вещественна. Параметр
X' задается выражением A0.5.22), где X Ф Г. Учитывая, что г= ±1 и
5 = ± 1, получаем
т=0, s =(-)", Zl...zn = r. A0.7.15)
Асимптотическая формула A0.7.7) становится непригодной, если дей -
ствительная часть Re(w) оказывается отрицательной или обращается в
нуль. В таком случае нужно использовать выражения
0(ш) =* 1, H(iu) ~ 2i q{ sinh(^/2/) A0.7.16)
при IRe(u//')l < 1. Тогда из выражений A0.6.8) и A0.5.16) при

230 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
lRe(y//')l < 2 получаем
п
Ф) = П 2?' &Щф - vj)/4I] A0.7.17)
/=i
Полагая
z = ехр(-яу/2/), A0.7.18)
выражение для q(v) можно записать в виде
q{v) = {-Yq^z-^iz,. . . г„)-»П(г -zj). (Ю.7.19)
/ = i
Перепишем его еще раз, используя A0.7.12) и A0.7.13):
q(v) = q^z-^iz,. . . 2я)-»{(-2)" + (z,. . . zn)-'} . A0.7.20)
Определим теперь асимптотический вид уравнения A0.6.1) в низкотем-
низкотемпературном пределе. Если lRe(i;)l < min(X, 2Г — 2Х), то мы получим, ис-
используя выражения A0.5.24), A0.6.8), A0.5.22), A0.5.16) и A0.7.7), следую-
следующее уравнение:
A(v)q(v) = pNqmx-NqnlAz-nl2{zx. . . zn)\Rx + R2) , A0.7.21)
где
/?i = (-zy\ R2 = (zi...znyl. A0.7.22)
Первое слагаемое в правой части A0.6.1) дает член К{ в уравнении
A0.7.21), а второе слагаемое — член /?2. Но, как видно из A0.7.20),
функция q(v) также содержит множитель R{ + /?2, поэтому в уравнении
A0.7.21) он сокращается. При этом уравнение A0.7.21) принимает вид
...zn, A0.7.23)
а в пределе низких температур с учетом A0.7.8) и A0.7.15) получаем
/i(v) = rcN, A0.7.24)
Выражение A0.7.24) действительно определяет правильное максималь-
максимальное собственное значение трансфер-матрицы в пределе низких температур.
Фактически имеется два собственных значения, соответствующие случаям
г = ±\. Для г = +1 (-1) соответствующий собственный вектор сим-
симметричен (антисимметричен) относительно обращения всех стрелок, а
собственное значение положительно (отрицательно). Указанные два
собственных значения асимптотически вырождены в том смысле, что раз-
разность между их модулями экспоненциально убывает при увеличении N. В
низкотемпературном пределе мы определим величины v{ , . . . , vn для
этих собственных значений. Из выражений A0.7.15), A0.7.10) и A0.7.11)
получаем
2il[2ji( l)]/ / = 1,...,л. A0.7.25)

ГЛАВА 10 232
В разд. 8.8 и 8.9 мы отметили, что свободная энергия аналитична при w
(или и) = 0, хотя выкладки при положительных w отличаются от выкла-
выкладок при отрицательных w. С помощью приведенных выше уравнений легко
видеть, как это происходит. Если v > 0, в пределе п — оо величина R{ экс-
экспоненциально мала по сравнению с /?2, так что в правой части уравнения
A0.6.1) преобладает второе слагаемое. Если v < 0, то имеет место
обратная ситуация: преобладает первое слагаемое. Таким образом, термо-
термодинамический предел уравнения A0.6.1) или аналогично (8.4.4) для случаев
v > 0 и v< 0 необходимо рассматривать отдельно.
Но поскольку множитель R{ + R2 содержится также в q(v), он
сокращается в уравнении A0.7.21), т. е. в A0.6.1); поэтому конечный
результат не зависит от того, какая из величин R{ или R2 больше. Конеч-
Конечно, мы рассмотрели только низкотемпературный предел, но проведенное
рассуждение дает обобщение на случай произвольной температуры.
10.8. ВЫЧИСЛЕНИЕ СВОБОДНОЙ ЭНЕРГИИ
Вернемся к случаю ненулевых температур, т. е. к случаю конечных
/', X, v, и посмотрим, как можно решить уравнения A0.6.10) в пределе
больших п.
Эти уравнения являются восьмивершинным обобщением уравнений
(8.9.12), причем в них у. = —/а-. В разд. 8.9 показано, что величины
ах , ... , ап действительны и лежат в интервале (-тг, тг), т.е. на
полупериоде функции sinh /a/2, входящей в соответствующие уравнения. В
случае восьмивершинной модели такой функцией является h(ia/2), и со-
соответствующий интервал равен (—2/, 21). Мы видели, что в низко-
низкотемпературном пределе (формула A0.7.25)) величины ivx , . . . , ivn дей-
действительно лежат в данном интервале.
Очевидный способ решения уравнений A0.6.10) состоит, следовательно,
в том, чтобы, предполагая равномерное распределение величин vx , . . . , vn
на интервале (-2/7, 2/7) при п — оо, получить, как в разд. 8.7 — 8.9, из
A0.6.10) линейное интегральное уравнение для функции распределения
величин v{ , . .. , vn.
Здесь я использую другой способ, который представляет собой усо-
усовершенствованный вариант метода, примененного в работе [25], и имеет
то преимущество, что в нем различаются два наибольших по модулю
собственных значения. Такой метод можно применить для вычисления
поверхностного натяжения [28].
Предположения
Отметим сначала, что при выбранных значениях чисел г, s, р, р'
выражения A0.6.7) и A0.7.11) определяют величины т и zx , . . . , zn.
Предполагая, что в основной области не происходит резких изменений,
этим числам следует придать их предельные значения, отвечающие
низкой плотности. Следовательно, равенства A0.7.15) должны выпол-
выполняться во всей основной области.

232 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Введем величину
p(v) = №у)д(у + 2Х) (ю gл)
<№+v)q{2k'y
Величина p(v) равна отношению первого слагаемого в правой части A0.6.1;
ко второму. В низкотемпературном пределе она равна Ry/R2, где R{ и R2
определяются формулой A0.7.22), поэтому справедлива асимптотика
р(и) -г(-)пехр(-пли/21). A0.8.2)
При Re(v) > 0 правая часть A0.8.2) экспоненциально убывает, когда п^ оо;
при Ke(v) < 0 она экспоненциально растет.
Кроме того, как следует из выражения A0.7.23), в низкотемпературном
пределе собственное значение A(v) постоянно (при конечных v). Поэтому
кажутся разумными следующие предположения (для всей основной
области).
I. Существует некоторое положительное число 5, такое, что функция
ln[l + p(v)] аналитична при 0 < Re(y) < б, а функция ln[l -h \/p(v)]
аналитична при 0 > Re(v) > -5.
И. Величины v{ , . . . , vn чисто мнимые.
III. Функция A(v) является аналитической, не обращающейся в нуль
функцией в вертикальной полосе, содержащей мнимую ось.
Факторизация Винера — Хопфа
Я покажу теперь, что уравнение A0.6.1) имеет решение, удовлетво-
удовлетворяющее предположениям I — III. Используем сначала предположение I для
проведения факторизации Винера — Хопфа [181, 188] функции 1 + p(v);
определим функции X+(v) и X_(v) следующим образом:
211 lnfl + p(v')]
lnX_{v) = __L Г г1"[1+Р;;;)/]1 Ло', Re(*)
где 0 < а < а' < 5. Сложим данные уравнения; используя тот факт, что
p(v) — периодическая функция с периодом 4тг/, правую часть полученной
суммы можно записать в виде интеграла по прямоугольнику а' — 2/7,
а' + 2/7, а + 2/7, а — 2/7. Из теоремы Коши о вычетах следует
X+(v) X-(v) = 1 + p(v). A0.8.4)
Данное выражение можно использовать для определения функции Х+.(и)
npta Re(v) ^ а и функции Х_ (и) при Re(v) ^ а'.
Уравнение A0.6.1) теперь можно записать в виде
и) q(v - 2k')X+(v) X-{v)/q(v). (Ю.8.5)

ГЛАВА 10 ^ 233
Из определений A0.8.3) следует, что Х+ (и) — аналитическая функция,
не обращающаяся в нуль' (АФНН) при Re(f) > 0, а функция X_ (v) —
АФНН при Кф) < <5. Другие члены в правой части A0.8.5) можно
представить в виде произведений аналитических функций, обладаю-
обладающих аналогичными свойствами. Чтобы сделать это, заметим, что из
A0.5.16) и A5 1.5) следует
00
h{u) = -h(-u) = уехр(яи/2/) Ц A ~ ?техр(-яи//)}
т=0 A0.8.6)
х{1-<7техр[-л(/' -«)
где
оо
У=Ч*&@)ЦA-д2тJ. (Ю.8.7)
т = \
Подстановка выражения A0.8.6) для h(u) в A0.5.24) и A0.6.8) при т = 0
дает
ф(и) = pNf exp{Nnvl4I)A{v) ЛBГ - v), A0.8.8)
q(v) = уп ехр[фи - vi - ... - vn)/4I]F(v) G(v - 2/') A0.8.9a)
= (- y)n exp[tt(ui + . . . + vn - nv)/4I]F(v + 2/') G{v), A0.8.96)
где введены обозначения
00
A(v) "IIU- ?техр(-яи/2/)]л', A0.8.10)
т = 0
р(») = П П U - Чт*М-ф - Vj)/2I}], A0.8.11a)
/ = 1 т=0
п оо
G(v) = П П [1 - Ят ехр{я(и - Vj)/2I}]. A0.8.116)
/ = 1 т=0
Подчеркнем, что функция A(v) известна, а величины v{ , . . . , vn и,
следовательно, функции F(f), G(f) не известны. Цель последующих выкла-
выкладок состоит в получении полезных выражений для F(v) и G(v).
Подставим выражения A0.8.10), A0.8.11) в A0.8.5), используя
выражения A0.8.9а) для a(v) и A0.8.96) для q(v — 2Х'). В результате, учи-
учитывая A0.5.22), A0.7.9) и A0.7.15), получим
Л(у) = rfxNfx-NL+{v) L-(v), A0.8.12)
где
L+(y) = Л (Я + v) F(v + 2Г - 2А) X^u)/F{u),
L_(y) = ЛB/' - А - у) G(y - 2А) X-(v)/G(v - 2/'). О0-8-1^

234 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Введем обозначение
<5' = min(<5,2A,2/'-A); A0.8.14)
используя выражения A0.4.1а), A0.8.10), A0.8.11) и предположение II,
легко обнаружить из A0.8.13), что функция L + (v) аналитична и не имеет
нулей при Re(f) > 0, a L_(v) аналитична и не имеет нулей при Re(f) < <5'.
Из последнего свойства, выражения A0.8.12) и предположения III следует,
что L + (и) аналитична и не имеет нулей- в полупространстве Re(v) > 0.
Окончательно получаем следующие свойства:
L+(y) АФИН приRe(y)^0,
' V } A0.8.15)
L-(v) АФНН при Re(u) < д'.
Повторим теперь проделанные выкладки, но начнем их с факторизации
Винера — Хопфа для функции 1 -I- l/p(v):
. __ . ч ±1 f-«+2
ln v±(») = 77
v -
Vp(v')] л ,
idt/> (Ю.8.16)
1
где верхний знак выбирается, если Re(f) > — а, а нижний знак, если
Re(f) < - а, причем 0 < а < д. Получаем соотношение
У+(у) Y.(v) = 1 + [Vp(v)], A0.8.17)
Функция Y+ (и) аналитична и не имеет нулей при Re(f) > - 5, а функция
У_(v) имеет эти свойства при Re(f) < 0. Уравнение A0.6.1) принимает вид
Л(у) = 0(А - v) q(v + 2А') Y+(u) Y-(v)/q(v) . A0.8.18)
Используя выражения A0.8.8), A0.8.9а), \l0.8.96) для ф(\ - v), q(v + 2Х')
и q(v)y получаем отсюда
Л(у) = rpAryiVJC"A'M+(i;) М-(у) , A0.8.19)
где
Af+(у) = ЛB/' - А + у) F(y + 2А) Y+(v)/F(v + 2/'),
Af-(y) = Л(А - v) G(v - 2Г + 2A) y_(y)/G(i7) . (Ю.8.20)
Уравнения для функций F(v), G(v), p(v)
Из выражений A0.8.20) следует, что функция M+(v) аналитична и не
имеет нулей при Re(u) > -5', a M_(v) обладает теми же свойствами в
области Re(f) < 0. С учетом выражения A0.8.19) и свойства III отсюда
следует
М+(у)АФНН при Re(u) > - <5\
М_(|;)АФННприЯе(о)«0. A0.S.21)
Сравнение выражений A0.8.12) и A0.8.19) показывает, что
L+(v)/M+(v) = M-{v)IL-{v). A0.8.22)

ГЛАВА 10 235
Левая часть данного уравнения является аналитической функцией, не имею-
имеющей нулей при Re(v) ^ 0. Она периодична с периодом 4/7 и стремится к
единице при Re(f) — оо (последнее свойство следует из определения).
Правая часть уравнения аналитична и не имеет нулей при Re(f) < 0,
периодична с периодом 4/7 и стремится к постоянной, когда Re(f) —
— -оо. Следовательно, обе части уравнения являются целыми, не имею-
имеющими нулей ограниченными функциями. По теореме Лиувилля они посто-
постоянны. Эта постоянная должна быть равна единице, поэтому
Af+(i7) = L+(y), Af-(i7)=L-(y). A0.8.23)
С помощью выражений A0.8.13) и A0.8.20) первое из уравнений
A0.8.23) можно записать в виде
5+(у) = S+(v + 2/' - 2А) X+(v)/Y+(u) , A0.8.24)
где
S+(v) = F(v) F(v + 2K)IA{v + A) . A0.8.25)
Будем считать, что функции X±(v), Y±(v) известны. Тогда уравнение
A0.8.24) можно рассматривать как рекуррентное соотношение для S+(v),
решение которого имеет вид
00
S+(v) = П *+[» + 2т(г ~ WY+[v + 2т(Г - А)]. A0.8.26)
Уравнение A0.8.25) теперь можно решить относительно функции F(v), что
дает
= ГГ А[у + Dт + l)k]S+(v + 4тХ)
{V) il>A[v + Dm + 3)А] S+[v + Dm + 2)A] * A°'8'27)
(Бесконечное произведение сходится, поскольку из определений следует,
что все функции X+(v), Y+(v), A(v) экспоненциально стремятся к единице
при Re(f) — оо.)
Аналогично из второго уравнения A0.8.23) следует
5-(у) = S.(v - 21' + 2А) Y.(v)/X-(v) , A0.8.28)
где
S-(v) = G(v) G(v - 2А)/Л(А - v) . (Ю.8.29)
Поскольку G(v) и А(- v) экспоненциально стремятся к единице при
Кф) — -оо, тем же свойством обладают и функции S_(v) и
У_ (v)/X_ (v). Отсюда получаем
S-(v) = 11 Y.[v - 2т(Г - X)]IX-[v - 2т(Г - A)], A0.8.30)
A A[(Am + 1)A - v] S-(v - 4mA)
(U) ii,A[Dm + 3)X-v]S-[v-(.4m + 2)X\' AO-831)

236 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
С помощью выражений A0.8.8) и A0.8.9) определение A0.8.1) функции
p(v) можно записать через A(v), F(v), G(v). Используя A0.8.9а) и A0.8.96)
для q(v + 2к') и q(v — 2\') соответственно, а также формулу A0.7.16),
получаем следующее выражение для p(v):
р(у) = г(-)пехр( - лли/2/) Л(А - v)'A{2I' - А + у) x
х F(v + 2А) G(v + 2А - 2/')/[Л(А + у) х A0.8.32)
х ЛBГ -X-v)F(v + 2V - 2А) G(v - 2A)].
Вычисление p(v) с помощью итераций
Полученные результаты точны даже при конечном п при условии, что
удовлетворяются предположения I — III. Можно применить итерационный
метод решения, в котором в качестве нулевого приближения используется
некоторая начальная функция р(у), удовлетворяющая предположению I.
Метод состоит в следующем: из A0.8.3) и A0.8.16) вычисляем функции
X±(v), Y ±(v), а из A0.8.26) и A0.8.30) — функцию S +(v); находим функции
F(v), G(v) из A0.8.27) и A0.8.31); определяем/?^) из A0.8.32) и повторяем
итерационный цикл.
Если удовлетворяется предположение I, указанная процедура дает функ-
функции F(v) и G(f), которые аналитичны и не имеют нулей в областях
Re(f) > 0 и Re(f) < 0 соответственно. Тогда из выражения A0.8.11)
следует, что величины v} , ... ? vn могут быть только чисто мнимыми;
следовательно, предположение II удовлетворяется. Кроме того, из A0.8.12)
или A0.8.19) видно, что функция A(v) аналитична в области —6' <
< Re(f) < 5', а значит, предположение III также удовлетворяется.
Рассмотрим теперь случай, когда число п велико. Допустим, что с ро-
ростом п функция p(v) экспоненциа1ьно стремится к нулю при 0 < Re(f) < д
и экспоненциально растет при 0> Re(f) > —5. Такое предположение под-
подтверждается формулой A0.8.2). Тогда из A0.8.3) и A0.8.16) следует, что
функции X+(v), X_(f), Y+(v), Y_(v) экспоненциально близки к единице
при условии, что v лежит в областях Re(f) > 0, Re(f) < 5, Re(f) > — 5,
Re(f) < 0 соответственно.
Следовательно, при Re(u) > 0 каждая функция S + (v) в выражении
A0.8.27) экспоненциально близка к единице; npn*Re(f) < 0 то же спра-
справедливо для функций S_(v) в A0.8.31). Из формулы A0.8.32) следует, что
при lRe(t;)l < minBX, 21' - 2\) имеем
Л[Dт + 1)А + у + 2Г] Л[4т + 1)А - у] Л[{4т + 3)А - у + 2Г]
Л[Dт + 3)А + у + 2/'] Л[Dт + 3)А - у] Л[Dт + 1)А - у + 2/']
х A -I- члены, экспоненциально стремящиеся к нулю при п — оо).

ГЛАВА 10 237
Используя определение A0.8.10) функции A(v) вместе с выражением
A0.7.9), получаем
A(u)/A(v + 2/') = [1 - ехр(-яу/2/)]дг. A0.8.34)
Замечательной особенностью выражения A0.8.33) является то, что функция
А (и) входит в него только в виде комбинации A0.8.34), поэтому при
I Re(f)l < minBX, 71' '- 2Х) имеем
. 00.8.35)
где х и z определены формулами A0.7.9) и A0.7.19) и отброшены экспо-
экспоненциально малые поправки.
Следовательно, параметр Якоби q не входит в выражение A0.8.35). С
другой стороны, сравнивая A0.8.34) с A5.4.13), мы видим, что p(v) связана
с эллиптической функцией, параметр Якоби которой равен х2 или л:. Дей-
Действительно, поскольку функция am(w) определена формулой A5.4.13), в ко-
которой параметр q заменен на q2, имеем
p(v) = r(-)nехр[-iNam(/i3,к)], A0.8.36)
где /с — эллиптический модуль, соответствующий параметру Якоби
<?=*, A0.8.37)
а
6/1 = v/BI). A0.8.38)
Модуль функции exp [-/am(/, vt /с)] меньше единицы при 0 <
< Re(v) < 2Х и больше единицы при 0 > Re(v) > -2Х. Кроме того,
exp [-/am(/ vt /с)] является мероморфной функцией v. Следовательно,
предположение I удовлетворяется, если функция p(v) задается выражением
A0.8.36), причем 0 < д < min BХ, 71' — 2Х); удовлетворяются и предполо-
предположения II и III. Справедливо также следующее утверждение: данная функция
p(v) при п — оо экспоненциально стремится к нулю в области
0 < Re(f) < 5 и экспоненциально растет при 0 > Re(f) > —д.
Если подставить выражение A0.8.36) для p(v) в A0.8.3) и A0.8.16) и про-
продолжить итерационную процедуру, то получим экспоненциально малые
поправки к A0.8.36), затем получим поправки к поправкам и т. д. По-
видимому, можно совершенно строго доказать, что такая процедура
сходится к решению уравнения A0.6.1), удовлетворяющему предполо-
предположениям I — III и при больших N имеющему вид A0.8.36).
Отметим, что величины v{ , ... , vn являются нулями функции
1 -I- p(v), лежащими на мнимой оси. Поэтому при больших N величины
vx/I, . . . , vn/I, так же как и p(v), зависят только от л:, но не от q (или z).
Я считаю данное свойство весьма интригующим; у меня нет простого
объяснения, почему так происходит.

238
ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
ФУНКЦИИ р{р), A(v) В ТЕРМОДИНАМИЧЕСКОМ ПРЕДЕЛЕ
Справедливые при больших п формулы A0.8.35) и A0.8.36) определяют
p(v) только при lRe(t;)|< min BX, 21' — 2\). Чтобы найти функцию p(v)
при других значениях у, отметим, что формула A0.8.27) определяет F(v)
для всех и; но лишь при Re(f) > 0 функции 5+ дают множитель, который
экспоненциально стремится к единице при больших п. Таким образом,
формула A0.8.27) «полезна» при Re(f) > 0, так как в этом случае в
ведущем члене разложения при больших п неизвестные функции X+(v),
Y+(v), S+(v) можно заменить на единицу. Аналогично выражение A0.8.31)
для G(v) полезно при Re(f) < 0.
Из второго соотношения периодичности в A0.6.2) следует, что функция
q(v) при любом v пропорциональна функции q(v*)> где 0 < Re(f*) < 21'. С
помощью выражения A0.8.9а) функцию q(v*) можно представить в виде
произведения функций. Такое произведение определяет q(v) через функцию
F(v) только при Re(f) > 0 и через функцию G(v) только при Re(f) < 0.
Проделав это в выражении A0.8.1) и используя A0.8.27) и A0.8.31),
получим следующие выражения, справедливые при больших п:
p(v)=p{0)(v) при |Re(y)|<minBA,2/' - 2А) , A0.8.39а)
p(v) = 1 при 2А < Re(y) < 2/' - 2А , A0.8.396)
p(v) =p@\v)p{0\v - 2/>ри2Г - 2A < Re(y) < 2A
A0.8.39b)
где p°(v) — правая часть выражений A0.8.35) и A0.8.36).
Полученные выражения вместе с условиями периодичности (которые
являются следствиями выражений A0.6.2), A0.5.24) и A0.8.1))
p(v + 4U) = p(v + 2Г) = p(v)
A0.8.40)
определяют функцию/?^) при произвольном значении v. Области примени-
применимости трех формул A0.8.39) показаны на рис. 10.5. Штриховой линией
показана граница области, в которой функция p(v) экспоненциально мала
при больших N. Из сказанного следует, что максимальное значение
21'
Рис. 10.5. Области применимости (а, Ь, с) различных форм уравнения A0.8.39).
Внутри области, ограниченной штриховой линией, функция p(v) экспоненциально
мала при больших п.

ГЛАВА 10 239
параметра д в предположение I равно
<5 = minBA,/'). A0.8.41)
Вычислим теперь L_(v), M+(v) и A(v) по формулам A0.8.13), A0.8.20) и
A0.8.12) соответственно, используя A0.8.23) для замены L+ наМ+. (Такой
путь позволяет получить выражение, которое, очевидно, аналитично и не
имеет нулей в области -6' < Re(v) < 5'.) Пренебрегая экспоненциально
малыми поправками, получаем следующий результат, справедливый при
условии lRe(i;)l < 5:
+ 3) А + у]
X
А[2Г + Dm - 1) Я + у]А[Dт + 3) Я - у]Л[2Г + Dт - 1) Я - у]
А[2Г + Dт + 1) Я + у] Л [Dт + 5) Я - у] Л[2/' + Dт + 1) А - у]
Мы решили функциональное уравнение A0.6.1) относительно, функций
q(v) и Л(у). Это эквивалентно решению данного уравнения относительно
fj , ... , vn. В самом деле, поскольку величины vx , ... , vn — нули
функции 1 + p(v), они могут быть найдены из выражения A0.8.35).
Уравнение A0.6.1) имеет много решений, соответствующих 2N различ-
различным собственным значениям A(v) трансфер-матрицы V(v). Мы получили
точно два таких решения, т. е. два собственных значения: одно с г = + 1
(симметрия относительно обращения всех стрелок), другое с г = — 1
(антисимметрия относительно обращения всех стрелок). Из выражения
A0.8.42) следует, что данные собственные значения равны по модулю и
имеют разные знаки (с точностью до экспоненциально малой поправки при
п — оо).
Мы видели, что в низкотемпературном пределе такие собственные
значения являются максимальными по модулю собственными значениями.
Из теоремы Перрона — Фробениуса [93], которая утверждает, что
матрица с положительными элементами имеет единственное максимальное
собственное значение, следует, что собственные значения A0.8.42)
максимальны по модулю во всей основной области A0.7.1), в которой
больцмановские веса а, Ь, с, d положительны и для которой справедлив
проведенный анализ.
Результат A0.8.42) можно, конечно, аналитически продолжить на
комплексную у-плоскость. Действительно, при I Re(f)l < h выражение
A0.8.42) имеет прежний смысл: A(v) представляет собой собственное значе-
значение, связанное с тем собственным вектором, который максимален в основ-
основной области (собственный вектор не зависит от и). В частности, данное
аналитическое продолжение удовлетворяет соотношению
А(у) ЛBЯ - у) = ф{к + у) ф{Ък - у), A0.8.43)
к которому я вернусь в гл. 13.

240 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Свободная энергия
С учетом выражения A0.8.10) логарифм от ^ правой части A0.8.42)
превращается в двойную сумму членов вида ln(l - qaxbz± !), где а и
Ъ — целые числа. Разложение каждого такого слагаемого в ряд Тейлора по
степеням qaxbz± x позволяет провести суммирование. При этом получаем
Кроме того, из выражений A0.4.24), A0.8.7) и A5.1.5) следует
V 2ат - х2т - Л - qm(xm + х~т) (zm + z~m)
In с = \п(ру/х) + 2, —г.—3Sv •
m = 1 m{l * ) A0.8.45)
Как обычно (уравнения A.7.6) и (8.2.4)), свободная энергия на один узел
/ связана с максимальным собственным значением Лтах соотношением
-f/квТ = lim ЛГ1 in Лтах, A0.8.46)
W-юо
где N — число столбцов решетки.
Из теоремы Перрона — Фробениуса [93] следует, что максимальное
собственное значение реализуется при г = + 1. Таким образом, Лтах равно
значению Л(у), определяемому выражением A0.8.44) с г = +1. Исключая
A(v) и ру/х из трех последних уравнений, получаем
v *"m(*2m- qmJ(xm + *~m -zm-z~m)
w(l - qlm) A + x2m) ' (Ю.8.47)
Используя выражения A0.4.24), A0.8.7) и A5.4.27), можно также
установить, что справедливо соотношение
^л х + а х~ — а (хт + х~т — z — z~m\
Не + d) = Hpy/x) - 2 -—q— qm(; * —z-^
m = l YYi\ I — Q )
v ч > A0.8.48)
и, следовательно, имеет место равенство
-f/квТ = Щс + d) +
) A - qml2x-m) (xm+x-m-zm-z~m) A0-8-49)
10.9. СЛУЧАЙ ИЗИНГА
В разд. 10.3 показано, что при J" — 0 восьмивершинная модель
распадается на две идентичные и независимые модели Изинга. Коэф-
Коэффициенты взаимодействия, соответствующие данным моделям, обоз-
обозначены в гл. 7 через К и L, а в настоящей главе через J/kBT, J'/kBf.
Обозначим через kly Uj, ql , . . . переменные к, и, q , . . . из гл. 7.

ГЛАВА 10 241
Тогда, согласно G.6.1),
kjl = sinhBJ/kBT) sinhBT/fcBr). A0.9.1)
Разложение правой части выражения A0.9.1) в сумму экспонент и
использование формул A0.3.9), A0.3.10) и A0.4.6) приводят к соотношению
кТ1 = (а2 + &-<?- d2)/4ab = А . A0.9.2)
Следовательно, ферромагнитно упорядоченное состояние модели
Изинга {J > 0, J' > 0, kj < 1) лежит в области А> \,a>b + c + d
восьмивершинной модели.
Данную область можно отобразить в основную область A0.7.5) с по-
помощью соотношения симметрии A0.2.14), т. е. с помощью перестановки
весов а с с и b с d. Сделаем это и определим величины р, к, X, v
в соответствии с выражениями A0.4.24) или A0.4.21). Получим следую-
следующие равенства:
snh A = ?"*, A0.9.3)
fc* snh и = exp(-2J'/kBT). A0.9.4)
Из формул A0.9.2) и A0.4.17) с учетом того, что величина А меняет знак
при перестановке а с с и b с d, следует
кТ1 = ? en /A dn /A. A0.9.5)
Тогда из A0.9.3), используя A5.4.32), получаем
А = \V , A0.9.6)
т. е. величина X лежит точно в середине интервала @, /'), задаваемого
выражением A0.7.1). Из A0.7.9) следует
q = x4. A0.9.7)
Кроме того, из A5.4.32) и A0.9.5) получаем
кг = 2fc*/(l + к) . A0.9.8)
Полученное соотношение между эллиптическими модулями представляет
собой преобразование Ландена (разд. 15.6). Если qf — параметр Якоби, со-
соответствующий модулю kl9 то из A5.6.2) и A0.9.7) получаем
qi = qk = x2. A0.9.9)
Следовательно, спонтанную намагниченность в модели Изинга можно
записать с помощью G.10.50) и A5.1.4) в виде
Мо=Д тт^=Д гт?^ • <10-9Л0>
Кроме того, применяя преобразование A5.6.4) к выражению A0.9.4) и
сравнивая результат с G.8.5), получаем
и/= (! + *)«. A0.9.11)

242 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Такие соотношения позволяют непосредственно проверить, что при J" - О
выражение A0.8.47) действительно принимает вид полученного выше для
модели Изинга результата G.9.16).
ШЛО. ДРУГИЕ ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
Поверхностное натяжение
В основной области восьмивершинная модель характеризуется дальним
антиферромагнитным упорядочением. При этом возможны две конфи-
конфигурации стрелок. Первая показана на рис. 8.3; вторая получается из пер-
первой при обращении всех стрелок.
Поверхностное натяжение между доменами указанных двух типов
можно получить так же, как в разд. 7.10. Если Ло, А1 — два наибольших
по модулю собственных значения, то они асимптотически вырождены в
том смысле, что
Ai/A0= -1 + €[zxp(-Ns/kBT)], A0.10.1)
где s — поверхностное натяжение.
Указанные собственные значения Ло, А1 — это как раз те собственные
значения, которые обсуждались в предыдущем разделе и которые связаны
с г = +1 и г = -1 соответственно. Мы видели, что при больших 7V они
равны по модулю и имеют разные знаки. Чтобы получить натяжение s,
мы должны сохранить экспоненциально малые поправки, которые были
отброшены в предыдущем разделе.
Выведем снова выражение A0.8.42), сохраняя все вклады в функции
%.(v), Y±(v) и используя формулы A0.8.3) и A0.8.16). Обозначим через
А%)) правую часть A0.8.42). Тогда при IRe(t;)l < а получим следующее
выражение:
а+2И
n[l+p(v')]D(v ~v')dv'~~
2/7
! f-a+TU A0.10.2)
-— \n[l + l/p(v')]D(v-v')dv',
Oil J-a-2iI
где введено обозначение
I ra+2L
~8ill-2u
AОлаз)
(величины z, х определены формулами A0.7.18) и A0.7.9)). Функция D(v)
удовлетворяет соотношениям
D(v) = -D(-v) = -D(v + 2A) ; A0.10.4)
кроме того,
D(v-X) = dn(iv/k), A0.10.5)
где dn (w, к) — эллиптическая функция, определенная в A5.1.6), а величины

ГЛАВА 10 243
к, С заданы выражениями A0.8.37) и A0.8.38). Мы видим снова, что
появляется эллиптическая функция с параметром Якоби ху а не д.
Выражение A0.10.2) является точным даже при конечном п. Основную
поправку к A(v) (при больших п) можно получить, подставляя в A0.10.2)
выражения A0.8.39) для p(v), справедливые при больших п.
При а < min BХ, 2/' — 2Х) указанные выражения принимают вид
A0.8.35) и A0.8.36). Функция p(v) имеет седловые точки при v = 2/7 ± X,
т. е. при z = —х±х. Положив в A0.10.2) а = X и проинтегрировав с по-
помощью метода перевала, получим
\n[A(v)/A{0\v)] -pBil + Я). A0.10.6)
Из выражения A0.8.35) при z = -х следует
pB*7 + A) = rA:f2, A0.10.7)
где
(|0ЛОЙ
(Величина к{ является эллиптическим модулем, отвечающим параметру
Якоби х1. Она связана с (с соотношением ? = 2А:]/2/A + к{).)
Величина A(v) в выражении (Г0.10.6) равна Ао при г — + 1 и Aj при
г= -1. Из A0.8.42) видно, что функции A°(v) в указанных случаях
различаются только знаками. Вычисляя разность и используя A0.10.7),
получаем
). A0.10.9)
Следовательно, рассматриваемые максимальные собственные значения
асимптотически вырождены: они удовлетворяют соотношению A0.10.1),
причем поверхностное натяжение s задается соотношением
Qxp(~s/kBT) = к\. A0.10.10)
Если X > 2/V3, то проведенные выкладки неприменимы, поскольку в
этом случае функция p(v') в A0.10.2) при а = X не задается выражением
A0.8.35). Тем не менее результат A0.10.10) остается справедливым, как это
показано в приложении D работы [30].
Если к -~ 0, то q — 0, / — 7г/2 и snh и — sinh и. Используя A0.4.23), мы
видим, что соотношение A0.4.21) принимает тот же вид, что и выражение
(8.9.7) при d = 0. Таким образом, восьмивершинная модель сводится к
шестивершинной, основная область A0.7.5) превращается в область IV из
разд. 8.10, и, следовательно, величины X, v имеют тот же смысл что и в
разд. 8.10.
Следовательно, поверхностное натяжение в шестивершинной модели
задается формулами A0.10.10) и A0.10.8) в пределе q — 0. Но поскольку
данные выражения не зависят от q, поэтому они дают полученный выше
результат (8.10.3). Определение A0.7.9) величины х сводится к выражению
(8.10.2).

244 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
КОРРЕЛЯЦИОННАЯ ДЛИНА
Кроме двух наибольших собственных значений A(v) трансфер-матрицы
V(v) в пределе больших 7V можно последовательно вычислять другие
собственные значения. Поскольку подобные вычисления связаны с проб-
проблемой нахождения статистической суммы XYZ-цепочш, обсуждаемой в
разд. 10.14, значительная их часть уже выполнена [95, 118, 119, 227 — 229,
264].
Я не буду воспроизводить здесь такие вычисления. Позвольте мне лишь
сделать следующее замечание. По-видимому, для каждого собственного
значения (при больших N) нули v l , ... , vn функции q(v) собираются в
группы в комплексной плоскости. Все нули, принадлежащие некоторой
группе, имеют одну и ту же мнимую часть; они расположены равномерно
с интервалами 2Х и симметрично относительно мнимой оси или вертикаль-
вертикальной линии Re(t;) = /\ Таким образом, группа из т нулей состоит из
комплексных чисел
w + //' + B/-m-l)A, /=l,...,m, A0.10.11)
где / — целое число, равное нулю или единице.
Для двух наибольших собственных значений (т. е. тех, которые рас-
рассматривались в разд. 10.8) каждая группа содержит только один нуль и
имеет / = 0. Обозначим через Л2 собственное значение, которое следует по
величине за максимальным. Джонсон и др. [120 — 122] показали, что тако-
такому собственному значению соответствует либо одна из групп с / =1, либо
две из них, заменяемые на группу удвоенной длины.
Существуют 2N таких собственных значений, соответствующих диаго-
диагональному оператору S, имеющему собственное значение s = -(-1)". В
пределе N — оо при условии X < /' /2 наибольшее из них определяется
формулой (8.10.10) или, что эквивалентно, формулой (8.10.11), т. е.
№ А* + Z) П A + *4m*)A+*4m*") (I0 ,0 12)
где величины X, v, x, z определены выражениями A0.4.24), A0.7.9) и
A0.7.18). (Подобно результатам A0.10.8) и A0.10.10) для поверхностного
натяжения данная формула не содержит q, поэтому она имеет один и тот
же вид для восьмивершинной и шестивершинной моделей.)
Рассуждения, приведенные после формулы (8.10.11), все еще приме-
применимы, поэтому корреляционная длина ? стрелок определяется выра-
выражением (8.10.12). С учетом A0.10.8) его можно записать в виде
r1 = Hn(l/^), A0.10.13)
если, как и раньше, X < Г /2.
Исключая кх из выражений A0.10.10) и A0.10.13), получаем
s%= kBT, A0.10.14)
где s — поверхностное натяжение. Теперь можно понять, почему соотно-

ГЛАВА 10 245
шение A0.10.14) выполняется как для модели Изинга (уравнение G.10.44)),
так и для шестивершинной модели (уравнение (8.10.13)). Обе модели
являются частными случаями восьмивершинной модели, для которой со-
соотношение A0.10.14) справедливо в общем случае при условии
0 < \/Г < Vi, (В модели Изинга \/Г = !/2, в шестивершинной модели
\/Г = 0.)
Вообще гипотеза скейлинга [2, 252] предсказывает, что для всех
систем, находящихся вблизи критической точки, величины s и ? должны
удовлетворять некоторому соотношению вида A0.10.14).
Джонсон и др. [122] получили также выражение для ? при 1/2 < X < /'
и обнаружили, что формулы A0.10.12) и A0.10.13) не выполняются при
X > 21'/3. Такое поведение типично для вычислений немаксимальных
собственных значений трансфер-матрицы восьмивершинной модели:
результаты, полученные при значениях X из разных частей интервала @,
/'), оказываются различными. Отчасти это обусловлено группами нулей,
имеющими длину, большую, чем период 2/' функции q(v), и появляющи-
появляющимися поэтому по другую сторону прямоугольника периодичности. Это
свойство сильно затрудняет изучение немаксимальных собственных зна-
значений.
Из приведенных рассуждений следует также, что многие из формул, на
первый взгляд не содержащих величину q (а содержащих только х и г), в
действительности, к сожалению, зависят от нее, поскольку q входит в
определение областей, в которых справедливы данные формулы. Если бы
отношения Лу/Л0 для любых собственных значений Лу зависели только от х
и i (как в A0.10.9), A0.10.12) и в уравнении (8) работы [120], то эти отно-
отношения можно было бы получать (при больших N) из точных результатов
модели Изинга.
Следует заметить, что результаты A0.10.10), A0.10.13) для поверхно-
поверхностного натяжения и корреляционной длины не сводятся к формулам
G.10.18), G.10.43) для случая чистой модели Изинга. Из формул A0.9.8),
A0.9.9) следует, что величина kf является эллиптическим модулем с
параметром Якоби х2, поэтому величина кх = кг равна модулю, использо-
использованному в гл. 7. Мы видим, что множители различаются в два раза. Такое
расхождение в величине поверхностного натяжения связано с изменением
масштаба длины: п в формуле G.10.17) соответствует N/2 в выражении
A0.10.9). Различие в значениях корреляционной длины происходит из-за
того, что в основной области (где система упорядочена) величины Л2,
обсуждаемые в работах [120, 122], не лежат в том же диагональ-
диагональном блоке трансфер-матрицы, что и Ло (соответствующее собственное
значение оператора 5 имеет противоположный знак); поэтому матричные
элементы /02, /20 в G". 10.33) равны нулю, и необходимо перейти к
следующей зоне собственных значений. Данное обстоятельство приводит к
тому, что необходимо возвести Л2/Л0 в квадрат и тем самым удалить мно-
множитель Vi из формулы A0.10.13). (В областях, где система находится в
неупорядоченном состоянии, собственное значение Л2 лежит в том же
диагональном блоке, что и Ло; выражение A0.10.13) справедливо в той

246 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
форме, в которой оно записано, при условии что величины к, \ v
определены так же, как в разд. A0.11). Этот результат можно сравнивать
с формулой G.11.4) для модели Изинга при низкой температуре.)
Спонтанная намагниченность
Мы видели, что восьмивершинную модель можно рассматривать либо
как модель сегнетоэлектрика (диполи представлены стрелками на ребрах
решетки), либо как модель ферромагнетика с изинговыми спинами на
гранях решетки. Параметр порядка зависит от принятой точки зрения.
Используем сначала картину изингова магнетика, рассмотренную в
разд. 10.3. Пусть о1 — некоторый спин, и пусть
М0 = (о1) A0.10.15)
представляет собой среднее значение данного спина, вычисленное в пределе
бесконечно слабого магнитного поля, как сделано в A.1.1).
Предположим, что рассматриваемая система ферромагнитна, так что^У
и J' положительны, a J" > -max (У, У). Тогда при достаточно низких
температурах Т больцмановские веса, заданные формулой A0.3.9), удов-
удовлетворяют соотношению
a>b + c + d. A0.10.16)
Используя свойства симметрии A0.2.14), указанную область можно
получить из основной области A0.7.5) с помощью перестановки весов асе
и Ь с d. Условие A0.10.16) определяет область ферромагнитного упорядоче-
упорядочения восьмивершинной модели.
Определим величины к, X, v, р, удовлетворяющие условиям A0.7.1),
учитывая перестановки acenbedu используя выражения
A0.4.21) — A0.4.24). Определим также q, х, z с помощью A0.7.9) и
A0.7.19), а параметр у — соотношением
q=x2y. A0.10.17)
Тогда Мо можно рассматривать как функцию х, у и z.
Барбер и Бэкстер [13] разлагали Мо в ряд по х, коэффициенты которого
априори являются функциями у и z. (Такое разложение представляет собой
частично просуммированный низкотемпературный ряд.) С точностью до
членов порядка х4 они получили выражение
Мо = 1 + 0.* - 2х2 + О.*3 + 2хА + A0.10.18)
Все вычисленные коэффициенты оказались постоянными.
Нетрудно видеть, что величина Мо не должна зависеть от z. Так же как
в G.10.48) и G.10.32), ее можно записать только через односпиновый диаго-
диагональный оператор и матрицу Р (U в гл. 7) собственных векторов трансфер-
матрицы. Данные собственные векторы не зависят от v и, следовательно,
от z, поэтому Мо также не зависит от z.
Не очевидно, что Мо не зависит от q. Но поверхностное натяжение,
корреляционная длина (при условии X < 2/V3) и первые пять членов

ГЛАВА 10 247
разложения Мо по степеням х не зависят от q. Поэтому Барбер и Бэкстер
[13] высказали предположение, что Мо зависит только от х.
Для чистой модели Изинга, которая получается с учетом A0.9.7) при
q - а-4, из A0.9.10) известно, что Мо имеет вид
A0.10.19)
поэтому из предположения Барбера и Бэкстера [13] следует, что формула
A0.10.19) справедлива при любых значениях q. Данное предположение
было проверено: намагниченность Мо вычислялась с помощью угловых
трансфер-матриц (гл. 13).
Напомним, что определенная в A0.10.8) величина к{ представляет со-
собой, согласно A5.1.4а), эллиптический модуль, соответствующий пара-
параметру Якоби х2. Из формулы A5.1.46) следует
Мо = к'"* = A - к2I18. A0.10.20)
Спонтанная поляризация
Вернемся к исходной формулировке модели с помощью стрелок. Введем
обозначение
Ро = <*!>, A0.10.21)
где aj — «стрелка-спин», лежащий на некотором ребре решетки (вер-
(вертикальном или горизонтальном) и принимающий значения ± 1 в зави-
зависимости от направления стрелки. Из A0.3.2) следует
Ро = (OiO2) , A0.10.22)
где ар а2 — изинговы спины на гранях, содержащих оба узла рассматрива-
рассматриваемого ребра решетки.
Величина Ро, подобно Мо, является «параметром порядка». Как следует
из рис. 10.1 и формулы A0.1.5), восьмивершинная модель без внешнего по-
поля не изменяется при обращении всех стрелок. Указанная симметрия нару-
нарушается при добавлении к полной энергии членов вида
-е2<*/, A0.10.23)
где Е — «электрическое поле» и суммирование проводится по всем
вертикальным (или горизонтальным) стрелкам.
В модели сегнетоэлектрика, в которой вес а или Ъ является наибольшим
среди больцмановских весов а, Ь, с, d> электрическое поле Е снимает вы-
вырождение основного состояния. Если теперь вычислить величину A0.10.21)
в пределе большой решетки и затем положить Е — 0 по положительным
значениям, то результирующее выражение для Ро будет отлично от нуля,
если вес а или Ь достаточно велик.
В модели антисегнетоэлектрика, когда вес с или d является наибольшим
из больцмановских весов (как в основной области A0.7.5)), члены вида

248 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
A0.10.23) не снимают вырождения основного состояния (рис. 8.3). Необхо-
Необходимо сделать поле Е непостоянным, изменяя его знак на ребрах,
следующих друг за другом. Тогда соответствующее предельное значение Ро
снова отлично от нуля при достаточно большом весе с или d.
Такие вычисления не проводились, и никакие модели, более сложные,
чем модель Изинга, не рашались с учетом магнитного поля. Фактически
величина Ро не вычислялась, но, подобно Мо, она должна быть функцией
только х и q и не зависеть от z> Бэкстер и Келланд [39] предположили, что
в основной области A0.7.5) справедливо выражение
A0-10-24)
Данное выражение согласуется с результатом (8.10.9), полученным для
шестивершинной модели (q = 0). В модели Изинга (q = х4) с учетом
A0.9.10) выражение A0.10.24) приводит к равенству Ро = Мо2, которое
справедливо, поскольку спины о1 и о2 в A0.10.22) лежат на разных
подрешетках, и поэтому в изинговом случае они независимы. Рас-
Рассматриваемое предположение справедливо также в пределе q = х2, X = /',
когда а = b = 0, с = d и система полностью упорядочена.
Бэкстер и Келланд [39] рассмотрели также случай q = ху (см. формулу
A0.10.17)) и вычислили Ро с точностью до членов порядка х4 в разложении,
коэффициенты которого зависят от .у. Результат согласуется с выражением
AQ. 10.24), поэтому весьма вероятно, что A0.10.24) выполняется точно во
всей основной области.
Отметим, что параметры Якоби q и х2 связаны с модулями к и к 1 со-
соответственно. Тогда с учетом A5.1.7) получаем, что выражение A0.10.24)
можно записать в виде
)9 A0.10.25)
где к' и к\ — соответствующие сопряженные модули, а /, 1Х — полные эл-
эллиптические интегралы первого рода.
10.11 КЛАССИФИКАЦИЯ ФАЗ
В основной области A0.7.5) свободная энергия задается выражением
A0.8.47). В данном случае мы видим, что из A0.2.16) следует
W3> W4> Wi> \W2\. A0.11.1)
При произвольных значениях а, Ь, с, d, используя свойства симметрии
A0.2.17), свободную энергию можно определить с помощью следующей
процедуры:
1. Вычислить Wj , . . . , vv4 по формулам A0.2.16).
2. Изменить знаки и расположить величины vv2 , . . . , vv4 так, чтобы
удовлетворялось условие A0.11.1).

ГЛАВА 10 249
3. Из формул A0.2.16) найти новые значения весов а, Ь, с, d. Получен-
Полученные значения будут лежать в основной области.
4. Вычислить параметры р, к, X, v из A0.4.16) — A0.4.24), величины q и
х из A0.7.9), аг из A0.7.18).
5. Вычислить свободную энергию/ по формуле A0.8.47) или A0.8.49).
Вычисленная таким способом функция f(a, Ь, с, d) аналитична всюду,
кроме поверхностей, на которых одна из величин а, Ь, с, d равна сумме
трех других. Таким образом, существует пять областей:
I. Сегнетоэлектрик: а > b + с + d, А > 1.
II. Сегнетоэлектрик: Ъ > а + с + d, A > 1.
III. Область беспорядка: а, Ь, с, d < Vi (a + Ъ + с + d), — 1 < Д < 1.
IV. Антисегнетоэлектрик: с > а + b + d, А < — 1 (основная область).
V. Антисегнетоэлектрик: d > а + b + с, А < - 1.
В областях I, II, IV V система упорядочена. Любая такая область
может быть получена из области IV с помощью элементарных свойств
симметрии A0.2.12) — A0.2.14). Поверхностное натяжением, корреляцион-
корреляционная длина ?, намагниченность Мо и поляризация Ро задаются формулами
A0.10.10), A0.10.13) (без множителя /г), A0.10.19), A0.10.23) со-
соответственно. Величины q, x, z определяются так, как указано для четвер-
четвертого этапа процедуры отображения.
Заметим, что система всегда упорядочена, если модуль параметра Д,
определенного в A0.4.6), больше единицы. Система разупорядочена при
IAI < 1.
Приведенная классификация фаз по областям станет более очевидной,
если мы точно решим уравнения A0.4.17) и A0.4.6) относительно модуля к.
Возведем в квадрат второе уравнение A0.4.17), используем свойства A5.4.4)
и A5.4.5) и исключим srA'X с помощью выражения A0.4.16). Тогда получим
2 1 уJ A0.11.2)
Решая полученное уравнение относительно к + к~х и используя A0.4.6),
найдем
fco + V-2= A0.11.3)
_ (а - Ъ - с - d) (а - Ъ + с + d) (а + Ъ - с + d) (а 4 b + с - d)
Aabcd
*0 + W, + 2,i^, «,0.„.4,
abed
где а', b', с', d' определены выражениями A0.2.5), а индекс 0 означает,
что величину к0 следует вычислять непосредственно по формуле A0.11.3)
или A0.11.4) не используя первые три этапа процедуры отображения.
Отсюда следует, что к0 не обязательно лежит в интервале @, 1).
В областях упорядочения I, II, IV, V правая часть выражения A0.11.3)
положительна. Она отрицательна в области беспорядка III.

250 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Чтобы отобразить область III в основную область, необходимо исполь-
использовать соотношение дуальности A0.2.11). В зависимости от того, являются
ли величины Ъ', с', d' положительными или отрицательными, возникают
разные случаи. Но оказывается, что свободная энергия / представляет со-
собой аналитическую функцию переменных а, Ь, с, d во всей области III.
Данная область является областью беспорядка: спонтанная намагничен-
намагниченность и спонтанная поляризация равны нулю, корреляционная длина
задается точно формулой A0.10.13).
Точки разупорядочения
Система разупорядочена во всей области III, но то же самое происхо-
происходит, если с' или d' равны нулю, т. е. если (используя A0.2.5)) точка (а, Ь,
с, d) лежит на одной из поверхностей
a + c = h + d1HjiH a + d = Ъ + с. A0.11.5)
Процедура 1 — 5 отображает данные поверхности в основную область IV
восьмивершинной модели, причем а = 0 или Ь = 0. Поскольку в этом слу-
случае к0 = 0, а величина к лежит на отрезке [0, 1], из A0.11.3) следует,
что к = 0. Точнее говоря, когда отображенная величина а (или Ь)
стремится к нулю, к — 0, у и у пропорциональны к~\ как это следует из
A0.4.9) — A0.4.21), величина X стремится к бесконечности, но разность
/' - X остается ограниченной. Из формулы A0.7.9) следует, что обе
величины q и х стремятся к нулю, причем величина а* пропорциональна qVl.
Как видно из выражений A0.10.8) и A0.10.13), кх и ? стремятся к нулю.
Таким образом, корреляционная длина (определяемая формулой G.10.41),
модифицированной с учетом аргументов, приведенных после (8.10.11))
обращается в нуль: система полностью разупорядочена.
Свободная энергия определяется выражением A0.8.47), в котором
величина с имеет смысл образа веса с при отображении 1 — 3, а все члены
в сумме равны нулю. Таким образом,
-flkBT=\n\{a + Ъ + с + d). A0.11.6)
(Полученный простой результат можно понять по крайней мере двумя спо-
способами. Первый состоит в том, что выражения A0.2.11) — A0.2.15) можно
использовать для отображения данной модели на шестивершинную модель
в замороженном сегнетоэлектрическом состоянии (области I или II в разд.
8.10). Второй состоит в том, чтобы проверить справедливость равенства
Vx = [Vi (a 4- Ъ 4- с + d)]Nx, где V — трансфер-матрица, х — вектор, все
элементы которого равны единице; такое вычисление особенно просто
выполнить, если V заменить трансфер-матрицей, которая строит решетку
по диагонали.)
Точки полного разупорядочения появляются также в модели Изинга с
антиферромагнитным взаимодействием на треугольной решетке [216].

ГЛАВА 10 25j_
10.12. КРИТИЧЕСКИЕ СИНГУЛЯРНОСТИ
Свободная энергия системы является аналитической функцией пере-
переменных a, by с, d, и корреляционная длина ? конечна при условии, что
больцмановские веса а, Ь, с, d не лежат на одной из поверхностей
а = b + с + d или Ъ = а + с + d,
c-a + b + d ипи d-a + b + c A0.12.1)
С — И \ U \ (А ИЛИ (Л — Uit/iC,
где все величины а, Ь, с, а неотрицательны. Поверхности A0.12.1) назы-
называются критическими поверхностями в (а, Ь, с, ^-пространстве.
Если фиксировать энергии ех , ... , ?8, удовлетворяющие условиям
A0.1.5), и изменять температуру Г, то точка (а, Ь, с, d) будет двигаться
вдоль некоторого пути в рассматриваемом пространстве. Когда одна из
величин ?j, ?3, ?5, ?7 (скажем, ех) меньше других, при достаточно малых Т
такой путь лежит в одной из областей упорядочения (область I). С другой
стороны, при достаточно больших Т(а = b = с = d = 1) этот путь лежит
в области разупорядочения III. Следовательно, рассматриваемый путь
должен пересечь некоторую критическую поверхность (причем только один
раз) в критической точке.
Если две или более из величин ?р ?3, ?5, ?7 Равны между собой и
меньше других, то путь всегда лежит в области беспорядка III и критиче-
критической температуры не существует.
Рассмотрим точку (а, Ь, с, d), лежащую вблизи одной из поверхностей
A0.12.1), и введем обозначение
_ (a-b-c-d)(a-b+c + d){a+b-c+d)(a+b+c-d)
\6abcd (Ю.12.2)
Величина / равна нулю на любой критической поверхности и обращается в
нуль при приближении к критической температуре в общем случае линейно
по Т — Тс, причем величина (Т — Tc)/t положительна. Следовательно, мы
можем рассматривать величину / как переменную, описывающую откло-
отклонение от критической температуры, и заменить выражение A.1.3) на
A0.12.2).
Все четыре критические поверхности A0.12.1) можно отобразить на
поверхность c = a + b + dc помощью тривиальных свойств A0.2.12) —
A0.2.14). Такие отображения просто меняют порядок расположения
величин а, Ь, с, d и отображают области порядка в области по-
порядка, а области беспорядка в области беспорядка. Следовательно, без
потери общности можно сосредоточить внимание на критических точках
поверхности с = а + b + d, разделяющей области III и IV. В остающейся
части данного раздела будет проведено такое рассмотрение.
Альтернативные выражения
для термодинамических характеристик
Рассмотрим сначала основную область IV, в которой величина /
отрицательна и к = к0. Из выражений A0.11.3) и A0.12.2) следует

252 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
k + k'l = 2-4t, A0.12.3)
так что к стремится к единице при / — 0_ .
Отсюда следует, что q — 1 и бесконечные произведения, входящие в
определения тэта-функций A5.1.5), становятся слабо сходящимися. Этого
можно избежать, подставляя A5.7.2) в A0.4.24) , чтобы выразить веса а,
Ь, с, d через тэта-функции модуля к', сопряженного модулю к.
Мы хотим также сравнить правильное выражение для свободной
энергии /, справедливое в области III, с аналитическим продолжением
функции / из области IV. Такое сравнение удобнее проводить, работая с
переменными wx , . . . , vv4, введенными в A0.2.16), а не с весами а, Ь, с, d.
Подставляя сопряженные к A0.4.24) выражения в A0.2.16), используя
A5.4.29) для факторизации правой части и применяя затем разложение в
произведение A5.1.5), окончательно получаем
= i(* -b) = -p -^2lA_pV)A_p%r
CO-12.4)
, cos(W2) n A +p2nz') A +p2nlz')
i(c + d) - p cQs(^2) 11
где
р 9 , A0.12.5)
x' = ехр(*>), z' = e?p(«iv),
а параметр pr — некоторый нормировочный множитель (пропорцио-
(пропорциональный /э), точное значение которого здесь не понадобится.
Эти уравнения вместе с ограничениями A0.7.1), т. е.
0<р<1, |w|<jm<jt, |>0, A0.12.6)
определяют р', \к, w и р. Очевидно, что при / ^0 р — 0 и величины ?, /х, V
стремятся к конечным пределам, которые являются критическими значе-
значениями этих величин. В частности, критическое значение /х определяется
формулой
tanOi/2) = (cd/aby. A0.12.7)
Свободная энергия задается выражением A0.8.47) или A0.8.49).
Последнее более удобно для наших настоящих целей, поскольку оно

ГЛАВА 10 253
содержит с + d (т. е. 2w3), а не с, что облегчает сравнение областей III и
IV.
Заметим, что \х и w стремятся к конечным пределам при / — 0 и к — 1.
Поскольку при этом /' — 7г/2, а /— оо, из выражений A0.12.5), A0.7.9) и
A0.7.18) следует, что все величины q, х, z стремятся к единице (снизу).
Поэтому сумма в выражении A0.8.49) превращается в интеграл. Его
поведение вблизи t = 0 можно изучить с помощью формулы суммирования
Пуассона A5.8.1). Для этого введем определение
[cosh (я - 2и)и - cosh ии] [cosh ии - cosh wu]
гш) — : ". (lU.lz.oj
и sinh ли cosh ии
Тогда, учитывая, что F(u) — четная функция и F@) = 0, а также используя
выражения A0.7.9), A0.7.19), A0.12.5), можно показать, что выражение
A0.8.49) принимает вид
00
-f/kBT = ln(c + d) + — 2 f(—] . A0.12.9)
4/m=-a> \2I j
Из формулы A5.8.1) видно, что это выражение можно записать в виде
00
-f/kBT= ln(c + d) + JG(O) + 2g(^) , (Ю.12.10)
где
G(k) = Г cxp(iku)F(u) du , A0.12.11)
и мы использовали тот факт, что G(k), подобно F(w), должна быть четной
функцией
При положительных к контур интегрирования в A0.12.11) можно
замкнуть в верхней полуплоскости и представить интеграл в виде суммы
вычетов в полюсах и = in, i (n — Vi)^/^ при п = 1, 2, 3, . . . . Подставляя
результат в A0.12.10) и вычисляя сумму по w, получаем
-//**r=ln(c + ?/)+iG@) +
00
_ v (cos 2nu - cos пл cos пи) (cos пи - cos nw) р
+ 2Z ,: V 2n, ^- + A0.12.12)
n = \ n cosnu A -p )
(-1У cot[(/i - 4) я2///] cos[(/i
Выражения A0.10.10), A0.10.13), A0.10.20) для поверхностного натяже-
натяжения 5, корреляционной длины ? и спонтанной намагниченности Мо имеют
вид
slkBT = \ 1пA/*0 , § = 2/ln(l/*i), Мо = A - А:?I/8, A0.12.13)

254 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
где величина кх, определенная формулой A0.10.8), представляет собой
эллиптический модуль, соответствующий параметру Якоби х2.
Для изучения поведения вблизи точки х = 1 мы просто перейдем к
сопряженному модулю и сопряженному параметру Якоби. Сопряженный
модуль равен кх' = A - кх2)у\ а сопряженный параметр Якоби, как это
следует из выражения A5.1.3) (при перестановке периодов / и /'), имеет
вид ехр [7г2/1п (х2)]. Следовательно, используя A0.7.9) и A0.12.5), для
сопряженного параметра Якоби получаем выражение
q[ = ехр(-л://Я) = рк11\ A0.12.14)
Заменяя в A5.1.4а) величины кх, qx на кх , qx и возводя в квадрат, име-
имеем
.. -.-г / 14- плп/^ \ 8
A0.12.15)
Спонтанная поляризация по-прежнему точно задается выражением
A0.10.25), т. е.
P0 = k[Il/(k'I). A0.12.16)
Перейдем снова к сопряженным параметрам. Заменяя к, Г, q в A5.1.8)
на А:', /, q' и используя A0.12.5), получаем
Аналогично, используя кх , /р qx и формулу A0.12.14), имеем
AОЛ2Л8)
Поведение вблизи критической точки
При заданных а, Ь, с, d в области IV величины р, \i и V определены
уравнениями A0.12.4) и A0.12.5). Свободная энергия, поверхностное
натяжение и другие характеристики заданы уравнениями A0.12.12) —
A0.12.18).
По другую сторону перехода в области III величины wx , . . . , vv4 необ-
необходимо перестроить в соответствии с процедурой 1 — 5, описанной в
предыдущем разделе. Указанная процедура приводит к тому, что, прежде
чем использовать уравнения A0.12.4) и A0.12.5), необходимо переставить
величины Wj и и>4. Свободная энергия снова определяется выражением
A0.10.12), а корреляционная длина ? —выражением A0.12.13). Величины
Мо и Ро равны нулю, а поверхностное натяжение s теряет смысл.
Но из уравнений A0.12.4) очевидно, что р, \х, V — аналитические
функции а, Ь, с, d даже при р = 0, т. е. при переходе из области IV в
область III. Значит, перестановка величин wx и vv4 эквивалентна просто
изменению знака только у величины р.

ГЛАВА 10 255
Отсюда следует, что р, \х, V могут быть аналитически продолжены из
области IV в область III, и это аналитическое продолжение отличается от
соответствующих правильных значений только знаком величины р.
Итак, при малых / из A0.12.3), A0.12.5) и A5.1.4а) следует
р= -гЛб + О^), A0.12.19)
так что р стремится к нулю линейно относительно /.
Обратимся к выражению A0.12.12) для свободной энергии. Первые три
члена содержат только аналитически меняющиеся при переходе границы
между областями III и IV величины vv3, /х, К и р2, которые являются
одними и теми же функциями а, Ь, с, d в обеих областях. Следовательно,
только последний член может быть в каком-то смысле сингулярным. При
малых р основной вклад в него имеет вид
-/sing/АгвГ = -4 cot(^) cosf^j p^. A0.12.20)
Величина /sing эффективно совпадает с величиной fs, определенной в
A.7.10а). Поскольку /х, w стремятся к конечным пределам при /-0 и
предельное значение функции \х не равно нулю, члены, содержащие
тригонометрические функции, постоянны. Из формулы A0.12.19) и
приведенных выше рассуждений следует, что при малых / правильное
поведение функции р в обеих областях III и IV имеет вид
р = |f|/16. A0.12.21)
Отсюда получаем
/sing ~ Ил/" , A0.12.22а)
где критическое значение \х задано формулой A0.12.7).
Особые случаи возникают при д = -к/т, где т — целое число. Если т
четно, то множитель cot Gг2/2/х) в A0.12.20) равен бесконечности. Такая
ситуация является следствием того, что два полюса функции F(u)
сливаются. При вычислении интеграла A0.12.11) следует правильно
определить вычет такого двойного полюса. Влияние двойного полюса сво-
сводится к появлению множителя In I /1, поэтому если 7г/)х — четное целое
число, то
/sing-M^lnM . A0.12.226)
Если критическое значение 7г//х равно нечетному целому числу, то мно-
множитель cot Gг2/2/х) в формуле A0.12.20) равен нулю. Чтобы получить вид
основной сингулярности в таком случае, необходимо рассмотреть зависи-
зависимость # от температурной переменной /.
Из выражений A0.12.13) - A0.12.18) и A0.12.21) следует, что в
упорядоченной области IV при малых (и отрицательных) /
s, Г1 - {-tYl2\ Мо ~ (-Г) я/1ь" , Ро ~ (-0(я-")/4" , A0.12.23а)
а в области беспорядка III (/ положительно)
Г1 - Гт2/\ A0.12.236)

256 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
(Формула A0.10.13) для корреляционной длины ? справедлива только
при X < 2/V3, т. е. \х < 2тг/3. Но Джонсон и др. [122] показали, что
данная формула правильно описывает критическое поведение ? даже при
д > 2тг/3.)
Критические показатели и скеилинг
Так же как в разд. 8.11, определим критический показатель (Зе для
поляризации Ро по аналогии с определением показателя /3 для намагничен-
намагниченности Мо. Чтобы не путать введенный выше параметр /х с критическим
показателем поверхностного натяжения в формуле A.7.34), обозначим
последний через ц5. Тогда из выражений A.1.4), A.7.9), A.7.25), A.7.34),
A0.12.23) следует, что критические показатели а, а', /3, /Зе, р, v', ц5 равны
ос = а* = 2 - к\\1, /3 = я/16/i ,
A0.12.24)
Д. = (я - /л)/4/л, v= v' = fis = лПц .
Поскольку восьмивершинная модель может быть решена только при
нулевом внешнем поле (как электрическом, так и магнитном), ее нельзя
использовать для полной проверки гипотезы скейлинга A.2.1). Но все
предсказания скейлинга, которые можно проверить, а именно выражения
A.2.15) и A.2.16), равенства а = а' и v = v\ действительно выполняются.
Если принять другие предсказания скейлинга, то из выражений
A.2.12) — A.2.14) можно вычислить соответствующие критические
показатели. В частности, «магнитные» показатели у, 6, -q равны
E=15, г] = \. A0.12.25)
Универсальность и слабая универсальность
Полезно сделать некоторые выводы об определении функции \х в
критических точках. При заданных энергиях вершин ер е3, ?5> е7 веса а> Ь>
с, d определяются формулами A0.1.2) и A0.2.1). Уравнения критических
поверхностей имеют вид A0.12.1). Если выполнено условие е5 < е{, е3, е7»
то критическая температура Тс определяется уравнением
ехр(-е5/квТс) = ехр(-ег/квТс) + exp(-f3/A:flrc) +
A0.12.26)
+ ехр(-е1/квТс).
Из формул A0.12.7) и A0.12.6) следует, что критическое значение \i дается
выражением
= exp[(?i + еъ - е5 - е7)/2квТс], 0 < \i < л . A0.12.27)
(Случаи, когда какая-нибудь другая из величин ер е3 или е7 является наи-
наименьшей, тривиально сводятся к рассматриваемому случаю с помощью со-
соотношений A0.2.12) — A0.2.14).)
При изменении энергий ер е3, е5, е7 величина \х. может принимать

ГЛАВА 10 257
любые значения в интервале @, 7г). Поэтому показатели а, /3, у, v> fis (но не
д и г)) непрерывно зависят от величин е1 , . . . , е7.
Указанное свойство противоречит приведенной в разд. 1.3 гипотезе
универсальности, утверждающей, что критические показатели не должны
зависеть от деталей взаимодействия. Каданов и Вегнер [135] показали, что
такая зависимость критических показателей от энергии вершин появляется
из-за особых свойств симметрии и размерности восьмивершинной модели
без внешнего поля. Предположим, например, что в рассмотренной в разд.
10.3 магнитной картине обе величины Jh и Jv не равны нулю одновременно
(в электрической картине это соответствует наличию внешнего поля).
Тогда из результатов Каданова и Вегнера следует, что магнитный
показатель в точности равен соответствующему показателю в модели
Изинга. С этой точки зрения свойство универсальности сохраняется в
«нормальных» условиях, а восьмивершинная модель является особым,
исключительным случаем. Данное утверждение подтверждается также
приближенными расчетами с помощью метода ренормализационной
группы [134, 150, 241].
Существуют две другие модели, которые, по-видимому, имеют
непрерывно изменяющиеся критические показатели, но эти модели нельзя
решить точно. Одна из них — модель Ашкина — Теллера [132, 267], рас-
рассматриваемая в разд. 12.9, другая — модель Изинга на квадратной решетке
с ферромагнитным взаимодействием между ближайшими соседями и анти-
фе*рромагнитным взаимодействием между соседями из следующей ко-
координационной сферы [12, 180, 182].
Сузуки [221] предложил использовать термин «слабая уни-
универсальность». Большинство показателей определяется как степени раз-
разности температур Т — Тс (показатели Ь и rj являются исключением).
Сузуки предположил, что в качестве переменной, описывающей отклонение
от критической точки, более естественно использовать обратную
корреляционную длину ?~*. Например, вместо выражения A.1.4) следует
принять
М0~Г^, A0.12.28)
где /3,— критический показатель. (Высказанная идея весьма привлекатель-
привлекательна, поскольку с математической точки зрения температура является неко-
некоторым малоинтересным делителем гамильтониана, в то время как корре-
корреляционная длина дает ценную информацию о поведении системы в окрест-
окрестности критической точки.)
Из формул A.1.4) и A.7.25) следует
$ = p/v. A0.12.29а)
Аналогично новые показатели для величин/sing, s и \ имеют вид
ф=B-а)/р, fis=lijv, y=ylv, A0.12.296)
в то время как показатели Ь и г) не изменяются. Для восьмивершинной мо-

258 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
дели из выражения A0.12.24) получаем показатели
Р = ~, 0=2, р,= 1, у=- 6=15, »,= !, A0.12.30)
которые являются фиксированными числами, не зависящими от д.
Таким образом, если сформулировать «слабую универсальность» как
предположение о том, что показатели /3 , ф , 'fi s, у , 6, rj не должны зави-
зависеть от деталей взаимодействий, то восьмивершинная модель согласуется с
такой гипотезой. Более того, данная гипотеза удачно связывается со скей-
лингом, покольку из соотношений A.2.12) — A.2.16) имеем
Р = ТТТ' Ф = d> fa=d-l,
°+l A0.12.31)
Отсюда следует, что если показатель д универсален, то должна выпол-
выполняться слабая универсальность.
10.13. ЭКВИВАЛЕНТНАЯ МОДЕЛЬ ИЗИНГА
В разд. 10.3 мы видели, что восьмивершинную модель можно рас-
рассматривать как две модели Изинга с взаимодействием между ближайшими
соседями (каждая из моделей на своей подрешетке), связанные между со-
собой с помощью взаимодействия между четырьмя спинами. Некоторые
авторы относятся скептически к введению таких четырехспиновых
взаимодействий, считая их в определенной степени «нефизическими».
Юнглинг [126] ответил на подобную критику, показав, что
восьмивершинная модель (в частности, восьмивершинная модель без
внешнего поля) эквивалентна модели Изинга на квадратной решетке с
взаимодействиями только между двумя спинами, которые представляют
собой взаимодействия между ближайшими соседями и соседями из третьей
координационной сферы.
Рассмотрим квадратную решетку, приведенную на рис. 10.6. На рисунке
показаны диагонали и выделены две подрешеки, узлы которых изо-
изображены светлыми и темными кружками. Обозначим через N число
темных кружков.
Разделим решетку на N квадратов, как это показано пунктирными ли-
линиями на рис. 10.6. Каждый такой квадрат содержит один темный узел.
Пусть полная энергия системы определяется выражением
где суммирование проводится по всем таким квадратам; через /, j, к, I, m
обозначены принадлежащие некоторому квадрату узлы, расположенные
так, как показано на рис. 10.6; сгД= ± 1) — спин, отвечающий узлу /.

ГЛАВА 10
259
Рис. 10.6. Формулировка восьмивершинной
модели, предложенная Юнглингом: модель Изинга
только с двухспиновыми взаимодействиями на
решетке, показанной сплошными линиями,
эквивалентна модели Изинга с двухспиновыми и
четырехспиновыми взаимодействиями на решетке,
показанной пунктирными линиями.
Приведенное выражение для энергии содержит взаимодействия только
между парами спинов: либо между ближайшими соседями (например,
°i am), либо между соседями из третьей координационной сферы
(например, а, ок). Как обычно, выражение для статистической суммы
имеет вид
Z = 2 ехр(-%/квТ), A0.13.2)
о
где суммирование проводится по всем значениям спинов.
Выражение под знаком суммы в A0.13.2) разбивается в произведение N
множителей, по одному на каждый квадрат. Каждый спин, отвечающий
темному узлу, входит только в один множитель, поэтому суммирование по
его значениям (±1) легко выполняется. Просуммировав по всем таким
спинам, получим
Z =
W(o, , а,, ок , о,),
A0.13.3)
, K=JlkBT, K'=J'/kBT,
то выражение для функции W в A0.13.3) примет вид •
W(au 02, 0з, о*) = 2 exp(KoiO3 + К'о2оА) х
где произведение берется по всем квадратам, а значок (О) показывает, что
суммирование проводится по всем спинам, отвечающим светлым узлам.
Если ввести обозначения
(Ю.13.4)
A0.13.5)
Поскольку спины dj , ч . . , ог4 принимают только два значения (+1 и
- 1), то любую функцию от них можно записать в виде
Li ~t~ %Li\O\ ~f~ . . . ~f~ Lj 13СТ1СГ3 "h . . . ~h /-'123401020304 •> A0.13.6)
где L , . . . , L1234 — постоянные коэффициенты.
Функция W(ox, a2, a3, a4) положительна; следовательно, ее логарифм^
действителен и может быть представлен в виде A0.13.6). Функция W
является четной функцией о{ , . . . , а4, так что в A0.13.6) должны входить
только четные слагаемые. Следовательно, можно найти такие величины L,

260 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
L12, L13, ^i4» ^23 > ^24» ^34» ^1234» чт0 выполняется равенство
,о2,оъ, а4) = exp L + X L,ya,-O/ + Li234<7i<7203<74 . A0.13.7)
[_ 1^/</^4 I
(Оно известно как преобразование «звезда — квадрат» и представляет со-
собой обобщение соотношения звезда — треугольник, рассмотренного в
разд. 6.4.)
Подставляя A0.13.7) в A0.13.3) и замечая, что каждая пара ближайших
спинов a, Oj входит в два квадрата, получаем
Z = exp(NL) E@) exp[(L12 + L34) 2 о& + (L23 + L14) 2 *fk
V a V V 1 (Ю.13.8)
^ ^1234 X OiOjOkOi \ ,
где суммирование в показателе экспоненты проводится по всем
вертикальным ребрам (/, у), горизонтальным ребрам (/, А:), диагональным
парам (/, к) и (/, /) и всем квадратам (/, У, А:, /).
За исключением множителя expGVL), выражение A0.13.8) представляет
собой статистическую сумму модели типа Изинга на квадратной решетке,
показанной на рис. 10.6 с помощью светлых кружков и пунктирных линий,
с диагональными и четырехспиновыми взаимодействиями между ближай-
ближайшими соседями. Это в точности совпадает с формулировкой восьми-
восьмивершинной модели A0.3.1), причем энергии взаимодействия Jh и Jv задают-
задаются выражениями
Jh/kBT = L{2 + LM, Jv/kBT = L23 + LH. A0.13.9)
В общем случае Jh и Jv не равны нулю, поэтому модель Юнглинга
эквивалентна некоторой восьмивершинной модели во внешнем электричес-
электрическом поле (верно и обратное утверждение).
Более интересен следующий факт. Если величины Jl% J2, J3> JA удов-
удовлетворяют не зависящим от температуры условиям
^1=/з, h=~h, A0.13.10)
то модель Юнглинга эквивалентна восьмивершинной модели без внешнего
поля.
Чтобы увидеть это, заметим, что из A0.13.10) следуют равенства
А^! = Къ и К2 = -К4. Тогда правая часть выражения A0.13.5) rfe изменяет-
изменяется при перестановке а{ и а3 или при перестановке и изменении знаков а2 и
а4. Отсюда следует, что формула A0.13.7) должна иметь следующий вид:
, a4) = exp[L+ LuOiO3 + L2aO2oa + Ln(oi + оъ)(о2 - a4) +
В частности, из нее следует
L12 + L34 = L23+ L,4 = 0, A0.13.12)

ГЛАВА 10 261
поэтому величины Jh и Jv, определенные выражениями A0.13.9), равны
нулю.
Рассмотренная формулировка восьмивершинной модели выдвигает на
первый план потенциальные трудности, связанные с универсальностью.'
Как показано в разд. 1.3, гипотеза универсальности допускает скачко-
скачкообразное изменение критических показателей при нарушении симметрии.
Данное свойство согласуется с выводом Каданова и Вегнера [135], отмечен-
отмеченным в предыдущем разделе: при наличии внешнего поля восьмивершинная
модель может иметь постоянные изинговы критические показатели, даже
если она не имеет их в отсутствие внешнего поля.
В формулировке Юнглинга это означает, что в общем случае модель
A0.13.1) имеет один набор показателей, а при У, = /3, /2 = -У4 — другой.
Хотя теперь мы видим, что при J{ = J3, J2 = -J4 модель обладает осо-
особой симметрией, априори это никоим ооразом не очевидно: симметрия
«скрыта». Вероятно, такое нарушение скрытой симметрии происходит и в
других моделях. Это трудно предвидеть.
10.14. ^yZ-ЦЕПОЧКА
С восьмивершинной моделью без внешнего поля тесно связана проб-
проблема определения собственных значений оператора
N
j
^ [Jxo}of+l + Jyo]oyj+l + JzVf°j + i], A0.14.1)
где Jx, Jyi Jz — постоянные величины,
of = ch о) = iCjSh of = Sj, A0.14.2)
a sl , . . . , sN, cl , . . . , cN — операторы, определенные формулой F.4.17).
Используя обозначения прямого произведения, получаем
of =
о) = е® ®e®d®e® ®e, A0.14.3)
где в каждом произведении имеется N членов, операторы с, d, s
появляются в позиции j, а е. с. d, s — спиновые матрицы Паули
J ( d ( ) ( -J- A014'4)
Все операторы о*, о?, of, ^представляют собой матрицы 2N x 2N.
Оператор jf в выражении A0.14.1) представляет собой гамильтониан
одномерной квантовомеханической модели ферромагнетика: N спинов
лежат на линии и пронумерованы индексом j' = 1 , . . . , TV; с каждым
спином j ассоциируется трехмерный вектор матриц Паули о- = (о?, о>\

262 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Энергия взаимодействия соседних спинов j и j' + 1 имеет вид
- ViUj • J • <jj + j, где J — диагональная матрица 3 х 3 с элементами Jх,
Jy, Jz. Статистическая сумма такой модели имеет вид
Хж = Trace ехр(-Ж/квТ). A0.14.5)
Если Jx = Jy = Jz, то получается модель Гейзенберга [57, 58, 109]. Если
Jx = Jy = 0, то оператор Ж диагоналей, и модель сводится к модели
Изинга с взаимодействием между ближайшими соседями (каждый спин
эффективно направлен вверх или вниз вдоль направления z). Такие модели
можно построить на решетке произвольной размерности, но с двумер-
двумерной восьмивершинной моделью связан одномерный случай A0.14.1).
Случай Jx = Jy = 0, отвечающий одномерной модели Изинга, рассмот-
рассмотренной в гл. 2, легко решается. Случай Л, = 0 известен как ЛТ-модель и
связан с моделью Изинга. Для всех собственных значений (при конечных
N) могут быть получены точные выражения и вычислена статистическая
сумма. Такие вечисления выполнены в работах [142, 161].
Случай Jx = Jy иногда называется моделью Гейзенберга — Изинга.
Бете [52] дал правильную форму выражений для собственных векторов
оператора <%*, в работе [263] строго доказана справедливость анзаца Бете и
в пределе больших N получено минимальное собственное значение га-
гамильтониана.
Когда Либ [157 — 159] решил модели типа льда, он обнаружил, что
собственные векторы трансфер-матрицы в точности совпадают с
собственными векторами оператора Гейзенберга — Изинга. Поэтому он
мог использовать многие результаты работы [263].
Сезерленд [220] прямо показал, что трансфер-матрица любой
восьмивершинной модели без внешнего поля коммутирует с оператором
Гамильтона XYZ-модепи. Поэтому они имеют одни и те же собственные
векторы. Я не был знаком с результатом Сезерленда, когда изучал восьми -
вершинную модель. (Большая часть работы была проделана на борту лай-
лайнера «Аркадия» в Атлантическом и Индийском океанах. Такая обстановка
помогает сосредоточиться, но затрудняет обмен информацией.) Из разд.
10.4 — 10.6 должно быть очевидно, что такие коммутационные соотноше-
соотношения тесно связаны с решением проблемы.
Действительно, можно показать [23, 26], что для любых Jx, Jyi Jz
оператор Нравен логарифмической производной от некоторой трансфер-
матрицы восьмивершинной модели. Поэтому можно вычислить минималь-
минимальное собственное значение оператора Ж Такое вычисление проводится в
настоящем разделе.
Для вычисления статистической суммы Z % нужно знать все
собственные значения оператора V. Найти все собственные значения очень
трудно, и в общем случае лучшее, что можно сделать, это свести данную
проблему к решению системы нелинейных интегральных уравнений (см.
замечания и ссылки на литературу в разд. 10.10, относящиеся к корреляци-
корреляционной длине).

ГЛАВА 10 263
СВЯЗЬ МЕЖДУ /ИК
Трансфер-матрица V восьмивершинной модели определена выражением
(9.6.1), в котором весовая функция w задана формулой A0.2.3) или
эквивалентной формулой A0.2.4). Такие определения можно записать в
следующем виде:
w(ia , а\Р , v) = Щ(а + с) + (а- фа] <5(д, /?) д(а, v) +
A0.14.6)
+ [{Ъ + d)-(b- d)tia] d{ii, -р) д(а,- v)},
где <5(а, 0) = 1 при а = C, д(а, C) = 0 при а* 0.
Рассмотрим сначала случай, когда выполняются условия
b = d = O, a = c = co>O. A0.14.7)
Тогда из A0.14.6) следует
w(fi, а\Р ,v) = c0 д(!л , /?) 6(or, i;). A0.14.8)
После подстановки A0.14.8) в (9.6.1) можно выполнить суммирование по
Hi , . . . , nN. Если через Ко обозначить матрицу V для данного случая, то
ее элементы (а, #) имеют вид
(VoU = <# в(«1, ft) <5(а2, Рз). . . d(aN, /3,). (Ю.14.9)
Таким образом, co~NVo представляет собой оператор левого сдвига, кото-
который переводит конфигурацию стрелок [а^ , ... , ctN] в конфигурацию
[aN, а, , . . . , aN _ ,}.
Рассмотрим теперь возмущение описанного выше случая и введем
величины
а = со+да, b = 6b, с = со+дс, d=6d, A0.14.10)
где да, bb, be, bd — бесконечно малые приращения весов а, Ь, с, d. Обозна-
Обозначим через 8w, 5V соответствующие приращения весовой функции w и
трансфер-матрицы V соответственно. Тогда из выражения (9.6.1) следует
/v
7-1 A0.14.11)
(заметим, что имеется два набора величин, обозначенных через 6s: прира-
приращения и символы Кронекера).
Умножим матрицу 8V слева на Vo~ К Из выражений A0.14.9) и
A0.14.11) тогда следует соотношение
t = c01^. . . d(ffy-i,#-i)dw(ffy, aj + i\Pj,pj+i) x
J~X A0.14.12)
Отсюда и из выражения (9.6.9), используя весовую функцию восьми-

264 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
вершинной модели, получаем
Vol 6V = Со1(диг + 6U2 + . . . + 6UN) , A0.14.13)
где 6Uj — приращение вершинного вектора Uj.
Подставляя выражение A0.14.6) для w в (9.6.9) и используя определения
F.4.17) величин Sj и cjy оператор Uj можно записать в виде
U,- = М(я + c)i + (а - c)SjSj+l + (b + d) CjCj + i - (b - d)sjCjsj + iCj + 1}
или, используя A0.14.2), в виде ' ' '
Ц = Ща + сK> + (b + d) ofof+l + (b-d) ofof+i + (a - c) ofo*+i},
A0.14.15)
где ./— тождественный оператор.
Добавка 8U- получается просто с помощью замены в A0.14.15) весов а,
Ь, с, d на ba, bb, be, bd. После выполнения такой замены выражение
A0.14.13) принимает вид
N
Vol 6V = BсоУг 2 {(& + 6с)» + FЬ + 6d) ojoj+\ +
i=l A0.14.16)
+ {6b - 6d) a,yof+l + (da - 6c) ojo;+1}.
За исключением аддитивного члена, пропорционального тождествен-
тождественному оператору ,У, выражение A0.14.16) представляет собой ATZ-оператор
вида A0.14.1).
Чтобы завершить такое отождествление, подставим значения величин
a, bt ct d A0.14.10) в A0.4.6). При этом с точностью до ведущего порядка
относительно приращений получим
поэтому формулу A0.14.16) можно записать в виде
V0-i 6V = 8Ь + 6d 2 \6"*df, $ + °]о*+, + Г а]о}+, + Д ojo]+ г} .
2cq y = i lob + od )
A0.14.18)
Если величины Jx, Jyi Jz связаны с Г и А соотношениями
Jx\Jy\Jz = 1 :Г: А, A0.14.19)
то получаем
Vo 6V = СоЧЩба + дс)$-FЬ + 6d) WJX}, A0.14.20)
где оператор Жъ точности равен оператору A0.14.1) для ^yZ-цепочки.
Предположим, что при изменении величин а, Ь, с, d параметры А и Г
сохраняются постоянными. Тогда все трансфер-матрицы V коммутируют
между собой и, как следует из A0.14.20), коммутируют с оператором Ж

ГЛАВА 10 265
Таким образом, если выражения A0.4.6) и A0.14.19) удовлетворяются при
одних и тех же значениях Г и А, то трансфер-матрица V восьмивершинной
модели коммутирует с гамильтонианом Jff А'У^-цепочки. Они имеют
одинаковые собственные векторы (это результат Сезерленда [220]).
Если с0, db, bd, Jx положительны, то из A0.14.20) следует, что
максимальное собственное значение Лтах матрицы V соответствует
минимальному собственному значению оператора Ж. При положительных
значениях величин а, Ь, с, d величина Лтах является тем собственным
значением, которое необходимо для вычисления свободной энергии для
восьмивершинной модели.
Энергия основного состояния Ео
Обозначим через NE0 минимальное собственное значение оператора Ж
Тогда Ео — энергия основного состояния на один узел. В пределе больших
N из формул A0.8.46) и A0.14.20) получаем следующее соотношение для
Ео:
d(-f/kBT) = Со Щба + 6с) - (db + dd) E0/Jx}, (Ю.14.21)
где / — свободная энергия восьмивершинной модели на один узел', а
8(—f/kBT) — соответствующее приращение величины —f/kBT.
До сих пор в настоящем разделе на величины А, Г, Jx, Jy, Jz не было
наложено никаких ограничений, за исключением условия Jx > 0. Рас-
Рассмотрим теперь основную область A0.7.5) восьмивершинной модели, в
которой выполняются условия (из A0.4.6))
|Г|<1, А<-1. A0.14.22)
Из выражений A0.14.19) и A0.14.22) следует
\Jy\<Jx< -Jz, A0.14.23)
поэтому я буду называть область значений Jx, Jy, Jv удовлетворяющих
условиям A0.14.23), основной областью для Л'УХ-цепочки. Из выражения
A0.7.1) следует, что параметры к, \ v эллиптической функции дей-
действительны и0<к<1,0<\<Г. При заданных значениях а, Ъ, с, d
свободная энергия / определяется формулами A0.4.21), A0.4.23), A0.7.9),
A0.7.18) и A0.8.47) или A0.8.49).
Постоянство величин Г и А эквивалентно постоянству параметров к и
X. В настоящем разделе без потери общности мы можем потребовать,
чтобы с = 1. Тогда из формул A0.4.21) и A0.4.23) получаем
а = snh i(A ~ v) /snh A, b = snh i(A + v) /snh A ,
A0.14.24)
c=l, d = ksnhi(k-v) snhi(A+y).
В качестве переменной остается величина v. Случай A0.14.7) со-
соответствует v = -X; увеличение v на 5v дает
v = -А+ до. A0.14.25)

266 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Из выражений A5.5.1а), A5.5.5) и A0.4.20) следует равенство
— snh v = en iv dn iv , A0.14.26)
dv
справедливое при всех комплексных v. Продифференцируем выражение
A0.14.24) по v с помощью данного равенства и положим v = -X; получим
6а!ди = -? сп /A dn /A /snh А, дЫди = i/snh A ,
&/би = О, &*/&; = ** snh А. (Ю.14.27)
(Теперь легко проверить, что выражения A0.14.17) и A0.4.17) экви-
эквивалентны.)
Вычислив b(—f/kBT) из A0.8.47) и A0.7.18) и подставив результат в
A0.14.21), получим следующее выражение для Ео:
Е - Ч _ ?Е V (*т-*-"УJA-*2т) A0.14.28)
где <7, х определены в A0.7.9), / — полный эллиптический интеграл первого
рода модуля к и
A0.14.29)
Используя A0.8.49) вместо A0.8.47), можно получить эквивалентное
выражение для Ео, а именно
E0 = i(-Jx + Jy + J2)-
_ m у х"т(хЪт - qml2) A - qmax~m) (I - х2т) A0Л4-30)
2/m = i (I -qm){\ +x2m)
Определим параметр / равенством
/ = 2**/A +к). A0.14.31а)
(Это эллиптический модуль, полученный с помощью преобразования
Ландена A5.6.1).) Исключая у2 (отрицательную величину) из двух
уравнений A0.4.12) и используя A0.4.9) и A0.14.19), получаем
/= (/2 _у2^/(<у2 _/2^ (Ю.14.316)
Разрешая A0.4.17) относительно sn /X и используя формулы A0.4.20) и
A0.14.19), получаем выражение
кк snh А = (Л ~ Jy)kl(Jx + Jy)k • A0.14.31b)
Подстановка A0.14.31в) в A0.14.29) дает выражение
г =k~\j2x- J2yY , A0.14.31r)
которое, используя A0.14.316), можно представить в виде
г= {Ilk)\j2-J2)\j2-J]y. A0.14.32)

ГЛАВА 10 267
Суммируем полученные до сих пор результаты. Если величины Jx, Jyi
Jz лежат в основной области A0.14.23), то приходящаяся на один узел
энергия основного состояния Ео ^fyZ-оператора ^A0.14.1) вычисляется по
формуле A0.14.28) или A0.14.30), где параметры к, X, г определены
выражениями A0.14.31), a q, x — выражением A0.7.9).
Симметрии
Три матрицы Паули оД оЛ of можно переставлять с помощью
простых преобразований, поэтому Ео является симметричной функцией Jx,
Jyi Jz. Предположим, что N четно, как в выражении A0.5.9), и рассмотрим
преобразование подобия
Ж-+ о\о\о\. . . Ж о\о\о\.... A0.14.33)
Поскольку oj антикоммутирует с aj и crj, но коммутирует со всеми другими
операторами Паули, влияние такого преобразования на оператор A0.14.1)
сводится к замене Jx и Jy на —Jx и — Jy. Следовательно, энергия Ео не
изменится при умножении на -1 любых двух величин из Jx, Jyi Jz.
Рассмотренные свойства симметрии можно использовать для отображения
произвольного ^fyZ-оператора #* в основную область A0.14.23). После
этого энергия основного состояния Ео вычисляется по формуле A0.14.28)
или A0.14.30).
Конечно, указанные свойства симметрии связаны с соответствующими
свойствами восьмивершинной модели. Из выражений A0.4.6), A0.14.19) и
A0.2.16) следует
Jx:Jy:Jz = ab + cd : ab - cd : \{a2 + b2 - с2 - d2)= A0.14.34)
= w\ - w\ + w2 - wl: Wi - и>2 - w2 + w\: w\ + w\ - w2 - w\.
Очевидно, что применение симметрии восьмивершинной модели
A0.2.11) — A0.2.15) или, что эквивалентно, A0.2.17) приводит просто к пе-
перестановке членов в правой части соотношения A0.14.34) и, возможно, к
умножению двух из них на - 1.
Сингулярности функции Ео
Из приведенных результатов следует, что Ео — аналитическая функция
переменных Jx, Jyi Jz всюду, кроме поверхности, на которой модули двух
наибольших переменных равны. Основным является случай —J7 = JX>
> \Jy\. Эти условия определяют границу основной области A0.14.23). Как
видно из формул A0.14.31), на этой границе к = 1. Поведение вблизи
границы можно получить, применяя формулу суммирования Пуассона
A5.8.1) к ряду, входящему в A0.14.28). Указанные выкладки весьма близки
к выполненным в A0.12.8) — A0.12.12) (фактически результат можно
получить из них с помощью дифференцирования по w). При -Jy > J >

268 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
> \Jy\ получаем
00 <л
^ р
- 4 2а (COS 2n\i - COS ПЛ COS П\1) tan П\1 _ 2n\
00
4.7Г ^ /
Z> COt[(n - \O^l\i\p{2n~XOllil A -pB"
где /г, /? определены формулами A0.12.5) и
[cosh (л - 2\i)u - cosh \ш\ sinh дм .._ ч , nn ы ^ч
sinh ли cosh \ш
Случай Jx> —Jz> \Jy\ можно отобразить в основную область, умно-
умножив на - 1 и переставив параметры Jx и Jz. При этом так же, как при
перестановке функций w{ и vv4 в восьмивершинной модели, \к не изменится,
а р перейдет в —р. Функции /г и /?2 аналитические при переходе через
границу —Jz = Jx, в то время как вблизи границы
р * —|у2 _у2| /(/2 _у2) ? A0.14.37)
т.е./? обращается в нуль линейно по I Уг + /^ I.
Заменив в формуле A5.6.6) модуль к' на А: и использовав A0.14.3Га) и
A0.12.5), получим ю
/'(Л//)* = *;гПA "Р2"J^1 +Р2ЛJ- A0.14.38)
Отсюда и из формулы A0.14.32) очевидно, что изменение знака и
перестановка величин Jx и Jz не изменяют множитель Jx/(rl') в A0.14.35), и
этот множитель является аналитической функцией на границе Jz= -Jx.
Таким образом, все члены в A0.14.35) аналитичны при пересечении этой
границы, кроме слагаемых в последней сумме. Доминирующий
сингулярный член имеет вид
(?o)sing = {2л2т1ра') сог(л2/2ц)р^. A0.14.39)
Если Jz— —Jx, то к = 1, / = 1, /' = тг/2, snh X = tan X поэтому из
формул A0.14.31в) и A0.12.5) следует, что величина \к определяется соотно-
соотношением
Jy/Jx = cos /i, 0<jU<;r, A0.14.40)
а для г из A0.14.32) получаем
A0.14.41)
так что выражение A0.14.39) упрощается и принимает вид
(?o)sing = 4Л/Г1 Jx sin ft со1(я2/2/|) р"">, (Ю.14.42)

ГЛАВА 10 269
где р определено выражением A0.14.37). При условии что функция
cot (тг2/2^) койечна и не равна нулю, из A0.14.42) следует, что при
Jz = —Jx функция Ео имеет степенную сингулярность
A0.14.43)
Сравнивая выражения A0.12.20) и A0.12.21) с выражениями A0.14.42) и
A0.14.37), видим, что (при всех значениях р) Ео имеет такую сингулярность
при Jz + Jx = 0, как и свободная энергия восьмивершинной модели при
t = 0.
Некоторые общие замечания о (/-мерных моделях
изинга и (d - 1)-мерных квантовомеханических
МОДЕЛЯХ
Уравнение A0.14.20) связывает ATZ-оператор Jfc трансфер-матрицей V
восьмивершинной модели. Здесь матрица V вычисляется при значениях ве-
весов a, Ъ, cf d, бесконечно близких к значениям A0.14.7), при которых
трансфер-матрица равна простому оператору сдвига.
Как показал Сузуки [222], подобные связи существуют для многих
моделей. Например, трансфер-матрица слой — слой модели Изинга на
простой кубической решетке имеет элементы
V(o, &) = cxpi 2j 2j [b(KiOijOi+\ j + K\<j\jOi+\ i +
U=l/=1
A0.14.44)
Здесь a = [an , . . . , aMN\ обозначает все спины в одном слое решетки, а
о> = [°"ii » • • • » °mn} — все спины в следующем слое.
Определяя операторы s-, ctj по аналогии с F.4.17) и используя тожде-
тождество F.4.22), получаем
B sinh 2К3УШ" V = exp[i(tfiA + К2В)\ ехрДОС] exp[i(A:^ + К2В)],
A0.14.45)
где tanh K3 = ехр (-2К3) и
М N М N м N
_ (,. A0.14.46)
i=l y=l ' ' i=ly=l i=ly=l
Если К{ = K2 = K3* = 0, то правая часть выражения A0.14.45) является
просто тождественным оператором. Если все величины Кх, К2, К^ малы,
то с точностью до первого порядка имеем
ln[B sinh 2КЪ)~Ш" V] = Ж , A0.14.47)
где теперь
Ж = КА + К В + К*С A0.14.48)
Как и в выражении A0.14.2), величины siJf ctj являются операторами

270 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Паули оу* и о^ соответственно. Поэтому правую часть A0.14.48) можно
рассматривать как некоторый двумерный оператор гейзенберговского
типа, в котором квантовомеханические спины взаимодействуют друг с
другом через свои z-компоненты, а внешнее поле напряженности К3*
приложено в направлении оси х.
Если К3* = 0, то оператор диагоналей, и его собственные значения
являются энергетическими уровнями двумерной модели Изинга. По этой
причине оператор ^известен как гамильтониан двумерной модели Изинга
в поперечном магнитном поле [183, 195, 217].
Из выражения A0.14.47) следует, что если бы мы могли вычислить
собственные значения трансфер-матрицы V трехмерной модели Изинга, то
могли оы также вычислить их для двумерного гамильтониана <Ж Наобо-
Наоборот, можно надеяться, что решение последней проблемы приведет к
решению первой. К сожалению, ни та, ни другая проблема не решена точ-
точно, хотя приближенные методы, рассмотренные в разд. 1.5, привели к
полному успеху.
Приведенные выше аргументы легко распространить на решетки других
типов и размерностей. Однако следует отметить, что двумерная
восьмивершинная модель без внешнего поля обладает одним исключи-
исключительным свойством: которое указанным способом не обобщается на другие
системы: трансфер-матрица V такой модели всегда коммутирует с некото-
некоторым ^fyZ-оператором, даже если V значительно отличается от Ко, со-
соответствующего оператору сдвига.
10.15. СВОДКА ОПРЕДЕЛЕНИЙ ДЛЯ ВЕЛИЧИН Д, Г,
к, X, vy q, x, z> p> [I, w
Результаты, полученные в настоящей главе, с неизбежностью
выражались через параметры эллиптических функций, такие, как q> x, p, fi.
Последние вводились по мере необходимости для восьмивершинной
модели, для модели ^fyZ-цепочки и для некоторых особых случаев,
рассмотренных выше. Представляется полезным представить со-
соответствующие определения в общем виде.
Величины Д и Г для восьмивершинной модели с больцмановским весами
а, Ьу с, d определяются выражениями A0.4.6), т. е.
а2 + Ь2 - с2 - d2 ab-cd (Ю.15.1а)
2(ab + cd) ' ab + cd
Для ^fyZ-цепочки с коэффициентами Jx, Jyi Jz те же величины
определяются выражениями A0.14.19), т. е.
Л:^:Л = 1:Г:Д. A0.15.16)
Собственные векторы трансфер-матрицы восьмивершинной модели и
^fyZ-гамильтониана представляют собой одни и те же функции, зависящие
только от Г и Д.

ГЛАВА 10 271
Процедура перестройки
Отобразим теперь рассматриваемые модели в соответствующие основ-
основные области. В случае восьмивершинной модели нужно воспользоваться
процедурой 1 — 3, описанной в разд. 10.11. Пусть а, Ь, с, d — исходные
значения больцмановских весов, a ar, br, cr, dr — их перестроенные значе-
значения. Тогда веса ar, br, cr, dr лежат в основной области A0.7.5) или на ее
границе (поскольку свободная энергия и другие характеристики системы
являются непрерывными функциями а, Ь, с, d, граничные случаи можно
рассматривать, переходя к подходящим пределам), т. е.
cr^ar+ br + dn яг^0, br^0, dr^0. A0.15.2)
Определим Аг, Гг по формулам A0.15.1а), заменяя а, Ь, с, d на ar, br, cr, dr.
Отсюда следует
Гг|^1, Дг^-1, A0.15.3)
где равенства достигаются только на границах области A0.15.2).
Для ATZ-цепочки процедура перестройки значительно проще. Нужно
просто переставить величины Jx, Jyi Jz и, возможно, изменить знаки у двух
из них так, чтобы отобразить их в область A0.14.23) или на ее границу.
Пусть f^ Jryt Jrz — перестроенные указанным способом величины. Тогда
имеем
\ry\^Jrx^-Jrz. A0.15.4)
Определим Д , Г по формуле A0.15.16), в которой J , J , J заменены на
f f f т е
jx, jy jv т. е.
Tr = Jry/Jrx, Ar = Jrz/Jx. A0.15.5)
Отсюда ясно, что такие величины Ar, Tr также удовлетворяют условиям
A0.15.3).
Как было показано в A0.14.34), преобразование симметрии вось-
восьмивершинной модели приводят просто к перестановке величин ab +
+ cd, ab — cd, Vi (a1 + b1 — c1 — d2) и, возможно, к изменению знаков
двух из них. Из формул A0.15.1) следует, что существует эквивалентный
способ определения Гг, Аг для восьмивершинной модели, состоящий в
следующем.
Определяем Г, Д по формулам A0.15.1а) и выбираем Jx, Jy, Jz так,
чтобы удовлетворялись соотношения A0.15.1а), и выбираем Jx, Jy, Jz так,
чтобы удовлетворялись соотношения A0.15.16), причем Jx > 0. Пере-
Переставляем Jx, Jyi Jz и изменяем знаки у двух из них так, чтобы удовлет-
удовлетворялись условия A0.15.4). Определяем величины Гг, Аг по формулам
A0.15.5).
Такое альтернативное определение окажется полезным в следующем
разделе.
Параметры эллиптических функций
Параметры эллиптических функций к, X определяются по формулам
A0.4.17) или, что эквивалентно, с помощью выражений A0.4.9), A0.4.12) и
A0.4.16), в которых используются перестроенные значения Гг, Аг величин

272 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Г, Д. Соответствующие уравнения можно записать в виде
2А*/A + к) = A - Г?)»/(Д? - Г?)', A0.15.6а)
snh А = АГ» A - Гг)*/A + Г,)*, A0.t5.66)
где snh и = — / sn ш, и &, X должны удовлетворять условиям
0*?**?1, О^А^Г. A0.15.7)
Величины / и /' — полные эллиптические интегралы первого рода модулей
к и к' = A - ?2I/2 соответственно. В A0.15.7) равенства достигаются
также только на границах области.
В случае восьмивершинной модели параметр v теперь легко получить из
выражений A0.4.21) и A0.4.23), используя перестроенные значения величин
а, Ь, Су d, например
snh i(A -v) = (ar/cr) snh A , A0.15.8)
причем должно выполняться условие
-А^у^А. A0.15.9)
Параметры q, х, z определяются из A0.7.9) и A0.7.18), т. е.
q = exp(-jzl'/l), х = ехр(-тгА/2/), z = ехр(-от/2/), A0Л5Л°)
и удовлетворяют условиям
0^q^x2^l, x^z^z'1. A0.15.11)
Наконец, параметры ру \к и w задаются выражениями A0.12.5), т. е.
р = ехр(-2я////), ц = лк/Г, w = jw/F, A0.15.12)
и удовлетворяют условиям
l, O^p^JZ, M^jU. A0.15.13)
Модели описывают критическое состояние тогда и только тогда, когда
к = 1. В этом случае, как следует из гл. 15, /= тг/2, I = ао, q = \9 р = 0,
в то время как X, v, \ky w конечны, согласно A0.15.6) — A0.15.13), Аг = — 1
и х = z = 1.
10.16. ЧАСТНЫЕ СЛУЧАИ
Существует три частных случая восьмивершинной модели, которые
были решены до решения общей модели без внешнего поля: модель Изинга
[184], рассмотренная в гл. 7, модель «свободных фермионов» [83] и модель
типа льда, или «шестивершинная модель» [157 — 159], рассмотренная в гл.
8. Указанные случаи связаны с XZ-, XY-моделями и моделью Гей-
зенберга — Изинга соответственно. В каждой модели соответствующее
критическое значение параметра \к равно 0, тг/2 или тт. Эти частные случаи
детально исследованы в работах [84, 123].

ГЛАВА 10 273
МОДЕЛЬ ИЗИНГА И ^ГУ-ЦЕПОЧКА
Как показано в разд. 10.3, обычная модель Изинга с взаимодействием
между двумя ближайшими спинами является частным случаем восьми-
восьмивершинной модели, который реализуется при выполнении условия
A0.3.10), т. е. cd = ah. Отсюда с учетом A0.15.1а) следует
Г = 0. A0.16.1)
Как видно из выражения A0.15.16), это условие соответствует Jy = 0,
т. е. .YZ-случаю .YyZ-модели. Процедура перестройки величин Jx, Jyi Jv
приводящая к условию A0.15.4), должна сохранить равенство нулю
коэффициента Jy. Поэтому из выражения A0.15.5) получаем
Гг = 0. A0.16.2)
Из A0.15.66), A5.4.32) и A0.15.12) получаем
А=*/', \1 = Ы. A0.16.3)
Таким образом, \к лежит точно в середине допустимого интервала
изменения @, тг).
Критические показатели а, 0, *>, /и5, определенные по формулам
A0.12.24), в точности совпадают с соответствующими значениями в
G.12.12) и G.12.14). Отметим, что рассматриваемый случай представляет
собой модель, в которой тг/ji — четное целое число; поэтому сингуляр-
сингулярность свободной энергии определяется множителем In 11\, как в выра-
выражениях A0.12.226) и G.12.10). Аналогично в выражении A0.14.43) появ-
появляется множитель In 1У^ + Jx\.
МОДЕЛЬ СВОБОДНЫХ ФЕРМИОНОВ
Фан и By [83] для решения восьмивершинной модели при условии
(DiO>2 + СО3Щ = (О5С06 + OO(Dg A0.16.4)
использовали метод пфаффиана, рассмотренный в разд. 7.13. Здесь ш1 , . . .
..., ы8 — больцмановские веса, определенные в A0.1.2). Указанный
метод применим, даже если не выполняются условия A0.1.5), т. е. он при-
пригоден для решения восьмивершинной модели во внешнем поле.
В случае когда внешнее поле отсутствует, ограничение A0.16.4) с учетом
A0.2.1) принимает вид
a2 + b2 = c2 + <f, AОЛ6.5)
поэтому из выражения A0.15.1) следует, что А = 0 и Jz = 0. Таким обра-
образом, эта модель соответствует ^У-цепочке. Процедура перестройки вели-
величин Jx, Jy) Jv приводящая к условию A0.15.4), должна давать Jy = 0, т. е.
^У-модель преобразуется в .YZ-модель. Тогда из A0.15.16) получаем
Гг = 0, A0.16.6)
что соответствует только что рассмотренной модели Изинга. Следо-
Следовательно, модель свободных фермионов без внешнего поля можно отоб-
отобразить на модель Изинга, поэтому параметр \к в модели фермионов ра-

274 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
вен тг/2. Но ограничение A0.16.5) приводит к тому, что веса а, Ь, с, d
всегда лежат в области беспорядка III (разд. 10.11), так что в данной
модели переход в упорядоченное состояние отсутствует.
Шестивершинная модель и цепочка
гейзенберга — изинга
Шестивершинная модель получается из восьмивершинной при d = 0,
поэтому из A0.15.1) следует Г = 1 и
Jx = Jy. A0.16.7)
Следовательно, такая модель соответствует цепочке Гейзенбер-
га — Изинга, и собственные векторы трансфер-матрицы должны совпа-
совпадать с собственными векторами гамильтониана Гейзенберга —
Изинга. Либ [157 — 159] определил такое состояние и использовал
его в своих расчетах.
Параметры гамильтониана Гейзенберга — Изинга выберем следующим
образом: (Jx, Jy, Jz) = A, 1, А). При таком выборе условие A0.15.16) удов-
удовлетворяется. Переставим величины Jx, Jy) Jz и изменим знак у двух из них
так, чтобы выполнялись требования A0.15.4). Определим параметры
эллиптических функций, в частности к, X и /г, с помощью выражений
A0.15.5) — A0.15.13). Существуют три различных случая, которые, как это
легко увидеть, соответствуют сегнетоэлектрически упорядоченной, неупо-
неупорядоченной и антисегнетоэлектрически упорядоченной фазам, рассмот-
рассмотренным в разд. 8.10:
1. А > 1 (сегнетоэлектрический порядок): Гг = -1, Аг = -А,
к = 0, А = Г = оо, \х = п .
2. - 1 < А < 1 (беспорядок); Г,. = -А, Аг = - 1,
к=1, A = ijU, A=-cosjU. A0.16.8)
3. А < -1 (антисегнетоэлектрический порядок): Гг = 1, Аг = А,
fc = 0, A =-cosh А, ^ = 0 .
Особенно интересен второй случай, поскольку здесь к = 1. При этом
восьмивершинная модель описывает критическое состояние. Значит, в
данной фазе шестивершинной модели корреляционная длина равна беско-
бесконечности (для случая свободных фермионов в рамках шестивершинной
модели последнее утверждение установлено точно [19]). Система не упо-
упорядочена только в том смысле, что спонтанная поляризация равна нулю.
Наоборот, критическое состояние восьмивершинной модели можно
отобразить на «неупорядоченное» состояние шестивершинной модели.
Шестивершинная модель имеет два перехода — при А = +1 и при
А = - 1. Первый переход имеет место в сегнетоэлектрических моделях,
таких, как модель KDP. В этом случае из A0.16.8) видно, что параметр \к

ГЛАВА 10 275
принимает свое максимально возможное значение, равное тг. Как показано
в разд. 8.11, данный переход является переходом первого рода, и
упорядоченное состояние заморожено. Указанное свойство затрудняет
интерпретацию результатов для общей восьмивершинной модели, но заме-
заметим, что формулы (8.11.8) и (8.11.10) правильно воспроизводятся в
A0.12.24).
Переход при А = - 1 имеет место в антисегнетоэлектрических моделях,
таких как F-модель. Из A0.6.8) следует, что параметр \к равен
нулю — своему минимальному возможному значению. Вывод критических
свойств A0.12.22) и A0.12.23) в данном случае не справедлив. Конечно,
правильный расчет приводит к существенным сингулярностям в
выражениях (8.11.14) — (8.11.25), но не позволяет разумно определить
критические показатели. Следует заметить, однако, что если просто поло-
положить \х = 0 в выражении A0.12.24), то получится бесконечный критический
показатель (8.11.18). Итак, «соотношения показателей» (8.11.26) дей-
действительно удовлетворяются в общей восьмивершинной модели.
10.17. ТОЧНО РЕШАЕМАЯ НЕОДНОРОДНАЯ
ВОСЬМИВЕРШИННАЯ МОДЕЛЬ
До сих пор восьмивершинная модель, рассматриваемая в настоящей
главе, считалась однородной, т. е. энергии вершин ех , ... , е8 были
одинаковыми для всех узлов решетки. Для точно решаемого случая, когда
внешнее поле равно нулю, однородность модели означает, что
больцмановские веса а, Ь, с, d, определяемые выражениями A0.1.2) и
A0.2.1), не зависят от узла.
Такое ограничение можно ослабить некоторым весьма специальным
способом и тем не менее вычислить свободную энергию и другие
характеристики путем прямого обобщения изложенных выше методов.
При этом применяются в точности те же уравнения, но используется
несколько более общая интерпретация переменных.
Различные столбцы
Предположим сначала, что больцмановские веса а, Ъ> с, d могут
изменяться при переходе от одного столбца к другому, но не зависят от
номера ряда решетки. Обозначим через ctj, bJf cjt dj значения весов, со-
соответствующие j-му столбцу. В решетке имеется N столбцов, так что
j = 1 , . . . , N.
Рассмотрим соотношение звезда — треугольник A0.4.1), которое
получается из выражений (9.6.5) — (9.6.8). Матрицы S и S' теперь зависят
от номера столбца j9 которому они соответствуют, т. е. от положения j в
матричных произведениях (9.6.5) и (9.6.6). Даже в этом случае еще
справедливо (при условии что матрица М не зависит от j) утверждение,'
что из соотношения (9.6.7) следует равенство выражений (9.6.5) и (9.6.6).
Отмеченное выше условие соответствует, тому, что w" и, следо-
следовательно, введенные в разд. 10.4 величины а", Ь", с", d" не зависят от j.

276 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
Величины А" и Г" также не зависят от j, поскольку они определяются
выражениями A0.4.6), в которых веса а, Ъ, с> d заменены на а", Ь", с",
d". Из A0.4.26) следует, что таким же свойством должны обладать
величины Д, Г, Д', Г'.
Определим для каждого столбца j параметры р, к, X, v с помощью
A0.4.24). Из формулы A0.4.17) следует тогда, что к и X не зависят от У и
одинаковы для трансфер-матриц V и V.
Поскольку равенства A0.4.26) удовлетворяются, соотношение
звезда — треугольник сводится к A0.4.30). Здесь переменные и, и' могут
зависеть от У, но и" не может зависеть от j. Обозначим через Vj(Vj) значе-
значение параметра v для 7-го столбца и трансфер-матрицы V (V). Тогда из
A0.4.23) следует
v\ ~ V] не зависит от у. A0.17.1)
Подведем итоги. Трансфер-матрица К определяется выражением (9.6.1),
где каждая функция и> зависит от номера столбца У, которому она со-
соответствует, т. е. от места в произведении матриц. Для У-го столбца
функция w задается выражениями A0.2.3) и A0.4.24), в которых параметры
к и X не зависят от j и
и, = 1>*+и. A0.17.2)
(Нормировочный множитель р входит в уравнения тривиально и может
изменяться любым способом; я буду считать его здесь постоянным, не
зависящим от узла решетки.)
Тогда две трансфер-матрицы коммутируют между собой, если они
имеют одинаковые значения параметров к, \ v{° , . . . , v%. Собственные
векторы таких матриц не зависят, следовательно, от v. Они зависят только
от к, X и от разностей величин v х , . . . , vN.
Будем рассматривать V как функцию V(v). Тогда снова выполняется
равенство A0.4.25).
Теперь легко обобщить выкладки, проведенные в разд. 10.5. Величины
а, Ь, с, d в A0.5.1) следует заменить на aJf bj, Cj, dj. Но параметры Д и у в
выражении A0.5.2) не зависят от У; поэтому^ все еще задается формулами
A0.5.14) и A0.5.8). Переменные и и и в A0.5.11) — A0.5.21) следует заме-
заменить на и- и Vj, все еще связанные равенством A0.4.23). Множители
{ph[Vi(k±v)]}N в выражении A0.5.23) следует заменить очевидным образом
на произведение величин pjh(Vi(K±Vj)]y У = 1 , . . . , N; увеличение v на
±2Х' нужно понимать как увеличение каждого параметра Vj на ±2Х\ Но
если Vj представлено в виде A0.17.2), где каждая величина Vj считается
постоянной, то увеличение каждого параметра v- на ±2Х' приводит в
точности к тому же, что и увеличение v на ±2Х\ Следовательно, мы сно-
снова получаем выражение A0.5.32), но теперь формула A0.5.24) заменяется
формулой
Л'

ГЛАВА 10 277
При условии что каждая величина Vj лежит в области (-Х, X), дальней-
дальнейшие выкладки проводятся фактически так же, как в разд. 10.8. Основное
изменение состоит в том, что определение A0.8.10) величины A(v)
заменяется на
00 N
A(v) = П Ш1 -<Texp[-jr(o70+ V)l2l]}. (\0МЛ)
т = О / = 1
Заметим также, что величины vl , . . . , vn, рассматриваемые в разд. 10.8,
отличны от величины v { , . . . , vN настоящего раздела.
Будем рассматривать правую часть уравнения A0.8.47) как функцию
больцмановских весов а, Ь, с, dy причем параметры q> x, z определены так
же, как в разд. 10.5. Введем для нее обозначение — ф(а, Ь, с, d)> т. е.
гр(а , & , с, d) = -Inс -
_ у х~т(х2т - дтJ (хт + х~т -zm- z~m) A0.17.5)
m = i m(l - q^) A + x^)
Тогда для рассматриваемой неоднородной системы выражение A0.8.44) (в
пределе больших N) принимает вид
N
In Лтах = - 2 УЦ , Ъ,, с,, dj). (Ю-17.6)
/=1
Замечательно простой результат!
Все другие свойства, рассматриваемые в разд. 10.10, не зависят от t\
поэтому полученные там выражения справедливы и для данной неоднород-
неоднородной модели.
Различные ряды
Рассмотрим теперь решетку, в которой больцмановские веса а, Ь, с, d
могут изменяться как при переходе от ряда к ряду, так и при переходе от
столбца к столбцу. Обозначим их значения для узла в /-м ряду и 7-м столб-
столбце через ajj, b^, c^, d^. Определим параметры о, к, X, v для каждого узла с
помощью A0.4.24) и потребуем, чтобы для всех /, j выполнялись условия
к Я не зависят от / и у,
A0.17.7)
= V® +
где vtj — значение параметра v в узле (/, j), a v°x , . . . , v°N и v\ , . . . ,
vlM— некоторые параметры, которые находятся в нашем распоряжении.
Теперь трансфер-матрица V зависит от номера ряда /, к которому она
относится, поэтому обозначим ее V{. Тогда выражение (8.2.1) принимает
вид
Z = Trace ViV2...VM. (Ю.17.8)
Заметим, что к, X и разности величин vn , vi2 , . . . , viN не зависят от /.
Из замечаний после формулы A0.17.2) следует, что собственные векторы
матрицы Vt не зависят от номера /: все матрицы К, , . . . , Vм коммути-

278 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ РЕШЕТКЕ
руют между собой. При условии что каждая величина vtj лежит в области
(-Х, X), все матрицы Vt имеют один и тот же максимальный собственный
вектор. Следовательно, обобщение выражения (8.2.4) имеет вид
Z ~ ЛтахA).... Лтах(М) , A0.17.9)
где Лтах(/) — максимальное собственное значение матрицы Vt. Поэтому из
формул A0.17.6) получаем
м N
In Z = - 2 2 VK , Ьч > сч > da) • A0.17.10)
Подобно формуле A0.17.6), данное выражение имеет изумительно про-
простой смысл: полная свободная энергия F = —квТ lnZ равна сумме свобод-
свободных энергий отдельных узлов (но только в пределе больших М и N и при
выполнении условий A0.17.7)). Ясно, что такое «расцепление» связано с
коммутационными свойствами трансфер-матриц.
Как и выше, все не зависящие от v свойства (поверхностное натяжение,
корреляционная длина, намагниченность, поляризация) должны быть
такими же, как соответствующие свойства однородных систем при тех же
значениях параметров /г и Л.
К сожалению, я не знаю физически интересных неоднородных систем,
удовлетворяющих условиям A0.17.7). Большой интерес представляет
восьмивершинная модель с различными весами на двух подрешетках,
поскольку она содержит как частные случаи модель Изинга в магнитном
поле [261] и модели Поттса и Эшкина — Теллера (гл. 12). Но такая модель
не удовлетворяет условиям A0.17.7).
Тем не менее с математической точки зрения рассмотрение обобщений
восьмивершинной модели на неоднородные системы может оказаться
полезным. При вычислении спонтанной поляризации в шестивершинной
модели антисегнетоэлектрика [29] широко использовалась такая форма
зависимости собственных векторов трансфер-матрицы от величин
vj°, . . . , Vfr Замечания, сделанные после формулы A0.17.2), играют
ключевую роль в гл. 13 при установлении мультипликативных свойств уг-
угловых трансфер-матриц.

11
ВОСЬМИВЕРШИННАЯ МОДЕЛЬ
НА РЕШЕТКЕ КАГОМЕ
11.1. ОПРЕДЕЛЕНИЕ МОДЕЛИ
Небольшое дополнительное исследование позволяет обобщить результаты
гл. 10 на особый класс восьмивершинных моделей на так называемой ре-
решетке кагоме 1\ показанной на рис. 11.1. Не все восьмивершинные модели
на решетке кагоме принадлежат к указанному классу; к нему относятся
только такие модели, больцмановские веса которых удовлетворяют огра-
ограничениям A1.1.7). Тем не менее данный класс моделей представляет инте-
интерес, поскольку он содержит как частные случаи модели Изинга на тре-
треугольной и шестиугольной решетках, критические модели Поттса на тех же
решетках (гл. 12) и трехспиновую модель на треугольной решетке [42, 43].
Восьмивершинная модель может быть построена на любом графе или
решетке, у которых в каждом узле сходятся четыре ребра. (Слово «граф»
используется здесь для обозначения любого набора узлов и соединяющих
их ребер; «решетка» представляет собой регулярный граф.) Расположим
стрелки на ребрах (по одной стрелке на каждом ребре). Разрешенными яв-
являются только такие конфигурации, в которых к любому узлу графа на-
направлено четное число стрелок. Для каждого узла / возможны восемь ти-
типов конфигураций стрелок. Припишем у-й вершинной конфигурации на /-м
\
P Q
¦*~в
л / л / V/
Рис. ILL Решетка кагоме с тремя разными типами A, 2, 3) узлов. Показаны также
три узла Р, Q, R и некоторые типичные стрелки с горизонтальными проекциями,
направленными вправо.
^ Эта решетка напоминает некоторые образцы японских плетений из бамбука, носящих такое
название. — Прим. ред.

280 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
узле энергию е- и больцмановский вес
щ = ехр(-Ец/квТ), A1.1.1)
где кв — постоянная Больцмана, Т — температура. Тогда статистическая
сумма имеет вид
= 2 Ц
(П-1.2)
где суммирование проводится по всем конфигурациям С стрелок данного
графа, произведение берется по всем узлам /, a j(i, С) — тип вершинной
конфигурации стрелок на узле /, соответствующий конфигурации С.
На каждом узле / мы всегда можем обозначить восемь типов вершин-
вершинных конфигураций так, чтобы каждый четный тип получался из предшест-
предшествующего нечетного с помощью обращения всех четырех стрелок. Тогда ус-
условие отсутствия внешнего поля имеет вид
«л = a>j2, а>,-з = а>,-4, a)i5= u>ib, а>,7 = а>й . A1.1.3)
Удобно ввести обозначения ai9 bi9 с,-, dt для величин ып, Ы|-3, ы/5, ы/7:
con ,. . . , (oiS = ah at, bh bh ch ch dh dt. A1.1.4)
Для однородной квадратной решетки, в которой вершинные конфигура-
конфигурации стрелок упорядочены так, как показано на рис. 10.1, величины ah bh с,,
di не зависят от номера / и соответствуют весам а> Ь, с, d в A0.2.1).
Рассмотрим теперь решетку кагоме. На рис. 11.1 видно, что существу-
существуют три типа узлов. Назовем их просто узлами типа 1, 2 и 3 и предполо-
предположим, что все узлы одного типа имеют одинаковые энергии взаимодействия
и одинаковые больцмановские веса. Тогда мы можем использовать символ
bj для обозначения величины Ъ для всех узлов типа 1 и аналогично av bv
Cj, flfj, a2, bv c2, d2, я3, Ь3, c3, dr
a, a, 6, 6, с, с, d, ' d,
az az b2 bz cz cz dz dz
xxxxxxxx
a3 a3 b3 b3 c3 c3 d3 d3
Рис. 11.2. Три типа вершин решетки кагоме и восемь вершинных конфигураций,
разрешенных для каждого типа. Под каждой конфигурацией указаны со-
соответствующие больцмановские веса.

ГЛАВА 11 281
1 ,i\
¦ v
г / s и \г
a v
Рис. 11.3. Три типа вершин решетки кагоме; д, а, /3, v — стрелки-спины на ребрах,
окружающих вершину; г, s, t, и — грани, окружающие вершину.
Порядок всех вершинных конфигураций стрелок для узлов типа / пока-
показан в i-й строке рис. 11.2. Такое расположение вершинных конфигураций
обладает следующим свойством симметрии: конфигурации любой строки
могут быть получены из конфигураций предыдущей строки с помощью по-
поворота на 120° против часовой стрелки.
Для каждого узла типа / полезно определить вершинную весовую функ-
функцию W; по аналогии с A0.2.3). Чтобы установить связь с соответствующи-
соответствующими уравнениями в гл. 9 и 10, удобно воспользоваться следующим асиммет-
асимметричным способом.
Каждому ребру т сопоставим «стрелку-спин» ат, принимающий значе-
значение + 1 (-1), если соответствующая стрелка имеет проекцию, направлен-
направленную вправо (влево). (Некоторые типичные, направленные вправо стрелки
показаны на рис. 11.1) Рассмотрим некоторый узел типа / и обозначим че-
через /х, а, /3, v стрелки-спины, лежащие на окружающих его ребрах, распо-
расположенных так, как показано на рис. 11.3. Обозначим через w/(/x, a I 0, v)
больцмановский вес соответствующей конфигурации стрелок, показанной
на рис. 11.2. Значения функций Wj, w2, w3 приведены в табл. 11.1.
Сравнивая данное определение функции н'Д/х, а I C, v) с A0.2.3), мы ви-
видим, что оно совпадает с определением каждой функции w,- по формуле
A0.2.3), в которой веса а, Ъ, с, d заменены на aif b{i cif d{ и величины аъ и
Ъъ переставлены. Теперь статистическую сумму можно записать в виде,
+ , +1
+ . -1
+ . -1
+ , +1
Значения функций w,
+, + И -,
-, + И -,
+ , - и -,
- , - и - ,
afifiv = -
-I-, -
+ I+, -
+ 1 -, +
-1
а 1/3,
v)
»х
ах
Ьх
с,
d\
0
w2
а2
b2
с2
d2
0
Таблица 11.1
w3
^3
cr3
с3
^3
0

282
ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
аналогичном A0.2.6), а именно
<Хт\<Хр
A1.1.5)
где суммирование проводится по всем наборам стрелок-спинов а = [а{,
а2» • • • )» произведение берется по всем узлам решетки, символ / для каж-
каждого узла обозначает тип данного узла, а индексы /, т, р, q обозначают
окружающие данный узел ребра, расположенные так же, как ребра /х, а, /3,
v на рис. 11.3.
Ограничение звезда — треугольник
Из рис. 11.1 очевидно, что в решетке кагоме имеется два типа треуголь-
треугольников: с вершинами, обращенными вверх и вниз. Рассмотрим треугольник
одного из этих двух типов и обозначим через alt. . . , а6 стрелки-спины на
внешних ребрах и через 0V /32, /33 стрелки-спины на внутренних ребрах, как
это показано на рис. 11.4.
Указанные два типа треугольников определяют в выражении A1.1.5)
слагаемые вида
, ar2|ft,
> ft
, ft 1*4,
соответвенно. В любом случае все остальные множители в A1.1.5) не зави-
зависят от j8j, j82, j83. Поэтому можно выполнить суммирование по j8j, j82, i33,
определяющее эффективный полный вес данного треугольника.
Полученный полный вес является функцией aj, . . . , а6. В следующем
разделе показано, что восьмивершинную модель на решетке кагоме можно
решить, если оба типа треугольников имеют одинаковые веса, т.е.
"' У А 2\**
<Хц
ОС л /f ОС с
g\ A /g5 ,
ос»
Pwc. 77.-4. Два типа треугольников на решетке кагоме. Стрелки-спины а1 , . . . , а6,
01» 02» 03 связаны с ребрами; изинговы спины а{ , . . . , а7 связаны с гранями. Усло-
Условия равенства полных весов данных треугольников A1.1.6) и A1.5.8).

ГЛАВА И 283
2 i(i, 2\p2, ft) w3(a6, ft|a5, ft) w2(ft , ft|a4, a3)=
AfAfA A1.1.6)
2 , ft) w3(ft , a2|ft ,
для всех значений величин av . . . , а6.
Соотношение A1.1.6) в точности соответствует соотношению звезда —
треугольник (9.6.8), в котором w, w", w', заменены на Wj, vv2, vv3. Следо-
Следовательно, оно эквивалентно шести уравнениям A0.4.1), в которых а, Ь, с,
d, а", Ь", с", <af", a', b't c't d' заменены на^^ b{i c{i dv a2, b2, c2, d2, Ь3,
аз> сз» dy В данных обозначениях уравнения A0.4.1) принимают более сим-
симметричный вид:
(fl/fly - bibj)ck = (CiCj - didj)bk ,
A1.1.7)
(fl/fey - 6|fly-)djk = (c/rf7 - djCj)ak
для всех перестановок (/, j, к) чисел A,2, 3).
Все следствия из A0.4.1), которые были получены в разд. 10.4, можно
применить теперь к уравнениям A1.1.7). В частности, так же как в A0.4.6),
введем определение
Д. = i(fl2 + Ь1 _ С2 _ d2)/{a.b. + Cjdj) 9
rj=(ajbj-cjdj)/(ajbj + cjdj) ALL8)
при j = 1, 2, 3. Тогда из A0.4.26) следует, что Aj = Д2 = Д3,
Tj = Г2 = Г3. Обозначив через Д и Г общие значения величин Ду и Гу, мы
можем записать
Ау = А, Гу = Г, /=1,2,3. A1.1.9)
Параметризация с помощью эллиптических функций
К уравнениям A1.1.7) можно применить параметризацию с помощью
эллиптических функций, введенную в разд. 10.4. (Она нам потребуется в
конце разд. 11.7 и в разд. 11.8.) Используя A0.4.21), мы можем определить
величины к, X, Wj, и2, м3 так, чтобы при у = 1, 2, 3 выполнялись условия
uj : bj: Cj: dj = snh(A - w7): snh u}: snh Я: к snh A snh Uj snh(A - w;).
A1.1.10)
Здесь snh и — гиперболическая эллиптическая функция аргумента и и моду-
модуля к, определенная выражениями A0.4.20) и A5.1.4) — A5.1.6). Из A0.4.17)
следует
А = -en /A dn ik/(I - к sn2/A)?
Г= A + fcsrAA)/(l -km2ik). (И.1.11)
Здесь переменные и {, и2, и3 сопоставляются соответственно величинам
w, и", X — и', определенным в разд. 10.4. (Перестановка а1 с Ь1 эквива-

284 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
лентна замене и' на X — и'.) Таким образом, соотношение A0.4.30) прини-
принимает вид
Mi + и2 + иъ = А. A1.1.12)
Это завершает параметризацию. Если величины aJf bJf cJt dj удовлетво-
удовлетворяют условиям A1.1.10) и A1.1.12), то удовлетворяются также условия
звезда — треугольник A1.1.7). Наоборот, из A1.1.7) следует, что существу-
существуют величины к, X, ult u2, w3, удовлетворяющие соотношениям A1.1.10) и
A1.1.12).
11.2. ПЕРЕХОД К МОДЕЛИ НА КВАДРАТНОЙ
РЕШЕТКЕ
В настоящем разделе будет показано, что ограничения звез-
звезда — треугольник A1.1.7) приводят к тому, что определенные свойства мо-
модели на решетке кагоме совпадают со свойствами модели на ассоциирован-
ассоциированной квадратной решетке. Поэтому можно воспользоваться результатами,
полученными в гл. 10.
Приводимые здесь соображения можно специализировать на случай мо-
модели Изинга [37] или обобщить на произвольный граф, построенный из пе-
пересекающихся прямых линий [32, 33].
Рассмотрим сначала любой обращенный вверх треугольник на решетке
кагоме, например треугольник PQR на рис. 11.1. Обозначим стрелки-спины
так, как показано на рис. 11.4. Вклад данного треугольника в статистичес-
статистическую сумму A1.1.5), просуммированный по всем значениям стрелок-спинов
на внутренних ребрах, равен левой части соотношения A1.1.6).
Заменим указанный вклад правой частью A1.1.6). Статистическая сумма
A1.1.5) равна теперь выражению, соответствующему графу, показанному
на рис. 11.5,я, в котором горизонтальная линия ЛВ сдвинута и проходит
выше узла R . Узел Р остается точкой пересечения линии ЛВ с прямой, про-
проходящей в направлении с юга-востока на северо-запад, и по-прежнему име-
имеет весовую функцию w j. Аналогично точки Q и R лежат на тех же линиях,
что и прежде, и имеют те же весовые функции (vv2 и vv3), что и прежде.
Такая процедура не только не изменяет статистической суммы Z, но со-
сохраняет также любую корреляцию, например
(азО^Од . . . О82> = Z 2 (ХъОСаОЬ ... ^82 П wi(<Xl > <*т\<Хр , <Xq) , (Н.2.1)
при условии что стрелки-спины с*3, а4» а9» • • • » а82 не лежат на внутренних
ребрах треугольника PQR.
Предположим, что решетка натянута на вертикальный цилиндр, и
выполним описанную выше процедуру с каждым треугольником, основа-
основание которого первоначально лежало на линии ЛВ. В результате получим
граф, показанный на рис. 11.5,6, где линия ЛВ сдвинута вверх.
Проделаем теперь такую процедуру с горизонтальной линией, лежащей
над ЛВ, затем с самой ЛВ и так до тех пор, пока ЛВ и все горизонтальные

ГЛАВА И 285
\ / \ / \
л \ / 0\ /Р \ /
(я
а 6
Рис. 11.5. Решетка кагоме, показанная на рис. 11.1; а — линия ЛВ поднята над уз-
узлом /?, б — вся линия ЛВ поднята как ряд. Статистическая сумма и все корреляции
в нижней половине решетки не изменяются.
линии выше нее не окажутся на вершине графа. Аналогично сдвинем ли-
линию CD и все горизонтальные линии ниже ее к основанию данного графа.
Конечный результат таков, что решетка кагоме (рис. И.6,а) превратится в
граф (рис. 11.6,6).
Рассмотрим любой набор ребер, лежащих между исходными линиями
ЛВ и CD (но не на них), т.е. ребер, примыкающих к среднему ряду узлов.
Примером может служить пара (/, ^)» показанная на рис. 11.6. Ни на какой
стадии преобразования через такие ребра не проходит какая-либо горизон-
горизонтальная линия. Следовательно, они являются внешними ребрами для всех
треугольников, вовлеченных в многочисленные преобразования звезда —
треугольник, поэтому соответствующие корреляции не изменяются при
описанном преобразовании.
Восьмивершинные модели на двух графах рис. 11.6 имеют не только
одинаковые статистические суммы Z, но и одинаковые корреляции между
спинами в среднем ряду, например (ajak).
Пусть число горизонтальных линий равно 2 А/. Тогда рис. 11.6,6 состо-
состоит из лежащей в центральной области квадратной решетки (показанной
диагональными линиями), содержащей 2 М рядов, обрамленной сверху и
\ /\ / \ /\
X
а' >
X
х
X
{>
X
(>
о
X
X
<)
X
х/
X
/ V
\ /\
*х
X
' \7 V7 V7 \/
а 6
Рис. 11.6. Решетка кагоме (а) и та же решетка после того, как все верхние
горизонтальные линии подняты до вершины, а все нижние горизонтальные линии
опущены до дна (б). Статистическая сумма и все корреляции вида (^ак) и (атапУ в
центральном ряду не изменяются.

286 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
снизу областями, каждая из которых содержит М горизонтальных линий.
Весовая функция всех узлов в центральной области равна vv3.
В пределе больших М ребра j и к лежат глубоко внутри квадратной ре-
решетки. Поэтому мы ожидаем, что корреляция (ctj(xk) будет той же, как в
случае обычной квадратной решетки. В частности, отсюда следует
{(XjQCk) зависит только от а3, Ьъ, с3, d3 A1.2.2)
и аналогично для любой корреляции спинов на ребрах, примыкающих к
центральному ряду узлов.
Граничные обрамляющие области
Результат A1.2.2) справедлив даже в том случае, если граничные об-
обрамляющие области также становятся большими. Чтобы увидеть это, вве-
введем трансфер-матрицу К3 ряд — ряд в центральной области и трансфер-
матрицу К12 в обрамляющих областях. Тогда
где Sj, sk — диагональные матрицы с элементами ау, ак, а ф — вектор,
компоненты которого определяются граничными условиями. Обозначим
через А12 максимальное собстэенное значение матрицы V п и положим
Тогда выражение A1.2.3) принимает вид
(а}ак) = фтУЬкУгз^ф/фтУ1м+хф. A1.2.5)
Последнее выражение в точности равно корреляции внутри квадратной ре-
решетки с весовой функцией vv3 и граничными условиями, соответствующими
вектору ф. При больших М вектор ф стремится к ненулевому пределу, а
именно к максимальному собственному вектору матрицы К12. Из теоремы
Перрона — Фробениуса [93] следует, что такой вектор имеет только неот-
неотрицательные компоненты; такими же свойствами обладает максимальный
собственный вектор матрицы К3. Поэтому максимальные собственные век-
векторы соответствующих матриц не ортогональны (если только не равны ну-
нулю все те компоненты одного из них, которые соответствуют ненулевым
компонентам другого, чего не следует ожидать). Следовательно, вектор ф
определяет непатологические граничные условия на квадратной решетке, и
правую часть выражения A1.2.5) можно вычислить при больших М с по-
помощью методов, изложенных в разд. 2.2. Использование таких методов
приводит к выражению
) ? М /) 5;С/СГС, A1.2.6)
где Л3, f — максимальное собственное значение и максимальный собствен-
собственный вектор матрицы К3. Полученный результат зависит только от К3, но
не от граничных условий ф.

ГЛАВА 11 287
В данном рассмотрении для простоты предполагалось, что матрицы
К12 и К3 симметричны (для верхних и для нижних граничных условий). Та-
Такое предположение не является необходимым ограничением.
11.3. КОРРЕЛЯЦИОННАЯ ДЛИНА
И СПОНТАННАЯ ПОЛЯРИЗАЦИЯ
Вернемся к формуле A1.2.2). Если ребра у и к лежат в центральной го-
горизонтальной полосе на рис. 11.6 и достаточно далеки друг от друга, то
(цаск) ~ ехр[-|/ - к\ЩКС], A1.3.1)
где ?KG — горизонтальная корреляционная длина решетки кагоме. Из фор-
формулы A1.2.2) следует
§то= &е(яз > Ъъ > съ, d3), A1.3.2)
где ?5g(tf, b, с, d) — диагональная корреляционная длина восьмивершин-
ной модели с весами а, Ь> с, d на квадратной решетке (рис. 11.2, третий
ряд). Насколько мне известно, эта корреляционная длина не вычислена
(для этого необходимо получить уравнения на собственные значения для
трансфер-матрицы диагональ — диагональ). Критическое поведение корре-
корреляционной длины ?Sq, по-видимому, аналогично поведению корреляцион-
корреляционной длины ?, введенной в разд. 10.10, поскольку вблизи критической точки
корреляции во всех направлениях затухают одинаково медленно.
Рассмотрим некоторый узел типа 3 в центральном ряду решетки каго-
кагоме, показанной на рис. И.6,а. Пусть спины /х, а, /3, v на окружающих дан-
данный узел ребрах расположены так, как показано на последней диаграмме
рис. 11.3. Все эти ребра лежат между линиями А В и CD, поэтому анало-
аналогично A1.2.2) имеем
(a), (afj) , . . . , {(ларр) зависят только от величин аз, Ь3, сз, d3, и
совпадают с корреляциями в модели с теми же весами
на регулярной квадратной решетке, построенной на
внутренней области решетки рис. 11.6,6.
Таким образом, все локальные корреляции вблизи узла типа 3 совпада-
совпадают" с соответствующими корреляциями на квадратной решетке. Вследствие
симметрии аналогичные соответствия имеются и для узлов типов 1 и 2. Ес-
Если выполняются ограничения A1.1.7), все локальные корреляции модели на
решетке кагоме могут быть представлены как корреляции на квадратной
решетке.
Это означает, что для ребра j решетки кагоме, примыкающего к узлу
типа 3,
(aj) = P0(a3,b3,c3,d3), A1.3.4)
где Р0(а, Ъ1, с, d) — спонтанная поляризация восьмивершинной модели с
больцмановскими весами а> Ь, с, d на квадратной решетке. Функция Р0(а,

288 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
Ь, с, d) задается выражением A0.10.24), причем величины q, x определены
в разд. 10.15. Зависимость от я, b, с, d входит в Ро только через величины
Д и Г, поэтому из A1.1.8) следует, что правая часть выражения A1.3.4) не
изменится при замене я3» ^з» сз» ^з на а\* ^i» ci» ^l или на аъ> ^2» С2» ^2- ^
учетом симметрии относительно поворотов отсюда следует, что выраже-
выражение A1.3.4) справедливо для всех ребер у. Таким образом, величина <ау>
имеет одинаковое значение для всех ребер решетки кагоме.
11.4. СВОБОДНАЯ ЭНЕРГИЯ
Хотя обрамляющие области на рис. 11.6,6 не влияют (на больших ре-
решетках) на центральные корреляции, они, несомненно, дают вклад в ста-
статистическую сумму и, следовательно, в полную свободную энергию решет-
решетки кагоме
FKG = -kBTlnZ. A1.4.1)
В пределе большой решетки объемная свободная энергия Fкс должна быть
равна просто сумме объемных свободных энергий трех областей, показан-
показанных на рис. 11.6,6, так как вклады от границ этих областей не существен-
существенны. Таким образом,
Fkg = Fsq + 2FFR , A1.4.2)
где FSq — полная свободная энергия центральной области, FFR — свобод-
свободная энергия верхней или нижней обрамляющей области.
Пусть N — число узлов типа 1 в решетке. Тогда (при больших N) су-
существует также N узлов типа 2 и N узлов типа 3. Следовательно, в цент-
центральной области имеется N узлов типа 3; поэтому
Q b3,c3,d3), A1.4.3)
где /(а, Ь, с, d) — приходящаяся на один узел свободная энергия восьми-
вершинной модели на регулярной квадратной решетке, которая определя-
определяется формулой A0.8.47) и рассматривается в разд. 10.15; величина квТ
здесь считается некоторой заданной постоянной.
Увеличенная картина одной из обрамляющих областей показана на
рис. 11.7. Ясно, что это также квадратная решетка, в которой узлы типа 1
и узлы типа 2 лежат на чередующихся столбцах. Всего имеется N узлов
обоих типов.
Согласно A1.1.8), все узлы имеют одинаковые значения Д и Г, поэтому
восьмивершинная модель в обеих обрамляющих областях представляет со-
собой модель с неоднородными столбцами, рассмотренную в разд. 10.17.
Следовательно, полная свободная энергия (при больших N) имеет вид
Ffr = ШАаг, Ъх , С!, dx) + \Nf{a2,b2,c2,d2). A1.4.4)
Подстановка выражений A1.4.3) и A1.4.4) в A1.4.2) дает весьма простой
результат, обладающий нужной симметрией:
c2,d2) +f(a3,b3,c3,d3)]. A1.4.5)

ГЛАВА И 289
Рис. 11.7. Увеличенный участок од-
одной из обрамляющих областей,
показанных на рис. 11.6,6. Показаны
два типа узлов. Обрамляющие
области представляют собой
квадратную решетку с различными
весами на чередующихся столбцах.
11.5. ПРЕДСТАВЛЕНИЕ В ВИДЕ МОДЕЛИ ИЗИНГА
НА ТРЕУГОЛЬНО-ШЕСТИУГОЛЬНОЙ РЕШЕТКЕ
С ВЗАИМОДЕЙСТВИЯМИ ДВУХ
И ЧЕТЫРЕХ СПИНОВ
Подобно модели на квадратной решетке, восьмивершинную модель на
решетке кагоме можно сформулировать на языке «магнитных» спинов на
гранях вместо «электрических» стрелок на ребрах.
Наиболее симметричный способ сделать это состоит в том, чтобы в ка-
качестве стандартной конфигурации рассматривать конфигурацию стрелок,
показанную на рис. И.8,я, которая соответствует антисегнетоэлектрику:
все вершины типа 5 (рис. 11.2, пятый столбец). С каждой гранью г свяжем
спин аг, принимающий значения +1 и -1. Рассмотрим ребро у, лежащее
между гранями г и s. Поместим на него стрелку в соответствии со следую-
следующим правилом:
если oras = + 1, направим стрелку в ту же сторонуу что и стрелка на
ребре j в стандартной конфигруации; в противном случае направим
ее в противоположную сторону. A1.5.1)
Используя A1.5.1), поместим стрелки на всех ребрах решетки.
л /\ а у V у
XXX
а 6
Рис. 11.8. а — стандартная антисегнетоэлектрическая конфигурация стрелок на ре-
решетке кагоме (показаны не все стрелки); б — соответствующая конфигурация на
треугольной решетке, полученной при стягивании в точки всех треугольников углом
вверх решетки кагоме. Показаны также три подрешетки А, В, С такой треугольной
решетки.

290 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
Представим себе наблюдателя, движущегося вокруг некоторого узла и
проходящего последовательно четыре грани. Если при переходе от одной
грани к следующей он видит изменение спина, то стрелка на расположен-
расположенном между гранями ребре не имеет стандартного направления; если спин
не изменяется, то стрелка имеет стандартное направление. Возвращаясь к
исходной точке, наблюдатель должен увидеть четное число таких измене-
изменений; следовательно, на четырех ребрах каждого узла имеется четное число
нестандартных стрелок. Поскольку в стандартной конфигурации две стрел-
стрелки направлены к узлу и две стрелки — от узла, в каждом возможном слу-
случае должно быть четное число стрелок, направленных к узлу, и четное чис-
число стрелок, направленных от узла. Полученный результат представляет со-
собой условие, характеризующее восьмивершинную модель.
Следовательно, каждой конфигурации спинов на гранях соответствует
конфигурация стрелок на ребрах, удовлетворяющая условию восьмивер-
шинной модели. Наоборот, с помощью таких же, рассуждений, как в
разд. 10.3, можно показать, что каждой конфигурации стрелок, удовлетво-
удовлетворяющей условию восьмивершинной модели, соответствуют две конфигура-
конфигурации спинов на гранях (переходящие одна в другую при обращении направ-
направлений всех спинов). Используя данное соответствие, выражение A1.1.2)
можно записать в виде
IWo). AL5-2)
a i
где суммирование проводится по всем конфигурациям о = ( av о2, • . . )
спинов на гранях, произведение берется по всем узлам /, a j(i, о) — вер-
вершинная конфигурация в узле / при конфигурации спинов а.
Пусть окружающие узел типа / грани /•, s, /, и расположены так, как по-
показано на рис. 11.3. Обозначим через W^o^ а^ оv au) больцмановский вес
вершинной конфигурации стрелок, соответствующей значениям спинов на
гранях ог Ор оv ои. Тогда из правила A1.5.1) и рис. 11.2, 11.3, 11.8 полу-
получаем
Щ+ + +) И0(+ + ,-)= а,,
A1.5.3)
где / = 1, 2, 3 и a,, o^ ot, ou = ±1. Данные выражения определяют функ-
функцию lVh и статистическую сумму A1.5.2) можно записать в виде
rs,Ot,ou), A1.5.4)
r,os,ot, au) = Wj(-or,-os,-o,, -au)

ГЛАВА 11
291
где произведение берется по всем узлам; / теперь обозначает тип узла, а /*,
s, t, и — окружающие узел / грани.
Из выражений A1.5.3) видно, что функцию Wi можно записать в виде
Wi(ar,as,ot, ou) = Miехр^до, + K\asau + К-о^ор»], (i 1.5.5)
где величины Mif Kt, K\, К" связаны с весами а{> bjt с,, di соотношениями
i - K[ - K'l), bi = М( exp( -K, + K[ - K'l),
Ci = Mi exp(Ki + K[ + K'l),
A1.5.6)
i = Mi exp( -Kt - K\ + K'!).
Из выражения A1.5.4) с учетом вида функции Wi A1.5.5) следует, что Z
(строго говоря, 2Z) представляет собой статистическую сумму модели
Изинга, определенной на гранях решетки кагоме, с взаимодействиями меж-
между двумя спинами на противоположных гранях и между четырьмя спинами
на гранях, окружающих узел.
Поместим точку в центр каждой грани решетки кагоме и соединим точ-
точки на тех гранях, спины которых включены в двухспиновые взаимодейст-
взаимодействия. При этом получится решетка, показанная на рис. 11.9. Она состоит из
шестиугольной решетки, переплетающейся с треугольной. На рис. 11.9 по-
показаны также коэффициенты взаимодействия Kit K\, связанные с различны-
различными ребрами. Пусть N — число узлов типа 1 (или типа 2, или типа 3) в ис-
исходной решетке кагоме. Тогда ассоциированная шестиугольная решетка
имеет 2N узлов, а треугольная — N узлов; каждая из решеток имеет 3N
ребер, и каждое ребро одной решетки пересекается с одним ребром другой.
Рис. 11.9. Шестиугольно-треугольная решетка, образованная точками, находящими-
находящимися в центрах граней решетки кагоме, и линиями, соединяющими центры тех граней,
спины которых вовлечены в двухспиновые взаимодействия. Указаны со-
соответствующие коэффициенты взаимодействия К{ , . . . , Ау,г г, s, t, и —точки,
отвечающие четырем граням на рис. 11.3,я; точки тип соответствуют граням т и
п на рис. 11.6,а.

292 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
Используя A1.5.5), выражение A1.5.4) можно записать в виде
Z = \{МХМ2МЪ)"^ exp{EKiOrot + 2К'(о5ои + ТЩа^а^, (П.5Л)
где первая сумма в показателе экспоненты оерется по всем ребрам (/*, /)
шестиугольной решетки, вторая — по всем ребрам (s, и) треугольной ре-
решетки и третья — по всем пересекающимся парам ребер (/*, t) и (s, и). Во
всех суммах номер /( = 1, 2, 3) определяет тип ребра, как показано на
рис. 11.9.
Таким образом, Z представляет собой с точностью до нормировочного
множителя объединенную статистическую сумму моделей Изинга на ше-
шестиугольной и треугольной решетках, взаимодействующих друг с другом с
помощью четырехспинового взаимодействия узлов, принадлежащих пересе-
пересекающимся ребрам.
Ограничение звезда — треугольник
Для разрешимости модели необходимо, чтобы коэффициенты Kv . . . ,
^'удовлетворяли ограничениям A1.1.7), где величины а^ Ь^ с? d{ определя-
определяются формулами A1.5.6).
Такие ограничения возникли из соотношения звезда — треугольник
A1.1.6). Интересно вернуться к этому соотношению и выразить его через
«магнитные» спины на гранях решетки кагоме вместо «электрических» спи-
спинов на ребрах.
Соотношение A1.1.6) утверждает, что после суммирования по всем раз-
разрешенным кофигурациям стрелок на внутренних ребрах два графа на
рис. 11.4 имеют одинаковый полный вес. Чтобы выразить данное соотно-
соотношение на «магнитном» языке, установим соответствие между гранями гра-
графов и спинами, как показано на рис. 11.4. Тогда требование равенства пол-
полных весов рассматриваемых графов имеет вид
2 Wi(o2 ,<Ъ,07,Ох) W2(a4 ,o5,o7, оъ) W3(a6 ,ox,on, о5) =
* A1.5.8)
= Z, Wi(gj ,O4,o5, a6) W2(a7 ,oe,Oi, о2) W3(a7 ,о2,о3, a4).
07
Полученное уравнение должно выполняться при всех значениях внешних
спинов <jj, . . . <т6. Суммирование проводится по значениям внутреннего
спина а7, что соответствует (см.( 11.1.6)) суммированию по всем допусти-
допустимым значениям величин /Зр /32, #з (условием восьмивершинной модели до-
допускаются только два набора значений).
Можно проверить непосредственно, используя A1.5.3), что уравнения
A1.5.8) совпадают с A1.1.6). Используя A1.5.5), их можно записать в виде
+ К3ав + К[охо2оъ
A1.5.9)
exp(A'iа4а6 + К2ава2 + К'ъо2оА) cosh(Ar1a5 + К
Къоъ + К{о4о5о6 + К2'оьохо2

ГЛАВА 11 293
Поскольку данное уравнение эквивалентно A1.1.6), из него следуют ра-
равенства A1.1.7) и A1.1.8), в частности Г{ = Г2 = Г3. Тогда из выражения
A1.1.9) следует, что отношение aibi/cidi не зависит от /, а из A1.5.6) следу-
следует
К" не зависит от /. A1.5.10)
Таким образом, все узлы независимо от их типа должны иметь один и
тот же коэффициент четырехспинового взаимодействия. Обозначим его че-
через К". Тогда, рассматривая все 64 набора значений спинов о{, . . . , а6,
найдем, что A1.5.9) эквивалентно следующим шести уравнениям:
+ ЯП - cosh(*< + */ + Кк- К")
) + 2Кк) - со _ + К + ,
A1.5.11)
для всех перестановок (/, у, к) из A, 2, 3).
Полученные уравнения совпадают с уравнениями A1.1.7). Они не неза-
независимы, поскольку вторую группу уравнений легко получить из первой.
Первая группа, содержащая три уравнения, очевидно, независима, посколь-
поскольку эти уравнения можно использовать для определения величин К[, К2, К'3
при заданных Kv K2, К^ К". С другой стороны, можно считать, что зада-
заданы величины К[, К'2, К'у К", и решать уравнения относительно Kl9 K2, К^.
С учетом A1.5.6) следствия A1.1.8) — A1.1.9) при у = 1, 2, 3 принимают
вид
А = - sinh 2Kj sinh 2K\ - tanh 2К" cosh 2K} cosh 2K] , A1.5.12а)
Г= - tanh2X". A1.5.126)
Исключая величину у1 (считая ее отрицательной) из уравнений A0.4.12) и
используя A0.4.9), получаем для эллиптического модуля к соотношение
2**/A +*)=/, A1.5.13)
ГДС I2 = A - Г2)/(А2 - Г2). A1.5.14)
Последнее выражение с учетом A1.5.12) можно представить в виде
,2 = q-^(i-o7J(w2J
16A JrlV]v'jv"){v" + VjV}){Vj + v'jV")(vj + VjV") '
где
Vj = tanh K}, v'j - tanh K'n v" = tanh K". A1.5.16)
Спонтанная намагниченность
Рассуждения разд. 11.2 можно повторить, используя спины на гранях
вместо стрелок на ребрах. Вместо уравнений A1.1.6) нужно использовать

294 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
A1.5.8). Аналоги результатов A1.2.2) и A1.3.3) можно представить следую-
следующим образом.
Обозначим через ov . . . , от набор спинов, лежащих между линиями
АВ и CD на рис. 11.6, а решетки кагоме. Пусть выполняются ограничения
A1.1.7) или, что эквивалентно, A1.5.11). Тогда для большой решетки
{о\. . . . от) равно корреляции в восьмивершинной модели с весами
Яз > Ьз, Сз, d3 на регулярной квадратной решетке, построенной
на внутренней области графа рис. 11.6,6. A1.5.17)
Таким образом, корреляция (ох . . . от) зависит только от я3, ^з» сз> ^з
или, что эквивалентно, от К3, К$, К".
В частности, отсюда следует, что среднее значение любого спина на
грани от равно
независимо от того, на какой грани решетки кагоме — треугольной или
шестиугольной — лежит спин от. Следовательно, однозначно определен-
определенную величину (от) мы можем назвать спонтанной намагниченностью.
В A1.5.18) величина М0(я3, Ь3, с3, d3) имеет смысл спонтанной намагни-
намагниченности в восьмивершинной модели с весами я3, Ь3, с3, d3 на квадратной
решетке. Она определяется формулой A0.10.19). Подобно спонтанной пб-
ляризации, Мо зависит от я3, 63, с3, tf3 только через величины Д и Г, кото-
которые имеют одинаковые значения для всех трех типов узлов решетки; поэ-
поэтому выражение A1.5.18) не изменится при замене я3, Ь3, с3, <af3 на av bv
cv dx или на я2, ^2» С2> ^2* Последнее очевидно из свойств симметрии ре-
решетки при поворотах на 120°.
Гиперболическая тригонометрия и параметризация с
помощью эллиптических функций
Определим параметры и и О следующим образом
coth 2K" = cosh Q, - A coth 2K' = cosh со . A1.5.19)
Тогда выражение A1.5.12а) можно записать в виде
cosh со = cosh 2Kj cosh 2Kj + cosh Q sinh 2K, sinh 2K- . A1.5.20)
Данное выражение представляет собой соотношение между сторонами
со, IKjy 2Kj гиперболического треугольника, причем угол между сторонами
2KJt 2Kj равен ж + /О [69, 184]. Другие следствия соотношения
звезда — треугольник A1.5.11), например
- cosh 2K2 cosh 2K3 + coth 2K[ sinh 2K2 sinh 2K3=
A1.5.21)
= cosh 2Кх cosh 2K" + coth 2K[ sinh 2KX sinh 2K'f,
можно интерпретировать с помощью гиперболической тригонометрии.
Представляется вероятным, что многие из свойств соотношения звез-
звезда — треугольник, особенно «четырехстороннюю теорему» [32], можно ин-

ГЛАВА 11 295
терпретировать таким способом. Насколько известно автору, это еще не
сделано.
Изложенные идеи дают также альтернативный подход к параметриза-
параметризации с помощью эллиптических функций, приведенной в разд. 10.4. Хорошо
известно [102], что соотношение A1.5.20) можно упростить, введя эллипти-
эллиптические функции модуля [102]
/ = sinh Q/sinh со . A1.5.22)
Онсагер [184] называл такую процедуру униформизирующей подстановкой.
Величина / в A1.5.22) в точности совпадает с параметром /, определен-
определенным выражением A1.5.15), поэтому она связана с модулем к, используе-
используемым в гл. 10, соотношением A1.5.13). Таким образом, как следует из
разд. 15.6, величины / и к связаны между собой преобразованием Ландена;
поэтому оба подхода, как и следовало ожидать, приводят к одинаковой па-
параметризации эллиптическими функциями.
11.6. ФАЗЫ
Из выражений A1.3.4) и A1.5.18) следует, что спонтанная поляризация
и намагниченность модели на решетке кагоме совпадают с соответствую-
соответствующими величинами в восьмивершинной модели на квадратной решетке при
тех же значениях параметров Д и Г. Как видно из разд. 10.11, модель на
решетке кагоме имеет упорядоченное состояние при \А\ > 1 и неупорядо-
неупорядоченное при IДI < 1.
Основная область упорядочения определяется условиями
ci>ai + bi + dh сц>0, bi>0, dt>0, AЬ6Л)
где / = 1, 2, 3. Из выражений A1.1.8) видно, что в данной области
Д < — 1. Основному состоянию соответствует антисегнетоэлектрическая
конфигурация стрелок, показанная на.рис. И.8,я, или конфигурация, полу-
получающаяся из нее при обращении направлений всех стрелок. Поскольку мы
использовали первую конфигурацию в качестве стандарта при установле-
установлении связи между стрелками-спинами и спинами на гранях, на «магнитном»
языке данная фаза интерпретируется как ферромагнитная: в основном со-
состоянии все спины на треугольных гранях одинаковы и все спины на ше-
шестиугольных гранях также одинаковы. Существует четыре таких основных
состояния.
Кроме области A1.6.1) в пространстве параметров существует семь дру-
других областей, в которых данная система упорядочена [32]. Все такие обла-
области можно получить из основной с помощью обращения направлений под-
подходящих наборов спинов. Например, обращение всех спинов на гранях тре-
треугольников углом вверх эквивалентно обращению всех стрелок на сторонах
таких треугольников. На рис. 11.2 видно, что при этом переставляются ве-
веса at с dt и bt с с,; поэтому область A1.6.11) отображается в
bi>ai + ci + db я,>0, с,>0, di>0, 01.6.2)
где Д > 1.

296 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
Иначе говоря, обращение спинов на гранях между чередующимися пара-
парами горизонтальных линий эквивалентно обращению всех горизонтальных
стрелок. При этом веса я3» ^з» сз» ^з не изменяются, но при / = 1 и / = 2
переставляются я. с bi и ci с dr Таким образом, область A1.6.1) отобража-
отображается в
di>fli + 6i + cb d2>a2 + Ь2 + съ d3>a3 + b3 + d3, (Н.6.3)
где все веса положительны и Д < — 1.
Очевидно, что два других отображения можно получить, используя
симметрию при поворотах. Комбинируя приведенные выше различные
отображения, можно получить все семь областей упорядочения.
Существует только одна область беспорядка, а именно
О < ah bh ch di<h(ai + b{ + с, + d,) , A1.6.4)
где / = 1, 2, 3, причем — 1 < A < 1.
11.7. AT" = 0: МОДЕЛИ ИЗИНГА НА ТРЕУГОЛЬНОЙ
И ШЕСТИУГОЛЬНОЙ РЕШЕТКАХ
В разд. 10.3 мы отметили, что восьмивершинная модель на квадратной
решетке разбивается на две независимые модели Изинга, если коэффициент
четырехспинового взаимодействия К" равен нулю.
Такая же факторизация происходит и в случае модели на решетке каго-
ме. Как видно из формульГ A1.5.10). мы можем одновременно положить
равными нулю все коэффициенты четырехспиновых взаимодействий К".
Тогда экспонента в выражении A1.5.7) разобьется на два сомножителя;
первый из них содержит только спины шестиугольной решетки, показан-
показанной на рис. 11.9, а второй — только спины треугольной решетки. Отсюда
получаем
Z = \{МХМ2МЪ)"Z^KX, К2, К3) ZT{K[, К'г, К$ , A1.7.1)
где ZH(K{i K2, К$) — статистическая сумма модели Изинга с взаимодейст-
взаимодействием между ближайшими соседями на шестиугольной решетке с коэффици-
коэффициентами взаимодействия Kv K2, Kv a ZT(K{, К'г, К'ъ) — статистическая сум-
сумма модели Изинга с взаимодействием между ближайшими соседями на
треугольной решетке с коэффициентами взаимодействия K'v K'v Ку Шести-
Шестиугольная решетка содержит 2N узлов, треугольная — N узлов.
Соотношения A1.5.11) можно записать в виде
вместе с двумя другими соотношениями, получающимися при перестановке
индексов 1, 2, 3. Полученные соотношения представляют собой соотноше-
соотношения звезда — треугольник F.4.8) модели Изинга (из которых исключена ве-
величина R и Kj, Lj заменены на Kj, Kj).
Указанная эквивалентность более ясна из исходного уравнения A1.5.9).

ГЛАВА 11 297
Если коэффициенты KJв нем положить равными нулю, то данное уравне-
уравнение разобьется на два уравнения, одно из которых содержит только спины
ai» °v а5» а ДРУгое — только спины а2, а4, а6. Эти уравнения имеют вид
K2O4 + К3а6) A1.7.3а)
= R ехр(К[аАа6 + К2а6а2 + К)
К2ох + А'заз)
A1.7.36)
где R — общая постоянная. Каждое из этих уравнений представляет собой
в точности соотношение звезда — треугольник F.4.4), F.4.5).
Из выражения A1.5.126) следует, что величина Г равна нулю. Поэтому,
учитывая A1.5.14) и A1.5.12а), мы можем выбрать
/-i = -A = sinh2XjSinh2X;, /=1,2,3. A1.7.4)
Полученная формула совпадает с F.4.13), где k, Kj, Lj заменены на /, Kj,
Kj. Из формул F.4.16) и F.3.5) следует
16A + v[vM) (v[ + v2v'3) (v'2
где v{9 V2, v^ определены в A1.5.16) с помощью коэффициентов взаимо-
взаимодействия К[, K'v К'ъ на треугольной решетке.
Альтернативно, используя F.4.12), величину / можно выразить через ко-
коэффициенты взаимодействия Klt K2, Къ шестиугольной решетки следую-
следующим образом:
где
,2 _ 16(! + ^1^2^з) Qi + z2z3) (z2 + z3zx) (z3 + zxz2)
A?J(l2J(iJ
2У = exp(-2A}), 7 = 1,2,3. A1.7.7)
(Одинаковый вид выражения A1.7.5) и выражения, обратного A1.7.6), от-
отражает соотношение дуальности, рассмотренное в разд. 6.3. Я не знаю, по-
почему они похожи также на одноузельное соотношение A1.5.15).)
Величина R в A1.7.3) совпадает с величиной R в разд. 6.4. Поэтому, за-
заменяя в F.4.14) k, Lj, Kj на /, Kj, Kj, получаем
Л2 = 2/2sinh 2Ki sinh 2K2 sinh 2Л:3 = 2/(P sinh 2K[ sinh 2Kb sinh 2К'Ъ).
A1.7.8)
Свободная энергия
В обозначениях данной главы тождество F.4.7) принимает вид
ZH{KX, К2, Къ) = RNZT{K[, Ki, К'ъ). AL7'9)
Подстановка A1.7.9) в A1.7.1), взятие логарифма и использование A1.4.1) и
A1.4.5) дает

298 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
2InZj(K[ ,Kt,,K$ =
A1.7.10)
где использовано обозначение/^ для функции/(^ bj, с., dj), которая пред-
представляет собой приходящуюся на один узел свободную энергию восьмивер-
шинной модели с весами a-t bj, c-t dj на квадратной решетке.
Данные веса определяются выражением A1.5.6). Поскольку коэффици-
коэффициент KJ равен нулю, восьмивершинная модель на квадратной решетке разби-
разбивается на две невзаимодействующие модели Изинга на соответствующих
подрешетках. Выбирая каждую величину Mj равной единице, из A0.3.11)
находим, что функция f- равна приходящейся на один узел свободной энер-
энергии модели Изинга с коэффициентами К* Kj на квадратной решетке.
Удобно работать с безразмерной свободной энергией
tl> = flkBT. A1.7.11)
Из формулы A.7.6) видно, что для решетки, имеющей N узлов, величина ф
связана со статистической суммой Z соотношением
т/>- -lim ATMnZ. A1.7.12)
N-* оо
Для модели Изинга с коэффициентами взаимодействия Kj, Kj на ква-
квадратной решетке функция ф зависит только от этих коэффициентов. Обо-
Обозначим ее через ф5д(К^ Kj). Аналогично для модели Изинга с коэффициен-
коэффициентами К[, К'г, К'ъ на треугольной решетке безразмерную свободную энергию
обозначим через фт( K'v K'v K^). Тогда из формул A1.7.10) — A1.7.12) сле-
следует
1, К'2, К'ъ) = i[lnЯ + Vsc?№ , ^0 + Vs?K2, KQ + Ц80{Къ, К'ъ)].
A1.7.13)
Используя формулу A1.7.9) и вспоминая, что шестиугольная решетка
имеет 2N узлов, для безразмерной свободной энергии, приходящейся на
один узел такой решетки, в модели Изинга с коэффициентами К[, К'1У Л^
получаем выражение
i[-\nR + xl)sQ{Kx, К[) + Vs^Ki, К'2) +
A1.7.14)
Функция Ф8д(К, К') получена в гл. 7 и (как частный случай восьмивер-
шинной модели) в гл. 10. Заменяя величины К, L, k на К', К, /, из уравне-
уравнений G.9.14), G.9.16) и G.6.1) для всех значений К и К' получаем
\I)Sq(K ,K') = -Bл:)-1 rin{2[cosh2/T cosh2#+
^^V Jo
A1.7.15)

ГЛАВА 11 299
где по аналогии с A1.7.4) имеем
rl = sinh2K sinh2tf\ A1.7.16)
Мы можем произвольно выбирать величины К[, К2, К'ъ или Kv К2> Кг\
поэтому формулы A1.7.13) или A1.7.14) позволяют вычислить свободную
энергию модели Изинга на любой регулярной треугольной или шестиуголь-
шестиугольной решетке. Другие параметры определяются тремя уравнениями A1.7.2)
и выражением A1.7.8).
Корреляции соседних спинов
При К" = 0 формула A1.5.17) связывает корреляции моделей Изинга на
треугольной и шестиугольной решетках с корреляциями той же модели на
квадратной решетке. Рассмотрим показанные на рис. 11.6 грани т> п.
Пусть ат> ап — соответствующие изинговы спины; применим формулу
A1.5.17) для вычисления (отоп)-
Так же как в разд. 11.5, поместим точку в центр каждой грани и соеди-
соединим точки тех граней, спины которых вовлечены в двухспиновые взаимо-
взаимодействия. Тогда вместо рис. И.6,я получим рис. 11.9, а точки тип ока-
окажутся ближайшими соседями на вертикальном ребре шестиугольной ре-
решетки; коэффициенты взаимодействий соответствующей модели Изинга
равны Kv K2, Ку С другой стороны, вместо рис. 11.6,6 получим две пере-
переплетающиеся квадратные решетки, точки тип окажутся ближайшими сосе-
соседями на вертикальном ребре; коэффициенты взаимодействия соответству-
соответствующей модели Изинга на квадратной решетке равны Kv К'у В обоих случа-
случаях ребру (т, п) соответствует коэффициент взаимодействия Ку Поскольку
корреляции (ат о п) в обеих моделях одинаковы, имеем
8н(К3, К,, Кг) = gse(K3, Ki), (n-7-17>
где gH, gSg — корреляции соседних спинов шестиугольной и квадратной ре-
решеток соответственно, а первый аргумент равен коэффициенту взаимо-
взаимодействия на рассматриваемом ребре.
Рассматривая точно так же корреляции между спинами на тех двух гра-
гранях рис. 11.6, которые граничат как с гранью т, так и с гранью л, полу-
получим
gj(Ki, К[, Щ = gSQ(Ki, Къ). A1.7.18)
Корреляции gSg, gH, gT являются производными от функций \I/Sq, фн,
фТ. Из формул F.2.1) (где величины К, L заменены на Аг/, #), A1.7Л2) и
A.4.4) следует
gsQ{K,K') = -dH)SQ{K,K')ldK. A1.7.19a)
Аналогично
ft*Ki ,К2,К3) = - дЫКх, К2, К3IдКх, (Н-7.196)
g,(K[ ,Ki,Ki) = - дЦт(К[, Ki, К$/дК[, A1.7.19b)
где каждое дифференцирование производится при фиксированных значени-
значениях других аргументов.

300 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
Альтернативный вывод свободной энергии модели
изинга
Соотношения A1.7.17) и A1.7.18) не являются просто следствиями со-
соотношений A1.7.19). Они содержат больше информации. Чтобы увидеть
это, заметим, что из A1.7.13) и A1.7.14) следует
Ы&1, К2, Къ) = 4[ - In Л + х1>т{К[, К'2, К'ъ)}. A1.7.20)
(Это выражение является простым следствием A1.7.9).) Продифференциру-
Продифференцируем A1.7.20) по Къ при постоянных Кх и К2.
Коэффициенты К[, К'г, К'^ определены соотношениями A1.7.2). Можно
показать, используя A1.7.2), A1.7.4) и A1.7.8), что
3 = 2w3, (И7 21)
дК[/дК3 = 2w2, дКУдКъ = 2w!,
где
w = / sinh 2К[ sinh 2К'2 sinh 2К'Ъ,
A1.7.22)
wr = wcoth2Ar;, r = 1,2,3.
Следовательно, дифференцируя выражение A1.7.20) и используя A1.7.17) —
A1.7.19), получаем
gsQ(K3 ,K$ = w3 + w2gSQ{K[ ,K0 +
+ wigsaW ; К2) - wgsdKi, К3). ( }
Поскольку коэффициенты Kv K2, Къ независимы, полученное уравнение
представляет собой уравнение с тремя переменными относительно функции
двух переменных g$Q(K, К'). Бэкстер и Энтинг [37] показали, что данное
уравнение вместе с выражением A1.7.19а) и свойством симметрии Ф$д(К,
К') = \I/Sq(K', К) полностью определяет функцию gSQ(K> К'). Читателя,
интересующегося деталями, мы отсылаем к упомянутой работе, в которой
уравнение (8) (с заменой К, L на Аг/, К,) совпадает с приведенным выше
уравнением A1.7.23). Приведем краткий вывод. Из уравнения A1.7.23) при
положительных К и К' следует
где в соответствии с A1.7.4)
Г1 = sinh 2K sinh 2K\ A1.7.25)
а аA) и b(l) зависят только от /. Правая часть A1.7.24) должна стремиться
к единице при К — оо, откуда следует линейное соотношение между функ-
функциями аA) й b(l).
Из симметрии функции Ф3д(К, К') и из A1.7.19а) следует, что аA) и
b(l) удовлетворяют некоторым дифференциальным уравнениям. Решение

ГЛАВА 11 301
их при 0 < / < оо дает
],
A1.7.26)
= 2A-/)/(/О/я,
где
/i = 2/*/A +/) , A1.7.27)
a /(/j), ^(/j) — полные эллиптические интегралы первого и второго рода
модуля /j, определенные в A5.5.9) и A5.5.13).
Поскольку теперь функция gSQ(K, К') определена, свободную энергию
можно получить из выражения A1.7.19а).
Привлекательной особенностью данного вывода является то, что ис-
используется только соотношение звезда — треугольник, которое представ-
представляет собой локальное свойство модели Изинга. Оно используется дважды:
сначала для установления свойства A1.5.17) и его следствий A1.7.17),
A1.7.18), а затем для установления равенства A1.7.20). (В работах [110,
111, 151] показано, что соотношение звезда — треугольник можно исполь-
использовать также для вывода критических свойств модели Изинга с помощью
метода ренормализационной группы.) Приведенный вывод подчеркивает еще
раз значение соотношения звезда — треугольник по крайней мере для моде-
модели Изинга. Я не уверен, что данный метод можно обобщить на полную
восьмивершинную модель.
Результат A1.7.24) — A1.7.27) согласуется, конечно, с результатом вы-
вычислений, выполненных в гл. 7 с помощью метода трансфер-матрицы, т.е.
с выражениями G.9.16) и A1.7.15).
Критические сингулярности при / = 1 возникают не из интеграла в
A1.7.24), а из свойств «коэффициентов» аA) и b(l). Вблизи / = 1 они ведут
себя как
71 1 — /
Отсюда ясно, что свободные энергии моделей Изинга на квадратной, треу-
треугольной и шестиугольной решетках имеют одинаковые критические сингу-
сингулярности, а именно те, которыми обладает &(/). Симметричная логариф-
логарифмическая расходимость удельной теплоемкости получается сразу, поэтому,
как в G.12.12), показатели а, а' равны нулю:
а=а' = 0. A1.7.29)
Намагниченность
Из формулы A1.5.18) следует, что все модели Изинга на треугольной
решетке с коэффициентами К[, К'г, К'ъ, на шестиугольной решетке с коэф-

302 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
фициентами Kv K2, К3 и на квадратной решетке с коэффициентами К{, К[
(или К2, К2, или К3, А'з) обладают одинаковыми спонтанными намагничен-
ностями. Поэтому мы можем использовать результат для квадратной ре-
решетки G.10.50). В обозначениях настоящей главы имеем
о () |
A1.7.30)
= 0 ПРИ |/|> 1.
(Каждая модель Изинга упорядочена при I/I ^ 1 и не упорядочена в про-
противном случае.)
Сравнивая выражения A1.7.30) и A.1.4) и замечая, что при критической
температуре разность / — 1 стремится к нулю линейно по Т — Тс, нахо-
находим, что для всех трех моделей критический показатель 0 равен
0=1/8. (п-7-31)
Другие критические показатели, вероятно, также одинаковы для всех
рассмотренных моделей Изинга и имеют значения, определенные выраже-
выражениями G.12.12) — G.12.16). Это находится в согласии с гипотезами скей-
линга и универсальности.
11.8; ТОЧНЫЕ РАЗЛОЖЕНИЯ РЕЗУЛЬТАТОВ,
ПОЛУЧЕННЫХ В МОДЕЛИ ИЗИНГА
Результаты A1.7.13) и A1.7.15) выражаются через элементарные функ-
функции и интегралы от них. Такая форма удобна для изучения, но не всегда
удобна для использования. Для некоторых целей, например для разложе-
разложения в ряд или даже для прямого вычисления, могут быть более полезными
эллиптические функции и их разложения в бесконечные произведения.
В настоящем разделе мы будем предполагать, что все коэффициенты
взаимодействия Кх, К2, К3, К[у К2У К'ъ неотрицательны. Такое предположе-
предположение означает, что для любой решетки нужно рассматривать только два
случая: случай низких температур @ < / < 1) и случай высоких температур
(/ > 1).
Квадратная решетка: низкие температуры
Рассмотрим сначала модель Изинга на квадратной решетке с коэффици-
коэффициентами взаимодействия Kjf Kj. Такая модель эквивалентна восьмивершин-
ной модели на квадратной решетке с весами ajy bjt cjt dj, заданными выра-
выражениями A1.5.6), причем величины Му и KJ равны единице и нулю соот-
соответственно.
Заменим веса я, Ьу с, d из гл. 10 величинами ajt bjt cJt dj. Заменим так-
также переменные «, v, z на Uj, Vj, Zj. Тогда из формул A0.4.21) и A1.5.6) сле-
следует, что параметры kt X, Uj определяются соотношениями
A1.8.1a)
ехр( - 2Kj) = dj/a) = fc* snh щ, A1.8.16)
ехр( -2KJ) = dj/bj = A:*snh(A - щ). A1.8.1в)

ГЛАВА 11 303
Пусть, так же как в гл. 15, / и /' — полные эллиптические интегралы
первого рода модулей к и к' = A - к2)Уг соответственно. Тогда из
A1.8.1а) и A5.4.32) получаем результат A0.9.6), т.е.
A=i/'. A1.8.2)
Из выражений A0.4.23), A0.7.9) и A0.7.19) следует
И/= *(*+?>/), ? = ехр(-я/7/), (П83)
х = ехр(- лА/2/), 2; = ехр(-
поэтому из A1.8.2) имеем
q = x\ (П.8.4)
При условии 0 < / < 1, которое вместе с уравнением A1.7.4) приводит
к неравенству sinh2Aysinh2Ay- > 1, свободная энергия дается выражением
A0.8.47). Поэтому с учетом A1.5.6) и A1.8.4) выражение для безразмерной
свободной энергии ф = f/kBT имеет вид
_ у х3тA - х2)V1 + х~т - z? - zjm)
Коэффициенты К- и Kj можно точно выразить через величины х и гу-,
используя разложение функции kVl snw, входящей в A1.8.16) и A1.8.1 в), в
бесконечное произведение A5.1.5), A5.1.6) и определения A1.8.3) и A1.8.4).
Полезно ввести параметр г и две функции фA) и g(z), определенные выра-
выражениями
-tof. (п-8-6а>
m = l /71^1 "" X )
/*УГГ A -*8"-7z)(l ~^""'г) П1Й^
где величина х считается постоянной. Затем, действуя так же, как выше,
получаем
ф(г[1), A1.8.7а)
j , к;) = - к}f - к; - г + g(z;) + g(z;^J). (i i .8.76)
Выражение A1.8.76) определяет функцию tSQ(Kjt Kj) для всех неотри-
неотрицательных чисел К» Kj9 таких, что величина /, заданная формулой A1.7.4),
меньше единицы. Параметры х, z> однозначно определяются выражением
A1.8.7а) и ограничениями A0.15.11), т.е.

304 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
Приведенные уравнения можно использовать для вычисления функции
ф8д или для разложения ф8д(К^ К-) + К- + К'- по степеням ехр(-2Ау) и
ехр(-2Ау'). Параметр х мал при достаточно низких температурах, (/ < 1) и
увеличивается до единицы при критической температуре (/ = 1).
(Индекс j не существен в настоящем и следующем подразделах; он дол-
должен учитываться ниже при изучении модели Изинга на треугольной и ше-
шестиугольной решетках.)
КВАДРАТНАЯ РЕШЕТКА: ВЫСОКИЕ ТЕМПЕРАТУРЫ
Самый легкий способ получения результата для высоких температур
(/ > 1) состоит в применении дуального преобразования F.2.14) к выраже-
выражениям A1.8.7). При этом получаем
tanh К; = 0(г;), tanh К} = ф(г[1), A1.8.9а)
xPsq(Kj , К;) = - ln[2 cosh Kjcosh К}] - т + g(zj) + g(zj~l). A1.8.96)
Величины х и Zj снова удовлетворяют ограничениям A1.8.8). Параметр х
теперь мал при достаточно высоких температурах.
Треугольная и шестиугольная решетки:
низкие температуры
Выражения для безразмерной свободной энергии моделей на треуголь-
треугольной и шестиугольной решетках можно теперь получить из A1.7.11) и
A1.7.12). Определим х и zj; с помощью выражений A1.8.7а) при у = 1, 2, 3.
Как видно из A1.7.4) и A1.5.13), величины /, к и, следовательно, <?, х не за-
зависят от у. Кроме того, из'выражений A1.1.12) и A1.8.3) следует, что zv
z2, z$ должны удовлетворять соотношению
ZiZ2z3=x~l. A1.8.10)
Основная проблема состоит в получении полезного выражения для ве-
величины In R из формулы A1.7.8). Из A1.8.16) следует
1). A1.8.11)
Модули к и / связаны между собой преобразованием Ландена A1.5.13). Из
формулы A5.6.3) вытекает соотношение
где
uj=(l+k)Uj. A1.8.13)
Таким образом, из A1.7.4) имеем
sinh 2Kj = -i snO'u/, /). A1.8.14)
(Этот результат можно было получить непосредственно из A1.8.1 в). Срав-
Сравнивая A1.8.14) и A1.8.12) с G.8.5), видим, что величины Kjt Kj, й} соот-
соответствуют величинам L, К, и в гл. 7.)

ГЛАВА 11 305
Мы можем снова использовать разложение функции sn в бесконечное
произведение A5.1.5), A5.1.6), но в данном случае модуль равен /, а не к.
Используя соотношения A5.6.2), A1.8.3) и A1.8.4), получаем
1 \lZjJ „М A - ХАп 3Zj *) A " ХАп lZj)
Подстановка данного результата в A1.7.8) вместе с использованием выра-
выражений (М.8.7) и A1.8.10) дает
з
V8n-5y\2/i v8«-3,,-l\2
-Угтгт( j) (
/I 1111/1 V8w-5r-l\2
7/ /=in-lU~* Zj )
( j
Из выражений A5.6.2) и A1.8.4) видно, что параметр Якоби, отвечаю-
отвечающий модулю /, равен qVl —а:2. Поэтому, используя модуль / в формуле
A5.1.4а), получаем выражение
(M.8.17)
= 1 \ 1тл /
которое можно переписать в виде
L-To,. я..-?о- (П.8.18)
Вычислим логарифмы выражений A1.8.18) и A1.8.16), разложим в ряд
Тейлора каждый член вида 1пA — х%п • const), просуммируем по всем п и
сравним с формулами A1.8.6); при этом получим
ln[2(*//)J]=2r, A1.8.19)
3 3
In R + 2 (К) - К,) = т + 2 \g(Zj) - g{zf1)]. A1.8.20)
С учетом последнего выражения для In/? вместе с A1.8.76) и A1.7.13)
безразмерную свободную энергию модели Изинга на треугольной решетке
можно записать в виде
Vb<Ki,K2,K3) =
= -*i - Кг - К'г - х + gfo) + g(z2) + g(z3), (И.8.21)
где величины ху z{, z2» ^3 определены через A'j, K'2, К'ъ соотношением
A1.8.10) и вторым из уравнений A1.8.7а), г.е.
Ziz2z3 = дГ1, ехр(-2«/) = <p(zfl), /= 1,2,3. A1.8.22)
Используя формулы A1.7.14) и первое из уравнений A1.8.7а), для ше-
шестиугольной решетки получим следующее выражение для свободной энер-
энергии:

306 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
Ъ ,Къ) = "* i -К2-К3-2т+ g(zV) + g^) + g(z^) ,
где A1.8.23)
ZiZ2z3=x-\ exp(-2Kj) = (Hzj), у = 1,2,3. A1.8.24)
Неравенства A1.8.8) должны выполняться и в данном случае; величины
х и / малы при достаточно низких температурах и возрастают до единицы
в критической точке.
Для изотропной системы zx = z2 = z^ = x~Yi. Уравнения A1.8.22) и
A1.8.24) для треугольной и шестиугольной решеток соответственно сводят-
сводятся в этом случае к одному уравнению для х.
Треугольная и шестиугольная решетки:
высокие температуры
При температурах выше критической модуль /, определенный A1.7.5) и
A1.7.6), больше единицы. Простейший способ рассмотрения данного слу-
случая состоит в применении дуального преобразования F.3.7) к полученным
выше низкотемпературным результатам. Для треугольной решетки получа-
получаем
хрт{К[ , К'г, К'ъ) =, -ln[2 cosh K[ cosh K'2 cosh К'ъ) -
- 2т + g{zTl) + g(z2l) + gC^1), (Н.8.25)
где Zj, z2y z3, x определены в A1.8.3) и
zlz2z3=x~\ tanhKj = 0(z/), /=1,2,3. A1.8.26)
Для шестиугольной решетки получаем
1, К2, Къ) = -ln[4 cosh Kx cosh K2 cosh Къ] -
g()g()g() (П.8.27)
где
zlz2z3=x~\ tanh^/=0(z>-1), / = 1,2,3. A1.8.28)
Параметр л" мал при достаточно высоких температурах. Для изотроп-
изотропных систем zx = z2 = z3 = х~ 1/з.
Намагниченность
Из выражений A1.5.13), A5.6.2) и A1.8.4) следует, что параметр Якоби,
соответствующий модулю /, равен qVl - х2. Следовательно, с учетом
A5.1.46) выражение A1.7.30) для спонтанной намагниченности эквивалент-
эквивалентно равенству
00 2 _ х*п~2
U
UtTZm2
"-»1'1'* A1.8.29)
= 0 при |/|>1,
которое согласуется с A0.10.19).

ГЛАВА 11 307
Последний результат справедлив для квадратной, треугольной и шести-
шестиугольной решеток. При 1/1 ^ 1, т.е. при температурах меньше критичес-
критической, величина х для квадратной, треугольной и шестиугольной решеток
определяется по формулам A1.8.7) и A1.8.22) и A1.8.24) соответственно.
Объединенные формулы для всех трех плоских решеток
Все полученные выше результаты для квадратной, треугольной и ше-
шестиугольной решеток можно представить в простой общей форме. То, что
такая возможность существует, мне кажется весьма интригующим.
Обозначим через q координационное число решетки, т.е. число соседей
каждого узла. Для квадратной, треугольной и шестиугольной решеток
<7 = 4, 6 и 3 соответственно. Обозначим через Кх, . . . , К- коэффициенты
взаимодействия моделей Изинга, ассоциированные с q реорами в каждом
узле, как это показано на рис. 11.10.
Отметим, что новые обозначения отличаются от обозначений в преды-
предыдущих разделах: для квадратной решетки Кх и К2 заменяют К- и Kj из
A1.8.7) и A1.8.9) и Кг = Кх, КА = К2\ для треугольной решетки Кх, К2, К3
заменяют К[, K'v К'ъ из A1.8.22) и A1.8.36) и К4 = Кх, К5 = Kv К6 = Ку
Для шестиугольной решетки изменений в обозначениях нет.
С каждым коэффициентом Кг свяжем параметр wr следующим образом:
Квадратная решетка: wx ,. . . , vv4 = zh z~\ z}, z~l;
Треугольная решетка: wx,. . . , w6 = Zi\ zi\ 23, zf1, zi\ Z31 ;
A1.8.30)
Шестиугольная решетка: vvb и>2, w$ = z\, Zj, 23.
Здесь Zj совпадает с Zj из A1.8.7) и A1.8.9); zx, z2, z3 совпадают cz,, z2, z3
из A1.8.22) — A1.8.28). Следовательно, из неравенств A1.8.8) получаем
0<*<1, x<wr<x~\ r=l,...,^. A1.8.31)
Все низкотемпературные (/< 1) результаты A1.8.7), A1.8.21) —
A1.8.24) можно теперь записать в виде
wiw2. . . Wq =x«-\ exp(-2Kr) = <#О, г = 1 ,. . . , q , A1.8.32а)
r-1), (и.8.326)
где суммирование проводится по г = 1, . . . , q; t, Ф(г), g(z) определены в
A1.8.6). При заданных Кх, . . . , Kq величины tv,, . . . , w- и х определены
Кг
Рис. 11.10. Используемые в A1.8.32) — A1.8.43) коэффициенты взаимодействий
моделей Изинга на квадратной, треугольной и шестиугольной решетках.

308 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
выражениями A1.8.31) и A1.8.32а). Приходящаяся на один узел решетки
(квадратной, треугольной или шестиугольной) безразмерная свободная
энергия определяется выражением A1.8.326), а намагниченность — выра-
выражением A1.8.29).
Аналогично все высокотемпературные (/ > 1) результаты A1.8.9),
A1.8.25) — A1.8.28) можно записать в виде
<Цп;х), A1.8.33а)
Kr+ т+ i2[g(wr)- т]. A1.8.336)
г г
АНАЛОГИЯ С ФОРМУЛАМИ ДЛЯ РЕШЕТКИ БЕТЕ
Полученные результаты для анизотропных плоских решеток очень по-
похожи по форме на результаты разд. 4.9 для анизотропной решетки Бете.
Действительно, если в разд. 4.9 положить h = 0 и заменить /, хг на х2,
(x/wr)Y2 соответственно, то выражения для свободной энергии D.9.4) и
D.9.6), модели на решетке Бете в точности примут вид A1.8.32). Но при
этом определения A1.8.6) заменяются на
A1.8.34)
Как для A1.8.6), так и для A1.8.34) справедливы соотношения
0(дс) = 1, ft*) =$(*-•) =0, g(*) = r. (П.8.35)
Выражение D.9.5) для намагниченности принимает вид
М = A - х2)/A + х1). A1.8.36)
Последнее выражение не совпадает с A1.8.29), но М снова зависит только
от х2.
Для ферромагнитной модели на решетке Бете при температуре ниже
критической должны выполняться неравенства A1.8.31). (Выше критичес-
критической температуры х = wx = ... = н^=1и модель на решетке Бете ста-
становится более тривиальной: ф = —In 2 — ViY, cosh/fr и М = 0.)
Удивительно, что существуют такие соответствия между анизотропны-
анизотропными моделями Изинга без внешнего поля на двумерных решетках и на беско-
бесконечномерной решетке Бете. Я использовал разложения в ряд, пытаясь най-
найти подобные свойства для трехмерных моделей и для плоских моделей во
внешнем поле, но без успеха.
Критическая температура
В моделях Изинга и на плоских решетках и на решетке Бете критическая
точка имеется в том случае, когда величины х, Wj, . .., w- бесконечно близ-
близки к единице. Введем обозначения
* = ехр(-б), wr = exp(-ar). A1.8.37)

ГЛАВА 11 309
Тогда из A1.8.6), A5.1.5) и A5.1.6) следует, что функция (f>(wr) для плоской
решетки имеет вид
<К™г) = -«Л* sn[/(arr+ 6)Ил], A1.8.38)
где к — модуль, введенный в данном разделе, с q = х4. Поэтому
я/74/= 6. A1.8.39)
Если х = 1, то к = 1 и/' = 7г/2. Используя A5.7.3а) и A1.8.39), выраже-
выражение A1.8.38) можно привести к виду
0(wr) = Ш[л(аг + д)/8д]. A1.8.40а)
Полученное выражение соответствует функции ф(н>г) для плоской ре-
решетки в пределе 6 — 0 при постоянном отношении аг/д.
С другой стороны, используя A1.8.34) и A1.8.37), легко проверить, что
для решетки Бете в таком пределе
ФЮ = (аг + <5)/2<5. A1.8.406)
В обоих случаях должны выполняться уравнения A1.8.32а), поэтому
*1+ ... + *j = E-4N, A1.8.41а)
ехр( - 2КГ) = ф(О, г = 1,. . . , q . A1.8.416)
Решая уравнения A1.8.416) и A1.8.40) относительно аг и подставляя реше-
решение в A1.8.41а), получаем следующие условия критического состояния для
модели Изинга на решетке с координационным числом q и коэффициента-
коэффициентами взаимодействия Кх, . . . , К-:
плоские решетки: artan(?i) + . . . + artan(^) = rtq- 2I А ,
A1.8.42)
решетки Бете: ?i + . . . + f$ = q - 2 ,
ГДС Сг=ехр(-2Л:Г), г=1,...,?. A1.8.43)
Для каждой конкретной плоской решетки условие A1.8.42) можно упро-
упростить. Пусть К{, К2 (Кх, К2, Кг) — коэффициенты взаимодействия на ква-
квадратной (треугольной или шестиугольной) решетке. Тогда условия крити-
критического состояния имеют вид
квадратная решетка: ?j?2 4- fj 4- f2 = 1 ,
треугольная решетка: ?2?з + Сз?1 + fi?2 = 1 , A1.8.44)
шестиугольная решетка: С1С2С3 - С2С3 - ?з? 1 ~ С?г - Сi ~ С2 ~ Сз + 1 = 0 .
Для изотропной модели, когда все коэффициенты одинаковы и равны
К, из формулы A1.8.42) следует, что критическое значение f = ехр( — 2К)
равно
плоские решетки: С= tan[;r(*7 — 2)/4Jl,
A1.8.45)
решетки Бете: ? = (q - 2)lq .

310 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
Таблица 11.2
Критические значения величины К = J/kB T для моделей Изинга
на разных решетках (д — координационное число)
я
3
4
6
8
12
Плоская
решетка
0,658479
(шестиугольная)
0,440687
(квадратная)
0,274653
(треугольная)
Трехмерная
решетка
0,369790
(алмаз)
0,22169
(простая кубическая)
0,15741
(ОЦК)
0,10209
(ГЦК)
Решетка
Бете
0,549306
0,346574
0,202733
0,143841
0,091161
Для конкретных плоских решеток значения f равны
квадратная решетка: 9 = 4, f = V2 - 1 = 0.414214,
треугольная решетка: q = 6,?= 1/Л/з = 0.577350, A1.8.46)
шестиугольная решетка: # = 3, С = 2 - VI = 0.267949 .
Соответствующие критические значения К = J/kBT даны в табл. 11.2
вместе с численными оценками для трехмерных решеток [98, 224] и значе-
значениями для решетки Бете. Поскольку решетка Бете является бесконечномер-
бесконечномерной (в смысле, определенном в разд. 4.2), при заданном координационном
числе оценки, сделанные для трехмерных решеток, должны лежать между
значениями для плоской решетки и решетки Бете. Они действительно ле-
лежат в этом интервале.
Результаты A1.8.42) — A1.8.45) относятся к ферромагнитной модели
Изинга, когда все коэффициенты взаимодействия неотрицательны. Любую
модель на квадратной и шестиугольной решетках, а также на решетке Бете
можно отобразить в данную область с помощью обращения подходящих
чередующихся слоев спинов. Таким способом можно изменить знак любого
коэффициента взаимодействия. В случае треугольной решетки можно изме-
изменять знаки только у пар коэффициентов взаимодействия: в пространстве

ГЛАВА 11 ЗП_
точек (f j, f2» Г3) существует четыре критические поверхности. Одна из та-
таких поверхностей задана уравнением A1.8.44), а три другие получаются из
первой при изменении знаков любых двух величин из f j, f2» Гз-
11.9. ТРИДЦАТИДВУХВЕРШИННАЯ МОДЕЛЬ
Очевидное обобщение модели типа льда, или шестивершинной модели
на квадратной решетке состоит в том, чтобы поместить стрелки на ребра
треугольной решетки так, чтобы в каждом узле три стрелки были направ-
направлены к вершине, а три стрелки — от нее. При этом существует 20 возмож-
возможных конфигураций стрелок на каждой вершине, поэтому такое обобщение
модели льда известно как «двадцативершинная» модель. Каждой конфигу-
конфигурации соответствует вес о?у, где j = 1, . . . , 20. Статистическая сумма име-
имеет вид
где суммирование выполняется по всем допустимым конфигурациям С
стрелок на ребрах треугольной решетки, произведение берется по всем
узлам / иу(/, С) — тип вершинной конфигурации стрелок в узле / при кон-
конфигурации С. Такая модель в общем случае точно не решена. Она может
быть решена точно при выполнении некоторых условий [18, 144, 145].
Восьмивершинная модель была получена из шестивершинной с по-
помощью введения дополнительных разрешенных конфигураций стрелок на
каждом узле: допускались вершинные конфигурации, в которых число стре-
стрелок, направленных к узлу, равно 0, 4 и 2. Таким же способом можно обоб-
обобщить и двадцативершинную модель, допустив конфигурации с любым не-
нечетным числом стрелок, направленных к узлу. Тогда на каждой вершине
существуют 32 возможные конфигурации стрелок.
Стрелки можно представлять с помощью связей: ребро пусто, если со-
соответствующая стрелка имеет составляющую, направленную вправо
Х--Х--Х--Х- *г-тС* У-
(V W OM6 OM6 U)JS UI5 Щ6 Шц; ШП пI3
U)Jlf UJ3 U)Z3 LQ25 WZ5 OK6 пK6 W34 UKtf CU35 CO35
* X- -tr
f
Щ5 Щ5 oj1z w1z u)Z6 wZ6 aI6 w}6
Рис. 11.11. Тридцать две допустимые вершинные конфигурации связей на треуголь-
треугольной решетке и соответствующие больцмановские веса.

312 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
(рис. 11.1); на ребре находится связь, если стрелка имеет составляющую,
направленную влево. Тогда в каждом узле имеется четное число связей. На
рис. 11.11 показаны 32 возможные конфигурации связей на вершине. Кроме
того, приведены веса w, . . . , а>16, соответствующие таким конфигурациям.
Случай свободных фермионов
Сакко и By [207] рассмотрели модель свободных фермионов и показали,
что ее можно решить методом пфаффианов, изложенным в разд. 7.13, при
условии что
(ой) = a>i2ft>i2 - <Oi3u)i3 + a>i4d>i4 - (Oi5a)i5 + w^Ota, О1 -9-2a)
(ой)тп = (OijCOki ~ VikPn + (Оцсо)к A1.9.26)
при всех перестановках /,у, к, /, т, п чисел 1, 2, . . . , 6, таких, что т < п
и / < j < к < /. Существует 15 подобных перестановок (соответствующих
15 возможностям выбора т и п); следовательно, всего имеется 16 условий.
Случаи, которые сводятся к восьмивершинной модели
на решетке кагоме
Другой интересный класс решаемых моделей можно получить из вось-
восьмивершинной модели на решетке кагоме. На рис. 11.1 треугольники углом
вверх имеют меньшие размеры, чем треугольники углом вниз. Представим
себе процесс, в котором размеры треугольников углом вверх становятся
бесконечно малыми. В результате решетка кагоме превратится в треуголь-
треугольную.
Каждый узел такой треугольной решетки представляет собой кластер,
состоящий их трех узлов исходной решетки кагоме.
Такой кластер показан на рис. 11.4,а. Окружающие его ребра имеют
спины «j, . . . , а6, равные -I-1, если ребро пусто, и — 1, если ребро содер-
содержит связь. Суммируя по внутренним стрелкам или конфигурациям связей
внутри треугольника, получим зависящий от а1? . . . , а6 полный больцма-
новский вес кластера, который появляется в левой части уравнения A1.1.6).
Отсюда следует, что если величины w, . . . , а>16 являются такими
больцмановскими весами при подходящих значениях а1? . . . , а6, то 32-
вершинная модель эквивалентна восьмивершинной модели на решетке ка-
кагоме. Если выполняются условия A1.1.6) или A1.1.7), то модель может
быть решена так же, как в разд. 11.2 — 11.5.
Рассматривая все 32-вершинные конфигурации, можно показать, что
модель решается точно при выполнении следующих соотношений:
cld2d3,
со = ахпгЪъ +
юн = схс2съ + Ьф2Ь3,

ГЛАВА 11
313
а>15 =
= сха2аъ
= схЪ2Ъъ + Ъхс2съ, A1.9.3a)
И ПРИ 1 < АИ < П
= о), (Ьтп =
A1.9.36)
Если можно найти такие al9 . . . , d3, что условия A1.9.3), которые
включают в себя ограничения A1.1.7), выполняются, то спонтанная поля-
поляризация 32-вершинной модели задается формулой A1.3.4), а из A1.4.5) сле-
следует, что свободная энергия на один узел равна
, Ьх, сх, dx) +f(a2,Ь2,с2, d2)
A1.9.4)
где/(а, Ъ, с, of) — свободная энергия на один узел восьмивершинной моде-
модели с весами а, Ь, с, d на квадратной решетке, а величина /г^Г считается
постоянной, одинаковой для всех /.
Из выражений A1.1.8) — A1.1.12) очевидно, что для величин ы, . . . ,
а>16 существует только пять степеней свободы: к, uv w2, w3 и один норми-
нормировочный множитель. Таким образом, условия A1.9.3) содержат 27 ограни-
ограничений на веса 32-вершинной модели. Как мы увидим в следующем разделе,
даже такая ограниченная модель представляет интерес.
При dx = d2 = d3 = 0 ограниченная модель сводится к решаемым слу-
случаям двадцативершинной модели, рассмотренным в работах [46, 145]. В
частности, сюда относится модель KDP на треугольной решетке [144], ко-
которая ведет себя аналогично сегнетоэлектрической модели на квадратной
решетке (гл. 8), имея переход первого порядка в замороженное сегнето-
электрическое состояние.
Формулировка в виде модели Изинга
с мультиспиновыми взаимодействиями
на шестиугольной решетке
Подобно восьмивершинной модели, 32-вершинную модель можно рас-
рассматривать как модель Изинга с мультиспиновыми взаимодействиями.
Каждой грани т треугольной решетки поставим в соответствие спин от со
значениями 4-1 или — 1. Как и в разд. 10.3 и 11.5, установим соответствие
вида два к одному между конфигурациями спинов ( а,, а2, . . . ) и допусти-
допустимыми конфигурациями стрелок, покрывающих решетку. Такое соответст-
соответствие можно установить, выбирая конфигурацию стрелок на рис. 11.8,5 в ка-

314 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
честве стандартной: если спины по обе стороны некоторого ребра одинако-
одинаковы (противоположны), то на данном ребре следует располагать стрелку,
указывающую в ту же (противоположную) сторону, что и стрелка в стан-
стандартной конфигурации. Проделаем такую процедуру для всех ребер. Тогда
в каждой вершине на шести ребрах должно быть четное число нестандарт-
нестандартных стрелок и, следовательно, нечетное число входящих (и выходящих)
стрелок.
Пусть ар . . . , ав — шесть окружающих узел спинов, расположенных,
как показано на рис. 11.4, а, причем треугольник стянут в точку. Обозна-
Обозначим через W(ax, . . . , о^ функцию, значение которой при спиновой конфи-
конфигурации ар . . . , ав равно весу соответствующей конфигурации стрелок в
данном узле. Тогда выражение A1.9.1) можно записать в виде
) (И.9.5)
О I
где суммирование проводится по всем значениям спинов на гранях тре-
треугольной решетки, произведение берется по всем узлам / и а1/} . . . ,
o6i — спины на гранях вокруг узла /.
Изменение знаков у всех спинов ои, . . . , а6/ оставляет неизменными
стрелки, входящие в узел или выходящие из него, т.е.
W( - <7i ,...,- аб) = Щох,. . . , о6). A1.9.6)
Используем теперь дуальную решетку: спины лежат в узлах шести-
шестиугольной решетки, произведение в A1.9.5) берется по всем гексагональным
граням / такой решетки и а1/} . . . , ав1 — шесть спинов, окружающих дан-
данную грань /. Таким образом, 32-вершинная модель эквивалентна модели
типа Изинга на шестиугольной решетке с взаимодействиями всех шести
спинов, принадлежащих каждой грани. Такие взаимодействия должны
быть четными, поэтому весовая функция грани удовлетворяет условию
A1.9.6). Указанная эквивалентность имеет весьма общий характер.
Рассмотрим теперь решаемый случай 32-вершинной модели, когда веса
удовлетворяют условиям A1.9.3). Можно, конечно, получить все значения
функции W, воспользовавшись определениями данного подраздела и соот-
соотношениями A1.9.3). Например, W( +, +, +, +, +, +) соответствует
стандартной вершинной конфигурации, показанной на рис. 11.8,6. Заменяя
направленные влево стрелки на связи, мы видим из рис. 11.11, что вес дан-
данной конфигурации равен а>14. Поэтому, используя A1.9.3), получаем
Щ+ , + , + , + , + ,+) = (ои = С\С2С3 + ЪхЪгЪъ. A1.9.7а)
Другими примерами являются следующие значения функции W\
A1.9.76)
Вспомним, что рассматриваемый случай 32-вершинной модели получа-
получается при стягивании в точки треугольников углом вверх решетки кагоме.

ГЛАВА 11 315
Проделав данную процедуру в мультиспиновой формулировке модели
разд. 11.5, мы сразу получим формулировку 32-вершинной модели с по-
помощью изинговых спинов, причем остаются те спины, которые не принад-
принадлежат внутренним граням треугольников углом вверх. Весовая функция
И^ар . . . , а6) представляет собой полный вес треугольника на
рис. 11.4,я, просуммированный по значениям центрального спина а7. Она
просто равна левой части A1.5.8). Записывая весовые функции W{, W2, W3
для решетки кагоме в виде A1.5.5) и используя выражение A1.5.10), полу-
получаем
, а6) = 2MiM2M3 exp(K[aia3 + Цого5Н- К'ъо5ох) х
A1.9.8)
К'оъоАо5 + Kf)
Данное выражение равно левой части A1.5.9), умноженной на постоянную
величину 2М1М2М3.
Если функция W задается формулой A1.9.8), то 32-вершинная модель
эквивалентна общей восьмивершинной модели на решетке кагоме: эти мо-
модели имеют одинаковые статистические суммы и, поскольку соседние изин-
говы спины ат, оп в первой модели являются соседними спинами и в по-
последней, одинаковые спонтанные намагниченности (от) и спонтанные по-
поляризации (отоп) .
Если удовлетворяются также условия A1.5.11) (которые означают, что
левые и правые части выражения A1.5.8) или A1.5.9) равны), то соответст-
соответствующая восьмивершинная модель на решетке кагоме решена в разд. 11.2 —
11.5. Следовательно, полная свободная энергия, спонтанная намагничен-
намагниченность и спонтанная поляризация 32-вершинной модели даются выражения-
выражениями A1.4.5), A1.5.18) и A1.3.4) соответственно, где N — число вершин и
а],..., </3 определяются формулами A1.5.6)
11.10.ТРЕХСПИНОВАЯ МОДЕЛЬ НА ТРЕУГОЛЬНОЙ
РЕШЕТКЕ
Историческое введение
Решение восьмивершинной модели [22, 25] возбудило интерес к моде-
моделям с мультиспиновыми взаимодействиями, особенно к модели с взаимо-
взаимодействием трех спинов на треугольной решетке.
В такой модели на каждом узле / треугольной решетки находится спин
О;, принимающий значения +1 или -1. Энергия определенной конфигура-
конфигурации спинов имеет вид
? = -/11G,^, A1.10.1)
где суммирование проводится по всем треугольным граням решетки. Как
следует из формулы A.4.1), статистическая сумма записывается в виде
Z = 2 ехр[к2 OiOjOk] , A1.10.2)
где °
K = J/k»T. A1.10.3)

316 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
Безразмерная свободная энергия на один узел равна
гр(К) = - lim N In Z , A1.10.4)
где N — число узлов в решетке.
Треугольную решетку можно разоить на три подрешетки Л, В, С, как
показано на рис. 11.8,5, так что каждая треугольная грань (/, i, k) содер-
содержит один узел типа А , один узел типа В и один узел типа С. Из формулы
A1.10.1) очевидно, что изменение знаков всех спинов одной подрешетки
эквивалентно изменению знака коэффициента J и, следовательно, измене-
изменению знака К. Без потери общности мы можем поэтому считать, что вели-
величина К неотрицательна.
Вуд и Гриффите [256] и Мерлини и Грубер [166] рассмотрели такую мо-
модель и показали, что она удовлетворяет соотношению дуальности
гр(К*) = 2К+ хр(К) - lnBcosh2A:*), A1.10.5а)
где
tanhA:* =exp(-2/O. A1.10.56)
Соотношение A1.10.5а) в точности представляет собой соотношение дуаль-
дуальности F.2.14) изотропной модели Изинга (с L = К) на квадратной решет-
решетке. Следовательно, справедливы рассуждения, предшествующие формуле
F.2.16): если существует только одна критическая точка, то она определя-
определяется условием К = Кс, где
sinh2A:c = 1, Кс = 0.44068679. . . . A1.10.6)
Гриффите и Вуд [103] использовали данный вывод и разложение в ряд
для оценки критических показателей рассматриваемой модели. Они получи-
получили 0,6 < а' ^ 0,8, 0,070 < 0 < 0,071, 1,25 < у' < 1,40 и правильно угада-
угадали значение а' = 2/з. Их оценки показателей /3 и у' были не совсем верны-
верными; в действительности величина /3 равна Ум, а (предполагая скейлинг) ве-
величина у' равна 7/б.
Предположим, что к энергии A1.10.1) добавлен член, отвечающий взаи-
взаимодействию с магнитным полем —//? о-. Обозначим через io^N H сред-
среднее значение спина а,, вычисленное по формуле A.4.4) для конечной решет-
решетки с N узлами при наличии внешнего поля Н\ пусть
<а,)= lim lim (o^n н , A1.10.7)
где предел при N ¦— оо означает, что решетка увеличивается во всех направ-
направлениях.
Величина <а;> представляет собой намагниченность при нулевом поле.
Так же как в модели Изинга, и в восьмивершинной модели она должна
быть равна нулю при достаточно высоких температурах.
Последнее утверждение сразу не очевидно: поскольку энергия A1.10.1)
не изменяется при обращении всех спинов, обычный аргумент разд. 1.7'для
модели Изинга (что М является нечетной функцией Я, непрерывной при
достаточно высокой температуре) не применим. Вместо этого заметим.

ГЛАВА 11 317
что при Я = О энергия A1.10.1) не изменяется при изменении знаков всех
спинов на любых двух подрешетках из А, В, С.
Обозначим через оА, ов, ос все спины на подрешетках Л, В, С соот-
соответственно. Тогда любой полной конфигурации (аА, о^ ос) спинов соот-
соответствуют три другие конфигурации, которые получаются при изменении
знаков у всех спинов на двух подрешетках. Таким образом, конфигурации
спинов можно сгруппировать в наборы из четырех конфигураций, имею-
имеющих одинаковую энергию:
(оА,ов,ос) Л°а, -ов, -ос) Л~Оа, ов, -ос) ,(-сгл, ~°в, ос) .
A1.10.8)
Для каждого отдельного спина ог сумма его значений в данных четырех
конфигурациях равна нулю. Следовательно, для конечной решетки должно
выполняться равенство
<<т,Уо = О. A1.10.9)
При достаточно высоких температурах пределы в A1.10.7) можно пере-
переставлять. При конечных N величина <^,->^,я является непрерывной функ-
функцией Я, поэтому из A1.10.9) следует
((Ji) = 0 при достаточно высоких температурах. A1.10.10а)
С другой стороны, Мерлини и др. [165, 167] использовали метод Пай-
ерлса [106, 192] для получения нижней границы величины <ау> Nн. Они по-
показали при этом, что
(а,) > 0 при достаточно низких температурах, A1.10.106)
т.е. существует ненулевая спонтанная намагниченность <а,>. Отсюда сле-
следует, что должна существовать критическая точка — температура Гс,
вблизи которой при понижении температуры величина <а^> скачком прини-
принимает отличное от нуля значение.
Аналогичные замечания применимы к величине {otOj) (где / и у отно-
относятся к ближайшим соседям), вычисленной с помощью двойного предель-
предельного перехода A1.10.7). Данная величина должна быть равна нулю при до-
достаточно высоких температурах и, по-видимому, должна отличаться от ну-
нуля при достаточно низких температурах. По аналогии с мультиспиновой
формулировкой восьмивершинной модели в разд. 10.3 и формулой
A0.10.22) величину {otOj) удобно назвать «поляризацией» трехспиновой
модели.
Бэкстер и By [42, 43] вычислили непосредственно свободную энергию
трехспиновой модели (при Я = 0), используя метод трансфер-матрицы и
обобщенный анзац Бете для собственных векторов. Бэкстер и др. [44] ис-
использовали разложения в ряд для выяснения вида точных выражений для
спонтанной намагниченности < а,> и спонтанной поляризации < о;о().
Бэкстер и Энтинг [36] заметили, что полученные результаты в точности
совпадают с результатами для частной восьмивершинной модели и что
восьмивершинная модель также обладает четырехкратной симметрией спи-

318 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
новых конфигураций. Руководствуясь обнаруженными свойствами, они на-
нашли преобразование трехспиновой модели на треугольной решетке в вось-
мивершинную модель на квадратной решетке. Следовательно, все резуль-
результаты, полученные для трехспиновой модели, являются следствием соот-
соответствующих результатов для восьмивершинной модели.
Позднее я показал [32], что трехспиновая модель представляет собой
особый случай разрешимой восьмивершинной модели на решетке кагоме.
Такая эквивалентность значительно проще, чем результат, полученный
Бэкстером и Энтингом; она и будет использоваться в настоящем разделе.
С этой точки зрения преобразование Бэкстера — Энтинга представляет со-
собой способ установления связи между частными восьмивершинными моде-
моделями на квадратной решетке и решетке кагоме, каждая из которых эквива-
эквивалентна трехспиновой модели. Такой способ является альтернативным по
отношению к способу, использованному в разд. 11.2.
Эквивалентность восьмивершинной модели
НА РЕШЕТКЕ КАГОМЕ
Выполним в A1.10.2) суммирование по всем спинам одной подрешетки,
скажем С. Такое суммирование легко выполнить, поскольку каждый спин
подрешетки С взаимодействует только со спинами подрешеток А и В. По-,
лучим выражение
Z=  \}Щои,...,оы), A1.10.11)
где
W{o\,. . . , Об) = 2 cosh К{о\О2 + ОгОг + Ого± + Ол,о$ + о&ь + ОьО\).
A1.10.12)
Суммирование в A1.10.11) выполняется по всем спинам подрешеток А и В.
Подрешетки А и В вместе образуют шестиугольную решетку (рис. 11.8,6).
Произведение в A1.10.11) берется по всем граням / такой шестиугольной
решетки; aw, . . . , оы — шесть спинов, окружающих грань /.
За исключением множителя Уг, который не существен для большой ре-
решетки, выражение A1.10.11) совпадает со статистической суммой A1.9.5)
32-вершинной модели. Далее прямые вычисления, использующие тот факт,
что спины or j, . . . , а6 принимают только значения + 1 или - 1, показыва-
показывают, что выражение A1.10.12) можно представить в виде
W(oi,. . . , Об) = 2 cosh К(а2 + о4 + о6 + охо2оъ + оъо±о5 + o5oboi) -
A1.10.13)
Но последнее выражение в точности совпадает с выражением A1.9.8) для
функции W\ где
Mi=l,K't=0,Kt = К" = К A1.10.14)
при / = 1, 2, 3. Таким образом, трехспиновая модель эквивалентна восьми-
восьмивершинной модели на решетке кагоме с указанными выше значениями ве-

ГЛАВА 11 319
личин Mt, Kt, AT/, К", рассмотренной в разд. 11.5. Интересно отметить,
что набор коэффициентов взаимодействия A1.10.14) весьма специфичен: те-
теперь равны нулю взаимодействия в A1.5.7) вдоль ребер треугольной решет-
решетки, а коэффициенты остающихся двух- и четырехспиновых взаимодействий
одинаковы.
Ограничения A1.5.11) выполняются автоматически, поэтому из замеча-
замечаний в конце предыдущего раздела следует, что приходящаяся на один узел
свободная энергия трехспиновой модели имеет вид
hsP,n=f(a,b,c,d), A1.10.15)
где через f(a, b, с, d) обозначена приходящаяся на один узел свободная
энергия восьмивершинной модели на квадратной решетке, веса а, Ь, с, d
которой заданы формулами A1.5.6) и A1.10.14) для любых значений номе-
номера /, т.е.
я, Ь, с, d = 1, exp(-2K), expBK), 1. (П.10.16)
Аналогично спонтанная намагниченность и спонтанная поляризация запи-
записываются в виде
(от) = M0(a,b,c,d), (aman) = Po(a,b,c,d), (П.10.17)
где тип — соседние узлы.
Следовательно, трехспиновая модель на треугольной решетке эквива-
эквивалентна восьмивершинной модели с весами а, Ь, с, d на квадратной решет-
решетке, причем для обеих моделей функции/, (от), (отоп) одинаковы. Пусть
далее все спины из некоторого набора ох, . . . , от лежат на толстой зигза-
зигзагообразной линии, показанной на рис. 1Ь8,б. Тогда, используя A1.5.17) и
приведенные выше аргументы, легко показать, что для трехспиновой моде-
модели и для восьмивершинной модели на квадратной решетке, полученной при
удалении всех горизонтальных ребер графа, показанного на рис. 11.8,6,
корреляции (а{ . . . от) одинаковы. Таким образом, рассматриваемые две
модели имеют одинаковые корреляционные длины ? вдоль показанной на
рис. 11.8,6 зигзагообразной линии.
УПОРЯДОЧЕННАЯ ФАЗА
Свойства функций /, М0, PQ B восьмивершинной модели на квадратной
решетке можно получить из результатов гл. 10. Если К > Кс, где Кс —
введенное в A1.10.6) критическое значение величины К, то из A1.10.16) сле-
следует
sinh2A:>l, Oa + b + d. A1.10.18)
Следовательно, веса а, Ъ, с, d лежат в основной области A0.7.5), и можно
использовать непосредственно соотношения разд. 10.4— 10.10; не нужно
никаких предварительных преобразований весов а, Ъ, с, d.
Из формулы A1.10.16) видно, что ad = be и а = d. Отсюда и из выра-
выражения A0.4.24) следует

320 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
ksnh2(k- и) = 1 , к snh A snh и = 1 A1.10.19)
Как видно из A0.7.1) и A0.4.23), величины к, \ и и действительны и
0 < и < \ < Г . Эллиптическая функция snh w, определенная в A0.4.20),
действительна, монотонно возрастает от нуля до бесконечности при воз-
возрастании и от нуля /' и, как следует из A5.2.5) и A5.2.6), удовлетворяет
уравнению
snh(/' - и) = (к snh и)~1. A1.10.20)
Из A1.10.19) следует
A-w = ?/', А+м = /'; A1.10.21)
поэтому, используя A0.4.23), A0.7.9) и A0.7.19), получаем
А = |/\ и**/', и = -*/', A1.10.22)
x = qm, z = q~m. A1.10.23)
Чтобы связать данные параметры с коэффициентом взаимодействия К,
заметим, что из выражений A0.4.21), A1.10.16) и A1.10.22) следует
ехр(-2А:) = - = *"Ь" . = ** snh(/74). A1.10.24)
a snh(A -и) у
Введем
р = <?1М. A1.10.25)
Тогда, используя A0.4.20), A5.1.6) и A5.1.5) для разложения kVl snh(/'/4)
в бесконечное произведение, получим
- р> ft d-
A1.10.26)
т.е. точное соотношение между величинами К и р.
Свободная энергия задается формулой A0.8.47). Используя A1.10.16),
A1.10.23) и A1.10.25), получаем
Выражение под знаком суммы можно записать в виде суммы двух рацио-
рациональных функциий отрт, имеющих знаменатели 1 - р8т и 1 -I- рЪт соот-
соответственно. Разложение в ряд Тейлора по степеням рт, суммирование по
всем т и взятие экспоненты дает
ТТ A -рЬп~3)A -р*п-УA -pSn)
ехр(-/ВД = ехрBК) Д (\ _РрЬп) {[ ./-sy^ _/-гу ¦ ("-Ю.28)
Для некоторых целей такая форма записи более удобна, чем A1.10.27): она

ГЛАВА 11 321
дает степенной ряд относительно р, в котором все коэффициенты являют-
являются целыми числами.
Для спонтанной намагниченности и спонтанной поляризации из формул
A0.10.19) и A0.10.24), используя A1.10.23) и A1.10.25), получаем
_ fll-p*-3
Рп=П14-^ \-С). (ПЮ.ЗО)
Подведем итоги: если величина К задана, то р определяется из
A1.10.26) и удовлетворяет неравенству 0 < р '< 1; в этом случае функции
/, Мо, Ро вычисляются [44] по формулам A1.10.28) — A1.10.30).
Можно исключить р и представить ехр(-//квТ), Мо, Ро в виде алге-
алгебраических функций от ехр(-2Аг). Результаты оказываются громоздкими
и дают мало нового; они приведены в работах [42, 43].
Неупорядоченная фаза
Если 0 < К < Кс, то веса а, Ь, с, d не лежат в основной области
A0.7.5). Они принадлежат области разупорядочения III (разд. 10.1.1). В
этой области отсутствуют спонтанная намагниченность и спонтанная поля-
поляризация:
Мо = Ро = О. A1.10.31)
Для получения свободной энергии мы должны использовать процедуру
перестройки 1 — 3, описанную в разд. 10.11. Такая процедура приводит к
перестановке функций Wj и w4 в формулах A0.2.16), что соответствует за-
замене весов а, Ь, с, d на
ar = i(a-b + c-d), br = \{-a + b + с -d),
A1.10.32)
cr = i(a +b + c + d), dr = i(-a -b + с + d).
Из выражений A1.10.16) следует
an bn cr, dr = sinh 2K, 2 sinh2^, 2 cosh2/C, sinh2A:. A1.10.33)
Подобно весам a, b, c, d, новые веса ап br, cn dr также удовлетворяют ра-
равенствам ardr = brcr и аг = dr. Выражения A1.10.33) можно представить в
виде
(аг, Ъг, cr, dr) = sinh2A:(l, exp(-2*:*), ехрBК*), 1), A1.10.34)
где величина К* определена в A1.10.56).
Новые веса совпадают с исходными весами A1.10.16), за исключением
того, что в них величина К заменена на А'* и каждый вес умножен на
sinh 2K. Следовательно, безразмерная свободная энергия ф = f/kBT опре-
определяется соотношением
гр(К) = - In sinh 2Я+!//(*:*), A1.10.35)

322 ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ
т.е. соотношением дуальности A1.10.5а). Используя данное соотношение и
результаты A1.10.26), A1.10.28) для упорядоченной фазы, получаем, что
если р определяется выражением
то свободная энергия равна
ехр(-//ад = 2 cosh2К Д
Д (\ _ Рр6п) J (_^/_5J^ ^/_3J •
Параметры ?, X, и задаются теперь формулами A0.4.21), в которых ве-
веса а, Ь, с, d заменены на ar> br> cr> dr Поскольку веса ar> br, cr, dr отлича-
отличаются от исходных величин в A1.10.16) только нормировочным множите-
множителем и выбором К, уравнения A1.10.19)—A1.10.23) остаются справедливы-
справедливыми. Из A0.12.5) следует, что как для упорядоченной, так и для неупорядо-
неупорядоченной фаз
/i = ?tt, w=-\n. A1.10.38)
Критическое поведение
Критическая точка трехспиновой модели соответствует значению
К = Кс. Поскольку функции /, Л/о, Ро данной модели совпадают с соот-
соответствующими функциями восьмивершинной модели на квадратной решет-
решетке с /х = Зтг/4, то, как следует из A0.12.24), критические показатели а, а',
/3, $е равны
a=af = i9 Р = Ре=&- A1.10.39а)
Корреляционная длина ? совпадает с корреляционной длиной восьми-
восьмивершинной модели в диагональном направлении. Она не равна рассмотрен-
рассмотренной в гл. 10 корреляционной длине вдоль ряда или вдоль столбца решетки,
но вблизи критической точки величина ?, по-видимому, ведет себя так же,
как в A.7.25), имея показатель v, который не зависит от направления изме-
измерения корреляции. Предполагая, что данное свойство выполняется, из
A0.12.24) получаем для трехспиновой модели
„=„' = §. A1.10.396)
Это согласуется с гипотезой скейлинга A.2.16). Если принять также другие
предсказания скейлинга, то критические показатели у, 5, т\ и показатель по-
поверхностного натяжения /х5 в трехспиновой модели равны
y=h E=15, rj=|, ц,= 1. O1.1O.39b)

12
МОДЕЛИ ПОТТСА И
ЭШКИНА — ТЕЛЛЕРА
12.1. ВВЕДЕНИЕ И ФОРМУЛИРОВКА
МОДЕЛИ ПОТТСА
В разд. 10.3 мы убедились, что восьмивершинная модель представляет со-
собой обобщение модели Изинга. Разумеется, существует неограниченное
число других таких обобщений. В этой главе рассматриваются два из них:
модель Поттса и модель Эшкина — Теллера, обе для двух измерений. Ни
одна из этих двух моделей не решена точно, но они могут быть представ-
представлены как вершинные модели с антипараллельным порядком, и их критиче-
критическое поведение изучено довольно хорошо.
Первую из указанных выше моделей определил в 1952 г. Поттс [196] по
предложению С. Домба. В действительности он определил две модели.
Первая из них в настоящее время называется Zyy-моделью. В этой модели
каждый узел решетки характеризуется двумерным единичным вектором,
направленным по одному из N равномерно распределенных по углам на-
направлений. Энергия взаимодействия двух векторов на соседних узлах про-
пропорциональна их скалярному произведению.
Здесь рассматривается вторая модель, называемая ниже просто мо-
моделью Поттса. Она может быть сформулирована для любого графа >/, т.е.
для любой совокупности вершин (узлов) и ребер (линий), соединяющих па-
пары вершин. Из соображений общности имеет смысл так и поступить. По-
Позднее мы конкретизируем формулировку на случай, когда ^представляет
собой двумерную решетку.
Пусть граф У содержит N вершин, пронумерованных 1, 2, . . . , N.
Каждой вершине поставим в соответствие величину а,, которая может
принимать q значений, скажем 1, 2, . . . , q. Как и в модели Изинга, в
восьмивершинной модели будем рассматривать о{ как «спин». Два сосед-
соседних спина oi и ay взаимодействуют с энергией взаимодействия —J8(ajf ay),
где
д(о,а') = 1 при о— <У,
= 0 при аФ d .
Поэтому полная энергия равна
Я= -/2 5(af-, а.-), A2.1.2)
О'.у)
где суммирование распространяется на все ребра (/, j) графа. Из A.4.1) еле-

324 МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА
дует, что статистическая сумма имеет вид
ZN = 2 ехр) К 2 д(о(, а,) 1, A2.1.3)
где
К = ЛквТ. A2.1.4)
Здесь сумма по о берется по всем значениям всех спинов ov . . . , oN. Та-
Таким образом, имеется qN членов.
Для определенности я предположил, что каждый спин oi принимает
значения 1, . . . ,<?, но с тем же успехом можно было взять любые q раз-
различных чисел. В частности, для q = 2 мы могли бы позволить каждому
спину а, принимать значения +1 или — 1. Тогда 5(а, а') = — A + оог);
иодставляя это выражение в A2.1.3) и сравнивая с A.8.2), мы видим, что
модель Поттса для q = 2 эквивалентна (с заменой К на 2К) модели Изинга
в отсутствие внешнего поля.
В разд. 12.2 — 12.8 будет показано, что модель Поттса может быть ре-
решена в критической области [30, 45, 231]. Имеется еще несколько точно ре-
решаемых случаев: q = 1 (тривиальный случай), q = 2 (модель Изинга), мо-
модель на квадратной решетке с q = 3 и К = - <х (задача о трехцветном рас-
раскрашивании, разд. 8.13) и модель на треугольной решетке с q = 4 и
К = -оо (задача о четырехцветном раскрашивании [20]).
12.2. МОДЕЛЬ ПОТТСА И БИХРОМАТИЧЕСКИЙ
ПОЛИНОМ
В работах [45, 92, 141] показано, что ZN можно представить как бихро-
матический полином [235]. Доказывается это очень просто; положим
v = exp(/Q - 1. A2.2.1)
Тогда A2.1.3) можно записать в виде
ZN = 2 П [1 + v did , ау)]. A2.2.2)
Пусть Е — число ребер графа У. Тогда выражение под знаком суммы в
A2.2.2) представляет собой произведение Е сомножителей. Каждый сомно-
сомножитель в свою очередь представляет собой сумму двух членов A и v5(ait
oj)), так что все произведение можно разложить в сумму 2Е членов.
Каждому из этих 2Е членов можно поставить в соответствие некоторую
часть графа S. Чтобы сделать это, заметим, что любой отдельно взятый
член представляет собой произведение Е сомножителей, по одному от каж-
каждого ребра .У. Этот сомножитель для какого-то ребра (/', j) равен либо 1,
либо v5(oj, Gj). В первом случае удаляем это ребро из графа, во втором
случае оставляем его на месте. Проделаем эту операцию для всех ребер (/,
j). В результате получим взаимно-однозначное соответствие между частя-
частями графа .^и членами разложения в сумму произведения в A2.2.2).

ГЛАВА 12 325
. Рассмотрим типичный граф G, содержащий / ребер и С связных частей
(компонент), причем изолированный узел рассматривается как одна компо-
компонента. Тогда соответствующий член разложения содержит множитель vl, a
дельта-функции обеспечивают равенство спинов в пределах одной компо-
компоненты. В результате суммирования по независимым спинам получаем, что
вклад этого члена в статистическую сумму ZN равен qcvl. Суммируя по
всем таким членам, т.е. по всем графам G, приходим к следующему выра-
выражению для статистической суммы:
ZN = ^qcul. A2.2.3)
G
Суммирование выполняется по всем графам G, которые можно изобразить
на ^f. Это выражение представляет собой бихроматический полином [235,
250].
Заметим, что q в A2.2.3) не обязательно должно быть целым числом.
Допустимы любые действительные положительные числа, что может быть
полезным обобщением. Например, рассматривая ZN как функцию q и v (a
также N), получаем
^-lnz) =2Ci7//2«>/, A2.2.4)
dq Jq = \ G I g
что совпадает со средним числом компонент в задаче о перколяции, где
каждое ребро присутствует с вероятностью р = v/{\ + v). Это знамени-
знаменитая нерешенная задача [80].
Если К = -оо, то соседние спины должны быть различными, так что
из A2.1.3) очевидно, что ZN представляет собой число способов раскраши-
раскрашивания q красками вершин графа ^так, чтобы никакие две соседние верши-
вершины не были раскрашены одной краской. Выражение для ZN является в
этом случае полиномом от q, который называется «хроматическим» поли-
полиномом. Мы видим из предыдущего, что он получается из A2.2.3), если по-
положить v = - 1.
Ребра регулярных решеток можно естественно сгруппировать в классы.
Например, ребра квадратной решетки либо горизонтальны, либо верти-
вертикальны. Часто бывает удобно обобщить модель Поттса, допуская для J (и,
следовательно, для Кии) различные значения в зависимости от принад-
принадлежности соответствующего ребра к тому или иному классу. Если
Jr — значение J для класса г, то легко видеть, что искомое обобщение
A2.2.3) имеет вид
Zn = 2 qcv\vZvll • • . A2.2.5)
Q 1 1 2 3 /
где суммирование выполняется по всем графам G; С — число связанных
компонент в G; 1Г — число линий класса г (г = 1, 2, 3, ...) и
Kr = JJkBT, vr = ьхЫКг) ~ 1. A2-2-6)

326
МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА
12.3. ПЛОСКИЕ ГРАФЫ: ЭКВИВАЛЕНТНАЯ МОДЕЛЬ
ТИПА ЛЬДА
Медиальный граф j}>
Все сказанное в предшествующих двух разделах применимо к любому
графу ^независимо от его структуры и размерности. В дальнейшем усло-
условимся считать Л плоским графом, т.е. таким, который можно изобразить на
плоскости, причем так, что никакие два ребра не пересекутся и никакие две
вершины не совпадут.
Мы можем поставить в соответствие графу ~/другой граф J1 , руко-
руководствуясь следующими правилами. Нарисуем простые полигоны, охваты-
охватывающие каждый узел ~/, так что:
1) никакие полигоны не перекрываются и ни один из них не окружает
другой;
2) полигоны для узлов, не являющихся ближайшими соседями, не име-
имеют общих узлов;
3) полигоны соседних узлов / и j имеют один и только один общий
угол; этот угол лежит на ребре (/, j).
Будем считать углы этих полигонов узлами J? , а их стороны — ребра-
ребрами У*. Ниже будем называть их базисными полигонами графа S.
Мы видим, что имеется два типа узлов У'. Во-первых, те, которые яв-
являются общими для двух базисных полигонов. Они лежат на ребрах У и
имеют четырех соседей в У . Мы назовем их «внутренними» узлами. Во-
вторых, могут существовать узлы, принадлежащие только одному базис-
базисному полигону. Они имеют двух соседей, и мы назовем их «внешними»
узлами. (Основания для такой терминологии станут ясны, когда мы перей-
перейдем к рассмотрению регулярных решеток.)
Вышеприведенные правила не определяют граф У однозначно, по-
Рис. 12.1. Граф .У (светлые кружки и штриховые линии) и его медиальный граф У
(темные кружки и сплошные линии). Заштрихованная область внутри каждого ба-
базисного полигона — «земля».

ГЛАВА 12 327
скольку сохраняется возможность изменения его формы и на любое ребро
можно добавить внешние узлы. Но топология соединений между внутрен-
внутренними узлами инвариантна, и общие соображения последующих разделов
применимы к любому допустимому выбору У . (Для регулярных решеток
имеется очевидный естественный выбор.) Граф У' называется медиальным
графом графа -/[187]. Типичный пример показан на рис. 12.1.
Внутреннюю часть каждого базисного полигона полезно заштриховать,
как это сделано на рис. 12.1, и каждой заштрихованной области дать ус-
условное название «земля», а незаштрихованной — «вода». Тогда У* будет
состоять из нескольких «островов». Каждый остров содержит один узел
У. Острова соприкасаются на ребрах ./в точках, являющихся внутренними
узлами У\
Разбиение У на полигоны
Установим теперь следующее взаимно-однозначное соответствие между
графами G на У и разбиениями У :
Если G не содержит связи на ребре (/, у), то в точке соответствую-
соответствующего внутреннего узла У раздвинем углы, образуемые двумя парами
ребер, так, чтобы «острова» / и у разделялись, как на рис. 12.2,я. Если
G содержит эту связь, то раздвинем углы так, чтобы острова соедини-
соединились, как на рис. 12.2,6. Проделаем эту операцию для всех ребер У.
Результатом этого будет разбиение У на совокупность несвязанных по-
полигонов, как это показано на рис. 12.3. (В данном случае мы называем по-
полигоном любую простую замкнутую ломаную линию на У'.)
Ясно, что теперь любая связанная компонента G соответствует какому-
то большому острову в У', образованному из соединившихся базисных
островов. Внешний периметр каждого такого большого острова представ-
представляет собой один из полигонов, на которые разбивается У\ Большой ост-
остров может содержать внутри себя «озера», внешний периметр которых
также является полигоном.
Каждый полигон относится к одному из этих двух типов. Таким обра-
образом, У' разбивается на р полигонов, причем
p = C + S, A2.3.1)
Рис. 12.2. Два возможных способа разделения ребер на внутреннем узде У
(расположенном на ребре (/, j) графа У): а — связь между / и j отсутствует;
б — связь есть.

328
МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА
Рис. 12.3. Граф G на ^(сплошные линии между светлыми кружками) и соответству-
соответствующее разбиение У на полигоны. Чтобы не усложнять рисунок, узлы -/' не пока-
показаны, но они находятся в тех же местах, что и на рис. 12.1.
где С — число связных компонентов в G, a S — число внутренних циклов,
замкнутых путей в G, не содержащих внутри себя линий.
Граф G имеет N узлов и / ребер (где / = 1Х + /2 + /3 + . . .). Числа С,
S, Л/, / не независимы, а должны удовлетворять соотношению Эйлера
S = C-N + l. A2.3.2)
В книге [187] vj обозначает полное число циклов, включающее внешний
бесконечный цикл, так что vj — S 4- 1.
Исключая С и S из уравнений A2.2.5), A2.3.1) и A2.3.2), получаем
A2.3.3)
где
Pd
xr = q
A2.3.4)
а символ pd означает, что сумма распространяется на все разбиения -/' на
полигоны. Здесь р — число отдельных полигонов в данном разбиении, а
1Г — число внутренних узлов из класса г, в которых произошло разделение
ребер, как на рис. 12.2,6.
Покрытия У стрелками
Выражение под знаком суммы в A2.3.3) можно рассматривать как про-
произведение различных множителей: множителей qVl (по одному для каждого
полигона в данном разбиении; например, в разбиении, показанном на
рис. 12.3, имеется четыре полигона) и множителей хг (по одному для каж-
каждого узла класса г, в котором ребра У разделились, как на рис. 12.2,6).

ГЛАВА 12
329
Множители хг являются «локальными» в том смысле, что они зависят
только от состояния соответствующего узла. Множители qVl не являются
локальными в этом смысле, но мы сделаем их такими с помощью следую-
следующего приема.
Определим величины X и z выражениями
= 2 cosh Я , z = ехр(АУ2лг).
A2.3.5)
Рассмотрим какое-то разбиение ^' на полигоны типа показанного на
рис. 12.3. Каждый полигон составлен из ребер ^ и имеет столько же
углов, сколько ребер. Например, полигон слева рис. 12.3 имеется 10 ребер
и 10 углов. Каждый угол полигона является пересечением двух его ребер.
Разместим стрелки на линиях ^ так, чтобы у каждого угла полигона
имелась одна стрелка, направленная к нему, и одна — от него. Припишем
каждому углу вес za, где а — угол, отсчитываемый влево, на который по-
поворачивается наблюдатель, движущийся по направлению стрелок, при про-
прохождении через угол. Поскольку линии не могут налагаться друг на друга,
а лежит в интервале — тг < а < ж. Два типичных примера представлены
на рис. 12.4.
Все еще рассматривая какое-то фиксированное разбиение Л' на полиго-
полигоны, составим произведение весовых множителей za по всем углам. Затем
просуммируем этот комбинированный вес по всем допустимым конфигура-
конфигурациям всей совокупности стрелок.
Результат, дол жен быть равен qp/1. Чтобы это увидеть, заметим, что
при обходе одного полигона все стрелки должны иметь одно направление:
либо против часовой стрелки, либо по часовой стрелке. В первом случае
наблюдатель при полном обходе полигона поворачивается на угол 2тг, так
что произведение весовых множителей углов этого полигона равно z2ir. Во
втором случае угол равен — 2тг, а комбинированный вес равен z~2x. Веро-
Вероятности той и другой ситуации для каждого полигона независимы, поэто-
поэтому полный вклад от каждого полигона составляет z2x + z~2ir. Согласно
A2.3.5), это равно в точности 2coshX, т.е. ql/2. Имеетсяр полигонов, так
что полная сумма должна быть равна qp/1.
Отсюда следует, что A2.3.3) можно записать в виде
_ nN/2
-q
ZN-q
Jill
х
2^
pd
A2.3.6)
Рис. 12.4. Углы полигона из -/", на которых
наблюдатель, движущийся в направлении стрелки,
поворачивается на угол а влево или на угол —а
вправо. Отметим, что -тг < а < тг и угол между
линиями равен тг - I a I.
0С>0

330 МОДЕЛИ ПОТТСА И ЭШКИНА - ТЕЛЛЕРА
где символы pd и ас означают, что внешняя сумма берется по всем разбие-
разбиениям ~f на полигоны, а внутренняя — по всем допустимым конфигураци-
конфигурациям стрелок на ребрах _^'. Произведение в A2.3.6) распространяется на все
т углов полигонов (ат — соответствующий угол, определенный выше).
Весовые множители zUm являются локальными характеристиками т углов;
локальным является и правило, согласно которому у каждого угла одна
стрелка направлена к нему, а другая — от него.
Модель типа льда на j"
Рассмотрим какой-нибудь внутренний узел ~/', расположенный на ребре
(/, j) графа S. Пусть а, /3, у, 6 — углы между четырьмя ребрами _^, как
показано на рис. 12.5. Имеется две возможности для разделения ребер, как
это показано на рис. 12.2. Для каждого из них имеется четыре допустимые
конфигурации стрелок. Результирующие восемь возможностей показаны на
рис. 12.6 вместе с произведением соответствующих множителей хг и zam.
Это произведение представляет собой полный вклад такой конфигурации
узла в выражение под знаком суммы в A2.3,6).
Заметим, что в каждом случае имеются две стрелки, направленные к
узлу, и две — от него. Таким образом, «правило льда» (раз/1. 8.1) выполня-
выполняется для всех внутренних узлов. Если мы игнорируем разделение ребер, то
получим обычные шесть допустимых конфигураций стрелок вокруг узла
(вершины), как показано на рис. 12.7.
Очередная хитрость состоит в том, чтобы поменять порядок суммиро-
суммирования в A2.3.6). Возьмем в качестве исходного неразделенный граф У'. На-
Нарисуем стрелки на его ребрах всеми допустимыми, согласно изложенному
выше, способами. Это означает, что правило льда должно соблюдаться
для каждого внутреннего узла, и у каждого внешнего узла одна стрелка
должна быть направлена к нему, а одна — от него.
Каждое такое покрытие стрелками содержится в комбинированной сум-
сумме в A2.3.6), но некоторые из них появляются более чем один раз. Это свя-
связано с тем, что каждая из конфигураций стрелок 5 и 6 на рис. 12.7 возника-
возникает двумя способами. Конфигурация 6 возникает из любой из двух крайних
справа картинок на рис. 12.6; аналогично конфигурация 5 возникает из двух
соседних картинок.
Предположим, что какое-то допустимое покрытие .У стрелками содер-
содержит / вершин типа 5 и 6. Каждая вершина типа 1, 2, 3 или 4 соответствует
единственному разделению линий в ее окрестности, в том время как каж-
каждая вершина типа 5 и 6 соответствует двум возможным выборам разделе-
Рис. 12.5. Типичный внутренний узел ~/'. Показаны углы
между ребрами. Обращаем внимание на то, что углы а и 7
лежат внутри базисных полигонов («островов») У t а углы
E и д — снаружи.

ГЛАВА 12
331
Z*'Y
-a-y
XZ
Рис. 12.6. Два возможных способа разделения линий на внутреннем узле J" и вос-
восемь допустимых конфигураций стрелок. Внизу приведено произведение соответству-
соответствующих множителей хг и т?. Индекс г у хг опущен; обозначения углов те же, что на
рис. 12.5.
ния. Таким образом, это покрытие стрелками соответствует 21 разбиениям
на полигоны и появляется в A2.3.6) 21 раз.
Но поскольку каждый выбор является независимым, при вычислении
полного вклада в A2.3.6) от этого покрытия стрелками не возникает ника-
никаких проблем: следует просто сложить два соответствующих весовых мно-
множителя на рис. 12.6. Таким образом, A2.3.6) можно записать в виде
яс
(весовые множители),
A2.3.7)
где сумма теперь берется по всем допустимым покрытиям J" стрелками, а
произведение охватывает все узлы J*'. Каждый внешний узел вносит в это
произведение весовой множитель za, где а — угол на рис. 12.4. Каждый
внутренний узел вносит весовой множитель ик, где к (= 1, . . . , 6) обозна-
обозначает конфигурацию стрелок для данного узла в последовательности, приня-
принятой на рис. 12.7, и
, . . . , йN =
(J2.3.8)
Рис. 12.7. Шесть допустимых конфигураций стрелок вокруг узла у . Конфигурации
ориентированы так, что заштрихованные области («земля») расположены справа и
слева.

332 МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА
Здесь г указывает класс внутреннего узла и а, /3, у, 5 — углы, показанные
на рис. 12.5. Важно отметить, что углы а и 7 лежат внутри базисных по-
полигонов («островов») графа У\ а углы /3 и 5 — снаружи.
Суммирование в A2.3.7) распространяется на все покрытия У стрелка-
стрелками, такие, что к каждому узлу направлено столько же стрелок, сколько и
от него. В случае внутренних узлов это соответствует правилу льда. Дейст-
Действительно, сравнивая A2.3.7) с (8.1.1) и (8.1.3), мы видим, что q~N/1ZN
представляет собой статистическую сумму для модели типа льда (или ше-
стивершинной), обобщенной таким образом, что весовые множители раз-
различных узлов могут быть разными и могут существовать «внешние» узлы
с координационным числом, равным двум. Таким образом, модель Поттса
на любом плоском графе У может быть представлена как модель типа
льда на медиальном графе У.
Задача о раскрашивании четырьмя красками
В кратком замечании, сделанном после A2.2.4), было отмечено, что ес-
если v = — 1, то статистическая сумма ZN равна числу способов раскрашива-
раскрашивания q красками плоского графа У. Было бы захватывающе интересно уз-
узнать, имеет ли наша формулировка A2.3.7) в терминах модели типа льда
какое-либо отношение к знаменитой задаче о раскрашивании четырьмя кра-
красками [187, 206], которая была решена лишь недавно [7,8], после того как
более чем столетие дразнила и притягивала к себе воображение математи-
математиков.
Несомненно, значение q — 4 является весьма особым случаем: параметр
X в A2.3.5) действительный при q ^ 4 и чисто мнимый при q < 4. В част-
частности, при q = 4 и v = —1 имеем z = 1 и хг = — — . Поэтому весовые
множители в A2.3.8) действительные, а ы3 и ы4 отрицательны. Чтобы по-
получить альтернативное решение задачи о четырехцветном раскрашивании,
мы должны были бы показать, что отрицательные члены в сумме A2.3.7)
численно меньше, чем положительные.
Имеется еще одно интригующее обстоятельство, указывающее на то,
что наше преобразование имеет отношение к этой проблеме. На основании
численных и других исследований предполагают, что действительные нули
полинома раскрашивания для произвольной плоской решетки группируют-
группируются вокруг предельных точек, когда решетка становится большой. Предпо-
Предполагают, что эти предельные точки являются «числами Берага» q =
= [2cos(tt/a2)]2, n = 2, 3, 4, . . . [48 - 50, 236 — 238]. Согласно A2.3.5),
это соответствует просто значениям /тг/2, /тг/3, /тг/4, . . . нашего пара-
параметра X.
12.4. МОДЕЛЬ ПОТТСА НА КВАДРАТНОЙ РЕШЕТКЕ
Эквивалентная модель типа льда
Для внутренней части регулярных решеток имеется очевидный естест-
естественный выбор при построении У , а именно нужно взять в качестве узлов

ГЛАВА 12 333
Рис. 12.8. Квадратная решетка ^ (светлые кружки и штриховые линии) и ее
медиальная решетка -/' (темные кружки и сплошные линии). Два класса ребер
./— горизонтальные и вертикальные — обозначены цифрами 1 и 2 соответственно.
-z^ средние точки отрезков, соединяющих узлы ~/, т.е. средние точки ребер
-2^, и условиться, что два узла ^' будут соседними в том и только в том
случае, если соответствующие ребра ^встречаются в общем узле и ограни-
ограничивают одну и ту же грань. Все узлы J" являются тогда «внутренними»,
за исключением тех, которые расположены на границах; с ними и связано
некоторое усложнение терминологии. Квадратная решетка -/показана на
рис. 12.8 вместе с ее медиальным графом -/'. Она имеет два класса линий,
горизонтальные и вертикальные, которые мы назовем классами 1 и 2 соот-
соответственно.
Определим параметр
5 = ехр(А/4). A2.4.1)
Тогда из A2.3.7), A2.3.8) и A2.3.5) мы видим, что q~N/2ZN представляет
собой статистическую сумму модели типа льда со следующими весовыми
множителями:
й>ь . . . ,fi>6= l,l,xnxns-2 + XrS2,s2+xf-2, A2.4.2)
1де г обозначает класс узла ./", а шесть конфигураций стрелок пронумеро-
пронумерованы, как на рис. 12.7.
Можно исключить дробные степени ех, приписывая дополнительные
взаимно-обратные весовые множители началу и концу некоторых стрелок.
Для каждой стрелки на линии «юго-запад — северо-восток» введем допол-
дополнительный весовой множитель s~l9 связанный с узлом, к которому эта
стрелка направлена, и весовой множитель 5", связанный с узлом, от которо-
которого она идет. Очевидно, что в ZN все эти весовые множители сокращаются,
но индивидуальные вершинные весовые множители ы5, ы6 изменяются: от-

334 МОДЕЛИ ПОТТСА И ЭШКИНА - ТЕЛЛЕРА
Рис. 12.9. Шесть допустимых конфигураций стрелок вокруг узлов квадратной решет-
решетки. Ориентация одинакова для всех узлов.
носящиеся к узлам типа 1 умножаются Has2, s^2 соответственно, а относя-
относящиеся к узлам типа 2 — на s~~2, s2 соответственно.
Следует обратить внимание на то, что весовые множители в A2.4.2)
пронумерованы так же, как на рис. 12.7, где заштрихованные области рас-
расположены справа и слева. Именно так изображены узлы типа 1 на
рис. 12.8, но для узлов типа 2 соответствующее изображение на рис. 12.7
следует повернуть на 90°.
Удобнее использовать всюду одну ориентацию. Пусть ы1э . . . , ы6 —
весовые множители шести стрелочных конфигураций, показанных на
рис. 12.9, причем всегда используется одна и та же ориентация этого ри-
рисунка и рис. 12.8. Для узлов типа 1 эта нумерация совпадает с исходной;
для узлов типа 2 имеем ыр . . . , о>6 = w3, ш4» <^2» Ы1> Ы6» Ы5- Учитывая
также упоминавшиеся выше дополнительные множители s2 и s~2, полу-
получаем
тип i: о)х ,. . . , (о6 = 1,1, дгь*ь 1 +*! е\ 1 +*1е"~я, A2.4.3а)
тип 2: 0)i ,. . . , 0)в = х2, Х2, 1,1, х2 + е\ х2 + е~я . A2.4.36)
Весовые множители внешних узлов справа и слева на рис. 12.8 теперь
всегда будут равны единице. Для тех же, которые расположены сверху и
снизу, они равны ехр(Х/2), если стрелки направлены вправо, и ехр(-Х/2),
если влево.
Альтернативный вывод эквивалентности
Эквивалентность модели Поттса на квадратной решетке и модели типа
льда впервые была получена в работе [231]. В ней использовались операто-
операторы, порождающие довольно изящную и интересную алгебру. Поэтому по-
полезно привести здесь краткое описание этого альтернативного подхода.
Рассмотрим модель Поттса на квадратной решетке У. Пусть J имеет
т рядов и п столбцов. Тогда, действуя обычным образом (разд. 2.1, 7.2,
8.2), мы можем записать статистическую сумму в виде
ZN = fVWVW. . . V%, A2.4.4)
где матричное произведение содержит т сомножителей V и тЛ сомножи-
сомножителей W\ % представляет собой ^-мерный вектор-столбец, все элементы
которого равны единице; V — трансфер-матрица, которая добавляет к ре-
решетке ряд горизонтальных линий связи, в то время как W добавляет ряд

ГЛАВА 12 335
вертикальных линий. Обе матрицы К и W имеют размер qn х qn, систему
индексов о = \ dp . . . , оп } и о' = [ aj, . . . , о'п } и элементы
л-1 п
Vo,& = ехр К, 2 <5(а,, ау + 1) П Щ , о?), A2.4.5а)
I 7 = 1 J 7=1
<12-4'5б>
(Заметим, что циклические граничные условия ни на ряды, ни на столбцы
^ не накладываются.)
Определим матрицы Ul9 . . . , Uln _ \ посредством соотношений
п
№-1^ = ?"'Пй(Gу^)> 02.4.6а)
,<t) • A2.4.66)
Таким образом, С/2/ — диагональная матрица с диагональными элемента-
элементами Qfl/26(a/, а,- + !>, а С/2/ _ j имеет структуру
U2t-i = е® е® . . . ®e®g® е® . . . ®е , A2.4.7)
где е — единичная матрица q x q, а. множитель g (стоящий в положении /
в произведении) является матрицей q x q, все элементы которой равны
Из A2.4.5) и A2.4.6) легко получить
V = txplq^K^Uz + UA + . . . + U2n-2)}, A2.4.8а)
П
W = П (^ + 9*1/2/-1) , A2.4.86)
где »У— единичная матрица ^л х qn, a t>2 = ехр (Я^) - 1, как в A2.2.1).
Выражение A2.4.8а) можно привести к виду, сходному с A2.4.86), ис-
используя равенство Ц2 = qulUr В свою очередь, A2.4.86) можно привести
к виду, сходному с A2.4.8а). При этом мы получим
л-1
У= Y[{* + q~*ViU2j}, A2.4.8b)
W= ?7?exp{9-*^(t/i + I/3 + . . . + U2n-i)}, A2.4.8D
где vx = exp(A'1)- 1 и
ехр AT? = (i72 + 9)/02 = (e^2 + q- l)/(e^2 - 1). A2.4.9)

336 МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА
Матрицы Gр..., U2n _ 1 удовлетворяют соотношениям
U} = q^Ui, i = 1 ,. . . , 2л - 1 ,
UiUi+1Ui = Ui, i = l,..., 2л -2,
A2.4.10)
UiUi.lUi = Ui, 1=2,...,2л-1,
UiUj=UjUi, \i~j>2.
Эти соотношения определяют алгебру, порождаемую операторами
C/j, . . . , C/2w _ i- В частности, они определяют собственные значения пол-
полной трансфер-матрицы К Ж (но не их вырождение). Поэтому они определя-
определяют максимальное собственное значение и, следовательно, поведение стати-
статистической суммы в пределе больших т.
В действительности они определяют ZN даже для конечного значения
т. Чтобы увидеть это, введем матрицу
R=UlU3U5... U2n-i. A2.4.11)
Используя явное представление A2.4.6а) или A2.4.7), мы получим, что R
представляет собой матрицу qn x qn, все элементы которой равны q~n/1.
Таким образом,
R = q~n/2^T A2.4.12)
гДе ? — вектор-столбец из A2.4.4), все элементы которого равны единице.
Теперь очевидно, что для любой матрицы X размера qn x qn имеем
RXR = t(X)R, A2.4.13)
где т(Х) — скаляр.
Точнее т(Х) = q~n/2?TX?. Отсюда и из A2.4.4) следует
ZN = qn/2 t(VWVW. ..V). A2.4.14)
Забудем теперь, что К, W, Uv . . . , U2n _ х были введены как матрицы
qn х qn', и будем рассматривать их просто как операторы, удовлетворяю-
удовлетворяющие соотношениям A2.4.8) и A2.4.10). Пусть X — любая сумма произведе-
произведений из U]t . . . , U2n _ i и единичного оператора ^. Тогда с помощью
A2.4.10) и A2.4.11) может быть установлено, что A2.4.13) выполняется и
скаляр т(Х) может быть вычислен. Поскольку произведение VWVW... К
можно записать в виде таких сумм в соответствии с A2.4.14), таким спосо-
способом в принципе можно вычислить ZN.
Разумеется, я не утверждаю, что эта программа может быть выполнена
для произвольно больших тип; отмечается только принципиальная воз-
возможность. Это означает, что мы не обязаны придерживаться представле-
представления A2.4.6): любой набор операторов U{, . . . , U2n _ p удовлетворяющих
A2.4.10), для которых произведение R не равно тождественно нулю, будет
в равной степени хорошим представлением.

ГЛАВА 12 337
В работе [231] показано, что одно такое альтернативное представление
получается, если в качестве U v . . . , Uln _ j взять матрицы 4п х 4п с си-
системой индексов а = [а{, . . . , а2п) и а' = {aj, . . . , а^), где каждая
переменная ау, aj принимает значения + 1 и — 1, a U; имеет элементы
A2.4.15)
а/+1)б(а/+2,а/+2).. • <5(*2Я, Огп),
где / = 1, . . . , 2/7 - 1,
= А(-,-) = 0,
A2.4.16)
А( + , -) = ехр(-Я/2),А(- , +) = ехр(Я/2),
а А определяется посредством A2.3.5).
Будем считать, что набор a{i . . . , а2п описывает состояние ряда вер-
вертикальных или почти вертикальных стрелок: о,- = + , если стрелка в
столбце j направлена вверх; «у = - , если она направлена вниз. Более
определенно, пусть набор ар . . . , а2п описывает типичный ряд стрелок
на линиях -z^', такой, как, например, верхний ряд линий на рис. 12.8, про-
пронумерованный 1, . . . , 2/i. Рассмотрим оператор j^+ xxU2j в а-
представлении A2.4.15). Он действует на стрелки, находящиеся в узлах 2у и
2у + 1, и может рассматриваться как «вершинная трансфер-матрица». Его
ненулевые элементы в точности равны весовым множителям ы^ . . . , ы6 в
A2.4.3а), соответствующим шести стрелочным конфигурациям на
рис. 12.9. Таким образом, этот оператор представляет собой вершинную
трансфер-матрицу узла типа 1 в модели типа льда. Из A2.3.4) и A2.4.8в)
мы видим, что произведение таких матриц для j = 1, ...,/?— 1 равно
как раз V. Таким образом, V в A2.4.8) является трансфер-матрицей для ря-
ряда узлов типа 1 в модели типа льда.
Аналогично из A2.4.86), A2.3.4) и A2.4.36) мы находим, что q~n/2W
является трансфер-матрицей для ряда узлов типа 2 в модели типа льда. За-
Замечая, что N = тпу и используя A2.4.14), получаем
Zn = qm x статистическая сумма модели типа льда. A2.4.17)
Мы можем проверить, что внешние узлы имеют весовые множители, при-
приведенные после A2.4.3). Поэтому эквивалентность выражению A2.3.7) сле-
следует из двух представлений A2.4.6) и A2.4.15) операторов Ul9 . . . ,
U2n - v
Некоторые общие замечания о модели типа льда
Для произвольных значений хх и х2 решение модели Поттса пока не по-
получено. Среди нерешенных моделей эта — одна из наиболее загадочных.
Например, как уже отмечалось в разд. 8.12, однородная модель типа льда
на квадратной решетке может быть решена методом анзаца Бете, описан-

338 МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА
ным в гл. 8, даже если ограничения (8.1.7), соответствующие ситуации в
отсутствие внешнего поля, нарушаются. В этом случае определение (8.3.21)
параметра Д принимает вид
А = (a)i(O2 + (O3CD4 - Ю5в>б)/2(а>1а>20>зв>4)', A2.4.18)
и собственные векторы трансфер-матрицы зависят только от этого Д и от
горизонтального электрического поля Е' .
Модель типа льда, которую мы здесь рассматриваем, не является одно-
однородной: ее весовые множители различны для двух подрешеток (типов 1 и
2). Даже в этом случае из A2.4.3), A2.4.18) и A2.3.5) мы видим, что
Д =-cosh A =-?<?* A2.4.19)
для узлов обоих типов. (На самом деле, согласно A2.3.8), последнее соот-
соотношение справедливо для произвольного плоского графа.) Таким образом,
параметр Д является однородным, тем не менее метод анзаца Бете (гл. 8)
оказывается неприменимым.
Интригующим обстоятельством здесь является то, что анзац не приме-
применим даже для q = 1 и q = 2, в то время как свободную энергию в этих
двух случаях можно подсчитать другими методами; первый из этих случаев
вообще тривиален, второй представляет собой модель Изинга. Следует за-
заметить также, что эта эквивалентная модель Изинга соответствует значе-
значению параметра /л, равному тг/4, в (8.8.1), т.е. в соотношении Д = — cos/*.
Это не согласуется с тем фактом, что модель Изинга эквивалентна также
модели свободных фермионов, как показано в разд. 10.16. Модель свобод-
свободных фермионов представляет собой восьмивершинное обобщение однород-
однородной шестивершинной модели сД = Ои/i = тг/2. Поэтому должна сущест-
существовать какая-то связь между этими вершинными моделями с \л = тг/4 и
II = тг/2.
Дуальность
Одно из преимуществ нашей формулировки модели Поттса как модели
типа льда состоит в том, что при этом очень легко показать, что модель
на квадратной решетке удовлетворяет соотношению дуальности.
Чтобы это сделать, заметим, используя A2.4.3), что весовые множите-
множители узлов типа 2 и типа 1 сходны по форме. Действительно, их можно по-
поменять местами, если заменить xl9 х2 на*^1, jcj соответственно, а затем
умножить все множители типа 1 на хь а типа 2 на xY.
С другой стороны, для достаточно большой решетки У' не имеет зна-
значения, какую из подрешеток мы назовем*!, а какую 2 (попросту говоря, мы
можем поменять местами черные и белые поля шахматной доски). Это
влияет на граничные условия, но мы не думаем, что это повлияет на харак-
характер экспоненциального роста ZN с ростом N. Сохраняя только такие экспо-
экспоненциальные множители и рассматривая ZN как функцию хх и х2 (при фик-
фиксированном q), мы получаем
ZN{x,, х2) = (XiXi^Zrfx? , V) • A2.4.20)

ГЛАВА 12 339
Точнее, мы ожидаем, что термодинамический предел
\р = - lim ЛГ1 In ZN A2.4.21)
существует. Аналогично F.2.10) и A.7.6) эта формула определяет безраз-
безразмерную свободую энергию на один узел, которая связана с обычной сво-
свободной энергией/ равенством ф = f/kBT. Подобно ZN, ф можно считать
функцией jCj и х2. Тогда из A2.4.20) следует
. V(*i > х2) = -Щххх2) + Ц(Х21, V). A2.4.22)
Это — соотношение дуальности, связывающее высокотемпературную и
низкотемпературную модели Поттса. Впервые оно было получено Пот-
тсом [196]. Мы могли бы вывести его также путем перестановки К{ и К^ъ
A2.4.8а) и A2.4.8г) и замены Ui на Ut + v Такая операция с точностью до
граничных условий и скалярных множителей просто меняет местами
трансфер-матрицы V и W.
Мы уже отмечали в разд. 12.1, что модель Поттса для q = 2 эквива-
эквивалентна модели Изинга. В этом случае соотношение A2.4.22) совпадает с со-
соотношением F.2.14) для модели Изинга на квадратной решетке.
Положение критической точки
Допустим теперь, что обе величины Jх и J2 положительны. Это означа-
означает, что система ферромагнитна: соседние спины «предпочитают» быть
одинаковыми. Согласно A2.2.6) и A2.3.4), все величины К{9 К2, vv v2 и xv
х2 также положительны.
Очевидно, что A2.4.22) связывает значение ф в точке (xl9 x2) со значени-
значением этой функции в точке (л:^1, л:]). Это отображение переводит область
0 < ххх2 < 1 в область ххх2 > 1. Каждая точка на линии ххх2 = 1 являет-
является самодуальной.
Мы ожидаем, что при высоких температурах (л^ и х2 малы)
ферромагнитная модель Поттса будет неупорядоченной и каждое из q воз-
возможных спиновых состояний будет равновероятно, а при низких темпера-
температурах (х{ их2 больше) она будет упорядоченной, причем какое-то одно спи-
спиновое состояние будет предпочтительным для всех спинов. Где-то в проме-
промежуточной области будет существовать критическая температура Гс, при
которой только начинает возникать спонтанное нарушение симметрии.
Следовательно, на плоскости (jcp x2) должна существовать линия, разделя-
разделяющая неупорядоченную и упорядоченную области. Мы ожидаем, что функ-
функция ф(хх, х2) аналитична на всей плоскости, за исключением, может быть,
этой линии.
Будем рассуждать так же, как в разд. 6.2. Если функция ф(х{, х2) неана-
литична на какой-то линии в области 0 < х{х2 < 1, то, согласно соотно-
соотношению дуальности A2.4.22), она должна быть неаналитична также на неко-
некоторой линии в области х{х2 > 1. Простейшее предположение состоит в
том, что она неаналитична на самодуальной линии ххх2 = 1. (Для изо-
изотропной системы с х{ = х2 это соответствует требованию единственности

340 МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА
критической температуры.) Было показано [112], что это действительно
так: критические точки модели Поттса на квадратной решетке определяют-
определяются условием
ххх2 = 1 • A2.4.23)
12.5. МОДЕЛЬ ПОТТСА НА КВАДРАТНОЙ РЕШЕТКЕ
В КРИТИЧЕСКИХ ТОЧКАХ
Предположим, что условие A2.4.23) выполняется, т.е. х2 = \/х{. Тогда
из A2.4.3) с очевидностью следует, что весовые множители типа 2 равны
соответствующим множителям типа 1, деленным на х{. Умножение всех
шести весовых множителей на любом заданном узле на один и тот же
множитель представляет собой тривиальную модификацию модели, при
которой статистическая сумма просто умножается на этот множитель. По-
Поэтому система по существу однородна. Точнее, используя A2.3.7) и заме-
замечая, что имеется TV узлов типа 2 в У, это можно выразить следующим об-
образом:
где Z'2N — статистическая сумма модели типа «льда» на решетке S' с 2N
узлами, каждый с больцмановским весом, определяемым A2.4.3а).
Свободная энергия-
В силу своей однородности (т.е. равенства весовых множителей для
всех узлов) эта модель типа «льда» может быть решена методами гл. 8.
Действительно, как было замечено в конце разд. 8.1, вершины типов 5 и 6
должны встречаться попарно, будучи соответственно стоками и истоками
горизонтальных стрелок. Таким образом, весовые множители ы5 и ы6 появ-
появляются только в виде комбинации w5w6. Это означает, что статистическая
сумма не изменяется при замене каждого из множителей w5 и w6 на их
среднее геометрическое. Тогда, используя A2.4.3а) и (8.3.3) (и замечая, что
последовательность вершин на рис. 12.9 совпадает с рис. 8.2 при подходя-
подходящем повороте изображений), получаем, что Z'1N представляет собой стати-
статистическую сумму модели типа льда на -/' в отсутствие внешнего поля со
следующими весовыми множителями:
я = 1, Ь=х1ч с = A + 2х2 cosh A+ *?)*. A2.5.2)
Безразмерная свободная энергия модели Поттса определена посредст-
посредством A2.4.21). С помощью A2.5.1), A.7.6) и A2.5.2) она приводится к виду
, A2.5.3)
g— безразмерная свободная энергия модели типа льда, вычислен-
вычисленная в гл. 8. Согласно (8.3.21) и A2.3.5),
А = -cosh А = -\q\ A2.5.4)

ГЛАВА 12 341
так что подлежат рассмотрению два случая: 0 > Д > -1 и Д < — 1. В
первом из них мы видим, что 0 < q < 4, и используем результаты
разд. 8.8; во втором (q > 4) используем результаты разд. 8.9. Поскольку
ф — непрерывная функция, случай q = 4 можно получить предельным пе-
переходом от любого из двух рассмотренных. Выполняя это, получаем
гр = -J In q - ф(хх) ~ ф{х2) , A2.5.5)
где х{ и х2 удовлетворяют условию критичности A2.4.23), величина q счи-
считается постоянной, а функция ф(х) определена следующим образом:
О < q < 4: qh = 2 cos \i, 0 < \i < л/2 ,
x = sin y/sin(fi - у), 0 < у < fi , A2.5.6а)
r sinh тй cosh
-t), 0<t<1,
Ф(х) = J
A2.5.66)
ixp(-y) stchy sinh 2ту dy ;
A>0,
jc = sinh /3/sinh(A - /J), 0 < /3 < A , A2.5.6b)
00
ф(х) = p + jS л ехр(-мА) sechмА sinh 2nj3.
Для всех значений <? эта функция ф(х) удовлетворяет тождеству
A2.5.6г)
Пусть 7У, т-у, Cj — значения параметров у, г, C при jc = Xj. Тогда из ус-
условия критичности A2.4.23) следует
7i+72 = iW, Ti + t2=1, /?i + /?2= A. A2.5.7)
Действительно, 7i и 72 совпадают с Vi^ + w) и ^(/х + w) в разд. 8.8, а
/3j и /32 совпадают с ViQ\ + v) и Vi(K - v) в разд. 8.9. Параметр X и в этой
главе тот же смый, что и в гл. 8.
Интеграл в A2.5.6а) можно вычислить аналитически, когда /х составляет
рациональную долю тг (например, тг/4, тг/3, 2тг/5). Для изотропной моде-
модели с хх = х2 = 1 некоторые из таких случаев были табулированы [231].
Внутренняя энергия и теплота перехода
Мы можем вычислить также внутреннюю энергию модели Поттса в
критической точке [30, 196]. Чтобы это сделать, вернемся сначала к рас-
рассмотрению общей модели Поттса, не обязательно удовлетворяющей усло-
условию критичности A2.4.23). Из A2.1.2), A2.1.3) и A.4.4) следует, что полная

342 МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА
средняя энергия .
(E) = kBT2^-lnZN 02.5.8)
01
в согласии с A.4.6). Статистическая сумма для квадратной решетки зависит
от Т через хх и х2. В соответствии с A2.1.4), A2.2.6) и A2.3.4) хг и Т связа-
связаны соотношением
xr = q-\txp(JrlkBT) - 1]. A2.5.9)
Рассматривая ZN как функцию хх и х2 (при постоянных д и N), полу-
получаем
2
(Е)= -$-*2Лехр(Л/ВД — lnZyv. A2.5.10)
r=l dJtr
Воспользуемся теперь выражением A2.3.7) для ZN, в котором весовые
множители определены с помощью A2.4.3). Для заданного покрытия
стрелками линий ^f' пусть пк(п'к) — полное число узлов типа 1 (типа 2),
имеющих стрелочную конфигурацию к на рис. 12.9; здесь к = 1, . . . , 6.
Тогда A2.3.7) можно записать в более развернутом виде:
ZN = qm 2 xV+ПАA + xi eA) A 4- jci е"А)Пбх
, ,aC A2.5.11)
xjc21+n2(jc2 + eA)n5(jC2 + e-A)n6,
где суммирование выполняется по всем покрытиям -/' стрелками, удовлет-
удовлетворяющим правилу «льда» на каждом узле.
Из A2.5.10), A2.5.11) и A.4.4) следует
2
(Е) = -q-> 2 Jr ехр(/г//квГ) lr, A2.5.12)
где '=1
j =
1+jci exp(A) 1+jci exp(-A) '
<# A2*5ЛЗ)
k + +
jc2 jc2+exp(A) jc2+exp(-A) '
(пр и <«j>, как обычно, — средние значения rij и nj.
Мы можем вычислить 1Х и /2, если выполняется условие критичности
A2.4.23), т.е. х{х2 = 1. Тогда ZN (для больших N) получаем из A2.4.21) и
A2.5.5), т.е.
In ZN = N[h \nq + ф{хх) + ф{х2)] , A2.5.14)
где функция ф(х) определена формулой A2.5.6), a q рассматривается как
константа. Подставляя это выражение для ZN в A2.5.11) и дифференцируя
логарифмически по Xj (помня, что х2 — l/*i), находим

ГЛАВА 12 343
МФЧ*О - xl ф'(х2)] = /i " хЦ2 • A2.5.15)
Здесь </>' (х) обозначает производную ф(х).
Мы получили одно соотношение, связывающее 1{ и /2. Еще одно можно
получить, рассматривая соотношения симметрии между 12 средними вели-
величинами <«!>,..., (п'в). Как мы отмечали в начале этого раздела, при
ххх2 = 1 весовые множители A2.4.3) можно ренормализовать так, чтобы
привести их к виду (8.3.3), где а, Ъ, с определены в A2.5.2). Это не влияет
на </tj>, . . . , (п'6), но выявляет то обстоятельство, что модель типа льда
(при ххх2 = 1) имеет два вида симметрии: она трансляционно инвариантна
(узлы типа 1 имеют такие же весовые множители, как узлы типа 2) и инва-
инвариантна по отношению к обращению всех стрелок (это условие связано с
отсутствием внешнего поля).
Строго показано [64], что если с > а + &, то обе эти симметрии спон-
спонтанно нарушаются. Как объяснено в разд. 8.10, в этом случае система ан-
тисегнетоэлектрически упорядочена и имеется спонтанная антипараллель-
антипараллельная поляризация Ро. Рассматривая систему в исчезающе малом антипарал-
антипараллельном электрическом поле (или фиксируя антипараллельную ориентацию
стрелок на границе), мы можем определить Ро как некоторое среднее < тг) .
Здесь т, — поляризация электрического диполя на линии /. Она определена
так же, как в разд. 8.10, будучи равной + 1 («правильной»), если направле-
направление стрелки совпадает со стандартным направлением на рис. 8.3, и -1
(«неправильной»), если направление стрелки другое.
Это значение Ро одинаково для всех 47V линий _/", поэтому
4NPq= среднему числу «правильных» стрелок ri25itfi
минус среднее число «неправильных».
Каждая стрелка связана только с одним узлом типа 1, и каждый узел типа
1 в свою очередь является местом, где встречаются чеырые стрелки («вер-
(«вершиной»). Пусть стандартная конфигурация на рис. 8.3 соответствует тому,
что все вершины типа 1 графа S* имеют стрелочную конфигурацию 6, со-
согласно рис. 12.9. Тогда из сравнения этих рисунков становится очевидным,
что каждая стрелочная конфигурация 1 — 4 содержит столько же непра-
неправильных стрелок, сколько и правильных. В то же время конфигурация 5 со-
содержит четыре неправильные стрелки, а конфигурация 6 — четыре пра-
правильные. Таким образом, A2.5.16) можно переписать в виде
A2.5.П)
Хотя оба вида симметрии — по отношению к перестановке подрешеток и
по отношению к обращению стрелок — по отдельности спонтанно наруша-
нарушаются при с > а + Ьу комбинированная симметрия сохраняется. Например,
основное состояние, показанное на рис. 8.3, не изменится, если одновре-
одновременно повернуть все стрелки и поменять местами узлы типов 1 и 2. Отсю-
да следует

344 МОДЕЛИ ПОТТСА И ЭШКИЙА — ТЕЛЛЕРА
Соотношения A2.5.17) и A2.5.18) остаются справедливыми, когда
\а - Ь\ < с < а + b. В этом случае модель типа льда является неупоря-
неупорядоченной в том смысле, что нет нарушения симметрии (хотя корреляцион-
корреляционная длина бесконечна, как было отмечено в разд. 8.10). Это означает, что
<л5> = <я6>, так что поляризация Ро в A2.5.17) равна нулю.
Имеется N узлов типа 1, каждый из которых может находиться в од-
одном из шести возможных состояний, так что пх + . . . + п6 = N. Обра-
Образуя выражение хх1х + x2l2, где 1Х и /2 определены посредством A2.5.13) и
используя соотношения симметрии A2.5.18) вместе с A2.5.17) и A2.4.23),
получаем
Jti/i + x2l2 = N{\ -2xx C(JCt) Ро}, <12-5Л9>
где
?(*) = sinh A/(l + х2 + 2х cosh Я). A2.5.20)
Мы получили второе необходимое нам соотношение для 1Х и /2. Вспо-
Вспоминая, что х2 = 1/aTj, мы легко устанавливаем с помощью A2.5.20) и
A2.5.6г), что
Решая A2.5.15) и A2.5.19) относительно 1Х и /2 и используя при этом
A2.5.21), находим
Ir = N[(f>'(xr)-!;(xr)Po], A2.5.22)
где г = 1,2. Поэтому, согласно A2.5.12), выражение для внутренней энер-
энергии на один узел U = <?> /N для модели Поттса на квадратной решетке
имеет вид
2
U = ?-¦ 2 Jrexp(Jr/kBT) [~ф'(хг) ± ?(*г) Ро] ¦ A2.5.23)
Г = 1
Я ввел знаки ±, поскольку знак правой части A2.5.17) еще не опреде-
определен. Если симметрия модели льда спонтанно нарушена в пользу стрелоч-
стрелочной конфигурации 6 E) на узлах типа 1 B), то правая часть A2.5.17) поло-
положительна, и это выражение определяет обычную спонтанную антисегнето-
электрическую поляризацию Ро. С другой стороны, если симметрия нару-
нарушена в пользу стрелочной конфигурации 5 F) на узлах типа 1 B), то знак
Ро становится отрицательным. Согласно A2.4.3), первая ситуация возника-
возникает (при X > 0), когда ххх2 приближается к единице снизу, а вторая, когда
ххх2 приближается к единице сверху. Поэтому в A2.5.23) должен быть взят
положительный знак, если Т приближается к Тс сверху, и отрицательный в
противоположном случае.
Спонтанная поляризация Ро вычислена [29], и соответствующие резуль-
результаты приведены в разд. 8.10 (см.(8.10.9), (8.10.2) и (8.9.1)). Из A2.5.4) вид-
видно, что следует рассмотреть два случая:

ГЛАВА 12 345
1.О<0<4:О>Д^ -1>Х — чисто мнимая величина. Модель типа
льда не упорядочена в том смысле, что отсутствует спонтанное нарушение
симметрии (хотя длина корреляции бесконечна). Таким образом, поляриза-
поляризация Ро равна нулю, а внутренняя энергия U непрерывна в точке Т — Тс.
(Мы все же ожидаем, что U неаналитична при Т = Тс\ это определенно
верно для Ц = 2, когда модель Поттса становится моделью Изинга.)
2. q > 4: А < -1,Х — действительная величина и должна быть взята
положительной. Имеется спонтанное нарушение симметрии. Поляризация
Ро положительна и-определяется выражением
00
Ро = nitanhmA]2. A2.5.24)
m = \
Поэтому, согласно A2.5.23), модель Поттса имеет фазовый переход перво-
первого рода при Т = Тс с теплотой перехода
2
L = 2q~^Jr exp(Jr/kBT) %xr) Po. A2.5.25)
Для изотропной модели cJl = J2 = Jnxl = x2 = 1 мы можем вычис-
вычислить ф'(хх) из A2.5.21). Используя A2.5.9) и A2.5.23), получим тогда про-
простую формулу
?/av = -(l+9"*)/. A2.5.26)
Здесь Gav — среднее из значений внутренней энергии чуть ниже и чуть вы-
выше Гс, т.е. C/av = - {U_ + G+). Для q ^ 4, когда нет скачка С/, это значе-
значение совпадает со значением внутренней энергии при Тс. Этот результат по-
получил Поттс [196].
12.6. МОДЕЛЬ ПОТТСА
НА ТРЕУГОЛЬНОЙ РЕШЕТКЕ
Для модели Поттса на треугольной и шестиугольной решетках мы мо-
можем выполнить программу, аналогичную описанной выше, т.е. мы можем
найти критические точки и вычислить свободную энергию и внутреннюю
энергию в этих точках [46].
Пусть Zjy и ZJy — статистические суммы для модели Поттса на тре-
треугольной и шестиугольной решетках соответственно, причем каждая из
этих решеток имеет N узлов. Эти статистические суммы определяются вы-
выражением A2.1.3) с тем уточнением, что каждая решетка имеет три типа
линий связи между узлами. Пронумеруем их 1, 2, 3; пусть Кх, К2, К3 — со-
соответствующие значения К. Тогда каждая статистическая сумма зависит
от Кх, К2, Къ> а также от N и q.
Треугольная решетка «^изображена на рис. 12.10 вместе со своим меди-
медиальным графом S1 (который представляет собой решетку кагоме). В соот-

346 МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА
ветствии с A2.3.7) и A2.3.8) имеем
ZTN(Kl,K2,Ki)=qmZ', A2.6.1)
где Z' — статистическая сумма модели типа льда на решетке ^' с весовы-
весовыми множителями
а>ь . . . ,d>6= l,l,xnxr,t~l+xrt\t +XJ-2. A2.6.2)
Здесь г = 1, 2 или 3 в зависимости от типа узла решетки ~^'\ шесть допу-
допустимых конфигураций стрелок для каждого г — это первые шесть в ряду г
на рис. 11.2. Решетка =/" имеет 3N узлов; / и хг определяются формулами
t = ехр(ДУЗ), xr = q-*[exp(Kr) - 1]. A2.6.3)
Дуальность треугольной и шестиугольной решеток
Рассмотрим решетку ~^D, дуальную к -/. Она представляет собой ше-
шестиугольную решетку, состоящую из 2N узлов, расположенных в центрах
незаштрихованных треугольных граней ^f' на рис. 12.10. Медиальным гра-
графом решетки ~/D снова является -/' (если пренебречь приграничной облас-
областью), но теперь заштрихованные грани на рис. 12.10 становятся незаштри-
хованными, и наоборот. Рассматривая модель Поттса на ~/D и снова ис-
используя A2.3.7) и A2.3.8), находим
^Z", A2.6.4)
где Z" — статистическая сумма модели типа льда на ^f' с весовыми мно-
множителями
Шь... ,Ы6 = упуп I,l,yrt-l+t2,yrt+t-2. A2.6.5)
Соответствующие конфигурации стрелок • упорядочены так же, как в
A2.6.2), t снова определяется посредством A2.3.5) и A2.6.3) и
*-l]. A2.6.6)
Допустим, что^ = х~\ Тогда весовые множители A2.6.5) отличаются
от A2.6.2) только общим множителем уг. Умножение всех весовых множи-
множителей типа г на произвольный множитель а приводит просто к умножению
статистической суммы на aN. Поэтому из A2.6.1) и A2.6.4) следует
., K2, К3) = (q4x]x2x3)NZ^N(Ll, L2,L3), A2.6.7)
где
xr = q~\txp{Kr) - 1] = <7*/[exp(Lr) - 1]. A2.6.8)
Это — соотношение дуальности, отображающее низкотемпературную (вы-
(высокотемпературную) модель Поттса на треугольной решетке на высоко-
высокотемпературную (низкотемпературную) модель на шестиугольной решетке.
Для модели Изинга, когда q = 2, полученное соотношение эквивалентно
F.3.7).

ГЛАВА 12
347
Рис. 12.10. Треугольная решетка Л (светлые кружки и штриховые линии) и ее
медиальная решетка кагоме У (темные кружки и сплошные линии).
ПОЛОЖЕНИЕ КРИТИЧЕСКОЙ ТОЧКИ
Мы можем приписать началам и концам стрелок взаимно обратные ве-
весовые множители и включить их в весовые множители вершин. Очевидно,
что это не влияет на Z', но меняет ыр . . . , ы6. Если мы используем оди-
одинаковые весовые множители для всех линий одного типа (например, для
всех горизонтальных линий У), то ыр . . . , п4 не изменяются, п5 умно-
умножается на аг, а со6 делится на аг, где г определяет тип соответствующего
узла и a jc^c^ = 1.
Мы можем поставить вопрос, позволяет ли этот произвол обеспечить
выполнение для модели типа льда условий Ы| = ы2, <^з = Ш4> Ы5 = ыб ПРИ
г = 1, 2, 3, соответствующих равенству нулю внешнего поля. Первые два
условия выполняются автоматически. Третье требует, чтобы произведение
трех весовых множителей о^ (при г = 1, 2, 3) было равно такому же произ-
произведению трех множителей ы6. Поскольку дополнительные весовые множи-
множители стрелок не влияют на эти произведения, то согласно A2.6.2), мы по-
получим
3 3
Г1
H
r=l
хгГ2).
A2.6.9)
Из A2.3.5) и A2.6.3) следует, что t и q связаны соотношением
Разлагая в ряд обе части A2.6.9), получим
A2.6.10)
1. A2.6. Л)
Это необходимое условие для приведения модели типа льда к форме, соот-
соответствующей отсутствию внешнего поля. Оно является также и достаточ-
достаточным.

348 МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА
Удивительно то, что A2.6.11) является одновременно условием пребы-
пребывания модели Поттса (или дуальной шестиугольной модели) в критическом
состоянии. Это не очевидно, поскольку в отличие от модели Изинга мо-
модель Поттса, вообще говоря, не удовлетворяет соотношению звезда —
треугольник. Поэтому мы не можем вывести соотношение дуальности тре-
треугольник — треугольник, как это сделано в разд. 6.5. Ким и Джозеф [148]
показали, что соотношение звезда — треугольник существует, когда вы-
выполняется условие A2.6.11) (на самом деле авторы рассматривали изотроп-
изотропный случай хх = х2 = х3, но приведенное там доказательство легко обоб-
обобщается). Результирующее отображение переводит треугольную модель
Поттса саму на себя (с теми же коэффициентами взаимодействия Кх, АГ2,
К3). Таким образом, модель является самодуальной при некоторой темпе-
температуре, определяемой условием A2.6.11). Авторы предположили [148], что
эта самодуальная точка является также и критической. Их соображения
были обобщены [46] на случай модели Поттса на треугольной решетке с
дополнительными трехузельными взаимодействиями на чередующихся тре-
треугольных гранях. Было показано, что для этой более общей модели всегда
существует соотношение дуальности треугольник — треугольник и что в
самодуальной точке трехспиновое взаимодействие исчезает и условие
A2.6.11) выполняется. Хинтерман и др. [112] показали, что критическая
температура, в самом деле, совпадает с самодуальной точкой.
Я буду пользоваться здесь переменными xl9 хг, х3, но следует заметить,
что весьма естественно вместо них употреблять /Зр /32, /33, где &г — значе-
значение /3 при х = хг. Условие A2.6.11) принимает тогда простую линейную
форму:
/8, + ft + ft-A. <12-6-12>
(По существу, 0Г соответствует иг из разд. 11.1, а A2.6.12) соответствует
A1.1.12).)
Критическая свободна* энергия
Свободная энергия модели Поттса на треугольной решетке (и на дуаль-
дуальной шестиугольной) может быть вычислена, если выполняется условие
критичности A2.6.11). Один из способов сделать это состоит в том, чтобы
свести в точку те треугольники решетки кагоме, один из углов которых на-
направлен вверх. В работе [46] разъясняется, что модель типа льда переходит
при этом в «двадцативершинную» модель на треугольной решетке. Кел-
ланд [145] исследовал условия, при которых такая двадцативершинная мо-
модель может быть решена методом анзаца Бете (гл. 8). Оказывается, что
при этих условиях двадцативершинная модель сводится к шестивершинной
модели на решетке кагоме с весовыми множителями, определяемыми урав-
уравнениями A2.6.2) и A2.6.11). Таким образом, этот результат позволяет ^вы-
^вычислить свободную энергию в том и только в том случае, когда двадцати-
двадцативершинная модель эквивалентна модели Поттса на треугольной решетке в
критической точке.
(Двадцативершинная модель решается еще в некоторых случаях, когда

ГЛАВА 12 349
она сводится к модели свободных фермионов, но при этом используются
другие методы [207].)
Мы можем также вычислить свободную энергию, используя результа-
результаты, полученные в гл. 11. Если условие A2.6.11) выполнено, то можно так
подобрать взаимно обратные весовые множители для начала и конца стре-
стрелок, что A2.6.2) переходит в
О)и . . . , щ = Яг, ап Ьп Ь„ сг, сг, A2.6.13)
где
вг=1, br = xr, с, = {1+х,^(
у, A2614)
и снова г = 1, 2 или 3 в зависимости от типа рассматриваемого узла ^/'.
Вершинные конфигурации стрелок, соответствующие а^ Ъ^ сп показаны на
рис. 11.2.
Модель типа льда стала теперь шестивершинной моделью на решетке
кагоме в отсутствие внешнего поля, что является частным случаем восьми-
вершинной модели, введенной в разд. 11.1, когда весовые множители d{9
d2, d3 равны нулю. Далее, если условие A2.6.11) выполнено, то можно убе-
убедиться, что все шесть соотношений «звезда — треугольник» A1.1.7) удов-
удовлетворяются.
Поэтому свободная энергия определяется выражением A1.4.5), из кото-
которого, учитывая, что решетка кагоме У имеет 37V узлов, получаем (для
больших значений N)
Z' = Z%(Xl) Z%(x2) Z#(jc3) , A2.6.15)
где ^$(хг) — статистическая сумма модели типа льда на квадратной ре-
решетке с весовыми множителями A2.6.14), причем все узлы считаются
принадлежащими к типу г. Используя результаты гл. 8 или просто обра-
обращаясь к Формулам A2.5.3) — A2.5.6), убеждаемся, что безразмерная сво-
свободная энергия на один узел для такой модели на квадратной решетке име-
имеет вид
' -N-llnZr3(x) = -<Kx). A2.6.16)
Поэтому в соответствии с A2.6.1) и A2.6.15) безразмерная свободная энер-
энергия на один узел для модели Поттса на треугольной решетке в критической
точке равна
VtfKi , К2, Къ) = -AT1 In Z\AKX, K2, К3) -
= -Hn q - ф(х{) - ф(х2) - ф(х3).
Критическая внутренняя энергия
Соотношения A2.5.8) — A2.5.13) легко обобщить на случай треугольной
решетки, что дает
з
(Е) = -q-* 2 Jrexp(Jr/kBT)Ir, A2.6.18)

350 МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА
где /г, согласно A2.6.1) — A2.6.3), определяется выражением
j = {пъ) + Ы + ехр(Я) (п5) + ехр(-А)(к6) A2.6.19)
jcr l+jtrexp(A) I 4- jtrexp(-A) '
Здесь г = 1, 2 или 3, a /ty в A2.6.19) равно числу узлов типа г в решетке „/",
которые имеют стрелочную конфигурацию j на рис. 11.2.
Поэтому отношение (пр /N представляет собой вероятность того, что
узел типа г имеет стрелочную конфигурацию j. Эта величина является ло-
локальной корреляцией узла, так что, согласно A1.3.3), она зависит только
от ап br сг и» следовательно, только от хг. (Как обычно, мы считаем q, a
потому и \, / константами.)
Действительно, значение 1Г должно быть таким же, как для квадратной
решетки из N узлов, у которой все узлы имеют весовые множители A2.6.2)
и принадлежат к одному типу г. Но это значение 1Г определяется формулой
A2.5.22). Поэтому из A2.6.18) для внутренней энергии на один узел
U = (Е) /N для модели Поттса на треугольной решетке получаем выра-
выражение
з
U = q~h 2 Jrtxp(JrlkBT) [-<Kxr) ± фс,)Р0]. A2.6.20)
12.7. ОБЪЕДИНЕННЫЕ ФОРМУЛЫ ДЛЯ МОДЕЛЕЙ
ПОТТСА НА ВСЕХ ТРЕХ ПЛОСКИХ РЕШЕТКАХ
В критической точке свободную энергию и внутреннюю энергию модели
Поттса на шестиугольной решетке легко получить из соответствующих
значений для треугольной решетки с помощью соотношений дуальности
A2.6.7). Результаты аналогичны по форме тем, которые получены для ква-
квадратной и треугольной решеток. Фактически мы можем объединить их в
одну формулу, как это сделано в разд. 11.8 для модели Изинга. Для всех
трех решеток условие критичности имеет вид
П [A + *г ехр{А})/A 4- jcrexp{-A})] = ехрDА). A2.7.1)
г
Тогда безразмерная свободная энергия на один узел равна
гр = f/квТ = -4 In q ~ 4 2 ф{хг) , A2.7.2)
а внутренняя энергия на один узел составляет
U = *?"' 2Лехр(/ДвГ)[-0'(Хг) ± ?(дс,)Ро] • A2-7-3)
В последнем, выражении верхний (нижний) знак выбирается, если темпера-
температура приближается к критической сверху (снизу).

ГЛАВА 12
Произведение в A2.7.1) и суммы в A2.7.2) и A2.7.3) распространяются
на все линии, сходящиеся к какому-то заданному узлу. Таким образом, г
принимает три значения для шестиугольной решетки, четыре для квадрат-
квадратной и шесть для треугольной решетки. Jr представляет собой коэффициент
взаимодействия для r-й линии в последней сумме, так что в очевидных обо-
обозначениях J3 = J{ и J4 = J2 для квадратной решетки и /4, /5, /6 = J{, /2,
/3 для треугольной решетки. Как обычно, хг определяется посредством
A2.3.4), т.е.
xr = q-\exp(Jr/kBT) - 1]. A2.7.4)
Параметр X определен в A2.3.5) (он чисто мнимый, если q < 4), а функ-
функции ф(х), f(x) определены в A2.5.6) и A2.5.20); поляризация Ро равна нулю
при q ^ 4^ а при q > 4 она определена формулой A2.5.24).
Пусть q — координационное число решетки (равное 3 для шестиуголь-
шестиугольной, 4 для квадратной и 6 для треугольной решеток). Тогда наибольшее г в
A2.7.1) — A2.7.4) совпадает с q. Определим величину в посредством ра-
равенства
в = 2X/Q. A2.7.5)
Для изотропной модели, где Jx = J2 = . . . = /, условие критичности
A2.7.1) принимает вид
exp(-J/kBT) = sinh(A - в) /sinh(A 4- в). A2.7.6а)
Если q = 2, то X = /тг/4, и это соотношение сводится к A1.8.45а) для мо-
модели Изинга.
Мы можем завершить сравнение с A1.8.45), замечая, что методы гл. 4
легко обобщаются на ^-компонентную модель Поттса на решетке Бете с
координационным числом q. Критическая температура этой модели опре-
определяется условием
txp(-JlkBT) = (q^ 2)l{q + q - 2). A2.7.66)
12.8. КРИТИЧЕСКИЕ ПОКАЗАТЕЛИ
ДЛЯ ДВУМЕРНОЙ МОДЕЛИ ПОТТСА
Мы вычислили свободную энергию / и внутреннюю энергию U для пло-
плоских моделей Поттса, но сделали это только для критической температуры
Тс и в отсутствие внешнего поля. (Точнее, мы вычислили U в пределе, ког-
когда Т приближается к Тс сверху или снизу.)
Эти результаты показывают, что фазовый переход будет первого рода
(со скрытой теплотой перехода), когда q > 4, и непрерывным (без скры-
скрытой теплоты) при q ^ 4. Они ничего не говорят нам о том, каковы крити-
критические показатели при q < 4. Чтобы выяснить это прямым способом, мы
должнь; были бы решить модель Поттса для произвольной температуры,
что до сих пор не сделано. (Это очень интригующая проблема, как я отме-
отмечал в разд. 12.4.)
Тем не менее некоторые данные имеются. Когда q = 2, модель Поттса
становится моделью Изинга, которая решена [184, 262]. Значения критиче-
критических показателей а, C и 5 определены в G.12.12), G.12.14) и G.12.16). Они

352 МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА
равны
а=0, /?=4, 6=15 при q = 2. A2.8.1а)
Александер [3] привел соображения в пользу того, что модель Поттса с
q = 3 и модель жестких гексагонов (каждая из которых имеет три упоря-
упорядоченных состояния) должны относиться к одному классу универсальности
и иметь одинаковые критические показатели. Тогда, используя результаты
для модели жестких гексагонов A4.7.12), A4.7.13), получаем
ос = 4, /3=4, 6=14 при q=3. A2.8.16)
Аналогично в работе [73] высказаны соображения в пользу того, что
модель Поттса с q = 4 и трехспиновая модель (каждая из которых имеет
четыре упорядоченных состояния) должны иметь одинаковые критические
показатели, так что из A1.10.39) следует
от = §, /}=¦&, 6=15 при q=A. A2.8.1b)
В разд. 12.3 — 12.5 мы убедились, что модель Поттса в критических
точках эквивалентна шестивершинной модели в отсутствие внешнего поля
с весовыми множителями A2.5.2). Можно рассматривать это как частный
случай восьмивершинной модели, для которой d = 0. Параметр А в
A0.15.1) описывается формулой A2.5.4). При q < 4 мы видим, что
0 > А > -1. Из A0.16.8) следует, что это соответствует восьмивершин-
восьмивершинной модели в критических точках с параметром д, определяемым посредст-
посредством равенства А = -cos/x. Вместе с A2.5.4) это означает, что
9* = 2cosjU, 0 <С ju <C ijr . A2.8.2)
Здесь д — тот же параметр, который входит в формулы A0.12.24) для кри-
критических показателей восьмивершинной модели. В работе [71) приведены
доводы в пользу того, что критические показатели модели Поттса также
должны иметь простую зависимость от ц. или, точнее, от
y = 2fjJx. A2.8.3)
(Значения этого параметра^ лежат между 0 и 1. В работе [71] он обозначен
у*т .) Для критического показателя а в модели Поттса (при q ^ 4) предло-
предложено выражение
а= B - 4у)/C - Ъу). A2.8.4)
Аналогичным образом в работах [179, 191] независимо предположено,
что
A2.8.5)
Тогда соотношения скейлинга A.2.12) и A.2.13) предсказывают, что
д = A5 - 8у + у2)/A - у2). 02.8.6)
При q = 1, 2, 3, 4 параметр у принимает значения , , - , 0 соот-
3 2 3

ГЛАВА 12 353
ветственно. Поэтому предположения A2.8.4) — A2.8.6) согласуются со зна-
значениями A2.8.1), а также предсказывают значения
*=-§, j8=ft, в =18* при 4=1, A2.8.7)
(Как отмечалось в связи с A2.2.4), случай q - 1 соответствует задаче о
перколяции.) Указанные выше предположения согласуются также с числен-
численными оценками показателей [59, 60] и с ренормгрупповыми разложениями
около q = 4 по теории возмущений [66]. Недавно справедливость A2.8.4)
подтверждена методами ренормализационной группы [56]. Представляется
весьма вероятным, что соотношения A2.8.5) и A2.8.6) также являются точ-
точными.
12.9. МОДЕЛЬ ЭШКИНА - ТЕЛЛЕРА
НА КВАДРАТНОЙ РЕШЕТКЕ
Эшкин и Теллер [10] предложили свою модель в качеств^ обобщения
модели Изинга на четырехкомпонентную систему. Каждый узел решетки У
в этой модели занят атомом одного из четырех сортов: А, В, С или D.
Энергия взаимодействия двух соседних атомов равна е0 для АА, ВВ,СС,
DD, е{ для АВ, CD, е2 для AC, BD и е3 для AD, ВС.
Фэн [82] показал, что модель может быть выражена через изинговские
спины. Каждому узлу / поставим в соответствие два спина: s, и <т,. Пусть
(s^, Gj) = (+, +), если в узле / находится атом А, (+, -), если атом В,
(-, +), если атом С, и (-, -), если атом D. Тогда энергия взаимодейст-
взаимодействия для ребра (/, j) имеет вид
e(i,;') = -JsiSj - J'OiOj - JaSiOiSjOj - /о, A2.9.1)
v w • A2.9.2)
/ ( )
Как обычно, мы хотим вычислить статистическую сумму. Согласно
A.4.1), она определяется выражением
ZAT = 2 2 ехр[- ^ e(iJ
A2.9.3)
где /rfi — постоянная Больцмана, Г — температура. Суммирование под
знаком экспоненты охватывает все линии (/, j) решетки, соединяющие со-
соседние узлы; внешние суммы берутся по всем значениям всех спинов slf s2,
53, . . . И OTj, <Т2» °» • • • •
Удобно ввести безразмерные коэффициенты взаимодействия
к = лквт, К'=г/квт, П294)

354 МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА
а также больцмановские весовые множители линий
(Oi = Qxp(-?i/kBT), i = 1,. . . , 4 . A2.9.5)
Из A2.9.2) получаем
а>о = ехр(/С + К' + К< + Ко), о)! = exp(/C - /С' - /С4 + /Со),
шг = ехр(-К + К' - К4 + Ко), <»з = ехр(-ЛС - /С' 4- /С4 + /Со).
Эквивалентность восьмивершинной модели с двумя
подрешетками
Сказанное выше применимо к любой решетке -/, не обязательно плос-
плоской. Ограничим теперь рассмотрение случаем, когда -/'является квадрат-
квадратной решеткой с N узлами. Тогда из A2.9.1) следует, что модель
Эшкина — Теллера (ЭТ) можно представить себе как две модели Изинга на
квадратной решетке (^-модель и а-модель), связанные посредством четы-
рехспинового взаимодействия.
Это похоже на восьмивершинную модель без внешнего поля с гамиль-
гамильтонианом A0.3.1), в котором Jv = Jh = 0. Но геометрия системы в этих
двух случаях различна. Спины восьмивершинной модели расположены, как
показано на рис. 10.4: s-спины занимают темные узлы, а а-спины — свет-
светлые. В модели ЭТ спины обоих сортов si и oi находятся на одном узле /.
Даже в этом случае оказывается возможным представить модель ЭТ
как восьмивершинную модель с двумя подрешетками [248]. Хитрость со-
состоит в том, что преобразование дуальности (рзд. 6.2) применяется только
к а-спинам.
Чтобы выполнить это, заметим, что с помощью A2.9.1) выражение
A2.9.3) можно записать в виде
exp[S (KsiSj + Ко)] Z^L}, A2.9.7)
ZAT =
где
Z^L} = 2 exp|"S LijOiOj] , A2.9.8)
а коэффициенты L^ определяются выражением
Lij = K' + KAsiSj. A2.9.9)
Здесь N — число узлов квадратной решетки ~/\ L — совокупность коэффи-
коэффициентов L;j, по одному для каждой линии S.
Ясно, что каждый коэффициент L^ зависит от спинов st и 5у, но мы вре-
временно фиксируем 5-j, . . . , sN и рассмотрим выражение в правой части
A2.9.8). Оно представляет собой стандартную статистическую сумму моде-
модели Изинга на квадратной решетке, но система является неоднородной, по-
поскольку коэффициенты взаимодействия L- изменяются при переходе от од-
одного ребра к другому.
Обратимся теперь к соотношению дуальности F.2.14). Используя

ГЛАВА 12
355
F.2.10) (и игнорируя граничные эффекты), его можно свести к следующему
утверждению: если ZN(K, L) является статистической суммой модели
Изинга на квадратной решетке с коэффициентами взаимодействия К для
вертикальных линий и L для горизонтальных линий и с общим количест-
количеством узлов N, то
г„(К* , L*) = [2 exp(-/C - L) coshК* cosh L*]NZu(K,L). A2.9.10)
Дуальные коэффициенты К*, L* определяются посредством F.2.14а).
Это выражение получено для однородной системы. Но вывод его в
разд. 6.2 непосредственно обобщается на случай неоднородной системы с
коэффициентом взаимодействия L- на ребре (/, j). Результат имеет вид
П
OV)
-^') cosh Ц
•где
tanh Ц = exp(-2L/y).
A2.9.11)
A2.9.12)
Здесь L обозначает совокупность всех коэффициентов L-, a L* — аналогич-
аналогичную совокупность всех L?; ZN [L] — исходная статистическая сумма для
решетки ^, определяемая выражением A2.9.8); ZN {L*} — то же для ре-
решетки ^fD, дуальной Л\ L*j — коэффициент взаимодействия на ребре ^D,
дуальном ребру (/, j) из У.
Пусть к, I — узлы решетки Уо, такие, что ребро (к, I) дуально ребру (/,
j), как это показано на рис. 12.11. Тогда
Zk{L*} = 2 ехр
[ 2 Lf}tkt(] ,
A2.9.13)
в узлах JD.
Выражая с помощью A2.9.11) ZN { L] через ZN [L*], подставляя резуль-
результат в A2.9.7) и используя A2.9.13), получаем
A2.9.14)
Рис. 12.11. Решетка У (темные кружки и
сплошные линии») и ее дуальная решетка Уо
(светлые кружки и штриховые линии); {к,
I) — линия Уп, дуальная линии (/, у) решет-
решетки У\ LtJ* и L,j — соответствующие этим
линиям коэффициенты взаимодействия.

356 МОДЕЛИ ПОТТСА И ЭШКИНА - ТЕЛЛЕРА
где произведение охватывает все ребра (/, j) решетки -4 причем
Wtj = 2"* sech Ц exp[L,y + KsiSj + K0 + LJwJ. A2.9.15)
Учитывая, что Ly определяется посредством A2.9.9), где stSj = ±1, а
J — посредством A2.9.12), мы можем представить Wy в виде
+ Btkfi + CsiSjtkti + D), A2.9.16)
где Л, 5, С, ?> определяются соотношениями
а = ехр(Л + В + С + D) =
С + D)
A2.9.17)
с = ехр(-Л + В - С + D) = 2"*(ш2 + ю3),
d = ехр(Л - В - С + D) = 2~*(шо - ^0 .
Поэтому в соответствии с A.4.1), A2.9.14) и A2.9.16) ZAT является ста-
статистической суммой модели с гамильтонианом
E(s , Г) = -квТ 2 (AstSj + BtkU + Cs^r^/ + D). A2.9.18)
Примем теперь, что -/является решеткой из темных узлов и сплошных
линий на рис. 10.4. Тогда -/D будет решеткой из светлых узлов и штрихо-
штриховых линий; 5-спины принадлежат решетке -/, а /-спины — решетке -4). Мы
видим, что A2.9.18) представляет собой гамильтониан модели с взаимо-
взаимодействиями между соседними 5-спинами и между соседними /-спинами и с
четырехспиновым взаимодействием между спинами на пересекающихся ли-
линиях.
Этот гамильтониан имеет общий вид A0.3.1), но с Jv ¦ Jh = 0, J" =
« квТС и с дополнительной постоянной энергией -kBTD для каждой ли-
линии. Чтобы избежать путаницы, обозначим J и J' в A0.3.1) и на рис. 10.4
символами J%y и J'%v> Эти величины, конечно, не те, которые входят в ра-
равенства A2.9.1)-A2.9.4).
Имеется одно существенное различие между A2.9.18) и A0.3.1): в
A2,9.18) А и В ассоциируются со сплошными и штриховыми линиями меж-
между узлами на рис. 10.4 соответственно; в A0.3.1) J%v и J'%v ассоциируются с
линиями юго-запад — северо-восток и юго-восток — северо-запад на том
же рисунке. Поэтому, чтобы привести A2.9.18) к виду A0.3.1), необходимо
допустить чередование J%v и J^v от узла к узлу. Можно положить
(J$y/(kBT)t J%y/(kBT)) равными (А, В) на одной подрешетке (сумма / + j
четнаяр A0.3.1)) и равными (В, А) на другой подрешетке (сумма#/ + j не-
нечетная). Поэтому модель Эшкина — Те л л ера эквивалентна восьмивершин-
ной модели с двумя подрешетками. Из A0.3.9.) (с учетом дополнительной
постоянной энергии -kBTD) следует, что больцмановские весовые множи-

ГЛАВА 12 3S7
тели этой восьмивершинной модели на одной подрешетке равны а, Ь, с, d в
A2.9.17), а на другой подрешетке они равны a, b, d, с.
То, что модель Эшкина — Теллера эквивалентна восьмивершинной мо-
модели с двумя подрешетками, является, конечно, интригующим обстоя-
обстоятельством. Во многих отношениях эта эквивалентность напоминает ту, ко-
которая была обнаружена в разд. 12.4 между моделью Поттса и шестивер-
шинной моделью с двумя подрешетками. Действительно, вершинные моде-
модели в этих двух случаях могут быть сведены в одну, эквивалентную модели
Поттса при q = 4 (которая является частным случаем модели Эшкина —
Теллера с е1 = е2 = е3).
Способ разделения рассматриваемой здесь восьмивершинной модели на
подрешетки состоит просто в том, что весовые множители end меняются
местами. Отсюда, а также из A0.15.1а) и A0.15.6) следует, что каждая из
величин Д, Г, к и X сохраняет одно и то же значение для обеих подреше-
ток. Разбиение на подрешетки влияет только на аргумент эллиптических
функций у, который меняет знак при переходе от одной подрешетки к дру-
другой. К сожалению, к, X, v не удается привести к виду A0.17.7), что являет-
является наиболее общим условием разрешимости восьмивершинной модели. Та-
Таким образом, модель Эшкина — Теллера в общей формулировке остается
нерешенной.
Несмотря на это, эквивалентность модели ЭТ восьмивершинной модели
с двумя подрешетками имеет некоторые интересные следствия, которые
будут рассмотрены ниже в этом разделе.
Дуальность
Очевидно, что статистическая сумма восьмивершинной модели с двумя
подрешетками не изменится, если с и d поменять местами на всех узлах
(это просто меняет местами подрешетки). Представим ZAT как функцию
больцмановских весовых множителей ы0, . . . , ы3 A2.9.6). Тогда из
A2.9.17) следует
ZAT(o>o , (о{ , о^ , о>з) = ZatOo , ft>i, ft>2, юз), A2.9.19)
если
cob = i(a>o + (О\ + (о2 + щ),
Ы{ = K^O + 0)i - (О2 - СОЪ) ,
, 1/ ч A2.9.20)
(О2= 2(^0+ СО2- (ОЪ~ (Ох) ,
&>з = Ь(щ + о>з ~ Щ - со2).
Это — соотношение дуальности, связывающее высокотемпературную
модель ЭТ с низкотемпературной. Оно получено в работе [81], где было
высказано предположение, согласно которому критическая температура
определяется условием самодуальности
а>о = (О\ + (о2 + (Оз . A2.9.21)

358 МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА
Однако Вегнер [248] обратил внимание на то, что условие однородности
соответствующей восьмивершинной модели с = d совпадает с написан-
написанным выше. Решение однородной восьмивершинной модели получено в
гл. 10. Оно не соответствует, вообще говоря, критической точке (даже ког-
когда с = d); то же можно сказать о модели ЭТ, удовлетворяющей условию
A2.9.21). (Спиновые переменные sv s2, • • • используются в обеих моде-
моделях; поэтому можно высказать следующее разумное предположение: состо-
состояние любой из этих двух моделей соответствует критической точке в том и
только в том случае, если корреляция (S;Sj) затухает в зависимости от рас-
расстояния rtj между узлами / и j не экспоненциально, а как отрицательная
степень этого расстояния. Это означает, что если одна модель находится в
критической точке, то и другая тоже.)
В самом деле, если У4 = 0 в A2.9.1), то очевидно, что модель ЭТ факто-
ризуется в две независимые модели Изинга: одна для 5-спинов с коэффици-
коэффициентом У, другая для ст-спинов с коэффициентом J'. При условии что
J Ф J' у они имеют две различные критические температуры. Поэтому мо-
модель ЭТ в этом случае имеет две критические температуры. Они располо-
расположены по обе стороны от температуры самодуальности, определяемой по-
посредством A2.9.21); отображение A2.9.20) переводит одну из них в другую.
Вегнер [248] высказал мысль, что, вообще говоря, и при У4 Ф 0 должны
быть две критические температуры, a By и Лин [260] рассмотрели возмож-
возможное расположение критических поверхностей в пространстве (wj/w0, а;2/^0,
Wj/wq). Одна из нерешенных на данный момент проблем состоит
в том, чтобы точно определить положение этих поверхностей. Предполага-
Предполагается, что гипотеза универсальности выполняется на этих поверхностях (за
исключением некоторых особых линий, обсуждаемых ниже). В этом случае
критические показатели должны быть такими же, как в случае /4 = 0» т-е-
такими же, как для модели Изинга.
Другие свойства симметрии
Кроме A2.9.19), статистическая сумма ZAT удовлетворяет ряду других
соотношений симметрии. Она не меняется при перестановке У, /', У4 в
A2.9.1), поскольку это соответствует просто перестановке si9 a7, siai на
каждом узле. (Любую пару из этих трех спиновых переменных можно рас-
рассматривать как независимые спины.) С учетом этих свойств симметрии из
A2.9.4) и A2.9.6) следует
ZAT(t0|, а);, п)к , (Oi) = ZAT(a)o ,(Oi,(O2, О)Ъ) A2.9.22)
для всех перестановок /, j, к, I чисел 0, 1,2, 3. Таким образом, ZAT не ме-
меняется при перестановке весовых множителей соо, . . . , со3.
Другой способ получения соотношений дуальности и симметрии
A2.9.19) и A2.9.22) состоит в том, чтобы ввести восьмивершинные весовые
множители Wj, w2, н>3, н>4, как в A0.2.16). Соотношения симметрии
A0.2.17) справедливы даже для неоднородной восьмивершинной модели.
Используя их, а также A2.9.17), мы снова получаем A2.9.19) и A2.9.22).

ГЛАВА 12 359
ИЗОТРОПНАЯ МОДЕЛЬ ЭШКИНА — ТЕЛЛЕРА В КРИТИЧЕСКИХ
ТОЧКАХ
Если J = J', то высказанные выше соображения о том, что модель ЭТ
должна иметь две критические точки, отпадают. Этот случай особенно ин-
интересен; мы будем называть его «изотропной моделью ЭТ». Из A2.9.6) мы
видим, что он соответствует условию
0I = о>2 A2.9.23)
для весовых множителей модели ЭТ.
Соответствие с двухподрешеточной восьмивершинной моделью, у кото-
которой порядок следования весовых множителей с, d чередуется на соседних
узлах и которая в общем виде не решена, все еще сохраняется. Но если ус-
условие самодуальности A2.9.21) выполнено, то с = d, и восьмивершинная
модель становится однородной. Согласно A0.2.16), ее весовые множители
w имеют вид
и>1 = h(a + b) = 2*ft>i,
и>2 = i(a - b) = 2-\щ + ft>3),
A2.9.24)
i( d) 2*( )
Из A0.2.17) следует, что ZAT не изменится, если поменять местами vv2 и
н>4. Пусть а'у Ь', с'у d' — новые восьмивершинные весовые множители по-
после такой перестановки. Тогда мы видим, что
я'= ft'= 2*юь С = 2\щ + ю3), rf' = 0. A2.9.25)
Поскольку d' = 0, эта модель сводится к шестивершинной модели (факти-
(фактически к F-модели). Пусть / — свободная энергия на один узел для модели
ЭТ, определяемая так же, как в A.7.6), а именно
-flkBT = lim N-1 In ZAT. A2.9.26)
Поскольку вершинная модель имеет вдвое больше узлов, чем исходная
модель ЭТ, из (8.3.3), (8.8.9), (8.8.17), (8.9.7) и (8.9.9) получаем, что при
выполнении условий A2.9.21) и A2.9.23) свободная энергия/ определяется
соотношениями
/ Oh \
О)Ъ<щ\ cos(ju/2) = J 1 + — ,
\ (Ох/
, , ч Г0
-f/квТ = 2 1пBЧ) +
J J-
A2.9.27a)
00 tanh fix smh (я - (л)х

360 МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА
юз = ft>i: -f/квТ = 2 111B*0)!) + 41п[ГD)/2Г(|)]; A2.9.276)
ffl3>ffll: cosh(A/2) = i(l + — V Я>0,
^ A2.9.27b)
oo
-/7*ЯГ = 21пBЦ) + Я + 2 2 m exp(-mA) tanh mA.
КРИТИЧЕСКИЕ ПОКАЗАТЕЛИ
Состояние однородной восьмивершинной модели соответствует крити-
критической точке в том и только в том случае, если в последовательности
I Wj I, I vv21, I w31, I vv41, расположенной в порядке убывания, две средние
величины равны. В этом случае можно воспользоваться соотношением
симметрии A0.2.17) для отображения на шестивершинную модель типа
рассмотренного в разд. 8.8, т.е. с -1 < А < 1. Критические показатели
тогда даются A0.12.24). Их связь с восьмивершинной моделью обозначим
верхним индексом 8V; кроме того, «магнитные» показатели (связанные с
введением поля -//? ot) будем отмечать индексом т. «Электрические» по-
показатели (связанные с полем — ?? OjOj, где / и у — соседние узлы) уже име-
имеют у нас индекс е. Тогда, согласно A0.12.24), имеем
/T=B-y)W,
где
у = 2fjJjz , A2.9.29)
ад — параметр, введенный в разд. 8.8 (у — ренормгрупповой показатель,
который мы уже использовали в разд. 12.8).
Применяя указанный выше общий критерий к самодуальной изотропной
модели ЭТ, устанавливаем с помощью A2.9.24), что модель можно счи-
считать находящейся в критической точке, если ы3 < wj. Ее свободная энергия
описывается выражением A2.9.27а), где параметр д тот же, что в A2.9.29).
Так же как в случае модели Поттса, свободную энергию / мы вычисли-
вычислили только в критической точке. Мы не знаем, как свободная энергия изме-
изменяется с температурой или полем, поэтому не можем непосредственно
определить какой-либо критический показатель. Разумеется, мы не можем
применить результаты A2.9.28) для однородной восьмивершинной модели
к модели ЭТ, поскольку эти модели эквивалентны только в критической
точке.
Несмотря на это, в работах [132 — 134] связь между критическими по-
показателями восьмивершинной модели и модели ЭТ была установлена с по-
помощью операторной алгебры и скейлинга [131]. Те же соотношения были
получены затем [150] методом ренормализационной группы; этот подход
получил дальнейшее развитие [70, 71], и было подтверждено предположе-

ГЛАВА 12 361
ние [78] о том, что дт = \5 для модели ЭТ. Некоторые из этих соотноше-
соотношений были проверены [267, 268] с помощью разложений по теории возмуще-
возмущений.
Все эти работы в совокупности дают следующие критические показате-
показатели для модели Эшкина — Теллера:
оЛт = B - 2уI{Ъ - 2у), № = B - >')/B4 - Щ),
/3?Т=A2-8уУ1.
Что касается восьмивершинной модели, то у нее имеется два набора
критических показателей: «магнитные» показатели, соответствующие по-
полю — HEoj, и «электрические» показатели, соответствующие полю
-?? ор(. Я использую индекс т для первых и индекс е для вторых. Таким
образом, /Зт является критическим показателем для параметра порядка
(о{), а Ре — для <<т15|1>.
Соотношения A.2.12) — A.2.16) между критическими показателями ос-
основаны на тех же соображениях, что и A2.9.30); поэтому их можно исполь-
использовать, чтобы получить 1туЬтУу\тУ ув, 5в, ч\е и v. Обе модели, восьмивер-
шинная и Эшкина — Теллера, не подчиняются принципу универсальности,
поскольку их критические показатели непрерывным образом зависят от па-
параметра у. Для обеих моделей имеют место соотношения
6т = B - а - /3m)//Sm = 15 , & = A - ог)/4. A2.9.31)
Условия критичности A2.9.21) и A2.9.23) можно выразить через коэф-
коэффициенты взаимодействия К, К', К4. Используя A2.9.6), получаем
К' = К, exp(-2K4) = sinh2A:, A2.9.32a)
условие ы3 < wj эквивалентно условию
К*<К, AZ9.326)
а определение параметра /х A2.9.27а) можно записать в виде
cos pi = i[expDA:4) - 1] , A2.9.33)
где 0 < II < 2тг/3.
Фазовая диаграмма модели Эшкина - Теллера
В действительности A2.9.32) является не единственной линией критиче-
критических точек для изотропной модели ЭТ. Полная фазовая диаграмма, полу-
полученная в работе [72], удивительно богата. Она показана на рис. 12.12. Име-
Имеется пять областей на плоскости (Я^, К). В области I система упорядочена
ферромагнитным образом, средние величины <aj>, <Sj> и (ajSj) все не
равны нулю; в области II все они равны нулю и система не упорядочена; в
области III имеется частичный порядок, величина <aj 5j> не равна нулю,
но <Gj> и <5j> обращаются в нуль; область IV сходна с областью III, но
упорядочение здесь является антиферромагнитным, происходит чередова-

362
МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА
0,5-
о-
-
; iv
D
A 1 I
' 1 '
II
1 1 1
' :
b\ m -
V "
1 1 1 1 1 1
с
G
G'
С
-0,5
0,5
Рис. 12.12. Фазовая диаграмма изо-
изотропной модели Эшкина — Теллера
на плоскости (К4, К).
ние величины {о{ sx) от узла к узлу; область V сходна с областью I, но ве-
величины (а{) и <$!> упорядочены антиферромагнитным образом.
Линия EF, которая разделяет области I и И, является линией A2.9.32),
обсуждавшейся выше. Это линия, вдоль которой критические показатели
меняются непрерывно: /х в A2.9.29) изменяется от 0 в точке F до 2тг/3 в
точке Е; F является точкой (Кп Kt), где Kt-- 1пЗ = 0,2746, . . . ; в точке
4
Е отношение КА/К равно - 1 при К -* оо.
На линии Е' F' критические показатели также меняются непрерывно.
Эта линия получается из EF просто изменением знака К. Действительно,
перемена знаков всех спинов st и оi на одной подрешетке ~/ эквивалентна
просто изменению знака А'; поэтому вся диаграмма рис. 12.12 симметрична
относительно оси КА.
Штриховая линия FG является продолжением линии EF'. Это линия са-
самодуальности с ы3 > wj. Она не является линией критических точек; вме-
вместо этого имеется две линии критических точек FB и FC с точкой бифурка-
бифуркации F. Положение этих линий точно не установлено, но точка В должна
быть точкой (Кр 0), а С — точкой (оо, —, Кс), где Кс — критическое значе-
значение К для модели Изинга, определяемое условием
sinh2Kc = l, tfc = 0.4406....
A2.9.34)
Линии FB, FC отображаются одна в другую при посредстве соотношения
дуальности A2.9.20). Ожидается, что вдоль этих линий критические показа-
показатели постоянны и совпадают со значениями для модели Изинга.
Аналогично предыдущему положение линии критических точек EDE'
точно не известно, но точка D является точкой (-А^, 0). Ожидается, что
критические показатели на этой линии также совпадают со значениями для
модели Изинга.

13
УГЛОВЫЕ ТРАНСФЕР-
МАТРИЦЫ
13.1. ОПРЕДЕЛЕНИЯ
Обозначения
В гл. 7 — 10 успешно использовалась трансфер-матрица V ряд — ряд.
Умножение на такую матрицу соответствует добавлению к решетке одного
ряда. Каждый элемент матрицы V представляет собой полный больцма-
новский вес ряда решетки (см. G.2.2) и (8.2.2)).
Другим полезным понятием является «угловая трансфер-матрица»
(УТМ), которая соответствует добавлению к решетке одного квадранта. В
настоящем разделе я введу определения для четырех таких матриц (по од-
одной на каждый угол), которые обозначу Л, В, С, D. Будут определены так-
также соответствующие нормированные матрицы Ап, Вп, Сп, Dn и нормиро-
нормированные и диагонализованные матрицы Ad, Bd, Cd, Dd. Здесь п и d не явля-
являются индексами, а просто означают «нормированная» и «диагональная»
матрица соответственно.
Элемент (а, о') одной из таких матриц обозначается с помощью двой-
двойного индекса ааг; например, Воо> и (Ап)аа, представляют собой элементы
(а, о') матриц В и Ап соответственно.
ВСГ-МОДЕЛЬ
Угловые трансфер-матрицы могут быть определены для любой плоской
решеточной модели с короткодействующими взаимодействиями. Для опре-
определенности рассмотрим квадратную решеточную модель, в которой взаи-
взаимодействуют «спины», расположенные в узлах каждой грани решетки. Для
краткости я буду называть ее ВСГ-модель. Она определяется следующим
образом.
С каждым узлом / квадратной решетки ассоциируется спин а(. В настоя-
настоящей главе предполагается, что каждый спин а,- принимает значение + 1 или
— 1; в следующей главе окажется более удобным считать, что соответству-
соответствующие значения равны 0 и 1. В общем случае можно выбирать любой под-
подходящий набор значений.
Пусть полная энергия равна
<Z=2e(oi,oj,ok,ol), A3.1.1)
где суммирование проводится по всем граням решетки; на каждой грани
узлы /, j, к, I расположены так, как показано на рис. 13.1,а. Из выражения

364
УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
а
Рис. 13.1. а — упорядочение узлов /, j, к, /, расположенных вокруг грани квадратной
решетки; б — квадрант решетки, которому соответствует статистическая сумма
Ааа. A3.1.8).
A.4.1) следует, что статистическая сумма имеет вид
2 = Е П w(oi-, о;, ок , oi),
A3.1.2)
где произведение берется по всем граням решетки, суммирование проводи-
проводится по всем значениям всех спинов и
w(a,b,c,d)= ехр[-ф , Ъ , с ,
A3.1.3)
Величина w(a, b, с, d) представляет собой больцмановский вес взаимо-
взаимодействий между спинами а, Ь, с, d, принадлежащими одной грани.
Пусть 7V — число узлов в решетке. Введем определение
к= limZlw.
A3.1.4)
Тогда из выражения A.7.6) следует, что свободная энергия, приходящаяся
на один узел, равна
f= -квТ\пк. A3.1.5)
Согласно A.4.4), среднее значение отдельного спина ох вычисляется по
формуле
en
(оч, о}, ok , at).
03.1.6)
Задача статистической механики состоит в том, чтобы в пределе боль-
больших решеток определять такие величины, как к и (о{). Следует ожидать,
что такие предельные значения не зависят от способа увеличения размеров
решетки, если она увеличивается во всех направлениях.

ГЛАВА 13 365
На данном этапе функция и» (я, Ь, с, d) произвольна, так что ВСГ-
модель включает в себя многие модели, представляющие интерес для ста-
статистической механики. Например, она включает случай, когда наряду с вза-
взаимодействием четырех спинов на каждой грани имеются взаимодействия
между парами спинов, лежащих на диагоналях, а это не что иное, как
сформулированная на языке спинов A0.3.1) восьмивершинная модель. Во-
Вообще ВСГ-модель включает в себя восьмивершинную модель как в «маг-
«магнитном», так и в «электрическом» поле, а также модель Изинга во внеш-
внешнем поле.
Основное состояние
Система может иметь одно или несколько основных состояний. Основ-
Основное состояние — это такая конфигурация всех спинов решетки, для кото-
которой энергия <f, определенная выражением A3.1.1), минимальна. В более об-
общем виде основное состояние можно определить как такую конфигурацию,
которая дает наибольший вклад в сумму по всем состояниям в A3.1.2).
Для ферромагнитной системы типа модели Изинга имеется не более
двух основных состояний: либо все спины направлены либо вверх, либо
вниз. Для системы с антиферромагнитным взаимодействием основное со-
состояние может состоять из областей с чередующимися спинами. Последнее
состояние не обладает трансляционной симметрией, даже если энергия
A3.1.1) трансляционно-инвариантна. В таком случае должно существовать
по крайней мере два основных состояния, поскольку трансляционный сдвиг
изменяет спиновую конфигурацию, но не изменяет ее энергию.
В настоящей главе я буду часто упоминать понятие «основное состоя-
состояние». Под этим я понимаю некоторое вполне определенное основное состо-
состояние. Существенно, чтобы всюду использовалось одно и то же основное
состояние полной решетки. Например, если основное состояние не является
трансляционно-инвариантным, то при вычислении по формулам A3.1.11),
A3.1.14) и A3.1.15) может оказаться, что {ах) зависит (при достаточно
низких температурах) от того, какое используется основное состояние. В
таком случае трансляционная инвариантность оказывается «спонтанно на-
нарушенной».
Матрицы А, В, С, D
Рассмотрим решетку, изображенную на рис. 13.1,6. Обозначим спины
левого столбца через ох% . . . , от, а спины верхнего ряда через aj, . . . , о'т,
как показано на рисунке. Ясно, что обозначения а{ и а{ соответствуют од-
одному спину, находящемуся в верхнем левом углу; поэтому
о{-01. A3.1.7)
Зафиксируем граничные спины, расположенные на узлах, обозначенных
на рис. 13.1,6 треугольниками, придав им значения, отвечающие основно-
основному состоянию. Например, для ферромагнитной модели Изинга все указан-
указанные значения могут быть выбраны равными +1.
Обозначим через о набор спинов (alf . . . , am)t а через а' набор

366
УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
о'т} .Введем определение
= 0 при охф а[ ,
A3.1.8а)
A3.1.86)
где произведение берется по всем —гп(гп + 1) граням на рис. 13.1,6, а
суммирование проводится по всем стшнам на узлах, обозначенных темны-
темными кружками. Отметим, что по спинам о{, . . . , о'т суммирование не
проводится; поэтому правая часть A3.1.8) является функцией о и о' .
Определим матрицу Вау тем же способом, что и Лоу, но при этом
повернем рис. 13.1,6 на 90° против часовой стрелки. Спины а{, . . . , от
окажутся на нижней границе, а спины а[, . •. . , а'т — на левой. Аналогично
с помощью двух поворотов на, 90° определим матрицы Соу и Day.
Рассмотрим теперь решетку, показанную на рис. 13.2. Разделим ее с по-
помощью двух разрезов, как показано на рисунке, на четыре квадранта оди-
одинакового размера. Пусть а{ находится в центре решетки, и пусть а, а', а",
о'" представляют собой наборы спинов (включая ох)у лежащих на соот-
соответствующих полуосях, показанных на рис. 13.2. Тогда по определению
матриц Л, В, С, D величина
AajBtsCrD*,, A3-1.9)
равна произведению больцмановских весов всех граней, просуммированно-
просуммированному по всем спинам, кроме тех, которые лежат на разрезах. Следовательно,
статистическая сумма оешетки, показанной на рис. 13.2, имеет вид
Z =
W,o"'
A3.1.10)
При суммировании по всем наборам спинов а, . . . , о'" имеется только
одно ограничение: а{ = о[ = о'[ = о'{\ поскольку каждый из этих спинов яв-
а"
Рис. 13.2. Решетка, статистическая
сумма которой выражается формулой
A3.1.10). Граничные спины (на узлах,
обозначенных треугольниками) имеют
фиксированные значения, отвечающие
основному состоянию; а{ — централь-
центральный спин; а — набор всех спинов
(включая а,) на нижнем луче жирной
вертикальной линии; а' — набор спинов
(включая (jj) на правом луче
жирной горизонтальной линии; о", а'"
определяются аналогично.
с
л
В

ГЛАВА 13 367
ляется центральным. Но указанное условие можно не учитывать, так как
из определения A3.1.86) следует, что слагаемые с несовпадающими значе-
значениями центральных спинов равны нулю, поэтому
Z = Trace ABCD . A3.1.11)
Из формулы A3.1.6) видно, что среднее значение спина а{ равно отно-
отношению правой части A3.1.10) с дополнительным множителем ох под зна-
знаком суммы к той же величине без множителя ох. Таким образом,
(ох) = Trace SABCD/Trace ABCD , A3.1.12)
где S — диагональная матрица, элемент (а, о') которой равен а{.
Матрицы S, А, В, С, D имеют блок-диагональную структуру, причем их
элементы (а, о') равны нулю при о{ Ф о[. Матрица S коммутирует с At Bt
С и D. В частности, для моделей типа Изинга, в которых каждый спин о-
равен +1 или -1, указанные матрицы имеют следующую структуру:
где / — единичная матрица. В данном случае (о{) представляет собой на-
намагниченность М.
Очевидно, что в A3.1.11) умножение на Л соответствует введению ниж-
нижнего правого квадранта, или «угла» решетки. Поэтому назовем А угловой
трансфер-матрицей нижнего правого угла. Аналогично В, С, D являются
угловыми трансфер-матрицами верхнего правого, верхнего левого и нижне-
нижнего левого углов соответственно.
Нормированные матрицы Л п, Вп, Сп, Dn
Обозначим через s, s', s", s"f значения, которые принимают спины из
наборов о у о', о" у о'", показанных на рис, 13.2, когда все спины находятся
в основном состоянии. Положим
ос=Л„; 0=В,,,. y=Csr; 6 = Drs 03.1.14)
и введем определения
А„ = а-1А, Bn = p~lB, Сп = у-'С, Dn = d'"D. A3.1.15)
Матрицы Лп, Вп, Сп, Dn называются нормированными угловыми
трансфер-матрицами. Их элементы, отвечающие основному состоянию,
т.е. (An)ss>, равны единице. Мы увидим, что данные матрицы полезны при
рассмотрении предела при т — оо.
Многие формулы, включающие угловые трансфер-матрицы, не зависят
от нормировки матриц Л, В, С, D. Очевидным примером является
A3.1.12). В'таких формулах матрицы Л, В, С, D можно заменить на Ап,
В,,' С„ Dn.

368 УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
Диагональные матрицы Аф Bd> Cd> Dd
Часто оказывается полезным использовать диагональные формы Аф
Вф Сф Dd матриц А, В, С, D (и Ап, Вп> Сп, Dn)t нормированные так, что
их максимальные элементы равны единице. Диагональные матрицы опре-
определяются соотношениями
A3.1.16)
С = y'R Cdr\ Dn = 6'TDdp-1,
где а', 0', у', б' — скаляры, Я, Q, /?, Т — несингулярные матрицы, Аф
Bdt Cdt Dd — диагональные матрицы, максимальные элементы которых
равны единице.
Матрица Р представляет собой матрицу собственных векторов произве-
произведения Ап ВпСп Dn% матрица Q построена аналогично из собственных век-
векторов произведения Вп Сп Dn An и т.д., причем все матрицы можно вы-
выбрать коммутирующими с 5. Другими словами, все матрицы Р, Q, /?, Т
имеют блок-диагональную структуру вида A3.1.13). Поэтому A3.1.12)
можно переписать в виде
<ai> - Trace SAdBdCdDd/TxMt AdBdCdDd. A3.1.17)
Для определенности предположим, что Аф Вф Сф Dd построены так, что
их максимальные элементы находятся в положениях A, 1);
{Ad)u = (Bd)ul = (Crf)ifi = (Drf)i,i = 1. A3.1.18)
Матрицы Р, С /?, T определены не однозначно, так как нормировка
собственных векторов произвольна. Следовательно, Р, Q, /?, Т можно ум-
умножить справа на диагональные матрицы. Это повлияет на матрицы Ad,
Bd, Сф Dd> но не на их произведение.
В некоторых случаях существует единственный естественный выбор
матриц Р, Q, R> Т. Например, для ферромагнетика, описываемого мо-
моделью Изинга с изотропным взаимодействием ближайших соседей, матри-
матрицы А, В, С, D равны друг другу и симметричны. В этом случае естествен-
естественно выбрать матрицы Р, Q, R, Т одинаковыми и ортонормированными.
Тогда Ad представляет собой матрицу собственных значений А, нормиро-
нормированную так, чтобы удовлетворить условию A3.1.18).
Если диагональные матрицы Аф Вф Сф Dd известны, то намагничен-
намагниченность легко вычислить по формуле A3.1.17). Основная цель настоящей гла-
главы состоит в том, чтобы показать, что для определенных моделей (особен-
(особенно для восьмивершинной) матрицы А& Вф Сф Dd довольно легко найти
при условии, что решетка бесконечно велика. В разд. 13.8 показано также,
что для диагональных и некоторых других матриц можно выписать само-
самосогласованные уравнения. Такие уравнения являются точными и бесконеч-
бесконечномерными. Но их можно свести к конечному набору приближенных урав-
уравнений, которые можно использовать для получения хороших численных
приближений для функции к и для разложения ее в ряд.

ГЛАВА 13
369
13.2. ПРЕДСТАВЛЕНИЕ В ВИДЕ
ПРОИЗВЕДЕНИЙ ОПЕРАТОРОВ
Рассмотрим матрицу Ui9 элемент (а, о') которой имеет вид
(-х) х
... д(от,&т).
A3.2.1)
Умножение на С/,- соответствует добавлению к решетке отдельной грани в
направлении с северо-востока на юго-запад, как это показано на рис. 13.3.
Матрицу Ut можно рассматривать как «трансфер-матрицу грани», или
«оператор грани». Она аналогична вершинному оператору (9.6.9); единст-
единственное отличие состоит в том, что здесь мы используем язык «спинов на
узлах», а не «стрелок на ребрах».
Два оператора Ui и Uj коммутируют, если модуль разности чисел / и j
больше единицы, т.е.
UiUj=UjUi,ecjiH |i-;|
A3.2.2)
Угловая трансфер-матрица А может быть записана в виде произведения
операторов граней, каждый из которых отвечает одной из Угт(т + 1)
граней, показанных на рис. 13.1,6. Чтобы учесть грани, лежащие вблизи
границы, определим С^как оператор Um, заданный выражением A3.2.1), в
котором спин от + j имеет фиксированное значение 5, т.е.
tfi) • • • <5(<7m-i, &m-x) w(om,s, &m,om-X). A3.2.3a)
Аналогично C/J{*+ x определим как оператор Um + v в котором a
m +
2. <r'm +
заменены на s, t, z, т.е.
oi)... 6(am ,oln)w(s,t,z, am).
A3.2.36)
Таким образом, (и%*+ х)аа, является диагональной матрицей.
Пусть s,/,,,,j,zh5',/',.,,,/- граничные спины, расположен-
Рис. 13.3. Графическое изображение влияния ум-
умножения слева на матрицу Uh определенную
выражением A3.2.1). Такое умножение соответствует
добавлению показанного на рисунке квадрата с подхо-
подходящей весовой функцией w и суммированию по всем
значениям спина а{. Мы использовали соглашение,
что спины, показанные светлыми кружками, фиксиро-
фиксированы, а по спинам, показанным темными кружками,
проводится суммирование.

370 УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
ные так, как показано на рис. 13.1,6. Тогда легко видеть, что
А = Щ5'ЧГ2Щ'2 прит=2, A
= Щ'Щи21Л'уЩЩу'2 при т = 3 ,
и вообще
где
mUm-lUm-l. • • U,. A3.2.6)
13.3. СООТНОШЕНИЕ ЗВЕЗДА — ТРЕУГОЛЬНИК
В разд. 9.6 с помощью «электрического» языка стрелок на ребрах пока-
показано, что в шестивершинной модели две трансфер-матрицы коммутируют
между собой, если выполняется соотношение звезда — треугольник (9.6.8).
Этот результат обобщен на восьмивершинную модель в разд. 10.4, а в
разд. 11.5 он сформулирован на «магнитном» языке изинговых спинов.
Последняя формулировка, конечно, могла быть введена сразу независи-
независимо от других. В действительности соотношение звезда — треугольник
можно записать (но не всегда решить) для любой ВСГ-модели. Пусть N
столбцов квадратной решетки натянуты на цилиндр так, что за TV-m
столбцом следует первый. Тогда элементы трансфер-матрицы V ряд — ряд
имеют вид
N
Уо,« = Д H°j
где oN + j = ov o'N + j = aj, о = {ov . . . , gn], о' = (aj, . . . , o'N] и ве-
весовые функции и»(я, b, c, d) произвольны.
Заменим в A3.3.1) функцию w на и»' и обозначим новую матрицу через
V . Тогда матричные элементы произведения VV имеют вид
A3.3.2)
где
s(a,a",a'\b,b\b')=w(a,b,b",a")w'(a",b",bt,a'). A3'3'3)
Функция s(a, a"', а'\Ь, Ъ", 6'), входящая в A3.3.2), представляет собой вес
двух примыкающих друг к другу квадратов, показанных на рис. 13.4.
При заданных значениях спинов av . . . , oN и aj, . . . , o'N правая часть
A3.3.2) равна произведению матриц. Обозначим через S(a, af \b, b') мат-
матрицу 2x2 (для спинов, принимающих два значения), элемент которой в
строке а" и в столбце Ь" равен s(а, а"', a'\b, b", bf). Тогда выражение

ГЛАВА 13
371
а о
Рис. 13.4. Соседние квадраты с весовыми функциями w и w'. Их
объединенный вес равен s(a, я", я' I Ь, Ъ", Ь') A3.3.3). а
A3.3.2) можно записать в виде
(V V')a& = Trace Sfa , о}|а2, &2) S(a2 , oj|a3, &ъ)
.. . S(aN,
A3.3.4)
Определим таким же способом матрицу S', но в выражении A3.3.3) по-
поменяем местами функции w и w'. Тогда VV задается формулой A3.3.4), в
которой S следует заменить на S' . Очевидно, матрицы V и V коммутиру-
коммутируют, если существует матрица М(я, а'), такая, что выполняется равенство
S(<z ,а'\Ь, Ъ') = Ща , a') S'(a ,а'\Ь,Ь') [ЩЬ , Ь')] ~\ A3.3.5)
поскольку матрицы М исключаются из A3.3.4).
Умножим A3.3.5) справа на МF, bf). Представим элемент (с, d) матри-
матрицы М(я, а') в виде w" (с, at d, а') и запишем подробно произведения мат-
матриц 2x2. При этом A3.3.5) принимает вид
2ф,Ь,с, я") w\a\c ,Ь',а') w\c ,b,b",b') =
= 2 w"(a" ,a,c,a') w'{a ,Ь ,b",c)w(c ,Ь",Ь',а')
A3.3.6)
для всех а, а', а", b, b'', Ь" .
На рис. 13.5 представлено графическое изображение уравнения A3.3.6).
Рис. 13.5. Графическое представление обобщенного соотношения звезда — треуголь-
треугольник A3.3.6): статистические суммы двух графов равны соответственно правой и ле-
левой частям соотношения.

372 УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
Определим операторы U\ и U", заменяя в определении A3.2.1) функцию w
на w' и w" соответственно. Тогда уравнение A3.3.6) эквивалентно опера-
операторному соотношению
Ui9 03.3.7)
где / = 2, . . . , т - 1. Очевидно, что равенство A3.3.7) представляет со-
собой обобщение для ВСГ-модели соотношений звезда — треугольник
F.4.27) для модели Изинга и (9.6.10) для шестивершинной модели.
При заданной функции w уравнение A3.3.6) в общем случае допускает
только тривиальное и не представляющее интереса решение относительно
w' и w" . Оно имеет вид
w' = w, w"(a,b ,c,d) = д(а,с), ПЗ.3.8)
что соответствует просто тому факту, что матрица V коммутирует сама с
собой.
МОДЕЛИ, ДОПУСКАЮЩИЕ РЕШЕНИЕ
Мы хотим найти классы коммутирующих трансфер-матриц и, следов-
тельно, функции w, такие, что уравнение A3.3.6) имеет бесконечно много
решений относительно w' и w". (Конечно, всегда можно умножить реше-
решение wf, w" на скаляр, поскольку такой множитель должен сократиться при
подстановке решений в A3.3.6); но такие решения нельзя рассматривать как
новые.)
Мы уже нашли одно семейство решений, а именно восьмивершинную
модель без внешнего поля. Действительно, A3.3.6) представляет собой
уравнение A,1.5.8), в котором ар . . . , а7 заменены на Ъ', а', а", а, Ь, Ъ",
с, функция W2 на w, 1Уг(а, Ь, с, d) на w" (с, d, а, Ь) и W\(а, Ь, с, d) на
w'(b, с, А а).
Определим параметры р, к, X, и так, чтобы выполнялись соотношения
w(a ,b ,a ,b) = psnh A,
w(a ,b , -a , -b) = pk snh A snh и snh(A - u),
A3.3.9)
w(a ,b,a, -b) = p snh(A - w),
w(a , b , -a , b) = p snh и
при а = ± 1, b = ± 1. Здесь snh w — эллиптическая функция, определенная
выражениями A0.4.20) и A5.1.6).
Определим теперь функции w' и w", заменив в A3.3.9) аргумент и на. и'
и и" соответственно. Из выражений A1.5.3.) и A1.1.10) видно, что эти ве-
величины w, м', и" соответствуют величинам м2, X - Wj, w3 в гл. 11. Из
A1.1.12) следует, что соотношение звезда — треугольник A3.3.6) удовлет-
удовлетворяется при условии
и' =
03-3.10)

ГЛАВА 13 373
Будем считать, что параметры р, к, X фиксированы, aw — комплексная
переменная. Тогда w(a, b, с, d) является функцией м, а также четырех спи-
спинов а, Ь, с, d. Запишем ее в виде w[u\a, b, с, d] или просто w[u]. Решение
уравнения A3.3.6) тогда имеет вид
w = w[u], w' = w[u + u"], w" = w[u"]. A3.3.11)
Записывая оператор Ui как функцию ?/Дм)> из A3.3.7) получаем эквивалент-
эквивалентное равенство
Ui+l(u) Щи + и") Ui+l(u") = Щи") Ui+1(u + и") U,(u), A3.3.12)
для всех комплексных чисел и им". Равенство A3.3.12) представляет собой
соотношение (9.7.14), выраженное с помощью спинов в узлах, а не стрелок
на ребрах решетки.
Поворот решетки на 90° эквивалентен замене а, Ь, с, d на Ь, с, d, а. Из
определения A3.3.9) видно, что указанная перестановка соответствует заме-
замене и на X — и. Таким образом,
и> [А — м] — весовая функция после поворота
решетки на 90°. A3.3.13)
Допустим, как в выражении A0.7.1а), что выполняются условия
р>0, 0<А:<1, 0<А</', A3.3.14)
где /' — полный эллиптический интеграл первого рода модуля
к' — A — к2)Уг. Тогда для всех значений спинов а, Ь, с, d из A3.3.9) сле-
следует
w[u\a,b,c,d] ^0 приО^м^А, A3.3.15)
Как видно из определения A3.1.3), больцмановские веса w при действитель-
действительных значениях энергии неотрицательны, поэтому «физические» значения и
лежат в интервале @, X) действительной оси.
В следующей главе будет показано, что аналогичными свойствами обла-
обладает ограниченная модель жестких квадратов. Хотя в указанной модели со-
соотношения A3.3.8) изменятся, но функцию w снова можно выразить через
комплексную переменную и (и некоторые «постоянные» к и X), так что
удовлетворяются уравнения типа A3.3.9) — A3.3.15). Поэтому представля-
представляет интерес изучение следствий, вытекающих из уравнений A3.3.10) —
A3.3.15).
Из соотношений звезда — треугольник A3.3.6) следует, что две
трансфер-матрицы ряд — ряд V и V коммутируют. Полученный резуль-
результат можно обобщить на модель с неоднородными столбцами решетки то-
того типа, который рассмотрен в разд. 10.17. Пусть больцмановские весовые
функции w различны для разных столбцов решетки, но при этом парамет-
параметры ? и X не зависят от номера столбца. Обозначим через ul9 . . . , uN соот-
соответствующие переменные, отвечающие столбцам у = 1, . . . , N, от кото-
которых зависит матрица V.

374
УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
Аналогично пусть и[у . . . , ufN — переменные для матрицы V . Тогда
вывод уравнений A3.3.1) — A3.3.6), связанный с коммутативностью мат-
матриц V и V, все еще применим, но при условии, что и" и, следовательно,
w" и М одинаковы для всех столбцов. Из A3.3.10) вытекает условие ком-
коммутативности
у у = V'V, если и- - Uj не зависят от у . A3.3.16)
Отсюда в свою очередь следует, что нормированные собственные векторы
матрицы V зависят только от разностей величин и{, . . . , uN.
Выражение для произведения
угловых трансфер-матриц
Рассмотрим теперь решетку, показанную на рис. 13.6, в которой весо-
весовая функция граней, расположенных справа от центральной линии, равна
w[w], а весовая функция граней, расположенных слева от нее, равна w[v] и
все грани решетки обладают одними и теми же значениями параметров к и
X.
Пусть о = ((jj, а2, • • • ) и °' — I ai» а2» • • • ) » где °'\ = °\- Тогда набо-
наборы а и а' вместе описывают все спины, принадлежащие нижнему ряду ре-
решетки. Введем определение
= 2 П
°j , °к
A3.3.17)
где произведение берется по всем М граням решетки и суммирование
проводится по всем спинам, расположенным в узлах, показанных на
рис. 13.6 темными кружками.
Мы рассмотрим два возможных граничных условия. Во-первых, приме-
применим граничные условия, показанные на рис. 13.1 и 13.2/ Тогда из определе-
определения матрицы А A3.1.7) и соответствующих определений матриц В, С оче-
очевидно, что
VW = [В(и) Civ)]* ,
A3.3.18)
°г
w[u]
Рис. 13.6. Решетка с весовой функцией w[w]
для граней, расположенных справа от
жирной линии, и весовой функцией w[v] для
граней, расположенных слева от этой
линии. Статистическая сумма решетки
равна фаа. A3.3.17).

ГЛАВА 13 375
где явно показана зависимость матрицы В от параметра и и зависимость
матрицы С от параметра v.
Во-вторых, допустим, что теперь используются цилиндрические гранич-
граничные условия, и фиксируем значения спинов, расположенных в верхнем ряду
решетки: . . . , s^y sf2, s^ s2, 5з» • • • • Пусть s = [s{, s2, • • • ) и s' =
= {sj, $2, . . .), причем s[ = s{.
Тогда имеем
VW = (V^aaV, A3.3.19)
где r — число рядов, V — введенная в настоящем разделе трансфер-
матрица ряд — ряд, а и а' вместе образуют индекс строки матрицы V в
выражении A3.3.19), а s и s' образуют индекс столбца этой матрицы.
В пределе больших г отсюда следует, что, если не учитывать нормиро-
нормировочный множитель, ф является максимальным собственным вектором мат-
матрицы V. Из замечания после формулы A3.3.16) следует, что собственный
вектор ф зависит только от разности и — v. Таким образом,
= ?'(" , v) [X'(u - v)]a& , A3.3.20)
где т'(и, v) — нормировочный множитель, не зависящий от а и а', а
[X' (и — v)]aa, зависит только от разности и — v. Для последующего срав-
сравнения с выражением A3.3.18) полезно рассматривать [X'(и - v)]aa, как
элемент (а, о') матрицы X'(и - v). Так как ох = о[, то можно считать,
что X' (и — v) имеет блок-диагональную структуру A3.1.13); отметим, что
матрица X'(и — v) не равна транспонированной матрице Х(и — v).
13.4. ПРЕДЕЛ БЕСКОНЕЧНОЙ РЕШЕТКИ
Чтобы продвинуться дальше, мы должны перейти к пределу, когда ре-
решетка становится бесконечно большой, а матрицы — бесконечномерными.
Нелегко математически строго рассмотреть этот предел, хотя соответству-
соответствующие методы развиты в работе [202]. Здесь я буду полагаться в основном
на физическую интуицию, приобретенную при рассмотрении низкотемпера-
низкотемпературных разложений, когда возбуждения лежат вблизи основного состояния
системы.
Параметр а, входящий в формулу A3.1.14), сам представляет собой ста-
статистическую сумму для решетки, изображенной на рис. 13.1,6, когда значе-
значения всех граничных спинов соответствуют основному состоянию. Посколь-
Поскольку имеется Vim(m -V 1) граней, на основании определения A3.1.4) можно
предполагать, что
К Л™. ' 03.4.1)
Если значения фиксированного числа граничных спинов а и а' отлича-
отличаются от значений, соответствующих основному состоянию, то мы ожида-
ожидаем, что появится лишь дополнительный множитель, который стремится к

376 УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
конечному ненулевому пределу при т — оо. Другими словами, существует
предел
lim (Aa&/Ass>), A3.4.2)
при условии, что имеется целое число г (не зависящее от т), такое, что
Oi = Si и &i = s- при i^r. A3.4.3)
Но A3.4.2) представляет собой просто элемент (а, о') матрицы Ап, опреде-
определенной* формулами A3.1.14) и A3.1.15). Таким образом, мы ожидаем, что
существует предел
lim {An)o& A3.4.4)
и что в этом смысле матрица Ап при т — оо стремится к предельной бе-
бесконечномерной матрице. На основании аналогичных рассуждений можно
ожидать, что матрицы Вп, Сп, Dn при т — оо также стремятся к своим
предельным значениям.
Расположим столбцы матриц Р, Q, R, Т так, чтобы диагональные эле-
элементы произведения Ad Bd Cd Dd в A3.1.16) находились в порядке убыва-
убывания их численных значений. Тогда матрицы Ad, Bd, Cd, Dd могут быть вы-
выбраны так, что элементы каждой из них также расположены в порядке
убывания их численных значений. Для широкого класса функций w(a, b, с,
d) и при достаточно низких температурах, по-видимому, можно считать,
что все величины а'', /3', у', 5', Р, Q, R, Т, Аф В# С& DdB A3.1.16) стре-
стремятся к соответствующим пределам при m — оо. Указанный предельный
переход следует понимать в том смысле, что матричные элементы вида
Poj и (Ad)jj стремятся к пределам при любом фиксированному и любом на-
наборе а, удовлетворяющем условию A3.4.3). (Область высоких температур
можно рассмотреть, используя граничные условия «свободных спинов», но
мы сосредоточимся на случае низких температур.)
В разд. 13.7 показано, что для восьмивершинной модели с ферромаг-
ферромагнитным упорядочением Cd = Ad, Bd = Dd,a. шесть наибольших диагональ-
диагональных элементов матрицы Ad (в пределе при m — оо) имеют вид
I,s,s2,s\s\s\ A3.4.5)
где s = (xz)l/2; x, z — параметры эллиптических функций, определенные
выражениями A0.4.23), A0.7.9) и A0.7.18). (Элементы матрицы Bd задают-
задаются путем замены z на г в определении величины s.) При низких темпера-
температурах величина s мала; она возрастает до единицы при увеличении темпе-
температуры до критического значения.
По-видимому, справедливо более общее утверждение. При достаточно
низких температурах для любой ВСГ-модели каждая угловая трансфер-
матрица имеет дискретный спектр собственных значений при m — оо. Это
означает, что для любого е > 0 имеется только конечное число собствен-
собственных значений, больших, чем е.

ГЛАВА 13 377
Совершенно другую структуру имеет спектр трансфер-матрицы V
ряд — ряд. Если решетка имеет N столбцов, то обычно за единственным
максимальным собственным значением следует зона из N близко располо-
расположенных собственных значений, затем другая зона из ViN{N — 1) собствен-
собственных значений и т. д. В пределе при N — оо спектр в указанных зонах стано-
становится непрерывным. Нормированная матрица собственных значений мат-
матрицы V не стремится «ни к какому пределу при N — оо.
13.5. СОБСТВЕННЫЕ ЗНАЧЕНИЯ УГЛОВЫХ
ТРАНСФЕР-МАТРИЦ
Вернемся теперь к разд. 13.3 и предположим, что весовая функция w та-
такова, что соотношение звезда — треугольник A3.3.6) допускает однопара-
метрический класс решений w', w". Члены этого класса имеют вид w[w],
где и — произвольное комплексное число, и справедливы"соотношения
A3.3.9) —A3.3.12).
Тогда справедливы также выражения A3.3.18) и A3.3.20). Для конечной
решетки эти выражения для фаа, различны, поскольку в них использова-
использовались разные граничные условия. Однако мы ожидаем, что в пределе беско-
бесконечной решетки влияние граничных условий можно не учитывать. Исклю-
Исключая фаа,, используя выражение A3.1.15) и собирая множители а и C в t'(w,
v)s получаем
Вп(и) Cn(v) = т\и , и) Х\и - и), A3.5.1)
где Вп(и) и Cn(v) — нормированные угловые трансфер-матрицы бесконеч-
бесконечной решетки.
Три уравнения, аналогичные A3.5.1), можно получить с помощью по-
последовательных поворотов решетки на 90°. В частности, поворот на 90° по
часовой стрелке дает
Лп(и) Bn(v) = т(м , и) Х(и - и), A3.5.2)
где т(и, v) — некоторый скалярный множитель, а матрица Х(и — v) зави-
зависит только от разности и — v. Я буду теперь рассматривать уравнение
A3.5.2) как исходное, а уравнение A3.5.1) — как один из его аналогов, по-
получаемых с помощью поворотов.
С данным уравнением связаны определенные проблемы, возникающие
из-за бесконечномерности входящих в него матриц. Сумма по всем элемен-
элементам, содержащаяся в произведении двух матриц в левой части уравнения,
вероятно, не сходится, давая расходящийся множитель. Но этот множи-
множитель оказывается общим для всех элементов произведения An(u)Bn(v); по-
поэтому его можно включить в t(w, у), и он не играет роли в последующем
анализе. Я предполагаю, что справедливо следующее утверждение. Если s
и s" — значения спинов а и а" в основном состоянии на рис. 13.2, если су-
существует целое число г (не зависящее от aw), такое, что справедливо усло-
условие
Oj = Sj и dj = S-' при j^r A3.5.3a)

378 УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
и если Лп(и) и Bn(v) снова определены для конечных т, то предел
Km {[А„(и) Bn(v)]O(f/[An(u) Bn(v)]sJ A3.5.36)
m—»»
существует и зависит от и и v только через их разность и — v.
Итак, я предполагаю, что имеются представления, в которых существу-
существуют подходящим образом нормированные бесконечномерные матрицы
Ап(и), Bn(v) вместе с их произведением An(u)Bn(v). Поэтому ниже я буду
рассматривать A3.5.2) как обычное матричное уравнение. Я предполагаю
также, что матрицы Ап(и) и Bn(v) не обладают одинаковыми особенностя-
особенностями при всех и и v и имеют полные наборы собственных векторов. Все эти
рассуждения, очевидно, весьма не строги. Тем не менее предположения, по-
видимому, оправдываются, и результаты оказываются точными.
Симметричный случай
В уравнении A3.5.2) содержится обширная информация. Это уравнение
легче всего исследовать в случае, когда нет спонтанного нарушения транс-
трансляционной инвариантности решетки и когда справедливы равенства
w(a , Ъ , с , d) = w(c , b , а , d) =w(a,d,c,b). A3.5.4)
В таком случае (который включает восьмивершинную модель с ферро-
ферромагнитным упорядочением) все граничные спины s, /, . . . , z на рис. 13.1
одинаковы, матрицы А и В симметричны и С = A, D = В. Кроме того,
поскольку матрица В получается из А с помощью поворота решетки на
90°, из A3.3.13) следует, что при всех значениях v имеем
BH(v)=AH(k-v). A3.5.5)
Замена v на X — v в уравнении A3.5.1) дает
An(u) An(v) = т(и , Я - v) X(u + v - Я). A3.5.6)
Переставляя и и v и исключая X, получаем
т(р , Я - и) Ап(и) An(v) = т(и , Я - у)Л„(у)Л^и). A3.5.7)
Рассматривая представление, в котором матрица Ап(и) диагональна, мож-
можно показать, что из A3.5.7) следует
т(и , Я - и) = т(и , Я - v), A3.5.8)
м). A3.5.9)
Из выражений A3.5.9) и A3.5.6) вытекает, что матрицы Ап(и), An(v),
Х(и + v — X) коммутируют и, следовательно, имеют общие собственные
векторы, не зависящие от и и v. Пусть р{, р2, ру . . . — собственные век-
векторы матрицы Ап(и) для некоторого физического значения м, скажем для
и = Х/2, которые пронумерованы так, что соответствующие собственные
значения ах(и), а2(и), . . . расположены в убывающем порядке. Пусть

ГЛАВА 13 379
х{(и), х2(и), ... — соответствующие собственные значения матрицы Х(и).
Введем определения
Ad(u) = P-lAn(u) Р1ах{и),
A3.5.10)
Xd{u) = р-'Х(и) Р/Х1(и).
Матрицы Ad(u) и Xd{u) диагональны, и верхние левые элементы в них рав-
равны единице. Приводя A3.5.6) к диагональному виду путем умножения слева
на Р~1 и справа на Р, для элементов A,1) получаем
r(w,A- v) = a1{u)al(v)/x1(u + v - Я), A3.5.11)
и уравнение A3.5.6) принимает вид
Ad(u) Ad(v) = X^u + v - Я). A3.5.12)
Каждый диагональный элемент матричного уравнения A3.5.12) пред-
представляет собой скалярное уравнение одного и того же вида, которое дол-
должно выполняться для всех действительных чисел w, v в интервале @, X).
Взяв логарифмическую производную, легко убедиться в том, что общее ре-
решение имеет вид
[Ad(u)]r,r = mrexp(-aru), A3.5.13)
где г = 1, 2, 3, . . . , а тп аг — постоянные, не зависящие от и.
Для каждой конкретной модели величины тг аг можно определить из
рассмотрения условий периодичности и частных случаев. Это будет проде-
проделано в следующем разделе для восьмивершинной модели с ферромагнит-
ферромагнитным упорядочением.
Из выражения A3.5.5) и равенств С = A, D = В очевидно, что все мат-
матрицы Ап(и), Вп(и), Сп(и)9 Dn(u) коммутируют друг с другом. Поэтому
можно считать, что все матрицы Р, Q, R, Т в формуле A3.1.13) одинаковы
и равны Р. Следовательно,
Cd(u)=Ad(u), Dd{u)=Bd(u)=Ad{k-u). A3.5.14)
Пусть Sr — собственное значение матрицы S, соответствующее собствен-
собственному вектору рг. Подставляя выражения A3.5.13) и A3.5.14) в A3.1.17), по-
получаем
00 00
<cti> = 2 Srmf ехрBаД)/Х т\ expBd>A). A3.5.15)
НЕСИММЕТРИЧНЫЙ СЛУЧАЙ
Даже если условия симметрии A3.5.4) и A3.5.5) не выполняются, из
уравнения A3.5.2) (и его аналогов, полученных с помощью поворотов) все
же можно получить точные формулы для матриц Ad, Bd, Cd, Dd. Для это-
этого требуются лишь несколько более длительные вычисления.
В выражении A3.5.2) заменим сначала величины и и v на X - v, X - w,

380 УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
а затем исключим матрицу Х(и - v). При этом получим
г(А- v ,к~и)Ап(и)Вп(и) = t(u,v)An(k-v)Bn(h-u). A3.5.16)
Пусть величина и равна некоторому фиксированному значению и0; пред-
предположим также, что матрица Ап(и^) обратима. Тогда уравнение A3.5.16)
можно разрешить относительно Bn(v). Подставив результат в A3.5.1) и
умножив справа на B~l(K — u^A~l(u^t получим
d(u) s?(A - v) = ф(и , v) Y{u - v), A3.5.17)
где
d{u) =An(u)A-\u0),
Y{u) = X(u) ЯДА - wo) An\u0), A3.5.18)
ф(и ,v) = т(и ,v) т{\- v ,X- wo)/t(wo , v).
Полученное уравнение A3.5.17) в точности совпадает с уравнением
A3.5.6), в котором величина v заменена на X - у. Оно может быть решено
теми же методами. Решение имеет вид
sl(u) = ах(и) РА^и) P~l, A3.5.19)
где Р не зависит от«,а матрица Ad(u) диагональна. Столбцы матрицы Р
расположены так, что для физических значений переменной и (или во вся-
всяком случае для некоторого физического значения) численные значения диа-
диагональных элементов матрицы Ad(u) убывают с ростом номера строки.
Верхний левый элемент матрицы Ad(u) равен единице. Элемент (л, г) запи-
записывается в виде
]гг = тгехр(од<), A3.5.20)
где тг otr не зависят от м.
Из выражения A3.5.19) и первого из трех выражений A3.5.18) следует
An(u)=ax{u)PAlu)Q'\ A3.5.21)
где Q, так же как и Р, не зависит от и (в действительности Q =
= А~{(и^Р). Подставим выражение A3.5.21) для матрицы Ап(и) в
A3.5.16). Решаем уравнение A3.5.16) относительно Bn(v), полагая и = и0
заменяя переменную v на и и используя коммутативность матриц
Ad(\ - и) и Ah(uq}\ получаем
Вп(и) = Ьг(и) Q All -u)R-\ A3.5.22)
где b{(u) скалярный множитель и матрица R не зависит от и.
Рассмотрим теперь первый аналог уравнения A3.5.2), получаемый пово-
поворотом на 90°, а именно уравнение A3.5.1). Подстановка выражения
A3.5.22) или Вп(и) в A3.5.1) в точности аналогична подстановке A3.5.^21)
для Ап(и) в A3.5.2) и A3.5.16) и приводит к следующему результату:

ГЛАВА 13381
Cn{u) = ci(u) RAAu) Г'1, A3.5.23)
где Cj(w) — скаляр, а Г не зависит от и.
Подобным образом, используя аналог уравнения A3.5.2) для произведе-
произведения матриц Cn(u)Dn(v), получаем
Dn(u) = dx(u) TA^k - и) W, A3.5.24)
где d{(u) — скаляр, a W не зависит от и.
Подстановка выражений A3.5.24), A3.5.21) для Dn(u), An(v) в аналог
уравнения A3.5.2), содержащий произведение Dn(u)An(v), дает
Ad(k - и) W~XPАЛр) = т"(и , v) Х"(и - v), A3.5.25)
где т"(и, v) — скалярный множитель. Поскольку матрица Ad(u) диаго-
нальна и ее элемент A,1) равен единице, из уравнения A3.5.25), записанного
для элемента A,1), следует, что множитель r"(w, v) можно выбрать рав-
равным единице. Отсюда видно, что элемент (г, s) матрицы WlP обладает
следующим свойством:
(W^P)rs = 0 при аг ф ос, . A3.5.26)
Таким образом, матрица W~lP блок-диагональная и не зависит от и.
Умножая введенные выше матрицы Pt Q, R, T, W справа на постоян-
постоянные матрицы, имеющие ту же блок-диагональную структуру, мы можем
привести W~lP к единичной матрице, а выражения A3.5.21) — A3.5.14) к
виду
>ln(w)=a1(u)PAd(u)Q-1, Blu)=biu)QBd{k-u)R~\
A3.5.27)
u)P~\
где все матрицы Ad(u)\ Bd(u), Cd(u), Dd{u) диагональны и их элементы
определены выражением A3.5.20). Для каждого целого числа г величина аг
имеет одно и то же значение для всех четырех матриц, но величины mr мо-
могут различаться. В любом случае при г = 1 имеем а{ = 0, тх = 1.
Так же как в симметричном случае величины аг и тг могут быть полу-
получены из условий периодичности и рассмотрения частных случаев. Такое
рассмотрение проведено в следующей главе для ограниченной модели жест-
жестких квадратов.
Подставляя A3.5.27), A3.5.20) в A3.1.17), мы снова получим формулу
A3.5.15) для намагниченности, но теперь тАг следует заменить произведени-
произведением величин тг относящихся к матрицам Ап, Вп, Сп и Dn.
13.6. СВОЙСТВА ОБРАТИМОСТИ: ВЫРАЖЕНИЕ ДЛЯ
ФУНКЦИИ к(и)
Если и = 0, то из A3.3.9) следует
w(a , Ь , с , d) = р snh Я д{а, с). A3-6Л)

382 УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
Предположим, что граничные условия таковы, что s = /=... = z и
s' = /' = . . . = у'. Тогда из A3.2.1) получаем
Ui = psnhk$, A3.6.2)
где У— тождественная матрица и / = 1, . . . , т - 1. Далее из A3.2.3)
следует, что A3.6.2) выполняется также для граничных матриц IP^
U%z+l, которые входят в соотношения A3.2.4) — A3.2.6). Отсюда следу-
следует
А@) = (psnhA)*m(m + 1)^ , A3.6.3а)
и, таким образом, из A3.1.14) и A3.1.15) получаем
Лп@) = 3> . A3.6.36)
Положив и = О в первом из уравнений A3.5.27), находим
Q = al@)PA(?0), 03.6.4)
поэтому
Лп(и) =[а1(М)/а1@)]РЛ^)Л,@)р-1. A3.6.5)
Из выражения A3.5.13) следует, что матрица Ad(u)Adl@) диагональна и
имеет элементы
[Ad(u)AtXWr = ехр(-а,л), A3.6.6)
где осг не зависят от и.
Пусть J^d — диагональная матрица с элементами «j, а2» аз» • • • • Опре-
Определим матрицу ^следующим образом:
~1. A3.6.7)
Тогда из выражений A3.6.5) и A3.1.15) следует
А(и) = т(м) ехр(-мЗе), A3.6.8)
где т(и) имеет вид
т{и) = аа1(и)/а1@). A3.6.9)
Величина а в выражении A3.6.9) может зависеть от и. Следует ожидать,
что при m — оо матрица Жъ функция ах{и) будут стремиться к соответст-
соответствующим пределам. Поэтому из выражения A3.4.1) получаем, что статисти-
статистическая сумма на один узел решетки имеет вид
к(и) = lim [riu)]2lm^ +'К A3.6.10)
Приведенные выше уравнения были получены при физических значениях
w, принадлежащих интервалу (О, X) действительной оси. Мы ожидаем, что
при таких значениях и существуют различные пределы при m — оо. В част-
частности, можно надеяться, что если диагональные элементы матрицы
Ad(u)Adl@) расположены в порядке убывания их численных значений и
наибольший из них равен единице, то любой данный элемент будет стре-

ГЛАВА 13 383
миться к некоторому пределу при т — оо. Это означает, что cxj, a2,
«з» • • • — неотрицательные числа, a Jff— неотрицательно определенная
матрица.
По-видимому, данные уравнения можно продолжить в область малых
отрицательных значений переменной и. Получающиеся при этом значения
к(и) совпадают, вероятно, со значениями аналитического продолжении к(и)
из области положительных м. (Для отрицательных и функция к(и) не опре-
определяется формулой A3.1.4), поскольку порядок собственных значений мат-
матрицы ехр(— uJ?f) обращается. В этом случае необходимо нормировать на
единицу наименьшее собственное значение, а не наибольшее.)
Допустим, что выражение A3.6.8) справедливо для достаточно малых
значений м, как положительных, так и отрицательных. Тогда, очевидно,
А(и)Л(-и) = т(и) т(-м) <?> . A3.6.11)
Последний результат можно получить непосредственно. Из выражений
A3.3.9) легко установить, что равенство
2 w(n\а , Ь , а', d) и>(-и \а', Ь , с , d) =g(u) д(а , а') A3.6.12)
а'
справедливо при всех знчениях спинов а, Ь, с, d и всех комплексных числах
и. В выражении A3.6.12) введено обозначение
g(u) = p(M)p(-M)(snh2A- snh2M), A3.6.13)
и для общности принимается, что нормировочный множитель р, введен-
введенный в A3.3.9), является некоторой заданной функцией и (однако к и X по-
прежнему считаются постоянными).
Из выражений A3.6.12) и A3.2.1) следует
Uiu)U{-u)=g(u)9. A3.6.14)
Равенство A3.6.14) справедливо при / = 2, . . . , m - 1, а также для мат-
матрицы Usm, при условии что величина s фиксирована. Оно не справедливо
для матрицы и%\ р определенной формулой A3.2.36). Но диагональную
матрицу и%\ j, без нарушения граничных условий можно заменить мат-
матрицей, для которой равенство A3.6.14) выполняется. Поскольку мы пред-
предположили, что s = t = . . . = z и s' = t' = . . . = у\ из выражений
A3.2.4) — A3.2.6) следует соотношение
A(u)A(-u) = [g(u)]^m + V$, A3.6.15)
которое имеет ту же форму, что и прежний результат A3.6.11). Сравнивая
их, получаем
т(и) т(-и) = [g(u)Ym(m + l\ A3.6.16)
Используя A3.6.10) и A3.6.13) и взяв корень степени х/гт(т 4- 1) из уравне-
уравнения'A3.6.16), находим
к{и) к(-и) = р(и) р(-и) [snh2A - snh2 и]. A3.6.17а)

384 УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
Аналогичное уравнение можно получить с помощью поворота решетки
на 90°. Из формулы A3.3.13) известно, что такой поворот эквивалентен за-
замене функций к(и), р(и) на к(\ - и) и р(Х - и) соответственно. Проделав
указанную замену в A3.6.17а), получаем
к(и) кBк -и) = р(и) рBА - и) [snh2A - snh2(A - и)]. A3.6.176)
Положим
р = р(м) = p'tfQifk) 0(ш) 0(*А - ш) , A3.6.18)
где р' — постоянная. Такое определение обеспечивает параметризацию
больцмановских весов A3.3.9) того же вида, что и в A0.4.24) (с заменой р
на р'); кроме того, при этом веса являются целыми функциями и. Исполь-
Используя формулы A5.4.19) и A3.6.17), получаем соотношения
к(и) к(-и) = p'2h{k - и) h(k + и), A3.6.19а)
к(и) кBк - и) = p'2h{u) hBk - и), A3.6.196)
где функция h(u) определяется формулой A0.5.16), т.е.
й(и) = -i 0@) H(iu) 0(ш). A3.6.20)
В действительности мы уже сталкивались со вторым из соотношений
A3.6.19). Как видно из A3.1.5), A0.8.46) и A0.4.23), функция Х(у), введенная
в гл. 10, связана с к (и) соотношением
у)]У\ A3.6.21)
где N — число столбцов в решетке в гл. 10. В уравнении A3.6.196) заменим
и на !/г(Х + v) и возведем его в N-ю степень; тогда уравнение примет вид
Л(у) ЛBА - v) = ф(к + v) 0(ЗА - v), A3.6.22)
где функция ф(у) определена в A0.5.24). Но это уравнение в точности со-
совпадает с A0.8.43).
Следовательно, соотношения A3.6.19), несомненно, справедливы для
восьмивершинной модели, что увеличивает доверие к тем допущениям, ко-
которые были использованы при их выводе. Аналогичные соотношения были
использованы Строгановым [218] для двух частных случаев «81-
вершинной» модели; другие соотношения используются в следующей главе
для модифицированной модели жестких квадратов.
В более общем случае для любойВСГ-модели мы всегда можем опреде-
определить «обратную» весовую функцию w, такую, что для всех спинов а, Ь, с, d
выполняется равенство
w{a , Ь ,/, d) w(f, b , с, d) = E(я , с). A3.6.23)
Определим матрицу Ui с помощью выражения A3.2.1), в котором w заме-
заменено на vv. Тогда из A3.6.23) следует
j $ , A3.6.24)

ГЛАВА 13 385
где / = 2, . . . , т. Запишем к как функцию k[w] от и\ Определим k[w] как
аналитическое продолжение функции k[w] от w к w. Тогда можно, исполь-
используя аргументы, аналогичные приведенным выше, установить, что функция
k[w] является обратной по отношению
фу] Kpv] = 1. A3.6.25)
(Простейший путь, по-видимому, состоит в том, чтобы рассмотреть тран-
трансфер-матрицу диагональ — диагональ (UlU3U5. . -UN_l)(U2U4U6. . .UN).
Затем можно определить к как корень N-й степени из того собственного
значения матрицы, для которого собственный вектор не имеет отрицатель-
отрицательных элементов. После этого обращение каждой матрицы Ui приведет к об-
обращению всех собственных значений и, следовательно, функция к перейдет
в обратную.)
Уравнение A3.6.25) является обобщением уравнения A3.6.17а). Обобще-
Обобщение уравнения A3.6.176) получается с помощью поворота решетки на 90°,
т.е. при использовании в определении функции w направления с северо-
запада на юго-восток вместо направления с северо-востока на юго-запад.
В следующем разделе для восьмивершинной модели будет показано,
что уравнения A3.6.17) и некоторые простые свойства аналитичности и пе-
периодичности определяют функцию к(и) и тем самым свободную энергию.
Очень интересно проверить, справедливо ли уравнение A3.6.25) для любой
ВСГ-модели, например для модели Изинга в магнитном поле. К сожале-
сожалению, для таких моделей к(и), по-видимому, является существенно более
сложной функцией, и, хотя уравнение A3.6.25) остается справедливым, его
уже недостаточно для определения к (и).
13.7. ВОСЬМИВЕРШИННАЯ МОДЕЛЬ
Свободная энергия
Воспользуемся определением функции p(w) (I3.6.Г8), в котором р' будем
считать постоянным множителем. Тогда параметризация больцмановских
весов A3.3.9) оказывается той же, что и в выражениях A0.4.24), в которых
нужно только р заменить на р'. Если справедливы выражения A3.3.14) и
A3.3.15), то система находится в упорядоченной ферромагнитной фазе. По-
Поэтому можно воспользоваться результатами разд. 10.8 для получения вы-
выражения для свободной энергии, и, следовательно, функции к(и). Из фор-
формул A3.6.15) и A0.8.44) получаем
где q, х, z определены выражениями A0.4.23), A0.7.9) и A0.7.18), т.е.
я/77), х = ехр(-яЛУ27), z = х~1ехр(-ли/1). A3.7.2)
Поскольку параметры р', к,\ постоянны, постоянны также и величины
q, х. Параметр z изменяется при изменении и. Из выражения A3.7.1) вид-

386 УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
но, что
In к(и) — аналитическая функция в области, содержащей вертикальную
полосу О ^ Re(w) ^ к, периодическая с периодом 2U. A3.7.3)
Указанные свойства аналитичности и периодичности вместе с соотношени-
соотношениями A3.6.17) действительно определяют функцию к(и).
Чтобы увидеть это, заметим, что из выражения A3.7.3) следует анали-
аналитичность \пк(и) как функции z в кольце х ^ z < x~l. Следовательно, раз-
разложение Лорана функции \пк(и) существует и сходится в области, содержа-
содержащейся в кольце, т.е. существуют коэффициенты сп, не зависящие от z и м,
такие, что
00
\пк(и)= 2 cnzn, x^z^x1. A3.7.4)
Кроме того, из выражения A0.8.6) получаем
In ft(ii) = In у + ли/21 - 2 xnzn/n(l - qn), A3.7.5)
где суммирование проводится по всем не равным нулю целым числам я, а
значения и лежат в полосе 0 < Re(w)< /'.
Уравнения A3.6.17) эквивалентны уравнениям A3.6.19). Возьмем лога-
логарифм от обеих частей уравнения A3.6.19а). В комплексной плоскости и су-
существует полоса, содержащая мнимую ось, внутри которой все функции
можно разложить в ряды с помощью выражений A3.7.4) и A3.7.5). При
этом получаем
2(с„ + х^с-п) zn = 2 In(p'y/Jt) - 2 (х3п + qnx~n) znln{\ - qn). A3.7.6a)
n ^0
В обеих суммах п изменяется от -оо до оо, ново второй сумме исключено
слагаемое с п = 0. Аналогично из выражения A3.6.196) получаем
2(с„ + х^с-п) zn=2 In(p'y/Jt) - 2 (хп + qnx~3n)zn/n(l - qn), A3.7.66)
л*0
для вертикальной полосы, содержащей прямую Re(w) = X. Сравнивая ко-
коэффициенты при одинаковых степенях zn в уравнениях A3.7.6а) и A3.7.66),
получим уравнения для Сп, которые можно решить. Решение имеет вид
с0 = ln(p'y/jt) >
УН Г } A3.7.7)
сп = с.п = ~(х3п + qnx~n)/[n(l + х2п) A - qn)] при п ? 0 .
Подстановка выражений A3.7.7) в A3.7.4) дает результат A3.7.1), получен-
полученный в гл. 10.
О свойствах аналитичности и периодичности можно было догадаться
при изучении низкотемпературных разложений, а затем получить выраже-
выражение для к(и) с помощью приведенных выше соображений. Если принять на-
начальные допущения, изложенный метод, несомненно, является простейшим

ГЛАВА 13 387
из известных путей получения функции к(и) и, следовательно, вычисления
свободной энергии в восьммивершинной модели.
Намагниченность
Конфигурация спинов в основном состоянии упорядоченной ферромаг-
ферромагнитной фазы может быть выбрана так, что все спины имеют значение 4-1.
Поскольку функция w(a, by с, d) симметрична по отношению к перестанов-
перестановкам а с с и b с d, угловые трансфер-матрицы А, В, С, D симметричны и
С = A, D = В. Такой случай рассмотрен выше (см. A3.5.4) — A3.5.15)).
Из выражений A3.5.10) и A3.5.5) следует
An(u) = Cn(u)=p-1Ad(u)P/a{u),
Вп(и) = Dn(u) = P~lAd{X - и) Plaik - и). '?* }
Диагональная матрица Ad(u) имеет элементы, определенные выражени-
выражением A3.5.13), в котором тх = 1, осх = 0. Но из A3.6.36) следует, что
тг = 1 для всех г; поэтому диагональные элементы матрицы Ad(u) имеют
вид
[Ad{u)]r,r = exp(-arw). A3.7.9)
Здесь «j, a2» • • • — не зависящие от и постоянные.
Больцмановские веса A3.3.9) являются периодическими функциями и с
периодом 4/7. По-видимому, рассуждения, проведенные в разд. 13.5, мож-
можно распространить на все комплексные числа м, лежащие в вертикальной
полосе 0 < Re(w)< X (в низкотемпературные разложения величина и вхо-
входит только через целые или полуцелые степени параметра z. определенно-
определенного в A3.7.2)). Отсюда следует, что матрица Ad(u) также периодична с пе-
периодом 4/7. Таким образом, из формулы A3.7.9) получаем
[Ad{u)]rj = ехр(-лп^/27), A3.7.10)
где /ij, /i2, . . . — целые числа.
Указанные целые числа можно найти, рассмотрев случай, когда к — 0
при фиксированных значениях \/Г и и. При этом первый и третий веса
A3.3.9) остаются одного порядка, а остальные два становятся пренебрежи-
пренебрежимо малыми по сравнению с первыми. Из A5.1.6) и A3.7.2) находим
w(a,b ,a,b)-
W(«,ft,-«,-*)-><>, A37П)
w(a,b , а , -b) -> \рх ~l exp( - mill),
w(a,b, -a ,b)->0.
Из A3.2.1) и A3.2.3) следует, что матрицы U( диагональны. Их элемен-
элементы имеют вид
~l ехр[-лиA - Oi-xOi;. i)/4/], A3.7.12)

388 УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
где / = 2, . . . , т 4- 1, а спины ат + v am + 2 равны значению 4-1, отвеча-
отвечающему основному состоянию. Из выражений A3.2.4) — A3.2.6) следует,
что матрица А также диагональна, так что Ad(u) получается с помощью
нормировки на единицу максимального диагонального элемента матрицы
А. При этом получаем
m + l
[Ad(u)]a,a = ехр[-лм g (i - 1) A - ff,-iffi+i)/4/]. A3-7ЛЗ>
Сравнивая полученный результат с общей формулой A3.7.10) и заменяя
отдельный индекс г мультипликативным индексом а = [ av а2, . . . , ат},
находим
m + l
*e = i2(i-l)(l-c*-iffi+i). <13-7Л4)
Отсюда следует, что выражение A3.7.13) справедливо для упорядочен-
упорядоченной ферромагнитной фазы в пределе больших т. Если мы рассмотрим г-й
наибольший диагональный элемент матрицы Ad(u) (при положительных и)
и устремим т к бесконечности, считая г фиксированным, то такой элемент
будет стремиться к пределу, который определяется выражением A3.7.13).
Если набор спинов а соответствует r-му наибольшему элементу, то должно
существовать целое число у, не зависящее от аи, такое, что
Oi=+l при i>j. A3.7.15)
Удобно ввести новый набор спинов jiv . . . , \лт с помощью соотноше-
соотношения
№= аА-+2, i-l,...,m. A3.7.16)
Здесь так же, как и выше, ат + х = ат + 2 = 4-1. Тогда Ad(u) является
диагональной матрицей, строки и столбцы которой обозначаются индек-
индексом \л = [ /ij, . . . , fim J, а диагональные элементы равны
ПЗ.7.17)
Кроме того, поскольку ах = fi^^s • • • » матРица S в A3.1.13) диагональна
и имеет элементы
^ = (iijU3jU5. ... A3.7.18)
Матрицы Ad(u) и S являются теперь прямым произведением матриц
2x2. Введем величины
s = (хгУ = ехр(-лм/2/),
t = {xlz)h = ехр(-я(Я - и)/21]. A3.7.19)
Тогда, используя A3.7.8) и A3.1.16), получаем

ГЛАВА 13389
,13.7.20,
*-(' VC VC V-
\0 -1/ \0 1/ \0 -1/
Выписанные выражения справедливы только в пределе т — оо, когда
имеется бесконечное число членов в каждом из прямых произведений.
Впервые я ввел их в 1976 г. [31], но не мог их тогда доказать.
Подстановка выражений A3.7.20) в A3.1.17) дает следующую формулу
для <ах):
= П A
1
- **-2)/(i + х4"-2), <13-7-21)
которая в точности совпадает с выражением A0.10.9) для спонтанной на-
намагниченности в восьмивершинной модели. Следовательно, мы доказали
результат, первоначально предсказанный в работе [13].
Проведенные рассуждения не легко обобщить для вычисления спонтан-
спонтанной поляризации; формула A0.10.24) пока остается не доказанной.
13.8. УРАВНЕНИЯ ДЛЯ УГЛОВЫХ
ТРАНСФЕР-МАТРИЦ
В этом разделе я вернусь к общей ВСГ-модели, описанной в разд. 13.1 и
13.2, и покажу, что существуют уравнения, которые связывают функцию
к (и) с угловыми трансфер-матрицами и в принципе определяют их. До сих
пор такие уравнения не использовались для точно решаемых моделей, но
они весьма успешно применялись для получения разложений в ряд [38, 47] и
для нахождения хороших численных аппроксимаций [17, 41, 146, 234].
Введем
Л* = 9^9Г'° • • • ТО,, Л** = 9Г'° • • • 9%'ti • A3.8.1)
Тогда из выражений A3.2.5) и A3.2.6) следует
А = 9?''А* , Л* = 9$иА** , 9?'' = 9$'* U2. A3.8.2)
Предположим для простоты, что основное состояние является трансля-
ционно-инвариантным, так что s, t, и, . . . и$', /', и', . . . , равны между
собой. (Данное предположение не является существенным, но для систем с
нарушенной трансляционной инвариантностью необходимо следить за гра-
граничными условиями, соответствующими разным угловым трансфер-
матрицам, что усложняет обозначения.) Исключая J*2 и ^ъ из уравнений

390 УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
A3.8.2), получаем
А = А* (А**)~1 U2A* . 03.8.3)
Матрицы А* и А** являются угловыми трансфер-матрицами для систе-
системы, в которой спины сдвинуты и т уменьшено. При этом справедливы со-
соотношения
(А*)О1...от\о1...от = <5(cti ,a[)AO2i^m\O2Omy A3.8.4a)
(А**)О1...от\о1...от = d(oi,o[)d((J2,O2)AO3^Om\O3^Omt A3.8.46)
Матрица А, входящая в правые части выражений A3.8.4а) и A3.8.46),
определяется формулой A3.1.8), в которой т заменяется на т — 1 и т — 2
соответственно.
Решеточный квадрант, показанный на рис. 13.1,6, будем называть ква-
квадрантом т х т. Тогда A3.8.3) определяет матрицу Л для любого квадран-
квадранта т х т через матрицы для квадрантов (т - \)х(т - 1) и
(т — 2)х(т — 2). Следовательно, A3.8.3) является рекуррентным соотно-
соотношением.
Существуют, конечно, аналогичные рекуррентные соотношения для
матриц В, Си/), получаемые из A3.8.3) с помощью последовательных по-
поворотов решетки на 90°.
Рекуррентные соотношения для матриц А# В# С^ Dd
Существует по крайней мере две причины, по которым для нас пред-
представляет интерес вычисление диагональных матриц А# В# CdyDd. Во-
первых, для моделей, которые могут быть решены точно, диагональные
матрицы имеют весьма простую структуру, например A3.7.20). Во-вторых,
для других моделей были проведены лишь приближенные вычисления, при
которых необходимо переходить от бесконечномерных угловых трансфер-
матриц к матрицам, имеющим подходящую конечную размерность. Как
будет показано ниже, такой переход лучше всего выполнить, работая с
диагональными матрицами.
Вместо того чтобы вычислять исходные угловые трансфер-матрицы А,
В, С, D из уравнения A3.8.3) и его аналогов, а затем с помощью A3.1.15) и
A3.1.16) находить диагональные матрицы Ad, Bd, Cd, Dd, можно сразу
подставить A3.1.15) и A3.1.16) в A3.8.3).
Введем сначала некоторые обозначения. Для любой 2т ~ l x 2m ~ 1-
матрицы X с элементами Х- определим 2т х 2т-матрицу X* с элементами
X*Maij=d(a1,o'1)Xii. A3.8.5а)
Здесь строки матрицы X* обозначены двойным индексом (аь /), а
столбцы — индексом-(aj, У). Используя очевидные обозначения, можно на-
написать
X*=ei®X=( ), A3.8.56)
где ех — единичная 2 х 2-матрица. ^ ^'

ГЛАВА 13
391
Аналогично для всякой 2т 2 х 2т 2-матрицы X определим
2т х 2т-матрицу X** с элементами
A3.8.6а)
или в других обозначениях
A3.8.66)
Приведенные определения согласуются с выражениями A3.8.4) дляЛ* и
Л** и являются их очевидными обобщениями.
Пусть матрицы Р, Q, Ad соответствуют решеточному квадранту
(т — \)х(т — 1). Определим матрицы Р*, Q*, А% согласно A3.8.5а),
A3.8.56). Аналогично определим матрицы Р**, Q**, А*,* через матрицы,
соответствующие квадранту (т — 2) х (т — 2). Пусть т^ = скх', где а,
а' — скалярные множители, входящие в A3.1.15) и A3.1.16), вычисленные
для квадранта m x m. Если теперь подставить A3.1.15) и A3.1.16) в урав-
уравнение A3.8.3), то, учитывая A3.8.4) — A3.8.6), получим
к
71 = А,,
где
РГ = (Р*У1Р,
Р* = (p**)-ip*,
&={Q**YlQ*,
К — ТтХ
- 2/vfn - 1
A3.8.8)
A3.8.9)
A3.8.10)
Все матрицы, входящие в выражения A3.8.7) — A3.8.10), имеют размер-
размерность 2т х 2т. Мы использовали тот факт, что матрица Р имеет блок-
диагональную форму A3.1.13); поэтому Р** и U2 коммутируют. Введенные
в A3.8.7) индексы г и t означают «отношение» и «полностью вычисленная
угловая трансфер-матрица» соответственно.
Чтобы понять последнее замечание, заметим, что A3.8.7) представляет
собой одно из четырех соотношений, получаемых с помощью последова-
последовательных поворотов решетки на 90°. Такие повороты приводят к цикличе-
циклическим перестановкам матриц А, В, С, D и Р, Q, R, Т. Эти четыре соотно-
соотношения имеют вид
A3.8.11)

392 УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
Они имеют в точности форму уравнений A3.1.16). Поскольку матрицы
Аф Bd, Cd, Dd являются диагональными угловыми трансфер-матрицами
для квадранта т х т, из A3.8.11) следует, что матрицы Ар Bt, Ct, Dt осу-
осуществляют некоторые допустимые представления угловых трансфер-
матриц. В общем случае они не диагональны, но, по-видимому, являются
«более диагональными», чем исходные матрицы Л, В, С, D: например, вы-
выявление сходимости соответствующих матричных произведений в пределе
бесконечномерной решетки, по-видимому, не вызывает трудностей. По-
Поскольку матрицы At и А связаны между собой соотношением
At*(P*YlAQ* , A3.8.12)
мы можем рассматривать At как «частично диагонализованную» форму
матрицы А.
Предположим, что мы вычислили 2т ~ 1 х 2т ~ !-матрицы Аф Вф Сф
Dd, Pr Qr R* Тп соответствующие квадрантам (т - 1)х(га - 1), и
2т ~ 2 х 2т ~ -матрицы Ad, Вф Сф Dd, соответствующие квадрантам
(т - 2)х(т - 2). Тогда из определений A3.8.5) и A3.8.6) можно найти
2т х 2т-матрицы A*d, P*9 Q*, A*d, подстановка которых в A3.8.8) позволя-
позволяет вычислить Аг Аналогично находятся матрицы Вр Ср Dr После этого
уравнения A3.8.11) можно решить относительно 2т х 2т-матриц Аф Bd,
Сф Dd, P^ Q^ R^ Тп соответствующих квадрантам m x m.
(Остается еще некоторая свобода в выборе нормировки векторов-
столбцов матрицы Pr Qj, Rr Tn но в каждом конкретном случае сущест-
существует обычно некоторый разумный выбор таких множителей. Например, в
простейшей изотропной, обладающей симметрией относительно отраже-
отражений модели, когда матрицы А = В = С = D симметричны, можно счи-
считать, что матрицы Рг = Qr = Rr = Тг ортогональны, а максимальное соб-
собственное значение матриц Ad = Bd=Cd = Dd равно единице. Полезно по-
помнить этот простой результат.)
Итак, для больших m мы ожидаем, что величина а', входящая в
A3.1.16), стремится к некоторому пределу, поэтому из A3.4.1) следует ра-
равенство тт = кх/2т^т + 1\ где к— статистическая сумма на один узел ре-
решетки. Следовательно, определения A3.4.1) и A3.8.10) для функции к экви-
эквивалентны.
Таким образом, уравнения A3.8.8) и A3.8.11) можно использовать в ка-
качестве рекуррентных соотношений для последовательного вычисления к,
Ad, Bd, Cd, Dd, Pr Qr Rr Tr при все больших значениях т.
Сокращенные уравнения
Рассмотрим несколько более подробно, как можно найти решение урав-
уравнений A3.8.11) при заданных Л,, Bt, Ct, Dr Умножая уравнения A3.8.11)
друг на друга, получаем
KAPrAdBdCdDdP;1 =AtBtCtDt. A3.8.13)
Таким образом, необходимо диагонализовать произведение AtBtCtDt:

ГЛАВА 13 393
KAAdBdCdDd — диагональная матрица собственных значений (И — наи-
наибольшее из них), а столбцы матрицы Рг — правые собственные векторы
произведения. Если Р9 Q^ R^ Ts — матрицы, обратные матрицам Pr Qr
Rr Tr соответственно, то строки матрицы Ps — левые собственные векто-
векторы произведения А( В( С( Dr Аналогичные утверждения для Qr . . . , Ts
можно получить с помощью циклической перестановки матриц Л, В, С, D.
Определение A3.8.8) матрицы А( записывается теперь в виде
At = A3Q?(A3*Vl U2P?AZ . A3.8.14)
Если рассматриваются все такие собственные значения и собственные
векторы, то размеры диагональных матриц Ad, Bd, Cd, Dd удваива'ются
при каждом шаге рекуррентной процедуры. Мы ожидаем, что данные мат-
матрицы стремятся к бесконечномерным пределам. Смысл такого предельного
перехода определен в разд. 13.4: если диагональные элементы матриц рас-
расположены в убывающем порядке, то каждый данный элемент (например,
шестой) будет стремиться к пределу.
Указанное свойство позволяет провести самосогласованное сокращение
уравнений: использовать только часть наибольших собственных значений
матрицы At Bt Ct Dt и соответствующих правых и левых собственных век-
векторов. Это означает, что мы рассматриваем уравнения
d = AtQr, A3.8.15а)
dQs = PsAt, A3.8.156)
QsQr = $ A3.8.16)
вместе с A3.8.14) и его аналогами, получаемыми при поворотах на 90°.
Если число оставленных собственных значений равно а?, то из A3.8.5),
A3.8.14) — A3.8.16) следует, что различные матрицы имеют следующие
размерности:
Ad:nxn; А%:2пх2п; АЗ*: 4л х 4л;
Ах\ 2л х 2л; Рг: 2л х л; Qs: л х 2л; A3.8.17)
Рг*:4лх2л; Q*: 2л х 4л; С/2:4лх4л;
при этом данные размерности не меняются при циклических перестановках
матриц А, В, С, D и Р, Q, R, Т.
Из выражения A3.8.14) следует, что матрицы Ар Bv Ct, Dt имеют блок-
диагональную структуру вида A3.1.13). Следовательно, диагональные эле-
элементы матрицы Ad (и матриц Bd, Cd, Dd) распадаются на два набора: эле-
элементы, соответствующие блоку с S = 4-1, и элементы, соответствующие
блоку с 5 = — 1. Обозначим диагональные элементы с помощью индекса
/ = 1, . . . , /?, и пусть fi = 4-1(—1), если диагональный элемент соот-
соответствует блоку с S = 4-1(—1). Тогда, используя выражение A3.2.1), эле-
элементы различных матриц можно записать в виде

394УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
i J) ;
J) ;
(li.o.lo)
sXioi,; = <5F
УМ^2 , 6 , ^ , ^l) •
Здесь, как обычно, индексы, отвечающие строкам и столбцам, имеют
сложную структуру. Вертикальная черта используется для разделения та-
таких индексов; например, матрица Р* имеет индекс строки (ох, о2, 0 и ин-
индекс столбца (a'j, j). Множители Of/Oj и aj/at введены для удобства даль-
дальнейших вычислений.
Матричные уравнения A3.8.14) — A3.8.16) и их аналоги, получаемые
при поворотах, имеют теперь конечную размерность. Задавшись разумным
начальным решением, данные уравнения можно решить с помощью итера-
итераций. При этом нужно из A3.8.14) и его аналогов вычислить Л,, Bt, Ct, Dt,
затем диагонализировать произведение AtBtCtDn выбрать п наибольших
собственных значений (и соответствующих собственных векторов) и полу-
получить величины к, Аф Вф Сф йф Pr Qr Rr Tr P^ Q^ R^ T^ входящие в
A3.8.15) и его аналоги. Тогда уравнение A3.8.16) служит условием норми-
нормировки различных собственных векторов.
Решение, полученное для данного значения п, является начальным реше-
решением для последующих значений п. Таким образом, можно в принципе ре-
решить уравнения при п = 1, 2, 3 . . . , во всяком случае при достаточно низ-
низких температурах, когда итерационная процедура сходится и когда выбор
начального решения достаточно удачен.
ТОЧНОСТЬ СОКРАЩЕННОЙ СИСТЕМЫ УРАВНЕНИЙ
Обычно уравнения A3.8.14) — A3.8.16) нельзя решить аналитически, но
при конечных значениях п их можно решить численно с помощью компью-
компьютера или использовать для получения низкотемпературных разложений. В
последнем случае функцию к и все матричные элементы разлагают по сте-
степеням некоторой низкотемпературной переменной х.
Конечно, для любого конечного п получающиеся значения к, Ad и т.д.
не совпадают с соответствующими значениями для бесконечной решетки.

ГЛАВА 13 395
Но мы надеемся, что имеет место сходимость к таким предельным значе-
значениям при п — оо.
Следовательно, представляет интерес оценка относительной ошибки в
определении функции /с, появляющейся вследствие использования сокра-
сокращенной системы уравнений. К счастью, по-видимому, существует простой
способ оценить указанную ошибку.
Как видно из выражений A3.1.11) и A3.1.17), существенная переменная
имеет вид
р, = Trace AdBdCdDd. A3-819>
Заметим, что п собственных значений матрицы Ad BdCd Dd находятся сре-
среди 2л собственных значений матрицы кА AtBt Ct Dn причем наибольшее из
них равно единице. Введем обозначение
Я — наибольшее собственное значение матрицы K~AAtBtCtpt,
не содержащееся среди собственных значений матрицы AdBdCdPd-
A3.8.20)
Величина X является в некотором смысле мерой относительной ошибки в
Рр связанной с сокращением числа уравнений до конечного числа п. По-
Поскольку величина (ах) равна производной от In ас и, как видно из уравнения
A3.1.17), пропорциональна рр отсюда следует:
относительная ошибка в определении к =* X. A3.8.21)
Конечно, такая оценка представляет собой значительное упрощение, по-
поскольку одно неучитываемое собственное значение влияет на все другие
собственные значения и фактически на все матричные элементы. Но в ре-
реальных численных расчетах оценка A3.8.21), по-видимому, оказывается
справедливой [41, 47, 234].
Далее в работах [38, 47], в которых изучались разложения в ряд, было
обнаружено, что если X ~ хр, где/? — некоторое положительное целое чис-
число, то относительная ошибка в определении к также порядка хр.
Отсюда следует, что можно получить достаточно длинные разложения
при довольно малых значениях п. Например, для восьмивершинной модели
без внешнего поля из A3.7.19) и A3.7.20) получаем
0\
J.... О3.8.Я,
где через х обозначен малый при низких температурах параметр, по кото-
которому можно вести низкотемпературное разложение.
Из формулы A3.8.22) следует, что четырнадцать первых собственных
значений матрицы Ad Bd Cd Dd, расположенные в убывающем порядке,
имеют вид
1 Jl V4 V6 V6 V8 V8 vl0 v10 v10 V12 V12 V12 v 12 (\г Q 014
Если сохранить три первые собственные значения, то наибольшее из
остальных имеет порядок л*6. Таким образом, даже при п = 3 сокращенные

396 УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
уравнения определяют к с точностью до х5. Если п = 10, то ас определяет-
определяется с точностью до х11.
Существуют другие примеры, когда собственные значения убывают еще
быстрее: в модели жестких квадратов удалось получить [47] первые 43 чле-
члена разложения к, используя лишь матрицы 13 х 13.
Вариационный принцип
Сокращенные уравнения A3.8.14) — A3.8.16) эквивалентны некоторому
вариационному принципу для функции к. Чтобы увидеть это, используем
явные выражения A3.8.18) для различных матриц. При этом выражение
A3.8.14) принимает вид
uqioi) = 2 и>F- > U , 6; > <7i) qikukPkj • A3.8.24)
Используя это определение, вместо уравнений A3.8.15) и A3.8.16) получаем
iPijbj = 2 wF , 6k, 6 , 6>) qikakPkibiqij, A3.8.25a)
iflj = 2 w(?k , 6/> 6;> ^i)Pikdkqkiaipij, A3.8.256)
2
«,/) при 6 = § • A3.8.26)
Три поворотных аналога данных уравнений могут быть получены с по-
помощью циклических перестановок at %b, с, d и р, q, r, t, а также четырех ар-
аргументов функций w. Первое такое уравнение, подобное A3.8.256), имеет
вид
кагЩ = 2 wF,- ЛкЛп 6>) qikuki-kibiqij. A3.8.27)
Сравнивая данное уравнение с A3.8.25а) и используя результаты сопостав-
сопоставления других уравнений, легко видеть, что уравнения допускают такие ре-
решения, для которых выполняются равенства
П} = Pij, Ц = qtj, pi] = Гц, qij = tij. A3.8.28)
Отсюда получается упрощенная запись
2 иьафъцщ = uibi8{i,j) при 6 = ?/, A3.8.29)
2 wF , 6* , 6/, ?/) UkdkPkibiqij = KuiPijbj. A3.8.30)
В обоих уравнениях /, j — целые числа от 1 до а?. Уравнение A3.8.29) спра-
справедливо лишь при f, = fy, а уравнение A3.8.30) — при любых / иу.
Полезно ввести новые матричные обозначения. Обозначим через а диа-
диагональную матрицу п х п с элементами а(Ь(и У), через р матрицу п х п с
элементами/?^ и т. д. Тогда уравнения A3.8.29) и A3.8.30) принимают вид

ГЛАВА 13 397
(tabq)^ = (ab),y при ?, = ?,, A3.8.31a)
2 vv(&, U , 6, §) f* (apb)w<7// = jc (apb)<,. A3.8.316)
Эти уравнения и соответствующие поворотные аналоги можно вывести
из некоторого вариационного принципа. Введем определения
pi = Trace abed ,
рг = Trace abqcdt,
A3.8.32)
р2 = Trace bcrdap ,
и рассмотрим величину
() A3.8.33)
Взяв логарифмическую производную от ас к по каждому элементу мат-
матриц я, ...,/, обнаружим, что такая производная обращается в нуль, если
удовлетворяются уравнения A3.8.31) и их аналоги, получаемые при помо-
помощи соответствующих циклических перестановок. Исходя из A3.8.31), легко
проверить, что рх = р2 — Р'г = к~1Рг* поэтому
kv = k. A3.8.34)
Таким образом, существует вариационный принцип для статистической
суммы на один узел к: функция к представляет собой стационарное значе-
значение к v. Приведенное утверждение является точным в пределе больших п и
служит хорошим приближением даже для малых значений п.
Уравнения A3.8.31) — A3.8.34) можно получить (по крайней мере для
достаточно симметричных систем) из вариационного приближения для
максимального собственного значения трансфер-матрицы V ряд — ряд.
Этим способом данные уравнения были получены первоначально [17, 34,
146].
Матрицы а, Ь, с, d he обязательно диагональны
Уравнения A3.8.31) не изменяют своего вида при следующем преобразо-
преобразовании:
A3.8.35)
Здесь а, 0, 7» $ — любые несингулярные матрицы, имеющие блок-
а—»
с—»
Р-*
г—*
5аа\
ара,
УГУ'1,
Ь->
<!->
q-*
t->
ab/Г1
ydS1
/Jq/s1

398 УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
диагональную структуру: их элементы (/, j) отличны от нуля только при
f, = f •. Если строки и столбцы различных матриц расположены так, что
f, = 4-1 при / = 1, . . . , п' и f, = - 1 при i = л' 4- 1, . . . , а?, то матри-
матрицы a, j8, 7» $ имеют вид
A3.8.36)
где верхний левый блок представляет сооои матрицу я' хп'.а нижний
правый блок — матрицу (п — nf) x (п — п').
Таким образом, преобразование A3.8.35) нарушает точный диагональ-
диагональный вид матриц at b, с, d, хотя блок-диагональный вид A3.8.36) сохраня-
сохраняется. (Фактически это эквивалентно снятию требования диагональности
матриц A d, Bd, Cd, Dd и сохранению условия блок-диагональности A3.1.13)
данных матриц.)
Может оказаться полезным работать в представлении, в котором мат-
матрицы a, b, ct d недиагональны. В частности, при разложениях в ряд диаго-
диагональная форма данных матриц не удобна, поскольку при этом могут появ-
появляться иррациональные коэффициенты. Лучше считать, что данные матри-
матрицы имеют блок-диагональный вид, причем все элементы блока имеют (в
ведущем порядке) одинаковые степенные зависимости от параметра разло-
разложения х, и каждый элемент (/, j) равен нулю при f,. Ф f..
Графическая интерпретация.
Уравнения A3.8.31) можно представить графически. Рассмотрим первый
квадрант решетки, показанный на рис. 13.7. Пусть индекс / обозначает спи-
спины, лежащие на левом ребре; f, — верхний из таких спинов. Аналогично У
обозначает спины, лежащие на верхнем ребре; fy — крайний левый из та-
таких спинов. Пусть a{j представляет собой элемент (/, j) матрицы а. По-
Поскольку матрица а не должна быть диагональной, а^ может отличаться от
нуля при / Ф j, но
ац ФО только при ?, = ?;. A3.8.37)
, l>
«У
Puc. 13.7. Сегменты решетки и со-
jj ответствующие им статистические
j I J суммы или полные веса. Через / и j
обозначены спины на соответствующих
rU fij ребрах.

ГЛАВА 13
399
Поскольку f, и fy- обозначают верхний левый спин, они должны быть
равными. Будем называть а^ полным весом квадранта. Вообще величины
а№ bij> cij> dy, Pjj, q{j, rijt ty будем называть весами, соответствующими сег-
сегментам решетки, показанным на рис. 13.7. При этом величина f, всегда со-
соответствует спину на том конце ребра, обозначенного через /, на котором
изображен кружок. Такой же смысл имеет величина fy.
Рассмотрим теперь составной сегмент решетки, показанный в левой ча-
части рис. 13.8,я. Он состоит из четырех участков с весами tik, akl, blm, qmJ.
Суммирование по всем внутренним спинам данного сложного сегмента эк-
эквивалентно суммированию по к, I, m при условии, что величина
fк = fj = fm представляет собой спин узла, показанного темным кружком.
Но такое суммирование дает просто элемент (tab q)., который равен
полному весу фигуры, изображенной в левой части рис. 13.8,я. Аналогично
вес фигуры в правой части рисунка равен (а Ь),у, так что на рис. 13.8,а гра-
графически представлено уравнение A3.8.31а).
Вспоминая, что w есть больцмановский вес квадратной грани решетки,
мы видим, что рис. 13.8,6 представляет графически уравнение A3.8.316).
Для бесконечно больших сегментов решетки данные графические уравнения
имеют очевидный смысл: при добавлении к полубесконечной решетке до-
дополнительного столбца статистическая сумма решетки не изменится, за ис-
исключением нормировочного множителя; указанный нормировочный мно-
множитель не зависит от выбора спинов на левом ребре.
Величины pj, p3, p2, Pi представляют собой веса составной решетки, по-
показанной на рис. 13.9; поэтому вариационный принцип A3.8.33) также мож-
можно представить графически, как это показано на том же рисунке.
Поскольку величина к v стационарна по отношению к малым возмуще-
возмущениям матричных элементов а^ . . . , ty, уравнение A3.8.33) дает достаточ-
достаточно хорошее приближение к величине к даже при довольно простом выборе
а у, . . ., ty. Один очевидный способ выбора состоит в том, чтобы данные
величины приравнять точным больцмановским весам конечных сегментов
решетки. Если считать, что продольное ребро на рис. 13.7 содержит г
узлов, то из равенства A3.8.34) и рис. 13.9 следует, что приближенное зна-
значение к равно
/(l,2r^2r,2r-l) , A3.8.38)
т
]\Я
i\t
I =
а 6
Рис. 13.8. 'Графическое представление уравнений A3.8.31а) и A3.8.316). Каждый ри-
рисунок представляет собой полный вес, который дается произведением весов сегмен-
сегментов (например, tabq), просуммированным по всем спинам внутренних линий.

400
УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ
К =
с
d
b ;
о- \
: С
: Г (
d
i
b
р
а
с.
d
t
о
а
\/
с
d
ъ \
i & ''
л \
j
Рис. 13,9. Графическое представление
вариационного принципа A3.8.33).
где Zmn — статистическая сумма прямоугольной решетки, имеющей т ря-
рядов и п столбцов. Необходимо ввести подходящие граничные условия. При
низких температурах можно считать, что граничные спины имеют фикси-
фиксированные значения, соответствующие основному состоянию.
При заданном размере матриц а, . . . , t полученное приближение мало
похоже на точное решение уравнений A3.8.31) и A3.8.32). Тем не менее его
можно считать удовлетворительным, как обсуждается в работе [79].
На протяжении всего раздела предполагается, что основное состояние
системы трансляционно-инвариантно. Если же трансляционная инвариант-
инвариантность основного состояния нарушена, то необходимо ввести несколько
угловых трансфер-матриц А и а, по одной для каждого значения углового
спина, отличающегося от значения в конфигурации спинов, отвечающей ос-
основному состоянию бесконечной решетки. То же относится к матрицам В,
СДЬ I.
Уравнения A3.8.31) можно распространить на другие типы плоских ре-
решеток; интересен случай треугольной решетки, рассмотренный в работе
[41]. (В некотором смысле этот случай самый простой, поскольку уравне-
уравнения имеют самую низкую степень.)
Данные уравнения можно применить для трехмерных решеток. При
этом очевидным образом записывается обобщение рис. 13.9, которое
включает куб, разрезанный на 27 частей с помощью шести разрезов. К со-
сожалению, получающиеся уравнения достаточно сложны и содержат «угло-
«угловые тензоры» с тремя индексами. Для таких тензоров не существует проце-
процедуры, аналогичной приведению матриц к диагональному виду, и эти урав-
уравнения до сих пор не изучены.

14
ЖЕСТКИЙ ГЕКСАГОН
И БЛИЗКИЕ МОДЕЛИ
14.1. ИСТОРИЧЕСКИЙ ПРИМЕР И ОСНОВНЫЕ
РЕЗУЛЬТАТЫ
Исторически превосходным примером использования угловых трансфер-
матриц является модель жесткого гексагона. Она представляет собой дву-
двумерную решеточную модель жестких (т. е. неперекрывающихся) молекул.
В данной модели частицы располагаются на узлах треугольной решетки,
так что никакие две из них не могут одновременно находиться ни на од-
одном и том же узле, ни на соседних узлах. Типичное допустимое расположе-
расположение частиц показано на рис. 14.1. Если мы представим себе, что каждая ча-
частица находится в центре гексагона, покрывающего шесть соседних граней
треугольной решетки (такие гексагоны на рис. 14.1 заштрихованы), то при-
приведенное выше правило допускает только неперекрывающиеся гексагоны;
отсюда и название модели.
Для содержащей N узлов решетки большая статистическая сумма имеет
вид
мз
Z= *Zzng(n,N), A4.1.1)
л = 0
где g(n, N) — допустимое число способов расположения п частиц на ре-
решетке, а суммирование проводится по всем возможным значениям п. (По-
(Поскольку может быть занято не более чем !/з всех узлов, п принимает значе-
значения от 0 до ЛУЗ.) Мы хотим вычислить Z или точнее приходящуюся на
один узел бесконечной решетки статистическую сумму
к= lim ZllN A4.1.2)
N-+oo
как функцию положительной переменной z, которую обычно называют ак-
активностью.
Указанную проблему можно перевести на «спиновый» язык, связывая с
каждым узлом / переменную ог Но в рассматриваемом случае удобно счи-
считать, что а, принимает значения 0 или 1: если узел пуст, то oi = О, если на
Рис. 14.1. Типичное расположение частиц v—^^77/ГК—7\ А А Л
(темные кружки) на треугольной решетке, \///ш/шК/ \/ \/ \/
такое, что никакие две частицы не находят-
находятся на одном и том же узле и не являются
соседями. Шесть граней, окружающих каж-
каждую частицу, заштрихованы; такие грани
образуют неперекрывающиеся («жесткие») /\ /\ /\ /\ /\ /\
гексагоны.

402 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
узле находится частица, то а1: = 1. Таким образом, величина а, представля-
представляет собой число частиц в узле /, или заселенность. На таком языке формулу
A4.1.1) можно переписать в виде
Z = 2 zai+ +а» П A " °i°j) , A4Л-3>
где произведение берется по всем ребрам (/, j) треугольной решетки, а сум-
суммирование проводится по всем значениям @ и 1) всех чисел заселенности
а]9 ... , aN.
Данное выражение для Z очень похоже на статистическую сумму A.8.2)
модели Изинга. Действительно, в разд. 1.9 показано, что общая модель
Изинга с взаимодействием между ближайшими соседями во внешнем поле
эквивалентна решеточному газу с взаимодействием между ближайшими со-
соседями. Модель жестких гексагонов представляет собой предельный случай
последней.
Мы ожидаем, что в такой модели происходит фазовый переход из одно-
однородного жидкого состояния при малых активностях z в неоднородное твер-
твердое состояние при больших активностях.
Чтобы увидеть это, разделим исходную решетку на три подрешетки 1,
2, 3 так, чтобы никакие два узла одного типа не были соседними
(рис. 14.2). Существуют три возможные плотноупакованные конфигурации
частиц; они соответствуют случаям, когда заполнены все узлы первого ти-
типа, все узлы второго типа или все узлы третьего типа.
Предположим, что мы фиксируем заполнение граничных узлов решетки
в соответствии с первой возможностью, т. е. все граничные узлы первого
типа заполнены, а все остальные граничные узлы пусты. Тогда для беско-
бесконечной решетки вторая и третья возможности дают пренебрежимо малый
вклад в сумму по состояниям в A4.1.3).
Очевидно, что теперь узлы различных подрешеток не эквивалентны.
Обозначим через рг локальную плотность частиц на узле типа г; тогда, ис-
используя A.4.4), получаем
рг = (а) = Z l 2 a/zai+ •+а» Д A " Ofjj) , A4.1.4)
где / — узел типа г.
При бесконечно больших z система плотно упакована, причем заполнены
все узлы типа 1; поэтому pj = 1, р2 = р3 = 0. Мы можем разложить каж-
Рис. 14.2. Три подрешетки треугольной решетки.
Подрешетка 1 состоит из всех узлов типа 1;
подрешетки 2 и 3 определены аналогично.
Соседние узлы лежат на разных подрешетках.
Показана некоторая плотноупакованная конфи-
конфигурация частиц (темные кружки): все узлы одной
подрешетки (в данном случае подрешетки 1)
заняты, все остальные узлы свободны.

ГЛАВА 14 403
дую функцию рг по обратным степеням z, рассматривая последовательные
возмущения плотноупакованного состояния. Для узла /, находящегося в
глубине большой решетки, получаем
Рг = 1 - z - 5z - 34z - 267z - 2037z
A4.1.5)
Pi = Ръ = z~2 + 9z + 80z + 965z + . . . .
Следовательно, система неоднородна, поскольку не все плотности рр
Р2> Рз Равны. Рассмотренная ситуация резко отличается от случая малых
активностей: начиная с состояния, в котором все узлы пусты, и последова-
последовательно вводя частицы, мы получаем разложения
Pi=p2 = P3 = z-7z2+ 58z3 - 519z4 + 4856z5 - .... A4.1.6)
Равенство рх = p2 = p3 справедливо во всех порядках данного разложения.
Следовательно, система находится в неоднородном состоянии при до-
достаточно больших z и в однородном состоянии при достаточно малых z. (В
предположении, что соответствующие ряды сходятся; доказательство это-
этого предположения можно, вероятно, построить с помощью рассуждений,
аналогичных аргументам Пайерлса [192].) Должно существовать критиче-
критическое значение zc активности г, выше которого система теряет однород-
однородность. Поскольку однородная фаза типична для жидкости, а неоднородная — для
твердого тела, можно сказать, что в данной модели при z = zc происходит пере-
переход жидкость — твердое тело.
Представляют интерес две величины: средняя плотность
Р = (pi + Рг + Рз)/3 = z(d/dz) In к A4.1.7)
и параметр порядка
Я = рг- р2= Р\~ Рз- A4.1.8)
Заметим, что по определению величина R равна нулю при z < zc. При
z > zc следует ожидать, что R больше нуля.
Численные расчеты
Прежде чем данная модель была решена точно [35], было проделано не-
несколько приближенных численных расчетов. Такие расчеты поучительны,
так как они помогли прийти к точному решению.
Раннелс и Комбс [204] вычислили максимальное собственное значение
трансфер-матрицы для решеток конечной ширины. При экстраполяции к
решетке бесконечной ширины они получили zc = 11,12 ± 0,10.
Гонт [96] продолжил разложения в ряд A4.1.5) и A4.1.6) до порядков
z~5 и z8 соответственно. Он получил следующую оценку:
zc= 11.05 ±0.15. (И. 1.9а)
Гонт обнаружил также, что в комплексной z-плоскости функция k(z) име-
имеет, по-видимому, только две сингулярности в точках z = Zc и z = ZNP. Ин-
Индекс NP обозначает «нефизическую» особенность, и величина zNP равна
zNP = 0.0900 ± 0.0003. A4.1.96)

404 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
Он предположил, что zc и zNP могут быть корнями некоторого простого
квадратного уравнения, и вычислил их произведение и сумму:
zc + zNP= 10.96 ±0.15,
A4.1.10)
zczNP = -0.995 ±0.014.
Гонт высказал также предположение, что точные значения суммы и произ-
произведения чисел zc и zNP равны И и — 1 соответственно. При этом zc опреде-
определяется из уравнения
z] - \\zc -1=0, zc = ?A1 + 5V5) = 11.09017.... A4.1.11)
К сожалению, последнее предположение Гонт не опубликовал. Как мы уви-
увидим ниже, оно в точности выполняется.
Для случая z = 1 Меткаф и Янг [168] выполнили дополнительные расче-
расчеты для решетки конечной ширины. С точностью до четвертого знака они
нашли
In к = 0.3333 A4.1.12)
и высказали предположение, что точное значение величины In к равно Уъ.
Бэкстер и Цонг [41] также рассмотрели случай z = 1, но они использо-
использовали модифицированные для треугольной решетки сокращенные уравнения
A3.8.31) для угловых трансфер-матриц. При этом учитывалось, что, по-
поскольку z < zc, метод угловых трансфер-матриц должен быстро сходиться
и давать хорошие численные результаты. Действительно, для метода угло-
угловых трансфер-матриц результаты были весьма обнадеживающими: сокра-
сокращение матриц до 2 х 2, 3 х 3, 5 х 5, 7 х 7, 10 х 10 дало значения
In к = 0.333 050 ,
0.333 242 657,
0.333 242 721958, A4.1.13)
0.333 242 7219761,
0.333 242 7219761
соответственно.
Очевидно, что предположение Меткафа и Янга ошибочно, но обнаружи-
обнаружились некоторые замечательные свойства. В табл. 14.1 даны собственные
значения а, сокращенных угловых трансфер-матриц А, нормированных так,
чтобы наибольшее собственное значение было равно единице.
Приведенные собственные значения естественным образом распадаются
на два класса, соответствующие двум диагональным блокам в выражении
A3.8.36). Один из таких блоков отвечает пустому угловому узлу,
другой — занятому. Пусть ^ = 0 соответствует случаю, когда а, принадле-
принадлежит первому .блоку, a f, = 1 — случаю, когда а, принадлежит второму бло-
блоку. Значения f,- также приведены в табл. 14.1.

ГЛАВА 14
405
Таблица 14.1
Собственные значения al9 ..., а10 угловой трансфер-матрицы для
модели жесткого гексагона при z = 1. Значения вычислены при-
приближенно из сокращенного матричного уравнения для треуголь-
треугольной решетки, аналогичного уравнению A3.8.31). Собственные
значения образуют группы близких по величине чисел, зависящие
от учета всех членов каждой группы. Поэтому использовались
матрицы вида 2 х 2, 3 х 3, 5 х 5, 7 х 7, 10 х 10. Каждое соб-
собственное значение а{ дано для последовательности матриц возрас-
возрастающего размера, и ясно видно, что а( стремится к пределу.
Этот предел равен точному значению at для бесконечномерной
угловой трансфер-матрицы.
I
1
2
3
4
5
6
7
8
9
10
2x2
0 1,0
1 0,7603903
0
0
1
0
1
0
0
1
3 x 3
1,0
0,7608436
-0,2548910
ai
5 x 5
1,0
0,7608440
-0,2549635
0,06499191
0,04944546
7x7
1,0
0,7608440
-0,2549636
0,06500641
0,04945972
-0,01657025
-0,01260704
10 x 10
1,0
0,7608440
-0,2549636
0,06500641
0,04945974
-0,01657427
-0,01261043
0,004225773
0,004224830
0,003214313
В табл. 14.2 даны значения величин а4/аз» а5/(а2аз)» аб/аз и ai^a2a\)-
Очевидно, что при увеличении размеров матрицы данные отношения стре-
стремятся к единице. Такое поведение согласуется с утверждением, что в преде-
Таблица 14.2
Значения величин аА/а\ и т.д. при
достаточно больших размерах матриц
5x5
7x7
10 х 10
аА/а\
ъ
аь/а\
ап/{а2а])
0,999777067 0,9999998^3
0,999711560 0,999999539
0,999757797
0,999730684
0,999999999
0,999999999
0,999999849
0,999999592

406 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
ле бесконечно больших матриц (когда уравнения точны)
а{ = а(&)хП1 при / ^ 1 9 A4.1.14)
где
х = аз/аг A4.1.15)
и ni — неотрицательное целое число.
Последнее утверждение заслуживало интереса потому, что соответству-
соответствующие я, в восьмивершинной модели представляют собой целые степени не-
некоторой переменной х (или 5), входящей в формулу A3.7.20). Если модель
жестких гексагонов обладает аналогичными свойствами, то она, очевидно,
может быть решена точно.
Поэтому Цонг повторил вычисления для z = 0,7, а я, используя прог-
программу разложения в ряд для компьютера, получил разложения нескольких
первых собственных значений ai в ряды по степеням z (при малых г)«и z~x
(при больших z). Наши результаты снова находились в полном согласии с
A4.1.14).
Точное решение
В действительности на данной стадии было нетрудно угадать точное
решение для функций k(z) и R(z). Определив х по формуле A4.1.5), я раз-
разложил z в ряд по степеням х до 30-го порядка (при z < zc). Затем, руко-
руководствуясь результатами для восьмивершинной модели, представил разло-
разложение в виде
00
2 = "* П A - *")с" A4.1.16)
П = \
и нашел
сг ,. . . , с29 = 5, -5, -5, 5, 0, 5, -5, -5, 5, О,
5, -5, -5,5,0,5, -5, -5,5,0, A4.1.17)
5,-5,-5,5,0,5, -5, -5,5.
После этого не трудно было догадаться, что
z = -x[H{x)IG{x)}\ A4.1.18)
где введены обозначения
A4.1.19)
n = \
Та же вычислительная серия дала разложения функции к в ряд по х до 29-
го порядка. Записывая его, подобно A4.1.16), в виде произведения, можно
было угадать, что с точностью до всех порядков

ГЛАВА 14 407
где
v ' *^ V / I Г > /\ /\ / /1/11 ОЛЧ
Q(x) = П A - xn). A4.1.21)
Приведенные бесконечные произведения того же типа, что и произведения,
которые появляются в эллиптических тэта-функциях A5.1.5). При больших
z я вычислил функции z, к, R с точностью до девятого порядка в их разло-
разложениях по х. Даже этого оказалось достаточно для подтверждения того,
что данные функции можно записать с помощью бесконечных произведе-
произведений того же вида:
z=x-l[G(x)/H(x)]\ A4.1.22)
;T1/3G3(jt) BV)
-Jt3"-2)A -
H\x) „M A-^J ' —
R = Q(x)Q(x5)/Q2(x3), A4.1.24)
При убывании jc до от 0 до - 1 величина z в A4.1.18) возрастает от 0 до
zc, где zc определена в A4.1.11). При возрастании х от 0 до -Hi величина z
в A4.1.22) убывает от оо до zc. Такое поведение показывает, что выраже-
выражения A4.1.18) и A4.1.20) применимы для жидкой фазы 0 < z < zc (при
0 > х > -1), а выражения A4.1.22) — A4.1.24) применимы для твердой
фазы z > zc (при 0 < х < 1). Полученные выражения согласуются также с
предположением Гонта A4.1.11) о положении критической точки.
На следующей стадии необходимо было найти способ доказательства
такого «угаданного» точного ответа. Такие вычисления с использованием
угловых трансфер-матриц даны в разд. 14.2 — 14.7. Они не строги в мате-
математическом смысле, поскольку предполагаются определенные аналитиче-
аналитические свойства функции к и используются результаты гл. 13 (которые зави-
.сят от предположения о возможности перестановки различных предельных
переходов к бесконечно большой рещетке). Но я верю, что такие предполо-
предположения и, следовательно, выражения A4.1.18) — A4.1.24) действительно
справедливы.
14.2. МОДЕЛЬ ЖЕСТКИХ КВАДРАТОВ
С ДИАГОНАЛЬНЫМИ ВЗАИМОДЕЙСТВИЯМИ
Как показано в разд. 10.4, первым этапом в решении восьмивершинной
модели было установление класса коммутирующих трансфер-матриц
ряд — ряд. Руководствуясь этим, я рассмотрел решеточную модель,
трансфер-матрицы которой коммутируют с трансфер-матрицами модели
жестких гексагонов. Изобразим треугольную решетку так, как показано на

408
ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
а
Рис. 14.3. а — треугольная решетка,
представленная в виде квадратной решетки
с одним набором диагоналей; б — диаго-
диагонали, ассоциированные в выражении
A4.2.1) с коэффициентами взаимодействий
L, М.
рис. 14.3,я. При этом модель жестких гексагонов переходит в модель на
квадратной решетке, в которой не могут быть заняты одновременно узлы,
являющиеся ближайшими соседями, и узлы, являющиеся соседями, следу-
следующими за ближайшими, и лежащие на диагоналях северо-запад — юго-
восток.
Затем я перешел к более общей модели, в которой не могут быть заня-
заняты одновременно узлы, являющиеся ближайшими соседями, а частицы, ле-
лежащие на диагоналях квадратных граней, взаимодействуют друг с другом.
Такая модель представляет собой частный случай ВСГ-модели, рассмот-
рассмотренной в гл. 13. Статистическая сумма определяется выражением A3.1.2),
где каждый спин а, принимает значения 0 или 1 и
при ab = bc = cd = da = O, A4.2.1)
= 0 в остальных случаях.
Здесь каждая величина я, ?, с, d принимает значения 0 и 1;
т — тривиальный нормировочный множитель; величина t сокращается в
выражении для статистической суммы; L и М — коэффициенты диагональ-
диагональных взаимодействий, как показано на рис. 14.3.6; z — активность. Модель
жестких гексагонов получается при т = 1, L = ОиМ = — оо.
Соотношение звезда — треугольник
Рассмотрим две такие модели с весовыми функциями w и w'. Как пока-
показано в разд. 13.3, трансфер-матрицы ряд — ряд данных моделей коммути-
коммутируют, если существует третья функция w", такая, что при всех значениях 0,
1 величин а, а\ а", 6, /?', Ь" удовлетворяется соотношение A3.3.6)
звезда — треугольник. Пусть весовая функция w' (w") определяется выра-
выражением A4.2.1), в котором z, L, My t заменены на z\ L\ M\ t' (z'\ L",
M", t"). Для удобства поменяем местами величины L' и Л/', заменим ве-
величину t' на обратную и введем параметр
= (zz'z")V(tt't").
A4.2.2)
Тогда соотношения A3.3.6) сведутся к семи отдельным уравнениям:

ГЛАВА 14 409
(zrzrry = s + s2cL, A4.2.3a)
(z"z)h = s + s2eL>, A4.2.36)
(zz'y = s+s2cL\ A4.2.3в)
z(z'z"ycM = s2 + s3eL> + L\ O4-2.3r)
z'{z" z)* tM> = s2 + s3 eL"+L , A4.2.3д)
L", A4.2.3ж)
которое мы будем обозначать здесь просто как (а) — (ж). Рассматривая
разность eL (a) — eLF), получаем
(z'* eL' - z* tL) z"* = (eL< - eL)s. A4.2.33)
Умножая уравнения (в), (е) и (ж) на s, s~l и s~l соответственно, мы ви-
видим, что данные уравнения линейны и однородны относительно пяти вы-
выражений
z"*, s, s2, s3tL\ s~lz"tM" A4.2.4)
с коэффициентами, которые не зависят от 5, z\ L", М".
Для любых пяти уравнений (или четырех уравнений, не содержащих
М") детерминант, построенный из таких коэффициентов, должен обра-
обращаться в нуль: данное требование эквивалентно исключению величин s, z",
L", М" из рассматриваемых уравнений. После исключения указанных вели-
величин остаются три уравнения
А, = А/, /=1,2,3, A4.2.5)
где
A2 = z*(eL + e"-e^), A4.2.6)
А3 = z"*(e"L + t~M - t~L~M - z eL+Af),
а величины Д|, A^, A3 определяются такими же выражениями, но с заме-
заменой z, L, М на z\ L'у М'
(Уравнения (а), (б), (г), (д) дают А! = Ар из уравнений (з), (в), (г), (д)
следует А2 = А2> а из C)» (г)» (д)» (е)' (ж) получаем А3 = А3.)
Три уравнения A4.2.5) представляют собой достаточные условия того,
что соотношения A4.2.3) имеют решение для 5, z", L", М". Следствие
уравнений A4.2.6) имеет вид
Д!Д2 - 1 = (Аз - Ai - А2) z» eL+M ¦ A4.2.7)
Предположим, что величины Aj, A2, А3 заданы. Тогда из выражения

410 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
A4.2.7) определим г2 exp (L + М). Затем из первого уравнения A4.2.6) по-
получим zVl, а из второго — L и М. Отсюда следует, что в общем случае ре-
решениями уравнений A4.2.5) являются z\ L\ M' — z> Л/, L и z\ L\
М' = z, L, М. Данные решения не очень интересны и не очень полезны,
поскольку они означают просто, что трансфер-матрица коммутирует сама
с собой и с обратной матрицей.
Но предположим, что Др Д2, Д3 не произвольны, а удовлетворяют
ограничениям
Д2 = ДГ1, Дз = Д1 + ДГ1. A4.2.8)
Тогда A4.2.7) уже не определяет zh exp (L + М), поэтому уравнения
A4.2.6) имеют бесконечно много решений для z, L, М. Все трансфер-
матрицы, соответствующие этим решениям, коммутируют между собой.
Из уравнений A4.2.6) видно, что оба ограничения A4.2.8) удовлетворя-
удовлетворяются, если
z = A - e"L) A - е~M)l(tL*~M - tL - tM). A4.2.9)
Положим Д = Aj, т.е.
Д = Z~\\ - ztL + M) . A4.2.10)
Если две модели различаются значениями z, L, М, но имеют одинаковые
значения Д, причем обе модели удовлетворяют условию A4.2.9), то
трансфер-матрицы таких моделей коммутируют.
Заметим, что A4.2.9) удовлетворяется при всех z в пределе L — 0 и
М — -оо, который соответствует модели жестких гексагонов. Данное ус-
условие не удовлетворяется при L, М — 0, что соответствует модели жест-
жестких квадратов. Действительно, численные решения Бэкстера и др. [47] мо-
модели жестких квадратов показали, что собственные значения угловой
трансфер-матрицы данной модели не обладают никакими простыми
свойствами типа A4.1.14).
Параметризация с помощью эллиптических
функций
Исключая z из выражений A4.2.9) и A4.2.10), получаем
При заданной величине Д данное выражение представляет собой симмет-
симметричное биквадратное соотношение между е1 и е^. Как показано в
разд. 15.10, такое соотношение можно параметризовать с помощью эллип-
эллиптических функций. Общая форма такой параметризации имеет вид
ем=ф(и-Х), A4.2.12)
где функция ф(и) определяется выражением
ф(и) = %H(v + a) H(v - a)l\H{v + b) H(v - b)]. A4.2.13)
Функция H(v) определена формулой A5.1.5) и представляет собой эллипти-

ГЛАВА 14 4П
ческую тэта-функцию аргумента v и модуля к. Величины к, X, ?, я, Ъ по-
постоянны. (Мы заменили символы м, /, т/, X, /х разд. 15.10 на v, к, X, а, Ъ и
выбрали нижний знак в формуле A5.10.14).)
Из выражения A5.2.3) следует, что функция ф(и) является периодиче-
периодической с периодами 2/ и ИГ, т.е.
ф(и + 21) = ф(и + ИГ) = ф(-и) = ф(и)у A4.2.14)
где / и /' — полные эллиптические интегралы первого рода модулей к и
к' = A - k2)Vl соответственно.
(Отсюда следует, что при заданном значении L первое из уравнений
A4.2.12) имеет много решений относительно переменной v; если известно
некоторое решение vy то для получения другого нужно к v прибавить пери-
периоды 2/ и ИГ, умноженные на целые числа, и, возможно, изменить знак.
Но все такие значения v дают только два различных решения уравнения
A4.2.12) для е^\ так и должно быть, поскольку выражение A4.2.11) квад-
квадратично по е^.)
Обозначим через v0 значение и, при котором eL = 1. Тогда из A4.2.12) и
A4.2.13) получаем
§ = H(v0 + Ь) H(v0 - b)/[H(v0 + a) H(v0 - а)]. A4.2.15)
Отсюда и из A4.2.14) следует, что функция ф(и)— 1 обращается в нуль при
v = v0 + 2ml Л- ИпГ; поэтому она содержит множитель H(v — v0). По-
Поскольку функция ф(и) четна, она содержит также множитель H(v + v0).
Используя рассуждения, приведенные в конце разд. 15.3, или просто при-
применяя тождество A5.3.10), получаем выражение
l _ 4 1 = _ Я(Д + Ъ) Н(а - Ь) Щи + ур) Щи - у0)
С Ф[и) H(a + Vo)H(a-vo)H(v+b)H(v-b)\l42A6)
Чтобы найти связь между величинами X, a, b, v0, рассмотрим некото-
некоторые частные значения L и М. Если eL = 1, то уравнение A4.2.11) дает
6м = 0 или 6м = оо. Из выражения A4.2.16) следует, что v = v0 или
v = ~v0. Подставляя данные пары значений для е1^ и v в A4.2.12) и
A4.2.13), получаем, что а и Ъ можно выбрать следующим образом:
а = ио~К Ь = -ио-к. A4.2.17)
Если е1 = оо, то оба решения для е^ уравнения A4.2.11) равны единице,
а из A4.2.12) получаем v = Ь или v = —b. Следовательно, правая часть
выражения A4.2.16) должна обращатья в нуль при v = —X±b. Отсюда
получаем дополнительное условие
ЯBА + 2i;0) = 0 . A4.2.18)
Общее решение последнего уравнения имеет вид v0 = - X + ml + inl', где
тип — целые числа. Но одновременное увеличение v, v0, я, —Ъ на
ml Л- inl' не изменяет ф(и) и ф(и — X); поэтому без потери общности

412 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
можно выбрать ^ = _л A4 2 19)
Подставляя выражения для / и^, в которых учтен выбор величин я,
/?, v0, в формулу A4.2.11) (используя A4.2.12) для левой части и A4.2.16)
для правой), получаем соотношение
Д^Я^А) Я2(ЗЯ) Щи + 2А) Щи - ЗА)/Я4BА) =
A4.2.20)
= Я4BА) Щи + А) Щи - 2А) - Н\к) Я^ЗА) Щи) Щи - А).
Оно должно быть тождеством, справедливым при всех комплексных значе-
значениях v. Полагая v = ЗХ и v = 0, имеем
Я(А) Я3(ЗА) = Я3BА) ЯDА), A4.2.21)
А = Я8BА)/[Я5(А) Я3(ЗАI. (Г4.2.22)
Отсюда следует, что отношение правой части A4.2.20) к левой пред-
представляет собой целую двоякопериодическую функцию v, которая равна еди-
единице при v = 0. Из теоремы Лиувилля следует, что данное отношение рав-
равно единице при всех комплексных значениях v, поэтому тождество действи-
действительно выполняется.
Положив в выражении A5.3.10) w, v, ху у = 0, X, 2Х, ЗХ,ололучим тожде-
тождество
Я3BА) ЯDА) - Я(А) Я3(ЗА) = Н\Х) ЯEА), A4.2.23)
поэтому условие A4.2.21) эквивалентно равенству
Я3(А)ЯEА)=0. A4.2.24)
Решения X = Ъп1 Л- ЪпГ (т, п — целые числа) данного уравнения нам
не подходят, поскольку из A4.2.12) и A4.2.14) следует тогда, что е1 = е^.
Следовательно, нужные решения имеют вид
к=Bт1+2Ш')/5, A4.2.25)
где тип — целые числа, которые не делятся одновременно на пять.
Мы можем выбрать для X одно из таких значений. В дальнейшем будем
считать, что
А = 27/5 . A4.2.26)
(Другие возможные значения X приводят к другим параметризациям, на-
например выбор X = ИГ /5 эквивалентен использованию эллиптических функ-
функций сопряженного модуля.)
В настоящей главе удобно перейти к новой переменной
u = JW/2I A4.2.27)
и к новой функции
00
0i(u , q2) = sin u П A - 2 q2n COS2м + /.") A - о2") = H(v)l{2qk\.
п = 1 A4.2.28)

ГЛАВА 14 413
(Приведенное обозначение не стандартно: обычно эллиптическая 0Г
функция содержит множитель 2qVA. Поскольку в наши уравнения входят
только отношения вида 0j(w, ср")/Вх(и\ q2), указанный множитель не су-
существен; его удобно не включать в определение 0j(w, q2), так как иногда
мы будем принимать q2 < 0. Настоящее определение обеспечивает дейст-
действительность функции 0j и в этом случае.)
Используя приведенное выше определение для замены функции Н в вы-
выражениях A4.2.13), A4.2.15), A4.2.22) на Вх и записывая 0j(w, q2) просто как
0j(w)> окончательно получаем параметризацию следующего вида:
где использовано тождество Вх(и) = ^(тг - и). Из формулы A4.2.9) сле-
следует
Данную параметризацию можно использовать для точного решения
полного набора соотношений A4.2.3) звезда — треугольник. Пусть величи-
величины L', М', z' (L\ M\ z" ) определяются формулами A4.2.29) и A4.2.31),
в которых переменная и заменена на и'(и"). При этом считаем, что вели-
величина q2 всюду одна и та же. Тогда все уравнения A4.2.3) удовлетворяются
при выполнении условий
и + и' + м" = я/5 , A4.2.32)
A4-2-33)
Области в плоскости параметров L, М
Для нас представляют интерес те значения L и М, при которых величи-
величина z, определяемая A4.2.9), положительна. Такие значения лежат в пока-
показанных на рис. 14.4 незаштрихованных областях (L, Л/)-плоскости. За-
Заштрихованные области соответствуют отрицательным значениям z-
Выражение A4.2.29) можно рассматривать как переход от переменных
L, М к переменным q2y и. Он очень похож на переход от декартовых коор-

414
ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
и=2я/5
II
и=-я/5
Рис. 14.4. Шесть областей в (L,
М)-плоскости, определенных в A4.2.37).
Заштрихованные области соответст-
соответствуют нефизическим значениям г, по-
поскольку в них, согласно A4.2.9),
активность z отрицательна. Области
I, III, V не упорядочены; в областях
II и VI имеется «треугольное упорядо-
упорядочение», а в области IV — «квадратное
упорядочение». Система находится в
критическом состоянии на границах (I,
II), • (III, IV) и (V, VI), где I Д I =
= Дс. Показаны значения переменной и
на осях L и М.
прямым из начала координат через незаштрихованные области, а и возра-
возрастает при движении против часовой стрелки вокруг начала координат. Три
области значений и:--к/5 <w<0, 0<w< 7г/5, 7г/5 < и < 2-к/Ь соот-
соответствуют незаштрихованным участкам нижнего правого, верхнего право-
правого, верхнего левого квадрантов соответственно.
Следовательно, мы рассматриваем такие L, А/, что выполняется огра-
ограничение
z>0, A4.2.34)
где z задается выражением A4.2.9). Мы также считаем, что q2 и и удовлет-
удовлетворяют условиям
-Kq2< 1, -я/5< и<2я/5.
Тогда отображение (L, М) в (q2, и) взаимно однозначно.
A4.2.35)
Если q = 0, то из A4.2.28) и A4.2.30) очевидно, что Д = ±ДС, где
5/2
A4.2.36)
Мы будем различать случаи положительных и отрицательных значений па-
параметра q2. Тогда незаштрихованные области плоскости (L, А/), показан-
показанные на рис. 14.4, разделятся на шесть новых областей:
I: А > Дс, q2 < О, -я/5 < и < 0 ,
II: 0 < А < Дс, q2 > 0, -я/5 < и < 0 ,
A4.2.37)
III: - Ас < А < 0, q2 > 0, 0 < и < я/5 ,
IV:A<-AC, q2<0, 0<м<я/5,

ГЛАВА 14 415
V: А > Дс, q2 < О, я/5 < и < 2я/5 ,
VI: О < А < Ас, q2 > О, я/5 < и < 2я/5 .
Области V и VI отличаются от областей I и II только тем, что пере-
переставлены параметры L и А/. Это эквивалентно просто повороту решетки
на 90°, поэтому без потери общности мы в дальнейшем будем рассматри-
рассматривать только области I, II, III и IV.
Указанные области можно классифицировать как области порядка или
беспорядка, рассматривая следующие пределы:
Г. L—> 0, М конечно: z, А —> 0.
II: L, -М->+оо: z-exp(-L-M); Д->0.
HI: L, М^> +оо: z ~ exp(-L - М); - Д -> 0 .
IV: z—» +», L и М конечны: -А —» 0 .
В таких предельных случаях основной вклад в статистическую сумму да-
дают соответственно следующие состояния:
I: вакуум;
II: состояние, аналогичное показанному на рис. 14.5,а, в котором занят
каждый третий узел; если образовать треугольную решетку, добав-
добавляя диагонали, как показано на рис. 14.3, то получится состояние,
показанное на рис. 14.2; существует три таких состояния, соответст-
соответствующих заполнению любой из трех подрешеток;
III: вакуум;
IV: состояние, соответствующее плотной упаковке на квадратной решет-
решетке (рис. 14.5, б); существует два таких состояния.
Состояния в областях II и IV упорядочены; в них происходит спонтан-
спонтанное нарушение трансляционной инвариантности решетки. По-видимому,
такое поведение сохраняется и при конечных значениях L, A/, z, достаточно
близких к соответствующим пределам.
При более строгом подходе мы вычислим параметр порядка R, кото-
который определен выражением A4.1.8). Он равен нулю в областях I и III и по-
положителен в областях II и IV. Таким образом, I и III — области беспоряд-
беспорядка, а II и IV — области порядка.
Мы обнаружим также, что параметр порядка R равен нулю на границах
между областями I и II и между областями III и IV, и свободная энергия
сингулярна на этих границах. Следовательно, в граничных точках, т. е. при
q1 = 0 и Д - ±ДС, рассматриваемая система находится в критическом со-
состоянии.
БОЛЫДМАНОВСКИЕ ВЕСА
Из выражения A4.2.1) следует, что больцмановские веса допустимых
спиновых конфигураций вокруг граней равны

416
ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
i
о,
о,
а б
Рис. 14.5. а — типичное основное состояние в области II; б — основное состояние в
области IV. Темные кружки обозначают частицы. Другие основные состояния мож-
можно получить с помощью однородных трансляций. При этом получаются три основ-
основных состояния типа а и два основных состояния типа б. Если мы добавим
диагонали, как показано на рис. 14.3,я, то частицы в состоянии а будут занимать
одну из подрешеток получающейся треугольной решетки. Следовательно, мы
можем называть состояния а треугольным упорядочением, а состояния б
квадратным упорядочением.
Жирные линии разделяют каждую решетку на четыре квадранта, со-
соответствующие (рис. 13.2) угловым трансфер-матрицам Л, В, С, D (форма внешней
границы изменилась, но в термодинамическом пределе это не существенно). Величи-
Величины а,, а2» аг » • • • в A4.4.16) равны показанным на данных рисунках значениям
спинов (jj, а2> аг » • • • » поэтому оба эти рисунка соответствуют к = 2 в формуле
A4.5.1).
= w@ , 0 , 0 , 0) = т ,
= w(l,0,0,0) =и>@,0,1,0) =
= w@ ,1 , 0 , 0) = *v@ , 0 , 0 ,1) = т z *f, П4.2.38)
Используя выражения A4.2.29) и A4.2.31) для L, М и z, мы можем вы-
выбрать т и t так, чтобы выполнялись равенства
A4.2.39)

ГЛАВА 14 417
я
Параметры т' и /' связаны с исходными величинами т и t. Они тривиаль-
тривиально входят в конечные выражения; статистическая сумма для решетки с N
гранями пропорциональна mrN и не зависит от t'.
Параметризация, использующая
сопряженный модуль
Будем предполагать и использовать определенные свойства аналитично-
аналитичности и периодичности статистической суммы на один узел к и собственных
значений угловых трансфер-матриц. Указанные свойства легче выразить и
понять, если проделать «преобразование сопряженного модуля» от пере-
переменных q2 и и к новым переменным х и w. (Переменную w не следует сме-
смешивать с больцмановской весовой функцией w(a, /?, с, d).)
Используем соотношения A5.7.2) и A5.1.5) для записи бесконечного
произведения в выражении A4.2.28) в терминах сопряженного параметра
Якоби q'. Результат удобно выразить с помощью функции
00
К»,Я) = ПA -<7"-V)(l -9\>~1)A -qn). A4.2.40)
Л = 1
По существу, это просто другой способ записи эллиптической тэта-
функции. Функция/(w, q) обладает следующим свойством симметрии:
f{w,q)=f{qw-\q). A4.2.41)
Функцию/(w, q) иногда будем записывать просто KaK/(w).
При положительных q2 выражение A4.2.28) можно свернуть непо-
непосредственно с помощью A5.7.2а). Если же q2 < 0, то мы должны сначала
разбить произведение в A4.2.28) на члены с четными и нечетными п, а по-
потом использовать формулы A5.7.2а) и A5.7.2г). При этом получаются
тождества
(и,е-)-*-7
A4.2.42)
Определим параметры х, w, а следующим образом:
IhIV (~Kq2<0): q2=-exp(-s)t
A4.2.43)
х = -ехр(-лг/5е), w = ехрBям/е);

418 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
II и III @ < q2 < 1): q2 = ехр(-г),
х = ехр(-4л2/5е), w = ехр(-4ям/е).
Тогда, подставляя тождества A4.2.42) в A4.2.30) и A4.2.39), можно
определить т' и V так, чтобы выполнялись равенства
I и IV (-1 < х < 0):
А = -x[f{x)lf{x2)}\ со, = f(xw)/f(x),
со, = ar-\-xyf(w)/[f(x)f(x2)]\ со3 = г/
СО, = Г
2
А-2 = дс
^2 = <xr-xx*f(w)l[f(x)f(x2)]\ щ = rf(xw~l)/f(x) , A4.2.446)
со, = г wf(x2w-l)/f(x2), co5 = г2 w-lf(xw)/f(x).
Здесь/(w) = /(w, jc5) — функция, определенная выражением A4.2.40), в
котором параметр q заменен на х5. Параметр г пропорционален t' и нахо-
находится в нашем распоряжении; значения а = ± 1 выбраны так, чтобы обес-
обеспечить положительность величины о>2.
Из выражений A4.2.33) и A4.2.39) следует
I: \>w>x2\ II: Kw<jc; A4.2.45)
III: l>w>x; IV: Kw<jc;
A4.2.46)
I и III: a= +1; II и IV: ar= -1.
Преимущество такой параметризации состоит в том, что параметр х
мал в пределе максимального порядка или беспорядка. Это значит, что
бесконечное произведение в определении A4.2.40) функции/(w, x5) быстро
сходится, и полученные результаты легко сравнивать с разложениями в
ряд при высокой и низкой плотностях.
14.3. СВОБОДНАЯ ЭНЕРГИЯ
Резюмируем сказанное выше. Параметризация A4.2.44) получается из
решения соотношения A3.3.6) звезда — треугольник. Если две модели име-
имеют одинаковые значения параметра jc, но разные значения и и г, то их
трансфер-матрицы ряд-ряд коммутируют. Больцмановские веса являются
целыми функциями и.
Перечисленные выше свойства очень похожи на свойства восьмивершин-
ной модели (разд. 10.4). Представим выражения A4.2.32) в симметричном

ГЛАВА 14 419
виде, переставляя L' и А/', что эквивалентно, как это следует из A4.2.29),
замене и' на 7г/5 — и'. После такой замены выражение A4.2.32), принима-
принимает вид
и' = и + и". A4.3.1)
Последнее выражение в точности совпадает с A3.3.10). Отсюда следует,
что формулы A3.3.16) и A3.5.16) — A3.5.27) справедливы для рассматрива-
рассматриваемой модели, если в них X заменить на 7г/5.
Постараемся теперь вычислить свободную энергию с помощью изло-
изложенного в разд. 13.6 приема, связанного с обращением матриц. Для этого
нам нужны аналоги уравнений A3.6.17а), A3.6.176) и A3.7.3) восьмивер-
шинной модели.
Первое соотношение обратимости
Определим трансфер-матрицу для отдельной грани Ui в соответствии с
выражением A3.2.1), в котором больцмановские веса w(a, b, с, d) заданы
формулами A4.2.38). Пусть набор спинов о = [olf ... , от] принимает толь-
только такие значения, что никакие два соседних спина не равны единице. Такое
ограничение соответствует игнорированию запрещенных конфигураций и
может быть записано в виде
ом + 1 = О при / = 1, 2 т - 1. A4.3.2)
Введем такое же ограничение и на набор спинов о' = [о\, ... , о^}. Тогда
при т = 3 имеется пять допустимых значений о и а':[0,0,0], [0,0, 1],
[0, 1,0], [1, 0, 0], [1,0, 1]. При таком упорядочении состояний U2 является
матрицей 5x5:
/
У
Oil
0
Oh
0
о
0
ft>3
0
0
0
oh
0
ft>4
0
0
0
0
0
ft>3
0
0
0
0
0
@5
\
J
A4.3.3)
(В дальнейшем мы будем считать, что все трансфер-матрицы действу-
действуют только между допустимыми состояниями некоторого ряда спинов, т. е.
состояниями, удовлетворяющими ограничению A4.3.2). Размерность мат-
матриц при этом уменьшается. Уменьшение размерности матриц характерно
для обобщенной модели жесткого гексагона и связано с ее разрешимостью,
так как уменьшается число условий, входящих в соотношение
звезда —: треугольник A3.3.7).)
Очевидно, что U2 можно привести к блочно-диагональной матрице, содер-
содержащей блоки
Г **),(«*), (а*). 04.3.4)
\О>2 Щ/

420 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
Справедливо более общее утверждение: к блочно-диагональному виду мож-
можно привести любую матрицу Ui при т > 3 и 2 < i < /w - 1. Отсюда сле-
следует, что если мы введем величины
Щ = 0)А1{Щ0)А ~ (D22), 6J = ~СО2/((О1СОА ~ 0)\) ,
^з = сиз, щ =
и определим матрицу Ut так же, как Ui9 но с заменой wlr... , ы5 на
шр ... , о>5, то получим
UiUi = $, A4.3.6)
где J^— единичная матрица.
Из определения A4.2.40) функции/(дг, q) с q = х5 мы можем установить
следующее тождество:
wf(x2w)f(x2lw) xf\w) ^
fix2) f(x)f(x2) f\x)
(Доказательство аналогично доказательству тождества A5.3.10): иозьмем
отношение левой и правой частей и рассмотрим его как функцию w; пока-
покажем, что такая функция аналитична при 0 < I w I < оо и не изменяется при
замене w на x5w, поэтому она ограничена и, как следует из простого обоб-
обобщения теоремы Лиувилля, постоянна; положив w = 1, найдем, что значе-
значение постоянной равно единице.)
Больцмановские веса w,- (при / = 1, ... , 5) определены в формуле
A4.2.44) как функции от г и w (считая х заданной постоянной); поэтому их
можно записать в виде соДг, w). Подставляя эти определения в A4.3.5) и ис-
используя тождество A4.3.7), находим
d>1=|ft>,(r-\w-1), i=l,...,5, A4-3.8)
где множитель ? задается следующим образом:
I и IV: S = /V)/[/Vh0/(*2/h0],
П4.3.9)
II и III: % = f2{x)l\f{xw)f(xlw)\.
Таким образом, замена wp ... ,о>5 на шр ... ,w5 эквивалентна замене в
A4.2.44) величин г, w на г, vv и умножению каждого веса на ?.
Очевидно, каждую матрицу Ui мы можем расматривать теперь как
функцию г и w. Поскольку матрица U,- линейна относительно ш,, ... , w5, из
выражений A4.3.8) следует, что Ut = {(/Дг, w). Тогда соотношение
A4.3.6) дает
%Ui(r,w)Ui(r\w-l) = 9. A4.3.10)
Данному соотношению удовлетворяют трансфер-матрицы граней G2,
t/3, ... , определенные как функции г и w выражениями A3.2.1), A4.2.38) и

ГЛАВА 14 421
A4.2.44). Фактически соотношение A4.3.10) представляет собой соотноше-
соотношение обратимости A3.6.24). Определим функцию к как корень N-й степени
из собственного значения трансфер-матрицы (U{U3 ... UN_{)(U2U4 ... UN)
диагональ — диагональ, соответствующего собственному вектору с неот-
неотрицательными элементами. Тогда легко видеть, что такая функция к не за-
зависит от г (изменение г эквивалентно просто некоторому диагональному
преобразованию подобия трансфер-матрицы). Функция к зависит от w и,
как следует из A4.3.10), удовлетворяет равенству
'1) = 1. A4.3.11)
Последнее равенство представляет собой соотношение обратимости
A3.6.25). Если переменная w имеет «физические» значения A4.2.45), то все
больцмановские веса ojj, ... , w5 положительны и величина к равна свобод-
свободной энергии на один узел, так же как в выражении A3.1.4). При других зна-
значениях w (особенно при тех, которые достигаются при прохождении через
точку w = 1) функция к, по-видимому, является аналитическим продолже-
продолжением «физической» k(w).
Второе соотношение обратимости
Соотношение обратимости A4.3.11) является аналогом соотношения
A3.6.17а) для восьмивершинной модели. Нам нужен также аналог соотноше-
соотношений A3.6.176), представляющий собой второе соотношение обратимости, кото-
который получается при рассмотрении направления юго-запад — северо-восток.
Напомним, что w(ah ojy ok, gj) — больцмановский вес взаимодействий
между спинами, принадлежащими одной грани и лежащими в узлах /, у, к,
/, как показано на рис. 13.1,я. Ясно, что поворот решетки на 90° эквивален-
эквивалентен замене w(a, /?, с, d) на w(b, с, dy а). Как следует из выражения
A4.2.40), указанная процедура эквивалентна перестановке о>2 с w3 и ы4 с ы5.
Обозначим через Vi трансфер-матрицу грани в направлении юго-
восток — северо-запад. Она задается выражением A3.2.1), в котором вес
w(a, by cf d) заменен на w(b, с, d, а). Обратная матрица Vi может быть по-
получена так же, как обратная матрица Ui для матрицы Ц: нужно лишь в
A4.3.5) поменять местами индексы 2 и 3 и индексы 4 и 5. Проделав указан-
указанные перестановки и повторив выкладки, приводящие к выражению A4.3.10), по-
получим
rj Vi(r, w) Vfrllr , wllw) = S> , A4.3.12a)
где
ri = ~х/ф(х),х-1ф(х),хф(х), -х~1/ф(х),
3 -3/2 2 A4.3.126)
wo= -x\x 5\x,x z
в областях I, II, III, IV соответственно, и
ri=f(x)f(x2)rl/[\x\f(w)f(Wyw)], A4.3.13)
000 = f(x)/f(x2) = H(x)/G(x), A4.3.14)
где функция G(x) и Н(х) определены формулами A4.1.19).

422 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
В действительности существует бесконечное число соотношений вида
A4.3.12), соответствующих умножению веса w0 на целые степени величины
хл. Приведенные выше соотношения гарантируют, что величина w0 близка
насколько это возможно к единице и лежит с той же стороны от единицы,
что и физическое значение веса w, определенное формулами A4.2.45).
Так же, как из A4.3.10) следует соотношение A4.3.11), из A4.3.12) следу-
следует соотношение
Г) k(w) k(wI/w) = 1. A4.3.15)
Аналитичность функции k(w)
При «физических» значениях w, т. е. при значениях, удовлетворяющих
условиям A4.2.45), функция k(w) в выражениях A4.3.11) и A4.3.15) является
статистической суммой на один узел A3.1.4). При других значениях w она,
по-видимому, является аналитическим продолжением «физической» k(w).
Более строго, из разложений в ряд, по-видимому, следует
lnLw^/^w)] аналитична в кольце a <\w\ < bf
A4.3.16)
содержащем точки w = 1 и w = Wq.
Здесь /х = 0, /з, 0, Vi в областях I, II, III, IV соответственно.
Приведенное свойство аналитичности аналогично свойству A3.7.3) вось-
восьмивершинной модели. Здесь не доказывается это свойство, но оно, по-
видимому, справедливо; соответствующие аргументы можно вывести из
уравнений A3.8.31) для угловых трансфер-матриц. В области I данное свой-
свойство приводит к результатам, которые согласуются с выражениями
A4.1.18) — A4.1.20) и, следовательно, с упомянутым в разд. 14.1 исходным
разложением в ряд до 29-го порядка для модели жестких гексагонов. В
дальнейшем будет предполагаться, что выражение A4.3.16) справедливо.
Вычисление функции k(w)
Уравнения A4.3.11), A4.3.12) и A4.3.16) являются аналогами уравнений
A3.6.17а), A3.6.176) и A3.7.3). Так же как последние уравнения можно раз-
разрешить относительно свободной энергии восьмивершинной модели, первый
набор уравнений можно разрешить относительно свободной энергии обо-
обобщенной модели жестких гексагонов.
Чтобы выполнить это, заметим, что из A4.3.16) следует
1п[ц>-ц k(w)] = 2 cnw\ A4.3.17)
П = — <х>
где сумма сходится, когда I w I лежит в окрестности единицы или в окрест-
окрестности w0. Если I w I лежит в окрестности единицы, то из выражений
A4.3.9) и A4.2.20) получаем

ГЛАВА 14 423
In § = d0 + X dn(wn + w-n), A4.3.18)
где при п > 0 введены обозначения
I и IV: d0 = 2 ln/(jc2), dn = (x2n + x3n)/[n(l - x5n)],
II и III: d0 = 2 In/(x), rfn = (л;" + x4n)/[n(l - x5n)].
Взяв логарифмы от обеих частей соотношения A4.3.11), подставляя в него
полученные выше разложения Лорана и приравнивая коэффициенты при
одинаковых степенях w, получаем
cn + c-n=-dn, n^O. A4.3.20)
Аналогично соотношение A4.3.15) дает
сп + Щ2пс-п = -d'n - 2\iIn w06„,0, A4.3.21)
где dn — коэффициенты ряда Лорана функции In rj в кольце, содержащем
точку w = vv0. Из формул A4.3.13), A4.2.45) и A4.2.46) получаем
d'n = A + x5<mwo2n)/[cm(l -x5an)l n=tO.
Уравнения A4.3.20) и A4.3.21) можно теперь разрешить относительно
коэффициентов сп. При этом получаем
Со= -Wo ,
A4.3.23)
сп = {wl?dn - dn)l{\ - wln) при п ? 0.
Точнее, из формул A4.3.19) и A4.3.22) вместе с приведенными выше
определениями а и w0, имеем
Со = — 1п/(;с2) в областях I и IV,
A4.3.24а)
= - 1п/(х) в областях II и III
и при п Ф О
I: cn=-x2n(l+xn)/[n(l-x5n)(l +JC3")],
И:. сп = - х3пA -хп + х2п - хАпI[п{\ - х5п) A - х3")]
1 A4.3.246)
III: сп=- х\\ -хп + х2п)/[пA - х5п)],
IV: сп = - х4пA + хпI[п{\ - х5п) A + х2")].
Статистическую сумму на один узел k(w) можно теперь сразу получить

424 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
из A4.3.17), учитывая, что ц = О, Уз, О, Уг для областей I, II, III, IV соот-
соответственно. Если вычислить величину ш}к/(ш4и>5), а не к, то разложение в
ряд получается более простое. Используя выражения A4.2.44), находим
= - In w -
L'
тт 11 V (xn-x2n)(wn- w~n)
11: = 4 In w + 2j ; ГТ "
i-l ПA-Х3п)
A4.3.25)
III: =0.
TV- 11 V Х^ ~ W
iv. iiS
--iinw-S пA+;с2и) •
Разложим в ряд Тейлора знаменатели в выражениях под знаком сумм в
A4.3.25), просуммируем каждый член по п и используем определение
A4.2.40). Полученные результаты можно записать в виде
1:(о1к/((о4(о5)= w-'fixw^6)^^ ,x6)/[f(xw-\x^f(x^-\x%
И: = wmf{xw~l ,x3)/f(xw,x3).
A4.3.26)
III: =1.
IV: = w-*/(jtw, x4)/f(xw ч , jc4) .
Выражения A4.3.26) справедливы при всех значениях w, удовлетворя-
удовлетворяющих условиям A4.2.45), даже если суммы в A4.3.25) расходятся при неко-
некоторых значениях w. (Нарушение сходимости связано просто с тем, что ш4 и
wj имеют нули в точках w = xhw = x~1b областях I и IV соответствен-
соответственно.)
14.4. ПОДРНШЕТОЧНЫЕ ПЛОТНОСТИ
И ПАРАМЕТР ПОРЯДКА R
С помощью изложенных в разд. 13.5 методов, использующих угловые
трансфер-матрицы, мы можем найти подрешеточные плотности, опреде-
определенные выражением A4.1.4), и вычислить параметр порядка R по формуле
A4.1.8).
Диагональная форма угловых трансфер-матриц
Как мы отмечали выше после выражения A4.3.1), уравнение A3.3.10)
удовлетворяется с помощью рассмотренной параметризации обобщенной
модели жестких гексагонов. Считая матрицы Ап, Вп, Сп, Dn функциями м,
можно снова получить соотношение A3.5.1) и его поворотные аналоги, ко-
которые приводят к выражениям A3.5.27), где Ad(u), Bd(u), Cd(u), Dd(u)

ГЛАВА 14 425
имеют диагональный вид A3.5.20), т. е.
A4.4.1)
и аналогично для Bd(u), Cd(u), Dd(u). Коэффициенты ау одни и те же для
всех четырех матриц, а величины rrij могут быть различными.
Нам нужно лишь вычислить коэффициенты а: и rrij. Как будет показано
ниже, коэффициенты ау- и rrij можно найти, рассматривая случай и = 0, ис-
используя свойство обратимости A4.3.12) и переходя к пределу при х -* 0.
Случай и = 0и первое сотношение обратимости
Из формул A4.2.43) ясно, что при и = 0 величина w равна единице. Как
следует из выражений A4.2.44) и A4.2.38), больцмановская весовая функция
(не путать с переменной w!) в данном случае равна
w(a , Ь , с , d) = rb + d-a-c <5(а, с). A4.4.2)
Отсюда в свою очередь при и = 0 следует
A = C = An=Cn = L, A4.4.3)
где L — диагональная матрица с элементами
Цог, ъ , .. \о[, О2 ,...)= г°1 <5(а!, &г) <5(а2, &2). . . A4.4.4)
Положив и = 0 в выражениях A3.5.27), получим
Q = al@)L-1PAj@),
A4.4.5)
r=c1@)Li?Cd@).
Все такие матрицы имеют блочно-диагональный вид, причем их элементы
равны нулю при ох Ф а/. Отсюда следует, что матрица L коммутирует с
ними. Подставляя выражения A4.4.5) для Q и Т в A3.5.27), можно переоп-
переопределить скалярные множители ах(и), bx(u), Cj(w), dx(u) и диагональные
матрицы Ad(u), Bd(u), Cd(u), Dd(u) так, чтобы выполнялись равенства
An(u) = (n(u)PAd(u)p-\ Bn(u) =b1(u)PBd(k-u)R-\
A4.4.6)
Cn(u) = Cl(u)RCd(u)R-\ Dn(u)=d1(u)RDd(k-u)p-\
где а{@) = Cj(O) = 1 и
= L . A4.4.7)
Данные матрицы могут зависеть от параметра л, входящего в выраже-
выражения A4.2.44), но такая зависимость весьма тривиальна: все матрицы Лп(и),
\ Сп(и\ Cd(u) имеют вид
L х (матрица, не зависящая от г); A4.4.8)

426 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
матрицы Вп(и), Bd(u), Dn(u), Dd(u) имеют такой же вид, но с заменой L
на L~x\ Р и R не зависят от г.
Все элементы диагональных матриц Ad(u), Bd(u), Cd(u), Dd(u) имеют
вид A4.4.1), причем коэффициент ау одинаков для всех четырех матриц.
Используя A4.4.7), получаем
[M«)h = [CdMIw = * ехрЦм), A4.4.9)
где otj не зависит от и и л, а величина 5у, принимая значения спина ох, отве-
отвечающего элементу (/.У)» равна 0 или 1. Из выражений A4.4.6), демонстри-
демонстрирующих зависимость матриц Ап и Сп от г, следует
An{r ,u)An{rl, -u) =ах(и)а{-и) $,
Сп(г , и) Сп(г~1, -и) = ci(n) ci( -и) i.
Следовательно, с точностью до скалярного множителя матрица Ап(г~\
— и) совпадает с матрицей, обратной Ап(г, и). Аналогичным свойством об-
обладает матрица Сп.
Мы могли бы предсказать полученное свойство обратимости непо-
непосредственно из A4.3.10), используя выражения A4.2.43) и тот факт, что
матрицы А и С, так же как в A3.2.4) и A3.2.5), равны произведениям опе-
операторов Uj.
Второе соотношение обратимости
Оператор Vi определяется выражением A3.2.1), в котором больцманов-
ская весовая функция w(a, b, с, d) заменена на wF, с, d, а). Последнее эк-
эквивалентно перестановкам аь с а>3 и а>4 с а>5. Тогда угловые трансфер-
матрицы В и D задаются выражениями A3.2.4) и A3.2.5), в которых каж-
каждый оператор Ui заменен на Vi и использованы подходящие граничные спи-
спины 5, /, ... , у'.
Мы хотим использовать второе свойство обратимости A4.3.12) и полу-
получить уравнения для матриц В и Z), аналогичные A4.4.10), но следует соб-
соблюдать осторожность. Если и = м0, то w = w0 и, как можно видеть из
A4.3.126) и A4.2.44), величина о>3 равна при этом нулю только в областях
III и IV. Следовательно, при и = и0 только в указанных областях оператор
Vi (а следовательно, В и D) диагоналей. Другими словами, мы не можем в
общем случае построить уравнения, аналогичные A4.4.6).
Рассмотрим конфигурацию частиц, показанную на рис. 14.5, а. Это одно из
трех возможных основных состояний системы в области II (два других получают-
получаются с помощью двух последовательных сдвигов всех частиц на один узел вправо).
Угловая трансфер-матрица В, отвечающая правому верхнему квадрату, в основ-
основном состоянии (х = 0) отображает спиновое состояние
OOIOOIOOI...
(на верхнем, выделенном жирной линией вертикальном луче, выходящем
из центра) в спиновое состояние
о#оо#оо#оо ...
(на горизонтальном, выделенном жирной линией луче).
Для бесконечной системы такой результат будет иметь место и при
х Ф 0. При этом матрица В отображает векторное пространство У в век-

ГЛАВА 14 427
торное пространство W. Здесь Г—пространство функций (ох, а2, ...)>
подчиненных условию
а3?->1, Оз*±1->0 при&-> оо ; A4.4.11а)
/? — соответствующее пространство, такое, что
^1, Оък и O3ik + i->0 при/;-» ос . A4.4.116)
Поскольку пространства У и Ж различны, умножение матрицы 5 са-
самой на себя не имеет смысла. Из рис. 14.5,я можно заключить, что матри-
матрица D отображает Ж в V. Вспоминая, что Вп и Dn отличаются соответст-
соответственно от В и D на скалярные множители, из выражений A4.3.12) и
A4.2.43) получаем
Вп(г , и) Dn{rllr , 2щ - и) ос » , A4.4.12)
где w0 — значение и, при котором w = vv0. Подстановка выражений
A4.4.6) для Вп и Dn в последнее соотношение дает
Bd{k - и) Dd{X - 2щ + и) = у(и) LgL, A4.4.13)
где 7(") — скалярный множитель, a Lo — значение матрицы L(r) при
г = г0.
Из замечаний, следующих после формул A3.5.27) и A4.4.9), вытекает,
что Bd(\ - и) и Dd(\ - и) являются диагональными матрицами, (/, J)-
элементы которых имеют вид
[Bd(X - u)]hi = т'}Г5> exp(-o-yw) ,
A4.4.14)
[Dd{X - u)]jj = m]" r~s> exp(-ayw),
где коэффициенты шуи wy не зависят от г и и. Рассматривая диагональный
(/', у)-элемент выражения A4.4.13) и подставляя в него A4.4.14), получаем
mjmj' = у(и) г$> ехрBаг/ио). A4.4.15)
Ясно, что величина у(и) не зависит от w, поэтому ее можно записывать
просто как у.
В A3.1.17) мы выразили локальную плотность <aj> через Ad, Bd, Cd и
Dd. Поскольку данное уравнение было получено из A3.5.27) и A3.1.12) (где
матрицы А у Ву С, D заменены на нормированные Ап, Вп> Сп> Dn), то мат-
матрицы Ad, Bd% Cd, Dd в A3.1.17) являются матрицами Ad(u), Bd(\ - w),
Cd(u). DH(\ - и) настоящего раздела.
(Параметр X не играет в настоящем разделе никакой роли. Он является
частью обозначений для'матриц Bd и Dd, рассматриваемых как функции и.)
Следовательно, можно подставить выражения A4.4.9) и A4.4.14) для
Ad, Bd, Cd, 7)^непосредственно в A3.1.17). Проделав это, обнаружим, что
величины г и и сокращаются в окончательном выражении. (Так и должно
быть, поскольку, используя результаты, аналогичные G.10.28) — G.10.48),
величину <Gj> можно записать в виде t]^S\l/R, где S — диагональный опера-

428 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
тор с элементами ох, a \pL и фк — левый и правый собственные векторы
трансфер-матрицы V ряд — ряд. Такая матрица определена в A3.3.1). Она
не зависит от л, а ее собственные векторы не зависят от и. Следовательно,
< ох > и все корреляции внутри отдельного ряда не должны зависеть от л и
и.)
Для < ох > получаем выражение
2 Sj-mlmJ'/j, m}m]'. A4.4.16а)
Используя A4.4.14), последний результат можно представить в виде
(ел) = 2 stf* expBojuo)/2 rfr ехрBа^0). A4.4.166)
Из A4.4.9) следует
(cji) = Trace 5 A2d(r0, и0) /Trace Л2d(r0, и0). A4.4.17)
Коэффициенты «у
Мы должны вычислить коэффициенты «у. Чтобы сделать это, сначала
используем свойство периодичности, так же как при выводе A3.7.10) для
восьмивершинной модели.
Из A4.2.43) следует, что увеличение и на /е (или /е/2 в областях II и III)
не изменяет w. Тогда, как видно из A4.2.44), не изменяются больцманов-
ские веса и, следовательно, диагональные матрицы Ad, Bd, Cd, Dd. Дан-
Данные матрицы, по-видимому, аналитичны в вертикальной полосе, содержа-
содержащей точки и = 0 и и = и0; поэтому выражения A4.4.9) и A4.4.14) спра-
справедливы в указанной полосе. Следовательно, данные выражения должны
быть периодичными с периодом /е (или /е/2), откуда следует
I и IV: ц = 2лп}/е,
1 } A4.4.18)
II и III: агу= -4ял/е,
где все я ¦ — целые числа. Из выражения A4.4.9) видно, что диагональные
элементы матрицы Ad(r4 и) равны
[Ad(r,u)]jj=r^wn^ A4.4.19)
Поскольку Sj и fij — целые числа, их можно вычислить, рассматривая
подходящий предельный или частный случай. Пусть х — 0, а величина w
остается фиксированной. Так как при этом о>2 в A4.2.44) стремится к нулю,
то из A3.2.1) и A4.3.3) следует, что матрицы Ut становятся диагональны-
диагональными. Поэтому диагональна и матрица Л. Далее из A4.2.43) видно, что
больцмановская весовая функция имеет вид
w(a,b,c,d)= rb + d-2awQ-xbd6{a , с), A4.4.20)
где
г = 0 в областях I и IV,
= 1 в областях II и III.

ГЛАВА 14 429
Подставив последнее выражение в A3.2.1), получаем, что элементы диаго-
диагональной матрицы U; равны
га1-1а1+^ A4.4.22)
Для конечной решетки матрица А, как следует из A3.2.1) — A3.2.3), за-
записывается в виде
ll A4.4.23)
где от + j и от + 2 равны значениям, отвечающим основному состоянию.
Отсюда, используя A4.4.22), получаем, что диагональные элементы матри-
матрицы А равны
Д] = riwb 3 w 2) A4.4.24)
Из выражений A3.1.15) и A4.4.6) видно, что матрицы А и Ad различаются
только скалярным множителем и связаны преобразованием подобия. Они
обе диагональны, поэтому преобразование подобия только переставляет
диагональные элементы.
Пусть <7j, а2, ... , ат + 2 — значения спинов о{, ... , от + 2, отвечающие
основному состоянию. Данные значения соответствуют максимуму выра-
выражения A4.4.24) при (г = 1); поэтому Ad можно рассматривать как диаго-
диагональную матрицу с элементами
H^,a = r!(V(°), A4-4.25)
где через о обозначен набор спинов [ох, ... , от] и
s{a) = ох,
Л A4.4.26)
п(а) = 2j i(Oi+i - + &)
i
Полученный результат имеет ожидаемый вид A4.4.19) с той лишь раз-
разницей, что индексу заменен на а. Ясно, что s(a) и п(а) — целые числа, поэ-
поэтому выражение A4.4.25) справедливо не только в пределе х -* 0, но и при
всех х (при условии что т — оо). Из A4.4.17) следует
(а,) = 2 аАМп(а)/2 frvW». <14-4-27)
а /а
Мы получили общую формулу для плотности на данном узле (узле 1).
При вычислении суммы следует помнить, что спины olf ... , от не полнос-
полностью произвольны: они должны удовлетворять условиям
О№ + 1 = 0 при i = 1 , т . A4.4.28)
Как отмечалось после формулы A4.3.3), данное условие учитывалось в
проведенных выше рассуждениях при определении векторных пространств,
на которых действуют трансфер-матрицы. Оно просто соответствует тому
факту, что никакие две частицы не могут находиться на соседних узлах.

430 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
Симметрии
Угловые трансфер-матрицы Лу Ву С, D удовлетворяют различным со-
соотношениям симметрии. В настоящем разделе мы не использовали такие
соотношения, но полезно иметь о них представление.
Из выражения A4.2.38) следует, что больцмановские весовые функции
удовлетворяют равенствам
w(a , Ъ , с, d) = w(c , b , а , d) = w(a , d , с, b\ A4.4.29)
которые в точности соответствуют соотношениям A3.5.4). Из них следует,
что модель симметрична по отношению к отражению от любой диагонали
решетки. Такая симметрия не нарушается спонтанно в областях I, III, IV
(область IV отвечает упорядоченным состояниям, но из рис. 14.5,6 очевид-
очевидно, что каждое основное состояние обладает указанной симметрией); сле-
следовательно,
I, III, IV: Л=ЛТ=С=СТ, B = BT = D = DT. A4.4.30)
Поэтому матрицы Р и R в A4.4.7) равны и ортогональны.
Основные состояния в области II показаны на рис. 14.5,я. Очевидно,
что они симметричны относительно отражения от диагонали, проведенной
с юго-востока на северо-запад, но не от диагонали юго-запад — северо-
восток. Отсюда следует, что в общем случае в области II выполняются
только соотношения
II: Л=Л\ С = СТ, B=DT. A4.4.31)
Матрицы Р и R ортогональны, но не обязательно равны.
С другой стороны, если центральный узел лежит на выделенной на
рис. 14.5,а подрешетке, то симметрия относительно отражения от диагона-
диагонали юго-запад — северо-восток фактически сохраняется и соотношения
A4.4.30) оказываются справедливыми. В соответствии с классификацией,
рассмотренной ниже, это случай, когда к = 1 в области II.
14.5. ТОЧНЫЕ ФОРМУЛЫ ДЛЯ
РАЗЛИЧНЫХ СЛУЧАЕВ:
ТОЖДЕСТВА РОДЖЕРСА — РАМАНУЯНА
Суммы, входящие в выражение A4.4.27), можно вычислить, но при
этом следует рассмотреть семь различных случаев. Одна из причин состо-
состоит в том, что величина п(о) имеет различный вид в A4.4.26) в зависимости
от равенства параметра т нулю или единице. Другая причина — граничные
условия: спины om + j и от + 2 должны иметь значения, отвечающие основ-
основному состоянию. В областях I и III основное состояние одно:
I и III: а; = 0, /=1,2,3,... A4.5.1а)
В области IV система находится в упорядоченном состоянии на квадрат-
квадратной решетке, показанном на рис. 14.5,6. Существует два основных состоя-
состояния

ГЛАВА 14 431
IV: Оц + ь - 1) 02/ + * +1 ~ 0, при всех целых /, A4.5.16)
где к = 1 для одного состояния и к = 2 для другого. В области II система нахо-
находится в упорядоченном состоянии на треугольной решетке (рис. 14.5,я); имеется
три основных состояния:
II: <J3; + * = 1, о3] + к±1 = 0, при все целых / , A4.5.1в)
где к = 1, 2, 3 для трех основных состояний соответственно.
Следовательно, чтобы вычислить A4.4.27), мы сначала фиксируем об-
область и (для областей II и IV) значение к. Затем можно провести суммиро-
суммирование по наборам о = (<7j, a2, ... , ат), удовлетворяющим условиям
A4.4.28). Мы обнаружим, что суммы сходятся к соответствующим преде-
пределам при т — оо. Результат равен плотности р или (в областях II и IV) под-
решеточным плотностям рк.
Выполнив суммирование по ар можно записать выражение A4.4.27) в
виде
Pk = (о,) = &{1)/[Щр) + rgFTCl)] , A4.5.2)
где введено обозначение
F(aO= 2 wl<°\ A4.5.3)
02,ОЗ,..,От
причем при рассмотрении областей I и III индекс к писать не нужно. Сле-
Следовательно, вычисления проводят в три стадии: вычисляют F@) и F(\) по
формуле A4.5.3), находят <aj> по формуле A4.-5.2) и (для областей с упоря-
упорядочением) вычисляют R по формуле A4.1.8).
Область I
Из A4.4.2П и A4.3.126) получаем
т = 0, wo= -x\ ti = -х G(x)/H(x) , A4.5.4)
где — 1 < х < 0, а G(x), Н(х) определены в A4.1.19). Из выражений
A4.5.3), A4.4.26) и A4.5.1а) следует
( ^ ...> A4.5.5)
О2,Оз,...,От
где q = Wq = х6, поэтому 0 < q < 1.
Рассмотрим сначала основное состояние, в котором все спины а2,
а3, ... равны нулю, затем рассмотрим состояния, в которых один из них
равен единице, а потом состояния, в которых два спина равны единице, и
т. д. Взяв предел при т — оо и вспоминая условия A4.4.28), получаем
<14-5-6>

432 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
Полученные ряды хорошо известны в математической теории распределе-
распределений ([5], гл. 7). Из выражения A4.5.5) легко видеть, что отношение
F(l)/F@) (которое входит в A4.5.2)) равно цепной дроби
1/A + ql{\ + q2/(l +q3/---))). A4.5.7)
Следующие равенства, полученные Роджерсом [200] и Рамануяном
[198], не столь очевидны:
F@) = 1/[A -q){\ -<74)A -<?6)A -q*){\ -<?") • • •] = G{q) ,
П4.5.8)
q12) • • •] = H(q),
где функции G(q) и H(q) определены формулами A4.1.19). Таким образом,
функции G и Н появляются не только в выражениях A4.5.4) для г\, но так-
также и в формулах, определяющих F@) и F(\). Используя тождество A5.9.2),
выражения A4.5.8) можно записать в виде
F@) =
л = 0
A4.5.9)
2 - qn+1).
2
где "-0
Тождества, вытекающие из A4.5.6) и A4.5.8), известны как тождества
Роджерса-Рамануяна. Существует много обобщений этих тождеств [210].
Замечательно, что многие из таких обобщений естественным образом воз-
возникают в ходе наших рассуждений. Например, подставляя A4.5.8) в A5.5.2)
и используя A4.5.4) и равенство q = х6, получаем
р=-хG{x)Щхь)/[Н(х) G(x6) -xG{x)H(x6)]. A4.5.il)
Заметим, что знаменатель этого выражения можно записать в виде бес-
бесконечного произведения того же типа, что и в разложениях тэта-функций
A5.1.5). Как установил Рамануян (см. [54]) и доказал Роджерс [201],
Н(х) G(x6) - х G(x) H(xb) = Р{хIР{хъ) , A4.5.12)

ГЛАВА 14 433
где
00
Р(х) = Hil-X2"-1). A4.5.13)
п ~ 1
Следовательно, окончательно находим, что плотность р равна
р = -х G(x) H(x6) Р(х3)/Р(х2) . A4.5.14)
Удивительно, ч^то тождества Роджерса — Рамануяна появились в рас-
рассматриваемой задаче; с их помощью очень удобно приводить результаты к
более простому виду. В частности, они полезны при рассмотрении крити-
критического поведения при 1x1 — 1; при этом G(x), Щх) и Р(х) связаны с эл-
эллиптическими функциями, и их поведение вблизи I a* I = 1 можно получить
из тождеств «сопряженного модуля», таких, как A5.7.2). Я не знаю других
прямых методов для изучения исходных выражений A4.5.6).
Область II
Если изучение области I проводится легче всего, то область II является
наиболее трудной. Величина п(о) существенно более сложна, и в данной
области имеется три основных состояния. В формуле A4.5.1в) им соот-
соответствуют значения к — 1, 2, 3 и каждому основному состоянию отвечают
свои функции F@) и F(\) и свои локальные подрешеточные плотности рк.
Из A4.4.21) и A4.3.126) следует
т=1, wo = Jr3/2, rl = x-lH(x)/G(x), A4.5.15)
где 0 < х < 1. Из A4.5.3), A4.4.26) и A4.5.1в) получаем
F{O\)= 2 ^¦(ад+г-а.-н+ф + О^ A4.5.16)
О2,ОЗ,...,От
где q = х3, внутреннее суммирование проводится по целым числам / от 1
до w, величины а; заданы в A4.5.1в) и а1э ... , от должны удовлетворять
условиям A4.4.28).
Для вычисления F@) и F(\) мы выведем рекуррентные соотношения.
Введем определение
G(oh а/+1) = 2 42'(a'a'+2~ai+1 + di+1), A4.5.17)
tf/ + 2,...,Om
где внутреннее суммирование проводится от / = / до / = т. Вычисляя сум-
сумму по Gj + г, легко проверить равенства
G/(O,1)=0#~'G,+,A,O), A4.5.18а)
G,(l ,0) = 0,[G/+,(O ,0) + q'Gl+l@ ,1)],

434 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
где
R, = <7'при(/ - к + 1)/3, равном целому числу,
A4.5.186)
= 1 в остальных случаях
F(O) = Go(O,O)=Go(l,O), F(l) =GO(O,1). A4.5.19)
Каждая из функций G/(o, о') при т — оо стремится к некоторому преде-
пределу. Эти пределы удовлетворяют равенствам
G,@,0)=(l-<?)-'
при условии, что / велико и (/ — к)/3 — целое число.
Рекуррентные соотношения A4.5.18) и граничные условия при больших /
A4.5.20) определяют G,. Функции F@) и F(l) можно получить затем из
A5.5.19). Обозначая зависимость от к в виде Fk@), Fk(l), находим
/7,@) = 1 + 2q + 2q2 + 4<?3 + 5<?4 + Sq5 + llq6 + . . . ,
Fi(l) = 1 + q2 + 2q3 + 3qA + 4q5 + lqb + . . . ,
v J ч ч ч ч ч 7 A4.5.21)
F2@) = F3@) = 1 + q + 2q2 + 3q3 + 5qA + lq5 + 10<?6 + . . . ,
F2(l) = F3(l) = q + <72 + 2G3 + 2g4*+ 4^5 + 5^6 + Sq1 + . . . .
В областях I, III и IV функции F@) и F(l) можно записать в виде рядов,
подобных рядам в A4.5.6) (это можно сделать, рассматривая Gt как функ-
функцию / и разлагая ее по степеням ql, как в.формуле A4.5.35)). Затем мы мо-
можем использовать подходящие аналоги тождеств Роджерса — Рамануяна
A4.5.6) — A4.5.8) для записи F@) и F(\) в виде простых произведений тэта-
функций.
В области II соответствующая программа более сложна. Однако Энд-
рюс [6] показал, что каждую функцию Fk@) и F^(l) можно записать в виде
двойного ряда, и, используя такие разложения, получил выражения
' 2 (-1)у5«с+1>/2[<7-4" - ч4п+4 + ч(я~п - чп+1)},
"-° A4.5.22а)
{)q \q q
п — О
A4.5.226)
F2@) = F3@) = [Q{q)Yx 2 (-1)у5„(„ + 1)/2^-бП -qt*+*) A4.5.22в)
п=0

ГЛАВА 14 435
F2(l) = F3A) =q[Q(q)]~1 2 (-l)^1^^1^-3"-^*3). 04.5.22т)
n = 0
Данные выражения похожи на A4.5.9): наиболее очевидное различие состо-
состоит в том, что два первых выражения содержат сумму двух разложений
тэта-функций вместо одного.
Рассмотрим сначала случаи к = 2 и к = 3. Используя A5.9.2) и опреде-
определения A4.5.8), A4.5.10) функций G, Hy Q, можно записать выражения
A4.5.22b) и A4.5.22г) в виде
F2(l)=F3(l)=qQ(ql5)/[Q(q)G(q3)]y
F2@) = F3@) = Q(ql5)/[Q(q) H(q*)]. ^'^
Из выражений A4.5.15) имеем r$ = x~ !//(.x:)/G(.x:) и q = x5. Подставляя
A4.5.23) в A4.5.2), получаем
Р2 = р3 = *2Я(х) H(jc9)/[G(jc) G(x9) + х2Н(х) Н(х9)]. A4.5.24)
Обратимся теперь к списку тождеств Рамануяна, приведенному Берчем
[54], и найдем, что из уравнения F) этой работы следует
G(x) G(x9) + хЩх) Н(х9) = [Q(x3)]2/[Q(x) Q(x9)]; A4.5.25)
поэтому выражение A4.5.24) упрощается и принимает вид
Р2 = р3 = хЩх) Н(х9) Q(x) Q(x9)/[Q(x3)]2. A4.5.26)
Случай к = 1 более сложен, но из A4.5.22а) и A4.5.226) можно устано-
установить следующее:
F,@) = [G(*9) Q(*9) - Н(х) Q(x)]/[x G(x3)],
A4.5.27)
( 29 93
(Для этого нужно разложить числители в правых частях A4.5.27) в ряды,
используя тождества, вытекающие из A4.5.8) и A4.5.9). Ряды, отвечающие
произведениям H(x)Q(x) и G(x)Q(x), разобьем на три части: члены с
п = За*, п = За* + 1 и я.= Зг + 2. После некоторых сокращений, вспоми-
вспоминая, что q — л:3, получим выражения A4.5.22). В частности, из проведен-
проведенных рассуждений следует, что правые части выражений A4.5.27) можно
разложить по степеням х3, что совершенно не очевидно.)
Подставляя выражения A4.5.27) для /^@) и Fj(l) в A4.5.2) и используя
A4.5.15), получаем
рх = Н(х) [G(x) Q(x) + x2H(x9) Q(x9)]/\Q(x9) [G(x) G(x9) +
A4.5.28)
Используем снова тождество Рамануяна A4.5.25) для упрощения знамена-

436 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
теля в A4.5.28); при этом получим
pi = Н{х) Q(x) [G{x) Q(x) + х2Н(х9) Q(x9)]/[Q(x3)]2. A4.5.29)
Подставляя выражения для р{ и р2 в A4.1.8), получим параметр порядка
R = Pl-p2= G(x) Щх) [Q(x)/Q(x3)]2
A4.5.30)
= Q(x) EУШ(')J
= П A - Л С1 -х5п)/A -х3пJ. A4.5.31)
п = 1
Последнее выражение весьма похоже на формулу A3.7.21) для параметра
порядка восьмивершинной модели.
Область III
В данном случае аналоги выражений A4.5.15) и A4.5.16) имеют вид
т=1, wo = x, ri = xH(x)/G(x), A4.5.32)
F(al)= X 9***+1-™+2) 9 A4.5.33)
О2,...,От
где 0<л:< 1,д = х2иаш+ j = а/й + 2= 0. Выражение A4.5.33) совпада-
совпадает с A4.5.16), где а, = 0 и параметр q заменен на q~l. Следовательно,
функции F@) и F(\) можно вычислить с помощью рекуррентных соотноше-
соотношений A4.5.8), в которых /3/ = 1 и проведена замена q на q~l, и используя
равенства A4.5.19). Снова рассмотрим предельный случай больших т. Тог-
Тогда граничные условия при больших / имеют вид
G{O,l)=G(q), 04.5.34)
Разложим функцию G/ по степеням ql и систематически будем вычис-
вычислять коэффициенты разложения, используя формулы A4.5.18) (с заменой q
на q~l). Проделав это, найдем
G,@,l)= Lqnl'2n-2an-x/{\-q2n-1), A4'535)
П 1

ГЛАВА 14 437
где а0 = 1 и
ап = q^-2an-xl[{\ - qn) (I - q2n'1)] A4.5.36)
при п > 1. Вычисляя ап из последнего соотношения и используя A4.5.19),
получаем
00
F@) = 2 qn{3n-l)/2/[(l-q)(l-q2).. • A "Я*)*
A4.5.37)
х A -
Выражения A4.5.37) можно упростить с помощью тождеств
Роджерса — Рамануяна D6) и D4) из списка Слэтера [210]. При этом получаем
F@) = G(q2) Q(q2)/Q(q),
A4.5.38)
Из выражений A4.5.2) и A4.5.32) следует
р = х Щх) H(xA)/[G(x) G(jc4) + х Щх) Щх')]. A4.5.39)
Рамануян (см. [54] установил, а Роджерс [201] доказал равенство
G(x)G(xA) +хЩх)Щх*) =[Р(-х)}\ A4.5.40)
где функция Р(х) определена формулой A4:5.13). Следовательно, выраже-
выражение A4.5.39) упрощается и приводится к виду
р = х Щх) ЩхУ[Р(-х)]2. (Н-5.41)
Область IV
Данная область является областью упорядочения, и в выражении
A4.5.16) мы должны различать два случая: к = 1 и к = 2. Из формул
A4.4.21), A4.13.126), A4.4.26) и A4.5.3) следует
т = 0, w0 = x~2, ri = -jc G(x)/H(x) , A4.5.42)
F(ol)= 2 qWb+i-**!)^ A4.5.43)
O2,..,Om
где — 1 < x < 0, q = x4. Величины а, определены в A4.5.16), и суммирова-
суммирование в A4.5.43) выполняется, как обычно, по всем значениям @ и 1) спинов
а2, ... , ат, которые удовлетворяют условиям A4.4.28), где
°т + 1 "= °т + 1 •

438 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
Так же, как в областях II и III, можно вывести рекуррентные соотноше-
соотношения, которые задают F@) и F(l). Введем определение
GiOi)^ 2 д*^-°'^у A4.5.44)
Ol+i,... ,От
где внутреннее суммирование проводится теперь по / = /, ... , т. Рассмат-
Рассматривая вклады от о{ + { = 0 и а1 + х = 1, получаем
G,(l) = /3,G,+1@), A4-5'45a)
где
pi - 1 при/ - /с четном,
A4.5.456)
= д'при/ — /: нечетном.
Очевидно, что
F@) = d@), F(l) = G,(l) . A4.5.46)
Каждая функция Gt(o) стремится к пределу при т — оо, и соответствую-
соответствующие предельные значения удовлетворяют граничному условию
G/(O)->A -q)~\ G/A)->1 при /^оо A4.5.47)
при условии, что / — к — четное число.
Разложим бДО) и G,(l) по степеням ql. Подставляя разложения в
A4.5.45) и сравнивая коэффициенты при четных / — к> находим
A4.5.48)
где а0 = 1 и
Последнее уравнение можно решить последовательно для а{, а2, аъ и
т. д. и определить F@) и F(\) из выражений A4.5.46) и A4.5.48). (При
к = 2 нам нужны G/ для нечетных I — к. Такие функции легко найти из
A4.5.45).) Указывая зависимость F@) и F(\) от к с помощью индекса, полу-
получаем
F,@) = 2 qn2+n/[(l -q)i\ ~q2). . . A ~q2n + 1)],
F,(l) = 5 qn2+nl[(\-q)(\-q2).. . A -g2")], A4.5.50)
0

ГЛАВА 14 439
F2@) = 2 qn2/[(l -q){l-q2)... A - q2n)) ,
2()
n=l
Используя тождества (94), (99), (98) и (96) Роджерса — Рамануяна из
списка Слэтера [210], находим
F1@)=H(-q)/P(q),
F,(l) = G{-q)IP{q),
F2@) = С{ЧУР(Ч), A4551)
F2(l)=qH(qyP(q),
где функции G, Я, Р, Q определены выражениями A4.5.8), A4.5.13) и
A4.5.10).
Подставляя эти результаты в A4.5.2) и используя A4.5.42) и равенство
q = х4, получаем
р, = G(*) G(-x4)/[G(x) G(-x4) -xH(x)H(-x*)]y
A4.5.52)
Знаменатель в первом из этих выражений, по-видимому, не изучался Ра-
мануяном, но он установил, а Уотсон [247] доказал уравнение
G(x) Щ-х) + G(-jc) H(x) = 2/[Р(х2)]2 A4.5.53)
(это уравнение B3) в работе Берча [54]). Далее Роджерс [200] показал, что
G(-*4) = Q(x2)[H(x) + Я(-д:)]/[2е(^8)], ^ ? ^
Н(-х') = Q(x2)[G{x) - G(-x)]/[2xQ(x*)}.
Из приведенных трех тождеств следует
G(jc)G(-jc4) -xH(x)H(-x*) =Р(-х2). A4.5.55)
Кроме того, Рамануян установил (см. [54]), а Роджерс [201] доказал
тождество
Н{х) G(jc16) - jc3G(jc) H(x16) = Р(-х2). A4.5.56)
Используя последние два тождества, мы можем упростить выражения
A4.5.52); они принимают вид
),
A4.5.57)
= -x3G(x) H(xl6)/P(-x2).

440 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
Роджерс [200] доказал, что
Н{ххь) = Q(x2)[H(x) - H(-x)]/[2x3Q(x8)]. A4.5.58)
Подставляя последнее выражение для Н(х16) и формулу A4.5.54) для
G( —х4) в A4.5.57), получаем среднюю плотность
Р = «Р. + Рг) = *ОД Щ-х) [Р(х2)J A4.5.59)
и параметр порядка
R = Pl-p2=G(x)H(x)[P(x2)]2
= [Q(x2)]2 Q(x5)/{Q(x) [Q(x*)J} (,4.5.60)
00
= П A -х2"J^ -*5")/[(l -x")(l -x*"J).
Параметр порядка в виде отношения произведений Q-функций имеет
форму, аналогичную выражению A4.5.30) для R в области II и выражению
A3.7.21) для параметра порядка восьмивершинной модели.
Таким образом, завершен вывод выражений для подрешеточных плот-
плотностей и параметра порядка обобщенной модели жесткого гексагона. Мы
рассмотрели отдельно четыре области, но теперь можно видеть некоторые
общие черты; нам удалось найти рекуррентные соотношения, определя-
определяющие Fk@) и Fk(l). В областях I, III и IV выражения для Fk@) и Fk(l) пред-
представлены в виде бесконечных рядов. Затем мы использовали подходящие
тождества Роджерса — Рамануяна из списка Слэтера [210] для записи Fk@)
и Fk(l) в виде бесконечных произведений типа тэта-функций. (В области II
программа оказывается более сложной, но в данном случае также удается
записать Fk@) и Fk(\) в виде суммы самое большее двух произведений типа
тэта-функций.) Далее, подставляя полученные результаты в A4.5.2), мы
обнаружили, что знаменатели соответствующих выражений можно упро-
упростить с помощью тождеств Рамануяна из списка Берча [54]. Наконец, най-
найдено, что в областях II и IV параметр порядка R = рх — р2 равен отноше-
отношению произведений Q-функций.
Удивительно, что тождества Роджерса — Рамануяна и тождества Раману-
Рамануяна появляются так часто в данной главе. Первые сигналы, предупрежда-
предупреждающие о появлении этих тождеств, можно увидеть в соотношениях
звезда — треугольник A4.2.3), в частности в параметризации с помощью
эллиптических функций A4.2.11). Такая параметризация автоматически ве-
ведет к выражениям A4.2.29) — A4.2.30) и, следовательно, к A4.2.44). По-
Последнее уравнение содержит много множителей/(л:, л:5) и/(л:2, л:5). Из вы-
выражений A4.2.40), A4.1.21) и A4.1.19) следует, что такие множители в точ-
точности равны функциям H(x)Q(x) и G(x)Q(x). Естественное возникновение
этих функций (особенно их отношений) должно подготовить нас к появле-
появлению тождеств Роджерса — Рамануяна.

ГЛАВА 14 441
14.6. АЛЬТЕРНАТИВНЫЕ ВЫРАЖЕНИЯ
ДЛЯ ФУНКЦИЙ к, р, R
Полученные результаты можно суммировать следующим образом. Для
заданной модели жестких квадратов с активностью z и коэффициентами
взаимодействий L, А/, удовлетворяющими условию A4.2.9), вычисляют ве-
величину А по формуле A4.2.10). Из соотношений A4.2.37) определяют об-
область, которой соответствует данная модель (если данная модель лежит в
областях V или VI, то следует поменять местами коэффициенты L и М).
Вычисляют х и w(w, / и г) из выражений A4.2.38) и A4.2.44). Тогда стати-
статистическая сумма на один узел к определяется формулой A4.3.26), а плот-
плотность р (или для областей II и IV подрешеточные плотности рк) и пара-
параметр порядка R определяются подходящими выражениями из разд. 14.5.
Все результаты выражены через бесконечные произведения, которые хо-
хорошо сходятся при малых х; малым значениям параметра х соответствуют
состояния системы вблизи полного беспорядка или полного порядка. Полу-
Полученные выражения удобно сравнивать с разложениями в ряд^при низкой
или высокой плотности. На рассматриваемые бесконечные произведения
сходятся очень плохо, когда I x I близки к единице, что происходит при
I Д I, близких к Ас, когда система находится в состояниях вблизи критичес-
критической точки. Поэтому удобно преобразовать произведения к виду, быстро
сходящемуся при I x I , близких к единице.
Часть такой процедуры уже выполнена: мы просто перейдем от уравне-
уравнений «сопряженного модуля» A4.2.44) для w и х к исходным уравнениям
A4.2.29) — A4.2:31) для q2 и и.
Статистическая сумма на один узел к
Чтобы преобразовать уравнения A4.3.26) для к, используем тождество
A4.2.42) для перехода от/-функций к ^j-функциям. Проделав это, мы обна-
обнаружим, что нам потребуется также эллиптическая тэта-функция
00
Ни ,Ч2) = П A - 2q2n~1 cos2h + tf4"-2)(l -q2n), A4.6.1)
П = \
которая удовлетворяет соотношению «сопряженного модуля»
в<(и, е-) = (^V ехр[- ф + М?Е^)]/(_е-4)Ш/е) е-^?) A4.6.2)
Из уравнения A4.3.26), используя A4.2.43) и A4.2.38) и применяя тож-
тождества A4.2.42) и A4.6.2), получаем следующие выражения для к в четырех
областях:
I: Kl(mzeL+M) = - ч" " ' w 3 '

442ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
II: = (
HI: = 1 , A4.6.3)
IV: = t
Здесь
p = e-e= |<72|, A4.6.4)
где величина q определена в A4.2.28) и A4.2.29). Таким образом, мы вы-
выразили результаты для функции к через параметры q2 и и, входящие в
A4.2.29) — A4.2.39).
Параметр т введен в A4.2.1) как простой множитель, на который умно-
умножается каждый больцмановский вес. Следовательно, он входит в виде мно-
множителя и в выражение для к, поэтому к/т не зависит от т. Таким обра-
образом, выражения A3.3.26) и A4.6.3) справедливы при всех значениях т (и
при т = 1), несмотря на то что в A4.2.44) был использован частный вы-
выбор т.
ПОДРЕШЕТОЧНЫЕ ПЛОТНОСТИ рк
И ПАРАМЕТР ПОРЯДКА R
Все результаты разд. 14.5 выражаются через функции G(x), H(x), Q(x),
Р(х), где
00
G(x) = П [A - х5"-4) A - л5"'1)]-1, A4.6.5а)
00
Н(х) = П [A - Х5п~ъ) A - х5")], A4.6.56)
я = 1
Q(x) = П A " хп) , A4.6.5в)
00
Р(х) = П (Г- х2п'1) . A4.6.5г)
Мы можем использовать тождества A4.2.42) и A4.6.2) для преобразова-
преобразования бесконечных произведений в A4.6.5) к виду, который быстро сходится
при х, близких к + 1 или - 1. (Для этого рассмотрим выражения A4.2.42) в
пределе и — 0 и извлечем кубический корень из обеих частей данных выра-
выражений. При этом получаем преобразованную формулу для Q(x). Осталь-
Остальные формулы можно получить затем непосредственно.)
При выполнении указанной процедуры возникают две новые функции:
Gj(x) и Нх(х), определяемые выражениями

ГЛАВА 14443
A4.б.5д)
Н1(х) = BsinyIn[l-2r"cosy + x2"l1. A4.6.5e)
Мы получаем тождества
Q{t~e) = Bл/е^ ехр \^- - —1 ??(ехр[ - 4л2/е]) , A4.6.6а)
Р(е'е) = 2*ехр - — - — /р(ехр[ -2т^1е\), A4.6.66)
G(^e) = ехр [ - ^ + — J Gi(exp[ - 4^/5e]), A4.6.6b)
Я(е"е) = ехр —^ 4- — Hi(exp[ - 4^/5^]), A4.б.6г)
Q{-t~?) = (л/е)*ехр [^-- —-1 С(-ехр[-я2/г]), A4.б.6д)
- e"«) = exp [ - ± + ^] P( - exp[ - я2/е]) , <14.6.6e)
J H( [ 2/5])A46.6ж)
G( - e"?) = exp [ - ^ + —J Hx( - exp[ - л2/5е]), A4.6.6
Я( - e"?) = exp [^ + ^J G,( - exp[ - я2/5?]). П4.6.6з)
Применяя эти тождества к формулам разд. 14.5 для р и /?, находим
I: р = Я,( - р) Нх(рт) Р( -р513)/Р( -р5),
II: ft = рз = Я,(р) Я^1'9) Q(p5) Q(p5l9)/Q4p5e),
R = р, - р2 = C/V5)p"9e(p5) 2(p)/Q2(p5/3).
A4.6.7)
III: p = Hl(p)Hl(pliyP2(-p5"),
IV: Pl = Я,( - p) Я,( - p1/4)/P( - p512),
= Hl(-p)H1(pw)/P(-p5>2),
= Kp, + p2) = я,( - p) нх{р*IР2(рь),
e( - p) Q2{pw)l[Q( - p5) Q2(p5)] ¦

444 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
В области II не существует простого выражения для рх и для
р = (pj + р2 + ръ)/Ъ в виде произведения функций, но можно показать,
что р разлагается по целым степеням параметра р/з.
Параметр р в формулах A4.6.3) и A4.6.7) определен в A4.6.4), где вели-
величина е в свою очередь задается выражением A4.2.43), a q2 — выражениями
A4.2.28) — A4.2.31). В частности, из A4.2.30) следует, что р можно опреде-
определить из соотношения
A2/5=Hl(±p)/Gl(±p), A4.6.8)
выбирая положительные знаки для областей II и III и отрицательные знаки
для областей I и IV. Подчеркнем, что параметр р неотрицателен.
Критические сингулярности
Наши результаты представлены теперь в таком виде, что можно об-
обсуждать поведение системы при пересечении границ между областями
I — II и III — IV. Из выражения A4.2.37) следует, что пересечение проис-
происходит при А = ±АС и q2 = р = 0.
Мы изучали модель жестких квадратов с диагональными взаимодейст-
взаимодействиями только при выполнении условия A4.2.9). Такое ограничение означа-
означает, что мы рассматриваем не полное (L, М, ^-пространство параметров, а
только двумерную поверхность1 в нем A4.2.9).
Рассмотрим линию на такой поверхности, пересекающую границу
А = ±АС в точке С и не являющуюся касательной к ней. Будем считать к,
р и R функциями от положения на данной линии. Они аналитичны всюду,
кроме точки С. Параметр порядка R тождественно равен нулю на той сто-
стороне от точки С, где находится область беспорядка (области I и III), и по-
положителен на той стороне, где находится область упорядочения (области II
и IV). Таким образом, С — критическая точка.
Параметры и и q1 определены выражениями A4.2.28) — A4.2.31). Они
оба являются аналитическими функциями положения вдоль линии даже в
точке С. В точке С параметр и не равен нулю, a q1 обращается в нуль ли-
линейно относительно положения на линии. Следовательно, мы можем рас-
рассматривать q2 (или —q2) как переменную, описывающую «отклонение от
критической точки» и соответствующую переменной t в разд. 1.1.
Определим величину t следующими выражениями:
Тогда переменная / положительна в неупорядоченных областях и отрица-
отрицательна в упорядоченных. Она линейно обращается в нуль в точке С. Мы
хотим получить ведущий член разложения функций к, р, R при малых t.
Это легко сделать, используя результаты A4.6.3) и A4.6.7), а также
определения A4,2.28), A4.6.1) и A4.6.5). Мы получаем

ГЛАВА 14 445
I и И:
mz
5)/3] _ 2V5 5/3 sjnAOu/3) + 0(,ю/з)} ^ A4.6.10)
=
sin[(tf + 5m)/3J
III: = 1 ,
IV: = 1 - 4( -1M'2 sin 5м + <S(t5),
I и II: p = pc - sgn(f) MM/V5 + 0X0 ,
III: p = Pc~ '1/4/V5 + O(f1/2), A4.6.11)
IV: p=pc+0@,
II: R = C/V5) ( - 01/9{l +t + 2(- 05/3 + 002)},
IV: R = B/V5) ( - 01/4U - f + Ч'2)}- A4-6-12>
Здесь критическая плотность рс равна
pc = E - V5)/10 = 0.27639 .... A4.6.13)
Мы ожидаем, что R и ведущие сингулярные члены функций к и р при
малых t ведут себя как
R ~ ( - 0', *sing~ Г2"", psing~ Г1"*, A4.6.14)
где /3, а, а — критические показатели из выражений A.1.14) и A.7.9). Из
формул A4.6.10) — A4.6.12) следует, что в рассматриваемой модели для
границы между областями I и II получаем
а=а= 1/3, /3= 1/9, A4.6.15)
а для границы между областями III и IV
*=-1/2, а =3/4, /3=1/4. A4.6.16)
Для общей модели жестких квадратов с весовой функцией A4.2.1) сред-
средняя плотность р связана с функцией к соотношением A4.1.7), причем диф-
дифференцирование выполняется при фиксированных коэффициентах взаимо-
взаимодействий L и М. Отсюда следует, что если рассматривать функции к, р, R
вдоль некоторой линии, параллельной оси z в (z, L, М)-пространстве, то
показатели а и а в A4.6.14) должны быть одинаковыми. Но такую линию
мы провести не можем, поскольку допустимыми являются лишь линии на
поверхности A4.2.9). Следовательно, показатели а и а не обязательно дол-
должны быть одинаковыми, и действительно мы видим, что они различаются
вдоль границы между областями III и IV.
Основное состояние в области IV совпадает с состоянием, показанным
на рис. 14.5,6, или получается из него с помощью сдвига всех частиц на од-

446 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
но межузельное расстояние вправо. Такие состояния являются также упо-
упорядоченными основными состояниями обычной модели жестких квадратов
A4.2.1), в которой L = М = 0. Кажется вероятным, что граничная линия
между областями III и IV лежит на той же критической поверхности, что и
критическая точка (z = 3,7962..., L = М = 0) модели жестких квадратов.
Поскольку значения критических показателей A4.6.16) справедливы только
для поверхности A4.2.9), нет ничего неожиданного в том, что они отлича-
отличаются от критических показателей модели жестких квадратов а = а = 0,
/3 = !/8 [47]. Тем не менее вызывает разочарование, что критические показа-
показатели двух данных моделей, по-видимому, совершенно не связаны между со-
собой.
14.7. МОДЕЛЬ ЖЕСТКОГО ГЕКСАГОНА
Мы начали данную главу с обсуждения модели жесткого гексагона, т. е.
газа на треугольной решетке, частицы которого не могут находиться на со-
соседних узлах. Чтобы найти решение для такой модели, мы перешли к более
общей модели жестких квадратов с диагональными взаимодействиями, ко-
которая обсуждалась в разд. 14.2 — 14.6. Вернемся теперь к исходной модели
жесткого гексагона. Для этого устремим величины т, L, М в A4.2.1) к
1,0, -оо соответственно. Из выражения A4.2.29) следует
и-»-лг/5, A4.7.1)
а из A4.2.10) и A4.2.30) получаем
где функция 0j определена в A4.2.28). При заданной активности z выраже-
выражения A4.7.1) и A4.7.2) можно понимать как определения параметров и и q2.
Необходимо рассмотреть два случая, которые отвечают положитель-
положительным и отрицательным значениям параметра q2. Как видно из A4.7.2), та-
такие случаи соответствуют в свою очередь z < zc и z > zc, где
zc = (sin-^/sin^j = [i(l + V5)]5 = i(ll + 5V5) = 11.09017 ....
V Ь 7 A4.7.3)
Мы видим, что это значение zn совпадает со значением, предложенным
Гонтом [96]. >
При z < zc в пределе и = -тг/5 модель лежит в области I, а при
z > zc — в области II. Определим х по формуле A4.2.43). Тогда из выра-
выражений A4.2.10) и A4.2.44) получаем, что величинах связана с z следующим
образом:
z<zc: z = -x[H(x)/G(x)}5,
A4 7 4)
z>zc: z = x-\G(x)/H(x)]5,

TT , f(xw,x)f(xw
II: CO4CO5/CO1 = 72—2 57-7 57
f(x2wx5)f(xx5)
ГЛАВА 14 447
где G(x) и Н(х) — функции Роджерса — Рамануяна, определенные в
A4.1.19) и A4.6.5). Выражения A4.7.4) в точности совпадают с формулами
A4.1.18) и (И.1.22), поэтому величинах в настоящем разделе та же, что и
в разд. 14.1.
Чтобы получить выражение для ку перенормируем сначала веса
сор ... , со5 в формуле A4.2.44) так, чтобы весо^ оказался равным единице.
Такая перенормировка означает, что в формулах A4.2.38) и A4.2.1) величи-
величина т равна единице. Используя перенормированные веса и вспоминая, что
/(w) в A4.2.44) обозначает/(w, x5), из выражений A4.2.44) получаем
f(xw~l , X5)f(x2w~l, x5)f(x , х5)
I: CO4CO5/CO1 = 727 57771 57 >
A4.7.5)
f(x2w-l,x5)f(xw,x5)f(x\x5)
= 72—2 57-7 57 .
f(x2w,x5)f(x,x5)
Используем теперь выражение A4.3.26) (которое справедливо при любых
нормировках весов сор ... , со5) и перейдем к пределу при и — -тг/5. Из
формул A4.2.43) следует, что в области I при ы — -тг/5 величина w стре-
стремится к х2, а в области II w — х~1. В обоих случаях правая часть A4.3.26)
содержит простой полюс при указанных значениях w, который сокращает-
сокращается с соответствующим нулем выражения A4.7.5). Мы видим, что функция к
действительно определяется формулами A4.1.20) и A4.1.23).
При z < zc плотность р задается выражением A4.5.14). При z > zc под-
решеточные плотности рх, р2» /°з и параметр порядка R определяются фор-
формулами A4.5.29), A4.5.26) и A4.5.30). Последняя формула совпадает с
A4.1.24); таким образом, предположения, высказанные в разд. 14.1, дока-
доказаны.
Критическое поведение
Чтобы изучить поведение системы вблизи z = zc, используем получен-
полученное в предыдущем разделе альтернативное представление результатов для
модели жесткого гексагона.
На первом этапе заметим, что параметр q2 задается выражением
A4.7.2). Используя A4.2.28) и A4.7.3), указанное выражение можно запи-
записать в виде
00
+ 4")/(l 22" +
U [( 7y 7)/( 7y qA4.7.6)
Выражение A4.7.6) определяет q2 при всех положительных z\ q2 < 0 прн
z < zc, q2 > 0 при z > zc.
Чтцбы получить разложение функции к при малых q, используем выра-
выражения A4.6.3), A4.2.29) и A4.2.31). Положим т — 1 и устремим и к -тг/5.
С помощью функций Q(x), P(x), G{(x), H{(x), определенных в A4.6.5), на-
находим

448 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
z<z. к _ 3V3 G\{q2) Q\q2) Q(p5) Р3(р1Ю) ^
A4.7.7)
_3V3 G\(q2)Q2(q2)Q(p5)
5H\{q2)Ql(p™) '
где р определяется по формуле A4.6.4), т. e. p = \q2\ . Критическое значе-
значение кс функции к получается из любой из формул A4.7.7) при q2 = р = 0:
Кс = 3V3 sin2B;r/5)/[10 sin3(;r/5)]
= [27B5 4- llV5)/250]* = 2.3144 .... A4.7.8)
При z < zc плотность р задается первой формулой A4.6.7). При z > zc
справедливы формулы, отвечающие области II; в частности, параметр по-
порядка равен
R = C/V5)/71/9e(p5) Q(p)/Q2(p5/3). A4.7.9)
Из выражения A4.7.6) следует, что q2 — аналитическая функция z при
z = zc, имеющая разложение Тейлора вида
q2 = (z - zc)/EV5 zc) + C[B - zcJ]. A4.7.10)
Приведенные результаты точны. Чтобы получить критическое поведе-
поведение, разложим их по степеням q2 и/7, удерживая первые два или три члена.
При этом получим
q2 = (z - zc)/EV^zc) + €{(z - zcJ},
/c=*:c{l + f(V5- l)^2 + 3|92|5/3 +
p = Pc+sgn(^)|92|2/3/V5 + O(^),
R = C/V5) (q2I19 {l-q2 + 2qim +
Здесь pc - E - V?)/10 — критическая плотность (разд. 14.6). Последнее
выражение (для R) применимо только при z > zc; три первых справедливы
как при z > zc, так и при z < zc. Определяя критические показатели а, а, /3
обычным образом с помощью A4.6.14) и заменяя / на z — zc, мы снова по-
получаем значения A4.6.15), т. е.
а=а= 1/3, р= 1/9. A4.7.12)
Используя эти значения и соотношения скейлинга A.2.12) — A.2.16), на-
находим другие критические показатели:
у =13/9, 6=14, jU=i/=5/6, rj = 4/15. A4.7.13)
В результатах A4.1.18) — A4.1.24) используются эллиптические функции
с различными параметрами Якоби х5, х6, х3 и х. Между такими функциями

ГЛАВА 14 449
можно получить алгебраические соотношения (так, преобразование Ланде-
на из разд. 15.6 связывает эллиптические функции с параметрами Якоби q
и #2) и, следовательно, исключить х из полученных выше выражений. Со-
Соотношение между z и параметром порядка /?, справедливое при z > zc,
найдено Джойсом [125]. Он получил соотношение
гр1\5 4- 105 4- 52K = B75 4- гр6) B43s 4- 1//6K, A4.7.14а)
где Г
\р = V5R, 5 = 125z/(z2 - llz - 1). A4.7.146)
Следовательно, параметр порядка R является алгебраической функцией ак-
активности z.
14.8. ЗАМЕЧАНИЯ И ПРЕДПОЛОЖЕНИЯ
В настоящей главе для вычисления свободной энергии использован прием, свя-
связанный со свойствами обратимости, а подрешеточные плотности и,параметр по-
порядка определены с помощью диагонализации угловых трансфер-матриц. В отли-
отличие от восьмивершинной модели, рассмотренной в гл. 10, мы не получили
точных уравнений для всех собственных значений трансфер-матрицы
ряд — ряд. В результате нам не удалось вычислить поверхностное натяже-
натяжение и корреляционную длину.
Недавно такие расчеты были выполнены [40]. Будем считать, что вели-
величины т' и С в выражении A4.2.39) фиксированы. Тогда больцмановские
веса озi и трансфер-матрица V ряд — ряд являются функциями переменной
и. Можно проверить, что справедливо равенство
\{и) V(m + А) = ф(А - и) ф(к 4- и) 9 4- ф(и) V(n - 2Х), (М 8 1}
где У — единичная матрица и
А = 2л/5 , ф(и) = [т'ОгМ/в^Х)]" . A4.8.2)
Как обычно, из соотношения звезда — треугольник следует, что при всех
комплексных значениях и и v матрицы V(u) и V(v) коммутируют. Следова-
Следовательно, можно выбрать представление, в котором матрица V(u) диаго-
нальна при всех и. Тогда равенство A4.8.1) представляет собой функцио-
функциональное соотношение для каждого собственного значения. Данное соотно-
соотношение с учетом свойств аналитичности и квазипериодичности V{u) позво-
позволяет в принципе вычислить любое собственное значение при конечном N.
Следовательно, можно определить свободную энергию, поверхностное на-
натяжение и корреляционную длину. Результаты, конечно, согласуются с
A4.3.26). Кроме того, для критических показателей /х, v, v' модели жестко-
жесткого гексагона получено значение
ц= v= v' = 5/6, A4.8.3)
С учетом выражения A4.7.12) отсюда следует, что выполняются соотноше-
соотношения скейлинга A.2.14а), A.2.15) и A.2.16).

450 ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ
В разд. 10.1 и 10.3 мы видели, что восьмивершинная модель содержит в
качестве частных случаев решенные ранее модель Изинга и шестивершин-
ную модель. Когда Ф. By и я решали в 1973 — 1974 гг. трехспиновую мо-
модель, казалось, что это новая модель. Однако, как было показано в
разд. 11.10, данная модель также является частным случаем восьмивершин-
ной модели.
Повторится ли это для модели жесткого гексагона? Точнее говоря, бу-
будет ли решена более общая модель, содержащая как частные случаи вось-
мивершинную модель и модель жесткого гексагона? Я сомневаюсь-в этом.
Первое обстоятельство, подтверждающее, что рассматриваемые модели
весьма различны, состоит в том, что критический показатель <5 равен 15
для восьмивершинной модели и 14 для модели жесткого гексагона. Кроме
того, соотношение звезда — треугольник A3.3.6) или A1.5.8) содержит
много больше уравнений, чем неизвестных величин. Свойства симметрии
восьмивершинной модели в четыре раза (от 64 до 16) уменьшают число
уравнений. В случае обобщенной модели жесткого гексагона требование,
чтобы никакие две частицы не занимали соседних узлов, исключает 44
уравнения из 64. При этом число уравнений и число неизвестных оказыва-
оказывается одинаковым. Таким образом, причины успеха в обоих случаях весьма
различны, и мне кажется невероятной возможность найти непрерывный
ряд решаемых моделей, соединяющих между собой восьмивершинную мо-
модель и модель жесткого гексагона.
Можно ли распространить рассмотренные методы на модели изингова
типа в трехмерном пространстве? Как показал Замолодчиков [266], соотно-
соотношение звезда — треугольник A3.3.6) или A1.5.8) можно обобщить, вводя
«соотношение тетраэдра». Трудность связана с тем, что в данном случае
нужно решить 214 уравнений (вместо 26\ Одно очень полезное свойство
двумерных моделей не сохраняется в трехмерных моделях. Если модель
разбивается на две независимые модели (каждая на соответствующей под-
решетке квадратной или простой кубической решетки), то весовые функции
представляются в виде произведений функций, отвечающих независимым
моделям. Соотношение звезда — треугольник для плоской решетки также
разбивается на два идентичных соотношения (каждое из которых является
соотношением звезда — треугольник для модели Изинга в разд. 6.4). Но
соотношение тетраэдра в трехмерном пространстве разбивается на два не-
неодинаковых соотношения, одно из которых тривиально, что, по-видимому,
препятствует существованию интересных решений.
Тем не менее Замолодчиков нашел строгое доказательство того, что со-
соотношение тетраэдра имеет некоторые (нефакторизуемые) решения. Было
бы крайне интересно найти такие решения и проверить, соответствует ли
они какой-нибудь представляющей интерес статистико-механической моде-
модели.
Конечно, желательно продвинуться как можно дальше в изучении пло-
плоских моделей. Модель Изинга в магнитном поле по-прежнему не решена.
Фактически единственными моделями, которые решены в присутствии на-
нарушающего симметрию внешнего поля, являются сферическая модель из

ГЛАВА 14 451
гл. 5 и модель сегнетоэлектрика (KDP) из разд. 8.12. Решение данных мо-
моделей дало возможность полной проверки гипотез скейлинга (разд. 1.2) и
позволило найти вид функций скейлинга hs(x).
По-видимому, метод «коммутирующих трансфер-матриц» нельзя ис-
использовать для решения модели Изинга и других моделей в присутствии
внешнего поля или даже для решения некритической модели Поттса. Мне
кажется, что единственная надежда решить восьмивершинную модель и
модель Поттса состоит в том, чтобы найти подходящие алгебраические
методы подобные тем, которые привели Онсагера [184] и Кауфман [143] к
решению модели Изинга без внешнего поля. (Вера в существование таких
методов основана на том, что диагонализованные угловые трансфер-
матрицы бесконечной решетки имеют простой вид прямого произведения
A3.7.20).)
Если такие методы существуют, то их можно применить для рассмот-
рассмотрения восьмивершинной модели, в которой две подрешетки имеют различ-
различные бельцмановские веса, но одинаковые комбинации Д и Г, определенные
в A0.4.6). В частности, для такой модели можно определить, используя
A0.4.17) и A0.12.5), один параметр д. Случай /х = тг/2 соответствует
Г = 0. При этом модель разбивается на две независимые модели Изинга
для антиферромагнетика, которые можно решить алгебраически. (Можно
решить также модель «свободных фермионов» Д = 0; см. разд. 10.16.)
Пытаясь обобщить алгебраические методы, естественно в первую очередь
обратить внимание на другие значения /х, являющиеся простыми долями тг,
например /х = тг/3, Зтг/4 и т. д.
Если такое обобщение удастся найти, то это будет гигантским шагом
вперед. Многие интересные модели можно представить как частные случаи
восьмивершинной модели с различными подрешетками. Особый интерес
представляют некритическая модель Поттса (разд. 12.4), модель Эшки-
на — Теллера (разд. 12.9) и модель Изинга в магнитном поле [259]. Было
бы глупо связывать все наши надежды только с данной возможностью, ко-
которая не осуществляется уже по крайней мере в течение десяти лет. В то
же время я чувствую, что столь же глупо упускать ее из виду.
14.9. БЛАГОДАРНОСТИ
Я получил большую помощь при нахождении различных тождеств
Роджерса — Рамануяна, которые использовались в разд. 14.5, особенно от
Джорджа Е. Эндрюса (который доказал равенства A4.5.22)), Ричарда Эски
и Дэвида Брессу (которые показали, что выражение A4.5.55) является
следствием A4.5.53) и A4.5.54), и помогали мне при поиске нужных тож-
тождеств из списка Берча), Майка Хиршхорна и Джефа Джойса. Я крайне при-
признателен всем им за поддержку и помощь.

15
ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
15.1. ОПРЕДЕЛЕНИЯ
Обычные эллиптические функции являются функциями двух переменных, в
качестве которых мы выберем параметр Якобы q и аргумент ы. Параметр
q считается заданной действительной величиной, лежащей в интервале
@,1), а аргумент ы рассматривается как комплексная переменная.
Тогда полуперыоды I и Г (в обычных обозначениях К, К') определяют-
определяются выражениями
Г = лГ1 I\n(q-1) , A5.1.2)
поэтому для параметра q справедливо выражение
q = ехр(-я/7/). A5.1.3)
Модуль к и сопряженный модуль к' равны
Тэта-функыыы определяются выражениями
00
Щи) = 2qi sin % П A - 2q2" cos ^ + qA (I
= 2<7* cos — П ( 1 4- 2qLn cos -
A5.1.5)
(и) = П (l - 2q2"-1 cos^ + ?4") A - f2»
i(«) = П (l + 2?2"-1 cos^ + ?4"-2) A - ?2
W = 1 \ i /

ГЛАВА 15 453
Эллиптические функции Якоби имеют вид
snw = Г* Н(и)/е(и),
сп и = (*'/*)'Я1(и)/в(ы), A5.1.6)
dn и = k'k 0i(u)/e(u).
Умножая A5.1.1) на A5.1.46), получаем
=m.. а5л.7)
Кроме того, из выражений A5.1.1), A5.1.2) и A5.1.4а) следует
\2
кГ =2qHn(\lq)X\U--^\ . A5Л.8)
15.2. АНАЛИТИЧНОСТЬ И ПЕРИОДИЧНОСТЬ
Тэта-функции //, //j, 9, Gj являются целыми функциями и (т.е. они
аналитичны всюду), имеющими только простые нули. В частности, нули
функций Н(и), G(w) задаются соотношениями
Щи)=0 при м = 2т/ + 2ш/', A5.2.1)
В(м) = 0 при и = 2/и/+ iBn - 1)/', A5.2.2)
где т, п — целые числа.
Таким образом, из определений A5.1.6) следует, что функции snw, cnw,
dnw мероморфны (т. е. единственными особенностями этих функций явля-
являются полюса). Все полюса функций Якоби простые и соответствуют точ-
точкам, удовлетворяющим равенству A5.2.2).
Функция Н(и) удовлетворяет квазипериодическим соотношениям
Н(и + 21) = -Н(и) , A5.2.3а)
Щи + ИГ) = -q~l ехр(-лгш/7) Щи). A5.2.36)
Другие тэта-функции связаны с Н(и) соотношениями
Hi(m) = Щи + /), ех(и) = в(м + /),
0(м) = -/?* ехр(?лш//) Я(м + //') , A5.2.4)
0i(m) = ^^ ехр(Ши/1) Щи + / + ?/').
Отсюда следует, что функции snw, cnw, dnw удовлетворяют соотношениям
sn(-w) = - sn м, cn(-w) = en м, dn(-w) = dn и ,
sn(w + 2/) = - sn и, cn(u + 21) = - en и, dn(w + 2/) = dn и, A5.2.5)
sn(w -f 2i/') = sn w, cn(w + 2W) = - спи, dn(w + 2il) = - dn и

454
ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
г
-/
-W
21
Рис. 15.1. Типичный прямоугольник
периодичности показан штриховыми линиями
в комплексной w-плоскости (ширина его 21, а
высота 2/7').
sn(u + //') = (к sn и) х,
сп(м + И') - —i dn м/(А: sn и),
dn(u + //') = -i en w/sn и .
A5.2.6)
Вертикальный прямоугольник шириной 2/ и высотой 2//' в комплек-
комплексной плоскости называется прямоугольником периодичности (рис. 15.1).
Любую функцию/(w), удовлетворяющую сотношениям
2/)=±/(и),
A5.2.7)
называют двоякопериодической (или двоякоантипериодической). Если та-
такая функция известна внутри и на границе прямоугольника периодичности,
то ее значение в любой точке комплексной плоскости можно получить с
помощью многократного применения соотношений A5.2.7). С точностью
до знака все значения, которые принимает функция/(w), достигаются при
значениях аргумента w, лежащих внутри и на границе прямоугольника пе-
периодичности.
15.3. ОБЩИЕ ТЕОРЕМЫ
Теорема 15 (а)
В теории функций комплексного переменного хорошо известна теорема
Лиувилля, которая утверждает, что ограниченная целая функция равна по-
постоянной. Для настоящей главы полезно следующее следствие из теоремы
Лиувилля:
Если функция двоякопериодична (или двоякоантипериодична) и анали-
тична внутри и на границе прямоугольника периодичности, то она равна
постоянной. A5.3.1)

ГЛАВА 15 455
Доказательство весьма простое: поскольку функция аналитична в зам-
замкнутой области, то она ограничена. Из свойства двоякопериодичности сле-
следует, что функция аналитична и ограничена всюду. Тогда из теоремы Лиу-
вилля вытекает, что данная функция постоянна.
Теорема 15F)
Если функция/(w) двоякопериодична (или двоякоантипериодична), меро-
морфна и имеет в прямоугольнике периодичности п полюсов, то она
имеет в прямоугольнике периодичности в точности п нулей. (Кратные
нули и полюса порядка г считаются г раз.)
Доказательство. Выберем прямоугольник периодичности так, чтобы
функция/(w) не имела полюсов и нулей на его границе (поскольку нули и
полюса изолированы, такой выбор возможен).
Рассмотрим интеграл
' [/'("Ж")] du , A5.3.3)
где С — граница прямоугольника, движение по которой совершается про-
против часовой стрелки, как показано на рис. 15.1. Подынтегральная функция
аналитична на С и строго двоякопериодична, поэтому вклады в интеграл
A5.3.3) от двух боковых сторон прямоугольника (а также от верхней и
нижней сторон) взаимно сокращаются. Следовательно, интеграл A5.3.3)
равен нулю.
С другой стороны, если/(w) имеет п полюсов и т нулей внутри прямо-
прямоугольника, то функция f'(u)/f(u) имеет п полюсов с вычетом — 1 и т по-
полюсов с вычетом +1. Поскольку других особенностей функция f'(u)/f(u)
не имеет, из интегральной формулы Коши следует
[f'(u)/f(u)]du=2jri(m-n). A5.3.4)
Так как левая часть A5.3.4) равна нулю, то т — /?, что и требовалось
доказать.
Теорема 15(в)
Если функция f{u) мероморфна и удовлетворяет условиям (анти-) перио-
периодичности
где г, s — целые числа, и если f(u) имеет п полюсов в прямоугольнике
периодичности в точках Mj, . . . , ип (считая полюс порядка г как г со-
совпадающих простых полюсов), то
п
/(и) = С ей" П [Н(и - о,)/Н(и - и,)] , A5.3.6)
i 1

456 ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
где С, X, v{, . . . , vn — постоянные, удовлетворяющие соотношениям
[>i + . . . + у„ = Mi + . . . + ия + (г + 2m)/ - i(s 4- 2п)Г , A5.3.7)
Я= ?л(.у + 2л)//, A5.3.8)
a w, n — целые числа.
Доказательство. Из теоремы 15F) следует,что/(w) имеет в прямоу-
прямоугольнике периодичности п нулей v{, . . . , vn. Обозначим через ф(и) произ-
произведение в правой части A5.3.6) и временно не будем учитывать ограничение
A5.3.7).
Рассмотрим функцию
[/'(")//(«)] -[ф'(и)/ф(и)]. A5.3.9)
Из A5.2.3) и A5.3.5) следует, что данная функция строго двоякопериодич-
на. Поскольку f(u) и ф(и) имеют одни и те же полюса и нули, функция
A5.3.9) аналитична. Из теоремы 15(а) вытекает, что данная функция равна
постоянной.
Проинтегрировав функцию A5.3.9), получим, что f(u) должна иметь
вид A5.3.6). Условия A5.3.7) и A5.3.8) необходимы для выполнения ра-
равенств A5.3.5).
Получается замечательный результат: всякую двоякопериодическую ме-
роморфную функцию можно представить в виде A5.3.6). Именно по этой
причине существует сбивающее с толку количество тождеств между эллип-
эллиптическими функциями: многие суммы и произведения таких функций удов-
удовлетворяют условиям рассмотренной теоремы; если удается найти их нули,
то данные суммы и произведения можно представить в виде A5.3.6).
Полезно рассматривать выражение A5.3.6) как обобщение основной
теоремы алгебры, которая утверждает, что всякий полином степени п
можно представить в виде произведения п линейных множителей.
Доказанные теоремы крайне эффективны. Они будут полезны в следу-
следующем разделе для получения ряда алгебраических тождеств, которым
удовлетворяют эллиптические функции; возможно, простейшим примером
использования теоремы 15(а) является тождество
Щи 4- х) Щи - х) Щи 4- у) Щи -у)-
- Щи 4- у) Щи - у) Щи 4- х) Щи -х)= A5.3.10)
= Щх - у) Щх 4- у) Щи 4- и) Щи - и).
Чтобы доказать данное тождество, зафиксируем величины х, у, v и рас-
рассмотрим и как комплексную переменную. Обозначим через/(w) отношение
левой части тождества A5.3.10) к правой. Из формул A5.2.3) следует, что
f{u) периодична с периодами II и 2/7'. Она мероморфна и, возможно, име-
имеет простые полюса в точках и = ±v + 2ml + ИпГ при любых целых т и
/?. Поскольку левая часть A5.3.10) обращается в нуль при и = ±v, полюса,
отвечающие данным точкам, исчезают. Из условия периодичности следует,
что исчезают также и все другие полюса. Следовательно, f(u) — целая дво-

ГЛАВА 15 457
якопериодическая функция. Из теоремы 15(а) вытекает, что/(^) постоянна.
Положив и = у, получаем, что данная постоянная равна единице. Тожде-
Тождество A5.3.10) доказано.
Заметим, что в проведенном доказательстве не использовалась точная
формула A5.1.5) для Щи). Требовались только следующие свойства:
а) Н(и) — целая функция, б) Н(и) удовлетворяет условиям квазиперио-
квазипериодичности A5.2.3), в) Н(и) — нечетная функция, т.е. //( — «) = —Н{и).
15.4. АЛГЕБРАИЧЕСКИЕ ТОЖДЕСТВА
Соотношения между функциями sn м, en w, dn и
Рассмотрим выражение
[НЩ 02(м) - 02(О) Н\{и)]1Н\и). A5.4.1)
Очевидно, что оно представляет собой мероморфную функцию w, возмож-
возможно, с двукратными полюсами в точках, где Н(и) = 0, т. е. при
и = 2ml + 2лпГ. Но при и = 0 числитель обращается в нуль, а также (по-
(поскольку числитель является четной функцией) обращается в нуль и его про-
производная. Таким образом, функция A5.4.1) аналитична при и = 0 и, следо-
следовательно, аналитична внутри и на границе прямоугольника периодичности,
центром которого является начало координат.
Из выражений A5.1.6) и A5.2.5) легко видеть, что функция A5.4.1)
(строго) двоякопериодична; поэтому из теоремы 15(а) следует, что она рав-
равна постоянной. Полагая и — /, находим эту постоянную и получаем равен-
равенство
Я?@) 02(и) - Q2@)H\(u) = &2ЩН\и). A5.4.2)
Используя формулы A5.1.5) и определения A5.1.4), можно выписать
следующие выражения:
\д = #i@)/ei@) , k* = 0(O)/0i(O). A5.4.3)
Разделив A5.4.2) на Я,2(ОH2(г/) и используя A5.1.6), получаем
cn2w + sn2w = 1. A5.4.4)
Увеличивая и на //' и используя A5.2.6), находим
dn2u + k2sn2u = 1. A5.4.5)
Тождества A5.4.4) и A5.4.5) позволяют использовать эллиптические
функции для параметризации выражений, содержащих квадратные корни
из квадратичных форм. Например, если имеется уравнение
у ( A5.4.6)
то очевидной параметризацией является
JC = snw, A5.4.7)

458 ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
а из A5.4.4) — A5.4.6) следует
у = snw cnw 4- dnw. A5.4.8)
Данная параметризация определяет х и у как однозначные мероморфные
функции w, которые весьма удобны для выполнения достаточно сложных
вычислений. При к2 Ф 0 и к2 =? 1 такая параметризация невозможна в тер-
терминах элементарных функций.
Легко проверить, используя A5.1.6), A5.4.3) и A5.2.4), что выполняются
равенства
sn/=l, dnl = k'. A5.4.9)
Положив в A5.4.5) и = /, получаем соотношение
к2 + к'2=\ A5.4.10)
между двумя модулями.
Если 0 < q < 1, то из A5.1.4) видно, что к и к' положительны. Из со-
соотношения A5.4.10) следует
0< Аг< 1, 0<к'<1. A5.4.11)
Модифицированная амплитудная функция
Другая полезная для наших целей функция имеет вид
Am(w) = -iln[ikhsn(u - Ji7')]. A5.4.12)
Из A5.1.6) и A5.1.5) следует
где
z = Qxp(iitu/I). A5.4.14)
Взяв логарифм от каждого сомножителя, разлагая его в ряд Тейлора и вы-
выполняя суммирование по /?, можно получить выражение
Am^ = Yi+ 2 Ж ТфТ^-) ^тжи11)' A5А 15)
где I Im I < УгГ .
При действительных и данная функция действительна, нечетна и моно-
монотонно возрастает с ростом и. Она удовлетворяет условию квазипериодич-
квазипериодичности
Am(w 4- 21) = Ат(и) + я. A5.4.16)
Функция Ат(ы) не является мероморфной, поскольку она имеет логариф-
логарифмические точки ветвления при и — 2ml + i(n - Vi)l'.

ГЛАВА 15 459
Обычная эллиптическая амплитудная функция am(w) определяется фор-
формулой A5.4.15) с заменой q на q2. Такие преобразования от эллиптических
функций с параметром Якоби q к эллиптическим функциям с параметром
q2 известны как преобразования Ландена; они обсуждаются в разд. 15.6.
Формулы сложения для тэта-функций
Тэта-функции удовлетворяют приводимому ниже ряду тождеств при
всех комплексных значениях и и v. Каждое из них можно доказать весьма
просто, рассматривая отношение левой и правой частей как функцию w, ис-
используя A5.2.4) и равенство Я@) = 0 для проверки того, что данная функ-
функция является целой и двоякопериодичной, а следовательно, как вытекает из
теоремы 15(а), постоянной. Полагая и = 0, находим, что указанная посто-
постоянная равна единице. Справедливы следующие тождества:
Щи) ©(и) Hx(v) Bi(v) - Щи) S(v) Нг(и) ©{и)=
A5.4.17)
= Щи - v) в(и 4- и) Нх@) 0i(O),
Щи) ех(и) нг(и) е(и) - нх(и) &(и) Щи) ег(и)=
A5.4.18)
= Щи - v) &{(и 4- и) Нг@) 0@),
Н\и) в\и) - e\u)H\v) = Щи - и) Щи + и) 02(О). A5.4.19)
Заменяя в A5.4.19) величину и на и + /7 и используя A5.2.4) и A5.2.3), по-
получаем
Q\u) @2(v) - Н\и) H\v) = в(и - v) S(u 4- и) 02(О). A5.4.20)
Разделив обе части выражения A5.4.17) на соответствующие части A5.4.20)
и использовав D5.1.6) и A5.4.3), находим формулу сложения для функции
snw:
sn и en v dn v - en и dn и sn и „ „ А ^
sn(w - v) = л—г 2 • A5.4.21)
1 - к1 sn2 и sn2 v
Другие формулы сложения имеют вид
—i sn(i/' - и - и) сп и en v - сп(П' - и - v) sn и sn v =
У ' v ' A5.4.22)
= k-ldn(W -u-v),
sn(a - и) sn(a - v) - sn и sn v , ч ,,еА„
п — Г^ ч 7 ч = sn a sn(« -u-v), A5.4.23)
1 - кг sn w sn v sn(a - w) sn(# - y)
sn t; sn(g - v) - sn и sn(fl - и) _ sn(g -u-v) A5424)
sn(fl - w) sn v - sn(fl - v) sn w sn й
0(w) ©(*;) S(a - u) S(a - v) - Я(и) Я(и) Ща - и) Ща - и) =
= 0@) в(в) в(и -v)e(a-u-v), A5.4.25)

460 ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
Щи) Ща - v) @(и) Q(a - и) - Q(v) 0(а - v) Щи) Ща - и)=
= Э@) ©(a) H(v -u)H{a-u-v), A5.2.26)
©(и) @(v) - Щи) H(v) = -2qkH[i(iI' +u-v)] Щ{И' - и + о)] х
х Щ{Ц + и + v)] Щ{1Г -и- еШВД) в,@)], A5.2.27)
в(и) H{v) + Щи) e(v) = 2 H[i(u + v)] в[Ци +v)]x
A5.2.2о)
х Я,[*(и - v)] e,[i(« - у)]/[Я1@) 0,@)],
Hl(u)Hl(v)-H(u)H(v)=2H[i(I + u+v)
x e[i(/ + u-v)] ®w
Я,(и) Я(У) + Я(и) Я,(») = 2 Я[*(и + v)] Нх[\{и + »)] х A5 2 29б)
х в\1(и - v)] в,[*(и -
Частные значения функций snw, cnw, dnu
Используя выражения A5.1.5), A5.1.6), A5.2.6), A5.4.4) и A5.4.5), легко
проверить равенства
snO = O, cnO = dnO = l, A5.4.30)
sn/=l, cn/ = 0, dn/ = A:', A5.4.31)
sn Ji/' = ik~\ enШ' = A4- Л)*, dnji/' = A4- k)K A5.4.32)
15.5. ДИФФЕРЕНЦИАЛЬНЫЕ И ИНТЕГРАЛЬНЫЕ
ТОЖДЕСТВА
Рассмотрим выражение
X=sri(u)/(cnu dnu), A5.5.1a)
где штрих означает дифференцирование по и при постоянном q. Дифферен-
Дифференцирование выражений A5.4.4) и A5.4.5) дает
X=-cri(u)/(snu dnu) A5.5.16)
= - dnf(u)/(k2snu спи). A5.5.1b)
Подставляя определения A5.1.6) функций snw, enw, dnu в A5.5.1) и вспо-
вспоминая, что тэта-функции являются целыми функциями, получаем
Х =
Я,(м) ©г(и) = Щи) в,(и) = Щи) Я,(и) '

ГЛАВА 15 461
где в каждом отношении многоточие обозначает целую функцию. Из пер-
первого выражения для X видно, что величина X имеет полюса там, где Нх(и)
и 9j(w) обращаются в нуль. Из второго выражения для X следует, что X не
имеет полюсов в точках, где Нх{и) - О, а из третьего выражения получа-
получаем, что X не имеет полюсов в точках, где Q{(u) = 0.
Следовательно, X не имеет полюсов и является целой функцией. Из вы-
выражения A5.2.5) вытекает, что X— двоякопериодическая функция, поэтому
она равна постоянной.
Получая sn и из A5.1.6) и A5.1.5) и полагая затем и — 0, находим
lim—=ртЙ?ПA-^K A5-5-3)
и—о и
Используя выражения A5.1.1), A5.1.4) и A5.1.5), получаем простой ре-
результат:
ton (sn u)lu = 1. A5.5.4)
(Фактически можно считать, что определение A5.1.1) величины / выбрано с
целью обеспечить соотношение A5.5.4).)
Из уравнения A5.5.4) следует, что sn'(O) = 1, а из A5.1.6) и A5.4.3) вид-
видно, что cn@) = dn@) = 1. Вычисление постоянной X по формуле A5.5.1а)
при и — О дает
Х=1. A5.5.5)
Если, используя A5.4.4) и A5.4.5), выразить сп и и dn и через sn w, то
выражение A5.5.1а) принимает вид дифференциального уравнения первого
порядка относительно sn и. Интегрируя его, получаем
A5.5.6)
Определим функцию ф так, чтобы выполнялось равенство
sn и = sin0. A5.5.7)
Тогда выражение A5.5.6) можно записать в виде
Д-1—т A5.5.8)
'о A - к2 sin2 *)*'
Последнее равенство представляет собой обычную интегральную форму
связи между и и snw. В A5.5.8) необходимо выбрать путь интегрирования и
знак подынтегрального выражения, но при действительном w, лежащем в
интервале @, 1), указанный выбор не вызывает трудностей: все функции
sn ы, en w, dn и положительны и 0 < sn и < 1. Таким образом, и определя-
определяется действительным интегралом A5.5.8) с положительной подынтеграль-
подынтегральной функцией и 0 < ф <.тг/2.

462 ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
Пусть теперь и — /. Из выражений A5.1.6), A5.2.4) и A5.4.3) следует
равенство sn / = 1. Поэтому ф = тг/2, и выражение A5.5.8) принимает вид
/=I (l-*w»)" A559)
т. е. представляет собой обычное выражение для полупериода / как полно-
полного эллиптического интеграла первого рода модуля к.
Если переменная и равна чисто мнимой положительной величине, то та-
таким же будет и значение функции sn w, в то время как функции сп и и dn и
действительны и имеют одинаковый знак. Следовательно, функция — / sn и
монотонно возрастает с ростом Im(w) и конечна при 0 < \т(ы) < Г. В
данном случае подходящим путем интегрирования в A5.5.8) является поло-
положительная мнимая ось. Подынтегральное выражение по-прежнему положи-
положительно.
Из выражений A5.1.5) и A5.1.6) следует, что функция sn и становится
бесконечной в пределе и — //'. Положив а = ф в A5.5.8), получаем
Это интегральное выражение для I', которое можно привести к стандарт-
стандартному виду с помощью подстановки
tany=sinh/?. A5.5.11)
Используя A5.4.10), находим
С nil ^у
~! A - к'2 sin2 у)*' 15'5'12)
Сравнивая формулы A5.5.9) и A5.5.12), видим, что связь между / и А
аналогична связи между Г и к': Г — полный эллиптический интеграл пер-
первого рода модуля к'.
Полный эллиптический интеграл второго рода модуля к имеет вид
Г я/2
Е= \ A - к2 sin2 у)* dy. A5.5.13)
Поведение sn и и Н(и) при малых и
Легко видеть из A5.5.6) и A5.1.6), что при I и I <^ 1 справедливы асимп-
асимптотики
snw~w, Я(и) ~ А:* 0@) и . A5.5.14)

ГЛАВА 15 463
15.6. ПРЕОБРАЗОВАНИЕ ЛАНДЕНА
Будем указывать зависимость функций <?, Л /', sn w, en w, dn w и т. д.
от модуля ку записывая их в виде qk, Ik, 1к, эп(и, к), cn(w, к), dn(w, к) и
т. д. Если ввести величины
/ = 2Л*/A + Jt), й = A+к)и, A5.6.1)
а затем заменить в A5.5.6) параметры и, к, t на й, /, A + k)t/{\ + АгГ2) со-
соответственно (замечая, что sn / = 1, sn //' = оо), легко проверить справед-
справедливость следующих равенств:
// = A+ *)/*, U = h(l+k)I'k, qi = ql, 05.6.2)
/ sn(w , /) = 2kl sn(w , k)/[l + A: sn2(w , A:)], A5.6.3)
kl sn(w , it) = [1 - dn(w , /)]/[/ sn(w , /)]. A5.6.4)
Решая уравнение A5.6.1) относительно к, используя A5.6.2) и заменяя к,
I на /77, к у получаем
т = A - *')/(! + *'), gm = ^. <15-6-5>
Из выражений A5.1.1) и A5.1.46) следует
00
т')* = 4л:ПA-<74''J/A +Ч*"J- A5-6'6)
15.7. СОПРЯЖЕННЫЙ МОДУЛЬ
Введем функцию
Х(и) = (///')' ехр[-лм2/D//')]. A5.7.1)
Тогда
9(мД)=х(«)ЩшД'), A5.7.2а)
Щи ,к) = ~ i)&u) Щш , к'), A5.7.26)
Щи , к) = Х(и) 0(ш , к'), A5.7.2в)
el(u,k) = x(u)@l(iu,k'), A5-7-2г>
sn(« ,k) = -i sn(iu , k')/cn(iu , к'), A5.7.3а)
сп(«Д) = 1/сп(шД'), A5.7.36)
dn(w , A:) = dn(iu , k')lcn(iu Л') ¦ A5.7.3b)

464 ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
Приведенные тождества можно доказать с помощью теоремы 15(а). На-
Например, обе части тождества A5.7.2а) являются целыми функциями и, име-
имеющими простые нули при и = 2ml + 2тГ для любых целых т, п. Следо-
Следовательно, их отношение — целая функция. С помощью A5.2.3) можно про-
проверить, что она двоякопериодическая, поэтому, согласно теореме 15(а), по-
постоянна.
Часто бывает значительно труднее получить значение этой постоянной,
чем доказать остальные тождества. Один из путей дальнейшего доказа-
доказательства состоит в следующем. Соотношения A5.7.26) — A5.7.2г) можно
получить из A5.7.2а), заменяя и на и + //' , и + /, и + / + //' соответст-
соответственно и используя A5.2.4). Отсюда следует, что все тождества справедли-
справедливы с точностью до возможного общего множителя в их правых частях.
Такой множитель не должен зависеть от и, однако он может зависеть
от к или, что эквивалентно, от
?=Г/1. A5.7.4)
Обозначим этот множитель через с(е) и введем функцию
R(e) = е1 е"то/12 П A - е"да) <15-7-5)
Л = 1
Из выражений A5.1.5), A5.5.9) и A5.5.12) получаем
q = ехр( - ле), q* = ехр( - л/е), A5.7.6)
где параметр Якоби q соответствует модулю к, а параметр Якоби q' соот-
соответствует сопряженному модулю к' = A — k2)Vl. Рассматривая A5.7.2а) с
учетом только что определенного множителя с(е) в пределе w-Ои исполь-
используя A5.1.5) и A5.7.5), находим соотношение
R\e) = c(e) tfV) • 05.7.7)
Аналогично, умножая A5.7.2а) на A5.7.26) и рассматривая предел при
и — 0, получаем
R\el2) R\e) = c\e) RzBle) R2(e~l). A5-7.8)
Можно получить третье уравнение, заменяя е в A5.7.7) на е/2. Исключе-
Исключение функций R(e) и R(e/2) из трех уравнений дает
с(е/2) = с\е). A5-7.9)
Далее из уравнения A5.7.7) следует, что с(е~1) = 1/с(е). Заменяя е в
A5.7.9) на 2/е и используя указанное свойство обратимости, находим
с(е) = с\е12). A5.7.10)

ГЛАВА 15 465
Отсюда следует, что с(е) = с\е). Поскольку множитель с(е) действителен и
не равен нулю, справедливо равенство
с(е) = 1. A5.7.11)
Таким образом, тождества A5.7.2) доказаны. Равенства A5.7.3) следуют из
A5.7.2) и A5.1.6).
15.8. ФОРМУЛА СУММИРОВАНИЯ ПУАССОНА
Имеет место тождество
2 f(n6) = 6-1 2 gBmlS), A5.8.1)
П= - °° П= - ос
где
g(k) = f exp(ita)/(*) dx . A5.8.2)
Данное тождество справедливо для любой аналитической при действи-
действительных х функции/(jc), для которой интеграл A5.8.2) сходится абсолютно
[68]. Формула суммирования Пуассона полезна для представления рядов
типа A5.4.15) в виде быстро сходящихся при q — 1 новых рядов. Такое
представление соответствует переходу от эллиптических функций модуля к
к эллиптическим функциям модуля к'.
15.9. РАЗЛОЖЕНИЯ ТЭТА-ФУНКЦИЙ В РЯД
00
Щи) = 2 2 (-1)"-У"~й2 sin[B« - l)mi/2I], A5.9.1a)
П — 1
оо
в(и) = 1 + 22 (-1)V2cos(«^m//) , A5.9.16)
00
#i(w) =2^ <7(""iJ cos[Bai - 1)ли/21] , A5.9.1в)
0i(m) = 1 + 2 2 <? cos(nm/I) , A5.9.1г)
00
A5.9.2)

466 ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
Чтобы установить тождества A5.9.1), заметим, что из A5.1.5) следует,
что Н(ы) — целая, нечетная и антипериодическая функция с периодом 2/.
Следовательно, ее ряд Фурье имеет вид
00
Щи) = 2 К sin[Bw - 1)тш/21]. A5.9.3)
Из выражения A5.2.36) видно, что hn + { = -qlnhn, поэтому справедливы
равенства
hn = 2c(-iy-lq(n-b\ A5.9.4)
где с — некоторая постоянная. Подставляя данный результат в A5.9.3), за-
заменяя и на и, и + //', и + /, и + / + //' соответственно и используя
A5.2.4), получаем четыре тождества A5.9.1а) — A5.9.1г), за исключением
множителя с в их правых частях.
Так же как и в разд. 15.7, вычисление множителя с создает наибольшие
трудности. Множитель с не зависит от w, но он может зависеть от к или,
что эквивалентно, от q. Обозначим такую зависимость через c(q) и введем
две функции:
%) = П A - <Я2/A - q2"), A5-9.5)
П = \
оо
T{q) = 1 + 2 2(-l)V2- A5-9-6>
П = \
Полагая и = 0 в тождестве A5.9.16) с учетом только что определенного
множителя c(q) и используя A5.1.15), получаем
S{q)=c{q)T{q). A5.9.7)
Аналогично, умножая A5.9.16) на A5.9.1г), полагая и = 0 и используя
A5.1.5), находим
A5.9.8)
Обозначим т = г + 5, п = г - s; тогда A5.9.8) принимает вид
A5.9.9)
Г S
Здесь г и s — либо одновременно целые, либо одновременно полуцелые
числа. В последнем случае сумма по s равна нулю, поскольку имеются па-
пары слагаемых, одинаковых по величине и противоположных по знаку. Зна-
Значит, мы можем вычислять сумму только по всем целым числам г и s (поло-
(положительным, равным нулю и отрицательным). При этом получаем
S\q2)=c2{q)T\q2). A5.9.10)
S\q2)=c\q) ? ? (-1Г^»г.
т = — ос п= — ос

ГЛАВА 15 467
Заменяя q в A5.9.7) на q2 и сравнивая с A5.9.10), находим
c(q2) = c{q). A5.9.11)
Но из формулы A5.9.7) видно, что функцию c(q) можно разложить в
окрестности q = 0 в ряд Тейлора с ведущим членом, равным единице.
Подставляя ряд Тейлора в A5.9.11) и сравнивая коэффициенты получаем
c{q) = \. A5.9.12)
Следовательно, тождества A5.9.1) доказаны. Тождество A5.9.2) является
следствием A5.9.1а), которое получается с помощью A5.1.5) при z —
= exp (iiru/I) и с заменой q на qVl.
15.10. ПАРАМЕТРИЗАЦИЯ СИММЕТРИЧНЫХ
БИКВАДРАТНЫХ СООТНОШЕНИЙ
При рассмотрении модели Изинга, восьмивершинной модели и модели
жесткого гексагона мы сталкивались с симметричными биквадратными со-
соотношениями вида
ах2у2 + Ь(х2у + ху2) + с{х2 + у2) +2dxy +e(x+y)+f = 0. A5.10.1)
Здесь х и у — переменные (комплексные числа); я, Ь, с, d, eyf— заданные
постоянные.
Любое такое соотношение можно параметризовать с помощью эллип-
эллиптических функций. Чтобы показать это, выполним сначала преобразования
д), A5.10.2)
где а, /3, у, 6 — числа (в общем случае комплексные), такие, что ад Ф (Зу.
Вообще мы можем выбрать а, /3, у, д такими, чтобы в выражении A5.10.1)
величины b и е обратились в нуль и выполнялось равенство а = f Ф 0.
(Возможные исключения следует рассматривать, переходя к соответствую-
соответствующим пределам.) Разделим A5.10.1) на а и получим биквадратное соотноше-
соотношение канонического вида
х2у2 + 1 + с(х2 + у2) + 2фсу = 0. A5.10.3)
Данное соотношение можно рассматривать как квадратное уравнение
относительно у. Его решение имеет вид
у = - {dx ± V[-c + (d2 - 1 - с2)х2 - сх*]}/(с + х2). ,A5.10.4)
Подкоренное выражение в A5.10.4) представляет собой квадратичный от-
относительно х полином. Переходя к переменной и с помощью соотношения
х = к**пи, A5.10.5)
данный полином можно записать как полный квадрат. В соотношении

468 ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
A5.10.5) sn и — эллиптическая функция Якоби аргумента и и модуля к, где
к определяется равенством
? + k~l = (d2- I -c2)/c. A5.10.6)
С учетом A5.4.4) и A5.4.5) подкоренное выражение в формуле A5.10.4) за-
записывается в виде
-с[\ - (?+ к~1)х2 + хА] =
1 V } J A5.10.7)
= - сA - sn2w) A - к2 sn2w) = - с cn2w dn2w .
Введем параметр т;, определяемый соотношением
с= - l/(ksn2rj). A5.10.8)
Тогда из A5.10.6) следует, что знак параметра у] можно выбрать так, что-
чтобы выполнялось равенство
2/?). A5.10.9)
Подставляя полученные выражения в A4.10.4), получаем
у = /c^n^cn^dnry±snyycn^dn^ A5.10.10)
1 - к2 sn2w svty)
С помощью теоремы сложения A5.4.21) данный результат приводится к
следующему простому виду:
у = k*sn(u ± rj). A5.10.11)
Таким образом, переменная у определяется уравнением того же вида, что и
уравнение A5.10.5) для всех А', но с заменой и на w ± у.
Рассмотрим другой способ. Если мы перейдем от переменных л% у к пе-
переменным w, v в соответствии с правилом
x = k*snu, y = k*snv, A5.10.12)
то каноническая биквадратная форма A5.10.3) сведется к паре линейных со-
соотношений
v = и + г\ и v = и - г\. A5.10.13)
Мы можем теперь, используя преобразование A5.10.2), вернуться к об-
общему биквадратному соотношению A5.10.1). При этом изменятся, конечно,
величины с и d. Следует помнить, что в выражениях A5.10.6) — A5.10.9) исполь-
используются те же величины с* и г/, что и в формуле A5.10.3). Тем не менее справедливо
утверждение, что существуют параметры к иг;, такие, что равенство A5.10.1) сво-
сводится к
х = ф(и), у = ф(и±г]), A5.10.14)
где функция ф(и) определяется выражением
ф(и) = (ak^snu + l3)/(yk*snU + 5). A5.10.15)

ГЛАВА 15 469
Определим два новых параметра X, д следующим образом:
snA= - к~*р/а, sniu= - к~Щ. A5.10.16)
Тогда A5.10.15) можно записать в виде
ф(и) = (а/у) (sn и - sn A)/(sn и - sn (л). A5.10.17)
Используя A5Л.6) для выражения функции sn с помощью отношения
тэта-функций и применяя тождество A5.4.28) (с заменой и на —и), полу-
получаем
т(и - Я) т(и - 21 + Я) /,с1люч
0(w) = constant x -) f-) — '- , A5.10.18)
где функция r(w) определена формулой
т(и) = Я(и/2) 0(и/2). A5.10.19)
Из выражения A5.1.5) следует, что с точностью до постоянного множи-
множителя функция т(ы) представляет собой эллиптическую Я-функцию, в кото-
которой q заменено на q1, а и/1 — на и/{21). Из формулы A5.6.2) следует, что
функция т(и) связана с Н'(и) с помощью преобразования Ландена. Спра-
Справедливо равенство
т(и) = constant хЯ(м',/), A5.10.20)
где
/ = 2kh/(l +к), и' = |A + к)и . A5.10.21)
Изменим каждую из величин и, Л, /л, вычитая из них / и умножая затем
на A + к)/2. Умножим на A + к)/2 также и параметр г). Тогда выражение
A5ЛОЛ8) примет вид
ф(и) = constant x
а выражение A5.10.14) останется неизменным.
Следовательно, общее симметричное биквадратное соотношение
A5.10.1) можно свести к A5.10.14), где функция ф(и) задана выражением
A5Л0.22) или эквивалентным выражением
0(м) = constant х nv ; А-^-2 . A5.10.23)
rv У ( /) 2( /)

470 ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
Постоянный множитель и параметры /, X, /л, г) не зависят от х и у и опре-
определяются коэффициентами я, . . . ,/ из A5.10.1). В каждом конкретном
случае можно подставить выражения A5.10.14) и A5.10.22) для х и у не-
непосредственно в A5.10.1) и, придавая различные значения переменной и.
найти указанные параметры.
Существует много превосходных книг по теории эллиптических функций
[61,178, 251]. Очень полезен список тождеств в разд. 8.110 — 8.197 справоч-
справочника Градштейна и Рыжика [101]. Я надеюсь, мне удалось показать, что
если достаточно хорошо ознакомиться с применением теорем из разд. 15.3,
то становится ясным прямой путь проверки любого тождества.

ЛИТЕРАТУРА
1. Abraham D.В., Phys. Lett., A43, 163 A973).
2. Abraham D.В., Phys. Rev., B19, 3833 A979).
3. Alexanders., Phys. Lett., A54, 353 A975).
4. Als-Nielsen J. et al., Phys. Rev., B12, 4963 A975).
5. Andrews G. E., The Theory of Partitions, Addison-Wesley, Reading,
Massachusetts, 1976.
6. Andrews G. E.y The hard hexagon model and new Rogers — Ramanujan
type identities, Penn. State University Math. Dept. Research Report 8167,
1981.
7. AppelK., Haken W., Bull. Am. Math. Soc, 82, 711 A976).
8. AppelK., Haken W., Illinois J. Math., 21, 429 A977).
9. AppelK., Haken W., Koch J., Illinois J. Math., 21, 491 A977).
10. AshkinJ., Teller E., Phys. Rev., 64, 178 A943).
11. Baker G. A., Phys. Rev., B15, 1552 A977).
12. BarberM. N., J. Phys. A: Math. Gen., 12, 679 A979).
13. Barber M. N., Baxter R. J., J. Phys. C: Solid State Phys., 6, 2913 A973).
14. Baxter R. J., Proc. Camb. Phil. Soc, 59, 779 A963).
15. Baxter R. J., Phys. Fluids, 7, 38 A964).
16. Baxter R. J., Phys. Fluids, 8, 687 A965).
17. Baxter R. J., J. Math. Phys., 9, 650 A968).
18. Baxter R. J., J. Math. Phys.,10, 1211 A969).
19. Baxter R. J., Phys. Rev., Bl, 2199 A970).
20. Baxter R. J., J. Math. Phys., 11, 784 A970).
21. Baxter R. J., J. Math. Phys., 11, 3116 A970).
22. Baxter R. J., Phys. Rev. Lett., 26, 832 A971).
23. Baxter R. J., Phys. Rev. Lett., 26, 834 A971).
24. Baxter R. J. — in: Phase Transitions and Critical Phenomena, eds. С
Domb, M. S. Green, Academic Press, London, Vol. 1, 1972, p. 461.
25. Baxter R. J., Ann. Phys. (N. Y.), 70, 193 A972).
26. Baxter R. J., Ann. Phys. (N. Y.), 70, 323 A972).
27. Baxter R. J., Ann. Phys. (N. Y.), 76, 1, 25, 48 A973).
28. Baxter R. J., J. Stat. Phys., 8, 25 A973).
29. Baxter R. J., J. Phys. C: Solid State Phys., 6, L94 A973); J. Stat. Phys.,
9, 145 A973).
30. Baxter R. J., J. Phys. C: Solid State Phys., 6, L445 A973).

472
ЛИТЕРАТУРА
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
Baxter R. J., J. Stat. Phys., 15, 485 A976).
Baxter R. J., Phil. Trans. Roy. Soc. (London), 289, 315 A978).
Baxter R. J., Ann. Israel Phys. Soc, 2A), 37 A978).
Baxter R. J., J. Stat. Phys., 19, 461 A978).
Baxter R. J., J. Phys. A: Math. Gen., 13, L61 A980).
Baxter R. J., Enting I. G., J. Phys. A: Math. Gen., 9, L149 A976).
Baxter R. J., Enting I. G., J. Phys. A: Math. Gen., 11, 2463 A978).
Baxter R. J., Enting I. G., J. Stat. Phys., 21, 103 A979).
Phys. C: Solid State Phys., 7, L403 A974).
Phys. A: Math. Gen., 15 A982).
Baxter R. J., Tsang S. K., J. Phys., A: Math. Gen., 13, 1023 A980).
Baxter R. J., Wu F. Y., Phys. Rev. Lett., 31, 1294 A973).
WuF. Y., Aust. J. Phys., 27, 357 A974).
Sykes M. F.t Watts M. G., J. Phys. A: Math. Gen., 8, 245
Baxter R. J., Kelland S. В., J
Baxter R. J., Pearce P. A., J
Baxter R. J.
Baxter R. J.
A975).
Baxter R. J.
A976).
Baxter R. J.
don), A358
Baxter R. J.
Kelland S. В., WuF. Y., J. Phys. A: Math. Gen., 9, 397
V., Ashley S. E., Proc. Roy. Soc. (Lon-
Temperley H. N.
535 A978).
Enting 1. G., Tsang 5. K, J. Stat. Phys., 22, 465 A980).
BerahaS., Kahane J., J.Combinatorial Theory, B27, 1 A979).
Beraha S., Kahane J., Weiss N. J., Proc. Nat. Acad. Sci. (USA), 72, 4209
A975).
Beraha S., Kahane J., Weiss N.J. — in: Studies in Foundations and Com-
Combinatorics, ed. C. G. Rota, Academic Press, New York, 1978, p. 213.
Berlin T. H., Kac M., Phys. Rev., 86, 821 A952).
Bethe H. /4., Zs. Physik, 71, 205 A931).
Bethe H. A., Proc. Roy. Soc. (London), A150, 552 A935).
Birch B. J., Math. Proc. Camb. Phil. Soc, 78, 73 A975).
Birgeneau R. J., Guggenheim H. J., Shirane G., Phys. Rev., B8, 304 A973).
Black J. L., Emery V. J., Phys. Rev., B23, 429 A981).
BlochF., Zs. Physik, 61, 206 A930).
BlochF., Zs. Physik, 74, 295 A932).
Blote H. W. J., Nightingale M. P., Derrida В., J. Phys. A: Math. Gen., 14,
L45 A981).
Blumberg R. L.f Shlifer G., Stanley H. E., J. Phys. A: Math. Gen., 13.
L147 A980).
Bowman F., Introduction to Elliptic Functions, with applications, English
Universities Press, London, 1953.
Bozorth R. M., Ferromagnetism, Van Nostrand, New York, 1951. [Имеется
перевод: Бозорт Р. М. Ферромагнетизм. —М.: ИЛ, 1956.]
Bragg W. L., Williams E. J., Proc Roy. Soc (London), A145, 699 A934).
Brascamp H. J., Kunz H., WuF. Y., J. Math. Phys., 14, 1927 A973).
Burley D. M. — in: Phase Transitions and Critical Phenomena, Vol.2, eds.
C. Domb, M. S. Green, Academic Press, London, 1972, p. 329.
Cardy J. L., Nauenberg M., Scalapino D. J., Phys. Rev., B22, 2560 A980).

ЛИТЕРАТУРА 473
67. Chen M.S., OnsagerL., Bonner J., Nagle J., J. Chem. Phys., 60, 405
A974).
68. Courant R., Hilbert D., Methods of Mathematical Physics, Vol. 1, Inter-
science, New York, 1953. [Имеется перевод: Курант Р., Гильберт Д.
Методы математической физики, т. 1. — М. — Л.: ГТИИ, 1951.]
69. Coxeter H. S. M., Non-Euclidean Geometry, Toronto University Press,
Toronto, 1947.
70. den NijsM. P. M., J. Phys. A: Math. Gen., 12, 1857 A979).
71. den NijsM. P. M., Phys. Rev., B23, 6111 A981).
72. DitzianR. V. et al., Phys. Rev., B22, 2542 A980).
73. DomanyE., Riedel E. K., J. Appl. Phys., 49C), 1315 A978).
74. Domb C, Adv..Phys., 9, 149 A960).
75. Domb C. — in: Phase Transitions and Critical Phenomena, Vol. 3, eds.
С Domb, M. S. Green, Academic Press, London, 1974, p. 357.
76. DombC, Hunter D. L., Proc. Phys. Soc. (London), 86, 1147 A965).
77. Eggarter T. P., Phys. Rev., B9, 2989 A974).
78. Entingl. G., J. Phys. A: Math. Gen., 8, L35 A975).
79. Entingl.G., Baxter R. J., J. Phys. A: Math. Gen., 10, L117 A977).
80. Essam J. N. — in: Phase Transitions and Critical Phenomena, Vol. 2, eds.
С Domb, M. S. Green, Academic Press, London, 1972, p. 197.
81. Fan C, Phys. Rev., B6, 902 A972).
82. Fan C, Phys. Lett., 39A, 136 A972).
83. Fan C, WuF. Y., Phys. Rev., B2, 723 A970).
84. FelderhofB. U., Physica, 65, 421; 66, 279, 509; Phys. Lett., 44A, 437
A973).
85. Fisher M. Ё., Phys. Rev., 124, 1664 A961).
86. Fisher M. E., Phys. Rev. Lett., 16, 11 A966).
87. Fisher M. E.y Rep. Progr. Phys., 30, 615 A967).
88. Fisher M. E., J. Phys. Soc. Japan (Suppl.), 26, 87 A969).
89. Fisher M. E., Commun. Math. Phys., 26, 6 A972).
90. Fisher M. E., Rev. Mod. Phys., 46, 597 A974).
91. FisherM. E., FelderhofB. V., Ann. Phys. (N. Y.), 58, 176 A970).
92. Fortuin С. М., Kasteleyn P. W., Phisica, 57, 536 A972).
93. Frobenius F. G. A908). Reprinted in Section 79 of Ferdinand Georg
Frobenius: Gesammelte Abhandlungen, Springer-Verlag, Berlin, 1968.
94. Гантмахер Ф. Р. Теория матриц. — M.: Наука, 1966.
95. GaudinM., Phys. Rev. Lett., 26, 1301 A971).
96. Gaunt D. S., J. Chem. Phys., 46, 3237 A967).
97. Gaunt D. S., Domb C, J. Phys. C: Solid State Phys., 3, 1442 A970).
98. Gaunt D. S., Sykes M. S., J. Phys. A: Math. Nucl. Gen., 6, 1517 A973).
99. Gibbs J. W. A902). Elementary Principles in Statistical Mechanics,
Reprinted by Dover. New York, 1960.
100. GlasserM. L., Abraham D. В., Lieb E. H., J. Math. Phys.. 13, 887
A972).
101. Градштейн И. С, Рыжик И. М. Таблицы интегралов, сумм, рядов и
произведений. — М.: Физматгиз, 1962.

474 ЛИТЕРАТУРА
102. Greenhill Л. G. A892). Applications of Elliptic Functions, Reprinted by
Dover, New York, 1959.
103. Griffiths H. P., Wood D. W., J. Phys. C: Solid State Phys., 6, 2533
A973).
104. Griffiths R. В., Phys. Rev., 158, 176 A967).
105. Griffiths R. В., Phys. Rev. Lett., 24, 1479 A970).
106. Griffiths R. B. —in: Phase Transitions and Critical Phenomena, Vol. 1,
eds. C. Domb, M. S. Green, Academic Press, London, 1972, p. 7.
107. Guggenheim E. A., Proc. Roy. Soc. (London), A148, 304 A935).
108. Hankey A., Stanley H. E., Phys. Rev., B6, 3515 A972).
109. Heisenberg W., Zs. Physik, 49, 619 A928).
110. Hilhorst H. /., Schick M., van Leeuwen J. M. /., Phys. Rev. Lett., 40,
1605 A978).
111. Hilhorst H. J., Schick M., van Leeuwen J. M. J., Phys. Rev., B19, 2749
A979).
112. HintermannA., Kunz H., WuF. Y., J. Stat. Phys., 19, 623 A978).
113. HockenR., Moldover M. /?., Phys. Rev. Lett., 37, 29 A976).
114. Houtappel R. M. F., Physica, 16, 425 A950).
115. Hultchen L.y Arkiv. Mat. Astron. Fysik, 26A, No. 11 A938)
116. Hurst C. A., Green H. S.t J. Chem. Phys., 33, 1059 A960).
117. IsingE., Zs. Physik, 31, 253 A925).
118. Johnson J. D., BonnerJ. C, Phys. Rev. Lett., 44, 616 A980).
119. Johnson J. D.y McCoy В. M., Phys. Rev., A6, 1613 A972).
120. Johnson J. D.y Krinsky S., McCoy B. M.,Phys. Rev. Lett., 29, 492 A972).
121. Johnson J. D.y McCoy B. M., Lai С К., Phys. Lett., 38A, 143 A972).
122. Johnson J. D., Krinsky S.t McCoy В. M.y Phys. Rev., A8, 2526 A973).
123. Jones R. В., J. Phys. A: Math. Nucl. Gen., 6, 928 A973); 7, 280, 495
A974).
124. Joyce G. S. — in: Phase Transitions and Critical Phenomena, Vol. 2, eds.
C. Domb, M. S. Green, Academic Press, London, 1972, p. 375.
125. Joyce G. 5., Private communication, 1981.
126. JunglingK., J. Phys. C: Solid State Phys., 8, L169, A975).
127. KacM.y Thompson C. /., Physica Norvegica, 5, 163 A971).
128. Kac. M., Ward J. C, Phys. Rev., 88, 1332 A952).
129. KacM., Uhlenbeck G. E., Hemmer P. L., Math. Phys., 4, 216 A963); 5,
60 A964).
130. KadanoffL. P., Physics, 2, 263 A966).
131. Kadanoff L. P. — in: Phase Transitions and Critical Phenomena, Vol. 5A,
eds. C. Domb, M. S. Green, Academic Press, London, 1976, p. 1.
132. KadanoffL. P., Phys. Rev. Lett., 39, 903 A977).
133. KadanoffL. P., Ann. Phys. (N. Y.), 120, 39 A979).
134. KadanoffL. P., Brown A. C, Ann. Phys. (N. Y.), 121, 318 A979).
135. KadanoffL. P., WegnerF. J., Phys. Rev., B4, 3989 A971).
136. KadanoffL. P. et al., Rev. Mod. Phys., 39, 395 A967).
137. Kadanoff L. P., Hought on A., Yalabik M. C, J. Stat. Phys., 14, 171
A976).
138. Kanamori J., Progr. Theor. Phys., 20, 890 A958).

ЛИТЕРАТУРА 475
139. Kasteleyn P. W., Physica, 27, 1209 A961).
140. Kasteleyn P. W., J. Math. Phys., 4, 287 A963).
141. Kasteleyn P. W., Fortuin С M., J. Phys. Soc. Japan (Suppl.), 26, 11
A969).
142. Katsura S., Phys. Rev., 127, 1508 A962).
143. Kaufman В., Phys. Rev., 76, 1232 A949).
144. KellandS. В., J. Phys. A: Math. Nucl. Gen.',v7, 1907 A974).
145. KellandS. В., Austral. J. Phys., 27, 813 A974).
146. KellandS. В., Canad. J. Phys., 54, 1621 A976).
147. KikuchiR., Phys. Rev., 81, 988 A951).
148. KimD.y Joseph R. /., J. Phys. C: Solid State Phys., 7, L167 A974).
149. Kirkwood J. G., J. Chem. Phys., 3, 300 A935).
150. Knops H. J. F., Ann. Phys. (N. Y.), 128, 448 A980).
151. Knops H. J. F., Hilhorst H. /., Phys. Rev., B19, 3689 A979).
152. Kramers H. A., Wannier G. H., Phys. Rev., 60, 252 A941).
153. Kumar AT., Austral. J. Phys., 27, 433, A974).
154. Kunz H., Ann. Phys. (N. Y.), 85, 303 A974).
155. Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — 3-е
изд. — М.: Наука, 1976.
156. Lenard A., J. Math. Phys., 2, 682 A961).
157. LiebE. H., Phys. Rev., 162, 162 A967).
158. LiebE. H., Phys. Rev. Lett., 18, 1046 A967).
159. LiebE. #., Phys. Rev. Lett., 19, 108 A967).
160. Lieb E. #., Mattis D. C, Mathematical Physics in One Dimension,
Academic Press, New York and London, 1966.
161. LiebE. #., SchultzT.D., Mattis D. C, Ann. Phys. (N. Y.), 16, 407
A961).
162. LiebE. H., Wu F. Y., Phys. Rev. Lett., 20, 1445 A968).
163. Lieb E. H., Wu F. Y. — in: Phase Transitions and Critical Phenomena,
Vol. 1, eds. C. Domb, M. S. Green, Academic Press, London, 1972,
p. 321.
164. McCoy B. M.y Wu Т. Т., The Two-Dimensional Ising Model, Harvard
University Press, Cambridge, Mass; 1973.
165. Merlini D., Lett. Nuovo Cim., 8, 623 A973).
166. Merlini D.y Gruber C, J. Math. Phys., 13, 1814 A972).
167. Merlini D.y Hinterman A., Gruber С, Lett. Nuovo Cim., 7, 815 A973).
168. MetcalfB. D., Yang С. Р., Phys. Rev., B18, 2304 A978).
169. Montroll E. W., Nuovo Cim., Suppl., 6, 265 A949).
170. Montroll E. M., Potts R. В., Ward J. C, J. Math. Phys., 4, 308 A963).
171. Muir Т., A Treatise on the Theory of Determinants, Macmillan, London,
1882, p. 197.
172. Muller-Hartmann E., Zittarts J., Phys. Rev. Lett., 33, 893 A974).
173. Мусхешвили Н. И. Сингулярные интегральные уравнения. Граничные
задачи теории функций и некоторые их приложения к матем.
физике. — 2-е изд. — М.: Физматгиз, 1962.
174. NagleJ. F., J. Math. Phys., 9, 1007 A968).
175. NagleJ. F., J. Chem. Phys., 50, 2813 A969).

476 ЛИТЕРАТУРА
176. NagleJ. F., Commun. Math. Phys., 13, 62 A969).
177. NagleJ. F., Temperley H. N. V., J. Math. Phys., 9, 1020, A968).
178. Neville E. H., Jacobian Elliptic Functions, Oxford University Press, Ox-
Oxford, 1944.
179. NienhuisB., Riedel E. K., Schick M., J. Phys. A: Math. Gen., 13, L189
A980).
180. Nightingale M. P., Phys. Lett., 59A, 486 A977).
181. Noble В., Methods Based on the Wiener — Hopf Technique, Pergamon,
London, 1958. [Имеется перевод: Нобл Б. Применение метода
Винера — Хопфа для решения дифференциальных уравнений в
частных производных. — М.: ИЛ, 1962].
182. OitmaaJ., J. Phys. A: Math. Gen., 14, 1159 A981).
183. OitmaaJ., Plischke M., Physica В 4- С, 86 — 88, 577 A977).
184. OnsagerL., Phys. Rev., 65, 117 A944).
185. OnsagerL., Nuovo Cimento (Supll.), 6, 261 A949).
186. Onsager L. — in: Critical Phenomena in Alloys, Magnets and Supercondu-
Superconductors, eds. R. E. Mills, E. Ascher, R. I. Jaffee, McGraw-Hill, New York,
1971.
187. Ore O., The Four-Colour Problem, Academic Press, New York, 1967.
188. Paley R. E. A., Wiener N., Fourier Transforms in the Complex Domain,
American Mathematical Society, New York, 1934. [Имеется перевод: Ви-
Винер H., Пэли Р. Преобразование Фурье в комплексной области. —
М.: Наука, 1964.]
189. Pathria R. К., Statistical Mechanics, Pergamon, Oxford, 1972.
190. Pearce P. A., Thompson С J., J. Stat. Phys. 17, 189 A977).
191. Pearson R., Phys. Rev., B22, 2579 A980).
192. Peierls R., Proc. Camb. Phil. Soc, 32, 477 A936).
193. PercusJ. K., Phys. Rev. Lett., 8, 462 A962).
194. PercusJ. K., Yevick G. J., Phys. Rev., 110, 1 A958).
195. Pfeuty P., Physica В + С, 86 — 88, 579 A977).
196. Potts R. В., Proc. Camb. Phil. Soc, 48, 106 A952).
197. Potts R. В., Ward J. C, Progr. Theor. Phys. (Kyoto), 13, 38 A955).
198. Ramanujan S., Proc. Camb. Phil. Soc, 19, 214 A919).
199. Riedel E. K., Physica, 106A, 110 A981).
200. Rogers L. J., Proc. Lond. Math. Soc, 25, 318 A894).
201. Rogers L. J., Proc. Lond. Math. Soc, 19B), 387 A921).
202. Ruelle D., Statistical Mechanics: Rigorous Results, Benjamin, New York,
1969. [Имеется перевод: Рюэль Д. Статистическая механика. Строгие
результаты. — М.: Мир, 1971.]
203. Runnels L. К., J. Math. Phys., 8, 2081 A967).
204. Runnels L. К., Combs L. L., J. Chem. Phys., 45, 2482 A966).
205. Rys F., Helv. Phys. Acta. 36, 537 A963).
206. Saaty T. L., Kainen P. C, The Four-Colour Problem, McGraw-Hill, New
York1, 1977.
207. SaccoJ. E., Wut. J., J. Phys. A: Math. Gen., 8, 1780 A975).
208. Schultz T. D., Mattis D. C, Lieb E. H., Rev. Mod. Phys., 36, 856 A964).
209. Slater J. C, J. Chem. Phys., 9, 16 A941).

ЛИТЕРАТУРА 477
210. Slater L. J., Proc. Lond. Math. Soc, 54, 147 A951).
211. Stanley H. E., Phys. Rev.,176, 718 A968).
212. Stanley H. E., Introduction to Phase Transition and Critical Phenomena,
Clarendon, Oxford, 1971. [Имеется перевод: Стенли Г. Фазовые пере-
переходы и критические явления. — М.: Мир, 1973.]
213. Stanley Н. Е. — in: Phase Transition and Critical Phenomena, Vol. 3, eds.
С Domb, M. S. Green, Academic Press, London, 1974, p. 485.
214. Starling S. G., Woodall A. J., Electricity and Magnetism, Longman,
London, 1953.
215. Stephen M. J., Mittag L., J. Math. Phys., 13, 1944 A972).
216. Stephenson J., Phys. Rev., Bl, 4405 A970).
217. Strinchcombe R. В., J. Phys. C: Solid State Phys., 6, 2459 A973).
218. Stroganov Y. G., Phys. Lett.. 74A, 116 A979).
219. Sutherland В., Phys. Rev. Lett., 19, 103 A967).
220. Sutherland В., J. Math. Phys., 11, 3183 A970).
221. Suzuki M., Progr. Theor. Phys., 51, 1992 A974).
222. Suzuki M., Progr. Theor. Phys., 56, 1454 A976).
223. SykesM. F., Essam J. W., Gaunt D. S., J. Math. Phys., 6, 283 A965).
224. SykesM. F. et aly J. Phys. A: Math. Gen., 5, 640 A972).
225. SykesM. F. et al.y J. Phys. A: Math. Gen., 6, 1507 A973).
226. SykesM. F. et al., J. Math. Phys., 14, 1071 A973).
227. TakahashiM., Progr. Theor. Phys., 50, 1519 A973).
228. TakahashiM., Progr. Theor. Phys., 51, 1348 A974).
229. TakahashiM., Suzuki M., Progr. Theor. Phys., 48, 2187 A972).
230. Temperley H. N. V., Fischer M. E.y Phil. Mag., 6, 1061 A961).
231. Temperley H. N. V., Lieb E. #., Proc. Roy. Soc. (London), A322, 251
A971).
232. Thompson C. J., J. Math. Phys., 6, 1392 A965).
233. Thompson С J., Mathematical Statistical Mechanics, Princeton University
Press, Princeton, N. J., 1972.
234. Tsang S. K., J. Stat. Phys., 20, 95 A979).
235. Tutte W. Т., J. Combinatorial Theory, 2, 301 A967).
236. Tutte W. Т., J. Combinatorial Theory, 9, 289 A970).
237. Tutte W. Т., Canad. J. Math., 25, 426 A973).
238. Tutte W. Т., Canad. J. Math., 26, 893 A974).
239. van der Waals J. D.y Over de Continuiteit van den Gas-en Vloeistoftoes-
tand, Thesis, Leiden, 1873.
240. van HoveL., Physica, 16, 137 A950).
241. van LeeuwenJ. M. J., Phys. Rev. Lett., 34, 1056 A975).
242. van Leeuwen J. M. J., Groeneveld J.y de Boer J., Physica, 25, 792 A959).
243. ВдовиченкоН. В. — ЖЭТФ, 1964, т. *!7, с. 715.
244. Vicentini-Missoni M. — in: Phase Transitions and Critical Phenomena,
Vol. 2, eds. С Domb, M. S. Green, Academic Press, London, 1972, p. 39.
245. Walker L. R., Phys. Rev., 116, 1089 A959).
246. WannierG. H., Rev. Mod. Phys., 17, 50 A945).
247. Watson G. N., J. Indian. Math. Soc, 20, 57 A933).
248. WegnerF. J., J. Phys. C: Solid State Phys., 5, L131 A972).

478 ЛИТЕРАТУРА
249. WegnerF. J., Physica, 68, 570 A973).
250. Whitney #., Ann. Math. (N. Y.), 33, 688 A932).
251. Whittaker E. Т., Watson G. //., A course of Modern Analysis, Cambridge
University Press, Cambridge, 1915. [Имеется перевод: Уиттекер Э. Т.,
Ватсон Г. Н. Курс современного анализа. — В 2-х частях. — М.: Физ-
матгиз, 1962 — 1963.]
252. WidomB., J. Chem. Phys., 43, 3892, 3898 A965).
253. Wilson К. G., Phys. Rev., B4, 3174 A971).
254. Wilson K. G., Fisher M. E., Phys. Rev., Lett., 28, 240 A972).
255. Wilson K. G., Kogut /., Phys. Reports, 12C, 75 A974).
256. WoodD. W., Griffiths H. P., J. Phys. C: Solid State Phys., 5, L253
A972).
257. Wrege D. E.y Spooner S., Gersch H. A., American Institute of Physics
Conference Proceedings, 5, 1334 A972).
258. WuF. Y., Phys. Rev., B4, 2312 A971).
259. Wu F. Y., J. Phys. C: Solid State Phys., 12, L637 A979).
260. WuF. Y.y LinK. Y., J. Phys. C: Solid State Phys., 7, L181 A974).
261. WuF. Y.y LinK. Y., Phys. Rev., B12, 419 A975).
262. Yang С N., Phys. Rev., 85, 808 A952).
263. Yang С N., Yang С. Р., Phys. Rev., 150, 321, 327; 151, 258 A966).
264. Yang С N., Yang С. Р., J. Math. Phys., 10, 1115 A969).
265. Yang С. Р., Phys. Rev. Lett., 19, 586 A967).
266. Замолодчиков А. Б., Commun. Math. Phys., 79, 489 A981).
267. ZisookA. В., J. Phys. A: Math. Gen., 13, 2451 A980).
268. ZittartzJ., Zs. Physik, B41, 75 A981).

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Антисегнетоэлектрическая фаза восьми-
вершинной модели 249
модели типа льда 154
Асимптотическое вырождение наиболь-
наибольших собственных значений трансфер-
матрицы 116, 155, 242
Берага числа 332
Бете анзац 142, 171
— решетка 20, 55—66, 308, 351
Бихроматический полином 325
Ван дер Ваальса уравнение состояния
20, 38
Винера — Хопфа факторизация 232, 234
Внутренняя энергия 16, 23
модели Поттса 344, 345, 349
сферической модели 71
Волновые числа 146, 147, 171, 180
Восприимчивость 11, 25
— для сферической модели 76
Восьмивершинная модель 205—322
Гейзенберга модель см. А^У^-модель
Гиперболическая тригонометрия 294
Гиперскейлинг 14
Гипотеза подобия (скейлинга) 12—14,
45, 53, 65, 77, 167
Двадцативершинная модель 313
Димера задача 128—130
Дуальная решетка 79, 80
Дуальность 82, 83
— восьмивершинной модели 209
— модели Поттса 338, 339, 346
Эшкина — Теллера 357
— плоской модели Изийга 82, 83, 91
Задача о раскрашивании четырьмя
красками 332
Звезда — треугольник, соотношение для
восьмивершинной модели 213—218,
282, 283, 292
ВСГ-модели 370—372
модели жесткого гексагона
408—410
типа льда 190—192
плоской модели Изинга 85,
98, 127
трехмерное 450
Кагоме решетка 279, 280
KDP модель 133
Кейли дерево 55—57, 62, 63
Корреляции 18, 26, 27
— одномерная модель Изинга 43, 44
— плоская модель Изинга 299, 300
Корреляционная длина 26
восьмивершинная модель 244, 245
модель жесткого гексагона 449
типа льда 157
одномерная модель Изинга 44
плоская модель Изинга 118, 122,
124
связь с собственными значениями
трансфер-матрицы 44, 119—122
Кривая сосуществования 36
Критическая точка 10, 18, 35
восьмивершинная модель 251
модель жесткого гексагона 444
Изинга на решетке Бете 62
Поттса 339, 340, 347, 348
среднего поля 52
типа льда 158
Эшкина — Теллера 360
одномерная модель Изинга 45
плоская модель Изинга 82, 83, 92,
125
сферическая модель 73
трехспиновая модель 316

480
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Критическая точка, численные значения
для изотропной модели Изинга 82,
83, 310
Критические показатели 11, 12. См.
также Гипотеза подобия и Соотно-
Соотношения подобия
восьмивершинная модель 256—258
классические значения 38, 39, 54,
65
модель жесткого гексагона 447,
448
Изинга на решетке Бете 65
Поттса 351, 352
среднего поля 53, 54
типа льда 159, 167, 168
Эшкина — Теллера 360, 361
непрерывно изменяющиеся 15,
256, 257
одномерная модель Изинга 46
плоская модель Изинга 126
сферическая модель 75, 76
трехспиновая модель 321, 322
Кюри точка 10, 52. См. также Крити-
Критическая точка
Ландена преобразование 463
Лиувилля теорема 454
Медиальный граф 326, 327, 333
Модель жесткого гексагона 401—451
— Изинга 21—40
на решетке Бете 55—66, 308—310
одномерная 40—46
плоская 78—130, 296—310
связь ^/-мерной модели
с d—1-мерной квантовомеханической
моделью 269, 270
— свободных фермионов 273
— среднего поля 47—54
— сферическая 67—77
— типа льда 131—182
— F 133
— XYZ (цепочка) 261, 262, 270, 271,
273
-^323
Намагниченность 9—12, 24, 25. См.
также Спонтанная намагниченность
— модели Изинга на решетке Бете
60—62
Намагниченность модели среднего поля
49
— одномерной модели Изинга 43
— сферической модели 71
Обратимости соотношения 381—385,
419—422, 425—427
Параметр порядка 403. См. также
Спонтанная намагниченность и
Спонтанная поляризация
модели жестких гексагонов 403,
436, 440, 448
Перколяции задача 325
Поверхностное натяжение 27, 115—118,
242, 243
Поляризация 164. См. также Спонтан-
Спонтанная поляризация
Поттса модель 321—352
Правило льда 131
Прохождение пары векторов через
вершину 196, 197, 218
Пуассона формула суммирования 465
Пфаффиан 129
Разложения в ряд 17, 29, 30, 394, 395
Разностное ядро, преобразование
к нему 148, 174
Разупорядочения точки 250
Раскрашивание квадратной решетки
168—181
Ренормализационная группа 18
Решеточный газ 31, 37
модель жестких гексагонов 401,
407, 408
среднего поля 54
Роджерса — Рамануяна тождества 430,
432, 440
Свободная энергия 23, 24
восьмивершинной модели 240, 288
модели жестких гексагонов 447
Изинга на решетке Бете 62,
63, 66
Поттса 340, 348, 349
среднего поля 50
типа льда 148—153
одномерной модели Изинга 42
плоской модели Изинга 114, 115
сферической модели 68
трехспиновой модели 321

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
481
Сегнетоэлектрическая модель типа льда
в поле 163—167
Скейлинг см. Гипотеза подобия и
Соотношения подобия
Слабое разложение графа 2209
Соотношения подобия (скейлинга) 14,
28, 126, 449
Сопряженный модуль 417, 418, 463, 464
Спонтанная намагниченность 9, 11, 30
восьмивершинная модель 246,
293, 294, 389
модель Изинга на решетке Бете
64
среднего поля 52
плоская модель Изинга 123, 302,
306
сферическая модель 74, 75
трехспиновая модель 321
— поляризация и спонтанная антисегне-
тоэлектрическая поляризация восьми-
вершинной модели 247, 248
модели типа льда 155,
156
трехспиновой модели
321
Статистическая сумма 16, 23, 33
Сферическая модель 67—77
Теплоемкость 23
Трансфер-матрица 41, 95
— восьмивершинной модели 188, 217
— ВСГ-модели 370
— модели жесткого гексагона 449
Трансфер-матрица модели типа льда
134
— одномерной модели Изинга 41, 42
— плоской модели Изинга 90, 94—99
— угловая см. Угловые трансфер-
матрицы
Трехспиновая модель 315—321
Тридцатидвухвершинная модель
на треугольной решетке 311—315
Угловые трансфер-матрицы 363—400
восьмивершинная модель 385—389
Универсальность 14—16, 256—258
— слабая 256, 258
Фазовый переход 9. См. также Крити-
Критическая точка
Шестивершинная модель см. Модель
типа льда
Эллиптические функции 452—470
в восьмивершинной модели 215,
216
модели жесткого гексагона
410—413
плоской модели Изинга 1, 107,
1087
Эшкина — Теллера модель 257,
353—362
Якоби параметр 464

ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА 5
ПРЕДИСЛОВИЕ 7
1. ОСНОВЫ СТАТИСТИЧЕСКОЙ МЕХАНИКИ 9
1.1. Фазовые переходы и критические точки 9
1.2. Гипотеза подобия (скейлинга) 12
1.3. Универсальность 14
1.4. Статистическая сумма 16
1.5. Приближенные методы 17
1.6. Точно решаемые модели 18
1.7. Обобщенная модель Изинга 21
1.8. Модель Изинга с взаимодействием между ближайшими сосе-
соседями 28
1.9. Решеточный газ 31
1.10. Уравнение ван дер Ваальса и классические показатели 38
2. ОДНОМЕРНАЯ МОДЕЛЬ ИЗИНГА 40
2.1. Свободная энергия и намагниченность 40
2.2. Корреляции 43
2.3. Критическое поведение вблизи Т = 0 44
3. МОДЕЛЬ СРЕДНЕГО ПОЛЯ 47
3.1. Термодинамические свойства 47
3.2. Фазовый переход 50
3.3. Свойства при Н = 0 и критические показатели 52
3.4. Критическое уравнение состояния 53
3.5. Модель среднего поля для решеточного газа 54
4. МОДЕЛЬ ИЗИНГА НА РЕШЕТКЕ БЕТЕ 55
4.1. Решетка Бете 55
4.2. Размерность 56
4.3. Рекуррентные соотношения для намагниченности центральной
точки 57
4.4. Предел при п — оо 59

ОГЛАВЛЕНИЕ 483
4.5. Намагниченность как функция Н 60
4.6. Свободная энергия 62
4.7. Результаты для низкотемпературной области в отсутствие
поля 63
4.8. Критическое поведение 64
4.9. Анизотропная модель 65
5. СФЕРИЧЕСКАЯ МОДЕЛЬ 67
5.1. Формулировка модели 67
5.2. Свободная энергия 68
5.3. Уравнение состояния и внутренняя энергия 70
5.4. Функция g'(z) 71
5.5. Существование критической точки при d > 2 73
5.6. Свойства в отсутствие внешнего поля: показатели а, /5, у, у' .... 75
5.7. Критическое уравнение состояния 76
6. ДУАЛЬНОСТЬ И ПРЕОБРАЗОВАНИЕ ЗВЕЗДА — ТРЕУГОЛЬ-
ТРЕУГОЛЬНИК ПЛОСКИХ МОДЕЛЕЙ ИЗИНГА 78
6.1. Общие замечания относительно двумерных моделей 78
6.2. Соотношение дуальности для модели Изинга на квадратной
решетке 78
6.3. Взаимная дуальность шестиугольной и треугольной решеток .... 83
6.4. Соотношение звезда — треугольник 85
6.5. Самодуальность треугольной решетки 91
7. МОДЕЛЬ ИЗИНГА НА КВАДРАТНОЙ РЕШЕТКЕ 93
7.1. Историческое введение 93
7.2. Трансфер-матрицы V, W 94
7.3. Два важных свойства матриц К и W 96
7.4. Соотношения симметрии 99
7.5. Коммутационные соотношения для трансфер-матриц 100
7.6. Функциональное соотношение для собственных значений 101
7.7. Собственные значения Л при Т = Тс 102
7.8. Собственные значения Л при Т < Тс 106
7.9. Общие выражения для собственных значений 112
7.10. Следующие за максимальным собственные значения; поверх-
поверхностное натяжение, корреляционная длина и намагниченность
при Т < Тс 115
7.11. Следующее за максимальным собственное значение и корреля-
корреляционная длина при Т > Тс 123
7.12. Критическое поведение < 124
7.13. Параметризованное соотношение звезда — треугольник 127
7.14. Задача димера 128
8. МОДЕЛИ ТИПА ЛЬДА 131
8.1. Введение 131
8.2. Трансфер-матрица 134

484 ОГЛАВЛЕНИЕ
8.3. Сохранение линий 135
8.4. Собственные значения для произвольного п 141
8.5. Максимальное собственное значение; определение zx , . . . , zn .. 143
8.6. Случай Д > 1 145
8.7. Термодинамический предел при Д < 1 146
8.8. Свободная энергия при -1 < Д < 1 148
8.9. Свободная энергия при Д < -1 151
8.10. Классификация фаз 153
8.11. Критические сингулярности 158
8.12. Сегнетоэлектрическая модель в присутствии поля 163
8.13. Раскрашивание квадратной решетки тремя красками 168
9. АЛЬТЕРНАТИВНЫЙ СПОСОБ РЕШЕНИЯ МОДЕЛЕЙ ТИПА
ЛЬДА 183
9.1. Введение 183
9.2. Коммутирующие трансфер-матрицы 183
9.3. Уравнения для собственных значений 184
9.4. Соотношение между матричными функциями, определяющее
собственные значения 185
9.5. Сводка матричных свойств 187
9.6. Прямой вывод матричных свойств: коммутация 188
9.7. Параметризация в целых функциях 193
9.8. Матрица Q(v) 195
9.9. Значения^, X, v 204
10. ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА КВАДРАТНОЙ
РЕШЕТКЕ 205
10.1. Введение 205
10.2. Симметрии 207
10.3. Формулировка восьмивершинной модели как модели Изинга с
взаимодействием между двумя и четырьмя спинами 210
10.4. Соотношение звезда — треугольник 213
10.5. Матрица Q(v) 218
10.6. Уравнения на собственные значения матрицы V(v) 225
10.7. Максимальное собственное значение: определение величин
. •••.»„ 227
10.8. Вычисление свободной энергии 231
10.9. Случай Изинга 240
10.10. Другие термодинамические свойства 242
10.11. Классификация фаз 248
10.12. Критические сингулярности 251
10.13. Эквивалентная модель Изинга 258
10.14. ATZ-цепочка 261
10.15. Сводка определений для величин Д, Г, ку X, vy q, xy z, р, д, w .. 270
10.16. Частные случаи '.. 272
10.17. Точно решаемая неоднородная восьмивершинная модель 275

ОГЛАВЛЕНИЕ 485
11. ВОСЬМИВЕРШИННАЯ МОДЕЛЬ НА РЕШЕТКЕ КАГОМЕ 279
11.1. Определение модели 279
11.2. Переход к модели на квадратной решетке 284
11.3. Корреляционная длина и спонтанная поляризация 287
11.4. Свободная энергия 288
11.5. Представление в виде модели Изинга на треугольно-шести-
треугольно-шестиугольной решетке с взаимодействиями двух и четырех спинов 289
11.6. Фазы 295
11.7. К" = 0: модели Изинга на треугольной и шестиугольной
решетках 296
11.8. Точные разложения результатов, полученных в модели
Изинга 302
11.9. Тридцатидвухвершинная модель 311
11.10. Трехспиновая модель на треугольной решетке 315
12. МОДЕЛИ ПОТТСА И ЭШКИНА — ТЕЛЛЕРА 323
12.1 Введение и формулировка модели Поттса 323
12.2. Модель Поттса и бихроматический полином 324
12.3. Плоские графы: эквивалентная модель типа льда 326
12.4. Модель Поттса на квадратной решетке 332
12.5. Модель Поттса на квадратной решетке в критических точках . 340
12.6. Модель Поттса на треугольной решетке 345
12.7. Объединенные формулы для моделей Поттса на всех трех
плоских решетках 350
12.8. Критические показатели для двумерной модели Поттса 351
12.9. Модель Эшкина — Теллера на квадратной решетке 353
13. УГЛОВЫЕ ТРАНСФЕР-МАТРИЦЫ 363
13.1. Определения 363
13.2. Представление в виде произведений операторов 369
13.3. Соотношение звезда — треугольник 370
13.4. Предел бесконечной решетки 375
13.5. Собственные значения угловых трансфер-матриц 377
13.6. Свойства обратимости: выражение для функции к(и) 381
13.7. Восьмивершинная модель 385
13.8. Уравнения для угловых трансфер-матриц 389
14. ЖЕСТКИЙ ГЕКСАГОН И БЛИЗКИЕ МОДЕЛИ 401
14.1. Исторический пример и основные результаты 401
14.2. Модель жестких квадратов с диагональными взаимодейст-
взаимодействиями 407
14.3. Свободная энергия 418
14.4. Подрешеточные плотности и параметр порядка R 424
14.5. Точные формулы для различных случаев: тождества
Роджерса — Рамануяна 430

486 ОГЛАВЛЕНИЕ
14.6. Альтернативные выражения для функций а:, р, R 441
14.7. Модель жесткого гексагона 446
14.8. Замечания и предположения 449
14.9. Благодарности 451
15. ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ 452
15.1. Определения 452
15.2. Аналитичность и периодичность 453
15.3. Общие теоремы 454
15.4. Алгебраические тождества 457
15.5. Дифференциальные и интегральные тождества 460
15.6. Преобразование Ландена 463
15.7. Сопряженный модуль 463
15.8. Формула суммирования Пуассона 465
15.9. Разложения тэта-функций в ряд 465
15.10. Параметризация симметричных биквадратных соотношений 467
ЛИТЕРАТУРА 471
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 479

УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании книги, ее
оформлении, качестве перевода и другие просим
присылать по адресу: 129820, Москва, И-110.
ГСП, 1-й Рижский пер., д. 2, изд-во «Мир».