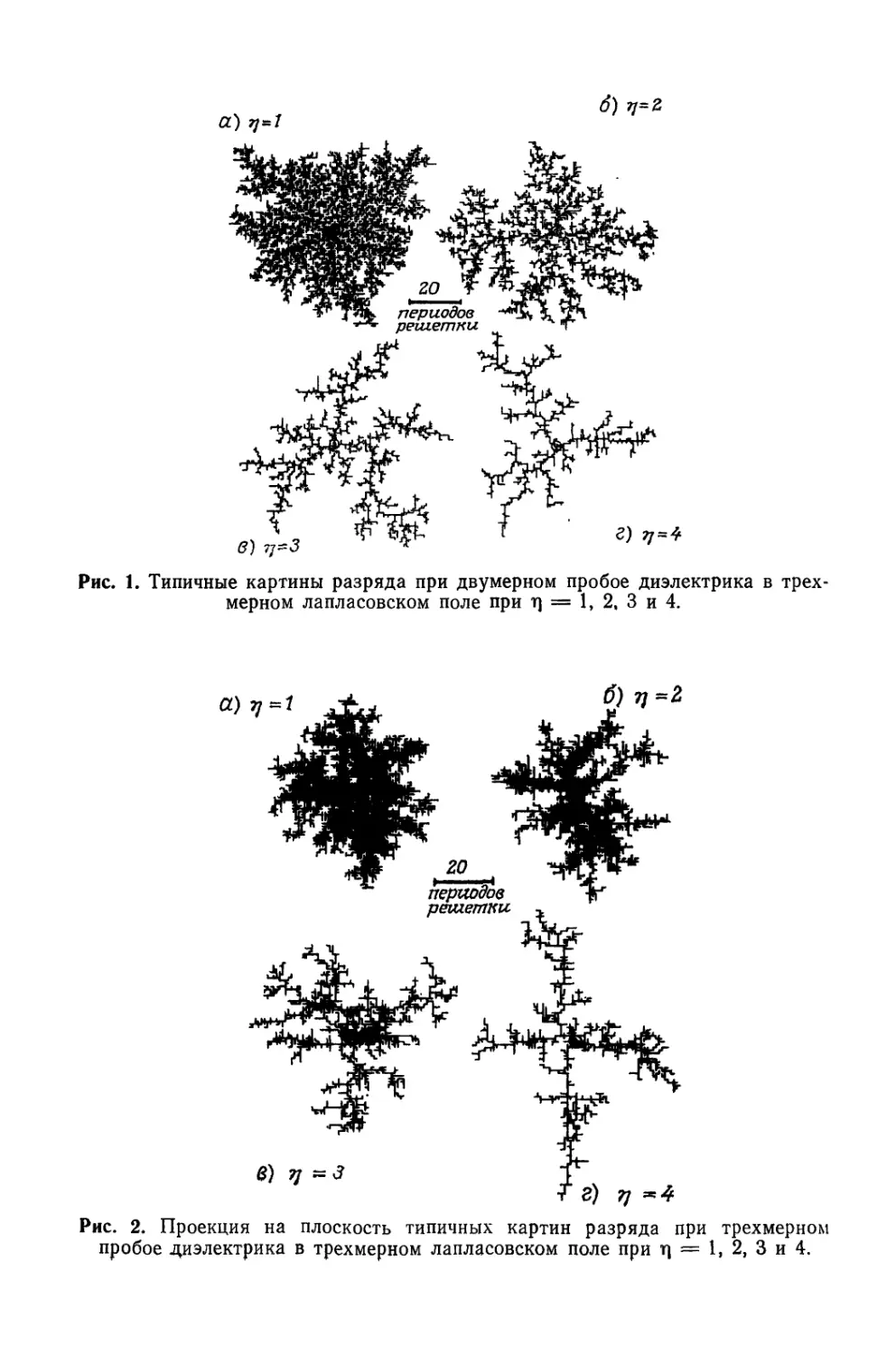
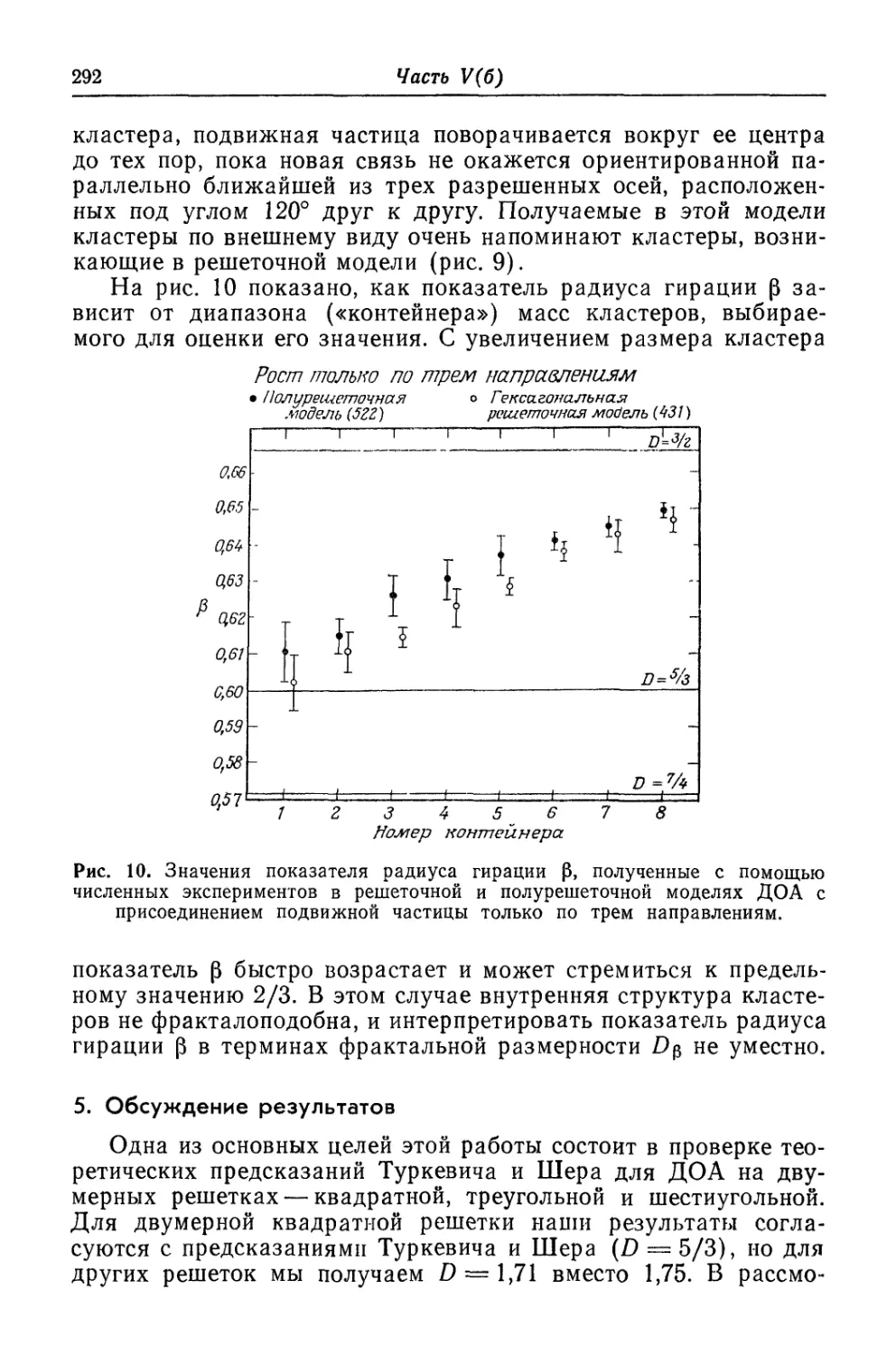
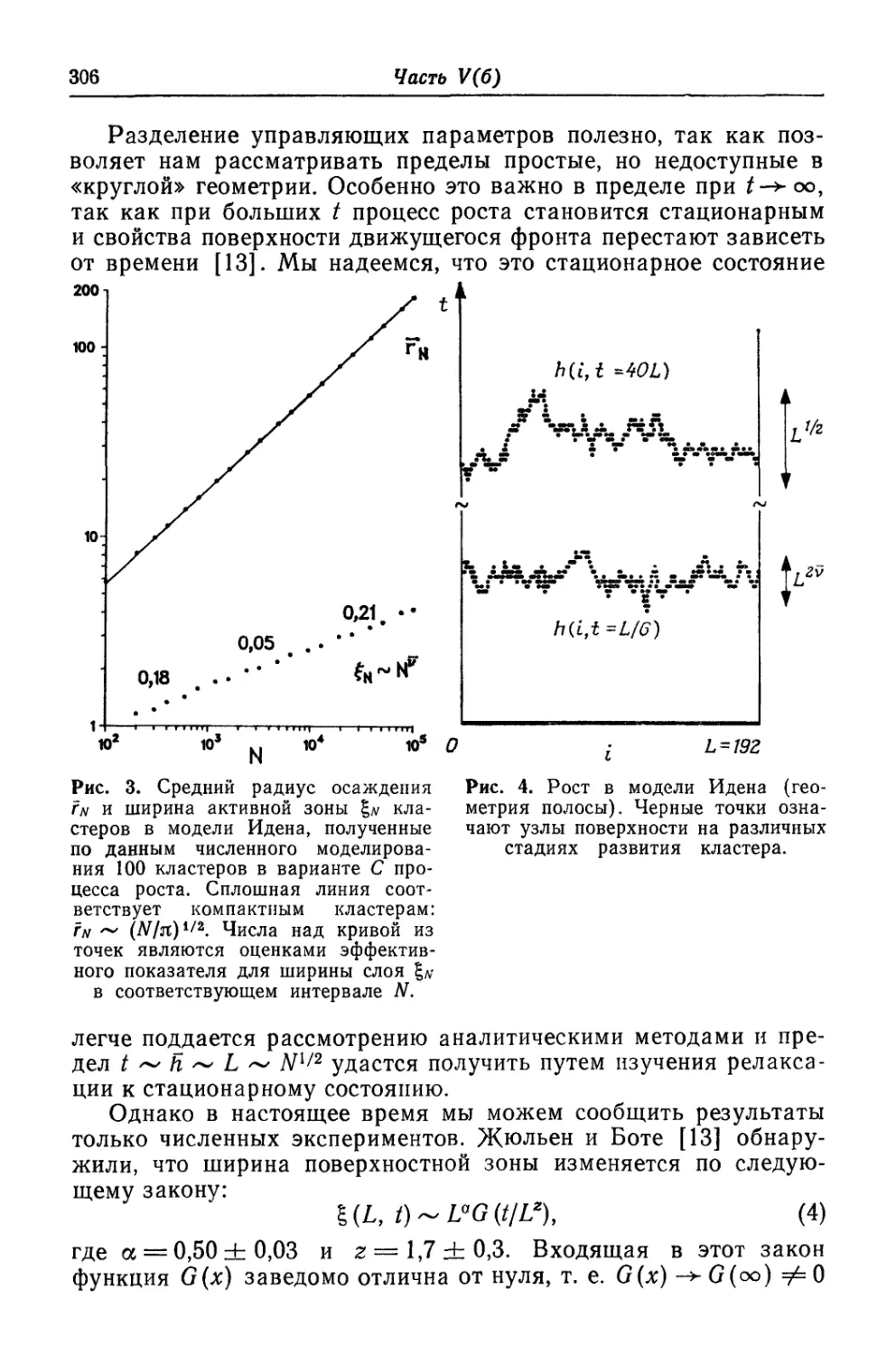
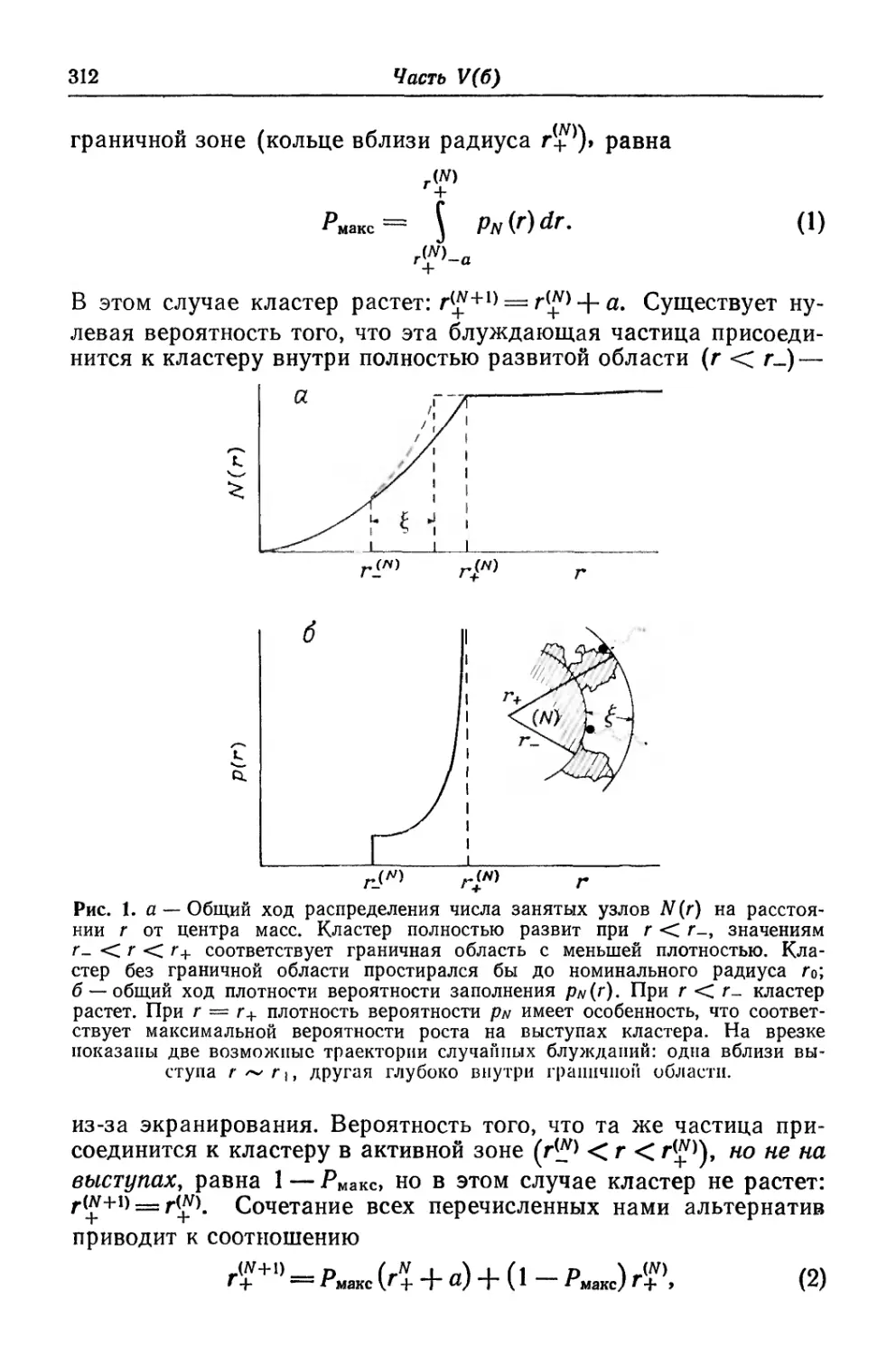
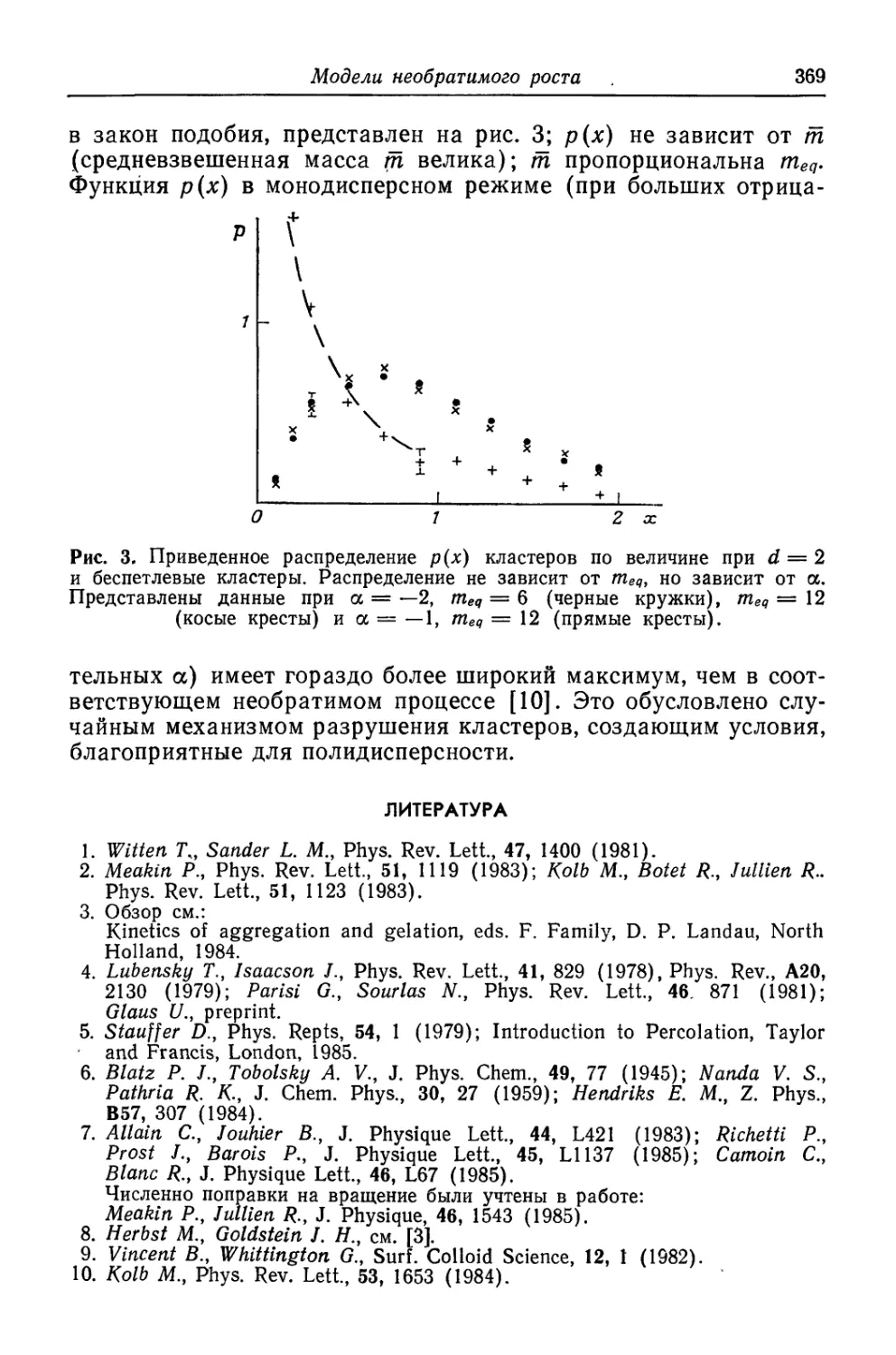
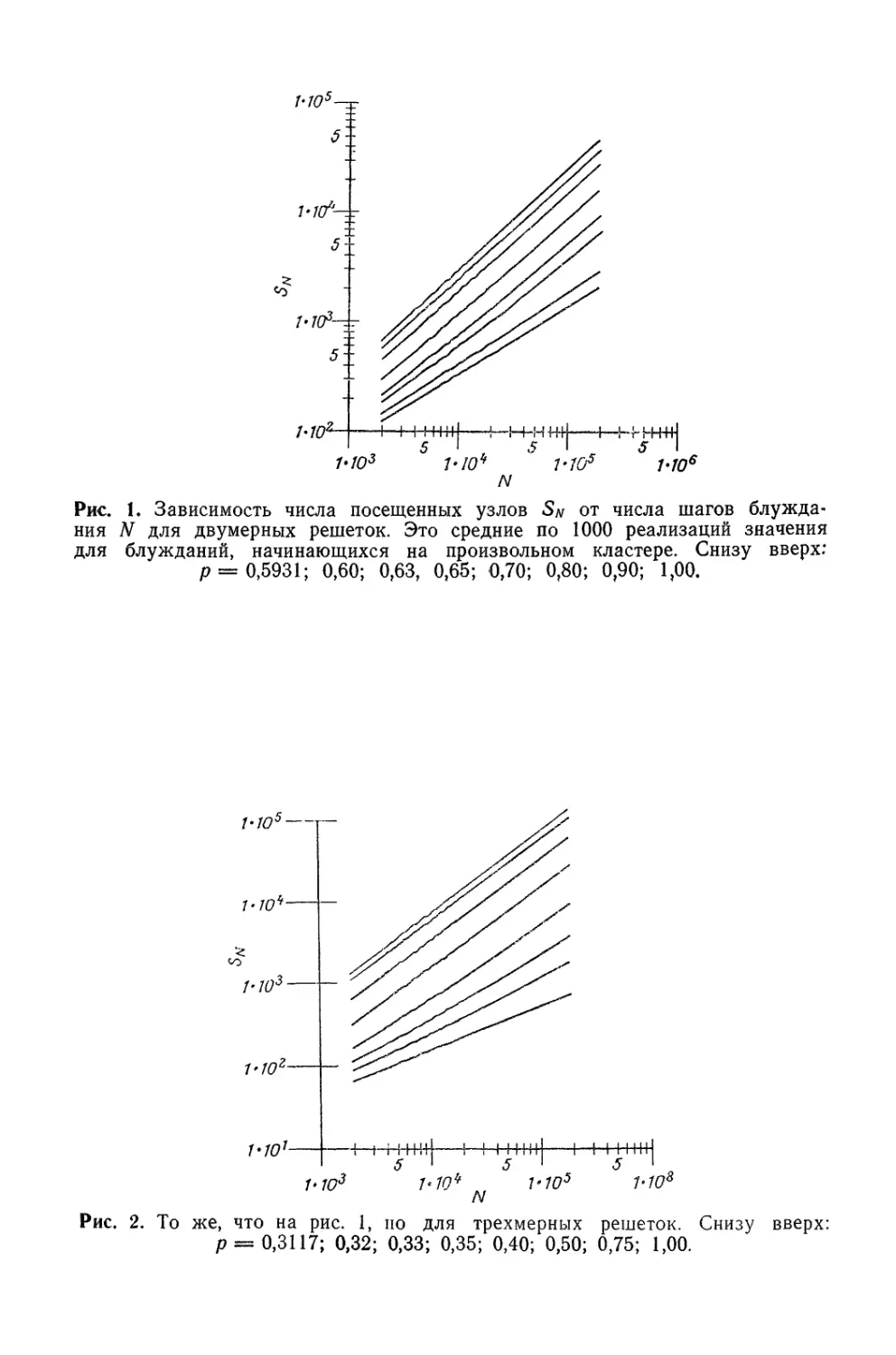
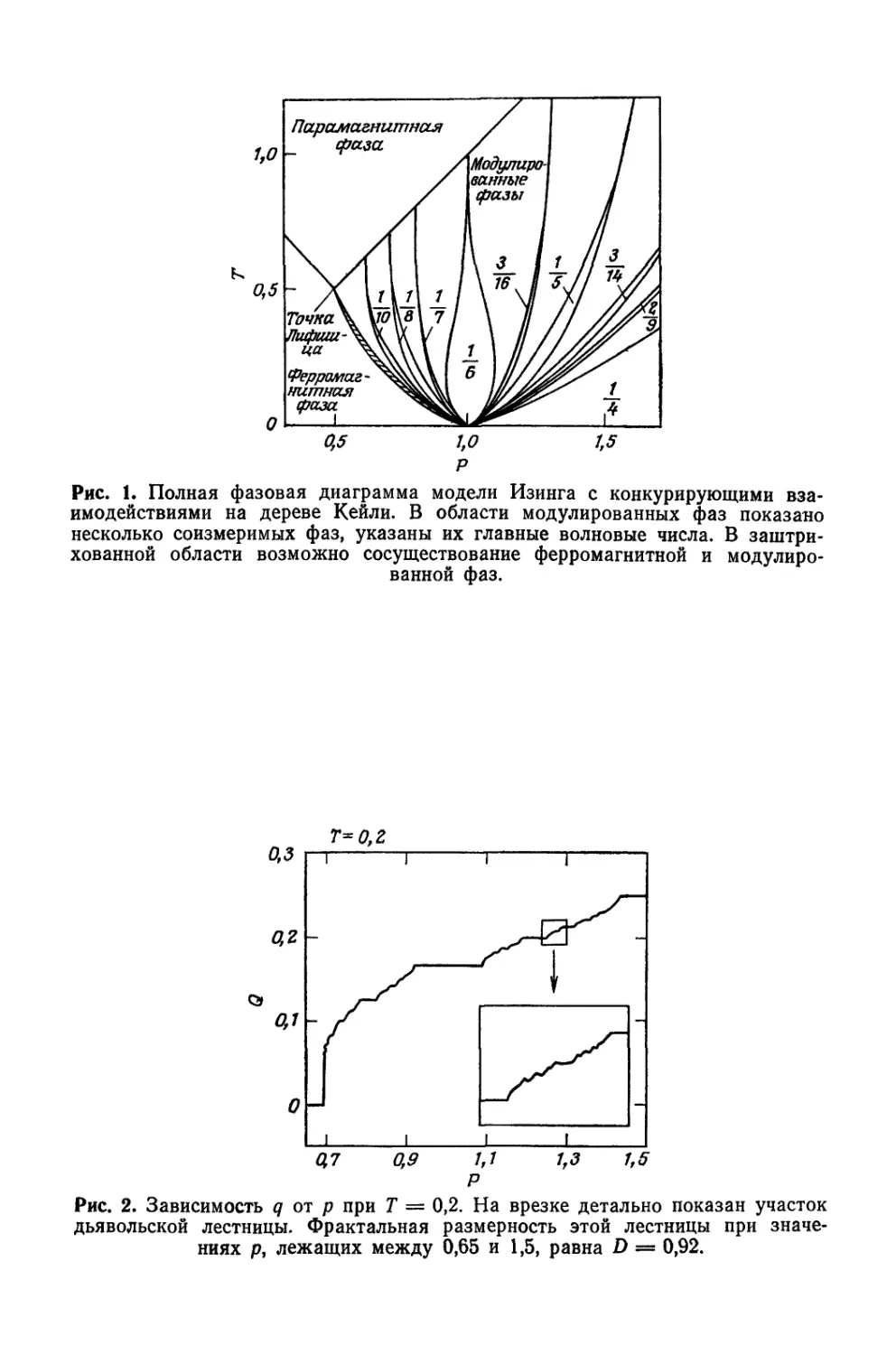
Текст
ISBN 503-001295-8 (русск.)
ISB1N 0444---— • (англJ
со
е
DQ
с:
®
ФРАКТАЛЫ В ФИЗИКЕ
V
ИЗДАТЕЛЬСТВО«МИР'
FRACTALS IN PHYSICS
Proceedings of the Sixth Trieste
International Symposium on
Fractals in Physics,
ICTP, Trieste, Italy, July 9—12, 1985
Edited by
Luciano PIETRONERO
Solid State Physics Laboratory
University of Groningen
The Netherlands
and
Erio TOSATTI
International School for Advanced Studies
Trieste
Italy
North-Holland
AMSTERDAM-OXFORD-NEW YORK-TOKYO
1986
ФРАКТАЛЫ
В ФИЗИКЕ
Труды VI международного симпозиума
по фракталам в физике
(МЦТФ, Триест,
Италия, 9 - 12 июля, 1985)
Под редакцией
Л. Пьетронеро и Э. Тозатти
Перевод с английского
под редакцией
д-ра физ.-мат, наук проф. Я. Г. Синая и
акад, И. М. Халатникова
Москва «Мир» 1988
ББК 22.3
Ф82
УДК 530.1
Переводчики: Веденова И. А., Данилов Ю. А., канд.
хим. наук Кучаиов С. И., канд. физ.-мат. наук
Соколов И. М., Третьякова Л. И.
Фракталы в физике: Труды VI международного
Ф82 симпозиума по фракталам в физике (МЦТФ, Триест,
Италия, 9—12 июля, 1985): Пер. с англ. / Под ред. Л.
Пьетронеро, Э. Тозатти. — М.: Мир, 1988.-—672 е., ил.
ISBN 5-03-001295-8
В книге, представляющей собой труды международного
симпозиума, собраны последние достижения в теории фракталов. Среди
авторов — крупнейшие специалисты из многих стран мира (США,
Англии, ФРГ, Франции, Италии и др.). По содержанию книга
охватывает почти все области физики, в которых обнаружены
фрактальные структуры — от квантовой теории поля и статистической
механики до турбулентности и хаоса в динамических системах, а также
приложения фрактальной геометрии в различных разделах химии,
биологии. На русском языке это первая книга по теории фракталов
и ее приложениям.
Для физиков, математиков, химиков и биологов,
. 1704020000-506 .. OQ f ____ ___
Ф 041(01)~88 64 -88' Ч' 1 ББК 22'3
Редакция литературы по физике
и астрономии
ISBN 5-03-001295-8 (русск.) © Elsevier Science Publishers В. V.,
ISBN 0-444-86995-6 (англ.) 1986
© перевод на русский язык, «Мир»
1988
ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
На русском языке выходит первая книга по теории
фракталов, получившей в течение последних десяти лет
огромное распространение. До фактического начала активной
деятельности в этой области в математике существовало понятие
размерности Хаусдорфа — Безиковича (рХБ). Теория такой
размерности была построена в 20-е годы, и затем она
эпизодически появлялась в отдельных работах. В связи с этим можно
вспомнить работы А. Реньи (Венгрия), П. Биллингсли (США)
и др. По самому характеру рХБ было ясно, что она связана не
с топологией, а с метрикой, т. е. со способом построения
рассматриваемого множества. Она может принимать любые
значения, что давало некоторый повод говорить о пространствах
дробной размерности. Наиболее известными примерами
служили канторовское множество на прямой с размерностью
1п2/1пЗ и броуновская кривая на плоскости, размерность
которой равна 2. Несколько более сложными примерами являются
ковер Серпинского, кривая Коха и др.
Принято называть фракталами множества, у которых рХБ
превышает их топологическую размерность. Сам термин
«фрактал» был предложен американским ученым Б. Мандельбротом,
автором известной книги «Фрактальная геометрия природы»
(Mandelbrot В. В. The Fractal Geometry of Nature, Freeman, San
Francisco, 1982). Мы рекомендуем эту книгу каждому, кто
захочет ознакомиться с первоначальными понятиями, идеями и
примерами, относящимися к фракталам. Сейчас несомненно, что
фракталы встречаются в огромном числе физических процессов
и явлений. Можно сказать, что идея фракталов была выдвинута
весьма вовремя: само развитие науки шло навстречу
фракталам. Первые примеры (форма облаков, изрезанность берегов
материков, сложные формы в живой и неживой природе) не
могли заинтересовать широкий круг исследователей. Положение
изменилось после того, как было обнаружено большое число
задач, где фрактальная структура и размерность служат
основными характеристиками системы. Так, в турбулентности теория
фракталов теснейшим образом связана с теорией масштабной
инвариантности Колмогорова. Если рассмотреть скорость тур-
6
Предисловие редакторов перевода
булентного потока как функцию пространственных переменных
и времени, то она представляет собой фрактал такого же в
сущности типа, что и броуновская кривая, хотя и с несколько иными
локальными свойствами.
В теории динамических систем появились «странные
аттракторы» (СА). По замыслу авторов этого понятия Рюэлля и Та-
кенса СА состоят из таких решений систем дифференциальных
уравнений, которые не заполняют никакой области, а образуют
сложную «дырявую» структуру, т. е. являются фракталами. Их
фрактальность и улавливает свойства этой структуры. Все это
можно увидеть уже на примере знаменитого аттрактора
Лоренца, с которого началось проникновение идеи СА в физику.
Различные видоизменения понятия фрактальной размерности, ее
нахождение по результатам эксперимента превратились в
самостоятельную область теории динамических систем. Можно,
например, упомянуть недавние эксперименты Ю. Н. Беляева,
И. М. Яворской (МГУ) по движению жидкости в шаровом слое,
в ходе которых фрактальная размерность выводилась как
непосредственный результат эксперимента. В недавних
исследованиях А. В. Гапонова-Грехова и М. И. Рабиновича и в
математических работах А. В. Бабина, М. И. Вишика, Ю. С. Илья-
шенко, О. А. Ладыженской эта размерность связывалась с
числом существенных параметров системы, определяющих
характер ее динамики.
Далее, у теории фракталов много точек соприкосновения с
методом ренормгруппы и теорией фазовых переходов. В
статистической физике метод ренормгруппы выделяет распределения
вероятностей, инвариантные относительно действия группы
масштабных преобразований. Такие распределения, как правило,
сосредоточены на фракталах. Это означает, что флуктуации
температуры, плотности и т. п. как функции пространственных
переменных также относятся к числу фракталов. В последнее
время здесь обнаружились новые связи. Прежде всего были
найдены интересные классы взаимодействий, для которых
пространство основных состояний имеет фрактальную структуру.
Так, для некоторых антиферромагпитпых взаимодействий
структура основных состояний описывается в терминах
фракталов. Отметим, что идея таких фракталов была высказана еще
Ландау около 40 лет назад. В теории фазовых переходов
соизмеримость— несоизмеримость Обри, Мэзер, Персиваль
показали, что в модели Френкеля — Конторовой при разрушении
регулярных основных состояний появляются кантороторы —
объекты, относящиеся к фракталам. В последнее время А. М.
Поляков неоднократно подчеркивал важность фрактальной
размерности в квантовой теории струн.
Предисловие редакторов перевода
7
При развитии теории фракталов обнаружились новые,
неизвестные ранее примеры. Недавно издательство «Шпрингер»
выпустило очень яркую, красочную книгу «Красота фракталов»,
содержащую полученные на ЭВМ изображения многих
фракталов. Остановимся на одном из примеров. В теории динамических
систем одним из самых замечательных открытий последнего
времени была универсальность Фейгенбаума, связанная с
последовательностью бифуркаций удвоения периода для семейства
отображений х-^х2— X. Если считать х, X комплексными, то
наряду с удвоениями периода равные права приобретают
бифуркации утроения, учетверения периода и т.д. Соответственно
возникают значения параметра Я, где происходят также
бифуркации. Область значений А,, где не происходит вообще никаких
бифуркаций, была впервые (численно) построена Мандельбро-
том, и ее граница и есть тот самый фрактал, который
изображен в книге издательства «Шпрингер» и называется
фракталом Мандельброта. Локальная структура этого фрактала
связана с универсальностями, обобщающими универсальность
Фейгенбаума.
Предлагаемая книга представляет собой перевод трудов
симпозиума, посвященного фракталам в физике. Сам симпозиум
был организован Л. Пьетронеро и Э. Тозатти. Профессор Пье-
тронеро чрезвычайно содействовал скорейшему появлению
перевода. Среди разделов книги многие относятся к физике и
химии полимеров, моделям роста, кинетике кластеризации,
неупорядоченным средам и др. Как это часто бывает, многие статьи
следует рассматривать скорее как конспективные заметки или
краткие тезисы, чем как систематические статьи. Прилагаемые
при этом списки литературы дают возможность достаточно
быстро войти в тот или иной круг вопросов. Для читателей,
желающих ознакомиться с первоначальными понятиями и
современной точкой зрения на теорию фракталов, мы рекомендуем
прекрасный обзор Я. Б. Зельдовича и Д. Д. Соколова в УФН
(1985, т. 146, с. 492).
Эта книга ликвидирует существенный пробел в
отечественной научной литературе. Мы надеемся, что она будет полезна
нашим физикам-теоретикам, химикам, биологам и математикам.
Я. Г. Синай
И. М. Халатников
ПРЕДИСЛОВИЕ
Настоящее издание содержит труды международного
симпозиума «Фракталы в физике», который проходил в
Международном центре теоретической физики (Триест, Италия) 9—
12 июля 1985 г. Это шестой симпозиум МЦТФ по физике
конденсированного состояния.
Понятия масштабной инвариантности (скейлинга) и
самоподобия возникли независимо в разных областях. Одна из них —
физика фазовых переходов, которая изучает критические
явления, другая — фрактальная геометрия, включающая понятие
фрактальной (нецелой) размерности. Целью настоящего
симпозиума было рассмотреть различные физические явления,
обнаруживающие масштабную инвариантность и фрактальные свойства,
и выявить общие математические черты в описании этих
явлений. Основное внимание уделялось теории и эксперименту,
связанным с явлениями, отчетливо выраженными. Динамические
системы и хаос рассматриваются довольно бегло, поскольку
этим вопросам были посвящены специальные конференции.
Значительная (если не большая) часть материалов сборника
относится к физике явлений необратимого роста, в результате
которого возникают фрактальные структуры. Эта область
«критических кинетических явлений» — одна из наиболее
захватывающих в сегодняшней теоретической физике.
Из-за того что число статей велико, мы разбили их на
части, названия которых лишь приближенно отражают тематику
работ. Многие статьи по своей тематике гораздо шире, чем те
части, в которые они включены, поэтому их точно так же можно
было включить в другие части сборника. Мы хотели бы
принести извинения за субъективность выбранного распределения
докладов.
В подготовке симпозиума нам помогали члены оргкомитета
С. Лундквист, Б. Мандельброт, X. Стенли и К- Эвертс
(секретарь), и мы им глубоко признательны. Мы хотели бы также
поблагодарить всех участников, — это из-за них симпозиум прошел
так интересно, с таким большим успехом.
Щедрым устроителем симпозиума был Международный центр
теоретической физики в Триесте. В организации и
финансировании принимали участие также фирма IBM (Италия),
Управление научных исследований ВМС (США), Национальный
исследовательский совет (Италия), Гронингенский университет
(Нидерланды), SOHIO (Кливленд, США) и Исследовательский
центр Брауна Бовери (Швейцария). От имени нашего
международного научного сообщества мы хотели бы выразить глубокую
благодарность всем этим организациям, а также отдельным
лицам— особо хотелось бы отметить Деизу Буранелло и Карлу
Карбоне, — которые обеспечили успешное проведение
симпозиума и издание его трудов. л Пъетронеро, Э. Тозатти
Часть |
ОБЩИЕ СВОЙСТВА
ФРАКТАЛОВ
Самоаффинные фрактальные множества
I. Основные фрактальные размерности
Б. Мандельброт *
Понятие фрактальной размерности исследуется для различных
фрактальных кривых и пыли, которые являются не
самоподобными, а диагонально самоаффинными. При диагональном аффинном
преобразовании коэффициенты растяжения вдоль разных
координатных осей различны. Показано, что в противоположность
случаю строго самоподобных множеств, когда фрактальная
размерность единственна, в общем случае необходимо несколько
различных фрактальных размерностей. Важнейшие из них:
размерность, полученная с помощью нахождения массы внутри сферы, и
размерность, полученная путем покрытия фрактала одинаковыми
клетками. Оказывается, что при любом определении существенно
лишь, что мы проводим: интерполяцию или экстраполяцию; при
этом получаются два совершенно различных значения размерности:
локальное (справедливое для масштабов, меньших некоторого
критического) и глобальное (справедливое для масштабов, больших
критического). От того, какой способ нахождения размерности
(нахождение массы или покрытие клетками) был использован, оба
этих значения не зависят.
1. Введение
В этой работе (в трех частях, соответствующих
различным уровням рассмотрения) исследуется, что происходит с
различным образом выбранными определениями фрактальной
размерности, когда эти определения обобщаются с класса
самоподобных фракталов на некоторый класс самоаффинных
фракталов. Статья содержит основные положения моей статьи [1].
Первоначально различные определения фрактальной
размерности были детально исследованы для самоподобных фракталов,
и оказалось, что величина размерности не зависит от выбора
определения [2]. Когда какой-либо метод хорошо работает при
определенных условиях, возникает искушение распространить
его на более широкую область. Этой областью в нашем случае
является класс самоаффинных фракталов.
* Benoit В. Mandelbrot -Physics Department, IBM Research Center;
Mathematics Department, Harvard University, Cambridge, MA 02138, USA.
Работа выполнена при частичной поддержке Управления научных
исследований ВМС США (контракт N00014-85-K-0188).
10
Часть I
Я ввел понятия «самоаффинный» и «самоподобный» в 1964 г.
(второе из этих понятий настолько широко принято теперь, что
трудно поверить в его юный возраст). Понятие «аффинный»
восходит еще к Эйлеру. В этой статье не используется никаких
специальных сведений из аффинной геометрии, но мне хочется
процитировать характеристику этой науки, данную Снаппером и
Тройером: «Грубо говоря, аффинная геометри — это то, что
останется от евклидовой геометрии, если из нее убрать
практически любую возможность измерения длин, площадей, углов и т. д.
Можно подумать, что аффинная геометрия — очень бедный
объект. Напротив, она очень богата». Я надеюсь убедить читателя,
что самоаффинные фракталы тоже удивительно богатый объект.
Одним очень известным, но очень специальным примером
самоаффинного фрактала является траектория винеровского
процесса броуновского движения — так называется начинающийся
в начале координат случайный процесс B(i), приращения
которого за непересекающиеся промежутки времени t независимы и
имеют нормальное (гауссовское) распределение. Эта
траектория обладает известным свойством инвариантности: процессы
B(t) и Ь~1/2В(Ы) имеют одинаковые распределения при
произвольном коэффициенте Ь > 0. Заметим, что при этом изменении
масштаба коэффициенты при t и В различны, следовательно,
переход от B(t) к Ь~1/2В(Ы) не является преобразованием
подобия, а есть более общее аффинное преобразование. Поэтому
в моей книге [2] процесс B(t) и был назван статистически
самоаффинным.
В то время как преобразование подобия сжимает или
растягивает геометрическую фигуру по всем направлениям в
одинаковом отношении, аффинное (линейное) преобразование
сжимает фигуру в различных направлениях по-разному. Более
точно, B(t) не меняется (статистически) при «диагональном
аффинном» преобразовании (это понятие будет объяснено в разд. 2).
В этой статье диагонально самоаффинные фрактальные
кривые, пылеобразные множества точек и другие множества
детально исследуются на различных уровнях общности сначала на
плоскости (графики функций случайных и не случайных,
аналогичных B(t), два уровня более общих множеств), а затем в
пространстве. В каждом случае выявляются новые и удивительные
усложнения фрактальной размерности.
Различные функции единственной фрактальной размерности
«общего назначения» вполне самоподобного множества теперь
выполняются различными фрактальными размерностями
«специального назначения».
В этой части рассматриваются размерность, связанная с
массой, заключенной в круге, размерность, связанная с покрытием
квадратами, и размерность, связанная с «дырами». Концептуаль-
Общие свойства фракталов
11
но и математически наиболее неожиданным обстоятельством
является то, что самоаффинные размерности, связанные с массой
и квадратами, оказываются различными в зависимости от того,
какой вариант мы рассматриваем — локальный или глобальный.
Например, в достаточно общем случае рекуррентного
построения фракталов единственное основание Ь заменяется двумя
основаниями 6' и 6", и вместо классического выражения для
фрактальной размерности log& N появляются выражения
\ogbf{Nb'lb") (локальная фрактальная размерность) и
\of*b"{Nb"jb') (глобальная фрактальная размерность). Часто
рассматривается также лежащая между ними размерность,
связанная с дырами, имеющая одно значение для всех масштабов,
а именно \ogNJ\og л]Ь'Ь".
В части II изучается размерность, получающаяся при
определении длины кривой с помощью измерительного циркуля или
при разбиении поверхности на треугольники. Получающиеся
величины «аномальны вдвойне», а именно отличны от величин,
полученных в части I.
Часть III начинается с рассмотрения и обобщения некоторых
новых математических фактов, касающихся определенных
случаев размерности Хаусдорфа — Безиковича Dhb\ далее
обсуждается смысл найденной в некоторых случаях «двойной
аномалии».
Богатство и сложность предмета нашего исследования не
носят чисто математического характера — они лишь являются
отражением богатства и сложности природы. И чем более
сложные фракталы мы рассматриваем, чем более точно хотим
описать их структуру, тем большее число фрактальных
размерностей оказывается необходимым.
2. Понятия: аффинное преобразование,
диагональное аффинное преобразование
и самоаффинное множество
2.1. Предварительные сведения о диагональной аффинности
Рассмотрим еще раз траекторию броуновского движения.
В интерпретации Винера / — это время, а В— координата
физической частицы на пространственной оси. Эти две координаты
играют совершенно различные роли, и единицы измерения В и
t (сантиметр и секунда?) могут быть выбраны независимо.
Производить поворот нельзя, так как это привело бы к
множествам, не являющимся траекториями. Составив выражение B(t) —
— 8t (еще одно применение аффинности), мы получим функцию
(описывающую броуновское движение со сносом), которая
сильно отличается от B{t). В интерпретации Луи Башелье
12
Часть I
(относящейся к 1900 г.) t — это время, а В — цена в франках, и
здесь верны все те же замечания. Однако мной позже была
предложена интерпретация, существенно отличная от этой: B(t)
описывает вертикальное сечение одного из моих броуновских
ландшафтов ([2], гл. 28); координаты здесь все еще играют
различную роль, так как гравитация определяет вертикальное
направление, исключает «нависание» выступов рельефа и делает
удобным представление рельефа однозначной функцией. В тоже
время в этом примере и В, и t — длины, и единицы их
измерения уже не могут быть выбраны независимым образом. По
причинам, которые станут ясны позже, лучше всего выбрать
единицу измерения tc для В и t таким образом, чтобы \B(t + tc) —
— B(t)\ ~ \tc\. Эту величину назовем промежуточным
масштабом. Такая величина для обычного броуновского движения
зависела бы от единиц, выбранных для t и для В, поэтому в
общем случае промежуточный масштаб не является внутренне
присущим задаче.
Локальная и глобальная размерности, которые будут
введены и исследованы ниже, разделены именно этим
промежуточным масштабом. Если бы его не было, то само введение
понятий локальный и глобальный было бы невозможным.
2.2. Диагональное аффинное преобразование
Разд. 2.1 показывает, что в случае, когда мы исследуем
график функции B(t) —и это справедливо для всех фракталов,
рассматриваемых в данной статье, — особую роль играют аффинные
преобразования, инвариантное множество которых состоит из
прямых, параллельных координатным осям. Такое аффинное
преобразование, которое я предлагаю называть диагональным,
действует в £-мерном аффинном пространстве АЕ. Каждое
аффинное преобразование определяется заданием неподвижной
точки с координатами фт(0<т<£'+1) и набором
коэффициентов преобразования rm(o< m < Е-\- 1) и действует
следующим образом:
Коэффициенты Гщ могут и не быть положительными. И все они
не должны быть равными, так как в этом случае
преобразование выродится в преобразование подобия (гомотетию).
Обратные величины l/|rm| ==6m, называемые основаниями, в
простейших примерах, которые строятся при помощи рекурсии,
являются целыми числами.
Примерами в основном будут множества на аффинной
плоскости А2 (£=2). Обозначим 6/==maxfew, &" = min&m, #==
= \ogb"/\ogb'. Величина Я, называемая аффинным показате-
Общие свойства фракталов
13
лем, удовлетворяет соотношению 0 < Н <; 1. При Е > 2 имеется
Е(Е—1)/2 аффинных показателей и промежуточных
масштабов.
Формально линейное преобразование получается при
последовательном выполнении параллельного переноса и умножения
на матрицу; нас интересуют только те случаи, когда матрица
диагональна и ее диагональные элементы не тождественны.
Композиция двух диагональных аффинных преобразований
будет диагональным аффинным преобразованием. Следовательно,
некоторое множество диагональных аффинных преобразований
может быть использовано в качестве базиса группы.
Коснемся значения слов «квадрат», «расстояние» и «круг» в
аффинной геометрии (см. разд. 1). Эти понятия имеют смысл
для сечений рельефа, но для графиков шума или цен единицы
измерения вдоль оси t и вдоль оси В выбираются независимо
друг от друга. Здесь нет смысла говорить о равенстве высоты
и ширины и квадрат определить нельзя. Аналогично, нельзя
датьопределениекруга, поскольку квадрат радиуса i?2 = (A^)2 +
+ (АВ)2 состоит из комбинации разных единиц. Более того,
нельзя пользоваться измерителем для анализа самоаффинного
графика шума, потому что расстояние, которое находится при
каждом шаге измерителя, содержит и Д£, и AS. Правда, тот же самый
график шума всегда можно представить как сечение некоторого
рельефа, т. е. как изотропное множество. Это, однако, не
устраняет различия между аффинным АЕ и евклидовым RE
пространствами, хотя иногда оно кажется настолько слабым, что
возникает соблазн вычислить различные «запрещенные»
величины «механически». Этого делать не следует.
2.3. Рекуррентное построение на сетке многих стандартных
самоподобных фракталов легко распространяется на самоаффинный случай
В качестве примера, обобщающего построение ковра Серпин-
ского, возьмем в качестве исходного множества (инициатора)
полуоткрытый единичный квадрат. (Полуоткрытый квадрат —
это квадрат, который содержит свои нижнюю и левую стороны
л не содержит правую и верхнюю. Прямоугольники, которые мы
будем рассматривать, тоже будут полуоткрытыми.) В качестве
генератора возьмем решетку, изображенную на рис. 1.
Таким образом, мы делим исходное множество на 3 X 4 = 12
прямоугольных частей и выбрасываем две части из середины
(они выделены черным цветом). Затем выбрасываем две
средние части из двенадцати, на которые делится каждый из
оставшихся прямоугольников, и т. д. Получившийся самоаффинный
ковер является объединением десятых (N = 10) частей. Каждая
десятая получается из целого при помощи диагонального
14
Часть I
аффинного преобразования с коэффициентами г'п= 1/3, г%= 1/4,
где п изменяется от 1 до N ~ 10. Можно объединить все эти
признаки преобразования, представляя генератор в форме
генератора со стрелками, рисуя стрелки на диагоналях десяти
прямоугольников. В рассмотренном примере стрелки нужно
разместить, как показано на рис. 1, чтобы быть застрахованным от
пересечения десятых. Неподвижными точками являются четыре
вершины, средние точки левой и правой сторон и точки 1/3 и 2/3
на верхней и нижней сторонах. В самом деле, неподвижной
точкой аффинного преобразования является точка пересечения
четырех прямых, соединяющих вершины исходного квадрата с их
-
Рис. 1.
образами, являющимися вершинами частей (прямоугольников).
Необходимо сделать замечание относительно выбора в
качестве инициатора единичного квадрата. При таком выборе
единица измерения координат t я В фиксируется по аналогии с
условием \B(t-\-tc)—B{t)\ ~ tc. Экстраполяция, приводящая к
масштабам, большим чем tc, обсуждается в разд. 2.6.
Произвольный фрактальный генератор на самоаффинной
решетке получается, если нарисовать Ъ' X Ь" прямоугольников и
оставить N<b'b" из них. Опять-таки |г'п\ = 1/6' и |>*"|=1/6
для всех п, но ориентация п-го аффинного преобразования,
определяющаяся знаками г'п и г", может зависеть от п. Можно
изображать это преобразование с помощью векторов,
направленных по диагоналям. Два примера преобразований, которые
понадобятся нам в дальнейшем и играют особенно важную роль,
приведены на рис. 2 и 3.
(Удивительно, но в части III будет показано, что DHb
зависит от того, какой вариант выбран!) Когда прямоугольники
генератора с их диагоналями выбраны, возникающий
результирующий фрактал получается как предел последовательности
вложенных прямоугольников. Термин «вложенный» означает,
что каждый из них содержится в предыдущем. Если рассмотреть
только диагонали и если эти диагонали образуют кривую, то
пределом последовательности ломаных линий будет самоаффин-
Общие свойства фракталов
15
ная фрактальная кривая. Заметим, что требование связности
генератора со стрелками налагает определенные ограничения на
расположение остающихся прямоугольников.
Однако, как можно понять из моей книги ([2], гл. 13),
генератор со стрелками может распадаться на несколько кривых,
порождая «острова» и (или) «озера».
Н ffl
Рис. 2. Рис. 3.
Следует отметить важный частный случай: когда N = b*\
порожденная генератором со стрелками фрактальная кривая
является графиком (однозначной) непрерывной функции.
2.4. Определение самоаффинного множества
Приведенные выше примеры достаточно хорошо поясняют
следующее определение.
Множество S является самоаффинным по отношению к
последовательности N диагональных аффинных преобразований
осп, если выполняется 5 = UanS, причем anS f| ocmS = 0 при
пфт. То есть S разбивается на N частей (никакие две из них
не пересекаются), каждая из которых получается из целого при
помощи одного из аффинных преобразований
последовательности.
2.5. Фрактальная однородная мера
Чтобы дать определение массовой размерности фрактала,
нужно дать определение массы внутри куба. Здесь легко
определить однородную меру на фрактале.
Графикам функций придадим вес (меру) пропорционально
прошедшему времени.
Для фракталов, полученных при помощи рекурсии на
решетке, на k-м этапе имеется Nk прямоугольников; придадим
равные веса этим прямоугольникам.
При этом для графиков функций, построенных при помощи
рекурсии, оба способа дают один и тот же результат, поскольку
проекция меры на ось X в соответствии со вторым определением
однородна.
16
Часть I
2.6. Экстраполяция
Понять экстраполяцию особенно важно в случае
самоаффинных фракталов, так как (это было уже сказано и будет
доказано) результат экстраполяции имеет свои собственные
глобальные фрактальные размерности. Вспомним, что экстраполяция
канторовской пыли не единственна, фактически такая
экстраполяция существует для каждой двоичной (N = 2) бесконечной
последовательности.
Так как при интерполяции каждая точка в канторовском
множестве определяется последовательностью, которая пишется
слева направо, экстраполяционную последовательность лучше
записывать справа налево, т. е. ...а_*...а_3, я-2, я~ь #о- Если
а0 = 0 (соответственно а0= 1), наше множество
рассматривается как левая (соответственно правая) часть множества, которое
было увеличено в Ь =3 раз, и т. д. Это же можно сказать обо
всех многомерных рекуррентных конструкциях; для них экстра-
поляционные последовательности должны быть записаны по
основанию N. В нашем самоаффинном случае значения п0
отождествляют исходный квадрат (инициатор) с одной из N частей
суперинициатора, который имеет основание 6' и высоту Ъ"\
таким образом, По определяет суперинициатор. Далее используем
метод рекурсии: когда известен супер^-инициатор, значения
n-k показывают, где он находится в супер*+1-инициаторе, и т. д.
3. Различные фрактальные размерности
самоаффинного множества
И в чисто математической литературе, и в литературе о
фракталах единственный широко известный факт, относящийся к
обсуждаемому вопросу, — это то, что размерность Хаусдорфа —
Безиковича Вив графика броуновского движения равна 3/2.
Этот результат становится менее загадочным, если его
распространить на более общий случай «дробного» броуновского
движения BH{t), где О < Н < 1. Если Вн(0) = 0, то случайные
процессы BH(t) и Ь~нВн(Ы) имеют одинаковые распределения. Для
дробного броуновского движения имеем DHb = 2— Я. Значение
Н = 1/2 дает нам B{i) как частный случай BH{t).
Но что можно сказать о DHb для самоаффипных множеств,
которые являются графиками других функций или же вовсе
не являются графиками функций, и об определениях
фрактальной размерности, отличных от Dhb'?
О (само) подобной размерности Ds достаточно сказать
несколько слов. Это понятие непосредственно приложимо к
самоподобным фрактальным множествам, состоящим из N частей,
каждая из которых получена из целого при помощи преобразо-
Общие свойства фракталов
17
вания подобия с коэффициентом \г\ =1/6. Для самоподобных
фрактальных множеств Ds = log N/log Ь. Для самоаффинных
фрактальных множеств, величина Ds просто не может быть
найдена. (В разд. 4, однако, будет введено естественное обобщение
величины Ds.)
В ряде работ были предприняты попытки найти замену
размерности Ds, однако высказанные в этих работах
предположения неоправданны. Для примера возьмем B(t). Если записать
Dhb как 1 4- 1/2, то значение оказывается численно равным
1 Ч- log6' b"\ где (снова) br большее, а Ь" меньшее основание. На
самом же деле DHB= 2 — logb'b", как показывает
исследование дробного броуновского движения BH(t). Ошибочность
других предположений не столь очевидна.
Основным фактом, который устанавливается в данной статье
(а частично был уже установлен ранее, см. [1]), является то,
что различные роли, которые в самоподобиом случае играет
одно число, называемое фрактальной размерностью, в
самоаффинном случае должны быть распределены между различными
величинами. Некоторые из них локальны (как Dhb), те же,
которые введены в последнее время, глобальны. Особого
внимания заслуживают глобальная массовая размерность Dmg и
локальная клеточная размерность DBl.
Напомню, что когда-то я определил фрактал как множество,
для которого Dhb>Dt (= топологическая размерность). Со
временем это «пробное» определение выглядело все менее и
менее привлекательным, и я от него отказался (см. книгу [2],
издание второе и последующие, с 458). Была альтернатива
рассматривать в качестве фракталов те множества, для которых
размерности из определенного набора совпадают. Эта
альтернатива отпала.
4. Размерность, связанная с лакунами (дырами)
Мы начнем с фрактальной размерности, которая проста, но
малоинтересна, поскольку имеет узкую область применимости.
Так как самоподобная размерность log N/log b теряет смысл для
самоаффинных множеств, можно попробовать «спасти» ее
формально, подставив вместо Ь какое-нибудь подходящее
«эффективное основание» &*, а затем попытаться интерпретировать
результат. Возьмем в качестве Ь* геометрическое среднее bm, a
именно b*= (bib2...bE)l/E, и покажем, что DG = logN/logb*
действительно представляет собой размерность в том случае, когда
можно определить лакуны (дыры) или острова. Формула для
DG симметрична по отношению к основаниям, поэтому DG n
фигурирует среди предположений о том, каким же должно быть D.
Мы увидим, что другие, более важные D не симметричны.
18
Часть I
Понятие лакунарнои размерности приложимо к
самоподобным фракталам в RE, представителями которых являются канто-
ровское множество на прямой и кривая Серпинского, а также
ковер Серпинского на плоскости. Эти фигуры имеют следующие
свойства. Они имеют меру нуль в RE («толстые фракталы» — см.
[2], гл. 15 — исключаются). Дополнение к ним расщепляется на
бесконечное число лакун (максимальных связных множеств,
которые являются областями (открытыми) в RE, подобными друг
другу и отличающимися единственно линейным размером).
и
Рис. 4.
Во всех этих случаях известно, что для произвольного L
выполняется следующее соотношение:
«Число лакун, имеющих линейный размер > L» ~ LTD°,
где DG < £.
Тогда показатель DG называется лакунарнои фрактальной
размерностью, и все другие определения фрактальной
размерности для самоподобных фракталов дают то же значение. Теперь
расмотрим самоаффинные фракталы, имеющие лакуны. Здесь
нас ожидают и хорошие, и плохие новости.
Хорошие новости состоят в том, что число лакун изменяется
как Nk, а их объем — как &i62...&£. Определим линейный размер
как объем в степени \/Е (геометрическое среднее длин сторон).
Тогда соотношение между числом и размером лакун или
островов остается степенным законом, справедливым при'любом L.
Показатель, не зависящий от L, можно по-прежнему называть
лакунарнои размерностью — это величина DG, определенная
выше.
Плохие же новости таковы: DG не имеет прямого отношения
к Dhb. Рассмотрим, например, генератор, изображенный на
рис. 4. Здесь мы имеем D0 = log8/log л]Ь • 6 = 1,30, в то время
как в части III будет показано, что DHb = 1,34, и вскоре мы
увидим, что основные фрактальные размерности имеют значения
Dbl =1,38 и Dmg = 1,20.
Для тощих пылеобразных множеств (множеств, имеющих
лебегову меру нуль) в частном случае Е = 1 (например, множе-
Общие свойства фракталов
19
ство Кантора; см. [2], с. 78) лакунарная размерность является
более сильной формой (действующей при всех масштабах)
показателя, который Безикович и Тейлор ввели для малых
масштабов и для которого показали, что он совпадает с DHB ([2],
с. 359). Известно, что обобщение совпадения Dbt = Dhb на
случай Е > 1 является правомерным в некоторых самоподобных
случаях (ковер Серпинского; см. [2], с. 134), но теперь мы
видим, что в самоаффинном случае DG стоит особняком,
5. Самоаффинные фрактальные кривые на плоскости,
определенные как графики функций
Разд. 5.1 и 5.2 являются по существу выдержками из
аннотации моей статьи [1], содержащими дополнительный материал
и более подробное обсуждение. Разд. 5.3 является новым и
важным.
Замечание относительно употребления буквы Н для logyb":
она очень подходит в этой части, потому что Я — показатель
Гёльдера (Holder) для BH(t) и для других функций, которые
мы изучаем. Однако изначально я выбрал Н в честь Хёрста
(Н. Е. Hurst; см. [2], гл. 27).
5.1. Локальное значение массовой размерности при малых R равно 2 — Н.
При больших R массовая размерность равна 1
Если множество S — самоподобный фрактал, то масса M(R),
содержащаяся в пересечении S с кругом или шаром радиуса R,
ведет себя как M(R) ~ R°M. Можно заменить круг (или шар)
квадратом (или кубом), стороны которых параллельны осям и
имеют длину 2R. Для некоторых физиков это свойство стало
чуть ли не определением понятия фрактала. На самом деле
нужно быть аккуратным по отношению к значению символа ~.
Наиболее важным является его значение для физика,
который думает в основном об экстраполяции к большим радиусам,
о спрямлении зависимости (в двойном логарифмическом
масштабе) массы от радиуса и о пределе lim log M {R)/\og R = DM.
R-+oo
Найдем этот предел для графика произвольной диагонально са-
моаффииной функции, такой как Вн^), или же функции,
определенной при помощи рекурсии. Когда R ^> tc, любой из этих
графиков можно приближенно считать горизонтальным
интервалом. В квадрате со стороной 2R он занимает очень тонкую
горизонтальную полосу. Поэтому если мы поступим, как было
сказано в разд. 2.5, и припишем нашему графику вес,
пропорциональный прошедшему времени, то получим, что M(R)~R.
То есть мы получили поразительный результат: Dmg = 1.
(Индекс G означает «глобальный».)
20 Часть I
Математик, однако, может рассмотреть и случай, когда
R <С tc. Здесь наш график может быть приближенно заменен
набором вертикальных интервалов, по интервалу на каждый нуль
функции. После некоторых вычислений получим значение для
локальной массовой размерности Цщ. = 2— Я, которое
встречалось нам как Вив для графика Bjj(l). (Индекс L означает
«локальный».)
Вывод: мы обнаружили, что два предела, совпадающих
между собой для самоподобных множеств, могут различаться.
Кроме того, 1 < 2— Я для всех Я в интервале 0 < Я < 1.
Оставшаяся часть статьи посвящена обобщениям этого
открытия.
5.2. Локальное значение клеточной размерности
при больших Ь равно 2— Н.
Глобальное значение равно 1
После того как построена решетка из квадратов (клеток) со
стороной г = 1/6, покрывающая некоторое множество,
обозначим через N(b) число клеток решетки, которые пересекаются с
этим множеством. В настоящее время я употребляю термин
«клеточная размерность» для показателя, характеризующего те
множества, для которых N(b) ведет себя как N(b) ~b°B.
Клеточная размерность — сокращенное название для «размерности,
связанной с подсчетом квадратов (клеток), покрывающих
множество». Название должно быть коротким и не иметь других
значений (термин «метрическая размерность» был бы
применим ко всем фрактальным размерностям, а термин «емкостная
(capacity) размерность» уже давно используется как синоним
размерности Фростмана).
Снова зададим вопрос: что означает символ ~?
Наиболее важным является его значение для математика,
исследующего локальное поведение, т. е. lim (log N(b)/logb) =
= DBL.B случае рекуррентно определенных объектов
попытаемся покрыть часть объекта шириной (b')~k = b~l и высотой {b")~k
квадратными клетками со стороной Ь~К Ясно, что эти квадраты
нужно сложить в вертикальные столбики. Число квадратов в
каждом столбике равно (b"/b')~k = 61_я, а число столбиков
равно Ь. Следовательно, DBl = 2 — Я. Аналогично в случае BH{t)y
эвристические доводы, приведенные в моей книге [2] внизу
слева на с. 237, приводят к тому, что Dbl = 2 — Я.
Физик, однако, может интересоваться и тем, что происходит
с пределом при б-*-0 или г-»-юо, для чего требуется
неограниченный график. Часть самоаффинного графика от 0 до г > 1 по-
п ,. log N(b) r,
крывается одним квадратом. Следовательно, lim —р—t-L:=DBg=
= 1.
Общие свойства фракталов
21
5.3. Поведение размерностей В r.i(t) при сечении.
Ограниченные локально самоподобные фракталы
Обычно (см. [2], с. 135), когда самоподобный фрактал на
плоскости рассекается прямой, фрактальная размерность
сечения оказывается меньше размерности исходного фрактала на
единицу. Это основное правило, но из него есть исключения.
В применении его к графику BH(t)t который не является
самоподобным, осторожность не только необходима, но и принесет
хорошие результаты. Мы предположим, что BH(t) имеет
некоторый внутренний масштаб, равный единице.
Горизонтальные сечения. Они самоподобны, и их локальная
размерность совпадает с глобальной. Она равна 1—Н = (2 —
— Н) — 1, т. е. ее можно получить из DBl, и тот факт, что
Dbg = 1, не имеет значения.
Вертикальные сечения. Они сводятся к одной точке,
размерность которой нужно считать исключением из правила.
Наклонные сечения прямыми Y = at, где О <С а < оо. Если
клеточка размера (b')-kY^(b")-~k увеличивается до единичного
квадрата, то Y = at заменяется на Y — a(b"/b')ki. Таким
образом, У = at локально можно заменить на К = 0. Это сечение
локально самоподобно, так как локально совпадает с
горизонтальным сечением. Но! Свойства самоаффинных множеств
побуждают нас отнестись более внимательно к глобальным
свойствам и внутреннему масштабу.
Глобально наклонное сечение не является самоподобным. На
самом деле оно ограниченно, и поэтому DMg = DBg = 0. Это
подтверждается тем, что глобально Y = at стремится к
вертикальной прямой. И действительно, из основного правила, если
его применить к DMg = DBg = 1 для исходной кривой, получаем
Dmg = Dbg — 0.
Признаюсь, что до сих пор я не обращал внимания на эти
особые свойства ограниченных локально самоподобных
фракталов. Между тем в природе они встречаются очень часто —
лучшими примерами являются береговые линии островов и DLA.
Теперь о внутреннем масштабе сечений. Для ограниченного
густого множества масштаб — это длина самого короткого из
интервалов, содержащих его. При а-^оо внутренний масштаб-v
->0, поэтому вертикальное сечение сводится к одной точке и
единственное, что может оказаться в пределе, это глобальная
размерность, которая равна нулю. Другими словами,
вертикальные сечения не считаются больше исключением. При а->0
внутренний масштаб -> оо, поэтому горизонтальные сечения
неограниченны и самоподобны. Это объясняет, почему горизонтальные
сечения вообще нечувствительны к глобальным
характеристикам.
22
Часть I
5.4. Поведение размерностей сечений самоаффинных фракталов,
полученных при помощи рекурсии
Эта тема, поразительно сложная и интересная, должна быть
отложена до части III.
6. Самоаффинные, построенные на плоскости
при помощи рекурсии фракталы,
проекции которых покрывают оси
6.1. Проекции на оси самоаффинных фракталов,
построенных рекуррентно
Если проекция генератора заполняет соответствующую
сторону исходного квадрата (инициатора), то в пределе проекция
фрактала заполняет собой всю ось. Если же проекция
генератора не заполняет целиком сторону исходного квадрата, то в
пределе проекция фрактала представляет собой пыль, имеющую
непокрытые интервалы. В частности если г'п > 0 и г" > 0 для
всех основных аффинных преобразований, то предел проекций
фрактала есть канторовская пыль. Эти оба случая исследуются в
разд. 6 и 7. Случаи, когда некоторые из г'п < 0 и (или) г" < О,
здесь не будут обсуждаться.
6.2. Глобальная массовая размерность 1 — \/Н + \ogbffN = log^,/ (Nb'/b").
Локальная массовая размерность 1 — # + logyN = logy (Nb")b')
Опять начнем с понятия, представляющего больший интерес
для физиков: с экстраполяционной глобальной массовой
размерности. В соответствии с разд. 2 возьмем в качестве
инициатора единичный квадрат и припишем ему единичную массу.
Экстраполяция (разд. 2.6) однозначно определяется
последовательностью увеличивающихся прямоугольников массой Nk и
площадью (b'b")k. Кажется, что это указывает на то, что лаку-
нарная размерность DG = logN/log 6* является массовой
размерностью. Но дело обстоит несколько сложнее, поскольку
зависимость массы от радиуса определяется для массы, находящейся
в квадрате, а не в специально выбранном прямоугольнике.
Если в прямоугольнике со сторонами Ъ'к и Ъ"к случайным образом
выбрать квадрат со стороной Ъ"к, то в среднем он будет
содержать массу Nk(b"/b')k. Следовательно, мы получим новый
удивительный результат D m=\og{b" N lbr)kl\ogb"k=\+\ogb>>{N )b') =
= l-l/H + logb»N.
В случае графика функции (разд. 5) N = Ь\ а значит,
только что полученное DMg принимает уже известное нам значение
Dmg = 1.
Общие свойства фракталов
23
Аналогичные рассуждения в локальном случае приводят к
DML = l-H + logb'N.
Далее, для случая графика функции (разд. 5) N = 6', а
значит, величина Dml принимает уже известное нам значение 2 — Я.
Полученные формулы трудно понять. Их главной особенностью
является то, что они, будучи симметричными одна относительно
другой, в то же время асимметричны относительно У и 6".
6.3. Глобальная и локальная клеточные размерности
принимают те же значения, что и соответствующие массовые размерности
Формула для Del уже давно была получена (неявно)
Клейном [6].
6.4. Имеем: DMQ = DBQ <DQ< DBL = DML
Доказательство: Dmg < DBl следует из того, что br > 6".
Действительно,
log(Nb'/b") ^ \og(Nb"lb')
\ogb' ^ log b" '
Взяв среднее от числителей и среднее от знаменателей, мы
получим величину, находящуюся строго между Dmg и Del и
равную log N/log У PF7 = DG.
7. Самоаффинные, полученные на плоскости
при помощи рекурсии фракталы,
у которых по меньшей мере одна проекция
является канторовской пылью
7.1. Определения и пример
Название этого раздела означает, что а) г'п > 0 и т"п > О
для всех п и б) Х- и/или У-проекция предельного фрактала яв-
Рис. 5.
ляется множеством Кантора, состоящим соответственно из N'
частей с г' = 1/6' и из N" частей с г"= 1/6".
24
Часть I
Рассмотрим простейший пример, генератор для которого
изображен на рис. 5. Ясно, что построенный фрактал глобально
представляет собой настоящее канторовское множество, которое
получается изъятием средних третей. Поэтому глобальные
размерности равны log3 2. С другой стороны, построенный фрактал
локально представляет собой канторовскую лестницу без
плоских ступенек. Локальные размерности равны 1.
7.2. Глобальная массовая размерность равна DMQ = (\ ~ \/H)logb,N' +
+ logb„N = \ogb„(NN'H-1).
Локальная массовая размерность равна DML == (1 — Н) log^N" + log^/ N =
Рассуждения относительно DMg проводятся точно так же,
как в разд. 6.2, до того момента, как определяется средняя
масса в квадрате со стороной b"k. Новой особенностью является то,
что масса теперь может иметь значение нуль, но квадраты без
массы не будут частью множества прямоугольников, при помощи
которого вычисляется размерность. Поэтому необходимо
исключить квадраты, не содержащие массы, и взять условную
среднюю массу, которая больше, чем усредненная масса. Заметим,
что b'kH == b"k. Полоса шириной b'k и высотой b"k разбивается
на (b'/b")k квадратов со стороной b"k, из которых N'k(l~H) не
пусты. Следовательно, условно усредненная масса равна
jsjkfji-kd-H) и
DMG = -(\- H)logb»N' + logb»N =
Аналогичные рассуждения для локального случая дадут
DML = (l ~ H)\ogb»N" + logb>N ==(1/Н -- l)logb>N" + logb> N.
Первая (вторая) формула для DMl является симметричной
относительно второй (первой) формулы для DMg-
7.3. За исключением случая, когда N = N'N", D^L > DMG
Обозначим выражение (1/log 6") — (1/log &') через F. Тогда
DMg - DML = log** N - (logy N' - logy N') -
- logy N - (logy N" - log6*AT) = F (log N - log N' - log N") =
Так как F > 0 и N < N'N", то DMg < DMr., за исключением того
случая, когда N = N'N";— при этом DMg = DMl, а наше канто-
Общие свойства фракталов
25
ровское множество на плоскости является прямым
произведением двух канторовских множеств на прямой. Таким образом,
простота самоподобного случая распространяется на
самоаффинный случай, когда последний может быть представлен в виде
прямого произведения.
7.4. Глобальное и локальное значения клеточной размерности совпадают
с соответствующими значениями массовой размерности
8. Самоаффинные поверхности
В этом разделе рассматриваются две функции:
Z(#> у) у где (х, у) -плоскость изотропна и имеется один
параметр масштаба Я, и
Т(х, у у г), где (х, у, г)-пространство аффинно и имеются два
параметра масштаба G и Я.
8.1. Фрактальные функции координат на изотропной плоскости.
Рельеф
Простейшая из предложенных мной моделей земной
поверхности (см. [2], гл. 28) — это дробная броуновская поверхность
Вн(х, у)у где точка с координатами х и у находится на
изотропной плоскости. Все свойства этой поверхности зависят от
единственного параметра Я. Легко видеть, что DBg = Dmg = 2, в то
время как DBl = DML — 3 — Я. Так же и DHb = 3 — Я.
Поведение размерностей при сечениях вертикальной и
горизонтальной плоскостями. Вспомним правило, согласно которому
размерность сечения фрактала плоскостью меньше размерности
фрактала на единицу. Повторю, что это правило
фундаментально, но тем не менее имеет множество исключений; покажем, как
некоторые из них могут быть устранены.
Вертикальные сечения Вн(Хуу) обладают как локальными,
так и глобальными свойствами, и наше правило, без сомнений,
применимо как к DBl, так и к DBG.
Горизонтальные сечения представляют собой береговые
линии всех островов, рассматриваемых в совокупности. Они само-
подобны и имеют только одну размерность, которая является
также локальной размерностью вертикальных сечений.
Внутренний масштаб горизонтальных сечений бесконечен. Таким
образом, размерность говорит о многом в случае горизонтального
сечения, но в случае вертикального сечения содержит лишь часть
информации.
Поведение размерностей при сечениях наклонной плоскостью.
Так же, как для наклонных линий в разд. 5.3, для наклонной
плоскости Z — ох имеем: локально она приближается горизон-
26
Часть 1
тальной плоскостью, а глобально — вертикальной плоскостью.
И локальная, и глобальная размерности уменьшаются на
единицу.
8.2. Фрактальные функции переменных в изотропной плоскости.
Облака и дождь
С. Лавджой эмпирически показал, что с помощью моей
модели фрактальной береговой линии можно описать форму
вертикальной проекции границ облаков на поверхность Земли. Это
в свою очередь привело Лавджоя и Мандельброта [7] к
двумерной модели областей, в которых идет дождь, или областей,
покрытых облаками. В этой модели используется «фрактальная
сумма импульсов» — термин, который я ранее ввел для других
целей и который описывает семейство самоаффинных
поверхностей. В этой модели такие величины, как температура,
непрозрачность облаков или интенсивность дождя, описываются
самоаффинной функцией ZH(x, у), аргументы которой (х, у)
принадлежат изотропной плоскости. Основным математическим
отличием по сравнению со случаем функции Вн(х, у), описывающей
рельеф, является то обстоятельство, что если высота гор, как
правило, есть непрерывная функция, то интенсивность дождя
терпит резкие разрывы во времени и пространстве. В простейшем
случае [7] единственный параметр в этой модели — величина Н.
8.3. Фрактальные функции переменной,
принадлежащей аффинной плоскости. Облака
t
Общеизвестно, что большие облака имеют форму блинов,
параллельных поверхности Земли, и в современной метеорологии
обычно считается, что на малых масштабах атмосфера
трехмерна, а на больших двумерна, и переход от трехмерного случая к
двумерному происходит при некотором промежуточном
масштабе. С другой стороны, Шертцер и Лавджой [8] указали на
существование экспериментальных фактов, свидетельствующих о
том, что атмосфера является самоподобной по переменным х и
у, но самоаффинной по переменным х (или у) и г. Мне
представляется чрезвычайно интересным как само это
предположение, так и те подходы, которые используются в [8] для такой
адаптации различных предложенных мной моделей, которая
делает их самоаффинными или даже полностью самоаффинными.
Размерностные свойства соответствующих фракталов
заслуживают в связи с этим подробного исследования.
К сожалению, в работе [8] отсутствует подробная
мотивировка приводящихся численных значений, а также недостаточно
четко подчеркнуты интересные усложнения, к которым приводит
рассматриваемая модель.
Общие свойства фракталов 27
Для простоты можно рассмотреть самоаффинные функции
Т(х, у, г), где горизонтальные переменные (х, у) являются
изотропными. Указанное основное свойство самоаффинности — это
инвариантность при преобразовании, диагональные элементы
которого можно записать как г, г, rG и rGH, где G < 1. Кроме
того, используя несколько тяжеловесные, но понятные
обозначения работы [8], имеем АГ(Ал:) ~ (Ax)GH, АТ(Ау) ~ (Ay)GH и
AT(Az) ~ (Аг)я, и мы находим, что Я< 1. Легко найти, что
для поверхности, описываемой функцией Г, DMg = DBg = 3
независимо от Я и G. Однако другие размерности этой
поверхности и размерности других объектов, связанных с этой функцией,
как правило, зависят и от самого объекта, и от Я и G.
Например, рассмотрим DBl. В кубе со стороной Ах == Ау =
= Az <C 1 величина AT(Az) ~ (Az)GH превышает ДГ(Дл;).
Поэтому чтобы покрыть поверхность, описываемую Т, кубами
со стороной Ах — Ау = Az, необходимо (Ал:)~3 столбиков по
~ (Az)GH~l кубиков в каждом. Итак, Dbl — 4— GH.
8.4. Покрытие прямоугольниками
и «эллиптическая размерность»
В случае £ = 3, 61 = &2 и b3 = b^ в работе [8] выделяется
величина Dei = 2 + Я, которую авторы называют эллиптической
размерностью пространства. Основанием для выделения такой
величины является то, что в изотропном трехмерном случае
Dei = 3, а в изотропном двумерном случае Dei = 2; авторы [8]
считают, что поэтому естественно рассматривать величину 2 + Я
как фрактальную размерность этого самоаффинного
пространства.
Однако одной этой привлекательной мотивировки
недостаточно, более того, она ослабляется другим аргументом,
выдвигаемым в [8] в качестве поддержки такого определения; этот
второй аргумент сводится к замечанию, что в случае £ = 2 и
Ь2 = Ь? при Я = 1/2 получаем «Dei = 1,5, т. е. то же самое
значение, что и для фрактальной размерности, предложенной»
[так!] мною для графика B(t). Мы знаем, однако, что для Вн(1)
размерность Ьнв скорее равна 2 — Я, а не 1 + Я; эти две
формулы лишь численно совпадают для Я = 1/2.
Первый аргумент в пользу введения эллиптической
размерности состоит в том, что «число вихрей с горизонтальным
характерным размером % пропорционально X~D», где D = Dcu Но если
рассмотреть характерные размеры в вертикальном направлении,
то D = 1 + 2/Я; почему же мы должны выбирать
горизонтальные размеры?
Поиски четкой интерпретации величины 2-\- Н как
размерности включали частые беседы с Ж. П. Кахане и Ж. Пейрьером,
28
Часть I
предложившими проверку с помощью «внутреннего» покрытия не
квадратами, а аффинными прямоугольниками высотой {b")~~k и
шириной {b')~k, причем «радиусом» является его большая
сторона. Локальные хаусдорфовы размерности такого типа
обсуждались Пейрьером [9].
Конкретный физический смысл покрытия прямоугольниками
в настоящее время не вполне ясен. Введение такого покрытия,
конечно, привело бы к дополнительным локальным и
глобальным размерностям, значения многих из которых оказываются
весьма сомнительными. Например, массовые размерности для
случая, исследовавшегося в разд. 6, оказываются равными
\ogb'N (глобальное значение) и \ogb"N (локальное значение).
Оба значения дают весьма искаженное и неполное
представление о структуре этих фракталов. В частности, возьмем
самоаффинный ковер Серпинского с Ь' = 9 и Ь" ==3, с одной большой
лакуной, образующейся при N = 20. Его глобальная средняя
размерность, получающаяся с использованием собственных
прямоугольников, равна logy N = 1,36. Это же самое значение
сохраняется при замене Ъ" любым целым числом от 3 до 9
(включительно), хотя ковры, которые при этом получаются, сильно
отличаются друг от друга. Запомнив это значение для будущего,
заметим, что /)0 = 1,81, DML = DBL = logb'N-\- 1 — Я = 1,86 и
DMo = DBQ = log*- tf + 1 - 1/Я = 1,72.
В работе [8], однако, в качестве единственной фрактальной
размерности этого ковра приводится (без объяснений)
величина logyN.
В предельном случае N = b'b" основные размерности,
получающиеся при покрытии прямоугольниками, упрощаются и
принимают значения: 1 + 2/Я— локальное и 2 + Я— глобальное.
Это последнее значение могло бы служить некоторым
элементом обоснования для введения эллиптической размерности, но
точно так же можно было бы думать о введении и другого
(неограниченного) значения 1 + 2/Я.
Заметим также следующее. Чтобы подтвердить
существование этих двух размерностей, глобальной 2 + Я и локальной 1 +
+ 2/Я, нужно заранее знать, какие именно прямоугольники
нужно использовать для покрытия, т. е. заранее знать величину Я.
В то же время, для нахождения размерностей с помощью
обычного покрытия квадратами имеются прямые алгоритмы.
9. Замечание о «физической» экстраполяции
и «математической» интерполяции
Все конструкции и процедуры, которые фрактальная
геометрия заимствовала у математики, содержат бесконечную
интерполяцию, однако в физике интерполяцию нельзя проводить до
Общие свойства фракталов
29
бесконечности, и конструкции в физике, как правило, возникают
при экстраполяции. В 1980 г., когда фракталы впервые были
использованы в физике, сами физики часто обращали мое
внимание на это различие. В самоподобном случае, к обоюдному
удивлению и математиков, и физиков, степенные законы, полученные
при интерполяции, оказываются справедливыми на всех
масштабах. В самоаффиином же случае эти две основные процедуры
существенно различны.
Самоаффинные фрактальные множества
II. Размерности длины и поверхности
Б. Мандельброт *
Для самоподобной кривой можно оценить фрактальную
размерность с помощью измерительного циркуля. Показано, что для
самоаффинных кривых такая процедура дает некоторые глобальное
и локальное значения, которые оказываются вдвойне аномальными.
Исследуются также другие вопросы, связанные с измерением
длины и площади.
1. Введение
Представляется соблазнительным попытаться измерить
длину кривой с помощью измерительного циркуля,
последовательно уменьшая его раствор, или измерить площадь
поверхности с помощью все более и более мелкой триангуляции. Для
обычных кривых такая процедура дает хороший результат.
В то же время известно, что уже для обычных поверхностей
(например, для цилиндра) возникают аномалии; основная
аномалия проявляется в так называемом парадоксе площадей
Шварца, который заслуживает широкой известности и будет
обсуждаться ниже. Для самоподобных кривых эта процедура снова
приводит к фрактальной размерности. Попытаемся использовать
такую процедуру для самоаффинных фракталов и покажем, что
размерности, к которым она приводит, отличаются от массовой
и клеточной размерностей.
2. Измерение длины самоаффинных фрактальных кривых,
являющихся графиками функций
2.1. Измерение длины с использованием «сосиски» Минковского
дает локальную и глобальную размерности, совпадающие с Dml и DMg
Следуя Минковскому и Булигану, определим приближенную
длину кривой В(ц)у используя «сосиску» Минковского,
содержащую все точки на расстоянии, меньшем чем т], от данной точки
кривой. Для обычной спрямляемой кривой и при т)< 1 В(г\) =
= (2г|)-1' (площадь сосиски). Для самоподобной кривой (см.
[2], с. 36) В(у\) ~ Y]1_D, для самоаффинной кривой площадь
сосиски при малых г] ведет себя как N(r\)r\-2 ~ г]я, и поэтому
локальная размерность равна 2 — Н. Глобальная размерность
равна 1. Оба этих значения встречались в части I данной статьи.
* Benott В. Mandelbrot-Physics Department, IBM Research Center;
Mathematics Department, Harvard University, Cambridge, MA 02138, USA.
Работа выполнена при частичной поддержке Управления научных исследований
ВМС США (контракт N00014-85-K-0I88).
Общие свойства фракталов
31
2.2. Нахождение длины с помощью измерительного циркуля
при фиксации последнего выхода кривой дает локальную
и глобальную размерности, совпадающие с DML и Dmg
В одном из многих методов нахождения длины спрямляемой
кривой используется измерительный циркуль, перемещающийся
вдоль кривой. На кривой могут быть узлы, т. е. кратные точки
произвольного порядка; достаточно, чтобы точки кривой были
упорядочены, например «во времени». Начнем с исходной точки
Pq. Первая точка Pi будет первым выходом кривой из круга с
центром в Pq и радиусом ц и т. д. Если обозначить через L(r\)
длину возникающей ломаной линии, приближенно описывающей
нашу кривую, то длина кривой будет Ишц^Ь(г\).
Можно выбрать в качестве Pi точку последнего, а не первого
выхода вдоль кривой. И можно также двигаться назад.
Для самоподобной кривой находим L(r\) ~ r\l~D, и снова по
желанию можно отмечать либо первый, либо последний выход
кривой.
Для наших самоаффинных кривых ситуация оказывается
совершенно иная. Кроме локальной размерности при ц-+0
имеется также глобальная размерность, которая, как мы увидим,
равна 1. И локальная размерность, полученная при помощи
измерительного циркуля, имеет два совершенно различных значения,
одно для последних, а другое для первых выходов. Прежде чем
двигаться дальше, заметим, что для самоподобных функций
рассмотрение становится проще (а результаты не меняются), если
круг с центром в точке Pk заменить квадратом.
Если воспользоваться этим обстоятельством, то рассмотрение
последних выходов становится простым. Покроем нашу кривую
(b"k)2-H квадратами со стороной (b")k <С 1; это дает D > 2 — Я.
Далее добавим кольцо из 8 таких же квадратов вокруг каждой
ячейки и тем самым увеличим сторону втрое. Ясно, что (b"k)2~H
шагов циркуля с раствором 3(6")~* достаточно, чтобы пройти
вдоль кривой, поэтому размерность, полученная с помощью
измерительного циркуля, меньше 2— Н. Следовательно, она равна
2-Я.
2.3. Нахождение длины с помощью измерительного циркуля
при фиксации первых выходов дает «аномальные размерности».
Локальное значение размерности при малых Г) равно 1/Я.
Эта величина совпадает с фрактальной размерностью
фрактального следа, связанного с функцией.
Для больших г] размерность равна 1
В этом разделе приведены результаты, полученные в
работе [1].
При г] >> tc (например, когда единица измерения Вн
достаточно мала) график по сути дела близок к горизонтальной
линии. При передвижении измерительного циркуля вдоль кривой
32
Часть 1
он в основном остается параллельным оси /, и Ь(ц) слабо
меняется с изменением rj. Если считать, что Ь(ц) ~ r\l~D, тогда то
обстоятельство, что Ь(ц) является константой, дает для
глобальной размерности значение 1 независимо от Н.
Если/ наоборот, ц <С tc (например, когда единица измерения
Вн велика), то ситуация оказываетя иной: измеритель,
передвигающийся вдоль кривой, в основном остается параллельным
оси В. В результате получаем размерность, равную 1/Я.
Это чрезвычайно странное значение может превышать 2 и
является аномальным вдвойне: оно противоречит значению 2—
—Я, которое получалось при других локальных определениях
фрактальной размерности. С другой стороны, те, кто знакомы
с фрактальным броуновским движением, могут отождествить
\/Н с фрактальной размерностью следа (в некотором £-мерном
евклидовом пространстве RE, при Е > 1/Я) движения, для
которого координаты Е представляют собой независимые
реализации BH(t).
В этом случае попытка использовать необычный путь для
измерения фрактальной размерности для одного множества в
действительности заканчивается измерением значения, которое все
пути дают для некоторого другого множества.
2.4. Размерности, связанные с покрытием аффинными
прямоугольниками
В этом разделе мы хотим связать измерение длины с
вопросами, обсуждавшимися в разд. 8, части I статьи. В обоих
предельных случаях ц ;> 1 или ц <С 1 число шагов измерителя
^(rl)/rl Для всех практических случаев равно числу
прямоугольных ячеек высотой т) = (6'/)""А и шириной (b')~k, используемых
для покрытия фрактала. При обычном определении
размерности фрактала выбираются квадратные ячейки, и число ячеек
находится как функция их диаметра. Аналогичную формулировку
можно применить и для величины Ь(ц)/ц, если в качестве
диаметра прямоугольной ячейки выбрать ее большую сторону.
В локальном случае наибольшей стороной является
вертикальная, и мы приходим, как и в разд. 2.3, к размерности 1/Я.
В глобальном случае наибольшей стороной является
горизонтальная, так что размерность равна 1.
3. Измерение длины других самоаффинных кривых,
в частности следов движения Пеано
К этому интересному случаю могут быть применены
аргументы, аналогичные использованным в разд. 2.3.
Локальное значение. Использование измерительного циркуля
раствором (Ь")~ <С 1 потребует Nk шагов, и поэтому показатель
Общие свойства фракталов 33
для приближенного значения длины равен log^(6//Ar~1)= 1 —
— logb"N> так что размерность равна log^N. В частности, в
случае Пеано N = b'b" и размерность равна 1 + 1/#.
Глобальная размерность. Она равна log*,' N и в случае Пеано
принимает значение 1 + Н.
4. Парадокс площадей Шварца
Триангуляция обычных поверхностей оказывается делом
гораздо более сложным, чем можно было бы ожидать. В
частности, в конце XIX в. Герман Амандус Шварц показал, что для
случая цилиндра единичного радиуса и единичной высоты
безобидный на первый взгляд метод триангуляции может дать для
площади боковой поверхности любую величину: от истинного
значения 2я до бесконечности!
Поступим следующим образом: разделим цилиндр по высоте
на п слоев плоскостями z = p/n (р — целое число больше нуля)
и выделим на окружностях с четным номером уровня точки 0 =
= (2<7+ l)n/m (q — целое),а на окружностях с нечетным
номером уровня —точки 8 = 2<7я/т. Соединим каждую точку (г, 0)
с точками (г±1//г, &±я/т). Таким образом, боковая
поверхность единичного цилиндра приближенно представлена 2тп
равными треугольниками. Теперь, чтобы получить истинную
площадь, кажется естественным сложить площади этих
треугольников и затем произвольным образом независимо устремить я->оо,.
Прямое вычисление показывает, что для больших т эта
площадь приближенно равна 2я Д/|1 + ("^")"^т • Если т->оо,
но я/т2->•(), то это приближенное выражение действительно
сходится к величине 2зх. Однако, если т ->• оо и п = Хт2 (К —
= const > 0), мы получим произвольное конечное значение,
превышающее 2я! И мы можем сказать, кроме того, что, выбирая
п ~ тР, р > 2, можно добиться, чтобы приближенное значение
площади возрастало как произвольная степень либо 1/т, либо
1/я, либо площади треугольника, пропорциональной 1/тп.
Цилиндр оказывается похожим на фрактал! Его площадь
неограниченно возрастает при таком способе измерения.
Причиной такого поведения является следующее
обстоятельство: при переходе к пределу т/п-* оо мы используем
треугольники, которые а) становятся все более и более узкими, т. е.
имеют хотя бы один угол, стремящийся к нулю, и б) лежат в
плоскостях, стремящихся стать перпендикулярно боковой
поверхности цилиндра. При этом возникающая поверхность становится
все более и более «волнистой» и все больше удаляется от
истинной поверхности.
34
Часть I
Реакция прагматика была бы следующей — избегать узких
треугольников. Ответ математика: «парадокс площадей
Шварца» относился к числу проблем, способствовавших развитию
современной математики. В частности, этот парадокс стимулировал
Минковского дать корректные определения длины и площади
через объемы все более тонких «сосисок» Минковского для
кривых и все более тонких «шарфов» Минковского для
поверхностей. Эти множества состоят из всех точек внутри е-окрестности
некоторой точки кривой или поверхности. Так, Минковский
определяет площадь обычной поверхности как
lim (1/2я) X (объем е-шарфа).
В отличие от треугольников все интервалы подобны друг
другу, и поэтому для обычной кривой в плоскости аналога
парадокса Шварца не существует. Его не существует также и для
самоподобных фрактальных кривых; действительно, в [2]
отмечено, что измерения длины с переменной точностью е могут быть
проведены многими различными путями, но во всех случаях
длина меняется по одному и тому же закону: пропорционально e1_D.
Но для самоаффинных кривых, как показано в разд. 2.1—2.3,
ситуация более сложная. Здесь длина растет как гх~°, но D =
= Dbl при подходе Минковского и D = DCl > DBl при
использовании измерительного циркуля. Может ли размерность D
принимать значения, отличающиеся от этих двух величин?
5. Измерение площади
самоаффинных фрактальных поверхностей,
полученных из графиков функций
5.1. Площадь фрактального рельефа Bff (x,y),
найденная с помощью «шарфа» Минковского
Мы возвращаемся к размерностям DBl и Dbg.
5.2. Определение площади фрактального рельефа
с помощью триангуляции
Выберем квадратные плитки с Ах=Ау= 1/6. Четыре
вершины каждой плитки определяют четыре значения Вн и дают
два способа аппроксимации небольшой части поверхности двумя
«треугольниками-близнецами». Возьмем среднее из этих двух
приближений для каждой ячейки и, кроме того, проведем
усреднение по Ь2 ячейкам.
Грубая триангуляция. Если пренебречь деталями с
размерами, меньшими чем критическое значение хс = {/с, то в этом
приближении моя броуновская модель рельефа Земли имеет
Общие свойства фракталов
35
вполне определенную площадь, ненамного превышающую
площадь проекции рельефа на идеализированную плоскость (или
сферу).
Эта ситуация резко отличается от той, которая имела место
для береговой линии.
Рассмотрим в качестве примера два негауссовских
ландшафта (см. [2], вклейка С13). Они получены из одного и того же
гауссовского ландшафта с помощью нелинейных
преобразований, в которых предполагалось, что величина tc очень мала для
долины на верхнем рисунке С13 и для плато на нижнем рисунке
С13, и в то же время величина tQ очень велика для горной цепи
на верхнем рисунке С13 и в каньоне на нижнем рисунке. Далее,
я уже указывал в своих лекциях, что хорошие взлетные полосы
аэропортов неровны в той же степени, что и Гималаи, только их
вертикальный масштаб значительно меньше. Теперь мы видим,
что эти количественные различия приводят к качественным
эффектам. Прежде всего, как подсказывают обычные наблюдения
и здравый смысл, у аэропорта имеется вполне определенная
площадь, даже при измерении самой точной линейкой. В Гималаях
же обычные фотографии, снятые издалека, показывают, что
«средний наклон» порядка я/4. Это в свою очередь показывает,
что в области переходного масштаба имеется ряд интересных
деталей; поэтому различные измерения площади, полученные с
различными линейками, меньшими чем tc, должны дать кривую,
график которой в двойном логарифмическом масштабе будет
заведомо отличаться от прямой.
Тонкая триангуляция. В этом случае площадь наверняка
может быть произвольно большой, но как быстро она будет расти
с уменьшением размера треугольников? Каждый из
треугольников-близнецов в ячейке имеет длину ~ b~Hk и высоту ~ &-*, он
очень узкий, и его площадь ~ 6-(#+i)fc. Полное число
треугольников b2k = а-2/(я+1) и приближенное значение площади (а) ~
~ а1-2/(я-и) Это соотношение аналогично выражению для длины
кривой Z.(t|) — Ti1_"1//f, но здесь аномальная размерность равна
2/(#+1),а не 1/#.
Следующая сетка, которую мы рассмотрим, самоаффинна и
включает {b'b")k прямоугольников шириной b'~k и высотой b"~k,
причем Ъ' > Ь". Площадь каждого из треугольников теперь
~ ((b")-l(b')l~H)k, а аномальная размерность равна
log (bfb") /log (b"b'H). Она может принимать значение между
2/(# + 1) и 1/Я, и это есть фрактальная форма парадокса
площадей Шварца.
Самоаффинные фрактальные множества
III. Аномалии хаусдорфовой размерности
и их смысл
Б. Мандельброт *
Для некоторых самоаффинных фракталов, построенных рекуррент-
но, размерность Хаусдорфа — Безиковича Dhb принимает «вдвойне
аномальное» значение: она представляет собой некоторую дробь и
оказывается меньше, чем Dbl< Возникает вопрос, указывает ли это
отличие Dhb от DBl на некоторые новые глубокие закономерности
или же это неравенство ставит под сомнение ту выделенную роль,
которую размерность Dhb играла до сих пор во фрактальной
геометрии? В работе также изучаются размерности сечений некоторых
самоподобных фракталов.
1. Введение
В части I мы не говорили о том, какое значение
принимает размерность Хаусдорфа — Безиковича Dhb для
построенных рекуррентно самоаффинных фракталов, поскольку в связи
именно с этими значениями Dhb возникают интересные вопросы,
на которые в настоящее время не имеется полного ответа.
Нашей исходной точкой будет теорема, принадлежащая Макмал-
лену [3, 4], который показал, что для данных Ь\ Ь" и данного
генератора при определенных комбинациях знаков г'п и г"
оказывается, что DHB < DBL, Эта «положительная аномалия»
Del — Dhb была для меня сюрпризом. Дополнительные
результаты по этому и близким вопросам были получены Бедфордом
[5]. Мы сможем, однако, либо доказать, либо привести
аргументы в пользу того, что для других комбинаций знаков (в
частности, для некоторых случайных комбинаций) оказывается, что
Dhb = DBl. Математический анализ этого различия Dhb и DBl,
как оказывается (довольно неожиданно), включает некоторые
фрактальные меры, введенные мною в 1974 г. при исследовании
турбулентности [10], которые в дальнейшем оказались весьма
полезными при изучении странных аттракторов [11]. Возможно,
существование указанной аномалии означает, что Dhb не
является величиной, имеющей физический смысл (в
противоположность тому, что я вначале предполагал). Кроме того, будут
приведены некоторые результаты, по-видимому новые,
относящиеся к сечениям самоподобных фракталов.
* Benoit В. Mandelbrot -Physics Department, IBM Research Center;
Mathematics Department, Harvard University, Cambridge, MA 02138, USA. Работа
выполнена при частичной поддержке Управления научных исследований
ВМС США (контракт N00014-85-K-0188).
Общие свойства фракталов
37
2. Теорема, определяющая Dhb, и следствие
ТЕОРЕМА А [3, 4}. Рассмотрим рекуррентный
самоаффинный фрактальный генератор на решетке с горизонтальным и
вертикальным основаниями Ъ' и Ь" и введем H=logb"/logb'. Пред*
положим г'п=± \\Ъ\ г"= ЦЪ" для всех п (это означает, что
все стрелки направлены вверх). Обозначим b't число клеток,
содержащихся в /-м горизонтальном ряду генератора. Тогда в
пределе Dhb фрактала определяется решением уравнения
b"D=Zib'i)H.
СЛЕДСТВИЕ В [3,4,5]. Для самоподобных фракталов,
удовлетворяющих условию теоремы A, DBh может быть строго
меньше, чем локальное значение клеточной или массовой
размерности, обсуждавшихся в части I.
Численный пример, в котором Dhb < DBl- Обратимся к
генератору, изображенному на рис. 2 части I. Здесь 6/ = 4, Ь" = 2,
Я =1/2, b[=l, Ь'2 = 3 и г'п (см. стрелки) обеспечивают
непрерывность фрактальной кривой. Согласно теореме А, 2 = 1 +
+ д/3, так что Dhb= 1,44998. В то же время Dbl — 2 — H =
= 1,5.
Замечание. Для этого примера проекция меры на ось У
оказывается сингулярной. Действительно, она совпадает с хорошо
известной мерой Безиковича (см. [2], с. 377) с pi = 1/4 и /?2 =
= 3/4.
3. Выражение для вертикальной аномалии А" = Dbl—Dhb
Аномалия A" = DBl — Dhb представляет собой меру разброса
ненулевых значений b'jt Например, генератор со стрелками
графика непрерывной функции может содержать либо несколько
больших изломов, либо много малых; аномалия будет больше
во втором случае. (Читателю предлагается построить
иллюстрирующие примеры.)
Теперь прежде всего мы выразим аномалию А" через
величины р. = b'lJN, связанные с вероятностями,
соответствующими проекции меры на ось У. Аномалию А" можно записать в
виде
Л''М1-#)(1о&6,,;Г'-/£), где /£ = (log^£pf)/(tf-l).
Член log&"N" есть размерность множества, которое является
носителем проекции меры на ось У. Это множество есть
интервал при N" = Ъ" и канторовское множество при N" < Ь". Что
касается 1"НУ то оно известно читателю, знакомому с мерой
38 Часть I
Безиковича, — это Я-информационная размерность проекции
меры на ось У.
Далее, заметим, что мера Безиковича представляет особый
случай случайной фрактальной меры [10], часто называемой
Л1-мерой (иначе ее называют мультипликативной мерой, или
мерой Мандельброта — по терминологии Пейрьера; в моей книге
[2], с. 378, она носит название нелакунарной, взвешенной
сгущенной меры). Рассматривая это обобщение, удобно ввести
обозначения Wf = b'fb"/N = pfb" и (Гя)= £ (b'T1 Wf. Такое
обозначение приписывает равные вероятности Ъ" возможным
значениям (случайного) «веса» W, удовлетворяющего условию <W>=
= 1. Тогда
А" = - logb„(WH) = - log** ((WHyiH) > 0.
СЛЕДСТВИЕ С [4]. При Ъ* = V необходимым и
достаточным условием отсутствия аномалии является совпадение всех
ненулевых Ь'г
Замечание. Проекция меры на ось Y однородна на своем
носителе, если А" = 0, и сингулярна на своем носителе, если
А" > 0.
4. Размерность горизонтального сечения
4.1. Горизонтальные сечения некоторых рекуррентных
самоподобных фракталов. Выражения для их аномалий
Чтобы оценить следующие ниже результаты, нужно
полностью понять соответствующие результаты, относящиеся к
самоподобным фракталам (b' = b ). Это, по-видимому, новые
результаты, и они сами по себе представляют интерес.
Напомним, что для обычного ковра Серпинского известно, что
размерности горизонтальных сечений нельзя получить, вычитая
1 из полной размерности log3 8. Эти сечения будем называть
аномальными. Чтобы найти их размерности, распределим
однородно на ковре массу, располагая ее на каждом шаге
конструирования ковра в восьми ячейках с плотностью 9/8. Ясно, что
проекции меры на оси X и У являются мерами Безиковича с
Ь = 3, р\ = 3/8, р2 = 2/8 и ръ = 3/8. Покажем, что размерности
сечений связаны с этими мерами.
Рассмотрим произвольные значения 6, N и р\ = bj/N, не
исключая возможности того, что некоторые р\ = 0. Пусть
ордината горизонтальной прямой, которой рассекается фрактал, по
основанию Ь равна */ = 0, t/if/2... , и пусть k\ есть число
повторений индекса / в первых k цифрах. Положим $(ун) равным
Ь/, если уь = /. В k-м приближении горизонтальная линия с ор-
Общие свойства фракталов
39
динатой у пересечет число ячеек со стороной b~k, равное
произведению р(#/г) от h = 1 до h = ft. Таким образом, ft-e
приближение горизонтального сечения имеет конечный показатель
размерности
log Nk (*/)/log (bk) = £ (ft,/*) l°Sb b,.
Если у таково, что ft//ft->-<7/ Для каждого /, то это выражение
имеет предел, этот предел совпадает с клеточной размерностью и
эта размерность зависит от у. Теперь выберем точку на нашем
фрактале с однородной мерой, т. е. выберем такое у, что
проекция меры на ось У, являющаяся мерой Безиковича, сингулярна
в точке у. В этом случае kj/k->pj. Добавляя и вычитая
£ (ft//ft) log6 N — 1 в обеих сторонах предыдущего равенства,
получим, что с большой вероятностью размерность сечения
равна
D = {logbN-l) + (l-I),
где
I = — TiPflogbPj.
Поскольку \ogb N представляет собой размерность нашего
исходного плоского фрактала, величина log&Af—1 представляет
собой размерность, которую мы получили бы, воспользовавшись
правилом «вычти единицу». Мы видим, что это правило
оказывается неверным: появляется аномалия, зависящая от / —
информационной размерности проекции меры на ось У; эта
аномалия либо равна 0, либо больше нуля.
Тогда (и только тогда), когда /= 1 (что предполагает р/ =
= N/b), аномалия исчезает.
Если р/= \/N" для N" значений / и р/ = 0 для других
значений, то аномалия равна 1 — log& N", в этом случае проекция
меры на ось У однородна на канторовской пыли. Горизонтальное
сечение является почти наверное пустым по отношению к
однородной мере на [0, 1], но по отношению к однородной мере на
канторовской пыли это сечение имеет размерность
log6JV-log,JV".
Это равенство представляет собой весьма интересное обобщение
стандартного правила на непустые сечения.
4.2. Горизонтальные сечения
некоторых рекуррентных самоаффинных фракталов
С очевидными изменениями результаты здесь аналогичны
результатам разд. 4.1. Мы коротко изложим их и в дальнейшем
прокомментируем в разд. 4.3.
40
Часть t
Если аномалия Л" исчезает, то горизонтальные сечения
фрактала, удовлетворяющего условиям теоремы Л, либо пусты, либо
являются канторовскими множествами размерности logy (N/N").
Если N" = Ь"у сечение никогда не пусто, имеет размерность
logy(Ntb") = DBL-l
и, следовательно, удовлетворяет стандартному правилу для
размерности сечений. Если N" < Ъ"\ то для непустых сечений
получаем размерность
logy (W) = (DBL - 1) + log^W",
которая представляет собой обобщенное стандартное правило
разд. 4.1 в случае самоаффинного фрактала. Однако это
равенство можно также записать в виде
logb,(N/N") = D*BL-l,
соответствующем стандартной записи для случая
самоаффинности, заменяя DBL на D*BL, где последнее значение — это
размерность, которая проявляется у фрактала после того, как он был
сжат по вертикали для исключения лакун.
Если А" > 0, то почти наверное размерность сечения есть
D = logft' N — Е Р/ log*' Pf.
Удобно переписать правую часть, введя некоторые
использовавшиеся ранее размерности. Поскольку
log*' N = DML — (1///— 1) log*- N" = DML - (Я - 1) logvN",
TO
D = DBL-(1-H) logrN" - HI»,
где
/f = ~ZP/ l°Zb»Pi = l ~ <w l°8 W)
— /-информационная размерность проекции меры на ось У.
Отсюда следует, что аномалия размерности сечения имеет вид
D - {DBl- \ogb„N") = Я [Iog6„JV"- I'{].
Эта величина больше 0, и больше Я [log^AT' — /£], поскольку
Г < Г
4.3. Заключение
В самоподобном случае у целого фрактала аномалия
отсутствует (т. е. Dbh = Dbl), даже если горизонтальные сечения
имеют аномалию (т. е. Dce4 не равна £>фР — !)•
Общие свойства фракталов
41
В самоаффинном случае целый фрактал обладает аномалией
в том и только том случае, когда горизонтальные сечения почти
наверное обладают аномалией.
5. Глобальный «двойник» D* размерности Хаусдорфа —
Безиковича Dhb и горизонтальная аномалия А' = D *—Dbg
В части I отмечалось, что формулы для Dbl = Dml и Dbg =
— Dmg симметричны: они получаются при замене ролей У и Ъ"
и N' и N". Приверженность к симметрии заставила меня искать
глобальный двойник D* размерности DBh как решение
уравнения
Соответствующую горизонтальную аномалию мы будем
рассматривать по отношению к величине DBg, так что она равна
А' = DBG - D* == - logr(WV«) < 0.
Случай графиков функций. Здесь Z)*=l; это значение мы
встречали в частях I и II для всех других глобальных
размерностей. Аномалия А' = 0 и размерность вертикальных сечений
равна нулю, как и должно быть. Аномалия А' играет для
вертикальных сечений ту же роль, какую А" играет для
горизонтальных сечений, но спрашивается, имеет ли величина D* какой-либо
дополнительный смысл кроме того, что она выступает как
размерность?
6. Самоаффинные непрерывные графики,
не удовлетворяющие условиям теоремы А
6.1. Пример, в котором Dhb = &bl, и вопрос
Два генератора, показанных на рис. 2 и 3 в части I,
отличаются лишь направлением стрелки во втором блоке.
Генератор, изображенный на рис. 3, используемый рекуррент-
но, дает фрактал, который является графиком координаты X(t)
хорошо известной кривой Пеано, изученной Чезаро и названной
в моей книге [2], с. 64, треугольным изгибом. График
координаты Y(t) есть 1—X(l — t). В этом случае, как было показано
в [4], Dhb =1,5.
Заметим, что проекция меры на ось X одинакова для
графика X(t) и для следа Пеано в плоскости (X, У). Поскольку
след Пеано заполняет («изгибами») однородно треугольник, мы
находим, что проекция меры дифференцируема и имеет
плотность 2(1 — х).
В более общем случае предположим, что проекция меры на
ось У имеет правую и левую производные f'+ и f\ Эвристиче-
42
Часть I
ское применение формулы теоремы А к генератору после k
шагов дает формулу, где суммирование пооизводится от р = 1 до
р = &"*:
Ъ"ы> = £ (А/ (*/))я &"* - J] (6"Г* (Г 0/+))я • &" (2~Я) * ~
~&''(2"*)* $(/'(#+))" ^.
При k > 1
D = 2-H + (l/k) log** J (/'(</+))"<ty,
асимптотически D = 2 — Я.
Тот же самый результат можно, очевидно, обобщить на
случай, где проекция меры на ось У является абсолютно
непрерывной на канторовской пыли.
Напоминание. Для процесса BH(t) DBh — 2— Я и,
следовательно, А" = 0. Кроме того, известно, что здесь проекция меры
на ось У дифференцируема. Заметим, что для случайных
процессов абсциссы горизонтальных сечений на высоте у образуют
множество возвратов к точке у (называемой также локальным
временем).
Вопрос. Имеется ли однозначная связь между тем
обстоятельством, что А = 0, и тем, что Я-информационная
размерность проекции меры на ось У является размерностью ее
носителя?
6.2. Случайные генераторы
Случайно выбранные генераторы удобно рассматривать, если
при их геометрическом построении использованы «процессы
рождения». (Эти процессы заслуживают более широкого
обсуждения их свойств, чем то, которое приводится ниже.)
Простейшая из таких функций, MH{t), приведена в моей
работе [1]. Эта «учебная» функция MH(t) получается, если
выбирать направления всех четырех стрелок на рис. 1 или рис. 2
случайным образом, с равными вероятностями для
направлений вверх и вниз. Частично эвристическое рассуждение,
приведенное ниже, показывает, что проекция меры на ось У функции
Мя(0 дифференцируема. Если предположить, что ответ на
вопрос, приведенный в конце разд. 6.1, является утвердительным,
то эта дифференцируемость меры предполагает, что DHb =
= DMl = 2 — Я (как утверждалось без доказательства в
работе [1], написанной в то время, когда я еще не представлял
себе всей сложности вопроса).
Первая часть рассуждений является строгой. Вклад в массу
интервала длиной (Ь"Ук на оси У осуществляется прямоуголь-
Общие свойства фракталов
43
никами шириной (bf) , высотой (Ь")~ и массой N~k = (b')~~k.
Их число определяется простым случайным процессом
рождения со средним числом потомков на одно поколение N/b" =
= b'/b" > I. Рассмотрим для каждого у последовательность
вложенных 6-адных интервалов длиной (b")~k, которая
определяет у (если у не является 6"-адным), или последовательности,
определяющие у+ и у- (если у является 6"-адным). Средняя
мера на интервалах в одной из этих последовательностей имеет
вид {b'jb")~k (число потомков в k-м поколении). Стандартная
теорема процессов рождения (см. [12], с. 13) утверждает,что эти
средние меры почти наверное сходятся к пределу, являющемуся
значением строго положительной случайной переменной W,
такой что (W} = 1.
Поэтому \х(у), определяемое как счетно-аддитивная мера
между 0 и у, обладает тем свойством, что на вложенных
интервалах длины (b")~k, определяющих у, у+ или у~, средний наклон
\х(у) сходится к пределу.
Следующий шаг гораздо проще сделать для У = 4, Ь" = 2
и N = 4. Выберем конечное 4>1 и рассмотрим приближенную
меру \ik(y) на диадном интервале (у', у") длиной 2~*. В левой
половине этого интервала число потомков для шага k= 1 равно
сумме 2kW независимых случайных переменных с
математическим ожиданием 2 и дисперсией а2. Это число можно записать
как 2k+xW + {2-2kW)V2GG, где G есть нормированная гауссов-
ская переменная. В правой половине этого интервала
справедлива та же формула с заменой плюса на минус. Поэтому
наклоны функции [ik+Ay) на двух половинах нашего интервала
равны W ± л/W G(<y/2)~h~l. Приближенная мера \Xk+i(y)
получается из \ik(y) путем смещения средней точки (см. [2],
гл. 26). То есть значение в средней точке \ik (y 2 y j нужно
сместить на величину 2~k~la л/W G(2 л/2)~к~\ Если k
достаточно велико, можно пренебречь изменениями W при переходе
от одного шага к другому, тогда для \х(у) мы получим ряд
И (У) ~ V (У) = Vk (У) + о W I о*0 {2hy\
h>k
где а==(2 д/2)-1, а а (у) — случайная пилообразная функция, а
именно такая функция, которая обращается в нуль при целых
значениях у, принимает независимые нормированные гауссовы
значения в полуцелых у и линейна на диадных интервалах
длиной 2-*-1. Возникающая функция \х*(у)—м*(#) известна. Для
а > 1/2 она непрерывна, но не дифференцируема (и в
некоторых грубых фрактальных алгоритмах служит моделью гор). Для
а< 1/2, в частности для нашего значения а = (2 л/2)~1, эта
44
Часть 1
функция непрерывна и имеет правую и левую производные.
(Фактически производная м^'С*/4) является почти броуновской;
это вариант рядов Радемахера, близких к рядам Фурье для
процесса Броуна — Винера.)
Можно ожидать, хотя у меня не было возможности проверить
все детали, что эвристики последнего параграфа можно строго
доказать, т. е. имеется альтернативное строгое короткое
доказательство.
Заключение. \х(у) является дифференцируемой. Приведенное
выше W есть ее производная для не 6"-адного у или ее правая
и левая производные для 6"-адного у. (В 6"-адных точках
правая и левая производные отрицательно коррелированы.)
6.3. Более общие M„(t) -подобные случайные функции
Причина, по которой в приведенном выше обсуждении
использовались величины Ь', Ъ" и N, а не 4, 2 и 4, состоит в том,
что приведенные аргументы справедливы и в более общем
случае, если только генераторы стрелок, порождающие
непрерывные графики, описываются некоторыми специальными
вероятностями. (При Ь" > 1 и 67>1 этим условиям удовлетворяют
случайные генераторы со стрелками.) Однако для других
распределений вероятностей ситуация оказывается более сложной.
Интервал длиной (&")-* может находиться в любом из Ъ"
«положений» внутри интервала длиной (b")~k+l9 и ожидаемое число
потомков обычно зависит от этого положения. Нельзя ожидать,
что соответствующая проекция меры на ось У будет
дифференцируемой.
Предположение. Анализ отдельных примеров позволяет
ожидать, что для рекуррентных самоаффинных непрерывных
случайных графиков можно получить и почти наверное DHb < Dbl,
и почти наверное DHb > DBl, и что А" = DBl — DHb есть
непрерывная функция вероятностей, введенных в генераторы со
стрелками.
7. Другие случайные самоаффинные множества,
не удовлетворяющие условиям теоремы А
7.1. Генераторы, получаемые сгущением при N/Ь" > 1
(соответственно рЬ' > 1)
Идея выбора полностью случайного генератора может быть
реализована в нескольких формах. С одной стороны, можно
приписать равные вероятности каждому из способов выбора N
ячеек из Ъ'Ъ" ячеек. Если все варианты выбора статистически
независимы, то возникающий в результате фрактал получается
Общие свойства фракталов
45
путем процесса, являющегося самоаффинным аналогом
процесса «микроканонического сгущения», введенного мной в
1974 г. (см. [2], гл. 10). С другой стороны, можно приписать
некоторую вероятность р тому событию, что выбранная ячейка
принадлежит генератору. Тогда генератор состоит в среднем из
pb'b" ячеек. Если все варианты являются статистически
независимыми, то возникающий в результате фрактал получается в
процессе, являющемся самоаффинным аналогом
«канонического» варианта процесса сгущения, также рассмотренного мною
в 1974 г. (см. [2], гл. 10).
В обоих случаях математическое ожидание числа потомков
на поколение равно N/b" (соответственно pb'). Процесс
рождения переходит в процесс рождения и гибели, но аргументы
разд. 3 остаются, вообще говоря, справедливыми, если N/b" > 1
(соответственно, если pb'> 1). Новым элементом является то,
что производная теперь может оказаться равной нулю с
вероятностью больше 0 и меньше 1. То есть в данном примере
производная может обращаться в 0 на некоторых интервалах у.
7.2. Генераторы, получаемые путем сгущения при N/b" < 1
(соответственно pb' < 1)
В сложном генераторе после k шагов Ь'} равно нулю для
большей части значений /. В первом приближении не будем
рассматривать эти значения, а рассмотрим только те, для которых
6< > 0. Стандартная теорема теории процессов рождения (см.
[4], с. 12) утверждает, что условное распределение величины Ь'}
(в случае, когда Ь^ > 0) стремится при &->-оо к
распределению случайной переменной. Если мы обозначим этот предел
через W (как это сделано в разд. 3), то мера на непустом
интервале длиной {b")~k снова окажется равной произведению W на
меру N~k ячейки (b")~k{b')~k. Поэтому среднее число неисче-
зающих b'f равно Nk(W). В пределе при &->-оо проекция меры
на ось У определяется фрактальным множеством размерности
logb"N (соответственно logy {pb'b")). Это можно было бы
угадать. Но что труднее угадать — это то, что на этом множестве
распределение меры оказывается почти однородным, а именно
однородным с точностью до множителя W. Это показывает, что
ситуация здесь аналогична той, которая была описана в разд. 7.1,
с той разницей, что здесь <W> > 1.
С другой стороны, можно исследовать меру на полученном
фрактальном множестве следующим образом: на каждом шаге
выберем те ячейки длиной (b")~kf для которых Ь^ > 0, плюс
такое число пустых ячеек, которое нужно, чтобы в сумме
получилось N. Это равносильно тому, что мы «разбавляем» W,
46
Часть I
разрешая значение W = Q, и обеспечиваем (W) = 1. В
результате мы приходим к ситуации, аналогичной рассмотренной
ранее в этом разделе.
При обоих подходах эвристическое использование теоремы А
приводит к предположению, что DHb сколь угодно близко к Dbl-
Итак, Dhb = Dbl.
Предположение. Можно ожидать, что равенство DHb = DBl
выполняется для широкого класса случайно генерируемых
самоаффинных множеств, не являющихся графиками функций.
Замечание. Каноническое сгущение генерирует специальную
плоскую Л1-меру (см. разд. 2). Интересно было бы исследовать
проекции более широкого класса М-мер, в самоподобном и
самоаффинном случаях.
8. Обсуждение
Значение Dhb, следующее из теоремы А, обычно аномально,
поскольку представляет собой дробь, но это обстоятельство
соответствует самому духу фрактальной геометрии. Вторая же
аномалия обусловлена тем, что Dhb оказывается неправильной
дробью. Однако теорема А изобретена вовсе не для этой цели.
Наоборот, встречавшиеся ранее специально изобретенные
«вторые аномалии» относились, например, к случаю высокой
неоднородности, подобно аномалии Булигана, рассмотренной выше
в разд. 1. Именно по этой причине в каждом рассмотренном
ранее случае, интересном для физики, фрактальная размерность
вначале находилась с помощью какого-либо «имеющегося под
рукой» грубого метода (обычно это были размерности Dbl или
Dml), и лишь затем это значение фрактальной размерности
«подтверждалось» более трудоемким и технически более
сложным вычислением Dhb-
Следующее наблюдение: когда мы имеем дело с графиками
функций, таких как B(t), естественно приписать равные меры
графикам, соответствующим интервалам равной длительности.
Это свойство удовлетворяется для случая B(t) при введении
хаусдорфовой меры относительно подходящей калибровочной
функции. Существует ли такая калибровочная функция для
рекуррентных самоаффинных функций, удовлетворяющих теореме
А? Если существует, то получающееся хаусдорфово время не
является реальным временем.
Моей первой инстинктивной реакцией было рассматривать
направления стрелок (знаки г'п и г£) в самоаффинных
фрактальных конструкциях как «нефизические» тонкие детали,
поэтому казалось, что величины, определяемые расположением
стрелок, не могут быть физическими. Далее, по-видимому,
история повторилась, когда оказалось, что эти тонкие детали влияют
Общие свойства фракталов
47
на (однозначную) размерность горизонтальных сечений,
которая имеет физический смысл. Но тогда приходят на ум
аргументы, приведенные в разд. 4.1, и аномалия Dhb снова кажется
нефизической. Даже если она, возможно, приведет к некоторым
новым физическим догадкам, я боюсь, что определение Хаус-
дорфа — Безиковича теряет свое выделенное значение.
Благодарности
Часть I. Для меня было весьма полезным обсуждение
разд. 5.1 и 5.2 (из работы [1]) с Ричардом Ф. Боссом.
Основным толчком для написания данной работы (весной
1985 г., когда я преподавал фрактальную геометрию) было
обсуждение обычных дифференцируемых функций, являющихся
самоаффинными. Я обнаружил, что, хотя определение объекта
было дано в моей книге еще в 1977 г., известно о нем мало.
В дальнейшем оказалось возможным связать эти
исследования с объяснением странных результатов и с теоретическими
трудностями, встречающимися в самоаффинных моделях
поверхностей (часть II) и облаков (разд. 7.3).
Часть II. Разд. 2.3 (это часть работы [1]), написанный
первым, возник из попыток разрешить загадку опубликованных
оценок фрактальных размерностей различных грубых
поверхностей. Глубокие замечания Майкла В. Берри побудили меня
расширить этот раздел.
Часть III. Чрезвычайно полезными были обсуждения с
Куртом Макмалленом.
ЛИТЕРАТУРА
1. Mandelbrot В. В., Physica Scripta.
2. Mandelbrot В. В., The Fractal Geometry of Nature, Freeman, New York,
1982
3. McMullen C., Nagoya Math. J., 96, 1 (1984).
4. McMullen С, в печати.
5. Wedford Т. /., Crinkly Curves, Markov Partitions and Dimension,
Ph. D. Thesis, Warwick University, U. K., 1964.
6. Kline S. A, J. London Math. Soc, 20, 79 (1945).
7. Lovejoy S., Mandelbrot В. В., Tellus, A37, 208 (1985).
8. Shertzer D., Lovejoy S., in: Turbulent Shear Flow 4, eds. L. J. S.
Bradbury et al.
9. Peyriere J., Bulletin Soc. Math. Fr., 114 (1986).
10. Mandelbrot В. В., Fluid Mech, 62, 331 (1974); C. R. Acad. Sc. (Paris),
278A, 289, 355 (1974).
11. Hentschel H. G. £., Procaccia /., Physica, 8D, 435 (1983).
12. Harris T. #., The Theory of Branching Processes, Springer, Berlin, 1963.
Случайные фракталы, пластичные фракталы
и ренормализационная группа
Цж. Мелроуз*
Показано, что метод ренормализационной группы является
мощным средством анализа и построения ансамблей, содержащих
самоподобные фракталы. Эти ансамбли являются иерархическими в
следующем смысле: в конечном пространстве параметров может
быть проведена ренормализация, при этом неподвижным точкам
ренормгруппы соответствуют самоподобные конструкции, а вдали
от неподвижных точек найдены несамоподобные конструкции,
названные пластичными фракталами. При обсуждении используется
пример «изинговой снежинки». Легко конструируются ансамбли,
являющиеся подмножеством хорошо известных моделей. Описана
конструкция иерархических ансамблей для случайных блужданий
без самопересечений.
1. Введение
Мандельброт [1] ввел случайные фрактальные
конструкции для моделирования природных фракталов. Такие
конструкции могут генерировать ансамбль конфигураций, и
оказывается полезным ввести производящую функцию [2] с
определенным весом для каждой из выбранных основных форм,
порождающих возможные конфигурации. В данной работе такие
производящие функции строятся как прямые комбинации
известных итеративных конструкций с простой схемой
ренормгруппы. При этом естественно возникают фрактальные матрицы
переноса [3].
2. Конструкция
Вводимые нами ансамбли и производящие функции будут
иерархическими.
Пусть Zn(r) есть производящая функция ансамбля для п-й
итерации, тогда ансамбль называют иерархическим, если Zn(r)
подчиняется рекурсии
Zn{r) = Zn^{R{f))K{f), (1)
где г есть некоторое конечное множество q весов, R(r) есть ре-
норма лизационное рекуррентное соотношение, и q и К (г) не
зависят от п (это прямое обобщение определения иерархической
решетки).
Обсудим пример «изинговой снежинки» [4]. Эта конструкция
представляет собой итеративную декорацию границ, разделяю-
* John Melrose Department of Chemistry, Royal Hollway College, Egham,
Surrey, TW20 OEX, UK. ~
Общие свойства фракталов
49
щих черные и белые области на плоскости. Исходя из черного
треугольника на белом фоне, мы на каждом шаге делим каждый
из черных треугольников на 9 равных треугольников. Затем
каждая граница каждого треугольника, получившегося в
результате деления, независимо декорируется в соответствии с
некоторым распределением возможных декораций.
На рис. 1 изображены возможные декорации треугольника,
у которого одна сторона является границей; декорации для
треугольников с двумя и тремя границами, очевидно, представляют
/// / ' / /
У/Л'
V/'/л/
'Л.
и' /// '//
/// // / // /
/ х
7 7/ / / / / / /
Рис. 1.
собой прямое произведение этих декораций [4]. Черные
области на рисунке заштрихованы.
Чтобы выбрать распределение декораций, вводятся веса г0,
*Ч, >*2, г$ для основных форм, порождающих конфигурации,—
черных треугольников с 0, 1, 2, 3 границами; всем белым
треугольникам приписывается вес 1.
Функции распределения для всех возможных декораций
каждой основной формы подчиняются ренормализационным
рекуррентным соотношениям. Пусть общее полиномиальное
рекуррентное соотношение имеет вид
г\=ЪЬЬ-'<->'*
rfc\
(2)
где ti обозначает вес из г.
Построение конфигураций n-го уровня с весом г выглядит
следующим образом: рекурсия (2) повторяется п раз, п = #(f),
г% = ЩИ (г)) ... гп; для t-ro веса в гР будем использовать обо-
50
Часть I
значение rlp. Тогда, исходя из первоначально выбранной
основной формы, мы проводим итеративную декорацию так, что на
&-й итерации каждая основная форма, например t'-ro типа,
декорируется /-м типом, выбираемым заново для каждого
появления каждой формы с вероятностью
Такая конструкция есть просто обращение ренормализации.
В неподвижных точках (2) описанная конструкция является
самоподобной ((3) = const) и генерируются случайные
фракталы, а вдали от неподвижных точек строятся несамоподобные
конфигурации, соответствующие «движению» вдоль некоторой
траектории ренормгруппы, и мы будем называть их
пластичными фракталами.
Если все коэффициенты Ъ в соотношении (2) равны 1, то все
конфигурации с одним и тем же числом основных форм
оказываются равновероятностными, для общего же случая это не так.
Для снежинки при Ь = 1 конфигурация я-го уровня дается весом
г1 • rf . rk • г1
Г0 Г* Г2 Г3 М)
если она содержит от i до / черных треугольников, имеющих от
0 до 3 границ соответственно. Рекуррентное соотношение можно
найти, декорируя каждую из основных форм всеми возможными
способами с соответствующими весами. Если все коэффициенты
Ъ = 1, то для снежинки г'0 = г* и из рис. 1
т\ = т\т\ + r\r\r2 + rtri + r Jrfra; (5)
соотношения для г'2 и r's даны в [4].
Мы не упомянули об одном тонком моменте: множество
декораций на рис. 1 выбрано так, что не разрешен никакой
выступ на расстоянии от концов матрицы декорации, равном его
высоте, поэтому при декорации различных границ не возникают
множественные края. В то же время пересечение вершин при
различных декорациях разрешено, но при определении весов в
ансамбле множество вершин игнорируется. При этом
геометрическая реализация иерархической конструкции оказывается
возможной.
3. Математическое ожидание
Математическое ожидание, определенное как производная
производящей функции, может быть найдено с помощью ренорм-
группорой матричной алгебры. Пусть некоторая интересующая
Общие свойства фракталов
51
нас величина Qx связана с сопряженным полем х и rt = fi(x, ср),
где ф означает некоторое множество других полей, также
присутствующих в задаче; тогда
{Q»)n = (xdZn (г (x))/dx)/Zn (г (*)). (6)
Используя иерархическое свойство (1), находим после
перестановки
(Qx)n = VnfifmV0, (7)
где i-й элемент Кп удовлетворяет равенству (Vn)/ = d^, й —
индекс основной формы, использованной в начале процедуры
декорации (V0)i = x d% , и Гт — множество (7X<7 матриц:
(Гш),/ = {г/ m_! ДО, (г)/*-,) |r-=fm_i}/r,m;
где (Гт)/у есть ожидаемое число основных форм /-го типа,
введенных на i'-й основной форме при п—m + 1 декорации. fm —
естественное обобщение (как на случай ансамбля, так и на
случай пластичных фракталов) фрактальной матрицы переноса,
введенной недавно в [3]. Для примера со снежинкой выбор
полей
Го = г9 rx = rs, г2 = г52, rs = rs? (8)
соответствует г, сопряженному с черной площадью, и s,
сопряженному с длиной границы.
Некоторые интересные значения математического ожидания,
не выражающиеся как производные Zn, могут быть вычислены
как суммы произведений Тт\ примером могут служить
множества вершин для конструкций снежинок.
4. Подмножества известных моделей
Подобно тому как были построены ансамбли с весами (4) и
(8), можно строить ансамбли, являющиеся подмножествами
известных моделей. Снежинка с весами (4) и (8) является
подмножеством низкотемпературных графов модели Изинга на
гексагональной решетке [4], однако подмножество снежинок —
плохое приближение для полной модели Изинга. Фазовая
диаграмма содержит неподвижную точку в инвариантном
подпространстве г= 1 (см. формулы (8)). Черные площади
конфигураций имеют размерность DA = 2 для всех значений параметра,
и фазовый переход происходит между ямами при (г = 1, s-^0)
и (г = 1, s-^oo), имеющими размерности границ DB=l и
Doo = 2 соответственно. Собственные значения и собственные
векторы снежинки и более общих конструкций (не удовлетво-
й
Часть t
ряющих условию Da = const) приведены в [4]. Неподвижная
точка обладает более чем двумя существенными, полями,
появления которых можно было бы ожидать в полной модели.
Критические особенности модулируются периодическими
множителями [4]. В конструкции снежинки величина k(r, 1) равна
единице.
Можно непосредственно построить и иерархические
ансамбли для случайного блуждания без самопересечения. Построение
основано на квадратной сетке; выбираются декорации
независимых ребер, непересекающиеся в вершинах.
Рассмотрим достаточный случай двух ребер под прямым
углом; чтобы образовать траекторию без самопересечений, две
-
А (
1
1
1
1
\ \
[
* 1
L-A-
1 1
1 1
I
Рис. 2.
Рис. 3.
декорации, встречающиеся вблизи от точки А, не должны
пересекать ни одну из диагональных связей, обозначенных
пунктирными линиями на рис. 2. Перенумеровав все пересекающиеся
кластеры для блуждания без самопересечений (рис. 3), можно
найти рекуррентные соотношения.
5. Заключение и перспективы
Были описаны элементарные шаги, необходимые для
объединения случайных фрактальных конструкций с традиционным
ренормализационным анализом ансамблей. Отмечено, что легко
могут быть найдены такие иерархические ансамбли, состоящие
из подмножеств хорошо известных моделей; это обстоятельство
может оказаться полезным при построении более
контролируемых ренормализационных приближений в реальном
пространстве.
Благодарность. Автор приносит благодарность
администрации Ройял-Колледжа (Игхэм, Сюррей) за представленную воз-
Общие свойства фракталов
53
можность исследования и г-же Дж. Ивенс за перепечатку
рукописи.
ЛИТЕРАТУРА
1. Mandelbrot В. В., The Fractal Geometry of Nature, Freeman, San Fransisco,
1982.
2. Feller W., Introduction to Probability Theory and its Applications, Wiley,
New York, 1950. [Имеется перевод: Феллер В. Введение в теорию
вероятностей и ее приложения. — М.: Мир, 1984.]
3. Mandelbrot В. В., Gegen У., Aharony A., Peyriere /., J. Phys. A: Math. Gen.,
18f 335 (1985).
4. Melrose J. R.y в печати.
О конечно разветвленных фракталах
и их обобщениях
Р. Хильфер, А. Б люмен *
С помощью генераторов с тетраэдрической симметрией строятся
детерминистические фрактальные решетки. Из соответствующего
уравнения для вероятности определяется спектральная размерность
й и показано, что й < 2. Далее это множество фракталов (такое,
что соответствующее ему множество размерностей й является
плотным на отрезке [1, 2]) расширяется с помощью прямого
перемножения, так что получаются фракталы, множество размерностей
которых является плотным в [1, оо).
В [1] было предположено, что многие случайные
среды являются фрактальными структурами. Это побудило нас
исследовать фрактальные детерминистические решетки, изучая
случайное блуждание на них. Основное наше внимание
сосредоточено на решетках с конечным ветвлением [1, 2]. Такие
решетки обладают следующим свойством: исключение конечного
определенного числа связей решетки оказывается достаточным
для того, чтобы изолировать некоторое произвольно большое
компактное подмножество этой бесконечной структуры.
Мы начнем с класса фракталов с конечным ветвлением и
тетраэдрической симметрией, наиболее типичным представителем
которых является кривая Серпинского. Мы вкратце опишем
конструкцию таких фракталов и найдем их фрактальные (хаус-
дорфовы) размерности. Анализируя уравнение для вероятности,
мы перейдем затем к их спектральной (фрактонной)
размерности.
В заключение мы рассмотрим также класс бесконечно
разветвленных фракталов, получаемых прямым перемножением.
Детерминистические фрактальные решетки полностью
описываются заданием геометрического генератора и итерационной
процедуры. На рис. 1 показано несколько двумерных (d = 2)
генераторов, сторона которых обозначается через Ь. Кривая
Серпинского соответствует специальному случаю 6 = 2. На рис. 2
приведен пример одного шага итеративного построения для
генератора с 6 = 5, изображенного на рис. 1. Бесконечное
повторение итерации дает полную фрактальную решетку. Результат
применения конечного числа итераций мы будем называть п-
структурой, где п = 1 соответствует генератору.
Теперь обратимся к хаусдорфовой размерности d [1],
которую можно найти из соотношения b^= lim N(n+ l)/N(n), где
П->оо
* R. Hilfer, A. Bfomett-Lehrstuhl f. Theoretische Chemie, Techn. Universitat
Munchen, Lichtenbergstr. 4, D-8046 Garching and Max-Planck-Institut f. Po-
lymerforschung, Jakob-Welder-Weg 15, D-6500 Mainz, FRG.
Общие свойства фракталов
55
N(n)—число точек решетки в /г-структуре. Из соотношения
N(n+l) =N(l) +N[N{n)—d—l] получаем
u = \nN/lnbt (l)
где N есть число треугольников (соответственно
гипертетраэдров) с одной вершиной вверху в генераторе. Заметим, что число
Ь=5 Ь=7 Ь=9
Рис. 1. Три генератора для конечно разветвленных фракталов.
Е(п) краев в л-структуре подчиняется рекуррентному
соотношению
E(n+l) = NE(n), (2)
из которого можно определить d через Е(п).
Чтобы найти спектральную размерность Я, мы воспользуемся
уравнением для вероятности, описывающим случайное
блуждание по ближайшим соседям в решетке. Допустим, что
блуждание точки начинается из положения г0 в момент времени £ = 0.
Рис. 2. Один шаг итерационного построения фрактала.
Вероятность P(r„ t) найти блуждающую точку в положении г*
в момент t удовлетворяет управляющему уравнению
4г р ^ О = /С Кр О* t) - ЩР (r„ t)], (За)
где суммирование ведется по всем Г/, являющимся ближайшими
соседями г*. Рассмотрим частный случай, когда плотность
56
Часть I
вероятности перехода хюц из г/ в г* удовлетворяет соотношению
Z (г,) <% = ку = const, (36)
где w — постоянная плотность, a Z(r;)—число ближайших
соседей для г/. Проводя преобразование Лапласа в уравнении (За)
с начальным условием P(ri9 0) = бГ/, г , получаем
(1 - а) Р (г,, и) - £ А(г;, а)/г (г,) = бГ£, rJw, (4)
/(О i « о/
где мы положили а = —u/w. Используя самоподобие рассма-
триваемых решеток, можно решить уравнение (4) с помощью
процедуры децимации, являющейся обратной итеративному
построению» Здесь будут рассматриваться только фракталы со
связными генераторами. Для таких генераторов можно достичь
каждой точки генератора, исходя из любой другой точки
генератора и проходя некоторую последовательность связей, в
которой две соседние связи имеют одну общую точку.
Для определенности запишем уравнение (4) для случая
простого генератора, углы которого s0, si, ..., Sd «выживают» на
каждом шаге процедуры децимации. Устраняемые внутренние
точки будем обозначать di, ..., d^ (M — N(l)—d—1),
начиная с d ближайших соседей точки s0, таких, что so, d* и s/ кол-
линеарны (1 ^ i ^ d). Вводя вектдры Qi = (Q(di, и), ...
..., Q(dM, и)) и Q2=(Q(s0, и), ..., Q(srf, и)), где Qfo и) =
~Р(г/, а)/г(п), мы получаем для простого генератора
[(l-aJD-^JQ^^A, (5)
где D — диагональная М ХМ-матрица, элементы которой
даются равенством Du = z(di). Матрицы А\ и Л2 — это подматрицы
матрицы А смежности генератора. МХМ-матрица А\
получается из А исключением строк и столбцов, соответствующих углам;
МX (d+ 1)-матрица А2 получается исключением d-fl строк,
соответствующих углам, и М столбцов, соответствующих
внутренним точкам.
Прежде чем переходить к децимации, нам нужно
исследовать возможность обращения матрицы (1—a)D — А\. Прежде
всего заметим, что матрица D — А\ является диагонально
домяла
нантной, т. е. | (D — Аг)п | > £ | (D — A{)if | для всех 1 ^ i < М.
Это можно показать следующим образом. Элемент {А{)ц равен
1 либо 0 в зависимости от того, связана точка d/ с d/ или нет,
.м м
Поэтому \(D-Al)il\ = z(di), а £ I Ф - А\)ц 1= £ (Аг)И.
Общие свойства фракталов
57
Более того, сумма по строке £ (А)// дает число ближай-
ших соседей точки d„ которые в то же время являются
внутренними точками генератора, и поэтому не превышает z(di). Кроме
того, D — А\ неприводима, т. е. нельзя найти матрицы
перестановок В такой, что B(D — А\)В~1 сводится к блочной форме.
Это эквивалентно связности генератора [3]. Теперь, зная, что
D — А\ является неприводимой диагонально доминантной
матрицей с положительными диагональными элементами и
неположительными недиагональными элементами, мы с помощью
теории неотрицательных матриц приходим к выводу, что обратная
ей матрица {D — Л1)-1 существует и имеет положительные
элементы [3]. Далее, так как для и ^ О мы имеем а ^ 0, то 1 —
--ос 135 1 и поэтому [(1 — a)D — A\]~l также существует и
выполнено соотношение
([(l-a)D-A]-%>0 (6)
для всех i, | и a < 0.
Теперь мы можем решить уравнение (5) для одного из
ближайших соседей So, например di, и получим
d
Q (di, и) = g (a) Q (s0, и) + £ ht (a) Q (s„ и), (7а)
где
g(a) = ([(l-a)D-AlrlA2)n (76)
и
ht (a) = ([(1 -a)D- A,]'1 A2\ w. (7в)
Учитывая вращательную симметрию тетраэдрического
генератора, можно получить те же самые результаты для всех
ближайших соседей so. Затем вычисления повторяются для /
генераторов, которым принадлежит so- Запишем теперь уравнение (4)
для P(s0, и) в виде
/ d
~К Ф + W 0 - «) Q («о, и) = £ E Q (df, и), (8)
где различные генераторы обозначены индексом k> \^k^.l.
Для Q(d/, и) мы подставляем вырал<ения (7) и получаем
-Кч№к(<*)] + W(1 -Ф(«))Q(so, и) = Е XQ(s/, а), (9)
где
#(а)=1-{[1-о-в(а)]/А(а)} и /ф)=ЕМ«).
£«1
58
Часть I
Уравнение (9) включает только s0 и углы соседних
генераторов, и это завершает децимацию.
Покажем теперь, что уравнения (8) и (9) для s0 в полной
и соответственно децимированной решетке действительно
совпадают в пределе при а-*0. Рассмотрим я-структуру для
больших п. Тогда стационарное решение (t-*oo) есть
Q (г,) = Р (г,)/2 (г,) = const, (1 Оа)
как можно видеть из уравнения (3). Значение константы
определяется законом сохранения для вероятности
N(n)
Z Р(г„ 0=1,
1*0.) <10б>
Const =1 £ 2 (Г;).
I *-1
Подставляя (10а) в (7), получаем g(0) + Л(0) =1, что в свою
очередь, согласно уравнению (9), дает ^(0) =0. С учетом ра-
N{n)
венства £ z(ri) = 2E(n)> где Е(п) есть число краев в /г-струк-
туре, мы подставляем значение Q из (10) в уравнение (8) для
Го = So и получаем
- 1/ш + И (1 - а)/2Е (п) = Ш/2Е (п)
в пределе /г-^оо и а-^-О. После одного шага децимации это
равенство переходит в уравнение (9):
— Ifiwh (а)] + Ш[1-ф (а)]/2Е (n—l) = td/2E (я - 1).
Исключая из этих уравнений w9 мы получаем /i(a) = <xN/<f>(a)
и после перехода а->-0 находим
h(0) = N/K, (И)
где % = ф'(0). Это равенство в работе [4] было названо
фрактальным соотношением Эйнштейна. Рассмотрим теперь
уравнение (9) для а, близких к 0, где можно положить ф (а) ^ ка.
В этой области уравнение (9) для ренормированных величин
NQ(Si,u) и w/к совпадает с уравнением (8) для исходных
величин Q и w.
Найдем теперь спектральную (фрактонную) размерность й,
которая для случайных блужданий определяется вероятностью
возвращения в начальную точку Р(г0, t). Для больших
значений времени имеем [5]
Я (Го, t)~(l/wt)*l*
Общие свойства фракталов
59
и после проведения децимации
NP(r0, t)~(klwtyi\
так что
d = 21n^/lnx = 2(l~-ln/i(0)/lniVr1, (12)
где при получении второго равенства была использована
формула (11). В предыдущих работах [6, 7] мы явно вычислили 5
Рис. 3. Тоблерон-решетка: результат перемножения кривой Серпинского с
одномерной решеткой.
для многих структур и показали также [7], как построить
фракталы для заданных значений 3(1^5^2), плотно
заполняющих интервал [1, 2].
Заметим, что для описанных в данной статье фракталов
3 < 2. Из неравенства (6) и того факта, что А2 неотрицательна,
мы видим, используя уравнение (7), что g(a) > 0 и h(a) > О
для всех а. Поскольку g(0) + /i(0) =1, то g(0), ft(0) < 1,
таким образом, —оо < In h(0) < О, a In N > 0, поскольку N > I.
Поэтому (1 — ln/i(0)/lnN)~l < 1 и ИЗ равенства (12) следует,
что Я < 2.
В заключение мы расширим класс фракталов путем прямого
перемножения и, следовательно, получим плотное множество d
на [1, оо). Как пример мы приводим на рис. 3 результат
второго этапа перемножения кривой Серпинского с одномерной
решеткой. Мы назвали этот объект тоблерон-решеткой [8]. Ее
спектральная размерность определяется низкочастотным
поведением ее собственных функций. В этой модели удобно
представить, что в узлах решетки находятся массы mz(rt), а на
связях размещены пружины с упругостью f. Для низких частот,
согласно [5, 9], плотность состояний определяется зависимостью
р(со) ~ со^-1. Уравнение движения для фурье-компоненты
смещения Р(г/, о) совпадает с уравнением (4) без правой части,
60
Часть I
Далее, величина а соответствует величине а = тсо2//.
Записывая явно Ti = (xt, у и z{), получаем
—*P(xh у и *ь ©)= Z [Р(*1> Ур zi> ©) —Р(х„ у и zi9 ©)], (13)
где учтено, что для тоблерон-решетки число ближайших
соседей г(т{) = 6. В уравнении (13) можно разбить суммирование
по ближайшим соседям на суммирование по линейной решетке
и по кривой Серпинского:
aPto, Уь zi) = 2P(xi, yh zJ — PiXi, уь zt+ 1) —
— P(xi9 Уь «/ —1)+ Yi[P(Xh Уь Zi) — P(xf. yh z,)], (14)
где мы предположили, что постоянная решетки равна 1, и
опустили для простоты зависимость от частоты. Для компоненты
Фурье по переменной zP(x, у, k)= ^eikzP(x, yy z) получаем
z -
(a-2 + 2cos*)P(*„ yt9 k)=*Z[P(Xi, Уь k)-P(xh yf, k)]. (15)
Для фиксированного k уравнение (15) в точности совпадает с
уравнениями для кривой Серпинского, если спектральный
параметр считать равным ak = a — 2(1—cos k). Поскольку мы
интересуемся пределом длинных волн (k -> 0), можно считать
ak = a — k2. Таким образом, из равенств a = m©|//, ak = /пю|//
и k2 = m(o2c/f мы получаем со2, = со2с + со|, где индексы Г, С и S
относятся к тоблерон-решетке, одномерной решетке и кривой
Серпинского. Чтобы вычислить рт (со), подсчитаем число
собственных функций с частотами меньшими со; NT(a>) = \ рг (со') da/.
Поскольку в уравнение (15) величина k входит как параметр, мы
можем получить величину NT (со), суммируя ps (со') dco'pc (<*>") d(d"
при условии а/2 + со"2 s^ со2.
Используя соотношения р5(со)~со s~l и рс(со) ~const,
получаем
NT (со) = $ $ ps (со') рс (©'О rf©W - ©J*+1.
Сй^+Сй"2<Сй2
Дифференцирование дает рг(со)~со^5 и, следовательно,
спектральная размерность тоблерон-решетки равна dT = ds + 1.
Очевидно, можно получить более высокие значения d,
перемножая наши фракталы с регулярными решетками более высоких
размерностей; соответствующие значения 3 плотно заполняют
полуось [1, оо).
Общие свойства фракталов
61
Итак, рассматривая общие свойства фракталов с конечным
ветвлением, мы показали, что для некоторого класса Я < 2.
Кроме того, мы указали, как можно построить бесконечно
разветвленные фракталы, для которых значения й превышают 2 и
образуют плотное множество.
Благодарность. Авторы приносят благодарность Фонду
химической промышленности и Немецкому исследовательскому
обществу за поддержку.
ЛИТЕРАТУРА
1. Mandelbrot В. В., The Fractal Geometry of Nature, Freeman, San Francisco,
1982.
2. Uryzohn P., Verhandelingen der Koninklijke Akademie te Amsterdam, XIII
No. 4 (1927).
3. Varga R. S.} Matrix Iterative Analysis, Prentice Hall, Englewood Cliffs,
1962.
4. Given /. A, Mandelbrot В. В., J. Phys., A16, L565 (1983).
5. Alexander 5., Orbach #., J. Physique Lett., 43, L625 (1982).
6. Hilfer R.t Blumen A., J. Phys., A17, L537 (1984).
7. Hilfer R.y Blumen A., J. Phys., A17, L783 (1984).
8. См. также: Маритан А., Стелла А. — наст, сб., с. 151.
9. Rammal R., Toulouse G., J. Physique Lett., 44, L13 (1983).
Часть ||
АНАЛИЗ ФРАКТАЛЬНЫХ
СВОЙСТВ МАТЕРИАЛОВ
Структура случайных силикатов:
полимеры, коллоиды
и пористые твердые тела
Д. Шефер, К. Кефер *
Для характеристики структур, растущих в ходе случайных
процессов в силикатных системах^ использовалось малоугловое рассеяние
света и рентгеновских лучей. Тонкие и грубые коллоиды, а также
разветвленные полимеры растут при полимеризации в растворе.
Кроме них изучались также гели, коллоидные жидкости, агрегаты
и другие надмолекулярные структуры.
1. Введение
Почти все материалы, за исключением монокристаллов,
являются в том или ином смысле неупорядоченными. Несмотря
на это, мало что известно о структуре неупорядоченных
материалов или о связи между структурой и процессом ее
образования. Этот недостаток знаний распространяется также на
соотношения между структурой и свойствами. Проблема здесь в
основном заключается в том, что лишь недавно были разработаны
как методы изучения случайных структур, так и модели,
связывающие эти структуры с условиями их роста.
Настоящая статья ставит своей целью показать, что из
данных по малоугловому рентгеновскому рассеянию (МУРР)
можно получить существенную информацию о случайных
структурах. Кроме того, наблюдаемые структуры часто можно
объяснить, пользуясь представлениями о процессах случайного роста,
таких, как полимеризация, агрегация коллоидов и разделение
фаз. Мы остановимся на силиконовых системах, которые
обладают большим богатством различных случайных структур,
получающихся в ходе процессов как химического, так и физического
роста.
На рис. 1 представлена схема, иллюстрирующая набор
структур, которые уже были найдены в силикатах.
Материаловеды в общем интересуются свойствами твердого материала,
который указан в правой части рисунка. Он может быть чем угод-
* D, W. Schaefer, К. D. Keefer -Sandia National Laboratories, P. О. Box
5800, Albuquerque, New Mexico 87185, USA.
Анализ фрактальных свойств материалов
63
но, начиная от плотного стекла и кончая сильно пористым сили-
кагелем. Основная цель заключается в контролировании
процессов роста, представленных в левой части рисунка, таким
образом, чтобы получать любую желаемую структуру.
Можно выделить два класса процессов роста: химические и
физические. Типичным процессом химического роста является
полимеризация, показанная слева на рис. 1. При полимеризации
Рис. 1. Пути образования стекол и керамических материалов.
спиртового раствора кремнийсодержащего мономера Si(OC2H5)4
(тетраэтилортосиликат, ТЭОС) можно получить разветвленные
полимеры (Л), плотные коллоидные частицы (В) и рыхлые
коллоидные частицы (С). Агрегация коллоидов (Е) представляет
собой пример процесса физического роста, в то время как геле-
образование (D) может протекать как по химическому, так и по
физическому механизму. Жидкокристаллические структуры (F),
показанные в центральной колонке рис. 1, можно индуцировать
физическими методами, прикладывая, например, электрическое
поле [1].
2. Методы рассеяния
В настоящем сообщении основное внимание уделяется
материалам с характерными пространственными масштабами от 5 А
до 1 мкм. Структуры в этом диапазоне масштабов можно
определить с помощью малоуглового рассеяния рентгеновских
лучей или нейтронов, а также рассеяния света. Во многих случаях
ключ к пониманию кривых рассеяния дает фрактальная геомет-
64
Часть It
рия, поэтому рассеяние от фрактальных объектов стало
предметом всестороннего обсуждения [2].
Фрактальная геометрия [3] количественно учитывает
случайность и поэтому позволяет характеризовать такие случайные
системы, как полимеры [4], коллоидные агрегаты [5], грубые
поверхности [6, 7] и пористые материалы [6—8]. Качественной
особенностью фрактальных объектов является присущая им ди-
латационная симметрия [3], означающая инвариантность
основных геометрических особенностей при изменении масштаба
(таких, как изменение увеличения в микроскопе).
Здесь мы используем метод МУРР для характеристики
фрактальных материалов. В основном для всех фракталов
характерна степенная зависимость [2, 8, 9] интенсивности рассеяния
/ от передаваемого импульса k = 4яАг1 sin (8/2) (где 6— угол
рассеяния):
I{k)~k~\ (1)
Заметим, что при данном k изучаются масштабы длины (в
смысле фурье-преобразования) порядка /Н. Назовем х показателем
Порода, а интервал выполнимости степенного закона (1)—по-
родовской областью кривой рассеяния [2]. Интерпретация
показателя х зависит от источника рассеяния. Для так называемых
массовых фракталов (т. е. структур типа полимеров) этот
показатель просто совпадает с фрактальной размерностью D,
которая связывает размер R объекта с его массой N:
N ~ RD. (2)
Для полимероподобного фрактального объекта с одномерным
скелетом величина D может принимать значение в интервале
1 <Д^З в зависимости от степени разветвленности и
гибкости; Для фрактального объекта листоподобного типа этот
интервал сужается до 2 ^ D ^ 3, причем D > 2 для
разветвленных и извилистых структур.
Для рассеяния от трехмерных объектов с фрактальными
поверхностями [7]
[* = 6-Ds (2<DS<3). (3)
Здесь Ds — фрактальная размерность поверхности, причем Ds =
= 2 для классической гладкой поверхности. Наконец, для
фрактальных пористых материалов [6,7, 10] значение х = 7 — у, где
у— это показатель, характеризующий распределение Р(г) пор
по радиусам г:
Р(г)~г~\ (4)
Эффект характеризуемой степенным законом полидисперсности
на кривые рассеяния был детально изучен Мартином [11].
Анализ фрактальных свойств материалов
65
3. Силикатные полимеры
На рис. 2 показаны профили МУРР для силикатов, заполи-
меризованных при различных условиях. Нижняя кривая (Е)
характеризует промышленный
TM/SM), который получен
в ходе процесса Штёбера
[12], где происходит
полимеризация ортофосфорной
кислоты Si (ОН) 4.
Предельный наклон, равный —4 для
этого материала, указывает
на то, что его частицы
представляют собой компактные
объекты с гладкими
поверхностями (Ds = 2 в
уравнении (3)). Ясно, что кривые
рассеяния согласуются с
общим представлением о
коллоидных структурах.
Кривая (£)) на рис. 2
относится к рассеянию от
рыхлых коллоидных частиц,
полученных в результате
гидролиза и полимеризации
ТЭОСа в присутствии
основного катализатора [13].
В этих условиях молекулы
ТЭОСа гидролизуются лишь
частично (например, до
Si(OC2H5MOH)4-«) и
полимеризация до плотных
структур не протекает, по-
коллоидный силикат (Ludox
*(1/А)
Рис. 2. Данные рассеяния в
координатах Порода для силикатов, заполимери-
зованных при различных условиях: А —
двухстадийный кислотный катализ [2,
14]; В — двухстадийный основной
катализ [2, 14]; С — одностадийный
основной катализ , W =* 1; D —
одностадийный основной катализ [13] W = 2; Е —
Ludox SM.
скольку спиртовые группы
плохо полимеризуются. Для катализируемой основанием системы
с W = [Н2О] / [Si] = 2 наблюдаемая кривая рассеяния
показывает грубые фрактальные структуры с Ds = 2,7, которые мы
называем рыхлыми коллоидными частицами [13]. Следует
отметить, однако, что, исходя из выражения (4), возможна иная
интерпретация этих данных, которые можно отнести к
полидисперсному набору плотных частиц, имеющих степенную функцию
распределения по размерам.
Силикаты полимерного типа могут быть синтезированы
двумя путями. В результате катализируемой основанием
полимеризации ТЭОСа при значениях W меньше стехиометрического
получаются кривые рассеяния типа (С) [13], где наклон (—2,8)
66
Часть И
указывает на объект, масса которого является фракталом.
Вероятно, это плотно сшитая полимерная молекула. Вблизи сте-
хиометрического значения W = 2 происходит плавный переход
от структур с фрактальной массой к структурам с фрактальной
поверхностью.
Полимеры можно синтезировать также двухстадийным
способом [4, 14]. На первой стадии в ходе полимеризации,
проводимой при недостатке воды в присутствии кислотного
катализатора, идет рост форполимеров (олигомеров) с размерами ~5 А
[14]. В ходе второй стадии, проводимой в условиях либо
кислотного, либо основного катализа, происходит сшивание этих
форполимеров друг с другом с образованием конечного полимера,
который характеризуется кривыми (А) и (В) на рис. 2.
Независимо от деталей полимеризации на второй стадии мы всегда
наблюдаем показатели Порода вблизи —2, что указывает на
структуры полимерного типа с фрактальной массой. Изучая
эволюцию кривых рассеяния по мере разбавления фракционной
системы, мы показали большую разветвленность в системах,
катализируемых основанием, нежели кислотой [4]. Фрактальная
размерность тем не менее остается равной 2. Этот результат
согласуется с ренормализационными расчетами Фэмили [15],
который показал, что в асимптотическом пределе больших структур
значение D нечувствительно к степени разветвленности.
4. Надмолекулярные структуры
Рассмотренные в предыдущем разделе полимерные
компоненты могут образовывать в ходе процессов гелеообразования,
агрегации, фазового разделения и упорядочения различные
надмолекулярные структуры, которые при последующем
высушивании, спекании или иным способом превращают затем в
требуемый сухой твердый материал.
Возможны по крайней мере два различных типа гелей:
полимерные, образующиеся при химическом сшивании
разветвленных полимерных кластеров, и коллоидные,
формирующиеся в ходе физической агрегации коллоидных частиц. В обоих
случаях кривые рассеяния совершенно нечувствительны (для
неразбавленных систем) к гель-точке. Например, на рис. 3
представлены кривые рассеяния полимерного силиката, измеренные
до и после точки гелеообразования. Несмотря на очень
значительное изменение в ее окрестности механических свойств, там
не наблюдается никакого изменения структуры профилей
рассеяния.
МУРР не фиксирует гель-точку, потому, что этот метод
чувствителен к электронной плотности, а не к связности. Вблизи
точки перехода золь—гель образование небольшого числа сши-
Анализ фрактальных свойств материалов
67
вок резко изменяет связность, практически не меняя при этом
пространственное распределение атомов. Чувствительные лишь к
нему профили МУРР остаются при этом практически
неизменными.
Картину рассеяния, наблюдаемую вблизи гель-точки, можно
понять, воспользовавшись аналогией с полуразбавленными
растворами полимеров [16]. На ранних стадиях полимеризации
вдали от точки гелеобразо-
вания разветвленные
кластеры рассеивают
независимо друг от друга. По мере
их роста в ходе
полимеризации происходит
увеличение радиуса Гинье /?о,
измеряемого по начальной
кривизне профилей рассеяния.
Однако при концентрациях,
когда начинается
перекрывание и зацепление
кластеров, величина RG перестает
меняться или даже
уменьшается при дальнейшем
росте числа звеньев в
кластерах. В таком
полуразбавленном режиме раствора
полимеров флуктуации
концентраций имеют радиус
корреляции порядка
масштаба между двумя
межцепными контактами [17].
Поскольку это расстояние
не меняется при гелеобразовании, расходимости RG в этой
точке не наблюдается. Однако ее можно ожидать в
разбавленном растворе, где величина RG по порядку совпадает с
радиусом кластеров.
В противоположность рассеянию в режиме Гинье профили
рассеяния в режиме Порода нечувствительны к корреляциям
Дальнего порядка, но чувствуют только локальную топологию
цепи. Однако поскольку локальная структура не меняется при
гелеообразовании, то показатели Порода остаются постоянными
при переходе через гель-точку.
Коллоидные системы, как видно из рис. 4, также дают
новые надмолекулярные структуры. Кривая (В) относится к
профилю рассеяния (света или рентгеновских лучей) коллоидного
агрегата, образованного при дестабилизации
стабилизированной зарядом суспензии частиц Ludox SM [5]. Эта кривая рас-
0,001
o,oi о
KU/A)
Рис. 3. Данные рассеяния в
координатах Порода для силиката, полученного
двух стадийным способом в присутствии
основного катализатора: А — до гелеоб-
разования; В — после гелеобразования.
68
Часть II
сеяния обнаруживает два описываемых степенным законом
режима с показателями Порода —2 и —4. Наклон —4 согласуется
с рассеянием от гладкой поверхности на масштабах длины,
меньших радиуса а первичных коллоидных частиц. С другой стороны,
наклон —2 характеризует структуру с фрактальной массой и
близок к значению,
найденному при моделировании
химически контролируемой
агрегации [18].
При деионизации
коллоидной суспензии в смешанном
слое ионообменной смолы
можно получить новые
упорядоченные структуры,
называемые коллоидными
кристаллами [19]. Они дают
резкое брэгговское
рассеяние в режиме
светорассеяния, аналогичное тому,
которое наблюдается при
рассеянии рентгеновских лучей
атомными кристаллами. Эти
упорядоченные структур ы
обязаны сильному кулонов-
скому отталкиванию между
коллоидными частицами.
Существует также ближний,
характерный для жидкостей
порядок [20], зависящий от
концентраций частиц и
соли (см. кривую (А) на
рис. 4). Такой профиль рассеяния очень напоминает профиль,
получаемый в атомных жидкостях, но то, что он наблюдается
здесь при рассеянии света, связано с разделением частиц на
расстояния в тысячи их радиусов.
К*2а
Рис. 4. Рассеяние от надмолекулярных
структур, полученных из коллоидных
систем: А — денонсированного полисти-
рольного латекса [19]; В — коллоидных
агрегатов частиц Ludox SM [5].
5. Пористые твердые тела
В качестве примера твердых силикатных материалов
рассмотрим пористый силиконовый аэрогель, полученный в ходе
образования геля из золя. В зависимости от деталей процедуры
получения образуются три различные структуры:
нефрактальная, с фрактальной массой и с фрактальной поверхностью.
^Рассмотрим сначала пористый твердый материал,
полученный сушкой на воздухе грубой фрактальной коллоидной
суспензии, описываемой кривой (С) на рис. 2. Рассеяние от этого ма-
Анализ фрактальных свойств материалов 69
териала [13] показано на кривой (С) рис. 5. То обстоятельство,
что в характеризуемом степенным законом режиме рассеяния
профиль по существу идентичен профилю исходного раствора,
указывает на сохранение фрактальной поверхности при сушке.
Такой материал можно рассматривать как имеющий
однородную пористость с грубыми фрактальными поверхностями.
Однако, имея данные лишь по одной кривой рассеяния, нельзя
исключить возможную
структуру однородных пор со
степенным законом
распределения по радиусам.
Кривая (С) на рис. 5
отличается от аналогичных
кривых для пористых
твердых тел, полученных из
исходных однородных
коллоидов с нефрактальными
поверхностями. Кривые
рассеяния {А) и (В) на рис. 5
отвечают двум таким
материалам, полученным в обоих
случаях при гидролизе и
конденсации Si(OCH3)4 в
присутствии основного
катализатора [21].При этом по-
лимеризующимся
компонентом является Si (ОН) 4 и
образуются плотные
коллоидные частицы. Кривая (В)
характеризует аэрогель
относительно высокой
плотности (0,21 г/см3). Пик
структурного фактора
напоминает характерный для
жидкостей структурный фактор на рис. 5. Мы интерпретируем
этот гель как набор упакованных сфер и связываем пик в
структурном факторе с тем, что сферы не могут перекрываться
(эффект коррелированных пустот) [22].
Совершенно иную кривую рассеяния (А) дает аэрогель
низкой плотности (0,09 г/см3) [10], где отвечающая большим
углам часть кривой имеет соответствующий коллоидной структуре
наклон —4. Однако в области промежуточных масштабов
(0,01 ^k ^0,08) виден второй характеризуемый степенным
законом режим с наклоном, близким к —2, характерным для
объектов с фрактальной массой. Наиболее приемлемая
интерпретация такого поведения связана с коллоидным агрегатом. По су-
0,007
Ог01 0,1
/ff//A)
Рис. 5. Кривые Порода для пористых
силикатов: Л — аэрогель, полученный из
коллоидной системы [10], 0,09 г/см3;
В ~ аэрогель, полученный из
коллоидной системы 0,21 г/см3; С — аэрогель,
полученный из фрактально-грубой
системы [13].
70
Часть II
ществу пористое твердое тело выглядит как случайный агрегат
первичных коллоидных частиц.
В поддержку такой агрегатоподобной структуры аэрогелей
низкой плотности говорят результаты сравнения кривых
рассеяниях этих аэрогелей и сформированного из раствора агрегата
(см. кривую (В)\ рис. 4). Так как последний получен при очень
низкой концентрации БЮг, то и промежуточный,
характеризуемый степенным законом режим намного более экстенсивен.
Сходство двух кривых подтверждает приведенную выше
интерпретацию структуры пористого твердого тела.
6. Заключение
В настоящем обзоре концепция фрактальной геометрии
привлечена для интерпретации кривых рассеяния силикатных
материалов. Кремнийсодержащие полимеры в зависимости от
химических условий их синтеза могут быть получены в виде
однородных структур, а также структур с фрактальной массой или
поверхностью. Из исходных полимерных растворов можно
сформировать как полимерные, так и коллоидные гели, а из них в
свою очередь получить пористые твердые тела различной
структуры. Наконец, при соответствующих условиях удается
сформировать жидкокристаллические образцы и коллоидные жидкости.
Такой набор различных структур показывает, как, используя
явления химического и физического роста в исходных растворах,
ученый, работающий в области создания новых материалов,
может контролировать их свойства.
ЛИТЕРАТУРА
1. Hard A. /., in: Ultrastructure Processing of Geramics, Glasses and
Composites, vol. 2, eds. L. L. Hench, D. R. Ulrich, Wiley-Interscience, New York,
1986.
2. Schaefer D. W.t Keefer K. ZX, Mat. Res. Soc. Pros., 12, 1 (1984).
3. Mandelbrot B. B.y Fractals, Form and Chance, Freeman, San-Fransisco,
1977.
4. Schaefer D. W., Keefer К D.y Phys. Rev. Lett., 53, 1383 (1984).
5. Schaefer D. W.y Martin /. E.y Wiltzius P., Cannel D. S.y Phys. Rev. Leet.,
52, 2371 (1984).
6. Pfeifer P., Avnir D.y J. Chem. Phys., 79, 3558, 3566 (1983).
7. Bale H. Z)., Schmidt P. W.y Phys. Rev. Lett., 53, 596 (1984).
8. Shaefer D. W.y Martin J. E.y Hard A. /., Keefer K. D.y in: Physics of Finely
Divided Matter, Springer-Verlag, New York, 1985.
9. Sinha S. Ky Freltort T.y Kjems /., in: Kinetics of Aggregation and
Gelation, eds. F. Family, D. P. Landau, North Holland, 1984, p. 87.
10. Schaefer D. W.y Keefer К D.y Structure of Porous Materials, будет
опубликовано.
11. Martin /. £., J. Appl. Cryst., будет опубликовано.
12. Stober W.9 Fink A, Bohn E.y J. Coll. Interface Sci., 26, 62 (1968).
Анализ фрактальных свойств материалов
71
13. Keefer К. D.y Schaefer D. W.y Growth of Fractally Rough Colloids, будет
опубликовано.
14. Brinker С. /., Keefer К. D.y Schaefer D. W., Assink R. A.y Kay B. P.y
Ashley C. S., J. Non Cryst. Solids, 63, 45 (1984).
15. Family F., J. Phys., A13, L325 (1980).
16. Daoud M., Cotton J. P.y Farnoux B.y Jannink G., Sarma G.y Benoit H.y
Duplessix R.y Picot R.y de Gennes P. G., Macromolecules, 8, 804 (1975).
17. Schaefer D. W.y Polymer, 25, 387 (1984).
18. Kolb Л1, Jullien R.t J. Physique Lett. (Paris), 45, L977 (1984).
19. Schaefer D. W.y Ackerson B. J., Phys. Rev. Lett., 35, 1448 (1975).
20. Schaefer D. W., J. Chem. Phys., 66, 3980 (1977).
21. Henning S.y Svensson L., Physica Scripta, 23, 697 (1981).
22. Freltoft Т., Kjems J. /(., Sinha S. K-y Power-Law Correlations and Finite
Size Effects in Aggregates, Phys. Rev., будет опубликовано.
Взаимодействие фракталов
с фракталами: адсорбция полистирола
на пористой поверхности АЬ03
П. Пфейфер*
Рассматривается вопрос, до какой степени фрактальная
поверхность (поверхностный фрактал или массовый фрактал размерности
D) может изменить фрактальную структуру гибких полимерных
цепей в результате адсорбции. Конформации цепи в растворе и в
адсобированном состоянии описываются фрактальными
размерностями £>Раств и Z)*AC соответственно. Показано, что, исследуя
зависимость числа адсорбированных цепей от их радиуса инерции в
растворе, можно получить величину D • D^acTB/^AC; показано
также, как из распределения пор адсорбента по размерам можно
найти D (размерность £)Раств определяется качеством
растворителя). Анализ системы полистирол — АЦОз дает £> = 2,90 ±0,10 и
Z)aAC/D^aCTB = 1,04 ±0,04. Отсюда следует, что конформация при
адсорбции не меняется и что при адсорбции полимерные цепи не
образуют квазимонослой на поверхности пор твердого тела. Этот
вывод резко отличается от ситуации на поверхностях с низким
значением Dt на которых монослой образуется, что приводит к
£адс__£) Такое сильное влияние величины D на (эффективное)
адсорбционное равновесие объясняется как результат увеличения
энтропийного барьера с увеличением Z), вследствие чего истинное
термодинамическое равновесие не достигается. Обсуждаются также
другие случаи взаимодействия двух неодинаковых фракталов.
1. Введение. Постановка задачи
Поверхность раздела между твердым телом и
окружающим его пространством может быть фрактальной (фрактальная
размерность D), причем возможны три случая. Это может быть:
а) поверхностный фрактал —в этом случае площадь
поверхности характеризуется показателем Д а объем твердого тела и
объем пор меняются как объем образца во всем интервале
рассматриваемых масштабов;
б) массовый фрактал — в этом случае площадь поверхности
и объем твердого тела меняются одинаково, т. е. оба
характеризуются показателем D, а объем пор меняется как полный объем;
б) фрактал пор — в этом случае площадь поверхности и
объем пор меняются одинаково (с показателем D), а объем
твердого тела меняется как полный объем.
[Когда мы говорим, что изменение происходит с
характерным показателем D или что величина ведет себя как полный
объем, это означает, что соответствующее множество подчи-
* Peter Pfeifer-Fakultat fur Chemie, Universitat Bielefeld, D-4800
Bielefeld, BRD.
Анализ фрактальных свойств материалов
73
няется соотношению масса — размер с показателем D или
показателем 3 соответственно. Таким образом, только для D->3
три рассмотренных выше класса фракталов совпадают. Более
подробное обсуждение будет проведено в другом месте.]
Большинство открытых к данному моменту фрактальных
поверхностей принадлежит к первым двум классам, и особый интерес с
точки зрения химии поверхностей представляют те из
поверхностей, фрактальные свойства которых проявляются, начиная
с атомных масштабов [2—9] и захватывая большие масштабы.
При этом фрактальная размерность D определяет природу
адсорбированных комплексов, распределение активных узлов,
поверхностную диффузию, перенос через поры и т. д. [4, 8].
Наиболее прямой метод анализа фрактальной поверхности при
размерах порядка ангстрем и выше (применимый и к
поверхностным, и к массовым фракталам) состоит в определении (из
экспериментов по адсорбции) зависимости плотности числа
молекул п в соответствующем монослое на поверхности от радиуса
молекулы г:
n(r)~r~D. (1)
При этом единственным требованием является химическая
однородность поверхности по отношению к используемым
«измерительным» молекулам. (При использовании других методов [2—
9] необходимо выполнение дополнительных условий.) Для
молекул малого и среднего размера, достаточно жестких, а
значит, обладающих вполне определенной формой, соотношение (1)
может быть установлено при г в интервале примерно 1—10 А.
Для химии поверхности этот интервал представляет
значительный интерес; примерами могут служить предсказание
адсорбционной емкости, ориентация адсорбционных несферических
молекул [9], сольватациоиные свойства поверхности [10],
микроскопические контактные углы между жидкостями и
поверхностью, эффективные коэффициенты диффузии для некоторых
материалов. Однако, чтобы наблюдать соотношение (1) при
г > 10 А, в качестве зондов нужно брать молекулы полимеров.
Для гибких цепных молекул (которые используются в
большинстве работ по адсорбции полимеров) форма молекулы в
адсорбированном состоянии не обязательно остается той, которую
она имеет в растворе, поэтому зависимость п от г (далее г
будет означать радиус молекулы в растворе) может отличаться от
(1). Действительно, хорошо известно, что на плоской
поверхности (D = 2) цепи (имеющие форму случайных клубков в
растворе) выпрямляются и образуют по сути дела монослой
мономеров (мономеры цепи взаимно отталкиваются и
притягиваются к поверхности). Экспериментальным подтверждением такой
картины является независимость адсорбированной массы от чис*
74
Часть II
ла мономеров в цепи N (см., например, [11] и цитированную
там работу; то обстоятельство, что измеренная толщина
адсорбированного слоя зависит от N [12], не противоречит этой
картине, а лишь отражает тот факт, что этот слой в
действительности является диффузным [13,
14] и включает петли и хвосты
неадсорбированных
сегментов).
Итак, вопрос состоит в том,
будет ли происходить такое же
распрямление клубков на
неровных пористых
поверхностях (D>2), как было
предложено в [15] (в этом случае
п(г) зависело бы лишь от
соотношения между г и N в
данном растворителе, но не от
размерности поверхности Z)),
или же адсорбция является
необратимой [14], так что
цепи, удерживаемые в порах
радиуса «г, сохраняют свою
исходную конформацию (2—6]
(в этом случае соотношение
(1) остается спр аведливым).
Эти два предельных случая
проиллюстрированы рис. 1.
В более общей постановке
вопрос состоит в том, насколько
процесс адсорбции может
изменить фрактальную
геометрию цепей. Таким образом,
если мы обозначим
размерности цепей в растворе и на
поверхности через DcacTB и ОсДС соответственно (см. также разд. 2),
то мы должны исследовать D**c как функцию D и DfCTB (и,
возможно, других факторов).
В этой работе впервые приводится результат определения
D*AC на фрактальной поверхности. В разд. 2 показано, как из
проведенного ранее анализа [2] данных [11] по адсорбции
полистирола на пористом А1203 можно найти величину D • D?acTB/
Д)сДС (а также какую информацию можно получить, используя
дополнительные данные). Размерность поверхности D
получается из распределения пор по размерам того же образца АЬОз
Рис. 1. Два крайних случая
адсорбции полимера на пористой
поверхности: а — цепь развертывается, как в
случае плоской поверхности; б — на
поверхности цепь сохраняет ту же
конформацию, что и в растворе (сте-
рическое препятствие). Из рисунка
можно также определить диаметр 2г'
области, занятой адсорбированной
одиночной полимерной цепью. Эта
величина входит в (4).
Анализ фрактальных свойств материалов
75
(разд. 3), а величина D*acrB определяется качеством
растворителя. Полученный результат (D*AC — £>Раств при q « 2,9)
является сильным аргументом в пользу сделанного ранее в [2, 16]
вывода о том, что (в общем случае) на поверхностях с большим
значением D остается справедливым соотношение (1) (как если
бы полимерные клубки были жесткими структурами). Детальное
обсуждение и интерпретация приводятся в разд. 4 и 5.
2. Зависимость функции п{г) от D, D£aCTB, DlAC
С феноменологической точки зрения процесс адсорбции
можно формально рассматривать как химическую реакцию.
Поверхность (D) + п • Полимер (D£acTB) -►
-► Поверхность (D) • [Полимер (Оас*с)]п. (2)
Фрактальные размерности, приведенные в скобках,
рассматриваются как заданные величины, п (г) описывает «баланс
массы и геометрии» в уравнении (2). Исходными реагентами
являются полимерные клубки, радиус инерции г и степень
полимеризации N которых связаны соотношением
/ раств
г~ЛГ * , (3)
где £)2аств = 5/3 (случайное блуждание без самопересечений)
для хорошего растворителя и D£aCTB = 2 (простое случайное
блуждание) для плохого растворителя (в-точка). Продуктами
реакции являются одиночные адсорбированные цепи
протяженностью г' (рис. 1), где в зависимости от N величина г' меняется
как
Это соотношение определяет фрактальную размерность
адсорбированной цепи £>сАС (соотношение длина — объем [1]).
Адсорбированный слой как целое представляет собой монослой
таких клубков радиусом г', плотно упакованных без перекрытия.
Тогда, по определению D-мерной поверхности, число п цепей на
монослой падает с увеличением г' как (г')-°. Поэтому из (4) и
(3) получаем
n~N ! с , (5)
праств/ аде
~r~D'Dc lDc . (6)
Соотношение (6) представляет собой искомое соотношение,
определяющее структурную реалаксацию адсорбированных моле-
76
Часть II
кул. В противоположность соотношению (5) оно применимо и
для различных измерительных молекул, состоящих из
различных мономеров при условии, что для всех их зависимость г' от
г одна и та же (это обстоятельство будет использованию ниже).
И наоборот, соотношение (5) (но не (6)) применимо для
различных растворителей при условии, что структура
адсорбированных цепей не зависит от растворителя. Таким образом,
соотношения (5) и (6) записаны так, чтобы можно было проверить
две отдельные гипотезы об универсальности, а в остальном же
они эквивалентны.
Два предельных случая, изображенных на рис. 1,
соответствуют
д!АС = £> (клубок растянут на поверхности), (7а)
/)*АС = dTctb (структура клубка не изменилась), (76)
и подстановка (7а) или (76) в (5) и (6) приводит к различным
возможностям, обсуждавшимся в разд. 1. Заметим, что в
случае (7а) цепь (изотропна) повторяет все детали поверхности,
более крупные чем мономер. Это показывает, что структура
двумерной адсорбированной цепи оказывается совершенно
различной в случаях (7а) (ОасЛС = 2, плоская поверхность) и (76) (£>сДС=
= 2, плохой растворитель). Далее, мы видим, что в случае
(7а) самоподобность адсорбированных цепей соответствует
структуре слоя, «параллельного» поверхности, тогда как
самоподобие, обсуждавшееся в [13—15] (для этого же случая),
соответствовало структуре слоя, «нормального» к поверхности.
Наконец, следует заметить, что, поскольку равенство (76) не
зависит от коэффициентов пропорциональности, опущенных в (3) и
(4), оно может реализоваться, скажем, при 50 %-ном
уменьшении радиуса всех клубков при адсорбции.
Возвратимся теперь к анализу [2] данных по адсорбции
полистирола на А1203 с помощью соотношения (6). В [2] было
показано, что экспериментальные данные Барнса и Карпентера
[11], для этой системы описываются степенным законом п(г)~
/^г~2,79±о,озпри g А < г < 380 А (значение г = 2 А относится к
азоту, который был единственной измерительной молекулой,
отличной от полистирола); отмечалось также, что точка,
соответствующая азоту, прекрасно ложится на кривую, полученную
экстраполяцией данных только по полистиролу. Поскольку
полистирол находился в ©-растворителе [11], нам дополнительно
известно, что DcacTp = 2 (ср. также данные для зависимости г от
N в [11]). Комбинируя эти данные с (6), мы приходим к
следующим заключениям:
Анализ фрактальных свойств материалов
77
I. Результаты D • Df^lDT = 2,8 и £>ГТВ = 2 исключают
(7а); вместо этого мы имеем £>/DcAC=1,4.
II. Для азота по понятной причине конформационная
перестройка отсутствует, так что точка, соответствующая азоту,
должна лежать на кривой (1). Но поскольку она лежит на кривой
для полистирола, то и для полистирола должно выполняться
соотношение £>*АС = £>ГСТВ. Поэтому из (I) получаем: D = 2,8.
Это усиливает аргумент, приведенный в [2], в пользу того,
что фрактальная размерность рассматриваемой поверхности
А120з « 2,8. Однако дополнительные определяющие сведения в
пользу этого следуют из экспериментальных данных [11], не
обсуждавшихся до сих пор. Они представлены в следующем
разделе.
3. Распределение пор по размерам для А1203
Наряду с экспериментами по адсорбции Барнс и Карпентер
[11] определили также распределение пор по размерам в
образце А120з. Исходя из изотермы десорбции азота (петля
гистерезиса для капиллярной конденсации), они вычислили Л(р) —
площадь поверхности пор с радиусом, большим чем р, для
25 А < р < 195 А. Площадь поверхности, измеренная по
адсорбции азота (в виде монослоя) дает доплнительное значение
А (р « 2 А). Величину А (р) можно отождествить с площадью
поверхности, измеренной с помощью (жестких) молекул
радиусом р. Тогда для поверхностного и массового фракталов из
соотношения (1) следует
Л(р)~р2-». (8)
В строгом выводе соотношения (8), который будет приведен в
другом месте, используется распределение по размерам объема
пор V(p) с радиусом, большим р. Эта величина для
произвольного множества К определяется как объем пространства вокруг
К, которое нельзя заполнить шарами радиусом р без
пересечения /(. Можно показать, что независимо от того, является ли
множество К фрактальной повернхостью, кривой и квантовым
множеством (т. е. в условиях гораздо более общих, чем
рассмотренные в [17]), справедливо соотношение
В частности, (9) справедливо для поверхностного и массового
фракталов. С учетом равенства
-dV(9) = A(P)d9
из (9) следует (8).
78
Часть It
Ч 1,6
<
0,8
0,1 0,5
0,9 1,3
Ц р, А
1J
2,1
На рис. 2 приведен в двойном логарифмическом масштабе
экспериментальный график зависимости А от р. Эта
зависимость хорошо описывается степенным законом и дает значение
размерности фрактальной по-
24|_ х верхности «3,0.
4. Обсуждение.
Энтропийный барьер
Теперь мы можем оценить
значение DlAC независимо от
способа, приведенное в
заключении II разд. 2. Из значений
Я.ЯГТВ/ДГ = 2,8, £ГТВ = 2
(разд. 2) и D = 3,0 (разд. 3)
мы получаем £>?АС = 2,1. Эта
величина практически
совпадает с полученной в выводе II
разд. 2 и, конечно, по
существу согласуется с выводами
Барнса и Карпентера.
И наоборот, мы можем
сказать, что с точностью до
экспериментальной ошибки два
значения поверхностной
размерности, D = 2,8 по
адсорбционной емкости и D = 3,0 из по-
розиметрии, совпадают. В
действительности совпадение этих двух значений нужно считать
замечательным, если учесть то обстоятельство, что при их
нахождении использовались совершенно различные данные,
характеризующиеся своими собственными экспериментальными
неопределенностями. [Значения экспериментальных ошибок
для D в разд. 2 и 3 представляют собой стандартные
отклонения коэффициентов регрессии и, по-видимому, недооцени-
вают действительные ошибки. См. также [1,18].] Надежной
оценкой исследуемого А1203 представляется значение D = 2,90+
±0,10 в интервале 2 А < р < 200 А. Это значение хорошо
согласуется с недавними результатами [19], полученными при
исследовании адсорбции спирта, и данными по малоугловому
рассеянию рентгеновских лучей для аналогичного образца А1203,
а также с тем обстоятельством, что поверхности силикагеля
(которые структурно аналогичны АЬОз) также близки к
трехмерным [4, 9, 20—22]. Однако ни в одном из этих случаев
исследования не охватывают столь широкого интервала значений г.
Рис. 2. Распределение пор по
размерам, Л(р), для поверхности оксида
АЬОз, на которой адсорбируется
полистирол. Величина р меняется в
пределах 2—195 А. Крайняя точка слева
соответствует удельной поверхности
катализатора, измеренной по методу
Брунауэра, Эммета и Теллера. Из
наклона прямой и соотношения (8)
определяем D = 3,04 ± 0,02.
Анализ фрактальных свойств материалов
79
Таким образом, мы видим, что все экспериментальные
данные дают /)*дс ~ /)?аств и D с* 2,9. Этот вывод противоречит
вышеупомянутому предсказанию [15] D^C = D (в обозначениях
данной работы) для всех D ^ 2. Основным аргументом [15]
является соображение о том, что адсорбция без существенного
искажения клубков (т. е. £>*дс = D?acTB) не может
соответствовать термодинамическому равновесию. Действительно, из общих
соображений следует, что конфигурационная энтропия должна
возрастать с увеличением D**c, так что равенство £>?дс = D
должно приводить к уменьшению свободной энергии как из-за
уменьшения энергии, так и из-за увеличения энтропии, если
D > D?aCTB> т. е. если D ^ 2. (Мы не рассматриваем коллапсиро-
ванные цепи, £)ГСТВ > 2.) Однако на очень пористой поверхности,
соответствующей значению размерности Д близкому к 3, такое
равновесие, по-видимому, оказывается невозможным.
Действительно, для достижения такого равновесия необходимо, чтобы
сегменты цепи, прикрепившиеся к поверхности при первом
контакте, могли снова отойти от поверхности и образовать
конфигурацию, в которой большее, чем раньше, число сегментов
войдет в малые поры, и т. д. При геометрических ограничениях,
создаваемых сетью пор, клубок радиусом г, первоначально
захваченный порой такого же радиуса, должен был бы претерпеть
маловероятное изменение формы, чтобы достичь истинного
равновесия Д?дс = D. На языке теории переходного состояния в
химической кинетике это соответствует непреодолимому
энтропийному барьеру между исходными веществами и продуктами
соответствующей реакции (2): переходное состояние,
представленное в виде напряженной цепи перед исходной порой радиусом г,
обладает нулевой энтропией. Другой пример состояний,
разделенных бесконечным энтропийным барьером, можно найти в
[23].
Таким образом, хотя равенство DTC = D*acTB действительно
не соответствует равновесию (в согласии с [15]), оно
соответствует эффективно устойчивому состоянию, т. е. фактическому
равновесию, на поверхностях с высоким значением D — точно
так же, как сама керамика А120з (и любое аморфное твердое
тело, стекло и т. д.) представляет собой устойчивую фазу во
всех практических приложениях. Можно ожидать поэтому, что
результат D**c c^ D*acTB справедлив не только для системы
полистирол— А1203, но что и в самом общем случае
Г D
Dc ~\d\
для D~2, (10a)
раств для D-3 (106)
80
Часть II
(вспомним в связи с (10а) разд. 2.1). Адсорбция случайных
сополимеров (в хорошем растворителе) на древесном угле [24]
является, по-видимому, вторым примером равенства (106): из
результатов [24] следует, что D^0 ~ D?acTB; в работе [16] при
том же допущении показано, что D ~ 2,8.
Следовательно, фундаментальный вопрос, на который
должны ответить будущие исследования, касается поведения £?дс в
промежуточном интервале значений Z). Из уравнения (10) и
неравенства £?аств^2 следует, что величина Оадс имеет
локальный максимум при некотором значении D между 2 и 3. В
частности, представляет интерес вопрос: испытывает ли DlAZ скачок
при этом значении D или же D?*c постепенно уменьшается до
значения D?aCTB при £>->-3; т. е. является ли изменение £)адс при
переходе от истинного равновесия к фактическому равновесию
разрывным или непрерывным? Если истинное (фактическое)
равновесие соответствует конечному (бесконечному)
энтропийному барьеру, то можно ожидать, что этот барьер
увеличивается с ростом D так, что он становится бесконечным при
некотором критическом значении DKpHT (2 < DKpHT < 3) и затем
сохраняет свое значение. Такому поведению должен соответствовать
скачок, а именно £>адс = /) для П < DKpHT и Da*c = D?acTB для
D^DKpHT, кроме того, при приближении D к DKPHt должно
наблюдаться критическое замедление установления равновесия.
5. Заключение
Показано, что
1) адсорбция гибких полимерных цепей на пористой
поверхности может быть естественно описана как взаимодействие двух
фракталов («гостя» с размерностью £>£аств и «хозяина» с
размерностью D);
2) фрактальная размерность Оадс адсорбированного
фрактала-гостя может быть найдена из эксперимента;
3) величина £>адс определяется только «родительскими»
размерностями D?aCTB и D (по крайней мер в исследованных до
настоящего времени случаях D ~ 2 и D ~ 3), причем решающее
значение имеет переменная Z);
4) эта зависимость от D и Z)?aCTB не является простым
аналитическим продолжением евклидова случая D = 2 — она
описывает существенное (возможно, разрывное) изменение Ладс,
соответствующее изменению природы (эффективного
адсорбционного равновесия при увеличении D от 2 до 3)?
Анализ фрактальных свойств материалов
81
Такая неаналитичность по отношению к размерности
фрактала-хозяина D (т. е. то обстоятельство, что физика для
нецелых D может отличаться от той, которую предполагает
интерполяция или экстраполяция евклидовой ситуации) известна из
исследований, посвященных другим случаям взаимодействий
между фракталами. Так, для фазовых переходов на фракталах
[25] фрактальная размерность критических изинговых
кластеров (гость) зависит не только от размерности D решетки, но
также и от ее порядка ветвления, лакунарности и т. д. Для
диффузии на фракталах [26] фрактальная размерность случайных
блужданий (гость) дается величиной D-min{l, 2/D} (без учета
мультипликативности), где дополнительный параметр Л есть
спектральная размерность решетки.
Благодарности. Автор приносит глубокую благодарность
Д. Авниру и С. Александеру за полезное обсуждение и Биле-
фельдскому университету за субсидии.
ЛИТЕРАТУРА
1. Mandelbrot В. В.у The Fractal Geometry of Nature, Freeman, New York,
1982.
2. Avnlr D.y Farln D.y Pfeifer P., Nature 308 (1984) 261.
3. Pfeifer P., Applic. Surf. Sci. 18 (1984) 146.
4. Pfeifer P, Avnir D.y Farin D., J. Stat. Phys. 36 (1984) 699; 39 (1985) 263.
5. Bale H. D.y Schmidt P. W.y Phys. Rev. Lett. 53 (1984) 596.
6. Avnir D., Farin D.y Preifer P., J. Colloid Interface Sci. 103 (1985) 112.
7. Pfeifer P., Welz U., Wippermann Я., Chem. Phys. Lett. 113 (1985) 535,
8. Pfeifer P, Chimia 39 (1985) 120.
9. Farin D., Volpert A.y Avnir D., J. Am. Chem. Soc. 107 (1985) 3368; 107
(1985), в печати.
10. Levy A., Avnir D.y Ottolenghi M., Chem. Phys. Lett (1985), в печати.
11. Burns Я., Carpenter D. К., Macromolecules 1 (1968) 384.
12. Kawaguchi M., Takahashi A., Macromolecules 16 (1983) 1465.
13. deGennes P. G.y Macromolecules 14 (1981) 1637.
14. Klein /., Pincus P., Macromolecules 15 (1982) 1129.
15. deGennes P. G.y C. R. Acad. Sc. Sen II 299 (1984) 913.
16. Avnir D., Farin D., Pfeifer P., J. Chem. Phys. 79 (1983) 3566.
17. Pfeifer P., Avnir D., J. Chem. Phys. 79 (1983) 3558; 80 (1984) 4573.
18. Weitz D. A.y Huang J. S., in: Kinetics of Aggregation and Gelation,
eds. F. Family and D. P. Landay, Elsevier, Amsterdam, 1984, p. 19—28.
19. Avnir D., Schmidt P. W.y частное сообщение.
20. Avnir D.y Pfeifer P., Nouv. J. Chim. 7 (1983) 71.
21. Schmidt P. W., Bale H. D.y in: Fractal Aspects of Materials, eds. В. В. Man-
delbrot and D. E. Panssoja, Materials Res. Soc, Pittsburgh, 1984, p. 14—16.
22. Drake M.y Sinha S. K.y частное сообщение.
23. Pfeifer P., Phys. Rev. A26 (1982) 701.
24. Hopkins A., Howard G. /., J. Polym. Sci. A9 (1971) 841.
25. Gefen Y., Aharony A, Mandelbrot В. В., J. Phys. A17 (1984) 1277; см.
также цитированную в статье литературу.
26. Rammal R.y J. Stat. Phys. 36 (1984) 547; см. также цитированную в
статье литературу.
Рассеяние
на фракталах
Э. Джейкмен*
Рассматриваются статистические характеристики флуктуации
интенсивности, возникающих при рассеянии волн на экранах с гауссов-
ской случайной фрактальной фазой.
1. Введение
Хотя понятия введенной Мандельбротом фрактальной
геометрии [1] нашли широкое применение в самых
современных областях физики, их практические приложения
представляют интерес и для более традиционных разделов физической
науки. Одним из таких разделов является рассеяние волн,
электромагнитных или скалярных, на случайных вариациях
показателя преломления, наибольшие характерные размеры которых
превышают длину падающей волны, что позволяет применять
физическую оптику или теорию дифракции Кирхгофа. Такое
рассеяние представляет интерес как для дистанционного
определения гладкости препятствия (т. е. дистанционного, или
бесконтактного, измерения шероховатости поверхностей) или
детектирования турбулентных слоев и протяженных областей, так и
при рассмотрении шума — моделировании шума и шумового
предела действия оптических, микроволновых и акустических
систем.
Простейшей рассеивающей системой физической оптики
можно считать экран с случайно изменяющейся фазой, который
вносит в падающую волну только пространственно-случайные
возмущения. Последующее распространение «рассеянной»
волны приводит к развитию флуктуации амплитуды, которые в
оптических экспериментах проявляются в виде более или менее
сложного распределения светлых и темных областей на экране,
поставленном на пути рассеянного света. Экран с случайной
фазой может быть использован в качестве модели шероховатых
поверхностей, тонких рассеивающих слоев, а в некоторых случаях
п более протяженных областей с переменным показателем
преломления.
В этом кратком обзоре мы обсудим свойства волн,
претерпевших рассеяние на экранах с гауссовской случайной фазой, для
которых характерен степенной спектр, — так называемых гаус-
совских случайных фракталах [2]. Такие инвариантные
относительно преобразования подобия (автомодельные) модели при-
* Eric 1акетап-Т1оуа] Signals and Radar Establishment, St Andrews
Road, Malvern, Worcestershire WR14, 3PS, UK,
Анализ фрактальных свойств материалов
83
водят к амплитудным флуктуациям со статистическими
свойствами, весьма отличными от статистических свойств
флуктуации, порождаемых экранами с гладко изменяющейся фазой. На
протяжении всего обзора мы будем предполагать, что
создаваемые экраном разности хода больше длины волны. В
следующем разделе мы определим модели рассеяния и геометрии,
обычно исследуемые теоретически и экспериментально. В разд. 3
и 4 обсудим предсказания, к которым приводят такие модели,
и сравним их с экспериментальными данными, а в разд. 5
рассмотрим более подробно коротковолновой предел одной из
моделей рассеяния. Краткое заключение и выводы изложены в
разд. 6.
2. Модель рассеяния
На рис. 1 представлена геометрия простого эксперимента по
рассеянию на экране с случайной фазой. В рамках физической
Экран
I
Z
Рис. 1. Геометрия рассеяния.
оптики решение задачи дается дифракционным интегралом
Гюйгенса — Френеля [3]
«Чг)~ J dY exp[ikr'42r-ik-r'sin Ъ + 1ф (г')] А {г')> (1)
— оо
где г и sin О указаны на рис. 1, ф — случайное возмущение
фазы, & = 2яД— волновой вектор и Л (г') —апертурная функция.
Если фазовый экран помещен в сужении лазерного пучка, то
Л(г') = ехр(-г'2/^2). (2)
Предположение о том, что соотношение (2) выполняется, часто
позволяет упростить вычисления. Обычно принято
рассматривать две геометрии рассеяния: 1) поле в дальней зоне, или пре-
84
Часть II
дел Фраунгофера, когда kW2 <C 1, и 2) предел Френеля
kW2/2z > 1. Хорошо известно [5], что в дальней зоне при
W > I, где | — наибольший характерный масштаб флуктуации
фазы, рассеянное поле представляет собой комплексный гаус-
совский процесс, поэтому интенсивность / = |<§Г|2 образует спекл-
картину с распределением
p(/) = -irexp(-1L-) (3)
и моментами
$£ = «1 (4)
Если величина W сравнима с £ или меньше £, то статистики
негауссовские, и нормированные моменты превышают значения,
задаваемые соотношениями (4). Проще всего для вычисления
предела Френеля положить Л(г/1)= 1. При распространении на
достаточно большие расстояния z поле в этом случае
представляет собой гауссовский процесс, но вблизи фазового экрана
геометрические и дифракционные эффекты ограничивают площадь,
дающую вклад в поле у детектора, и снова наблюдаются
негауссовские статистики. Именно эти негауссовские режимы и будут
интересовать нас в первую очередь. Они сложные и содержат
больше информации, чем гауссовские спекл-режимы [5], хотя
и накладывают более строгие ограничения на
функционирование системы.
Мерой информации, содержащейся в флуктуациях
интенсивности, служат их статистические свойства. В области
Фраунгофера они зависят от величины освещенной площади и угла
рассеяния Ф. В близкой зоне эти флуктуации являются функцией
длины распространения. Чтобы вычислить статистические
свойства рассеянного поля, для свойства ф необходимо принять
какую-то модель. Для простоты и из-за отсутствия лучшей
модели обычно предполагается, что ф — стационарный гауссовский
процесс. Остается выбрать спектр, или автокорреляционную
функцию (ф{0)ф(т)}. В случае фрактальных моделей более
подходящей является структурная функция. Возмущение фазы
полезно выразить через условную высоту Ф(г') =kh(r), где
D(r) = ((h(0)-h(r)r) (5)
— структурная функция. Для гладко изменяющихся
неограниченно дифференцируемых высот функция D(r) допускает
разложение в ряд по четным степеням г относительно г = 0. Но уже
для сравнительно простой по своей структуре неровной
фрактальной поверхности
D(x) = \x\vL2~v, 0<v<2. (6)
Анализ фрактальных свойств материалов
85
Показатель v связан с фрактальной размерностью D
соотношением v = 2(2 — D)6, причем масштаб длины L обычно принято
называть топотезой "[7]. Функция высоты, обладающая
свойством (6), непрерывна, но не дифференцируема. Другой
наглядной иерархической моделью может служить субфрактальная
поверхность, структурная функция наклона которой
определяется выражением [8, 9]
ЗД = |*Г7^-2, 2<v<4. (7)
Поверхность, обладающая свойством (7), однократно
дифференцируема и имеет наклон, изменяющийся от точки к точке
непрерывно.
3. Фрактальная модель высоты
Особенности спектра, связанные с рассеянием в моделях
этого типа, являются следствием недифференцируемости
поверхности. Тем самым исключаются понятие «луч» и эффекты
геометрической оптики. Так как принято считать, что угловое
распределение интенсивности рассеянного света в зоне, далекой от
шероховатой поверхности, определяется той частью поверхности,
которая обращена в соответствующем направлении, т. е.
распределением наклона поверхности, предположение о фрактальности
[6] должно приводить к важным следствиям даже для этого
простейшего из статистических свойств. Действительно,
обнаружено, что </('&)> — стабильное распределение sinfl:
(1(П~рЛ[Щ1~^*тъ), (8)
где
pv (х) ехр (Их) dy = ехр (-— AXV).
— оо
Для гладко изменяющейся поверхности
</W)~Pm(sind), (9)
где рт — распределение наклона поверхности. «Хвост»
распределения (8) при аргументе, превышающем величину (kL)1-2^^
Xsinft ~ 1, спадает как sin^'fr. В принципе такой характер
убывания можно использовать для определения обоих
параметров модели v и L по измерениям </('&)> способом, не
зависящим от абсолютного значения этой величины. В этом
проявляется отличие распределения (8) от распределения (9) для гладко
изменяющейся поверхности, из которого следует, что экспери-
86
Часть И
ментальные результаты позволяют определить только свойства
распределения наклона.
Поведение второго нормированного момента интенсивности
</2>/</>2 и в пределе Фраунгофера, и в пределе Френеля
отражает отсутствие эффектов геометрической оптики. Ни в одном
из пределов теория не предсказывает существенного
превышения гауссовского момента над 2 (соотношение (4)) [2, 3, 6].
Для фрактальных поверхностей получены только отдельные
^кривые произведений k, L и W или г, в то время как в случае
непрерывно изменяющихся поверхностей удалось построить
семейства кривых как функции среднеквадратичного отклонения
высоты. При больших значениях этой величины теория
предсказывает очень большие флуктуации, которые действительно
наблюдаются в случае гладко изменяющейся поверхности и
соответствуют наличию каустик, или геометрических особенностей,
в распределении интенсивности [10]. Фрактальная модель [6]
не предсказывает такие флуктуации, и они не наблюдаются в
экспериментах по рассеянию инфракрасного излучения на
искусственно построенной броуновской фрактальной поверхности
(v = l;Z) = l,5) [11,12].
4. Фрактальная модель наклона
В отличие от фрактальной модели высоты субфрактальная
модель, или фрактальная модель наклона, приводит к
элементарной геометрической оптике, или эффектам, описываемым с
помощью понятия луча. Как и в случае моделей гладкой
поверхности, угловое распределение интенсивности как функция
угла определяется распределением наклона поверхности, и
статистика высокого порядка позволяет обнаружить интересные
особенности, характерные для иерархии масштабов, присущей
природе поверхности. Например, в далекой зоне режим
геометрической оптики преобладает при условии, если освещенная
область меньше характерного внешнего размера, но больше
размеров апертуры, необходимой для того, чтобы дифракционная
угловая ширина превышала угловую ширину пучка лучей при
заданном диапазоне наклонов поверхности [13]. В таком режиме
геометрической оптики падающий пучок преломляется на угол
Qi, средний квадрат которого определяется значением
структурной функции наклона при аргументе, равном характерному
внешнему масштабу, т. е. Qi = VS(S); угловая ширина пучка
Q2 определяется значением структурной функции при аргументе,
равном апертуре, т. е. Q2 = ^S(W). Нетрудно показать, что
при грубом приближении, в котором пучок по предположению
имеет прямоугольную форму (интенсивность, видимая детекто-
Анализ фрактальных свойств материалов
87
ром, имеет форму квадратной волны), выполняется соотношение
[2, 14]
W. = fJLVv-2)/2 (Ю)
(/)2 \w2 ) ' {l '
и аналогичные результаты могут быть получены для старших
моментов. Степенная зависимость от W, характерная для
рассматриваемой модели, может быть выведена и из более точных
вычислений. Эта зависимость отличается от зависимости,
предсказываемой для гладко изменяющихся поверхностей, которая
порождает отклонение от гауссовской статистики, обратно
пропорциональное площади освещенной поверхности (т. е. ~W~2).
Замечательный результат получается для области Френеля:
если модель не содержит внешнего масштаба, то флуктуации
амплитуды выходят на насыщение при значении, большем чем
в случае гауссовского спекла [15]. Обусловлено это тем, что
флуктуации плотности луча не усредняются даже на больших
расстояниях распространения, где вклад в распределение
интенсивности дает большая часть поверхности, так как наклон
поверхности коррелирован в «бесконечном» диапазоне. Если же
ввести внешний масштаб, то флуктуации интенсивности в
конечном счете оказываются ниже значения гауссовского спекла, так
как некоррелированные области поверхности начинают давать
вклад в рассеянное поле. Можно показать, что в рассматривае
мой модели интенсивность имеет приближенное
^-распределение в значительном диапазоне расстояний распространения
(особенность, наблюдавшаяся во многих экспериментальных
исследованиях) и что в отсутствие внешнего масштаба флуктуации
интенсивности в броуновском случае (v — 3) допускают точное
описание [15] с помощью формулы
р(/) = 2/Со(2л//). (И)
Возможно, наиболее важная отличителньая особенность
рассматриваемой модели состоит в том, что, хотя наклон
поверхности вполне определен, этого нельзя сказать о кривизне
поверхности, поэтому возникают флуктуации плотности лучей, но
отнюдь не их фокусировка или каустики. Отсюда следует, что
статистики в коротковолновом пределе не расходятся и отпадает
необходимость учитывать в вычислениях дифракционное
сглаживание. Значительное упрощение анализа в этом предельном
случае позволяет, в частности, прийти к выводу о том, что
флуктуации плотности лучей конечны и могут быть исследованы как
простое геометрическое свойство случайных фрактальных
функций.
88
Часть II
5. Флуктуации плотности излучения
Такие флуктуации могут быть исследованы с помощью
функционала (случай волнистой поверхности) [15]
Ц-оо
К(У,г) = Т \ * (т{х)-■*=*-) dx, (12)
—оо
из которого следует, что
<Я>=1; 0R*> = 2/(4-v). (13)
Высшие моменты могут быть вычислены в предположении, что
т(х)—гауссовский процесс. Оказалось, что эти моменты
близки к соответствующим моментам класса гамма-распределений с
О 50 ЮО
Рис. 2, Рассеяние на двух экранах (соотношение (15)).
тем же средним и той же дисперсией. В частном случае при
v = 3 (броуновский субфрактал) вся статистическая задача
становится точно разрешимой:
где \g(jn)} —• перестановки величин {#/}. Это показывает, что
R — интенсивность комплексного гауссовско-марковского
процесса [16].
Из-за относительно простой математики более сложные
задачи геометрической оптики удается проанализировать для
субфрактальной модели. Одна из задач, представляющих
заведомый интерес, — задача о рассеянии на нескольких фазовых
экранах. Флуктуации плотности излучения порождаются
последовательно двумя субфрактальными экранами,
характеризуются, например, в приближении малого угла вторым моментом
(R2) __ 2г 1 7° \x\^-2V2dx
{R}> « 4-v J [l-(l+r)*j4|*r2(l-*)2' { '
Анализ фрактальных свойств материалов
89
где r = li/l2, h — расстояние между экранами, 12 — расстояние
между вторым экраном и детектором. Заметим, что в то время
как соотношения (13) для одного экрана не зависят от длины
распространения (хотя пространственная структура картины с
расстоянием увеличивается в размерах, как видно из
формулы (14)), соотношение (15) зависит от отношения г.
Зависимость (15) при различных значениях v представлена на рис.2.
Рис. 3. Распространение лучей за диффузором с броуновским фрактальным
наклоном.
При больших г (детектор находится у второго экрана) и при
малых г (оба экрана разделены небольшим промежутком)
зависимость (15), как и следовало ожидать, сводится к
аналогичной зависимости для одного экрана, но при г от 1 до 10
обнаруживает значительно более сильные флуктуации.
Наконец, стоит, по-видимому, заметить, что численное
моделирование распределений плотности излучения проводится
достаточно прямо и может быть использовано для подтверждения
теории. Пример распространения лучей от броуновского
субфрактала с конечным внешним масштабом показан на рис. 3.
6. Выводы
В настоящем кратком обзоре мы смогли упомянуть лишь
несколько наиболее существенных особенностей, характерных
для рассеяния с образованием ореола на гауссовских
случайных фракталах. На этих особенностях наглядно видны
качественные отличия от более знакомого рассеяния на объектах с
гладко изменяющейся поверхностью. Например,
экспериментально обнаружено, что поверхности большинства твердых тел
90
Часть II
характеризуются диапазоном масштабов, который может
простираться и ниже уровня длины волны, и обнаруживают фрак-
талоподобные свойства рассеяния (по крайней мере при
некоторых геометриях). Однако в поведении жидкостей
обнаруживается тенденция к более гладким изменениям, хотя в некоторых
случаях субфрактальные модели могли бы оказаться вполне
пригодными для описания турбулентных систем. Ясно, однако,
что общепринятая модель Колмогорова (v = 5/3 в соотношении
(6)) не позволяет предсказывать эффекты геометрической
оптики, нередко возникающие при прохождении волн через
турбулентные среды: при вычислении рассеяния необходимо
учитывать внутренний масштаб сглаживания.
ЛИТЕРАТУРА
1. Mandelbrot В. B.f The Fractal Geometry of Nature, Freeman, San
Francisco, 1982.
2. Jakeman E., Coherence and Quantum Optics V, Plenum, New York, p. 1039,
1984.
3. Jakeman £., McWhirter J. G., J. Phys. A10, 1599 (1977).
4. Lasey Speckle and Related Phenomena, ed. J. C. Dainty, vol. 9 of Topics
in Applied Physics, Springer-Verlag, Berlin, 1975.
5. Jakeman £., Optical Engineering, 23, 453 (1984).
6. Berry M. V.% J. Phys., A12, 781 (1979).
7. Sayles R. S., Thomas T. R„ Nature, 271, 431 (1978).
8. Rino C. L., Radio Science, 14, 1135 (1979).
9. Jakeman £., J. Phys., A15, L55 (1982).
10. Walker J. G., Jakeman £., Optica Acta, 29, 313 (1982).
11. Jordan D. I., Hollins R. C, Jakeman E., Appl. Phys., B31, 179 (1983).
12. Jordan D. L., Hollins R. C, Jakeman E., Opt. Commun., 49, 1 (1984).
13. Jakeman E„ Optica Acta, 30, 1207 (1983).
14. Walker J. G., Jakeman E., Optica Acta, 31, 1185 (1984).
15. Jakeman £., J. Opt. Soc. Am., 72, 1034 (1982).
16. Glauber R. /., Phys. Rev., 131, 2766 (1963).
Оптические преобразования
Фурье фракталов
/С. Аллен, М. Клуатр *
Дифракционные эксперименты проводились на одномерных и
двумерных детерминистических фракталах. Показано, что такой метод
позволяет осуществить прямое измерение нескольких
геометрических характеристик фракталов, в том числе размерности Хаусдор-
фа D. Рассмотрены применения метода к экспериментально
получаемым объектам.
1. Введение
Большинство фракталов, встречающихся в
экспериментальных ситуациях, обладают автомодельностью, т. е. их
геометрические характеристики инвариантны относительно
растяжений. Одна из целей любого эксперимента такого рода состоит,
вообще говоря, в определении размерности Хаусдорфа D и
пределов 6 и L, в которых структура проявляет фрактальные
свойства. Например, в случае кластера частиц такими пределами
являются характерный размер е отдельной частицы и наибольший
масштаб кластера L. Размерность Хаусдорфа D можно
определить исследуя характер возрастания массы, заключенной в шаре
радиусом R, с увеличением радиуса: M(R) ~ RD [1]. Другой
метод основан на использовании корреляционной функции
плотность— плотность, изменяющейся по степенному закону:
g(R) ~ RD~d [2]. Для лабораторных исследований особенно
удобным оказался метод рассеяния света. Он был использован
при изучении силикагелей [3] и коллоидов [4].
В настоящей работе приведены результаты оптического
преобразования Фурье (ОПФ), выполненного нами на фрактальных
решетках. ОПФ служит мощным методом при анализе и
манипулировании с пространственными частотами объекта. В
частности, ОПФ позволяет осуществить прямое измерение размерности
Хаусдорфа D. Сначала мы кратко опишем общую
последовательность экспериментальных процедур, позволяющих
осуществить ОПФ на двумерных объектах. Затем мы подробно обсудим
применения ОПФ к детерминистическим фрактальным
решеткам и сравним полученные экспериментальные данные с
результатами точных вычислений преобразований Фурье. В
заключение обсудим обобщение аналогичного метода для двумерных
экспериментально наблюдаемых кластеров.
* Catherine Attain, Michel Cloitre -Laboratoire cTHydrodynamique et Me-
canique Physique UA CNRS/857, ESPCI, 10 rue Vauquelin, Paris, France.
92
Часть II
2. Экспериментальные процедуры
Исследуемые в нашей работе фракталы являются
одномерными и двумерными автомодельными объектами, которые
могут быть построены рекуррентно, как, например, канторовское
множество отрезков [1J и фрактал Вичека [5], изображенные
на рис. 1. Эти объекты были вычислены на персональном
компьютере и вычерчены графопостроителем, а затем
сфотографированы на слайдах размером 24 X 35 мм с высоким
разрешением. Из-за толщины линий, наносимых нашим
графопостроителем, нам приходилось ограничиваться фракталами, которые
Рис. 1. Канторовское множество отрезков и фрактал Вичека.
получаются примерно после 7 итераций. Отношение L/e
наибольшего масштаба L фрактала к его наименьшему масштабу
е составляет при этом около 1000. Такое же ограничение
реализуется и в том случае, если мы обратимся к анализу слайдов
с фотографиями реального экспериментального фрактала.
Существенное ограничение при анализе реального фрактала
обусловлено конечными размерами элементарного зерна в фотопленке,
определяющими наименьший масштаб е, который может быть
зафиксирован на пленке (еМИн ~ 2 мкм), и наибольший масштаб
L, который определяет разрешение измерений /(Q). Величина
отношения L/e, равная максимальному числу масштабов,
которые могут быть запечатлены на пленке, составляет примерно
10 000. На практике увеличение выбирается с таким расчетом,
чтобы изображение исследуемого объекта оказалось в
указанных пределах.
Схема оптической установки, на которой выполнялись
дифракционные эксперименты, представлена на рис. 2. Луч Л от
аргонового лазера (488 нм, 600 мВт) проходит через линзу
микроскопа ЛМ. В ее фокусе помещен экран с отверстием О
(диаметром 25 мкм), действующим как пространственный фильтр,
который отбирает поперечную моду ТЕ^. СЛ — собирающая
линза («Никкор», 690 мм, f/П). В дальнейшем мы будем
пренебрегать всякого рода дифракционными ограничениями,
которые могут возникать из-за линзы СЛ. Исследуемая фрактальная
решетка ФР помещается между линзой СЛ и экраном Э.
Наблюдаемая на экране Э дифракционная картина /(Q) есть не
Анализ фрактальных свойств материалов
93
что иное, как преобразование Фурье решетки ФР [6] (Q —
пространственная частота координат р, q). Распределение
интенсивности /(Q) записывается с помощью фотоумножителя ФУ.
Рис. 2. Принципиальная схема экспериментальной установки.
Перемещение его по плоскости Фурье контролируется
высокоточными микрометром ММ. Наконец, полученные данные
хранятся в многоканальном анализаторе (МКА).
3. ОПФ канторовского множества отрезков
В работе [6] мы показали, что преобразование Фурье
любого автомодельного фрактала может быть вычислено
аналитически. Например, распределение интенсивности на
дифракционной картине от канторовского множества отрезков после п
итераций (D = log 2/log 3) одномерно и определяется выражением
/Л9) = »[Псоз(2^в)]2[^1]2,
где коэффициент 22пе2 — итенсивность, прошедшая при q = 0.
Нетрудно показать, что она изменяется как
Экспериментально величина ^/ln(0) служит мерой массы М,
заключенной в фрактале с линейным размером L. Используя
диафрагмы с различными апертурами для ограничения
эффективно освещенной части фрактальной решетки ФР, мы
получаем возможность изменять L и, следовательно, определить D.
Этот метод аналогичен определениям D на основе измерений
массы, описанным во введении. В дальнейшем мы нормировали
/,(0) на 1.
Как обычно в дифракционных экспериментах, In(q) состоит
из формфактора F(q) и структурного фактора S(q). Формфак-
тор F(q) соответствует интенсивности света, дифрагировавшего
на единичном элементе (в рассматриваемом случае — на отрезке
94
Часть II
(«черте») шириной е):
'«-(т?)"
Величина F(q) обращается в нуль при #макс = 1/8. В
дальнейшем МЫ будем СЧИТаТЬ, ЧТО (/макс = 1.
Структурный фактор S(q) описывает, каким именно образом
единичные элементы распределены по фракталу:
S(flf) = [ilcos(2nflf3'e)]
0,2 0,4 0,6 0,в
Пространственная чистота q
1,0
Этот структурный фактор подробно исследован в нашей
предыдущей работе [6]. Напомним просто, что автомодельность
объекта в реальном
пространстве отражается в ОПФ
существованием п—1
частотных полос,
масштабно-инвариантных относительно
растяжений с коэффициентом
3(6/). Средняя энергия
(S{q)y, рассеянная по
полосе частот 5/, изменяется
как
(S(q))~q~D. (1)
Это соотношение,
выведенное после усреднения,
предназначенного для того,
чтобы разрушить любую
регулярность, которая только
может возникнуть из-за
детерминистической природы
канторовского множества
отрезков, совпадает с одним
из распределений
интенсивности, наблюдавшихся на
случайных структурах [7].
На рис. 3, а и б
показано, как выглядят
экспериментальный и вычисленный
спектры канторовского множества отрезков (п = 7). Так как
первый нуль формфактора F(q) приходится на q = 1, при
высоких пространственных высотах F(q) замазывает структуру
решетки; масштаб в мы находим, измеряя фмакс- Наоборот, при
малых углах (q < 0,25) формфактор F{q) ~ 1, и им можно
пренебречь. Частота осцилляции интенсивности продифрагировав-
0,2 0,4 0,6 0,8
Пространственная частота а
ЬО
Рис. 3. Дифракционные спектры
канторовского множества отрезков (п = 7):
а — экспериментальный; б —
вычисленный.
Анализ фрактальных свойств материалов
95
шего излучения на спектрах а и б связана с 1/L, что позволяет
производить прямое измерение L. Наконец, вычисление (S(q)}
для экспериментального -спектра приводит к степенному закону
изменения (1): значение D совпадает с ожидаемым в пределах
10 %-ной погрешности.
4. Обобщение на двумерные фракталы
Предыдущий метод допускает обобщение на любой
детерминистический или случайный фрактал в случае двух измерений.
Описанная выше экспериментальная процедура остается в силе
с той лишь оговоркой, что для полной записи I(q) необходимо
сканирование по двум измерениям фурье-плоскости. Следует
заметить, что интенсивность излучения, продифрагировавшего на
одной оси (например, на оси q), определяется выражением
I(p)= \ eMq4 \ Т(х, у)йЛйу,
где Т(х, у)—коэффициент оптического пропускания
исследуемого фрактала. Эту формулу можно интерпретировать как ОПФ
оптической проекции фрактала на ось у. Следует иметь в виду,
что эта проекция может не быть фракталом. Если же она
является фракталом, то ее фрактальная размерность,
определяемая по измерениям I(q), не обязательно совпадает с
фрактальной размерностью исходного объекта. Вейтц и др. показали [8],
что в общем случае эти две величины совпадают лишь при
условии, если
D<d+l9
где d — размерность евклидова пространства, в котором лежит
фрактал.
На рис. 4 приведено ОФП фрактала Вичека (п = 5).
Отчетливо видна инвариантность относительно растяжений в 3 раза.
Для определения размерности Хаусдорфа D можно
воспользоваться соотношением (1), усреднив интенсивность
продифрагировавшего излучения по каждой из масштабно-инвариантных
частотных полос.
Обратимся теперь к случайным фракталам. На рис. 5
представлено ОПФ кластера из 1024 частиц [9], образовавшегося из
решетки в модели Виттена — Сандера [9]. Яркие кольца вокруг
центрального пика обусловлены формфактором, т. е.
дифракционной картиной от одной сферической частицы, промодулиро-
ванной структурным фактором. Как и в рассмотренном выше
случае, формфактор спадает до нуля при волновых векторах Q
с Q = 1/е, где е — диаметр отдельной частицы. Из-за случайно-
96
Часть И
сти исходного фрактала никакой дискретной структуры на
дифракционной картине на наблюдается. Для определения D
можно воспользоваться формулой (1), если под <S(<7)> понимать
Рис. 4. ОФП фрактала Вичека Рис. 5. ОФП кластера из 1024 ча-
(п = 5). стиц, образовавших решетку в
модели Виттена — Сандера.
интенсивность продифрагировавшего излучения, усредненную по
окружностям радиуса Q.
5. Выводы
Резюмируя, можно сказать, что нами предложен метод
получения ОФП двумерных фрактальных объектов, аналогичный
применяемому для получения ОФП одномерных фрактальных
объектов. Наш метод позволяет непосредственно измерять L, е
и D. Приложения метода подробно продемонстрированы на
примере канторовского множества отрезков. Произведено сравнение
экспериментальных спектров с спектрами, получаемыми с
помощью точных аналитических вычислений. Рассмотрены
обобщения на более сложные случаи двумерных детерминистических
или случайных фракталов. Изложенный выше метод мы
намереваемся применить для получения ОПФ экспериментально
наблюдаемых кластеров, например двумерных кластеров,
образующихся при агрегации малых частиц, плавающих в жидкости
[Ю].
ЛИТЕРАТУРА
1. Mandelbrot В. В., The Fractal Geometry of Nature, W. H. Freeman and
Company, New York, 1982.
2. Witten, T. A, Sander L. M., Phys. Rev. Lett., 47, 1400 (1981).
3. Shaefer D. W.y Keefer К D., Phys. Rev. Lett., 53, 1383 (1984).
4. Shaefer D. W.y Martin J. E., Cannel D., Wiltzius P., Phys. Rev. Lett., 52,
2371 (1984).
5. Vicsek Т., J. Phys., A16, L647 (1983).
Анализ фрактальных свойств материалов
97
6. Allain С, Cloitre М., препринт направлен в Phys. Rev. В.
7. Kjems J. К., Freltoft Т., работа направлена в Proceedings of the NATO
ASI (Geilo, 1985).
8. Weitz D. A., Oliveira M., Phys. Rev. Lett., 52, 1433 (1984).
9. Этот кластер был получен в численном эксперименте Р. Жюльеном и
М. Кольбом (Орсэ).
10. Аллен /С., Клуатр М. — наст. сб. с. 395.
Об измерении фрактальных
размерностей по физическим свойствам
Л'. Цаллис *
Измерение фрактальных размерностей реальных веществ путем
прямого применения математических определений может оказаться
чрезвычайно трудоемким. Мы утверждаем, что в случае произвола
но шероховатых и иррегулярных проводников задача
экспериментального определения фрактальных размерностей может быть
существенно упрощена, если воспользоваться обычным
скин-эффектом. Дело в том, что и электрическое сопротивление; и диссипация
электромагнитной энергии должны обнаруживать аномальные
степенные зависимости от приложенной частоты и соответствующие
показатели степеней непосредственно связаны с теми
фрактальными размерностями, которые требуется измерить*
1. Введение
Огромное число реальных физических систем обладает
(в соответствующих диапазонах масштабов) фрактальной
природой, характеризуемой значениями одной или нескольких
соответствующих фрактальных размерностей. Полезность такого
подхода в случае пористых углей [1], протеинов [2, 3], спеченных
металлических порошков [4], цементных гелей [5] и многих
других веществ не нуждается в дополнительных
доказательствах. Однако практическое определение фрактальных
размерностей весьма часто оказывается весьма трудоемким занятием, что
в свою очередь приводит к результатам, надежность которых не
всегда удовлетворительна. Мы утверждаем [7], что обычный
скин-эффект может быть превосходным средством для
преодоления упомянутых выше трудностей при рассмотрении веществ,
обладающих значительной электропроводностью.
Существуют физические свойства (например, релаксация
спина [2], удельная теплоемкость [8]), тесно связанные как с
статическими (чисто геометрическими), так и с динамическими
фрактальными размерностями. Например, время t\
низкотемпературной (Т — температура) спин-решеточной релаксации
некоторых гемопротеинов определяется [2] зависимостью l/t\ ~ Тп,
где нецелый показатель п может быть связан с нецелой
размерностью d соотношением [2, 3] п = 3 + 2d. При определенных
условиях размерность d может быть отождествлена [3] с
фрактальной размерностью [9] dfr = 2df/dWt где df — структурная
* Constantino Tsallis -Centro Brasiliero de Pesquisas Fisicas/CNPq, Rua
Xavier Sigaud, 150; 22290 —Rio de Janeiro, Brazil (постоянный адрес);
Centre de Recherches sur les Tres Basses Temperatures/CNRS, B. P. 166, Centre
de Tri, 38042 Grenoble, France.
Анализ фрактальных свойств материалов
99
размерность траекторий случайных блужданий (без
самопересечений) по фракталу (dw определяется из соотношения
(r2)dw ~ /2^ где ^ _ средний квадрат расстояния между
концами траектории случайного блуждания после t шагов). Мы
видим, что экспериментальные данные (например, п) дают
информацию о чисто геометрической размерности dfy но взаимосвязь
между данными и размерностью носит весьма косвенный
характер и затрагивает «динамическую» размерность dw
(отражающую диффузионный и колебательный аспекты проблемы).
Следовательно, измерения спиновой релаксации вряд ли можно
считать практическим средством определения df.
Вместе с тем существуют другие физические явления
(например, малоугловое рассеяние рентгеновского излучения [1,
6]), дающие экспериментальные данные, которые
непосредственно связаны с чисто геометрическими фрактальными
размерностями системы и, следовательно, удобны для определения этих
величин. Например, в экспериментах по малоугловому
рассеянию рентгеновского излучения, о которых упоминалось выше,
интенсивность / рассеянного излучения пропорциональна [1]
qds~Q, где q— угол рассеяния (в радианах). Следовательно,
построив график зависимости In / от In q по экспериментальным
данным, можно непосредственно получить фрактальную
размерность поверхности ds (равную 2 в евклидовом случае, что
приводит к хорошо известному закону I ~ 1/?~4). В настоящей
работе мы покажем, что обычный скин-эффект принадлежит к той
же категории методов и, следовательно, представляет удобный
способ определения фрактальных размерностей сколь угодно
шероховатых и нерегулярных проводников, позволяющий заменить
математические определения этих величин относительно
простыми физическими измерениями.
2. Скин-эффект
Рассмотрим проводник, имеющий цилиндрообразную форму
(рис. 1). Пусть lL и 1Т — его фрактальные длины, продольная и
поперечная (периметр), a S — фрактальная площадь
поверхности, заключенной между поперечными сечениями, отстоящими
Друг от друга на расстояние /L. Для произвольной фрактальной
поверхности должно, вообще говоря, выполняться неравенство
^ Мг' предположим, чт0 вдоль цилиндра приложен
переменный электрический потенциал с амплитудой V и частотой со.
Соответствующая глубина скин-слоя определяется
выражением [10].
100
Часть II
где коэффициент пропорциональности зависит от
электромагнитных свойств (таких, как электропроводность) вещества
(однородного) .
Рис. 1. Цилиндроподобный проводящий образец с фрактальной внешней
поверхностью; 1т — периметр. Переменный потенциал приложен между двумя
(эквипотенциальными) основаниями. Толщина скин-слоя 6 изображена без
соблюдения масштаба (слишком большой) для удобства проверки фрактально-
сти шероховатой поверхности.
Фрактальные величины lLf 1т и S порождают фрактальные
размерности du dT и ds, задавая их с помощью соотношений
ln(/L/6)
Ul~ In (1/6) ' W
откуда
откуда
откуда
Ш(Уб)
йт— In (1/6) ' W
ln(S/6*) M)
"5— In (1/6) ' w
Анализ фрактальных свойств материалов
101
В общем случае справедливы неравенства 1 ^ dL, dr < 2
(равенство выполняется для гладких дифференцируемых
кривых) и 2 <; ds < 3 (равенство выполняется для гладких
дифференцируемых поверхностей). Интересный частный случай
возникает, когда 5 = lLlT: в этом случае ds =dL-\- dT^ 2. Другой
интересный частный случай представляет (статистически)
однородная изотропная фрактальная поверхность: в этом случае
dh = dj = ds — 1 ^ 1.
Энергия Р, рассеиваемая веществом, определяется
выражением
P=$j(r)E(r)tf3r, (5)
где j(r) —плотность тока, а Е(г) —электрическое поле в точке
г. По закону Ома j(r)=aE(r) (a — электропроводность), что
позволяет записать соотношение (5) в виде
Р = в\Е*с(3г = о(Е\КЙН J rf»r = о<£•>«-.«*, (6)
ко-
где «скин» означает объем as= \ cPr = S6 слоя вещества, в
скин
тором электрическое поле существенно отлично от нуля
(напомним, что электрическое поле убывает экспоненциально по мере
продвижения в глубь материала).
Если мы производим эксперимент с фиксированной
плотностью электромагнитного поля, то из соотношения (6)
получаем
Р ~ S6 = 63~ds (7)
(равенство следует из соотношения (4')). Используя
соотношение (1), преобразуем (7) к виду
P = -sV (8)
(О 2
При dsj=2 это соотношение воспроизводит стандартное (Р =
= 1/лЛ°)- Заметим также, что из соотношения (7) следует
зависимость i/ = 63~ds, что при подходящем изменении
характеристической длины воспроизводит соотношение (4) из
работы [1].
Выполнив эксперимент с прохождением электрического тока,
мы получим (Е2)скш = У2[12ь. Тогда, с учетом соотношения (6),
имеем
oVJSb
/2
P = ^f. (9)
102
Часть II
Сравнивая (9) с формулой Р= V2/R (R— электрическое
сопротивление), получаем
*-т1- (10)
Наконец, из соотношений (2') и (4') мы находим, что
R = ads-*dL-\ (11)
или с учетом соотношения (1)
{+2dL-dS
R~a 2 . (12)
При ds = 2 и dL = 1 это соотношение переходит в стандартное
Резюмируя, можно сказать, что, нанося экспериментальные
данные на графики в координатах (InP, In со) и (In/?, In со), мы
получаем прямые с угловыми коэффициентами (ds — 3)/2 и
(l + 2dL — ds)/2, что позволяет непосредственно измерить ds
и dL-
В упомянутом выше частном случае, а именно при ds = db +
+ dTi из соотношений (8) и (12) получаем
Р~ aJL-*r (13)
со 2
И
Я~Сй * . (14)
В другом частном случае (весьма часто встречающемся в
природе), а именно rfL ==rfr = ds— 1, из соотношений (8) и (12)
следует, что
со 2
R~(*dL'\ (16)
В этом случае один эксперимент, например измерение R как
функции от 0, позволяет определить db.
В экспериментах обоих типов (с прохождением
электрического тока и фиксированной плотностью электромагнитного
излучения в полости) пространственное распределение
электромагнитного тока эволюционирует с частотой со, и именно эта
эволюция позволяет полю «прощупать» фрактальную размерность
системы. Качественно-пространственное распределение
электромагнитного поля снаружи (внутри) вещества в эксперименте с
Относительно низкая со
Относительно высокая си
Рис. 2. Увеличенное изображение поверхности проводника: штриховой линией показан скин-слой
в веществе при определенной частоте. В эксперименте с фиксированной плотностью
электромагнитного излучения в полости показано электрическое поле снаружи проводника (а и б); в
эксперименте с прохождением электрического тока показано электрическое поле внутри проводника (в
и г).
104
Часть II
фиксированной плотностью электромагнитного излучения в
полости (прохождением электрического тока) представлено на
рис. 2, а (2,6).
3. Выводы
Изложенные выше соображения относительно масштабной
инвариантности показывают, что скин-эффект является
перспективным средством измерения фрактальных размерностей прово-
б
4
3
г
г
О 1 г 3 4 5 6 ln_OL
Рис. 3. Возможный результат измерения электрического сопротивления
шероховатости проводящего образца. На кривой виден фрактальный режим (с
угловым коэффициентом, отличным от 1/2), переходящий в стандартный режим
(с угловым коэффициентом 1/2); (do(Ro)—опорная частота (опорное
сопротивление), подобранное для исследуемого образца.
дящих материалов. Разумеется, не следует ожидать, что
реальные вещества обнаруживают аномальный скин-эффект
указанного типа при всех частотах. В реальном эксперименте,
например при измерении электрического сопротивления, будут
наблюдаться различные режимы, переходящие один в другой при
соответствующих частотах. Всегда будет наблюдаться
низкочастотный режим, при котором сопротивление не зависит от
частоты со (б больше поперечного размера образца). Этот режим
прекращается, когда толщина скин-слоя б становится сравнимой с
этим размером. Высокочастотный режим также существует
всегда. Он соответствует случаю, когда нарушается условие со «<
<С а/г (е — диэлектрическая постоянная), необходимое для того,
чтобы выполнялось соотношение (1) (при © > а/г сама
поляризуемость начинает зависеть от со и возникает нетривиальный
эффект). Между указанными режимами, низко- и
высокочастотным, могут наблюдаться один или несколько фрактальных и
Анализ фрактальных свойств материалов
105
(или) евклидовых скин-режимов в соответствии с масштабами б,
в пределах которых поверхность проводника кажется
«шероховатой» или гладкой. На рис. 3 мы изобразили сказанное для
случая, когда промежуточный частотный режим фрактальный
(с угловым коэффициентом (l + 2dL — ds)/2, отличным от 1/2)
и сменяется стандартным режимом (с угловым коэффициентом
1/2).
В заключение скажем, что эксперименты по проверке
соотношений (8) и (12) были бы весьма кстати. Хорошими
кандидатами для измерений являются такие системы, как пористые
образцы меди, золота, серебра [4], пористые угли,
металлические губки.
Благодарности. Я признателен за интересные обсуждения
А. Кариде, К. Боллини, Ж. Джамбиаги, Дж. Хелмену, А. Крайе-
вичу и Г. Герману, а также Л. Пьетронеро, Л. Сандеру и
П. Пфейферу за ценные замечания.
ЛИТЕРАТУРА
1. Bale Я. £>., Schmidt P. W., Phys. Rev. Lett., 53, 596 (1984).
2. Stapleton H. J, Allen J. P., Fly tin C. P., Stinson D. (?., Kurtz S. R.} Phys.
Rev. Lett, 45, 1456 (1980).
Allen J. P., Colvin J. 7\, Stinson D. (?., Flynn C. P., Stapleton H. J.,
Biophys. J, 38, 299 (1982).
3. Helman J. S., Coniglio A., Tsallis C, Phys. Rev. Lett., 53, 1185 (1984);
54, 1735 (1985).
Cates M. £., Phys. Rev. Lett., 54, 1733 (1985).
Stapleton H. /., Phys. Rev. Lett., 54, 1734 (1985).
4. Franco #., Bossy /., Godfrin #., Cryogenics, September 1984, p. 477.
5. Allen A. /., Schofield P., preprint (1985), будет опубликовано в Ргос.
NATO meeting on Scaling Phenomenon in Disordered System, Geilo, April
1985, Plenum.
6. Pfeifer P., Avnir £>., J. Chem. Phys., 79, 3558 (1983).
Avnir O., Farin D.y Pfeifer P., J. Chem. Phys., 79, 3566 (1983); Nature
(London), 308, 261 (1984).
7. Tsallis C, Caride A. O., Bollint C. G., Giambiagi /. /., Helman J. 5., будет
опубликовано.
8. Dillon L. D.} Rapp R. E., Vilches O. £., J. Low Temp. Phyt., 59, 35 (1985).
Rapp R. £., Dillon L. D., Godfrin #., Cryogenics, 25, 152 (1985).
9. Alexander 5., Orbach R.} J. Physique Lett, 43, L625 (1982).
10. Jackson /, /)., Classical Electrodynamics, 2nd edition, J. Wiley and Sons.
1975.
Часть К)
СТАТИСТИКА ПОЛИМЕРОВ
И БЛУЖДАНИЯ
БЕЗ САМОПЕРЕСЕЧЕНИЙ
Случайные блуждания
с памятью
Л. Пелити *
Случайные блуждания с памятью представляют собой
своеобразную арену для иллюстрации методов описания явлений
необратимой агрегации. Образующиеся топологически простые агрегаты
погружаются затем в окружающее пространство, что можно описать
с помощью фрактальных понятий. Достаточно хорошо
установленная аналогия со скейлинговыми свойствами критических явлений
приводит здесь к более полному пониманию их свойств, чем в
случае общих процессов агрегации.
1. Введение
Траектория броуновской частицы представляет собой
один из простейших фракталов, которые образуются при
физических процессах. Она приводится в недавней книге Мандель-
брота [1] в качестве единственной иллюстрации, взятой из
эксперимента. Развертку такой траектории можно моделировать
как простой процесс агрегации, называемый случайным
блужданием (СБ). Объяснение свойств СБ, исходя из теории
фракталов, сводится к простому упражнению. Эта модель,
допускающая, с одной стороны, детальное исследование и, с другой —
физическую реализацию, демонстрирует простые, хотя и
нетривиальные, фрактальные свойства.
Благодаря ее успеху стали разрабатываться различные
вариации на тему СБ в надежде найти допускающие анализ
модели с различными фрактальными свойствами. Такая
программа становится еще более привлекательной, если обратиться к
приведенному де Женом [2] доказательству точной аналогии
между фазовым переходом в общей модели ферромагнетика и
статистическими свойствами самонепересекающихся
конфигураций длинных цепей. Последние в свою очередь легко
моделируются траекториями неких случайных блужданий с памятью,
* L. Ре/Ш-Dipartimento di Fisica, Universita «La Sapienza», Piazzalo Aldo
Moro, 2? 1-00185. Roma (Italy) and GN$M-CNR, Unita di Roma,
Статистика полимеров и блуждания без самопересечений 107
носящих название блуждания без самопересечений, или
самонепересекающегося блуждания (СНБ). Таким образом, мы
становимся свидетелями расцвета моделей случайных блужданий
с памятью, для которых различные «правила игры» приводят к
различным геометрическим свойствам получающихся агрегатов.
Как правило, эти модели не предназначены для описания
реальных физических процессов, а используются для того, чтобы
изучить те их особенности, которые лежат в основе фрактальных
свойств. Прямая аналогия с критическими явлениями здесь
весьма эффективна, так как в большинстве случаев позволяет
использовать методы ренормгруппы. Однако эти же достижения
могут стать в будущем источником ошибок, поскольку они
приводят к искушению объявить универсальными те черты
процессов агрегации, которые наиболее легко интерпретируются
сточки зрения современных представлений о скейлинге в
критических явлениях. Случайные блуждания с памятью в противовес
этой тенденции основаны на ошеломляющем (и все еще
совершенно необъяснимом) успехе самосогласованных подходов
(Флори [3], Пьетронеро [4]). Они приводят, в
противоположность теории критических явлений Ландау, к зависящим от
размерности пространства нетривиальным показателям, которые в
общем находятся в хорошем согласии с результатами как
экспериментов, так и моделирования. Эти подходы характерны для
теории линейных агрегатов, так что объяснение их
эффективности применительно к большому кругу систем все еще служит
вызовом теоретикам.
В данной работе блуждания рассматриваются как
кинетический процесс образования топологически линейных агрегатов.
Автор не обсуждает равновесные свойства линейных полимеров
при различных ограничениях, упоминая лишь о том, что они
точно описывают асимптотические свойства блужданий. В разд. 2
СБ вводятся как простейшие среди блужданий, а также кратко
обсуждаются эффекты добавления в модель конечной памяти.
Самонепересекающиеся блуждания — процесс агрегации,
который воспроизводит статистику цепей с исключенным объемом, —
вводятся и обсуждаются в разд. 3. В следующем разд. 4
описываются так называемые истинные самонепересекающиеся
блуждания (ИСНБ). Дальнейшие модификации и разработки
кратко сформулированы в разд. 5, а несколько заключений — в
последнем разд. 6.
Общая структура настоящей статьи и большая часть ее
содержания взяты из обзора [5], который был написан автором
совместно с профессором Л. Пьетронеро. К этому обзору автор
отсылает читателей, интересующихся деталями приведенного
ниже материала.
108
Часть III
2. Случайные блуждания с короткой памятью
СБ на решетке моделируют диффундирующую броуновскую
частицу. Рассмотрим дискретные моменты времени to, /ь ..., в
каждый из которых tn частица находится в узле г простой
кубической d-мерной решетки. В момент tn+i частица может
находиться в любом из соседних узлов г' = г + 6 узла г, где вектор
6 направлен от г к одному из его ближайших соседей. Для
случайных блужданий без памяти условная вероятность p(r', tn+\\r,
tn) того, что частица в момент tn+i находится в точке г' при
условии, что в момент tn она находилась в г, полностью описывает
процесс и зависит лишь от г, г' (и, возможно, от tn). В
простейшем случае она постоянна и равна l/qf где q — координационное
число решетки. Для этого случая можно непосредственно
вычислить асимптотическое распределение плотности вероятности
P(r, t) обнаружения в момент t в окрестности точки г частицы,
вышедшей из начала координат при to = 0. Это распределение
оказывается гауссовским с дисперсией %2{t) — Dt, причем
коэффициент диффузии D простым образом выражается через At =
= tn+i — tn и постоянную решетки а = |б| согласно выражению
D = a2/At. (I)
Фракталом в данном случае является траектория {0 = r(t0),
r(£i), ..., r(t)}, оставленная движущейся частицей. Этот
фрактал имеет линейную протяженность в пространстве порядка |(£),
а для длин I в интервале а<С/<С|(0 0Н обладает свойством
самоподобия, характеристикой которого служит фрактальная
размерность df, равная в данном случае 2 для евклидова
пространства любой размерности. Можно рассмотреть
последовательность узлов, посещаемых частицей в моменты, разделенные
интервалом времени Af, который много больше At, но мал по
сравнению с t. Эти узлы разделены один от другого
расстоянием / порядка (DAt')l/2, поскольку процесс движения частицы
в течение каждого интервала времени At' сам представляет
собой случайное блуждание с тем же коэффициентом диффузии.
Следовательно, всю траекторию можно покрыть М клетками
радиусом /, где
M = t/At' = Dt/l2 (2)
в соответствии с обычной процедурой «подсчета клеток»,
используемой для определения фрактальной размерности. По этой
причине можно связать фрактальную размерность df с
показателем, характеризующим увеличение расстояния частицы от
начала при возрастании времени блуждания, который по аналогии
с теорией критических явлений обозначается через v:
VV) = <\T(f)f)~t*>. (3)
Статистика полимеров и блуждания без самопересечений 10§
Указанная связь имеет вид
d,= l/v. (4)
Это выражение будет охватывать более общие случаи
рассматриваемых далее блужданий при условии, что самоподобие
остается справедливым для всех их траекторий. Второй
показатель, обозначаемый у, связан с полным числом Jf блужданий,
которое может произойти за время t:
jr~(q*fNy-1, (5)
где N = t/At— общее число шагов. В частном случае СБ имеем
q* = q и у = 1.
Легко убедиться, что указанные свойства сохраняются для
систем с конечной памятью. В данном случае процесс
описывается условными вероятностями р (гл+ь *n+i|rn, tn; vn_u tn_x\...
...; гл_л, tn_k) того, что частица находится в момент tn+i в
точке гл-н, если ее траектория в моменты времени между tn-k и
tn проходит через точки (г„_А, Гд-л+ь •••» гл). Таким образом,
память о недавней истории блуждания (в течение времени At' =
= kAt) характеризует вид переходных вероятностей.
Рассмотрение подобной траектории в моменты времени, разделенные
между собой интервалами, заметно большими At', приводит к
результатам предыдущей модели. Отсюда следует заключение о
том, что наличие конечной памяти не влияет на
асимптотические свойства СБ.
3. Самонепересекающиеся блуждания
СНБ являются кинетическим процессом, который
асимптотически воспроизводит равновесную статистику линейных
полимеров в хорошем растворителе. В ходе этого процесса частица
перемещается по решетке случайного ей запрещено (и
соответствующие траектории не включаются в статистический
ансамбль) попадать в узлы, через которые она уже проходила
ранее. Свойства этого процесса удается проанализировать из
простых соображений самоподобия [4], которые воспроизводят
результаты, полученные ранее Флори [3] для равновесных
свойств полимеров. Определим G(r, t) как плотность
распределения вероятностей обнаружить в момент / в точке г частицу,
которая начала при t = 0 свое блуждание из начала координат.
Она может быть представлена в виде произведения аналогичной
функции Go(r, t) для стандартных СБ с теми же самыми
переходными вероятностями на вероятность выживания 5 (г, t). Эта
функция равна вероятности попасть блуждающей частице за
время t в точку г без самопересечений. Ясно, что S (r, t) является
110
Часть III
возрастающей функцией |г|, поскольку для более
продолжительных блужданий вероятность самопересечения
соответственно меньше. Функция Go (г, t) для длительных интервалов
времени t и не слишком больших значений |г| может быть
аппроксимирована гауссовским распределением
G0 (г, /) ~ (2nDtydl2 ехр (-1 г |2 2Dt). (6)
Вычислим теперь 5 (г, t). Траектория блуждания локализована
в объеме порядка |г
ней плотностью р —t
\d и, следовательно, характеризуется сред-
jr|-rf. Проследим генезис блуждания к
моменту времени t. На каждом шаге вероятность вторичного
попадания в какую-либо точку имеет порядок р. Вероятность того,
что на любом шаге этого не произойдет, равна 1 — р, и, следова-*
тельно, на всей траектории после N = t/At таких независимых
шагов будет
S(r, /)~(1-P)"~exp(--Wp). (7)
Эту формулу можно переписать в виде
S(r, 0~ехр(-£/2|гГ*)> (8)
где g — некоторая положительная постоянная. Теперь вычислим
средний квадрат расстояния l2(t) между начальной и конечной
к моменту / точками траектории:
t(t)^(\r\2)=\ddT\r\2G(r) t)=\ddr\rfG0(r, t)S(r, 0 =
= \ddr\rfexp[-F(r, /)], (9)
^0-^ + *^. (10)
Вычисление интеграла (9) методом перевала приводит к
зависимости
Ut)~(gDt)v*, (П)
где показатель vf дается соотношением Флори
V-7TI <12>
и соответствует фрактальной размерности df =(rf + 2)/3.
Заметим, что в случае размерности пространства d > 4, когда
формула (12) дает показатели v меньшие, чем отвечающее СБ
значение 1/2, приведенные выше рассуждения оказываются
неприменимыми. Причиной этого служит неприменимость в этом
случае метода перевала, поскольку значение F(10) в
перевальной точке здесь уменьшается с ростом t. При этом в выражении
(10) доминирующим оказывается первое слагаемое, а следова-
Статистика полимеров и блуждания без самопересечений 111
тельно, асимптотическое поведение в рассматриваемом случае
СНБ совпадает с гауссовским поведением при СБ. Поэтому
значение 4 является верхней критической размерностью^ для СНБ.
Формула (12) находится в отличном согласии с результатами как
эксперимента, так и компьютерного моделирования. Она
приводит к значению dc =4, правильно предсказывает v = 1 при d =
= 1, дает при d = 3 и d = 2 соответственно значения 3/5 и 3/4,
первое из которых с точностью менее 1 % совпадает с
результатами моделирования, а второе, вероятно, вообще может быть
найдено из точного аналитического решения. В настоящее
время не имеется убедительного объяснения впечатляющего успеха
этого приближения [6]. С помощью аналогичных соображений
было получено схожее с (12) выражение
для определяемого (5) показателя у. Согласие величины у,
вычисленной по формуле (13), с результатами компьютерного
моделирования оказывается хуже, чем для показателя v. Разница
здесь составляет ~ 3 % и ~ 10% для d = 3 и d = 2
соответственно.
Теоретико-полевое рассмотрение [8, 9] СНБ позволяет
доказать, что их асимптотическое поведение воспроизводит
равновесную статистику полимеров в хорошем растворителе и,
следовательно, может быть изучено, согласно подходу де Жена [2],
исходя из рассмотрения обобщенной модели Гайзенберга для
ферромагнетика с параметром порядка размерности я->0. Это,
следовательно, позволяет использовать мощные ренормгруппо-
вые методы для получения разложений показателей у и v в
ряды по степеням параметра е = 4— d. Указанные методы можно
заменить применением формализма Мартина, Сиджо и Розе [9],
предложившими его для описания классических уравнений
эволюции с помощью интегралов по траекториям. Такой формализм
в более удобном для целей настоящей работы виде использовал
Дой [10] при рассмотрении химических реакций. На эту тему
можно рекомендовать также статью Грассбергера и Шейнерта
[Н], а для первоначального ознакомления — работу [12].
Таким образом, удается формально установить эквивалентность
асимптотических свойств СНБ и равновесных свойств
полимерных цепей в хорошем растворителе.
4. Истинные самонепересекающиеся блуждания
Здесь рассматривается предложенная в работе [13] модель
роста на ^-мерной решетке цепи с самонепересекающимися
конфигурациями;
112
Часть 111
I. частица начинает блуждание в нулевой момент
времени в начальном узле d-мерной простой кубической решетки;
II. на каждом временном шаге частица может перейти из
узла г в один из ближайших соседних узлов г + 6;
III. вероятность перехода на узел г+ 6 определяется числом
я (г+ 6) предшествующих попаданий в него блуждающей
частицы таким образом, чтобы ей было невыгодно попадать в
узлы, в которых она уже ранее побывала. Автор, в частности,
использует для вероятности экспоненциальную зависимость
р(г+ 6 |г) ~exp[-gn(r + 6)], (14)
нормировка которой выбирается таким образом, чтобы
блуждающая частица на любом шаге разыгрывала каждый раз
исходы попадания в те или иные узлы решетки. Положительный
множитель g характеризует интенсивность отталкивания от
областей, которые частица уже успела посетить.
Сформулированные выше закономерности блуждания
частицы не запрещают ей бывать дважды или более раз в том же
самом узле решетки даже при g> стремящемся к бесконечности.
В последнем случае, однако, частица будет выбирать с равной
вероятностью среди узлов те, в которые она попадала наименее
часто. Совершенно удивительно, что рассматриваемое
блуждание имеет асимптотическое поведение, отличное от поведения
СНБ. Оно было неудачно названо истинным
самонепересекающимся блужданием, хотя, вероятно, название «блуждание Хау-
дини», предложенное М. Ф. Шлезингером в ходе настоящей
конференции, более подходит, поскольку частица предпочитает
избегать все ловушки, в которые она может нечаянно попасть.
(Можно рассмотреть модель [14, 15], когда в случае отсутствия
на каком-либо шаге у частицы не посещенных ею ранее
соседних узлов она прекращает свое блуждание. Оказывается, что
асимптотическое поведение блужданий в рамках такой модели
не отличается от СНБ.)
Восходящие к Пьетронеро [16] эвристические соображения
дают для таких блужданий значения верхней критической
размерности и показателя v (а следовательно, и фрактальной
размерности rff = l/v). Предположив, что среднеквадратичное
расстояние | (3) между концами траектории является
единственным пространственным масштабом блуждания, для плотности
р(г, t) узлов, в которые попала за время / частица, можно
написать следующую скейлинговую формулу:
р(г, t)~trdf{\r\ll). (15)
Из обычного предположения о степенном характере
зависимости | ~ tv следует, что увеличение £ вследствие продления вре-
Статистика полимеров и блуждания без самопересечений 113
мени блуждания на Ы; будет определяться зависимостью
Al~f-'A*. (16)
Вместе с тем это же увеличение А£, связанное с направленным
наружу давлением из-за эффектов отталкивания, можно
считать пропорциональным градиенту плотности р на расстоянии
порядка | от начального узла. Дифференцируя выражение (15),
получаем
•&1 . t~T(d+I)f(l)~',4d+,)v. (17)
Сравнение (16) и (17) приводит к формуле
Эта формула становится неприменимой при d > 2, так как в
этом случае эффекты отталкивания дают пренебрежимый по
сравнению с обычной диффузией вклад в давление.
Следовательно, верхняя критическая размерность dc рассматриваемой
модели равна 2, так что в двумерных системах ожидаются
логарифмические поправки к поведению СБ [13, 16]. Такие
поправки были вычислены методом ренормгруппы и могут быть
найдены при тщательном анализе степенных разложений [17, 18].
Ситуация все же остается дискуссионной. Заметим, что для
размерностей пространства 1 <Zd<z2 формула (18) дает значения
фрактальной размерности df = 1/v большие, чем rf. Это не
является противоречием, поскольку df в данном случае
характеризует распределение массы, т. е. меру, а не множество.
Можно рассмотреть два интересных нетривиальных случая
ИСНБ: одномерный случай [19—21] и ИСНБ на фрактале [22].
Первый из них оказывается менее тривиальным, чем поначалу
можно предположить. Для него получается значение v
неотличимо близкое к значению 2/3, которое следует из формулы (18).
Хотя в его подтверждение были приведены определенные
эвристические соображения [21], вопрос их обоснованности
остается, несмотря на впечатляющий и совершенно необъяснимый
успех, открытым в той же мере, что и соображения Флори для
описания СНБ. С помощью компьютерного моделирования
изучалось ИСНБ на кривой Серпинского. Полученные данные
сопоставлялись затем с результатами скейлингового анализа на
основе подхода, обобщающего рассмотренный выше. Условие для
определения критической размерности
2-dJ2**dJdf (19)
содержит спектральную размерность ds [23]. Когда правая
часть этого выражения оказывается меньще левой, то показа-
114
Часть III
тель v, как показано, определяется выражением
Это выражение основано, с одной стороны, на требовании, чтобы
величина drv была для фрактала внутренней, т. е. не
зависящей от его погружения во внешнее (евклидово) пространство, а
с другой стороны, на наблюдении, что ds есть простейшая
внутренняя размерность. Замена d на ds в формуле Пьетронеро (18)
дает нужный результат, который удивительно хорошо
согласуется с результатами компьютерного моделирования на
двумерном ковре Серпинского.
5. Вариации
Модель ИСНБ имела определенный успех вследствие ее
простоты, легкости компьютерной реализации, а также того, что
она демонстрирует нетривиальное, хотя и допускающее
необходимый анализ поведение при низкой размерности. Это
стимулировало появление некоторых других моделей случайного
блуждания с памятью, которые мы кратко рассмотрим в
настоящем разделе. Выше уже упоминался один из вариантов ИСНБ
[14, 15], который принадлежит к тому же самому классу
универсальности, что и СНБ. Другая модификация, при которой
блуждающая частица на двумерной решетке узнает ловушки
до попадания в них, была предложена Кремером и Ликлемой
[24], которые назвали эту модель «неограниченно растущее
самонепересекающееся блуждание» (НРСНБ). (Она может быть
получена в соответствующем пределе из лапласовых блужданий
(ЛБ), которым посвящен доклад Ликлема на настоящей
конференции [25].) Эта модель явно не попадает ни в один из
классов универсальности, которые мы обсуждали до сих пор. Все это
еще более сбивает с толку, поскольку версия НРСНБ на сотовой
решетке оказывается отвечающей равновесной статистике
самонепересекающихся цепей с соответствующими взаимодействиями
между ближайшими и следующими за ними соседями
[26].Действительно, некоторые равновесные конфигурации не
образуются при заданном кинетическом механизме роста, так что ничто
не препятствует модели ИСНБ принадлежать своему
собственному классу универсальности, а отнюдь не тому, в который
входит поведение полимеров в 8-растворителе, как это ранее
предполагалось.
ИСНБ с дальнодействующим отталкиванием [27, 28]
рассматривалось как с помощью соображений Флори —
Пьетронеро, так и на основе теоретико-полевого подхода. Вполне
возможно, что использование эвристических соображений имеет
здесь больше оснований, так ж? как в случае линейных поли-
Статистика полимеров и блуждания без самопересечений 115
меров с дальнодействующими взаимодействиями 129, 30J.
Результаты, полученные на основе подхода Флори, достаточно
близки к данным компьютерного моделирования, чего нельзя
сказать (за исключением тривиальных случаев) о результатах
вычислений с помощью е-разложения.
Соображениями Флори все же следует пользоваться с
некоторой осторожностью. Это подтверждается при рассмотрении
так называемых ^-толерантных блужданий [31], где
разрешаются все конфигурации с не более чем k пересечениями
траектории в любом узле. Для такой модели, принадлежащей,
очевидно, к одному и тому же классу универсальности с равновесным
ансамблем полимеров в хорошем растворителе, соображения
Флори приводят к иному асимптотическому поведению. По
этому же признаку не ясно, до какой степени можно принять на
веру предсказания, сделанные Оттипгером [32] об
асимптотическом поведении одного из вариантов ИСНБ с переходной
вероятностью
Р(г+6|г)~ехр[-#1«(г+6)]. (21)
Нет основания ожидать, так же как в случае ^-толерантных
блужданий, различного асимптотического поведения при а = 1
(обычное ИСНБ) и, скажем, при а = 2, С другой стороны,
моделирование подтверждает предсказания, сделанные исходя из
соображений Флори — Пьетронеро. По мнению автора, углубление
нашего понимания этого подхода крайне необходимо.
6. Заключения
Одной из основных задач теории фракталов является
выяснение того, какие характеристики физического процесса
приводят к образованию фрактальных структур. В этом смысле
теория случайных блужданий с памятью снимает вопрос, так как
она дает достаточно простое решение задачи. С одной стороны,
траектории частицы, совершающей случайные блуждания с
памятью, очевидно, имеют пустоты, с другой стороны, их
самоподобие обычно можно объяснить таким же образом, как и в
случае критических флуктуации, а именно существованием
неподвижной точки преобразования соответствующей ренормгруп-
пы. По этому же признаку в подобных моделях не следует
ожидать такого интересного явления (наблюдаемого в ДОА-класте-
рах на перколяционных сетках), как сосуществование
нескольких популяций с различным скейлинговым поведением,
отличающихся между собой при наблюдении разных статистических
моментов распределения по массе. По мнению автора,
достижения в нашем понимании поведения случайных блужданий с
памятью скрывают тот факт, что, несмотря на успехи в
кинематике агрегации (а ее изучение, несомненно, улучшило наши
116
Часть III
представления в этой области), мы не имеем ключа к
пониманию наиболее важных аспектов динамики. А добыть этот ключ
мы можем лишь в результате наблюдения этого своенравного
мира реальных процессов агрегации.
Благодарности. Я признателен Л. Пьетронеро, который
поделился со мной своими взглядами на этот предмет. Я
благодарен также Д. Амиту, Л. Аркангелису, А. Конильо, П. Грассбер-
геру, С. Обухову, X. Оттингеру, Ш. Паризи и И. Ликлеме за
плодотворные обсуждения.
ЛИТЕРАТУРА
1. Mandelbrot В. B.f The Fractal Geometry of Nature, Freeman, San
Francisco, 1982.
2. de Gennes P. G., Scaling Concepts in Polymer Physics, Cornell Univ.
Press, Ithaca, N. Y., 1979. [Имеется перевод: де Жен П. Идеи скейлинга
в физике полимеров. — М.: Мир, 1982.]
3. Flory P., Principles of Polymer Chemistry, Cornell Univ. Press, Ithaca,
N. Y., 1971, Chap. XII.
4. Pietronero L., Phys. Rev. B27 (1983) 5887; Phys. Rev. Lett. 55 (1985)
2025.
5. Peliti L., Pietronero L., Random Walks with Memory, La Rivista del Nuovc
Cimento, в печати.
6. Obukhov S. P., J. Phys. A: Math. Gen. 17 (1984) L-965.
7. Pietronero L., Peliti L., Phys. Rev. Lett. 55 (1985) 1479.
8. Peliti L., J. Physique Lett. 45 (1984) L-925.
9. Martin P. C, Siggia E. D., Rose H. A., Phys. Rev. A7 (1973) 423.
10. Doi M.t J. Phys. A: Math. Gen. 9 (1976), 1465; 9 (1976) 1479.
11. Grassberger P., Scheunert Ai, Fortschritte der Physik, 28 (1980) 547.
12. Peliti L., Path Integral Approach to Birth Death Processes on a Lattice,
J. Physique, в печати.
13. Amit D. /., Parisi G., Peliti L., Phys. Rev. B27 (1983) 1635.
14. Majid /., Jan N.t Coniglio A., Stanley H. £., Phys. Rev. Lett. 52 (1984)
1257.
15. Lyklema /. W., Kremer K, J. Phys. A: Math. Gen. 17 (1984) L-691; a
также в печати.
16. Obukhov S. P., Peliti L., J. Phys. A: Math. Gen. 16 (1983) L-147.
17. Byrnes C, Guttman A. /., J. Phys. A: Math. Gen. 17 (1984) 3335.
18. Adler /., частное сообщение. Ряды были получены Р. Декейзером (не
опубликовано).
19. Bernasconi /., Pietronero L.t Phys. Rev. B29 (1984) 5196.
20. Rammal R., Angles /. C, d'Auriac, Benoit A., J. Phys. A: Math. Gen. 17
(1984) L-9.
21. Obukhov S. P., J. Phys. A: Math. Gen. 17 (1984) L-7.
22. Angles /. C. d'Auriac, Rammal R.f J. Phys. A: Math. Gen. 17 (1984) L-15.
23. Rammal R., Toulouse G.y J. Physique Lett. 44 (1983) L-13.
24. Kremer K., Lyklema J. W., Phys. Rev. Lett. 54 (1985) 267.
25. Ликлема И. — наст, сб., с. 131.
26. Coniglio A, Jan N., Majid /., Stanley H. E.t будет опубликовано.
27. Zhang Y. C, Brookhaven preprint.
28. Peliti L., Zhang Y. C, J. Phys. A: Math. Gen. 18 (1985) L-709.
29. Grassberger P., J. Phys. A: Math. Gen. 18 (1985) L-463.
30. Halley /. W., Nakanishi H., Phys. Rev. Lett. 55 (1985) 551.
31. Стелла А., Декейзер Р., Маритан А. — наст, сб., с. 141.
32. Ottinger H. С, J. Phys. A: Math. Gen. 18 (1985) L-363.
Вероятность выживания и фактор
усиления в статистике
полимеров
Л. Пьетронеро, Л. Пелити *
Метод рассмотрения вероятности выживания открывает новые
перспективы для приближений типа предположения Флори и
позволяет дать их математическое обоснование. Он позволяет также
вычислить точное выражение для показателя у = 3 — dv,
завершая построение теории среднего поля для описания статистики
полимеров.
1. Введение
В предшествующей статье [1] было показано, как ряд
кинетических задач с памятью удается рассмотреть на основе
теорий самосогласованного скейлинга. Известно также, что
стандартная равновесная задача самонепересекающихся цепей
(СНЦ) [2] может быть сформулирована на кинетическом языке
с использованием понятия вероятности выживания [3, 4]. В
первой части этой короткой заметки обсуждается, как наилучшим
образом определить с этих новых позиций приближения,
которые делаются в рамках подхода Флори. Во второй части
показано, как следует обобщить теорию Флори для вычисления
второго независимого показателя у, характеризующего статистику
полимеров.
2. Приближения, характеризующие подход Флори
Рассмотрим подход Флори аналогично тому, как это было
сделано в разд. 3 предыдущей статьи [1], — путем введения
вероятности выживания. Здесь вместо времени ty использованного
в [1] при описании кинетических блужданий, мы будем
рассматривать длину цепи N. Основная идея заключается в том, чтобы
дать теоретическое описание метода, который применяется в
численном моделировании для воспроизведения статистики
самонепересекающихся цепей. Запускается множество обычных
случайных блужданий, каждое из которых продолжается до тех
пор, пока блуждающая частица не попадет на узел, в котором
она уже успела побывать ранее. В этот момент
рассматриваемое блуждание прекращается, и его траектория исключается из
статистического ансамбля. Основной вопрос, следовательно,
заключается в том, как вычислить вероятность того, что данное
* L. Pietronero-University of Groningen, Groningen, Melkweg 1, 9718 EP
Groningen, The Netherlands; L. Peliti-Departimento di Fisica, Universita «La
Sapienza», /-00185 Rome, Italy and GNSM —CNR, Unita di Roma.
114
Часть III
тель v, как показано, определяется выражением
Это выражение основано, с одной стороны, на требовании, чтобы
величина df v была для фрактала внутренней, т. е. не
зависящей от его погружения во внешнее (евклидово) пространство, а
с другой стороны, на наблюдении, что ds есть простейшая
внутренняя размерность. Замена d на ds в формуле Пьетронеро (18)
дает нужный результат, который удивительно хорошо
согласуется с результатами компьютерного моделирования на
двумерном ковре Серпинского.
5. Вариации
Модель ИСНБ имела определенный успех вследствие ее
простоты, легкости компьютерной реализации, а также того, что
она демонстрирует нетривиальное, хотя и допускающее
необходимый анализ поведение при низкой размерности. Это
стимулировало появление некоторых других моделей случайного
блуждания с памятью, которые мы кратко рассмотрим в
настоящем разделе. Выше уже упоминался один из вариантов ИСНБ
[14, 15], который принадлежит к тому же самому классу
универсальности, что и СНБ. Другая модификация, при которой
блуждающая частица на двумерной решетке узнает ловушки
до попадания в них, была предложена Кремером и Ликлемой
[24], которые назвали эту модель «неограниченно растущее
самонепересекающееся блуждание» (НРСНБ). (Она может быть
получена в соответствующем пределе из лапласовых блужданий
(ЛБ), которым посвящен доклад Ликлема на настоящей
конференции [25].) Эта модель явно не попадает ни в один из
классов универсальности, которые мы обсуждали до сих пор. Все это
еще более сбивает с толку, поскольку версия НРСНБ на сотовой
решетке оказывается отвечающей равновесной статистике
самонепересекающихся цепей с соответствующими взаимодействиями
между ближайшими и следующими за ними соседями
[26].Действительно, некоторые равновесные конфигурации не
образуются при заданном кинетическом механизме роста, так что ничто
не препятствует модели ИСНБ принадлежать своему
собственному классу универсальности, а отнюдь не тому, в который
входит поведение полимеров в 0-растворителе, как это ранее
предполагалось.
ИСНБ с дальнодействующим отталкиванием [27, 28]
рассматривалось как с помощью соображений Флори —
Пьетронеро, так и па основе теоретико-полевого подхода. Вполне
возможно, что использование эвристических соображений имеет
здесь больще оснований, так ж? как в случае линейных поди-
Статистика полимеров и блуждания без самопересечений 115
меров с дальнодействующими взаимодействиями [29, 30J.
Результаты, полученные на основе подхода Флори, достаточно
близки к данным компьютерного моделирования, чего нельзя
сказать (за исключением тривиальных случаев) о результатах
вычислений с помощью 8-разложения.
Соображениями Флори все же следует пользоваться с
некоторой осторожностью. Это подтверждается при рассмотрении
так называемых ^-толерантных блужданий [31], где
разрешаются все конфигурации с не более чем k пересечениями
траектории в любом узле. Для такой модели, принадлежащей,
очевидно, к одному и тому же классу универсальности с равновесным
ансамблем полимеров в хорошем растворителе, соображения
Флори приводят к иному асимптотическому поведению. По
этому же признаку не ясно, до какой степени можно принять на
веру предсказания, сделанные Оттипгером [32] об
асимптотическом поведении одного из вариантов ИСНБ с переходной
вероятностью
p(r+6|r)~expbg/z«(r+6)]. (21)
Нет основания ожидать, так же как в случае ^-толерантных
блужданий, различного асимптотического поведения при а = 1
(обычное ИСНБ) и, скажем, при а = 2. С другой стороны,
моделирование подтверждает предсказания, сделанные исходя из
соображений Флори — Пьетронеро. По мнению автора, углубление
нашего понимания этого подхода крайне необходимо.
6. Заключения
Одной из основных задач теории фракталов является
выяснение того, какие характеристики физического процесса
приводят к образованию фрактальных структур. В этом смысле
теория случайных блужданий с памятью снимает вопрос, так как
она дает достаточно простое решение задачи. С одной стороны,
траектории частицы, совершающей случайные блуждания с
памятью, очевидно, имеют пустоты, с другой стороны, их
самоподобие обычно можно объяснить таким же образом, как и в
случае критических флуктуации, а именно существованием
неподвижной точки преобразования соответствующей ренормгруп-
пы. По этому же признаку в подобных моделях не следует
ожидать такого интересного явления (наблюдаемого в ДОА-класте-
рах на перколяционных сетках), как сосуществование
нескольких популяций с различным скейлинговым поведением,
отличающихся между собой при наблюдении разных статистических
моментов распределения по массе. По мнению автора,
достижения в нашем понимании поведения случайных блужданий с
памятью скрывают тот факт, что, несмотря на успехи в
кинематике агрегации (а ее изучение, несомненно, улучшило наши
120
Часть III
представляет собой асимптотическую вероятность встречи,
имеющую порядок единицы, а малая поправка к ней
оо
Лр (АО = \ Pn (1) dN ~ N~v (d+e)+{ (10)
N
связана с конечностью величины N.
Проследим теперь за блужданием от его начала (п = 1) до
момента п = N и вычислим его полную вероятность выживания.
При данной длине п она равна 1 — р(п), так что полная
вероятность выживания определяется выражением
5л, = П[1-р(«)]=-П[1-р(оо) + Ар(^)] =
= [1 - Р (оо)]* Цх(п)сх ехр [-р (оо) N] П х (я), (11)
где использовано обозначение
л (я) * + /»("> (12)
Сравнивая выражения (11) и (6), можно установить связь
р (оо) = In (2/г) (13)
между параметрами гиг. Член
f* = n*(«)^^~' (14)
соответствует усилению вероятности выживания из-за того, что
цепь в действительности конечна на каждом шаге. Требование,
чтобы асимптотика fN имела степенное поведение, приводит к
зависимости
^^*fH+i-h = fHW+l)-l]-fH¥-p(-) • (15)
Отсюда следует скейлинговое условие
bp(N)~l/N, (16)
которое ведет к соотношению
v(d + g) = 2. (17)
Подставив сюда определяемое формулой де Клуазо [2]
значение g=(y—l)/v, получим окончательный результат
y = 3 — 4v<» (18)
Статистика полимеров и блуждания без самопересечений 121
Аналогичным образом можно получить значение у для 0-точки
[4] :
Y6 = 2(2-ved). (19)
Эти результаты завершают построение теории среднего поля
для описания статистики полимеров. Более детальное
рассмотрение содержится в работе [4].
Наконец, мы хотим отметить интересный подход
Александровича [6], который также получил формулы v^(4 + d)/4d
и y ^ 8/(4 + d) для показателей v и у. Использованный им
метод ближе по духу к разложению по отклонению от верхней
критической размерности, чем к стандартной теории среднего поля.
Полученные таким способом результаты очень близки к точным
значениям и хорошо согласуются с первым порядком е-разложе-
ния. Суммируя приведенные результаты, можно отметить, что
понятие вероятности выживания ведет к более глубокому
пониманию приближений, лежащих в основе подходов типа
использованного Флори. Исходя из этого понятия, впервые удалось
в рамках теории среднего поля получить выражение для второго
независимого показателя у, характеризующего статистику
полимеров.
ЛИТЕРАТУРА
1. Пелити Л.— наст, сб., с. 106.
2. de Gennes P. G.,, Scaling Concepts in Polymer Physics, Cornell Yniv. Press,
1979. [Имеется перевод: де Жен Я. Идеи скейлинга в физике полимеров. —
М.: Мир, 1982.]
3. Pietronero L.t Phys. Rev. Lett. 55 (1985) 2025.
4. Pietronero L., Peliti L., Phys. Rev. Lett. 55 (1985) 1479.
5. Обухов С. Я., в печати. Этот автор сделал аналогичные замечания
относительно важности «вытянутых» конфигураций.
6. Alexandrowicz Z„ Phys. Rev. Lett. 53 (1984) 1088.
Лапласово случайное блуждание
Я. Ликлема, К. Эвертс *
Вводится однопараметрическое (с параметром г\) семейство
случайных блужданий, которые являются истинно кинетическими и в
точности самонепересекающимися. Эти блуждания представляют
собой пример явления линейной агрегации и близко связаны с
задачей диэлектрического пробоя. Они сводятся при ц=0 к
предложенным недавно неограниченно растущим самонепересекающимся
блужданиям в пространстве произвольной размерности. Установлен
непрерывный характер изменения с ростом г\ показателя v от 1/2
до 1.
1. Введение
Последнее время явления агрегации привлекают к себе
широкое внимание [1]. Их простым частным примером
является так называемое неограниченно растущее
самонепересекающееся блуждание (НРСНБ) [2], которое действительно
самонепересекающееся (так как в каждый узел траектория может
заходить только один раз) и истинно кинетическое (так как все
траектории имеют бесконечную длину). Следовательно, НРСНБ
служит примером линейной агрегации. Описания других
кинетически растущих блужданий можно найти в [3].
Это блуждание имеет важное значение с точки зрения
теории безотносительно к его возможным физическим
применениям. Хотя агрегация численно изучена очень хорошо,
аналитических результатов даже в рамках теории самосогласованного
поля типа предложенной ранее Флори имеется пока не так
много. Поскольку эффект самоусреднения может завуалировать
последствия сделанных приближений, для развития теории этих
явлений легче изучать задачу типа НРСНБ, где нет ветвлений.
К сожалению, пока не имеется алгоритма, применимого к
описанию трехмерного варианта этой модели.
В настоящей статье предлагается линейная версия задачи
диэлектрического пробоя [4] и обсуждается ее связь с НРСНБ
[11]. Показывается также, что свойства НРСНБ можно
воспроизвести с помощью одношаговой вероятности перескоков,
которая связана с решением уравнения Лапласа при
соответствующих граничных условиях. Это новое блуждание, так называемое
лапласово случайное блуждание (ЛСБ) можно определить в
пространстве любого числа измерений. Как и в задаче полного
* /. М. Liklema-Institut fur Festkorperforschung der Kernforschunsanlage
Julich, D-5170 Julich, BRD; Carl Evertsz-Laboratorium voor Vaste Stof Fy-
sica, Rijks Universiteit Groningen, Melkweg 1, 9718 EP Groningen, The
Netherlands.
Статистика полимеров и блуждания без самопересечений 123
диэлектрического пробоя, вероятность перескоков при ЛСБ
зависит от напряженности поля в некоторой степени г). При г| = О
получается НРСНБ, в том числе в пространстве трех и
большего числа измерений. Затем посредством точного перечисления
изучается ЛСБ на квадратной решетке и анализируется
асимптотическое поведение среднего квадрата расстояния между
концами траектории ((R2(N)} ~ N2v). Здесь, в частности, изучено
влияние параметра ri на критический показатель v. В разд. 2
дается определение ЛСБ и описывается его построение. В разд. 3
анализируются численные данные и обсуждаются результаты.
^
/К
Рис. 1.
2. Определение и построение лапласова случайного блуждания
Связь между НРСНБ и задачей диэлектрического пробоя
иллюстрируется на рис. 1, где изображена возможная
конфигурация НРСНБ на квадратной
решетке. Перескок в узел 2 не
разрешен, потому что в этом случае
блуждающая частица
впоследствии оказывается захороненной.
Следовательно, вероятности pi
перескоков из узла / в соседний
с ним узел i оказываются
следующими: рб = 0 (из условия
самонепересечения), р2 = 0 (из
условия истинной кинетики),
рг = Р4 = 1/2 (из условия
равновероятности всех разрешенных переходов). Согласно такому
определению, разрешенные для переходов узлы должны быть
свободными и не приводить в клетку, где осуществляется
захоронение растущего конца траектории. Рассмотрим теперь тот же
самый рисунок, но поместим его в центр большого круга с
радиусом Re, много большим типичного размера блуждания R.
Для такой конфигурации решим уравнение Лапласа V2<D = О,
считая траекторию блуждания и окружность радиуса Rc
идеальными проводниками со значениями потенциала на них: Ф
(траектории) = 0 и Ф(#с) = 1. Потенциал на других узлах
находится из решения конечно-разностного аналога уравнения Лапласа
ф« = т21ф„ (1)
^ пп
где сумма берется по всем ближайшим соседям (пп) узла и
Отсюда сразу получим систему Ф2 = Фе/4 иФ6 = Фг/4, решение
которой ф2 = Ф6 = 0 отражает так называемое фарадеевское
экранирование, которое будет иметь место в клетках любых
размеров и конфигураций. Потенциал всех узлов внутри клетки ока-
124
Часть III
зывается равным нулю до тех пор, пока она может быть
заполнена непрерывной последовательностью идущих вперед связей
между ближайшими соседями или следующими за ними
соседями. Если допустить, что вероятность перескоков блуждающей
частицы пропорциональна потенциалу, то мы получим свойства
такого блуждания, аналогичные свойствам НРСНБ. Оно будет
самонепересекающимся и истинно кинетическим, поскольку
Ф = 0 на узлах траектории и внутри клеток. Мы обобщим его,
как в процессе полного диэлектрического пробоя, положив
р,= ф?1Еф?. (2)
/ пп
Разница между рассматриваемым блужданием и задачей
полного диэлектрического пробоя заключается в том, что в первом
случае рост осуществляется только с конца структуры, и поэтому
образуются линейные фракталы вместо разветвленных. С
позиции диэлектрического пробоя наше определение pi (2) имеет
«нефизическую» особенность, заключающуюся в том, что новый
разряд зависит от напряженности поля только вблизи конца.
Однако со статистической точки зрения рассматриваемая модель
представляет собой корректно определенное случайное
блуждание с нетривиальными взаимодействиями дальнего порядка.
Параметр г\ управляет асимметрией между разрешенными
направлениями. При т] = 0 вероятность р,- не зависит от
напряженности поля и мы приходим к НРСНБ, а при rj > 0 имеем
блуждание с отталкиванием. Вероятность возрастает вместе с
напряженностью поля, и, следовательно, ориентированные
наружу направления будут предпочтительнее других. В
предельном случае г) ->■ оо траекторией является прямая линия, которая
дает показатель v = 1. Для случая т] < 0, отвечающего
блужданию с притяжением, предпочтительными становятся
ориентированные внутрь направления, что приводит к увеличению плот-
ностя. Для того чтобы предотвратить коллапс цепи, следует из
определения вероятности (2) исключить точки с Ф* = 0. Тогда
для т] <С 0 блуждание также останется в точности
самонепересекающимся и истинно кинетическим. В пределе т]->—оо его
траектория будет представлять собой правильную спираль,
поскольку всегда будет выбираться направление, ближайшее к объекту.
Это дает асимптотическое поведение (R2(N)} ~ N, т. е. v = 1/2.
Известно, что для случая ц = 0 (НРСНБ) показатель v = 0,567
[1]. Возникает вопрос о том, меняется ли показатель v от 1/2
(при т|->—оо) до 1 (при т]->оо) непрерывным образом, или
он равен 0,567 для всех конечных значений г\ и претерпевает
скачки лишь на бесконечности. Поскольку траектории для всех
значений г| в точности одинаковые, этот вопрос можно
переформулировать иначе. А именно: изменится ли критическое поведе-
Статистика полимеров и блуждания без самопересечений 125
ние блуждания, если приписать больший статистический вес не
компактным, а растянутым траекториям? Аналогичный вопрос
изучался ранее для обычных СНБ [5] и для ИСНБ [6], где в
обоих случаях было показано, что локальное взаимодействие не
меняет асимптотических свойств. С другой стороны, для ЛСБ
вычисление вероятности перескоков основано на учете
дальнодействия (математически это отражено оператором Лапласа) и
поэтому можно ожидать, что вариация параметра т] приведет
к изменению критического поведения. Это предсказание вроде
бы согласуется с результатами [4] для полного
диэлектрического пробоя. Однако заранее не ясно, останется ли этот
результат справедливым при изучении линейных фракталов вместо
разветвленных.
3. Анализ и результаты
Как отмечалось выше, мы хотим изучить асимптотическое
поведение среднего квадрата расстояния между концами
траектории из N шагов <jR2(AT)> = AN2v. Для этого на квадратной
решетке было осуществлено точное перечисление всех
конфигураций с N ^ 18, а также (для сопоставления) проведены расчеты
с помощью метода Монте-Карло. Мы применили первый подход
из-за его огромного преимущества, заключающегося в том, что
можно использовать решение уравнения Лапласа для
конкретной конфигурации при вычислении скоростей переходов для
целой серии различных значений ц, число которых было взято 49.
Ясно, что это невозможно при вычислениях методом
Монте-Карло, где для одного значения времени следует генерировать
целую серию блужданий. Неудобство заключается в том, что мы
имеем только относительно короткие серии. Для случая т] = О
(НРСНБ) известно, однако, что результаты перечисления в
точности согласуются с данными Монте-Карло {N ^ 100), и можно
ожидать аналогичного совпадения для ненулевых значений г).
Решение дискретного аналога уравнения Лапласа (1)
находится методом итераций, при котором новое значение потенциала
Ф/ в £-м узле вычисляется по старому значению потенциалов в
ближайших соседних его узлах. Если ввести структуру подре-
шетки [7], то удается сделать алгоритм векторным. Только
благодаря этой особенности возможно осуществить точное
перечисление в сериях такой длины. Действительное компьютерное
время, требуемое для этой программы на машине Gray X-MP, было
75 ч. Намного большее время необходимо для нахождения
показателя v с помощью точного моделирования методом
Монте-Карло цепей длины N ^ 1002>5, даже если ограничиться гораздо
меньшим числом различных значений г\. Ясно, что желательно
иметь точные результаты для более длинных цепей, как, напри-
126
Часть III
мер, при N ^.22 для случая г| = 0. Однако для каждой новой
генерации общее машинное время увеличивается в 2,7 раза, и
мы, таким образом, прекратили перечисление на 18-м поколении
генерации. Это требует решения уравнения Лапласа для 9-Ю6
различных траекторий. Мы ожидаем, что максимальная длина
iV = 18 достаточна для изучения наиболее важной зависимости
от г] критического показателя v.
Для анализа среднего квадрата расстояния между концами
траектории мы воспользовались хорошо известными методами
Рис. 2. Зависимость эффективного показателя v(N) от l/(N) на квадратной
решетке. Значения ц сверху вниз следующие: 2,0; 1,75; 1,5; 1,25; 1,0; 0,9; 0,8;
0,7; 0,65; 0,6; 0,55; 0,5; 0,4; 0,3; 0,2; 0,1.
[2, 5, 8, 9] анализа рядов. Предположив асимптотическое скей-
линговое поведение
(R2(N))==AN^(l + BN~A + CN~l +
определим эффективный показатель v(N):
In {{R>{K+l))l<R2(M - !)>} _
.),
(3)
v(N) =
2\n{(N+\)/(N-\)}
= v
4-д£#-л--4--слг1+
(4)
Откладывая зависимость v(N) от 1/JV, в результате
экстраполяции l/Af->0 можно найти значение v. На рис. 2 показаны
результаты для случая отталкивания при 16 различных значениях
г\. Эти данные в значительной степени указывают на
непрерывный характер изменения показателя v, подтверждая, таким
образом, более ранние результаты для задачи диэлектрического
пробоя [4].
Обсудим теперь несколько специальных результатов. Для
т| = 7,5 (не показано) мы нашли v = 0,997, практически
совпадающее с предельным значением v = 1, при котором траектория
Статистика полимеров и блуждания без самопересечений 127
вырождается в прямую линию. Линейный «эквивалент»
диффузионно-ограниченных агрегатов (ДОА), для которого т| = 1,
имеет показатель v = 0,8. Это соответствует фрактальной
размерности df — 1,25, которую можно сравнить со значением df ^
~ 1,75 для разветвленных ДОА. Здесь не следует понимать
«эквивалентность» буквально, поскольку граничные условия не
л.7-
i 1
0,6
0,5-\
0,4-
ttiiiiiii!
i
i
»•:;;;'. \
о,г
7/N
о,г
I
0,3
Рис. 3. Зависимость эффективного показателя v(N) от 1/iV на квадратной
решетке. Значения т] сверху вниз следующие: 0,1; 0,05; 0,03; 0,01; 0,0; —0,01;
—0,03; —0,05; —0,1; —0,2; —0,3; —0,4; —0,5; —0,55; —0,6; —0,65; —0,7;
—0,8; —0,9; —1,0.
идентичны. Для формирования ДОА фрактала [10] следует
запустить на окружность Rc случайно блуждающие частицы и
позволить им двигаться до тех пор, пока они не достигнут
фрактала. Здесь каждая из них приклеивается к нему в узле,
соседнем с узлом, где траектория впервые сталкивается с фракталом.
При ЛСБ приклеивание возможно только на конце фрактала,
а при столкновении со всеми остальными его точками
блуждающая частица бесследно исчезает, т. е. в этих точках она теряет
свою способность к приклеиванию. Иная ситуация получается,
когда хвост блуждания выступает в роли твердой стенки, от
которой блуждающая частица при столкновении отскакивает и
продолжает свое движение дальше. Такие граничные условия
более в духе задачи ДОА, а в контексте ЛСБ они пока что не
были реализованы.
Показатель v = 3/4 обычных СНБ получается при т) = 1п2.
Для осознания этого факта нужно понимать, что хотя
траектории ЛСБ составляют ничтожно малое подмножество
траекторий СНБ, но его мощность бесконечна и именно входящие в
него траектории определяют асимптотическое поведение. Наконец,
несколько необычным является значение ц = 0,6, где
асимптотическое поведение наблюдается с самого начала (v = 0,73).
На рис. 3 показан второй набор значений т), первые 5 из
которых соответствуют отталкиванию, а остальные 15 — притяже-
128
Часть III
нию. При rj = 0, естественно, получается присущее НРСНБ
значение v = 0,567, а в интервале —0,1 <rj < 0,5 зависимость v
от rj оказывается линейной. Поэтому молено ожидать, что при
малых отрицательных значениях ч\ линейная экстраполяция
v(N) от 1/N все еще применима. При больших отрицательных ц
она становится непригодной, что легко заметить из рис. 3. Для
двумерных систем наименьшее возможное значение v — это 1/2,
а функция v(iV) экстраполируется при ц = —0,3 к значению v,
меньшему чем 1/2. Это ясно показывает некорректность
линейной экстраполяции в данной области и необходимость
генерирования цепей с большими значениями N. Следовательно, можно
заключить, что v(N) проходит через минимум и будет
увеличиваться при больших N, стремясь к асимптотическому значению
v ^ 1/2. Такое поведение может наблюдаться при ц = —1, для
которого указанный минимум достигается при N ~ 12.
Подобный характер зависимости предполагает возможность того, что
скейлинговый показатель Д в уравнении (3) оказывается
меньшим единицы. Аналогичное поведение наблюдалось ранее для
обычных СНБ [9]. Предположение Д > 1 делалось неявно при
линейной экстраполяции ЛСБ с отталкиванием. Это
подтверждается в случае rj = 0 (НРСНБ) данными моделирования
методом Монте-Карло цепей с ЛГМакс = 100 [2]. Поскольку
обнаружен непрерывный характер изменения основного показателя v,
можно ожидать аналогичного поведения и для поправочного
скейлингового показателя Д. Таким образом, на основании
наших данных возникает искушение сделать вывод о том, что в
случае отталкивания величина Д больше единицы, но становится
меньшей единицы при переходе к режиму притяжения. Конечно,
такие детали не могут быть количественно установлены из
наших степенных разложений, для чего, возможно, требуются
точные расчеты методом Монте-Карло. К дополнительным
усложнениям при больших отрицательных значениях ri приводят
осцилляции в поведении v{N), причиной которых является
дискретная структура решетки. Тот факт, что осцилляции
проявляются только при таких т|, связан с большим статистическим
весом для этих т) спиральных траекторий среди остальных.
Зависимость критического показателя v от т) для ЛСБ с
отталкиванием показана на рис. 4. Асимптотические значения v =
— l/df (df — фрактальная размерность) найдены линейной
экстраполяцией из степенных разложений v(N), представленных на
рис. 2 и 3. В результате получается гладкая кривая, идущая от
v = 0,567 при ц = 0 к v = 1,0 при г| == 10. К сожалению, мы не
можем объяснить эот результат, потому что для такого типа
явлений пока не существует даже теории среднего поля.
Естественно попытаться описать полученную зависимость
v(r|) некоторой эмпирической рациональной функцией. Мы подо-
Статистика полимеров и блуоюдания без самопересечений 129
брали такую функцию v(r|) = (1 + ц + г]2)/(ф + г] + Л2)»
которая с точностью около 2 % воспроизводит найденную нами
зависимость v от г). Из приведенной формулы следует v(—0,4) =
= 0,5. Это означает, что ЛСБ с ц = —0,4 имеет верхнюю
критическую размерность dc = 2. Хотя такое предсказание по
описанным выше причинам не может быть проверено на основе
наших данных, его нельзя исключить. Так как мы установили
непрерывный характер изменения показателя v, то вправе
ожидать также аналогичного изменения величины rfc.
Следовательно, заранее нет никаких причин полагать, что показатель v
достигает своего предельного значения 1/2 только при т]-*-—оо.
Т9Оп —г
^
0,J-| , 1
О '6 70
V
Рис. 4. Зависимость найденных значений v и т].
Итак, мы показали, что введение взаимодействий дальнего
порядка, таким образом как это осуществляется при ЛСБ,
влияет на асимптотические свойства. Кроме того, мы нашли, что
перераспределение вероятностей среди всех возможных
траекторий не меняет критического показателя v. Более детальный
анализ результатов, в том числе и для трехмерного ЛСБ, будет
опубликован в другом месте.
ЛИТЕРАТУРА
1. Kinetis of Aggregation and Gelation, eds. F. Family, D P. Landau, North
Holland, Amsterdam, 1984.
CECAM-Workshop on Kinetic Models for Cluster Formation.
Yullien #., Kolb M.t Herrmann Я., Vannimenus J., J. Stat. Phys. 39 (1985)
241.
2 Kretner /(., Lyklema J. W.t Phys. Rev. Lett. 54 (1985) 267.
Kremer K, Lyklema J. W., J. Phys. A18 (1985) 1515.
3 Pelitl L., Pietronero L, La Rivista del Nuovo Cimento, в печати.
Ликлема PI. — наст, сб., с 131.
4. Niemeyer L, Pietronero L., Wiesmann И. /., Phys. Rev. Lett. 52 (1984)
1033.
Pietronero L., Wiesmann //. /., J. Stat. Phys. 36 (1984) 881.
5. Lyklema /. W., Kremer /(., J. Phys. A17 (1984) L691,
130
Часть Iff
Kremer /(., Lyklema J. W.y Phys. Rev. Lett., в печати.
Lyklema /. W.y Kremer /(., J. Phys. А, в печати.
6. Bernasconi /., Pietronero L.f Phys. Rev. B29 (1984) 5196.
7. Oed W., Angewandte Informatik 7 (1982) 358.
8. Djordjevic Z. V., Majid /., Stanley H. £., dos Santos R. /., J. Phys. A16
(1983) L519.
9. Lyklema L W., Kremer K., Phys. Rev. B31 (1985) 3182.
10. Witten T. A., Sander L. M., Phys. Rev. Lett. 47 (1981) 1400; Phys. Rev.
B27 (1983) 5686.
11. Pietronero L., будет опубликовано.
Кинетически растущие
самонепересекающиеся
блуждания
Я. Лыклема *
Автор обсуждает самонепересекающиеся случайные блуждания с
зависящей от локального окружения вероятностью перескоков.
Такие блуждания благодаря их линейности представляют собой
простейшие примеры явления агрегации. Используя анализ скей-
линговых степенных разложений для обработки данных
моделирования методом Монте-Карло, изучалось асимптотическое поведение
этих блужданий. Результаты анализа указывают на существование
по крайней мере трех различных классов универсальности: (I) СНБ
(dc = 4) cv = 0,75 при d = 2 и v = 0,59 при d = 3; (II)
растущие трейлы (dc = 3) с v = 0,535 при d = 2 и v = 0,5 при d = 3;
(III) неограниченно растущие СНБ с v = 0,567 при d = 2.
1. Введение
В настоящем сообщении мы обсудим асимптотическое
скейлинговое поведение кинетически растущих
самонепересекающихся блужданий. Они отличаются от обычных
самонепересекающихся блужданий (СНБ) тем, что их одношаговая
переходная вероятность зависит от окружения. Для обычных СНБ
ата вероятность равна (q—I)-1 (для первого шага равна q~\
где q — координационное число решетки). Такое блуждание
описывает, например, равновесный ансамбль полимеров, все связи
которых имеют один и тот же статистический вес. Изучены
некоторые модификации этого блуждания. Они включают &-толе-
рантные СНБ [1] (где блуждающая частица может попасть в
один и тот же узел не более k раз), ^-толерантные
самонепересекающиеся трейлы (СНТ) [2] (блуждающая частица не может
пройти вдоль одной и той же связи более k раз) и циклический
вариант самонепересекающегося блуждания (ЦСНБ) [3]. Все
эти модификации приводят к одному и тому же
асимптотическому поведению, такому, как у обычных СНБ, при котором
верхняя критическая размерность dt. = 4, а показатель v равен
соответственно 3/4 и 0,588 при d = 2 и d = 3.
Впервые отличное от этого критическое поведение на
схожих моделях обнаружил Амит с соавт. [4], предложивший
так называемое истинное самонепересекающееся блуждание
(ИСНБ), в котором вероятности перескоков на соседние узлы
зависят от того, сколько раз траектория уже попадала в них до
этого. Для ИСНБ верхняя критическая размерность dc = 2, а
* /. М. Zift/ema-Institut fur Festkorperforschung der Kernforschungsanlage
Julich, Postfach 1913, D-5170, Julich, Federal Republic of Germany,
132
Часть III
v = 2/3 в одномерных системах [5]. Такое блуждание истинно
кинетическое в том смысле, что оно никогда не прекращается, и
поэтому оно могло бы моделировать явления роста. Однако,
поскольку траектория может приходить в один и тот же узел
более одного раза, это блуждание не в точности
самонепересекающееся и поэтому не подходит для описания реальных
процессов роста.
2. Растущее самонепересекающееся блуждание
В качестве попытки устранить этот недостаток была
предложена [6] версия растущих СНБ. С целью исключить
захоронение для этой модели РСНБ мы модифицируем вероятность
перескоков модели СНБ ри взяв ее в виде 1/а, где а — число
свободных соседних узлов. Однако, если во все ближайшие
соседние узлы траектория уже попадала ранее, блуждание
обрывается. Обычное СНБ обрывается уже в том случае, когда мы
попытаемся попасть в посещенный ранее узел. Поначалу
думали, что эта модель принадлежит к новому классу
универсальности. Однако было показано [7], что это неправильно,
поскольку плотность ловушек, как и для обычных СНБ,
пропорциональна плотности посещенных блуждающей частицей узлов. Поэтому
РСНБ будут принадлежать тому же самому, что и обычные
СНБ, классу универсальности. То что это именно так,
продемонстрировали Кремер и Ликлема [8] многочисленными расчетами
методом Монте-Карло. После этой работы стало ясно, что
асимптотический режим не может быть изучен перечислением серий,
которые чересчур коротки и содержат обычно порядка 20
шагов на квадратной решетке. Так, в работе [8] показано, что на
этой решетке требуется по крайней мере 200 шагов для анализа
РСНБ. Если мы предположим для среднего квадрата
расстояния между концами траектории справедливость обычной скей-
линговой формулы
(R2(N)) = AN*>(1 + BN-* +CN-1 + ...), (1)
то сможем вычислить из наклона зависимости \n(R2(N)} от
In TV значение показателя v. Однако по виду этой кривой очень
трудно определить, достаточно ли велико значение N для
попадания в область применимости асимптотической зависимости
(1). Слегка искривленная линия может быть легко
интерпретирована как прямая, описывающая асимптотическое поведение.
Эта проблема была решена с применением различных методов:
от анализа рядов до полученных с высокой точностью данных
метола Монте-Карло [9]» В связи с этим определим эффектив»
Статистика полимеров и блуждания без самопересечений 133
ный показатель v(N)
\n{(R2(N+l))/(R*(N-\))}_
v(N):
2\n{(N+\)/(N-l)}
= v-^Mf-*-^.N-t+uu9m (2)
Предположив, что поправочный скейлинговый показатель А ^ 1,
можно найти v путем экстраполяции при 1/N-+0 зависимости
(2). Кроме того, одновременно из анализа v(N) при разных N
можно заметить, попадают или нет данные моделирования в
область применимости асимптотической формулы (2).
3. Растущий самонепересекающийся трейл
Мы установили, что любая модификация СНБ, которая
строго сохраняет свойство самонепересекаемости, принадлежит к
одному с ней классу универсальности. Следующая модель, которую
можно изучить, — это растущий самопепересекающийся трейл
(РСНТ), являющийся версией растущих СНТ. По аналогии с
РСНБ мы модифицировали одношаговые вероятности СНТ к
виду pi= l/ac, где ас — число свободных связей. Хотя это
блуждание допускает самопересечения, его не следует путать с
^-толерантным СНБ. РСНТ нигде не может оборваться, кроме как
в начальном узле, потому что, когда частица попадает в узел,
там имеется либо одна, либо три связи, через которые она
может уйти. Начальный узел представляет собой особую точку.
После второго попадания в него остается только одна смежная
с ним непройденная ранее связь, так что блуждание обрывается
при третьем попадании в начальный узел. Это блуждание
может быть определено лишь на решетках с четным числом связей.
Согласно способу его построения, можно ожидать отличного от
СНБ асимптотического поведения, потому что это блуждание
имеет возможность оборваться только в одной начальной точке,
в то время как все другие блуждания могут это сделать на
любом узле решетки.
Выполненные автором методом Монте-Карло многочисленные
расчеты этой модели на квадратной и простой кубической
решетках подтвердили ожидаемое отличие в критическом
поведении от класса универсальности СНБ. Были найдены значения v,
равные 0,535 и 0,5 в пространствах размерности 2 и 3
соответственно. Последний результат явно указывает на то, что
критическая размерность равна 3. В таком случае ожидаются
логарифмические поправки следующего вида:
ШМ)) = АЖ(\пЮпа-
(3)
134
Часть III
Эта скейлинговая формула при значениях а = 0,025, А\ = 1,5 и
А2 = 3,75 дает идеальное согласие с данными, полученными
методом Монте-Карло. При критической размерности, кроме того,
ожидается гауссовское поведение, для которого отношение
(R*(N))/(R2(N))2 = A2/A] должно быть равно 5/3. Именно такое
значение получил автор в результате моделирования блужданий
методом Монте-Карло. Следовательно, он обнаружил
самонепересекающееся блуждание с асимптотическими свойствами,
отличными от класса универсальности обычных СНБ, к которому
принадлежат другие блуждания, за исключением ИСНБ.
4. Неограниченно растущие самонепересекающиеся блуждания
Последними мы рассмотрим неограниченно растущие
самонепересекающиеся блуждания (НРСНБ) [11], для которых од-
ношаговая вероятность равна Pf=l/orny» где апу ~~ число
прыжковых узлов, т. е. ближайших соседей, не ведущих в
клетку. Это безобрывное блуждание сочетает два важных свойства,
необходимых для модели роста. Оно истинно кинетическое и
действительно самонепересекающееся. Траектории НРСНБ
составляют ничтожно малое подмножество от траекторий
общеизвестного СНБ. Возникает интересный вопрос о том, изменится ли
критическое поведение, если использовать иное определение
вероятности перескоков р,- [12, 13]? Мы установили, что это
обязательно произойдет в случае лапласовых случайных блужданий
(ЛСБ) [12], которые являются обобщением НРСНБ. Для
последних мы нашли значение v = 0,567, которое отличается как
от СНБ, так и от РСНТ. Здесь возникает также вопрос о
значении верхней критической размерности. К сожалению, пока он
остается без ответа, потому что все еще не найден алгоритм
построения этой модели (см., однако, работу [12]).
Второй момент, заслуживающий внимания, — это
поведение числа Y(N) различных траекторий длины N. Для СНБ оно
имеет следующую асимптотику [14]:
ПЛО-^ффЛЛ-1. (4)
Параметр у, имеющий смысл критического показателя
восприимчивости, может быть определен исходя из /г-векторной модели
в пределе /z-*- 0 [14]. В формуле
хГмагц - Е Z (N) = S Г (/V) qoN =ZHI[Pi (5)
N N N CN i = \
величина Z(N) равна вероятности найти блуждание длины N.
Здесь T(N) означает число всех возможных конфигураций CN
длины Nf a pi= l/qo = l/(q— I), где q — координационное
Статистика полимеров и блуждания без самопересечений 135
число решетки. Ясно, что Z(N) и число блужданий T{N) имеют
одинаковое асимптотическое поведение, поскольку вероятность
перескоков pi постоянна. При снятии этого ограничения
естественно предположить, что Z(N) имеет асимптотику типа ^фЛЛ"1,
где параметр у снова имеет смысл показателя восприимчивости
(см. работы Ликлемы и Кремера [6]). В случае НРСНБ из-за
сохранения вероятности имеем Z(N) = 1, и соответственно
показатель восприимчивости -у = 1.
Обратимся снова к асимптотическому поведению числа
блужданий Г(Л/Г), которые, как уже упоминалось выше,
представляют собой подмножество траекторий СПБ. Несомненно, что
оно содержит в основном асимптотически длинные блуждания,
поскольку блуждания конечных размеров, которые обрываются
вследствие захоронения, удаляются из статистического
ансамбля. Поэтому можно ожидать, что число Y(N) НРСНБ
асимптотически ведет себя как д^фф^у~\ где ^эфф и у имеют
характерные для СНБ значения: ^эфф = 2,64 и у = 43/32. Это в точности
подтверждается результатами расчетов методом Монте-Карло
[13]. Параметр у может, однако, и не интерпретироваться как
показатель восприимчивости. Это указывает на то, что НРСНБ
можно использовать для изучения критического поведения СНБ,
если разыгрывать испытания с выборочными оценками. Работа
в этих направлениях в настоящее время развивается [13].
ЛИТЕРАТУРА
1. Malakis A, J Phys. А8 (1975) 1885; А9 (1976) 1283.
Guttmann А. /., Byrnes С, Frankel N. £., J. Phys. A17 (1984) L457.
Dekeyser R., Maritan A, Stella Л. /,., Phys. Rev. B31 (1985) 4659.
2. Malakis A, J. Phys. A17 (1984) L837.
Guttmann A. /., J. Phys A18 (1985) 567, 575.
Rapaport D. С J. Phys A18 (1985) L475.
3. Cujrati P. D., Phys. Rev. B27 (1983) 4507.
Guttmann A. /., J. Phys. A17 (1984) 455.
4 Amit D /., Parisi G., Peliti L, Phys. Rev. B27 (1983) 1635.
5. Pietronero L., Phys. Rev. B27 (1983) 5887.
6. Majid /., Jan N.t Coniglio A., Stanley H. £., in: Kinetics of Aggregation
and Gelation, eds. F. Family, D. P. Landau, Norlh Holland, Amsterdam,
1984, p. 51.
Lyklema J. W., Kremer K., in: Kinetics of Aggregation and Gelation,
eds. F. Family, D. P. Landaw, North Holland, Amsterdam, 1984, p. 241.
Majid /., Jan M, Coniglio A., Stanley И. Е., Phys Rev. Lett. 52 (1984)
1257.
Lyklema /. W, Kremer /0, J Phys A17 (1984) LG91
Hemmer S., Hemmer P. C, /. Chem Phys. 81 (1984) 584.
7. Peliti L, J. Physique Lett 45 (1984) 45.
Pietronero L, Phys. Rev. Lett, 55, 2025 (1985).
8. Kremer /0, Lyklema J. W.9 Phys. Rev. Lett. 55 (1985) 2091.
Lyklema J. W.t Kremer K, J. Phys. А, в печати.
9. Lyklema J. W., Kremer K, Ppys. Rev. B31 (1985) 3182.
136
Часть III
10. Lyklema J. W., J. Phys A18 (1985) L617.
11. Kremer K, Lyklema J. W., Phys. Rev Lett. 54 (1985) 267; J. Phys. A18
(1985) 1515. '
12. Ликлема #., Эвертс К.— наст, сб., с. 122.
13. Lyklema I. W., Kremer К., готовится к печати.
14. de Gennes P. G., Scaling Concepts in Polymer Physics, Cornell Univ.
Press, Ithaca, 1979. [Имеется перевод: де Жен Я. Идеи скейлинга в
физике полимеров. — М.: Мир, 1981.]
Переход клубок — глобула
в двумерной системе
Н. Ян, А. Конильо, И. Маджид,
X. Стенли *
Авторы показали, что взаимодействующее самонепересекающееся
блуждание (полимерная цепь при 0-температуре) может быть
отображено на неограниченно растущее самонепересекающееся
блуждание («разумное» кинетическое блуждание). Для показателя v,
характеризующего зависимость расстояния RN между концами
полимерной молекулы от числа звеньев в ней N, полученные
авторами численные результаты вместе с очень точным статистическим
анализом этих блужданий приводят к значению v = 0,57 («4/7).
Критические свойства самонепересекающегося
блуждания (СНБ) известны точно для пространств размерности d = l,
d = 2 [1] и d = 4 [2], которая является верхней критической
размерностью dc этой модели. Для трехмерных систем имеются
лишь приближенные решения, точность которых, однако,
достаточно высока [3—5]. Теория Флори [2] дает значения v =
= 3/(2 + d) показателя v, который характеризует зависимость
Rl-AN*- (1)
радиуса инерции RN от степени полимеризации ;V.
Взаимодействующее СНБ обнаруживает другие критические
свойства при в-температуре, которая соответствует появлению
сколапсированной фазы. Для полимерной цепи в в-условиях
dc = 3, так что критические показатели теории среднего поля
дают в случае трехмерных систем с логарифмической точностью
правильные значения [2]. Двумерная задача представляет
особый интерес, так как здесь ожидаются неклассические
показатели. Эта задача определения критических свойств при
в-температуре является серьезным вызовом теоретикам. Например,
де Жен [6], используя е-разложение Стефена и Макколи [7],
получил v = 0,505, что согласуется с прямым полимерным
рассмотрением Дюплантье [8]. Данные Монте-Карло, полученные
методом рептации, тоже хорошо согласуются с упомянутыми выше
результатами е-разложения. Холоденко и Фрид [10] получили
v = 0,55 используя иную теорию возмущений. В недавнем
препринте Деррида и Салье [11] с помощью метода матрицы
переноса и скейлинга конечных масштабов получили значение v =
= 0,55. Соображения Флори применительно к в-точке приводят
к v = 2/3 [12], в то время как экспериментальные данные
•' Naeem Jan, Antonio Coniglio, Imtiaz Majid, H Eugene Stanley-Center
for Polymer Studies, Boston University, Boston, MA 02215, USA.
138
Часть III
Вилановы и Ронделеса [13] в полимерных монослоях дают
значение v = 0,56.
Нашей исходной точкой служит хорошо известная
зависимость между числом я самонепересекающихся многоугольников
с N + 1 стороной и расстоянием RN между концами
J 2эфф/?ЛГ ,
"W + D-V^J" ' 1%
где гЭфф — эффективное координационное число. Если
многоугольникам приписать правильные статистические веса (т. е.
каждой из Ann пар соседних монометров приписывается весовой
множитель ехр(—е/т), а всему многоугольнику — множитель
ехр(—Ллглге/т)), то придем к формуле
nw{N+\)~R-v{%)dy (3)
где из общих соображений можно ожидать
VCHB Т > в,
v(x)-S V° Г1 Т = 0' (4)
VKo^ =-J T < в.
Рассмотрим «разумное» кинетическое блуждание на сотовой
решетке. Оно строится следующим образом. Сначала
выбираются два произвольных шестиугольника, в центры которых
помещаются буквы «о» и «х» соответственно. Делается шаг вдоль
связи, разделяющей эти шестиугольники. Второй шаг
определяется исходом подбрасывания монеты. В рассматриваемом на
рис. 1 примере этот исход соответствует «о» и второй шаг
сделан в показанном там направлении. Таким же образом делаются
остальные шаги. Они разыгрываются, как и при СНБ, с
вероятностью 1/2 везде, кроме случаев, при которых блуждающая
частица находится вблизи уже посещенной ею ранее области,
когда у частицы может не быть свободы выбора кроме как
переместиться с вероятностью 1 в заднном направлении. Это
происходит, когда все остальные возможности приводят либо к
самопересечению, либо к самозахоронению траектории. Такое
блуждание может быть рассмотрено как блуждание на периметре
кластера треугольной решетки при Рс. Шаги, которые избегают
самопересечения, дают вклад ехр(е), где г — In 2 —
притягивающее взаимодействие между парой соседних мономеров. В то же
время шаги, избегающие самозахоронения, дают тот же самый
вклад, но уже в результате взаимодействия следующих за
ближайшими соселними мономерами. Таким образом, статистиче-
Статистика полимеров и блуждания без самопересечений 139
ский вес конкретного многоугольника W{N -\- 1) равняется
W (N ± 1)= ГснвехрГЕ 8+ £''el. (5)
L пп ппп J
Отсюда число взвешенных многоугольников равно
-v (%) d
tiw{N+ l)~RNU~N-y™a, (6)
где, согласно общим ренормализационным соображениям, мы
ожидаем, что v(t) принадлежит одной из трех стационарных то-
о •
о *—* о . .
. . о . . о . . . .
Рис. 1. Шестиугольник I указывает первый шаг. Состояние шестиугольника 2,
определяемое исходом бросания монеты, предопределяет второй шаг, который
в данном примере есть «о», так что блуждание продолжается вдоль
периметра кластера из «х»-в. Отметим, что «о» и «х» являются частью треугольной
решетки. Используются обозначения для взаимодействий: между ближайшими
соседями (волнистая линия) или между следующими за ближайшими
соседями (штриховая линия). Например, 18-й шаг определяется без рассмотрения
состояния какого-либо шестиугольника, поскольку исход его однозначен в
отличие от предшествующих шагов, которые идентичны СНБ.
чек (4). Показатель vpkb Для «разумных» кинетических
блужданий был определен с высокой степенью точности и оказался
близок к 4/7. Поскольку это блуждание отображается на
взаимодействующее СНБ, а отвечающий ему показатель vpkb
отличается от значений vchb и vKc^, to, следовательно, МКБ имеет
такой же показатель v, как в в-точке.
Для проверки этого результата мы использовали
предложенное недавно кинетически растущее блуждание (КРБ), которое
совсем исключает возможность взаимодействий между
ближайшими соседями, но может подвергнуться захоронению в тупике.
Можно эффективно генерировать очень длительные СНБ с
притяжением лишь между ближайшими соседями. Эти блуждания
имеют характеристики СНБ [15], но при усилении притяжения
мы получили v = 0,57 в хорошем согласии с результатами
приведенного выше анализа.
140
Часть IIJ
ЛИТЕРАТУРА
1. Nienhuis В., Phys. Rev. Lett, 49, 1062 (1982).
2. de Gennes P. G, Scaling Concepts in Polymer Physics, Cornell U. P,
Ithaca, 1979. [Имеется перевод: де Жен Я. Идеи скейлинга в физике
полимеров. — М.: Мир, 1981.]
3. Le Guillou J. С, Zinn-Justin /, J. Physique Lett, 46, L137 (1985).
4 Majid I., Djordjevic Z, Stanley H. E., Phys. Rev. Lett, 51, 1282 (1983).
5 MacDonald В., Jan A/, Hunter D. L, Steinitz M. 0, J. Phys, A18, 2627
(1985).
6. de Gennes P. G, J. Physique Lett, 36, L55 (1975).
7. Stephen M. J, McCauley J. L, Phys. Lett, 44A, 89 (1973).
8. Duplantier В., в печати.
9. Baumgartner A, J. Physique, 43, 1407 (1982).
10. Kholodenko A. L, Freed K. F., J. Chem. Phys, 80, 900 (1984).
11. Derrida В., Salem H., в печати.
12. Majid I, Jan N., Coniglio A., Stanley EL E., Phys. Rev. Lett, 52, 1257
(1984).
13. Villanove R, Rondelez F.t Phys. Rev. Lett, 45, 1502 (1980).
14. Kremmer K, Lyklema J. W.t Phys. Rev. Lett, 54, 267 (1985).
Weinrib A , Trugman 5. A, Phys. Rev, B31, 2993 (1985).
15. Lyklema J W.t Kremmer K, J. Phys, A17, L691 (1984).
Самоподобие взаимен
и самопересечений
случайных фракталов
А. Стелла, Р. Декейзер, А. Маритан *
Обсуждаются фрактальные размерности множеств пересечений
различных типов случайных фракталов. Это позволяет лучше понять
результаты, касающиеся верхней критической размерности,
приближений Флори или универсальности критического поведения при
различных способах учета исключенного объема. В ходе общего
обсуждения этих вопросов рассматривается также диффузия на
самопересекающихся фракталах и на фракталах с локальными
мостиками, где приводятся точные значения относительных
показателей, полученные из анализа данных Монте-Карло.
1. Введение
Для многих статистических задач критического
поведения на решетках, таких, как самонепересекающиеся блуждания
(СНБ) или модели линейных и разветвленных полимеров,
оказываются важными свойства случайных фракталов,
связанные с их взаимо- и самопересечениями. Хорошо известно, что
верхняя критическая размерность задачи должна быть связана
со свойствами взаимного пересечения двух реплик
рассматриваемого случайного фрактала. С другой стороны, концепция
самопересечения фрактала входит как основной ингредиент в
широко применяемое приближение Флори [1] для вычисления
показателя v в полимерных задачах. Связанная с исключенным
объемом энергия отталкивания в этом приближении считается
пропорциональной среднему числу самоконтактов полностью
случайной линейной или разветвленной цепи.
Во втором разделе настоящего сообщения дается обзор
основных результатов первого (насколько нам известно)
систематического исследования скейлинговых законов, которые
управляют статистической геометрией различных сортов
взаимодействий случайных фракталов на решетке [2]. Этому вопросу,
несмотря на его важность (что будет проиллюстрировано далее),
до настоящего времени уделялось лишь незначительное
внимание [3] в математической и физической литературе. Кроме того,
что изучение законов, определяющих фрактальные размерности
само- и ваимопересечений, проливает новый свет на важные
результаты (типа упомянутой выше связи между пересечениями и
критической размерностью или универсальностью показателя v
* A. L. Stella, A. Maritan. Dipartimento di Fisica della Universita di Pa-
dova, 1-35100 Padova, Italy; R. Dekeyser, Instituut voor Theoretische Fysica,
Katholieke Universiteit Leuven, B-3030 Leuven, Belgium.
142
Часть III
по отношению к различным способам проявления
исключенного объема), оно с необходимостью приводит нас к более
глубокому пониманию и новой нетривиальной интерпретации
приближения Флори, как это показано в третьем разделе.
Случайные фракталы с разрешенными самопересечениями,
подобные ^-толерантным блужданиям (при которых
блуждающая частица может попасть в один и тот же узел не более k
раз), представляют интерес не только для обсуждения
упомянутых выше статистических свойств. Важным вопросом здесь
является, могут ли такие самопересечения привести к
нетривиальному значению (отличному от 1) для спектральной размерности,
определяемой диффузией на фрактале [4, 5]. Такой связанный
с динамикой вопрос, для которого вступают в игру новые
аспекты геометрии самопересечений, представляет
самостоятельный интерес в связи с недавними дебатами о возможном
механизме, приводящем к нецелым значениям спектральной
размерности ферродоксина и гемопротеинов, которая следует из
экспериментов по измерению спин-решеточной релаксации [6].
2. Фрактальная размерность взаимо-
и самопересекающихся множеств
Следует ожидать, что фрактальная размерность D (А[\В)
множества точек взаимного пересечения двух случайных
фракталов А и В с фрактальными размерностями D(A) и D(B) будет
даваться законом аддитивности коразмерностей [3], согласно
которому
D(A[\B) = D(A) + D(B)-d (1)
при условии, что правая часть равенства неотрицательна и
D(A(]B) =0 в остальных случаях. Здесь d — это размерность
евклидова пространства, в которое погружен фрактал. Этот
закон можно вывести из простых скейлинговых рассмотрений.
Чтобы быть конкретными, рассмотрим блуждания (СБ, СНБ,
^-толерантные и т. д.) на d-мерной решетке. Обозначая через W
общее блуждание с экстремумом в заданном начальном узле
г = 0 и числом шагов \W\> можно написать формулу для гранд-
канонической вероятности, т. е. производящей функции
вероятности блуждания попасть в узел г
Р^Ек'^г.^ГЕ^Т'' (2)
w L w J
где К — активность шага, а функция %(r, W) равна 1, если W
попадает в г, и равна 0 в остальных случаях. Если 1(К) —гранд-
каноиическое среднеквадратичное расстояние между концами
Статистика полимеров и блуждания без самопересечений 143
блуждания, то обычные скейлинговые рассуждения приводят к
формуле
Я(г)~г-*/(г/£), 1(К)^(КС-КГ\ (3)
справедливой при /*->- оо и К~> К7. Считается, что функция f {у)
стремится к константе при у-*0. Показатель х легко выразить
через v и d. Действительно, сумма Я (г) по всем г равна
среднему числу <||W1I> различных точек, через которые прошла
блуждающая частица. Из определения [3] следует <||W||> ~ £1/v =
s= £D, где D — фрактальная размерность блуждания. Поэтому
на основе вышеупомянутых свойств можно сделать вывод, что
1^ „ %d-x или x=d_[)
Рассмотрим теперь два независимых блуждания Wi и W2 с
одинаковой фрактальной размерностью и, для простоты, с
общим началом. В этом случае при К-+К7 получим асимптотику
< I! W, П W21|) = S Р, (г) Р2 (г) ~ l2D-d, (4)
что находится в согласии с выражением (1).
Закон аддитивности коразмерностей был прямо
подтвержден моделированием методом Монте-Карло fe-толерантных
блужданий с4<5 в двумерных и трехмерных системах [2].
В случае полностью случайных блужданий Р(г) можно
вычислить точно. Найденная таким образом функция удовлетворяет,
естественно, скейлинговой формуле (3), причем x — d — 2 при
d > 2 и х = О при d ^ 2, как это и должно быть, поскольку
фрактальная размерность D — 2 при d > 2 и D — d при d^2
[2]. Для двух независимых случайных блужданий W и W' с
общим началом величина <||^П Wil> стремится при £~>-оо либо
к бесконечности, либо к некоторой константе в зависимости от
того, меньше или больше размерность пространства
критического значения, которое равно четырем. Замечательным при
этом является то, что величина <||№П№"11> оказывается
пропорциональной интегралу, представляющему поправку первого
порядка к четырехточечной одночастичной неприводимой
вершинной функции в теории «ф4» с ультрафиолетовым обрезанием.
При ^том видно, что появление в такой теории инфракрасных
расхол^имостей непосредственно связано с расходимостью
величины <||Wf] №"ll> Для двух случайных блужданий W и W.
Эквивалентное этому утверждение состоит в том, что пересечение
W и W представляет собой фрактал с положительной хаусдор-
фовой размерностью [2].
Более трудная ситуация возникает, когда мы рассматриваем
фрактальную размерность самопересечений данного фрактала.
Ранее предполагалось [3, 7], что фрактальную размерность
точек кратного самопересечения /п-го порядка (m-кратных точек)
144
Часть III
следует определять так, как если бы эти точки представляли
собой взаимные пересечения m независимых реплик данного
фрактала. Фрактальная размерность в этом случае, согласно (1),
должна быть равна mD—(m—\)d, где D — фрактальная
размерность самопересекающегося фрактала. Эта репличная идея,
однако, находится в противоречии с точными результатами для
случайных блужданий и с обширными численными
исследованиями ^-толерантных блужданий в двумерных и трехмерных
системах [2]. В первом случае известно, что среднее число
m-кратных точек (т = 2, 3, ...) для всех случайных блужданий
с \W\=N растет при N-^oo как конечная доля от N [8].
С другой стороны, при К-^Кс можно точно найти асимптотику
корреляционной длины для вероятности того, что в каждый из
двух данных узлов блуждающая частица попадала, например,
дважды [2]. Вид этой асимптотики (Кс — К)~х/2 вместе с
приведенными выше результатами указывают на то, что
фрактальная размерность двукратных точек совпадает с фрактальной
размерностью самого случайного блуждания.
Случай ^-толерантных блужданий представляет собой
интересный пример нетривиальных фракталов, где численно
возможно проверить самоподобие га-кратных точек (га ^ k). Такое
исследование является очень трудной задачей, потому что уже
только для того, чтобы найти асимптотические скейлинговые
свойства расстояния между концами этих блужданий,
необходимо установить (например, методом Монте-Карло)
статистические закономерности крайне длительных блужданий, в
особенности при больших k. Эти трудности намного возрастают, если,
как в данном случае, попытаться дать скейлинговое
рассмотрение среднего радиуса инерции относительно центра масс,
например двукратных точек. Здесь успешная стратегия [2],
аналогичная развитой независимо в работе [9], заключается в
вычислении с высокой степенью точности среднего радиуса
инерции m-кратных точек для блужданий с малым и
промежуточным числом шагов (обычно до N ~ 50) с помощью выборочной
оценки [10]. Такие N, конечно, не пригодны при точном
перечислении, но они не требуют слишком большого числа серий для
достижения необходимой точности. Мы применили некоторые
стандартные методы асимптотического анализа рядов. В то
время как отдельные методы (такие, например, как метод
отношений) слишком чувствительны к неопределенностям в
последовательности данных для систематического использования их в
нашем случае, другие методы, использующие все данные
одновременно (типа аппроксимации Паде), оказываются гораздо
менее чувствительными к шуму и способными поэтому давать
достаточно хорошие результаты. Исходя из них, со всей ясностью
установлен факт, что репличный метод неприменим к т-крат-
Статистика полимеров и блузадания без самопересечений 145
ным точкам. При любом т, как и при случайных блужданиях,
среднее число т-кратных точек растет пропорционально N, а их
средний радиус инерции увеличивается пропорционально
расстоянию между концами траектории блуждания. Это четко
показывает, что фрактальная размерность m-кратных точек такая
же, как и у блуждания в целом.
3. Новый взгляд на приближение Флори
Согласно этому приближению, энергия отталкивания
линейной самонепересекающейся цепи (полимера) из N шагов
(мономеров) полагается пропорциональной среднему числу
двукратных точек случайного блуждания [1J, которое имеет порядок
величины N2R~d, где R — характерный размер цепи, например
расстояние между ее концами. Вычитая из этой энергии
энтропийный член ~R2/N, учитывающий эластичность гауссовской
цепи с удлинением R, и минимизируя полученную свободную
энергию по R, можно получить при ЛГ->оо асимптотическую
зависимость N ~ RD с D= {2 + d)/3 [l, 11].
Первое важное замечание заключается в том, что
асимптотическая зависимость ~N2R~d для среднего числа двукратных
точек не соответствует нашим знаниям о самопересечениях.
Известно [2], что это число должно быть пропорционально N. С
другой стороны, поскольку N ~ RD, выражение N2R~d удобно
представить в эквивалентном виде R2D~d, который можно
интерпретировать, согласно закону аддитивности коразмерностей, как
число взаимных пересечений двух независимых реплик цепи.
Подобная интерпретация отличается от той интуитивной
идеи, которая была заложена в основу аппроксимации
Флори.
Для того чтобы понять, каким образом можно согласовать
эти два кажущихся противоречивыми аспекта
(взаимопересечение и самопересечение), нужно прибегнуть к новой
интерпретации указанной аппроксимации в целом, что будет сделано ниже.
Необходимость такой реинтерпретации наиболее очевидна при
рассмотрении случая fe-толерантных блужданий, для которых
наивное применение стандартных рассуждений Флори ведет к
неправильным результатам. Перенося эти рассуждения со
случая k=\ на произвольные k, следует записать выражение для
энергии отталкивания ^-толерантного блуждания, связанной со
столкновениями (& + 1) мономера, в виде Л^+1/?--ы. Это
приводит к зависящему от k значению фрактальной размерности D =
= (2 + kd)/{k + 2) [7], что оказывается неправильным
предсказанием, поскольку в действительности величина D остается
при всех k равной ее значению для k== 1 при обычных СНБ [12,
13]. Ясно, что для написания члена, учитывающего отталкива-
146
Часть III
ние в выражении для свободной энергии в рамках приближения
Флори, требуется более подходящий критерий. Как мы покажем
ниже, этот критерий не может игнорировать истинную
геометрию как взаимо-, так и самопересечений случайных
фракталов.
Для того чтобы найти свободную энергию цепи из N
мономеров, мысленно разобьем ее на N/I сегментов таким образом,
чтобы каждый сегмент содержал большое число / мономеров и
мог рассматриваться как отдельный фрактал. Свободная
энергия цепи может быть найдена как сумма свободных энергий
всех N/1 сегментов плюс вклады от межсегментных
взаимодействий. Первая часть может быть записана как (N/l)F0(l), где
^о (0 — свободная энергия сегмента размера /, которая,
естественно, не зависит от удлинения R всей цепи. В духе
приближения Флори мы будем рассматривать различные сегменты как
независимые случайные цепи (СБ) длины /. Энергия их
взаимного отталкивания определяется эффектами отталкивания
между сегментами. Число их соударений в духе теории среднего
поля будет пропорционально (N/l)2(R/ll/2)-d с учетом того, что
удлинение каждого сегмента должно быть ~ /1/2. Поскольку
сегменты являются фракталами, среднее число точек пересечения
какой-либо их пары должно быть пропорционально величине
(/1/2)4~rf, которая получается в результате возведения удлинения
11/2 сегмента в степень (2X2 — d)> равную фрактальной
размерности взаимных пересечений двух случайных блужданий.
Энтропию сегментов легко найти, поскольку она представляет
собой энтропию случайной цепи (N/1) сегментов с общим
удлинением (R/ll/2). В результате можно написать выражение
р = (М/1) F0 (/) + a {Nllf (R/l{/Td {lxl2f~d + b {Rim21 {NII) (5)
для полной свободной энергии, где а и Ь — некоторые
размерные слабо зависящие от / коэффициенты. Замечательной
особенностью выражения (5) является то, что оно дает ту же самую
зависимость свободной энергии от N и R, которая получается
при использовании приближения Флори для
самонепересекающихся цепей. Уравнение (5), в котором / играет роль
масштабного параметра, действительно напоминает неоднородное скей-
линговое уравнение для свободной энергии спиновой модели
вблизи неподвижной точки ренормгруппового преобразования
[14]. Следовательно, в обычном выражении Флори для
свободной энергии скрыта масштабная инвариантность, которая
проявляется, однако, при соответствующей форме записи ее в виде
выражения (5).
В приведенном выше выводе формулы для свободной
энергии используются те же самые основные допущения, что и в
стандартном выводе [1], кроме точного учета пересечения фрак-
Статистика полимеров и блуждания без самопересечений 147
талов. Последнее обстоятельство дает то важное преимущество,
что оно позволяет понять, почему свободная энергия в виде (5),
приводящая к показателю модели СНБ, описывает также &-то-
лерантные блуждания с k>\. Действительно, второй член в
(5) должен оставаться неизменным при любом k. Это
заключение мы можем сделать, исходя из рассуждений, приведенных в
предыдущем разделе, о том, что (k -f- 1)-кратные точки
взаимных пересечений двух случайных блужданий из / шагов будут
расти в среднем как (ll/2)4-d при всех к. Эти точки можно,
конечно, представить как простые пересечения /Zi-кратных точек
первого блуждания с ^-кратными точками второго при условии
fti + n2 = k-\- 1. Для каждого п множество я-кратных
самопересечений фрактала образует фрактал с той же самой
размерностью.
Соображения, аналогичные представленным в настоящем
разделе, можно сформулировать и для решения других задач на
основе приближения Флори, таких, например, как описание
разветвленных полимеров [2].
4. Спектральная размерность ^-толерантных
и случайных блужданий
Как отмечалось во введении, самопересекающиеся фракталы
(подобные, например, ^-толерантным блужданиям)
представляют интерес также с точки зрения динамики. Очень важными
стимулами для общего изучения динамики фракталов [4, 5]
послужили хорошо известные экспериментальные результаты по
низкочастотному поведению плотности колебательных состояний
в ферродоксине и некоторых гемопротеинах [6]. Специфическая
проблема, возникающая при интерпретации этих экспериментов,
состоит в понимании того, до какой степени присутствие сшивок
(например, за счет водородных связей) между различными
сегментами боковых привесков белка может изменить его
существенно одномерный характер динамического поведения и
привести к спектральной размерности, большей чем
единица [15].
Эквивалентный этому вопрос можно сформулировать на
языке решеточных моделей диффузии на случайных фракталах
относительно того, изменится или нет показатель,
характеризующий, например, случайное блуждание на
самонепересекающейся цепи, если разрешить сверхпрыжки между несмежными
узлами цепи. Такие прыжки рассматривались только через
короткие мостики, т. е. между соседними узлами, в которые цепь
попадала с интервалом в определенное число шагов. Другой путь,
приводящий к отклонению от закона диффузии на
самонепересекающейся цепи, заключается в рассмотрении случайного
148
Часть III
блуждания, например на 2-толерантном блуждании.
Фрактальная размерность последнего будет такая же, как и СНБ [12, 13],
но диффузия на 2-толерантном блуждании может заметно
усилиться из-за множества сверхпрыжков, совершаемых из
двукратных точек.
Задача диффузии на самоиепересекающихся блужданиях с
короткими мостиками была совсем недавно исследована
несколькими авторами [2, 16]. Достаточно точное определение
показателя, характеризующего такую диффузию в двух
измерениях, было найдено из анализа серии около 107 случайных
блужданий длиной от 1 до 50 шагов, начинающихся в середине
самонепересекающихся блужданий длиной в 200 шагов, что
позволяет исключить граничные эффекты [2]. Для каждой
группы из 50 случайных блужданий использовались блуждания с
различными конфигурациями. Применение упомянутого в
предыдущем разделе метода анализа серий дало нам значение
Dw = 2,65 d= 0,03. Фрактальная диффузионная размерность Dw
определяется соотношением / ~ R°w между средним смещением
R и числом шагов /, за которое оно произошло. Тот факт, что
найденное нами значение показателя Dw не отличается от того,
который получается при простой диффузии на
самонепересекающейся цепи, означает, что спектральная размерность в данном
случае равна единице.
Аналогичное исследование диффузии было проделано на
2-толерантных блужданиях в двумерном пространстве. При
этом получено Dw = 2,65 ± 0,15, что дает достаточно четкое,
хотя и не столь точное подтверждение сходности со случаем
СНБ.
Типичная картина 2-толерантного блуждания,
согласующаяся с этим результатом и с результатами предыдущего раздела,
показывает, что конфигурации, в которых большинство петель
образовано блужданием между двумя попаданиями в его
двукратные точки, имеют малые пространственные масштабы.
После нескольких усреднений этих мелкомасштабных петель
блуждание выглядит как соответствующая самонепересекающаяся
структура. Появление больших петель предотвращается неким
эффектом экранировки, обязанным присутствию плотной и
однородной последовательности малых петель вдоль структуры.
Согласно такой картине, фрактальная размерность двукратных
точек в точности идентична, как и должно быть, фрактальной
размерности всего блуждания, а диффузия должна иметь
асимптотическое поведение, такое же как на простом
самонепересекающемся блуждании.
Для диффузии на чисто случайном блуждании мы должны
ожидать иного поведения. В этом случае, где нет fe-толерантно-
сти для осуществления экранирования, можно ожидать появле-
Статистика полимеров и блуохдания без самопересечений 149
ния петель всех пространственных масштабов, которые
оказывают существенное влияние на динамические показатели.
Многочисленные данные моделирования для этого случая приводят
при d = 2 к диффузионной размерности Dw = 2,99 ± 0,04. Этот
результат явно подтверждает значение Dw = 3, которое непрямо
и менее четко следует из расчетов сопротивления случайной
цепи [17], но находится в противоречии с результатами работы
[18]. Спектральная размерность [4, 5] случайного блуждания
в двух измерениях, таким образом, равна 2D/Dw — 4/3, где
D = 2 есть фрактальная размерность случайного
блуждания.
5. Заключительные замечания
Приведенные выше результаты показывают, что короткие
мостики или самоконтакты в первоначально
самонепересекающейся структуре не влияют на диффузионные свойства на ней. Этот
вывод подтверждает догадки некоторых авторов, высказанные
ими в ходе простых объяснений экспериментальных фактов,
касающихся белков [15]. Для того чтобы получить значение
спектральной размерности, большее единицы, мы должны полностью
отказаться от самонепересечения или ограничений типа &-толе-
рантности.
Альтернативная возможность, позволяющая сохранить
самонепересекающуюся структуру, заключается в разрешении
дальних прыжков между различными узлами цепи. Это было
показано на основе точных ренормгрупповых вычислений для
модели двумерной диффузии на детерминистическом фрактале,
которые привели к неуниверсальным спектральным размерностям
во всем диапазоне между 1 и 4/3 [19]. Длинные мосты для
перескоков в этой модели по существу играют роль петель
всевозможных длин, которые влияют на диффузию на абсолютно
случайной, ничем не ограниченной цепи.
ЛИТЕРАТУРА
1. de Gennes P. G., Scaling Concepts in Polymer Physics, Cornell U. P.,
Ithaca, 1979. [Имеется перевод: де Жен П. Идеи скейлинга в физике
полимеров.—М/ Мир, 1981.]
2. Dekeyser R., Maritan A., Stella A. L., будет опубликовано.
3. Mandelbrot В. В., The Fractal Geometry of Nature, Freeman, San Fran-
sisco, 1982.
4. Alexander S.t Orbach R., J. Physique Lett., 43, L625 (1982).
5 Rammal R., Toulouse G., J. Physique Lett., 44, L13 (1983).
6. Stapleton H. /., Allen /. P., Flynn C. P., Stinson D. G., Kurtz S. R., Phys.
Rev. Lett, 45, 1456 (1980).
7. Turban L., J. Phys., A16, L643 (1983).
8. Montroll E. W.t Weiss G. Я., J. Math. Phys., 6, 167 (1965).
150
Часть III
9. Lyklema /. W., Kremmer /(., Phys. Rev., B31, 3182 (1985).
10. Rosenbluth M. N., Rosenbluth A. W., J. Chem. Phys., 23, 356 (1955).
11. Flory P. /., Principles of Polymer Chemistry, Cornell U. P., Ithaca, 1969.
12 Guttmann A /., Byrnes C, Frankel N. E., J. Phys., A17, L457 (1984).
13. Dekeijser R., Maritan A, Stella A. L., Phys. Rev., B31, 4569 (1985).
14. Niemeijer Th., van Leeuwen /. M. /., Physica, 71, 17 (1974).
15 Helman /. 5., Coniglio A., Tsallis C, Phys. Rev. Lett., 53, 1195 (1984).
16. Yang Y. S , Liu Y. Lam P. M , Z. Physik, B59, 445 (1985)
Chowdhury D , Chakrabarli B. K., J. Phys., A18, L377 (1985).
17. Bancuar J. R., Harris A. B.y Koplik /„"Phys. Rev. Lett., 51, 1115 (1983).
18. Halvin S., Weiss G. H., Ben-Avraham £>., Movshovitz ZX, J. Phys., A17,
L849 (1984).
19. Maritan A., Stella A, Univ. of Padua preprint DFPD 17/85 (1985).
Статистическая механика
самонепересекающихся
случайных поверхностей
А. Маритан, А. Стелла *
Самонепересекающиеся случайные поверхности (ССП) получаются
в пределе п-+0 из соответствующих решеточных калибровочных
моделей с га-компонентными переменными связей. Точно вычислен
показатель v для ССП на решетке с фрактальной размерностью
1 + In 3/In 2.
1. Введение
Модели случайных поверхностей и их фрактальные
свойства представляют интерес в нескольких отношениях. На
основании ряда экспериментов теперь совершенно ясно, что
поверхности многих материалов представляют собой случайные
образования, которые обладают свойством самоподобия,
начиная с масштабов в несколько молекулярных радиусов [1—3].
Случайные поверхности являются также естественными
обобщениями более знакомых моделей случайного блуждания. Можно
ожидать, что первые будут играть такую же важную роль в
калибровочных теориях, какую играют вторые в спиновых
задачах.
ССП по аналогии с самонепересекающимися блужданиями,
определяются как связанные множества плакетов
(элементарных ячеек) гиперкубической d-мерной решетки. Не более двух
плакетов может встретиться вдоль общего ребра, а каждый пла-
кет решетки может входить в множество только однажды
(исключенный объем). Недавно [4, 5] для ССП была предложена
скейлинговая теория, основанная на соответствующих
обобщениях концепций и методов статистики полимеров. Здесь будет
дана предварительная оценка новых результатов, касающихся
связи ССП с калибровочными решеточными теориями (разд. 2),
и приведены точные результаты в нетривиальной модели ССП
на фрактальной решетке (разд. 3) [6].
Используя формализм большого канонического ансамбля для
ССП, можно рассмотреть однопетлевую корреляционную
функцию
Wr(K)= И K]S\ (1)
S:dS=T
где через К обозначна активность плакета, а каждое S — это
ССП с |S| плакетами и контуром dS (ребра, принадлежащие
* Amos Maritan, Attilio L. Ste/Za-Dipartimento di Fisica dell'Universiln di
Padova, Italy.
152
Часть III
одному плакету), совпадающим с самонепересекающимся
замкнутым путем Г [5]. Часто в качестве Г можно выбрать контур
др элементарного плакета р, а определение (1) можно,
очевидно, обобщить на случай более чем одной петли, например для
того, чтобы ввести корреляционную функцию связи между
двумя плакетами. Ее радиус ЦК) определяет масштаб длины,
характеризующий, например, поверхности, которые дают основной
вклад в сумму (1).
Можно ожидать, что как WoP(K), так и ЦК) будут иметь
сингулярное поведение при приближении активности К снизу к
ее критическому значению Кс. Ведущие сингулярные члены при
этом имеют вид Wdp(K)~(Kc-Ю~у+\ %(Ю~(КС-КГУ.
Показатель v равен обратной фрактальной размерности, а у
имеет энтропийный смысл. Действительно, согласно (1), число
поверхностей с |S| плакетами и с контуром др будет иметь при
больших |S| асимптотику | 5 |Y~2/<7l S' [4, 5].
Для односвязных поверхностей приближение типа сделанного
Флори дает v = 3/(4 + d) при d < 8 и v= 1/4 при d ^ 8 [4].
Эта зависимость находится в отличном количественном согласии
с результатами вычислений методом ренормгруппы в реальном
пространстве [4]. Значение v = 1/4 для ССП выше верхней
критической размерности dc = 8 подтверждается асимптотическими
расчетами в пределе d->oo, которые дают v = 1/4 и у = 1/2
[5, 7]. Известно также, что для случайных поверхностей без
ограничений, связанных с исключенным объемом, точные для этой
модели вычисления приводят к значению v= 1/4 [8].
Используя соображения типа примененных ранее к перколя-
ции и решеточным животным [9], можно предугадать
нарушение гиперскейлинга у = 2— v(d — 2) в случае ССП [6].
2. ССП и калибровочные решеточные теории
Связь между калибровочными теориями и случайными
поверхностями может быть установлена точно, если последние
являются самонепересекающимися. Действительно, ССП может
быть получена в пределе я->0 соответствующих калибровочных
моделей с /г-компонентными векторными переменными,
характеризующими связи [6, 10]. Для того чтобы исключить трудности,
возникающие при предельном переходе п~+0, нужно
использовать не матричные, а векторные переменные [10, 11].
В целях иллюстрации основного результата рассмотрим
калибровочную модель на решетке. Каждой связи, которая
соединяет пару ближайших соседних узлов (1У /), поставим в
соответствие переменные S?/(а = 1, 2, ..., п), являющиеся компонен-
Статистика полимеров и блуждания без самопересечений 153
тами вектора с 2/г возможными орнентацнями S^(o, .. ., О, ±
+ V^, 0, ..., 0).
С помощью рассуждений, аналогичных приведенным в
работе [12], можно показать, что для гамильтониана
h-kZZ П4 (2)
где произведение берется по всем парам (/, /), принадлежащим
dp, а сумма — по всем плакетам, справедливо следующее
выражение:
lim (Usli\=WT(K). (3)
Здесь p — произвольная метка, Г — самонепересекающийся
замкнутый путь, а произведение берется по всем
принадлежащим ему парам (&, /). Функция в правой части (3) определена
выражением (1) и содержит вклады от одно- и многосвязных
поверхностей.
Гамильтониан (2) обладает глобальной симметрией по
отношению к перестановкам компонент. Его локальная
калибровочная инвариантность относительно преобразований типа S//->
-> 6/S//8/ с е/ = ±1 характеризуется группой симметрии j£2-
Приведенные выше результаты могут быть легко обобщены на
другие корреляции или на случай векторных переменных, который
включает в рассмотрение все возможные ориентации в
n-мерном пространстве.
3. ССП на фрактальной решетке
Рассмотрим фрактальную решетку в трехмерном
пространстве, типа схематически изображенной на рис. 1. Она состоит из
последовательности кривых Серпинского, уложенных
параллельно плоскости XY. Каждый узел на данной кривой соединен
также связями с соответствующими ближайшими соседними узлами
на смежных кривых. Такую же решетку, которую мы назовем тоб-
лерон-решеткой, рассматривали независимо Хильфер и Блюмеи
в другом контексте [13]. Для построения ССП можно
использовать все квадратные плакеты, которые содержат связи,
ориентированные в направлении оси г. При том же построении в
качестве плакетов могут быть использованы лишь направленные вверх
(незаштриховаиные) параллельные плоскости XY треугольники.
С помощью метода рекурсии, который по существу
равносилен ренормгрупповым расчетам, можно точно вычислить
показатель v для ССП на данной решетке, что дает v = In 2/lnf 7—
— у 5 ) ex. 0,44. Легко заметить, что это значение v соответст-
154
Часть III
вует увеличенной на единицу фрактальной размерности одного
из самонепересекающихся блужданий на ковре Серпинского в
двумерном пространстве (14). Плоский ковер Серпинского и тоб-
лерон-решетка имеют соответственно фрактальные
размерности In 3/ln 2 и 1 + 1пЗ/1п2, отличающиеся на единицу.
Приближение Флори для ССП [4] и для самонепересекающихся
блужданий [15] демонстрирует аналогичное свойство. Фрактальная
размерность поверхностей в (d +
+ 1)-мерном пространстве (d ^
^ 4) получается при добавлении
единицы к фрактальной
размерности блужданий в d-мерном
пространстве.
Подставляя в полученное
нами в рамках приближения
Флори выражение v = 3/(4 + d)
вместо d значение фрактальной раз-
Рис. 1. Тоблерон-решетка. мерности тоблерон-решетки,
получим величину V —0,45, которая
находится в удовлетворительном качественном согласии с
точным результатом.
4. Заключительные замечания
Развитием разд. 2 является нетривиальное обобщение на
поверхности хорошо известного результата, касающегося предела
/г->0 для О (я)-спиновой модели [16]. В разд. 3 впервые,
насколько авторам известно, приведены точные результаты по
нетривиальной модели ССП. Более того, они дают дальнейшее
подтверждение применимости ренормализационпого подхода и
приближения Флори при общем изучении ССП [4, 5].
ЛИТЕРАТУРА
1. Avnir £>., Farin D.y Pfeifer P., Nature (London), 308, 261 (1984).
2. Pfeifer P., Avnir D.y Farin D., Wipperman #, Fractal Surfaces and Pore
Size Distribution of Disordered Materials; см. Пфейфер П. — наст, сб
с. 72.
3. Schaefer D. W., Structures of Random Materials from Scattering
Techniques; см. Шефер Д, Кефер К. — наст, сб., с. 62
4. Maritan A., Stella A. L., Phys. Rev. Lett., 53, 123 (1984).
5. Maritan A, Stella A. L, in: Applications of Field Theory to Statistical
Mechanics, ed. L. Garrido, Springer, Berlin, p. 316, 1985.
6. Maritan A, Stella A. L, будет опубликовано.
7. Drouffe J. M, Parisi G.t Sourlas N.t Nucl. Phys, B161, 397 (1980).
8. Eguchi Т., Filk Г., Phys. Lett, 149B, 381 (1984).
9. Family F, J. Phys, A15, L538 (1982).
10. Maritan A, Topics on Static and Dynamic Properties of Fractals,
Ph. D. Thesis, International School for Advanced Studies, Trieste, 1985.
Статистика полимеров и блуждания без самопересечений 155
11. Durhuus В., Frohlich /., Jcnsscn /., Nucl. Phys., B225, 185 (1983).
12. Hilhorst H. /., Phys. Rev., B16, 1253 (1977).
13. Хильфер Р., Блюмен А.— наст. сб. с. 54.
14. Klein D. J., Seitz W. A, J. Physique Lett., 45, L241 (1984).
15. de Gennes P. G., Scaling Concepts in Polymer Physics, Cornell Univ.
Press, Itaca, 1979. [Имеется перевод: де Жен П. Идеи скейлинга в
физике полимеров. — М.: Мир, 1982.]
16. De Gennes P. G.} Phys. Lett., 38A, 339 (1972).
Приближение типа аппроксимации
Бете для самонепересекающихся
случайных блужданий и поверхностей
(и фрустрации)
А. Каппелли, Р. Лава,
А. Маритан, С. Руффо *
1. Введение
Стандартное применение метода среднего поля (СП) к
решеточным статистическим моделям предполагает:
(I) свести многочастичную задачу к одночастичной в
эффективном поле,
(II) определить это поле из самосогласованного уравнения
относительно локального параметра порядка типа
намагниченности.
Во многих статистических моделях типа случайных
блужданий и моделей фрустрации трудно использовать метод СП,
потому что соответствующий параметр порядка либо неизвестен,
либо даже вообще не существует.
Здесь мы обсудим некоторые методы типа приближения Бете,
которые исключают эти трудности. Основная идея заключается
в использовании уравнения согласования между
корреляционными функциями кластеров со многими узлами. Член,
ответственный за нарушения симметрии, заменяется эффективным
взаимодействием на границе кластера.
Для самонепересекающихся блужданий и поверхностей, а
также для полностью фрустрированных двумерных спиновых
моделей параметр порядка еще требует идентификации, в то время
как для решеточных калибровочных теорий более аккуратная
идентификация параметра порядка — фрустрация — возможна
благодаря использованию преобразования дуальности. В
последнем из трех случаев основная особенность этого метода
заключается в том, что он сохраняет калибровочную
инвариантность.
2. Блуждания и поверхности
Рассмотрим модель самонепересекающихся случайных
блужданий на квадратной решетке. Производящая функция блу-
* Andrea Cappelli, Roberto Livi, Stefano /faffo-Dipartimento di Fisica and
TNFN Sczione di Firenze, Largo E. Fermi 2 1-50125 Firenze, Italy; Amos Ma~
ntatt-Dipartimento di Fisica and INFN Sezione di Padova, Via Marzolo 8
1-35131 Padova» Italy.
Статистика полимеров и блуждания без самопересечений 157
жданий определяется как [1]
0(х9у\К)= I K|FI. (2Л)
W:6W={x, у}
где сумма распространяется на все самонепересекающиеся
блуждания из х в у длиною в \W\ шагов между ближайшими
соседними узлами, а К — активность мономера.
Для определения приближения типа аппроксимации Бете на
кластере (рис. 1) введем
поверхностную эффективную активность К' [2]
и наложим следующее условие
согласования между корреляциями
ближайших соседей [2]:
0(1, 2;/С, K') = G(0,S;K, /СО- (2.2)
Решение этого уравнения К'(К)
пропадает при значении /Сс = 0,406,
которое можно интерпретировать как
точку перехода, выше которой сумма
(2.1) расходится (теорема Хаммерсли
[37]). В настоящее время принято
значение Кс = 0,38. В окрестности точки
перехода «внутренняя энергия»
d
U(K) = KZ G(x, х + \х\ К) (2.3)
(где \х — единичные векторы решетки) имеет асимптотику
U(K) = K-+Kcconst'(Kc-K){~a при а =1/2. (2.4)
Обобщением предыдущей модели служат
самонепересекающиеся случайные поверхности, которые строятся из
элементарных квадратов (плакетов) Р на гиперкубической решетке.
Ограничение заключается в том, что каждая связь b поверхности S
входит в состав двух плакетов. Исключение составляют
граничные связи Ъ е 6S, каждая из которых принадлежит только
одному плакету. Активность К связана с каждым плакетом.
Функция Грина, соответствующая замкнутому непересекающемуся
пути у, которая называется здесь контурной функцией,
определяется формулой
G(Y)= £ K]S\ (2.5)
где сумма берется по всем самонепересекающимся поверхностям
площади |S|, ограниченным контуром 6S «а^
1
1 1
1\ 2\ 3
Го
---/JLj
4
5
1 л }
\ 1
1 1
1 1
•
1
1
Рис. 1. Пример кластера,
рассматриваемого в задаче
двумерных
самонепересекающихся блужданий.
Эффективная активность
приписывается связям,
изображаемым двойными
линиями.
158
Часть III
Этот метод можно применить в простейшем случае rf = 3
для расчета кластеров, приведенных на рис. 2. Активности К и
К' относятся соответственно к
объему и границе. В этом случае мы
также наложим условие согласования
G(6P; К, tf') = G(6P'; К, К'), (2.6)
Рис. 2. Пример кластера, рас
сматриваемого в задаче само
непересекающихся
поверхностей. Объемные плакеты за
штрихованы.
где Р и Р/ обозначают один из
граничных и внутренних плакетов
соответственно. Решение уравнения
(2.6) пропадает при Кс = 0,537.
Согласно обобщению теоремы Хаммер-
сли [4], это можно
интерпретировать как сигнал фазового перехода.
Метод Монте-Карло приводит к
Кс = 0,588 [5], а метод ренормгруп-
пы дает 0,62 -f- 0,64. Критический
показатель внутренней энергии а снова равен 1/2.
В обоих рассмотренных нами случаях можно добиться
улучшения результатов либо увеличением размера кластера, либо
введением дальнейших условий согласо- ш^
вания.
3. Треугольная фрустрированная модель
Антиферромагнитная модель Изинга
на треугольной решетке не имеет при
нулевой температуре упорядоченной фазы
[7], что свидетельствует о
неприменимости для этого случая стандартного
метода СП.
Мы применим здесь наш метод для
простого кластера показанного па рис. 3.
Его приведенное действие запишется в
виде
А\ = — $ахов — Р' Z otai¥Xy оь = ох.
Рис. 3. Пример кластера,
рассматриваемого в
треугольной фрустрирован-
ной модели.
Наложим условие согласования между «внутренними» и
«внешними» двухточечными функциями Грина:
(^^з)л = (°'1сг2)л. (3.1)
Решение (J'flJ) уравнения (3.1) существует всегда, и поэтому
здесь при всех температурах, кроме нулевой, не ожидается
фазового перехода, что согласуется с точным результатом [7]. (В фер-
Статистика полимеров и блуждания без самопересечений 159
ромагнитном случае переход найден при Рс = 0,346.) Мы
получили приемлемое значение энтропии при нулевой температуре
S0 = 0,2877, которое можно сравнить с точным значением S0 —
= 0,3231 [7; 8]. Сейчас изучаются возможности улучшений и
расширений нашего метода применительно к другим фрустриро-
ванным решеточным моделям.
4. Решеточная калибровочная теория
Ограничимся описанием нашего метод для 22-решеточной
калибровочной модели при d — 3. (Более общий анализ имеется
в работе [9].)
Рис. 4. Пример кластера, рассматриваемого в Z2 калибровочной теории при
d = 3, и его дуальный спиновый кластер (сплошные линии).
На простом изинговском кластере Л, изображенном на рис.4,
мы определим приведенное действие
лЛ = р (s0sf0 + E 50s2 + s'Qs') + ь I st + s;, (4. i)
где член ~by ответственный за нарушение симметрии, вводится
в самом начале. С помощью преобразования дуальности
величины Л л отображается на калибровочное действие
ЛХ = Р Z ap + b Z <тр, (4.2)
Pel Ре=Л
определенное на дуальном кластере Л, где thjj = exp(—2р),
th Ь = ехр(—2&), а аР — ооао — переменная, характеризующая
плакеты.
Условие согласования Бете—Пайерлса для намагничивания
на изинговском кластере превращается в результате
преобразования дуальности в следующее уравнение:
<ехр[- 2 (р + 5) ар])АК = <ехр [~2Ьор]>лх. (4.3)
160
Часть III
Левая сторона (4.3) является ^ фрустрацией (11 sign р=
= П sign 6 == — 1) на внутреннем к Л кубе, а правая сторона
соответствует фрустрации на внешнем к Л кубе, которые имеют
общий плакет на их границе Р е 6Л.
Уравнение (4.3) указывает при |3С = 0,805 на фазовый
переход второго рода между упорядоченной фазой с нулевыми
средними значениями (рс = 0,761) в обеих частях уравнения (4.3) и
ио
0,9
0,8
0,7
0,6 tc О J 0,8 i
Рис. 5. Среднее значение плакета как функция от t — th p для кластера
3X3X2 в сравнении с результатами расчета методом Монте-Карло (точки)
и с разложением в ряд теории возмущений в приближении слабой связи
(штриховая линия).
неупорядоченной фазой, где изолированные на кубах
фрустрации конденсируются.
Нарушенная симметрия может быть названа симметрией
дуальной эквивалентности [9].
Уравнение (4.3) представляет собой приближение СП,
сохраняющее калибровочную инвариантность. Улучшение метода
может быть достигнуто рассмотрением больших кластеров (рис. 5).
Исследование случая d = 4 приводит к фазовому переходу
первого рода и дает возможность предложить новую, более фи-
зичную интерпретацию приближения «средней связи» [10] для
калибровочных решеточных теорий, которые не сохраняют
калибровочную инвариантность.
ЛИТЕРАТУРА
1. De Gennes P. G, Scaling Concepts in Polymer Physics, Cornell Univ.
Press, 1979. [Имеется перевод: де Жен П. Идеи скейлинга в физике
полимеров. — М.: Мир, 1982]
2. Livi /?., Martian Л., Ruffo S.t J. Phys. А, в печати.
Статистика полимеров и блуждания без самопересечений 161
3 Har.n.iersiey J. M., Proc. Camb. Phyl. Soc, 57, 516 (1961).
4. Durhuus £., Frohlich /., Jonsson Г., Nucl. Phys., B225, 185 (1983).
5. Greensite /., Sterling 7\, Phys. Lett, 121B, 345 (1983).
6. Maritan A., Stella Л., Phys. Rev. Lett., 53, 123 (1984).
7. Wannier G. H„ Phys. Rev., 79, 357 (1950).
8. Caracciolo 5., Parisi G.y Sourlas N.t Nucl. Phys., B205, 345 (1982).
9. Cappelli A, Livi R.y Maritan A, Ruff о S., Mean Field for Topological
Excitations of Z2 Spin and Gauge Models, Univ. of Florence, preprint,
1985.
10. Drouffe J. M.t Zuber J. B.9 Phys. Rev., 102, 1 (1983).
О самонепересекающихся блужданиях
на неупорядоченных решетках
С. Милошевич, А. Черновцам, *
Изучались самонепересекающиеся блуждания (СНБ) на случайной
манхэттенской квадратной решетке (СМР), представляющей собой
прототип неупорядоченных решеток. С помощью теории ренорм-
группы в реальном пространстве авторы показали, что СНБ на
СМР и на обычной квадратной решетке принадлежат одному и
тому же классу универсальности. Эти результаты обсуждаются в
связи с недавними противоречивыми предсказаниями относительно
СНБ на фракталах.
1. Введение
Статистические свойства модели СНБ заключают в себе
множество хорошо поставленных для исследования задач [1, 2].
Задача СНБ на бесконечном перколяционном кластере вблизи
точки перехода привлекла недавно особое внимание, поскольку
здесь был высказан ряд взаимопротиворечивых утверждений
(всеобъемлющее введение в эту проблему можно найти,
например, в работе Надала и Ваннименуса [3]). Бесконечные перко-
ляционные кластеры дают возможность реализации фрактальных
структур в физике, но на вопрос, возникающий при сравнении
критических свойств СНБ на таких структурах и на
однородных решетках, имеются противоречивые ответы.
В данной работе мы изучим задачу СНБ на квадратной СМР.
Прототип этой решетки (рис. 1) можно создать, если все
дорожные знаки одностороннего движения на улицах нижнего Ман-
хэттена рандомизировать на каждом перекрестке [4]. Такая
решетка, задуманная как транспортное ограничение, находится
в точке перколяционного перехода. Действительно, анализ
методом ренормгруппы в реальном пространстве (РГРП) [5]
показывает, что изменение сколь угодно малой части
ориентированных, например, на восток (В) и север (С) связей (улиц) вызовет
направленную перколяцию в юго-западном (ЮЗ) направлении.
В то же время, лишив СМР одинаково малых частей, которые
по отдельности вносят перколяционный вклад в СВ- и ЮЗ-
направлениях, мы не вызовем перколяции совсем.
(Рандомизированный подобным образом нижний Манхэттен оказывается
непроезжим для сквозного движения.) Кроме того, введение
неориентированных связей вместо одинаково малых долей связей,
которые вносят вклад в СВ- и ЮЗ-перколяции, будет
способствовать изотропной перколяции. Следовательно, СМР находит-
* S. Milosevic, A. Chernoutsan-Department of Physics and Meteorology,
University of Belgrade, P. O. Box 550, 1101 Belgrade, Yugoslavia; настоящий
адрес второго автора Москва, физический факультет МИНХиГП
им. И. М. Губкина.
Статистика полимеров и блуждания без самопересечений 163
ся в точке множественного перколяционного перехода, и по этой
причине она может служить основой для проверки свойств СНБ.
Имея это в виду, мы применили РГРП-анализ, аналогичный
предложенному недавно Прентисом [6]. В результате удается
показать, что СНБ на СМР и на обычной квадратной решетке
—Л—4—О—*—О—<—О—4—О—>—О—
—6—►—6—►—6—«—О—<—6—►—6—
—6—►—6 4—6—►—Q—►—Q—►—9—
—Л 4 (V-»—6—►—6—*—О—«-
Рис. 1. Часть случайной манхэттенской решетки (СМР).
принадлежат к одному и тому же классу универсальности. Этот
результат обсуждается в связи с взаимоисключающими
утверждениями, упомянутыми перед этим.
2. Ренормгрупповой анализ
Статистика СНБ определяется общим числом Си траекторий
из N шагов и соответствующим средним квадратом расстояния
(R2N) между их концами. Критичность СНБ проявляется в
степенном характере зависимостей при больших N:
C-^N*-1, (Rl)~W
2v
О)
где |ы — константа связности, а у и v — критические показатели,
причем 1/v — фрактальная размерность СНБ. Вводя параметр
активности /С, весьма важный при скейлинговом рассмотрении,
производящие функции для (1) можно записать в виде формул
большого канонического ансамбля:
z(K)=Z KNcN>
N=0
с»
14k)=Zk»(ri)cn/z(k).
N=0
(2)
(3)
Из этих формул при К меньших, но очень близких к
критической активности
Кс=Щ, (4)
164
Часть III
асимптотический анализ позволяет установить следующее
критическое поведение:
Z(K)~(Kc-KT\ l2{K)~{Kc-KV2\ (5)
По определению СНБ, составляющие некую группу (например,
СНБ на различных двумерных решетках), принадлежат к
одному классу универсальности, если все участники этой группы
имеют одинаковые значения критических показателей у и v.
Сначала сравним значения v для СНБ на СМР и на
обычной квадратной решетке, вычисленные РГРП-методом. Чтобы
построить РГРП для СНБ на СМР, вначале преобразуем
изменением масштаба исходную СМР в новую более
крупномасштабную СМР. Для этой цели мы используем отображение ячейки на
0 о О
т Т
-»—о ► о-^-о
1 I сг> ▲
«-О—►—о—<»—о 6 ► О
Рис. 2. Рескейлинг ячейки размера 6 = 3 СМР.
связь с масштабным множителем 6 = 3 и воспользуемся
правилом большинства [6], которое иллюстрируется на рис. 2. Затем
сконструируем для активности преобразование ренормгруппы
K' = F(K) таким образом, чтобы активность К? приписывалась
в качестве статистического веса каждому шагу на новой СМР.
Указанное преобразование должно сохранять общий
статистический вес всех СНБ, которым является, скажем, Z(K). Этого
можно приближенно добиться с помощью правила связности
[8], которое требует, чтобы F(K) вычислялось как общий
статистический вес всех возможных СНБ, которые пересекают ре-
нормируемую ячейку, например, в северном направлении. При
этом каждое блуждание из п шагов дает вклад Кп в функцию
F(K). Мы используем здесь вариант «равноусреднения» правила
связности, согласно которому разрешены три возможных
попадания блуждающей частицы на дно ячейки размера 6=3 и все
СНБ учитываются с равным весом 1/3. Далее мы должны
усреднить F(K) no 214 различным ячейкам размера 6 = 3, которые
соответствуют ориентированным на север перенормированным
связям. Эта трудная программа может быть облегчена
отдельным усреднением каждого члена в F(K), т. е. каждого СНБ,
которое пересекает ячейки.
В рамках однопараметрической (с параметром К) РГРП-схе-
мы мы разрешаем СНБ на каждом шаге двигаться только в на-
Л
С
Статистика полимеров и блуждания без самопересечений 165
правлении, которое определяется соответствующей связью на
СМР. Тогда описанная выше программа ведет к следующему
преобразованию ренормгруппы:
^ = 1[(Ю944/(3 + 21888/С4 + 21888Д:5 +
+ 9120 К6 + 4608 К7 + 936 К8 + 482 #9)/2и], (6)
которое имеет неподвижную точку К* = 0,9078, определяющую
критическое значение активности Кс = К*. Критический
показатель v= 0,7234 получается из формулы [9] v = ln6/lnX, где
Я = dF/dK — собственное значение линеаризованного в
окрестности К = К* преобразования (6). Сравнение указанного выше
значения v с соответствующим значением для СНБ на обычной
квадратной решетке [6] v = 0,7283 показывает малое (хотя и
конечное) их отличие. Последнее не позволяет сделать
определенного заключения относительно классов универсальности этих
двух СНБ.
Для решения вопроса о классах универсальности расширим
пространство параметров таким образом, чтобы обе
рассматриваемые модели включались в одну и ту же РГРП-схему. Для
этого введем, следуя Прентису [6], вероятность W того, что
СНБ сделает шаг в направлении соответствующей связи, и
соответственно вероятность 1 — W того, что этот шаг делается против
направления связи. В каждом из этих двух случаев
статистический вес одного шага СНБ соответственно равен WK и (1 —
— W)K. Следовательно, при изменении W от 1 до 1/2 мы
совершаем эволюцию от СНБ на СМР (с активностью К) к СНБ на
обычной квадратной решетке (с эффективной активностью К/2).
Соответствующее преобразование ренормгруппы описывается
схематическими формулами
W'K' = Fx (К, W, \ — W)\ (1 - W) К' = F2 (К, W, 1 - W), (7)
где W и К! — ренормируемые параметры. Функция fi (функция
F2) соответствует общему статистическому весу множества СНБ,
усредненных по всем ячейкам, которые дают ориентированные
на север (на юг) перенормированные связи. Мы установили
следующее свойство:
F2(K,x,y) = Fl(Kiy,x), (8)
а также нашли точное выражение
g p i
Л (К, xty) = i^- £ £ ацх'-'у'ЪК' Й
*«3 /-0
166
Часть III
с соответствующими наборами точных коэффициентов
{6Л = {192, 384, 384, 160, 64, 8, 2},
Ы = {57, 126, 66, 7},
Ы = {57, 183, 192, 73, 7},
{а5у} = {57, 240, 375, 265, 80, 7},
{^ = {57, 297, 615, 640, 345, 87, 7},
{a7i} = {72, 444, 1137, 1565, 1235, 543, 116, 8},
{a8y} = {117, 831, 2526, 4307, 4480, 2861, 1058, 193, 11},
{а9/} = {241, 1924, 6701,13609,17551, 14705,7895,2515,380,15}.
Диаграмма потоков, которая отвечает преобразованиям (7),
изображена на рис. 3. Она показывает только одну
нетривиальную неподвижную точку W* — 1/2, К* ==0,8788 с
соответствующими ей значениями %к = 4,5198 и v = 0,7283. Кроме того,
критическая линия несомненно пересекает линии W = 1 и W = 0,
/
W
0j5i
—^ 2С—
-ч/-
-J —
*i
0,5
_U
К
/А
Рис. 3. Диаграмма потоков, отвечающая РГ преобразованию (7). Точки на
критической линии входят в нетривиальную неподвижную точку А при
W = 0,5. Тривиальные неподвижные точки обозначены В.
которые отвечают СНБ на СМР и на обращенной СМР
соответственно. Этот факт и вид РГ потока на критической линии
приводят к заключению о том, что СНБ на СМР принадлежит тому
же самому классу универсальности, что и СНБ на обычной
квадратной решетке.
3. Обсуждение
Основным результатом предыдущего раздела является
заключение о том, что СНБ на СМР и на обычной квадратной
решетке принадлежат, если рассматривать их критический
показатель v, к одному классу универсальности. Для того чтобы
удостовериться в справедливости этого заключения, поставим
Статистика полимеров и блуждания без самопересечений 167
два вопроса. Во-первых, не является ли характер полученной
диаграммы потоков следствием использованного
параметрического представления СНБ и, во-вторых, находится ли эта
диаграмма в согласии с аналогичными результатами, полученными
в других более простых моделях? В ходе ответа на первый
вопрос возникает желание ввести более физичный параметр U
вместо параметра W. Таким новым параметром U может быть,
например, вероятность того, что блуждающая частица сделает шаг
против направления связи, в то время как с вероятностью 1 — U
она свободна от ограничений связью ее движения. Можно
показать, что соответствующая диаграмма потоков в (К, U)
-плоскости подтверждает сделанное выше заключение. Единственным
отличием будет новое положение критической линии, которая
теперь оказывается уже не прямой и не содержит точки,
отвечающей СНБ на обращенной СМР.
Касаясь нашего второго вопроса, напомним недавнюю
работу Сахими [10], который применил метод РГРП к изучению
СНБ на квадратной решетке с долей 1 —р выколотых узлов.
Сахими установил, что для всех р выше перколяционного перехода
(р > рс) рассматриваемая им модель находится в классе
универсальности СНБ на обычной квадратной решетке, в то время
как СНБ на бесконечном перколяционном кластере (р = рс)
описываются другим (большим по значению) показателем vi.
Можно утверждать, что наши результаты подтверждают работу
Сахими на том основании, что, используя при отображении
правило большинства вместо примененного Сахими [10]
перколяционного правила, мы вынудили решетку вести себя так, как
если бы она находилась выше рс- С другой стороны, мы не
применяли при отображении перколяционное правило, потому что
оно приводит к решетке, которая содержит ориентированные и
неориентированные связи и вакансии. Для изучения СНБ
такая решетка будет, очевидно, представлять собой неподходящую
основу.
ЛИТЕРАТУРА
1. Domb С, Adv. Chem. Phys., 15, 229 (1969).
2. McKenzie D. S, Phys. Rep., 27C, 35 (1976).
3. Nadal J. P., Vannimenus /., J. Physique, 46, 17 (1985).
4. Redner S., in; Percolation Structures and Processes, eds. G. Deutscher,
R. Zallen, J. Adler, Adam Hilger, Bristol, p. 447, 1983.
5. Redner S, Phys. Rev., B25, 3242 (1982).
6. Prentis /. /., J. Phys., A17, L21 (1984).
7. Redner S.f Reynolds P. /., J. Phys., A14, L55 (1981).
8. Redner S.} Reynolds P. /., J. Phys, A14, 2679 (1981). -
9. Stanley H. £., Reynolds P. /, Redner S, Family F.y in: Real Space Re-
normalization, eds. T. W. Burkhardt, J. M. J. van Leeuwen, Springer,
Berlin, p 171, 1982.
10. Sahimi M.t J. Phys., A17, L379 (1984).
Эксперименты
с белками
Е. Янг *
СНБ в двух и трех измерениях предлагаются для описания
скелетов ферредоксина и гемопротеинов. Однако процессы
спин-решеточной релаксации ионов Fe3+ не могут быть описаны чисто
фрактальной моделью. Наблюдаемые экспериментально спектральные
размерности определяются выражением ds = df/a, где величина а
находится из скейлинговой формулы <d(bL) = ba(d(L) для
низкочастотной моды системы в целом (которая включает белки и
растворитель), выведенной при изменении пространственного
масштаба.
В спин-решеточной релаксации ионов Fe3+ в ферредок-
сине и гемопротеинах с низким содержанием спинов при
температурах Т > g\iBH/k доминируют двухфононные процессы.
Температурная зависимость времени релаксации % определяется
скейлинговой формулой [1,2]
1/т~Г3+2^(7"/в, d8)% (l)
где F(x, у)—гладкая функция х> а 0 — дебаевская
температура. Фрактонная, или спектральная, размерность d$ [3, 4]
входит в (1) благодаря зависимости
р(со)~сЛ-1 (2)
фононной плотности состояний при низких частотах от частоты
о). Для обычных d-мерных объектов ds совпадает с евклидовой
размерностью d, а уравнение (1) находится в хорошем
согласии с экспериментом.
Однако эксперименты [2, 5 — 7] показывают, что ds и
фрактальная размерность df равны 4/3 для ферредоксина и 5/3 для
гемопротеинов. Некоторые авторы [2, 6] отождествляли d$ с
фрактальной размерностью df и постулировали справедливость
(1) также для нецелых значений ds- Поскольку эти значения
совпадают с фрактальными размерностями двух- и трехмерных
самонепересекающихся блужданий (СНБ), они также полагали,
что скелеты белков могут моделироваться СНБ. Однако
спектральная размерность ds отличается, вообще говоря, от
фрактальной размерности df и пространственной размерности d [8].
В случае СНБ ds = 1 и подстановка этого значения в выражение
(1) дает результат, который противоречит эксперименту.
* Y. S. Yang^ International Centre for Theoretical Physics, Trieste, Italy;
настоящий адрес: Institute of Physics, Chinese Academy of Sciences, Bejing,
China.
Статистка полимеров и блуждания без самопересечений 169
Для разрешения этого противоречия Хелман с соавт. [9]
предложил фрактальную модель, которая использует понятие
безмассовых мостиков. Они полагали, что при достаточно
высокой концентрации этих мостиков ds будет равна df. Однако
теоретический анализ и компьютерное моделирование [12, 13]
показывают, что включение в рассмотрение мостиков конечной
длины не меняет спектральной размерности системы.
Расхождение между теорией и экспериментом связано, по
мнению автора, с тем, что предшествующая теория основывалась
на «чисто» фрактальных моделях,
а эксперименты делались в
растворителе (воде). Фононная плотность
состояний различна в этих двух
случаях. Релаксационные процессы
включают модуляцию орбитальной
электронной волновой функции
структурными колебаниями,
поскольку спины связаны с
колебаниями за счет спин-орбитальных
взаимодействий. Следовательно, вклад в
релаксационный процесс вносят
только те фононные моды, которые
влияют на орбитальную волновую
функцию ионов Fe3+. Для этого
релаксационного процесса автор
предложил фрактальную модель,
которая учитывает эффекты, связанные
с растворителем. Молекулы белка, а
следовательно, и ионы Fe3+
образуют конфигурацию
самонепересекающегося блуждания, остальные узлы которой заняты
молекулами растворителя (см. рис. 1).
Поскольку спины могут менять состояние лишь при
изменении расстояния между ионами Fe3_r, вклад в релаксационный
процесс вносят только колебательные моды этих ионов. Следуя
скеилинговым соображениям Раммала и Тулузе [4], можно
предположить, что при изменении масштаба длины L-+bL
концентрация ионов Fe3+ меняется по закону
N{L) = b~dfN(bL), (3)
где df — фрактальная размерность белка. Если считать скелеты
белка самонепересекающимися блужданиями, то df = (rf + 2)/3.
Предполагая, что при указанном изменении масштаба частота
мод также характеризуется скеилинговым поведением
Рис. 1. Решеточная модель
белков в растворителе. Молекулы
белка, обозначенные
соединяющими узлы жирными линиями,
образуют конфигурации
самопересекающегося блуждания.
Остальные узлы решетки
заняты молекулами растворителя.
<j>L = b aa>bl>
(4)
170
Часть III
и учитывая, что число фононных мод пропорционально числу
ионов, получим формулу
Pl К) = b~%bL (щь) ^ = ba~%bL KJ, (5)
Положив Ь = со~"1/а, легко заметить, что спектральная
размерность дается выражением
ds = df/a. (6)
Из приведенного выше анализа видно, что влияние
растворителя проявляется в скейлинговой формуле (4) для частоты
моды. Если взаимодействия белок — белок, белок —
растворитель, растворитель — растворитель одинаковы, то колебательный
спектр будет таким же, как в гомогенной системе, так что а=\.
Предположим, что тот же самый результат получается в случае,
когда все три типа взаимодействий конечны. Именно этот
случай соответствует эксперименту, так что согласие его с теорией
восстанавливается. При изотропном характере взаимодействий
между молекулами уравнение движения системы имеет вид
т* т=£ **. ^ ш+«- и^ (7>
б
где индекс i означает тип и положение атомов, Кц — силовая
постоянная между атомами i и /, mi — масса i-vo атома, б —
вектор расстояния между ближайшими соседями. Преобразование
Фурье уравнений (7) дает
- со2"*А = £ Ki% м (Ui+6 - и(). (8)
б
Вспомним преобразование Лапласа управляющего уравнения
для задачи случайного блуждания
— «Л = Е Wt, i+6 (Рм — Pi)> (9)
б
где pt(t)—вероятность обнаружить блуждающую частицу в
точке i в момент времени t, Wi,j — вероятность ее перескока за
один шаг из узла i в узел /. При больших t среднее перемещение
частицы за время t определяется скейлинговой формулой
R(t)~tlldw. (10)
Аналогия уравнений (8) и (9) приводит к соотношению
a = dw/2. (11)
Перенесенные из задачи колебаний в задачу случайных
блужданий вероятности перескоков Wij, хотя и зависят от i и /, но
имеют конечные значения, ограниченные сверху и снизу величц-
Статистика полимеров и блуждания без самопересечений 171
нами И^макс и №мин. Если рассмотреть два СНБ с постоянными
вероятностями перескоков И^макс и 1^МИн, то их средние смещения
/?макс(0 и /?мин(0 будут, очевидно, ограничивать интервал
аналогичного смещения исходного СНБ:
(/). (12)
Из того, что
Ru»*(t)~tv\ RuaKC(t)~txl\ (13)
следует зависимость
R(t)~t^, (14)
что доказывает сделанное выше предположение об изотропных
взаимодействиях.
Итак, чисто фрактальная модель не может объяснить
экспериментальные результаты для ферредоксина и гемопротеинов.
Фрактальная размерность этой модели отличается от той,
которая следует из эксперимента. Следовательно, применяя
результаты чисто фрактальной модели к реальным физическим
системам, необходимо соблюдать осторожность.
ЛИТЕРАТУРА
1. Orbach R.t Proc. Roy. Soc. London 264 (1961) 458.
2. Allen /. P., Colvin J. T.y Stinson D. G.y Flynn C. P., Stapleton H. /.,
Biophys. J. 38 (1982) 299.
3. Alexander S., Orbach R. /., J. Physique Lett. 43 (1982) L625.
4. Rammal R., Toulouse G., J. Physique Lett. 44 (1983) L13.
5. Mailer C, Taylor C. P. S.y Biochimica et Biophysica Acta 322 (1973) 195.
6. Stapleton H. /., Allen J. P., Flynn C. P., Stinson D. G., Kurtz S. R.t
Phys. Rev. Lett. 45 (1980) 1456.
7. Colvin J. Г., Stapleton H. /., Chem. Phys. 82 (1985) 4699.
8. Stanley H. E.t in: N. B. S. Conference on Fractals, J. Sta. Phys. 35,
Sept. 1984.
9. Helman J. S., Coniglio A, Tsallis C, Phys. Rev. Lett. 53 (1984) 1195;
54 (1985) 1735.
10. Cates M. E., Phys. Rev. Lett. 54 (1985) 1733.
11. Stapleton H. /., Phys. Rev. Lett. 54 (1985) 1734.
12 Yang У. S., Lam P. AL, Commun. Theor. Phys., в печати.
13. Yang У. S, Liu Y.t Lam P. Al, Z. Phys. B-Condensed Matter 59 (1985)
445.
Часть |V
РАЗВЕТВЛЕННЫЕ ПОЛИМЕРЫ,
ГЕЛЕОБРАЗОВАНИЕ
И ПЕРКОЛЯЦИЯ
Размерность фракталов
и синтез разветвленных полимеров
3. Александрович *
1. Введение
Статистическое поведение разветвленных полимеров
принято идентифицировать с поведением решеточных зверей —
так называется ансамбль различных невзвешенных графов,
образованных М связями на решетке. Такая идентификация
основана на том, что как полимеры, так и звери состоят из случайно
ориентированных, не перекрывающихся связей. Представляется,
однако, что подобное догматическое отождествление
разветвленных полимеров с решеточными зверями остается открытым
для следующей критики (см. работу [1]). Разветвленные
полимеры могут образовываться в результате обратимого либо
необратимого связывания отдельных функциональных групп,
принадлежащих мономерам. В первом случае мы имеем дело с
ансамблем из N свободных и связанных в кластеры (полимеры)
мономеров, причем полимеры здесь выступают в роли
промежуточных топологических характеристик. Такое обратимое
связывание, или гелеобразование, как уже давно было отмечено де
Женом [2], соответствует перколяции. Поэтому ясно, что для
понимания сходства полимеров с «зверями» следует обратиться ко
второму случаю, когда связывание мономеров протекает
необратимо. Но здесь мы сталкиваемся с той трудностью, что
структура ансамбля зверей предполагает равновесие по отношению к
перегруппировкам связей в системе. Необратимый синтез
разветвленных полимеров происходит большей частью по
ступенчатому механизму, когда бифункциональные и
полифункциональные мономеры последовательно присоединяются необратимым
образом к «активным концам» цепей. Поскольку здесь
образование различных топологических структур контролируется
кинетикой, то остается неясным вопрос о равенстве статистических
весов этих структур, как это имеет место в равновесном ансамбле
* Z. Лlexandrowicz- Department of Polymer Research, Weizmann Institute
of Sciences. Rehovot 76 100, Israel.
Разветвленные полимеры, гелеобразование и перколяция
животных. Поэтому становится понятной важность изучения
влияния конкретных особенностей кинетических моделей на
распределение топологических структур и, следовательно, на
статистику их формы. Одним из возможных типов кинетического
поведения является неограниченный рост. В течение заданного
интервала времени все активные концы растут линейно или с
разветвлениями (соответственно присоединяя бифункциональные
или полифункциональные мономеры), что ведет к
экспоненциальному увеличению массы полимеров со временем. Подобный рост
привел бы к переполнению реактора и преждевременному
исчерпанию мономера. Поэтому в кинетическую схему следует
добавить какие-либо механизмы, ограничивающие рост цепей.
2. Модели синтеза полимеров
В этом разделе обсуждаются две очень упрощенные
кинетические модели. В первой из них, модели S, рост
ограничивается заданной скоростью расхода однородно распределенного по
системе мономера. В течение данного интервала времени не все,
а лишь определенное число концов (например, один)
присоединяет бифункциональные и трифункциональные мономеры. Это
число случайно распределено среди текущего набора G концов.
С ростом массы полимера величина G увеличивается в
результате появления новых разветвлений, пополняя список способных
к активации и ожидающих для этого своей очереди концов.
В отсутствие взаимодействий G ~ М для размерностей
пространства D ^ Dc. Модель S соответствует той, которая
изучалась ранее Рэндером [3]. Во второй кинетической модели (Т)
рост ограничивается введением в кинетическую схему обрыва,
когда растущий конец может либо присоединять
бифункциональный и трифункциональный мономер соответственно с
вероятностями pi и р2 или стать с вероятностью 1 — (pi + P2)
неактивным вследствие реакции обрыва. Обрыв может осуществляться
как в результате присоединения монофункционального мономера,
так и вследствие потери активности радикалом. При
выполнении критического условия р* + 2р£=1, когда ветвление в
точности компенсируется обрывом, в отсутствие флуктуации
должен осуществляться линейный рост массы полимера при
постоянном значении G. Однако G из-за флуктуации будет тем не
менее увеличиваться вместе с М. Если последовательные
стохастические _шаги не коррелированы, то G возрастает
пропорционально VМ. Поскольку в этом случае G/M-+0 при М->оо, то
ограничение, связанное с фиксированием скорости подачи
мономера, становится несущественным. Фрактальная размерность
df = l/vM, определяющая зависимость среднего радиуса R
174 Часть IV
кластера от его массы
R~Mmy (1)
изучалась в настоящей работе для разветвленных полимеров,
синтез которых описывается кинетическими моделями S или Т.
3. Время t как независимая переменная
В ходе предшествующего обсуждения неоднократно
упоминалось «время» роста разветвленной цепи, которое здесь можно
определить следующим образом. Цепь в момент £ = 0 начинает
свой рост в выделенном начальном узле решетки. Ближайшие
к нему соседние мономеры, образующие первое окружение,
могут присоединиться к цепи на первом шаге t= 1. В свою
очередь, на следующем шаге такое присоединение возможно уже
для мономеров второго окружения t = 2 начального узла, к
которым относятся соседи узлов первого окружения. Переход к
большим значениям t очевиден. (При реальной кинетике,
описываемой, например, моделями S или Т, последовательность
попаданий активного конца в узлы решетки не соответствует,
естественно, последовательности переходов от предшествующего
окружения к следующему; некоторые ветви могут в реальном
времени расти быстрее других, т. е. уходить на большее число t
шагов от начального узла.) Время t предусматривает некую
переменную, имеющую смысл длины, которая дает возможность
изучать (как и для линейных цепей) зависимость среднего
радиуса от контурной длины:
R~?*\ (2)
R и t могут быть измерены между любой точкой цепи и
начальным узлом или любыми двумя точками, одна из которых
выбирается за начальную. В отсутствие петель длина t между любой
парой точек определяется однозначно, а при наличии циклов для
этого требуется усреднение по различным путям на
молекулярном графе. Скейлинговая зависимость
(M)~tyt (3)
вместе с (1), (2) дает связь vt = VMyt между критическими
показателями. Если рост полимера, как здесь, не совпадает с
последовательностью переходов по ^-окружениям начального узла,
то показатель l/yt может быть измерен по зависимости
{t)~ Mxlyf. Использование переменной t и показателей v*, 7*ДЛЯ
описания разветвленных полимеров впервые было предложено
автором в связи с построением перколяционных кластеров как
«критически разветвленных цепей» [5]. Потом этот подход был
заимствован в последующих работах, посвященных перколяции
Разветвленные полимеры, геле образование и перколяция 175
и решеточным зверям [6 (а—е)]. (В некоторых из них t носит
название «химического» или «топологического» расстояния.)
Сравнение моделей S и Т в значительной мере осуществляется
на основании измерений зависимости характеристик этих
моделей от t,
4. Результаты
Разветвленные полимеры были построены методом Монте-
Карло в соответствии с моделями S и Т. На каждом шаге
построения проводятся три испытания. При первом выбирается
один из текущего набора растущих концов. При втором в
соответствии с вероятностями р\ и рч определяется, одна или две
связи растут из этого конца. В отличие от модели S (где р\ +
+ р2=1) в модели Т помимо присоединения мономера
возможен еще обрыв с вероятностью 1— (Р1+Р2). При третьем
испытании определяется направление связи в £)-мерном
пространстве. Окончания связей образуют новые концы. Если последний
попадает в свободный узел решетки, то рост продолжается.
Если, однако, попадание приходится на узел, уже занятый
предшествующим сегментом цепи (попадание в исключенный
объем), то последовательное построение полимера прекращается и
процесс начинается сначала.
С помощью метода «обогащения» [7] при размерности
пространства Л от 2 до 8 были построены серии из (2— 10) -103
цепей, имеющих максимальную массу в интервале от 150 до
2000. Для того чтобы четко различать неоднородность
плотности сегментов относительно начала, показатель vm измерялся
тремя различными способами: (I) vMg определялся из среднего
радиуса инерции сегментов; (II) vMo — из среднеквадратичного
расстояния М сегментов от начального узла; (III) фрактальная
размерность df определялась с помощью недавно предложенной
техники [8]. Находилась также определяемая зависимостью
G ~ М8 степень разветвленности g.
Эти результаты представлены в табл. 1; верхние индексы S
и Т означают тип одной из двух моделей, а результаты
последней строки, относящиеся к идеальной цепи (аббревиатура I),
построены без учета исключенного объема в пространстве
размерности D = 8. Из анализа данных табл. 1 вытекают
следующие наблюдения.
а. Ветвление. Можно ожидать, что в отсутствие эффекта
исключенного объема x?s = 1, a gT должно быть приблизительно
равно 1/2 [1]. Это подтверждается данными, приведенными в
табл. 1. При уменьшении D возрастает роль исключенного
объема, приводящего к образованию менее разветвленных цепей, я
црзтому g уменьшаете^.
176
Часть IV
б. Зависимость (t) от М. Величина l/yt, наоборот,
минимальна в отсутствие исключенного объема; когда D уменьшается,
l/yt растет, приближаясь к единице, что соответствует линейной
топологии. Для модели Т с хорошей точностью выполняется
равенство y^1 = 1 — gy выведенное недавно для разветвленных
цепей, растущих в критических условиях [9]. Отчетливо видно
выполнение при всех D неравенства 1/yJ> 1/vf, означающего, что
по сравнению с моделью S в модели Т всегда образуются менее
Таблица /.
D
2
3
4
5
6
7
8
I
S
g
0,83
0,91
0,96
0,97
0,98
0,99
0,99
1,0
т
g
0,25
0,34
0,38
0,41
0,44
0,46
0,46
0,46
i/ s
0,57
0,46
0,38
0,33
0,30
0,26
0,24
0,20
i/vj
0,74
0,66
0,63
0,60
0,58
0,54
0,54
0,52
S
0,44
0,32
0,24
0,20
0,17
0,14
0,13
0,10
S
vMg
0,57
0,42
0,32
0,26
0,23
0,19
0,17
0,13
■/-?
0,57
0,42
0,34
0,30
0,27
0,24
0,23
0,22
T
*M0
0,62
0,47
0,40
0,35
0,31
0,29
0,28
0,26
T
vMg
0,62
0,47
0,40
0,35
0,31
0,29
0,28
0,26
./<y
0,63
0,50
0,43
0,38
0,35
0,32
0,30
0,28
3B
0,64
0,50
0,42
0,36
0,32
0,28
0,25
0,25
разветвленные структуры. Это отличие может быть следствием
кинетики получения полимера. В модели Т нет избыточного
образования концов (G/M->-0), которое, однако, наблюдается в
модели S, где рост происходит на активированных случайным
образом концах из быстровозрастающего набора ожидающих
активации концов. Это приводит к образованию большого числа
относительно коротких цепей, т. е. к более объемной по
сравнению с линейной топологии молекул полимера. Далее, из-за
повторяющегося во времени характера выбора активных концов
среди неактивных мономеры с большей вероятностью
присоединятся к тем из концов, которые образовались на ранних
стадиях полимеризации. В результате получается распределение
плотности сегментов, имеющее более высокое значение вблизи
начального узла.
в. Зависимость радиуса от массы. Объемный характер
топологии кластеров в модели S еще ярче проявляется в значениях
радиуса инерции, так как vTMg > v%g при всех Z). Тот факт, что
в модели S значения vf^0 значительно ниже, чем v^g, указывает
на увеличение с ростом М плотности сегментов в окрестности
начального узла. В модели Т это явление не наблюдается,
поскольку vTm ex vTMg. Дальнейшее подтверждение указанные
наблюдения находят при анализе значений фрактальной
размерности df, измеренной среди соседей произвольно выбранного
Разветвленные полимеры, гелеобразование и перколяция 177
сегмента [8], безотносительно к ступенчатому росту М. Это
нивелирует выделенное положение начального узла в модели S.
Найденные таким образом значения l/df оказываются
сравнимыми или даже большими, чем v^ . (Приведенные в табл. 1
величины l/df измерены относительно сегментов, выбранных
случайным образом; если выбрать для этой цели начальный узел,
то получается в пределах погрешности эксперимента та же
величина l/df, хотя можно было ожидать несколько меньшее ее
значение.) В модели Т величины l/dj, как это и должно быть, при-
близительно равны vmo и v^g. (Все же l/df получается хотя и
ненамного, но заметно больше значения, приведенного на
сноске 12 работы [1].) В общем, показатель vm зависимости (1)
оказывается аналогичным (возможно, чуть меньшим при низких D)
v™y вычисленному для решеточных зверей [10].
5. Заключение
Оказывается, что кинетика образования разветвленных
полимеров, несомненно, влияет на распределение их топологических
структур и среднюю форму молекул. Применимость для их
описания критических показателей зверей ограничена только
определенными классами разветвленных полимеров, не
синтезированных по необратимому ступенчатому механизму, а также,
возможно, и теми из них, которые хотя получены этим
способом, но растут, как в модели Т, без переизбытка концов.
Действительно, модели S и Т отражают две крайние ситуации:
огромный переизбыток равнодоступных концов и полную
компенсацию их роста обрывом. Истинные кинетические модели
представляют, вероятно, промежуточные типы поведения. Так, в
модели S концы, образовавшиеся в начальных стадиях процесса,
оказываются захороненными внутри цепи и, следовательно,
менее доступными, т. е. в некоторой степени подвергнувшимися
обрыву. Также можно ожидать отклонения от условия
равнодоступности концов за счет диффузионного контроля реакций.
ЛИТЕРАТУРА
1. Alexandrowicz Z., Phys. Rev. Lett., 54, 1420 (1985).
2. de Gennes P. G., J. Physique Lett., 37, LI (1976).
3. Redner S., J. Phys., A12, L239 (1979).
4. Flory P., Principles of Polymer Chemistry, Cornell Univ., Ithaca, 1953,
chap. IX, sect. 1.
5. Alexandrowicz Z., Phys. Lett., 80A, 284 (1980).
6. Pike R.y Stanley H. £., J. Phys. A14, L169 (1981).
Chalupa /, Krausz F G., Phys. Lett., 115 (1984).
Havlin 5, Nossal R., J. Phys., A17t L427 (1984).
Grassberger P., Math. Biosci., 63, 157 (1983).
178
Часть IV
Havlin S, Djordjevic Z. V.y Majid /., Stanley Я. E.t Weiss G. #., Phys.
Rev. Lett, 53, 178 (1984).
7. Wall F. Т., Erpenbeck J. /., J. Chem. Phys, 30, 634 (1959).
8. Termonia У, Alexandrowicz Z, Phys. Rev. Lett, 14, 1265 (1983).
9. Alexandrowicz Z, Phys. Lett, 109A, 169 (1985).
10. Lubensku Т. С, Issacson /., Phys. Rev. Lett, 41, 829 (1978); Phys. Rev
A20, 2130 (1979).
Parisi, Sourlas N., Phys. Rev. Lett, 46, 871 (1981).
Dhar D.9 Phys. Rev. Lett, 51, 853 (1983).
Derrida B.t De Seze L., J. Phys. (Paris), 43, 475 (1982).
Фрактальные размерности
скелетов и кластеров
в кинетической модели
гелеобразования
А. Чабра, Г. Герман, Д. Ландау *
Представлены результаты изучения с помощью компьютерного
моделирования фрактальной размерности наибольшего кластера,
скелета и упругого скелета в рамках трехмерной кинетической модели
необратимого гелеобразования при радикальной полимеризации.
Причиной появления данной работы послужили более ранние
наблюдения того, что, несмотря на совпадение объемных критических
показателей этой модели с перколяционными, распределение
кластеров по размерам в ней заметно отличается (затухающие
осцилляции) и описывается иной скейлинговой формулой. Сравнение
фрактальных размерностей рассматриваемой модели и перколяции
показывает, что для упругих скелетов и наибольшего кластера они
совпадают, а для скелетов значительно различаются.
1. Введение
Недавно было обращено внимание [1] на то, что
фракталы можно использовать как модели случайной среды.
Кластеры, образованные согласно механизмам различных моделей
роста (например, перколяции, кинетического гелеобразования,
ДЛА), служат примерами таких фракталов. Описание
геометрической структуры таких кластеров близко к задаче описания
распространения упорядочения в критической точке. Такие
вопросы, как описание потока жидкости через пористую среду,
электропроводность случайной сетки сопротивлений,
эластичность полимеров, — все они относятся к модификациям
указанной выше задачи.
Ниже приводятся результаты вычислений фрактальных
размерностей наибольшего кластера, скелета и упругого скелета
в кластерах, образующихся в рамках кинетической модели
необратимого гелеобразования. Эти размерности сопоставлены с
теми, которые были получены ранее для модели случайной
перколяции по связям.
2. Описание модели роста [2]
В данной модели тетрафункциональные мономеры
размещены на узлах простой кубической решетки с периодическими гра-
* A. Chhabra-Department of Physics, University of Georgia, Athens GA
30602, USA; Masoa Laboratory, Yale University, New Haven, CT 06520, USA.
H. J. Herrmann-Service de Physique Theorique, CEN Saclay, Gifsur-Yvette
Cedex, France; D. P. Landau-Department of Phvsics, University of Georgia,
Athens, GA 30602, USA.
180
Часть IV
ничными условиями. Заданное число молекул инициатора
случайным образом рассеянно по узлам этой решетки.
Концентрация инициатора Cf определяется как отношение
общего числа его молекул к числу потенциально возможных
связей на трехмерной решетке [3]. Каждая молекула инициатора
разрывает одну двойную связь в мономере и присоединяется к
ней, в результате чего образуется мономер с одной
ненасыщенной связью, называемой активным центром. Последний образует
связь со случайно выбранным узлом при условии, что тот
содержит ненасыщенную связь. Число активных центров в
результате их рекомбинации и захвата уменьшается со временем.
Одновременный рост кластеров и их слияние ведут к образованию
бесконечного кластера, что проявляется в фазовом переходе
золь — гель. Дальнейшие детали этой модели можно найти в
работах [2, 4].
3. Определения и процедура расчета
фрактальных размерностей
Как только выбирается бесконечный кластер, он разрезается
на несколько кусков в соответствии с периодическими
граничными условиями. Затем отыскиваются концевые точки
наибольшего среди них. Кластеры, которые разрезались на множество
Рис. 1. Схематическая диаграмма наибольшего кластера (1), скелета (2) и
упругого скелета (3).
малых кусков или содержали концевые точки, расположенные
слишком близко друг к другу, отбрасываются для обеспечения
необходимой однородности образцов. Затем продолжается
построение скелетов и упругих скелетов.
Для того чтобы определить скелет, рассмотрим две концевые
точки Pi и Р2, которые разделены расстоянием, сравнимым с
корреляционной длиной системы (рис. 1). Если заставить
жидкость перетекать из точки Pi в точку Р2> она сможет сделать
Разветвленные полимеры, гелеобразование и перкоАяция 181
это по некоторому набору путей (связей); этот набор связей
называется «скелет». С ними связан другой фрактальный объект,
«упругий скелет», название которого появилось в ходе попыток
описания упругости неупорядоченных систем. При рассмотрении
связей между узлами Pi и Р2 есть основания предположить, что
среди всех путей, соединяющих эти узлы, лишь кратчайшие
будут давать основной вклад в сопротивление при любой
деформации системы. Совокупность этих путей (связей) и составляет
упругий скелет.
Числа узлов, петель и т. д. в наибольшем кластере и в
скелетах вычислялись с помощью метода «выжигания» кластеров,
детали алгоритма которого можно найти в статье [3]. Средняя
плотность узлов в скейлинговом пределе имеет вид
Рз(р)~(р — Рс)*-
Воспользовавшись скейлинговой теорией для кластеров
конечного размера, число узлов в типичном среди них можно
записать в виде
S{Pc) = Ld9s{Pc)~Ld-*h = LD,
где d и D — соответственно пространственная и фрактальная
размерности. Следует заметить, что показатели (3 и v здесь
относятся к описанию критического поведения той или иной среди
изучаемых величин, т. е. к скелету, упругому скелету и т. д. Для
каждой из них, построив в двойной логарифмической шкале
зависимость соответствующей величины от размера решетки,
находим различные фрактальные размерности.
4. Причина сопоставления результатов
с перколяцией
Хотя объемные критические показатели кинетической
модели гелеобразования и перколяции согласуются между собой,
существуют некоторые интересные различия между двумя
моделями. В то время как отношение амплитуд восприимчивости
ниже и выше критической точки является для перколяции
универсальной величиной, для кинетической модели гелеобразования
это отношение меняется с концентрацией инициатора. Другим
отличием является поведение распределения кластеров по
размерам, которое монотонно спадает в первой из указанных
моделей и имеет характер затухающих осцилляции во второй [4].
Это приводит к различным скейлинговым формулам для
каждой из моделей. Представляется интересным посмотреть,
имеются ли отличия ь критическом поведении и фрактальных
размерностях кластеров и скелетов в кинетической модели
гелеобразования от тех, что наблюдаются в перколяции.
182
Часть IV
5. Результаты и заключение
Результаты изучения влияния размера решетки и числа
серий, по которым проводится усреднение различных величин,
следующие.
Статистика для С^3«10"~4
Размер решетки Число серий Скелеты
20 4000 653
30 1000 164
40 500 50
60 200 15
На рис. 2 в двойном логарифмическом масштабе показаны
зависимости числа узлов от размера решетки. Найденные по на-
ю:
5
10'
10
20 30 40 60
L
Рис. 2. Зависимости в двойном логарифмическом масштабе среднего числа
узлов в наибольшем кластере (/), скелете (2) и упругом скелете (3) от
размера решетки.
клонам прямых на этом рисунке фрактальные размерности
сравниваются ниже с перколяциоиными.
Сравнение фрактальных размерностей
Фрактальная
размерность
^наиболып. кластер
•^скелет
^упр. скелет
Кинетическое
гелеобразование
2,34±0,14
2,22 ±0,10
1,47±0,08
Перколяция
2,49±0,01
1,74±0,04
1,37±0,07
Разветвленные полимеры, гелеобразование и перколяция 183
Можно заметить, что фрактальные размерности упругого
скелета и наибольшего кластера с точностью до ошибки
эксперимента совпадают с их перколяционными значениями, а
фрактальная размерность скелета от них значительно отличается.
ЛИТЕРАТУРА
1. Mandelbrot В. В., The Fractal Geometry oi Nature, Freeman, New York,
1983.
2. Herrmann H. /., Stauffer /)., Landau D. P., J. Phys., A16, 1221 (1983)
3. Herrmann H. /., Hong D. C, Stanley H. £., J. Phys., A17, L261 (1984)
4. Chhabra A, Matthews-Morgan /)., Landau D. P., Herrmann H. J. J Phvs
A18, L575 (1985). ' ' У "
Решеточная магнитная модель
для разветвленных полимеров
и перехода золь — гель
Л. Гонзалес *
Показано, что ^-компонентная спиновая решеточная модель в
пределе п = 0 соответствует модели системы разветвленных
полимеров в хорошем растворителе на некоторой решетке. С помощью
этой модели можно описать режимы как ниже, так и выше точки
перехода золь — гель.
1. Введение
Характерный для разветвленных полимеров при
определенных условиях переход золь — гель изучался ранее в
течение долгого времени. В точке перехода образуется
«бесконечная» молекула (размера, сравнимого с реакционным объемом)
за счет объединения в ходе химических реакций разветвленных
полимеров. В 40-х годах Флори [1] и Стокмайер [2]
предложили теорию золь — гель-перехода, хорошо описывающую
положение точки перехода и значения различных средних
молекулярных весов полимера. Отказавшись от допущения этой теории
об отсутствии циклов и петель, авторы [3, 4] в 70-х годах
попытались моделировать гелеобразование с помощью задачи о
случайной перколяции, где учет циклов осуществляется
естественным образом. Перколяционная задача случайных узлов (или
случайных связей) на решетке имеет, однако, всего одну степень
свободы — вероятность узлу (связи) быть занятым.
Образующиеся в этой модели кластеры (разветвленные полимеры) имеют
вполне определенную фрактальную размерность (компактность)
как ниже, так и выше точки перколяционного перехода [5]. При
этом разветвленные полимеры, которые образуются в процессах
истинного гелеобразования, могут иметь самые различные
фрактальные размерности в зависимости от механизма роста молекул
полимера. В некоторых случаях можно полагать, что он
осуществляется путем межкластерной агрегации [6], которая
интенсивно изучается в настоящее время. В этом случае имеются по
крайней мере две фрактальные размерности, описывающие
агрегаты ниже точки перехода, которые не совпадают с
фрактальными размерностями перколяционных кластеров ниже точки
перколяционного перехода. В настоящей работе предполагается
устранить этот недостаток на основе рассмотрения магнитной
модели [7], подразумевающей введение активностей трех
компонент: мономеров (занятых узлов), полимерных молекул (кла-
* Agastin E. Gonzalez-Institute) do Fisica UNAM, Apdo Postal 20-364,
Delegation Alvaro Obregon, 01000 Mexico, D F., Mexico,
Разветвленные полимеры, гелеобразование и пёркоЛяция 1SS
стеров), петель. Варьируя число последних, можно менять
компактность кластеров по своему усмотрению. Хотя подобная
теория в ее нерешеточном теоретико-полевом варианте была
предложена ранее Любенским и Изаксоном [8] 1), имеются по
крайней мере две причины рассмотреть настоящий вариант
соответствия между полимерами и магнетиками. Во-первых, потому что
он более легок для понимания, по крайней мере для тех, кто не
владеет методами теории поля, и, во-вторых, потому что он
позволяет провести ренормгрупповые преобразования в реальном
пространстве в физически важных случаях размерности d = 2
и 3, которые достаточно далеки от верхней критической
размерности dc этих систем (например,- dc = 8 для разбавленного
раствора разветвленных полимеров [8]).
2. Модель
Рассмотрим для простоты двумерную регулярную решетку
из N узлов, каждому из которых отвечает переменная Oia
характеризующая состояние покомпонентного спина, где 1 = 1, 2, ...
. .., q\ а = 1, 2, . .., п; а сумма о21а по всем / и а равна nq.
Далее выбирается следующий гамильтониан:
-Р# = /е1 £ Е<г|в(/,)...*,«(/,) + *£ £а„(/), (1)
I / a it
где индексы I =(/i, ..., If) и i спиновой переменной указывают
координату спина на решетке, а остальные два нижних индекса
дают значения его компонент. Первое суммирование в
описывающем взаимодействие члене (1) распространяется на все
расположенные через одну ячейки, такие, что никакие две из них не
содержат более одного общего спина и каждый спин
принадлежит двум ячейкам. Первый член в гамильтониане [1] описывает
f-спиновое взаимодействие между f спинами, принадлежащими
каждой из ячеек. На рис. 1 приведен пример для / = 4
(квадратная решетка). Заметим, что, как следует из второго члена в
(1), магнитное поле h сопряжено с q компонентами спина.
Статистическая сумма Z рассматриваемой системы имеет
вид
Z/Q = (exp(-p#))o,
где
{A\^{\li\AdQt)/(jli\dQ)
означает усреднение по спиновым переменным, dQi —
дифференциал телесного угла в пространстве размерности nq, a Q =
*> Подробная библиография работ по использованию решеточных и
континуальных моделей магнетиков для описания статистики разветвленных
полимеров, в том числе и с привлечением теоретико-полевых методов, имеется
в сокращенном [1*] и более полном [2*] вариантах обзора Кучанова,
Королева и Панюкова. — Прим. перев.
186
Часть IV
= ПЛ dQt. Можно показать [7], что в пределе п = О
Z/Q = [2V/(2V-q)]N5py (2)
Sp=E E Z^[Np\nq + S\nU + NR\nV]Q(Np9S9NR)9 (3)
Np S NR
где выражение (3) представляет собой большую статистическую
сумму раствора разветвленных полимеров в хорошем
растворителе, размещенных на новой решетке с М = 2N/f узлами,
отвечающими расположенным через одну ячейкам старой решетки
ItifyfJ
С XXI
• в4
II
ill
X Т1
ill
f Т Т
ill
I Ti
L_ А. ...^^
т т
*х" 1
1 1 j
Рис. 1. Слева: фрагмент исходной решетки с чередующимися ячейками и
двумя кластерами. На этом фрагменте представлено: 5 = 20 мономеров
(кресты), Nv = 36 вершин (непрореагировавшие функциональные группы), NR =
= 22 связи (черные пятна), Ni = 1 полимерные молекулы. Справа: те же
самые кластеры на новой решетке.
(см. рис. 1). При этом Q(NP, S, NR) представляет собой число
способов размещения Np полимеров на новой решетке с М
узлами при заданных полных числах мономеров S и реакций
(связей) NR. Наконец, U и V определяются выражениями U =
= Ш/ (1 + gh2/2) f и V = g/2 + ft-2.
3. Соответствие
Определив свободную энергию gslim(l/N)ln(Z/Q), намаг-
ничивание га= {dg/dh)q, k и внутреннюю энергию и =
= —$-lk(dg/dk)q>h магнитной системы, можно выразить через
них концентрации мономеров ф, полимеров срр и связей cpR с
помощью следующих формул:
Ф = --[|3"> (4)
*—Н4-+4г»«-«(£)...-¥Ч <5>
»»=-4[/(i-^-)P" + (1+-sr)»«-e**]- <«>
Разветвленные полимеры, гелеобразование и перколяция 187
Значение конверсии р можно определить из (4) и (6),
используя выражение р = 2фр//ф. Наконец, осмотическое давление я
определяется формулой яа0р = (f/2)g— (f/2) In (1 -f gh2/2), где
Vq — объем (поверхность при d = 2) единичной ячейки новой
решетки.
С помощью равенства NR = S — Np + Nt в большой
статистической сумме можно перейти от числа связей к числу петель
[7] и получить набор активностей мономеров, полимеров и
петель, о котором шла речь выше. Следовательно, NR также
является мерой компактности кластеров.
Ясно, что в пространстве активностей (g, k, h) существует
критическая поверхность, отделяющая неперколяционную фазу
(где существуют только конечные кластеры) от перколяционной
фазы (где помимо конечных кластеров имеется бесконечный
кластер, протянувшийся по всей решетке). Можно выделить две
точки этой критической поверхности [7]:
а) {<7= 1, А = д/2 , k= 2f,2pc(\ — рс)~1}- Эта точка отвечает
задаче о случайной перколяции по узлам. Здесь рс соответствует
перколяционному переходу на новой решетке;
б) {q = 0, h = 1, k = kc). Эта точка отвечает задаче о
случайных решеточных животных по узлам, т. е. точка, где
изолированный кластер узлов решетки становится бесконечным.
Также можно указать аналогичные точки, отвечающие
задаче о перколяции на дереве и задаче о случайных решеточных
зверях без петель [7].
Двухвершинные корреляционные функции между вершинами,
принадлежащими либо одной, либо разным полимерным
молекулам, можно также выразить через переменные магнитной
системы [9]. В частности, коррелятор Рц между вершинами,
входящими в состав одной молекулы, называемый парной
связностью, определяется простой формулой
Р" =i™0 qk (exp (- P*))0 ' (?)
где a/1 — перпендикулярная направлению поля компонента
спина в 1-м узле.
В качестве обобщения рассмотрим гамильтониан
-ря-fe.E Е £<тг„(/,)••• <x,„(/f) +
I г а
+ ^SSS%(0<тга(/) + h E 2 а/.(О, (8)
(г/> /а i I
где первая сумма та же самая, что и раньше в (1), а <*'/>
означает суммирование по соседним узлам решетки. В этом случае
магнитная система с гамильтонианом (8) соответствует развет-
188
Часть IV
вленным гетерополимерам, состоящим одновременно из
бифункциональных и f-функциональных мономеров [9]. В пределе к2-+
->0 получим рассмотренный выше случай, а в пределе ^i-^0
придем к известному случаю раствора линейных полимеров [10].
Кроссовер между этими случаями можно изучить с помощью
гамильтониана (8).
ЛИТЕРАТУРА
1 Flory Р. /., J. Am. Chem. Soc, 63, 3083, 3091, 3096 (1941).
2. Stockmayer W. H, J. Chem. Phys,, 11, 45 (1943); 12, 125 (1943).
3. de Gennes P. G., J. Phys. (Paris), 37, LI (1976).
4. Stauffer £>, J. Chem. Soc. Faraday Trans. II, 72, 1354 (1976).
5. Stauffer D. et al., Adv. Polym. Sci., 44, 103 (1982).
6. Kolb AT, Botet R., lullien R., Phys. Rev. Lett., 51, 1123 (1983); см. также
наст, сб., с. 360.
7. Gonzalez Л. £., J. Phys. (Paris), в печати.
8. Lubensky Т. С, Isaacson /., Phys. Rev. Lett., 41, 829 (1978); Phys. Rev.,
20A, 2130 (1979); J. Phys. (Paris), 42, 175 (1981).
9. Gonzales A. E., будет опубликовано.
10. de Gennes P. G., Scaling Concepts in Polymer Physics, Cornell U. P,
Ithaca, 1979. [Имеется перевод: де Жен П. Идеи скейлинга в физике
полимеров. — М.: Мир, 1982.]
ЛИТЕРАТУРА, ДОБАВЛЕННАЯ ПРИ ПЕРЕВОДЕ
I*. Кучанов С. И., Королев С. В., Панюков С. В. Графы в химической
физике полимеров. — В кн.: Применение теории графов в химии/Под ред
Зефирова Ы. С. и Кучанова С. И —Новосибирск: Наука, 1988, с. 144—
299.
2*. Kuchanov S. /., Korolev S. V., Paniukov S. V. Graphs in Chemical Physics
of Polymers — In: Advances in Chemical Physics, vol. 72, eds. I. Prigogine,
S. Rice, N. Y., John Wiley, 1988, p. 115—325.
Перколяция в градиенте
концентрации
Ж.-Ф. Гуйе, М. Россо, Б. Саповал *
Рассмотрение задачи о перколяции по узлам на решетке с
градиентом концентрации приводит к многообещающему подходу для
изучения диффузионных фронтов и для определения перколяцион-
ных параметров, таких, как точка перехода и критические
показатели. Здесь приводятся основные результаты для двумерных
систем и некоторые предварительные результаты для трехмерных
систем.
1. Введение
Изучение перколяции по узлам на решетке с
градиентом концентрации представляет большой интерес для понимания
особенностей диффузионных фронтов [1], а также приводит к
существенным упрощениям при нахождении специфических пер-
коляционных характеристик [2].
При постоянном градиенте концентрации вдоль оси х, когда
концентрация линейно уменьшается от значения, равного
единице при х = 0у до нуля, бесконечный кластер появляется в
области больших заполнений. Он имеет внешнюю границу, которая
расположена в области концентраций, близких к критическому
перколяционному значению рс [1].
С использованием метода численного моделирования в
настоящей работе изучена общая структура этой границы.
Во-первых, показано, что на двумерной решетке она является
фракталом в области, размеры которой возрастают по мере
уменьшения градиента концентрации Vp. Фрактальная размерность
границы йн = 1,75 [1, 3]. Во-вторых, установлено, что число
частиц, входящих в эту границу, и ее ширина зависят от Vp
степенным образом. Соответствующие показатели и фрактальная
размерность могут быть простым образом выражены через
критические показатели двумерной перколяционной задачи [1].
Исходя из адекватного определения границ, можно
определить критическую перколяционную вероятность рс с очень
высокой точностью при малых затратах машинного времени. Эти
результаты в случае двумерной решетки приведены в разд. 3, а
некоторые предварительные данные для трехмерных систем —
в разд. 4.
Однако, прежде чем перейти к обсуждению этих
результатов, необходимо напомнить некоторые определения,
используемые в задачах перколяции.
* lean-Frangois Gouyet, Michel Rosso, Bernard Sapowal -Laboratoire de
Physique de la Matiere Condenses. Ecole Polytechnique 91128 Palaiseau,
France»
190
Часть IV
2. Определения
Далее в качестве примера рассматривается квадратная
решетка. Кластер из занятых узлов (Л-узлов), соединенных
между собой связывающими соседние узлы связями (возможное
их число 4), называется Л-кластером. Перколяциоиная
вероятность— это минимальная вероятность концентрации, при
которой появляется бесконечный Л-кластер. Рассматривая теперь
B-t/зел
ХрА
/
XfAB
Хгв
А-узел
Рис. 1. Границы \а (черные кружки, соединенные черной линией) и fe (белые
кружки, соединенные белой линией) на квадратной решетке с градиентом
концентрации.
оставшиеся пустые узлы (В-узлы), определим аналогичным
образом В-кластер как набор незаполненных узлов, которые
соединены друг с другом связями. Однако в отличие от Л-класте-
ров эти связи соединяют в В-кластерах каждый узел не только
с его ближайшими соседями, но и с их соседями (число
возможных связей 8). Л-кластеры и В-кластеры определены на двух
решетках (LA и LB) с различными координационными числами
(4 и 8 связей на каждый узел). Говорят, что эти решетки
образуют «подходящую пару» [4].
Мы имеем дело с монотонно убывающей вероятностью
концентрации Л-узлов, начинающейся с концентрации р = 1 при
х = 0 (рис. 1) и достигающей значения р = 0 при достаточно
больших х. В отличие от обычной задачи перколяции здесь на
двумерной решетке одновременно существуют два бесконечных
(в пределе неограниченной системы) кластера, один из которых
состоит из узлов Л, а другой — из узлов В. Бесконечный
Л-кластер находится в области высоких концентраций, а бесконечный
В-кластер— в области низких концентраций. При этом они
находятся в контакте друг с другом, как это можно увидеть на
рис. 1.
Границу между ними, согласно определению работы [1],
составляют узлы бесконечного Л-кластера, соединенные с узлами
Разветвленные полиМеры, гелеобразов ан'ие it перколяцйя 191
бесконечного В-кластера связями между ближайшими и
следующими за ними соседями. Такая граница называется /д.
Аналогично определяется граница /в, которую составляют узлы
бесконечного В-кластера, соединенные связями через одного соседа
с узлами бесконечного Л-кластера (см. рис. 1).
Для каждой из границ fA и fB определяется соответствующая
функция pfA(x) и Pfe{x). Например, pfA{x)—это вероятность
найти узел границы /U на расстоянии х. Для этой границы
можно определить следующие характеристики: ее среднее
положение в пространстве х?а, ширину о>л, число входящих в нее
узлов NfAl
оо оо
*fA = \ *PfA (*) dx A pfA (x) dx,
о /о
оо оо
°)а = \ (х "" xfA)2 PfA (x) dx ^ pfA (x) dx,
о /о
оо
NfA = L^ pfA (x) dx.
о
Толщина границы Of по своему смыслу должна быть
существенно меньше толщины решетки L.
Как показано на рис. 1, удобно рассмотреть двойную границу
Jab, которая получается в результате объединения границ fA и fB;
ее среднее положение XfAB есть просто среднее положение точек
решетки, принадлежащих границам fA и fB. Аналогично можно
определить ofAB и NfAB с помощью функции
PfAB(x) = PfA(x) + pfB(x).
Градиенты концентрации могут появиться в различных
физических ситуациях. Так, в рассмотренной в работе [1]
диффузионной задаче концентрация частиц меняется вдоль оси х по
закону, дополнительному к функции ошибок благодаря
используемым граничным условиям. Легко показать, однако, [5], что
асимптотическое поведение границ полностью определяется их
локальным градиентом. Далее представлены результаты
изучения перколяции в постоянном градиенте концентрации.
3. Постоянный градиент в двумерных системах
При постоянном градиенте Vp концентрация падает по
линейному закону
p(x)=l—x\Vp\
192
Часть IV
от р = 1 при х = 0 до р =0 при х= | Vpl"1. Показано [1, 2, 5],
что границы локализованы около критической точки рс перко-
ляционного перехода, а параметры Xf, <Xf, Л/f зависят от Vp по
степенным законам. Концентрации р(*м), p{XfB), р(х?ав) в
средних положениях границ очень быстро выходят на значение рс.
I. Исключительно резкий характер зависимости р(х?ав)
может быть использован для точного определения величины рс. На
основании численного анализа работы [2] получена зависимость
XfAB c*{l—Pc) (Vp)"1 + в*ма>
в которой рс и 8xfAB для квадратной решетки равны
рс = 0,59280 ± 10~5, 6xfAB ~ 0,0162.
Используя аналогичную процедуру, авторы работы [6]
получили для сотовой решетки
рс = 0,69703 ± 10"5.
II. Для XfA и XfB найдены [5] более точные поправки к скей-
лингу:
хиы{\- рс)(VP)"1 - 0,250(Vp)(1-V)/(1+V) + Ьхив,
xfB с* (1 - ре) (VP)-1 + 0,250 (vp)(I-v)/(1+v) + 6xfAB,
где v = 4/3 есть критический показатель корреляционного ра
диуса в двумерной задаче перколяции.
III. Простое рассмотрение [1, 5] показывает, что
<rM~0fs~ 0,500 |Vpf4
NfA/Pc -NfBf(l - pc) с* NfAB ы | Vp Г",
где dH — фрактальная размерность границы при Vp->-0.
На основании численных [1] и скейлинговых [3]
аргументов было сделано предположение
tf*=l + l/v=l,75.
Эта фрактальная размерность, единая для всех границ /л, /в и
1аву характеризует масштабы от нескольких постоянных решетки
до ширины Of границы. При больших масштабах происходит
кроссовер к размерности единица. Размерность йн очень близка
к той, которая найдена [7] для оболочки, т. е. внешней границы
бесконечного перколяционного кластера. Точнее говоря, граница
fA оказывается совпадающей с этой оболочкой в пределе Vp =
= 0 [1].
Разветвленные полимеры, гелеобразование и перколяция 1&J
Для систематического построения указанных границ и
лучшего понимания их структуры можно рассматривать «одетые
самонепересекающиеся случайные блуждания» [5, 8].
4. Постоянный градиент в трехмерных системах
Трехмерный случай является более сложным, нежели
двумерный, поскольку для него имеются два различных перколяцион-
ных перехода. При заданной постоянной концентрации в
пространстве размерности D = 2 существует только один бесконечный
Концентрация р А-узлов
f 1-РсВ Р Рса О
1 0,20 0,W 0,60 0,80
Приведенная координата
Рис. 2. Нормированные распределения вероятностей pfA(x)lp(x) или PfB(x)/
[1 — р(х)] при Vp = 1/256 и размерах образца 64X64X256. Пунктирная
линия соответствует пределу Ур ■
:0.
кластер из узлов или Л, или В. Поэтому значения перколяцион-
ных переходов рсА и рсВ на паре «подходящих» решеток LA и Lb
для D = 2 в сумме всегда дают единицу. В отличие от этого для
0 = 3 существует диапазон концентраций 1 — рсВ > р > 1 —
— Рса, где совместно существуют бесконечные Л-кластер и В-
кластер. Поэтому при наличии градиента концентрации граница
здесь более не локализована при определенном значении р, а
лежит между рх = рсА и р2 = рев-
Это отчетливо проявляется при переходе к приведенным
распределениям вероятностей Ргл{х)/р(х) и PfB(Jc)/(l — р{х))у
которые сливаются в одну кривую (рис. 2). Иными словами,
приведенные распределения для бесконечного Л-кластера и для ко-
печного ^-кластера идентичны. Аналогичное утверждение
получится, если буквы Л и В поменять местами.
Отсюда вытекает следующий удивительный результат: почти
все узлы типа Л (соответственно В) в интервале (рь, р2)
входят в состав границы fA (соответственно fB).
194
Часть IV
Это ясно видно из рис. 2. При концентрации рмин только 2,5 X
X Ю~~4 узлов не входят в состав никаких границ. Это значение
можно легко найти с помощью дуального рассмотрения, из
которого следует, что вблизи Рмин не принадлежащие границам узлы
представляют собой изолированные узлы типов А или В,
окруженные со всех сторон узлами, входящими в состав границы }л
Концентрация р
1-РсВ
А - узлов
РсА
0,5 г
Приведенная координата
Рис. 3. Производная нормированных распределений, приведенных на рис. 2.
или fB. Приведенная вероятность подобного изолированного узла
равна Pl= (1 — рМин)6= (1— 0,73256)6^2,5-Ю-4.
Благодаря существованию двух перколяционных переходов
концентрация в точке Xf заметно отличается от каждой из
величин рсА и 1 —рев. Однако при расмотрении графика приведенной
плотности вероятности на границе можно убедиться, что в
пределе Vp->-0 эта зависимость будет стремиться к штриховой
кривой на рис. 2. Отсюда следует способ нахождения рс с помощью
производной распределения pf{x), график которой имеет два
экстремума, асимптотически приближающихся при Vp-^О к рсл
и 1—рев (рис. 3). При этом пики, отвечающие указанным
экстремумам, несимметричны.
Проведя усреднение по 100 реализациям на решетке 64 X
X 64X256 при значении градиента Vp = 1/256, получили
первые предварительные значения:
д.в~ 0,091, рсЛ~0,31,
которые можно сравнить с принятыми в настоящее время [9]:
рсВ~ 0,098, рсЛ~0,3117.
Как и для двумерных решеток [3], здесь можно использовать
ограниченные реализации, поскольку система рассматривается в
далекой от критических точек области параметров, где радиус
корреляции флуктуации достаточно мал.
Разветвленные полимеры, гелеобразование и перколяция 195
ЛИТЕРАТУРА
1. Sapoval В., Rosso M, Gouyet J.-E.y J. Physique Lett., 46, L149 (1985).
2. Rosso AT, Gouyet J.-F.y Sapoval В., Phys. Rev. B, September 1985.
3. Bunde A, Gouyet 7.-F., J. Phys., A18, L285 (1985).
4. Sykes M. F., Essam J. W., J. Math. Phys., 5, 1117 (1964).
Shante V. K. S., Kirkpatrlck S, Adv. Phys., 20, 325 (1975).
5. Gouyet /.-F., Rosso M.f Sapoval В., будет опубликовано.
6. Cassereau S., Couture В., частное сообщение.
7. Voss R. F., J. Phys., A17, L373 (1984).
8. Gouyet J.-F.y Bunde A, Harder //., будет опубликовано.
9. Heermann D, W.> Stauffer D„ Z. Phys., B44, 339 (1981).
Saleur //., Derrida В., J. Physique, 46, 1043 (1985).
Поверхностное натяжение
в моделях Поттса
и перколяция
С. Харрис *
Используя выражение Костелена — Фортуина для модели Поттса
с s состояниями дается простое доказательство соотношения
Ра? = 1 между корреляционной длиной в выделенном
направлении плоской решетки и поверхностным натяжением
соответствующим образом ориентированной поверхности на дуальной решетке.
Это соотношение, являющееся обобщением хорошо известного
результата для модели Изинга, используется также для
интерпретации поверхностного натяжения в задаче перколяции в
пространстве произвольной размерности.
1. Введение
Статистическая сумма и корреляционная функция
модели Поттса с 5 состояниями при различных взаимодействиях
могут быть представлены в виде взвешенных сумм на
множествах графов, образованных занятыми или свободными связями
[1] или узлами [2, 3] решетки. После предельного перехода
s-M в формулах модели Поттса они перейдут в
соответствующие выражения, описывающие задачи перколяции по связям и
узлам.
Такая процедура обобщается здесь для статистической
суммы модели Поттса при условии фиксированного состояния
границы. Через эту статистическую сумму определяется поттсовская
межфазная свободная энергия на единицу площади
(поверхностное натяжение) и дается ее непосредственная физическая
интерпретация применительно к задаче перколяции.
2. Общая теория
Рассматриваются следующие поттсовские гамильтонианы:
-№B = ksT,[6(oi9af)-l]9
~Р#5 = ь£[6{аа}<--1],
i
где t, /—координаты узлов и (ij) —связи между ближайшими
соседями на решетке L, а а—координаты узлов на покрывающей
решетке Lc, которые расположены в серединах связей решетки!.
Символ {aa}i введен для сокращенного обозначения набора потт-
* С. К. Harris-Department of Physics, University of Edinburgh, King's
Buildings, Mayfield Road, Edinburgh EH9 3 it, UK*
Раззетвленные полимеры, гелеобразование и перколяция 197
совских состояний узлов решетки Lc, которые являются
смежными с i-м узлом решетки L. Поттсовские переменные а* и аа
пробегают для каждого узла значения 1, 2, ..., 5, а
дельта-символы определены следующим
образом:
Мог*, <гу) =
( 1, если at — а/
\о в остальных случаях,
1, если все
состояния набора {aa)i
б iao]i = \ одинаковы,
~ в остальных
случаях.
Для того чтобы определить
поверхностное натяжение,
рассмотрим конечные части L(^
решетки L и LSp решетки LC9
которые изображены на рис. 1,
а и б соответственно. Там же
показаны произвольная
выпуклая область R и плоскость 5
с единичным вектором
нормали я, площадь пересечения
которых обозначена через А.
Обратившись к рис. 1, обозначим
через Z^v статистическую
сумму модели Поттса на L(f) или
UJ\ граничные узлы типа С\ и
С2, в которых находятся
соответственно В СОСТОЯНИЯХ [Л И
v. Тогда поттсовское
поверхностное натяжение на
нормальной к вектору п поверхности
можно определить с помощью
следующей формулы:
Pa (A, s) =
= -lim (l/A\n(ZV2/Zn)).
А->оо
Теперь установим соответствие правой части этой формулы с
взвешенными суммами графов на решетке для гамильтонианов
Нв и Hgi
Рис. 1. Иллюстрация построений для
определения поттсовского
поверхностного натяжения для
гамильтонианов Нв (а) и Hs (б). При этом
использованы следующие
обозначения: / — внутренние поттсовские
узлы, т. е. расположенные внутри
области на вершинах (а) или связях
(б) ячеек решетки L; 2 — граничные
узлы, тип которых Ci или С2
зависит от того, с какой стороны 5 они
расположены; 3 — периметрические
узлы типа Pi или Р2 на решетке L
для задачи узлов с гамильтонианом
Hs. Для задачи связей с
гамильтонианом Нв по определению считается
Pi = С4, Р2 = С2.
198
Часть IV
2.1. Перколяция по связям
Zi2=Sp[II'6((7f, l)6(a}, 2)]ехр(-0Яв) =
= Sp[II,6((Tf, 1)б(07, 2)Щ[1-р + р6(в1) о,)],
где р = 1—ехр(—sk), символ Sp означает сумму по всем
состояниям системы, a W — произведение по принадлежащим С\
узлам i и принадлежащим С2 узлам /.
Каждый член разложения в ряд второго произведения в
правой части отвечает графу G, содержащему занятые и свободные
связи на решетке L. При этом связь (//) в G занята, если в этом
члене содержится множитель б (а/, ау), и свободна в его
отсутствие. При нахождении следа по состояниям каждому кластеру
занятых узлов в зависимости от характера его связности с
граничными узлами типа С\ и С2 соответствует один из трех
множителей 5, 1,0. Первый —когда таких связей вообще нет,
второй — при условии наличия связей только с узлами одного из
типов, третий — в случае, когда имеются связи с узлами обоих
типов. При этом получаются формулы
Z12 = <6[tf(G,CbC2), 0K'(*%, (1)
Z" = (f*<°%, (2)
где N(G, Си Сг)—числа кластеров в G, связанных с
граничными узлами только одного типа С\ или С2, ft/(G)—число
кластеров в G, связанных только с не входящими в состав границ
узлами, NB(G) —число занятых связей в графе G, а операция
усреднения по множеству этих случайных графов соответствует
суммированию
(V(G))0- £ V(Gfp°<0)(1 - р)"в-^°>.
G И
2.2. Перколяция по узлам
ZI2=Sp[IT6((7a, 1)б((т3, 2)]exp(-ptfs) =
-Spill'в (а., Пв(*э, 2)Ш[1-р + рв{*вМ,
где произведение П' берется по всем узлам из L{J\ таким, что
а принадлежит Си а р принадлежит С2.
В этом случае каждый член разложения в ряд правой части
соответствует графу G, содержащему занятые и свободные
связи на решетке L. При этом i-й узел занят в графе G, только
когда в отвечающем этому графу члене разложения имеется
множитель 6{oa}i- При вычислении следа по состояниям в Z12
каждый кластер занятых узлов и каждая связь между парой
Разветвленные полимеры, гелеобразование и перколяция 109
свободных узлов входит с множителем s. Исключение
составляют периметрические связи и присоединенные к ним кластеры,
которым соответствует множитель 1, а также кластеры,
присоединенные по крайней мере одной связью к узлам каждого из
периметрических классов С\ и Сг, которым отвечает
множитель 0.
Тогда можно получить формулы
Z12<6[JV(G, Cl9 C2), Q]f'{a»n»m)Q9
Zu = (sniiG)+nv{G%,
где rtu(G)—число пар смежных незанятых узлов в графе G,
NS{G)—полное число в нем свободных узлов, а операция
усреднения по случайному набору графов G представляет собой
суммирование такого вида:
<У (О)- I V(G)pN^a)(l-pf-Nsia\
G
3. Предельный переход
к случаю одного состояния и перколяция
Осуществляя такой предельный переход s-M, можно
получить
Zi2/Z"=<6[tf(G, pu P2), 0]) = Q(A, p),
где Q(A, p)—вероятность того, что в задачах перколяции по
связям или узлам ни один узел Pi не связан ни с каким узлом
Рис. 2. Перколяционный кластер с большой «дырой».
Р2. Через эту величину выражается поверхностное натяжение в
перколяционной задаче
р(т(/г, 1) = —Hm U"llriQ(4, р)\,
А->оо
200
Часть IV
которое всегда неотрицательно и обращается в нуль при всех
р < рс. Выбрав из скейлинговых соображений
Q(A, p) = Avf(A/td-1),
получим в окрестности критической точки р = рс
cr(A, l)~(p-pcf-l)\
Пусть P(S) означает вероятность того, что при р > рс впер-
коляционном кластере вдоль поверхности 5 имеется большая
дыра площадью А (рис. 2). Тогда, используя (3), получим
lim [A-{lnP(S)]=-[$e(A, l)dS/[dS.
Применив подобные соображения к распределению больших
мертвых концов, можно показать, что оно асимптотически
совпадает с распределением больших конечных кластеров.
4. Соотношение дуальности для перколяции
на плоских решетках
4.1. Перколяция по связям
Рассмотрим ограниченную часть (L*)(f) дуальной решетки L*,
каждая связь которой пересекает связь решетки L(f), как это по-
Рис. 3. Построение рис. 1 с конечным фрагментом (L*)<f> дуальной
решетки L, показанной штриховыми линиями.
казано на рис. 3. Узлы а и Ь на (L*)<f> принадлежат тем
поверхностям на решетке L, в которые входят поттсовские узлы типа
С\ и С2 границы поверхности. Любому графу G на L(f) можно
поставить в однозначное соответствие граф G* на (L*)(f) таким
Разветвленные полимеры, гелеобразование и перколяция 201
образом, что каждая занятая связь графа G пересекает
свободную связь графа G*, и наоборот. Легко заметить, что G, точки
Pi и Р^ которого связаны, соответствует графу G* с не
связанными точками а и 6, и наоборот. Поэтому
б [N (G, Ри Р2), 0] = 1 - б [N (G\ a, 6), 0], (4)
и поскольку
NB(G) = NB-NB(G*), (5)
то с учетом р* = 1 — р получим
(б [N (G, Ри Р2), 0]) = (1 - б [N (G\ а, Ь), 0]>. (6)
4.2. Перколяция по узлам
В этом случае G является графом занятых и свободных
узлов на L(f), а связь в G считается занятой, если она соединяет
пару смежных занятых узлов. Множество (L*)(f) образует
решетку взаимодействующих вершин, через которую занятые узлы
графа G* на L взаимодействуют с другими занятыми узлами той
же самой поверхности L^K К занятым узлам графа G* относятся
свободные узлы графа G и взаимодействующие вершины, а связь
в G* считается или занятой, если она соединяет занятые
вершины, или свободной, — во всех остальных случаях. Рассмотрим
поверхность, образованную парой соседних узлов (L*)(f) и парой
узлов Uf\ соседних к ним обоим. Если G связывает последние
через поверхность, то G* не связывает первые около нее, и
наоборот. При этом приведенные выше выражения (4) — (6) с
учетом замены NB на Ns останутся справедливыми. Усреднение
<.. .> по множеству G* проводится по вероятностной мере пер-
коляционной задачи узлов L^\ в которой занятые узлы одной
поверхности связаны.
Таким образом, в задачах связей и узлов величина <1 —
-6[N(G\ a, ft), 0])G„ равная вероятности того, что точки а и о
связаны, убывает экспоненциально ехр(—Л/|*) с
корреляционной длиной £*, отвечающей дуальной решетке. Отсюда следует
важное равенство рог^* = 1.
5. Соотношение дуальности при произвольных 5
Оно легко устанавливается для модели Поттса с
взаимодействиями ближайших соседей. Связи L(f) могут быть поставлены
во взаимно однозначное соответствие со связями дуальной к
(L*)(f) решетки, в которой Pi и Р2 слились в один внешний узел
е. Используя инвариантность ft/(G), можно связать величины,
входящие в правые части (1) и (2), с соответствующими
величинами на указанной решетке. Графы на L{f\ в которых Р\ и Р2
202
Часть IV
не связаны, соответствуют графам, в которых проходящие через
е циклы не пересекают внутри области R линию 5 нечетное
число раз. Исходя из стандартных соображений о дуальности [5J
и выражения (3) можно показать, что Zl2/Zn равно коррелятору
поттсовских состояний точек а и & на (L*)(f> со всеми
вытекающими отсюда результатами. Детальные вычисления и
обсуждения указанных вопросов приведены в работе [6].
ЛИТЕРАТУРА
1. Kasteteyn P. W., Fortuin С. М, J. Phys. Soc. Japan SuppL, 16 11 (1969).
Fortuin С. M.y Kasteteyn P. W., Physica, 57, 536 (1972).
2. Giri M. R., Stephen M. J.t Grest G. S., Phys., Rev., В16, 4971 (1977).
3. Essam J. W., J. Math. Phys., 20, 1769 (1979).
4. Можно упомянуть более раннюю работу математиков: Fontaine /. #.,
Gruber Ch., Commun. M. ath. Phys., 70, 243 (1979), где поверхностное
натяжение в произвольных спиновых системах, включая модели Поттса,
рассматривалось с точки зрения установления в них строгих критериев
существования фазового перехода.
5 Wu F. У., Rev. Mod. Phys., 54, 235 (1982) и ссылки в ней.
6 Harris С. /С, J. Phys. A: Math. Gen, 18, 2259 (1985).
Перколяция на РМП
Р. Дьюар, С. Харрис*
Обсуждаются различные алгоритмы перечисления свойств перко-
ляционных кластеров на параллельном компьютере с помощью
распределенного матричного процессора (РМП). На основании
полученных результатов проверяется недавнее утверждение Г. Джага
относительно критического поведения при перколяции в двумерном
пространстве.
1. Введение
РМП представляет собой машину параллельного
действия, с помощью которой могут быть эффективно проведены
вычисления многих физических величин. Несмотря на
ограниченное применение, она принадлежит к расширяющемуся классу
машин с новой архитектурой, предназначенных для решения
крупномасштабных задач вычислительной физики и других
дисциплин.
РМП (рис. 1) представляет собой массив 64X64
действующих элементов (ДЭ), каждый из которых обладает 4096 бит
памяти и связан с четырьмя своими ближайшими соседями (север,
юг, восток, запад). Крайние связи массива можно выбрать так,
чтобы удовлетворить плоским или цилиндрическим граничным
условиям в любом направлении. Процессоры работают
синхронно.
Для программного обеспечения используется РМП
ФОРТРАН, который представляет версию обычного ФОРТРАНа,
приспособленную для работы на РМП. Например, сложение матриц
размера 64X64 выполняется при помощи команды
С = А + В,
где сложение и присвоение осуществляются одновременно для
всех элементов. Процессоры действуют во времени на одной
плоскости размером 64 X 64 бита так, что наиболее быстрыми
среди операций являются булевы операции с логическими
матрицами, элементами которых служат ИСТИНА или ЛОЖЬ. Это
объясняет причину того, почему РМП особенно эффективен при
решении задач с двумя состояниями, таких, как моделирование
изинговских систем [1] и перколяции.
* R. Dewar, С. К. Harris-Department of Physics, University of Edinburgh,
Mayfield Road, Edinburgh EH9 3JZ, UK.
204
Часть IV
Рис.
1. Схематическая
РМП.
диаграмма
Логические массивы крайне полезны в качестве условных
масок для выключения определенных процессоров во время
выполнения операции. Например, можно написать
A(LMASK) = B,
что присваивает элементы В только тем элементам А, у которых
LMASK есть ИСТИНА, а остальные А остаются неизменными.
Процессоры взаимодействуют друг с другом посредством
общих операций сдвига. Например, в результате выполнения
команды циклического сдвига
д «восток» с логическими масси-
I вами L, М, N
4096 L = M.AND.SHEC(N,3)
UJ" происходит присвоение элемен-
1 там L логической суммы
соответствующего элемента N и
элемента М, сдвинутого на 3
позиции на «запад». При этом
используются циклические
граничные условия по
направлению «восток — запад».
Классическая перколяцион-
ная задача рассматривает
кластеры занятых узлов или связей на правильной решетке.
Неотъемлемая трудность здесь заключается в нелокальной природе
связности кластеров. Для того чтобы извлечь из перколяцион-
ных конфигураций интересующую информацию (типа
распределения кластеров по размерам), узлы должны быть помечены
таким образом, чтобы можно было следить за развитием тех из
них, которые входят в состав одного и того же кластера. Кроме
того, указанные метки должны быть обновлены при выборе двух
кандидатов для связывания кластеров в один.
В такой процедуре нельзя полностью использовать
параллельную структуру РМП, хотя в случае направленной перколя-
ции (когда запрещено прохождение в обратном направлении
путей, связывающих пары узлов) можно написать эффективный
параллельный алгоритм, который учитывает связность кластеров
[2]. Однако локальное окружение на уровне ближайших
соседей отдельных узлов может быть эффективно проанализировано,
что используется в следующем алгоритме для подсчета числя
кластеров в перколяционных двумерных конфигурациях.
2. Параллельный алгоритм для подсчета кластеров
Этот алгоритм легче всего проиллюстрировать на примере
перколяции по узлам на квадратной решетке линейного размера
Разветвленные полимеры, гелеобразование и перколяция 205
L —64 узла с плоскими граничными условиями. Конфигурация
занятых узлов с концентрацией р генерировалась как случайная
логическая матрица на РМП. Итерация на основе центрального
алгоритма переводит кластеры
занятых узлов в единичные
кластеры, каждый из которых
увеличивает число кластеров на еди-
Эта
i—т—i—i
—тт—
т———
1—1—I—i
Кластеры=0
Кластеры-I
■>
—?
*—L
?{ластерьг=3
Остановка
ницу, а затем удаляется
процедура показана на рис. 2 на
примере типичной 4X4
конфигурации, содержащей 3
кластера.
Этапы указанной процедуры,
заключающиеся в
использовании параллельной булевой
логики и операций сдвига на РМП
ФОРТРАНе, таковы:
1. Идентифицируются все занятые узлы, не имеющие занятых
соседних узлов на «севере» и «востоке». Четыре возможных
здесь случая приведены ниже
о о
а) о • о 6) •—• о
о
о
Рис. 2. Иллюстрация кластерного
алгоритма.
О
о
в) о t о г)
Г 8,Ч
Для каждого узла типа "я" общее число кластеров
увеличивается на единицу.
Удаляются все найденные на этапе 1 узлы с одновременной
заменой узлов типа "г" на новые занятые узлы, лежащие на
«юго-западе» (если только последние свободны)
т^п
Заметим, что, поскольку операции осуществляются параллельно,
никакие два кластера не могут на этом этапе соединиться
нечаянно. Далее этапы 1—3 повторяются до тех пор, пока не
останется занятых узлов.
Когда применяются циклические граничные условия,
некоторые кластеры, образуя бесконечные петли вокруг решетки,
никогда не выводятся из системы. В этом случае алгоритм
обрывается после некоторого числа итераций, достаточного для
гарантированного выведения всех способных к нему кластеров.
206
Часть IV
Тогда все оставшиеся узлы предполагаются входящими в состав
единственного основного кластера, который дает вклад, равный
единице, в общее число кластеров.
Этот алгоритм и аналогичный ему алгоритм для перколяции
по связям могут быть использованы для решеток различных
типов вплоть до их размеров L = 64, но особенно эффективны они
при L = 8, 16, 32, когда можно размещать в памяти и
анализировать одновременно много подобных решеток. Для таких
значений L число анализируемых в час конфигураций падает, грубо
говоря, как Lr2 и составляет приблизительно 2-Ю6 (1,5-106) для
перколяции по связям (узлам). Эти цифры полезно сравнить со
значением 0,07-106, которое достигается на мощной серийной
машине CRAY1 [3] при расчетах перколяции по связям на решетке
с L = 30.
3. Критическое поведение в случае двумерной перколяции
3.1. Среднее число кластеров
В задаче перколяции по связям или узлам среднее число
кластеров на один узел К(р) при заданной концентрации р
служит аналогом удельной свободной энергии в термической
задаче. Вблизи перколяционного перехода рс эта величина имеет
сингулярную часть
К*(р) = С\р-рс?-а, (1)
где для двумерных систем в настоящее время принято значение
а=-2/3. (2)
Однако недавно Джаг [4] поставил под сомнение это
значение, а следовательно, либо справедливость гиперскейлинга, либо
значения других показателей двумерной перколяции. Начав с
двумерной модели Изинга с разбавлением по связям с помощью
метода грассмановского интеграла по траекториям, который
является точным при малых разбавлениях, он вычислил свободную
энергию /(Г, р). Эта функция, как показано в [4], описывает
критическое поведение модели Изинга с разбавлением повсюду
вдоль критической кривой Тс{р), включая перколяционный
переход Тс = 0, р = рс, вблизи которого ее сингулярная часть
дается асимптотической формулой
Ks(p) = C(p - рс)2\п\1п\р - рс\\. (3)
Итак, теория, основанная на грассмановских интегралах,
предсказывает отличное от (2) значение а = 0 и ставит под вопрос
существование [5] отдельного класса универсальности для
двумерных перколяционных процессов.
Разветвленные полимеры, гелеобразование и перколяция 207
Джаг [3] для подтверждения этого спорного результата
воспользовался численными данными и вновь проанализировал
степенные разложения. В оставшейся части статьи обсуждаются
эти данные вместе с оригинальными результатами авторов,
полученными с помощью РМП.
3.2. Численное исследование
Сингулярное поведение (1) или (3) проявляется в
расходимости третьей производной К"'{р) функции К(р) в точке р = рс.
Скейлинговый анализ для
системы конечных размеров L
ведет при L ->■ со к асимптотикам
К'"{р,
,L) = {
А + BLX>\ (4)
A + B(L)Ll»,
(5)
40
30
^ 20
$
i
10
9
7
6
- А]
Наклон = /-__/<? Т
^-"Х. Наклон- 7/4
( >М
L ^^^^
1111 1 1
7 8 9 10
го зо
Рис. 3. Закон расходимости
K'"{pci L) при увеличении L.
первая из которых получается
в обычной теории, а вторая —
в теории Джага. Фактор B(L)
учитывает логарифмические
поправки. В отличие от
работы [3], численные результаты
которой подтверждают
формулу (5) с показателем v =1
модели Изинга с
разбавлением, данные настоящей
работы отдают предпочтение общепринятой формуле (4). Следуя
[3], случайным образом были генерированы конфигурации для
моделей перколяции по узлам и связям на решетках различных
размеров. Затем по флуктуационной формуле
К'" (Р, L) = С{ {(N0nc) - (NQ)(nc)} +
+ С2 {(Nine) - 2 (N0) (N0nc) + 2 (N0f (nc) - (Nl) (nc)} +
+ C3 {(Nlnc) - 3 (NQ) (Nlnc) + 6 (Nl) (N0nc) -
- 3 (Nl) (Nonc) - 6 (Nl) (nc) + 6 (No) (Nl) (nc) - (Nl) (nc)} (6)
вычисляли К!" {pc,L). Здесь угловые скобки означают
усреднение по большому числу конфигураций, N0 и пс — число занятых
связей (или узлов) и соответственно число кластеров на один
узел в каждой конфигурации, а константы Си С?, С3 дакугся фор-
208
Часть IV
мулами
2(/Г3 + <7-3),
с2=- з (р~3+р~ У - р~ У2 - <Г3)> (7)
СзЧ/гЧ?-1)3,
где q = 1 — р.
На рис. 3 представлены оригинальные результаты для пер-
коляции по связям на квадратной решетке (квадратики)
размерами до L = 32. Там же для сравнения приведены аналогичные
данные из работы [3]
(кружки) и похожие результаты для
перколяции по узлам на
треугольной решетке
(треугольники). По мнению авторов,
несоответствие результатов на
рис. 3 обязано недооценке в
работе (3) шума,
генерированного уравнением (6). Для того
чтобы устранить
статистические флуктуации, предложена
следующая процедура.
К{р) содержит
аналитическую часть
20 30
Рис. 4. Гистограмма К'"(рс, 16) для
перколяции по связям. 1 «ящик»
соответствует среднему по I 638 400
конфигурациям. Полная гистограмма
содержит 62 «ящика», а —-
Необработанные данные; б — шум снят.
К(р) = а + Ь(р-рс) +
+ c(p-Pcr + d(p-Pcr+...,
(8)
где константы а, 6, с, d либо
известны аналитически, либо
могут быть найдены из
степенных разложений [6]. Второе и
третье слагаемые не вносят вклад в К{рс), но они дают
значительный вклад в шум при вычислении средних в формуле (6)
по конечному набору конфигураций. Этот шум может быть
вычтен заменой пс в правой части формулы (6) на
гСс = пс - Ъ (N0 - Npc)/N -c(N0- Npcf/N2,
(9)
где N— общее число вершин (ребер) решетки в случае задачи
узлов (связей). Четвертый член в формуле (8) вносит вклад в
константу А в (4) или (5) и для облегчения интерпретации
данных может быть вычтен аналогичным образом.
Эффект вычитания этого шума показан графически на рис. 4,
откуда можно заключить, что приведенные в работе [3] ошибоч-
Разветвленные полимеры, гелеобразование и перколяция 209
ные данные имеют заниженные значения. Прямые линии,
проведенные через точки, полученные в настоящей работе для пер-
коляции по узлам и по связям, имеют соответственно наклоны
0,25 + 0,02 и 0,28 ±0,03, согласующиеся с зависимостью (4).
ЛИТЕРАТУРА
1. См., например, Pawley G. S. et ai, Phys. Rev., B29, 4030 (1984).
Williams J. /(., J. Phys., A18, 49 (1985).
2. Williams J. /C, McKenzie N. D., J. Phys., A17, 3343 (1984).
3. Jug С, в печати.
4. Jug G.t Phys. Rev. Lett, 53, 9 (1984).
5. Stauffer D.y Z. Phys., B22, 161 (1975).
Birgeneau R. J. et a/, Phys. Rev. Lett., 37, 940 (1976).
6. Domb C, Pear се С. /., Phys. A9, LI 37. (1976).
Часть V (а>
МОДЕЛИ НЕОБРАТИМОГО РОСТА:
ЛАПЛАСОВСКИЕ ФРАКТАЛЫ, ПРОБОЙ
ДИЭЛЕКТРИКОВ, РАСТРЕСКИВАНИЕ
И ВЯЗКИЕ «ПАЛЬЦЫ» В ЖИДКОСТЯХ
Свойства лапласовских фракталов
при пробое диэлектриков
в двух и трех измерениях
Г. Висман, Л. Пьетронеро *
Исследованы свойства случайных фрактальных структур S в
случаях одного, двух и трех измерений. Процесс роста определяется
вероятностной мерой, задаваемой решениями краевой задачи
теории потенциала (лапласовские фракталы). Соотношение между
вероятностью роста и локальным электрическим полем имеет вид
р~Ец. Фрактальная размерность D, средний радиус и зона
роста характеризуются первым и вторым моментами распределения
заряда на S. Особое внимание уделено нетривиальной зависимости
D от т|.
1. Введение
Известно много различных разновидностей пробоя
диэлектриков от молний в атмосфере до электрических стримеров
в полимерах. В зависимости от диэлектрика (газ, жидкость,
твердое тело или полимер) микроскопический процесс,
приводящий к пробою, может быть различным. Тем не менее мы
наблюдаем весьма похожие между собой глобальные, или
структурные, свойства картины разряда, и наши основные усилия
направлены на понимание этих аспектов пробоя.
Пробой диэлектрика служит примером процесса случайного
роста. Если электрическое поле, наложенное на изолирующий
материал, превышает некоторое критическое значение Ес, то в
материале возникает проводящая фаза. Со временем эта фаза
растет стохастически и образует характерные картины разряда.
Наблюдаются различные геометрии от диффузных
квазиоднородных до нитевидных со слабым или сильным ветвлением.
Как научный, так и технический интерес представляют
следующие вопросы. 1) Каково значение критического поля £с? Си-
* Я. /. Wiesmann- Brown Boveri Research Centre, CH-5405 Baden,
Switzerland; L. Pietrenero-University of Groningen, Melkweg 1, 9718 EP Cronin-
gen, The Netherlands,
Модели необратимого роста
211
туация в газах досконально изучена и понятна [1]. Что же
касается критического поля инжекционного пространственного
заряда в полимерах [2], то известно лишь несколько недавно
полученных результатов. 2) Охватывает ли процесс роста
глобальный (катастрофический) пробой или распространяется
только на некоторую ограниченную область пространства? Ответ на
этот вопрос, разумеется, зависит от геометрической
конфигурации электродов, но, что более интересно, обладает и внутренним
аспектом: максимальная протяженность области, охваченной
процессом роста, и критическое поле тесно взаимосвязаны.
3) Можно ли описать геометрию картины пробоя и объяснить ее
исходя из закона роста? Для того чтобы хотя бы частично
ответить на этот вопрос, мы ввели математическое описание
процесса разряда, приводящего к фрактальным структурам [3]. Такое
описание позволяет охарактеризовать картины пробоя числами:
фрактальными размерностями и критическими показателями.
Оказывается, что эти числа нетривиальным образом зависят от
специфической формы закона роста и, следовательно, не
универсальны. В настоящей работе изложены результаты обширных
исследований этой проблемы для евклидовой размерности d = 2
и новые результаты для d = 3.
2. Реальный процесс и его идеализация
Для того чтобы понять (с физической точки зрения)
ограничения модели и направления возможных обобщений,
необходимо хотя бы в общих чертах дать «реалистическое»
феноменологическое описание процесса разряда. При пробое материал
разделяется на две различные фазы: Pd (диэлектрическую, или
изолирующую, фазу) и Рс (проводящую фазу). Фазы разделены
границей, которая является динамическим объектом более или
менее сложной стохастической формы. В каждой из фаз нам
необходимо ввести систему уравнений, позволяющих определять
те физические величины, которые представляют интерес:
электрическое поле Е, потенциал </>, плотность заряда q и, возможно,
некоторые другие величины. Если исключить процессы
фотоионизации, то такие уравнения имеют вид
-Аф = д, £=-grad^, (1)
q = e Yj ant, (2)
a, k
nl = 0 в РЛ, (3)
hl = Dlnl в Ре, (4)
где п% означает плотность носителей заряда с зарядом а-е,
индекс к позволяет в случае необходимости различать различные
212
Часть V(a)
виды носителей, D\ — локальный, но нелинейный оператор,
зависящий от £ и п%. Правая часть уравнения (4) описывает
процессы рождения, уничтожения и переноса зарядов (поле и
диффузионные токи). Динамика поверхности, разделяющей
диэлектрическую и проводящую фазы, разумеется, зависит от
скоростей частиц в ее окрестности.
Так как в фазе Ра плотность заряда равна нулю, уравнение
(1) переходит в уравнение Лапласа: для того чтобы найти ф,
необходимо решать краевую задачу теории потенциала с
граничными условиями на поверхности раздела диэлектрической и
проводящей фаз.
Решение системы уравнений (1) (Пуассона) и (2)
(переноса) в проводящей фазе Рс — весьма многообещающая
программа в попытке понять пробой диэлектриков. Множество
теоретических работ посвящено рассмотрению этих уравнений при
самых различных, более или менее искусственных граничных
условиях. К сожалению, задача оказалась слишком сложной,
чтобы позволить понять происхождение наиболее характерных
структур разряда. Кроме того, описываемая выше теория не
содержит элемента, порождающего явно стохастическую природу
процесса пробоя.
Наша идеализированная теория приводит к пониманию этих
важных аспектов ценой отказа от всех деталей, описываемых
уравнением (4). Вместо них мы принимаем предположение о
том, что ф = ф° = const в Рс (заметим, кстати, что это
выражение является тривиальным решением уравнения Лапласа).
Можно сказать, что оно эквивалентно утверждению об
идеальной проводимости фазы Рс. Такое предположение находится в
весьма хорошем согласии с наблюдениями, например для
разрядов проводников в газах. В результате плотность заряда
отлична от нуля только на поверхности раздела фаз
(индуцированный заряд на поверхности проводника Рс)- Кроме того, q
пропорциональна напряженности поля в фазе Ра на поверхности
раздела и, следовательно, определяется решением граничной
задачи в фазе Ра- Мы интерпретируем это поле на поверхности
раздела в стохастическом смысле как вынуждающую силу для
процесса роста: точки поверхности раздела, на которой
напряженность поля велика, в среднем движутся быстро; точки в поле
малой напряженности движутся медленно или стационарны.
3. Решеточная модель лапласовских фракталов
Изложенные выше идеи мы реализуем в решеточной модели,
чтобы упростить численное моделирование на компьютерах и
уменьшить число возможных конфигураций разряда. Предметом
Модели необратимого роста
213
исследования служит решеточная структура 5 ^-мерной
(кубической) решетки, представляющая проводящую фазу Рс, в то
время как Ра соответствует дополнению структуры Zd \ S.
Полезно отличать структуру узлов и структуру связей. Пусть Sn
Рис. 1. Решеточная структура разряда: Sn (узлы, черные точки) и Sn
(связи, сплошные линии). Каждой связи из dSn (поверхностные связи,
штриховые линии) поставлена в соответствие определенная вероятность,
зависящая от поля.
означает связную конфигурацию узлов, содержащую (я + 1)
узлов (изображенных на рис. 1 черными точками), a S'n
соответствует структуре связей, содержащей п связей (изображенных
на рис. 1 сплошными линиями). Тогда
Sn = {km\km<^Zd, m = 0, ..., п}у
S; =={(£> £')l|fc--fe'l=l, k,k'<==Sn}. {Ь)
Необратимый процесс роста происходит элементарными
шагами Sn ->■ S/i+i, Sn <= 5я+1. Чтобы сохранить связность структуры
Sn, мы после каждого шага накладываем ограничения
Sft+i = SttU{A}, dist(A, Sn)=l,
S^i^Utt*,*)}, {k,h}^dS'n, U
где
dS'„ = {(k9h)\\k-h\=l9 k^Sn, h0Sn] (7)
— множество поверхностных связей структуры Sn (штриховые
линии на рис. 1); dist (Л, Sn) — расстояние от узла h до
структуры Sn- Таким образом, на каждом шаге мы случайным
образом выбираем одну связь из множества «кандидатов» dSn-
214
Часть V(a)
Сопоставляемая связи вероятности \is определяется решением
граничной задачи для ф на d-мерной решетке:
А^= Z (Фы-е-2ёфн) = 0, (8)
h^Zd \S
с граничными условиями Дирихле
фк = ф°, k^Sny (8a)
Фк~>0> |Л|-^оо при d>3, (86),
Фк~— Ф°\п\к\, |ft|->oo при d = 2.
Пусть по определению
^(А.Л)=Г*^-^ ПРИ <к>">ед& (9)
ft (0 в противном случае
с нормирующим множителем
ZSn= Z !(Фь-Фн), (90
(*,/i)€=ds;;
т. е. вероятность выбрать поверхностную связь (ft, h) на (п +
+ 1)-м шаге определяется функцией / локального поля,
приписываемого этой связи в конфигурации Sn- При выборе функции
f у нас еще остается неиспользованная степень свободы. Для
того чтобы определить /, существуют две различные
возможности: либо на основе микроскопических соображений вычислить
по крайней мере пороговое значение Ес> либо моделировать
различные структуры на основе тех или иных функций /, стремясь
достичь удовлетворительного согласия с экспериментально
наблюдаемыми структурами. Мы предпочитаем двигаться вторым
путем и ограничиваем выбор f однопараметрическим семейством
функций
/(*/) = const *Д (10)
Мера \х в этом случае определяется выражением
ц3п(ft, h) = Zsln(фк - фн)\ (ft, h) e dSn. (11)
При таком выборе f мы в действительности пренебрегаем
существованием критического поля Ес. Мера \х не зависит от
приложенного напряжения ф°, так как потенциал линеен по ф°. В
рассматриваемой задаче не существует естественной физической
единицы (такой, как поле или напряжение), и \i зависит только
от геометрической конфигурации S„. Соотношение (10) в
действительности представляет собой самый общий вид функции f,
согласующейся с мерой, заданной чисто геометрически. Почему?
Модели необратимого роста
215
Дело в том, что \х не зависит от ^° в том и только том случае,
если / удовлетворяет соотношению типа
f№) = gWf(y) (12)
при некоторой функции g, эквивалентному соотношению
F{%y) = F{X)F{y)y (120
где F(y) = f(y)/f(l). Единственным измеримым решением
уравнения (12х) является степенная функция, откуда и следует
зависимость (10).
Соотношения (8) и (11) полностью определяют процесс
роста, если тот начинается с заданной начальной конфигурации
5Ло. В дальнейшем мы всегда будем выбирать за 5«0 начало
решетки: Sn0—{0}. Возникающие в процессе роста бесконечно
протяженные структуры обладают, как оказывается,
фрактальными свойствами. Мы называем их лапласовскими фракталами,
так как порождающий их динамический процесс тесно связан
с уравнением Лапласа.
4. Вероятностная мера и индуцированный заряд
Структура Sn и ее динамическое поведение характеризуются
двумя различными функциями плотности, связанными между
собой граничной задачей (8). Мы имеем в виду плотность
заполнения р:
f 1 при k^Sn,
го« I 0 в противном случае,
и если предположить, что в рассматриваемом случае т) = 1,
плотность заряда q:
<7sraW = -A^ = - E (Фн-tk). (И)
п h,\h-k\ = \
Разумеется, плотность (14), как следует из краевой задачи (8),
равна нулю при k e Sn, но, вообще говоря, не на Sn. Так как
потенциал на Sn постоянен, мы можем отбросить в сумме (14)
слагаемые с A g Srt, и тогда из (11) следует, что
qSn(k) = ZSn £ »(k, h). (15)
К (krh) <=TdSr
п
Наконец, суммируя по всем k e 5Я, мы получаем
Qsn = ZSn, (16)
т. е. нормирующий множитель меры \х есть не что иное, как
суммарный заряд, сосредоточенный на структуре S*. В силу соот«
216
Часть V(a)
ношений (15) и (16) нормированную плотность заряда qsJQsn
можно интерпретировать как распределение вероятности того,
что (п + 1)-й шаг роста начнется в узле k конфигурации 5Я.
Определим следующие моменты этого распределения:
r? = QZlnTlqsn(b)-\kr, m=l, 2, ... . (17)
k
Определяемый соотношением (17) момент г™ представляет
собой среднее по заданной конфигурации Sn. Заменяя плотность
Ф О р(Г)
* О /МП, # а р-(Г)
Рис. 2. Картина разряда, характеризуемая числом ветвей р(г), пересекающих
окружность данного радиуса г, и плотность точек ветвления р+(г) и
свободных концов о-(г).
заряда qSft ее средним qn по всем возможным реализациям,
получаем (г%\. Моменты с пг = 1 и m = 2 имеют практическое
значение, так как допускают численные реализации. Обозначим
для краткости (г]^ через (гп}у а флуктуации
{{гп-{гп))Т (18)
через (дгпу. В то время как (гп) можно интерпретировать как
радиус средней структуры из п элементов, (8гп) — мера
радиальной толщины растущей зоны. Относительно п эти величины
ведут себя в соответствии с законами подобия
{гп)~агп\ (6rn)~(wy. (19)
Прежде чем переходить к изложению результатов, следует
упомянуть о том, что в случае п Ф 1 плотность заряда q
надлежит заменить «обобщенной» плотностью заряда
qfn(k)= £ (Фн~ф№ (20)
допускающей процедуру, аналогичную применяемой при т) = 1,
Модели необратимого роста
21?
Наконец, как видно из рис. 2, показатель vi существен для
конфигурации разряда в случае сферически симметричной
геометрии электродов. Асимптотическая структура S = limSn ха-
П-±оо
рактеризуется своей фрактальной размерностью Д связанной
с показателем vi соотношением
D = vT\ (21)
как отмечали еще Плишке и Рац [4] в предположении о гаус-
совском радиальном распределении заряда. Если р(г)—число
линий разряда, пересекающих окружность данного радиуса г,
р±(г)—радиальная плотность точек ветвления (+) и
свободных концов (—), a L(r) —полная длина линий разряда в
окружности радиуса г, то выполняются следующие соотношения
подобия
L{r)~rD, p(r)~rD-1, p±(r)~rD-2. (22)
Результаты
Мы далеки от полного решения задачи динамического роста
для лапласовских фракталов. Точные решения известны только
для размерности rf= 1. При d — 2 и й = Ъ мы располагаем
результатами численного счета. Они ограничены радиальными
плотностями.
При d = 1 задача эквивалентна обычной задаче о
случайном блуждании в одномерном случае. Структурная сложность,
столь характерная для более высоких размерностей, в
одномерном случае отсутствует. Структура (связная) Sn
характеризуется своими свободными концами («висячими вершинами»),
каждый из которых несет нормированный заряд 1/2. Если гп —
координата (правого) конца, то независимо от х\
п
'.»=t£(1+M. (23)
где £*е (—1, +1) —случайные величины. Из соотношения (23)
мы получаем хорошо известные показатели vi = 1, V2=0,5 и
распределение вероятности для конфигураций
Prob{r„ = *} = 2-«(*). (24)
Установлено, что при d = 2 и d = 3 картины разряда
обладают следующими характерными свойствами относительно
параметра г]. Большие значения ц приводят к малым плотностям
заполнения с небольшим числом ветвлений, глубоким
проникновением поля в структуру и, следовательно, широкому радиальному
218
Часть V(a)
распределению зарядов. Отчетливо выражена тенденция к
предпочтительному росту на концах в направлении сильного поля.
В отличие от этого при малых значениях параметра г\ мы
получаем сильно разветвленные плотные структуры, резко
экранирующие внешнее поле. Соответствующие радиальные плотности
заполнения р£ад и заряда ^ад определяются выражением
QT4r)=I,qn(k)b(\k\-r) (25)
к
(и аналогичным выражением для р) и представлены на рис. 3
при d = 2, ц = 0,5; 1; 2 и соответственно п « 30 000, 10 000, 3000.
Можно различить две области.
Внутренняя область, в которой
структура достигла своего
асимптотического предела,
характеризуется типичным
возрастанием рРад по степенному
закону с показателем (D—1) и
малостью jj£aA. Растущая, или
флуктуирующая, зона
является носителем зарядов, и
заполнение в ней убывает.
Наиболее важным
результатом является установление
нетривиальной зависимости
показателей vi и v2 от
характеристического параметра ц рас-
и V2 с увеличением к\
возрастают. Мы получаем неравенство V2 <C vi, причем
отношение v2/vi возрастает. На рис. 4 показана ситуация при
d = 3 (при d = 2 результаты качественно такие же). Кроме
того, на рис. 5 показана в дважды логарифмическом масштабе
зависимость 1п<г„> и ln<8r„> от In я при d==2, d = 3 и q=l.
Зависимость показателей от г), как нетрудно понять,
непрерывна с точностью до единственного возможного исключения —
значения т] = 0. При г) = 0 возможны два различных определения
процесса роста. Грубо говоря, процесс роста зависит от того,
положить ли величину уч в соотношении (10) при j/ = 0 ht) = 0
равной 1 или 0. Определение «1» соответствует равному весу
каждой поверхностной связи независимо от того, лежит ли
поверхностная связь внутри петли в конфигурации 5«, где поле в
точности равно нулю, или не лежит. Такую модель можно
назвать моделью связи Идена. Определение «0» соответствует
пределу г) = 0 нашей модели, но, к сожалению, существующие ныне
численные методы не позволяют проанализировать ее. Мы пола-
0 60 100 150
Радиус
Рис. 3. Плотность заполнения (р„аА»
сплошные линии) и плотность заряда
(<?5ад»А штриховые линии) в
произвольных единицах при d = 2 и г] =
= 0,5; 1 и 2.
пределения вероятности. И ;ь
Модели необратимого роста
219
гаем, что при более высоких размерностях различие между
двумя определениями становится несущественным, но при d=2
необходимо соблюдать известную осторожность.
Зависимость показателей роста от у\ позволяет по-новому
взглянуть на спор по поводу диффузионно-ограниченной
агрегации (ДОА) [5], управляется ли процесс одним или несколькими
масштабами. Из математической эквивалентности ДОА и
модели пробоя диэлектриков в частном случае при т) = 1 [6] мы
Рис. 4. Показатели роста vi, v2 и их Рис. 5. Средний размер </*„><* и флук-
отношение как функции характери- туации <6гя><* как функции от л в
стического параметра ч) распределе- дважды логарифмическом масштабе
ния вероятности. при г| = 1 и d = 2, d = 3.
заключаем, что обе модели должны приводить к одинаковым
результатам. Если бы показатель v2 стремился к показателю vi
при больших п, мы могли бы ожидать, что это происходит при
среднем радиусе, меньшем при малых rj (резкое экранирование)
и большем при больших rj (слабое экранирование). Такой
тенденции нам обнаружить не удалось.
Наконец, табл. 1 позволяет составить общее представление
о показателях v, фрактальной размерности Д приближенных
размерах образца яМакс и числе образцов я, использованных для
получения средних значений, при d=l, 2, 3 и различных
значениях т|. Следует подчеркнуть, что приведенные в табл. 1
показатели вычислены на основе соотношения (17). В ограниченных
пределах нам удалось провести исследования при d = 3 (гмаКс~
~ 25). Аналогичные вычисления в рамках модели ДОА [7, 8]
приводят к несколько иным значениям (vi = 0,39; v2 = 0,29;
D = 2,55).
Приведенные выше результаты позволяют нам прийти к
следующим выводам.
220
Часть V(a)
1) Показатели и фрактальная размерность не универсальны,
а зависят от данного вида распределения вероятности,
отражающего некоторые физические свойства процесса пробоя
диэлектриков. Следовательно, и показатели, и фрактальную
размерность можно рассматривать как числовые характеристики
исследуемого физического процесса.
2) Неравенство v2 < vi показывает, что лапласовские
фракталы стремятся при больших п образовать поверхность или
фигуру. Структуры Sn и Sn' при пфп! не подобны, автомодель-
на только асимптотическая структура S. Анализ растущей зоны
Таблица 1. Показатели роста vi, v2 и фрактальная размерность D
при d= 1, 2, 3 и нескольких значениях т|. Кроме того, приближенно
указан размер образца /гмакс и число образцов, использованных
при вычислении средних значений.
d x\ vi v2 D "макс образцов
Все
0
0,5
1
2
0
0,5
1
2
1
0,497
0,52
0,59
0,70
0,325
0,36
0,38
0,44
0,5
0,145
0,41
0,50
0,64
0,073
0,23
0,28
0,35
1
2
1,92
1,70
1,43
3
2,78
2,65
2,26
20 000
30 000
10 000
3 000
20000
10 000
4 000
1500
Точный
результат
20
20
20
20
20
40
40
40
с точки зрения различных показателей или линейных
масштабов проводится в другой работе настоящего сборника [9].
ЛИТЕРАТУРА
1. Kunhardt E. £., Luessen L. #., Electrical Breakdown in Gases, Plenum
Press, New York and London, 1983.
2. Hibma Т., Pfluger P., Zeller H. R.y in: Electronic Properties of Polymers
and Related Compounds, eds. H. Kozmany, M. Mehring, S. Roth, Springer,
Berlin, Heidelberg, New York, 1985, p. 317—326.
3. Niemeyer L., Pietronero L., Wiesmann H. /., Phys. Rev. Lett., 52, 1033
(1984).
4. PUschke M., Rdcz Z., Phys. Rev. Lett, 53, 415 (1984).
5. Meakin P., Sander L. M., PUschke M., Rdcz Z., Phys. Rev. Lett., 54, 2053
(1985).
6. Pietronero L., Wiesmann H. /,, J. Stat. Phys., 36, 909 (1984).
7. Meaking P., Phys. Rev., A27, 1495 (1983).
8. PUschke M., Rdcz Z., Phys. Rev., A31, 985 (1985).
9. Пьетронеро Л., Эвертс К., Висман Г. —наст, сб., с. 221.
Свойства подобия растущей зоны
и емкость лапласовских фракталов
Л. Пьетронеро, К. Эвертс, Г. Висман *
Следуя численным результатам, рассмотренным в нашей
предыдущей работе, мы пытаемся выяснить, почему существование
различных линейных масштабов в лапласовских фракталах не только не
приводит к каким-либо противоречиям, но и является вполне
естественным для задач данного типа. Мы рассматриваем также
задачу о представлении полного заряда (или емкости) лапласовских
фракталов как функции их размеров и показываем, что главный
степенной член зависит тслько от размерности евклидова
пространства, в которое они вложены. В двумерном случае получено явное
выражение для логарифмической поправки, дающей хорошее
согласие с численными результатами.
1. Введение
Лапласовские фракталы (ЛФ) были введены в
предыдущей работе [1] как фрактальные структуры, вероятность
роста которых удовлетворяет уравнению Лапласа. В нескольких
докладах на настоящем симпозиуме сообщалось об
исследованиях систем, относящихся к этому классу, и в большинстве из
них авторы пытаются выяснить природу механизма роста [2—6].
Дальнейшее продвижение, насколько можно судить, в
значительной мере зависит от более полного понимания свойств
растущей зоны. Вопрос этот весьма спорный. Основная проблема
состоит в том, справедлив ли для характерной длины,
определяющей толщину растущей зоны, закон подобия, как для
характерного размера системы [7, 8]. В предыдущей работе [1] мы
привели численные результаты в двумерном и трехмерном случаях
для показателя V2 растущей зоны как функции показателя т),
связывающего локальное поле с вероятностью роста. Эти
результаты убедительно свидетельствуют о том, что растущая зона
удовлетворяет закону подобия с показателем, отличным от
радиуса. Однако возникли вопросы о том, сколь согласовано
существование более одного линейного масштаба с требованием
автомодельное™ [8]. Как будет показано ниже, существование двух
характерных линейных масштабов не только не приводит к
противоречию, но и весьма естественно следует для задач
рассматриваемого типа. Такое заключение согласуется с выводами
Плишке и Раца [2, 7]. Мы также обсудим, какие следствия
проистекают из того, что и vi = 1/Z), и v2 явно зависят от tj.
Наконец, мы рассмотрим еще одно свойство растущей зоны, имеющее
* L. Pietronero, С. Evertsz-University ot Groningen, Melkweg 1, 9718 ЕР
Groningen, The Netherlands; tf. /. Wiesmann ■ Brown Boveri Research Center,
CH-5405 Baden, Switzerland*
222
Часть V(a)
самое непосредственное отношение к задаче о пробе
диэлектриков [9, 10], — электрическую емкость. Вопрос состоит в
том, какому закону подобия удовлетворяет полный заряд на
фрактале при изменении N или R. Как будет показано, ведущий
показатель обусловлен только размерностью d евклидова
пространства, в которое вложен фрактал. Что же касается
фрактальной размерности D, то от нее зависит только коэффициент
закона подобия.
2. Свойства растущей зоны
Рассмотрим лапласовский фрактал с центром в начале
координат. Его фрактальная размерность D измеряется путем
подсчета числа элементов (точек или связей) N(R), содержащихся
в гиперсфере радиуса R при
различных R:
N(R)=\(>(r)r<d-»dr = Rt>.
о
а)
Отсюда следует, что плотность
р(г) удовлетворяет закону
подобия
p(r)~r-W-D>. (2)
Рассмотрим гиперсферу
радиуса R. Для случая d = 2
она изображена на рис. 1.
Общее число ветвей,
пересекающих эту гиперсферу, равно
N{R) = A^^R(D-i). (3)
Мы придерживаемся здесь
варианта задачи со связями, как
в первоначальной модели пробоя диэлектриков [9, 10], поэтому
все ветви одинаково толстые и нет необходимости вводить
эффективную толщину ветви, как в варианте задачи с узлами
[2, 7]. Средняя «площадь» гиперповерхности, приходящаяся на
каждую ветвь, равна
<<T(tf)> = TOT~*W-D). (4)
Рис. 1. Схематическое изображение
некоторых ветвей лапласовского
фрактала: величины %i и Яг
указывают расстояния между парами
ветвей вдоль окружности радиуса R.
Размер растущей зоны
характеризуется величиной £.
где среднее <а(/?)> берется по всем ветвям.
Модели необратимого роста
m
Это понятие аналогично понятию многогранников Вороного
для неупорядоченных систем. Среднее расстояние между
ближайшими ветвями равно поэтому
<* (Л)> = (р (R))m~l) = д(4=г). (5)
Смысл к можно пояснить на рис. 1, где показаны два
расстояния k\(R) и Я2(Я). в двумерном случае Xi(R) —расстояние
между i-й ветвью и следующей вдоль окружности радиуса R. С
точки зрения процесса ограниченной диффузией агрегации ясно,
что эти расстояния играют важную роль в процессе роста.
Нетрудно видеть, что по сравнению с R характеристическая
длина <Л(#)> в общем случае удовлетворяет другому закону
подобия. Действительно, из требования (k(R)} ~ R следует,что
D = 1. Обозревая картину пробоя, мы можем определять
характерный линейный масштаб, который в нетривиальных случаях
удовлетворяет не такому закону подобия, как R. Уже одно это
обстоятельство вынуждает нас весьма скептически относиться
к гипотезе об одном линейном масштабе, определяющем
процесс роста.
Попытаемся теперь связать линейный масштаб,
определяемый соотношением (5), со свойствами роста системы. Мы
ограничимся обсуждением двумерного случая (см. рис. 1).
Рассмотрим две параллельные ветви, разделенные расстоянием X.
Можно показать, что распределение вероятности, с которой
совершающий случайные блуждания проникает на единичное
расстояние в глубь «новой территории» (мы придерживаемся
модели ДОА), приближенно может быть представлено в виде [12]
РЛ(1) = ^[1п(Я2/4+12)-1п(12)]. (6)
Следовательно, характеристическая глубина проникновения
удовлетворяет соотношению £ ^ X. Простейшее обобщение этого
соотношения, необходимое для получения закона подобия, состоит
в предположении
<£(*)> «<ЧЮ>. (7)
Однако в связи с таким соотношением возникает ряд проблем.
Действительно, если рассмотрим распределение вероятности,
задаваемое соотношением (6), и обобщим его на случай ц Ф 1, то
получим соотношение [Р^О)]4, по-прежнему приводящее к
характеристической глубине проникновения порядка % [12].
Отсюда следует, что теория, опирающаяся на соотношение (7), не
могла бы учитывать зависимость D от т|. С другой стороны, не
приходится сомневаться в том, что для конкретной пары
ближайших ветвей выполняется равенство & = Л/. Эту загадочную
ситуацию удается разрешить, рассматривая распределение
224
Часть V(a)
W[k(R)] различных значений X(R) в интервале от 0 до ^макс,
что дает
Лмакс
<Ч*)> = \ W[l(R)]l(R)d[K(R)\, (8)
О
но вычисление среднего от ^(R) требует более тонких
соображений. Дело в том, что распределение значений k(R) приводит
к появлению дополнительного весового множителя порядка
l(R) для среднего от £(#), так как совершающий случайное
блуждание с большей вероятностью заканчивает свой путь в
более широком «заливе», соответствующем большему Ki{R) на
рис. 1, чем в более узком «заливе», соответствующем меньшему
значению faiR)- Производя вычисления, мы получаем
^макс
<£(*)>= \ W[X(R)]^(R)d[X(R)}. (9)
О
Ясно поэтому, что введение распределения для X(R) приводит в
общем случае к неравенству <£(/?)> ф (X(R)}. Это в принципе
позволяет разрешить противоречия, о которых мы упоминали
выше. Таким образом, задача сводится к определению
самостабилизирующегося асимптотического распределения W [X (R) ].
Через различные соотношения это распределение оказывает
воздействие на фрактальную размерность D и толщину граничной
поверхности £(R). Естественно поэтому ожидать, что R и t>(R)
по-разному ведут себя при преобразовании подобия. В свою
очередь это порождает своего рода ограниченную автомодельность
в том смысле, что, поскольку отношение t>(R)/R отлично от
постоянной, система автомодельна только асимптотически
относительно преобразований радиуса с неподвижным центром.
Следовательно, рассматриваемая система не обладает
свойствами однородности перколяционных кластеров, но у нее
существуют вполне определенные свойства подобия. Такое
заключение полностью согласуется с выводами Плишке и Раца [2, 7]
и подкреплено результатами исследования анизотропии
корреляционной функции [11].
3. Электрическая емкость лапласовских фракталов
Интересным свойством рассматриваемых систем,
заслуживающим изучения, является электрическая емкость как функция
от N или R. Этот вопрос играет важную роль в модели пробоя
диэлектриков, где он может иметь прикладной интерес. В
предыдущей работе мы показали, как распределение заряда,
вычисляемое по локальному полю с помощью дискретного варианта
теоремы Гаусса, модулирует вероятность роста. Сейчас нас инте-
Модели необратимого роста
225
ресует, что представляет собой полный заряд на таких
фракталах, как функция их размера. Начнем с рассмотрения
двумерного случая, два предельных примера которого, допускающих
аналитическое решение, изображены на рис. 2. В двумерном
случае существует одна тонкость: из-за логарифмической
природы функции Грина необходимо соблюдать особую
осторожность при выборе граничных условий. На рис. 2, а мы имеем
Рис. 2. Два предельных примера системы, для которых емкость может быть
точно вычислена.
окружность радиуса г0 с внешней границей — окружностью
радиуса ги в то время как на рис. 2, б мы рассматриваем отрезок
длиной 2/*0 с теми же граничными условиями. Если считать, что
структура содержит не только окружность радиуса г0, но и все
заключенные внутри окружности точки, то приведенные нами
два примера могут рассматриваться как предельные случаи всех
систем, которые могут быть вложены в окружность радиуса Го.
Круг, ограниченный этой окружностью, является наиболее
компактной из этих структур (D =2), а отрезок — наиболее
«разреженной» из них (D = 1). Электростатические задачи могут быть
решены методом конформных отображений [12]. Заряд на
единицу напряжения оказывается равным
0, = 2я/1п(г,/го) (10)
для окружности и
Qs = 2n/ln(2r1/r0) (11)
для отрезка. Аналитическое поведение в обоих случаях
одинаково. Рассматривая окружность радиуса го и отрезок длиной 2г0
как предельные случаи, мы заключаем, что любая фрактальная
структура, вписанная в ту же окружность, будет иметь емкость,
ограниченную сверху и снизу величинами (10) и (И). Такой
вывод станет более понятным, если мы примем во внимание, что при
добавлении к структуре, состоящей из N элементов с зарядом
Q(jV), еще одного элемента полный заряд (полная емкость) мо-
226
Часть V(a)
жет только возрасти:
^F>°- (12)
Этот результат интуитивно очевиден и может быть к тому же
строго доказан [12]. Аналитическое поведение указанного типа
можно обобщить, чтобы получить зависимость от N полного
заряда на фрактале (в (2 — d)-мерном случае):
Q(N) = 2л/\п [a (D)r{/(r0)N], (13)
где
(rQ)N = ANW, (14)
a a(D) —коэффициент, зависящий только от D. Мы проверили
несколько фракталов, построенных с помощью компьютеров, и
их полный заряд оказался в прекрасном согласии с
формулой (13).
Обратимся теперь к случаю, когда евклидова размерность
больше двух. Можно показать [12], что соотношение между
зарядом и размером имеет вид
Q = Rd~2. (15)
Используя приведенные выше соображения относительно
верхней и нижней границ емкости фрактальной структуры, мы
можем записать, что в общем случае для фрактала справедливо
соотношение
Q (ЛО = A (D) Rd~2 = A' (D) N{d~2)ID. (16)
Итак, мы показали, что даже для фрактала ведущий член
степенной зависимости полного заряда (полной емкости) как
функции характерного размера определяется только
размерностью евклидова пространства, в котором вложен фрактал.
Что же касается фрактальной размерности, то от нее зависит
только коэффициент при степенном члене (если d > 2) или
логарифмический член (если d = 2).
ЛИТЕРАТУРА
1. Висман Г.у Пьетронеро Л.— наст. сб. с. 210.
2. Плитке М., Рац 3. — наст. сб. с. 301.
3. Микин П. — наст, сб., с. 283.
4. Туркевич Л., Шер Г. — наст, сб., с. 310.
5. Росса Дж. и др. — наст, сб., с. 330.
6. Жюльен Р., Боте Р. — наст, сб., с. 350.
7. Plischke M., Racz Z., Phys. Rev. Lett., 53, 415 (1984); С54, 2054 (1985).
8. Meakin P., Sander L. M., Phys. Rev. Lett., C54, 2053 (1985).
9. Niemeyer L., Pietronero L.y Wiesmann H. /., Phys. Rev. Lett., 52, 1033
(1984).
10. Pietronero L., Wiesmann H. /., J. Stat. Phys., 36, 909 (1984).
11. Микин П.у Вичек Г.— наст, сб., с. 296.
12. Пьетронеро Л., Эвертс К., Висман Г. — наст, сб., с. 221.
Бесконечная иерархия показателей
для описания явлений роста
А. Конильо *
Модель роста характеризуется набором вероятностей {р^}/ер того,
что каждый узел на внешнем периметре Г в данный момент
времени становится частью кластера. Уравнения для /?, в рамках
модели ДОА и других моделей роста получены с использованием
электростатической аналогии с моделью пробоя диэлектриков.
Масштабно-инвариантный подход развит для распределения
вероятности. Проведено сравнение полученных результатов с
распределением напряжения в случайной сетке резисторов и случайной
сверхпроводящей сетке на пороге перколяции. Для полного задания
моментов распределения, связанных с структурой поверхности
кластера, необходим бесконечный набор показателей.
1. Введение
В основу настоящего сообщения положена работа,
выполненная совместно с К. Амитрано, Л. де Аркангелисом, Ф. ди
Либерто, П. Микином, С. Реднером, X. Стенли и Т. Виттеном.
Его можно рассматривать как дополнение к лекции [1],
прочитанной на школе в Каргезе по росту и форме за неделю до
начала этой конференции. Основные идеи моей лекции в
настоящем сообщении сформулированы заново и развиты на основе
более общего подхода к фрактальным мерам, предложенного Ка-
дановом [2] на той же школе.
Какие параметры наиболее пригодны для полного описания
существенных особенностей процесса роста? Ответ на этот
вопрос чрезвычайно важен для понимания сложности и
разнообразия столь захватывающей области, как явления роста. Ясно,
например, что кластер не может быть полностью охарактеризован
своей фрактальной размерностью. Кластеры, возникающие в
модели ДОА [3], и перколяционные кластеры в трехмерном случае
имеют примерно одинаковую фрактальную размерность, хотя их
структура совершенно различна.
Один из возможных способов полностью охарактеризовать
модель роста состоит в задании на каждом временном шаге
распределения вероятности роста узлов (РВРУ) {pi}i^Tf где
pi — вероятность того, что узел I станет частью кластера.
В большинстве случаев рост происходит по периметру Г
кластера.
* Antonio Coniglio-Instituto di Fisica Teorica, Mostra D'Oltremare, Pad. 19,
80125 Napoli, Italy; Center for Polymer Studies and Department of Physics,
Boston University, Boston, Massachusetts 02215, USA.
228
Часть V(a)
2. Свойства подобия распределения вероятности роста узлов
Из РВРУ можно не только вывести интересующие нас
статические и динамические свойства, но и получить гораздо более
подробную информацию о способности каждого узла,
находящегося на периметре кластера, к росту и тем самым достичь более
точного представления о структуре поверхности. Например, в
модели ДОА самыми «горячими» узлами («прорастание» которых
наиболее вероятно) являются узлы, расположенные на выступах
кластера, для которых вероятность роста принимает наибольшие
значения, в то время как самые «холодные» узлы, находящиеся
в глубине фиордов, характеризуются весьма малыми значениями
вероятности роста.
Для того чтобы охарактеризовать фрактальную структуру
кластера, рассмотрим следующие моменты и соответственные
показатели [4—7]:
Z(q)^ Z p7~Zr(«-1)D(* (i)
где L — размер кластера, который может совпадать, например,
с радиусом. Величину Z(q) удобно представить следующим
образом:
zfo) = E«(rt*-£**<»*>, (2)
р р
где п(р) —число узлов с вероятностью роста, равной р, и
F(py q) = lnn(p) + q\nq. (3)
Так как при больших L можно ожидать расходимости F(p> q)>
сумму в правой части (2) удобно вычислять методом
быстрейшего спуска. Если р* — значение, при котором F(p, q) достигает
максимума, то
д In п {р)
din p
р=р'
„--Я- W
При каждом значении q существует соответствующее ему
значение p* = p*(q). Введем следующие законы подобия [2]:
Р* ~/Га«>, (5)
n(pm)~Lf(q). (6)
Тогда
Z(q)~eF{*-0~L-l4a{q)-,m, (7)
и из соотношения (1) мы получаем, что
(q-l)D(q) = qa(q)-f(q). (8)
Модели необратимого роста
229
Заметим, что, так как р*—функция от q (в силу соотношения
(4)), справедливо соотношение
д^ _ „да
и поэтому
dq~q dq '
-±.(q-l)D(q) = a(q). (9)
Такой же результат получен в работе [2]. Следовательно, если
функция D(q) задана, то мы можем с помощью соотношений
(8) и (9) вычислять a(q) и f(q)> и наоборот. Величина f(q) —
фрактальная размерность множества узлов с вероятностью
роста р = р*, a(q) характеризует закон подобия, которому
удовлетворяет р* при изменении L. В работе [6] было введено понятие
плотности особенностей f и «силы» особой точки а, но в рамках
модели ДОА a{q) и f (q) считались не зависящими от q.
Зная a(q) и f(q), мы можем предсказать закон подобия,
которому удовлетворяет п(р). Из соотношения (5) следует, что при
больших L
х^ ^р* = <*(?) (10)
1прМакс а(оо) * '
Если a(q)—монотонная функция от q, то соотношение (10)
можно обратить, и мы получим q = q(x). Таким образом, из
соотношения (6) следует закон подобия
n{p)~L*{x\ *<1, (11)
где х = In p/lnрмакс, ц)(х) =f(q(x)) и п(р) при х^\ очень
быстро стремится к нулю. Заметим, что если f(q) = const, то
ф(лг) = const. Соотношение (11) означает, что узлы в кластере
могут быть разделены на различные множества, каждое из
которых характеризуется своим значением х = In p/ln рмакС.
Каждое такое множество имеет свою фрактальную размерность
ф(лг). Самые «горячие» узлы имеют большую вероятность роста,
соответствующую л;=1, в то время как наиболее
«холодные» узлы характеризуются минимальным значением хМИН =
= а(—oo)/a(-f°°).
В модели Идена вероятности роста отличны от нуля на
поверхности, и все равны pi = р*. Следовательно, п(р*) ~ Ld~l,
так как 2 р,- = 1, р* ~ Ll~d. Таким образом, в модели Идена
D(q) = a(q) = f(q) =d—1 не зависит от q. Для описания
фрактальной структуры в модели ДОА требуется бесконечный
набор показателей. Чем сложнее структура, тем сильнее разброс
показателей. При d-+oo модель ДОА переходит в модель
Идена, в которой для описания структуры кластера необходим
только один показатель. Наличие бесконечного ряда показателей —
230
Часть V(a)
ситуация, весьма отличная от той, с которой мы встречаемся в
обычных критических явлениях, например в модели Изинга.
В этой модели фрактальная размерность критических капель
одинакова независимо от их размеров. Именно эта фрактальная
размерность, доминируя, порождает единственный показатель
степени «отклонения от критического параметра», который
описывает все моменты параметров порядка.
3. Уравнения для РВРУ
Показатели (8) были измерены с помощью численного
моделирования [7] в рамках модели ДОА для d = 2 при k = 2, ...
..., 8. В этих экспериментах NT точек совершали случайные
блуждания по кластеру в модели ДОА, и подсчитывалось, сколько
раз (Nt) блуждающие точки сталкиваются с данным узлом i
периметра. При больших Nl справедлива оценка pi « Ni/Nt- По
известным вероятностям р,- был вычислен набор показателей.
Обнаружено, что множество независимых показателей стремится
к D(oo) = df— 1.
• Другой подход был использован в [8] для вычисления РВРУ.
Если воспользоваться электростатической аналогией, то в
непрерывном варианте плотность вероятности р(х) в точке х
поверхности определяется выражением
р(х) = -п(х)-\ф(х) = \Е(х)\9 (12)
где п(х) —нормаль в точке х к поверхности кластера, ф(х) —
электростатический потенциал поверхности, удовлетворяющий
уравнению Лапласа с условием ф = const на проводнике и ф — 0
в бесконечности (постоянная выбирается с таким расчетом,
чтобы полный заряд проводника был равен единице). Решение ф(х)
имеет вид
^Hj^T^ (I3)
при d > 2, а при d = 2 множитель \х — xf\2~d в
подынтегральном выражении заменяется множителем In \х — л:']-1; о(х') =
= —п(л;') • Уф(х') —плотность заряда. Из соотношения (12)
следует, что
р(х) - - п(х) V, J ]хР_%-г М- (14)
Это уравнение может быть дискретизовано и решено численно
относительно р(х). Вычисление моментов приводит к
результатам, согласующимся с результатами численного моделирования
в работе [7]. Уравнения для РВРУ на решетке приведены
также в работе [9].
Модели необратимого роста
231
4. Распределение напряжения в случайной сетке резисторов
на пороге протекания
Теория, развитая в разд. 2, применима и к распределению
напряжения в случайной сетке резисторов на пороге протекания
рс [5]. Действительно, учитывая аналогию между ДОА и
пробоем диэлектриков, можно ожидать, что свойства распределения
Напряжения имеют много общего со свойствами РВРУ в модели
ДОА. И действительно, модель ДОА непосредственно связана
с моделью пробоя диэлектриков [10], в которой вероятности
роста имеют прямое отношение к распределению напряжения на
поверхности кластера.
Рассмотрим d-мерную гиперкубическую решетку с
характерным размером L. Предположим, что каждая связь активна с
вероятностью р и неактивна с вероятностью 1 — р. Из теории
протекания известно, что в пределе бесконечной системы
существует порог протекания рс, выше которого существует
бесконечный кластер активных связей. Непосредственно на пороге
протекания рс связи в образующих «мост» конфигурациях, как
заметил Стенли [11], могут быть разделены на свободные
(«висячие») связи, не дающие вклада в электрическое
сопротивление, и закрепленные («скелетные») связи. Закрепленные связи
в свою очередь можно разделить на линейные (односвязные)
проводники и многосвязные блоки («блобы»). Можно ли
пренебрегать блоками, как в модели Скала — Шкловского — де Жена
[12], или линейными проводниками, как в модели ковра Сер-
пинского [13], — вопрос нетривиальный. На основе точных
результатов ныне установлено, что и линейные проводники, и блоки
могут иметь решающее значение. Число линейных
проводников L\ расходится как L\ ~ L1/v в любой размерности, если v —
показатель длины связности [14]. По мере приближения
евклидовой размерности d к 6 блоки становятся все менее
существенными. Пусть d ^ 6 блоками можно пренебречь. Численные
результаты убедительно подтверждают правильность
нарисованной нами картины [15].
Чтобы охарактеризовать более подробно структуру
скелетных связей, поставим в соответствие каждой связи единичное
электрическое сопротивление и приложим единичное
напряжение к противоположным границам ячейки, соединенным
протекающим кластером. Каждая связь характеризуется падением
напряжения У, равным текущему по связи току /. Максимальное
падение напряжения (VMaKc = /MaKc) происходит на линейных
проводниках.
Фрактальные структуры можно также характеризовать
моментами распределения напряжения [5]:
Z(q)=Y,n(V)Vq~L-{q-l)Diq). (15)
232
Часть V(a)
Эти моменты были вычислены аналитически в рамках
иерархической модели, дающей весьма хорошее описание свойств
протекающего кластера. Выражение для величины v(q—l)D(q)
(обозначенной в [5] через p(q)) имеет вид
<7 in 4-in (1+2-4)
v(q-l)D(q) = (q-l) + —ш (16)
и весьма точно воспроизводит данные численного
моделирования двумерного случайного протекания. Из формулы (13)
следует, что существует бесконечное множество показателей,
описывающих моменты распределения напряжения. Физически это
означает, что не существует никакого характерного значения
напряжения, которое доминировало бы над остальными. В
действительности при каждом значении q существует значение
V*(q), при котором F(V, q) = n(V)VQ достигает максимума. Из
соотношений (5) и (6) получаем
F*(<7)~L-a4 n(V)~Di*\ (17)
где
va(<7) = — Цг, (18)
W/ In 2 1+2-4
1 W' 1 + 2~q In 2 V '
Тем самым соотношения (8) и (9) выполнены. Установлено
также, что
n(V)~LP<#, (20)
где
__ in У _ <х(?)
in f макс a (oo)
(21)
и <р{х) —f(q(x)), а q(x)—функция, получаемая при
обращении соотношения (21) с помощью равенства (18).
Когда евклидова размерность d превышает верхнюю
критическую размерность dc = 6, все показатели совпадают с
показателями относительно связей vD(q) = 1. Этот результат
допускает физическое объяснение: при d > dc = 6 блоки становятся
несущественными и основное значение обретают только
линейные проводники. Следовательно, моменты распределения
напряжения подавляются одной величиной — падением напряжения
V = Умакс на проводниках. С другой стороны, максимальный
разброс D(q) достигается при d = 2, когда блоки становятся
наиболее существенными. Следует подчеркнуть сильное сходство
данной ситуации с той, которая возникает в модели ДОА.
В заключение еще раз отметим, что для описания моментов
распределения напряжения необходим бесконечный набор неза-
Модели необратимого роста
233
висимых показателей. Они связаны с образованием бесконечного
кластера. Чем сложнее структура, тем сильнее разброс
показателей.
В настоящем сообщении основной упор делался на
распределение вероятности роста узлов. Это распределение
вероятностей изменяется по степенному закону аналогично
распределению напряжения в случайных сетках резисторов, в которых для
полного описания разнообразия структуры геометрических
свойств кластера необходим бесконечный набор показателей.
Я хотел бы выразить благодарность моим коллегам,
работающим в той же области: К. Амитрано, Л. де Аркангелису, Ф. ди
Либерто, П. Микину, С. Реднеру, X. Стенли и Т. Виттену.
ЛИТЕРАТУРА
1. Coniglio A, In: Proc of Cargese Summer School on Growth and Forms
1985, eds. H. E. Stanley, N. Ostrowsky.
2. Kadanoff L. P., in: Proc. of Cargese Summer School on Growth and
Forms 1985, eds. H. E. Stanley, N. Ostrowsky.
Halsey T. C., Jensen M. #., Kadanoff L. P., Procaccia /., Shraiman B. /.,
preprint.
3. Witten T. A, Sander L. M„ Phys. Rev. Lett., 47, 1400 (1981).
4. Hentshel H. G. £., Procaccia /., Physica, D8, 835 (1983).
5. deArcangelis L., Redner S., Coniglio A, Phys. Rev., B31, 4725 (1985).
6. Halsey Т. С, Meakin P., Procaccia /., будет опубликовано.
7. Meakin P., Stanley H. E.y Coniglio A., Witten Г., Phys. Rev., A32, 2364
(1985); а также — в печати.
8. Amitrano С, Coniglio Л., diLiberto F., будет опубликовано.
9. Turkevich L. A, Scher #., Phys. Rev. Lett., 55, 1026 (1985).
10. Niemeyer L., Pietronero L., Wiesmann H. /., Phys. Rev. Lett., 52, 1033
(1984).
11. Stanley H. £., J. Phys., A10, L211 (1977).
12. Skal A. 5., Shklovskii B. /., Sov. Phys. Semicond., 8, 1029 (1975).
de Gennes P. C, La Recherche, 7, 919 (1976).
13. Gefen У., Aharohy A., Mandelbrot В. В., Kirkpatrick S., Phys. Rev. Lett.,
47, 1771 (1981).
14. Coniglio A, Phys. Rev. Lett., 46, 250 (1981); J. Phys., A15, 3824 (1982).
15. Pike R., Stanley Я. £., J. Phys., A14, L169 (1981).
Herrmann H. J Stanley H. £., Phys. Rev. Lett 53, 1121 (1984).
Двумерный пробой диэлектриков
между параллельными линиями
М. Мюрат *
Пробой диэлектрических материалов в двумерном случае,
помещенных между параллельными линиями с большой разностью
потенциалов, воспроизводится в модели пробоя диэлектриков.
Внешнее сходство явлений подкрепляется сравнением геометрических
свойств структур в обоих случаях.
Формирование электрического разряда в материале,
поддерживаемом при высоком потенциале и заземленном с
помощью точечного электрода, недавно было промоделировано
Нимейером, Пьетронеро и Висманом [1]. Такая модель пробоя
диэлектриков позволяет воспроизвести формирование открытых
древовидных структур, весьма напоминающих ограниченные
диффузией кластеры (в модели ДОА) [2]. В двумерном
случае фрактальные размерности структур, возникающие в такой
модели пробоя диэлектриков и в модели ДОА, оказались
равными примерно 1,7. Подобие структур подтверждается сравнением
управляющего уравнения для многочастичной функции
распределения для задачи в модели ДОА с уравнением Лапласа,
имеющим основополагающее значение в модели пробоя
диэлектриков [3].
Обе модели первоначально рассматривались в круговой
геометрии: затравка (в модели ДОА) или заземленный электрод (в
модели диэлектрического пробоя) представляют собой одну
точку. Позднее модель ДОА применялась также к случаю, в
котором «затравкой» была плоскость (или прямая в двумерном
случае) [4], что позволило воспроизвести с помощью этой модели
выпадение осадка на поверхности. Фрактальная размерность
при этом оказалась такой же, как в исходной геометрии. Были
измерены и другие геометрические свойства осадка, такие, как
высота и среднеквадратичная толщина. Оказалось, что они
изменяются как некоторая степень числа частиц, выпавших в
осадок. Опубликованы полученные значения показателей.
В настоящей работе мы применяем модель пробоя
диэлектриков к случаю, когда двумерный диэлектрический материал
помещен между двумя линиями, поддерживаемыми при
различных потенциалах. Высокая разность потенциалов приводит к
электрическому разряду, который мы моделируем с помощью
модели пробоя диэлектриков. Геометрические свойства картин
разряда мы сравниваем с геометрическими свойствами
ограниченных диффузией осадков, исследованием которых занимался
Микин [4].
* Michael Murat- School of Physics and Astronomy, Raymond and Beverly
Sackler Faculty of Exact Sciences, Tel Aviv University, Tel Aviv 69978, Israel.
Модели необратимого роста
235
Опишем кратко модель пробоя диэлектриков,
приспособленную к нашей геометрии. Квадратная решетка изображает
диэлектрический материал. Узлам в верхнем (нижнем) ряду
решетки приписан потенциал V = 1(0). Разряд распространяется
снизу вверх постепенно, шаг за шагом. Узлам, до которых
доходит заряд, приписывается потенциал V = 0. Связь (линия,
соединяющая узлы), добавляемая на каждом шаге к картине
разряда, выбирается следующим образом. Для каждого узла
решетки решается уравнение Лапласа
V2l/ = 0 (1)
с граничными условиями: V = 1 для узлов верхнего ряда и
V = 0 для узлов нижнего ряда и всех разряженных узлов.
Вероятность выбора данной связи, соединяющей разряженный узел
с одним из соседних узлов, пропорциональна разности
потенциалов между этими двумя узлами. Связь выбирается случайно
из всех возможных связей с использованием распределения
вероятности, о котором упоминалось выше. Весь процесс
повторяется до тех пор, пока возникающая структура не достигнет
верхнего ряда.
Одна из таких картин разряда изображена на рис. 1.
Фрактальную размерность структур мы находили, вычисляя сначала
величину р(г), задаваемую средней плотностью разряженных
узлов в r-м ряду снизу. Установлено, что для рядов, не
слишком близких к верхнему,
р(г)~г-«. (2)
Среднее по 10 численным экспериментам на решетках размером
100 X ЮО составляет а = 0,35 ± 0,05. Фрактальная размерность
df определяется соотношением
df = 2 — a, (3)
из которого мы заключаем, что df = 1,65 + 0,05 (в соответствии
с значением df, полученным в модели ДОА).
Мы проследили также, как ведут себя в зависимости от шага
по времени t (равного числу узлов, принадлежащих картине
разряда) средняя и среднеквадратичная высота картины разряда и
его среднеквадратичная толщина. На протяжении довольно
большого временного интервала обе величины удовлетворяют
степенному закону. Были вычислены нами и показатели 8/ каждого
такого закона
Xi ~ ft, (4)
где %i — любая из только что указанных характеристик.
Оказалось, что показатели е* зависят от размера L решетки. Значения,
вычисленные путем экстраполяции на бесконечную решетку
236
Часть V(a)
(1/L — параметр экстраполяции), представлены в табл. 1 вместе
с значениями, полученными в модели ДОА [4].
Резюмируя, можно сказать следующее. Мы выполнили
численное моделирование формирования разрядов в двумерном ма-
Рис. 1. Картина разряда, полученная на решетке 200 X 200. Кажущиеся не
связанными между собой структуры у левого и правого краев решетки в
действительности соединены посредством периодических граничных условий.
териале, помещенном между двумя параллельными
эквипотенциальными линиями, между которыми поддерживается высокая
разность потенциалов. Полученные формы разряда обладают
Таблица L Показатели &i в моделях ДОА и пробоя диэлектриков
Среднеквадра- Средняя
Среднеквадратичная высота тичйгая
толщина высота
ДОА [4] 1,36 ±0,05 1,45+0,05 —
Пробой диэлектри- 1,3±0,1 1,45±0,1 1,4-0,1
ков
Результаты согласуются с предположением о том, что обе модели приводят к
статистически тождественным структурам.
Свойство
Модель
Модели необратимого роста
237
специфическими геометрическим свойствами. Как показывают
результаты, формы разряда в модели пробоя статистически
тождественны ограниченным диффузией осадкам на поверхности.
Благодарности. Автор выражает свою признательность проф.
Амнону Аарони, предложившему провести это исследование, и
проф. Р. Энгману и Д. Штауфферу за ценные замечания. Эта
работа частично финансировалась Израильской академией
естественных и гуманитарных наук, Американо-израильским двух-
национальным научным фондом и Научно-исследовательским
центром Израильской комиссии по атомной энергии в Сореке.
ЛИТЕРАТУРА
1. Niemeyer L., Pietronero L., Wiesmann H. /., Phys. Rev. LetL, 52, 1033
(1984). (Мы имеем в виду только случай т| = 1, где величина г\
определена в данной работе.)
2. Witten Т. A., Sander L. At., Phys. Rev. Lett., 47, 1400 (1981).
3. Pietronero L., Wiesmann H. /., J. Stat. Phys., 36, 909 (1984).
4. Meakin P., Phys. Rev., A27, 2616 (1983); B30, 4207 (1984).
Пробой диэлектриков
в трехмерном случае
С. Сатпати *
Фрактальные свойства форм пробоя диэлектриков в трехмервхш
пространстве исследованы в рамках модели Нимейера — Пьетроне-
ро — Висмана путем прямого численного моделирования.
Проанализированы два случая: 1) двумерные фигуры в трехмерном лап-
ласовском поле и 2) трехмерные фигуры в трехмерном лапласов-
ском поле.
1. Введение
Образование разветвленной фигуры траекториями тока в
процессе пробоя диэлектрика хорошо известно по столь
распространенному явлению, как молнии во время гроз [1]. Но, как
стало недавно известно [2—6], та же разветвленная фигура
допускает описание и как объект нецелой размерности —
фрактал.
Савада и др. [3] были, по-видимому, первыми, кто ввел
стохастическую модель для описания ветвлений фигур пробоя
диэлектриков путем произвольного сопоставления априорных
факторов с ростом концов в уже имеющейся растущей фигуре.
Однако в такой модели фрактальная размерность [2, 7] оказалась
равной евклидовой размерности. Такое совпадение не
удивительно, так как в модели Савады концы и внутри кластера, и на
его периферии имеют одну и ту же скорость роста. Позднее Ни-
мейер, Пьетронеро и Висман (НПВ) предложили [4, 5]
правдоподобную стохастическую модель, в которой рост кластера явно
зависит от локальных электрических полей. Кластеры,
полученные при численном моделировании, оказались фракталами и по
внешнему виду напоминали фигуры разряда, получаемые в
физических экспериментах. Выполненное НПВ численное
моделирование проводилось для пробоя диэлектриков в двумерном
случае, помещенных в двумерное лапласовское поле. В настоящей
работе мы приводим результаты численного моделирования
пробоя в трехмерном лапласовском поле. Мы рассматриваем два
случая — когда пробой растет в трех измерениях и когда его
рост ограничен плоскостью. Исследование последнего случая
мотивировано тем, что во многих лабораторных экспериментах
картина пробоя диэлектриков растет только в двух измерениях,
хотя уравнения поля трехмерны.
* S. Satpathy-Max-Planck-Institut fur Festkorperforschung, Heisenberg-
strasse 1 7000 Stuttgart 80, Federal Republic of Germany.
Модели необратимого роста
239
2. Модель НПВ и метод моделирования
Мы моделировали пробой диэлектриков на кубической
решетке в сфере диаметром около 120 периодов решетки.
Поверхность сферы образует эквипотенциальный электрод. Разрядный
кластер образуется в центре и распространяется, захватывая
ближайшие связи ■— по одной связи за один раз, —
примыкающие к уже имеющемуся кластеру. Вероятность пробоя связи
пропорциональна разности потенциалов на концах связи в
степени т). Наши численные эксперименты проводились при целых
значениях ц от 1 до 4. На каждом этапе распространения
разрядного кластера потенциалы Vqu в узлах решетки
определялись путем решения методом итераций дискретизованного
уравнения Лапласа V2V = 0, например по формуле
Vifk = -g- IVi+i, /, k + Vi-u f,k + Уi, /+i, k + Vif /_i, k +
На каждом шаге роста кластера потенциал изменяется
всюду. Однако мы вычисляли новый потенциал, сохраняя
предыдущие значения потенциала неизменными всюду, за исключением
непосредственной окрестности последней пробитой разрядом
связи в объеме 20Х20Х 120 периодов решетки. Внутри сферы
потенциал вычислялся только на каждом пятом шаге. Такая
процедура позволяла достаточно быстро производить вычисления и
не сказывалась сколько-нибудь заметно на фрактальной
размерности разрядного кластера.
Фрактальная размерность D определялась из соотношения
масса — длина, имеющего вид степенной зависимости
N(r)~rD,
где N(r) —общее число пробитых разрядом связей в сфере
радиуса г. Линейная часть графика In N ~ In r была проведена
методом наименьших квадратов. Угловой коэффициент
построенной прямой позволяет непосредственно оценить D.
3. Результаты
На рис. 1 и 2 показаны типичные кластеры, полученные с
помощью численного моделирования, в случаях двумерного и
трехмерного пробоя диэлектриков. Лапласовское поле в обоих
случаях трехмерно. В наших численных экспериментах счет
прекращался после того, как кластер достигал размеров ~5000
периодов решетки или касался сферической границы. С увеличением
Л размеры кластера уменьшались и точнось оценки фрактальной
a)q*i
6)7J-Z
Рис. 1. Типичные картины разряда при двумерном пробое диэлектрика в
трехмерном лапласовском поле при т) = 1, 2, 3 и 4.
Рис. 2. Проекция на плоскость типичных картин разряда при трехмерном
пробое диэлектрика в трехмерном лапласовском поле при ц = 1, 2, 3 и 4.
Модели необратимого роста
241
размерности D понижалась. Однако мы привели все полученные
результаты, так как других пока не имеется.
На рис. 3 общее число «пробитых» связей N(r) показано как
функция от г на трех
различных стадиях роста кластера,
изображенного на рис. 1,а. На
этом рисунке видно, что
кластер растет не только наружу,
но и продолжает расти в уже
занятой области. Подгонка по
методу наименьших
квадратов дает для этого кластера
фрактальную размерность D =
= 1,93. Аналогичный анализ
для кластера, изображенного
на рис; 2; г, относящийся к
трехмерному пробою (DB = 3)
в трехмерном лапласовском
поле, при т] = 4 приводит к
результатам, представленным на
рис. 4.
Полученные оценки
фрактальных размерностей и
средние размеры кластеров приведены в табл. 1. Эти результаты
были получены путем усреднения по 5—10 различным кластерам.
*°| 1 1 1 » 1 f ГП
Рис. 4. То же, что на рис. 3, для разрядного кластера, изображенного на
рис. 2, г.
Оцениваемые ошибки представляют собой среднеквадратичные
отклонения от среднего и не включают в себя возможные ощиб*
кн из-за конечных размеров кластера,
-I i i l_
1,0 2,0 3,0 4,0
In г
Рис. 3. Общее число N(r) попавших
в пробой связей в сфере радиуса г
с центром в затравке на различных
стадиях роста для кластера,
изображенного на рис. 1, а. Величина N
означает характерный размер
кластера на последовательных стадиях
роста, Db — размерность
пространства, в котором растет кластер.
242
Часть V(a)
При г) = 0 электрическое поле эффективно не влияет на рост
разрядного кластера, и рассматриваемая модель эквивалентна
модели Савады и соавт. [3], в которой приоритетный множитель
роста концов равен единице, т. е. рост ни одного из концов не
имеет приоритета перед другим. Получающийся в результате
кластер имеет евклидову размерность. Как можно было бы
ожидать, исходя из интуитивных соображений, фрактальная
размерность равномерно убывает с возрастанием значений г\ (см.
Таблица 1. Фрактальные размерности кластеров, образующихся
при пробое диэлектриков в модели НПВ
МЧ
3/3
3/2
2/2*
г\
0
1
2
3
4
0
1
2
3
4
0
0,5
1
2
ЛГ, %
5000
5000
2600
1750
4500
2150
1300
850
5000
D
3
2,48±0,06
2,11 ±0,06
1,96±0,08
1,75±0,06
2
1,96=Ь0,03
1,82±0,05
1,78±0,06
1,69±0,08
2
1,89*0,01
1,75±0,02
-1,6
Dy~размерность уравнения Лапласа для поля; Dg — размерность пространства, в котором
происходит рост кластера при пробое; АГ, %—средние размеры кластеров, полученных
при численном моделировании.
* Результаты, заимствованные из работы [4].
табл. 1). При г) = 1, т. е. в том случае, когда вероятность пробоя
связи прямо пропорциональна локальному электрическому полю,
модель НПВ аналогична модели ограниченной диффузией
кластеризации (ОДК), для которой в последнее время были
проведены обширные вычисления [8—10]. Численное моделирование
на основе ОДК в трехмерном случае, проведенное Рихтером и
соавт. [10], привело к значению D = 2,39 ±0,2. Микин [9]
получил для этого случая более точное значение Z> = 2,51 ±0,06.
Это значение и следует сравнивать с нашим значением
2,48 ±0,06 (см. табл. 1).
Благодарность. Выражаю свою признательность П. Келли за
полезные обсуждения.
Модели необратимого роста
243
ЛИТЕРАТУРА
1. Feynman R. P., Leighton R. В., Sands М., Lectures on Physics, vol. II,
Addison-Wesley, London, 1964.
2. Mandelbrot B. B.y The Fractal Geometry of Nature. Freeman, San
Francisco, 1982.
3. Sawada Y., Ohta S., Yamazaki M.y Honjo #., Phys. Rev., A26, 3557 (1982).
4. Niemeyer L., Pietronero L., Wiesmann #. /., Phys. Rev. Lett., 52, 1033
(1984).
5. Pietronero L., Wiesmann H. /., J. Stat. Phys., 36, 909 (1984).
6. Пьетронеро Л. и др. — наст, сб., с. 221; Мюрат М., — наст. сб. с. 234.
7. Hausdorff F., Math. Ann., 79, 157 (1919); Besicovitch A. S., Math. Ann.,
110, 321 (1935).
8. Witten T. A., Sander L. M.y Phys. Rev. Lett., 47, 1400 (1981); Phys. Rev.,
B27, 5686 (1983).
9. Meakin P., Phys. Rev., A27, 604, 1495 (1983).
10. Richter R, Cheng Z. M, Sander L. M., Witten T. A., Bull. Am. Phys. Soc,
28, 261 (1983).
Фрактальная природа
трещин
Э. Луис, Ф. Гита, Ф. Флорес *
Конфигурации трещин в материалах исследовались с помощью
модели, включающей в себя уравнения упругости и простые правила
распространения трещин. Рассмотрены различные граничные
условия. Автомодельные конфигурации получены при фрактальных
размерностях, близких к 1,6.
1. Введение
Как было показано [1—3], множество конфигураций,
возникающих в различных процессах роста, обладает
фрактальной структурой. Появившиеся недавно полуэмпирические
соображения и некоторые измерения наводят на мысль о том, что
поверхности трещин в металле также могут иметь фрактальный
характер [4]. Хотя было предпринято несколько теоретических
попыток [5, 6] выяснить, можно ли считать геометрию
поверхности трещин фрактальной, глубокого понимания существа
проблемы (по крайней мере на уровне, достигнутом в последнее
время в теории пробоя диэлектриков (ПД) [2] и
диффузионно-ограниченной агрегации (ДОА) [3]) пока еще нет.
В данной работе мы предлагаем модель, которая
воспроизводит распространение трещины в идеальном моно- или
поликристалле (см. ниже). Явления растрескивания принадлежат к
числу наиболее интересных процессов в материаловедении [7].
Решающую роль в них играют многие факторы, такие, как
природа материала, примеси, дефекты, внутренние и внешние
границы и т. д., что обусловливает существование обширного
семейства механизмов растрескивания [7] от трещин в
пластических материалах до спайности в кристаллах. Несмотря на столь
сложную феноменолгию, начать следует с простой модели,
позволяющей довести до конца анализ возможной фрактальной
природы поверхности трещин.
Полученные нами результаты показывают, что конфигурации
образующихся в нашей простой модели трещин действительно
обладают фрактальным характером, что стимулирует
дальнейшие исследования более реалистических систем.
2. Модель и метод вычислений
Начнем с уравнений упругой сплошной среды [8]
(Я+ ^ (Z д/«/) + ^ (2 3?) «1 = 0, (1)
* Е. Louis -Departamento de Fisica, Universidad de Alicante, Apdo 99,
03080 Alicante, Spain; F. Guinea, F. Flores- Departamento de Fisica del Estado
Solido, Universidad Autonoma, Cantoblanco, 28049 Madrid.
Модели необратимого роста
245
где % и [г — коэффициенты Ламе, di — частная производная по
i-й компоненте вектора г, щ — компоненты поля деформаций.
Эти уравнения выведены в гармоническом приближении, а в
остальном совершенно общие и позволяют исследовать различные
изотропные материалы при изменяющемся отношении
коэффициентов Ламе. Уравнения (1) допускают различные граничные
условия: деформацию сдвига, одноосное сжатие, равномерное
сжатие и т. д. Следующий шаг состоит в принятии
предположения о том, что вероятность образования трещины в данной
части образца пропорциональна rj-й степени действующего на нее
напряжения. В нашей работе выбрано значение т|=1.
Уравнения (1) мы заменили дискретной системой, используя
треугольную решетку с пружинками, соединяющими ближайшие
соседние узлы. Такая модель позволяет воспроизводить либо
монокристалл (в этом случае пружинки соответствуют
межатомным силам), либо поликристалл (в этом случае пружинки
соответствуют напряжениям на границе кристаллических зерен).
Континуальный предел такой системы характеризуется
равенством К = |х. Хотя в этой работе мы излагаем результаты для
этого простого случая, более общие случаи также могут быть
исследованы, если выбрать более сложную элементарную
ячейку. Например, выбрав ячейку д/З X V^ мы получаем
возможность описывать изотропную систему в определенном диапазоне
значений отношения Х/\х, в то время как анизотропию удобно
исследовать, выбрав ячейку 2X1-
Дискретизация уравнений (1) на треугольной решетке легко
осуществляется, если за базисные векторы выбрать два вектора
решетки ai = а(1, 0) и a2 = a(l/2, V3 /2). В таком базисе
уравнения движения представимы в виде
Ащ(/, гп) — щ(I + 1, т) — щ(1—1, т) — щ(I + 1, т + 1) —
— Ui{l— 1, т— 1) + 2uf(l9 /я) —«/(/+ 1, т+ 1) —
— «/(/— 1, т— 1) = 0, (г, /=1,2), (2)
где ut(l, т))—/-я компонента (вдоль вектора смещения а,) в
узле решетки (/, т). Эта система уравнений решается методом
итераций на всей решетке. Исследовались решетки размером до
100ХЮ0. Граничные условия мы выбирали в виде
равномерного растяжения и деформации сдвига. Практическая
реализация граничных условий сводилась к удержанию в процессе
растрескивания неподвижными узлов решетки на внешней оболочке.
В исходной решетке связи были растянуты на 10 % по
сравнению с их равновесной длиной. Одну связь мы разрывали, и
предоставляли решетке релаксировать (в силу уравнений (1)) к
новому положению равновесия. Затем мы разрушали связи,
соседние с уже разорванным, выбирая их случайно и пропорцио-
246
Часть V(a)
нально сосредоточенному в них напряжению. Так повторялось
до тех пор, пока число разорванных связей не становилось
достаточно большим. Мы построили конфигурации трещин с
числом разорванных связей до 1200, что меньше числа, обычно
достигаемого в моделях ПД [2] и ДОА [3]. В этой связи
необходимо заметить, что, хотя некоторые аналогии между моделью
ПД и настоящей работой, несомненно, существуют, два
основных различия приводят к гораздо большим затратам машинного
времени при расчетах по нашей модели: 1) уравнения (2)
содержат векторное поле, а не скалярный электростатический
потенциал [2] и 2) в настоящей работе релаксирует вся сетка, в том
числе и ее фрагмент в зоне разрушения, тогда как в моделях
ПД или ДОА динамика области внутри кластера заморожена.
3. Результаты и их анализ
На рис. 1,а, б показаны характерные конфигурации трещин,
образующихся при равномерном растяжении и деформации
сдвига. Конфигурации автомодельны с фрактальной размерностью
1,62 ± 0,05 при растяжении и 1,64 ± 0,05 при сдвиге. Положения
узлов решетки, соответствующие конфигурациям трещин на
рис. 1, показаны на рис. 2. Обращаем внимание на следующие
характерные особенности: 1) решетка релаксирует в области
разрушенных связей; 2) на активных концах конфигурации
наблюдаются большие деформации; 3) симметрия, налагаемая
граничными условиями, отчетливо заметна на конфигурациях
трещин, что соответствует общему результату, согласно которому
поле деформаций в изотропной среде зависит от граничных
условий, хотя и не зависит от упругих постоянных [7, 8].
Один из наиболее привлекательных результатов, описанных
в предыдущем разделе, состоит в том, что фрактальная
размерность слабо зависит от граничных условий, хотя поле
деформаций существенно зависит от граничных условий. При сравнении
приведенных выше фрактальных размерностей с фрактальными
размерностями кластеров, полученных в двумерном случае при
ограниченной диффузии кластеризации и пробое диэлектриков,
обращает на себя внимание превосходное совпадение всех трех
размерностей [2, 3].
Итак, мы исследовали распространение трещин в идеальной
треугольной решетке, в которой ближайшие узлы соединены
между собой пружинками. Оказалось, что конфигурация трещин в
такой системе имеет фрактальную природу. Проведенная нами
работа могла бы стать началом серии исследований постепенно
усложняющихся моделей растрескивания. Используя
фрактальную геометрию [1], такие исследования могли бы
способствовать лучшему пониманию явлений растрескивания в материалах.
Модели необратимого роста
247
Благодарности. Часть вычислений, результаты которых
приведены в настоящей работе, были выполнены в Лаборатории
Рис. 1. Разрушенные связи: Рис. 2. Перемещенные атомов: а —при
а— при растяжении; б —при растяжении; 5 —при сдвиге,
сдвиге.
квантовой химии Университета в Аликанте. Выражаю свою
признательность заведующему лабораторией проф. Ф. Москардо,
предоставившему мне возможность воспользоваться
лабораторными компьютерами,
248
Часть V(a)
ЛИТЕРАТУРА
1. Mandelbrot В. В., The Fractal Geometry of Nature, Freeman, San
Francisco, 1983.
2. Niemeyer L., Pietronero L., Wiesmann H. /., Phys. Rev. Lett., 52, 1033
(1984); см. также наст, сб., с. 210.
3. Witten Т. A, Sander L. M., Phys. Rev., B27, 5686 (1983); см. также наст,
сб., с. 336.
4. Mandelbrot В. В., Passoja D. Е., Paullay A. /., Nature, 308, 721 (1984).
5. Termonia У., Meakin P., The Formation of Fractal Cracks in a Kinetic
Fracture Model, preprint.
6. Лунг Ч. — наст, сб., с. 260.
7. Fracture Mechanics Current Status, Future Prospects, Pergamon Press,
Oxford, 1979.
8. Ландау Л. Д., Лифшиц Е. М. Теория упругости. Изд. 3-е, испр. и до-
полн. — М.: Наука, 1965.
Формирование конфигураций
дендритных фракталов при растрескивании
и электрическом пробое
X. Такаясу *
Процесс роста трещин и конфигураций электрического пробоя
анализируется численно на простой решеточной модели. В обоих
случаях случайные дендритные фракталы образуются по
детерминистическому правилу эволюции, а случайность добавляется только
в самом начале. Отмечены сходство и различие между двумя
явлениями: растрескиванием и электрическим пробоем.
1. Введение
Образование конфигураций случайных фракталов —
возможно, одна из наиболее интересных задач современной
неравновесной статистической физики. Простые модели позволили с
помощью численных экспериментов успешно исследовать
диффузионно-ограниченную агрегацию (ДОА) [1] и электрический
пробой [2]. В этих моделях случайные конфигурации растут
стохастически с вероятностью, тесно связанной с решением
уравнения Лапласа. Было установлено, что фрактальный характер
конфигураций обусловлен случайным ростом в сочетании с
эффектом экранирования [3].
В отличие от этих стохастических моделей мною недавно
была предложена детерминистическая модель электрического
пробоя [4]. В моей модели начальная малая флуктуация полевой
переменной усиливалась детерминистически, и в результате
возникали случайные фрактальные конфигурации. Это, возможно,
указывает на то, что случайный процесс роста несуществен для
образования фрактальной конфигурации.
В следующем разделе мы кратко рассмотрим предложенную
мной модель электрического пробоя. В разд. 3 мы займемся
анализом хрупкого растрескивания тонкой пластины. Показано,
что предложенная мной модель электрического пробоя
переходит в модель хрупкого растрескивания при изменении только
одного параметра.
2. Электрический пробой
Рассмотрим сначала элементарный процесс электрического
пробоя. Мы разделяем здесь точку зрения, согласно которой
элементарный процесс электрического пробоя моделируется
следующими нелинейными и необратимыми характеристиками прово-
* Hideki Takayasu- Department of Physics, Faculty of Science, Kyoto
University, Kyoto, 606, Japan.
250
Часть V(a)
димости. Предположим, что постоянное напряжение V
приложено к резистору, причем V меньше некоторого критического
напряжения Vc, G — проводимость резистора. Когда V
превосходит Vc, происходит пробой резистора
и проводимость повышается до XG
(Я > 1). Параметр К означает
отношение увеличившейся проводимости к
проводимости в идеальном' случае К =
= оо. После пробоя резистор
сохраняет увеличившуюся проводимость
независимо от величины приложенного
напряжения V (рис. 1).
Рассмотрим далее квадратную
решетку из таких резисторов (см. рис. 1
в работе [4]). В этой решетке
электрический потенциал и удовлетворяет следующему уравнению
для любого узла решетки (i, j):
Рис. 1. Отклик
проводимости G на приложенное
напряжение V.
Z Gk (i, j) {uk (i, j) - и (i, /)} = 0,
(1)
Л-1
где индекс k указывает направление (рис. 2), Gk(i, j) означает
проводимость соответствующего резистора. Это уравнение пред-
)
,Uj(i,j) = u(j,j-l)
Gz(U)
(=iz(t-/fj))
tGd(i,j-l))
4(w)
MU)
Рис. 2. Смысл величин uk(i, j) и Gk(i, j). Индекс к означает направление:
1 — вверх; 2 — влево; 3 — вниз и 4 — вправо.
ставляет собой не что иное, как комбинацию закона Ома и
законов Кирхгофа. В случае если узел решетки расположен на
границе, то для отсутствующего резистора необходимо положить
Gk = 0. При произвольно заданных {Gk} и надлежаще
выбранном граничном условии на {и} уравнения (1) при всех комбина-
Модели необратимого роста
251
циях (i, j) образуют систему линейных уравнений для {и} и
могут быть решены численно.
Временная эволюция такой системы определяется
следующим алгоритмом:
1) задать {G} и граничное условие на {и}\
2) решить уравнения (1) и найти {и};
3) проверить каждый резистор (за исключением уже
разрушенных пробоем): если выполняется условие пробоя \uk(i>j) —
— и(/,/)]> Vc, то произвести замену Gk(i,j) на №ь(/,/);
tfffl fffii
I
11
т 1
'Bill 1 1 1 U
] 11 1 1 О. J
I 1 1 I 1 1 1 1 1 1 111 1 1
ill L.LI 4
11 111ftiIJ
I 1 In i II11
r«/
T=Z
T=3
T-4
!■■■■■■■■■■■ I ■ ■ ■
■■■■■■■■■■■■■■I
■ ■■■■■■■ ■■■■■■■
Ш
d
T=5
T=6
T = 7
Рис. 3. Эволюция конфигурации электрического пробоя на решетке 10 X Ю.
На последнем «кадре» показана конфигурация перколяционного кластера при
Т = 4. Параметры имеют следующие значения: G = 2,0; G* = 2,0; Vc = 1,0
иЫ 100.
4) остановиться, если при выполнении предшествующих
этапов процедуры не был разрушен пробоем ни один новый
резистор, в противном случае вернуться к п. 2 и продолжать
выполнение процедуры.
Из приведенного нами алгоритма ясно, что мы предоставляем
системе эволюционировать, неоднократно решая уравнения (1)
и проверяя условие пробоя.
Пример такой эволюции на решетке 10 X Ю показан на
рис. 3. Граничное условие здесь задано соотношениями
u(i, 0) = 0 и u{i, 10) = U (/=1, 2,
Ю),
(2)
где напряжение U выбрано достаточно большим для того, чтобы
происходил пробой по крайней мере одного резистора, а
начальные значения {G} выбраны случайно по формуле
О* (Л /) = G + G*2, (3)
где G и G* — постоянные, Z — случайная величина, равномерно
распределенная на полуоткрытом интервале [0, 1). Такую эво-
252
Часть V(a)
люцию можно рассматривать как своего рода динамический
фазовый переход, т. е. переход из непроводящего состояния в
проводящее, при котором управляющим параметром служит шаг по
времени. Критической точкой такого фазового перехода должен
быть момент времени, когда впервые возникает перколяцион-
ный кластер из пробитых резисторов (Г = 4 на рис. 3).
Вычисления подтвердили, что критические перколяционные кластеры
рассматриваемой нами системы являются фракталами с
размерностью около 1,6 [4].
Хотя шаг по времени в нашей модели отличается от
реального времени, вполне интересная задача — количественная
оценка скорости роста пробоя. При исследовании решеток 32X32
был обнаружен следующий экспоненциальный рост:
N (Т) = ехр (ЬТ), Ь = 0,85 ± 0,03, (4)
где N(T) —усредненное число разрушенных пробоем резисторов
на Г-м шаге по времени. Это соотношение выполняется при
числе шагов по времени меньшем, чем время образования перколя-
ционного кластера.
В образовании фрактальной конфигурации пробоя
существенную роль играет необратимый отклик проводимости. В этом
можно убедиться, рассматривая случай, когда проводимость
имеет обратимый линейный характер, т. е. ступенеобразный
отклик на напряжение. При таком отклике перколяционные
фазовые переходы не происходят и фрактальная структура не
возникает— обычно появляются колебания. Эту особенность нашей
электрической системы полезно иметь в виду.
3. Растрескивание
Изложение в этом разделе во многом параллельно
изложению в предыдущем разделе.
Рассмотрим сначала элементарный процесс растрескивания.
Предположим, что один конец тонкого хрупкого стержня зажат
неподвижно, а другой конец свободен. Если перемещение d
свободного конца меньше критического значения dCi то модуль
жесткости стержня G постоянен. Когда же d превышает dc,
стержень может сломаться и G внезапно падает до очень малого
значения eG, 0<е<1, как показано на рис. 4.
Рассмотрим далее плоскую квадратную решетку,
составленную из таких хрупких стержней. Если предположить, что
перемещения в узлах такой решетки перпендикулярны плоскости
(задача об антиплоском сдвиге), то уравнение равновесия сил
совпадает с уравнением (1), в котором {и} и {G} означают
соответственно перемещения и модули жесткости. Такое совпадение
не случайно; в в пределе непрерывной среды уравнения (1) пе-
Модели необратимого роста
253
реходят в уравнение
V • (GVu) = О,
(5)
если G и и достаточно гладкие функции. Это фундаментальный
закон сохранения и одно из наиболее широко известных
уравнений в физике. (Уравнение Лапласа
получается из уравнения (5) в частном
случае, когда G = const.)
Временную эволюцию хрупкой
решетки можно воспроизвести с
помощью алгоритма, описанного в
предыдущем разделе, если Vc заменить на
Я, a ok —на е. Граничное условие (2)
и начальное условие (3) также могут
быть использованы. Граничное
условие (2) соответствует такой
физической ситуации, когда к верхнему краю
квадратной хрупкой пластинки приложено растягивающее
усилие, в то время как нижний край пластинки закреплен
неподвижно. Из-за отмеченного сходства электрического пробоя и
хрупкого растрескивания численное моделирование электриче-
Рис. 4. Отклик модуля
жесткости G на
перемещение d.
Г = 7
Г=2
Т= 3
В
Г = 4
r=j
Рис. 5. Пример эволюции трещин при хрупком растрескивании. Все условия,
за исключением параметра X (Я = 0,01 (= е)), тождественны с условиями
электрического пробоя на рис. 3. На последнем «кадре» показана перколяци-
онная трещина при Т = 5.
ского пробоя практически оказывается численным
моделированием хрупкого растрескивания с единственным различием,
состоящим в замене больших значений параметра Я на очень малые.
На рис. 5 показано, как эволюционирует трещина при тех же
условиях, что и электрический пробой на рис. 3. На рис. 3 рост
кластера происходит по вертикали, на рис. 5 трещина
развивается по горизонтали. Рост останавливается, когда конфигура-
254
Часть V(a)
ция трещины образует перколяционный кластер. С точки
зрения математики интересно отметить, что эти различия
проистекают только из-за параметра Я.
Фрактальные свойства таких перколяционных кластеров
были изучены, и по полученным оценкам их фрактальная
размерность составляет
D= 1,65 ±0,05. (6)
Усредненное число разрушенных связей N(T) в этом случае
следует степенному закону
N(T) = Tat a = 2,4 ±0,2. (7)
Такой степенной закон указывает, что процесс роста трещины
обладает фрактальными свойствами не только в
пространственных, но и во временных характеристиках.
В отличие от электрического пробоя при упругом
растрескивании необратимый отклик несуществен. Трещины растут почти
тождественно даже в том случае, если отклик жесткости
заменить обратимым. Различие между электрическим пробоем и
упругим растрескиванием отчасти можно понять, если обратить
внимание на полную энергию систем: при упругом
растрескивании полная энергия убывает со временем, при электрическом
пробое она возрастает. Можно утверждать поэтому, что чем
больше растут трещины, тем стабильнее становится система.
Более подробные сведения относительно хрупкого растрескивания
будут опубликованы нами позднее [5].
Благодарность. Эта работа частично финансировалась
Исследовательским фондом министерства образования и Комитетом
по проектам в области образования для японских специалистов
по математическим наукам.
ЛИТЕРАТУРА
1. Witten Т. A., Jr., Sander L. Af„ Phys. Rev. Lett., 47, 1400 (1981).
2. Niemeyer L, Pietronero I., Wiesmann H. /., Phys. Rev. Lett., 52, 1033
(1984).
3. Meakin P., Phys. Rev., B28, 6718 (1983).
Pietronero L, Wiesmann H. /., J. Stat. Phys., 36, 909 (1984).
4. Takayasu #, Phys. Rev. Lett, 54, 1099 (1985).
5. Takayasu Я, Prog. Theor. Phys, в печати.
Разрушение нагруженных
фрактальных деревьев
С. Солла *
Фрактальное дерево с статическим распределением длин ветвей
служит иерархической моделью разрушения структуры под
действием внешней нагрузки. Перенос нагрузки с разрушенных ветвей
на еще целые приводит к дальнейшему разрушению, а при
критическом значении приложенной нагрузки — к катастрофическому
разрушению всей структуры.
Исследования разрушения материалов и структур под
действием приложенной нагрузки имеют важное практическое
значение и сопряжены с определенными концептуальными
трудностями. Обычный подход, опирающийся на теорию упругости
сплошной среды, не дает простых средств для анализа
существенных нелинейностей данной проблемы. Цель настоящей статьи
состоит в изложении альтернативного подхода: статистического
описания распространения области разрушения [1].
Нагруженное фрактальное дерево используется для введения масштабно-
инвариантного механизма переноса нагрузки, приводящего к
катастрофическому разрушению при достижении приложенной
нагрузкой критического порога [2].
Рассмотрим простое фрактальное дерево, у которого из
каждой вершины выходят два ребра, образующие между собой угол
<h Вертикальная нагрузка V приложена к вершине п = 0 у
основания. На п-ы уровне существуют 2п ребер, соединяющих
каждую вершину (п—1)-го порядка с двумя вершинами п-го
порядка. Высота п-го уровня равна hn = h\/2n-l9 что вдвое меньше
высоты (п—1)-го уровня. Полная высота дерева равна Н =
оо
= 2 hn = 2hi. Если разрушения нет, то нагрузка на каждое
ребро на п-м уровне составляет Vn=V cos('&/2)/2rt.
Флуктуации размеров, форм и других внутренних
параметров ребер реальной структуры приводят к статистическому
распределению значений разрушающего напряжения Vnf ребер п-го
уровня. Разнообразие значений мы моделируем распределением
Вейбулла [3]. Вероятность разрушения рп (того, что нагрузка
Vn превосходит разрушающую нагрузку Vnf) определяется
выражением
рп = Prob (Vnf < Vn) = 1 - exp [- (Vn/V0n)m], (D
* Sara A. Solla-IBM Thomas J. Watson Research Center, Yorktown
Heights, New York 10598, USA.
256
Часть V(a)
где Von — некая стандартная нагрузка для ребер п-го уровня, а
целое число m — порядок распределения. Распределения Вейбул-
ла часто используются для представления статистических
флуктуации разрушающих нагрузок [4].
Существенной отличительной особенностью нашей модели
является масштабно-инвариантный механизм переноса нагрузки:
если одно из ребер /г-го уровня разрушается, то приложенная к
нему нагрузка переносится на соседнее ребро /г-го уровня,
выходящее из той же вершины (п—1)-го уровня. Второе ребро в
паре может при этом разрушиться от дополнительной нагрузки
с условной вероятностьюР1^2 того, что Vnf^2Vn, если Vnf > Vn.
Такая условная вероятность легко вычисляется для
распределения Вейбулла (1) и равна
Pln2=l-(l-pnfm-1. (2)
Разрушение ребер п-го уровня полностью снимает нагрузку с
вершины (п—1)-го уровня, из которой они выходят, и
приводит к разрушению ребра (п—1)-го уровня, входящего в эту
вершину. Вероятность разрушения ребра на (п—1)-м уровне
определяется выражением
Рп-1 = Р2п+2рп(1-Рп)Рп2. (3)
Первое слагаемое описывает прямой процесс, вызванный
разрушением двух ребер п-го уровня, образующих пару, а второе
слагаемое описывает индуцированное разрушение и возникает
только в том случае, если разрушается непосредственно одно
из двух ребер п-го уровня, образующих пару. Подставляя
условную вероятность (2) в формулу (3), получаем рекуррентное
соотношение
Р^1 = 2рЛ1-(1-Р«Л-Р- (4)
описывающее распространение разрушения по дереву (от
низшего уровня к высшему) и применимое ко всем уровням
структуры.
Функциональная зависимость р/г_1 от рп при m = 2 показана
на рис. 1. Уравнению неподвижной точки рп-\ = рп
удовлетворяют значения рл, равные 0, 1 и рс. Критическая точка рс =
= 0,2065 описывает переход от режима, в котором области
разрушения остаются ограниченными (рп < рс), к режиму, в
котором области разрушения неограниченно растут и структура не
может выдерживать внешнюю нагрузку (рл5>рс). В качестве
конкретного примера упомянем о том, что при m = 2
рекуррентное соотношение (4) переводит p„ = 0,l в p«_i = 0,0588, рп-2=
= 0,0218, ря_з = 0,0032. При убывании п вероятность
разрушения стремится к нулю, и структура устойчива. Но при рп = 0,6
Модели необратимого роста
257
то же соотношение (4) порождает последовательность
вероятностей рп-\ = 0,8093, рп-г = 0,9615, рЛ_3 = 0,9985. При убывании п
к вершине дерева вероятность разрушения стремится к единице,
и вся структура, не выдерживая приложенной нагрузки,
разрушается.
Катастрофическое разрушение структуры при рс обусловлено
резким ростом разрушенной части структуры при увеличении
нагрузки. Такое поведение можно охарактеризовать длиной
распространения L, т. е. число
уровней, на которые распространяется
вверх по дереву разрушение от
данной нагрузки. Ниже рс длина
распространения конечна и при
приближении к рс снизу
расходится с критическим показателем v.
В ситуации, изображенной на рис.
1 (т = 2), разрушение структуры
происходит при рс = 0,2063 с
показателем v = 1,439.
Соответствующую критическую нагрузку
можно вычислить по формуле (1):
Vc = 0,4807 Von- Она значительно
меньше средней нагрузки на
ребро л-го уровня V = 0,8862 VW
Рассмотренные выше
характерные особенности решения при
т = 2 носят весьма общий характер. При увеличении т
распределение (1) разрушающей нагрузки становится более узким, и
в пределе при т-+оо все ребра разрушаются при Vn= VW Но
при сколь угодно больших конечных значениях т рекуррентное
соотношение (4) порождает S-образную кривую, качественно
похожую на кривую, изображенную на рис. 1.
pc=l-(l/2)i/(2m-i)
соответствует критической нагрузке
Fc = [ln2/(2m-l)]V-l/te.
Хотя критическая вероятность разрушения быстро убывает
с увеличением т, разрушающая нагрузка почти не зависит от т
и остается почти вдвое меньше средней нагрузки
V = (llm)lV0n. (7)
При т > 5 критический показатель v почти не зависит от /п.
Результаты при различных значениях т представлены в табл. 1.
Иерархическая модель, приводящая к рекуррентному
соотношению (4) для распространения разрушения, предсказывает
о рп 1
Рис. 1. Рекуррентное соотношение
для распространения разрушения
по дереву (соотношение (4) для
вероятности разрушения (1)).
Кривая соответствует т == 2.
Критическая точка
(5)
(6
258
Часть V(a)
разрушение структуры через расходимость характеристической
длины распространения. Основным механизмом такого
катастрофического поведения является индуцированное разрушение,
обусловленное переносом нагрузки. Разрушающая нагрузка для
системы почти не зависит от разрушающих нагрузок в
подсистемах и ниже своего характеристического значения. Полученные
нами результаты применимы к разиличным задачам, в которых
Таблица 1. Критические параметры
m
2
3
5
10
20
oo
Рс
0,2063
0,0943
0,0221
0,7-10"'
0,7 • 10~6
0
vc/von
0,4807
0,4626
0,4676
0,4821
0,4909
0,5
v/von
0,8862
0,8930
0,9182
0,9513
0,9735
1
V
1,439
1,368
1,328
1,317
1,316
1,316
распространение разрушения происходит ирерархически из-за
корреляции между размером разрушенной области и размером
прилегающей области, не затронутой разрушением, но
находящейся под действием нагрузки.
Интересная возможность предотвратить разрушение
структуры открывается при включении в структуру некоторой доли
особо прочных ребер. Рассмотрим распределение разрушающих
нагрузок с двумя характеристическими нагрузками Von и yVm с
у> 1. Вероятность разрушения для ребер «-го уровня в этом
случае равна
рп = Prob (Vnt < Vn) = (1 - а) {1 - ехр [- (VJV0n)m]} +
+ a{l-exp[-(VjyV0n)m)}. (8)
Введены два дополнительных параметра: доля а прочных ребер
и отношение у характеристической нагрузки прочных ребер к
характеристической нагрузке непрочных ребер. Рассмотренное
ранее распределение (1) содержится в распределении (8) как
частный случай (а = 0). При а=^0 условная вероятность Р]^2
не представима через рп простым аналитическим выражением.
Численное исследование возникающего при а Ф 0 рекуррентного
соотношения как функции от а и у обнаруживает режим,
характеризуемый двумя критическими точками, как показано на рис. 2
при а = 0,15, у = 10 и m = 2.
Нижняя критическая точка pCw = 0,2343 (VCw = 0,5671 Von)
соответствует разрушению непрочных ребер. Верхний порог
pcs = 0,8809 (1/С5 = 4,8067У0«) достигается, когда разрушение
Модели необратимого роста
259
структуры происходит с достоверностью. Промежуточный
интервал pew < рп < pes контролируется неподвижной точкой рь —
= 0,7205. Значения рп в этом интервале порождают
последовательность вероятностей разрушения, стремящуюся к рь при
убывании п к вершине дерева. Таким образом, рь определяет
эффективность механизма сопротивления разрушению,
осуществляемому прочными ребрами. При фиксированном параметре у
вероятность рь убывает от единицы по мере того, как доля а прочных
ребер возрастает от нуля.
Неподвижные точки рь и pcw при
увеличении а сближаются до
полного слияния при а = ас и
последующего исчезновения. При а >
> ас критической точки,
связанной с непрочными ребрами, не
существует и разрушение
структуры зависит только от прочных
ребер. Диапазон 0 < а < ас
характеризуется существованием
двух критических точек pcw и pcs.
При т = 2, 7 = Ю (см. рис. 2)
ас « 0,29.
Рис.
ДЛЯ
2. Рекуррентное соотношение
распространения разрушения
вверх по дереву (соотношение (8)
для вероятности разрушения).
Кривая соответствует а = 0,15,
у = 10 и m = 2.
Резюмируя, мы утверждаем,
что нагруженное фрактальное
дерево может служить простой
моделью при исследовании
разрушения структуры под действием приложенной извне
нагрузки. Бимодальная вероятность разрушения, описываемая
соотношением (8), служит примером одного из возможных
обобщений модели, учитывающих характерные особенности тех
физических систем, к которым применимы развитые выше соображения.
Благодарности. Эта работа выполнена при участии Р. Смэл-
ли-мл. и Д. Теркотта (геологический факультет Корнеллского
университета). Выражаю свою признательность им обоим за
сотрудничество, оставившее самые приятные воспоминания.
ЛИТЕРАТУРА
1. Smalley R. F., Jr., Turcotte D. L., Solla 5. Л., J. Geophys. Res., 90, 1894
(1985).
2. Turcotte D. L, Smalley R. F.t Jr., Solla S. A, Nature, 313, 671 (1985).
3. Weibull W.t J. Appl. Mech., 18, 293 (1951).
4. Harlow D. G., Phoenix S. I., Adv. Appl. Probab., 14, 68 (1982).
Фракталы и разрушение
металлов с трещинами
Ч. Луна *
Предложена модель межкристаллитных поверхностей при хрупком
и вязком разрушении металлов с трещинами. Показано, что в
металлах с мелкозернистой структурой критическая сила
растяжения трещины быстро возрастает (быстрее, чем следует из
соотношения Холла — Петча) из-за увеличения истинной площади
нерегулярной поверхности трещин.
1. Введение
Поверхность трещины, образующейся после отрыва,
весьма неровна и иррегулярна. Мандельброт и другие авторы
[1,2] установили, что структура поверхности трещин в металле
превосходно моделируется фрактальными поверхностями, хотя
поверхность трещин лишь весьма извилиста (предел
извилистости ограничен снизу характерным размером микроструктурных
неоднородностей), в то время как фракталы бесконечно
извилисты. Проведенные этими авторами эксперименты по разрушению
металла показали, что фрактальная размерность D имеет вполне
определенное значение для различных образцов одного и того
же металла, подвергшихся аналогичной термомеханической
обработке.
Мы считаем, что размеры и ориентация зерен во многих
поликристаллических металлах «нерегулярны» (распределение
примесей, дефектов и других источников внутренних
напряжений также «нерегулярно»). Эти нерегулярности, возможно, и
являются физической основой того, что поверхности трещин в
металле успешно моделируются фракталами.
В настоящей работе мы анализируем, как размер зерна
влияет на разрушение металла в фрактальных моделях.
2. Критическая сила растяжения трещины
В теории Гриффитса идеально упругого разрушения [3] для
разрыва необходимо превзойти работу 2ys, которую требуется
совершить для разделения двух поверхностей. В подходе
Ирвина к механике разрушения критическая скорость
высвобождения энергии деформации Gc, т. е. критическую силу растяжения
трещины [3], можно записать в виде
<?c = 2ys (при хрупком разрушении) (1)
* С. W. Lung-International Centre for Theoretical Physics, Trieste, Italy;
Institute of Metal Research, Academia Sinica, Shenyang, People's Republic
of China (постоянный адрес),
Модели необратимого роста
261
Gc = 2vs + Yp (при квазихрупком разрушении),
(2)
где ур— энергия, затрачиваемая на работу пластической
деформации, необходимую для создания неустойчивого
распространения трещины на ее концах.
В отличие от стекла
поверхности трещин в металлах
неровные и нерегулярные.
Истинные площади поверхностей
трещин металла больше, чем
данные, получаемые с помощью
макроскопических измерений.
Площадь поверхности
трещины на единицу толщины
образца составляет величину [L(e) /
/L0(e)]-1 (в механике
разрушения трещину всегда
упрощенно представляют в виде
линии в двумерной системе).
Следовательно, вместо
соотношений (1) и (2) мы получаем
соотношения (рис. 1,а, б)
G, = 2(L(e)/L0(e))Y5, (3)
Ос = 2 (ш-а)"1 [Lite)+
+ Me2)]Ys + YP, (4)
где ее — масштабы длин.
Другие параметры указаны также
на рис. 1.
3. Фрактальная модель
межкристаллитных
поверхностей при хрупком
разрушении металлов
В случае межкристаллитно-
го разрушения трещина
распространяется вдоль зигзагообразных границ зерен. В более
мелком масштабе трещина распространяется вдоль более мелких
зигзагообразных границ субзерен. В более крупном масштабе
трещина распространяется по более крупному слабому проходу
в направлении, близком к генеральному направлению
распространения трещин. Такой проход образуют нерегулярные
распределения кластеров вакансий, микропустоты, включения,
6
\с
-*] L1 \*~Ьг -А
V^/__ 2a _~д_у
,,._. ^ nj j-
1
'0
Рис. 1. а — Идеальное хрупкое
разрушение в стекле; б — упругопластиче-
ское разрушение в металле.
262
Часть V(a)
микротрещины и т. д. Все перечисленные нами поверхности
нерегулярны, их можно считать автомодельными и, следовательно,
моделировать с помощью фракталов (рис. 2). Кроме того, я
считаю, что фрактальная размерность D может быть однозначно
определена для различных образцов одного и того же металла,
не только подвергшихся аналогичной термомеханической
обработке [1], но и при одних и тех же температурных условиях и
скорости нагружения при испытаниях на растяжение.
Существуют две формы межкристаллитного хрупкого
разрушения (рис. 3, а и б). Их фрактальные размеры можно
определить с помощью формального определения
D = logtf/log(l/r), (5)
где N = 1//ео/, г = е0//£<н (см. рис. 3):
а) # = 2, г^-^, D=l,26;
б) N = 4, r = y, D=l,26.
Фрактальные размерности обеих форм одинаковы и равны 1, 2,
6, но размеры зерен различны. Размер зерна d определяется
выражением
d = Lqi = 1 >73e0I = 3,46е02, (6)
где L\ =2е0ь £oi = 1,73еоь L2 = 4е02, £о2 = Зе02. Из соотношения
(3) получаем
Gc = 2Ys [LJLi0] = 2Y5 (LQi/eoi)»-K (7)
а) Gc=1,73°.*.2y5,
б) Gc = 30.26. 2Y5.
Нетрудно видеть, что в случае а) образование поверхности
трещин требует меньших затрат энергии, чем в случае б) и поэтому
предпочтительнее. С учетом этого в основу фрактальной модели
в нашей работе положен случай а).
С уменьшением размера зерна истинная площадь
поверхности трещины все увеличивается. По Мандельброту [2]
L,(et0~Fe!-D, (F = L0D), (8)
Gc = 2ys(Li/L0) « 2ysFLolE\-D « 2ysd-°*
(заметим, что 1,730,26 « 1,1; FL£l = Lo~l=l9 если L0 выбрать
за единицу длины, например LQ=l см). Следовательно,
Gc = 2ys- 10,96 .'при й=1(Г4см),
Gc = 2ys • 20 (при d = 1(Гб см),
Gc = 2Y5 • 36,3 (при d = 10"6 см).
Модели необратимого роста
263
Член, связанный с ys в соотношении (2), теперь сравним по
порядку величины с членом, связанным с ур (обычно ур ^ IOys)
при хрупком разрушении, или меньше его, но еще не достаточно
Рис. 2. Все более мелкие зигзагообразные трещины, образующиеся в
фрактальной модели металла.
Рис. 3. Межкристаллитное хрупкое разрушение.
велик, чтобы повысить сопротивление материала разрушению.
Возможно, в этом заключается одна из причин того, почему
поверхностные энергии металлов, оцениваемые измерениями
низкотемпературного хрупкого разрушения, неизменно оказываются
более высокими, чем энергии, получаемые другими
методами.
264
Часть V(a)
4. Фрактальная модель поверхности трещины
при межкристаллитном вязком разрушении металла
Как показывают фрактографические наблюдения межкри-
сталлитного разрушения, поверхность трещин при вязком
разрушении покрыта микровпадинами — следами дыр, образующихся
перед основной трещиной. По современным представлениям эти
дыры образуются в реальных марках стали главным образом
Рис. 4. Дополнительный угол, возникающий при пластической деформации
в зерне.
в тех местах, где в матрице находятся осевшие частицы.
Большие пустоты в среде часто бывают связанными полосами
интенсивного сдвига, образующимися при движениях дислокаций. Что
касается нашей упрощенной фрактальной модели, то вследствие
пластических деформаций в зернах границы зерен ab и be
становятся кривыми ab' и Ус. Кроме того, аУ и Ус проходят круче,
чем ab и be: после нагружения образца возникает
дополнительный угол # (рис. 4). Но
Lp = 2e,
L0 = 2ecos(30° + #).
В нашем случае N = 2, г = [2cos (30° + #) ] -1,
D = log 2/log [2 cos (30° + 0)1. (9)
Величину угла ft можно оценить как
# = (P6L)/L = p6, (10)
где р — линейная плотность подвижных дислокаций.
Характерные величины полной линейной плотности дислокаций
колеблются в диапазоне от 106—107 см-1 для кристаллов,
подвергшихся холодной обработке, до 103 см-1 для отожженных
кристаллов. При b » 3-Ю-8 см угол в соотношении (10) заключен
в пределах от 3-10-5 рад до 0,03—0,3 рад (1,7—17°).
Соответственно фрактальные размерности могут изменяться в диапазоне
1,26—2,23.
Модели необратимого роста
265
Выбирая D = 2,23, получаем
Gc ~ 2уз4-1* ,
Gc = 2y5X8,3. 104 (при ^=1СГ4см),
Gc = 2ysX1,4- lO6 (при d=lCT5 см).
Оцениваемая по нашей модели критическая сила растяжения
трещины быстро возрастает с уменьшением размеров зерен. Она
возрастает быстрее закона Холла — Печа d~I/2, если плотность
подвижных дислокаций достаточно велика. По нашим
наблюдениям, размеры зерен большинства суперпластических сплавов
очень малы (^ Ю-4 см). Это явление, по-видимому, может быть
объяснено нашей фрактальной моделью.
Благодарности. Автор хотел бы поблагодарить проф. Аб-
дуса Салама, Международное агентство по атомной энергии и
ЮНЕСКО за гостеприимство, проявленное во время его
пребывания летом 1985 г. в Международном центре теоретической
физики в Триесте, где была выполнена эта работа. Автор выражает
также свою признательность проф. С. Лундквисту и проф.
Б. Б. Мандельброту за полезные обсуждения. Работа
финансировалась Научным фондом китайской Академии наук.
ЛИТЕРАТУРА
1. Mandelbrot В. В.у Passoja D. £., Paullay A. /., Nature, 308, 721 (1984).
2. Mandelbrot 5. В., The Fractal Geometry of Nature, Freeman, San-Fransisco,
1983, p. 25, 29, 469.
3. Knott J. F.y Fundamentals of Fracture Mechanics, Butterworths, 1976, p. 109.
4. Lung C. W., Gao H.y Phys. Stat. Sol. (a), 87, 565 (1985).
Когда вязкие «пальцы»
имеют фрактальную
размерность?
И. Нитман, Ж. Даккор, X. Стенли *
Показано, что вытеснение водой сильновязкой неньютоновской
жидкости в линейной и радиальной ячейках Хеле — Шоу приводит
к фрактальному росту. Наши эксперименты с линейной ячейкой
позволяют утверждать, что фрактальная размерность df
неустойчивых структур есть функция ширины ячейки. С увеличением
ширины ячейки размерность df стремится к значению 1,7,
получаемому в рамках модели ДО А. Это значение было проверено во втором
независимом эксперименте с радиальной ячейкой, в которой
граничные эффекты несущественны. Для размерности Хаусдорфа
радиальных вязких «пальцев» нами получено значение df=l,70±0,05.
Мы также произвели первые экспериментальные измерения точек
роста и сравнили полученные результаты с данными численных
экспериментов в рамках модели ДОА. Нами обнаружено, что
толщина пальца есть линейная функция величины зазора между
пластинами. Чтобы понять фрактальный рост вязких пальцев, мы
провели также сравнение моделей ДОА и управляемого
градиентом роста.
1. Введение
В последнее время большое внимание привлекли как
экспериментальные [1—7], так и теоретические [8—15]
исследования разнообразных физических явлений, происходящих при
вытеснении жидкостью с малой вязкостью другой жидкости с
большой вязкостью в ячейке Хеле — Шоу. В общем случае
первоначально плоская поверхность раздела жидкостей переходит
в поверхность, напоминающую по форме пальцы перчатки,
откуда и название — вязкие пальцы. Недавно нами были
установлены физические условия, при которых вязкие пальцы имеют
весьма разветвленную структуру. Из-за последовательного
случайного дробления кончиков пальцев вязкие пальцы
перерастают в разветвленные кластеры, плотность которых убывает со
временем. Нам удалось установить, что эти структуры являются
фрактальными и что фрактальные пальцы могут быть
количественно охарактеризованы размерностью Хаусдорфа. Цель
настоящей статьи состоит в определении физических условий, при
которых развиваются фрактальные пальцы, и в обсуждении того,
насколько фрактальная модель роста применима для
воспроизведения основных особенностей роста.
* Johann Nittmann, Gerard Daccord-Etudes et Fabrication Dowell Schum-
berger, B. P. 90, 42003 Saint Etienne, France; H. Eugene Stanley-Centre
for Polymer Studies and Department of Physics, Boston University, Boston,
MA 02215 USA,
Модели необратимого роста
267
Образование вязких пальцев впервые наблюдалось при
интенсифицированной добыче нефти. Для повышения полноты
извлечения нефти в нефтеносный пласт закачивают воду, которая
вытесняет нефть, удерживаемую пористой средой. Но
вытеснение жидкости с большой вязкостью другой жидкостью с малой
вязкостью в среде, оказывающей сопротивление потоку, —
процесс неустойчивый, и в потоке возникают пальцеподобные
структуры. Саффмен и Тейлор [15] исследовали это явление в ячейке
Хеле — Шоу. Так называет-
Вход
Выход
Выход
Выход
ся прибор, состоящий из
двух прямоугольных
стеклянных пластин с
небольшим (обычно 0,5 мм)
зазором между ними. Вдоль
длинных сторон пластины
склеены, и жидкость может
поступать в зазор между
ними через небольшое
отверстие в центре одной из
коротких сторон и выходить из
ячейки через другую
короткую сторону (рис. 1).
Ячейка Хеле — Шоу
часто используется для
моделирования течения двух
жидкостей в пористой среде.
Для обеих жидкостей существует эмпирический закон,
связывающий скорость течения v одной жидкости с градиентом
давления \Р в жидкости. Это соотношнеие известно под названием
закона Дарси:
Рис.
1. Схема линейной и радиальной
ячеек Хеле — Шоу.
(1)
где k и ju — проницаемости среды и жидкости. Закон Дарси по
существу просто констатирует, что скорость течения
пропорциональна приложенному градиенту давления. В пористой среде
проницаемость является функцией точки пространства, в то
время как в ячейке Хеле —Шоу k — константа. (Можно показать,
что & = 62/12, где Ь — ширина зазора между пластинами.)
^Ранние эксперименты были сосредоточены на вытеснении
одной жидкости другой, с ней не смешивающейся, при котором
капиллярные силы препятствуют росту очень мелких пальцев.
Отношение вязких сил к капиллярным силам может быть
выражено некоторым безразмерным числом — капиллярным
числом NCa:
*с.=^. (2)
268
Часть V(a)
где а — поверхностное натяжение границы между двумя
жидкостями. Чуоке и другие [16] показали, что поверхностное
натяжение границы между двумя жидкостями вводит минимальный
масштаб длины. Расти могут только возмущения с длиной
волны Я, превышающей критическую длину волны Хс> где
Xc = 2nb/(l2NCa)-l(*. (3)
Соотношение (3) показывает, что Кс — линейная функция
ширины зазора между пластинами и для любой конкретной пары
жидкостей убывает с увеличением скорости течения.
Повторяя классический экперимент Саффмена — Тейлора с
системой вода — нефть, мы заметили, что при уменьшении Кс
Рис. 2. Вязкий палец, возникший при инжектировании воды в ячейку Хеле —
Шоу с ньютоновской жидкостью нефтью. Показано, как выглядит картина
течения при двух различных капиллярных числах: а) iVca=0,08; б) iVca=0,16.
(например, при увеличении скорости течения) пальцы на
концах делятся (рис. 2). По-видимому, дальнейшее увеличение
вязкой силы должно приводить к еще более интенсивному
ветвлению. Однако реально увеличить скорость течения нам не
удалось, поскольку экспериментальная установка определяет
пределы прилагаемых к системе вязких сил. Учитывая это, мы
полностью изменили геометрию эксперимента.
2. Эксперименты
Мы занялись поиском двухжидкостной системы, обладающей
следующими свойствами:
1) поверхностное натяжение границы между двумя
жидкостями пренебрежимо мало;
2) большое отношение вязкостей;
3) поршнеобразные (течение — пробка) профили
перемещений в направлении, перпендикулярном к стеклянным
пластинкам.
Чтобы свести к минимуму поверхностное натяжение
границы между двумя жидкостями, мы использовали смешивающиеся
Непрямой,
свет
ТВ камера
Белый матерчатый,
экран
Сжатый воздуос
(вязкая аюидкость)
Волюметрическии
насос (жидкость
смолой вязкостью)
Радиальная ячейки
Мнжекция в центре
{снизу)
И
О
Контрольны^
экран
ВиВеозаписывающии.
аппарат
Рис. 3. Схема экспериментальной установки.
270
Часть V(a)
жидкости. Но поскольку смешивающиеся жидкости
смешиваются, важно, чтобы продолжительность эксперимента была мала
по сравнению с временем смешивания. Близкое к нулю
поверхностное натяжение границы раздела позволяет расти любой
малой флуктуации. Преобладание рандомизирующих эффектов над
стабилизирующими чрезвычайно важно для фрактального
роста.
Отношение вязкостей (вязкости толкающей жидкости к
вязкости вытесняемой жидкости) — своего рода вынуждающая сила
неустойчивости, следовательно, желательно, чтобы отношение
вязкостей было побольше. Третье свойство предотвращает
образование трехмерных пальцев. В смешивающихся
ньютоновских жидкостях наблюдалось частичное вытеснение одной
жидкости другой с менее разветвленными неустойчивыми
структурами [8].
Первой системой двух жидкостей, которую мы использовали
в своих экспериментах [1], была вода, вытесняющая водный
полимерный раствор полисахарида с большой молекулярной
массой, для которого время смешивания с водой очень велико по
сравнению с продолжительностью эксперимента (коэффициент
диффузии £)=10~5 см2/с). Ячейка заполнялась полимерным
раствором, а вода принудительно инжектировалась в ячейку
либо через небольшое отверстие в середине одного из коротких
торцов (в линейном эксперименте, см. рис. 1,а), либо в центре
ячейки (в радиальном эксперименте, см. рис. 1,6).
Растущие структуры снимались телевизионной камерой [6].
Сигналы передавались на систему, преобразовывавшую их в
цифровую форму и записывавшую отснятые структуры на
решетке 256X256. В цифровой форме структуры подавались на
вход компьютера VAX 11/785 для дальнейшего анализа. Схема
экспериментальной установки приведена на рис. 3.
3. Результаты экспериментов и анализ
3.1. Определение фрактальной размерности
На рис. 4 и 5 показаны два типичных результата,
получаемых при вытеснении водой раствора полимера с большой
молекулярной массой. На рис. 3 вы видите снимок линейной ячейки
Хеле — Шоу длиной 1 м и высотой 10 см. На рис. 5 вязкие
пальцы получены в радиальной ячейке Хеле — Шоу. Зазор между
пластинами в обоих случаях составляет 0,5 мм. Количественный
анализ вязких пальцев, представленных в цифровой форме,
производился несколькими методами.
1. Метод «ящика с песком» [17]. Вокруг каждого узла
решетки в пальцеобразной структуре мысленно строим квадрат-
Модели необратимого роста
271
ный ящик размером L X L, подсчитываем число N{L) точек
структуры внутри каждого ящика и усредняем по всем узлам
решетки, которые служат центрами ящиков. График двойного
Рис. 4.^ Типичные вязкие пальцы, образующиеся при распространении воды
в линейной ячейке Хеле — Шоу, заполненной раствором полимера (склеро-
глюкана).
логарифма от N(L) как функции от L имеет угловой
коэффициент, равный df.
2. Корреляционная функция плотность — плотность
[18].Вокруг каждой точки структуры, как вокруг центра, проводим
окружность радиуса R. Подсчитываем число точек пальцеобразной
Рис. 5. Типичные вязкие пальцы, образующиеся при распространении воды в
радиальной ячейке Хеле — Шоу, заполненной раствором полимера (склеро-
глюкана).
структуры, лежащих на окружности. Это число, деленное на
общее число точек жидкости в кластере, зависит от радиуса R как
R f , где d — евклидова размерность.
3. Радиус гирации [19]. Берем несколько снимков, на
которых запечатлены последовательные стадии роста пальца. На
каждом снимке измеряем Rg и откладываем на графике как
функцию массы пальца. Угловой коэффициент равен l/df.
272
Часть V(a)
Для пальцеобразной структуры на рис. 4
—г h
!
I
1000
Число точек
$ too У
I
§ 10 (=-
0,? / 70 /00
Яидыус
Рис. 6. Определение фрактальной
размерности: а — метод
корреляционной функции плотность —
плотность (угловой коэффициент
1,70); б — метод радиуса гирации
(начальный угловой коэффициент
1,6); в — метод «ящика с песком»
(угловой коэффициент 1,70).
нами получена
оценка df = 1,4 ± 0,4, однако это
значение сильно зависит от
высоты модели [1]. При увеличении
высоты модели фрактальная
размерность возрастает. Ясно, что
верхняя и нижняя границы
ячейки ограничивают рост
неустойчивости. Проведенные нами
параллельно численные исследования
показали, что с увеличением
высоты ячейки фрактальная
размерность df, по-видимому,
стремится к величине df = l,7,
получаемой в модели, ограниченной
диффузией кластеризации
(ОДК). Чтобы получить
фрактальную размерность без
ограничительного влияния границ, мы
сконструировали другую ячейку
Хеле — Шоу с радиальной
геометрией. На рис. 5 показана
типичная структура, получаемая в
такой ячейке диаметром 1м [3].
Используя три перечисленных
выше метода, мы получили [3]
для фрактальной размерности
вязких пальцев в радиальной
геометрии (рис. 6, а —в) оценку
df= 1,70 ±0,05.
Как показали более ранние
[1] и последние [2, 3]
эксперименты, это значение df не
зависит от скорости течения (в
исследованном диапазоне скоростей
0,4—40 мл/мин) и концентрации
полимера (в исследованном
диапазоне концентраций 2,4—12г/л).
Полученное значение df
воспроизводилось для различных
типов полимеров (эксперименты
проводились с склероглюканом,
производным гуарового каучука
Кроме того, фрактальные струк-
и гидроксиэтилцеллюлозой).
туры с аналогичными размерностями df были получены в ла
Модели необратимого роста
273
тексе, представляющем собой
суспензию полимерных
шариков (диаметром 0,1 мкм) в
воде.
3.2. Как растут вязкие пальцы?
Чтобы выяснить, где
именно происходит рост за
конечный промежуток времени, мы
взяли два последовательных
снимка растущих вязких
пальцев (с интервалом времени в
1 с). «Вычитая» более ранний
снимок из более позднего
(рис. 7, а), мы получаем
«точки роста» кластера. Рис. 7, б
качественно напоминает
эквивалентные структуры больших
кластеров, возникающих в
модели ДО А [19]. В обоих
случаях точки роста структур
располагаются на выступах и
почти никогда — в «фиордах».
Обращает на себя внимание,
что в столь различных
физических механизмах, как
кластеризация и образование вязких
пальцев, процесс роста почти
неотличим. Сходство обоих
механизмов подтверждается и
количественно: произведя
корреляционный анализ плотности,
Микин обнаружил, что
угловой коэффициент равен —1,1.
Нами для сравнительно
небольших кластеров в вязких
пальцах получено значение
—1,3 ±0,1 [3]. Вязкие пальцы
растут путем
последовательного нерегулярного дробления
*
,«,
к
t
4и
€
и
*
Э
Л
Fiiii"
Рис. 7. Представленная в цифровой
форме «область роста» типичной
структуры вязких пальцев в
радиальной ячейке Хеле — Шоу (а),
полученная путем вычитания из одного
снимка другого, снятого с
небольшим упреждением по времени.
Концентрация «точек роста» (б) на
концах пальцев убедительно
свидетельствует о наличии сильного
экранирования.
концов ведущих пальцев. Такой
механизм отличен от роста кристаллов, в котором у дендритов
часто наблюдаются устойчивые концы с нерегулярными
боковыми ветвлениями [211,
274
Часть V(a)
3.3. Как ширина пальцев зависит от величины зазора между пластинами?
Мы уже упоминали о том, что в процессе роста ширина
пальцев, по нашим наблюдениям, оставалась вполне определенной,
т. е. постоянной. В качестве первого шага к пониманию этого
явления мы исследовали, как ширина пальцев зависит от
величины зазора Ь между пластинами. В теории Чуоке и др.
критической ширины пальца для несмешивающихся жидкостей
толщина пальцев линейно зависит от величины зазора между
пластинами (см. соотношение (3)). Патерсон недавно предложил
теорию для смешивающихся
жидкостей. По его мнению, за
то, что способностью расти
обладают длины волн,
превышающие определенное
пороговое значение, отвечает
механизм вязкой диссипации.
Патерсон также обнаружил
линейную зависимость толщины
пальцев от величины зазора
между пластинами. Однако его
теория предсказывает, что
толщина пальцев не зависит от
скорости течения.
На рис. 8 представлены
результаты, полученные нами
при различной величине
зазора между пластинами. В
пределах точности эксперимента
мы обнаружили линейную
зависимость. Полученное значение углового коэффициента равно
4,6, что очень близко к значению, предложенномуПатерсоном
для ньютоновских жидкостей. Столь точное совпадение угловых
коэффициентов и то, что в наших экспериментах толщина
вязких пальцев не зависит от скорости течения, свидетельствуют
в пользу теории Патерсона. Однако механизм диссипации в
растворах полимеров отличается от механизма диссипации в
ньютоновских жидкостях.
4, Стохастическое моделирование
4.1. ДОА как модель РВП
Как уже упоминалось, между радиальными вязкими
пальцами (РВП) и ДОА наблюдается количественное согласие в
фрактальной размерности и качественное согласие в распреде-
0 0,2 Q4 0,6 0,8 1,0 7,2 7,4
Зазор между пластинами., мм
Рис. 8. Зависимость ширины пальцев
(«критической длины волны») от
величины зазора Ъ между пластинами
в ячейке Хеле — Шоу для
ньютоновской жидкости склероглюкана
(показатель затухания сдвига п' = 0,15).
Модели необратимого роста
275
лении точек роста. Кроме того, чисто внешнее сравнение «на
глаз» вязких пальцев, изображенных на рис. 5, и кластеров ДОА
(рис. 9)' обнаруживает дополнительные общие особенности
роста:
1) главные ветви расходятся из центра, как спицы в колесе,
и образуют скелет структуры;
Рис. 9. Типичный кластер из 10 000 точек в модели ДОА.
2) по мере роста структуры концы некоторых из главных
ветвей разделяются на две главные ветви;
3) на всех главных ветвях растут боковые ветви, концы
которых также делятся;
4) угол, под которым отходят боковые ветви, гораздо
меньше 90°.
Помимо отмеченного выше поразительного сходства между
РВП и кластерами в модели ДОА нетрудно усмотреть и
определенные различия:
1) у фрактальных пальцев главные ветви более прямые, чем
у кластеров;
2) ветви, на которые расщепляется конец пальца, расходятся
под меньшим углом, чем ветви в кластере;
3) «спицы» кластера в модели ДОА покрыты более густой
«листвой», чем сравнительно голые главные ветви РВП.
Почему РВП так похожи по своей структуре на кластеры,
возникающие в модели ДОА? Можем ли мы объяснить
различия между пальцами и кластерами?
Можно показать [18, 20], что в модели ДОА вероятность
<£(г, /) оказаться при случайном блуждании в момент времени /
в точке г удовлетворяет уравнению Лапласа
V2^ = 0.
(4)
276
Часть V(a)
Скорость роста и кластера пропорциональна локальному
градиенту вероятности между точкой кластера и соседней точкой:
u ~ Уф. (5)
Течение двух ньютоновских жидкостей в ячейке Хеле — Шоу
описывается аналогичными уравнениями. Если предположить,
что одна жидкость значительно более вязкая, чем другая, то
потенциал или давление менее вязкой жидкости можно считать
постоянными [9]. Нормальная скорость граничной поверхности
между жидкостями равна в этом случае локальному градиенту
давления:
ид = —n- VP. (6)
Учитывая условие несжимаемости ?а = 0, получаем уравнение
Лапласа для поля давления:
V2P = 0. (7)
Соотношение (6) отличается от соотношения (5), поскольку
представляет предел среднего поля (ПСП) соотношения (5).
Тан [11] показал, что ПСП обращенной во времени ДОА
порождает устойчивые пальцы Саффмена — Тейлора, которые,
однако, не являются фракталами. Подобно поверхностному
натяжению ПСП приводит к сглаживанию профиля роста. Однако
поверхностное натяжение отнюдь не обязательно предотвращает
фрактальный рост, хотя и вводит масштаб длины, ниже
которого рост заведомо не имеет фрактального характера. Для того
чтобы мы могли наблюдать фрактальный рост при наличии
поверхностного натяжения на границе между двумя жидкостями,
размеры экспериментального устройства должны во много раз
превосходить критическую длину волны роста. Удовлетворить
этому требованию практически для многих систем двух
жидкостей весьма трудно. В нашей системе поверхностное натяжение
на границе между двумя жидкостями априори отсутствует, так
как выбранные нами две жидкости смешиваются. Существование
вполне определенной толщины пальца, возможно, объясняется
некоторым остаточным натяжением границы между жидкостями
или какими-то другими еще не понятыми физическими
явлениями. Сходные особенности, отличающие РВП и ДОА,
свидетельствуют о том, что в пределе, когда характерный размер
вязкого пальца много меньше характерного размера
экспериментальной установки, рост вязких пальцев следует
соотношению (5).
До сих пор наше внимание было сосредоточено только на
ньютоновских жидкостях. Следующий вопрос, который мы хотим
поставить, можно сформулировать так: как изменяются при
переходе к ньютоновским жидкостям соотношения (6) и (7)? В на-
Модели необратимого роста
277
ших экспериментах использовались неньютоновские жидкости с
затухающим сдвигом, в которых вязкость \л убывает с
увеличением скорости сдвига у (у= —dv/dz, где z— ось координат,
нормальная к стеклянным пластинам). В исследованном диапазоне
скоростей течения логарифмическое соотношение между
скоростью сдвига и вязкостью линейно. Такие жидкости часто
называются жидкостями со степенным законом из-за соотношения
V = c'yn'-\ (8)
где с' и п' — постоянные, характерные для данного раствора
полимера [22]. Показатель затухания сдвига п' для жидкостей в
наших опытах был заключен в диапазоне от 0,4 до 0,1.
Соотношение (8) позволяет записать уравнения (6) и (7) в виде
Ma = -n.(|VPr-IVP)f . (9)
V(|VPr"1VP) = 0, (10)
где m = \jn!. Неясно, каким образом уравнения (9) и (10)
можно представить в модели случайных блужданий. Кроме того,
если мы предполагаем, что отношение вязкостей наших
жидкостей конечно, то необходимо учитывать градиент давления в
менее вязкой жидкости. В модель ДОА также требуется внести
некоторые существенные изменения.
Модель ДОА обладает еще и чисто феноменологическим
недостатком: рост кластеров в ней происходит путем агрегации, в
то время как рост РВП начинается из центра структуры.
Аналогичная морфология фрактального роста наблюдалась недавно
в явлении пробоя диэлектриков Нимейером и соавт. [23].
Предложенная ими модель позволяет воспроизводить фрактальный
рост без использования случайных блужданий.
4.2. Модель управляемого градиентом роста (УГР)
Модель пробоя диэлектриков (МПД) представляет собой
альтернативный способ решения уравнений (4) и (5). Как и
модель ДОА, она исходит из предположения о том, что в * менее
вязкой жидкости градиент давления равен нулю. Первый шаг
состоит в нахождении численного решения уравнения Лапласа
для более вязкой жидкости. Эта задача решается с помощью
конечно-разностного дискретного аналога уравнения (4) с
граничными условиями Дирихле. Приняв за исходное
аналитическое решение при t = 0, мы шаг за шагом решаем уравнение
(4) методом итераций.
Второй шаг состоит в обращении к уравнению (5). После
того как известно распределение поля давления между
поверхностью раздела жидкостей и границей, мы вычисляем
локальные градиенты давления между любой потенциальной точкой
278
Часть V(a)
роста и соседней точкой. Новая точка выбирается произвольно,
пропорционально локальному градиенту. Затем решается
конечно-разностный аналог уравнения (4), и цикл завершается.
Получаемые в результате структуры имеют фрактальную
размерность, несколько большую, чем в модели ДОА. Прямое
сравнение машинного времени показывает, что в модели ДОА
кластеры растут значительно быстрее, чем в МПД. Однако МПД
обладает тем большим преимуществом, что легко обобщается на
более сложные системы [23]. Один из интересных вопросов
состоит в том, как влияет на рост конечное отношение вязкостей.
Ясно, что профиль границы жидкости с большей вязкостью,
вытесняющей жидкость с малой вязкостью, устойчив.
Следовательно, переход от фрактального роста к нефрактальному росту
должен происходить как функция отношения вязкостей. Чтобы
проследить этот переход, Шервуд и Нитман [24], обобщив МПД,
построили обобщенную модель управляемого градиентом роста
(ОУГР). На рис. 10, а — г показаны полученные с помощью
численного моделирования радиальные неустойчивые структуры
при отношениях вязкостей г) =0,0001; 0,01; 0,1; 10 (г) —
отношение вязкости вытесняющей жидкости к вязкости вытесняемой
жидкости). Мы наблюдаем переход к фрактальной размерности
как функцию отношения вязкостей. Мы обнаружили, что при
rj = 0,0001 фрактальная размерность df = 1,90 ± 0,05. При ц =
= 0,01 структура не является фракталом. Переход произошел
вследствие того, что давление в жидкости с малой вязкостью не
является более постоянным, а имеет угловой коэффициент того
же знака, что и жидкость с большой вязкостью. Вследствие этого
у точек, расположенных в «фиордах» структуры, повышается
вероятность роста.
Нам хотелось бы вернуться к проблеме более точного
представления неньютоновских свойств вытесняемой жидкости.
Уравнения (4) и (5) обладают перед уравнениями (9) и (10)
существенным преимуществом, ибо они линейны. Неньютоновский
характер придает уравнению (9) сильную нелинейность, и как его
решать, пока не известно. Однако изучение аналитического
решения уравнений (9) и (10) для системы при / = 0 позволяет
сделать кое-какие выводы о процессе роста. Действительно,
решение уравнений (9) и (10) имеет вид
n(m-l)/m __ r(m-l)/m
R{m_l)fm_{ при пгф\9 (И)
Р(г)-
1 —-fnT при m=1 (12)
с граничными условиями Р == 1 при г = 1 и Р = 0 при г = R.
Случай m = 1 соответствует ньютоновским жидкостям (модель
100,0-
-100,0-
-к
100,0
-WqO-75fQ-50,0-Z5jO 0 25,0 50,0 75,0100,0
a
4QO,0-7$,0-50P-Z5p 0 Z5,0 50ft 75,0 100,0
6
-Wfl-75,0-50,0-Z5p 0 25ft 50ft 75,0100,0
100,0
-100,0
-100ft-75ft'50fl-Z5,Q 0 Z5ft 50ft 75,0100,0
г
Рис. 10. Типичные структуры, возникающие в модели управляемого
градиентом роста. Компактность структуры определяется отношением вязкостей х\\
а) 1-| = 0,0001, df — 1,90 ± 0,05; б) 11 = 0,01, структура нефрактальная;
а) г] = 0,1; г) устойчивый случай — жидкость с большой вязкостью
вытесняет жидкость с малой вязкостью, у\ = 10.
0,8
0,6
ъ>
%
■Ч 0,2
О
Н N^V m = 5
\. /77 = 5 ^""■"-—««^^^ ^^^^
^Гг- 1- 1 ' Г^^^.1
0,2
0,8
W
О,* 0,6
Радиус (r/R)
Рис. 11. Зависимость поля давления Р(г) от г (расстояния от центра
радиальной ячейки Хеле —Шоу). Построено несколько кривых при различных
значениях параметра т = \1п\ Рассмотренные ранее ньютоновские жидкости
соответствуют случаю т = 1. В нашич экспериментах жидкости с большой
вязкостью имели пг в диапазоне от 0,1 до 0,4, поэтому т < 1,
280
Часть V(a)
ДОА и МПД). При т = 1 скорость в начале роста
пропорциональна 1//\ Интересно отметить, что неньютоновские жидкости
следуют тому же закону роста 1/г. Рассмотрим случай m > 1
(аналогичные рассуждения применимы и при /л < 1). Хотя и
из-за уравнения (9) становится функцией m-й степени давления,
что указывает на более сильный рост на концах, где градиенты
обычно велики, распределение давления становится более
плоским из-за уравнения (10). Чтобы показать это, мы построили
графики зависимости полей давления от радиуса при m = 0,5;
1; 3 и 5 (рис. 11). Тем самым мы полагаем, что неустойчивые
структуры, получающиеся при использовании неньютоновских
жидкостей, не должны особенно отличаться от структур,
возникающих в ньютоновских жидкостях. Правильность нашего
предположения можно проверить только путем численного
решения уравнений (9) и (10).
5. Выводы
Наши эксперименты показали, какие поразительные
фрактальные структуры, могут возникать в ламинарном течении
жидкости. Имеющиеся у нас данные позволяют утверждать, что эти
структуры обусловлены преобладанием рандомизирующих
процессов над стабилизирующими силами. Флуктуации на
граничной поверхности между двумя смешивающимися жидкостями
могут расти хаотически, не испытывая на себе ограничивающего
влияния сглаживающих поверхностных сил. Рост управляется
глобальным полем давления, и конкуренция между ростом
соседних элементов граничной поверхности между двумя
жидкостями пропорциональна локальному градиенту давления.
Фрактальные пальцы наблюдались и в случае неустойчивого
вытеснения одной жидкости другой жидкостью в пористых
средах. Ленорман и Зарконе [25], а недавно Чен и Уилкинсон [26]
обнаружили пальцеобразование типа ДОА в моделях
двумерных пористых сред в тех случаях, когда вязкие силы
доминируют над капиллярными силами. Чен и Уилкинсон высказали
предположение о том, что фрактальность поведения
наблюдавшихся ими структур обусловлена случайностью распределения
размеров пор. Для проверки своей гипотезы они провели
исследования на моделях с более узкими распределениями размеров
пор и обнаружили в пределе только одного размера высокоупоря-
доченную структуру. В частности, рис. 1, а и 2, а из их работы
напоминают наш рис. 12, полученный путем введения
анизотропии и поверхностного сглаживания в модель управляемого
градиентом роста. Цель, которую мы при этом преследовали,
состояла в моделировании роста вязких пальцев в условиях
пространственной анизотропии. Ленорман [6] и Бен-Жакоб с соавт,
Модели необратимого роста
2Ы
[7] недавно, протравливая каналы в одной из пластинок,
получили в ячейке Хеле — Шоу структуры, напоминающие по виду
снежинки. Структура на рис.
12, хотя на первый взгляд
и кажется высокоупорядо-
ченной, имеет фрактальную
размерность df « 1,64.
Работа по анализу и
осмыслению экспериментальных
данных продолжается.
Самые последние
новости позволяют надеяться на
то, что открытые нами
фрактальные вязкие пальцы —
не более чем верхушка
айсберга, ниже которой лежит
новое понимание роста и
форм случайных и
упорядоченных структур.
Благодарности. Мы
хотели бы поблагодарить наших
коллег из Etudes et
Fabrication Dowell Schlumberger
P. Ленормана, Ф. Ронделе,
Дж. Шервуда, Э. Тубула и д-ра Р. Гаскелла (Лидский
университет) за ценные обсуждения и М. Бурлион за техническую
помощь.
ЛИТЕРАТУРА
1. Niitmann /., Daccord G., Stanley Я. £., Nature, 314, 141 (1985).
2. Daccord G., Niitmann /., Stanley H. E.t in: On Growth and Form, eds.
H. E. Stanley, N. Ostrowsky, Martinus Nijhoft Pub., Dordrecht, 1985,
p. 175.
3. Daccord G., Nittmann /., Stanley E. #., Phys. Rev. Lett., в печати.
4. Maker /., Phys. Rev. Lett., 54, 1498 (1985).
Maxworthy Т., preprint.
5. Parks C. W.f Homsy G. M, Phys. Fluids, 28, 1583 (1985).
6. Lenormand R., частное сообщение.
7. Ben Jacob £., Godbey R., Goldenfeld N. D., Koplik /., Levine #.,
Mueller Г., Sander L. M., Phys. Rev. Lett., 55, 1315 (1985).
8. Paterson L., Phys. Rev. Lett., 52, 1621 (1984).
9. Paterson L., Phys. Fluids, 28, 26 (1985).
10. Kadanoff L. P., J. Stat. Phys, 39, 267 (1985).
11. Tang C, Phys. Rev., A31, 1977 (1985).
Liang S., preprint.
12. Bensimon D., preprint.
13. Ti/gravson G, Aref tf, J. Fluid Mech., 154, 287 (1985).
DeGregoria A. /., Schwartz L. W., preprint.
100,0-
, . н 1 г"" ' '*» i г
400,0-75,0-50,0-25,0 О 25,0 50,0 75,0 700,0
Рис. 12. Моделирование образования
вязких пальцев в ячейке Хеле — Шоу с
протравленной пластиной. Введение
пространственной анизотропии и
поверхностного сглаживания превратило
первоначально неупорядоченную
структуру типа ДОА в сильно упорядоченную
структуру с осью 4-го порядка.
282
Часть V(a)
14. Kessler D. Л., Levine #., preprint.
15. Saffmann P. G.y Taylor G. /., Proc. Roy. Soc, A245, 312 (1958).
16. Chuoke R. JL, Van Meurs P., Van der Poet C. /., J. Petrol. Tech., 11, 64
(1959).
17. Forrest L.t Witten T. A, J. Phys., A12, L109 (1979).
18. Witten Г. A., Sander L. M, Phys. Rev. Lett., 47, 1499 (1981).
19. Meakin P., Stanley H. E.f Coniglio A., Witten Т., Phys. Rev., A32, 2364
(1985).
Meakin P., in: On Growth and Form, eds. H. E. Stanley, N. Ostrowsky,
Martinus Nijhoff Pub., Dordrecht, 1985, p. 81.
20. Witten T. A.f Sander L, M.y Phys. Rev., B27, 5685 (1983).
21. Honjo #., Ohta S., Sawada Y., Phys. Rev. Lett., 55, 841 (1985).
22. Bird R. В., Armstrong R. C, Haffager D.> in: Dynamics of Polymeric
Liquids, vol. 1, Wiley, 1977.
23. Niemeyer L., Pietronero L., Wiesmann #., Phys. Rev. Lett., 52, 1033
(1984).
24. Sherwood J. D.t Nittmann /., J. Physique, 47 (1986).
25. Lenormand R., Zarcone C, Phys. Chem. Hydro., 6, 497 (1985).
26. Chen /.-D., Wilkinson D.t preprint.
Часть V (б)
МОДЕЛИ НЕОБРАТИМОГО РОСТА:
ОГРАНИЧЕННАЯ ДИФФУЗИЕЙ
АГРЕГАЦИЯ, РОСТ ДЕНДРИТОВ,
МОДЕЛЬ ИДЕНА И КЛАСТЕР-
КЛАСТЕРНАЯ АГРЕГАЦИЯ
Некоторые последние достижения
в моделировании ограниченной
диффузией агрегации
и родственных процессов
П. Микин *
На различных решетках с помощью усовершенствованных
алгоритмов в модели диффузионно-ограниченной агрегации (ДОА)
получено большое число (сотни) крупных (состоящих из ~ 105
точек, или частиц) двумерных кластеров. В случае квадратной
решетки наши результаты согласуются с теоретическими
результатами Туркевича и Шера (D = 5/3). В случае гексагональной и
треугольной решеток результаты численного моделирования
расходятся с теорией указанных авторов, но это несогласие можно
объяснить в терминах понятий, содержащихся в их теории.
Наши результаты приводят к предположению о том, что
фрактальная размерность моделей ДОА с высокой симметрией
принадлежит к тому же классу универсальности, что и внерешеточная
ДОА, но что модели с низкой симметрией не универсальны.
Исследованы эффекты анизотропии присоединения и диффузионной
анизотропии, а также анизотропии решетки.
1. Введение
В последние годы наблюдается резкое возрастание
интереса к неравновесному росту и процессам агрегации. В
частности, интенсивно исследовались модели, приводящие к
образованию фрактальных структур [1]. Значительная часть этой
работы была стимулирована моделью Виттена — Сандера [2]
ДОА, которая и поныне остается наиболее важной моделью при
исследовании неравновесного роста и процессов агрегации.
Первоначально энтузиазм, с которым была встречена модель
Виттена—Сандера, был вызван главным образом интересными
свойствами масштабной инвариантности и универсальности [3, 4],
* Paul Meakin-Central Research and Development Department, E. I. du
Pont de Nemours and Company, Experimental Station, Welmington, Delaware
19898,
284
Часть V(6)
которыми обладали порождаемые этой моделью структуры.
Впоследствии интерес еще более возрос, когда обнаружилось,
что модель ДОА и родственные модели применимы к
электролитическому осаждению [5, 6], морфологии тонких пленок [7],
процессам вытеснения одной жидкости другой [8—10], пробою
диэлектриков [11], росту- дендритов [12—14] и другим
явлениям. Были предложены различные теоретические подходы
[15—17]. Хотя все эти теории дают результаты, находящиеся в
хорошем согласии с численным моделированием, если говорить
о зависимости фрактальной размерности D от евклидовой
размерности d решетки или пространств вложения, эти результаты
трудновычислимы и не могут быть легко распространены на
другие модели аналогичного типа.
Недавно Туркевич и Шер [19, 20] разработали новый
теоретический подход, основанный на идеях, согласно которым
фрактальная размерность определяется порядками особенностей
вероятностей заполнения узлов решетки в процессе роста в модели
ОДК, а эти порядки в свою очередь определяются структурой
решетки, используемой при численном моделировании.
Аналогичные идеи высказывали также Болл и др. [21] и Холси и др.
[22]. В отличие от ранее существовавших теорий метод Турке-
вида и Шера может быть легко обобщен на другие модели того
же типа и позволяет делать конкретные предсказания, которые
допускают проверку с помощью численного моделирования.
Наиболее поразительное предсказание модели Туркевича— Шера,
по:видимому, состоит в том, что фрактальная размерность D
неуниверсальна в том смысле, что зависит не только от
размерности решетки, используемой при численном моделировании, но и
от структуры решетки. В частности, Туркевич и Шер
предсказывают, что фрактальная размерность должна быть равна 5/3 для
двумерной квадратной решетки и 7/4 для двумерной
гексагональной и треугольной /«пчелиные сотьЫ решеток. Одна из ос-
новых целей излагаемой ниже работы состоит в проверке этих
предположений.
Для того чтобы мы могли отличить предсказанные (Ьракталь-
ные размерности 1.Р67 и 1,750 от фрактальной пязмерт-юсти
1,715 ±0,002 [23], получаемой путем крупномасштабного
моделирования, для снижения статистических иеоппеделенногтей и
выхода на асимптотический предел (большую массу кластера)
необходимо генерировать большое число Гсотни) кпупньтх
(состоящих из ~ 105 частиц, или точек) кластеров.
2. Модели
В модели ДОА Виттена — Сандера частицы (часто
изображаемые занятыми узлами решетки) присоединяются к
растущему кластеру или агрегату частиц по одной через траектории слу-
Модели необратимого роста
285
чайного (броуновского) блуждания. Траектории частиц
начинаются вне области, занятой кластером, и заканчиваются, когда
частица приходит в соприкосновение с кластером и кластер
вырастает на одну частицу.
Недавно были описаны эффективные алгоритмы,
позволяющие моделировать двумерные внерешеточные и полурешеточные
агрегаты в модели ДОА [24]. В этих алгоритмах подвижная
частица совершает случайное блуждание не по ребрам решетки и
может перемещаться сразу на большое расстояние, когда
находится далеко от любого занятого узла, или частицы, кластера.
В такой внерешеточной модели агрегация происходит, когда
траектория вынуждает частицу войти в соприкосновение с
частицей, уже принадлежащей растущему кластеру. В
полурешеточной модели растущий кластер состоит из занятых узлов
решетки, а его рост происходит, когда частица (нулевого
диаметра) попадает в вакантный узел, ближайший сосед которого
занят, т. е. принадлежит кластеру. Ни на одной стадии в ходе
моделирования блуждающая частица не может оказаться в уже
занятом узле решетки. В связи с работой, излагаемой в
настоящем сообщении, были разработаны два новых алгоритма. В
одном из чих подвижная частица переносится в ближайший узел
решетки, после чего совершает случайное блуждание по ребрам
решетки, если оказывается на заданном расстоянии хотя бы от
одного занятого узла (обычно на расстоянии 6—7 постоянных
решетки). Рост происходит в том случае, когда блуждающая
частица попадает в свободный узел с занятым ближайшим
соседом. Таким образом, в окрестности кластера эта модель
действует так же, как обычная решеточная модель ДОА [2, 3]. На
больших расстояниях от кластера частица совершает внереше-
точное случайное блуждание. Величина шага возрастает по мере
увеличения расстояния от кластера, но остается недостаточно
большой для того, чтобы частица могла проникать более чем на
одну постоянную решетки внутрь области, в которой случайное
блуждание происходит по ребрам решетки. Поскольку такая
модель должна давать результаты, неотличимые от результатов,
получаемых в рамках модели с случайными блужданиями,
происходящими только по ребрам решетки, она называется
решеточной моделью ДОА. Схематически эта модель изображена на
рис. 1.
По второму алгоритму моделирование пповолится так же,
как в случае внерешеточного моделирования [241. Но после
присоединения к кластеру частица движется по окружности с
центром в центре мясе той частины, с которой она «пришпа в
соприкосновение», по тех пор, пока не займет ближайший к той
свободный узел решетки. Дня случая квадратной решетки эта
модель изображена на рис, 2. Такую модель мы назвали вторым
286
Часть V(6)
вариантом полурешеточной модели, чтобы отличить ее от более
ранней полурешеточной модели, которую уместно назвать первым
Рис. 1. Решеточная модель ДО А. Показана возможная траектория на ранней
стадии моделирования. Вблизи кластера движение подвижной частицы
переходит в случайное блуждание по ребрам решетки.
вариантом [24]. Обе описанные выше модели были реализованы
для квадратной решетки, трехкоординатнои, или треугольной
Рис. 2. Второй вариант полурешеточной модели на квадратной решетке.
Штриховая окружность указывает положение, в котором подвижная частица
первоначально присоединилась к кластеру. Затем эта частица начала
двигаться по окружности вокруг центра той частицы, с которой она пришла в
соприкосновение, и продолжала движение до тех пор, пока не оказалась в
ближайшем к той не занятом узле решетки (сплошная окружность).
решетки («пчелиные соты») и шестикоординатной, или
шестиугольной (гексагональной), решетки.
3. Результаты
На рис. 3 представлены некоторые из результатов анализа
более 300 кластеров, порожденных с помощью двумерной
решетчатой модели (см. выше), и примерно такого же количества
кластеров первого варианта полурешеточной модели [24] для
квадратной решетки. Каждый из кластеров содержит 80 000
занятых узлов решетки. Фрактальная размерность D$ оценивается
по зависимости радиуса гирации от числа занятых узлов решет-
Модели необратимого роста
287
ки Л/, или массы кластеров. Результаты разделены на
«контейнеры»: в 8-й контейнер попадают кластеры, содержащие от
40 000 до 50 000 (т. е. от N(max)/2 до ЛГ(тах)) узлов, в 7-й
контейнер попадают кластеры, содержащие от 20 000 до 40 000
(т. е. от i\f(max)/4 до ЛГ(тах)/2) узлов, в 6-й контейнер
попадают кластеры, содержащие от 10 000 до 20 000 узлов, и т. д.,
Квадратная решетка
• Полуреилеточная модель (363) ° Решеточная модель (327)
(80000) (8000Q)
Р^/З ■■»''»■!
\ | \\ \i]'
р=7А
— i L i i i i i iZJ
/ г 3 4 5 6 7 8
Номер контейнера
Рис. 3. Зависимость показателя радиуса гирации Р от массы кластера,
полученная из численных экспериментов в рамках решеточной модели и первого
варианта полурешеточной модели на квадратной решетке. Здесь и далеее
(на рис. 4, 5, 7 и 10) приведены данные о числе кластеров (363 для
полурешеточной и 327 для решеточной модели) и их размерах (80 000 занятых
узлов решетки). Горизонтальные линии указывают значения показателя
радиуса гирации, предсказанные Туркевичем и Шером [16] для квадратной
(£>р=5/3, Р = 0,6) и гексагональной (Dp = 7/4, р = 0,5714) решеток.
Коридор ошибок на рис. 3—5, 7 и 10 соответствует 95 %-ному доверительному
интервалу.
где /V(max) —число занятых узлов решетки при максимальных
размерах кластера. Эффективная фрактальная размерность /)р
[25] определялась для кластеров в каждом контейнере путем
подгонки методом наименьших квадратов прямых к зависимости
\n(Rg) oTln(tf).
На рис. 3 показаны значения показателя р, полученные в
предположении, что
Rg~№. (1)
Эффективная фрактальная размерность D$ равна 1/р. Значение
Р при малых массах кластера равно 0,585 (что очень близко к
значению р для кластеров всех размеров, вычисляемому в
рамках внерешеточной модели) [23, 26]. Однако при больших
значениях массы кластеров эффективное значение р возрастает, и
оМ
0,59\
Р
0,58 \
Треугольная решетка
» Попурешеточиал модель 0 рвШето¥нал модель (Щ
(второй вариантпК425) Г ,опппп\
(50000) (80000)
0,60
G,59 \
Р
0,58
0,57
DxS/j " i " "" i i i I ill
т
/7=1
0 т
<
1 •
i
> т
с
" Г
• i
[ и [i Р ^!
i i j i 1
8
2 3 4 5 6
Номер контейнера
Рис. 4. Зависимость показателя радиуса гирации р от возрастающей массы
кластера при численных экспериментах в модели ДОА на треугольной
решетке. Размеры кластеров, порождаемых полурешеточной и решеточной
моделями, в этом случае не равны.
Гексагональная решетки
• Полуреъиеточная модель о нешет'очная модель (865)
{второй, вариант)(Ш)
(50000)
3 4 5 6
Номер контейнера
Рис. 5. Нечувствительность показателя (3 и соответствующей эффективной
размерности D$ к размерам кластера при численных экспериментах на
гексагональной решетке в рамках решеточной и полурешеточной моделей ДОА.
Модели необратимого роста
289
наши результаты согласуются с предельным значением 0,6, со-
ртветствующим одному из предсказаний Туркевича и Шера
.(Я»=1/р = 5/3).
На рис. 4 представлены аналогичные результаты,
полученные при моделировании ограниченной диффузией
кластеризации на треугольной решетке (или на ребрах {связях) решетки
типа «пчелиные соты»). В этом случае показатель Ji почти не
зависит от размеров кластеров, используемых для его оценки. Не
существует никаких признаков того, что эффективная
фрактальная размерность (Dp = 1/f}) стремится к значению 7/4, как
предсказывают Туркевич и Шер. В действительности если
какая-то вариация фрактальной размерности от массы кластера и
существует, то D§ скорее убывает с увеличением массы
кластера.
На рис. 5 представлен аналогичный набор результатов,
полученных с использованием шестиугольной решетки. В этом
случае нет сколько-нибудь заметной зависимости р или D§ от
массы кластера, и численные значения показателя р и эффективной
фрактальной размерности D§ очень близки к тем, которые
получаются при внерешеточном моделировании. Эти результаты не
согласуются с предсказаниями Туркевича и Шера для
шестиугольной решетки (Z)p = 7/4).
4. Результаты, получаемые из других моделей
Для исследования того, как влияет анизотропия на
ограниченную диффузией кластеризацию, было предложено несколько
других моделей. На рис. 6 показана модификация
шестиугольной решеточной модели, в которой шаги при случайном
блуждании вблизи кластера разрешаются только в 3 из 6 возможных
направлениях. Такая модель порождает кластеры, имеющие
«треугольную» форму. На рис. 7 показано, как в этой модели
показатель радиуса гирации р зависит от массы кластера.
Совершенно отчетливо видно, что в этом случае с увеличением
массы кластера показатель р возрастает и что предельное
значение р при N-+- оо превышает 0,6 (т. е. Dp < 5/3).
Были проведены также численные эксперименты на
шестиугольной решетке, в которой присоединение подвижной частицы
разрешается только по 3 из 6 возможных направлений. Эта
модель изображена на рис. 8. На рис. 9 показан случайно
выбранный кластер, полученный с помощью такой модели.
Аналогичные численные эксперименты были проведены и в рамках
полурешеточной модели, в которой подвижные частицы, придя в
соприкосновение с частицами кластера, описывают вокруг них
дуги окружностей с тем, чтобы связи располагались только по
трем разрешенным направлениям. Соприкоснувшись с частицей
Рис. 6. Показана типичная траектория, приводящая к присоединению
частицы. Закрашенные шестиугольники принадлежат растущему кластеру, а
незакрашенный шестиугольник показывает, где в результате прохождения
траектории к кластеру присоединяется новый занятый узел. Вдали от кластера
случайное блуждание, вообще говоря, происходит не по ребрам решетки, и
шаги могут быть большими.
Гексагональная решетка с присоединением
по трем направлениям
Решеточная модель (204) 60000 узлов
0,60
0,59
0,58
П5Т
D=$5
Т
<
i
{D=7A
I
I
,
I j
<
i 1 1 1 :
j
»
<
>
*
>
<
\
i
>
J 1 L 1 1 1 J ..._. 1 ._ 1
/
в
г з 4 5 б :
Номер контейнера
Рис. 7. Значения показателя радиуса гирации р, полученные с помощью
модели ДОА на двумерной гексагональной решетке с случайным блужданием
только по трем направлениям.
Рис. 8. Начальная стадия моделирования ДОА на гексагональной решетке
с присоединением только по трем направлениям. Незанятые узлы на
периферии («поверхности») кластера, в которых может присоединяться подвижная
частица («точки роста»), отмечены черными кружками. Подвижная частица
может занимать также другие узлы на «поверхности» кластера, но при этом
присоединения к кластеру не происходит. Ни на какой стадии подвижная
частица не может попасть в занятые (закрашенные) узлы кластера.
1000 постоянных решетки
Рис. 9. Типичный кластер из 40 000 точек, возникающий в модели,
изображенной на рис. 8. (ДОА на гексагональной решетке с присоединением
подвижной частицы только по трем направлениям).
292
Часть V(6)
кластера, подвижная частица поворачивается вокруг ее центра
до тех пор, пока новая связь не окажется ориентированной
параллельно ближайшей из трех разрешенных осей,
расположенных под углом 120° друг к другу. Получаемые в этой модели
кластеры по внешнему виду очень напоминают кластеры,
возникающие в решеточной модели (рис. 9).
На рис. 10 показано, как показатель радиуса гирации (3
зависит от диапазона («контейнера») масс кластеров,
выбираемого для оценки его значения. С увеличением размера кластера
Рост только по трем направлениям
• iЧолурешеточная о Гексагональная
модель (5ZZ) решеточная лгос/ель (43 J)
0,66
0,65
0,64
0,63
C16Z
0,61
С, 60
0,59
0,58
Г ' "т"'~'"""т ' "■ ' ' ' 0L%|
tll'i
1
~
L... 1
I
т-i
\
—i
I
i
—i—•
4
—I
-1
if J*1
27=%
-j
, °-A
/2345678
fiojvrep контейнера
Рис. 10. Значения показателя радиуса гирации р, полученные с помощью
численных экспериментов в решеточной и полурешеточной моделях ДОА с
присоединением подвижной частицы только по трем направлениям.
показатель (3 быстро возрастает и может стремиться к
предельному значению 2/3. В этом случае внутренняя структура
кластеров не фракталоподобна, и интерпретировать показатель радиуса
гирации р в терминах фрактальной размерности Dp не уместно.
5. Обсуждение результатов
Одна из основных целей этой работы состоит в проверке
теоретических предсказаний Туркевича и Шера для ДОА на
двумерных решетках — квадратной, треугольной и шестиугольной.
Для двумерной квадратной решетки наши результаты
согласуются с предсказаниями Туркевича и Шера (D = 5/3), но для
других решеток мы получаем D —1,71 вместо 1,75. В рассмо-
Модели необратимого роста
293
тренных нами случаях статистические погрешности гораздо
меньше расхождения между теоретическим предсказанием и
результатами численного эксперимента, и нет никаких признаков,
говорящих о статистически значимом влиянии конечных
размеров. Несмотря на расхождение между теорией и данными чис-
сленного моделирования, полученные нами результаты могут
быть интерпретированы с помощью идей, содержащихся в
теории Туркевича и Шера. Согласно этой теории, рост кластера в
модели ДОА управляется областями наиболее быстрого роста
(выступами кластера). Таким образом, скорость роста
кластеров в модели ДОА (и их фрактальной размерности)
определяется порядком особенностей в распределении вероятностей роста,
связанных с этими выступами. Предполагается, что порядок
особенностей такой же, как у регулярного объекта, имеющего
форму решетки. Следовательно, порядок особенностей определяется
характерным углом ft решетки данной структуры (для
квадратной решетки ft = 90°, для гексагональной и треугольной
решеток [27] ft =120°). Согласно теории Туркевича и Шера,
фрактальная размерность определяется соотношением
/) = (3я —Ф)/(2я —О).
Чем выше порядок старшей особенности в распределении
вероятности (чем меньше угол ft), тем меньше фрактальная
размерность.
В случае внерешеточного моделирования фрактальная
размерность, составляющая примерно 1,71, может быть связана с
эффективным углом, равным примерно 108° [16, 19]
(внутренний угол правильного пятиугольника). Особенность в
распределении вероятности во внерешеточной модели ДОА имеет более
высокий порядок, чем вычисленная для модели ДОА на
шестиугольной и треугольной решетках (ft =120°). Следовательно,
неразумно ожидать, что кластеры в модели ДОА растут с
фрактальной размерностью 1,71 вместо 1,75, так как с полностью
случайной внерешеточной ДОА связаны особенности более вы-
ского порядка, чем с решеточной ДОА. Эта позволяет нам
прийти к выводу о том, что ДОА на решетках с высокой симметрией
(ft ^ 108°) порождает структуры, принадлежащие тому же
классу универсальности (имеющие tv же фрактальную
размерность), что и внерешеточная ДОА. Для решеток с низкой
симметрией фрактальная размерность зависит от структуры
решетки, и эти модели принадлежат другому классу универсальности,
чем внерешеточная ДОА.
Результаты, полученные путем введения в модель ДОА
других разновидностей анизотропии (см. выше), указывают на то,
что эти же выводы, по-видимому, могут быть распространены и
на те случаи. Для анизотропных вероятностей присоединения на
294
Часть V(6)
квадратной решетке Болл и др. [21] показали, что образуются
компактные иглообразные структуры, в которых рост по
«легким» направлениям характеризуется соотношением х ~ М2/3, а
по «трудным» направлениям — соотношением у ~ Nl/Z.
Теория Туркевича и Шера подкрепляется наблюдением,
состоящим в том, что в модели ДОА большие кластеры на
квадратной решетке имеют ромбовидную форму с характерным
углом 90° [24, 28]. Однако мы не знаем, устойчива ли эта форма
или переходит в «крестообразную», возможно, не обладающую
нефрактальной внутренней структурой. Приведенные выше
результаты для анизотропных вероятностей присоединения, а
также полученные Боллом и др. показывают, что такой переход
возможен. Возможно также, что убывание эффективного
значения фрактальной размерности Dp с увеличением размеров
кластера связано с искажением ромбовидной формы и что Dp
возвращается к своему значению, составляющему около 1,71, по
завершении этого процесса. Для того чтобы ответить на эти
вопросы, необходимы численные эксперименты в гораздо большем
объеме и гораздо более тщательный анализ.
Следует также отметить, что при малых размерах кластеров
эффективные значения фрактальной размерности D$ оказались
по существу равными для всех моделей, рассмотренных в
настоящей работе. Это обстоятельство объясняет, почему в ранних
работах с малыми кластерами [2, 4] не было обнаружено
никаких признаков иеуниверсальности в фрактальной размерности
ДОА.
ЛИТЕРАТУРА
1. Mandelbrot В. В, The Fractal Geometry of Nature, W. H. Freeman and
Company, San Francisco, 1982.
2. Witten t. A, Sander L. M, Phys. Rev. Lett., 47, 1400 (1981).
3. Meakln P., Phys. Rev, A27, 604 (1983); A27, 1495 (1983).
4 Witten T. A, Sander L. M., Phys. Rev., B27, 5686 (1983).
5. Brady R M., Ball R. C, Nature, 309, 225 (1984).
6 Matsushita M.y Sano M., Hayakawa Y., Honjo #., Sawada Y.y Phys. Rev.
Lett:, 53, 286 (1984).
7. Elam W. Г., Wolf S., Sprague 5. A., Gubser D. V., VanVechten Z)„
Barz G G., Jr., Meakln P., Phys. Rev. Lett., 54, 701 (1985).
8. Kadanoff L. P, preprint
9. Ntttmann /., Daccord G., Stanley H. E, Nature, 314, 141 (1985).
10. Tang C, Phys. Rev., A3!, 1977 (1985).
11. Nlemeyer L.y Pietronero L, Wiesmann А. Г., Phys Rev. Lett., 54, 1346
(1985).
12. Vicsek 7\, Phys. Rev. Lett., 53, 2281 (1984).
13. Szep Г., Cserti Г., Kertesz Г.,
14. Bern-Jacob £., Godbey R. B.} Mueller J E, Sander L M., Bull. Am. Phys
Soc, 30. 269 (1985).
15. Gould tf., Family F., Stanley H. £., Phys. Rev. Lett., 50, 686 (1983).
16 Muthukumar M.t Kawasaki K., Phys. Rev. Lett., 50, 839 (1983).
Модели необратимого роста
295
17. Tokuyama М, Kawasaki К., Phys. Lett., 100A, 337 (1984).
18. Hentschel H. G. E., Phys. Rev. Lett., 52, 212 (1984).
19. Turkevich L, Sher #., preprint.
20. Туркевич Л, Шер Г. — наст. сб. с. 310.
21. Ball R. С, Brady R. М„ Rossi G, Thompson В. R., preprint.
22. Halsey Т. С, Meakin P., Procaccia /., preprint.
23. Meakin P., in: On Growth and Form. Proc, 1985, Cargese NATO ASI,
eds. H. E. Stanley, N. Ostrowsky, Martinus Nijhoft, Amsterdam.
24. Meakin P., J. Phys, A18, L661 (1985).
25. Stanley H. E9 J. Phys, A10, L211 (1977).
26. Meakin P., Sander L. M, Phys. Rev. Lett, 54, 2053 (1985).
27. Хотя треугольная решетка обладает осями 3-го порядка, окружение
узлов решетки не эквивалентно и связано между собой поворотом на 180°.
Вследствие этого процессы роста на треугольной решетке происходят
так, как если бы решетка обладала осями симметрии 6-го, а не 3-го
порядка.
28. Brady R. M., Ball R. С, СЕСАМ Workshop, Orsay, 1984 (не
опубликовано).
Внутренняя анизотропия кластеров,
ограниченных диффузией
П. Микин, Г. Вичек *
Корреляции внутри слоя на расстоянии R от начала больших
кластеров, ограниченных диффузией, были исследованы путем
установления зависимости тангенциальной корреляционной функции
£я(д) от угла О. Мы обнаружили, что при О <С 1 функция cR($)
убывает как степень угла О с показателем а± = — 0,41 ± 0,04,
отличным от соответствующего показателя для радиальных
корреляций, что свидетельствует о внутренней анизотропии кластеров.
Последняя сказывается на результатах, полученных относительно
фрактальной размерности, в виде появления поправки к
масштабному члену.
1. Введение
Модель ДОА была введена Виттеном и Сандером [1]
как простая модель широкого класса процессов роста, в которой
скорость роста ограничивается диффузией и не допускается
перераспределение материала внутри кластеров. Кластеры в этой
модели представляют собой крупные случайным образом
разветвленные объекты с фрактальной размерностью D [2],
меньшей евклидовой размерности пространства, в котором
происходит кластеризация.
Фрактальная размерность является глобальным свойством
кластера и ничего не говорит о деталях его структуры. С
другой стороны, мы ожидаем, что ограниченный диффузией
механизм, посредством которого растут кластеры в модели ДОА,
оказывает весьма характерное воздействие на корреляции ветвей
и взаимосвязь между ними внутри большого кластера.
В настоящей работе мы исследуем внутреннюю структуру
ограниченных диффузией кластеров путем установления
корреляций Cr($) плотность — плотность на расстоянии R от начала
кластера как функции угла О с вершиной в начале кластера,
где Ф/? — расстояние между точками в слое.
2. Результаты относительно с R (Ф)
В проведенных нами численных экспериментах большие
(состоящие из 50 000—100 000 частиц) двумерные кластеры в
модели ДОА были порождены с помощью усовершенствованных
* Paul Meakin-Central Research and Development Department,
Experimental Station, E. I. du Pont de Nemours and Company, Wilmington, DE 19898,
USA; Tamds Vicsek-Department of Physics, Emory University, Atlanta, GA
30322, USA (постоянный адрес Research Institute for Technical Physics,
Budapest, Ujpest 1, Pf. 76, N-1325, Hungary).
Модели необратимого роста
297
алгоритмов [3]. Зная координаты частиц в кластере, состоящем
из N частиц, мы вычисляем тангенциальную корреляционную
функцию плотность—плотность Cr{®) в слое шириной Д# на
расстоянии R от начала кластера (рис. 1) по формуле
с* (*) = ЛМ £ рЛ (О + *') Р* (*'), 0)
О'
где ряС^) = й, если в «ящике» размером ARA® в точке (/?, *&)
находятся & частиц; в противном случае р*(Ф) =0. Суммирова-
Рис. 1. Центральная часть внерешеточного ограниченного диффузией
кластера. Тангенциальные корреляции определяются в слое толщиной AR на
расстоянии R от начала как функции угла О. Аргументами зависящей от
ориентации корреляционной функции с (г, ф) в точке Л служат расстояние г от
точки А и локальный угол 0.
иие в правой части формулы (1) проводится по значениям ft',
возрастающим с шагом ЛФ' от <К = 0 до #' = я.
Выражение (1) впервые было использовано для обработки
данных, полученных для 168 кластеров, выросших на
квадратной решетке с внерешеточными траекториями случайного
блуждания частиц [3] и состоявших из 80 000—100 000 частиц.
Результаты этих крупномасштабных численных экспериментов
представлены на рис. 2. (Кривые негладкие из-за статистических
ошибок.) В отличие от радиальной корреляционной функции
тангенциальные корреляционные функции, представленные на
рис. 2, обладают четко выраженным минимумом и вторым
максимумом, обостряющимся с увеличением расстояния R от слоя,
для которого определяется корреляционная функция £#(#),
до начала кластера. Положение второго максимума, задаваемое
приближенным соотношением 1п(дМин) = 0,45 « ln(jt/2), соответ-
298
Часть V(6)
ствует анизотропной структуре с четырьмя большими ветвями и
общей конфигурацией, обладающей симметрией квадрата.
Как и ожидалось, угловая корреляционная функция при не
слишком больших углах ft убывает по степенному закону с не-
Рис. 2. Тангенциальные корреляции cR($) как функции от угла О на
различных расстояниях R от начала. Результаты получены при обработке данных по
168 ограниченным диффузией кластерам, выросшим на квадратной решетке
и содержавшим 80 000—100 000 частиц. При построении кривых а —г
данные усреднены по интервалам 6R = R ± 0,05/?, где R имеет следующие
значения: a) R = 100, б) R = 200, в) R = 300 и г) R = 400. Второй максимум
при О = я/2 указывает на то, что общие очертания кластеров складываются
под определяющим влиянием квадратной решетки, на которой они выросли.
которым показателем ах- Этот показатель мы определили при
нескольких значениях R, чтобы учесть влияние конечных разме-
*4^5| J ! J J \ 5 1 1 1 1 1 Г—Т
in (0)
Рис. З. Тангенциальные корреляции во внерешеточных ограниченных
диффузией кластерах. Кривые а — г построены по 44 кластерам, состоящим из
50 000 частиц, путем усреднения по интервалам &R = R ± 0,5/?, где R имеет
значение: a) R = 75, б) R = 150, в) R = 225 и г) R = 300. Положение
минимума этих корреляционных функций не изменяется с увеличением
расстояния R от начала кластера. Это свидетельствует о том, что кластеры состоят
из небольшого числа крупных древовидных ветвей. Угловой коэффициент
прямой, проведенной через кривую г, равен а^ = —0,42.
ров кластера. Как видно из рис. 4 при R < 200 показатель а±
убывает с увеличением R. При 200 < R < 400 значения а±
выходят на насыщение (около 0,39). Если предположить, что
последняя тенденция сохраняется и при гораздо больших
радиусах, то наша экстраполированная оценка для кластеров в мо-
Модели необратимого роста
299
0.5
0.4
дели ДОА, выросших на квадратной решетке, приводит к
значению показателя ах = 0,39 ± 0,04, Это значение заметно
отличается от значения ах = 0,29 ± 0,02, описывающего степенной
закон убывания обычной радиальной корреляционной функции
*(г) = лг|£Р(г' + г)р(г') [1, R
3].
Естественно пр едпо л ожить,
что ромбовидные кластеры в
наших экспериментах
возникали из-за сильного влияния
квадратной решетки. Для
проверки такой гипотезы нами
были проведены дополнительные
численные эксперименты на
основе внерешеточной модели.
На рис. 3 показаны угловые
корреляции крупных внереше-
точных кластеров в нескольких
слоях. Эти данные получены
по 44 кластерам, содержавшим
по 50 000 частиц. Как и в
предыдущих случаях, угловая
корреляционная функция имеет
минимум, но четко
выраженного максимума на этих
кривых не наблюдается.
Линейные участки графиков
описывают степенное убывание
угловой корреляционной
функции с некоторым показателем
ах- На рис. 4 приведены
значения а, полученные при
различных R. Зависимость а от R
во внерешеточном случае
слабее. При R > 60 значение а флуктуирует вокруг — 0,41. Это
наводит на предположение о том, что в пределе при R-+oo
показатель определяется выражением ах = —0,41+0,04.
, , ,
А {
о 1
V
А
А
° о"» ° о
\4Г
—. 1
о
Т 1
о 1
J
0.0 0.01 0.02
Рис. 4. Нарушение масштабной
инвариантности оценок показателя а± как
функций обратного расстояния i?_1
для квадратной решетки и
внерешеточной модели. Данные имеют смысл
угловых коэффициентов прямых,
проведенных по методу наименьших
квадратов через экспериментальные
точки мя тангенциальных
корреляций на интервале 0,035 < О < 0,135.
Для сравнения приведена недавно
полученная оценка показателя а
радиальной корреляционной функции
[3].
3. Обсуждение результатов
Согласно полученным нами численным результатам,
корреляции вокруг данной частицы, принадлежащей кластеру и
находящейся в точке R, убывают как функция того направления, в
котором измеряются корреляции плотность — плотность.
Покажем, как это влияет на фрактальную размерность D и
радиальную корреляционную функцию с (г), определяемую обычным об-
300
Часть V(6)
разом. Для этого предположим, что корреляционная функция
с (г, ф) зависит от г (расстояния от данной частицы) и
локального угла ф (ф = 0 вдоль радиального направления R, как
показано на рис. 1). Если такое предположение соответствует
нашим данным, то при неслишком больших г корреляции в
направлении, параллельном R, должны убывать как г""аи, а в
направлении, перпендикулярном R, как г-а±. Учитывая это, мы
воспользуемся выражением
с (г, Ф) = f (г, ф) (г"а» cos2 ф + рхГа± sin2</>), (2)
#
где pj — постоянная. Соотношение (2) становится
приближенным, если предположить, что медленно меняющаяся функция
f(r, ф) равна постоянной ро.
Из (2) следует, что фрактальная размерность определяется
выражением D== lim {In N (a)/ln a} = lim {2 — щ\+0{(а)}—2—щ
а->оо а->ос
с поправочным (к масштабному преобразованию) членом D{ (а)=
= 1п{р0я(1 +plaa[{~a±)}/lna. Следовательно, радиальная
функция распределения (т. е. корреляционная функция с (г, ф),
усредненная по углам ф) и значение фрактальной размерности D
определяются корреляциями по радиальным направлениям
кластера и тем, что неравенство оси < осх проявляется только в
появлении члена низшего порядка, убывающего при а->оо. Этот
эффект искажения масштабной инвариантности, по-видимому,
является одной из причин завышения значений показателя,
получаемых в первых попытках численного моделирования
ограниченных диффузией кластеров, которые содержали гораздо
меньше частиц, чем в настоящей работе.
Благодарности. Один из авторов (Т. В.) выражает свою
признательность Ф. Фэмили за полезные обсуждения. Работа
проводилась в Университете Эмори на субсидии
Научно-исследовательского фонда Университета Эмори и Национального
научного фонда (контракт № DMR-82-08051).
ЛИТЕРАТУРА
1. Witten Т. Л., Sander L. М, Phys. Rev. Lett., 47, 1400 (1981); Witten T. Л.,
Jr., Sander L. M.f Phys. Rev., B27, 5686 (1983).
2. Mandelbrot B. B.y The Fractal Geometry of Nature, Freeman, San
Francisco, 1982.
3. Meakin P., не опубликовано.
Активная зона в модели ДОА
и в модели Идена
М. Плишке, 3. Рац*
Рост описывается как движение активной зоны, определяемой как
та область, в которой к кластеру присоединяются новые частицы.
Показано, что активную зону можно охарактеризовать двумя
параметрами: средним радиусом осаждения N-н частицы (р^ ~ Nv —
где D — фрактальная размерность бесконечного кластера)
и шириной активной зоны, изменяющейся независимо (g^ ~ ft*,
где v < v). Показано, что в случае ограниченной диффузией
агрегации (ДОА) небольшое различие в v — v может возникнуть из-за
внутренней анизотропии кластеров. Более прозрачна модель
Идена в которой появление второго масштаба длины удается связать
с неравновесной динамикой процесса.
1. Введение
Из предыдущих лекций [1] теперь совершенно ясно, что
существует несколько процессов роста (таких, как ДОА [2]),
приводящих к возникновению масштабно-инвариантных структур, и
что основной теоретический вопрос состоит в том, как вычислить
величины, характеризующие эту масштабную инвариантность,
например, как вычислить фрактальную размерность
образующейся структуры.
По предыдущим докладам [3, 4] можно было заметить одну
общую особенность интересующих нас процессов роста: рост
происходит во внешних слоях кластеров. Причиной этого может
быть экранирование, как в случае ОДК, или запрет, как в
случае модели Идена [5]. Но главное в том, что всегда существует
внешняя активная зона [6], собирающая все присоединяющиеся
к кластеру новые частицы. Эта активная зона распространяется
по направлению от центра кластера наружу и оставляет за
собой вмороженную структуру, свойства которой мы и хотели бы
вычислить. А поскольку вмороженная часть формируется в
активной зоне, для того, чтобы понять ее свойства, нам необходимо
понять свойства активной зоны. Именно это соображение лежит
в основе мотивации исследований структуры поверхности
растущих кластеров. (Другие побудительные мотивы, более
непосредственно связанные с экспериментом, приведены в работах [3]
и [4].)
Первый шаг к пониманию любого объекта всегда сводится к
его описанию. Поэтому наша первая задача состоит в том, как
* М. Plischke- Physics Department, Simon Fraser University, Burna-
by, В. С, Canada, V5A 1S6; Z. Rdcz-The Institute for Theoretical Physics,
Eotvos University, H-1088 Budapest, Hungary.
302
Часть V(6)
охарактеризовать активную зону. В качестве упрощенного
подхода [7] можно попытаться исследовать только радиальные
(усредненные по сферам) свойства кластеров и задать себе
следующий вопрос: какова вероятность P(r, N)dr того, что iV-я частица
присоединяется на расстоянии г от центра масс уже
существующего кластера из N—1 частиц? Если представление об активной
0.15-1 P(r,N)
N=100
о,ю
0,05
N=900
0,00
Рис. 1. Плотность вероятности, вычисленная при d = 2 в модели ДОА по
методу Монте-Карло. Сплошные линии соответствуют гауссовским кривым,
подогнанным под экспериментальные данные. Подробности см. в работе [6].
зоне верно, то плотность вероятности P(r, N) должна быть
равна нулю и во вмороженной зоне (г << RN)j и вдали от кластера
(г > /?лг), где Rn — характерный радиус М-частичного кластера.
Как видно из рис. 1, такого рода ожидание вполне оправданно
в случае двумерной (d = 2) ДОА. Аналогичные кривые могут
быть продемонстрированы и при других размерностях, и в
других моделях [6, 8].
Рис. 1 обладает одной замечательной особенностью:
сплошными линиями на нем обозначены гауссовские кривые, с
высокой точностью аппроксимирующие данные, вычисленные по
методу Монте-Карло. Это означает, что если речь идет о свойствах,
усредненных по сферам, то процесс роста полностью
характеризуется двумя параметрами: средним радиусом осаждения rN
Модели необратимого роста
303
(центром гауссовского распределения) и шириной активной
зоны gtf (шириной гауссовского распределения). Этот вывод
обладает большой общностью. Он выполняется для модели ДОА и
модели Идена при d = 2 и d = 3 (d— евклидова размерность)
и для различных обобщений [8] модели Идена при d — 2.
Описание процесса роста сводится тем самым к пониманию
функций, выполняемых величинами fN и £#. Так как rN
практически совпадает с радиусом Af-частичного кластера, при
больших N должно выполняться соотношение
rN~N*-N{lDf (1)
где D — фрактальная размерность вмороженной структуры.
В общем случае можно было бы ожидать, что £# изменяется по
какому-то степенному закону
tN~N\ (2)
Если наше предположение верно, то исследование поведения
кластеров при больших N упрощается, так как сводится к
исследованию двух показателей v и v.
Теория равновесных критических явлений в изотропных
системах наводит на мысль о том, что в действительности мы
располагаем только одним параметром, так как в таких
системах существует только одна характерная длина и,
следовательно, v=v. В этой лекции я хотел бы особенно подчеркнуть, что
растущие кластеры не являются, вообще говоря, ни
изотропными, ни равновесными, поэтому появление еще одной
характерной длины неудивительно. Неравенство v^v — скорее правило,
чем исключение.
2. Ограниченная диффузией кластеризация при d Ф 2
Вопрос о том, выполняется ли при d — 2 равенство v = v или
v Ф v, остается открытым. Численные эксперименты,
проводимые с помощью метода Монте-Карло (МК) над сравнительно
небольшими кластерами [6], подтверждают неравенство v < v, но
эффективное значение v возрастает с увеличением размера
кластера [9], и для самых больших кластеров (содержащих около
50 000 частиц) разность v — v составляет 0,05. Возрастание
эффективного значения v отнюдь не означает, что v->-v при N-*
->оо, так как из-за слабой анизотропии, наблюдаемой у
ограниченных диффузией кластеров [10], можно ожидать разности
v — v порядка 0,05 [10].
Такого рода ожидание основано на том, что если в
структуре имеются зазоры величиной /, то диффузия проникает в
поглощающую структуру на глубину /. Применительно к ДОА это
означает, что глубина проникновения налетающих частиц и,
304
Часть V(6)
следовательно, ширина активной зоны | может быть вычислена
как среднее расстояние между соседними ветвями на расстоянии
от центра кластера, равном радиусу осаждения (рис. 2). Среднее
расстояние между ветвями может быть найдено следующим
образом. Прежде всего подсчитаем число ветвей на радиусе
осаждения fN. Так как плотность частиц р(г#) изменяется по
степенному закону р ~ rivd+D> число частиц в оболочке шириной dr
Рис. 2. Ограниченный диффузией кластер с средним радиусом осаждения
(штриховая линия). Ширина активной зоны g вычисляется как среднее
расстояние между соседними ветвями.
изменяется по закону dN ~?n~x dr. Число частиц dNx в
оболочке, принадлежащих данной ветви, также изменяется по
степенному закону dNx^r^dr, но показатель а неизвестен. Если
кластер ежеобразный и состоит из «голых» одномерных ветвей
(крайняя анизотропия), то а = 0; в случае же изотропных
ветвей a = Z)—1. В общем случае можно ожидать, что 0 < a <
< D— 1. Затем мы находим число ветвей п ~ dNjdNx ~?n~1~°'
и, распределяя это число ветвей равномерно по d-мерной сфере
радиуса rN, получаем среднее расстояние между ветвями
g = f#-z>+«)/w-0 (3)
Можно показать, что равенство v = v выполняется только в
изотропном случае (a = D—1) и слабая анизотропия может
привести к небольшому различию между v и v. Анизотропия
ограниченных диффузией кластеров действительно была измерена
[11]. Судя по полученным результатам, можно заключить, что
а ж 0,59 приводит к оценке v ^ 0,51 [10]. Этот результат пока-
Модели необратимого роста
305
зывает, что если анизотропия обусловлена не влиянием конечных
размеров кластера, то v - v « 0,07.
Сам по себе феномен существования двух различных
масштабов длины, порождаемых анизотропией, ненов. Он
наблюдается и в равновесных критических явлениях (в качестве
простого примера сошлемся хотя бы на направленную перколяцию
[12]). Однако, как показывает следующий пример, для
появления в процессах роста второго масштаба длины существует
более общая и более глубокая причина, а именно: неравновесная
природа процесса.
3. Модель Идена в двумерном случае (d = 2)
Существует несколько незначительно отличающихся друг от
друга вариантов алгоритмов роста кластеров в модели Идена.
Мы рассмотрим вариант С, предложенный Жюльеном и Боте
[13]. В этом варианте занятые узлы на поверхности кластера
выбираются случайным образом, а новая частица «садится»
равновероятно в один из соседних незанятых узлов. Результаты
проведенного нами численного моделирования этого процесса
представлены на рис. 3. Данные о радиусе гирации (Rg ~ Nv ~ N1'2)
убедительно свидетельствуют о том, что кластеры компактны
[14]. Ясно также, что другой масштаб длины — ширина
поверхностной зоны I ~ Nv — расходится с показателем v, отличным
от v.
Чтобы понять, насколько «шероховата» поверхность
кластеров в модели Идена, удобно исследовать процесс роста в
геометрии полосы [13], т. е. ограничить рост полосой ширины L.
В качестве начального условия можно выбрать субстрат, в
котором все узлы до высоты ft0 = 0 заняты (рис. 4). Геометрия
полосы позволяет удобным образом разделить управляющие
параметры. Ширину полосы L и среднюю высоту осаждения Я, или
(в подходящих единицах) время роста t — Я, мы можем
изменять независимо. Нетрудно видеть, что такая ситуация
существенно отличается от обычно рассматриваемой «круглой»
геометрии [6, 15, 16], в которой кластер растет из затравочной
частицы и один-единственный параметр N управляет и «высотой»,
которую можно считать средним радиусом R ~ Nl/2, и
«шириной» полосы, эквивалентной длине окружности среднего радиуса
2nR ~ N1/2. Разумеется, следует ожидать, что при ЛГ-voo
перестанет сказываться влияние кривизны. Таким образом, свойства
кластеров в модели Идена относительно масштабных
преобразований в «круглой геометрии» могут быть выведены из
аналогичных свойств в геометрии полосы, если выбрать t ~ К ~ L ~
~ ЛИ/2.
306
Часть V(6)
Разделение управляющих параметров полезно, так как
позволяет нам рассматривать пределы простые, но недоступные в
«круглой» геометрии. Особенно это важно в пределе при £->оо,
так как при больших t процесс роста становится стационарным
и свойства поверхности движущегося фронта перестают зависеть
от времени [13]. Мы надеемся, что это стационарное состояние
200
юо н
h(i,t ~40L)
in
w
jT Чяяд л ffrTt
1/z
.«„та ■<Пп.у •.. s».. я • sru& .'ti
h{i,t=L/6)
t2v
0 i L = 192
Рис. 3. Средний радиус осаждения Рис. 4. Рост в модели Идена (гео-
fN и ширина активной зоны %N кла- метрия полосы). Черные точки озна-
стеров в модели Идена, полученные чают узлы поверхности на различных
по данным численного моделирова- стадиях развития кластера,
ния 100 кластеров в варианте С
процесса роста. Сплошная линия
соответствует компактным кластерам:
?n ~ (N/n)i/2. Числа над кривой из
точек являются оценками
эффективного показателя для ширины слоя gA-
в соответствующем интервале N.
легче поддается рассмотрению аналитическими методами и
предел t ~ h ~ L ~ Nl/2 удастся получить путем изучения
релаксации к стационарному состоянию.
Однако в настоящее время мы можем сообщить результаты
только численных экспериментов. Жюльен и Боте [13]
обнаружили, что ширина поверхностной зоны изменяется по
следующему закону:
Z(L,t)~L°G(t/L% (4)
где а = 0,50 ± 0,03 и г = 1,7 ± 0,3. Входящая в этот закон
функция д(х) заведомо отлична от нуля, т. е. G(x) ->■ G(oo) Ф О
Модели необратимого роста
307
при х-*- со, в то время как в менее очевидном пределе при х-^-0
она по предположению [13J ведет себя как G(x) ~ xa/z (тем
самым зависимость £ от L при малых t выпадает). Поведение
функции G(x) при малых х важно для нахождения предела
t ~ L ~ Nl/2-*oo и тем самым нахождения показателя v:
I (L, L) ~ L*G (Ll~z) ~ № ~ N*№ ~ N* (5)
и, следовательно,
v = a/(2z). (6)
Так как масштабное преобразование (4) наводит на
интересные аналогии с динамическими критическими явлениями итак
как непроверенный предел х->0 существен при выводе
соотношения (6), мы предприняли более подробное исследование
поверхности, разлагая ее на моды Фурье и анализируя статические и
динамические свойства этих мод.
Для того чтобы мы могли воспользоваться анализом Фурье,
высота поверхности должна быть однозначной функцией. Хотя
число выступов и дыр в варианте С модели Идена весьма
ограниченно, все же поверхность в итоге состоит более чем из одной
точки над каждой точкой субстрата. Один из способов
преодоления этой трудности состоит в определении локально
усредненной высоты h(i, t) для точки субстрата i в момент времени t:
ns a, t)
*<'•*>-"ОТ!) £ h'{i't]' (7)
где A/ (i, t) —высота /-го узла поверхности в t-м столбце, ns{i,
t) —число узлов поверхности в i-м столбце, а время t
измеряется по числу частиц, осевших на узел субстрата. Анализ Фурье
такой «сглаженной поверхности» производится путем введения
величины
L
h (q, t) = -1т У [ft (/, t)-h (I)} eiq\ (9)
где q = db 2kn/L, k=l, 2, ..., L — 1 и ft (/) — средняя высота,
т. е. ft(/)= X ft(/,/)/L. Величина h(q,t) позволяет записать
соотношение
L
t{Li /)==j-l>(/, o-mo]2=tZImm)I2. (g)
Мы видим, таким образом, что квадраты амплитуд мод Фурье
определяют ширину поверхности.
308
Часть V(6)
Результаты наших численных экспериментов [16]
относительно | h (q, t) | показывают, что в стационарном состоянии
(t^-oo) эта функция практически не зависит otL и \h(q, oo)|2~
~ q~2. Отсюда непосредственно следует, что
я
1ЩУ оо)~ J dqlq*~L. (10)
Этот результат согласуется с значением а = 0,50 ± 0,03,
полученным в работе [13]. Полученное нами соотношение l~^L
напоминает одно из свойств граничных поверхностей в моделях
шероховатости и Изинга [17, 18]. Однако подобие касается
только статических аспектов явления. Как показали
проведенные нами численные эксперименты [16], величина \ft(q7t)\2
обладает динамической масштабной инвариантностью [19]
\h(q,t)\2~jrl\-g{qzt)\, (И)
но динамический критический показатель г = 1,55 ±0,15
отличен от показателей (г ^2), найденных для динамических
обобщений моделей шероховатой поверхности [17] и Изинга [20].
Масштабная функция g(x) экспоненциально мала при x->-oo, в
то время как 1—g(x) ~ х при х->0. Следовательно,
подставляя соотношение (11) в правую часть равенства (9), мы
получаем для |(L, t) масштабное преобразование (4) с а = 0,5 и z =
= 1,55 ±0,15, и поведение масштабной функции G(x)~xa/Z
при х->-0 перестает быть гипотезой, так как следует из
соотношения (11).
Масштабно-инвариантные свойства поверхностных мод в
модели Идена имеют много общего с свойствами мод в
термодинамической системе вблизи критической точки. Дальнейшие
исследования этих мод будут полезны при построении
феноменологической теории поля, которая позволит получить а и г с помощью
надлежащего ренормгруппового подхода.
Отождествление z с динамическим критическим показателем
(11) и связь показателя поверхности v с динамическим
показателем z подтверждают наше утверждение о том, что второй
масштаб длины естественно возникает как следствие неравновесной
природы процесса. Мы считаем, что связь между v и z носит
весьма общий характер и будет весьма полезной при выяснении
тех средств, которые позволяют осуществить классификацию
процессов роста.
ЛИТЕРАТУРА
1. См. предыдущие доклады на этой конференции.
2. Witten Т. Л., Sander L. Л1, Phys. Rev. Lett., 47, 1400 (1981).
3. Пьетронеро Л. и др. — наст, сб., с. 221.
Модели необратимого роста
309
4. Микин П. — наст, сб., с. 283.
5. Eden М., Proceedings of the Fourth Berkeley Symposium on Mathematical
Statistics and Probability, ed. F. Neyman, University of California,
Berkeley, vol. IV, p. 223, 1961.
6. Plischke M., Rdcz Z., Phys. Rev. Lett., 53, 415 (1984).
Rdcz Z., Plischke M, Phys. Rev., A31, 985 (1985).
7. Более сложные определения поверхностной зоны см.:
Meakin P., Wltten Т. A., Phys. Rev, A28, 2985 (1983); Meakln P., Phys.
Rev., B30, 4207 (1984); Phys. Rev., A32, 453 (1985).
8. Bunde Л., Herrmann H. /., Margolina A, Stanley H. £"., preprint 1984.
9. Meakin P., Sander L. M.t Phys. Pev. Lett., 54, 2053 (1985).
10. Plischke M.t Rdcz Z., Phys. Rev. Lett., 54, 2054 (1985).
11. Meakin P, Vicsek Т., Phys. Rev. А, в печати.
Кольб М. — наст, сб., с. 360.
12. Kinzel W., Yeomans J. Af., J. Phys., A14, L163 (1981).
J3. Jullien /?., Botet R., Phys. Rev. Lett, 54, 2055 (1985); J. Phys. А, в
печати.
14. Dhar /)., Phys. Rev. Lett., 54, 2058 (1985).
15. Peters H. P. et al, Z. Phys., B34, 399 (1979).
16. Plischke M., Rdcz Z., preprint 1985.
17. Weeks J. ZX, Gilmer G. #., Adv. Chem. Phys., 40, 157 (1979).
18. Jasnow /)., Rep. Prog. Phys., 47, 1509 (1984).
19. Hohenberg P. C, Halperin B. /., Rev. Mod. Phys., 49, 435 (1977).
20. Bausch R., Dohm V., Janssen Я. /C, Zia R. K. P., Phys. Rev. Lett, 47, 1837
(1981).
Закон масштабного преобразования
вероятности присоединения частицы
в модели ДОА
Л. Туркевич, Г. Шер*
Масштабное преобразование связывает размерность Хаусдорфа
ограниченных диффузией кластеров с вероятностями заполнения
узлов периметра на выступах кластеров. Для двумерной квадратной
решетки мы получили D = 5/3 в модели ДОА, D = 2 в модели
Идена и D = 2 — У|/3 в модели пробоя диэлектриков Брауна —
Бовери степени tj. При одноосной анизотропии в модели ДОА
D = 3/2. Полученные результаты были обобщены на случай d ^ 2.
Мы не обнаружили верхней критической размерности в ДОА,
хотя D-+d — 1 при больших d. Полученные нами значения D
полностью согласуются с результатами численных экспериментов
Микина на прямоугольных решетках для 2 ^ d ^ 6. При
одноосной анизотропии верхняя критическая размерность d = 3, выше
нее D = d — 1.
1. Введение
В настоящей работе показано, какую важную роль
играют вероятности заполнения при ограниченной диффузией
агрегации [1, 2]. Эти вероятности — не что иное, как вероятности
окончания случайного блуждания в узлах растущего периметра
ограниченного диффузией кластера. В разд. 2 мы устанавливаем
связь вероятностей заполнения для узлов в точках роста [3] с
фрактальной размерностью D кластера. Физика, воплощенная
в простом соотношении подобия [3], приводит к выводу о том,
что весь рост происходит на выступах кластеров и управляется
выступами. Это замечание позволяет свести ДОА к классической
электростатике и считать все остальные модели вариантами,
лишенными реального содержания. Для вычисления размерности
Хаусдорфа D нам необходимо знать только закон масштабного
преобразования вероятности заполнения РМакс(№) наиболее
выступающих концов кластера в зависимости от его массы N.
В разд. 3 мы воспользуемся предположением о том, что
крупномасштабная структура кластера определяет длину остриев
кластерных выступов. Такое предположение позволяет с помощью
простой электростатической аналогии вычислить закон
преобразования вероятности PMaKc(N) в двумерном случае, используя
конформные преобразования. Теория предсказывает не слишком
сильную неуниверсальность (зависимость от решетки)
размерности Хаусдорфа D. В разд. 4 мы обобщим [4] эти результаты
на более высокие размерности. В соответствии с высказывав-
* Leonid Л. Turkevich, Harvey Scher-The Standard Oil Company,
Corporate Research Center, 4440 Warrensville Center Road, Cleveland, Ohio 44128.
Модели необратимого роста
311
шимися ранее идеями [2] наша теория не позволяет вычислить
верхнюю критическую размерность в модели ДОА на
прямоугольных решетках. К аналогичным результатам приводят и
проведенные Микином обширные численные эксперименты на
прямоугольной решетке [5, 8]. При наличии одноосной
анизотропии верхняя критическая размерность понижается до d = 3.
2. Связь вероятностей заполнения с D
Рассмотрим ограниченный диффузией кластер, состоящий из
N частиц. Пусть (Л/"+1)-я точка, совершающая случайные
блуждания, запускается из бесконечности и с вероятностью pi
может занять один из узлов (обозначенный индексом i) на
периметре кластера. Эти вероятности заполнения распределены не
равномерно, как было бы в модели Идена [6], а тесно связаны
с диффузионным (фрактальным) характером случайного
блуждания. В частности, совершающая случайное блуждание
частица с гораздо большей вероятностью присоединяется к узлу,
расположенному на выступе периметра кластера, чем к узлу,
расположенному в глубине «фьорда». Такое экранирование
находит отражение и в нашем масштабно-инвариантном подходе.
Если бы ограниченный диффузией кластер был полностью
развит вплоть до самых дальних от центра выступов, то он имел
бы номинальный радиус r0 = W1/Z)a, где а — постоянная
решетки. Но внутренняя часть кластера заэкранирована (с длиной
экранировки |): новые точки, совершающие случайное
блуждание, захватываются только узлами, лежащими на периметре в
«активной зоне». Таким образом, ограниченный диффузией
кластер полностью развит (т. е. число частиц в радиусе г внутри
кластера изменяется по закону N(r)~rD) только до радиуса
г^ = г0 — £. Чтобы собрать все N частиц, кластер должен
простираться дальше — до радиуса г+> г0 (рис. 1,а). В силу
автомодельное™ все характерные длины r0, r+, | изменяются в
зависимости от N по одному и тому же закону.
Рассмотрим теперь ограниченные диффузией кластеры при
d = 2. Вероятности заполнения можно представить с помощью
некоторой плотности pN{r)dr того, что (N -\- 1)-я частица,
совершающая случайное блуждание, закончит свой путь и
присоединится к кластеру в кольце шириной dr на радиусе г. Ясно, что
плотность вероятности ры{г) максимальна на выступах кластера
(в действительности ры{г) расходится при г^>~г+ (см. врезку на
рис. 1,6)).
Эта расходимость в плотности вероятности заполнения
определяет размерность Хаусдорфа D. Если дан кластер, состоящий
из N частиц, то вероятность того, что (ЛГ+ 1)-я частица,
совершающая случайное блуждание, присоединится к кластеру в его
312
Часть V(6)
граничной зоне (кольце вблизи радиуса г^), равна
г+
Л*акс = \ PN{r)dr. (1)
В этом случае кластер растет: г^+{) = г(_^> + а. Существует
нулевая вероятность того, что эта блуждающая частица
присоединится к кластеру внутри полностью развитой области (г <С rJ) —
Рис. 1. а — Общий ход распределения числа занятых узлов N(r) на
расстоянии г от центра масс. Кластер полностью развит при г < г_, значениям
г- < г < г+ соответствует граничная область с меньшей плотностью.
Кластер без граничной области простирался бы до номинального радиуса г0;
б — общий ход плотности вероятности заполнения pyv(r). При г < г_ кластер
растет. При г = г+ плотность вероятности /?лг имеет особенность, что
соответствует максимальной вероятности роста на выступах кластера. На врезке
показаны две возможные траектории случайных блужданий: одна вблизи
выступа г~Г\, другая глубоко внутри граничной области.
из-за экранирования. Вероятность того, что та же частица
присоединится к кластеру в активной зоне (rW < г < г^), но не на
выступах, равна 1 — РМакс, но в этом случае кластер не растет:
/•(лн-1) _ r{N)m Сочетание всех перечисленных нами альтернатив
приводит к соотношению
Г{Г1) - Ямакс {Л + а) + (1 - Рмакс) г!Г, (2)
Модели необратимого роста
313
которое при больших ./V переходит в уравнение
dr{N)
~Jr = P»*Kc(N)a. (3)
Уравнение (3) облекает в количественную форму физические
соображения, согласно которым рост кластеров в модели ДОА
определяется вероятностью заполнения на выступах кластера.
Уравнение (3) выражает также и то, что в процессе роста
pN+i(r) (плотность вероятности заполнения для (N + 2)-й
частицы, совершающей случайное блуждание) отличается от ры{г)>
тогда как в отсутствие роста pN+i(r) & Рлг(г)- Наконец, так как
r+ ~ Nl/Da, особенность в плотности вероятности заполнения
ры(г) при г-*-г+ (приближении к выступу кластера) полностью
определяет фрактальную размерность D.
Поскольку нам необходимо знать pN(r) только в окрестности
выступов, все тонкие особенности структуры случайного
разветвленного кластера несущественны: весь рост происходит на
выступах кластера, что позволяет нам воспользоваться любым
объектом, обладающим такой же структурой выступов, как и
ограниченный диффузией кластер. Это — наиболее существенная
отличительная особенность нашего подхода к выводу закона
преобразования вероятности заполнения: размерность Хаусдорфа D
зависит не от нерегулярной структуры кластера, а от его более
регулярного роста. Таким образом, допустимо рассматривать
любой объект, обладающий структурой решетки (например, для
квадратной решетки — «ромб с прямыми углами»), или, иначе
говоря, случайное блуждание при наличии расположенных в
узлах квадратной решетки поглощающих ловушек. Вероятности
заполнения мы вычисляем как функцию расстояния 8s от
вершин квадрата.
В пределе при / -»■ оо задача о диффузии при случайном
блуждании сводится [7] к уравнению V2u = 0, где и — поле
концентрации случайно блуждающих частиц. Поскольку узлы на
периметре являются идеальными ловушками, на периметре кластера
выполняется условие // = 0. Так как совершающие случайное
блуждание частицы запускаются из бесконечности изотропно,
существует дополнительное граничное условие и=1 при r=R<x>.
Плотность вероятности заполнения р(т) пропорциональна потоку
Vw случайно блуждающих частиц в узле периметра г.
Следовательно, чтобы найти плотность вероятности р(г), мы в принципе
решаем электростатическую задачу \2ф = 0 для проводящего
кластера (0 —0) внутри проводящей окружности бесконечного
радиуса (ф = 1):
p(r) = |E(r)|/J|E(r)|<fe, (4)
и
314
Часть V(6)
где Е = —V<j> есть электрическое поле и плотность вероятности
нормирована по периметру кластера II. Кроме того, можно
рассмотреть [7] целый класс моделей, в котором соотношение (4)
заменено более общим соотношением
р(г)=|Е(г)рА|Е(г)|пЛ. (5)
/ и
При ц = 0 мы получаем модель Идена [6], при rj = 1 — модель
ДОА и при цФ I — класс моделей пробоя диэлектриков,
рассмотренных группой из Центра Брауна — Бовери [7].
3. Предположение о крупномасштабной структуре
Задача электростатики о случайно разветвленном
проводящем кластере внутри проводящего цилиндра слишком трудна для
того, чтобы ее можно было решить точно. Но наш закон роста
(3) требует соответствующего поведения плотности вероятности
только на выступах кластера. Внутренность кластера
заэкранирована. Следовательно, закон преобразования Рмакс должен быть
нечувствителен к деталям разветвленной случайной внутренней
части кластера. Чтобы найти закон измедения Рмакс, достаточно
рассмотреть любой объект, обладающий такой же структурой
выступов, как и ограниченный диффузией кластер.
Для кластера, выросшего на двумерной квадратной решетке,
направления легкого роста ориентированы точно по осям
решетки. Структура выступов кластера неизбежно отражает
симметрию решетки. Например, в крупномасштабных вычислительных
экспериментах Микина [8] и кембриджской группы [9]
кластеры принимают четко выраженную ромбическую форму
(квадрата, повернутого на угол я/4 относительно прямоугольных осей).
Мы принимаем предположение о том, что в модели ДОА
структура выступов кластера, выросшего на квадратной решетке,
тождественна структуре выступов ромбовидного контура,
образованного узлами решетки.
Это предположение позволяет нам вычислить с помощью
конформного преобразования электростатический потенциал вблизи
острия выступа кластера в модели ДОА. Вблизи вершины
квадрата со стороной длины L
E~L-W6s-W, (6)
где 8s — расстояние от вершины. Нормируя величину (4) по
длине экранирования £w, мы получаем плотность вероятности
Mr)~fSW-2/V+W)-r)-1/3. (7)
Модели необратимого роста
315
Используя соотношение (1), получаем вероятность заполнения
на вершине выступа! г макс rsu (я/Е)2/3- Из масштабного
уравнения (3) для роста следует, что N ~ (г/а)5/3, т. е. £)=5/3 для
двумерных кластеров в модели ДОА на квадратной решетке.
Непротиворечивость предположения о ромбической структуре
выступов была проверена нами [3] путем изучения зависимости
Pm2lkc{N) ~ £-2/3 ~ Af-2/5 на небольших реализациях
ограниченных диффузией кластеров, выращенных «по рецепту»
случайных блужданий с присоединением частиц к выступам кластера.
Аналогичный закон масштабного преобразования (Рмакс ~ Af~0,39)
наблюдался Микином [10] в крупномасштабных численных
экспериментах (Af~5-104).
Результаты, полученные нами на двумерных квадратных
решетках, непосредственно переносятся на более общий класс г\-
моделей [7]. Нормируя закон преобразования (6) с учетом
соотношения (5), получаем
рАг)~Ъ^-{(г+-г)-^у (8)
в силу чего из (1) следует, что РМакс ~ (а/£)1-Т1/3.
Интегрирование масштабного уравнения роста (3) приводит к закону N ~
~ (r/а)2-^3, т. е. Z)ti==2 — rj/З. Последняя зависимость дает
значения />0 = 2 для модели раковой опухоли Идена [6] и
D\/2= 11/6 и D2 = 4/3 для соответствующих моделей пробоя
диэлектриков Брауна — Бовери [7] на двумерной квадратной
решетке. Последние результаты находятся в превосходном
согласии с численными экспериментами Микина [8] (Da = l,86=fc
± 0,02; Db = 1,92 ± 0,05 при ц = 1/2 и Da = 1,44 ± 0,02; Dp =
= 1,39 ± 0,10 при т) = 2). При у\ > 3 распределение вероятности
(8) становится ненормируемым, что свидетельствует о
невозможности поддержания фрактальной структуры при столь
экстремальном законе роста [11].
Наше предположение о крупномасштабной структуре
кластера, определяющей структуру выступов, применимо и к ДОА
на других решетках. Можно ожидать, что на двумерной
треугольной решетке кластер в модели ДОА «в большом» будет
напоминать шестиугольник с углом при вершине, равным 2я/3.
Рассуждения, тождественные приведенным выше для случая
квадратной решетки, приводят к размерности Хаусдорфа D —
= 7/4. Последние численные результаты Микина [8] для
кластеров, выросших на гексагональной решетке, указывают на то,
что Dp = 1,71, и согласуются с данными по внерешеточной ДОА
с малой погрешностью, позволяющей исключать статистически
(но не систематические D = l,75. Сколько-нибудь выпаженной
гексагональной структуры в этих кластеоах не возникает. Либо
кластеры, о которых идеть речь (N ~ 103), недостаточно велики
Для того, чтобы по ним можно было надежно определить D,
316
Часть V(6)
либо шестиугольник никогда не образуется. Последняя
альтернатива указывает на то, что более сильная особенность,
характерная для внерешеточиой ДОА, доминирует над особенностью,
порождаемой треугольной решеткой (в то время как еще более
сильная особенность, характерная для двумерной ДОА на
квадратной ре!петке, обусловливает переход от неподвижной точки
внерешеточиой ДОА к ромбообразной структуре).
Заметим, что виерешеточные результаты [8] (£> = 1,71)
могут быть качественно поняты как усреднение по относительному
расположению присоединившихся к кластеру частиц,
совершавших случайное блуждание. Две возможные двумерные
изотропные решетки стоят в одном ряду с результатом, полученным для
внерешеточного блуждания: D = 5/3 (решетка с осью
симметрии 4-го порядка) и /5 = 7/4 (решетка с осью симметрии 6-го
порядка). Интересно отметить, что внерешеточная структура с
гипотетической осью симметрии 5-го порядка обладает D =
= 12/7^ 1,7143... В переводе на этот язык адекватная теория
внерешеточиой ДОА позволит получить информацию о
локальном относительном расположении частиц в кластере.
Наконец, приведенные выше результаты могут быть
распространены на анизотропные (но сохраняющие симметрию 4-го
порядка) косоугольные решетки (с углом |3). Прямые вычисления
приводят к размерности Хаусдорфа D = (Зя — Р)/(2я— (5),
заключенной в узких пределах: 1,50 <£< 1,67.
Неуниверсальность (слабая) этого результата может быть объяснена
«выпрямлением» косоугольной решетки. Наивное объяснение
состоит в том, что мы должны были бы получить ДОА со
структурой изотропной прямоугольной решетки, но «выпрямление»
воздействует на распределение источников в бесконечности,
выстраивая источники случайно блуждающих частиц вдоль одной
оси. Это предсказание достаточно впечатляет, чтобы оправдать
проверку с помощью численного моделирования. В случае
экстремальной одноосной анизотропии общий класс т]-моделей [7|
должен был бы обладать D^ — 2— ц/2 с недолговечными
фрактальными структурами при я > 2.
4. Высшие размерности
Применим теперь изложенные выше геометрические идеи к
высшим размерностям [4]. Для простоты будем рассматривать
только прямоугольные решетки. При d — 3 нам необходимо
проинтегрировать распределение вероятности до выступов кластера,
чтобы получить
Ямакс= \ PN(r)rdr. (9)
Модели необратимого роста
317
Масштабное уравнение роста (3) остается неизменным.
Принятое нами предположение о крупномасштабной структуре служит
обоснованием существования решения электростатической
задачи для октаэдра (дуального простой кубической решетке),
поддерживаемого при потенциале ф = О внутри проводящей
сферы бесконечно большого радиуса, поддерживаемой при
потенциале ф=1. Поскольку дивергенция электрического поля
вблизи краев меньше, чем вблизи вершин выступов, мы
находим главный член решения, описывающий поведение поля
вблизи острия конуса с прямым углом при вершине. В случае
азимутальной симметрии переменные разделяются: ф = Жг)в('б');
радиальная часть изменяется по закону R ~ rv, т. е. Е = rv~x,
поэтому из соотношения (9) мы получаем D = 2 + v. Константа
разделения v входит в записанное в полярных координатах
уравнение Лежандра
и определяется граничным условием (означающим, что конус
поддерживается при постоянном потенциале [12])
Pv(cosfl) = F(-v, v + 1; 1,2) = 0, (11)
где Pv(cos'Oi) —функция Лежандра порядка v, F(a, (3; у; z) —
гипергеометрическая функция и г = (1 —cos &)/z. Следует иметь
в виду, что угол раствора конуса измеряется вне, а не внутри
конуса (для конуса с прямым углом раствора p==3jt/4).
Сказанное допускает непосредственное обобщение и на более
высокие размерности [4]. Чтобы найти РМакс, распределение
вероятности следует проинтегрировать до острия гиперконуса:
г+
Л.«с~ 5 PN(r)rd~4r. (12)
Г| -fl
В гиперсферических координатах переменные в случае
азимутальной симметрии разделяются: ф = R(г)в(О); радиальная
часть изменяется по закону R ~ rv-rf+3, поэтому из соотношения
(12) мы получаем D = 2~\-v- Константа разделения v входит в
уравнение в гиперсферических координатах
и определяется граничным условием, означающим, что
гиперконус находится под постояным потенциалом
^(rf-3-v, 1+v; ^~-; г) = 0. (14)
318
Часть V(6)
Зависимость показателя гирации р = 1/D как функции от
евклидовой размерности d представлена на рис. 2. Здесь же
нанесены данные, полученные Микином [5] с помощью численных
экспериментов для прямоугольных решеток с 2 ^ d ^ 6.
Согласие между результатами численных экспериментов и теорией
замечательное.
На рис. 3 показана сама размерность Хаусдорфа — график
отклонения D от ее значения по гипотезе среднего поля d—1
(нижней границы причинности [13]). Мы видим, что D-+d—1
при больших d, но при этом неизменно выполняется
неравенство D > d— 1. Следовательно, верхней критической границы
на изотропных прямоугольных решетках при DOA не
существует. Отсутствие верхней критической размерности
предполагалось с самого начала [2], что согласуется с инвариантностью
закона изменения средней длины пути в зависимости от массы,
наблюдавшейся у ограниченных диффузией кластеров [14].
Верхняя штриховая линия на рис. 3 соответствует основанной на
соображениях среднего поля гипотезе о том, что D = (d2 +
+ l)/(rf+ 1) [15]. Нетрудно видеть, что наши значения D (14)
стремятся к нижней границе причинности d— 1 быстрее, чем
значения, вычисляемые по формуле «среднего поля». На рис. 3
представлены также результаты численных экспериментов Ми-
кина на прямоугольных решетках [5]. Вертикальными
отрезками указаны доверительные интервалы, с которыми Микин
определял размерность Хаусдорфа D при соответствующих
значениях евклидовой размерности d. В тех случаях, когда границы
доверительного интервала не установлены, данные о
размерности Хаусдорфа для отдельных кластеров изображены
квадратами [5]. Представленные на рис. 3 результаты численных
экспериментов получены при обращении данных Микина о
показателе радиуса гирации р. Для широкого класса г]-моделей [7]
справедливо соотношение D^ — d=r|(Di— d). При r\> \/{d —
— Di) фрактальный рост становится неустойчивым. В частности,
модель пробоя диэлектриков Брауна — Бовери при к\ = 2 не
должна обладать фрактальными решениями при d ^ 3.
Наконец, нами был рассмотрен и вопрос о том, в какой мере
влияет на полученные результаты одноосная анизотропия, а
именно, как наши результаты зависят от решетки. Выяснить это
несложно: необходимо лишь проварьировать внешний угол р
при вершине гиперконуса. В одноосном пределе (при р->0)
получаем: D — (d+ 1)/2 при d ^ 3 и D ==d— 1 при d ^ 3.
Следовательно, для таких анизотропных решеток размерность
Хаусдорфа при d ^ 3 понижается до значения, к которому приводит
гипотеза среднего поля, хотя верхней критической размерности
для изотропных решеток не существует.
1,0 г
o,«j-
0,7 l-
o,el
0,4 I
0,3 [
0,2 I
0,1 |
0,0 1
0,0
5,0 10,0
Евклидова размерность d
15,0
Рис. 2. Показатель радиуса гирации р для кластера в модели ДОА,
выросшего на ^-мерной прямоугольной решетке. Данные из работы Микина [5J
(вертикальные линии указывают ширину доверительных интервалов,
квадраты соответствуют отдельным кластерам).
1,0
0,0 1,0 2,0 3,0 4,0 5,0 6,0 7,0 8,0 9,0 10,0
Евклидова размерность d
Рис. 3. Отклонение размерности Хаусдорфа D от ее значения по гипотезе
среднего поля d— 1 (нижняя граница причинности [13]). Верхняя штриховая
кривая соответствует гипотезе среднего поля [15]. Данные (квадраты и
вертикальные линии) заимствованы из работы Микина [5]. Нижняя штриховая
кривая соответствует случаю одноосной анизотропии.
320
Часть V(6)
5. Выводы
Резюмируя, мы можем утверждать, что нами предложена
масштабно-инвариантная формулировка модели ДОА. На
каждой стадии роста мы сосредоточиваем внимание на вероятности
присоединения случайно блуждающей частицы в вакантный узел
на периметре кластера. Рост в основном происходит на
выступах кластера и управляется вероятностью заполнения РМакс
наиболее выступающих вершин. Закон изменения РМакс определяет
размерность Хаусдорфа D кластера и может быть получен из
главного члена, описывающего особенность в плотности
вероятности регулярного объекта с такими же выступами, как у
ограниченного диффузией кластера. Мы установили, что D — 5/3 для
ДОА на плоской квадратной решетке ий= 7/4 на плоской
треугольной решетке. Это свидетельствует о слабой
неуниверсальности. Полученное решение мы распространили на высшие
размерности и не обнаружили верхней критической размерности
для ДОА на прямоугольных решетках: D-+d—1. Но в случае
одноосной анизотропии верхняя критическая размерность
понижается до d = 3.
ЛИТЕРАТУРА
1. Witten Т. A., Jr., Sander L. M.t Phys. Rev. Lett., 47, 1400 (1981);
Meakin P., Phys Rev., A27, 604 (1983).
2. Witten T. A., Jr., Sander L. M., Phys. Rev., B27, 5686 (1983).
3. Turkevich L A., Scher H., Phys. Rev. Lett., 55, 1026 (1985).
4. Turkevich L. A., Scher #., Phys. Rev. А, будет опубликовано.
5. Meakin P., Phys. Rev., A27, 1495 (1983).
6. Eden M., in: Proc. Fourth Berkeley Symp. on Mathematical Statistics and
Probability, ed. J. Neyman, Univ. of California Press, Berkeley, 1961,
vol. 4, p. 223; Peters H. P., Stauffer D., Holters II. P., Loewenich K., Z.
Phys., B34, 399 (1979).
7. Niemeyer L., Pietronero L., Wiesmann H. /., Phys. Rev. Lett., 52, 1033
(1984).
8. Meakin P., in: On Growth and Form. A Modern View, eds. H. E. Stanley,
N. Ostrowski, M. Nijhoff, Dordrecht, 1985.
9. Ball R. C, Brady R. M., будет опубликовано.
10. Meakin P., частное сообщение.
11. Мы признательны Л. Сандеру за вопрос, заданный на этом симпозиуме
и вызвавший это замечание.
12. Jackson /. D., Classical Electrodynamics, 2nd edition, Wiley, New York,
1975, p. 94; Hall R. N., J. Appl. Phys., 20, 925 (1949).
13. Ball R. C, Witten T. A, Jr., Phys. Rev., A29, 2966 (1984).
14 Meakin P., Majid I, Havlin S., Stanley H. E., J. Phys., A17, L975 (1984).
15. Muthukumar M., Phys. Rev. Lett., 50, 839 (1983).
Tokuyama M., Kawasaki K., Phys. Lett, 100A, 337 (1984).
Модель «угол конуса»
и анизотропия роста
ограниченных диффузией
кластеров
Дж. Росси, Б. Томпсон, Р. Болл,
Б. Брэди *
Результаты численного моделирования ограниченных диффузией
кластеров, выросших в соответствии с анизотропными правилами
присоединения, свидетельствуют в пользу новой модели роста
кластеров, ограниченных диффузией. Эта модель ДОА устанавливает
связь между показателями, управляющими ростом ограниченного
диффузией кластера, и его общей формой. В случае одноосного
анизотропного присоединения модель предсказывает существование
универсальных показателей. В случае обычной ДОА модель
позволяет получить хорошую оценку фрактальной размерности.
1. Введение
Мы излагаем в настоящей работе новую модель,
которую в дальнейшем условимся называть моделью «угол конуса»,
для описания роста ограниченных диффузией кластеров [1, 2].
Она состоит из некоторого набора масштабно-инвариантных
соображений, позволяющих установить связь между
крупномасштабными свойствами кластера (в особенности формой его
выступов) и показателями, характеризующими его рост. Наша
картина основана на детерминистической модели роста, но в то же
время учитывает усредненно (эффективно) стохастическую
природу процесса.
Идеи, лежащие в основе нашей модели, мы апробировали,
исследуя ограниченные диффузией кластеры, выросшие в
соответствии с анизотропными правилами присоединения [3] на
двумерной квадратной решетке. Правила, использованные нами при
численном моделировании роста кластеров, сводятся к
следующему. Частица запускается из случайно выбранного узла на
окружности, внутри которой находится кластер, и совершает
случайное блуждание [4] до тех пор, пока не попадет в узел
решетки, соседней с кластером. Частица присоединяется к
кластеру (а новая частица запускается), если ближайший сосед
справа или слева от достигнутого узла решетки занят. В
противном случае присоединение происходит только с вероятностью
р (рис. 1). Если частица не присоединяется к кластеру, она
продолжает совершать случайные блуждания, но не может
попадать в уже занятые узлы решетки. Частица уничтожается
* Giuseppe Rossi, Bernard R. Thompson, Robin C. Ball, Robert M. Brady
TCM Group, Cavendish Laboratory, University of Cambridge, Madingley Read,
Cambridge CB3 OHE, UK.
322
Часть V(6)
(а новая частица запускается),
если она, совершая случайное
блуждание, удаляется от центра
кластера более чем на 200
радиусов кластера.
Результаты проведенного
нами численного моделирования
убедительно свидетельствуют в
пользу модели «угол конуса».
Полученные данные показывают,
что при любом значении р,
меньшем единицы, характерные
размеры кластера в направлении
легкого (л:) и трудного (у)
роста в пределе при iV->oo (N—
число частиц в кластере)
возрастают соответственно как N2/s и
Nl/Z. Это означает, что при
любой наложенной одноосной
анизотропии кластер в конечном
счете вырастает в компактный
объект, напоминающий по форме
стержень (компактность в
данном случае означает, что
площадь, покрываемая кластером,
возрастает линейно по N).
Соображения, опирающиеся на модель
«угол конуса», позволяют
предсказать такой результат.
Если те же рассуждения,
которые были использованы нами
для случая анизотропного
присоединения, применить к обычной
ДО А (р = 1), то возникают
приближенные оценки фрактальной
размерности Д весьма близкие к
значениям, полученным с
помощью численного
моделирования. В частности, в двумерном
случае модель угол конуса
предсказывает значение D = 5/3.
2. Модель «угол конуса»
Начнем с рассмотрения
обычного ограниченного диффузией
Модели необратимого роста
323
кластера, состоящего из N частиц и имеющего максимальный
радиус R. Вероятность ф(т) найти диффундирующую частицу в
определенном месте г вне кластера удовлетворяет уравнению
Лапласа V2^(r) =0 с поглощающим граничным условием # —0
в точках, смежных с кластером. Поток диффундирующих частиц,
приходящий к данному поглотителю, пропорционален
нормальной (относительно поверхности кластера) производной от ф в
точке, где находится поглотитель.
Электростатическим аналогом такой ситуации является
задача о заряженном проводнике, имеющем форму кластера.
В частности, электрическое поле (или плотность поверхностного
заряда) в точке на поверхности проводника служит аналогом
потока, приходящего в эту точку. Электростатической аналогией
можно воспользоваться для того, чтобы сформулировать на
знакомом языке такие задачи, как, например, нахождение
зависимости производной dN/dR от R. Действительно, dN/dR =
= (dN/dt) (dt/dR), где полный поток частиц dN/dt, приходящий
к кластеру, соответствует полному заряду, а скорость роста
наиболее далекого от центра выступа dR/dt пропорциональна
потоку случайно блуждающих частиц, приходящему к этому
выступу, т. е. плотности заряда на выступе.
Так как ограниченные диффузией кластеры являются
стохастическими фракталами, можно ожидать, что N ~ RD, т. е.
dN/dR ~ RD~K Сравнивая это выражение с выражением для
dN/dR, полученным из электростатики, мы должны получить
оценку фрактальной размерности D. Например, в двумерном
случае, так как D — нецелое число, можно ожидать, что решение
электростатической задачи приведет к зависимости dN/dR от
R, выражающейся нецелой степенью R.
Модель «угол конуса» состоит в замене электростатической
задачи, связанной с сложной фрактальной геометрией
ограниченного диффузией кластера, более простой задачей, связанной с
вполне обозримой геометрией, которая, однако, позволяет
получить вполне удовлетворительную оценку степенной зависимости
от R для dN/dR. Оказывается, что по крайней мере в случае
кластеров, выросших в соответствии с правилом анизотропного
присоединения, вводимая таким образом простая
легкообозримая геометрия непосредственно связана с крупномасштабной
формой кластера.
В двумерном случае простейшей геометрией, порождающей
нецелую степенную зависимость от R производной dN/dR,
является геометрия конуса. Действительно, рассмотрим решение
уравнения Лапласа для проводящего бесконечного конуса с
половиной внешнего угла р (рис. 2), задаваемое выражением
ф (г, $) = Cr*№ cos (яФ/2р),
(1)
324
Часть V(6)
где С—нормирующий множитель. Таким образом, поток
совершающих случайное блуждание частиц, надвигающийся на острие
конуса, на расстоянии р от его вершины равен
г/(р) = (я/(2р))Ср^)-1. (2)
Производную dN/dt мы найдем, интегрируя а(р) от р = 0 до
верхней границы обрезания р ~ /?, а производную dR/dt—
интегрируя и(р) до нижней границы обрезания р ~ а (а —
размеры диффундирующей частицы или постоянная решетки, в даль-
Рис. 2. Геометрия модели «угол конуса».
нейшем принимаемые за единицу). Таким образом, из
выражения (2) мы получаем, что dN/dt ж СЯл/{2^ и dR/dt = С,
поэтому
dR/dN ~ /J-*/<*>. (3)
Отсюда мы заключаем, что для получения нецелой степенной
зависимости dN/dR от R необходимы геометрии с острыми
углами (такие, как конусы и многоугольники). Что же касается
гладких геометрий (например, окружностей), то они порождают
только целые степени. Иначе говоря, для воспроизведения
неаналитических свойств стохастического фрактала необходима
структура с особенностями, связанными с острыми углами.
До сих пор мы не предпринимали никаких попыток связать
угол р с геометрическими характеристиками кластера. В
действительности же уравнение (3) можно рассматривать просто
как определение эффективного угла (Зэфф, связанного с
размерностью D соотношением
/>=1 + я/(2Рафф). (4)
Наша модель не позволяет предсказывать значение D.
В случае ограниченных диффузией кластеров, выросших в
соответствии с анизотропным правилом присоединения, введенный
выше угол конуса допускает естественную интерпретацию: угол
Р нетрудно связать с ромбовидными очертаниями таких
фракталов. Трудно удержаться от искушения рассматривать
ромбовидную геометрию как имеющую самое непосредственное
отношение к определению показателей. Как будет показано в даль-
Модели необратимого роста
325
неишем, такой подход вполне разумен, т. е. позволяет
предсказывать значения показателей, согласующиеся с результатами
проведенных нами численных экспериментов.
3. Предсказания на основе модели «угол конуса»
Для решения задачи электростатики с ромбовидной
геометрией можно воспользоваться отображением Шварца — Кристоф-
феля [3, 5]. Однако тот же результат может быть получен и с
помощью того же рассуждения на уровне здравого смысла,
которое привело к уравнению (3), т. е. к вершинам ромба,
обращенным по направлениям осей х и у (рис. 3). Для скорости ро-
Рис. 3. Ромбическая геометрия.
ста расстояний X и У между противоположными вершинами
ромбовидного кластера получаются следующие уравнения:
dX
■dN-AR-«V>*\ (5)
= в#-л/(21Ч (6)
dY
dN
где R== (1/2) (X2 + У2)1/2 есть длина стороны ромба, А и В —
масштабные множители порядка единицы (они могут быть
медленно изменяющимися функциями от Ху У и р). Так как (3* —
= я —arctg(y/X) и ру = я/2 +arctg(y/X), показатели в
правых частях уравнений (5) и (6) зависят только от отношения
Y/X ширины ромба к его длине.
Следует подчеркнуть, что уравнения (5) и (6) являются
континуальными: они относятся к средним скоростям роста длины
и ширины кластера [5].
Можно ожидать, что для ограниченных диффузией кластеров,
выросших при р < 1, углы будут удовлетворять неравенству
&х > ру, т. е. dX/dN > dY/dN. Иначе говоря, уравнения (5) и
(6) показывают, что у ограниченных диффузией кластеров,
выросших в соответствии с анизотропным правилом присоединения,
326
Часть V(6)
поперечник X растет быстрее, чем поперечник У.
Следовательно, с увеличением N кластер приобретает все более вытянутую
форму и в пределе напоминает стержень, характеризуемый
углами р* = я и $у = я/2. Соответственно уравнения (5) и (6)
переходят в соотношения dX/dN ~ Х-1/2 и dY/dN ~ Х"19 откуда
в пределе при JV-> oo получаем
X~N2*\
Y~N4*9 (7)
и область, занятая кластером, растет линейно по N.
При обычной ДОА никакого различия между
направлениями роста X и У не существует: если экстраполировать на этот
случай описание роста при анизотропном присоединении частиц,
то окажется, что на протяжении всего процесса роста А = 5,
Р* = Ру = Зя/4, из чего в свою очередь следует, что R ~ N3/5,
т. е. D = 5/3. (Заметим, однако, что обычные ограниченные
диффузией кластеры, выращиваемые отдельно, не обнаруживают
сколько-нибудь выраженной ромбовидной формы.) Этот вывод
находится в удовлетворительном согласии с результатами самых
последних численных экспериментов [2, 6], дающих D = 1,71 ±
±0,01.
Приведенные выше соображения допускают обобщение на
случай евклидовой размерности больше 2 (см. [3]), например
при rf = 3 мы получаем D=2,46, а при d = 4 — размерность
Хаусдорфа D = 10/3, что также хорошо согласуется с
результатами численного моделирования [7].
4. Результаты численного моделирования кластеров,
выросших в соответствии с правилом
анизотропного присоединения
С помощью описанного во введении алгоритма мы в ходе
численных экспериментов вырастили по крайней мере семь
кластеров, содержавших до 10б частиц, при семи различных
значениях р от р = 1/50 до р = 2/3. (Остальные результаты этих
экспериментов обсуждаются в [5].)
Показатели, управляющие ростом таких кластеров, могут
зависеть от числа частиц N и вероятности р присоединиться в
направлении у. Пусть Xg — среднеквадратичная длина, Yg —
среднеквадратичная ширина (эти величины можно рассматривать
как анизотропные аналоги радиуса гирации). Показатели Dx и
Dy можно измерить, предположив, что
Ye~Nu\
(8)
Модели необратимого роста
327
Если изложенная выше модель угол конуса правильна, то
можно ожидать, что 1) при достаточно больших N показатели
Dx и Dy стремятся соответственно к 3/2 и 3 независимо от
величины р и что 2) Dx и Dy — две универсальные функции
отношения Y/X ширины кластера к его длине. Для проверки этой
возможности мы измерили Dx, Dy и Y/X как функции от N для
каждого кластера. Для каждой серии кластеров при
определенном значении р мы получили средние <£>*> и <Д,> при заданных
Т.1 1 I 1 1 L-I 1—1 1 1 1 1 L-I I I I \ t » ' t
Рис. 4. Измеренные значения Dx (нижние данные) и Dy (верхние данные)
как функции от <УД>. Различные группы экспериментальных точек
соответствуют различным значениям р (слева направо): р = 1/50 (кружки), р =
= 1/20 (треугольники), р = 1/10 (квадраты), р = 1/5 (кружки), р = 1/3
(треугольники), р = 1/2 (квадраты), р — 2/3 (кружки). Данные при
различных значениях р, обозначенные одинаковыми символами, не перекрываются.
Непрерывные кривые соответствуют теоретическим предсказаниям.
N и нанесли их на график в зависимости от среднего
отношения (У/Ху ширины кластера к его длине. Результаты такого
построения представлены на рис. 4. Оказалось, что данные о
кластерах, выросших при различных значениях р, в хорошем
приближении можно считать лежащими на одной кривой. Это
свидетельствует о том. что вывод «2» действительно верен.
Показатели Dx и Dy по мере того, как кластеры становятся все более
удлиненными, по-видимому, выходят на свои асимптотические
значения.
328
Часть V(6)
Если воспользоваться уравнениями (5) и (6), предположив
дополнительно, что коэффициенты А и В не зависят от р, то
возникает возможность теоретических предсказаний вида
зависимостей Dx и Dy от Y/X. Действительно, рассмотрим, например,
уравнение (5): при Y/X, принадлежащих достаточно малой
окрестности некоторого значения УоДо, Для показателя
vx(Y/X) = n/(2.px(Y/X)) (9)
допустимо разложение в ряд Тейлора по степеням {{Y/X) —
— (Yo/Xo)). Пренебрегая членами первого порядка, получаем
^~АХ-"*, (10)
где v^— значение показателя v* при Y/X = YQ/X0. Следовательно,
Dx<yjX0) = v»+l. (И)
Аналогичное рассмотрение уравнения (6) приводит к
Dy (YQ/X0) = (v*0 + l)/(v*0 - v„. + 1). (12)
Эти приближенные выражения для Dx и Dy порождают
непрерывные кривые, изображенные на рис. 4 (заметим, что обе
кривые не зависят от значений А и В). Согласие с результатами
численных экспериментов и на этот раз превосходное.
Следует подчеркнуть, что для получения своих результатов
мы использовали наложенную одноосную анизотропию, но не
тип решетки, на которой росли кластеры. Это в равной мере
относится и к показателям анизотропной ДОА в пределе при N-+-
->■ оо (как мы надеемся, точном), и к нашим оценкам
фрактальной размерности обычной ОДК (которые можно
рассматривать только как приближенные). В действительности мы
выращивали наши анизотронпые кластеры на квадратной решетке,
но считаем, что их общие ромбовидные очертания (игравшие
важную роль в наших рассуждениях) являются следствием
введенной нами одноосной анизотропии [8] и в той же мере
присущи кластерам, выращенным вне решетки или на решетках
конфигурации, отличной от квадратной.
5. Выводы
Резюмируя, можно утверждать, что предложенная нами
модель «угол конуса» связывает показатели ДОА с
крупномасштабной формой кластеров. Анизотропные правила присоединения
позволяют дать естественное определение того, что понимается
под крупномасштабной формой, и тем самым открывают путь к
количественным предсказаниям. В частности, предсказанное на
основе нашей модели универсальное поведение X ~ N2/3, Y ~
Модели необратимого роста
329
~ Nl/3 (при N-+oo) согласуется с всеми имеющимися данными
численного моделирования.
Благодарности. Дж. Росси хотел бы выразить свою
благодарность SERC (Великобритания), а Б. Томпсон — NSERC
(Канада) за финансовую поддержку. Б. Томпсон признателен также
Королевскому колледжу в Кембридже и Кембриджскому фонду
Британского содружества наций.
ЛИТЕРАТУРА
1. mtten Г. Л., Sander L. M., Phys. Rev. Lett., 47, 1400 (1981).
Witten Т. Л., Sander L. M., Phys. Rev., B27, 5686 (1983).
2. Meakin P., Sander L. M., Phys. Rev. Lett., 54, 2053 (1985).
3. Ball R. C, Brady R. M., Rossi G., Thompson В. Д., Phys. Rev. Lett., 55,
в печати.
4. Brady R M., Ball R. C, J. Phys. А, в печати.
5. Томпсон Б. и др. — наст. сб. с. 330.
6. Meakin P., Bull. Amer. Phys. Soc, 30, 222 (1985).
7. Meakin P., Phys. Rev., A27, 1495 (1983).
8. На этом симпозиуме П. Микин сообщил данные о росте кластеров в
условиях симметрии с различной анизотропией.
Рост анизотропных ограниченных
диффузией кластеров
Б. Томпсон, Дж. Россы,
Р. Болл, Р. Брэди*
Выведены уравнения, описывающие эволюцию ограниченных
диффузией кластеров, выросших в соответствии с правилами
анизотропного присоединения. Показано, что предсказания, сделанные
на основе этих уравнений, дают хорошее согласие с результатами
численного моделирования.
В первой части этой работы мы опишем результаты
численного моделирования роста кластеров в модели ДОА [1] для
двумерного случая с правилами анизотропного присоединения
[2, 3]. Затем мы выведем уравнения описывающие рост таких
кластеров в рамках модели «угол конуса» (в предположении,
что общие очертания кластера имеют ромбовидную форму). Ив
заключение—сравним решения выведенных уравнений с
результатами численного эксперимента и убедимся в
превосходном согласии. Нашу работу надлежит читать после работы [2],
помещенной в этом же сборнике. В работе [2] изложены
модель «угол конуса» роста ограниченных диффузией кластеров и
алгоритм, используемый для построения ограниченных
диффузией кластеров, растущих по правилам анизотропного
присоединения.
На рис. 1 показаны различные стадии развития кластера при
р = 1/5 (здесь р — вероятность присоединения в направлении у;
вероятность присоединения в направлении х равна 1). Нетрудно
видеть, что кластер становится все более продолговатым
(отношение его ширины к длине Y/X убывает) и компакным по мере
того, как возрастает число частиц N. Крупномасштабные
очертания кластера вырисовываются все более четко по мере того,
как увеличиваются его размеры.
Нам удалось вырастить по крайней мере 7 двумерных
кластеров, содержащих 50 000 и более частиц, при каждом из
следующих значений р: 1/50, 1/20, 1/10, 1/5, 1/3, 1/2 и 2/3. Для
каждого кластера мы измеряли расстояния X и У между
выступами (т. е. разности (в постоянных решетки) между
максимальной и минимальной абсциссами и ординатами) как функции
числа частиц N в кластере. На рис. 2 среднее отношение ширины
кластера к его длине представлено как функция от N для
кластеров, выросших при различных значениях р. Мы видим, что
при любом значении р величина (Y/X} при возрастании N
убывает. Модель угол конуса предсказывает, что в пределе при
* Bernard R. Thompson, Giuseppe Rossi, Robin С. Ball, Robert M. Brady-
TCM Group, Cavendish Laboratory, Madingley Road, Cambridge CB3 OHE, UK.
Модели необратимого роста
331
JV ->- оо и всех значениях р, меньших единицы, <Х> « N2/z и
<У> ~ N1/3, вследствие чего <У/Х> ~ Л^/3 и <*><У> ~ N. Таким
•^^^^^
Рис. 1. Кластер, выросший в соответствии с правилами анизотропного
присоединения (р = 1/5), на различных стадиях развития. Кластеры содержат
(сверху вниз) N = 5, 10, 20, 30, 40 и 50 тыс. частиц. Отрезок вверху
соответствует 500 постоянным решетки.
образом, при N-+-oo кластер становится компактным стержне-
видным объектом. На рис. 2 мы видим, что асимптотический
угловой коэффициент близок к теоретическому значению —1/3 при
малых р уже при N ~ 104. На рис. 3 отношение ширины
кластера к его длине <У/Ху представлено как функция от <Х>.
Модель угол конуса предсказывает, что (Y/X} ~ <Х>~1/2 в пределе
<Y/X)
1,00 A
0,99 4
0,9Br
» t » i t it ■
100
ttttj-
10000
100000
Рис. 2. Средние измеренных отношений ширины кластера к его длине <УД>
как функция числа частиц N. В выбранных точках указаны интервалы
ошибок. Кривые соответствуют р = 2/3, 1/2, 1/3, 1/5, 1/10, 1/20 и 1/50 (сверху
вниз). Линейные участки имеют предсказанный угловой коэффициент, равный
-1/3.
'I ' ' ■ ' ' I ' ■ ' J • • ч |
100 ЮОО X
Рис. 3. Средние измеренных отношений ширины кластера к его длине <Щ>
как функция от <Х>. В выбранных точках указаны интервалы ошибок.
Кривые соответствуют р = 2/3, 1/2, 1/3, 1/5, 1/10, 1/20 и 1/50 (сверху вниз).
Линейные участки имеют предсказанный угловой коэффициент, равный -—1/2.
Модели необратимого роста
333
при <Х> ~ оо. И на этот раз согласие теории с численным
экспериментом при малых р превосходное.
Воспользуемся теперь соображениями, исходящими из
модели угол конуса, для вывода уравнений, описывающих
эволюцию ограниченных диффузией кластеров, растущих по правилам
анизотропного присоединения частиц. Это позволит нам
сравнить теорию с данными численного эксперимента вдали от
асимптотического режима.
Ограниченные диффузией кластеры, выросшие в
соответствии с правилами анизотропного присоединения, имеют общие
очертания, поразительно напоминающие по форме ромб (в чем
легко убедиться, взглянув на рис. 1), поэтому их естественно
моделировать как идеально поглощающие ромбы. Проблемы,
возникающие в связи с такой моделью, мы рассматриваем ниже.
На этом уровне рост кластера полностью описывается
величинами dX/dN и dY/dN — скоростями роста длины и ширины
кластера по мере присоединения к нему новых частиц. Чтобы найти
скорость роста ширины X и длины У, рассмотрим сначала
стационарные потоки частиц их и иу, приходящие к выступам
кластера по оси х я у. Затем отождествим их и иу с скоростями
роста длины и ширины кластера (ромба) по времени —
величинами dX/dt и dY/dt. Компоненты их и щ мы находим, решая с
помощью отображения Шварца — Кристоффеля уравнение
SJ2<}> = 0 с граничными условиями ф = 0 на границе ромба и
ф(т)-^\пг при г->оо. Полученное нами решение имеет вид
ux~cm){9*iRp2*x)-{> (о
uy^C(l/R)(9yfRf/2^-\ (2)
где (см. рис. 3 в работе [2]) R = (1/2) {X2 + У2)1/2 —длина
любой из сторон ромба, X и У—его длина и ширина, измеряемые
от вершины (выступа) до вершины, $х = п — arctg(y/X), py ф
= (it/2) + arctg(УД"), р* и ру — расстояния вдоль сторон ромба
от его вершин, лежащих на оси, параллельной оси х и оси у. Мы
находим также, что по теореме Гаусса общий поток частиц,
приходящий к ромбу, dN/dt ~ С, не зависит от R.
Во избежание расходимости в потоке на вершинах ромба
обрезание мы производим на малом расстоянии р ~ а, где а —
радиус выступа кластера или постоянная решетки. Это необходимо
из-за конечных размеров диффундирующих частиц: выступ
кластера должен иметь конечную кривизну в отличие от
бесконечной кривизны «колющихся» вершин ромба, порождающих
расходимости в потоках их и иу в вершинах ромба. Заметим, что,
умножив стационарные потоки, приходящие к вершинам ромба,
на диаметр частиц, мы получим временные скорости
распространения выступов (\/2)dX/dt и (l/2)dY/dt. Таким образом, спра-
334
Часть V(6)
ведливы следующие уравнения:
dX/dN = (dX/dt) {dt/dN) = Л/ГЯ/(2|Ч (3)
dY/dN = (dY/dt) (dt/dN) = BR~n№y\ (4)
Коэффициенты Л и В по порядку величины равны 1, но могут
быть медленно меняющимися функциями от X, Y и от р.
Относительно уравнений (3) и (4) следует сделать несколько
замечаний, а) Моделирование кластеров, выросших в
соответствии с правилами анизотропного присоединения, как идеально
поглощающих ромбов означает, что мы заменили проблему
описания стохастического роста объектов иррегулярной формы
простой задачей описания детерминистического роста. При этом нас
интересует рост не всего ромба, а лишь то, каким образом
растут его «выступы» — вершины. Заметим, что при наших
предположениях форма ромба не сохраняется, б) Мы исходили из
предположения о том, что ограниченные диффузией кластеры,
выросшие с анизотропными вероятностями присоединения, допустимо
моделировать как идеальные поглотители, хотя при р < 1
приходящие частицы не обязательно присоединяются к кластеру с
первого соприкосновения. Идеальность поглотителя в данном
случае означает, что каждая частица присоединяется к кластеру
вблизи точки первого контакта с ним. Среднее расстояние
между точками первого и последнего контактов не зависит от
размеров кластера, и поэтому в том масштабе, в котором
выполняются наши уравнения, присоединение частиц носит локальный
характер, в) Следует заметить, наконец, что уравнения (3) и
(4) континуальные; они относятся к средним скоростям роста
длины и ширины кластера.
Для проверки уравнений (3) и (4) путем сравнения
основанных на них предсказаний с результатами численного
эксперимента мы заметили, что исключение N позволяет свести эти
уравнения к следующему:
d (Y/X)/dX = (В/А) (1/Х) R~n№y)+n№*) - (ГД2). (5)
Это уравнение было проинтегрировано численно. Коэффициент
(В/Л) мы предполагали постоянным, выбирая его значения так,
чтобы кривая Y/X как функция от X проходила через
экспериментальные точки (результаты численного моделирования) при
значениях X, соответствующих N = 10 000 и N = 50 000 частиц.
Такая подгонка кривых производилась при р= 1/3, 1/10 и 1/50.
Результаты подгонки кривых представлены на рис. 4.
Непрерывные кривые на рис. 4 получены с помощью интегрирования
уравнения (5), а интервалы ошибок указаны для результатов
численного моделирования, представленных на рис. 3. Согласие
превосходное, если учесть приближения и допущения, принятые
Модели необратимого роста
335
при выводе уравнений (3) и (4). При больших значениях р
согласие ухудшается. Мы в праве ожидать, что любой алгоритм
подгонки кривых будет лучше работать при меньших значениях
<У/*>
7,00-
0,99 Л
гооо гбоо
Рис. 4. Двухпараметрическая подгонка уравнения (5) к результатам
численного эксперимента. Кривые соответствуют р= 1/3, 1/10 и 1/50 (сверху вниз).
р, так как с убыванием р выход на асимптотический режим
происходит быстрее.
ЛИТЕРАТУРА
1. Witten Т. Л, Sander L. М, Phys. Rev. Lett, 47, 1400 (1981).
Witten T. A., Sander L. AT, Phys. Rev, B27, 5686 (1983).
2. Росси Дж. и dp.— каст. сб. с. 321.
3. Ball R. С, Brady R. M, Rossi G, Thompson B. R.y Phys. Rev. Lett, 55,
в печати.
Континуальная ДОА:
случайный фрактальный рост,
порождаемый детерминистической
моделью
Л. Сандер *
С теоретической и экспериментальной точек зрения рассмотрена
роль шума в ограниченной диффузией агрегации. Предложена
детерминистическая модель, показывающая, что фрактальный рост от
случайного начала обладает многими характерными особенностями
ДОА.
1. Введение
В последнее время внимание исследователей привлекло
необратимое объединение частиц в кластеры. Стало понятно, что
именно кластеризация является одним из способов
возникновения фракталов в необратимых процессах. Виттен и Сандер [1,
2] предложили модель такого рода — модель
диффузионно-ограниченной агрегации (ДОА), ставшей предметом интенсивных
исследований. Модель очень проста: совершающие случайное
блуждание частицы в результате аккреции образуют кластер,
приходя по одной издали и присоединяясь либо к точечному
центру кластеризации, либо к ранее аккретировавшим частицам.
Интенсивные компьютерные исследования показали, что в
результате такого процесса образуются сложные разветвленные
фракталы (рис. 1).
Для того чтобы по достоинству оценить модель ДОА, лучше
всего рассмотреть начавшую складываться в последние годы
общую феноменологию других кинетических процессов,
сопровождающихся переходом из равновесного состояния в
неравновесное. Обычно мы можем выделить три динамических режима
(конвекция Рэлея —Бенара служит.хорошим примером): 1)
режим, близкий к равновесному; 2) образование структур иЗ)
хаотический режим. В задаче Рэлея — Бенара они соответствуют
режимам теплопроводности, образованию конвективных
валиков и турбулентности. Как будет показано дальше, эти же
режимы удается обнаружить и в процессах, ограниченных
диффузией. Это обстоятельство позволяет понять существенные
особенности модели ДОА, которая до сих пор, несмотря на свою
предельную простоту, упорно сопротивлялась попыткам
аналитического объяснения.
Связь между ДОА и затвердеванием в виде дендритов
известна уже в течение некоторого времени [1]. В дальнейшем мы
* Leonard M. Sander • University of Michigan, Department of Physics, Ann
Arbor Michigan, 48109—1120.
Модели необратимого роста
337
Рис. 1. Кластер в модели ДО А.
рассмотрим ее более подробно, а пока достаточно сказать, что
диффузию скрытой теплоты от растущего кристалла мы
отождествляем с движением случайно блуждающих частиц к кластеру.
Ясно, что неравновесный кристалл, форма которого определяется
построением Вульфа, соответствует режиму «1», о котором
говорилось выше. Изящные формы снежинок соответствуют режиму
«2». Неупорядоченный,
хаотический рост кристалла,
отождествляемый нами с ДОА,
доведенной до конечного предела,
служит примером режима «3»
и порождает фрактальные
структуры.
В следующем разделе мы
обсудим некоторые конкретные
реализации процессов типа
ДОА, допускающих описание
на единой общей основе. Затем
мы рассмотрим роль шума и
анизотропии в ДОА с учетом
последнего эксперимента Бен-
Жакоба и др. [3]. Наконец, в
заключительном разделе мы с
помощью численного эксперимента рассмотрим модель
граничной поверхности для ограниченных диффузией процессов,
позволяющую достичь фрактального роста в отсутствие внешнего
шума.
2. Реализации ограниченного диффузией процесса
Наиболее точным из известных нам экспериментальных
примеров ДОА является электролитическое осаждение металлов на
небольшой электрод. Первым экспериментом такого типа,
проанализированным в терминах фрактального роста, был
эксперимент Брэди и Болла [4]. Наблюдавшийся ими процесс имел
много общего с трехмерной ДОА. Последовавшая затем работа
Мацуситы и др. [5] дала пример двумерного роста. Аналогия
с описанным выше процессом прямая: ионы меди или цинка
диффундируют, совершая случайные движения, в электролите при
соответствующих условиях до тех пор, пока не присоединяются
к уже осажденному металлу. Но поскольку осажденный металл
имеет поликристаллическую структуру, с кристаллитами
макроскопически малыми, но содержащими много атомов,
по-видимому, уместно отождествить размеры кристаллитов с размерами
частиц в исходной модели [4].
Для удобства дальнейших ссылок мы можем записать
систему уравнений, описывающих средний рост при таких уело-
338
Часть V(6)
виях. Для плотности ионов и (г, t) справедливо стационарное
уравнение диффузии с поглощающими граничными условиями
V2w = 0, (1)
и \s = 0 + обрезание, (2)
дополненными условием роста на границе
vn~nVu\St (3)
где \п — нормальная скорость роста частицы на границе.
Другой реализацией того же процесса является пробой
диэлектрика [6]. В этом случае введенную выше величину и мы
можем отождествить с электростатическим потенциалом в
материале. Условие (2) соответствует тому, что канал пробоя
приближенно можно считать эквипотенциальным с обрезанием на
расстоянии, определяемом характерным размером канала.
Наконец, условие (3) означает физическое допущение, согласно
которому скорость дальнейшего пробоя пропорциональна
электрическому полю в канале.
Используя величину vn, задаваемую соотношением (3), как
вероятность при численном моделировании, удалось показать
[6], что исследуемый процесс действительно эквивалентен ДОА.
В этом случае, как и в предыдущем, удается отождествить
макроскопическое обрезание и в явном виде понять роль
дискретности и шума (соответствующего дробовому шуму налетающих
частиц) в процессе. Однако и в данном случае, и в описываемых
далее случаях необходимо объяснить, каким образом дробовому
шуму удается породить крупномасштабные структуры
фрактальной природы, которые затем не усредняются.
В задаче об отвердевании мы можем отождествить и с Тт —
— Г, где Т— температура переохлажденного расплава, а Тт —
температура плавления. В пределе при очень медленном росте
скрытая теплота (производство которой на поверхности
задается соотношением (3)) диффундирует в соответствии с
уравнением (1). (В общем случае в левую часть уравнения (1) входит
член, зависящий от времени.) Однако обрезание в
рассматриваемой системе не связано явно с характерным размером
кристаллитов. Обычное поверхностное натяжение приводит к
обрезанию даже в случае роста отдельного кристалла. Напрашивается
вывод о том, что так происходит по следующей причине: в
рассматриваемом случае, когда не существует в явном виде ни
дробового шума, ни дискретности и система не может перейти в
режим «3» без какого-нибудь интенсивного внешнего источника
дробового шума, всегда наблюдается рост упорядоченных
структур, но никогда не наблюдается рост фракталов. На первый
взгляд кажется, что такое утверждение соответствует широкой
Модели необратимого роста
339
распространенности дендритов (к числу которых относятся,
например, снежинки). Как будет показано ниже, такое заключение
неверно, и физика отвердевания может в надлежащих условиях
порождать фракталы даже в отсутствие внешнего шума.
Наиболее ярким экспериментальным подтверждением этого
служит не эксперимент по отвердеванию, а некая разновидность
течения жидкости. Патерсон [7] заметил, что выписанное выше
уравнение с граничными условиями в точности совпадает с
уравнением и граничными условиями Саффмена и Тейлора [8],
рассматривавших образование вязких «пальцев» в жидкости.
В работе Саффмена и Тейлора речь идет о вытеснении вязкой
жидкости, текущей либо в пористой среде, либо в узком зазоре
между параллельными пластинками (ячейке Хеле-Шоу). В такого
рода системах скорость течения пропорциональна градиенту
давления в жидкости.
v ~ VP. (4)
Если одна вязкая жидкость вытесняется другой, вязкостью
которой можно пренебречь (и течет под более или менее
постоянным давлением), то граница раздела между жидкостями
обретает сложную структуру: возникают так называемые
вязкие пальцы.
Мы можем принять и = Р — Ро, где Ро— постоянное
давление вторгающейся жидкости. Тогда в случае несжимаемой
жидкости уравнение (1) следует из уравнения (4). Соотношение (2)
выполняется для скачка давления на границе жидкости с
обрезанием, обусловленным обычным граничным условием
поверхностного натяжения:
u\s = d%, (5)
где d — капиллярная длина, % — кривизна. Ясно, что
соотношение (2) служит подходящим граничным условием для
соотношения (4).
Указанное течение жидкости имеет особое значение для
понимания ДОА, так как в такой системе на масштабе,
превосходящем размеры отдельных молекул, нет дискретности. Если в
ней образуются сложные ветвящиеся структуры,
напоминающие ограниченные диффузией кластеры, и если структуры имеют
фрактальную природу, то это означает, что нам удалось достичь
существенного продвижения в понимании процесса роста.
Действительно, в большинстве исследований процесса роста
не удалось получить разветвленные структуры, так как
эксперименты производились в обычной геометрии Хеле-Шоу —
длинном канале с непроницаемыми стенками. Стенки канала
направляли поток и порождали единственный «палец». Но Патерсон
показал экспериментально [9], что радиальная геометрия
(менее вязкая жидкость впрыскивается в центре пластины, откры-
340
Часть V(6)
той по краям) не обладает указанной особенностью и что
ветвящиеся структуры могут быть получены. Бен-Жакоб и др. [3]
также занялись этой проблемой и показали, что фрактальная
размерность структур приблизительно совпадает с фрактальной
размерностью ограниченных диффузией кластеров. Тем самым
была показана возможность кластеризации частиц без частиц.
3. Неустойчивости, шум и анизотропия
Приведенные выше соображения позволяют нам
предположить, что дискретность и шум несущественны для возникновения
случайных фрактальных структур типа ограниченных диффузией
кластеров. Разумеется, для того чтобы в системе могли
возникнуть фрактальные хаотические структуры, некоторая
случайность все же необходима. Однако мы считаем, что процесс роста
в основном имеет детерминистический характер и что начальные
стадии роста, когда дробовой шум существует в масштабе
кластера, служат своего рода начальным условием для
последующих стадий. Случайные начальные условия в свою очередь
создают зародыши неустойчивостей, которые развиваются и
взаимодействуют, порождая фрактальные структуры. Такая точка
зрения принята в работе [3], где на основе экспериментальных
наблюдений высказывается предположение о том, что
существенной является именно та неустойчивость, которая приводит к
разделению концов вязких пальцев в отсутствие направляющего
механизма, например стенок-сторон в ячейке Хеле-Шоу.
В задаче о росте дендритов структуры, напоминающие по
внешнему виду снежинки, возникают из-за другого
направляющего механизма — анизотропии кристалла [10, 11]. Самые
первые исследования по этому вопросу проводились в пределе,
противоположном тому, который связан с моделью ДОА, где правая
часть уравнения (1), которую нам пришлось положить равной
нулю, указывает на физику процесса и вводит в задачу еще один
масштаб — длину диффузии. Именно существование этого
нового масштаба исключает фрактальную автомодельность
рассматриваемой разновидности отвердевания, но при малой
анизотропии разделение концов существует и наблюдается.
Экспериментальное доказательство того, что такой переход
происходит даже в пределе бесконечной длины диффузии (т. е.
когда выполняется уравнение (1)), приведено в работе [3].
Авторы нанесли решетку на одну из пластин радиальной ячейки
Хеле-Шоу. Наблюдался четкий переход от разделения концов
пальцев при малых скоростях течения к ориентированным
структурам, напоминающим по виду снежинки, при быстром течении.
Таким образом, проблема роста кристалла с превалирующим
образованием структуры, по-видимому, получает свое решение, воз-
Модели необратимого роста
341
можно, не окончательное. В большинстве случаев анизотропия
кристалла слишком велика для того, чтобы можно было
наблюдать фрактальные структуры.
4. Континуальная ДОА
Опираясь на изложенные выше представления, мы пришли к
необходимости пересмотреть теоретические основы фрактальной
кластеризации так, чтобы четко выделить роль шума в
создании начальных условий и управлении ростом. Для этого мы
предложили формулировать задачу в терминах движения
поверхности раздела, подпитываемой случайно блуждающими
частицами. Введенные ранее уравнение и условия удобно записать
в следующем виде:
V2^ = 0, (6a)
Уп = — nVu |5/4я, (66)
u(R0) = 09 (6в)
u(xs)=l —k(xs), (6г)
*Фвнутр)=К (6д)
На большом расстоянии R0 поле и поддерживается равным
нулю; внутри области, ограниченной поверхностью раздела, оно
равно единице; n(xs) означает кривизну поверхности раздела в
точке xs, vn — нормальная скорость поверхности раздела.
Форма обрезания соответствует задаче о вязких пальцах, но
пригодность ее в рамках модели ДОА остается под сомнением.
Действительно, граничное условие при численном
моделировании на основе ДОА включает только обрезание на малом
расстоянии, соответствующем размерам частиц. К этому вопросу
мы еще вернемся. Но какое-то обрезание все же необходимо —
в противном случае на поверхности раздела возникают
нефизические острия [12]. Решать уравнения (6) прямыми (например,
релаксационными) методами достаточно трудно. Однако
недавно было показано [13], что более эффективное решение может
быть достигнуто путем перехода к интегро-дифференциальному
уравнению
1 + 1ST j dxs'% (Xs'}dG (*s> х$')1дп'=
= J dxs'G (xS) xS') vn (xs')> (7)
где G(xy у)—функция Грина для двумерного уравнения
Лапласа. Интеграл в левой части уравнения (7) есть не что иное,
как потенциал двойного слоя величины —к/4к, создающий
скачок поля от 1 до 1—%{xs) на поверхности раздела. Уравнение
342
Часть V(6)
(7) мы обращаем численно, заменяя непрерывные величины
дискретными и переходя к матричному уравнению. Найдя vn,
сдвигаем поверхность раздела на один шаг по времени.
Результат численного моделирования показан на рис. 2, где
при асимметричных начальных условиях образовалась
разветвленная структура. К сожалению, из-за ограниченных
возможностей компьютера мы не можем продолжить решение
достаточно далеко для того, чтобы посмотреть, напоминает ли оно
Z000
юоо U
-1000
-2000
-2000 -1000 Q 7000 2000
Рис. 2. Численное решение уравнений (6).
тонкие разветвленные структуры, возникающие в модели ДОА.
Предположим, однако, что мы произвольно модифицировали
уравнение (7) следующим образом:
1
+ -^ \ dxKN dG/dn = J dxGvn.
(8)
Мотивы такой замены в случае ДОА ясны, так как большие
кривизны и ^ 1/а запрещены, а меньшие не приводят к нужному
эффекту. При больших N мы достигаем указанного предела, и
скорость разделения концов значительно возрастает. Но для
течения жидкости условие (6г) физически корректно.
Теперь мы можем обратиться к вопросу о характере
структур, порождаемых уравнениями (6) при различных граничных
условиях, задаваемых уравнением (8). Значения N до 5
достаточно велики для того, чтобы прояснить вопрос. Выбрав
начальное условие с осью симметрии 4-го порядка при R = 20 и бт =
= 0,05, решим уравнения (6) с учетом уравнения (8) при N = 5.
Мы получим результаты, представленные на рис. 3. Отчетливо
видно существование разветвленной структуры с
последовательным разделением концов выступов и сходство между
численными результатами и структурами, наблюдаемыми в ячейке Хеле-
Модели необратимого роста
343
Шоу в экспериментах Бен-Жакоба и др. [3] и Патерсона [9].
Мы считаем, что если бы нам удалось продолжить рост нашей
структуры, то она достигла бы тонкости, присущей структурам
ДОА. Заметим, например, что толщина ветвей на рис. 3 не
возрастает столь же быстро, как размеры структуры. Мы
убеждены, хотя нам и не удалось доказать это, что даже при N = 1
наша структура может стремиться к фрактальному пределу.
k . i .... i .... i.... i i..-
-200 -100 О 10Q 20Q
Рис. 3. Численное решение уравнений (6) при ЛГ = 5.
Фрактальную размерность объектов на рис. 3 можно
вычислить, измеряя закон изменения площади в зависимости от
радиуса гирации Rg:
A~RDg. (9)
Для структур, изображенных на рис. 3, мы получили Z> = 1,72.
Аналогичная ситуация наблюдается и при N = 3.
Наконец, мы подвергли пересмотру роль вводимой
анизотропии [10, 11], варьируя граничное условие:
u(xs)=l —к~ vnf(0)9
f(0) = P(l —cosfl). ( }
Уравнение (7) при этом переходит в уравнение
1 + ^Г\ dx%dG/dn =\dx[G-(//4я)dG/дп]vn. (11)
Выбирая в качестве начального условия R = 200, бт = 0,05
и т=4 с параметром анизотропии (3 = 0,004, мы получаем
структуру с параболическим выступом и боковым ветвлением,
типичным для кристаллических дендритов в рассматриваемом
случае [10, 11]. Скорость вершины выступа по нашим наблюдениям
осциллирует с периодичностью, определяемой наступлением
бокового ветвления, и неустойчивость разделения выступа
оказывается превзойденной.
344
Часть V(6)
Выводы
В настоящей работе мы стремились показать, что модель,
тесно связанная с ДОА, достаточно неустойчива для того, чтобы
порождать фрактальный рост, и конкретные особенности
процесса кластеризации не играют сколько-нибудь существенной
роли. Полученные нами с помощью численных экспериментов
данные о фрактальной размерности и общем виде структур очень
напоминают аналогичные данные численных экспериментов по
ДОА и натурных экспериментов по образованию вязких
пальцев. Мы пытались пролить свет на эту проблему с помощью
континуальной аппроксимации ДОА. Заметим, что, даже если кто-
нибудь склонен принять наше рискованное предположение об
аналогии между случаем TV = 1 и всеми другими случаями, нам
удалось доказать возможность получения объектов,
напоминающих по своей структуре ограниченные диффузией кластеры,
вводя обрезание на некоторых коротких расстояниях.
ДОА реализуется путем увеличения числа неустойчивостей.
Если какая-то неустойчивая мода начинает расти, ее рост имеет
детерминистический характер, хотя чувствительная зависимость
его от начальных условий отнюдь не исключается. Короче
говоря, модель сама порождает свой собственный шум.
Благодарности. Вычисления, результаты которых приведены
в этой статье, выполнены совместно с Э. Бен-Жакобом и Р. Ра-
манлалом [14]. Мы хотели бы поблагодарить Р. Болла и Д. Кес-
слера за полезные обсуждения. Работа выполнена на средства
DoE (контракт DE-FG02-85ER45189).
ЛИТЕРАТУРА
1. Witten Т. A, Sander L. Ж, Phys, Rev. Lett, 47, 1400 (1981).
2. Witten Г. A, Sander L. M., Phys. Rev., B27, 5686 (1983).
3. Ben-Jacob E., Godbey R., Goldenfeld N.t Koplik /., Levine #., Mueller T.y
Sander L., Phys. Rev. Lett, 55, 1315 (1985).
4. Brady #., Ball R. C, Nature, 309, 225 (1984).
5. Matsushita M., Sano M., Hayakawa У., Honjo #., Sawada У., Phys. Rev.
Lett, 53, 286 (1984).
6. Neimeyer L., Pietronero L., Weisman #., Phys. Rev. Lett., 52, 1033 (1984).
7. Paterson L., Phys. Rev, Lett., 52, 1621 (1984).
8. Saffman P., Taylor G., Proc. Roy. Soc, A245, 312 (1958).
9. Paterson L., J. Fluid Mech., 113, 513 (1981).
10. Brower R. C, Kessler D. A,, Koplik /., Levine #., Phys. Rev., A29, 1335
(1984).
11. Ben-Jacob £., Goldenfeld N., Langer /. 5., Schon G., Phys. Rev., A29, 330
12. Shraiman B.y Bensimon D., Phys. Rev., A30, 2840 (1984).
(1984).
13. Kessler D. A., Koplik /., Levine #., Phys. Rev., A30, 2820 (1984).
14. Sander L., Ramanlal P., Ben-Jacob £., Phys. Rev. А, в печати.
Формирование структур
отвердевания в моделях агрегации
Т. Вичек*
Рассмотрены обобщения модели ДОА, позволяющие
воспроизводить формирование структур при отвердевании. Двумерные
кластеры, выросшие из затравочной частицы, первоначально имеют
круглую форму, а на более поздних стадиях роста они начинают
расти как дендриты. Эффекты анизотропного поверхностного
натяжения исследованы в предположении, что вероятность
присоединения частиц зависит от локальной ориентации поверхности раздела.
Направленное отвердевание моделируется присоединением частиц,
совершающих несимметричные случайные блуждания. При учете
основных особенностей экспериментов по направленному
отвердеванию образуются линейные устойчивые структуры. Получающиеся
структуры очень похожи на структуры, наблюдаемые
экспериментально.
1. Введение
Формирование структур растущими поверхностями —
один из основных процессов в широком диапазоне явлений,
изучаемых наукой и используемых техникой. Такой процесс
наблюдается, в частности, при отвердевании, когда кристаллическая
фаза растет в перенасыщенном паре или переохлажденном
расплаве [1]. К числу примеров формирования структур
отвердевания относятся эволюция снежинки в атмосфере или
направленное отвердевание в ряде процессов, играющих важную роль
в металлургии [2].
Ход отвердевания описывается нелинейными
дифференциальными уравнениями в частных производных, решение которых
как аналитическими, так и численными методами наталкивается
на большие трудности. Именно поэтому многие из вопросов,
относящихся к формированию структур при отвердевании, до сих
пор не получили удовлетворительного ответа. Один из возможных
способов изучения таких вопросов состоит в исследовании
модельных систем, способных порождать структуры [3—7].
Для моделирования поведения фронта отвердевания в
присутствии нелокальных вынуждающих сил необходимы новые
численные методы й модели. Модель ограниченной диффузией
агрегации Виттена и Сандера [2] представляется особенно
пригодной для изучения эффектов нелокального поля диффузии.
В нашей последней работе [3] было предложено простое
обобщение ДОА, в которой стабилизирующее действие
поверхностного натяжения учитывалось с помощью введения вероятности
* Tamds Vicsek-Department of Physics, Emory University, Atlanta, GA
30322, USA. Постоянный адрес: Research Institute for Technical Physics,
Budapest, Ujpest 1, Pf. 76, H-1325, Hungary.
346
Часть V(6)
присоединения, зависящей от локальной кривизны. В настоящей
работе предложенная в работе [3] обобщенная модель ДОА
используется для получения структур отвердевания.
2. Модель
При моделировании процесса отвердевания мы будем
придерживаться следующих правил [3]:
1) частицы совершают случайные блуждания (как в ДОА);
2) присоединение частицы к поверхности растущего кластера
происходит с вероятностью, зависящей от локальной кривизны
поверхности раздела;
3) релаксация в положение с наибольшим числом занятых
ближайших соседей.
Первое правило моделирует эффекты нелокального поля
диффузии в таком виде, в каком оно было рассмотрено Виттеном и
Сандером [8] и Кадановом [9]. Эта дестабилизирующая сила
компенсируется поверхностным натяжением, которое
учитывается правилом «2» (рост замедляется в местах с большой
кривизной). Третье правило необходимо для того, чтобы получать
компактные кластеры с низкой плотностью локальных дефектов
(дыр). Подробное описание этой модели см. в работе [3].
Применение нашей модели к задаче отвердевания обладает
рядом преимуществ. Численный метод прост и эффективен.
Модель позволяет легко воспроизводить сравнительно сложные
геометрии. Кроме того, флуктуации, всегда присутствующие в
любой термодинамической системе (и играющие важную роль в
процессе роста), естественно, могут быть включены через
случайные блуждания частиц. Наконец, модель может быть легко
модифицирована с тем, чтобы учесть различные
экспериментальные условия. Например, эффекты анизотропного поверхностного
натяжения или наложенный на систему градиент температуры
могут быть непосредственно воспроизведены в модели.
3. Дендритный рост
Для воспроизведения дендритного роста мы использовали
модель, описанную в разд. 2, с одной затравочной частицей на
квадратной решетке. Процесс начинается с роста почти круглого
кластера, так как на первой стадии доминирует влияние
кривизны, зависящей от вероятности присоединения частицы,
которое приводит к минимизации площади поверхности
кластера.
По мере продолжения процесса первоначально
бесструктурный рост переходит в дендритный рост, как показано на рис. 1.
Число узлов поверхности Ns представлено как функция общего
Модели необратимого роста
347
числа узлов N в кластере (в дважды логарифмических
координатах). При сравнительно малых размерах кластеров угловой
коэффициент прямых, проходящих через экспериментальные
точки, приближенно равен 1/2 — в соответствии с ростом
круглого кластера. Однако на более поздних стадиях число узлов
Угловой
=0,5
Угловой
jio3cp<pu циенгп
1,0
6 7 8
ln(N)
Рис. 1. Зависимость числа
поверхностных частиц Ns от общего числа
частиц в кластере N. Изменение в
наклоне указывает на переход от
компактного кластера к дендриту.
Рис. 2. Влияние вероятности
присоединения, зависящей от локальной
ориентации поверхности. На рисунке
изображен кластер из 25 000 частиц,
выросший при условии, что
вероятность присоединения максимальна
вдоль осей квадратной решетки.
Показаны только частицы на
поверхности раздела (имеющие менее четырех
ближайших соседей).
поверхности становится примерно равным N (угловой
коэффициент почти достигает единичного значения), что соответствует
росту дендритов.
Эффекты анизотропного поверхностного натяжения могут
быть исследованы в рамках нашей модели путем введения
вероятности присоединения рап, зависящей от локального наклона
поверхности.
На рис. 2 изображен кластер из 25 000 частиц, выращенный
с использованием анизотропного поверхностного натяжения,
усиливающего рост вдоль главных осей решетки. Изображенная на
нем структура обладает рядом свойств, типичных для
дендритного отвердевания, и, насколько можно судить, устойчива, так
как разделения концов не наблюдается. Тем не менее кластер
на рис. 2 не столь регулярен, как большинство структур
отвердевания, наблюдавшихся в экспериментах. Меньшая регулярность
обусловлена флуктуациями, сравнительно большими при малом
поверхностном натяжении. В принятой нами модели появления
348
Часть V(6)
более регулярных структур можно ожидать при больших
значениях Л. С другой стороны, для получения больших кривизн и
более сложных структур в наших численных экспериментах
средних масштабов параметр А должен быть сравнительно
малым.
4. Направленное отвердевание
В этом разделе мы рассмотрим вариант модели, в котором
частицы не присоединяются к одной отдельной частице, а
осаждаются на прямую, что позволяет воспроизводить условия
экспериментов по направленному отвердеванию [10, 11]. В этих
экспериментах рабочий материал (обычо длинный стержень
Рис. 3. Структура, возникающая при несимметричном случайном блуждании
частиц: вероятность переместиться на один узел вниз относится к вероятности
переместиться на один узел вверх как R = 1,1. На врезке справа вверху
показаны экспериментальные результаты Эсло и Либхабера [11] по
направленному затвердеванию сукцинонитроля.
или тонкая полоса) протягивается с заданной скоростью через
выбранный градиент температуры.
Для учета движения рабочего материала мы вводим
несимметричное случайное блуждание, увеличивая вероятность
перескока по направлению к поверхности раздела («вниз») pd по
сравнению с вероятностью перескока «вверх» pw. Моделирование
при нескольких значениях отношения ра/Ри приводит к
структурам, отличающимся большей регулярностью при R > 1, чем в
случае симметричного блуждания. Эти структуры по виду очень
похожи на те, которые наблюдали Эсло и Либхабер [11] в
экспериментах по направленному отвердеванию тонких образцов
сукцинонитроля. Сходство структур отчетливо видно на рис. 3,
где приведены экспериментальные результаты и данные
численного моделирования.
Модели необратимого роста
349
Выводы
Несколько обобщений модели ограниченной диффузией
кластеризации применены к задаче об отвердевании. Показано, что
предложенная в работе [3] модель кластеризации порождает
структуры, обладающие свойствами, которые согласуются с
экспериментальными данными. Эти структуры возникают в
результате случайного процесса, приводящего либо к фрактальным
объектам, либо к почти регулярным структурам отвердевания
в зависимости от значения параметра, соответствующего
поверхностному натяжению.
Благодарности. Автор выражает признателньость Ф. Фэмили,
Л. Каданову и А. Либхаберу за полезные обсуждения. Эта
работа выполнена при поддержке Исследовательского фонда
Университета Эмори и Национального научного фонда (контракт
No. DMR-82-08051).
ЛИТЕРАТУРА
1. hanger J. S., Rev. Mod. Phys., 52, 1 (1980).
2. См., например, Crystal Growth, ed B. R. Tamplin, Pergamon, New York,
1975.
3. Viscek 7\, Phys. Rev. Lett. 53, 2281 (1984).
4. Ben-Jacob E., Goldenfield N., hanger J. S., Schon G., Phys. Rev. Lett., 51,
1930 (1983), Phys. Rev., A29, 330 (1984).
5. Brower R. C, Kessler D. A., Koplik /., hevine Я., Phys. Rev. Lett., 51,
1111 (1983); Phys. Rev., A29, 1335 (1984).
6 Kessler D. A, Koplik /., hevine #., Phys. Rev., A30, 2820 (1984).
7. Szep /., Cserti /., Kertesz /., J. Phys., A18, L413 (1985).
8. Witten T. A., Sander h. M.t Phys. Rev. Lett., 47, 1400 (1981); Phys. Rev.,
B27, 5686 (1983).
9. Kadanoff h. P., будет опубликовано.
10. Jackson К. A., in: Solidification, American Society for Metals, Metals Park,
Ohio, 1971.
11. Heslot F., hibchaber A.y Phys. Scr., T9, 126 (1985).
Масштабно-инвариантные
свойства поверхности
в модели Идена
Р. Жюльен, Р. Боте*
Поверхность в модели Идена исследуется численно путем введения
конечного масштаба с помощью ленточной геометрии. Рассмотрены
три варианта модели и показано, что наиболее часто
использовавшийся ранее вариант обладает значительными корреляциями на
конечном масштабе. Установлено, что толщина поверхности а
имеет следующий масштабно-инвариантный вид ff (/, h) ~ laf(hll Y)
где / — ширина полосы, h = NJl, N — число частиц в кластере,
/ (х) ->■ const при #->оо и f(x)~xaly при *->0. Показано, что
в двумерном случае у = 0,50 ± 0,03 и у = \J dz 0,3.
Многие модели необратимого роста (модель Идена, ДОА,
баллистическая модель и т. д.) (обзор см. в сборнике [1])
были введены в «сферической» геометрии с сферической затравкой,
играющей роль зародыша роста в центре координат бесконечной
решетки. Другой способ исследования таких моделей состоит в
изучении полосочной геометрии и введении конечного масштаба.
Этот метод был применен к исследованию ДОА [2],
баллистической модели [3] и (недавно) моделей Идена [4].
В d-мерном пространстве наш метод состоит во введении
бесконечной полосы с периодическими граничными условиями,
сечение которой имеет вид (d— 1)-мерного гиперкуба с ребром
длиной /. В начале процесса все узлы в полосе заняты до высоты
2 = 0. Процесс роста начинается с этой гиперплоскости.
Мы рассмотрим здесь три варианта модели Идена.
В варианте А всем вакантным узлам, расположенным в
непосредственной близости от поверхности, приписывается равная
вероятность, и мы случайным образом выбираем один из этих
узлов, после чего его занимает новая частица. Вариант А
(«модель Идена для физиков») широко изучался в прошлом [5].
В варианте В мы приписываем равные вероятности всем
открытым связям (соединяющим занятый узел с вакантным) и
выбираем случайным образом одну из них, после чего новая
частица присоединяется к кластеру, заполняя вакантный узел.
Этот вариант соответствует исходной модели Идена [6].
В варианте С мы считаем равновероятными все занятые узлы
поверхности и выбираем случайным образом один из этих узлов.
Затем мы рассматриваем все открытые связи, исходящие из
выбранного узла, как равновероятные и выбираем случайным
образом одну из них,
* R. Jullieriy R. .BofeM-aboratoire de Physique Solides, Bat 510, Univer-
site Paris —Sud, Centre d'Orsay, 91405 Orsay, France.
Модели необратимого роста
351
Все три варианта различны в том смысле, что хотя
множества разрешенных узлов для данной конфигурации у них одно
и то же, статистический вес одного состояния (вероятность
выбрать это состояние) во всех трех вариантах, вообще говоря,
различен. ,..4v-: .-....„,
В настоящей работе мы ь4^^КЙЩи.-Г^% . »:»..„.!."
приведем некоторые результа- !-В||й^Й .
ты при d = 2. Все три модели ^^Xi2MM:!^s^;:!tZc-J:
приводят к компактным
кластерам (с фрактальной размер- л t fr. ;''!f^V.'**'-a
ностью, равной размерности ^^§!^^Шнй"^Ш^-™^12.гы
пространства) с единичной
плотностью. На рис. 1
представлены верхние слои типичных liilSllli;-. , ^.^М^шеШЬ
кластеров при / = 96. Под
этими слоями во всех трех случаях Рис- *• Типичные двумерные приме-
располагаются полностью за- ^Z^JS^S^S £
полненные полосы высотой 41) L верхностные узлы. Сверху вниз: ва-
Если фрактальная размер- рианты Л, Я, с.
ность тривиальна, то этого
нельзя сказать о толщине поверхности. Она определяется по
формуле
где
s t
суммирование проводится по its поверхностным узлам,
перенумерованным индексом i, a z-t означает высоту узла и
Поверхность зависит от двух характерных масштабов:
ширины I полосы и эффективной высоты h = N/l кластера, где N—
общее число частиц.
При больших / и ft, как показывают общие соображения
относительно автомодельности, а принимает следующий
масштабно-инвариантный вид [7]:
а(/> A)~/a?(A//Y)>
где
/ (х) -> const при х -> оо,
f{x)-+x$ при х->0
и у = a/р (чтобы обеспечивалась независимость о от / при
1^>К). Из этого масштабно-инвариантного отношения следует,
что при ft ;» / существует стационарное состояние, для которого
cr~Ja.
352
Часть V(6)
Прямое оценивание показателя а в случае С приводит к
величине
а = 0,50 ± 0,03.
В других случаях (особенно в варианте А) обнаруживаются
сильные корреляции на конечных расстояниях [4]. В варианте
А показатель а достигает минимума а = 0,37 между / = 24 и
/ = 48, после чего медленно возрастает. Аналогичную слабую
сходимость для модели А отмечали ранее Микин и Виттен [5].
Те же глобальные характерные особенности обнаруживает
дважды логарифмический график зависимости а (/, -^ I) от I
(подробности см. в работе [4]), из которого следует, что
р = 0,30 ± 0,03,
откуда в сочетании с предыдущим результатом для а находим
Y=f = l,7±0,3.
Полученные значения а и у очень близки к значениям,
найденным аналитически для аналогичной модели роста [8]: а =
= 1/2, 7 = 2. Но, хотя значения показателя а находятся в
хорошем согласии, этого нельзя сказать о у. Несмотря на
заметное расхождение между нашим значением р и значением р = 1/4,
характерным для некоторых точно решаемых моделей роста,
окончательный вывод о значимом расхождении был бы
преждевременным. Необходимы новые более обширные численные
эксперименты (недавно проведенные вычисления [9] до 224 узлов
для дискриминации моделей недостаточны).
ЛИТЕРАТУРА
1. Kinetics of Aggregation and Gelation, eds. F. Family, D. P. Landau, North
Holland, 1984.
2. Jullien ft, Kolb M., Botet R., J. Physique, 45, 395 (1984).
Racz Z.y Vicsek Г., Phys. Rev. Lett., 51, 2385 (1983).
Turban L., Debierre J. M., J. Phys. A17, L289 (1984).
3. Getband P., Strenski P. N., J. Phys., A18, 611 (1985).
4. Jullien #., Botet #., Phys. Rev. Lett, 54, 2055 (1985).
Lullien R., Botet i?., J. Phys., A18, -2279 (1985).
5. Peters tf. P., Stauffer D.y Holters H. P., Loewenich /C, Z. Phys., B34, 399
(1979); Meakin P., Colloid /., Interface Sci., 96, 415 (1983), Meakin P.,
Witten T. A, Phys. Rev., A28, 2985 (1983); Plischke M., Racz Z., Phys.
Rev. Lett, 53, 415 (1984).
6. Eden M., in: Proceedings of the Fourth Berkeley Symposium on
Mathematical Statistica and Probabilities, ed. F. Nevman, Univ. of California Press,
Berkeley, 1961, vol. IV, p. 233.
7. Family P., Vicsek Г., J. Phys., A18, L75 (1985).
8. Richardson ZX, Proc. Camb. Phil. Soc, 74, 5151 (1973); Dhar D., Phys. Rev.
Lett., 54, 2058 (1985).
9. Freche P., Stauffer Z)., Stanley H. £., J. Phys. A Lett., будет опубликовано.
Агрегация кластеров
Р. Боте, Р. Жюльен, М. Кольб*
Процесс агрегации кластеров мы вводим как модель для описания
агрегации коллоидных или аэрозольных частиц в режиме низких
концентраций. Исследованы модификации параметров модели.
В частности, уточнены различные обратимые модели агрегации и
рассмотрены возможные соотношения между ними (классы
универсальности).
1. Введение
Изучение фдрмирования кластеров путем агрегации
отдельных частиц играет важную роль во многих областях
естествознания [1]. В коллоидах и аэрозолях кластеры обнаруживают
геометрическую скейлинговую структуру с многими вполне
определенными характерными масштабами [2, 3]. Исходный пункт
для теоретического исследования был найден с помощью
численного моделирования. Мы до сих пор не знаем, почему кластеры
являются фракталами, но начинаем понимать, как реализуется
их фрактальная структура и как их фрактальная размерность
связана с физикой процесса.
В настоящей работе мы излагаем модель необратимой
агрегации кластер — кластер, дающей реалистическое описание
процесса образования коллоидов и аэрозолей.
2. Модель агрегации кластеров
Эта модель была предложена независимо Микином [4] и
нами [5]. Мы описываем здесь только трехмерный вариант
модели, так как именно он наиболее удобен для прямого
сравнения с экспериментами [6]. Тем не менее все размерности
меньше 6 были исследованы численно [7], так же как и
размерности, превышающие верхнюю критическую размерность (8] dc —
= In 36/ln(3/2) =8,8... . Модель определяется следующим
образом. В ячейке L X L Х^ с периодическими граничными
условиями, составляющей часть бесконечной кубической решетки, мы
выбираем случайным образом N0 тождественных частиц.
Каждая из этих частиц совершает случайное блуждание по решетке.
Модель воспроизводит бесконечную среду, статистически
однородную с начальной плотностью N0/Lz монодисперсных
броуновских частиц. • :
Сталкиваясь (т. е. приходя в два соседних узла решетки),
две такие частицы соединяются необратимо и образуют неболь-
* R. Botet, R. J allien, M. Kolb • Laboratoire de Physique des Solides; Bat.
510, Universite Paris-Sud, Centre d'Ofsay, 91405 Orsay, France. -'■*
354
Часть V(6)
шой жесткий димер. Такой кластер также совершает случайное
блуждание со скоростью, зависящей от его массы. При
столкновении два кластера соединяются и образуют жесткий кластер
больших размеров, после чего весь процесс продолжается. Так
Рис. 1. Типичный кластер из 1024 частиц, выросший в результате
присоединения кластеров к кластерам на решетке.
как соединение кластеров необратимо, число кластеров со
временем убывает, и процесс заканчивается, когда в ячейке
остается только один кластер.
В рассматриваемом варианте опорная решетка запрещает
вращение кластеров при движении вдоль траектории. При
численном моделировании кластерам также не разрешалось
вращаться. Было проведено и внерешеточное моделирование с
обобщенным случайным блужданием. Такие численные
эксперименты показали, что кластеры обладают той же фрактальной
структурой даже с учетом вращения по траектории [9].
Аналогичным образом зависимость между скоростью
кластера и его массой несущественна для геометрических свойств
кластера, если эта зависимость реалистична, т. е. если
скорость— не возрастающая функция массы [10]. Разумеется,
распределение размеров кластеров как функция времени зависит
от соотношения между скоростью и массой [11).
На рис. 1 показан типичный кластер из 1024 частиц,
выросший указанным выше образом в ячейке размером 70X70X70.
При усреднении по большому числу кластеров график
зависимости радиуса гирации от массы в дважды логарифмическом
масштабе обнаруживает закон подобия вида
N~RD
при всех масштабах, превышающих несколько радиусов
мономера. Показатель D здесь — фрактальная размерность,
принимающая значение D = 1,78 ± 0,05. Это значение очень близко
Модели необратимого роста
355
к экспериментальным значениям Форреста и Виттена [2] D =
= 1,8 ±0,1 (на переохлажденных парах железа) и Вейца и Оли-
вейры [3] D = 1,75 ± 0,05 (на коллоидном золоте).
3. Физические параметры модели
Интересно отметить, как мало параметров необходимо,
чтобы охватить все экспериментальные результаты.
Начальные условия: монодисперсные частицы при низкой
концентрации.
Условия диффузии: броуновская диффузия.
Условия присоединения: сталкиваясь, два кластера
соединяются необратимо и образуют новый жесткий
кластер.
Что произойдет, если мы изменим некоторые из параметров
модели?
4. Модификация начальных условий
Если полидисперсность мономеров допустима (т. е. шары
имеют определенное распределение радиусов), то численные
эксперименты, аналогичные тем, о которых шла речь выше,
показывают, что образующиеся кластеры по-прежнему являются
фрактальными объектами с такой же фрактальной
размерностью, как и в монодисперсном случае [12]. Эти численные
результаты с успехом выдержали сравнение с данными недавних
экспериментов по полидисперсным кластерам железа [13].
Кроме того, со временем эффективная плотность
i по всем кластерам
становится величиной порядка единицы, так как средний радиус
R кластера возрастает со временем. Броуновская экранировка
становится неэффективной из-за запутанности структуры. Мы
оказываемся в так называемом кинетическом режиме гелеобра-
зования, и характерная для этого режима фрактальная
размерность составляет (при d = 2) величину D = 1,75 ±0,07 [14].
5. Модификация условий диффузии
Можно представить себе молекулярную (а не броуновскую)
диффузию кластеров, при которой средняя длина свободного
пробега ограничена только соударениями между кластерами.
Здесь также экранировка менее эффективна, чем в броуновском
355
Часть У(б)
случае, и в среднем кластеры проникают друг в друга глубже.
Фрактальная размерность получающихся при этом кластеров
составляет величину D = 1,91 ± 0,03 [15].
6. Модификация условий присоединения
Условия присоединения можно варьировать, изменяя три
параметра: вероятность присоединения при столкновении,
жесткость кластеров и необратимость процесса присоединения.
Если вероятность присоединения устремить к нулю, то
получится химическая модель. В этой модели кластеры прежде, чем
соединиться, претерпевают многочисленные соударения, но
соединяются необратимо, т. е. образовавшийся новый кластер не
распадается. Химическая модель исследовалась численно [16]
и экспериментально [17] (высоту отталкивательного барьера
между двумя золотыми коллоидными частицами можно менять
химическим путем). Фрактальная размерность образующихся
кластеров составляет величину D = 2,00 ± 0,06 (при численном
моделировании) и D = 2,01 ± 0,10 (в натурном эксперименте).
Некоторые аспекты изменения структуры кластеров при
деформации в ходе их агрегации были исследованы Микином и
Жюльеном [18], и мы на них не останавливаемся.
Последнее, что остается рассмотреть, — это вопрос о
необратимости. Если в приведенной выше модели разрешить распад
кластеров так, чтобы могло существовать стационарное
состояние (например, чтобы каждая связь имела конечное время
жизни), то фрактальная размерность кластеров [19] оказывается
весьма близкой к фрактальной размерности «решеточных
зверей» [20].
В связи с этим возникает задача: как распознать, приводят
ли две модели (обратимая агрегация кластер — кластер и
решеточные звери) к одному и тому же классу универсальности. Пока
мы располагаем для проверки такого соответствия только
фрактальной размерностью. А как обстоит дело с другими
кинетическими моделями агрегации — фрагментации в состоянии
равновесия?
Исследованием обратимой модели Идена занимался в
другом контексте (перколяция) Штауффер [21]. Это модель
связных кластеров, из которых мы извлекаем частицу (если кластер
в результате проделанной операции не распадается на два
несвязных фрагмента) и помещаем ее в (случайно выбранную)
точку поверхности кластера (агрегация типа Идена), после чего
все повторяется сначала. Стауффер обнаружил, что
фрактальная размерность кластеров в обратимой модели Идена
оказывается такой же, как фрактальная размерность решеточных
зверей.
Модели необратимого роста
357
Обратимая модель ДОА была исследована двумя из
авторов настоящей статьи [22]. В этом варианте агрегации
частица— кластер [23] мы начинаем с любого замкнутого кластера,
не содержащего замкнутых петель, на решетке. Выбираем
случайным образом частицу в множестве односвязных кластеров и
О 160 ЗбООО
Рис. 2. Общий ход обратимой ДОА на компактном беспетлевом кластере (а)
или типичном беспетлевом кластере, ограниченном диффузией (б), из
100части. Число итераций, указанное внизу, возрастает слева направо.
разрываем соответствующую связь, после чего частица
отправляется в случайное блуждание до тех пор, пока снова не
присоединится к кластеру, — ДОА (рис. 2).
Для того чтобы получить структуру без петель, мы
придерживаемся следующего правила. Присоединение происходит в том
случае, когда диффундирующая частица (например, А)
достигает узла, занятого частицей кластера (например, В), после
чего частица А отступает на один шаг по своей броуновской
траектории, а мы соединяем ее только с частицей В кластера (у
частицы А может быть несколько соседей, но мы проводим
только одну связь — между Л и В). Этот процесс был введен ранее
Кадановом [25] для ДОА.
Какой бы ни была начальная конфигурация, в итоге через
очень большой промежуток времени мы придем к одному и
тому же статистическому распределению кластеров. В этом
стационарном состоянии фрактальная размерность, как оказалось,
очень близка к фрактальной размерности решеточных зверей.
Все четыре обратимые модели (решеточных зверей, обратимой
358
Часть V(6)
агрегации кластер — кластер, обратимой модели Идена,
обратимой ДОА) различны в том смысле, что статистический вес
данного конечного кластера в каждой модели различен. Однако это
отнюдь не означает, что скейлинговые свойства каждого
большого кластера также различны. Фрактальные размерности
делают весьма правдоподобным предположение о том, что все
перечисленные нами обратимые модели принадлежат к одному и
тому же классу универсальности (решеточных зверей). Но до
сих пор эта гипотеза не подкреплена никакими теоретическими
соображениями.
Выражаем нашу благодарность за сотрудничество и
обсуждения Г. Герману и П. Микину. Нашу работу субсидировали АТР
C.N.R.S. и CCVR, Палезо.
ЛИТЕРАТУРА
1. Обзор по процессу агрегации см. в сб.: Kinetics of Aggregation and
Gelation, eds. F. Family, D. P. Landau, North Holland, 1984.
2. Forrest S. R.t Witten А. Т. Л, J. Phys., A12, L109 (1979).
3. Weitz D. Л, Oliveria M, Phys. Rev. Lett., 52, 1433 (1984); Weitz D, A.,
Lin M. Y„ Sandroof C. /., Surface Sci., 158, 147 (1985).
4. Meakib P, Phys. Rev. Lett., 51, 1119 (1983).
5. Kolb M., Botet R., Jullien R., Phys. Rev. Lett, 51, 1123 (1983).
6. Последние эксперименты проводились в двумерном ограниченном
пространстве (слое). Они описаны в работе:
Hurd A., Schaefer D, Phys. Rev. Lett., 54, 1043 (1985). Возможное
объяснение полученных результатов см. в работе: Jullen R. G.y в печати.
7. Jullien R.y Kolb М.у Botet Я, Physique Lett, 45, L211 (1984); Meakin P,
Phys. Lett, A107A, 269 (1985).
8. Ball R. C„ Witten Т. Л, Phys. Rev, A29, 2966 (1983); Ball R. C, J. Stat.
Phys., 36, 873 (1984).
Obukhov S. P., Kinetically aggregated clusters, preprint (1984); Botet R.y
J. Phys., A18, 847 (1985).
9. Meakin P, J. Chem. Phys., 81, 4637 (1984).
10. Botet R.t Jullien R., Kolb M, Phys. Rev, A30, 2150 (1984); Meakin P,
J. Coll. and Interface Sci, 102, 491 (1984).
11. Botet R., Jullien R., J. Phys, A17, 2517 (1984); Kolb M, Phys. Rev. Lett,
53, 1653 (1984); Meakin P, Vicsek Г, Family P, Phys. Rev, B31, 564
(1985).
12. Chevalier J. P, Colliex С, Тепсе М., Jullien R.y Botet R., Fractal structure
of polydisperse iron aggregates: STEM analysis and numerical simulations,
будет опубликовано.
13. Chevalier J. P, Colliex C, Tence M.y Jullien R., Botet R., Analysis of
digitalized STEM micrographs: Application to the calculation of the fractal
dimension of iron aggregates, стендовый доклад на: Colloque annuel de
la Societe Francaise de microscopie electronique, Strasbourg 28—31 mai
1985.
14. Kolb M, Herrmann /, J. Phys, A18, L435 (1985).
15. Meakin P., J. Coll. and Interface Sci, 102, 505 (1984); Phys. Rev, A29,
997 (1984); Ball R. C, Jullien R., J. Physique Lett, 45, L1031 (1984).
16. Jullian R.y Kolb M, J. Phys, A17, L639 (1984); Kolb M, Jullien R.,
J. Physique Lett, 45, L977 (1984).
17. Weitz D. A., Huang /. 5, Lin M. Y, Sung /, The Limits of the fractal
dimension colloids, preprint (1985).
Модели необратимого роста
359
18. Meakin P., Jullien R., J. Physique, 46, 1543 (1985).
19. Kolb M., Reversible diffusion limited cluster aggregation, preprint (1985).
20. Peters H. P., Stauffer Z)., Holters H. P., Loewenich K., Z. Physik, B34, 399
(1979); Derrida £., de Seze L.y J. Physique, 43, 475 (1982); Privman V.
Family F.y Margolina A.f J. Phys., A17, 2837 (1984).
21. Stauffer D., Phys. Rev. Lett, 41, 1333 (1978).
22. Botet R., Jullien R., Diffusion limited aggregation with disagregation,
preprint (1985).
23. Обзор см. в [1] и трудах конференций в Гейло («Scaling phenomena in
disordered systems», ed. R. Pynn, 1985), Лезуше (Finely divided matter,
ed. M. Daoud, 1985), и Каргезе (On growth and forms, eds. H. E. Stanley,
N. Ostrowski, Martinus Nijhoff publishers, 1985).
24. Подчеркнем, что во внерешеточной модели ДОА кластеры не содержат
петель. Петли являются артефактом, порождаемым решеткой.
25. Kadanoff Leo P., J. Stat. Phys., 39, 267 (1985).
Анизотропия в кластерах
и агрегация частиц
М. Кольб *
Анизотропия, обусловленная и решеткой, и механизмом роста,
анализируется в рамках моделей ДОА и агрегации кластеров. В
модели агрегации кластеров существует только анизотропия
амплитуды, обусловленная решеткой, в то время как в случае агрегации
частиц скейлинг в направлении роста и в перпендикулярном
направлении происходит по различным законам. Показатели
корреляционной функции отличаются по этим двум направлениям на
АЛ = 0,16 ± 0,05.
Хотя в последние годы было предложено и исследовано
немало различных моделей роста и найдено много показателей
в соответствующих законах подобия, особого продвижения в
понимании первопричин, определяющих характеристики роста,
достигнуто не было [1]. После того как первые попытки дать
качественное описание модели Виттена — Сандера [2] диффузионно-
ограниченной агрегации частиц не привели к достаточно ясной
картине, исследователи принялись за более подробное изучение
этой модели численными методами и в конечном счете сумели
прийти к полному описанию ее наиболее характерных
особенностей.
С самого появления модели Виттена — Сандера ДОА возник
вопрос о том, приводит ли радиальный поток частиц, идущий
снаружи внутрь сферически-симметричного кластера,
ограниченного диффузией, к эффектам анизотропии, если даже визуально
малые части кластера кажутся изотропными. Этот вопрос
возник снова после того, как были установлены решеточные
анизотропии у очень больших кластеров [3]. Такого рода
наблюдения означали, что автомодельная картина, обычно применяемая
к таким кластерам по аналогии с статическими критическими
явлениями, нуждается в уточнении.
Одним из критериев, одновременно простым и решающим,
является анизотропия корреляционных функций. В соответствии
с этим критерием корреляционные функции кластеров,
ограниченных диффузией, были измерены в зависимости от угла с
вершиной в центре кластера, отсчитываемого от некоторого
направления. Особое внимание обращалось на то, чтобы избежать
ложных эффектов, обусловленных конечными размерами,
незавершенностью роста и статистическими погрешностями. Аналогичный
анализ проводился и в случае агрегации кластер — кластер [4],
* М. Kolb • Laboratoire de Physique des Solides, Bat. 510, Universite de
Paris-Sud, 91405 Orsay, France; Institut fur Theorie der Kondensierten Mate-
rie, Freie Universitat Berlin, Arnimalle 14, 100 Berlin, West Berlin.
Модели необратимого роста
361
но оказалось, что малость анизотропии характерна для
агрегации кластер — частица.
Рис. 1. Определение угловых корреляций с(р, г)= с (г, Ф). Вектор р,
проведенный из начала затравочной частицы для АЧ и частицы, ближайшей
к центру масс кластера, в случае АК означает радиус-вектор частицы
кластера, корреляционные функции с(р, г) = <я(р + г)л(р)> = (п(р + г> —
среднее от плотности п в точке р + г и зависит только от г и Ф (на
рисунке 1 слева). На решетке корреляционная функция с(р, г) зависит также от
угла а между р и одной из осей решетки, а вектор г ограничен узлами
решетки. Были вычислены аксиальная (Фа) и диагональная (Ъ&) корреляции
(на рисунке 1 справа).
Полученные данные позволяют утверждать, что в случае
ДОА существует слабая, но четко выраженная анизотропия кор-
Кольиф Кольцо
\7
Рис. 2. Аксиальные корреляции са{г = б, ft) (нормированные на среднее от
са по углам). Вычислены для всех точек кластера и затем усреднены по
отдельности по концентрическим кольцам (кольца 1—7) с одним и тем же
числом частиц (общий центр всех колец совмещен с началом). Начальные
условия и поверхностные эффекты, как видно из приведенных данных, сильно
сказываются на угловой зависимости са. Данные для агрегации частиц
приведены слева, для агрегации кластеров — справа.
реляционной функции: вдоль направления роста корреляция
спадает по степенному закону с показателем, который на зеличину
362
Часть V(6)
АЛ =0,16 ± 0,05 меньше, чем в перпендикулярном направлении
[5]. В случае агрегации кластеров, которую следует ожидать,
Агрегация
- частиц
Аксиальная
V корреляция
IZ
Агрегация
кластеров
Аксиальная
корреляция
12\Диа.гокалъная Т.
' корреляция а-
Диагональная
корреляция
Рис. 3. Аксиальная и диагональная
корреляции с (гу ft) (нормированные)
для агрегации частиц и кластеров
как функции угла Ф (г — параметр).
Данные относятся к точкам,
расположенным глубоко внутри кластера,
где выполняются неравенства (1)
(корреляции усреднены только по
точкам четвертого кольца).
Результаты в случае агрегации частиц
(слева) заметно отличаются от
результатов в случае агрегации
кластеров (справа). Это расхождение
свидетельствует о различных законах
преобразования в направлениях,
параллельном и перпендикулярном
направлению роста, только для
агрегации частиц. Сравнение аксиальных
корреляций (вверху) с
диагональными корреляциями (внизу)
показывает также, что решетка изменяет
амплитуды корреляций и при
агрегации кластеров. Статистическая
ошибка даных менее 0,04. Для
диагональных корреляций масштаб по г
выбран в л/2 раз больше, чем
постоянная решетки.
су
0,4
0,3
o,z\
o,t
о
-of
Агрегация
£ частиц
* . + - Агрегация
+ о *о ^о+1 кластеров
~'0
7 2
In г
Рис. 4. Зависимость
отношения Сц/с± = [с (г, Ф == 0) + с (г, Ф =
= к)]/2с (г, <д, = зт/2) как функция от
г в дважды логарифмическом
масштабе для агрегации частиц,
позволяющая определить показатель
ДЛ = А± — А{{ = 0,16 ± 0,05.
Прямая имеет угловой коэффициент 0,16.
При больших г аксиальная и
диагональная корреляции выходят на
прямую с одинаковым наклоном.
Постоянство отношения для агрегации
кластеров свидетельствует о том, что
АЛ = 0. Автомодельность
нарушается при г ^ 30 для аксиальной и
г ^20 для диагональной корреляций
в основном на границе кластера (в
случае агрегации частиц). Черными
кружками обозначены аксиальные,
косыми крестами — диагональные
корреляции в случае агрегации
частиц, белыми кружками аксиальные
и прямыми крестами — диагональные
корреляции для агрегации кластеров.
если приписывать анизотропию механизму роста, такого
эффекта не обнаружено: агрегация частиц не имеет фиксированного
центра роста, как это обычно бывает у кластера,
образовавшегося при соединении двух кластеров сравнимых размеров.
Кроме того, и в случае агрегации частиц, и в случае агрегации
кластеров существует дополнительная анизотропия амплитуды для
Модели необратимого роста
363
корреляций, обусловленная структурой квадратной решетки, на
которой происходит рост. Все вычисления проводились для
двумерного случая.
Результаты анализа кластеров, образовавшихся в результате
агрегации частиц (АЧ) и агрегации последовательно
укрупняющихся кластеров (АК), представлены на рис. 1 (АЧ-кластер
содержал 5000 частиц, АК-кла-
стер — 4096 частиц). Здесь R —-
радиус кластера, р — радиус-
вектор точки кластера, г —
направление, в котором
производится измерение
корреляционной функции. Вне решетки в
области автомодельности, где
1<г<р</?, (1)
корреляция может зависеть
только от г = | г | и $ — угла,
образуемого вектором г с
направлением роста р.
Поскольку кластеры выращены на
квадратной решетке, аксиальная
и диагональная корреляции
вычислялись отдельно, чтобы
исключить возможные эффекты,
обусловленные решеткой. На
рис. 2 представлены
результаты вычисления осевых
корреляций для агрегации частиц и
агрегации кластеров. Данные
о всех углах были
сгруппированы в пять сегментов — от
до направленного назад (ф = гс). Измерения производились
отдельно по семи концентрическим кольцам с центром в
затравочной частице, причем в кольцах 3 и 4 автомодельность была
наиболее полной (область, задаваемая неравенствами (1)). Между
кольцами 1 и 7 отклонения наиболее заметны.
На рис. 3 аксиальная и диагональная корреляции в области
автомодельности показывают, что с возрастанием г анизотропия
между направлениями Ф = 0, Ф = я и д = я/2 усиливается в
случае агломерации частиц. В случае агломерации кластеров
такого эффекта не существует.
Чтобы получить количественную оценку анизотропии, мы
представили на рис. 4 в дважды логарифмическом масштабе
отношение с„/с± = г-(лн-л-^ = гАЛ, где с\\ = с(г, * = 0, п), с± =
= с(гу ф = я;/2). И аксиальная, и диагональная корреляции сви-
а
ьг
V
7
0,9
Агрегаиия
частиц
- ^V
j
Кольцо
т .
Л/8
Ttfr ос
Рис. 5. R (N, а) — средний радиус
N-к частицы, присоединяющейся к
кластеру под углом а к одной из
осей квадратной решетки. На рис. 5
представлена нормированная
величина а(а) = R2(N, a)/R*(N)t где
R2 (N) — среднее по улам от R2(N,a),
причем усреднение проводится
отдельно по кольцам возрастающего
радиуса для агрегации частиц в
интервале 0 ^ а <; я/4. Отчетливо
видна анизотропия формы кластеров.
Статистическая ошибка меньше 0,03.
направленного вперед ($ = 0)
364
Часть V(6)
детельствуют о существовании анизотропии в случае агрегации
частиц с АА = 0,16 ± 0,05, но не в случае агрегации кластеров.
Наконец, наблюдавшуюся анизотропию формы [3] кластеров
в случае агрегации частиц можно оценивать количественно,
вычисляя средний радиус R2(a,N) (N + 1)-й частицы,
присоединяющейся к кластеру под углом а к одной из осей решетки. Для
того чтобы иметь меру, не зависящую явно от N, мы вычисляли
отношение a — R2(a, N)/R2(N), где R2(N) —среднее по углу от
R2(a, N). При возрастании радиуса колец (1—7) анизотропия
монотонно возрастает, как видно из рис. 5. Как показывают
приведенные данные, анизотропия становится все более
отчетливо выраженной по мере увеличения размеров кластера.
Проведенные измерения отличаются особой тонкостью, так как
визуально кластеры исследуемых размеров продолжают казаться
изотропными.
ЛИТЕРАТУРА
1. Общее представление можно составить по аннотациям докладов на
рабочем совещании «Кинетические модели образования кластеров» (17—28
сентября 1984 г., СЕКАМ, Орсэ), вышедших под редакцией Р. Жюльена,
М. Кольба, Г. Германа и И. Ваннименуса; см. J. Stat. Phys., 39, 241
(1985).
2. Witten Т. Л., Sander L. M., Phys. Rev. Lett., 47, 1400 (1981).
3. Brady R., Ball R., не опубликовано. Эти авторы высказали предположение
о том, что большие кластеры на квадратной решетке визуально имеют
ромбовидную форму.
4. Meakin P., Phys. Rev. Lett., 51, 1123 (1983).
5. Kolb Ai, J. Physique Lett., 46 L361 (1985). П. Микин и Т. Вичек и
независимо от них Р. Фосс с помощью аналогичных методов также
обнаружили анизотропию кластеров при агрегации частиц.
Обратимость при агрегации кластеров
М. Кольб *
Работа посвящена систематическому введению обратимости в
диффузионную агрегацию кластер — кластер. Скейлинговый анализ
больших кластеров позволяет утверждать, что обратимость
нарушает характерные особенности необратимой кластеризации,
приводящей к фрактальным размерностям D = 1,57(2,03) в двумерном
(трехмерном) случае независимо от кинетики. Эти значения
согласуются с чисто статической статистикой кластеров. В то же время
распределение размеров кластеров зависит от кинетики.
Необратимость — то, что затрудняет теоретические
исследования процессов роста. Обычные методы равновесной
статистической механики не допускают простого обобщения на
сильнонеравновесные ситуации. Вместе с тем, по всеобщему
убеждению, именно необратимость обусловливает то необычайное
разнообразие новых скейлинговых свойств, наблюдаемых во
многих процессах роста [1—3].
Таким образом, исследования роста в условиях, когда
необратимость частично подавлена, вполне обоснованны.
Сохраняются ли при этом свойства необратимой агрегации? Появлятся ли
новые скейлинговые свойства или лишь те, которые знакомы по
хорошо известным статическим моделям кластеров {4, 5] ?
Частичная необратимость представляет интерес и с точки зрения
эксперимента как фрагмент обычно наблюдаемого процесса [6—
9]. Ответ, подсказываемый кластер-кластерной агрегацией с
разрывом связи, как это предлагается ниже, состоит в том, что
геометрические фрактальные свойства кластеров становятся
численно сравнимыми с аналогичными свойствами статических
моделей и полностью не зависят от кинетики. Это
свидетельствует о том, что любая необратимость полностью разрушает
скейлинговые особенности кластер-кластерной агрегации.
Рассматриваемая нами модель является моделью
кластеризации кластеров [2]. Частицы диффундируют независимо и
соединяются при столкновениях. Образовавшиеся димеры также
диффундируют и кластеризуются при столкновениях. Поскольку
связи не разрушаются и необратимы, кластеры растут и все
более увеличиваются в размерах. Новая отличительная
особенность, привносимая нами в модель, состоит в том, что каждая
связь имеет конечное (хотя и большое) время жизни.
Необратимая кластеризация соответствует т=оо. При разрыве связи
кластер распадается на два меньших кластера (если нет пе-
* М. /Co/6-Laboratoire de Physique des Solides, Bat. 510, Universite de
Paris-Sud, 91405 Orsay, France; Institut fur Theorie der Kondensierten Mate-
rie, Freie Universital Berlin, Arnimallee 14, 1000 Berlin 33, West Berlin.
366
Часть V(6)
тель). Предполагается, что эти два кластера диффундируют
независимо, так как если бы связь между ними никогда не
существовала. Предполагается также, что разрыв каждой из связей
происходит независимо: в единицу времени каждая связь
разрушается с вероятностью 1/т. Процесс агрегации доминирует на
первой стадии, когда рост начинается с отдельных частиц, между
которыми не существует никаких связей. По мере роста
образуется все больше связей, и некоторые из них начинают
разрываться. Наступает момент, когда связей имеется достаточно
много, так что время, которое необходимо на образование в процессе
агрегации одной новой связи, становится равным времени, в
течение которого разрывается одна из многих существующих
связей. Устанавливается динамическое равновесие. Ранние стадии
такого процесса соответствуют необратимой кластеризации,
долговременное поведение — обратимой кластеризации. Именно
последняя и послужит предметом исследования в настоящей
работе. Средний размер кластера в рассматриваемой области
увеличивается с возрастанием т. При анализе скейлинговых свойств
фрактальная размерность больших кластеров определяется
путем вычисления их радиуса гирации как функции массы
кластера (масса изменяется при изменении среднего времени жизни
связи т). Полученные результаты свидетельствуют о том, что
обратимость разрушает фрактальный аспект необратимой
кластеризации. Свойства кластеров оказываются свойствами,
известными из статистики статических кластеров («решеточные
звери») безотносительно к кинетике диффузионного движения
кластеров и вероятностям присоединения как в двумерном, так
и в трехмерном случае. Образование петель в рассматриваемом
процессе роста несущественно.
Модель, исследованная нами численно в двумерном и
трехмерном случаях, представляет собой решеточный вариант
агрегации кластеров. Частицы и кластеры движутся случайным
образом в гиперкубической решетке с ребром L и периодическими
граничными условиями. В начальный момент времени N0
частицы распределяются случайным образом по решетке, причем
никакие две из них не занимают один и тот же узел. Затем
частица случайным образом перескакивает в ближайшие
соседние узлы. Если две частицы находятся в двух ближайших
соседних узлах, между ними образуется связь, и в дальнейшем они
движутся как димер. Аналогично, если два кластера
соприкасаются (оказываются ближайшими соседями), между ними
образуется жесткая связь. Кластер всегда движется как жесткий
объект. В то время как при численном моделировании внереше-
точной кластеризации вероятность образования петель
обращается в нуль, при моделировании на решетке петли могут
образовываться при одновременном соприкосновении двух класте-
Модели необратимого роста
367
ров в двух точках. В действительности образование петли не
сказывается на результатах. Чтобы продемонстрировать это, мы
рассмотрели два случая. В беспетлевом варианте мы просто
выбираем случайным образом пару соприкасающихся частиц (если
одновременно соприкасаются несколько частиц кластеров) и
помещаем между ними связь. В варианте с петлями между
частицами устанавливаются все возможные связи. Вместе с тем
необходимо заметить, что при удалении одной связи кластер не
обязательно распадается на части: при разрушении связи
распадается либо кластер, либо только петля.
Качественно, при низкой концентрации кластеров, можно
провести следующий анализ. Пусть D означает фрактальную
4
Z
О 1 Z 3 i/ieq
Рис. 1. Переход от роста (необратимой кластеризации) к равновесной
агрегации (обратимой кластеризации). На рис. 1 представлена зависимость средней
массы m (нормированной на meq) как функция времени t (нормированного
на teq). Для сравнения приведены данные при а = — 2, meq = 6 (жирные
точки); а = —2, meq = 12 (косые кресты) и а = О, meq = 12 (прямые
кресты). Данные усреднены по 100 независимым численным экспериментам для
двумерного случая.
размерность кластеров, d — размерность пространства. Пусть,
кроме того, скорость диффузии кластеров зависит от массы по
закону v(m) ~ пга. В приближении среднего поля для времени
образования пары %а ~ ml-a~(d-2)/D и среднего времени разрыва
одной связи %f ~ %/гп (индекс указывает на процесс агрегации
или фрагментации) условие равновесия ха = Xf определяет
характерную массу кластера m как функцию от т: meq ~
^ Ti/(2-a-(^-2)/D)< Характерное время, определяющее наступление
равновесной агрегации, равно teq = T/meq. На временах t<^teq
процесс агрегации необратим, при t ^> teq наступает равновесие.
В нашей работе последний режим был промоделирован при
различных значениях т и, следовательно, т.
На рис. 1 показан переход между двумя режимами в
приведенных координатах (m/meq как функция от t/teq) при
различных meq и а. При заданном параметре а точки, отвечающие
различным т, лежат на одной кривой, что свидетельствует об
одном законе подобия. На рис. 2 радиус гирации R представлен в
дважды логарифмических координатах как функция массы т.
'*?—. i I г
368
Часть V(6)
И в случае агрегации с петлями и без петель, и в случае
данных, полученных при усреднении по всем кластерам и для
самого большого кластера, экспериментальные точки ложатся на
прямые с угловым коэффциентом /)= 1,57 ±0,06 (2,03 + 0,05)
в двумерной (трехмерной)
модели. Изменяя параметр а, мы
можем влиять на кинетику
диффузии, но в пределах
погрешности эксперимента это
изменение не сказывается на
измеряемом значении D. Другой
способ воздействия на
кинетику состоит эо введении
вероятности присоединения: связь
образуется с вероятностью р < 1
при столкновении двух частиц.
Численное моделирование с
р = 0,05 показывает, что при
такой модификации
сохраняются приведенные выше
значения фрактальной
размерности.
Вывод, который можно
сделать на основе проведенных
измерений в широком диапазоне
условий, состоит в том, что
обратимость оказывает весьма
сильное влияние на рост.
Фрактальная размерность
принимает другое значение, чем
при необратимой
кластеризации: кластеры становятся
более компактными, но
нечувствительными к кинетике. Ни структура петель, ни диффузия, ни
условия присоединения не имеют сколько-нибудь решающего
значения. Это позволяет сделать вывод о том, что
фрактальные свойства определяются только конфигурационными
(статическими) аспектами обратимости. В пользу такого заключения
свидетельствует и то, что полученное значение D согласуется
с соответствующими значениями для статических решеточных
зверей.
Тем не менее кинетика оставляет свой отпечаток, если
перейти к распределению кластеров по величине. Числр N(m)
кластеров с массой т, если записать его в виде закона подобия
N(m) = fn-2p(m/in), обнаруживает зависимость от кинетики, где
m — средневзвешенная масса. График функции р{х), входящей
tntf
г J
i ±
* /
/ i
О
и
_j
6 In/77
Рис. 2. График зависимости радиуса
гирации R от массы /п. Кривая /
соответствует d = 2, кривая 2 —
d = 3. Данные приведены при а =
= —2 (черные кружки) и а = 0
(косые кресты) для средних по всем
кластерам и при а = —2 (прямые
кресты) для наибольшего кластера,
для беспетлевых кластеров. Средние
по кластерам представлены при а =
= —2 (белые кружки). Согласно
полученным оценкам, фрактальная
размерность при d = 2(3) равна D =
= 1,57 z+= 0,06 (2,03 ± 0,05). Эта
величина получена в результате
усреднения по 2000 измерениям в
стационарном режиме.
Модели необратимого роста 369
в закон подобия, представлен на рис. 3; р(х) не зависит от in
(средневзвешенная масса in велика); m пропорциональна meq.
Функция р(х) в монодисперсном режиме (при больших отрица-
Р
7
О 7 2 ос
Рис. 3. Приведенное распределение р(х) кластеров по величине при d = 2
и беспетлевые кластеры. Распределение не зависит от meq, но зависит от а.
Представлены данные при а = —2, meq = 6 (черные кружки), meq = 12
(косые кресты) и а = — 1, meq = 12 (прямые кресты).
тельных а) имеет гораздо более широкий максимум, чем в
соответствующем необратимом процессе [10]. Это обусловлено
случайным механизмом разрушения кластеров, создающим условия,
благоприятные для полидисперсности.
ЛИТЕРАТУРА
1. Witten 7\, Sander L. М., Phys. Rev. Lett., 47, 1400 (1981).
2. Meakin P., Phys. Rev. Lett., 51, 1119 (1983); Kolb M., Botet R., Jullien R..
Phys. Rev. Lett., 51, 1123 (1983).
3. Обзор см.:
Kinetics of aggregation and gelation, eds. F. Family, D. P. Landau, North
Holland, 1984.
4. Lubensky Г., Isaacson /., Phys. Rev. Lett., 41, 829 (1978), Phys. Rev., A20,
2130 (1979); Parisi G., Sourlas N., Phys. Rev. Lett., 46, 871 (1981);
Glaus U., preprint.
5. Stauffer D., Phys. Repts, 54, 1 (1979); Introduction to Percolation, Taylor
and Francis, London, 1985.
6. Blatz P. /., Tobolsky A. V., J. Phys. Chem., 49, 77 (1945); Nanda V. S.,
Pathria R. K.y J. Chem. Phys., 30, 27 (1959); Hendriks E. M., Z. Phys.,
B57, 307 (1984).
7. Allain C, Jouhier В., J. Physique Lett., 44, L421 (1983); Richetti P.,
Prost J., Barois P., J. Physique Lett., 45, LI 137 (1985); Camoin C,
Blanc R.y J. Physique Lett., 46, L67 (1985).
Численно поправки на вращение были учтены в работе:
Meakin P., Jullien R., J. Physique, 46, 1543 (1985).
8. Herbst M., Goldstein J. Я., см. [3].
9. Vincent Б., Whittington G., Surf. Colloid Science, 12, 1 (1982).
10. Kolb M.t Phys. Rev. Lett., 53, 1653 (1984).
i \
\
V
, \
\ *
+
*
1
5
+
•
X
+
+
X
•
+
9
+ 1
Фильм о процессах агрегации
М. Кольб*
Фильм о нескольких механизмах роста был снят для того, чтобы
сделать их наглядными. В основу фильма положено численное
моделирование по соответствующим теоретическим моделям. В
фильме показано, как в зависимости от различных механизмов роста
образуются разные структуры фрактального типа.
Фильм о явлениях агрегации необходимо было снять по
двум причинам. Во-первых, процессы в природе, приводящие к
образованию неупорядоченных фрактальных структур,
допускают моделирование с помощью весьма простых стохастизи-
рующих правил. Во-вторых, теоретическое осмысление таких
процессов во многом опирается на численные эксперименты (с
использованием метода Монте-Карло). Эти численные
эксперименты позволяют реально воспроизводить в несколько
упрощенном варианте движения частиц в процессах, происходящих в
природе.
Наш фильм преследует педагогические цели. Утверждение
о том, что лучше один раз увидеть, чем тысячу раз услышать, в
особенности относится к процессам роста.
Чтобы сюжет фильма не был слишком отрывочным, мы
выбрали четыре важные модели роста, экспериментально
охватывающие широкий диапазон приложений и вместе с тем тесно
связанные между собой в теоретическом плане, т. е. модели,
которые можно рассматривать, как частные случаи одной общей
модели агрегации. Наш выбор пал на следующие четыре
модели: 1) модель Идена, пригодную для описания роста
поверхности, аналогичную росту биологических систем; 2) модель Вит-
тена — Сандера, или ограниченной диффузией кластеризации,
используемую при описании молнии, электроосаждения и
вытеснения жидкости жидкостью; 3) модель ограниченной диффузией
агрегации кластеров, или кластеризации кластеров,
описывающую агрегацию в аэрозолях и коллоидах; 4) модель химической
кластеризации, также используемую при описании коллоидных
систем.
Причина, по которой эти модели тесно связаны между собой,
состоит в том, что они могут быть представлены как частные
случаи единой обобщенной модели кластеризации кластеров с
двумя параметрами. Один из этих параметров управляет
механизмом агрегации — присоединением отдельных частиц к
кластеру или кластера к кластеру. Осуществляется управление по-
* М. Kolb • Laboratorie de Physique des Solides, Bat. 510, Universite de
Paris-Sud, 91405 Orsay, France; Institut fur Theorie der Kondensierten Mate-
rie, Freie Universitat Berlin, Arnimallee 114, 1000 Berlin 33, West Berlin.
Модели необратимого роста
371
средством коэффициента диффузии, зависящего от величины
кластера. Второй параметр устанавливает, какой процесс
доминирует в необратимом образовании связей между кластерами:
диффузия или химические реакции. Вероятность присоединения
есть та переменная, которая теоретически позволяет различать
эти два случая.
Фильм начинается с модели Идена. Отчетливо видна одна
ее характерная особенность: рост, начинающийся от
центрального зародыша, приводит к образованию концентрических
колец, аналогичных годовым кольцам на срезе спиленного дерева.
Структура, компактность, величина неровности на поверхности
постепенно убывают по сравнению с размерами кластера.
Динамика растущей поверхности продемонстрирована на растущей
зоне.
Второй в фильме показана модель Виттена — Сандера в той
же сферической геометрии, как и модель Идена. Рост
обнаруживает на двух различных масштабах одновременно и
(приближенную) масштабную инвариантность, и влияние решетки,
которое сказывается на общей форме объекта. Активная
поверхность в процессе роста по Виттену — Сандеру имеет совершенно
иную структуру, чем в модели Идена. Это различие отражает
существенную роль диффузии и проявляется в том, что кластеры
в модели Виттена — Сандера внешне выглядят как фракталы.
Съемка с различных расстояний обнаруживает инвариантность
объекта, рассматриваемого в различных масштабах. В модели
Виттена — Сандера форму кластера определяет геометрия, в
которой он растет. В качестве примера в фильме показан кластер,
выросший в модели Виттена — Сандера на поверхности и
поразительно напоминающий образования окислов металлов,
встречающиеся в горных породах. Наконец, при введении стока
(точки, поглощающей частицы) возникает возможность изучать
свойства отдельной ветви дендритной структуры.
Третьей в фильме показана модель кластеризации
кластеров, в которой ансамбль случайно движущихся частиц образует
все более крупные объекты с сильно разветвленной
волокнистой структурой. Это объясняет, почему частицы дыма
собираются в нитевидные струйки. Важнейшую информацию о кинетике
экспериментов можно извлечь из распределения кластеров по
размерам. Качественные особенности такого распределения
отчетливо видны в фильме благодаря тому, что кластеры
различных размеров «кодированы» различным цветом.
Теоретическую связь с моделью Виттена — Сандера можно
продемонстрировать способом, не лишенным занимательности,—
путем обращения закона, связывающего массу кластера и
коэффициент диффузии: после такого обращения более крупные
372
Часть V(6)
кластеры начинают диффундировать быстрее, чем мелкие. Чем
больше растут кластеры, тем «прожорливее» они становятся!
Другие физические ситуации описываются двумя вариантами
модели кластеризации кластеров. Когда концентрация кластеров,
становится большой, начинается гелеобразование, при котором
рост (в отличие от обычного моделирования в терминах перко-
ляции) определяется кинетикой. Если образование связей не
является необратимым, то система достигает динамического
равновесия, а кластеры имеют несколько более компактный вид.
Последняя из представленных в фильме моделей —
химическая (ограниченная протеканием реакции) кластеризация. Как
и в реальных коллоидных системах, модель показана для
кластеров, растущих за счет диффузии, но в случае, когда
вероятность присоединения с образованием связи (при столкновении
двух кластеров) настолько мала, что рост определяется не
диффузией, а скоростью реакции. И в этой модели образующиеся
кластеры имеют заметные отличия от кластеров, возникающих
в модели Виттена — Сандера: они более компактны (хотя
остаются фракталами).
В фильме показаны только по две двумерные численные
реализации названных выше процессов агрегации (основные
понятия в двумерном и трехмерном случаях совпадают, в то время
как двумерные проекции или сечения трехмерных структур, как
оказалось, не позволяют составить достаточно полное
представление о процессе их роста). Для передачи динамики роста при
съемке использовался цвет: со временем экран начинает
переливаться всеми цветами радуги!
Технически съемка фильма производилась следующим
образом. На компьютере путем моделирования одного из четырех
описанных выше процессов роста порождалась серия последова?
тельных конфигураций. В модели Идена новая конфигурация
отличается от предыдущей примерно несколькими сотнями
частиц, осевших на поверхность. В модели агрегации кластеров
промежуток времени между двумя последовательными
конфигурациями выбран с таким расчетом, чтобы большинство
кластеров успело продиффундировать на расстояние порядка
размеров частицы.
Полученные конфигурации одна за другой проецировались
на цветной экран с высоким разрешением. После того как
очередная конфигурация полностью прорисовывалась на экране,
перед ним ставилась камера и производилась съемка одного кадра.
Затем вся процедура повторялась с следующей конфигурацией
и т. д. На каждую секунду экранного времени приходится 25
снятых таким образом кадров.
Для тех, кто интересуется, сообщаем, что продолжительность
фильма составляет около 25 мин. Все процессы агрегации сопро-
Модели необратимого роста
373
вождаются подробным объяснением. Для прослеживания
деталей любой структуры не требуется производить «экспертизу на
месте». Копии фильма высылаются по требованию в двух
вариантах: на 16-миллиметровой пленке или на цветной
видеоленте.
В съемке фильма принимали участие ZEAM (производство),
факультет географии и ZEDAT (Свободный университет
Западного Берлина) и ZUSE Zendum (Западный Берлин). Фотоснимки
предоставили Лемма, Пьетронеро, Рац и Вейц. Фирма Pathe
Marconi (EMI Records), Париж, также оказала нам содействие.
Особую признательность мы выражаем У. Холлу и К. Пенсону.
Мы благодарны DFG (Бонн) за финансовую поддержку.
Теоретико-полевой подход
к моделям Идена и ДОА
Л. Пелити, Й.-Ч. Дзен *
Предложены полевые теории таких моделей роста, как модель
Идена и модель диффузионно-ограниченной агрегации (ДОА) на
языке формализма Дон — Грассбергера — Шейнерта пространства
Фока для классических объектов.
Кинетические модели агрегации являются в настоящее
время предметом интенсивных исследований. К числу наиболее
популярных среди такого рода моделей принадлежат модель
Идена (1) и модель Виттена —Сандера (ДОА) [2, 3].
Значительная часть этих исследований осуществляется путем
численного моделирования [4], хотя нет недостатка и в различных
теоретических подходах. Так, несколько точных результатов в
моделях Идена и ДОА в пределе многих измерений были
получены Паризи и Дзеном [5] и Ваннименусом и др. [6].
Одна из главных целей современных исследований этих
моделей состоит в установлении механизма, лежащего в основе
замечательной автомодельности кластеров, и в разработке способа
вычисления их фрактальной размерности. Опираясь на опыт
теории критических явлений, мы в праве ожидать, что теоретико-
полевые методы станут могучим вычислительным аппаратом,
способствующим осуществлению такой программы.
Действительно, теоретико-полевые подходы к процессам рождения и
уничтожения на решетке во многом напоминают появившиеся в
литературе модели агрегации. Теоретико-полевые подходы к
процессам рождения и уничтожения с памятью и без памяти недавно
были рассмотрены в работах [7—9]. Предложена также
теоретико-полевая интерпретация модели Шлёгля [10] химической
реакции (связанной с направленной перколяцией), имеющая
непосредственное отношение к полевой теории Редже в физике
высоких энергий [11]. Позднее Карди [12] ввел в модель Шлёгля
эффекты иммунизации и рассмотрел соответствующий
немарковский процесс с помощью полевой теории, аналогичной
«истинному» случайному блужданию без самопересечений [13].
Выводы этой работы были затем пересмотрены Карди и Грассбер-
гером [14] и Ианссеном [15], которые пришли к выводу, что
статистические свойства этой модели принадлежат тому же
классу универсальности, что и статистика перколяционных кла-
* Luga РеШ£-Dipartiamento di Fisica, Universita «La Sapienza», Piazzale A.
Moro 2, 1-00185 Roma (Italy) and GNSM — CNR, Unita di Roma; Zhang Yi-
Cheng- Physics Department, Brookhaven National Laboratory, Upton, NY 11973
USA. При поддержке министерства энергетики США (контракт № DE-AC02-
76Н00016).
Модели необратимого роста
375
стеров. С другой стороны, исходя из эвристических
соображений, Паризи и Дзен [16] предложили полевые теории,
описывающие модели Идена и ДОА. Эти авторы пришли к выводу о
том, что модель Идена допускает описание с помощью теории
Редже с локальными взаимодействиями глубоко внутри
упорядоченной области, в то время как ДОА соответствует
обобщенной теории Редже с нелокальными взаимодействиями. Шапир и
Дзен [17] развили систематический гамильтонов подход к
модели Идена и разработали полевую теорию, локальную по
пространству и нелокальную (немарковскую) по времени. Как
будет показано ниже, единый вполне однозначный метод
оказывается достаточным для получения последовательного
теоретико-полевого описания моделей Идена и ДОА. Этот метод есть не
что иное, как формализм пространства Фока для классических
объектов, предложенный впервые Дои [18] и впоследствии
переформулированный Грассбергером и Шейнертом [19].
По существу метод, о котором идет речь, сводится к
представлению эволюционных уравнений модели в виде следующего
уравнения для многочастичной функции распределения:
■ЩР- = ь\Ф№ (1)
где фЦ) —макроскопическое состояние системы,
характеризуемое вероятностями ф (п; /) найти систему в микроскопическом
состоянии, определяемом! набором чисел заполнения n = {ftr,a}
(г — радиус-вектор узлов D-мерной решетки, а — индекс,
указывающий «сорт» частицы, входящей в систему). Оператор
эволюции L (лиувиллиан) можно выразить через операторы
уничтожения ar, a и рождения яг, а, определяемые соотношениями
аг,а!{Яг.а'}>==Яг,а|{..., Яг.а—1, ...}>> (2)
Яг,а|{Яг'.а'}) = |{..., Лг,а+1, ...}). (3)
Операторы уничтожения и рождения удовлетворяют
обычному коммутационному соотношению
[Яг, a, *V. а'] = бгг'6аа'. (4)
В пространство макроскопических состояний структура
гильбертова пространства вводится так, чтобы оператор a+a,
эрмитово сопряженный с оператором уничтожения a a, определялся
соотношением
а£а = Яг,а— 1. (5)
Если оператор L записан в виде нормального произведения,
т. е. линейной комбинации мономов относительно операторов
рождения и уничтожения с операторами уничтожения, стоящими
376
Часть V(6)
справа от операторов рождения, то соответствующий интеграл
по траекториям определяется лагранжианом
#= Z 'Чг.а'фг.а - L [*$, ф] (6)
г, а
как функция двух вещественных классических полей $ = {фг, a},
г() = {<фг \ Точка сверху означает производную по времени.
Функция 3?(ity> ф) получается из представления оператора Лиу-
вилля в виде нормального произведения путем подстановки
/<фг а вместо а+а и г|)г а вместо аг а с учетом соотношения (5).
Рассмотрим теперь следующую формулировку модели Идена
[1]. В исходной модели Идена на каждом шаге по времени к
кластеру присоединялась ровно одна частица. Мы же считаем,
что на каждом шаге по времени каждый элемент кластера
может присоединить по частице в ближайший узел, если тот
свободен, с определенной вероятностью \i. Таким образом, «время»
в исходной модели Идена пропорционально массе кластера в
этой модели. Нетрудно записать представление оператора Лиу-
вилля в виде нормального произведения для такого процесса:
°° к
1 = ^ Y Y Y kl (Яг — 1) Яг + еЯгЯг +еЯг. (7)
г е fe=0
Множитель
у(яг. «г)=х;-^^ягч6 (8)
не позволяет частицам присоединяться к кластеру в уже
занятые узлы. Сумма по е берется по векторам всех ближайших
соседей, т. е. по всем векторам, идущим из данного узла ко всем
его ближайшим соседям. Применяя изложенную выше схему,
мы приходим к лагранжиану
г = |Y *м*- *Y Y -Цг-(^) х
^ г е fc=0
X (*Фг+е + 1) 0"*г + 1У Фг+в*?}. (9)
Чтобы сделать это выражение более удобообозримым, выделим
члены низшего порядка по полям:
& = Е {'ФгФг — Ц Z [4i4r+e + (*$>г) О'Фг+е) *|'г+е —
г I e
—/фгФг+еЧ>] + члены старшего порядка.} (10)
Модели необратимого роста
377
Перегруппировав явно выписанные члены, преобразуем (10) к
следующему виду:
& = Z fa$r*r — |*?АМг — МЛ'фгЛ'Фг — М- (^г)2 Фг +
г
+ Ц/'фгФг — Ц'Фг А (*фгФг) — Ц/'Фг'Фг А^г + . . .}, (11)
где q — координационное число решетки, А — дискретный
оператор Лапласа:
Л^г=Е(^г+е-Фг). (12)
е
Выписанные в правой части разложения (11) члены
соответствуют полевой теории Редже с отрицательной «массой» (глубоко
в упорядоченной области). Пренебрегая членами старшего
порядка, мы приходим к теории Редже в непрерывном пределе.
Следует заметить, что наша полевая теория с лагранжианом (9)
локальна (марковская) по времени и квазилокальна по
пространству, поскольку содержит производные только до второго
порядка. Кроме того, в нашу теорию не входят другие поля,
кроме поля плотности -ф и сопряженного с ним поля и[).
Обратимся теперь к модели ДОА, которую мы сформулируем
следующим образом. Имеется стационарный (но слабый) поток
диффундирующих частиц D и кластер из частиц Л. Если частица
D оказывается в узле, не занятом частицами Л, но ближайшем
к узлу, занятому одной из частиц Л, то она может превратиться
в частицу Л и перестать диффундировать с вероятностью [л.
Обозначим через ф, г|) поля плотности соответственно частиц D и Л,
через i<f>, *'$— сопряженные поля. В этих обозначениях
лагранжиан имеет вид:
& = 2 \1ФтФг + 1фгФг — <* Е (#г+е — 1фт) Фт +
г I e
+ V Е (1 + *Фг+е) (*фг — 1фт) Фг+е^г +
е
k Л
+ Ц £ £ ■Цг-(1 + *+е) 0+г - ih) (1 + '♦г)*Фг*+г+е*г[ • (13)
е &=1 ' '
Мы не выписываем в явном виде члены, соответствующие
источникам на бесконечности, которые обеспечивают стационарность
потока частиц D. Опустив пропорциональные *фг+е члены,
описывающие взаимодействие, мы придем к теории среднего поля
для ДОА, предложенной Науэнбергом [20].
Итак, показано, что метод Дои — Грассбергера — Шейнерта
позволяет строить полевые теории наиболее известных моделей
необратимой агрегации.
378
Часть V(6)
Выражаем свою признательность. И. Шапиру за ценные
обсуждения.
ЛИТЕРАТУРА
1. Eden M., ed., J. Proc. of the 4th Berkeley Symposium on Mathematical
Statistics and Probability (Berkeley, University of California Press,
vol. IV, 1961, p. 223.
2. Witten T. A., Sander L. M, Phys. Rev. Lett., 47, 1400 (1981).
3. Witten Т. Л, Sander L. M., Phys. Rev., B27, 5686 (1983).
4. Family F, Landau D. P., eds., Kinetics of Aggregation and Gelation,
Amsterdam, North Holland, 1984.
5. Parisi G, Zhang У. C, Phys. Rev. Lett., 53, 1791 (1984).
6. Vannimenus /., Nickel В., Hakim V., Phys. Rev., B30, (1984), 391 (1984).
7. Grassberger P, De La Torre A., Ann. Phys., NY, 122, 373 (1979).
8. Cardy /. L, Sugar R. L„ J. Phys. A: Math. Gen., 13, L423 (1980).
9. fanssen #. K, Z. Physik, B42, 151 (1981).
10. Schlogl /\, Z. Physik, 253, 147 (1972).
11. Amati D.7 Ciafaloni M., Marchesini G., Parisi G., Nucl. Phys. 448, 483
(1976).
12. Cardy J. L., J. Phys. A: Math. Gen., 16, L709 (1983).
13. Obukhov S. P., Peliii L., J. Phys. A: Math. Gen, 16, L167 (1983).
14. Cardi J. L, Grassberger P, J. Phys, A18, L267 (1985).
15. Janssen H. /(., Z. Physik, B58, 311 (1985).
16. Parisi G, Zhang Y. C, Brookhaven preprint (1985), направлен в J. Stat.
Phys.
17. Shapir F, Zhang Y. C, Lett. J. de Phys, June Issue, 1985.
18. Doi M., J. Phys. A: Math. Gen, 9, 1465 (1976).
19. Grassberger P, Schuenert M., Fortschritte der Physik, 28, 547 (1980).
20. Nauenberg M.t Phys. Rev, B78, 449 (1983).
Распространение эпидемических заболеваний,
приводящее к фрактальным структурам
П. Грассбергер*
Рассмотрены модели роста популяций, позволяющие
воспроизводить распространение эпидемий и приводящие к образованию
фрактальных кластеров. Все известные модели такого рода
позволяют описывать не только рост, но и спад эпидемии и связаны с
направленной или ненаправленной перколяцией. В случае
близкодействующей инфекции численные эксперименты на основе метода
Монте-Карло позволяют получать очень точные оценки
критических параметров обычной перколяции. Для близко- и дальнодей-
ствующих инфекций рассмотрены 8-разложения динамических
критических показателей.
1. Введение
В моем докладе речь пойдет о моделях роста кластеров,
которые могут служить моделями распространения эпидемий в
популяциях с малой мобильностью и с инфекциями,
обладающими не слишком большим радиусом действия [1—3]. Такие
модели (с весьма незначительными модификациями)
применимы и к многих другим явлениям — от лесных пожаров до
образования звезд. Для большей связности изложения я буду
говорить об эпидемиях.
Простейшей моделью распространения эпидемий может
служить модель Мальтуса экспоненциального роста. Учет эффектов
насыщения приводит (если пренебречь пространственным
распределением) к модели Ферхюльста. Приняв во внимание
пространственную кластеризацию, мы получим модель Идена [4].
Последняя приводит к компактным кластерам, поэтому я не буду
на ней особо останавливаться (хотя границы кластеров в
модели Идена растут по нетривиальным законам подобия [5]).
Более реалистические модели должны учитывать, что
кластер инфицированных индивидов не всегда растет. Например,
больные индивиды менее приспособлены к самозащите, и
поэтому потомство здоровых индивидов может их вытеснять.
Условно это можно записать в виде схемы «реакции»
f больной + больной
(инфекция с коэффициентом
больной + здоровый -> { (1)
здоровый + здоровый
I (смерть и замещение с
( коэффициентом Ъ < а).
* Peter Grassberger • Physics Department, University of Wuppertal, Wup-
pertal, FRG.
380
Часть V(6)
Эта схема была предложена в качестве модели роста опухолей
[6]. Она также не приводит к образованию фрактальных
кластеров, но мы в праве ожидать, что поверхность кластеров
будет обнаруживать интересные и нетривиальные законы подобия,
аналогичные тем, которые были найдены в работе [5].
Для получения фрактальных кластеров, необходимо учесть
выздоровление или смерть как «одночастичную» реакцию
больной-> здоровый (или смерть). (2)
Основное различие между уравнениями (1) и (2) состоит в
том, что в случае уравнения (1) кластер больных может
«сморщиваться» только с периферии — периметра, в то время как в
случае уравнения (2) внутри кластера могут возникать дыры.
Существуют две качественно различные модели.
I. «Простая эпидемия с выздоровлением» [1],
характеризуемая только двумя типами индивидов и следующими реакциями,
происходящими между соседями:
больной + здоровый -> больной + больной
(инфекция с коэффициентом а),
больной -► здоровый
(выздоровление с коэффициентом Ь).
Если отношение а/6 превышает некоторое критическое значение,
то возникает эпидемическая ситуация, т. е. стационарное
состояние с ненулевой плотностью больных. Критическое поведение
системы вблизи порога описывается, как будет показано ниже,
направленной перколяцией в (d + 1)-мерном пространстве, где d—
размерность пространства.
II. «Общая эпидемия», или «эпидемия с выбыванием» [1], в
которой существует третье состояние «выбывших» (т. е.
иммунизированных или умерших) индивидов, с реакцией
больной + восприимчивый -> больной + больной
(инфекция с коэффициентом а),
больной -> выбывший
(смерть или выздоровление с иммунизацией,
коэффициент Ь).
Следует иметь в виду, что резервуар восприимчивых не
восполняется. Поэтому в конечной популяции всякая эпидемия рано
или поздно затухает. Но в бесконечной популяции эпидемия
может распространяться неограниченно долго как уединенная
волна, оставляя после себя кластер иммунизированных индивидов.
Если эти индивиды не движутся, то образуется
(ненаправленный) перколяционный кластер.
Модели необратимого роста
381
Таким образом, все известные модели распространения
эпидемий, приводящие к фрактальным структурам, связаны с пер-
коляцией.
В разд. 2 мы остановимся подробно на двух последних
моделях и приведем результаты численных экспериментов по методу
Монте-Карло. Полевая теория и е-разложения для этих теорий
будут рассмотрены в разд. 3, а обобщения (в основном на
случай дальнодействующих инфекций) — в разд. 4.
2. Связь с перколяцией и численное моделирование
по методу Монте-Карло
2.1. Чтобы понять связь между моделью (I) и направленной
перколяцией, рассмотрим квадратную решетку в (1 + 1)-мерном
пространстве-времени, ориентированную, как на рис. 1.
Рис. 1.
Каждый индивид занимает один узел решетки, и болезнь
продолжается ровно один шаг по времени. Инкубационным, или
латентным, периодом мы пренебрегаем. Если предположить, что
каждый больной индивид инфицирует обоих ближайших соседей
независимо и с вероятностью р, то можно проследить, как один
зародыш болезни порождает перколяционный кластер с
направленными связями. С другой стороны, если инфекция всегда
поражает либо обоих ближайших соседей, либо ни одного из них, то
получается перколяция узлов. Как выглядит типичная картина,
порождаемая при р ж рс в одномерном пространстве, когда в
начальный момент времени все узлы инфицированы, показано
на рис. 2.
Критические показатели в рассматриваемой модели
вычислялись различными способами, например методом подобия с
конечным масштабом [7], разложения в ряд [8] и Монте-Карло
[9]. При р = рс фрактальная размерность кластера больных в
любой заданный момент времени определяется по формуле
dF = d-$/v9 (3)
382
Часть V(6)
из которой следует [7, 8], что rf/r = 0,749±0,001 при d=l и
dp = 1,119 ± 0,004 при d = 2. Можно предположить, что в
одномерном случае dp = 3/4, но точное значение фрактальной
размерности неизвестно, несмотря на простоту модели. При всех
Рис. 2.
размерностях d ^ 1 типичные кластеры не связаны, как на рис. 2
(при d — 1).
2.2. Воспользуемся той же решеткой для модели с
иммунизацией. Нетрудно видеть, что в случае одного пространственного
измерения процесс всегда затухает (рис. 3).
Рис. 3.
При d ^ 2 процесс может неограниченно долго не затухать,
если р > рс, и иммунные узлы при t = оо образуют связный
кластер. Ясно, что статистики этих кластеров совпадают с
статистиками (ненаправленной) перколяции связей [10].
Если начать с инфицированной гиперплоскости и следить за
распространением инфекции от нее, то наиболее эффективным
методом численного моделирования является метод
Монте-Карло. Типичная картина, которая при этом возникает (при rf = 2),
Модели необратимого роста
383
изображена на рис. 4. Выбывшие узлы показаны серым цветом,
больные — черным, инфекция распространяется снизу вверх.
При d = 2 величина рс и статические критические показатели
точно известны. Существует только один независимый
кинетический показатель, например показатель v*f определяемый из
соотношения vKopp ~ | р — рс |v*. Измеряя среднее число больных
узлов и их среднее расстояние от исходной линии как функции от
Рис. 4.
t, мы получили [11] V* = 1,509 ± 0,004, что наводит на мысль
о точном значении v*=3/2 (другие оценки [12, 13] содержат
большую погрешность). При более высоких размерностях
численное моделирование по методу Монте-Карло [12, 14]
позволяет получать рс и статические критические показатели
примерно с той же точностью, что и другие методы. Для кинетического
показателя мы получили [14] оценку v/vt = 0,725 ± 0,006 (d =
= 3) и 0,625 ± 0,01 (rf = 4). Более подробное сравнение с
другими оценками критических параметров см. в работе [14]
(расхождение в рс при d = 4, о котором упоминалось в предыдущем
варианте работы [14], было вызвано ошибкой в программе).
3. Теория поля и е-разложения
Хотя полевые теории эпидемических процессов могут быть
получены исходя из соображений, аналогичных развитым
Мартином— Сиджа — Розе [15], более систематический подход,
использующий теорию поля для описания процессов агрегации
частиц, был развит Дои и другими авторами [16].
В случае эпидемии без иммунизации вводятся полевой
оператор г|)(х) и сопряженный ему оператор г|)+(д:), играющие
соответственно роль операторов уничтожения и рождения для
инфицированных индивидов. Плотность последних при условии, что
384
Часть V(6)
в начальный момент времени единственный инфицированный
индивид находился в точке пространства-времени (х, t) = (0, 0),
задается функцией Грина
(0|++(х)^г*(0)|0>, (4)
где оператор Лиувилля L = \ 2Б (х) dx содержит следующие члены:
L = — DV^ • Vo|) — 6ф + г|э + а (1 + г|э+) г|э+\|э —
(диффузия + выздоровление) (инфекция)
— с(1 + Ф+)Ф+Ф2. (5)
(насыщение из-за конечной плотности
восприимчивых индивидов)
Некоторое время назад эта теория была подробно
исследована под названием теории Редже в физике высоких энергий
[17]. Верхняя критическая размерность при таком подходе
равна dc = 4. Полученные в его рамках е-разложения (e = dc — d)
и петлевые разложения [17] приводят к результатам,
находящимся в хорошем согласии с результатами других методов.
В случае иммунизации необходимо ввести еще одну пару
полевых операторов ф(х) и Ф+(х). Эти операторы описывают
дырки в распределении восприимчивых индивидов и не
распространяются в пространстве. Оператор Лиувилля содержит в этом
случае следующие члены:
L = — DV\|>+ -Щ + а(1 +ip+)i|)+il5 +
(диффузия) (инфекция)
+ с (1 + ф+) ^+я|> - с' (1 + ф+) ф+ДО. ( '
(рождение дырок) (столкновение
инфекции и дырок)
На этот раз верхняя критическая размерность составляет
dc = 6. е-Разложения для статических показателей согласуются
с разложениями, полученными в рамках Ф3-теории [18]. Для
кинетического показателя мы получаем v* = 1 + е/28 + О (s2)
[15, 19]. Численное согласие с показателями, полученными
другими методами, находится в разумных пределах [14].
4. Дальнодействующая инфекция и другие модификации
4.1. В реалистических ситуациях инфекция редко передается
только между ближайшими соседями. Более удачным следует
считать приближение, предложенное в работе [2], согласно
которому вероятность инфекций убывает как некоторая степень
Модели необратимого роста
385
обратного расстояния:
вероятность инфекции ~ r~a-d.
При а > 2 такая гипотеза не влияет на критические
показатели. При а < 2 оказывается, что диффузионные члены в
операторах Лиувилля (5) и (6) должны быть заменены в
пространстве Фурье членами
^dkk^+(k)^(k). (7)
Иначе говоря, взаимодействующие броуновские блуждания
должны быть заменены взаимодействующими пробегами Леви [20].
Показатели v и v* должны определяться при этом через
геометрические средние:
<1п /корр) ~ — v <ln I P - Рс 1>> /8ч
<ln/Kopp>~--^<ln|p~-pc|).
Верхние критические размерности в этом случае равны dc =
= 2а (без выбывания) и dc = 3a (с выбыванием). s-Разложе-
ния по степеням e=dc — d, как и прежде, могут быть получены
непосредственно. Для процесса I (без выбывания, направленная
перколяция) находим
1 . 2е 1 /1 . 4е \
2е
для процесса II аналогичным образом получаем
^ = 1 + w> v-bt(1+"s)- (10)
В последнем случае статические показатели были приведены
ранее в работе [18].
Трудность состоит в том, что при а = 2 эти показатели не
аналитичны (см. [21]). Тем самым ставится под сомнение
область применимости выписанных выше разложений [22].
При d> dc может существовать более чем один
бесконечный кластер. Следовательно, вероятность Р(р) того, что данный
узел является источником бесконечной эпидемии при р> рс
(т. е. принадлежит некоторому бесконечному кластеру), больше,
чем плотность р(р) инфицированных (соответственно
выбывших) узлов в данном бесконечном кластере:
Р (р) ~ (Рс - Р)\ 9 (Р) ~ (Рс - Pf\ где р' > р. (11)
386
Часть V(6)
Рассмотрим теперь модель с иммунизацией. В этом случае
локазатели v*, p и распространяющаяся размерность Й [11]
являются «внутренними» характеристиками, т. е. не зависят от
решетки и показателя а, при d>dc: v* = р = 3/2=1. С другой
стороны, показатели v, (3' и dp зависят от решетки и от a: v =
= 1/а, fi' = d/a — 2, dF = 2a. Эти результаты остаются в силе
л в случае близкодействующей инфекции при замене а на 2.
4.2. Разумеется, реальные эпидемии протекают гораздо слож-
лее, чем это описывают приведенные выше простые модели.
Существуют, например, скрытые периоды, инкубационные периоды,
носители инфекции, векторы и т. д. [1]. Все эти эффекты не
изменяют критических показателей, если не сопряжены с бесконеч-
лыми временными или пространственными масштабами. Вместе
€ тем они влияют на диапазон, в котором можно ожидать
выполнения законов подобия. Однако критическое поведение
может изменяться, если иммунность сохраняется в течение
интервалов времени, распределенных как некоторая обратная степень.
Наконец, мы можем рассмотреть случай, когда иммунные
индивиды диффундируют, и поставить вопрос о форхме образуемого
лми кластера. Так как диффузия происходит медленно по
сравнению с эволюцией эпидемического процесса, должны
существовать промежуточные масштабы времени, на которых она
существенна, с переходов к бесструктурному кластеру при /->оо.
В качестве последнего примера мы можем рассмотреть
эпидемии (такие, как некоторые гельминтовые инфекции), в
которых тяжесть заболевания (число гельминтов на одного
индивида) варьируется в широких пределах и изменяется только под
воздействием многократной инфекции [23]. Возможно, что в
этом случае фрактальный кластер инфицированных индивидов
следует заменить фрактальной размерностью другого порядка —
а-мерным [24]. Каждый из критических показателей при этом
подлежит замене целой иерархией показателей, аналогичной
иерархиям, рассмотренным Конильо [25].
ЛИТЕРАТУРА
1. Baily N. Т. J., The Mathematical Theory of Infections Diseases, Griffin,
London, 1975.
2. Mollison D., Roy /., Stat. Soc, B39, 283 (1977).
3. Liggett T. M.y Interacting Particle Systems, Springer, New York, 1985.
4. Eden M., in: Proc. 4th Berkeley Symp. on Mathem. Statistics and
Probability, vol. IV, p, 233, ed. F. Neyman, Univ. of California Press, Berkeley,
1961.
5. J Mien R., Botet R, J. Phys., A18, 2279 (1985).
6. Williams 7\, Bjerknes #., Nature, 236, 19 (1972).
7. Kinzel W., Yeomans J. M., J. Phys., A14, L163 (1981).
8. Brower R., Furman M. A, Moshe M.t Phys. Lett, 76B, 213 (1978).
Модели необратимого роста
387
9. Grassberger P., de la Torre Л., Ann. Phys., N. Y., 122, 373 (1979).
10. Grassberger P., Math. Biosci., 62, 157 (1983).
11. Grassberger P., J. Phys., A18, L215 (1985).
12. Alexandrowicz Z., Phys. Lett., 80A, 284 (1984).
13. Pike R.y Stanley H. £., J. Phys., AlO, L169 (1981); Hong D. C, Stan-
ley H. £., J. Phys., A16f L475, L525 (1983); Havlin S., Nossul #., J. Phys.,
A17, L427 (1984); Rammal R.f Angles d'Auriac J. C, Benoit A., J. Phys.,
A17, L491 (1984).
14. Grassberger P., J. Phys. А, в печати.
15. Janssen К. Я., Z. Phys., B58, 311 (1985).
16. Dot M.9 J. Phys., A9, 1456, 1479 (1976); Grassberger P., Scheunert M.,
Fortschr. Phys., 28, 547 (1980) ;РеШ/ L., Univ. Rome preprint.
17. Moshe M.9 Phys. Rep., C37, 255 (1978).
18. Priest R. G., Lubensky T. C, Phys. Rev., B13, 4159 (1976); Amit D. /.,
J. Phys., A9, 1441 (1976).
19. Cardi J. L.y Grassberger P., J. Phys., A18, L267 (1985).
20. Mandelbrot Bt В., The Fractal Geometry of Nature, Freeman, San
Francisco 1982.
21. Fisher M. £., Ma S.-/(., Nickel B. G., Phys. Rev. Lett., 29, 917 (1972).
22. Theumann W. K.y Gusmao M. A., Phys. Rev., B31, 379 (1985).
23. Dietz K.y частное сообщение.
24. Grassberger P., Phys. Lett., 97A, 227 (1983); 107A, 101 (1985).
25. Конильо А. — наст, сб., с. 227.
Моделирование дендритного
роста на основе
«случайного дождя»
Б. Каприле, А. Леей, Л. Лиджери*
В рамках модели «случайного дождя», в которой кандидаты на
присоединение приближаются к растущему кластеру вдоль
случайных прямых, описаны численные эксперименты по
воспроизведению роста в двумерном случае. Исследованы изотропный рост от
центрального зародыша и рост на опорной прямой, на которую
наклонно падают «атомы» с параллельной прямой. Образующиеся
кластеры оказываются сильно разветвленными, хотя и меньше, чем
в модели ДОА. Оценена их размерность Хаусдорфа — Безиковича.
Выведены интегро-дифференциальные уравнения для локальной
плотности как функции положения и времени. Рассмотрено
несколько модификаций модели, позволяющих учесть различные
физические эффекты: 1) испарение; 2) поверхностное натяжение (учет
его достигается путем введения вероятностей присоединения,
различных по разным направлениям); 3) теплопроводность в твердых
телах; 4) поверхностная диффузия вдоль границы. В итоге
удается достичь отчасти реалистической картины роста двумерного
кристалла.
1. Введение
Хотя дендритный рост кристаллов долгое время
считался моделью порождения разветвленных объектов, численные
эксперименты но воспроизведению дендритного роста на
микроскопическом уровне производились отнюдь не часто и теория в
значительной степени оставалась макроскопической [1]. Было
показано [2], что ограниченная диффузией агрегация (ДОА) с
точки зрения математики имеет много общего с ростом
кристаллов; но дендритные кристаллы гораздо более компактны и
менее разветвлены (за исключением особых случаев), чем
кластеры, выросшие в рамках модели ДОА. Кроме того,
численные эксперименты на основе ДОА чрезвычайно дороги (из-за
высокой стоимости случайных блужданий). Наконец, поскольку
в нашей лаборатории проводились исследования рассеяния
атомов на поверхности, рост из пара представлял для нас больший
интерес, чем рост из раствора, который лучше всего
моделировать с помощью ДОА.
По всем этим причинам мы решили провести численные
эксперименты, в которых «атомы» — кандидаты на присоединение —
падают на растущий кластер, как капли дождя, вдоль некоторых
* В. Caprile, А. С. Levi, L. Liggieri-Universita di Genova, Dipartimento
di Fisica and Gruppo Nationale di Struttura della Materia del CNR, Via Do-
decaneso 33, 16146 Genova, Italy.
Модели необратимого роста
389
случайных прямых, а не по броуновским траекториям,
характерным для ДОА. Нашу модель мы назвали моделью «случайного
дождя».
2. Модель «случайного дождя»
Модель «случайного дождя» (СД) нельзя назвать
совершенно новой. У нее долгая история, восходящая к работам
Марджори Волд [3] и Сазерланда [4]. Недавно она была
использована для численного моделирования Бенсимоном и др. [5] и
Рис. 1. Кластер, полученный в модели «случайного дождя» на квадратной
решетке.
двумя из авторов настоящей работы [6]. Нами рассмотрены
здесь две геометрии (обе в двумерном случае). В первой из них
зародыш помещался в центре, после чего «атомы» (кандидаты
на агрегацию) начинали двигаться с большой окружности внутрь
ограничиваемого ею круга. Каждый «атом» стартовал из
случайно выбранной точки и двигался по случайной хорде. Во
второй геометрии «атомы» по случайным направлениям падали на
прямой, соединяясь при соприкосновении либо с
линией-основанием, либо с растущим кластером. Характерный пример
кластера, выросшего в первой геометрии, показан на рис. 1. Модель
«случайного дождя» порождает разветвленные структуры (хотя
и не столь разветвленные, как в случае ДОА), потому что
вероятность присоединения к ветви выше вероятности
присоединения к центру.
390
Часть V(6)
3. Размерность Хаусдорфа — Безиковича
3.1. Рост из зародыша
Размерность Хаусдорфа — Безиковича D кластера
измерялась путем подсчета «атомов» в кругах возрастающих радиусов
(рис. 2). Полученное значение составляет величину D = 1,86 ±
3Г
z\
ir
i
* 1
_L
_L
I
J
J_
_L
_L
4 6
_L
Z 3 4 5 О 1 Z в 4
In (расстояние от зародыила)
Рис. 2. Вычисление размерности Хаусдорфа — Безиковича по формуле D (г) —
= \n[AiN(r)-n]/\nry где А\ — площадь единичной ячейки, N(r)—число
занятых узлов в круге радиусом г для кластеров, изображенных: / — на рис. 1;
2 — на рис. 3; 3 — на рис. 4 и 4 — на рис. 5.
=Ь 0,03. Но и обширные численные эксперименты Микина [7],
и математические аргументы, развитые Боллом и Виттеном [8],
указывают на то, что кластеры в модели «случайного дождя»
имеют тривиальную размерность Хаусдорфа — Безиковича, т. е.
что D =2. Поэтому значение D = 1,86, по-видимому, не следует
считать окончательным, и по мере увеличения размеров
кластеров оно, возможно, будет медленно возрастать до 2.
3.2. Рост на прямой
В этом случае размерность Хаусдорфа — Безиковича D
измерялась путем подсчета «атомов» в полосках длиной / и
возрастающей шириной z по формуле N(z) ~ lzD~l. И в этом случае
полученное значение составляет величину D = 1,86 ± 0,02, но,
как и в случае роста из зародыша, следует ожидать, что с
увеличением размеров кластера D будет стремиться к 2.
Модели необратимого роста
391
4. Интегро-дифференциальные уравнения
Средняя радиальная плотность cp(r, t) кластера, растущего
из зародыша в модели «случайный дождь», возрастает со
временем в соответствии с интегро-дифференциальным
уравнением [6]
-|^ = Лф^ ^Ф(/?2 + г2 —2/?rcos^)-x/2exp{5 ^ln [1 — ф(К, /)]},
(1)
где (R, г|э)—- полярные координаты точечного источника на
окружности большого круга, dl — дифференциал длины пути.
Уравнение (1) выполняется при условии, если размеры кластера
велики по сравнению с шагом решетки. Экспонента описывает
непрозрачность кластера.
Уравнение (1) принадлежит к интересному классу
эволюционных уравнений, простейшим представителем которого может
служить уравнение
^ = [t(x) + g (х) ф {х, /)] exp |- J dx'y (*', t) J, (2)
легко решаемое аналитически в случаях a) g* = 0, б) g"=l,
/ = 0. При t-*oo решение ф стремится к некоторой функции
фоо. Интеграл от последней расходится на больших расстояниях.
Непрозрачность внешних частей кластера обращается в
бесконечность, вследствие чего плотность ф в каждой точке х
перестает возрастать через определенное время t (? зависит от х).
5. Испарение
Присоединение без испарения соответствует бесконечной
разности химического потенциала Ар, между жидкостью и твердым
телом. В реальной жизни А|л конечна, и атомы испаряются.
Присоединение с испарением допускает моделирование с помощью
случайного отрыва атомов от периферии кластера.
Оторвавшись, они движутся по прямым до тех пор, пока либо не
столкнутся с какой-нибудь другой частью кластера, либо не исчезнут
вдали от него.
6. Теплопроводность и дифференциальное присоединение
Описанное выше численное моделирование не воспроизводит
многие физические свойства, играющие весьма существенную
роль в реальных кристаллах. К числу наиболее важных из таких
свойств относятся:
а) поверхностное натяжение;
392
Часть V(6)
б) теплопроводность в твердых телах;
в) макроскопическая симметрия кристалла;
г) поверхностная диффузия.
В выполненных недавно численных экспериментах
предпринята попытка учесть эти эффекты.
а) Эффекты поверхностного натяжения удается частично
учесть, просто приписывая большую вероятность присоединению
Рис. 3. Кластер, выращенный на шестиугольной решетке. Вероятность
присоединения «атома» считается равной 0,02; 0,3 или 1 в зависимости от того,
приводит ли оно к достраиванию отрезка, треугольника или шестиугольника.
в узел, имеющий много ближайших соседей. Если кластер
растет на гексагональной решетке, то дифференциальная
вероятность присоединения достигается путем приписывания в порядке
возрастания вероятностей присоединения «атома», приводящего
к достраиванию отрезка, треугольника или шестиугольника.
Такая процедура способствует образованию минимальных границ
и тем самым позволяет моделировать поверхностное натяжение.
б) При соединении «атомов» образуется скрытая теплота,
которая распространяется по кластеру так, что поток тепла
пропорционален разности температур между соседними ячейками.
Избыток тепла отводится с плоскости через излучение.
в) Проводимые в настоящее время численные эксперименты
не позволяют воспроизвести макроскопическую гексагональную
симметрию кристалла, но относящаяся к симметрии физическая
информация, как и в случае «а», должна быть связана с
дифференциальным присоединением.
Рис. 4. Кластер, полученный путем введения: 1) дифференциальных
вероятностей присоединения; 2) переноса тепла внутри кластера; 3) потерь тепла
на излучение; 4) «поверхностной» диффузии присоединяющегося «атома».
Рис. 5. Кластер, выращенный при тех же условиях, что и кластер на рис. 4,
с дополнительным учетом испарения.
394
Часть V(6)
г) Поверхностная диффузия может быть учтена при
численном моделировании, если разрешить «атому» блуждать по
периметру кластера до тех пор, пока он не окажется в узле,
присоединение в который предпочтительно либо а) по числу соседей,
либо б) вследствие легкой диссипации энергии.
Численные эксперименты проводились с учетом различных
комбинаций эффектов а — г и (или) испарения. Приводимые
примеры показывают кластеры, выросшие с учетом только
дифференциального присоединения (рис. 3), дифференциального
присоединения с учетом теплопроводности и поверхностной
диффузии (рис. 4) и всех этих условий и испарения (рис. 5).
Соответствующие размерности Хаусдорфа — Безиковича
представлены на рис. 2: по мере увеличения числа учитываемых
физических эффектов наблюдаемая размерность D имеет тенденцию к
возрастанию.
ЛИТЕРАТУРА
1. Langer /. S.y Rev. Mod. Phys., 52, 1 (1980).
2. Witten T. A., Sander L. M., Phys. Rev. Lett, 47, 1400 (1981); Phys Rev.,
B27, 5686 (1983).
3. Void M. 7., J. Colloid Sci., 18, 684 (1963).
4. Sutherland D. N., J. Colloid Sci., 22, 300 (1966); 25, 373 (1967).
5. Bensimon /)., Domany E.y Aharony A., Phys. Rev. Lett., 51, 1394 (1983).
6. Levi A C, Liggieri L., Surf. Sci., 148, 212 (1984).
7. Meakin P., частное сообщение.
8. Ball R. C, Witten T. A., Phys. Rev., A29, 2966 (1984).
Экспериментальное исследование
двумерной агрегации
К. Аллен, М. Клуатр *
Изложены результаты экспериментальных исследований двумерной
агрегации мелких сферических частиц, плавающих по поверхности
раздела воздух — вода. Дается количественное описание
взаимодействий типа притяжения (капиллярных эффектов) между
частицами. Показано их существенное влияние на эволюцию системы.
Образующиеся структуры автомодельны с фрактальной
размерностью D = 1,65 ± 0,05.
1. Введение
Образование кластеров частиц — весьма
распространенный процесс, встречающийся, например, при выпадении хлопьев
в коллоидных системах, коагуляции аэрозолей или в химических
реакциях с участием радикалов. Помимо численного
моделирования, приводящего к различным моделям необратимой
агрегации [1—3], недавно было выполнено несколько
экспериментальных исследований кластеризации [4—7]. В настоящей работе
мы излагаем последние экспериментальные результаты,
полученные на системе, претерпевающей двумерную агрегацию [8].
2. Эксперимент
Наша система состоит из сферических частиц одинакового
диаметра, плавающих по поверхности раздела воздух — вода.
В качестве таких частиц мы использовали шарики из
полипропилена или воска диаметром 3,1 мм; кювета, в которой
проводился эксперимент, имела форму квадрата размером 600 X
X 600 мм. Случайные градиенты скорости были малыми: G <
< Ю-2 с-1; влияние этих градиентов скорости на агрегацию
было исследовано в нашей лаборатории Бланком и др. [9],
занимавшимися изучением процесса кластеризации таких же
частиц в сдвиговом течении.
Равновесие шарика на поверхности раздела воздух —
жидкость достигается при обращении в нуль равнодействующей его
веса, архимедовой силы и сил поверхностного натяжения. Из-за
капиллярного притяжения две частицы, соприкоснувшись,
соединяются необратимо. В начале эксперимента частицы
случайным образом распределялись по поверхности. Положение и
движение частиц фиксировались на кинопленке.
* Catherine Attain, Michel Cloitre -Laboratoire d'Hydrodynamique et Me-
chanique Physique UA CNRS/857, ESPCI, 10 rue Vauquelin, Paris 75005,
France.
396
Часть V(6)
3. Взаимодействия между частицами
Связь между шариками осуществлялась только за счет
капиллярных сил. Количественное описание взаимодействия между
шариками достигалось путем измерения деформаций
поверхности раздела воздух — вода вокруг частицы. Мы применили
методику, основанную на использовании методики муаровых узоров.
Рис. 1. Зоны деформации вокруг Рис. 2. Изоклины вокруг кластеров
двух различных частиц (Х0,3). (Х0,3).
Периодическая решетка полос проецировалась через
оптическую систему на поверхность S. После отражения от S
производилось фотографирование, изображение анализировалось с
помощью оптических фильтров, и мы находили линии равной
кривизны и изоклины. На рис. 1 черные круги, охватывающие
различные частицы Л и В, соответствуют областям поверхности
раздела с радиусом кривизны меньше 60 м (вдали от частиц радиус
кривизны бесконечен). Диаметры этих зон (^л = 50 мм и de —
= 30 мм) связаны с радиусами действия капиллярных
эффектов, обусловленных частицами Л и В. На рис. 2 кластеры
(состоящие из частиц типа А) окружены тонкими черными линиями,
повторяющими их очертания, — изоклинами.
Ясно, что зоны деформации вокруг кластеров не изотропны.
Из качественных соображений следует, что новые частицы или
кластеры присоединяются к растущему кластеру, приближаясь
к нему по линии наибольшей крутизны. Этим и объясняется
разветвленная структура кластеров.
4. Результаты
Первый результат относится к существованию двух режимов
агрегации в зависимости от начальной концентрации частиц Ф
[8]. В режиме разбавленной взвеси (Ф» 1—3%) один-един-
Модели необратимого роста
397
ственный кластер образуется по истечении довольно длительного
промежутка времени (через 12 ч). Когда Ф превышает
критическую концентрацию Фс, через конечное время возникает
кластер, соединяющий два противоположных борта кюветы. По
нашим наблюдениям при уменьшении капиллярного притяжения
между шариками критическая концентрация Фс возрастает;
например, Фс ~ 8 % Для частиц А и Фс ж 12 % для частиц В.
Рис. 3. Снимок, сделанный перед ге- Рис. 4. Снимок, на котором запечат-
леобразованием: для образования лена заключительная стадия экспери-
бесконечного кластера недостает мента, выполненного с частицами
только двух связей. двух типов: А и В.
Снимок, представленный на рис. 3, сделан на пороге гелеобразо-
вания через 20 мин после начала эксперимента; начальная
концентрация составляет Ф ^ 10 %.
Чтобы продемонстрировать масштабную инвариантность
кластеров и определить размерность Хаусдорфа, мы находим число
N частиц в данном кластере как функцию его диаметра А (для
каждого из кластеров, наблюдаемых на снимке, аналогичном
рис. 3). Относительно диаметра А заметим следующее. Мы
берем среднее наибольшего линейного размера кластера и его
ширины в перпендикулярном направлении. График зависимости
In TV от In А показывает, что Af(A) изменяется по степенному
закону N(A) ~ AD в достаточно широком диапазоне [8]. Наши
эксперименты в режиме гелеобразования приводят к D = 1,65 ±
± 0,05. Каждый кластер также обладает автомодельностью.
Например, в случае бесконечного кластера мы измеряли массу
М (L) в квадратных кюветах со стороной L и центром в
заданной точке и получили D = 1,7 ±0,1. Это значение согласуется с
предыдущими измерениями. Следует заметить, что полученная
398
Часть V(6)
нами размерность D больше значений, найденных при
численном, моделировании кластер-кластерной агрегации, при которой
D » 1,4 [2, 3]. Мы полагаем, что увеличение размерности может
быть связано^ с обусловленными гибкостью ветвей кластера
внутренними перестройками и внутри кластерной агрегацией. Кроме
того, по нашим наблюдениям по мере убывания капиллярных
взаимодействий кластеры становятся все более компактными.
В настоящее время мы занимаемся исследованием влияния
капиллярности на кластеризацию. Например, в экспериментах по
агрегации двух сортов частиц, обладающих различной
смачиваемостью, наблюдается новый эффект — существование
процесса сегрегации. На рис. 4 показана заключительная стадия
эксперимента с частицами А и В при начальных концентрациях
Ф(Л)=5% и Ф(В)=10%. Из-за различия в свойствах
поверхности частиц А и В взаимодействия А — В носят характер
отталкивания, а взаимодействия А—Ли В — В — характер
притяжения. Мы наблюдаем образование большого кластера из
частиц Ву в который внедрены небольшие кластеры из частиц Л.
Заметим, что, по-видимому, из-за отталкивания в случае
взаимодействий Л — В кластер, состоящий из частиц В, более
компактен, чем в экспериментах, производимых только с частицами В
(без частиц Л).
5. Выводы
Изложены некоторые последние результаты, полученные в
экспериментах с системой, претерпевающей двумерную
агрегацию. Получены количественные характеристики межчастичных
взаимодействий, обусловливающих кластеризацию.
Экспериментально показано существование критической концентрации, выше
которой наблюдается гелеобразование. Кластеры обладают
масштабной инвариантностью с фрактальной размерностью, равной
в режиме гелеобразования 1,65 + 0,05. Наконец, отмечено
существенное влияние капиллярных взаимодействий на
окончательную структуру кластеров; в частности, при смешивании частиц,
по-разному смачиваемых водой, наблюдается процесс сегрегации.
ЛИТЕРАТУРА
1. Witten Т. Л., Sander L. Л1, Phys. Rev. Lett., 47, 1400 (1981).
й. Kolb M.\ Botet R., Jullien R., Phys. Rev. Lett., 51, 1123 (1983).
3. Meakin P., Phys. Rev. Lett., 51, 1119 (1983).
4. Shaefer D. W., Keefer K. D., Phys. Rev. Lett. 53, 1383 (1984).
5. Shaefer D. W., Martin J. E., Cannel D.y Wiltzius P., Phys. Rev. Lett., 52,
- 2371 (1984).
6. Richetti P., Prost /., Barois P., J. Phys. Lett., 45, LI 137 (1984).
7. Weitz D. Л., Oliveira M.t Phys. Rev. Lett., 52, 1433 (1984).
8. Allain C, Jouhier B.y J. Phys. Lett., 44, L421 (1983).
•9. Blanc R., Camoin C, J. Phys. Lett., 46, L67 (1985).
Часть VI
КИНЕТИКА ОБРАЗОВАНИЯ
КЛАСТЕРОВ
Кинетика образования кластеров
при необратимой агрегации
М. Эрнст *
Приведены аналитические результаты расчетов распределения
кластеров по размерам, полученные исходя из описывающего
коагуляцию уравнения Смолуховского. Поведение решения сильно
зависит от констант Кц скорости коагуляции в рассматриваемой
модели. Обсуждены следующие аспекты: точные результаты в
полностью и частично решаемых моделях и вопросы их
существования и единственности; возможность гелеобразования;
асимптотические решения: (I) в скейлинговом (автомодельном) пределе /г,
t-+oo при постоянном отношении k/s(t), где s(t) —средний размер
кластера; (II) поведение при больших k при фиксированном
времени t и (III) поведение при больших t при фиксированном
значении k.
1. Введение
Предложенное Смолуховским уравнение коагуляции с
самого момента его появления в 1914 г. широко используется
для описания явлений агрегации во многих областях науки и
технологии. Исчерпывающие обзоры старой литературы по этому
вопросу были даны Дрейком [1] и Фридландером [2], а более
недавней литературы — Зиффом [3] и автором (4) 1\ Однако за
последние несколько лет появились многие новые аналитические
результаты, дающие полную картину поведения Ck(t) во всей
(&, t) -плоскости, что оправдывает появление нового обзора.
Рассмотрим суспензию агрегирующих частиц, взвешенных в
жидкой или газообразной среде, которые непрерывно растут
путем формирования кластеров или полимеров в результате
образования парных контактов частиц и последующего их слипания
или связывания.
Для статистического описания макроскопических свойств
системы необходимо знать распределение кластеров по размерам,
т. е. концентрацию Ck{t) как функцию времени при различных
* М. Н. /TrnsMnstitute for Theoretical Physics, University of Utrecht,
P. O. Box 80.006, 3508 ТА Utrecht, The Netherlands.
l) Большие пробелы, которые имеются в указанных обзорах в
цитировании статей, опубликованных в советских журналах, частично восполняются
отечественными монографиями [1*, 2*, 3*]. — Прим. перев.
400
Часть VI
k = 1, 2, ... . Нулевой момент M0(t) этого распределения задает
осмотическое давление (статистические моменты определяются
формулой Mn(t)— Yi knCk(t))\ первый момент M\(t) =M задает
k
общую массу или общую концентрацию мономерных единиц;
средний размер кластера s(t) = M2{t)/M\(t) определяет
вязкость суспензии и интенсивность светорассеяния в ней. Итак,
мы хотим описать совместную систему химических реакций:
А1 + А1->А2,А1 + А2-->А3, ..., А2 + А2->А4, ..., А, + АУ-*А/+/,
где Ai, Аг, .. •, Ak обозначают соответственно мономеры, диме-
ры и &-меры. Эти реакции считаются необратимыми, поскольку
предполагается отсутствие диссоциации и дробления.
В таких реакциях можно выделить по крайней мере два
характерных времени: диффузионное tD и реакционное tR. Первое
из этих времен требуется двум частицам для того, чтобы
прийти в контакт друг с другом посредством диффузии. Оно
включается в общее время tRi протекающее до момента образования
химической связи, которое связано с вероятностью реакции
(слипания) в единицу времени Р0, где tR ~ 1/Р0 при Л)->0.
Если оба масштаба времени сильно отличаются, то возможны
упрощения в описании системы. Здесь мы различаем два
предельных случая: (I) диффузионно-контролируемая агрегация
(ДКА, или ДОА) с Id > tRy где при каждом столкновении связь
образуется мгновенно (Ро=1); (II) кинетически-контролируе-
мая агрегация (ККА) с tR » tD, что соответствует малой
вероятности слипания Ро.
В этих предельных случаях можно описать агрегацию на
масштабах времени протекания медленных процессов
посредством системы зацепляющихся кинетических уравнений для
'функций Ck(t), содержащих набор констант Кц скоростей
коагуляции. Скорость конкретной (ij) -реакции равна KijCiCj, где
предполагается, что вероятности найти /-кластер и /-кластер в
любых точках статистически некоррелированы. Таким образом,
получается уравнение коагуляции Смолуховского, описывающее
изменение со временем концентраций Ck(t):
оо
-df = ~2 zl ^nCiCi — ckl^Kk!C}. (1.1)
Эта нелинейная система (k = 1, 2, ...) дифференциальных
уравнений первого порядка должна решаться при общем начальном
условии Cfc(0), частный случай которого Ck(0) » 6*i
(отвечающий монодисперсной исходной смеси) наиболее соответствует
физическому смыслу.
Каковы же дальнейшие ограничения обоснованности
уравнения коагуляции? Оно имеет типичную для приближения среднего
Кинетика образования кластеров
401
ноля структуру, где частицы реагируют независимо от
расстояния между ними. При этом пренебрегается пространственными
флуктуациями и корреляциями между положениями
реагирующих частиц.
Во многих приложениях уравнения (1.1), таких, например,
как коагуляция аэрозолей [1, 2], обычно рассматривают
распределение по размерам С(х, t)dx как функцию от непрерывной
переменной— размера х — и используют континуальный аналог
уравнения коагуляции. В настоящем обзоре размер
рассматривается как дискретная переменная, хотя большинство
приведенных здесь асимптотических результатов применимо также к
континуальной форме уравнения коагуляции.
Возвращаясь к этому уравнению, следует заметить, что
средний размер кластера s(t) все время увеличивается и агрегация
происходит до тех пор, пока все мономеры не образуют
единственный макроскопический агрегат. Распределение кластеров
по размерам Ck{t) при фиксированном k приближается к
тривиальному стационарному решению С&(оо)=0 для всех & =
= 1, 2, .... В течение этого процесса агрегации масса
сохраняется, что выражается условием
оо
Afi(0=Z kCk(t) = M=l, (1.2)
где kCk(t)/M — вероятность того, что мономер содержится в
й-мере. Единица объема выбрана таким образом, чтобы полная
плотность М равнялась единице. Общее число кластеров M0(t)
при этом, разумеется, не сохраняется.
Закон сохранения (1.2) может быть просто выведен
умножением уравнения Смолуховского на ka, суммированием по всем
k и свободной переменой порядка суммирования. Если допустить
такую перемену, то можно получить при произвольном а общие
уравнения для моментов
^=JEW/fc + i)a-'a-r]- (1-3)
из которых при а= 1 получается условие сохранения массы.
Одним из наиболее интересных свойств этого уравнения
является соответствующее гелеобразованию нарушение сохранения
массы после конечного интервала времени, как это может
проявляться з определенных классах моделей коагуляции.
Математические особенности, вытекающие из уравнения Смолуховского
для некоторых типов его коагуляционных ядер Кц (когда Mo(t)
отрицательно или M2(t) расходится за конечное время), были
рассмотрены ранее с целью выявления ограничений на
временной интервал, в течение которого уравнение Смолуховского
402
Часть VI
имеет физический смысл. Надлежащая интерпретация этих
особенностей как признаков гелеобразования была не так давно-
дана Лушниковым [6] и Зиффом |7].
План этого обзора следующий. В разд. 2 различные коагуля-
ционные ядра Кц подразделяются на три класса с разными
асимптотическими свойствами. В разд. 3 рассматриваются немногие
точно решаемые модели /С//, частично решаемые модели и
строгие результаты, касающиеся существования и единственности.
В разд. 4 обсуждаются критерии гелеобразования. В остальных
разделах проводится обсуждение асимптотических свойств
решения Ck(t): в разделе 5 скейлинговый предел, где k, t-^oo
при сохранении фиксированного значения k/s(t) (s(t)—это»
средний размер кластера); в разд. 6 поведение в области
больших t при заданном k, а в разд. 7 поведение в области больших
k при заданном t. Показано, что различные асимптотические
решения имеют общие области применимости. Заканчивается
статья кратким обсуждением результатов.
2. Классификация процессов коагуляции
Перед формальной классификацией различных типов коагу-
ляционных ядер обсудим некоторые характерные примеры.
Типичный пример ДКА — процесс броуновской коагуляции. Если
кластеры являются компактными объектами, то частота
столкновений Кц может быть вычислена из решения уравнения
диффузии на поглощающую сферу [2]. Это дает в случае
пространства размерности d = 3 выражение Кц = АпОцЯц с Оц = Di +
+ Dj и /?// = /?/ + /?/, а в более общем случае d>2 имеем
Kij = DuRdii2. При d = 2 сформулированная выше
диффузионная задача не имеет стационарного решения. В приведенных
выражениях Rk означает радиус инерции кластера, причем Rk ~ kv
при k ->• оо. Для компактных кластеров v = l/d. Если к ним
применима формула Эйнштейна для коэффициента Dk, то имеем
Dk ~ l/Rk.
Примерами процессов ККА являются реакции, протекающие
в непрерывном реакторе идеального перемешивания, где
медленные диффузионные процессы исключаются за счет
перемешивания. Другими примерами служат реакции полимеризации, где
Флори привел оценки значений вероятностей слипания Р0 ~
~ Ю-9 и Р0 ~ Ю-13 для реакций соответственно между
мономером и кластером и двумя кластерами [8].
В реакциях ККА константа скорости коагуляции Кц будет
тем больше, чем больше в кластере реакционных групп
(обозначаемых здесь как А) являются доступными. Чтобы
проиллюстрировать это, рассмотрим предложенную Флори RAf-модель
(«модель /-функциональной поликонденсации»). Здесь каждый
Кинетика образования кластеров
403
мономер имеет / групп А, где / — это функциональность или
координационное число; полимеры образуются посредством АА-
связей; любой &-мер не имеет циклов и, следовательно,
содержит Ok = (/ — 2)& + 2 непрореагировавших групп А, а два
полимера при их взаимодействии предполагаются полностью
взаимопроницаемыми. Тогда константа коагуляции пропорциональна
числу потенциально возможных пар АА в обоих кластерах, т. е.
Kij ~ а*6/!), что сводится для больших кластеров к Кц ~ f2ij.
В случае, когда кластеры в противоположность фракталам
представляют собой компакты, они имеют «дыры» и «фьорды»
характерной длины и два кластера проникают один в другой
лишь на конечное расстояние. Теперь доступными являются
лишь группы А, находящиеся в поверхностном слое, число
которых будет Ok ~ Л® с со = 1 — drl. Это дает для больших
кластеров оценку kij ~ {i})®. Размерность пространства, в котором
рассматриваются кластеры, проявляется в такой «модели
поверхностного взаимодействия» только через «поверхностный»
показатель ю.
Как эти аргументы должны быть модифицированы для того,
чтобы описать ККА фрактальных кластеров, остается неясным.
В табл. 1 собраны вместе данные об основных коагуляционных
ядрах, приведенные в литературе.
Для обсуждения асимптотических свойств различных
моделей коагуляции удобно классифицировать их в соответствии с
двумя признаками: (I) как некий большой кластер реагирует с
другим большим кластером и (II) как большой кластер
реагирует с малым кластером. Эти два признака характеризуются
соответственно показателями % и \i> исходя из чего определим:
Ki,ai~l% O'^l» значение а фиксированно),
Так как среднее число реакционных центров в кластере не
может увеличиваться быстрее, чем его размер, то наложим
физические ограничения X ^2 и v^l, никак не ограничивая при
4> Стокмайер впервые нашел более 40 лет назад точное решение
уравнения коагуляции с таким ядром в случае, когда вначале присутствуют только
мономеры [4*]. Однако он пришел к этому решению косвенным путем в
результате статистических рассуждений и, только получив таким способом
аналитическую формулу, доказал затем непосредственной подстановкой, что она
удовлетворяет коагуляционному уравнению. Точное аналитическое решение
этого уравнения при произвольных начальных условиях в наиболее общем
случае модели Флори — Стокмайера (когда имеется любое число типов
мономеров, каждый v-й из которых RvAtvl, A2v2, ..., A^m содержит
произвольные количества fvl, fv2, ..., fvtn групп типов Aj, A2, ..♦, Am) было
найдено в работе [5*]. — Прим. перее. ,
404
Часть VI
Таблица 1. Однородные коагуляционные ядра
Процессы
(/*/3 _|_ ;l/3)^-l/3 _|_ /-!/з) Броуновская коагуляция в непрерывном
режиме [1] (jx = —ГЗ)
(i*/3 _[_ jl/3)2^-i j^ .-iy/2 Броуновская коагуляция в свободном
молекулярном потоке [1] (jx == —1/2)
| ji/з _ yl/з | ^i/з _|_ yi/3^2 Коагуляция при гравитационном
осаждении [2] (ц== 1/3)
0 + У1^3) Коагуляция в потоке со сдвигом [2] (ц = 0)
// Модель разветвленной поликонденсации:
со связями типа АА (ц=?\) [7]
(ij)® (® = 1 — \/d) Та же модель, но с поверхностным
взаимодействием функциональных групп [9]
/ + / Модель разветвленной поликонденсации
со связями типа АВ [7] (ц = 0)
jQ _j_ .со Та же модель, но с поверхностным
взаимодействием функциональных групп [9]
1 Модель линейной поликонденсации [7J
(И = 0)
(i + /)w Математическая модель [10] (ц — 0)
jMyv _|_ j\y.£t Математическая модель с v > \i [11]
(/yjM' (/ _|- ;yv-n Математическая модель с произвольными
v и \i
/ °б// Иерархическая модель [12] (ц = +оо)
/^б/! + г°°6/1 Модель присоединения [13] (ц = — со)
этом величину \х. Верхние пределы этих неравенств могут быть
достигнуты, только если кластеры полностью проницаемы.
Никакие дальнейшие физические или математические ограничения
на \i и Я, определяющие на рис. 1 область допустимых моделей,
автору не известны.
Как видно из табл. 1, большинство использованных в
литературе коагуляционных ядер являются, по крайней мере для
кластеров больших размеров, однородными функциями i и /.
Поскольку далее основное внимание будет сосредоточено на
свойствах Ck(t) при больших k, естественно рассматривать ядра,
которые асимптотически однородны:
limrt^^Jtf, /). (2.2)
а->оо
В данной статье рассмотрение ограничивается ядрами, которые
строго однородны:
KtJ = a-bKat9a, = X(i,j). (2.3)
Степень однородности X является наиболее важным параметром,
но некоторые свойства Ck(t) определяются также параметром (я.
Кинетика образования кластеров
405
Таким образом, можно различать, как это показано на рис. 1,
класс I с [I > 0, класс II с и, = 0 и класс III с \i < 0. Типичными
для класса I являются реакции ККА подобные полимеризации;
Класс I
(М>0)
(преобладают
взаимодействия
между большими,
кластерами)
— Класс II(ju^O)
Класс III
(Преобладают
взаимодей ствия
болъшиос кластеров
с малыми)
Рис.1. Разделение на классы однородных коагуляциопных ядер Kij ^^Г W^>
^> /, X = \i + v) в зависимости от их асимптотического поведения. Класс I
содержит модели, которые как описывают, так и не описывают гелеобразо-
вание.
для класса III типичны реакции ДКА, протекающие при
коагуляции аэрозолей, т. е. броуновская коагуляция.
3. Точные результаты
За. Точно решаемые случаи
В отдельных подразделах ниже дается краткое описание: (I)
точно решаемых моделей; (II) частично решаемых моделей, для
которых либо (а) возможно последовательное вычисление
распределения кластеров по размерам, хотя и без расчета его
статистических моментов, либо (б) только один из таких моментов
может быть вычислен; (III) строгих результатов относительно
существования, единственности и положительности решений.
В случае произвольных начальных условий такие решения
известны только при Кц = const [1]; i + / [14]; ij [15—17]. Для
последней из этих трех моделей общее решение при произволь-
406
Часть VI
ных начальных условиях было найдено всего лишь несколько лет
назад [16] ]). Подобное решение для билинейного ядра Кц =
= Л*/+ £(/ + /) + С известно только в случае монодисперсного
начального распределения C*(0)=6*i [1, 18—20]. Например,
при С Ф 0, А = 5 = 0 имеем Ck(t) =tk~{(l + О"*"1, где путем
соответствующего выбора единиц времени можно выбрать С =
Гель-фаза
G-1-M,
tc —^1
Рис. 2. Поведение трех статистических моментов в модели Кц
= 2. Однако при АфО известное из работы [15] решение
справедливо лишь в течение конечного интервала времени.
Душников [6] и Зифф [7], по-видимому, первыми обратили внимание
на существование фазового перехода в этой модели2). Легче
всего это понять, изучая поведение во времени среднего размера
кластера s(t) =M2{t)/Mi(t). В случае простейшей среди таких
моделей Кц = ij уравнения (1.3) для моментов
АГо = —1/2; Mi = 0; Af2 =
••Ml
(3.1)
показывают, что средний размер кластера становится
бесконечным через конечное время tc = 1/M2(0). Такое поведение
моментов на временах t <Ctc иллюстрируется на рис. 2. Физической
интерпретацией этой сингулярности является наступление при
1} Это утверждение неточно, поскольку гораздо более общее решение
было получено ранее в работе [5*] (см. замечание 2). — Прим. перев.
2) Впервые наличие гелеобразования как фазового перехода установили
независимо Флори [8, р. 374] и Стокмайер [5*], которые даже привели решения
для распределения конечных кластеров Ck за гель-точкой. Аналогичное
решение в общей модели Флори — Стокмайера (см. замечание 4) приведено в
работе [6*]. — Прим. перев.
Кинетика образования кластеров
407
t = tc фазового перехода, называемого гелеобразованием. Для
понимания того, что происходит при t-+tc, следует с помощью
(1.1) вычислить поток массы J(Lyt) от кластеров размеров fe<
< L к кластерам с k > L. Это дает
/ (I, о = Z *с* = - £ £ *2/ед. (3.2)
Пока С& экспоненциально убывает при больших k,
предельное значение потока /(оо,/)=0 и общая масса сохраняется,
M\{t) = 1, что имеет место для t < tc. Однако, если Ck убывает
по степенному закону Ck ~ /г~т(&->-оо), то поток массы в
пределе больших L имеет асимптотику /(L, /) ~ L5_2t [17, 21]. Как
будет видно из дальнейшего, точное решение дает т = 5/2 для
t > tc. Таким образом, /(оо, t) фО при t ^ tc. Это означает, что
здесь существует конечный, не исчезающий поток массы от
кластеров конечного размера (частиц золя) к бесконечному
кластеру (гелю) и общая масса конечных кластеров (золя) M\(t) =
оо
= £ kCk{t) не остается постоянной, а начинает уменьшаться
при t > tc. Гель имеет исчезающе малую концентрацию, но
конечную массу, называемую гель-фракцией G(t) = l—M\(t)y
которая служит параметром порядка для этого фазового
перехода.
В качестве иллюстрации можно привести заимствованное из
работ [16, 18] выражение для распределения кластеров по
размерам при их начальном монодисперсном распределении
С*(0)=6Ы:
Ck (t) - [ {kk~2/kl) e-k/t {t>x)y <3-3)
где tc = 1 соответствует гель-точке. Догелевое решение впервые
было получено Маклеодом [15]. Более информативным
является асимптотическое поведение этого решения при больших k:
_Г(2яГ1/2АГ5/2(^-')* (/<1),
Ck{t)~\(2n)-1<2k-5'2rl (*>1). (3-4)
Эти результаты показывают, что распределение по размерам при
&->оо экспоненциально ограничено (С&<ехр(—ak)) в ходе
догелевой стадии (золь-фаза) и имеет алгебраический хвост
распределения (Ck~k-V2) в послегелевой стадии гель-фаза).
Соответственно все статистические моменты ограничены в золь-
фазе, в то время как в гель-фазе Ма (t) с а ^ 3/2 расходятся
и сохранение массы нарушается, поскольку M\(t)= \/t.
408
Часть VI
Асимптотика (3.4) распределения по размерам при больших
k показывает, что производящая функция/ (x,t)=£kCk(t)exp(kx)
при х = 0 характеризуется регулярным поведением для t < tc и
имеет при t>tc точку ветвления типа квадратного корня,
приводящую к алгебраическому хвосту распределения Ck ~ к~ъ/2.
Для более общих ядер Кц = Aij-{- B(i: + /)+ С и
монодисперсных начальных условий также найдены решения для до- и
послегелевых областей [19, 20, 22]. Можно добавить в
уравнение коагуляции источники мономеров [23—25] 1\ включить в
рассмотрение дробление [26—28] 2), обобщить билинейные ядра на
модели сополимеризации с различными типами мономеров [29]3),
включить в билинейные константы скорости Кц зависимость не
только от размера, но и от формы кластера, как, например, от
числа в нем точек ветвления [30] 4).
Существует также взаимно однозначное соответствие [31]
решений уравнения Смолуховского для модели I с Кц = (ai +
+ b){aj + b) и модели II с Кц = а(1 + /) + b. Если Ck{t) и
1) Более ранней работой, где найдено точное решение уравнения
коагуляции с ядром типа Kij = OiOj при наличии подпитки мономером, является
[7*]. Недавно появилась теоретическая работа [8*], в которой скорость такой
подпитки менялась по периодическому закону. Близкие по постановке задачи
решались в работах [9*, 10*], где рассматривалась агрегация
(поликонденсация) в проточных открытых системах, на входе которых подаются мономеры,
а на выходе имеется некое распределение агрегатов (полимеров) Ck.
Основной задачей теории здесь является нахождение стационарного распределения
С|т из уравнения агрегации при различных режимах гидродинамического
перемешивания. В случае, когда система состоит из единственной ячейки
(реактора) с идеальным перемешиванием в ней для ядра Kij = const Бисен-
бергером найдено точное решение [9*]. Аналогичная более общая задача в
каскаде из нескольких таких ячеек решалась в работе [10*] для ядер Kij =
= const и Kij = GiG;, где, в частности, найдены точные значения
коэффициента полидисперсности Ж' = M2Mq/M2{ и положения гель-точки в
зависимости от кинетических и гидродинамических параметров системы, а также от
числа ячеек в ней. — Прим. перев.
2) В работе [11*] впервые строго показано, что включение в
кинетическую схему агрегации (поликонденсации) бифункциональных мономеров
трех различных механизмов дробления не приводит к изменению вида
распределения молекул полимера С*, а лишь меняет зависимость его
параметров от времени. — Прим. перев.
3) Общая задача такого рода решена в работе [5*]. Этому вопросу
посвящена также недавняя публикация [12*]. — Прим. перев.
4) Впервые кинетические уравнения для распределений кластеров по
числам в них мономерных звеньев, образующихся в ходе подобных процессов
агрегации, а также уравнения в частных производных первого порядка типа
Гамильтона — Якоби для производящих функций указанных распределений
были приведены в работах [13*, 14*]. На примере поликонденсации мономера
RAf с кинетически зависимыми группами был указан алгоритм построения
приближенного решения этих уравнений [15*], а также выписаны две
системы из нескольких кинетических уравнений, решение каждой из которых дает
точное значение гель-точки [16*]. — Прим. перев.
Кинетика образования кластеров
409
tik{t) — соответственно решения для этих моделей, то
nk (t) = a(ak + b) tce~atCk (tc (1 - е~*% (3.5)
где tc определяется начальным распределением Ck{0) или /u(0).
Это преобразование отображает догелевое решение на конечном
интервале 0 < t < tc описывающей гелеобразование модели I
на общее решение во всей полуоси 0 < t < оо модели II, в
которой образование геля отсутствует.
36. Частично решаемые случаи
Для коагуляционных ядер Кц некоторого специального вида
распределение по размерам может быть рассчитано
последовательно, но его моменты найти точно не удается.
Первая из таких моделей была рассмотрена Лушниковым и
Пискуновым [32]. Коагуляционное ядро в их работе [32] имело
довольно общую форму Кц = ioi + /а/, где ak — произвольная
положительная функция с ak<ck (fe-^сю). Подстановка
Ck(t) = Vk(t)exp[kM0(t)] вместе с условием сохранения массы
Mi (t) = 1 (для систем с гелеобразованием это применимо при
t < tc) преобразует уравнение коагуляции в следующее:
Т= Е ^v,-W. (3.6)
Эта система уравнений может быть решена последовательно,
начиная с k=l, 2, ..., при общих начальных условиях, что дает
vi (t) = vi (0) X exp (—ait) и т. д. Если у (х, t) = £ vk (t) exp (kx),
то M0(t) можно вычислить из уравнения M0(t) = y[M0(t),t].
Второй пример был приведен Эрнстом с соавт. [33],
использовавшими ядро Кц = oi + Of с указанными выше
ограничениями на ok. В этом случае подстановка
v*(T) = C*(0/Af0(0, dx = Mt(t)dt (3.7)
преобразует уравнение коагуляции (3.1) в такое:
с ограничением 2^=1>Эта система также может быть
решена последовательно для общих начальных условий с
последующим нахождением зависимости M0(t) от исходной
переменной t из условия'сохранения массы.
Ниже рассматриваются некоторые предложенные Зиффом
[7] модели, в которых один из моментов вычисляется точно, что
позволяет найти точное значение гель-точки для моделей с
гелеобразованием.
410
Часть VI
В модели (а) Кц = Aftf/[(i + /) — ft — /] со степенью
однородности X = р < 2 момент M$(t) можно вычислить точно,
исходя из (1.3): Mfl(t) = Mp(0)/[l — 0,5AM$(0)t]. Если р>1
и А > 0, то имеем модель класса I (|х = р— 1; v= 1), а р-й
момент расходится в гель-точке через конечное время tc =
= 2/ЛМр(0). Если же р < 1 и А < 0, получается ядро модели
класса II (fx = 0; v = P), где M$(t) остается все время
ограниченным.
В модели (б) Кц = A(ift + jft)/[(i + jft - ft - ft] со
степенью однородности Я= 1 имеем M${t) =M$(0)exp(At) до тех
пор, пока M\{t) =1. При любых значениях р это ядро модели
класса II.
В модели (в) Кц = Aij/[(i + jft — ft — ft] с Я = 2 — p
получаем Mfi(t) =M$(0) + 0,5At пока Mx{t) = 1. При р > 1 и А >
> 1 имеем jm = 0 (класс II), а при р < 1 и А < 0 имеем jut =
= 1 —р (класс I). В последнем случае момент M$(t) принимает
нефизическое отрицательное значение через конечное время (ср.
с экстраполяцией на малые времена поведение M0(t) на рис. 2),
что указывает на образование геля еще до этого момента.
Зв. Существование и единственность
Ниже приведено то немногое, что известно о существовании
и единственности решения задачи Коши коагуляционного
уравнения для общих классов его ядер:
(I) Для ядер Кц ограниченных сверху величиной Aij, на
конечном интервале времени существует единственное решение,
удовлетворяющее условиям положительности и нормировки [15].
Значение этого интервала, в котором доказана единственность,
в общем случае не превышает t > Л-1. Далее все константы,
подобные Л, будут исключены путем соответствующего выбора
единицы времени,
(II) Для ядер, удовлетворяющих неравенству Кц < (* + /)>
включающему о(0; ^ V'7> Уайт доказал [34] существование
общего решения задачи Коши, все моменты которого ограничены
на конечном промежутке времени.
(III) Для ядер Kij = OiOj с a^/fe-^О при &->оо Левраз и
Тшуди [18] установили существование общего решения, но не
его единственность.
Проблема существования и единственности решений в
данном случае не является математическим ухищрением. Например,
в близкой к рассматриваемой задаче с коагуляционным ядром
ktj = const Айзенмаи и Бак [26] доказали, что существует
только одно положительное глобальное решение Ck(t) уравнений
(1.1) в классе функций kzCk(t) ->-0 при £->-оо.
Кинетика образования кластеров
'411
Иные математические трудности возникают для коагуляцион-
ных ядер cv> 1, где снова Fq = 0. Некоторые численные и
аналитические результаты показывают [16], что в нефизическом
случае v > 1 не существуют ни глобальные, ни локальные
решения задачи Коши.
4. Образование геля
4а. Границы гель-точки
Как следует из предыдущего раздела, в точно решаемой
модели Кц — Ц имеет место гелеобразование, сопровождаемое
следующими интересными явлениями:
(I) размер среднего кластера s(t) расходится при t-*-tc\
(II) нарушается закон сохранения массы при конечных tc;
(III) распределение по размерам спадает при больших k
экспоненциально и алгебраически соответственно ниже и выше tc;
(IV) производящая функция распределения С&, вначале
регулярная при х = 0, после конечного интервала времени tc имеет
там точку ветвления.
Возникает вопрос о том, существует ли в других процессах
коагуляции аналогичный переход с образованием геля? Иными
словами, какие коагуляционные ядра Кц в уравнении Смолухов-
ского приводят к гелеобразованию?
Поскольку точные решения неизвестны, необходимо
разработать иные тесты на проявление гелеобразования, способные
продемонстрировать, какие из характерных его особенностей
(I—IV) проявляются, а какие нет [35]. (В этом подразделе
изучается возможность расходимости среднего размера кластера
s(t).)
Определим некоторую меру для среднего размера кластера,
такую, как s = M2, поскольку Mi = 1. Если можно указать его
верхнюю границу s(2)(£), которая остается ограниченной сверху
для всех конечных /, то для них s(t) ^sW(t) <oo и
образование геля не происходит (рис. 3). С другой стороны, если можно
указать ограничивающую снизу функцию s(1)(0> расходящуюся
при t-+t\ < сю, то s(t) ^s^(t) расходится за конечное время
tc ^ t\ и гель образуется.
Для иллюстрации метода можно привести ряд примеров.
Начнем с предгелевой стадии, где по предположению все Ck(t)
убывают при больших k экспоненциально и все моменты
Ма (0 = Yj kaCk (t) конечны. Поэтому из уравнений для них
(1.3) при ос = 2 можно найти s(t) =M2(t). Рассмотрим первый
пример Kif = iv>jv + Р]'11 (v^m,), для которого (1.3) приводит к
выражению
M2=2MV+1M^+1. (4.1)
412
Часть VI
В случае \х ^ v < 1 из неравенства Иенсена следует Afv+1<yVf2
(при v > 1 знак этого неравенства обратный), так что М2 < 2NU
с i = ix-\-v [35]. Используя начальные условия, показанные на
рис. 3, можно найти ограничивающую сверху функцию
М{22) (/) = [Л + 2(1~-Я)/]1/(1-Я).
При К = [х + v ^ 1, когда эта функция ограничена при всех t <
< оо, гелеобразования не будет. Если Я, > 1, то она расходится
Рис. 3. Схематическое поведение статистического момента Ма (t) (сплошная
линия), а также ограничивающих его сверху (пунктир) и снизу (штриховая
линия) функций, когда все они имеют одно и то же начальное значение:
а — гелеобразования нет; б — неопределенный случай; в — гелеобразование.
Для верхней границы а = 2, так что М^ > М2, а для нижней границы
а = |х + 1, так что m[/+i < М|Х+1 < М2, где также М^+{ (0) < М2 (0).
В случае гелеобразования U < tc < h\ в неопределенном случае гель может
образоваться при tc > h.
при/->/с = {2(А— ЩЛМО)]*^1} и сделать вывод о том, будет
или нет гелеобразование, невозможно.
В нефизическом случае v > 1 (см. рис. 1) с v ^ \х ^ 0
можно указать расходящуюся нижнюю границу, и, следовательно,
гелеобразование наступит до некоторого конечного момента t\.
Однако есть указания на то, что в этих нефизических моделях
гель образуется мгновенно при tc =0 [35, 36].
Для того чтобы решить вопрос о гелеобразовании при % > 1
в физически реализуемом случае v ^ 1, следует указать
расходящуюся нижнюю границу. До сих пор успехи здесь достигнуты
Кинетика образования кластеров
413
только для ядер с v = 1 [36]. Ниже этот метод иллюстрируется
на примере Кц = ij*1 + j№ (ji^: 1) с использованием неравенств
ir + i?>(iir(i + i)1-*,
(i + ff _ ? _ f > 4 (l - 21-") (/ + jf-%
справедливых при 1 << a < 2. Подставляя эти неравенства при
■a = l + |i в (4.1), получим A/^+i > 2(l — 2"^) Afji+i. Для
положительных fjt (k= 1 + [i > 1) можно установить расходящуюся
нижнюю границу М{^+1 < М^ < М®^. Таким образом,
указанное выше ядро Ktf с 0 < |л ^ 1 или 1 < X ^ 2 описывает
модель гелеобразования со следующим диапазоном локализации
гель-точки:
(2ц [М2(0)f}~' < U < {2 (1 - 2-") Мй+, (О)}"1. (4.2)
Пока рассматривалось гелеобразование для ядер с v = 1 и
О < [х ^ 1, поскольку при v < 1 требуются иные подходы.
46. Нарушение сохранения массы
Теперь найдем решение уравнения Смолуховского с
зависящей от времени массой золя Мх (t) = £ kCk (t), что имеет место
после начала гелеобразования. Для иллюстрации метода
рассмотрим модель поверхностного взаимодействия Кц = (ij)& с
о) < 1 [35]:
оо
Удобно ввести производящие функции g(x> t)= ]С С* (0 exp (&*)
и f(xt t) = X ft^Cfe if) exp (fex), которые имеют при малых л:
следующее асимптотическое поведение:
g (х, t) ~ М0 (t) + хМ{ (t) + О (х),
f{x9t)*M„{t) + 0(l). ( }
Из (4.3) следует, что g и / удовлетворяют соотношению
jf(g-M0) = ^(f-M(Of, (4.5)
которое можно использовать для проверки того, имеет или нет
коагуляционное уравнение (4.3), описывающее гелеобразование,
решение с зависящей от времени массой золя М\ Ф 0. Для этой
цели следует подставить (4.4) в (4.5) и решить его относительно
f(x, t). Это дает формулу
f (xf t) *> М« (t) - [2хМ{ (t)]112 (x -> 0),
414
Часть VI
приводящую к следующей асимптотике для распределения
кластеров по размерам
Ck(t)^[-Mt(t)/2n]l/2^\ т = © + |. (4.6)
Данный результат заведомо непротиворечив при условии со <
< 1/2, когда масса золя Mx(t) < оо. Следовательно, при 1/2 <
< со < 1 коагуляционное ядро Кц= Щ)® описывает
образование геля в системе, поскольку в этом случае за гель-точкой
существует самосогласованное решение (4.6) с зависящей от
времени неизвестным образом функцией M\(t). В гель-фазе t>tc
(где tc также неизвестно) распределение по размерам имеет
алгебраический хвост Ck{t) ~ krx с известным показателем т =
= со + 3/2. Из теоремы Уайта [34] в разд. Зв мы уже знаем, что
ядро (i/)® с со<1/2(Я^1) не приводит к гелеобразованию
вследствие 2 <y/ij <i + j.
Ван Донген и автор [37] использовали дополнительные
соображения при рассмотрении специального автомодельного
решения уравнения Смолуховского, которое обсуждается в
следующем разделе. Найденное ими поведение во времени среднего
размера кластера
s{t)~\(tc-trm-l) (я.>1)
также указывает на то, что гелеобразование наступает или нет
в зависимости от того, больше или меньше единицы величина X.
На основании этих и аналогичных им аргументов (см.
разд. 36) можно сделать заключение о том, что однородные
коагуляционные ядра (2.3) с 1 < X ^ 2 описывают гелеобразующие
системы (см. рис. 1).
5. Распределение по размерам при больших k и t
5а. Автомодельные решения
В экспериментах по коагуляции аэрозолей и эмульсий [38]
наблюдалось, что после переходного периода распределение
кластеров по размерам стремится к скейлинговой форме, как это
показано на рис. 4. Используя уравнение коагуляции
Смолуховского, Фридландер [2] сформулировал теорию
самосохраняющегося спектра, которая удовлетворительно объяснила
экспериментальные данные. Все рассмотренные им коагуляционные
процессы, однако, моделировались ядрами, принадлежащими к
классу III. Та же самая теория применялась во многих областях
науки [И, 40—44] и была обобщена на коагуляционные модели
классов I и II рядом авторов [21, 35, 37]. Приближение распре-
Кинетика образования кластеров
415
деления к скейлинговой форме было также замечено недавно
при имитационном моделировании процессов межкластерной
агрегации [43—45].
Остановимся вкратце на теории для ядер класса III. Здесь
можно искать асимптотическое решение уравнения Смолухов-
ского в скейлинговой, т. е. автомодельной, форме
Ck(t)~s-\(k/s\
(5.1)
где ф(х) —универсальная функция, не зависящая от начального
распределения, а средний размер кластера 5(0 —возрастающая
Рис. 4. Экспериментальная проверка скейлинговых законов в эмульсии типа
«масло в воде» [38]. Данные измерений в различные моменты времени после
первых 15 мин коагуляции все приблизительно ложатся на одну кривую,
если объем капель масла k относить к его среднему значению s(t). Здесь
оо
дй = \ ф (х) dx — это доля капель, которые имеют объемы, большие к.
функция времени, которая в отсутствие гелеобразования
остается всегда конечной. Предполагается, что такая скейлинговая
форма будет правильно описывать решение в так называемом
скейлинговом пределе, когда fe, t-^oo при фиксированном их
отношении k/s(t). Общая масса при этом нормирована на
единицу:
М
i = \ лгф (л:) dx = 1.
416
Часть VI
Для определения скейлинговой функции ф(л;) нужно
подставить выражение (5.1) в уравнение коагуляции и перейти к скей-
линговому пределу. Скейлинговая функция при этом
удовлетворяет нелинейному интегральному уравнению
оо
— wxy' (х) — 2шф (х) = — ф (х) \ Ж (х, у) ф (у) dy +
о
х
+ j \ Ж {у, x — y)q>(x — y)q>(y) dy, (5.2)
о
а средний размер кластера находится из уравнения 5 = wsK с
X, определяемым из (2.2). Его решением служит s(t) ~ tz9 где
г = 1/(1—к). Константа w, возникающая в процессе
применения при решении метода разделения переменных, может быть
выражена через моменты ф(х) путем умножения (5.2) на ха(а >
> 0) и последующего интегрирования по всем х. Для моделей
без гелеобразования классов I и II два члена в правой части
уравнения (5.2) содержат взаимно уничтожающиеся
бесконечности, что требует большей осторожности при формулировке
интегрального уравнения [37]. Подобная формулировка в работе
Свифта и Фридландера [38] для ядер класса II при описании
коагуляции в сдвиговом гидродинамическом поле (см. табл. 1
разд. 2) содержит «бесконечности» и поэтому является плохо
определенной. Более того, скейлинговая гипотеза должна быть
переформулирована для моделей гелеобразования класса I.
Распределение по размерам в скейлинговом пределе (fe, s(/)->oo
при фиксированном k/s(t)) имеет вид
Ck(t)~s-4p{k/s), (5.3)
где показатель степени т еще должен быть определен. В
системах с гелеобразованием автомодельное решение уравнения Смо-
луховского в виде (5.3) существует только во время догелевой
стадии, пока не расходится при t-*-tc средний размер кластера
s(t).
56. Асимптотические свойства решения
Что же известно об интегральном уравнении? Его общее
решение содержит две произвольные положительные константы
интегрирования, так что ф(л:) =aq(bx) также удовлетворяет
уравнению (5.2). Для трех точно решаемых моделей: Ж(х, у) —
= const, x + у и ху, автомодельными решениями соответственно
являются ф (х) ~ е~х, x~z/2e~x и at~5/2£~*, причем последнее из
них справедливо лишь до гель-точки. Численные решения урав-
Кинетика образования кластеров
417
нения (5.2) пока найдены только для некоторых моделей
класса III [39,43].
Аналитические результаты, касающиеся однородных коагу-
ляционных ядер более общего вида, имеются лишь при
описании поведения решений в областях малых и больших х. Ниже
дается краткое резюме этих результатов. Средний размер
кластера увеличивается в системах без гелеобразования (к < 1)
[37—43] и с гелеобразованием (1 < К ^ 2) [21, 35, 37]
соответственно как
if (/-oo), z=l/(l -Л) (Я<1),
\(te-tT4a(t->te), а = (Л— 1)/2 (К>1).
На граничной линии (Х = 1) между указанными двумя типами
систем зависимость s(t) имеет экспоненциальную форму s(t) ~
~ ехр(/а), где а = 1/2 в классе I (fx > 0) и а = 1 для [i = 0.
Асимптотическое поведение при больших х скейлинговой
функции для систем с гелеобразованием и без него имеет при % < 1
(см. рис. 1) следующий вид:
<р{х)~х~ке-* (x-^oo). (5.5)
Можно также найти следующий член асимптотики при больших
х. На границе (v = 1) между физичиой и нефизичной областями
поведение ф(л;) может быть самым различным в зависимости от
деталей ядра Ж{х, у) [47]. Асимптотическое поведение ср{х) при
малых х очень сильно зависит от \х. Для класса III (fx < 0)
скейлинговая функция спадает экспоненциально:
Ф {х) ~ х~х ехр (— лг-1 м.I + ...) (* -> 0), (5.6)
где т зависит от коагуляционного ядра [37, 39, 40].
Скейлинговая функция для ядер класса III имеет типичную колоколооб-
разную форму и спадает экспоненциально как на малых, так и
на больших х. Например, Ж{х, у) = (ху)а с а<0 дает т = 2,
а Ж{х, у) =ха + уа с а> О дает т = 1 [37]. Для броуновской
коагуляции в непрерывном режиме и в кинетическом режиме
(см. первый и второй примеры табл. 1 разд. 2) Фридландер с со-
авт. [39] нашли при л;-*-0 соответственно
Ф(л:) ~*-U06exp(— л;-1'3), <р(дг) ~х~2ехр(— х~Х12 — ах~1^).
Результаты Лушникова [40] для первого из ядер с т = 2
некорректны.
В классе I (jli > 0) следует различать системы с
гелеобразованием (X > 1) и без него (Ж 1):
(А+1 (А<1),
*(х)~х-*(х-+0), т = ( {к>{)я (57)
418
Часть VI
Скейлинговая функция при /->0 увеличивается (по крайней
мере для Я, >—1) в противоположность экспоненциальному
спаду в классе III. В моделях без гелеобразования в принципе
допустимы значения Я<—1, так что q>(x) может при х-^0
уменьшаться по степенному закону. Математическим примером
здесь может быть Ж(х> у) — (ху)»(х + y)v~^ с fx>0 и! =
= |j, + v<—1. Автору не известны, однако, физические
примеры в этом диапазоне значений \х и v.
Следует обратить внимание на существование точного
нефизического решения уравнения (5.2) для всех не приводящих к
гелеобразованию ядер класса I [11]:
у{х) = Ах-{~х. (5.8)
Это решение нефизично, потому что полная масса £ kC^
расходится, что нетрудно заметить, если воспользоваться
выражениями (5.1) и (5.7).
Класс II (м- = 0), образуя граничную линию между
классами I и III, не имеет четкого различия между основными
механизмами роста. Асимптотика на малых х все еще имеет
алгебраическую форму (5.7), но показатель т выражается через
моменты скейлинговой функции и не может быть вычислен без
решения интегрального уравнения [11, 37]. В некоторых
случаях, как, например, Ж(х, у) = хк + ух и Ж(х, у) — {х + у)х,
оказывается, можно указать достаточно резкие верхнюю и
нижнюю границы для показателя т в случае ядер класса II [47].
Для всех приводящих к гелеобразованию ядер, всех не дающих
гелеобразования ядер классов II и III, а также для тех не
приводящих к гелеобразованию ядер класса I типа Ж(х, у) =
= л;я+1Х6(л; — у), которые имеют достаточно резкий максимум
на диагонали, можно найти поправки высшего порядка в
асимптотике на малых х, которая является здесь алгебраической
функцией [37]. Для более общих не приводящих к
гелеобразованию ядер класса I, таких, как Ж(х, у) = хауъ + уахь,
предположение об алгебраических поправках к (5.7) ведет к
противоречиям [37] в отличие от предположений, сделанных в работе
[11]. В этом случае аналитическая структура первого
поправочного члена к основному выражению (5.7) остается неизвестной.
5в. Дальнейшие результаты и проблемы
Существует также обширная литература по процессам
коагуляции в присутствии источников мономеров или олигомеров, в
которой изучены автомодельные или стационарные решения
уравнения Смолуховского [5, 24, 25, 29].
В теории коагуляции аэрозолей обычно используется
непрерывный вариант уравнения коагуляции [2], которое инвариант-
Кинетика образования кластеров
419
но относительно полугруппы автомодельных преобразований
[4]. Эта симметрия допускает точное автомодельное решение
вида (5.2) при условии, что оно существует. Строго говоря, пока
мало что известно о типах ядер, для которых положительное
решение уравнения (5.2) существует.
Трудности при нахождении высших поправок к выражению
(5.7), которые отмечались в конце предыдущего подраздела,
могут быть связаны с отсутствием имеющего физический смысл
скейлингового решения уравнения Смолуховского. Нельзя
исключить возможность того, что точное нефизичное решение Луш-
никова и Пискунова [11] есть единственное решение для
определенных моделей класса I, так что физически приемлемые скей-
линговые решения могут для таких моделей вообще не
существовать.
Более того, существование автомодельных решений
уравнения Смолуховского не дает гарантии того, что по истечении
переходного периода распределение по размерам обязательно
будет стремиться к скейлинговой форме. Для точно решаемых
случаев из разд. За можно показать, что решение Ck{t) в скейлин-
говом пределе стремится к автомодельному в случае, когда
начальное распределение С*(0) убывает экспоненциально. Однако
Малхолланд с соавт. [50] показали для модели с ядром Ж(х,
у) — const, что начальное распределение С/е(0) с
алгебраическим хвостом не переходит в универсальную скейлинговую
форму, которая для этой модели имеет экспоненциальный вид
ц)(х) ~ е~х. Аналогичный результат был получен для
приводящей к гелеобразованию модели Ж(х, у) — ху Зиффом с соавт.
[16], которые показали, что начальное распределение с
алгебраическим хвостом стремится в скейлинговом пределе к неуни-
версальиой скейлинговой форме с показателями, определенно
зависящими от начального распределения. Аналогичные
результаты имеют место для не приводящей к гелеобразованию модели
Ж{х, у)=х + у. Можно применить отображение (3.5) ядра-
произведения на ядро-сумму и сделать заключение на
основании предыдущих рассуждений о том, что начальное
распределение с асимптотикой Ck(0) ~Ak~a(a > 2) при k-*- oo
стремится при /-vooh*>^k распределению
Ck(t)c^Ak~aexp[(a- l)t].
Для начальных распределений, ограниченных экспоненциально
{Ck(0) ^ сехр(—efe) с е > 0), имеются серьезные указания на
то, что в случае не приводящих к гелеобразованию ядер с 0<
^ v <С 1 после достаточно длительного времени установится
автомодельное решение [46]. При v < 0 и v = 1 ситуация не
совсем ясна. В системах с гелеобразованнем (v <С 1) имеются
соображения о конечности времени to, при котором происходит крое-
420
Часть VI
совер к универсальному поведению, что не исключает
возможности условия to ^ tc. В этом случае скейлинговое решение
вблизи гель-точки будет зависеть от начального распределения.
6. Распределение по размерам при больших k
6а. Инфинитезимальные интервалы времени
В настоящем разделе рассматривается асимптотическое
поведение кластеров больших размеров в фиксированный момент
времени tf существенно меньший гель-точки tc. Следует иметь в
виду, что понятие «большой» означает здесь большой по
сравнению со средним размером кластера s(t), который сам
является возрастающей функцией времени.
Общая задача конечных промежутков времени и
произвольных начальных распределений рассматривается в следующем
подразделе. Здесь же внимание сосредоточено на задаче на ин-
финитезимальных (бесконечно малых) временных интервалах
и монодисперсных начальных распределениях С&(0)=6и, где
«большой» кластер достаточно велик по сравнению с кластерами
единичного размера.
В основанных на понятиях статистической механики теориях
полимеризации и перколяции [51, 52] обычно принято
представлять асимптотическую форму распределения по размерам
кластеров в золь-фазе в виде
Ck ~ Ak~Q exp (— ck1) (k -* oo), (6.1)
где А и с — положительные константы, а 8 и £
—характеризующие распределение геометрические показатели.
Аналогичное (6.1) выражение использовалось для описания
распределения по размерам, «решеточных животных» в перко-
ляционных теориях [51]. В статистико-мехаиических моделях
решеточной перколяции показатели 8, £ не связаны с
показателями, которые характеризуют Ck в гель-точке. Более того, они
не зависят от доли р уже образовавшихся связей,
выражающейся здесь неявным образом через переменную t. Применив
ренормгрупповые методы [52] к указанным решеточным
моделям, можно установить, что показатели 8, £ решеточных
животных определяются в неподвижной точке р = 0, которой
соответствует здесь t — 0 и монодисперсное начальное распределение.
Основываясь на этих результатах, авторы [32, 53]
вычислили показатели 8, £ из решения уравнения Смолуховского на
малых временах при монодисперсном начальном распределении.
Это решение дает при /->-0 асимптотику Ck(t) ^ Nktfc~l{l +
+ #(')}» гДе Ni == 1 и Nk удовлетворяют рекуррентным соотно-
Кинетика образования кластеров
421
шениям
(*-1)ЛГА=1 £ *,/JV,tfy. (6.2)
/ + У-Л
Поведение решения этого уравнения при больших k
определяется поведением Кц при больших i и /. Если снова ограничиться
асимптотически однородными ядрами степени % (см. (2.2)), то
для всех из них с v<l получается асимптотическое решение
[32]
1
Nk~ak-KR-k(k->oo), аГх=±\Ж{х, 1 - х)[х(1 - х)]~х dx,
(6.3)
где радиус сходимости R ряда, получающегося в результате
рекуррентного использования соотношения (6.2), может в общем
случае быть найден только численно. Таким
образом,распределение по размерам имеет асимптотическую форму
Ck(t)~(a/t)k-K(t/R)k (fc->oo) (6.4)
и, следовательно, в формуле (6.1) 0 = А,, £ = 1.
66. Конечные временные интервалы
66.1. Догелевая стадия
В предыдущем подразделе обсуждалось утверждение о том,
что асимптотика (6.4), полученная на основе выведенных для
малых времен рекуррентных соотношений (6.2), может быть
применима для описания при больших k решения уравнения Смолу-
ховского на длительном временном интервале. Это утверждение,
как было недавно показано [46], оказалось правильным.
Однако при этом следует принять во внимание несколько
уточнений. Первое из них требует экспоненциальной
ограниченности начального распределения Ck(0) ^Лехр(—ek) с е>0
и fe->oo. Если при наличии алгебраического хвоста
распределения Cfc(O) это неравенство не выполняется, то функциональная
зависимость (6.1) и, в частности, показатели 0, £, как
ожидается, будут неуниверсальными и зависящими от С&(0), что также
случается в скейлинговом пределе (см. разд. 5в). Во-вторых, все
результаты относятся только к золь-фазе и, в-третьих, для того
чтобы исключить добавочные усложнения [46] на граничной
линии v = 1, рассматривались лишь ядра cv< 1.
С этими ограничениями асимптотическое выражение
распределения по размерам на конечном интервале времени можно
найти из аналогичных (6.2) рекуррентных соотношений. Здесь
422
Часть VI
следует различать переходное и универсальное решения. По
истечении времени tQy продолжительность которого зависит от
начального распределения, переходный режим выходит на
универсальную асимптотическую зависимость
-А,
Ck (/) ~ azA; exp [кг (/)] {к » s (*)),
(6.5)
где постоянная а и показатель 6 = X те же самые, что
получаются из рекуррентных соотношений (6.2). Зависимость от
начальных условий проявляется только через функцию z(t) (со
т
т т т t т т
е
<—
<
t
tc.«
Рис. 5. Схематическое изображение асимптотических решений Ck(t) в золь-
фазе (т. е. при t <c tc в системах с гелеобразовнием) с их частично
перекрывающимися областями применимости. Направления стрелок указывают
различные предельные случаи: (I) вверх: &->оо при фиксированном t
(разд. 66.1); (II) влево- /->0 при фиксированном k (разд. 6а); (III вправо:
t-^oo при фиксированном k (разд. 7); (IV) вверх-направо: t, &->oo при
фиксированном отношении k/s(t) (разд. 5).
свойствами г(/) <0иг(/) >0), остающуюся при этом
рассмотрении неопределенной. В чем-то похожий результат был также
получен Боте и Жюльеном [54].
Этот результат, возможно, не так удивителен, потому что он
относится к тем моментам времени, когда хвост распределения
по размерам находится на начальной стадии своего развития.
Здесь Ck{t) задается аналитической формулой, которая для всех
k ^> s(t) определяется только одной неизвестной функцией z(t).
Следует отметить, что универсальная аналитическая формула
(6.5) при /->-0 сводится к результату (6.4) разд. 6а [46].
Таким образом, области применимости двух предельных решений:
а) сначала t-*- О, затем fe->oo и б) сначала &->оо, затем £->0,
перекрываются (см. верхний левый угол диаграммы на рис. 5).
Кинетика образования кластеров
423
Можно показать, что (I) универсальное асимптотическое
решение (6.5) для моделей с гелеобразованием и без него при
фиксированном t совпадает с (II) скейлинговым решением (5.1),
(5.3) и (5.4) для больших значений автомодельного аргумента
x = k/s(t) ^> 1. Здесь снова имеются частично
перекрывающиеся области применимости двух предельных решений: (I) £->»оо,
t фиксированно и (II) сначала k-+ оо, s(t) ->■ со с х
фиксированным, затем я->-оо. Это иллюстрируется в верхнем правом углу
диаграммы на рис. 5.
В заключение этого раздела можно высказать следующие
соображения. Принимая во внимание огромное количество
вычислительных работ [55], посвященных решению нелинейных
уравнений коагуляции аэрозолей (безопасность реакторов, ядерные
аварии), очень полезной для улучшения численных программ с
целью повышения их эффективности при расчетах на больших
временах распределения кластеров больших размеров может
служить аналитическая информация о поведении решений при
больших k. Трудность здесь заключается в вычислении
бесконечной суммы в последнем члене уравнения Смолуховского
(1.1). После каждого шага интегрирования следует
"модернизировать" результаты для z{t) и воспользоваться аналитической
формулой (6.5) для улучшенного определения бесконечной
суммы в (1.1), улучшая таким образом сходимость процедуры
вычисления и сокращая тем. самым время решения на ЭВМ
уравнения коагуляции.
66.2. Послегелевая стадия
Асимптотика (6.5) при конечных временах экспоненциально
ограничена и относится к догелевой области. Если в момент tc
происходит гелеобразование, то при t>tc решение для
больших k имеет алгебраический хвост
Ck (/) ~ В (t) kTx (k -> оо). (6.6)
Этот результат уже иллюстрировался выше в (3.4) и (4.6) для
специального вида ядра Кц=(ф(*. Для однородных коагуля-
ционных ядер (2.2) с ^> 1 коэффициент B(t) можно
определить путем вычисления потока массы J(L,t) от малых
кластеров (k < L) к большим (k > L) (см. разд. За). Этот поток в
данном случае получается заменой произведения kj на Ж(k, j)
в правой части выражения (3.2). Подставив туда (6.6) и
потребовав ограниченности потока /(оо, t) =—tit\(t) частиц золя в
гель, получим т = (X + 3) /2 и
1 оо
B(t) = [-Ml(t)/b]V2, b=^dx J Ж(х, y)xi-ty-xdy, (6.7)
424
Часть VI
причем зависимость М\ от времени остается неопределенной.
Асимптотические результаты (6.6), (6.7) для распределения по
размерам были получены в работах [21, 35, 37].
В следующем разделе будет показано, что существует
частное решение за гель-точкой, для которого lA\(t) = (а + bt)~l,
а при произвольном начальном распределении имеет место
асимптотический результат М\(t) ~ l/t(t-*oo).
Последний результат относится к случаю, когда переменная
k является дискретной. Если же она непрерывная, то вес золь-
фракции может уменьшаться сколь угодно медленно в
зависимости от поведения начального распределения по размерам
C(k\ 0) в окрестности точки k = 0. Это показано на примере
точно решаемой модели Ж{х, у) =ху в работе [17].
7. Распределение по размерам при больших t
Для определения поведения решения Ck(t) на больших
временах можно использовать два различных метода, которые
приводят к частично дополняющим друг друга результатам. Один
из них использует скейлинговые функции, о которых
упоминалось в разд. 5, а другой — низкочастотные рекуррентные
соотношения (в противоположность высокочастотным рекуррентным
соотношениям (6.2)).
Эти соотношения дают при t-*oo предельные значения
11m Ck(t)/Ci(t) = bky но не позволяют определить закон
приближения к ним. Они применимы только к моделям класса I.
Метод скейлинговых функций, применимый лишь к догелевой
области, предсказывает поведение распределения только при
больших k. В данном контексте последний метод является
единственно пригодным для моделей, не описывающих гелеобразование.
Метод рекуррентных соотношений описывает весь диапазон
изменения k и для систем с гелеобразованнем дает результаты в
послегелевой области.
Вначале приведем установленный в работах [35, 47, 48, 56]
результат о существовании у уравнений коагуляции частного
решения Ck(t)= C\(t)bk (k= 1,2, ...):
оо
-wbk = \ £ Ktfltbt-hYtKkfa, *i = l. (7Л)
-w = Ci(t)/(fi(t)9
где w — положительная константа, получающаяся при
разделении переменных в исходном уравнении. Концентрация мономера,
согласно (7.1), меняется по закону C\(t) = (А + wt)~x.
Поскольку первое из уравнений (7.1) должно выполняться при k = l,
Кинетика образования кластеров
425
то отсюда следует w = X ^1 А- Исключив неизвестную до,
можно получить низкочастотные рекуррентные соотношения
оо
6* £(**/-*«) 6/=4 £ *<М- (7-2)
/=1 i + j = k
Их область применимости не ограничивается асимптотически
однородными ядрами (2.2), хотя только для них был проведен
анализ. Его результатом [47] является установление
существования строго положительного решения уравнения (7.2) для
систем класса I с гелеобразованием (%> 1) и без него (К < П.
Для ядер класса II также изучено решение этого уравнения [47,
48]. Для некоторых ядер коэффициенты bk строго положительны,
в то время как для других они не имеют определенного знака.
Однако величины bk не имеют для класса II того
универсального значения, как в классе I, где их асимптотика имеет вид
**~*М*-оо), * = Ь+1 (Ж1). (7'3)
Рассмотрим полную массу частиц золя М{ (t) = Cx (i) X kbk. Для
систем с гелеобразованием (К > 1) эта бесконечная сумма
сходится, что отвечает уменьшению общей массы золя по закону
M\{t) ~ C\{t) ~ 1/7. Здесь мы вынуждены иметь дело с таким
послегелевым решением, где гель-точка остается
неопределенной. Рекуррентные соотношения (7.2) фактически были
приведены в работе [35] с целью определения критического
показателя т для модели Кц= (ij)® после гель-точки. Для систем без
гелеобразования бесконечная сумма расходится, так что
решение Ck{t) =C\(t)bk не имеет физического смысла. Это
фактически соответствует нефизическому скейлинговому решению
(5.8), полученному Лушниковым и Пискуновым. Однако в
системах без гелеобразования асимптотические решения такого
вида физически допустимы, потому что Ck(t)/C\(t) может
стремиться к bk неравномерно по k. При этом J] kCk— 1, хотя сумма
Ys kbk расходится.
Частное решение, определяемое низкочастотными
рекуррентными соотношениями, имеет универсальное значение в качестве
асимптотики при больших t решений систем класса I. То есть
произвольные начальные распределения эволюционируют таким
образом, что при t-^oo обязательно существуют предельные
значения
WmCk{t)lCx{t) = bk (£ = 2, 3, ...), (7.4)
которые не зависят от Ck(0). Комбинируя (7.1), (7.3) и (7.4),
можно получить Ck(t) ~ t~lk-b-1 для не описывающих гелеоб-
426
Часть VI
разование моделей класса I. Тот же самый результат следует
из (5.1), (5.4) и (5.7) в скейлинговом пределе. Таким образом,
два предельных решения: (I) сначала t-*oo, затем &->оо, и
(II) сначала, kyt-*oo с x = k/s(t) фиксированным, затем х->09
имеют общую область применимости, как это видно в правой
части диаграммы на рис. 5.
Простым примером ядра класса I служит /G/ = (*7)co> когда
рекуррентные соотношения упрощаются до вида
?«(*"--о**=4 £ (чти*!* р»=2>%.
Они изучены как для описывающих гелеобразование систем
(X = 2(о > 1) [35, 36], так и для систем без гелеобразования
(% = 2ы< 1) [48].
В коагуляционных моделях класса II (|х = 0) отношение
Ck{t)/C\(t) при t-^oo стремится к константе, которая, однако,
зависит от С/г(0) и не может быть определена из рекуррентных
соотношений (7.2). Концентрация мономера уменьшается по
закону C\(t) ~ t~v(t->oo) быстрее, чем в классе I. Показатель
степени у, согласно скейлинговой формуле (5.1), равен (2—
— т)/(1—к). Для ядер класса II величина т выражается через
моменты скейлинговой функции у(х) (см. текст после формулы
(5.8)), так что для определения т следует сначала найти
решение интегрального уравнения для у(х). В точно решаемых
случаях Kij-= const и /(//==/ + / моделей класса II получается
соответственно С\ (t) ~ t~2 и С\ (t) ~ e~f. Можно, следуя [47],
отметить также некорректность результата Ck\t)/C\{t) ~
~ &-i~co/2 (£->-оо), приведенного в работе [48] для ядра Кц =
= ^ + i40- В коагуляционных моделях класса III отношение
Ck(t)/Ci(t) для всех k стремится к бесконечности при ^->оо,
а концентрация мономера выходит на нулевое значение быстрее
по сравнению с классами I и II. Физически это понятно,
поскольку большие кластеры растут в основном за счет убыли малых
кластеров.
8. Заключение
В настоящее время имеется достаточно полная
аналитическая информация об асимптотических свойствах решения Ck(t)
уравнения коагуляции, что лучше всего видно из рис. 1 и 5. Для
асимптотически однородных ядер степени X на рис. 1 показано,
какие именно из моделей приводят к гелообразованию, а на
рис. 5 указаны асимптотические результаты, известные для золь-
фазы. Аналогичные результаты для гель-фазы приведены в
разделах 66.2 и 7.
Больше всего результатов получено при использовании идей
самосогласования, несмотря на их неполноту и отсутствие мате-
Кинетика образования кластеров
427
матической строгости. Ряд нерешенных проблем отмечен в
различных разделах обзора К К их числу относится, например,
вопрос о том, всегда ли решение коагуляции выходит на
автомодельную форму, если она существует, или вопрос о том, при
всех ли негелеобразующих ядрах класса I существует
автомодельное решение.
Пока численные решения интегрального уравнения для скей-
линговой функции ц)(х) имеются только для некоторых моделей
класса III. Было бы интересно получить численные решения для
более реалистических моделей, а также для моделей классов I
и II. Подобная информация, несомненно, дает возможность
провести более детальное сопоставление со множеством данных,
полученных из экспериментов [38, 39. 57] и имитационного
моделирования явлений агрегации. Известно, что многие свойства
распределения кластеров по размерам, полученного в реальных
и компьютерных экспериментах, уже нашли свое объяснение на
основе уравнения Смолуховского [38, 39, 54, 57, 58].
ЛИТЕРАТУРА
1. Drake R. L., In: Topics in Current Aerosol Research, vol. 3, eds. G. M. Hidy,
J. R. Brock, Pergamon Press, New York, part 2, 1972.
2. Friedlander S. K., Smoke, Dust and Haze, Wiley-Interscience, New York,
1972.
3. Ziff R. M., in: Kinetics of Aggregation and Gelation, eds. F. Family,
D. P. Landau, Elseviers Sc. Publ. B. V., Amsterdam, 1984.
4. Ernst M. H., in: Fundamental Problems in Statistical Mechanics VI,
ed. E. G. D. Cohen, Elseviers Sc. Publ. B. V., Amsterdam, 1985.
5. Klett J. D., J. Atmosph. Sci., 32, 380 (1975).
6. Лушников А. А. — Изв. АН СССР, Физика атмосферы и океана, 1978,
вып. 10, с. 1046.
7. Ziff R. М, J. Stat. Phys., 23, 241 (1980).
8. Flory P. J., Principles of Polymer Chemistry, Cornell Univ. Press, N. Y.,
1953.
1} К сожалению, в настоящем обзоре автор совершенно не упоминает
одну из основных и наиболее сложных проблем теории агрегации
(поликонденсации), связанную с корректным учетом в ней реакций между группами
одного и того же кластера. В процессах поликонденсации или полимеризации
такие внутримолекулярные реакции приводят к образованию в молекулах
полимеров (кластерах) циклических фрагментов, корректный учет которых
требует выхода за рамки приближения среднего поля. Построение здесь
универсальной теории агрегации, осложненной интенсивным протеканием
внутримолекулярных реакций, представляется маловероятным. Более
конструктивными являются подходы, включающие в рассмотрение иерархическую
последовательность приближений, когда на каждом ее этапе учитываются
вполне определенные циклические фрагменты. Алгоритмы построения этой
последовательности, два из которых сформулированы в обзоре [17*], могут быть
различными в зависимости от физико-химических особенностей
рассматриваемой системы. Менее последовательные подходы к учету
внутримолекулярных взаимодействий, типа использованного в работе [18*], не позволяет
количественно оценить степень сделанных в ходе их приближений. — Прим.
перев.
428
Часть VI
9. Hendrics E. AT, Ernst M. Я., Ziff R. Af., J. Stat. Phys., 31, 519 (1983).
10. van Dongen P. G. /., Ernst Af. Я, Phys. Rev., A32, 670 (1985).
И. Лушников А. А., Пискунов В. Я. — ДАН СССР, 1976, т. 231, с. 1166.
12. Botet R.y Jullien Я., Kolb М., J. Phys. A: Math. Gen., 17, L75 (1984).
13. Hendriks E. Af., Ernst Af. Я., J. Colloid Interf. Sci., 97, 176 (1984).
14. Головин A. Af. — Изв. АН СССР, сер. Геофизика, 1963, вып. 5, 783.
15. McLeod J. В., Quart. J. Math., Oxford, 13, 119, 193 (1962).
16. Ziff R. Af, Ernst Af. Я., Hendriks E. Af, J. Phys. A: Math. Gen., 16, 2293
(1983).
17. Ernst M. Я., Ziff R. Af, Hendriks E. Af, J. Colloid Interf. Sci., 97, 266
(1984).
18. Leyvraz F., Tschudi Я. R., J. Phys. A: Math. Gen., 14, 3389 (1981).
19. Ziff R. Af, Siell G, J. Chem. Phys., 73, 3492 (1980).
20. Spouge /. L., J. Phys. A: Math. Gen., 16, 767 (1983); J. Stat. Phys., 31,
363 (1983); van Dongen P. G. /., Ernst Af. Я., J. Phys. A: Math. Gen., 16,
L327 (1983).
21. Leyvraz F., Tschudi Я. R., J. Phys. A: Math. Ren., 15, 1951 (1982).
22. van Dongen P. G. J., Ernst M. Я., J. Phys. A: Math. Gen., 17, 2281
(1984).
23. Лушников А. А., Пискунов В. Я. — ДАН СССР, 1976, т. 231, с. 1403;
Лушников А. Л, Токарь Я. Я., Цицкишвили М. Ц. — ДАН СССР, 1981,
т. 256, с. 1155
24. Crump J. G, Seinfeld /. Я., J. Colloid Interf., Sci., 90, 469 (1982).
25. White W. Я., J. Colloid Interf. Sci., 87, 204 (1982).
26. Aizenman Af, Bak T. A., Commun Math. Phys., 65, 203 (1979); Ernst M.H.,
in: Studies in Statistical Mechanics, vol. X, eds. E. Montroll, J. L. Lebo-
witz, North-Holland, Amsterdam, 1983, chap. 3.
27. Srivastava R. C„ J. Atmosph. Sci., 39, 1317 (1982).
28. van Dongen P. G. / , Ernst Af. Я., J. Stat. Phys, 37, 301 (1984).
29. Домиловский Е. Р., Лушников А. А., Пискунов В. Я. — ДАН СССР, 1078,
т. 243, с. 407.
30. Samsel R. Г., Perelson A S., Biophysics J., 37, 493 (1982; 45, 805 (1984);
van Dongen P. G. /, Ernst Af. Я, in: Kinetics of Aggregation and
Gelation, cds. F. Family, D. P. Landau, Elsevier Sci. Publ, Amsterdam, p. 205,
1984.
31. Ziff R. Af, Ernst Я. M, Hendriks E. Af, J. Colloid Interf. Sci, 100, 220
(1984).
32. Лушников А. Л, Пискунов В. Я. — Коллоид, журнал, 1975, т. 37, с. 285.
33. Ernst M. Я, Hendriks E. Af, Ziff R. M, Phys. Lett, 92A, 267 (1982).
34. White W. Я, Proc. Am. Math. Soc, 80, 273 (1980).
35. Ziff R. M, Hendriks E. M, Ernst M. Я, Phys. Rev. Lett, 49, 593 (1982);
Hendriks E. M., Ernst M. Я, Ziff R. M, J. Stat Phys., 31, 519 (1983).
36. van Dongen P. G. /, Ernst M. Я, будет опубликовано.
37. van Dongen P. G. /, Ernst M. Я, Phys. Rev. Lett., 54, 1396 (1985).
38. Swift D. L, Friedlander S. K, J. Colloid Interf. Sci, 19, 621 (1964).
39. Friedlander S. tf, Wang C. S, J. Colloid Interf. Sci, 22, 126 (1966);
Lai F. S., Friedlander S. K, Pick /, Hidy G. M, J. Colloid Interf. Sci,
39, 395 (1972).
40. Lushnikov А. Л, J. Colloid Interf. Sci, 45, 549 (1973).
41. Binder K., Phys. Rev, B15, 4425 (1977); Silk /., White S. D, Astrophys
J. 223, L59 (1978).
42. Rosen J. Af, J. Colloid Interf. Sci., 99, 9 (1984).
43. Kolb Af, Phys. Rev. Lett, 53, 1653 (1984).
44. Ziff R. Af, McGrady E. D, Meakin P., J. Chem. Phys, 82, 5269 (1985).
45. Vicsek Т., Family F, Phys. Rev. Lett, 52, 1669 (1984); Meakin P., Vic-
sek Т., Family F, Phys. Rev, B31, 564 (1985).
46. ван Донген П., Эрнст М. — наст, сб., с. 430; van Dongen P. G. /,
Ernst Af. Я. J. Colloid Interf. Sci.
Кинетика образования кластеров
429
47. van Dongen P. G. /., Ernst M. #., Phys. Rev., A32, 670 (1985); J. Phys. A:
Math. Gen., 18, 2779 (1985).
48 Leyvraz F., Phys. Rev., A29, 854 (1984).
49. Л ушников А. А., Пискунов В. Н. — Коллоид, журнал, 1977, т. 39, с. 1076.
Душников А. Л., Токарь Я. Я. — ДАН СССР, 1980, т. 252, с. 136.
50. Mulholland G. W.y Baum Я. R, Phys. Rev. Lett., 45, 761 (1980); Mulhol-
land G. W.y Lee T. G., Baum H. R.y J. Colloid Interf. Sci., 62, 406 (1977).
51. Stauffer D.y Coniglio A, Adam M., In: Advances in Polymer Science,
vol. 44, ed. K. Dusek, Springer Verlag, Berlin, 1982, p. 103.
52. Stanley H. E., Reynolds P. /., Redner «S.,. Family F.y in: Real Space Renor-
malization, eds. T. W. Burkhardt, J. M. J. van Leeuwen, Springer Verlag,
Berlin, 1982, ch. 7.
53. Ernst M. Я, Hendriks E. M.t Leyvraz F.t J. Phys. A. Math. Gen., 17,
2137 (1984).
54. Botet R., Jullien #., J. Phys. A: Math. Gen., 17, 2517 (1984).
55. Loyalka 5. K„ Progress in Nuclear Energy, 12, 1 (1983); Emani A, Loyal-
ka S. K.f Nuclear Technology, 52, 162 (1981); Gelbard F.t Seinfeld R. /.,
J. Colloid Interf. Sci., 78, 785 (1980); Middelton Л. F., Brock /. #., J.
Colloid. Interf. Sci., 54, 2 (1963).
56. Leyvraz F., J. Phys. A: Math. Gen., 16, 2861 (1983).
57. Weitz D., Huang J. S., Lin M. У., Sung /., Phys. Rev. Lett., 53, 1657
(1984); 54, 1416 (1985); Martin J. £., Schaefer D. W., Phys. Rev. Lett, 53
2457 (1984); Feder /., Jossang /., Rosenqvist £., Phys. Rev. Lett., 53,
1403 (1984).
58. Kolb M. et al.9 J. Phys., A18, L435 (1985).
ЛИТЕРАТУРА, ДОБАВЛЕННАЯ ПРИ ПЕРЕВОДЕ
1*. Волощук В. М, Седунов Ю. С. Процессы коагуляции в дисперсных
системах.—Л.: Гидрометеоиздат, 1975.
2*. Волощук В. М. Кинетическая теория коагуляции. — Л.:
Гидрометеоиздат, 1984.
3*. Кучанов С. И. Методы кинетических расчетов в химии полимеров. —• М.:
Химия, 1978.
4*. Stockmatjer W. Я. —J. Chem. Phys., 1943, v. 11, p. 45.
5*. Кучанов С Я. -ДАН СССР, 1976, т. 229, с. 135.
6*. Королев С. В., Кучанов С. Я., Слинько М. Г. — ДАН СССР, 1981, т. 258,
с. 1157.
7*. Кучанов С. И. — Высокомолек. соед., сер. Б., 1974, т. 16, с. 136.
8*. Душников А. Д., Пискунов В. Я., Осидзе И. Г. — ДАН СССР, 1986,
т. 287, с. 679.
9*. Biesenberger J. Л.— A. I. Ch. Eng. Journ., 1965, v. 11, p. 369.
10*. Кучанов С. Я. — TOXT, 1981, т. 15, с. 855.
И*. Кучанов С. Я., Письмен Д. М. — Высокомолек. соед., 1971, т. 13, с. 689.
12*. Пеньков Н. В. — ЖПХ, 1986, т. 59, с. 1129.
13*. Кучанов С. И., Письмен Д. М. — Высокомол. соед., 1972, т. 14, с. 886.
14*. Кучанов С. Я. - ДАН СССР, 1979, т. 249, с. 899.
15*. Кучанов С. Я., Поволоцкая Е. С. — Высокомолек. соед., 1982, т. 24,
с. 2179.
\6*. Кучанов С. Я., Поволоцкая Е. С. — Высокомолек. соед., 1982, т. 24,
с. 2190.
17*. Кучанов С. И. Современные представления о статистической теории ге-
леобразования. — В кн.: Процессы студнеобразования в полимерных
системах. — Саратов: Изд-во Саратовского университета, 1985, Часть 1,
с. 61-78.
18*. Lloyd А. С, Stepto R. F. Т. — Brit. Polym. Journ., 1985, v. 17, p. 190.
Хвост распределения
для больших кластеров
при необратимой агрегации
#. Ван Донген, М. Эрнст *
Исходя из коагуляционного уравнения Смолуховского [1],
определен хвост распределения кластеров по размерам в области
размеров достаточно больших по сравнению со средними. Константа
скорости К{и j) этого уравнения предполагается однородной
функцией / и /. Показано, что хвост имеет экспоненциальную
форму Ck(t) = Ak(t)exp[kz(t)], где функции Ak(t), имеющие порядок
роста \nAk(t) — О(k) при &->оо, могут быть вычислены из
рекуррентных соотношений. В зависимости от начального
распределения Ck(0) и константы скорости K(i, j) предложено различать
универсальное решение, совпадающее со скейлинговым решением
в случае расходимости среднего размера кластера, и
неуниверсальные решения. Справедливость оригинальных общих результатов
подтверждена на примере двух точно решаемых моделей.
1. Введение
В настоящей статье коагуляционное уравнение
Смолуховского
оо
Т = Т £ *(U) ОД-С* £*(*,/) С, (1)
* + / = & / = 1
используется для нахождения функциональной зависимости
распределения кластеров по размерам Ck(t) при больших k для
различных типов начальных распределений C&(0) и коагуля-
ционных ядер K{i> j). В данном контексте термин «большие»
означает «много больше среднего размера кластера s(/)».
Асимптотические свойства распределения кластеров по размерам
изучались в различных предельных случаях: (I) кратковременные
решения при монодисперсных начальных условиях [2], (II)
долговременное поведение при фиксированном k [3] и (III) скей-
линговое поведение в пределе &->оо, s(£)->oo при сохранении
конечного значения их отношения k/s(t) [4]. В дополнение к
указанной информации о решениях уравнения Смолуховского
(1) ниже вычисляется асимптотика распределения по размерам
Ck{t) для конечного фиксированного времени. В описывающих
гелеобразование системах, где s(t) расходится в гель-точке при
конечном времени /с, приведенное далее рассмотрение
ограничено этим моментом t < tc. Полученные ниже асимптотические
результаты совпадают, с одной стороны, с кратковременными
решениями (см. (I)), а с другой стороны, со скейлинговыми ре-
* P. G. J. Van Dongen, M. H. Ernst Institute for Theoretical Physics,
University of Utrecht, P. O. Box 80.006, 3508 ТА Utrecht, The Netherlands.
Кинетика образования кластеров
431
шениями (см. (III)), взятыми в обоих случаях в пределе
больших кластеров (k ^> s(t)). Такое соответствие связывает и
объединяет между собой более ранние результаты.
Структура распределения кластеров по размерам при
больших значениях k зависит от поведения константы скорости
K(i, j) при больших размерах кластеров i и /. Поскольку
большинство встречающихся в литературе [1] коагуляционных ядер
являются однородными функциями i и /, то далее можно
ограничиться (по крайней мере для кластеров больших размеров)
такими ядрами и характеризовать K(i, j) двумя показателями,
определяющими его зависимость от i и / при / >> i:
К (ai, aj) = &К (i, j) = а*К (/, /), (2а)
К (/, j) zc iY (j > /, Я = |i + v). (26)
Поскольку реакционная способность больших кластеров не
может расти быстрее чем их размер, то v ^ 1, А, ^ 2, хотя никаких
ограничений на [i не накладывается. Предполагается далее, что
К(х, 1—х) является непрерывной и положительной функцией
х в интервале от 0 до 1.
Основной полученный результат заключается в том, что
распределение кластеров по размерам имеет универсальный
экспоненциальный хвост:
Ch(t) = Ak(t)e*n (z(0<0), (За)
Urn In [Ak (t)/k] = 0, (36)
где поведение при больших k предэкспоненциального фактора
Ak(t) можно вычислить из рекуррентных соотношений. При этих
вычислениях различаются ядра cv<l и v=l, В обоих
случаях, кроме того, следует отличать универсальные решения,
которые переходят в скейлинговые в одноименном пределе, от не-
универсальных (промежуточных) решений. При &-><х>
универсальные решения имеют вид Ak(t)c^A(t)k~d, за исключением
некоторых моделей с v = l, где Ak(t) ~ехр[—A(t)k$]. Сама
возможность существования неуниверсальных решений и их
форма определяются видом начального распределения С&(0).
2. Метод
Рассмотрим общие решения вида
Ck(t) = Ak(t)exp№z(t)) с £>0, 2(f)<0, (4а)
Iim [In Ak (t)/k] = 0. (46)
432
Часть VI
Если начальное условие экспоненциально ограничено с
константами С, 8 > О
Ck(0)<ce-*k (£=1,2, ...), (5)
то можно показать [5], что только допущение £= 1 или (За, б)
приводит к согласованным решениям. Подставляя (За, б) в
уравнение Смолуховского (1), получим, что z(t) и Ak{t) связаны
следующим уравнением:
оо
zkAk + Ak = 1 £ K V> Л AiAi ~ 4k £ * (ft, />Cr <6>
М-/-Л /=1
При решении этого уравнения для больших k следует делать
различие между моделями cv< 1 и v = 1.
3. Решения для v < 1
Решения имеют различное поведение при z Ф 0 и z = 0.
Если z ф 0, то уравнение (6) сводится при больших k к
рекуррентному соотношению
zkAk ~ -~ £ К (i, 1) AtA, (k -* оо) (7)
i + j^k
При выводе (7) использовалось вытекающее из (36) при k -> оо
условие Ak/Ak = C?(k), а также £ /((ft,/)C/~ftvAf^, где Ма(/)=
= 2^aCfe обозначает a-й момент распределения Cfe(0-
Удовлетворяющее условию (36) решение уравнения (7) имеет общий
вид
Ak(t) = A(t)k-* (ft->oo). (8)
Для определения А и 6 следует подставить асимптотическое
выражение (8) в (7) и приравнять главные члены одинакового
порядка по ft. В сочетании с (За) это дает
Ck(t)^az(t)k-Kekz{t) (ft-*oo), (9а)
где z < 0, г > 0, а постоянная а определяется сходящимся при
v = 1 интегралом
1
7 = tS*(*. 1-*)[*(1-*)]"*<**. (96)
о
Следующим рассматривается случай i = 0 или z(t) =Zo при
v ^ 0, когда уравнение (6) допускает асимптотическое решение
Ak(t)~Ak(0)exp№A(t)] (ft->oo) (10а)
Кинетика образования кластеров
433
с |3 = v и Д(0) =0. Зависимость А от времени определяется
формулой
Д(')=Е k»Ak(l-ekZo)>0. (106)
Анализ выражений (10а, б) при v > 0 показывает, что это
решение возможно только в случае A(t)<C сх> при t-*Q> т.е. когда
начальное условие удовлетворяет требованию положительности
выражения —k-vlnAk{0) при &-^оо. Аналогично при v = 0
необходимо потребовать ограниченности суммы J] k^A-k (0) Для ог~
раниченности величины А(0). Можно показать, что при 0 ^ v <
<С 1 решения (10а, б) являются промежуточными, переходящими
в выражения (9а, б) за конечное время. По этой причине можно
отнести (9) к классу универсальных асимптотических решений.
Для случая £ = 0 и v < 0, допустив ограниченность суммы
Yj ^4а(0), из (10а, б) можно вывести, что Ak(t)/Ak(0) ->■ 1 при
£->оо. Следовательно, зависимость от времени Ak(t) при
фиксированном k не может быть объяснена только исходя из
асимптотики решения при &->~оо. Более того, из такого анализа
нельзя даже сделать вывод о том, является ли решение (10)
переходным или же неуниверсальным долговременным.
Следующими рассматриваются начальные распределения вида Ak(0) ^
~Л£~а (&-»- оо) са< 1 + ^' так что сумма ]Г) k^Ak(Q) остается
конечной. Допустив Ak(t) ~A(t)k-a при &->-оо, из (6) получим
-^~Lkl+b-a\K{x, 1-х)[х([-х)Гас1х. (11)
о
Для ограниченных неравенством 1 + X < а < 1 + \х значений а
получается при &->~оо то же самое асимптотическое поведение
А -> 0 или А и (t) /Ak{0) -->-1, что и для а > 1 + \х. Мгновенный
переход для а < 1 + % к универсальному решению вытекает из
неограниченности производной Л(0), которая следует из (11).
В специальном случае а = 1 + % промежуточная асимптотика
Ck{t)~ A(t)k~l~xexp(kz0) с A(t) = (t0 — t)~l переходит при
t-^toB универсальное решение.
4. Результаты для v = 1
Для этого специального случая расчеты технически сложнее,
чем для v < 1. Ниже приводятся только основные их
результаты. При этом необходимо различать случаи 2 = 0 и z Ф 0,
поскольку уравнение (6) содержит два члена одного порядка
малости O(k). Для v= 1 асимптотическое поведение Ak(t)
зависит от более детальной структуры ядра K(i, /), чем только
434
Часть VI
указание его порядка роста (26). Для дальнейшего анализа,
исходя из определения
K(i, /) = (*Vf (*• + /)'_tl[l +Q(i, /)], (12a)
вводится функция Q(i9 /), такая, что асимптотическое поведение
Q{x, 1 —х) при малых х имеет вид
Q(x, l — x)~qx<>+ ... (*~>0, р>0). (126)
Как легко заметить из (12а), Q(i, j) является однородной
функцией степени нуль.
В случае v = 1 различаются универсальное и
неуниверсальное решения. Критерием универсальности поведения является
то, что в этом случае решение сводится к скейлинговому (см.
ниже), когда средний размер кластера s(t) неограниченно
возрастает. В обоих случаях зависимость z (t) определяется полным
видом распределения кластеров по размерам
2(0=S ft%(/)(l-e-fa)>0. (13)
Асимптотическое поведение Ak{t) при &->-оо, однако,
различается для универсальных и неуниверсальных решений.
Универсальное асимптотическое поведение Ak{t) приведено
для различных значений р и q в табл. 1. Это поведение при боль-
Таблица 1
Ak(t)*A(t)k-Q
l + H<Q<m(\)
/(8) = 0
Ak{t)**A(t)k-*
Ak(t)*A(t)k-Q
m(2)<Q<\i-q
Ak(t)~exp[-k*fii(tj\
P = l —P
ших k либо алгебраическое Ak—AkrQ, либо растянутое
экспоненциальное
Л*(/)~ехр[-Д(0^] (ft-*oo) (14)
с 0<р<1 и Д(£)>0. Заметим, что в противоположность
(10а) показатель экспоненты в (14) отрицателен.
Из табл. 1 видно, что в классах А, В, С имеет место
алгебраическое, а в классе D —растянутое экспоненциальное распре-
Ар>1
Р = 1,
<7 > -2, / (2 + ix) > 1
р< 1, <7>0
B. р = 1,
q ==-2, /(2 + ц)<0
C. р = 1, <7<-2
D. р < 1, q < 0
Кинетика образования кластеров
435
деление. Показатель 9 в классе А находится как решение
трансцендентного уравнения
7(6) = 0, (15а)
лежащее в интервале 1 + ^ < б < m(\) = min {2 + М" 1 +М- +
+ р}. Здесь 7(6) определяется формулой
1/2 оо
/(6)=j {К(х, I ~ х)[х(1 - х)]~* - x»-Q) dx - J x»~Qdx. (156)
О 1/2
В классе В согласованное алгебраическое решение имеется при
6 = 2 +(л, а для моделей класса С — при значении &, лежащем
в интервале т (2) < & < \х — q, где m (2) = max {2 + jx, |л — ^ —
-1}.
Поскольку в классе С параметр q может быть отрицательным
и сколь угодно большим по модулю, показатель 6 > 0 также
может быть произвольно большим. Наконец, в классе D получается
растянутое экспоненциальное поведение с р=1—р. В
специальном случае р = 1, q = —2 имеются некоторые сложности,
которые здесь не будут обсуждаться.
Наконец, при k-^oo рассматриваются переходные решения
в виде Ak{t) ex F(t)Ak(0) с ^(О) =1, которые могут быть
найдены при условии Ak(0) ~ k~Qo с 60 > m(3) = max{2 + \l, \x — q)
и q ^ 1. Зависимость функции F(t) от времени может быть
выражена через моменты распределения кластеров по размерам.
Если km^Ak(0) ограничено и keAk{0) ->0 при fe->oo, решение
мгновенно выходит на универсальное. С другой стороны, если
начальное распределение имеет при £->оо вид Ak(0) ~
~ ехр [—D0№] с D0 > 0 и 1 > р > m(4) = max {0, 1 — р}, то
переходное решение определяется формулой Ak(t) ~
~ ехр[—D(t)№ — A(0*m(4>].
В случае р^т(4) осуществляется мгновенный выход на
универсальное решение.
5. Связь с кратковременными и скейлинговыми решениями
В этом разделе обсуждается вопрос о том, каким образом
универсальное асимптотическое поведение при больших k
распределения кластеров по размерам Ck{t) связано с 1)
кратковременным решением при монодисперсном начальном условии и
2) скейлинговым решением. Основные рассуждения относятся к
классам моделей с v < 1, хотя выводы применимы также к
моделям с v = 1.
Кратковременные решения уравнения Смолуховского для
монодисперсного начального распределения Ck(0)—8k\ имеют при
t->-0 вид Ck(t) ^Nktk~ly где коэффициенты Nk удовлетворяют
436
Часть VI
рекуррентному соотношению
(*-1)лъ=4£ K{ij)NiNh л^ = 1. (16)
i+j=k
Асимптотическое поведение величин Nk при больших k,
определяемое таким же способом, как и Ak, имеет вид Nk ^ ak~xR-k,
где постоянная а задается формулой (96), а значение R остается
неопределенным. Отсюда следует, что при k >> 1 распределение
Ck{t) в пределе £->0 описывается выражениями (За, б) с
Ak(t)~ak-% (17а)
z(t)~ln(t/R). (176)
Те же самые выражения (17а, б) получаются, если сначала
перейти к пределу Л-*оо, т. е., начав с выражений (9а, б),
положить в них z(i) =- In (t/R) при t->-0. Отсюда можно сделать
заключение о существовании общей области применимости, где
совпадают два предельных решения: а) сначала /->0, затем
fe->-oo и б) сначала fe-^оо, затем /->0.
Аналогично можно показать, что существуют
перекрывающиеся области применимости асимптотического при fe-^oo
решения и скейлингового решения. Последнее получается в скей-
линговом пределе, когда текущее k и среднее s(t) значения
размера кластеров устремляются к бесконечности при сохранении
конечным их отношения k/s(t). Для гелеобразующих систем
(1 < % ^ 2) скейлинговое решение имеет вид
Ch(t)~[s{t)rx<f[k/s№ (18а)
s = ws2-v+\ (186)
где т= (1 + 3)/2, a w — константа, возникающая при
разделении переменных. В гель-точке i = tc средний размер кластера
расходится. Асимптотическое поведение скейлинговой функции
ф(х) (18а) описывается выражением
ф(х) ~ wdax~Kexp(— дх) (#->oo), (19)
где константа а определяется формулой (96). Сравнение (18а,
6), (19) с асимптотическим при больших k решением (9а, б)
показывает, что оба они приводят к одному и тому же выражению,
если положить z(t) ~—8/s(t) при z-^О или s-^oo. Те же
самые соображения применимы при s(t) ->оок негелеобразующим
системам (Я<1), где т в (18а, б) должно быть заменено на 2-
6. Точно решаемые случаи
Ниже обсуждается асимптотическое при больших k
поведение в двух точно решаемых моделях, а именно: K{i, /) =2 с
v = 0 и K(i,j)=ij с v = 1. Детальные вычисления для первой
Кинетика образования кластеров
437
из них имеются в работе [5], а для второй — будут
опубликованы позже. Здесь приведены только окончательные результаты.
Асимптотическое поведение в модели /C(i, /) =2 (значение 2
выбрано для удобства) определяется производящей функцией
V (х) начального распределения
V{x)~f,Ck(0)x*. (20)
Мы различаем два случая: V(xc) расходится и V(xc) ограничена
в точке хс = ехр [—z (0) ].
(I) При V(xc) = оо асимптотическое поведение
универсальное:
Ck(t)~[t2V'(xo)xoV{Xok (fc-*oo), (21a)
зависимость xo(t) от времени определяется выражением
V(x0)-V(l)=l/L (216)
Легко показать, что (21а, б) переходят в (9а, б).
(II) При ограниченных V(xc) или X ^U(O) < °° асимптотика
имеет вид
Ck(l)~(l-t/t0r2Ck(0) (*-*«,), (22)
где кроссовер происходит при /0 = [V (хс) — V (l)p1. Согласно
предположению (5) или 2(0) < 0, величина t0 является
конечной.
В модели /C(i, /) =ij поведение решения Ck(t) при больших
k может быть найдено из точного решения [6], где результаты
выражаются через производящую функцию £/(je) = £ kCk(0)ekx.
Здесь снова следует различать две возможности: (I) U'(—z0) =
= оо и (II) £/'(—Zq) < оо, где 2o = z(0). Первая из них ведет
к универсальному асимптотическому поведению
Ck(t) ~ [2nt3Uff(sc)]-ll2k-5'2ekz{t\ (23)
где зависимость от времени sc(t) определяется неявным
образом из решения уравнения
U'(sc)=l/t. (24)
В этой точно решаемой модели удается проинтегрировать
уравнение (13) при jut = 1, что дает
z(t) = -[sc + tU(se)-t]. (25)
В случае (II) ограниченной производной U'(—z0) уравнения
(23) —(25) применимы только при t > t0 = \/U'{—z0), когда
имеется корень sc(t) уравнения (24). При 0 < t < t0 существует
переходное решение, зависящее от формы начального распреде-
438
Часть VI
ления. Если последнее имеет при 6->-оо вид Ck(0) — A(0)k e° X
Xexp(&20), то переходное решение задается формулами
Ck (t) ~ A (t) АГе° exp [kz (/)] (k -> oo), (26a)
z(t) = zQ+[U(-zQ)-l]t, (266)
A(t) = A (0) [1 -ф0Г{в°-1). (26в)
Другие начальные условия приводят к иному переходному
поведению. Например, при С&(0) ~ ехр [—Д(0)&Р + kzo] оно
описывается
Ск (t) — ехр [- А (0 k? + kz (/)] (27а)
с z(l), определяемой (266), и A(t)9 задаваемой выражением
Д(0 = Д(0)(1-/Д0Д (276)
Следовательно, промежуточная асимптотика переходит в
универсальную (23) — (25) за конечное время t0= l/U'(—z0),
меньшее времени гелеобразования tc = \/U/(0) в этой модели.
Итак, можно сделать заключение, что асимптотическое при
й->-оо поведение в моделях /C(t, /) = 2 и /((/, /) = lj находится
в полном согласии с предсказаниями для моделей с v<l и
v = 1 соответственно.
7. Заключение
Показано, что для общих однородных ядер cv<l решение
уравнения Смолуховского имеет вид Ck{t) = Л^(/)ехр [kz(t)],
где In Л/г возрастает медленнее чем k при й->оо. Для значений
k много больших, чем средний размер кластера, величины Ak{t)
можно вычислить из рекуррентных соотношений. Структура этих
вычисленных величин различна для v < 1 и v = 1. В
зависимости от типа начального распределения по размерам С&(0)
различаются универсальные и неуниверсальные промежуточные
решения. Первые переходят в скейлинговые решения при
возрастании среднего размера кластера s(t) -^оо, а последние
выходят на универсальные решения за конечное время. В некоторых
особых случаях (v < 0, v = 1) нельзя исключить
долговременный характер неуниверсальных решений.
Результаты здесь следующие. Для всех ядер с v< 1 найдено
универсальное асимптотическое поведение Ck~ z (t) k~~K exp [kz (t)]
(9a, 6), когда при А->оо начальное распределение
удовлетворяет условию k-v\nAk(0)-+0 (v > 0) или й1+МА(0)->0 (v <
< 0). С другой стороны, если k"v In Л*(0) > const и 0 < v < 1
или v = 0 и J] ^Ак({Ц) < °°, то имеется промежуточное
асимптотическое решение Ck{t) ~ Ck(0)exp[kvA(t)], которое переходит
Кинетика образования кластеров
439
в универсальное за конечный интервал времени. Для v < 0 при
условии Ak{0) = 0{k~l-%) найдены асимптотические решения,
удовлетворяющие при k-+ оо условию \im[Ak{t)/Ak(0)] = 1.
Наконец, для класса ядер с v = 1 в зависимости от деталей коагу-
ляционного ядра K(i, j) возможны самые разнообразные типы
универсального и неуниверсального поведения решений.
Кроме того показано, что в течение малых интервалов
времени универсальное асимптотическое решение при больших k
для монодисперсного начального условия совпадает с
кратковременным решением в области кластеров больших размеров.
Аналогично универсальная асимптотика для достаточно крупных
кластеров совпадает со скейлинговым решением в области
больших значений его аргумента, когда средний размер кластера
s(t)-+оо. Таким образом, область применимости асимптотики
&->-оо перекрывается с областями применимости
кратковременного решения и скейлингового решения, если каждое из них
рассматривать при больших размерах кластеров.
Для таких кластеров предсказания предложенной в
настоящей работе теории проверены в двух точно решаемых моделях
/("(/, /) =2 и К{1, j) = ij. Сделано заключение о том, что
результаты этой теории вместе с результатами работ [2—4] дают
замечательно полное аналитическое описание асимптотических
свойств распределения кластеров по размерам, если только коа-
гуляционное ядро K(i,j) является однородной функцией i и / по
крайней мере для больших i и /.
ЛИТЕРАТУРА
1. Drake R. L, in: Topics in Current Aerosol Research, vol. 3, eds. G. M. Hidy,
J. R. Brock, Pergamon Press, New York, 1972, part 2.
2. Lushnikov A. A, J. Coll. Interface Sci., 45, 549 (1973); Ernst M. #., Hend-
riks E. M, Leyvraz F.t J. Phys. A: Math. Gen., 17, 2137 (1984).
3. Leyvraz F., Phys. Rev., A29, 854 (1984); van Dongen P. G. /., Ernst M. H.,
J. Phys. A: Math. Gen., 18 (1985).
4 Friedlander S. K., Wang C. S., J. Coll. Interface Sci., 22, 126 (1966);
Leyvraz F., Tschudi H. R., J. Phys. A:Math. Gen., 15, 1951 (1982); van Don-
gen P. G. /., Ernst M. #., Phys. Rev. Lett., 54, 1396 (1985).
5. van Dongen P. G. /., Ernst M. #., J. Coll Interface Sci., будет
опубликовано.
6. Zlff R M, Ernst M. H., Hendriks E. M., J. Phys. A: Math. Gen., 16, 2293
(1983).
Скейлинговое обобщение
уравнения Смолуховского
3. Рац*
Исследуется диффузионно-ограниченная межкластерная агрегация
при условии, что мономеры вводятся в систему с постоянной
скоростью h, а кластеры размером больше некоторого
фиксированного удаляются из системы. Флуктуационные эффекты в ней
рассмотрены на феноменологическом уровне путем скейлингового
обобщения уравнения Смолуховского. Найдено, что распределение
кластеров по размерам подчиняется скейлингу, а все критические
показатели выражаются через единственный индекс однородности
Он определяется на основании доводов, что процесс с h — 0
принадлежит к тому же классу универсальности, что и задача
диффузионно-ограниченной аннигиляции. Скейлинговая теория
продемонстрирована на примере одномерной диффузионно-ограниченной
аннигиляции в присутствии источников частиц. Точно вычислены
стационарная плотность частиц а и время релаксации т се
флуктуации, котрые имеют при А->-0 масштабы ii ~ /i1/3 nt^ h~zlz в
согласии со скейлннговой теорией.
1. Введение
Необратимая агрегация относится к довольно общим
механизмам роста. Полимеризация, образование аэрозолей, рост
коллоидов, агрегация красных кровяных телец и образование
зародышей при фазовых переходах [1] —все это может быть
описано некоторыми модификациями агрегационных моделей.
Большинство из них являются, однако, непринципиальными
обобщениями предложенного Смолуховским приближения среднего
поля [2, 3], которое основано на предположении о бинарном
характере столкновений и пренебрежении пространственными
флуктуациями плотности этих объектов. Поскольку известно, что
такие флуктуации становятся существенными в пространствах
с низкой размерностью (d ^ dc), то следует ожидать нарушения
теории Смолуховского при d ^ dCi причем для большинства
процессов агрегации критическая размерность dc точно не известна.
Как следует из теории критических явлений, пространственные
флуктуации могут быть учтены на феноменолгическом уровне
скейлинговым обобщением теории среднего поля. Ниже показало,
каким образом это скейлинговое обобщение может быть
проведено для агрегирующих систем с источниками и стоками
частиц.
2. Скейлинговые свойства уравнения Смолуховского
Из допущения Смолуховского о том, что коалесценция
кластеров происходит путем их случайных бинарных столкновений,
* Zoltdn Rdcz-Department of Physics, Simon Fraser University, Burnaby,
В. С, Canada V5A 1S6.
Кинетика образования кластеров
441
вытекает закон эволюции во времени плотности /^-частичных
кластеров tik(t):
оо
^зг- = il *</"' W ду W - Л* W Z */*"'(/)- (1)
Ядро Kij этой системы уравнений частично учитывает такие
детали процесса, как зависимость сечения столкновений от
размеров и подвижности кластеров. Если, следуя обычной
процедуре, предположить [4] однородность функции Кц относительно
ее аргументов Кы, ь\ = ЬЩц> то можно использовать степень
однородности К как параметр при сопоставлении скейлинговых
результатов с экспериментальными данными. Эта процедура в
чем-то напоминает феноменологический метод получения
критических показателей в равновесной критической точке
посредством введения в рассмотрение соответствующим образом
выбранных дальнодействующих сил. Из дальнейшего будет
видно, однако, что такой подход может быть применен к задачам,
где, кроме того, имеются источники и стоки, которые
соответствуют наличию внешнего поля в окрестности равновесной
критической точки.
Далее рассматриваются простейшие типы источников и
стоков. Предполагается, что частицы единичного размера
генерируются со скоростью h штук в единице объема в единицу времени,
а кластеры с более чем k0 звеньями одновременно отводятся из
системы. Соответствующее уравнение Смолуховского [5, 6]
обладает при скорости А-*0 простыми скейлинговыми
свойствами, которые фактически определяются тем, что столкнови-
тельные члены квадратичны по плотности кластеров.
Следовательно, Кц нельзя использовать для нахождения
соответствующих показателей. Переходя путем введения соответствующих
масштабов к скейлинговым времени и распределению кластеров
по размерам [7]:
f = AI/2/, nk(t) = nk(t)/hm9 ' (3)
можно заметить, что величина h в уравнении (2) пропадает и,
следовательно, в пределе больших времен (когда уже можно
пренебречь зависимостью от начальных условий) решение
записывается в виде
nk(t, h) ~ tii\k{hX,2t). (4)
Из него следует, что стационарное распределение кластеров по
размерам пи и время релаксации к нему т/г имеют характерные
442
Часть VI
масштабы hk ~ h{/2 ит^ ft~l/2, в то время как закон
релаксации при h = 0 является неэкспоненциальным n,k{t,0)~ \/t.
Моделирование этой системы методом Монте-Карло [8] дает,
однако, при Л->0 асимптотики nk ~ Л1/б, тЛ~/г~А и nk(ty 0)~t~^>
а полученные из уравнения (4) среднеполевые значения
показателей применимы только для пространств с размерностью выше
критической do которая в данном случае оказывается равной 2.
3. Скейлинговое обобщение уравнения Смолуховского
Для развития теории, учитывающей отклонения от
приближения среднего поля, заметим, что уравнение (2) можно
записать в виде
dnb it)
—ft— = hbk\ — Gk {nu n2, ..., tikX (5)
где Gk — однородная функция степени 2, именно Gk (Хщ> Хп2, ...
..., knkQ)==h2Gk(nb n2i ..., fiko). Поскольку аналогично
производным свободной энергии величина Gk является «обобщенной
силой», движущей систему к ее равновесному состоянию, и
поскольку скейлинг является общей особенностью полученных
методом Монте-Карло результатов [8], будет совершенно
естественно постулировать, следуя теории критических явлений, скей-
линговый вид функции Gk
Gk (Аль Хп2, ..., Xtiko) = №Gk {пи п2, ..., п^), (6)
где степень однородности б служит свободным параметром.
Анализ уравнений (5) и (6) такой же, как и уравнения (2). Теперь,
однако, выбор скейлинговых времени и распределения кластеров
по размерам, при которых величина h исчезает из уравнений (5),
будет таким:
t = hl-lt*t и nk(i) = nk(t)/hm.
Следовательно, решение уравнения (5) при больших временах
имеет вид
nk(t,h)~h1!\(hl-m(), (7)
из которого получаются асимптотические зависимости
hk~til\ rh~h-A ипкУ,0)~Г1 cA=l-l/fi, £=1/(6-1).
(8)
Из этих формул видно, что все показатели выражаются через
индекс однородности б. Скейлинговая формула (7) и скейлин-
говые законы (8) были подтверждены [8] для
диффузионно-ограниченной агрегации при d = 1, 2 и 3. Более строгим тестом для
теории является ее применимость в частном случае k0 = 1, кото-
Кинетика образования кластеров
443
рый представляет собой диффузионно-ограниченную
аннигиляцию в присутствии источников частиц. Эта задача интенсивно
изучалась [9—14] при h = О, а для одномерного случая d=l
она решена точно [9]. Точный результат n\(t,0) ~ t~1/2
означает, что если скейлинговая теория верна, то б = 3 и А = 2/3.
Ниже путем прямого вычисления б и А подтверждается
применимость скейлинговых законов (8) для d=\.
4. Одномерная диффузионно-ограниченная аннигиляция
в присутствии источников
Рассматривается следующая модель. Частицы совершают
случайные блуждания со скоростью перескоков Г в единицу
времени вдоль одномерной решетки и аннигилируют при
одновременном попадании в один и тот же узел. Кроме того, частицы
непрерывно генерируются со скоростью Th на каждом узле.
Наша цель — вычисление стационарной плотности частиц Я и
времени релаксации ее флуктуации. Эта задача решается
сведением рассматриваемой модели к обобщенной кинетической
модели Изинга.
Для понимания этой процедуры последняя модель
рассматривается при d = l, исходя из предложенного Глаубером [15]
вида для скоростей переориентации спина
где at = ± 1 — стохастическая спиновая переменная,
приписываемая узлу i решетки, а у— параметр, связанный с
температурой системы. При нулевой температуре y = 1> так чт0 *'-й спин
переворачивается со скоростью Г/2 при at-+i = —a/-i или со
скоростью Г при 0/+1 = <Т/_1 =—о*,-. Это означает, что доменная
стенка движется налево и направо с равной скоростью Г/2, в
то время как две соседние доменные стенки аннигилируют друг
с другом со скоростью Г. Идентифицируя, таким образом,
доменные стенки с частицами, можно увидеть, что в пределе
пулевой температуры кинетическая модель Изинга описывает
диффузионно-ограниченную аннигиляцию. Источники частиц можно
ввести в эту схему, если разрешить процессы переворота спина,
при которых одновременно могут менять ориентацию все спины
at с / ^ и В ходе такого процесса возникает доменная стенка, а
следовательно, и частица между узлами i и i+ 1. Если между
ними уже существует доменная стенка, то происходит ее
разрушение. Это соответствует тому, что рождение частицы на
занятом другой частицей узле ведет к его освобождению. Если
выбрать скорость этого процесса независящей от i
W^Th, (Ю)
444
Часть VI
то получится кинетическая модель Изинга с динамикой
доменных стенок, эквивалентной динамике частиц при ограниченной
диффузией аннигиляции с равномерно распределенными
источниками.
Поскольку плотность частиц между узлами i и i + 1 равна
гы=(1 —a/aii+i)/2, то необходимо лишь вычислить <(Ti0i+1> в
кинетической модели Изинга со скоростью переориентации спинов,
определяемой формулами (9) и (10). В случае трансляционно-
инвариантных начальных состояний /г = </г;> уравнение для
<сг;07+1> содержит лишь двухточечные корреляционные функции
п = (niOi+i). Следуя статье Глаубера [15], можно получить
уравнение для ti [16]
^/Г = г|_1 + г/ + 1-2(1 + «)г, (/>0), (11)
причем r0 = (of}=l и rt — r_l при / < 0,
Стационарное решение этого уравнения имеет вид
h = h+h-^h-{)IJh^{h~{), (12)
где Jv(z) —функция Бесселя [17] первого рода порядка v. Для
п= (1 — г\)/2 в пределе h->■ 0 получим
п «0,46л1/3, (13)
так что 6 = 3 в соответствии со скейлинговым предсказанием.
Для того чтобы найти времена релаксации флуктуации
однородной плотности, нужно искать решение уравнения (11) в виде
Гк = Гк + дн^хр(—t/x). Подстановка этого rk в (11) приводит
к бесконечному набору времен релаксации, наибольшее из
которых в скейлинговом пределе А->0 имеет вид
xh ~ 0,27Г_1/Г2/3. (14)
Следовательно, второе предсказание скейлинговой теории А =
= 2/3 также подтверждается.
5. Заключительные замечания
Поскольку при переходе от k0 = 1 к k0 = 2, 3, . . . никаких
новых законов сохранения или симметрии не вводится в систему,
можно предположить, что критические показатели, вычисленные
в случае ограниченной диффузией аннигиляции, остаются теми
же самыми для других диффузионно-ограниченных процессов
агрегации. Это предположение подтверждается также
результатами имитационного моделирования методом Монте-Карло,
который в случае одномерной ограниченной диффузией аннигиляции
дает с хорошей точностью значения б = 3, Д = 2/3,
Кинетика образования кластеров
445
■-{
Диффузионно-ограниченная аннигиляция изучалась также в
пространствах более высоких размерностей [10—14], где
установлено существование критической размерности dc = 2, выше
которой £ = 1, а ниже — £ = d/2. На основании скейлинга и
соображений универсальности можно сделать предположение о
том, что задача об ограниченной диффузией агрегации в
присутствии источников и стоков имет решение (5) и (6) со скейлинго-
вым показателем
2 d>2y
(d + 2)/d d<2. (15)
Поскольку dc = 2, флуктуации не играют существенной роли в
реальных агрегационных системах. Следует заметить, однако,
что химические реакции часто протекают на имеющих низкую
размерность фрактальных поверхностях, где развитая выше
теория непосредственно применима.
ЛИТЕРАТУРА
1. Kinetics of Aggregation and Gelation, eds. F. Family, D. P. Landau, North-
Holland, Amsterdam, 1984.
2. von Smoluchowski M., Phys. Z., 17, 557 (1916).
3. Эрнст M. — наст, сб., с. 399.
4. van Dongen P. G. /., Ernst M. #., Phys. Rev. Lett., 54, 1396 (1985).
5. von Smoluchowski M., Z. Phys. Chem., 92, 129 (1918).
6. Эксперименты, где источники и стоки частиц играют важную роль,
описаны в работах:
Madelaine G. /., Perrln M. L., Itoh M., J. Aerosol Sci., 12, 202 (1979);
Mocros L. F., Quon /. £., Hjelmfelt А. Г., J. Colloid Interface Sci., 23, 90
(1967).
7. Rdcz Z., Phys. Rev. A, August 1985.
8. Vicsek Г., Meakin P., Family F.t Phys. Rev. A, August 1985; Anacker L. W.,
Kopelman R.y J. Chem. Phys., 81, 6402 (1984).
9. Torney D. C, McConnel H. M., J. Phys. Chem., 87, 1941 (1983).
10. Toussaint /)., Wiczek f.t J. Chem. Phys., 78, 2642 (1983).
11. Torney D. C, J. Chem. Phys., 79, 3606 (1983).
12. Meakin P., Stanley Я. E., J. Phys., A17, L173 (1984).
13. Kang K., Redner S.y Phys. Rev. Lett., 52, 955 (1984).
14. Kang /C, Redner S., Phys. Rev., A30, 2833 (1984).
15. Glaujber R. /., J. Math. Phys., 4, 294 (1963).
16. Rdcz Z., будет опубликовано.
17. Handbook of Mathematical Functions, eds. M. Abramowitz, I. A. Stegun,
Dover, New York, 1965.
Кластеризация во Вселенной
Ф. Луккин *
Сгустки материи встречаются во Вселенной в радиусе порядка
102 Мпс, причем фрактальная размерность кластеров в
широком диапазоне составляет примерно D « 1,2. Дается краткий
обзор кластеризации и ее значения для космологии.
1. Введение
Кластеризация (скручивание) галактик в последние
60 лет была предметом интенсивных исследований. Цвикки [1],
Лик [2] и астрономы Краковской обсерватории [3],
составившие каталоги положений галактик, подвели итог этим
исследованиям. Накопленный материал позволил существенно
продвинуть статистический анализ кластеризации. Эта работа была
выполнена главным образом Пиблзом и его сотрудниками [4].
Недавно в изучении кластеризации началась новая эра, связанная
с появлением значительно усовершенствованных спектрографов
и эмульсий, что позволило измерять радиальные скорости v
слабых галактик и, следовательно, расстояния до них (хорошо
известный закон Хаббла v = H0d устанавливает связь между
скоростями далеких галактик, обусловленными расширением
Вселенной, и расстоянием до них d\ постоянная Хаббла Я0 равна
100 (км/с)/Мпс, где 0,5с<Лс<^ 1; 1 пс ^ 3,3 св. года). В свою
очередь это позволило недавно составить каталоги красного
смещения (красное смещение г = v/c — полезный параметр для
оценки расстояний и обращенного назад времени), например
Калифорнийский каталог [5]. Прогресс в анализе кластеризации
галактик всегда тесно связан с прогрессом, достигнутым теорией
в изучении возникновения космических структур. Эта область в
последние годы переживает бурное развитие, главным образом
из-за притоков идей «новой физики» (теорий Великого
объединения, суперсимметрии и т. д.) в традиционную космологию (см.
работы [6, 7]).
2. Кластеризация во Вселенной
2.1. Морфологическое описание
Распределение галактик имеет сгустки и разрежения во всех
масштабах. Галактики представляют собой системы с массой
107— 1012Мо(Мо —-масса Солнца) размером 10—102 кпс и
превышениями до 10б раз по сравнению с средней плотностью. При-
* Francesco Lucchin-Dipartamento di Fistca «G. Galilei», Via Marzolo
8,35100 Padova, Italy.
Кинетика образования кластеров
447
мерно половина всех галактик является членами групп или
скоплений. Группы состоят из нескольких десятков галактик, имеют
массу 1012—1014 Мо, размеры КН—10 Мпс и превышение над
средней плотностью в 103 раз. Местная группа состоит примерно
из 20 членов, из которых самыми крупными являются наша
Галактика и Туманность Андромеды. Скопления представляют
собой агломерации из нескольких тысяч галактик с массой
порядка 1015 Ме, размерами порядка 10 Мпс и превышением
плотности над средней в 102 раз и более; структура их неоднородна,
с разрешениями и сгущениями. В одних случаях плотность
галактик в центре мала (нерегулярные скопления в Деве), в
других распределена гладко и симметрично (регулярные скопления
типа Волос Вероники). Наиболее важные каталоги скоплений
составлены Цвикки [1] и Эйбеллом [8].
За последние 30 лет были получены данные,
свидетельствующие о существовании сверхскоплений [9]. Они содержат по
несколько скоплений и имеют неправильную форму.
Сверхскопление имеет массу порядка 10п М© и размеры порядка 102 Мпс;
плотность превышает среднюю примерно в 2—3 раза.
Концентрация галактик в сверхскоплениях часто имеет волокнистое или
сплющенное распределение. Местное сверхскопление с центром
в Деве служит типичным примером сверхскопления.
Преобладающая часть объема Вселенной практически лишена галактик.
Было бы интересно иметь каталоги сверхскоплений и полостей
(таких, например, как огромная полость в Волопасе [10]). Это
позволило бы изучить их статистические свойства; пока мы
располагаем только одним таким каталогом, в который включены
сведения о 20 сверхскоплениях [11].
Резюмируя, можно сказать, что распределение вещества во
Вселенной, весьма неоднордное на малых масштабах, становится
все более однородным по мере приближения к масштабам
порядка 102 Мпс. На еще больших (причем существенно больших)
масштабах Вселенная весьма однородна, о чем мы можем судить
главным образом по сильной изотропности трехградусного
космического фонового излучения [12]: АГ/Г^Ю-4. Космическое
фоновое излучение — своего рода «ископаемое», запечатлевшее
«последнее рассеяние» (через 105 лет после Большого взрыва)
перед возникновением космических структур.
2.2. Статистический подход
Основная работа в этом направлении состояла в измерении
корреляционных функций между галактиками низкого порядка
и кластерами на основе каталогов [1—3], содержащих сведения
о положении около 106 галактик. Результаты этой работы [4]
были углублены и подтверждены анализом корреляционных
448
Часть VI
функций, построенных на основе каталогов красного смещения
[И, 13].
Спорные статистические данные о том, насколько характерны
для суперкластерной морфологии нити, полосы и пустоты, и
острые дискуссии о различных сценариях возникновения галактик
(некоторые из этих сценариев довольно естественно
воспроизводят те самые нити, полосы и полости [14, 15J) лишний раз
подчеркивают настоятельную необходимость альтернативной и
дополнительной статистики, более чувствительной к
топологическим свойствам кластеризации галактик. Среди вновь
предложенных подходов наиболее важным является выборочная
проверка на перколяцию [16], заимствованная из теории перколя-
ции в физике твердого тела.
2.3. Корреляционные функции
Двухточечная пространственная корреляционная функция
1(г\2) для галактик определяется из соотношения
6P = n*[l+l(rX2)]6Vl6V29 (1)
где 8Р — совместная вероятность найти галактики в объемах
6V\ и 5V2, разделенных расстоянием r,2, n — средняя численная
плотность галактик. Аналогичным образом определяются
корреляционные функции высших порядков: трехточечная £123,
четырехточечная т)1234> • • • корреляционные функции:
6Р = /г3 (1 + 6,2 + 623 + 631 + £,28) *ух 6У2 6К8, (2)
SP = /г4 (1 + 61S + баз + £з4 + 6« + Eai + ^ + Ым + 613624 +
+ 614623 + £123 + £,24 + £234 + Ч1234) bV{ 6V2 6V3 6V4, (3)
где ln = t{rif), %,ik = £(r,7, rik, rki),
Наблюдаемая двухточечная корреляционная функция
галактик хорошо аппроксимируется соотношением
Цг)~(г/г0)~у (4)
в диапазоне 0,1/г-1 Мпс < г << lO/i-1 Мпс с показателем у « 1,8
н радиусом корреляции галактик г0 ~ 5,5 h~l Мпс; величина £(г)
становится отрицательной при г ^ 30/г-1 Мпс. Данные по трех-
и четырехточечным функциям весьма хорошо
аппроксимируются подходящей симметричной суммой произведений
двухточечных функций (так называемой иерархической формой)
6l23 ~ Q (5l2&13 + 621623 + 631632)7 (5)
Л1234 ~ Ra [612623^34 + циклическая перестановка (12 членов)] +
+ Rb [£126,36,4 + циклическая перестановка (4 члена)] (6)
Кинетика образования кластеров
449
в том же диапазоне с Q » 1, Ra ~ 2,5 и Нь & 4,3. Критический
анализ теоретических следствий из иерархической формы
приведен в работах Пиблза [4] и Фрая [17],
Кластеры (скопления), содержащие большое число
галактик, коррелируют примерно по тому же закону (4), но с
большей амплитудой [11, 13, 18]: в диапазоне 1Ьгх Мпс < г <
< 150А-1 Мпс двухточечная корреляционная функция таких
кластеров определяется соотношением
tc(r)~(r/rc)~*c (7)
с радиусом корреляции кластеров rc ~ 25/г-1 Мпс и у ж 1,8. По
поводу этого результата ведутся споры [19, 20], так как из него
следует, что галактики и кластеры не могут быть хорошими
метками распределения масс: по-видимому, постоянный наклон
двухточечных корреляционных функций галактик и кластеров
указывает на возникновение галактик и кластеров в ходе единого
масштабно-инвариантного процесса, в то время как различные
амплитуды корреляций обусловлены неодинаковостью
последующих процессов. Аналогичные масштабно-инвариантные процессы
известны под названием фракталов [21]: фрактальная
размерность D, соответствующая законам подобия (4) и (7), равна
D = 3-y~ 1,2 (8)
(ясно, что на масштабах г > 102 Мпс D » 3). В настоящее
время известны следующие масштабно-инвариантные процессы [19]:
а) образование галактик происходит в пиках поля плотности
материи и начинается с первичного масштабно-инвариантного
спектра возмущений («несимметричное» образование галактик
[22]); б) галактики возникают от первичных флуктуации,
создаваемых космическими струнами (Виленкин [23]); в)
образование галактик вызвано перколированным взрывом первичных
затравок [20, 24]. Для получения приведенной выше фрактальной
размерности были предложены некоторые геометрические
модели (степенная кластерная модель [25]; модель непрерывной
масштабно-инвариантной иерархии [26]; нитевидная модель
[27]).
2.4. Перколяционный анализ
В заданной выборке из N галактик в кубе объемом /,3_вокруг
каждой галактики проводится сфера радиусом r = rd (d =
= L/Nl/S — среднее расстояние между соседними галактиками).
Длина перколяции L(r) ^ L есть максимальное расстояние
между двумя галактиками, которое можно пройти, оставаясь в
сферах; при L(f) = L в выборке поисходит перколяционный
переход, и соответствующая безразмерная величина p = r(L) назы-
450
Часть VI
вается параметром перколяции. Равномерное распределение
галактик характеризуется величиной р = 1; распределению
Пуассона с N > 103 соответствует [28] р = 0,86; для легко
перколируемого распределения (типа сплошных нитей или полос)
получается р < 0,86, а для трудно перколируемого распределения
(типа отдельных сгустков материи) р > 0,86. Перколяционный
анализ некоторых «игрушечных» модельных распределений был
проведен Декелем и Вестом [29], отметившими некоторые
трудности перколяционного теста. В настоящее время произведен
перколяционный анализ окрестности Местного сверхскопления
[30]: оказалось, что р « 0,65.
3. Возникновение космических структур
3.1. Набросок модели большого взрыва
Классическая космология большого взрыва дает
удовлетворительное описание эволюции Вселенной от планковских времен
(когда температура достигала Г = 1019 ГэВ) до современной
эпохи (когда Г = 3 К) примерно через 15 млрд лет [31]. Модель
большого взрыва опирается на следующие краеугольные камни:
а) изотропное расширение Хаббла; б) трехградусное
космическое фоновое излучение; в) наблюдаемая распространенность
легких элементов (существует «чудесное» согласие между
распространенностью наблюдаемой и распространенностью,
предсказанной на основе модели). Теоретические предпосылки
модели большого взрыва сводятся в конечном счете к общей
теории относительности и общей изотропии и однородности
горячей Вселенной на ранней стадии ее существования. Тем не
менее долгое время несколько проблем оставалось неразрешимыми
для классической модели [6]: а) происхождение барионной
асимметрии (наблюдаемое в настоящее время отношение числа
барионов к числу фотонов Пь/пу ~ 109); б) происхождение
спектра первичных флуктуации плотности (которым обусловлены
наблюдаемые космические структуры); в) «избыточная»
плоскостность современной Вселенной (приблизительно через 15 млрд. лет
после планковской эпохи все еще продолжает сохраняться
природное равновесие между расширением и гравитационным
притяжением; это следует из того, что современное значение
параметра плотности Q0 = 8ttGpo/3#o » 1, где р0 «* Ю"29 г/см3—
полная современная плотность Вселенной); г) проблема горизонта
(введенное специально предположение о первичной
однородности). Все эти проблемы удалось разрешить непротиворечивым
образом, хотя до сих пор их решения носят качественный
характер, путем применения идей «новой физики» к космологии [6],
позволивших объяснить происхождение барионов [32] и получить
Кинетика образования кластеров
451
несколько сценариев расширения Вселенной [33]. В частности,
из «новой» космологии следует, что на раннем этапе развития
Вселенной а) параметр плотности Q0 очень близок к единице, и
поэтому в соответствии с некоторыми данными существует
огромное количество не собранной в кластеры «темной» материи
(наблюдаемая кластеризация соответствует £2Кл ~ 0,1—0,3) не-
барионного типа (из нуклеосинтеза легких элементов следует,
что для барионов Q&<0,1): небарионная компонента,
по-видимому, состоит из реликтовых слабо взаимодействующих
массивных частиц [14, 15]; б) спектр первичного возмущения
адиабатический (возмущения плотности приближенно одни и те же для
всех компонент: барионов, фотонов, слабо взаимодействующих
массивных частиц, ...) и масштабно-инвариантный (флуктуации
среднеквадратичной глубины потенциала
масштабно-инвариантны). Такой первичный спектр надлежащей интенсивности был
предложен [34] за 10 лет до теорий Великого объединения и
«революции» в расширении Вселенной для получения менее
неудовлетворительных сценариев возникновения галактик. К
сожалению, предложенные до сих пор модели расширения
предсказывают требуемые темпы расширения только при тонкой
«настройке» физики, лежащей в основе процесса [6, 7].
3.2. Сценарии возникновения галактик
По множеству начальных данных, как показывает
традиционная космология, можно построить подробный сценарий эволюции
возмущений; такой подход является по существу
гидродинамическим на линейном этапе, когда материя и излучение еще связаны,
в то время как численное моделирование на основе задачи N
тел часто используется на заключительных нелинейных этапах.
Теоретические результаты подлежат сравнению с наблюдаемыми
свойствами Вселенной. Основные наблюдательные ограничения
определяются тем, что галактики существуют при z ^ 3 (из
наблюдений квазаров [35]), космическое фоновое излучение
изотропно, а также кластерными свойствами Вселенной и
индивидуальными свойствами типичных галактик и скоплений.
Особенности сценариев возникновения галактик зависят от
природы слабо взаимодействующих массивных частиц. В
настоящее время существуют два сценария: сценарии «горячей» и
«холодной» темной материи [14, 15]. По сценарию горячей темной
материи слабо взаимодействующие массивные частицы
образовались при распадах остальных частиц Вселенной «недавно»,
поэтому их средний импульс составляет сейчас р0 = 3 К, а
плотность (число частиц в единице объема) п0 « пу. В этом
сценарии свободное течение разрушает любые флуктуации, масштаб
которых меньше типичного характерного размера кластера, по-
452
Часть VI
этому первые объекты с массой М « 1015Мо фрагментируются
при первом же коллапсе на галактике (сценарий «сверху вниз»).
Кандидатом на роль слабо взаимодействующих массивных
частиц могли бы быть массивные нейтрино (mv » 30 эВ). Холодные
слабо взаимодействующие массивные частицы вступают во
взаимодействия менее интенсивно и образуются раньше, поэтому
теперь имеют импульс р0 < 3 К и плотность п0 < пу (но для того
чтобы fio « 1> их масса должна быть больше mv: mw>my).
В этом случае свободное течение уничтожает флуктуации, не
представляющие космологического интереса: первые объекты с
массой около 1016Мо быстро кластеризуются в более крупные
структуры, образуя иерархически упорядоченную шкалу
объектов (сценарий «снизу вверх»). Кандидатами в слабо
взаимодействующие массивные частицы в этом случае могли бы быть
фотино или аксионы [15, 36].
Все сценарии с слабо взаимодействующими массивными
частицами (с некоторыми несущественными ограничениями на
параметры теории) удовлетворяют требованию изотропности
космического фонового излучения [37]. В настоящее время
«горячие» модели переживают определенные трудности, так как
численное моделирование на основе задачи тел показывает, что
галактики образуются слишком поздно, а кластеризация приводит
к большим сгусткам материи [14, 38]. «Холодные» сценарии
более многообещающи, несмотря на то что в недавних численных
экспериментах на основе задачи N тел обнаружились небольшие
трудности [39]. В последнее время были предложены и другие
модели с слабо взаимодействующими массивными частицами
[18] для преодоления более существенных трудностей в теории
возникновения галактик. В современной космологии такая
теория представляет более важную и пока открытую проблему,
надежды на решение которой принято связывать с будущими
достижениями в космологии и физике частиц как в теории, так и в
эксперименте.
ЛИТЕРАТУРА
1. Zwlcky F., Herzog £., Wild P., Karpowicz M., Kowal С. Г., Catalogue of
Galaxies and Clusters of Galaxies, Caltech, Pasadena, 1961—68.
2. Shane C. D., Wirtanen C. A, Astron. /., 59, 647 (1954); Publ. Lick Obs.,
22 (1967).
3. Rudniki K, Dworak T. /0, Flirt P., Baranowski £., Sendrakowski A, Acta
Cosmologica, 1, 7 (1973).
4. Peebles P. J. E., The Large-Scale Structure of the Universe, Princeton
Univ. Press, Princeton Univ. Press., Princeton, 1980.
5. Huchra J. P., Davis M., Latham D. W, Tonry L. /., Astrophys. J. Suppl.,
53, 89 (1983).
6. The Very Early Universe, eds. G. Gibbons, S. Hawking, S. Siklov,
Cambridge Univ. Press., Cambridge, 1983.
Кинетика образования кластеров
453
7. Large-Scale Structure of the Universe, Cosmology and Fundamental
Physics, eds. G. Setti, L. Van Hove, ESO and CERN, Geneva, 1984.
8. Abell G. O., Astrophys. J. Suppl., 3, 211 (1958).
9. Oort J. Af, Ann. Rev. Astron. Astrophys., 21, 373 (1983).
10. Kirshner R. P, Oemler A., Schechter A., Schectman P. L, Astrophys. J.,
248, L57 (1981).
11. Bahcall N. A., Soneira R. M., Astrophys. J., 270, 20 (1983).
12. Uson J. M, Wilkinson D. Г, Astrophys. J., 277, LI (1984).
13. Davis M.y Peebles P. J. £., Astrophys. J, 267, 465 (1983); Shanks Г.,
Bean A. /, Efstathiou G., Ellis R. «S., Fong R.y Peterson B. A., Astrophys.
J., 274, 529 (1983); Клыпин А. А., Копылов А. Т. — Письма в Астр, ж.,
1983, т. 9, с. 41.
14. Primak J. #., Lectures of the Int. School of Phys. «E. Fermi», Varenna,
1984.
15. Hogan С #, Kaiser N„ Turner M. S, Vittorio N.9 White S. M., The
formation of Structure in the Universe, Fermilab-Conf, 85/57-A, 1985.
16. Zeldovich Ya. В., Einasto J., Shandarin S.y Nature, 300, 407 (1982).
17. Fry J. N.y Astrophys. J., 279, 499 (1984).
18. Hauser M. G.y Peebles P. /. E., Astrophys. J., 185, 757 (1973).
19. Schramm D. #., Dark Matter, tooth faires, Fractals and Strings, Fermilab-
Conf, 85/42 A, 1985.
20. Szalay A., Schramm D. M.y Are Galaxies More Strongly Correlated than
Clusters? Fermilab-Pub, 85/24 A, 1985.
21. Mandelbrot B.y The Fractal Geometry of Nature, Natur Freeman, San
Francisco, 1982.
22. Kaiser N., Astrophys. J., 284, L9 (1984).
23. Vilenkin A., Phys. Reports, 121, 263 (1985).
24. Carr B. /., Bond J. R.t Arnett £>., Astrophys. J., 277, 445 (1984).
25. Peebles P. /. £., Astron Astrophys., 32, 197 (1974).
McClelland /., Silk /., Astrophys. J, 217, 331 (1977).
26. Maldebrot R. В., С. R. Acad. Sci., Paris, 280A, 1551 (1975); Soneira R. M.,
Peebles P. /. £., Astron. J., 83, 845 (1978).
27. Fry J. N., Astrophys. J., 270, L31 (1983).
28. Шкловский Б. И., Эфрос А. Л. Электронные свойства легированных
полупроводников. — М.: Наука, 1979.
29. Dekel Л., West М. /., Astrophys. J., 228, 411 (1985).
30. Einasto /., Klypin A. A., Saar E., Shandarin P., Mon. Not. Roy. Astron.
Soc, 206, 529 (1984).
31. Zeldovich Ya. В., Novikov L D.y Relativistic Astrophys, vol. II, The Univ.
of Chicago Press, Chicago, 1983.
32. Kolb E., Turner M., Ann. Rev. Nucl. and Part. Sci, 33, 645 (1983).
33. Linde A. D.y Rep. Prog. Phys., 47, 925 (1984).
34. Zeldovich Ya. 5, Mon. Not. Roy. Astron. Soc, 160, IP (1972).
35. Faber S. M., Galaxy Formation and Cosmology in ref. 8, pp. 187—203.
36. Shramm D. N., Nucl. Phys, V 252, 53 (1985).
37. Bonometto S. Л, Lucchin P., Valdarnini R., Astron. Astrophys, 140, L27
(1984); Vittorio N., Silk /., Astrophys. J, 285, L39 (1984); Bond /. /?.,
Efstathiou G., Astrophys. J, 285, L44 (1984).
38. Frenk C, White S. D. M, Davis M., Astrophys. J., 271, 417 (1983).
39. Davis M., Efstathiou ft, French С 5., White S. M., Astrophys, J., 293, 371
(1985),
Стохастический подход
к крупномасштабной кластеризации
материи во Вселенной
«Когда молодой человек
произносит в моей лаборатории слово
«Вселенная», я говорю ему, что нам
уже пора расстаться».
Э. Резерфорд*
Л. Пьетронеро, Р. Купере **
Сформулирована стохастическая модель, которая при подходящих
предположениях относительно входящих в нее вероятностей
порождает автомодельную кластеризацию во всех масштабах.
Отсюда следует, что система с начальным распределением
однородным и случайным может спонтанно переходить в фрактальное
распределение с корреляционными функциями, изменяющимися по
степенным законам. Это обстоятельство позволяет по-новому
взглянуть на происхождение крупномасштабной кластеризации
материи во Вселенной,
1. Введение
Распределение материи во Вселенной представляется
кластеризованным на всех масштабах — от галактических до
существующих в настоящее время пределов наблюдений [1].
(Современный анализ кластеризации во Вселенной см. в
предыдущей статье Луккина [2].) Отсюда следует, что определение
средней плотности существенно зависит от выбранного конкретного
объема и свидетельствует об иерархическом распределении.
Наблюдаемая корреляционная функция плотности может быть с
достаточной точностью описана степенным соотношением
C(r) = (p(r0)p(ro + r)>-r-v, (1)
где у « 1,8. Так как для фрактала [3] С (г) ~ r~(d~D\
соотношение (1) можно интерпретировать как подтверждение фракталь-
ности распределения с фрактальной размерностью D = 1,2 (d =
= 3 — евклидова размерность пространства). Во избежание
недоразумения заметим, что р(г) относится не к отдельному
элементу системы, как это обычно принято при анализе моделей
кластер-кластерной агрегации [4, 5], а описывает распределение в
пространстве всех элементов рассматриваемой системы.
Обсуждение в литературе обычно строится на основе так называемой
* Из статьи Дж. А. Уилера, опубликованной в журнале Physics Today,
October 1985, p. 66.
** L. Pietronero, R. Kupers ♦ University of Groningen, Melkweg 1, 9718 EP
Groningen, The Netherlands.
Кинетика образования кластеров
455
безразмерной двухточечной корреляционной функции £(г),
связанной с С (г) соотношением [6]
Эта функция описывает отклонения от средней плотности <р> и
при I » 1 по существу совпадает с С (г). Так как для
иерархических распределений определение средней плотности <р>
зависит от выбранного объема, мы предпочитаем пользоваться
непосредственно корреляционной функцией С (г). Степенной закон
(1) изменения С (г), охватывавший на протяжении более чем
трех десятилетий все более широкий диапазон масштабов, в
последние годы стал предметом интенсивных исследований [2].
Однако пока удовлетворительного теоретического объяснения
степенного закона (I) не существует [7, 8]. Часто допущение о су
ществовании такого закона просто принимается для того, чтобы,
исходя из других свойств, вычислить его характеристики [6—8].
Что касается его происхождения, то наиболее распространенная
точка зрения опирается на данные численных экспериментов на
основе задачи п тел, согласно которым большие флуктуации
плотности возникают от усиления первичных не зависящих от
масштабов флуктуации [9—11]. В свою очередь усиление
связано с конкуренцией между расширением и гравитационным
притяжением. При таком подходе вопрос о происхождении этих
флуктуации сдвигается по времени к свойствам ранней
Вселенной [11]. Основная проблема такого подхода состоит в том, что
изотропность трехградусного фонового излучения накладывает
жесткие ограничения на величину первичных флуктуации.
Вычисления на основе задачи п тел состоят в моделировании
молекулярной динамики с явным учетом расширения и всех
гравитационных взаимодействий. Если начальные распределения
случайны, то такого рода численные эксперименты не приводят
к автомодельным иерархическим структурам [7, 9].
Относительно реальной Вселенной они накладывают весьма жесткие
ограничения и по пространству, и по времени. Действительно, одна
отдельная галактика состоит примерно из 1010 звезд, тогда как
численные эксперименты на основе задачи п тел охватывают
всего лишь несколько тысяч частиц и порождаемый в
результате экспериментов средний объект содержит около 30
начальных частиц [9]. Ясно, таким образом, что может существовать
серьезная проблема масштабов, так как не исключено, что
некоторые флуктуации не могут развиваться полностью.
Чтобы исследовать такую возможность, мы рассмотрим здесь
упрощенные стохастические модели, в которых гравитация
учтена только через вероятность необратимой агрегации (слияния)
двух объектов (галактик), сближающихся на достаточно малое
456
Часть VI
расстояние. Влияние гравитации на траектории считается
пренебрежимо малым. Столь сильные упрощения обладают тем
преимуществом, что надлежащий выбор правил для вероятностей
необратимого присоединения позволяет воспроизводить
реальное поведение систем более крупных масштабов. В частности,
такой подход позволяет управлять и исследовать достаточно
подробно асимптотическое развитие флуктуации. По своему духу
этот подход аналогичен другим стохастическим моделям, о
которых сообщалось в других докладах на данной конференции, и
предназначен для описания систем, в структуре которых
доминируют полностью развитые флуктуации. Сошлемся, в
частности, на перколяцию [12], пробой диэлектриков [13], рост ден-
дритов [14], кластер-кластерную агрегацию [15] и т. д. По
аналогии с этими явлениями мы рассмотрим возможность того, что
масштабно-инвариантные флуктуации могут спонтанно
порождаться каким-нибудь конкретным механизмом. Мы
намереваемся показать, что простая модель, воспроизводящая влияние
динамического трения [15] на процесс агрегации, обладает
следующим свойством: однородное случайное начальное
распределение спонтанно эволюционирует в фрактальное распределение
(без учета расширения). Новая картина, проистекающая из
этого результата, кратко обсуждается в п. 4.
2. Простые модели агрегации
Рассмотрим эволюцию в рамках простых моделей агрегации,
берущую начало от случайных распределений, аналогичных
распределению, изображенному на рис. 1.
Все результаты, о которых пойдет речь в настоящей работе,
относятся к двумерной решетке с периодическими граничными
условиями, но большинство из них подтверждается более
реалистической динамикой без решетки [16]. В начальный момент N
частиц (как правило, N ~ 1000) равной массы случайное
распределены по решетке (рис. 1). Для каждой частицы выбрано
случайное направление, в котором она будет двигаться. Все
частицы передвигаются по своим прямолинейным траекториям
дискретными шагами. При столкновении двух частиц они с
вероятностью ра необратимо соединяются и с вероятностью 1 — ра
претерпевают рассеяние. После столкновения вылетающая
частица с удвоенной массой или две исходные частицы движутся,
вообще говоря, по новым случайным направлениям. Такая
модель напоминает модели кластер-кластерной агрегации [4, 5],
но отличается от последних в двух важных отношениях. 1)
Частицы между двумя последовательными столкновениями
движутся по прямолинейным траекториям ( а не совершают
случайные блуждания); изменение направления может происходить
Кинетика образования кластеров
457
только после столкновения с другой частицей. Это устанавливает
определенную связь между пространственным распределением
и динамическими свойствами, которой нет в моделях кластер-
кластерной агрегации. 2) Мы пренебрегаем нутренной структу-
■ •• •• ... . • • • •
Рис. 1. Пример случайного распределения 750 точек на двумерной решетке
(50X50). Выбираемые нами начальные конфигурации всегда принадлежат
к таким случайным конфигурациям.
рой отдельных кластеров, рассматривая их как точки и
принимая во внимание только их глобальное распределение в
пространстве.
Гравитация моделируется только с помощью вероятности
агрегации раУ которая сделана зависящей от масс налетающих
частиц. Как правило, мы использовали функции вида
■(Af,Af;)e
(3)
с показателем а, выбираемым в пределах от 0 до 2. В качестве
грубого приближения к закону сохранения импульса,
обусловленного случайностью скоростей, вводилось правило: частицы,
начиная с определенной массы, просто останавливаются. В
численных экспериментах, о которых говорится в настоящем докладе,
мы останавливали все частицы, массы которых втрое
превосходили начальную массу. Рассмотренный нами класс моделей
порождает распределения такого типа, который изображен на
рис. 2, с агрегацией начальных частиц в более крупные, но без
настоящей кластеризации. Анализ корреляционной функции для
распределения на рис. 2 показывает, что в действительности эта
458
Часть VI
система однородна, начиная с некоторого масштаба, и поэтому
не является фракталом. Обусловлена такая однородность тем,
что большая масса возникает в определенной точке независимо
Р~- « ^0 '•
Г . • • . о
L • е • • •
'
1 •
ф в •.
0
* о
в ©
1 0
ь ' е
Т © в
е 'в
• ' о
е
о
1 .е- •'« : °
-& - - е—* (
О в •
*о • • •
•
0 • • 1
0 # |
о
0 * j
© • .
« ©
'.©••
е
ее> ' :
в •
в
е 8'
Рис. 2. Типичное конечное распределение для класса моделей, описанных
в разд. 2. Радиус частиц соответствует их массе. В такого рода
распределении не возникает иерархической кластеризации. Оно приводит к
равномерному распределению по всем крупным масштабам.
от окружения последней. В следующем разделе мы опишем
механизм, создающий зависимость массы от окружения.
3. Влияние обмена энергией на кластеризацию
Рассмотрим две точечные массы, сближающиеся с большого
расстояния под действием классического распределения. Если
не существует канала для рассеяния кинетической энергии, то
эти две частицы не могут образовать связанное состояние.
В большинстве случаев диссипация энергии обусловлена
короткодействующим рассеянием частиц на других частицах. В
космических масштабах сечение короткодействующих столкновений
двух тел может быть чрезвычайно мало, и другой механизм
становится более важным. Термализация орбит звезд в галактике
обусловлена не столько двухтельными столкновениями, сколько
флуктуациями гравитационного поля [17]. Этот эффект
наводит на мысль о том, что столкновение, происходящее в
окрестности других масс (в точке А на рис. 3), приводит к агрегации
с большей вероятностью, чем столкновение в изолированной
области (в точке В на рис. 3). Объясняется это тем, что столкнр-
Рис. 3. Схема, показывающая, как эффект динамического трения,
обусловленный наличием других масс, влияет на вероятность возникновения связанного
состояния. Столкновение В происходит в пустой области пространства.
Напротив, столкновение Л, происходящее в окрестности масс М2 и Мз,
сопровождается диссипацией энергии и с большей вероятностью приводит к
образованию связанного состояния.
^—
О
1 *
1 • 0
ф effl ф
L° о *
Г© •
1 а °
U® в©
Р
О О
1 «
д о
о
.
о
•
о
ч©
^ го •
*>.
О 0
_<л>
•
•
о
0
в
О
о ©
в
\ ' в
0
о
о
9 |
©
т
о
о
°о
О
©1
О 1
О
т
Рис. 4. Типичное конечное распределение для стохастической модели с учетом
описанного в разд. 3 эффекта динамического трения. Наблюдается
кластеризация во всех масштабах и развитие больших пустот. Такое распределение
действительно фрактально.
460
Часть VI
вение в точке А с большей вероятностью сопровождается
рассеянием энергий, чем столкновение в точке В. Это
предположение соответствует приписыванию большей вероятности слиянию
частиц, когда оно происходит в населенной области.
Предположение допускает проверку с помощью детального исследования
процесса слияния в различных конфигурациях. Чтобы учесть
2,50 |
2,00 К
!
1,50
1,00
14--... Лг *- А- —|
A A A A AJ
I 1 1 1 I I I l i I
Время
Рис. 5. Фрактальная размерность D на различных временах в модели с
динамическим трением, приводящая к конечному распределению, показанному
на рис. 4. Фрактальная размерность получается из анализа
корреляционной функции плотности (соотношение (1)).
этот эффект в нашей модели, мы вводим для каждой массы Mi,
находящейся в точке Г/, функцию fifflt, г*)» задающую
количественную меру влияния массы Mi на вероятность слияния. Так
как имеются данные [18], свидетельствующие о локальном
характере эффектов подобной природы, мы можем использовать
резко спадающие функции, например схематически
изображенную на рис. 3 ступенчатую функцию или экспоненциальные
функции типа
Мг)=Лехр{—[1ц^У (4)
Суммарное влияние конкретного распределения масс задается в
этом случае функцией /7(г)= X ft (г). Не располагая подробной
теорией этого эффекта, мы связываем функцию F(r) с
вероятностью агрегации степенным законом
Pa{r)~[F(r)f.
Ясно, что наличие других масс влияет на вероятность
возникновения новой большой массы в данной точке. Наша новая модель
приводит к распределениям, аналогичным изображенному на
рис. 4, с различными комбинациями параметров р и у. Обычно
Кинетика образования кластеров
461
мы использовали р = 1/2 и 1 и 6 = 1, 2 и 3; остальные
подробности будут опубликованы в другой работе [19]. Распределение
на рис. 4 свидетельствует о развитии кластеризации во всех
масштабах и наличии больших пустот. Анализ его в терминах
корреляционной функции плотности С (г) показывает спонтанное
развитие фрактального распределения из однородного
начального распределения. Фрактальная размерность D как функция
времени показана на рис. 5. Асимптотическое значение D
зависит от конкретных предположений, заложенных в модель.
Итак, мы установили динамический процесс, способный
спонтанно порождать фрактальное распределение из однородного без
расширения системы. Разумно ожидать, что учет расширения не
изменит качественные особенности такого поведения. Это
показывает, что расширение отнюдь не обязательно является
существенным признаком развития фрактального распределения.
4. Выводы
Итак, мы перечислили результаты, к которым приводят
стохастические модели. Их можно описать следующим образом. Мы
начинаем с плотной однородной системы в соответствии с
изотропностью космического фонового излучения (Т = ЗК). Из-за
высокой плотности двухтельное рассеяние является основным
механизмом энергетических потерь, и агрегация развивается
однородно, как на рис. 2. Позднее из-за расширения и агрегации
сечение двухтельного рассеяния сильно понижается, и
доминирующим механизмом энергетических потерь становится обмен
энергией через гравитационные флуктуации. В этом режиме в
системе возникают существенные неоднородности и спонтанно
переходят в фрактальное распределение, как на рис. 4, без
каких бы то ни было начальных флуктуации специального типа.
Эта новая картина позволяет в принципе решить ряд проблем,
давно стоявших в затронутой области [6—8, 11], но, разумеется,
для того чтобы окончательно принять или отвергнуть ее,
необходима еще дополнительная работа.
ЛИТЕРАТУРА
1. de Vaucouleurs G., Science, 167, 1203 (1970).
2. Луккин Ф. — наст, сб., с. 446.
3. Mandelbrot В., The Fractal Geometry of Nature, W. H. Freeman & Co.,
New York, 1983.
4. Ziff R. AT, in: Kinetics of Aggregation and Gelation, eds. F. Family,
P. Landau, Elsevier Publisher, 1984, p. 191.
5. Боте Р. и др. — наст, сб., с. 353.
6. Peebles P. /. £., The Large-Scale Structure of the Universe, Princeton
Univ. Press, 1980. .
7. Davis M.. Peebles P. J. £., Astrophys. J., 267, 465 (1983).
462
Часть VI
8. Bouchet F. R., Pellat R., Astron. Astrophys., 141, 77 (1984).
9. Efstathiou G., Eastwood J. M.y Mon. Not. R. Astr. Soc, 194, 503 (1981).
10. Frenk С S.t White S. D. M.t Davis M.9 Astrophys. J., 271, 417 (1983);
Barnes /., Dekel A, Efstathiou G., Frenk C. S.t Astrophys. J., 295, 368
(1985); Davis Л1, Efstathiou G., Frenk C. S.t White S. D. M.y Astrophys.
J., 292, 371 (1985).
11. The Very Early Universe, eds. G. W. Gibbons, S. W. Hawking, S.T.C. Sik-
los, Cambridge Univ. Press, 1983.
12. См., например, работы X. Стенли и А. Конильо в наст. сб.
13. Висман Г.у Пьетронеро Л. — наст, сб., с. 210.
14. См., например, Микин П. —наст, сб., с. 283.
15. Chandrasechar S., Principles of Stellar Dynamics, Univ. of Chicago Press,
1947.
16. Taraglio S., thesis, Univ. of Rome, 1985.
17. Tremaine S., in: The Structure and Evolution of Normal Galaxies,
eds. S. M. Fall, D. Lynden-Bell, Cambridge Univ. Press, 1980, p. 67.
18. Tremaine S.t Weinberg M. D.t Mon. Not. R. Astr. Soc, 209, 729 (1984).
19. Pietronero L.t Kupers R.f будет опубликовано.
Часть VII
ДИНАМИЧЕСКИЕ СВОЙСТВА
ФРАКТАЛЬНЫХ СТРУКТУР
Фрактальные поверхности
и модель «термита»
для двухкомпоиентных случайных материалов
X. Стенли *
Этот доклад представляет собой простой рассказ, начинающийся с
обзора задачи о случайной смеси. Мы описали новый подход к
этой задаче — моделирование ее с помощью случайного блуждания
с двумя масштабами времени, соответствующими движению в
областях с хорошей и плохой проводимостью. Предельный случай,
в котором отношение этих масштабов расходится, соответствует
случайной сверхпроводящей сетке: в этом случае один компонент
является сверхпроводящим, а другой — нормальным (де Жен
называет этот случай моделью „термита", поскольку движение
совершающей случайные блуждания частицы напоминают движение
термита). В заключение мы кратко обсудили недавно
обнаруженный факт, заключающийся в том, что для описания поверхности
кластеров, образовавшихся при диффузионно-ограниченной
агрегации, требуется бесконечная иерархия скейлинговых показателей.
Вначале отмечу, что результаты, о которых пойдет речь,
получены при реализации двух исследовательских проектов.
Первый из них—модель «термита» для электропроводности
двухкомпоиентных случайных материалов — разрабатывался в
сотрудничестве с А. Бунде, А. Конильо и Д. Хонгом (детали см.
в работах [5, 6, 13]). Исследования в этом направлении
показали, что для описания физических процессов, лежащих в основе
электропроводности, необходимо учитывать различия между
экранированными участками («впадинами») и неэкранированными
участками («выступами») на поверхности кластеров. Эта идея
привела к возникновению второго направления исследований —
исследованиям фрактальных поверхностей, проводившимися в
соавторстве с А. Конильо, П. Микином и Т. Виттеном
(подробно— в работах [6, 18, 19]). Чрезвычайно полезными были для
нас контакты с Ж. Адлер, А. Аарони, Ш. Александером, П.-Ж.
де Женом, Ф. Леивра и Д. Штауффером. Мы благодарим ONR
и Национальный научно-исследовательский фонд за
финансовую поддержку.
* // Eugene Stanley-Center for Polymer Studies and Department of
Physics, Boston University, Boston, Massachusetts 02215, U$A.
464
Часть VII
Задача о термите
Как изменяются фундаментальные законы диффузии и
переноса, если рассматривается среда, представляющая собой
случайную смесь компонентов Л и В, в которой имеются хорошо
и плохо проводящие участки? В последнее время особое
внимание привлекали два предельных случая этой задачи:
1) случайная сетка резисторов (ССР), или предел
«муравья». В этом сучае предполагается, что участки, занятые
плохим проводником В, имеют нулевую проводимость;
2) случайная сверхпроводящая сетка (ССС), или предел
«термита». В этом случае проводимость хорошего проводника А
бесконечна.
Происхождение терминов «муравей» и «термит» таково.
Задача о проводимости с помощью соотношения Нернста —
Эйнштейна может быть сведена к задаче о диффузии. В пределе ССР
диффузия в областях с нулевой проводимостью невозможна.
Поведение частицы, совершающей диффузионное движение при
наличии геометрических ограничений, действительно напоминает
поведение муравья в лабиринте [8]. В предельном случае ССС
геометрические ограничения отсутствуют, и частица совершает
свое движение во всем пространстве, однако диффузия в
областях, занятых проводником типа А с бесконечной
проводимостью, имеет совершенно необычный характер. Для этого
весьма тонкого явления де Жен [9] несколько лет назад придумал
название «диффузия термита». В отличие от хорошо изученной
задачи о муравье для этого случая на сегодня у нас нет четких
утверждений о том, как можно описать и измерить это явление.
В настоящее время мы наблюдаем рост интереса к таким
задачам, и этому есть несколько причин.
1. Первая причина состоит в том, что многие
экспериментальные системы являются случайными и неоднородными.
Например, горные породы состоят из зерен, имеющих различную
теплопроводность, электропроводность, проницаемость для
влаги. Если такие неоднородные материалы являются к тому же
неупорядоченными, то для описания образованной ими системы
естественно использовать модель с узельным беспорядком —
модель решеточного газа. Вначале мы вводим огрубленное
решеточное описание материала, затем присваиваем каждой клетке
проводимость, принимающую одно из двух значений — о„ и <ть.
Результаты вычислений, основанных на таком прямом подходе,
сравнивались с иелым рядом экспериментов. Это и
эксперименты по проводимости тонких пленок свинпа на изоляционной
подложке (этот случай грубо описывается ппелепом CCPV и
эксперименты по проводимости систем, полуденных пли вакуумном
напылении сверхпроводника на подложку из нормального ме*
Динамические свойства структур
465
талла (что грубо описывается пределом ССС), и исследование
смесей ионных проводников с дисперсной диэлектрической
фазой, для описания которых нужны оба предельных случая.
2. Вторая причина, вероятно, близка к причине того, почему
всегда был велик интерес к модели Изинга: это чрезвычайно
простая модель, схватывающая основные черты реальных
физических систем. Аналог модели Изинга для
случайно-неоднородных материалов — это смесь узлов (или связей), случайно
распределенных на решетке. Для простоты предполагается, что
узлы (или связи) имеют одно из двух возможных значений
проводимости:
f aa с вероятностью р,
{ аь с вероятностью I — р.
Мы примем соглашение, в соответствии с которым аа > <т&, так
что отношение h = вь/ва всегда меньше единицы.
Если речь идет о магнитной задаче, то в ней обычно хотят
узнать макроскопическую намагниченность изинговского
ферромагнетика, состоящего из элементов спинов, микроскопическое
состояние каждого из которых описывается принимающей два
значения переменной. Точно так же теперь мы интересуемся
макроскопической проводимостью, зависящей от всех
возможных конфигураций микроскопических элементов (проводников),
проводимость которых и в этом случае является величиной,
принимающей два значения (аа и а&). Точно так же, как
намагниченность связана с магнитным полем Я, проводимость связана
с полем h.
Обсудим теперь упомянутые выше предельные случаи более
подробно, а) В пределе ССР большая проводимость полагается
равной единице, меньшая — равной нулю. При приближении
концентрации компонента А к порогу протекания vc сверху,
макроскопическая проводимость стремится к нулю, ее поведение
описывается критическим показателем jut:
2~(Р-Р<Г. (2а)
б) В пределе ССС меньшая проводимость равна единице, а
большая проводимость бесконечна. При приближении к перко-
ляционному порогу снизу проводимость стремится к
бесконечности по закону
2~(Рс-рГ8. (26)
Традиционный подход к случаю ССР заключается в замене
системы уравнений Кирхгофа эквивалентной задачей о
диффузии. Как уже говорилось, макроскопическая проводимость
связана с коэффициентом диффузии D соотношением Нернста —
466
Часть VII
Эйнштейна
2~nD, (3)
где п — плотность носителей заряда.
Рассмотрим движение путешественника, совершающего
случайные блуждания по решетке, на которой имеются связи двух
видов — Л и В. Ограничимся рассмотрением только одномерного
случая (случай произвольных d см. в работе [13]). У
путешественника имеются две монеты, нормальная и «взвешенная» (о
свойствах которой мы поговорим позже), и часы. Без потери
общности мы можем считать, что начальная точка путешествия
выбрана внутри области А с более высокой проводимостью.
С каждым тиканьем часов путешественник бросает монету и
движется вправо или влево в зависимости от исхода бросания.
Когда путешественник попадает на узел, лежащий на границе
областей Л и В, он бросает другую монету, «взвешенную» так,
что вероятность остаться в области А оказывается равной
Р« = Ш« + Ь)=1/(1+А), (4)
а вероятность перейти в область В равна
Pb = fb/(fa + fb) = h/(l+h). (5)
Если путешественник уходит из области Л, он замедляет шаги
в fa/fb = h~l раз. Например, если проводимость области В в
10 раз меньше, чем в области Л, то fb в 10 раз меньше, чем
fa(h = 0,1), и путешественник делает свой новый шаг только
после того, как часы протикают 10 раз.
Предельные случаи нашей модели случайных блужданий
следующие:
1) й=1. В этом случае нет ни различия между областями,
ни отражения на границе (Ра = Рь), ни различия в скорости
шагов внутри и вне кластеров Л.
2) h<^l. Если путешественник находится в области Л, он
делает 1 шаг, пока часы протикают 1 раз, а подойдя к границе
областей, почти всегда поворачивает назад. Изредка он
выходит из области Л и попадает в область Ву где его шаги очень
сильно замедляются: 1 шаг совершается только после того, как
часы протикают /Н раз. Статистически за очень большое время
путешественник сделает 0(fa) шагов в областях Л и 0(fb)
шагов в областях В.
Предположим, что мы сняли фильм о движении
путешественника. Просматривая его, мы увидим, что путешественник
отражается от границ почти при каждой встрече с ними и только
очень редко — примерно один раз за /Н встреч — выходит из
кластера [13]. Когда это случается, его движение замедляется
в h раз. Цели мы будем смотреть наш фильм дальше, у нас мо-
Динамические свойства структур
467
жет не хватить терпения наблюдать за движением
путешественника в области Б, и мы ускорим движение ленты при показе в
\/h раз. Теперь попавший в область В путешественник будет
делать один шаг в единицу времени, и наше нетерпение не будет
мешать наблюдению за ним. Однако, когда он, наконец,
доберется до кластера А и проникнет в него (что произойдет с большой
вероятностью 1/(1+ й)), его движение в этом кластере также
будет ускорено в 1/h раз. Таким образом, движение, вначале
нормальное на кластере А и очень медленное на кластере В,
превратится в движение термита, который движется с
нормальной скоростью в кластере В и очень быстро на кластерах А.
Действительно, единственная разница между двумя случаями —
муравья и термита (ССР и ССС)—заключается в различном
выборе временного масштаба. Это простое наблюдение может
быть формализовано в терминах некоторого строгого
преобразования [13]. Такое преобразование в свою очередь составляет
базис для формулировки скейлинговых законов для обоих
пределов в общем случае двухкомпонентной смеси.
Таким образом, исследование двухкомпонентной случайной
смеси требует понимания того, как надо обращаться с
диффузионным процессом с двумя, а не одним, как обычно,
характерными масштабами времени. Этот вопрос ранее не исследовался
и во многих аспектах является весьма тонким. Вплоть до
недавнего времени предполагалось, что физика, определяющая
перенос в ССС, или в пределе термита, существенно отличается от
той, что управляется поведением транспортных свойств в
пределе муравья (ССР). Теперь мы понимаем, что эти две области
связаны простым изменением временного масштаба [13] (см.
также [1,5, 16, 33]).
Поверхности, границы раздела и экранировка
фрактальных структур
Следующая часть нашего рассказа посвящена тонкому и
чрезвычайно занимательному вопросу о случайных
поверхностях. Что мы понимаем под поверхностью фрактального
объекта? Мы увидим, что на самом деле имеется множество
различных определений этой поверхности. Выбор подходящего
определения зависит от того, какой именно физический процесс нас
интересует (рис. 1). Мы обсудим эти понятия приблизительно в
том порядке, в каком возрастает их утонченность.
Внешний периметр {«кожура»): dn> Полное число узлов,
принадлежащих внешней поверхности, или «кожуре», кластера
растет с ростом его максимального размера или радиуса инерции
468
Часть VII
L как
Nh~Ldh [фрактальная размерность № 1]. (6)
Для перколяционных кластеров при rf==2 ^ оказывается
примерно равно 1,74 ±0,02 [30], что явилось основой для
предположения, что
dh=l + dr = 7/4, (7)
так как в двумерном случае dr = 1/v = 3/4 (точно), где dr —
размерность множества красных связей, о которых см. ниже.
Полный периметр: df. Мы знаем, что полное число узлов
периметра Np ведет себя так же, как и полное число узлов в
кластере [14]:
Np~ Nf~ Ldf [фрактальная размерность № 2], (8)
где для d = 2 df = 91/48 = 1,896. Тот факт, что dh < df
означает, что отношение числа узлов внешнего периметра к полному
Внешний периметр, или „кожура."
{океанское побережье)
Иеэкранированныи
' периметр
Узлы
роста.
Внутренний периметр
(побережья озер)
Частица, совершающая
блуждания
Рис. 1. На этом рисунке показаны четыре различных вида фрактальных
поверхностей, возникающих при описании перколяционных кластеров: а —
внешний «океанский» периметр, или «кожура». Фрактальная размерность этого
периметра равна йк\ б — полный периметр. Его размерность df равна
фрактальной размерности всего кластера. Поскольку dh<df, внутренний
периметр («побережья озер») имеет ту же размерность, что и полный периметр;
в -— иеэкранированныи периметр (области, где велика вероятность
столкновения блуждающей частицы с границей кластера) показан штриховой линией.
Размерность этого множества равна du\ г — узлы роста. Это те узлы
периметра, которые образуют «живую» границу кластера. Фрактальная
размерность их множества равна de\ конкретный вид фрактала, образованного этими
узлами, зависит от механизма роста (см., например, [3, 4, 12, 30]).
числу узлов периметра у больших кластеров на пороге
протекания стремится к нулю. С ростом кластеров их внутренний
периметр («побережья озер») составляет все большую и большую
по сравнению с внешним периметром («океанским побережьем»)
Динамические свойства структур
460
величину. При компьютерном моделировании конечной системы
в пространстве с размерностью большей двух узлы внутреннего
периметра встречаются реже: чтобы полностью окружить
трехмерное озеро, требуется слишком много узлов. Вопрос о
значении dh при d>2 остается открытым. Может быть, dh = dft
Требуется работа, чтобы проверить эту возможность.
Неэкранированный периметр: du- Понятие неэкранированного
периметра было введено Конильо и Стенли [6], чтобы описать
ту часть кожуры кластера, которая эффективна с точки зрения
движения термита:
Nu ~ Ь*и [фрактальная размерность № 3]. (9)
Они показали, что критический показатель проводимости ССС
просто связан с du. Рассматривая, как преобразуется
соотношение Нернста — Эйнштейна при преобразовании масштаба, мы
получим
2~ЯМ/?класт)2т-1. (Юа)
Частота перескоков х-1 меняется при этом как доля узлов
кластера, принадлежащая неэкранированному периметру,
%-*~(NjNt). (106)
Подставляя в это выражение формулу Штауффера для
среднего радиуса конечных кластеров, Якласт, получим
2 ~ L2-(d-df)Ld"-di. (11)
Поскольку Е ~ е-*, где s = \р — рс|, имеем
5 = s/v = du — (d — 2). (12)
Проводимость между двумя точками ведет себя в зависимости
от расстояния между ними как L-CCG, где |ссс = s + (d — 2). Из
(12) получаем чрезвычайно простой результат: критический
показатель проводимости в этом случае в точности равен
фрактальной размерности неэкранированного периметра
lccc = du. (13)
Случай ССР соответствует совершенно иному поведению, здесь
мы тоже можем сопоставить критический показатель
проводимости с некоторой фрактальной размерностью. Соотношение
Эйнштейна (3) справедливо и в этом случае, но теперь мы должны
положить п = Роо, т. е. концентрация носителей заряда равна
вероятности того, что случайно брошенный в лабиринт муравей
попадет на бесконечный кластер. Поведение Р<х> определяется
470
Часть VII
коразмерностью (d— df), а коэффициент диффузии ведет себя
как (Ь2/время). Следовательно,
2 = P0OD~L*r*L2-rf» (14)
[2, 10]. Вспоминая, что в пределе ССР 2 ~ е*\ получаем
д = ф = (d - 2) + (dw - df). (15)
Проводимость между двумя точками зависит от расстояния
между ними как LSccp, где £сср = и — (d — 2). Таким образом, для
задачи о ССР выражение (13) заменяется на
Sccp = dw-df. (16)
О сопротивлении между двумя точками удобно думать как о
«массе» резисторов сопротивлением в 1 Ом каждый, включенных
ч ) сетки
< ^сопротивлении
Синие V4
связи —\ S
(блобы) \/
а) ССР б) ССС
Рис. 2. Схематическая иллюстрация основных черт структуры кластеров в
двух предельных случаях описания проводимости двухкомпонентных смесей:
а — случайная сетка резисторов; б — случайная сверхпроводящая сетка.
Согласно [6].
последовательно между этими точками. В этом случае мы
можем рассматривать fccp как нормальную фрактальную
размерность некоторого фрактального объекта (множества
резисторов):
NR~LdR [фрактальная размерность № 4]. (17)
Из (13) и (16) получаем для этой величины
( - du (ССС),
**-U.-rf,(CCP). (I8)
Из (18) видно, что в обоих случаях показатель сопротивления
просто выражается через фрактальные характеристики среды.
Выражения эти, однако, совершенно различны, поскольку
совершенно различны механизмы переноса (рис. 2). Из рис. 2, а мы
видим, что перенос в ССР определяется структурой типа рыбац-
Динамические свойства структур
471
кой сети, размер ячейки которой порядка длины связности
(корреляционной длины) |. Нити сети сделаны из недублированных
(«красных») и дублированных («синих») связей, статистические
свойства которых мы вкратце обсудим позже. Из рис. 2, б мы
видим, что в случае ССС при концентрации чуть ниже рс
перенос от одной шины к другой определяется движением носителей
заряда от одного кластера к другому, точнее, от неэкранирован-
ного периметра одного кластера к неэкранированеому периметру
другого. Кластеры в пределе ССС играют, таким образом, ту же
роль, что узлы сети в пределе ССР. В задаче о ССР вблизи рс
критическими связями являются красные (наиболее горячие)
связи. В задаче же о ССС критическими являются те связи
решетки, включение которых соединяет два кластера. Я всегда
называл их розовыми: это зарождающиеся красные связи; будучи
включенными, они становятся красными. Штауффер недавно
назвал их антикрасными, поскольку в некотором смысле они
дополнительны по отношению к красным связям. Красные связи
определяют физику задачи о ССР при концентрации чуть выше
Рс, в то время как антикрасные связи определяют поведение
ССС при концентрации чуть ниже критической. В
неопубликованной работе Конильо показал, что множество этих связей
имеет ту же размерность, что и множество красных связей:
rfe_r = l/v. (19)
Между пределами ССР и ССС имеется, таким образом,
некоторая симметрия, которая следует из упомянутых выше теорем.
Работа в этом направлении только начинается, и, возможно, кто-
то из присутствующих на нашей встрече поможет достичь
прогресса в этом направлении.
Можно ли вычислить фрактальные размерности du и dw,
появляющиеся в (2), зная фрактальную размерность среды dr?
В разрешении этого вопроса было достигнуто определенное
продвижение, однако используемые аргументы основаны на
некоторых дополнительных предположениях. В настоящем разделе мы
рассмотрим аргумент в пользу того, что
dtt = (df-l) + (d-df)/dw, (20)
основанный на приближении среднего поля [6].
Нам необходимо было разработать метод исследования
фрактальных объектов. Использованный нами метод [18]
заключался в следующем. В систему по одной выпускались случайно
блуждающие частицы. Как только частица достигала
периметрического узла £, показание счетчика на этом узле увеличивалось
на единицу (было ЛГ/, стало N, 4 1). Статистика набиралась по
блужданиям примерно миллиона частиц. Наш анализ
основывался на предположении о том, что большая часть частиц по-
472
Часть VII
глощается весьма малой частью полного периметра. Чтобы
проанализировать функцию распределения Nt (i= 1, 2, ..., Р, где
Р — полное число узлов периметра), мы рассмотрели моменты
ji/, определяемые соотношением
\\4\'=Y^H=YWr^N,fX (21)
i i
Здесь
NT^Y,Ni (22)
i
есть полное число блуждающих частиц, а
Pi = NJNT (23)
— вероятность того, что частица попадет на узел и В силу (22)
Pi нормирована на единицу. Вначале мы вычислили у}- для / =
= 1 — 3 и обнаружили, что полученное в приближении среднего
0,50
Уз
0,45
~'г~0 0,1 0,Z 0,3 0,4 0,5
r/j
Рис. 3. Показатели Y/» характеризующие поведение моментов распределения
Pi. Pi (основная величина, характеризующая рост поверхности) есть
вероятность того, что узел i — это следующий узел, который будет присоединен
к кластеру. Чтобы показать, что иерархия, или спектр, показателей сходится
при / = оо к ожидаемому пределу 1 — 1/ф, мы изобразили на графике
значения показателей у}- в зависимости от 1//. Из работы [19].
поля соотношение (20) выполняется в пределах точности наших
вычислений. Мы заметили также систематическую зависимость
7/ от /, и для того, чтобы понять, может ли у/ зависеть от /,
продолжили наши вычисления вплоть до / = 8. Поведение, намек
на которое мы увидели при /= 1 —3, проявилось яснее (рис. 3).
Мы пришли к выводу, что речь идет не об одном показателе, а о
целой иерархии показателей [18, 19]. Этот результат был
подтвержден Халси и др. [11].
Почему же несправедливо соотношение Конильо — Стенли?
По-видимому, дело в том, что оно соответствует допущению о
том, что граница, или «активная зона», кластера
рассматривается как некий опоясывающий кластер обруч, и затем
предполагается, что вероятность захвата частицы любым из узлов этого
Динамические, свойства структур
473
обруча одинакова. В действительности же узлы периметра
имеют непрерывный ряд «температур»: выступающие части
кластера являются очень горячими, во впадинах же чрезвычайно
холодно. Ситуация напоминает рассмотренную де Архангелисом
и др. [7] задачу об определении N(V)—распределении числа
связей скелета, падение напряжения на которых равно V. Здесь
тоже имеется плавная градация температур — от наиболее
горячих красных связей, на которые приходится почти все
падающее на кластере напряжение, до очень холодных связей,
принадлежащих большим петлям, включающим блобы.
Обнаружение бесконечной иерархии критических
показателей— как в задаче о распределении напряжений в скелете пер-
коляционного кластера, так и в задачах о ДОА (диффузионно-
ограниченной агрегации) — вызвало большое удивление,
поскольку обычно считается, что для описания критического
объекта достаточно всего двух показателей. Например, выше мы
отметили, что показателей yh(=df) и ут{=с1г) достаточно для
описания перколяции. Однако, если мы «что-то делаем» с
фракталом — подключаем его к батарее или населяем блуждающими
частицами, — мы фактически вводим на нем некую новую меру.
Вес, приписываемый каждому узлу, уже не равен просто
единице, а зависит от того, что мы делаем с фракталом (например,
каждому узлу соответствует напряжение на нем или то число
раз, которое на него попала частица). Несколько групп (Ми-
кин, Стенли, Конильо и Виттен (не опубликовано), Туркевич и
Шер [31], Халси и др. [11]) пытаются разобраться с тем, что
представляет собой эта новая мера и что мы можем узнать, зная
эту бесконечную иерархию показателей.
Оглядываясь назад, мы понимаем, что с самого начала могли
предвидеть появление такой иерархии показателей. Дело в том,
что для двух предельных значений /, / == — 1 и j = оо показатели
отличаются более чем в 2 раза: у(—1) = 1 и y(°°) = * — 1/Ф-
Первый результат следует из того, что при ДОА полная
поверхность масштабируется с тем же показателем df, что и полная
масса. Второй следует из недавно доказанной теоремы [15] о
том, что Рмакс (максимальное значение Р£) масштабируется в
зависимости от массы кластера с показателем 1 — 1/df. Это
предсказание подтверждается нашими расчетами для / = 1 — 8.
Наша иерархия, или спектр, фрактальных размерностей
поверхности сходится к числу, весьма близкому к предсказанному
значению 1 — l/df (см. рис. 3).
Рост фракталов
Как можно охарактеризовать рост фрактальных систем?
Этому вопросу мы посвятим последнюю часть доклада.
Необходимо сразу же отметить очевидный факт: различные механиз-
474
Часть VII
мы роста иногда приводят к появлению одинаковых
фрактальных объектов (см., например, обсуждение в работе [3]).
Сейчас мы рассмотрим простейший кинетический механизм роста,
связанный с муравьем. Вместо того чтобы пускать муравья по
заранее приготовленной фрактальной структуре, как мы это
делали раньше, мы можем бросить его на евклидову решетку,
снабдив набором правил, по которым он, двигаясь на решетке,
будет создавать фрактал. Во-первых, если движение происходит
на квадратной решетке, мы должны дать ему четырехгранную
игральную кость. Во-вторых, нужен какой-то динамический
механизм, с помощью которого создавался бы окончательный
фрактал. Для того чтобы создать перколяционный фрактал,
например, нужна взвешенная монета, для того чтобы с
вероятностью 1—рс заблокировать каждый рассматриваемый узел.
Механизм движения муравья подробно описан в работе Бунде
и др. [31.
В области пространства, по которой движется муравей,
можно выделить узлы трех типов. Названия этих типов узлов
соответствуют интерпретации общей задачи о росте кластера в
терминах распространения эпидемии. Итак, в системе имеются:
1) уже посещенные (зараженные) узлы, принадлежащие
кластеру;
2) уже посещенные, но заблокированные при бросании
взвешенной монеты узлы (невосприимчивые);
3) еще не посещенные узлы, являющиеся соседями
посещенных (узлы роста).
С точки зрения муравья узлы роста обладают той
особенностью, что только их наличие позволяет расширить доступную
территорию.
Чем интересны узлы роста? Субъективно, тем, что они
образуют «открытую границу» фрактала [20]. Объективно, это
множество несвязанных узлов имеет хорошо определенную
фрактальную размерность dg, означающую, что число, или масса,
узлов роста подчиняется скейлинговому соотношению
Ng~Lds [фрактальная размерность №25]. (24а)
Здесь, как и раньше, L — это диаметр кластера или его радиус
инерции. Можно определить число узлов роста как функцию
массы кластера Nf. Для внутреннего показателя х,
определяющего связь этих величин, Ng ~ N*, имеем
х = djdf. (246)
Стенли и др. [30] получили первые оценки для х: в двумерной
задаче х = 0,49.
Оценим dg, используя два известных предположения
относительно связи между dw и df. Выше мы уже упоминали гипотезу
Динамические свойства структур
475
Александера — Орбаха (АО) о том, что dw = {3/2)dfi и
предположение Аарони и Штауффера (АШ), что dw = 1 + df.
Используя эти предположения, имеем
( df/2 = 91/96 = 0,9479 (АО),
d* ~ \df - 1 = 43/48 = 0,8958 (АШ). (25а)
Для внутреннего показателя х тогда получаем
_( 1/2 = 0,5000 (АО),
Х — \ 1 - Щ = 0,4725 (АШ). (2Щ
Мы видим, что вычисленное значение х лежит между
значениями, предсказываемыми с помощью соотношений АО и АШ.
Леивра и Стенли [17] рассмотрели условие, при котором
соотношение АО могло бы оказаться точным. Важным условием
этого оказалась статистическая независимость вкладов в Ng.
Такая независимость всегда имеет место на дереве Кейли,
поскольку на фрактале без петель корреляции появиться не
могут. Таким образом, был понят тот численный результат, что
гипотеза АО оказывается справедливой для дерева Кейли (dw = 6,
df = 4). Если предположить, что на очень большом кластере —
скажем, размером с Корсику — корреляции между вкладами в
Ng9 несмотря на наличие замкнутых петель, ослабевают и в
асимптотическом пределе эти вклады становятся независимыми,
то распределение Ng будет нормальным, причем x — dg/df будет
равно в точности 1/2, как и предсказывает соотношение
Александера — Орбаха.
Вопрос об узлах роста неоднократно возникал в последнее
время в контексте разных задач. Некоторые из них связаны с
целым семейством моделей распространения эпидемий. Эти
модели соответствуют росту статических перколяционных
кластеров [3, 4, 12]. В зависимости от правил роста динамические
критические показатели dg в этих моделях различны, хотя
статический показатель df одинаков для всех моделей. Одну из таких
моделей мы уже рассмотрели выше. Другая модель является
вариацией только что рассмотренной, с той разницей, что
муравей посещает теперь только узлы роста, никогда не возвращаясь
на уже посещенные узлы кластера. Для этого требуется, чтобы
муравей мог совершать длинные прыжки. В простейшей версии
этой модели муравей выбирает с равной вероятностью один из
всех имеющихся узлов роста и переходит на этот узел.
Численная реализация такой модели требует очень мало времени (по
крайней мере в 100 раз меньше, чем для обычной модели
блуждающего муравья). Полагая р = 1, мы получили бы иденов-
ский кластер с df = d. Если же доля 1 — р всех узлов роста
отравлена (недоступна), наш летающий муравей ведет себя как
476
Часть VII
бабочка, тщательно выбирающая узел, на который она
собирается сесть, и никогда не садящаяся на отравленные узлы.
Типичный кластер при р — рс, полученный таким способом,
показан на рис. 4.
Я должен принести извинения за то, что ограниченность
пространства и времени не позволили мне дать то связное и полное
Рис. 4. Типичный перколяционный кластер, полученный с помощью «бабочки»
в случае, если перескоки на все узлы периметра равновероятны. Эта модель
эквивалентна модели Идена на разбавленной решетке, на которой доля
1 — Рс узлов удалена или «отравлена». Из работы [3].
изложение свойств фрактальных материалов, которое мне
хотелось бы дать. Поскольку ранние работы уже нашли свое
отражение в обзорах [21—29], я решил остановиться на тех идеях,
что появились в самые последние месяцы, поскольку лекция,
отвечающая состоянию науки на момент времени —т, в момент
времени +т уже устаревает.
Динамические свойства структур
477
ЛИТЕРАТУРА
1. Adler /., Aharony A, Stauffer />., J. Phys., A18, L129 (1985).
2. Ben-Avraham D., Havlin 5., /. Phys., A15, L691 (1982).
3. Bunde A., Herrmann Я. /., Margolina A, Stanley Я. E., Phys. Rev. Lett.,
55, 653 (1985).
4. Bunde A., Herrmann H. /., Stanley H. £., J. Phys., A18, L532 (1985).
5. Bunde A., Coniglio A., Hong D. C, Stanley H. £., J. Phys., A18, L137
(1985).
6. Coniglio A., Stanley Я. £., Phys. Rev. Lett., 52, 1068, (1984).
7. de Arcangelis L., Redner S., Coniglio A., Phys. Rev., B31, 4725 (1985).
8. de Gennes P. <?., La Recherche, 7, 919 (1976).
9. de Gennes P. <?., J. Phys. (Paris) Colloq., 41, C3 (1980).
10. Gefen Y., Aharony A., Alexander S., Phys. Rev. Lett., 50, 77 (1983).
11. Halsey Т. С, Meakin P., Procaccia /., Phys. Rev. Lett., 56, 854 (1986).
12. Herrmann H. /., Stanley H. £., Z. Phys., B60, 165 (1985).
13. Hong D. C, Stanley H. £., Coniglio A., Bunde A, Phys. Rev., B33, 4564
(1985).
14. Kunz Я., Souillard В., J. Stat. Phys., 19, 77 (1978).
15. Leyvraz P., J. Phys., A18 (1985).
16. Leyvraz P., Adler /., Aharony A, Bunde A., Coniglio A, Hong D. C,
Stanley H. £., Stauffer D., Preprint for J. Phys. A Lett. (1985).
17. Leyvraz P., Stanley H. E., Hhys. Rev. Lett., 51, 2048 (1983).
18. Meakin P., Stanley H. E., Coniglio A., Witten T. A, Phys. Rev., A32,
2364 (1985).
19. Meakin P., Stanley H. £., Coniglio A, Witten T. A., Preprint, 1985.
20. Rammal R., Toulouse G., J. Phys. Lett. (France), 44, L13 (1983).
21. Stanley H. £., in: Int. Conf. on Disordered Systems and Localisation,
eds. С Castellany, С DiCastro, L. Peliti, Springer Verlag, Heidelberg,
1981.
22. Stanley H. E., in: Proc. NATO Advanced Study Institute on Structural
Elements in Statistical Mechanics and Particle Physics, eds. K. Fredenha-
gen, J. Honerkamp, Plenum Press, New York, 1982.
23. Stanley Я. £., in: Physics as Natural Philosophy: Festschrift in Honor of
Laszlo Tisza, eds. A. Shimony, H. Feshbach, MIT Press, Cambridge, 1982.
24. Stanley H. E.} Prog. Physics (Beijing), 30, 95 (1982) (на китайском
языке).
25. Stanley Я. E.} J. Phys. Soc. Japan Suppl., 52, 151 (1983).
26. Stanley Я. £., in: Kinetics of Aggregation and Gelation eds. F. Family,
D. Landau, North Holland, Amsterdam, 1984.
27. Stanley Я. £., J. Stat. Phys., 36, 843 (1984).
28. Stanley H. E., in: Encyclopedia on Polymer Science, Wiley, New York,
1985.
29. Stanley Я. £., Coniglio A, in: Percolation Structures and Processes, eds.
G. Deutscher, R. Zallen, J. Adler, Adam Hilger, Bristol, 1983.
30. Stanley Я. £., Majid /., Margolina A, Bunde A, Phys. Rev. Lett., 53, 1706
(1984).
31. Turkevich L. A, Scher Я, Phys. Rev. Lett., 55, 1026 (1985).
32. Sapoval В., Rosso M., Gouyet /. F., J. Phys. Lett. (France), 46, L149
(1985),
Динамические свойсства случайных
и неслучайных фракталов
Р. Стинчком *
С помощью скейлинговых методов рассмотрена нормальная и
аномальная критическая динамика случайных и неслучайных
фракталов. Обсуждается поведение характерных частот, динамических
показателей, плотности состояний, спектральной размерности и
линейного отклика в динамике диффузии, колебаний решетки и
спиновых волн в одномерных цепочках, на не случайных фракталах, а
также на случайных фракталах (перколяционных кластерах).
Приведены недавние результаты по анизотропной диффузии на кривой
Серпинского (включая диффузию со сносом); обсуждаются
фрактальные модели, соответствующие блужданиям Леви.
1. Введение
Масштабная инвариантность случайных фракталов [1],
таких, как перколяционная сетка на пороге протекания, и
неслучайных фракталов, таких, как кривые Серпинского [1],
приводит к аномалиям динамических свойств таких систем. Ниже эти
свойства будут рассмотрены с помощью скейлинговых методов
[2], развитых с тех же позиций, что и скейлинговые методы для
обычных критических явлений.
При непрерывных термодинамических фазовых переходах
динамика становится аномальной (критической) из-за того, что
в точке перехода расходится корреляционная длина £.
Расходимость характерной длины и соответствующая аномальная
динамика возникают и в других ситуациях, из которых мне хотелось
бы обратить внимание на следующие:
1) геометрические фазовые переходы, из которых наиболее
известным является перколяционный переход [3] в
разбавленных решеточных системах (например, в разбавленных
магнетиках [4], представляющих собой почти идеальный объект для
экспериментальных исследований);
2) неслучайные фрактальные системы, например кривые
Серпинского, которые интересны как сами по себе, так и в качестве
моделей [5] реальных случайных фракталов, таких как
перколяционная сетка или ее скелет.
Отметим, что рассмотренные подходы могут оказаться
полезными и в других ситуациях, в которых появляется большая
характерная длина, например при исследовании несоизмеримых
систем (получающихся в пределе из периодических решеток со
все большей и большей длиной периода) или для систем (таких,
как некоторые смолы и стекла), имеющих «окно» масштабной
* Robin Stinchcombe- Theoretical Physics Department, 1 Keble Road,
Oxford 0X1, 3NP, UK.
Динамические, свойства структур
479
инвариантности, в котором может обнаружиться аномальная
динамика, связанная с так называемыми фрактонами [6].
Наше обсуждение динамических процессов на случайных и
неслучайных фракталах, упомянутых в пп. «1» и «2», мы
начнем с рассмотрения нормальной и критической (аномальной)
динамики в масштабно-инвариантных системах и связанных с
этим понятий скейлинга и кроссовера (разд. 2). Затем, в разд. 3,
мы дадим простую иллюстрацию пространственного скейлинга,
а в разд. 4 применим скейлинговые методы для исследования
динамики неслучайных фракталов. В следующем разделе (разд. 5)
мы продолжим обсуждение более сложного примера случайных
фракталов, в частности обсудим поведение разбавленных
магнетиков на пороге протекания. Заключительные разделы будут
посвящены изложению последних результатов по двум
специальным вопросам: а) анизотропная диффузия на кривой Серпин-
ского (разд. 6) и б) диффузия во фрактальной модели с
перелетами (разд. 7).
2. Нормальная и аномальная (критическая) динамика
Для того чтобы иметь возможность единым образом описать
сразу три важнейших динамических процесса — диффузию,
спиновые волны и колебания решетки, — мы введем [2] частотную
переменную Q, которая равна ко для диффузии, со для спиновых
волн и со2 для колебаний решетки (со —это обычная частота).
Соотношение между частотой и волновым вектором k в
длинноволновом пределе при этом во всех случаях принимает вид
Q = Dk2. (1)
Этот результат справедлив в том случае, если длина волны
велика по сравнению со всеми остальными характерными длинами
в системе (приближение сплошной среды). Соотношение (1),
конечно, нарушается при расходимости корреляционной длины.
В этом случае, обычном при рассмотрении критических явлений,
можно воспользоваться гипотезой о скейлинге (справедливость
ее обычно подтверждается скейлинговыми методами), которая
в данном случае соответствует зависимости
Q = **/(«), (2)
где z — динамический показатель. Это соотношение справедливо
для любого значения переменной кроссовера k\ при условии
малости каждой из величин k и 1/| по отдельности. Переменная
kl выражает соотношение двух больших длин (£ и длины
волны) и определяет влияние корреляционной длины на
критическое поведение. Необходимо потребовать, чтобы в предельных
случаях соблюдались следующие асимптотические зависимости:
480
Часть VII
1) Q ~ kz при Л|-^оо. Эта зависимость описывает
аномальное (критическое) поведение; для выполнения этого условия
требуется, чтобы функция / стремилась на бесконечности к
конечному пределу.
2) Q ~ k2l2~z при &£-^0. Это нормальное поведение,
описываемое формулой (1). Для его воспроизведения требуется,
чтобы при малых х f(x) ~ x2~z. Коэффициент Ъ2-2 стремится к
нулю при £->оо, поскольку обычно z > 2; это хорошо известное
явление смягчения мод в критической области.
Все эти явления — смягчение мод, кроссовер (переход к
критической области) и аномальная зависимость,
характеризующаяся динамическим показателем г, — имеют место при
геометрическом фазовом переходе. Для фракталов, которые являются
строго самоподобными, всегда имеет место предел аномального
(критического) поведения k\ = оо.
3. Скейлинг в реальном пространстве при исследовании
динамических свойств
Динамические свойства рассмотренных выше систем удобно
исследовать методами, основанными на масштабном
преобразовании. Рекурсивная природа таких методов позволяет
исследовать расходимость длины, ответственной за критические
явления, а также работать с системами (неслучайными
фракталами), само построение которых задается рекурсивной процедурой.
Эти методы непосредственно приводят к скейлинговому
поведению, кроссоверу, результатам для критических показателей
и т. д. Кроме того, если масштабное преобразование делается
в реальном пространстве, как это описано ниже, такие методы
позволяют исследовать динамику неоднородных и случайных
систем, таких, как неслучайные фракталы или перколяционные
сетки.
Проиллюстрируем использование такой техники на
простейшем примере. Возьмем одномерную решетку — цепочку узлов,
разделенных расстоянием а. Пусть Un — динамическая
переменная, соответствующая узлу п, например смещение атома, если
мы рассматриваем задачу о колебаниях решетки. Вводя
частотную переменную й, как это было описано в предыдущем
разделе, мы получим уравнение движения
-QUa = Un+x-2Un + Un+l9 (3)
применимое ко всем трем случаям: диффузии, спиновым волнам
и фононам. Это уравнение было бы проще всего исследовать с
помощью методов, работающих в ^-пространстве, однако такие
методы нельзя обобщить на случай неоднородных систем или
систем, обладающих масштабной инвариантностью, что понадо-
Динамические свойства структур
481
бится нам при исследовании неслучайных и случайных
фракталов. Поэтому мы будем использовать другой подход,
применимый и в таких, более сложных ситуациях. Этот метод
(децимация) основан на исключении, например, каждого второго из
уравнений движения. Вместо (3) мы тогда получаем уравнение того
же вида, но с заменой Un±\ па Un±2 и й на £¥, равную
Q' = 4Q-Q2. (4)
Такова, следовательно, частотная переменная для
преобразованной решетки, постоянная которой теперь равна
а' = 2а (5)
(здесь мы рассматриваем преобразование с масштабным
множителем 6=2). Из уравнений масштабного преобразования (4),
(5) следует, что Й = /(а) (соотношение между частотной
переменной Йиа) удовлетворяет условию
/(2а) = 4/(а)-/(а)2. (6)
Это уравнение имеет решение f(a) =2(1 — cos ka), где k —
произвольная постоянная, которая легко идентифицируется с
волновым вектором, возникающим при использовании подходов,
связанных с рассмотрением задачи в обратном пространстве.
Таким образом, рекуррентного уравнения (4) достаточно, чтобы
получить известное соотношение, дающее полный закон
дисперсии. Уравнение (4) представляет собой особый случай (с
управляющим параметром, равным 4) квадратичного отображения,
исследованного Фейгенбаумом и др. [8]. Более сложные случаи
появятся в следующем примере — при рассмотрении фракталь
ной кривой Серпинского.
Простейшая треугольная кривая Серпинского получается
следующим образом: равносторонний треугольник делится на
четыре равных треугольника; центральный треугольник
выбрасывается, с каждой из оставшихся частей проделывается та же
самая процедура — и так до бесконечности [1]. Обобщение этой
кривой на df-мериое пространство получается при применении
той же процедуры к гипертетраэдру. Получившаяся система
является неслучайной, но, очевидно, неоднородной, так что методы,
использующие ^-пространство, неприменимы. Децимация —
исключение узлов, появившихся на данной стадии построения,—
обращает рекуррентную процедуру, так что введенный выше
метод масштабного преобразования идеально подходит для
исследования таких фракталов.
Процесс децимации удваивает расстояние между узлами (ср.
(5)) и приводит к следующему точному преобразованию для
частоты [2, 9, 10]:
Q' = XQ~Q2, (7)
482
Часть VII
где к = d + 3 для фрактала, построенного в d-мерном
пространстве.
Получившееся функциональное уравнение для закона
дисперсии / в £l = f(a) теперь (для d > 1) не имеет
аналитического решения. Тем не менее мы можем найти динамический
показатель г, поскольку он описывает лишь низкочастотную
динамику. При Q->0 мы можем пренебречь в (7) нелинейным
слагаемым. При этом окажется, что при удвоении а величина
Q преобразуется с коэффициентом К = d + 3, так что
Q~az, z = log2(d + 3). (8)
Плотность состояний, которую также можно найти из (7),
сосредоточена на фрактальном множестве, поскольку все значения,
лежащие в области Q > 4, переводятся преобразованием в
нефизические значения [11]. Применяя масштабное преобразование
к неоднородным уравнениям движения, можно исследовать
также скейлинговые свойства функции Грина [10]. Недавно были
получены и решены численно [12] скейлинговые уравнения для
полной, зависящей от частоты и волнового вектора функции
отклика. Эта функция степенным образом зависит от
произведения k на обладающую иерархической структурой функцию
переменной со/&2, где z дается формулой (8). Кроме того, функция
отклика периодически зависит от log2 k. Эта периодическая
зависимость связана с тем, что при децимации на
рассматриваемом регулярном фрактале допускается изменение масштаба
только в 2п раз. Детальное рассмотрение другого недавно
полученного результата, связанного с анизотропной диффузией на
кривой Серпинского, дано в разд. 5.
4. Динамика случайных фракталов: спиновые волны
на пороге протекания и т. д.
Дадим краткое описание применения скейлинговых методов
[2] к динамике случайных фракталов, рассмотрев случай пер-
коляционной сетки. Хотя формально она является фракталом
только при концентрации, равной порогу протекания рс,
динамические процессы на ней можно изучать при произвольной
концентрации р, обсудив затем свойства кроссовера. В этом случае
следует получить скейлинговые уравнения не только для Q, но
и для концентрации р:
//=ад, (9)
Q' = S(p, Q). (Ю)
Эти уравнения, как и рассматривающиеся выше, нужно
получать с помощью децимации. Однако в отличие от
рассмотренного выше случая теперь следует рассмотреть распределение
Динамические свойства структур
483
вероятностей переменных, характеризующих узлы или связи
(это распределение зависит от конкретного вида масштабного
преобразования), и использовать какое-либо кластерное
приближение [2, 10, 13].
Для конкретности мы рассмотрим задачу о спиновых волнах
в одно- и двумерных разбавленных системах, однако наши
выводы будут приложимы и к диффузии, и к простой фононной
задаче (без сдвиговых мод).
В одномерном случае, если параметр преобразования Ъ
равен 2, первое скейлинговое уравнение имеет вид р' = р2
(точно). В фиксированных точках р = 0,1 (пустая или заполненная
цепочка) второе уравнение принимает вид (7) cl = 3 и 4 при
р = 0 и 1 соответственно [13].
При интегрировании квадратичного отображения (7)
величина Q принимает в первом случае дискретный набор значений
(периодическое поведение), а во втором — непрерывный спектр
значений (хаотическое поведение). Можно показать, что
плотность распределения Q дает плотность состояний. Плотность
состояний, таким образом, дискретна при р ~ 0, что
соответствует уровням энергии состояний, локализованных на малых
кластерах, и непрерывна при р = 1, что соответствует
энергетической зоне идеальной цепочки. Подробности даны в работе [13].
Были получены полные точные скейлинговые выражения для
динамических функций отклика как для ферромагнитного [14],
так и для антиферромагнитного [15] случая.
С помощью скейлинговых методов был рассмотрен также
двумерный случай [10]. Один из результатов заключается в том,
что спиновые волны на перколяционной сетке при р = рс имеют
закон дисперсии © ~ kz, где г — 2,76. Этот динамический
показатель получается из (10) линеаризацией (9), (10) в
фиксированной точке (р, Q) = (рс, 0):
(ж)Рс,о^Я = ^ <">
Аномальная динамика, связанная с этим показателем,
приводит к аномальной плотности состояний и, следовательно, к
аномальным термическим свойствам слоистых гейзенберговских
магнетиков при р = рс. Для чисто ферромагнитной спиновой
системы в пространстве с d = 2 плотность состояний р(©)
постоянна при малых со. Изменение размерности бесконечного
кластера приводит к расходимости плотности состояний [16]
р(©)~©-\ (12)
где ^==0,32± 0,01.
Аномальная динамика спиновых волн, характеризующаяся
показателем z, будет вскоре изучаться с помощью рассеяния
484
Часть VII
нейтронов [17]. Уже имеются эксперименты [18] по рассеянию
нейтронов на изинговских возбуждениях на перколяционной
сетке при р = рс, давшие скейлинговое выражение для
характерного времени релаксации т. Последние теоретические работы
[19, 20], однако, предсказывают, что этот скейлинг будет
нарушаться по мере перехода к более низким температурам.
5. Анизотропная диффузия на фрактальных кривых
Серпинского
В этом и последующем разделах представлены последние
результаты по диффузии на фракталах. Вначале рассмотрено
влияние анизотропии вероятностей перескоков на диффузию по
двумерной кривой Серпинского [21]. Причиной постановки
такой задачи явилось желание выяснить, не вызывает ли наличие
сноса перехода к новому поведению. Рассмотрена также
анизотропия относительно вращений.
Система нелинейных уравнений скейлинга для вероятностей
перескоков может быгь получена методом децимации,
обсуждавшимся в разд. 3. Эти уравнения имеют изотропную
фиксированную точку (соответствующую равенству вероятностей
перескоков). Линеаризация уравнений вблизи этой фиксированной
точки дает четыре собственных значения, одно из которых
определяет критический показатель аномальной диффузии z = \og2%
(ср. (8)). Другие показывают, что фиксированная точка дважды
неустойчива по отношению к сносу (соответствующий показатель
кроссовера Ф=1) и устойчива по отношению к вращательной
анизотропии (соответствующий показатель, дающий поправку к
скейлингу, равен £ = log25/3). Если величины d и г,
характеризующие соответственно снос и вращательную анизотропию,
малы, можно получить точное скейлинговое выражение для
диффузионной длины R на больших временах:
R = tl,zF(dt*tz, rCllz). (13)
Хотя наша модель совершенно неадекватна для описания
перколяционной сетки, этот результат находится в качественном
соответствии с результатами моделирования методом Монте-Карло
[22] диффузии со сносом на перколяционном кластере при р ==•
= рс в том смысле, что он показывает наличие перехода к
дрейфовому поведению.
6. Диффузия во фрактальной модели с перелетами
Вторая проблема, которая недавно была рассмотрена с
помощью фрактальной модели, — это задача о влиянии на
диффузию перескоков на произвольно большие расстояния («переле-
Динамические свойства структур 485
тов») [23]. Как и в хорошо известной задаче о полетах Леви
[24], в этом случае должна, как мы увидим, появиться
аномальная зависимость диффузионной длины от времени.
Рассматриваемый фрактал строится с помощью следующей
рекурсивной процедуры. Каждая связь заменяется
последовательно соединенными г + s связями, причем внутренние 5
связей шунтированы еще одной «длинной» связью (перелет длины
s). Получившийся фрактал допускает перелеты произвольно
большой длины L, распределение вероятностей которой P(L)
обладает тем свойством, что его моменты Мт равны нулю при
отрицательных и бесконечности при положительных значениях т.
Диффузионный процесс на таком фрактале является негауссов-
ским [24].
Точное скейлинговое соотношение между временами
диффузии tut' на двух последовательных стадиях п и п + 1
построения фрактала может быть получено [23] с помощью децимации
уравнений движения, исключающей внутренние узлы структуры,
получившиеся при замене одной связи п-к стадии связями п+ 1-
стадии. Линеаризация полного скейлингового соотношения в
окрестности фиксированной точки, соответствующей пределу
больших времен, приводит к следующему аномальному соотношению
между диффузионной длиной R и временем t на больших
временах:
R~tyz, (14)
где
2 = Л <* + !) 1. (15)
In(r + s) v '
Этот показатель зависит от г и s, а его аномальный вид связан
с двумя чертами рассмотренной фрактальной системы —
наличием сколь угодно длинных перелетов (приводящим к
расходимости среднего квадрата смещения за прыжок) и тем фактом,
что в системе есть две иерархии масштабов. Эта последняя
черта не позволяет выразить z через показатели, характеризующие
распределение P(L) длин перелетов, как это можно сделать в
более простых случаях, таких, как блуждание Вейерштрасса
[24].
7. Заключение
Сделав этот краткий обзор основных понятий и некоторых
последних результатов, мы попытались показать, что динамика
масштабно-инвариантных систем удивительно богата новыми и
экзотическими явлениями. Наиболее фундаментальные из них
связаны с переходом от нормальной к (аномальной) критиче-
486
Часть VI/
ской динамике. Эти явления можно изучать с помощью методов,
основанных на масштабном преобразовании, использующих
фундаментальную масштабную инвариантность или иерархическую
природу таких систем. Эти методы непосредственно позволяют
получить основные характеристики этих систем — аномальные
показатели, скейлинговые формы и т. д. Хотя некоторые из
рассмотренных систем и были слишком идеализированными
(неслучайные фракталы), они дали некоторое представление и о
поведении случайных фракталов (таких, как перколяционная сетка
при рс), которые представляют огромный экспериментальный
интерес. Эти случайные системы сами по себе могут быть
исследованы скейлинговыми методами, описанными в разд. 4, в
котором была рассмотрена разбавленная гейзенберговская
спиновая система на пороге протекания. Замечательно, что столь
простые системы (и близкие к ним масштабно-инвариантные фо-
нонная и диффузионная задачи), описываемые линейными
уравнениями, могут демонстрировать такое богатство явлений.
Впрочем, основной причиной этого богатства является именно
масштабная инвариантность. Если включить в рассмотрение еще и
нелинейные эффекты, ситуация становится еще интереснее. При
этом появляются такие дополнительные возможности, как
нарушение динамического скейлинга, имеющее место, скажем, в
разбавленной модели Изинга при рс. Эти нелинейные масштабно-
инвариантные системы, так же как, впрочем, и несоизмеримые
системы, бросают вызов теории; для их изучения требуется
дальнейшее развитие скейлинговых методов.
ЛИТЕРАТУРА
1. Mandelbrot £., Fractals: Form, Chance and Dimension, Freeman, San
Francisco, 1977.
2. Stinchcombe R. В., in: Highlights of Condensed Matter Physics, cds.
F. Bassani, F. Fumi, M. P. Tosi, North Holland, 1985; Stinchcombe R. #.,
in: Static Critical Phenomena in Inhomogcneous Systems, eds. A. Pekalski,
J. Sznajd, Springer, Lect Notes in Physics, 206, 1984; Stinchcombe R. £.,
in: Scaling Phenomena in Disordered Systems, eds. R. Pynn, A. Skjeltorp,
Plenum, 1985 и ссылки в этих работах.
3. Essam /. IP., Rept. Prog. Phys., 43, 833 (1980).
4. Stinchcombe R. В., Dilute Magnetism, in: Phase Transitions and Critical
Phenomena, Vol. 7, eds. C. Domb, J. L. Lebowitz, Academic Press, 1983.
5. Gefen У., Mandelbrot £., Aharony Д., Phys. Rev. Lett., 45, 855 (1980).
6. Orbach R., in: Scaling Phenomena in Disordered Systems, eds. R. Pynn,
A. Skjeltorp, Plenum, 1985.
7. Hatperin B. /., Hohenberg P. C, Phys. Rev., 117, 953 (1969).
8. Feigenbaum AT., J. Stat. Phys., 19, 25 (1978), ibid., 21, 669 (1979).
9. Rammed /?., Toulouse G., J. Phys. (Paris) Lett., 44, L13 (1983).
10. Harris C. /C, Stinchcombe R В., Phys. Rev. Lett., 50, 1399 (1983).
11. Domamj £., Alexander S., Bensimon D.t Kadanoff L. P., Phys. Rev., B28,
3110 (1983).
12. Maggs А., готовится к публикации.
Динамические свойства структур
487
13. Stlnchcombe R. В., Phys. Rev. Lett., 50, 200 (1983).
14. Stlnchcombe R. B.t Harris С. K.y J. Phys., A16, 4083 (1983).
15. Maggs A. C, Stinchcombe R. £, J. Phys., A17, 1555 (1984).
16. Lewis S. /., Stinchcombe R. B.y Phys. Rev. Lett., 52, 102 (1984).
17. Aeppli G., частное сообщение.
18. Aeppli G.t Guggenheim H. /., Uemura У. /., Phys. Rev. Lett., 52, 942
(1984).
19. Henley C. L, Phys. Rev. Lett, 55, 1653 (1985).
20. Harris C. K, Stinchcombe R. В., Phys. Rev. Lett., 56, 869 (1986).
21. Stinchcombe R. В., J. Phys., A18, L591 (1985).
22. Pandey R., Phys. Rev., B30, 489 (1984).
23. Stinchcombe R. В., J. Phys., A18, LI 169 (1985).
24. Montroll E. W.y Schlesinger M. F.y in: Non-Equilibrium Phenomena II.
From Stochastics to Hyrodynamics, eds. J. L. Lebowitz, E. W. Montroll,
North-Holland, 1984.
Упругое поведение
фрактальных структур
И. Уэбман*
Построена теория упругих свойств перколяционных сеток и других
фракталов. Показано, что скейлинговые свойства упругих модулей
иные, чем у электропроводности, — их поведение в критической
области описывается новым критическим показателем. Теоретические
результаты сопоставлены с результатами экспериментов и
численного моделирования. Динамическое поведение таких систем
характеризуется спектральной размерностью меньшей единицы, что
соответствует расходимости плотности колебательных мод на низких
частотах. Следствием этого является существование границ
внутренней стабильности фрактальных объектов. Рыхлые фрактальные
объекты очень чувствительны к внешним нагрузкам. Обсуждается
влияние таких нагрузок на упругий отклик и основные черты
нелинейного упругого поведения таких систем.
1. Линейная упругость
При агрегации малых частиц могут образовываться
макроскопические материалы, имеющие малую плотность и
характеризующиеся на большом интервале масштабов — от
размера частицы до корреляционной длины |—фрактальной
геометрией [1—4]. Примерами таких материалов являются
коллоидные агрегаты золота и кремния [2, 4], а также
высокопористые композиты, получаемые спеканием субмикрометровых
частиц серебра [3]. В настоящей работе изложена теория упругих
свойств таких систем, пригодная также для описания некоторых
других рыхлых структур, например гелей.
Чтобы построить решеточную модель для физических свойств
разуиорядоченного фрактального материала, необходимо задать
на решетке кластеры узлов или связей, имеющие
соответствующую статистику геометрических характеристик, и определить
гамильтониан, соответствующий рассматриваемому свойству. Для
определенности я буду рассматривать модель, соответствующую
перколяции по связям- Такая модель описывает
неупорядоченный материал, состоящий из твердых частиц, промежутки между
которыми пусты или заполнены мягким веществом.
Гамильтониан, описывающий упругие свойства такой системы, должен
удовлетворять следующим условиям:
а) условие упругой связности: кластеры на решетке должны
обладать конечной жесткостью. В перколяционной модели
решетка при р > рс должна иметь конечные макроскопические
модули упругости, обращающиеся в нуль при р->-рс;
* Itzhak Webman-Serin Physics Laboratory, Rutgers University, Piscata-
way, N. J. 08854 USA.
Динамические свойства структур
489
б) должны правильно воспроизводиться тензорные свойства
упругости длинных цепочек, из которых в основном состоит
система;
в) в отсутствие существенных внешних воздействий
гамильтониан механически устойчивой системы должен быть
инвариантен относительно вращений.
Простейший гамильтониан, удовлетворяющий этим
критериям, имеет для случая двумерной решетки вид [5]:
h = g See^* + -^E([ii,-tt/)i. (i)
i,l,k a if
Здесь в первом члене суммирование производится по всем узлам
i и по узлам / и k, являющимся ближайшими соседями i, а во
втором — по всем парам соседних узлов i и /. (u/ — u/)n есть
разность смещений узлов i и / в направлении, параллельном
связи (i, /). а Ьфцн — изменение угла между связями (i, /) и (/*,
6), соединенными с узлом и Символ ]£с означает, что
суммирование проводится по узлам, принадлежащим кластеру.
Величины G и Q — это локальные постоянные, характеризующие
упругость решетки, а — постоянная решетки.
Если в гамильтониане оставить только члены, описывающие
центральные силы, действующие между ближайшими соседями,
то получившийся гамильтониан не будет удовлетворять условию
упругой связности. Концентрация, при которой у решетки
появится макроскопическая упругость рг, будет выше перколяцион-
ного порога рс [6]. Для кубических решеток рг=\.
Для описания упругости гелей [7] часто применялся
скалярный гамильтониан Борна, приводящий к аналогии между
задачами об упругости и электропроводности случайных сеток. Этот
гамильтониан не обладает инвариантностью относительно
вращений. Он может явиться подходящей моделью для тех систем,
механическая устойчивость которых обеспечивается за счет
взаимодействий, не включенных в гамильтониан упругой сетки.
В гелях такими причинами могут быть осмотическое давление и
эффекты исключенного объема [8, 9].
Основными элементами, из которых состоят рыхлые
фрактальные структуры, являются тонкие извилистые цепочки
связей. Полный упругий отклик такой цепочки можно вычислить
как для непрерывной модели, так и для соответствующего
кластера на решетке. Упругое поведение цепочки описывается
тензорной силовой постоянной К, зависящей как от длины цепочки,
так и от ее геометрической конфигурации. В пространстве двух
измерений изменение упругой энергии длинной цепочки при
относительном перемещении ее концов на вектор 6R дается соот-
490
Часть VII
ношениями
£ = -i-6R/?6R, (2)
K = G
2
ZS~2Z
N
Здесь S2 — тензор инерции цепочки, определяемый
соотношением
&_J_
5 — N
и
x2ds 0
0 \y2ds
где интегрирование ведется по длине цепочки (величина S2
порядка квадрата ее длины), а 2 — оператор поворота на 90°.
Константа G зависит от ширины цепочки: G ~ ad. Обобщение этих
полученных для двумерной системы результатов на случай
большего числа измерений очевидно.
При вычислении К я опустил то слагаемое в (1), которое
описывает центральные силы, поскольку их вклад становится
малым при больших N. Результат легко обобщается на случай
неоднородных цепочек, у которых локальный модуль
сопротивления связи изгибу G(s) меняется по длине цепочки. Константу
Gv в выражении (2) в этом случае следует заменить на вели-
N
чину l/\ G~l(s)ds.
Наиболее удивительным свойством полученного результата
является зависимость упругого поведения при малых
растяжениях от конфигурации цепочки. В скалярной модели Борна,
напротив, К ~ l/N> и упругость определяется только длиной
цепочки. В качестве простейшей иллюстрации этого различия
рассмотрим упругость тонкого длинного стержня длины /. Тензор К
имеет продольную компоненту, ведущую себя как Н, и
поперечную, ведущую себя как /-3. В скалярной модели Борна обе
компоненты ведут себя как М (так же, как и проводимость
стержня).
Скелет перколяционного кластера в пространстве шести и
более измерений практически не содержит многосвязных
областей размером меньше |. Таким образом, результаты,
полученные для цепочек, могут быть непосредственно использованы для
определения жесткости K{L) участка скелета размером L.
Учитывая, что при rf = 6 хаусдорфова размерность скелета /)& = 2,
и используя равенство (2) с 5~2 ~ L~2 и N (L) ~ L ь, получаем
K(L)~L Ч
(3)
Динамические свойства структур
491
где
££ = А, + 2 = 4. (4)
Используя пространственный скейлинг, можно получить
значение показателя т, описывающего зависимость упругих модулей
от концентрации вблизи порога перколяции:
К(Р — Ре) = К0(р — Рс)\ /5ч
T = [(d-2) + flv = 4.
Обратите внимание на различие между этим значением
показателя т = 4, полученным в приближении среднего поля, и
получаемым в том же приближении значением показателя
проводимости t = 3.
В общем случае упругие модули куска фрактала с
характерным размером L зависят от структуры скелета, который в
низкоразмерных пространствах состоит как из недублированных, так
и из многократно дублированных путей. Предполагая, что
упругость области определяется только недублированными связями
(т. е. считая куски, состоящие из дублированных связей,
абсолютно жесткими), можно использовать выражение, полученное
выше для неоднородной цепочки [5], и найти для жесткости
участка размера L следующую оценку сверху:
*Ю<ТмЩГ. (6)
где NS{L)—число недублированных связей в куске фрактала
размером L, NS{L) ~ Lv [10, 11]. Это приводит нас к тому, что
K(L)~L~^E с показателем ^ = 2 + l/v. Следовательно,
нижний предел для показателя т будет равен
x = dv+l. (7)
Соответствующие значения т равны т = 3,6 для d = 2 и т =
= 3,55 для d = 3. Эти значения сильно отличаются от значений
показателя проводимости t = 1,28 для d = 2 и t = 2,05 для
d = 3.
После опубликования работы [5] было выполнено несколько
работ, в которых значения т были получены из численного
эксперимента. Для двумерных решеток получены значения т = 3,5 ±
±0,2 [12], т = 3,3 ±0,5 [13, 14] и т = 3,5 + 0,4 [15]. Расчет
Заболицки и др. [16] дал для d = 2 т = 3,96 ± 0,04.
Недавно появились и два реальных эксперимента по
определению т, их результаты хорошо согласуются с теорией. Бенгиджи
[17] исследовал упругость и электропроводность металлических
пластин с отверстиями. Для пластин из алюминия и меди он
получил т = 3,3 ± 0,5 и т = 3,5 ± 0,4 соответственно. Позже Деп-
492
Часть VII
так и др. [3j исследовали поведение вблизи порога протекания
модуля Юнга пористых брусков, полученных спеканием
субмикронных частиц серебра. Этой группой был получен результат
т = 3,8 ± 0,5 в хорошем согласии с теоретическими
предсказаниями для трехмерного случая,
В обоих экспериментах измерялась также и
электропроводность. Полученные значения показателя / согласуются с
известными из численного моделирования, что подтверждает различие
между характером критического поведения упругости и
электропроводности.
2. Динамические свойства
Свойства низкочастотных мод колебаний фрактальных
объектов определяются структурой не только скелета, но и ветвей —
мертвых концов. Скелет определяет упругие модули, а вклад в
массу дают и скелет, и мертвые концы. Рассмотрим участок
размером L фрактальной структуры с хаусдорфовой размерностью
D. Изменение масштаба длины в % раз приводит к следующему
изменению К: К (AL) = Х~^ЕК (L). Показатель ££ зависит от
конкретных геометрических свойств данной фрактальной структуры.
Масса М рассматриваемого участка ведет себя как M(kL) =
— %DM(L). Из этих соотношений можно получить выражение
для скейлинговых свойств частоты колебаний:
(о(Я1) = Я"^+^/2(о(1). (8)
Плотность колебательных состояний ведет себя
приблизительно как р(со, L) ~ l/L°Ao), где Асо —разность частот низших
колебательных собственных состояний в системе размером L.
Разность Асо есть величина порядка частоты наинизшего
собственного состояния; при масштабном преобразовании она ведет себя
так же, как и co(L) в уравнении (8). Комбинируя эти скейлин-
говые соотношения, можно определить показатель д,Е,
описывающий зависимость от частоты плотности колебательных
состояний на низких частотах:
~ __ 2D О)
Приближение среднего поля (d = 6) дает значение Яе=1. Для
d = 2 и rf = 3, ds = 0,8 и 0,9 соответственно. Таким образом,
для перколяционного кластера при р = рс величина N((d)
является расходящейся функцией. В скалярной модели Борна,
напротив, никакой расходимости нет: М(ю) ~ оУ*-1, 3 = 4/3 [18].
К аналогичным выводам мы придем и при рассмотрении ветвя-
Динамические свойства структур
493
щихся фракталов, таких, какие возникают при диффузионно-
ограниченной агрегации [19].
Плотность колебательных состояний в перколяционных
кластерах и фракталах, возникающих при ДОА, была численно
определена Уэбманом и Грэстом [15]. Для спектральной
размерности dE, описывающей упругие свойства, они получили
следующие значения: в случае перколяционных кластеров 3£ = 0,82±
± 0,05, в случае ДОА йЕ = 0,6 ± 0,05. Оба этих значения
находятся в хорошем согласии с полученными на основе скейлинго-
вых аргументов [15].
Наиболее интересным аспектом этих результатов является
то, что значения упругой спектральной размерности йЕ
оказались меньше единицы: в динамике рыхлых фракталов
доминируют низкочастотные моды. Две рассмотренные системы
совершенно различны, но демонстрируют одинаковое поведение;
можно думать, что это поведение является весьма общим.
Расходимость плотности состояний заставляет поставить
вопрос об устойчивости фрактальных объектов. Действительно, из
нашего результата следует, что, если размер объекта
достаточно велик, так что частота наинизшей моды опускается ниже не-
которого критического значения, объект не будет сохранять
своей первоначальной формы и станет неустойчивым по отношению
к термическим флуктуациям. Этот аргумент приводит к
критерию стабильности фрактальных агрегатов, аналогичному
предложенному Кантором и Виттеном [20]. Такой критерий
устанавливает верхний предел размера неравновесных фрактальных
агрегатов. На масштабах, больших этого критического размера,
конфигурация фрактала определяется релаксацией к
термическому равновесию, как в ветвящихся полимерах: это приводит
к кроссоверу к другой фрактальной размерности. Расходимость
плотности состояний при этом обрезается на соответствующей
частоте.
3. Упругость при больших деформациях
Рыхлые фрактальные объекты, подвергнутые сильным
внешним воздействиям, деформируются. На больших масштабах их
первоначальное геометрическое устройство при этом сильно
изменяется. Примером такого эффекта может служить поведение
фрактального агрегата, помещенного в термостат. На
пространственных масштабах, больших критической длины, о которой
говорилось выше, агрегаты становятся мягкими, как полимеры в
растворе. Изменение структуры на больших масштабах
означает, что при приложении фиксированной внешней нагрузки
упругое поведение системы будет изменяться. Другим следствием
малости упругих модулей фрактальных сеток является появле-
494
Часть VII
ние уже при малых напряжениях нелинейного упругого отклика.
Общее условие, что переход к нелинейному поведению
осуществляется при пространственных деформациях порядка единицы,
выполняется, конечно, и в этом случае. Нелинейное поведение
рыхлых фрактальных материалов связано с деформацией
системы на больших пространственных масштабах, а не с
изменениями на микроскопическом уровне, как это имеет место в
плотных твердых телах. Эта черта тесно связана с зависимостью
упругого поведения системы от ее геометрического устройства,
обсуждавшейся в разд. 1. Ясно, что большинство рассматриваемых
явлений не может быть получено из скалярной модели
упругости. Ниже мы попытаемся также рассмотреть связь между
тензорной упругостью и скалярной упругостью, изначально
подвергнутой действию внешних напряжений сетки,
рассматривавшейся Александером [9].
Излагаемый подход основан на следующей эвристической
картине. При приложении нагрузки к фрактальному объекту
его деформация затрагивает только масштабы длин,
превышающих некоторую определенную длину, которая уменьшается по
мере увеличения нагрузки. На меньших масштабах деформация
очень мала. Таким образом, наличие внешней нагрузки
приводит к появлению в задаче нового масштаба длины. Сходная идея
была выдвинута Пинкусом [21] и де Женом [22] при изучении
упругости макромолекул. Рассмотрим извилистую тонкую
длинную цепочку длиной N с характерным пространственным
размером L, растягиваемую силой Т. Цепочка будет реагировать на
эту силу как большая случайная пружина. Линейный отклик
пружины зависит от ее конфигурации: в соответствии с (2)
К (L) ~ l/NS2±J где S2± — квадрат радиуса инерции,
определенного для направления, перпендикулярного вектору,
соединяющему концы пружины. Пусть приложенная сила достаточно
велика (настолько, что полная относительная деформация цепочки
много больше единицы). Цепочку при этом можно
рассматривать как последовательность блобов, центры которых лежат в
точках {Rr}. Теперь можно сконструировать «гамильтониан
блобов» [23]
^=Е[^(^)2+-4-(^)2]- (ю)
Здесь х1( и % —размеры блоба в направлениях, параллельном
и перпендикулярном растяжению Г; 6R/— смещения точек R*;
g-—средняя химическая длина блоба (число звеньев в участке
цепи, образующем блоб). Для упрощения можно положить %1( ||
— % =%, Константа G определяет сопротивление изгибу. Она
зависит от свойств цепочки, например от ширины ее звеньев.
Динамические свойства структур
495
Размер х определяется из условия, что относительная
деформация блоба равна единице:
х-да"^- (id
Здесь D — хаусдорфова размерность цепочки (остающаяся
неизменной вплоть до масштабов порядка %). Соответствующая
силовая постоянная (коэффициент упругости блоба) равна по
порядку величины
КВ(Т)~ GD+lTD+l. (U)
Теперь мы можем переписать (10) в виде
Н ==4"? Кв(Т)№* + 6R/-2). (13)
Влияние внешней нагрузки, следовательно, формально сводится
к тому, что упругая энергия (2) заменяется перенормированной
упругой энергией, описываемой выражением скалярного типа.
Переход от упругого поведения, характерного для малых
напряжений, к «скалярному» поведению происходит при таких
напряжениях, при которых вся цепочка представляет собой один
блоб. Это напряжение кроссовера равно по порядку величины
Т ~ GLT(Z)+I). (14)
Для внешней нагрузки, меньшей^ Г, упругость системы остается
линейной. Для заданного Т > Т поведение под действием
дополнительной малой нагрузки определяется гамильтонианом
(13). Рассматривая отклик на большую силу при большом
растяжении, находим, что длина сильно растянутой цепочки
зависит от Т нелинейным образом:
р~\
Эту картину можно приложить и к такой фрактальной сетке,
как перколяционный кластер выше рг. При данном значении
напряжения 7 кроссовер от нескалярной к скалярной упругости
происходит, когда корреляционная длина становится порядка
размера блоба. Соответствующее соотношение между £с и Т
имеет вид
r = Ggc~(D+1), (16)
где D — хаусдорфова размерность скелета на масштабах,
меньших £. Зависимость от £ макроскопического модуля линейной
496
Часть VII
упругости К дается соотношением
К{1)~{ (i)(^s)/(I+D)^r4 1»ып (17)
где £s — показатель, определяющий масштабную зависимость
скалярной упругости (равный соответствующему показателю для
электропроводности). Для перколяционного кластера при d<6
соответствующая хаусдорфова размерность D — это размерность
множества недублированных связей, D=l/v, где v —
критический показатель длины корреляции. Для d = 6 это значение
совпадает с хаусдорфовой размерностью скелета Db = 2.
Наконец, применим эти результаты, чтобы получить
зависимость линейного макроскопического модуля упругости
перколяционной системы выше рс от р — рс. Переход к скалярной
упругости происходит при концентрации р = /?^, достаточно близкой
к рс- р+ дается соотношением
1
Р*
Чт)'"- <«>
Поведение макроскопического модуля упругости К{р — рс) при
Р< Р* и Р> Р* следующее:
\ (P~Pcf\ Р>Р*>
К(р-Рс)~)/ т \(x-mi+v)/ .t ^ ^ (19)
I VG'J (Р — Рс), Рс<Р<Р*-
Здесь t — критический показатель проводимости перколяционной
сетки. Таким образом, макроскопическое поведение упругости
сетки при заданной внешней нагрузке соответствует скалярной
модели упругости при концентрациях, очень близких к рС) и
описывается тензорной моделью при более высоких концентрациях.
Требуется сделать несколько комментариев.
Картина упругости при больших нагрузках очень упрощена.
При больших деформациях отдельные участки решетки могут
сталкиваться и перепутываться, что делает систему более
жесткой. По этой причине изложенные выше аргументы лучше
применимы для сеток, почти все связи которых принадлежат
скелету, с небольшим количеством мертвых концов или вовсе без
них. Требует дополнительного исследования вопрос о том,
насколько широка в различных системах область нелинейного
поведения, т. е. какая деформация вызывает разрушение системы
Для этого нужна более детальная информация о флуктуациях
структуры скелета.
Термин «внешнее напряжение», употребляемый в этом
разделе, понимается в широком смысле. Он подразумевает любое
Динамические свойства структур
497
воздействие, растягивающее сетку, первоначально
находившуюся в равновесной конфигурации [9]. Ясно, однако, что для
достижения кроссовера к скалярному поведению это растяжение
должно быть достаточно большим на макроскопических
масштабах. Это указывает на возможность того, что в полимерных
сетках, состоящих из цепей с достаточно высоким локальным
сопротивлением изгибу и большой персистентной длиной, переход
от скалярного к тензорному поведению происходит при
концентрации, заметно превосходящей точку гелеобразования. В этом
случае в соответствующих режимах появятся оба показателя (т
и t). Проведенные недавно исследования модуля сдвига
казеинового геля, по-видимому, подтверждают это предсказание [24].
Благодарности. Я хотел бы поблагодарить Ш. Александера
и Д. Бергмана за ценные обсуждения.
ЛИТЕРАТУРА
1. Kinetics of Aggregation and Gelation, eds. F. Family, D. P. Landau, North
Holland, Amsterdam, 1984.
2. Weitz D. A. S., Oliveira AT., Phys. Rev. Lett., 52, 1433 (1984).
3. Deptuck D., Harrison J. P., Zawadski P., Phys. Rev. Lett., 54, 913 (1985).
4. Schaeffer D. W.t Martin /. £., Wiltzius P., Cannell D. S., Phys. Rev. Lett.,
52, 2371 (1984).
5. Kanior У., Webman /., Phys. Rev. Lett., 52, 1891 (1984); Webman /.,
Kantor У., см. в fl].
6. Feng S., Sen P. N.9 Phys. Rev. Lett., 52, 216 (1984).
7. de Gennes P. G„ J. Phys. (Paris) Lett, 37, LI (1976).
8. Alexander S., J. Phys. (Paris), 45, 1939 (1984).
9. Alexander S., in: Proc. of Les-Houches Conference on Finely Divided Mat-
tar, March, 1985.
10. Coniglio A., Phys. Rev. Lett., 46, 250 (1981); см. также работу Конильо
в наст, сб., с. 227.
11. Pike R., Stanley E. #., J. Phys., A14, L169 (1981).
12. Bergman D. /., Phys. Rev., B31, 1696 (1985).
13. Feng S., Sen P. N., Hatperin B. /., Lobb C. /., Phys.. Rev., B30, 5386
(1984).
14. Sen P. N.y in: Proc. of the Les-Houches Conference on Finely Divided
Matter, March, 1985.
15. Webman /., Grest G. 5., Phys. Rev., B31, 1689 (1985).
16. Zabolitsky /., Bergman D. /., Stauffer D., не опубликовано.
17. Benguigi L., Phys. Rev. Lett., 53, 2028 (1984).
18. Alexander 5., Orbach #., J. Phys. (Paris) Lett., 43, L625 (1982).
19. Witten Т. Л, Sander L M., Phys. Rev. Lett., 47, 1400 (1982).
20. Kantor У, Witten Т. Л, J. Phys. (Paris) Lett., 45, L675 (1984).
21. Pincus P., Macromolecules 9, 386 (1976).
22. de Gennes P. G.t Scaling Concepts in Polymer Physics, Cornell University
Press, 1979. [Имеется перевод: де Жен Я. Идеи скейлинга в физике
полимеров. — М.: Мир, 1982.]
23. Webman /., не опубликовано.
24 Tokita M, Niki /?., Nikichi К., J. Chem. Phys., 83, 2583 (1985).
Статические и динамические
свойства фрактальных агрегатов,
не содержащих петель
С. Хавлин *
Исследованы статические и динамические свойства нескольких
разновидностей агрегатов, не содержащих петель. Предложена модель
роста случайных деревьев (случайных агрегатов без петель). С
помощью этой модели можно получать кластеры с различными
значениями внутренней (химической) размерности di и фрактальной
размерности df. Найдено общее соотношение между показателем
диффузии dw и фрактальной размерностью дерева df. Эти новые
результаты получены с помощью скейлинговых методов и
подтверждены данными численного моделирования. Рассмотрена
также модель одномерной диффузии, аналогичная диффузии на
агрегатах без петель. Решение этой модели воспроизводит полученные
скейлинговыми методами результаты для показателя диффузии.
Модель основана на параметрах, характеризующих структуру
дерева.
1. Введение
Геометрические и топологические свойства случайных
агрегатов представляют большой интерес. Активно исследуются
такие системы, как перколяционные кластеры, решеточные
«звери» и кластеры, возникающие в процессе
диффузионно-ограниченной агрегации (ДОА). Цель этих исследований состоит в
нахождении показателей, определяющих физические свойства
таких систем [1—12]. Значителен также интерес к внутренним
свойствам случайных агрегатов [3, 5, 10, 13—17], знание
которых позволяет понять динамические свойства таких систем [3,
5,8, 14, 15].
Чтобы охарактеризовать случайные агрегаты, можно
использовать два внутренних показателя di и tf/. Внутренняя
размерность di показывает, как меняется масса системы в зависимости
от характерного химического расстояния /:
М~Л (1.1)
где химическое расстояние между двумя узлами кластера —это
длина кратчайшего пути, соединяющего эти узлы; показатель
df — внутренняя размерность скелета [9]. Скелет кластера
можно определить как совокупность всех кратчайших путей,
соединяющих узлы кластера с окружающей его оболочкой,
расположенной на химическом расстоянии L <С 1 от рассматриваемой
области. Масса скелета растет с химическим расстоянием как
Ms~td*. (1.2)
* S. Havlin-Department of Physics, Bar-Пап University, Ramat-Gan
Israel
Динамические свойства структур
499
Было обнаружено [9J, что скелеты перколяционных кластероз
в пространстве любого числа измерений при критической
концентрации линейны в смысле химического расстояния, т. е. df = 1.
Это доказывает справедливость качественных аргументов в
пользу того, что перколяционные кластеры на пороге протекания
имеют конечную разветвленность. Недавно было показано, что
для кластеров (т. е. решеточных «зверей») с конечной развет-
вленностыо и без замкнутых петель показатели,
характеризующие диффузию, могут быть выражены через фрактальную и
внутреннюю размерности [5]:
dlw = dt + l, d9 = df(l + l/dl)9 d = 2dl/(dl+l). (1.3)
Здесь dw — показатель диффузии, dlw — химический показатель
диффузии [3], d — фрактонная размерность. Возникает вопрос
[8], существуют ли бесконечно разветвленные фрактальные
агрегаты (т. е. такие, для которых df > l), в частности деревья?
Недавно появились работы [18, 19], в которых описана
модель роста деревьев. Эта модель позволяет получать деревья с
наперед заданным значением di на решетке любой раамерности,
в том числе и на дереве Кейли (ДК). В разд. 2 мы исследуем
свойства скелетов этих деревьев при d =2 и на ДК и покажем,
что dSi > U если величина dt превосходит некоторое критическое
значение.
Большое внимание уделяется также анализу транспортных
свойств фрактальных агрегатов [20—24]. В настоящем обзоре
представлены два подхода к исследованию транспортных свойств
агрегатов, не содержащих петель. Первый подход [25],
изложенный в разд. 3, основан на гипотезе скейлинга и соотношении
Эйнштейна между диффузией и проводимостью. Второй подход
(разд. 4) представляет собой феноменологическую модель
диффузии, основанную на параметрах, характеризующих
геометрическую структуру дерева [26]. В обоих подходах мы получаем
одни и те же общие соотношения между динамическими
показателями, описывающими диффузию, и статическими
показателями, описывающими структуру дерева:
dl^Z + dt-dt d. = ^ (2+ </|-df), J= 2dl (1.4)
Заметим, что в частном случае df=l (1.4) переходит в (1.3).
2. Модель роста древовидных кластеров
Общая модель, которая позволяет получить дерево с
заданной внутренней размерностью, следующая. Выберем на d-мер-
ной решетке узел («семечко» дерева) и затем выберем случайно
500
Часть VII
и заблокируем В(\) ближайших соседей этого узла. Эти
занятые узлы представляют собой первую химическую
координационную сферу; химическое расстояние от них до исходного узла
/ = 1. Следующая координационная сфера получается
аналогичным образом — пересмотром всех незанятых и незаблокирован-
ных ближайших соседей узлов первой сферы. Случайно
выбранные В (2) из них затем объявляются занятыми с тем
ограничением, что новый узел может быть занят лишь при условии, что
он имеет ровно одного уже занятого ближайшего соседа. Если
у узла больше одного занятого ближайшего соседа, он
полагается заблокированным. Это ограничение исключает
возможность появления петель —замкнутых петель по кластеру.
Последующие стадии построения осуществляются аналогичным
образом. Похожая модель без этого ограничения рассмотрена в [27].
Чтобы получить структуру с заданной размерностью, выберем
В(/) = В0/а. (2.1)
Из (2.1) следует, что
М (/) = 2 В (Г) - /а+1 = ld*, (2.2)
где di — внутренняя размерность кластера. На рис. 1 показаны
выращенные на двумерной решетке деревья с di = 1,3; 1,5 и 1,8.
Фрактальная размерность этих деревьев вычислялась
следующим образом. Поскольку М ~ fl ~ Rdf, то R ~ ldildf. Таким
образом, если мы численно определим радиус инерции R(l)
кластера
/?(/)-/*, (2.3)
то сможем вычислить df из соотношения v = di/df. Результаты
для vh df при различных значениях di представлены в табл. 1.
Скелеты кластеров, показанных на рис. 1, изображены на
рис. 2. Структуры, изображенные на рис. 2, а и 2, б (di= 1,3 и
1,5 соответственно), не ветвятся вплоть до значений /, близких
к L, в то время как на рис. 2,6 (dt = 1,8) мы видим, что
ветвление начинается при / <С L. Мы вычислили внутренние
размерности скелетов этих и других кривых. Результаты также
представлены в табл. 1.
Интересно сравнить наши результаты для df с результатами
для перколяции. При di ^ 1,65 получаем di = 1, как это имеет
место для перколяционпых кластеров в критической области
[9]. При di> 1,65 мы нашли di > 1. Показатель df — 1
характеризует разветвленность кластера [12]. Таким образом, при
di<: 1,65 наши деревья имеют конечную разветвленность
(показатель разветвленности равен нулю), в то время как при
di > 1,65 их разветвленность бесконечна.
Рис. 1. Древовидные кластеры, полученные с помощью процедуры, описанной в тексте (L:
==^макс = 300): а) d/=l,3; б) d/ = l,5; в) di = \fi.
а
Рис. 2. Скелеты структур, показанных на рис. 1: a) d/=l,3; б) di=\, 5, в) d/ = l,8.
502
Часть VI!
Таблица 1. Показатели, характеризующие деревья и их скелеты. Значения
фрактальной размерности dfy отношения v = di/d/ и внутренней размер-
ности скелета dl для кластеров, имеющих внутреннюю размерность d/.
Погрешности этих величин определены по экстремальным наклонам
прямых при линейной аппроксимации соответствующих зависимостей
dl df v df
1,3
1,5
1,6
1,7
1,8
1,9
2,0
1,71 ±0,03
1,82±0,03
1,8б±0,03
1,91 ±0,03
1,95±0,03
2 0+0
Аи—0,03
2 0+0
z'u-0,03
0,76 ±0,02
0,82 ±0,02
0,86 ±0,02
0,89±0,02
0,92±0,02
0,95±0,02
i+0,0
-0,02
С помощью аналитических методов недавно было показано
[19], что аналогичные структуры, построенные на ДК, имеют
df = 1 при dt ^ 2 и df = dt — 1 при dt ^ 2. Эти результаты
вместе с теми, что представлены на рис. 3, согласуются со
следующими соотношениями между dt и df:
df = 1 при di^dci,
dSt = 1 + dt — dci при di^d°i,
где d\ — критическое значение размерности dt [18]. Поскольку
для деревьев, построенных на решетке Кейли (соответствующей
пределу высоких размерностей), соотношение (2.4) с d/ = 2
было доказано аналитически и поскольку на основании численного
моделирования можно предположить, что оно выполняется при
d = 2 (если положить d/~l,65)> мы можем заключить, что
оно, вероятно, справедливо (при соответствующем значении d°i)
для деревьев, построенных в пространстве любой размерности.
Заметим, что d°i = 2 равно значению внутренней
размерности di перколяционного кластера на ДК. Аналогично значение
dcl= 1,65 dz 0,05, полученное в настоящем исследовании, близко
к значению d/=l,64, характеризующему перколяционный кла-
i,o;
1,0
+0,03
-0,0
+0,03
—0,0
, о+0'05
ljU-0,0
1,1 ±0,05
1,2±0,05
1,27±0,04
1,37±0,03
Динамические свойства структур
503
стер на пороге протекания при d = 2 [3]. Таким образом, мы
можем предположить, что d°i в модели роста деревьев равно
•а
1,0
1 ' » I I I I I I 1 .
7,2 1,3 1,4 1,5 1,6 7,7 1,8 1,9 2,0
Рис. 3. Внутренняя размерность скелета dt кластеров, имеющих внутреннюю
размерность du Критическая размерность d% по-видимому, приблизительно
равна ^ = 1,65 + 0,05.
значению di критических перколяционных кластеров в
пространстве того же числа измерений.
3. Скейлинговое рассмотрение переноса на деревьях
В этом разделе мы получим соотношения между
показателями, характеризующими транспорт на деревьях. Рассмотрение
будет основано на скейлинговых аргументах и соотношении
Эйнштейна [20]
d9 = dt + l (3.1)
где £—показатель сопротивления, определяющий зависимость
сопротивления р от размера кластера R: р~#§. Определим
р/(/) как полное сопротивление, измеренное между узлом А и
всеми узлами /-го химического слоя, показатель сопротивления
определим соотношением р* ~ fiK Пусть pi(/)—сопротивление,
измеренное между узлом А и одним узлом, находящимся от А
на химическом расстоянии /.
Пусть В (I) — число связей в /-м слое скелета. Ясно, что
В° (/) ~ dMs(l)/dl ~ lai -\ Поскольку петлевые пути на дереве
по определению отсутствуют, величина р*(/) оказывается непо-
V *—*-
. I .
504
Часть VII
средственно связанной с Bs(l):
1
Pi (I) = [ *L г (df < 2). (3.2)
WW J BS(l') df-2
В силу отсутствия петель имеем также pi (/) ~ I и,
следовательно,
li = 2~dl (3.3)
Теперь мы можем использовать соотношения [3]
d-^ = vdw, d/ = vdf, £j = v| (3.4)
и соотношение Эйнштейна (3.1), чтобы получить аналогичное
соотношение в /-пространстве. Общие соотношения,
приведенные в (1.4), получается из (3.3), (3.5) и определения фрактон-
ной размерности d = 2df/dw = 2di/dlw. В частном случае
деревьев с конечной разветвленностью, для которых rf;=l,
получаем (1.3).
4. Модель диффузии на агрегатах без петель
Предшествующие исследования аномальной диффузии на
фрактальных агрегатах и древесных структурах были основаны
на соотношении Эйнштейна, с помощью которого показатели
аномальной диффузии связывались с поведением проводимости.
В этом разделе мы рассмотрим феноменологический подход,
позволяющий непосредственно вычислить некоторые свойства
диффузии на деревьях.
Рассмотрим дерево, состоящее из корня, или начала,
бесконечного разветвленного скелета и ответвляющихся от него
конечных мертвых концов. Для простоты будем вначале считать
нашу структуру дискретной, с единицей длины А/, а затем
перейдем к континуальному пределу. Будем считать, что при
блуждании частица с данного узла может перейти только на
соседние. Таким образом, частица, находившаяся в точке, расстояние
от которой до корня равно /, может перейти в точки, лежащие
на расстояниях / ± А/ от корня. Вероятности соответствующих
перемещений обозначим р±(/). В общем случае эти величины не
равны друг другу, сумма их может отличаться от единицы.
Вероятность того, что частица останется на данном шаге
неподвижной, равна р0(1) = 1 + р+(/) — р_(/). Чтобы определить
вероятности ро, р+ и р_, воспользуемся величинами В(1) и Bs(l)9
характеризующими дерево: эти вероятности связаны с ними со-
Динамические свойства структур
505
отношениями
Ро (/) = 1 - Р+ (/) — Р_ (/) = 1 — В* (1)1В (I), (4.1)
P+(l)IP-(D = B*{l+\)lB*(l). (4.2)
Первое из этих соотношений означает, что, оказываясь на
мертвом конце, совершающая блуждания частица прекращает свое
движение по скелету. Второе означает, что отношение
вероятностей шага вперед и шага назад равно отношению чисел
связей, по которым можно двигаться вперед и назад. Соотношения
(4.1) и (4.2) и известные скейлинговые свойства B(l)~ldl~l и
В (I) ~ I l , ^ справедливые при больших I, позволяют найти
асимптотическое выражение
Р±(/) = ^г(1±£), Л(0=1—£. (4.3)
где А — постоянная, связанная с коэффициентами
пропорциональности в асимптотических выражениях для М(1) и Ms(l), a
параметры а и В связаны с dt и df соотношениями
a = d,-rf?, B = df — 1. (4.4)
Из (4.4) следует, что диффузия частицы замедляется по мере
того, как она уходит от начальной точки. Это и понятно,
поскольку с удалением от начала растет вероятность того, что
частица будет «поймана» мертвым концом. Член в скобках в
выражении (4.3) появляется из-за того, что, если скелет ветвится,
т. е. df > 1, частица сносится туда, где эти ветвления
происходят чаще. Предположение о том, что частица может
перемещаться только на соседние узлы, позволяет нам написать
рекуррентные соотношения для вероятностей {Un(l)} того, что на
я-шаге блуждания частица находится на расстоянии / от начала:
Un+i (0 = Р+ (* - ДО Un (I - АО + р_ (/ + М) Un (I + А/) +
+ РоЮ */„(/). (4.5)
В качестве дифференциального аналога (4.5) получаем
диффузионное уравнение
дп 2 д12\р) 2 d/^/a+iJ' v*-°J
решение которого, удовлетворяющее начальным условиям
£/(/, 0) =6(1), имеет вид
U* Ю = И(1+а + Д)/(2 + а)] СХР (" ^Г-) ' <4'7>
где X = 2/[Л(2 + а)2]. Численное решение (4.5) хорошо
согласуется с этим выражением.
506
Часть VII
Выражение для Un{l) позволяет получить соотношения
между различными показателями. Показатель dlw легко
получается вычислением а2(/) из (4.7). Для временной зависимости этой
величины находим
1
а2 (/) = (I2) - (I)2 = Сп 2+а, (4.8)
где С — числовая постоянная. Из этого соотношения следует, что
dlw= 2 + а = 2 + di — di. Далее, величина U при большом, но
фиксированном I и при л^-оо ведет себя как я-о+а+щг+а^
откуда следует, что фрактонная размерность d равна
7 = 2 (1 + a + В)/{2 + а) = 2dl/(dl -d? + 2). (4.9)
Значения показателей dw и d согласуются со значениями,
полученными в разд. 3.
ЛИТЕРАТУРА
1. Mandelbrot В. В., The Fractal Geometry of Nature, Freeman,
San-Francisco, 1982.
2. Alexander S., Orbach R.y J. Phys. (Paris) Lett., 43, L625 (1982).
3. Havlin S, Nossal ft, J. Phys., A17, L427 (1984); Havlin S, in: Kinetics
of Aggregation and Gelation, eds. F. Family, D. P. Landau,
North-Holland, Amsterdam, 1984.
4. Witten Т. A, Sander L. Af.f Phys. Rev. Lett., 47, 1400 (1981); Meakin P.,
Phys. Rev. Lett, 51, 1119 (1983).
5. Havlin 5., Djordjevic Z. V.t Majid /, Stanley Я. £., Weiss G. Я, Phys.
Rev. Lett., 53, 178 (1984).
6. Pike A, Stanley Я. £., J. Phys., A14, L169 (1981).
7. Cates M. £., Phys. Rev. Lett, 53, 926 (1984).
8. Witten Г. Л, Kantor У., Phys. Rev, B30, 4093 (1984).
9. Havlin 5, Nossal R., Trus 5, Weiss G. tf„ J. Phys, A17, 1957 (1984).
10. Meakin P., Majid /, Havlin 5, Stanley H. £., J. Phys, A17, L975 (1984).
11. Havlin S, Trus В., Weiss G. #, Ben-Avraham D.f J. Phys, A18, L247
(1985).
12. Gefen У, Aharony A, Mandelbrot В. В, Kirkpatrick S.} Phys. Rev. Lett,
47, 1771 (1981).
13. Alexandrowicz Z, Phys. Lett, A80, 284 (1980).
14. Herrmann Я. /., Hong D., Stanley H. E., J. Rhys, A17, L261 (1984).
15. Ritzenberg A L, Cofien R. /, Phys. Rev, B30, 4036 (1984).
16. Vannimenus /, Nadal J. P., Martin #, J. Phys, A17, L351 (1984)
17. Djordjevic Z. V., Havlin 5, Stanley H. £, Weiss G. Я, Phys. Rev, B30,
478 (1984).
18. Havlin S, Nossal /?., Trus B, Phys. Rev, A31, 3829 (1985).
19. Havlin 5, Keifer /, Weiss G. Я, Ben-Avraham D., Glazer У, J. Stat.
Phys, 41, 489 (1985).
20. Alexander S, Orbach R., J. Phys. (Paris) Lett, 43, L625 (1982).
21. Ben-Avraham Z), Havlin 5, J. Phys, A15, 2691 (1982); Havlin S, Ben-
Avraham D., Sompolinsky #, Phys. Rev, A27, 1730 (1983).
22. Gefen У, Aharony A, Alexander 5, Phys. Rev. Lett, 50, 77 (1983).
23. Rammal R.y Toulouse G, J. Phys. (Paris) Lett, 44, L13 (1983).
24. Pandey R.t Stauffer Z), Phys. Rev. Lett, 51, 527 (1983).
25. Havlin S., Nossal R., Trus B, Weiss G. Я, Phys. Rev. B31, 7497 (1985).
26. Havlin 5, Trus B, Weiss G. Я, J. Phys, A18, L1043 (1985).
27. Hong Z), Havlin 5, Stanley Я. £, J. Phys, A18, LI 103, (1985).
Фрактальная размерность
периметра роста
Л. Марголина *
Рассмотрена фрактальная размерность do периметра кластера,
получаемого в модели блужданий бабочки — недавно предложенной
модели роста кластеров. В пределе дальнодействия генерируемая
такими блужданиями граница перколяционного кластера имеет
размерность, по-видимому, равную размерности множества недубли-
рованных связей Ug = 1/v. Предложено новое соотношение для
химической размерности: di = df/(df— do). В пределе близкодей-
ствия «блуждания бабочки» по евклидовой решетке принадлежат
тому же классу универсальности, что и обычные случайные
блуждания. Обсуждаются динамические аспекты блуждания,
генерирующего кластер. Спектральная размерность, соответствующая
такому блужданию, плавно зависит от параметров модели. В обоих
предельных случаях — дальнодействия и близкодействия — эти
случайные блуждания отличаются от обычной диффузии на перколя-
ционном кластере.
1, Введение
Диффузию и транспорт в неупорядоченных средах
можно моделировать случайными блужданиями по фрактальным
структурам. Один из способов исследования таких явлений
связан с переформулировкой соответствующих задач как задач о
росте. Рассмотрим блуждание, которое само строит
фрактальную среду, выбирая посещаемые узлы согласно некоторым
вероятностным законам. След, оставляемый таким блужданием,
образует кластер посещенных узлов S. Получающаяся
структура наряду с обычными статическими и динамическими
фрактальными размерностями [1] (фрактальной размерностью самой
среды dfy «химической» размерностью di, фрактальной
размерностью минимального пути dMJIH, фрактальной размерностью
множества недублированных связей rfr, фрактальной размерностью
блужданий dw, спектральной размерностью ds) характеризуется
фрактальной размерностью периметра роста do. Кластер растет
за счет узлов, которые являются ближайшими соседями уже
посещенных узлов, но еще не были использованы блуждающей
частицей. Эти узлы называются узлами роста [2], а их
множество— периметром роста G. Периметр роста зависит от среднего
радиуса кластера R как
G~RdG~SdGfdf. (1)
Чрезвычайно важно обнаружить соотношения между
различными фрактальными размерностями, например между статиче-
* Alia E. Margolina-E. I. du Pont de Nemours and Company, Control
Research and Development, Experimental Station Wilmington, Delaware 19898.
508
Часть VII
скими фрактальными размерностями df, di и динамическими
размерностями dw, dG. В настоящей работе предложена новая
модель роста кластеров — модель блужданий бабочки [3],
которая посещает только узлы роста. Будут получены некоторые
новые соотношения между фрактальными размерностями df, di,
dr и dG. Мы обсудим также некоторые аспекты задачи о
диффузии, связанной с этой моделью роста, и сравним диффузию
бабочки с обычной диффузией на перколяционном кластере
(диффузией муравья).
2. Модель
Рассмотрим на квадратной решетке задачу о
распространении инфекции от первоначально зараженного узла [S].
Представим себе, что инфекция переносится бабочкой, перелетающей
" V."... ;у ••. • ; t, W"
Рис. 1. Кластер из 1500 узлов, построенный бабочкой с а = —3 на
евклидовой решетке (р=1). Показаны только узлы роста *. Сходство кластера
с бабочкой случайное.
с одного узла роста на другой, случайно выбираемый в
соответствии с распределением вероятности
Р(г)~1/Л (2)
где г—расстояние от узла, зараженного последним, до данного
узла роста, а а — параметр, определяющий притяжение или
отталкивание между узлами роста G. Выбранный узел G
превращается в зараженный узел 5. Типичный кластер узлов 5 с
периметром роста G показан на рис. 1. Если соответствующая
процедура реализуется для перколяционного кластера, должен
делаться еще один случайный выбор: узел G преобразуется в узел
S с верояностью рс и с вероятностью 1—рс — в
невосприимчивый узел /. Зараженные и невосприимчивые узлы остаются
таковыми все дальнейшее время, периметр же роста G постоянно
изменяется: каждую единицу времени добавляется новый
зараженный узел, и все не определенные ранее его соседи
превращаются в узлы G. Будем считать, что время увеличивается на
единицу только тогда, когда происходит рост, т. е. при появле-
Динамические свойства структур
509
нии нового узла G; бабочка движется в некоем искусственном
времени роста t = S. После t временных шагов образуется
большой разветвленный кластер из 5 узлов. Фрактальная
размерность df полученного кластера такая же, как у перколяцион-
ного кластера при р = рс {df = 91/48 при d = 2), поскольку
получившиеся узлы связаны так же, как связаны занятые узлы в
задачах перколяции. Наиболее интересной характеристикой
рассмотренного типа блужданий является фрактальная размерность
периметра роста do.
3. Пределы дальнодействия и близкодействия
и переход между ними
Рассмотрим влияние изменения параметра а в (2) на
структуру растущего кластера. Случай а = 0 приводит к модели Иде-
на на перколяционной системе: узлы G выбираются совершенно
случайно, с вероятностью 1/G. Следует выделить два
предельных случая поведения бабочки — предел дальнодействия, когда
бабочка стремится улететь возможно дальше (насколько
позволяет ей размер кластера), и предел близкодействия, когда
бабочка совершает лишь короткие перелеты (в основном на
соседние узлы). Разделяющее эти типы поведения значение а можно
получить, рассмотрев среднюю длину перелета r=\drrP(r),
что дает ас = 2. Дальнодействующее поведение имеет место при
а < 2, случай а > 2 соответствует близкодействию. При а > 8
поведение устанавливается, и при всех а > 12 периметр роста
ведет себя одинаково. Как отражаются изменения а на росте
кластеров? Основной результат состоит в том, что с ростом а
величина do непрерывно возрастает от значения do с* 0,76 (а <
< 2) до значения do = 1,04 (а > 8). Таким образом, изменение
последовательности, в которой узлы присоединяются к кластеру,
может ускорить или замедлить рост числа узлов G. Таким
образом, мы обнаружили, что кинетический показатель dG может
непрерывно изменяться, в то время как статический показатель
df остается неизменным. Из этого следует, что динамические
классы универсальности совершенно независимы от статических.
Модель бабочки (по-видимому, первая модель, обладающая
таким свойством) дала нам возможность узнать об одной из
важнейших черт моделей роста.
4. Фрактальная размерность в пределе дальнодействия
Гипотезу о значении dG в пределе дальнодействия можно
сформулировать [4], основываясь па предположении, что скей-
линговые свойства [5] периметров кластеров, рост которых уже
510
Часть VII
закончился, и кластеров, которые еще растут, одинаковы, коль
скоро сами кластеры достаточно велики. Зависимость периметра
кластера от числа узлов в нем дается соотношением
p = S_Lzi£<L + ASa, (3)
рс v ;
где o=l/vdf, v — показатель длины корреляции, А —
постоянная. Первое слагаемое в (3) соответствует числу
заблокированных узлов в растущем кластере размера S. Таким образом,
периметр роста G, равный числу всех ближайших соседей узлов
кластера 5 минус число узлов, уже определенных как
заблокированные, должен быть пропорционален «избыточному»
периметру:
G~Sa~7?l/v. (4)
Сравнивая (2) и (4), получаем
dG=Uv = dr. (5)
Наша гипотеза находится в прекрасном согласии с численными
данными для предела дальнодействия в двух- и трехмерном
случае и выполняется точно на дереве Кейли. Заметим, что
фрактальная размерность периметра роста в пределе дальнодействия
равна фрактальной размерности множества недублированных
связей [6], что может привести к интересным догадкам о
динамике связности растущих перколяционных кластеров.
Мы рассмотрели также [4] новое соотношение между
«химической» фрактальной размерностью di (определенной как
S ~ I 1> где / — «химическая длина»)
1 df
df-dQ
(6)
ранее предсказанное на основании численных наблюдений [7].
Заметим, что, поскольку di = df/dmiHy можно получить также,
что
dMmi = df — dG. (7)
Мы видим, что фрактальная размерность периметра роста de
является важной величиной и может уменьшить число
«независимых» фрактальных размерностей.
5. Интерпретация предела короткодействия
Получающееся в пределе короткодействия значение do ^
~1,04 ±0,04, по-видимому, соответствует иному классу
универсальности, чем модель муравья, для которой мы нашли, что
Динамические свойства структур
511
dG = 0,93 [8]. Проверим, выполняется ли это утверждение для
блужданий короткодействующей бабочки на евклидовой
решетке. При а > 16 блуждание бабочки на двумерной решетке — это
хорошо определенное блуждание, заполняющее пространство
(рис. 2). Это блуждание генерирует периметр, свойства которого
аналогичны свойствам периметра роста обычного случайного
блуждания: G ~ S/\nS.
Полученный результат делает еще
более интригующим отличие
динамики короткодействующей
бабочки и муравья в случае
перколяционной системы.
Удовлетворительного объяснения
этому отличию мы в настоящее
время не имеем.
6. Свойства диффузии
в модели бабочки
Перейдем от времени роста
t = S к обычному времени
t~S f, что соответствует
возможности повторного
посещения уже посещенных узлов
(здесь dm — размерность
блуждания, определенная как t ~ R*w). Это предположение
означает, что случайное блуждание происходит обычным образом,
пока не встречает узлы роста. В этот момент решение занимать
или не занимать соответствующий узел принимается в
соответствии с распределением (2). Если принято решение не
занимать узел, повторное посещение узлов продолжается, пока не
встретится новый узел роста. Я предложила назвать такой тип
блуждений процессом диффузии, лимитированной ростом. Если
мы предположим, что полученное для муравья соотношение [1]
dJdf = 2-dG/df (8)
справедливо при любых а, мы получим,-что спектральная
размерность ds = 2df/dw блуждания бабочки на перколяционном
кластере при d = 2 меняется от d5~l,25 (дальнодействие) до
ds ^ 1,38 (близкодействие); значение ds ^ 1,32, соответствующее
блужданию муравья, лежит между этими двумя значениями.
Таким образом, обычный процесс диффузии соответствует
умеренно дальнодействующей бабочке с а ^ 4. Это вполне
соответствует нашему пониманию того, что случайные блуждания
•—* 9 > ♦
I
t N
4 н-t \
О О
Рис. 2. Типичная «ловушка» из 7
шагов для близкодействующего
кинетического блуждания. Бабочка
выбирается из ловушки, перелетая на один
из узлов роста (кружок) в
соответствии с распределением (2).
Наиболее вероятен выбор узла 1.
512
Часть VII
имеют конечную вероятность посетить и достаточно удаленные
узлы роста. Комбинируя (7) и (8), я получила выражение для
#мин*
du1iH = df — dW9 (9)
а комбинируя (6) и (8), — выражение
djdf=l + l/dt. (10)
Благодарности. Эта работа была выполнена в
сотрудничестве с А. Бунде, Г. Германом, Дж. Маджидом и X. Стенли. Мне
хотелось бы поблагодарить А. Аарони, Ш. Хавлина, Ф. Леивра,
Р. Рубина и Д. Штауффера за полезные обсуждения.
ЛИТЕРАТУРА
1. Stanley H. £., J. Stat. Phys., 36, 843 (1984).
2 Leyvraz F.t Stanley H. £., Phys. Rev. Lett., 51, 2048 (1983).,
3. Bunde A, Herrmann H. /., Margolina A, Stanley H. E., Phys. Rev. Lett.,
55, 653 (1985).
4. Margolina A., J. Phys., A18, L651 (1985).
5. Stauffer D., Phys. Rep., 54, 1 (1979).
6. Coniglio A. /. Phys., A15, 3829 (1982).
7. Havlin S., Nossal R., J. Phys., A17, L427 (1984).
8. Stanley H. E.y Majid /., Margolina A, Bunde A, Phys. Rev. Lett., 53,
1706 (1984).
Перколяция и фрактальное поведение
в неупорядоченных решетках
//. Лргиракис *
С большой точностью вычислены фрактальные показатели для
случайных блужданий на двумерных и трехмерных решетках со
случайно занятыми узлами. Мы использовали эффективный алгоритм
роста кластеров в процессе диффузии и определили число узлов,
посещенных частицей за N шагов блуждания, и ее
среднеквадратичное смещение в пределе больших времен. Показано, что переход
к евклидову поведению происходит при концентрациях, очень
близких к порогу протекания.
1. Введение
В недавно появившемся цикле работ [1—4] было
показано, что случайные блуждания на неупорядоченных решетках
представляют собой чрезвычайно интересный предмет
исследований, особенно если речь идет о связи их свойств с теми
фрактальными свойствами, которыми обладают такие решетки. Со
случайными блужданиями связано множество физических
процессов— процессы диффузии [6], тушение возбуждений
[^химические реакции [5] и т. д. Особенно интересными являются
эти задачи в применении к перколяционным системам,
поскольку свойства таких систем на пороге протекания представляют
собой прекрасный пример фрактального поведения. В настоящей
работе суммированы результаты вычислений свойств случайных
блужданий по перколяционным системам при концентрациях,
равных и превосходящих критическую, в частности даны
значения фрактальных показателей, определенных по зависимости
числа посещенных блужданием узлов Sn от числа шагов
блуждания N. Даны оценки погрешностей определения этих
величин, полученные на основании статистического анализа.
Представлены также результаты для показателя диффузии Д
полученные из вычисления среднего квадрата смещения за N шагов
R%. Наконец дана картина перехода от критического поведения
к поведению в идеальном кристалле (при отсутствии
беспорядка) [6].
2. Метод вычислений
Для определения свойств случайных блужданий мы
использовали метод Монте-Карло. Детали алгоритмов подробно
обсуждаются в работе [6]. Размер рассматривавшихся решеток
* Panos Argyrakis- Department of Physics, University of Crete, Iraklion,
Crete, Greece.
514
Часть VII
составлял 4ХЮ6 узлов, т. е. 2000X2000 в двумерном и 160 X
X 160 X 160 в трехмерном случаях. Рассматривались блуждания
длиной до 2-Ю5 шагов. Использование таких больших систем
гарантирует отсутствие граничных эффектов, поэтому
полученные результаты свободны от всяких приближений или
экстраполяции. Особое внимание уделено начальной стадии блужданий,
поскольку для ее описания требуются дополнительные
показатели [7].
3. Результаты
Необходимо различать неэквивалентные спектральные
размерности. Хорошо известны формулы
SN~Ndsl\ (1)
/&~JV2/D (2)
Моделирование случайных блужданий на пороге протекания
может проводиться при различных условиях:
а) частица первоначально помещена на наибольший перко-
ляционный кластер, характеризуемый показателями ds и D\
б) частица может попасть на любой кластер, в том числе и
на кластер малого размера. Множество таких кластеров
характеризуется показателями drs и D'.
Для исследования поведения в пределе больших времен
удобно использовать алгоритм выращивания кластеров [6],
приводящий к случаю б). Показатели ds и d's связаны
соотношением [4]:
4 = ^(2-^), (3)
где d — евклидова размерность, а р и v — статические перколя-
ционные показатели. Если известен один из показателей (ds или
d's), второй может быть легко вычислен. Величина d's
определялась по наклону нижних кривых на рис. 1 и 2, на которых
показана зависимость \nSN от \nN для двумерного и
трехмерного случаев соответственно. Эти кривые соответствуют
критической точке, т. е. рс = 0,5931 и рс = 0,3117; другие графики
соответствуют более высоким концентрациям р (см. ниже).
Наклоны кривых дают:
d's == 1,23 ± 0,02 (двумерный случай), (4)
d's — 1,06 ± 0,02 (трехмерный случай). (5)
ыо3
ыо1*
N
+-Н f tH—+—Н- W-+HJ
1-Ю6
ыо5
Рис. 1. Зависимость числа посещенных узлов Sn от числа шагов
блуждания N для двумерных решеток. Это средние по 1000 реализаций значения
для блужданий, начинающихся на произвольном кластере. Снизу вверх:
р = 0,5931; 0,60; 0,63, 0,65; 0,70; 0,80; 0,90; 1,00.
U10° г-
1-Ю
Г-Ю1
V10
1-Ю
Рис. 2. То же, что на рис. 1, но для трехмерных решеток. Снизу вверх:
р = 0,3117; 0,32; 0,33; 0,35; 0,40; 0,50; 0,75; 1,00.
516
Часть VII
С помощью соотношения (3) и значений (4) и (5) получаем
ds = 1,30 ± 0,02 (двумерный случай), (6)
ds= 1,33 ±0,02 (трехмерный случай). (7)
Значение ds для двумерного случая, определенное здесь
косвенным методом, находится в прекрасном согласии с результатами
предыдущих работ, в которых ds вычислялось непосредственно
для блуждания из N = 5000 шагов на наибольшем кластере.
Погрешности ±0,02 в равенствах (6) и (7), соответствующих
блужданию на наибольшем кластере, определялись с помощью
обычных методов оценки погрешностей, т. е. исходя из
стандартного отклонения а распределения 5V и числа реализаций. В
равенствах (4) и (5) погрешность определена графически по
экстремальным наклонам кривых. Нам пришлось поступить таким
образом, поскольку теперь распределение Sn не является
гладким, как в предыдущем случае, а содержит много значений Sat,
близких к нулю, связанных с вкладами малых конечных
кластеров. Из-за этого величина а в этом случае очень велика.
Например, для N = 4000 шагов:
случай (a) SN = 189,8 or = 114,0, (8)
случай (б) SN = 249,8 or = 81,7. (9)
На рис. 3 показан график зависимости In R2N от In N для
двумерного блуждания. Из наклона кривой определяем значение
показателя D':
D' = 2,89 ±0,05. (10)
Погрешность и в этом случае вычислена графически по рис. 3,
значение D находится в хорошем согласии с полученным ранее
для малых N (N = 300 шагов) [8].
На рис. 4 показана зависимость эффективного значения
показателя ds от концентрации р для двумерной и трехмерной
решеток. Точки вычислены по наклонам кривых на рис. 1 и 2 в
пределе больших времен (N = 200 000). Видно, что переход к
евклидову поведению и в двумерном, и в трехмерном случаях
происходит при концентрациях, достаточно близких к
критической. В двумерном случае ожидаемое значение ds = 2 не
достигается из-за наличия логарифмических поправок. Из вида
кривых на рис. 4 можно заключить, что скейлинг справедлив
только в узкой области, где кривые имеют большую производную,
т. е. при концентрациях 0,31—0,35 в трехмерном и 0,59—0,65 в
двумерном случае. Этот вывод подтвержден в работе [6].
Подводя итоги, отметим, что вычисленные нами двумя
различными способами с помощью очень точных алгоритмов
значения ds хорошо согласуются с предсказанием Аарони и Штауф-
V10[
ию5
**
1-Ю4'
U10
f-10'
1
•JOG
Рис. З. Среднеквадратичное смещение R2N как функция числа шагов N для
тех же значений р, что и на рис. 1 (двумерный случай).
/ifUU-
1,60-
ds -
1tZ0-
оло
о
- О
о
- о
о
О
О
—t—
о
О
—+-
О
„о©0
о
о
о
о
о
8
0
!
о
о
о
~ч
0,25
0,50
0,75
Ш
Рис. 4. Эффективное значение ds как функция концентрации для двумерных
(нижняя кривая) и трехмерных (верхняя кривая) решеток.
518
Часть VII
фера [9], т. е. полученное для двумерных решеток значение ds
немного (примерно на 2'%) ниже, чем предполагавшееся
значение ds — 4/3. Двумя различными способами получены оценки
погрешностей этих величин ±0,02. Значение показателя
диффузии Z)', определенное в пределе больших времен, совпало с
ожидаемым.
ЛИТЕРАТУРА
1. Blutnen A, Klafter /., White B.f Zumofen /., Phys. Rev. Lett., 53, 1301
(1984).
2. Pandey R. #., Stauffer £>., Margolina Л., Zabolitzky J. G., J. Stat. Phys.,
34, 427 (1984).
3. Havlin S., Ben-Avraham ZX, Sompolinsky #., Phys. Rev., A27, 1730 (1983).
4. Webman /., Phys. Rev. Lett., 52, 220 (1984).
5. Kopelman /?., Klymko P. W., Newhouse L S., Anacker L. W., Phys. Rev.,
B29, 3747 (1984).
6. Argyrakis P., Kopelman R., J. Chem. Phys., 81, 1015 (1984); J. Chetn.
Phys., в печати.
7. Keramiotis A., Argyrakis P., Kopelman #., Phys. Rev., B31, 4617 (1985).
8. Ben-Avraham D., Havlin 5, J. Phys., A15, L691 (1982); J. Phys., A15, L311
(1982).
9. Aharony A., Stauffer D.t Phys. Rev. Lett., 52, 2368 (1984).
Иерархические фрактальные
графы и блуждания на них
Дж. Мелроуз *
На иерархических решетках очень легко проводятся ренормализа-
ционные преобразования. Дано краткое обсуждение структуры
иерархий. Приведены результаты для блужданий без
самопересечений и случайных блужданий на иерархиях: ограничение на
термический показатель в модели Изинга, накладываемое значением
показателя для блужданий без самопересечений, сходимость этих
показателей при D-^oo, доказательство фрактального соотношения
Эйнштейна для простого класса иерархий. Особое внимание
уделяется объяснению свойств и аномалий блужданий на таких
решетках, связанных с их иерархической структурой. Приведены
результаты моделирования случайных блужданий на иерархиях
Мигдала — Каданова методом Монте-Карло.
1. Введение
Самоподобные иерархические решетки [1, 2] обладают
конечной разветвленностью по отношению к узлам, n-e, n + 1-е
и т. д. поколения этих решеток, получаемых итеративной
процедурой, мы будем называть соответственно я-й, п + 1-й и т. д.
единицами. Узлы, лежащие на поверхности единиц и связывающие
несколько т-х единиц в одну я-ю (п > т) единицу, мы будем
называть соединениями. По определению иерархии число g
соединений является постоянной, не зависящей от т величиной;
для такой системы может быть проделана точная процедура
перенормировки в конечном пространстве параметров (пример:
треугольная кривая Серпинского — иерархия с тремя
соединениями). Иерархии связей [3] имеют два соединения и получаются
декорированием связей. Этот простейший класс иерархий и
будет рассмотрен ниже. На рис. 1 показана единица с п ~4
иерархии связей Мигдала — Каданова (алмазной иерархии).
В литературе можно найти много других примеров иерархий
[10]. На этих решетках исследовано много различных
физических задач [10]. Анализ поведения случайных блужданий на
фракталах выявил их аномальный характер. В настоящей
работе после некоторых общих замечаний о структуре иерархий
представлены результаты для блужданий на иерархиях.
Иерархии могут иметь бесконечную разветвленность по
отношению к связям. Следовательно, на них могут иметь место
фазовые переходы с Тс >> 0. Используя внутреннюю метрику,
Мелроуз [4, 5] определил внутреннюю размерность D и
связность Q иерархий связей: D = lng"/ln 6, где g— число связей и
* John Melrose-Department of Chemistry, Royal Holloway and Bedford
New College, University of London, Egham, Surrey, TW20 OEX, UK.
520
Часть VII
b — кратчайшее расстояние между соединениями в единице с
п= I. Величина D характеризует, как число связей в /г-й
единице gn растет с ростом линейного масштаба Ьп (в примере на
рис. 1 g = 4, 6 = 2).
За бесконечную разветвленность по отношению к связям при
конечной разветвленности по отношению к узлам приходится
платить наличием бесконечного
ряда координационных чисел
узлов (см. рис. 1). Таким же
свойством обладают решетки,
дуальные к хорошо известным
фрактальным решеткам [5]. Пусть
w — координационное число
соединений в единице с п = 1 (на
рис. 1 w = 2). Тогда в m-й
единице будут два соединения с
координационным числом wm и узлы
с координационными числами
kiW\ где 0 < i < m — 1, a kt не
зависит от m и равно числу
узлов, не являющихся
соединениями, в первой единице. Узел с
координационным числом ktwp мы
будем называть узлом р-го
порядка. Узел р-го порядка окружен
kt р-ми единицами, kiw р—1-ми
единицами и т. д. Структура,
окружающая такой узел,
фиксирована вплоть до расстояния Ьр.
На больших расстояниях эта
структура различна для
различных узлов р-го порядка и зависит от положения узла внутри
больших единиц.
Рис.
2. Блуждания без самопересечений
Автор исследовал поведение показателя длины блужданий
без самопересечений (ББС) vBBC на нескольких иерархиях
связей и обнаружил, что собственное значение Xs, соответствующее
фиксированной точке ББС, vBBC = In й/ln Xs является верхней
границей для термического показателя %t в модели Изинга.
Более того, при рассмотрении семейства иерархий со все
увеличивающимися значениями D было обнаружено, что Xs и Xt
сходятся при £)->оо, если только при этом также Q->oo. Тем не
менее показатель vBBC не сходится к показателю vCB, характе-
Динамические свойства структур
521
ризующему обычные случайные блуждания (см. ниже), как это
имеет место на евклидовых решетках.
Тот факт, что показатели v для обычных случайных
блужданий и ББС на иерархических решетках в пределе D->oo не
равны друг другу, можно понять, рассмотрев структуру таких ре-
шеток. Рассмотрим узел с большим координационным числом,
лежащий на поверхности большой единицы. С точки зрения
обычных блужданий этот узел аналогичен поверхности большой
«единицы» — куска обычной решетки, содержащей много узлов
и связей. С точки зрения же ББС поверхность, состоящая из
одного узла, накладывает сильные ограничения на блуждание и
сильно отличается от поверхности единицы обычной решетки,
3. Случайные блуждания
На иерархиях связей легко может быть проделана процедура
перенормировки производящей функции блужданий [6].
Рекуррентные соотношения для весового параметра ансамбля z дают
производящие функции для первого прохода через первую
ячейку. Собственное значение %г в фиксированной точке z* = 1 дает
ожидание числа шагов Х™у необходимых блужданию,
начинающемуся на одном соединении m-й единицы, чтобы достичь ее
другого соединения. Перенормировка случайного блуждания
эквивалентна [6] перенормировке гауссовской модели [8] и
гармонических уравнений движения, в которых узлам соответствуют
члены (т. е. массы), перенормирующиеся как их
координационное число. С помощью матричной алгебры можно доказать [6],
что для рассматриваемого класса иерархий связей справедливо
фрактальное соотношение Эйнштейна [7]
К = ёК, (1)
где Хг — собственное значение, описывающее скейлинг
сопротивления.
На фрактальных решетках вводится спектральная
размерность [8, 9] F = 2DvCB, где vCB = In (\)/ln (6). На фракталах
число узлов A(N), попавших в область пространства размером
порядка среднеквадратичного смещения блуждающей частицы
за N шагов R(N), удовлетворяет соотношению [9] A(N) ~
~ R(N)D = NFt2. Число различных узлов, посещенных
блужданием за N шагов, S{N), ведет себя как S(M) ~ A (N) при F < 2
и как S(N) ~ N при F > 2. Однако в случае, когда узлы имеют
бесконечный набор координационных чисел, внутренняя
размерность D, определенная выше, не характеризует рост числа узлов
иерархии вокруг данного узла с ростом пространственного
масштаба [5], и соотношение A (N) ~ NF/2 не выполняется.
522
Часть VII
Автор исследовал случайные блуждания на иерахии,
показанной на рис. 1 с помощью метода Монте-Карло. Иерархии
Мигдала — Каданова имеют линейную природу, позволяющую
легко занумеровать узлы по слоям, что упрощает вычисления.
На рис. 2 показана зависимость In S (N) от InN для блужданий,
начинающихся на узле высокого порядка. S(N) получалось
усреднением по 103 блужданий из 103 шагов. Для N > 50 этот
график выходит на прямую линию, усреднение наклона по 10
таким графикам дало S(N) ~
~ЛГ0, в = 0,866 ±0,001. Мы
также рассмотрели случайные
блуждания, начинающиеся на
узлах нулевого порядка.
Усреднение наклона линейного
участка для 10 различных
узлов дало 0 = 0,856 ± 0,002.
Поскольку в нашем случае F = 2,
соотношение 5 (N) ~ NF/2 не
имеет места. (Исследования
поведения блужданий на ие-
in (ло °'и рархиях Мигдала — Каданова
Рис 2. с большими значениями
множественности М (на рис. 1
М = 2) показали, что Q-+1 при М, D-+oo.) Статистика
возвратов блуждания к начальной точке также имеет для
иерархических решеток аномальный характер. Если блуждание
начинается на узле р-го порядка, с помощью ренормгруппы можно
получить производящую функцию для блужданий, возвращающихся
не позднее чем за Ьр шагов (т. е. не проходящих через другие
соединения окружающих р-х единиц). Рассмотрение блужданий,
возвращающихся после более чем Ьр шагов, требует учета
различных возможностей расположения начального узла в более
крупной единице, как это уже обсуждалось в разд. 1.
Линейная структура объекта на рис. 1 приводит к тому, что
статистика возвратов к начальному узлу р-го порядка
блужданий длиной не более чем в Ьр шагов такова же, как и в
одномерной решетке. Для блужданий, которые возвращаются через
более чем Ьр шагов, простые эвристические аргументы
подсказывают, что эта вероятность пропорциональна N~F/2. Этот
результат подтвержден методом Монте-Карло. Построенный в
двойном логарифмическом масштабе график зависимости
вероятности возврата через N шагов от N для блужданий,
начинающихся на узлах 0-го порядка для иерархии, показанной на рис. 1
(f = 2), имеет наклон —0,95 + 0,06 (статистика набиралась по
102 начальным точкам и (3~4)-103 блужданиям из 200
шагов).
5,0 И
ЬО
I I I i > I 1 •
I * I
I * I
Г •• 1
I « I
I * I
I * I
Г* • I
I * I
I • ^
I * 1
I * I
I * i
I * I
Г" • \
i • I
I * 1
1 • 1
г- • "Л
Динамические свойства структур
523
4. Выводы
Показано, что блуждания на иерархических решетках с
бесконечным набором значений координационных чисел узлов
имеют еще более аномальное поведение, чем блуждания на
фрактальных решетках, не обладающих этим свойством.
Благодарность. Автор благодарит S.E.R.C. за
предоставленную стипендию.
ЛИТЕРАТУРА
1. Berker A. N.t Ostlund 5., J. Phys, C12, 4961 (1979).
2. Griffiths R. В., Phys Rev, B25, 5022 (1982), см. также работу [10] и
ссылки в этой работе.
3. Melrose /. R.f J. Phys, A18, L17 (1985).
4. Melrose J. R., J. Phys, A16, 3077 (1983).
5. Melrose J. R., J. Phys., A16, L407 (1983).
6. Melrose /. R.t J. Phys, A18, 3407 (1985).
7. Given /. Л, Mandelbrot В. В., J. Phys, A16, L565 (1983).
8. Dhar Z), J. Math. Phys, 18, 577 (1977).
9. Rammal R., Toulouse G.t J. Phys. (Paris) Lett, 44, L13 (1983).
10. Griffiths R. B.y Kaufman M.y Phys. Rev, B30, 244 (1984).
Динамика экситонов,
напоминающая фрактальную:
геометрический и энергетический беспорядок
Р. Копельман*
Кинетика возбуждений, напоминающая фрактальную, наблюдалась
в образцах нафталина со сложными геометрическими
ограничениями. Исследованы системы: 1) нафталин в каналах пористого
стекла викор или пористых полимерных (например, нейлоновых)
мембран; 2) границы зерен в свежеприготовленных и подвергнутых
старению пленках нафталина при Т = б К. Пленки были получены
быстрым осаждением из пара при низкой температуре; 3)
нафталин, заключенный в полостях полимерного стекла (например,
плексигласа). Аномальная кинетика возбуждений описывается
значениями эффективной спектральной размерности, лежащими между
1 и 2. Получены оценки относительных вкладов влияния
геометрических ограничений и энергетического беспорядка.
1. Введение
Кинетика экситонов, напоминающая фрактальную,
четко наблюдается в изотопических сплавах нафталина [1, 2].
Перенос экситонов здесь ограничен перколяционными кластерами
компоненты с более низкой энергией уровня (молекулы
нафталина) в бинарном сплаве. В этом случае энергетические
ограничения приводят к появлению фрактального пространства (пер-
коляционный кластер на пороге протекания) с хорошо
определенным фрактальным показателем случайных блужданий [3],
который на практике дается значением фрактонной
(спектральной) размерности [4, 5], равным 4/3 (с поправками на наличие
конечных кластеров [6—9]). В то время как эксперименты по
стационарному переносу [10, 11] в основном связаны с
характеристиками, описываемыми фрактальной размерностью df (т. е.
перколяционными критическими показателями (3, у и б),
кинетика аннигиляции экситонов связана в основном со
спектральной размерностью ds [1, 12, 13]. Еще раз подчеркнем, что
простой спектр энергий возбуждений (с двумя резкими пиками)
в таких сплавах и наличие идеальной кристаллической решетки
(если отвлечься от беспорядка замещения) позволяют
заключить, что кинетика аннигиляции, напоминающая фрактальную,
действительно отражает наличие фрактальной геометрии
(случайных кластеров). Мы покажем, как можно использовать
значение эффективной спектральной размерности, полученной из
кинетики аннигиляции экситонов, для того чтобы охарактеризо-
* Raoul Kopelman-Department of Chemistry, The University of Michigan,
Ann Arbor, Michigan 48109.
Динамические свойства структур
52S
вать неоднородность образцов, скажем, их пористость или
наличие межзеренных границ. Мы покажем также, как можно
разделить вклады геометрической и энергетической неоднородности.
2. Методы и материалы
Мы исследовали аннигиляцию триплетных экситонов в
агрегатах нафталина, находящихся в порах различных мембран или
X
_„.„__ I I
""Ч# -3,0 -2,0 "'-4,0 -3,0 -2,0
Логарифм времени Логарифм времени
Рис. 1. Зависимость коэффициента скорости реакции k = F/P2 от времени в
двойном логарифмическом масштабе для свежеприготовленной (слева) и
подвергнутой старению (справа) пленки нафталина, полученной осаждением из
пара при Т = 50 К. Температура пленки 6 К. Наклон h равен 0,44 у левой
и 0,45 у правой кривой (см. табл. 1).
стекла викор, полостях полимерных стекол или на границах
зерен. Общим свойством этих систем является неклассическая,
напоминающая фрактальную кинетика аннигиляции. Коэффициент
скорости аннигиляции k не постоянен, а зависит от времени: k ~
~' t~h, где h—показатель неоднородности (0<А<1),
обращающийся в нуль только для однородных образцов; поведение
при этом возвращается к классическому: k = const.
Эффективная спектральная размерность среды дается соотношением
rf^ = 2(1 — /г). Мы провели также измерение зависимости h от
температуры.
Коэффициент скорости реакции k определяется из данных по
временному ходу затухания флуоресценции (F) и
фосфоресценции (Р) [1, 16]; k ~ F/P2 (величину k можно получить, зная
лишь одну из величин F или Р как функцию времени [12, 16]).
Примеры полученных результатов показаны на рис. 1. В табл. 1
приведены значения показателей неоднородности h и
эффективной спектральной размерности drs для различных образцов при
разных температурах.
и,и \
3
| -щ
3
| -щ
I
_«»/iL.
_f<?/l
626
Часть VII
3. Результаты и обсуждения
Из табл. 1 мы видим, что при низких температурах все
образцы демонстрируют похожее на фрактальное (неоднородное)
поведение: h > 0. С ростом температуры величина h
уменьшается. Это соответствует теореме о субординации [14]: d's = $ds, где
Таблица 1
Материал
Ацетат А8
Ацетат А1
Ацетат A3
Нейлон В214
Пористое стекло викор
Плексиглас (РММА)
Пленка (границы зерен)
Стекло — фильтровальная бумага
Стекло — фильтровальная бумага
Бумага — фильтровальная бумага
Бумага — фильтровальная бумага
Размер
пор,
мкм
0,2
0,5
1,2
0,2
0,04
?
— __ __ __
0,6
0,6
0,6
0,6
т, к
4
4
4
4
6
77
6
6
80
6
80
Показатель
h
0,16
0,47
0,44
0,21
0,44
0,1
0,45
0,50
0,20
0,33
0,06
Спектральная
размерность
*S
1,2—1,7
0,8-1,1
0,9-1,1
1,2-1,6
U
1,8
1,1
0,6-1,2
1,2-1,6
0,8-1,3
1,9
Р — параметр, характеризующий распределение времен
прыжков (например, для случайных блужданий с непрерывным
временем). Мы видим также, что в некоторых образцах с
повышением температуры h->0. Это означает, что все фракталоподоб-
ные эффекты связаны с энергетическим беспорядком, так как
при) повышении температуры параметр W, характеризующий
беспорядок, становится малым в сравнении с Г. В других
образцах эффективная геометрия остается фрактальной и при
комнатной температуре. Очевидно, наше значение дает только
оценку снизу для реальной (геометрической) ds. Заметим, что
для пористого стекла викор при низких температурах d£~l,l,
что согласуется с известными из литературы [15] значениями
df ^ 2 (напомним, что для фракталов ds ^df ^ d, где d —
размерность евклидова пространства, в котором находится
система). Подчеркнем, что во всех этих системах, особенно в тонких
пленках, большая часть объема может иметь кристаллическую
структуру (т. е. является евклидовой), но большие времена
наблюдения приводят к тому, что мы видим только наиболее
медленную кинетику затухания, соответствующую фрактальным
областям.
Динамические свойства структур
527
У мембран с более крупными порами при более высоких
температурах мы наблюдаем такое же поведение, как и у
осажденных пленок, — никакой замедленной флуоресценции намил-
лисекундных масштабах времен. Мы обнаружили прекрасную
корреляцию между фрактальной кинетикой и следующим
набором спектроскопических характеристик: 1) шириной
спектральных линий W] 2) свечением суперловушек (бета-метилнафта-
лин); 3) свечением типичных продуктов фотофизических реакций
(эксимеров); 4) свечением типичных продуктов фотохимических
реакций (радикалов).
Мы четко установили наличие корреляции между
фрактальной кинетикой аннигиляции экситонов и геометрическими
ограничениями и/или энергетическим беспорядком во многих
образцах чистого нафталина. Было обнаружено поведение,
аналогичное поведению изотопических смесей нафталина (связанному в
них с наличием перколяционных кластеров) и существенно
отличающееся от поведения идеальных кристаллов чистого
нафталина. Целью дальнейших работ является разделение вкладов
фрактальной геометрии и энергетического беспорядка (т. е.
фракталоподобного поведения из-за фрактальной структуры
поверхностей постоянной потенциальной энергии или
«фрактального» распределения времен перескока возбуждения).
Благодарности. Экспериментальные результаты были
получены Л. Хармоном, С. Парусом, Дж. Прашадом и Е. Ньюхау-
зом.
ЛИТЕРАТУРА
1. Klymko P. W.} Kopelman R., J. Phys. Chem., 87, 4565 "(1983).
2. Evesque P., Duran /., J. Chem. Phys., 80, 3016 (1984).
3. Aharony Л., Stauffer D., Phys. Rev. Lett., 52, 2368 (1984).
4. Alexander S., Orbach #., J. Phys. (Paris) Lett., 43, L625 (1982).
5. Rammal R.t Toulouse G.y J. Phys. (Paris) Lett., 44, L13, (1983).
6. de Gennes P. G., С R. Acad. Sci., A296, 831 (1983).
7. Ben-Avraham ZX, Havlin S., J. Phys., A15, L691 (1982).
8. Webman /., Phys. Rev. Lett., 42, 220 (1984).
9. Argyrakis P., Kopelman #., Phys. Rev., B29, 511 (1984).
10. Ahlgren D. C, Ph. D. Thesis, University of Michigan, 1979.
11. Newhouse /. $., Ph. D. Thesis, University of Michigan, 1985.
12. Kopelman R., Klymko P. W., Newhouse J. S., Anacker L. W., Phys. Rev.,
B29, 3747 (1984).
13. Anacker L. W., Kopelman #., J. Chem. Phys., 81, 6402 (1984).
14. Klafter /., Blumen A., Zumofen G., J. Stat. Phys., 35, 561 (1984).
15. Even U., Rademann K, Jortner /., Manor N., Reisfeld R., Phys. Rev. Lett.,
52, 2164 (1984).
16. Harmon L. A., Pht D. Thesis, University of Michigan, 1985.
Найквистовский, диффузионный
и фликкер-шум (1//-шум)
в фрактальных системах
и перколяционных сетках
Р. Раммал *
Изложены недавно полученные результаты для мощности найкви-
стовского и фликкер-шума (l/f-шума) в фрактальных случайных
сетках сопротивлений. Результаты, относящиеся к континуальной
модели протекания, сравниваются с экспериментальными данными,
полученными для смесей металл-изолятор.
1. Введение
Важнейшим для понимания поведения неупорядоченных
систем понятием является понятие статистического самоподобия.
Для описания, например, различных физических свойств
перколяционных сеток введены понятия фрактальной размерности,
спектральной размерности и размерности распространения.
Интуитивно ясно, что для того чтобы охарактеризовать фрактал,
может понадобиться бесконечное число показателей. Недавно
было показано, что это действительно так: величина (но не
частотная зависимость) шума, вызванного флуктуациями
сопротивления (l/f-шума, или фликкер-шума), связана с новым
показателем, характеризующим фрактальные решетки. Этот
показатель Ь можно рассматривать как один из членов бесконечного
семейства показателей, включающего фрактальную и
спектральную размерности. Подробное рассмотрение соображений
относительно фликкер-шума во фракталах и в перколяционных сетках
дано в работах [1—5]. Поэтому в дальнейшем мы ограничимся
рассмотрением двух задач, для которых имеются
экспериментальные результаты: 1) тепловой (найквистовский) шум во
фрактальной перколяционной сетке и 2) фликкер-шум в
континуальных моделях перколяции.
2. Найквистовский шум
2.1. Общие соображения
Будут рассмотрены два типа шума в макроскопических
образцах: тепловой или найквистовский шум, не зависящий от
плотности тока в образце, и фликкер-шум, интенсивность
которого пропорциональна квадрату плотности тока. Для модели-
* Rammal Rammal- Centre de recherches sur les Tres Basses Temporal
tins, C. N. R. S., B. P. 166 X, 38042 Grenoble Cedex, France,
Динамические свойства структур
529
рования шума в этих случаях рассматриваются соответственно
микроскопические флуктуации локальных напряжений или
локального сопротивления. В данном разделе мы рассмотрим
только найквистовский шум. Предположение о справедливости
и для фрактальных сеток сопротивлений флуктуационно-дисси-
пационной теоремы приводит к следующему выражению для
спектральной плотности разности потенциалов V на образце:
2
= 2kBT/Q(L, со).
Здесь G(Ly S) означает действительную часть удельной
электропроводности на линейном масштабе L и на частоте со. Тот факт,
что 5у(со) ведет себя как величина, обратная G(L, со), может
быть подтвержден следующим рассуждением. Предположим, что
в каждой ветви а цепи, содержащей резистор га, имеется
включенный последовательно с этим резистором генератор
случайного напряжения Va{t). Будем считать, что все эти генераторы
создают шум с одинаковой стационарной спектральной
плотностью s(со). Не представляет труда вывести следующие
комбинационные правила для флуктуации напряжения:
при последовательном включении s = Zj sa, r=Y* ra>
а а
при параллельном включении s = J] sa (r/ra)2t г""1 = £ Га1.
а а
Если все га и sa одинаковы, то 5 ведет себя так же, как
полное сопротивление. Интересно сравнить эти правила с теми, что
получены в работе [1] для модели с флуктуациями
сопротивления.
2.2. Модель
В дальнейшем мы будем рассматривать типичную модель
сетки сопротивлений, эквивалентную задаче о диффузии на той
же структуре. Узлы заданной решетки, являющиеся
ближайшими соседями, соединим проводниками, каждый из которых
имеет чисто активное сопротивление /?. Каждый не соединенный
с электродами узел, соединен с землей через цепочку,
состоящую из емкости С и ЭДС I/x-eto'. ЭДС на электродах равна
внешнему потенциалу. Шум вводится в систему следующим
образом [6]. В каждом проводнике, соединяющем соседние узлы k
и /, появляется случайная компонента тока (генерируемая
тепловыми флуктуациями) Jki(t) с равным нулю средним значе-
Sv (со) = lim -д-
е-»оо °
ei<dtV(t)dt
530
Часть VII
нием и с корреляционной функцией
2k Т
</«(0/«О=-^-б(^-п,
где Т — температура. Основное уравнение для такой сетки
получается из закона сохранения заряда Qt на узле /:
Здесь Vi — напряжение на узле i; Qt = C(Vi— Ut).
2.3. Евклидовы решетки
Рассмотрим сначала случай евклидовой решетки с линейным
размером L, содержащей Ld узлов. О флуктуациях токов будем
предполагать, что они имеют спектры типа белого шума и не
коррелированы в пространстве. К сетке присоединены два
больших плоских электрода, перпендикулярных оси х и
находящихся на расстоянии L друг от друга. Спектр мощности шума
измеряется между этими электродами. В этом случае для
величины 5у(со) = Р(ы) легко получить результат:
2k T
Здесь /(со) = (2D/co)1/2 обозначает диффузионную длину, D =
= a2/RC — коэффициент диффузии; а — постоянная решетки,
G(L) —макроскопическая проводимость сетки на частоте со =0.
Этот результат можно записать также в форме F((x>) =
= (A/DLd-2)ty(l(ti)) /L), где Л — постоянная, а г|) — скейлинговая
функция, удовлетворяющая условиям ф(и<с1)~£г и ф(а^>
^> 1) —' 1. В пределе низких частот в этом случае
воспроизводится результат Найквиста: F((d) не зависит от со. На частоте
со = o)D ss o)o(a/L)2, где о)о = 1/#С, осуществляется переход к
диффузионному режиму. Физический смысл различных
режимов следующий:
а) со <С сод. В этом пределе флуктуации во всем образце
становятся коррелированными. Пространственно-временная
корреляционная функция У (г, t) не зависит от о;
б) cod <С со <С со0: /(со) > L. Флуктуации коррелированы лишь
в областях с линейным размером /(со). Вклад в F(co) в этом
случае могут дать только два тонких слоя толщиной /((о),
прилегающих к электродам. В полученном для предыдущего случая
выражении Ld~2 следует заменить проводимостью внешних
областей Ld~l/l((u), откуда следует результат, приведенный выше;
в) о) ^> (оп. На очень высоких частотах, когда /(со) <С я,
конденсатор накоротко соединяет узел с землей. По аналогии со
Динамические свойства структур
531
случаем "б" Ld~2 надо заменить на Ld~x/a. F(co) приобретает
вид
Необходимо отметить, что аргументы, использованные в случаях
„б" и „в", можно использовать и в том случае, когда вместо
плоских электродов используются точечные. Соответствующие
результаты для этого случая записываются без затруднений.
2.4. Фрактальные сетки
Рассмотрим теперь случай фрактальной сетки, на которой
и в отсутствие всякого беспорядка имеет место аномальная
диффузия. Показатель vCB, характеризующий эту диффузию, дается
отношением й/2й спектральной 3 и фрактальной d размерностей
[7, 8]. Зависимость удельной проводимости образца от его
размера L дается соотношением G(L)~L?L, где PL = d+l/vcB.
Используя те же рассуждения, что и в предыдущем случае, мы
придем к выводу, что скейлинговая форма F((u) определяется
скейлинговыми свойствами функции G(L, со):
а) на очень низких частотах, когда /(со) ^> L (где /(со) ~ co-vC
обозначает диффузионную длину), имеет место режим нулевой
частоты, и F (со) ~ kBTL~^L. В этом пределе со < со^ = со0 (a/L)1/VCB
и пространственно-временная корреляционная функция
напряжения становится независимой от частоты, в противоречии с
неверным утверждением, сделанным в работе [9]. Этот результат
совершенно не зависит от геометрических свойств контакта
электрода с образцом;
б) a<i((o)CL. Предполагая, что контакты электродов с
образцом точечные (две точки на расстоянии L), получаем, что
F((d) дается тем же выражением, что и в предыдущем случае, с
заменой L на /(со): F(со) ~ kBT (/(co)~Pl ~ (o~1+rf/2 (d < 2). В этом
пределе вклад в ^(со) дают только две области с линейным
размером /(со) вокруг контактов;
в) /(со) <С а. Как и в случае „б", зависимость от L
определяется геометрией контактов, зависимость же от частоты будет
такой же, как и для евклидовой решетки: F(cd) ~ (coo/со)2.
Следует заметить, что вне области частот, соответствующей
статическому пределу со <С ®d, зависимость ^(со) от размера системы
определяется скейлинговой формой проводимости, в нашем
случае G(L, со) = L?Lf Г—^- J , и формой контактов. Поэтому
проделанный нами анализ может быть обобщен на более сложные
сетки с произвольными импедансами в ветвях цепи [10].
S32
Часть VH
2.5. Перколяционные сетки
Обратимся к случаю перколяционных сеток при Др = р—
— рс ^ь 0. В этом случае существенны четыре масштаба длины:
постоянная решетки а, диффузионная длина /(со), перколяцион-
ная корреляционная длина lp = a(Ap)~vp и линейный размер
образца L. В соответствии со значением отношения \PjL можно
выделить различные режимы.
а) Случай \р «С L. Образец можно рассматривать как
евклидову решетку, каждая элементарная ячейка которой содержит
ld узлов. Таким образом, а->£р, co^cd* = cd£*/vcb, a
перенормированная диффузионная длина становится равной /*(со) ~
с g,cD*-i/2. Здесь vCB = vp/(t + 2vp - рр).
I. /*(со)»|р. В этом пределе надо различать два случая.
Первый соответствует /* (со)» L >> £р, т. е. низкочастотному
режиму на евклидовой решетке. В этом случае
F (о) = —г-4 Р (р) ^т (Ар)2^"'.
v ' Ld-2D{p) УН Ld~2 и/
о
Здесь Р (р) ~ (Ар) р означает вероятность того, что данный узел
принадлежит бесконечному кластеру, a D(p) ~ а2а>0(Др)'~рр есть
коэффициент диффузии. Второй случай соответствует обратному
соотношению gp << /*(со) <С L. Тогда
*И- ,а-2
ЛР(р) t Г (со)
Ld"2£) (p) ^
II. /*(со)<С £Р. С помощью приведенных выше результатов
нетрудно получить, что
\2 6Р Р (Р)
Ld~2D (p)
Обратим внимание, что вблизи рс высокочастотный шум,
пропорциональный со~1/2, наблюдается, начиная с частоты, для
которой о)*/соо ас |р, т. е. для частот со ^ со0 {a/L)2 (Др)'-1Ч а не
(о0/(a/L)2, как было бы для идеальной сетки (р = 1). Мощность
этого избыточного высокочастотного шума следует сравнить с
экспериментальными данными. Физическая причина его
появления связана с перенормировкой коэффициента диффузии
D(p > pc)/D(p= 1) = (Др)*~рр из-за наличия беспорядка.
б) Случай gp » L. Очень близко к рс корреляционная длина
1Р становится больше, чем L. В этом пределе начинает
сказываться фрактальная структура бесконечного кластера.
Выражение для F((o) следует из результатов предыдущего раздела.
Динамические свойства структур
533
3. Фликкер-шум
3.1. Модель флуктуации сопротивления
Фликкер-шум во фрактальных или случайных сетках можно
описать в рамках модели флуктуирующих сопротивлений [1—б].
В этой модели считается, что сопротивление каждой ветви а
цепи имеет малую флуктуирующую часть 6ra(t). Эти 8га
считаются зависящими от времени некоррелированными
случайными величинами с равным нулю средним значением. Фурье-
образ их ковариации равен ^бга(со)бГр(—со)^ = барр2 (со).
Механизмы, порождающие эти флуктуации, могут быть самыми
различными. Предполагая, что ра(<о) одинакова во всех ветвях
цепи, можно определить относительную величину шума в сетке:
Sr/R2 = (8R8R)/R2. Здесь R и 8R— это соответственно полное
сопротивление и его временная флуктуация, измеренные по од-
ноканальной схеме. Определенная таким образом Sr
характеризует величину l/f-шума при постоянном внешнем токе. Если
флуктуации сопротивления в каждой из ветвей независимы и
имеют одинаковый спектр, вопроса о частотной зависимости не
возникает.
Для фрактальной сетки сопротивлений с линейным размером
(L > 1) было показано, что Sr ведет себя по степенному
закону: SR~L~b, где Ь — новый показатель, характеризующий
фрактальную структуру. Оба показателя (Ь и |3l) связаны с
моментами распределения токов {ia} в сетке:
*~Z#~i"4 sR~Z&~irb (-р* <*<<*)•
а а
В приложении к перколяционным сеткам это означает, что
вблизи рс и Ry и относительная величина шума расходятся, но эти
расходимости описываются различными показателями.
Вычисления Ь с помощью различных методов представлены в работах
[1-5].
3.2. Экспериментальные результаты
Недавно были проведены очень аккуратные исследования
1//-шума вблизи рс в смесях угля с воском [11]. Вблизи рс как
сопротивление /?, так и спектральная плотность шума Sr
расходятся в соответствии со сделанными выше предположениями.
Измеренные значения показателей t и к (R~ {&р)~* и Sr/R2 ~
~ (Др)"~н) равны t = 2,3 ± 0,4 и %. = 5 ± 1. Исследование
зависимости Sr от R показывает, что Sr ~ RQ, где Q ^= 2 + %jt =
= 3,7 ±0,2 есть показатель, определяющий зависимость шума
от сопротивления. Аналогичные измерения для двумерных
пленок были проведены двумя другими группами исследователей
[12, 13]. На островковых пленках серебра [12], полученных оса-
534
Часть VII
ждением паров и подвергнутых ионному травлению,
наблюдалось большое значение Q = 4. Еще большие значения (5,4 ^
^Q^8,l) были получены [13] в металлических пленках (А1,
Cr, In), в которых часть металла удалялась при обработке
пескоструйным аппаратом. Эти значения t и к отличаются от
предсказываемых решеточной теорией перколяции. Эти отличия
должны быть приписаны существующим в континуальной теории
перколяции поправкам. Как будет показано ниже, трехмерные
данные являются, по-видимому, первым количественным
подтверждением континуальной теории перколяции.
3.3. Показатели для моделей континуальной перколяции
Прежде всего отметим, что измеренные в эксперименте
показатели лежат вне тех интервалов, которые можно получить для
них в решеточной теории протекания. Используя хорошо
известные неравенства для показателя Ь1~г Ъ = d — x/v = d — t(Q —
— 2)/v : —|3l ^ b ^ —2fiL— 1/v, нетрудно получить, что в
двумерном случае 2,82 < Q < 3,05 (при v =4/3, —pL = 0,973) и
в трехмерном случае 2,84 ^ Q ^ 2,85 (при v = 0,88, —Pl =
= 1,16). Здесь pL = d — 2 — t/vy d— размерность евклидова
пространства, v — показатель длины корреляции. Теория
эффективной среды дает для Q значение Qm = 3.
Как указывалось различными авторами [14—16], в отличие
от статических показателей, таких, как v, показатели /их,
описывающие перенос, могут различаться в решеточных и
континуальных моделях. Аналогом простейшей континуальной модели
будет решеточная модель, в которой распределение вероятностей
p(g) проводимости связи g имеет вид: p(g) = (1 — p)6(g)-\-
+ p-h(g). Здесь h(g) —некоторая нормированная функция.
Модели «швейцарского сыра» [14] —одна из возможных
реализаций системы с аномальным распределением h(g) :h(g) ~
~ ё~а(ы < 1) вблизи g — 0. Для этого класса моделей
показатель t{a) = v(d— 2) + 1/(1 — а) при O^a^l и t(a) =
= v(d—-2)+l при а ^ 0. Этот результат неявно содержится
в работе [15] и совпадает в пределе больших d с результатом
работы [16]. Простейший вывод этого результата основан на
следующем соображении. Проводимость g= (2j gT ^
резисторов с проводимостями {g/}, 1 ^ / < L, выбранными наудачу,
согласно распределению h(g), соединенных последовательно,
совпадает при g ~ 0 с min{gi}. Простое вычисление показывает
114], что g ~ L1/^-1) при 0 ^ а < 1 и g ~ Lrx при а ^ 0, и
приводит к тому, что —vPl равно 1/(1 — а) и 1 соответственно.
Заметим, что полученное таким образом значение t(a) отличается
от получаемого в приближении эффективной среды [16]
значения tm = t (а) — v{d — 2).
Динамические свойства структур
535
Вычисление х может быть проведено аналогично [4] с
использованием правила для последовательного соединения
генератора шума [1]: s=Yisi (g/ei)2- Для простоты мы будем
рассматривать модели типа швейцарского сыра и предполагать
[17], что £/~б" и Si~6Tv, где и = 1/(1—a), a v —
показатель, связывающий относительную величину шума Si связи I с
шириной 6/ перемычки /. В зависимости от и и v следует
выделить три различных случая: а) при и> 1 и v -\-2u> \ к —
= dv-\-v\ б) при и < 1, и+2«>>1 K = dv + (2u-{-v — 2) и
в) при и <. I, v ~\- 2и<. I к = dv — I. Эти значения %
отличаются от результатов приближения эффективной среды [17]: Qm =
= 2 + о/и при и > 1 и Qm = 3+ (v—l)/u при а < 1, которые,
по-видимому, справедливы вдали от рс [1—3].
В рамках моделей швейцарского сыра, в которых u = d —
— 3/2 и v = d— 1/2, получаем следующие результаты. При d =
= 2 (случай „б") t = tm = 1, и = 3,16, Km = 2 и Q = 5,16, Qm =
= 4. При d = 3 (случай „а") ^ = 2,38, fm=l,50, x = 5,14, xm =
= 2,5 и Q = 4,16, Qm = 3,67. Данные работы [11] хорошо
согласуются с этими оценками. Результаты работы [12], похоже,
совпадают с вычисленными в рамках метода эффективной среды
[17], результаты же работы [13] существенно превосходят
сделанные выше оценки. Обратим внимание, что во всех случаях
наблюдается увеличение Q по сравнению с решеточной моделью.
В двумерном случае требуется провести более подробные
исследования. Необходимо одновременное измерение обоих
показателей t и %. Кроме того, полезным было бы измерение SR при
различных температурах. Это позволило бы определить механизм
проводимости и микроскопическую причину наблюдаемого шума.
ЛИТЕРАТУРА
1. Ratnmal #., Tannous С, Tremblay А. М. S., Phys. Rev., A31, 2662 (1985).
2. Ratnmal R., J. Phys. (Paris) Lett., 46, L129 (1985).
3. Rammal /?., Tannous C, Breton P., Tremblay A. M. S., Phys. Rev. Lett.,
54, 1718 (1985).
4. Rammal R., Phys. Rev. Lett., 55, 1428 (1985).
5. Rammal R.y in: Physics of finely divided matter, Les Houches winter school,
ed. M. Daoud, Springer, Berlin, в печати.
6. Stephen M. /., J. Phys., Cll, L965 (1978).
7. Alexander S., Orbach R., J. Phys. (Paris) Lett., 43, 623 (1982).
8. Rammal Я., Toulouse G., J. Phys. (Paris) Lett., 44, L13 (1983).
9 Rammal R., J. Phys. (Paris) Lett., 45, L1007 (1984).
10. Luck J. M., J. Phys., A18, 2061 (1985).
11. Chen C. C, Chou Y. C, Phys. Rev. Lett., 54, 2529 (1985).
12. Koch #., Laibowitz R., Phys. Rev., В, в печати.
13. Garfunkel G.y Welssman M. В., Phys. Rev. Lett., 55, 296 (1985).
14. Halperin B. /., Feng S., Sen P. N., Phys. Rev. Lett., 54, 2391 (1985).
15. Ben-Mizrahi A, Bergman D. /., J. Phys., C14, 909 (1981).
16. Kogut P. M., Straley /. P., J. Phys. C12, 2151 (1979).
17. Tremblay A. M. S.y Feng 5., Breton P., Phys. Rev., B33, 2077 (1986).
Исследование электрических и шумовых
свойств перколяционных кластеров
методом ренормгруппы
в реальном пространстве
Дж. Лакк *
Электрические свойства перколяционных кластеров в пространстве
двух и трех измерений исследованы в рамках схемы
перенормировки в реальном пространстве Мигдала — Каданова. Этот метод
эквивалентен точному решению задачи протекания на некоторой
иерархической решетке. Кратко рассмотрены статические свойства
перколяционных кластеров на таких решетках. Исследовано
поведение комплексной проводимости смесей резисторов и
конденсаторов на этих решетках. Особое внимание уделяется критическому
поведению (при р->рс) и частотной зависимости угла потерь б,
величина которого может быть измерена для системы микрочастиц
в стеклянной матрице и для микроэмульсий. Изучено усиление
шума сопротивления (фликкер-, или l/jF-шум), имеющее место в
критической области. Показано, что это усиление при
концентрациях, близких к критической, и на низких частотах подчиняется
универсальным скейлинговым законам. Эти законы содержат два
новых критических показателя —- X и Y. Вычислены значения этих
показателей. Новые показатели X и У связаны с недавно
введенной Раммалом и др. шумовой размерностью Ь.
1. Введение
В работе представлены результаты вычислений
частотной зависимости проводимости на переменном токе и усиления
фликкер-шума в случайных сетках сопротивлений вблизи порога
протекания методом группы перенормировок в реальном
пространстве. План моего доклада совпадает с планом нашей
оригинальной статьи [1], к которой я и отсылаю читателя за
подробностями вычислений и полной библиографией. Двух- и
трехмерный случаи мы будем рассматривать параллельно.
2. Иерархические решетки и перколяция
В нашей работе мы воспользуемся приближением Мигдала —
Каданова. Эта схема перенормировки в реальном пространстве,
являющаяся приближенной для регулярных решеток (т. е.
решеток, инвариантных относительно некоторой группы трансляций),
становится точной (для неслучайных моделей) на некоторых
иерархических решетках, построение которых задается
рекурсивной процедурой. Способы построения решеток, которые мы бу-
* /. М. Luck-Servica de Physique Theoretique, CEN-Saclay, 91191 Gif-sur-
Yvette Cedex France.
Динамические свойства структур
537
дем использовать в случае двух и трех измерений, показаны на
рис. 1 и рис. 2 соответственно.
Статические свойства в задаче протекания по связям на этих
иерархических решетках определяются очень легко. Эти решетки
а о
Рис. 1. Рекурсивная процедура построения двумерной «алмазной»
иерархической решетки.
допускают точное ренормгрупповое преобразование Г,
действующее на вероятность р того, что данная связь является занятой:
решетка N-yo поколения с вероятностью р эквивалентна решетке
А А
В В
а 6
Рис. 2. То же, что на рис. 1, для трехмерной решетки.
N—1-го поколения с перенормированной вероятностью Т(р).
Преобразование Т имеет вид
Г2д(р)=1-(1-р2)2,
Гз/>(р)=1-(1-Р2)4-
(1а)
(16)
Отображение Т имеет две суперустойчивые фиксированные
точки р = 1 и р = 0, соответствующие фазам с наличием и
отсутствием протекания, и неустойчивую фиксированную точку рс,
соответствующую перколяционному порогу. Пусть р, = Т (рс) есть
производная Т в фиксированной точке. Можно показать, что
показатель длины корреляции v связан с \х следующим образом:
v = In 2/ln ц. (2)
Численные значения рс и показателей приведены в таблице в
конце доклада.
Atg 5 (двумерный.
Рис. 3. Зависимость tg6 от со/соо в двойном
логарифмическом масштабе для двумерной модели.
Значения р — рс указаны на кривых.
Atg 6 {трехмерный
случай)
Рис. 4. То же, что на рис. 3, для трехмерного»
случая.
Динамические свойства структур
539
3. Электропроводность на переменном токе
Рассмотрим следующую задачу: какова макроскопическая
проводимость 2 на переменном токе нашей решетки, если
каждая занятая связь представляет собой резистор (с импедансом
/?о), а каждая пустая связь — конденсатор (с импедансом
(шСо)-1). Такая задача моделирует широкий класс случайных
сред, таких, как порошки, микроэмульсии и т. д. Не вдаваясь
в детали, отметим, что эта задача слишком сложна и не может
быть решена в общем виде даже на иерархических решетках,
поскольку она сводится к нелинейному интегральному
уравнению для распределения вероятностей проводимости связей.
Необходимо упростить задачу. Критические свойства
проводимости 2(р, со) правильно описываются при сведении_полной задачи
к пятимерному действительному отображению Г. Здесь будут
представлены только результаты, относящиеся к критическому
режиму: р-+рс и со/со0->0, где ©0 = (RoC0)~l (проводимость 2
имеет очень похожие критические режимы при со <С оо0 и р-*рс
и при со ^> ооо и р->-1 —рс). Низкочастотный критический режим
характеризуется скейлинговой функцией ф±:
2 = Яо"11 р- рcU± (tofa>[Р-РсГ~0> (3)
где t и s — обычные показатели для статических задач
проводник— изолятор и нормальный проводник — сверхпроводник, а
индексы ± соответствуют знаку (р — рс). Проиллюстрируем
наши результаты более детальным рассмотрением поведения
угла потерь, определяемого соотношением
{g6 = Re2/Im2. (4)
Эта величина является безразмерной и допускает
экспериментальное измерение. При р = рс и о)<Со>о Угол потерь принимает
универсальное значение бс:
Зависимость tg S от частоты для различных значений р выше и
ниже рс для двух- и трехмерного случаев показана
соответственно на рис. 3 и 4.
4. Усиление фликкер-шума
В данном разделе рассмотрен вопрос о наблюдаемом спектре
шума в макроскопическом образце нашей смеси резисторов и
конденсаторов. Обычно рассматривают два типа шума — тепло-
вой (найквистовский) шум, связанный по теории Найквиста с
действительной частью импеданса, и фликкер-шум. Мы
рассмотрим усиление этого шума, определяемое структурой перколя-
ционных кластеров вблизи порога. Предположим, что микроско-
IG (двумерный
* случаи)
Рис. 5. Зависимость фактора усиления фликкер-шума G(p, o>) от о)/о>р в
двумерной модели. Значения р — рс указаны на кривых.
д G{трехмерный
ф случай)
Рис. 6. То же, что на рис. 5, для трехмерного случая.
Динамические свойства структур
541
пическое сопротивление каждой занятой связи имеет малую
флуктуирующую добавку До(0:
/? = /?0(l+AoW), (6)
характеризуемую спектральной плотностью
S0(co)=JA(co)|2. (7)
В рамках схемы расцепления Т, уже обсуждавшейся в разд. 3,
можно показать, что макроскопический шумовой сигнал от
образца с объемом (числом связей) V имеет вид
SMaKpoN = So(CD)l/-lG(p, «>)> (8)
где 5макро((о)—определенная по аналогии с So (со)
нормированная спектральная плотность флуктуации проводимости:
Змакро(со) =cos/S2. Наш метод позволяет определить
коэффициент усиления G(p9 со) при произвольных значениях
параметров. В критической области (когда и (р — рс) и со/coo малы) эта
величина имеет следующее скейлинговое поведение:
G(р, ©) = Iр- ft ГХ%± (i;\p-PcГ"') • (9)
В пределе со-^0 величина G(p, со) расходится при р-+рс со
своим собственным показателем X. При р — рс коэффициент
усиления G расходится при со->~0 как со_у. Показатели X и У
связаны с показателем шума 6, недавно введенным Раммалом
и др. [2]:
X = (s + t)Y = (D — b)v. (10)
На рис. 5 и 6 показаны графики зависимости G(p, со) от частоты
при различных значениях р > рс в двумерном и трехмерном
случаях.
5. Выводы
Числовые значения порогов протекания и показателей,
обсуждавшихся в настоящем обзоре, приведены в следующей
таблице:
D = 2 D = 3
Рс
V
S
t
X
Y
b
0,618
1,635
1,135
1,135
1,339
0,590
1,181
0,282
1,227
0,440
2,243
2,343
0,874
1,091
542
Часть VII
Эти числа, как и всегда при подобного рода приближениях,
следует воспринимать лишь как грубые оценки.
С помощью изложенного метода можно дать ответ и на
более сложные вопросы, связанные с электрическими свойствами
перколяционных кластеров, таких, как распределение
напряжений, отклик на произвольный внешний сигнал, поверхностные
эффекты и т. д. В конце отмечу, что нами в содружестве с мар-
сельской группой [3] были исследованы электрические свойства
детерминистической модели перколяционных кластеров.
ЛИТЕРАТУРА
1. Luck /. М„ J. Phys, A18, 2061 (1985).
2. Rammal R., Tannous С, Tremblay A. M. S, Phys. Rev, A31, 2662 (1985).
3. Clerc J. P, Giraud G., Laugier J. M.t Luck I. M.f J. Phys, A18, 2565
(1985).
Отклик шероховатых поверхностей
на переменном токе
С. Лиу, Т. Каплет, Я. Грэй *
Уже более шести десятилетий известно, что эквивалентная схема,
описывающая импеданс поверхности раздела инертного электрода
и водного (или твердого) электролита, часто содержит элемент,
обеспечивающий постоянство угла потерь, — элемент постоянной
фазы (ЭПФ), импеданс которого зависит от частоты как
Z ~ (/со)-11, 0 < х\ < 1. В последние годы было экспериментально
показано, что показатель ц связан с шероховатостью поверхности.
По мере того как поверхность становится все более гладкой,
показатель ц приближается к единице. Мы показали, что наличие ЭПФ
связано с фрактальной геометрией шероховатостей поверхности.
На основании рассмотрения ряда моделей мы получили, что г\ =
= 3 — ds, где ds — фрактальная размерность поверхности.
1. Введение
Электрические свойства поверхности контакта
металлического электрода и водного (или твердого) электролита
чрезвычайно важны для электрохимии и электрохимических
технологий, поскольку они влияют на характеристики
электрохимических устройств. В классической теории влияние границы на
прохождение через систему переменного тока описывается
граничной емкостью, включенной последовательно с омическим
сопротивлением электролита. Предсказываемая частотная
зависимость импеданса очень проста: его действительная часть не
зависит от частоты, а мнимая обратно пропорциональна частоте.
С 1926 г. известно, что реальные системы ведут себя
совершенно иначе [1]. Оказывается, что почти во всех таких
системах, по крайней мере в ограниченном диапазоне частот, в
частотной зависимости импеданса доминирует член (/со)-11, где
у = /у/—1, а показатель г\ удовлетворяет неравенству 0 < г\ <
< 1. Этот добавочный член был назван элементом с
постоянным углом потерь, или просто элементом постоянной фазы
(ЭПФ). В последнее десятилетие многие исследователи
обосновали связь между ЭПФ и шероховатостью поверхности [2—
6]. По мере того как поверхность становится более гладкой,
величина г] приближается к единице. Де Леви предложил
имитировать шероховатость поверхности порами, электрические
свойства которых моделируются линиями передачи [3]. В моделях
такого типа, однако, всегда г| = 1/2, если только не предпола-
* S. H. Liu, Т. Kaplan-Solide State Division, Oak Ridge National
Laboratory, Oak Ridge, TN 37831, USA; L. /. Gray-Engineering Physics and
Mathematics Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA
544
Часть VII
гать специальной пространственной структуры распределения
сопротивления и емкости [7].
Последние успехи теории неупорядоченных систем сделали
возможным использовать при решении задач, связанных со
случайной геометрией, статистический подход. Коэн и Томкиевич
предположили, что на поверхности полупроводникового
электрода имеет место некоторый новый перколяционный процесс,
что и является причиной наблюдаемого поведения [8, 9]. Ле
Мео и Крепи предположили наличие связи между ЭПФ и
фрактальной геометрией поверхности [10]. В настоящей работе нами
проделаны точные модельные вычисления отклика фрактальных
поверхностей на переменном токе. Мы получили, что показатель
г\ = 3 — ds, где 2 < ds < 3, есть фрактальная размерность
поверхности. Поскольку этот результат получился при
рассмотрении различных моделей, можно надеяться, что такое
соотношение между ц и ds является общим.
2. Фрактальная природа реальных поверхностей
Пфейфером с соавт. было показано, что поверхности
твердых частиц, используемых в гетерогенном катализе, на
микроскопическом масштабе являются шероховатыми. Эта
шероховатость может быть описана с помощью фрактальной размерности,
Рис. I. Поверхность Ag-p-Al203 под электронным микроскопом.
лежащей между 2 и 3 [11—13]. Фрактальную размерность
можно измерить, определив число адсорбированных молекул,
необходимых для образования монослоя. Авторы работ [11—13]
обнаружили, что число молекул в монослое пропорционально
диаметру молекулы в степени —d, 2<d<3. Это означает,. что
эффективная поверхность образца для адсорбции меньших
молекул больше, поскольку малые молекулы сильнее чувствуют
иррегулярность поверхности. Степень d есть по определению
фрактальная размерность поверхности [14, 15].
Динамические свойства структур
545
Качественно определить, является ли данная поверхность
фрактальной, можно, рассматривая ее под электронным
микроскопом при различных увеличениях. У фрактальных
поверхностей отсутствует естественный масштаб длины, и при различных
увеличениях они выглядят одинаково. На рис. 1 показана
поверхность Ag-p-Al203, хорошо известного твердого
электролита [6]. На фотографии видны выступы и впадины различных
размеров. На каждом выступе и впадине имеются меньшие
выступы и впадины. В следующих разделах работы мы построим
модели, обладающие похожей самоподобной структурой, и
покажем, что это самоподобие и является причиной явлений,
связанных с ЭПФ.
3. Простейшая модель
Простейшая модель, в рамках которой ЭПФ оказался
связанным с фрактальной геометрией поверхности, была основана
Рис. 2. Модель границы раздела шероховатого металлического электрода и
электролита, основанная на канторовом множестве.
на канторовом множестве. Соединив друг с другом отрезки,
получающиеся на различных стадиях построения канторова
множества [16], мы получим объект, изображенный на рис. 2. На
каждой последующей стадии построения множества от каждого
исходного отрезка остаются два отрезка, длина каждого из
которых составляет l/а (а < 2) от длины исходного.
Фрактальная размерность такого множества равна d = ln2/ln a < 1;
размерность несимметричной границы между черным и белым на
рис. 2 равна, как нетрудно показать, ds = 2 + d [14, 15].
Будем считать, что черная часть рисунка соответствует
области, занятой электролитом. Отрезки на рис. 2 соответствуют
гладким поверхностям, перпендикулярным плоскости страницы.
Эта модель навеяна наблюдениями де Леви [3], показавшими,
что на полированной поверхности твердого тела имеется
множество царапин с зазубренными краями. Мы ввели в модель
фрактальную геометрию, сделав царапины самоподобными.
546
Часть VII
Переменный ток, текущий от электролита (черная сторона
рисунка) к электроду (белая сторона), встречает омическое
сопротивление электролита и поверхностную емкость на каждом
участке поверхности. Эквивалентная электрическая схема такой
системы показана на рис. 3. Каждая новая стадия построения
канторов а множества
соответствует разветвлению цепи.
Сопротивление каждой
последующей ветви увеличивается в а
раз, поскольку во столько же
раз уменьшается толщина
соответствующего выступа.
Число конденсаторов,
соответствующих поверхностной
емкости выступов, на каждой
последующей стадии также
увеличивается, емкости всех
конденсаторов одинаковы. Это
предположение соответствует
пренебрежению поверхностной
емкостью, связанной с дном
впадин. На дальних стадиях
построения поверхность этих
донышек действительно
становится очень малой, и в
асимптотическом пределе ее вклад
не существен.* Общее
заземление обозначает электрод.
Входной импеданс цепи, показанной на рис. 3, можно
записать в виде бесконечной цепной дроби:
2(ш) = Я + -
Рис. 3. Эквивалентная электрическая
схема для модельной поверхности,
показанной на рис. 2.
(О
;о»с +
aR +
I
/<»С +
о*Я + ...
Функция Z((o) удовлетворяет следующему скейлинговому
соотношению [17]:
2 ("5") = * + j«>cz (Г) + 2 • (2)
В низкочастотном пределе уравнение (2) переходит в
Это соотношение удовлетворяется при
Z (e>)=* A (fa)-\ (4)
Динамические свойства структур
547
где А — постоянная, а
г\ = 1 — d (5)
и rf = ln2/lna есть фрактальная размерность канторова
множества. Эта цепь, таким образом, и есть ЭПФ. Поскольку d лежит
между нулем и единицей, показатель ц также ограничен 0 и 1,
В терминах фрактальной размерности границы
4 = 3-rf,. (6)
У гладкой поверхности ds = 2, что дает г\ = 1 (в качественном
согласии с экспериментом).
Лучше понять поведение, связанное с ЭПФ, можно,
рассмотрев цепь, получающуюся на конечной стадии построения.
Входной импеданс вычисляется с помощью рекуррентного
соотношения для цепной дроби (1) [18].
Поведение действительной
части Z(co) показано на рис. 4.
На низких частотах эта
величина выходит на плато,
высота которого для каждой
последующей стадии увеличивается
в а/2 раз. На высоких
частотах предельное значение
импеданса равно R. Между
этими двумя пределами система
обладает свойством ЭПФ.
Мнимая часть Z обратно
пропорциональна частоте на высоких
и низких частотах и имеет
поведение, соответствующее
ЭПФ, в промежуточной
области. Эти результаты
показывают, что степенная
зависимость импеданса от частоты
связана с конкуренцией рези-
стивного и емкостного путей протекания тока. Сигнал более
низкой частоты распространяется по цепи дальше, прежде чем он
сможет уйти через поверхностную емкость, поэтому импеданс
на более низких частотах больше. Реальные поверхности
являются самоподобными лишь в конечном интервале масштабов;
это определяет диапазон частот, в котором имеет место
постоянство угла потерь.
Модель легко обобщается на случай, когда на каждой новой
стадии построения появляется N <С а ветвей. Показатель ц в
этом случае равен г| == 1 — In N/In а. Фрактальная размерность
канторова множества d = In N/\n а, размерность поверхности
io*i 1 1 1 1 1 1 J
ои(в единицах (ВС)'1)
Рис. 4. Зависимость от частоты
действительной части входного
импеданса цепи, изображенной на рис. 3.
Число N — количество стадий
построения конечной цепи.
548
Часть VII
ds = 2-\- d. Уравнение (6), следовательно, справедливо и в этом
случае.
Результат — уравнение (5)—полностью согласуется с
теорией аномальной диффузии для перколяционных кластеров
[19—22]. Если каждая связь перколяционного кластера
образована резистором R и между каждым узлом кластера и землей
включен конденсатор С, полученная сложная /?С-цепь будет
обладать свойством ЭПФ с
л=1_й/(2 + е), (7)
где d—фрактальная размерность перколяционного кластера,
Э — показатель аномальной диффузии. Рассмотрим случайное
блуждание на перколяционной сетке. Средний квадрат
расстояния, на которое уходит блуждающая частица, связан с числом
шагов соотношением
(г*)~№№+*\ (8)
Показатель 0 определяется геометрией кластера. Если в единицу
времени частица делает фиксированное число шагов, (8)
определяет средний квадрат ухода частицы за данное время, или,
что то же самое, диффузионную длину для сигналов различных
частот. Появление величины Э в выражении для показателя т),
характеризующего ЭПФ, поэтому совершенно естественно.
Формула (7) отличается от формулы, полученной Гефеном
и др. [21]. Эти авторы использовали динамическое скейлинговое
соотношение для исследования проводимости сеток на
переменном токе. Клерк и др. [23], однако, показали, что на кривых
Серпинского в D-мерном пространстве динамическому скейлин-
говому соотношению, напоминающему (3), удовлетворяет
полный импеданс. Поскольку в любой сетке низкочастотный сигнал
распространяется на большие расстояния, чем высокочастотный,
мы полагаем, что можно применить динамический скейлинг к
полному импедансу диффузионного объема в перколяционном
кластере. Из этого соображения и следует результат (7).
Рассмотрим теперь случайное блуждание по сетке,
показанной на рис. 3, начинающееся на произвольном узле этой сетки.
Если шаги вправо и влево равновероятны, результатом таких
блужданий будет дрейф вправо, т. е. <r> = N/3. Если положить,
что вероятность шага на данную ветвь обратно
пропорциональна сопротивлению ветви, результатом блужданий будет дрейф
влево с <г> = — (а — 2)N/(a + 2). В любом случае из (8) мы
получим, что 8===—1; при этом уравнение (5) становится
эквивалентным (6). Таким образом, модельная поверхность,
подобно другим фрактальным системам, обладает аномальными
диффузионными свойствами.
Динамические свойства структур
549
4. Случайные фрактальные системы
Реальные системы не обладают регулярностью, присущей
канторову множеству. Рассмотрим, например, поверхность,
показанную на рис. 1. Она самоподобна лишь в статистическом
смысле, т. е. увеличенное изображение одного ее участка
напоминает любой другой. Мы исследовали несколько фрактальных
моделей, приближенно отражающих это свойство [17]. Для
начала предположим, что на различных стадиях построения
поверхности числа ветвления равны N\, Af2, NZy ..., а
коэффициенты изменения масштаба — это а\, а2, а3, ... . Выражение для
входного импеданса при этом имеет вид
Z(*) = R + Ц^г • (9)
/шС + f*!_
ai* + -
/соС +
N2
axa2R +
Можно показать, что для низких частот имеет место следующее
соотношение:
l/Z(co) = (iV1/a1)l/Z1(a1(o), (10)
где Zi(co)—входной импеданс каждой ветви системы,
оставшейся после удаления цепочки, соответствующей первой стадии
построения.
Предполагая, что наборы {Щ и [а] — множества случайных
переменных с заданным распределением, и усредняя по
ансамблю систем, получаем
(l/Z(«.)> = (iV)(l/aZI(a(o)). (11)
Поскольку Z и Z\ имеют одинаковую степенную зависимость от
частоты, получаем, что
{N){a^x)=\. (12)
Нетривиальное решение для ц имеется, если выполняется
неравенство
(а-') < 1/<Л0 < 1 (13)
(условие того, что поверхность, представляемая эквивалентной
цепью, является фрактальной). Фрактальная размерность
границы дается аналогичным соотношением:
<Л0<а2-"*>=1- (14)
Из (14) и (13) немедленно следует т]=3 — ds. Интересно
отметить, что показатель г] зависит только от среднего числа ветвле-
550
Часть VII
ний <Af>, но чувствителен к виду распределения масштабного
коэффициента а.
Следующий шаг на пути к построению модели случайной
поверхности— сделать случайными масштабные коэффициенты а
для разных ветвей, получаемых на одной стадии построения.
После достаточно трудоемких вычислений получаются результаты,
совпадающие с (12) — (14). Детали этой работы были
опубликованы в статье [17]. Мы также показали, что можно сделать
случайной и высоту выступов на каждой стадии, что приводит
к случайным значениям не только для R, но и для С.
Соотношение между показателем т] и фрактальной размерностью при этом
не изменяется [24].
5. Модель канторова блока
Выступы и впадины на поверхности, показанной на рис. 1,
лучше воспроизводятся моделью, которую мы назвали канторо-
вым блоком. Эта модель основана на двумерном обобщении
канторова множества и строится по следующему алгоритму. Начнем
с квадратной пластины площадью w X w и толщиной Ь. На
первой стадии построения из пластины вырезается крест,
разделяющий ее на четыре конгруэнтных квадрата, каждый
площадью (w/a) X (w/a)> где а > 2. Процесс этот повторяется до
бесконечности. Модель поверхности, которую мы будем
рассматривать, получится, если сложить друг с другом объекты,
полученные на разных стадиях построения множества, как мы
делали это в предыдущем случае. Фрактальная размерность
поверхности ds = 1 + In 4/ln a, 2 < а < 4. Для а > 4 получаем
ds = 2, хотя поверхность не является гладкой: шероховатости
очень быстро уменьшаются от стадии к стадии и не вызывают
"заметного эффекта.
Эквивалентная электрическая цепь для такой поверхности
имеет ту же структуру, что и показанная на рис. 3, с тем
отличием, что на каждой стадии имеются 4 ветви, сопротивления
соответствующих резисторов увеличиваются в а2 раз, а емкости
конденсаторов уменьшаются в а раз. На низких частотах можно
получить следующее скейлинговое соотношение для импеданса:
Z(co/a) = (a2/4)Z(co), (15)
соответствующее ЭПФ с показателем
г] = 2 — 1п4/1па = 3 — ds. (16)
Построение канторова блока можно начинать и с
прямоугольника со сторонами w* X wyj который разрезается на NxNy
меньших прямоугольников со сторонами (wx/a) X (wy/a). По-
Динамические свойства структур
551
скольку NxNy > а > Nx, Ny> получаем ds = 1 + \r\{NxNy)/[n a,
a rj = ln(NxNy)/\na — 3 — ds. Кроме того, в эту модель, как и
в модель, рассмотренную выше, можно внести элемент
случайности, введя случайные число ветвлений, масштабный коэффициент
и толщину на каждой стадии. При этом обнаруживается
замечательный факт, что простое соотношение (7) между т)и^
справедливо, коль скоро ds > 2, т. е. поверхность остается
фрактальной. Детали этой работы будут опубликованы [24].
6. Обсуждение
Поскольку соотношение (6) между ц и ds справедливо для
множества моделей регулярных и случайных фракталов, мы
можем предположить, что оно справедливо и в общем случае. Это
предположение должно быть проверено экспериментально.
Неизвестным параметром теории является фактор преобразования
от масштаба длин к масштабу частот. Один из способов
определения этого фактора состоит в том, чтобы приготовить
поверхности с заданной фрактальной размерностью и измерить их им-
педансы в различных электролитах. Мы надеемся, что загадка
ЭПФ будет, таким образом, решена.
Благодарности. Авторы многим обязаны д-ру Дж. Бейтсу,
который предложил нам провести это исследование, не терял к
нему интереса и поддерживал нас. Мы хотим также
поблагодарить д-ра Дж. Уанга за полезные обсуждения.
ЛИТЕРАТУРА
1. Wolfe /., Phys. Rev., 27, 755 (1926).
2. Bottelberghs P. H., Low-Frequency Measurments on solid Electrolytes and
Their Interpretations, in: Solid State El Electrolytes, eds. P. Hagenmuller,
W. van Gool, Academic Press, New York, 1978, p. 145—172.
3. de Levie R., Ebectrochimica Acta, 10, 113 (1965).
4. Bottelberghs P. #., Briers G. H. /., J. Electroanal. Chem., 67, 155 (1976).
5. Armstrong R. D., Burnham R. A, J. Electroanal. Chem., 72, 257 (1976).
6. Bates J. £., Wang J. C, Chu Y. 7\, in: Proc. of the 5th International
Conference on Solid State Ionics, Lake Tahoe, USA, 1985.
7. Wang J. C, Bates J. В., in: Proc. of the 5th International Conference on
Solid State Ionics, Lake Tahoe, USA, 1985.
8. Cohen M. #., Tomkiewicz M.y Phys. Rev., B26, 7097 (1982).
9. Lyden /. /C, Cohen M. #., Tomkiewicz M., Phys. Rev. Lett., 47, 961 (1981).
10. Le Mehaute A, Crepy G., Solid State Ionics, 9 and 10, 17 (1983).
11. Pfeiffer P., Avnir D.t J. Chem. Phys., 79, 3558 (1983).
12. Avnir ZX, Farin D., Pfeiffer P., J. Chem. Phys., 79, 3566 (1983).
13. Pfeiffer P., Avnir D., Farin D., Surf. Sci., 126, 569 (1983).
14. Mandelbrot B, £., Fractals: Forms, Chance and Dimension, Freeman, San
Francisco, 1977.
15. Mandelbrot B. £., The Fractal Geometry of Nature, Freeman,
San-Francisco, 1983.
552
Часть VII
16. Liu S. tf, Phys. Rev. Lett, 55, 529 (1985).
17. Kaplan 7\, Gray L. /., Phys. Rev., B32, 7360 (1985).
18. Handbook of Mathematical Functions, National Bureau of Standards,
Washington D. C, 1964, p. 19.
19. de Gennes P. G, Recherche, 7, 919 (1976).
20. Alexander S.f Orbach R.y J. Phys. (Paris) Lett, 43, L625 (1982).
21. Gefen Y, Aharony Л., Alexander S, Phys. Rev. Lett, 50, L13 (1983).
22. Rammal R.y Toulouse G, J. Phys. (Paris) Lett, 44, L13 (1983).
23. Clerc /. P, Tremblay Л. M. S, Albinet G, Mitescu C. /)., J. Phys.
(Paris) Lett, 45, L913 (1984).
24. Kaplan Т., Gray L. /, Liu S. H., будет опубликовано.
Чась VIII
ИЕРАРХИЧЕСКИЕ И ФРАКТАЛЬНЫЕ
СВОЙСТВА НЕУПОРЯДОЧЕННЫХ СИСТЕМ
Природа временных иерархий,
определяющих релаксацию
в неупорядоченных системах
М. Шлезингер, Дж. Клафтер*
С 1970 г. стало ясно, что диэлектрическая релаксация во многих
стеклах и полимерах следует растянутому экспоненциальному
закону. Оказалось, что такой закон описывает самые различные типы
релаксации (ЯМР, механической, диэлектрической, релаксации
оптических корреляций) во многих сложных случайных материалах.
Для объяснения этого вездесущего закона было предложено
несколько теорий: 1) прямой перенос на фрактале; 2) динамика с
иерархическими ограничениями; 3) диффузия с фрактальным
временем. Физика, лежащая в основе этих моделей, совершенно
различна, однако всем им можно придать одинаковую
математическую форму. Концепция, объединяющая эти модели, связана с
наличием иерархии времен релаксации, распределение которых
достаточно широко, так что время появляется в окончательных
формулах в нецелой степени. Эта единая концепция справедлива несмотря
на то, что различные физические механизмы соответствуют
параллельной, последовательной и некоторым другим комбинациям
каналов релаксации,
1. Введение
Большое внимание в последние годы уделяется
исследованию процессов релаксации в сложных конденсированных
системах. Это связано с тем удивительным экспериментальным
фактом, что во многих самых различных системах спадание
корреляционных функций следует одному и тому же растянутому
экспоненциальному закону:
*(/) = ехр[-(</т)*], 0<р<1. (1)
Параметры |3 и т зависят от материала и могут быть функциями
внешних переменных, например температуры. Закон (1) был
впервые предложен Кольраушем [1] в 1864 г. для описания пол-
зучести материалов, а в 1970 г. был использован Уильямсом и
* Michael F. Shlesinger- Physics Division (Code 012), Office of Naval
Research, 800 North Quincy Street, Arlington, Virginia 22217-5000; Joseph Klaf-
ter- Corporate Research Science Laboratories, Exxon Research and Engineering
Company, Route 22 East, Clinton Township, Annandale, New Jersey 08801.
554
Часть VIII
Уоттсом [2] при описании диэлектрической релаксации в
полимерах. С тех пор растянутый экспоненциальный закон
использовался при обработке экспериментальных данных по
различным системам, например для остаточной намагниченности
спиновых стекол [3] или для затухания люминесценции в пористых
стеклах [4]. Этот вездесущий закон спадания может быть
следствием различных физических механизмов. В статистической
теории разрушения этот растянутый экспоненциальный закон
известен как распределение Вейбулла [12]. Цель настоящей
статьи — найти связь между тремя различными физическими
моделями, приводящими к такому закону, и определить, какое
их общее свойство ответственно за его появление.
Вначале мы рассмотрим форстеровский механизм прямого
переноса возбуждения [13], дающий пример процесса
релаксации, протекающего по параллельным каналам. Мы рассмотрим
связь математической структуры этой модели с моделью
динамики с иерархическими ограничениями Пальмера и др. [10].
Еще одна рассматриваемая теория — это модель диффузии
дефектов Шлезингера и Монтролла [9]. В этих трех теориях
растянутый эконенциальный закон получается естественным
образом. Мы покажем, что причиной его появления является
существование в каждой из этих моделей масштабно-инвариантных
скоростей релаксации.
2. Форстеровская модель прямого переноса
А. Много параллельных каналов
Эта модель появилась в результате исследований переноса
возбуждений от доноров к статическим дефектам в
конденсированных средах [13].
Рассмотрим закон затухания возбуждения на выделенном
доноре, находящемся в начале координат, за счет прямого
переноса энергии к дефекту, расположенному в узле Ri решетки
с заданной структурой. Функция релаксации
Ф/(0—вероятность того, что по прошествии времени t донор останется в
возбужденном состоянии, — равна
(DtW^expl-tWiRi)], (2)
где W{Ri) —скорость релаксации, зависящая от расстояния
между донором и дефектом и определяющая время релаксации
x(Ri) = \/W(Ri). Для фиксированной конфигурации многих
дефектов, расположенных в узлах Ri (исключая начальный),
получаем
<${R]=Yl'exp\-tW(R()]. (3)
* 1=1
Иерархические и фрактальные свойства неупорядоченных систем 555
Усредним (3) по всем возможным конфигурациям дефектов.
В случае, когда все дефекты расположены совершенно
случайно, и вероятность того, что данный узел занят дефектом, равна
р, имеем [13]
Ф (0 = П' (1 - Р + Р ехр НУ («, (4)
что для р <С 1 дает
Ф(/)^ехр[-р £'{1 -ехрl-twm]}]. (5)
Вводя плотность узлов
Р (#)=!' б (R-Rt), (6)
i
преобразуем сумму в интеграл
Ф (t) = ехр [-р J dR9 (R) {1 - ехр [-tW (*)]}]. (7)
Рассмотрим два типа взаимодействия:
W(R) = aR~s, (8a)
Г(Я) = Яехр(-уЯ). (86)
Если пространственная структура системы однородна, т. е.
p(R) = const, для случая (8а) получим
Ф (t) = ехр [(—t/x)D!s] (в пространстве D измерений), (9)
что соответствует растянутому экспоненциальному закону. В фор-
стеровской модели переноса энергии 5^6. Для случая (86)
имеем
<b(t) = (Bt)-AXn {Bt) (в пространстве D измерений). (10)
Это выражение соответствует «ускоренному» степенному закону
спадания, в одномерном случае принимающему вид
алгебраического закона.
Неэкспоненциальное затухание (выражения (9) и (10))
является результатом параллельных процессов релаксации и
наличия иерархии расстояний. Чтобы обобщить этот результат на
случай переноса по фрактальной структуре с фрактальной
размерностью Я, достаточно просто заменить D на d [14]. Если
структура является однородной на масштабах, больших |, и
фрактальной на меньших масштабах, переход от характерного
для фрактального случая поведения к поведению,
соответствующему однородному случаю, происходит на временах, для
которых №(Ш~ 1 [И1-
556
Часть Vllt
Б. Только самый быстрый канал
Те же типы релаксационного поведения могут быть получены
и при рассмотрении системы, в которой перенос возбуждения
возможен только на соседние дефекты. Тогда
оо
4>NN=\f(R)eiLp[-tW(R)]dR, (11)
О
где f(R) —вероятность найти ближайший дефект на расстоянии
R. Для случайно расположенных дефектов в одномерном случае
имеем
f(R) = pexp(-pR). (12)
Для W(R) вида (8а) получаем
ф^ = р J <f "*exp {-taR~s) dR. (13)
Метод перевала дает
фш = ре-(С1) в (14)
Это снова растянутый экспоненциальный закон, но с
показателем меньшим, чем дает для одномерного случая выражение (9).
Это связано с исключением влияния удаленных дефектов. Если
же W(R) имеет вид (86), то
Фмм=(^)вГр%(ру, Bt), (15)
где 7i — неполная гамма-функция. На больших временах при
D = l (15) ведет себя так же, как (10). Свойства релаксации,
связанной с прямым переносом, одинаковы как при наличии
многих параллельных каналов, так и при учете только самого
быстрого канала распада: при W{R) = aR~s зависящее от
расстояния время релаксации является масштабно-инвариантным.
3. Динамика с иерархическими ограничениями
Недавно Пальмер и др. [10] предложили модель
релаксации, которую можно назвать не параллельной, а
последовательной-: Иерархическая модель подразумевает, что релаксация
совершается в несколько стадий, причем более быстрая степень
свободы должна релаксировать прежде, чем может релаксиро-
вать более медленная. Это означает, что масштаб времен
релаксации на уровне п подчинен релаксации на более низком
уровне.
В качестве одной из возможных реализаций модели была
рассмотрена система [10] с дискретным набором уровней п =
Иерархические и фрактальные свойства неупорядоченных систем 557
= 0,1,2, ... . На каждом уровне система имеет степени
свободы, представленные Nn спинами, которые могут быть
направлены вверх или вниз. Спины на уровне п + 1 могут изменить
свое состояние только тогда, когда \лп спинов на уровне п
находятся в одном определенном из своих 2**п возможных
состояний. Время релаксации на уровне п + 1 (хп+\) тогда равно
тп+1 = 2"*»тп= (16а)
= т0ехр( Ё Ы. (166)
\fe=0 /
где ji/fe == |л^ In 2. Функция релаксации <f>(t) дается выражением
оо
^)=Z«>rtexp(-//T„), (17)
где ©л = #п/2 Nn — весовой множитель для уровня п. Обра-
тим внимание, что иерархия времен релаксации, даваемая
выражением (16а), похожа на иерархию скоростей переходов,
рассмотренную нами для модели переноса.
Задав конкретную форму \лп и аь, можно вычислить
соответствующую функцию релаксации. Выбор \in = Мю дает
т„ = т0ехр(М), (18)
что в точности соответствует случаю (86). Выбрав
©П = <М,-П, (19)
что соответствует распределению (12), и преобразуя сумму (17)
в интеграл, получаем
оо
ф (/) = со0 J е~п 1п * ехр [-* ехр (-jv*)/t01 dn. (20)
о
Этот интеграл приводит к алгебраическому закону релаксации
(15), а именно j>{f) „t~{lnH)(k\ Такой же тип релаксационного
поведения был получен при исследовании дифузии в
иерархической системе [15].
Тот же выбор (On совместно с условием [in = \хс/п (п ^ 1,
k ^ 1) дает
Tn==T0exp(jlo Ё/~*J~
~т0^°(при *=1), (21)
558
Часть VIII
что соответствует случаю (8а). При k= 1 это приводит к
интегралу
оо
ф (t) = co0 J e~n ln> ехр [-/л~До/т0] dn, (22)
о
который, как и (13), соответствует растянутому
экспоненциальному закону с показателем (3 = 1/(1 + До)•
Хотя физические картины релаксации в последовательности
иерархически подчиненных уровней и релаксации за счет
прямого переноса возбуждения на соседний дефект совершенно
различны, оба этих случая приводят к одинаковым интегралам
релаксации. Весовой множитель юя и время релаксации %п для
каждого уровня в иерархической модели соответствуют
весовому фактору f(R) для расположения дефектов и скорости
переноса W(R) в модели прямого переноса.
4. Модель диффузии дефектов
В 1960 г. Гларум [16] предложил концепцию, согласно
которой мигрирующие дефекты могут включать релаксацию
вмороженных диполей в аморфных материалах. Предполагалось,
что релаксация происходит мгновенно, как только ближайший
дефект в первый раз достигнет диполя. В дальнейшем эта идея
была обобщена [17]: теперь предполагалось, что любой дефект
может запустить релаксацию. Такая модель в одномерном
случае дает растянутый экспоненциалньый закон с (3=1/2, а в
трехмерном случае — обычный экспоненциальный закон.
Шлезингер и Монтролл [9] показали, как можно обобщить эти
результаты, чтобы получить все (3 из диапазона 0<(3<1: это
можно сделать, введя иерархию времен ожидания перескоков в
случайном окружении. В рамках задачи о мишени было также
исследовано обобщение такой модели на случай фрактальной,
самоподобной геометрии [Па, 18]. В работе [Па] было
указано, что модель диффузии дефектов содержит параллельные
каналы релаксации, каждый из которых сам по себе является
последовательным.
С помощью приближенных аргументов Реднера и Канга [19]
мы можем придать модели диффузии дефектов ту же
математическую форму, что была рассмотрена в предыдущих разделах.
Пусть мишень расположена в начале координат, а дефекты
случайно распределены вокруг нее. Пусть f(R\)—вероятность
отсутствия дефектов на расстоянии меньше Ri от мишени.
Вероятность того, что дефект, первоначально расположенный в точке
Ri, не достиг начала координат за время t, равна ехр (—//4/??)
(коэффициент диффузии дефектов положен равным единице).
Иерархические и фрактальные свойства неупорядоченных систем 559
Закон релаксации для мишени тогда будет иметь вид
ф {Rl9 t) ~ ехр(—p/?i)Пехрf - j~\ ~
~ ехр (—pRi) ехр ( —/р J ^) =
= ехр(~^1 + р1^-). (23)
Усредняя по Rt, получаем
оо
фЦ)=\ ехр (-/*,) ехр (- -g-) d#,. (24)
О
Выражение (24) имеет такой же вид, как выражение (13) для
модели Форстера и выражение (22) для модели Пальмера и др.
с x(R) = {4/p)R, и приводит к растянутому экспоненциальному
закону с р= 1/2. Обобщение этого результата на другие
размерности дает [9, Па, 18, 19]
*(*) = exp(-pS(/)), (25)
где S(t) —среднее число различных узлов решетки, посещенных
блуждающей частицей за время L Для регулярных решеток
S(t) ~p/*(D = l), S{t) ~ t/lnt(D=2) и S{t) ~ t{D=3).
Релаксация мишени происходит, следовательно, по
растянутому экспоненциальному закону с р = 1/2 при D = 1 и по
экспоненциальному закону при D=3. Если дефекты мигрируют по
самоподобной фрактальной структуре [20], то
Г f*2, d<2,
If, d > 2,
S{t)~\ - (26)
I /, d > 2,
где 3 — спектральная (фрактонная) размерность [21]. Если
структура, по которой мигрируют дефекты, является
фрактальной только до масштаба |, мы ожидаем наличие кроссовера от
растянутого экспоненциального закона к обычному
экспоненциальному на временах, за которые диффундирующая частица
смещается на величину |.
Рассмотренные выше результаты были обобщены также
введением распределения времен ожидания i|)(f) движения
дефектов [9, 22]. В случае очень широкого распределения времен
ожидания, для которого первый момент бесконечен [9], г|)(0 ~ f~a_1,
0 < а < 1, получим S(t) ~ £а/2(£> = 1), что соответствует (24)
с x(R) ~ Я2'*"1 и S(t) ~ t«(D = 3).
Это приводит, согласно (25), к растянутым
экспоненциальным законам с р = а/2 и р=а соответственно. Теория Коэна
560
Часть VIII
и Треста [6] для растянутой экспоненциальной релаксации в
стеклообразных металлах принадлежит к тому же
математическому классу, что и рассмотренные выше теории. Времена
релаксации в этой теории обладают масштабной инвариантностью того
же типа, что и в равенствах (8а) и (21), хотя физические
принципы, лежащие в основе этой модели, совершенно иные.
5. Заключение
Мы продемонстрировали общую математическую основу
различных физических моделей, приводящих к растянутому
экспоненциальному закону релаксации, часто наблюдаемому в
эксперименте. Общей чертой всех этих теорий является наличие
масштабно-инвариантного распределения времен релаксации.
Различные физические механизмы релаксации можно разделить по
различной зависимости |3 и т в (1) от внешних параметров,
таких, как температура и давление.
Благодарности. Мы благодарим Дж. Бендлера и А. Блюмена
за полезные обсуждения.
ЛИТЕРАТУРА
1. Историю вопроса и ссылки можно найти в работе: Montroll Е. W.,
Bendler L Г., J. Stat. Phys., 34, 129 (1984).
2. Williams G.y Watts D. C, Trans. Faraday Soc, 66, 80 (1970).
3. Chamberlin R. V., Mozurkewich G., Orbach /?., Phys. Rev. Lett, 52, 867
(1984).
4. Even U.y Rademann K., Jortner /., Manor N.t Reisfeld R., Phys. Rev. Lett.,
52, 2164 (1984).
5. Shore /. £., Zwanzig R.y J. Chem. Phys., 63, 5445 (1975).
6. Cohen M. #., Grest G. S. in: Structure and Mobility in Molecular and
Atomic Glasses, eds. J. M. O'Reilly, M. Goldstein, Academic Press, New
York, 1981, p. 199.
7. Ngai К L., White С. Т., Phys. Rev., B20, 2475 (1979).
8. Skinner /. L., J. Chem. Phys., 79, 1955 (1983).
9. Shlesinger M. F., Montroll E. W., Proc. Nat. Acad. Sci. (USA), 81, 1280
(1984).
10. Palmer R. G., Stein D., Abrahams E. S., Anderson P. W.y Phys. Rev. Lett.,
53, 958 (1984).
11. a) Klafter /., Blumen A., Chem. Phys. Lett., в печати; b) Huber D. L., Phys.
Rev., B31, 6070 (1985).
12. Cox D. R.y Renewal Theory, Chapman and Hall, London, 1962.
13. a) Forster Г., Z. Naturforsch. Teil, A4, 321 (1949); b) Blumen A, Nuovo
Cimento, B63, 50 (1981).
14. Klafter /., Blumen Л., J. Chem. Phys., 80, 875 (1984).
15. Huberman B. A, Kerszberg M., J. Phys., A18, L331 (1985).
16. Gtarum S. Я., J. Chem. Phys., 33, 1371 (1960).
17. Bordewijk P., Chem. Phys. Lett, 32, 592 (1975).
18. Zumofen G., Blumen A., Klafter /., J. Chem. Phys., 82, 3198 (1985).
19. Redner 5., Rang K., J. Phys., A17, L451 (1984).
20. Rammal R., Toulouse G, J. Phys. (Paris) Lett., 44, L13 (1983).
21. Alexander 5., Orbach R,y J. Phys. (Paris) Lett., 43, L625 (1982).
Реакции в фрактальных моделях
неупорядоченных систем
Л. Блюмен, Дж. Клафтер, Г. Цумофен*
Исследована динамика реакций в неупорядоченных системах.
Исследование проведено в рамках фрактальных моделей,
учитывающих наличие пространственного (а) и временного (у) беспорядка.
Рассмотрено влияние пространственного (а) и временного (у)
беспорядка на псевдомономолекулярные (задача о мишени, тушение
возбуждений на ловушках) и бимолекулярные реакции. На
больших временах для большинства реакций имеет место субординация
Ф (0 ~ f (tay)y в случае же тушения на ловушках доминирует
влияние временного беспорядка.
1. Введение
Многие интересные процессы в неупорядоченных
системах — перенос энергии в конденсированных молекулярных
средах и выжигание провалов в их спектрах [1—3], перенос
электронов и дырок в неупорядоченных полупроводниках [4, 5],
диффузия в пористых материалах и процессы, происходящие при
хроматографическом разделении веществ [6] —имеют на
больших временах неэкспоненциальное поведение. Такие процессы
нельзя описать одним временем релаксации. Основные типы
законов релаксации, встречающихся при изучении сложных
систем, следующие:
а) растянутый экспоненциальный закон Кольрауша или
Уильямса и Уоттса [7—10]
ф(/) = ехр[-(г/т)а] (0<а<1, t>%); (1)
б) экспоненциально-логарифмическая форма Инокути и Хи-
райямы [11] и Шера, Лэкса и Монтролла [4, 12]
Ф(/) = ехр[-В1пр(г/т)] (р>1, t>x); (2)
в) алгебраическое затухание [5]
0>(t)~(t/T)-y (у>0, t>%). (3)
Эти типы законов перечислены в порядке все более медленного
спадания.
В настоящей работе мы рассмотрим способы моделирования
перечисленных систем фрактальными системами с учетом как
пространственного, так и временного беспорядка [13]. Как бу-
* A. Blumen-Max Planck Institute fur Polymerforschung, D-6500 Mainz,
and Lehrstuhl fur Theoretische Chemie, Technische Universitat, D-8046 Gar-
ching, BRD; /. Ktafter • Corporate Research Science Laboratories, Exxon
Research and Engineering Co., Clinton Township, Annandale, NJ 08801, USA;
G. Zumofen -Laboratoriumfur Physicalische Chemie, ETH-Zentrum, CH-8092
Zurich, Switzerland,
562
Часть VIII
дет показано в нашей работе, фрактальные понятия легко
приводят к поведению типа „а" — „в". С самого начала следует
заметить, что пространственная неоднородность, связанная,
например, со случайным расположением примесных молекул в
матрице или с расположением атомов в аморфном полупроводнике
и определяющая распределение межатомных расстояний,
приводит к тому, что диапазон микроскопических скоростей переходов
оказывается весьма широким: пространственный беспорядок
приводит к временному, и иногда и к энергетическому
беспорядку. Такую' сложную ситуацию невозможно исследовать
аналитически. Необходимы модели, такие, как рассмотренные ниже
фракталы.
2. Фракталы в пространстве и во времени
Основной чертой фракталов является их самоподобие [14],
т. е. инвариантность каждого отдельного объекта или их
ансамбля относительно группы масштабных преобразований. В
трудах нашего симпозиума представлено уже много примеров
геометрических, т. е. пространственных фракталов, поэтому мы
считаем разумным начать с рассмотрения временных фракталов.
Как было недавно отмечено, рассмотрение процессов
переноса заряда в аморфных средах в рамках модели случайных
блужданий с непрерывным временем (СБНВ), такой, какая
использовалась Шером и Монтроллом [4], фактически основано
на введении фрактального множества времен событий [15, 16].
Пусть г|) (t) — плотность вероятности того, что следующее
событие случится через время t после того, как произошло
предыдущее. Простейший пример — пуассоновский процесс
г|)*(г) = &ехр(-&/). (4)
Нетрудно сконструировать масштабно-инвариантное
распределение, приняв во внимание события, проиходящие на всех
масштабах времен [16]:
^(0 = 1^Е^,ехрМбО, (5)
где N <С 1. Очевидно, что распределение (5) —это
нормированная сумма пуассоновских членов и что
г|) (Ы) = ф (t)l{Nb) - (1 - ЛО exp (—tb)IN. (6)
В дальнейшем мы будем рассматривать случай b < N, так что
Ъ < 1 и на больших временах rp(bt) с~ ty(t) /Nb. Последнее
выражение эквивалентно тому, что
♦w-tW- (7)
Иерархические и фрактальные свойства неупорядоченных систем 563
где у = In N/ln b. Выражение (7) показывает наличие
временного скейлинга для функции ty(t), т. е. ее фрактальную во
времени природу.
Чтобы показать, что распределение (5) получается вполне
естественным образом, рассмотрим распределение времен
освобождения носителей заряда с низколежащих ловушек в зону
проводимости [17]. Это распределение лежит в основе
формализма многократного захвата. Скорости перехода активацион-
ных процессов экспоненциально зависят от энергии, так что
эквидистантное расположение уровней Е\ = jAE приводит к
скоростям переходов, пропорциональным ехр(—Ej/kT)—b}\ где
&=ехр(—AE/kT). Кроме того, плотность состояний в хвосте
зоны часто сама экспоненциально зависит от энергии (как
ехр(—Ej/kTo), где Т0 — описывающая это спадение характерная
температура), так что плотность состояний ведет себя как Nf
с JV=exp(—AE/kTo). Таким образом, в данном примере при
Т < Т0 у = In N/ln b = Т/То: при Т < Т0 имеет место
дисперсионный транспорт.
Скейлинг распространяется также на величины, связанные с
ф(0- Пусть %n(t)—вероятность того, что за время t
совершается ровно п событий. Эта важнейшая для формализма СБНВ
величина весьма просто связана с лапласовским образом ^(t):
&[%n(t)]^xn(u) = №(u)]n[l -ЪШи, (8)
На рис. 1 показаны зависимости %n{t) для пуассоновского
процесса (4). На кривых видны отчетливые максимумы, которые
по мере увеличения п сдвигаются в сторону больших времен. На
графике, построенном в двойном логарифмическом масштабе,
ясно видно отсутствие скейлинга.
Чтобы получить скейлинг, необходимо взять такую г|з(^),
которая на больших временах ведет себя алгебраически. Типичным
примером такой функции является функция ^(t),
принадлежащая семейству функций, определенных как [4, 18]
+« (0 = спа2 [exp (a2/)] in erfc (at"2), (9)
где inevfc(z) —повторные интегралы от функции ошибок, а сп —
нормировочные постоянные. Функция if>2(t) не имеет первого
момента, г|)2(н) = (1 + ul/2/a)-2, и в выражении (7) у = 1/2. На
рис. 2 показано поведение соответствующих %n(t). Как
непосредственно видно из графика, на больших временах имеет место
скейлинговое поведение, наклон всех кривых дается у = 0,5. Для
качественного рассмотрения на больших временах можно с
хорошей точностью приблизить %n(t) функцией зсо(0"> это свойство
мы будем использовать в дальнейшем.
0,1 1 ГО
t/re
Рис. 1. Вероятности %n(t) того, что за время t частица сделала ровно пшагов
пуассоновского распределения времен ожидания typ(t) (4). хе определено
соотношением l|)p(te) = lie.
Рис. 2. То же, что на рис. 1, но для распределения времен ожидания ^z{t)y
даваемого формулой (9). Здесь также я|)2(ге)= 1/е.
Иерархические и фрактальные свойства неупорядоченных систем 565
Теперь рассмотрим более привычные геометрические
фракталы. Многие стохастически разупорядоченные системы, такие,
как перколяционные кластеры на пороге протекания, агрегаты,
возникающие в процессе диффузионно-лимитированного роста,
линейные и ветвящиеся полимеры, эпоксидные смолы и
различные пористые материалы, как оказалось, обладают свойством
геометрического самоподобия [19]. Однако мы хорошо знаем,
что фракталы вовсе не обязаны быть случайными. Известным
примером являются построенные с помощью детерминистической
процедуры кривые Серпинского. • Основой для построения этих
кривых являются гипертетраэдры в d-мерном евклидовом
пространстве, состоящие из d-\- 1 гипертетраэдров с вдвое меньшей
длиной ребра. Обобщения этой процедуры можно получить,
выбрав отличный от 2 коэффициент масштабного йреобразования
и изменив способ покрытия исходного тетраэдра [20, 21]. Такая
процедура позволяет построить напоминающие кривые
Серпинского фрактальные структуры с заранее определенной
фрактальной размерностью. Кроме того, детерминистические фракталы
можно получать как прямые произведения множеств. Например,
произведение кривой Серпинского и линейной цепочки дает тоб-
лерон-решетку [21,22].
После того как мы определили фракталы в пространстве и во
времени, мы можем объединить эти два аспекта. Как уже
говорилось, пространственный беспорядок часто сопровождается
временным беспорядком. Оба типа беспорядка возникают в
рассмотрении таких динамических процессов, как движение
жидкости в пористых горных породах или миграция возбуждений в
перколяционных системах, в которых случайными являются
энергии узлов или величина их взаимодействия (барьеры). В
предыдущих работах мы обобщили СБИВ на фрактальные решетки и
исследовали для нескольких классов распределений ty(t)
поведение среднего квадрата смещения (r2(t)} и закон спадания
числа возбуждений в системе, связанного с их тушением на
ловушках. Мы показали, что наличие как временной, так и
пространственной случайности приводит к новым интересным аспектам
поведения [13, 23].
В качестве примера рассмотрим средний квадрат смещения
частицы, блуждающей на геометрическом фрактале. В случае,
когда времена ожидания между шагами фиксированны, имеем
[24]
(rl)~nW, (10)
где п — число шагов, a J и Я — фрактальная и спектральная
(фрактонная) размерности соответственно. Аналог выражения
566
Часть VIII
(10) для блужданий с непрерывным временем имеет вид
(r2(t))=t(rl)xn(t), (11)
/г=0
где %n(t) —вероятность сделать за время i ровно п шагов. Ла-
пласовский образ этой величины дается выражением (8).
Соотношение (11) приводит в общем случае к сложным выражениям,
однако для фракталов поведение величины (r2(t)} на больших
временах получить довольно легко. Если %n(t) удовлетворяет на
больших временах скейлинговаму закону (см. рис. 2), для
фиксированного t имеем
*"(/Ио »>/w(/). (12)
Используя условие нормировки для %n(t) и равенство (12),
можно восстановить временную зависимость яМакС:
°° "макс
i = Zx„(0^ £ Хо(0 = Хо(Олы.«(0, (13)
/г=0 «=0
откуда, поскольку %0(t) ~ М, получаем пмакс ~ ty.
Тот же аргумент в применении к равенству (11) дает
"макс _. _
<r2(0)~ £ nMMt)~K,(t)nl+jld, (14)
откуда с помощью (13) получаем
(г2(Ф~пШ~РШ. (15)
Это выражение подтверждает наличие субординации [13], т. е.
мультипликативное поведение показателей для двух видов
беспорядка.
Сходные аргументы можно использовать и для определения
S(t) —среднего числа узлов, посещенных блужданием за время
t. Для блужданий с фиксированным временем ожидания имеем
Sn ~ п^2 при й<:2и8п~пв противном случае. Таким
образом,
*«>~{Г,при^' <16»
( г, при d > 2,
что дает еще один пример субординации [13].
3. Реакции
В этом разделе мы проанализируем влияние фрактального
поведения на реакции некоторых типов. Будут рассмотрены как
псевдомономолекулярные, так и бимолекулярные реакции. При-
Иерархические и фрактальные свойства неупорядоченных систем 567
мером реакции первого типа является реакция Л + Б->Б, при
которой частица типа А аннигилирует, встречаясь с частицей В.
Примерами бимолекулярных реакций являются реакции А +
+ Л->-0 и Л + jB-^O. В первом случае в рамках кинетической
схемы плотность частиц типа А зависит от времени квазиэкспо-
ненциально, в то время как при реакции А + Л->-0 она следует
на больших временах закону \/t [25]. Такое же спадание
концентрации получается и для реакции типа Л + В->0 при
равном числе частиц А и В. Как мы покажем ниже, область
применимости кинетического подхода (предполагающего протекание
реакции в условиях хорошего перемешивания) ограничена. Мы
продемонстрируем отклонения от рассмотренных выше законов
затухания.
Начнем с псевдомономолекулярной схемы реакции и
покажем наличие отклонений от экспоненциальное™. Как уже
упоминалось в наших предыдущих работах, особый интерес
представляют два случая, а именно те, в которых частицы одного
из типов неподвижны. Случай, в котором неподвижны частицы
A (DA =0, ОвфО), приводит к задаче о мишени, случай, когда
неподвижны частицы В (Da ф 0, DB = 0), соответствует задаче
о ловушках [23].
Для регулярных трансляционно-инвариантных решеток мы
показали, что задача о мишени имеет точное решение,
выражающееся через 5(0 — среднее число посещенных узлов [25, 26].
Для случая фиксированных времен ожидания можно определить
Нп(т)—вероятность того, что первое достижение точки 0
блужданием, стартовавшим из точки г, случится за п первых
шагов. Если частица А расположена в начале координат, а
частица В — в точке г, для вероятности того, что В не достигнет
точки 0 за первые п шагов, имеем
^(г)=1-#Лг). (17)
Таким образом, если частицы В распределены на решетке по
Пуассону, закон спадания числа частиц А будет
Ф„ = ГГ {£ (е-У//!)[^(г)К} = ехр[-р S' #„ (г)], (18)
где р— концентрация частиц В. Далее, Нп(т) связана с Sn
(средним числом посещенных'за п шагов узлов) соотношением
£'#„(r) = S„-l (19)
г
и, следовательно,
<P„ = exp[-p(S„-l)]. (20)
Для СБНВ воспользуемся величиной %n(t), даваемой
выражением (8), и получим вероятность посещения точки 0 из точки
568
Часть VIII
г за время U
Я(/5 r)=Zxn(t)Hn(r). (21)
/г=0
Вместо уравнения (20) для задачи о мишени в случае СБИВ
находим
<b(t)~exp[—pS(t)). (22)
Для фрактальной ty(t) (см. (7)) S(<) дается соотношением (16).
Тот же результат (22) приближенно справедлив и для
фрактальных решеток, поскольку для них имеется усреднение по
неэквивалентным положениям мишени. Отметим, что спад
концентрации в задаче о мишени следует закону Кольрауша — Уильям-
са — Уоттса (1).
Совершенно иной вид имеет обобщение на случай СБИВ
задачи о ловушках. Снова начнем с простых случайных
блужданий с фиксированным временем ожидания. Теперь движутся
частицы Л, частицы В остаются неподвижными. Пусть Rn означает
число различных узлов, посещенных за п шагов в данной
конкретной реализации блуждания. Пусть Fn — вероятность того,
что для той же реализации частица еще не поймана ловушкой.
Если частицы типа В распределены по Пуассону, вероятность
того, что данный узел не занят частицей В, равна е~р и,
следовательно [25],
Рп = е-р1*п-г\ (23)
Наблюдаемой величиной будет вероятность выживания
частицы, равная среднему от Fn по всем возможным реализациям
блуждания:
= е-"ехр[Е^)Л-р)//л]> (24)
где /С/, л — кумулянты распределения Rn. Взяв два первых
кумулянта, например, получим
Фж~в-" (*»-•)./^ (25)
Как и раньше, мы можем перейти к случаю СБНВ,
используя %n(t) [27]:
ф(0=Еф»х»(0. (26)
/г=0
Глядя на (26) как на результат дополнительного усреднения
(24), в пределе коротких времен получаем выражение (22) как
первый член кумулянтного разложения:
Ф(0~ехр[-/?5(0]. (27)
Иерархические и фрактальные свойства неупорядоченных систем 569
Поведение же на больших временах следует из свойств
фрактальной %п (/):
пмакс
Ф(0~Хо(0 I Ф„~Хо (*)<»>, (28)
где <я>— среднее число шагов, которое делает до захвата
ловушкой частица, совершающая обычные случайные блуждания
с фиксированным временем ожидания:
<«> - £ п (Ф„_, - Ф„) = £ Ф„. (29)
В (29) мы использовали тот факт, что Фп образуют убывающую
суммируемую последовательность и что пмаКс для больших
времен также велико^ (см. (13)). Замечательным результатом,
следующим из (28), является то, что на больших временах кривая
Ot(t) идет параллельно зависимости %0(0= 1 -— \ ^{t')dtf (см.
о
(8)), определяющей вероятность того, что к моменту времени t
не сделано ни одного шага. Это свойство проявилось и в наших
предшествующих численных исследованиях законов спадания
концентрации и привело к тому, что соответствующие, зависящие
от концентрации законы следуют непересекающимся кривым
[28]. Интересно, что на больших временах зависимость от числа
частиц В и от структуры решетки входит только через величину
<я>. Простая оценка для случая малых концентраций дает
<л> = £ Фп ~ £ e~p (s»-') ~ \ dx ехр (- р&) = р-Ч*Т (1 + ±) .
п=0 п=0 О
(30)
В (30) мы использовали выражение (16), согласно которому
Sn ~ па\ Г (л:)—эйлерова Г-функция. Отметим, что при d = \
соотношение <n> ~ р~2 является точным [29], и что оно
достаточно хорошо выполняется и в высших размерностях. Объединяя
(28), (30), (13) и (16), имеем
Ф(0Чг7(Л при!<2' (3D
{:-■
}/р, при d > 2.
Таким образом, зависимость от времени числа возбуждений в
системе с ловушками и фрактальным временем перескоков
является алгебраической, как в (3). Долговременные асимптотики
спадания концентрации в моделях мишеней и ловушек, таким
образом, совершенно различны.
570
Часть VIII
Теперь обратимся к бимолекулярным реакциям и проследим
за отклонениями от предсказываемого формальной кинетикой
закона S(t). Начнем с реакции Л + Л->0. Из рассмотренной
выше теории псевдомономолекулярных реакций мы знаем, что
в режиме малых времен кинетическая экспонента
модифицируется за счет появления 5(0- Поэтому можно ожидать, что для
реакции Л+Л->0 закон спадания на больших временах будет
1/5(0 [25,30].
Для случая блужданий с фиксированным временем
ожидания мы показали, что закон спадания концентрации хорошо
описывается следующей формулой [25]:
<tfA = (l + 2pSnrt- (32)
Здесь р — плотность частиц Л. Долговременная асимптотика
спадания, таким образом, следует алгебраическому закону
ФпА ~ п~а/р- В качестве эвристического аргумента мы можем
использовать предположение, что (32), являющееся решением
многочастичной задачи, связано с вероятностью встречи двух
частиц, которая в свою очередь выражается через Sn — объем,
посещенный каждой из них. Тогда, поскольку в схеме СБНВ Sn
заменяется на S{t), можно ожидать, что в пределе больших
времен ФЛА ~[pS(t)]~K
Чтобы проверить это предсказание, мы численно
смоделировали и проанализировали реакцию Л + Л->0 при СБНВ. Мы
рассмотрели блуждания на трехмерной простой кубической
решетке и взяли фг(0 из (9)> так что у = 1/2. Соответствующий
закон спадания приведен на рис. 3. Этот закон значительно
отличается от приведенного на том же рисунке закона спадания
концентрации частиц, совершающих обычные случайные
блуждания. В то время как при обычных блужданиях спадание
следует закону Н, при СБНВ с распределением ty2(t) на больших
временах концентрация спадает как /~1/2. Это видно из того же
рис. 3, на котором показаны асимптотические наклоны кривых.
Для получения дополнительных примеров мы смоделировали ту
же реакцию на нескольких кривых Серпинского и на линейной
цепочке. Результаты соответствующих численных экспериментов
представлены на рис. 4. Как видно из этого рисунка, спадание
концентрации на больших временах действительно следует
закону №А, а не №2> как было бы для обычных блужданий. Все
эти данные согласуются с предположением, что <&AA(t) ~
~ [5(f)]-1, т. е.
ГуЯ/2 при d < 2,
( /-ч
ф^(|)~|^
(33)
при d > 2.
Выражение (33) дает еще один пример субординации [13].
Ю'1 b
70'с -
70''
FV
h
г
L
p
p
p
г
F
L
г
L
\\
\\
\\
\\
\ \
\\
\\
CB
1
d = 3
\ \
\ \
\\
\\
\\
\\
\\
\\
\ "Лл
\ СБИВ \ч
%"*-' \
\\ \\
\\ V
\\
\\
1 1 1 1 1
70z
70*
n, i/te
to6
Рис. 3. Закон спадания концентрации ФАА (t) из-за аннигиляции Л + Л -*- О
на простой кубической решетке, d = 3, для простых случайных блужданий и
СБНВ с распределением ^i{t). Начальная концентрация частиц р = 0,1. Для
наглядности отдельно показаны асимптотические наклоны кривых в пределе
больших времен.
Рис. 4. То же, что на рис. 3, для СБНВ с распределением ^%(t) на
нескольких кривых Серпинского и на линейной цепочке.
572
Часть VIII
В качестве последнего примера рассмотрим строго
бимолекулярную реакцию А +£-►• 0 при одинаковом числе частиц А
и В. В этом случае известно [25, 31, 32], что, если частицы А и
В совершают случайные блуждания с фиксированным временем
ожидания, долговременное спадание концентрации следует не
закону пг1, а закону n~3li. Критическая размерность 3 = 4
связана с появлением крупномасштабных пространственных
флуктуации [25, 31, 32]. Поскольку мы уже показали, что закон
I I III» I I I L
Ю'° Ю~г Ю'* W6 Ю'8
п, t/re
Рис. 5. Закон спадания ФАВ(1) строго бимолекулярной реакции A + B-+Q,
Д(0) = В(0) для частиц, совершающих СБНВ на линейной цепочке. Также
показаны наклоны кривых на больших временах.
n~dfA хорошо выполняется для кривых Серпинского в
пространствах различной евклидовой размерности dy нам остается только
изучить влияние СБНВ. Как и в предыдущих случаях, мы
ожидаем наличие субординации по отношению к временной
переменной, т. е. закона
флв(/)~Г^/4 (для<2<4). (34)
На рис. 5 показан закон спадания числа частиц,
совершающих СБНВ с распределением фг(0 на линейной цепочке. Из
рис. 5 видно, что предположение о субординации действительно
хорошо выполняется.
4. Выводы
В нашем сообщении мы рассмотрели поведение псевдомоно-
молекулярных (задачи о мишени и ловушках) и
бимолекулярных реакций в системах с пространственным и временным бес-
Иерархические и фрактальные свойства неупорядоченных систем 573
порядком. Для моделирования стохастических свойств таких
систем мы использовали пространственные и временные фракталы.
Мы показали, что классическая кинетика не слишком хорошо
описывает такие реакции, поскольку отклонения от
экспоненциального закона спадания или закона \/t встречаются
довольно часто.
Таблица 1. Законы спадания концентрации со временем
Тип реакции
Случайные блуждания
Большие
времена
Малые времена
СБИВ
Большие
времена
А + В->В
Ловушки
Z)B = 0)
Мишень
e~ctd/2(d<2)
e~ct (d > 2)
-ct
310+2)
ГУ
Нет
субординации
e-Ci3l2(d<2)
e~ct (d > 2)
-ct
№ ~ „Yd/2 _
(d<2) e~ct (d<2)
-Qt (d > 2)
e~ct\d>2)
Есть
субординация
А + А->0
Бимолекулярная
[l + Ct3,12]-1 (d<2) t~3/2(d<2)
[\+Ctrl {d>2) Г1 (d>2)
ry3/2 (3 < 2)
Г У (d > 2)
Есть
субординация
А + В->0
Л(0) = В(0)
BZ°nu?J~ [l + Ctd*2]-l(d<2) rd^(d<2) Г^/*(3<2)
лярная
(DA
= 0)
[l + Ct]
'l (d > 2)
-1 (d>2)
ГV [d > 2)
Есть
субординация
В качестве итога возьмем табл. 1, в которой приведены
законы спадания концентрации для различных типов реакций. Во
всех случаях (кроме достаточно специфической задачи о
ловушках) законы спадания демонстрируют наличие
субординации, т. е. наличие различных видов случайности приводит к
тому, что в окончательный ответ соответствующие скеилинговые
коэффициенты входят мультипликативно. Для задачи о
ловушках поведение на больших временах целиком определяется
временным беспорядком. Такое же поведение будет наблюдаться и
в случае энергетического беспорядка, свойства которого
обсуждались в разд. 2. В этом случае скейлинговый коэффициент
пропорционален температуре.
574
Часть VIII
Благодарности. Авторы благодарят д-ра М. Шлезингера за
многочисленные полезные и приятные обсуждения. Мы
благодарим Немецкое общество научных исследований и Фонд
химической промышленности за финансовую поддержку и
компьютерный центр ЕТН в Цюрихе за предоставление машинного
времени.
ЛИТЕРАТУРА
1. Klafter /., Blumen Л., in: Energy Transfer Processes in Condensed Media,
ed. B. di Bartolo, Plenum, New York, 1984, p. 621.
2. Brenl W., Friedrich /., Haarer D., J. Chem. Phys., 81, 3915 (1984).
3. Friedrich L, Blumen Л., Phys. Rev., B32, 1434 (1985).
4. Scher #., Montroll E. №., Phys. Rev., B12, 2245 (1975).
5. Tauc /., Semicond. and Semimetals, 21B, 299 (1984).
6. Weiss G. Я., Separation Sci., 5, 51 (1980).
7. Kohlrausch #., Ann. Phys. (Leipzig), 12, 393 (1847).
8. Williams G., Watts D. C, Trans. Faraday Soc, 66, 80 (1970).
9. Kgai K.L., Comments Solid State Phys., 9, 127 (1979); 9, 141 (1980).
10. Shlesinger M. F., Montroll E. W., Proc. Natl. Acad. Sci. USA, 81, 1280
(1984).
11. Inokuti M., Hirayama F., J. Chem. Phys., 43, 1978 (1965).
12. Scher #., Lax M,, Phys. Rev., B7, 4491 (1973).
13. Blumen Л., Klafter /., White B. S., Zumofen G., Phys. Rev. Lett., 53, 1301
(1984).
14_ Mandelbrot В. В., The Fractal Geometry of Nature, Freeman,
San-Francisco, 1982.
15. Shlesinger M. F., J. Stat. Phys., 36, 639 (1984).
16. Montroll E. W., Shlesinger M. F., in: Monequilibrium Phenomena II From
Stochastics to Hydrodynamics, eds. J. L. Lebowitz, E. W. Montroll, North
Holland, Amsterdam, 1984, p. 1.
17. Pfister G., Scher #., Adv. Phys., 27, 747 (1978).
18. Shlesinger M. F., J. Stat. Phys., 10, 421 (1974).
19. См. наст. сб.
20. Hilfer /?., Blumen A., J. Phys., A17, L537; L783 (1984).
21. Хильфер Р., Блюмен А. — наст, сб., с. 54.
22. Маритан Л., Стелла Л.— наст, сб., с. 151.
23. Klafter /., Blumen Л., Zumofen (?., J. Stat. Phys., 36, 561 (1984).
24. Alexander S., Orbach #., J. Phys. (Paris) Lett., 43, L625 (1982).-
25. Zumofen G., Blumen Л., Klafter /., J. Chem. Phys., 82, 3198 (1985).
26. Blumen A., Zumofen G.} Klafter /., Phys. Rev., B30, 5379 (1984).
27. Blumen Л., Zumofen G., J. Chem. Phys., 77, 5127 (1982).
28. Zumofen G., Klafter /., Blumen Л., J. Chem. Phys., 79, 5131 (1983).
29. Montroll E. W., J. Phys. Soc. Japan Suppl., 26, 6 (1969).
30. Klymko P. W., Kopelman R., J. Phys. Chem., 87, 4565 (1983).
31. Ovchinnikov А. Л., Zeldowich Ya. В., Chem. Phys., 28, 215 (1978).
32. Toussaint D.. Wilczek F, J. Chem. Phvs.. 78, 2642 (1983).
Самоподобное временное поведение
случайных блужданий
в одномерной случайной среде
Дж. Бернаскони, У. Шнейдер *
С помощью новой ренормализационной процедуры в реальном
пространстве исследованы случайные блуждания в одномерной
случайной среде. Для асимметричных распределений вероятностей
перехода показано, что перенормированное блуждание стремится к
направленному движению частицы; получающееся в этом пределе
распределение времен перехода вычислено с помощью метода
Монте-Карло. При определенных условиях множество времен перехода
имеет самоподобную кластерную структуру со средней
фрактальной размерностью v < 1. В пределе больших времен
асимптотическое поведение среднего смещения частицы описывается законом
х (t) ~ t~v F(\n t), где F — периодическая функция.
Случайные блуждания в случайных средах в последнее
время вызывают большой интерес [1, 2]. Соответствующие
модели демонстрируют многие замечательные особенности
поведения и используются для исследования аномальных
транспортных свойств различных неупорядоченных материалов. В
настоящей статье мы рассмотрим случайные блуждания с дискретным
временем на одномерной решетке со случайными вероятностями
переходов. Пусть Xt = n есть положение частицы в момент
времени t. Тогда Xt+\ = п ± 1 с вероятностями рп и 1 — рп
соответственно. Таким образом, мы имеем
Рп (t + 1) = Рп^Рп^ «) + (1- Ря_х) Рп+1 (О,
где Pn(t) —вероятность того, что Xt = n\ мы будем всегда
считать, что Рп(0) =6no. Вероятности переходов рп будем считать
независимыми случайными переменными, одинаково
распределенными с данной плотностью вероятности р(р).
Соответствующие модели и их обобщения для случайных
блужданий с непрерывным временем исследовались с помощью
различных методов [1—8]. Был сделан замечательный вывод о
том, что при определенных условиях среднее смещение
x(t)= £ nPn(t)
/1= — оо
асимптотически растет медленнее, чем линейно по времени. Для
некоторых специальных типов беспорядка было обнаружено еще
более удивительное явление [2, 3, 6]: на этот сублинейный рост
наложены незатухающие осцилляции x(t) как функции \ogt.
* J. Vernasconi, W. R. Scneider- Brown Boveri Research Centerg, CH-5405
Baden, Switzerland.
576
Часть VIII
Эти асимптотические осцилляции были интерпретированы в
терминах самоподобной кластеризации времен ожидания, и их
свойства могут быть определены для моделей, содержащих конечную
долю «диодов».
Для того чтобы детально исследовать асимптотическое
поведение x{t) при произвольном беспорядке, мы предложили и
проанализировали новую процедуру перенормировки в реальном
пространстве для случайных блужданий в случайной среде. Эта
1-Ро Ро
7-pZ *
Ро
Рис. 1. Схематическое представление основного шага ренормализационной
процедуры.
процедура непосредственно приводит к цели и более наглядна,
чем прежние ренормгрупповые подходы [7—9]. Метод основан
на простой децимации одномерной решетки (рис. 1);
перенормированная вероятность перехода, связанная с узлом 0, р0 равна
Выражение (1) получено суммированием по всем возможным
путям блуждания, приводящим от узла 0 к узлу 2 через
промежуточные узлы— 1 и 1. Поскольку число шагов этих блужданий
меняется от 2 до бесконечности, перенормировка приводит в
принципе к широкому распределению времен перехода. Чтобы
упростить процедуру, мы определим среднее время перехода,
усредняя по этому распределению после каждого шага ренормали-
зационного преобразования. Соответствующее преобразование
для времени перехода имеет вид
-' — - i - i Р-1 (1 — Ро) (T-i + qo) + Ро П — РО <то + вО /оч
где Т/г и On означают средние времена перехода для прыжков
вправо и влево соответственно.
Начальные вероятности перехода рп независимы и одинаково
распределены; плотность вероятности соответствующего
распределения р(р)=р°(р); все времена переходов равны единице,
т. е. р*0)((т> а}) = 6 (т—1)6 (а — ^.Соответствующие плотности
вероятностей после k шагов ренормализационного преобразова-
Иерархические и фрактальные свойства неупорядоченных систем 577
ния обозначим р(й)(р) и р&Щх, <*})• Мы будем интересоваться
поведением этих величин в пределе k ~> оо.
Мы проанализировали поведение системы при различных
начальных распределениях р(0)(р) методом Монте-Карло,
проделав до k = 7 шагов преобразования. Наши результаты
показывают, что
р(*)(р)^б(р_1) (3)
Я -> оо
для любых асимметричных распределений р(0)(р), для которых
$dpp<°>(p)ln-^<0. (4)
о
Выражение (3) означает, что перенормированное блуждание
стремится к предельному блужданию, совершающему только
7,0
t
0,5
О 0,5 р—*- 1,0
Рис. 2. Перенормированные функции распределения /?(А)(р) (см. (6)) для
модели, задаваемой выражением (5) с х = 0,4, у = 1/я.
шаги вправо (если интеграл в (4) оказывается больше нуля,
предельное блуждание направлено влево). С ростом k
случайность в вероятностях переходов исчезает и заменяется
случайностью во временах переходов.
Соответствующие результаты подробно представлены на
рис. 2—4. Все они относятся к «бинарному» распределению
вероятностей перехода типа
р0(р) = *6(р-у) + (1-*)д(р-(1-у)). (5)
На рис. 2 показаны функции распределения i?(*> (p):
#»(P)=$<W*>(//). (6)
о
Видно, что после 6 шагов преобразования 90 % вероятностей
перехода по величине оказываются больше, чем 0,95. Поскольку
578
Часть VIII
p{k)(p) приближается к б(р—1), зависимость свойств
блуждания от времен перехода для прыжков влево исчезает, и
предельное распределение времен перехода легко определяется
вычислением интеграла
pik4x)=\dppik4p)\doPW({T, a})
(7)
для достаточно больших k. Соответствующая гистограмма,
полученная после & = 5 шагов преобразования, показана на
б 10 15 20 1пчг
\ Наклон v
\
О
-г
-4
-6
-8
-10
Рис. 3. Плотность распределения времен перехода как функция 1пт после &=
= 5 шагов ренормализационного преобразования для модели, определяемой
(5) с х = 0,2 и у = 0,047.
рис. 3. На нем ясно виден фрактальный характер распределения
времен перехода, подразумевающий [2, 6, 10], что во множестве
времен перехода имеет место самоподобная кластеризация,
характеризующаяся масштабным множителем ехр(р) и средней
фрактальной размерностью v.
Модели, привлекающие движение во фрактальном времени,
уже использовались при объяснении аномального поведения
переноса и релаксации в некоторых аморфных системах [10, 11].
В этих моделях, однако, фрактальная структура времен
перехода предполагалась априори, в то время как в нашей модели
случайных блужданий она возникает в процессе перенормировок
как естественное следствие беспорядка.
Предположим теперь, что после k перенормировок наше
случайное блуждание приблизительно представимо направленным
Иерархические и фрактальные свойства неупорядоченных систем 579
движением частицы с плотностью распределения времен
перехода p(fe)(t) и что корреляциями между временами
последовательных переходов можно пренебречь. Тогда лапласовский
образ x{z) среднего смещения x{t) приблизительно равен
' P(.fc)(*)
x(z) =
г l-p<ft)(z) '
(8)
где p(fe) (z) — лапласовский образ р^> (т). Если, как на рис. 4,
поведение p(ft)(z) при малых z имеет вид
l-pf^-z^Gr'M, (9)
где G периодическая функция с периодом 1, то среднее
смещение асимптотически ведет себя как
лг(0~^(р-'М, (10)
где F тоже периодична с периодом 1. Наша ренормализацион-
ная процедура дает, таким образом, не только показатель v, но
in(7-/>J*Vim*
t
Zfi.
г,7
2,6
S/
V^OfiZ £s'
.••/^C.»** I
л ' I _1 ! 1
-7$
-1*
-10
-5 In z
Рис. 4. Поведение лапласовского образа плотности распределения времен
перехода после k = 4 шагов преобразования для модели с х = 0,2 и у = 1/17.
и период осцилляции р. Сравнение с точными результатами для
моделей с «диодами» [2, 6] показывает, что значения v и р
определяются достаточно точно уже после нескольких шагов
преобразования. Мы заметим также, что осцилляции наблюдаются,
только если р(0)(р) дискретно и приводит к значениям v < 1, как
это и ожидалось в соответствии с общими представлениями
[2,4,6].
19*
580
Часть VIII
Мы применили нашу ренормализационную процедуру и к
случаю с симметричными вероятностями перехода, т. е. к таким
р(0)(р), для которых интеграл (4) обращается в 0 [12]. В этом
случае (см., например, рис. 5) мы обнаружили, что
P(*,(p)rrti-[*(P) + e(P-i)], (П)
ft -> оо Z
и соответствующее предельное блуждание ведет себя весьма
странным образом. Это поведение очень трудно проанализиро-
Рис. 5. Перенормированные функции распределения R<k)(p) (6) для
равномерной плотности начального распределения времен перехода.
вать количественно; по-видимому, оно находится в качественном
соответствии с предсказаниями Синая [12].
ЛИТЕРАТУРА
1. Alexander S., Bernasconi /., Schneider W. R., Orbach R., Rev. Mod. Phys.,
53, 175 (1981), см. также ссылки в этой работе.
2. Bernasconi /., Schneider W. R., Helv. Phys. Acta, 58, 579 (1985).
3. Solomon F., Ann. Prob., 3, 1 (1975).
4. Kesten #., Kozlov M. V., Spitzer F., Composition Math., 30, 145 (1975).
5. Derrida В., Pomeau У., Phys. Rev. Lett., 48, 627 (1982).
6. Bernasconi /., Schneider W. R., J. Phys., A15, L729 (1982).
7. Machta /., Phys. Rev., B24, 5260 (1981); J. Stat. Phys., 30, 305 (1983).
8. Guyer R. A.t Phys. Rev, A29, 2114 (1984).
9. Napiorkowski M., J. Phys., A16, 3065 (1981).
10. Shlesinger M. F., Hughes B. D.t Physica, 109A, 597 (1981).
И. Шлезингер М., Клафтер Дж. — наст, сб., с. 553.
12. Sinai Ya. О., Lect. Notes Phys., 153, Berlin, Springer, 1982, p. 12; Theor
Prob. Appl, 27, 256 (1982).
Наблюдение скейлинга
в реакции с ловушками
3. Джорджевич *
Исследована временная зависимость концентрации C(t)
химического вещества, частицы которого свободно диффундируют в растворе,
в котором случайно расположены практически неподвижные нена-
сыщаемые ловушки. Показано, что концентрация С(t) следует
зависящему от размерности пространства закону спадания C(t) '=
= exp (—At — £/W+2>) с d = 3.
1. Введение
В последние несколько лет мы стали свидетелями
заметного возрастания интереса к исследованию
диффузионно-ограниченных реакций [1—11], Этот интерес (по крайней мере
среди физиков) во многом определяется тем, что концентрации
химических веществ (физических частиц), принимающих
участие в реакциях, спадают, как выяснилось, по аномальным
законам. Наиболее подробно исследованы процессы рекомбинации
[7], реакции со статическими ловушками и «реакция
мусорщика» [2, 12]. Каждая из этих реакций имеет свои особенности
поведения, но физическая причина аномалий во всех случаях
одна и та же.
В качестве примера рассмотрим реакцию, в которой частицы
Р химического вещества диффундируют в среде, содержащей
случайно расположенные статические ненасыщаемые ловушки Т.
При контакте частицы Р с ловушкой Т частица исчезает.
Ненасыщаемость ловушки означает, что реакция Р + Т-*Т может
повторяться бесконечное число раз. Обычно считается, что, если
концентрация частиц и ловушек велика или реакция происходит
при интенсивном перемешивании, процесс может
рассматриваться как классическая реакция первого порядка. В этом случае
можно считать, что закон спадания концентрации частиц C(t)
будет иметь вид
С(^ехр(-Л/), (1)
где А — константа, пропорциональная концентрации ловушек.
Однако, если концентрация случайно расположенных ловушек
мала, с необходимостью существуют области пространства,
практически свободные от ловушек. Частицы,,попавшие в эти
области, могут достичь ловушек лишь за весьма большое время, и,
следовательно, спадание их числа со временем будет более мед-
* Zoran В. Djordjevic- «Boris Kidric» Institute of Nuclear Scienses, Vitica,
Laboratory for Solid State and Radiation Chemistry, P. 0. Box 522, 11001
Belgrade, Yugoslavia.
582
Часть VIII
ленным. Формальный анализ [13] этой задачи показывает, что
концентрация частиц спадает по закону
C(t)~exp(-Btdld+2)> (2)
зависящему от размерности пространства d. Читатель, конечно,
заметил, что сингулярная зависимость От времени в (2)
появилась одновременно с крупномасштабными флуктуациями
(неоднородностью) плотности ловушек. Эта взаимосвязь не случайна:
в ее основе лежат те же физические механизмы, что действуют
вблизи точки фазового перехода второго рода.
Если ловушки могут двигаться, их движение как бы
усредняет влияние пространственной неоднородности, так что
предположения, приводящие к (1), будут выполняться лу^шб. С
помощью весьма нетривиальных аргументов било показано [12],
что в этом случае концентрация частиц спадает по
комбинированному закону
С (t) ~ exp (~ At) • ехр (- Btdfd+% (3)
где А пропорционально коэффициенту диффузии ловушек.
Цель настоящей работы — проверить применимость этих
теоретических предсказаний к реальным экспериментальным
системам.
2. Экспериментальная система
Наблюдавшаяся нами реакция — это реакция переноса
электрона от однозарядного катиона метилового фиолетового (1,1'-
диметил 4,4'-бипириДин) к коллоидным частицам платины в
водйом растворе [14]. Первоначально система содержит
трижды дистиллированную воду с небольшим количеством (2Х
X Ю-4 моль/дм3) дикатиОнов метилового фиолетового MV2+,
немного 2-пропанола (Ю-1 моль/дм3) и 5/10~5 моль/дм3 платины.
Коллоидная платина получалась в реакции [17] между
цитратом натрия и гексахлорплатиновой кислотой. Измерения
среднего радиуса коллоидных частиц дали величину 3 нм, что
соответствует среднему числу агрегации 7,5-103.
Активные частицы в растворе создавались его импульсным
радиолизом, который происходил при облучении раствора
импульсным пучком электронов с энергией 2 мэВ
продолжительностью 20 не. При таком облучении образуется некоторое
количество [(1 Ч-З) -Ю-6 моль/дм3] монокатионов MV+. При
контакте с коллбидными частицами платины эти монокатионы
отдают один электрон и исчезают, превратившись в стабильный
дикатиои MV2+. Одна платиновая частица способна собрать до
104 электронов и с практической точки зрения может считаться
ненасыщаемой ловушкой. Относительно большой размер этих
Иерархические и фрактальные свойства неупорядоченных систем 583
частиц приводит к тому, что их коэффициент диффузии
примерно на порядок меньше, чем у частиц MV+. Перед
использованием проводилась деаэрация раствора продуванием аргона.
Рассматриваемая реакция может быть формально
представлена в виде
mMV+ + (р« -> (PC" + mMV
2+
(4)
где т — «произвольное» целое число. Реакция (4) наблюдалась
по уменьшению оптического поглощения в растворе на линии
поглощения MV+ (длина волны 605 нм, 8б05= 12 6Q0 моль-1-см-*1)
[16]; поглощение MV++ на этой длине волны пренебрежимо
мало. Концентрация C(/)MV+ определялась из закона Бугера —
Ламберта — Бэра /(/)== /о ехр(—DC(t)), где I(t)—
интенсивность прошедшего через раствор света, a D — константа,
пропорциональная толщине образца и величине молекулярного
поглощения MV+. Измерение I(t) проводилось от 1300 до 2000 раз
через каждые 0,5 мкс.
3. Результаты и обсуждение
Зависимость от времени концентрации активных, быстро
диффундирующих частиц MV+ показана на рис. 1. Частицы возни-
ZOO WO 600
Время, л?/<с
Рис 1. Зависимость концентрации монокатионов MV+ от времени.
кают в момент времени / = 0; время лх генерации меньше, чем
временное разрешение при наших измерениях. Мы интересуемся
зависимостью от времени логарифма C(t); эта зависимость
представлена на рис. 2. Согласно классической кинетике
реакций первого порядка, эта зависимость должна была бы быть
линейной. На графике же, представленном на рис 2, отчетливо
заметна кривизна, так что неприменимость классического
рассмотрения очевидна.
Чтобы проверить применимость уравнений (2) и (3), мы
нашли наилучшее в смысле метода наименьших квадратов
приближение экспериментальных точек функций — At — Btc с
неизвестными значениями коэффициентов Л и В и показателя С.
584 Часть У 111
Наилучшие результаты получились при конечных значениях А
и В и значениях показателя С, лежащих между 0,5 и 0,6.
Осторожная оценка наилучшего значения с дает С = 0,56 ± 0,06.
Наилучшие значения А и В указаны в подписи под рис. 2 и
связаны с выбранным масштабом по оси времени. Следует
отметить, что в рассматриваемом диапазоне времен сингулярная
'■V
""' ^О 250 500 7*50
Время, мне
Рис. 2. Логарифм функции C(t), показанной на рис. 1: / —
экспериментальные данные; 2 — подгоночная кривая log С fit) = —1,1825-10~3^ — 6,08 X
X Ю-2-М
часть функции lnC(t) дает более чем 90 %-ный вклад в ее
величину.
В рамках точности наших измерений и сделанных нами
приближений мы можем сказать, что закон аномального спадания,
полученный Реднером и Кэнгом [12] для реакции в системе с
подвижными ловушками, дает удовлетворительное описание
кинетики такой реакции в трехмерном случае.
Нам известны трудности, встречающиеся при попытках
подтвердить такой закон спадания с помощью численного
эксперимента. В таком эксперименте он может наблюдаться лишь в
пределе очень больших времен. Надо отметить, что в наших
опытах выбраны такие значения концентрации, при которых
численное моделирование становится невозможным. Например, мы
имеем порядка 10~9 молей платиновых частиц на литр раствора.
Если перевести это на язык решеточной модели, это
соответствует примерно одной ловушке на 109 узлов решетки. Ясно, что
эффективно смоделировать реакцию на такой большой решетке
невозможно. Использование столь малых концентраций дало нам
возможность достичь той области, в которой неаналитический
член/d/(d+2) начинает играть определяющую роль. Коэффициент
диффузии наших ловушек оказался, по-видимому, мал или
велик ровно* настолько, чтобы сделать возможцьдо наблюдение
обоих членов в формуле (3).
II
г,о\
Иерархические и фрактальные свойства неупорядоченных систем 585
Благодарности. Автор благодарен своим коллегам д-ру Ми-
лице Неданович и д-ру Ольге Мицич за помощь в постановке
этих экспериментов.
ЛИТЕРАТУРА
1. Балагуров В. #., Вакс В. Г., ЖЭТФ, 65, 1939 (1973).
2. Shlesinger M. F.t J. Chem. Phys., 70, 4813 (1979).
3. Boxon M., Zwanzig R., J Chem. Phys., 75, 234 (1981).
4. Kirkpatrick T. #., J. Chem, Phys., 76, 4255 (1982).
5. Grassberger P., Procaccia /., J. Chem. Phys., 77, 6281 (1982).
6. Calef D. F., Deutch J. M., Ann. Rev. Phys. Chem., 34, 493 (1983).
7. Kang K., Redner S., Phys. Rev. Lett., 52, 955 (1984).
8. Meakin P., Stanley H. E.f J. Phys., A17, L173 (1984).
9. Anacker L. №., Kopelman R.y J. Chem. Phys., 81, 6402 (1984).
10. Blumen A., Zumofen G., Klafter /., Phys. Rev., B30, 5379 (1984).
11. Havlin S., Weiss G. #., Keifer /. £., Dishon M., J. Phys., A17, L347 (1984).
12. Redner 5., Kang K.y J. Phys., A17, L451 (1984).
13. Donsker M. D., Varadhan S. R. S.f Commun. Pure Appl. Math., 28, 525
(1975).
14. Matheson M, S., Lee P. C, Meisel D., Pelizzetti £., J. Phys. Chem., 87,
394 (1983)
15. Markovic V., Nikolic N.y Micic 0. /., Int. J. Rad. Phys. Chem., 6, 227
(1974).
16. Nenadovic M. Г., Micic 0, /., Adzic R. R., J. Chem. Soc. Faraday Trans. I,
78, 1065 (1982).
17. Bond G. C.f Trans. Faraday Soc, 5£, 1235 (1956),
Термодинамика с иерархическими
ограничениями в метастабильных системах
и стеклах
Л. Пьетронеро *
Недавно была предложена картина, согласно которой
конфигурационные степени свободы в стеклах и вообще в метастабильных
системах могут быть иерархически связаны. Мы показали, что
такая картина приводит к тому, что объем доступной области
фазового пространства зависит от температуры. Следствия этого
результата согласуются с низкотемпературным поведением различных
свойств стекол.
1. Введение
Стекло представляет собой метастабильное состояние
твердого тела, в котором отсутствует дальний порядок. С
практической точки зрения это состояние можно рассматривать как
стабильное, поскольку время релаксации к упорядоченному
состоянию может быть очень большим (в некоторых случаях
больше возраста Вселенной). Вопрос об относительной стабильности
стекла может поэтому казаться не имеющим практических
оснований. С другой стороны, именно неравновесность делает столь
трудной задачей формулировку статистической механики и
термодинамики стеклообразного метастабильного состояния. Эта
задача в основном еще не разрешена [1]. Главная трудность
связана с тем, что рассматриваемые системы являются неэрго-
дическими, так что одного только исследования равновесных
распределений недостаточно: в теорию должна быть явно
включена динамика. На настоящий момент не ясна даже природа
перехода стекло — жидкость (термодинамический он или чисто
динамический) [1].
Интересная попытка явно включить динамические эффекты
в описание свойств стекол недавно была сделана Пальмером и
др. [2]. Эти авторы рассмотрели влияние на динамику
релаксации иерархических ограничений и получили закон релаксации
Кольрауша ехр[—(t/x)*]. Основная идея подхода заключается
в том, что атом не может двигаться, пока другой атом,
блокирующий его движение, не освободит путь.
Нами будет рассмотрено влияние таких ограничений на
термодинамические свойства стекол. Мы покажем, что эффективно
доступная область фазового пространства зависит от
температуры [3]. Этот факт сказывается на различных свойствах —
ширине примесных уровней, теплоемкости, теплопроводности, — по-
* L. Pietronero-University of Groningen, Melkweg 1, 9718 ЕР Groningen,
The Netherlands.
Иерархические и фрактальные свойства неупорядоченных систем 587
ведение которых можно сравнить с экспериментальными
данными. Кроме того, такой подход позволяет по-новому взглянуть
на переход стекло — жидкость. Этот переход соответствует
некоторой задаче о просачивании, когда доступные степени
свободы постепенно заполняют все фазовое пространство.
2. Динамика с иерархическими ограничениями
В терминах фазового пространства образование
стеклообразного состояния может быть рассмотрено следующим образом.
При остывании стекла его состояние оказывается связанным с
-о
Рис. 1. Схематическая иллюстрация динамических ограничений в паре
двухуровневых систем". Если ДУС, обозначенная через а, находится в локальном
минимуме /, она блокирует путь релаксации системы Ь. Если она находится
в минимуме 2, система Ь может релаксировать.
некоторой областью фазового пространства, одной из многих
равновозможных; остальные области становятся недоступными.
Доступность означает, что соответствующее время релаксации
не превосходит времени наблюдения. С понижением температуры
«вымораживается» все больше и больше степеней свободы;
остаются только колебательные и релаксационные степени
свободы, соответствующие той области фазового пространства, в
которой связана система. При описании стеклообразного состояния
мы можем ограничиться рассмотрением лишь
конфигурационных степеней свободы. Для простоты и конкретности мы будем
описывать их в терминах двухуровневых систем (ДУС) [4].
Рассмотрим стекло при низкой температуре, скажем 1 К.
Стандартный способ описания в терминах ДУС состоит в том,
чтобы, начиная с локального основного состояния, указать число
возбуждений, время релаксации которых xR меньше, чем время
эксперимента хЕ. Ситуация осложняется, если на динамику ДУС
наложены ограничения. Тип ограничений, которые мы хотим
обсудить, схематически представлен на рис. 1.
Конфигурация двух ДУС, показанная на рис. 1, состоит из
свободной ДУС (а) и ДУС (6), потенциальный барьер которой
зависит от положения а, как это показано на рис. 2. Отметим,
Рис. 2. Схематическое изображение потенциала в ДУС (6) на рис. 1. Если
система а находится в состоянии /, барьер в системе Ь очень высок, и
переход блокирован, если же система а находится в состоянии 2, барьер в
системе b становится ниже, и переход возможен. Заметим, что эта связь чисто
динамическая, так как она не затрагивает энергий локальных минимумов.
Быстрая релаксация
Уровень
- N-1
■ N+2
Медленная релаксация
Рис. 3. Схематическое представление иерархии степеней свободы. Каждая
стрелка означает ограничение того типа, что показан на рис. 1, 2. С ростом
N степени свободы становятся все более медленными.
Иерархические и фрактальные свойства неупорядоченных систем 589
что эта связь является чисто динамической, т. е. на рис. 2
меняется только барьер, но не энергии локального равновесия.
Ограничение является иерархическим в том смысле, что а
действует на 6, но 6 не действует на а; это нетрудно обобщить на
последовательности уровней, как это показано на рис. 3.
Для простоты мы ограничимся обсуждением только одной
пары ДУС. Пусть х^ — доступная степень свободы. Это
означает что %Е ;> т<*>. Поставим вопрос: при каких условиях, х^
тоже доступна? Поскольку х^ предполагается доступной, за
время хЕ она достигает термодинамического равновесия, и
вероятность заселения состояния х2 будет
р (*« = **)-в-*-/0+«-••«), (1)
где р = \/kBT и 8а — расстояние между уровнями а,
«Эффективное» время эксперимента т^>, в течение которого может
измениться состояние Ь> будет
^ (•«. Т) = хЕр (х{а) =* х2) = VTР8*/0 + е~*Ч (2)
Теперь мы можем ввести «функцию доступности» Р,
определяющую, является ли степень свободы системы Ъ доступной за
эффективное экспериментальное время. Эта функция зависит
также от свойств а:
1, если т<*>(еа, Т) > т£>,
О, если tg>(ee, Т) < т<|>. (3)
РЫФ'*аУ
Для данной функции распределения W(ea) расстояний между
уровнями га вероятность того, что xib) доступна, равна
оо
(Р\%в; xf; ej )0=\W (е.)Р[v, tg»; eJ d*a. (4)
О
Если приближенно положить 1 — е"^а с* 1, то условием
доступности будет просто
ев<Г1п[тв/т<|>], (5)
и для равномерного распределения W(ea) = W0 получим
<^[V. ^ «J >. ^ J ^ («.) d% * ™0 1П КК>]. (6)
о
Теперь можно просто вывести выражение для эффективной
плотности доступных степеней свободы
Р СП - Рй [1 + Т (p6/pfl) W In (VTg»)], (7)
590
Часть VIII
где ра и рь — соответственно плотности ДУС типа а и 6. Этот
результат показывает, как иерархические ограничения приводят
к тому, что доступная область фазового пространства растет с
температурой. Он также проливает свет на ту важнейшую роль,
которую играет динамика для квазиравновесных свойств мета-
стабильных систем.
3. Связь с экспериментом
Свойство (7) влияет на многие физические характеристики
системы. Учитывая сделанные нами приближения, выражение
(7) следует рассматривать как справедливое в пределе низких
температур.
Наиболее изученной характеристикой стекол при низких
температурах является их теплоемкость [4]. Для нее мы
предсказываем зависимость
С(Г)-р0Г + 5р^. (8)
Недавно проведенный анализ имеющихся данньцс по
низкотемпературной теплоемкости стекол дает в качестве наилучшего
приближения именно такое выражение [5].
Другим хорошо изученным свойством является
теплопроводность, для которой получаем
/С(Г)-Г2(1-ЯРоГ). (9)
Такое выражение согласуется с экспериментом, данные которого
обычно приближаются степенным законом с показателем около
1,8 [4].
Эти два эффекта, однако, наблюдаемы лишь при очень
низких температурах (T^l К), когда влияние дополнительного
квадратичного члена мало. Совершенно иная ситуация имеет
место для однородной ширины примесного уровня [6, 7], которую
можно измерить и при промежуточных (Г = 10 К), и при
относительно высоких температурах (Г = 100 К). Для ширины
линии мы получили
Г~р0Г + 5р2Г. (10)
Этот результат согласуется с тем, что «кажущийся показатель»
возрастает для данного материала с температурой; поведение
меняется от Т при низких до Г2 при высоких температурах
[6,7].
Сделаем, наконец, несколько спекулятивных замечаний о
применимости представленной картины к переходу стекло —
жидкость. Такой переход соответствует температуре, при которой
доступные степени свободы заполняют все фазовое
пространство. Это означает, что такой переход больше похож на некото-
Иерархические и фрактальные свойства неупорядоченных систем 591
рую задачу протекания (на что с совершенно иной точки зрения
указывали Греет и Коэн [1]), чем на обычный равновесный
фазовый переход.
Для описания этого явления недостаточно ограничиться лишь
учетом возмущений при низких температурах, как это было
сделано в настоящей работе; следует рассмотреть всю иерархию
связанных уровней, показанную на рис. 3. Реальная ситуация
может оказаться еще сложнее, так как в иерархии могут
существовать замкнутые петли. Интересно отметить, что наличие
петель приводит к гистерезисным эффектам при переходе. Такие
эффекты действительно наблюдались [1]. Для того чтобы
подтвердить или опровергнуть эти предположения, необходим
тщательный анализ.
ЛИТЕРАТУРА
1. Grest G. S.t Cohen M. #., Adv. Chem. Phys., 48, 55 (1981).
2. Palmer R. (?., Stein D. L., Abrahams E., Anderson P. W., Phys. Rev. Lett.,
53, 958 (1984).
3. Более детальные обсуждения см. в работе: L. Pietronero, в печати.
4. См., например, Amorphous Solids, ed. W. A. Phillips, Topics in current
Physics Springer, Berlin, 1981.
5. Varma C. M.y Dynes R. C, Banavar J. R„ J. Phys., CI5, L1221 (1982).
6. Thijssen H. P. #., van den Berg R. £., Volker 5., Chem. Phys. Lett., 103,
23 (1983); ibid, 97, 295 (1983).
7. Hegerty /., Broer M. M., Golding В., Simpson J. R., MacCheshey J. В., Phys.
Rev. Lett, 51, 2033 (1983).
Фрактальные кластеры
и скейлинг в модели Изинга
Дж. Камбье, М. Науэнберг *
Численное моделирование двух- и трехмерной модели Изинга
методом Монте-Карло показало, что кластеры спинов являются
фракталами и что распределение кластеров большого размера обладает
скейлинговыми свойствами. Скейлинговые показатели этой
функции распределения — поверхностный показатель и фрактальная
размерность — связаны с критическими показателями модели
Изинга.
1. Введение
В этой лекции мы продемонстрируем результаты
численных экспериментов по моделированию свойств кластеров, или
капель, одинаково направленных спинов в модели Изинга и
обсудим связь их свойств с критическими явлениями. Следуя
капельной модели Фишера [1], которая затем была развита Дом-
бом с соавт. [2, 3], рассмотревшими влияние разветвленных
кластеров, Биндер [4] расширил границы скейлинговой теории
кластеров и проверил с помощью метода Монте-Карло многие
предлагавшиеся скейлинговые соотношения. Однако после
работы Мюллер-Крумхаара [5], обнаружившего в трехмерной
модели Изинга перколяционный кластер при температуре,
меньшей критической (хотя и близкой к ней), полезность такого
подхода к описанию критических явлений стала подвергаться
сомнениям. Чтобы сдвинуть этот кажущийся перколяционный
переход в критическую точку, были предложены различные
модификации кластерной модели [4, 6, 7]. Границы этих новых
кластеров могут, однако, не соответствовать парам
антипараллельных спинов на решетке и не дают поэтому вклада во
внутреннюю энергию. Следовательно, эти модифицированные кластеры
не дают полного описания критического поведения в модели
Изинга. Позднее Брюс с соавт. [8, 9] развили
микроскопическую теорию капель в низкоразмерном случае. Эта теория
приводит к иным скейлинговым соотношениям для
характеризующих изинговские кластеры показателей, чем
феноменологическая теория [4]. Далее, используя теорию скейлинга в системах
конечного размера и некоторые непроверенные допущения
относительно свойств кластеров, Сузуки [10] получил соотношение
между фрактальной размерностью [11] наибольшего кластера
и критическими показателями, похожее на соответствующее
соотношение для перколяционных кластеров [12, 13].
* /. L. Cambler, M. Nauenberg- Physics Department, University of
California, Santa Cruz, CA 95064, USA.
Иерархические и фрактальные свойства неупорядоченных систем 593
Чтобы прояснить некоторые из возникающих в связи с этой
задачей вопросы, мы исследовали с помощью метода Монте-
Карло поведение кластеров одинаково направленных спинов.
Нами исследованы распределение кластеров по размерам и
зависимость от числа спинов в кластере его средней поверхности
и радиуса инерции для модели Изинга в пространстве двух и
трех измерений при температуре, несколько меньшей
критической. Мы использовали новый подход, позволяющий получить
такое распределение для кластеров большого размера, что
особенно важно при исследовании скейлингового поведения. Ниже
будет изложена скейлинговая теория для распределения
кластеров по размерам и представлены результаты численных
экспериментов для нулевого магнитного поля.
2. Формализм
Рассмотрим систему при температуре ниже критической.
Пусть N(n, t, h) есть распределение кластеров из п спинов,
направленных против магнитного поля A, t — приведенная
температура t=(Tc — Т)/Тс. Распределение нормировано условием,
что полная доля перевернутых спинов на решетке равна
ОО
X tiN (n> t, А), а намагниченность в точности дается соотноше-
нием
оо
m(ty A)=l-2£ nN(n> U К). (1)
Аналогично, если s(n, t, А) соответствует средней поверхности
кластера, определенной как полное число антипараллельных
спинов, или разорванных связей, связанных с границей кластера,
внутренняя энергия e(ty А) будет равна
оо
e(U) = 2Zs (л, /, А) N (п, /, А) - Am(/, А). (2)
Вблизи критической точки (при / = 0 и А=0) намагниченность
и внутренняя энергия удовлетворяют известным скейлинговым
соотношениям
m(t, h) = fim(z)9 (3)
e(t, h) = t{l-a)e(z) + eQ(t, A), (4)
где z = h/t*f a a, p и ф—критические показатели. Скейлинго-
вые функции fn{z) и e(z) регулярны при 2 = 0, а e0(t, А)
—несингулярная часть энергии. Чтобы получить критическое
поведение из кластерных сумм (1) и (2), надо предположить, что
распределение кластеров N(n,t,h) и поверхность s(nttth) зависят
594
Часть VIII
от своих переменных скейлинговым образом при больших п.
Такое скейлинговое поведение было предложено Фишером [1]
и в более общем виде обсуждалось Биндером [4],
предположившим, что при большом п и малых t и h распределение N(n, t, h)
принимает вид
N(n, U h) = n~xN(tnYTf hnYfI\ (5)
где N (х, у)—скейлинговая функция, регулярная при х = 0 и
*/ = 0, а т, Ут и Ун — показатели. Для поверхности s(n, t, h) мы
использовали простую асимптотическую форму
s(n9 t, h) = Sn°, (6)
впервые предложенную Фишером [1], где а — поверхностный
показатель, а 5 — постоянная. В более общем случае
скейлинговая форма для 5 должна быть такой же, как в (5) :S (thYT,hnYH).
Покажем теперь, что асимптотические формулы (5) и (6)
приводят к обычному скейлинговому поведению (3) и (4), и
выведем соотношения между новыми скейлинговыми и хорошо
известными критическими показателями. Предположим, что
асимптотические скейлинговые выражения (5) и (6) верны для п >
> пСу где пс — некоторая нижняя граница, в точном определении
которой нет необходимости, и приблизим в (1) и (2) суммы при
п> пс интегралами по п. Для удобства рассмотрим частичную
сумму Мг(п, t, К) для r-го момента распределения:
Mr(ny U h)=Z nrN(n, U h\ (7)
где г — постоянная. Это выражение можно переписать в виде
пс п
Mr(n, U h) = Yj nNf<n> {> h)+\ dn-n-xN{tnYTy hnYH)r (8)
л = 1 nc
где мы подставили в интеграл асимптотическую скейлинговую
зависимость (5) для N(n> t, ft). Заменяя переменную
интегрирования п на х = tnfTy получаем
Mr{n, t, А) = £ nN(n9 /, Л) + уЧ dxx~u~XM{x, х*г)9 (9)
ft-i т *с
где u = (x-r-l)/YT, x = tnYT, ф = Ун/Ут. Для и > 0 и #(0,
0) Ф 0 интеграл в (9) расходится при стремлении к нулю
нижнего предела интегрирования. Регуляризируя его вычитанием из
подынтегрального выражения /7(0, 0), получаем
Мг (л, /, А) = gr ЦП) + ffr {х, z), (Ю)
Иерархические и фрактальные свойства неупорядоченных систем 595
где
X
fr(x9 z)=~l-\dxx-»-l[N(xy x+z)-N(09 0)], (11)
т о
Пс -uYT _
SAU h) = YnrN(n, U A)--i-_tf(o, 0)-
£i T
- J dnnr~x [N (tnYT, hnYH) - N (0, 0)]. (12)
о
Последнее выражение определяет не обладающий скейлинго-
выми свойствами вклад малых кластеров. Хотя постоянная пс и
появляется в верхнем пределе суммы и интеграла в (12), gr(t, h)
на деле не зависит от этой величины, что нетрудно показать,
взяв ее частную прозводную по пс. Если N(x9 у) регулярна при
я = 0 и у = 0, интеграл в (12) также регулярен по t и /г, и
сингулярности Мг(п, t, К) связаны только со вторым членом
выражения (10).
Намагниченность m(t, Л), даваемая выражением (1), может
быть определена с помощью выражения (10), если положить
г = 1 и перейти к пределу я->-оо, помня о дополнительном
условии gi(0, 0) = 1/2. При этом мы придем к скейлинговой форме
(3), в которой
m (z) = - 2Af, (оо, г\ Р = (т - 2)/YT. (13)
С помощью аналогичной процедуры, используя соотношение (6)
и полагая г = 0, можно определить внутреннюю энергию e(ty h).
При этом мы получаем скейлинговую форму (4), где
e(z) = 2M0(oo, z)9 а=1-(т — а — l)/YT. (14)
Термодинамическое соотношение
-J-mtf, h) = -£-e(t, h) (15)
приводит к обычному соотношению для критических
показателей а + р + ^ = 2 и соотношению
a=l+YT-YH=l-YT(f-l). (16)
3. Результаты численного моделирования
и их интерпретация
Данные о свойствах кластеров в модели Изинга в магнитном
поле были получены при моделировании системы методом
Монте-Карло на квадратной решетке со стороной L = 64 и 128 в
двумерном и на кубической со стороной L= 16 и 32 в трехмерном
596
Часть VIII
i
I
I
1 H
j 111 и 111111111 j 1111 j 11111111111
случае. При каждом значении температуры делалось в
типичном случае 10000 итераций. Через каждые 50 итераций
анализировалась структура кластеров для получения данных о рас-
о пределении кластеров по
° I I I I I I I I I I I I I I I I I I II 1 I I I I I I I I I I II I I I I М 1 I I I I I I I I I I I «
размерам и о полной
поверхности. Поверхность
определялась как число
разорванных связей как
на внешних, так и на
внутренних границах.
Зависимость площади
поверхности кластеров от
числа узлов при
температурах ниже критической
в двойном
логарифмическом масштабе
представлена для двумерного
случая на рис. 1.
Аналогичные результаты получены
и для трехмерного
случая. Для наглядности
графики, соответствующие
различным температурам,
сдвинуты на единицу по
вертикали. Нижний
график изображен в
правильных координатах.
Разброс точек для
двумерного случая гораздо
больше, чем для
трехмерного, что отражает
наличие в этом случае
перехода, связанного с
появлением шероховатости. Для
среднего значения
поверхности кластеров мы
использовали аппроксимацию предложенной Фишером степенной
функцией (6). Естественно, что диапазон размеров кластеров
в нашем случае ограничен. Для кластеров среднего размера
п ^ 200, исключая малые кластеры с п < 20, мы получили
следующие значения показателей: в двумерном случае 02d =
= 0,68 ± 0,04, в трехмерном оы — 0,88 ± 0,04. Наши результаты
для d = 2 (и d = 3) согласуются с результатами Домба и др.
[3], но не с результатами Биндера [4].
Чтобы получить скейлинговую функцию М(х)
непосредственно из распределения N(n, t> 0), получаемого в численном экспе-
м nil i nl 111 il 11 nil 111111111111111 и ilmili in
0123456789 10
Логарифм размера /кластера
Рис. 1. Зависимость логарифма площади
поверхности от логарифма размера кластера
в двумерном случае. Данные для Т = 2,15
сдвинуты вверх на две единицы, для Т =
= 2,25 — на одну единицу. Точки,
соответствующие температуре Т = 2,35 (нижняя
зависимость) изображены в правильных
координатах.
Иерархические и фрактальные свойства неупорядоченных систем 597
рименте, требуется слишком много компьютерного времени.
Вместо этого мы определили из частичной суммы Мх{п, t, 0)
интегральную скейлинговую функцию f(x, 0) (см. (10), (11)), из
которой N(x) находится дифференцированием. Результат для
We
10
-*
10'
10'
10'
Скейлинговал функция при Т~ 4,05,... t 4,2
1 г
S*
ОА
L^otCp^
>#г
&
?
#
J L
• Г = 4,05
о Т= 4,1
▼ т= 4,15
v Г = 4,2-
J I L
0,1
0,2
0,3
in*
0,4
Vt
Рис. 2. Зависимость скейлинговой функции f%(x) от x = tn
для трехмерного случая. На врезке показана скейлинговая функция N(x),
полученная из полиномиальной аппроксимации для f% (х) (сплошная линия).
Указанные на этом же графике экспериментальные точки получены
непосредственным измерением N (х) = tixN (n, t) для кластеров среднего размера.
d = 3 показан на рис. 2, демонстрирующем, что в указанном на
этом рисунке интервале температур скейлинг действительно
имеет место. Скейлинговые показатели равны: x2d = 2,05 + 0,03
и Y2a = 0,40 + 0,02 в двумерном и %zd = 2,07 ± 0,03 и Уы =
= 0,21 ±0,02 в трехмерном случае (предполагается, что
критические температуры равны Гс = 2,25 в двумерном и Гс = 4,52 в
трехмерном случае соответственно). Подставляя эти значения
показателей в скейлинговое соотношение (13), мы получаем для
критического показателя р значения, согласующиеся с извест-
598
Часть VIII
ными для d = 2 и 3. В трехмерном случае, однако, при 4,3 <
< Т < 4,52 в системе появляется перколяционный кластер (что
ранее наблюдалось Мюллер-Крумхааром [5]), и это
скеилинговое поведение нарушается.
Мы определили также радиус инерции кластеров /?, чтобы из
соотношения R — n{ld' получить их фрактальную размерность
d'\ d'2d = 1,9 ± 0,06 и d'M = 2,3 ± 0,05. Следует отметить, что,
хотя эти результаты и удовлетворяют приблизительно
соотношению df = d — p/v, аргументы, с помощью которых это
соотношение было получено Сузуки, не согласуются со свойствами
распределения кластеров, полученными в наших численных
экспериментах.
4. Выводы
С помощью численного моделирования мы показали, что
распределение размеров кластеров в модели Изинга имеет в узкой
области температур ниже критической температуры Тс при
нулевом магнитном поле скеилинговое поведение, одинаковое при
d = 2 и d = 3. Определены значения критических показателей т
и Ут, связанных с этим распределением. Значения этих
показателей с хорошей точностью удовлетворяют соответствующим
скейлинговым соотношениям. При d = 3 такое скеилинговое
поведение имеет место только ниже кажущегося порога
протекания, соответствующего Гр = 4,3. Существование этого порога
кажется на первый взгляд весьма удивительным в свете
современной скейлинговой теории перколяции [13], предсказывающей
скейлинг по отношению к Тр. Мы рбнаружили, однако, что
зависимость распределения размеров кластеров от приведенной
температуры t'= (Тр— Т)/Тр также имеет приблизительно скей-
линговый характер, но с показателем Y'T ~ 0,4. Похоже, что
существует более сложная скейлинговая форма, учитывающая
наличие обоих порогов. При температурах выше Тр, но ниже Тс
какое-либо простое скеилинговое поведение, по-видимому,
отсутствует. Влияние конечности решетки может изменить
распределение кластеров по размерам. В дальнейшем мы намерены
исследовать это влияние. Мы обнаружили также, что изинговские
кластеры являются фракталами, и вычислили поверхностный
показатель. Как выяснилось, этот показатель не зависит от
температуры, но несколько возрастает с ростом размера кластеров.
Интересно узнать, связано ли это с тем, что кластеры
становятся все более разветвленными, или же с ростом их внутренних
границ. Полученные результаты необходимо обобщить, изучив
скейлинговые зависимости во внешнем магнитном поле и, что
особенно интересно, влияние случайных полей [14], поскольку
Иерархические и фрактальные свойства неупорядоченных систем 599
считается, что в этом случае свойства кластеров спинов, или
доменов, играют определяющую роль. В заключение отметим, что
недавние попытки построить микроскопическую теорию капель
в низкоразмерной системе [8, 9] привели к соотношениям между
показателями, не согласующимся с нашими результатами при
d = 2. В этих работах ошибочно предполагалось, что
характерный размер кластеров соответствует изинговской
корреляционной длине.
Благодарности. Мы благодарны А. Конильо, В. Клейну,
Дж. Карди и А. Янгу за полезные обсуждения.
ЛИТЕРАТУРА
1. Fisher M. Я., Physics, 3, 255 (1967).
2. Domb С, J. Phys., A9, L141 (1976).
3. Domb С, Schneider Т., Stoll £., J. Phys., A8, L90 (1975).
4. Binder K, Ann. Phys., 98, 390 (1976).
5. Muller-Krumbhaar #., Phys. Lett., 48A, 459 (1974).
6. Coniglio A., Klein W„ J. Phys., A13, 2775 (1980).
7. Heermann D. W., Stauffer D., Z. Phys., B44, 339 (1981).
Heermann D. W., Coniglio A, Klein W., Stauffer £>., J. Stat. Phys., 36, 447
(1984).
8. Bruce A. D., Wallace D. /., J. Phys., A16, 1721 (1983).
9. Sim J. 5., Bruce A. £>., J. Phys., A18, 1119 (1985).
10. Suzuki M, Prog. Theor. Phys., 69, 65 (1983).
11. Mandelbrot В. В., The Fractal Geometry of Nature, Freeman, San-Francisco,
1982.
12. Kapitulnik A, Aharony Л., Deutscher G., Stauffer D., J. Phys., 16, L269
(1983).
13. Stauffer ZX, Phys. Rep., 54, 1 (1979); обзор современного состояния
теории протекания см. Kertesz /., Stauffer D., Coniglio Л., Annals of the
Israel Phys. Soc, 5, 101 (1983). Percolation Structures and Processes,
ed. G. Deutcher, R. Zallen, J. Adler.
14. Cambier J. L., Nauenberg M., U. C. S. C. preprint, 1985.
«Дьявольская лестница»
и странный аттрактор
в модели Изинга
с конкурирующими взаимодействиями
М. де Оливейра, С. Салинас,
/С. Йокои*
Сформулировано соответствие между моделью Изинга с конкури
рующими взаимодействиями на дереве Кейли в пределе
бесконечной координации и двумерным нелинейным отображением. Фазовая
диаграмма такой модели имеет точку Лифшица и множество
модулированных фаз. Проделаны вычисления, свидетельствующие
о существовании при низких температурах полной «дьявольской
лестницы». Представлены результаты расчетов, явно
свидетельствующие о существовании хаотических фаз, связанных со
странным аттрактором.
Модель Изинга с конкурирующим анизотропным
взаимодействием представляет собой обычную модель Изинга со
взаимодействием ближайших соседей, усложненную наличием
конкурирующего взаимодействия со следующими за
ближайшими вдоль одной выделенной оси соседними узлами. Такая
модель является, по-видимому, простейшей нетривиальной
моделью, имеющей богатую фазовую диаграмму с точкой
Лифшица и множеством пространственно модулированных фаз
[1—6]. Значительные усилия были направлены на исследование
глобальной фазовой диаграммы этой модели в координатах
Т — р, где Т — температура, а р = —/2//1 есть отношение
величин конкурирующих обменных взаимодействий. По результатам
численного исследования, основанного на приближении среднего
поля, было сделано предположение о существовании при низких
температурах бесконечной последовательности соизмеримых
фаз, так называемой дьявольской лестницы.
В настоящей работе представлены результаты расчетов для
модели Изинга на дереве Кейли в пределе бесконечного
координационного числа z с ферромагнитным взаимодействием между
ближайшими соседями (Л > 0) и антиферромагнитным
взаимодействием со следующими вдоль ветвей дерева соседями (72 <
< 0) [7]. Как было показано Ваннименусом, рассмотревшим
такую модель на дереве с z = 3, эта модель, хотя и не
тождественна, но похожа на анизотропную модель Изинга с
конкурирующим взаимодействием.
Вначале мы обобщим вычисления Ваннименуса [8] на
дерево с произвольным координационным числом. Затем с помощью
* М. J. de Olivetra, S. R. Salinas, С S О. УоЫ-Instituto de Fisica Unb
versfdade de Sao Paulo, С. Р. 20516, CEP 01498, Sao Paulo, Brazil
Иерархические и фрактальные свойства неупорядоченных систем 601
процедуры Инавасиро, Томпсона и Хонды [9] запишем для этой
модели систему из трех рекуррентных уравнений первого
порядка. В пределе бесконечного координационного числа, который в
нашем случае соответствует г->оо, /i->0, /г->0, но zJ\ = const
и 2/2 = const, в этой системе остается только два простых
рекуррентных соотношения первого порядка. Переход к пределу
бесконечного координационного числа необходим именно для
того, чтобы получить простые уравнения, поддающиеся
аналитическому и очень подробному численному исследованию. Границы
парамагнитной фазы на изображенной на рис. 1 фазовой
диаграмме в координатах Т — р (где в нашем случае р = — 22/2/^/ь
а температура Т измерена в единицах zJ\/k) могут быть
найдены аналитически из условий устойчивости парамагнитной
фиксированной точки. Легко найти также положение точки Лифши*
ца и границу устойчивости ферромагнитной фазы. Критическое
значение волнового числа плавно меняется вдоль Я-линии,
разделяющей парамагнитную и модулированные фазы, и
обращается в нуль в точке Лифшица. Фазовая диаграмма оказалась
гораздо богаче, чем та, что была получена Ваннименусом, а
структура модулированных фаз качественно согласуется с
результатами работ по исследованию анизотропной модели с
конкурирующим взаимодействием [5, 6].
В настоящей работе проделаны детальные расчеты,
позволившие получить, например, дьявольскую лестницу (зависимость
главного волнового числа q от параметра р) при различных
температурах и вычислить соответствующие фрактальные
размерности D (см. рис. 2). При низких температурах D < 1, и мы
получаем настоящую дьявольскую лестницу, т. е. несоизмеримые
фазы занимают области меры нуль на фазовой диаграмме.
Величина Д однако, возрастает с температурой. Это означает, что
существует температура, выше которой значительная доля
фазовой диаграммы занята несоизмеримыми фазами [10].
Совершенно неожиданным явилось наблюдение в области
сосуществования ферромагнитной и модулированной фаз фиксированных
орбит. Мы получили также сильное численное подтверждение
существования хаотических траекторий, характеризуемых
положительными показателями Ляпунова. Эти траектории имеют
фрактальную структуру, напоминающую структуру странных
аттракторов Карри и Йорке [11]. Численные данные показывают
наличие последовательности бифуркаций (т. е. модулированных
фаз с удвоением периода), приводящей к хаотическому
состоянию и характеризующейся универсальным показателем Фейген-
баума б 112].
Рассмотрим введенную Ваннименусом модификацию модели
Изинга с конкурирующими взаимодействиями между
ближайшими и следующими за ближайшими вдоль ветвей дерева Кейли
Парамагнитном
I фаза
Рис. 1. Полная фазовая диаграмма модели Изинга с конкурирующими
взаимодействиями на дереве Кейли. В области модулированных фаз показано
несколько соизмеримых фаз, указаны их главные волновые числа. В
заштрихованной области возможно сосуществование ферромагнитной и
модулированной фаз.
Г* 0, г
Рис. 2. Зависимость q от р при Т = 0,2. На врезке детально показан участок
дьявольской лестницы. Фрактальная размерность этой лестницы при
значениях р, лежащих между 0,65 и 1,5, равна D = 0,92.
Иерархические и фрактальные свойства неупорядоченных систем 603
соседями (см. рис. 1 работы [8]). Чтобы получить
итерационную схему, проведем суммирование по спинам, находящимся в
узлах внешних слоев дерева (от г = 0 до r = N, r—поколение
узлов дерева). В пределе бесконечного координационного числа
мы получим простые соотношения
Xr = H/T + (l/T)thXr^ + Yr^
Yr = -(p/T)thXr_u
где Н — внешнее поле, а Хг можно интерпретировать как
эффективное поле в расчете на один узел в рассматриваемом r-м слое.
Удобно ввести также эффективную намагниченность на один
спин в г-м слое, Mr = thXn и написать разностное уравнение
второго порядка:
Мг = th [Г"1 (Мг_х - рМг„2 + Я)]. (1)
Границы модулированных фаз, показанные на рис. 1, получены
при численном исследовании (1) в нулевом внешнем поле.
Равновесное состояние при заданных Тир находится
итерированием этого рекуррентного соотношения при начальных
условиях Мо = М\ — 1. При последовательных итерациях
намагниченность стремится к одному из следующих аттракторов: 1)
тривиальной фиксированной точке Л1* = 0 (парамагнитная фаза);
2) нетривиальной фиксированной точке М* Ф 0
(ферромагнитная фаза); 3) циклу с хорошо определенным периодом
(соответствующему периодической фазе с данным периодом); 4)
одномерной орбите (связанной с несоизмеримой фазой) и 5)
странному аттрактору фрактального характера. Для периодических
орбит (соизмеримые фазы) показатель Ляпунова отрицателен,
для одномерных аттракторов он с точностью, достижимой в
наших расчетах, обращается в нуль. Для фрактальных
аттракторов вычисленные нами показатели Ляпунова положительны.
В заштрихованной области фазовой диаграммы намагниченность
стремится или к ферромагнитной критической точке, или к
аттрактору, соответствующему модулированной фазе, в
зависимости от начальных условий. Переход между ферромагнитной и
модулированной фазами является, следовательно, переходом
первого рода, поскольку допускает сосуществование различных
фаз. В этой же области были обнаружены и странные
аттракторы, существующие, однако, и за границей устойчивости
ферромагнитной фазы.
Самый замечательный результат наших вычислений показан
на рис. 3, а — г, полученных при Т = 0,2, р = 0,69662 и при
начальных условиях M0 = Mi = 1. На этой последовательности
рисунков хорошо видна фрактальная природа странного аттрак-
604
Часть VIII
тора. Показатель Ляпунова для этой орбиты положителен (К =
= 0,12), и фурье-анализ показывает, что соответствующие
значения намагниченности имеют шумовой спектр. Мы проанали-
Т = О, Z Р =0, C9PG2
0,08 у
0,05
0,46
0,47
T~0,Z P -0,69662
0,073
С, J 75
0,074
0.073
Т = 0,2 Р~0,6965 Z
' 1 1
1 1
1 1
1 1
i 1
/ \
7 L/
7
/ '
/
/
/
/ |
0,466
Рис. 3. а — Аттрактор, связанный с отображением (/) при Т = 0,2 и р =
= 0,69662 и при начальных условиях Мо = Mi = 1. Первые 104 итераций
опущены, показанные на рисунке точки соответствуют последующим 5000
итераций; б — увеличенное изображение участка аттрактора, отмеченного
прямоугольником на рис. 3, а. Показаны точки, полученные в 3000 из 49 439
итераций, результаты первых 104 итераций опущены; в — увеличенное
изображение участка, отмеченного на рис. 3, б. Точки получены в 2000 из примерно
105 итераций, первые Ю4 итераций не учитываются; г — увеличенное
изображение участка, отмеченного на рис; 3, в. Рисунок соответствует 1000 из
порядка. 106 итераций. Эта последовательность рисунков демонстрирует
самоподобие странного аттрактора.
зировали путь перехода к хаосу. В пределах точности
вычислений мы наблюдали девять бифуркаций (т. е. соизмеримых фаз
с удвоением периода), по которым определили показатель Фей-
генбаума 6=4,669 + 0,001 (табл. 1).
Таким образом, исследование модели Изинга с
конкурирующими взаимодействиями на дереве Кейли в пределе бесконеч-
Иерархические и фрактальные свойства неупорядоченных систем 605
ного координационного числа сводится к изучению двумерного
нелинейного отображения. Полная фазовая диаграмма такой
модели похожа на фазовую диаграмму модели Изинга с
анизотропным конкурирующим взаимодействием, полученную в
приближении среднего поля. Численное исследование отображения
показало наличие при низких температурах полной дьявольской
Таблица 1. Положение точек бифуркации при Т = 0,2
П Рп 6n==:(f>n+l-Pn)/(Pn + 2-Pn+l)
1 0,69595967544 4,4934
2 0,696021075024 4,6345
3 0,6960347394183 4,6609
4 0,6960376878381 4,6675
5 0,69603832041215 4,6688
6 0,6960384559389 4,6691
7 0,69603848496684 4,668
8 0,6960384911838
9 0,6960384925155
лестницы, а также появление во внутренних областях дерева при
определенных условиях на его границе хаотических фаз.
ЛИТЕРАТУРА
1. Elliot R. /., Phys. Rev., 124, 346 (1961).
2. Hornreich R. M.t Luban M.t Shtrikman 5., Phys. Rev. Lett., 35, 1678
(1975).
3. Redner S., Stanley H. £., Phys. Rev., B16, 4901 (1977).
4. Selke W., Z. Phys., B29, 133 (1978); Selke W., Fischer M. £, Phys. Rev.,
B20, 257 (1979).
5. Bak P., von Boehm /., Phys. Rev., B21, 5297 (1980).
6. Fischer M. E.f Selke W.f Phys. Rev. dett., 44, 1502 (1980).
7. Предварительный отчет об этих расчетах см.: Yokoi С. S. О., de Oti-
veira М. /., Salinas S. R., Phys. Rev. Lett., 54, 163 (1985).
8. Vannimenus /., Z. Phys., B43, 141 (1981).
9. Inawashiro S., Thompson C. /., Honda G., J. Stat. Phys., 33, 419 (1983).
10. Такая же зависимость фрактальной размерности от температуры для ки-
ральной модели Поттса на дереве Кейли получена в работе:
Yokoi С. S. О., de Oliveira M. /., J. Phys., A18, L153 (1985).
11. Curry Я., Yorke Л., In: The Structure of Attractors in Dynamical Systems,
ed N. G. Markley, J. C. Martin, W. Perrizo, Lect. Notes Math., 668,
Springer, Berlin, 1978, p. 48.
12. Feigenbautn M, /., Physica (Utrecht), 7D, 16 (1983).
О самоподобной структуре
волновых функций
в неупорядоченных системах
Л. Сибесма, Л. Пьетронеро *
Рассмотрено несколько вопросов, связанных с недавно
появившейся гипотезой о существовании фрактальных свойств у внутренней
структуры локализованной волновой функции. Проведенный нами
анализ свидетельствует против такой возможности, хотя и не
позволяет сделать окончательных выводов.
1. Введение
Недавно Сукулис и Эконому [1] рассмотрели
возможность того, что мелкомасштабные осцилляции локализованных
беспорядком волновых функций имеют фрактальную структуру.
Распределение вероятности, соответствующее локализованной по
Андерсону волновой функции, экспоненциально спадает на
расстояниях порядка длины локализации к. Эта длина, однако,
может быть гораздо больше постоянной решетки а, так что может
существовать интервал масштабов длины величиной в
несколько порядков, на котором могут наблюдаться самоподобные
флуктуации. Авторы [1] проанализировали поведение волновых
функций в этом режиме и пришли к выводу, что эти флуктуации
действительно имеют фрактальную структуру, а их фрактальная
размерность D зависит от степени беспорядка. Ввиду
ограничений, накладываемых условиями численного эксперимента,
точность данных будет выше всего в одномерном случае, поскольку
в двух- и трехмерном случае максимальный размер
моделируемой системы оказывается гораздо меньше.
Мы начали работу с того, что повторили расчеты,
проделанные в [1] для одномерного случая. Наш результат заключается
в том, что мы получили на первый взгляд аналогичную картину,
однако более тщательный анализ данных выявил неизменное
наличие на построенных в двойном логарифмическом масштабе
графиках малой отрицательной кривизны. Это означает, что
наблюдаемые отличия D от единицы (т. е. от нефрактального
поведения) могут быть связаны с влиянием конечного размера
системы, а не со свойствами самоподобия волновой функции.
Чтобы разобраться в этом вопросе, мы рассмотрели
идеализированные примеры самоподобных нормированных распределений
вероятности, построенные детерминистическим образом. Анализ
таких систем показал, что их нельзя рассматривать как
однородные фракталы, поскольку масштабная инвариантность имеет ме-
* А. Р. Siebesma, L. Pietronero-University of Groningen, Melkweg 1, 9718
EP Groningen, The Netherlands.
Иерархические и фрактальные ceoucfea неупорядоченных систем 607
сто только по отношению к выделенным начальным точкам.
Трудно себе представить, чтобы распределения вероятности,
соответствующие реальным локализованным волновым функциям,
обладали свойствами однородных фракталов, как это
предполагается при анализе, основанном на использовании
корреляционной функции плотность — плотность [1]. Поэтому нам
представляется, что доводы в пользу того, что локализованные волновые
функции обладают фрактальными свойствами, вызывают
сомнения.
2. Анализ локализованных волновых функций
одномерной системы
В этом разделе мы рассмотрим метод, использованный Су-
кулисом и Эконому [1], и укажем на некоторые несоответствия,
ставящие под вопрос применимость такого подхода.
Идея подхода заключается в том, что на масштабах,
ограниченных постоянной решетки а и длиной локализации Я, могут
иметь место самоподобные флуктуации. При численном
моделировании максимальный интервал масштабов достижим в
одномерном случае. Именно его мы и будем здесь рассматривать. Мы
будем рассматривать стандартную модель Андерсона для
приближения сильной связи, характеризующуюся прямоугольным
распределением энергий узлов шириной W. Точно такая же
модель рассматривалась и в работе Сукулиса и Эконому [1]. С
помощью метода обратных итераций мы вычислили несколько
собственных функций для системы из 5000 узлов с периодическими
граничными условиями. Типичное распределение вероятности,
соответствующее волновой функции с Е ~ 0 (центр зоны) для
W = 0,5 показано на рис. 1.
Гипотеза состоит в том, что, если флуктуации
распределения вероятностей, соответствующего этой волновой функции, са-
моподобны, фрактальны, это распределение при а < х < X
может быть описано в среднем степенным законом р(лг) =
= | *ф (х) |2 ~ х~а. При х^Х (в случае волновой функции,
показанной на рис. 1, % ^ 400а) спадание будет определяться в
основном экспоненциальной функцией. Фрактальная размерность
D = 1 — а может быть определена из соотношения
L
\9(x)dx~L{{-a) = LD. (1)
о
Анализ распределения вероятностей такого типа, как
показанное на рис. 1, с точки зрения определения (1) предполагает
необходимость выбора центра распределения и приводит к
значительным флуктуациям, устранить которые можно лишь усред-
60S
Часть Vllt
нением по очень большому ансамблю систем. Чтобы избежать
этих трудностей, Сукулис и Эконому [1] предложили
рассмотреть корреляционную функцию, которая является адекватной
характеристикой для однородных фракталов [2]. Величина
фрактальной размерности может при этом быть определена из
соотношения
I (L) = \ (р (х0) р (хо + х))0 dx ~ IJ>9 (2)
о
где усреднение <.. .>0 проводится по положениям начала отсчета
л;0. При таком определении даже одна волновая функция дает
0,60
0,Ь5 Ь
b 0,30 ь
0,15 У
О 7000 2000 3000 4000 5000
Узлы
Рис. 1. Пример распределения вероятностей, соответствующего
локализованной волновой функции в одномерном случае. Диагональный беспорядок с
шириной W = 0,5.
достаточно гладкую зависимость ln/(L) от InL.
Соответствующая зависимость для волновой функции, показанной на рис. 1,
дана на рис. 2. Если эта зависимость линейна, ее наклон дает
фрактальную размерность D. На первый взгляд функция на
рис. 2 достаточно близка к линейной, с другой стороны, ее
наклон достаточно близок к D = 1, что соответствует
нефрактальному поведению. Чтобы аккуратно исследовать этот вопрос, мы
нашли наилучшее линейное приближение для этой зависимости
в интервале от In £мин = 1,7, что соответствует LMHH ^ 5
постоянным решетки, до некоторого In £Макс и рассмотрели
получающиеся значения фрактальных размерностей как функцию верхней
границы интервала. Для фрактальной системы следовало бы
ожидать наличие хорошо определенного значения D со случай-
Иерархические и фрактальные свойства неупорядоченных систем 609
ными статистическими флуктуациями и резкого изменения
поведения при приближении Ьыакс к длине локализации К. В табл. 1
о
-1,50
^ - 3,00
5 -k,5Q
-6,00
~7 ЪП
I I
-
/'
-
I I
I I" I
•""" I
н
—I
I I J
1,50 3,00
4,50
In L
6,00 7,50 9,00
Рис. 2. Корреляционная функция (см. (2)) распределения вероятностей,
показанного на рис. 1. Линейная зависимость с наклоном, отличным от
единицы, давала бы подтверждение фрактального поведения. Обратите внимание
на небольшую кривизну (см. подробно в табл. 1). По нашему мнению
наличие этой кривизны свидетельствует против фрактальной интерпретации.
мы вместо этого видим плавное изменение „D" от 1 до ~0,86 —
значения, очень близкого к полученному Сукулисом и Эконому
Таблица 1. Наклон кривой на рис. 2
как функция длины рассматриваемого
интервала. Плавное изменение
наблюдаемой фрактальной размерности
свидетельствует скорее в пользу
эффектов конечного размера,
чем в пользу истинного фрактального
поведения
макс
20
33
55
90
148
245
403
665
1П LM3KC
3
3,5
4
4,5
5
5,5
6
6,5
„Д"
0,971
0,958
0,941
0,918
0,902
0,892
0,880
0,859
ыо
Часть VIII
для этого типа беспорядка. Такое систематическое изменение
наклона дает с нашей точки зрения сильный аргумент против
наличия фрактальной структуры у волновой функции. Такой же
анализ был проделан для многих других волновых функций
(всего около 50); было получено точно такое же поведение с тем
же типом кривизны. Это означает, что усреднение по многим
волновым функциям (что также было проделано нами) не исправит
ситуацию. Наш результат означает, что кажущееся изменение
наклона по сравнению с D = 1 может быть просто следствием
эффектов конечного размера. Рассмотрение большего значения
Wy которое должно соответствовать меньшему D [1], не снимает
проблемы, поскольку в этом случае интервал возможного
фрактального поведения ограничен меньшим значением длины
локализации.
Встретившись с этими трудностями, мы решили рассмотреть
основной вопрос: может ли локализованная волновая функция
обладать свойствами однородного фрактала? Мы обсудим этот
вопрос в следующем разделе, в котором будет рассмотрено
идеализированное детерминистическое распределение.
3. Идеализированные самоподобные
нормированные распределения
Чтобы выяснить природу возможной самоподобной структуры
локализованной волновой функции, рассмотрим
детерминистическую процедуру построения самоподобного распределения
вероятностей, сохраняющего нормировку. Такое распределение
можно получить, рассмотрев обобщение способа построения кан-
торова множества, при котором различным точкам канторова
множества [2] приписываются различные веса. Начнем с
канторова множества Ck{K*])> гДе ^ — число интервалов, <п — их
длина, k — порядок итерации. Определим Uk=i(x), приписав
веса каждому из Я интервалов С\(%, rj):
tf*-i(*) =
wu если х е [0, т)],
w2> если х
Г 1 — Ti (Я-1)ц+1-тП
хв>ь, если х е [1 — ц, 1]>
0 в остальных случаях.
В силу нормированное.™
E«W=1. (4)
Иерархические и фрактальные свойства неупорядоченных систем 611
При следующей итерации
мы поступаем
совершенно таким же образом, с
тем же распределением
весов. Для простоты
рассмотрим частный случай
А, = 3, т|= 1/4 и W(wu
w2> ау3) = (йУ, 2оу, ш),
показанный на рис. 3.
В силу нормированно-
сти распределения
соотношение между г] и w
имеет вид 4wv\ = l. Для
Uk(x) имеет место
следующее скейлинговое
соотношение
Uk+i(w) = -^Uk(x).
(5)
При малых х (заметим,
что начало координат
совпадает с краем рис. 3)
U(x) можно описать
гладкой функцией
U(x)~xD-1 (x->0\
(6)
где D = —1п4/1пг| = 1
для г] = 1/4. Такое
скейлинговое поведение имеет
место только при данном
выборе начала координат.
Покажем, что, изменив
начало отсчета, можно
получить другие скейлин-
говые свойства.
Рассмотрим трансляцию *->•* —
— 1/2. Теперь начало
координат лежит в центре
распределения. В этом
случае мы приходим к
задаче, исследованной
Шиллингом [3]. Для функции
U(x) теперь справедливо
н ^
Л 8
12
3
16
1Z
S 8
4
к = 4
11111 шшщ
к'З
ШпНШпНп
пИп ИНН Щ
к =2
Пг^ ПМП
п_
*=7
0,5
Рис. 3. Пример обобщения канторова
множества, построенный для того, чтобы
смоделировать возможные свойства
самоподобия локализованной волновой функции.
Детальное описание см. в тексте.
612
Часть VIII
скейлинговое соотношение
иш(ЧХ) = -щик(х). (7)
так что D =—1п2/1п т] = 0,5 (при ц = 1/4), что вдвое меньше,
чем в предыдущем случае. Такая зависимость от начала
координат связана со введением различных весов. Мы приходим,
таким образом, к выводу» что построенное нами множество в
отличие от обычного канторова множества не является
однородным фракталом. Если предположить, что локализованная
волновая функция представляет собой обобщенное канторово
множество, обладающее стохастическими свойствами, трудно
представить себе, как она может обладать свойствами однородного
фрактала. Для нашего идеализированного случая
интегрирование вблизи точек л: = 0 и х = 1/2 дает две различные
фрактальные размерности, если же х выбрана на локальном пике, хорошо
определенного степенного закона вообще не существует.
Использование корреляционной функции, даваемой (2), дает некоторую
усредненную фрактальную размерность, лежащую между двумя
указанными выше значениями, однако совершенно неясно, как
следует интерпретировать это число с точки зрения тех скейлин-
говых закономерностей, которые мы использовали при
построении системы. Другие методы анализа приводят при усреднении
к другим значениям фрактальной размерности [4].
4. Выводы
В заключение мы должны отметить, что анализ поведения
локализованной волновой функции с помощью корреляционной
функции (2) не может дать строгого доказательства
фрактального поведения. Чтобы смоделировать возможные скейлинговые
свойства локализованной волновой функции, мы построили
некоторое обобщение канторова множества. Из построенных нами
идеализированных примеров невозможно понять, как реальная
волновая функция может обладать свойствами однородного
фрактала. Наш анализ, таким образом, свидетельствует против
существования у локализованной волновой функции свойств
самоподобия, хотя и не позволяет сделать окончательных выводов.
ЛИТЕРАТУРА
1. Soukoulls С. AL, Economou E. ЛГ., Phys. Rev. Lett., 52, 565 (1984).
2. Mandelbrot В. В., The Fractal Geometry of Nature, Freeman, San Francisco,
1983
3. Schilling R., Phys. Rev Lett., 53, 2258 (1984).
4. Siebesma A. P., Pietronero L., в печати-
Часть |Х
ХАОС# ТУРБУЛЕНТНОСТЬ
И РОДСТВЕННЫЕ ВОПРОСЫ
Отображения окружности
на комплексной плоскости
И. Цвитанович, М. аенсен,
Л. Каданов, И. прокачча *
Отображения окружности полиномиального, экспоненциального и
рационально-полиномиального типов исследованы численно на
комплексной плоскости. Показано, что универсальность золотого
сечения для вещественных отображений окружности не может быть
продолжена на комплексную плоскость.
1. Введение
Открытие универсальности удвоения периода в
итерациях одномерных отображений [1, 2] послужило толчком к
поиску универсальных масштабно-инвариантных закономерностей
в других динамических системах малой размерности (обзор
теоретических результатов и экспериментальных данных по
удвоениям периода см. в работах [3—5]). Класс задач, в котором идеи
универсальности получили подтверждение, образуют переходы
к хаосу в диффеоморфизмах на окружности (отображения
окружности). Отображения такого рода моделируют различные
физические системы. Подробное обсуждение физических
приложений отображений окружности читатель найдет в работах
[6,7].
Первый пример универсальности критических отображений
окружности был обнаружен при исследовании отображений с
числом вращений, равным золотому сечению [8—10]. Изящная
формулировка таких асимптотически универсальных
автомодельных законов может быть получена с помощью уравнения
неустойчивого многообразия [3, 11 — 14].
Для отображений окружности уравнение неустойчивого
многообразия имеет вид (пример см. в работах [12, 15])
2р(г) = аё1+р/б(аё1+Чб+Р1бЛФ2)У (Ы)
* Predrag Cvitanovlc- Institute of Theoretical Physics, Chalmers University
of Technology, $-41296, Goteborg, Sweden; Mogens H. Jensen, Leo Kadanoff-
The James Franck and Enrico Fermi Institutes, University of Chicago, Chicago,
Illinois 60637, USA; Itamor Procaccia-Department of Chemical Physics, The
Weizmann Institute of Science, Rehovot 76100, Israel.
614
Часть IX
Однако численное решение этого уравнения затрудняют тонкие
вопросы сходимости. Насколько нам известно, существуют
только две успешные попытки численного решения уравнения
неустойчивого многообразия [16]. Именно эти проблемы
сходимости, а также стремление понять другие универсальности,
связанные с отображениями окружности [15], побудили нас
исследовать структуру комплексифицированных отображений
окружности. Такие исследования уже позволили по-новому взглянуть
на некоторые универсальные законы подобия [13, 14, 17, 18] и
привели к красивым математическим результатам (см.,
например, работы [19—24]).
Введение в круг вопросов, связанных с отображениями
окружности, читатель может найти в работах [6, 15] и [25]. В
настоящей работе мы сосредоточим внимание на некоторых
общих свойствах комплексифицированных отображений
окружности.
2. Кубическое отображение окружности
В качестве первого примера комплексифицированного
отображения рассмотрим критическое кубическое отображение
Zn-H = ^ + 44> Re (г+1/2) (modi) (2.1)
(кубическое отображение окружности называется критическим,
если оно имеет кубическую точку перегиба z' = z" = 0). Такое
отображение периодично вдоль вещественной оси и
претерпевает разрывы в точках z = ±l/2 + iy при всех уфО. Это
простейший пример полиномиальных аппроксимаций отображений
окружности того типа, который используется при численном
решении уравнения неустойчивого многообразия (1.1).
Множество Мандельброта (множество всех значений
параметра, при которых итерации критической точки стремятся к
бесконечности) полиномиального кубического отображения
изображено на рис. 2.1. Граница большой центральной компоненты
(значения параметра, при которых итерации критической точки
сходятся к устойчивой неподвижной точке) определяется
кардиоидой значений параметра, для которых неподвижная точка
обладает критической устойчивостью: ]dz'/dz} = 1. Отображение z
монотонно при вещественных z и, следовательно, не может
порождать удвоение периода вдоль вещественной оси, но на мнимой
оси бифуркации удвоения периода существуют, порождая пару
2-циклов («сердец»). Одно из таких сердец показано на рис. 2.2.
Бифуркация с переходом к устойчивой периодической орбите
происходит при каждом рациональном значении фазы
производной dzr/dz вдоль границы кардиоиды. Это порождает множество,
состоящее из подобных сердец, аналогичное множеству Ман-
Хаос, турбулентность и родственные вопросы 615
дельброта квадратичного отображения z-+c + z2. Как и в
квадратичном случае [14], центр каждой компоненты лежит на
Рис. 2.1. Множество Мандельброта Рис. 2.2. Увеличенное изображение
критического полиномиального куби- 2-цикла («сердца») с рис 2.1.
ческого отображения z ->- с + 4z3.
сверхустойчивом m/n-цикле, и для бесконечной
последовательности бифуркаций можно ожидать универсальный закон
подобия.
Форма множества Мандельброта для отображений
окружности описана в следующем разделе.
Область притяжения (множество всех начальных значений г,
итерации которых не стремятся к бесконечности)
сверхустойчивой неподвижной точки кубического отображения (2.1)
изображена на рис. 2.3.
Нетрудно понять, как выглядят области притяжения
комплексных отображений окружности в общем случае. Границей
критической устойчивости \dz'/dz\=\ отображения (2.1)
является окружность радиусом \z\ = 1/2. Это условие определяет
центральный круг. Условие периодичности Re(2 + 1/2) (mod l)
порождает бесконечную последовательность таких кругов — по
одному при каждом целом значении Re z. Остальная автомо-
616
Часть tX
дельная структура возникает из этой периодичности: она
порождается всеми прообразами кругов \z\ = 1/2 вдоль
вещественной оси. Отображение гъ переводит начальные точки с фазой
ехр (± 2ш/3), ехр (± in/З) на
вещественную ось. Это порождает четыре
радиальных последовательности
меньших кругов вдоль лучей,
расположенных под углами ±60°, ± 120° к
вещественной оси. Аналогичным образом
итерации отображения (2.1) более
высокого порядка отображают на
вещественную ось другие
последовательности кругов, видимых на рис. 2.3.
(Резкий обрыв вблизи Im z = 0,95 носит
искусственный характер и вызван
условием периодичности на Re z в
отображении (2.1).
3. Стандартное отображение
окружности
В качестве второго примера комп-
лексифицированного отображения
окружности рассмотрим синусное
отображение
у
zn+l = Q + zn—-^ sin (2nzn) (mod 1)
(3.1)
(в критическом случае £=1).
Области притяжения обладают по
существу такой же структурой, как в
предыдущем примере; область
притяжения сверхустойчивой неподвижной
точки изображена на рис. 3.1, а область притяжения
сверхустойчивого 1/3-цикла — на рис. 3.2 как типичные примеры.
Комплексифицированное синусное отображение может
служить примером экспоненциального отображения [26]: при
подстановках
и = ехр (2niz), с = ехр (2ш'й)
отображение (3.1) переходит в отображение
и' = си ехр [- к (и - 1/и)/2] (3.2)
(здесь k = 1). В отличие от полиномиальных отображений типа
(2.1) или рациональных отображений, о которых пойдет речь в
Рис. 2.3. Верхний правый
квадрант области
притяжения сверхустойчивой
неподвижной точки кубического
отображения (2.1) (Q=0).
Остальные квадранты
получаются из данного при
отражении относительно осей
х и у.
Рис. 3.1. Область притяжения
сверхустойчивой неподвижной точки
синусного отображения (3.1).
Рис. 3.2. Область притяжения
сверхустойчивого 1/3-цикла синусного
отображения (3.1).
Рис. 3.3. Множество Мапдельброта синусного отображения (3.1). Нижняя
комплексная полуплоскость получается при отражении относительно
вещественной оси. Черная область соответствует значениям параметра, при
которых итерации критической точки не уходят в бесконечность. Различные
оттенки серого цвета соответствуют скорости убегания: чем большее число
итераций необходимо для достижения линии обреза, тем светлее оттенок.
Большие «сердца» на концах интервала отвечают неподвижной точке сердца
р середине — орбитам с числом вращений 1/2 и т. д.
618
Часть IX
следующем разделе, экспоненциальные отображения обладают
областями притяжения, простирающимися в бесконечность и
всюду плотными на комплексной плоскости. Например, образы
тчэчек z = ±1/4 + 1у при больших у лежат вблизи вещественной
оси на рис. 3.2, и точно так же
любой луч из кругов, являющийся
прообразом вещественной оси, уходит
на бесконечность.
По тем же причинам
изображенное на рис. 3.3 множество Мандель-
брота синусного отображения
всюду плотно на всей комплексной
плоскости.
Об общей структуре множества
Мандельброта критических
отображений окружности можно судить по
рис. 3.3. Вдоль вещественной оси
лля любого рационального числа
существует интервал синхронизации
мод. Поскольку отображение имеет
кубическую точку перегиба,
каждый интервал синхронизации мод
доходит на комплексной плоскости
до множества сердец,
изображенного на рис. 2.1. Переход из
центральной компоненты в одно из
сердец сопровождается га-кратным
увеличением периода отображения без
изменения числа вращений
(например, число вращений 1/2 после
удвоения периода переходит в 2/4).
Следовательно, множество
Мандельброта любого отображения
окружности состоит из двух основных
блоков: во-первых, это отображение
имеет кубическую точку перегиба,
поэтому комплексные увеличения периода в п раз
характеризуются последовательностью подобных сердец, изображенной
на рис. 2.1; во-вторых, отображение периодично, и это
порождает бесконечную последовательность копий основных сердец
вдоль вещественной оси и некоторых лучей на комплексной
плоскости.
Аналогичным образом области притяжения для критических
отображений окружности строятся из соответствующих блоков:
во-первых, из области притяжения критического кубического по
линомиального отображения; во-вторых, из бесконечной последо-
Рис. 3.4. Область притяжения
сверхустойчивого цикла
удвоения периода отображения (3.1)
с числом вращений 0/1.
Центральная часть области
притяжения такая же, как в случае
2-периода полиномиальных
кубических отображений.
Остальную часть множества образуют
копии, порождаемые
периодичностью по вещественной оси,
и прообразы на комплексной
плоскости.
Хаос, турбулентность и родственные вопросы 619
вательности ее прообразов, порождаемой условием
периодичности. Это показано на рис. 3.4 для сверхустойчивого цикла
удвоения периода с числом вращений 0/1. Треугольное
расположение четырех центральных кругов типично для областей
притяжения 2-периодических полиномиальных кубических отображений;
остальная часть множества порождена периодичностью вдоль
вещественной оси и прообразами вещественной оси на
комплексной плоскости.
4. Рационально-полиномиальное отображение
В качестве третьего примера рассмотрим
рационально-полиномиальное отображение
t£ = cu{3- ku)/{3 - k/u) (4.1)
(здесь k=l). Вид этого отображения определяется членом
низшего порядка, на котором обрывается разложение в степенной
Рис. 4.1. Множество Мандельброта рационального отображения (4.1). Центр
множества сердец неподвижной точки расположен на с = 1, число вращений
1/2 соответствует с= — 1. Остальное бесконечное множество других
синхронизации мод расположено на единичной окружности.
ряд экспоненты из отображения (3.2). Это критическое
отображение окружности с кубической точкой перегиба при и = \:
и'~с{\—г3/2- г5/4 + г6/8 + ...),
г = Ъиг. (4.2)
Множество Мандельброта такого отображения изображено на
рис. 4.1.
Рациональные отображения отличаются от
экспоненциальных в одном важном отношении: их множества Мандельброта и
области притяжения имеют конечную протяженность, так как
620
Часть 1К
при больших \и\ рациональные отображения ведут себя как
полиномиальные. Прообразы вещественной оси при отображении
окружности (точнее, поскольку (4.1)—экспоненциальное
отображение окружности) сами являются замкнутыми петлями.
Рис. 4.2. Область притяжения рационально-полиномиального отображения
(4.1) для значений параметра, соответствующего числу вращений, равному
золотому сечению.
Примером может служить изображенная на рис. 4.2 область
притяжения отображения (4.1) для числа вращений, равного
золотому сечению.
5. Неустойчивое многообразие золотого сечения
Уравнение неустойчивого многообразия (1.1) означает, что
в окрестности значения параметра (соответствующего числу
вращений), равного золотому сечению, множество Мандельброта
инвариантно относительно преобразований подобия,
удовлетворяющих универсальному закону Шенкера с параметром б. Мы
исследовали это численно, растягивая окрестность значения
параметра, соответствующего золотому сечению, и сравнивая
размеры множеств сердец, отвечающих последовательным
отношениям чисел Фибоначчи. В этой окрестности множество
Мандельброта действительно претерпевает преобразование подобия с
таким же универсальным коэффициентом, как и в вещественном
случае. Однако универсальность золотого сечения не допускает
обобщения на комплексную плоскость в нескольких важных
отношениях.
Первая неуниверсальность известна из теории итераций
полиномиальных отображений [24, 27]: чем длиннее цикл, тем
«волосатее» внешность множества сердец. В этом нетрудно убедить-
Хаос, турбулентность и родственные вопросы 621
ся, сравнив рис. 2.1 (множество сердец неподвижной точки) с
рис. 5.1.
Другая неуниверсальная особенность комплексных
отображений окружности состоит в том, что внешности множеств
сердец .различных отображений безошибочно различимы, во сколько
бы раз мы ни увеличивали окрестность значения параметра,
соответствующего золотому сечению. В этом нетрудно убедиться,
Рис. 5.1. Множество Мандельброта (изображенное на рис. 3.3) синусного
отображения (3.1) в окрестности значения параметра, соответствующего
числу вращений, равному золотому сечению. Множество самых больших
сердец соответствует отношению 55/89 чисел Фибоначчи. В то время как
множества сердец последовательных отношений чисел Фибоначчи удовлетворяют
универсальному закону подобия Шенкера, их внешние области покрываются
все большим числом «волос».
сравнив рис. 5.1 с рис. 5.2. В то время как все внешние лучи
синусного отображения уходят в бесконечность, внешние области
множеств сердец рационально-полиномиального отображения
украшены петлеобразными прообразами единичной окружности.
Численно эти петлеобразные «украшения» удовлетворяют
универсальному закону подобия Шенкера с тем же параметром, как
и внутренние области множеств сердец, поэтому тип исходной
аппроксимации неустойчивого многообразия мы можем
определять независимо от «коэффициента увеличения». Отсюда мы
заключаем, что уравнение неустойчивого многообразия (1.1) не
имеет единственного аналитического продолжения в
комплексную плоскость.
Благодарности. Мы признательны Дж. Хаббарду и Б. Бран-
неру за вдохновляющие обсуждения. Предраг Цвитанович вы-
622
Часть IX
ражает благодарность Дж. Хаббарду и математическому
факультету Корнеллского университета за доступ к компьютеру VAX и
Б. Виттнеру за любезную помощь в программировании
двумерных итераций, позволивших получить почти все иллюстрации,
приведенные в этой работе. П. Цвитанович выражает свою
признательность М. Фейгенбауму за гостеприимство, оказанное ему
Рис. 5.2. Изображенное на рис. 4 1 множество Мандельброта рационально-
полиномиального отображения (4.1) в окрестности значения параметра,
соответствующего числу вращений, равному золотому сечению. Множество
самых крупных сердец соответствует отношению чисел Фибоначчи 21/34. В то
время как множества сердец последовательных отношений чисел Фибоначчи
удовлетворяют универсальному закону подобия Шенкера, их внешние
области отличаются от внешних областей сердец экспоненциального отображения
(показанных, например, на рис. 5.1).
в Лаборатории физики твердого тела, и благодарит за
предоставленную ему финансовую поддержку (по контракту DOE No.
DE-AC02-83-ER13044). И. Прокачча благодарит за частичную
поддержку Фонд «Минерва» в Мюнхене. М. Иенссен и Л. Када-
нов пользовались частично поддержкой Управления научных
исследований ВМС США и Научно-исследовательской
лаборатории материалов.
ЛИТЕРАТУРА
1. Feigenbaum M. /., J. Stat. Phys., 19, 25 (1978).
2. Feigenbaum M. /., J. Stat. Phys., 21, 669 (1979). [Имеется перевод: Фей-
генбаум М. -УФН, 1983, т. 141, с. 345.]
3. Cvitanovic P., ed., Universality in chaos, Hilger, Bristol, 1984.
4. Chaos, ed. Bai-Lin Hao, World Scientific, Singapore, 1984.
Хаос, турбулентность и родственные вопросы
623
5. Cellet Р, Eckmann /.-P., Iterated Maps on Interval as Dinamical Systems,
Birkhauser, Boston, 1980.
6. Jensen M. #., Bak P., Bohr Г, Phys. Rev., A30, 1960 (1984).
7. Bohr Г, Jensen M. Я, Bak P., Phys. Rev, A30, 1970 (1984).
8. Shenker S. /., Physica, 5D, 405 (1982).
9. Felgenbaum M. /., Kadanoff L. P., Shenker S. /., Physica, 5D, 370 (1982).
10. Ostlund S., Rand D., Sethna /., Siggia E. D, Physica, D8, 303 (1983).
11. Daido Я, Phys. Lett., 83A, 246 (1981); 86A, 259 (1981).
12. Daido Я, Prog. Theor. Phys., 67, 1698 (1982).
13. Гольберг A. #., Синай Я. Г., Ханин К. М. — УМН, 1983, т. 38, с. 159.
14. Cvitanovic P., Myrheim /, Nordita preprint 84/5 (1985); опубликовано в
Commun. Math. Phys. (Feb. 1984).
15. Cvitanovic P, Jesnen M. Я, Kadanoff L. P., Procaccia /., Phys. Rev. Lett.,
55, 343 (1985).
16. Gunarathne О., не опубликовано; Felgenbaum M. /., не опубликовано.
17. Manton N. S, Nauenberg M., Commun. Math. Phys, 89, 555 (1983).
18. Widom M., Commun. Math. Phys. 92, 121 (1983).
19. Douady Л, Hubbard J. Я, С R. Acad. Ssi, Paris, 294, 123 (1982).
20. Fatou P., Bull. Soc. Math, France, 47, 161 (1919); 48, 33, 208 (1920).
21. Julia G, J. Math. Pures et Appl, 4, 47 (1918).
22. Mandelbrot В. В., Ann. N. Y. Acad. Sci, 357, 249 (1980).
23. Mandelbrot В В., The Fractal Geometry of Nature, Freeman, San
Francisco, 1982.
24. Milnor 7, IHEE preprint, may 1985.
25. Cvitanovic P, Shraiman В., Soderberg В., Phys. Scripta, в печати.
Дж. Хаббард (частное сообщение).
27. Douady A., Hubbard J. Я., частное сообщение; Mandelbrot В. 5,
неопубликованная гипотеза.
Фрактальные модели двух-
и трехмерной турбулентности
Дж. Паладин, Л. Вульпиани*
Принято считать, что диссипация энергии в трехмерных
турбулентных течениях сосредоточена на множестве с нецелой
(фрактальной) размерностью. Однако экспериментальные данные о моментах
флуктуации скоростей свидетельствуют о том, что
мелкомасштабные свойства турбулентного потока не могут быть описаны с
помощью обычного фрактала, порождаемого некоторым набором
правил, связывающих его статистические свойства в определенном
масштабе со статистическими свойствами в большем масштабе. Мы
вводим поэтому «неоднородные фракталы», правила образования
которых на каждом шаге по иерархии масштабов выбираются
случайным образом в соответствии с некоторым распределением
вероятности. Перенос энергии описывается при этом с помощью
модели случайной фрагментации в предположении, что между
различными этапами процесса нет корреляции.
Такая модель не может быть распространена на двумерный
случай путем рассмотрения локального каскада энсртофии вместо
энергии, поскольку из точных результатов следует, что
перемежаемость не влияет на закон подобия структурных функций. Учитывая
это, мы вводим новую модель, в которой механизм фрагментации
оказывается запрещенным всякий раз, когда плотность диссипации
энстрофии превышает некоторое критическое значение.
Мы воспроизводим некоторый промежуточный режим, но без
поправок к двумерному степенному закону Колмогорова и находим,
что области нулевой диссипации энстрофии так же, как и области
больших градиентов завихренности, имеют в Я2 фрактальную
размерность, совпадающую с топологической размерностью.
1. Введение
Фрактальные объекты в последнее время стали входить
в анализ широкого класса явлений в физике и других
естественных науках [1].
Геометрическим аспектам турбулентности особенно
необходимы исследования в рамках автомодельных, а не евклидовых
методов.
Обычно принято рассматривать однородные фракталы (т. е.
фракталы, обладающие глобальной точной инвариантностью
относительно растяжений). Мы же хотим предложить простые
модели, в которых автомодельность выполняется только в
среднем, имея в виду воспроизведение перемежающихся режимов в
двух- и трехмерной турбулентности. Точнее говоря, мы
воспользуемся неоднородными фракталами, порождаемыми по
правилам, которые на любом масштабе длин не фиксированы, а выби-
* G. Paladin, A. l/tt/ptam-Dipariimento di Fisica, Universita «La Sapien-
za», Piazzale Aldo Moro 2, 1-00185 Roma, Italy and GNSM-CNR, Unit* di
Roma, Italy.
Хаос, турбулентность и родственные вопросы
625
раются случайным образом в соответствии с заданным
распределением вероятностей.
Поясним нашу терминологию на примере (рис. 1). Двумерный
ковер Серпинского получается путем итерации процесса
фрагментации. На каждом шаге i квадрат масштаба U порождает
п2 масштабов U+\ = U/n, из которых «заполненные» составляют
лишь долю (5 (см. рис. 1, где п = 2).
Ковер называется однородным, если число заполненных
клеток фиксировано (т. е. если $п2 = пор), и неоднородным, если
Рис. 1. Схематическое представление однородного фрактала (а) по
сравнению с неоднородным фракталом (б). Заштрихованы зоны, активные в
процессе фрагментации.
это число не постоянно, т. е. если р— случайная величина,
зависящая от конкретного квадрата и рассматриваемого шага.
Ясно, что фрактальная размерность, даже если она
однозначно определена (например, для ковра Серпинского DF = 2 +
+ log„{p}, где { } означает усреднение по распределению
вероятности для р), не может быть характеристикой неоднородности.
С другой стороны, фрагментация определяется распределением
вероятностей долей р, которое в принципе известно по моментам
{р*7}. Эти моменты могут быть естественно связаны с
показателями структурной функции в трехмерной турбулентности. В
двумерном случае установить такую связь уже невозможно, так как
фрагментация приводит к автомодельной структуре.
2. Трехмерная перемежаемость
Уравнения Навье — Стокса
^u + (u-V)u = -|vjt7 + vAi| (1)
626
Часть IX
формально инвариантны относительно преобразований подобия
г->Лг, и->ЛАи, t^ll~ht,
,~x»V <2)
Заметим, что средняя диссипация энергии e =
v(Vu)2изменяется под действием преобразования подобия (2) по закону
е-»*,3*""1!. (3)
Знаменитый закон Колмогорова (2) может быть получен,
если потребовать инвариантность ё относительно преобразования
подобия (2) с h = 1/3. Из этого следовало бы, что
Нт _*" = Hm |U(X + AX1)/3^U(X)1 Ф 0. (4)
Величина Ах в соотношении (4) означает Ах ~ длине
диссипации, поэтому в пределе бесконечно больших чисел Рейнольдса
градиенты скорости имеют особенность. Заметим, что в теории
Колмогорова существует неявное предположение о заполнении
множеством особых точек (тех, в которых выполняется
соотношение (4)).
Можно считать (как впервые заметил Ландау [3]), что
диссипация энергии е(х) = (1/2) ■ v • £ (д{и} + д}щ)2 испытывает
*./
сильные флуктуации. Так происходит, например, если множество
точек, в которых градиенты скорости имеют особенность,
обладает нецелой фрактальной размерностью.
Подход к этой проблеме, использующий однородные
фракталы, был предложен в так называемой р-модели [4]. Суть
такого подхода состоит в замене соотношения (4) новым
соотношением
Дм Dv — 2
Hm —ТФ0, Л=-£ . (5)
Множество точек, где выполняется неравенство (5), имеет
фрактальную размерность DF < 3. Практически в этой модели
диссипация энергии е(х) равномерно распределена по однородному
фрактальному объекту. В р-модели для флуктуации скорости
получаются следующие соотношения:
<|Д«(/)!'>~/Ч £p = -^V^P + (3-DF). (6)
На рис. 2 приведены экспериментальные данные о зависимости
Ер от р [5].
Линейная аппроксимация пригодна только при р с< 7. При
больщих значениях р показатель £р ведет себя нелинейно. От-
Хаос, турбулентность и родственные вопросы 627
сюда мы заключаем, что область, в которой происходит
диссипация энергии, не является однородным фракталом и что
существует много структур с особенностями, соответствующих различ-
Рис. 2. Зависимость £р от р. Жирными точками и кружками обозначены
экспериментальные данные из работы [5]. Сплошная линия соответствует р-мо-
дели с DF = 2,83. Штриховая линия изображает зависимости (13) и (14)
при х — 0,125.
ным значениям h. Недавно [6, 7] для учета более сложных
структур была предложена многофрактальная модель.
Определим S(h) как множество точек, в которых
,. I и (х) — и (у) I . л
lim J—-г1 )^J-L ф 0,
х+у |х —у|л
(7)
и обозначим через d(h) фрактальную размерность множества
S(h). Так как вероятность принадлежать к множеству S(h) в
масштабе / пропорциональна /3-ад, справедливо соотношение
(\&u(l)f)~\dt(h)t
ph+3-d (ft)
fa.
Методом перевала мы получаем для ^:
lp = va\n{ph + Z-d(h)}.
(8)
(9)
Физически соотношение (5) означает, что при заданном
значении р показатель £р зависит от конкретного значения А.
Следовательно, характер неустойчивостей, необходимых для создания
множеств S(A), отбирается моментами разностей скоростей.
Рис. 2 можно поэтому интерпретировать как подтверждение
существования различных действующих на течение механизмов
отбора распределения вероятности переноса энергии и диссипации.
Введем теперь обобщение [7] |3-модели для получения
неоднородного фрактального объекта с особенностями различного
рода, т. е. с различными показателями А, градиентов скорости.
Рассмотрим масштабы /я=2_?/о, где /0 — масштаб, в котором в
систему поступает энергия. Если в масштабе 1п в системе суще-
628
Часть IX
ствует N активных вихрей, то каждый вихрь ln(k) порождает
вихри масштаба ln+i {k нумерует «материнские» вихри, к =
= 1, ..., Nn). Так как скорость переноса энергии между
вихрями ln(k) и tn+\(k) постоянна, справедливо соотношение
VI Шя <*) = K+i (*) K+i (Win+l (k), (io)
где, как в стандартной р-модели, Vn(k) — разность скоростей в
активном вихре между точками, находящимися на расстоянии 1п
друг от друга, pft+i(&)—доля объема (в процентах),
занимаемая активными вихрями масштаба /я+ь порожденными вихрем
масштаба /я. Из соотношения (10) следует, что разность
скоростей Vn в вихре, порожденном заданным набором
фрагментации рь ..., рл, имеет порядок
( п ч-1/З
Vn~lT\Jl$i) • (И)
В свою очередь из соотношения (11) следует, что
я
<| Ли (/„) |р> = J П dfilP (р„ ..., р„) р, | Уя f. (12)
Так как по предположению между различными шагами фрагмент
п
тации не существует корреляции, т. е. p(Pi, ... , PJ = Пр(Р,),
мы получаем для показателя %р:
?P==p/3-log2{p(1-p/3)}. <13)
где {...} означает усреднение по распределению Р(р). Заметим,
что если р — постоянная (2(D/7~3)), то мы приходим к
результатам стандартной р-модели (т. е. к соотношению (7)). Знание
распределения вероятности Р(Р) связано с пониманием природы
особенностей, допускаемых уравнениями Навье — Стокса. Как
показывает рис. 2, простое соотношение
Р(Э)==лгб(р —0,5) + (1 —ж)б(Р— 1), (14)
где х = 0,125 приводит к хорошему согласию с имеющимися
экспериментальными данными, х — единственный свободный
параметр. Не существует сколько-нибудь глубоких причин, по
которым следовало бы отдать предпочтение распределению (14) для
Р(Р). Выбирая распределение (14), мы следовали простой
феноменологической идее, согласно которой один активный вихрь
может породить либо полосы скорости (Р = 0,5), либо вихри
типа колмогоровских, заполняющие пространство (р = 1).
Заметим, что фрактальный объем, порождаемый согласно
приведенным выше правилам, не обладает свойствами глобаль-
Хаос, турбулентность и родственные вопросы 629
ной инвариантности относительно преобразования подобия. Тем
не менее можно вычислить фрактальную размерность DF,
определяемую соотношением
где Nn — число активных вихрей на /г-м шаге фрагментации.
Нетрудно показать с помощью простых вычислений [7], что
D^ = 3 + log2{P} = 3-b. (16)
Заметим, что фрактальная размерность Dp, определяемая
соотношением (15), отличается от размерности D*, часто
используемой в экспериментальных работах и вычисляемой по
корреляции диссипации энергии. С показателем £р величина D* связана
соотношением D* = 1 + Ее. Нетрудно видеть, что в общем
случае DF > D*. Равенство DF = D* выполняется только для
стандартной (5-модели (т. е. для однородного фрактала). Например,
DF = 2,91 и/)* = 2,83, если экспериментальные данные
аппроксимировать кривой (14) с л: = 0,125. Это косвенная проверка
многофрактальной природы полностью развитой
турбулентности.
3. Двумерная перемежаемость
Описанная в предыдущем разделе случайная (J-модель не
может столь легко распространяться на двумерную
турбулентность путем рассмотрения локального каскада энстрофии
вместо энергии.
Если предположить, что процесс фрагментации не
перемежающийся (т. е. колмогоровского типа, заполняющий
пространство), то в инерционном диапазоне [9] для структурной функции
получается обычный степенный закон
<|Д«(/)|Р)~/Ч £Р = Р. (17)
Покажем, что поправка на перемежаемость к закону
подобия (17) не может быть получена в рамках р-модели.
Напомним, что центральную роль играет предположение о
постоянстве переноса энстрофии, из которого путем подсчета
размерности мы получаем
£з = 3. (18)
Кроме того, можно показать, что t# — выпуклая функция от р
[10]. Следовательно, существует точный результат для
двумерного уравнения Эйлера [9], который без труда может быть
распространен на вязкий случай:
| Ли (г) |< const -r\ In r |, (19)
откуда £р > р.
630
Часть IX
Последнее неравенство согласуется с соотношением (18) и
выпуклостью £р, только если £р = р.
Может показаться весьма удивительным, что перемежаемость
не влияет на показатели структурной функции. Тем не менее
некоторые численные данные подтверждают столь странное
поведение, совершенно необычное для двумерной турбулентности.
Таким образом, случайную (3-модель необходимо
модифицировать, если мы хотим воспроизвести хотя бы известные
феноменологические аспекты.
Поскольку мы постулировали постоянную скорость переноса
энстрофии, формула (10) переходит в соотношение
-7з77Г= Ря+lW ,3 m - (2°)
Неравенству (19) можно удовлетворить, наложив еще одну связь
РЯ+1=1> если 7Г>*]макс. (21)
Условие (21) представляет собой модификацию старого бер-
нуллиевского процесса фрагментации в марковский процесс,
поскольку стадии процесса не являются более независимыми.
В этой марковской случайной (3-модели режим
перемежаемости не возникает, даже если t,p = р.
Действительно, в R2 существуют области с нулевой
диссипацией энстрофии, имеющие фрактальную размерность D/? = 2,
а также активные вихри с большим градиентом скорости.
Грубо говоря, мы имеем дело не с многофрактальной
структурой, а с структурой, напоминающей «шахматную доску».
Фрагментация заполняет пространство при масштабах
достаточно малых, но все же больших, чем масштабы вязкой
диссипации, и перемежаемость должна проявить себя как некое
«макроскопическое» явление в двумерном случае.
Как показывают недавно полученные численные результаты
[11], сценарий двумерной турбулентности качественно
согласуется с нашей моделью. Каскад энстрофии действительно
ослабляется в некоторых когерентных структурах, доминирующих
в энергетическом спектре при всех масштабах.
ЛИТЕРАТУРА
1. Mandelbrot В., The Fractal Geometry of Nature, Freeman, San Francisco,
1982.
2. Колмогоров Л. Я. — ДАН СССР, 1941, т. 30, с. 299; Избранные труды.
Математика и механика. — М.: Наука, 1985, с. 281—287.
3. Ландау Л. Д., Лифшщ Е. М. — Механика сплошных сред. Изд. 2-е, пе-
рераб. и дополн. — М.: ГТТИ, 1954; Гидродинамика, Изд. 3-е,
переработанное. — М.: Наука, 1986.
Хаос, турбулентность и родственные вопросы
631
4 Frisch U., Salem P., Nelkin AT., J. Fluid Mech., 87, 719 (1978).
5. Anseltnet F., Gagne Y., Hopfinger E. J., Antonia R. A., preprint, Institute
de Mecanique de Grenoble, 1983.
6. Frisch V., Parisi G., Vagenna Summer School LXXXVIII, 1983.
7. Benzi R., Paladin G., Parisi G., Vulpiani Л., J. Phys. A: Math. Gen. 17,
3521 (1984).
8. Paladin G.y Vulpiani A.y Lett. Nuovo Cimento, 41, 82 (1984).
9. Rose H. A., Salem A, J. Physique, 39, 441 (1978).
10. Feller W., An Introduction to Probability Theory and its Applications,
vol. 2, Wiley, New York, 1971. [Имеется перевод: Феллер В. — Теория
вероятностей и ее приложения. В 2-х томах. Изд. 3-е. Т. 2.— М.: Наука,
1984.]
П. Benzi R., Paladin G, Paternello S., Santangelo P., Vulpiani А., будет
опубликовано.
Численное исследование
неоднородных фракталов
Р. Бадии, Л. По лит и *
Помимо понятия размерности, дающей первую осредненную
характеристику фракталов, предлагается и обсуждается вторая
характерная величина — коэффициент неоднородности. Теоретические
вычисления выполнены для канторовского двоичного множества, чтобы
продемонстрировать интуитивный смысл неоднородности как рас-
плывания распределения вероятностей Я (б, я), заданного на
расстояниях б между ближайшими соседями среди п точек, по
различным скоростям сокращения линейных масштабов. Подробно
исследовано отображение Синая как прототип отображения с
непостоянным якобианом как в обратимой, так и в необратимой
области параметров.
1. Введение
В последнее время исследование фрактальных множеств
[1] стало вызывать большой интерес во многих областях физики.
Для характеристики фрактальных множеств были предложенрл
различные величины типа размерности [2—4]. Их можно грубо
расклассифицировать на две группы, отнеся к первой размер-
ностные характеристики, выведенные из чисто геометрических
соображений, и ко второй — характеристики, связанные с
теорией информации. Определения первой группы обычно приводят
для физических систем к одинаковым результатам, в то время
как различия между величинами, принадлежащими ко второй
группе, служат мерой степени «неоднородности» [4—6]
рассматриваемого фрактала.
Чтобы лучше понять это понятие и придать ему
количественный характер, недавно был предложен континуум размерностей
(называемый функцией размерности) через моменты
распределения Р(8,п) попарных расстояний б между ближайшими
соседями среди п точек фрактала. Поскольку можно доказать, что
функция размерности при подходящем выборе точек порождает
такие величины, как размерность самоподобия,
информационную размерность и все остальные размерности Реньи [4Ь],
вычисление ее служит полезным средством исследования
неоднородности в физических системах.
2. Функция размерности и неоднородность
Для удобства напомним определение размерности Реньи
порядка q. Предположим, что фазовое пространство разделено на
* Re/no Badu-Physik-Institut der Universitat, Schonberggasse 9, 8001
Zurich, Switzerland; Antonio Politi- Institute) Nazicnale di Ottica, Largo E.
Fermi 6, 50125 Firenze, Italy.
Хаос, турбулентность и родственные вопросы 633
ячейки размером е, и пусть Pi {&) — вероятность попасть в i-ю
ячейку. Реньи ввел [2] обобщенные энтропии Kq(s), q = 0y 1,
2, ..., я, определив их следующим образом:
*,(«) = { In ZPi (в) }/(l-q). (1)
Соответственно размерности Реньи определяются как
D, = -limtf,(e)/lne. (2)
В частности, DQ есть не что иное, как размерность самоподобия
(обычно вычисляемая с помощью алгоритма счета ячеек), D\
называется информационной размерностью [За], а
£>2—показателем корреляционного интеграла [Зь]. Размерности Реньи
удовлетворяют неравенству Dq > Dp (если р > q). Равенство
достигается в случае однородных множеств, т. е. таких множеств,
в которых вероятность Pi удовлетворяет закону подобия Pi(v) ~
~ &D, где D — любая размерность [6]. Поскольку прямое
вычисление размерностей Реньи Dq в общем случае пракически
неосуществимо из-за недостаточного объема памяти современных
компьютеров и отсутствия статистической сходимости, мы
избрали другой подход. Рассмотрим точку отсчета х в d-мерном
евклидовом пространстве плюс (п—1) других точек, из
которых все выбраны случайно относительно заданной на множестве
естественной меры 1). Определим 8(п) как расстояние между
точкой х и ее ближайшим соседом среди (п—1) остальных точек.
Ясно, что 8(п) —невозрастающая функция от п> и в общем
случае некоторое среднее по всем точкам х будет вести себя как
<6(я)> ~ rrXID. Точнее говоря, мы вводим распределение
вероятности Р(6, п) на расстояниях между ближайшими соседями среди
п точек. Следуя работам [4], вычислим моменты распределения
вероятности Р(6, п) как
оо
<6V («)> = Му (п) = J Р (6, ft) db = Kn-y,D (v\ (3)
О
где D(y)—зависящее от у определение размерности,
называемое в дальнейшем функцией размерности. Коэффициент К
зависит от у и пу но его зависимость от у по определению не имеет
значения для интересующей нас задачи, а зависимость от п
сводится для широкого класса систем к несущественной
периодичности по In (я) [8]. Было показано [4], что при y — D{y)f т. е.
4) В случае динамической системы точки порождаются последовательно.
Для таких фракталов, как перколяционные решетки или кластеры полимеров,
точки можно выбирать по любому правилу, чтобы получить информацию
о структуре. Следует иметь в виду, однако, что различные правила
соответствуют заданию различных вероятностей весов на различных частях объекта.
634
Часть IX
когда выполняется соотношение неподвижной точки, значение
функции размерности совпадает с значением размерности
самоподобия (по крайней мере в случае автомодельных фракталов
[Ь\). Кроме того, для того же класса систем можно доказать
общее соотношение D{y = (1 — q)Dq) = Dq, где Dq —
размерность Реньи порядка q. При q = 0 последнее соотношение
переходит в соотношение неподвижной точки. Таким образом,
вычисление моментов (3) позволяет определять любые размерности
Реньи Dq рекуррентно: начальное значение y выбирается для
получения первой оценки требуемой размерности, которая в
свою очередь используется как начальное значение для
следующего приближения и т. д., пока не будет достигнута
удовлетворительная точность. Однако, вообще говоря, в таком процессе
нет особой необходимости, так как оценка размерности D(y) в
некоторых заранее заданных точках позволяет получить ту же
информацию. Для проверки стабильности метода необходимо
вычислить наклон функции размерности в неподвижных точках.
В работе [4bJ было показано, что производная D' (у) всегда
ограничена и заключена между 0 и 1, для равномерных фракталов
равна 0 и все размерности совпадают. Кроме того, наклон в
неподвижной точке X = D'(D0) связан с соответствующей
энтропией [4] и может быть использован для получения степени
неоднородности фракталов, так как с увеличением неоднородности
А стремится к 1. В соответствии с этим Я получила название
«коэффициент неоднородности». Некоторые свойства
распределения вероятности Р(8, п) расстояний б между ближайшими
соседями среди п точек заслуживают особого изучения. Во-первых,
распределение Р(б, п) гладкое в отличие от распределения
точек в евклидовом пространстве, содержащем фрактал.
Во-вторых, в некоторых физических системах отдельные точки могут
быть недоступными, но распределение Р(б, п) остается
вычислимым либо аналитически, либо численно, если его
интерпретировать следующим образом. Рассмотрим покрытие фрактала п
неравными шарами с диаметрами 6* (i= 1, 2, ..., п) и перейдем
к более тонкому покрытию, взяв большее число шаров меньших
размеров. Для перколирующей системы, например, величина
Р(б, п) означала бы вероятность найти кластер размером б в
ячейке (размером L), содержащей п кластеров. Затем нам
следовало бы рассмотреть более крупную ячейку (т. е. взять
большее число п) и ренормировать ее к масштабу L так, чтобы при
п-+оо расстояние 6-^0. Наконец, заметим, что при увеличении
п распределение Р(б, п) расплывается. Действительно, как
показано в работе [4Ь], относительное среднеквадратичное
отклонение Л (я) распределения Р(б, п) ведет себя при малых X как
l^(n) = [M2Du — M2Do)U2/MDo = n%. Это объясняет смысл
неоднородности как расплывания по различным скоростям сокращения
Хаос, турбулентность и родственные вопросы
635
масштабов при п->оо. В однородных множествах (т. е. при
% = 0) все расстояния убывают с одной и той же скоростью.
Функция размерности ограничена двумя горизонтальными
асимптотами, соответствующими наибольшей (у = —=) и
наименьшей (y = oo) скоростям сокращения линейных масштабов.
3. Фрактальные меры
Исследуем теперь вид функции Р(б, п) в простом случае:
однородном канторовском множестве, возникающем при
оставлении двух сегментов длиной а и выбрасывании средней части
единичного отрезка. Обоим сегментам приписывается одинаковая
вероятность. Для распределения Р(б, п) такого множества было
получено следующее выражение [4Ъ]:
Р (б, п) = 2D0n (26)D°-~l exp {- п (26)D°). (4)
Выясним, как неоднородность проявляется в форме
распределения Р(б, п). Для этого рассмотрим двоичное канторовское
множество [За], т. е. множество точек х (0 < х < 1), таких, что
их двоичные разложения содержат нули с вероятностью р\ и
единицы с вероятностью p2(pi + Рг = 1). Приведем пример
фрактальной меры [9], или «нелакунарного фрактала» [1]: весь
единичный отрезок заполнен (т. е. Dq== 1), а мера Хаусдорфа [1]
и информационная мера {А = — {р\ In рг + р2 In p2) /In 2 < 1}
совпадают. Нас интересует суммарная вероятность S(6, ft), что
для точки отсчета х найдется среди ближайших соседей,
выбранных среди (п—1) точек, такая точка, которая отстоит от х на
л
расстояние б, т. е. интеграл 5(6, п) — \Р(у, ri)dy. В работе
о
[4Ь] мы получили для дополнительного распределения 5=1—
— 5 следующее выражение:
-log р2
5 ~ [~ log 26]I/2 J ехр [- п (26)°] X
-log pi
где log означает двоичный логарифм и р2< Рь Первый член в
интеграле совпадает с результатом, который мы получили бы
для троичного канторовского множества размерности D [4Ь].
Следовательно, все выражение для S можно интерпретировать
как суперпозицию распределений однородных канторовских
множеств с различными размерностями. Заметим, что размерность
D принимает значения от —lor pi до —logp2, и эти пределы
совпадают с асимптотами функции распределения D(—оо) и
636
Часть IX
D(oo). Кроме того, весовая функция есть гауссовское
распределение, центрированное на информационной размерности,
которая, как выясняется, играет особую роль. Аналогичные
соображения должны быть применимы и к фракталам, вложенным в
пространстве более высокой размерности. Действительно, как
видно из некоторых приведенных в работе [4Ь] графиков
распределения Р(б, л), отклонения от вида (4) свидетельствуют о
неоднородности.
4. Ляпуновская размерность в необратимых отображениях
В качестве более физического примера фрактальной меры
рассмотрим отображение Синая [4, 10]
х' = х + у + g cos (2m/) (mod 1),
у' = х + 2у (modi), ( '
итерации которого при достаточно малом g покрывают весь
единичный квадрат. Однако, поскольку сумма показателей Ляпу-
г
о о,1 о,г о,в
9
Рис. 1. Ляпуновская размерность DL (сплошная линия) и функция
размерности D(y) (точки) как функции от g. Функция размерности вычислена при
5 различных значениях у (—2, —1, 0, 1, 2).
нова всегда отрицательна, элемент площади со временем
стягивается к нулю. Это означает, что распределение вероятности
сильно изрезано пиками, т. е. аттрактор является фрактальной
мерой. Другая причина, по которой следует ожидать
неоднородности в случае отображения Синая,— непостоянство его якобиана
J = 1 +2jtgsin(2m/). Действительно, как показали Грассбергер
и Прокачча [11], флуктуации в дельта-образных значениях по-
Хаос, турбулентность и родственные вопросы
637
казателей Ляпунова в таких системах сильны, и именно с этим
связано различие режимов в различных масштабах. Кроме того,
информационная размерность D\ аттрактора может быть
выражена через показатели Ляпунова: DL = 1 + A,i/|ta| ^ D\.
Равенство выполняется для двумерных обратимых отображений
[12], в то время как для более общих систем размерность
Ляпунова Dl дает хорошее приближение к D\. Следовательно,
интересно исследовать поведение размерности Ляпунова как
функции параметра g. На рис. 1 DL (сплошная линия) и пять
значений функции размерности D(y) (центральная точка
соответствует информационной размерности) показаны как функции от
g. В точке g = 1/(2я) (указанной вертикальной штриховой
линией) отображение становится необратимым, и при больших
значениях g размерность Ляпунова Dl, как и ожидалось, только
указывает верхнюю границу для D\ =D(0). Кроме того, уже при
gp = 0,l система весьма неоднородна, и наибольшее расплывание
по различным масштабам достигается в точке перехода g =
= 1/(2я). Ясно, однако, что неоднородность изменяется в
зависимости от g весьма гладко и не имеет отношения к
необратимости отображения.
ЛИТЕРАТУРА
1. Mandelbrot В. В.у The Fractal Geometry of Nature, Freeman, San
Francisco, 1983.
2 Renyi A, Probability Theory, North-Holland, Amsterdam, 1970.
3. a> Farmer J. D.y Z. Naturforsch., 37A, 1304 (1982); b> Grassberger P.,
Procaccia /., Phys. Rev. Lett., 50, 346 (1983); c> Farmer /. D.y Ott E.y
Yorke J. A.y Physica, 7D, 153 (1983); d> Termonia У., Atexandrovitch Z.,
Phys. Rev. Lett., 51, 1265 (1983); e> Guckenheimer /., Buzyna G., Phys.
Rev. Lett., 51, 1438 (1983).
4. Badli R., Politi A, a> Phys. Rev. Lett., 52, 1661 (1984); ь> j. stat. Phys.,
40, 725 (1985).
5. Grassberger P., Phys. Lett., 97A, 227 (1983).
6. Hentschel H. G. E.y Procaccia /., Physica, 8D, 435 (1983).
7. Tricot C.y Math. Proc. Camb. Phill. Soc, 91, 57 (1982).
8. Badii #., Politi A.9 Phys. Lett., 104A, 303 (1984).
9. Мандельброт Б. — наст, сб., с. 36
10. Синай Я. Г. - УМН, 1972, т. 4, с. 2.
П. Grassberger P., Procaccia /., Physica, 13D, 34 (1984).
12. Young L. 5., J. Ergodic Theory and Dynam. Sys., 2, 109 (1982).
Обобщенная масштабная
инвариантность и анизотропные
неоднородные фракталы
в турбулентности
Д. Шертцер, Ш. Лавджой*
Предложено обобщение масштабной инвариантности, позволяющее
учитывать анизотропию и (многомерную) перемежаемость.
Обсуждаются следствия из нового понятия, в особенности для
метеорологических полей.
1. Введение
Многие геофизические поля подвержены сильным
изменениям в широком диапазоне временных и пространственных
масштабов. Вариабельность атмосферы велика в диапазоне,
охватывающем по крайней мере 9 порядков (от ~ 1 мм до
~1000 км), и создает сильно перемежающиеся и анизотропные
структуры: энергетический спектр (£(£)) горизонтального
ветра по горизонтали изменяется как ~&_5/3, в то время как по
вертикали он изменяется сильнее—по закону ~/Н1/5. Это
различие представляет собой спектральную аналогию
(крупномасштабной) стратификации по вертикали.
И анализ, и численное моделирование таких структур
делают необходимым обобщение как понятия масштабной
инвариантности и перемежаемости (путем введения анизотропных
метрик и размерностей), так и масштабно-инвариантных мер,
характеризуемых целым спектром (фрактальных) размерностей.
Существование многих размерностей приводит к интересным
следствиям: оно непосредственно связано с расходимостью
высших статистических моментов средних характеристик каскада,
мультипликативными процессами и новыми вопросами
относительно детектируемости и предсказуемости.
2. Обобщенная масштабная инвариантность
2.1. Мотивировка
Чтобы избежать ничем не обоснованного противопоставления
двумерного и трехмерного случаев при больших (и малых)
масштабах, мы предложили альтернативную
масштабно-инвариантную модель [1—3] (нематематический обзор см. также в
* Daniel Sc/terteer-EERM/CRMD, Meteorologie Nationale, 2 avenue Rapp,
750007 Paris, France; Shaun Love joy- Department of Physics, McGill
University, University St., 3600 University St., Monreal, Que. НЗА 2Т8, Canada.
Хаос, турбулентность и родственные вопросы 639
работах [4—5J) динамики атмосферы: анизотропия,
обусловленная гравитацией через выталкивающую силу, приводит к
дифференциальной стратификации и последующему изменению
эффективной размерности пространства (от значения D = 3 для
изотропного случая к D = 23/9 = 2,5555 ...).
Для учета этого и других эффектов (таких, как
обусловленное силой Кориолиса дифференциальное вращение) необходим
обобщенный механизм масштабной инвариантности. Основная
проблема состоит в нахождении семейства «шаров»,
представляющего статистические свойства вихрей в различных
масштабах посредством (математических) случайных мер, таких, как
поток энергии через структуры в данном масштабе.
2.2. Обобщенное понятие масштаба
Внимательное изучение феноменологии турбулентных
каскадов позволило выделить основные свойства, связанные с
понятием масштаба, и привело [6] к следующему абстрактному
определению в терминах группы («масштабной группы») операторов
7\, действующих на топологическом пространстве М:
I. {7\} — мультипликативная группа (A g j?*+)
преобразований, действующих из М в М:
Тм = ТкоТк>9 VA, А'е=7г; (1)
(в частности, Т1 = 1 — тождественный оператор, и Тк{ = Тк-^У
II. Существует семейство В\ шаров (открытых подмножеств
множества М), таких, что В = ТкВ\— базис топологии в М.
III. Существует возрастающая функция ф, отображающая В
в /?+> ограниченная на В\ и факторизующаяся на (De/?+):
Ткф = Х°ф, VA (2)
(оператор Тк определен естественно: Ткф(В) =ф(ТкВ), VX, В).
Подчеркнем, что выражение XD возникает из групповых свойств
оператора Тк (оно следовало бы из предположения о
существовании в (2) непрерывной функции g(h)).
Как нетрудно показать, в случае метрического пространства
D играет роль размерности, а ф можно рассматривать как
радиус шаров, определяемых метрикой, Тк в случае изотропии —
обычное растяжение. В более общем плане мы можем
воспользоваться свойством измеримости шаров. Например, в
пространстве Rd мы можем рассматривать ф как меру Лебега (d-объем),
предполагая, что множества В измеримы по Лебегу, а
размерность D равна размерности d, если шары являются обычными
шарами или кубами. В случае сильно анизотропных шаров
(таких, как самоаффинные, но не самоподобные эллипсоиды) это
640
Часть IX
уже неверно. Может представиться случай, когда шары еще
более анизотропны (и/или нерегулярны): (анизотропные)
фрактальные множества. Во всех случаях ф можно рассматривать
как меру, конечную и положительную на шарах (меру Лебега
или Хаусдорфа), а масштаб задается выражением ф1/£>.
2.3. Случай линейной обобщенной масштабной инвариантности
Группа 7\ порождена в этом случае (ограниченным)
линейным отображением G по формуле
оо
Т = exp (G In Я) = £ (ln)"G7"I (3)
Следующие условия [6] необходимы и достаточны для
получения группы преобразований подобия.
а) Измеримый случай: A>* = Tr(G) > 0. Величину Dei
можно рассматривать как эффективную размерность пространства
или его эллиптическую размерность [1—3]. Нелинейные
примеры приведены в работе [6].
б) Метрический случай: inf Re g(G) ^ 1, где a(G) —спектр
отображения G. Если единичный шар определяется эллипсоидом,
порожденным симметричным оператором А, то получается
следующее условие:
inf or (sym (AG)) >1 (4)
(sym(AG) означает симметричную часть оператора AG).
Особенно простые примеры линейной обобщенной
масштабной инвариантности возникают при использовании кватернионов
[6] и применяются для построения [7] в рамках модели
фрактальной суммы импульсов [8—9] примеров (мономерных) полей,
обладающих линейной метрической обобщенной масштабной
инвариантностью.
3. Обобщенная масштабная инвариантность
и многомерная перемежаемость
3.1. Введение
Обычные стохастические процессы (например, броуновское
движение) получаются при сложении (с соответствующими
весами) независимых одинаково распределенных случайных
величин (например, интегралов от белого шума). Напротив,
мультипликативная группа 7\ наводит на мысль, что в случае
обобщенной масштабной инвариантности наиболее естественно
воспользоваться процессами, которые возникают при умножении,
соответствующем нелинейному распаду вихрей.
Хаос, турбулентность и родственные вопросы
641
Если первый случай мономерный, то последний обычно
приводит к многим размерностям. Немало усилий было
предпринято, чтобы связать наиболее заметную особенность
перемежаемости— ее «пятнистость» [10] —с турбулентным носителем,
обладающим одной фрактальной размерностью [11, 12]. Но, как
отмечалось в работах [1, 2], феноменологические модели
перемежаемости [11, 13, 14] обычно приводят к многим
размерностям, что соответствует различным (тензорным) степеням меры
потока энергии. Действительно, последовательность
размерностей легко получается [2, 3, 15, 16] при рассмотрении
расходимости высших моментов плотности ел потока энергии
относительно различных Д4-мерных мер Хаусдорфа:
<е*> = оо при DA < С (Л) = Del-D (А), (5)
C(h) = logk(wh)/(h-l)f (6)
где w — случайная величина, распределяющая плотность на
протяжении одного этапа каскада. Заметим, что условие (6) по
существу соответствует условию непересечения множеств А и S (ft)
коразмерности С (Л) (так как обычно для множеств А и В
выполняется соотношение
0(А[\В) = 0(А)-С(В)9 (7)
где D — размерность, а С — коразмерность соответствующих
множеств). Увеличение h соответствует исследованию более
интенсивных областей. Коразмерность С (Л) — возрастающая
функция от А, т. е. наиболее интенсивные области распределены
наиболее редко.
3.2. Обобщенная масштабная инвариантность
и мультипликативные процессы — мультипликативный хаос
Вместо сложения случайных инкрементов все более тонкого
разрешения по каскаду (как в фрактальной сумме импульсов
[8, 9]) можно умножить инкременты все более тонкого разре-*
шения. Эта мультипликативная процедура соответствует
нелинейному распаду вихрей на подвихри (предложенная Мандёль-
бротом каскадная модель перемежаемости на жесткой решетке
соответствует дискретному произведению).
Вопрос о том, что представляет собой предел таких
процессов, является математической проблемой (так называемый
мультипликативный хаос). Недавно в теории мультипликативного
хаоса были получены некоторые результаты [17]. Однако
мультипликативность операторов Т и способ построения процесса
позволяют ввести функцию коразмерности С (К) (f —- мультиплй'-'
642
Часть IX
кативный инкремент плотности):
(ПТ) = Ь1Н-1)С(Н)(?) (8)
и тем самым обобщить предыдущие результаты (соотношения
3.3. Следствия из многомерности
Для изучения поведения стохастической меры m введем
вместо классической структурной функции «структурный интеграл»
5(Л, А):
S(h, A) = (mh(A))/(m(A))h, (9)
где А есть /)-мерное опорное множество, на котором мы берем
среднее. Из обобщенной масштабной инвариантности следует,
что
S (/г, ТкА) = Л"р <*• D4S (/г, Л). (10)
В простом случае, когда явление мономерно с размерностью
Ds (коразмерность = Dei — DS = CS), показатель p(h, DA)
линеен по h:
P(h, DA) = C8{h-l) при DA>CS9 (И)
В других случаях Cs следует заменить функцией
коразмерности C(h) (показатель p(h, DA) при этом перестает быть
линейным по А), и (физические) меры становятся чувствительно
зависящими от DA (в особенности из-за условия пересечения).
Анализ радиолокационных наблюдений [18] (с DA = l\ 1,5; 2;
3; 4) подтверждает многомерное поведение для дождя.
Условие детектируемости размерности следует из условия
невырожденности статистики (статистика должна быть ненулевой
и конечной), т. е. (см. соотношение (6)) пересечения множества
наблюдений А и множеств-носителей S(h). Таким образом,
разрешение масштабов недостаточно для оценки детектируемости
явления, например, самые интенсивные явления окажутся
утраченными, если множество наблюдений будет редким. Показано
'[19], что сети точек, в которых производятся наблюдения,
должны иметь размерность меньше 2 (всемирная сеть
метеорологических станций имеет DA = 1,75). Из-за нелинейных
взаимодействий возникают новые проблемы, связанные с
предсказуемостью, которая до сих пор исследовалась только в терминах
масштабов.
4. Выводы
Имея в виду сильную анизотропность и перемежаемость
атмосферы, мы разработали формализм, который назвали
обобщенной масштабной инвариантностью. В основе его лежат два
Хаос, турбулентность и родственные вопросы 643
множества элементов, и наш формализм можно рассматривать
как продолжение более ранних работ по каскадным процессам
(в особенности [3, 10]).
Первое множество представляет собой группу изменяющих
масштабы операторов, второе множество образуют
перемежающиеся меры, инвариантные относительно таких операторов.
В турбулентном каскаде изменяющий масштабы оператор
преобразует вихри в подвихри, оставляя инвариантным физически
существенный поток энергии (которому в модели соответствует
масштабно-инвариантная мера). Следует заметить, что явное
знание геометрии требуется не всегда, так как достаточно
свойств измеримости.
Подчеркнем, что многомерность для мультипликативных
процессов — правило, а не исключение; она была подтверждена
радиолокационными наблюдениями дождевых полей [18].
Зависимость от размерности порождает новые вопросы относительно
детектируемости и предсказуемости турбулентных явлений.
Благодарность. Считаем своим долгом выразить
благодарность за плодотворное обсуждение Г. Остину, Д. Лилли, Р. Ка-
халану и П. Мюллеру.
ЛИТЕРАТУРА
1. Schertzer Z>., Love joy 5., preprint vol., IUTAM Symp. on Turbulence and
Chaotic Phenomenon in Fluids, Kyoto, Japan, p. 141, 1983.
2. Schertzer /)., Lovejoy 5., in: Turbulent and Chaotic Phenomena in Fluids,
ed. T. Tatsumi, North-Holland, 1984, p. 505.
3. Schertzer ZX, Lovejoy S., in: Turbulent Shear Flow 4, ed. B. Launder,
New York, Springer, 1985, p. 7.
4. Schertzer D.y Lovejoy 5., Sciences et Techniques, 69 (1984).
5. Lovejoy S.y Schertzer D.y AMS Bulletin, 67, (1985).
6. Schertzer D., Lovejoy 5., PCH Journal, 6, 5/6, 623 (1985).
7. Lovejoy S., Schertzer D., Wat. Resour. Res., 21, 8, 1233 (1985).
8. Mandelbrot £., Fractal Sum of Pulses (получено от автора).
9. Lovejoy S., Mandelbrot B.y Tellus, 37A, 209 (1985).
10. Batchelor G. /., Townsend A. A.y Proc. Roy. Soc, A199, 238 (1949).
11. Mandelbrot B. B.y J. Fluid Mech., 62, 331 (1974).
12. Fridch U.y Salem P. L., Nelkin M.y J. Fluid Mech., 87, 719 (1978).
13. Новиков Е. A.y Стюарт P. — Изв. АН СССР, сер. геофиз., 1964, т. 3,
с. 408.
14. Яглом А. М. — ДАН СССР, 1966, т. 2, с. 266.
15. Schertzer D., Lovejoy 5., Note CRMD № 69, Met. Nat., Paris.
16. Mandelbrot В. В., J. Stat. Phys., 34, 895 (1984).
17. Kahane J. P., Multiplicative Chaos, готовится к печати.
18. Lovejoy S., Schertzer D.y in: Digital Image Processing in Remote Sensing,
ed. P. J. Muller, Taylor and Frencis, London, 1985, ch. 14.
19. Lovejoy S., Schertzer D.y Ladoy P., Nature, в печати.
Анализ фрактальной размерности
облаков с мощными
конвективными токами
Ф. Рис, А. Вальдфогель *
Анализ радиолокационных данных по градовым облакам
показывает, что более крупные облака имеют фрактальную форму с
фрактальной размерностью (размерность Хаусдорфа) Z>i =
= 1,36 ±0,1. Это согласуется с более ранним анализом формы
облаков, проведенным Лавджоем [9], и теорией относительной
турбулентной диффузии [10]. Кроме того, дрейф (снос) частиц при
сильных ветрах и в центре градовых облаков, по-видимому,
обусловливает более резкий переход к гладкому режиму (Z>i = l),
обладающему четко выраженным характерным линейным масштабом.
1. Введение
С 1977 г., когда математическое понятие «размерность
Хаусдорфа» было переименовано в фрактальную размерность и
введено в физическую литературу [1], выяснилось, что оно
является важным геометрическим понятием, позволяющим
количественно описывать неупорядоченные структуры в простых
моделях и физических системах в целом. Все возрастающее число
работ по экспериментальным система (таким, как полимерные
растворы или расплавы [2], адсорбирующие области [3],
электрические разряды [4] и т. д.) и численному моделированию
(например, агрегирующих систем [5]) убедительно доказывает
полезность нового понятия.
Фрактальная размерность D характеризует любую
самоподобную систему: при изменении линейных размеров в / раз
фрактальная величина (например, «длина» контура или
«площадь» поверхности) изменяется (при любом /) в fD раз.
Значение фрактальной размерности поверхности Ds заключено между
2 и 3 (размерность Z)s = 2 имеет гладкие поверхности), в то
время как фрактальные размерности контурной линии
заключены в пределах 1 ^ D\ ^ 2 (D\ = 1 соответствует гладким
линиям). Плоское сечение фрактальной поверхности имеет,
вообще говоря (если отбросить патологические случаи [6]),
размерность D\ = DS—1. До сих пор существуют
немногочисленные чисто академические модели, для которых удается точно
вычислить их фрактальную размерность, поэтому ценность
последней определяется возможностью находить ее из
многочисленных экспериментальных наблюдений [7].
* Franz S. /tys-Fritz-Haber-Institut der Max-Planck-Gesellschaft, Faraday-
weg 4—6, D-1000 Berlin 33, West Berlin; A. Waldvоgel-Institut fur Atmo-
spharphysik, ETZ-Zurich, Honggerberg, CH-8093, Zurich, Switzerland.
Хаос, турбулентность и родственные вопросы
645
В настоящей работе мы покажем, что облака с мощными
конвективными токами (такие вертикальные токи возникают в
градовых облаках) также имеют фрактальную форму. Анализ
данных по радиолокации таких облаков позволяет обнаружить:
1) нетривиальную фрактальную структуру более крупных
частей облаков;
2) существование четко выраженного характерного
масштаба.
Удивительно, что фрактальная размерность D периметра
сечения облака в пределах ошибки наблюдений имеет такое же
значение D ж 4/3, как для дождевых полей и полей облаков
вплоть до очень крупных размеров порядка 106 км2, которые
были обнаружены с помощью спутниковых наблюдений в
инфракрасной области и радиолокационных наблюдений. С другой
стороны, небольшие градовые облака имеют гладкую форму.
Кроме того, заметное сглаживание формы облаков происходит
во время бурь с градом, когда сильные ветры вызывают быстрое
перемещение средней части градового облака (со скоростями
до 15 м/с). Хотя теоретического объяснения этого наблюдения
не существует, мы предполагаем, что наличие сильных ветров
сглаживает форму облака так же, как анизотропный
коэффициент диффузии сглаживает форму ограниченных диффузией
кластеров. Аналогичные эффекты анизотропии наблюдаются в
электрических разрядах в полях с одноосной симметрией [12].
2. Метод
Экспериментальные данные были собраны в 1976—1982 гг.
во время проведения научно-исследовательской программы
Grossversuch IV по предотвращению градообразования.
Радиолокационная информация поступала в виде планов индикации
положении, т. е. спроектированных на плоскость ху почти
горизонтальных линий постоянного коэффициента отражения
радиосигнала. Планы индикации положения получались при полном
обороте антенны с постояным углом возвышения 5,5°. Время
измерения для съемки одного плана составляло 1 мин, разрешающая
способность радара составляла Г по азимуту, 0,3 км по
расстоянию и 1 дБ по коэффициенту отражения.
Последний определяется как
Z=^N{d)d*d{d)9 (1)
где N(d) означает распределение Рэлея диаметров
гидрометеоров (т. е. таких рэлеевских рассеивателей, как дождевые капли
и градины) на 1 м3 и в интервале диаметров от d до d + d(d)
(в единицах мм6/м3, т. е. 10~18 м3). Обычно используется вели-
646
Часть IX
чина
/=101nZ (в дБ). (2а)
Для распределения Пуассона N(d)~exp(—Ы)у которое
хорошо описывает наблюдения, получаем
/ = const — 70 In Я, (26)
т. е. значения (в дБ) монотонно возрастают с размером частиц
(при Ы (медиана) = const). Подробности обработки
радиолокационных данных и др. см. в работе [8].
Типичный план индикации положений представлен на рис. 1,
на котором показаны линии равного коэффициента отражения
15. 7.
198Z
161ZH
45-
55 -L
60 1
65-
45 60
-15
-ю
Z5
20
15
10
%
§
8
*
1
|
£
10
15
Расстояние к бостону, км
Рис. 1. Пример горизонтального сечения поверхностей постоянного
коэффициента отражения радиосигнала для мгновенной формы градового облака.
Каждое сечение характеризуется определенным значением / (в дБ).
при / = 45, 55, 60 и 65 дБ. В частности, кривая с / = 65 дБ
указывает на область сильного дождя (со скоростью выпадения
осадков R = 500 мм/ч) с выпадением града.
Фрактальная форма наблюдаемых градовых облаков
проявляется в фрактальных свойствах контуров с постоянными
значениями / (в дБ). Площадь F, заключенная внутри контура,
фрактально зависит от длины контура (периметра) U:
F = F0UE,
(3)
где показатель Е связан с фрактальной размерностью D\
контура соотношением
E = 2/Dx (4)
Хаос, турбулентность и родственные вопросы 647
и соответственно с фрактальной размерностью Ds = D\ + 1
поверхности постоянного коэффициента отражения и тем самым
градового облака.
3. Результаты
На рис. 2 в дважды логарифмических координатах показана
зависимость площади F, заключенной внутри контура, от
периметра U контура / = 45 дБ. Значения F и U измерялись с
интервалами в 1 мин в наиболее характерный период эволюции
10г
W1
и."
Cj
I
1 ю-'
Ю'г
Ю-1 10° Ю1 70z
Перилтетр V, км
Рис. 2. Зависимость между площадью F, заключенной внутри контура, и
периметром U контура при / = 45 дБ в дважды логарифмических
координатах. Каждая точка соответствует вполне определенному интервалу времени
(J мин), в течение которого происходит временное развитие бури. Из
прямых, проведенных через 24 различные точки, получены оценки (5) и (6).
градовой бури. Аналогичные кривые были построены при / =
= 55, 60 и 65 дБ. Точки, соответствующие меньшим контурам,
располагаются на прямой, соответствующей степенному закону,
с угловым коэффициентом Е = 2 (т. е. Z)i = l). Следовательно,
эти контуры гладкие. Точки, соответствующие большим
контурам, располагаются на другой прямой с угловым коэффициентом
Е = 1,5, т. е. D\ = 133, что свидетельствует о фрактальной
структуре больших контуров.
При обработке 24 градовых бурь мы получили следующие
результаты :
1) При меньших значениях U фрактальная размерность
£<=1,0±0,1 (£><=2,0±0,1) (U<С/0) (5)
описывает гладкую форму.
р
ттптпг
U
ь
ТТТПТГ
! 111
/у
о/о
/,,Л , ,
| ,
jff
\
\
t I t 111
J?
«To
0
1 1 LJ_LlLlJ
648
Часть IX
2) При больших значениях U фрактальная размерность
DT = 1,36 ± 0,1 (D> = 2,36 ± 0,04) (U > С/0) (6)
описывает фрактальную форму.
3) Весьма резкий переход в точке U = £/0 указывает на
существование характерной длины
L = U0/n = 3 ± 1 км.
4) Сильные ветры при градовой буре приводят к смещению
порогового значения £/0 в сторону больших значений, отчего
большие контуры кажутся гладкими.
4. Обсуждение результатов
1. Фрактальная размерность больших контуров U > t/0,
задаваемая оценкой (6), как показал недавно Лавджой [9], с
точностью до ошибки эксперимента равна 4/3. Полученная им
оценка D = 1,35 ± 0,05 справедлива в интервале 10 ^ U ^ 104 км.
Опубликована также попытка интерпретировать фрактальную
размерность D формы облаков в рамках теории относительной
турбулентной диффузии [10].
2. Наблюдаемый переход при (J=Uq свидетельствует о
существовании в проблеме градовых облаков характерной длины
L. Значение L не зависит от линии уровня коэффициента
отражения, т. е. от размера частиц, но изменяется в зависимости от
силы ветра. Заметим, что значение L на один порядок величины
превосходит разрешающую способность радара (~0,3 км).
Следовательно, маловероятно, чтобы переход в точке L был
обусловлен конечной разрешающей способностью радара. В то же
время зависимость L от силы ветра указывает на то, что
переход к гладкой форме отражает существование дрейфа частиц
(или конвективных токов). Установлено, что особенно сильные
вертикальные восходящие и нисходящие точки существуют в
центральной части грозовых и градовых облаков. Это позволяет
объяснить гладкость меньших контуров вблизи центра облака.
Имея в виду все это, мы предполагаем, что сглаживание (1)
меньших облаков и (2) контуров больших облаков при сильном
ветре обусловлено наличием конвективных токов. Можно
ожидать, что при больших скоростях дрейфа частицы будут
двигаться по гладким траекториям (вместо броуновских траекторий при
нулевом дрейфе). Это один из возможных механизмов
сглаживания форм облаков. Аналогичное сглаживание
соответствующих структур наблюдалось недавно в условиях ограниченной
диффузией кластеризации [11] и электрических разрядах в
сильных однородных внешних полях [12].
Обобщение теории относительной турбулентной диффузии
на случай ненулевого дрейфа частиц должно описывать это яв-
Хаос, турбулентность и родственные) вопросы 649
ление количественно. Интересно, что значение £/0 при слабых
ветрах соответствует нижнему концу диапазона длин контуров,
наблюдавшихся в работе [9]. Из этого факта, а также из
равенства фрактальных размерностей (градовых) облаков с
мощными конвективными токами, легких дождевых облаков и
облаков в ясную погоду мы заключаем, что полученные нами
результаты описывают в общем случае фрактальную природу облаков
при наличии ветров.
3. Эти наблюдения могли бы стать основой полезного
феноменологического метода определения полей облаков с сильными
ветрами путем измерения соответствующих фрактальных
размерностей облаков.
Следует заметить, что сбор данных, на которые мы
опирались, проиводился в течение всей бури с градом, и поэтому
временные вариации силы ветров могли быть важным источником
отклонений от средних значений, заметных на рис. 2. Для
улучшения статистики необходимы дополнительные наблюдения в
различных масштабах с строго определенными скоростями
ветра. Кроме того, для количественного описания форм облаков при
наличии ветров в общем случае необходимы количественные
теоретические соображения.
Благодарности. Один из нас (Ф. Рис) выражает
признательность за финансовую поддержку Deutsche Forschungsgemeins-
chaft (контракт Sfb-6 TP A7/2). Считаем своим приятным
долгом поблагодарить Ж.-П. Экмана, М. Кольба, П. Пфейфера,
П. Пьетронеро и Г. Висмана за различные информативные
обсуждения.
ЛИТЕРАТУРА
1. Mandelbrot В. В., Fractals, Freeman, San Francisco, 1977.
2. de Gennes P. /., Scaling Concepts in Polymer Physics, Cornell University
Press, Ithaca, N. Y., 1979. [Имеется перевод: де Жен П. Идеи скейлинга
в физике полимеров. — М.: Мир, 1982.]
3. Elam W. Г., Wolf S. A., Sprague /., Gubser D. U.t von Vechten D.,
Barz G. L., Jr., Meakin P., Phys. Rev. Lett., 54, 701 (1985). *
4. Nlemeier L., Pietronero L., Wiesmann H. /., Phys. Rev. Lett., 52, 1033
(1984).
5. Witten T. A, Sander L. M., Phys. Rev. Lett., 47, 1400 (1981).
6. Mattila P., preprint.
7. См., например, Ргос 3 rd Conf. on Fractals in the Physical Sciences, NBS
Gaithersburg, MD USA; November 1983.
8. Waldvogel A., Schmid W., J. Appl. Meteorology, 21, 1228 (1982).
9. Love joy S., Science, 216, 186 (1982); см. также Ргос. 20th Conf. on Radar
Meteorology, Boston, MS, USA, November, 1981.
10. Hentschel H. G. £., Procaccia /., Phys. Rev., A29, 1461 (1984).
11. Meakin P., Phys. Rev., B28, 5221 (1983).
12. Wiesmann H. /., частное сообщение (1985).
Конечные автоматы с вставками:
континуальные аспекты
дискретных систем
У. Квастхофф *
Клеточные автоматы по определению состоят из дискретных
клеток, содержащих эти автоматы, и работают в дискретном времени.
Для моделирования непрерывных процессов мы описываем
процедуру вставки, заменяющую клетки другими клетками монотонно
убывающих размеров и позволяющую получать сколь угодно
малые клетки и сколь угодно малые единицы времени при
сохранении макроскопической структуры. Автоматы с простой структурой
окружения исследованы для выявления вопроса, допускают ли они
такую процедуру вставки.
1. Введение
На рис. 1 показан до 128 треугольник Паскаля вычетов
по модулю 2 (mod 2). Точки соответствуют единицам, а
пропуски— нулям. Хотя наша картина состоит из конечного числа
Рис. 1.
дискретных клеток, ясно, что существует гораздо более тонкая
фрактальная структура, порождающая такую же
макроскопическую картину.
Структуру, изображенную на рис. 1, можно мыслить как
образовавшуюся в результате функционирования следующего
клеточного автомата. Чтобы найти состояние клетки в момент
времени £+1, необходимо сложить по модулю 2 состояние этой
клетки и ее соседа справа в момент времени t. Получающееся
состояние изображается под исходными клетками строкой ниже.
Построение всей фигуры начинается с одной клетки,
находящейся в состоянии 1.
* Uwe Quasthoff-Karl-Marx-Universitat Leipzig, Sektion Mathematik,
DDR-7010 Leipzig, DDR.
Хаос, турбулентность и родственные вопросы
651
На рис. 2 изображен тот же клеточный автомат, но с
случайной начальной конфигурацией. По этой картине уже трудно
судить, можно ли получить гораздо более тонкую структуру с
помощью того же правила перехода, которая порождала бы ту же
макроскопическую структуру. Хотя картины, подобные
изображенной на рис. 2, возникают и при других правилах перехода,
Рис. 2.
процесс вставки возможен только для описанного выше
автомата. Мы дадим полную классификацию клеточных автоматов
с двумя состояниями, одно- или двусторонним взаимодействием
и функцией вставки одного и того же типа. Пример с сложением
состояний по модулю 2 обобщается на большее число состояний,
большее число соседей и более высокие размерности.
Обсуждаются приложения к модельным непрерывным пространствам
состояний. Доказательства теорем желающие могут найти в
работе [1].
2. Процедура вставки
Рассмотрим клеточные автоматы с клетками,
расположенными в виде d-мерной решетки, изоморфной Zd. В этом и в
следующем разделах мы будем считать, что d = \.
Пространство состояний У клетки предполагается конечным. Переходная
функция Т клетки задает состояние этой клетки в момент
времени f-fl в зависимости от состояния соседних клеток в
момент времени t. Для простоты мы будем предполагать, что
окрестность U(x) клетки х состоит из нескольких примыкающих
друг к другу клеток, включая клетку х> т. е. U(x) = {х — &, х —
— k + 1, ..., х + I] при некоторых натуральных числах &, /.
Окрестности с более сложной структурой исследованы в
работе [1].
Процесс вставки протекает следующим образом. Мы
заменяем (одновременно) каждую клетку m меньшими клетками с
одной и той же переходной функцией Т. Назовем m порядком
процесса вставки. Окрестность каждой малой клетки
представляет собой уменьшенную копию исходной окрестности. Назовем
функцией вставки функцию N: Ym-+Y, устанавливающую со-
652
Часть IX
стояние большой клетки в зависимости от состояний меньших
клеток внутри ее (предполагается, что эти меньшие клетки
каким-то образом упорядочены).
Определение. Пара (Г, N), состоящая из переходной функции
Т и функции вставки N, называется совместимой, если
существует натуральное число п, такое, что
T-N = N-Tn.
Величина п называется скоростью роста.
Существование функции вставки N для данной переходной
функции Г, такой, что пара (Г, N) совместима, приводит к
нескольким следствиям. Процесс вставки можно итерировать,
рассматривая каждый раз меньшие клетки как исходные большие
и строя все меньшие и меньшие клетки. Малая клетка,
построенная на k-м шаге, представляет собой не что иное, как nf-\o часть
исходной клетки, и единица времени такой малой клетки
представляет собой не что иное, как я*-ю часть единицы времени
исходной клетки. Таким образом, мы можем аппроксимировать с
помощью клеточных автоматов с вставками процессы,
непрерывные во времени и в пространстве. С другой стороны, мы
можем интерпретировать функцию вставки N: Ym-+Y как
отображение пространства состояний #(У)Л на пространство
состояний ф(У) (ф(У) означает число элементов множества У).
Объединяя эти две точки зрения, можно даже предположить, что
меньшие автоматы обладают большим числом состояний, а это
позволяет нам аппроксимировать также непрерывные
пространства состояний. В этом случае необходима другая переходная
функция для автоматов с большим пространством состояний.
Пример приведен в разд. 5.
В дальнейшем мы будем предполагать, что я = #-М+1,
т. е. число элементов в окрестности любой точки равно числу
малых клеток, заменивших большую клетку.
3. Полный анализ автоматов с двумя состояниями и одно-
и двусторонним взаимодействием с ближайшилли соседями
В случае одностороннего взаимодействия с ближайшим
соседом мы можем предположить, что U(x) = {х, х-\-1}, а в случае
двустороннего взаимодействия положим U(x) = {х— 1, х, х+ 1}.
Присваивая имена различным переходным функциям, мы
следуем Вольфраму [3]. Условимся считывать пару или тройку s
состояний в окрестности в их естественном порядке как
двоичное число b(s)y и пусть T(s) —преобразованное состояние.
Присвоим переходной функции Т имя ^ T(s) • 26(5),где
суммирование проводится соответственно по всем 22 или 23 возможным
парам состояний.
Хаос, турбулентность и родственные вопросы
653
Например, при одностороннем взаимодействии мы получим
имена 6, 10 и 12 для переходной функции введения, левого
сдвига и тождества. Таким же способом нумеруются и функции
вставки. Мы будем рассматривать только переходные функции
и функции вставки с одинаковыми именами, поскольку нам
необходимо, чтобы глобальное состояние, в котором все автоматы
находятся в состоянии 0, было устойчиво.
Справедлива следующая теорема.
Теорема L (1) В случае одностороннего взаимодействия с
ближайшим соседом совместимыми являются только пары (6, 6),
(6, 10), (6, 12), (8, 8), (10, л), (12, п) и (14, 14), где я = 2,
4, .. ., 14.
(2) В случае двустороннего взаимодействия совместимыми
являются только пары (128, 128), (136, 128), (170, л), (192, 128),
(204, я), (238, 254), (240, п)у (252, 254) и (254, 154), где п =
= 2,4,..., 254.
Таким образом, переходная функция совместима со всеми
функциями вставки в том и только том случае, если переходная
функция есть тождественная функция или сдвиг. Все другие
переходные функции, за исключением функции 6 в (1),
принадлежат к классу 1 (см. работу [4]), т. е. они переводят
начальное состояние в некоторое единственное однородное состояние
и обладают простым поведением. Единственная оставшаяся
переходная функция приведена во введении (сложение по
модулю 2). Она принадлежит к классу 3 (т. е. приводит к
«хаотическим» структурам) и является единственной функцией,
оставляющей неинвариантным глобальное состояние, в котором все
автоматы находятся в состоянии 1.
4. Различные скорости роста и высшие размерности
Чтобы построить совместную пару со сколь угодно большой
скоростью роста log n, воспользуемся процессом вставки п-го
порядка. Если Т — левый сдвиг (это означает, что состояние в
точке х в момент времени t + 1 совпадает с состоянием в точке
х-\- 1 в момент времени t) и N— любая функция вставки п-го
порядка, то пара (Г, N)—совместимая пара, причем T-N =
= N-Tn, т. е. скорость роста равна п. Тот же результат остается
в силе и для высших размерностей.
Чтобы привести менее тривиальный пример, обобщим
преобразование по модулю 2. Пусть У = {0, 1, ..., р— 1} при
некотором нечетном р, Up(х) = {х — р~ , ... , х = р~ ] , и пусть
Тр — функция, суммирующая р своих аргументов (состояния
клеток в окрестности) по модулю р. Определим функцию вставки
Np порядка р также путем суммирования по модулю р. При р =
654
Часть IX
= 2 и слегка отличающейся окрестности пара (Г2, N2) есть пара
(6, 6). По теореме 1 она совместима. Справедлива следующая
более общая теорема.
Теорема 2. (1) Для каждого простого числа р существует
совместимая пара (Гр, Np), удовлетворяющая условиюТр • Np=
= NP-TPP.
(2) Пусть N' - функция вставки /?-го порядка,
удовлетворяющая при некотором q: 1 ^ q ^ р равенству Np(siy ... , sp)=
= sq. Тогда пара (Тр, Np) также совместима и имеет скорость
роста р.
Эти примеры могут быть следующим образом обобщены на
случай более высокой размерности. Рассмотрим Up = Up X .. -
... X Up (d множителей) как d-мерную окрестность. В процессе
вставки каждая клетка имеет форму d-мерного куба и подлежит
замене pd малыми кубами. Пусть Тр9 Np, как и прежде,
функции, суммирующие свои аргументы по модулю р. Тогда
(Тр, Np) — совместимая пара.
5. Модель непрерывного пространства состояний
Существует еще одна точка зрения на процедуру вставки:
после замены большой клетки m малыми клетками мы можем
интерпретировать набор из m состояний внутри большой клетки
как одно сложное состояние этой клетки. Вместо разбиения
каждой клетки на большее число клеток мы строим для каждой
клетки новое пространство состояний. Это индуцирует новую
переходную функцию, которая может иметь более простую
структуру окрестностей, как показывает следующий пример. Процесс
в этом случае также допускает интерации.
Начнем с переходной функции Т5 из теоремы 2. Замена
каждой клетки 5 меньшими клетками с 5 возможными состояниями
эквивалентна расширению пространства состояний исходной
клетки с 5 до 55 возможных состояний. Пусть V: У5-> (О, 1, ...
..., 55 — 1} есть функция V{s\, • • > s5) = 54Si + 53s2 + • • • + s5,
считывающая пять примыкающих друг к другу состояний на
некоторое число в пятиричной системе счисления. Новая
переходная функция V на этих автоматах с большим числом состояний
индуцируется функцией Т5 по формуле Г'= VT5V~l. В отличие
от Т5 функция Т имеет взаимодействие с следующим
ближайшим соседом.
Пусть N—функция вставки N(s\, ..., s5) =S\. Тогда пара
(Т5, N) совместима по теореме 2. Из соотношения Г5 ■ N = N • Т%
получаем: VNV'Y5 = Г • UNU~l = UTN~\ где UNU'1 -
функции, отображающая число х в наибольшее кратное чис-
Хаос, турбулентность и родственные вопросы 655
ла 5\ не превосходящее л:. Таким образом, преобразованная
функция вставки UNU~l уменьшает пространство состояний
способом, аналогичным округлению.
ЛИТЕРАТУРА
1. Quasthoff £/., Nested Cellular Automata, preprint, 1985.
2. Wilson S. /., Discrete Appl. Math, 8, 91 (1984).
3. Wolfram 5., Rev. Mod. Phys., 55, 601 (1983).
4. Wolfram 5, Physica. 10D, 1 (1984).
Гипотеза гиперболической спирали:
фрактальная мера Стэплтона
на распределениях мод
гидрофобной свободной энергии
аллостерических белков
А. Манделл*
1. Предварительные сведения
Развитый Пуанкаре геометрическо-топологический
подход к задаче о числе п периодических и почти периодических
семейств Fn орбит z(n) на R2 привел к гипотезе о том, что
пРп = со. Из первоначальной работы Пуанкаре, основанной на
продолжении аналитических рядов, следовало, что для меры т
на пространстве параметров (г, к) каждой орбиты zi
справедлива оценка mi (г Д) Zi-~ In tiFn. В настоящей программе
исследований наше внимание сосредоточено на свойствах этого
распределения орбит Pz{nFri), его динамическом происхождении
и значении для поведения белков.
Биркгоф [1] исследовал ограниченные линейные
отображения кольца ф{: R2-+R2> которые сохраняют меру: ф*2 = еА*,
deL4 = l. Одновременные движения парных образов одной
орбиты вдоль отождествленных границ, внутренней и внешней,
происходят в противоположных направлениях; фг есть
множество зеркально-симметричных представлений одностороннего
преобразования. Как будет показно, два сильных условия на
симметрию— энтальпийио-энтропийная компенсация и стереоизомер-
ное ограничение на обмен информацией между полипептидами и
белками — превращают эти орбиты в попарно соответствующие
геодезические с собственньши значениями, симметричными
относительно единичной окружности. R2 есть банахово пространство
E = ES<8> Еи\ \ф*и (г)] с= Es, [$l (z)] cz Eu — разложение
касательного пространства многообразия Е на устойчивое и неустойчивое
многообразия [2] ;ри е Ф*и{г) и р0е^* (г)—
зеркально-симметричные образы гиперболической неподвижной точки. Вихреобраз-
ный генератор nFn вместе с условием det A = 1 составляет
биологически ориентированной реконструкции доказательство Бирк-
* Arnold J. MandelU Laboratory of Biological Dynamics and Theoretical
Medicine (M-003), University of California, San Diego, La Folia, California
92093, USA. Работа написана во время пребывания автора в качестве
прикомандированного сотрудника в Institut des Hautes Etudes Scientifique, Bures-
sur-Yvette, France. Численное моделирование на аналоговых и цифровых
компьютерах проводилось при поддержке U. S. Army Research Contract
DAAG-20-83-K-0069, а также Department of Defence Instrumentation Grant
DAAG-29-84-G-0072.
Хаос, турбулентность и родственные вопросы
657
гофа последней геометрической теоремы Пункаре. Любое
взаимно однозначное преобразование кольца, допускающее
инвариантный интеграл и вращающее границы в противоположных
направлениях, имеет по крайней мере две различные
инвариантные точки с симметрично противоположными по знаку
индексами. В диссипативном пределе конструкции, связанной с
отображением кольца, можно говорить о суперпозиции устойчивого
(Я—) и неустойчивого (А,+ ) многообразий окружности
(спирали) в резонансе. Это условие равномерной гиперболичности на
неподвижные точки и орбиты в R2 находит непосредственное
выражение в термодинамических свойствах белков.
«Гидрофобная» свободная энергия (поверхностное натяжение
между эллиптическими белками и их водным окружением)
разлагается на несколько компонент. К ним относятся 1) свободная
энергия наблюдаемой средствами рентгеновской
кристаллографии структуры, содержащей энтальпию (устойчивое
многообразие ф*и} — она вычисляется по измерениям поверхности белка и
составляет от 25 до 35 кал/моль на А2; 2) свободная энергия
«айсбергов» в окружающем растворителе и ненаблюдаемая,
оцениваемая по косвенным данным дестабилизирующая потеря
энтропии полипептидной цепью при складывании — так
называемая деформация энтропии (неустойчивое многообразие ^), —
она составляет от 2 до 3 ккал/моль на остаток [4]; 3) очень
слабые, обычно пассивные вариации Н+-связей самого
растворителя: из 600 возможных связей меняются 3 или около того,
ги ~ 15 ккал на моль белка. Гиперболический второй закон для
среднего белка и окружающее его «гало» энтальпийно-энтропий-
ной компенсации в окружающем растворителе (в ккал/моль)
[5] имеет вид
Ф*и — аф1±ги=0, (la)
350- 350 ± 15 = 0. (16)
Такая энтальпийно-энтропийная компенсация состоит в
уничтожении больших членов противоположных знаков, характерна
для самой воды и всех органических соединений в водных или
аналогичных водным растворах [6], представляет собой
скрытую симметрию, которая сводит проблему структуры белка и
дицамики к двумерному фазовому пространству, для которого
выполняется теорема Пункаре—Биркгофа. Нас будут
интересовать значения а — показателя, входящего в закон подобия, и
отношения мод невидимой комплексной молекулярной энтропии
и энтропии растворителя: Ф^(г) ~ еа~1(0<\
Важный шаг в указанном направлении был сделан группой
Стзплтона [7, 8], получившей значение а-1 как размерность
Фурье плотности спектра мод состояний, используя преобразо-
658
Часть IX
вание температурной зависимости скорости релаксации спина
электронов низкоспинового Fe3+ железосодержащих белков. Эн-
тальпийно-энтропийная симметрия предстает при этом как
соотношение взаимности между вещественной и мнимой частями
собственных значений распределения комплексной энтропии
р (z) ~ £а"~1(°а. Полученное значение было равно 1,65 ± 0,04.
Относительно вездесущего фликкер-шума (1Д-шума) флуктуации
ионной проводимости мембранных белков и степенного спектра
Стэплтона для белков заметим, что£~а_1~а = 1 в том и только
том случае, если а = 0,618... . Эквивалентные значения были
получены для пространственной размерности dim* с помощью
стробоскопических снимков динамики белков по рентгенокри-
сталлографическим отображениям на R2: а ~ dim*.
Это отношение между последовательными модами
согласуется с обычными целочисленными модами, найденными в наших
преобразованиях Фурье последовательностей аминокислот в
гидрофобных свободных энергиях более чем 100 полипептидов и
белков [9] с использованием их энергий спиртово-водного
распределения [10] (2, 3, 5, 7—8, 11 и 13) (Zi/zi+i} ~ а. Как
отражение динамики агрегатов белков мембранной ионной
проводимости головного мозга величина а входит в отношение полос
основных частот варьирующихся во времени колебаний
электроэнцефалограмм: А = 2 — 3; <& = 5 —7; а = 11 — 13; р = 17 —
— 19, а также в характерный степенной закон za.
2. Семейство зеркально-симметричных рекуррентных
гидрофобных гиперболических геодезических Fn
Пуанкаре свел изучение поведения однопараметрических
преобразований плоскости в окрестности точки равновесия к
изучению фундаментального семейства стоков, источников и седел.
Однако вырождения решений, неустранимые малыми
возмущениями (такие вырождения появляются в самой малой
окрестности), имеют положительную меру в коразмерности 2. Обозначив
энтальпию через и, энтропию через и, нелинейную гидрофобную
связь г ~ {и} ({и} — средняя гидрофобность на остаток в
ккал/моль), мы исследовали численно уравнение Картрайт —
Литтлвуда [11] в (и + v) sa и = /(г, X):
и - г (1 — и2) и + и = гЯ cos М. (2)
Дифференцируя и производя масштабное преобразование
(v/r->-v) с неявным шагом по временной переменной Д/ = 'б,/я,
мы получаем нелинейные уравнения для энтальпии и энтропии:
^ = 1>-г(«-а3/3), (За)
^ = -tt/r + *cosM. (36)
Хаос, турбулентность и родственные вопросы
659
На рис. 1,а показано результирующее отображение кольца,
как в теореме Пуанкаре — Биркгофа, множество
зеркально-симметричных геодезических и гиперболических неподвижных точек.
Скрытая зеркальная симметрия лево-право, верх-низ становится
1 ■*.■"
Л
^>j
Ж-
р*
>V
Рис. 1.
заметной при малом изменении г (рис. 1, б). Во то время как
область параметров вырожденных геодезических свидетельствует
о существовании хаотических математических решений и
чувствительности к начальным условиям, в гиперболической
спирали гидрофобной свободной энергии почти периодические моды
белков — семейство геодезических <j>fv^ Fn— стереоизомериче-
ски обращено и существует только в зеркале растворителя. Мае-
660
Часть IX
штабно-инвариантный спектр мод Стэплтона представляет собой
не 1//-шум хаоса, а дискретные моды универсального спектра с
степенным законом и последовательностью низкочастотных
пиков, изменяющихся по закону а-1, а. Как мы увидем дальше,
эти моды Фибоначчи последовательностей Фарея описывают
разбиение гиперболической единичной окружности как
некоторое совершенное множество [12, 13].
Дзета-функция £(г) позволила показать, что распределение
гиперболических геодезических на R2 аналогично распределению
простых чисел Фп [14]. В настоящее время мы изучаем эту
теорему в контексте соотношения (3) и полагаем, что
распределение орбит zt e <j>*v ведет себя как Фп при низком порядке п:
Pz {nFn) ~ £ (z) = (1 - е-<2+*>а <*>). (4)
Мы используем также другой подход, рассматривая
преобразование Фурье — Лапласа от Си(х) как зависящее от времени
убывания корреляционной функции:
t t t
Си {%) = lim -т \ ZiZf dt — lim -r \ zt dt \ z* dt, (5a)
*-»~ oJ <->* oJ о
C&=2_Zjle«z+f(*)- (56)
Спектр мод Стэплтона мы можем получить непосредственно,
разлагая эитальпийную компоненту гидрофобной свободной
энергии в тригонометрический ряд |^(2)|а-
ф*я = Г (а + I)-1 J г (иТ{а+Х)ег dz (и), (6а)
X
оо
r(a+l)=$(^)V"d«, (66)
о
и предсказать распределение Леви устойчивых относительно
свертки тождественно распределенных мод гидрофобной
свободной энергии с масштабной инвариантностью и
характеристическими показателями a-1, a [15]:
In Pz = idz - сГ1 \z |~a (1 + fp2), (7)
где б задает спектр, а р описывает его асимметрию.
Если p/q и r/s — последовательные члены ряда Фарея
порядка п — несократимые дроби, заключенные между 0 и 1, с
знаменателем, который не превосходит я, то семейство
геодезических Fn = f(r, X) можно задать с помощью матрицы А отобра-
Хаос, турбулентность и родственные вопросы
661
жения ф*и = еА*9 det Л = 1, норма (К—, %+) Ф\, например,
Матрица А в неподвижной точке сильной связи Fn = 1, если ее
возвести в степень:
(! loJA\ DG з)(з DCs 1У (9)
порождает накопление орбит как элементов SpA, по закону
Согласующийся с диапазоном спиральных рефлексов,
обнаруженных при рентгеноструктурном исследовании белков,
диапазон значений а =(1/3 — 2/3), о котором недавно сообщила
группа Стэплтона, изучившая более 70 белков [16], может быть
интерпретирован в терминах преобразования </>*и как двухпара-
метрическое (г, X) -отображение кольца в динамику на
эллиптической кривой С, параметризованной с помощью гармонического
треугольника. Приращение Аи ориентировано вдоль
наименьшего, Av— вдоль наибольшего диаметра, отношение Au/Av
определяет, сходится или разложение в ряд Тейлора (или
тригонометрический ряд) возмущения кривой С одновременно к Аи и
Av или утрачивает свой гиперболический характер, сходясь
всегда только к Аи. Пусть теперь Аи и Av — комплексные числа
Аи = zu> Av = zv, где Imz = n/k, k — число циклов кривой С
(k<Cn/2 и k взаимно просто с п), Re г — модули г. Возникает
вопрос: каким должен быть предел на модули разностей
modj^u — zu\, чтобы не сходиться гладко к zu при возмущении?
Используя аналитический и геометрический подходы, Кэйли
[17] доказал, что
то(1|г0 — zu\ = amodiZu. (10)
Пространство перекрытия вырожденности
зеркально-симметричных геодезических, т. е. то место, где «живет» гидрофобная
гиперболическая спираль, лежит в области значений а,
найденных группой Стэплтона: две трети каждой моды расположены
в средней трети классического (получающегося при повторном
разбиении отрезка на три равные части и выбрасывании
средней трети) канторовского множества в комплексном
пространстве. Распределение Фарея — Фибоначчи мод гидрофобной
свободной энергии, а также спектральная и фрактально-размерност-
ная изометрия устанавливают связь между совершенным
множеством Салема единственности тригонометрического ряда,
являющегося распределением бесконечно многих функций
независимых распределений Бернулли [18], распределением Леви мод,
662
Часть IX
устойчивых относительно свертки [15], масштабной
инвариантностью критических модулей уравнения Картрайт — Литтлвуда
для вырожденных решений [11] и универсальным спектром [12,
13], с одной стороны, и степенным законом изменения
гидрофобной моды на плотности спектра состояний некоторых белков
Стэплтона [7] —с другой. В другой нашей работе мы изложили
соображения, из которых следует, что именно зона между
топологическим сопряжением (непрерывность по Гёльдеру) и диф-
ференцируемостью по Липшицу выделяет окрестность, в которой
с наступлением макромолекулярных фазовых переходов
утрачивает силу масштабно-инвариантный спектр. Спектр еа~1(*а
может быть отличительным свойством аллостерических белков с
их специфической способностью к низкоэнергетическим конфор-
мационным переходам. Всего лишь 3,7 ккал/моль необходимо
для трансконформации гемоглобина (размерность Стэплтона
dim*= 1,65) из состояния с низким в состояние с высоким
средством к кислороду. Аналогичными динамическими свойствами
обладает миоглобин (размерность Стэплтона dim* = 1,67).
Напротив, трипсин (размерность Стэплтона dim* = 1,34) не
обладает аллостерическими свойствами.
3. Оптическая изометрия и энтропия растворителя
Так как ф*и — ф[ ~ О, (Я —) е ф1и и (X —) <= ф[ описывают
зеркально-симметричную экспоненциальную расходимость zu и zv
(см. рис. 1,а, б). Эти отображения можно представить как
спаренные спиральные орбиты возрастающих (убывающих)
радиусов г, вращающихся с постоянной угловой скоростью t (в
радианах). Пусть 7 — постоянный угол, образующийся в тех точках,
где пересекаются 8г — приращение длины последовательных
радиусов— и касательные к кривой. Так как ±(6r/r) ~ е(Ь+«-),
7^T~ctgY, (Па)
lnr~/ctga + lnr0, (116)
\x\X{%-l)~i{rl)cig4. (Ив)
Кривая, на которой касательная в любой точке образует
постоянный угол с радиусом, проведенным в эту точку из
некоторой неподвижной точки, есть почти периодическое двухпарамег-
рическое (t, у) растягивающее (сжимающее) преобразован^
плоскости, самоподобное по масштабам, обладает симметрией
относительно растяжения и имеет последовательные модули
mod \zi — zj\ =azf. Так как обратное относительно полюса
преобразование есть также спираль, оно соответствует стереоизо-
мерному растворителю, двойственному гидрофобной гиперболи-
Хаос, турбулентность и родственные вопросы
663
ческой спирали. Заметим, что и на этот раз ф*и(г)— белковая
энтальпийная наблюдаемая, а f*v(z) — ненаблюдаемая и
зеркально-симметричная энтропия растворителя. Изменение в
растворителе пассивно относительно его индуцированной стериоизо-
метрии, так как чистая вода обладает осью симметрии второго
порядка Si, поэтому поворот на 180° = 360°/2 переводит ее в
состояние, неотличимое от исходного. Оптически активные полосы
поглощения часто являются следствием нарушения симметрии и
перехода ее в асимметрию под действием молекулярного
окружения [19].
Если молекула обладает спиральной структурой, то ее
поляризуемость, измеряемая по вращению оптического излучения,
предварительно право- или левополяризованного, зависит от
того, приложено ли поле пробного излучения в направлении
спирали. Молекулы, обладающие спиральной структурой, не могут
быть совмещены с своим зеркальным отражением. Семейства
геодезических ф*и(г) и <t>*v(z) — зеркально-симметричны и
вращают поляризованный свет по часовой стрелке (+) и
против часовой стрелки (—). Оптическая активность белков
количественно оценивается по оптической активности единичной массы,
выражаемой в процентах спиральности, и зависит от гидрофоб-
ности белка и структуры окружающего растворителя.
Увеличивая среднее гиперболическое гидрофобное «давление» <ц>
путем добавления 2-хлорэтанола в растворитель, можно увеличить
процент спиральности белка в 3—4 раза, в то время как
разрушение структуры воды с помощью такого хаотизующего агента,
как мочевина, позволяет исключить всю оптическую активность
макромолекул. Обозначив через <ц> среднюю гидрофобную
свободную энергию на остаток аминокислот белка (в ккал/моль)
и через zi — моды свободной гидрофобной энергии белка, можно
обнаружить интересное соотношение между оптической
активностью и показателями Стэплтона. В качестве примера
выберем два наиболее тщательно исследованных белковых фермента
(табл. 1).
Таблица 1
Белок
Лизоцим
Рибонуклеаза
<и>
1,15
1,01
zi
2,2 3,3
5,7 13,3
5,7 10,1
Спиральности,
%
29
16
dimx
1,69
1,33
Гипотеза гиперболической спирали допускает частичную
проверку путем установления корреляции между удельной оптиче-
664
Часть IX
ской активностью белков в стандартных условиях и их
значениями в размерностях Стэплтона dim*: a = f{y) (как в (11)).
Работа в этом направлении продолжается.
Тень растворителя энактиоморфного дополнения к фги
(именно </>£) существует в обычно обладающем осью симметрии 2-го
порядка запасе водной энтропии. Этот резервуар энтропии имеет
(+)- и (—)-отсеки для необходимо-стереоспецифических
обменов энтропией между субстратами, гормонами, трансмиттерами
и фармакологическими препаратами с спиральным рецептором и
белками ферментов. Хорошо изученным контрпримером такого
рода взаимодействия может служить асимметрия энтропийного
окружения в растворителе, достигаемая с помощью таких
сильно гидрофобных, стереохимически специфических «хозяев», как
циклодекстрин или краун-эфиры, и позволяющая оптически
разрешить путем вытеснения из раствора (+)- и (—)-членов
рацемических смесей аминокислот и аминосолей [20]. Количественно
эти процессы зависят от <ц> [21].
Так как энтропийное состояние гелеобразных перегородок
принадлежит к глобальным свойствам биологических объектов,
может оказаться, что некоторая обобщенная хаотичность
функции белка проистекает из замены условия симметрии 52
растворителя на плоскости энтропии — энтальпии R2 оптически
активным зеркально-симметричным смещением (как на рис. 1,6).
В качестве гипотетического и противоречащего медицинской
интуиции примера приведем следующий: высокие уровни титров
антител «постороннего» стереохимически специфического белка
могут привести к оптическому смещнию энтропии растворителя,
уменьшив оптически активную область для обмена
стереохимически специфической энтропийно-энтальпийной информацией
между белковым антигеном нового, проникающего в организм
патогенного агента и мембранным белком, ответственным за
приведение в действие защитного каскада в лимфатической ткани.
Системы, порождающие гиперфункционирующие антитела, и
иммунологический паралич, делающий организм уязвимым со
стороны других обычно безвредных организмов, могут
парадоксальным образом сосуществовать.
Бифуркация от расходящегося потока к периодичности
происходит из-за потери математическими решениями
гиперболической устойчивости — перехода от зеркально-симметричных
геодезических к структуре с синхронизацией мод. Мы постулируем,
что это состояние в белковых рецепторах мембран порождает
стереотипное поведение и приводит к утрате регуляторной
чувствительности клеток. На рис. 2 приведены для сравнения спектр
мощности временных рядов препаратов гормона роста,
выделенного из чисто клеточного типа перфузионных систем нормаль-
Хаос, турбулентность и родственные вопросы
665
ных и опухолевых клеток гипофиза [22]. В ряду опухолевых
клеток отчетливо заметно исчезновение гиперболического не-
Динамический ртклик нормальных клеток гипосриза крыс
нес химические агенты
Контроль
6(ш)г
j
w (мин)
Соматомедин АВ
А
Ингибитор
фоссродиэстеразы
ltflb™ rnrilWlW
Контроль
GRF
GRF + Сэ/латосглзтин м
1шк
Ш,
Як
гЛПп-ГТТтП
Рис. 2.
прерывного спектра и возникновение периодичности с
синхронизацией мод и без отклика на активные агенты.
ЛИТЕРАТУРА
1. Birkhoff G. D.t Acta Math., 43, 1 (1920).
2. Smale S., Bull. Am. Math. Soc, 73, 747 (1967).
3. Reynolds J. A. et al., Proc. Natl. Acad. Sci., USA, 71, 2925 (1974).
4. Chothia C, Nature, 248, 338 (1974).
5. Privalov P. L., Khenichinashvili N. N., J. Mol. Biol., 86, 665 (1974).
6. Hinshelwood C. H., J. Chem. Soc, 538, 858 (1937).
7. Stapleton H. J. et al, Phys. Rev. Lett, 45, 1456 (1980).
8. Allen J. P. et al, Biophys. J, 38, 299 (1982).
9. Mandell A. J., Ann. Rev. Pharmacol. Toxicol., 24, 237 (1984).
10. Nozaki Y„ Tanford £., J. Biol. Chem., 246, 2211 (1971).
11. Cartwright M. L., Littlewood J. E., J. Lond. Math. Soc, 20, 180 (1945).
12. Shenker S. /., Physica, 5D, 405 (1982).
13. Rand D. et al., Phys. Rev. Lett., 49, 132 (1982).
14 Parry W., Pollicott AL, Ann. Math., 118, 573 (1983).
15. Гнеденко Б. В., Колмогоров Л. Я. Предельные распределения для сумм
независимых случайных величин. — М.-Л.: Гостехиздат, 1949.
16. Wagner G. С. et al, J. Am. Chem. Soc, 1985.
17. Cayley C, Quart. J. Pure Appl. Math., 16, 179 (1879).
18. Salem R., Trans. Am. Math. Soc, 54, 218 (1943).
19. Crabbe P., Optical Rotary Dispersion and Circular Dichroism in Organic
Chemistry, Holden-Day, San Francisco, 1965.
20. Kyba E. P. et al, J. Am. Chem. Soc, 99, 2564 (1977).
21. Sugimoto Т., Baba N., Isr. J. Chem., 18, 214 (1979).
22. Guillemin R. et al., In: Synergetics of the Brain, eds. E. Basar, H. Flohr,
H. Haken, A. J. Mandell, Springer-Verlag, Berlin, 1983, p. 155.
СОДЕРЖАНИЕ
Предисловие редакторов перевода 5
Предисловие (Перевод Л. И. Третьяковой) 8
Часть I. ОБЩИЕ СВОЙСТВА ФРАКТАЛОВ
Самоаффинные фрактальные множества. I. Основные фрактальные
размерности. Б. Мандельброт (Перевод И. А. Веденовой) 9
Самоаффинные фрактальные множества. II. Размерности длины и
поверхности. Б. Мандельброт (Перевод И. А. Веденовой) 30
Самоаффинные фрактальные множества. III. Аномалии хаусдорфовой
размерности и их смысл. Б. Мандельброт (Перевод PL А.
Веденовой) 36
Случайные фракталы, пластичные фракталы и ренормализационная
группа. Дж. Мелроуз (Перевод И. А. Веденовой) 48
О конечно разветвленных фракталах и их обобщениях. Р. Хильфер,
А. Блюмен (Перевод (И. А. Веденовой) 54
Часть II. АНАЛИЗ ФРАКТАЛЬНЫХ СВОЙСТВ МАТЕРИАЛОВ
Структура случайных силикатов: полимеры, коллоиды и пористые
твердые тела. Д. Шефер, К. Кефер (Перевод С. И. Кучанова) 62
Взаимодействие фракталов с фракталами: адсорбция полистирола на
пористой поверхности А1203. П. Пфейфер (Перевод Л. И. Третьяковой) 72
Рассеяние на фракталах. Э. Джейкмен (Перевод Ю. А. Данилова) ... 82
Оптические преобразования Фурье фракталов. К. Аллен, М. Клуатр
(Перевод Ю. А. Данилова) 91
Об измерении фрактальных размерностей по физическим свойствам
К. Цаллис (Перевод Ю. А. Данилова) 98
Часть III. СТАТИСТИКА ПОЛИМЕРОВ И БЛУЖДАНИЯ
БЕЗ САМОПЕРЕСЕЧЕНИИ
Случайные блуждания с памятью. Л. Пелити (Перевод С. И. Кучанова) 106
Вероятность выживания и фактор усиления в статистике полимеров.
Л. Пьетронеро, Л. Пелити (Перевод С. И. Кучанова) 117
Лапласово случайное блуждание, й. Ликлема, К. Эвертс (Перевод
С. И. Кучанова) 122
Кинетически растущие самонепересекающиеся блуждания. Й. Ликлема
(Перевод С. И. Кучанова) 131
Содержание 667
Переход клубок — глобула в двумерной системе. Н. Ян, А. Конильо,
И. Маджид, X. Стенли (Перевод С. И. Кучанова) 137
Самоподобие взаимо- и самопересечений случайных фракталов. А.
Стелла, Р. Декейзер, А. Маритан (Перевод С. И. Кучанова) 147
. Статистическая механика самонепересекающихся случайных
поверхностей. А. Маритан, А, Стелла (Перевод С. И. Кучанова) 151
Приближение типа аппроксимации Бете для самонепересекающихся
случайных блужданий и поверхностей (и фрустрации). А. Каппелли,
Р. Ливи, А. Маритан, С. Руффо (Перевод С. И. Кучанова) .... 156
О самонепересекающихся блужданиях на неупорядоченных решетках.
С. Милошевич, А. Черновцан (Перевод С. И. Кучанова) 162
Эксперименты с белками. Е. Янг (Перевод С. И. Кучанова) 168
Часть IV. РАЗВЕТВЛЕННЫЕ ПОЛИМЕРЫ, ГЕЛЕОБРАЗОВАНИЕ
И ПЕРКОЛЯЦИЯ
Размерность фракталов и синтез разветвленных полимеров. 3.
Александрович (Перевод С. И. Кучанова) 172
Фрактальные размерности скелетов и кластеров в кинетической модели
гелеобразования. А. Чабра, Г. Герман, Д. Ландау (Перевод С. И.
Кучанова) 179
Решеточная магнитная модель для разветвленных полимеров и перехода
золь —гель. А. Гонзалес (Перевод С. И. Кучанова) 184
Перколяция в градиенте концентрации. Ж.-Ф. Гуйе, М. Россо, Б. Саповал
(Перевод С. И. Кучанова) 189
Поверхностное натяжение в моделях Поттса и перколяция. С. Харрис
(Перевод С. И. Кучанова) 196
Перколяция на РМП. Р. Дьюар, С. Харрис (Перевод С. И. Кучанова) . . 203
Часть V(a). МОДЕЛИ НЕОБРАТИМОГО РОСТА:
ЛАПЛАСОВСКИЕ ФРАКТАЛЫ, ПРОБОЙ ДИЭЛЕКТРИКОВ,
РАСТРЕСКИВАНИЕ И ВЯЗКИЕ «ПАЛЬЦЫ» В ЖИДКОСТЯХ
Свойства лапласовских фракталов при пробое диэлектриков в двух и трех
измерениях. Г. Висман, Л. Пьетронеро (Перевод Ю. А. Данилова) 210
Свойства подобия растущей зоны и емкость лапласовских фракталов
Л. Пьетронеро, К. Эвертс, Г. Висман (Перевод Ю. А. Данилова) .221
Бесконечная иерархия показателей для описания явлений роста. А.
Конильо (Перевод Ю. А. Данилова) 227
Двумерный пробой диэлектриков между параллельными линиями. М. Мю-
рат (Перевод Ю. А. Данилова) 234
Пробой диэлектриков в трехмерном случае. С. Сатпати (Перевод
Ю. А. Данилова) 238
Фрактальная природа трещин. Э. Луис, Ф. Гинеа, Ф. Флорес (Перевод
Ю. А. Данилова) 244
Формирование конфигураций дендритных фракталов при растрескивании
и электрическом пробое. X. Такаясу (Перевод Ю. А. Данилова) . . 249
Разрушение нагруженных фрактальных деревьев. С. Солла (Перевод
Ю. А. Данилова) 255
Фракталы и разрушение металлов с трещинами. Ч. Лунг (Перевод
Ю. А. Данилова) 260
Когда вязкие «пальцы» имеют фрактальную размерность? И. Нитман,
Ж. Даккор, X. Стенли (Перевод Ю. А. Данилова) . 266
668
Содержание
Часть V(6). МОДЕЛИ НЕОБРАТИМОГО РОСТА: ОГРАНИЧЕННАЯ
ДИФФУЗИЕЙ АГРЕГАЦИЯ, РОСТ ДЕНДРИТОВ, МОДЕЛЬ ИДЕНА
И КЛАСТЕР-КЛАСТЕРНАЯ АГРЕГАЦИЯ
Некоторые последние достижения в моделировании ограниченной
диффузией агрегации и родственных процессов. П. Микин (Перевод
Ю. А. Данилова) .283
Внутренняя анизотропия кластеров, ограниченных диффузией. П. Микин,
Т. Вичек (Перевод Ю. А. Данилова) 296
Активная зона в модели ДОА и в модели Идена. М. Плишке, 3. Рац
(Перевод Ю. А. Данилова) 301
Закон масштабного преобразования вероятности присоединения частицы
в модели ДОА. Л. Туркевич, Г. Шер (Перевод Ю. А. Данилова) . .310
Модель «угол конуса» и анизотропия роста ограниченных диффузией
кластеров. Дж. Росси, Б. Томпсон, Р. Болл, Р. Брэди (Перевод
Ю. А. Данилова) 321
Рост анизотропных ограниченных диффузией кластеров. Б. Томпсон,
Дж. Росси, Р. Болл, Р. Брэди (Перевод Ю. А. Данилова) 330
Континуальная ДОА: случайный фрактальный рост, порождаемый
детерминистической моделью. Л. Сандер (Перевод Ю. А. Данилова) . . 336
Формирование структур отвердевания в моделях агрегации. Т. Вичек
(Перевод Ю. А. Данилова) 345
Масштабно-инвариантные свойства поверхности в модели Идена.
Р. Жюльен, Р. Боте (Перевод Ю. А. Данилова) 350
Агрегация кластеров. Р. Боте, Р. Жюльен, М. Кольб (Перевод Ю. А.
Данилова) 353
Анизотропия в кластерах и агрегация частиц. М. Кольб (Перевод
Ю. А. Данилова) . 360
Обратимость при агрегации кластеров. М. Кольб (Перевод Ю. А.
Данилова) 365
Фильм о процессах агрегации. М. Кольб (Перевод Ю. А. Данилова) . . 370
Теоретико-полевой подход к моделям Идена и ДОА. Л. Пелити,
Й.-Ч. Дзен (Перевод Ю. А. Данилова) 374
Распространение эпидемических заболеваний, приводящее к фрактальным
структурам, П. Грассбергер (Перевод Ю. А. Данилова) 379
Моделирование дендритного роста на основе «случайного дождя».
Б. Каприле, А. Леви, Л. Лиджери (Перевод Ю. А. Данилова) . . . 388
Экспериментальное исследование двумерной агрегации. К. Аллен,
М. Клуатр (Перевод Ю. А. Данилова) 395
Часть VI. КИНЕТИКА ОБРАЗОВАНИЯ КЛАСТЕРОВ
Кинетика образования кластеров при необратимой агрегации. М. Эрнст
(Перевод С. И. Кучанова) 399
Хвост распределения для больших кластеров при необратимой агрегации.
П. Ван Донген, М. Эрнст (Перевод С. И. Кучанова) 430
Скейлинговое обобщение уравнения Смолуховского. 3. Рац (Перевод
С. И. Кучанова) 440
Кластеризация во Вселенной. Ф. Луккин (Перевод Ю. А. Данилова) . . 446
Стохастический подход к крупномасштабной кластеризации материи во
Вселенной. Л. Пьетронеро, Р. Купере (Перевод Ю. А. Данилова) . . 454
Часть VII. ДИНАМИЧЕСКИЕ СВОЙСТВА ФРАКТАЛЬНЫХ СТРУКТУР
Фрактальные поверхности и модель «термита» для двухкомпонентных
случайных материалов. X. Стенли (Перевод И. М. Соколова) . . . 463
Содержание
669
Динамические свойства случайных и неслучайных фракталов. Р. Стинч-
ком (Перевод И. М. Соколова) 478
Упругое поведение фрактальных структур. И. Уэбман (Перевод И. М.
Соколова) 488
Статические и динамические свойства фрактальных агрегатов, не
содержащих петель. С. Хавлин (Перевод И. М. Соколова) 498
■Фрактальная размерность периметра роста. А. Марголина (Перевод
И. М. Соколова) 507
Перколяция и фрактальное поведение в неупорядоченных решетках.
П. Аргиракис (Перевод И. М. Соколова) 513
Иерархические фрактальные графы и блуждания на них. Дж. Мелроуз
(Перевод И. М. Соколова) 519
Динамика экситонов, напоминающая фрактальную: геометрический и
энергетический беспорядок. Р. Копельман (Перевод И. М. Соколова) 524
Найквистовский, диффузионный и фликкер-шум (1// шум) в
фрактальных системах и перколяционных сетках. Р. Раммал. (Перевод
И. М. Соколова) 528
Исследование электрических и шумовых свойств перколяционных
кластеров методом ренормгруппы в реальном пространстве. Дж. Лакк
(Перевод И. М. Соколова) 536
Отклик шероховатых поверхностей на переменном токе. С. Лиу, Т. Кап-
лан, П. Грэй (Перевод И. М. Соколова) 543
Часть VIII. ИЕРАРХИЧЕСКИЕ И ФРАКТАЛЬНЫЕ СВОЙСТВА
НЕУПОРЯДОЧЕННЫХ СИСТЕМ
Природа временных иерархий, определяющих релаксацию в
неупорядоченных системах. М. Шлезингер, Дж. Клафтер (Перевод И. М.
Соколова) 553
Реакции в фрактальных моделях неупорядоченных систем. А. Блюмен,
Дж. Клафтер, Г. Цумофен (Перевод И. М. Соколова) 561
Самоподобное временное поведение случайных блужданий в одномерной
случайной среде. Дж. Бернаскони, у. Шнейдер (Перевод И. М.
Соколова) 575
Наблюдение скейлинга в реакции с ловушками. 3. Джорджевич
(Перевод И. М. Соколова) 581
Термодинамика с иерархическими ограничениями в метастабильных
системах и стеклах. Л. Пьетронеро (Перевод И. М. Соколова) .... 586
Фрактальные кластеры и скейлинг в модели Изинга. Дж. Камбье, М. Нау-
энберг (Перевод И. М. Соколова) 592
«Дьявольская лестница» и странный аттрактор в модели Изинга с
конкурирующими взаимодействиями. М. де Оливейра, С. Салинас,
К. йокои (Перевод И. М. Соколова) 600
О самоподобной структуре волновых функций в неупорядоченных
системах. А. Сибесма, Л. Пьетронеро (Перевод И. М. Соколова) . . . 606
Часть IX. ХАОС, ТУРБУЛЕНТНОСТЬ И РОДСТВЕННЫЕ ВОПРОСЫ
Отображения окружности на комплексной плоскости. И. Цвитанович,
М. йенсен, Л. Каданов, И. Прокачча (Перевод Ю. А. Данилова) . . 613
Фрактальные модели двух- и трехмерной турбулентности. Дж. Паладин,
А. Вульпиани (Перевод Ю. А. Данилова) 624
670
Содержание
Численное исследование неоднородных фракталов. Р. Бадии, А. Полити
(Перевод Ю. А. Данилова) 632
Обобщенная масштабная инвариантность и анизотропные неоднородные
фракталы в турбулентности. Д. Шертцер, Ш. Лавджой (Перевод
Ю. А. Данилова) 638
Анализ фрактальной размерности облаков с мощными конвективными
токами. Ф. Рис, А. Вальдфогель (Перевод Ю. А. Данилова) .... 644
Конечные автоматы с вставками: континуальные аспекты дискретных
систем. У. Квастхофф (Перевод Ю. А. Данилова) 650
Гипотеза гиперболической спирали: фрактальная мера Стэплтона на
распределениях мод гидрофобной свободной энергии аллостерических
белков. А. Манделл (Перевод Ю. А. Данилова) 656
Научное издание
Бенуа Мандельброт,
Джон Мелроуз, Р. Хильфер и др.
ФРАКТАЛЫ В ФИЗИКЕ
Труды VI Международного симпозиума
по фракталам в физике (МЦТФ, Триест,
Италия, 9—12 июля, 1985)
Под редакцией Лучано Пьетронеро и Эрио Тозатти
Заведующий редакцией проф. А. Н. Матвеев
Зам. зав. редакцией С. М. Жебровский
Научный редактор Л. И. Третьякова
Мл. редакторы: В. Н. Цлаф, В. И. Аксенова,
И. А. Зиновьева
Художник А. А. Лукьяненко
Художественный редактор К. В. Радченко
Технический редактор А. Л. Гулина
Корректор С. С. Суставова
ИБ № 6571
Сдано в набор 25.03.88. Подписано к печати 28.11.88. Формат
О0Х90!Дб. Бумага типографская № 1. Печать высокая.
Гарнитура литературная. Объем 21,00 бум. л. Усл. печ. л. 42,00.
Усл. кр.-отт. 42,00. Уч.-изд. л. 36,77. Изд. № 2/5466. Тираж 4600
экз. Зак. 2827. Цена 5 р* 90 к.
Издательство «Мир» В/О «Совэкспорткнш а»
Государственного комитета СССР но делам издательств, полиграфии и
книжной торговли 129820, ГСП, Москва, 1-й Рижский пер., 2.
Отпечатано с набора Ленинградской типографии № 2
головного предприятия ордена Трудового Красного Знамени
Ленинградского объединения «Техническая книга» им.
Евгении Соколовой Союзполиграфпрома при Государственном
комитете СССР по делам издательств, полиграфии и
книжной торговли. 198052, г. Ленинград, Л-52, Измайловский
проспект, 29 в Ленинградской типографии № 4 ордена
Трудового Красного Знамени Ленинградского объединения
«Техническая книга» им. Евгении Соколовой
Союзполиграфпрома при Государственном комитете СССР по делам
издательств, полиграфии и книжной торговли. 191126, Ленин*
град, Социалистическая ул., 14.