Автор: Булавин Л.А. Выгорницкий Н.В. Лебовка Н.И.
Теги: физика моделирование
ISBN: 978-5-91559-101-0
Год: 2011
Текст
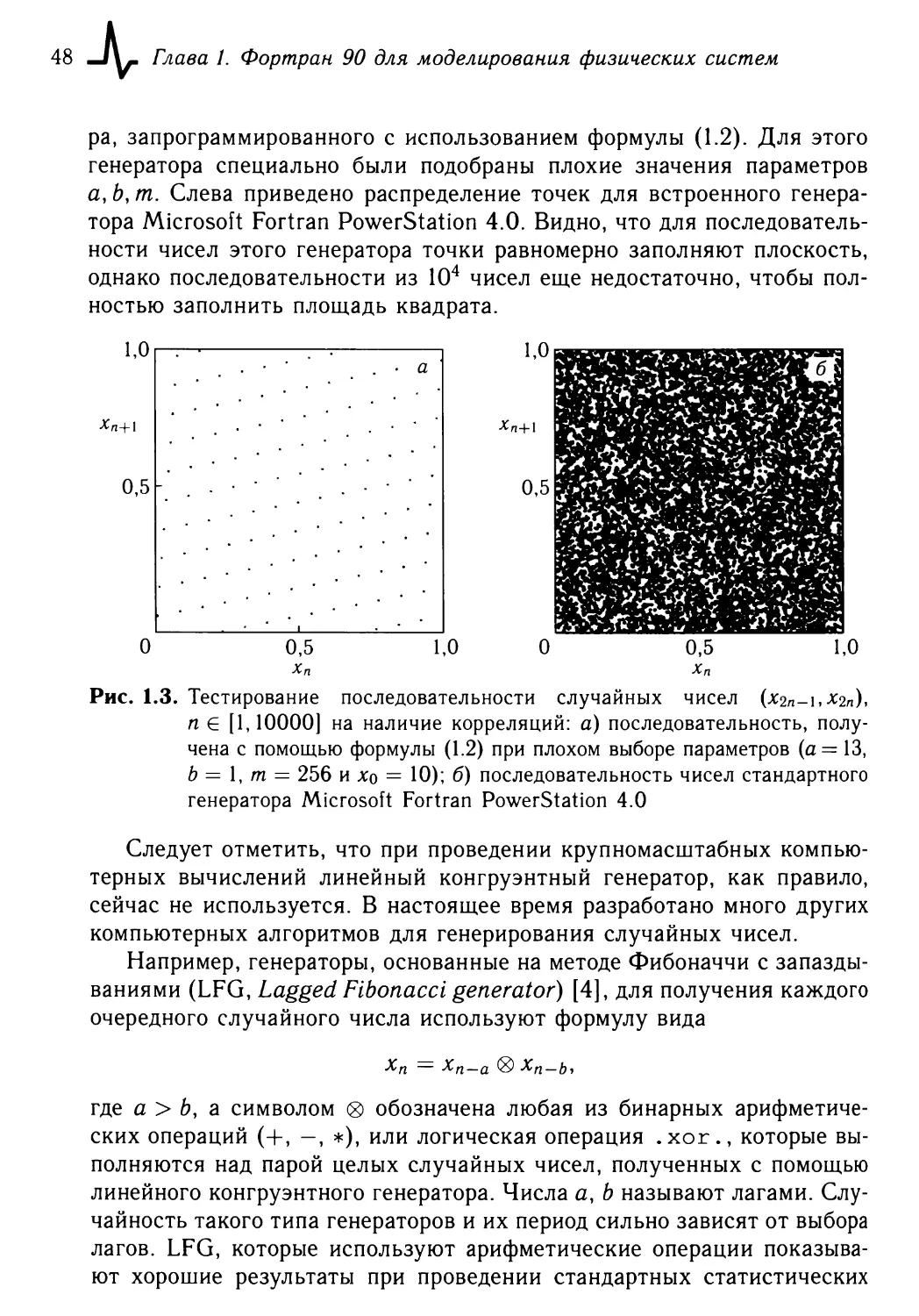
л
Издательский Дом
ИНТЕЛЛЕКТ
Л. А. БУЛАВИН, Н.В. ВЫГОРНИЦКИЙ, Н.И. ЛЕБОВКА
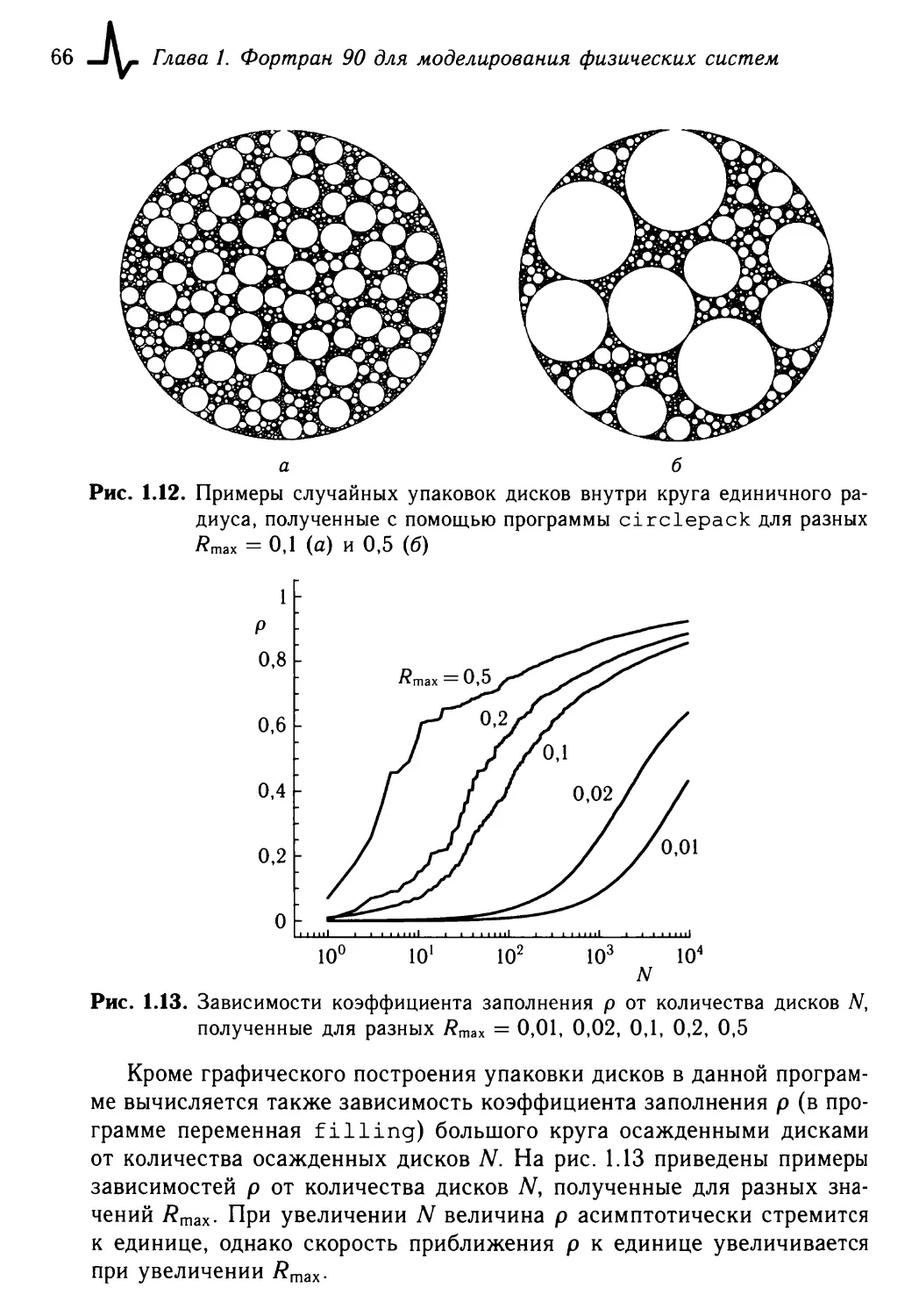
КОМПЬЮТЕРНОЕ
МОДЕЛИРОВАНИЕ
ФИЗИЧЕСКИХ СИСТЕМ
Л. А. БУЛАВИН. Н.В. ВЫГОРНИЦКИЙ, Н.И. ЛЕБОВКА
КОМПЬЮТЕРНОЕ
МОДЕЛИРОВАНИЕ
ФИЗИЧЕСКИХ СИСТЕМ
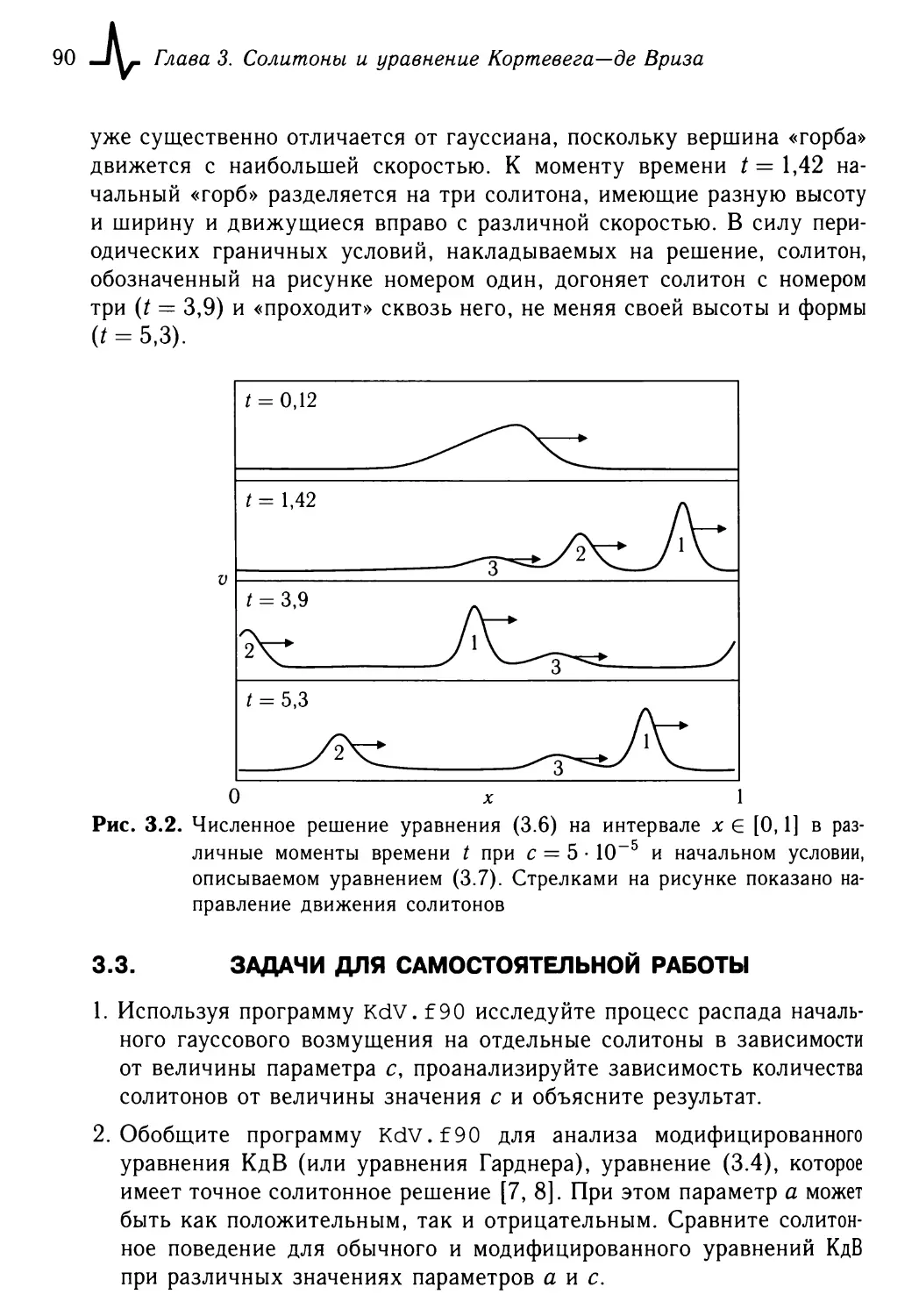
Издательский Дом
ИНТЕЛЛЕКТ
ДОЛГОПРУДНЫЙ
2011
JI.A. Булавин, H.B. Выгорницкий, Н.И. Лебовка
Компьютерное моделирование физических систем: Учебное
пособие / JI.A. Булавин, Н.В. Выгорницкий, Н.И. Лебовка -
Долгопрудный: Издательский Дом «Интеллект», 2011. — 352 с.
ISBN 978-5-91559-101-0
В учебном пособии изложен материал по применению методов компью¬
терного моделирования для исследования физических систем. В каждой
главе рассмотрена самостоятельная физическая задача, в ней содержится
введение в суть проблемы, изложены рецепты и алгоритмы ее решения, дано
описание рабочей программы на языке Фортран 90, а также приведены
примеры ее использования. Рассмотренные задачи относятся к областям
статистической физики и физики конденсированных систем, физики фрак¬
талов, перколяционных и хаотических явлений. Для более глубокого усво¬
ения материала, к каждой главе прилагаются задачи и упражнения для са¬
мостоятельной работы.
Для студентов, аспирантов и преподавателей физических, физико-хими¬
ческих специальностей, а также научных сотрудников.
ISBN 978-5-91559-101-0
© 2011, JI.A. Булавин, Н.В. Выгорницкий,
Н.И. Лебовка
© 2011, ООО «Издательский Дом
«Интеллект», оригинал-макет,
оформление
ОГЛАВЛЕНИЕ
Предисловие 11
Глава 1. Использование языка программирования
Фортран 90 для компьютерного моделирования физических
систем 13
1.1. Краткое введение в язык программирования Фортран 14
1.1.1. Первичные понятия 14
1.1.2. Основные типы величин, их представление и описание в
программе 17
1.1.3. Программирование арифметических выражений 23
1.1.4. Операции отношения и логические выражения 25
1.1.5. Операторы присваивания и управления 26
1.1.6. Особенности работы с массивами 30
1.1.7. Программные единицы 33
1.1.8. Операторы ввода-вывода и работа с файлами 38
1.1.9. Генерация случайных чисел 44
1.1.10.Использование графики 49
1.2. Примеры 53
1.2.1. Табуляция и построение графика функции 53
1.2.2. Построение спирали Улама 55
1.2.3. Вычисление многомерных интегралов и числа я методом
Монте-Карло 59
1.2.4. Построение эквипотенциальных линий для распределения
электрических зарядов 61
1.2.5. Аполлониевы упаковки 63
1.3. Задачи для самостоятельной работы 67
1.4. Литература 69
Глава 2. Задача Ферми-Паста-Улама 70
2.1. Колебания в цепочке связанных осцилляторов 70
4 -/U Оглавление
2.1.1. Линейная цепочка 71
2.1.2. Нелинейная цепочка 72
2.2. Алгоритм и описание работы программы 73
2.2.1. Алгоритм 73
2.2.2. Описание работы программы 74
2.2.3. Пример работы программы 79
2.3. Задачи для самостоятельной работы 80
2.4. Литература 81
Глава 3. Солитоны и уравнение Кортевега—де Вриза .... 83
3.1. Развитие представлений о солитоне 83
3.1.1. Распространение уединенной волны в узком канале 83
3.1.2. Уравнение Кортевега—де Вриза 84
3.1.3. Роль нелинейного и дисперсионного вкладов 84
3.1.4. Точное солитонное решение 85
3.2. Алгоритм и описание работы программы 86
3.2.1. Алгоритм 86
3.2.2. Описание работы программы 87
3.2.3. Пример работы программы 89
3.3. Задачи для самостоятельной работы 90
3.4. Литература 91
Глава 4. Логистическое отображение и показатель
Ляпунова 92
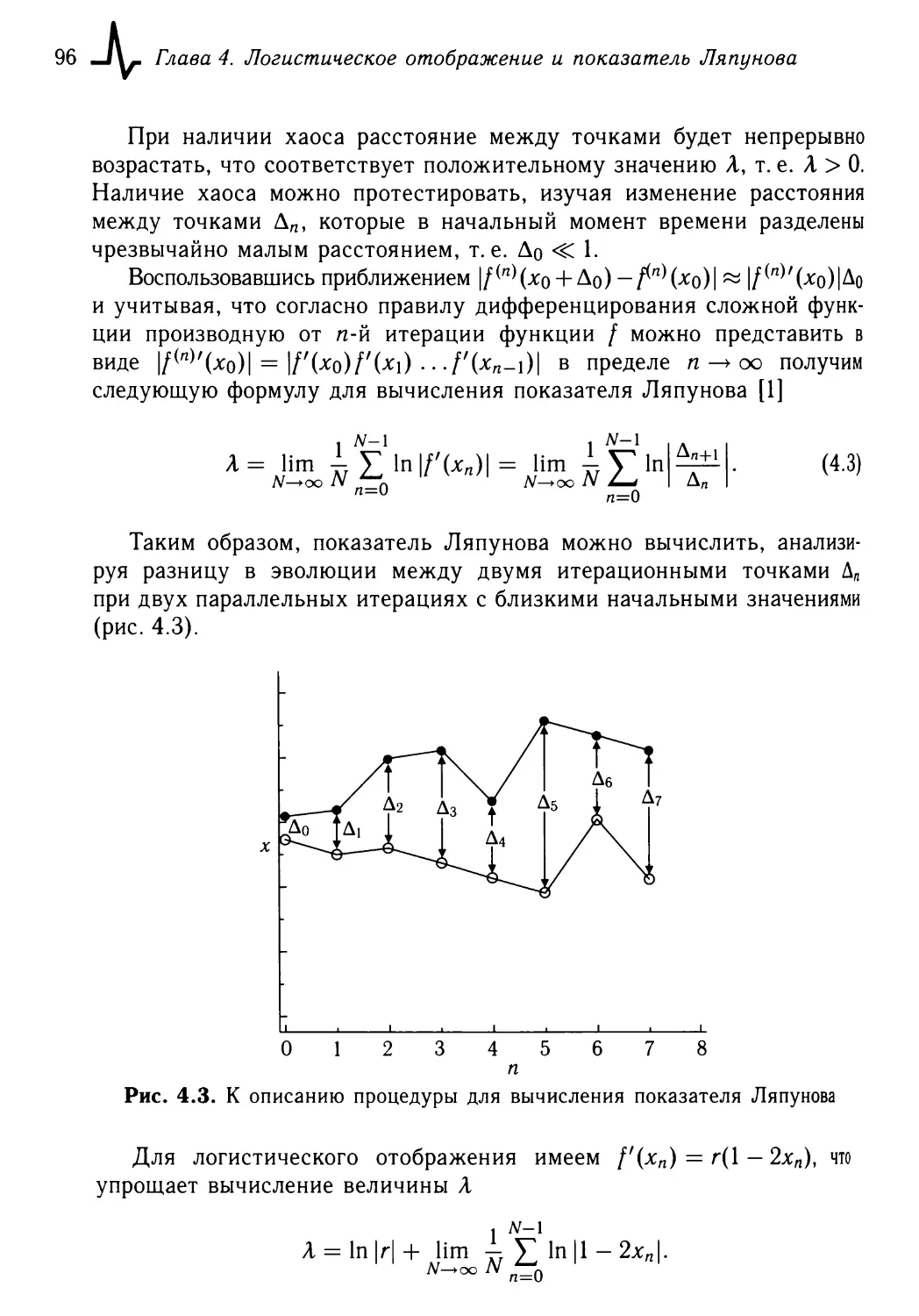
4.1. Хаотическое поведение 92
4.1.1. Логистическое отображение 92
4.1.2. Показатель Ляпунова 95
4.2. Описание работы программ 97
4.2.1. Бифуркационная диаграмма и поведение показателя Ляпунова 97
4.2.2. Пример работы программы 98
4.3. Задачи для самостоятельной работы 98
4.4. Литература 100
Глава 5. Множества Жюлиа и Мандельброта 101
5.1. Нелинейные отображения в комплексных координатах 101
5.1.1. Множество Жюлиа 101
5.1.2. Множество Мандельброта 105
5.2. Алгоритмы и описание работы программ 107
5.2.1. Алгоритм для построения множества Жюлиа 107
5.2.2. Алгоритм построения множества Мандельброта 107
5.2.3. Описание работы программ 107
5.2.4. Примеры работы программ 109
5.3. Задачи для самостоятельной работы 110
5.4. Литература 110
Оглавление -i\, 5
Глава 6. Детерминистические фракталы 112
6.1. Примеры детерминистических фракталов 112
6.1.1. Кривые Коха и Мандельброта-Гивена 113
6.1.2. Треугольник и ковер Серпинского 114
6.1.3. Пирамида Серпинского и губка Менгера 115
6.1.4. Канторовская пыль 116
6.2. Алгоритмы и описание программ 116
6.2.1. Рекурсивный алгоритм 117
6.2.2. Алгоритм на основе систем итерируемых функций (IFS) . . 119
6.2.3. Описание работы программ 121
6.2.4. Примеры работы программ 125
6.3. Задачи для самостоятельной работы 125
6.4. Литература 126
Глава 7. Рост бактериальных колоний: Модель Идена .... 128
7.1. Типы моделей стохастического роста 128
7.1.1. Базисная модель Идена 128
7.1.2. Модель с подавлением шума 129
7.1.3. Нерешеточные модели Идена 130
7.1.4. Структура кластеров Идена 130
7.1.5. Перколяционная модель 131
7.1.6. Модель экранированного роста 132
7.1.7. Модель случайного последовательного роста 132
7.1.8. Модель «летающей бабочки» 132
7.2. Алгоритм для базисной модели Идена и описание работы программы 133
7.2.1. Алгоритм 133
7.2.2. Описание работы программы 133
7.2.3. Пример работы программы 135
7.3. Задачи для самостоятельной работы 136
7.4. Литература 136
Глава 8. Агрегация, контролируемая диффузией 138
8.1. Варианты модели агрегации, контролируемой диффузией 138
8.1.1. Базисный вариант модели DLA 138
8.1.2. Модель DLA с подавлением шума 141
8.1.3. Рост на множественных центрах 142
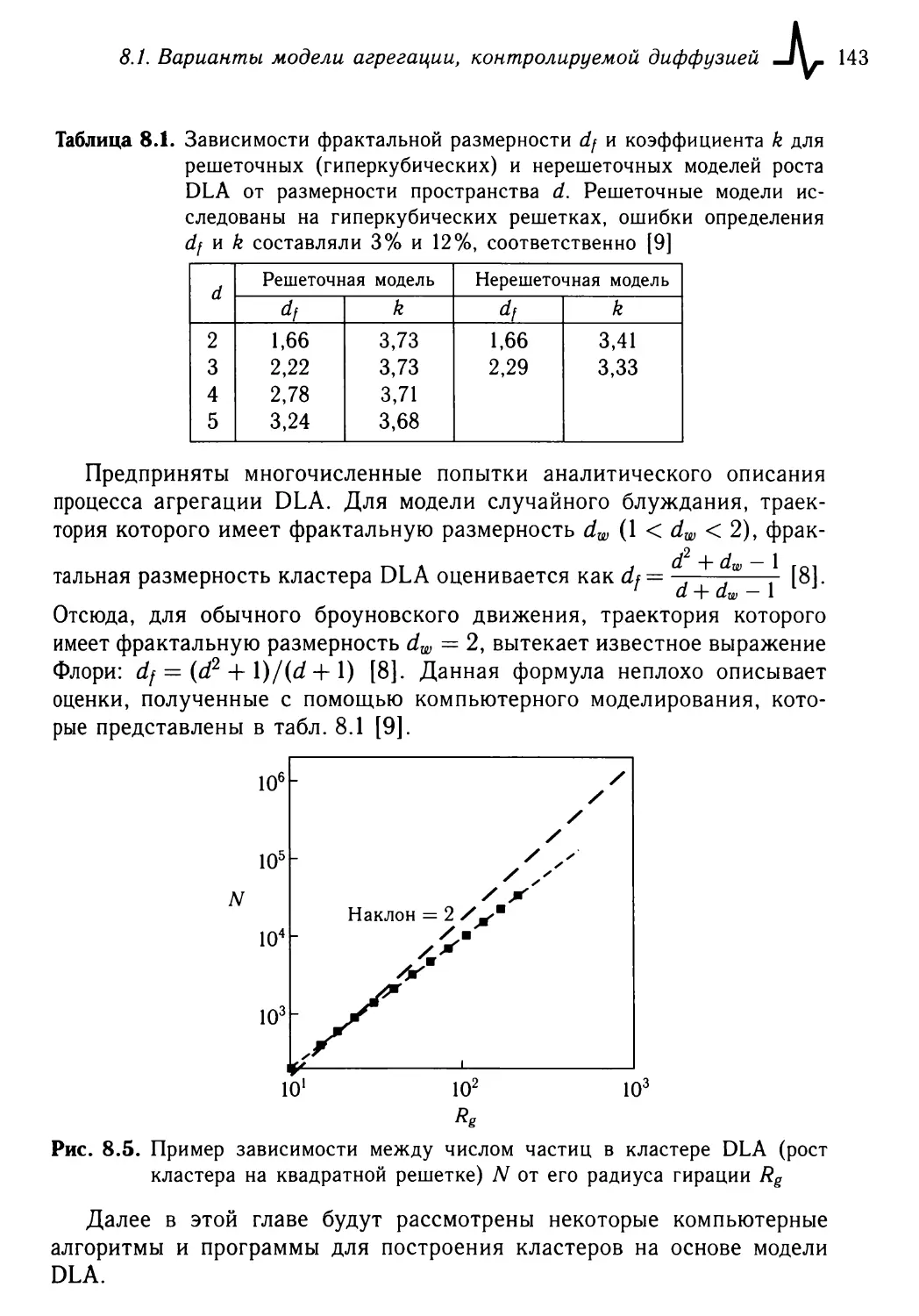
8.1.4. Фрактальная размерность 142
8.2. Алгоритмы и описание работы программ 144
8.2.1. Алгоритм для базисного варианта 144
8.2.2. Алгоритм для ускоренного варианта 145
8.2.3. Описание работы программы для базисного варианта .... 147
6 -Jb Оглавление
8.2.4. Описание работы программы для ускоренного варианта . . . 149
8.2.5. Примеры работы программ 157
8.3. Задачи для самостоятельной работы 157
8.4. Литература 159
Глава 9. Имитация роста шероховатых поверхностей 160
9.1. Структура и свойства шероховатых поверхностей 160
9.1.1. Характеристики фронта роста поверхности 161
9.1.2. Концепция пространственно-временного скейлинга 162
9.1.3. Основные типы компьютерных моделей 164
9.1.3.1. Случайное осаждение (RD) 164
9.1.3.2. Осаждение с поверхностной релаксацией (RDR). . . 166
9.1.3.3. Баллистическое осаждение (BD) 166
9.1.3.4. Смешанные модели 168
9.2. Алгоритмы и описание работы программ 169
9.2.1. Описание алгоритмов для моделей осаждения RD, RDR и BD 169
9.2.2. Описание работы программ для моделей осаждения RD, RDR
и BD 170
9.2.2.1. Модель RD 172
9.2.2.2. Модель RDR 172
9.2.2.3. Модель BD 173
9.2.3. Примеры работы программ 173
9.3. Задачи для самостоятельной работы 174
9.4. Литература 176
Глава 10. Случайная последовательная адсорбция 178
10.1. Необратимая адсорбция и джамминг 178
10.1.1. Определение базисной модели RSA 178
10.1.2. Концентрация джамминга для разных вариантов модели RSA 180
10.1.3. Модель RSA для объектов анизотропной формы 181
10.1.4. Влияние формы частиц и полидисперсности 183
10.1.5. Кинетика осаждения для решеточных и непрерывных моделей 185
10.2. Алгоритм и описание работы программы 186
10.2.1. Алгоритм RSA для одномерной модели 186
10.2.2. Быстрый алгоритм RSA для двумерной квадратной решетки 186|
10.2.3. Описание работы программы для определения порога
насыщения 187
10.2.4. Описание работы программы для моделирования кинетики
насыщения 189
10.2.4.1. Одномерная модель RSA 189
10.2.4.2. Двумерная модель RSA 191
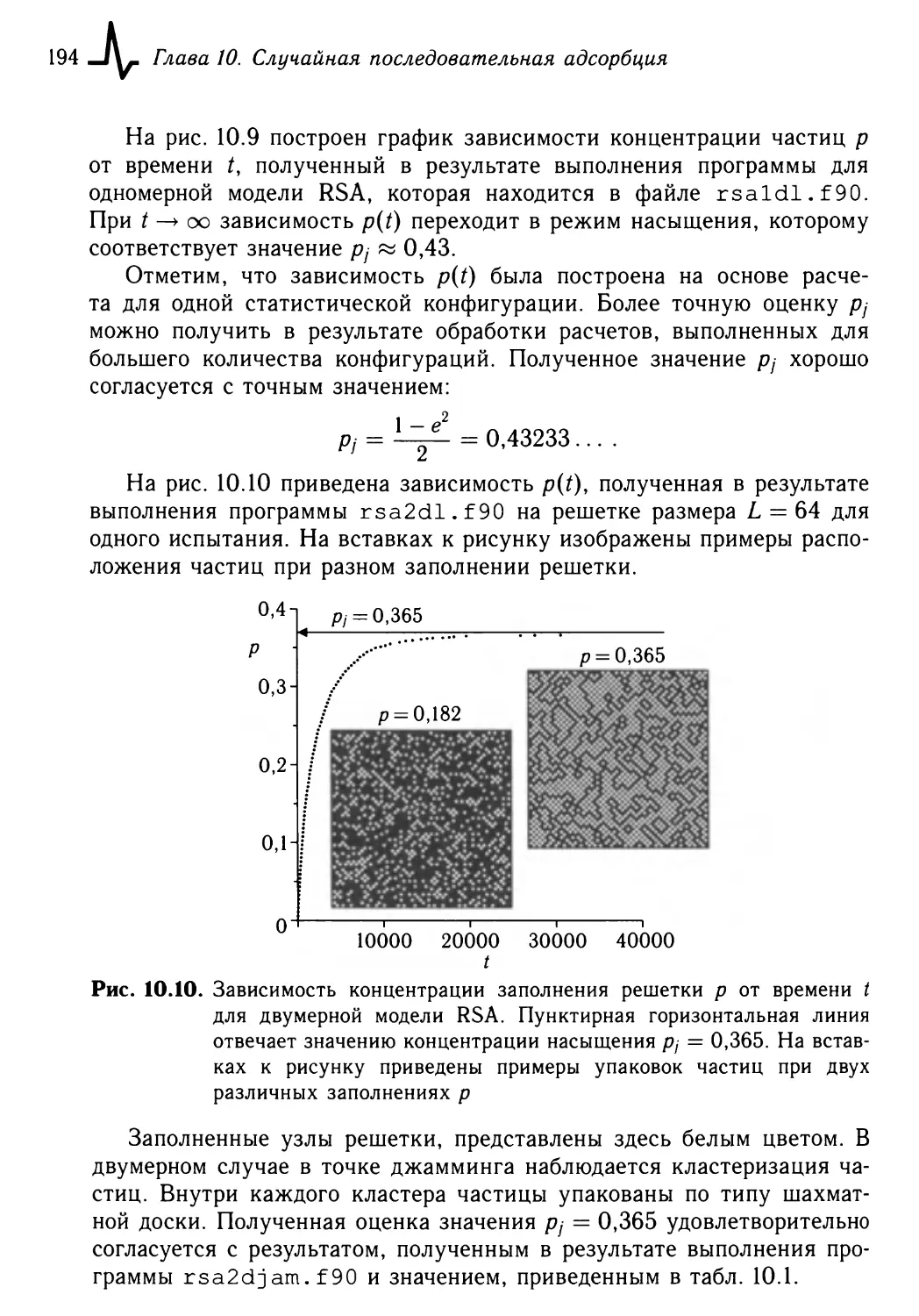
10.2.5. Примеры работы программ 193
10.3. Задачи для самостоятельной работы 195
10.4. Литература 195
Оглавление -l\r 7
Глава 11. Аномальная диффузия и диффузия в
неупорядоченных средах 198
11.1. Модели диффузии в различных конденсированных средах 198
11.1.1. Случайные блуждания и движение броуновской частицы . 198
11.1.2. Классификация типов диффузионного движения 199
11.1.3. Модель «прыжков Леви» 199
11.1.4. Модель диффузии с памятью 200
11.1.5. Модель Эдвардса 201
11.1.6. Модель решеточного газа 201
11.1.7. Диффузия при наличии дрейфа частицы 201
11.1.8. Диффузия в неупорядоченных средах и модель де Жена. . 202
11.1.9. Диффузия на фрактальных объектах 203
11.2. Алгоритм и описание работы программы для изучения диффузии
на перколяционном кластере 206
11.2.1. Алгоритм 206
11.2.2. Описание работы программы 206
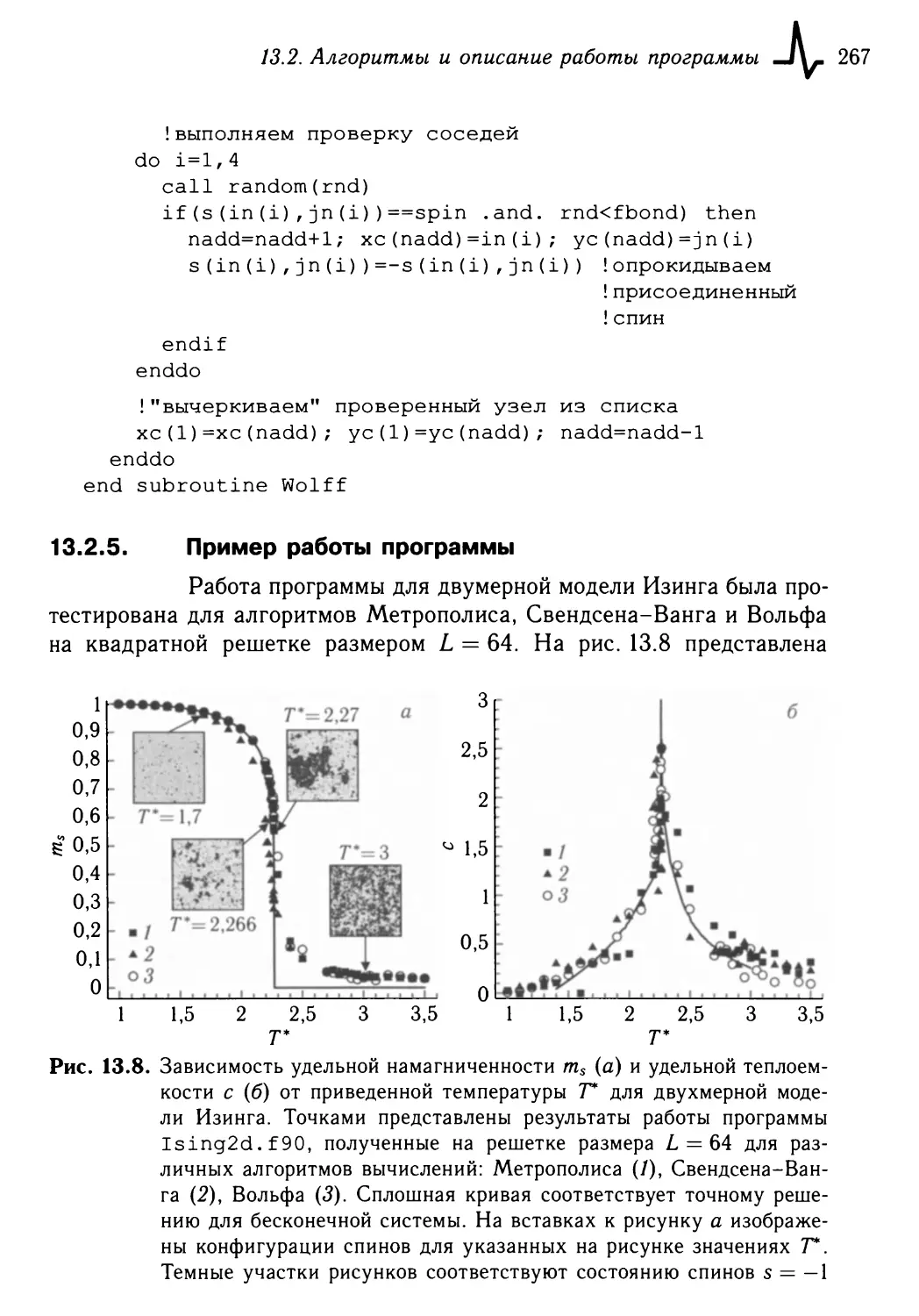
11.2.3. Пример работы программы 214
11.3. Задачи для самостоятельной работы 215
11.4. Литература 217
Глава 12. Алгоритмы кластерного анализа 219
12.1. Постановка задачи 219
12.2. Кластерный анализ методом прожига 221
12.2.1. Алгоритм 221
12.2.2. Программа кластерного анализа методом прожига 222
12.2.3. Пример работы программы кластерного анализа методом
прожига 225
12.3. Кластерный анализ с использованием метода Хошена-Копельмана 226
12.3.1. Решеточный вариант 226
12.3.1.1. Алгоритм 226
12.3.1.2. Описание программы 227
12.3.2. Нерешеточный вариант 229
12.3.2.1. Формирования списка связности 229
12.3.2.2. Алгоритм Хошена-Копельмана с использованием
списка связности 230
12.3.2.3. Описание программы, основанной на использова¬
нии списка связности 231
12.4. Вспомогательные программы 235
12.4.1. Случайное заполнение плоскости 235
12.4.1.1. Узлы квадратной решетки 235
12.4.1.2. Перекрывающиеся диски 235
Оглавление
12.4.2. Формирование списка связности 236
12.4.2.1. Узлы квадратной решетки 236
12.4.2.2. Перекрывающиеся диски 238
12.4.3. Визуализация кластеров 240
12.5. Примеры работы программ для кластерного анализа с использова¬
нием метода Хошена-Копельмана 240
12.6. Задачи для самостоятельной работы 242
12.7. Литература 242
Глава 13. Метод Монте-Карло для анализа модели Изинга:
Алгоритм Метрополиса и кластерные алгоритмы 244
13.1. Фазовые переходы в магнитных материалах и модель Изинга . . . 244
13.1.1. Определение Модели Изинга на квадратной решетке .... 245
13.1.2. Точное решения Модели Изинга на квадратной решетке . . 246
13.1.3. Простейшее обобщение модели Изинга: модель Поттса. . . 247
13.1.4. Конечномерный анализ для модели Изинга и метод куму¬
лянт Биндера 248
13.1.5. Алгоритм Метрополиса для решения модели Изинга .... 248
13.1.6. Замедление процедуры Метрополиса вблизи критической
точки 251
13.1.7. Преодоление проблемы критического замедления с помощью
кластерных алгоритмов 251
13.2. Алгоритмы и описание работы программы 253
13.2.1. Алгоритм Метрополиса 253
13.2.2. Алгоритм Свендсена-Ванга 253
13.2.3. Алгоритм Вольфа 254
13.2.4. Описание работы программы 255
13.2.4.1. Процедура Метрополиса 263
13.2.4.2. Процедура Свендсена-Ванга 264
13.2.4.3. Процедура Вольфа 266
13.2.5. Пример работы программы 267
13.3. Задачи для самостоятельной работы 268
13.4. Литература 269
Глава 14. Задача коммивояжера 272
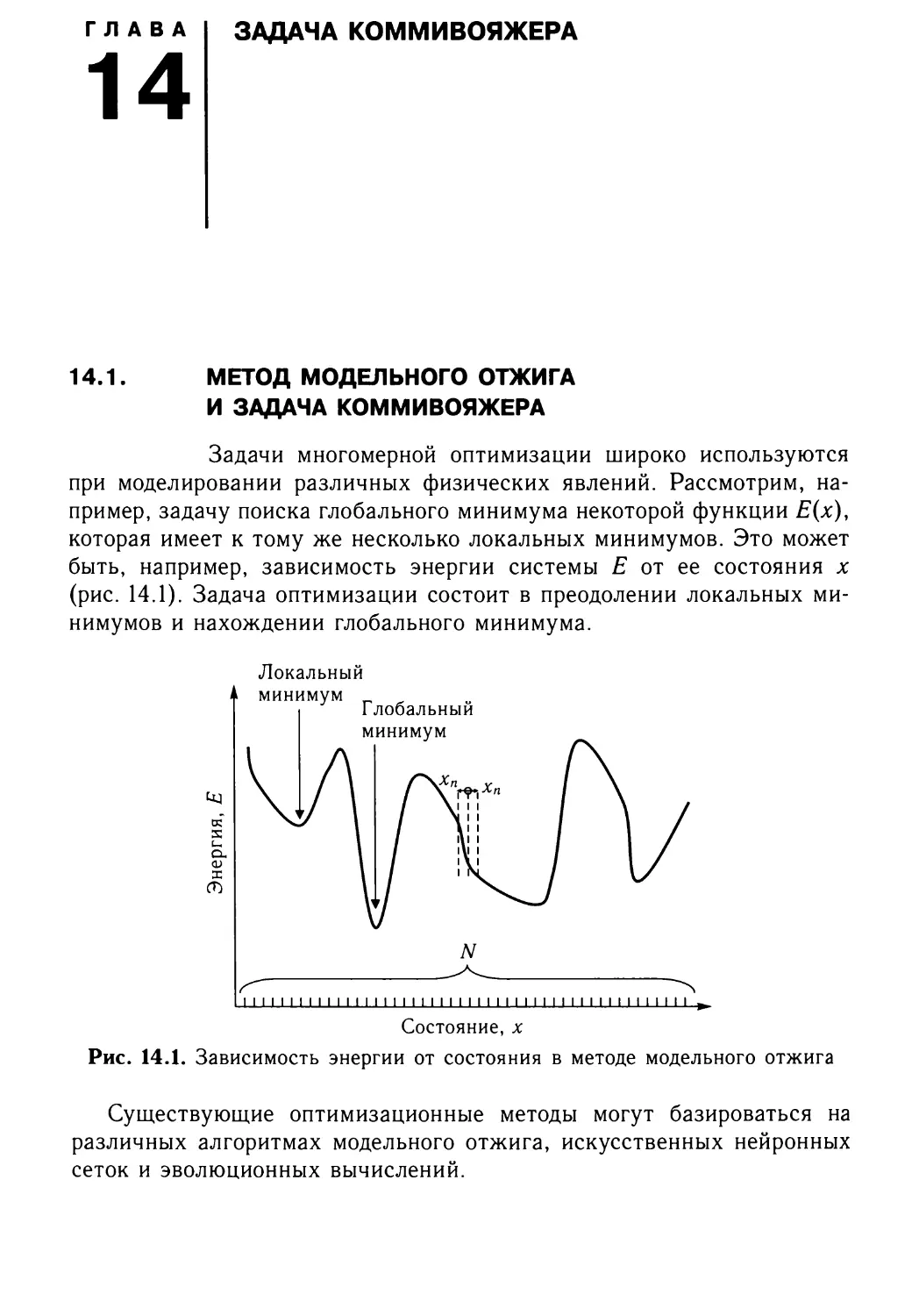
14.1. Метод модельного отжига и задача коммивояжера 272
14.1.1. Метод модельного отжига 273
14.1.1.1. Вероятность перехода 273
14.1.1.2. Уменьшение температуры со временем 274
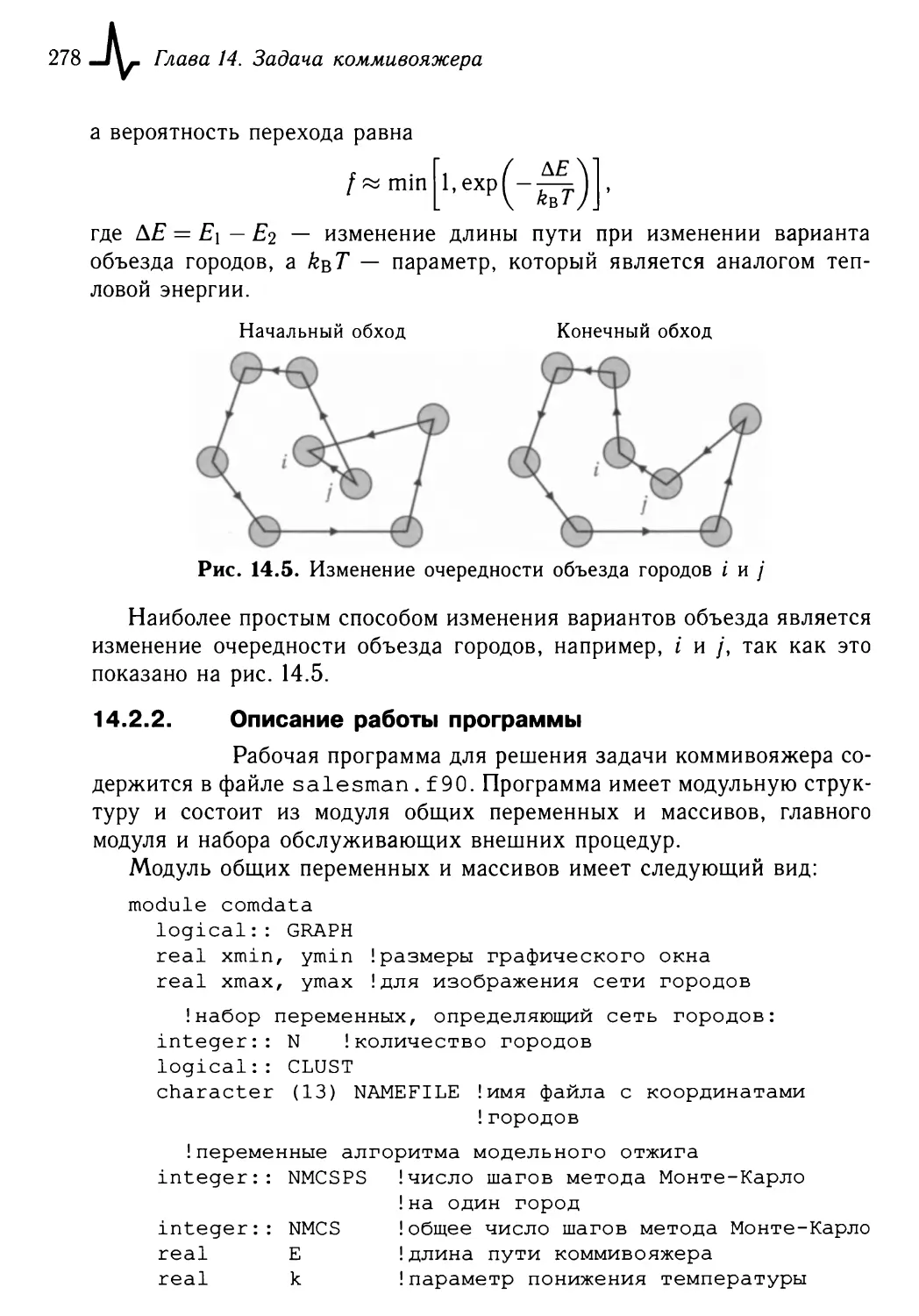
14.1.2. Задача коммивояжера 275
Оглавление -l\r 9
14.2. Алгоритм для решения задачи коммивояжера и описание работы
программы 277
14.2.1. Алгоритм 277
14.2.2. Описание работы программы 278
14.2.3. Примеры работы программы 282
14.3. Задачи для самостоятельной работы 283
14.4. Литература 285
Глава 15. Вычисление электропроводности
композиционных систем 287
15.1. Методы расчета электропроводности композиционных систем . . . 287
15.2. Алгоритм Франка-Лобба для расчета электропроводности и опи¬
сание работы программы 289
15.2.1. Алгоритм Франка-Лобба 289
15.2.1.1. Элементарные преобразования 289
15.2.1.2. Преобразование звезда-треугольник и их обобщение 290
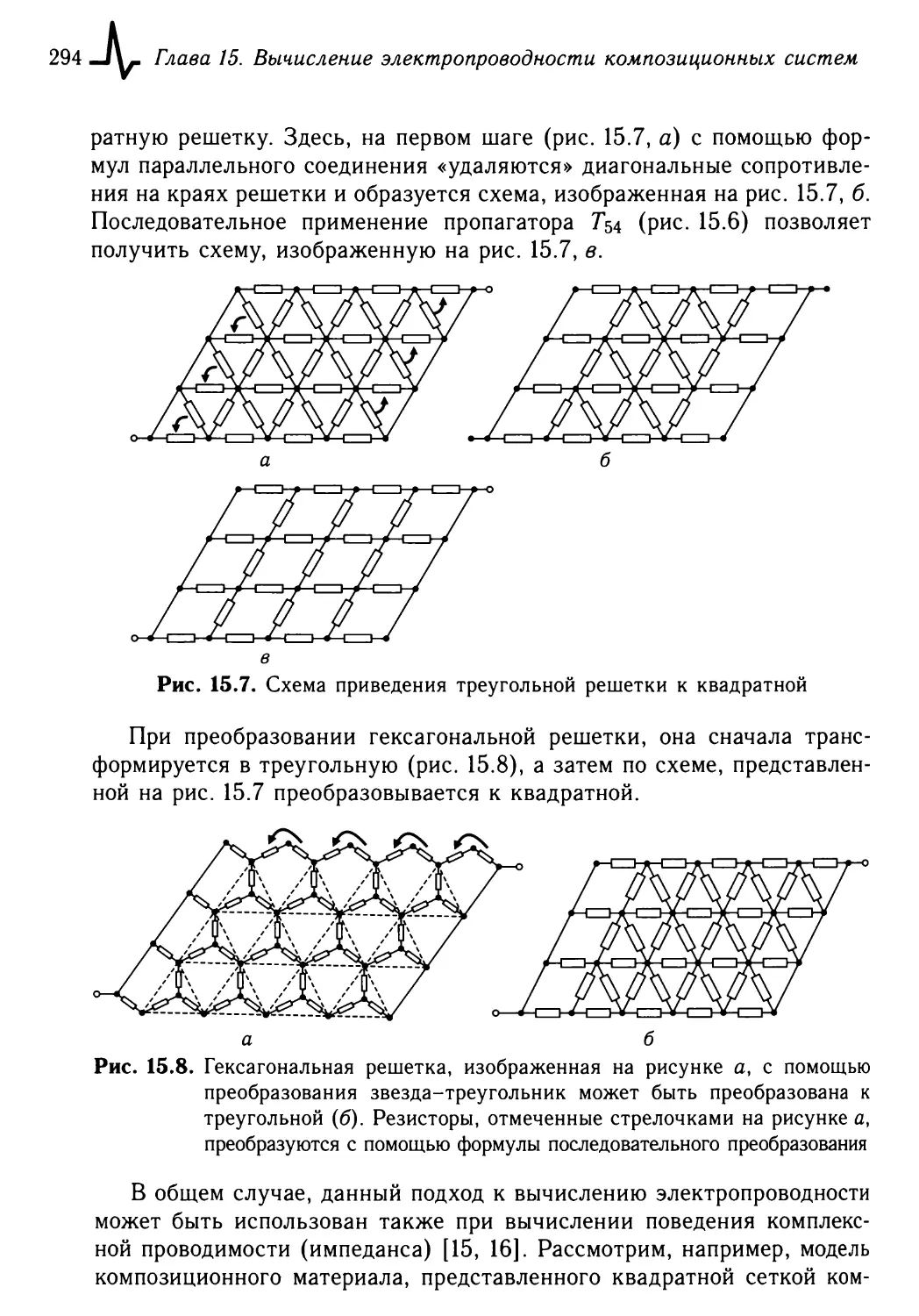
15.2.1.3. «Сворачивание» квадратной сетки сопротивлений 291
15.2.1.4. Применение метода Франка-Лобба для более слож¬
ных плоских решеток 293
15.2.2. Описание работы программы 295
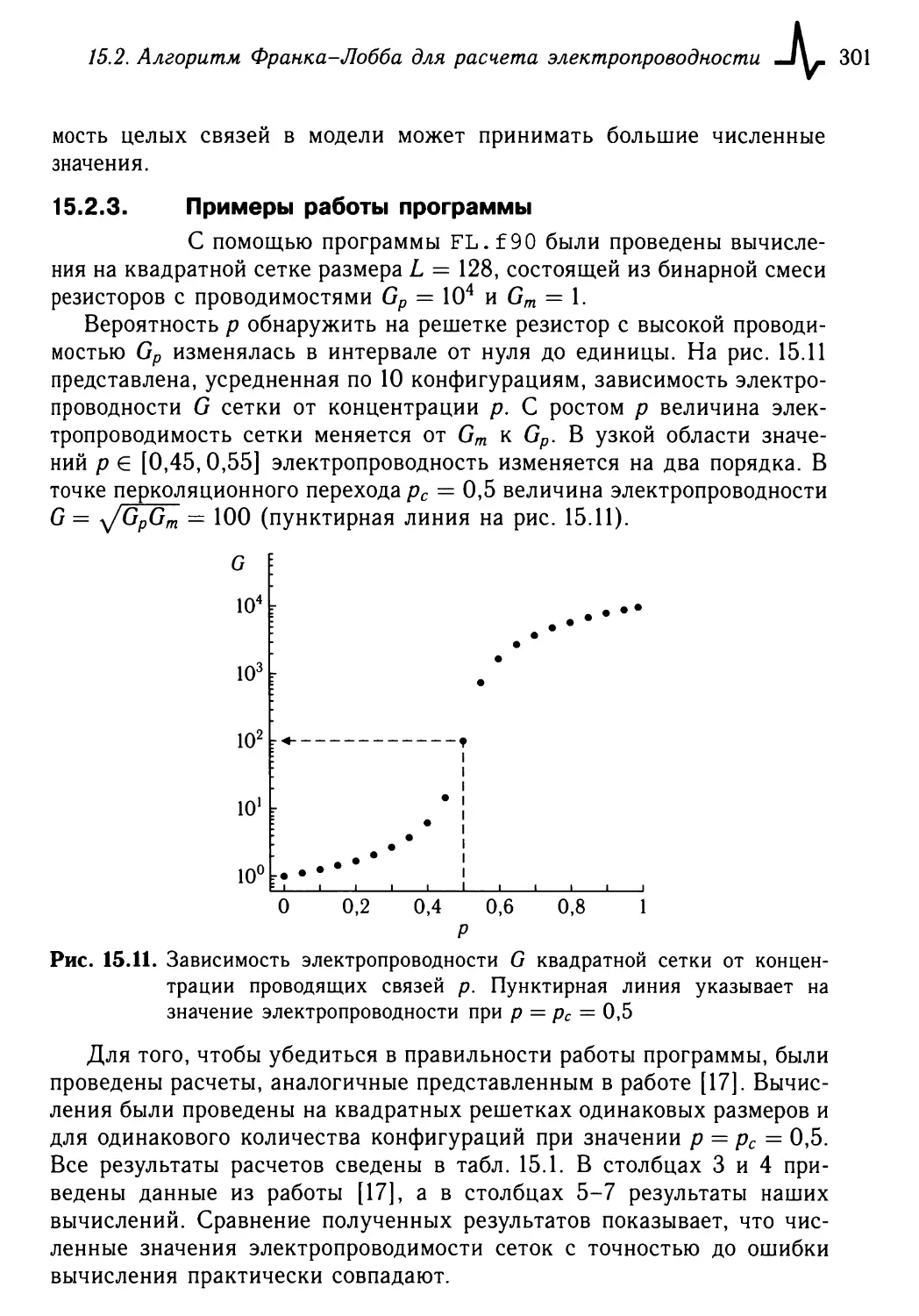
15.2.3. Примеры работы программы 301
15.3. Задачи для самостоятельной работы 302
15.4. Литература 304
Глава 16. Электрический пробой 306
16.1. Простейшие модели электрического пробоя 306
16.1.1. Модели типа резистор-изолятор (модель RI) и резистор-
сверхпроводник (модель RS) 307
16.1.2. Стохастические и детерминистические модели 308
16.1.2.1. Стохастическая модель (модель NPW) 309
16.1.2.2. Детерминистическая модель (модель Такаясу). . . 310
16.1.3. Термоактивационная модель 311
16.2. Алгоритмы и описание работы программ 312
16.2.1. Стохастическая модель NPW 312
16.2.2. Обобщенная модель Такаясу 313
16.2.3. Термоактивационная модель 314
16.2.4. Описание работы программ 314
16.2.4.1. Стохастическая модель NPW 314
16.2.4.2. Обобщенная модель Такаясу 320
16.2.5. Примеры работы программ 324
16.3. Задачи для самостоятельной работы 325
16.4. Литература 326
10 -J\, Оглавление
Глава 17. Самоорганизованная критичность 328
17.1. Модели самоорганизованной критичности 328
17.1.1. Обвал кучи с песком 329
17.1.2. Землетрясения 333
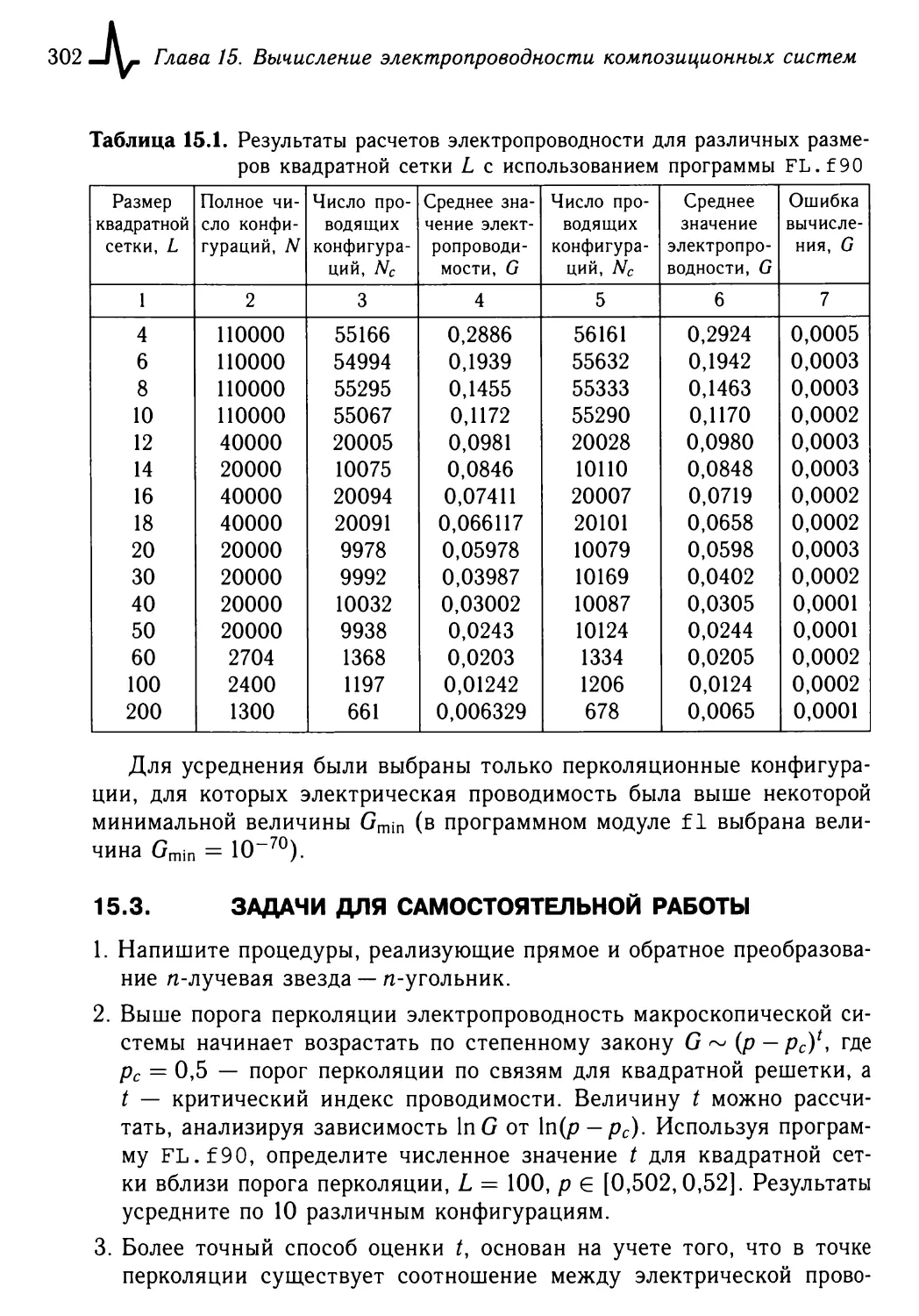
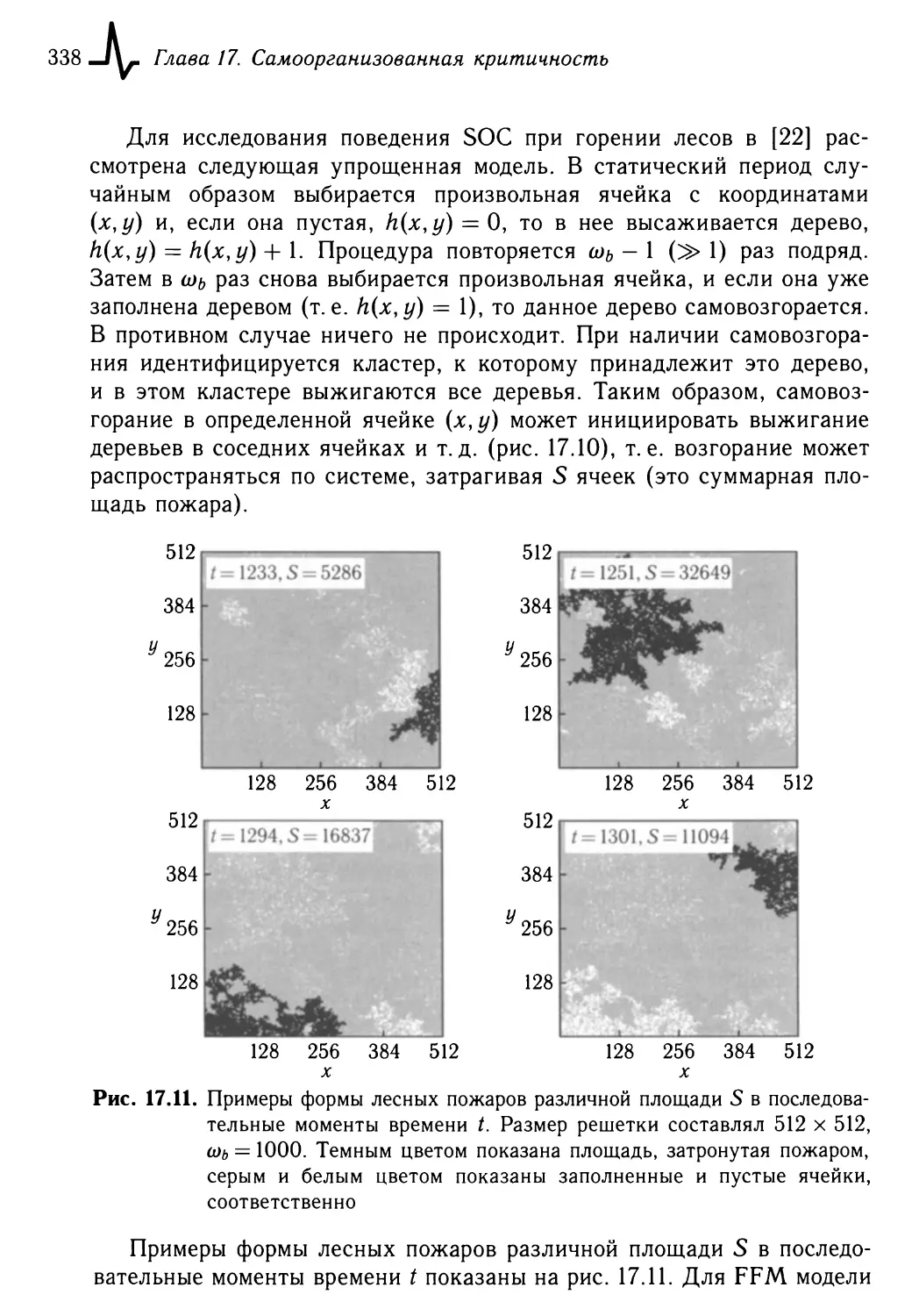
17.1.3. Горение лесных массивов 335
17.1.4. Игра «Жизнь» 339
17.2. Алгоритмы и описание работы программ 340
17.2.1. Обвал кучи с песком 340
17.2.2. Лесной пожар 341
17.2.3. Описание работы программ 341
17.2.3.1. Обвал кучи с песком 341
17.2.3.2. Лесной пожар 343
17.2.4. Примеры работы программ 345
17.3. Задачи для самостоятельной работы 347
17.4. Литература 347
ПРЕДИСЛОВИЕ
Компьютерное моделирование является неотъемлемой ча¬
стью современной физики. Моделирование физической природы или
«численный эксперимент» в настоящее время широко используется как
теоретиками, так и экспериментаторами. Компьютерные методы нахо¬
дят все более широкое применение при моделировании свойств слож¬
ных физических систем, а их внедрение позволило получить совершен¬
но новые результаты и рассмотреть классы задач ранее традиционно от¬
носимых к «нерешаемым». Значительные успехи получены в таких фун¬
даментальных областях как статистическая физика и физика конденси¬
рованных систем, физика твердого тела и квантовая механика, физика
фракталов и хаотических явлений, финансовая физика. Для решения
таких задач были развиты специфические рецепты, алгоритмы, модели
клеточных автоматов, что позволило значительно ускорить получение
конечных результатов. Однако, по нашему мнению, в традиционных
изданиях, посвященных применению вычислительных и компьютерных
методов, многие из таких алгоритмов анализируются не достаточно
детально.
Предлагаемая вниманию читателя книга является фактически учеб¬
ником для студентов-физиков, который основан на многолетнем опыте
преподавания курса «Моделирование физических систем» в ряде веду¬
щих украинских вузов. Книга состоит из 17 глав и посвящена анализу
некоторых компьютерных рецептов, используемых при моделировании
физических систем. В качестве основного языка программирования вы¬
бран язык Фортран 90, который, как известно, хорошо адаптирован для
решения физических задач, имеет хорошую библиотечную поддержку
в физических приложениях и широко используется в настоящее время.
Каждая глава книги представляет собой отдельную сформулирован¬
ную вычислительную задачу и организована по сходному принципу:
введение, теоретическое изложение материала на уровне справочного
пособия, алгоритм решения, описания рабочей программы и примеры
12 -»Ъ- Предисловие
ее применения. Приведенные в книге программные листинги следует
рассматривать как текст, предназначенный для чтения и детального
анализа. Полные листинги протестированных программ можно найти
на сайте кафедры молекулярной физики Киевского национального уни¬
верситет имени Тараса Шевченко (http:/molphys.univ.kiev.ua в разде¬
ле публикации). Для понимания приведенных в книге кодов программ
обязательным является прочтение первой главы, где кратко изложены
основы программирования на языке Фортран 90. Читатели, для кото¬
рых этот язык хорошо знаком, могут эту главу пропустить. Все осталь¬
ные главы книги практически автономны, и их материал может быть
использован независимым образом без прочтения остального матери¬
ала. Все главы также снабжены дополнительными задачами, многие
из которых сформулированы на основании статей, опубликованных в
научных журналах физического профиля.
Основное внимание уделено дискретным математическим моделям
сложных и многочастичных систем, которые широко применяются в
термодинамике, статистической физике и смежных областях. В част¬
ности, в книге рассмотрены некоторые алгоритмы, широко использу¬
емые в качестве вспомогательных инструментов при анализе струк¬
туры многочастичных систем. Приведены примеры применения рекур¬
сивных алгоритмов для построения фракталов. Описаны программы
для построения множеств Мандельброта и Жюлиа. Методы Монте-
Карло проиллюстрированы на примере рассмотрения модели Изинга
и решения оптимизационной задачи коммивояжера. Проанализированы
классические задачи о нелинейных связанных осцилляторах (Ферми-
Улама-Паста), солитонном решении уравнения Кортевега—де Вриза и
хаотическом поведении нелинейных систем. Рассмотрены алгоритмы,
используемые для анализа связности кластеров, роста кластерных, пер-
коляционных, дендритных систем и бактериальных колоний. Рассмот¬
рены также основные алгоритмы для имитации явлений электрического
пробоя, роста поверхностей, диффузии в неупорядоченных и фракталь¬
ных средах, а также явлений самоорганизованной критичности.
В конце каждой главы приведен список литературы, который ни в
коей мере не претендует на полноту, а используется только для ссылок
на обсуждаемые модели. Книга предназначена для студентов и аспи¬
рантов физических, физико-химических специальностей, а также на¬
учных сотрудников. По стилю изложения эта книга является скорее
учебником, и ее материал может быть использован в преподавательских
курсах посвященных применению компьютерного моделирования для
решения физических задач.
ГЛАВА
1
ИСПОЛЬЗОВАНИЕ ЯЗЫКА
ПРОГРАММИРОВАНИЯ ФОРТРАН 90
ДЛЯ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ
ФИЗИЧЕСКИХ СИСТЕМ
На протяжении почти 60 лет язык программирования Фор¬
тран остается основным языком программирования, используемым в
научных вычислениях. Фортран был создан специалистами фирмы IBM
в начале 50-х XX века и его название происходит от слов FORmula и
TRANslation. Само название языка означает, что Фортран был разра¬
ботан специально для решения численных задач физики и математики.
Высокая эффективность проведения численных вычислений оказывает
содействие тому, что этот язык программирования по-прежнему ис¬
пользуют большинство физиков всего мира. С момента своего создания
Фортран претерпел ряд существенных изменений. На протяжении ис¬
тории своего развития было принято несколько стандартов этого языка:
Фортран 66, Фортран 77, Фортран 90, Фортран 95, Фортран 2003,
Фортран 2008. Фортран считается одним из наиболее удачных языков
программирования в применении для решения вычислительных задач.
Современный Фортран содержит также некоторые элементы объектно-
ориентированного программирования, и включает много средств, кото¬
рые делают его идеальным для проведения вычислений на многопро¬
цессорных компьютерах.
В этой главе изложены только наиболее важные возможности со¬
временного Фортрана, которые можно использовать для иллюстрации
алгоритмов компьютерного моделирования в физике. Более детальное
изложение возможностей Фортрана 90 можно найти в существующих
учебных пособиях [1, 2], или полном описании стандарта [3]. Изла¬
гаемый в этой главе материал был отобран таким образом, чтобы по¬
знакомить читателя только с теми элементами Фортрана 90, которые
необходимы для понимания работы программ, излагаемых в этой книге.
Большая часть излагаемого материала справедлива для любой реализа¬
ции Фортран 90. Исключение могут составлять генераторы случайных
чисел и графические операторы, которые излагаются для реализации
Фортран 90 Microsoft Fortran PowerStation 4.0.
14 ->\r Глава 1. Фортран 90 для моделирования физических систем
1.1. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК ПРОГРАММИРОВАНИЯ
ФОРТРАН
1.1.1. Первичные понятия
Первичными элементами Фортрана являются символы, ко¬
торые могут быть разделены на основные и дополнительные. Основные
символы — включают 52 символа латинского алфавита, десять симво¬
лов цифр, а также спецсимволы. Основные символы языка использу¬
ются для построения всех конструкций языка. Набор дополнительных
символов не фиксирован и используется для построения символьных
констант, либо снабжения программы комментариями. В табл. 1.1 при¬
веден набор специальных символов.
Таблица 1.1. Специальные символы Фортран
Символ
Название
Символ
Название
Пробел
Двоеточие
=
Равно
|
Восклицательный знак
+
Плюс
Точка с запятой
-
Минус
&
Амперсенд
*
Звездочка
%
Процент
/
Слэш
<
Меньше
(
Левая скобка
>
Больше
)
Правая скобка
Вопросительный знак
,
Запятая
"
Кавычки
/
Точка
Апостроф
$
Денежный знак
Последовательности символов языка Фортран образуют слова, ко¬
торые могут обозначать числа, имена величин, некоторые действия и
т. д. Различают два типа слов: служебные слова и слова пользователя.
Служебные слова имеют раз и навсегда заданный смысл. Слова поль¬
зователя создаются разработчиком программы по его усмотрению, но
с учетом правил принятых в языке Фортран. Слова пользователя не
должны совпадать со служебными словами по начертанию.
Основные конструкции языка являются операторы, которые могут
быть выполняемые и невыполняемы. Выполняемые операторы служат
для указания действий и порядка их выполнения, а невыполняемые
операторы используются для указания типа и структуры величин, для
задания информации о распределении памяти и т. д.
В простейшем случае программа может включать только основной
модуль. В более сложных случаях программа может состоять из моду¬
лей, основной программы и подпрограмм. Выполнение программы все¬
гда начинается с основной программы. Подпрограмма подключается к
/./. Краткое введение в язык программирования Фортран -»\г 15
работе основной программы путем вызова ее с основной программы,
либо вызова ее из других подпрограмм.
Приведем пример программы, которая выполняет сложение двух
чисел и печатает результат на экран дисплея:
1 program exOl
2 integer a, b !определяем a, b и с
3 integer с !как переменные целого типа
Фактически этот пример иллюстрирует ряд определений, о которых
говорилось выше. Проанализируем их более детально. Для удобства
анализа каждая строка кода программы была пронумерована. Данная
программа начинается со служебного слова program, а заканчивает¬
ся служебными словами end program. Служебное слово program
определяет программную единицу как основную программу. В данном
случае программа состоит всего лишь с одной программной единицы —
основной программы. Слово пользователя exOl является названием
основной программы и присутствует в начале и в конце программы.
В начале программы все величины, которые используются программой,
должны быть описаны. Служебное слово integer является примером
невыполнимого оператора, который используется для описания типа ве¬
личин а, Ь, с. Слова пользователя а, Ь, с являются также именами пе¬
ременных. В программах операторы описания могут использоваться как
для описания типа отдельной переменной, так и списка переменных,
как это показано в этом примере. Для разделения переменных в списке
используется спецсимвол запятая. Для комментирования кода програм¬
мы используется спецсимвол восклицательного знака, который может
находиться в любой позиции программной строки и всегда стоит в нача¬
ле любого комментария. Пятая строка кода содержит примеры двух вы¬
полнимых операторов присваивания, в которых спецсимвол = использу¬
ется для обозначения операции присваивания. Два и более оператора в
одной строке разделяются друг от друга точкой с запятой. С помощью
этих операторов присваивания величины а и b принимают значения 10
и -2 соответственно. Более сложный оператор присваивания содержит¬
ся в строке кода с номером семь. В данном случае переменной с присва¬
4
5 а=10; Ь=-2
6
7 с=а+Ь
!присваиваем переменным а и b значения
!присваиваем с результат сложения
! переменных а и b
!печатаем на экран дисплея
!значение переменной с, равной 8
8
9 write(*,*) с
10
11 end program exOl
12
16 ->\r Глава 1. Фортран 90 для моделирования физических систем
ивается результат вычисления арифметического выражения а+b. Девя¬
тая строка кода содержит оператора вывода write (*,*), который осу¬
ществляет печать на экран значения переменной с. Приведенный при¬
мер также иллюстрирует наличие пустых строк в коде программы, ко¬
торые удобно использовать для повышения читабельности программы.
В рассмотренном выше примере использовались простые слова для
имен переменных. Но в общем случае имена переменных могут включать
символы цифр и символ подчеркивания. Например, имена переменной
а_1, Ь2 является вполне корректным именами переменных. Следует
отметить, что символ подчеркивания не может быть первым в имени
переменной. Компилятор Фортрана не различает больших и малых сим¬
волов в именах переменных и операторов. Например, операторы вывода
WRITE (*, *) и write (*, *) полностью эквивалентны. Использование
больших или малых букв при кодировании программы скорее зависит
от «вкуса» программиста. В приведенных в этой книге программах
для кодирования операторов используются малые символы, а для имен
переменных, которые обозначают параметры модели большие символы.
Программы для компилятора Фортрана могут быть написаны с ис¬
пользованием фиксированного или свободного формата кодирования. Все
программы, представленные в этой книге, написаны с использованием
свободного формата кодирования, однако сегодня еще можно встретить
много библиотечных функций и процедур, использующих фиксирован¬
ный формат кодирования, который является стандартом Фортрана 77.
Фиксированный формат кодирования накладывает ряд ограничений на
представление кода программы. Кратко опишем эти ограничения:
• длина программной строки не может превышать 72 символа;
• первый символ программной строки используется для комментиро¬
вания кода программы, в качестве которых используют любой из
символов: *, С, с.
• позиции с 1-й по 5-ю используются для обозначения меток. После
метки не должно быть пустой программной строки;
• если 6-я позиция содержит любой символ, то это указывает на
продолжение предыдущей программной строки кода;
• операторы кода могут содержаться с 7 по 72 позицию строки;
• в программе не допускается наличие пустых строк.
Файлы с программами, которые написаны в фиксированном форма¬
те, обычно имеют, расширения * . for, или * . f. Например, myprog.f.
Свободный формат кодирования снимает ряд предыдущих ограни¬
чений на код программы, но не все:
• длина программной строки не может превышать 132 символа;
• для продолжения длинной строки используют спецсимвол &, кото¬
рый ставится в конце строки кода.
1.1. Краткое введение в язык программирования Фортран •Аг 17
Файлы, которые написаны в свободном формате кодирования, обыч¬
но, имеют расширение *.f90. Например, my.f90.
Отметим, что в обоих стандартах кодирования меткой является по¬
следовательность цифровых символов, которая не превышает, пяти зна¬
ков. В свободном формате кодирования позиция метки не ограничена
первыми пяти позициями.
1.1.2. Основные типы величин, их представление
и описание в программе
В программах Фортрана могут использоваться величины
следующих типов: целого, вещественного, комплексного, логического и
символьного. Значениями целых и вещественных величин могут быть
положительные, отрицательные числа соответствующих типов. Ком¬
плексные величины определяются парой чисел. Первое из них означает
действительную часть комплексной величины, а второе — коэффициент
при мнимой единице i. Логические величины могут принимать только
два значения: истина или ложь. Величины символьного типа опреде¬
ляются последовательностью символов основного и дополнительного
наборов.
Величины целого, вещественного и комплексного типа могут ис¬
пользоваться в виде констант, простых переменных, или переменных с
индексами (массивов). Данные типы величин могут также иметь стан¬
дартную и нестандартную длину. Длина величины определяет количе¬
ство байт, необходимых для представления ее в оперативной памяти
компьютера и соответственно диапазон допустимых значений, которые
она может принимать.
Константы используются для представления постоянных значений
величин, а также в арифметических выражениях. В табл. 1.2 приведены
примеры представления констант разных типов.
В приведенных примерах для представления констант стандартной
длины используется экспонента е, а нестандартной d. Величины стан¬
дартной длины занимают четыре байта оперативной памяти, а нестан¬
дартной восемь.
Переменная — это величина, которая в программе может принимать
различные значения. Для описания типа переменных стандартной дли¬
ны в программах используются служебные слова:
integer (целые),
real (вещественные),
complex (комплексные),
character (символьные),
logical (логические).
18 Глава 1. Фортран 90 для моделирования физических систем
Таблица 1.2. Примеры представления констант разных типов в Фортран 90
Тип константы
Примеры
Целый
0 (означает число ноль),
-15,
133,
В' 110010' , О'62' , Z' 32' (означают число 50, пред¬
ставленное в системах исчисления с основанием: 2, 8, 16
соответственно)
Вещественный
0 . (означает число ноль),
-.123 (означает число —0,123),
311. (означает число 311,0),
3 . 52е4 (означает число 3,52 • Ю4),
3 . 52d4 (означает число 3,52 • Ю4),
-. 1е-3 (означает число —0,1 • 10_3)
Комплексный
(-2 ., 3 .) (означает число —2,0 + 3,0/),
(.1е5,-3.е12) (означает число Ю4 — 3 • Ю12/)
(1. d5, 7 . d-2) (означает число 105 + 0,07/)
Логический
.true., .false.
Символьный
'32', 'book', 'х=', 'a+b='
Переменные целого, вещественного и логического типа стандартной
длины занимают в памяти четыре байта, а величины комплексного
типа используют вдвое большее количество байт. Переменные сим¬
вольного типа стандартной длины занимают один байт. Для описания
переменных нестандартной длины, приведенные выше служебные сло¬
ва, используются вместе со скобками. В этом случае числа в скобках
указывают на количество байт, которые используются для размещения
переменной в оперативной памяти. Альтернативный способ описания
переменных, оставшийся от стандарта Фортран 77, заключается в ис¬
пользовании спецсимвола звездочка. Например, два следующих описа¬
ния переменной
integer(2) my
integer*2 my
полностью эквивалентны и означают, что переменная с именем ту яв¬
ляется величиной целого типа и занимает в оперативной памяти два байта.
Для корректного описания длины переменных в программе нуж¬
но правильно оценить диапазон значений, которые она может прини¬
мать в ходе вычислений. Неправильная оценка и соответственно непра¬
вильное описание переменных может приводить иногда к получению
«удивительных» результатов, или к «непонятной» работе программы. В
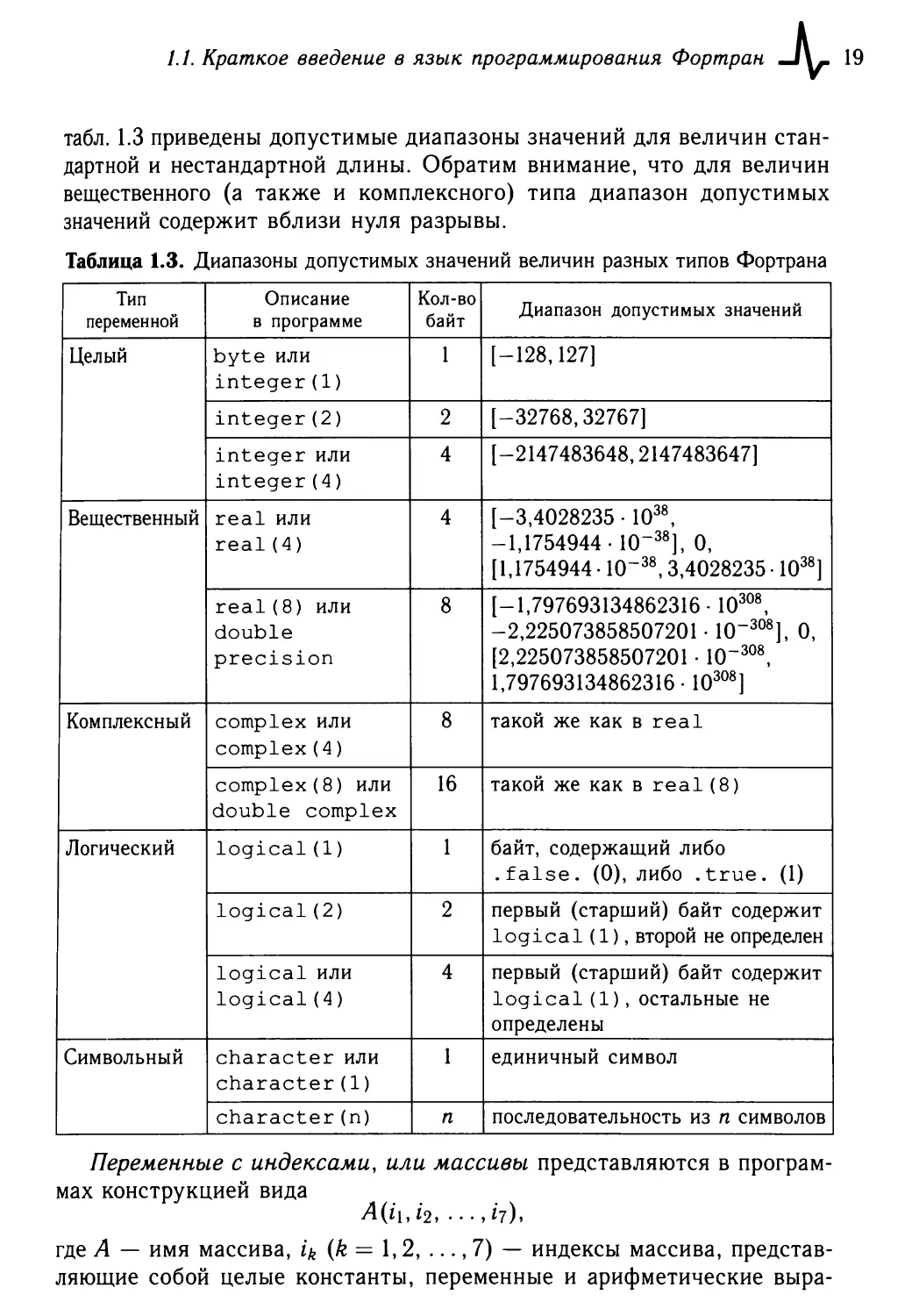
/./. Краткое введение в язык программирования Фортран •Аг 19
табл. 1.3 приведены допустимые диапазоны значений для величин стан¬
дартной и нестандартной длины. Обратим внимание, что для величин
вещественного (а также и комплексного) типа диапазон допустимых
значений содержит вблизи нуля разрывы.
Таблица 1.3. Диапазоны допустимых значений величин разных типов Фортрана
Тип
переменной
Описание
в программе
Кол-во
байт
Диапазон допустимых значений
Целый
byte или
integer(1)
1
[-128,127]
integer(2)
2
[-32768,32767]
integer или
integer(4)
4
[-2147483648,2147483647]
Вещественный
real или
real(4)
4
[-3,4028235 • 1038,
—1,1754944 -10-38], 0,
[1,1754944 • 10-38,3,4028235 • 1038]
real (8) или
double
precision
8
[-1,797693134862316 • Ю308,
-2,225073858507201 • lO”308], 0,
[2,225073858507201 • lO"308,
1,797693134862316 • Ю308]
Комплексный
complex или
complex(4)
8
такой же как в real
complex (8) или
double complex
16
такой же как в real (8)
Логический
logical (1)
1
байт, содержащий либо
.false. (0), либо .true. (1)
logical (2)
2
первый (старший) байт содержит
logical (1), второй не определен
logical или
logical (4)
4
первый (старший) байт содержит
logical (1), остальные не
определены
Символьный
character или
character (1)
1
единичный символ
character(n)
n
последовательность из п символов
Переменные с индексами, или массивы представляются в програм¬
мах конструкцией вида
A{i\, h, • • •, h),
где А — имя массива, ik {k = 1,2, ..., 7) — индексы массива, представ¬
ляющие собой целые константы, переменные и арифметические выра-
X
20 ->V Глава 1. Фортран 90 для моделирования физических систем
жения целого или вещественного типа. В случае величин веществен¬
ного типа значение индекса округляется до ближайшего целого. Ко¬
личество измерений (индексов) массива называют его рангом. Оно не
может быть больше семи. В Фортране массивы бывают статического,
или динамического типа. Статические массивы во время выполнения
программы занимают строго фиксированный объем памяти, который не
может быть изменен в ходе выполнения программы. Напротив, объем
памяти, который занимают массивы динамического типа, может быть
изменен во время исполнения программы.
В начале любой программы все величины, которые в ней исполь¬
зуются, должны быть описаны. Для описания переменных и массивов
используют следующий формат:
type [,attribute ::] list,
где type — оператор описания типа величины, list — список имен пе¬
ременных или массивов, разделенных запятыми, a attribute — атри¬
бут, который описывает природу величины и способ ее использования
и не является обязательным, поэтому взят в квадратные скобки. Ниже
содержится несколько примеров описания переменных и массивов без
использования атрибутов
real b(10), с (5,4), d(-l:2,3:5)
integer (2) е
character(8) name
complex compl_val
Первый оператор иллюстрирует описание в программе массивов. По
умолчанию нижняя граница изменения индекса массива равна единице,
поэтому описание с (5, 4) означает, что массив с состоит из двадцати
элементов. Границы изменения индекса могут быть указаны явно, как
это показано в случае массива d.
Использование атрибутов при описании величин в программе поз¬
воляет придавать им дополнительные свойства. Простейшим примером
атрибута может служить служебное слово parameter. После исполь¬
зования этого атрибута данные воспринимаются программой, как име¬
нованные константы и не могут быть изменены в ходе выполнения
программы. Например, допустимо такое объявление:
real, parameter:: pi=3.14159
В этой программной строке одновременно происходит описание веще¬
ственной константы pi и инициализация ее значения. В этом случае
после атрибута нужно использовать последовательность из двух симво¬
1.1. Краткое введение в язык программирования Фортран 21
лов двоеточия. При объявлении массивов можно использовать атрибут
dimension. Например, строка:
integer, dimension (1:4) :: d,e
описывает в программе два одномерных массива d и е индексы которых
изменяются от единицы до четырех.
Начальные значения величин могут быть заданы в операторах опи¬
сания типа, или с помощью оператора data. Оператор data имеет
следующий синтаксис:
data список имен /список значений/
[, список имен /список значений/]
где список значений может иметь множители повторяемости. Например:
real eps, стах
integer а(10)
logical (1) fl
data eps, стах, fl, a /1.0e-8, 2.4e6, .true., 10*5/
Этот пример содержит множитель повторяемости 10, который исполь¬
зуется при инициализации начальных значений массива а.
Важным понятием Фортрана является конструктор массивов, ко¬
торый имеет следующий формат:
(/список значений элементов массива/) .
Конструкторы массивов используется при инициализации значений
элементов небольших массивов, а также как элементы выражений.
Ниже приведен пример, который иллюстрирует использования кон¬
структора массивов в этих случаях:
real :: а(5)=(/1.1, -2.3, 5.6, 4.1, 7.3/)
integer b (4)
Ь=3*(/1, -2, б, 7/)
В первой строке приведенного кода осуществляется одновременно опи¬
сание массива и инициализация его значений с помощью конструктора
массива. Следует обратить внимание, что при одновременном описа¬
нии и инициализации величин после оператора описания должна все¬
гда использоваться последовательность из двух символов двоеточия.
После выполнения программой последней строки приведенного кода
элементам массива b будут присвоены значения: Ь(1)=3, Ь(2)=-6,
b (3) =18, b (4) =21.
Отметим, что в Фортране существуют правила описания величин
по умолчанию. Допускается не описывать величины целого и веще¬
ственного типов. Так величины, имена которых начинаются символами:
22 Глава 1. Фортран 90 для моделирования физических систем
i, j, к, 1, m, n, I, J, К, L, M, N — считаются целыми, а все другие
вещественными стандартной длины. Изменить правила по умолчанию
можно, если использовать оператор implicit. Например, в программе
может присутствовать строка кода
implicit integer (a, c-f), logical (g)
Это означает, что все величины, имена которых начинаются из букв а, А,
или из букв диапазона c-f, C-F будут иметь тип integer, а величи¬
ны, имена которых начинаются из букв g, G будут иметь тип logical.
Чтобы отменить все правила описания по умолчанию, достаточно в
начале программы использовать оператор implisit none. Использо¬
вание этого оператора автоматически означает, что все переменные и
массивы обязательно должны быть описаны явно, в противном случае
это приведет к ошибке при компиляции программы. Отметим, что
оператор implisit none используется практически во всех кодах
программ, приведенных в этой книге.
Выше были рассмотрены стандартные типы величин, однако этим не
исчерпываются все возможности Фортрана. Множество других типов
данных можно создать с помощью конструктора type. Например, мы
можем создать новый тип данных book:
type book
character(40) author
character(40) title
character(40) publishing
integer year
integer pages
end type book
Таким образом, сконструированный тип book представляет объединение
в одно целое разных стандартных типов Фортрана. Если в программе
используется переменная с именем bk, которая принадлежит к этому
типу, то ее описание в программе должно выглядеть следующим образом:
type (book) bk
Доступ к отдельным полям сконструированного типа осуществляется с
использованием спецсимвола точки. Например, операторы
bk.author='Бартеньев О.В.'
bk.title='Современный Фортран'
bk.publishing='M.: ДИАЛОГ-МИФИ'
bk.уеаг=2000
bk.pages=449
1.1. Краткое введение в язык программирования Фортран -1\г 23
осуществляяют присваивание значений отдельным полям переменной
Ьк типа book.
Сконструированные типы широко используются в объектно-ориен¬
тированном программировании. В данной книге они используются в
некоторых программах (см., например, программу fpu.f90 в гл. 2),
а также в графических процедурах Microsoft Fortran PowerStation 4.0.
1.1.3. Программирование арифметических выражений
Арифметические выражения состоят из отдельных опе¬
рандов знаков арифметических выражений и круглых скобок. В каче¬
стве отдельных операндов могут использоваться константы, переменные,
массивы, указатели библиотечных функций и функций пользователя.
Для кодирования математических операций сложения, вычитания,
умножения и деления используются общепринятые во всех языках про¬
граммирования высокого уровня символы: +, —, *, / соответственно.
Для возведения чисел в степень используется последовательность из
двух символов **. Например, х**2 математически эквивалентно х2.
Арифметические выражения могут состоять всего лишь с одного
операнда. Примерами таких выражений являются:
ь
2.52
sin(х)
М (х, у)
где sin — указатель библиотечной функции, М может быть указа¬
телем функции пользователя с аргументами М(х,у), или элементом
матрицы М с индексами *, у, т. е. Мху. Однозначный ответ по поводу
последней ситуации можно дать, имея полный листинг программы.
Более сложные арифметические выражения состоят из нескольких
операндов, которые соединены между собой знаками арифметических
операций. Примерами таких выражений являются:
a+b*sqrt (х) (означает а + Ьу/х)
х+2 . 52*у- (х+у) ** (1/3) (означает х + 2,52 • у - fyx + у)
sin (х) **2 (означает sin2*)
sin(x**2) (означает sin*2)
Приведенные примеры иллюстрируют, что любые арифметические вы¬
ражения могут быть заключены в круглые скобки и могут выступать
как части более сложных арифметических выражений. Приоритет вы¬
числений в арифметических выражениях соответствует принятым в
арифметике правилам.
При программировании арифметических выражений с величинами
целого типа следует обращать особое внимание на то, что результатом
24 -»\r Глава /. Фортран 90 для моделирования физических систем
их деления всегда будет целая величина или ноль, если знаменатель
больше числителя. В некоторых случаях это может приводить к ре¬
зультатам, не имеющим физического смысла. Эту ситуацию удобно
проиллюстрировать на примере конкретной задачи. Пускай, например,
имеется квадратная решетка, общее число узлов которой L х L. Вы¬
делим случайным образом из общего числа узлов решетки некоторую
часть, скажем N узлов. Теперь, чтобы ответить на вопрос какова доля
выделенных узлов решетки, нам нужно запрограммировать арифмети¬
ческое выражение вида
N/L* *2
В приведенном примере величины N и L — являются целого типа,
поэтому результат вычисления данного выражения будет нуль. Чтобы
получить правильный ответ можно воспользоваться библиотечными
функциями Фортрана real (), которые преобразовывают величины це¬
лого к вещественному типу. Таким образом, в результате вычисления
арифметического выражения вида
real(N)/real (L**2)
получим правильный ответ.
В табл. 1.4 приведены указатели некоторых математических функ¬
ций, которые часто используются при программировании арифметиче¬
ских выражений.
Таблица 1.4. Некоторые библиотечные функции Фортрана
Указатель
функции
Означает
Указатель функции
Означает
log(х)
In X
asin(x)
arcsinx
loglO(х)
IglO*
acos(x)
arccosjt
ехр(х)
е*
atan(x)
arctgx
sqrt(х)
V*
abs(x)
\x\
sin(х)
sin jc
min(xl,.
..,xN)
минимальная величина
списка аргументов
из
cos(х)
cosx
max(xl,.
..,xN)
максимальная величина
списка аргументов
из
tan(х)
t gx
mod(i,j)
остаток от деления целых
чисел i на /
Отметим, что при вычислении тригонометрических функций угол
должен быть задан в радианах. Полный список библиотечных функций
Фортрана довольно обширен. Информацию, о синтаксисе и правилах
1.1. Краткое введение в язык программирования Фортран 25
использования конкретной функции можно получить, воспользовав¬
шись справочной системой. Следует отметить, что указатели имен биб¬
лиотечных функций Фортрана хорошо продуманы и имеют практически
очевидный смысл. Большинство из приведенных в табл. 1.4 функций
используют аргументы вещественного типа стандартной длины, и ре¬
зультат вычисления этих функций есть также величина вещественного
типа стандартной длины. Для других типов величин указатели библио¬
течных функций отличается только префиксом или суффиксом. Напри¬
мер, полный список библиотечных функций для вычисления функции
синуса различных типов аргументов следующий:
Указатель функции
Тип аргумента
Тип результата
sin(х)
dsin(х)
csin(х)
cdsin(х)
sind(х)
dsind(х)
real (4) (в радианах)
real (8) (в радианах)
complex (4) (в радианах)
complex (8) (в радианах)
real (4) (в градусах)
real (8) (в градусах)
real (4)
real(8)
Complex(4)
Complex(8)
real (4)
real (8)
1.1.4. Операции отношения и логические выражения
Наряду с арифметическими выражениями очень важную
роль в программах играют отношения. Отношения очень часто встре¬
чаются в операторе управления if. Отношения включают в себя два
операнда и одну операцию отношения. В качестве операндов могут вы¬
ступать константы и арифметические выражения целого и веществен¬
ного типа. Результатом операций отно¬
шения являются величины логического
типа. В Фортране для обозначения зна¬
ков операций отношения можно исполь¬
зовать либо последовательности букв,
которые начинаются и заканчиваются
точкой, либо последовательности спец¬
символов. Эти последовательности при¬
ведены в табл. 1.5. Отметим, что по¬
следовательности спецсимволов недопу¬
стимы в стандарте Фортран 77. В приведенных в этой книге про¬
граммах отдано предпочтение последовательностям спецсимволов, по¬
скольку они имеют более наглядный смысл и повышают читабельность
программы.
Фортран позволяет также программирование логических выраже¬
ний. Логические выражения образуются из операндов логического ти¬
Таблица 1.5. Обозначение опе¬
раций отношения в Фортране
.EQ.
==
равно
.NE.
/ =
не равно
.LT.
<
меньше
.LE.
<=
меньше равно
.GE.
>=
больше равно
.GT.
>
больше
26 -J\r Глава 1. Фортран 90 для моделирования физических систем
па, знаков логических операций и круглых скобок. К операндам ло¬
гического типа относятся константы, переменные, указатели функций
логического типа и отношения. Для обозначения логических операций
используются следующие последовательности символов:
.not. (означает отрицание)
.and. (означает логическое умножение)
. or. (означает логическое сложение)
.хог. (означает исключающее ИЛИ)
. eqv. (означает эквивалентность)
.neqv. (означает отрицание эквивалентности)
Простейшое логическое выражение состоит либо из одного логического
операнда, либо одного логического операнда перед которым стоит знак
операции отрицания, т. е. логическая операция .not. является унар¬
ной. Все остальные логические операции являются бинарными.
Результат выполнения некоторых логических операций легко по¬
нять, если при выполнении операций вместо двух возможных значений
операндов .true, и .false, воспользоваться их эквивалентными
числовыми значениями 1 и 0. Тогда при выполнении логических опе¬
раций .and. (умножение) и .or. (сложение) можем воспользоваться
мнемонической табличкой из арифметики:
1 .and. 0
1x0 = 0
1 .or. 0
1 + 0 = 1
В этой табличке приведено только по одному примеру использования
операций .and. и .or., результаты всех возможных других вариан¬
тов использования этих операций понятны по аналогии. Исключение
составляет разве что случай:
1 . or. 1
1 + 1/1
Результат выполнения операции .or. в этом случае есть .true.,
т. е. 1. Операция .not. изменяет значение операнда на противополож¬
ное. Другие логические операции при программировании физических
задач практически не используются, поэтому мы не будим останавли¬
ваться на них детально.
1.1.5. Операторы присваивания и управления
Исполнимая часть программы может состоять только из
последовательности операторов присваивания. Пример такой програм¬
1.1. Краткое введение в язык программирования Фортран ->\г 27
мы был рассмотрен в п. 1.1.1. В общем случае оператор присваивания
имеет синтаксис:
N а=Ь,
где N — либо метка оператора, либо пусто (отсутствие каких-либо
символов), а — переменная или массив, b — константа или выражение,
символ = используется для обозначения операции присваивания. При
выполнении оператора присваивания сначала осуществляется вычис¬
ление значения величины Ь, а затем ее значения приводится к типу
и длине величины а. Преобразование типов величин выполняется в
соответствии со следующими правилами:
• если а — целого типа, а b — вещественного, то выбирается целая
часть Ь;
• если а — целого типа, а b — комплексного, то выбирается целая
часть действительной компоненты Ь;
• если а — вещественного типа, а b — целого, то выбирается значе¬
ние Ь;
• если а — вещественного типа, а b — комплексного, то выбирается
действительная часть компоненты Ь;
• если а — комплексного типа, а b — вещественного или целого, то
действительной части а присваивается значение Ь, а мнимая часть
полагается равной нулю.
Фортран выполняет операторы программы последовательно, но эту
последовательность можно изменить с помощью управляющих опера¬
торов. Простейшим управляющим оператором является оператор без¬
условного перехода:
goto N
При выполнении этого оператора управление передается оператору,
помеченному меткой N. Кроме безусловного оператора перехода goto
в Фортране существует также устаревший оператор перехода goto по
назначению, который имеет следующий формат:
goto i,(list)
где i — переменная целого типа, list — список меток операторов. К
моменту выполнения этого оператора переменной i должно быть при¬
своены значения одной из меток списка с помощью оператора assign.
Например, пусть задана последовательность операторов:
assign 5 to i
goto i, (3,5,10,15)
После выполнения оператора goto управления выполнением програм¬
мы будет передано оператору с меткой 5.
28 -»\л Глава 1. Фортран 90 для моделирования физических систем
В языке Фортран имеется несколько вариантов синтаксиса управ¬
ляющего оператора if. Условный логический оператор if имеет сле¬
дующий синтаксис:
if(е)s
где е — логическое выражение, s — выполнимый оператор.
При выполнении условного логического оператора if выполняется
вычисление логического выражения и управление передается операто¬
ру s, если значение логического выражения е есть истина, а в против¬
ном случае происходит выполнение операторов следующей строки кода.
Фрагмент кода, приведенный ниже, иллюстрирует совместную работу
условного оператора if и оператора stop:
if (b==0) stop 'b=0!'
c=a/b
Данный фрагмент кода иллюстрирует, каким образом можно из¬
бежать в программе критической ситуации, связанной с делением на
ноль. Если значение переменной b в программе вдруг окажется равным
нулю, то управление будет передано оператору stop, работа программы
будет приостановлена и на экран дис¬
плея будет выведено текстовое сообще¬
ние Ь=0 !. В противном случае будет вы¬
числено значение переменной с.
Более сложный синтаксис имеет блоч¬
ный оператор if. Работу этого операто¬
ра удобно объяснить на примере модели¬
рования случайного движения частицы.
Пускай у нас имеется некая частица, ко¬
торая совершает плоское движение и в
единицу времени может смещаться на
единичное расстояние случайным обра¬
зом в одном из четырех направлений со¬
гласно схеме, представленной на рис. 1.1.
Направление смещения определяется зна¬
чением целой переменной direct, кото¬
рая может принимать четыре возможных значения: 1, 2, 3, 4. Тогда
вычисление нового положения частицы при смещении можно запро¬
граммировать следующим образом:
if(direct==l)then
у=у+1
else if(direct==2)then
x=x+l
1
A
4<=
О
=>2
V
3
Рис. 1.1. Схема вариантов дви¬
жения частицы для вычисле¬
ния ее нового положения
1.1. Краткое введение в язык программирования
Фортран 29
else if(direct==3)then
y=y-l
else
x=x-l
end if
В данном фрагменте кода в зависимости от значения переменной
direct осуществляется выполнение одного из четырех блоков опе¬
ратора if. Данный пример предусматривает анализ четырех значений
переменной direct, поэтому используется наиболее общий вариант
синтаксиса оператора. В случае меньшего числа вариантов анализа
значения управляющей переменной, синтаксис оператора if намного
упрощается.
Приведенные ниже примеры иллюстрируют синтаксис оператора в
случае одного, или двух вариантов анализа:
В примере, показанном слева, переменной у будет присвоено зна¬
чение единица, а переменной а значение арифметического выражения
b+с только тогда, когда значение переменной х будет больше нуля.
В противном случае часть кода, которая стоит внутри оператора if
будет проигнорирована. В примере, показаниям справа, если значение
переменной d больше нуля, то переменной а будет присвоено значение
единица, а иначе два.
Отметим, что в сложных программах нередки ситуации, когда
внутрь одного из блоков, или даже в каждом блоке операторы if могут
быть вложены другие блочные операторы if.
При работе с векторами или матрицами, при суммировании рядов и
в других ситуациях возникает потребность в повторении однотипных
вычислений заданное число раз. В этих случаях используют опера¬
торы цикла. В Фортране существует два оператора цикла: do и do
while. Варианты синтаксиса оператора do иллюстрируют приведенные
ниже примеры:
do 100 n=start,stop,step do n=start,stop,step
a(n)=2*n+l a(n)=2*n+l
100 continue end do
If(x>0)then
У=1
a=b+c
end if
if(d>0)then
a=l
else
a=2
end if
Оба примера кода выполняют вычисление элементов массива а(п) по
формуле: ап = 2п + 1. Начальное и конечное значение индекса п, а так¬
30 •Ar Глава 1. Фортран 90 для моделирования физических систем
же шаг изменения определяются значением переменных start, stop,
step соответственно. В случае если значение переменной step не
задано то полагают, что шаг прироста индекса равен единице. Отметим,
что в Фортран 77 допустим только оператор do вместе оператором
continue в конце цикла. Число 100 в варианте слева является меткой
окончания цикла. При работе с массивами, которые имеют два или
большее число индексов операторы цикла do вкладывают друг в друга.
В этом случае, предпочтительным является вариант синтаксиса опера¬
тора, приведенный слева, поскольку он позволяет легко увидеть начало
и окончание каждого цикла.
Для досрочного прекращения выполнения цикла do в Фортран 90
можно использовать внутри цикла оператор exit. Он передает управ¬
ление первому оператору, которые находится после окончания цикла.
Например:
loopl: do n=l,10
if(n==3) exit loopl
write(*,*) n
end do loopl
a=l
При выполнении этого примера на дисплее будут напечатаны значения
переменной п=1,2, а затем будет выполнен оператор присваивания
а=1. Начало и окончание цикла при использовании оператора exit
должно быть помечено меткой (в приведенном примере loopl).
Проиллюстрируем синтаксис использования оператора цикла do
while на примере вычисления суммы ряда я-2:
s=0; п=1
do while(n<=100)
s=s + l/n* *2
n=n+l
end do
В данном примере, переменная s используется в качестве накопителя
значения суммы ряда. Операторы внутри цикла будут выполняться до
тех пор, пока отношение п<=100 истинно.
1.1.6. Особенности работы с массивами
Одной из особенностей Фортрана является наличие мас¬
сивов динамического типа. Массивы динамического типа используются
во многих программах этой книги. Их использование предусматривают
соблюдение некоторых обязательных правил. Проиллюстрируем их на
конкретном примере. Пускай, имеем набор рыбацких сетей с квадрат¬
ными ячейками, каждая из которых состоит из L х Н узлов. В общем
1.1. Краткое введение в язык программирования Фортран 31
случае значения L и Н могут быть разными. Положение каждого узла
сети может быть охарактеризовано парой целых чисел, а его состояние
еще одним числом, равным 0 для разрушенного узла и 1 — для целого.
Для описания состояния узлов каждой сети можно воспользоваться
массивом динамического типа. Пускай имя этого массива будет s, тогда
описание массива в программе имеет вид
integer(1),allocatable:: s(:,:)
Такая запись означает, что s — двухиндексный массив динамиче¬
ского типа, каждый элемент которого занимает в памяти один байт.
Принадлежность массива в Фортране к динамическому типу опреде¬
ляется с помощью атрибута allocatable. Конечно, для описания
состояния узла (целый или разрушенный) достаточно было бы и одного
бита, но, к сожалению, в Фортране нет стандартных величин длиной
в один бит. Приведенное описание массива s достаточно сделать один
раз. Оно пригодно для сетей любых размеров. Размер конкретной сети
должен быть указан на этапе размещения массива в оперативную па¬
мять, которая осуществляется с помощью оператора allocate:
allocate(s(1:1000,1:50))
В приведенном примере размер сети составляет 1000 х 50 узлов.
В операторе allocate дополнительно указаны границы изменения
каждого индекса массива от 1 до 1000 для величины L и от 1 до 50
для величины Н.
Для того чтобы освободить оперативную память, занимаемую дина¬
мическим массивом достаточно выполнить в программе оператор:
deallocate (s)
Отметим, что в приведенных примерах операторы allocate и
deallocate используются для загрузки и выгрузки только одно¬
го массива, однако их можно использовать сразу и для нескольких
массивов.
Сразу после размещения массива в оперативную память всем его
элементам присваивается нулевое значение, что фактически означает
полностью разрушенную сеть. Если сеть цела, то для описания состо¬
яния всех ее узлов достаточно выполнить один оператор присваивания
s=l, который означает, что всем элементам массива s будет присвоено
единичное значение. Понятно, что подобным образом всем элементам
массива можно присвоить и любое другое значение.
Представим себе несколько искусственную ситуацию: пусть у на¬
шей сети в одном ряду, скажем 10, все нечетные узлы разрушены,
а в других рядах все узлы целы. Для того чтобы описать состояние
32 •Ar Глава 1. Фортран 90 для моделирования физических систем
такой сети после размещения массива s в оперативной памяти нужно
выполнить два оператора присваивания:
s=l; s(1:1000:2,10)=0
В этом примере используется индексный триплет 1:1000:2 в ко¬
тором, первая цифра обозначает начальное значение индекса, вторая
конечное, а третья — шаг прироста. Триплеты очень мощное средство
Фортрана. Их использование при работе с массивами позволяет многие
задачи запрограммировать в несколько строк.
Зададимся теперь вопросом: сколько целых узлов в нашей сети? В
Фортране ответ на вопрос может быть получен и напечатан на экране
двумя способами:
write (*,*) sum(s)
write (*,*) count(s>0)
Эти примеры иллюстрируют работу двух библиотечных функций
sum и count. Функция sum осуществляет суммирование всех эле¬
ментов массива, а функция count — подсчет количества элементов в
массиве s, значения которых больше нуля. В табл. 1.6 приведен список
некоторых других функций Фортрана для работы с массивами.
Таблица 1.6. Некоторые функции Фортрана для работы с массивами
Функция
Назначение
dot_product(a,b)
Выполняет скалярное произведение двух векторов а и
Ъ (одномерных массивов)
matmul(а,b)
Выполняет умножение двух матриц а и b (двухмер¬
ных массивов)
maxval(а)
Находит максимальное значение элемента в массиве а
minval(а)
Находит минимальное значение элемента в массиве а
transpose(а)
Выполняет транспонирование матрицы а (двухмерно¬
го массива)
where(s)a=b
Всем элементам массива а, для которых значение ло¬
гического выражения s истинно, присваивается зна¬
чение b (константа, переменная или арифметическое
выражение). Например, where (а>0) а=1
Многие другие операции с элементами массивов также програм¬
мируются легко. Пускай, например, имеем три вектора x,y,z. Для их
представления в программе удобно воспользоваться массивами веще¬
ственного типа, описав их следующим образом:
real х (1: 3) , у (1: 3) , z (1: 3)
1.1. Краткое введение в язык программирования Фортран ->\г 33
Тогда строки кода означают:
z=x+y (означает г — х + у)
у=3*х (означает у = Зх)
a=sum(x*y) (означает а =х - у)
1.1.7. Программные единицы
При написании программы исходная задача, как правило,
разбивается на отдельные подзадачи, которые реализуются в виде от¬
дельных программных единиц. В Фортране к ним относятся: главная
программа, процедуры и модули. Процедуры, в свою очередь могут быть
реализованы в виде функций, или подпрограмм и бывают внешними и
внутренними.
Рассмотрим теперь более детально синтаксис основных программ¬
ных единиц.
В каждом проекте может быть только одна главная программа. Она
имеет следующий формат:
program [ имя программы ]
[операторы описания]
[выполнимые операторы]
[contains
внутренние процедуры]
end [program [имя программы] ]
Здесь и дальше квадратные скобки используются для обозначения
необязательных элементов синтаксиса. Пример программы, которая со¬
стоит только из одной программной единицы — главной программы
был приведен в п. 1.1.1. После оператора contains, который может
использоваться в главной программе, а также во внешних процеду¬
рах и модулях, могут быть заданы внутренние процедуры. Внутрен¬
ние процедуры могут быть вызваны только с программной единицы-
носителя, или из других внутренних процедур той же самой про¬
граммной единицы. Внутренние процедуры в отличие от внешних и
модульных процедур не могут содержать в себе других внутренних
процедур.
В Фортране могут быть определенны два типа процедур: подпро¬
граммы и функции. Синтаксис, который нужно использовать при коди¬
ровании процедуры, часто понятен из конкретной подзадачи, которую
решает процедура. Но, обычно, процедуру оформляют в виде функции,
если результат ее выполнения можно записать в одну переменную.
34 -»\r Глава 1. Фортран 90 для моделирования физических систем
В других случаях для оформления процедуры нужно использовать под¬
программу. Общий формат процедур имеет следующий вид:
subroutine имя подпрограммы (список формальных параметров)
[операторы описания]
[выполнимые операторы]
[contains
внутренние процедуры]
end [subroutine [имя подпрограммы] ]
function имя функции (список формальных параметров)
[операторы описания]
[ выполнимые операторы ]
[contains
внутренние процедуры]
end [function [имя функции] ]
Список формальных параметров процедур может содержать также
имена других процедур. Процедуры-функции имеют одну результирую¬
щую переменную, которая в Фортран 77 совпадает с именем функции.
В Фортран 90 можно задать другое имя результирующей переменной,
которое отличается от имени функции с помощью оператора result.
В качестве примера, иллюстрирующего использование функции и ра¬
боту оператора result, приведем код небольшой программы, который
состоит из двух программных единиц: главной программы и внешней
процедуры-функции:
program my
integer mysum !описываем внешнюю функцию
integer:: c=l,d=2, res
res=mysum(c, d)
write (*, *)res
end program my
function mysum(a,b) result (s)
integer a,b,s
s=a+b
end
В главной программе осуществляется вызов внешней функции mysum
и результат ее выполнения присваивается переменной res, а затем
печатается на дисплей. Обратите внимание, что внешняя функция
описывается в главной программе как обычная переменная. Функция
mysum осуществляет сложение двух чисел. Результат сложения присва¬
1.1. Краткое введение в язык программирования Фортран •Аг 35
ивается результирующей переменной s. В случае отсутствия оператора
result функция mysum должна иметь вид
integer function mysum(a, b)
integer a,b
mysum =a+b
end
В этом случае имя результирующей переменной совпадает с именем
функции, а ее тип описан в заголовке функции. Выполнение опера¬
тора end в конце процедуры приводит к передаче управления в вы¬
зывающую программную единицу (в данном случае в главную про¬
грамму). В приведенных примерах в конце функции не используется
служебное слово function, которое не является обязательным для
внешних процедур. Во внутренних и модульных процедурах, закры¬
вающие операторы обязательно должны содержать служебные слова
subroutine и function. Выход из процедуры в любом месте можно
осуществлять также с помощью оператора return. Очень часто этот
оператор используется в блоках оператора if, для выхода из проце¬
дуры по достижению определенного условия. Процедура в этом случае
может содержать несколько операторов return, которые обеспечивают
альтернативные варианты прекращения ее выполнения.
Рассмотренную выше задачу сложения чисел можно было бы ре¬
шить, воспользовавшись также внешней подпрограммой. В этом случае
программа могла бы выглядеть следующим образом:
program my
integer mysum !описываем внешнюю функцию
integer:: c=l,d=2, res
call mysum(c, d, res)
write (*,*)res
end program my
subroutine mysum(a, b, s)
iteger a, b, s
s=a+b
end subroutine mysum
Вызов внешней подпрограммы из главной программы осуществля¬
ется с помощью оператора call.
Следует обратить внимание, что в самих процедурах и операторах
вызова их из главной программы имена в списке параметров, могут
отличаться. Имена параметров, которые используются при описании
процедуры, называют формальными, а те, которые используются при
36 -»\r Глава 1. Фортран 90 для моделирования физических систем
вызове процедуры — фактическими. При вызовах процедур нужно сле¬
дить, чтобы списки формальных и фактических параметров были со¬
гласованны между собой по типу и длине.
Рассмотрим теперь на конкретном примере, как происходит пере¬
дача массивов у процедуры. Пускай нам нужно написать программу,
которая вычисляет расстояние между двумя точками в п-мерном про¬
странстве. Для описания координаты точек удобно воспользоваться
массивами. Программа, решающая поставленную задачу, может иметь
следующий вид:
program dist
real, dimension(1:3) :: a=(/1.1,2.4,7 . 2/), &
b=(/4.2,5.6,9.3/)
real r
write (*,*) r(a,b,3)
end program dist
real function r(pl,p2,n)
integer n, index
real, dimension(1:n):: pl,p2
real:: s=0.
do index=l,n
s=s +(pi(index)-p2(index))**2
end do
r=sqrt(s)
end
В данном примере функция г используется для вычисления рассто¬
яния в трехмерном пространстве, однако она пригодна и для общего
случая.
Модули используются для описания в программах глобальных вели¬
чин проекта, а также модульных процедур. В приведенных в этой книге
программах модули, в основном, используются только для описания
глобальных переменных и массивов. Такое использование модулей поз¬
воляет сократить списки передаваемых в процедуры параметров и тем
самым повысить читабельность программ. Модули имеют следующий
формат:
module имя модуля
[раздел описаний]
[contains
модульные процедуры]
end [module [имя модуля] ]
1.1. Краткое введение в язык программирования Фортран -*\г 37
Доступ к модулю с программной единицы (главной программы,
внешней процедуры, или другого модуля) осуществляется с помощью
оператора:
use имя модуля
Оператор use должен стоять в начале программной единицы. При
включении одного модуля в другой необходимо следить, чтобы модуль
не ссылался сам на себя ни прямо, ни через другие модули. По умолча¬
нию все переменные модулей имеют атрибут public, т. е. они являют¬
ся доступными во всех программных единицах, которые ссылаются на
данный модуль с помощью оператора use. Если возникает потребность
сделать определенную переменную доступной только внутри модуля,
то при описании переменной необходимо воспользоваться атрибутом
private.
В заключение этого раздела приведем пример программы, которая
иллюстрирует использование модулей в Фортране:
module myl
integer:: a=l,b=l
integer, private :: c= 1
contains
subroutine mosub(d)
integer:: d,c2=l
write (*,*) 'mosub:', d,b
d=2; b=c+l
call mosubl (d)
write (*,*) 'mosub:', d,b
contains
subroutine mosubl(d)
integer d
write (*,*) 'mosubl:', d,b
d=d+l; b=b+c2
end subroutine mosubl
end subroutine mosub
end module myl
program pm
use myl
integer с
write (*,*) 'promt_l:', a, b, с
call mosub(a)
write (*,*) 'promt_2:', a, b
end program pm
В данном примере программа состоит из модуля myl и главной
программы pm. Модуль myl кроме описания переменных содержит
38 •Ar Глава 1. Фортран 90 для моделирования физических систем
определение модульной процедура mosubl, а та в свою очередь содер¬
жит внутреннюю процедуру mosubl. В результате выполнения этой
программы на экране будет напечатано:
promt_l: 1 10
mosub: 1 1
mosubl: 2 2
mosub: 3 3
promt_2: 3 3
Из этого примера видно, что значения переменных а, и b доступны в
главной программе благодаря использованию оператора use. Значения
переменной с остается неизвестно, поскольку она описана в модуле
myl с использованием атрибута private. Значения переменных b и
с2 доступны в процедурах модуля. Такая передача данных в процедуры
модуля осуществляется через тело модуля.
1.1.8. Операторы ввода-вывода и работа с файлами
В Фортране существует два универсальных оператора
ввода-вывода данных. Они имеют следующий формат:
read (a,b) с
write (a,b) с
где а — номер устройства ввода-вывода, на который ссылается набор
данных, b — метка оператора формата, с — список величин, read-
оператор ввода, a write — оператор вывода.
В приведенных выше примерах программ оператор вывода write
использовался в виде write (*,*). Такая форма записи оператора
вывода означает, что программа будет выводить значения величин из
списка с на дисплей в свободном формате. Это замечание справедливо
и по отношению к оператору read, только в этом случае устройством
ввода по умолчанию является клавиатура. Например, для последова¬
тельности операторов вида
read (*,*) myvar
write(*,*) myvar
значение переменной myvar будет считываться с клавиатуры в свобод¬
ном формате, и затем печататься на экране также в свободном формате.
При необходимости вывода данных в заданном формате использу¬
ются спецификаторы формата. Они могут задаваться в виде последова¬
тельности символов непосредственно в операторах ввода-вывода, или
внутри оператора format. В табл. 1.7 приведены основные специфика¬
торы формата, которые часто используются в программах.
1.1. Краткое введение в язык программирования Фортран ->v 39
Таблица 1.7. Спецификаторы формата Фортрана
Спецификатор формата
Назначение
Iw, Bw, Ow, Zw
Служит для представление величин целого типа в
десятичной, двоичной, восьмеричной и шестнадца¬
теричной системах исчисления соответственно
Fw. d
Служит для представления вещественных и ком¬
плексных чисел в фиксированной форме
Ew.d, ENw.d, ESw.d
Служит для представления вещественных и ком¬
плексных чисел в экспоненциальной форме
Dw. d
Служит для представления вещественных и ком¬
плексных чисел двойной точности
Lw
Служит для представления величин логического
типа
Aw
Служит для представления величин символьного
типа
Gw.d
Универсальный формат, который используется для
представления величин целого, вещественного,
комплексного и логического типа по умолчанию
В приведенной таблице используются следующие обозначения: w —
целая константа без знака, означающая общую длину поля (в симво¬
лах) для представления величин, d — часть (количество знаков после
запятой) от общей длины поля w, которая используется для представле¬
ния дробной части величин вещественного и комплексного типа. Длина
поля w должна выбираться с учетом наличия знака у величин и деся¬
тичной точки, для которых выделяется по одной позиции. Для величин
вещественного типа, представленных в экспоненциальной форме, длина
поля w также должна учитывать одну позицию для вывода символа е,
одну для знака порядка и еще две для вывода его значения. Специ¬
фикаторы формата EN и ES соответствуют экспоненциальной форме
представления вещественных чисел, принятой в инженерных и научных
расчетах. В этих спецификаторах для представления порядка числа
отводится три позиции. С помощью спецификатора EN мантисса числа
формируется таким образом, чтобы целая часть числа принадлежала
интервалу значений от 1 до 1000. Спецификатор ES формирует целую
часть мантиссы в интервале значений от 1 до 10. При выводе величин
логического типа в правой части поля длинной w позиций печатается
символ Т, или F. Для величины символьного типа длина поля должна
соответствовать фактической длине (в символах) константы или пере¬
менной. Отметим, что при неправильно выбранной длине поля w вместо
числа на печать будет выводиться последовательность звездочек. При
40 •Ar Глава 1. Фортран 90 для моделирования физических систем
выводе величин комплексного типа используются два спецификатора
формата для действительной и мнимой части числа.
По умолчанию ввод-вывод выполняется с использованием специфи¬
катора Gw.d, который в зависимости от типа величин и их значения
преобразует их к рассмотренным выше форматам. При этом малые
вещественные числа выводятся на печать в фиксированной форме, а
большие преобразуются к экспоненциальной форме.
Рассмотрим пример использования некоторых спецификаторов фор¬
мата для вывода величин разных типов. Пускай, имеется набор величин:
-1234, -123.456 , 'book' .
Поставим себе задачу напечатать эти величины на одной строке.
Для печати целого числа -12 34, нужно воспользоваться спецификато¬
ром I. Длина поля для первой величины в строке должна быть больше
на единицу, поскольку первая позиция каждой строки вывода исполь¬
зуется для символов управления кареткой печатающего устройства.
Таким образом, для целого числа должен использоваться специфика¬
тор 16. Отметим, что если воспользоваться спецификатором 15, то
вместо ожидаемого числа -1234 будет напечатано положительное чис¬
ло 12 34. Для вывода действительного числа -123.4 56 воспользуемся
спецификатором F9.3, а для печати символьной константы 'book'
спецификатором А5. Программа, которая выполняет поставленную за¬
дачу, имеет следующий вид:
program simpleprint
integer:: а=-1234
real:: b=-123.456
write (*,'(i6, f9.3, a5)') a, b, 'book'
write (*,1) a,b,'book'
1 format (i6, f9.3, a5)
end program simpleprint
Данная программа иллюстрирует два возможных варианта исполь¬
зования оператора write: в первом варианте спецификатор формата
задан в самом операторе вывода, а второй вариант предусматривает
использование оператора формата с меткой 1.
В приведенном примере искусственно завышена длина полей для
вещественной и символьной величины в спецификаторе формата на
единицу для того, чтобы выводимые на печать величины были отделены
друг от друга символом пробела. В случае, если бы были выбраны спе¬
цификаторы F8.3 и А4, то последние две величины будут напечатаны
слитно с целым числом. Чтобы исключить данную ситуацию нужно
уметь управлять размещением информации внутри текущей строки.
1.1. Краткое введение в язык программирования Фортран •Аг 41
Для этого в языке Фортран 90 существует ряд дополнительных специ¬
фикаторов форматов. Одним из них является пХ, который используется
для вставки п пробелов в текущей строке. Спецификаторы Tn, TRn,
TLn используются для смещения каретки внутри строки. Тп позволяет
начать печать с n-й позиции текущей строки, а спецификаторы TRn и
TLn используются для относительного смещения каретки от текущего
положения на п позиций вправо, или влево соответственно. Переход
на новую строку можно осуществить с помощью символа обратного
слэша \, а последовательность из двух символов \\ позволяет создать
пустую строку. Приведенная ниже программа иллюстрирует, каким
образом с помощью этих операторов осуществляется управление раз¬
мещением информации в строке:
program pi
integer:: а=1, b=3, с=415
character(3):: sl='Pi='
character(1):: s2='.'
write(*,l) a, b, c, si, s2
1 format (T6,I2, TL4,I2 ,TR2,13,T2,A3,TR1,A1 )
end program pi
В результате выполнения этой программа на экране будет напеча¬
тана последовательность символов:
Pi=3.1415
При вводе-выводе больших массивов удобно использовать цикличе¬
ские списки ввода-вывода. Такие списки имеют следующий формат:
(список объектов цикла, var=start, stop [, inc] )
где каждый объект списка может быть переменная или новый цикли¬
ческий список, var — счетчик цикла, start, stop, inc — начальное,
конечное значение счетчика цикла и шаг его прироста соответствен¬
но. Проиллюстрируем использование циклического списка примерами
нескольких операторов вывода:
write (*,'(lx,80al)') к=1,80)
write (*,2) г к=1, 40)
2 format (lx,40(lx, al))
Первый оператор осуществляет печать на экран сплошной, а второй
пунктирной линий. В данном примере при определении спецификаторов
формата используются коэффициенты повторяемости, которые могут
использоваться не только к отдельным спецификаторам формата, но и
к списку спецификаторов, взятому в круглые скобки.
42 -iV Глава 1. Фортран 90 для моделирования физических систем
В Фортране 90 несколько величин можно объединить в именован¬
ный список ввода-вывода, который создается в разделе описаний про¬
граммной единицы с помощью оператора namelist и имеет следую¬
щий формат:
namelist /имя списка/ список переменных
[/имя списка/ список переменных]
Ввод-вывод именованных списков осуществляется операторами
read и write:
program nl
integer:: a,b
complex:: z
namelist /my/ a,b,z
read(*,my); write(*,my)
end program nl
Данная программа осуществляет чтение с клавиатуры именованного
списка ту, состоящего из двух величин целого типа а, b и одной
величины комплексного типа z, а затем печатает набранный список
на экран. Набор именованного списка должен осуществляться с со¬
блюдением определенных правил. Так, например, при выполнении этой
программы именованный список может быть набран на клавиатуре с
помощью следующих последовательностей символов:
&my а=1 b=2 z=(3,4) /J
или
&myj
z=(3,4)J
b=2 J
a=lj
/J
где J означает Enter. Обязательным условием является наличие в
начале именованного списка символов &ту, а в конце спецсимвола /.
Порядок набора значений величин не играет роли. Набранный список
в любом случае будет напечатан на экране в виде
&MY
А = 1
В = 2
Z = (3.000000, 4.000000)
/
1.1. Краткое введение в язык программирования Фортран -*\г 43
Именованный список очень удобен при проведении компьютерного
моделирования. Например, можно объединить все входные параметры
модели в один именованный список и оформить его в отдельном файле,
который может дополнительно содержать любой текст, поясняющий
смысл того, или иного параметра модели. В начале работы программа
считывает именной список из файла, а затем выполняет его обработку.
Использование такой технологии позволяет проводить исследование по¬
ведения модели при любых допустимых значениях входных параметров
без повторной компиляции программы.
Для того чтобы считать или записать данные в файл нужно пред¬
варительно его открыть с помощью оператора open. Каждому файлу,
который открывается программой оператором open, должен быть при¬
своен свой индивидуальный номер. Все дальнейшие операции чтения и
записи в файл, а также закрытие файла оператором close осуществля¬
ются с использованием этого номера. Оператор open позволяет задать
довольно большое количество параметров при открытии файла. Полный
список его опций можно посмотреть в справочной системе. Однако, для
осуществления простейших операций ввода-вывода достаточно знать
лишь некоторые из них.
Например, для считывания числовых данных, представленных в
текстовом файле с именем my.dat в виде двух столбцов вещественных
чисел можно использовать следующую программу:
program FileRead
implicit none
integer, parameter:: N=100 !количество пар чисел
integer:: i=0
real, dimension (1:N):: x, у
open (1, file='my.dat') !открываем файл
do while (.not. eof(l))
i=i + l
read (1,*) x(i),у(i)
write(*,*) x(i),у(i)
end do
close (1)
end program FileRead
В данной программе файлу my.dat при открытии присваивается
логический номер 1. Значения чисел из файла сначала считываются
оператором read, присваиваются элементам массивов х (), у (), а за¬
тем печатаются на экран оператором write. Количество пар чисел в
файле может быть произвольным, однако не должно превышать чис¬
ло 100. Для обработки файлов с большим количеством чисел нужно
увеличить значение параметра N. Считывание числовой зависимости
44 ->\r Глава 1. Фортран 90 для моделирования физических систем
продолжается внутри цикла do while до тех пор, пока не будет до¬
стигнут конец файла. Проверку на достижение окончания файла вы¬
полняет логическая функция eof (). Она устроена таким образом, что
при обработке данных внутри файла возвращается значение ложь, а в
противном случае истина. Поэтому чтобы согласовать работу функции
eof с циклом do while в заглавии цикла используется логическое
выражение (.not. eof(l)). Отметим, что для правильной работы
программы FileRead с данными нужно проверить, чтобы файл не
содержал пустых строк без чисел.
1.1.9. Генерация случайных чисел
В настоящее время существует два хорошо известных
класса методов генерирования случайных чисел. Первый из них осно¬
ван на использовании реальных физических явлений, например под¬
счета времени между щелчками счетчика Гейгера. Достоинством этого
класса методов является то, что числа, получаемые этим методом, дей¬
ствительно полностью случайны. К недостатку следует отнести то, что
данный класс методов, как правило, является достаточно «медленным»
и получаемые числа не поддаются воспроизведению, что утрудняет
отладку программ.
Второй класс методов основан на компьютерных алгоритмах. Для
этого класса методов все выглядит с точностью до наоборот: достоин¬
ства и недостатки меняются местами. Из-за того, что числа в этом ме¬
тоде можно подобрать, если конечно известен алгоритм их получения,
то строго называть их случайными нельзя. Чаще всего их называют
псевдослучайными. Однако в дальнейшем изложении на этом не будет
акцентироваться внимание, и данные числа будут называться случайными.
Сегодня существует много алгоритмов для получения случайных
чисел и некоторые из них достаточно сложны. Ниже будет описан
алгоритм конгруэнтного генератора, который позволяют генерировать
случайные числа, равномерно распределенные на интервале от 0 до 1.
Для получения последовательности случайных чисел вначале берется
некоторое целое число хо, которое называют зерном (seed). Затем
выполняются вычисления, использующие формулы:
хп = mod(ax„_i, m), (1.1)
или
хп = mod(ax„_i + b, т) (1.2)
и получается новое целое число хп, п > 1. Величины а,Ь и т — целые
положительные числа, a mod(ii,i2) ~ функция, вычисляющая оста¬
ток от деления двух целых чисел i\ и Алгоритм (1.1) называют
мультипликативным конгруэнтным генератором, а (1.2) — линейным,
1.1. Краткое введение в язык программирования Фортран -*\г 45
или смешанным (из-за наличия в формуле (1.2) операций умножения
и сложения) конгруэнтным генератором. Формулы (1.1) и (1.2) легко
запрограммировать. Ниже представлен код программы, реализующий
эти алгоритмы:
module comdata
!параметры линейного конгруэнтного генератора
integer:: а=7
integer:: b=5
integer:: m=15
integer х01,х02 !зерно генератора
end module comdata
program rndnum
use comdata
implicit none
integer i
integer numseed !зерно
integer xnl, xn2 !случайные числа
numseed=4
write(*,*) ' '
write(*,*) ' numseed=',numseed
write (*,*) ' i xnl xn2'
call initseeds(numseed)
do i=l,12
call rnum (xnl,xn2)
write (*,*) i, xnl, xn2
enddo
end program rndnum
!процедура инициализации генератора
subroutine initseeds (numseed)
use comdata
integer numseed !зерно генератора
x01=numseed
x02=x01
end subroutine initseeds
!процедура генерации случайных чисел
subroutine rnum(xnl,xn2)
use comdata
integer xnl,xn2
x01=mod(a*x01,m) !формула (1.1)
x02=mod(a*x02+b,m) {формула (1.2)
xnl=x01
xn2=x02
end subroutine rnum
46 •Ar Глава 1. Фортран 90 для моделирования физических систем
Данная программа находится в файле rndnum. f 90. Параметры
формул (1.1) и (1.2), а также начальное число хо определены в модуле
общих переменных comdata.
Результат работы данной программы представлен на рис. 1.2, где
приведены первые 12 чисел, полученных с помощью генератора rnum
для обеих формул. При анализе полученных последовательностей чи¬
сел видно, что первая последовательность начинает повторяться с чет¬
вертого числа, а вторая с двенадцатого, таким образом, период пер¬
вой последовательности tp\ = 4, а второй tp2 = 12. Такой малый период
обусловлен неудачным выбором параметров а,Ь и т в формулах (1.1)
и (1.2). Следует отметить, что главное условие проведения корректного
компьютерного моделирования заключается в выборе такого генератора
случайных чисел, который имеет период намного больше количества
случайных чисел, необходимых для проведения моделирования. В зада¬
че 1 к этой главе описан способ оценки периода генератора случайных
чисел.
nuaseed=
4
i
хп1
хп2
1
13
3
2
1
11
3
7
7
4
4
9
5
13
8
б
1
1
7
7
12
8
4
14
9
13
13
10
1
6
11
7
2
12
4
4
13
13
3
14
1
11
15
7
7
Рис. 1.2. Результат работы программы rndnum. f 90 при численных значениях
параметров формул (1.1) и (1.2): а = 7, Ъ = 5 и т = 15. Численное
значение зерна хо = 4
Числа, генерируемые с помощью формул (1.1) и (1.2) не превыша¬
ют численного значения т. Поэтому, для получения случайных чисел
распределенных на интервале от 0 до 1, достаточно их нормировать
на т. Хороший генератор случайных чисел должен генерировать числа,
равномерно распределенные на этом интервале.
В Фортране 90, реализованном для Microsoft Fortran PowerStation 4.0,
содержится две стандартных процедуры, с помощью которых реализо¬
1.1. Краткое введение в язык программирования Фортран •Аг 47
ван конгруэнтный генератор случайных чисел: seed и random. Опи¬
сание этих процедур содержатся в модуле msflib, поэтому любая
программная единица, которая использует встроенный генератор слу¬
чайных чисел, в блоке объявлений должна содержать оператор use
msflib.
Процедура seed инициализирует первое число последовательности
случайных чисел, а процедура random генерирует случайные числа.
Ниже приведен пример программы, которая объясняет правила исполь¬
зования встроенного генератора случайных чисел Microsoft Fortran
PowerStation 4.0:
program fps4rnum
use msflib
implicit none
real rndnum
integer:: i,iseed
integer, parameter:: NMAX=10
read(*,*) iseed
call seed(iseed)
do i=l,NMAX
call random(rndnum)
write (*,' (lx,F8.5)') rndnum
end do
end program fps4rnum
В данной программе с клавиатуры считывается целое число iseed,
инициализирующее стандартный генератор случайных чисел. Генера¬
ция последовательности из десяти случайных чисел выполняется в
цикле do с помощью процедуры random. Следует отметить, что если
процедура seed отсутствует в программе, то стартовое число iseed
всегда полагается равным единице. Чтобы стохастизировать его зна¬
чение при вызове процедуры seed можно использовать специальную
переменную rnd$timeseed, которая описана в библиотечном модуле
msflib.
Очень важным требованием, предъявляемым к генераторам случай¬
ных чисел, является отсутствие корреляций между числами последо¬
вательности. Для проверки наличия корреляций можно использовать
метод отображения пары последовательных случайных чисел на плос¬
кости. Для хорошего генератора, в которого отсутствуют корреляции,
точки будут равномерно заполнять площадь квадрата единичной дли¬
ны. На рис. 1.3 приведены результаты тестирования двух генерато¬
ров случайных. Слайд справа демонстрирует регулярное распределе¬
ние точек на плоскости для нормированного конгруэнтного генерато¬
48 -»\r Глава 1. Фортран 90 для моделирования физических систем
ра, запрограммированного с использованием формулы (1.2). Для этого
генератора специально были подобраны плохие значения параметров
а, Ь, т. Слева приведено распределение точек для встроенного генера¬
тора Microsoft Fortran PowerStation 4.0. Видно, что для последователь¬
ности чисел этого генератора точки равномерно заполняют плоскость,
однако последовательности из Ю4 чисел еще недостаточно, чтобы пол¬
ностью заполнить площадь квадрата.
0 0,5 1,0 0 0,5 1,0
Хп Хп
Рис. 1.3. Тестирование последовательности случайных чисел (Х2л-ь*2л).
п G [1,10000] на наличие корреляций: а) последовательность, полу¬
чена с помощью формулы (1.2) при плохом выборе параметров (а = 13,
b = 1, т — 256 и xq = 10); б) последовательность чисел стандартного
генератора Microsoft Fortran PowerStation 4.0
Следует отметить, что при проведении крупномасштабных компью¬
терных вычислений линейный конгруэнтный генератор, как правило,
сейчас не используется. В настоящее время разработано много других
компьютерных алгоритмов для генерирования случайных чисел.
Например, генераторы, основанные на методе Фибоначчи с запазды¬
ваниями (LFG, Lagged Fibonacci generator) [4], для получения каждого
очередного случайного числа используют формулу вида
Хп — Хп—а С> Хп — ЬУ
где а > Ь, а символом ® обозначена любая из бинарных арифметиче¬
ских операций (+, -, *), или логическая операция .хог., которые вы¬
полняются над парой целых случайных чисел, полученных с помощью
линейного конгруэнтного генератора. Числа а, Ъ называют лагами. Слу¬
чайность такого типа генераторов и их период сильно зависят от выбора
лагов. LFG, которые используют арифметические операции показыва¬
ют хорошие результаты при проведении стандартных статистических
1.1. Краткое введение в язык программирования Фортран •Аг 49
тестов. Отметим, что операция .хог. является наихудшей для генера¬
торов этого типа [5].
Очень часто используют также комбинированные генераторы, ко¬
торые сочетают в себе несколько алгоритмов получения случайных
чисел. Примером такого генератора является RANMAR, предложенный
в работе [6]. Этот генератор сочетает LFG генератор и генератор Вейля
и имеет период 2144.
В последнее время широкое распространение получил также гене¬
ратор «вихрь Мерсенна», алгоритм которого предложен Мацумото и
Нисимурой в работе [7]. Этот генератор имеет колоссальный период
219937 _ ^ что более чем достаточно для большинства задач компью¬
терного моделирования. Реализацию это генератора для разных языков
программирования, в том числе и Фортран можно найти на сайте [8].
Отметим, что хорошим методом испытания современных генерато¬
ров случайных чисел является использование их для моделирования
двухмерной модели Изинга (см. гл.13), для которой известно точное
решения. Всестороннее тестирования и анализ работы разных типов ге¬
нераторов применительно к данной модели был выполнен в работе [9].
1.1.10. Использование графики
Отладка работы программ, реализующих физические мо¬
дели, становится значительно проще, когда в программе присутствует
графика. Для построения графических изображений в программах, на¬
писанных для Microsoft Fortran PowerStation 4.0 достаточно знать и по¬
нимать работу небольшого числа операторов. Важно подчеркнуть, что
графические процедуры Microsoft Fortran PowerStation 4.0 работают
корректно, если качество цветопередачи графического адаптера не пре¬
вышает 16 бит на пиксель. В Microsoft Fortran PowerStation 4.0 суще¬
ствует всего два типа проектов: Standard Graphics Application
и QuickWin Application, которые позволяют работать с графиче¬
скими процедурами. Графические процедуры описаны в модуле msflib,
поэтому он должен быть подключен в начале любой программной
единицы, которая их использует, с помощью оператора use.
При написании графической программы в самом начале с помо¬
щью процедуры setviewport открывается графический порт. Вы¬
зов этой процедуры осуществляется следующим образом:
call setviewport (xl,yl,х2,у2),
где xl,yl — координаты левой верхней, а х2,у2 — нижней правой
точек экрана. Координаты указанных двух точек описывают замкну¬
тый прямоугольник, внутри которого и будет происходить построение
50 ■Ar Глава 1. Фортран 90 для моделирования физических систем
графического изображения. Допустимые значения координат указан¬
ных точек, которые являются величинами целого типа, определяются
режимом работы видеоадаптера.
Для определения системы координат и масштабирования изоб¬
ражения, внутри графического порта используют функцию setwindow:
res=setwindow(finvert, Xmin, Ymax, Xmax, Ymin),
где величина логического типа finvert определяет положения нача¬
ла системы координат и направление осей. Если finvert присвоено
значение .true., то начало координат находится в левом нижнем
углу графического порта. В случае, когда finvert присвоено значение
.false., то начало координат, находится в верхнем левом углу и
ось ординат направлена вниз. Значения Xmin, Ymax, Xmax, Ymin —
вещественных величин типа real (8) определяет границы допустимых
координат объекта. Величина целого типа res является результатом
выполнения этой функции и принимает ненулевое значение, если ра¬
бота функции завершена успешно. В противном случае res принимает
нулевое значение.
Перед построением любого графического объекта нужно выбрать
цвет его отображения с помощью функции setcolor:
res=setcolor(numcol) ,
где numcol — индекс, определяющий цвет изображения. Значение
индекса изменяется в пределах от 0 до 15, что соответствует таблице
стандартных цветов, которая определена в модуле msflib.
В случае успешного выполнения данной функции величине res
присваивается предыдущий индекс цвета, а в противном случае зна¬
чение — 1.
Другой способ определения цвета объекта заключается в использо¬
вании функции setcolorrgb:
res=setcolorrgb(col),
где col — шестнадцатеричная константа, определяющая цвет. Напри¬
мер, для получения некоторых чистых цветов наивысшей интенсивно¬
сти значение col должны быть следующими:
Значение col=#^00^^00^JD0^
В G R
Цвет
#ff0000
голубой
#00ff00
зеленый
#0000ff
красный
1.1. Краткое введение в язык программирования Фортран •Аг 51
Данный пример иллюстрирует принцип получения чистых цветов с
помощью функции setcolorrgb. Каждые две позиции в значении
шестнадцатеричной константы col слева направо используются для
задания различной интенсивности голубого, зеленого и красного цве¬
та соответственно. Допустимые значения интенсивности для каждого
цвета в шестнадцатеричной системе исчисления находятся в интер¬
вале значений от 00 до ff (от 0 до 255 в десятичной системе ис¬
числения). Путем комбинирования значений интенсивности чистых
цветов, можем получить любой требуемый цвет. Например, желтый
цвет наивысшей интенсивности получим при смешивании голубого и
красного (col=#00ffff), а белый при смешении всех трех цветов
(col=#ffffff). Рисунок 1.4 иллюстрирует способ получения различ¬
ных оттенков черного цвета.
#000000 #333333 #666666 #999999 #СССССС
Рис. 1.4. Получения различных оттенков черного цвета с помощью графиче¬
ской функции setcolorrgb. Внизу под каждым цветом приведены
значения шестнадцатеричной константы col
Простейшим графическим примитивом является точка, которую
можно изобразить, воспользовавшись функцией setpixel_w:
res=setpixel_w(х,у)
где х,у — величин вещественного типа real (8). Данная функция
фактически изменяет предыдущий индекс цвета на текущее значение
индекса цвета, поэтому при успешном ее выполнении величине res
присваивается предыдущий индекс цвета, а в противном случае зна¬
чение -1.
Построение отрезка {линии) осуществляется с помощью двух гра¬
фических процедур:
call moveto_w(xl,yl,wxy); res=lineto(x2,y2)
Процедура moveto осуществляет перенос графического курсора
в начальную точку отрезка с координатами (xl,yl), а процедура
lineto соединяет линией начальную и конечную точки отрезка. Для
представления начальных и конечных координат точек отрезка исполь¬
зуются величины вещественного типа real (8). Величина wxy являет¬
ся сконструированным типом данных, описание которого содержится в
52 ->\r Глава 1. Фортран 90 для моделирования физических систем
модуле ms f lib. В случае успешного завершения работы line to, пере¬
менной res присваивается ненулевое значение, а в противном случае —
нуль.
Для построения прямоугольников (квадратов) используется функция:
res=rectangle_w(option,xl,yl,х2,у2)
где xl,yl — координаты верхнего левого угла, а х2,у2 — нижнего
правого угла прямоугольника. Величина option может принимать два
значения: $gfillinterior и $gborder, которая определяют будет
ли дополнительно залит прямоугольник текущим цветом, или будет
только нарисован.
Эллипсы и окружности строятся с помощью функции ellipse_w:
res=ellipse_w(option, xl,yl, х2,у2)
Смысл всех переменных этой функции таков же, как и в функции
rectangle_w. В Microsoft Fortran PowerStation 4.0 для построения
эллипсов и окружностей реализован алгоритм, который вписывает их
внутрь прямоугольников и квадратов соответственно.
Графический порт, или даже все окно можно очистить с помощью
процедуры:
call clearscreen(option)
где параметр option может принимать значения: $gclearscreen,
или $gviewport. Первое значение используется для очистки всего
экрана, а второе лишь для очистки текущего графического порта.
Приведем теперь текст небольшой программы draw, f 90 для по¬
строения точки, диска, квадрата и отрезка прямой линии, которая ил¬
люстрирует применение рассмотренных графических процедур:
program draw
use msflib
implicit none
logical(2):: direct=.true.
integer(2) res
real (8) :: r=20.
real (8) :: xl=70., yl=70.
type (wxycoord) wxy
!очищаем экран
call clearscreen($GCLEARSCREEN)
!открываем графический порт
call setviewport(10,10,400,400)
res=setwindow(direct,0.,100.,100.,0.)
1.2. Примеры -*\r 53
!выбираем для рисования желтый цвет
res=setcolor(14)
!изображаем точку
res=setpixel_w(10.,10.)
! строим отрезок
call moveto_w (xl, yl, wxy)
res=lineto_w(50.,50.)
!рисуем прямоугольник
res=rectangle_w($gborder,30.,30.,80.,80)
!рисуем заполненную окружность
res=ellipse_w($gfillinterior,30.-r,30.+r,30.+r,30.-r)
end program draw
В приведенной выше программе строка кода type (wxycoord) wxy
означает принадлежность величины wxy к сконструированному типу
wxycoord. На рис. 1.5 приведен дамп экрана, полученный после окон¬
чания работы программы draw, f 90.
Рис. 1.5. Результат работы программы draw, f 90
Следует отметить, что в этом разделе были рассмотрены лишь не¬
сколько графических процедур, из их большого многообразия, доступ¬
ного в модуле msflib Microsoft Fortran PowerStation 4.0. Однако,
этих процедур вполне достаточно для представления разнообразных
моделей, представленных в данной книге.
1.2. ПРИМЕРЫ
Проиллюстрируем примеры использования языка Фортран
для программирования некоторых вычислительных задач.
1.2.1. Табуляция и построение графика функции
Проанализируем программу для табуляции функции вида
f(x) = (е~х + + 3,7)/3 на интервале значений х от 0 до 2 с шагом
0,01 и вывода ее графика на экран.
Глава 1. Фортран 90 для моделирования физических систем
Данная программа может выглядеть следующим образом:
program ftab
use msflib
type (wxycoord) wxy
logical(2):: direct=.true.
real f {описание функции
integer i, n
real (8):: a=-2., b=4., st=0.01 {интервал и прирост
!аргумента
real (8) xi, ymin, ymax
real(8), allocatable:: x(:),y(:)
!определяем число точек функции
n=int( (b-a)/st)
I загружаем в оперативную память массивы
allocate(х(1:n), у(1:n))
!табулируем функцию
i=l
do xi=a, b, st
x(i)=xi; у(i)=f(xi)
i=i + l
end do
{вычисляем минимальное и максимальное значение
ymin=minval(у); ymax=maxval(у)
1 открываем графический порт
call setviewport(10,10,400,400)
res=setwindow(direct,a,ymax,b,ymin)
res=rectangle_w($gborder,a,ymax,b,ymin)
!строим график функции
call moveto_w (x(l), y(l), wxy)
do i=2,n
res=lineto_w(x(i), y(i))
end do
end program ftab
real function f(x)
real (8) x
f=(exp(-x)tsqrt(exp(x))+3.7)/3.0
end
Приведенная программа состоит из главной программы ftab и
внешней процедуры-функции f, которая используется для кодирования
конкретной функции. Значения аргумента и соответствующее значение
1.2. Примеры ->\r 55
/ Рис. 1.6. График функции f(x) = (е~х + Ve* + 3,7)/3,
/ построенный с помощью программы ftab на интер-
вале значений х от 0 до 2 с шагом 0,01
функции записываются в массивы динамического типа, количество
элементов которых вычисляется вначале работы программы. После
окончания табуляции функции, вычисляется ее минимальное и мак¬
симальное значение на заданном интервале. Данные значения исполь¬
зуются для масштабирования окна графического порта с помощью
процедуры setwindow. График функции строится отрезками, кото¬
рые соединяют протабулированные точки. Результат работы программы
ftab представлен на рис. 1.6.
1.2.2. Построение спирали Улама
Однажды, присутствуя на длинном и скучном докладе,
Станислав Улам придумал себе следующее развлечение. На клетчатой
бумаге он начал записывать все числа по спирали против часовой
стрелки, как это показано на рис. рис. 1.7, а затем закрасил в ней
клеточки, принадлежащие простым числам. В этой спирали в сосед¬
них диагоналях чередуются четные и нечетные числа. Таким образом,
простые числа в этой спирали лежат в чередующихся диагоналях, что
и не удивительно, так как все простые числа являются нечетными (за
исключением числа 2).
14
13
5
4
3
12
6
1
2
11
7
8
9
10
14-
-13
t
5 -
1
-4 -
- 3
t
I
12
t
i
6
1
1 -
I
- 2
I
II
t
1
7 -
- 8 -
- 9-
I
-10
Рис. 1.7. Построение спирали Улама. В этой спирали в соседних диагоналях
чередуются четные и нечетные числа, а простые числа лежат в
чередующихся диагоналях
Однако, Улам с удивлением обнаружил, что простые числа в череду¬
ющихся диагоналях расположены не хаотично, а образуют некоторый
56 •Ar Глава 1. Фортран 90 для моделирования физических систем
узор и вытянуты в довольно длинные цепочки. В дальнейшем эта зада¬
ча настолько заинтересовала Улама, что он продолжил исследования на
ЭВМ Maniac Лос-Аламосской лаборатории [10, 11]. Данное построение,
которое в литературе еще иногда называют скатертью Улама, отражает
существование определенной закономерности в последовательном рас¬
положении простых чисел, но этот феномен еще не получил какого-
либо математического объяснения.
Программу, реализующую алгоритм построения спирали Улама, удоб¬
но разбить на две подзадачи, которые осуществляют: 1) проверку нату¬
рального числа на принадлежность к простому числу; 2) графическое
построение спирали. В соответствии с таким разбиением код главной
программной единицы выглядит следующим образом:
program Ulam !главная программа
use comdata
implicit none
integer Np, Eratosphen
call init
Np=Eratosphen (); call UlamSpiral(Np)
end program Ulam
Приведенная программа использует модуль общих переменных и
массивов:
module comdata
implicit none
integer:: N=100000 !максимальное значение
!натурального числа
!массив простых чисел
integer, allocatable:: prime(:)
end module comdata
В данном модуле определяется максимальное значение натурально¬
го числа N и описывается массив динамического типа prime (), кото¬
рый используется для хранения всех простых чисел, значения которых
меньше натурального числа N.
Размещение массива prime () в оперативную память выполняет
процедура init:
subroutine init() !процедура инициализации начальных
!значений величин
use comdata
implicit none
integer imax !число элементов массива prime()
1.2. Примеры 57
if(N>200) then
imax=int(real(N)/(log(real (N))-2.) + 1.)
else
imax=int(1.6*real(N)/log(real(N)) + 1.)
end if
allocate(prime(1:imax)) !располагаем массив prime()
end subroutine init
В этой процедуре для определения количества элементов fmax в
массиве prime () используется следующая оценка:
Поиск простых чисел выполняется во внешней функции Eratosphen:
integer function Eratosphen() !метод Эратосфена
use comdata
implicit none
integer i, j, k !индексы
real sqrk !sqrk=sqrt(k)
prime(1)=1; prime(2)=2; prime(3)=3 !первые 3 простых
j=3
do 2 k=3,n,2
i=2; sqrk=sqrt(real(k))
1 i=i+l
if(prime(i)>sqrk) then
prime(j)=k; j=j+l; goto 2
endif
if((k/prime(i))*prime(i)/=k) goto 1
2 continue
Eratosphen=j-1
end function Eratosphen
В данном случае поиск простых чисел осуществляется с помощью
метода, который получил название «Решето Эратосфена». Суть метода
заключается в том, что любое целое число N ф\ является простым, если
оно не делится ни на одно простое число, которое меньше y/N. Резуль¬
тирующей переменной данной функции является количество найден¬
ных простых чисел, которое хранится внутри функции в переменной j.
!в оперативной памяти
*тах — int
intfr^7 + 1l- N<200-
L In N J
^max —
!числа
Глава 1. Фортран 90 для моделирования физических систем
Рис. 1.8. Спираль Улама, полученная с по¬
мощью программы Ulam для N = Ю5
Графическое построение спирали Улама осуществляет процедура
UlamSpiral:
subroutine UlamSpiral(Np)
use comdata
use msflib
implicit none
logical(2):: direct=.true.
integer
res
integer
Np
!количество простых чисел
integer
move
!направление движения
integer
lenside
!длина стороны спирали
real
lenmax
!максимальное значение длины стороны
!спирали
integer
ip
!индекс простого числа
integer
primemax
!максимальное значение простого числа
integer
i, j, k
!индексы
real
x, у
!координаты
! таблица
сдвига координат:
integer::
: dx(1:4)=
(/1,0,-1, 0/)
integer:
: dy(1:4)=
(/0,1, 0,-1/)
primemax=
=prime(Np)
; lenmax=sqrt(real(primemax))+1
!открываем графический порт
call setviewport(10,10,700,700)
res=setwindow(direct, 0.,lenmax, lenmax,0.)
!изображаем три первых простых числа
x=lenmax/2; y=lenmax/2 !координаты первого числа
res=rectangle_w($gfillinterior,х-.4,у+.4, х+.4, у-.4)
do move=l,2
x=x+dx(move); y=y+dy(move)
res=rectangle_w($gfillinterior,x-.4, y+.4, x+.4, y-.4)
enddo
1.2. Примеры •Ar 59
!изображаем остальные простые числа <N
i=4; ip=4;lenside=2; move=3
do while(i<primemax)
do j=l,2
do k=l,lenside
x=x+dx(move); y=y+dy(move)
if(i==prime(ip)) then
ip=ip+l; res=rectangle_w($gfillinterior,x-.4, &
У+.4, x+.4, y-.4)
endif
i=i + l
enddo
move=move+l; if(move>4)move=l
enddo
lenside=lenside+l
enddo
end subroutine UlamSpiral
Простые числа на спирали отмечаются заполненными квадратами.
На рис. 1.8 представлена картина распределения простых чисел, значе¬
ние которых меньше числа 105.
1.2.3. Вычисление многомерных интегралов и числа лг
методом Монте-Карло
Вычисление многомерных интегралов методом Монте-Кар¬
ло удобно проиллюстрировать на примере нахождении объема я-мерно-
го шара Vn радиуса R. Точное значение его объема известно:
Vt(n) = CnRn,
где Сп = лп/2/Г(п/2 + 1) — постоянная, выраженная через Гамма-
функцию. Для парных п имеем, Сп = лп/2/(п/2)\, а для непарных
Сп = я('1_1)/22(г1+1)/2/(/2)!!. Например, С\ =2, C<i = я, Сз = 4я/3. Со¬
гласно этой формуле объем шара радиуса R = 1 равен Vt = л для п = 2
и Vt = я8/8! для п = 16.
Впишем я-мерный шар внутрь л-мерного куба объемом (2R)n. Если
случайным образом выбирать точки внутри п-мерного куба, то вероят¬
ность fn обнаружить точку внутри я-мерного шара равна отношению Nh
числа благоприятных исходов (попадание внутрь шара) к общему числу
испытаний Nt, когда Nt —> оо. С другой стороны fn равна отношению
объемов шара к кубу. Поэтому V(ri) объем я-мерного шара радиуса
R= 1, вычисленного методом Монте-Карло, будет равен:
V(n) « 2nfn.
60 ->\r Глава 1. Фортран 90 для моделирования физических систем
Рис. 1.9. Зависимости объема /2-мерного шара V от числа испытаний Nt при
/г = 2 (а) и п = 16 (б), полученные с помощью программы integ.
Горизонтальные линии соответствуют точным значениям Vt = п
(п = 2), Vt = л8/8! (п = 16)
Ниже приведен код программы integ, реализующей вычисление
объема /2-мерного шара методом Монте-Карло:
program integ
use msflib
implicit none
integer:: n=16 !мерность
!числа попаданий и испытаний
!максимальное число испытаний
'расстояние, координата
!объем n-мерной сферы
!вычисляем объем
integer Nh, Nt
integer:: NMAX=le8
integer(2) i
real (8) r,x
real rnd
real (8) Vn
open(1,file='V.dat')
Nt=0
do while(Nt<NMAX)
r=0 .
do i=l,n
call random(rnd); x=dble(rnd)
r=r+x*x
end do
if(r<l.dO)Nh=Nh+l
Nt=Nt+l
Vn=(dble(Nh)/dble(Nt))*2**n
if (mod(Nt,100000)==0)write(*,*) Nt
if (mod(Nt,10000)==0) write(l,*) Nt, Vn
enddo
close (1)
end program integ
1.2. Примеры -l\r 61
В данной программе число испытаний и соответствующее ему зна¬
чение объема /г-мерного шара записываются в выходной файл V.dat.
На экран также периодически печатается число испытаний Nt для
контроля выполнения программы. На рис. 1.9 приведены зависимости
объема шара V от числа испытаний Nt при п = 2 (а) и п = 16 (б). С
ростом числа испытаний приближенное значение объема шара посте¬
пенно приближается к точному значению.
1.2.4. Построение эквипотенциальных линий
для распределения электрических зарядов
Рассмотрим некоторое пространственное распределение
точечных зарядов qi на плоскости. Положение каждого /-го заряда
определяется вектором г/. Задача состоит в построении картины распре¬
деления эквипотенциальных линий. Для решения поставленной зада¬
чи можно просканировать интересующую пространственную область,
вычислить в каждой точке г, значения потенциала и(г) и отметить
точками только определенные, заранее заданные значения потенциала.
Величина и(г) рассчитывается по формуле u(r) = £"=1 qi/\r — г,-|.
Ниже приведена программа charges, реализующая поставленную
задачу для трех зарядов, расположенных на плоскости:
program charges
use msflib
implicit none
logical(2):: direct=.true.
integer(2) i, res
integer(2):: density=10000
real rnd, x, y, R, ri
real u !потенциал
!определяем величины зарядов и их координаты
real:: q(l:3)=(/l, -2, 1 /)!величины зарядов
real:: yq(1:3)=(/0.75, 0.25, 0.75/)
real:: xq(1:3)=(/0.25, 0.5, 0.75/)
!открываем графический порт
call setviewport(10,10,700,700)
res=setwindow(direct,0.,1.,1.,0.)
!изображаем положение зарядов
do i=l,3
R=.01*abs(q(i)) !радиус окружности
res=ellipse_w($gborder,xq(i)-R,yq(i)+R,xq(i)+R,yq(i)-R)
enddo
!осуществляем построение эквипотенциальных линий
do
call random(rnd);x=rnd
62 -*\r Глава 1. Фортран 90 для моделирования физических систем
call random(rnd);y=rnd
u=0.
do i=l, 3
ri=sqrt((x-xq(i))*(x-xq(i))+(y-yq(i))*(y-yq(i)))
if(ri/=0) u=u+q(i)/ri
enddo
if (mod(int(u*density),density)==0) res=setpixel_w (x, y)
enddo
end program charges
В данной программе для присвоения значений зарядам и коорди¬
натам их положения используются конструкторы массивов. Каждый
заряд изображается окружностью, радиус которой пропорционален аб¬
солютному значению заряда. Сканирование единичного квадрата (обла¬
сти распределения зарядов) осуществляется случайным образом внутри
бесконечного цикла do. Значения потенциала и(г) преобразуются к
величинам целого типа и на картине отображаются только значения
потенциала, кратные значению параметра density. Параметр целого
типа density использован для регулирования плотности расположе¬
ния эквипотенциальных линий и его значение подбирается вручную.
При увеличении величины density плотность расположения линий
уменьшается. На рис. 1.10 представлен результат работы программы
charges для системы трех зарядов: q\ = 1, <72 = —2, q% = 1 (а) и для
системы 20 зарядов (q = ±1) равномерно расположенных на кольце (б).
В последнем случае программа была незначительно модифицирована с
целью задания значений 20 зарядов и их пространственных координат.
Рис. 1.10. Картины эквипотенциальных линий, полученная с помощью про¬
граммы charges, для системы трех зарядов: q\ = 1, q<i = —2 (вни¬
зу)» Чъ = 1 (а) и для системы 20 зарядов (q = ±1), равномерно
расположенных на кольце (б)
1.2. Примеры ->\r 63
1.2.5. Аполлониевы упаковки
Задачи компактной упаковки традиционно вызывают боль¬
шой научный и практический интерес. В III веке до нашей эры Аполло¬
ний, древнегреческий геометр из Перги, рассмотрел упаковку дисков на
плоскости, конструируемую путем итера¬
ционного заполнения пор образуемых меж¬
ду тремя касающимися дисками (рис. 1.11).
В данном случае полость между любыми
тремя касающимися дисками внутри кру¬
га заполняется дисками меньшого разме¬
ра так, чтобы они касались сторон поло¬
сти и т.д. Для каждой полости процесс
можно продолжить до бесконечности. В
работе [12] впервые было отмечено, что та¬
ким образом полость между любыми тремя
дисками может быть практически полно¬
стью заполнена дисками меньшего разме¬
ра. Отметим, что подобные упаковки могут
быть построены и в многомерных пространствах. Полученные упаковки
для дисков и сфер имеют самоподобную структуру.
Детальные исследования показали, что число объектов N, радиус
которых больше г, удовлетворяет асимптотическому соотношению:
N~r~df,
где фрактальная размерность равна df = 1,30568 [13], df = 2,4739465
[14], df« 3,5848 [15] для двух-, трех- и четырехмерного случаев,
соответственно.
В идеальной аполлониевой упаковке центры дисков расположены
регулярным образом. Другой тип упаковки можно получить, если рас¬
полагать центры дисков случайным образом внутри круга, выбирая их
радиусы так, чтобы не происходило пересечений с ранее осажденными
дисками [16]. Допускаются только касания между ближайшими диска¬
ми. Любопытно, что фрактальная размерность для случайных упаковок
дисков равна df « 1,64 [16], что существенно превышает значение для
идеальной упаковки df = 1,30568 [13].
Текст программы circlepack для построения случайной аполло¬
ниевой упаковки дисков представлен ниже:
program circlepack
use msflib
implicit none
integer:: ND=10000 !максимальное число дисков
Рис. 1.11. Аполлониева упа¬
ковка дисков внутри круга
Глава 1. Фортран 90 для моделирования физических систем
real :: Rmax=0.4
logical(2) inside
logical(2):: direct=.true.
integer res
integer i,n
real PI2
real filling
real Rmin
real Rn
real rho,phi,xn,yn
!максимальный радиус диска
!коэффициент заполнения
!минимальный радиус диска
!радиус n-го диска
!координаты положения центра
!п-го диска
!расстояние между центрами
!i-ro и n-го дисков
real
nn
real
real
rnd
x(10000),y(10000),R(10000) !координаты
!центров дисков
!и их радиусы
PI2=8.*atan(1.) ! вычисляем 2*Pi
!открываем графический порт
call setviewport(10,10,900,900)
res=setwindow(direct, -1., 1., 1., -1.)
!рисуем окружность единичного радиуса
res=ellipse_w($gborder, -1., 1., 1., -1.)
!инициализируем генератор случайных чисел
call seed(rnd$timeseed)
open(1,file='packing.dat')
filling=0; n=0
do while(n<ND)
!генерируем случайным образом положение центра
!очередного n-го диска и выполняем проверку на
!попадание его внутрь какого-либо i-ro диска (i<n)
inside=.true.
do while(inside)
call random(rnd); rho=rnd
call random(rnd); phi=Pi2*rnd
xn=rho*sin(phi); yn=rho*cos(phi)
inside=.false.
loop: do i=l,n
rin=sqrt((xn-x(i))**2+(yn-y(i))**2)
if(rin<R(i)) then
inside=.true.; exit loop
endif
enddo loop
enddo
1.2. Примеры 65
!вычисляем радиус n-го диска: он должен касаться
!ближайшего к нему диска
Rmin=l.-rho
do i=l,n
Rn=sqrt((xn-x(i))**2+(yn-y(i))* * 2)—R(i)
if(RrKRmin) Rmin=Rn
enddo
!запоминаем положение и радиус n-го диска
n=n+l
if(Rmin>Rmax) Rmin=Rmax
x(n)=xn; y(n)=yn; R(n)=Rmin
!рисуем n-й диск
res=ellipse_w($gborder,x(n)-R(n),у(n)+R(n) , &
x(n)+R(n), у (n)-R(n))
!вычисляем коэффициент заполнения и записываем
!данные в выходной файл
filling=filling+R(n)*R(n)
write(l,*) n, filling
enddo
close (1)
end program circlepack
В данной программе максимальное число дисков определяется пере¬
менной ND, а также вводятся массивы для х () , у () , R () для описания
координат центров дисков и их радиусов. В процессе работы внутри боль¬
шого круга единичного радиуса генерируется случайная точка (хп,уп),
которая не должна попадать на ранее осажденные диски. Для проверки
этого условия перебираются все ранее осажденные диски, вычисляется
расстояние rin=sqrt ( (xn-x (i) ) **2 + (yn-y (i) ) **2) и проверяется
выполнение условия rin<R (i). Если это условие выполняется хотя бы
для одного диска, то генерируется новая случайная точка. В противном
случае, снова перебираются все диски, и вычисляется минимальное зна¬
чение rmin величины sqrt ( (xn-x (i) ) **2 + (yn-y (i))**2)-R(i).
Число осажденных дисков увеличивается на единицу, и после
этого запоминаются координаты и радиус вновь осажденного диска
x(n)=xn; y(n)=yn; R(n)=rmin. Процедура завершается после оса¬
ждения требуемого количества дисков ND.
В программе введено также ограничение на максимальный ради¬
ус диска, т. е. R < Rmах> в простейшем варианте, проанализированном
в [16], /?тах = 1. Примеры упаковок, полученных при случайном оса¬
ждении дисков с помощью программы circlepack представлены на
рис. 1.12.
66 ->\r Глава 1. Фортран 90 для моделирования физических систем
а б
Рис. 1.12. Примеры случайных упаковок дисков внутри круга единичного ра¬
диуса, полученные с помощью программы circlepack для разных
Я шах = 0,1 (а) и 0,5 (6)
N
Рис. 1.13. Зависимости коэффициента заполнения р от количества дисков N,
полученные для разных /?тах = 0,01, 0,02, 0,1, 0,2, 0,5
Кроме графического построения упаковки дисков в данной програм¬
ме вычисляется также зависимость коэффициента заполнения р (в про¬
грамме переменная filling) большого круга осажденными дисками
от количества осажденных дисков N. На рис. 1.13 приведены примеры
зависимостей р от количества дисков N, полученные для разных зна¬
чений Ятах. При увеличении N величина р асимптотически стремится
к единице, однако скорость приближения р к единице увеличивается
при увеличении /?тах.
1.3. Задачи для самостоятельной работы •А, 67
1.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Один из способов определения периода генератора случайных чисел
основан на построении графика зависимости полного смещения слу¬
чайных блужданий от количества шагов. При этом каждый очередной
шаг случайных блужданий с вероятностью /= 0,5 имеет длину ±1.
Оценка периода выполняется путем визуального анализа полученной
зависимости. Напишите программу, реализующую данный метод, и
оцените период стандартного генератора, используемого в компиля¬
торе Вашего Фортрана.
Рис. 1.14. К описанию задачи Бюффона
2. Задача Бюффона. На плоскую поверхность, разграфленную парал¬
лельными линиями на расстоянии г, бросается случайным образом
игла длины £. Для описания положения иглы можно использовать
координату ее центра у и угол в (рис. 1.14), которые случайным
образом распределены в интервалах: 0 < у < г/2 и 0 < в < п. Игла
может пересечь линию, если выполняется условие у < (i/2) sin0. На¬
пишите программу, моделирующую бросание иглы, и вычислите ме¬
тодом Монте-Карло вероятность / пересечения иглы с линиями плос¬
кости. Для упрощения задачи положите равным г= 1. Рассмотрите
два возможных случая отношения размеров иглы и шага: a) i < г,
б) i > г. Сравните полученные значения / с точными значениями:
(2А е<п
f I nr
I = ) r(n - 2arcsin(r/£) + 2i( 1 - VI ~r2/i2)
^i>r.
^ nr
Воспользуйтесь соотношением / для случая i < г и вычислите зна¬
чение 71.
68 -*\r Глава 1. Фортран 90 для моделирования физических систем
3. Напишите программу для вычисления методом Монте-Карло инте¬
грала вида
/(л) = J dr 1 J dr2J drn,
D(r0) D(r0,r\) D(r0,ri,...,rn_i)
где D(r0) — единичный диск с центром го = (0,0) (т. е. х2 + У2 < 1,
рис. 1.15, a), D(ro,r\) объединение двух единичных дисков с цен¬
трами в точках го и причем центр второго диска попадает в
первый диск r\ е D(r0) (т. е. х2 + у2 < 1 или (х - х2) + (у — У2)2 < 1,
рис. 1.15, б), D(ro,ri,ri) — объединение трех единичных дисков, при¬
чем r\ е D(r0), г2 е D(r0, г\) (т. е. х2 + у2 < 1, (х - х\)2 + (у - у\)2 < 1
или (х - Х2)2 + (у — У2)2 < 1, рис. 1.15, в).
Рис. 1.15. К вычислению многомерного интеграла методом Монте-Карло
Для вычисления интеграла /(1) центр диска t\ случайным образом
помещается в квадрат размером 2, и если r\ е D(ro) (т. е. х\ + у2 < 1),
то счетчик удачных попаданий Nh увеличивается на единицу. Значе¬
ние интеграла оценивается как /(1) = (1 х 2)2Nh/N, где N — общее
количество испытаний. Для вычисления интеграла /(2) нужно слу¬
чайным образом поместить центр г\ в квадрате размером 2, а центр Г2
в квадрате размером 4. Если r\ е D(ro) и Г2 G D(ro,n), то счетчик
удачных попаданий s увеличивается на единицу. Значение интеграла
оценивается как /(2) = (2 х 4)2Nh/N (рис. 1.15, г). Аналогично этому
значение интеграла /(3) оценивается, как 1(3) = (3х 6)2Nh/N и т.д.
1.4. Литература 69
Вычислите интегралы 7(1), 7(2), 7(3), оцените ошибки метода Монте-
Карло и сравните полученные результаты с точными значениями: 7(1) =
= я, 1(2) = (4 + 3\/3/л)(л/2)2, /(3) = (8 + 14^3/л+ 44/л2)(л/2)3. [17].
I.4. ЛИТЕРАТУРА
1. Бартеньев О. В. Современный Фортран. — 3-е изд., доп. и перераб. — М.:
ДИАЛОГ-МИФИ, 2000. - 449 с.
2. Рыжиков Ю. В. Программирование на Фортран PowerStation для инжене¬
ров. Практическое руководство. — СПб.: Корона-Принт, 2000. — 160 с.
3. Фортран 90. Международный стандарт / Ред. перев. А. М. Горелик. — М.:
Финансы и статистика, 1998. — 379 с.
4. James F. A Review of Pseudorandom Number Generators // Computer Phys.
Comm. - 1990. - V. 60, No. 3. - P. 329-344.
5. Marsaglia G.A. // In: Computational Science and Statistics: The Interface /
Ed. by L. Balliard. — Amsterdam: Elsevier, 1985.
6. Marsaglia G., Zaman A. and Tsang W.-W. Toward a universal random num¬
ber generator // Stat. Prob. Lett. — 1990. — V. 9, No. 1. — P. 35-39.
7. Matsumoto М., Nishimura T. Mersenne twister: A 623-dimensionally equidis-
tributed uniform pseudorandom number generator // ACM Trans, on Model¬
ing and Computer Simulations. — 1998. — V. 8, No. 1. — P. 3-30.
8. http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/emt.html.
9. Coddington P. D. Tests of random number generators using Ising model simu¬
lations // Computational Physics and Physical Computation. — 1996. — V. 7,
No. 3. - P. 295-303.
10. Stein M.L., Ulam S. М., Wells M.B. A Visual Display of Some Properties of
the Distribution of Primes // American Mathematical Monthly (Mathematical
Association of America). — 1964. — V. 71, No. 5. — P. 516-520.
II. Stein М., Ulam S.M. An Observation on the Distribution of Primes 11 Ameri¬
can Mathematical Monthly (Mathematical Association of America). — 1967. —
V. 74, No. 1. - P. 43-44.
12. Leibniz G. W. and Look B. The Leibniz—Des Bosses correspondence. — New
Haven, Conn. [u.a.]: Yale Univ. Press, 2007.
13. Manna S. S. and Hermann H.J. Precise determination of the fractal dimen¬
sions of Apollonian packing and space-filling bearings // J. Phys. A: Math.
Gen. - 1991. - V. 24. - P. L481-L490.
14. Borkovec М., Paris W. and Piekert R. The fractal dimension of the Apollonian
sphere packing // Fractals. — 1994. — V. 2, No. 4. — P. 521-526.
15. Farr R. S., Griffiths E. Estimate for the fractal dimension of the Apollonian
gasket in d dimensions // Phys. Rev. E. — 2010. — V. 81. — P. 061403.
16. Manna S. S. Space filling tiling by random packing of discs // Physica A. —
1992. - V. 187. - P. 373-377.
17. Dickman /?., Wang J. -S., Jensen I. Random sequential adsorption: Series and
virial expansions // J. Chem. Phys. — 1990. — V. 94, No. 12. — P. 8252-8257.
ГЛАВА ЗАДАЧА ФЕРМИ-ПАСТА-УЛАМА
2
2.1. КОЛЕБАНИЯ В ЦЕПОЧКЕ
СВЯЗАННЫХ ОСЦИЛЛЯТОРОВ
Хорошо известно, что в термодинамически-равновесном
состоянии все колебательные моды системы имеют одинаковую (усред¬
ненную по времени) энергию. Однако, для системы осцилляторов свя¬
занных линейными силами, все моды являются независимыми и пере¬
распределения энергии не должно происходить. В задаче сформулиро¬
ванной Ферми Уламом и Пастой (ФПУ) впервые была предпринята по¬
пытка дать объяснение явлению перераспределения энергии и термали-
зации для системы осцилляторов, связанных нелинейными силами [1].
Исторически данная проблема впервые возникла при расчете тепло¬
проводности твердого тела. В 1914 г. Дебай предположил, что наблю¬
даемая конечная теплопроводность твердых тел может быть связана с
нелинейностью (ангармоничностью) возвращающих сил, возникающих
при тепловом возбуждении кристаллической решетки. В линейном при¬
ближении, колебания решетки можно представить в виде суперпозиции
нормальных мод. В этом случае нормальные моды переносят энергию со
скоростью звука, эффективная теплопроводность является бесконечной
и для передачи тепла с одного конца решетки на другой не нужно
никакого перепада температуры. Таким образом, поток энергии не под¬
чиняется закону Фурье, согласно которому теплопроводность реальных
кристаллов пропорциональна градиенту температур.
Для разрешения этого парадокса Дебай предположил включить в
рассмотрение нелинейные силы межатомного взаимодействия, действу¬
ющие в кристаллической решетке. В данном случае возможно вза¬
имодействие нормальных мод (вычисленных для линеаризированных
упругих сил), и суммарный эффект нелинейных взаимодействий (со¬
ударений фононов) может привести к ограничению переноса энергии и
коэффициента теплопроводности.
2.1. Колебания в цепочке связанных осцилляторов •Аг 71
2.1.1. Линейная цепочка
На рис. 2.1 изображена цепочка N частиц массы М, свя¬
занных между собой пружинками с жесткостью k. Смещение п-й ча¬
стицы из положения равновесия обозначим через уп. Концы цепочки
II II.
Г-Н н ни
У\ У2 yN-1 Ум
Рис. 2.1. Цепочка связанных осцилляторов
закреплены неподвижно, поэтому уо = уы+ \ = 0. Уравнения движения
имеют вид
Муп = k[(yn+\-уп) - (уп-уп-\)), n = \,...,N. (2.1)
Общее решение для такой системы записывается в виде суперпозиции
Уп = \J дщЕД' sin (nfi) cos ((Oit + (Pi) (n = 1,2, (2.2)
где амплитуды Д- и начальные фазы колебаний для каждой моды
определяются из начальных условий, /; = in/(N+ 1), а частоты колеба¬
ний o)i определяются соотношением
щ = 2^/^|51П(Л/2)|. (2.3)
В нормальных координатах, связанных с уп соотношениями
Г~2~ N
at = V лГП £ Уп sin("
» п= 1
система уравнений движения упрощается:
di + (D^ai = 0, i = 1, ..., N,
где частота i-й моды определяется формулой (2.3), а ее энергия равна
Ei = Ua?+ (ofd*). (2.4)
Энергия всей цепочки связанных осцилляторов может быть пред¬
ставлена в виде суммы энергий отдельных мод При этом каждая
из мод является отражением коллективного движения всей цепочки.
72 -J\r Глава 2. Задача Ферми-Паста-Улама
В отсутствии нелинейных взаимодействий перераспределения энергии
между нормальными модами не происходит, а энергия каждой моды
постоянна.
2.1.2. Нелинейная цепочка
В качестве простейшей модели кристаллической решет¬
ки Э. Ферми, Дж. Пасту и С. Улама (ФПУ) [1] выбрали одномерную
цепочку, состоящую из N одинаковых ангармонических осцилляторов,
связанных со своими соседями нелинейными пружинками. Для квад¬
ратично-нелинейной системы уравнение движения связанных осцилля¬
торов имеет следующий вид
M'i/n = k[(yn+1 - I/„) - (уп - уп-\)] + а[(уп+1 - Уп)2 - (уп - Уп-1>2],
n = l,...,N. (2.1')
Следует отметить, что вместо квадратичного нелинейного члена в
уравнении (2.1') часто также рассматривают кубичную нелинейность
или нелинейности более высокого порядка, например [2]:
Щп = к\(Уп+1 - Уп) - (Уп - Уп-1)] + а[(Уп+1 - Уп)2 - (Уп - Уп-\)2] +
+ Р\(уп+\ -Уп)3 - (Уп -Уп-l)3] +•••, n=i,...,N, (2.1")
где а, /2 — параметры, характеризирующие амплитуду нелинейности,
а соответствующие модели называют как ФПУ a-модель или ФПУ
/2-модель.
Так как для нелинейной постановки задачи отсутствовало аналити¬
ческое решение, эта задача была исследована численно [1]. При поста¬
новке задачи ФПУ предполагалось, что в начальный момент времени
энергия сосредоточена в низшей моде, а\ = y/2/(N+ 1) ^=\ yi sin(//i).
Вначале предполагалось, что небольшие нелинейные взаимодействия
между осцилляторами могут приводить к перераспределению энергии
между различными модами и система будет постепенно термализиро-
ваться. К удивлению авторов [1] данная система не приближалась к
равновесному состоянию. При начальном возбуждении энергия распре¬
делялась только между несколькими нижними начальными модами.
Происходил периодический обмен энергии между модами и наблюдался
возврат приблизительно в начальное состояние, т. е. энергия не тер-
мализовалась. Такое поведение наблюдалось как для а-, так и для
/2-моделей. Позднее было показано [3, 4], что при начальном возбуж¬
дении /-й нормальной моды (для начального условия yi\t=o = A sin(/,))
время возврата в начальное состояние tr возрастает с увеличением
длины цепочки N, и уменьшается с увеличением начальной амплиту¬
2.2. Алгоритм и описание работы программы ->\г 73
ды Ai или коэффициента нелинейности, например, для a-модели оно
определяется выражением
tr = 0,88(Af + 1 )Nz/2^/M/kaAi.
Постулат эргодичности предполагает, что средняя по времени энер¬
гия для одной частицы должна совпадать со средней энергией усред¬
ненной по всем частицам в любой момент времени. Отсюда следует,
что наблюдаемый возврат системы в начальное состояние и отсутствие
термически равновесного состояния свидетельствует о том, что система
ангармонических осцилляторов, изученная в задаче ФПУ не является
эргодичной.
В дальнейшем предпринимались многочисленные попытки улучшить
термализацию рассмотренной нелинейной цепочки [2]. Более быстрая сто-
хастизация наблюдалась для решетки ангормонически связанных частиц
с дополнительным потенциалом твердосферного типа [5]. Было показано,
что так называемые стохастические области с быстрой термализацией
могут наблюдаться только при соблюдении специальных условий для
начального возбуждения и достаточно высоком коэффициенте ангар¬
моничности [6, 7]. Показано также, что обмен энергией между различ¬
ными модами может происходить даже в случае малых нелинейностей
при выполнении условия их соизмеримости или резонансности [8]
£ ицгц = О,
где щ — целые числа, из которых не все равны нулю.
Если частоты являются несоизмеримыми, тогда перераспределения
энергии практически не происходит и наблюдается явление возврата
в начальное состояние. Оказалось, что условие соизмеримости не вы¬
полняется, если N является степенью числа 2 или является простым
числом [9]. Это и объясняет слабую термализацию в экспериментах
ФПУ, которые были выполнены для случаев N = 16, 32 и 64, т. е. для
нерезонансных случаев.
Для более подробного ознакомления с проблемой ФПУ можно ре¬
комендовать следующую литературу [7, 10-13].
В этой главе мы познакомим читателей с простейшим алгоритмом
и программой решения задача ФПУ, а также проиллюстрируем резуль¬
таты работы программы для различных начальных условий.
2.2. АЛГОРИТМ И ОПИСАНИЕ РАБОТЫ ПРОГРАММЫ
2.2.1. Алгоритм
Для решения нелинейной системы уравнений движения
(2.1') применяется алгоритм Эйлера. Вычисление усредненной по вре¬
74 ->\r Глава 2. Задача Ферми-Паста-Улама
мени приведенной энергии отдельной моды Et осуществляется по
формуле
i
Bi=jf [Ei(t)/E] dt.
(2.5)
где Е — полная энергия цепочки, равная сумме энергий всех N мод.
2.2.2. Описание работы программы
Текст программы решения задачи ФПУ находится в файле
fpu.f90. Программа имеет модульную структуру. Основные парамет¬
ры программы и массивы определяются в модуле comdata:
module comdata
implicit none
!определяем тип графического окна
type grafwindow
[экранные координаты графического окна
integer xl, yu, xr, yd
[физические координаты графического окна
real(8) xmin, ymin, xmax, ymax
end type grafwindow
type (grafwindow) gw (1:2)
real :: PI=3.14159265
!переменные цепочки
integer:: N0=32
real :: ALPHA=0.1
real
integer
real(8)
PIN1
N1
Etot
[число осцилляторов
[параметр нелинейности
!PIN1=PI/(N0+1)
!N1=N0+1
!полная энергия цепочки
[переменные интегрирования
real(8):: dt=0.1
real (8):: Tmax=le6
[массивы программы
real(8), allocatable::
real(8), allocatable:
real(8), allocatable:
real(8), allocatable:
real (8), allocatable:
end module comdata
[шаг интегрирования
[максимальное время интегрирования
у(:), yold(:) [смещения
!осцилляторов
I с положения
I равновесия
!скорости осцилляторов
[ускорения осцилляторов
!энергия мод осцилляторов
[усредненная по времени
I
v (:)
а(:)
Е(:)
Еа ( : ;
!энергия мод
2.2. Алгоритм и описание работы программы 75
Назначение переменных и массивов описано в комментарии к коду.
На экране дисплея для отображения результатов вычислений формиру¬
ется два графических окна. В верхнем окне строится конфигурация ос¬
цилляторов в цепочке, а в нижнем — зависимости приведенной энергии
от времени для первых четырех мод. С этой целью был сконструирован
тип данных grafwindow и описан массив gw, состоящий из двух
элементов этого типа.
Главный модуль программы в основном состоит из вызова внешних
процедур:
Program FPU
use comdata
use msflib
implicit none
integer it !счетчик временных шагов
real(8) t !время
open (1,file='Em.dat')
open (2,file='Ema.dat')
t=0.; it=0
call initial
call Emode
call EnergySave(t)
call Graf(t)
write (*,*) 'E=',Etot
do t=0,Tmax,dt
call Euler
call Emode
it=it+l
if(mod(it,500)==0) then
call EnergySave(t)
call Graf(t)
endif
enddo
close (1)
close(2)
end program FPU
В главном программном модуле при начале работы программы на
экран выводится значение Etot полной энергии цепочки, равной сумме
энергий всех N мод.
В процедуре initial осуществляется размещение массивов про¬
граммы в оперативной памяти, определяются размеры графических
окон и вычисляются начальные положения осцилляторов цепочки, соот¬
76 •Ar Глава 2. Задача Ферми-Паста-Улама
ветствующие первой возбужденной моде, или суперпозиции нескольких
первых мод цепочки:
subroutine initial ()
use comdata
use msflib
implicit none
integer n !индекс осциллятора
!вычисляем постоянные
N1=N0+1
PIN1=PI/real(N1)
!размещаем массивы в оперативной памяти
allocate (у(О:N1),yold(О:N1)); у=0; yold=0
allocate (v(О:N1),а(О:N1)); v=0; a=0
allocate (E(l:NO), Ea(l:NO)); E=0; Ea=0
!возбуждаем одну, или несколько первых мод колебаний
!цепочки
do п=1,N0
у(n)=sin(PI*real(n)/real(N1)) !1-я мода
!у(n)=у(n)+sin(2.*PI*real(n)/real(N1)) !1,2-я моды
!у(n)=у(n)+sin(3.*PI*real(n)/real(N1)) !1,2,3-я моды
!у(n)=y(n)+sin(4.*PI*real(n)/real(N1)) !1,2,3,4-я моды
enddo
!определяем размеры графических окон:
!верхнее окно
gw(l).xl=20; gw(l).yu=20
gw(1).xr=820; gw(l).yd=420
gw(1).xmin=0.; gw(1).ymin=-2.
gw(1).xmax=Nl; gw(l).ymax= 2.
!нижнее окно
gw(2).xl=20; gw(2).yu=430
gw(2).xr=820; gw(2).yd=820
gw(2).xmin=0.; gw(2).ymin=0.
gw(2).xmax=Tmax; gw(2).ymax=l
!очищаем экран
call clearscreen($GCLEARSCREEN)
end subroutine initial
Начальное смещение t = О отдельного осциллятора вычисляется по
формуле (2.2). При этом полагается, что амплитуда для каждой моды
равна Ai = y/(N + 1)/2, а начальные фазы равны нулю, т. е. (pt = 0.
Это соответствует нулевым начальным скоростям всех осцилляторов
в цепочке. Исходный текст программы составлен таким образом, что
возбуждается только первая мода. Для возбуждения более высоких мод
необходимо снять комментарий с соответствующих строк кода.
2.2. Алгоритм и описание работы программы ->\г 77
Вычисление энергии отдельных мод и полной энергии цепочки вы¬
полняется в процедуре Emode:
Subroutine Emode()
use comdata
implicit none
integer m, n !индексы
real Q, Qv !нормальные координата и скорость
real sinmn
do m=l,NO
Q=0; Qv=0
do n=l,NO
sinmn=sin(m*n*PINl)
Q =Q +y(n)*sinmn !нормальная координата
Qv=Qv+v(n)*sinmn !нормальная скорость
enddo
! энергия моды
E(m)=0.5*Qv*Qv+2.0*Q*Q*sin(m*PINl/2)*sin(m*PINl/2)
enddo
Etot=sum(E(1:NO)) !полная энергия цепочки
!интегрируем зависимость энергии от времени
!для каждой моды
do m=l,NO
Еа(m)=Еа(m)+Е(m)*dt/Etot
enddo
end subroutine Emode
Энергия отдельных мод вычисляется с использованием формул (2.4)
и (2.5). Усредненные по времени зависимости энергии всех мод колеба¬
ний записываются в выходной файл Ema. dat процедурой EnergySave
через каждые 500 шагов интегрирования. Временные зависимости
приведенной энергии нескольких первых мод записываются в выходной
Em.dat:
subroutine EnergySave(t)
use comdata
implicit none
real (8) t
integer m !индекс моды
write (1,1) t, (E(m)/Etot+(m-1), m=l,5)
if (t/=0) write (2,2) t,(Ea(m)/t, m=l,NO)
1 format(6(el2.5,' '))
2 format(33(el2.5,' '))
end subroutine EnergySave
Глава 2. Задача Ферми-Паста-Улама
Интегрирование уравнений движения (2.1') выполняется в процеду¬
ре Euler:
subroutine Euler ()
use comdata
implicit none
integer i !индекс
real (8) ypl, yml
do i=l,NO
ypl=y(i+1)-y(i)
yml=y(i)-y(i-1)
a(i)=ypl-yml+ALPHA*(ypl*ypl-yml*yml)
enddo
do i=l,NO
v(i)=v(i)+a (i)*dt
у(i) =y(i)+v(i)*dt
enddo
!переписываем новое положение осцилляторов в старое
yold(0:N1)=у(0:N1)
end subroutine Euler
Использование в программе двух массивов yold(), у() для хра¬
нения координат осцилляторов используется для имитации движения
цепочки в процедуре Graf.
Коды процедур Graf и инициализации графического порта initgraf
представлены ниже:
subroutine Graf(t)
use comdata
use msflib
implicit none
type (wxycoord) wxy
real (8) t
integer n, m
integer (2) res, j
!рисуем цепочку осцилляторов
j=l; call initgraf(j)
!сначала затираем старое положение осцилляторов
res=setcolor(0)
do n=l,NO
res=ellipse_w($gborder, dble(n)-.l, dble(yold(n)) + .05, &
dble(n) +.1, dble(yold(n))-.05)
enddo
2.2. Алгоритм и описание работы программы •Аг 79
!затираем пружинки
call moveto_w(dble(0), dble(yold(0)), wxy)
do n=l,N1
res=lineto_w(dble(n), dble(yold(n)))
enddo
!а затем рисуем новое
res=setcolor(15)
do n=l,NO
res=ellipse_w($gborder, dble(n)-.l, dble(y(n))+.05,&
dble(n)+.l, dble(y(n))-.05)
enddo
!рисуем пружинки
call moveto_w(dble(0), dble(y(0)), wxy)
do n=l,Nl
res=lineto_w(dble(n), dble(y(n)))
enddo
!рисуем зависимости энергии от времени для первых 4-х мод
j=2; call initgraf(j)
do m=l,4
res=setcolor(8+m)
res=setpixel_w(t,E(m)/Etot)
enddo
end subroutine Graf
subroutine initgraf(j)
use comdata
use msflib
implicit none
integer (2) j !индекс окна
integer (2) res
logical (2):: direct=.true.
call setviewport(gw(j).xl, gw(j).yu, gw(j).xr, gw(j).yd)
if (j==l) call clearscreen($gviewport)
res=setwindow(direct, gw(j).xmin, gw(j).ymax,&
gw(j).xmax, gw(j).ymin)
res=setcolor(3)
res=rectangle_w($gborder, gw(j).xmin, gw(j).ymax,&
gw(j).xmax, gw(j).ymin)
end subroutine initgraf
2.2.3. Пример работы программы
Для тестирования работы программы была выбрана це¬
почка, состоящая из N = 32 осцилляторов при а = 0,1, М = 1, k = I,
е = 0,039 (е = Е/N это удельная энергия цепочки) (уравнение (2.1')).
80 -»\л Глава 2. Задача Ферми-Паста-Улама
Рис. 2.2. Зависимости приведенной энергии EJE (а) и усредненной по вре¬
мени Ei (б) (см. уравнение (2.5)) энергии мод от времени t. В ком¬
пьютерном эксперименте вначале возбуждалась только первая мода
и затем отслеживалось перераспределение ее энергии по остальным
модам. Номера мод обозначены на рисунке цифрами. Расчеты вы¬
полнены для цепочки N = 32
На рис. 2.2 представлены зависимости энергии мод от времени.
Выбранное значение удельной энергия цепочки (е = Е/N) является до¬
вольно низким, е = 0,039, и при этом наблюдается периодическое доми¬
нирование нескольких первых мод. Период такого доминирования для
первой моды равен примерно Т « 104 (см. рис. 2.1, а). Энергия по очере¬
ди перекачивается между несколькими первыми модами. Для удобства
анализа истинное значение приведенной энергии i-Й моды на рис. 2.1, а
смещено вверх на / —1 единиц по оси ординат. На рис. 2.1, б пред¬
ставлена зависимость усредненной по времени Et (см. уравнение (2.5))
энергии мод от времени t. Из этого рисунка видно, что со време¬
нем происходит лишь частичная термализация нескольких наинизших
мод. Полной термализации цепочки не происходит, поскольку энер¬
гия высоких мод после примерно одного периода повторения остается
практически постоянной. Такое поведение энергии мод подтверждает
результаты, полученные в экспериментах ФПУ [1].
2.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Проанализируйте колебания одномерной линейной цепочки при на¬
личии случайных возбуждений. Для этого на каждом шаге к скоро¬
стям частиц прибавьте величину, случайно распределенную в интер¬
вале между —du и +du, где du — некоторый параметр. Исследуйте
2.4. Литература -J\r 81
изменение полной энергии системы. Для тестирования работы про¬
граммы выберите цепочку, состоящей из N = 32 осцилляторов при
M = l,k = l.
2. Сравните поведение усредненной по времени энергии мод для а-
и ^-моделей ФПУ. Для тестирования работы программы выберите
цепочку, состоящей из N = 32 осцилляторов при а = 0,1 или /3 = 0,1,
М = 1, k = 1, е = 0,039 (е = E/N — удельная энергия цепочки).
3. Исследуйте перераспределение энергий между модами для а-моде-
ли ФПУ при учете взаимодействия с окружающей средой, вызван¬
ного, например, наличием трения. Для этого введите в уравнения
движения дополнительно силу, пропорциональную скорости частицы
Fn = ~ТУп, п = 1,
4. Обобщите рассмотренную задачу для исследования колебаний дву¬
мерной сетки связанных осцилляторов. Эта задача может соответ¬
ствовать колебаниям мембраны. Рассмотрите квадратную сетку свя¬
занных осцилляторов, т. е. предположите, что каждый осциллятор
связан с четырьмя ближайшими соседями и смещения масс проис¬
ходят только в вертикальном направлении.
2.4. ЛИТЕРАТУРА
1. Fermi Е., Pasta J.R. and UlamS.M. Studies on nonlinear problems, Los
Alamos Scientific Laboratory Report No. LA-1940, 1955 (unpublished); cm.
также Ферми Э. Научные труды. Т. 2. Сер. «Классики науки». — М.:
Наука, 1972. - 717 с.
2. Gallavotti G. (Ed.) The Fermi-Pasta-Ulam Problem: A Status Report //
Lecture Notes in Physics. — V. 728. — Berlin-Heidelberg: Springer, 2008. —
302 p.
3. Zabusky N.J., Kruskal M.D. Interaction of «solitons» in a collisionless plasma
and the recurrence of initial states // Phys. Rev. Lett. — 1965. — V. 15. —
P. 240-243.
4 .Zabusky N.J. Nonlinear Partial Differential Equations. — Academic Press,
1967. - 223 p.
5. Northcote R. S. and Potts R. B. Energy sharing and equilibrium for nonlinear
systems 11 J. Math. Phys. - 1964. - V. 5. - P. 383-393.
6. Израилев Ф.М., Чириков Б. В. Статистические свойства нелинейной стру¬
ны // ДАН. Сер. Математика. Физика. — 1966. — Т. 11. — С. 30-34.
7. Заславский Р. М., Сагдеев Р. 3. Введение в нелинейную физику. От ма¬
ятника до турбулентности и хаоса. — М.: Наука, 1988; Zaslavsky G. М.,
Sagdeev R.Z., Usikov D. A., Chernikov A. A. Weak Chaos and Quasi-Regular
Patterns. — Cambridge: Cambridge University Press, 1991. — 265 p.
82 ->\r Глава 2. Задача Ферми-Паста-Улама
8. Ford J. and Waters J. Computer studies of energy sharing and ergodicity for
nonlinear oscillator systems 11 J. Math. Phys. — 1963. — V. 4, No. 10. —
P. 1293.
9. Hemmer P. C. Dynamic and stochastic types of motion in the linear chain:
Ph.D. thesis. — Trondheim, 1959.
10. Уизем Дж. Линейные и нелинейные волны. — М.: Мир, 1977. — 624 с.
11. Года М. Теория нелинейных решеток. — М.: Мир, 1984. — 264 с.
12. Додд Р., Эйлбек Дж., Гиббсон Дж., Моррис X. Солитоны и нелинейные
волновые уравнения. — М.: Мир, 1988. — 694 с.
13. Ньюэлл А. Солитоны в математике и физике. — М.: Мир, 1989. — 326 с.
ГЛАВА солитоны
о И УРАВНЕНИЕ КОРТЕВЕГА-ДЕ ВРИЗА
3.1. РАЗВИТИЕ ПРЕДСТАВЛЕНИЙ О СОЛИТОНЕ
3.1.1. Распространение уединенной волны в узком канале
На возможность распространения уединенной волны или
солитона впервые обратил внимание британский инженер Расселл
1834 г. [1-3]. Данную волну он назвал волной трансляции. В результате
более детальных экспериментальных исследований Расселл предло¬
жил эмпирическую формулу для зависимости скорости уединенной
волны от ее максимальной высоты уо (рис. 3.1) над уровнем воды в
канале
», = \Ц| + !)«<»о(| +1).
где vo = y/gh, g — гравитационная постоянная, h — глубина воды.
Приближенное соотношение в данной формуле получается при усло¬
вии невысокой волны, т. е. yv h.
Величина Vo = yfgh соответству¬
ет скорости Релея при распростра¬
нении волн в неглубоком канале,
т. е. глубина воды h намного мень¬
ше, чем длина распространяющей¬
ся волны Я (h <С Я).
Результат Рассела сначала был
воспринят скептически. Г. Р. Эйри
построил теорию волн на мелкой
воде и показал, что такие волны
должны быть неустойчивы, а Джон
Гершель охарактеризовал уединенную волну как «отсеченную половину
обычной волны».
//////// / пппипптпп////////////
Рис. 3.1. Распространение импульса
возмущения на поверхности воды в
84 ->V Глава 3. Солитоны и уравнение Кортевега—де Вриза
3.1.2. Уравнение Кортевега—де Вриза
Противоречие было разрешено в 1895 г. Кортевегом и де
Вризом (КдВ), которые предложили для описания формы слабо нели¬
нейной волны у(х, 0 на мелкой воде (h А) [4] следующее дифферен¬
циальное уравнение
yt + v0(l + ^)yx + v-?^ = 0, (3.1)
где vo = y/gh- В данном уравнении учтены нелинейные (слагаемое УУх)
и дисперсионные (слагаемое уххх), эффекты.
В случае пренебрежения нелинейными и дисперсионными эффекта-
ми, имеем волновое уравнение вида
yt + УоУх = О,
общим решением которого является произвольная функция вида у(х, t) =
= f(x-vot). Это решение соответствует распространению волнового им¬
пульса произвольной формы в определенном направлении со скоростью vv.
3.1.3. Роль нелинейного и дисперсионного вкладов
При учете только нелинейного слагаемого получим урав¬
нение вида
y, + v0(l + ^£)ух = 0.
В этом уравнении скорость распространения волны v(y) = vo[l + 3y/(2h)\
не является постоянной, максимальную скорость будут иметь частицы
на вершине горба, а минимальную на поверхности воды. В данной
ситуации, если на поверхности воды образуется импульс возмущения,
то со временем будет увеличиваться крутизна его переднего фронта.
При этом нижняя часть импульса будет «отставать» и со временем
импульс будет опрокидываться, т. е. терять свою форму. Таким образом,
нелинейность не является достаточным условием для формирования
солитона. Необходим дополнительный стабилизирующий фактор, кото¬
рый задается дисперсионным членом в уравнении КДВ (3.1).
При учете только дисперсионного члена получим уравнение вида
У1 + Vo Ух + УХХх = 0.
Это обобщение волнового уравнения, полученное добавлением произ¬
водной высшего порядка. Решение такого уравнения можно получить
с помощью подстановки у(х, t) = exp[ikw(x + ^oOL гДе kw — 2njX -
волновое число. Отсюда получим дисперсионное соотношение
3.1. Развитие представлений о солитоне -*\г 85
Это свидетельствует о том, что фазовая скорость v не является по¬
стоянной и зависит от kw = 2л/А, т. е. от длины волны А. Таким об¬
разом, дисперсионное слагаемое учитывает зависимость скорости от
длины волны А, которая определяется физическими и геометрическими
свойствами среды. В общем случае форму кривой, которая описывает
импульс возмущения можно разложить в ряд Фурье по различным
длинам волн А. При наличии дисперсии различные составляющие вол¬
ны движутся с различными скоростями и волна «расплывается». При
определенной форме импульса и его скорости дисперсионный эффект
может полностью подавлять нелинейную нестабильность, связанную
увеличением крутизны переднего фронта.
3.1.4. Точное солитонное решение
где vs = УоП + */o/(2/z)] — скорость солитона, а Д = 2hyJh/{3yo) — его
ширина, cosh г = (ez + е~г)/2 [5, 6]. Отсюда следует, что при увеличе¬
нии высоты солитона уо не только увеличивается его скорость, но и
уменьшается его ширина. Важными свойствами солитона является его
способность сохранять свою форму неизменной, а также локализация
его энергии, что является свойствами частицы.
В 1965 г. Забуски и Крускал [7] в результате численного интегриро¬
вания уравнения КдВ продемонстрировали, что солитонная волна вида
(3.2) может возникать при произвольных начальных условиях, и она
сохраняется при столкновениях с другими солитонными волнами.
Для численного интегрирования уравнение КДВ (3.1) удобно преоб¬
разовать к скоростной форме. Полагая v(y) = оо[1 + Зг//(2/г)] и исполь¬
зуя соотношение vxxx = 3voyxxx/{2h), получим
где c = voh2/6. Отметим, что с = kyf3yog/\2, при этом величина с
пропорциональна ширине солитона.
Существуют и другие примеры уравнений, имеющих солитонные
решения, например, модифицированное уравнение КдВ [8, 9]
где а,с — параметры, или уравнение sin-Гордона (СГ) [5, 6]
Vtt — Vxx + sin v = О,
которое описывает распространение дислокаций в кристаллах или волн
плотности заряда.
Уравнение КДВ (3.1) имеет точное солитонное решение
(3.2)
Vt + vvx + CVXXX = О,
(3.3)
Vt + v(\ + av)vx + cvxxx = 0»
(3.4)
86 -»\r Глава 3. Солитоны и уравнение Кортевега—де Вриза
В настоящее время найдено значительное количество примеров про¬
явления солитонных явлений в электронике, оптике, биологии, физи¬
ке твердого тела и теории поля. В природных явлениях солитонами
являются цунами и вихревые кольцеобразные образования, например
Большое красное пятно Юпитера [10, 11].
В этой главе мы более подробно проанализируем пример численного
решения уравнения КдВ.
3.2. АЛГОРИТМ И ОПИСАНИЕ РАБОТЫ ПРОГРАММЫ
3.2.1. Алгоритм
Для численного решение уравнения КДВ (3.3) представим
его в конечно-разностной форме, используя следующие соотношения:
Vj,i+I - Vj,i .
д<
Vj+l,i — vj~U
ы*= ; (3-5)
\ (vi+2,i - 2vi+и + Щ-и - vi-2,i)
- 2дз
где индекс / используется для узлов пространственной сетки, a i —
временной. Постоянные Д* и Д* используются для обозначения шага
интегрирования по координате и времени соответственно.
Подстановка выражений (3.5) в уравнение (3.3) приводит к конечно¬
разностному уравнению вида
Vj,i+1 = Vjj - ^-VjjiVj+n - vHli) - 7^{Vj+2,i - 2W/+U + 2У/-1,,' - Vj-2,i)-
(3.6)
Это наиболее простая явная схема, которая была использована в
классической работе [7]. Данная схема позволяет аппроксимировать
дифференциальную задачу с порядком 0(т2 + h<i) и она устойчива при
выполнении условия [12]:
А, <
4Д*
Ъсу/Ъ
В литературе обсуждаются также более сложные явные и неявные
конечно-разностные схемы для численного решение уравнения КДВ,
которые позволяют более точно выдерживать законы сохранения (так
называемые консервативные схемы) [13].
3.2. Алгоритм и описание работы программы 87
3.2.2. Описание работы программы
Рабочая программа для численного решения уравнения
КдВ в скоростной форме находится в файле KdV. f 90. Программа име¬
ет модульную структуру и ниже приведено описание основных модулей
и набора процедур. Переменные и массивы программы определяются в
модуле comdata:
module comdata
real(8) :: с = 0.00005 !параметр скоростного уравнения
!КдВ (3 солитона)
integer :: N = 200 !число узлов пространственной
!сетки
real (8):: dt = 0.0004 !шаг интегрирования по времени
!вспомогательные переменные
integer N1 !N1=N-1
integer N2 !N2=N-2
real PI !число Пи
!постоянные разностной схемы
real (8) dtdxl !dtdxl=dt/(2*dx)
real (8) dtdx2 !dtdx2=c*dt/(2*dx**3)
real (8) dx !шаг по координате dx=l/N
!таблица сдвига индекса
integer:: dj(-2:2)=(/-2,-l,0,1,2/)
!массив ближайших индексов
integer j n(—2:2)
!массивы для хранения решения уравнения КдВ
real (8), allocatable:: v (:) !текущее решение
real (8), allocatable:: vo(:) !старое решение
end module comdata
При численном интегрировании и использовании разностного урав¬
нения (3.6) нужно вычислять значения индексов ближайших соседей
по отношению к узлу с индексом /. Поэтому удобно ввести таблицу
относительных координат ближайших соседних узлов, которая пред¬
ставлена массивом dj (). Численные значения индексов ближайших
соседей записываются в массив jn(). Для графического построения
профиля солитона и имитации его движения используются два массива
v () и vo ().
Начальные условия определяются в процедуре инициализации init:
Subroutine init()
use msflib
use comdata
implicit none
integer j !индекс пространственного узла
real (8) x !пространственная координата
88 ->\r Глава 3. Солитоны и уравнение Кортевега—де Вриза
!параметры начального решения уравнения:
real (8):: xm = 0.5 !центр горба
real (8):: А = 0.5 !амплитуда горба
real (8):: s = 0.08 !ширина горба
!вычисляем постоянных разностной схемы интегрирования
!и вспомогательных переменных
dx = dble(1.0/N) !шаг интегрирования по координате
dtdxl = dt/(2*dx)
dtdx2 = c*dt/(2*dx**3)
N1 = N-l
N2 = N-2
!располагаем массивы для хранения решения
!в оперативной памяти
allocate(v (1:N)); v=0
allocate(vo(1:N)); vo=0
!определяем начальное значение для скорости v(x,0)
do j = 1,N
x=j *dx
v(j)=A*exp(-(x-xm)**2/(2*s**2))
enddo
end subroutine init
В качестве профиля начального возмущения у(х, 0) на поверхности
воды можно выбрать, гладкую функцию, например гауссову. Поскольку
v(xj) ~ у(х, t), то начальное условие для скорости можно представить
в виде
где А = 0,5 — амплитуда «горба», хт = 0,5 — координата его максиму¬
ма, и s = 0,08 — полуширина.
Численное интегрирование уравнения КдВ осуществляется в глав¬
ном модуле программы:
program KdVmain
use comdata
use msflib
implicit none
type (rccoord) curpos
character (1) key
integer i,j !индексы сетки
real(8) t
real (8) vnl, vd !нелинейный и дисперсионный вклад
(3.7)
!в скорость
call init
call initgraf
3.2. Алгоритм и описание работы программы •Аг 89
do i=l,100000 !цикл интегрирования по времени
t=i*dt
do j =1,N !цикл интегрирования по координате
!вычисляем значения ближайших индексов
!пространственной сетки
if(j==l) then
j n(-2)=N1; j n(-1)=N; jn(0:2)=j+dj (0:2)
elseif(j==2) then
jn(-2)=N; jn(-1:2)=j+dj (-1:2)
elseif(j==N-l) then
jn(-2:1)=j +dj (-2:1); jn(2)=l
elseif(j==N) then
jn(-2:0)=j+dj (-2:0); jn (1)=1; jn (2)=2
else
jn(-2:2)=j+dj (-2:2)
endif
!вычисляем значения скоростей в узлах
!пространственной сетки
vnl =-dtdxl* v(jn(0))*(v(jn(1))-v(jn(-1)))
vd =-dtdx2*(v(jn(2))-2.0*v(jn(l))+&
2.0*v(jn(-1))-v(jn(-2)))
v (j)= v(jn(0))+vnl+vd
enddo
if(mod(i,50)==0) then
call Plot() !рисуем решение
vo=v !переписываем текущее решение в старое
call settextposition (1,3,curpos);
write (*,' (a3, f8.5)')'t=', t, ' '
key=getcharqq()
endif
enddo
end program KdVmain
При интегрировании использовались периодические граничные усло¬
вия. Результат численного решения выводится на экран дисплея через
каждые 50 шагов интегрирования по времени с помощью графической
процедуры Plot. Для просмотра вида решения на дисплее в про¬
грамме используется библиотечная функция getcharqqO, которая
приостанавливает выполнение программы до нажатия любой клавиши
клавиатуры.
3.2.3. Пример работы программы
На рис. 3.2 приведен результат работы программы KdV. f 90,
полученный при использовании численного значения с = 5 • 10-5 в
уравнении (3.6). В момент времени / = 0,12 форма кривой решения
90 -iV Глава 3. Солитоны и уравнение Кортевега—де Вриза
уже существенно отличается от гауссиана, поскольку вершина «горба»
движется с наибольшей скоростью. К моменту времени t= 1,42 на¬
чальный «горб» разделяется на три солитона, имеющие разную высоту
и ширину и движущиеся вправо с различной скоростью. В силу пери¬
одических граничных условий, накладываемых на решение, солитон,
обозначенный на рисунке номером один, догоняет солитон с номером
три (t = 3,9) и «проходит» сквозь него, не меняя своей высоты и формы
(t = 5,3).
0 х 1
Рис. 3.2. Численное решение уравнения (3.6) на интервале х £ [0,1] в раз¬
личные моменты времени t при с = 5 • 10-5 и начальном условии,
описываемом уравнением (3.7). Стрелками на рисунке показано на¬
правление движения солитонов
3.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Используя программу KdV.f90 исследуйте процесс распада началь¬
ного гауссового возмущения на отдельные солитоны в зависимости
от величины параметра с, проанализируйте зависимость количества
солитонов от величины значения с и объясните результат.
2. Обобщите программу KdV.f90 для анализа модифицированного
уравнения КдВ (или уравнения Гарднера), уравнение (3.4), которое
имеет точное солитонное решение [7, 8]. При этом параметр а может
быть как положительным, так и отрицательным. Сравните солитон¬
ное поведение для обычного и модифицированного уравнений КдВ
при различных значениях параметров а и с.
3.4. Литература 91
3. В реальных ситуациях солитонные волны могут возникать в про¬
странственно неоднородных средах, что может быть связано, напри¬
мер, с изменением глубины океана h при прохождении солитонной
волны (цунами) [10]. В простейшем обобщении уравнения КдВ для
неоднородной среды можно учесть зависимость параметра с от про¬
странственной координаты х. В связи с этим обобщите программу
KdV.f90 для анализа пространственно неоднородного уравнения
КдВ. Проанализируйте солитонное поведение для пространственной
неоднородности барьерного (гауссов барьер) и синусоидального типа.
3.4. ЛИТЕРАТУРА
1. Scott Russell J. Report on waves. Rept. 14th meetings of the British Assoc, for
the Advancement of Science. — London: John Murray, 1844. — P. 311-390;
см. также Буллаф P., Кодри П. Солитон и его история // В кн.: Солитоны /
Под ред. Р. Буллафа и П. Кодри. — М.: Мир, 1983. — С. 11—77; Губан¬
ков В. Н. Солитоны. — Либроком, 2011. — 120 с; Филиппов А. Т. Много¬
ликий солитон. — М.: Наука, 1986. — 224 с. (Б-чка «Квант»; Вып. 48).
2. Уизем Дж. Линейные и нелинейные волны. — М.: Мир, 1977. — 622 с.
Ъ.ЛэмДж.Л. Введение в теорию солитонов. — М.: Меркурий-ПРЕСС,
2000. - 294 с.
4. Korteweg D.J., de Vries G. On the change form of long waves advancing
in a rectangular channel and on new type of long stationary waves // Phyl.
Mag. - 1895. - V. 36, No. 5. - P. 422-443.
5. Додд P., ЭйлбекДж., Гиббон Дж., Моррис X. Солитоны и нелинейные
волновые уравнения. — М.: Мир, 1988. — 694 с.
6. Заславский Г. М., СагдеевР.З. Введение в нелинейную физику. — М.:
Наука, 1988. — 368 с.
7. Zabusky N.J., Kruskal M.D. Interaction of «Solitons» in a Collisionless Plas¬
ma and the Recurrence of Initial States // Phys. Rev. Lett. — 1965. — V. 15,
No. 6. - P. 240-243.
8. Desanto J. A. Mathematical and Numerical Aspects of Wave Propagation. —
Philadelphia: SIAM, 1998.
9. Biswas A., Zerrad E. Soliton Perturbation Theory for the Gardner Equation //
Adv. Studies Theor. Phys. - 2008. - V. 2, No. 16. - P. 787-794.
10. Grimshaw R., Pelinovsky E. and Talipova T. Modeling internal solitary waves
in the coastal ocean // Surveys in Geophysics. — 2007. — V. 28. —
P. 273-298.
11. Незлин M.B. Солитоны Россби // УФН. — 1986. — Т. 150. — С. 3-60.
12. Березин Ю. А. О численных решениях уравнения Кортевега—де Вриза //
Численные методы механики сплошной среды. — Новосибирск, 1973. —
Т. 4. - С. 20-31.
13. de Frutos J., Sanz-Serna J.M. Accuracy and conservation properties in nu¬
merical integration: the case of the Korteweg—de Vries equation 11 Num.
Math. - 1997. - V. 75. - P. 421-445.
ГЛАВА ЛОГИСТИЧЕСКОЕ ОТОБРАЖЕНИЕ
Л И ПОКАЗАТЕЛЬ ЛЯПУНОВА
4.1. ХАОТИЧЕСКОЕ ПОВЕДЕНИЕ
В настоящее время выражение «эффект бабочки» стало
чрезвычайно популярным для определения наличия хаоса. При наличии
хаоса, любые, даже самые незначительные детали или изменения на¬
чальных условий могут приводить к глобальным изменениям в времен¬
ной эволюции событий. Существует масса примеров проявления хаоти¬
ческих процессов, например, поведение вихрей в турбулентных потоках,
шумов в электронных схемах, в сложных атмосферных явлениях, в хими¬
ческих реакциях, в экономике, биологии, экологии, медицине и т.д. [I].
Отметим, что большинство хаотических систем контролируется детер¬
министическими, но, вместе с тем, существенно нелинейными закона¬
ми. Одним из примеров могут служить псевдо-случайные числовые по¬
следовательности, которые основаны на использовании детерминисти¬
ческих формул итерационного типа. Результат работы хорошего гене¬
ратора псевдо-случайных чисел практически невозможно предсказать,
и многие статистические тесты подтверждают случайное происхожде¬
ние достаточно длинных последовательностей генерируемых чисел. В
литературе иногда высказывается мнение, что некоторые природные
случайные процессы могут быть также организованы подобным обра¬
зом, т. е. в их основе могут быть заложены детерминистические законы.
4.1.1. Логистическое отображение
На возможность генерации хаотических последовательно¬
стей при использовании нелинейных итерационных формул впервые об¬
ратил внимание Фейгенбаум в 1975 г. [2]. Используя программируемый
калькулятор он исследовал появление хаотизации для квадратичной
итерационной формулы типа
Хп+1 = ГХ„( 1 - хп), (4.1)
где величина г (0 < г < 4) является управляющим параметром.
4.1. Хаотическое поведение
X
93
Впоследствии оказалось, что подобная хаотизация является доволь¬
но общим явлением, характерным для нелинейных отображений раз¬
личного вида, и может наблюдаться, например, для отображения вида
х„+1 = хпег(Х-Хп) или хп+\ = г(1 - (1 - 2хп)4).
Нелинейное отображение, описываемое соотношением (4.1), называ¬
емое логистическим может служить в качестве математической модели
для описания динамики развития популяций. Численность популяций
может возрастать за счет естественного прироста, что соответствует
хл+\ ~ хп, но вместе с тем рост может быть ограничен, что учиты¬
вается введением множителя (1 — хп). Ограничение роста может быть
связано с перенаселением, отсутствием ресурсов или распространением
болезней.
Обычно область возможных значений хп ограничивают интерва¬
лом [0,1]. Управляющий параметр г характеризует скорость роста по¬
пуляции. Впервые логистическое уравнение для описания эволюции
биологических популяций предложил Ферхюльст в 1838 г.
г = 0,4
10 20 30 40
п
50
10 20 30 40
п
10 20 30 40 50
п
Рис. 4.1. Зависимости хп от п для 50 первых итераций для итерационной
формулы (4.1), при различных значениях параметра роста г
На рис. 4.1 представлен пример поведения хп для первых 50 итера¬
ций при разных значениях параметра «роста» г.
94 ->V Глава 4. Логистическое отображение и показатель Ляпунова
В качестве начального значения итерации во всех случаях было вы¬
брано хо = 0,5. В зависимости от значения г можно выделить несколько
основных типов поведения. При 0 < г < 1 величина хп быстро умень¬
шается и при больших значениях п приближается к 0 (рис. 4.1, а). В
интервале 1 < г < 3 величина хп после некоторого начального количе¬
ства итераций приближается к некоторому стационарному значению
Xfi—yQQ = х* (рис. 4.1, б). Точка х* называется устойчивой и она опре¬
деляется из уравнения х* = f(x*), где f(x) = гх(\ — х). Отсюда получим
х* = 1 — 1/г. Отметим, что для некоторых г известны точные аналити¬
ческие решения, описывающие поведение хп. Например,
Принципиально другое поведение наблюдается при дальнейшем
увеличении г (г > 3). В данном случае величина хп в пределе больших
значений п не сходится к определенному значению х*. Для интервала
3 < г < 1 + у/б (см., например, рис. 4.1, в) значение хп повторяется
через одну итерацию, т. е. наблюдаются осцилляции и происходит удво¬
ение периода осцилляций. При дальнейшем увеличении г могут наблю¬
даться более сложные осцилляции хПу и наконец при г = « 3,56995
число периодических точек становится бесконечным, и после чего
далее наблюдается переход к хаотическому режиму (рис. 4.1, г). Таким
образом, с ростом г осуществляется постепенный переход от детерми¬
нированного к хаотическому поведению.
Первое удвоения периода наблюдается при г\ = 3, второе удвоение
г = 1 + \/б, третье удвоение при г = 1 + \/8, а последовательность зна¬
чений гл, при которых происходит удвоения периода, когда п —► оо,
сходится геометрически к гпо закону
cLf
где величины dp « 2,637 и 6р = limл_>00(гл — гп-\)/(гп+\ — гп) « 4,6692
называют постоянными Фейгенбаума. Примечательно, что величина 6р
является одинаковой для всех отображений второго порядка.
Выполнив замену переменных 2 = г(1/2 — х) логистическое отобра¬
жение можно представить в форме
1 - (1 - 2х0 f
для г = 2,
2
1 — cos[2n arccos(l — 2хо)]
2
для г — 4.
Z„+1 = 4 + с,
(4.2)
где с = г{\ - г/2)/2.
4.1. Хаотическое поведение -Jb 95
Отметим, отображение (4.2) выраженное в комплексных коорди¬
натах используется для построения фрактальных множеств Жюлиа и
Мандельброта. Для отображения (4.2) первый период удвоения наблю¬
дается при с = —3/4, а второй период — при с = -5/4, а третий — при
с =-7/4.
г
Рис. 4.2. Бифуркационная диаграмма для логистического отображения, опи¬
сываемого итерационной формулой (4.1)
На рис. 4.2 представлена зависимость х = = х* от г для логи¬
стического отображения, описываемого итерационной формулой (4.1).
Отметим, что в интервале хаотичности при г > « 3,56995 суще¬
ствуют узкие «окна периодичности», которые предсказал в 1964 г.
А. Н. Шарковский [3], исследуя унимодальные отображения.
4.1.2. Показатель Ляпунова
Для характеризации хаотического поведения удобно ис¬
пользовать показатель Ляпунова А.
Для определения показателя Ляпунова рассмотрим две параллель¬
ные итерации, которые начинаются из двух близких начальных точек,
разделенных расстоянием До, например хо и хо + До- Расстояние между
этими точками после п итераций будет равно
Д„ = \fin)(x0 + До) - /(п)(*о)| « До<?пА-
Здесь f^n\x) = /(/(.../(*) • • •)) соответствует п-й итерации, а величи¬
на А (показатель Ляпунова) характеризует скорость разбегания точек
при увеличении количества итераций.
96
Глава 4. Логистическое отображение и показатель Ляпунова
При наличии хаоса расстояние между точками будет непрерывно
возрастать, что соответствует положительному значению А, т. е. Л > 0.
Наличие хаоса можно протестировать, изучая изменение расстояния
между точками Д„, которые в начальный момент времени разделены
чрезвычайно малым расстоянием, т. е. До 1.
Воспользовавшись приближением |/(^(хо + До)— /*лЧ*о)| ~ |/(ai)/(*o)|Ao
и учитывая, что согласно правилу дифференцирования сложной функ¬
ции производную от п-й итерации функции / можно представить в
виде |/(n)/(jco)| = \f'(xo)ff(x\) .. .f'(xn-\)\ в пределе п —> оо получим
следующую формулу для вычисления показателя Ляпунова [1]
Таким образом, показатель Ляпунова можно вычислить, анализи¬
руя разницу в эволюции между двумя итерационными точками Д„
при двух параллельных итерациях с близкими начальными значениями
(рис. 4.3).
Рис. 4.3. К описанию процедуры для вычисления показателя Ляпунова
х
О
2 3 4 5 6 7 8
п
Для логистического отображения имеем f'(xn) = r( 1 — 2хп), что
упрощает вычисление величины Я
4.2. Описание работы программ -1\г 97
4.2. ОПИСАНИЕ РАБОТЫ ПРОГРАММ
4.2.1. Бифуркационная диаграмма
и поведение показателя Ляпунова
Программа для графического построения бифуркационной
диаграммы и поведения показателя Ляпунова А в зависимости от па¬
раметра роста г содержится в файле logistic. f 90.
Ниже представлена основная часть кода этой программы:
program logistic
use msflib
implicit none
integer:: N=2000 !количество итераций
real r !параметр "роста"
real lambda !показатель Ляпунова
real x
integer i
integer(2) res
!инициализация графического окна
call initgraf
open (1,file='lyapunov.dat')
!выполняем итерации при разных г
do r=0.01,3.99,0.001
х=0.1 !начальное значение хО
lambda=0.
do i=l,N
x=r*x*(1-х)
lambda=lambda+log(abs(r*(1.-2.*x)))
if(i>1800)res=setpixel_w(r, x);
enddo
lambda=lambda/real(N)
write(1,*) r, lambda
enddo
close(1)
end program logistic
Итерационные вычисления в программе выполняются во внутрен¬
нем вложенном цикле do ... enddo по i. Во внешнем цикле присваи¬
ваются значения параметра г с шагом 10_3, и для каждого начального
значения jco = 0,1 выполняется 2 • 103 итераций во вложенном цикле.
Для отображения установившего режима первые 1800 итераций не
отображается на экране дисплея. Отображение численных значений хп
осуществляется с помощью графического оператора setpixel_w мо¬
дуля msflib.
98 •Ar Глава 4. Логистическое отображение и показатель Ляпунова
4.2.2. Пример работы программы
На рис. 4.4 представлены результаты вычисления зависи¬
мостей х — хп^оо и Л от г для логистического отображения, описывае¬
мого итерационной формулой (4.1) с помощью программы logistic . f 90.
Рис. 4.4. Зависимости х = хп^оо и Я от г для логистического отображения,
описываемого итерационной формулой (4.1), которое получено с по¬
мощью программы logistic, f90
Численные значения Л в зависимости от г выводятся во внешний
файл, что может быть полезно для дальнейшего анализа.
4.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Изучая расстояние между двумя точками Ь.п—х\—х\, которые в
начальный момент времени разделены чрезвычайно малым рассто¬
янием, например, xlQ = 0,5, х\ — 0,50000001, напишите программу
для тестирования наличия хаоса в логистическом отображении (4.1).
2. Постройте бифуркационные диаграммы и зависимости Я от г для
следующих отображений
хп+\ — rsin(7rxn), 0 < г < 1;
хп+1 = -гхп 1п(х„), 0 < г < е — 2,71829;
хп+\ = хпег^~Хп), 0 < г < е = 2,71829;
хп+\ — г + е~х\ — 1 < г < 1, k — 1,2,3;
x„+i = rxn( 1 - хп)а, 0 < а < 1, 0 < г < 1.
(4.4)
(4.5)
(4.6)
(4.7)
(4.8)
4.3. Задачи для самостоятельной работы 99
Модель (4.7) называется гауссовой. Модель (4.8) при а = 1 сводится
к логистической, а при а = О сводится к экспоненциальной.
3. Проанализируйте возможность использования логистического отоб¬
ражения для генерирования случайных чисел. Для этого, исполь¬
зуя соотношение (4.1) выполните 100000 итераций для различных
значений г из интервала хаотичности (г > « 3,56995). Сравните
равномерность распределения данной серии чисел с равномерностью
распределения, которое получается с помощью встроенного генера¬
тора случайных чисел. Объясните наблюдаемые различия.
4. Пусть логистическое отображение хп+\ = rxn{ 1 — хп) определено на
интервале 0 < хп < 1. Определите соответствующий интервал zn для
отображения zn+\ = z2n + с и постройте бифуркационную диаграмму
для этого отображения.
5. Постройте бифукарционную диаграмму и зависимость Л(г) для ло¬
гистической модели с запаздыванием, определяемой отображением
Хп+\ = гхп( 1 -*„_*),
где k = 0 соответствует обычному логистическому отображению.
Проанализируйте отличия в хаотическом поведении при k = 0,1,2.
6. Одним из широко известных примеров запаздывающего отображения
является отображение Хенона [5], для которого хп+\ — bxn-\ +1 — ах\.
Это отображение является стабильным при 0 < b < 1 и его можно
представить в виде двухмерного отображения
хп+1 =Уп + 1 - ах2п;
уп+1 = Ьхп.
Пример двумерного отображения Хенона в координатах у(х) пред¬
ставлен на рис. 4.5. Напишите программу для построения двумерно¬
го отображения Хенона и проанализируйте его хаотичность.
Рис. 4.5. Отображение Хенона при а = 1,4, b = 0,3
100
Глава 4. Логистическое отображение и показатель Ляпунова
7. Стандартное двумерное отображения (или отображение Чирикова-
Тейлора), определяется следующей системой уравнений [1, 4]
где г < 1 (параметр возмущения). Данная система уравнений описыва¬
ет движения ротатора, возбуждаемого периодическими толчками. На¬
пишите программу для построения стандартного отображения и про¬
анализируйте его хаотичность.
1. Шустер Г. Детерминированный хаос: Введение / Пер. с англ. — М.: Мир,
1988. - С. 68-71.
2. Фейгенбаум М. Универсальность в поведении нелинейных систем //
УФН. - 1983. - Т. 141, №2. - С. 343-373.
3. Шарковский А. Я., Коляда С. Ф., Спивак А. Г., Федоренко В. В. Динамика
одномерных отображений. — Киев: Наукова думка, 1989. — 216 с.
4. Заславский Г. М., Сагдеев Р. 3., Усиков Д. А., Черников А. А. Слабый хаос
и квазирегулярные структуры. — М.: Наука, 1991. — 41 с.
5. Мун Ф. Хаотические колебания. — М.: Мир, 1990. — 312 с.
хп+1 =хп- rs'm(yn) (mod 2л);
Уп+i =Уп+хп - rsin(j/„) (mod 2л),
4.4.
ЛИТЕРАТУРА
ГЛАВА МНОЖЕСТВА ЖЮЛИА И МАНДЕЛЬБРОТА
5
5.1. НЕЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
В КОМПЛЕКСНЫХ КООРДИНАТАХ
Ранее при рассмотрении хаотических явлений (см. гл. 4)
был проведен детальный анализ свойств нелинейного логистического
отображения. В настоящее время известно, что нелинейные отобра¬
жения, выраженные в комплексных координатах, могут приводить к
чрезвычайно интересному хаотическому поведению и проявлению са¬
моподобия генерируемых структур (паттернов) [1-3]. Рассмотрим более
детально такое поведение на примере множеств Жюлиа и Мандельбро¬
та, которые основаны на использовании логистического отображения,
обобщенного для комплексной области
Z„+1 = f{zn) = z\ + с,
где 2 = х + iy и с = сх + icy — комплексные числа, п — номер итерации.
Эволюция изменения величины гп зависит от начального значения zo
и значения с.
Для действительных чисел это соотношение можно переписать в
виде системы уравнений
Хп+1 = х2п - у2п + сх;
Уп+\ = 2 хпуп + Су.
5.1.1. Множество Жюлиа
Рассмотрим простейший случай с — 0 (сх = 0, су = 0) и
будем последовательно выполнять итерации zo —> z\ —► 23, ..., —> zn.
В экспоненциальном представлении величины zn выражаются как
zn+1 = (|z0|^)n, где п — номер итерации, a |zo| и ср — модуль и фаза
вектора.
102
Глава 5. Множества Жюлиа и Мандельброта
Когда \zo\ > 1, то изображающие точки zn итераций непрерывно
удаляются от начала координат и стремятся к бесконечности (в этом
случае говорят, что гп притягиваются к бесконечно удаленной точке).
ческое движение по множеству, а точки вне множества последова¬
тельно удаляются от множества. В случае, когда множество состоит
всего лишь с одной точки, то такую точку называют аттрактором.
В общем случае множество Жюлиа может состоять из конечного или
бесконечного числа точек, называемого циклом. Количество точек цик¬
ла определяет его период. Притянувшись к циклу, функциональная
итерация в дальнейшем не покидают этот цикл. В случае, когда пери¬
од цикла бесконечен, говорят, что итерации переходят в хаотический
режим.
Для каждого значения с = сх + icy имеется определенное множе¬
ство Жюлиа, ограничивающее значения комплексных чисел г, которые
в процессе итераций не уходят на бесконечность [1, 2].
Можно показать, что если в процессе итераций величина z выхо¬
дит за пределы области г > 2 (т. е. х2 + у2 > 4), то она в дальнейшем
довольно быстро уходит на бесконечность. Таким образом, для постро¬
ения множества Жюлиа необходимо при каком-то определенном зна¬
чении сх,Су просканировать область начальных значений х, у (обычно
выбирают интервал —2... 2) и разделить точки на те, которые уходят
и не уходят на бесконечность через достаточно большое количество
итераций.
Для \zo\ < 1, точки zn стремится
к нулю (рис. 5.1). При |zo| = 1 все
точки zn находятся на окружно¬
сти, а пограничная область в виде
круга единичного радиуса состав¬
ляет множество Жюлиа.
Рис. 5.1. Пример построения кругово¬
го множества Жюлиа для последова¬
тельных итераций zn+\ = z2n
При ненулевых значениях с
наблюдается аналогичная карти¬
на. В этом случае можно выде¬
лить пограничную область между
двумя различными типами пове¬
дения, когда при последователь¬
ных итерациях точки zn стремят¬
ся или к бесконечности, или к ну¬
лю (рис. 5.2).
Отметим, что в общем случае
с ф 0 точки на множестве Жюлиа
при итерациях совершают хаоти-
5.1. Нелинейные отображения в комплексных координатах ->\г 103
На рис. 5.2 черным цветом показаны области, из которых начальные
точки не уходят на бесконечность, а белым — из которых уходят. Мно¬
жество Жюлиа соответствует только границе между данными точками.
Отметим, что если величина с не имеет действительной части (сх = 0),
то изменение знака су приводит к зеркальному отображению картины
относительно оси х или у.
с — 0,0 -И-0,636
ООО
с — —0,25 + / • 0,0 с = 0,0— / 0,0 с = +0,25 + /0,0
с = 0,0-/-0,636
Рис. 5.2. Характерные примеры множества Жюлиа в комплексной плоскости
z = х + iy при различных сХу су
Если величина с не имеет мнимой части (су = 0), то изменение зна¬
ка сх приводит к изменению вида картины, отображающей множество.
Примеры эволюции множества Жюлиа при изменении сх приведены на
рис. 5.3.
Анализ структуры множеств Жюлиа показывает, что при опреде¬
ленных значениях с, она может быть достаточно сложной и проявлять
самоподобные (фрактальные) свойства. На рис. 5.4 представлен пример
самоподобия структуры множества Жюлиа с = —0,5 + i • 0,5, рассмат¬
риваемого при последовательном увеличении.
При некоторых значениях с = сх + icy могут формироваться ден-
тритоподобные и несвязные (так называемая пыль Фату) множества
Жюлиа, примеры которых приведены на рис. 5.5.
Вполне закономерно возникает вопрос, при каких значениях с, фор¬
мируются связанные множества Жюлиа? Ответ на этот вопрос связан
со свойствами множества Мандельброта.
104 -»\г Глава 5. Множества Жюлиа и Мандельброта
с — 0,0 +1• 0,0
с— -0,70 + / 0,0 с — -0,75 + /0,0
с — —0,80 + / • 0,0
Mil.i .Int.Ml
с——1,00+ /0,0 с——1,20 + /*0,0 с——1,50 + /-0,0
Рис. 5.3. Примеры эволюции множества Жюлиа с нулевой комплексной ча¬
стью су — 0 при изменении сх
Рис. 5.4. Самоподобность множества Жюлиа, с = —0,5 + / • 0,5
б
¥
ц* ***
с = 0,11031 + / 0,67037
Рис. 5.5. Примеры дентдритоподобного (с = 0 + /-1) и несвязного (с = 0,11031+
+ / • 0,67037) множеств Жюлиа
5.1. Нелинейные отображения в комплексных координатах ->\г 105
5.1.2. Множество Мандельброта
Множество Мандельброта определяет области значений
c = cx + icy для которых формируются только связные множества
Жюлиа (рис. 5.6). Здесь показаны также характерные множества
Жюлиа, которые наблюдаются при некоторых определенных значениях
с- сх + icy. Для любой точки с = сх + icy вне множества Мандельбро¬
та связные структуры Жюлиа рассыпаются на бесконечное число точек
(так называемая пыль Фату).
0,8
.. lAj.I. .Xljtti.il. LlLi ..
'Т’тутт “Т q ^
0,2
Рис. 5.6. Множество Мандельброта в плоскости z — х + iy. Здесь показаны
также характерные множества Жюлиа, которые наблюдаются при
определенных значениях с — сх + icy
Множество Мандельброта является примерно самоподобным и при
последовательном увеличении в его структуре можно обнаружить боль¬
шое количество миниатюрных копий.
Множество Мандельброта пересекает реальную ось в интервале
-2... 0,25. Для его построения нужно просканировать всю комплексную
область значений с (обычно это делается в интервале с* = —1,5, ..., 0,5,
су = —1,0, ..., 1,0) и определить, связным или не связным является
множество Жюлиа. Согласно теореме, доказанной Жюлиа и Фата,
106 Глава 5. Множества Жюлиа и Мандельброта
множество Жюлиа является связным только в случае, когда при старте
из начала координат (го = 0), последовательность гп не уходит на
бесконечность [1, 2]. Это означает, что в процессе итераций величина г
не должна выходить за пределы области г > 2 (т. е. х2 + у2 >4).
Отметим, что существует соответствие между итерациями в комплекс¬
ной области, порождаемыми квадратичным соотношением zn+\ — z2-\-c
и логистическим отображением хп+\ = rxn{ 1 — хп) (г = 0 ... 4), которое
определяется соотношением с = (1 — (г — I)2)/4. На рис. 5.7 представ¬
лена диаграмма, показывающая соответствие между логистическим
отображением и множеством Мандельброта. Область нулевых стацио¬
нарных решений х = 0 (г = 0... 1) соответствует с = 0 ... 0,25, область
ненулевых устойчивых решений х = 1 — \/г (г = 1 ... 3) соответствует
с = 0,25 ... — 0,75. Область первой бифуркации (г = 3, ..., 3,448) со¬
ответствует с = —0,75 ... — 1,248. Начало перехода к хаосу (г « 3,57)
соответствует с = —1,401.
Сх
Рис. 5.7. Соответствие между логистическим отображением и множеством
Мандельброта
Численные оценки показывают, что площадь множества Мандель¬
брота равна 1,50659177 ± 0,00000008, а центр тяжести находится в
точке (-0,28676844,-0,000000025) [4]. В 1998 г. Шишикура показал,
что фрактальная размерность (размерность Хаудорфа) для границы
множества Мандельброта равна 2 [5].
5.2. Алгоритмы и описание работы программ ->\г 107
Каким же образом можно определить, принадлежит ли конкретное
значение с множеству Мандельброта или нет? Мандельброт показал,
что данному множеству принадлежат такие значения с, для которых
функциональные итерации [6-8], стартующие с zq = 0, не уходят на
бесконечность.
Далее в этой главе приведены компьютерные алгоритмы и програм¬
мы для построения заполненных множеств Жюлиа и Мандельброта.
Заполненные множества отличаются от истинных тем, что определяют
на комплексной плоскости только те начальные точки функциональных
итераций, для которых итерации не уходят на бесконечность.
5.2. АЛГОРИТМЫ И ОПИСАНИЕ РАБОТЫ ПРОГРАММ
5.2.1. Алгоритм для построения множества Жюлиа
Для построения этого множества определяется значение
комплексной постоянной с = сх + icy и сканируется область значений
переменных х и у в интервале [—2,2], которые определяют начальную
точку zo = х + iy итераций. В ходе выполнения итераций zn+\ = z2n + с,
п = 1, ... ,Мпах проверяется условие |zn_|_i|<2. Если это условие не
нарушается после достижения значения п = jVmax, то координаты на¬
чальной точки итераций (х,у) изображаются черным цветом. Если же
в ходе выполнения итераций значение |zn+i| > 2, то итерации прекра¬
щаются, и итерационная процедура стартует в новой начальной точке
zo = х + iy.
5.2.2. Алгоритм построения множества Мандельброта
В данном случае начальная точка итераций всегда равна
го = 0, а с является переменной. Область значений с = сх + icy на
комплексной плоскости сканируется в интервалах сх = —1,5, ..., 0,5,
Су = —1,0, ..., 1,0. В ходе выполнения итераций z„+i = z2n + с, п =
= l,...,Nmax проверяется условие |zn+i| < 2. Если это условие не
нарушается после достижения значения п = Nmax, то координаты точки
(сХусу) изображаются черным цветом. Если же в ходе выполнения ите¬
раций значение |zn+i| > 2, то итерации прекращаются, и итерационная
процедура стартует с новым значением с = сх + icy.
5.2.3. Описание работы программ
Программы, реализующие алгоритмы для построения мно¬
жеств содержаться в файлах Julia . f 90 и Mandelbrot. f 90. Данные
программы состоят из основного модуля и процедуры инициализации
графического окна, которая является одинаковой для обеих программ
и выглядит следующим образом:
108 Глава 5. Множества Жюлиа и Мандельброта
subroutine initgraf()
use msflib
implicit none
integer (2) res
logical (2):: direct=.true.
!определяем размеры графического окна
call setviewport(20,20,700,700)
!определяем физические координаты графического окна
res=setwindow(direct,-2.,2.,2.,-2.)
!заливаем белым цветом графическое окно
res=setcolor(15)
res=rectangle_w($gfillinterior,-2.,2.,2.,-2.)
res=setcolor(0) !устанавливаем черный цвет для
!изображения точек множества
end subroutine initgraf
Код главного модуля программы для построения заполненного мно¬
жества Жюлиа представлен ниже:
program Julia
use msflib
implicit none
integer(2) res
integer n, nmax
real (8) x, y, cx, cy
complex(8) z,c
!инициализация:
Nmax=20 !максимальное количество итераций
cx=0.11031
cy=0.67037
c=cmplx(сх,су) !комплексная константа итераций
call initgraf !графическое окно
!построение множества:
do х=-2,2,0.005
do у=-2,2,0.005
z=cmplx(x, у); п=0
do while (cabs(z)<2 .and. n<Nmax)
z=z**2+c; n=n+l
enddo
if (cabs(z)<2) res=setpixel_w(x, y)
enddo
enddo
end program Julia
Для построения множества в программе используются внутренние
функции Фортрана преобразования действительных чисел в комплексные
сшр1х() и функция вычисления модуля комплексного числа cabs().
5.2. Алгоритмы и описание работы программ •Лг 109
Программа построения заполненного множества Мандельброта по¬
добна предыдущей программе. Ниже приведен код основного модуля
этой программы:
program Mandelbrot
use msflib
implicit none
integer(2) res
integer n, nmax
real(8) cx, cy
complex (8) z, с
инициализация:
Nmax=20
call initgraf
[максимальное количество итерации
!графическое окно
[построение множества:
do сх=-2,2,0.005
do су=-2,2,0.005
c=cmplx(сх,су);z= (0.,0); п=0
do while (cabs (z)<2 .and. n<Nmax)
z=z**2+c; n=n+l
enddo
if(cabs(z)<2) res=setpixel_w(cx, cy)
enddo
enddo
end program Mandelbrot
5.2.4. Примеры работы программ
На рис. 5.8 представлены результаты работы программ
Julia.f90 и Mandelbrot.f90.
с = 0 + /0.1
•
б
с = 0,31 + /-0,04
*
а !’5:
1:
0,5:
N max — 20
Nmax =20
су о-
с = 0 4- /
г
c = 0,\-i-0,7
т ¥*
-0,5:
>v
Nmax =15
&
#тах = 20
-1:
-1,5 -
-2 -1 с, 0
Рис. 5.8. Примеры множеств Жюлиа (а-г) и множества Мандельброта (д),
полученных в результате выполнения программ Julia, f 90 и
Mandelbrot. f 90, соответственно
110 -l\r Глава 5. Множества Жюлиа и Мандельброта
5.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Численные оценки показывают, что площадь множества Мандель¬
брота равна 1,50659177 ±0,00000008, а центр тяжести находится в
точке (-0,28676844,-0,000000025) [4]. Напишите программу для
вычисления площади и центра тяжести множества Мандельброта.
2. В 1998 г. Шишикура показал, что фрактальная размерность df для
границы множества Мандельброта равна 2 [5]. Напишите программу
для определения df используя для определения фрактальной размер¬
ности метод покрытия квадратами [6].
3. Модифицируйте программу Julia, f 90 и исследуйте поведение
нелинейного отображения вида zn+\ = (z\ + c)/z\ для разных зна¬
чений с (рис. 5.9).
Рис. 5.9. Множество Жюлиа для Рис. 5.10. Градиентная раскраска
отображения zn+\ = (z\ ± c)/z3nt области, не принадлежащей мно-
где с = 0,0001 ± /0,0001, построен- жеству Мандельброта
ное на интервале х, у € [—1,2,1,2]
4. Модифицируйте программу Mandelbrot. f 90 таким образом, чтобы
она задавала раскраску начальных точек итераций, не принадле¬
жащих множеству Мандельброта, в соответствии со скоростью их
«убегания» на бесконечность (рис. 5.10) [9].
5.4. ЛИТЕРАТУРА
1. Пайтген X. -О., Рихтер П.Х. Красота фракталов. Образы комплексных ди¬
намических систем. — М.: Мир, 1993. — 176 с.
2. Юрген X., Пайтген X.-О., Заупе Д. Язык фракталов // В мире науки. -
1990. — №10. — С. 32; Peitgen Н. -О., Jtirgens Н., Saupe D. Chaos and Frac¬
tals — New Frontiers of Science. — New-York: Springer, 2004. — 864 p.
5.4. Литература ->\r 111
3. Мандельброт Б. Фрактальная геометрия природы. — М.: Институт ком¬
пьютерных исследований, 2002. — 656 с.; Mandelbrot В. Fractal aspects of
the iteration of for complex // Annals NY Acad. Sci. — 1980. — V. 357. —
P. 249-259.
4. Lesmoir-Gordon N., Rood W. and Edney R. Introducing Fractal Geometry. —
Icon Books UK & Totem Books USA, 2000.
5. Shishikura M. The Hausdorff dimension of the boundary of the Mandelbrot set
and Julia sets 11 Ann. of Math. — 1998. — V. 147. — P. 225-267.
6. Федер E. Фракталы. — М.: Мир, 1991. — 260 с.
7. Шредер М. Фракталы, хаос, степенные законы. Миниатюры из бесконеч¬
ного рая. — Ижевск: НИЦ Регулярная и хаотическая динамика, 2001. —
528 с.
8. Кроновер Р. М. Фракталы и хаос в динамических системах. Основы тео¬
рии. — М.: Постмаркет, 2000. — 352 с.
9. Romera М., Pastor G., and Montoya F. Drawing the Mandelbrot set by
the method of the escape lines 11 Fractalia. — 1996. — V. 5. — P. 11-13
(http://www.iec.csic.es/~miguel/Preprint3.ps).
ГЛАВА ДЕТЕРМИНИСТИЧЕСКИЕ ФРАКТАЛЫ
6
6.1. ПРИМЕРЫ ДЕТЕРМИНИСТИЧЕСКИХ ФРАКТАЛОВ
Многие объекты, которые окружают нас, являются эвкли¬
довыми. В качестве примеров можно привести линии, плоскости, дуги
цилиндры, сферы и т. п. Топологическая размерность объекта определя¬
ется числом координат, необходимых для определения положения точки
на этом объекте. Например, квадрат является двумерным объектом, а
куб — трехмерным. Примером 0-мерного объекта является конечное
распределение точек в пространстве, а одномерного объекта — линия.
Обычный эвклидов объект, например, окружность не является само¬
подобным и при последовательном увеличении линия выглядит менее
скругленной и приближается к прямой. Однако, существует ряд при¬
родных объектов, которые не могут быть охарактеризованы в терминах
традиционной эвклидовой геометрии. Такие объекты, впервые детально
исследованные Бенуа Мандельбротом, были названы фракталами [1].
Фракталы, с одной стороны являются крайне нерегулярными, но с
другой стороны, они проявляют самоподобный тип структуры на раз¬
личных масштабах. Например, для фрактальной линии последующее
увеличение выявляет новые детали, и она выглядит примерно одина¬
ково на различных масштабах. Во многих случаях фракталы можно
сгенерировать повторением одинаковых структур на разных масшта¬
бах, применяя рекурсивные или итерационные процедуры. При этом
сначала определяется базисная геометрическая фигура, которая потом
размножается самоподобным образом. Такие фракталы называют еще
детерминистическими и они являются строго самоподобными. В каче¬
стве примеров детерминистических фракталов можно привести кривые
Коха или Мандельброта-Гивена, треугольник и квадрат Серпинского,
канторовскую пыль, дерево Кейли и др. аналогичные детерминистиче¬
ские фракталы.
6.1. Примеры детерминистических фракталов ->\г 113
6.1.1. Кривые Коха и Мандельброта-Гивена
Построение кривой Коха было предложено в 1906 г. швед¬
ским математиком Кохом [2]. Кох предложил пример нигде недиффе¬
ренцируемой кривой, которая является непрерывной и в тоже время
в любой ее точке не существует касательной к этой кривой. Впервые
существование таких кривых предсказал Карл Вейерштрасс в 1872 г.
п = 1
п = 3 п = 10
Рис. 6.1. Этапы построения триадной кривой Коха
п = 1
п = 2
ft
п= 1
п = 2
тт
гг
иг
п = 10
Рис. 6.2. Кривые Мандельброта-Гивена без петель (а) и с петлями (б)
Для построения триадной кривой Коха отрезок прямой линии раз¬
бивается на три части и центральное звено заменяется двумя зве¬
ньями как показано на рис. 6.1. В дальнейшем эта процедура повто¬
ряется. Если начальная длина отрезка равна 1, то после п итераций
число звеньев кривой Коха равно А7 = 4", а размер каждого звена
равен 6 = (1/3)". Исключая п из данных соотношений, можно полу¬
чить степенную зависимость между N и 6: N(6) = 6~df, где величина
df — In 4/In 3^ 1,262 определяется отношением логарифма числа зве¬
ньев (4) к логарифму делителя масштаба (3) и является фрактальной
размерностью. Общая длина фрактальной кривой п-го поколения рав¬
на £(6) = (4/3)" = N(6)6 = 6x~df и непрерывно возрастает. В пределе
п —> оо длина фрактальной кривой равняется бесконечности. Более то¬
114 •Ar Глава 6. Детерминистические фракталы
го, длина кривой между двумя любыми ее точками также является
бесконечной, так как всегда существует копия кривой Коха между
двумя любыми ее точками.
Более сложные операции используются для построения фракталь¬
ных кривых Мандельброта-Гивена. На рис. 6.2, а и б представлены,
соответственно, фрактальные кривые Мандельброта-Гивена без петель
и с петлями [3]. В данном случае масштаб делителя остается равным
три, однако число звеньев равно 8 (а) и 6 (б). Таким образом, фрак¬
тальные размерности данных кривых равны df = In 8/In 3 (рис. 6.2, а)
и df = In 6/ In 3 (рис. 6.2, б).
6.1.2. Треугольник и ковер Серпинского
На рис. 6.3 приведены построения для треугольной сал¬
фетки [4] (а) и квадратного ковра [5] (б) Серпинского, которые яв¬
ляются примерами фрактальных кривых на плоскости. Салфетку Сер¬
пинского также называют треугольником Серпинского. На рис. 6.3, а
изображены построения для первых трех поколений этой фигуры. На
первом шаге (рис. 6.3, а, п = 1) построения салфетки Серпинского рав¬
носторонний треугольник делиться на четыре одинаковых равносто¬
ронних треугольника с длиной стороны в два раза меньшей, чем в
исходного. При построении следующего поколения салфетки централь¬
ный треугольник выбрасывается из рассмотрения. Поэтому для тре¬
угольника Серпинского масштаб делителя равен 2, а множитель числа
элементов — 3. Отсюда следует, что фрактальная размерность данного
объекта равна df = In 3/ In 2 = 1,58.
Рис. 6.3. Салфетка df = In 3/ In 2 = 1,58 (а) и ковер df = In 8/ In 3 = 1,89 Сер¬
пинского (6)
6.1. Примеры детерминистических фракталов •Аг 115
На рис. 6.3, б проиллюстрирована процедура построения квадратно¬
го ковра Серпинского. Построение этой фигуры впервые было описано в
диссертации С. Мазуркевича в 1913 г. в его диссертации, выполненной
под руководством В. Серпинского. Для квадратного ковра Серпинско¬
го масштаб делителя равен 3, а множитель числа элементов — 8,
и фрактальная размерность равна = In 8/ In 3 = 1,89. Отметим, что
фрактальная размерность квадратного ковра Серпинского (рис. 6.3, б)
равна фрактальной размерности кривой Мандельброта-Гивена без пе¬
тель (рис. 6.2, а).
6.1.3. Пирамида Серпинского и губка Менгера
На рис. 6.4, а представлена пирамида (губка) Серпинско¬
го, которая является трехмерным аналогом треугольника Серпинского.
Эта пирамида строится путем разделением исходной пирамиды на 4
меньшие части (масштаб делителя равен 2), при этом центральная
часть пирамиды удаляется. Описанная процедура деления повторяется
на оставшихся 4 пирамидах и т. д. В данном случае, множитель числа
элементов равен 4, а масштаб делителя равен 2 при этом фрактальная
размерность определяется как df = In 4/ In 2 = 2. Каждая сторона пира¬
миды Серпинского является треугольником Серпинского.
Рис. 6.4. Пирамида Серпинского {df = In 4/ In 2 = 2, а) и губка Менгера
(^ = In 20/In 3 и 2,727, б)
На рис. 6.4, б изображена губка Менгера, способ построения ко¬
торой впервые описан в работе [6]. Губка Менгера строится путем
разделением куба на 27 меньших кубов и удалением центрального
куба, а также его шестерых ближайших соседей. Описанная процедура
деления повторяется на оставшихся 20 кубах. В данном случае, умно¬
житель числа элементов равен 20, а масштаб делителя равен 3 при этом
фрактальная размерность определяется как df = In 20/In 3 « 2,727. Ка¬
ждая сторона губки Менгера является ковром Серпинского. Пирамида
Серпинского и губка Менгера имеют бесконечную площадь поверхно¬
сти и нулевой объем.
116 •Ar Глава 6. Детерминистические фракталы
6.1.4. Канторовская пыль
Для построения триадного канторовского множества отре¬
зок прямой линии разбивается три части и центральное звено удаляется
как показано на рис. 6.5. В дальнейшем эта процедура повторяется [7].
При бесконечном повторении получается канторовское множество, или
канторовская пыль. Для этого множества масштаб делителя равен 3, а
множитель числа элементов равен 2, и фрактальная размерность равна
df = In 2/ In 3 < 1.
п = 1
п = 2
□
□
п
□
п = 3
□□ □□ □□ 00
п = 4
INI IIII ни 1111
Рис. 6.5. Канторовская пыль (df = In 2/In 3 = 0,63093)
Далее в данной главе будут рассмотрены примеры построения раз¬
личных детерминистических фрактальных объектов, основанные на
применении рекурсивных алгоритмов и метода систем итерируемых
функций (IFS).
6.2. АЛГОРИТМЫ И ОПИСАНИЕ ПРОГРАММ
Алгоритмы построения строго самоподобных фрактальные
объектов основаны на применении инвариантных преобразований, поз¬
воляющих смещать или поворачивать объекты, а также изменять их
масштаб. Рассмотрим линейное отображение Т точек на плоскости,
которое соответствует преобразованию (х,у) —> (х\,у\)
х\ = ах + by -1- е\
yi=cx + dy + /.
Отображение Т сохраняет площадь, если detZ = 0, где Z =
матрица, соответствующая данному преобразованию.
6.2. Алгоритмы и описание программ -Аг 117
Смещение объекта определяется простейшей системой уравнений
= х + е, У\ = у + f, или на комплексной плоскости z\ = z + где
z\ = х\ + iyu z = x + iynzd = e + if.
Изменение масштаба объекта (его сжатие или растяжение) опре¬
деляется соотношениями х\ = k(x — хо) + хо, t/i = k(y — уо) + уо, где
k — коэффициент масштабирования. \k\ > 1 — соответствует растяже¬
нию, a \k\ < 1 — сжатию. В частности, при преобразовании относи¬
тельно начала координат хо = 0, уо = 0, имеем х\ — kx, у\ = ky или
на комплексной плоскости z\ = kz.
Поворот на угол ср против часовой стрелки относительно начала ко¬
ординат определяется уравнениями х\ = jc cos </> — г/ sin (/>, у\ = л: sin <р+
+ycos(p, или на комплексной плоскости — z\— zexp(/<p).
6.2.1. Рекурсивный алгоритм
В основе рекурсивного алгоритма лежит процедура
Rec(xa,уа,хь,Уь, • • •, я), которая рекурсивно обращается сама к себе.
Здесь переменными ха, уа,хь, Уь • • • обозначены некоторые базисные
точки (табл. 6.1), а п соответствует глубине рекурсии.
Суть рекурсивного алгоритма можно представить в виде следующей
схемы:
0) инициализируем графическое окно;
1) определяем численные значения глубины рекурсии п и
определяем положение базисных точек фрактала;
2) вызываем рекурсивную процедуру, например
CALL Rec(ха,уа,xb,yb,...,п)
В подпрограмме (Rec (ха, уа, xb, yb, . . ., п) ) в случае п>0 вы¬
полняется вычисление узловых точек фрактального объекта и происхо¬
дит рекурсивное обращение подпрограммы самой к себе, а иначе рису¬
ются графические примитивы. Далее происходит передача управления
в вызывающую программу. Например, схема алгоритма для построения
триадной кривой Коха выглядит следующим образом:
1) Если п > 0, тогда выполняется рекурсивное обращение
подпрограммы самой к себе. При этом:
а) Вычисляются координаты узловых точек, в данном
случае xl=xa+dx, yl=ya+dy, x2=cos<pdx-sin<pdy+xl,
y2=sin<pdx+cos<pdy+yl, x3=x2+dx, y3=y2+dy, где
dx=(xb-xa)/3, dy=(yb-ya)/3.
б) Подпрограмма n раз обращается сама к себе,
перебирая все узловые точки, и уменьшая п, т.е.
CALL Rec(ха,уа,xl,yl,n-1);CALL Rec(xl,yl,х2,у2,п-1);
CALL Rec(х2,у2,хЗ,уЗ,n-1);CALL Rec(хЗ,уЗ,xb,yb,п-1).
2) Если п = 0 тогда рисуется отрезок, соединяющий точки
{xl,yl}, {х2,у2} и происходит выход из процедуры.
118 -IV Глава 6. Детерминистические фракталы
Таблица 6.1. Базисные и узловые точки, используемые в рекурсивных алго¬
ритмах построения фракталов
Координаты точек
Схема расположения точек
Триадная кривая Коха
Две базисные точки:
{Ха,Уа},{хЪ,Уь}
Узловые точки:
х\ = ха + dx, у\ = уа + dy,
Х2 = cos tpdx — sin <pdy + х\,
г/2 = sin <р dx + cos (pdy + г/i,
хз = *i + dx, #3 = #1 + dy, где
dx = (xb - Xa)/3, dr/ = (r/6 - Г/а)/3,
cos<p = 0,5, sin<p = 0,866
Начальные условия:
Xa = 0, ya = 0, Xb = 1, Уь = 0
Х2» У2
О -о
Ха» У а Хх, ух Х3,Г/3 Xft.y*
Треугольник Серпинского
Три базисные точки:
{ха,Г/а}, {Хь,Уь}, {хс,Ус}
Узловые точки:
XI = (хь + Хс)/2, ух = (уь + Ус)/2,
х2 = (хс + ха)/2, г/2 = (г/с + г/а)/2,
Х3 = (ха + Хь)/2, г/3 = (г/а + Г/6)/2
Начальные условия:
Ха = 0, уа = 0, Хь = 0,5,
Уь = 1, хс = 1, Ус = 0
Ъ
а 2 с
Квадрат Серпинского
Две базисные точки:
{Ха,Уа}, {Хь,Уь}
Узловые точки:
Xl = Ха + dx, ух = уа-\~ df/,
Х2 = ха + 2 dx, г/2 = г/а -1- 2 dy,
где
dx = (х& - Ха)/3, dr/ = (уь - Уа)/Ъ
Начальные условия:
Ха = 0. уа— 0:
хь = 1: уь = 1
j>6
уо -
XI, у Ь
Ха, У2
Х2,УЬ
xi, г/2
Хб,Г/б
Х2, г/2
Г/2 *
XI, г/2
Ха, г/1
Xft,r/2
Х2, г/1
Г/1 *
а
УаЩ
;
XI, г/1
Ха, У а
Х2, г/1
XI, У а
Хь,у\
Х2, У а
Р 1
Са Л
'1 Л
•2 А
Канторовская пыль
Две базисные точки:
Узловые точки:
Xl = Ха + dx, Г/1 = Г/а 4- dr/,
Х2 = xa + 2 dx, г/2 = 1/a + 2 dy, где
dx = (x6 - Xa)/3, dr/ = (уь - Уа)/3
Начальные условия:
xa = 0: уа = 0: хь = 1: уь = 0
о о о о
Ха» Уа XI, г/1 х2, г/2 х6,уь
6.2. Алгоритмы и описание программ ->\г 119
6.2.2. Алгоритм на основе систем итерируемых
функций (IFS)
Метод «Систем Итерируемых Функций» (IFS — англий¬
ская аббревиатура от iterated functions system) в настоящее время ши¬
роко используется для генерации фрактальных структур [8-10]. Наи¬
более простая IFS состоит из аффинных преобразований плоскости:
х' = ах + bu -I- е\
(6.1)
у = сх + dy + f.
В данном случае фрактальный объект кодируется несколькими про¬
стыми аффинными преобразованиями, т. е. коэффициентами этих пре¬
образований (в нашем случае а, Ь, с, d, e,f). Если задать какую-либо
начальную точку (например, х = 0, у = 0) и запустить итерационный
процесс, то после нескольких десятков итераций совокупность получен¬
ных точек будет описывать закодированный фрактальный объект. Ос¬
новная проблема состоит в нахождении коэффициентов IFS, использу¬
емых для кодирования заданного фрактала. Для построения IFS кроме
аффинных применяют и другие классы простых геометрических преоб¬
разований, которые задаются небольшим числом параметров, например,
квадратичные:
х’ = а\х2 + b\xy + с\у2 + d\x + е\у + /ь
у' = CL2X2 + Ь2Ху + С2У2 + ^2* + ^2 У + /2-
Для детерминистических фрактальных объектов наблюдается гло¬
бально е самоподобие и нахождение коэффициентов IFS не слишком
сложно. Метод IFS можно использовать для сжатия обычных изобра¬
жений (например, фотографий), что основано на выявлении локального
самоподобия, сохранении соответствующих локальных IFS коэффици¬
ентов и координат, характеризующих их местоположение [11].
Проиллюстрируем использования метода IFS для генерации тре¬
угольника и ковра Серпинского, а также куста папоротника. Для по¬
строения данных фракталов используются аффинные преобразования,
которые задаются уравнениями (6.1) с коэффициентами, приведенными
в табл. 6.2.
Отметим, что для построения треугольника и квадрата Серпинского
используется линейное отображение точек на плоскости, соответству¬
ющее сжатию и смещению треугольников и квадратов, соответственно.
Например, для треугольника Серпинского значение i = 1 соответству¬
ет сжатию треугольника с коэффициентом 0,5 (х —> 0,5х; у —> 0,5*/),
120 -J\r Глава 6. Детерминистические фракталы
значение i = 2 соответствует сжатию со смещением вдоль оси х на ве¬
личину 0,5 (х —► 0,5л: + 0,5; у —> 0,5у), а значение i = 3 соответствует
сжатию со смещением вдоль оси х на величину 0,25 и вдоль оси у
на величину 0,5 (х —> 0,5л: + 0,25; г/ —0,5г/ + 0,5). Аналогично, для
ковра Серпинского коэффициент сжатия равен 1/3, а коэффициенты
смещения равны 1/3 и 2/3.
Таблица 6.2. Коэффициенты IFS для генерации треугольника и ковра Сер¬
пинского, и куста папоротника
Треугольник Серпинского
i
bi
Ci
di
e-i
П
/*->0,5x+0,2tk
/ y—>0,5^ + 0,5 \
/ \ /1 = \
/ x^0,5x\ /-0,5x+o\
/ у -► 0,Ъу \/ y-> 0,Ъу \
1
2
3
0,5
0,5
0,5
0,0
0,0
0,0
0,0
0,0
0,0
0,5
0,5
0,5
0,0
0,5
0,25
0,0
0,0
0,5
Ковер Серпинского
i
а/
bi
Ci
di
ei
fi
1
2
3
4
5
6
7
8
1/3
1/3
1/3
1/3
1/3
1/3
1/3
1/3
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
1/3
1/3
1/3
1/3
1/3
1/3
1/3
1/3
0,0
0,0
0,0
1/3
2/3
2/3
2/3
1/3
0,0
1/3
2/3
2/3
2/3
1/3
0,0
0,0
i = 3
x-(* + 0)/3
y-(y + 2)/3
1 = 4
x-(x + l)/3
y-> {y+2)/Z
i = 5
x-(x + 2)/3
У^(у + 2)/3
i = 2
jt-(x + 0)/3
y-»(i/+l)/3
i = 6
x-(* + 2)/3
У—0/+0/3
i = 1
*-(* + 0)/3
1/ —(y+0)/3
i = 8
x —»(x +1)/3
(/-*(y+0)/3
i = 7
x —► (x + 2)/3
У^(у + 0)/3
Лист папоротника
i
Cli
bi
Ci
di
ei
fi
S'
1
2
3
4
0,0
-0,139
0,17
0,781
0,0
0,263
-0,215
0,034
0,0
0,246
0,222
-0,032
0,27
0,224
0,176
0,739
0,5
0,57
0,408
0,1075
0,0
-0,036
0,0893
0,27
6.2. Алгоритмы и описание программ -1\г 121
Можно описать простую геометрическую схему для построения тре¬
угольника Серпинского:
0) инициализируем графическое окно;
1) определяем вершины равностороннего треугольника
в массивах x(i),y(i), i=1...3;
2) выбираем на плоскости произвольную точку х, у;
3) случайным образом выбираем координаты i-й вершины
треугольника (i=int(3*rnd+l.)) ;
4) вычисляем координаты новой точки, используя
соотношения:
х—► (х+х (i) ) /2, y->(y+y(i) )/2;
5) рисуем новую точку на экране;
6) продолжаем шаги 3)-5) заданное число раз.
Несколько иначе выглядит геометрическая схема для построения
квадрата Серпинского:
0) инициализируем графическое окно;
1) задаем на плоскости произвольную точку х, у;
2) выбираем случайным образом два числа i и j в
интервале 0-2 (i=int(3*rnd), j=int(3*rnd));
3) в случае если \.фj : вычисляются координаты новой точки:
х—► (x+i) /3, у-> (y+j ) /3
и она рисуется на экране;
4) продолжаем шаги 2)-3) заданное число раз.
6.2.3. Описание работы программ
Программы, реализующие рекурсивные алгоритмы для по¬
строения триадной кривой Коха, треугольника Серпинского, квадрата
Серпинского и канторовской пыли содержаться в файлах KochRec. f 90,
STriangleRec . f 90, SSquareRec . f 90 и CantorRec . f 90, соот¬
ветственно. Данные программы имеют унифицированную модульную
структуру и состоят из главного модуля, рекурсивной процедуры и
процедуры инициализации графического окна. Пример главного модуля
для программы построения триадной кривой Коха приведен ниже:
Program KochRec !программа построения триадной кривой Коха
implicit real(8) (a-z)
call initgraf
xa=0; ya=0; xb=l; yb=0; n=4
call Rec(xa,ya,xb,yb,n)
end program KochRec
Для других программ, реализующих рекурсивные алгоритмы по¬
строения фрактальных объектов, структура главного модуля имеет ана¬
122 ->\r Глава 6. Детерминистические фракталы
логичную структуру. В начале программы вызывается внешняя проце¬
дура инициализации графического окна (initgraf):
subroutine initgraf()
use msflib
implicit none
integer (2) res
logical (2):: direct=.true.
real xmin,ymin !размеры графического окна
real xmax,ymax
call clearscreen($GCLEARSCREEN)
res=setcolor(3)
res=rectangle($GBORDER, 18,18,872,872)
call setviewport(20,20, 870, 870)
!определяем физические координаты графического окна
xmin=-0.5; ymin=-0.5
xmax=l.5; ymax= 1.5
res=setwindow(direct,dble(xmin),dble(ymax),&
dble(xmax),dble(ymin))
res=setcolor(15)
end subroutine initgraf
Данная процедура для других программ полностью идентична. Ни¬
же приведены коды рекурсивных процедур для построения указанных
фрактальных объектов.
Триадная кривая Коха
recursive subroutine Rec(ха,уа,xb,yb,n)
use msflib
implicit real (8) (a-z)
type (wxycoord) wxy
integer (2) res !результирующая переменная
!графических функций
if(n>0) then
dx=(xb-xa)/3.; dy=(yb-ya)/3.
xl=xa+dx; yl=ya+dy
x2=0.5*dx-0.866*dy+xl; y2=0.5*dy+0.866*dx+yl
x3=xl+dx; y3=yl+dy
call Rec(xa,ya,xl,yl,n-1)
call Rec(xl,yl,x2,y2, n-1)
call Rec(x2,y2,x3,y3,n-1)
call Rec(x3,y3,xb,yb,n-1)
else
call moveto_w(xa,ya,wxy) !вычерчиваем линию
res=lineto_w(xb,yb)
endif
end subroutine Rec
6.2. Алгоритмы и описание программ
Треугольник Серпинского
recursive subroutine Rec(ха,уа,xb,yb,хс,ус,n)
use msflib
implicit real (8) (a-z)
type (wxycoord) wxy
integer (2) res !результирующая переменная
!графических функций
if(n>0) then
xl=0.5*(xb+xc); yl=0.5*(yb+yc)
x2=0.5*(xc+xa); y2=0.5*(yc+ya)
x3=0.5*(xa+xb); y3=0.5*(ya+yb)
call Rec(xa,ya,x3,y3,x2, y2, n-1)
call Rec(x3,y3,xb,yb,xl,yl,n-1)
call Rec(x2,y2,xl,yl,xc,yc,n-1)
else
call moveto_w(xa,ya,wxy) !вычерчиваем треугольник
res=lineto_w(xb,yb); res=lineto_w(xc,yc);
res=lineto_w(xa,ya)
endif
end subroutine Rec
Квадрат Серпинского
recursive subroutine Rec(xa,ya,xb,yb,n)
use msflib
implicit real(8) (a-z)
integer (2) res !результирующая переменная
!графических функций
if (n>0) then
dx=(xb-xa)/3.; dy=(yb-ya)/3.
xl=xa+dx; yl=ya+dy
x2=xa+2.*dx; y2=ya+2.*dy
call Rec(xa,ya,xl,yl,n-1)
call Rec(xa,yl,xl,y2,n-1)
call Rec(xa,y2,xl,yb,n-1)
call Rec(xl,y2,x2,yb,n-1)
call Rec(x2,y2,xb,yb,n-1)
call Rec(x2,yl,xb,y2,n-1)
call Rec(x2,ya,xb,yl,n-1)
call Rec(xl,ya,x2,yl,n-1)
else
res =rectangle_w($gborder,xa,yb,xb,ya) !вычерчиваем
!квадрат
endif
end subroutine Rec
124 ->\r Глава 6. Детерминистические фракталы
Канторовская пыль
recursive subroutine Rec(ха,уа,xb,yb,n)
use msflib
implicit real (8) (a-z)
integer (2) res !результирующая переменная
!графических функций
if (n>0) then
dx=(xb-xa)/3.; dy=(yb-ya)/3.
xl=xa+dx; x2=xa+2*dx
yl=ya+dy; y2=ya+2*dy
call Rec(xa,ya,xl, yl, n-1)
call Rec(x2,y2,xb,yb,n-1)
else
!вычерчиваем отрезок
res=rectangle_w($gfillinterior,xa,yb+0.05,xb,ya)
endif
end subroutine Rec
Программы, реализующие алгоритмы IFS для построения треуголь¬
ника Серпинского, квадрата Серпинского и листа папоротника содер¬
жаться соответственно в файлах STrianglelFS . f 90, SSquarelFS . f 90
и FernIFS.f90. Данные программы имеют модульную структуру
и состоят из модуля общих переменных comdata, главного модуля
и процедуры инициализации графического окна, код которой пол¬
ностью совпадает с тем, который использовался для рекурсивных
программ.
В модуле общих переменных с помощью конструктора массивов
фортрана определяются численные значения итерационных коэффици¬
ентов и максимальное количество итераций. Например, для программы
FernIFS.f90 модуль общих переменных имеет вид
module comdata
!определяем коэффициенты
real (8)
: a (1
4)=(/0.,
-0.139,
0.17,
0.781/)
real (8)
: b (1
4) = (/ 0 .,
0.263,
-0.215,
0.034/)
real (8)
: с (1
4)=(/0.,
0.246,
0.222,
-0.032/)
real (8)
: d(l
4) = (/0.27,
0.224,
0.176,
0.739/)
real (8)
: e (1
4)=(/0.5,
0.57,
0.408,
0.1075/)
real (8)
: f (1
4) = (/0 . ,
-0.036,
0.0893,
0.27/)
integer
: nmax=le7 ! число итераций
end module comdata
Ниже в качестве примера представлен основной модуль программы
FernIFS.f90 для построения листа папоротника:
6.3. Задачи для самостоятельной
работы 125
Program FernlFS
use comdata
use msflib
implicit none
integer i, res
integer:: n=0
real(8):: x=0,y=0 !координаты начальной точки
real(8) хп,уп
real rnd
call initgraf
do while (n<nmax) !выполняем итерации
call random(rnd); i=int(4.*rnd+l.)
xn=a(i)*x+b(i)*y+e (i)
yn=c(i)*x+d(i)*y+f(i)
res=setpixel_w(yn,xn) !рисуем точку
x=xn; y=yn
n=n+l
enddo
6.2.4. Примеры работы программ
Описанные в этой главе рекурсивные процедуры были ис¬
пользованы нами для подготовки рисунков 6.1, 6.3 и 6.5, а также приве¬
дены на рис. 6.6. Пример работы программы FernlFS. f 90 содержится
в табл. 6.2.
Рис. 6.6. Изображения триадной кривой Коха (а), салфетки (б) и ковра
{в) Серпинского, полученной с помощью программ KochRec. f 90,
STriangleRec . f 90, SSquareRec. f 90 при глубине рекурсии
n = 4
1. На рис. 6.7 представлена структура дерева Кейли, состоящего из двух
веток. На каждом новом уровне ствол данного дерева разделяется на
две части, а длина веток уменьшается вдвое. Если п — количество
удвоений, то общая высота дерева будет конечна и равна 1 + 1/2 +1/4+
+1/8 + ... = 2. Напишите программу для построения дерева Кейли.
6.3.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
126
Глава 6. Детерминистические фракталы
dx 1 = dx/2
*2, г/2
*з,г/з
► dy 1 = dy/2
Х\,у\ 6'
Рис. 6.7. Структура узловых точек дерева Кейли. Узловые точки: Х2 = х\ — dx,
хз = xi + dx, г/2 = у + dy\, уз — у dy\, где dx\ = dx/2, d#i = dy/2
2. Наряду с триадной кривой Коха (рис. 6.6, а), можно построить также
и другие типы фрактальных кривых, представленных на рис. 6.8.
Напишите программы для построения этих кривых и вычислите их
фрактальные размерности.
Рис. 6.8. Фрактальные кривые с различным числом узловых точек. Жирной
линией под каждым фракталом показана схема расположения узло¬
вых точек
3. Напишите программы для построения треугольника и квадрата Сер¬
пинского, используя геометрические алгоритмы, описанные в тексте.
4. На рис. 6.2 приведены изображения фрактальных кривых Мандель¬
брота-Гивена. Напишите рекурсивные процедуры построения этих
фракталов.
1. Мандельброт Б. Фрактальная геометрия природы. — М.: Институт ком¬
пьютерных исследований, 2002. — 656 с.
2. von Koch Н. Une methode geometrique dlementaire pour l’etude de certaines
questions de la theorie des courbes planes // Acta Math. — 1906. — V. 30. —
P. 145-174.
6.4.
ЛИТЕРАТУРА
6.4. Литература •Ar 127
3. Федер Е. Фракталы. — М.: Мир, 1991. — 260 с.
4. Sierpinski W. Sur une courbe dont tout point est un point de ramification //
Compt. Rendus Acad. Sci. Paris. — 1915. — P. 160.
5. Sierpinski W. On a Cantorian curve which contains a bijective and continuous
image of any given curve 11 Mat. Sb. — 1916. — V. 30. — P. 267-287.
6. Menger K. Allgemeine Raume und Cartesische Raume // Proc. Koniklijke
Akademie van Wetenschappen te Amsterdam. — 1926. — V. 29. —
P. 1125-1128.
7. Cantor G. Ober Unendliche, Lineare Punktmannigfaltigkeiten V // Mathema-
tische Annalen. — 1883. — Bd. 21. — S. 545-591.
8. Barnsley M. F. Fractals Everywhere. — San Diego, Calif, [u.a.]: Morgan
Kaufmann, 2000. — 534 p.
9. Пайтген, X.-O., Рихтер П.Х. Красота фракталов. — М.: Мир, 1993. —
176 с.
10. Божокин С. В., Паршин Д. А. Фракталы и мультифракталы. — Ижевск:
НИЦ «Регулярная и хаотическая динамика», 2001. — 128 с.
11. Уэлстид С. Фракталы и вейвлеты для сжатия изображений в действии. —
М.: Триумф, 2003.
ГЛАВА
7
РОСТ БАКТЕРИАЛЬНЫХ КОЛОНИЙ:
МОДЕЛЬ ИДЕНА
7.1. ТИПЫ МОДЕЛЕЙ СТОХАСТИЧЕСКОГО РОСТА
В настоящее время стохастические модели роста широко
используются для имитации разнообразных физических, химических
и биологических процессов. Первую модель такого типа предложил
Тьюринг в 1952 г., в которой генерировались стохастические пятна,
подобные черно-белым пятнам на шкуре животных [1]. Немного позд¬
нее Иденом была разработана упрощенная модель роста бактериальных
колоний. Образование этой колонии было наглядно продемонстриро¬
вано в виде прямоугольных отверстий на перфокарте Холлерита [2].
Вместе с тем первоначально данная модель привлекла мало интереса.
Она рассматривалась как слишком упрощенная, а кроме того мощности
компьютеров в те годы не позволяли провести достаточно информатив¬
ных исследований.
7.1.1. Базисная модель Идена
В простейшем варианте модели Идена, которая проиллю¬
стрирована на рис. 7.1, рост бактериальной колонии имитируется по¬
следовательным заполнением узлов квадратной решетке по периметру
кластера.
Заполненный узел
Узел на периметре
кластера (соседний
с кластером
незаполненный узел) Ч У\ У
Рис. 7.1. К описанию решеточного варианта модели Идена
7.1. Типы моделей стохастического роста -J\r 129
В начальный момент времени (t = 1) кластер состоит всего из одной
частицы («зерна» роста). В дальнейшем рост кластера происходит за
счет последовательного присоединения новых частиц в узлах по его
периметру. Для квадратной решетки в начальный момент времени кла¬
стер состоит из 1 частицы и имеет периметр, состоящий из 4 узлов.
В последующий момент заполняется, какой либо из этих узлов, далее
определяется новый периметр и т. д. В процессе моделирования состав¬
ляется список узлов, принадлежащих к периметру, которые потенци¬
ально могут быть заполнены. На рис. 7.1 показан кластер, состоящий
из 4 частиц с периметром, включающим 8 узлов. Отметим, что бо¬
лее сложных вариантах модели случайным образом можно выбирать
не только узлы, но также связи между узлами, расположенными на
периметре [3].
7.1.2. Модель с подавлением шума
Решеточные модели допускают чрезвычайно простую про¬
граммную реализацию и позволяют проводить крупномасштабные вы¬
числения для больших размеров кластеров. Вместе с тем существен¬
ным их недостатком является потенциальная возможность влияния
симметрии решетки на структуру образуемого кластера [4, 5]. Это
влияние легко продемонстрировать с помощью, так называемой модели
Идена с подавлением шума. В данной модели узел на периметре кла¬
стера занимается не сразу, а только спустя определенное количество
визитов т в определенный узел. Для этого включается счет числа
визитов в каждый узел на периметре, но список потенциальных узлов
на периметре пополняется только после удачной попытки заполнения.
Примеры кластеров, полученных при различных значениях т, приведе¬
ны на рис. 7.2. При увеличении т кластер приобретает форму квадрата,
что отражает влияние симметрии подложки на структуру кластера.
Рис. 7.2. Структура кластеров Идена для решеточной модели с подавлением
шума (рост на квадратной решетке). Для иллюстрации динамики
роста кластера, его цвет циклично изменялся при пополнении кла¬
стера определенным количеством частиц
130 -*\r Глава 7. Рост бактериальных колоний: Модель Идена
7.1.3. Нерешеточные модели Идена
Нерешеточные модели Идена являются сложнее в про¬
граммной реализации и требуют существенно больших вычислитель¬
ных ресурсов. Один из вариантов такой модели продемонстрирован на
рис. 7.3 [6]. В данной модели случайным образом выбирается пробная
клетка, и идентифицируются ее соседи на расстоянии, не превышаю¬
щем двух диаметров. Затем, вокруг выбранной клетки с определенным
шагом (2л/k) сканируются углы с целью выбора удачного направле¬
ния роста. Каждая соседняя клетка исключает определенный интер¬
вал направлений роста вблизи выбранной клетки. При наличии такого
направления новая клетка присоединятся к выбранной клетке на рас¬
стоянии, равному ее диаметру. При отсутствии удачного направления
выбранная клетка объявляется «мертвой» и далее не рассматривается.
Процедура в дальнейшем повторяется.
Рис. 7.3. К описанию нерешеточного варианта модели Идена [6]
Выбор параметра k является довольно критичным, так как при ма¬
лых значениях k некоторые из клеток могут объявляться «мертвыми»
преждевременно, что может приводить к уменьшению плотности кла¬
стера. Расчеты показывают, что для данной модели при k « 24, до¬
стигается асимптотический режим с предельным значением плотности
заполнения р = 0,8276. Эта плотность превышает плотность случайной
упаковки для дисков р = 0,772, но ниже максимально достижимой
р = 0,9069 [7].
7.1.4. Структура кластеров Идена
Детальные исследования показали, что кластеры Идена
обладают компактной внутренней структурой, т. е. зависимость меж¬
ду количеством частиц в кластере и его радиусом гирации Rg опи¬
7.1. Типы моделей стохастического роста -1\г 131
сывается соотношением N ~ Rg, где величина d практически совпа¬
дает с эвклидовой размерностью. Радиус гирации определяется, как
/?g= (г* —г)2/ЛД где г= ^=\ n/N соответствует координатам цен¬
тра масс кластера. Вместе с тем поверхность кластеров Идена сильно
изрезана, имеет фрактальные свойства, а число узлов на периметре рас¬
тет как Ns ~ Rg , где df (> 1) — фрактальная размерность периметра.
К настоящему времени изучено значительное количество различ¬
ных вариантов модели Идена, применяемых для изучения роста бак¬
териальных колоний. Эти модели включают учет миграции клеток, их
вращения, особенностей роста, деления и другие аспекты клеточной
динамики [8]. Модель Идена используется для симулирования процес¬
сов излечения и регенерации биотканей [9], изучения роста популяции
раковых клеток [10] а также других природных стохастических про¬
цессов, таких как агрегация магнитных и заряженных частиц [11, 12],
эволюции бассейнов рек [13], роста городов [14].
В качестве иллюстрации рассмотрим некоторые простейшие вари¬
анты модели Идена.
7.1.5. Перколяционная модель
В этой модели предполагается, что часть центров роста
на периметре кластера может с определенной вероятностью / блоки¬
роваться [15] (рис. 7.4, а). Блокировка приводит к ограничению роста,
нарушению компактности кластеров, а при достаточно высоких значе¬
ниях / > fc после некоторого начального периода возможно полное пре¬
кращение роста. Величина /с совпадает со значением перколяционной
концентрации рс для данного типа решетки, например, для квадратной
решетки рс ~ 0,5927 (см. гл. 12). Таким образом, модель с блокировкой
может быть использована для генерации перколяционного кластера.
+\ Заполненный
.1 ; узел
ш
Заблокированный щ V
узел на периметре I Д /
кластера ч-— у
а б
Рис. 7.4. К описанию модели с блокировкой (а) и модели экранированного
роста (б)
132 Глава 7. Рост бактериальных колоний: Модель Идена
7.1.6. Модель экранированного роста
В модели экранированного роста [16, 17] предполагается,
что частицы и кластеры имеют «заряд» и учитывается отталкивание
между кластером и присоединяющейся частицей. Вероятность роста
на периметре /,- определяется выражением /*• = YljLieM-a/fy/L^ х
х П/li ехр(—a/r-у), где N,NS — число частиц в кластере и число узлов
на периметре, соответственно, гц — расстояние между занятым (/)
узлом и узлом на периметре (/); а, у/ — параметры, характеризующие
потенциал взаимодействия (рис. 7.4, б). Для данной модели может на¬
блюдаться рост некомпактных кластеров, при у/ < d (где d — евклидова
размерность пространства) кластеры проявляют фрактальные свойства
с фрактальной размерностью df « у/.
7.1.7. Модель случайного последовательного роста
В модели случайного последовательного роста пробный
узел на периметре заполняется только с некоторой вероятностью /, при
этом вводится дополнительное ограничение на степень заполнения ре¬
шетки (условие максимального сгущения) [18]. При очередной попыт¬
ке вычисляется локальная плотность заполнения р = N/Nmax, где N и
Л/max — соответственно количество заполненных и максимальное число
узлов внутри окружности с центром на пробном узле и радиусом R.
Кластеры, полученные с помощью данной модели, могут проявлять
фрактальные свойства. Примеры структуры кластеров, полученных с
помощью этой модели, представлены на рис. 7.5.
/=0,62, р = 0,24 /= 1,0, р = 0,24 /= 1,0, р = 1,0
Рис. 7.5. Примеры структур кластеров, выращенных при использовании моде¬
ли случайного последовательного роста [18]
7.1.8. Модель «летающей бабочки»
В модели «летающей бабочки» вводится ограничение на
расстояние г между последовательно присоединяющимися частицами
на периметре [19]. Предполагается, что вероятность присоединения в
7.2. Алгоритм для базисной модели Идена и описание работы программы
определенном узле на периметре меньше 1 и равна /(г) ~ 1 /гу, где
величина у/ характеризует среднюю длину скачков. При у/ = 0 дан¬
ная модель соответствует обычной модели Идена, при у/ > d скачки
происходят только преимущественно между ближайшими узлами. Для
данной модели компактность внутренней структуры кластеров сохра¬
няется, но структура периметра существенно зависит от у/.
В заключение отметим, что для процессов роста бактериальных
колоний, морфогенеза, и других биологических процессов может быть
использована идеология клеточных автоматов [20, 21].
Далее в этой главе будет проанализирован компьютерный алгоритм
и программа для построения кластеров на основе базисной модели
Идена.
7.2. АЛГОРИТМ ДЛЯ БАЗИСНОЙ МОДЕЛИ ИДЕНА
И ОПИСАНИЕ РАБОТЫ ПРОГРАММЫ
7.2.1. Алгоритм
Алгоритм построения кластера модели Идена можно пред¬
ставить в виде следующей схемы:
0) размещаем в оперативной памяти массивы
и инициализируем графическое окно;
1) размещаем в центре решетки зерно роста кластера;
2) выполняем проверку на достижение кластером границ
решетки и в случае достижения переходим к пункту 8;
3) выбираем случайным образом ячейку периметра кластера;
4) присоединяем к кластеру новую частицу;
5) исключаем выбранную ячейку из списка периметр кластера;
6) вычисляем новый периметр кластера;
7) рисуем частицу на экране и переходим к пункту 2;
8) заканчиваем работу программы.
7.2.2. Описание работы программы
Полный код программы для модели Идена содержится в
файле eden.f90 и выглядит следующим образом:
program Eden
use msflib
implicit none
integer:: L=1024 !размер квадратной решетки
integer:: NCOL=le5 !количество частиц для изменения
!цвета
integer (2) res
Глава 7. Рост бактериальных колоний: Модель Идена
logical (2):: direct=.true.
integer
integer
integer
integer:
integer:
integer
integer
L2,LL,L100
i
col
n =0
np=0
XP j УР
xn, yn
real
rnd
!массивы:
L2=L/2, LL=L*L, L10=L2-100
индекс
цвет частиц
счетчик числа частиц кластера
счетчик ячеек периметра
координаты ячейки периметра
координаты соседней ячейки
периметра
случайное число
integer,allocatable:
integer,allocatable:
x (:) , у (:)
site (:, :)
integer:: dx(l:4)=(/l, 0,-l,0/)
!списки ячеек периметра
!кластера
!массив для хранения
!координат частиц
!таблица сдвига
!координат
integer:: dy(1:4) = (/0,-1, 0,1/)
L2=L*L; L2=L/2; LL=L*L; L100=L/2-10
!0)размещаем в оперативной памяти массивы
!и инициализируем графическое окно
allocate(site(-L2:L2,-L2:L2))
allocate(x(l:LL),y(l:LL))
res=setcolor(3); res=rectangle($GBORDER, 18,18,872,872)
call setviewport(20,20,870,870)
res=setwindow(direct,dble(-L2),dble(L2),dble(L2),dble(-L2))
res=setcolor(15);
res=rectangle_w($gfillinterior,dble(-L2),dble(L2),&
dble(L2),dble(-L2))
col=0; res=setcolor (col) !цвет частиц (черный)
!1)размещаем в центре решетки зерно роста кластера
n=0; site(0,0)=1; хр=0; ур=0
do i=l,4
np=np+l; х(np)=dx(i); y(np)=dy(i)
enddo
!2)выполняем проверку на завершение роста кластера
do while (xp<L100 .and. yp<L100)
!3)выбираем случайным образом ячейку периметра кластера
call random(rnd); i=int(rnd*np+l); xp=x(i); yp=y(i)
!4)присоединяем к кластеру новую частицу
n=n+l;site(хр,ур)=1
!5)исключаем выбранную ячейку из списка периметр кластера
х (i)=х(пр); у(i)=у(np); пр=пр-1
1.2. Алгоритм для базисной модели Идена и описание работы программы
!6)вычисляем новый периметр кластера
do i=l,4
xn=xp+dx(i);yn=yp+dy(i)
if (site(xn,yn)==0) then
np=np+l; x(np)=xn; y(np)=yn
endif
enddo
!7)рисуем частицу на экране
if(mod(n,NCOL)==0)then
if (col==0) then
col=7 !серый цвет
else
col=0 !черный цвет
endif
res=setcolor(col)
endif
res=setpixel_w (dble (xp) , dble (yp) )
enddo
!8)заканчиваем работу программы
write (*, *) n
end program Eden
В приведенном коде окончание работы программы происходит при
достижении кластером границ решетки. Частицы кластера рисуются
поочередно темным и серым цветом. Смена цвета частиц определяется
значением переменной NCOL.
7.2.3. Пример работы программы
На рис. 7.6 приведен кластер Идена, полученный с помо¬
щью программы eden. f90, размер которого составляет N = 2 • 106.
Рис. 7.6. Кластер модели Идена 2-106 ча¬
стиц, полученный с помощью программы
eden. f90. Цвет частиц кластера изме¬
няется через каждые Ю5 частиц
136 -*\r Глава 7. Рост бактериальных колоний: Модель Идена
7.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. При исследовании эволюции внешней границы кластера для модели
Идена удобно исследовать шероховатость поверхности, которая опре¬
деляется, как w = Vг2 — г2. Здесь г£ = yjxf + y2t это расстояние от
данной точки на поверхности до зерна роста, усреднение проводится
по i узлам, расположенным на поверхности кластера /= 1, ...,NS.
Исследуйте зависимость до (г) и проверьте, выполняется ли соотно¬
шение [22]. Какой должна быть величина показателя для
кластера квадратной формы, показанной на рис. 7.2?
2. Модифицируйте программу eden. f 90 для исследования модели
Идена с подавлением шума (см. рис. 7.2). Величина т при неболь¬
шой модификации алгоритма может принимать также нецелые зна¬
чения. Для нецелого т, узел занимается с вероятностью / = [т] - т
после [т] визитов и с вероятностью 1 — / после [т] -I-1 визитов.
Здесь [т] означает целую часть числа т. Степень анизотропии кла¬
стера а можно определить, например, как отношение средних рассто¬
яний г = yjх2 + у2 частиц до центра кластера в направлении осей ре¬
шетки (г0,90) И ПОД углом 45° К НИМ (г45,135), Т. е. а = Г0,9о/г45,135 > 1.
Вычислите зависимости а от количества частиц в кластере N при
различных значениях т. Наблюдается ли отклонение величины а
от 1 для обычной модели Идена, т = 0?
3. Напишите программу для реализации нерешеточного варианта мо¬
дели Идена, описанного в тексте. Исследуйте зависимости шерохо¬
ватости поверхности до (г) (см. задачу 1), и проверьте, выполняется
ли соотношение до ~ ?&. Как зависит величина /3 от параметра k и
наблюдается ли режим насыщения при достаточно больших k?
7.4. ЛИТЕРАТУРА
1. Eden AL, Thevenaz P. History of a stochastic growth model 11 Proc. SPIE. —
1998. - V. 3346. - P. 43-54.
2. Eden M. Proceedings of the Fourth Berkeley Symposium on Mathematics,
Statistics and Probability / Ed. by F. Neyman. V. 4: Biology and Problems of
Health. — Berkeley: University of California Press, 1961. — P. 223-239.
3. Jullien R., Botet R. Scaling properties of the surface of the Eden model in
D = 2,3,4 // J. Phys. A18. - 1985. - P. 2279-2287.
4. Zabolitzky J. G., Stauffer D. Simulation of large Eden clusters 11 Phys. Rev.
A. - 1986. - V. 34, No. 2. - P. 1523-1530.
5. Batchelor М. Т., Henry В. I. Limits to Eden growth in 2-dimensions and
3-dimensions // Phys. Lett. A. - 1991. - V. 157. - P. 229-236.
7.4. Литература •Ar 137
6. Wang С. Y., Liu P. L., Bassingthwaighte J. B. Off-lattice Eden-C cluster growth-
model // J. Phys. A28. - 1995. - P. 2141-2147.
7. Wang C. Y., Bassingthwaighte J. В. Biological Growth on a Surface // Math¬
ematical Biosciences. — 1997. — V. 142. — P. 91-106.
8.MainiP.K., Othmer H.G. ed. Mathematical models for biological pattern
formation. — New York, Berlin, Heidelberg: Springer-Verlag, 2000. — 317 p.
9. Savakis A.E. and Maggelakis S. Models of Shrinking Clusters with Applica¬
tions to Wound Healing 11 Mathematical and Computer Modeling. — 1997. —
V. 25. - P. 1-6.
10. Drasdo D., Kree R., and McCaskill J. Monte carlo approach to tissue-cell
populations // Phys. Rev. E. — 1995. — V. 52. — P. 6635-6657.
11. Ausloos M., Vandewalle N. and Cloots R. Magnetic Eden Model // Europhys.
Lett. - 1993. - V. 24. - P. 629-634.
12. Lebovka N.I., Ivanenko Ya. V., and Vygornitskii N. V. Deterministic Eden
model of charged-particles aggregation 11 Europhys. Lett. — 1998. — V. 41. —
P. 9-24.
13. Leheny R. Simple model for river network evolution // Phys. Rev. E. —
1995. - V. 52. - P. 5610-5620.
14. Benguigui L. A new aggregation model: Application to town growth // Phys-
ica A. - 1995. - V. 219. - P. 13-26.
15. Hammersley J. М., Handscomb D.C. Monte Carlo methods. — London: Met¬
huen, 1964. — 178 p.
16. Meakin P. Formation of Fractal Clusters and Networks by Irreversible Diffusion-
Limited Aggregation 11 Phys. Rev. Lett. — 1983. — V. 51. — P. 1119-1122.
17. Rikvold P. A. Simulations of a stochastic model for cluster growth on a square
lattice // Phys. Rev. A. - 1982. - V. 26. - P. 647-650.
18. Ziqin W.y Boquan L. Random successive grown model for pattern formation //
Phys. Rev. E. - 1995. - V. 51, No. 1. - P. R16-R19.
19. Margolina A. The fractal dimension of cluster perimeters generated by a
kinetic walk 11 J. Phys. A: Math. Gen. - 1985. - V. 18. - P. L651-L656.
20. Тоффоли Г., Марголус H. Машины клеточных автоматов. — М.: Мир,
1991.
21. Исаева В. В., Каретин Ю.А., Чернышев А. В., Шкуратов Д. Ю. Фракталы
и хаос в биологическом морфогенезе. — Владивосток: Институт биологии
моря ДВО РАН, 2004. - 128 с.
22. Batchelor М. Т., Henry В. I. and WattS.D. Continuum model for radial in¬
terface growth // Physica A. — 1998. — V. 260. — P. 11-19.
ГЛАВА АГРЕГАЦИЯ, КОНТРОЛИРУЕМАЯ ДИФФУЗИЕЙ
8
8.1. ВАРИАНТЫ МОДЕЛИ АГРЕГАЦИИ,
КОНТРОЛИРУЕМОЙ ДИФФУЗИЕЙ
Агрегация частиц, возникающая в результате их броунов¬
ской диффузии или агрегация, контролируемая диффузией (DLA — ан¬
глийская аббревиатура от diffusion limited aggregation), наблюдается в
разнообразных природных явлениях. Даже при первоначально однород¬
ном распределении частиц в пространстве в результате интенсивного
броуновского движения и слипания частиц при контакте могут обра¬
зовываться агрегаты, включающие большое число первичных частиц.
Скорость агрегации может существенно зависеть от вязкости среды ц
и первоначальной концентрации частиц. В классической теории агре¬
гации, развитой Смолуховским половинное время агрегации t\j2 (т. е.
время, за которое количество первичных частиц уменьшается вдвое)
определяется соотношением
*1/2 = 3/7/4/гв7р,
где т] — вязкость среды, kв — постоянная Больцмана, Т — абсолютная
температура и р — численная плотность частиц.
Обычно, при слипании индивидуальных частиц, имеющих нано-
или микронный размер, образуются термодинамически — неравновес¬
ные агрегаты, имеющие сложную внутреннюю структуру [1, 2]. Для
таких агрегатов характерной является степенная зависимость между
количеством частиц в кластере N и его радиусом R, N ~ RdK При этом
степенной показатель df или фрактальная размерность агрегата может
быть нецелым числом.
8.1.1. Базисный вариант модели DLA
Значительный толчок в исследовании фрактальных свойств
агрегатов сыграла экспериментальная работа Форреста и Виттена [3],
8.1. Варианты модели агрегации, контролируемой диффузией -*\г 139
в которой наблюдалось образование разветвленных кластеров, образо¬
ванных из частиц железа. Для описания механизма образования этих
кластеров Виттен и Сандер в 1981 г. предложили компьютерную модель
диффузионно-контролируемой агрегации DLA (diffusion limited aggre¬
gation) [4]. В данной модели рост агрегата начинается с первоначаль¬
ной фиксированной частицы (так называемое «зерно» роста кластера),
к которой потом присоединяются другие частицы, диффундирующие в
пространстве.
На рис. 8.1 дано схематическое пояснение сущности модели DLA.
В данной модели предполагается, что в каждый момент диффундирует
только одна частица, т. е. концентрация диффундирующих частиц яв¬
ляется чрезвычайно малой (практически нулевой). Диффундирующие
частицы запускают одну за другой со случайного положения, располо¬
женного достаточно далеко от растущего кластера.
Новая диффундр
Рис. 8.1. К объяснению роста агрегата для модели DLA. «Зерно» роста кла¬
стера изображено частицей темного цвета. В процессе броуновской
диффузии частица 1 присоединяется к кластеру, а частица 2 уходит
на бесконечность
В частности, для показанного на рис. 8.1 двумерного варианта моде¬
ли DLA это положение можно выбрать на окружности достаточно боль¬
шого радиуса R, который должен превышать максимальный текущий
радиус кластера Rmах, например, R = Rmax + 5. При этом случайное
блуждание частиц может завершиться либо:
• «прилипанием» частицы к кластеру;
• либо уходом частицы на очень большое расстояние от кластера
R » Rmaxi например, на расстояние равное Rmax + 100 (рис. 8.1).
В случае прилипания частицы к кластеру вычисляется новое значе¬
ние /?тах> запускается новая частица, и процесс диффузии повторяется.
Если частр
уходит дал<
она «уничтож
частица
Новая диффундирующая
частица
Присоединение
новой частицы
к кластеру
140 Глава 8. Агрегация, контролируемая диффузией
Вследствие диффузионной природы транспорта присоединение но¬
вых частиц, как правило, происходит на периферии кластера, проник¬
новение вглубь кластера происходит редко и поэтому кластер имеет
разветвленную структуру. Примеры кластеров DLA для двухмерных и
трехмерных систем приведены на рис. 8.2.
а
Рис. 8.2. Примеры двух- (а) и трехмерных (б) кластеров, построенных с
помощью алгоритма DLA [1]
В определенном смысле модель DLA явилась «революционной», так
как она вызвала огромнейшее количество исследований, посвященных
изучению ее свойств [5]. К настоящему времени в мировой литературе
опубликованы тысячи работ, посвященных этой модели. DLA подобные
структуры были экспериментально обнаружены в различных физиче¬
ских системах: при электрохимическом осаждении металлов на элек¬
тродах, при вытеснении вязких жидкостей с помощью воды в радиаль¬
ных ячейках Хеле-Шоу, в процессах получения тонких пленок, при
электрическом пробое диэлектриков и т.п. [2, 6].
Отметим, что существуют, как дискретный (решеточный), так и
континуальный варианты модели DLA. В решеточной модели DLA,
которая является менее сложной в компьютерной реализации, пред¬
полагается, что частицы могут располагаться и двигаться только в
узлах решетки, например, квадратной треугольной, кубической и т.д.
Для континуальной модели DLA, которая ближе к действительности,
алгоритм роста кластера точно таков же, за исключением того, что
координаты частиц являются действительными числами.
Однако, решеточные модели могут обладать существенным недо¬
статком, в частности структура агрегатов может зависеть от симметрии
решетки и для достаточно больших агрегатов начинают, проявляются
так называемые решеточное эффекты, т. е. зависимость от типа решет¬
ки на которой формируется агрегат (явление решеточной анизотропии).
8.1. Варианты модели агрегации, контролируемой диффузией 141
X
Существует множество модификаций модели DLA, в которых учи¬
тывается анизотропия формы частиц, специфика межчастичных потен¬
циалов взаимодействия, возможность реструктуризации при формиро¬
вании агрегата (в частности, поверхностное натяжение) и т.д. В част¬
ности, структуры подобные структурам DLA возникают в так называе¬
мых процессах лапласовского роста (пробоя, вязкого пальцеобразова-
ния, роста дендритных структур), которые задаются полем потенциала
и, являющегося решением уравнения Лапласа Ьи = 0 [5].
8.1.2. Модель DLA с подавлением шума
Эффект существования решеточной анизотропии наибо¬
лее легко продемонстрировать с помощью модели DLA с подавлением
шума [7]. В этой модели предполагается, что какой либо узел на пери¬
метре кластера может заполниться только после т попыток присоеди¬
нения частицы в этом узле.
т = 10
1024 решеточных единиц
St = 0,1
st = 0,02
Рис. 8.3. Изменение структуры кластеров DLA при изменении фактора подав¬
ления шума т (а) и параметра прилипания st (6)
Для обычной модели DLA т — 1 и узел на периметре кластера за¬
полняется при первом же контакте с диффундирующей частицей. При¬
меры, демонстрирующие изменение структуры кластеров при увеличе¬
нии т показаны на рис. 8.3, а. При больших значениях т кластер про¬
являет «крестообразную» структуру, отражающую рост на квадратной
142 -l\r Глава 8. Агрегация, контролируемая диффузией
решетке. Аналогично, при росте на треугольной решетке возникают
кластеры с гексагональной структурой.
Учет конечной вероятности «прилипания» диффундирующей части¬
цы кластеру st (<1) также может приводить к изменению структуры
DLA (рис. 8.3, б). При уменьшении st ветки кластеров становятся более
плотными.
8.1.3. Рост на множественных центрах
В природных явлениях могут проявляться процессы роста
на множественных зернах роста, которые распределены, например, на
окружности (рис. 8.4, а) или на линии (рис. 8.4, б).
1024 решеточных единиц 1024 решеточных единиц
Рис. 8.4. DLA агрегация на множественных центрах роста, распределенных
на окружности (а) или линии (б). Диффундирующие частицы вы¬
пускаются из центра окружности (а) или на большом удалении от
линии (б)
8.1.4. Фрактальная размерность
При анализе фрактальной структуры обычно исследуют
зависимость среднего числа N частиц в кластере от его радиуса Rg
гирации с использованием соотношения
N=kRg',
где k — некоторая постоянная (рис. 8.5). Радиус гирации определяется,
как Rg = yjY^=\ (П — r)2/N, где г = fi/N соответствует координа¬
там центра масс кластера. Величина df зависит от пространственной
размерности d.
Значения фрактальной размерности df и коэффициента k для реше¬
точных и нерешеточных моделей представлены в табл. 8.1.
8.1. Варианты модели агрегации, контролируемой диффузией -J\r 143
Таблица 8.1. Зависимости фрактальной размерности df и коэффициента k для
решеточных (гиперкубических) и нерешеточных моделей роста
DLA от размерности пространства d. Решеточные модели ис¬
следованы на гиперкубических решетках, ошибки определения
df и k составляли 3% и 12%, соответственно [9]
d
Решеточная модель
Нерешеточная модель
df
k
df
k
2
1,66
3,73
1,66
3,41
3
2,22
3,73
2,29
3,33
4
2,78
3,71
5
3,24
3,68
Предприняты многочисленные попытки аналитического описания
процесса агрегации DLA. Для модели случайного блуждания, траек¬
тория которого имеет фрактальную размерность dw (1 < dw < 2), фрак-
d% _|_ (jj j
тальная размерность кластера DLA оценивается как df= ——-р—- [8].
d “I- dm 1
Отсюда, для обычного броуновского движения, траектория которого
имеет фрактальную размерность dw = 2, вытекает известное выражение
Флори: df = (d2 + \)/{d + 1) [8]. Данная формула неплохо описывает
оценки, полученные с помощью компьютерного моделирования, кото¬
рые представлены в табл. 8.1 [9].
106
Ю5
N
104
103
101 102 103
Я*
Рис. 8.5. Пример зависимости между числом частиц в кластере DLA (рост
кластера на квадратной решетке) N от его радиуса гирации Rg
Далее в этой главе будут рассмотрены некоторые компьютерные
алгоритмы и программы для построения кластеров на основе модели
DLA.
144 -»\r Глава 8. Агрегация, контролируемая диффузией
8.2. АЛГОРИТМЫ И ОПИСАНИЕ РАБОТЫ ПРОГРАММ
Алгоритмы для кластеров DLA основаны на применении
описанной выше схемы случайных блужданий. Процедура для реализа¬
ции случайных блужданий, как правило, требует больших вычисли¬
тельных ресурсов. В связи с этим, обычно, используют различные
ухищрения для ускорения расчетов. Ниже будут рассмотрены два ва¬
рианта для реализации процедуры построения кластеров DLA: базис¬
ный, в котором непосредственно реализуются случайные блуждания
на плоскости и скоростной, в котором реализуются скачки диффунди¬
рующей частицы на большие расстояния.
8.2.1. Алгоритм для базисного варианта
Базисный алгоритм, предложенный в работе [4], хотя и
является простым, однако, его применение для «выращивания» боль¬
ших кластеров (> Ю5 частиц) требует большого времени и является
достаточно проблематичным. В реализации модели DLA необходимо
непрерывно определять минимальное расстояние между диффундиру¬
ющей частицей и кластером. В простой, но неэффективной процедуре
после каждого случайного смещения перебираются координаты всех
частиц кластера. Понятно, что при существенном увеличении размера
кластера программа, основанная на таком подходе, будет выполняться
очень медленно.
Для решеточных задач повышения эффективности можно достичь
путем введения специального массива, в котором определено состояние
ячеек, но такой путь требует больших ресурсов памяти. Ниже описан
именно такой вариант базисного алгоритма, который можно предста¬
вить в виде следующей схемы:
0) инициализируем графическое окно;
1) размещаем первую частицу в центре решетки и задаем
параметры роста кластера: Rs — радиус стартовой
окружности и Rt — радиус окружности прерывания
случайных блужданий;
2) выполняем проверку на достижение кластером границ
решетки и в случае достижения переходим к пункту 8;
3) выбираем случайным образом начальное положение новой
частицы на окружности радиусом Rs;
4) смещаем ее случайным образом в ближайший узел,
вычисляем расстояние к зерну роста кластера г.
5) при удалении от зерна роста на достаточно большое
расстояние (r>Rt) переходим к пункту 3.
5) если частица находится вблизи кластера (r<Rs), то
проверяем условие контакта с кластером (сумма s
состояний ближайших ячеек должна быть отличной от нуля);
8.2. Алгоритмы и описание работы программ 145
6) при наличии контакта присоединяем частицу к кластеру,
изображаем ее на экране, вычисляем новые значения Rs,
Rt и переходим к пункту 2;
7) при отсутствии контакта переходим к пункту 4;
8) заканчиваем выполнение программы.
8.2.2. Алгоритм для ускоренного варианта
Ускоренные алгоритмы для построения кластера DLA был
описаны в [10-12]. Эффективность данных алгоритмов обусловлена
тем, что в них используется иерархия «карт» для определения кратчай¬
шего расстояния между блуждающей частицей и кластером. В частно¬
сти, в алгоритме [10] комбинируются длинные шаги для блуждающей
частицы вдалеке от растущего кластера с эффективным способом запо¬
минания информации необходимой для определения длины этих шагов.
При применении ускоренных алгоритмов компьютерное «время» растет
только слегка быстрее, чем размер кластера, что позволяет выращивать
довольно большик кластеры, включающие порядка Ю9 частиц [12].
Работу ускоренного алгоритма можно условно разделить на два этапа.
На первом этапе, когда диффундирующая частица находится от зерна
роста на расстоянии r>Rmaxi то ей совершенно необязательно совершать
случайные блуждания, смещаясь при этом в ближайшую соседнюю
ячейку. Диффузию частицы можно «ускорить», если совершать случай¬
ным образом прыжки на расстояние г — Rmax. Теоретически было пока¬
зано, что такой подход не нарушает структуру кластера базовой модели.
На втором этапе, когда г < Rmax и частица, скажем, находится меж¬
ду ветвями кластера, она может осуществлять прыжки на расстоя¬
ние, которое немного меньшее от минимального расстояния частицы к
кластеру. На рис. 8.6 показано, каким образом может быть вычислено
это минимальное расстояние и как осуществляется прыжок частицы в
этом случае. Поиск расстояния к кластеру можно существенно уско¬
рить, если построить так называемые карты кластера DLA на разных
масштабах. На рис. 8.6, а-в показано три уровня карт одного и того
же кластера. Карта уровня 2 на рис. 8.6, а отвечает самому крупному
масштабу, а карта уровня 0 на рис. 8.6, в самому мелкому. На карте
нулевого уровня структура кластера полностью детализирована. При
переходе с нулевого на более высокий уровень масштаб карты увеличи¬
вается в два раза. Ячейка карты первого уровня (рис. 8.6, б) покрывает
четыре ячейки нулевого уровня, ячейка карты второго уровня — четыре
ячейки первого и т. д. Если хотя бы одна из ячеек более низкого уровня
принадлежит к кластеру, то и покрывающая ячейка карты более высо¬
кого уровня будет принадлежать этому кластеру. Кластерные ячейки на
рис. 8.6, а и б изображены серым цветом. Допустим, мы имеем частицу,
146 ->V Глава 8. Агрегация, контролируемая диффузией
находящуюся вблизи кластера и обозначенную на рис. 8.6, а цифрой
один. Для каждого уровня карт положение частицы характеризуется
ячеечными координатами, численные значения которых определяются
положением ячейки относительно левого нижнего угла карты. Так,
на карте второго уровня координаты частицы 1 равны (4,4), перво¬
го — (7,7), а нулевого — (13,13). Зная координаты частицы на каждом
уровне, мы легко определяем расстояние для прыжка. Действительно,
анализ положения частицы на карте второго уровня (рис. 8.6, а) пока¬
зывает, что на этом масштабе длины прыжок невозможен, поскольку
ячейка, в которой находится частица, соприкасается по диагонали с
ячейкой кластера на этом уровне карты. Однако на первом уровне
карты (рис. 8.6, б) такой прыжок возможем. Мы можем осуществить
случайным образом прыжок на расстояние размера ячейки карты этого
уровня. Возможные ячейки для прыжка попадают внутрь пунктирной
окружности на рис. 8.6, б. Положим, частица совершила случайным
образом прыжок и оказалась в положении, обозначенном на рис. 8.6,6
цифрой 2. Проводя дальше анализ положения частицы, заключаем, что
дальнейшие прыжки невозможны и тогда переходим к карте нулево¬
го уровня (рис. 8.6, в). На карте нулевого уровня частица соверша¬
ет блуждание, случайным образом переходя в ближайшую соседнюю
ячейку. На рис. 8.6, в возможные смещения частицы из положения 2
показаны стрелками.
1
*)
'ч
1
2
К
У
а б в
Рис. 8.6. К объяснению скоростного алгоритма построения кластера модели DLA
Ускоренный алгоритм построения кластера DLA можно представить
в виде следующей схемы:
0) выполняем расчеты характеристик карт всех уровней и
инициализируем графическое окно;
1) размещаем первую частицу в центре решетки и задаем
параметры роста кластера: Rs — радиус стартовой
окружности и Rt — радиус окружности прерывания
случайных блужданий;
8.2. Алгоритмы и описание работы программ ->\г 147
2) выполняем проверку на достижение кластером границ
решетки и в случае достижения переходим к пункту 9;
3) выбираем случайным образом начальное положение новой
частицы на окружности радиусом Rs;
4) вычисляем расстояние от частицы к зерну роста
кластера г;
5) при удалении частицы от зерна на достаточно большое
расстояние (r>Rt) переходим к пункту 3;
5) продолжаем анализ значения г и определяем возможность
выполнения прыжка. Если прыжок возможен, выполняем его
и переходим к пункту 4;
6) осуществляем проверку условия присоединения частицы к
кластеру. Если условие присоединения выполняется, то
переходим к пункту 8
7) при отсутствии контакта смещаем частицу случайным
образом в ближайший узел и переходим к пункту 4;
8) присоединяем частицу к кластеру, изображаем ее на экране,
вычисляем новые значения Rs, Rt и переходим к пункту 2;
9) заканчиваем выполнение программы.
8.2.3. Описание работы программы
для базисного варианта
Программа, реализующая базисный вариант для построе¬
ния кластера DLA, содержится в файле dla_bas.f90. Полный код
этой программы представлен ниже:
program DLAbas
use msflib
implicit none
type (rccoord) curpos
integer (2) res
logical (2):: direct=.true.
integer:: L=512 !размер квадратной решетки
integer L2,L10 !L2=L/2; L10=L2-10
real
PI2
! 2*PI
integer:: n=0
счетчик числа частиц
integer x,y
координаты частицы
integer i
направление смещения частицы
integer s
сумма состояния соседних узлов
real
rnd
случайное число
real
phi
угловая координата стартующей частицы
real
r
расстояние частицы от центра роста
real
Rmax
максимальный радиус агрегата
real
Rs
радиус стартующей окружности
real
Rt
радиус окружности прерывания случайных
блужданий
Глава 8. Агрегация, контролируемая диффузией
!массивы:
real:: dx(l:4)=(/l, 0,-1,0/) !таблица сдвига координат
real:: dy(1:4)=(/0,-1, 0,1/)
real,allocatable:: site (:,:) !массив для хранения
!координат частиц
PI2=8.*atan(1.); L2=L/2
allocate(site(-L2:L2,-L2:L2))
!инициализируем графическое окно для отображения роста
!агрегата
res=setcolor(3)
res=rectangle($GBORDER, 18,18,872,872)
call setviewport(20,20, 870, 870)
res=setwindow(direct,dble(-L2),dble(L2),dble(L2), &
dble(-L2))
res=setcolor(15)
res=rectangle_w($gfillinterior, dble(-L2),dble(L2),&
dble (L2) , dble (-L2) )
res=setcolor(0) !цвет частиц (черный)
!размещаем первую частицу
site(0,0)=l; Rmax =0.; Rs=Rmax+5.; Rt=Rmax+100.
!рост кластера DLA
L10=L2-10
do while(Rmax<L10)
!стартуем новую частицу
call random(rnd); phi=PI2*rnd
x=int(Rs*cos(phi)); y=int(Rs*sin(phi))
r=sqrt(real(x*x)+real(y*y))
!осуществляем случайные блуждания частицы по узлам
!решетки
s=0 ;
do while(s==0 .and. r<Rt)
call random(rnd); i=int(4.*rnd+l.)
x=x+dx(i); y=y+dy(i)
r=sqrt(real(x*x)+real(y*y))
if(r<Rs) then
do i=l,4; s=s + site(x+dx(i),y+dy(i) ) ; enddo
if(s>0)then !присоединяем новую частицу к
!кластеру если s>0
n=n+l; site(x,y)=l
!изображаем присоединенную частицу
res=ellipse_w($gfillinterior, &
dble(x-0.4),dble(y+0.4),&
dble(x+0.4),dble(y-0.4))
8.2. Алгоритмы и описание работы программ •А, 149
if(r>Rmax)then
!вычисляем новые значения: Rmax, Rs, Rt
Rmax=r; Rs=Rmax+5.; Rt=Rmax+100.
endif
endif
endif
enddo
enddo
!печатаем на экране дисплея число частиц
call settextposition(1,10,curpos);
write(*,*)' n=' , n, ' '
end program DLAbas
В начале программы определяются переменные и массивы. Назначение
большинства переменных описано в комментарии. Переменная целого
типа res и переменная логического типа direct используется графи¬
ческими функциями программы.
Рост кластера начинается с размещения в начале координат «зер¬
на» роста. После этого в соответствии с алгоритмом вычисляются на¬
чальные радиусы стартовой окружности Rs и окружности прерывания
случайных блужданий Rt. Построение кластера происходит внутри
цикла do while (Rmax<L10) . . . enddo до тех пор, пока значение
его максимального радиуса Rmax не достигнет значения L/2 — 10, где
L — размер решетки. В начале этого цикла для каждой новой части¬
цы вычисляются начальные координаты ее положения на стартующей
окружности, а затем осуществляются случайные блуждания частицы
по узлам решетки до тех пор, пока она не коснется узла решетки,
который принадлежит кластеру, или ее расстояние от центра роста не
превышает значение Rt. В программе задано Rt=Rmax+100. Отметим,
что радиус прерывания случайных блужданий Rt должен быть очень
большим и в идеальном случае равным бесконечности. Невыполне¬
ние этого условия может приводить к определенным искажениям в
структуре кластера DLA. Данные искажения можно устранить, внося
поправку на выбор очередного угла для новой блуждающей частицы на
окружности радиуса Rmax (см., например, [12]).
Присоединение частицы к кластеру происходит только в том случае,
когда сума s состояний ближайших четырех узлов квадратной решетки
отлична от нуля.
8.2.4. Описание работы программы
для ускоренного варианта
Текст программы для двухмерной решеточной модели DLA,
реализующей ускоренный алгоритм, содержится в файле dla_ac. f 90.
150 ->\r Глава 8. Агрегация, контролируемая диффузией
Здесь будет рассмотрена работа только основных процедур программы
без описания ее графической части. Программа состоит из модуля общих
переменных comdata, главного модуля и обслуживающих процедур.
Код модуля общих переменных имеет вид
module comdata
real, parameter:: PI = 3.14159265
integer, parameter:: LEVELMAX = 10 !количество уровней
! карт
integer, parameter:: NMAX = 1E5 !максимальное число
!частиц
integer n !число частиц в кластере
integer L [размер квадратной решетки
!структура карты
type structmap
integer sc [размер ячейки карты
integer lm [размер карты (в ячейках)
integer si [начальный индекс ячейки карты
integer fi
integer nc
end type structmap
type (structmap), allocatable :: sm(:)
[массив для хранения информации о состоянии ячеек карт
integer (1), allocatable :: maps(:)
[таблица относительного сдвига координат
integer (1) :: dx(l:8)=(/0, 1, 0, -1, 1, 1, -1, -1/)
integer (1) :: dy(l:8)=(/l, 0, -1, 0, 1, -1, -1, 1/)
end module comdata
В приведенном модуле сконструирован нестандартный тип данных
structmap для описания структуры карт. Информация о характери¬
стиках карт всех уровней записывается в динамический массив sm
типа structmap. Количество структурных элементов в массиве sm
совпадает с количеством карт кластера. Массивы dx и dy используются
программой для оперативного вычисления координат ближайших ячеек
по отношению к заданной на всех картах. Элементы динамического
массива maps характеризуют состояния ячеек карт всех уровней и
могут принимать всего лишь два значения: 1 — ячейка кластера, 0 —
пустая ячейка.
Главный модуль программы включает вызов трех процедур:
program dla2d
use msflib
use comdata
type (rccoord) curpos
8.2. Алгоритмы и описание работы программ •Аг 151
call init ()
call seedparticle ()
call clustergrow()
!печатаем на экране дисплея число частиц
call settextposition(1,10,curpos);
write(*, *)'n=', n, ' '
end program dla2d
В конце выполнения основной программы на экране печатается ко¬
личество частиц в кластере. Отметим, что заданное в модуле общих
переменных число частиц NMAX не всегда может быть достигнуто, если
значение переменной LEVELMAX выбрано неудачно.
Процедура init является подготовительной. В ней осуществляют¬
ся расчеты характеристик карт всех уровней и размешаются в опе¬
ративной памяти все динамические массивы программы. Процедура
seedparticle осуществляет размещение в центральную ячейку кар¬
ты нулевого уровня «зерно» роста кластера и записывает информации
об этом на карты более высокого уровня. Построение кластера выпол¬
няет процедура clustergrow. Рассмотрим более детально коды для
этих процедур.
Процедура инициализации начальных значений представлена ниже:
subroutine init()
use comdata
implicit none
integer level !уровень карты
!располагаем массив структур в памяти
allocate(sm(0:LEVELMAX))
!вычисляем размеры ячеек карт всех уровней
do level=0, LEVELMAX
sm(level).sc=2**level
enddo
!вычисляем число ячеек карт всех уровней и их размеры
sm(LEVELMAX).nc=4
sm(LEVELMAX).lm=2
do level=LEVELMAX-l,0,-1
sm(level).nc=4*sm(level+1).nc
sm(level).lm=2*sm(level+1).lm
enddo
!вычисляем начальные и конечные индексы ячеек карт
!всех уровней
sm(0).si=l; sm(0).fi=sm(0).nc
152 Глава 8. Агрегация, контролируемая диффузией
do level=l,LEVELMAX
sm(level).si=sm(level-1).fi + 1
sm(level) .fi=sm(level) .si + sm(level) .nc-1 .
enddo
!размещаем массив для хранения информации о состоянии
!ячеек карт
allocate(maps(1:sm(LEVELMAX).fi))
!вычисляем размер квадратной решетки
L=2 * sm(LEVELMAX) .sc
!инициализируем графическое окно
call initgraf()
end subroutine init
Здесь уместно сделать несколько важных замечаний. Размер квад¬
ратной решетки L (по сути, размер карты нулевого уровня), на кото¬
рой выращивается кластер, не задается в программе, а вычисляется и
определяется значением переменной LEVELMAX. Значение переменной
LEVELMAX подбирается, исходя из требуемого количества частиц в
кластере. В модуле comdata этой переменной присвоено значение 10,
что является оптимальным для кластера размера Ю5 частиц. Размер
одномерного массива maps также вычисляется. Количество элементов
этого массива определяется общим количеством ячеек, необходимым
для карт всех уровней. Порядок распределения элементов этого мас¬
сива под карты разных уровней, а также его связь с массивом sm,
иллюстрируется на рис. 8.7.
sm(0).si=l
sm(0).fi=sm(0).nc
i
1
maps: | |
и l(
A J
V V
Кол-во ячеек = sm(0).nc sm(l).nc sm(LEVELMAX).nc
Рис. 8.7. Порядок распределение элементов массива maps и его связь с масси¬
вом sm в программе dla_ac.f90. Фигурная стрелка условно обо¬
значает количество ячеек карты каждого уровня, начиная с нулево¬
го. Наибольшее количество элементов массива maps приходится на
карту нулевого уровня, количество ячеек которой равно sm(0) .nc.
Информация об индексе первой и последней ячейке карты каждого
уровня содержится в массиве структур sm и записана в выделенных
для этого элементах sm (level) .si и sm (level) .fi. На рисунке
это проиллюстрировано только для карты нулевого уровня
При анализе связи и назначения элементов массивов sm и maps
можно воспользоваться аналогией с организацией файловой системы
8.2. Алгоритмы и описание работы программ ->\г 153
на жестком диске. Массив sm в этом случае исполняет роль таблицы
размещения файлов, а массив maps подобен поверхности винчестера,
разбитой на отдельные кластеры.
Процедура генерации зерна кластера имеет вид
subroutine seedparticle ()
use comdata
implicit none
integer xs,ys !координаты зерна роста
xs=L/2; ys=L/2; n=l
call particledraw(xs, ys)
call markmaps(xs, ys)
end subroutine seedparticle
В процедуре seedparticle вычисляются координат (xs, ys) зер¬
на роста кластера, рисуется его положение на экране, а затем вы¬
полняется нанесение положения зерна роста на карты всех уровней.
Последняя операция выполняется путем вызова процедуры markmaps:
subroutine markmaps(х,у)
use comdata
implicit none
integer x,y !координаты частицы
integer xc,yc !ячеечные координаты частицы
integer level !уровень карты
integer ic !индекс ячейки карты
do level=0,LEVELMAX
xc=x/sm(level).sc
yc=y/sm(level).sc
ic =sm(level).si+(yc-1)*sm(level).lm+xc-1
maps(ic)=1
enddo
end subroutine markmaps
Внутри цикла по переменной level координаты частицы (х,у)
пересчитываются в ячеечные координаты карты заданного уровня, а за¬
тем вычисляется индекс ic соответствующего элемента массива maps,
которому присваивается единичное значение.
Прежде чем переходить к объяснению работы процедуре clustergrow,
которая собственно и реализует скоростной алгоритм роста кластера,
рассмотрим работу некоторых вспомогательных функций и процедур,
которые используются в процедуре clustergrow.
Логическая функция clustercell (level, х, у) используется для
определения принадлежности ячейки с координатами (х,у) на карте
уровня level к кластеру. Эта функция имеет следующий вид:
154 •Ar Глава 8. Агрегация, контролируемая диффузией
logical function clustercell(level, x, у)
use comdata
implicit none
integer level !уровень карты
integer x, у !координаты ячейки
integer ic !индекс ячейки карты
ic=sm(level).si +(y-1)*sm(level).lm+x-1
if(maps(ic)==1) then
clustercell=.true.
else
clustercell=.false.
endif
end function clustercell
Функции целого типа emptylevel (x, у) осуществляет проверку
ближайших ячеек карты по отношению к ячейке карты, где находится
частица. Код этой функции имеет вид
integer function emptylevel(х, у)
use comdata
implicit none
integer x, у !координаты частицы
integer mx, my !ячеечные координаты частицы
integer mxn,myn !координаты соседней ячейки
integer level !уровень карты
integer i, lmap
logical clustercell
level=LEVELMAX-l
do while (level>0)
lmap =sm(level).lm
mx=x/sm(level).sc; my=y/sm(level).sc
do i=l,8 !осуществляем проверку соседних ячеек
mxn=mx+dx(i); myn=my+dy(i)
if(mxn>=l.and. mxn<= lmap .and. myn>=l .and.&
myn<= lmap) then
if(clustercell(level,mxn,myn)) goto 1
endif
enddo
emptylevel=level; return
1 level=level-l
enddo
emptylevel=0
end function emptylevel
Результатом ее работы является численное значение уровня карты,
на котором возможен прыжок (см. рис. 8.6, б). Для этого осуществляет¬
8.2. Алгоритмы и описание работы программ
ся проверка карт всех уровней, начиная с максимального. В ходе про¬
верки вычисляются координаты ячейки, в которой находится частица
на карте заданного уровня, далее проверяются все соседние ячейки на
принадлежность их кластеру. Если все соседние ячейки на карте пусты,
то прыжок возможен и выполнение функции прекращается. В против¬
ном случае осуществляется переход к более детализированной карте.
Код процедуры clustergrow выглядит следующим образом:
subroutine clustergrow()
use comdata
use msflib
implicit none
integer
i
integer
level
!уровень карты
integer
LI 0
IL/2-10 - ограничитель роста кластера
real
PI2
! 2*Р1
real
rnd
!случайное число
real
Rs
!радиус стартовой окружности
real
Rt
!радиус окружности прерывания блужданий
real
Rj
!радиус окружности для выполнения прыжка
real
Rmax
!максимальный радиус кластера
integer
xO, yO
!начало координат
integer
х,У
!координаты блуждающей частицы
integer
move
!направление блуждания
real
phi
!угловая координата частицы
integer
r
!расстояние частицы от начала координат
integer
xn, yn
!координаты соседнего узла
integer
s
!сумма состояний соседних узлов
logical
startnewparticle !переменная-переключатель,
!определяющая старт новой
!частицы
logical clustercell
integer emptylevel
PI2=2*PI; L10=L/2-10
xO=L/2; yO=L/2 !начало координат
Rmax=l; Rt=Rmax+100; Rs=Rmax+10
do while (RmaxCLlO .and. n<NMAX)
!старт новой частицы
call random (rnd); phi=PI2*rnd
x=int(rs*cos(phi)+x0); y=int(rs*sin(phi)+y0)
startnewparticle=.false.
!осуществляем прыжки и блуждания по узлам решетки
do while (.not. startnewparticle)
r=sqrt(real(x-xO)*real(x-xO)+real(y-yO)*real(y-yO) )
156 -»\л Гшва 8. Агрегация, контролируемая диффузией
if(r>Rt)then
Rj=0; startnewparticle=.true.
elseif(r>Rs .and. r<=Rt)then
Rj =r-Rmax-l
else
level=emptylevel(x, y)
if(level==0) then
!проверяем состояние соседних узлов
s=0
do i=l,4
xn=x+dx(i); yn=y+dy(i)
if (clustercell(level, xn, yn)) s=s + l
enddo
!присоединяем новую частицы к кластеру
if (s>0)then
n=n+l; call markmaps(x, y)
if(r>Rmax) then
Rmax=r; Rt=Rmax +100; Rs=Rmax+10
endif
!рисуем новую частицу кластера
call particledraw(x, у)
Rj=0; startnewparticle=.true.
else !осуществляем случайное блуждание
call random(rnd)
move=int(4.*rnd+l.) !выбор направления
x=x+dx(move); y=y+dy(move)
Rj =0
endif
else
Rj=sm(level).sc
endif
endif
!осуществляем прыжок
call random (rnd); phi=PI2*rnd
x=x+int(Rj *cos(phi)); y=y+int(Rj *sin(phi))
enddo
enddo
end subroutine clustergrow
В приведенной процедуре рост кластера происходит внутри двух
вложенных циклов do while . . . enddo. Внешний цикл осуществ¬
ляет контроль размеров кластера. Предполагается, что рост класте¬
ра прекращается при достижении заданного числа частиц или, ког¬
да размер кластера достигает границ решетки. Во внутреннем цикле
частица осуществляет прыжки и диффузию вблизи кластера. Выпол¬
8.3. Задачи для самостоятельной работы ->\г 157
нение внутреннего цикла продолжается до тех пор, пока частица не
присоединится к кластеру, или не достигнет окружности прерывания
случайных блужданий. В этих случаях значение логической перемен¬
ной startnewparticle принимает истинное значение. Случайные
блуждания частицы осуществляется только в том случае, когда значе¬
ние результирующей переменной level функции emptylevel равно
нулю и не выполняется условие присоединения частицы к кластеру, т. е.
сумма состояния ячеек карты нулевого уровня s=0.
8.2.5. Примеры работы программ
На рис. 8.8 приведены кластеры DLA, полученные с помо¬
щью программы dla_ac.f90 (основанной на использовании скорост¬
ной процедуры), размер которых составлял N = 104,105,106. Затрачен¬
ное время было примерно пропорционально размеру кластера. Можно
заметить, что при увеличении N внешний периметр кластера решеточ¬
ной модели DLA изменяет форму от ромбоподобной до крестообразной,
что является проявлением решеточной анизотропии. Для континуаль¬
ной модели этого не наблюдается, и внешний периметр всегда остается
кругообразным.
N= 10
Рис. 8.8. Изображения кластеров DLA различного размера, полученные с
помощью программы dla_ac.f90
8.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Исследуйте модель DLA для роста в замкнутой полости (см. рис. 8.4, а).
Предположите, что случайные блуждания начинаются из центра,
а зерна роста расположены на внешней окружности радиуса R.
Рост прекращается при достижении центра окружности. Исследуйте
зависимость числа частиц в полости N от ее радиуса R и, используя
соотношение (1), оцените значения k и df. Постройте для нескольких
значений R зависимости плотности р числа частиц в кластере от
х = r/R, где г — расстояние от центра окружности. Определите
значение х, соответствующее минимуму р.
158 -»\r Глава 8. Агрегация, контролируемая диффузией
2. Представим, что на квадратной решетке случайным образом распола¬
гается Ns зерен роста. Их концентрация определяется, как р = Ns/L2.
Частицы последовательно осаждаются в произвольные незанятые
узлы и начинают случайные блуждания с учетом периодических
граничных условий. Блуждания прекращаются при первом контак¬
те с любым кластером (это вариант модели множественного роста
DLA [13]). После осаждения Np частиц образуется перколяционный
кластер (см. гл. 12). Исследуйте зависимость Np от L при различ¬
ных р. Выполняется ли степенная зависимость Np ~ Ldf?
3. Исследуйте модель DLA для частиц, которые последовательно оса¬
ждаются на прямую линию, как это описано в тексте (см. рис. 8.4, б).
Проверьте, являются ли образуемые «деревья» фракталами. Для это¬
го исследуйте зависимость числа частиц N дерева, которые содер¬
жатся внутри рамки размера b (это метод «ящика с песком» для
вычисления фрактальной размерности).
4. Напишите программы для моделей DLA с подавлением шума (см.
рис. 8.3, а) и с разной вероятностью / прилипания частиц к кластеру
(см. рис. 8.2, б). Используя соотношения (1), постройте зависимости
фрактальной размерности df от параметров т и /.
Предыдущее
положение частицы
Направление преимущественного дрейфа
Рис. 8.9. К описанию обобщенных моделей DLA с преимущественным дрей¬
фом в направлении центра кластера (а) и дрейфа в магнитном поле
с «закрученной» траекторией под влиянием силы Лоренца (б) [12]
5. Интересным обобщением модель DLA является модель, в которой ве¬
роятность диффузии зависит от направления движения, т. е. частица
дрейфует в определенном направлении, которое может быть задано
электрическим или магнитным полем. На рис. 8.9 показан случай
преимущественного дрейфа в направлении центра кластера (а) и
8.4. Литература •Ar 159
дрейфа в магнитном поле с «закрученной» траекторией под влиянием
силы Лоренца (б) [14]. В модели а на каждом шаге вычисляется
угол в между направлением движения и центром кластера. В моде¬
ли б вычисляется среднее направление движения за определенное
количество предыдущих шагов (например, Af=10), а направление
преимущественного дрейфа на очередном шаге определяется путем
«закручивания» траектории на угол /3. Параметр а определяет ин¬
тенсивность дрейфа. Исследуйте изменения морфологии и фракталь¬
ной размерности кластеров для моделей а и б в зависимости от
параметра а. Какая характерная особенность формы кластеров DLA
начинает проявляться для модели б при (5 ф О?
8.4. ЛИТЕРАТУРА
1. Meakin P. Progress in DLA research 11 Physica D86. — 1995. — P. 104-112.
2. Федер E. Фракталы. — М.: Мир, 1991. — 261 с.
3. Forrest S. R., Witten T. A. Long-range correlations in smoke-particle
aggregates 11 J. Phys. A. — 1979. — V. 12. — P. L109-L117.
4. Witten T. A., Sander L.M. Diffusion limited aggregation, a kinetic critical
phenomenon 11 Phys. Rev. Lett. — 1981. — V. 47. — P. 1400-1403; Сан¬
дер Л.М. Фрактальный рост 11 В мире науки. — 1987. — №3. — С. 62-69.
5. Vicsek Т. Fractal Growth Phenomena. — Singapore: World Scientific, 1992. —
488 p.
6. Bunde A. and Havlin S. (eds.) Fractals and Disordered Systems. — 2nd ed. —
Berlin: Springer, 1996.
7. Meakin P. Noise-Reduced diffusion-limited aggregation // Phys. Rev. A. —
1987. - V. 36, No. 1. - P. 332-339.
8. Honda K., Toyoki H., Matsushita M. A theory of fractal dimensionality for gene¬
ralized diffusion-limited aggregation 11 J. Phys. Lett. — 1986. — V. 55. — P. 707.
9. Sorensen C.M., Roberts G.C. The prefactor of fractal aggregates // Journal
of Colloid and Interface Science. — 1997. — V. 186. — P. 447-452.
10. Ball R. C., Brady R. C. Large scale lattice effect in diffusion-limited aggrega¬
tion // J. Phys. A: Math. Gen. - 1985. - V. 18. - P. L809.
11. Tolman S., Meakin P. Off-lattice and hypercubic-lattice models for diffu¬
sion-limited aggregation in dimensionalities 2-8 // Phys. Rev. A. — 1989. —
V. 40. — P. 428-437; Meakin P., Tolman S. Diffusion-limited aggregation //
Proc. R. Soc. London. A423. - 1989. - P. 133-148.
12. Menshutin A. Yu., Shchur L. N. Test of multiscaling in a diffusion-limited-ag-
gregation model using an off-lattice killing-free algorithm 11 Phys. Rev.
E73. - 2006. - P. 011407.
13. Meakin P. Formation of Fractal Clusters and Networks by Irreversible Diffusion-
Limited Aggregation 11 Phys. Rev. Lett. — 1983. — V. 51. — P. 119-1122.
14. Mizuseki //., Tanaka K.y Ohno K. and Kawazoe Y. A new crystal growth
model based on a stochastic method under an external field // Modelling
Simul. Mater. Sci. Eng. — 2000. — V. 8. — P. 1-11.
ГЛАВА ИМИТАЦИЯ РОСТА
Л ШЕРОХОВАТЫХ ПОВЕРХНОСТЕЙ
9.1. СТРУКТУРА И СВОЙСТВА
ШЕРОХОВАТЫХ ПОВЕРХНОСТЕЙ
Идеально гладких поверхностей не существует, а потому,
даже внешне гладкие поверхности являются шероховатыми на микро¬
скопическом масштабе. Шероховатые поверхности или границы раз¬
дела можно наблюдать во многих природных явлениях и процессах,
например, на рис. 9.1 границы раздела, возникающие при росте лес¬
ного массива, распространении капли чернила на бумаге, образовании
ржавчины на поверхности металла, при отрыве коры с дерева, росте
лишайников.
9.1. Структура и свойства шероховатых поверхностей ->\г 161
9.1.1. Характеристики фронта роста поверхности
Для простоты рассмотрим рост так называемых (1 + 1)-по-
верхностей, которые образуются, например, при вертикальном осажде¬
нии частиц на линию. Шероховатость такой поверхности в опреде¬
ленный момент времени t можно охарактеризовать функцией высо¬
ты h{x, t) фронта поверхности, где х — пространственная координата в
горизонтальном направлении. Тогда средняя высота h(t) определяется
с помощью соотношения
hV)='th(x,t)/L, (9.1)
X— 1
где L — общая длина поверхности в горизонтальном направлении. В
данном случае предполагается, что высота измеряется через единич¬
ный интервал, а величина х в горизонтальном направлении принимает
дискретные значения, х = 1,2, ... ,L. Для непрерывной функции вели¬
чина h(t) вычисляется как интегральное среднее.
При условии постоянства потока осаждаемых частиц средняя вы¬
сота h(t) пропорциональна общему количеству осажденных частиц и
времени, т. е. h(t) ~ t. Обычно в расчетах за единицу «компьютерного»
времени принимается время, необходимое для осаждения L частиц.
Важной характеристикой поверхности является ее шероховатость а),
которая характеризует структуру поверхности и определяется как
W2(L, о = Е [М*. 0 - Wif/L = Щ)~ (Щ)2- (9.2)
*=1
Если переопределить вертикальную координату таким образом,
чтобы h(t) = 0, тогда w2(L, t) = h2(t).
Для определения степени корреляций положения частицы в лате¬
ральном (горизонтальном) направлении используют автокорреляцион¬
ную функцию, которая определяется как
<pl(r,t) = J^’t)h{x + r’t),
(1)
где <pi(0,0 = 1.
Величина <pi(r, t) обычно является экспоненциально убывающей функ¬
цией расстояния в латеральном направлении г, т. е. <p/(r, t) = exp(—r/£),
где <*; — корреляционная длина. Корреляционная длина £ определяет
пространственный масштаб при превышении которого теряется скорре-
лированность расположения высот в латеральном направлении.
162 -»\r Глава 9. Имитация роста шероховатых поверхностей
Можно определить также корреляционную функцию высота-высота
(Ph(f'J), которая определяется как
4>ht) = (h(x 4- rj) - h(x, t))2y
но эта функция не является независимой и связана с автокорреляцион¬
ной функцией соотношением (ph(r, t) = 2ш2(1 — (pi(r, t)).
При осаждении на неровную (холмистую) исходную поверхность
вводят также характеристическую длину А, соответствующую масшта¬
бу неровностей (рис. 9.2).
Рис. 9.2. К определению основных параметров, характеризующих шерохова¬
тую поверхность. Здесь а) — шероховатость, £ — корреляционная
длина, а величина А характеризует среднее расстояние между неров¬
ностями или холмами на исходной поверхности
Важной характеристикой структуры поверхности является также
среднеквадратичный наклон, определяемый как
ф = |V/i(x, t)\2
lim
r—>0
h(x + r, t) — h{r, t)‘
9.1.2. Концепция пространственно-временного скейлинга
При изучении роста шероховатых поверхностей широко
используется концепция пространственно-временного скейлинга. Идея
скейлинга (гипотезы подобия) не является новой, и раньше она ши¬
роко использовалась в физике фазовых переходов [1]. Следует отме¬
тить, что впервые идея о возможности применения гипотезы подобия
в теории фазовых переходов была высказана Паташинским и Покров¬
ским [2]. Еще раньше гипотезу подобия для объяснения «неклассиче¬
ских» свойств макроскопических систем в физике впервые использова¬
ли в теории турбулентности Колмогоров и Обухов (см., например, [3]).
9.1. Структура и свойства шероховатых поверхностей •Аг 163
Характерный вид функции шероховатости a)(L, t) представлен на
рис. 9.3 [4]. В начальный момент времени, при формировании первых
монослоев (t < ti) шероховатость w возрастает пропорционально корню
квадратному из времени, т. е. а) ~ уД. При малом заполнении рост коло¬
нок является некоррелированным, что соответствует режиму случай¬
ного роста. В последующие моменты времени, при ^ < t < tx возможен
скоррелированный рост и шероховатость возрастает по закону ш ~
где /3 < 0,5. При относительно больших временах (при t > tx) наблюда¬
ется режим насыщения и дальнейший рост а> прекращается (рис. 9.3).
Рис. 9.3. Зависимость шероховатости ш от времени t
Максимальное значение шероховатости а)^ = a)(t —> оо) также воз¬
растает по степенному закону при увеличении размера подложки L,
т. е. (Ооо ~ Lа. Величина а называется показателем шероховатости, а
величина ft — показателем роста. Переходное время tx можно оценить,
учитывая, что Ьау откуда получим tx ~ La/P- Величина z = а//3
называется динамическим показателем. Скейлинговые показатели а,
Р и z являются аналогами критических индексов в теории фазовых
переходов.
Зависимость шероховатости а) от L и t можно представить в виде
следующего закона динамического скейлинга [5]
o)(Lyt)=Laf(t/Lz)y (9.3)
где f(x) — некоторая универсальная функция, для которой справедливы
асимптотики
f(x) ~ х^ при х < 1;
f(x) = const при х > 1.
164 •Ar Глава 9. Имитация роста шероховатых поверхностей
Существуют различные классы универсальности, характеризующи¬
еся определенными значениями скейлинговых показателей а и /3. Поня¬
тие класса универсальности фактически предполагает, что физическое
поведение совершенно разных систем может описываться подобными
математическими уравнениями.
9.1.3. Основные типы компьютерных моделей
В современной литературе проанализированы различные
компьютерные модели для описания формирования и роста шерохова¬
тых поверхностей [4]. Здесь будут рассмотрены процессы роста осадков
для некоторых простейших двумерных (1 + 1)-моделей осаждения. Во
всех моделях предполагается, что частицы случайным образом оса¬
ждаются вдоль вертикального направления на ранее сформированный
осадок (линию) и фиксируются в узлах квадратной решетки, которая
содержит L колонок в горизонтальном направлении.
9.1.3.1. Случайное осаждение (RD)
В модели случайного роста (random deposition, RD) все
колонки заполняются случайным образом, т. е. рост различных колонок
является некоррелированным. После случайного осаждения N частиц
вероятность обнаружения колонки с высотой h в осадке можно вычис¬
лить с помощью следующего соотношения
/(/о = <й/л(1-/)*-*,
где величина / = \/L соответствует вероятности заполнения произволь¬
ной колонки, a ChN = N\/(h\(N— h)\) определяет число сочетаний для
данного события.
Величина /(/г) является функцией распределения высот, что позво¬
ляет рассчитать среднюю высоту осадка
W='£hf(h) = Nf=t, (9.1')
h=1
и его шероховатость
U)2{t) = mt) - (Ш? = t(l-l/L). (9.2')
Здесь учтено определение «компьютерного» времени t = N/L, а так¬
же соотношение для среднего квадрата высоты осадка
¥ = £ h2f{h,N) = 1 - /) + т2.
/1=1
9.1. Структура и свойства шероховатых поверхностей ->\г 165
В термодинамическом пределе, т. е. для бесконечной системы (L —► оо)
из (9.2') следует, что
a>(t) ~ tx/2. (9.4)
Для модели RD режим насыщения отсутствует и величина а явля¬
ется неопределенной, а показатель роста р равен 0,5.
Для получения аналитического описания поведения случайного ро¬
ста RD можно использовать также альтернативный подход. Данный
подход основан на рассмотрении поведения стохастического диффе¬
ренциального уравнения, пригодного к описанию модели случайного
роста. Он применим только в континуальном приближении для опи¬
сания поведения поверхности осадка на расстояниях, которые намного
превышают размеры постоянной решетки. Стохастическое дифферен¬
циальное уравнение для модели RD имеет вид
=V + J(9.5)
где v — средняя скорость движения фронта, a r/(x, t) — стохастическая
(шумовая) функция.
Стохастическая (шумовая) функция rj(x, t) обладает следующими
свойствами:
rj(x, 0 = 0;
r/(x, t)r](x\ t') = 2D6d(x - x')6(t - t'),
где 6d(x — xf) и 6(t — t') — дельта-функции Дирака, d — размерность
пространства a 2D — некоторая постоянная.
Последнее условие соответствует полному отсутствию корреляций
в пространстве и во времени. Стохастический шум такого типа назы¬
вается белым.
В дальнейшем будет удобно рассматривать рост поверхности в си¬
стеме координат, движущейся со средней скоростью фронта и, в кото¬
рой h = 0 и уравнение (9.5) можно переписать в виде
d-b^±=T]{xj). (9.50
Отсюда, интегрируя h(x,t) = JqT]{x, t')dt\ можно получить h2 = 2Dt
(одномерное уравнение диффузии Эйнштейна), и следующее соотноше¬
ние для шероховатости
w(t) = \l¥-h2 = V2Dt, (9.40
которое фактически совпадает с ранее полученным соотношением (9.4).
166 ->\r Глава 9. Имитация роста шероховатых поверхностей
9.1.3.2. Осаждение с поверхностной релаксацией (RDR)
Данная модель является модификацией модели RD. В мо¬
дели RDR учитывается возможность релаксации частицы в ближай¬
шую левую или правую колонку с более низкой высотой. Учет поверх¬
ностной релаксации в модели RDR приводит к сглаживанию высоких
«выступов», характерных для нескоррелированной модели RD, что фак¬
тически соответствует приближенному учету поверхностного натяже¬
ния. Данную модель можно приближенно описать с помощью стоха¬
стического дифференциального уравнения Едвардса-Вилкинсона (ЕВ),
которое подобно уравнению RD (9.5). В уравнении ЕВ учитывается
слагаемое, соответствующее наличию поверхностного натяжения [6]:
= vV2h(x, 0 + т](х, 0, (9.6)
где v — поверхностное натяжение.
Скейлинговые показатели а и ft для этой модели можно оценить
из условий инвариантности уравнения (9.6) при растяжении системы в
латеральном направлении на величину k, т. е. при изменении масштаба
хо —> х = kxQ. В данном случае из (9.3) следуют, что время t и высота
h перемасштабируются: to —> t = kzto\ ho —> h = kaho. При этом шу¬
мовое слагаемое тоже перемасштабируется: rj(x,t) —> k~(d+z^2r\{xo, to),
что следует из того, что 6(kx) = 8(x)/k и T}(kx, kzt)r]{kx',kzt') = 2D x
x6d(x-xf)8(t-t')/kd+z.
Применяя данные масштабные преобразования ко всем слагаемым
в уравнении (9.6), получим
k-*8h(X,t) = ka~2vV2h(Xt t) + k-(d+z)/2ф ty (9.6')
ot
Условие инвариантности (9.6) и (9.6') соответствует равенству
нулю всех степенных коэффициентов при k, откуда вытекает, что
а = (2 — d)/2, р = (2 — d)/A, z = 2. В частности, для двумерной мо¬
дели осаждения (так называемое (1 + 1)-осаждение), d = 1, из данных
соотношений получим а = 1/2, ft = 1/4, г = 2.
9.1.3.3. Баллистическое осаждение (BD)
Еще одной модификацией модели RD является модель
баллистического осаждения (BD). В данной модели частица фиксирует¬
ся в точке первого контакта с осадком. При осаждении проверяется вы¬
сота ближайших (левой и правой) колонок. Квадратная частица может
прилипать боковой поверхностью к уже существующему осадку [5].
В модели баллистического осаждения учитывается возможность роста
9.1. Структура и свойства шероховатых поверхностей •Аг 167
вдоль локальной нормали к поверхности. В работе [7] показано, что
наличие такого механизма роста должно приводить к появлению допол¬
нительного нелинейного слагаемого в стохастическом уравнении, кото¬
рый пропорционален (Vh(xJ))2. Появление данного слагаемого можно
понять, проанализировав схему, представленную на рис. 9.4. Влияние
нелинейного слагаемого (V/i(jc, О)2 может приводить к уширению ло¬
кальных выступов на поверхности фронта с течением времени, т. е. к
усилению роста поверхности в латеральном направлении.
Рис. 9.4. К выводу уравнения KPZ. За время dt фронт, движущийся со скоро¬
стью v, продвигается на расстояние vdt. При этом смещение поверх-
ности в вертикальном направлении составляет dh — у/(vdt)2 + а2,
где а — катет треугольника. Учитывая подобие большого и за¬
штрихованного треугольников, получим (а/vdt) = (Vhdx/dx) — V/г.
Отсюда, в приближении V/г 1, следует dh = vdt( 1 + (V/z)2/2) или
dh/dt = v + v(S7h)2/2). В системе координат, движущей со скоро¬
стью у, постоянный член v можно опустить
Обобщенное уравнение RD, в котором учитываться механизмы уси¬
ления латерального роста и поверхностного натяжения, получило на¬
звание уравнения KPZ [7]. Оно обычно записывается в виде
= vV2h(x, t) + v(V/i(*, t)f/2 + T](x, t), (9.7)
где v — скорость роста вдоль локальной нормали к поверхности.
К сожалению, степенные показатели а, /3 и z для модели KPZ
нельзя оценить, из скейлинговых соображений подобных тем, которые
применялись для модели ЕВ. Более сложный анализ, основанный на
применении метода ренорм-группы и флуктуационно-дисипационной
теоремы к одномерному варианту уравнения (9.7) (т. е. для модели
168 -»\л Глава 9. Имитация роста шероховатых поверхностей
осаждения (1+1)) позволил показать (см., например [4]), что а = 1/2,
р = 1/3, z = 3/2.
Таблица 9.1. Степенные показатели для простейших моделей осаждения
Модель
Стохастическое уравнение
Степенные
показатели
Случайное осаждение
(RD)
Осаждение с поверхност¬
ной релаксацией (RDR)
Баллистическое осажде¬
ние (BD)
dh 1 А
й=ч(лс>/)
^ = vV2ft + т](х, t)
dh —о. u(V/i)2 .
= vV ft + + tj(x, t)
1
a = oo, p = -
2-d Й a
a = —-—, p = —
2 K 2
d=\, a=1-, 5=\
2 3
В табл. 9.1 представлены степенные показатели для рассмотренных
выше простейших моделей осаждения.
9.1.3.4. Смешанные модели
В смешанных моделях предполагается, что осаждаются
частицы разных сортов. На рис. 9.5 представлена модель осаждения
для бинарной системы, состоящей из частиц А и С, осаждаемых с
вероятностями 1 - / и /, соответственно.
Частицы А, Частицы С,
вероятность выбора вероятность выбора а
1
\
/
|
+
I
\ >
+1
У
У
У
I
1 1
У
Рис. 9.5. Модель осаждения для бинарной системы [8, 9]. Осаждение ча¬
стиц А (белые квадраты) считается успешным, если они в осадке
контактируют с частицами А. Неуспешное осаждение частиц пока¬
зано зачеркнутым белым квадратом. Частицы С (серые квадраты)
могут осаждаться в любом месте. Частицы А после успешного оса¬
ждения всегда жестко фиксируются. Частицы С после осаждения
могут жестко фиксироваться [8] (а) или быть диффузионно-подвиж¬
ными (б) [9]
9.2. Алгоритмы и описание работы программ -1\г 169
Эта модель представляет некое обобщение модели RD, в которой
частицы С могут соответствовать частицам примеси. При / = 0 модель
строго соответствует модели RD. Вначале осаждаемая линия заполнена
частицами А. Осаждение этих частиц считается успешным, если в
осадке они контактируют с частицами А. При этом частицы С могут
осаждаться в любом месте, и предыдущее условие на них не распро¬
страняется. Частицы А после успешного осаждения всегда жестко фик¬
сируются. Частицы С после осаждения могут жестко фиксироваться [8]
или быть диффузионно-подвижными [9].
Для модели I (когда частицы С диффузионно-неподвижны) обра¬
зованные пространственные структуры (паттерны) имеют компактный
вид. Временная зависимость ширины фронта для промежуточных вре¬
мен со tPW , где показатель роста р является немонотонной функцией /
(относительной доли частиц С). В режиме насыщения величина со зави¬
сит от величины / как со ~ /_г [8], где у — некоторая постоянная. Для
модели II (когда частицы С диффузионно-подвижны) проявляется пове¬
дение, характерное для класса универсальности Эдварса-Вилкинсона,
т. е. р = 1/4 и не зависит от /. Для этой модели в режиме насыщения
наблюдаются немонотонная зависимость со от /[91-
Далее в главе анализируются компьютерные алгоритмы для рас¬
смотренных выше моделей осаждения: случайного (RD), с релаксацией
(RDR) и баллистического (BD).
9.2. АЛГОРИТМЫ И ОПИСАНИЕ РАБОТЫ ПРОГРАММ
9.2.1. Описание алгоритмов для моделей осаждения RD,
RDR и BD
На рис. 9.6 представлены двумерные (1 + 1)-модели оса¬
ждения RD (a), RDR (б) и BD (б). Рассмотрен простейший решеточный
вариант, в котором частицы квадратной формы (квадраты 1 х 1) оса¬
ждаются вдоль вертикального направления на ранее сформированный
осадок (линию) и фиксируются в узлах квадратной решетки. Осажде¬
ние частиц происходит последовательным образом в любой из случайно
выбранных колонок. Рост осадка прекращается при условии, что общее
количество осаждаемых частиц N или «компьютерное» время t = N/L
достигают требуемых значений.
В модели случайного роста (RD) при осаждении частицы в колонке
х ее высота увеличивается на единицу, т. е. h(x) = h(x) + 1 (рис. 9.6, а).
В релаксационной модели RDR при осаждении частицы проверяется
высота ближайших (левой и правой) колонок [5]. При этом разрешена
диффузия (релаксация) по поверхности осадка из положения с большей
высотой в положение с более низкой высотой (рис. 9.6, б).
170
X
Глава 9. Имитация роста шероховатых поверхностей
RD
[j] « RDR[^
воф
Г
Рис. 9.6. К описанию алгоритма моделей случайного осаждения RD (а), оса¬
ждения с поверхностной релаксацией RDR (б) и баллистического
осаждения BD (в)
В модели баллистической агрегации (BD) частицы могут «прилипать»
к другим частицам осадка (рис. 9.6, в). Высота колонки в данном случае
определяется с помощью оператора присваивания h (х) =max (h (х-1) ,
h (х)+1, h(х+1)).
Во всех моделях для хранения информации о профиле высоты до¬
статочно одномерного массива h (L).
9.2.2. Описание работы программ для моделей осаждения
RD, RDR и BD
Программы, реализующие алгоритмы моделей осаждения
RD, RDR и BD содержатся в файлах RD.f90, RDR. f 90 и BD.f90.
Данные программы имеют модульную структуру и состоят из модуля
общих переменных comdata, главного модуля и набора процедур.
Модуль общих переменных имеет вид
module comdata
implicit none
integer:: L =600
integer:: NMAX =150000
integer:: NSAVE =2000
integer:: NDRAW =50000
integer:: n
integer partcol
integer, allocatable:: h(:
end module comdata
размер системы
максимальное число частиц
интервал записи данных
в выходной файл
интервал смены цвета
число частиц кластера
цвет частицы
) !массив для хранения
!информации о высоте осадка
!в точке с координатой х
Для того, чтобы изобразить поверхность роста в различные момен¬
ты времени в программе используется переменная NDRAW, определяю¬
щая количество частиц, при котором происходит очередная смена цвета
осадка (рис. 9.7).
9.2. Алгоритмы и описание работы программ -1\г 171
Ниже приведен код основного модуля программы для модели RD.
program RD
use comdata
use msflib
implicit none
!располагаем массивы в оперативной памяти
allocate (h(l:L)); h=0
call initgraf () !инициализируем графическое окно
open(1,file='rd.dat')
do while (n<=NMAX)
n=n+l
call newparticle() !новая частица
if (mod(n,NSAVE)==0) call saveresult()
enddo
close (1)
end program RD
Код основного модуля для двух других моделей полностью иден¬
тичен, за исключением названия главного модуля и выходного файла.
Формирование осадка происходит до тех пор, пока число частиц не
превысит значение, определяемое переменной NMAX.
Вычисление среднего значения высоты и шероховатости осадка вы¬
полняется по формулам (9.1) и (9.2) в процедуре saveresult, которая
также полностью идентична для всех трех моделей. Код данной проце¬
дуры имеет следующий вид:
subroutine saveresult()
use comdata
implicit none
integer i
real hm !средняя высота осадка
real w !шероховатость поверхности
hm=real(sum(h(1:L)))/real(L)
w=0
do i=l,L
w=w+(h(i)-hm)*(h(i)-hm)
enddo
w=sqrt(w/real(L))
write (1,*) hm, w
end subroutine saveresult
Вычисленные величины записываются в выходной файл.
Различные алгоритмы осаждения реализуются путем вызова раз¬
личных процедур newparticle.
172 •Ar Глава 9. Имитация роста шероховатых поверхностей
9.2.2.1. Модель RD
Ниже приведена процедура newparticle для модели
случайного осаждения RD.
subroutine newparticle()! RD
use comdata
implicit none
integer x !координата частицы
real rnd !случайное число
!генерируем случайным образом координату осаждения
!частицы
call random(rnd); x=int(rnd*L+l.)
!определяем высоту осаждения частицы
h(х) =h(х)+1
!рисуем частицу
call particledraw(х, h(x))
end subroutine newparticle
9.2.2.2. Модель RDR
Ниже приведена процедура newparticle для модели
случайного осаждения с поверхностной релаксацией RDR.
subroutine newparticle() !RDR
use comdata
use msflib
implicit none
integer x !координата частицы
integer i, xt, ht
real rnd !случайное число
!таблица относительного сдвига координат
integer (2) :: dx(l:3) = (/ -1, 0, 1/)
!массив для хранения координат ближайших соседей
integer хп(1:3)
!генерируем случайным образом координату осаждения
!частицы
call random(rnd); x=int(rnd*L+l.)
!вычисляем координаты соседних столбцов
!с учетом периодических граничных условий
xn=x+dx
if (хп(1)<1) хп (1)=L
if(xn(3)>L) хп(3)=1
!определяем положение осаждения частицы
ht=h(xn(l)); xt=xn(l)
do i=2,3
9.2. Алгоритмы и описание работы программ -*\г 173
if(h(хп(i))<ht) then
ht=h(xn(i)) ;xt=xn(i)
endif
enddo
h(xt)=h(xt)+1
!рисуем частицу
call particledraw(xt, h(xt))
end subroutine newparticle
Для оперативного вычисления координат ближайших соседних
столбцов по отношению к координате осаждения частицы в программе
используются массивы dx и хп. Вычисления координат ближайших
соседей выполняется с учетом периодических граничных условий. Ко¬
нечное положение частицы xt определяется в цикле do ... enddo.
9.2.2.3. Модель BD
Ниже приведена процедура newparticle для модели
баллистического осаждения BD.
subroutine newparticle()! BD
use comdata
implicit none
integer x !координата частицы
real rnd !случайное число
!таблица относительного сдвига координат
integer (2) :: dx(1:3)=(/ -1, 0, 1/)
!массив для хранения координат ближайших соседей
integer хп(1:3)
!генерируем случайным образом координату осаждения
!частицы
call random(rnd); x=int(rnd*L+l.)
!вычисляем координаты соседних столбцов
!с учетом периодических граничных условий
xn=x+dx
if (хп(1)<1) хп(1)=L
if(xn(3)>L) хп(3)=1
!определяем высоту осаждения частицы
h(x)= max(h(хп(1)), h(xn(2))+l, h(xn(3)))
!рисуем частицу
call particledraw(x, h(x))
end subroutine newparticle
9.2.3. Примеры работы программ
Результаты работы программ, реализующих описанные
выше модели, представлены на рис. 9.7.
174 •Ar Глава 9. Имитация роста шероховатых поверхностей
а б в
18
18
18 г
16
16
16
14
14
14
12
12
12
10
10
10
8
8
8
6
■ / 6
6
4
■ / 4
4 -
2
2
••••••• • • • • •••« *•••••• О -
О 50 100150 200 250 0 50 100150 200 250 0 50 100150 200 250
t t t
Рис. 9.7. Результаты работы программ, реализующих модель случайного оса¬
ждения RD (а), случайного осаждения с релаксацией RDR (6) и
баллистического осаждения BD (в). Вверху представлены паттерны,
характеризирующие структуру осадков. Внизу представлены зави¬
симости шероховатости со осадка от времени осаждения t (средней
высоты). Размер решетки составлял L = 600, суммарное число оса¬
жденных частиц N равно 1,5 • Ю5. Смена цветов, осуществлялась
при осаждении каждых 50000 частиц
Для моделей случайного осаждения RD и модели случайного
осаждения с релаксацией RDR образовывались осадки с компактной
структурой (рис. 9.7, а и б соответственно), а для модели баллистиче¬
ского осаждения BD образовывался пористый осадок (рис. 9.7, в).
9.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. В тексте данной главы описан алгоритм смешанной модели осажде¬
ния частиц двух сортов А и С. Напишите компьютерную программу,
реализующую данный алгоритм для моделей I и II.
2. При изучении формирования поверхности осадков, состоящих из
смесей частиц разного сорта, иногда используют комбинированные,
или смешанные модели. Смешенные модели можно описать общей
формулой A^Bi_/, где А и В — символическое обозначение прими¬
тивных моделей, а / — вероятность или доля частиц, которые оса¬
9.3. Задачи для самостоятельной работы ->\г 175
ждаются по правилам примитивной модели А. Напишите программы
для смешенных моделей осаждения: a) RD^RDRi_^; б) RD/BDi_^;
в) BD/RDRj_/ [13].
3. Модифицируйте рассмотренную в этой главе программу для модели
случайного осаждения пластинок. В простейшем случае можно при¬
нять, что размер осаждающейся частицы в k раз больше постоянной
квадратной решетки (рис. 9.8). Исследуйте, каким образом меняется
пористость осадков и шероховатость их поверхности при увеличении
значения k.
а б
Рис. 9.8. Осадки, образуемые из пластинок различной длины k = 4 (а) и
k = 16 (б)
4. Обобщите рассмотренную в предыдущей задаче программу на слу¬
чай осаждения прямоугольных частиц размерами k х т (т < k) по¬
стоянных решетки. Исследуйте, как зависит пористость и шерохова¬
тость поверхности осадка от размера k и отношения (k/m).
5. Обобщите модель баллистического осаждения на случай, когда рост
осадка инициируется всего лишь одной частицей — затравкой. В
данном случае вы получите осадок, внешне напоминающий куст
(рис. 9.9, а).
Рис. 9.9. Осадок в виде куста (а) и в виде отдельных регулярно высаженных
кустов (б)
176
Глава 9. Имитация роста шероховатых поверхностей
Оцените среднее значение внешнего угла куста, в котором он фор¬
мируется. Далее рассмотрите случай, когда на решетке отдельные
кусты «высажены» регулярно с одинаковым шагом. Определите вы¬
соту /г, на которой кусты начинаются смыкаться. Совпадает ли ее
значение с оценкой, которую можно получить, зная средний угол
формирования отдельного куста и шаг между ними?
6. Обобщите программу для модели баллистического осаждения на
случай, когда осаждение частиц происходит на подложку, накло¬
ненную под углом в по отношению к горизонтали. Оцените эф¬
фективный угол роста осадка ф относительно нормали к подложке.
Выполните расчеты для больших (в > 85°) и малых (0 < в < 55°)
значений в. Проверьте, выполняются ли законы [10]: ф = С\в — для
малых углов и ф = в — С2 — для больших, где Ci, С2 — постоянные,
которые чувствительны к деталям модели осаждения. Альтернатив¬
ный закон роста осадков, который часто наблюдают при напылении
пленок: tg0 = O,5tg<p [11]. Проверьте, выполняется ли этот закон
для модифицированной модели баллистического осаждения?
7. Напишите программу для моделирования осаждения частиц на ли¬
нию по механизму модели диффузионно-контролируемой агрегации
(см. гл. 8). Используя формализм закона динамического скейлинга
для осаждения, вычислите показатели а и fi для этой модели.
8. Напишите программу для моделирования осаждения частиц на ли¬
нию по механизму модели Идена (см. гл. 7). Определите значения
показателей а и /3 для этой модели.
9. Модифицируйте программу для модели случайного осаждения в слу¬
чае осаждения частиц на линию, когда вокруг каждой частицы суще¬
ствует исключенный объем. Наличие данного исключенного объема
приводит к запрету осаждения частиц в ячейки, в которых имеются
соседние заполненные ячейки. При идеальном осаждении осадок мо¬
жет иметь структуру, подобную структуре шахматной доски, однако
в реальной ситуацию проявляется дефектная структура осадка. Ис¬
следуйте осаждение частиц для данной модели и определите закон
изменения концентрации дефектов с высотой [12].
1. Булавин JJ.A., Сысоев В. М. Физика фазовых переходов. — К.: ВПУ «Ки¬
евский университет», 2000. — 420 с.
2. Паташинский А. 3., Покровский В. Л. Флуктуационная теория фазовых
переходов. — М.: Наука, 1982. — 382 с.
9.4.
ЛИТЕРАТУРА
9.4. Литература •Ar 177
3. Рабинович М. И., Сущик М. М. Регулярная и хаотическая динамика струк¬
тур в течениях жидкости // Успехи физических наук. — 1990. — Т. 160,
№1. - С. 3-64.
4. Barabdsi A.-L., Stanley Н.Е. Fractal concepts in surface growth. — Cam¬
bridge: University Press, 1995. — 392 p.
5. Family F. and Vicsek T. Scaling of the active zone in the Eden process on
percolation networks and the ballistic deposition model // J. Phys. A. —
1985. - V. 18. - P. L75-L81.
6. Edwards S. F. and Wilkinson D. R. The surface statistics of a granular aggre¬
gate // Proc. R. Soc. London A. - 1982. - V. 381. - P. 17-31.
7. Kardar М., Parisi G. and Zhang Y.C. Dynamic scaling of growing inter¬
faces // Phys. Rev. Lett. - 1986. - V. 56. - P. 889-892.
8. Wang W'., Cerdeira H.A. Kinetic growth of randomlike and ballisticlike depo¬
sition models // Phys. Rev. E. — 1993. — V. 47. — P. 3357-3361.
9. Wang W., Cerdeira H. A. Surface growth of two kinds of particle deposition
models 11 Phys. Rev. E. - 1995. - V. 52. - P. 6308-6313.
10. Meakin P. Ballistic deposition onto inclined surfaces // Phys. Rev. A. —
1988. - V. 38. - P. 994-1004.
11. Nieuwenhuizen J. H. and. Haanstra H. B. Microfractography of thin films //
Philips Tech. Rev. - 1966. - V. 27. - P. 87-91.
12. Bulavin L.A., Lebovka N.I., Starchenko V. Y., Vygornitskii N. V. Interparti¬
cle interaction and structure of deposits for competitive model in (2 + 1)
dimensions // Physica A. — 2003. — V. 328. — P. 505-512.
13. Lebovka N.I., Manna S. S., Tarafdar S. and Vygornitskii N. V. Percolation in
deposits for competitive models in (l-bl)-dimensions 11 Physica A. — 2004. —
V. 339. - P. 385-391.
ГЛАВА СЛУЧАЙНАЯ ПОСЛЕДОВАТЕЛЬНАЯ
Л Л АДСОРБЦИЯ
10.1. НЕОБРАТИМАЯ АДСОРБЦИЯ И ДЖАММИНГ
Модель случайной последовательной адсорбции (RSA —
английская аббревиатура от random sequential adsorption) в последнее
время широко используется в физике, химии, биологии для описания
процессов формирования тонких пленок при осаждении на поверхность
наночастиц, адсорбции на поверхности молекул белков, изучении свя¬
зывания больших лигандов на полимерных цепях и т.д. [1]. Впервые
эта модель была предложена Флори в 1939 г. в связи с исследованиями
кинетики необратимых реакций в полимерных системах [2]. Он теорети¬
чески исследовал последовательное заполнение d-мерной решетки диме¬
рами, когда исключалось их взаимное перекрытие. Позднее были рас¬
смотрены более общие случаи случайной последовательной адсорбции
на решетках тримеров, тетрамеров и /г-меров, а также частиц других
различных форм: дисков, квадратов, прямоугольников и эллипсов [3-6].
10.1.1. Определение базисной модели RSA
В модели RSA предполагается, что частицы случайным об¬
разом осаждаются на поверхность, занимая определенную площадь [1].
Попытки осаждения частиц, которые перекрываются или соприкасают¬
ся с раннее осажденными частицами, не принимаются во внимание.
Последнее правило означает, что латеральные взаимодействия адсор¬
бированных объектов в модели сводятся к простому отталкиванию от
адсорбированной частицы в окрестности заданного радиуса. В базисном
варианте модели осаждение частиц есть необратимым и десорбция или
дальнейшая релаксация частицы на поверхности невозможна. Предпо¬
лагается также, что поверхностная диффузия адсорбированных частиц
очень медленна.
С увеличением концентрации адсорбированных на поверхности ча¬
стиц, постепенно увеличивается количество неуспешных попыток оса¬
10.1. Необратимая адсорбция и джамминг
ждения частицы. При некоторой критической концентрации на по¬
верхности не остается больше свободного места, и все дальнейшие по¬
пытки осаждения становятся неуспешными. В этом случае говорят, что
система достигла точки насыщения, или джамминга. На рис. 10.1 при¬
веден пример расположения частиц в точке джамминга, осажденных
на квадратной решетке для модели RSA с исключенными ближайшими
соседями.
Различают два типа моделей RSA: непрерывные и решеточные. В
непрерывных моделях координаты частиц — вещественные числа, а в
решеточных — целые, кратные периоду решетки. Модели можно также
классифицировать по типу объектов, которые осаждаются (учитывая
форму и размеры частиц). На рис. 10.2 приведены примеры располо¬
жения на поверхности частиц разной формы в точке джамминга для
непрерывной модели RSA.
стиц на квадратной решетке в точке
джамминга для модели RSA с исключен¬
ными ближайшими соседями. Размер ре¬
шетки L = 64. На рисунке видны класте¬
ры конечного размера, в которых наблю¬
дается идеальная упаковка типа шахмат¬
ной доски
а б
Рис. 10.2. Примеры расположения на поверхности дисков [3] {а) и иголок [7]
(б) в точке джамминга для непрерывной модели RSA
180 •Ar Глава 10. Случайная последовательная адсорбция
Адсорбированные частицы могут иметь конечную, или нулевую пло¬
щадь. Последний случай реализуется, например, при осаждении игл.
При этом аспектное отношение (т. е. отношение длины частицы к диа¬
метру), которое характеризует анизотропию формы частиц, равно бес¬
конечности.
В базисном варианте модели RSA частицы необратимо фиксируются
после осаждения, а в расширенных вариантах RSA они могут десорби¬
роваться, вращаться или мигрировать по поверхности, занимая более
энергетически удобные положения. В последнем случае довольно часто
наблюдается тенденция к образованию доменов [1].
10.1.2. Концентрация джамминга
для разных вариантов модели RSA
В табл. 10.1 приведены значения концентрации джаммин¬
га pj для разных вариантов модели RSA. Видно, что в общем случае
величина ру зависит от формы осаждающихся частиц, симметрии ре¬
шетки и размерности пространства.
Таблица 10.1. Концентрация джамминга pj для разных элементарных объек¬
тов. NN отвечает заполнению с исключенными ближайши¬
ми соседями; RO отвечает случайной ориентации; О отвечает
ориентированному
состоянию [1-8, 12—15
Объект
Решетка, размерность
Pi
/г-мер, к— 2
ld-решетка
1-е~2 = 0,864665
/г-мер, к = 3
ld-решетка
0,823653
/г-мер, к = 4
ld-решетка
0,803893
Аг-мер, к = 5
ld-решетка
0,792276
/г-мер, к = оо
ld-непрерывная
0,747597
RO, /г-меры, к = 2
Квадратная, 2d
0,9068
RO, /г-меры, к = 2
Кубическая
0,799 ± 0,002
RO, /г-меры, к = 2
Треугольная, 2d
0,9139
RO, &-меры, к = 3
Треугольная, 2d
0,8362
RO, /г-меры, к = 4
Треугольная, 2d
0,7886
RO, /г-меры, к = 5
Треугольная, 2d
0,7587
RO, /г-меры, к = 6
Треугольная, 2d
0,7372
RO, /г-меры, к = 7
Треугольная, 2d
0,7212
Квадраты 1 х 1 с NN
Квадратная, 2d
0,364
Кубы 1 х 1 с NN
Кубическая, 3d
0,304
Треугольники 1 х 1 с NN
Треугольная, 2d
0,23136
Квадраты 2x2
Квадратная, 2d
0,74788
0, Квадраты
Непрерывная, 2d
0,564 ± 0,002
0, Кубы
Непрерывная, 3d
0,4219 ±0,008
10.1. Необратимая адсорбция и джамминг
X
181
Таблица 10.1. (Продолжение)
Объект
Решетка, размерность
Pi
RO, квадраты
Диски
Сферы
Сферы
Полидисперсные диски,
а дисперсия
Непрерывная, 2d
Непрерывная, 2d
Непрерывная, 3d
Непрерывная, 4d
Непрерывная, 2d
0,532
0,547
0,3841 ± 0,0002
0,2598 ± 0,0003
0,547 + 0,53а
10.1.3. Модель RSA для объектов анизотропной формы
Одним из основных параметров в задаче RSA, который
определяет величину pj а также кинетику осаждения есть степень
анизотропии формы частиц. На данное время проведено детальное ис¬
следование задач, связанных с осаждением на плоскость квадратов [8],
дисков [9] , ИГЛ [6] и эллипсов [10].
Простейшим примером анизотропного объекта есть fe-мер, который
последовательно занимает на решетке k узлов. При осаждении fe-меров
на ld-решетке концентрация насыщения pj убывает с ростом k и опи¬
сывается уравнением [1]
... . . , 0,216181 , 0,362559 ,
Pj(k) = Pj(oo) + ~k + -2 + ...,
где pj(оо) = 0,747597 — концентрация насыщения для непрерывной
ld-модели RSA. Отметим, что RSA модель для осаждения &-меров на
ld-решетке допускает точное решение [11].
Детальные исследования RSA адсорбции fe-меров на квадратной ре¬
шетке проведено в [12]. Концентрация насыщения неориентирован¬
ных fe-меров постоянно уменьшается с увеличением длины k приблизи¬
тельно по степенному закону. При этом наблюдается тенденция парал¬
лельного упорядочения fe-меров и формирование компактных класте¬
ров, между которыми образуются пустоты, незаполненные /г-мерами.
На рис. 10.3 приведены примеры расположения на квадратной решетке
ft-меров в точке джамминга с разной степенью ориентационного упоря¬
дочения. При этом степень ориентационного упорядочения определяет
выражение
Q=Ni^k’ (10Л)
где NVlNh — количество /г-меров ориентированных в вертикальном и
горизонтальном направлениях, соответственно. Видно, что тенденция
формирования компактных кластеров с размером порядка величины k
усиливается с уменьшением параметра Q.
X
182 ->\r Глава 10. Случайная последовательная адсорбция
а б в
Рис. 10.3. Расположение на квадратной решетке /г-меров (к = 16) в точке
джамминга для Q = 0 (а), 0,5 (б) и 1 (в). Степень ориентационно¬
го упорядочения определяется по формуле (10.1). Размер решетки
L = 512
Накамура [13] детально проанализировал задачу RSA для осажде¬
ния на квадратной решетке ориентированных квадратов размера k х к.
На рис. 10.4 приведена зависимость pj от обратной длины квадрата
\/k [13]. Эта зависимость удовлетворительно описывается степенной
функцией вида pj(k) = рДоо) + ak~b, которая позволяет оценить зна¬
чение pj для непрерывной модели RSA (к = оо), р/(оо) = 0,569(0,002).
т
Рис. 10.4. Зависимости концентра¬
ции джамминга от обратной длины
квадрата 1//г, полученная для модели
RSA при осаждении на квадратную
решетку квадратов размера к х к [13]
Рис. 10.5. Зависимости концентрации
джамминга pj от аспектного отноше¬
ния г для случайно ориентированных
прямоугольников [29] и эллипсов [15]
Величина р/(оо) была потом уточнена при исследованиях непрерывной
модели RSA для параллельных квадратов, р} = 0,562009 ± 0,000004 [14].
X
10.1. Необратимая адсорбция и джамминг -*\г 183
При осаждении случайно ориентированных прямоугольников и эл¬
липсов величина pj зависит от аспектного отношения (рис. 10.5). Мак¬
симальное значение pj наблюдается при аспектном отношении г « 2.
Зависимости pj(r) для прямоугольников и эллипсов есть качественно
подобными, хотя при осаждении эллипсов достигается более высокая
степень заполнения чем при осаждении прямоугольников.
10.1.4. Влияние формы частиц и полидисперсности
Детальное исследование модели RSA для случая осажде¬
ния смеси полидисперсных объектов на треугольных и квадратных
решетках проведено в [16]. Изучено влияние количества компонентов
смеси и их формы на кинетику процессов осаждения. Показано, что
поздняя стадия кинетики осаждения отвечает экспоненциальному за-
кону pj - p(t) exp(—t/tr) не только для всей смеси, но и для каждой
компоненты. Авторами обсуждается в деталях как концентрация джам¬
минга и время релаксации tr зависит от состава смеси.
в [17] была изучена конкурентная модель RSA адсорбции на ld-
линию из бинарной смеси больших и малых частиц. Авторы показали
наличие сильной корреляции между парными функциями распределе¬
ний для малых и больших частиц. Показано, что дисперсия покрытия
линии малыми частицами существенно увеличивается при увеличении
отношения размеров частиц b/а, что обусловлено флуктуациями раз¬
меров щелей между большими частицами, которые служат в качестве
вакантных мест для осаждения малых частиц. Для b/а > 5 дисперсия
в распределении малых частиц практически для всех значений доли
малых частиц в общем потоке на адсорбирующую линию превышает
значение, характерное для пуассоновского распределения. Полученные
результаты являются важными для объяснения особенностей работы
полупроводниковых детекторов гамма излучения высоких энергий. Эти
же авторы в [18] провели детальные исследования ld-модели RSA, в ко¬
торой частицы после адсорбции могут увеличиваться или уменьшаться
в размерах.
Модель RSA, в которой размер объектов может изменяться со вре¬
менем, также детально проанализирована в [19]. В этой модели при¬
нимается, что размер объектов R (2б-диски, или ld-сегменты) после
осаждения может со временем уменьшаться по закону
/?(0 = 2/?oo[l + exp(-^)]I
где ta = l/fjR^) — время заполнения адсорбционного слоя, j — поток
на единицу площади в единицу времени. При этом для t = 0, R = 4/?^,
а для t = оо, R = 2R00. Таким образом, в данной модели одновременно
184 •Ar Глава 10. Случайная последовательная адсорбция
протекают два процесса: а) осаждение частиц, которое приводит к
уменьшению размеров пустот и б) уменьшение радиуса частиц, которое
приводит к увеличению размеров пустот. Отметим, что уменьшение
размера частиц увеличивает размер пустот, но с другой стороны это
вызывает интенсификацию процесса осаждения. Методом численного
моделирования в этой работе проанализированы корреляционная функ¬
ция плотность-плотность и функция распределения пор по размерам.
В [20, 21] детально исследованы свойства плотно упакованных ори¬
ентированных «супердисков» в джамминговых состояниях, сформиро¬
ванных этими объектами по механизму модели RSA. Изученные «су¬
пердиски» являются двухмерными объектами, которые ограничены кри¬
выми формы \x\2qd + \y\2qd = 1 при qd > 0. При этом значение qd = 1
отвечает обычным дискам, a qd = 0,5, оо отвечает квадратам. Примеры
таких фигур показаны на рис. 10.6.
9d 0 qd = 0,3 qd = 0,5 qd = 0,7
qd -> 1,0 qd = 1,3 qd = oo
Рис. 10.6. Форма «супердисков» при разных значениях параметра qd. Случай
qd = 0,5 разделяет вогнутые и выпуклые объекты [20, 21]
Для квадратов (^ = 1/2) и дисков (qd = 1) приведенные оценки
Pj = 0,5620 ± 0,0001 и pj = 0,5468 ± 0,0005 соответствуют значениям,
полученным раньше и приведенным в литературе. Показано, что вели¬
чина pj уменьшается при увеличении qd, причем для qd = 1/2 наблюда¬
ется излом первой производной джамминговой плотности pj(qd)- Такое
аномальное поведение при qd = 1/2 объясняется спецификой поведения
исключенной площади супердисков.
Самоорганизация бидисперсных смесей твердых дисков в двумерной
непрерывной модели RSA с ограниченной поверхностной диффузией
детально проанализирована в [22]. В работе [23] были исследовано
образование фракталов и упорядочение во время RSA процесса для
частиц со степенным распределением по размерам.
10.1. Необратимая адсорбция и джамминг
10.1.5. Кинетика осаждения для решеточных
и непрерывных моделей
На данное время в литературе довольно детально про¬
анализированы разные случаи решеточных и непрерывных вариантов
осаждения [24]. Доказано, что кинетика осаждения существенно от¬
личается для решеточных и непрерывных моделей. Например, для оса¬
ждения й-кубов на d-мерной решетке (&-меров для ld-случая и k х k
квадратов для 2d-cлyчaя) выполняется экспоненциальный закон
где ta = I/OV) — время заполнения адсорбционного слоя, V — объем
частицы, / — поток на единицу площади и времени.
Для модели RSA, в которой осаждаются длинные иглы на квад¬
ратной решетке также показано, что при приближении к концентрации
джамминга кинетика заполнения описывается экспоненциальным вре¬
менным законом [25, 26].
Для непрерывных моделей кинетика осаждения описывается услож¬
ненным степенным законом, вид которого зависит от размерности про¬
странства и формы частиц [27]. Например, для d-мерных кубов объе¬
ма V это
где ta = \/(jV) — время заполнения адсорбционного слоя, V — объем
частицы, j — поток на единицу площади и времени.
Для одномерных систем (так называемая задача парковки автомо¬
билей) выполняется степенной закон
В этой главе будут изложены некоторые простейшие алгоритмы,
используемые при моделировании процессов RSA. Ниже будут про¬
анализированы алгоритмы и программы для определения концентрации
насыщения и кинетики процесса RSA.
а для сферических частиц
186 Глава 10. Случайная последовательная адсорбция
10.2. АЛГОРИТМ И ОПИСАНИЕ РАБОТЫ ПРОГРАММЫ
10.2.1. Алгоритм RSA для одномерной модели
Рассмотрим одномерную дискретную модель RSA, в ко¬
торой координаты осаждаемых частиц могут принимать только цело¬
численные значения. Будем предполагать, что при заполнении любой
ячейки какой-то частицей, ближайшие соседние ячейки блокируются
для осаждения других частиц. Дополнительно наложим периодические
граничные условия для частиц, осаждаемых на внешних границах ре¬
шетки. В качестве примера на рис. 10.7 продемонстрировано объясне¬
ние процесса RSA для осаждения на одномерную решетку длины L = 9.
Частицы пронумерованы в порядке их осаждения. Видно, что между
осажденными частицами могут находится одна или две пустых ячейки.
ш
1
X
3
X
X
2
X
X
1 ^ \
Рис. 10.7. Одномерная дискретная модель RSA. Заблокированные ячейки обо¬
значены на рисунке крестиками. Первая частица заблокировала
левого соседа с учетом периодических граничных условий. Воз¬
можная позиция для осаждения четвертой частицы изображена
пунктирным кругом
10.2.2. Быстрый алгоритм RSA для двумерной
квадратной решетки
Рассмотрим алгоритм быстрого определения концентра¬
ции насыщения квадратной решетки L х L узлов с исключенными
ближайшими соседями. В начальный момент времени все узлы неза¬
няты и их количество равно Ns = L2. Пройдем последовательно всю
решетку по строкам и запишем декартовые координат всех узлов
в массивы х (i), y(i), где значение i = l,...,L2. Состояние ка¬
ждого узла решетки будем определять с помощью двухиндексно-
го массива Site (х (i) , у (i) ). Для занятых узлов будем полагать
Site (х (i) , у (i) ) =1, а для пустых — Site (х (i) , у (i) ) =0.
В процессе моделирования будем выбирать случайным образом i-й
узел i=int (rnd*Ns + l.), где Ns — число узлов, которые могут быть
заняты, a rnd — случайное число. После выбора узла проверим со¬
стояние четырех его ближайших соседей. Для этого вычислим сумму
значений соответствующих элементов массива Site (x(i) , у (i) ) по
координатам ближайших соседей, учитывая периодические граничные
10.2. Алгоритм и описание работы программы ->\г 187
условия. Если сумма равна нулю, то данный узел можно занимать и
элементу массива Site (х (i) , у (i) ) присваивается единичное значе¬
ние. Для исключения проверки данного узла в дальнейшем обмениваем
его координаты с координатами последнего узла в списке и уменьшаем
количество проверяемых узлов на единицу:
x(i)=x(Ns); y(i)=y(Ns); Ns=Ns-l.
Отметим, что для изучения кинетики процесса RSA такая процеду¬
ра неприменима, и в данной ситуации необходимо многократно прове¬
рять одни и те же узлы. Для высоких концентраций частиц, особенно
вблизи концентрации насыщения, вычислительный процесс становится
достаточно длительным и, обычно, для его завершения используют
определенные критерии остановки. В приведенных ниже программах
используется условие завершения RSA процесса, когда время осажде¬
ния (или число попыток осаждения частицы) достигает некоторого
большого значения ТМАХ = 106. Отметим, что конкретное значение
ТМАХ для каждого варианта модели RSA должны подбираться таким
образом, чтобы зависимость концентрации частиц от времени имела
асимптотический вид и выходила на полку.
10.2.3. Описание работы программы для определения
порога насыщения
Программа определения порога насыщения для квадрат¬
ной решетки содержится в файле rsa2djam. f 90. Полный код про¬
граммы приведен ниже:
program rsa2djam
use msflib
implicit none
integer:: NRAN=10000 !количество испытаний
integer L !размер решетки
integer L2 !L2=L*L
real pj !концентрация насыщения
integer xi,yi !координаты узла
integer xr,xl
integer yu,yd
integer s !сумма значений состояний ближайших
!соседей
integer i !индекс узла
integer Ns,Nf !счетчики узлов
real rnd !случайное число
integer j,k
integer, allocatable:: x(:),y(:) !списки координат
!узлов-кандидатов
Глава 10. Случайная последовательная адсорбция
integer(1),allocatable:: site (:,:) !матрица состояния
!узлов (заполненный
!или пустой)
open(1,file='rsa2djam.dat')
do к=4,12
L=2**k; write (*,*) 'L=',L !новый размер решетки
!размещаем массивы в памяти
L2=L*L
allocate(х(1:L2),у(1:L2))
allocate(site(1:L,1:L))
!выполняем испытания для заданного L
pj=0.
do j=l,NRAN
!новая последовательность случайных чисел
call seed(j)
Ns=0; Nf=0 !обнуляем счетчики узлов
!формируем список узлов решетки
do yi=l,L
do xi=l,L
Ns=Ns+l; x(Ns)=xi; y(Ns)=yi
site(xi,yi)=0
enddo
enddo
!заполняем узлы решетки
do while (Ns>0)
!выбираем случайным образом узел из списка
call random(rnd); i=int(rnd*Ns+l.)
xi=x (i); yi=y(i)
!вычисляем координаты соседей
xr=xi + l; if (xr>L) xr=l
xl=xi-l; if(xl<l) xl=L
yu=yi+l; if(yu>L) yu=l
yd=yi-l; if(yd<l) yd=L
!вычисляем сумму
s=site(xr,yi)+site(xl,yi)+site(xi,yu)+site(xi,yd)
if(s==0)then
site(xi,yi)=1
Nf=Nf+l !количество занятых узлов
endif
!исключаем узел из списка
x(i)=x(Ns); y(i)=y(Ns); Ns=Ns-l
enddo
!накапливаем значение концентрации насыщения
pj=pj+real(Nf)/real(L2)
enddo Следующее испытание
10.2. Алгоритм и описание работы программы ->\г 189
!усредняем и записываем результат расчетов в файл
Pj=Pj/real(NRAN)
write (1,*) L, pj
!освобождаем из памяти массивы
deallocate(х, у, site)
enddo !следующее значение L
close (1)
end program rsa2djam
В начале программы определяются переменные и массивы, назначе¬
ние которых понятно из комментария. Для хранения списка координат
и матрицы состояния узлов используются массивы динамического типа.
Для каждого нового значения L вычисляются новые границы изменения
их индексов, а далее происходит размещение их в оперативной памяти.
Во внешнем цикле do ... enddo по индексной переменной к с целью
контроля выполнения программы печатается на дисплей значение раз¬
мера решетки. Основная вычислительная часть программы содержится
внутри цикла по j и реализует описанный выше алгоритм вычисления
концентрации джамминга.
10.2.4. Описание работы программы для моделирования
кинетики насыщения
10.2.4.1. Одномерная модель RSA
Полный код программы моделирования кинетики процесса
насыщения на одномерной решетке содержится в файле rsaldl.90.
Данная программа имеет модульную структуру и состоит из модуля
общих переменных и массивов comdata, главного модуля rsaldl,
который осуществляет вызов внешней процедуры RSAld, реализующей
заполнение решетки по механизму модели RSA, и процедуры saveresult
записи результатов расчета в выходной файл.
Ниже приведен код модуля общих переменных:
module comdata
implicit none
integer:: L = 4096 !размер решетки
integer:: TMAX = 1е6 !максимальное время осаждения
integer n !счетчик частиц
integer(2), allocatable:: site (:) !массив для хранения
!координат частиц
integer, allocatable:: Nt(:) !массив для записи
!кинетики осаждения
integer(2):: dx (0 : 2) = (/0,-1, 1/) !таблица сдвига
!координат
integer хп(0:2) !координаты ближайших соседей
end module comdata
190 -»\r Глава 10. Случайная последовательная адсорбция
Назначение всех переменных и массивов описано в комментариях.
Остановимся более детально лишь на назначении массива dx (). При
выполнении проверки занятости ячейки нам необходимо регулярно вы¬
числять координаты ближайших соседей, которые будут смещены от
основной ячейки на —1 и +1. В связи с этим относительные смещения
координат удобно записать в массив dx (). Таким образом, для текущей
координаты ячейки х, координаты соседей можно вычислять и хранить
в массиве хп () с помощью одного оператора:
xn=x+dx.
Проверка на возможность осаждения частицы осуществляется с
помощью логической функции empty(х). Результатом ее работы есть
истина в случае, когда ячейка и два ее ближайших соседи незаняты,
или ложь в противном случае. Код этой функции приведен ниже:
logical function empty (х)
use comdata
implicit none
integer x, i
xn=x+dx
if(xn(l)<l) xn(l)=L !периодические граничные условия по х
if(хп(2)>L) хп(2)=1
!выполняем проверку соседей
do i=0, 2
if(site(хп(i))/=0)then
empty=.false.; return
endif
enddo
empty = .true.
end function empty
Код, в котором реализован алгоритм одномерной модели RSA, со¬
держится в процедуре RSAld:
subroutine RSAld()
use comdata
use msflib
implicit none
type (rccoord) curpos
integer n !счетчик частиц
integer t !время
integer x !координата частицы
real rnd !случайное число
logical empty !функция проверки ячейки на заполнение
10.2. Алгоритм и описание работы программы 191
!загружаем массивы в оперативную память
allocate (site(l:L)); site =0
allocate (Nt(l:L)); Nt=0
!реализуем RSA процесс
t=0; n=0
do while(t<TMAX)
t=t+l
call random(rnd); x=int(rnd*L+l.)
if(empty(x)) then !пустая ячейка
site(x)=1
n=n+l; Nt(n)=t
call settextposition (1,1,curpos);
write(*,*)'n=', n, ' '
endif
enddo
end subroutine RSAld
Заполнение решетки происходит до тех пор, пока отсчет времени t
(т. е. число попыток осаждения частицы) не превысит максимального
значения ТМАХ = 106. Для контроля процесса выполнения программы
внутри цикла do while . . . enddo на дисплее печатается число
осажденных частиц.
10.2.4.2. Двумерная модель RSA
Программу одномерной модели RSA можно обобщить на
случай двумерной квадратной решетки. Остановимся лишь на основ¬
ных моментах программы, которые нуждаются в переработке. Массив
site удобно сделать двохиндексным. В этом случае у каждой части¬
цы, которая осаждается на поверхность, появляется два дополнитель¬
ных ближайших соседа. Поэтому в модуле comdata нужно допол¬
нить таблицу сдвигов и массивы для хранения координат ближайших
соседей:
module comdata
!массив для хранения координат частиц
integer (2), allocatable:: site (:, :)
!таблица относительного сдвига координат
integer(2) :: dx(0:4)=(/0, 0, 1, 0,-1/)
integer(2) :: dy(0:4)=(/0, 1, 0,-1, 0/)
!массивы для хранения координат ближайших соседей
integer хп (0:4),уп(0:4)
end module comdata
192 ->\r Глава 10. Случайная последовательная адсорбция
Функция empty в этом случае будет иметь следующий вид:
logical function empty(х,у)
use comdata
integer x, у, i
!вычисляем координаты ближайших соседей
xn=x+dx; yn=y+dy
if(xn(2)>L) xn(2)=l
if(xn(4)<1) xn(4)=L
if(yn(1)>L) yn(1)=1
if(yn(3)<1) yn(3)=L
!выполняем проверку соседей
do i=0,4
if (site(xn(i), yn(i))/=0) then
empty=.false.; return
endif
enddo
empty=.true
end function empty
Процедура, заполнения узлов квадратной решетки выглядит следую¬
щим образом:
subroutine RSA2d()
use comdata
use msflib
implicit none
type (rccoord) curpos
integer t !время
integer x, у !координаты частицы
real rnd !случайное число
logical empty !функция проверки заполнения ячейки
!загружаем массивы в оперативную память
allocate (site(l:L, 1:L)); site =0
allocate (Nt(l:L*L)); Nt=0
!реализуем RSA процесс
t=0; n=0
do while(t<TMAX)
t=t+l
call random(rnd); x=int(rnd*L+l.)
call random(rnd); y=int(rnd*L+l.)
if(empty(x, y)) then !пустая ячейка
site(x,y)=1
n=n+l
10.2. Алгоритм и описание работы программы •Аг 193
Nt (n)=t
call settextposition (1,1,curpos);
write(*,*)'n=', n, ' '
call drawparticle(x,у)
endif
enddo
end subroutine RSA2d
Кроме указанных принципиальных изменений программа дополнена
графическими процедурами, которые позволяют рисовать расположение
частиц на экране дисплея. Полный код программы содержится в файле
rsa2dl.f90.
10.2.5. Примеры работы программ
Для тестирования работы программы rsa2djam.f90 бы¬
ли проведены расчеты по определению концентрации насыщения ру
на решетках различного размера в интервале значений L = 16 -=- 4096.
Величины pj усреднялись по Ю4 независимым компьютерным экспе¬
риментам. На рис. 10.8 представлена зависимость ру от Х/L. В дан¬
ных координатах эта зависимость является примерно линейной, т. е.
pj ~ 1/L. Для бесконечной системы (L —> оо) было получено значение
Pj « 0,36413 ± 0,00001. Данный результат согласуется с опубликован¬
ной ранее оценкой pj « 0,364 [1] (см. табл. 10.1).
0,3656
0,3654
0,3652
0,3650
0,3648
0,3646
0,3644
0,3642
0,3640
Pi
у
У
*№-Pi = 0,36413 ±0,0001
о
0,01
0,02
1 /L
0,03
0,5 -|
0,4-
0,3
0,2-
0,1-
Pj« 0,43
0
10000
20000
t
30000 40000
Рис. 10.8. Зависимости концентрации
насыщения ру от обратного размера ре¬
шетки 1/L
Рис. 10.9. Зависимость концентра¬
ции заполнения решетки р от вре¬
мени t для одномерной модели RSA.
Пунктирная горизонтальная линия
отвечает значению концентрации на¬
сыщения pj « 0,43
194 -»\r Глава 10. Случайная последовательная адсорбция
На рис. 10.9 построен график зависимости концентрации частиц р
от времени t, полученный в результате выполнения программы для
одномерной модели RSA, которая находится в файле rsaldl.f90.
При t —> сю зависимость p(t) переходит в режим насыщения, которому
соответствует значение pj « 0,43.
Отметим, что зависимость p(t) была построена на основе расче¬
та для одной статистической конфигурации. Более точную оценку pj
можно получить в результате обработки расчетов, выполненных для
большего количества конфигураций. Полученное значение pj хорошо
согласуется с точным значением:
Pi
\-ег
0,43233....
На рис. 10.10 приведена зависимость p(t), полученная в результате
выполнения программы rsa2dl.f90 на решетке размера L = 64 для
одного испытания. На вставках к рисунку изображены примеры распо¬
ложения частиц при разном заполнении решетки.
0,4-1
10000
30000 40000
20000
t
Рис. 10.10. Зависимость концентрации заполнения решетки р от времени t
для двумерной модели RSA. Пунктирная горизонтальная линия
отвечает значению концентрации насыщения = 0,365. На встав¬
ках к рисунку приведены примеры упаковок частиц при двух
различных заполнениях р
Заполненные узлы решетки, представлены здесь белым цветом. В
двумерном случае в точке джамминга наблюдается кластеризация ча¬
стиц. Внутри каждого кластера частицы упакованы по типу шахмат¬
ной доски. Полученная оценка значения pj = 0,365 удовлетворительно
согласуется с результатом, полученным в результате выполнения про¬
граммы rsa2djam.f90 и значением, приведенным в табл. 10.1.
10.4. Литература -»\r 195
10.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Модифицируйте приведенную в данной главе программу rsaldl. f 90
для случая адсорбция fe-меров на одномерной решетке, когда каждая
из частиц может занимать на решетке одновременно k соседних
ячеек. Постройте зависимость концентрации насыщения pj от длины
частицы k. Сравните полученное Вами значение pj при k —> оо с
точным значением ру = 0,7476 —
2. Модифицируйте программу rsa2djam. f 90 для вычисления концен¬
трации насыщения при осаждении k-меров на двухмерной квадрат¬
ной решетке для заданного значения параметра порядка Q (см. (10.1)).
Вычислите зависимости ру от Q при фиксированном k и от k при
фиксированном Q на решетке размера L = 512. Проследите, наблю¬
дается ли соответствие между заданным и вычисленным значениями
параметрами порядка. Дайте объяснение полученному результату.
3. Промоделируйте адсорбцию двухкомпонентных смесей на поверхно¬
сти субстрата. Модифицируйте программу rsa2dl.f90 для иссле¬
дования адсорбции частиц из двухкомпонентной смеси типа АВ. В
этой модели частицы типа А адсорбируются на поверхности субстра¬
та с вероятностью /, а частицы типа В с вероятностью 1 — /. При этом
контакты между частицами А и В запрещены [28].
10.4. ЛИТЕРАТУРА
1. Evans J.W. Random and cooperative sequential adsorption // Rev. Mod.
Phys. - 1993. - V. 65. - P. 1281-1329.
2. Flory P. J. Intramolecular Reaction between Neighboring Substituents of Vinyl
Polymers // J. Am. Chem. Soc. — 1939. — V. 61, No. 6. — P. 1518-1521.
3. Danwanichaku P., Glandt E. D. Percolation and jamming in structures built
through sequential deposition of particles // J. Coll. Int. Sci. — 2005. —
V. 283. - P. 41-48.
4. Kondrat G., Pekalski A. Percolation and jamming in random sequential ad¬
sorption of linear segments on a square lattice // Phys. Rev. E. — 2001. —
V. 63. - P. 051108.
5. Lebovka N. /., Vygornitskii N. V., Palikhov A. V. Percolation phenomena in
adsorption layer for the modified random sequential adsorption model // J.
Mol. Liq. - 2006. - V. 127. - P. 93-95.
6. Vandewalle N., Galam S., Kramer M. A New Universality for Random Se¬
quential Deposition of Needles 11 Eur. Phys. J. B. — 2000. — V. 14. —
P. 407-410.
7. Ziff R. М., Vigil R.D. Kinetics and fractal properties of the random sequential
adsorption of line segments // J. Phys. A. — 1990. — V. 23, No. 21. —
P. 5103.
196 -l\r Глава 10. Случайная последовательная адсорбция
8. Nakamura М. Percolational and fractal property of random sequential packing
patterns in square cellular structures 11 Phys. Rev. A. — 1987. — V. 36. —
P. 2384-2388.
9. Meakin P., Jullien R. Random-sequential adsorption of disks of different
sizes // Phys. Rev. A. — 1992. — V. 46, No. 4. — P. 2029-2038.
10. Talbot /., Tar jus G., Schaaf P. Unexpected asymptotic behavior in random
sequential adsorption of nonspherical particles // Phys. Rev. A. — 1989. —
V. 40, No. 8. - P. 4808-4811.
11. Gonz'alez J. J., HemmerP.C., HpyeJ.S. Cooperative effects in random se¬
quential polymer reactions 11 Chem. Phys. — 1974. — V. 3. — P. 228-238.
12. Bonnier B. Random sequential adsorption of k-mers on a square lattice: The
large к regime // Phys. Rev. E. — 1996. — V. 54, No. 1. — P. 974-976.
13. Nakamura M. Random sequential packing in square cellular structures 11 J.
Phys. A19. - 1986. - P. 2345-2351.
14. Brosilow B.J., Ziff R. М., Vigil R.D. Random sequential adsorption of parallel
squares // Phys. Rev. A. - 1991. - V. 43, No. 2. - P. 631-638.
15. Sherwood J. D. Random sequential adsorption of lines and ellipses 11 J. Phys.
A23. - 1990. - P. 2827.
16. Budinski-Petkovid L. /., Vrhovac S.B., Loncarevid I. Random sequential ad¬
sorption of polydisperse mixtures on discrete substrates // Phys. Rev. E. —
2008. - V. 78. - P. 061603.
17. Subashiev A. V., Luryi S. Fluctuations of the partial filling factors in compet¬
itive random sequential adsorption from binary mixtures 11 Phys. Rev. E. —
2007. - V. 76. - P. 011128.
18. Subashiev A. V., Luryi S. Random sequential adsorption of shrinking or ex¬
panding particles 11 Phys. Rev. E. — 2007. — V. 75. — P. 011123.
19. Gromenko O., Privman V. Random sequential adsorption of objects of decreas¬
ing size // Phys. Rev. E. — 2009. — V. 79. — P. 011104.
20. Gromenko O., Privman V. Random sequential adsorption of oriented su¬
perdisks // Phys. Rev. E. - 2009. - V. 79. - P. 042103.
21. Jiao Y., Stillinger F. H., Torquato S. Optimal Packings of Superdisks and the
Role of Symmetry 11 Phys. Rev. Lett. — 2008. — V. 100. — P. 245504.
22. Doty R.C., Bonnecaze R.T., KorgelB.A. Kinetic bottleneck to the self-or¬
ganization of bidisperse hard disk monolayers formed by random sequential
adsorption I j Phys. Rev. E. — 2002. — V. 65. — P. 061503.
23. Brilliantov N. V., Andrienko Yu. A., Krapivsky P.L., Kurths J. Fractal Forma¬
tion and Ordering in Random Sequential Adsorption // Pys. Rev. Lett. —
1996. - V. 76, No. 21. - P. 4058-4061.
24. Shelke P. B., Khandkar M. D., Banpurkar A. G., OgaleS.B., LimayeA.V.
Universality of the power-law approach to the jamming limit in random se¬
quential adsorption dynamics 11 Phys. Rev. E. — 2007. — V. 75. — P. 060601.
25. Manna S. S., Svrakic N.M. Random sequential adsorption: Line segments on
the square lattice // J. Phys. A. - 1991. - V. 24. - P. L671-L676.
10.4. Литература 197
26. Svrakic N.M., Henkel M. Kinetics of irreversible deposition of mixtures // J.
Phys. I. - 1991. - V. 1. - P. 791-795.
27. Cadilhe A., Araujo N.A.M., Privman V. Random Sequential Adsorption:
From Continuum to Lattice and Pre-Patterned Substrates 11 J. Phys. Cond.
Matt. - 2007. - V. 19. - P. 065124.
28. Sinkovits R. S. and Pandey R. B. Computer Simulations of Random Sequential
Adsorption of Two Interacting Species on a Lattice 11 J. Stat. Phys. — 1994. —
V. 74. - P. 457-463.
29. Vigil R. D. and Ziff R. M. Random sequential adsorption of unoriented rect¬
angles onto a plane // J. Chem. Phys. — 1989. — V. 91. — P. 2599.
ГЛАВА
11
АНОМАЛЬНАЯ ДИФФУЗИЯ
И ДИФФУЗИЯ В НЕУПОРЯДОЧЕННЫХ СРЕДАХ
11.1. МОДЕЛИ ДИФФУЗИИ В РАЗЛИЧНЫХ
КОНДЕНСИРОВАННЫХ СРЕДАХ
11.1.1. Случайные блуждания и движение
броуновской частицы
Впервые случайное движение микроскопических частиц
(пыльцевых зерен) в воде наблюдал шотландский ботаник Роберт Бро-
ун в 1827 г. Это движение было впоследствии названо броуновским.
Теоретическое объяснение данного явления было предложено в работе
Эйнштейна, опубликованной в 1905 г., который показал, что средне¬
квадратичное смещение броуновской частицы {r2(t)) пропорционально
времени t,
(r2^)) =2dDt, (11.1)
где d — эвклидова размерность пространства, D = k^T/{bm]R) — коэф¬
фициент диффузии броуновской частицы, &в — постоянная Больцмана,
Т — абсолютная температура, т] — вязкость жидкости, R — средний
радиус частицы.
Данное объяснение базировалось на предположении о хаотическом
тепловым движением молекул в жидкости. Случайные перемещения
молекул в жидкости, которые определяют их коэффициент самодиффу-
зии, могут быть изучены с помощью квазиупругого рассеяния медлен¬
ных нейтронов [1, 2]. Отметим, что для частиц, несущих электрический
заряд, существует прямая связь между электропроводностю среды С и
коэффициентом диффузии:
DeV
къТ '
где е — заряд электрона, ар — плотность носителей заряда.
11.1. Модели диффузии в различных конденсированных средах -*\г 199
Броуновское движение, описываемое законом (11.1), может быть про¬
моделировано с помощью метода случайных блужданий, в котором
броуновская частица смещается в единицу времени на единичное рас¬
стояние г = 1 в случайном направлении. Пример таких блужданий для
двухмерного случая показан на рис. 11.1, а.
11.1.2. Классификация типов диффузионного движения
В реальных системах часто наблюдаются ситуации, когда
закон (11.1) нарушается и между (r2(t)) и t существует нелинейная
зависимость типа,
<Г*(0> ~ Г, (11.2)
где 0 < у < 2.
Диффузия такого типа, когда 7 ^ 1, но находится в пределах
0 < 7 < 2 называется аномальной. Случай у = 1 соответствует обычной
диффузии, 7 < 1 соответствует медленной или субдиффузии, а случай
1 < 7 < 2 соответствует быстрой или супердиффузии. Предельное зна¬
чение 7 = 2 соответствует баллистическому движению, когда частицы
движутся по прямолинейным траекториям.
В некоторых случаях наблюдается также ультрамедленная диффу¬
зия типа
(Г2(0)~(1п0в,
где а > 0.
Аномальная диффузия обычно наблюдается для систем, в которых
существует определенная корреляция или когерентность диффузион¬
ных движений, распределение длин (либо времен) последовательных
смещений или эффекты «памяти» [3]. Нормальная диффузия предпо¬
лагает полную статистическую независимость последовательных слу¬
чайных блужданий при условии не очень широкого распределения для
длин или времен.
11.1.3. Модель «прыжков Леви»
В качестве простейшего примера случайных блужданий с
аномальной диффузией можно привести модель «прыжков Леви» [4],
для которой длина шага £ не являясь постоянной, может, с определен¬
ной вероятностью f(£) принимать целые значения £ е [1, оо]:
№ =
где 1 < р < оо, а с (с = 6/л2 при р = 2) — постоянная нормировки,
определяемая из соотношения L£i/W — 1-
200 Глава 11. Аномальная диффузия и диффузия в неупорядоченных средах
Модель «прыжков Леви» успешно использовалась для объяснения
различных экспериментальных результатов (турбулентные течения, фо¬
топроводимость аморфных материалов, смешивание полимерных ми-
целлярных систем [5]). Для диффузии по механизму «прыжков Леви»
выполняется закон аномальной диффузии (11.2) с коэффициентами
у = 2 при 1 < /1 < 2 (баллистическая диффузия);
7 = 4-// при 2 < р < 3 (супердиффузия);
7 = 1 при 3 < р (обычная диффузия).
Отметим в дополнение, что для модели «прыжков Леви» при р = 2 и
р = 3 наблюдаются модифицированные законы аномальной диффузии
{r2(t)) ~t2/\nt и (г2(0) tint, соответственно.
Рис. 11.1. Обычная диффузия (р = 3, а) и аномальная диффузия («прыжки
Леви», р = 2,2, б)
Ситуация р > 3 всегда соответствует нормальной диффузии, когда
7= 1 (рис. 11.1, а), т. е. в данном случае распределение длин являет¬
ся достаточно узким и среднеквадратическое смещение для большого
времени является средним эффектом от всех скачков. Для диффузии
по механизму «прыжков Леви» при р < 3, эта величина определяет¬
ся только самыми длинными прыжками (рис. 11.1, б) и средняя длина
прыжка равна бесконечности, т. е. (£2) = ^2/W — °о.
11.1.4. Модель диффузии с памятью
В качестве примера модели диффузии с памятью рас¬
смотрим модель, использованную для изучения электропроводности
смешанных А и В ионопроводящих стекол [6]. Для стекол данного
типа, вероятность смещения определенного иона зависит от состава его
ближайшего окружения. Предполагается, что смена «своего окруже¬
ния» на «чужое» всегда приводит к уменьшению коэффициента само-
11.1. Модели диффузии в различных конденсированных средах -1\г 201
диффузии. Частицы разного сорта, А и В, соответствующие разным ти¬
пам проводящих ионов совершают случайные блуждания по узлам ре¬
шетки. Наличие двух частиц одновременно в одном узле исключается.
Вероятность перехода частицы в соседний узел зависит от истории по¬
сещения узла и состава ближайшего окружения. Отметим, что данная
модель, несмотря на свою простоту, качественно правильно описывает
зависимость электропроводимости стекла от концентрации ионов.
11.1.5. Модель Эдвардса
Интересным примером скоррелированных случайных блуж¬
даний является модель Эдвардса, в которой вводится определенное
ограничение на самопересечения траектории диффузии [7]. В этой мо¬
дели в процессе случайных блужданий контролируется число самопере¬
сечений траектории N и вероятность последующих самопересечений /
экспоненциально убывает /~ехр(—aN). Случай а = 0 соответствует
модели нормальной диффузии, а случай а — оо соответствует модели с
запрещением самопересечений траектории.
Модель Эдвардса используют для изучения макромолекулярных
конформационных превращений, где параметр а характеризует эффек¬
ты, связанные с исключенным объемом. Для полимеров среднеполевая
теория Флори предсказывает у = 6/(d + 2), где d — размерность про¬
странства. По данным численного моделирования в двумерном случае
(d = 2) при а > 0 величина у не зависит от а и равна у = 3/2 [8], что
хорошо согласуется с теорией Флори.
11.1.6. Модель решеточного газа
Простейшим обобщением модели броуновского движения
на случай многочастичной задачи, является модель решеточного газа
[9, 10]. В этой модели рассматриваются случайные блуждания коллек¬
тива частиц по узлам решетки. Число частиц определяется заданной
концентрацией р и размером решетки L. Попадание двух частиц в один
узел решетки исключается, поэтому движение частиц в модели ре¬
шеточного газа является скоррелированным. Большой интерес данная
модель представляет для изучения диффузии в нанопористых матери¬
алах и в твердых телах, находящихся в кристаллическом состоянии,
где диффузия обусловлена наличием точечных дефектов в структуре
кристаллической решетки [11-13].
11.1.7. Диффузия при наличии дрейфа частицы
В модели смещенной или дрейфовой диффузии (biased dif¬
fusion) вводится преимущественное направление для случайных блуж¬
даний. Такая диффузия соответствует диффузии во внешнем поле Е
202 -»\r Глава 11. Аномальная диффузия и диффузия в неупорядоченных средах
(например, электрическом или гравитационном). При этом предполага¬
ется, что вероятность диффузии в направлении поля /+ является более
высокой, чем направлении противоположном полю /_,
/± = 1±£,
а движение в направлении перпендикулярном полю, не изменяется.
В работах [14, 15] в качестве варианта модели дрейфовой диффузии
рассмотрена модель, в которой вероятность диффузии в направлении
поля (например, вправо) равна /, а во всех остальных 1 — /. Показано,
что для этой модели зависимость (г2) от t может проявлять аномальный
осциллирующий характер.
11.1.8. Диффузия в неупорядоченных средах
и модель де Жена
Явление аномальной диффузии является широко распро¬
страненным для различных типов неупорядоченных материалов, типич¬
ными примерами которых являются пористые среды, случайно разбав¬
ленные магнитные системы, аэрогели, ионопроводящие стекла, аморф¬
ные полупроводники, и т.д. Отметим, что немаловажную роль в изу¬
чении транспортных свойств неупорядоченных сред сыграло развитие
теорий фрактальных и перколяционных кластеров. Структура дан¬
ных кластеров часто используется для геометрического моделирования
строения большинства неупорядоченных материалов [16].
1/3
t
б
1/3 —
1
-1/3
Рис. 11.2. К описанию моделей «слепого» (а) и «близорукого» (б) мура¬
вья. Узлы перколяционного кластера представлены заполненными
квадратами
Идея изучение транспортных свойств неупорядоченной среды была
предложена французским физиком де Женом в 1976 г. [17]. Он предста¬
вил случайного блуждателя на решетке, как маленького муравья в ла¬
биринте, образованного кластером. Для этой задачи де Жен придумал
название «муравей в лабиринте». В литературе обсуждается два раз¬
личных правила для данной модели. Они известны как модель «слепого
муравья» (рис. 11.2, а) и модель «близорукого муравья» (рис. 11.2, б).
11.1. Модели диффузии в различных конденсированных средах •Аг 203
Муравей может передвинуться с определенной вероятностью в ближай¬
ший разрешенный узел, принадлежащий перколяционному кластеру,
либо остаться в исходном узле. В первой из упомянутых моделей му¬
равей слепой и каждый из соседних узлов выбирается им с одинаковой
вероятностью равной 1/4 (рис. 11.2, а). В модели «близорукого мура¬
вья», осуществляется предварительный анализ состояния ближайших
ячеек. Например, если имеются только три разрешенных направления,
как показано на рис. 11.2, б, то вероятность перехода в одном из этих
направлений будет равна 1/3.
11.1.9. Диффузия на фрактальных объектах
Для диффузии на фрактальных и перколяционных кла¬
стерах выполняется закон аномальной диффузии (11.2) с показателем
у = 2jdw, который определяется фрактальной размерностью диффузи¬
онного пути dw [16]. Соотношение (11.1) можно переписать в виде
*~<г*-(0>. (11.3)
Для случайных блужданий в однородной среде наблюдается нор¬
мальная диффузия, для которой dw = 2. Это, в частности соответствует
квадратичному увеличению времени диффузии при удвоении масштаба.
Для диффузии на фрактальных объектах, в том числе и на перколяци¬
онных кластерах, обычно наблюдается замедленная диффузия (субдиф¬
фузия), что соответствует dw > 2.
Г
Рис. 11.3. К вычислению фрактальной размерности dw случайных блужданий
на треугольнике Серпинского
Величину dw для регулярных фракталов иногда можно вычислить
точно. В качестве примера рассчитаем увеличение времени диффузии
из вершины треугольника Серпинского к одному из узлов О в основа¬
нии треугольника при удвоении масштаба (рис. 11.3). Здесь буквенные
обозначения Т, А и В у каждого узла соответствуют неизвестным вре¬
менам, которые необходимы для диффузии частицы из заданной точки,
204 •Ar Глава 11. Аномальная диффузия и диффузия в неупорядоченных средах
в конечные точки О. Если Т соответствует времени, затрачиваемом
на проход одной связи, то V = Т + А. Составим теперь уравнение для
вычисления неизвестного времени А. Для этого проанализируем все
возможные пути диффузии частицы с узла А в О. Таких путей всего
четыре. Частица сразу может перейти в узел О, или перейти в другие
ближайшие соседние узлы А, В, V и продолжить диффузию с этих
узлов. Поэтому 4А = 47 +Л + В + Т. Проделав такой же анализ для
узла Б, окончательно получим систему трех линейных уравнений
Т = 7ЧЛ;
4А = 4Г+Б + Л + 7У;
4В = 4Т + 2А,
решение которых имеет вид Т = ЪТ (А = 4Т,В = 3Т). Таким образом,
при удвоении масштаба, время диффузии возрастает в пять раз, что
соответствует dw = In 5/ In 2 = 2,322 в уравнении (11.3).
Рис. 11.4. Построение ковров Серпинского для двух типов генераторов с фрак¬
тальными размерностями df = In 8/ In 3 (а) и df = In 6/ In 3 (б)
Множество других фрактальных объектов для исследования на них
диффузии можно сконструировать, используя различные типы «гене¬
раторов». В качестве примера на рис. 11.4 продемонстрировано постро¬
ение ковров Серпинского для двух типов генераторов, которые имеют
различную фрактальную размерность. Диффузия на этих объектах осу¬
ществляется по узлам, представленных заполненными ячейками.
11.1. Модели диффузии в различных конденсированных средах •Аг 205
Таблица 11.1. Фрактальные размерности случайных блужданий dw для моде¬
лей «слепого» и «близорукого» муравьев и различных генерато¬
ров, представленных на рис. 11.5, а-г
Генератор
dw, тип
[ модели
«слепого»
муравья
«близорукого»
муравья
а
2,71 ±0,01
2,68 ± 0,02
б
2,54 ±0,01
2,52 ± 0,02
в
2,48 ±0,01
2,47 ± 0,02
г
2,47 ±0,01
2,47 ± 0,02
В табл. 11.1 приведены данные по вычисленным значениям dw для
моделей «слепого» и «близорукого» муравьев на коврах Серпинского,
построенных таким способом для других типов генераторов представ¬
ленных на рис. 11.5, а-г [18]. Как ви¬
дим, наблюдается существенная зави¬
симость величины dw от типа генера¬
тора, но вместе с тем модели «слепо¬
го» и «близорукого» муравьев для од¬
ного типа генератора приводят прак¬
тически к одинаковым результатам.
К настоящему времени проведены
интенсивные исследования диффузии
и других транспортных свойств на
различных типах фрактальных и пер-
коляционных кластерах [5, 16]. Для
диффузии на случайном перколяцион-
ном кластере (двумерная квадратная
решетка) проведенные численные рас¬
четы дают оценку для величины dw
в интервале 2,65 <dw< 3,03, что находится в удовлетворительном
согласии с теоретической оценкой dw = 2,87. Отметим, что случай¬
ный перколяционный кластер является фракталом, фрактальная раз¬
мерность которого равна
df = d-£.
1 V
где d — эвклидова размерность, ft и v — экспоненты параметра по¬
рядка и корреляционной длины. Для двумерных систем известны точ¬
ные значения для этих величин, р = 5/36 и v = 4/3, и df = d — j8/v =
= 2-15/144 « 1,895833.
Рис. 11.5. Различные типы гене¬
раторов для ковра Серпинского с
одинаковой фрактальной размер¬
ностью df = In 10/ In 4 « 1,661
206 -»\r Глава 11. Аномальная диффузия и диффузия в неупорядоченных средах
Для диффузии на кластерах без петель с фрактальной размерно¬
стью df получено соотношение dw = df + 1, из которого следует, что для
диффузии на DLA кластерах dw = 2,56 ± 0,10 (2d) и dw — 3,33 ± 0,25
(3d) [5, 16].
В качестве важной характеристики аномальных диффузионных
процессов может служить также среднее количество различных уз¬
лов sm(t), посещенных за время t, которое масштабируется как
где ds = 2df/dw — фрактонная или спектральная размерность.
Отметим, что для нормальной диффузии величина ds = 2, а для
диффузии на перколяционных кластерах ds примерно равна 4/3 для
размерностей пространства в интервале 1 < d < 6. Таким образом, для
диффузии на перколяционном кластере, получим, что
~ Z2'3.
В этой главе в качестве примера будет рассмотрено применение ме¬
тода случайных блужданий для анализа задачи «муравей в лабиринте».
11.2. АЛГОРИТМ И ОПИСАНИЕ РАБОТЫ ПРОГРАММЫ
ДЛЯ ИЗУЧЕНИЯ ДИФФУЗИИ
НА ПЕРКОЛЯЦИОННОМ КЛАСТЕРЕ
11.2.1. Алгоритм
В качестве модели неупорядоченной среды выберем перко-
ляционный кластер, построенный на квадратной решетке по алгоритму
Хаммерсли-Лисса-Александровича (см. разд. 7.1.5). Броуновская ча¬
стица помещается в начало координат, которое совпадает с центром ро¬
ста кластера. Случайные блуждания частицы на перколяционном кла¬
стере выполняются с использованием алгоритма «слепого муравья». На
каждом шаге случайным образом выбирается направление смещения.
Частица смещается в соседний узел, если он не заблокирован, а время t
(количество шагов) увеличивается на единицу. Выполнение расчета
продолжается до тех пор, пока время t не достигнет требуемой величины.
11.2.2. Описание работы программы
Программа для исследования диффузии в плоских системах
содержится в файле diffusion, f90. Она имеет модульную структуру
и состоит из модуля общих переменных и массивов comdata, главного
модуля diffusion и набора процедур.
11.2. Алгоритм изучения диффузии на перколяционном кластере ->\г 207
Код модуля общих переменных и массивов имеет вид
module comdata
implicit none
logical:: GRAPH
logical:: CLUST
character (13) NAMEFILE !имя файла с координатами
!кластера
integer L, L12 !размер квадратной решетки
!L12=(L-1)/2
!переменные, связанные со случайными блужданиями
integer NPROBE
integer ТМАХ
integer TSTEP
!количество испытании
!количество шагов блужданий
!шаг вычисления характеристик случайных
!блужданий
integer NTSTEP !число временных шагов
integer NDS !число посещенных узлов кластера хотя бы
!один раз
integer х, у !координаты частицы
integer xnew, ynew !координаты пробного смещения
!массив для хранения информации о состоянии узла с
!координатами (х,у): site(x,y)> 1-узел кластера
integer, allocatable:: site(:,:)
!массивы для расчета усредненных временных зависимостей:
среднее число посещенных
узлов кластера
среднее значение
х-проекции смещения
среднее значение
у-проекции смещения
среднее значение квадрата
х-проекции смещения
!среднее значение квадрата
!у-проекции смещения
!таблица относительного сдвига координат
integer (2):: dx(l:4)=(/0, 1, 0,-1/)
integer (2):: dy(1:4)=(/1, 0,-1, 0/)
!массив для хранения координат ближайших соседних узлов
integer xn(1:4),уп(1:4)
!список параметров программы
namelist /prgparam/ GRAPH,CLUST,NAMEFILE,L,NPROBE,&
TMAX,TSTEP
end module comdata
real,
allocatable::
: NDSt(:)
real,
allocatable::
: Xt(:)
real,
allocatable::
: Yt(:)
real,
allocatable::
: X2t ( :)
real,
allocatable::
: Y2t ( : )
208 •Ar Глава 11. Аномальная диффузия и диффузия в неупорядоченных средах
Логическая переменная GRAPH введена для разрешения или бло¬
кировки работы графических процедур. Поскольку графические про¬
цедуры замедляют исполнение программы, то графику целесообраз¬
но использовать, либо в демонстрационных целях, либо на этапе
подбора размера кластера, на котором будут выполняться случайные
блуждания. Пример работы программы при подключении графического
режима (GRAPH=. TRUE.) для случайных блужданий на кластере
(CLUST=. TRUE.) показан на рис. 11.6.
Символьная переменная NAMEFILE указывает на имя файла, в ко¬
тором записан кластер. В программе для имени файла зарезервировано
13 символов. Если планируется использование длинных имен файлов,
то длина этой переменной должна быть увеличена.
Координаты узлов кластера считываются с входного файла и запи¬
сываются в двухиндексный массив site (х, у). Файл с информацией о
кластере представляет собой обычный текстовый файл, в котором в две
колонки записаны координаты узлов кластера. Случайные блуждания
всегда стартуют с узла с координатами (0,0).
Перед началом работы программы элементы массива, отвечающие
узлам кластера, полагаются равными единице. В конце модуля общих
переменных и массивов объявляется набор управляющих переменных
программы, который объединен в именной список prgparam.
Главный модуль программы имеет вид
program Diffusion
use comdata
use msflib
implicit none
type (rccoord) curpos
integer:: j=l !индекс частицы
integer t !время блужданий (количество шагов)
call init ()
!читаем кластер с входного файла
call readcluster()
!инициализируем графическое окно
if(GRAPH) then
call initgraf()
if (CLUST) call drawcluster !рисуем кластер
endif
!выполняем случайные блуждания на кластере
do j = 1,NPROBE
!печатаем на дисплей номер частицы
call settextposition (1,1, curpos)
11.2. Алгоритм изучения диффузии на перколяционном кластере •Аг 209
write(*,*)'Np=', j, ' '
!стартуем блуждания новой частицы
call rwinit (j);
!осуществляем случайные блуждания отдельной частицы
do t=0, ТМАХ
!смещаем частицу по алгоритму "слепого муравья"
call RW2D
[накапливаем результаты расчетов
if(mod(t, TSTEP)==0) call accumulate(t)
enddo
end do
call saveresults [записываем результаты расчетов
end program Diffusion
Для контроля хода выполнения программы в цикле по j печатает¬
ся номер очередной частицы, выполняющей случайные блуждания на
кластере. В начале основного модуля программы осуществляется вызов
внешней процедуры init:
subroutine init()
use comdata
implicit none
[читаем файл параметров
open(l, file='diffusion.txt')
read(1,prgparam)
close (1)
NTSTEP=TMAX/TSTEP
allocate (NDSt(1:NTSTEP)); NDSt=0
allocate ( Xt (1:NTSTEP)); Xt =0
allocate ( Yt (1:NTSTEP)); Yt =0
allocate (X2t (1:NTSTEP)); X2t =0
allocate (Y2t (1:NTSTEP)); Y2t =0
end subroutine init
В процедуре init осуществляется чтение управляющих параметров
программы, объединенных в именной список prgparam, из текстового
файла diffusion.txt. Такой подход весьма удобен, поскольку поз¬
воляет достаточно быстро изменять режим работы программы путем
простого редактирования текстового файла и повторного запуска про¬
граммы без выполнения компиляции. Управляющие параметры ТМАХ
и TSTEP используются процедурой для вычисления размеров масси¬
вов NDSt, X2t и Y2t, в которых накапливаются результаты расчетов.
После вычисления размеров эти массивы располагаются в оперативной
памяти, а затем обнуляются.
210 ->V Глава И. Аномальная диффузия и диффузия в неупорядоченных средах
Чтение кластера из входного файла осуществляется путем вызова
из основного модуля процедуры readcluster:
subroutine readcluster()
use comdata
implicit none
integer k
if(CLUST) then
[открываем файл первый раз и считываем координаты
[узлов кластера для определения размеров массива
I site(х,у)
L=0
open (1,file=NAMEFILE)
do while (.not. eof(l))
read (1,*) x, у
if(abs(x)>L) L=x
if (abs(y)>L) L=y
enddo
close (1)
k=l
do while (2**k<2*L)
k=k+l
enddo
L=2 * * k
endif
[располагаем массив узлов решетки в оперативной памяти
L12=(L-1)/2
allocate (site (-L12:L12, -L12:L12)); site=0
if (CLUST) then
[открываем файл второй раз и считываем координаты
[узлов кластера для записи в массив site (х, у)
open (1,file=NAMEFILE)
do while (.not. eof(l))
read (1,*) x, у
site(x,y)=1
enddo
close (1)
else
site=l
endif
end subroutine readcluster
Ход выполнения этой процедуры контролируется значением управля¬
ющей переменной CLUST. Если ее значение истинно, то чтение кла¬
стера с входного файла NAME FILE происходит в два этапа. Во время
11.2. Алгоритм изучения диффузии на перколяционном кластере ->\г 211
первого этапа чтения определяются максимальные по абсолютной ве¬
личине координаты узлов кластера и записываются в переменную L.
Затем значение переменной L корректируется к большему ближайшему
числу степени двойки. Откорректированное значение L используется
для вычисления размеров массива site. Если значение переменной
CLUST ложно, то в этом случае используется значение переменой L,
записанное в файле diffusion.txt. При втором чтении входного
файла координаты кластера записываются в массив site: соответ¬
ствующим элементам этого массива присваивается единичное значение,
а остаток имеет нулевое значение. Если значение переменной CLUST
ложно, то в этом случае всю квадратную решетку можно рассматривать
как кластер, поэтому всем элементам массива site следует присвоить
единичное значение.
Перед началом случайных блужданий для каждой новой частицы
выполняется вызов процедуры rwinit из главного модуля программы:
subroutine rwinit(ip)
use comdata
use msflib
implicit none
integer ip !индекс частицы
!помещаем частицу в центр решетки на перколяционный
!кластер
х=0; у=0
!обнуляем счетчик посещенных узлов
NDS=0
!инициализируем новую последовательность случайных чисел
call seed(ip)
!очищаем информацию, оставшуюся от предыдущего испытания
!в массиве site(х,у)
where (site>l) site=l
end subroutine rwinit
Поскольку в программе вычисляется среднее число sm узлов, кото¬
рые одна частица может посетить за время t, то перед запуском каждой
новой частицы, или началом нового испытания информация, оставша¬
яся от предыдущего испытания, должна быть удалена. С этой целью
в процедуре rwinit обнуляется счетчик узлов NDS (аббревиатура ан¬
глийских слов number distinct sites), которые посетила преды¬
дущая частица на кластере, и стирается информация о посещении уз¬
лов кластера в массиве site. Информация о числе посещений опре¬
деленного узла накапливается в соответствующие элементы массива
site.
212 -J\r Глава 11. Аномальная диффузия и диффузия в неупорядоченных средах
Один шаг блуждания каждой частицы соответствует вызову проце¬
дуры RW2D:
subroutine RW2D()
use comdata
use msflib
implicit none
integer direct !направление смещения
real rnd !случайное число
call random(rnd)
direct=int(4.*rnd+l.)
xnew=x+ dx(direct); ynew=y+dy(direct)
if(xnew<L12 .and. ynew<L12) then
if(site(xnew, ynew)>=1)then
!увеличиваем счетчик посещенных узлов
if(site(xnew, ynew)==l) NDS=NDS+1
x=xnew; y=ynew !смещаем частицу в новое положение
if(GRAPH) call rwdraw !рисуем смещение
endif
!накапливаем число посещений узла кластера
site(x,y)=site(x,y)+l
else
stop 'out of lattice'
endif
end subroutine RW2D
В этой процедуре в соответствии с алгоритмом «слепого муравья»
делается попытка перехода в один из четырех соседних узлов, выбран¬
ных случайно. Переменная direct определяет номер этого соседа в
соответствии с таблицей относительных смещений (массивы dx и dy,
определенные в модуле comdata). Для проверки условия достижения
граничных узлов решетки проводится сравнение координат нового по¬
ложения частицы с половинным размером решетки L12. При достиже¬
нии границы решетки работы программы останавливается с выдачей на
дисплей сообщения: out of lattice. Такой жесткий контроль по¬
ложения частицы необходим для случайных блужданий при значении
переменной CLUST=. FALSE ..
Если размер решетки L выбран неудачно и частица выходит за ее
границу, то это влечет за собой попытку записи информации в эле¬
менты массива site, которые ему не принадлежат, и соответственно к
аварийному останову программы. Если новое пробное положение части¬
цы (xnew, ynew) не выходит за границы решетки, тогда необходимо
выполнить две дополнительных проверки: во-первых, проверить, при¬
11.2. Алгоритм изучения диффузии на перколяционном кластере ->\г 213
надлежит ли новый узел решетки к кластеру и, во-вторых, посещался
ли он раньше. Признаком того, что данный узел кластера посещается
впервые, является равенство соответствующего элемента массива site
единице. В этом случае значение счетчика NDS следует увеличить на
единицу.
Накопление результатов расчета, усреднение и запись в выходной
файл выполняются в процедурах accumulate и saveresults:
subroutine accumulate(t)
use comdata
implicit none
integer t !время блужданий (количество шагов)
integer it
it=t/TSTEP
NDSt(it)=NDSt(it)+NDS
Xt (it)=Xt (it)+x
Yt (it)=Yt (it)+y
X2t (it)=X2t(it)+x*x
Y2t (it)=Y2t(it)+y*y
end subroutine accumulate
subroutine saveresults()
use comdata
implicit none
integer it, t
real factor
real R2t
factor=l./real(NPROBE)
open(1,file='rw.dat')
write (1,*) ' "t" "<гЛ2 (t)>" "<s_m(t)>" '
do it=l,NTSTEP
t=it*TSTEP
NDSt(it)=NDSt(it)*factor
Xt (it)=Xt (it) *factor
Yt (it)=Yt (it) *factor
X2t (it)=X2t(it) *factor
Y2t (it)=Y2t(it) *factor
R2t=X2t(it)+Y2t(it)-Xt(it)*Xt(it)-Yt(it)*Yt(it)
write (1,4) t, R2t, NDSt(it)
enddo
close (1)
4 format( i6, 4fl2.5)
end subroutine saveresults
214 -Лг Глава 11. Аномальная диффузия и диффузия в неупорядоченных средах
Выходной файл rw.dat состоит из трех колонок. В первую колонку
записывается время t, во вторую — среднее значение полного квадрата
смешения (г2) частицы, и в третью среднее значение числа узлов sm,
посещенных частицей за время t.
11.2.3. Пример работы программы
Работа программы тестировалась путем проведения вычис¬
лений на квадратной решетке (103 частиц по 104 шагов блужданий) и
на 10 перколяционных кластерах, построенных по алгоритму Хаммерс-
ли-Лисса-Александровича (см. разд. 7.1.5) на решетке с L = 1024 при
вероятности заполнения узлов / = fc = 0,5927 [19].
Рис. 11.6. Случайные блуждания на перколяционном кластере. Темным цве¬
том показаны узлы кластера, которые посетило Ю3 частиц. Кластер,
построенный по алгоритму Хаммерсли-Лисса-Александровича на
квадратной решетке с L = 1024 при вероятности заполнения уз¬
лов / = 0,5927 (изображен серым цветом). Число узлов в кластере
А=105. Время блужданий каждой частицы равно 104 шагов. В
данном случае размер кластера выбран достаточно большим и на
протяжении времени расчета ТМАХ отдельные частицы при блуж¬
даниях практически не достигали внешней границы кластера. Для
кластеров малых размеров частицы могут «отражаться» от внешней
границы кластера, что приводит к искажению временной зависимо¬
сти среднеквадратичного смещения (г2^))
Число узлов в каждом кластере было выбрано N = 105. Пример од¬
ного из таких кластеров, на котором проводилось моделирование, пред¬
ставлен на рис. 11.6. На каждом кластере для испытания было выбрано
по тысяче частиц, каждая из которых выполняла Ю4 шагов блужданий.
11.3. Задачи для самостоятельной работы 215
Результаты расчетов по каждому кластеру были записаны в отдельные
файлы, а затем усреднены по всем кластерам.
t
Рис. 11.7. Результаты тестирования работы программы dif fusion. f 90
На рис. 11.7 приведены зависимости среднеквадратического смеще¬
ния (г2) и среднего количества посещенных различных узлов sm от
времени t для блужданий на перколяционном кластере. Из этих дан¬
ных были получены следующие значения у = 2/dw = 0,738 ± 0,003 и
ds = 1,32 ±0,01. Для перколяционного кластера полученное значение
фрактальной размерности диффузионного пути dw = 2/0,738 « 2,71 на¬
ходится внутри интервала, приведенных в литературе численных оценок
2,65 < dw < 3,03 [5]. Вычисленное значение фрактонной размерности
перколяционного кластера ds = 1,32 ± 0,01 « 4/3 довольно хорошо со¬
гласуется с теоретическим значением ds = 2df/dw = 2*91 /48/2,87 = 1,321.
11.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Исследуйте случайные блуждания на кластере DLA. Для этого по¬
стройте кластер с количеством узлов 5 103, используя программу
dla2d.f90 (см. гл. 8). После этого воспользуйтесь программой
dif fusion. f 90 и рассчитайте усредненные по тысяче частиц вре¬
менные зависимости (г2) и sm. Максимальное число шагов положи¬
те равным 5 • 103. Найдите из полученных зависимостей значения
dw и ds. Сравните вычисленные вами значения с литературными
численными оценками, dw = 2,56 ± 0,1, ds = 1,2 ± 0,1 [20].
2. Исследуйте случайные блуждания на фрактальных коврах Серпин¬
ского, генераторы для которых показаны на рис. 11.4. Вычислите за¬
висимости среднеквадратического смещения от времени. Фракталь¬
216 •Ar Глава 11. Аномальная диффузия и диффузия в неупорядоченных средах
ная размерность для этих ковров равна df = In я/In 3, где п — коли¬
чество диффузионных узлов, показанных темным цветом.
3. Исследуйте дрейфовую диффузию на плоской квадратной решетке
[14, 15]. В качестве выделенного направления, задаваемого внеш¬
ним полем, выберете направление слева направо. Модифицируйте
программу dif fusion. f 90 с учетом того, что вероятность диффу¬
зии в выделенном направлении /, отличается от вероятности пере¬
хода в остальных направлениях 1 — /. Для этого на каждом шаге
блужданий генерируется случайное число rnd и если rnd < /, то
частица сдвигается в соседний узел направо (direct=2). В против¬
ном случае случайным образом (с помощью процедуры по формуле
direct=int (3 . *rnd+l.)) выбирается одно из трех оставшихся
направлений. Указанные изменения должны быть внесены в про¬
цедуру случайных блужданий RW2D. Постройте зависимости (г2)
от t для разных значений параметра 0,4 < / < 1 для диффузии на
перколяционных кластерах.
4. Модифицируйте программу dif fusion. f 90 для случайных блуж¬
даний на кубической решетке и рассчитайте среднее время t\, необ¬
ходимое частице для того, чтобы покинуть сферу радиусом R. За¬
тем рассчитайте зависимость среднего времени необходимого N
частицам для того, чтобы покинуть сферу R для различных значе¬
ний N. Постройте график зависимости tu/h от N, после чего ап¬
проксимируйте ее степенной функцией вида t^/h =Na. Проведите
анализ аппроксимации и сравните значение а с теоретическим зна¬
чением а = 2/3 [21].
5. Исследуйте случайные блуждания для модели решеточного газа с
ненулевой концентрацией блуждающих частиц р. Используйте пе¬
риодические граничные условия. Вычислите коэффициент диффузии
D = (d(r2(t))/dt)/2d (здесь d — размерность пространства) при фик¬
сированных концентрациях р = 0,1, 0,2, 0,3, 0,5 и 0,7, наблюдая за
какой-то одной выбранной частицей. Объясните наблюдаемую зави¬
симость D(p).
6. Напишите программу для моделирования аномальной диффузии в соот¬
ветствии с рассмотренной в тексте моделью «прыжков Леви». Для
генерации случайной длины прыжка распределенной по степенному
закону f(£) ~ 1/£Р можно воспользоваться формулой £ ~ г1/(1-^)? где
г — случайное число, равномерно распределенное в интервале 0 -И.
Случайные смещения координат равны Дх = ^sin<p, Дг/ = £cos(p, где
угол ср принимает случайное значение в интервале 0 -=- 2л. Иссле¬
дуйте зависимость коэффициента диффузии D = {d{r2(t))/dt)/A от
времени при различных значениях р.
11.4. Литература 217
11.4-
ЛИТЕРАТУРА
1. Булавин Л. А., Кармазина Т. В., Клепко В. В., Слисенко В. И. Нейтронная
спектроскопия конденсированных сред. — К.: Академпериодика, 2005. —
2. Булавин Л. А., Чалый К. О. Нейтронная оптика мезомасштабных жидко¬
стей. — К.: Наукова думка, 2006. — 210 с.
3. Bouchaud J. P. and Georges A. Anomalous diffusion in disordered media:
statistical mechanisms, models and physical applications // Phys. Rep. —
1990. - V. 195. - P. 127.
4. Weeks E. R. Experimental Studies of Anomalous Diffusion, Blocking Phenom¬
ena, and Two-Dimensional Turbulence Dissertation Doctor of Philosophy The
University of Texas at Austin 1997.
5. Havlin S. and Ben-Avraham D. Diffusion in disordered media // Advances in
Physics. - 2002. - V. 51, No. 1. - P. 187-292.
6. Bunde A., Ingram M.D. and Ngai K.L. Diffusion with memory: a model for
mixed alkali effects in vitreous ionic conductors // J. Phys. A: Math. Gen. —
1991. - V. 24. - P. L881-L886.
7. Edwards S. F. The statistical mechanics of polymer with excluded volume //
Proc. Phys. Soc. - 1965. - V. 85. - P. 613-24.
8. de Forcrand P., Pasche J. and Petritis D. Critical behaviour of the Edwards
random walk in two dimensions: a case where the fractal and Hausdorff
dimensions are not equal? // J. Phys. A: Math. Gen. — 1988. — V. 21. —
P. 3771-3782.
9. Demontis P., PazzonaF.G., and Suffritti G. B. Diffusion in tight confine¬
ment: A lattice-gas cellular automaton approach. I. Structural equilibrium
properties // The Journal of Chemical Physics. — 2007. — V. 126. —
P. 194709.
10. Demontis P., Pazzona F. G. and Suffritti G. B. Diffusion in tight confinement:
A lattice-gas cellular automaton approach. II. Transport properties // The
Journal of Chemical Physics. — 2007. — V. 126. — P. 194710.
11. Gupta D. (Ed.), Diffusion processes in advanced technological materials. —
Norwich, NY: William Andrew, Inc., 2005. — 532 p.
12. Jackson K. A. Kinetic Processes. — KGaA, Weinheim: Wiley-VCH Verlag
GmbH & Co., 2004. - 407p.
13. Shewmon P. Diffusion in Solids, Minerals, Metals, and Materials Society. —
KGaA: Wiley-VCH Verlag GmbH & Co., 2010. - 246 p.
14. Stauffer D., Sornette D. Log-periodic oscillations for biased diffusion on ran¬
dom lattice // Physica A. - 1998. - V. 252. - P. 271-277.
15. Stauffer D. New simulations on old biased diffusion // Physica A. — 1999. —
V. 266. - P. 35-41.
16. Ben-Avraham D., Havlin S. Diffusion and Reactions in Fractals and Disor¬
dered Systems. — Cambridge: University Press, 2000. — 315 p.
17. de Gennes P. G. La percolation: un concept uni_cateur (Percolation a unifying
concept) // La Recherche. — 1976. — V. 7, No. 72. — P. 919-927.
640 c.
218 ->\r Глава 11. Аномальная диффузия и диффузия в неупорядоченных средах
18. Dasgupta R., Ballabh Т.К., and Tarafdar S. Scaling exponents for random
walks on Sierpinski carpets and number of distinct sites visited: A new
algorithm for infinite fractal lattices // J. Phys. A: Math. Gen. — 1999. —
V. 32, No. 37. - P. 6503-6516.
19. Stauffer D., and Aharony A. Introduction to Percolation Theory. — 2nd ed. —
London: Taylor and Francis, 1992. — 182 p.
20. Meakin P., Stanley H. E. Spectral Dimension for the Diffusion-Limited Ag¬
gregation Model of Colloid Growth 11 Phys. Rev. Lett. — 1983. — V. 51,
No. 16. - P. 1457-1460.
21. Bendler J. T., Fontanella J. /., Shlesinger M. F. Sources of exponents 11 Phys-
ica D. - 2004. - V. 193. - P. 67-72.
ГЛАВА АЛГОРИТМЫ КЛАСТЕРНОГО АНАЛИЗА
12
12.1. ПОСТАНОВКА ЗАДАЧИ
Необходимость анализа связности кластеров возникает в
разнообразных физических приложениях, например, в задачах моле¬
кулярной физике, физике магнитных явлений, при анализе разнооб¬
разных спиновых моделей и решении перколяционных задач. Рассмот¬
рим для примера перколяционную задачу на квадратной решетке раз¬
мером LxL [1, 2]. Пусть узлы квадратной решетки случайным об¬
разом заполнены N частицами. Концентрация или численная плот¬
ность частиц определяется как p = N/(LxL). Эта величина также
является вероятностью заполнения узлов. Отметим, что с увеличе¬
нием концентрации частиц р отдельные частицы могут образовывать
конечные кластеры (рис. 12.1). При некоторой критической концентра¬
ции частиц рс появляется достаточно большой кластер, который «про¬
низывает» всю систему и такой кластер называется перколяционным
(рис. 12.1, в).
а б в
Рис. 12.1. Заполнение узлов частицами (обозначены серым цветом) на квад¬
ратной решетке размером L — 10 для разных значений вероятности
заполнения р = 0,46 (а), 0,61 (б) и 0,62 (в). Черным цветом пока¬
заны частицы, принадлежащие к перколяционному кластеру
220 •Ar Глава 12. Алгоритмы кластерного анализа
Основной проблемой является определение минимальной вероятно¬
сти рс, при которой наблюдается перколяция в горизонтальном или в
вертикальном направлении. Интенсивные исследования данной задачи
показали, что величина рс зависит как от симметрии решетки, так
и от размерности пространства и изменяется при изменении размера
решетки L по скейлинговому закону [1, 2]
pc(L)=p?+AL-[/\
где р^° соответствует значению перколяционной концентрации в преде¬
ле L —> оо, А — амплитуда, v — экспонента корреляционной длины.
Для рассмотренной на рис. 12.1 случайной перколяции на квадрат¬
ной решетке перколяционный порог равен рс = 0,5927... [1, 2]. Зна¬
чение v является универсальным, оно не зависит от симметрии ре¬
шетки, но зависит от размерности системы и типа задачи перколяции.
Например, для задачи случайной перколяции в двумерных системах
эта величина равна v = 4/3. Однако, эта величина может существенно
изменяться при скореллированном заполнении узлов. Задачи скорел-
лированной перколяции возникают при учете взаимодействия между
частицами, их притяжение может приводить к образованию достаточно
компактных, а отталкивание — более разреженных кластеров. Скор¬
релированные кластеры возникают, например, при анализе спиновых
систем.
На рис. 12.2 приведен пример непрерывной перколяционной моде¬
ли. В данном случае на плоскость случайным образом разбрасывается
N дисков единичного диаметра (D = 1). Концентрация или численная
плотность частиц определяется как р = N/(L х L). Предполагается, что
при перекрытии дисков (т. е. когда расстояние между их центрами
г < 1) образуются связанные кластеры. Здесь задача также заключа¬
ется в нахождении минимальной численной плотности дисков рс при
которой наступает перколяция. В приведенном на рис. 12.2 примере
плотность дисков р = 0,46 является недостаточной для образования
перколяционного кластера.
Для полностью проницаемых дисков перколяционная плотность
равна примерно рс = 1,436, что соответствует доли поверхности, кото¬
рая покрывается этими дисками рс = 1 — ехр(— pcnD2/А) « 0,676 [3, 4].
Визуальный анализ перколяционных задач является достаточно уто¬
мительным и теряет смысл, когда число узлов или дисков становится
достаточно большим. Компьютеризация задачи состоит в проведении
маркировки кластеров, при которой частицам в отдельных кластерах
присваивается один и тот же номер (кластерная метка). Если на про¬
тивоположных границах системы существуют узлы пронумерованные
12.2. Кластерный анализ методом прожига -*\г 221
одним и тем же номером то это соответствует существованию перколя¬
ционного кластера.
Рис. 12.2. Заполнение плоскости перекрывающимися дисками единичного
диаметра для непрерывной перколяционной модели. Размер систе¬
мы составляет 10 х 10, число дисков равно 46
В этой главе будет рассмотрено два популярных алгоритма для марки¬
ровки кластеров с использованием метода прожига и метода Хошена-
Копельмана.
12.2. КЛАСТЕРНЫЙ АНАЛИЗ МЕТОДОМ ПРОЖИГА
12.2.1. Алгоритм
Главная идея метода «прожига» заключается в последова¬
тельном анализе состояния ближайших соседей в решетке и выявление
связных кластерных конфигураций. Процесс исследования отдельного
кластера чем-то напоминает процесс горения леса, при котором огонь
переносится от дерева к дереву, полностью охватывая отдельно стоя¬
щий массив леса. Отсюда исходит и название данного алгоритма.
В качестве примера проанализируем применения данного алгоритма
для анализа связности кластеров на квадратной решетке. Информация
о занятых частицами узлах квадратной решетки с координатами (х, у)
содержится в массиве site(х,у): site(x,y)=l для занятых узлов
и site(x,y)=0 для пустых. При выполнении кластерного анализа
этот массив используется также для записи информации о принад¬
лежности каждого узла к определенному кластеру. Элементы масси¬
ва site (х, у), принадлежащие к одному кластеру имеют одинако¬
вые значения. На рис. 12.3 представлено пример распределения частиц
222 ->\r Глава 12. Алгоритмы кластерного анализа
на квадратной решетке размером L = 10 перед началом кластерного
анализа.
а б в
ю
1
1
1
1
1
10
1
1
1
1
1
10
10
10
10
10
10
9
1
1
1
9
1
1
1
9
9
8
8
8
1
1
1
1
1
8
1
1
1
1
1
8
8
8
8
8
8
7
1
1
1
1
1
1
1
1
7
X
1
1
1
1
1
1
1
7
2
8
8
8
8
8
8
8
6
1
1
1
1
1
6
2
2
1
1
1
6
2
2
8
8
8
5
1
1
1
1
5
2
1
1
1
5
2
8
8
8
4
1
1
1
1
4
2
2
1
1
4
2
2
7
6
3
1
1
1
1
3
2
2
1
1
3
2
2
5
6
2
X
2
2
2
2
I
2
X
1
1
1
1
2
2
1
1
1
1
2
2
3
4
4
I
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
Рис. 12.3. К объяснению работы алгоритма кластерного анализа методом выжига
Обход решетки осуществляется последовательно по строкам: слева
направо, начиная с левого нижнего угла и снизу вверх. При обна¬
ружении занятого узла с начальной кластерной меткой 1 начинается
процесс анализа («выжига») нового кластера. На рис. 12.3, а при ана¬
лизе первого узла с координатами (1,1) элементу массива site (1,1)
присваивается кластерная метка 2 и проверяется состояние его бли¬
жайших соседей. В данном случае существуют два соседних узла,
занятые частицами. Они отмечены на рис. 12.3, а крестиками. Коорди¬
наты отмеченных узлов заносим в список периметра — массивы хр (i),
yp(i). Список координат периметра будем продолжать исследовать
до тех пор, пока он не будет исчерпан. На каждом этапе элементам
старого списка присваивается текущая кластерная метка (в данном
случае 2), далее они исключаются из списка, и проверяется состояние
соседних узлов. В случае, когда узлы заняты частицами, их координаты
дополняют в список. На рис. 12.3, б изображена ситуация, когда список
состоит всего лишь из одного узла (помеченного крестиком). Дальней¬
ший процесс исследования этого списка приводит к его исчерпанию.
Таким образом, на решетке помечены все узлы кластера с номером 2.
После завершения обследования этого кластера счетчик кластерных
меток увеличивается на единицу и продолжается процесс исследования
решетки. На рис. 12.3, в представлена маркировка всех занятых узлов
после окончания обхода решетки.
12.2.2. Программа кластерного анализа методом прожига
Рассмотрим теперь программную реализацию данного ал¬
горитма. Код программы находится в файле burn, f90 и выглядит
следующим образом:
12.2. Кластерный анализ методом прожига -*\г 223
program burn
implicit none
integer
: L =100
размер квадратной решетки
real :
: prob=0.59
вероятность протекания узлов
решетки
integer
x, У
координаты узла
integer
xn, yn
координаты соседнего узла
integer:
: label=l
счетчик кластерных меток
integer
P, Pn
счетчики заполненных узлов
на периметре кластера
integer
i/ j
индексы
real
rnd
случайное число
integer
site(0:101,0
101) !массив для хранения
! информации о .состоянии
!узлов
!массивы для хранения координат периметра кластера
integer хр(1:10000), ур(1:10000)
integer xpnew(1:10000), ypnew(1:10000)
!таблица относительного сдвига координат
integer (1) :: dx(l:4)=(/0, 1, 0, -1/)
integer (1) :: dy(l:4)=(/l, 0, -1, 0/)
!открываем выходной файл и формируем матрицу,
!которая содержит информацию о заполнении узлов
open (1,file='coord.dat')
do у=1,L
do x=l,L
call random(rnd)
if(rnd<prob) then
site(x,y)=1
write (1(2i6)') x,y
endif
enddo
enddo
close (1)
!выполняем маркировку кластеров
do у=1,L
do x=l,L
if(site(x,y)==1)then !обнаружен новый кластер
label=label+l !увеличиваем счетчик
!кластерных меток
site(х,у)=label
Р=1; хр(Р)=х; ур(Р)=у
224 Глава 12. Алгоритмы кластерного анализа
!осуществляем поиск новых узлов кластера до тех
!пор, пока число присоединенных к кластеру узлов
!не будет равным нулю
do while(Р>0)
Рп = О
do i=l,P
do j =1, 4
xn=xp(i)+dx(j)
yn=yp(i)+dy(j)
if (site(xn, yn)==l) then
site(xn, yn)=label
Pn=Pn+l; xpnew(Pn)=xn; ypnew(Pn)=yn
endif
enddo
enddo
xp(l:Pn)= xpnew(l:Pn); yp(l:Pn)= ypnew(l:Pn)
P=Pn
enddo
endif
enddo
enddo
!записываем кластерные метки заполненных узлов
!в выходной файл
open(1,file='label.dat')
do y=l,L
do x=l,L
if(site(x,y)>0) write(l,*) site(x,y)-l
enddo
enddo
close (1)
end program burn
В начале программы определяются основные переменные и массивы.
Информация о заполнении узлов решетки с заданной вероятностью prob
записывается в массив site (х, у) и в выходной файл coord.dat.
Чтобы исключить при работе программы проверки на выход координат
узлов за границы решетки, пределы изменения индексов массива site
должны отличаться на единицу от размера решетки L (в программе
L = 100). Массивы хр (i), ур (i), xpnew (i), ypnew (i) служат для
хранения списка координат узлов решетки, присоединяемых к кластеру
во время анализа его периметра. Пределы изменения индексов данных
массивов должны учитывать ситуацию, когда р = 1 и на решетке нахо¬
дится всего лишь один кластер. Поэтому в программе значения индек¬
сов изменяются от единицы до L2. Маркировка кластеров реализована
внутри двух вложенных операторов цикла do ... enddo. При обходе
12.2. Кластерный анализ методом прожига
решетки и обнаружении занятой ячейки осуществляется исследова¬
ние нового кластера. Каждый новый кластер первоначально состоит
всего лишь с одного узла. Построение, анализ и обновление списка
координат узлов, принадлежащих к текущему кластеру, выполняется
внутри цикла do while . . . end do в соответствии с описанным в
предыдущем параграфе алгоритмом. Отметим, что обновление списка
ячеек кластера осуществляется переписыванием на его место вновь
обнаруженных ячеек с помощью двух операторов присваивания:
хр(1:Pn)=xpnew(1:Рп)
ур(1:Pn)=ypnew(1:Рп)
В конце работы программы метки всех кластеров записываются в вы¬
ходной файл label .dat. Поскольку маркировка кластеров начинается
с метки, равной двум, то при записи в выходной файл мы вычитаем со
всех значений меток единицу.
12.2.3. Пример работы программы кластерного анализа
методом прожига
Работа программы была протестирована на квадратной ре¬
шетке размера L = 100, когда концентрация заполненных ячеек равна
р = 0,59, т. е. близка к перколяционному порогу рс = 0,5927... [1,2].
В результате работы программы burn. ехе было создано два выходных
файла coord.dat и label.dat.
Информация, содержащаяся в файлах coord.dat и label.dat в
графическом виде представлена на рис. 12.4. Данный рисунок представ¬
ляет собой дамп экрана, полученный в результате выполнения програм-
Рис. 12.4. Результат кластерного
анализа методом «прожига» (про¬
грамма burn, f 90) для задачи
случайной перколяции на квад¬
ратной решетке, размер решетки
равен L — 100, концентрация за¬
полнения ячеек равна р = 0,59
226 •Ar Глава 12. Алгоритмы кластерного анализа
мы viewdisc-bw.exe (см. разд. 12.4.3). Ячейки решетки, принадле¬
жащие к разным кластерам, представлены на данном рисунке дисками,
заполненными оттенками черного цвета. При данном значении р на ре¬
шетке был обнаружен перколяционный кластер, который пронизывает
решетку по горизонтали и вертикали.
12.3. КЛАСТЕРНЫЙ АНАЛИЗ С ИСПОЛЬЗОВАНИЕМ
МЕТОДА ХОШЕНА-КОПЕЛЬМАНА
12.3.1. Решеточный вариант
12.3.1.1. Алгоритм
В алгоритме Хошена-Копельмана [5], также как и ранее,
информация о занятых частицами узлах квадратной решетки с коорди¬
натами (х,у) содержится в массиве site (х, у).
Для нумерации связных узлов решетки используется переменная
ncl (счетчик числа кластеров на решетке). В начале этой переменной
присваивается значение ncl=0. При прохождении решетки по стро¬
кам слева на право и снизу вверх узлы нумеруются последовательно
(рис. 12.5). В случае обнаружения каждого нового занятого узла ре¬
шетки, который не связан с соседями в левом столбце или в нижней
строке, переменная ncl увеличивается на единицу. Если занятый узел
связан только с одним соседом слева или снизу, то ему присваивается
метка соседа.
а б в
10
1
1
1
1
1
10
12
12
12
12
12
10
12
12
12
12
12
9
1
1
1
9
11
7
7
9
11
7
7
8
1
1
1
1
1
8
10
7
7
7
7
8
7
7
7
7
7
7
1
1
1
1
1
1
1
1
7
1
10
10
7
7
7
7
7
7
1
7
7
7
7
7
7
7
6
1
1
1
1
1
6
8
1
9
7
7
6
1
1
7
7
7
5
1
1
1
1
5
1
7
7
7
5
1
7
7
7
4
1
1
1
1
4
1
1
6
5
4
1
1
6
5
3
1
1
1
1
3
1
1
4
5
3
1
1
4
5
2
1
2
1
2
1
1
1
1
1
1
1
1
1
1
2
3
3
1
1
1
2
3
3
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
Рис. 12.5. Расположение узлов на квадратной решетке размера L = 10, заня¬
тых с вероятностью р = 0,46 (а). Значения кластерных меток узлов
после первого (б) и второго проходов решетки (в)
Первая нетривиальная ситуация при обходе решетки возникает для
узла с координатами (2,6). Данный узел связан с соседом слева, ко¬
торый имеет метку 8 и соседом снизу, метка которого 1. Для решения
подобных конфликтных ситуаций создается список связей меток в виде
12.3. Кластерный анализ с использованием метода Хошена-Копельмана
массива LL (). В начале работы алгоритма все элементы этого массива
равны нулю. Присвоим узлу с координатами (2,6) минимальную мет¬
ку 1, а элементу массива LL () с индексом 8 значение 1, т. е. LL (8) =1.
Поступая, таким образом, можно сформировать список связей меток
между собой.
Более сложная ситуация возникает в узле с координатами (6,7). Дан¬
ный узел связан с соседом слева, который имеет метку 10, и соседом
снизу, метка которого 9. Кроме того, метки 9 и 7 связаны между собой,
поскольку значение элемента массива LL (9) =7. В данном случае узлу
с координатами (6,7) присваивается метка 7, а элементу массива связей
с индексом 10 присваивается значение LL (10) =7.
Результат применения такой нумерации после первого прохода ре¬
шетки представлен на рис. 12.5, б. Все метки узлов решетки можно
разделить на правильные и неправильные, исходя из значений элемен¬
тов массива LL (). Так, например, метки узлов 8, 9 и 10 являются
неправильными, поскольку соответствующие элементы массива LL ()
равны соответственно: LL (8) =1, LL (9) =7, LL (10) =7. Все остальные
метки узлов являются правильными и соответствующие им элементы
массива LL () равны нулю. Исправить неправильные метки узлов мож¬
но во время второго прохода решетки, воспользовавшись информацией
о связях меток, хранящейся в массиве LL (). Результат выполнения
кластерного анализа после второго прохода решетки представлен на
рис. 12.5, в.
12.3.1.2. Описание программы
Программа, реализующий решеточный вариант алгоритма
Хошена-Копельмана, находится в файле hk.f90 и выглядит следую¬
щим образом:
program hk
implicit none
integer:: L =512
integer:: label=0
integer left, down
integer labmin
integer s
integer x, у
integer site (0:512,0:512)
integer LL(1:100000)
размер квадратной решетки
счетчик кластеров
метки ближайших соседних
узлов
значение минимальной метки
сумма меток
координаты узла
массив, содержащий
информацию о заполнении
узлов
список связности меток
узлов
Глава 12. Алгоритмы кластерного анализа
!открываем входной файл и формируем матрицу,
!которая содержит информацию о заполнении узлов
open (1,file='coord.dat')
do while (.not. eof(l))
read (1,*) x, у
site(x,y)=1
enddo
close (1)
!выполняем маркировку узлов
do y=l,L
do x=l,L
if (site(x,y)==1) then
left=site(x-1,y); down=site(x,y-1)
s=left+down
if (s==0) then
label=label+l; site(x,y)=label
else if(s==left) then
site(x,y)=left
else if (s==down) then
site(x,y)=down
else
do while (LL(left)/=0); left=LL(left); enddo
do while (LL(down)/=0); down=LL(down); enddo
labmin=min(left, down)
site (x,y)=labmin
if(down/=labmin) LL(down)=labmin
if(left/=labmin) LL(left)=labmin
endif
endif
enddo
enddo
!исправляем неправильные кластерные метки и записываем
!кластерные метки заполненных узлов в выходной файл
open(1,file='label.dat' )
do y=l,L
do x=l,L
label=site(x, y)
if (label>0) then
do while (LL(label)/=0); label=LL(label); enddo
site(x,y)=label
write(l,*) site(x,y)
endif
enddo
enddo
close (1)
end program hk
12.3. Кластерный анализ с использованием метода Хошена-Копельмана
В начале программы объявляются переменные и массивы, назначе¬
ние которых описано в комментариях. Значение переменной L=512 со¬
ответствует тестовому примеру, проиллюстрированному на рис. 12.8, а.
Отметим, что координаты заполненных узлов решетки для данного
значения L могут изменяться в пределах от 1 до 512, однако нижние
пределы индексов в массиве site выбраны равными нулю. Такой выбор
сделан для того, чтобы избежать дополнительных проверок на выход
индекса за пределы массива при определении меток соседних узлов
на левой и нижней границе решетки. Пределы изменения индекса в
массиве LL () выбраны з запасом. Однако если использовать данную
программу для решеток большого размера, то может возникнуть си¬
туация, когда количество кластеров на решетке превысит количество
элементов массива LL (). В этом случае в программу должна быть
введена дополнительная проверка на выход числа кластеров ncl за
границы массива LL ().
При выполнении маркировки занятых узлов решетки мы вычисляем
сумму меток соседних узлов, а затем анализируем ее значение. Наибо¬
лее сложная ситуация возникает, когда сумма меток отлична от нуля
и не равна ни одной из соседних меток, что соответствует наличию у
занятого узла двух соседей. В этом случае для каждой из соседних
меток ищется ее правильное значение с помощью списка связности
меток. Процесс такого поиска в программе реализуется внутри циклов
do while ... end do.
12.3.2. Нерешеточный вариант
В предыдущем разделе было дано объяснение работы ре¬
шеточного варианта алгоритма Хошена-Копельмана. В реальных си¬
туациях часто возникает необходимость анализа связности кластеров
в более сложных случаях, когда связи между частицами являются не
такими прозрачными, как для квадратной решетки. В качестве подоб¬
ного примера можно привести анализ связности для решеток сложных
симметрий в пространствах более высоких размерностей или нереше¬
точных задач. Пример такой задачи представлен на рис. 12.2. Более
универсальный подход для реализации Хошена-Копельмана в таких
ситуациях был предложен в работе [6]. Данный подход основан на
использовании списка связности, в котором для каждой частицы ука¬
зывается набор ее ближайших соседей.
12.3.2.1. Формирования списка связности
На рис. 12.6 показан пример процедуры для формирова¬
ния списка связности при заполнении плоскости перекрывающимися
дискообразными частицами единичного диаметра. Частицы пронуме¬
рованы в соответствии с порядком их заполнения так, как показано
230 -Ar Глава 12. Алгоритмы кластерного анализа
на рис. 12.6, а. Список связности записывается в отдельном файле. На
рис. 12.6, б представлена его структура. В первой строке файла запи¬
сано количество объектов в списке связности и максимальное число
связей объекта. Для приведенной на рис. 12.6, а конфигурации частиц
эти значения равны соответственно десяти и двум. Во второй и сле¬
дующих строках файла представлена информация о связях частиц в
порядке нумерации их в соответствии с рис. 12.6, а.
Структура файла списка связности
Число частиц Максимальное число связей
10ч
2 *
1
0
2
2
7
10
3
0
4
1
8
5
0
6
0
7
1
2
8
1
4
9
1
10
10
2
2
9
N Число Связанные
1234567 частицы связей частицы
Рис. 12.6. К описанию процедуры для формирования списка связности
В первом столбце каждой строки файла указан номер частицы; во
втором столбце указано число связей этой частицы с другими части¬
цами конфигурации. В следующих столбцах указаны номера частиц,
связанных с заданной частицей. Так, например, частица под номером 1
не связана с другими, поэтому число ее связей равно 0. Частица под
номером 2 связана с двумя частицами, номера которых 7 и 10 и т. д.
Следует отметить, что в общем случае, для формирования списка связ¬
ности составляется специальная программа, которая учитывает детали
модели, мерности пространства и т. д.
12.3.2.2. Алгоритм Хошена-Копельмана с использованием
списка связности
Кластерный анализ методом Хошена-Копельмана с ис¬
пользованием списка связности выполняется следующим образом. Вна¬
чале всем элементам из списка связности присваиваются начальные
значения кластерных меток, соответствующие порядку их следования
в списке связности. Такая операция присваивания позволяет сразу же
выполнить маркировку всех объектов, которые лишены связей. Поэто¬
му маркировка кластеров выполняется лишь для связанных объектов.
12.3. Кластерный анализ с использованием метода Хошена-Копельмана
X
Для наглядности работы алгоритма, введем в рассмотрение массивы
NLAB () и LL (). Назначение массива LL () такое же, как и в решеточ¬
ном варианте. Элементам массива NLAB () будем присваивать значения
кластерных меток, с которыми связан каждый объект из списка связ¬
ности. Процесс маркировки кластеров заключается в последовательном
просмотре списка связности и выполнении для каждого элемента этого
списка однотипных операций:
1) выбор очередного элемента списка связности;
2) формирование в массиве NLAB () списка кластерных меток, с кото¬
рыми связан очередной элемент списка связности;
3) проверка правильности кластерных меток в массиве NLAB () и при¬
сваивание элементам этого массива правильных значений кластер¬
ных меток;
4) нахождение минимального значения правильной кластерной метки
в массиве NLAB ();
5) установление связи на минимальную метку в массиве LL ();
6) маркировка связанных объектов минимальной меткой;
7) переход к пункту 1).
Отметим, что большинство из перечисленных пунктов програм¬
мируются в одну строку при использовании возможностей языка
Фортран 90.
12.3.2.3. Описание программы, основанной на использовании
списка связности
Рабочая программа кластерного анализа Хошена-Копель¬
мана, основанная на использовании списка связности находится в фай¬
ле hk-lc.f90. Данная программа имеет модульную структуру и со¬
стоит из двух модулей и трех внешних процедур.
Код модуля общих переменных и массивов comdata представлен ниже:
module comdata
implicit none
integer n
integer zmax
integer, allocatable::
integer, allocatable::
integer, allocatable:
integer, allocatable:
!число объектов модели
!максимальное число
!связей объекта
LC (:, : )
!список связности
!объектов
LL ( : )
!список связности меток
LAB(:)
!список кластерных меток
!объектов модели
NLAB(:)
!список меток с которыми
!связан отдельный
!объект модели
end module comdata
232 -»\л Глава 12. Алгоритмы кластерного анализа
Главный модуль программы hklc содержит вызов процедуры чтения
списка связности readconnectivity, процедуры алгоритма Хошена-
Копельмана hkalgo и процедуры записи кластерных меток в выходной
файл savelabel:
program hklc
call readconnectivity
call hkalgo
call savelabel
end program hklc
Процедура чтения списка связности выглядит следующим образом:
subroutine readconnectivity()
use comdata
implicit none
integer i, j
open (1,file='Lc.dat')
read (1,*) n, zmax
!размещаем массивы в оперативной памяти
allocate(LC(1:n,0:zmax)); LC=0
allocate(LL(1:n)); LL=0
allocate(LAB(1:n))
allocate(NLAB(1:zmax+1))
!переписываем список связности в массив
do i=l,n
read (1,*) i, LC(i,0), (LC (i, j),j =1,LC (i,0))
enddo
close (1)
end subroutine readconnectivity
В начале выполнения процедуры readconectivity мы считыва¬
ем из входного файла Lc.dat значения переменных п и zmax. Эти
переменные определяют размеры массивов модуля comdata, и далее
используются при размещении массивов в оперативной памяти. В конце
исполнения процедуры список связности из входного файла переписы¬
ваем в массив LC ().
Код процедуры hkalgo имеет следующий вид:
subroutine hkalgo()
use comdata
implicit none
integer nlinks !число связей объекта
integer labobj !метка объекта
integer i,j !индексы
integer ncl !счетчик кластеров
integer labmin !значение минимальной метки
12.3. Кластерный анализ с использованием метода Хошена-Копельмана
!присваиваем начальные значения кластерных меток
do i=l,n; LAB(i)=i; enddo
!выполняем маркировку кластеров
do i=l,n
nlinks= LC(i,0)
if(nlinks/=0) then
!формируем список кластерных меток,
!с которыми связан объект
NLAB=0; NLAB(1)=LAB(i)
do j=2,nlinks+1
NLAB(j)=LAB(LC(i, j-1) )
enddo
!выполняем проверку правильности кластерных меток
do j=l,nlinks+1
do while (LL(NLAB(j))/=0)
NLAB(j)=LL(NLAB(j))
enddo
enddo
!ищем значение минимальной правильной кластерной
!метки
labmin=minval(NLAB(1:nlinks+1))
!устанавливаем связи между кластерными метками
where (NLAB(1:nlinks+1) /=labmin) &
LL(NLAB(1:nlinks+1))=labmin
!присваиваем значение минимальной правильной
!кластерной метки
LAB(i)=labmin; LAB(LC(i,1:nlinks))=labmin
endif
enddo
!исправляем неправильные кластерные метки
do i=l,n
labobj=LAB(i)
do while (LL(labobj)/=0)
labobj=LL(labobj)
enddo
LAB(i)=labobj
enddo
!устраняем промежутки между метками
where(LL>0) LL=-1
ncl=0
do i=l,n
if(LL(i)==0) then
ncl=ncl+l
LL(i)=ncl
endif
enddo
234
Глава 12. Алгоритмы кластерного анализа
do i=l,n
labobj =LAB(i)
labobj=LL(labobj)
LAB(i)=labobj
enddo
end subroutine hkalgo
Более детально остановимся на этапе проверки правильности кла¬
стерных меток, j-я метка из массива NLAB(j) считается правильной,
если значение элемента массива LL (NLAB (j) ) равно нулю. В про¬
тивном случае поиск правильной метки осуществляется по цепочке
ссылок с использованием информации о связях меток, записанной в
массиве LL (). Схематически процедура поиска правильной метки про¬
иллюстрирована на рис. 12.7.
Рис. 12.7. Пример поиска правильной кластерной метки для метки с номе-
Исправление неправильных кластерных меток осуществляется при
повторном просмотре массива LAB () и использовании алгоритма поис¬
ка правильных меток.
Кластерные метки после исправления могут следовать с разрывами.
Так, например, анализ рис. 12.5, в показывает, что между кластерными
метками 7 и И существует разрыв. При дальнейшем исследования
распределения кластеров по размерам представляется более удобным
устранить пробелы между кластерными метками. Остаток кода проце¬
дуры hkalgo решает эту задачу. В ходе устранения пробелов между
кластерными метками мы еще раз используем принцип организации
массива LL ().
Процедура savelabel осуществляет запись кластерных меток всех
объектов, содержащихся в массиве LAB () в выходной файл label. dat
в соответствии с порядком их следования в файле coord.dat. Код
процедуры savelabel имеет следующий вид:
subroutine savelabel()
use comdata
implicit none
integer i
a) LL(7)=5
LL(5)=3
6) do while(LL(NLAB(j))/=0
NLAB(j)=LL(NLAB(j))
enddo
LL(3)=0
ром 7 из массива NLAB (). Метка 7 связана по цепочке ссылок с
правильной меткой 3 (а); код фортрана, реализующий поиск пра¬
вильной кластерной метки (б)
12.4. Вспомогательные программы ->\г 235
open(1,file='label.dat' )
do i=l,n
write (1,*) LAB(i)
enddo
close (1)
end subroutine savelabel
12.4. ВСПОМОГАТЕЛЬНЫЕ ПРОГРАММЫ
12.4.1. Случайное заполнение плоскости
12.4.1.1. Узлы квадратной решетки
В файле site . f 90 содержится программа для случайного
заполнения узлов квадратной решетки с вероятностью р. Координаты
протекающих узлов решетки в данной программе записываются в вы¬
ходной файл coord.dat и могут быть использованы другими програм¬
мами для дальнейшей обработки или графического отображения. Код
этой программы выглядит следующим образом:
program site
use msflib
implicit none
integer:: L=512 !размер квадратной решетки
real :: p=0.6 !вероятность протекания узлов решетки
integer х, у !координаты узла решетки
real rnd !случайное число
call seed(l)
open (1,file='coord.dat')
do y=l, L
do x=l,L
call random(rnd)
if(rnd<p) write(1,' (2i6)') x,y
enddo
enddo
close (1)
end program site
12.4.1.2. Перекрывающиеся диски
В файле disc. f 90 содержится программа для случайного
заполнения плоскости перекрывающимися дисками с плотностью р.
Вначале программы вычисляется число дисков птах, соответствую¬
щее заданной плотности (ятах = Р^2)- Далее случайным образом ге¬
нерируются координаты их центров, которые записываются в выходной
файл coord.dat и могут быть использованы другими программами
236 •Ar Глава 12. Алгоритмы кластерного анализа
для дальнейшей обработки или графического отображения. Код этой
программы выглядит следующим образом:
program disc
use msflib
integer n, nmax
real:: L=64
real:: p=l.5
real x, у
real rnd
call seed(l)
open (1,file='coord.dat')
n=0; nmax=int(p*L*L)
do while (n<nmax)
call random(rnd); x=rnd*L+l.
call random(rnd); y=rnd*L+l.
n=n+l
write (1,*) x, у
enddo
close (1)
end program disc
12.4.2. Формирование списка связности
12.4.2.1. Узлы квадратной решетки
В файле lc-site.f90 содержится программа форми¬
рования списка связности для заполнения узлов на квадратной ре¬
шетке. Координаты узлов считываются из файла coord.dat, кото¬
рый получен благодаря программе site, f90. В результате работы
этой программы формируется список связности и создается выходной
файл Lc.dat. Координаты узлов загружаются в двухиндексный мас¬
сив site (х, у). Индексы ненулевых элементов этого массива равны
координатам узлов, а значение самих элементов равно порядковым
номерам узлов в соответствии с записью их в файле coord.dat. Такое
представление координат узлов позволяет очень быстро сформировать
список связности, поскольку в этом случае для каждого узла не нужно
просматривать координаты всех узлов, а достаточно лишь просмотреть
состояние четырех элементов массива site (). Перед записью списка
связности определяется максимальное число связей zmax, которые
имеют частицы. Числа п и zmax определяют действительные границы
изменения индексов массива LC () и способствуют быстрой загрузке
списка связности в программу, которая реализует алгоритм Хошена-
Копельмана. Код программы, формирующей список связности для
заполненных узлов, выглядит следующим образом:
!количество дисков
!размер системы
!плотность дисков
!координаты диска
12.4. Вспомогательные программы ->\г 237
program lcsquare
implicit none
integer:: n=0
integer:
integer
integer
integer
integer
integer
integer,
MAXLINKS=4
i, j, к
x,y,xn,yn
xmin, ymin
xmax, ymax
zmax
allocatable
!счетчик узлов
!максимальное число связей
!индексы
!координаты узла
integer,
integer:
site (:, :)
LC (:, :)
dx(1:4) = (/0, 1, 0, -1/)
allocatable:
!массив координат
!узлов
!список связности
!узлов
!таблица сдвига
!координат
integer:: dy(l:4)=(/l, 0,-1, 0/)
!определяем количество узлов в конфигурации
!и размеры системы для записи координат узлов в массив
open (1,file='coord.dat')
do while (.not. eof(l))
read (1,*) x, у
if(n==0) then
xmin=x; ymin=y
xmax=xmin; ymax=ymin
else
if(x<xmin) xmin=x
if(y<ymin) ymin=y
if(x>xmax) xmax=x
if(y>ymax) ymax=y
endif
n=n+l
enddo
close (1)
!размещаем массивы в оперативной памяти
allocate(site(xmin-1:xmax+l,ymin-1:ymax+1)); site=0
allocate(LC(1:n,0:MAXLINKS)); LC=0
!переписываем координаты узлов из файла в массив site
open (1,file='coord.dat')
do i=l,n
read (1,*) x,y
site(x,y)=i
enddo
close (1)
238 -»\л Глава 12. Алгоритмы кластерного анализа
!формируем список связности
do y=ymin, ymax
do x=xmin, xmax
i=site(x,y)
if (i>0) then
do k=l,4
xn=x+dx(k); yn=y+dy(k)
j =site(xn, yn)
if (j>0) then
LC (i,0)=LC(i,0)+1
LC(i, LC(i,0))=j
endif
enddo
endif
enddo
enddo
!записываем список связности в выходной файл
zmax=maxval(LC(1:n,0))
open(1,file='Lc.dat')
write (1,*) n, zmax
do i=l,n
write (1,*) i, LC(i,0), (LC(i, j),j=1,LC(i,0))
enddo
close (1)
end program lcsquare
12.4.2.2. Перекрывающиеся диски
В файле lc-disc.f90 содержится программа форми¬
рования списка связности для непрерывной модели при заполнении
плоскости перекрывающимися дисками. Координаты дисков считыва¬
ются из файла coord.dat, который получен с помощью программы
disc, f 90. В результате работы этой программы формируется список
связности и создается выходной файл Lc.dat.
Список связности в программе формируется в двухиндексном мас¬
сиве LC (), значения которого в конце программы записываются в
выходной файл Lc.dat. Границы изменения первого индекса массива
LC () определяются после исследования входного файла coord.dat.
Интервал изменения второго индекса определяется значением пере¬
менной MAXLINKS=2 0. Отметим, что интервал изменения второго ин¬
декса выбран с запасом, однако может оказаться недостаточным при
очень больших плотностях дисков. В этом случае значение переменной
MAXLINKS следует увеличить.
12.4. Вспомогательные программы ■Аг 239
Процесс формирования списка связности осуществляется в двой¬
ном вложенном цикле путем вычисления расстояний между дисками
и сравнения его с единицей. Число связей i-ro диска записывается в
элемент массива LC(i,0), который служит также для определения в
i-й строке индекса столбца для записи номера очередного j-ro диска,
связанного с i-м.
Перед записью списка связности определяется максимальное число
связей zmax, которые имеют частицы. Числа п и zmax определяют
действительные границы изменения индексов массива LC () и способ¬
ствуют быстрой загрузке списка связности в программу, реализующую
алгоритм Хошена-Копельмана. Код программы lc-disc.f90 пред¬
ставлен ниже:
program lcdisc
implicit none
integer:: n=0
integer:: MAXLINKS=20 !максимально возможное число
!счетчик дисков
1, 3
г
xi, yi
dx, dy
allocatable:
allocatable:
!связей в списке связности
!максимальное число связей диска
!в конфигурации
!индексы
!расстояние между дисками
х(:), у(:) !координаты дисков
LC(:,:) !список связности
конфигурации
integer
integer
real
real
real
real,
integer,
!определяем количество объектов
open (l,file= 'coord.dat')
do while (.not. eof(l))
read (1,*) xi, yi
n=n+l
enddo
close (1)
!размещаем массивы в оперативной памяти
allocate(LC(l:n,0:MAXLINKS)); LC=0
allocate(x(1:n),у(1:n)); x=0; y=0
!переписываем координаты дисков из файла в массивы
open (l,file= 'coord.dat')
do i=l,n
read (1,*) x(i),у(i)
enddo
close (1)
240 -l\r Глава 12. Алгоритмы кластерного анализа
!формируем список связности
do i=l,n
do j=l,n
if (i/ = j) then
dx=x(i)-x (j)
dy=y(i)-y(j)
r=sqrt(dx*dx+dy*dy)
if (r<=l.) then
LC (i, 0) =LC (i, 0) +1
LC(i, LC(i,0))=j
endif
endif
enddo
enddo
!записываем список связности в выходной файл
zmax=maxval(LC(1:n, 0))
open(1,file='Lc.dat')
write(1,*) n, zmax
do i=l,n
write (1,*) i, LC(i,0), (LC(i, j),j=1,LC (i,0))
enddo
close (1)
end program lcdisc
12.4.3. Визуализация кластеров
В файлах viewsite-bw.f90 и viewdisc-bw.f90 со¬
держаться программы для визуализации кластеров, что существен¬
но помогает кластерному анализу. Данные программы изображают
различные кластеры оттенками черного. Отметим, что для построе¬
ния цветных изображений распределения кластеров можно восполь¬
зоваться аналогами этих программ, которые содержаться в файлах
viewsite.f90 и viewdisc. f 90. При выполнении этих программ,
координаты частиц кластеров считываются из файла cord.dat, а их
кластерные метки из файла label.dat.
12.5. ПРИМЕРЫ РАБОТЫ ПРОГРАММ ДЛЯ КЛАСТЕРНОГО
АНАЛИЗА С ИСПОЛЬЗОВАНИЕМ МЕТОДА
ХОШЕНА-КОПЕЛЬМАНА
Описанный набор программ для кластерного анализа Хо¬
шена-Копельмана был протестирован для дискретной и непрерывной
модели. Результаты тестирования представлены в графическом виде на
12.5. Кластерный анализ с использованием метода Хошена-Копельмана
рис. 12.8. Объекты, имеющие одинаковую кластерную метку, изобра¬
жены одним цветом. Для цветопередачи было выбрано шесть оттенков
черного, поэтому некоторые цвета кластеров на рисунке повторяются.
а б
Рис. 12.8. Графическое представление кластеров в разных моделях: а) запол¬
нение узлов на квадратной решетке с плотностью р = 0,6 (размер
решетки L = 512, перколяционная концентрация рс = 0,5927 [1, 2]);
б) заполнение плоскости перекрывающимися дисками с числен¬
ной плотностью р — 1,5 (диаметр диска равен 1, размер подложки
L = 64, перколяционная плотность рс = 1,436 [3, 4])
Оба слайда на рис. 12.8 представляют собой дампы экрана про¬
грамм: viewsite-bw.exe и viewdisc-bw.exe. Данные программы
осуществляют графическое представление результатов расчетов.
Слайд на рис. 12.8, а был получен путем последовательного выполне¬
ния цепочки программ: site.exe —> lc-site.exe —► hk-lc.exe —►
—> wiewsite-bw.exe, а слайд на рис. 12.8, б с помощью программ:
disc.exe —► lc-disc.exe —> hk-lc.exe —>wiewdisc-bw.exe.
В результате выполнения каждой цепочки программ на диске фор¬
мируются три текстовых файла: coord.dat, Lc.dat и label.dat.
Для практического использования приведенных программ представля¬
ется более целесообразным объединить каждую цепочку в одну про¬
грамму, тем самым, оформив каждую из программ цепочки отдельной
процедурой.
Пример такого объединения для задачи узлов квадратной решет¬
ки содержится в файле hksqdemo. f 90. Данная программа на входе
осуществляет генерацию координат протекающих узлов на квадратной
решетке, или считывает ее с входного файла, а на выходе представляет
результаты расчетов в графическом виде, или записывает в выходной
242 -»Ъ- Глава 12. Алгоритмы кластерного анализа
12.6. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Обобщите программу кластерного анализа с помощью метода Хоше¬
на-Копельмана для изучения перколяционной задачи на кубической
решетке (т. е. создайте трехмерный аналог программы hk2d.f90).
2. Напишите программу для логической функции, с помощью которой
можно определить наличие перколяционного кластера после выпол¬
нения кластерного анализа. В качестве входного аргумента выберите
переменную целого типа direction, которая может принимать три
значения: 1 — для перколяции в горизонтальном направлении, 2 —
для перколяции в вертикальном направлении и 3 — для перколяции
в обоих направлениях. Напишите процедуру для расчета функции
распределения кластеров по размерам (количество занятых ячеек)
для случая квадратной решетки.
3. Простейшим обобщением задачи перколяции на квадратной решетки
является принятие правила связности ближайших занятых узлов
не только в горизонтальном или вертикальном направлении, но и
по диагонали. Обобщите программу решеточного варианта метода
Хошена-Копельмана для выполнения кластерного анализа в этом
случае. Вычислите значение перколяционной концентрации для этой
задачи.
4. Напишите вспомогательные программы, которые выполняют запол¬
нение узлов с заданной вероятностью р а также запись их координат
в выходной файл для треугольной, сотовой и кубической решеток.
Используя полученные файлы, напишите программы, формирующие
списки связности. Протестируйте известные пороги перколяции для
указанных решеток: треугольной (0,50), сотовой (0,6970413), куби¬
ческой (0,3116081).
12.7. ЛИТЕРАТУРА
1. Stauffer D., Aharony A. Introduction to Percolation Theory. — London, Wash¬
ington: Taylor & Francis, 1992.
2. Тарасевич Ю. Ю. Перколяции: теория, приложения, алгоритмы. — М:
Эдиториал УРСС, 2002. — 112 с.
3. Quintanilla J.A., Torquato S., Ziff R. М. Efficient measurement of the percola¬
tion threshold for fully penetrable discs // J. Phys. A: Math. Gen. — 2000. —
V. 33. - P. L399-L407.
4. Quintanilla J.A., Ziff R.M. Asymmetry of percolation thresholds of fully pene¬
trable disks with two different radii // Phys. Rev. E. — 2007. — V. 76, No. 5. —
P. 051115.
12.7. Литература •Ar 243
5. Hoshen J., Kopelman R. Percolation and Cluster distribution. 1. Cluster multi¬
ple labeling technique and critical concentration algorithm // Phys. Rev. B. —
1976. - V. 14, No. 8. - P. 3438-3445.
6. van der Marck S. C. Percolation thresholds and universal formulas // Phys.
Rev. E. - 1997. - V. 55. - P. 1514-1517.
ГЛАВА
13
МЕТОД МОНТЕ-КАРЛО
ДЛЯ АНАЛИЗА МОДЕЛИ ИЗИНГА:
АЛГОРИТМ МЕТРОПОЛИСА
И КЛАСТЕРНЫЕ АЛГОРИТМЫ
13.1. ФАЗОВЫЕ ПЕРЕХОДЫ В МАГНИТНЫХ МАТЕРИАЛАХ
И МОДЕЛЬ ИЗИНГА
Магнитные материалы при нагревании размагничиваются
и переходят в немагнитное состояние при определенной температу¬
ре Тс, называемой точкой Кюри. Точка Кюри зависит от структуры
магнитных материалов и может изменяться в широких пределах. На¬
пример, она равна 631 К для никеля, 1026 К для железа, 1400 К для
кобальта и 289 К для гадолиния. На практике часто требуются матери¬
алы, которые бы сохраняли магнитные свойства в широком интервале
температур.
В начале XX века большой спрос на магнитные материалы со сто¬
роны промышленности привлек внимание исследователей к изучению
магнитных фазовых превращений. В 1920 г. заведующий кафедрой тео¬
ретической физики Гамбургского университета профессор Вильгельм
Ленц (1888-1957) предложил в качестве темы докторской диссертации
для Эрнста Изинга (1900-1998) рассмотрение одномерной спиновой мо¬
дели для объяснения природы магнитных фазовых переходов. Предпо¬
лагалось изучение поведения бесконечной одномерной цепочки магнит¬
ных моментов (спинов), каждый из которых взаимодействует только с
ближайшими соседями. Результаты исследования этой модели были из¬
ложены в 1924 г. Изингом в его докторской диссертации [1], а в 1925 г.
опубликованы в работе [2]. Главный вывод проведенных Изингом ис¬
следований заключался в том, что намагниченное состояние возможно
только при нулевой температуре, т. е. для одномерной модели точка
Кюри равна нулю, Тс = 0 К. Изинг сделал попытку обобщить рассмот¬
рение на случай двухмерной и трехмерной моделей, однако, в послед¬
ствии оказалось, что эти результаты были ошибочными [2]. История
развития этой проблемы изложена в [3].
13.1. Фазовые переходы в магнитных материалах и модель Изинга -»\г 245
13.1.1. Определение Модели Изинга на квадратной решетке
В простейшем варианте модели Изинга каждый узел на
решетке занимается спином st, и взаимодействия рассматриваются толь¬
ко между ближайшими соседями. Здесь каждый узел, ассоциируется с
частицей, которая может иметь два состояния, +1 или —1. Рассмотрим
более детально описание этой модели на примере двухмерной модели
Изинга на квадратной решетке (рис. 13.1). Гамильтониан системы Н
определяется выражением
Я=-£Л/^/-£1> (13.1)
(ч)
где Jij — величина, соответствующая энергии взаимодействия ближай¬
ших спинов i и /, (/,/) обозначает суммирование по соседним узлам,
второе слагаемое в данном уравнении соответствует взаимодействию
с внешним магнитным полем В. Обычно допускают, что является
постоянной величиной, = /, причем для ферромагнетиков / > 0, а для
антиферромагнетиков / < 0.
5 О
©
©
о
©
40
О
/Ш\
©
©
©
©
1 (3.3)
О
©
©
2 ©
о
о
©
м 1 о © © о о
I I 1 2 3 4 5
Рис. 13.1. К объяснению модели Изинга. В каждом узле находится спин st,
который направлен вверх (+1) или вниз (—1). Пунктирной лини¬
ей показаны ближайшие соседи для спина с координатами (3,3).
Энергия взаимодействия этого спина с ближайшими соседями при
В = 0, согласно (13.1), равна 4/. Размер решетки L = 5, число спи¬
нов N = L2
Рассмотрим более детально случай ферромагнетика, / > 0, для ко¬
торого минимальная энергия реализуется в состоянии с одинаковым
направлением спинов. В данном случае переворот любого из спинов
увеличивает минимальную энергию на 8/ и, таким образом, размаг¬
246 •Ar Глава 13. Метод Монте-Карло для анализа модели Изинга
ничивание является энергетически невыгодным. Несмотря на простоту
формулировки модели Изинга, точное решение данной проблемы оказа¬
лось непростой задачей даже для двухмерной модели, а для трехмерной
модели точного результата до сих пор не получено.
13.1.2. Точное решения Модели Изинга
на квадратной решетке
В 1936 г. Пайерлсом была показана принципиальная воз¬
можность существования фазового перехода при Тс ^0 [4], а в 1941 г.
для двумерной модели Изинга на квадратной решетке было получено
следующее значение для Тс [5]
Г = квЪ = 2— = б9 (13 2)
J 1п(1 + у/2)
где &в — постоянная Больцмана.
Точное решение двухмерной модели Изинга на квадратной решетке
в нулевом поле В = 0 было получено Онсагером в 1942 г. Детали этого
исследования были опубликованы два года спустя в работе [6]. Точные
решения в термодинамическом пределе, L —> оо, являются достаточ¬
но сложными, например, полученные зависимости внутренней энер¬
гии Е и теплоемкости с на один спин выражается через эллиптические
интегралы:
Е = -/coth(2/r)(l + 2fe'/C/(fel));
2 \ л J (133)
с = к(2/л) - 2 E,(h) - (1 - k\) (J + ВД*,))],
raeK/(ki)= J^2(l-k2 sin2 (p)~l/2d<p, J^2 (1 - k\ sin2 <p)l/2d<p —
полные эллиптические интегралы первого и второго рода, a k\ =
= 2sinh(2/7’*)/cosh2(2/7’*), k\ = y/T^ki.
Эллиптический интеграл K/(k\) имеет особенность при k\ = 1, по¬
этому термодинамические функции также имеют особенность при неко¬
тором значении Г* = 7£. Это значение определяется из уравнения
k\ = 2sinh(2/T£)/ch2(2/T£) = 1 и в точности соответствует значению
в уравнении (13.2).
Температурная зависимость спонтанной намагниченности ms, при¬
ходящейся на один спин, описывается соотношением [7]
тя(Г) = {1 - [sinh(2/r)]-4}1/8 для Г < Гс и 0 для Т>ТС.
(13.4)
13.1. Фазовые переходы в магнитных материалах и модель Изинга 247
Таблица 13.1. Критические индексы для двумерной и трехмерной модели Изин¬
га. Величины а и v связаны гиперскейлинговым соотношением,
а = 2 — dv (закон Джозефсона [8]), величины а, /3 и у связаны
скейлинговых соотношением, а = 2 — 2/3 — у (закон Рашбрука [9])
Размерность
а
Р
Г
V
d = 2
0 (log)
1/8
7/4
1
d = 3
0,10985
0,326448
1,23717(28)
0,63005(18)
Точные решения вблизи критической точки (Т —> Гс) удобно аппрок¬
симировать степенными (скейлинговыми) соотношениями вида
с ~ 1Г— Тс\~а, ms^(Tc-T)P, Т < Тс, х~\Т-Тс\-г,
l-1/v (135)
I >
где а, /3, у и v — критические индексы, ^ — удельная магнитная
восприимчивость, £ — корреляционная длина. Значения критических
индексов для двумерной и трехмерной модели Изинга приведены в
табл. 13.1.
13.1.3. Простейшее обобщение модели Изинга:
модель Поттса
Простейшим обобщением модели Изинга является ^-мо¬
дель Поттса, в которой каждая частица может иметь q состояний [10].
При q = 2 модель Поттса соответствует модели Изинга. Модель Поттса
проявляет более сложное поведение по сравнению с моделью Изин¬
га. Например, при увеличении q увеличивается экспонента удельной
теплоемкости а (а = 0 для двумерной модели Изинга). Для обычной
модели Изинга проявляется фазовый переход второго рода, но при
увеличении q выше некоторого критического значения, q > 4, модель
Поттса проявляет уже фазовый переход первого рода [И].
Большой интерес представляет так называемая разбавленная мо¬
дель Поттса, когда на решетке занимается только определенная часть
узлов [12]. Отметим, что формально случай разбавленной модели для
q = 1 соответствует модели обычной перколяции. Фазовые переходы в
модели Изинга и перколяционный переход имеют много общих харак¬
теристик. В целом модель Изинга и ее различные обобщенные вари¬
анты можно рассматривать как модель скорелированной перколяции,
в которой узлы занимаются не случайно, а соответствии с правилами,
определяемыми взаимодействиями между частицами.
Детальные исследования разбавленных моделей показали, что вели¬
чина температуры перехода Тс монотонно уменьшается до нуля при уве¬
личении степени разбавления до перколяционного предела (рс = 0,5927
(~\Т-ТС
248 ->\r Глава 13. Метод Монте-Карло для анализа модели Изинга
для квадратной решетки, рс = 0,3113 для кубической решетки). Кроме
того, критические экспоненты случайных систем связаны с экспонен¬
тами исходных решеточных систем без разбавления и данные Монте-
Карло и ренорм-групового анализа не дают явных изменений в крити¬
ческом поведении при разбавлении систем [13, 14].
13.1.4. Конечномерный анализ для модели Изинга
и метод кумулянт Биндера
Приведенные выше точные результаты для обычной мо¬
дели Изинга £, с и ms справедливы для бесконечных систем. При
выполнении моделирования приходится иметь дело с решетками конеч¬
ного линейного размера L. В этой связи приходится аппроксимировать
полученные величины, используя скейлинговые соотношения. Так, на¬
пример, для оценки критической температуры Тс бесконечной системы
используют соотношение TC(L) — Тс ~ L-1/v, где TC(L) — критическая
температура, вычисленная на решетке размера L. Вычислив точное зна¬
чение критической температуры Тс бесконечной системы, и воспользо¬
вавшись тем, что при Т = Тс корреляционная длина составляет порядка
размера решетки £ ~ L, выражения (13.5) можно также представить в
виде: с(Тс) ~ La/V, ms(Tc) ~ L-/3/v, хЪ'с) ~ Ly!v. Последние выражения
позволяют вычислять критические индексы а, jS, у для системы с из¬
вестными значениями Тс и v.
Эффективной способом оценки величины Тс является метод куму¬
лянтов Биндера [16]. При данном подходе вычисляется кумулянт 4-го
порядка, определяемый как Ub(L) = 1 — )/3(т^)2), где ms — намаг¬
ниченность. Для двумерной модели Изинга при Т > Тс величина Ub(L)
убывает до нуля по степенному закону, а при Т < Тс величина Ub(L)
стремится к Uoo=2/3 в термодинамическом пределе (при L —> оо).
На рис. 13.3, а показана зависимость Ub от L-1,5 в критической точке
« 2,269, откуда можно получить оценку Uc ~ 0,61069 [15].
Величину Тс удобно определять как точку общего пересечения
кривых зависимостей U&(T) при различных L (рис. 13.3, б). При изу¬
чении скейлинга исследуется поведение величины Ur как функции
(Т - Тс)1}!у [16].
13.1.5. Алгоритм Метрополиса для решения модели Изинга
Скейлинговый анализ для двумерной модели Изинга был
впервые выполнен с помощью компьютерного моделирования [17] с
использованием алгоритма Метрополиса [18]. При моделировании вна¬
чале формируется случайная конфигурация спинов. Далее, на каждом
шаге выбирается случайным образом спин s и производится попытка
изменения его направления на противоположное, s —> —s.
Ub(Tc)
13.1. Фазовые переходы в магнитных материалах и модель Изинга •Аг 249
Локальный переход ДЕ
4/ i
-4/i
1 т
1
— ill
i
-8/
ехр(8/Г)
2/Т
-2/Т
1 т
1
— Hi
i
-4/
ехр(4/Г)
о/Т
o/T
i т
i
— i i T
i
0/
1
-2/Т
2/ T
1 т
т
— i i T
T
+4/
ехр(-4/Г)
-4/Т
4/ T
11
т
— TiT
t
+8/
exp(—8/7"*)
Рис. 13.2. Анализ возможных локальных конфигураций спинов на квадратной
решетке для модели Изинга. При наличии внешнего поля вероят¬
ность / нужно умножить на величину ехр(—2В*/Т*). Здесь показан
только случай, когда в начальном состоянии центральный спин
направлен вверх, т. е. s = 1. Если в начальном состоянии спин
направлен вниз, т. е. s = — 1, в формулах для вероятности следует
сделать замену / —► /_1
1/L1,5 Г
Рис. 13.3. Зависимость кумулянта Биндера 4 порядка Ub от L-1,5 в критиче¬
ской точке Т*с « 2,269 (а) и Ub от Т* при различных L для двумер¬
ной модели Изинга. При вычислениях применялись периодические
граничные условия в направлениях х и у [15]
250
Глава 13. Метод Монте-Карло для анализа модели Изинга
При этом вычисляется изменение энергии, связанной с переворо¬
том Д£. При Д£ < 0 новая конфигурация принимается с вероятно¬
стью / = 1, при увеличении Д£ > 0 вероятность (/ < 1) вычисляется как
/= ехр[-Д£/(£вТ)), что можно записать как
В методе Монте-Карло величина / сравнивается со случайным чи¬
слом г е [0,1) и новая конфигурация принимается при / < г. Один
шаг Монте-Карло включает N попыток переворотов спина, где N —
общее количество спинов в системе. Основные затраты компьютерного
времени связаны с вычислением вероятности (13.6), причем их можно
значительно уменьшить путем предварительной табуляции значений /,
так как это показано на рис. 13.2.
Геометрические g-кластеры спинов на квадратной решетки, полу¬
ченные с помощью алгоритма Метрополиса при Т < Тс, Т « Тс и Т > Тс
показаны на рис. 13.4. Интересно отметить, что для двумерной модели
Изинга термический фазовый переход при Т = Тс соответствует пер-
коляционному переходу для g-кластеров, но это свойство не является
общим для спиновых систем и оно нарушается уже для трехмерных
систем. Более того, перколяционный переход для g-кластеров в двумер¬
ной модели Изинга не является эквивалентным обычной перколяции по
узлам или связям и критические перколяционные экспоненты g-кла-
стеров не связаны прямо с критическими термальными экспонентами
приведенными в табл. 13.1 [19].
Рис. 13.4. Конфигураций спинов на квадратной решетке для модели Изинга при
(13.6)
Т< Тс
Ttt Те
Т> Тс
различных температурах (= &вTc/J = 2/ 1п(1 + у/2) = 2,269...)
Однако такая связь существует для стохастических FK-класте-
ров [20], которые можно выделить из геометрических. FK-кластер яв¬
ляется кластером связей, которые выделяются в g-кластере с вероятно¬
13.1. Фазовые переходы в магнитных материалах и модель Изинга •Аг 251
стью равной fc = 1 — ехр(—2/Т£). Результирующий кластер FK-кластер
имеет меньший размер, чем порождающий его g-кластер и он является
менее связным. Критическая температура Тс в модели Изинга связана
с вероятностью образования перколяционного FK-кластера fc. В при¬
ближении метода ренорм-группы эта связь выражается соотношением
fc = 1 - ехр(-2/Т£) [21]. Отсюда, при Т*с « 2,269 получим fc = 0,5858,
что достаточно близко к значению fc = 0,5927, полученному для задачи
случайно перколяции на квадратной решетке [22]. В критической
точке геометрические и FK-кластеры являются фракталами, и их
фрактальную размерность можно вычислить с помощью соотношений
df{g) = 187/96 и 1,9479 и df(FK) = d- p/v{= 15/8 = 1,875) (см., на¬
пример, [23]).
13.1.6. Замедление процедуры Метрополиса
вблизи критической точки
Важной характеристикой процедуры Метрополиса для зада
чи Изинга является корреляционное время т. Обычно, после достиже¬
ния теплового равновесия, вычисляемые величины усредняются по кон¬
фигурациям, разделенным между собой заданным числом шагов Монте-
Карло, которое больше чем т. Усреднение по меньшим промежуткам вре¬
мени может приводить к неверным результатам. Это связано с сущест¬
вованием сильных корреляций в динамике поведения спиновых систем.
Особенно сильно такие корреляции проявляются вблизи критической
температуры, и это поведение в литературе называется критическим
замедлением. Корреляционное время т (измеряемое в шагах Монте-
Карло) вблизи критическое точки расходится по степенному закону
т~ IТ-ТсГ2, (13.7)
где z — динамический критический индекс. Для алгоритма Метропо¬
лиса динамический критический показатель 2^2 и практически не
зависит от размерности задачи.
Для двумерной модели Изинга v=l и при Т = Тс, когда корреля¬
ционная длина сопоставима с размером решетки £ ~ L, расходимость
(13.7) имеет приблизительно квадратичный характер, т. е. r(7c)~L2.
Подобное поведение затрудняет использование алгоритма Метрополиса
для больших систем вблизи критической точки.
13.1.7. Преодоление проблемы критического замедления
с помощью кластерных алгоритмов
Для преодоления данного затруднения были предложены
кластерные алгоритмы Свендсена и Ванга [24] и Вольфа [25], в кото¬
рых все спины решетки связываются в кластеры и в процессе моде¬
252 •Ar Глава 13. Метод Монте-Карло для анализа модели Изинга
лирования опрокидываются не отдельные спины, а целый кластер. В
качестве кластера можно определить набор однонаправленных спинов,
которые непрерывно связаны. Вероятность спина принадлежать к кла¬
стеру зависит от температуры [20].
При опрокидывании, конфигурация спинов сохраняется внутри кла¬
стера, и изменения энергии происходит только за счет изменения кон¬
фигураций на периметре кластера. Было показано, что такая динами¬
ка опрокидывания спинов не нарушает условий детального равнове¬
сия [24, 25]. Вместе с тем кластерные подходы позволяет значитель¬
но уменьшить корреляционное время т и в значительной мере снять
проблему расходимости т вблизи критической точки. Так, например,
динамический показатель для алгоритма Свендсена-Ванга равен 2 = 0,
0,3 и 0,5 для одномерной, двухмерной и трехмерной моделей Изинга.
Это обстоятельство позволяет выполнять расчеты намного быстрее, чем
с помощью алгоритма Метрополиса даже для больших значений L.
Некоторой проблемой данных алгоритмов является определение
аналога физического времени, используемого при вычислениях. В алго¬
ритме Метрополиса и Свендсена-Ванга в качестве единицы «компью¬
терного» времени можно выбрать единицу, соответствующую перебору
всех спинов в системе. Для решетки N х N, это соответствует перебору
N2 конфигураций за единицу времени. Однако для алгоритма Вольфа
ситуация не является настолько простой. Здесь в единицу времени
переворачивается целый кластер спинов. Но размер кластера сильно за¬
висит от температуры (на самом деле он обратно пропорционален тем¬
пературе) и такое определение единицы времени не является оправдан¬
ным. Альтернативным способом определения единицы времени в алго¬
ритме Вольфа является следующий. В алгоритме Свендсена-Ванга еди¬
ница времени соответствует ситуации, когда переворачивается пример¬
но половина спинов. В алгоритме Вольфа каждый кластер спинов пере¬
ворачивается одновременно. За единицу времени в алгоритме Вольфа
можно принять такую последовательность переворотов кластеров, для
которой сумма их масс примерно равна (в среднем) половине всех
спинов в системе. Таким образом, можно согласовать единицу времени
в алгоритме Вольфа и алгоритме Свендсена-Ванга. Для применения
алгоритма Свендсена Ванга в ^-модели Поттса единица времени про¬
порциональна относительному количеству (q — 1 )/q перевернутых спи¬
нов (= 0,5 для обычной модели Изинга), поэтому вероятность принятия
новой спиновой конфигурации отличной от старой равна (q — 1 )/q.
В заключение отметим, что алгоритм Метрополиса используется не
только для моделирования модели Изинга, но и множества других си¬
стем, например, для изучения структуры жидких кристаллов и фазовых
приращений в них (см. задачу в конце главы).
13.2. Алгоритмы и описание работы программы •Аг 253
Далее в данной главе будут рассмотрены примеры реализации ал¬
горитмов Метрополиса, Свендсена-Ванга и Вольфа для исследования
поведения двумерной модели Изинга.
13.2. АЛГОРИТМЫ И ОПИСАНИЕ РАБОТЫ ПРОГРАММЫ
13.2.1. Алгоритм Метрополиса
Алгоритм Метрополиса можно представить в виде следую¬
щей схемы:
1) Для заданной конфигурации спинов выбираем случайным
образом спин и вычисляем для него сумму состояний
соседних спинов с учетом периодических граничных
условий. Вероятность принятия новой конфигурации f
вычисляем с использованием рис. 13.2;
2) Генерируем случайное число г и проверяем выполнение
неравенства r<f. Если оно выполняется, то опрокидываем
выбранный спин.
13.2.2. Алгоритм Свендсена-Ванга
Рассмотрим более детально работу этого алгоритма для
квадратной решетки размером L = 5 (рис. 13.5, а). В каждой ячейке
находится спин, направленный вверх, или вниз. Решетка просматри¬
вается по строкам, начиная с левого нижнего угла. Два соседние,
одинаково направленные спины связываются в кластер с вероятностью
/ = 1 — ехр(—2/Т*) [24]. При последовательном просмотре решетки у
каждого спина проверяется состояние двух ближайших соседей, на¬
пример, нижнего и левого. При этом учитываются периодические гра¬
ничные условия.
9
9
7
7
7
8
8
7
7
7
4
5
7
7
7
4
5
6
6
3
1
2
3
3
3
а б в г
Рис. 13.5. К объяснению алгоритма Свендсена-Ванга
На рис. 13.5, б представлен пример распределения кластеров спинов,
образовавшихся в результате такого связывания. Кластер спинов может
состоять из одного или большего количества спинов. После формирова¬
ния кластеров спинов выполняется их маркировка. Наиболее удобно ис¬
254 -»\r Глава 13. Метод Монте-Карло для анализа модели Изинга
пользовать для этого алгоритм маркировки кластеров Хошена-Копель¬
мана (см. гл. 12). В результате выполнения маркировки (рис. 13.5, в)
создается список, в котором каждой кластерной метке сопоставляется
значение спина кластера. Затем список кластеров просматривается, и
спины всех кластеров опрокидываются с вероятностью 1/2. Возмож¬
ный результат такого опрокидывания представлен на рис. 13.5, г, где
при просмотре списка кластеров были опрокинуты спины кластеров с
метками 1, 3, 4, 5 и 8.
Ниже приведен алгоритм Свендсена-Ванга:
1) Последовательно просматриваем решетку и связываем два
ближайших спина i и j с вероятностью f=l-exp(-2/Т*),
если Si=Sj. Соседние спины, для которых Si^Sj считаем
несвязанными;
2) Идентифицируем на решетке кластеры, как множества
спинов, соединенных связями. Считаем, что два любых
спина принадлежат к одному кластеру, если существует
путь по связям, который их соединяет;
3) Присваиваем каждому кластеру новые значения спина с
равной вероятностью и в соответствии с этим изменяем
значения всех спинов, которые ему принадлежат.
Шаги 1-3 для алгоритма Свендсена-Ванга соответствуют одному
шагу МК для алгоритма Метрополиса.
13.2.3. Алгоритм Вольфа
В работе Вольфа [25] был предложен кластерный алго¬
ритм, немного отличающийся от алгоритма Свендсена и Ванга [24].
В отличие от алгоритма Свендсена и Ванга, в алгоритме Вольфа на
решетке формируется только один кластер, начиная с произвольно вы¬
бранного спина, а затем с равной вероятностью ему присваивается но¬
вое значения: 1 или -1.
Рассмотрим более детально работу этого алгоритма для квадрат¬
ной решетки размером L = 5 (рис. 13.6, а). Для иллюстрации рабо¬
ты алгоритма была избрана та же начальная конфигурация, что и
на рис. 13.5, а. В начале выполнения алгоритма в качестве зерна ро¬
ста кластера случайным образом был избран спин, отмеченный на
рис. 13.6, а пунктирным кружком. В алгоритме Вольфа ближайшие со¬
седние (с учетом периодических граничных условий) спины зерна роста
могут принадлежать к этому кластеру с вероятностью /= 1 — ехр(—2/71*),
если их спины одинаково направлены со спином зерна. Если спины
соседей направлены противоположно, то они не могут быть присоеди¬
нены к растущему кластеру. В ходе роста кластера ближайшие соседи
13.2. Алгоритмы и описание работы программы -1\г 255
каждого нового спина, присоединенного к кластеру, тестируются на
их принадлежность к кластеру. Такое тестирование для каждой пары
узлов (кластерный спин и один из его соседей) выполняется только
один раз. Тестирование выполняется до тех пор, пока все потенци¬
ально возможные спины-кандидаты на участие в кластере не будут
протестированы. На рис 13.6, б жирными линиями изображены связи,
которые были образованы соседними спинами в ходе такого тестиро¬
вания, а на рис. 13.6, в «выращенный» кластер выделен серым цветом.
После формирования кластера ему было присвоено с вероятностью 1/2
новое значение, равное —1, т. е. в данном конкретном случае произошло
опрокидывание спина кластера. На рис. 13.6, г изображена новая кон¬
фигурация спинов, полученная в результате работы этого алгоритма.
-1
-1
—1—
1
1 ■
■ 1
1
1
1
1
1
-1
1 ■
■ 1 ■
■ 1 ■
■ 1
-1
1
-1
-1
1
-1
-1
1 ■
■ 1
1
-1
-1
1
1
1
1
1
1
1
1
-1
1
1
1
1
-1
1
-1
-1
1
-1
-1
1
1
■ 1 :
-1
-1
1
1
1
1
1
1
-1
-1
1
1
1
1
1
1
-1
-1
-1
-1
-1
1
1
1
1
1
1
1
1
-1
-1
1
-1
-1
1
-1
-1
-1
-1
1
-1
-1
1
1
1
1
1
1
1
-1
а б в г
Рис. 13.6. К объяснению алгоритма Вольфа
Ниже приведен алгоритм Вольфа:
1) Выбираем на решетке случайным образом i-й спин и в
дальнейшем рассматриваем его как зерно роста кластера.
Присоединяем к зерну ближайшие соседние спины с
вероятностью f=l-exp (-2/Т*), если Si=Sj. Соседние
спины, для которых Si^Sj считаем несвязанными. Рост
кластера продолжается до тех пор, пока список
спинов-кандидатов на членство в кластере, полностью
исчерпывается;
2) Присваиваем «выращенному» кластеру новые значения
спина 1 или -1 с равной вероятностью и в соответствии
с этим изменяем, значения всех спинов, в этом кластере.
13.2.4. Описание работы программы
Полный код программы двухмерной модели Изинга для
квадратной решетки содержится в файле Ising2d. f 90. Здесь описана
работа программы без учета графических процедур. Программа имеет
модульную структуру: состоит из модуля общих переменных comdata,
главного модуля Isingmain и набора процедур. В программе реализо¬
ваны все описанные алгоритмы, которые оформлены в виде отдельных
256 JV Глава 13. Метод Монте-Карло для анализа модели Изинга
процедур. Опишем в начале общую часть программы, а потом проце¬
дуры для алгоритмов Метрополиса, Свендсена-Ванга и Вольфа.
Код модуля общих переменных имеет вид
module comdata
use msflib
type (rccoord) curpos
!тип алгоритма:
logical:: mea= .true. !Метрополиса
logical:: swa= .false. !Свендсена-Ванга
logical:: wolffa=.false. !Вольфа
!параметры модели
real :: Jij=l. !константа спинового взаимодействия
! (J>0 - случай ферромагнетика)
integer:: L=64 !размер решетки
integer:: NM=100 !количество "измерений" величины
!для усреднения
!набор значений приведенной температуры
real:: Т(1:41)=(/1.,1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,&
1.9.2.0.2.1.2.2.2.21.2.22.2.23.2.24.6
2.25.2.26.2.262.2.264.2.264.2.266.6
2.268.2.27.2.3.2.4.2.5.2.7.2.75.2.8.6
2.85.2.9.2.95.3.0.3.05.3.1.3.2.3.3.6
3.4,3.57)
integer
N !
!число спинов
real
M !
!намагниченность
real
E :
!энергия конфигурации
real
Em
!среднее значение энергии
real
E2m
!среднее значение квадрата энергия
real
Mm
!среднее значение намагниченности
real
M2m
!среднее значение квадрата намагниченности
!таблица сдвига индексов
integer::
dj (1
:4)=(/1, 0,-1, 0/)
integer::
di (1
:4)=(/0, 1, 0,-1/)
!массивы для хранения значений индексов
!ближайших соседей
integer in(1:4),jn(1:4)
!таблица вероятностей принятия в алгоритме Метрополиса
real f(-1:1,-4:4)
!вероятность связывания спинов в алгоритмах
!Свендсена-Ванга и Вольфа
real fbond
13.2. Алгоритмы и описание работы программы -1\г 257
!массив для хранения информации о состоянии спинов
!квадратной решетки
integer, allocatable:: s (:, :)
!массивы, использующиеся в алгоритме Свендсена-Ванга:
integer, allocatable:: scl (:) !список спинов кластеров
integer, allocatable:: cl (:,:) !массив меток кластеров
integer, allocatable:: LL(:) !список связности
!меток кластеров
!массивы, использующиеся в алгоритме Вольфа:
integer, allocatable:: хс (:), ус(:) !списки координат
!спинов кластера
end module comdata
Значение логических переменных: mea, swa, wolf fa, приведенных
в начале этого модуля, определяет тип алгоритма вычислений. В дан¬
ном случае программа настроена на использование алгоритма Метро-
полиса. Массивы di () и dj () используются для оперативного вычис¬
ления координат ближайших соседей, а массивы in(l:4),jn(l:4) —
для хранения их координат в оперативной памяти.
Ниже приведен код основного модуля программы:
program Ising2d
use comdata
use msflib
implicit none
integer NMCS !счетчик шагов Монте-Карло на один спин
integer STEPM !число шагов Монте-Карло на один спин
!между "измерениями"
integer iT,i,im,res
logical thermalization
!инициализируем начальные значения массивов и переменных
call init ()
!вычисляем температурные зависимости
do iT=l,41
!печатаем на экран значение температуры
call settextposition (1,1,curpos);
write(*,*) 'T=', T(it)
call initgraf
if(mea) then
call calcf(T(it)) !вычисляем вероятности f
!принятия для заданных Т
else
fbond=l.-exp(-2./Т(it)) !вероятность связывания
endif
258 -»\r Глава 13. Метод Монте-Карло для анализа модели Изинга
!обнуляем значения вычисляемых величин
Em=0; Е2т=0; Мт=0; М2т=0
!уравновешиваем систему
NMCS=0; thermalization=.true.
do while (thermalization)
call mcstep; NMCS=NMCS+1
call drawM(NMCS)
if(mod(NMCS,500)==0) then
if(getcharqq()=='e') thermalization=.false.
endif
end do
!выполняем измерения
call settextposition (1,30,curpos);
write (*,*) 'Enter measure step= '
call settextposition (1,50,curpos); read (*,5) STEPM
5 format(i5)
res=setcolor(15)
do im=l,NM
do i=l,STEPM
call mcstep
NMC S =NMC S+1
end do
call measure()
call drawM(NMCS)
enddo
!записываем вычисленные значения в файл
call output(iT)
enddo
end program Ising2d
Вычисления средних значений намагниченности и энергии конфи¬
гурации выполняются в главном модуле для набора значений темпера¬
туры Г*, приведенных в модуле общих переменных. Процесс моделиро¬
вания начинается с низких температур. В этом случае наиболее веро¬
ятными являются конфигурации, имеющие минимальную энергию, т. е.
все спины конфигурации направлены в одном направлении. Начальная
конфигурация спинов генерируется в процедуре init. Дальнейшее
повышение температуры осуществляется в цикле do iT=l,41 ...
end do. В начале этого цикла процесс вычислений разветвляется. При
истинном значении логической переменной теа вычисляются значения
вероятностей принятия новой конфигурации с помощью внешней про¬
цедуры calcf. В случае, когда переменной теа принимает ложное зна¬
чение, вычисляется значение вероятности связывания спинов, необхо¬
димой для алгоритмов Свендсена-Ванга и Вольфа. При каждом новом
13.2. Алгоритмы и описание работы программы •Аг 259
значении температуры в качестве начальной автоматически выбирается
конфигурация, оставшаяся от предыдущего расчета.
Перед началом вычисления требуемых физических величин, конфи¬
гурация спинов уравновешивается для каждого нового значения темпе¬
ратуры Т* путем повторения выполнения процедуры mcstep. Принятие
решения об окончании уравновешивания осуществляется на основании
наблюдения за поведением зависимости намагниченности конфигура¬
ции от «времени», которая строится с помощью графической процедуры
drawM (). Через каждые 500 шагов Монте-Карло выполнение програм¬
мы приостанавливается и она находится в ждущем режиме. Нажатие
клавиши с символом ‘е’ соответствует положительному ответу, свиде¬
тельствующему об окончании процесса термализации. В случае нажа¬
тия любой другой клавиши уравновешивание системы продолжается.
После окончания термализации в программе происходит вычисле¬
ние намагниченности и энергии конфигурации, которое выполняется
процедурой measure. Для этого в начале вычислений нужно ввести с
клавиатуры численное значение шага между измерениями (переменная
STEPM в программе).
Усреднение и запись результатов расчета в файл выполняется с
помощью процедуры output.
Рассмотрим теперь более детально работу отдельных процедур.
Процедура init инициализации начальных значений и процедура
calcf вычисления таблицы вероятностей принятия новой конфигура¬
ции представлены ниже:
subroutine init()
use comdata
implicit none
N=L*L !число спинов
!располагаем массивы в оперативной памяти
allocate(s(l:L,l:L))
if(swa) then !алгоритм Сендсена-Вонга
allocate(scl(1:N))
allocate(cl(1:L,1:L))
allocate(LL(1:N))
endif
if(wolffa) then !алгоритм Вольфа
allocate(xc(1:N),ус(1:N))
endif
!генерируем начальную конфигурацию спинов
!(холодный старт)
s=l
end subroutine init
260
Глава 13. Метод Монте-Карло для анализа модели Изинга
subroutine calcf(Ti)
use comdata
implicit none
real Ti
integer nnsum
!температура
!сумма состояния спинов
!ближайших соседей
f=0.
do nnsum=-4,4,2
f(-1,nnsum)=exp(+2.*nnsum/Ti)
f(+1,nnsum)=exp(-2.*nnsum/Ti)
end do
end subroutine calcf
В процедуре init в зависимости от типа алгоритма располагаются
в оперативной памяти необходимые массивы. Массив s () является
общим для всех трем алгоритмов. В начале моделирования мы при¬
сваиваем всем элементам этого массива единичное значение, что со¬
ответствует «холодному старту». Процедура calcf представляет собой
запрограммированные формулы, приведенные на рис. 13.2.
Процедура mcstep, реализующая выполнение одного шага Монте-
Карло, осуществляет N раз вызов процедуры Metropolis алгоритма
Метрополиса, или вызовы процедур SWalgo, Wolff для алгоритмов
Свендсена-Ванга и Вольфа соответственно. Код этой процедуры пред¬
ставлен ниже:
subroutine mcstep()
use comdata
implicit none
integer i
if(mea)then
do i=l,N
call Metropolis
enddo
endif
if(swa) call SWalgo
if(wolffa) call Wolff
end subroutine mcstep
Процедура для вычисления энергии и намагниченности конфигура¬
ции выглядит следующим образом:
subroutine measure()
use comdata
implicit none
13.2. Алгоритмы и описание работы программы -»\г 261
integer i,j
integer pbc !функция корректировки координат
!с учетом п.г.у.
!вычисляем энергию конфигурации без учета
!магнитного поля
Е=0 .
do j =1,L
do i=l,L
jn(1:2)=j+dj (1:2) !сосед сверху
in(1:2)=i+di(1:2) !сосед справа
jn(1)=pbc (jn (1)); in (2)=pbc (in (2)) !периодические
!граничные уел.
E=E-Jij*s(i, j )*(s(in(1),jn (1))+S(in(2) , jn (2) ) )
enddo
enddo
M=sum(s) !намагниченность конфигурации
!накапливаем значения вычисленных величин
Em =Em +Е
E2m=E2m+E*E
Mm =Mm tabs(M) !накапливаем абсолютное значение
!намагниченности
M2m=M2m+abs(М)*abs(М)
end subroutine measure
В этой процедуре намагниченность М конфигурации вычисляется
суммированием значения всех спинов. Отметим, что для конфигураций
с малым значением N возможна ситуация, когда последовательность
переворотов спинов в алгоритме Метрополиса может приводить к из¬
менению знака намагниченности конфигурации. Это означает, что сред¬
няя намагниченность на спин (ms) для конечных систем при большом
времени моделирования даже при температурах ниже точки Кюри будет
равна нулю. Для больших систем время перемагничивания растет, и в
пределе limyv^00(ms) ф О при Т < Тс. Поскольку нас в первую очередь
интересует поведение макроскопических систем, а выполняем мы мо¬
делирование на конечных системах, то при вычислении (ms) значение
намагниченности М отдельной конфигурации для накопления берется
по абсолютной величине. Энергия конфигурации вычисляется в со¬
ответствии с формулой (13.1). Для того чтобы не учитывать дважды
взаимодействие ближайших соседних спинов, при вычислении энергии
мы проходим по всем узлам решетки слева направо и снизу вверх и
учитываем взаимодействие только с верхним и правым ближайшими
соседними узлами. В данной процедуре и ряде других используется
262 •Ar Глава 13. Метод Монте-Карло для анализа модели Изинга
функция pbc корректировки координат соседних спинов с учетом пе¬
риодических граничных условий, налагаемых на решетку. Она имеет
следующий вид:
integer function pbc(coord)
use comdata
implicit none
integer coord
if(coord>L) coord=coord-L
if(coord<l) coord=coord+L
pbc=coord
end function pbc
Процедура для записи результатов расчета в выходной файл пред¬
ставлена ниже:
subroutine output(i)
use comdata
USE msflib
implicit none
integer i
real fact
real C,CHI !теплоемкость, восприимчивость
!усредняем результаты вычислений
fact=l./real(NM)
Em =Em *fact
E2m =E2m*fact
Mm =Mm * fact
M2m =M2m*fact
!рассчитываем:
C=(E2m-Em*Em)/(T(i)*T(i)) !теплоемкость
CHI=(M2m-Mm*Mm)/Т(i) !магнитную восприимчивость
!рассчитываем средние значения величин на один спин
fact=l./real(N)
Em =Em *fact
Mm =Mm * fact
С =C *fact
CHI=CHI*fact
open (1,file='Ising.dat',access='append')
write (1,1) T (i), Em, Mm, C, CHI
close (1)
1 format(5(f12.4))
end subroutine output
13.2. Алгоритмы и описание работы программы Аг 263
В приведенной процедуре дополнительно вычисляются удельные
значения теплоемкости с и магнитной восприимчивости х• Эти ве¬
личины вычисляются, используя известные флуктуационные формулы
с = д(Е)/дТ= ((£2) - (Е)2)/№вР Н х = д(М)/дН=((М2)-(М)2)/№Т,
где &в — постоянная Больцмана (здесь полагается kв = 1). Все ре¬
зультаты расчетов для каждого значения температуры дописываются в
конец выходного файла Ising.dat.
Проанализируем работу внешних процедур, реализующих алгорит¬
мы Метрополиса, Свендсена-Ванга и Вольфа.
13.2.4.1. Процедура Метрополиса
Ход выполнение этой процедуры соответствует алгоритму
Метрополиса и достаточно полно описан в комментариях.
subroutine Metropolis()
use comdata
use msflib
implicit none
integer i,j !координаты спина, выбранного
!для опрокидывания
integer k
integer nnsum !сумма состояний спинов ближайших соседей
real rnd
integer pbc
!случайным образом выбираем спин для опрокидывания
1 call random(rnd); i=int(L*rnd+1.); if(i>L) goto 1
2 call random(rnd); j=int(L*rnd+1.); if(j>L) goto 2
!вычисляем индексы соседних спинов с учетом
!периодических граничных условий
in(1:4)=i+di(1:4); j n(1:4)=j +dj (1:4)
jn(1)=pbc(jn(1))
in(2)=pbc (in (2))
jn(3)=pbc(jn (3))
in(4)=pbc (in (4))
!вычисляем сумму состояний спинов ближайших соседей
nnsum=0.
do k=l,4
nnsum=nnsum + s(in(k),jn(k))
enddo
!опрокидываем спин в соответствии с вероятностью
!принятия новой конфигурации
call random(rnd)
if(rnd<f(s(i,j),nnsum)) s(i,j)=-s(i,j)
end subroutine Metropolis
264 Глава 13. Метод Монте-Карло для анализа модели Изинга
13.2.4.2. Процедура Свендсена-Ванга
При описании алгоритма Свендсена-Ванга выделены три
шага, однако при кодировании этого алгоритма первые два шага можно
выполнять одновременно. В приведенной процедуре основную часть
составляет код Хошена-Копельмана для маркировки кластеров (см.
гл. 12). Данная часть кода процедуры была адаптирована с учетом спе¬
цифики алгоритма Свендсена-Ванга. В основном это касается опреде¬
ления меток соседей. Если в обычном алгоритме Хошена-Копельмана
соседние заполненные узлы всегда являются связанными, то в алгорит¬
ме Свендсена-Ванга соседние узлы с одинаковыми спинами связаны
лишь с некоторой вероятностью. Следует также обратить внимание на
то, что в начале анализа соседей каждого очередного узла их метки
заранее должны быть обнулены, поскольку точно неизвестно, сколько
соседей окажется у этого узла.
Еще одно отличие заключается в том, что в алгоритме Свендсена-
Ванга для запоминания состояния спина кластера дополнительно ис¬
пользуется массив scl (). Каждому элементу этого массива определя¬
ется значение спина, вновь обнаруженного на решетке кластера. Число
ненулевых элементов массива scl () в точ¬
ности равно числу спиновых кластеров, об¬
наруженных по окончанию сканирования
решетки. Список спинов кластеров scl()
используется для опрокидывания принад¬
лежащих каждому кластеру спинов узлов
решетки. Рисунок 13.7 иллюстрирует прин¬
цип организации связей между массивами
в процедуре SWalgo. Массив s() состо¬
яний спинов узлов решетки связан с мас¬
сивом cl () кластерных меток через коор¬
динаты узлов, а массив scl() связан с массивом с1() посредством
кластерной метки. Изменение спинов узлов решетки происходит при
втором проходе решетки. Спинам узлов решетки присваиваются новые
значения в соответствии со значениями элементов массива scl ().
subroutine SWalgo()
use comdata
use msflib
implicit none
real rnd
integer spin !состояние спина в узле
!переменные алгоритма маркировки кластеров:
integer i !индекс
integer х,у !координаты узла
s(x,y) = ( I’
II 1
cl(х,у)=label
1 /
scl(label) = < ^
Рис. 13.7. Принцип органи¬
зации связей между масси¬
вами в процедуре SWalgo
13.2. Алгоритмы и описание работы программы ->\г 265
integer xleft, ydown !координаты соседнего узла
integer ncl !счетчик кластеров
integer label !метка узла
integer left, down !метки ближайших соседних узлов
integer labmin !значение минимальной метки
integer summa !сумма меток
integer pbc !функция корректировки
!координат с учетом п.г.у.
!1 — 2) Сканируем решетку и создаем связи между двумя
!ближайшими спинами, если они находятся в одном
!состоянии. Одинаковые спины связываются с вероятностью
!f=l-exp(-2/Т). Параллельно со связыванием выполняем
!маркировку кластеров спинов
ncl=0
cl=0; scl=0; LL=0
do y=l,L
do x=l,L
left=0; down=0; spin=s(x,y)
xleft=pbc(x-1); ydown=pbc(y-1)
call random(rnd)
if(s(xleft,y)==spin .and. rnd<fbond) left=cl(xleft,y)
call random(rnd)
if(s(x,ydown)==spin .and. rnd<fbond) down=cl(x,ydown)
summa=left+down
if(summa==0) then
ncl=ncl+l; cl(x,y)=ncl
scl(ncl)=spin
else if (summa==left) then
cl(x,y)=left
else if (summa==down) then
cl(x,y)=down
else
do while (LL(left)/=0); left=LL(left); enddo
do while (LL(down)/=0); down=LL(down); enddo
labmin=min(left, down)
cl(x,y)=labmin
if(down/=labmin) LL(down)=labmin
if(left/=labmin) LL(left)=labmin
endif
enddo
enddo
!3) Сканируем список спинов кластеров и опрокидываем
!спин кластера с вероятностью 1/2
do i=l,ncl
call random(rnd); if (rnd<0.5) scl(i)=-scl(i)
enddo
266 -l\r Глава 13. Метод Монте-Карло для анализа модели Изинга
!После опрокидывания присваиваем новые значения спина
!каждому кластеру спинов
do у=1,L
do х=1,L
label=cl(х,у)
do while (LL(label)/=0); label=LL(label); enddo
s(x,y)=scl(label)
enddo
enddo
end subroutine SWalgo
13.2.4.3. Процедура Вольфа
Процесс опрокидывания спинов кластера можно осуществ¬
лять одновременно с ростом самого кластера. Для этого в начале опро¬
кидывания в переменной spin запоминается начальное значение спина
для зерна кластера. Такой подход позволяет существенно упростить код
и повысить скорость расчетов.
subroutine Wolff()
use comdata
use msflib
implicit none
real rnd
integer spin !состояние спина в узле
integer nadd !число присоединенных к кластеру спинов
integer i !индекс
integer х,у !координаты узла
integer pbc !функция корректировки координат
!с учетом п.г.у.
!1) Случайным образом выбирается узел решетки,
!который затем принимается в качестве затравки
!для роста кластера
3 call random(rnd); x=int(L*rnd+1.); if (x>L) goto 3
4 call random(rnd); y=int(L*rnd+1.); if (y>L) goto 4
!2) Осуществляем рост спинового кластера и
!опрокидываем спины узлов кластера
nadd=l; xc(nadd)=x; ус(nadd)=у
spin=s(х,у);s(х,у)=-s(х,у) !опрокидываем спин затравки
do while(nadd>0)
!вычисляем координаты соседей и корректируем их
!значения с учетом п.г.у.
in(1:4)=хс(1)+di(1:4); jn(1:4)=ус(1)+dj(1:4)
jn(1)=pbc(jn(1))
in (2)=pbc(in(2))
jn (3)=pbc (jn(3))
in (4)=pbc(in(4))
13.2. Алгоритмы и описание работы программы •Аг 267
!выполняем проверку соседей
do i=l,4
call random(rnd)
if(s(in(i), jn(i))==spin .and. rnd<fbond) then
nadd=nadd+l; xc(nadd)=in(i); yc(nadd)=jn(i)
s(in(i) , j n(i))=-s(in(i),j n (i)) !опрокидываем
!присоединенный
! спин
endif
enddo
!"вычеркиваем" проверенный узел из списка
хс(1)=хс(nadd); ус(1)=ус(nadd); nadd=nadd-l
enddo
end subroutine Wolff
13.2.5. Пример работы программы
Работа программы для двумерной модели Изинга была про¬
тестирована для алгоритмов Метрополиса, Свендсена-Ванга и Вольфа
на квадратной решетке размером L = 64. На рис. 13.8 представлена
Г= 2,27 а
3
7
'*-* -vJ- '
Гъ
Аж
щ
2,5
2
▲у
Рис. 13
Зависимость удельной намагниченности ms (а) и удельной теплоем¬
кости с (б) от приведенной температуры Т* для двухмерной моде¬
ли Изинга. Точками представлены результаты работы программы
Ising2d.f90, полученные на решетке размера L = 64 для раз¬
личных алгоритмов вычислений: Метрополиса (/), Свендсена-Ван¬
га (2), Вольфа (3). Сплошная кривая соответствует точному реше¬
нию для бесконечной системы. На вставках к рисунку а изображе¬
ны конфигурации спинов для указанных на рисунке значениях Т*.
Темные участки рисунков соответствуют состоянию спинов s = — 1
268 •Ar Глава 13. Метод Монте-Карло для анализа модели Изинга
зависимость рассчитанной удельной намагниченности ms (а) и удель¬
ной теплоемкости с (б) от приведенной температуры Г*. Численные
данные для всех трех алгоритмов вычислений обозначены на рисунке
разными символами. Вычисленные данные усреднены по 20 различным
начальным конфигурациям для каждого значения Т*. Полученные дан¬
ные неплохо согласуются с точным решением для бесконечной системы
(сплошная кривая) для Г <ГС. Для зависимости ms(T*) при Т* >
наблюдается некоторое расхождение, которое можно объяснить нали¬
чием масштабных эффектов.
13.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Исследуйте вариант разбавленной модели Изинга на квадратной ре¬
шетке. Для этой модели, немагнитные частицы (s = 0), концентра¬
ция которых равна р, распределены случайным образом по узлам ре¬
шетки. Модифицируйте программу таким образом, чтобы опрокиды¬
вание спинов выполнялось только для магнитных атомов. Исследуй¬
те зависимость температуры перехода Тс от степени разбавления р.
Наблюдается ли монотонное уменьшение величины Тс до нуля при
приближении величины р к перколяционному значению рс ~ 0,5927?
Из анализа зависимости 1 - Tc(L)/Tcoo ~ L-l/v определите скейлин-
говый показатель v.
2. Обобщите модель, рассмотренную в предыдущей задаче на трех¬
мерный случай. Рассмотрите простую кубическую решетку, размер
которой составляет N х N х L, L < N и в плоскости х-у применены
периодические граничные условия, N = 32. При L = 1 данная модель
вырождается в двумерную модель, при увеличении L происходит
постепенный переход к трехмерной модели [26]. Исследуйте зависи¬
мости температуры перехода Тс от L и р. Наблюдается ли монотонное
уменьшение величины Тс до нуля при приближении величины р
до перколяционного значения, характерного для заданной толщины
пленки (рс « 0,5927 при L = 1 и рс « 0,3113 при L = 32)? Определи¬
те зависимость скейлингового показателя v (см. предыдущую зада¬
чу) от р.
3. Исследуйте поведение двумерной модели Изинга для случаев, когда
спины жестко зафиксированы в определенном состоянии, s = -hi на
одной из границ системы (рис. 13.9, а) или на поверхности немагнит¬
ного квадратного включения, размером R, расположенного в центре
решетки (рис. 13.9, б). Определите характерную пространственную
длину £, вносимую данными возмущениями. Исследуйте, как зави¬
сит £ от Т.
13.4. Литература -l\r 269
граничные условия
Рис. 13.9. Варианты двумерной модели Изинга с жестко фиксированными
состояниями спинов на внешней границе (а) и на поверхности
квадратного включения (б)
4. Одним из широко исследуемых вариантов модели Изинга являет¬
ся векторная модель Лебволя-Лашера [27], в которой допускаются
непрерывные состояния спинов, определяемые их ориентацией в про¬
странстве. Гамильтониан данной системы определяется соотношени¬
ем Н = — J'L(ij) Я2(cos б//), где ву — угол между соседними спина¬
ми, P2(cos6ij) = (3cos2ву — 1)/2 — полином Лежандра второй сте¬
пени. Данная модель позволяет описать нематическое упорядочение
в жидких кристаллах. Исследуйте поведение данной системы при
различных температурах, вычислите среднюю величину (P2(cos в у))
и определите критическую температуру Т*с.
5. Для так называемой ±J модели Изинга величина J в уравнении (13.1)
не является постоянной, а случайно распределена по связям между
значениями +/ и -J. Таким образом, в данной системе одновре¬
менно присутствуют ферромагнитные (/ > 0) и антиферромагнитные
(J < 0) связи [28]. Пусть относительная доля ферромагнитных свя¬
зей составляет р. Исследуйте зависимость температуры перехода в
ферромагнитное состояние от р.
13.4. ЛИТЕРАТУРА
1. Ising Е. Beitrag zur Theorie des Ferro und Paramagnetismus. — Hamburg,
1924. Полный текст диссертации Э. Изинга приведен по веб-адресу:
http://www.fhaugsburg.de/~harsch/germanica/Chronologie/20Jh/Ising/
isi\_feOO.html.
2. Ising Е. Beitrag zur Theorie des Ferromagnetismus // Z. Phys. — 1925. —
Bd. 31. - S. 253-258.
270 -»\r Глава 13. Метод Монте-Карло для анализа модели Изинга
3. Brush S. G. History of the Lenz-Ising Model 11 Rev. Mod. Phys. — 1967. —
V. 39. - P. 883-893.
4. Peierls R. On Ising Model of Ferromagnetism // Mathematical Proceedings of
the Cambridge Philosophical Society. — 1936. — V. 32, No. 3. — P. 477-481.
5. Kramers H. A. and Wannier G. H. Statistics of the Two-Dimensional Ferro-
magnet. Part I 11 Phys. Rev. — 1941. — V. 60. — P. 252-262.
6. Onsager L. Crystal statistics. I. A two-dimensional model with an order-dis-
order transition 11 Phys. Rev. — 1944. — V. 65. — P. 117-149.
7. Yang C. N. The Spontaneous Magnetization of a Two-Dimensional Ising Mo¬
del // Phys. Rev. - 1952. - V. 85, No. 5. - P. 808-816.
8. Josephson B. Inequality for the specific heat: I. Derivation 11 Proc. Phys.
Soc. - 1967. - V. 92. - P. 269-275.
9. Rushbrooke G. On the Thermodynamics of the Critical Region for the Ising
Problem // J. Chem. Phys. - 1963. - V. 39. - P. 842-843.
10. Potts R. B. Some generalized order-disorder transformations 11 Mathemati¬
cal Proceedings of the Cambridge Philosophical Society. — 1952. — V. 48,
No. 1. - P. 106-109.
11. Стенли Г. Фазовые переходы и критические явления. — М.: Мир, 1973.
12. Wu F. Y. Dilute Potts model, duality and site-bond percolation // J. Phys. A:
Math. Gen. - 1981. - V. 14. - P. L39.
13. Ching W. Y. and Huber D. L. Monte Carlo studies of the critical behavior of
site-dilute two-dimensional Ising models // Phys. Rev. B. — 1976. — V. 13,
No. 7. - P. 2962-2964.
14. Jayaprakash C., Eberhard K. R. and Wortis M. Critical and thermodynamic
properties of the randomly dilute Ising model 11 Phys. Rev. B. — 1978. —
V. 18. - P. 2244.
15. Selke W., Shchur L.N. Critical Binder cumulant in two-dimensional anisotropic
Ising models 11 J. Phys. A. - 2005. - V. 38, No. 44. - P. L739-L744.
16. Binder K. and Heerman D. W. Monte Carlo Simulation in Statistical
Physics. — Berlin: Springer Verlag, 1988.
17. Landau D. P. Finite-size behavior of the Ising square lattice // Phys. Rev.
B. - 1976. - V. 13. - P. 2997-3011.
18. Metropolis N. A., Rosenbluth A. W., Rosenbluth M. N., Teller A. H. and
Teller E. Equation of state calculation by fast computing machines // J.
Chem. Phys. - 1953. - V. 21. - P. 1087-1092.
19. Janke WWeigel M. Geometric and stochastic clusters of gravitating Potts
models 11 Physics Letters B. — 2006. — V. 639. — P. 373-377.
20. Fortuin C.M., Kasteleyn P. W. On the random-cluster model. I. Introduction
and relation to other models 11 Physica. — 1972. — V. 57. — P. 536-564.
21. Coniglio A., Klein W. Clusters and Ising critical droplets: a renormalisation
group approach 11 J. Phys. A. — 1980. — V. 13, No. 8. — P. 2775.
22. Stauffer D., Aharony A. Introduction to Percolation Theory. — London,
Washington, DC: Taylor & Francis, 1992.
13.4. Литература -*\r 271
23. Janke W. and Schakel A.M.J. Fractal structure of spin clusters and domain
walls in the two-dimensional Ising model // Phys. Rev. E. — 2005. — V. 71. —
P. 036703.
24. Swendsen R. Wang J.-S. Nonuniversal critical dynamics in Monte Carlo
simulations // Phys. Rev. Lett. — 1987. — V. 58, No. 2. — P. 86-88.
25. Wolff U. Collective Monte Carlo Updating for Spin Systems 11 Phys. Rev.
Lett. - 1989. - V. 2, No. 4. - P. 361-364.
26. Soukoulis С. Af., GrestG.S., Velgakis M. Monte Carlo study of randomly
diluted ferromagnetic thin films 11 Phys. Rev. B. — 1989. — V. 40, No. 1. —
P. 467-470.
27. Lebwohl P. A., Lasher G. Nematic-Liquid-Crystal Order-А Monte Carlo Cal¬
culation // Phys. Rev. A. — 1972. — V. 6. — P. 426-428.
28. Ozeki Y., Nishimori H. Phase Diagram of the ±J Ising Model // Journal of
the Physical Society of Japan. — 1987. — V. 56, No. 9. — P. 3265-3269.
ГЛАВА ЗАДАЧА КОММИВОЯЖЕРА
14
14.1. МЕТОД МОДЕЛЬНОГО ОТЖИГА
И ЗАДАЧА КОММИВОЯЖЕРА
Задачи многомерной оптимизации широко используются
при моделировании различных физических явлений. Рассмотрим, на¬
пример, задачу поиска глобального минимума некоторой функции Е(х),
которая имеет к тому же несколько локальных минимумов. Это может
быть, например, зависимость энергии системы Е от ее состояния х
(рис. 14.1). Задача оптимизации состоит в преодолении локальных ми¬
нимумов и нахождении глобального минимума.
Локальный
Рис. 14.1. Зависимость энергии от состояния в методе модельного отжига
Существующие оптимизационные методы могут базироваться на
различных алгоритмах модельного отжига, искусственных нейронных
сеток и эволюционных вычислений.
14.1. Метод модельного отжига и задача коммивояжера •Аг 273
14.1.1. Метод модельного отжига
Метод модельного отжига (simulated annealing) широко
применяется для решения задач многомерной оптимизации [1, 2]. На¬
звание метода модельного отжига связано с имитацией процесса отжи¬
га металлов. При таком отжиге металл сначала раскаляют до высокой
температуры, а затем медленно охлаждают. При высокой температуре
система равновероятно может находиться в различных состояниях и
попадать в различные локальные минимумы. При плавном уменьшении
температуры Т амплитуда тепловых колебаний атомов около положений
равновесия постепенно уменьшаться и в результате система будет ре-
лаксировать в состояние, соответствующее глобальному минимуму.
Метод модельного отжига фактически является обобщением алго¬
ритма Метрополиса, предложенного в 1953 г. [3] на случай постоянно
уменьшающейся температуры. Впервые схемы модельного отжига исполь¬
зовалась Н. Метрополисом для вычисления многомерных интегралов,
а также С. Киркпатриком для оптимизации разводки микросхем [4].
Преимуществом метода модельного отжига является то, что он,
в принципе, позволяет найти глобальный минимум, избегая ловушек
в локальных минимумах, но определенной «платой» за это является
необходимость использования больших вычислительных ресурсов.
14.1.1.1. Вероятность перехода
ние хп и, система с вероятностью / переходит в это состояние, или в
противном случае процесс генерации хп повторяется. При уменьшении
энергии переход в новое состояние (вправо на рис. 14.1) происходит с
вероятностью /(Д£, Т) = 1, а при ее увеличении (влево на рис. 14.1) этот
переход может произойти с меньшей вероятностью /(Д£, Т) < 1, которая
определяется в классической процедуре модельного отжига, как
где Д£ обозначает приращение энергии Д£ = Е(хп) — Е(х), а темпера¬
тура Т уменьшается по некоторому закону.
Таким образом, процедуру выбора вероятности можно определить
соотношением
Последнее соотношение можно записать в приближенном виде
В методе модельного отжига генерируется новое состоя-
(141)
274 -*\r Глава 14. Задача коммивояжера
Эффективность процедуры отжига может быть значительно ускоре¬
на при специальном выборе функции /(Д£, Г), например, при использо¬
вании статистики Тсаллиса
где величина q может зависеть от Т.
Отметим, что в пределе q —> 1 соотношение (14.2) сводится к соотно¬
шению (14.1), а ускорение процедуры отжига наблюдается при q < 1 [5].
В начальные моменты времени при высоких температурах систе¬
ма может часто преодолевать большие барьеры, но при достаточно
медленном понижении температуры локализуется вблизи глобального
минимума, независимо от того, в какой точке она находилась сначала.
Схема метода отжига задается выбором вероятности /(Д£, Г) и зако¬
на уменьшения температуры со временем T(t). К настоящему времени
разработано большое количество различных вариантов метода модель¬
ного отжига. Показано, что этот метод в большинстве случаев является
эффективным способом нахождения глобального минимума. Однако
строгого математического обоснования условия нахождения глобаль¬
ного минимума пока не существует, и поэтому использование метода
модельного отжига не дает абсолютной гарантии и требует тщательной
проверки.
14.1.1.2. Уменьшение температуры со временем
Для описания уменьшения температуры Т со временем t
могут применяться различные законы, например, логарифмический или
больцмановский
/ТЧ rp In to
Ti = т°~ы’
где to — начальное время, соответствующее начальной температуре Го.
Больцмановская схема, хотя и гарантирует нахождение глобально¬
го минимума при определенных условиях, но является достаточно
медленной.
Более предпочтительной является экспоненциальная схема, которая
в дискретном варианте реализуется как
1 = (14.3)
Эффективность работы данной схемы сильно зависит от типа задачи,
а также величин &, Го. Эмпирически установлено, что хорошим зна¬
чением является k — 0.95, а величина to выбирается из условия, что
начальная вероятность перехода в среднем равна 0,8 [б].
(14.2)
14.1. Метод модельного отжига и задача коммивояжера ->\г 275
Иногда применяются более сложные законы, например, пилообраз¬
ный [7] или адаптивный, в котором температура в следующий момент
времени зависит от характеристик системы в данный момент [1, 8].
Метод модельного отжига широко используется для оптимизации
кластерных структур, поиска глобальных минимумов на поверхностях
потенциальной энергии больших молекул (например, белков), нахожде¬
ния оптимального пути в задаче коммивояжера, решения задач схемо¬
техники и конструировании микросхем, решения математических задач
в теории графов, анализе численных рядов, задач фильтрации, модели¬
ровании нейронных сеток, решении задач в области физики неупоря¬
доченных систем и спиновых систем, при моделировании сейсмических
явлений а также для анализа социальных процессов [9-11].
14.1.2. Задача коммивояжера
В задаче коммивояжера необходимо найти минимальный
путь (минимальной длины £min или минимальной стоимости) при про¬
хождении через N городов, при условии, что в каждом городе можно
побывать только один раз. Фактически задача состоит в нахождении
глобального минимума функции Е в зависимости от вариантов обхода
городов. Если мы начинаем обход с заданного города, то существует
(N — 1)! вариантов обхода в прямом и обратном направлении. Для сим¬
метричной задачи, т. е. когда путь в прямом и обратном направлениях
равны, число вариантов с разной длиной пути равно (Л7 — 1)!/2. При
прямом переборе всех возможных вариантов обхода задача усложняет¬
ся даже при небольших значениях N.
Отметим, что величина N\ увеличивается гораздо быстрее, чем лю¬
бая степень числа N и даже быстрее чем еР. При N = 100 всего полу¬
чается около ю155 вариантов обходов городов, что представляет собой
очень большое число и поэтому прямой перебор для данного случая
практически неприменим даже на современных компьютерах.
Можно попытаться уменьшить количество переборов, выбирая, на¬
пример, на каждом шаге только ближайший город, или анализируя
минимальный путь для определенных выделенных кластеров городов,
однако такие подходы не гарантируют правильности конечного резуль¬
тата, и их применимость может существенно зависеть от характера
распределения городов.
Пример оптимального тура по 40 городам Европы приведен на
рис. 14.2. При увеличении количества городов вид тура оказывается
довольно запутанным и его сложно интуитивно предсказать. К на¬
стоящему времени разработано большое количество точных и при¬
ближенных алгоритмов для решения задачи коммивояжера, которые
позволяют анализировать данную проблему при довольно больших
276 Глава 14. Задача коммивояжера
ИСЛАМ л мо Р*
Рейкьявик
° °°f Хельсинк1^Санкт|ПетеРбУРг
аг |С,ятШцши г Таллин
л ...... I Стокгольм^^ /~ч'^ о
о° 3 , Рига
йр Копенганен фсг" о ^ ш ^
л ~ . «™*1 --Вильнюс .д ттлШ~
ин 1 о ■ ^ — Москва
Лондон , Амстердам 1 fan о/n ta..f„L^T^\/^H,HCK ° /
"||^ГГ1П т " ьА Берлин ,'4ГВаршава\ ®- J
^ ^ г... ж «ir-со..»^ _ Ло _ X.,.. . ■
МШ$
значениях N. Например, в 2004 г. решена задача обхода всех 24978 го¬
родов в Швеции, и показано, что длина минимального тура составляет
примерно 72500 км [12]. Отметим, что тур по всем городам Земного
шара включает примерно 1904711 городов и эта задача все еще остается
достаточно сложной для точного решения [12].
o’ f Пра^а, \львов »-■ -4
«Ри^<^юксембрр№Бр^ла^в М ХаЕьк°в
:фра«н 1ГНц_,.' D Кишинев
Вена -Г » Будапешт п ' "
люксем°УРг ЦлЬратнслэзаХ ° - а
р аон inN^|K-,:Кишинев •
, .. ■ Одесса
° .'° ш Белград|я|р^- 0 о ; ,
. о «Любляна^Ч^ r^ArfJiГу °
о"" о О ® ч Ьухарест
0 , <4 v - if—- ■— ' * СараевоСофия •
1 ' ° .к ^0^7 а —• I >u-W7:y- -
• p"v \
»*£> • -ji-yC ■»-- ■ -• f “Ч . _ Т
О* 'т. _ (1 Г> А гК 1Л и UI
4Ссабон^<,
Риг 1/1 9
Очевидно, что величина Етш зависит от характера распределения
городов и увеличивается с увеличением количества городов N. При слу¬
чайном распределении городов на плоскости минимальный путь £mjn
является пропорциональным корню квадратному из числа городов N,
т.е. выполняется соотношение £min ~ y/N [12]. Если города расположены
случайным образом на прямоугольнике площади S, то Ет\n = Ky/NS,
где К « 0,7120 ± 0,0002 в пределе большого числа городов, N—> оо
[13-15]. Для случайного расположения в объеме V выполняется аналогич¬
ное соотношение Emin = Ky/NV, где К « 0,6979 ± 0,0002 при Af—► оо [15].
На рис. 14.3 представлен пример «острова», который образован
при оптимальном туре через 500 точек, случайно расположенных на
плоскости.
14.2. Алгоритм для решения задачи коммивояжера •Аг 277
Рис. 14.3. Оптимальный путь через 500 то¬
чек, случайно расположенных на плоскости
Стоимость пути можно определить в специальной матрице Гц. В
случае, когда стоимость пути не зависит от направления (т. е. для путей
/ —> / и / —/ их стоимости равны) и матрица гц является симметрич¬
ной, гц = гр задача коммивояжера называется симметричной. В случае,
когда Гц ф r-ц задача называется ассиметричной (рис. 14.4).
0
21
32
14
11
21
0
7
16
12
32
7
0
9
8
14
16
9
0
6
11
12
8
6
0
0
21
32
14
11
22
0
7
16
12
18
6
0
9
8
12
15
9
0
6
10
11
7
6
0
а б
Рис. 14.4. Примеры симметричной (а) и несимметричной (б) матриц стоимо¬
сти пути в задаче коммивояжера при N = 5
Задача коммивояжера называется геометрической, когда величи¬
ны гц пропорциональны евклидовому расстоянию между городами i и /.
В этом случае матрица стоимости удовлетворяет неравенству треуголь¬
ника, Гц + Гik > rik.
В этой главе мы хотели бы познакомить читателей с одним из примеров
применения метода модельного отжига для решения задачи коммивояжера.
14.2. АЛГОРИТМ ДЛЯ РЕШЕНИЯ ЗАДАЧИ КОММИВОЯЖЕРА
И ОПИСАНИЕ РАБОТЫ ПРОГРАММЫ
14.2.1. Алгоритм
При реализации алгоритма коммивояжера будем предпо¬
лагать, что матрица гц определяется расстояниями между городами
Гц = \J(xt -X,)2 + (у,- у,)2,
278 -l\r Глава 14. Задача коммивояжера
а вероятность перехода равна
/ « min
1, exp
ш
где АЕ = Ei — £2 — изменение длины пути при изменении варианта
объезда городов, a k^T — параметр, который является аналогом теп¬
ловой энергии.
Начальный обход
Конечный обход
Рис. 14.5. Изменение очередности объезда городов i и j
Наиболее простым способом изменения вариантов объезда является
изменение очередности объезда городов, например, i и /, так как это
показано на рис. 14.5.
14.2.2. Описание работы программы
Рабочая программа для решения задачи коммивояжера со¬
держится в файле salesman, f 90. Программа имеет модульную струк¬
туру и состоит из модуля общих переменных и массивов, главного
модуля и набора обслуживающих внешних процедур.
Модуль общих переменных и массивов имеет следующий вид:
module comdata
logical:: GRAPH
real xmin, ymin !размеры графического окна
real xmax, ymax !для изображения сети городов
!набор переменных, определяющий сеть городов:
integer:: N !количество городов
logical:: CLUST
character (13) NAMEFILE !имя файла с координатами
!городов
!переменные алгоритма модельного отжига
integer:: NMCSPS !число шагов метода Монте-Карло
!на один город
integer:: NMCS !общее число шагов метода Монте-Карло
real Е !длина пути коммивояжера
real к !параметр понижения температуры
14.2. Алгоритм для решения задачи коммивояжера
real КВТ !"тепловая энергия"
real KBTMIN
!массивы программы
real, allocatable:: х(:), у(:) !координаты городов
real, allocatable:: r(:,:) !расстояния между
!городами
integer, allocatable:: visit(:) !последовательность
!обхода городов
!список параметров программы
namelist /prgparam/ GRAPH, CLUST, NAMEFILE, N,&
KBTMIN, NMCSPS, k
end module comdata
Код основной части, который содержится в главном модуле, приве¬
ден ниже:
program salesman
use comdata
use msflib
implicit none
type (rccoord) curpos
integer i,j
call init
!записываем начальную последовательность
!обхода городов в файл
open (1,file='inittour.dat')
do i=l,N
write(l,*) x(visit(i)), y(visit(i))
enddo
write(l,*) x(visit(l)), y(visit(l))
close (1)
!печатаем начальные значения длины пути коммивояжера
!и "тепловой энергии"
call settextposition (1,1,curpos)
write (*,*) 'E0=', E, ' ','T0 = ', KBT, '
if(GRAPH) then
call initgraf !инициализируем графическое окно
call drawtour !рисуем начальный путь коммивояжера
endif
!оптимизируем путь коммивояжера и записываем в файл
!зависимость длины пути от температуры
open (1,file='ET.dat')
do while (KBT>KBTMIN)
do i=l,NMCS
call MonteCarlo
enddo
280 -»\r Глава 14. Задача коммивояжера
!печатаем текущие значения длины пути
!коммивояжера и "температуры"
call settextposition (1,60,curpos);
write (*,*) 'E=', E, ' KBT, ' '
KBT=k*KBT !уменьшаем "температуру"
j=j+l
if (mod(j,100)==0) then
write (1,*) КВТ, E
if(GRAPH) call drawtour !рисуем путь
end if
enddo
close (1)
!рисуем оптимизированный путь коммивояжера
if(GRAPH) call drawtour
!записываем оптимизированную последовательность
!обхода городов в выходной файл
open (1,file='finaltour.dat')
do i=l,N
write (1,*) x(visit(i)),у(visit(i))
enddo
write (1,*) x(visit(l)),y(visit(l))
close(1)
end program salesman
В процедуре init координаты городов считываются с входного
файла, или генерируются случайным образом (массивы x(i),y(i)),
а затем вычисляются расстояния между ними г (i, j). Начальная по¬
следовательность посещения задается в соответствии с порядком гене¬
рирования координат и сохраняется в массиве visit (i).
subroutine init ()
use comdata
use msflib
implicit none
real distance !функция вычисления пути коммивояжера
integer i,j !индексы
!инициализируем начальное число последовательности
!случайных чисел случайным образом
call seed(RND$TIMESEED)
!читаем управляющий файл программы
open(l, file='salesman.txt')
read(l, prgparam)
close (1)
!считываем координаты городов или генерируем
!случайным образом
call readcluster()
14.2. Алгоритм для решения задачи коммивояжера -»\г 281
!вычисляем расстояния между городами
do i=l,N
do j =1,N
r(i, j)=sqrt((x(i)-x(j))**2+(y(i)-y(j))**2)
enddo
enddo
!определяем начальную последовательность
!обхода городов
do i=l,N
visit(i)=i
enddo
!выполняем вычисление начальных значений:
E=distance() !длины пути
КВТ=1000./Е !"тепловой энергии"
!вычисляем общее число шагов метода Монте-Карло
NMCS=NMCSPS*N
end subroutine init
Расчет длины пути тура, что отвечает заданной последовательности
посещения городов, осуществляется во внешней функции distance.
После этого вычисляется начальная «температура» и начинается оп¬
тимизация пути коммивояжера, которая происходит в средине цик¬
ла do while . . . enddo основного модуля. В середине этого цикла
осуществляется вызов процедуры Метрополиса MonteCarlo и через
каждые NMCS вызовов происходит снижение «температуры». Код про¬
цедуры Метрополиса приведен ниже:
subroutine MonteCarlo()
use comdata
use msflib
implicit none
integer i,j !индексы
integer is, js !индексы городов в последовательности
! тура
real rnd !случайное число
real distance !функция вычисления длины пути
real Enew !новая длина пути
real dE !прирост длины пути
!выбираем случайным образом два города
!и изменяем маршрут визита путем перестановки
!выбранных городов
1 call random(rnd); i=int(N*rnd+1.О);
if (i>N) goto 1
j=i
282 -»\r Глава 14. Задача коммивояжера
do while (j ==i)
2 call random(rnd); j=int(N*rnd+1.0)
if (j>N) goto 2
enddo
is=visit(i); js=visit(j)
visit(i)=js; visit(j)=is
!вычисляем новую длину пути
Enew=distance()
dE=Enew-E
if(dE>0) then
call random(rnd)
if(exp(-dE/KBT)<rnd) then
visit (i)=is; visit(j)=js; return !старый тур
endif
endif
E=Enew !новый тур
end subroutine MonteCarlo
После завершения работы программы оптимизированная последова¬
тельность посещения городов, что отвечает минимальному пути, запи¬
сывается в выходной файл finaltour.dat.
14.2.3. Примеры работы программы
Для тестирования работы программы salesman, f 90 бы¬
ли проведены вычисления минимального пути для городов, случайно
распределенных на окружности, координаты, которых заданы в файле
circle.dat.
Рис. 14.6. Пример работы программы salesman, f 90 по оптимизации пути
для N = 100 точек, случайно распределенных на окружности единич¬
ного радиуса: начальный (а) и оптимизированный (б) путь обхода
-0,5
0,5
-1
0
-1
1 -0,5 0 0,5 1 -1 -0,5 0 0,5 1
14.3. Задачи для самостоятельной работы ->\г 283
kBT
Рис. 14.7. Зависимость длины пути Е от «тепловой энергии» к^Т при различ¬
ных значениях коэффициента к. N — 1000
На рис. 14.6 представлен начальный и конечный тур. Вычисления
проведены при следующих значениях параметров N = 100, к^Т = Ю-5
(минимальная «тепловая энергия»), NMCSPS = 100 (число шагов Монте-
Карло на один город), к = 0,9999 (параметр в уравнении (14,3), харак¬
теризующий скорость снижения «тепловой энергии»). Отметим, что при
выбранных значениях параметров используемая процедура оптимиза¬
ции позволяет найти глобальный минимум, соответствующий обходу
городов по кругу. Однако, при уменьшении к глобальный минимум
может достигаться не всегда. На рис. 14.7 показаны зависимости длины
пути Е от параметра k^T полученные для 15 различных начальных ини¬
циализаций при к = 0,9997. В данном случае процедура оптимизации
приводила к туру с минимальной длиной только примерно в половине
случаев, а для неоптимальных путей их длина была примерно в два
раза выше минимальной.
14.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Используйте программу Salesman.f90 для изучения зависимости дли¬
ны минимального пути Е от количества точек N для случайного
распределения их на плоскости. Аппроксимируйте зависимость фор¬
мулой Е = ay/N + Ъ и определите коэффициенты а и Ь. Обобщите
программу Salesman, f 90 для проведения оптимизации в трехмер¬
ном случае, когда города распределены в трехмерном пространстве
и исследуйте аналогичную зависимость E(N).
284
Глава 14. Задача коммивояжера
2. Используйте программу Salesman, f 90 для построения минималь¬
ного пути на двумерных кластерах перколяционном (см. рис. 12.4)
и DLA (см. рис. 8.8). Для генерации кластеров используйте про¬
граммы, описанные в главах 12 и 8. Минимальный путь позволяет
определить эффективную площадь, занимаемую кластером. Как и в
предыдущей задаче исследуйте зависимости E(N). Примеры мини¬
мального пути для этих кластеров представлены на рис. 14.8.
Рис. 14.8. Примеры оптимального пути на перколяционном (а) и DLA (б)
3. Обобщите программу Salesman, f 90 для расчета оптимального
значения Е, в случае, когда матрица стоимости имеет несиммет¬
ричной вид (как, например, изображено на рис. 14.4, б). Несиммет¬
ричную матрицу можно задать, например в виде
где величина Я может принимать некоторое значения, характерное
для данного города.
В задаче коммивояжера несимметричные матрицы стоимости мо¬
гут возникать при необходимости пересечения рек, необходимо¬
сти посещения складов, которые расположены только в опреде¬
ленных городах. Пусть величины А, распределены случайным об¬
разом в интервале 0-^1. Исследуйте зависимость E(N) в данном
случае.
4. Используйте метод модельного отжига для решения задачи ферзей.
В данной задаче на шахматной доске размером п х п нужно раз¬
местить п ферзей таким образом, чтобы они не «били» друг друга
(рис. 14.9). Каждая неприемлемая позиция соответствует увеличе¬
нию «энергии» на +1. При решении данной задачи можно пере¬
мещать ферзей только вдоль горизонтальной оси, обменивая гори¬
кластерах
14.4. Литература -l\r 285
зонтальные позиции двух случайно выбранных ферзей и вычисляя
изменение «энергии».
HL
а б
Рис. 14.9. Примеры решения задачи ферзей на шахматной доске размеров
8 х 8 (а) и 32 х 32 (б)
14.4. ЛИТЕРАТУРА
1. van Laarhoven P.J.M., and Aarts E.H.L. Simulated Annealing: Theory and
Applications. — Dordrecht, Holland: D. Reidel, 1987.
2. Arts E. H. L. and Korst J. H. M. Simulated Annealing and Boltzmann Ma¬
chines. — New York: Wiley (Interscience), 1989.
3. Metropolis N.. Rosenbluth A.W., Rosenbluth M.N., Teller A.H. and Teller E.
Equations of State Calculations by Fast Computing Machines 11 J. Chem.
Phys. - 1953. - V. 21. - P. 1087-1092.
4. Kirkpatrick S., Galatt C.D., Vecchi M.P. Travelling salesman problem. Opti¬
mization by simulated annealing 11 Science. — 1983. — V. 220. — P. 671-680.
5. Penna T.J.P. Traveling salesman problem and Tsallis statistics // Phys. Rev.
E. - 1994. - V. 50, No. 6. - P. R1-R3.
6. Kirkpatrick S., Gerlatt C.D.Jr., and Vecchi M.P. Optimization by Simulated
Annealing 11 IBM Research Report RC 9355, (1982).
7. Foreman K.W., Phillips A.Т., Rosen J.B., Dill K.A. Comparing Search Strate¬
gies for Finding Global Optima on Energy Landscapes // J. Comput. Chem. —
1999. - V. 20, No. 14. - P. 1527-1532.
8. Wales D.J., Berry R. S. Melting and freezing small argon clusters // J. Chem.
Phys. - 1990. - V. 92, No. 7. - P. 4283-4295.
9. Ingber L. Simulated annealing: Practice versus theory 11 Journal of Mathe¬
matical Computation Modelling. — 1993. — V. 18, No. 11. — P. 29-57.
10. Московский А. А. Методы оптимизации структуры молекулярных класте¬
ров: Дис. ... канд. хим. наук. — М.: МГУ, 2001.
11. GunnJ.R., Monge A., Friesner R. A., Marshall С.Н. Hierarchical Algorithm
for Computer Modeling of Protein Tertiary Structure 11 J. Phys. Chem. —
1994. - V. 98. - P. 702-711.
286 Глава 14. Задача коммивояжера
12. Applegate D., Bixby R., Chvatal V., Cook W., Helsgaun К. The traveling
salesman problem: http://www.tsp.gatech.edu; David Applegate, Robert Bix-
by, Vasek Chvatal and William Cook. On the Solution of Traveling Salesman
Problems // Documenta Mathematica Extra Volume ICM 1998, III, 645-656;
David L. Applegate, Robert E. Bixby, Vasek Chvatal & William J. Cook
The Traveling Salesman Problem: A Computational Study. — Princeton, NJ:
Princeton University Press, 2006. — 606 p.
13. Beardwood J., HaltonJ.H. and Hammersley J. M. The shortest path through
many points // Proc. Cambridge Philos. Soc. — 1959. — V. 55. — P. 299-327.
14. Johnson D. S., McGeochL.A. and Rothberg E. E. Asymptotic experimental
analysis for the Held-Karp traveling salesman bound // Proceedings of the
seventh annual ACM-SIAM symposium on Discrete algorithms Atlanta, GA,
USA, January 28-30, 1996. - P. 341-350.
15. Percus A. The Traveling Salesman and Related Stochastic Problems: PhD
dissertation. — Universite Paris, 1997.
ГЛАВА ВЫЧИСЛЕНИЕ ЭЛЕКТРОПРОВОДНОСТИ
15 КОМПОЗИЦИОННЫХ СИСТЕМ
15.1. МЕТОДЫ РАСЧЕТА ЭЛЕКТРОПРОВОДНОСТИ
КОМПОЗИЦИОННЫХ СИСТЕМ
Задача по определению электропроводности композицион¬
ных материалов, состоящих из проводящих и непроводящих компонен¬
тов, является достаточно сложной и требует применения специальных
вычислительных методов. Интерес вызывает поведение электропровод¬
ности для двухкомпонентных систем с большим электрическим кон¬
трастом (электропроводность одной фазы значительно больше другой)
вблизи точки перколяционного перехода [1]. В последнее время эта
задача приобрела особенно важное значение в связи с созданием ком¬
позитов на основе диэлектрических материалов, наполненных части¬
цами металлов, нанотрубок, сажи. В точке перколяционного перехо¬
да электропроводность таких композитов скачкообразно изменяться на
несколько порядков в очень узком интервале значений концентрации
наполнителя.
Задача электропроводности вблизи порога перколяции также интен¬
сивно обсуждалась в случае разорванных случайным образом сеток
резисторов. В качестве примера рассмотрим квадратную сетку одина¬
ковых резисторов с проводимостью G = 1. Часть резисторов удалим из
сетки случайным образом и положим проводимость разорванных связей
равной нулю. Пусть концентрация целых связей сетки равна р и сетка
состоит из L х L узлов. При низком значении р электропроводимость
сетки равна нулю. Когда р растет и достигает критического значения рс,
формируется токопроводящий (перколяционный) кластер и сетка ста¬
новится проводящей. Значение рс строго определено только в пределе
бесконечной решетки, когда L —> оо. Для бесконечной квадратной ре¬
шетки рс = 0,5 (см. гл. 12).
Строгого аналитического решения задача электропроводности для
случайно разбавленных резисторных решеток не имеет. Поэтому для
288 -»\r Глава 15. Вычисление электропроводности композиционных систем
приближенных оценок используют итерационные методы [2, 3], мето¬
ды аналогового эксперимента [4, 5] и методы ренорм-групповых при¬
ближений [6-10]. Для приближенной оценки эффективной электро¬
проводности можно также использовать метод случайных блужданий,
предложенный в [11]. Суть этого алгоритма заключается в том, что
электропроводимость G композиционной системы, состоящей из N ком¬
понентов, может быть вычислена по формуле
где ki — весовой коэффициент, определяющий вклад /-го компонента
в общую электропроводимость композита, a G; — его электропроводи¬
мость. Задачу можно свести к дискретной, если использовать суще¬
ствующую сетку (плоскую, или объемную зависит от геометрии образ¬
ца). Каждой ячейке сетки припишем электропроводимость G;, которая
соответствует локальной электропроводности композита. Весовые ко¬
эффициенты ki в (15.1) можно вычислить методом случайных блужда¬
ний, а затем определить общую электропроводность композита (см. за¬
дачу 9 в конце главы). Эти коэффициенты зависят как от концентра¬
ции компонентов, так и от топологической структуры композиционного
материала.
Рис. 15.1. Схема перехода от композита (а) к решетке связей (б), которая
используется для расчета его электропроводимости [12]
Сеточные модели можно использовать при оценке электропроводно¬
сти композиционных материалов. Рассмотрим, например, модель компози¬
ционного материала, в которой ячейки сетки заполнены случайным обра¬
зом частицами проводящего и непроводящего материалов (рис. 15.1, а).
Каждую частицу можно заменить некоторым набором проводимостей,
который имитирует локальную проводимость данного композиционного
материала [3, 12]. Например, при использовании квадратной решетки
это можно сделать так, как показано на рис. 15.1, б, заменяя частицу
проводника или диэлектрика четырьмя связанными резисторами, про¬
водимости которых Gp и Gm соответственно. Таким образом, исходная
N
G = £k,Gh
(15.1)
1=1
15.2. Алгоритм Франка-Лобба для расчета электропроводности ->V 289
задача может быть сведена к расчету электропроводимости квадратной
решетки связей.
В этой главе проанализирован один из наиболее эффективных ме¬
тодов расчета электропроводимости случайно разорванных сеток рези¬
сторов, основанный на использовании алгоритма Франка-Лобба [13].
15.2. АЛГОРИТМ ФРАНКА-ЛОББА ДЛЯ РАСЧЕТА
ЭЛЕКТРОПРОВОДНОСТИ И ОПИСАНИЕ РАБОТЫ
ПРОГРАММЫ
15.2.1. Алгоритм Франка-Лобба
Главная идея алгоритма Франка-Лобба заключается в ис¬
пользовании серии преобразований проводимостей связей решетки, в
результате которых вся сетка может быть свернута и заменена все¬
го одним резистором, проводимость которого полностью эквивалентна
проводимости всей сетки. Таким образом, формально в этом методе
проводимость рассчитается без каких либо приближений, а точность
метода определяется лишь только ошибками округлении в вычислениях
преобразований.
15.2.1.1. Элементарные преобразования
Рассмотрим основные преобразования и особенности их
применения при трансформации сетки резисторов.
G\ С?2 Gs
Gx
Рис. 15.2. Набор элементарных преобразований проводимостей сетки: а) по¬
следовательное преобразование; б) параллельное преобразование;
в) преобразование звезда-треугольник
На рис. 15.2 представлен набор элементарных преобразований про¬
водимостей сетки, которые основаны на хорошо известных трансфор¬
мациях для последовательных и параллельных соединений, а также
преобразовании звезда-треугольник.
290 -l\r Глава 15. Вычисление электропроводности композиционных систем
Для последовательного соединения имеем
Gs = (15.2)
С/1 + С/2
а для параллельного
Gp = Gl + G2. (15.3)
В обеих случаях, замена двух проводимостей одной, рассчитанной
по формулам (15.2) и (15.3) полностью эквивалентна по отношению к
внешней электрической цепи.
15.2.1.2. Преобразование звезда-треугольник и их обобщение
Для преобразований звезда-треугольник имеем следую¬
щие соотношения
G2G3
Ga
G\ + G2 + G3 ’
°'-ЗйЗЬ5‘ <154)
Gc —
G\ + G2 + G 3
и для обратного к нему преобразования треугольник-звезда:
c'=°‘4<s; + i + i>
°^°M.T, + i + £)- (155)
0, = ОлОв(^ + ^ + ^).
Формулы преобразования трехлучевая звезда — треугольник (15.4)
и (15.5) могут быть обобщены на случай /г-лучевая звезда —/2-угольник.
Рисунок 15.3, а иллюстрирует случай прямого, а рис. 15.3, б обрат¬
ного преобразований, когда п = 6.
При прямом преобразовании величина проводимости G£/, которая
образуется путем удаления центральной точки звезды между лучами,
имеющими проводимости G* и Gj равна [14]
Сц = (15.6)
L Gk
k—\
Формула для обратного преобразования имеет вид
Gkm = GkGmj^ ОГ1. (15.7)
/=1
15.2. Алгоритм Франка-Лобба для расчета
электропроводности 291
а
б
Рис. 15.3. Обобщенные преобразования я-лучевая звезда — я-угольник и я-уголь-
ник — я-лучевая звезда
Как и в предыдущих случаях, замена одной электрической цепи на дру¬
гую с учетом формул (15.6) и (15.7) не нарушает токов и распределения
потенциала во внешней электрической цепи.
15.2.1.3. «Сворачивание» квадратной сетки сопротивлений
Теперь рассмотрим две последовательности элементарных
преобразований, представленных на рис. 15.4. Обозначим эти последо¬
вательности для удобства символически Г55 и Т43 и назовем их про-
пагаторами. Индексы пропагаторов обозначают начальное и конечное
количество резисторов, полученное в результате применения пропа-
гатора к участку цепи квадратной сетки. Пропагатор Г55 состоит из
последовательности преобразований треугольник-звезда и обратного к
нему преобразования.
2
5
5
8 5
Рис. 15.4. Диагональный пропагатор Т55 (а-г), который «переносит» диаго¬
нальную связь 1 (а), в положение 11 (г); пропагатор Т43 (д-з)
используется на границе сетки, где отсутствует сопротивление 4
292 •Ar Глава 15. Вычисление электропроводности композиционных систем
Комбинация этих преобразований позволяет «перенести» диагональ¬
ное сопротивление, обозначенное номером 1 на рис. 15.4, а через узел
квадратной сетки в положение, обозначенное номером 11 на рис. 15.4, г.
При этом происходит пересчет участка цепи таким образом, чтобы
начальную конфигурацию сопротивлений 1-5 можно было заменить
эквивалентной по отношению к внешней цепи конфигурацией 6-11.
На границах сетки, где отсутствуют сопротивления, обозначенные на
рис. 15.4, а номером 4, используется пропагатор Г43 (последователь¬
ность преобразований д-з на рис. 15.4).
Рис. 15.5. Преобразование сетки резисторов при использовании алгоритма
Франка-Лобба
На рис.15.5 приведена последовательность преобразований прово¬
димостей в алгоритме Франка-Лобба для квадратной сетки размером
3x3 узла. Проводимость сетки рассчитывается в горизонтальном на¬
правлении. Сворачивание сетки происходит, начиная с левого верхнего
горизонтального сопротивления. Применяя последовательно пропагато-
ры Г55 и Г43, можно «перенести» это сопротивление в левый нижний
угол сетки, как показано на рис. 15.5, б. В результате получим экви¬
валентную схему, приведенную на рис. 15.5, в. Применив затем про¬
пагатор Г43, можно исключить следующее горизонтальное сопротивле¬
ние в левом ряду и прийти к схеме, показанной на рис. 15.5, г. Теперь
верхние горизонтальное и вертикальное сопротивления в следующем
15.2. Алгоритм Франка-Лобба для расчета электропроводности •Ar 293
ряду можно заменить одним, используя формулу для последовательно¬
го соединения. Полученное диагональное сопротивление «переносим»
в правый нижний угол с помощью пропагатора Г55. Продолжая про¬
цесс сворачивания сетки в соответствии с последовательностью преоб¬
разований изображенной на рис. 15.5, д, получим схему, изображенную
на рис. 15.5, е. Крайняя правая часть сетки сворачивается с помощью
применения формул последовательного и параллельного соединений в
соответствии с рисунками 15.5, ей ж.
Таким образом, в результаты выполненных преобразований, квад¬
ратная сетка будет свернута к цепочке последовательно соединенных
сопротивлений, изображенной на рис. 15.5, з, которую можем заменить
одним сопротивлением, используя дважды формулу для последователь¬
ного соединения.
15.2.1.4. Применение метода Франка-Лобба
для более сложных плоских решеток
С помощью формул (15.6) и (15.7) можно построить пропа-
гаторы, которые будут удобны при расчете электропроводности для
других типов плоских решеток (треугольной, гексагональной или со¬
товой). На рис. 15.6 проиллюстрирована работа пропагатора Т54, кото¬
рый можно использовать при расчете электропроводимости треуголь¬
ной решетки.
Рис. 15.6. К иллюстрации работы пропагатора Г54
Вначале треугольник сопротивлений 1, 2, 5 преобразовывается в
звезду 6, 7, 8. Затем можем преобразовать четырехугольник 3, 4, 7, 8
в звезду 9, 10, 11, 12 с помощью формулы (15.7). Сопротивления 6, 9
можем заменить одним эквивалентным, используя формулу для после¬
довательного соединения. Выполнив преобразование звезда-четырех¬
угольник, получитм схему изображенную на рис. 15.6, д.
Рисунок 15.7 иллюстрирует последовательность преобразований ре¬
зисторов на треугольной решетке, которая преобразовывает ее в квад¬
294 -»\r Глава 15. Вычисление электропроводности композиционных систем
ратную решетку. Здесь, на первом шаге (рис. 15.7, а) с помощью фор¬
мул параллельного соединения «удаляются» диагональные сопротивле¬
ния на краях решетки и образуется схема, изображенная на рис. 15.7, б.
Последовательное применение пропагатора Т54 (рис. 15.6) позволяет
получить схему, изображенную на рис. 15.7, в.
а б
в
Рис. 15.7. Схема приведения треугольной решетки к квадратной
При преобразовании гексагональной решетки, она сначала транс¬
формируется в треугольную (рис. 15.8), а затем по схеме, представлен¬
ной на рис. 15.7 преобразовывается к квадратной.
а б
Рис. 15.8. Гексагональная решетка, изображенная на рисунке а, с помощью
преобразования звезда-треугольник может быть преобразована к
треугольной (б). Резисторы, отмеченные стрелочками на рисунке а,
преобразуются с помощью формулы последовательного преобразования
В общем случае, данный подход к вычислению электропроводности
может быть использован также при вычислении поведения комплекс¬
ной проводимости (импеданса) [15, 16]. Рассмотрим, например, модель
композиционного материала, представленного квадратной сеткой ком¬
15.2. Алгоритм Франка-Лобба для расчета электропроводности ->\г 295
плексных сопротивлений (рис. 15.9). Комплексную проводимость G;^
можно представить в виде
Gi,j,k — Gi,j,k “I" I(*)Ci,j,ky
где / — комплексная единица; /, j — индексные координаты узла, а
k = 1,2 (рис. 15.10), а) — частота внешнего напряжения, приложенного
к измерительным электродам. В зависимости от характера исследо¬
вательской задачи численные значения GIt/>& и могут быть либо
одинаковы, либо распределены на решетке по определенному закону.
Рис. 15.9. Квадратная сетка комплексных проводимостей (импедансов)
Рис. 15.10. Фрагмент квадратной сетки с элементами массива электропровод¬
ностей G(i,j,k). Узел с координатами (/,/) и два его резистора
(верхняя и левая связи) выделены жирным. Удаленные резисторы,
распределенные на решетки случайным образом с вероятностью
1 — р, обозначены пунктиром, и имеют нулевую электропроводи¬
мость. В соответствии с рисунком значения элементов массива
G(i,j +1,1) и G(i + 1,/, 2) равны нулю
15.2.2. Описание работы программы
Рабочая программа расчета электропроводимости квадрат¬
ной сетки сопротивлений содержится на диске в файле FL.f90. Про¬
грамма имеет модульную структуру и состоит из модуля общих пе¬
ременных и массивов comdata, главного модуля flmain и набора
внешних процедур.
296 •Ar Глава 15. Вычисление электропроводности композиционных систем
Опишем сначала назначение основных массивов и параметров про¬
граммы, определенных в модуле comdata:
module comdata
implicit none
!параметры программы
integer
integer
integer
real
NPROBE
NPC
P
real(8):: Gb=1.0
!переменные стат
real
real
real
(8)
(8)
(8)
real (8)
линейный размер квадратной сетки
(число узлов)
количество конфигураций
количество проводящих конфигураций
вероятность, обнаружения на решетке
целой связи
проводимость целой связи
обработки результатов расчета:
среднее значение электропроводимости
сетки
среднее значение квадрата
электропроводимости сетки
стандартная ошибка вычисления
электропроводимости
allocatable:: G(:,:,:) !массив для хранения
!значения
!электропроводимостей
!связей
Gm
G2m
dGm
!список параметров программы
namelist /prgparam/ L, Р,NPROBE
end module comdata
Для хранения информации о проводимости резисторов используется
массив G(i,j,k). Данный массив организован таким образом, что
первые два индекса используются для записи координат узла сетки,
а трений индекс к может принимать значения 1, или 2 (рис. 15.10).
Основными параметрами программы являются размер сетки L, коли¬
чество конфигураций NPROBE и вероятность обнаружения на решетке
целого резистора Р. Данные параметры объединены в именной список
namelist /prgparam/. Их значения записаны во входном текстовом
файле f 1. txt и считываются процедурой init в начале работы основ¬
ного модуля программы, который выглядит следующим образом:
program fl
use comdata
use msflib
implicit none
integer probe !счетчик испытаний
real (8) Gc !проводимость конфигурации
15.2. Алгоритм Франка-Лобба для расчета электропроводности 297
real (8) FLA !внешняя функция расчета проводимости
!квадратной сетки
type (rccoord) curpos
call init ()
do probe=l,NPROBE
!печатаем на экран номер конфигурации
if (mod(probe,100)==0) then
call settextposition(1,10,curpos);
write(*,20)'probe=',probe, ' '
20 format(a7,i6,a4)
endif
call newconfig(probe) !генерируем новую конфигурацию
Gc=FLA() !рассчитываем ее проводимость
!накапливаем результаты расчета для усреднения
if (GO1D-70) then
NPC=NPC+1
Gm =Gm +Gc; G2m=G2m+Gc*Gc
end if
end do
!записываем результаты в выходной файл
call saveresults()
end program fl
Формирования очередной конфигурации целых связей, которые слу¬
чайным образом распределены на решетки с вероятностью Р, осу¬
ществляется путем вызова из основного модуля внешней процедуры
newconfig:
subroutine newconfig(probe)
use comdata
use msflib
implicit none
integer probe !номер испытания
integer i,j !индексы
real rnd !случайное число
G=0 !обнуляем массив связей
call seed(probe) !генерируем новую последовательность
!случайных чисел
!генерируем новую конфигурацию целых связей
do j =1,L
do i=l,L
call random(rnd)
if(rnd<P) G(i,j,2)=Gb
end do
end do
298 -»Ъ» Глава 15. Вычисление электропроводности композиционных систем
do j =1,L-l
do i=l,L-l
call random(rnd)
if(rnd<P) G(i,j,l)=Gb !вертикальные связи
end do
end do
end subroutine newconfig
Алгоритм Франка-Лобба оформлен в виде внешней процедуры-
функции FLA (). В результате ее выполнения вычисляется значение
электропроводимости конфигурации резисторов на квадратной сетке:
real (8) function FLA()
use comdata
implicit none
integer i,j,k,m [индексы
real (8) G1 [проводимость связи сетки
real (8) GL [проводимость квадратной сетки
real (8) parallel, series [внешние функции вычисления
[эквивалентной проводимости
[параллельного и
[последовательного соединений
!сворачиваем квадратную сетку
GL=0
do 1 i=l,L-l
do 2 j=L-l,1,-1
I определение значения диагональной проводимости
if (i==l) then
G1=G(i,j+1,2) [случай: рис.15.5a,в
else
[случай: рис.15.5г,д
Gl=series(G(i,j+1,2),G(i-1,j,1))
end if
[переброска диагональной проводимости через решетку
k=i; m=j
if(m==l) then
[случай: рис.15.56, д (нижнее диагональное
1 сопротивление)
call Т43(Gl,G(k,m,2),G(k,m,1),G(k+l,m,2)); goto 1
else
call T55(G1,G(k,m,2),G(k,m,1),G(k,m-l,l),G(k+l,m,2))
end if
k=k+l; m=m-l
15.2. Алгоритм Франка-Лобба для расчета электропроводности -1\г 299
!случай: рис.15.5г (нижнее диагональное сопротивление)
if(k==L) then
G(к,m,2)=parallel (G1, G (k, m, 2)); goto 2
end if
!случай: рис.15.56 (нижнее диагональное сопротивление)
if(m==l) then
call T43(Gl,G(k,m,2),G(k,m,1),G(k+l,m,2)); goto 2
end if
goto 3
2 continue
1 continue
!сворачивание связей на правой стороне сетки
!(рис.15.5е,ж)
i=L
do j=L—1,1,-1
G(i,j,2)=parallel(series(G(i,j+l,2) , G(i-1, j , 1) ) , &
G(i,j,2))
end do
{сворачивание последовательной цепочки (рис.15.5з)
GL=series(G(1,1,2),G(2,1,2))
do i=3,L
GL=series(GL,G(i,1,2))
end do
FLA=GL !(рис.15.5и)
end function FLA
Функция FLA, пожалуй, самая сложная для понимания часть про¬
граммы. Лучше всего, анализировать работу данной функции поша¬
гового, сопоставляя с последовательностью преобразований, показан¬
ных на рис. 15.5. Выполнение пропагаторов в соответствии с приняты¬
ми нами обозначениями реализуется путем вызова внешних процедур
Т55, Т43.
Внешние функции и процедуры, которые использует функция FLA,
представляют собой запрограммированные формулы (15.2)—(15.5), по¬
этому нет смысла описывать их все. Рассмотрим, лишь в качестве
примера, программный код для пропагатора Т55:
subroutine Т55(Gl,G2,G3,G4,G5)
implicit none
real (8) Gl,G2,G3,G4,G5 {проводимости связей сетки
real (8) G6,G7,G8
real (8) G9,G10,Gil
real (8) G123,G4 58
300 ->\r Глава 15. Вычисление электропроводности композиционных систем
!накладываем ограничения на величину
!проводимости связей сетки
if(G1>1D80) G1=1D80
if (GK1D-80) Gl=lD-80
if (G2>1D80) G2=1D80
if (G2<lD-80) G2=lD-80
if(G3>1D80) G3=1D80
if(G3<lD-80) G3=lD-80
if (G4>1D80) G4 = 1D80
if (G4<lD-80) G4 = lD-80
if (G5>1D80) G5=1D80
if (G5<lD-80) G5=lD-80
!преобразование треугольник-звезда
G123=(1./G1+1./G2+1./G3) !формула (15.5)
G6 =G1*G2*G123
G7 =G1*G3*G123
G8 =G2*G3*G123
!преобразование звезда-треугольник
G458=G4+G5+G8 !формула (15.4)
G9 =G4*G8/G458
G10 =G5*G8/G458
Gil =G4 *G5/G458
(определяем значения проводимостей после пересчета
Gl =G11
G2 =G6
G3 =G7
G4 =G9
G5 =G10
end subroutine T55
В данной процедуре все переменные обозначены в соответствии с
рис. 15.4, а-г. Хотелось обратить внимание читателей на две важные
детали. Поскольку в перколяционной модели связей некоторые прово¬
димости могут принимать нулевое значение, поэтому чтобы избежать
деление на нуль, и вытекающих отсюда последствий, можно заме¬
нить такие проводимости очень маленьким числом е\ (здесь выбрано
£\ = Ю-80). При сворачивании больших сеток, в которых число узлов
может достигать значения ~ 104, значение проводимостей отдельных
связей при пересчете могут быстро возрастать, превышая даже допу¬
стимый диапазон чисел двойной точности. Поэтому приходится так¬
же огранивать значение проводимостей связей сверху большим чис¬
лом £2 (здесь выбрано £2 = 1/fi), чтобы избегать ошибки переполнения.
Последнее замечание справедливо лишь для случая, когда проводи¬
15.2. Алгоритм Франка-Лобба для расчета электропроводности -1\г 301
мость целых связей в модели может принимать большие численные
значения.
15.2.3. Примеры работы программы
С помощью программы FL.f90 были проведены вычисле¬
ния на квадратной сетке размера L = 128, состоящей из бинарной смеси
резисторов с проводимостями Gp = 104 и Gm = 1.
Вероятность р обнаружить на решетке резистор с высокой проводи¬
мостью Gp изменялась в интервале от нуля до единицы. На рис. 15.11
представлена, усредненная по 10 конфигурациям, зависимость электро¬
проводности G сетки от концентрации р. С ростом р величина элек¬
тропроводимость сетки меняется от Gm к Gp. В узкой области значе¬
ний р G [0,45,0,55] электропроводность изменяется на два порядка. В
точке перколяционного перехода рс = 0,5 величина электропроводности
G = y/GpGm = 100 (пунктирная линия на рис. 15.11).
0,2 0,4 0,6 0,8 1
Р
Рис. 15.11. Зависимость электропроводности G квадратной сетки от концен¬
трации проводящих связей р. Пунктирная линия указывает на
значение электропроводности при р = рс = 0,5
Для того, чтобы убедиться в правильности работы программы, были
проведены расчеты, аналогичные представленным в работе [17]. Вычис¬
ления были проведены на квадратных решетках одинаковых размеров и
для одинакового количества конфигураций при значении р = рс = 0,5.
Все результаты расчетов сведены в табл. 15.1. В столбцах 3 и 4 при¬
ведены данные из работы [17], а в столбцах 5-7 результаты наших
вычислений. Сравнение полученных результатов показывает, что чис¬
ленные значения электропроводимости сеток с точностью до ошибки
вычисления практически совпадают.
302 •Ar Глава 15. Вычисление электропроводности композиционных систем
Таблица 15.1. Результаты расчетов электропроводности для различных разме¬
ров квадратной сетки L с использованием программы FL.f90
Размер
квадратной
сетки, L
Полное чи¬
сло конфи¬
гураций, N
Число про¬
водящих
конфигура¬
ций, Nc
Среднее зна¬
чение элект¬
ропроводи¬
мости, G
Число про¬
водящих
конфигура¬
ций, Nc
Среднее
значение
электропро¬
водности, G
Ошибка
вычисле¬
ния, G
1
2
3
4
5
6
7
4
110000
55166
0,2886
56161
0,2924
0,0005
6
110000
54994
0,1939
55632
0,1942
0,0003
8
110000
55295
0,1455
55333
0,1463
0,0003
10
110000
55067
0,1172
55290
0,1170
0,0002
12
40000
20005
0,0981
20028
0,0980
0,0003
14
20000
10075
0,0846
10110
0,0848
0,0003
16
40000
20094
0,07411
20007
0,0719
0,0002
18
40000
20091
0,066117
20101
0,0658
0,0002
20
20000
9978
0,05978
10079
0,0598
0,0003
30
20000
9992
0,03987
10169
0,0402
0,0002
40
20000
10032
0,03002
10087
0,0305
0,0001
50
20000
9938
0,0243
10124
0,0244
0,0001
60
2704
1368
0,0203
1334
0,0205
0,0002
100
2400
1197
0,01242
1206
0,0124
0,0002
200
1300
661
0,006329
678
0,0065
0,0001
Для усреднения были выбраны только перколяционные конфигура¬
ции, для которых электрическая проводимость была выше некоторой
минимальной величины Gmin (в программном модуле fl выбрана вели-
чина Gmin = 10“70).
15.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Напишите процедуры, реализующие прямое и обратное преобразова¬
ние я-лучевая звезда — я-угольник.
2. Выше порога перколяции электропроводность макроскопической си¬
стемы начинает возрастать по степенному закону G~ (р — рсУ, где
рс = 0,5 — порог перколяции по связям для квадратной решетки, а
t — критический индекс проводимости. Величину t можно рассчи¬
тать, анализируя зависимость InG от \п(р — рс). Используя програм¬
му FL. f 90, определите численное значение t для квадратной сет¬
ки вблизи порога перколяции, L = 100, р Е [0,502,0,52]. Результаты
усредните по 10 различным конфигурациям.
3. Более точный способ оценки t, основан на учете того, что в точке
перколяции существует соотношение между электрической прово¬
15.3. Задачи для самостоятельной работы -1\г 303
димостью и размером системы G ~ L_f/V, где v — критический ин¬
декс связности, который не зависит от типа решетки и определяется
пространственной размерностью системы. Для двухмерных систем
v = 4/3 [1]. Определите численное значение ty анализируя зависи¬
мости G(L) для квадратной сетки, L = 4 - 200, р = 0,5. Результаты
усредните по 10 различным конфигурациям.
4. Напишите процедуру, которая реализует работу пропагатора Т54
(см. рис. 15.6).
5. Напишите программы для трансформации треугольной и гексаго¬
нальной решеток в квадратную (рисунки 15.7 и 15.8).
6. Используя комплексный тип данных Фортрана, обобщите программу
FL. f 90 для расчета импеданса модели композиционного материала,
представленного на рис. 15.9.
7. Модифицируйте программу FL.f90 для расчета электропроводимо¬
сти композиционного материала. Для этого напишите процедуру,
заполняющую ячейки квадратной решетки случайным образом ча¬
стицами проводника и диэлектрика с проводимостями Gp и Gm, соот¬
ветственно и выполняющую преобразование, показанное на рис. 15.1.
а б
Рис. 15.12. К вычислению электропроводимости композиционной среды, ко¬
торая имеет включение в виде фрактального кластера DLA (а),
или компактного кластера (б). Радиус компактного кластера равен
радиусу Rg гирации кластера DLA
8. Используя программу, полученную при решении предыдущей задачи,
вычислите электропроводность композиционной среды, которая име¬
ет включение или в виде фрактального кластера DLA (рис. 15.12, а),
или в виде компактного кластера (рис. 15.12, б). Предполагается, что
частички кластера являются проводящими (проводимость Gp), а сре¬
да является плохопроводящей (проводимость Gm Gp). Для генера-
304
Глава 15. Вычисление электропроводности композиционных систем
ции кластера DLA используйте программу dla_bas.f90 (гл. 8) и
допишите соответствующие процедуры для записи и считывания ко¬
ординат частиц в файл. Проанализируйте зависимости электропро¬
водности композита от степени наполнения р и размера системы L.
9. Напишите программу для оценки электропроводности композита,
показанного на рис. 15.1, а, с помощью метода случайных блужда¬
ний. При вычислении электропроводности необходимо использовать
уравнение (15.1). На решетку в произвольном месте помещается
случайно блуждающая частица и вероятность перехода между со¬
седними ячейками / и k определяется, как /у* = 2GyG*/(Gy -f G^),
где Gi — Gi/Gmax нормированные значения проводимостей, Gmax =
= max{G;, i = 1,2}. Коэффициенты ki вычисляются, как kt = (.Ni)/N,
где (Ni) соответствует среднему числу посещений ячеек компози¬
та с электропроводностью Gi, N — количество шагов случайных
блужданий. Счетчики Ni и N увеличиваются на 1 после каждой
попытки перехода: удачной, или неудачной. После того, когда вре¬
мя 7V достигает некоторой максимальной величины Afmax, на решетке
в произвольном месте выпускается новая частица и расчет продол¬
жается. Сравните эффективность применения данного алгоритма и
алгоритма Франка-Лобба для вычисления электропроводности ком¬
позиционного материала, рассмотренного в задаче 8. Для расчетов
возьмите сетку размером 100 х 100 ячеек, заполненную проводящим
компонентом с вероятностью р = 0,59. Выберите для проводящего
компонента Gp = 1, а для диэлектрика Gm = 0.
1. Stauffer D., Aharony A. Introduction to Percolation Theory. — 2nd ed. —
London: Taylor and Francis, 1992; см. также Тарасевич Ю.Ю. Перколяция:
теория, приложения, алгоритмы. — М: Эдиториал УРСС, 2002. — 112 с.
2. Kirkpatric S. Percolation and Conduction 11 Reviews of Modern Physics. —
1973. - V. 45, No. 4. - P. 574-588.
3. Ciobanu C., Liu Y., Wang Y., Patton B.R. Numerical Calculation of Electrical
Conductivity of Porous Electroceramics 11 J. Electroceramics. — 1999. —
V. 3. - P. 17-23.
4. Watson B. P., Leath P. L. Conductivity in the two-dimensional-site percolation
problem // Phys. Rev. B. — 1974. — V. 9. — P. 4893.
5. Tobochnik /., Dubson M. A., Wilson M. L., Thorpe M. F. Conductance of a
plane containing random cuts 11 Phys. Rev. A. — 1989. — V. 40. —
P. 5370-5376.
6. Derrida B., Vannimenus J. A transfer-matrix approach to random resistor net¬
works // J. Phys. A15. - 1982. - P. L557-L564.
15.4.
ЛИТЕРАТУРА
15.4. Литература -*\r 305
7. Derrida В., Zabolitzky J.G., Vannimenus J., Stauffer D. A transfer matrix
program to calculate the conductivity of random resistor networks 11 J. Stat.
Phys. (USA). - 1984. - V. 36. - P. 31-42.
8. Paredes R. V., Alvarado V. Scaling of heterogeneous distributions of conduc¬
tances: Renormalization versus exact results // Phys. Rev. E. — 1998. —
V. 58, No. 1. - P. 771.
9. Byshkin M.S., Turkin A. A. A new method for the calculation of the conduc¬
tivity of inhomogeneous systems 11 J. Phys. A38. — 2005. — P. 5057-5067.
10. ClercJ.P., Podolskiy V.A., Sarychev A. K. Precise determination of the con¬
ductivity exponent of 3D percolation using exact numerical renormalization //
Eur. Phys. J. - 2000. - V. B15. - P. 507-516.
11. McCarthy J. F. Effective conductivity of many-component composites by a
random walk method // J. Phys. A23. — 1990. — P. L749-L753.
12. Yuge Y., Onizuka K. Monte Carlo experiment for the two-dimensional site
percolation network // J. Phys. Cl 1. — 1978. — P. L763-L768.
13. Frank D.J., Lobb C.J. Highly efficient algorithm for percolative studies in two
dimensions 11 Phys. Rev. B. — 1988. — V. 37. — P. 302-307.
14. Fogelholm R. The conductivity of large percolation network samples // J.
Phys. C: Solid St. Phys. - 1980. - V. 13. - P. L571-L574.
15. Han D. G., ChoG.M. Simulation of impedance for 2-D composite // Elec-
trochimica Acta. — 1999. — V. 44. — P. 4155-4161.
16. Bouamrane R., Almond D. P. The «emergent scaling» phenomenon and the
dielectric properties of random resistor-capacitor networks // J. Phys. C15. —
V. 2003. - P. 4089-4100.
17. Lobb C.J., Frank D.J. Percolative conduction and Alexander-Orbach conjec¬
ture in two dimensions // Phys. Rev. B. — 1984. — V. 30, No. 7. —
P. 4090-4092.
ГЛАВА ЭЛЕКТРИЧЕСКИЙ ПРОБОЙ
16
16.1. ПРОСТЕЙШИЕ МОДЕЛИ ЭЛЕКТРИЧЕСКОГО ПРОБОЯ
Явление электрического пробоя (молния, искровой разряд
в газовой среде, пробой диэлектрика) обычно развивается путем обра¬
зования узких каналов, которые имеют сложную, случайно разветвлен¬
ную структуру. Пробой развивается, если напряженность электриче¬
ского поля превышает электрическую прочность материала. Например,
для воздуха она составляет 30 кВ/см, для пропитанного картона и
полиэтилена — это 40-55 кВ/мм, для слюды — более 100 кВ/мм и для
трансформаторного масла не менее 280 кВ/см.
Обычно, при электрическом пробое происходит рост древовидных
структур (дендритов), которые преимущественно образуются в местах
с повышенной локальной напряженностью электрического поля (высту¬
пы на поверхности электрода, проводящие включения, микротрещины,
полости и т.д.). Одним из примеров являются разрядные фигуры Лих-
тенберга, которые впервые наблюдались в 1777 г. при скользящем ис¬
кровом разряде на поверхности изолятора, покрытого порошком. Дан¬
ные фигуры удобно визуализировать, проявляя фотопластинку, подло¬
женную во время разряда под слой изолятора. Любопытные картины
свечения газового разряда или так называемого «эффекта Кирлиан»
наблюдаются вблизи поверхности биологических объектов в электри¬
ческом поле высокой напряженности [1].
Помимо чисто научного интереса, исследования механизмов элек¬
трического пробоя в различных конденсированных средах представля¬
ют также и практический интерес. К настоящему времени разрабо¬
тано ряд импульсных электроразрядных технологий, таких как элек-
троимпульсное бурение, дробление и дезинтеграция, такие технологии
применяются для очистки поверхностей, интенсификации экстракции и
ряда других целей. С историей развития этой области исследований и
основных представлениях о механизмах возникновения и развития раз¬
ряда в импульсных полях можно познакомится, например, в работе [2].
16.1. Простейшие модели электрического
пробоя 307
В последнее время для изучения электрофизических свойств ма¬
териалов и моделирования процессов пробоя все чаще используются
компьютерные методы. Компьютерные модели применяются для иссле¬
дования неупорядоченных сред, например, гранулярных сверхпроводни¬
ков, композиционных материалов (металл-диэлектрик) и др [3]. В про¬
стейших случаях используются решеточные модели, в которых среда
моделируются с помощью токопроводящих элементов различной при¬
роды (резисторы, конденсаторы, диоды). Эти элементы располагаются
на связях квадратных, треугольных, кубических или гексагональных
решеток. Континуальные модели до настоящего времени используют¬
ся крайне редко, так как для них сложно составлять программные
алгоритмы, учитывающие изменение топологии системы в процессе
разрушения.
16.1.1. Модели типа резистор-изолятор (модель RI)
и резистор-сверхпроводник (модель RS)
По характеру пробоя токопроводящих элементов сущест¬
вующие модели можно условно разделить на пробой типа резистор-
изолятор (модель RI) и пробой типа резистор-сверхпроводник (мо¬
дель RS) (рис. 16.1). В модели пробоя RI [4] предполагается, что если
приложенное к токопроводящему элементу напряжение и превышает
некоторое критическое значением, то он становится диэлектриком (т. е.
«плавится»). В модели пробоя RS [5] при и > ис, токопроводящий эле¬
мент становится сверхпроводником, т. е. замыкает накоротко цепь, что
соответствует развитию стримера.
Вероятности / разрушения (пробоя) резистора может зависеть от при¬
ложенного напряжения и по различным законам, например f(u) ~ ит?,
№ пи exp(—ис/и), f{u) ~ th{u/uc) или f(u) = Н(и — ис). Здесь 7] —
степенной показатель, а Н(и — ис) — ступенчатая функция Хевисайда,
Н(и — ис) = 1 при и > ис и Н(и — ис) = 0 при и < ис. Если разрушение
происходит по термоактивационному механизму, то в этом случае
используют формулу ехр(-Д£/£вТ), где &Е(ис) — энергия актива¬
ции, которая в общем случае может довольно сложным образом зави¬
сеть от ис.
Рис. 16.1. Два типа моделей электрического разрушения
резисторных сеток: резистор-изолятор (RI) [4] и резистор-
сверхпроводник (RS) [5]
308 ->\r Глава 16. Электрический пробой
16.1.2. Стохастические и детерминистические модели
По характеру развития электрического пробоя различа¬
ют стохастические и детерминистические модели пробоя. В стоха¬
стических моделях решетки первоначально заполняются одинаковыми
резисторами, затем вычисляется распределение потенциалов, случай¬
ным образом выбирается резистор, который разрушается с вероятно¬
стью f(u) [6, 7]. В процессе эволюции пробоя система постепенно
наполняется резисторами с более низкой (модель RI [4]) или более
высокой (модель RS [5]) электропроводностью, т. е. система становится
неоднородной. В детерминистических моделях система первоначально
является неоднородной, т. е. наполнена резисторами имеющими раз¬
ную электропроводность и эта неоднородность усиливается в процес¬
се эволюции пробоя. Однако характер развития пробоя для детерми¬
нистических моделей может полностью определяться спецификой на¬
чального распределения резисторов по решетке [8]. Возможности ис¬
следования кинетики развития пробоя для моделей различного типа
обсуждаются в [9].
В литературе проанализированы различные варианты моделей про¬
боя, в которых учтено влияние начальной замороженной неоднородно¬
сти, барьеров и включений с различной электропроводностью, диэлек¬
трической проницаемостью прочностью и различные вероятностные за¬
коны разрушения [10-12].
В последнее время проведены детальные экспериментальные и тео¬
ретические исследования фрактальной структуры разрядных картин
[6, 13-18]. Фрактальная размерность df является одной из наиболее
важных характеристик, которые исследуются при теоретическом мо¬
делировании. Из анализа фотографий электрических молний получено
значение фрактальной размерности df = 1,34 ±0,05 [13]. В [14] прове¬
дены детальные исследования извилистости и разветвленности кана¬
лов молнии. Сообщалось, что фрактальная размерность картин пробоя
уменьшалась с уменьшением диэлектрической постоянной изолято¬
ра [15]. Для двумерной стохастической модели показано, что разрядные
картины характеризуются фрактальной размерностью df= 1,75±0,02 [6].
Авторы [16] для стохастической модели электрического разряда полу¬
чили величину, близкую к df ^ 1,66. В [17] двумерная стохастическая
модель была обобщена на трехмерный случай, при этом рассчитана
средняя фрактальная размерность трехмерных разрядов и их двумер¬
ных проекций. В [18] развита компьютерная модель для описания путей
каналов молнии в грозовой туче, основанная на численном решении
уравнения Пуассона и для фрактальной размерности получены значе¬
ния, находящиеся в интервале от 1,1 до 1,4.
16.1. Простейшие модели электрического пробоя -1\г 309
Рассмотрим некоторые популярные модели, используемые для компью¬
терной симуляции явлений электрического пробоя. Более детальный
обзор различных компьютерных моделей такого типа можно найти в [3].
16.1.2.1. Стохастическая модель (модель NPW)
Модель NPW [6] является стохастической моделью лапла-
совского роста, в которой используется формализм, подобный исполь¬
зуемому при изучении роста кластеров в модели диффузионно-контро¬
лируемой агрегации Виттена и Сандера (см. гл. 8). Вероятность роста
кластера контролируется скалярным полем потенциала и, удовлетво¬
ряющим уравнению Лапласа Ди = 0 с граничными условиями и=0 на
поверхности кластера и фиксированным значением и = 1 на круговом
электроде. В модели NPW предполагается, что развитие пробоя про¬
исходит в однородной среде, т. е. электропроводности всех связей на
решетке первоначально являются одинаковыми. Пробой инициализиру¬
ется случайным образом путем разрушения связи вблизи центрального
электрода. В дальнейшем эволю¬
ция пробоя происходит за счет раз¬
рушения связей, лежащих на пери¬
метре кластера, образуемого разру¬
шенными связями.
Пример разрядной картины, об¬
разуемой для модели NPW, пред¬
ставлен на рис. 16.2. Процесс раз¬
вития пробоя можно формально
рассматривать как рост кластера,
происходящий путем присоедине¬
ния к кластеру одного из узлов пе¬
риметра (незаполненные узлы на
рис. 16.2). На каждом временном
шаге к кластеру пробоя присоеди¬
няется по одному случайно выбран¬
ному узлу i. Вероятность присоеди¬
нения к кластеру (т. е. вероятность
пробоя) определяется с помощью степенного соотношения /= cuj, где
щ — потенциал выбранного узла, c = Y,jU- — константа нормировки.
Здесь суммирование проводится по всем узлам j на периметре кластера
пробоя, а г] является подгоночным параметром. Величина rj подбирается
таким образом, чтобы картина пробоя наиболее реалистично описывала
экспериментальные результаты.
После присоединения нового узла к кластеру пробоя, он приоб¬
ретает потенциал равный потенциалу кластера, и = 0. Это означает,
Рис. 16.2. К описанию стохастиче¬
ской модели электрического пробоя
NPW [6]
310 -»\л Глава 16. Электрический пробой
что проводимости всех связей, соединяющих данный узел с кластером
пробоя, равны бесконечности, т. е. модель NPW принадлежит к модели
пробоя типа RS.
16.1.2.2. Детерминистическая модель (модель Такаясу)
В детерминистической модели Такаясу [8] предполагает¬
ся, что резисторы, соединяющие узлы решетки, имеют неравные элек¬
тропроводности Gkjj, которые равномерно распределены в интервале
Gm( 1 — 6) < Gk,ij < Gm( 1 + 5), где Gm(= 1) — средняя проводимость свя¬
зи, а параметр 0 < 6 < 1 характеризует степень электрической неодно¬
родности системы.
Распределение потенциалов в узлах решетки вычисляется на основе
уравнения Лапласа. С учетом того, что сумма токов в ij узле сетки
равна нулю, iktij = 0, и ik,ij = Gk,ij(uktij - ut/), получим
Un =
У Gk,ijUk,ij
У Gb,ij
k
(16Л)
где суммирование по k выполняется по ближайшим соседям узла ij в
соответствии с рис. 16.3.
/
L
I 1 1
L 1 1
‘‘
/
о '
II 1
и 1
9 1
2<
1 «
п
и
i
1 2
L
U\
U2
/
' g2
, ^
\ Сз
\
\
Uij j
/
/
У
Щ
из
G\ = Go,i,j\ G2 = Gijj
G3 = Go,t,/-i; Ga = G\
Рис. 16.3. К описанию детерминистической модели Такаясу [8]
При моделировании пробоя на каждом временном шаге t вычисля¬
ется падение потенциала на каждой связи и и проверяется условие
и > ис. Связи, для которых это условие выполняется, разрушаются
и их электропроводность значительно возрастает. В модели Такаясу
при пробое резистора (и > ис) его электропроводность изменяется по
закону Gk,ij —> AGktij, где Л > 1. Таким образом, эта модель при Л = оо
эквивалентна модели пробоя типа RS [5].
16.1. Простейшие модели электрического пробоя 311
Для однородной системы (8 = 0) ее электропробой инициируется при
общем напряжении U, приложенном к электродам, равном ucL. Поэто¬
му, при моделировании удобно использовать нормированное значение
приложенного напряжения и* = U/ucL.
t= 12 t= 17 t = 25
L = 100
Рис. 16.4. Развитие электрического пробоя для детерминистической модели
Такаясу [8] при 8 = 0,9 и и* = 0,53. Момент времени t = 17 соот¬
ветствует образованию перколяционного кластера
На рис. 16.4 показан пример развития пробоя для детерминистиче¬
ской модели Такаясу при (5 = 0,9).
16.1.3. Термоактивационная модель
Интересный подход, сочетающий в себе оба типа пробоя
RS и RI предложен в работе Пенетты [19]. В этой работе рассмотрена
модель, в которой разрушение токопроводящих элементов происходит
за счет выделения на них тепла. Данная модель позволяет рассмат¬
ривать процессы разрушения как проводящих, так и непроводящих
пленок, что особенно важно для прогнозирования надежности работы
современных интегральных схем. Тонкая пленка моделируется квад¬
ратной сеткой резисторов, начальные значения сопротивлений которых
одинаковы и равны Zq. Тип пленки (проводящая, или непроводящая)
определяется начальной величиной Zq. Общее количество резисторов
равно N = 2L2, где L — линейный размер решетки. В модели рассмат¬
ривается два случая граничных условий: постоянного приложенного
напряжение U (непроводящая пленка), или постоянного тока /, про¬
ходящего через пленку (проводящая пленка). Общее сопротивление Z
пленки может быть вычислено с использованием уравнения баланса
мощности
i2z=iiizn,
п=1
312 •Ar Глава 16. Электрический пробой
где in — ток, проходящий через отдельное сопротивление сетки. Пленка
помещается на подложку, температура которой равна То. Сопротивле¬
ние каждого резистора Zn изменяться в зависимости от его температу¬
ры Тп по закону Zn(Tn) = Z0[l + jz{Tn - Г0)], где yz — температурный
коэффициент сопротивления (ТКС). Изменение температуры резисто¬
ра Zn происходит за счет тепловыделения на нем, а также теплопереда¬
чи от ближайших соседних резисторов Zm>n и вычисляется с помощью
уравнения
Тп — То + А \^п^п “I XI (Zm,ni2m,n — Zni2) >
L V m—\ J
где v (= 6 для квадратной решетки) — количество ближайших соседей,
im,n — токи соседних сопротивлений, В = 3/4 и соответствует равно¬
мерному распределению тепла между горизонтальными и вертикальны¬
ми сопротивлениями, а параметр А [К/Вт] — коэффициент пересчета
мощности в температуру. В данной модели разрушение пленки происхо¬
дит случайным образом за счет генерации дефектов, которые могут воз¬
никать и восстанавливаться с вероятностью foxR) — ехР(—£д(/?)Ав7л)>
где индексы D(R) соответствуют образованию (восстановлению) дефек¬
та, а Е — энергия активации. При генерировании дефектов для непро¬
водящей пленки текущее сопротивление Zn резко падает и происходит
RS пробой сопротивления, т. е. величина сопротивления становится
равной AZ„, где А <С 1. В случае генерирования дефекта восстановле¬
ния текущее значение дефектного сопротивления увеличивается, т. е.
становится равным A~{Zn. Для проводящей пленки в случае генерации
дефекта или его восстановления величина сопротивления изменяется в
обратном порядке.
Далее в данной главе будут рассмотрены алгоритмы и программы
для реализации стохастической модели Ниемеера-Пьетронеро-Вей-
смана (NPW) [6], детерминистической модели Такаясу [8] и термо¬
активационной модели [19].
16.2. АЛГОРИТМЫ И ОПИСАНИЕ РАБОТЫ ПРОГРАММ
В описанных ниже решеточных алгоритмах предполагает¬
ся, что узлы связаны между собой резисторами. На каждом итерацион¬
ном шаге определяется распределение потенциалов по узлам решетки,
определяется падение потенциала на каждом резисторе, а затем прини¬
мается решение о возможности его разрушения (пробоя).
16.2.1. Стохастическая модель NPW
В стохастической модели NPW начальные электропровод¬
ности всех резисторов принимаются одинаковыми, а вероятность раз¬
16.2. Алгоритмы и описание работы программ Аг 313
рушения f(u) возрастает при увеличении падения потенциала на рези¬
сторе. Здесь приведен вариант алгоритма стохастической модели NPW
для пробоя между центральным и внешним круговым электродами.
1) задаем начальные значения электропроводностей для
всех связей на решетки {G=l}, определяем потенциал
в центральном узле (и=0) и потенциал на узлах
кругового электрода (и=1). Вычисляем распределение
потенциалов {и} для всех остальных узлов решетки;
2) выбираем случайным образом узел на периметре кластера
пробоя и вычисляем вероятность присоединения этого
узла к кластеру / =сил. В случае присоединения этого
узла ереходим к пункту 3), а противном случае
выбираем случайным образом следующий узел на периметре
и продолжаем эту процедуру до тех пор, пока какой-либо
из них не присоединится к кластеру;
3) вычисляем новое значение потенциала во всех узлах
решетки, в узлах кластера пробоя полагаем и=0, в узлах
внешнего кругового электрода полагаем и=1; переходим
к пункту 2);
4) заканчиваем выполнение программы после образования
проникающего кластера пробоя, который достигает
внешнего кругового электрода.
16.2.2. Обобщенная модель Такаясу
Рассмотрим компьютерный алгоритм для обобщенной
модели Такаясу. В данной модели начальные электропроводности
всех резисторов не являются одинаковыми. Функция распределения
электропроводностей является ступенчатой (равномерной), а вероят¬
ность пробоя связи не носит порогового характера (как в исходной
модели Такаясу) и равна /= 1 при и>ис\ / = иц при и < ис, где
ис = 1. При jj —► оо данная обобщенная модель приобретает порого¬
вый характер и вырождается в обычную детерминистическую модель
Такаясу.
1) задаем начальные электропроводности резисторов G,
а также потенциалы в узлах решетки и на электродах
(рис. 16.3);
2) находим распределение потенциалов {и} по узлам решетки
и с вероятностью f(и) разрушаем каждый резистор,
увеличивая его электропроводность Gk.ij—>Л Gk,ij, где Л^>1;
3) выполнение программы останавливается при условии
отсутствия вновь пробитых резисторов, в противном
случае возвращаемся к п.2.
314 -*V Глава 16. Электрический пробой
16.2.3. Термоактивационная модель
Алгоритм для термоактивационной модели выглядит сле¬
дующим образом:
1) Моделирование начинается с рассмотрения однородной
решетки с одинаковыми величинами сопротивлений Zo всех
резисторов. Вычисляется распределение потенциала в
узлах решетки и токов, проходящих через отдельные
резисторы, а затем общее сопротивление Z решетки.
После этого вычисляется температура всех резисторов
решетки.
2) Решетка сканируется, и на ней генерируются дефекты с
вероятностью fD. Сопротивления незатронутых дефектами
резисторов изменяется в соответствии с их ТКС
зависимостью. Вычисляются новые значения потенциалов
узлов, токов и температур резисторов.
3) Решетка снова сканируется, и дефектные сопротивления
восстанавливаются с вероятностью fR. После
восстановления дефектов выполняется перевычисление
потенциалов узлов, токов и температуры сопротивлений,
а также общего сопротивления решетки.
4) Шаги 2 и 3 повторяются требуемое число раз.
Выполнения второго и третьего шага соответствует приросту «вре¬
мени» t на единицу.
Для расчета потенциалов в узлах решетки можно использовать под¬
ход, описанный для предыдущих моделей. В качестве подходящего кри¬
терия завершения процесса моделирования можно выбрать относитель¬
ное изменение сопротивления Z(t)/Z(0) — 1 проводящей пленки, а для
непроводящей пленки изменение тока i(t)/i(0) — 1. Процесс моделиро¬
вания закончивается если данные величины достигают определенного
заданного значения.
16.2.4. Описание работы программ
16.2.4.1. Стохастическая модель NPW
Программа для стохастической модели NPW содержится в
файле npw. f 90. Она состоит с модуля общих переменных и массивов
comdata, главного модуля npwmodel и набора внешних процедур.
В модуле comdata определяются основные параметры модели и
массивы программы. Код для этого модуля имеет вид
module comdata
implicit none
integer:: L=128 !размер сетки
16.2. Алгоритмы и описание работы программ ->\г 315
real:: ETA =1. !степенной показатель в формуле
!вероятности пробоя
real:: V=1. !потенциал кругового электрода
!число итераций
!относительная ошибка
!вычисления потенциала
!параметр сверхрелаксации
!радиус кругового электрода
!координаты центрального
!электрода
и(: , :) !потенциал узла сетки
G(:,:,:) !проводимость связи
!сетки
site (:, :) !состояние узла сетки
integer, anocataoie: : рх(:),ру(:) ! координаты узлов
!периметра паттерна
integer (2) :: di(l:4)=(/0, 1, 0,-1/)
integer (2) :: dj(1:4)=(/1, 0, -1, 0/)
integer in (1:4), jn(l:4) !координаты ближайших
!соседних узлов
end module comdata
Массив site(i, j) используется программой для хранения информа¬
ции о состоянии узлов квадратной решетки, которые могут быть пусты¬
ми (site (i, j ) =0), занятыми (т. е. принадлежать к разрядному клас¬
теру, (site (i, j ) =1)), или находиться на периметре (site (i, j ) =2).
Для вычисления координат ближайших соседей исследуемого узла с
координатами (i, j ), вводятся две таблицы сдвига координат, которые
оформлены в виде массивов di (), dj (). Координаты ближайших со¬
седних узлов запоминаются в массивы in (1:4), j n (1: 4). При работе
со списком узлов периметра разрядного кластера удобно использовать
одномерные массивы рх (), ру (), в которые записываются их коор¬
динаты. Основными параметрами задачи являются размер квадратной
решетки L, параметр т/, обозначенный в программе переменной ЕТА,
число итераций NITER и относительная ошибка вычисления потенци¬
ала UERROR. Приведенные массивы и переменные являются общими
для всех процедур программы.
Основной модуль программы включает вызовы нескольких процедур:
program npwmodel
!1) задаем начальные значения {G} и {и}, граничные
!условия для {и}, а также инициализируем графическое
! окно
call init(); call initgraf()
integer:: NITER =1000
real:: UERROR =0.001
real:: ALPHA =0.9
real Rc
integer ic,j с
!массивы:
real,allocatable::
real,allocatable::
integer,allocatable::
316 -l\r Глава 16. Электрический пробой
!2) моделируем развитие пробоя
call patterngrowth()
end program npwmodel
В процедуре init () осуществляется инициализация начальных зна¬
чений переменных и массивов программы, а в процедуре initgraf ()
инициализация графического окна для визуализации разрядной карти¬
ны. Код процедуры init () представлен ниже:
subroutine init()
use comdata
use msflib
implicit none
integer L2 !L2=L*L
real i,j !координаты узла сетки
real г !расстояние от центрального электрода
!размещаем массивы в оперативной памяти
allocate(u( 1:L,0:L)); u=0
allocate(G(0:1,1:L,0:L))
allocate (site(1:L, 0:L)); site=0
L2=L*L
allocate (px(l:L2)); px=0
allocate (py(l:L2)); py=0
G=1 !определяем начальные значения
!проводимостей
ic=L/2; jc=L/2 !координаты центрального электрода
Rc=0.9*L/2. !радиус кругового электрода
!задаем приближенные значения потенциала в узлах
do j =0,L
do i=l,L
r=sqrt((i-ic)*(i-ic)+(j-jc)*(j-jc))
u (i, j)=V*(r/Rc)
if(r>=Rc)u(i, j)=V
enddo
enddo
!находим точные значения потенциала в узлах
call solve()
end subroutine init
В приведенной процедуре начальные значения потенциала аппрок¬
симированы с помощью функции u(r) = ur/R, где и = 1 — потенциал
кругового электрода, г — расстояние от центрального электрода, a R —
радиус кругового электрода.
16.2. Алгоритмы и описание работы программ •Аг 317
Потенциалы в углах решетки вычисляются с помощью итерацион¬
ной процедуры solve ():
subroutine solve()
use comdata
implicit none
integer m !счетчик числа итераций
integer i,j !индексы
real Uijm,Uijml, Uij !значение потенциала в узле
real 01,02,03,04,014 !электропроводности
!сопротивлений узла (i,j)
real U1,U2,U3,U4 !потенциалы соседей узла (i,j)
real GU
real ErUij, ErmaxUij !ошибка вычисления потенциала
do m=l,NITER
ErmaxUij=0.
do j =1,L-l
do i=l,L
Uijm=u(i, j)
if(Uijm/=0 .and. Uijm/=V) then
Ul=u(i,j+1); U3=u(i,j-1)
01=0(0,i,j); 02=0(1,i,j); 03=0(0,i,j-1)
if (i==l)then
U2=u(L, j)
else
U2=u (i-1,j)
endif
if(i==L)then
U4=u (1,j); 04=0(1,1,j)
else
U4=u(i+1,j); G4=G(1,i+1,j)
endif
GU=G1*U1+G2*U2+G3*U3+G4*U4; G14=G1+G2+G3+G4
Uij=GU/G14
Uijml=ALPHA*Uij+(1-ALPHA)*Uijm
u(i, j)=Uijml
ErUij=abs(Uijml-Uijm)/Uijm
if(ErUij>ErmaxUij) ErmaxUij =ErUij
endif
enddo
enddo
if (ErmaxUijCUERROR) return
enddo !next m
end subroutine solve
318 -»\r Глава 16. Электрический пробой
В этой процедуре для ускорения сходимости итераций используется
метод верхней релаксации. Значение потенциала в узлах сетки вычис¬
ляется с помощью соотношения
<+‘ = аЩ + (I - a)u?j,
где т — номер итерации, а — параметр релаксации (в программе
переменная ALPHA), а Щ вычисляется по формуле (16.1). Вычисление
потенциала осуществляется только для тех узлов сетки, которые не
принадлежат к кластеру или круговому электроду с учетом периоди¬
ческих граничных условий. Вычисления с помощью данной процедуры
продолжается до тех пор, пока максимальная относительная ошибка
вычисления потенциала в узле сетки не будет меньше заданного значе¬
ния UERROR.
Рассмотрим теперь работу процедуры patterngrowth (), в кото¬
рой реализован алгоритм для стохастической модели NPW:
subroutine patterngrowth()
use comdata
use msflib
implicit none
integer
t
счетчик шагов разряда
real
r, rmax
радиус паттерна
integer
ip
индекс узла периметра
integer
np
счетчик узлов периметра паттерна
real
usum
сумма потенциала в узлах периметра
паттерна
real
f
вероятность присоединения узла
периметра к паттерну
real
rnd
случайное число
integer
i
!1)размещаем стартовый узел паттерна в центре сетки и
!вычисляем сумму потенциала в узлах периметра
px(l)=ic; РУ(1)=j с; ip=l; пр=1
call newsite(ip, np)
usum=0.
do i=l,np
usum=usum + u (px(i),py(i))**ETA
enddo
!2) продолжаем рост паттерна до требуемого размера
do while (rmax<Rc)
!2.1) выбираем случайным образом узел периметра
!паттерна
1 call random(rnd); ip=int(rnd*np+l.)
16.2. Алгоритмы и описание работы программ -Аг 319
!2.2) вычисляем вероятность присоединения в
!выбранном узле
f=u(рх(ip),ру(ip))**ETA/usum
!2.3) проверяем условие присоединения
call random(rnd); if(rnd>f) goto 1
!2.4) присоединяем выбранный узел сетки к паттерну
!разряда
call newsite(ip, np)
r=sqrt(real((px(ip)-ic)*(px(ip)-ic))+&
real((py(ip)-jc)*(py(ip)-jc)))
if(r>rmax) rmax=r
t=t+l
!2.5) находим новое распределение потенциала в
узлах и вычисляем сумму потенциала в узлах периметра
call solve ()
usum=0.
do i=l,np
usum=usum + u(px(i),py(i))**ETA
enddo
enddo
end subroutine patterngrowth
Рост разрядного кластера реализуется в цикле do while . . .
end do и продолжается до тех пор, пока максимальный радиус раз¬
рядного кластера rmax не достигнет радиуса кругового электрода Rc.
После присоединения нового узла решетки к разрядному кластеру
с помощью процедуры newsite вычисляется новое распределение
потенциалов (процедура solve) и определяется сумма потенциалов
по узлам периметра на разрядном кластере.
Процедура, используемая для присоединения нового узла к разряд¬
ному кластеру, приведена ниже:
subroutine newsite(ip, np)
use comdata
implicit none
integer ip !индекс узла периметра паттерна
integer np !счетчик узлов периметра паттерна
integer i,j !координаты узла сетки
integer к
i=px(ip); j=py(ip)
u(i,j)=0 !приравниваем нулю потенциал занятого узла
site(i,j)=l !помечаем занятый узел сетки
call dischargedraw(i, j) !рисуем новый узел паттерна
!исключаем занятый узел из списка периметра паттерна
px(ip)=рх (np); py(ip)=ру(np); пр=пр-1
320 -Ar Глава 16. Электрический пробой
!вычисляем координаты соседних узлов
!и дополняем список периметра паттерна
in=i+di; jn=j+dj
do k=l,4
if (site (in(k),jn(k))==0) then
np=np+l; px(np)=in(k); py(np)=jn(k)
endif
enddo
end subroutine newsite
В процедуре newsite исключение занятого узла периметра реа¬
лизуется переписыванием на его место координат последнего узда из
списка и уменьшением счетчика пр на единицу. После этого список
периметра дополняется, только теми узлами сетки, которые соответ¬
ствуют состоянию пустых узлов.
16.2.4.2. Обобщенная модель Такаясу
Программа для обобщенной модели Такаясу содержится
в файле mixmodel.f90 и имеет модульную структуру подобную той,
которая описана в предыдущей программе. Модуль comdata общих
переменных и массивов имеет вид
module comdata
implicit
none
!параметры:
integer::
: L =100
размер решетки
real ::
: ETA=1000.
степенной показатель в функции
вероятности пробоя
real ::
: DELTA=0.9
степень неоднородности
проводимостей сетки
real ::
: V =0.53
нормированное напряжение,
приложенное к сетке (V<=1)
real ::
: LAMBDA=100.
параметр увеличения
проводимости при пробое
real ::
: Gm=l
среднее значение проводимости
резистора
real
GBR !минимальное значение проводимости
!пробитого резистора
real
Vc=l !критическое напряжение пробоя
!резистора
integer::
: NITER =1000 !число итераций
real::
UERROR =0.001 !относительная ошибка
!вычисления потенциала
real::
ALPHA =0.9
!параметр сверхрелаксации
16.2. Алгоритмы и описание работы программ -Аг 321
!массивы:
real,allocatable:: u(:,:) !потенциал узла сетки
real,allocatable:: G(:,:,:) !проводимость связи сетки
end module comdata
Алгоритм вычислений для смешанной модели реализован в основ¬
ном модуле программы:
program mixedmodel
use msflib
implicit none
type (rccoord) curpos
integer it, t !"компьютерное" время
integer N(0:1000) !число пробитых сопротивлений
!на шаге t
integer verifyresistors !внешняя функция проверки
!сопротивлений сетки на пробой
!1) задать начальные значения {G} и {и}, граничные
!условия для {и}, а также инициализировать графическое
! окно
call init (); call initgraf()
!2) решить систему уравнений и найти {и}
1 t=t+l; call solve()
!3) проверить каждый резистор сетки (за исключением
!разрушенных пробоем): если выполняется условие пробоя,
!то произвести замену резистора на пробитый
N(t)=verifyresistors(); N(t)=N(t)+N(t-1)
call settextposition(1,1,curpos);
write(*,*) 't=',t,' ','N(t)=', N(t),' '
!4) остановить выполнение программы, если нет пробитых
!сопротивлений, в противном случае вернуться к п.2 и
!продолжить выполнение процедур
if(N(t)-N(t-1)>0) goto 1
!5) записываем результаты расчетов в выходной файл
open(1,file='Nt.dat')
do it=l,t-1
if(N(it)>0) write(l,*) it, N(it)
enddo
close (1)
end program mixedmodel
Вначале путем вызова внешней процедуры init задаются электро¬
проводности резисторов на решетке и начальные (пробные) значения
потенциала в узлах решетки. Код этой процедуры имеет следующий вид:
322 Глава 16. Электрический пробой
subroutine init()
use msflib
use comdata
implicit none
integer i, j
real rnd
real Gmin, DELTA2
!размещаем массивы в оперативной памяти
allocate(u( 1:L,0:L)); u=0
allocate(G(0:1,1:L,0:L)); G=0
!определяем начальные значения проводимостей
Gmin=Gm*(1-DELTA);DELTA2=2 *DELTA;GBR=LAMBDA*Gmin
do j =0,L
do i=l,L
call random(rnd); G(0,i,j)=Gmin+DELTA2 * rnd
call random(rnd); G(1,i,j)=Gmin+DELTA2*rnd
enddo
enddo
!определяем начальные значения потенциала
V=V*L
do j=0,L; do i=l,L
u(i, j)=V*real(j)/real(L)
enddo; enddo
end subroutine init
Начальные значения электропроводностей записываются в 3-индекс-
ный массив G (). Первый индекс данного массива принимает два
значения: 0 и 1, которые используются соответственно для обозначения
вертикально и горизонтально направленных резисторов (см. рис. 16.3).
Начальные пробные значения потенциала в узлах сетки задаются
равными для каждой строки узлов и линейно убывающими от верхнего
к нижнему электроду. Такое пробное распределение соответствует
распределению потенциалов для однородной системы (6 = 0). Точные
значения потенциала вычисляются в процедуре solve (). Процедура
solve () полностью идентична использованной ранее для модели NPW.
Проверка условия пробоя осуществляются во внешней процедуре-
функции verifyresistors ():
integer function verifyresistors()
use comdata
implicit none
integer i,j !индексы
real dU !разность потенциалов в узле
integer Nbreak !счетчик пробитых сопротивлений
logical break
16.2. Алгоритмы и описание работы программ •А, 323
Nbreak=0
do j =0,L-l
do i=l,L
if(G(0,i,j)<GBR) then !вертикальный резистор
!узла (i,j)
dU=u(i,j+1)-u (i, j)
if(break(dU))then
G(0,i,j)=LAMBDA*G(0,i,j);Nbreak=Nbreak+l
call breakresistor (0,i,j)
endif
endif
if(G(1,i,j)<GBR) then !горизонтальный резистор
!узла (i, j)
if(i==l) then
dU=u(L, j)-u (i, j)
else
dU=u(i-1,j)-u (i, j)
endif
if(break(dU)) then
G(1,i,j)=LAMBDA*G(1,i,j);Nbreak=Nbreak+l
call breakresistor(1,i,j)
endif
endif
enddo
enddo
verifyresistors=Nbreak
end function verifyresistors
В результате вызова данной функции определяется число пробитых
сопротивлений, которое возвращается в главный модуль программы
и служит в качестве критерия завершения программы, если в ходе
выполнения функции verif yresistors () не будет разрушено хотя
бы одно сопротивление. Для определения условий пробоя вычисляется
приложенное к резистору напряжение dU, которое анализируется в ло¬
гической функции break (). Напряжения на горизонтальных резисто¬
рах вблизи внешних границ решетки вычисляются с учетом периоди¬
ческих граничных условий. Электропроводность пробитых резисторов
увеличивается в Л(= 100) раз (в программе А соответствует перемен¬
ной LAMBDA). Процедура breakresistor служит для графического
представления пробитых резисторов.
Код логической функция break () представлен ниже:
logical function break(dU)
use msflib
use comdata
324 ->\r Глава 16. Электрический пробой
implicit none
real dU !разность потенциалов
real f !вероятность пробоя
real rnd
logical br
br=.false.
if(abs(dU)>Vc)then
br=.true.
else
f=abs(dU)**ETA; call random(rnd)
if(rnd<f) br=.true.
endif
break=br
end function break
16.2.5. Примеры работы программ
На рис. 16.5 приведены примеры картин разрядов, по¬
строенных для стохастической модели NPW с помощью программы
npw. f 90. Размер квадратной решетки составлял L = 128. Образуемые
разрядные кластеры имеют сложную структуру, которая подобна струк¬
туре кластеров, полученных с помощью модели DLA (см. гл. 8). Число
узлов N в круге радиуса г, центр которого находится на центральном
электроде, описывается степенной зависимостью вида N ~ г*г где df —
фрактальная размерность кластера разряда.
L = 128
Рис. 16.5. Картины разряда на квадратной решетке в стохастической модели
NPW [6] при разных значениях параметра г/ в формуле для вероят¬
ности / пробоя резистора
Величина df убывает при возрастании г/, изменяясь от df — 2 при
rj = 0 до df = 1,6 при 7} = 2 [6]. Отметим, что при ij = 0 вероятность
роста не зависит от локального распределения потенциала и данная мо¬
дель соответствует модели роста компактных кластеров Идена (см. гл. 7).
16.3. Задачи для самостоятельной работы 325
Программа для обобщенной модели Такаясу [8] тестировалась для
значения параметра г] = 103, что соответствовало приближению исход¬
ной детерминистической модели Такаясу. Результаты работы данной
программы представлены на рис. 16.4.
16.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Используя программу для стохастической модели NPW [6], иссле¬
дуйте зависимость фрактальной размерности df кластеров пробоя от
параметра г\ при ц = 0 -г-10.
2. Обобщите программу для модели NPW [6] с плоскими электродами.
Инициируйте пробой на нижнем электроде, потенциал и которого
равен нулю. Изменяя размер решетки, L, исследуйте зависимость
фрактальной размерности df кластеров пробоя от параметра т] при
q = 0-=-10.
Рис. 16.6. Кластеры пробоя для модели NPW [6] с плоскими электродами при
различных значениях т]. Пробой инициирован на нижнем электро¬
де, потенциал которого и равен нулю
3. С помощью программы для обобщенной модели Такаясу [8] иссле¬
дуйте развитие пробоя при следующих параметрах задачи ц = 103,
А — 100. Качественно охарактеризуйте развитие пробоя в зависимо¬
сти от параметров 6 и и* = U/ucL. Обратите внимание, что для силь¬
но неоднородной системы (5 = 0,9) возможна ситуация, когда разви¬
тие пробоя заканчивается без образования перколяционного класте¬
ра. Постройте зависимость величины umin, которая соответствует
минимальному напряжению, необходимому для развития пробоя от
параметра 6. Исследуйте зависимость фрактальной размерности df
кластеров пробоя от параметра неоднородности г].
326
Глава 16. Электрический пробой
4. Напишите программу для моделирования электрического пробоя
тонких проводящих и непроводящих пленок для термоактивацион¬
ной модели Пенетты [19]. Рассмотрите случай пробоя диэлектри¬
ческой пленки. Для этого используйте следующие значения пара¬
метров: L = 50, Z0 = 107 Ом, yz = 0, Т0 = 300 К, А = 5 • 105 К/Вт,
Ed = 0,19 эВ, Er = 0,13 эВ, А = 10“7. Вычислите зависимости изме¬
нения относительного тока i(t)/i(0) — 1, проходящего через пленку,
от t для значений U = 0,8, 1,0 и 1,2 В. Исследуйте, при каком мини¬
мальном значении U возможны скачкоподобные изменения тока.
1. Кирлиан В. X., Кирлиан С. Д. В мире чудесных разрядов. — М.: Знание,
2. Ушаков В. Я. Импульсный электрический пробой конденсированных сред
(Достижения высоковольтников ТПУ за 60 лет) // Известия Томского
политехнического университета. — 2006. — Т. 309, №2. — С. 58-63.
3. Sahimi М. Heterogeneous Materials Nonlinear and Breakdown Properties and
Atomistic Modeling. — New York: Springer-Verlag, 2003. — 637 p.
4. de Arcangelis L., Redner S. A random fuse model for breaking processes //
J. Physique Lett. - 1985. - V. 46. - P. L585-L590.
5. Duxbury P.M., Beale P.D. and Leath P.L. Size Effects of Electrical Break¬
down in Quenched random Media // Phys. Rev. Lett. — 1986. — V. 57,
No. 8. - P. 1052-1055.
6. Niemeyer L., Pietronero L., Wiesmann H.J. Fractal Dimension of Dielectric
Breakdown // Phys. Rev. Lett. — 1984. — V. 52, No. 12. — P. 1033-1036.
7. Family F., Zhang Y.C., Vicsek T. Invasion percolation in an external field:
dielectric breakdown in random media // J. Phys. A: Math. Gen. — 1986. —
V. 19, No. 12. - P. L733.
8. Takayasu H. Simulation of Electric Breakdown and Resulting Variant of Per¬
colation Fractals // Phys. Rev. Lett. — 1985. — V. 54, No. 11. — P. 1099-1101.
9. Meakin P. Models for Material Failure and Deformation 11 Science. — 1991. —
V. 252. - P. 226-234.
10. Sweeney P.J., Dissado L.A., Cooper J. M. Simulation of the effect of barriers
upon electrical tree propagation // Journal of Physics D: Applied Physics. —
1992. - V. 25, No. 1. - P. 113-119.
11. Kyxma В. P, Лопатин В. В., Носков М. Д. Применение фрактальной моде¬
ли к описанию развития разряда в конденсированных диэлектриках //
ЖТФ. - 1995. - Т. 65, №2. - С. 63-75.
12. Карпов Д. И., Лопатин В. В., Носков М. Д. Влияние высокопроводящих ба¬
рьеров на развитие дендритов в диэлектрике // Электричество. — 1995. —
№7. - С. 59-61.
13. Tsonis A. A. A fractal study of dielectric breakdown in the atmosphere //
In: Scaling, Fractals and Non LinearVariability in Geophysics / Ed. by
D. Schertzer and S. Lovejoy. — 1991. — P. 167-174.
16.4.
ЛИТЕРАТУРА
1964.
16.4. Литература 327
14. Lupo G., Petrarca C., Tucci V. and Vitelli M. EM fields associated with light¬
ning channels: on the effect of tortuosity and branching 11 IEEE Transactions
on Electronic Computers. — 2000. — V. 42, No. 4. — P. 394-404.
15. Kebbabi L. and Beroual A. Fractal analysis of creeping discharge patterns
propagating at solid/liquid interfaces: influence of the nature and geometry
of solid insulators // Journal of the Physics D: Applied Physics. — 2006. —
V. 39, No. 1. - P. 177-183.
16. Barclay A. L., Sweeney P. /., Dissado L. A. and Stevens G. C. Stochastic mod¬
elling of electrical treeing: fractal and statistical characteristics 11 Journal of
Physics D: Applied Physics. — 1990. — V. 23. — P. 1536-1545.
17. SanudoJ., Gomez J. B., Castano F. and Pacheco A. F. Fractal dimension of
lightning discharge 11 Nonlinear Processes in Geophysics. — 1995. — V. 2. —
P.101-106.
18. Kawasaki Z. and Matsuura K. Does a lightning channel show a fractal? //
Applied Energy. - 2000. - V. 67, No. 1. - P. 147-158.
19. Pennetta C., Reggiani L., Trefaan Gy., Cataldo R. and de Nunzio G. A Per-
colative Approach to Reliability of Thin Film Interconnects and Ultra-thin
Dielectrics // VLSI Design. - 2001. - V. 13, No. 1-4. - P. 363-367.
ГЛАВА САМООРГАНИЗОВАННАЯ КРИТИЧНОСТЬ
17
17.1. МОДЕЛИ САМООРГАНИЗОВАННОЙ КРИТИЧНОСТИ
Что может быть общего между такими различными при¬
родными или социальными явлениями как снежные обвалы, обвалы в
горах, финансовые обвалы, землетрясения, цунами, внезапные ливни
или лесные пожары? Как известно, эти явления достаточно непредска¬
зуемы, имеют различную интенсивность и могут охватывать различные
пространственные и временные масштабы. Важность описания таких
стихийных явлений человечество осознает уже на протяжении многих
столетий, а количественные статистические данные о них тщательно
собираются и документируются. При тщательном анализе этих явлений
обнаружилось, что все они обладают некоторой общностью. Оказалось,
что размер или интенсивность события, его продолжительность и вре¬
мя ожидания события характеризуются унифицированными скейлин-
говыми законами, когда отсутствуют характерные пространственные
или временные масштабы. Так возникло понятие о самоорганизован-
ной критичности, которое впервые было предложено П. Баком [1, 2].
Самоорганизованная критичность (SOC — английская аббревиатура от
self organized criticality), обычно, проявляется в системах, в которых
амплитуда флуктуаций какого-либо параметра достигает границы ста¬
бильности системы. В состоянии SOC, даже при постоянном характере
внешних возбуждений отклик системы на эти возбуждения характери¬
зуется лавиной непредсказуемых событий, или «обвалов».
Законы эволюции таких систем, как правило, характеризуются дву¬
мя общими чертами:
1) способностью накапливать определенное количество энергии (или
массы) на протяжении определенного временного интервала;
2) резким высвобождением энергии (или массы) при достижении гра¬
ницы стабильности системы.
17.1. Модели самоорганизованной критичности -*\г 329
Концепция SOC позволяет понять природу разнообразных явлений,
таких как обвалы снежных лавин в горах, сдвиги грунтов, землетря¬
сения, обвалы биржевых курсов, возгорание лесных массивов, возник¬
новение облаков и ливней, распространение эпидемий, возникновении
«пробок» в транспортных потоках. Эти и другие применения концеп¬
ции SOC всестороннее обсуждаются в работах [3-6]. С обсуждением
философских аспектов концепции SOC можно познакомится в [7].
В SOC состоянии система самоорганизуется в сбалансированном
(критическом) состоянии, характеризуемом безмасштабным поведени¬
ем, а статистическое поведение такой системы напоминает статистиче¬
ское поведение вблизи точки фазового перехода.
Для SOC системы количество событий N, как правило, зависит
степенным образом от его «размера» (масштаба) или интенсивности.
Так в ряде природных явлений выполняется следующее соотношение
между N и площадью S
N~S~a, (17.1)
где степенной показатель а зависит от характера явления, например,
а & 2 для землетрясений, а = 1,3 -г 1,5 для возгорания лесных масси¬
вов, а = 2,3 -г- 3,3 для сдвигов грунтов [5].
Аналогичные степенные соотношения выполняются между N и про¬
должительностью события At
N(At) ~ ДГ^,
и между N временем ожидания очередного события Т
М(Т) ~ Т~г. (17.2)
17.1.1. Обвал кучи с песком
Наиболее известной моделью SOC является модель обвала
кучи частиц (например, частиц песка, риса, и т.п.) [2]. В данной моде¬
ли частицы опускаются на вершину кучи одна за другой и спускаются
по ее склону. При этом, частицы могут фиксироваться в определенных
местах или вызывать обвалы различного пространственного масштаба.
Подобную картину можно наблюдать, рассматривая постепенное осы¬
пание кучки с песком в песочных часах (рис. 17.1).
В процессе роста этой кучи достигается некоторое стационарное
«критическое» состояние, когда угол наклона кучи по отношению к го¬
ризонту начинает флуктуировать возле среднего значения. В критиче¬
ском состоянии любая из осажденных частиц может вызвать обвал про¬
извольного размера, который невозможно предсказать заранее. Можно
сказать, что система имеет бесконечную восприимчивость к малому
330
—Глава 17. Самоорганизованная критичность
возмущению. Интересно отметить, что такое сложное поведение возни¬
кает для простой неравновесной системы, которая состоит из большого
количества частиц, взаимодействующих на
локальном уровне.
На рис. 17.2 представлена одномерная
(1 + 1)-модель кучи с песком.
В данной модели состояние системы
определяется одномерным массивом чисел,
представляющих высоты h(x), х = \ + L,
где L — размер системы в горизонталь¬
ном направлении. Слева находится стен¬
ка и на каждом временном шаге вбли¬
зи нее в позицию 1 добавляется песчин¬
ка. Это соответствует увеличению высоты,
h( 1) = h( 1) + 1 в этой позиции. На каж¬
дом временном шаге одновременно срав¬
ниваются высоты в соседних узлах. Если левая высота выше правой,
т. е. h(x) — h(x -1-1) > 1, то песчинка из верхнего угла может пере¬
катываться в нижний, что соответствует уменьшению левой высоты
(h(x) = h(x) — 1) и увеличению правой (h(x +1) = h(x + 1) + 1). Любая
песчинка, попадающая в крайний правый элемент массива h(L), уходит
за пределы системы и считается потерянной навсегда.
Рис. 17.1. Осыпание кучки с
песком в песочных часах1*
Рис. 17.2. К описанию одномерной (1 + 1)-модели обвала кучи с песком
Чрезвычайно популярной при исследовании явлений SOC является
(1 + 2)-модель обвала кучи с песком (SPM — английская аббревиатура
** Акварель В. Мельник.
17.1. Модели самоорганизованной критичности -1\г 331
от sand pile model) [1, 2]. Рассмотрим квадратную решетку, каждый
узел которой с координатами х,у представляет собой колонку, напол¬
ненную частицами песка. В процессе моделирования выбираем случай¬
ным образом произвольную ячейку и добавляем к ней одну песчинку
h(x,y) = h(x,y) + 1.
Предполагается, что максимальная высота в колонке не может превы¬
шать некоторое критическое значение /гс, скажем hc = 3. При h(x,y) > hc
происходит обвал, при котором все песчинки из данной колонки переда¬
ются ближайшим колонкам. При этом высота соседних колонок увели¬
чивается, т. е. h{x ± 1, у) = h(x ± 1, у) + 1, h{x, у ± 1) = h{x, у ± 1) + 1,
а высота данной колонки уменьшается, т.е. h(x,y) = h(x,y) — 4 (рис. 17.3).
В модели предполагается, что частицы, выходящие за пределы решетки
«уходят» из системы навсегда. При проверке обвалов решетка последо¬
вательно сканируется, например, начиная из верхнего угла в нижний
(рис. 17.4).
Перед «обвалом»
h(x,y) = 4
После «обвала»
h(x,y) = О
h(x— \,у) = 2 h(x+\,y) = \
h(x,y — 1) = 1
h(x, у+1) = 3
h(x—\,y) = 2 h(x+\,y) = \
h(x,y — 1) = 0
h(x, y +1) = 2
Рис. 17.3. К описанию двумерной модели обвала кучи с песком. В момент
обвала колонка х,у имеет высоту h(x,y) = 4, которая превышает
критическую. После обвала содержимое этой колонки перераспре¬
деляется между ближайшими соседями
Отметим, что обвал в определенной колонке (х,у) может иницииро¬
вать обвалы в соседних колонках и т.д. (рис. 17.4), т.е. «обвал» может
распространяться по системе. Таким образом, при каждом добавлении
каждой новой частицы может инициироваться па обвалов, которые
затрагивают S ячеек (это суммарная площадь обвалов).
332
X
Глава 17. Самоорганизованная критичность
Перед «обвалом»
Первый «обвал»
Второй «обвал»
1
1
О
1
1
1
1
1
2
2
3
0
+ .
2
2
3 -
1
-4-
1
- 1
2
1
i
0
2
Третий «обвал»
Четвертый «обвал»
После «обвала»
1
1
1
1
1
1
1
1
Я
vvL
i
i
ш
i
s
1
В
1
2
Ш
2
Рис. 17.4. Обвал определенной колонки при добавлении новой частицы (здесь
данная колонка отмечена кружочком) может инициировать серию
других обвалов в соседних ячейках. Нестабильные ячейки показаны
серым цветом. После второго обвала, решетка сканируется заново,
в результате чего возникает третий и четвертый обвал. Для рас¬
смотренного примера общее число обвалов па равно 4, а общее
число ячеек затронутое «обвалами» (площадь обвалов S) равно 12
Примеры формы обвалов различной площади для системы размером
256 х 256 приведены на рис. 17.5, а и б. Кластеры обвалов являются
компактными, однако, их периметр может иметь довольно сложную
форму.
Детальные исследования модели SPM показали, что частота воз¬
никновения кластеров N убывает по степенному закону с увеличением
их площади S, т. е. N(S) ~ S-a, где степенной показатель а « 1 [5].
Данная модель SPM является абелевой, т. е. конечное состояние
системы не зависит от того, каким образом это состояние было до¬
стигнуто [9]. Таким образом, конечная структура обвала не зависит от
последовательности, в которой выполняются перераспределения содер¬
жимого между ячейками и единственным контролирующим параметром
в этой модели является размер системы, который определяется раз¬
мер максимального обвала, но не влияет на масштабно инвариантное
соотношение между А/ и S. В описанной абелевской модели обвала
кучи с песком частицы случайным образом добавлялись в различные
узлы решетки. При добавлении частиц только в определенный узел,
например в центр решетки, обычно генерируются довольно сложные
17.1. Модели самоорганизованной критичности -*\г 333
128 192 256 64 128 192 256
х х
Рис. 17.5. Примеры формы обвалов различной площади (а) и перколяционный
обвал, проникающий через всю систему (б). На рисунке указаны
общее число па и площадь обвалов 5. Размер решетки составлял
256 х 256
Рис. 17.6. Симметричные обвалы,
генерируемые при добавлении но¬
вой частицы в центре решетки.
Здесь показана структура обвалов
с увеличивающейся площадью
5 = 5113 (1), 9549 (2), 16953 (3),
21217 (4), 29761 (5), 31957 (6). Сред¬
ний диаметр обвала d увеличива¬
ется при увеличении количества
осажденных частиц Np, примерно
как d ~ yJWp [8]
симметричные структуры обвалов (рис. 17.6). В этом случае после до¬
стижения состояния SOC образуются детерминистические структуры,
исследование которых представляет самостоятельный интерес [8].
17.1.2. Землетрясения
Другим примером модели SOC является модель связанных
скользящих блоков, которая была предложена для описания землетря¬
сений. Вариант одномерной модели такого типа схематически представ¬
лен на рис. 17.7 [10-14]. В данной модели геологический сдвиг описы¬
вается с помощью одномерной сетки связанных блоков. Блоки находят¬
334 Глава 17. Самоорганизованная критичность
ся между двумя плитами, из которых верхняя фиксирована, а нижняя
может двигаться. Каждый блок массой т (= 1) связан пружинами с
коэффициентами упругости k с двумя ближайшими соседями и пружи¬
ной с коэффициентом упругости kp с верхней фиксированной плитой.
Блоки находятся в контакте с шероховатой нижней плитой, движущей¬
ся со скоростью v влево. Предполагается, что сила трения F между
блоком и плитой зависит от относительной скорости х между блоком
и плитой. В простейшем приближении при v = 0 статическая сила тре¬
ния равна Fo и при v ф 0 динамическая силы трения равна F&. В мо¬
дели [10] величина F имеет функциональную форму F(x) = Fo<p{x/v),
где (p(x/v) = sgn(x/v)/(\ + \x/v\), а величина v характеризует зависи¬
мость F от скорости. Здесь сила трения максимальная (F = ±Fo) при
х = 0 и монотонно уменьшается до нуля при больших x/v.
Движущаяся плита ;
У///////Г7УТ*Г////////////7Г7
* Fi-1 Fi Fi+1 Fi+2
V L J L_ L J L J
Г H п г г П ГЛ
Xi-1 Xi Xi+1 Xi+2
Рис. 17.7. Модель скользящих блоков, связанных между собою пружинами,
которая используется для описания землетрясения
Уравнение движения блоков можно записать в виде
Xi = k(xi+1 - 2Xi + Xi-\) — kpXi — F(v -f Xi),
где Xi — смещения блоков относительно равновесных положений.
Позднее было дано обобщение данной модели на двумерный слу¬
чай [15]. Было показано, что для данной модели могут проявлять¬
ся нестабильности в характере движения блоков и развиваться «цеп¬
ная реакция» (землетрясение). Это связано с тем, что при возникно¬
вении скольжения определенного блока (когда сила действующая на
него превышает Fo) силы действующие на его соседей изменяются и
они могут также скользить. Общее число скольжений различных бло¬
ков, которые вызваны относительным сдвигом, является мерой энер¬
гии Е, выделенной при землетрясении. Исследования показали, что
для этой модели для частоты землетрясений N выполняется эмпири¬
ческий закон Гуттенберга-Рихтера [16], описываемый соотношением
N~E~a.
17.1. Модели самоорганизованной критичности -*\г 335
17.1.3. Горение лесных массивов
Еще одним примером модели SOC является модель горе¬
ния леса FFM (английская аббревиатура от forest fire model). В лите¬
ратуре описано большое количество различных модификаций этой мо¬
дели [5, 17] и здесь будет рассмотрена только наиболее популярная из
них. Рассмотрим квадратную решетку размером L х L, каждая из ячеек
которой, может быть либо пустой (е), либо занятой зеленым (t) или
горящим (Ь) деревом [17]. На каждом временном шаге узел с горящим
деревом превращается в пустой (Ь —> е), существует вероятность fet
роста дерева в пустой ячейке (е —> t) и конечная вероятность са¬
мовозгорания зеленого дерева (t —> Ь). Кроме того, предполагается, что
вероятность возгорания зеленого дерева (t —► b) при наличии горящих
соседей равна 1 — g, где g — «иммунитет» дерева к возгоранию, стиму¬
лированному ближайшими соседями. При g = 0 зеленое дерево всегда
возгорается при наличии хотя бы одного ближайшего горящего соседа.
Обновление всех ячеек происходит одновременно. Определенные выше
три состояния ячейки называют также рефракторным (е — пустая ячей¬
ка), статическим (t — зеленое дерево) или возбужденным (b — горящее
дерево) [17].
X X
Рис. 17.8. Эволюция картин роста для модели FFM при fet = 0,005, ftb = 0,
g = 0. Темным цветом показан фронт горения, серым и белым
цветом показаны заполненные и пустые ячейки, соответственно
336 -Ar Глава 17. Самоорганизованная критичность
512
384
'256
128
let = 0,010
I S
V ( ? ■ -1 v 1
.j
512
384
'256
128
fet = 0,020 '
r ' . Л.
С > 'v. £ ,
ЛД —■ >* * * *
'<V‘^ y:'r '
-/ %i.• '^*АЛлГЧ V* *
> 4 • ».ч » •,
С -V V». , )/Л-> ^
4 . A hJ ^«T
■a>VV,
*CH
rVJ
128 256 384 512
X
128 256 384 512
x
Рис. 17.9. Картины роста для модели FFM при фиксированном времени t— Ю4,
ftb = 0, g = 0 и различных значениях fet. Темным цветом показан
фронт горения, серым и белым цветом показаны заполненные и
пустые ячейки, соответственно
Поведение системы для модели FFM определяется значениями ее
параметров /*&, g и fet. При = 0, g = 0, когда отсутствует самовоз¬
горание и иммунитет, огонь распространяется только за счет стиму¬
лированной передачи огня между ближайшими соседями. Интересное
поведение проявляет система с постоянным точечным источником воз¬
буждения (источником огня), расположенным в центре решетки. При
малых значениях вероятности роста fet и постоянном источнике огня в
центре, фронт огня с течением времени становится все более регуляр¬
ным и может приобретать спиральную форму [17]. Эволюция картин
роста для модели FFM при fet = 0,005 представлена на рис. 17.8. Де¬
тальный анализ пространственных и временных корреляций показыва¬
ет, что для данной системы существуют характеристическая длина и
шкала времени, пропорциональные 1 /fet, которые становятся более раз¬
личимыми при малых fet. При увеличении fet фронт горения становится
крайне нерегулярным уже на начальных этапах эволюции (рис. 17.9).
Спиральные волны, подобные тем, которые характерны для моде¬
ли FFM, наблюдаются в осциллирующих химических реакциях и для
определенных процессов распространения эпидемий [18-21].
17.1. Модели самоорганизованной критичности -*\г 337
Поведение SOC для модели FFM проявляется только при ненулевой
вероятности самовозгорания, ftb ^ 0. Исследования показали, что при
L 1 после определенного переходного периода данная система при¬
ходит в стационарное состояние SOC, которое практически не зависит
от начальных и граничных условий и в котором среднее число горя¬
щих деревьев Nb равно среднему числу растущих деревьев fetNe, т. е.
Nb = fetNe [17].
Перед высадкой Первое дерево Второе дерево
*
А
0
А
0
0
0
0
*
0
0
*
А
0
*
0
Третье дерево
1
1
0
0
0
0
1
0
1
0
1
1
1
©
1
0
1
1
0
1
0
0
©
0
1
0
0
1
1
0
1
0
Самовозгорание
1
1
0
1
0
0
1
0
ф
0
1
1
1
1
1
0
1
1
0
0
0
0
1
0
1
0
©
1
1
0
1
0
После пожара
IpJ
О
1?|
I
о
1
о
Рис. 17.10. К описанию модели SOC горения леса. Сначала в произвольные
ячейки высаживается три дерева (шь = 4), затем выбирается про¬
извольный узел и если он заполнен деревом, то это дерево за¬
жигается (если узел пустой, то попытка самовозгорания счита¬
ется неуспешной и высаживается следующая партия деревьев).
После этого выжигаются все деревья, входящие в лесной связный
массив. Ячейки, затронутые пожаром, показаны штриховкой. Для
рассмотренного примера общее число ячеек, затронутое пожаром
(площадь пожара S) равно 7
В стационарном состоянии SOC для системы FFM характерно по¬
ведение, наблюдаемое при обвалах кучи с песком. При этом довольно
длительный период роста деревьев без пожаров (статический период),
перемежается быстро протекающим пожаром (возбужденный период),
охватывающим как угодно большие площади. Поведение SOC контро¬
лируется частотой возникновения пожаров (оь —let/ftb (> 1), которая
пропорциональна среднему количеству деревьев S, уничтожаемых при
одном самовозгорании в стационарном состоянии S = a)b(Ne/Nt) [17].
338
Л
Глава 17. Самоорганизованная критичность
Для исследования поведения SOC при горении лесов в [22] рас¬
смотрена следующая упрощенная модель. В статический период слу¬
чайным образом выбирается произвольная ячейка с координатами
(х,у) и, если она пустая, h(x,y) = 0, то в нее высаживается дерево,
h(x,y) = h(x,y) + 1. Процедура повторяется свь — 1 (» 1) раз подряд.
Затем в а)ь раз снова выбирается произвольная ячейка, и если она уже
заполнена деревом (т.е. h(x,y) = 1), то данное дерево самовозгорается.
В противном случае ничего не происходит. При наличии самовозгора¬
ния идентифицируется кластер, к которому принадлежит это дерево,
и в этом кластере выжигаются все деревья. Таким образом, самовоз¬
горание в определенной ячейке (х,у) может инициировать выжигание
деревьев в соседних ячейках и т.д. (рис. 17.10), т.е. возгорание может
распространяться по системе, затрагивая 5 ячеек (это суммарная пло¬
щадь пожара).
512
384
256
128
128 256 384 512 128 256 384 512
х х
512
t= 1294, S =16837
512
П=1301,5 = 11094И
384
-
384
и
256
-
У 256
щ
128
км.
128
L — J- 1
128 256 384 512 128 256 384 512
х х
Рис. 17.11. Примеры формы лесных пожаров различной площади S в последова¬
тельные моменты времени t. Размер решетки составлял 512 х 512,
о)ь = 1000. Темным цветом показана площадь, затронутая пожаром,
серым и белым цветом показаны заполненные и пустые ячейки,
соответственно
t= 1251, S = 32649
Примеры формы лесных пожаров различной площади S в последо¬
вательные моменты времени t показаны на рис. 17.11. Для FFM модели
17.1. Модели самоорганизованной критичности -»\л 339
в режиме SOC количество пожаров N убывает по степенному закону с
увеличением их площади 5, т. е. N(S) ~ S~a, где степенной показатель
а « 1,02 -г-1,17 [5].
17.1.4. Игра «Жизнь»
Еще одним примером модели, в которой наблюдается пове¬
дение SOC, является известная игра «Жизнь», предложенная Джоном
Конвеем и описанная в [23]. В данной модели каждая ячейка решетки
имитирует живой организм, который может быть живым или мертвым
(пустая ячейка). На каждом временном шаге состояние всех ячеек
решетки изменяется параллельно и определяется состоянием девяти
ближайших соседей. На рис. 17.12 схематически изображены прави¬
ла изменения состояния ячеек для этой модели, которая относится к
разряду моделей, называемыми клеточными автоматами. Для произ¬
вольного начального состояния после некоторого переходного процесса
в системе устанавливается динамическое равновесие. В работе [24]
было показано, что SOC поведение в этой модели наблюдается, когда
динамическое равновесие нарушается путем случайного выбора одной
ячейки и принудительного изменения ее состояния на противополож¬
ное. После этого в системе возникает лавина «смертей» и «рождений».
Новый организм рождается Живой организм умирает, если
в пустой ячейке, если вблизи находится меньше двух
рядом есть три соседа или больше трех соседей
©
©
(о^о)
©
©
Живой организм живет вечно, если
вблизи находятся два или три соседа
©
©
1 о_о
©
Рис. 17.12. Правила изменения состояния ячеек в игре «Жизнь»
Более детально, различные аспекты применения клеточных автома¬
тов для моделирования разнообразных физических явлений рассмотре¬
ны в [25, 26].
340 -*\r Глава 17. Самоорганизованная критичность
В данной главе будут проанализированы алгоритмы и программы
для исследования явлений SOC для двух примеров описанных в тексте:
модели обвала кучи с песком (SPM) и модели горения леса (FFM).
17.2. АЛГОРИТМЫ И ОПИСАНИЕ РАБОТЫ ПРОГРАММ
Описанные ниже алгоритмы используют идеологию мо¬
делей клеточных автоматов (КА), для которых содержимое каждой
ячейки последовательно обновляется с учетом состояния ее соседей в
предыдущий момент времени.
17.2.1. Обвал кучи с песком
Рассмотрим более детально алгоритм для реализации мо¬
дели обвала кучи с песком при последовательном падении частиц на
плоскость (модель (1 + 2)) (рис. 17.4). Будем полагать, что в начальный
момент все ячейки являются пустыми, т.е. h(x,y) = 0. При добавле¬
нии частицы в определенную ячейку будем увеличивать ее высоту
на единицу, h(x,y) = h{x,y) + 1. При превышении критической высоты
h(x,y) > 3 содержимое данной ячейки будем перераспределять между
ее ближайшими соседями. При таком перераспределении для ячеек,
находящихся вблизи границ, возможна потеря 1 или 2 частиц. Таким
образом, при добавлении новых частиц, общее их количество Np может
уменьшаться.
Ниже описан последовательный вариант алгоритма для (1 + 2)-мо-
дели кучи с песком, который можно представить в виде следующей
схемы:
1) выбираем случайным образом ячейку (х,у) и добавляем в
нее частицу (h(х,у)=h(х,у)+1) и увеличиваем счетчик
добавленных частиц Np=Np+l;
2) сканируем всю решетку (x=l-L, y=l-L), при h(x,y)>3
содержимое нестабильной ячейки перераспределяем
между ее ближайшими соседями: h(x±l,y) = h(x±l,y)+l,
h(x,y±l) = h(x,y±l)+l, h(x,y)= h(x,y)-4. Этот пункт
повторяем до тех пор, пока при сканировании
обнаруживаются нестабильные ячейки. При отсутствии
нестабильных ячеек переходим к пункту 3;
3) накапливаем информацию о характеристиках обвала
(количестве обвалов па, и их общей площади S).
Переходим к пункту 1).
Выполнение программы заканчивается после осаждения требуемого
количества частиц.
17.2. Алгоритмы и описание работы программ -*\г 341
17.2.2. Лесной пожар
Алгоритм лесного пожара (рис. 17.10), можно представить
в виде следующей схемы:
0) инициализируем графическое окно;
1) увеличиваем счетчик времени на единицу. Выбираем
случайным образом ячейку (х,у). В случае если она
пустая (h(x,y)=0), высаживаем в нее дерево
(h (х, у) =h (х, у) +1) . Этот пункт повторяем а)ь~ 1 раз.
2) выбираем случайным образом ячейку (х,у). В случае
если она пустая (h(x,y)=0), переходим к пункту 1.
Если она заполнена(h(х,у)=1), идентифицируем кластер,
к которому принадлежит данное дерево, и полностью
выжигаем этот кластер, полагая h(x,y)=0.
3) накапливаем информацию об общей площади S пожара.
Переходим к пункту 1.
17.2.3. Описание работы программ
17.2.3.1. Обвал кучи с песком
Программа, для реализации модели обвала кучи с пес¬
ком, содержится в файле sandpile. f 90. Полный код этой программы
представлен ниже:
program sandpile
use msflib
use portlib
implicit none
type (rccoord) curpos
integer:: L =50 !размер решетки
integer:: Np, NMAX=le5 !число частиц
integer:: he =3 !критическое число частиц в ячейке
integer LI, L2 !L1=L+1,L2=L*L
integer x, у !координаты ячейки
integer S !площадь(количество ячеек),
!которую затронула лавина
integer NA !количество обвалов
integer unstable !количество нестабильных ячеек
real rnd !случайное число
integer,
allocatable:: h(:,:)
integer, allocatable:: u(:,:)
!число частиц в ячейке
! <х,у)
!матрица для записи
!координат ячеек,
!которые находились в
!нестабильном состоянии
Глава 17. Самоорганизованная критичность
integer, allocatable:: n(:) !n (S) - число лавин,
!которые затронули
!S ячеек
!0) располагаем в оперативной памяти массивы
!и инициализируем графическое окно
L2=L*L; L1=L+1
allocate (h(0:LI, 0:L1)); h=0
allocate (n(l:L2)); n=0
allocate (u(1:L2,1:L2)); u=0
!1)проверяем значение времени наблюдения Np. Если
!Np<Nmax переходим к пункту 2, а при Np=Nmax переходим
!к пункту 6;
do Np=l,NMAX
if(mod(Np,100)==0) then
call settextposition(1,1,curpos);
write (*,*)' Np =', Np,' '
endif
!2) выбираем случайным образом ячейку и добавляем
!в нее частицу
call random(rnd); x=int(rnd*L+l.)
call random(rnd); y=int(rnd*L+l.)
h (x, y) =h (x, y) +1
!3) выполняем проверку ячеек решетки на стабильность.
!При обнаружении нестабильных ячеек переходим
!к пункту 4, а в противном случае к пункту 5
S=0; NA= 0; u=0
unstable=count(h>hc)
do while (unstable>0)
!4) сканируем решетку и при обнаружении критических
!ячеек. Выполняем перераспределение частиц
do у=1,L
do x=l,L
if(h(х,у)>hc) then
NA=NA+1
h (x, y) =h (x, y) -4
h(x+1,у)=h(x+1,у)+1; h(x-1,у)=h(x-1,у)+1
h(x,y+1)=h(x,y+1)+1; h(x,у-1)=h (x,у-1)+1
if(u(x,y)==0) then
S=S + 1;u(x,y)=1
endif
endif
enddo
enddo
unstable=count(h>hc)
enddo {окончание цикла do while
17.2. Алгоритмы и описание работы программ •Аг 343
!5) накапливаем информацию о характеристиках лавины
if (S>0) n (S)=n (S)+1
enddo !окончание цикла по переменной NP
!6) записываем результаты расчетов и заканчиваем
!выполнение программы
open (1, file='sandpile.dat')
do S=1, L2
if (n (S)>0) write (1,*) S, n(S)
enddo
close (1)
end program sandpile
В данной программе для проверки наличия на решетке нестабиль¬
ных ячеек используется внутренняя функция count () Фортрана 90.
Новые частицы добавляются только в ячейки с координатами в ин¬
тервале 1 — L. Границы массива h(x,y) выбраны большими на еди¬
ницу, т. е. h (0 :L+1, 0 :L+1), что позволяет накапливать в граничных
элементах этого массива частицы вышедшие за пределы решетки. В
заключительной части программы в выходной файл записывается за¬
висимость числа лавин N от их площади S.
17.2.3.2. Лесной пожар
Программа, для исследования явления SOC в модели лес¬
ного пожара, содержится в файле forestfire. f90. Полный код этой
программы представлен ниже:
program socffm
use msflib
implicit none
type (rccoord) curpos
integer:: t, TMAX=le5
integer:: L=512,L2
integer:
integer
integer
integer
integer
real
integer,
integer,
integer,
WB=1000
S
i, na
x, у
xn, yn
rnd
allocatable:
allocatable:
allocatable:
!время наблюдения
!L - линейный размер квадратной
!решетки, L2=L*L
!частота воспламенения дерева
!площадь пожара
!координаты узла
!координаты соседнего узла
!случайное число
h (:, :)
ха (:), уа(:)
п ( : ) ! n(S)
число пожаров
integer:: dx(1:4)=(/0,1, 0,
integer:: dy(1:4)=(/1,0,-1,
!площади S
-1/)
0/)
Глава 17. Самоорганизованная критичность
!0) размещаем в памяти массивы
allocate (h (0:L+1,0:L+l)); h=0
L2=L*L
allocate (ха(1:L2),уа(1:L2),n(1:L2)); ха=0;уа=0; п=0
do t=l,TMAX
if(mod(t,100)==0) then
call settextposition(1,1,curpos);
write(*,*)'t=', t, '
endif
!1)Выбираем случайным образом ячейку (х,у). В случае,
!если она пустая (h(x,y)=0), то высаживаем в нее
!дерево (h(x,y)=l). Этот пункт повторяем WB-1 раз.
do i=l,WB-1
call random(rnd); x=int(rnd*L+l.)
call random(rnd); y=int(rnd*L+l.)
if(h(x,y)==0) h(x,y)=1
enddo
!2)выбираем случайным образом ячейку (х,у). В случае,
!если она пустая (h(x,y)=0), переходим к пункту 1.
!Если она заполнена (h(x,y)=l), идентифицируем
!кластер, к которому принадлежит данное дерево и
!полностью выжигаем этот кластер, полагая (h(x,y)=0).
call random(rnd); x=int(rnd*L+l.)
call random(rnd); y=int(rnd*L+l.)
if (h(x,y)==1)then
h(x,y)=0; S=1; na=l; xa(na)=x; ya(na)=y
do while(na>0)
do i=l,4
xn=xa(1)+dx(i); yn=ya(1)+dy(i)
if(xn>=l .and. xn<=L .and. yn>=l .and. yn<=L)then
if(h(xn, yn)==l)then
h(xn, yn)=0; S=S + 1
na=na +1; xa(na)=xn; ya(na)=yn
endif
endif
enddo
xa(1)=xa(na); ya(1)=ya(na); na=na-l
enddo
!3)накапливаем информацию об общей площади S
!пожара. Переходим к пункту 1.
S=int(S/50); N(S)=N(S)+1
endif
17.2. Алгоритмы и описание работы программ Аг 345
!4)записываем результаты расчетов и заканчиваем
!выполнение программы
open (1, file='socffm.dat')
do S=1,L*L
if (n(S)>0) write (1,*) S*50, n(S)
enddo
close (1)
end program socffm
В приведенной программе переменная WB соответствует отношению
вероятности fet роста деревьев к вероятности ftb их воспламенения. Для
хранения состояния узлов решетки используется массив h (х, у). Для
узлов, оккупированных деревьями, значения элементов этого массива
приравниваются единице, а для пустых узлов — нулю. В процессе
«выжигания» отдельного кластера деревьев соответствующим элемен¬
там массива h (х, у) присваивается нулевые значения. Массивы ха (),
уа() служат для хранения списков координат отдельного кластера, а
переменная па определяет количество узлов, которые к нему принад¬
лежат. Процесс исследования соседних узлов по отношению к узлу, с
которого начинается «возгорание» продолжается до тех пор, пока зна¬
чение переменной па>0. При исследовании длина списков координат
ха (), уа () увеличивается при обнаружении каждого нового узла, ок¬
купированного деревом, и уменьшается на единицу после исследования
каждого очередного узла. Уменьшение списка осуществляется путем
переписывание на место исследованного узла (всегда имеет индекс,
равный единице) последнего из списка, т. е. путем исполнения после¬
довательности операторов
ха(1)=ха(па); уа(1)=уа(па); па=па-1.
В заключительной части программы в выходной файл записы¬
вается зависимость частоты пожаров N от площади S, затронутой
пожаром.
17.2.4. Примеры работы программ
На рис. 17.13 представлены зависимости частоты возник¬
новения N лавин от их суммарной площади S, которая получена с по¬
мощью программы sandpile. f 90. Приведенную зависимость можно
аппроксимировать степенным законом N ~ S-a, где а = 0,994 ±0,003,
что согласуется с литературными данными [3].
На рис. 17.14 представлена аналогичная зависимость частоты воз¬
никновения пожаров N от их площади S, полученная с помощью про¬
граммы forestfire. f 90 для а)ь — Ю3 на решетке размера L = 512.
346 Глава 17. Самоорганизованная критичность
Рис. 17.13. Зависимость количества лавин N от их суммарной площади 5.
Размер решетки составлял L = 50, общее количество частиц, до¬
бавленных к куче с песком, равно Np = Ю5
Рис. 17.14. Зависимость количества пожаров N от их площади S. Размер ре¬
шетки составлял L = 512, ^& = Ю3, время наблюдения равно £=105
Полученная зависимость, за исключением начального участка, хорошо
аппроксимируется степенным законом N ~ S~a, где а = 1,15 ± 0,01, что
согласуется с литературными данными [5].
17.4. Литература -J\r 347
17.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Напишите программу, реализующую алгоритм одномерной модели
кучи с песком, описанной в тексте. Исследуйте зависимость ста¬
ционарного угла кучи от локального условия стабильности, когда
h(x) — h(x + 1) > 1.
2. Напишите программу для клеточного автомата, реализующего алго¬
ритм игры «Жизнь» [23]. Исследуйте зависимость между частотой
и площадью лавины и вычислите степенной показатель для этой
модели.
3. В тестовом примере для программы горения леса приведена зависи¬
мость N(S) для значения параметра щ = 103. Вычислите несколь¬
ко аналогичных зависимостей для других значений соь. Исследуйте,
каким образом изменяется степенной показатель а при росте соь.
Отметим, что истинное SOC поведение для этой модели должно
выполняться в предельном случае, когда шь —> сю. Вычислите зна¬
чение а для этого предельного случая.
4. Для модели горения леса постройте зависимость площади кластера
выгорания 5 от радиуса гирации кластера Rg = ^/zf=i (п — r)2/S,
где г = Y,f=\ri/S соответствует координатам центра масс кластера.
Определите, является ли кластер выгорания фракталом?
5. Для модели горения леса постройте зависимость площади выгорания S
от параметра а)ь. Проверьте, выполняется ли зависимость S « са>ь,
где c = (\ — pt)/pt, a pt — плотность деревьев в режиме SOC.
Вычислите значение pt.
6. Исследуйте, является ли фракталом кластер обвала для двумерной
модели кучи с песком?
7. Для двухмерной модели кучи с песком исследуйте зависимость меж¬
ду количеством N и временем Т ожидания очередной лавины площа¬
ди S. Вычислите степенной показатель у для этой модели.
8. Напишите программу, реализующую одномерную модель землетря¬
сений. Вычислите для этой модели степенной показатель а в зави¬
симости N ~ Е~а.
17.4. ЛИТЕРАТУРА
1. Bak P., Tang С., Wiesenfeld К. Self-organized criticality: An explanation of
1/f noise // Phys. Rev. Lett. - 1987. - V. 59. - P. 381-384.
2. Bak P., Tang C. and Wiesenfeld K. Self-organized criticality // Phys. Rev.
A. - 1988. - V. 38. - P. 364-374.
348 -Ar Глава 17. Самоорганизованная критичность
3. Bak P. How Nature Works: The Science of Self-Organized Criticality. — New
York: Springer-Verlag, 1996. — 212 p.
4. Jensen H. J. Self-Organised Criticality: Emergent Complex Behaviour in Phys¬
ical and Biological Sciences. — Cambridge: Cambridge University Press,
1998. - 153 p.
5. Turcotte D. L. Self-organized criticality 11 Rep. Prog. Phys. — 1999. — V. 62,
No. 10. - P. 1377-1429.
6. Sornette D. Why Stock Markets Crash, Critical Events in Complex Financial
Systems. — Princeton, N.J.: Princeton University Press, 2003.
7- Frigg R- Self-organised criticality —what it is and what it isn’t 11 Stud. Hist.
Phil. Sci. - 2003. - V. 34. - P. 613-632.
8. Dhar D., Sadhu T. and Chandra S. Pattern formation in growing sandpiles //
Europhys. Lett. - 2009. - V. 85, No. 4. - P. 48002.
9. Dhar D. Self-organized critical state of sandpile automaton models // Phys.
Rev. Lett. - 1990. - V. 64, No. 14. - P. 1613-1616.
10. Burridge R., Knopoff L. Model and theoretical seismicity // Bull. Seism. Soc.
Am. - 1967. - V. 57. - P. 341-371.
11. Carlson J. M. and LangerJ.S. Properties of earthquakes generated by fault
dynamics 11 Phys. Rev. Lett. - 1989. - V. 62, No. 22. - P. 2632-2635.
12. Carlson J. M. and Langer J. S., Mechanical model of an earthquake fault //
Phys. Rev. A. - 1989. - V. 40, No. 11. - P. 6470-6484.
13. Carlson J. М., Langer J. S. and Shaw B.E. Dynamics of earthquake faults //
Rev. Mod. Phys. - 1994. - V. 66. - P. 657-670.
14. Xia /., Gould H. and Klein W. Simulations of the Burridge-Knopoff Model //
3rd ACES Workshop Proceedings 3rd ACES (APEC Cooperation for Earth¬
quake Simulation) Workshop in Maui, Hawaii 5-10 May 2002. — P. 225-230.
15. Olami Z., Feder H.J. S. and Christensen K. Self-organized criticality in a con¬
tinuous, nonconservative cellular automaton modeling earthquakes 11 Phys.
Rev. Lett. - 1992. - V. 68, No. 8. - P. 1244-1247.
16. Gutenberg B. and Richter C. Seismicity of the Earth and Associated Phenom¬
ena. — Princeton, N.J.: Princeton University Press, 1954. — 310 p.
17. Clar S., Drossel B. and Schwabl F. Forest fires and other examples of self-or¬
ganized criticality 11 J. Phys.: Condens. Matter. — 1996. — V. 8, No. 37. —
P. 6803-6824.
18. Earle S. Scott, Rodney Schreiner, Lee R. Sharpe, Bassam Z.Shakhashiri,
and Glen E. Dirreen. Oscillating Chemical Reactions in Chemical demonstra¬
tions: A handbook for teachers of chemistry. V. 2 (Shakhashiri, Basaam A.)
Madison: The University of Wisconsin Press, 1985. — P. 232-247.
19. D’Innocenzo A., Paladini F., Renna L. A numerical investigation of discrete
oscillating epidemic models // Physica A: Statistical Mechanics and its Ap¬
plications. - 2006. - V. 364. - P. 497-512.
20. White S.H., del Rey A.M., Sanchez G.R. Modeling epidemics using cellular
automata // Applied Mathematics and Computation. — 2007. — V. 186,
No. 1. - P. 193-202.
17.4. Литература 349
21. Volpert V., Petrovskii S. Reaction-diffusion waves in biology 11 Physics of
Life Reviews. - 2009. - V. 6, No. 4. - P. 267-310.
22. Sornette D. Critical Phenomena in Natural Sciences, Chaos, Fractals, Self¬
organization and Disorder: Concepts and Tools. — 2nd ed. — Heidelberg:
Springer Series in Synergetics, 2004.
23. Gardner M. Mathematical Games: The Fantastic Combinations of John Con¬
way’s New Solitaire Game «Life» 11 Scientific American. — 1970. — V. 223,
No. 4. — P. 120-123; Гарднер М. Крестики-нолики. — М.: Мир, 1988. —
С. 287-343.
24. Bak P.P., Chen P. and Creutz M. Self-organized criticality in the «Game of
Life» // Nature. - 1989. - V. 342. - P. 780-782.
25. Тоффоли Т., Марголус Т. Машины клеточных автоматов. — М.: «Мир»,
1991.
26. Беркович С. Я. Клеточные автоматы как модель реальности: поиски новых
представлений физических и информационных процессов. — М.: Изд-во
МГУ, 1993. - 112 с.
4 Р. П. Федоренко
/\ u-i_ Введение в вычислительную физику
У ИНТЕЛЛЕКТ 2-е, дополн. и исп. изд.
Книга посвящена описанию методов приближенного решения задач математической
физики, возникающих в различных областях. Изложение основных понятий и средств
численного анализа доводится до описания специальных алгоритмов решения важных
прикладных задач, разработка которых продолжается в настоящее время. Приближенные
решения сложных задач получаются как общими средствами вычислительной математики,
так и специфическими для данного узкого класса задач приемами, которые позволяют
обходить существенные трудности в современной вычислительной работе и делают
расчеты посильными для ЭВМ.
Для студентов и аспирантов факультетов прикладной математики и физико-технических
специальностей вузов с достаточно высоким уровнем преподавания математики, а также
для научных работников, специализирующихся в области применения численных методов
в научных исследованиях.
Предисловие редактора второго издания
Предисловие автора
Часть 1
ОСНОВЫ ВЫЧИСЛИТЕЛЬНОЙ
МАТЕМАТИКИ
1. Решение систем нелинейных
уравнений
2. Численное дифференцирование
3. Интерполяция функций
4. Вычисление определенных интегралов
5. Численное интегрирование задачи
Коши для систем обыкновенных
дифференциальных уравнений
6. Абстрактная форма приближенного
метода
7. Исследование сходимости методов Рунге
- Кутты
8. Приближенное решение краевых задач
для систем обыкновенных
дифференциальных уравнений
9. Метод дифференциальной прогонки
10. Прогонка в разностной задаче Штурма
- Лиувилля
11. Численное интегрирование задачи
Коши для уравнений с частными
производными
12. Спектральный признак устойчивости
13. Метод переменных направлений
14. Решение эллиптических задач
методом сеток
Часть 2
ПРИБЛИЖЕННЫЕ МЕТОДЫ
ВЫЧИСЛИТЕЛЬНОЙ ФИЗИКИ
15. Спектральная задача
Штурма - Лиувилля
16. Главная спектральная задача для
краевых задач математической физики
17. Жесткие системы обыкновенных
дифференциальных уравнений
18. Жесткие линейные краевые задачи
19. Осреднение быстрых вращений
20. Одномерные уравнения газовой
динамики и их численное
интегрирование
21. Нелинейное уравнение
теплопроводности
22. Реализация разностной схемы для
уравнений газовой динамики с
теплопроводностью
23. Приближенное решение двумерных
задач газовой динамики
24. Приближенное интегрирование
уравнения Власова
25. Некорректные задачи и их
приближенное решение
26. Поиск минимума
27. Дифференцирование функционалов
28. Задачи оптимального управления
29. Вариационные задачи механики с
недифференцируемыми функционалами
30. Псевдодифференциальные уравнения
31. Метод конечных суперэлементов
Список литературы
X
Издательский Дом
ИНТЕЛЛЕКТ
Глава 1.
АНАЛИЗ РАЗМЕРНОСТЕЙ
И ФИЗИЧЕСКОЕ ПОДОБИЕ
1.1. Размерность
1.2. Анализ размерностей
1.3. Физическое подобие
Глава 2.
АВТОМОДЕЛЬНОСТЬ
И ПРОМЕЖУТОЧНАЯ АСИМПТОТИКА
2.1. Пологое течение грунтовых вод.
Математическая модель
2.2. Очень интенсивное сосредоточенное
заводнение: автомодельное решение
2.3. Промежуточные асимптотики
Глава 3.
ЗАКОНЫ СКЕЙЛИНГА
И АВТОМОДЕЛЬНЫЕ РЕШЕНИЯ,
КОТОРЫЕ НЕ МОГУТ БЫТЬ ПОЛУЧЕНЫ
ПРИМЕНЕНИЕМ АНАЛИЗА
РАЗМЕРНОСТЕЙ
3.1. Формулировка модифицированной
задачи о расплывании бугра грунтовых вод
3.2. Прямое применение анализа
размерностей к модифицированной задаче
3.3. Численный эксперимент. Автомодельная
промежуточная асимптотика
3.4. Автомодельное предельное решение,
нелинейная задача на собственные
значения
Глава 4.
ПОЛНАЯ И НЕПОЛНАЯ АВТОМОДЕЛЬ¬
НОСТЬ. АВТОМОДЕЛЬНЫЕ РЕШЕНИЯ
ПЕРВОГО И ВТОРОГО РОДА
4.1. Полная и неполная автомодельность
4.2. Автомодельные решения первого и второго
рода
4.3. Практический рецепт приложения анализа
законов подобия
Глава 5.
СКЕЙЛИНГ И ГРУППЫ
ПРЕОБРАЗОВАНИЙ.
РЕНОРМАЛИЗАЦИОННАЯ ГРУППА
5.1. Анализ размерностей и группы
преобразований
5.2. Задача: пограничный слой на плоской
пластине в равномерном потоке
Г. И. Баренблатт
Автомодельные явления - анализ
размерностей и скейлинг
пер. с англ. 3-го изд.
5.3. Ренормализационная группа и неполная
автомодельность
5.3.1. Ренормализационная группа и
неполная автомодельность
5.3.2. Разложение теории возмущений
Глава 6.
АВТОМОДЕЛЬНЫЕ РЕШЕНИЯ И
БЕГУЩИЕ ВОЛНЫ
6.1. Бегущие волны
6.2. Ударные волны Бюргерса -стационарные
бегущие волны первого типа
6.3. Пламёна - стационарные бегущие волны
второго рода. Нелинейная задача на
собственные значения
6.3.1. Схематическая формулировка
задачи о распространении пламени
6.3.2. Нелинейная задача на собственные
значения
6.4. Автомодельная интерпретация
солитонов
Глава 7.
ЗАКОНЫ СКЕЙЛИНГА И ФРАКТАЛЫ
7.1. Фракталы Манделброта и неполная
автомодельность
7.2. Неполная автомодельность фракталов
7.3. Скейлинговые соотношения для
зависимости интенсивности дыхания
животных от их массы. Фрактальность
органов дыхания
Глава 8.
ЗАКОНЫ СКЕЙЛИНГА
ДЛЯ ПРИСТЕНОЧНЫХ ТУРБУЛЕНТНЫХ
СДВИГОВЫХ ПОТОКОВ ПРИ ОЧЕНЬ
БОЛЬШИХ ЧИСЛАХ РЕЙНОЛЬДСА
8.1. Турбулентность при очень больших числах
Рейнольдса
8.2. Математический пример Чорина
8.3. Стационарные сдвиговые течения при
очень больших числах Рейнольдса.
Промежуточная область течения в трубе
8.4. Модификация вывода закона
распределения скорости в
промежуточной области данного
Изаксоном-Милликаном-фон
Мизесом. Асимптотика исчезающей
вязкости
8.5. Турбулентные пограничные слои
Учебное издание
Заявки на книги присылайте по адресам:
zakaz@id-intellect.ru
solo@id-intellect.ru
id-intellect@mail.ru
тел. (495) 579-96-45
факс (495) 617-41-88
В заявке обязательно указывайте
свои реквизиты (для организаций) и почтовый адрес!
Подробная информация о книгах на сайте
http://www.id-intellect.ru
Леонид Анатольевич Булавин
Николай Викторович Выгорницкий
Николай Иванович Лебовка
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
ФИЗИЧЕСКИХ СИСТЕМ
Компьютерная верстка — А.А. Пярнпуу
Корректура авторов
Художник — С.Ю. Биричев
Ответственный за выпуск — Л.Ф. Соловейчик
Формат 60x90/16. Печать офсетная.
Гарнитура Ньютон.
Печ. л. 22. Тираж 1000 экз. Зак. № 1070
Бумага офсетная № 1, плотность 80 г/м2
Издательский Дом «Интеллект»
141700, Московская обл., г. Долгопрудный,
Промышленный пр-д, д. 14,
тел. (495) 617-41-85
Отпечатано в ООО «Чебоксарская типография № 1»
428019, г. Чебоксары, пр-т И. Яковлева, д. 15
БУЛАВИН ЛЕОНИД АНАТОЛЬЕВИЧ
Академик НАН Украины, зав. кафедрой
молекулярной физики КГУ им.
Т.Г. Шевченко. Автор около 600 научных
статей, 18 учебников и монографий.
ВЫГОРНИЦКИЙ НИКОЛАЙ ВИКТОРОВИЧ
Старший научный сотрудник Института
биоколлоидной химии НАН Украины.
Автор одного учебника, около
20 научных статей.
ЛЕБОВКА НИКОЛАИ ИВАНОВИЧ
Профессор, зав. отделом Института
биоколлоидной химии НАН Украины.
Автор свыше 340 научных статей,
4 монографий и учебников.
ISBN 978-5-91559-101-0
www.id-intellect.ru