Основы теории оптимального управления - Ф., Кротова В

Автор: Ф. Кротова В
Теги: дифференциальные, интегральные и другие функциональные уравнения конечные разности вариационное исчисление функциональный анализ управление экономикой математика дифференциальное исчисление математический анализ основы теории оптимального управления
ISBN: 5-06-000622-0
Год: 1990
Похожие
Исследование операций
Управление роботами
Численные методы и программное обеспечение
Математические основы кибернетики
Текст
                    ББК 65.050
0-75
УДК 517.977
Авторы:
В. Ф. Кротов, Б. А, Лагоша. С. М. Лобанов, Н. И. Данилина,
С. И. Сергеев
Рекомендовано
"Государственным комитетом СССР
по народному образованию
для использования в учебном процессе
Рецензенты:
<» кафедра математических методов анализа экономики МГУ
им. М. В. Ломоносова:
д-р физ.-мат. наук, проф. Ю. П. Иванилов
1402060000(4309000000)—368
О---------------------------85—-90
001(01)—90
ISBN 5-06-000622-0
© Коллектив авторов, 1990
ПРЕДИСЛОВИЕ
Предлагаемая книга написана на базе исследований, состави-
вших основу курса лекций по теории оптимального управления
и ее приложений к исследованию экономических процессов,
прочитанных на факультете экономической кибернетики Московс-
кого экономико-статистического института.
Изложение различных методов оптимального управления ве-
дется с единых методологических позиций. Теоретической основой
всех рассматриваемых методов и алгоритмов служат достаточные
условия оптимальности. Эти условия проявляются как признак
оптимальности для непрерывных и дискретных (многошаговых)
управляемых процессов в общем виде. Ставя при постановке
задачи оптимального управления ряд дополнительных требований,
получаем соотношения в форме Лангранжа — Понтрягина, кото-
рые являются необходимыми условиями оптимальности. Приме-
нительно к непрерывным управляемым процессам они известны
как принцип максимума Понтрягина.
Из достаточных условий оптимальности с помощью специаль-
ного выбора функции <р(Ц %) (результат решений дифференциаль-
ного уравнения Беллмана в частных производных для непрерыв-
ных и конечно-разностного—для многошаговых процессов) полу-
чаем алгоритмы динамического программирования для непрерыв-
ных и дискретных управляемых систем. Таким образом,
разработанные ранее как независимые принципы максимума
и динамичного программирования увязываются через достаточные
условия оптимальности.
В целом теоретическая часть книги отражает совокупность
математических методов теории оптимального управления, кото-
рые могут использоваться в различных прикладных направлениях.
Но так как базовый курс читается в экономическом вузе
и ориентирован главным образом на применение в макроэкономи-
ческих исследованиях, то указанные методы применяются к за-
дачам экономической динамики. Большинство приведенных при-
меров также имеет экономическое содержание.
Цель книги - - познакомить читателя с методами оптимизации
и их приложениями к макроэкономическому моделированию.
Исходя из этого была выбрана следующая структура изложения
материала.
В гл. 1 излагаются понятийный аппарат теории систем,
общие принципы моделирования и место методов экономико-
математического моделирования. Материал этой главы может
рассматриваться как введение в основные понятия экономической
3
кибернетики, необходимые как предпосылка для последующего
изложения конкретных методов оптимального управления.
Гл. 2 в соответствии с отмеченной общей направленностью
посвящена изложению некоторых типовых оптимизационных
моделей экономической динамики. Эти модели подготавли-
вают читателя для последующего применения оптимизационных
методов.
В гл. 3 рассматриваются методы качественного исследования
моделей экономических систем. Проведение таких исследований
обычно сопровождает решение задач оптимизации. В главе
также изучаются вопросы построения и оптимизации траекторий
сбалансированного экономического роста.
В гл. 4 дается общая постановка задачи оптимального
управления для непрерывных и дискретных процессов, и на ее основе
в гл. 5 формулируются и доказываются теоремы о достаточных
условиях оптимальности. Приводится пример одного из типов задач
оптимального управления, для которых алгоритм основывается на
непосредственном применении достаточных условий. Можно сказать,
что гл. 5 является теоретическим фундаментом излагаемого курса.
В гл. 6 описывается однопродуктовая макроэкономичес-
кая модель. Алгоритм оптимизации при этом отвечает ре-
зультатам § 5.5.
Гл. 7 посвящена исследованию классической задачи Эйлера
на основе достаточных условий оптимальности. В § 7.4 выводится
уравнение вариационного исчисления Эйлера с помощью идей,
которые далее развертываются в соотношения принципа максиму-
ма Понтрягина. Эти вопросы в виде соответствующей теории
излагаются в гл. 8 для непрерывных процессов.
В гл. 9 рассматривается аналог принципа максимума для
многошаговых (дискретных) процессов. В его основе лежит
использование сопряженных переменных в качестве аналога
множителей Лангранжа.
В гл. 10 приведен ряд задач оптимизации непрерывных и диск-
ретных процессов, которые иллюстрируют возможности при-
менения на практике метода Лангранжа — Понтрягина. За исклю-
чением первой — примера механического прямолинейного движе-
ния— остальные задачи имеют экономическое содержание. При
этом две из них (§ 10.2, 10.3) но постановке почти совпадают, но
относятся соответственно к непрерывным и дискретным процессам.
В гл. 11 реализуются достаточные условия оптимальности
в форме метода динамического программирования Гамильтона—-
Якоби — Веллмана. Глава завершается примером применения
метода при оптимизации распределения капитальных вложений
между предприятиями.
Гл. 12—16 при первом чтении можно опустить. Они
в некотором смысле носят специальный характер „ и посвящены
численным методам оптимизации многощаговых процессов или
4
специальным алгоритмам для частных классов задач дискретного
программирования.
Гл. 17 посвящена исследованию оптимальных режимов
экономического роста с помощью динамической многоотраслевой
модели народнохозяйственного развития. Глава носит, с одной
стороны, иллюстративный характер — в ней применены изложен-
ные ранее методы оптимального управления, с другой стороны,
в ней, что имеет самостоятельное значение, дан экономический
анализ полученных оптимальных траекторий. Эта глава требует
от читателя больших усилий вследствие повышенной сложности
излагаемого в ней материала.
В Приложении приведен справочный математический аппарат,
содержащий необходимый минимум для решения и понимания
учебных задач.
Книга написана коллективом авторов — преподавателей
Московского экономико-статистического института. Предисловие
написано В. Ф. Кротовым, гл, 1, 7, 10, Приложение — Б.А. Лаго-
шей, гл. 2, 6 — Н. И. Данилиной, гл, 3, 4, 5, 8 — С.М. Лобановым,
гл. 11, 17- В. Ф. Кротовым и С. М. Лобановым, гл. 12, 14 —
В. ф. Кротовым и С. И. Сергеевым, гл. 9, 12, 15, 16 — С. И. Серге-
евым. Научное руководство осуществлял проф, В. Ф. Кротов.
Книга предназначена в первую очередь для студентов, ас-
пирантов и преподавателей по специальностям «Экономическая
кибернетика» и «Информатика и АСУ», но может использоваться
и в специальности «Прикладная математика», и в других
направлениях управленческого профиля. Вместе с тем, так как
большинство глав книги (3, 5, 6, 8, 10, 14, 17) содержат новые
научные результаты, то она также может быть полезной
и научным работникам, занимающихся вопросами оптимизации
и моделирования экономических процессов.
Авторы
Глава 1
Основы моделироввния
экономических процессов
Объектами применения теории и методов оптимального
управления, раскрываемых в предлагаемом учебном пособии,
являются управляемые системы, описываемые дифференциаль-
ными или конечно-разностными уравнениями соответственно
для непрерывных или дискретных (многошаговых) процессов.
Понятия и определения системы, модели, обратной связи,
внешней среды, замкнутой и разомкнутой систем, существенных
или несущественных факторов, обусловленных целевой ориен-
тацией при изучении объекта исследования,— эта совокупность
исходных положений составляет обычно предмет введения
в курсы основ управления и, в частности, экономической
кибернетики для студентов, обучающихся по специальности
«Экономическая кибернетика».
Принимая во внимание, что учебное пособие может исполь-
зоваться и при подготовке специалистов по другим указанным
в предисловии специальностям, в том числе и в тех случаях,
когда курс основ экономической кибернетики не читается,
данная глава может рассматриваться как вводная, отражающая
содержательную сущность и формализованное представление
понятий и принципов формирования структур систем управления.
Так как речь идет именно об общих понятиях и принципах,
то и соответствующие примеры заимствуются из различных
областей, начиная с физического движения материальной точки
и кончая характеристиками сложных производственно-техноло-
гических и особенно социально-экономических систем. Послед-
нее особенно важно, поскольку прикладная ориентация учебного
пособия — прежде всего исследование экономических процессов,
§ 1.1. Система. Модель
Наблюдение, анализ и моделирование являются средствами
познания и прогнозирования процессов, явлений и ситуаций во
всех сферах объективной действительности. Наблюдения за явле-
ниями природы, постановка экспериментов позволили установить
физические законы. Эти законы проявляются в определенных
количественных соотношениях между параметрами процесса или
6
явления независимо от того, происходят ли они в действитель-
ности или их реализацию можно только представить. Например,
если на твердое тело массой т действует сила F, то ускорение,
с которым это тело движется, равно a = Fjm. Данное соотношение
отражает один из важнейших законов механики — второй закон
Ньютона. Отсюда исходя из известных в механике кинематических
соотношений могут быть получены скорость и пройденный путь
в каждый момент времени. Соответствующие величины могут
быть предсказаны или вычислены заранее, до начала реального
движения.
Так же обстоит дело в других физических и естественно-науч-
ных приложениях: знание физических законов позволяет облечь
их в ту или иную конкретную математическую форму, после
чего, решая дифференциальные, алгебраические уравнения или
производя другие вычисления, мы получим значения интересу-
ющих нас параметров или показателей.
В рассмотренном примере мы встретились, по существу, хотя
об этом прямо пока не говорили, с двумя важными понятиями:
системы и модели.
Говоря, например, о системах застройки города или района,
кровообращения, управления предприятием, уравнений, мы прежде
всего имеем в виду некую совокупность. Но любая ли совокуп-
ность может быть названа системой? Вряд ли кто назовет
системами совокупность выброшенных на свалку старых вещей
или луж на асфальте после дождя. Ни то, ни другое никак не
упорядочено, не отвечает определенной цели, в соответствии
с которой эта совокупность сформирована. Первое свойство
систематизации, системного представления о рассматриваемом
объекте—это наличие цели, для реализации которой предназ-
начается данная совокупность предметов, явлений, логических
представлений, формирующих объект. Цель функционирования
системы редуцирует системные признаки, с помощью которых
описываются, характеризуются элементы системы. Вновь об-
ратимся к примеру с движением твердого тела. Здесь цель
состоит в описании движения центра тяжести тела, без учета
его вращения вокруг этого центра, а также упругие перемещения
одних элементов относительно других. Последнее и характеризует
тело как «твердое», когда упругие деформации игнорируются.
Так как речь идет только о движении центра масс точки, не
имеющей геометрических размеров (точнее, мы их не принимаем
в расчет), то становятся несущественными все характеристики
конкретного объекта, за исключением его массы. Масса —
единственный важный системный признак, обусловленный постав-
ленной целью исследования движения тела.
Теперь проанализируем, что характеризует взаимосвязь рас-
сматриваемого твердого тела с внешней средой. Как сказано
выше, на тело действует сила F. Она может иметь один
7
источник, например тягу двигателя, или несколько источников
разного вида с соответствующей результирующей. Так как мы
игнорируем вращение ['ела вокруг центра масс, то существенна
только результирующая сила, которая характеризует взаимосвязь
тела с внешней средой. Из каких компонент состоит резуль тирующая
сила F, какова их физическая природа и т. д. - несущественные
признаки, если исходить из [[оставленной вначале цели.
Рассмотрим другой пример. Допустим, что целью является
совершенствование или разработка эффективной системы управле-
ния предприятием. Нужно ли для этого знать фамилии и размеры
получаемой зарплаты всех работников предприятия? Нет, так
как эти данные хотя в определенной мере и влияют на режим
управления, но не являются наиболее важными. Выделим сущест-
венные системные признаки. К ним относятся; число наименова-
ний выпускаемой продукции, потребность в ней народного
хозяйства, производственные мощности предприятия по выпуску
продукции различных наименований, обеспеченность материаль-
ными, трудовыми ресурсами, общий фонд заработной платы
и условия его использования и т. д. Особо следует выделить
«узкие места». К ним относятся факторы и условия, сдер-
живающие повышение эффективности производства. Сущностью
системы управления предприятием с точки зрения отражения
условий управляемости последним является установление и описа-
ние взаимосвязей и взаимозависимостей между наиболее сущест-
венными факторами и характеристиками предприятия. Еще раз
подчеркнем, что речь идет о предприятии как производствен-
но-экономической системе с точки зрения управляемости им,
т. е. предприятие рассматривается как объект управления. Именно
исходя из этого мы и определили существенные признаки объекта.
При изменении цели другими могут стать как существенные
признаки, так и связи с внешней средой. Например, если на
том же предприятии мы будем анализировать уровень квали-
фикации работников и организацию оплаты труда, то ведомость
на получение заработной платы, в предыдущем случае не
представлявшая первостепенного значения, станет теперь основ-
ным документом.
Подводя итог рассмотренным примерам, мы приходим к вы-
воду, что для выделения системы требуется наличие: а) дели,
для реализации которой формируется система; б) объекта иссле-
дования, состоящего из множества элементов, связанных в единое
целое важными, с точки зрения цели, системными признаками;
в) субъекта исследования («наблюдателя»), формирующего систе-
му; г) характеристик внешней среды по отношению к системе
и отражения ее взаимосвязей с системой.
Наличие субъекта исследования и некоторая неоднозначность,
субъективность при выделении существенных системных признаков
вызывают значительные трудности для однозначного выделения
8
системы и соответственно ее универсального определения. Поэ-
тому необходим более подробный анализ, который приведен в [3].
Изложенный выше содержательный подход дает возможность
определить систему как упорядоченное представление об объекте
исследования с точки зрения поставленной цели. Упорядоченность
заключается в целенаправленном выделении системообразующих
элементов, установлении их существенных признаков, характерис-
тик взаимосвязей между собой и с внешней средой. Системный
подход, формирование систем позволяют выделить главное,
наиболее существенное в исследуемых объектах и явлениях;
игнорирование второстепенного упрощает, упорядочивает в целом
изучаемые процессы. Для анализа многих сложных ситуаций
такой подход важен сам по себе, однако, как правило, построение
системы служит предпосылкой для разработки или реализации
модели конкретной ситуации.
Описанный подход предполагает ясность цели исследования
и детерминированное к ней отношение всех элементов системы,
взаимосвязь между ними и с внешней средой. Такие системы
называют детерминированными. Именно они являются предметом
изучения нашего курса. Это не означает, что все предпосылки,
лежащие в основе их построения, на практике выполняются.
Однако во многих случаях, и это характерно для экономики,
цель исследований — изучение и анализ природы усредненных
и устойчивых в среднем показателей. Это приводит к детер-
минированному подходу к построению системы.
Альтернативу представляют системы со стохастической струк-
турой (случайной природы), когда либо отсутствует ясно выражен-
ная цель исследования, либо по отношению к ней нет полной
определенности, какие признаки считать существенными, а ка-
кие — нет; то же относится и к связям элементов системы
с внешней средой.
Методы построения и исследования стохастических систем,
как правило, более сложные, чем детерминированных. В неко-
торых случаях существуют способы сведения стохастических
систем к специальным образом построенным детерминированным.
Стохастические системы обычно являются объектом специального
исследования, что не является нашей целью.
По настольной модели самолета нельзя определить, например,
его прочностные, аэродинамические характеристики, характерис-
тики системы управления. Следовательно, для реализации назван-
ных целей данная модель не годится. Эта модель подошла бы,
если бы наша цель была—добиться внешнего подобия. Таким
образом, и это главное, структура и свойства модели зависят
от целей, для достижения которых она создается. В этом
органическое единство системы и модели. Если неизвестна цель
моделирования, то неизвестно и с учетом каких свойств и качеств
надо строить модель.
9
Допустим, что цель известна. Построим модель предприятия
для расчета с ее помощью напряженного, но реального плана
производства. При этом, формируя систему, как уже отмечалось,
нужно знать: номенклатуру продукции, которую предприятие
может и заинтересовано выпускать, его производственные возмож-
ности, т. е. парк станков и оборудования, имеющиеся трудовые
и материальные ресурсы, принятый коэффициент сменности
загрузки оборудования и др. Нужно ли знать при этом фамилии
всех работников предприятия? Не нужно. Т. е. с точки зрения
поставленной цели свойства объекта моделирования могут быть
существенными и несущественными (здесь полная аналогия между
системными и модельными представлениями). Изменится цель
моделирования — и важные свойства могут стать несуществен-
ными, и наоборот. Возьмем, например, ведомость на выплату
заработной платы—это готовая модель распределения зарплаты,
фамилии работников — наиболее важное ее свойство, тогда как
при расчете плана производства это свойство несущественно.
Рассмотренные примеры позволяют определить модель как
формализованное представление об объекте исследования с точки
зрения поставленной цели. Различия между определениями систе-
мы и модели состоят в том, что систематизация предполагает
лишь упорядочение, тогда как моделирование — формализацию
взаимосвязей между элементами системы и с внешней средой.
Под моделированием понимается исследование объектов познания
не непосредственно, а косвенным путем, при помощи моделей.
Рассмотрим основные типы моделей [см. 3]. Слово «модель»
(фр. modele) означает; образцовый экземпляр какого-либо изделия;
вид, тип конструкции (например, автомобиля); материал, натура
для художественного произведения; копия, воспроизведение пред-
мета, обычно в уменьшенном размере; исследуемый объект,
представленный в наиболее общем виде.
В качестве примеров моделей можно привести глобус как
модель земного шара, карту как модель местности, маленькую,
например настольную, модель самолета, внешне подобную своему
натуральному образцу, и т. д.
Модели можно различать по ряду признаков: характеру
моделируемых объектов, сферам приложения, глубине моделиро-
вания. Остановимся на специфике моделей в зависимости от
средств моделирования. По этому признаку методы моделирова-
ния делятся на две группы: материальное (предметное) и иде-
альное моделирование:
Материальное моделирование, основывающееся на материаль-
ной аналогии моделируемого объекта и модели, осуществляется
с помощью воспроизведения основных геометрических, физичес-
ких, других функциональных характеристик изучаемого объекта.
Частным случаем материального моделирования является физи-
ческое моделирование, по отношению к которому, в свою
10
очередь, частным случаем является аналоговое моделирование,
Оно основано на аналогии явлений, имеющих различную физичес-
кую природу, но описываемых одинаковыми математическими
соотношениями. Пример аналогового моделирования изучение
механических колебаний с помощью электрической системы,
описываемой теми же дифференциальными уравнениями. Так
как эксперименты с электрической системой обычно проще
и дешевле, она исследуется в качестве аналога механической
системы (например, при изучении колебаний мостов).
Идеальное моделирование отличается от материального прин-
ципиально, Оно основано на идеальной, или мыслимой, аналогии.
В экономических исследованиях это основной вид моделирования.
Идеальное моделирование, в свою очередь, разбивается на два
подкласса: знаковое (формализованное) и интуитивное модели-
рование.
При знаковом моделировании моделями служат схемы, гра-
фики, чертежи, формулы. Важнейшим видом знакового модели-
рования является математическое моделирование, осуществляемое
средствами логико-математических построений.
Интуитивное моделирование встречается в тех областях науки,
где познавательный процесс находится на начальной стадии или
имеют место очень сложные системные взаимосвязи. Такие
исследования называют мысленными экспериментами. В эконо-
мике в основном применяется интуитивное моделирование; оно
описывает практический опыт работников.
§ 1.2. Управление. Обратная связь.
Замкнутая система
Введенные в §1,1 понятия не дают возможности разделить
системы на управляемые и неуправляемые, В широком смысле
под управлением понимается конкретная организация тех или
иных процессов для достижения намеченных целей. Управляемая
система призвана обеспечивать целенаправленное функционирова-
ние при изменяющихся внутренних или (и) внешних условиях.
Неуправляемой системе целенаправленное функционирование не
свойственно.
Примеры управляемых систем: движение автомобиля, работа
предприятия по установленному плану или в соответствии с опре-
деленными стимулами, плановое ценообразование как средство
целенаправленного воздействия на производство продукции и рас-
пределительные процессы в народном хозяйстве. Примеры неуп-
равляемых систем: движение ветра, стихийные явления в природе.
В системе, структура которой установлена ее целевой ориентацией
(для решения каких задач создается система), управление сводится
к поддержанию расчетных значений выходных параметров при
отклонениях внешних условий и внутренних параметров от
U
расчетных. Так устроено большинство технических управляемых
систем.
В экономической системе выбор и формирование как структу-
ры, так и способа функционирования являются задачами управле-
ния, обеспечивающими динамику социально-экономического раз-
вития. Однако соотношение типов задач — формирование произ-
водственно-организационной структуры самой системы и способа
ее функционирования — различно на разных уровнях иерархии
управления.
Рассмотрим общую принципиальную схему систем управления.
Любое управление предполагает наличие объекта управления
(управляемой системы), аппарата, который непосредственно осу-
ществляет процессы управления (управляющей системы), и внеш-
ней среды.
Объект управления производит те или иные действия для
реализации намеченных целей. Сложность объекта управления
зависит от количества входящих в него элементов и природы
взаимосвязей между ними. В процессе функционирования объект
управления подвергается воздействию внешней среды, которая
может способствовать или препятствовать достижению намечен-
ных целей.
Основное назначение управляющей системы — поддерживать
установленный и по каким-либо свойствам признанный нормаль-
ный режим работы объекта управления, а также обеспечивать
нормальное функционирование отдельных элементов объектов
управления в условиях воздействия внешней среды.
Объект управления во взаимодействии с управляющей систе-
мой образует замкнутую систему управления (рис. 1.1).
На рис. 1.1. Х--этО воздействие внешней среды на объект
управления; К—реакция системы на воздействие X. Связь,
с помощью которой управляющая система воздействует на
объект управления, если она имеется, называется обратной.
Входным сигналом для обратной связи является выходной сигнал
системы К. Если Этот сигнал не соответствует целям управления
замкнутой системой, то управляющая система вырабатывает
воздействие обратной связи &Х, которое вместе с X поступает
на вход объекта управления (X, У, &Х в общем случае — векторы
соответствующих размерностей).
В правильно работающей, с точки зрения поставленной цели,
системе сигнал Х+/ХХ должен
способствовать улучшению ка-
чества функционирования за-
мкнутой системы управления.
Количественные оценки
степени достижения цели в мо-
дели управления даются в ви-
де значений целевой функции
Рис. 1.1
12
(функционала), а условия, в рамках которых функционирует
система,— в виде ограничений модели. Цель оптимального упра-
вления — нахождение наилучшего, с точки зрения принятого
условия, критерия оптимизации. Для конкретных ситуаций при
выборе способа управления, хозяйствования или ведения де-
ятельности он реализуется в виде экстремального значения
функционала.
В технике воздействия управляющих систем на объекты
управления осуществляются через обратную связь с помощью
разного рода усилителей, рулевых приводов и других механизмов.
В экономике это могут быть, например, дополнительные фонды
на сырьевые и материальные ресурсы, изменение плановых
показателей и другие факторы управления производственными
процессами.
Обратная связь является средством гибкого управления, когда
конкретное управляющее решение вырабатывается в зависимости
от сложившейся ситуации — возмущения установленного функцио-
нирования системы.
Однако не в каждой системе управление осуществляется
с помощью обратной связи. Другими словами, управляющее
воздействие не всегда бывает связанным с конкретным состоянием
на выходе системы. Простейшая из таких систем без обратной
связи — управление уличным движением с помощью светофора.
В этом случае движение регулируется по заранее заданной
программе независимо от фактических потоков автомобилей,
т. е. состояния системы на выходе. Другие примеры управления
без обратной связи: уставы, кодексы, наставления, регламе-
нтирующие функционирование объекта управления в заданных
условиях. При этом может оказаться, что управленческое
решение, принятое согласно регламентирующему документу,
с учетом конкретной ситуации, характеризующей состояние
системы на выходе, когда решение было принято, не является
наилучшим по сравнению с другими возможными. Но оно
тем не менее считается верным, правомочным, гак как в точности
отвечает регламентирующему документу. Подобные случаи по-
рождают порой ситуации, когда, как иной раз говорят,
возникает альтернатива — принять решение «по закону» или
«по совести». Решение «по совести» может отражать учет
неординарных обстоятельств, уводящих в сторону от решения
«по закону».
В каких случаях система управления создается с обратной
связью, а в каких — без нее, зависит прежде всего От целей
функционирования системы. Здесь могут приниматься во внима-
ние экономические условия альтернативных вариантов и т. п.
Пример альтернативных вариантов —управление уличным движе-
нием с помощью автоматически переключающегося светофора
или регулировщика. Нетрудно представить, в каких случаях
13
целесообразно управление по первому, в каких — по второму
вариантам.
Итак, в структуре системы управления можно выделить:
— объект управления — непосредственное устройство, агрегат,
подсистема общей системы, в которой реализуется цель функцио-
нирования всей системы;
— управляющая система — орган управления (в экономичес-
кой литературе его иногда называют субъектом управления),
фиксирующий параметры объекта управления и вырабатываю-
щий при необходимости управляющие воздействия на объект
управления для приведения его функционирования к режиму,
который в соответствии с целью управления принято считать
нормальным. Если достижение такого режима в условиях име-
ющихся ресурсов системы невозможно, то в качестве нормального
может быть- принят режим, отклоняющийся от желаемого
минимально?-
— обратная связь — объект, подсистема, с помощью которой
реализуется воздействие управляющей системы на управляемый
объект.
Эти элементы, формирующие в совокупности замкнутую
систему управления, находятся под воздействием внешней среды,
которая может способствовать или препятствовать достижению
целей системы.
Представленное схематичное описание замкнутой системы
управления весьма упрощено и отражает только принцип ее
построения. В действительности каждый из указанных элементов,
в свою очередь, может включать объект, субъект управления
с обратной связью или без нее, вся система будет иметь, таким
образом, иерархическую структуру. Подобное характерно для
экономических систем. Например, в системе управления отраслью
в качестве объекта управления следует рассматривать подведо-
мственные министерству предприятия, а управляющего орга-
на— аппарат министерства. Обратная связь при этом осуществля-
ется через систему учета, контроля и оперативного управле-
ния в отношении предприятий со стороны министерства. Каж-
дое предприятие, являясь, таким образом, объектом управ-
ления со стороны министерства, в свою очередь, представляет
замкнутую систему управления со всеми необходимыми струк-
турными элементами. Объект управления- цехи, производствен-
ные участки; управляющая система—дирекция, заводоуправление;
обратная связь осуществляется также через систему учета,
контроля и оперативного управления со стороны руководства
предприятия.
Если спускаться по этой иерархической лестнице, то по
аналогичной схеме можно рассмотреть систему управления цехом.
В управлении народным хозяйством такие иерархические построе-
ния могут быть многоступенчатыми.
14
§ 1.3. Экономическая система как объект управления
(некоторые аспекты математического моделирования)
Изложенное вьпне относится к характеристике систем управле-
ния без учета их природы — физической, производственно-техноло-
гической, социально-экономической. Методы оптимального управ-
ления, которые мы будем изучать в следующих главах, также
не связаны с природой системы, скорее они ориентированы на
определенную форму модели. Для показа широких прикладных
возможностей изучаемых методов оптимального управления в ку-
рсе будут рассматриваться различные примеры. Однако преоб-
ладающей будет экономическая ориентация курса, что наклады-
вает свой отпечаток на характер и методологию практического
использования результатов математического моделирования.
С этой целью рассмотрим наиболее существенные характеристики
экономических систем как объектов управления.
Экономическая система охватывает параметры и характеристи-
ки общественного производства, распределения, обмена и потреб-
ления материальных благ. Она является подсистемой социально-
экономической суперсистемы, т. е. цели ее функционирования
подчинены социальным целям и вытекают из них, по крайней
мере согласуются с последними. Целенаправленное функциони-
рование социалистической экономической системы, за исключе-
нием, может быть, простейших частных случаев, по своей природе
многокритериально. Это означает, что в процессе функционирова-
ния, например, предприятия одновременно ставятся цели: до-
биться максимально возможных прибыли и выпуска продукции
в натуральном или в стоимостном выражении, одновременно
с этим выдержать установленные показатели по номенклатуре
или ассортименту, снизить себестоимость, добиться определенного
уровня качества и рентабельности производимой продукции и т. д.
Некоторые из этих показателей по тенденциям их реализации
могут быть противоречивыми. Например, стремление к мак-
симальному выпуску продукции (в стоимостном или натуральном
выражении) одновременно ведет и к суммарному росту себесто-
имости. Иначе быть не может, так как производство каждого
дополнительного изделия сопряжено с дополнительными затра-
тами, т. е. чем больше выпускается продукции, тем больше
становится и суммарная себестоимость производства. Ограничение
такой себестоимости — противоположное требование к росту вы-
пуска продукции. Минимизировать себестоимость производства
имеет смысл только тогда, когда точно установлен необходимый
плановый объем производства. Подобные противоречия могут
иметь место и в отношении других частных критериальных
показателей. В целом можно представить себе одну из двух
альтернатив; либо все принимаемые в расчет частные критери-
альные показатели ведут себя качественно сходным образом,
15
достигая одновременно своих экстремальных значений, либо не
существует такого возможного плана производства, которому
соответствовали бы экстремальные значения одновременно всех
частных критериальных показателей. Свидетельство тому — при-
веденный выше пример.
Первой альтернативе отвечает однокритериальная по существу
ситуация, когда используется основной в содержательном отноше-
нии критерий, а остальные игнорируются, так как они, ничему
не противореча, не влияют на оптимизацию основного принятого
в модели критерия.
Вторая альтернатива заключается в выработке разумного,
с практической точки зрения, компромисса, когда для принятого
плана производства не достигаются потенциально возможные
оптимальные значения отдельных целевых критериев, но каждый
из них для этого плана принимает в той или иной мере близкое
к оптимальному значение. Мы не будем рассматривать сейчас
практические детали формализованного отражения компромис-
сов—это самостоятельная теория, но в конечном итоге проблема
компромисса сводится конструктивно к выработке некоторою
комплексного критерия, в котором названные выше частные
критерии присутствуют как отдельные составляющие.
Пользуясь современной терминологией, можно сказать, что
экономические управленческие задачи плохо структуризованы и не
всегда модель может быть построена однозначным образом.
Что это может означать? Прежде всего цели функционирования
многих экономических и особенно социально-экономических си-
стем не всегда можно четко сформулировать. Причем это
относится не к каким-либо особым условиям или ситуациям,
а к самым обычным, ординарным. Например, каким конкретно
показателем выражается степень достижения цели неуклонного
повышения уровня жизни населения? Вопрос на первый взгляд
ясный, но в то же время каждый исследователь проблемы, если
поставить ее под конкретным углом зрения, может подойти
к пей по-разпому.
Один из наиболее простых подходов -это ориентация на
критерий роста денежных доходов населения. Однако за этой,
вроде бы естественной, постановкой стоят многие сложные
социально-экономические проблемы, такие, как обеспечение опере-
жающего роста производительности труда по отношению к за-
работной плате, укрепление покупательной способности рубля
и насыщение сферы потребления качественными товарами и услу-
гами, решение жилищной проблемы и обеспечение социальной
справедливости и т. п. Итак, как именно конструктивно реализо-
вать сформулированную выше цель, вообще говоря, содержатель-
но понятную, остается далеко не ясным. Не больше ясности,
или уже во всяком случае однозначности, в постановке той же
проблемы будет при других, более односторонних подходах.
16
Итеративный режим использования в экономике математичес-
ких моделей — один из характерных приемов при моделировании
плохо структуризованных задач. Процесс сходимости искомых
показателей в и теративном режиме понимается как целенаправлен-
ный человеко-машинный диалог с возможными изменениями
исходных данных и, если необходимо, отдельных элементов
модели. Другими словами, происходит уточнение (самообучение)
самой модели объекта с помощью имитации его функциониро-
вания.
Управление подразделениями народного хозяйства построено
по иерархическому принципу. На верхних уровнях — Госплана
СССР и Госпланов союзных республик, Государственных комите-
тов и других межотраслевых органов- осуществляется управле-
ние народным хозяйством в целом и его крупными межотрасле-
выми комплексами. Руководство отдельными отраслями относит-
ся к среднему уровню иерархии и осуществляется отраслевыми
министерствами и ведомствами. Нижний уровень иерархии, как
уже сказано, представляют предприятия и производственные
объединения.
Построение математических моделей управления производст-
вом на каждом уровне иерархии связано с использованием
агрегированной (укрупненной) информации: чем выше уровень
иерархии, тем большая степень агрегирования данных. И соответ-
ственно должны существовать относительно простые методы,
алгоритмы дезагрегирования (разукрупнения) информации яри
переходе к более низким уровням управления.
Нами рассмотрены некоторые общие положения, связанные
с математическим моделированием экономических систем. Их
учет привносит определенную специфику в методологию постро-
ения и использования на практике математических моделей
в экономике.
В настоящей главе нет возможности рассмотреть эти вопросы
более подробно, такая задача выходит за рамки курса, к изучению
которого мы приступаем. Наша цель в другом: изучая математи-
ческую теорию оптимального управления и указывая читателю
на общие условия применения ее положений и результатов,
дать возможность увидеть среди них место для экономических
приложений.
Желающие проанализировать и обсудить более подробно
специфику применения ма тематических методов в экономических
исследованиях могут обратиться, например, к [3, 4].
Глава 2
Оптимизационные модели
экономической динамики
Социалистическая экономика — сложная иерархическая дина-
мическая система. В зависимости от цели исследования ее
представляют в различных разрезах. Так, на верхнем уровне
иерархии экономику рассматривают как систему общественного
производства, распределения, обмена и потребления. Такое
разбиение удобно для исследования общественных отношений,
складывающихся в процессе производства.
Это описание служит основой политэкономического способа
соединения факторов производства: средств производства, рабо-
чей силы —и определяет непосредственно положение произво-
дителя в общественном производстве.
В процессе труда люди воздействуют друг на друга, соединя-
ясь определенным образом для совместной деятельности. Отно-
шение людей в производстве определяет социальную структуру
общества и распределение результатов. Общественный способ
соединения работников и средств труда характеризует тип
производственных отношений.
§ 2.1. Однопродуктовая динамическая
макроэкономическая модель
Исследование взаимосвязей элементов производства вне об-
щественной формы приводит к рассмотрению производствен-
но-технологической интерпретации экономики.
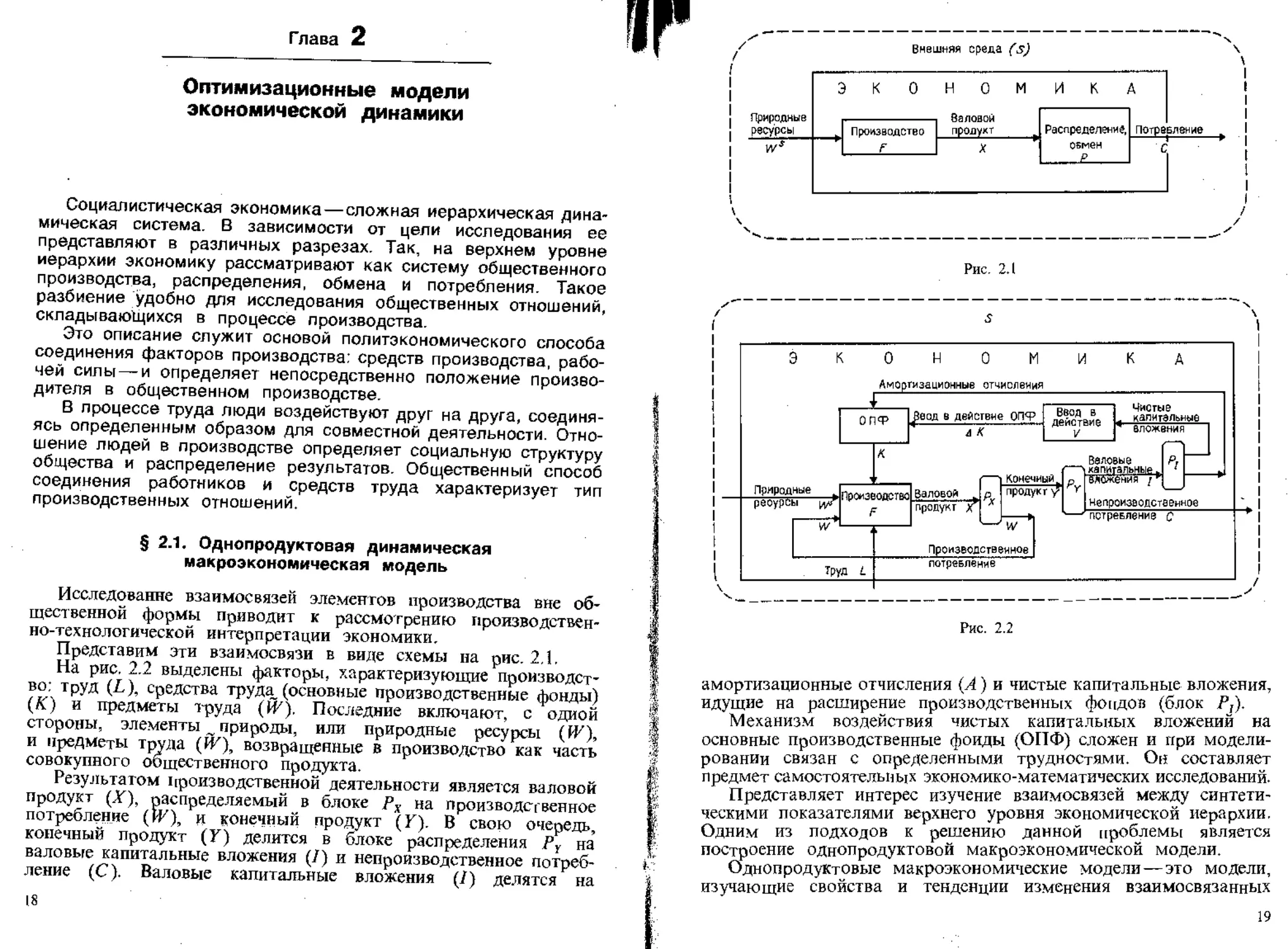
Представим эти взаимосвязи в виде схемы на рис. 2.1.
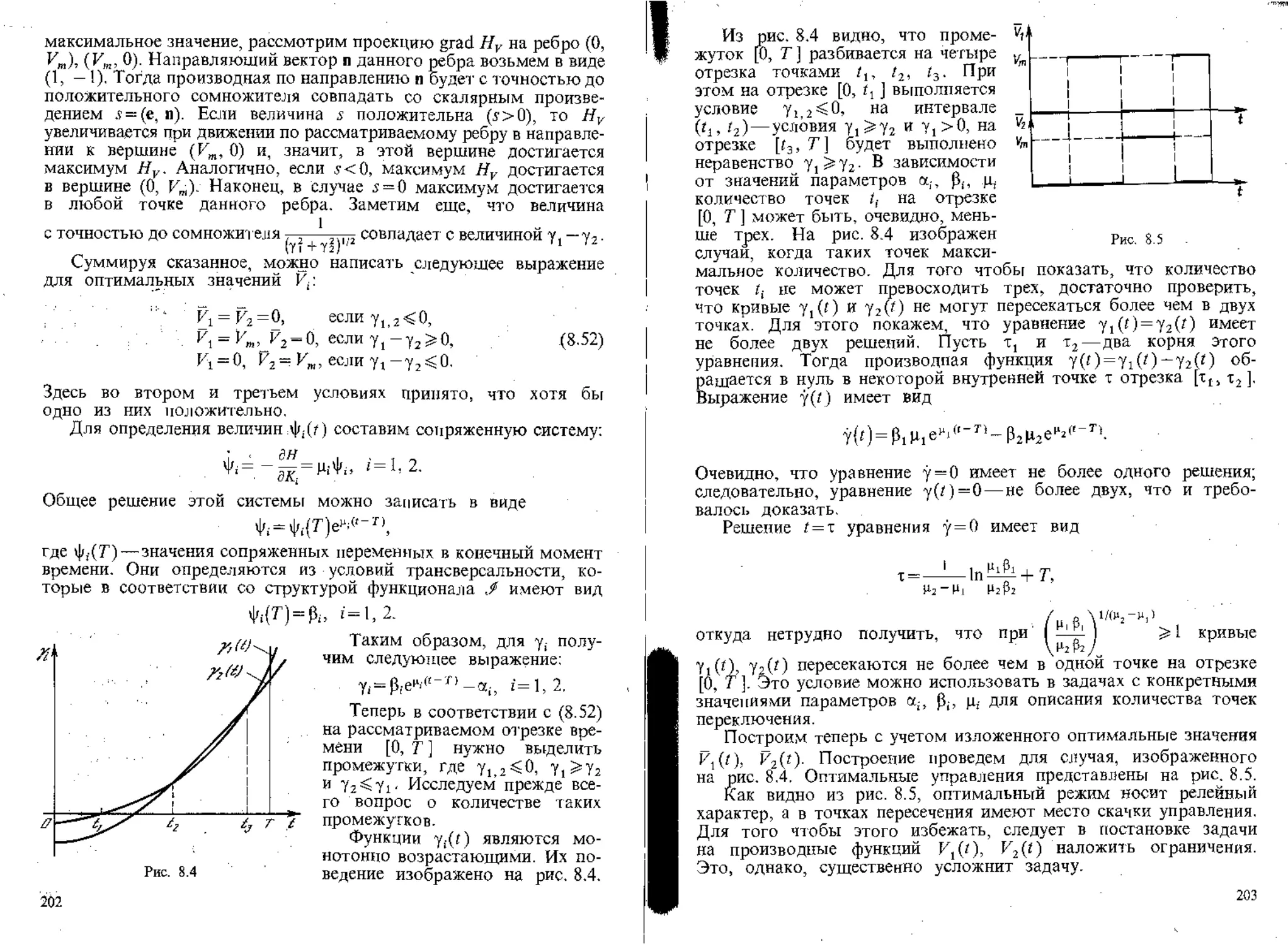
На рис. 2.2 выделены факторы, характеризующие производст-
во: труд (L), средства труда (основные производственные фонды)
(К) и предметы труда (Й7). Последние включают, с одной
стороны, элементы ~ природы, или природные ресурсы (И7),
и предметы труда (IT), возвращенные в производство как часть
совокупного общественного продукта.
Результатом производственной деятельности является валовой
продукт (X), распределяемый в блоке Рх на произведет венное
потребление (И7), и конечный продукт (К). В свою очередь,
конечный продукт (Y) делится в блоке распределения PY на
валовые капитальные вложения (7) и непроизводственное потреб-
ление (С). Валовые капитальные вложения (7) делятся на
18
t
Внешняя среда (s)
Рис. 2.1
Рис. 2.2
амортизационные отчисления (Л) и чистые капитальные вложения,
идущие на расширение производственных фондов (блок Р,).
Механизм воздействия чистых капитальных вложений на
основные производственные фонды (ОПФ) сложен и при модели-
ровании связан с определенными трудностями. Он составляет
предмет самостоятельных экономико-математических исследований.
Представляет интерес изучение взаимосвязей между синтети-
ческими показателями верхнего уровня экономической иерархии.
Одним из подходов к решению данной проблемы является
построение однопродуктовой макроэкономической модели.
Однопродуктовые макроэкономические модели — это модели,
изучающие свойства и тенденции изменения взаимосвязанных
19
агрегированных макроэкономических показателей, таких, как
валовой продукт, конечный продукт, трудовые ресурсы, произ-
водственные фонды, капитальные вложения, потребление и т, д.
Рис, 2.2 помогает выявить эти взаимосвязи, Так, на макроуровне
блок распределения Рх показывает взаимосвязь между валовым
продуктом X, производственным потреблением И7 и конечным
продуктом У:
X=W+Y.	(2,1)
Блок Ру делит конечный продукт на две составляющие; .
валовь!е капитальные вложения I и непроизводственное потребле-
ние С, т. е,
Y=I+C.	(2.2)
Капитальные вложения составляют материальную основу
наращивания и перевооружения производственного аппарата и яв-
ляются средством решения задач повышения народного благо-
состояния.
За счет капитальных вложений осуществляется ввод в действие
основных производственных фондов. Однако формализация взаи-
мосвязи «капитальные вложения — ввод в действие основных
производственных фондов» сопряжена с определенными труднос-
тями, одной из которых является учет распределенного запазды-
вания прироста основных фондов от капитальных вложений.
В экономико-математическом моделировании существует ряд
подходов к описанию этой взаимосвязи.
В простейшей однопродуктовой модели делают предположе-
ние, что валовые инвестиции полностью расходуются на прирост
основных производственных фондов в том же году и на
амортизационные отчисления:
а)	в дискретном варианте эта взаимосвязь имеет вид
I, = qXKt + А,	(2.3)
где ДК,=Ю + 1——прирост основных производственных фондов
в году г; q— параметр модели; Л—цК)—амортизационные отчис-
ления; ц—коэффициент амортизации; ^ — основные производст-
венные фонды в году г;
б)	аналогом этого уравнения в непрерывном варианте является
2=^+^.	(2.3')
Отсюда можно получить уравнение движения фондов:
“	(2.3-)
Объединяя уравнения связи (2.1)—(2.3), получим однопродук-
товую динамическую микромодель в дискретном варианте:
20
A, = Wt +	+ цА) + Ct.
Если считать производственные затраты W пропорциональны-
ми выпуску продукции X, т. е,
W=aX,	(2.4)
то дискретная однопродуктовая динамическая модель примет вид
A, =аХ. -ус/АК, рА) А С-),
или
(?
а в непрерывном варианте — соответственно
«=![(, -а)х-цк:-с].
В некоторых случаях используют упрощенные варианты одно-
продуктовои динамической модели.
Случай 1. Открытая однопродуктовая динамическая модель \
Леонтьева. Предполагают, что все валовые капитальные вложения \
идут на ввод в действие новых основных производственных 1|
фондов (основные фонды не изнашиваются). Считая, что прирост /
выпуска продукции ДА)—A1 + i —А( пропорционален капитальным/
вложениям, т. е.
4=хДА),	(2.5)
из уравнений (2.1), (2.2), учитывая (2.4), (2.5), получим однопро-
дуктовую открытую динамическую модель Леонтьева;
А( =яА( + к ДА, А С,,
В непрерывном варианте однопродуктовая динамическая мак-
ромодель Леонтьева имеет вид
Х=аХ+ъ^- + С.	(2.6)
dr
С математической точки зрения эта модель представляет
собой линейное неоднородное дифференциальное уравнение.
Случай 2. Замкнутая однопродуктовая модель Леонтьева.
Предполагают, что непроизводственное потребление С (t) идет
полностью на восстановление рабочей силы £(/). Тогда, введя
норму потребления у (/), получим
С(/) = у(/)£(0.	(2.7)
Далее, если считать, что затраты труда пропорциональны
выпуску продукции, то
E(r) = 6(r)A(t),	(2.8)
где b(l)— норма трудоемкости.
21
Подставляя (2.7) в (2.6) с учетом (2.8), получим «замкнутую
по потреблению» модель расширенного воспроизводства
Z=a(z)jr(r) + x(z)^^ + y (t)b(i)X(t),
которая описывается однородным дифференциальным уравнением
^-Л(02Г(0 = 0,	(2.9)
где
Тогда развитие экономики определяется решением уравнения (2.9):
АЛ(/) = АЛое~Й,ск
Случай 3. Предполагают, что непроизводственное потребле-
ние является известной функцией времени. Тогда закон развития
экономики определим из модели (2.6), которая с математической
точки зрения является неоднородным дифференциальным уравне-
нием вида
^+Р,ЫИ')=Л‘).
где р,(1)-----f(t)~
С 6
-44, с решением
о
Итак, можно сделать следующий вывод. Выделение из конечно-
го продукта У накапливаемой части / приводит к рассмотрению
динамических моделей и применению для исследования в качестве
математического аппарата теории дифференциальных (в непрерыв-
ном случае) и конечно-разностных уравнений (в многошаговом
варианте).
§ 2.2. Двухпродуктовая динамическая
макроэкономическая модель
Предположим, что экономика представлена двумя отраслями
народного хозяйства, каждая из которых выпускает валовую
продукцию X1, X2 и затрачивает на воспроизводство труд,
средства труда и предметы труда. Валовой продукт каждой
отрасли распределяется в блоках Р и ру2 (рис. 2.3) соответствен-
но на конечный продукт У1, У2 отраслей и производственное
потребление Wy.
22
Рис. 2.3
X2=IV2 + Y2.
Однако в двухпродуктовой модели промежуточный продукт
W' (i~ 1, 2) расходуется на воспроизводство валового продукта
не только своей отрасли, но и другой. На рис. 2.3 распределение
промежуточного продукта осуществляется в блоках Pw% и Pwi'-
ИЛ1 = ИЛ} + П''1,
Если предположить, что межотраслевые потоки W} (i, у=1,
2) из /-Й отрасли в ,/-ю отрасль пропорциональны объему
валовой продукции Xj-тл отрасли:
где Д/—норма затрат продукции ьй отрасли на воспроизводство
единицы продукции у-й отрасли,—то распределение валовой
продукции отраслей можно представить в виде
Xl^a[X'+a'2X2+Yl,
Х2=а2Х1+ a2X2+Y2.	{	’
23
Из схемы на рис. 2.3 видно, что блоки и участвуют
в межотраслевом обмене промежуточного продукта и образуют
систему межотраслевых связей. Вычленение этой системы из
рассматриваемой динамической модели приводит к модели меж-
отраслевого баланса, имеющей самостоятельное значение. Модель
межотраслевого баланса для п—2 отраслей представлена на рис. 2.4.
Дальнейшее деление конечного продукта У1, Y2 отраслей I и II
соответственно на валовые капитальные вложения I1,I2 и непроиз-
водственное потребление С *, С2 осуществляется в блоках и Руг:
Y1—Ii + C1,
V2_t2 j_/M	(2-И)
что приводит к вводу в балансовое уравнение составляющих
I1,I2, связь которых с валовым продуктом выражена конечно-раз-
ностными (в дискретном варианте) или дифференциальными (в
непрерывном варианте) уравнениями.
В двухпродуктовой модели в простейшем варианте будем
считать, что все валовые капитальные вложения идут на развитие
экономики (амортизационные отчисления в этом случае не
учитываем). Тогда расход валовых капитальных вложений /*,
12 каждой отрасли на увеличение основных фондов осуществ-
ляется соответственно в блоках Р t и PfZ:

(2.12)
В простейшей динамической модели считаем, что поток
валовых капитальных вложений j== 1, 2) из /-отрасли в у-ю
пропорционален приросту валовой продукции у-й отрасли:
24
r}^bXj, i, J=l, 2.	(2.13)
Подставляя в (2.10) формулы (2.11) —(2.13), получим открытую
двухпродуктовую модель в дискретном варианте:
(XI=a'X1-|-«lA'2+xJAX1+xUA'2 + CI,
[X2 = ajX1 + а2Х2 + х2 АХ1 + х^ДХ2 + С 2.
В непрерывном варианте модель (2.14) примет вид
[х1 =с|Х1+й2Х2 + Х1 +х)^+С1,
(	d( d<
^2=^XI+«lX2 + x2^-+z^+C2.
dr dz
Задавая в базисном году /0 X1 (ц) —Xq, X2(?q) — X2 и пред-
полагая известными потребления во времени С1^) и С2(/),
видим, что задача развития экономики, заданной двумя отрасля-
ми, сводится к системе линейных неоднородных уравнений.
С математической точки зрения эта задача является задачей
Коши для обыкновенных дифференциальных уравнений.
§ 2.3. Многопродуктовая модель экономики.
Межотраслевой баланс
В § 2.1 была построена однопродуктовая макромодель произ-
водства и распределения общественного продукта на уровне всего
народного хозяйства. Эта модель позволяет увязать основные
макроэкономические показатели, такие, как валовой продукт,
конечный продукт, капитальные вложения, трудовые ресурсы,
потребление и др. Однако для эффективного управления экономи-
кой, имеющей сложную структуру, необходимо установить плано-
вые пропорции не только на народнохозяйственном уровне, но
и на отраслевом. Это движение общественного продукта на
всех стадиях воспроизводства учитывает метод межотраслевого
баланса.
Межотраслевой баланс служит базой определения взаимо-
сбалансированной системы основных показателей. Он отражает
кругооборот общественного продукта в целом но народному
хозяйству и на межотраслевом уровне.
Первый межотраслевой баланс разработан Центральным ста-
тистически.м управлением СССР (ныне Госкомстат СССР)
в 1925 г- как составная часть баланса народного хозяйства за
1923— 1924 гг. Тем самым была сделана первая попытка провести
анализ структурных взаимодействий в развитии народного хо-
зяйства. Эти идеи нашли отражение в математической модели
межотраслевого баланса В. Леонтьева (США). В СССР со второй
половины 50-х годов межотраслевой баланс стал использоваться
25
как инструмент анализа н планирования темпов и пропорций
общественного воспроизводства.
Широкую известность получил составленный в ЦСУ СССР
отчетный межотраслевой баланс производства и распределения
общественного продукта за 1959 г. Этот баланс послужил
основой для ряда экономических расчетов и исследований
структуры советской экономики, ценообразования, эффективности
капитальных вложений, использования основных производст-
венных фондов и т. п.
Данные этого баланса были использованы для составления
экспериментальных плановых межотраслевых балансов, разра-
батываемых Научно-исследовательским экономическим институ-
том при Госплане СССР, Центральной экономико-математической
лабораторией (теперь Центральный экономико-математический
институт АН СССР) и др.
Идея межотраслевого баланса состоит в следующем.
Каждый производимый в народном хозяйстве продукт должен
быть рассмотрен с точки зрения его распределения и использова-
ния. С другой стороны, каждый продукт может быть представлен
по элементам стоимости как сумма затрат различных продуктов,
расходуемых на его изготовление (сырья, полуфабрикатов, топли-
ва, электроэнергии и др.), амортизацию основных фондов, вели-
чину заработной платы работников, создающих продукт, и вели-
чину чистого дохода (прибыли и налога с оборота, полученного
при производстве этого продукта).
Межотраслевые балансы могут разрабатываться на плановый
и отчетный периоды в стоимостном, натуральном и натурально-
стоимостном выражении; в зависимости от этого меняются
характер и форма отраженных в них экономических процессов.
Наряду с балансами, охватывающими все народное хозяйство,
разрабатываются региональные межотраслевые балансы по союз-
ным республикам и экономическим районам. Принципы меж-
отраслевого баланса используются для построения внутриотрасле-
вых межпродуктовых балансов, характеризующих связи между
подотраслями и видами производства внутри крупных отраслей
народного хозяйства.
В межотраслевом балансе понятие отрасли отличается от
общепринятого в практике планирования. В этом балансе выде-
ляют «чистые отрасли» — совокупность производств, выпускаю-
щих однородную продукцию.
Под номенклатурой межотраслевого баланса понимается пе-
речень отраслей (продуктов), которые по вертикали и горизонтали
входят в сводную таблицу межотраслевого баланса (табл. 2.1).
Правильность выбора номенклатуры во многом определяет
точность отражения в межотраслевом балансе реальных произ-
водственно-экономических связей и, следовательно, аналитические
возможности баланса.
26
		14 >м		Е >4	л	я Ег,. i • ]	i- [
					
5	 k4	-» <-< —, J7 *Lsj7	сК)7	К [xj7	= ><F
	1. Металлургия	х'	...	х‘	...	х’	j 2. Строительство	...	х?	п.	х* j	V V	п	-	 xj	.„	х"	... j	Итого	" I
27
Продолжение табл. 2,1
а
г
а
S4
Ю
о
3
i
Конечный продукт	Всего ва- лового продукта		
	Итого		
	Экспорт (+) Импорт (-)		
	Возмещение выбытии и капитального ремонта ос- новных фондов		
	Национальный *' доход		фонд но- фонд на- трсбле- копле- ния	ПИЯ
Текущее производственное потребление в отраслях (промежуточный продукт)		о 1	
			
			
			
			
			
		Строи- тельство	
		Метал- лургии	
ha
з ?5
g s
				
С				
Риз		N		S
				'К1.;
		N		
		N		’Sr
|и				
£		и N		
		N		Sr
	3		р	
	KKHVCHldl	ый ироду	о а о Е? § о	1 и
	Амс	числ	Веет	О U С
28
Плановый межотраслевой баланс производства и распреде-
ления продукции является, с одной стороны, дальнейшей конкре-
тизацией баланса народного хозяйства, с другой — обобщением
системы частных материальных балансов, разрабатываемых по
широкому кругу материальных ресурсов.
На предварительной стадии разработки народнохозяйственного
плана могут быть осуществлены многовариантные расчеты взаи-
мосбалансированных объемов производства важнейших видов
продукции в зависимости от различных вариантов конечного
продукта, намеченного на планируемый период. На этой же
стадии целесообразно осуществлять проверку пропорциональности
между развитием производственных мощностей по выпуску
различных видов продукции на начало планового периода
и степени ее изменения в результате намеченной производственной
программы. На заключительной стадии осуществляют комплекс-
ную проверку сбалансированности производственной программы
народнохозяйственного плана как с точки зрения пропорциональ-
ности выпуска важнейших видов продукции, так и с точки
зрения развития производственных мощностей по каждой из
отраслей, включаемых в номенклатуру межотраслевого баланса.
Отчетные межотраслевые балансы фиксирую! межотраслевые
потоки продукции и их направление, формы использования
конечного продукта по назначению, а также процесс создания
и использования национального дохода. Исходной информацией
для отчетных балансов являются данные текущей статистики
и специального обследования. Отчетный межотраслевой баланс
на народнохозяйственном уровне составляется Госкомстатом
СССР.
Основными исходными данными для расчетов плановых
межотраслевых балансов производства и распределения продукции
являются нормы затрат материальных ресурсов на производство
тех или иных видов продукции. Они представляют собой
отраслевые нормативы расхода сырья, материалов, топлива,
электроэнергии, непосредственно используемых на производство
продукции, соответствующих уровню развития техники, техноло-
гии и организации труда планового периода.
Важным фактором изменения нормативов является техни-
ческий прогресс. Введение новой техники, совершенствование
технологии, организации труда ведет к снижению расходов
материально-энергетических ресурсов на производство единицы
продукции, изменяет структуру материальных затрат.
Большинство позиций межотраслевого баланса являются агре-
гированными, особенно в отраслях машиностроения. При расчете
нормативов расхода материальных затрат на производство про-
дукции этих отраслей нужно учитывать не только влияние
технического прогресса, но и изменение структуры самого
производства. Таким образом, расчет плановых нормативов
29
предполагает учет намеченных отраслевых мероприятий по со-
вершенствованию технологии производства и его организации,
внедрению новой техники, а также соответствующих структурных
сдвигов в производстве.
Особенностью нормативов, употребляемых при разработке
межотраслевых балансов, является и то, что они включают
помимо технологических затрат общепроизводственные (цеховые
и общезаводские) и в непроизводственные материальные затраты,
приходящиеся на единицу продукции. Эти нормативы должны
отвечать ряду принципиальных требований:
— материальные затраты и продукция должны строго соот-
ветствовать номенклатуре межотраслевого баланса;
- материально-энергетические ресурсы и продукция, на произ-
водство которой они расходуются, должны быть показаны
в единых измерениях номенклатуры межотраслевого баланса.
Стоимостные отраслевые балансы характеризуют процессы
воспроизводства в денежном выражении (табл. 2.1). По своей
структуре межотраслевые балансы могут быть укрупненными
и детальными. Межотраслевой баланс в денежном выражении
охватывает все четыре раздела принципиальной схемы.
В I разделе фиксируются межотраслевые потоки продукции
текущего производственного потребления. Здесь дана одинаковая
классификация отраслей, производящих продукцию, и отраслей,
потребляющих ее. За счет этого обеспечивается шахматная
структура первого раздела схемы.
Во II разделе содержится информация о структуре
используемого конечного продукта, под которым понимается
сумма фонда непроизводственного потребления (личного
и общественного), фонда валовых накоплений (капитальные
вложения, капитальный ремонт, прирост оборотных фондов,
товарных запасов и резервов, прочие расходы), экспортно-
импортное сальдо.
Раздел III включает амортизационные отчисления и чистую
продукцию.
Раздел IV показывает, как используется национальный доход
на потребление, накопление и амортизационные отчисления на
простое и расширенное воспроизводство.
Межотраслевой баланс в натуральном выражении разраба-
тывается по важнейшим видам продукции. Его номенклатура
включает несколько сотен наименований продукции и не охваты-
вает всего общественного производства. Схема межотраслевого
баланса в натуральном выражении содержит показатели только
1 и II разделов схемы межотраслевого баланса общественного
продукта.
При построении статической открытой модели межотраслевого
баланса используется следующая система предпосылок.
Первая предпосылка
30
Все народное хозяйство (район и т. д.) можно разбить на
п отраслей (или п продуктов). Реализация этой предпосылки на
практике требует серьезной содержательной работы.
Вторая предпосылка
В каждой отрасли производится только одни продукт и одним
способом. Иными словами, не существует других вариантов,
кроме фиксированного варианта получения продукции. Эта пред-
посылка, существенная с точки зрения балансовой модели,
снимается в оптимальных моделях.
Третья предпосылка
Всю продукцию народного хозяйства можно разделить на
промежуточную и конечную. Промежуточной называют ту часть
валовой продукции, которая идет в дальнейшую переработку
в отрасли и образует текущие материальные затраты. Конечной
называют оставшуюся часть валовой продукции, которая оконча-
тельно уходит из производственного процесса годового произ-
водства и используется для потребления, накопления, экспорта.
Так, например, ткань, идущая на продажу, является конечной
продукцией. Сахар, идущий на переработку, является промежуточ-
ным продуктом, а сахар, идущий в торговую сеть,— конечным
продуктом.
Отобразим математически межотраслевые связи с учетом
сделанных предпосылок. Для этого проведем предварительную
формализацию взаимосвязей.
Обозначим:
1,	2, ..., ^-—интенсивность валового продукта z-й
отрасли;
У(г = 1, 2, ..., п]— интенсивность конечного продукта i-й
отрасли;
х}(г = 1, 2, ..., n,j=\, 2, ..., н)— интенсивность межотраслевого
потока продукции из /-й отрасли на воспроизводство валовой
продукции /-й отрасли.
Тогда распределение валовой продукции п отраслей примет вид
'.У =х1 +х1 + ...+х* + ... + Х* + У,
Т2=Х1+х1 + ... + х; + ...+х^+ К2,
Х1=х\ +xl2 + ... + xij+... + xill+ Y\
[Хп = хл1+хл2 + ... + х}+... + <+Уп
Однако полученная система уравнений связи дает бесчисленное
множество сбалансированных решений, так как ее математический
аналог — система из п уравнений — содержит 2л + и2 неизвестных
X1, ..., Хп, У1, ..., У и матрицу межотраслевых потоков
(ху). Рассматриваемая модель нуждается в доопределении. Для
того чтобы сократить число переменных, предполагают, что
31
межотраслевые поставки xj продукции /-Й отрасли в j-ю отрасль
зависят линейно от объема валовой Xj продукции /-го потреби-
теля и от нормы материалоемкости я), определяющей затраты
продукции /-Й отрасли на воспроизводство единицы валовой
Продукции /-й отрасли, т. е.
x^ajXj, /=1, 2, п, /=1, 2, ..., п. (2.16)
Система уравнений (2.15) с учетом (2.16) принимает вид
'X' ~а\Х1+а\Х2 + ...+а]ХЧ..-+агпХп+¥',
' A'i = «,1X1+aU2 + ... +4Г+-.-+аив+Л	t2‘17^
;\A'n==n^r1+fln2A'2 + ...+«jA'J + ...+^X'i+y'1,
или
Х‘ = f я)Л7+У‘, г=1, 2, п,	(2.17)
j=i
Экономико-математическую модель межотраслевого баланса
представляют также в матричной форме:
где
у=
х=
Г у1!
У2
— вектор
х=ях+у,
интенсивности
валового
(2.17')
продукта;
--вектор интенсивности конечного продукта;
-а\ а\ ...а) ...^
«i al...aj...a2

^я" «2-.а‘]...а" 7
— нормативная матрица материалоемкости (матрица коэффициен-
тов прямых затрат), или затраты продукции r-й отрасли на
воспроизводство единицы продукции /-й отрасли.
Система уравнений (2.17) или (2.17'), (2.17") в отличие от
системы уравнений (2.15) содержит 2п неизвестных (компоненты
32
валового и конечного продуктов	г-------1
и Отраслей). Для получения --------------► (г -а) ------
единственного решения н каких-	--------
либо переменных задают экзо-	рис. 2.5
генно, т. е. фиксируют, напри-
мер, компоненту вектора валового продукта X и по ней
определяют компоненты вектора конечного продукта Y (X->Y)
! либо, наоборот, по фиксированному вектору конечного продукта
Y определяют вектор валового продукта X(Y->X). Таким образом,
из уравнений связи (2.15) получают две задачи.
Задача 1. Задача наблюдаемости (X—>Y) отражает процесс
распределения валового продукта. Она является основой для
составления отчетных балансов. Здесь входом в модель (или
экзогенным фактором) является вектор валового продукта X,
а выходом — вектор конечного продукта Y. Матричное пред-
ставление этой модели
(£-Л)Х=У,
где Е—единичная матрица, элементы главной диагонали которой
суть единицы, а остальные элементы матрицы—нули.
Кибернетическая модель задачи наблюдаемости Представлена
на рис. 2.5.
Здесь (Е~Л)— матричный оператор преобразования вектора
валовой продукции X в вектор конечной продукции Y.
Задача 2. Задача синтеза (Y-+X) отражает содержание процесса
планирования валовой продукции X по заданному вектору
конечной продукции Y. Она отвечает на вопрос, в каком объеме
надо планировать валовую продукцию отраслей X, чтобы обеспе-
чить желаемый выпуск конечной продукции Y.
В задаче планирования валовой продукции X синтез уравнений
связи разрешается относительно вектора валовой Продукции X:
(Е-Л)-‘У=Х.	(2.18)
Кибернетическим аналогом задачи планирования является
преобразователь вектора конечного продукта Y в вектор валового
продукта X (рис. 2.6).
Здесь (£—Л)-1—оператор планирования, преобразующий эк-
зогенный вектор конечного продукта Y в вектор валового продукта X.
Из сопоставления кибернетических моделей видно, что линей-
ные балансовые модели задач распределения валовой про-
дукции и задача планирования
являются взаимно обратными. Модель планирования валовой	Y	(Е-А)"'	
			
продукции X (рис. 2.6), так же
как и модель распределения	Рис- 2.6
2 Зак 456
33
валовой продукции X, является открытой. Эти модели позволяют
построить систему взаимосвязанных показателей, однако они не
отвечают на вопрос, насколько эффективен тот или иной план.
Эту задачу решают с помощью оптимизационных моделей.
Остановимся на проблеме решения задачи планирования (2.18).
По экономическому содержанию матрица_материалоемкости не-
отрицательна, так как
Неотрицательность решения X определяется продуктивностью
матрицы А. Условие продуктивности неотрицательной матрицы
А эквивалентно одному из следующих условий:
1)	максимальное собственное число Х(Л) матрицы А меньше
единицы: Х(А )< 1;
2)	матрица (Е —А) неотрицательно обратима, т. е. существует
обратная матрица (Е— А)и все ее элементы неотрицательны:
3)	матричный ряд Е+А + А2 + А3+... = X Л1 сходится и
^А‘=(Е-А)~1-,
г-0
4)	последовательные главные миноры определителя матрицы
(Е — А) “1 положительны.
Выясним экономическое содержание элементов матрицы (Е—
В модели планирования (2.18) обозначим элементы матрицы
(Е-Л).-1 через С}, i= 1,2,..., л, j= 1,2,..., п. Тогда
Y1+c2Y24-... + c)Yj + ... + c„LYn = X1,
с2Y1 + c|Y2 + ... + Cj Y-'+... + с2Yn = X2,
c)Y1+c^Y2 + ... + cjY4^ + c'Y'1 = Xi!
с" Y1 + cb2Y2 + ... + cJYj + ... + c”Y" = Xb.
Положим
34
Тогда
с2
ci
1
О
О
О
характеризует затраты валовой продукции всех
: отраслей на
воспроизводство единицы конечной продукции первой отрасли.
Положим
О
1
Тогда затраты валовой продукции всех отраслей на воспроиз-
водство единицы конечной продукции второй отрасли составят
соответственно
а
воспроизводство
единицы конечной продукции п-й отрасли
/ 0
Y=| 0
т
ребует затрат валовой продукции всех отраслей в объеме
компонент вектора:
35
Иными словами, коэффициенты с}, /=1,2,	/“1,2, мат-
рицы (Е—Л)-1 представляют собой затраты валовой продукции
Ей отрасли, идущей на воспроизводство единицы конечной
продукции у-й отрасли. Их называют коэффициентами полных
затрат.
матрица коэффициентов косвенных затрат определяется как
разность между матрицей коэффициентов полных затрат (Е — А)'1
и прямых затрат А.
Пример 1. На плановый год задаются матрица коэффициентов
прямых затрат
0,3
0 09 0,08
А = [ 0Д8 0,24 0
\0,07 0,06 0
и вектор коиечиого продукта
/153 4\
Y =	17,2 . ,
\ 38,4/
Найти вектор валового продукта X и межотраслевые потоки
Для определения вектора валового продукта и межотраслевых
потоков воспользуемся экономико-математической моделью зада-
чи планирования производства и распределения продукции
Расчет
ществить,
(Е-АГ1
коэффициентов матрицы полных затрат можно осу-
например, методом прямого обращения матрицы
или итерационными методами по формуле
(Е-Ау1 =Е+А + А2 + ... +Ак +
/1,461 0,|82 0,Ц7\
(Е-А)~1 = 1 0,153 1,334 0,012 .
\0,111 0,092 1,009/
36
Найдем вектор валового продукта:
/1,461 0,182 0,117\ /153,4\ /231,7\
Х = 0,153 1 334 0,012	17,2 =	46,9 .
\ 0,111 0,092 |,009/ \ 38,4/ \ 57,4/
Определим межотраслевые потоки:
xlj = aljX\
Тогда
х}=69,5, *2=4,2, х! =4,6,
*^ = 18,5, Х2 = 11,2, хз=0,
*1 = 16,2, *2 = 2,8, *з =0.
Схема планового межотраслевого баланса примет такой вид:
Производил 1ЯЯ отрасль	Раснрвделеиие	потребляющим отраслям			Ко|/ечнь{й продукт	Валовой продукт
	1	2	3		
1	69,5	4,2	46	153,4	231,7
2	18,5	11,2	0	17,2	46,9
3	16.2	2.8	0	38.4	57,4
Отметим, что расчеты затрат труда и основных производствен-
ных фондов на реализацию плана не осуществляются в модели
межотраслевого баланса. Эти расчеты проводят только тогда,
когда найден планируемый вектор валовой Продукции X.
Для составления баланса труда введем коэффициенты трудоем-
кости для каждой отрасли, полученные на основании отчетных
балансов:
где /Д — норма трудоемкости ьй отрасли в отчетном году;
Ц, — затраты труда 1-й отрасли в отчетном году; Х10- валовой
продукт 1-й отрасли в отчетном году.
Коэффициенты Ь'о. 1=1, 2, ..., п. сведем в строку трудоемкости:
(bl, Ь2О, Ь”).
При составлении баланса труда нормы трудоемкости (Ьг0,	...
Ь"), полученные расчетным путем из отчетного баланса,
корректируют для планового баланса (Ь*, Ь;;, ..., откуда
баланс труда принимает вид
L,=blXl+btXl+...+bVa.	(2.19)
Прогнозируя трудовые ресурсы на планируемый период £.*,
оценим обеспеченность плана по труду. Если окажется, что
Ln>L*, то планируемый вектор валового продукта Xn-(xl, XI, ...
не обеспечивается трудовыми ресурсами; следовательно,
надо выбирать новый вариант и изменить вектор конечного про-
дукта Уп=(Уп, У„,  , Уп), снова вычислить вектор валовой про-
дукции и проверить обеспеченность его трудовыми ресурсами.
В модели (2.19) рассматривается редуцированный труд. Если
в каждой отрасли трудовые ресурсы представить по видам
деятельности, то баланс труда будет интерпретирован системой
уравнений.
Можно пересчитать коэффициенты полных затрат труда
(затраты груда на единицу конечной продукции). Математически
эти коэффициенты определяем из произведения вектора коэффи-
циентов трудоемкости на матрицу коэффициентов полных затрат:
1 (**, ъ\
И=(йп, ь1...,
.. I .л Л г
"2 el г2
- 1	2 - " L tt
или
6;=ад+вд+...+ад,
b2 = b\c\ + b2cl + ...+bnncn2,
bn-blc^+blcl + ...+bnncnn,
Где &'(г= I, 2,	n)—затраты живого труда всех отраслей на
воспроизводство единицы конечной продукции ьй отрасли.
Такая же работа проводится по обеспеченносги плана основ-
ными производственными фондами. Определим нормы фондоем-
кости из отчетного баланса:
>
где К'о— основные производственные фонды /-й отрасли на конец
отчетного периода.
Скорректировав эти нормы на планируемый период (/?„, /г2,
..., /г"), составим баланс основных производственных фондов:
А,( = /г'У'+/г2^ + ...+/гГ,Уп,
где планируемые основные производственные фонды сравниваются
сих прогнозным значением К. В случае Klf> К* расчеты повторяются
для нового варианта конечного продукта Уп=(Уп, У„, , У£)-
38
* ' ' '
 Так же как для баланса труда, основные производственные
В фонды можно развернуть по видам. Например, основные произ-
В водственные фонды разделить на активную и пассивную части,
™ в свою очередь, представив каждую из них по видам.
Зная коэффициенты прямых затрат фондов, определим затраты
фондов на единицу конечной продукции й(/=1, 2,	.как
Произведение строки фондоемкости на матрицу коэффициентов
полных затрат (Е—Л)~1:
2	7	2
П cl...с2
" сп2...с
где	—коэффициент полной фондоемкости, Приходя-
щейся на единицу конечной продукции г-й отрасли планируемого
периода.
Тогда коэффициенты полной фондоемкости будут равны:
h_l=h^cl1 + h2c2 + ...+h"c,,i,
h2^hlnci. + h2ci+ ...+hn„cn2,
hn =	с 1 + h2 с2 +... +hnncn„.
Иными словами, получили затраты производственных фондов
на воспроизводство единицы конечной продукции в i-й отрасли.
При моделировании межотраслевых связей важным является
вопрос агрегирования нормативных показателей.
Рассмотрим пример. Пусть задана таблица межотраслевых
потоков для четырех отраслей (табл. 2.2).
Таблица 2.2
Производящая отрасль	Распределение до потребляЕощим отраслям				Конечный продукт	Валовой продукт
	1	2'	3	4		
1		Х2		х;	У1	X'
2	х]			л	г2	х1
3	х?	Х2		*4	у’	X3
4		X4 Л 2			У4	X4
39
Определим параметры агрегирования при объединении второй
и третьей отраслей.
Выделим в табл. 2.2 отрасли, подлежащие агрегированию.
Присвоим новой отрасли индекс к и составим другую таблицу,
введя в нее отрасль к (табл. 2.3).
Та б лица 2.3
Производящая отрасль	Распределение по потребляющим отраслям			Конечной продукт	Валовой продукт
	1		4		
.  J	Л 1	-Г*	4	У1	X1
к		к	К 4	Ук	х“
4		4 л к	4- Л4	У4	хл
Агрегированными окажутся те межотраслевые потоки, которые
содержат индекс к.
Определим поток из г-й отрасли в отрасль к. Поток
л! объедини! все потоки из /-й отрасли в отрасли, которые
образовали /с-ю отрасль. Для нашего случая
4 = %‘2+х13, ;е(1,4).
Сформируем поток из /с-й отрасли в /-ю. Поток л) объединяет
потоки всех отраслей, направленных в у-ю отрасль, т. е. входящих
в к-ю отрасль. Для нашего случая
+	/е(1, 4).
Поток £-й отрасли на собственное воспроизводство включит
все межотраслевые потоки, оставшиеся внутри этой отрасли, т. е.
xkh=xl + xl + xl + xl.
Зная агрегированные потоки, найдем коэффициенты прямых
затрат агрегированных отраслей. Тогда коэффициент прямых
затрат г-й отрасли на воспроизводство единицы продукции л-й
отрасли равен отношению потока из гй отрасли к валовой
продукции fc-й отрасли:
Произведя замену, получим
।	2 "И 3  /1 j \
У‘4-13	3 ’ 7
Введя коэффициенты прямых затрат исходных отраслей, получим
а*гл4ч-а(№ .	..
,е0.4).
40
Соответственно,
fe -Д Xi+X?
<4=—г=—
X* . Х‘
или
Найдем коэффициент прямых затра т /с-й отрасли иа собствен-
ное воспроизводство;
пк = —	+ л’з+Л^ + ?;з
к~х*~ Х* 2 + т3 ’
или
к_(4~й1)х2-1-(й1 + о1)л3
а*---- ЛЧГ ........“•
Коэффициенты прямых затрат агрегированной матрицы можно
вычислить и матричным способом.
По таблице межотраслевых потоков (см. табл. 2.2) построим
матрицу коэффициентов прямых затрат А:
г	з
а{ а 2	al
h	а] а$ а% ai
	al al al
И	4 4 4	4
	а г al al al
В	' •
гДе	£’2=M'
Далее сформируем . оператор агрегирования Т. Для этого
произведем деформацию единичной матрицы четвертого порядка
(размерность единичной матрицы совпадает с размерностью
исходной таблицы межотраслевого баланса) по следующему
правилу; выделим в единичной матрице Б4 те строки, номера
которых совпадают с номерами агрегируемых отраслей, и просум-
мируем их. Результат внесем в к-ю строку матрицы Т. Все
остальные строки, номера которых в исходной таблице соответст-
вуют номерам отраслей, не подлежащих агрегированию, перепи-
сываем в матрицу Т без изменения.
Для нашего примера
1
О
О
О
ООО
1 О О
О 1 О
О О I
О 0 0 0\
110 0
0 0 0 17
41
Таким образом, матрица Т есть результат «горизонтальной
деформации» матрицы £4.
В более общем случае число строк деформированной матрицы
равно
m—n—q+ 1,
где т~ число строк матрицы Г; п-—размерность исходной
таблицы межотраслевого баланса; q— число отраслей, подлежа-
щих агрегированию.
Если одновременно формируют две агрегированные отрасли,
то число строк деформированной матрицы Т равно
т=п — (? + /) + 2,
где /-—число отраслей, агрегируемых в отрасль L.
Построим деформированную весовую матрицу ]¥. Для этого
введем веса ИИ, означающие вклад валовой продукции исходной
l-й отрасли в валовую продукцию отраслей, представленных
в новой агрегированной таблице.
Так, 1-я и 4-я отрасли в нашем примере (см. табл. 2.3) не
подлежат агрегированию. Следовательно,
^’ = 1, 1У4=1,
Составим весовую матрицу
W-.
I
О
О
О
О
W2
О
О
О
О
ррз
О

о
о
о
Деформируем матрицу W по
и третий столбцы. Тогда
столбцам, объединив второй
Wf =
1
о
о
о
О
W2
JT3
О
о
о
о
1
где W* — весовой оператор агрегирования.
Число строк весового оператора агрегирования W* совпадает
с размерностью исходной таблицы межотраслевого баланса,
число столбцов равно количеству строк деформированной ма-
трицы Т.
Для получения матрицы коэффициентов прямых затрат с уче-
том агрегирования достаточно умножить исходную матрицу
А материалоемкости слева на деформированную матрицу
42
; Т и справа на деформированную весовую матрицу И7*, т, е.
Лгр=тя^*>
где Лагр — агрегированная матрица материалоемкости,
§ 2.4. Моделирование запаздывания
при освоении капитальных вложений
? При идентификации процессов на макроуровне одним из
£ главных вопросов является формирование взаимосвязей факторов
: с учетом запаздывания, Так, например, цепочка «капитальные
£ вложения — ввод в действие основных производственных фондов»
« относится к числу таких взаимосвязей,
[ Имеется два подхода при моделировании запаздывания в нро-
? цессе освоения капитальных вложений. Первый из них предпо-
• лагает наличие промежутка времени т, по прошествии которого
капиталовложения превращаются в основные фонды. В этом
• случае можно считать, что изменение основных фондов в момент
г происходит за счет инвестиций, выделенных в момент / —т.
Тогда модель прироста основных фондов К(1) в непрерывном
; варианте принимает вид
Дг)= -рХ(0 + 7(?-т).
Это уравнение представляет собой уравнение с запаздыванием,
или, как принято в теории дифференциальных уравнений, уравне-
ние с отклоняющимся аргументом. Величина т называется
параметром запаздывания и определяет значение лага, т. е.
времени, необходимого на освоение инвестиций.
Наряду с данной моделью в настоящее время используется
подход к моделированию запаздывания, основанный на введении
так называемого распределенного лага. При этом предполагается,
что инвестиции, выделяемые на развитие основных фондов,
осваиваются постепенно. Это значит, что если в момент времени
т выделены инвестиции 7(т), то в момент времени t будет
освоена доля ЛХ^т) основных фондов. Если теперь взять все
моменты времени т</, то получим следующую формулу для
ввода в действие основных фондов К(Г) в момент времени г.
Г(0= f W,T)Z(T)<h.	(2.20)
- со
В случае дискретной (многошаговой) модели, когда инвестиции
образуются в моменты времени ф >t2	, формулу
(2.20) можно переписать следующим образом:
о
И(0 = £	+	(2.21)
i - — со
43
Если доля инвестиций, образованных в момент времени
т и вводимых в действие в момент времени t, зависит лишь
от промежутка времени освоения г—т, то говорят о стационар-
ности процесса ввода инвестиций в действие. В этом случае
функция	будет, очевидно, зависеть лишь от / —т и,
следовательно, равна N(t~т). Формула (2.20) тогда примет вид
Е(/) = j N(t— т)/(т)с!т.
- со
Введем новую переменную 0 = / — т. Если т-> —оо, то 0-юо,
а если т = /, то 0 = 0. Тогда выражение для V(i') примет вид
И(О=р(/-0Ж0)а0.	(2.22)
о
Функция W(0) является важной характеристикой процесса
ввода в действие капиталовложений. Одним из предположений
о ее поведении, которое может быть принято, является пред-
положение о монотонном убывании Л?(0), г. е. доля вводимых
в заданный момент времени t инвестиций, выделенных в момент
времени 6, будет тем меньше, чем больше промежуток времени
6. При моделировании инвестиционного лага используются раз-
личные способы задания функции А(0). Зададим ее в виде
Л(0) = Хе^®.	(2.23)
Если процесс освоения инвестиций является стационарным
и /(r) = /=const при — оо<г<д то естественным является требова-
ние И(/) = А Подставляя 2(т) = / и V(t) = I в формулу (2.22), получим
/-J/7V(0)d0,
О
откуда, сокращая на /, будем иметь
f/V(0)dr=l.	(2.24)
о
При 0->-с© доля вводимых инвестиций должна убывать к нулю,
иначе говоря, должно иметь место соотношение
НтМ6)=0.
Очевидно, что рассматриваемая функция распределения лага
7V(0) = Хе “кв перечисленным условиям удовлетворяет, так как
J\e“^ed0 = l, lime'w = 0.
о
Получим теперь уравнение для скорости ввода капитальных
вложений F(t). Для этого вычислим производную левой и правой
44
частей соотношения (2.22). Вычисляя производную правой части
по правилу дифференцирования интеграла по параметру, получим
СО
й(/)=
о
(2.25)
Подставим соотношение —-—\ — в равенство (2.25).
5/	rtf)
Получившийся при этом интеграл можно вычислить по частям:
А
й(0= - ~/(/~e)M6)de= fM6)d/(;-e)=
J	о
о
= A(0)7(f - 0)1 - J J(t - 0)d7V(0) =
o
= -?W(0-f /G-6)W)d0.	(2.26)
0
При вычислении было использовано равенство lim Д0) = О,
& —'СО
Соотношение (2.26) дает искомое уравнение для J-(f):
- V(i) = ЛГ(О)/(Г) +{/(/- 0)M6)d6	(2-27)
о
Для экспоненциального закона запаздывания уравнение (2.27)
упрощается. В этом случае Л)9)= — л2е^'Л6 = лЛ'(9) и 77(0) = Х.
Поэтому уравнение (2.27) можно переписать в виде
' V(f) = 7.7(f) - X J /(? - 0)N(0)df.
о
Но с учетом (2.22) последнее слагаемое будет равно — ХИ(Г),
поэтому окончательно получим
"И(г) = Х/(г)-?^(Г).	(2.28)
Как видно из соотношения (2.28), в случае экспоненциального
закона запаздывания объем вводимых в действие капитальных
вложений может быть найден с помощью решения обыкновенного
дифференциального уравнения (2.28). При этом необходимо задать
значение 7(f) и начальное значение K(f0)=C0. После этого Т(г)
определяется как решение задачи Коши. Теперь модель роста
основных фондов будет выглядеть так:
5 9	2
45
Таким образом, в случае экспоненциального распределения
лага основные производственные фонды ьй отрасли К‘(1) могут
быть найдены из системы дифференциальных уравнений (2.29).
Зависимости типа (2.28), (2.29) могут быть получены и в дис-
кретной модели ввода в действие основных фондов (2.21).
Аналогом соотношения (2.23) является при этом функция
А(9) = Ц1 - X)’,	(2.30)
которая, как нетрудно проверить, удовлетворяет [ср. с (2.24)]
условию
9 = 0
Рассмотрим соотношение (2.21). Предположим, как и в не-
прерывном случае, что фигурирующая в нем функция
зависит лишь от разности t — tt. Обозначая эту разность через
9 и используя для А(9) формулу (2.30), перепишем соотношение
(2.21) в виде
И(0= £	'	(2А1)
9 = 0
Последнее равенство можно записать в виде
C(/) = U(/) + £ Л(1 — X)eZ(r — 0).	(2,32)
9 = 1
Второе из слагаемых в правой части, если обозначить 9—1 =т,
можно представить в виде
ос-	GO
£ X(l-W-9)41-A)£ X(1-X)V((/-1)-T).	(2.33)
9=1	т=0
Сравнивая выражение (2.33) с (2.31), легко заметить, что оно
равно (1 — Х)И(/ — 1). Сопоставляя соотношения (2,29)— (2.31),
получим следующую формулу:
r(0=V(r)+(i -x)c(/-i).
Последнее уравнение позволяет определить, каким будет ввод
в действие капитальных вложений jz(f), если известно, какими
были сами капитальные вложения. Оно является дискретным
аналогом уравнения (2,28).
§ 2.5. Однопродуктовая оптимизационная динамическая
микроэкономическая модель
Социалистическая экономика содержит в себе объективную
необходимость и возможность оптимального развития.
46
Развитие экономики подчинено целостной системе экономи-
ческих законов, отражающих глубинные, внутренние, существен-
ные ее связи.
Ядром системы экономических законов является основной
экономический закон, определяющий направленность экономичес-
ких процессов. Он отражает высшую цель общественного произ-
водства при социализме, Сама по себе высшая цель не является
движущей силой. Для ее достижения необходимы высокоэффектив-
ная форма производства, высокая степень развития материаль-
но-технической базы, всемерное повышение эффективности народ-
ного хозяйства, опирающиеся на оптимальные темпы роста
производительных сил, технический прогресс и повышение произ-
водительности труда,
Количественный анализ и математическая формулировка
экономических законов служат переходной ступенью от их
качественной трактовки к разработке моделей оптимального
развития.
При математической интерпретации основного экономического
закона социализма следует исходить из того, что закон, представ-
ляющий причинно-следственную связь производственных отноше-
ний, имеет некоторую количественную форму выражения. В ка-
честве материального носителя основного экономического закона
социализма отдельные экономисты предполагают рассматривать
различные формы общественного продукта.
В конечном итоге содержание критерия развития сводится
к Определению максимального «съема» с экономики, наибольшей
эффективности общественного производства.
В рассматриваемой нами оптимизационной модели в качестве
критерия оптимальности предполагается максимизировать дискон-
тированную сумму потребления, создаваемого в течение всего
срока планирования:
г
J = J 0(/)C(r)d/-»-niax,	(2.34)
го
где C(t) — непроизводственное потребление; ©(f)—функция дис-
контирования, отражающая меру предпочтения потребления
в данный момент относительно потребления того же продукта
в последующие моменты.
Итак, если стоит задача оптимального развития экономики,
то ее можно сформулировать следующим образом: определить
такой вариант выпуска продукции Х(1) и такое непроизводственное
потребление C(f), которые обеспечат наибольшее интегральное
дисконтированное потребление.
Модель примет следующий вид.
Для экономики, распределение продукции которой определено
дифференциальным уравнением связи	".
47
У=аДг)+^+цК+С(О,
Си	/
выпуск продукции ограничен производственными возможностями
F(l, К, L)*;
К, L),
а рост производственных фондов ограничен снизу:
и Ш>) = А0.
Найти такой вариант развития, который обеспечивает максимум
функционала (2.34).
Итак, однопродуктовая модель, рассмотренная в данном
параграфе, учитывает це только динамику, но и цель развития
экономики.
Количественное определение оптимального варианта развития
с помощью этой модели связано с использованием аппарата
теории оптимального управления.
§ 2.6. Нелинейная оптимизационная модель развития
многоотраслевой экономики
Дезагрегирование динамической однопродуктовой макроэконо-
мической модели приводит к рассмотрению развития много-
отраслевой экономики.
Рассмотрим экономику, представленную п отраслями, каждая
из которых идентифицируется отраслевым уравнением воспроиз-
водства основных фондов в предположении, что валовые капи-
тальные вложения полностью расходуются без учета запаздывания
на прирост основных производственных фондов и на амортиза-
ционные отчисления:
Г = Л-р7Г,	(2.35)
где -интенсивноеть валовых капитальных вложений ый отрас-
ли; ц1—коэффициент амортизационных отчислений нй отрасли;
К1 — основные фонды г-й отрасли.
При известном уровне основных производственных фондов
в базисном году
К'(О) = К‘о	(2.36)
производственные возможности отраслей ограничены производ-
ственной функцией отрасли
0<1'Чг(г, К\ L‘),	(2.37)
где X*—интенсивность валовых инвестиций г-й отрасли; L'— тру-
довые ресурсы Лй отрасли.
* Производственная функция F(t, К, L) подробно рассматривается в § 6.1.
48
Межотраслевые связи представлены балансовыми соотноше-
ниями
(2.38)
>=1
Г’= £	z=T?^	(2.39)
jm 1
где У1 — интенсивность конечного продукта г-й отрасли; d}—
структурные коэффициенты основных производственных фондов;
С1 — интенсивность производственного потребления г-й отрасли.
Трудовые ресурсы отраслей ограничены неравенством
£ !?<£*.	(2.40)
i = f
[Кроме того, из экономических соображений
I	/'>0, C>CL,	(2.41)
В качестве исходной информации задаются начальные значения
основных производственных фондов А'Ь, коэффициенты аморти-
зации отраслей ц‘, матрица коэффициентов прямых затрат
\А = («}(0), матрица структуры фондов (j)), суммарные трудовые
'ресурсы £?), определяемые демографическим прогнозом, произ-
водственные функции отраслей F!(t, K. L).	_
Необходимо найти модель процесса i; = (JV(/), Y(t), I(t), С(1),
K(t), L(f)), оптимального в смысле
^/(ц)=) e~dtg(t, C)dz-MTiax,
о	D
где D — множество процессов (планов), определяемых условиями
'(2.35) — (2.41); 5 — коэффициент дисконтирования; g(t, Q.функ-
ция полезности, вогнутая с положительным градиентом.
Введение нелинейных производственных функций в межотрас-
левой баланс позволяет учесть возможность взаимного замещения
труда и фондов в отраслях и зависимость производительности
труда от фондовооруженности (в нелинейных моделях произво-
дительность труда считается заданной функцией времени).
Рассмотренная нелинейная оптимизационная модель развития
многоотраслевой экономики также является задачей, решаемой
с помощью теории оптимального управления.
Глава 3
Некоторые вопросы
качественного исследования
моделей упрввляемых
экономических процессов
Задачи управления экономическими процессами тесно связа-
ны с изучением свойств этих процессов. При исследовании
экономических систем с помощью моделей изучение свойств
сводится к анализу поведения траекторий модели, имитирующих
реальные процессы, протекающие в данной системе. Один из
наиболее существенных вопросов при таком анализе заключа-
ется в исследовании устойчивости траекторий модели.
При реализации программ управления в экономической
системе возможны отклонения от заданной расчетной траекто-
рии. Эти отклонения скажутся и на дальнейшем поведении
системы. При этом имеется два принципиально различных
исхода, вызванных этими отклонениями. Первый состоит в том,
что небольшие отклонения от траектории в настоящий момент
времени приведут также к небольшим изменениям траектории
в будущем. При этом отклонения в будущем могут быть
сделаны сколь угодно малыми за счет их уменьшения в насто-
ящем. Во втором случае происходит противоположное. Сколь
угодно малые отклонения от траектории в настоящий момент
неизбежно приводят к ее изменению не меньше чем на
определенную величину в будущем.
В первом случае траектория называется устойчивой, во
втором— неустойчивой.
В данной главе будут рассмотрены также определение
и исследование траекторий сбалансированного роста и отыс-
кание оптимальной постоянной нормы накопления. Последняя
задача может быть сведена к задаче статической оптимизации—-
отысканию экстремума некоторой функции при ограничениях.
Изложение этого материала будет вестись на примере одно-
продуктовой нелинейной макромодели экономического роста,
рассмотренной выше,
§ 3.1. Понятие устойчивости
Рассмотрим процесс, модель которого описывается системой
дифференциальных уравнений
50
 Пусть x(z) = (xl(O, •.х"(0)—изучаемая нами траектория сис-
темы (3,1), являющаяся ее решением с начальными условиями
I	х1(0) = х)>,	хп(0) = хпо.	(3-2)
I Рассмотрим наряду с этой траекторией траекторию xl(t),
gc"(r), определяемую начальными условиями
I	х1(0) = х^, • хв(0) = хо.	(3,3)
ъудем называть траекторию х(г) устойчивой, если для любого
наперед заданного числа е > 0 можно подобрать такое число
5>0, что из ]xj)-xo|<8, /=1, п, следует
|х!(/) —х'(г)|<£, /=1,н,
при всех значениях te [0, оо].
Введенное определение имеет следующий содержательный
смысл. Пусть имеется процесс х[(0? , ^"(0, определяемый си-
стемой (3,1) и начальными условиями (3.2). Следовательно,
система может отклоняться от заданного начального состояния.
Если эти отклонения достаточно малы, то траектории, отвечаю-
щие новым начальным условиям (3.3), будут отклоняться от
исходной траектории также достаточно мало. Если же нельзя
обеспечить, чтобы отклонение от исходной траектории было
достаточно мало даже при сколь угодно малом отклонении
начальных данных (3.3) от (3.2), то траектория х(0 называется
неустойчивой.
Рассмотрим примеры устойчивых и неустойчивых траекторий.
Пример 1. Пусть система (1.1) имеет вид.
Х,=Х2-1,
х2 = ~х1 + 1.
Рассмотрим траекторию (хт(г), х2(г)), отвечающую начальным
условиям Xj(0)=l, х2(0)=1. Таким решением системы будет
xf(0=1, х2(/) = 1.
Чтобы ответить на вопрос, является ли заданное решение
устойчивым, найдем множество всех решений системы (3.4). Ее
общее решение задается соотношениями
x^CjSinr+CiCos/-]-!,
х 2~ С jCos z -f- C2sin	1,
где Clf С2 — произвольные постоянные.
Можно проиллюстрировать поведение траекторий системы
(3.4) геометрически, изобразив их на фазовой плоскости (хь х2).
Для этого исключим t из соот-
ношений (3.5). Проведя неслож-
ные выкладки, получим
(х1-1)2 + (х2-1)2 = С2, (3.6)
где С = (С'? + С,2)1,'2--1фОизволь-
ная постоянная. Равенство (3.6)
представляет собой уравнение
траекторий, изображенных на
рис. 3.1.
Из рис. 3.1 видно, что при
отклонении начальных данных
от единичных на величину, не
превосходящую 8, траектория не может отклониться больше
чем на 28 (более точно — на ^/28). Таким образом, исходная
траектория оказывается устойчивой.
Это можно проверить исходя из определения устойчивости,
данного выше. Пусть е>0 - - произвольное число. Положим 8 = е/2.
Пусть Х[(0) и х2(0)--начальные значения для траектории лД/),
х2(1) системы (3.4), удовлетворяющие неравенствам
|х1(0)-1|<8, 1х2(0)-1|<8.
Тогда, как следует из (3.5), ]C1J<8 и ]С2|<8.
Разность |х(0 — х(0( можно оценить следующим образом:
|xJ(0-Xi(0l=|Clsin/ + C2cos/j ICjSin +)C2cos <|C, | + |C2| <28,
откуда, так как 28 = получим [х,(г) — хДг)! <s. Аналогично,
1-х2(0 —х2(01 <Е' Следовательно, исследуемая траектория устой-
чива.
Пример 2. Рассмотрим частное решение х1=х2 = 0 системы
Х|=Л2; s	(3-7)
Х2= — 2xj — 5х2.
Все решения данной системы можно записать в виде
X, =e'''(C1cos2/+-C2sin2t),
х2=е 'Г(СД — cos 2t - 2sin 2t) + C2(2cos 2t — sin 2?)),
Рассмотрим решение x/zj, x2(t) с произвольными начальными
условиями xf(0), x2(0). Подставляя эти условия в формулы
общего решения и выражая произвольные постоянные, будем
иметь
Ci=xi(0), С2 (х [(0) +х2(0)).
Отсюда следует, что если -4(0) и х2(0) не более чем на величину
8 отличаются от нуля, т. е. [х^О)! <8, |х2(0)| <8, то это относится
и к значениям Сг и С2: ICJ <8, |С2| <8. В результате, аналогично
52
[тому, как было сделано в при-
мере 1, получаем, что выбирая
!8 достаточно малым можно до-
биться, что х,(?) и x2(f) от-
личались от нулевого решения
не более чем на а, где в -любая
наперед заданная величина. Та-
ким образом, нулевое решение
системы (3.7) оказывается устой-
чивым.
Повеление траекторий (3.8)
системы (3.7) представлено на
рис. 3,2, Эти траектории пред-
ставляют- собой спирали, «на-
кручивающиеся» на начало ко-
ординат.
Пример 3. Динамическая од-
нопродуктовая модель Леонтьева
описывается уравнением
(1 -д)У=^Х+С,
| где У—валовой выпуск; С —конечное потребление; а- -коэффи-
к циент прямых (производственных) затрат; Ь — коэффициент при-
| ростной фондоемкости.
t Предположим, что заданы потребление в виде зависимости
F С(г) и начальное состояние системы Э'(0) = .?о. Тогда модель
I однозначно определяет траекторию экономического роста л(г).
Г Исследуем ее на устойчивость.
Разрешив уравнение модели относительно производной, по-
лучим
X==^jy-lc(r).	(3,9)
Уравнение (3.9) имеет частное решение X(t). Из-за линейности
этого уравнения множество всех его решений можно представить
в виде
X=Cle!'! + T(/),
(3.10)
ч 1 — а
где Сj — произвольная постоянная, а А,=—
о
Если подставить в формулу для общего решения (3,10)
начальное значение, то она примет вид
У=(Уо-Г0)е1(+Х(0.	(З.И)
Для исследования устойчивости решения Х(т) вычислим раз-
ность между этим решением и решением X(t) с другим начальным
условием XQ. Из (3.11) получим
53
(3.12)
Равенство (3.12) показывает, что, как бы ни была мала
величина |2f0 — У0|_Огклонения в начальных условиях, отклонение
решения ,¥(/) от X(t) будет неограниченно возрастать при /-><».
Отсюда следует вывод о том, что любое частное решение
уравнения (3.9) оказывается неустойчивым.
Обратимся снова к примерам 1 и 2. Мы показали, что
в каждом из них исследуемые траектории устойчивы. Однако,
сравнивая рис. 3.1 и 3.2, можно заметить, что характер поведения
траектории систем по отношению к исследуемым траекториям
различен. В примере 2 отклонение любого решения от исследуемо-
го стремится к нулю при /->оо. В примере же 1 это отклонение
к нулю не стремится. Тип устойчивости, с которым мы имели
дело в примере 2, называется асимптотической устойчивостью,
Дадим определение асимптотической устойчивости. Устойчивое
решение (траекторию) х’(т), ..., xn(t) системы (3.1) с начальными
условиями Хд, ..., Xq будем называл!» асимп тотически устойчивым,
если существует такое число 5о>0, что любое решение с началь-
ными данными хр, ..., х о, удовлетворяющими неравенствам
Хо]<6о, г=1, л, обладает свойством
l-v'(Z)— х‘(/)|->0 при /->оо.
Таким образом, асимптотическая устойчивость решения ,х(?)
означает, что оно, во-первых, устойчиво и, во-вторых, что любое
другое решение, достаточно мало от него отличающееся в началь-
ный момент времени (не более чем на величину 50), будет при
Мао неограниченно к нему приближаться.
§ 3.2. Исследование устойчивости
При изучении экономических процессов речь, как правило,
идет об исследовании асимптотической устойчивости. Поэтому
в данном параграфе приводится метод исследования асимптоти-
ческой устойчивости некоторого частного решения.
Исследование устойчивости решения х(/) системы (3.1) может
быть сведено к исследованию устойчивости нулевого решения
некоторой системы. Это может быть выполнено с помощью
надлежащим образом произведенной замены переменных. Так
как при исследовании устойчивости нас интересует отклонение
решений системы дифференциальных уравнений от заданного
частного решения х(/), можно перейти от исходных переменных
t, х1, ..., хп к переменным t, у, у" по формулам
/=х’—х‘(/), /= 1, п.	(323)
Если теперь xl(t) — некоторое решение системы (3.1), то полу-
чаемые по формулам (3.13) величины У(/) имеют смысл
отклонений х(/) от заданного частного решения х(/).
54
Чтобы перейти' в уравнениях (3.1) к новым переменным,
разрешим (3.13) относительно х1 и подставим полученные выра-
жения в соотношения (3.1):
у1 4-x40=/4f, / + *40, ->/ + хл(0),
y2+x2(f)=f2(t, yl4-xl(Z), ..., у"4-х”(/)),
ул + .ИЛ>ЛЛ/ + *4П, ...,уя+хШ
Учитывая, что x(t) удовлетворяет системе (3.1), т. е, х=/‘((,
х*(0>	ХЧ(/)), получим
J5'=/Ч^ /З-хЧО, , У’ + *"Ч))-./’1(Л *40, *40),
>2=720, / +*40, -,/+*40)-/4', *40, -, *40),
у"=Г0, А +*Ч0, /+*(0)-/в(', *40,..., *п(0).
Обозначив правые части уравнений (3.14) g‘(r, у1, ..., у"), получим
окончательный вид системы уравнений (3.14) для новых перемен-
ных у’:
/=/0, У1, •••,/)
y2 = g2(J, У1, -, у")
(ЗЛ5)
/=/(6 у1, -, /)•
Системы уравнений (3.14) и (3.15) имеют, как нетрудно видеть,
частное решение уг=0. В этом легко убедиться непосредственной
подстановкой. Из формул замены переменных (3.13), в свою
очередь, следует, что решение у1 = 0 системы (3.15) отвечает решение
xj) = *V) системы (3.1). Следовательно, исследование устойчивости
последнего сводится к исследованию устойчивости решения у‘ = 0.
В исследовании асимптотической устойчивости важную роль
играют уравнения, полученные с помощью линеаризации системы
(3.15). Чтобы пояснить сущность процедуры линеаризации, будем
рассуждать следующим образом, Пусть решение х(г) системы
(3.1) является асимптотически устойчивым. Тогда вместе с ним,
как отмечено выше, является асимптотически устойчивым и реше-
ние у(б) = 0 системы (3.15). Это, в частности, означает, что при
достаточно малых отклонениях начальных условий от нулевых
значений отклонение соответствующего решения у(г) от нулевого
будет также достаточно мало. Поэтому появляется возможность
упростить систему (3.15) с помощью разложения ее правых
частей в степенной ряд и отбрасывания слагаемых высших
порядков.
Предположим, что при каждом фиксированном t правые
части системы (3.15) можно разложить в ряд Тейлора. Это
означает, что система (3.15) может быть записана в виде:
55
>1 = a{y1+«ly2 + ... + a „УЧ'пЧх у1, /),
y2 = alyY +aly2 + ...+a^yn + r]2(i, yl, ..., /),
yn = a"гу1 + a '{y2 +... + a + T]”(l, у1, ..., y'[),
; dg‘
тде a'j^ —
J dyJ
—коэффициенты линейной части разложения в сте-
пенной ряд, зависящие, вообще говоря, от времени; p‘(r, у1,
у”) не содержат членов ниже второго порядка малости.
Оказывается, что об устойчивости нулевого решения системы
(3.15), а следовательно, и решения х(/) системы (3.1) можно судить
ограничиваясь рассмотрением лишь уравнений первого приближения:
у1 =a'ty1+a12y2 + ..,+a^y!',
y2 = ajyi+ay2 +... + а2уп,
уя = аи1у1+аи2у2 + ,„ + а^я.
Уравнения (3,17) получаются отбрасыванием в (3.16) слагаемых
выше первого порядка малости.
В матричной форме система (3.17) может быть записана в виде
У = Лу,	(3.18)
где у = (у;1, > У’У А—матрица с элементами (а)).
При исследовании устойчивости важную роль играет гот
часто встречающийся случай, когда матрица А постоянна. В этом
случае ответ на вопрос, является ли асимптотически устойчивым
нулевое решение системы (3.18), может бьтп, получен с помощью
исследования .матрицы А.
Исследование асимптотической устойчивости нулевого решения
системы (3.18) сводится к исследованию собственных значений
матрицы Л, т. е. корней уравнения
det (А -к£) = О,
Это уравнение имеет, как известно, п корней в комплексной
области Х,2, Хп. Оказывается, что если действительные
части всех корней отрицательны (ReXs<0), то нулевое решение
системы (3.18) асимптотически устойчиво. Наиболее существенное
е точки зрения приложений излагаемой теории к решению задач
условие ReX;<0 также является достаточным для асимптотичес-
кой устойчивости нулевого решения системы (3.15) и, следователь-
но, решения х(/) системы (3.1).	•’
Если же хотя бы одно собственное значение X, матрицы
А имеет положительную действительную часть, то нулевое
решение, а вместе с тем и х(г), неустойчиво.
Если же корни характеристического уравнения таковы, что?
их действительные части неположительны (т. е. действительные'
56
части некоторых из них нулевые, а остальные—-отрицательные), то
может иметь место как устойчивость, так и неустойчивость
исследуемого решения. Этот случай называется поэтому критическим.
Для иллюстрации рассмотрим нулевое решение системы
Данная система линейна. Нетрудно проверить, что характеристи-
ческое уравнение матрицы ее правых частей X2 = 0. Оба его
корня —нулевые; следовательно, мы имеем критический случай.
Общее решение рассматриваемой системы имеет вид Xj = С\/+ С2,
= Отсюда следует, что >оо при и при любых
С; и С2, одновременно не равных нулю, иначе говоря, при
любых ненулевых условиях. Следовательно, нулевое решение
является неустойчивым.
В то же время в критическом случае может быть получен
и противоположный результат. Иллюстрацией может служить
рассмотренный в § 3.1 пример 1, где характеристическое уравнение
имеет корни X,12=+z с нулевыми действительными частями,
а исследуемое решение, как было показано, устойчиво.
Теперь можно сформулировать следующий способ исследования
устойчивости. Пусть требуется исследовать устойчивость некоторого
решения х(£) системы (3.1). Производим замену переменных (3.13)
и составляем систему (3.15). Линеаризуя ее, переходим к системе
(3-17) или, что то же, к (3.18). Составляем характеристическое
уравнение det (Л — Х,£)=0 и находим его корни Х,„. Если все
действительные части корней Rek; отрицательны, то решение x(t)
асимптотически устойчиво. Если же действительная часть хотя бы
одного корня положительна, то x(t) неустойчиво.
Еще раз подчеркнем, что данный метод исследования устойчи-
вости применим в том случае, когда система (3.17) имеет
постоянные коэффициенты.
В описанном способе исследования устойчивости, который
в прикладных задачах является наиболее распространенным,
самые большие трудности возникают при отыскании корней
характеристического уравнения и исследовании знака их дейст-
вительных частей. Оказывается, что данное исследование можно
выполнить не прибегая к решению характеристического уравнения,
что может оказаться чрезмерно трудоемким. Приведем ниже
критерий Гурвица отрицательности действительных частей со-
бственных значений матрицы А.
Запишем характеристическое уравнение det(/l — А,Е) = 0 в виде
я0А.п + а1лл 1 + ...+«„_1Х.+й!„ = 0,	(3.19)
где для определенности
изменим знаки всех
будем считать
коэффициентов
«о>0 (в противном
flf). Вычислим п опре-
делителей:
57
Al=an
Д2=бй[ йу
\«3
я0
я2.
	Г		
	«1	я0	0...0
Д„ = det	я3	«2	яг..О
	Я2л- 1	а2п-2	Я2л - 1/"Яп
в которых я; = 0, если 1>п. Тогда, для того чтобы все корни
уравнения (3.19) имели отрицательную действительную часть,
необходимо и достаточно, чтобы определители Д; были поло-
жительными.
Для иллюстрации введенных понятий и методов приведем
пример исследования устойчивости. Рассмотрим решения xI(t)=l,
х2(С~2, х3(/)=1 следующей системы:
JCj = ~~ х2 — Х3 + З,
х2 = — Xj — х2 + 3,	(3.20)
Х3 = аД-Х3.
Переходим, согласно (3.13), к новым переменным щ = х} — I,
у2=х2— 2, т3=л'3 —1 и подставляем их в (3.20). Получаем
[ср. с (3.17)]"
Л = -У2-У3,
Уг=-У1-У2,	О-21)
Уз=У1+2уг-Уз-
Теперь исследование решения лД) системы (3.20) сводится к ис-
следованию устойчивости нулевого решения системы (3.21). Для
линеаризации уравнений (3.21) вычисляем матрицу производных
их правых частей при >\ = 0. Матрица А системы (3.18) в рас-
сматриваемом случае имеет вид
/0-1 -1\
Я= -1 -1	0 .
\ 2	0 -1/
Характеристическое уравнение det (А — LE) = 0 может быть, как
нетрудно вычислить, записано следующим образом:
2? + 2V + 2Z+l=0.
Применив к исследованию корней этого уравнения критерий
Гурвица, вычислим определители Д;:
/2 1\
Д,=2 Д2 = 0ец , „ =3, Д3 = det
1	\1 2/	’
Г
2 1 0
1 2 2
0 0 1
58
Так как определители положительны, из критерия Гурвица
следует, что все корни характеристического уравнения имеют
отрицательнее действительные части. Следовательно, исследуемое
решение x(z) = (l, 2, 1) является асимптотически устойчивым.
§ 3.3. Поведение траекторий в линейных моделях
экономической динамики
Применим методы исследования устойчивости к изучению
процессов, описываемых линейными системами.
Рассмотрим предварительно процесс, описываемый системой
линейных уравнений
х = Ах + В,	(3.22)
где х=(л'1, х2,	л"), А =(aj), ду = 1, п, B = (bl, Ь2, Ьп).
Пусть имеется частное решение х (?) системы (3.22), устойчивость
которого мы исследуем. Проведем исследование по изложенной
выше схеме. Для этого необходимо сдела ть замену переменных (см.
3,13) у =х1 —х‘(/). После подстановки в (3.22) получим [ср. с (3.15)]
для переменных у = (у1, у2, ..., у") систему уравнений
У = Яу,	(3.23)
а задача сведется к исследованию его нулевого решения.
Нетрудно заметить, что система (3.23) одна и та же для
любого частного решения х(/) системы (3.22), г. е. при исследо-
вании устойчивости любого частного решения х(/1 результат
одинаков. Иными словами, либо все решения системы неустой-
чивь[, либо все устойчивы.
. Применим теперь изложенные методы к исследованию устой-
чивости траекторий макроэкономических моделей. Ранее при
рассмотрении линейной однопродуктовой модели народного хо-
зяйства (см. §3.1, пример 3) бь[до показано, что при непосред-
ственном нахождении траекторий модели она не имеет устойчивых
решений. Покажем, как этот результат может быть получен
с помощью применения аппарата исследования устойчивости.
Система (3.23) в рассматриваемом примере имеет вид
уравнения
Для исследования устойчивости теперь нужно вычислить
собственное значение, которое здесь одно и равно	Так
как оно действительно и положительно, то отсюда вытекает
неустойчивость траекторий модели.
Рассмотрим более интересный пример, когда народное хозяй-
ство разбито на две группы отраслей. Первая из них производит
59
средства производства, а вторая — предметы потребления. Урав-
нения модели в этом случае таковы:
Xl=a1tX1 + a^Xz+b1^l+b2X2 + Cl,
Х'ЧЧаЧ	. +С2.
Исключая из системы с помощью второго уравнения X2, получим,
что система в данном случае сводится к одному дифференциаль-
ному уравнению. Это уравнение после некоторых преобразований
будет иметь вид
Х'г~аХ1+р,
где
6(1- az)+b2
(3.24).
Исследование устойчивости в данном случае сводится к опре-
делению знака а. В случае отрицательного знака траектории
данной модели устойчивы, в противном случае — неустойчивы.
Так как знаменатель 6(1 -alJ+Oz положителен, то знак а со-
впадает со знаком числителя этой дроби 1 — а\ — а2 + а|а2 —
— а2а2. Воспользуемся для определения знака последнего выраже-
ния свойством продуктивности матрицы прямых затрат в модели
Леонтьева (см. гл. 2). Из этого свойства вытекает, что максималь-
ное собственное значение матрицы А должно быть меньше
единицы. Характеристический /(A,) = det(4 —А,£) многочлен мат-
рицы А имеет вид
/(А.) = А,2 — (й J + а 2) А, — а 2 а 2.
Поэтому значение этого многочлена при А, = 1 должно быть
положительно, В противном случае, если /(1)<0, то, так как
Нш/'(А,)= + оо, существует корень уравнения /(А,) = 0, больший
единицы, что невозможно.
Условие /(1)>0 имеет вид
1 — а\ — аЧа ia2 — Й2Н1>0-
Тогда из (3.24) вытекает, что п>0. Следовательно, как и в од-
нопродуктовом случае, траектории модели Леонтьева для двух
отраслей являются неустойчивыми.
Рассмотрим еше одну линейную модель, являющуюся модифи-
кацией модели Леонтьева с учетом запаздывания капиталовложе-
ний и выбытия основных фондов. Принимая, что лаг капитальных
вложений имеет экспоненциальное распределение (см. гл. 2),'
получим следующие соотношения модели:
60
X=aX+I+C,
K=-^K+V,
V=-'kV+kI.
Предполагая, что связь между основными фондами и валовым
выпуском линейна, т. е. X^fK, где /—фондоемкость продукции,
после преобразований получим для данной модели уравнения
£=_pjt+K,
V^{\-a}fK-XV-XC.	(3.25)
Будем считать, что потребление С (г) — заданная функция
времени. Как отмечалось вьнпе, устойчивость любой траектории
системы (3.25) в силу ее линейности зависит От корней характе-
ристического уравнения матрицы
А=( 1 \
уХ,(1—-X/
Характеристическое уравнение для матрицы А имеет вид
0>
где а[=Х + р,, а2 = А,(ц—(1—а)/). Применяя критерий Гурвица,
получим, что необходимым и достаточным условием отрицатель-
ности действительных частей корней характеристического уравне-
ния будет положительность его коэффициентов, т. е. alt а2.
Первый из них, очевидно, положителен, а второй будет положи-
тельным при условии (]—«)/'< ц. Данное неравенство является
условием устойчивости системы (3.25). Заметим, что это условие
не выполняется, если ц = 0.
Предположим теперь, что потребление в рассматриваемой
модели задается не в заранее заданном виде, а как определенная
часть конечного продукта. Обозначая эту часть (долю потребле-
ния) через и, получим
С=и(\-а)Х;
следовательно, уравнения модели (3.25) можно переписать в виде
K=-[iK+v,
У=Ц1-а)(}-и)/К-к¥. .	(3.26)
Получена система линейных дифференциальных, уравнений,
которая может быть устойчива или неустойчива. В первом
случае все ее решения при г=ых> будут стремиться к нулю.
Как нетрудно видеть, характеристическое уравнение р2 + а(р +
+ а2 = 0 системы (3.26) имеет следующие коэффициенты: й[=А, + ц,
<г2 = Х(ц — (1 — й)(1 — и)). Отсюда получаем, что при достаточно
близкой к единице доле накопления, т. е. при 1>ц>1—	,
1— а
61
коэффициент будет положителен. Следовательно, система (3.26)
в этом случае устойчива и, как отмечалось,	И(/)->0
ПрИ /-+ОО.
Из полученного результата видно, что доля потребления не
должна быть слишком высока. Он дает оценку ее максимальной
величины и=1—	. В противном случае основные фонды
стремятся к нулю («проедание» фондов).
§ 3.4. Сбалансированный рост в однопродуктовой
макроэкономической модели
Рассмотрим однопродуктовую модель развития народного
хозяйства. Уравнения модели можно записать в следующем виде
(см. гл. 2): '
X = aX+Y,
Y=I+C.
K=-ilK+I,	<3'27)
X=F(K, L).
Здесь X—валовой национальный продукт; Y—конечный (чистый)
продукт; /—инвестиции в развитие производства; С—непроиз-
водственное потребление; АГ—основные непроизводственные фон-
ды; L -трудовые ресурсы; а — коэффициент прямых затрат;
ц— норма выбытия основных фондов; F(K, А) —производственная
функция народного хозяйства.
В данной модели трудовые ресурсы L(() задаются экзогенно.
Предположим, что рост трудовых ресурсов происходит с постоян-
ным темпом, равным л, тогда
(3.28)
или L = Lttent.
Введем величину s с помощью соотношения s = I}Y, Эта
величина представляет собой долю конечной продукции, вклады-
ваемую в расширение производства, и называется долей накопле-
ния. Ее связь с величиной u = CiY—долей потребления — выра-
жается соотношением s=и -у 1.
Для производственной функции F(K, L} будем предполагать,
что она и ее производные удовлетворяют требованиям, сфор-
мулированным в гл. 2.
Данная модель — это модель экономики как управляемой
системы. Управление системой ведется заданием доли потребле-
ния и накопления. Из соотношений (3.27) следует, что, задавая
с помощью зависимостей С(/), 7(z), связанных соотношением
62
I+C=Y, программу потребления и расширения производства,
мы тем самым получаем однозначный ответ, какими будут
остальные экономические показатели, характеризующие в рамках
данной модели народное хозяйство.
Для математического исследования модели удобно ввести
«относительные» переменные. Переход к новым переменным
задается формулами
теперь
виде
(3.29)
X=xL,
х , X с
*=L’ k-f C = L-
Эти переменные имеют следующий экономический смысл: х —
производительность труда, т. е. количество произведенной продук-
ции в расчете на одного рабочего; к-—фондовооруженность
! труда; с—потребление на одного рабочего. Исключая
1 из системы (3.27) переменные Y и Z, представим ее в
(1-а)У=Х+цК+С.
Производя в уравнении (3.29) замену переменных
K=kL, C = cL, получим
(1 — л) xL = kL 4- kt + pt L + c L.
. Учитывая (3.28) и сокращая обе части равенства на L, будем иметь
(1 — a)x = k + kn+yik + c.	(3.30)
В свою очередь, выражение для производственной функции
1 также может быть преобразовано. Воспользуемся приведенным
; выше свойством линейной однородности производственной функ-
ции и положим k = l/L. ’Тогда =	) ИЛИ’ вводя соответ"
ствующие обозначения,
х=/(£).
Здесь функция f(k\ как вытекает из свойств производственной
функции, будет обладать следующими свойствами:
1-/(0) =0.
2.	^>0.
дк
3	^<0
4.	при k~+Q,
дк г
df А ,
^2->0 при А."~»оо.
(3.31)
63
Заменим теперь с помощью (3.31) величину х в (3.30).
Получим уравнение, описывающее модель Солоу:
А=-(р+и)/с4-(1-~а)/(А)-с.	(3.32)
Используя введенную выше долю накопления з, можно
написать следующее равенство:
c=W{=(l-s)(l-«)/(A).	(3.33)
Подставив это равенство в (3.32), получим другую форму
уравнения модели:
к— -(р + и) Л+л’(1 -а)/(£).	(3.34)
Таким образом, исследование величин X, Y, I, С, К, описы-
вающих поведение экономической системы, сводится к решению
уравнения (3.34). Дейстительно, с помощью решения уравнения
(3.34) определена величина к (ф. Так как L(f) является известной
функцией времени, из равенства (3.33) можно получить величину
с(ф, а вместе с ней и С (f) = с (г) L (/). Основные производственные
фонды также могут быть легко определены: Яф)=£ (/) L (/).
Аналогично, X(/) =./(А (/)) L (У).
Введем понятие сбалансированного роста. Под сбалансирован-
ным ростом понимается такой процесс экономического развития,
при котором показатели, характеризующие экономику, растут
с постоянным темпом. Применительно к данной модели это
значит, что с постоянным темпом должны возрастать величины
У, Г, К, /, С, L.
Оказывается, что темны роста данных показателей не только
постоянны, но и одинаковы. Обозначим ..., п. темпы роста
первых пяти показателей и сохраним принятое в (3.28) обозначе-
ние для темпа роста трудовых ресурсов. Тогда рост показателей
носит экспоненциальный характер:
Х=Хоеп1г, Y= ToeV К=Коеп^
f=foe”*{, С=Сое”Л Т = Тое"‘.	<3-35)
Так как У=(1— а)Х, то Тоел21 = (1 — a) JVoe"i!, откуда «i = h2-
С учетом (3.27)
I=K+liK—K0 (р + «3)ев<
Учитывая, что /=/ое"*г, получаем п3 = и4. Используя уравнение
(3.29) и подставляя в’него сбалансированное решение (3.35),
будем иметь
(1—а) .¥ое”|' = Ау (н3+ ц) е"У + Сое"-<	(3.36)
Покажем, что последнее равенство возможно лишь при
Н1=«3 = и5. Разделим обе части (3.36) на eV. Получим
£0 (н3 + р) е<"з-VЧСо е<"= - V! = (1-а) Хо.
64
Так как левая часть последнего равенства постоянна при любом
f, ее производная обращается в нуль. Отсюда после некоторых
преобразований получим
М"з + Н) (н3-«1)е(в’~П1), = С0 (И1~л5)е<"5’Я1>1-
Следовательно, так как показатели экспонент в последнем
равенстве должны совпадать, то получаем =л5. Подставляя
полученный результат в (3.36), будем, аналогично рассуждая,
иметь п1 = п3. Сопоставляя теперь полученные соотношения между
темпами роста, получим, что все они совпадают, т. е.
Н1 = «2 = ... = и5.
Покажем, что все эти величины равны п — темпу роста
трудовых ресурсов. Действительно, так как величины X, К
и L связаны производственной функцией, то
yoeV = F(Koe4 ^оепг).
Используя линейную однородность производственной функции,
получим
Уоев? = евз'/-(ЛГО,/,0е(в-вз)').
Так как пг=п3, то отсюда следует
X0 = F(K0, Тое(в-зН).	(3.37)
Как отмечено выше, производственная функция монотонно
возрастает по каждой переменной. А так как первый аргумент
Ко и значение самой функции ,¥0 постоянны, равенство (3.37)
при всех значениях t может выполняться лишь при и3 =н.
Отсюда с учетом полученного выше вытекает
и,- = п, /=1,5.
Таким образом, мы получили, что определение траектории
сбалансированного роста данной модели приводит к тому, что
темпы прироста всех показателей оказываются одинаковыми.
Отсюда, в частности, вытекает, что на траектории сбалансирован-
ного роста доля накопления s =	постоянна.
Из равенства темпов роста показателей следует, что на
данной траектории показатели фондовооруженности труда бу-
дут постоянными. Это означает, что траектории сбалансирован-
ного роста в рассматриваемой модели отвечает решение (3.34),
имеющее вид к = const при s = const. Найдя решение к = к.
остальные переменные модели получаем с помощью следующих
формул:
K[t) = kL^n\ X(t)=f(k)Loem,
Г(<)=(1 — a)/(^)Loe"!, f(r)=41-«W)^eBt,
C(0 = (l-5)(l-n)/(fc)£oe"'.
3 3 ак 456
65
Искомое решение к = к обращает в ноль левую часть уравнения
(3.34). Следовательно, для отыскания к (при заданном постоянном
значении нормы накопления 5) требуется решить уравнение
л(1 - a) f(k} - (р+и) к = 0.	(3.38)
Покажем, что это уравнение имеет в области к>0 (только
такие значения имеют экономический смысл) единственное реше-
ние, Прежде всего рассмотрим вопрос о существовании решения
уравнения (3.38). Для этого рассмотрим производную левой
части (3.38), которая равна 5 (1 — a}f' (к.) —(р+и). Как было
отмечено выше, при к->0 значение	Следовательно,
в некотором промежутке 0<к<е величина .$(1 — a}f' (к) — (р+«)
будет положительной, т. е. левая часть (3.38) -возрастающая
функция. Так как при к = 0 значение левой части равно нулю,
то в полученной окрестности 0 < к < а это значение будет по-
ложительным. Таким образом, в некоторой точке кх (любой
из окрестности 0<k<s) будет выполняться неравенство
.s (1 —	—(щ-w) fct >0.	(3.39)
При к->од в силу свойств функции /(к) производная f (к)
становится сколь угодно малой. Следовательно, начиная с некото-
рого значения к=к’ выражение s (1 — a]fr (к) — (р+п) будет строго
отрицательным и меньше некоторого отрицательного числа —8.
Тогда для значений к^к' будет выполняться неравенство
интегрируя которое в пределах от к' до к получим	-
к	к
.' к'	к'	
или
5(1 - a)f'(k)~ (р + «)к^С-8к,	(3.40/
где С= -(8 + ц + п)к' + 5(1-п)/(к').
Правая часть неравенства (3.40) при к->од стремится к — oo;i
(так как 8>0). Следовательно, и левая часть этого неравенства!
также стремится к —од. Отсюда вытекает, что при некотором
k = k2 значение левой части будет отрицательным, т. е.
^0 ~Ф"Ш-(р+й)&2<0.	,
Сопоставив этот результат с (3.39), получим, что выражение
g(k) = T{1-d)/(k)-{p4-H)k	/
на концах промежутка ki^k^/c2 имеет различные знаки. Тогд^
по известной теореме о том, что функция принимает все свшу
промежуточные значения в некоторой точке (по крайней мер^,
одной) этого промежутка & = &, оно обратится в ноль, т. ё.
уравнение (3.38) имеет по крайней мере одно решение. ,,
66
Покажем, что это решение един-
ственно^ Предположим противное.
Пусть к2— положительнее кор-
ни уравнения (3.38). Так как к = §
также есть решение этого уравне-
ния, у него, следовательно, не менее
трех, неотрицательных корней: к = 0,
k=kit к = к2.
Характер поведения левой части
уравнения (3.38) g(&) показан на
рис. 3.3, Как следует из рисунка,
по меньшей мере в двух точках к2 производная левой части
(3.38) должна обратиться в ноль по известной теореме о функциях,
принимающих одинаковые значения на концах промежутка.
В то же время вторая производная левой части (3.38)
с точностью до положительного сомножителя ,v(l—п) совпадает
с f" (Д-), которая в силу свойс тв функции /(&) отрицательна. Отсюда
вытекает, что левая часть уравнения (3.38) является выпуклой
функцией, а ее первая производная монотонно убывает. Последнее
означает, что производная левой части (3.38) не может принимать
одинаковых значений при различных к. Следовательно, и в ноль
тоа производная не может обратиться в двух различных точках
к2. Это, в свою очередь, противоречит сделанному предположению
о наличии двух положительных решений к2 уравнения (3.38).
Таким образом, мы установили, что в рассматриваемой
модели для каждой фиксированной нормы накопления существует
единственная траектория сбалансированного роста.
Режим сбалансированного роста — это, вообще говоря, одна
из возможных траекторий развития экономической системы. Если
данная модель используется для описания реальной экономики,
то любая конкретная траектория будет определяться как решение
дифференциального уравнения (3.34) с начальным условием
&(0) = fco — значением фондовооруженности в начальный момент
времени и не обязательно является траекторией сбалансирован-
ного роста.
Вместе с тем, как будет показано ниже, траектория сбаланси-
рованного роста играет важную роль среди множества траекторий
однопродуктовой микромодели. А именно, исследуя поведение
траекторий модели, можно выяснить, что любая из них по
прошествии достаточно большого времени неограниченно прибли-
жается к траектории сбалансированного роста. Следовательно,
режим сбалансированного роста может быть использован для
расчетов экономических показателей при достаточно больших
значениях времени независимо от начальных значений этих
показателей.
С математ ической точки зрения описанное свойствоуграекторий
модели выглядит следующим образом. Пусть к — значение
з*
67
Рис. 3.5
фондовооруженности на траектории сбалансированного роста; k(t}
— траектория модели [решение уравнения (3,34)] с начальным
условием-л(0) = А:0>0, Тогда независимо от значения к0 справед-
ливо соотношение
lim&(/) = £	(3.41)
Соотношение (3.41) гарантирует асимптотическую устойчи-
вость сбалансированного роста. Вместе с тем отметим, что
описываемое им свойство траектории модели является значи-
тельно более сильным, так как асимптотическая устойчивость
означает сходимость к к только тех траекторий, начальные
значения которых достаточно близки к этому к.
Для доказательства свойства (3.41) исследуем траекторию
k(i)— решение уравнения (3.34) с начальным условием k(Q] = k(,.
Рассмотрим сначала_случаи, когда начальное значение к0 лежит
в области 0<ко<к. Изобразим графически функцию g(C| =
= — (р+и) fc+s(l — являющуюся правой частью уравнения
(3.34). Выше было выяснено, что эта функция обладает двумя
участками монотонности: до некоторого значения к монотонно
возрастает, затем монотонно убывает. При этом функция gU)
имеет единственный положительный корень к = к. График g(k)
изображен на рис. 3.4.
Из Этого графика, в частности, видно, что в рассматриваемой
области 0<к<к, где лежит начальное значение fc0, g(k)>Q, т. е.
правая часть уравнения (3.34) положительна. Следовательно, на
некотором интервале 0<г<е fc(t) будет монотонно возрастать.
При этом монотонное возраст ание к (г) сохранится до тех _пор,
пока к (?) будет продолжать находиться в области 0 < к < к.
Покажем, что в действительности к (И не покинет данной
области ни при каком t. Для этого изобразим поведение k(t}
графически (рис. 3.5).
Из данного графика видно, что если в некоторый момент
времени значение kfy станет больше к, то j силу ее непрерьшности
найдется такая точка в которой к(1^ = к. Но так как к = к также
является решением уравнения (3.34), то в точке будет нарушаться
единственность решения уравнения (3.34), поскольку но меньшей
мере два решения к (к) и к этого уравнения будут проходить через
данную точку. Но этого не может быть, так как с учетом свойств
функции,/(&) правая часть уравнения (3,34) удовлетворяет условиям
теоремы существования и единственности решений дифференциаль-
ных уравнений. Таким образом, мы получили, что при всех те [0, оо]
исследуемое решение k(t) остается в области Q<k[t)<k. Следовате-
льно, к. (/) монотонно возрастает, так как в этой области правая часть
g(A;) уравнения (3.34) и производная к (/) положительны (см. рис. 3.4),
Итак, мы выяснили, что любое решение к (г) с начальным
условием &(0) = &о, удовлетворяющим неравенству ^<к^<к, явля-
ется монотонно возрастающей функцией. Тогда, по теореме
Вейерштрасса, существует 1пп к (/). Покажем, что этот предел
। совпадает с к.
I Предположим, что это не так, т. е.
|	Нт к (1) = к\ <к.	(3.42)
Тогда, если учесть, что решение Л (г) монотонно возрастает
и ограниченно, то
lim/c(f) = 0.
Подставляя теперь k{t) в обе части уравнения (3.34) и переходя
в полученном равенстве к пределу при /~*оо, с учетом последнего
соотношения получим
0=1пп ( —(ц + «)А;(г)+г(1 -я) f{k(г))).
Отсюда, учитывая непрерывность правой части уравнения (3.34)
: и соотношение (3.42), будем иметь
-(ц + и)А;1+5(1-а)/^1) = 0,
Следовательно, величина /сь так же как и к, является
решением уравнения (3,38). Но, как было установлено выше,
это уравнение^ имеет единственное решение. Следовательно, кг
совпадает с к. Полагая теперь в (3.42) кг = к, получим (3.41),
что и требовалось доказать.
Таким образом, мы цолучили, что все траектории k(t)
(модели Солоу, начинающиеся в точке к(0] = ко. при 0<ко<к
 являются монотонно возрастающими функциями и неограниченно
приближаются к траектории сбалансированного роста. Аналогич-
но можно показать, что если начальное значение кЮ) = к0 лежит
в области к0>к. то соответствующая траектория k(t) является
монотонно убывающей функцией, причем при г-юо также имеет
68
69
место свойство (3.41). Полученный
результат изображен на рис. 3.6.
Более слабая по сравнению
с (3,33) асимптотическая устойчи-
вость сбалансированного роста мо-
жет быть легко получена с помо-
щью изложенных в данной главе
общих методов исследования устой-
чивости. Для этого запишем урав-
нение модели (3.34) в линеаризован-
ном виде, введя для этого перемен-
ную у=к — к:
у = { -(д + «) + л’ (I —а).Л
Таким образом, вопрос об асимптотической устойчивости сво-
дится к определению знака выражения — (ц +«) + ,s’ (I — a)f’ (£),
который, как было уже показано, отрицателен. Следовательно^
согласно результатам, изложенным в § 3.3, траектория к = к
является асимптотически устойчивой.
В заключение рассмотрим случай задания производственной
функции F в виде функции Кобба — Дугласа (см. гл. 2). В этом
случае f(k)=aka. Тогда решения к(г) уравнения (3,34) могут
быть найдены аналитически. Уравнение (3.34) для рассматрива-
емого случая будет иметь вид
к--(ц+и)& + л(1-й)<зАЛ	(3.43)
Произведя замену переменных по формуле ? = и продиффе-
ренцировав ее, получим z — (l-^k~sk. Тогда уравнение (3,43)
можно переписать в следующем виде:
z=-(ц+л)(1-a)z+5(l-a)o(l-а).
Это линейное неоднородное дифференциальное уравнение
первого порядка. Его решение есть сумма общего решения
однородного уравнения и частного решения неоднородного урав-
нения. В качестве частного решения уравнения можно взять
следующее:
у 7 ц-п
Тогда общее решение выражается формулой
27Д = (Ус-(и + И) (1 -a) t ,/(1 -ф g
U "	(u+n) ’
где С — произвольная постоянная.
Переходя к исходной переменной к (/), получим формулу для
общего решения уравнения (3.43):
70
/	h \ \ 1/(1 ~“)
k(i) = Ce"(M+nH1~g); + J( 1
'	\	Ц+п /
ПрИ t^-CQ
стремиться к
получим, что первое слагаемое в скобках будет
нулю, следовательно,	-
.	(3.44)
I Вычислим значение к. отвечающее сбалансированному росту
(я рассматриваемого случая производственой_ функции Кобба —
/гласа. Уравнение (3.38) для определения к примет вид
5 (1 — й) а/с“ — (ц + я) Zr = О
скомый положительный корень этого уравнения к будет опре-
ляться выражением
к=
' ,, \ \
5(1 — а) ст \
j.i+n !
Сравнивая это выражение с (3,44), получим для рассмаривае-
мого случая
lim к (/) —к,
что совпадает с полученным выше результатом (3.41) для
произвольной линейно однородной производственной функции.
§ 3.5. Сбалансированный рост в однопродуктовой
макроэкономической модели с запаздыванием
В § 3.4 рассматривались вопросы устойчивости решений в од-
нопродуктовой макромодели. В этой модели валов продукт,
произведенный в течение заданного промежутка времени, делится
на три части: производственное потребление, непроизводственное
потребление и инвестиции. Последние являются источником
увеличения основных производственных фондов. Главное допуще-
ние модели состоит в том, что инвестиции превращаются
в основные фонды мгновенно. Это предположение, однако, не
может быть принято безоговорочно, так как известно, что
в экономике освоение капитальных вложений всегда происходит
с определенным лагом (запаздыванием). Поэтому можно поста-
вить вопрос о том, как влияет этот лаг на основные показатели
экономического роста.
В данном параграфе мы рассмотрим однопродуктовую модель
с учетом запаздывания ввода в действие основных производствен-
ных фондов. Предположим, что ввод в дейстивие основных
71
фондов осуществляется поэтапно. Возникающий при этом лаг
будем считать непрерывным. Тогда, как указано в гл. 2, если
обозначить через /(/) инвестиции, вкладываемые в развитие
основных производственных фондов в момент времени t, а через
1/(?)— освоенные (введенные в действие) основные производствен-
ные фонды в момент времени /, то
/(/)== J 7V(/, т)7(/-т)dr,
о
где N(t, т)—доля вводимых в момент t инвестиций, вложенных
в момент времени t — г.
Если задать Л?(г, т) в виде jV((, т) = Ае:и'~:', то последнее
уравнение (см. гл. 2) равносильно уравнению
V=XV=XI.	(3.45)
Здесь параметр X характеризует продолжительность запаздывания.
Используя принятые обозначения, уравнения модели (3.45)
можно записать так:
Х=аХ+1+С,
К=-р/С+К,	(3.46)
X=F(K, L).
Предположим, как и прежде, что роет трудовых ресурсов
происходит с постоянным темпом, равным п, тогда
L = nL,	(3.47)
или Е = Еое',!.
Соотношения (3.45) —(3.47) представляют собой замкнутую
систему уравнений, позволяющую определить траекторию разви-
тия экономики, т. е. величины X(п, К(г), /(/), L{t}, задавая
связанные первым уравнением (3.46) величины /(/) и С (г).
Последние, если данную модель рассматривать как управляемую
систему, играют роль управляющих воздействий.
Перейдем для удобства исследования свойств модели
к новым переменным к = КЩ v=V/L, x=XjL= F(K, L)l
[L=F(K[L, V)= /(/c), s=II (1 - a) X, c=G/L. Тогда соотношения
(3.45) —(3.47) примут вид
^-^ + n)k + v,
v = -(X+n)i>+X(l — a)sf(k),	' ’
а удельное потребление будет равно
О-49)
Выше было показано, что в однопродуктовой модели без
учета запаздывания существует траектория сбалансированного
роста. Покажем, что аналогичным свойством обладает и модель
с запаздыванием.
72
И Пусть доля накопления j постоянна. Предположим, что
И переменные модели К’р), А (г), описывающие развитие эконо-
 мики, — сбалансированно растущие, т. е. Х/ЛГ=Е/Е=п, где п —
И теми роста. Тогда фондовооруженность, отвечающая этим величи-
И нам, постоянна: к = Ki L = const. Из первого уравнения (3,48)
И получим £=0, f=const, а из уравнения (3.49), очевидно, С=const.
И Отсюда, в частности, следует, что вводимые в действие основные
И фонды и потребления растут с таким же постоянным темпом
В п. Режим сбалансированного роста с точки зрения _ системы
В уранений (3.48) является ее точкой равновесия. Если к и v от-
В вечают сбалансированному росту, то их значения можно получить
В решая систему уравнений
I	-(м+пД+^0,
В	— (Х+л) i?+X(l — д)$/(£)=0.
В Система (3.50) сводится к уравнению
К	Х(1 —	— (Х +	+ к = 0.	(3.51)
С Левая часть этого уравнения G (X), график которой изображен
р на рис. 3.7, имеет с учетом свойств производственной функции
F в точке к = 0 производную С7 (А)-+со при Х->0, а при
'• Х-^сс- G' — (ц+«) (Х-рл). Функция G(/c) выпуклая, так как
таковой является функция f(k). Следовательно, уравнение
(3.51) и система (3.50) имеют ровно два решения, из
которых одно является тривиальным (Х = 0), т. е. траектория
сбалансированного роста модели (3.48) существует, и она
 единственная.
| В случае функции Кобба —Дугласа= решение уравне-
 ния (3.51) может быть легко получено:
Так же как и
вопрос: обладает
роста свойством
/ <А(1 — a)s \ л
к =	\/ "Ц . р = I - а.
в модели Солоу без запаздывания, возникает
ли полученная траектория сбалансированного
устойчивости? Ответ оказывается положитель-
ным, причем устойчивость лосит асимптотический характер.
Для исследования устойчивости составим уравнения первого
приближения. Линеаризуя_уравнение (3.48) в окрестности решения
к, v и обозначив г^ — к — к, v = v-v, будем иметь
Т] = - (|1+н) Г| + V,
v = X (1 — я) sf (X) р — (Хщи) v.
Матрица А правых частей системы (3.52)
А=( -^ + л) _	1 А
ухр -ajsf’ (X) -(Х+п)у
(3.52)
73
I
Рис. 3.7
является постоянной. Для доказатель-
ства асимптотической устойчивости
решения к, v достаточно провери ть
(см. § 3.2), что действительные части
корней ее характеристического урав-
нения det (А —рЁ} = 0 отрицательны.
Характеристическое уравнение бу-
дет иметь вид
рЁ + Тл2 — О,
где =к + ц + 2п,
й2 = (Х-]-н)(ц4-и) — л(1 — a)sf'(ic).
Применим к данному характеристическому уравнению крите-
рий Гурвица. Тогда, чтобы установить отрицательность действи-
тельных частей корней уравнения, достаточно проверить положи-
тельность коэффициентов «н «2. Первый из этих коэффициентов
положителен. Для проверки условия «2>0 поступим следующим
образом. Рассмотрим уравнение (3.51), которое будет выполняться
в точке к. Левая часть этого уравнения (рис. 3.7) имеет при
к = к отрицательную производную. Следовательно,
к (1 - и) af (А7)-(л.+«) (ц + п) < 0.
Так как левая часть этого неравенства равна — й2, то отсюда
вытекает д2>0.
Таким образом, установлено, что в случае запаздывания
освоения капитальных вложений траектория сбалансированного
роста является асимптотически устойчивой. Аналогичным свойст-
вом обладает сбалансированный рост в модели Солоу без
запаздывания. Таким образом, наличие лага капитальных вложе-
ний не нарушает устойчивости сбалансированного роста.
Покажем теперь, что корни характеристического уравнения
действительны. В самом деле, дискриминант этого уравнения
после преобразований можно записать следующим образом:
D =(Х. — р)2 +4Х.(1 —
Первое слагаемое в этом выражении неотрицательно, а вто-
рое —положительно. Таким образом, корни характеристического
уравнения действительны, различны и, как показано выше,
отрицательны.
На рис. 3.8 показано поведение решений системы (3.52) на
фазовой плоскости.
Поведение системы (3.48) в окрестности сбалансированного
роста /с, v носит тот же характер, что и поведение системы
(3.52) в окрестности начала координат. Траектории системы
(3.48) изображены на рис. 3.9.
74
§ 3.6. Оптимальная норма накопления
в однопродуктовой макромодели
В § 3.5 исследован вопрос о поведении траекторий однопро-
дуктовой макромодели в том случае, когда норма накопле-
ния—заданная постоянная величина. Сама же норма накопления
может быть выбрана различной по значению, и это сказывается
на характеристиках роста фигурирующих в данной модели
экономических показателей.
С экономической точки зрения норма накопления является
важнейшим фактором, определяющим показатели экономического
роста. В конечном итоге рациональный выбор нормы накопления
и определяет стратегию экономического развития. В однопродук-
товой макромодели норма накопления однозначно задает все
остальные показатели, основные производственные фонды вало-
вого и конечного продукта и потребления.
Возникает вопрос о том, какова оптимальная норма накоп-
ления, т. е. при каких пропорциях накопления и потребления
обеспечивается наилучшее развитие экономики. Чтобы ответить
на этот вопрос, нужно сформулировать критерий развития
экономики. Это позволит сравнивать различные варианты раз-
вития и выбирать наилучший из них.
При одно продуктовой макромодели такая задача может быть
пос тавлена различным. образом. В данном параграфе мы будем
считать, что норма накопления постоянна, хотя в дальнейшем
это ограничение будет снято. Как вытекает из результатов,
полученных раньше, данной постоянной норме накопления от-
вечает определенный режим сбалансированного роста. Если
вычислить потребление с на одного рабочего, то в режиме
сбалансированного роста эта величина будет постоянной. Если
к — фондовооруженность на траектории сбалансированного роста,
75
то потребление с на этой траектории задается формулой
[см. (3.33)]
(3.53)
Определим теперь значение з = 5 и отвечающую ему величину
к^=к, которые обеспечили бы максимальное значение выражения
(3.53). Тогда мы получаем задачу о выборе постоянной опти-
мальной нормы накопления,
С математической точки зрения данная задача является
задачей на условный экстремум. Требуется найти максимум
(3.53) при ограничении [см, (3.38)]
s(l+	=	(3-54)
Решение данной задачи может быть проведено с помощью
метода множителей Лагранжа. Для этого составим функцию
Лагранжа: '
£(л,зД) = (1 -j)(l-«)/(£ ) + X(,s(l-й)/(Л)-(ц+и)А;)
— и приравняем нулю ее частные производные по s и к:
Получим систему уравнений
ДI —а)/(/с)(Х.—1) = 0,	'	(3.55)
^ = (! -з-)(1 -a)f'(k) + Ц - (ц+л) + л(1 -a)f'(k))-0.
Вместе с (3.54) эта уравнения образуют систему трех уравнений
для определения трех неизвестных: з, /с, к.
Первое уравнение (3.55) имеет очевидное решение Х.= 1 (так
как /(/с)^0). Подставляя это значение во второе уравнение (3.55)
и преобразуя его, получим
(1-й)/'(^) = ц+л.	(3.56) 1
Это соотношение вместе с (3.54) представляет собой систему
двух уравнений для накопления искомых оптимальных значений
величин и и к. Данная система имеет единственное решение
к=^к. Действительно, так как f"(k)<Q, то левая часть уравнения
(3.56) является монотонно убывающей функцией. Следовательно,
решение уравнения (3.56) единственно. Что касается его сущест-
вования, то в этом легко убедиться используя свойства функции
f(k). При этом рассуждения аналогичны приведенным в § 3.5.
Итак, уравнение (3,56) имеет единственное решение к. Подстав-
ляя его в (3,54), получим и искомое значение величины ^ = з;
(ц+»)Г
(1-Ф/Д)'
Для расчета оптимальной нормы накопления теперь нужно
задать конкретную производственную функцию. После этого
(3.57)
76
f значение оптимальной нормы накопления однозначно определя-
? елся соотношениями (3.56), (3.57).
! Подчеркнем, что после определения J необходимо проверить
 s< 1.
Проведем в качестве примера эти расчеты для случая
производственной функции Кобба—Дугласа /(/с) = о/ся. Из (3.56)
.' получаем
(1-а)аа/ся-1 = (ц + н),
• откуда
7? (	+	)
। ' \ (1 —/
L Подставляя k в (3.57), будем иметь
[ »+п У'**-1”
f	(I — alal  -- 
|	1	7 V1 —Фса/
। откуда после сокращений получим
г.	$ = «.
| Таким образом, для производственной функции Кобба—Дуг-
(ласа оптимальная норма накопления совпадает с ее эластичностью
(по основным производственным фондам.
г Задача об оптимальной норме накопления может быть
I.поставлена и в однопродуктовой модели с запаздыванием. В этом
[случае она сводится к нахождению максимума потребления,
[вычисляемого по формуле (3.53) при ограничениях (см. § 3.5):
|.	-(p.+«)^ + v = 0,
i	-(X.=0.
IL Это задача на условный экстремум. Для ее решения, как
к в предыдущем случае, составим функцию Лагранжа:
Г = (1 -s)(1	(p+n)^ + t:z) + X,2(.s'X(l-ajffkj-l'k + njvj
И-и уравнения для отыскания точки экстремума:
I	g=(xA-i)(i-»)/(*)=<>.
Со
 Из первого и второго уравнений получим
	А2 = 1Д, Xr
77
а из третьего уравнения с учетом найденных значений
Л, найдем
(3.58)
Из соотношения (3.58) при Л-^со, т. е. когда запаздывание
при вводе капитальных вложений исчезает, получаем для оп-
тимального значения к уравнение

(.1 + »!
Т^’
что совпадает с полученным ранее результатом для модели без
запаздывания.
Если к — решение уравнения (3.58), то оптимальная норма
накопления . J выражается соотношением

(3.59)
Для производственной функции Кобба — Дугласа нетрудно
получить решение уравнения (3.58) в явном виде. Оно будет
иметь вид
I — а) \
ур.+фф+л)/
где о, а и 0=1— а — параметры функции Кобба — Дугласа.
Подставив это значение в соотношение (3.59), получим после
преобразований
5 = а, а<1,
т. е. оптимальная норма накопления совпадает с эластичностью
производственной функции по основным производственным фон-
дам. Интересно отметить, что для производственной функции
Кобба- - Дугласа в модели без запаздывания получается в то-
чности такой же результат для оптимальной нормы накопления,
хотя для других производственных функций это, вообще говоря,
не так.
Глава 4
Математическая модель
оптимальных управляемых
процессов
В этой главе рассматривается общая постановка матема-
тической задачи, к которой приводят проблемы, возникающие
при оптимизации систем, в частности экономических. Будем
считать, что имеется система, состояние которой может изме-
ниться под воздействием некоторого количества управляющих
воздействий. Задавая тем или иным способом эти воздействия,
мы получим определенный процесс изменения состояния си-
стемы. Первая задача, которая возникает при управлении
системой, — выбор таких воздействий на систему, чтобы проис-
ходящий процесс удовлетворял заданным условиям. Подобные
процессы принято называть допустимыми.
Решение этой задачи неоднозначно. Допустимые процессы
в системе образуют множество. Тогда возникает следующая
задача-—выбор из этого множества процесса, который является
в некотором смысле наилучшим. Другими словами, это задача
выбора оптимального процесса.
Чтобы решать оптимизационные задачи с помощью мате-
матических методов, нужно прежде всего сформулировать
на математическом языке рассматриваемые процессы и их
математические модели. Далее требуется дать математическое
выражение понятию «наилучший» — свойству, которым должен
обладать искомый процесс. Наконец, необходимо с помощью
математических средств уметь отразить те ограничения, которые
накладываются на состояние системы и управления. Математи-
ческой формализации всех этих понятий и посвящена данная
глава.
$4.1. некоторые математические понятия
Введем некоторые понятия и обозначения, которые будут'
использованы в дальнейшем. Рассмотрим множество М с эле-
ментами v(veM), причем элементы v можно представить как
пары следующего вида:
* = (х, >)=
79
где хеУ, ye Y, а X, У—некоторые заданные множества. Проек-
цией множества М на множество X назовем подмножество Мх,
обладающее тем свойством, что для каждого хеЛ/, существу-
ет такой элемент уеК, что пара v = (x, у) содержится в мно-
жестве М.
На рис, 4.1 множества X и Y—соответственно оси абсцисс
и ординат. Множество всех пар (Ху), хеХ, уе К—точки
координат плоскости. Множество М является его некоторым
подмножеством. Точка xt принадлежит проекции Мд., так как
найдется такая точка (например, уД что (xb yL)eM. Точка
таким свойством не обладает, так как не существует ни одной
точки уе У такой, что пара (х2,у) принадлежи г множеству М.
Следовательно, хг еМх.
Введем понятие сечения Мх множества М при данном х.
Сечением Л/'1 будем называть множество всех у, при которых
пара v=(x, У) принадлежит множеству М- На рис. 4,1 сечение
МД есть отрезок на оси ординат.
Введем понятие функционала. Будем говорить^ что на мно-
жестве М задан функционал если известно правило, которое
каждому элементу v е М ставит в соответст вие определенное
действительное число J (v). Можно сказать, что функционал
осуществляет отображение множества М (имеющего произволь-
ную природу) на множество действительных чисел.
Понятие функционала является обобщением понятия функции,
когда аргументом является элемент произвольного множества.
С другой стороны, функция у=/(х) сама является примером
функционала, заданного на множестве хеХ, являющемся под-
множеством «-мерного евклидова пространства R".
Понятие функционала является одним из главных в задачах
оптимизации. Приведем примеры функционалов.
Пример 1. Рассмотрим на плоскости (х, у) множество об-
ластей, представляющих собой фигуры, ограниченные замк-
нутыми кривыми (одна из таких областей изображена на
рис. 4.1).
Обозначим множество таких областей через М. Зададим на
этом множестве функционал
Xi	Если У(=4/—некоторая область.
Ряс. 4.1
то значение У(х) равно площади
этой области. Таким образом,
установлено соответствие между
элементами множества М и дей-
ствительными числами, причем
каждой фигуре из множества
М однозначно соответствует дей-
ствительное число — ее площадь.
Пример 2. В данном приме-
ре М — множество функций
SO
С [а, b ], заданных, и непрерывных на отрезке [а, b ]. Таким
образом, элементы v этого множества — непрерывные функции
у=/(х), определенные на данном числовом промежутке. Пусть
у некоторая такая функция. Зададим значение функци-
онала У формулой
6
У = №)dx.	(4.1)
Л
Тогда каждой функции поставлено в соответствие определенное
действительное число, равное ее интегралу на отрезке (а, b ]
(он существует, так как f(x) непрерывна). Следовательно, соот-
ношение (4.1) задает функционал на множестве М.
Пример 3. Множество Л/ то же, что и в примере 2, но
функционал У определяется формулой y=f(b), т. е. равен зна-
чению функции у=/(х) в конечной точке промежутка [а, 6].
Эта зависимость также однозначно задает значение функционала
на заданном элементе множества И.
Приведенные примеры показывают, что функционалы могут
быть заданы различными способами, причем на одном и том
же множестве могут быть заданы разные функционалы. В даль-
нейшем для нас особый интерес будут представлять функционалы
заданных на множествах функции, подобно рассмотренных в при-
мерах 2 и 3,
§ 4.2. Общая задача оптимизации
В общем виде задача оптимизации формулируется как задача
отыскания минимального (или максимального) значения функ-
ционала У(у) на множестве М. Эта задача ставится аналогично
задаче об отыскании экстремума функции.
Предположим, что требуется минимизировать функционал
У(у) на множестве М. Под решением такой задачи мы будем
понимать значение v такое, что для остальных элементов
v множества М выполняется неравенство
У(у)^У(¥).
Если решение этой задачи существует, w v называется опти-
мальным элементом множества Л/, а величина -J = ./(v)—опти-
мальным значением функционала. Решения поставленной задачи
У и у будем записывать следующим образом:
I	У = У(у)^ ттУ(у).
I Аналогично формулируется задача о нахождении максималь-
ного значения функционала. Решение задачи о максимизации
[функционала — У (г) сводится к задаче о минимизации функцио-
нала — У (v), т. е. если на элементе v множества М достигает
81
минимума функционал — J(y), то J(y) достигает на v искомого
максимума.
Введем понятие точной нижней и верхней границы функцио-
нала. Точной нижней границей функционала ,/(v) на множестве
М назовем такое число т, если:
1)	для любого veM;
2) существует последовательность {уДеМ, па которой /"(vj-*
->т.
Точная нижняя граница функционала обозначается
т = inf T(vj.
vfjW
Последовательность {v5} называется минимизирующей после-
довательностью.
Точно так . же определяется точная верхняя граница п функ-
ционала ,/(v):
И= sup>(v).
veM
Аналогично задачам о минимизации и максимизации функ-
ционала задачи о нахождении точной нижней и верхней границ
функционала сводятся одна к другой. Например, для нахождения
точной верхней границы п функционала y(v) достаточно найти
точную нижнюю границу т функционала — У(у). Тогда т = — п
— искомое значение точной нижней границы, а последователь-
ность	максимизирующая—У(т), будет минимизирующей
для >(v).
Назовем функционал ,/(v) ограниченным снизу (сверху) на
множестве М, если существует такое число Л, что при всех
уеМ УАууз>А (Л(у)^Т). Если функционал является ограниченным
снизу (сверху), то решение задачи о нахождении его точной
нижней (верхней) границы существует, т. е. имеет место следую-
щая теорема.
Теорема 4.1. Пусть на множестве М задан ограниченный снизу
функционал Ху). Тогда реализуется одна из двух возможностей:
Т. Существуют^ элемент уеМ и число при которых
,/(у) = ,Т и XV)5X При всех УеМ.
2!'. Существуют последовательность {у,} элементов множе-
ства М и_ число , удовлетворяющее условиям ХД-ХХ
и >(т)>У при всех уеМ.
Доказательство. Рассмотрим множество I значений функ-
ционала У (у) на числовой прямой. Это множество ограничено
снизу, так как каждый его элемент не меньше А. Тогда, по
теореме о существовании точной нижней границы ограниченного
снизу множества, она существует для множества J. Обозначим
ее т и покажем, что это и есть искомая точная нижняя граница
функционала ,/(v) на множестве М. Для этого нужно проверить,
82
что ,/(v)^m для всех veM и существует минимизирующая
последовательность {ys}. Первое из этих утверждений очевидно,
так как, будучи точной нижней границей множества значений
функционала -/(у), число т будет удовлетворять требуемому
неравенству.
Докажем теперь существование минимизирующей последова-
тельности, для чего рассмотрим два возможных случая: когда
число m принадлежит множеству I (в, следовательно, является
его минимальным элементом) и когда не принадлежит ему.
В первом случае, так как множество I состоит из значений
функционала ,/ (у), существует элемент v е М, при котором
./(v) = m. Тогда очевидно, что он удовлетворяет условию 1°
доказываемой теоремы.
Во втором случае, по свойству точной нижней границы
числового множества, существует последовательность
состоящая из элементов множества I. Так как любой элемент
множества I есть значение функционала У(у) при некотором
veM, то для каждого ms существует v.eW, при котором
,У'(у3) = ш5. Построенная последовательность {vsJ является мини-
мизирующей, так как >(у^)_>щ, и, следовательно, удовлетворяет
условию 2°. Теорема доказана.
Доказанная теорема, несмотря на простоту, имеет важное
значение по двум причинам. Во-первых, она говорит о том,
что постановка задачи об отыскании наименьшего (наибольшего)
значения ограниченного снизу (сверху) функционала имеет смысл.
Во-вторых, она проливает свет на природу решения такой
задачи. А именно: решением будет либо определенный элемент
v множества М, минимизирующий (максимизирующий) функци-
онал ,/(v), либо последовательность {у,} элементов множества
М, являющаяся минимизирующей (максимизирующей) последо-
вательностью. В первом случае можно говорить о точном
решении задачи, а во втором — о приближенном, так как при
, достаточно большом .$ значение У (vs) будет сколь угодно мало
i отличаться от своей точной нижней (верхней) границы, В этом
! случае у, будет приближенным решением задачи с заданной
точностью.
Задачу о нахождении минимального или максимального
значения функционала в дальнейшем будем называть задачей
об оптимизации функционала (v) па множестве М. Рассмотрим
обе возможные постановки задачи оптимизации—об отыскании
элемента у е Л/, на котором достигается оптимальное значение
функционала, и минимизирующей (максимизирующей) последо-
вательности.
Вторая постановка задачи обладает большей общностью по
сравнению с первой, которая не всегда имеет решение. Чтобы
первая постановка задачи была корректной, ее нужно дополнять
теоремой существования, в то время как вторая постановка
83
задачи об оптимизации ограничен-
ного функционала всегда имеет
решение.
Рассмотрим несколько приме-
ров.
Пример 1. Функционалом явля-
ется функция одной переменной.
Рассмотрим задачу о минимуме
монотонно возрастающей непре-
рывной функции y=f(x): а) на от-
резке [0. 1 ]; б) на интервале
В случае а) множество М есть отрезок [0, 1 ], Тогда функция
/(х) достигает минимального значения при х=0 (рис, 4.2).
Таким образом, значение точной нижней грани m =/(()) достигается
на элементе .'(=0 множества М, который и является оптимальным,
В случае б) множество М есть интервал (0, 1), В этом случае
значение гп =/((]) также является точной нижней границей значений
функции y~j\x\ но элемент х = 0 уже ие принадлежит множеству М.
Поэтому задачу надо ставить в форме отыскания минимизирующей
последовательности. Для этого можно взять любую сходящуюся
к нулю последовательность, например х3=1Д, 5=1,2,...,
Пример 2. Множество М представляет собой множество не-
прерывных на отрезке [a, b ] функций у=Г(х), удовлетворяющих
ограничениям: а)/(х)^1 при хе [0,1]; б)/(х)>] при хе [0,1].
Зададим функционал с помощью соотношения
0
и оу дем рассматривать задачу о нахождении его минимума:
J -► ПИП ./ (v), v=/(x).
те Л/
Геометрический смысл функционала (4,1) (рис. 4.3) — площадь
криволинейной трапеции, ограниченной кривой y-fix).
В случае а) искомый минимум функционала достигается при
/(х) = 1 и равен (й— а). Действитель-
но, так как /(х)>1, то, по свойству
интеграла,
ь	ь
J/(x)dx J 1 dx = 6 — а.
Таким образом, в данном случае
задача оптимизации функционала
имеет точное решение. Минимизи-
рующий элемент v множества
М есть функция /(х)=1.
Рис, 4.3
84
В случае б), как и в примере 1, точного решения не существует.
Точная нижняя граница т функционала равна Ь — а и может
быть достигнута с любой наперед заданной степенью точности
на минимизирующей последовательности /я(х)=1+^. При этом
последовательность значений функционала
Л = J/л (x)d х = А + ~ Vi - а}
Q	\	/
стремится при к значению т-b — а своей точной нижней
границы.
Пример 3. Важным частным случаем общей задачи оптими-
зации является задача математического программирования. Эле-
ментами v множества М здесь являются точки «-мерного
пространства R" («-мерные векторы):
х = (х15 ..., х„).
Множество М задается системой ограничений типа равенств
и неравенств:
= г' = 1> 2, ..., к,
•П-Э- ..., х„)<0, г = ^+1, т,	(4.2)
1 = 1, 2, и,
где gf(x,, ..., х„)-непрерывные функции.
Функционал > в данной задаче задается функцией у=/(х1(
..., х„) (целевая функция). Задача оптимизации состоит в отыска-
нии оптимального элемента v множества М, который миними-
зирует данный функционал. Иными словами, надо найти вектор
х = (Х[, ..., х„), удовлетворяющий ограничениям (4.2), который
минимизирует функцию у~((хг, ..., х„).
Эта задача может, как и в предыдущих примерах, иметь
точное решение и решение в классе минимизирующих последо-
вательностей, Наличие точного решения гарантируется, если
множество М, задаваемое условиями (4.2), ограничено (и, сле-
довательно, замкнуто), а целевая функция y=/'(xls ..., х„) непре-
рывна. Тогда, по теореме Вейерштрасса о существовании мак-
симума и минимума непрерывной функции в замкнутой огра-
ниченной области, существует точка х = (х1; ..., хл), в которой
рассматриваемая функция минимальна.
Пример 4. Рассмотрим задачу о линии наименьшей длины.
Для этого возьмем множество кривых, соединяющих точки
плоскости А и В, и поставим задачу выбрать из них кривую,
имеющую наименьшую длину.
В этой задаче множество М есть множество всех кривых,
соединяющих точки А и В, а значением функционала на данной
кривой является ее длина.
85
ВИЯМ Дл-л) = >*л, f{Xs)=yB.
равенством
Чтобы записать эту задачу
аналитически, изобразим на плос-
кости систему координат (рис. 4.4)
и будем рассматривать в качестве
элементов множества М те кри-
вые, которые задаются непрерыв-
но дифференцируемыми на отрез-
ке [хл.Л'л] функциями у = /'(л),
удовлетворяющими краевым усло-
Для таких кривых длина задается
•/ = J V^"+(j'*)2dx,	(4.3)
А,
что и является значением искомого функционала.
Таким образом, искомый оптимальный элемент множества
М в данной задаче—удовлетворяющая перечисленным выше
условиям функция j’=/(x), минимизирующая функционал (4.3).
Данная задача имеет точное решение. Оптимальным элемен-
том множества М, т. е. кривой наименьшей длины, будет прямая,
соединяющая точки А и В.
§ 4.3. Задача оптимизации управляемых процессов
Задачи оптимизации управляемых процессов, иди, как они
будут в дальнейшем называться, задачи оптимального управления
представляют' собой важный класс задач оптимизации. Эти
задачи являются частными по отношению к сформулированной
выше общей задаче оптимизации. Именно о методах решения
задач оптимального управления и будет в основном идти речь.
В настоящем параграфе дается постановка задач оптимального
управления.
Необходимость управлять процессом оптимально, т. е. на-
илучшим в определенном смысле образом, возникает в системах,
характеристики которых меняются во времени под влиянием
управлений. К такому классу систем относится и экономическая
система. Для того чтобы сформулировать на математическом
языке задачу управления в таких системах, необходимо ввести
некоторые понятия и построить соответствующую математи-
ческую модель.
Важнейшими понятиями в теории оптимального управления
являются понятия состояния системы и управления. Будем
рассматривать системы, состояние которых может быть в любой
момент времени определено вектором х д-мерного векторного
пространства с координатами х = (лл, х2, ..., хл), хе А'. Пространст-
во X будем называть пространством состояний системы.
86
Так как система изменяется во времени, то ее поведение можно
описать последовательностью состояний. Такую последовательность
системы x(/)=(xt(z), х2(ф, ..., хп(/)) называют траекторией системы.
Переменную /, которая является независимой, назовем аргу-
ментом процесса. Аргументом процесса может быть любая
величина, но чаще всего —время. Переменная t может пробегать
некоторый отрезок числовой прямой, если /е [r0, А ], или отрезок
натурального ряда t=/0, д + 1, Т. В первом случае процесс,
происходящий в системе, называется непрерывным, во втором
случае — многошаговым. Системы в Этих случаях назовем соот-
ветственно непрерывными и дискретными.
Изменение состояния системы, т. е. процесс в ней, может
происходить под воздействием управляющих воздействий. Будем
рассматривать системы, управляющие воздействия в которых
моделируются с помощью элементов r-мерного векторного про-
странства U:
н=(м], и2, ..., iZ), ue(/cR',
Управляющие воздействия могут задаваться в виде функций
от t. Тем самым реализуется Определенный способ управления
системой- В этом случае будем говорить о задании программы
управления u(/) = (i?(f), u2(t),..., и,(Г)).
На возможные (допустимые) состояния системы х(/) и управ-
ления u(z) могут быть наложены ограничения. Рассмотрим
множество троек (/, х, и) — совокупность (и + г 4-1) -мерных векто-
ров в пространстве R"+ г +1. Тогда ограничения на состояние
системы и управления в самом общем случае могут быть
записаны в виде
(t, х, «)еУ,
где p'eR"+,'+ !—некоторая область (подмножество) рассматривае-
мого (n + г +1 )-мерного пространства. Ограничения на величины
х(/), u(Z) в каждый фиксированный момент времени t могут
быть заданы и в виде
(x(f), u(r))eP,
где V*—сечение множества V при заданном значении t.
Пару функций v = (x(f), u(/)) назовем процессом. Между функ-
циями x(z), u(z) имеется связь: как только задано управление
u(Z) системой, последовательность ее состояний (траектория
системы) х(/) определяется однозначно. Связь между x(t) и н(?)
моделируется по-разному в зависимости от того, является система
непрерывной или дискретной.
Для непрерывных систем модели процессов задаются системой
Дифференциальных уравнений вида
х' к1, ..., х", и1, ..., wr), /=1, 2, ..., п,
или в векторной форме
87
x=/(r, x, u).	(4.4)
В дальнейшем для компактности будем пользоваться вектор-
ной записью переменных и систем уравнений. Однако иногда,
если эго будет диктоваться соображениями удобства, воспользу-
емся записью системы (4.4) в виде
х'=/£(1, х, и), 1 = 1,2,	и.
Пусть задано состояние, в котором система находилась
в начальный момент 10. Этот момент в дальнейшем для
определенности примем равным нулю, а момент окончания
процесса Z,—равным Т. Тогда аргумент процесса t изменяется
в пределах	а начальным состоянием системы будет
вектор
)?.	x(0)=x0-(xj, xg,	(4.5)
где хо = х'(0)—начальное значение г-й координаты вектора со-
стояния системы.
Проанализируем, каким образом модель отражает связь между
управлениями и состоянием системы, изменяющимся под их
воздействием. Пусть на промежутке	задано управление
u(z). Подставляя его в правую часть системы (4.4), получим
x = f(z, х, 11(f)).	(4.6)
Имеем систему дифференциальных уравнений относительно неиз-
вестной вектор-функции х = (х1, х2, ..., xrt). Решая ее с учетом
начальных условий (4.5), получим х(г). Это решение и есть
траектория, отвечающая заданному управлению u(f). При этом
мы предполагаем, что для системы (4.6) выполнены условия,
обеспечивающие существование и единственность ее решения при
заданных начальных условиях (решение задачи Коши).
Итак, задание управления в непрерывной модели однозначно'
определяет ее поведение. Задавая различные законы управления,
получаем, следовательно, различные траектории системы.
Модель дискретной управляемой системы имеет вид системы
рекуррентных уравнений;
х’(/4- l)=/'(z, xl(z), x"(z), и1 (/), .,,, ur[t)), i= 1, 2, n,
В векторной форме эту модель, как и в непрерывном случае,
будем записывать в виде
x(f+l)=/(f, х(/), «(/)),
или
?(£+l)=/(z,x(f),u(r)), 1=1,2, ...,н.	(4.7)
Здесь t принимает значение Z = 0, 1, ..., Т—\. Начальное зна-
чение х(0) = хо будем, как и выше, считать известным.
В дискретной системе, как и в непрерывной, задание програм-
мы управления u(f) при / = 0, 1, ..., Г-1 позволяет однозначно
88
определить отвечающую ей траекторию системы. При этом
в дискретном случае не требуется наложение каких-либо условий
на правые части уравнений (4.7), как в непрерывном случае,
где требовалось обеспечить существование и единственность
задачи Коши, В самом деле, при подстановке значения и (г)
в правую часть (4.7) получаем систему уравнений, которая
позволяет при известном значении состояния х(/) в момент
времени t определить состояние х(? +1) в следующий момент
времени. Так как в начальный момент / = 0 состояние х(0) = хо
известно, то, подставив его в правую часть (4.7), получим
x(l)=f(0, х0, и(0)).
Подставляя затем найденное значение х(1) и t=} в (4.7), так
же найдем значение х(2). Продолжая этот процесс, через Т шагов
получим последнее искомое значение х(Т).
Таким образом, и в дискретном случае уравнения модели
(4.7) позволяют однозначно определить траекторию системы
х(/) если задано управление «(/).
Следовательно, процесс v = (x(Z), u(z)) должен удовлетворять
следующим ограничениям:
Г". (х(/), u(/))e V1 при всех
2е. Пара (х(/), н(г)) удовлетворяет системе уравнений процесса:
а) системе (4.4) в непрерывном случае при te [О, Т]\ б) системе
(4.7) в дискретном случае при / = 0, 1, ..., Т—1.
3°. Заданы начальные условия (4.5).
4°. В непрерывном случае на вектор-функции х(/). и(/) накла-
дываются некоторые дополнительные ограничения, связанные
с применимостью употребляемых здесь математических записей.
Вектор-функцию и(7) будем считать кусочно-непрерывной, а век-
тор-функцию х(/)—непрерывной и кусочно-дифференцируемой.
Процессы v = (x(r). и(/)), удовлетворяющие условиям Г—-4а, будем
называть допустимыми. Таким образом, допустимый процесс это
программа управления и (/) и соответствующая ей траектория системы
х(/), удовлетворяющие перечисленным ограничениям.
Множество допустимых процессов в задаче оптимального
управления и представляет собой множество М допустимых
элементов, о которых шла речь выше при обсуждении общей
задачи оптимизации. Теперь для постановки оптимизационной
задачи необходимо ввести в рассмотрение функционал У, задан-
ный на множестве М. Задача оптимального управления будет
состоять в выборе элемента v = (х (г), й (г)) множества М, на
котором функционал ./ достигает минимального значения. Такой
процесс мы будем называть оптимальным процессом, управление
«(/) — оптимальным управлением, а траекторию х(/)— оптималь-
ной траекторией.
Функционал У, заданный на множестве допустимых процессов,
описывает цель, согласно которой оптимизируется процесс.
89
Значение ./(у), которое функционал принимает на данном
процессе, характеризует качество процесса и позволяет сравнить
два любых процесса. С точки зрения принятого функционала
более предпочтительным является процесс, на котором его
значения меньше. А оптимальным, т. е. более предпочтительным
но сравнению с любым другим процессом, будет тот, где
значение функционала минимально.
В задачах оптимального управления для непрерывных систем
будем рассматривать функционалы следующего вида:
x,u)d/ + F(x(7')),	(4.8)
О
где /°(/, х, и)=/°(/, №, ...,	и1, .... if); F(x)=F’(xJ, ..., х")— задан-
ные функции. Выражение (4.8) позволяет вычислить для каждого
допустимого процесса (х(Г), и(/)) определенное значение и тем
самым задать-функционал на множестве допустимых процессов.
Для этого необходимо подставить x(Z), u(f) вместо аргументов
функции f°(j, х, и), которая становится функцией времени, после
чего вычислить ее интеграл. Зачем к значению интеграла
прибавляем значение функции F(x) при х = х(7").
Функционал >(v) состоит из двух частей; j/°(z, х, u)dt
о
и функции конечного состояния 7г(х(Т')) — терминальной со-
ставляющей. Первое из этих слагаемых оценивает качество
процесса на (х'ф), «(/)) на всем промежутке [О, Г], второе
слагаемое — качество конечного состояния системы. Иногда в за-
дачах оптимального управления конечное состояние системы
х(2г) = х1 задается. В этом случае второе слагаемое функционала
(4.8) есть величина постоянная и, следовательно, не влияет на
его минимизацию. Такие задачи называются задачами с фик-
сированным правым концом траектории. Условие x(T) = xf
следует добавить в качестве дополнительного ограничения к усло-
виям Г—4е', определяющим множество допустимых процессов.
Функционал (4.8) выбирается таким образом, чтобы содержа-
тельный смысл входящих в него слагаемых отвечал цели
управления в конкретной задаче.
В частных случаях любое из слагаемых в (4.8) может
отсутствовать. Тогда функционал будет иметь вид
г
j?(v)= х, u)d/,
о
или
Возникающие в этих случаях оптимизационные задачи могут
быть сведены одна к другой и, следовательно, ни одна из них
не является более общей.	г
9(1
Функционалы вида (4.8) охватывают широкий класс прило-
жений задач оптимального управления, в том числе и оптими-
зации экономических процессов.
Для задач оптимизации многошаговых процессов в дискретных
системах функционал имеет вид
лх «ю)+^(х(П)-	(49>
г = 0
К функционалу (4.9) относятся все замечания и комментарии,
сделанные к функционалу (4.8).
Итак, мы определили все понятия, необходимые для поста-
новки задач оптимального управления. Поставим задачу о ми-
нимуме функционала (4.8) в непрерывном и (4.9) в дискретном
случае на множестве М допустимых процессов v = (x(r), и(Г)),
удовлетворяющих ограничениям Г'—4°.
Как следует из §4.2, сформулированная выше задача может
решаться в двух вариантах.
1. Определить оптимальный процесс г=(хД), «(/)), чтобы
minjf(v).
vcM 7
2. Определить минимизирующую последовательность {vs} =
= {is(0> us(O)}eM, чтобы ^(vs)^ inf ,/(v).
veM
Задача оптимального управления, как правило, ставится
в первом варианте. Но тогда она, как мы убедились, це всегда
имеет решение. В то же время во взором варианте задача
оптимального управления всегда имеет решение, если только
функционал ./ ограничен снизу на множестве М. Последнее условие
часто удается проверить достаточно просто. Например, в большом
количестве экономических приложений функции /°(/, х, u), F(x)
в (4.8) и (4.9) являются неотрицательными при любом наборе
аргументов. В этом случае функционал J не может принимать
отрицательных значений. Следовательно, он ограничен снизу.
В теории оптимального управления термины «состояние»
и «управление» имеют наглядный содержательный смысл. Он
заключается в том, что, как отмечалось выше, задавая управление
и(0, задаем и траекторию процесса х(г), а. изменяя программу
u(z) —«управляем» процессом.
Кроме того, имеются и некоторые формальные отличия:
в непрерывном варианте состояние x(Z) входит в уравнение
процесса вместе со своей производной х(/), а управление
«(^--непосредственно. Это обусловливает различные математи-
ческие требования к классам функций, к которым принадлежат
x(z), и0)п сформулированные в 4°. В дискретном случае состояние
i: x(z) входит в отличие от управления и(г) в управление процессом
(вместе со своим значением х(г+!) в момент времени (г+1).
91
Множество V‘ пар векторов (х, и)—сечение заданного мно-
жества V при данном г — определяется априорными ограниче-
ниями, вытекающими из содержательного (физического, эконо-
мического) смысла задачи. Это есть множество возможных «в
принципе» состояний системы управлений.
Из условия ve V'' можно выделить ограничения на состояние
и управление:
х(/)е И, и(Г)б	(4.10)
где Vx— проекция множества V1 на пространство X; Р"1 — сечение
множества У1 при данном х.
В задачах оптимального управления область Ух возможных
состояний часто является постоянной или совпадает со всем
пространством, а область У1Х возможных управлений не зависит от
х. Эти предположения выполняются в большом числе прак тических
случаев и упрощают решение задачи оптимального управления.
Из ограничений па состояние в (4.10) рационально выделить
граничное условие х(Т)еУх, накладываемое на состояние x(z)
в конечный момент времени. Как мы увидим ниже, множество
Ух при часто существенно иное, чем при t<T, из-за
дополнительных ограничений па конечное состояние системы,
как правило присутствующих в задачах. Обычно содержательные
условия, задающие У'х при z = Г, связаны с целью управления
(перевод системы в заданное состояние или область), тогда как
при КТ—с его возможностями.
Наконец, последнее замечание по постановке задачи опти-
мального управления. До сих пор мы предполагали, что про-
межуток времени	фиксирован, т. е. задай момент Г окон-
чания процесса. Возможны постановки задач, где этот момент
не задан, а является сам по себе решением задачи. Это относится,
в частности, к так называемым задачам о быстродействии,
когда требуется перевести систему (4.4) из заданного начального
состояния х(0)-хо в заданное конечное состояние x(T) = xt,
минимизируя при этом время Т протекания процесса, Методы
решения задач быстродействия будут рассмотрены ниже наряду
с методами решения задач с дискретным временем протекания
процесса.
§ 4.4. Примеры задач оптимального управления
Приведем примеры, иллюстрирующие постановку задач опти-
мального управления. В дальнейшем эти и другие задачи будут
решены математическими методами оптимального управления.
В числе примеров и модели экономических процессов, рассмот-
ренные в гл. 2.
Пример 1. Рассмотрим модель Леонтьева, которая представ-
ляет собой балансовое соотношение
92
X-aX+iX+C.	(4.11)
Экономика описывается интенсивностью выпуска валовой про-
дукции X, (количество валовой продукции, производимой в единицу
времени), интенсивностью потребления С, коэффициен том произво-
дственных материальных затрат а, коэффициентом приростной
фондоемкости 6. Соотношение (4.11) показывает, как валовая
продукция X распределяется на производственные затраты «X,
прирост основных производственных фондов ЬХ и потребление С.
Если рассматривать развитие экономики на некотором про-
межутке времени /е [0. Г], то различные альтернативы ее разви-
тия определяются тем, как задается потребление С. Задав ее
на промежутке [0, Т], найдем однозначно из уравнения модели
траекторию роста валового продукта Х(т),
Чтобы пояснить последнее, представим уравнение (4.11) в виде
Х=^Х-|с.	-	(4.12)
У о
Из (4.12) видно, что при задании C(t) это соотношение
превращается в дифференциальное уравнение относительно Х(/)
с заданной правой частью, откуда величина Х(г) может быть
найдена. Кроме того, известны начальное состояние, т. е. интен-
сивность валового выпуска в начальный момент времени, и Огра-
ничения на минимальную и максимальную величину потребления.
Если учесть и вытекающую из их экономического смысла
неотрицательность переменных в рассматриваемой модели, то
перечисленные ограничения можно представить в виде
X(0) = Xo, Cmin^C^Cnax, Х^О.	(4.13)
Если теперь воспользоваться терминологией, введенной ранее
для постановки задач управления, то соотношение (4.12) пред-
ставляет собой уравнение процесса, С — управление, X —состояние
системы. Накладываемые на процесс v = (x(/), C(z)) ограничения
(область И), определяются соотношениями (4.13).
Таким образом, соотношения (4.12), (4.13) определяют мно-
жество допустимых в данной системе процессов.
Чтобы определить наиболее эффективный путь экономического
роста, т. е. выбрать из множества допустимых процессов наилуч-
ший, требуется, как мы знаем, задать функционал У, определяю-
щий качество процесса. В гл. 2 было отмечено, что построение
критерия оптимальности развития экономической системы—са-
мостоятельная, имеющая важное значение проблема моделирова-
ния экономики.
Критерий, предусматривающий рост потребления и возмож-
ность наращивать определенный экономический потенциал к ко-
нечному моменту времени, может быть выражен функционалом
следующего вида:
93
т
У(у) = а fe_s'C,dz+₽y(7’)^max.	(4.14)
О	те Af
Здесь первое слагаемое представляет собой суммарное взвешенное
потребление на промежутке [О, Г], терминальный член имеет
смысл интенсивности выпуска в конечный момент времени.
Весовые коэффициенты а, 0 говорят о приоритете, который
имеет каждое из этих слагаемых. Если мы отдаем предпочтение
потреблению, то а>Р, а если предпочтение отдается накоплению
производственного потенциала, то а<р. Подынтегральное выра-
жение е -s' С—дисконтированное потребление, е -s' —взвешива-
ющая функция, 8 -коэффициент дисконтирования.
Итак, рассмотренная однопродуктовая динамическая модель
распределения валового продукта с учетом цели развития эконо-
мического объекта является задачей оптимального управления
с функционалом У (v), заданным соотношением (4.14) и ограниче-
ниями (4.12), (4.13), которым должен удовлетворять допустимый
процесс. Эта задача полностью соответствует сформулированной
выше общей задаче оптимального управления. Отметим, что
речь идет о максимизации функционала ./(*), что, как отмечалось
выше, эквивалентно минимизации функционала — У(т).
Пример 2. Рассмотрим задачу оптимального распределения
капитальных вложений в отрасли на заданном интервале
планирования.
Обозначим через А'(7) величину основных производсгвенных
фондов отрасли в году I. В процессе воспроизводства основных
производственных фондов их количество будет расти за счет
капитальных вложений, а уменьшаться за счет физического
и морального износа.
Будем считать, что ввод в действие основных фондов в году
t, численно равный 7{ г), удовлетворяет ограничениям
(4-15)
где минимальное 7т1Л и максимальное 7шах значения ввода
в действие основных фондов—известные постоянные иди зави-
сящие от времени функции, а величина выбытия фондов в году
t равна цА(т). Тогда уравнение баланса основных фондов,
отражающее равенство прироста основных производственных
фондов в году t вводу их в действие за счет выбытия примет вид
(4.16)
или
ДА(/+1) = (1-ц)А(/) + 7(т),	(4.17)
где ДА(т) = Х(/ +1) —	—прирост основных фондов в году.
Уравнение (4.17) является моделью (дискретной) роста основ-
ных фондов отрасли.
94
Будем считать заданным начальное значение основных фондов.
| Учитывая естественное условие их неотрицательности, имеем
f	Я(0) = Ао,	/ = 0, 1,..., Т.	(4.18)
Теперь можно рассматривать в качестве характеристики проис-
ходящего в системе пролесса пару v=^K(f), /(В), считая K(i')
состоянием системы,	т) — управлением, а (4.17) — уравнением
процесса. Тогда множество М допустимых процессов задается
: условиями (4.15), (4.17), (4.18).
Качество протекающего в системе процесса изменения основ-
ных фондов зададим функционалом
,	т-1
.	J = a £ /(/) +0 А (7")-»min,	(4.19)
где а, 0—-некоторые неотрицательные числа.
Выражение (4.19), являющееся критерием оптимальности про-
; цессов, состоит из двух слагаемых. Для того чтобы пояснить
: экономический смысл критерия, положим а=1, 3 = 0. Тогда
; У = £ /(?) и минимизация этого функционала отражает требова-
ло
ние максимальной экономии капиталовложений. Если же а = 0,
:	1, то У=— К(Т) и минимизация такого функционала равно-
; сильна максимизации А(Т) значения основных фондов в конце
1 планового периода.
Таким образом, в функционале (4.19) отражены два, вообще
; говоря, противоположных требования к процессу—экономии
; капиталовложений, с одной стороны, и увеличения основных
I производственных фондов отрасли—с другой. Числа <х, р явдя-
< ются весовыми коэффициентами. Если ос>0, то приоритет
( отдается первому требованию, если х<0 — второму.
( Таким образом, имеем задачу оптимального управления
 многошаговым процессом, заданным уравнением (4.17) с функцио-
 налом (4.19), ограничениями на управление (4.15) и на состояние (4.18).
’ В данной постановке задачи оптимального управления правый
? конец траектории А ( г) является свободным, так как отсутствуют
1 ограничение на значение А(/). Вместе с тем если положить
в функционале (4.19) а=1, 3 = 0, то при этом естественно
) наложить требование на значение А(Т). Иначе 7(г) = 0 и задача
1 теряет экономический смысл. В рассматриваемом случае будем
; считать заданным А"(/) = Л\, где величина А, задает наряду
1 с функционалом цель управления системой.
> Пример 3. Рассмотрим непрерывный вариант модели оптималь-
1 ного распределения капитальных вложений. Такая модель пред-
. ставляет интерес для теоретических исследований. Составим
I уравнение баланса основных фондов отрасли в непрерывном
К варианте.
95
Величина А К прироста основных фондов на промежутке	t
[t, / + Д/] будет равна K(t + At) — K(t\ В отличие от введенных	|
в дискретной модели переменных обозначим через I(() интенсивнос ть ’
ввода основных фондов в момент времени t, Под интенсивностью i
будем понимать количество вводимых в единицу времени фондов.
Тогда иа рассматриваемом промежутке будет введено /(г) Дт единиц
основных фондов. Обозначим через ц интенсивность выбытия
основных фондов. Тогда общее количество выводимых из производ-
ства за время At фондов будет равно цДт/(т), С учетом сказанного
уравнение баланса (4.16) можно записать в виде
K(t+&t)-K(t)= ~iiAtK(l) + l(t)At.	(4.20) '
Если разделить обе части последнего уравнения на At и перейти
к пределу при Дt->0, слева получим значение производной,
а уравнение (4.20) перепишем следующим образом:
К=-[хК+!.	(4.21)
К этому нужно добавить начальное условие и ограничения '
на значения переменных;
£(0) = ко, KZ0,	(4.22)
Рассматривая данный процесс как управляемый, будем, как
и в примере 2, считать K(t) состоянием процесса, /(;) — управле-
нием. Процесс описывается уравнением (4,21), которое вместе 1
с ограничениями (4.22) определяет множество М допустимых
процессов	/(/)).
Обобщением функционала (4.19) на непрерывный случай будет
функционал вида
т
> =	/d/-pK(T)-*min,	(4.23)
q	veAf
Теперь задача оптимального уравнения заключается в отыска-
нии оптимального процесса v = (Af(z), /(г)), являющегося допусти-
мым и минимизирующего функционал (4.23).
Как и в примере 2. если в выражении (4.23) Р = 0, требуется
задать конечное состояние K(t} = Кх.
Пример 4. Рассмотрим задачу оптимального распределения
капитальных вложений между отраслями,
Этот пример является обобщением примеров 2 и 3 для
нескольких отраслей. Как и выше, речь пойдет о распределении
ограниченного объема вводимых в действие основных производст-
венных фондов на некотором интервале времени te[0, Г].
Отличие состоит в том, что распределение нужно осуществить
не только во времени, но и между отраслями, которые являются
в данном случае «конкурентами».
Пусть имеются отрасли с номерами 1,2, ..., н. Если в г-й
отрасли Kl(t) — основные производственные фонды в году t,
96
ц*— коэффициент ежегодного выбытия фондов, /'(()— объем
вводимых в действие в году / основных фондов, то для каждой
из отраслей можно написать уравнение баланса основных фондов,
аналогичное (4J 7):
+ 1) = (1	+ P(t), 7 = 0, 1,	Г-1. (4.24)
Известны основные фонды отраслей на начальный год t = 0:
/Г(0)=Лф, г=1, 2, я.	(4.25)
Это будет начальным условием для системы уравнений (4.24).
Кроме того, суммарная величина вводимых в действие
основных фондов ограничена, С учетом перечисленных ограниче-
ний на переменные модели можно записать
f/Ч/тах>	/=1, 2, ..., п. (4.26)
i = I
Соотношения (4.24)—(4.26) описывают ограничения на мно-
жество допустимых процессов v=(№(t), ..., К” it},	...,
Обобщением на случай п отраслей функционала (4.19) будет
У = f а, Г (t ) - f ₽t. /С (T) -mm.	(4.27)
r = O i= l	i = L	,еЛ/
Функционал (4.27) вместе с ограничениями (4.24)—(4.26)
определяет задачу оптимального управления, Состоянием процес-
са здесь является вектор К=(№, К2, ..., Кп} основных фондов
отраслей, управлением—вектор 1=(Д, Г2,	7") вводимых
в действие фондов.
Сформулированная задача оптимального управления относится
к классу задач оптимизации многошаговых процессов. Может
быть также поставлена аналогичная задача и в непрерывном
времени. Для этого необходимо заменить систему разностных
уравнений (4.24) системой дифференциальных уравнений
Ю=~^Ю + Р, /=|, 2, п,	(4,28)
а функционал (4,27)—выражением
= И Z а;1‘)dz - Z ( Т) -min.	(4.29)
О i - I	i = I	Ч
Тогда получим непрерывную задачу оптимального управления,
описываемую функционалом (4.29), уравнениями процесса (4.28)
и ограничениями (4.25), (4.26).
Пример 5. Рассмотрим задачу оптимального управления меха-
ническим объектом.
Данный пример иллюстрирует задачи оптимального управ-
ления из той области, где они первоначально возникли,— физики
и механики.
4 Зак 456	97
Рассматривается движение мате-
риальной точки массой т под дей-
ствием силы F на интервале времени
[О, Т]. Состояние этой простейшей,
состоящей из одной материальной
точки механической системы в каж-
дый момент времени задается
(рис, 4.5) вектором х=(х3, х2, х2)
координат точки и вектором ее ско-
рости х=(х\ х2, X'3).
Сила F=(FC F2, г3)— векторная
величина, изменением которой мы
можем управлять. Тогда уравнение движения точки массой
т под действием силы F в соответствии со вторым законом
Ньютона будет иметь вид ma = F, где а — вектор ускорения,
т, е. вектор с координатами а= (х1, х2, л;3). Уравнение движения
можно записать в следующей координатной форме:
mx = F‘, /=], 2, 3.
(4-30)
Эта система состоит из уравнений второго порядка. Чтобы
записать ее в стандартном виде, содержащем только первые
производные, обозначим через у‘ компоненты вектора скорости
Я1. Тогда х‘ = у‘ и уравнение (4.30) вместе с формулами замены
переменных можно переписать в виде системы
У=у'.
yl=F* jm, i=l, 2, 3.
(4.31)
Итак, мы имеем систему, состояние которой описывается
переменными (х‘, у'), а уравнением является вектор F с коор-
динатами F‘, /=], 2, 3, На уравнения, как правило, накладываются
ограничения. Например, может быть ограничена максимальная
сила, которая выражается неравенством
((F‘)4(F2)4(F3)2)‘'4fm„.	(4.32)
Кроме того, задаются начальное и конечное состояния системы
в момент времени Г:
-Н°) =4, /(0) =у-0,
^) = <.НГ)=^=1. 2, 3.	'
Ограничения (4.3])—(4.33) задают множество М допустимых
процессов в рассматриваемой задаче.
Критерий оптимальности процесса задается в виде функциона-
ла
г
У= х', у1, Fi)dr->niin.	(4.34)
О	«еМ
98
Задание этого функционала вместе с ограничениями (4,31) —
(4.33) полностью определяет задачу оптимального уравнения.
Функционал (4.34) может иметь различный физический смысл.
Подобными функционалами описываются задачи на минимизацию
топливных затрат, перегрузок при маневре летательных аппаратов
и т. п.
Одним из часто встречающихся задач оптимального управле-
ния являются задачи на быстродействие. Чтобы получить поста-
новку этой задачи, будем считать момент времени Т окончания
процесса заранее не заданным, а подынтегральную функцию
в (4.34)—тождественно равной единице. Тогда функционал (4.34)
Примет вид
¥ЕЛ/
а задача будет состоять в выборе оптимального управления Г,
переводящего систему из заданного начального состояния Хо,
уЬ в заданное конечное состояние х‘о, yi (4.33) за минимальное
время Т.
Пример 6. К задачам оптимального управления могут быть
сведены различные оптимизационные задачи, исходная постановка
которых отличается от постановки задачи оптимального управле-
ния. В качестве примера рассмотрим упомянутую в данной
главе задачу о линии наименьшей длины, где требовалось
отыскать линию, задаваемую функцией y=f(x) с заданными
значениями на концах промежутка [хл, хв], равными уЛ=Дл:л),
ув=Дхв). При этом длина кривой, выражаемая функционалом
(4.3), должна быть минимальной.
Чтобы свести эту задачу к задаче оптимального управления,
введем обозначения: x—xA = t, х№—хл = Т, ул=Уо, ун=Ух- Тогда
Дх) становится функцией от г. При этом / изменяется на
промежутке te [О, Г], а с учетом формул замены переменных
y'x=y't=y функционал (4.3) будет иметь вид
J =	(4.35)
°
Краевые условия в данной задаче в новых обозначениях
примут вид
3,(0)=7о, y(T)=yt- '	(436)
Введем еще дополнительную переменную
у = и.	(4-37)
Тогда функционал (4.35) с учетом требования его минимизации
перепишем в виде
4*	99
7'
> = к/ 1 +tz2df ->min.	(4.38)
J	v e №
0
Здесь процессом v является пара (>’(/), и(/)). Состояние
системы задается величиной у, управление величиной и, мно-
жество М допустимых процессов—уравнением (4.37) и граничны-
ми условиями (4.36), а критерий оптимальности — функционалом
(4.38). Таким образом, исходная задача сведена к задаче оптималь-
ного управления.
Следует отметить, что к задачам оптимального управления
могут быть сведены задачи линейного программирования, задачи
целочисленного программирования и многие другие оптимиза-
ционные задачи.
§ 4.5. Построение траекторий управляемых процессов
В подавляющем большинстве задач оптимального управления
непрерывными системами функция и (/), как уже отмечалось, не
является непрерывной. Вместе с ней не будут непрерывны, что
обычно предполагается в теории дифференциальных уравнений,
правые части уравнений процесса.
В данном параграфе мы введем понятие траектории управляе-
мого процесса для случая, когда управление и(/) представляет
собой разрывную функцию времени, а также рассмо трим вопросы
практического построения таких траекторий.
Пусть имеется управляемый процесс, описываемый системой
дифференциальных уравнений
x = f(/, X, и),	(4.39)
где х= (х1, х2, ..., хл), и= (и1, м2,	г/).
Процесс протекает в промежутке времени [О, T]t причем
известно начальное состояние системы
х(°) = хо= (-4, хЗ).	(4.40)
Будем считать, что в математической модели процесса (4.39)
правые части этой системы уравнений f(r, х, и) = (у1(/, х, и),
...,/п(/, х, и)) являются непрерывными функциями, удовлетворяю-
щими достаточным условиям существования и единственности
решения, если u(f) задано в классе непрерывных функций.
Если задать программу управления некоторой непрерывной
функцией u(/j, то этой программе будет отвечать определенная
траектория х(/). Чтобы найти х(0, нужно подставить й(г)
в (4.39) и решить для получившейся системы задачу Коши
с начальным условием (4.40). Такое решение х(/) в силу
непрерывности й(7) будет существовать и определено единствен-
ным образом.
100
| Рассмотрим теперь
[случай, когда управление
; fi (z)—разрывная	функ-
:Ция. Будем в качестве
рассматри-
‘дня. Будем
допустимых
;вать такие управления,
f которые имеют на про-
межутке [О, Т] конечное
Нисдо точек разрыва пер-
i вого рода, т. е, имеющих
: в этих точках пределы
Рис. .4.6
слева и справа (рис, 4.6). Пусть fi(z)
(терпит разрыв веточках t;\ 0<tl<t2<.., <in^T. Тогда в этих
точках существуют односторонние пределы u(z):
limu(z) = u; и lining) = ц;+.
f<(;	t>ij
Чтобы однозначно задавать значения управления й(г) в точках
разрыва потребуем, чтобы fi(z) была непрерывна справа. Тогда
= и график ее будет выглядеть так, как представлено
!на рис. 4-6.
; Для построения решения, соответствующего заданному закону
(управления, рассмотрим последовательно отрезки [0, tL ], [zb
J, [zn, Т], на которые точки разрыва z; разбивают
(промежуток [О, Т\. На промежутке [О, Д ] функция u(z) будет
(непрерывна во всех точках, если дополнить ее при t=tl значением,
равным ее пределу слева. Тогда на этом промежутке будет
(определена траектория х (/), отвечающая и (')) и начальному
Гусдовию (4.40).
| Рассмотрим теперь отрезок [zI; Z2 ]. Если на нем доопределить
^функцию йД) в точке Z2 пределом слева, она также будет
| непрерывна. Если в качестве начального условия на этом
(промежутке взять конечное значение x(z), вычисленное раньше,
)то мы снова получим однозначно траекторию системы (4.39)
на отрезке [zT, z2 ] При этом ее начальное значение совпадает
с конечной точкой траектории, построенной на предыдущем
участке.
Продолжая этот процесс, мы в итоге подучим траекторию
x(z), изображенную на рис. 4,7.
101
Отметим некоторые свойства построенной траектории х(г).
Во-первых, эта траектория, как следует из правила ее построения,
однозначно соответствует заданным управлению й(/) и начально-
му условию (4.40), поэтому ее можно считать обобщением
решения задачи Коши на случай разрывных управлений. Во-вто-
рых, полученное решение х(г) будет непрерывным. В-третьих,
на каждом интервале (th ti + 1] х(г) имеет непрерывную произ-
водную в любой точке, а в точках — производную слева
и справа. Производная этой функции, следовательно, будет
кусочно-непрерывна.
В качестве примера рассмотрим управляемую систему, задан-
ную системой уравнений
Xj =Х2 + И1,
х2 = 2м2
на промежутке t е [ 0, 6 ]. Начальные значения переменных
х1(0]=х1О, х2(0) = х2О примем равными х10=1, х20=1, а упра-
вления зададим в виде
(0 при 1е [0,4),	Г — 0,5 при te [0,2),
Ul [1 при <е[4,6],	[ 0 при Iе[2,6].
Точки разрыва управлений делят отрезок [0,6) на три части
точками tL = 2, 12 =4. Эти точки и являются точками разрыва
управления.
Рассмотрим промежуток [0, 2). При таких значениях t управле-
ния имеют значения Wj=0, м2 = —1. Система после подстановки
имеет вид
X1 = х2,
х2 = -1.
Начальные условия на этом промежутке заданы условием задачи.
Найдем общее решение полученной системы:
х( =—у + Cj / + С2,
х2 = — t + Cj.
Подставляя сюда начальные условия, найдем значения произволь-
ных постоянных <?£=—1, с2=1. Следовательно, траектория систе-
мы на рассматриваемом промежутке имеет вид
Х£=— у— Z+1, х2 = — z — 1.
Определяем отсюда начальное значение Xj(2) = xI2, х2(2) = х23
на следующем промежутке [2, 4). Для этого нужно подставить
( = 2в полученные выражения для х15 х2. Начальными значениями
будут х12=—3, х22=—3.
102
Система уравнений процесса, которой удовлетворяет искомая
траектория, на этом промежутке будет следующей:
х2 = 0.
Общее решение Xj=C(? + C2, х2 = С( после подстановки на-
чальных условий даст уравнение траектории на промежутке [2, 4):
=3t + 3, х2= —3,
откуда получим Xj(4)=x14= — 9, х2(4) = х24= —3.
Наконец, траектория на участке [4, 6) определяется как
решение системы
-*т =х2 +1,
х2 = 0,
откуда с учетом найденных начальных значений х14, х24 получим
Xj= — 2г — 1, х2= —3.
Окончательно полученная траектория, изображенная на
рис. 4.8, имеет вид
-	L-/+1 при ге[0, 2),
—	3t+3 при ?е[2, 4),	х2(?) =
—	2г— 1 при te [4, 6],
— t — 1 при ге[0, 2),
— 3 при Ге[2, 6].

Графическое представление траекторий управляемой системы
часто дает ценную информацию для решения задач управления.
Изображение траекторий на плоскости [х, г], как сделано на
рис. 4.8,— один из возможных способов их графического пред-
ставления. Часто более информативным бывает представление
траекторий на фазовой плоскости (х1? х2).
Рассмотрим в качестве примера систему второго порядка
(4-41)
плоскости
значений
xt =x2 + w2,
Х2= —Xj +w2
и изобразим на фазовой
все ее траектории для
управления н( = --1, и2 = 1. Подста-
вляя эти значения управлений
в уравнение процесса, находим об-
щее решение полученной системы:
х, = С, sin/ + C2cos t+ 1,
(4.42)
-х2-С1 cosr + C2sin t+ 12
Эти уравнения задают в парамет-
рическом виде искомое семейство
траекторий, Параметр t можно
исключить, перенеся единицу в ле-
вую часть и сложив возведенные
в квадрат части уравнений:
Q2 + (x2 _ 1)2 =	+ С2-
Теперь видно, что кривые данного
семейства — окружности радиусом
г = (С1 + Сг) 1/2 с центром в точке
(11).
Аналогично можно построить
семейство кривых, отвечающих
значению ^управления = 1, и2=~ 1- Проводя такие же вычисле-
ния, получим уравнение в виде + ] )2 + (х2 + П2 = С2 + С%, т. е.
семейство окружностей с центром в точке (— I, -1).
На фазовой плоскости системы оба семейства траекторий
изображены на рис. 4,9, Стрелками показано направление движе-
ния точки (хх (t), х2(/)) [i0 траектории при возрастании i,
С помощью построений можно решать более сложные задачи,
например построение траекторий отвечающих кусочно-постоян-
ным управлениям. Это часто бывает необходимо в задачах
оптимального управления.
Например, пусть известно начальное состояние системы (4.4)
х1(0) = 2,
л2(0)=1,
и требуется
промежутке
отыскать траекторию системы,
времени
управлениям
отвечающую на
о, -
’ 2
I при
О,- ,
’ 2 /
Ze
te
л Зл
2’ 7
«2= )
— I при
л Зл
2’ Т
< — 1 при
“1 = )
1 1 при
При /е[0, тс/2) управления будут иметь значения ut = — 1, и2 = 1.
Так как мы уже построили все множество траекторий с такими
значениями управлений, остается выяснить, какая из них проходит
через начальную точку (2, ]). Мы знаем, что это ркружпость;
следовательно, нужно определить ее радиус. Это нетрудно
сделать, заметив, что он равен расстоянию от точки (2, 1) до
центра, т, е. точки (1, 1), Это расстояние и вместе с ним радиус
г—1. Таким образом, на первом участке ге[О, л/2) траектория
системы —дуга окружности радиусом г = 1 с центром в точке
t е
t Е
104
[1, 1), Далее мы можем воспо-
льзоваться вытекающим из формул
(4.42) соображением, что радиус-
вектор точки (xr ((],	трае-
ктории, проведенной из ее центра,
'за промежуток времени описывает
угол, численно равный длительности
|промежутка. Следовательно, радиус-
[вектор по отношению к начальному
состоянию в конце промежутка Г О,
л/2) поворачивается на угол к/2.
Нетрудно видеть (рис. 4.10), что
тогда при ( = тг/2 система оказывается
Рис. 4.10
в состоянии х1(тс/2)=1,
х2(л/2) = 0. Теперь, пользуясь изложенными соображениями, мож-
но построить участок траектории на промежутке [л/2, Зл/2].
Этот участок — половина дуги окружности радиусом
Л/5 с центром в точке (—1, — 1), начинающаяся в точке (1,
0) (рис. 4.10).
Глава 5
Достаточные условия
оптимальности
В теории оптимального управления для решения задач
применяется специфический математический аппарат, который
использует различные идеи отыскания оптимальных процессов,
использующие свойства и признаки, отличающие их от остальных
допустимых, процессов.
В настоящей главе излагается содержание методов решения
задач оптимального управления на основе достаточных условий
оптимальности. Эти методы отличаются от других методов
своим подходом. В них формулируются такие свойства до-
пустимого процесса, которые являются достаточными, т. е.
гарантируют его оптимальность. Из опыта решения различных
математических задач известно, что наиболее эффективным
средством отыскания решений являются необходимые условия.
Поэтому, если мы хотим применять достаточные условия, нужно
быть уверенным в их близости к необходимым. Этому требова-
нию и отвечают предлагаемые ниже достаточные условия
оптимальности. Поэтому их можно использовать как при ана-
литическом, так и при численном решении задач.
Для нас в дальнейшем достаточные условия оптимальности
будут иметь особое значение. Это связано с методикой, принятой
для изложения других методов отыскания оптимальных процес-
сов. Достаточные условия оптимальности будут в этом случае
играть существенную роль при выводе количественных соотно-
шений, характерных для этих методов, а также при их
обосновании.
§ 5.1, Вспомогательные математические конструкции
Рассмотрим вспомогательную задачу оптимизации, решение
которой будет нами использоваться в дальнейшем.
Пусть задан функционал
# =	u(0Hmin.	(5/1)
/ = о
где =	x2(t}... *"(/))—вектор состояния системы; и(?) =
= («*(/),	игщ)— вектор управления, на которые наложены
условия
106
условие (0.2) не выполняется, дто означает, что
существует такое значение (х(?*), “(Л)’ чт0
(x(z), u(r))e I/!, / = 0, 1, ,,,, Г—].
। Требуется отыскать минимальное значение функционала (5.1)
при заданных ограничениях.
Эту задачу можно рассматривать как частный случай задачи
оптимального управления в тривиальном случае, когда среди
ограничений, определяющих множество М допустимых процессов,
отсутствуют уравнения процесса.
В данной задаче нетрудно получить необходимые и доста-
точные условия, которым должно удовлетворять оптимальное
решение (х(/), минимизирующее функционал (5.]). Эти
условия можно сформулировать в виде теоремы.
Теорема 5.1. Для того чтобы процесс (хД), й(г)) был оп-
тимальным т. е. минимизировал функционал (5.1), необходимо
и достаточно, чтобы при всех t = 0, I, ..., Т— 1
/°(/, (x(f), й(г))=	х, и).	(5.2)
X, U Е Р
Доказательство.
1. Необходимость. Пусть (х(Д, й(/Д— оптимальный процесс,
т. е. удовлетворяющий условию (5-1). Это значит, что
^(х(0, й(г)) ^(x(r), u(z))	(5.3)
при всех (x(r), u(z))e V‘. Требуется доказать, что он удовлетворяет
и условию (5.1).
Допустим противное, т. е. существует такое t = Z*, при котором
при i=t*
(5.4)
определим
Рассмотрим новый процесс (х°(г), u°(t)), который
так:
х(Д, й(Д1 если
х(Д, й 1 , если /= t*.
Вычислим значение функционала (5.1) -/ на этом процессе:
^(0,	Л/, х(?), й(0)+гAt, Л)>
й(/))+л**, Л*), й(Л)'
Разбив выражение (5.1), для У(х((), Л)) аналогичным образом
получим
у(х(/), o(t))=	Л)> й('))+(_£ Л'>
й(0)+/°(1*, Л*)> “(Л)-
107
Сравним теперь правые части двух последних равенств.
Первые два слагаемых в них совпадают, а третьи удовлетворяют
сделанному предположению (5.4). Следовательно,	'
./(х(/), й(/))> ^(х°(г), и°(г)),
что противоречит условию (5.3) оптимальности процесса (х(Д,
й(0).
Необходимость доказана.
2. Достаточность, Пусть процесс (х(/), й(г)) удовлетворяет
условию (5.2) теоремы. Требуется доказать, что для него будет
выполнено и условие (5.1), т. е. процесс (х(/), й(/)) будет
оптимальным.
Рассмотрим произвольный допустимый процесс (x(z), и(/)).
Тогда из (5.2) можно вывести, что при каждом /=0, 1, Т— 1
/°(0, х(0), й(0))^/°(0, х(0), и(0)), .
/°(1, х(1), й(1))^/°(1, х(1), и(1)),
/°(Г  Г, х(Т-7)/й(Т-'1))^/°(Т-'1\''х(Т-1), и; 7 — 1)).
Складывая эти неравенства почленно, получим
Е f\t, *(4 й(0)^ Е /°(^ х(0’ «(О)-
1=0	1=0
Левая и правая части в этом неравенстве — -значение функци-
онала (5.1) для процессов (х(г), й(/)) и (x(r), и(т)), т. е.
^(х(г), й(/))^./(х(г), u(r)),
откуда из-за [зроизвольности процесса (x(z), u(/)) и вытекает
условие (5.1) для процесса (х(г), й(г)), который, следовательно,
и является оптимальным.
Достаточность доказана.
Доказанная теорема сводит решение поставленной задачи
(5.1) к минимизации функции fa\t, х, и) при всех r = 0, 1, ...,
Т— ] по переменным (х, и) на множестве (х, и)е V‘. При этом
существование минимума функции /°(д х, и) при всех t есть
необходимое и достаточное условие существования решения
задачи (5.1).
Отметим, что условия теоремы могут быть аналщ'ичпо
сформулированы и для задачи максимизации функционала.
Теорема 5.1 может быть обобщена и на непрерывный случай,
когда функционал задается соотношением
т
,./=J/°(r, х, u)dz->min.	(5.5)
о
Однако формулировка теоремы в этом случае нуждается в уточ-
нении. Что касается достаточности условия (5.2), то и в непрерыв-
ном случае это также остается справедливым (доказательство
108
[ дословно повторяет приведенные выше с заменой суммирования
I интегрирование). Необходимым же это условие, вообше
I говоря, не является, что показывает следующий пример.
| I Рассмотрим функционал
|	i	1
I 1	,/= J x2dz -» min,	(5.6)
I	о
'i заданный на множестве кусочно-непрерывных функций х(г),
| удовлетворяющих ограничению 1 й x(t) 2. Так как в данном
! примере вследствие ограничений л2(/)> 1 при всех Г, то, очевидно,
и значение ./ не может быть меньше единицы. Таким образом,
если при некотором будет достигнуто значение У(х[/)) = 1,
то можно сделать вывод, что функционал (5,6) достигает
минимального значения.
Возьмем в качестве х(0 следующую функцию:
Г 1, если 0 t < 0, 5,
x(f) = < 2, если t = 0, 5,
( 1, если 0, 5 < г 1.
Очевидно, что значение равно единице. Следовательно, х(г)
минимизирует функционал ,А Но данная функция, как легко видеть,
не минимизирует подынтегральную функцию x2(t) в (5.6) при всех
/е [0, I ]. В частности, этого не происходит при / = 0, 5, где значение
х=2. Подынтегральную функцию минимизирует значение х= 1.
Таким образом, в данном примере необходимость условия
теоремы не выполняется,
Для того чтобы условие теоремы в непрерывном случае
стало не только достаточным, но и необходимым, его нужно
уточнить. А именно нужно потребовать, чтобы оно выполнялось
не обязательно в каждой точке t интервала [0, Г], а «почти
всюду», т, е. за исключением, быть может, точек интервала,
значение функции в которых не влияет на величину интеграла
(5.5).
Возможен и другой путь, Если дополнительно наложить
требование непрерывности на процесс (x(r), и(/)) и на функцию
/°(/, х, и), то формулировка теоремы в непрерывном случае
сохраняется дословно с заменой соотношения (5.1) на (5.5).
Однако требование непрерывности (x(r), и(/)) является слишком
сильным в задачах оптимального управления и не выполняется
даже в простейших случаях, что мы увидим из следующего
примера.
Пример 1. Рассмотрим следующую задачу;
2л
J =. j =sjn tx1 wdr -> min,
о
где 0, 5<л<1, |«|^Г для всех /е[0, 2л].
109
Рис. 5.1
Для решения задачи воспользуемся
достаточным условием доказанной te-
оремы, откуда следует, что если
минимизировать подынтегральную
функцию при всех t е [0, 2 л], то
значения (xf/), й(/)), являющиеся точ-
кой минимума, и будут оптимальным
процессом.
Значения x(t) и a(t), при которых
функция /° = sin tx2и достигает мини-
мума, будет зависеть от знака sin/.
При sin / > О минимизирующими бу-
дут те значения х и й, которые
минимизируют функцию у1 = х2иу при
sin/<0 значения х, й нужно выбирать
из условия максимума х2 и, при
sin/ = 0 можцо в качестве х, й взять
любые значения.
Очевидно, в задаче минимизации
/' в качестве х следует взять х=1.
Значение же й(/) выбирается равным
t или — t (рис. 5.1) в зависимости от
знака sin /. Окончательный результат
можно записать следующим образом;
х(/)=1,
О SC t 2 л,
— / при 0 sS t < Я,
t при л t 2п.
Подчеркнем, что процесс (х(/), й(/)) удовлетворяет доста-
точному условию, что гарантирует его оптимальность. При этом
решение оказалось разрывным,
Введем теперь еше некоторые понятия, которые потребуются
в дальнейшем для формулировки теоремы о достаточных
условиях оптимальности для задачи оптимального управления
общего вида.
Рассмотрим систему дифференциальных уравнений
х1 =/’(/, х1, х2,	х“),
х2=/2(/, х1, х2’	Xя),	(5.7)
хя=у(/, х1, х2, ..., х"),
или в векторной форме
x = f(/, х).
Предположим, что имеется частное решение этой системы
х(г) = (.х1 (г), хя(/)), Пусть х) = ф(/, х1, х2, хп) —функция
л + 1 переменной, имеющая непрерывные частные производные
НО
по каждой из них. Если подставить в качестве значений
аргументов функции х) решение х(г), получим функцию,
за!	....
1исящую только от t:
Вычислим теперь в точке t производную функции Это
можно сделать пользуясь правилом дифференцирования сложной
функции:
''«Р, г
dr St (—j дх1 '
(5-8)
VW VW .	. л
где производные -г—., /=1 2, п, вычисляются в точке
at ax' ’
(г, .X1 (т), x2(l),	х"(/)). Так как мы имеем дело с решением
системы (5.7), то производные х' в правой части (5.8) можно
заменить с помощью соответствующего уравнения системы (5.7).
Выполнив эту замену, получим
р	ЦЕ	VI '	1
| Теперь рассмотрим выражение
©(/, х‘,Х2, ..., х")=^(^	—>
х(г, х1, х2, ..., х^/^'х1, х2, ..., х"),	(5.9)
или в векторном виде * *
ш(1,	f(,, х)).
Если подставить в выражение (5.9) вместо аргументов х‘
' решения x'(t) системы (5.7), то получим найденное ранее выражение
° производной функции ср (г, х) на решении x(t) системы. Этот
! результат является важным свойством выражения ©(/, х1, .... х”).
Пример 2. Рассмотрим систему уравнений
)	x' = -.V\
;	X —X1
функцию ф(г, х) = (х')2+(х2)2.
Выражение (5.9)
в этом случае
>удет иметь вид
©(г, х1, x2) = 2xJ(—х2) + 2х2х’ =0.
И
* Здесь и далее (а, Ь)—скалярное произведение £ а’Ь* векторов
ii—fa1. а1, а")п Ь = (6*, й2,	t>“).	* *
III
Отсюда мы получаем, что производная данной функции ср (г, эд
обратится в ноль при подстановке любого решения в эру
функцию, т. е, функция ср (Л, х) постоянна на любом решении
системы (5.7).	!
В этом можно убедиться и непосредственно на данном
примере, так как мы можем множество решений рассматриваемой
системы уравнений записать в виде
х1 = С1 sin г + С2 cos г,
х2 = — С1 cos / 4- С 2 sin г,
где С1, С2 —произвольные постоянные. Подставив это решение
в данную функцию ср (f, х), получим
<р(;.х)=(с')г+(сТ,
т. е. <p(Z, х) постоянна.
Рассмотрим теперь управляемый процесс, описываемый систе-
мой уравнений (в векторной форме)
x=f(/,x,u), х = (х1,х2, ..., х"), и = (м1, и2,	и"), (5.10)
и связанную с ним задачу оптимального управления с функцио-
налом
= х, u)dZ + F(x(r))->rnin.	(5.11)
о
Введем две вспомогательные функции для сформулированной
задачи: 7?р, х, и) и Ф(х),
Функция R (г, х, и) формально вводится следующим образом:
возьмем некоторую функцию cp(t, х), которая должна иметь
непрерывные частные производные по всем аргументам. Запишем
следующее выражение:
х, u) = |+^||,y(;,x,	х, н).	(5.12)
Нетрудно видеть, что в (5,12) первые два слагаемых совпадают
с выражением (5.9). Таким образом, функция К (г, х, и), отвечаю-
щая данной функции х), есть производная функции ср(?, xj
на решениях уравнении процесса за вычетом подынтегральной
функ[(ии в (5.11).
Определим функцию Ф(х):
Ф(х) = ср(Т, х)-Т(х),	(5.13)
где F(x)—терминальная функция в (5.11).
Рассмотрим пример, в котором система уравнений процесса
имеет вид
*1 = -х2 + «ь
. -Г 2 =“ Xj j 21^2 *
Функционал зададим соотношением
112
\	10
\	j (x?+2x2(«i-l-«2))d/4-2x?(10)4-4x2(10)-»inm,
0
Тогда для произвольной функции ф(/, х,, хЛ согласно сформули-
рованным правилам образования функций R(t, х, и) и Ф(х), получим
х, и)=^+^-(-х2 + н1)+^-(-х2+х2и1-2и2)-х|-2х2(и?+«1),
vf <7Л"1
Ф(х)=ср(10, х15 x2) + 2xf + 4x2.
Если взять теперь в качестве функции ср (г, хь х2) какую-нибудь
конкретную функцию, например ф(г, х15 х2)= — г(х2 -|-х2), то пос-
ледние два выражения примут вид
х; u)= — 2х| — х2 + 2/ Xj (х2 — м1) + 2(х2 (х2 — х2у, Р2и2) —
-2x2(wf + «l),
Ф(х)= —8X1 —6x1.
При другом задании ф(г, х1; х2) мы получим другие выра-
жения.
§ 5.2.	Достаточные условия оптимальности
для непрерывных процессов
Рассмотрим задачу теории оптимального управления в следую-
щем виде:
г
У = |/°(г, х, u)dr+F(x(7’))->min,	(5.14)
о
*, Ч	(515)
x(0) = xo, (x(/),u^))e
Требуется найти допустимый, удовлетворяющий ограничениям
(5.15) процесс (x(f), й(/)), минимизирующий функционал (5.14).
Пусть ф(л х) — непрерывная функция « + 1 переменной (л х1,
х2, хп), имеющая непрерывные частные производные по этим
переменным. Построим с помощью ф (г, х) введенные выше
функции ф(х) и R(t, х, и), определяемые соотношениями (5.12),
(5.13).
Рассмотрим следующую теорему.
Теорема 5.2 (достаточные условия оптимальности непрерывных
роцессов). Пусть допустимый процесс v—(x(f), я(/))еМ и неко-
торая функция Ф (<- х) удовлетворяют условиям:
Г. Я(Л x(f), u(f))= тах К(г, х, и) при всех fe[O, 7].
2“. Ф(х(Т)>™(х)Ф(х).
”огда процесс (x(t), 6(f)) является оптимальным.
113
Доказательство, Введем вспомогательный функционал /
J^(x, н, <р)= - J Яр, х, u)dr +Ф (х (Т)) - ср (0, х0).	(5.10
° / 1
Функционал (5.16) определен на множестве троек функций (хр),
up), фр, х). Если фиксировать значение ф(г. х), то получим
функционал, заданных на парах (х(>), up)).
Мы будем рассматривать множество D таких пар (хр), up)),
которые удовлетворяют прн всех /е[0, Г] ограничениям (хр),
up))e V1 [но могут не удовлетворять остальным ограничениям
(5.12)], и множество М допустимых, т, е. удовлетворяющих всем
ограничениям (5.12), процессов. Очевидно, М ~ D.
Введенный нами функционал У7 (х, и, ф) будем при фиксирован-
ном значении <р (Д х) считать заданным на множестве D. Функцио-
нал J, определяемый соотношением (5.16), будем также рассмат-
ривать не Только на множестве М, но и на множестве D.
Функционал ,У7(х, и, ф) обладает следующим свойством, свя-
зывающим его с функционалом У.
Лемма 1. Для любой функции фр, х), имеющей непрерывные
частные производные, на множестве допустимых процессов значе-
ния функционалов У и 3 совпадают, т, е.
^(хр), up), фр, х))=^(хр), up)), (хр), ир))еМ. (5.17)
Доказательство. Преобразуем выражение (5.16) для функ-
ционала =2’(х, а, ф), учитывая, что процесс (хр), up)), на котором
вычисляется его значение, принадлежит множеству М. Подставим
в (5J 6) выражения Лр, х, и) и Ф(х(Г)) из соотношений (5,12) и (5,13).
По отмеченному выше свойству функция Лр, х, и) представля-
ет собой разность величины top, х, и) [ср, с (5.9)] и подынтеграль-
ной функции /°р, х, и) в (5,14).
Если в выражении top, х, и) подставить допустимый, а следо-
вательно, удовлетворяющий системе уравнений (5.15) процесс
(х(0> “Р))>' то мы получим равенство
®р,хр),ир))=1фр,хр)).
Таким образом, функцию Яр, х, и) при подстановке в нее
допустимого процесса (хр), йр)) можно представить в виде
R(f, х(0> и(0)=^Фр, х(0)“/°('> х('Х “('))•
Тогда интегральный член в (5.16) оказывается равным
114
Вычисляя первое слагаемое в правой части по
на — Лейбница, получим
формуле Ньюто-
"ф(Г> х(0)1о=<Р(°> Х(°))-Ф(^ х(г))-
о
г Следовательно, выражение (5.] 8) преобразуется к виду
|	г	т
к	л	/*
I - R(i, x(t), u(r))d?= /°(z,x(?), и(г))^+ф(0, х0)-ф(Г, х(Т)),
I	о	о
I Вернемся к соотношению (5.16), преобразуя его правую часть
R с учетом предыдущего равенства. Получим
т	г
L ^(xfr), u(z), p(z, х))~ /°(г, x(f), и(г))бг+ф(О, х(0)-ф(0, х0) +
к	о
+Ф(х(7'))-ф(Г,х(П).
Второе и третье слагаемые обращаются в ноль, так как
х(0) = хо. Два последних слагаемых преобразуем с учетом равенст-
ва (5.13):
®(x(7'))-<p(7',x(Z))=F(x(7-)J.
Отсюда окончательно имеем
г
^(x(r),u(t), ф(г, х)) =	x(r), u(z))dz + F(x(7’)),
о
что совпадает с соотношением (5.17), справедливость которого
и следовало доказать.
Лемма 2. При выполнении условий Г, 2° теоремы 5.2
функционал ^(х, и, <р) достигает минимального значения на
множестве D при x = x(f), u = fi(z), т. е.
5’(x(i), й(?), ф(>, х))—-	min =S?(x, и, <р).	(5.19)
(x([),u(t))eD
Действительно, функционал (5,16) состоит из трех слагаемых,
последнее из которых — постоянная величина.
Рассмотрим первое слагаемое
115
о
Так как предполагается
выполненным условием
Iе, то при x = x(z), u = u(f)
подынтегральное выра-
жение J? (г, х, и) достига-
ет для всех Ге [О, Г]
максимального значе-
ния. а следовательно,
— /?(£, х, и) — минималь-
ного. В соответствии
с теоремой 5.1 (для не-
прерывного Случая) значения будет минимальным.
Что касается второго слагаемого в (5.16), оно также примет
минимальное значение при х=х(Т).
Таким образом, каждое из слагаемых в (5.16) достигает на
процессе (х(/), й(/)) минимального значения по сравнению с лю-
бым другим процессом (х(г), и (г)) на множестве D. Следовательно,
этим свойством обладает и сумма этих слагаемых, что и тре-
бовалось доказать.
Результат двух доказанных лемм проиллюстрирован на
рис. 5.2.
Рассмотрим теперь функционал (ф, заданный соотношением
4 = mjn j^(x, a, m).
Тогда свойство (5.19), доказанное в лемме 2, можно записать
в виде
=S?(x(z), u(f), ф(/, х))^4, (x(z), u(z))e£>,	(5.20)
^(x(f), u(f), ф(г, х)) = 4-	(5.21)
Эти соотношения также проиллюстрированы на рис. 5.2.
Теперь утверждение теоремы 5.2 доказывается совсем просто.
Во-первых, так как множество М является подмножеством Р,
то на нем также выполняется (5.20), т. е.
J?(x(f), и(г), ф(/,	(х(г), u(t))eM.
Но в силу леммы 1 последнее неравенство можно переписать так:
У(х(г), n(f))>Zr (x(r), n(f))eM	(5.22)
Так как, по условию теоремы, (х(г), й(г))еЛ/, то (5.21), в свою
очередь, также равносильно равенству
^(х-(г),й(г)) = /ф.	(5.23)
116
Сопоставляя соотношения (5.22) и (5.23), получим, что при
всех (х (t), и (/)) е М
откуда и вытекает оптимальность процесса (х(г), й(/)).
Теорема доказана.
Отметим, что соотношения (5.22) можно трактовать как
оценку снизу возможных значений функционала У. Как мы
доказали, эта оценка будет справедлива при любой наперед
заданной функции tp(z, х).
Если удастся подобрать tp (г, х) так, что для некоторого
процесса (х (?), и(/))
У(х(/), й(/))-/ф^е,	(5.24)
где е — некоторые достаточно малое число, то данный процесс
можно считать приближенно оптимальным.
Действительно, так как вследствие оптимальности процесса
(x(f), й(/)) и оценки (5.22),
У(х(/), и(г))^У(х(/),й(())^/ф,
то с учетом неравенства (5.24) получим
У(х(/), и'(г))-У(х-(/),
Таким образом, соотношение (5.24) гарантирует, что точность
(по функционалу) приближенного решения (x(r), и(/)) в данной
задаче оптимального управления будет не [шже г.
Отмеченное свойство оценки (5.24) находит самостоятельное
применение при приближенном численном решении задач опти-
мального управления. Общая схема такого решения выглядит
следующим образом. Задается некоторый класс функций <р(?, х)
(например, линейные по х функции (р(^х) = й0()),-|-а,(/)х1 +
... + ап (г) х„) и осуществляется направленный перебор функций
в этом классе для получения максимально возможного (и,
следовательно, наиболее близкого к оптимальному значению
функционала) значения величины /ф. При этом решается задача
минимизации функционала =5? на множестве D, которая сущест-
венно проще исходной задачи оптимального управления. В резуль-
тате получаем значение функции ср (/, х) из заданного класса.
Затем строится допустимый процесс (х (/), 6(f)), который с мак-
симальной возможной точностью удовлетворяет условиям Г, 2°
теоремы 5.2 при найденной функции ср (г, х). При этом величина
Д = ^(х(/), й(?))-/ф
является гарантированной оценкой точности приближенного руле-
ния (x(f), и(/)). Другими словами, реальная точность данного
решения заведомо не ниже Д. Таким образом, если Д достаточно
мало и удовлетворяет требованиям, предъявляемым к точности
JJ7
решения задачи, то оно на этом завершается, В противном
случае требуется изменить класс функций ср (г, х) и повторить
процедуру.
Другое значение касается областей допустимых значений
переменных х(1), u(l). В теореме 5.2 предполагается, что процесс
(х(?), 6(f)), для которого выполняются условия Г, 2°, сравнивается
со всеми процессами (x(f), иМ). для которых выполняется
единственное ограничение (хр), и (/)) е И1. Такие процессы, вообще
говоря, не являются, как отмечалось выше, допустимыми.
Для установления оптимальности процесса 11(7)) доста-
точно предположить, что условия теоремы 5.2 выполняются
лишь на множестве М допустимых процессов. Как легко
убедиться, все доказанные утверждения и, следовательно, сама
теорема остаются верны.
В различных задачах оптимального управления бывает удобно
проверять условия теоремы 5.2 либо на множестве Z), либо на
множестве М. Проверка условий теоремы на множестве D может
оказаться проще, если данное множество имеет более простую
структуру, чем множество М, В то же время в отдельных
задачах оказывается предпочтительнее проводить проверку усло-
вия теоремы на множестве М, которое бывает значительно уже
множества D, так как содержит больше ограничений на процесс
(*(*),«(*))
В заключение сделаем замечание, относящееся к формулировке
теоремы для задач оптимального управления, в которых конечное
состояние х(Т)=х1 задано. В этом случае множество ИГ состоит
из одной точки. Таким образом, область определения функции
Ф (х) — единственное значение х = х,, которое и есть ее точка
минимума. В связи с этим условие 2° теоремы 5.2 в задачах
с фиксированным конечным состоянием выполняется тривиально.
Поэтому для задач данного класса формулировка этой теоремы
содержит лишь условие i°.
§ 5.3. Достаточные условия оптимальности
для многошаговых процессов
Для задач оптимального управления в дискретных системах,
так же как и в рассмотренных выше непрерывных системах,
может быть сформулирована и доказана теорема о достаточных
условиях оптимальности. Используемые при этом математические
конструкции аналогичны введенным выше и являются их качест-
венным аналогом для многошаговых процессов.
Задача оптимального управления дискретной системой форму-
лируется следующим образом.
Пусть управляемый процесс описывается системой разностных
уравнений
!)=/'(/, х(г),«(?)), Г=0, 1, ..., Т-1, /=1, 2, ..., п,
118
с начальным условием
х(0)=хо.	(5.26)
На возможные значения состояния системы хр) и управления
u(t) наложены ограничения
(хр), up)) 6 К	(5.27)
Соотношения (5.25) — (5.27) можно рассматривать как ограни-
чения, определяющие множество Л/ допустимых процессов (хр),
и(гВ в данной системе.
Требуется найти такой процесс (хр), й(/)), который минимизи-
рует функционал
£ /°(^ *(0- u(0)+Mx(7’)hmin-	<5-28)
1 = 0
Так же как и в непрерывном случае, для формулировки
теоремы достаточных условий оптимальности вводятся две функ-
ции: 7i(f, х, и) и Ф(х), Д™ их построения рассмотрим, как
и выше, функцию фр, х) переменных р, х1, х2, ..., Xя). В отличие
от непрерывного случая от функции ф р, х), вообще говоря, не
требуется наличия каких-либо аналитических свойств типа непре-
рывности или дифференцируемости.
Функцию Яр, х, и) определим в дискретном случае следующим
образом:
R(t, х, и) = фр +1, fp, х, и))-фр, х)-/°р, х, и),	(5.29)
а функцию Ф(х), как и раньше, зададим в виде
Ф(х)=ф(Т, x)-bf’(x),	(5.30)
Если считать аналогом производной в дискретном случае
для функции /р) выражение Д/р)=/р-|-1)—/р), то первые два
слагаемых в (5.29) могут рассматриваться как «производная»
Дфр, хр)) функции фр, хр)), если хр) является решением системы
(5.25), т. е. траекторией рассматриваемого процесса.
Если это так, то в выражении фр+l, fp, х, и)) после
подстановки х = хр), u = ир) можно, учитывая (5.25), fp, хр), up))
заменить на x(f-|-l). В результате получим, что на траектории
хр) процесса первые два слагаемых в (5.29) будут равны
Дфр, хр)) = фр + 1, хр+1))-фр, хр)).	(5.31)
Для дискретного случая имеет место теорема о достаточных
условиях оптимальности, формулировка которой почти дословно
совпадает с формулировкой теоремы 5.2 для непрерывного случая.
Теорема 5.3 (достаточные условия оптимальности для много-
шаговых процессов). Пусть допустимый процесс v = (xp), up))еМ
и некоторая функция ф р, х) удовлетворяют условиям:
Г. R(t, хр), йр))= max R(t, х, и) при всех t=0, 1,	Т-1.
х, пеК'
119
2°. Ф(х(Т))= max ф(х).
х,€И*
Тогда процесс (х (1), й(/)) является оптимальным.
Доказательство. Теорема доказывается аналогично теоре-
ме 5.2.
Рассмотрим вспомогательный функционал 3^(х, и, ср) с по-
мощью соотношения
JT(x, и, р)=- X х(г), и(/)) + Ф(х(т))-(р(0, х0). (5.32)
г = О
Как и раньше, оба функционала и / будем рассматривать
на множестве D процессов (х (1), u (1)), удовлетворяющих ограни-
чению (5.27), и множестве допустимых процессов М с D.
Покажем, что на множестве допустимых процессов значения
функционала У? совпадают со значениями функционала У (х, и)
(аналогичный результат был получен для непрерывного случая).
Лемма 1. Для любой функции ф(г, х) значения функционалов
и Д’ на множестве М допустимых процессов совпадают, т. е.
u(l), ф (f, х)) = У(х(1), u(/)), (х(1), и(/))еМ.	(5.33)
До казатедьст во. Проведем преобразование выражения
(5.32) для функционала , учитывая, что процесс (х(z), и(/))
является допустимым.
Соотношение (5.32), подставляя в него	с учетом
(5.29), можно привести к виду
. ^(х(1 ),□(/),ф(/,х))=- X (р(т)ЛО, х(г),«(/)))-ср(/, х(/)) +
+ Z /°C, х(г), ц(г)) + Ф(Г, х)-ф(0, х0).	(5.34)
/ = о
Выражения под знаком суммы в первом слагаемом вследствие
(5.31) при значениях 1 = 0, 1, ..., Т — I будут равны:
ф(1, х(1))-ф(0, х(0)) при 1 = 0,
ф (2, х(2))-ф(1, х 1 при 1 = 1,
ф (3, х (3J) - ф (2, х (2JJ при t = 2,
х(Т-1))-ф(Т-2, х(Т-2))при 1=Т-2,
ф(Г, х(7))-ф(Г-1, х(Т-1)) при 1=Т-1.
Складывая эти выражения, мы видим, что после попарных
сокращений их сумма будет равна ф(т, x(7jj —ф(0, х(0)). После
ее подстановки в (5.34) с учетом х (0) = х0 и равенства (5.30)
получим
^*(x(t), и(1), ф(1, х))= £ /°(1, х(г), u^J+FfxfT’)),
t=i
120
что совпадает с равенством (5.33), которое и требовалось
установить.
Лемма 2. При выполнении условий 1° и 2° теоремы 5.3
функционал «Й’(х, и, ср) достигает минимального значения на мно-
жестве D при х = х(/), и = йр), т. е.
^(хр), йр),Фр,х))= min ^(Х, и, ф).	(5.35)
(х(;), и(г ))е £>
Доказательство. Рассмотрим каждое из трех слагаемых
в выражении (5.32) для функционала «S7.
По условию I6 теоремы 5.3 стоящая под знаком суммы
в первом слагаемом в (5.32) функция Яр, хр), up)) достигает
при всех z = 0, 1, ..., Т— 1 своего максимального значения на
процессе (хр), Это является вследствие теоремы 5.1 до-
статочным^ условием того, что максимальной будет и вся сумма
значений У /?р, х (г), и(/)). Так как знак перед этой суммой
1=0
отрицателен, то первое слагаемое в (5.33) достигает на процессе
(х р), й р)) своего минимального значения.
Второе Слагаемое (5.32) также будет минимально при х = х(Д)
по условию 2е теоремы 5.3, а третье слагаемое- -постоянная
величина. Таким образом, все три слагаемых одновременно
достигают минимального значения на процессе (х р), й(7)). Следо-
вательно, минимальной будет и их сумма, равная «Й’(хр ),
«р)>	*))-
Справедливость соотношения (5.35) доказана.
Если теперь мы обозначим
Р = min ^(х, и, и),
то, повторяя рассуждения для непрерывного случая, получим
с учетом леммы 2 соотношения (5.20) и (5.21). Применяя лемму'
1, получим оценку (5.22) функционала У (х, и), откуда с учетом
допустимости процесса (хр), up)) вытекает его оптимальность.
В дискретном случае остаются справедливыми и сделанные
в конце § 5.2 замечания, т. е., используя оценку (2.22), можно
построить алгоритм поиска приближенного решения задачи
оптимального управления данным многошаговым процессом.
При этом важно то, что после получения решения можно
оценить его точность, т.е. определить отклонение значения
функционала от оптимального.
Далее, как и в непрерывном случае условий 1°, 2° теоремы
5.3, можно рассматривать лишь на множестве процессов
(хр), up)) и принадлежащих множеству М допустимых процессов.
При этом теорема остается верной.
121
§ 5.4. Обобщенная теорема о досаточных условиях
оптимальности
В гл. 4 мы установили, что если на некотором множестве
задан ограниченный снизу функционал, то при решении задачи
о его минимизации имеет место альтернатива: либо существует
элемент этого множества, минимизирующий данный функционал,
либо существует минимизирующая последовательность элементов
множества, на которой функционал стремится к своей точной
нижней грани. Это полностью относится к задачам оптимального
управления, являющимся частным классом задач отыскания
экстремумов функционалов,
В § 5.2 и 5.3 речь шла об условиях, гарантирующих оптималь-
ность данного процесса (х(/), йД)). Здесь же мы рассмотрим,
при каких -условиях последовательность допустимых процессов
(хДг), уДД)}. будет минимизирующей последовательностью в дан-
ной задаче оптимального управления.
Рассмотрим сначала задачу оптимального управления для
непрерывного случая, когда ограничения, определяющие множест-
во допустимых процессов, задаются соотношениями (5.16), а фун-
кционал имеет вид (5.14), В задаче оптимального управления
для непрерывного случая достаточные условия оптимальности
такой последовательности могут быть сформулированы в виде
следующей теоремы.
Теорема 5.4 (обобщенная теорема о достаточных условиях
оптимальности для непрерывных процессов). Пусть имеется
последовательность (х Д), йДД} допустимых процессов, принадле-
жащих множеству М при всех $=1, 2, ,,,, Предположим, что
существует непрерывно дифференцируемая функция <р Д, х), кото-
рая при 5->оо удовлетворяет условиям'.
1°. 7?Д, хДД, йД/))-> sup R(t, х, о) равномерно но /б[0, Т].
(х, u) е V1
Г. Ф(«,(Т)Ы МгФ(х).
л е г х
Тогда последовательность (хтД). й,(г)} является минимизирующей
для функционала.
Доказательство проводится с помощью тех же вспомогатель-
ных конструкций, что и в § 5,2.
Область М допустимых процессов расширяется с помощью
рассмотрения таких процессов (х(Д, иДД которые удовлетворяют
условию (хД), иД))е V* при всех г е Гб, Т], но не обязательно
удовлетворяют уравнению процесса. Эти процессы составляют
множество D, и М является его подмножеством.
Введем определенный на множестве D (следовательно, и на
множестве М) функционал 2?(х и, <р) с помощью соотношения
(5.16). О функционале и, ф) известно (лемма 1 § 5.2), что
122
I
на множестве М его значение совпадает со значениями функ
ционала > [соотношение (5.17)].
Обозначим /ф аналогично тому, как было сделано выше:
/ = inf ^?{х, и, ср).
(х, u,)eZ)
Так как М есть подмножество D, то
inf =S?(x, u, <p)sj inf =S?(x, u, <p),
(x, u,)eZ)	(x, u,)evW
откуда
inf ,/(x, u)>/m.
(x.uJeM 	’ ф
(5.36)
С другой стороны, из условия 1° доказываемой теоремы 5.4
для первого слагаемого в соотношении (5.16) получаем
Следовательно, взятое с обратным знаком, это слагаемое стремит-
ся к inf [ - 7?(/, х(7), u(7))d/1.
(х, u,)eZ)\ J	/
о
Из условия 2" сразу получаем, что второе слагаемое функцио-
нала (5.16) также стремится к своей нижней грани.
Так как последнее слагаемое в (5.16) — постоянная величина,
то можно сделать вывод, что
й5, при ,5-юо.	(5.37)
Но так как (хД/), йДг))еМ, то на основе (5.17) при всех s
•/е(х„ us)=^(xs, й5, <р),
откуда с учетом (5.37) получим
./(xs, us)->Z„ при 5^ от.
Сравнивая последнее соотношение с (5.36) и пользуясь опреде-
лением точной нижней грани функционала, можно написать
й5)-э inf сф,«),
(х, и,)еМ
т. е. последовательность (хД/), йДД) является минимизирующей
для функционала > на множестве М, что и утверждается
в теореме.
Теорема 5.4 остается справедливой, если несколько видоизме-
нить ее условия.
Как отмечалось выше, иногда бывает удобно в условиях
теоремы предполагать, что верхняя грань функции х, и)
123
рассматривается при данном значении t только на множестве
(x(r), и(?)), где (х(/), u(t))еМ. Это множество уже множества V‘
и является его подмножеством. При таком изменении форм-
улировка теоремы остается справедливой.
Условие Г теоремы 5.4 может быть ослаблено, если сформули-
ровать его в виде
т	т
us(0)d* = f 8ЧРЛ Я(г, х(г), u(f))cU.
I"'
о	О
Если же при всех t [О, 7] существует шах /? (/, х, и), то
х, ие V'
утверждение теоремы остается верным при замене условия 1°
также более слабым
г
к'(г, *,(0, «J0)d^
max х, n)dt
(х. uje И'
(5.38)
Использованное в формулировке теоремы 5.4 условие Г
является достаточным условием выполнения соотношения (5.38),
так как равномерная сходимость подынтегральных функций
обеспечивает- и сходимость интеграла, однако диапазон примени-
мости этого условия шире, чем условия Г теоремы 5.4. Например,
условие (5.38) можно проверять для таких процессов, где
управление и (г) или состояние х(/) не являются ограниченными
по величине на отрезке [О, Г]. В этом случае даже если верхняя
грань функции А и не существует при всех ie [О, 7], то для
проверки соотношения (5.38) требуются лишь существование
и конечность интегралов в этом соотношении.
Перейдем теперь к обобщенной теореме о достаточных
условиях оптимальности для многошаговых процессов в дискрет-
ных системах.
Постановка задачи оптимального управления определяется
функционалом (5.28), который требуется минимизировать на
множестве М допустимых процессов, задаваемом ограничениями
(5.25) (5-27).
Так как доказательство теоремы для дискретных процессов
может быть проведено аналогично доказательству теоремы для
непрерывного случая, ограничимся ее формулировкой.
Теорема 5.5 (обобщенная теорема о достаточных условиях
оптимальности для многошаговых процессов). Пусть имеется
последовательность (Т), us())} допустимых процессов, которая
принадлежит множеству М при всех j=l, 2, ... и Z = 0, 1, ...,
Т. Предположим, существует функция <р (г, х), которая при
удовлетворяет условиям'.
Iе. R(t, xs(z), SUP ^х, и), /=0> Ь T~L
х, ue V‘
124
2°. Ф(хДГ))^Ыф(х).
Тогда последовательность {xs(/)} iis(?)} является минимизирующей
для функционала Т.
§ 5.5. Непосредственное применение
достаточных условий оптимальности
к решению задач
Доказанные выше теоремы могут использоваться не только
для проверки оптимальности некоторого процесса (х(/), и (Д),
но и для отыскания оптимального процесса. В данном параграфе
мы рассмотрим класс оптимизационных задач, где применение
достаточных условий позволяет эффективно строить оптимальное
решение.
Рассмотрим процесс, описываемый уравнением
x = P[t, x)+Q{t, х)и.	(5.39)
Данный процесс (х(/), где х(Д и — скалярные
функции, протекает на промежутке времени [О, Т], причем
начальное состояние системы при Г = 0 и конечное состояние
при t—Т, в которое ее требуется перевести, заданы:
х(0) = хо, х(Г)=х1.	(5.40)
Функционал в данной задаче задается соотношением
г
У = |(Р0(г, х)+£?°(?, x)w)dz'->min.	(5.41)
о
В соотношениях (5.39), (5.41) Р(г, х), Q{t, х), Р° (г, х), Q° [t, х)—
заданные непрерывные функции, причем Q[t, х)=£0.
Рассматриваемый класс задач характеризуется линейной зави-
симостью от управления правой части уравнения процесса (5.39)
и подынтегральной функции (5.41). Зависимость же от t и х может
быть, вообше говоря, произвольной.
Предположим, что в данных задачах отсутствуют ограничения
на х (/) и и (t). Для нахождения оптимального процесса (х (/),
; й(/)) применим к подобным задачам теорему 5.2.
Запишем функцию R для данной задачи:
R(t, х, u) = ||+g(P(/, x)+Q(f, x)u)-P°(f, x)-QG{t, x)u. (5.42)
Здесь <p(f, x)—некоторая функция, которую надо определить.
Наша цель будет состоять в подборе функции <р(г, х) таким
образом, чтобы процесс (х(/), «(/)) при каждом максимизиру-
ющий выражение (5.42), был допустимым. При таком подходе
мы получим, что процесс (х (tj, й (/)) является оптимальным.
Действительно, условие 1° теоремы 5.2 будет выполнено для
125
процесса (x(t),	а условие 2°, как отмечалось выше,
выполняется тривиально, так как в данной задаче, согласно
(5.40), правый конец траектории зафиксирован.
Зададим функцию <р (/, х) так, чтобы функция R(t, х, w) не
зависела от и. Из (5.42) видно, что зависимость R от и линейна,
поэтому независимость от и означает равенство нулю коэффици-
ента при и, т. е.
х) = 0.	(5.43)
При таком задании <р ((, к) функция R становится функцией
двух переменных т. е. к = /?({, х). Если теперь при каждом
1 найти max R(f, х), получим некоторую траекторию х(/). В случае
допустимостй-хД), т, е. если она удовлетворяет условиям (5.40),
эта траектория м есть искомое оптимальное решение. Соответству-
ющее управление «(/) мы получим, подставляя х(г) в уравнение
процесса (5.39). Выражая затем оттуда м(г), будем иметь
(544>
При этом управление w будет допустимым из-за отсутствия
в задаче ограничений на управление.
Найденный процесс (х(/), и(jj) будет удовлетворять условию 1°
теоремы 5.2. Если окажутся выполненными краевые условия
(5.40), то по этой теореме (х(<), “(0) будет оптимальным
процессом.
Для реализации показанной идеи требуется найти функцию.
<р (/, х) из уравнения (5.43). Преобразуя его, получим
х)
дх Q(t, х)'
Данное уравнение является простейшим уравнением с частными
производными. Его общее решение находится интегрированием:
<р(Ах)=
(5.45)
где х0— произвольное число, которое можно, например, принять
равным пулю; С(/) — произвольная функция времени.
Равенство (5.45) задает множество всех решений уравнения
(5.39), любые два из которых отличаются друг от друга только
па функцию, зависящую от времени. Чтобы с помощью найденной
функции (р (/, х) составить функцию 7?, вычислим слагаемые
в выражений (5.42). Чтобы вычислить слагаемое воспользуемся
126
правилом дифференцирования интегралов по параметру. Из
(5.45), где параметром в подынтегральной функции является
t, будем иметь
JC
st J Це(ьt,})	1'
X
Подставляя значения производных функций <р (/, х) в (5.42),
получим
Md5+C(,). (Ш)
V V’ ’ '	J 4,1 \ *v’ VJ /
х.
Эта формула позволяет получить выражение для функции /?(/, х)
в любой задаче рассматриваемого класса. Отметим, что искомое
значение х(Д максимизирующее /?(/, х), не зависит от вида
функции С'(/), так как она не зависит от х. Поэтому ее можно
считать равной нулю.
В рассматриваемой задаче ограничений на величину х нет,
поэтому необходимым условием максимума функции R (t, х)
по x будет
Зх х=х(/)
Это уравнение с учетом (5.45) можно переписать так:
±	x)-P°(z, x)C(z, х)\ d(Qa{t, х}\ = 0
йД	0(,х)	4 4
Равенство (5.47), которое должно выполняться при х = х(г),
можно использовать для отыскания x(zj.
Предположим, что решение х(г) найдено. На рис. 5.3 оно
изображено на плоскости (х, /).
Из рис. 5.3 видно, что траектория x(z) не обязательно
допустима. Действительно, при ее построении мы не учитывали
краевых условий (5.40). Им она в общем случае и не будет
удовлетворять.
Если же окажется, что траектория х(г) является допустимой,
т. е. х(О)=хо и х(Г)=х[5 то она является и оптимальной, так
как в этом случае она удовлетворяет теореме 5.2.
В общем случае, когда краевые условия не выполнены,
решение задачи может быть найдено в классе минимизирующих
последовательностей. Для построения последовательности посту-
пим таким образом. Рассмотрим Произвольную последователь-
ность моментов времени rs-»0 и г',->Т (рис. 5.4). Соединим
начальную точку х0 прямой с точкой х^), точку прямой
127
l2—с точкой х(т2) 11 т- Д- То же проделаем и с конечной точкой
соединив ее с точкой xfi)) прямой /), с точкой х(т2) - прямой
1'2 ит. д, В результате получим последовательность кривых xs(z),
каждая из -которых состоит из трех участков:

ls, если O^/CTj,
< х, если
если
(5.48)
Прямые ls и l's задаются уравнениями
ts-T '	'
(5-49)
Полученные значения xs (г) будем рассматривать как траекто-
рии системы (5'39). Реализующие их уравнения й5 (г) можно
получить подставляя значения xs(r) в (5,44). После определения
йД/) мы получаем последовательность (хДД й (/)) допустимых
процессов, удовлетворяющих ограничениям (5.39), (5.40) данной
задачи. Построенная последовательность процессов является ми-
нимизирующей и, следовательно, представляет собой решение
задачи. Покажем это.
Воспользуемся обобщенной теоремой 5.4. Как отмечалось
выше, в данной задаче требуется для последовательности
(МД ЫДГ)) проверить выполнение лишь условия 1° теоремы
5.4. Условие 2П выполняется автоматически, так как хДтМх;
при всех 5.
Как видно из рис. 5.4, сходимость xs(/) к x(t) на интервале
[О, Т] не является равномерной; следовательно, равномерная
сходимость функции R(t, х5(/)) в (5.46) к своей верхней грани
R(г, х(г)) не гарантирована, а в точках / = 0 и t=T вообще
может не иметь места. Поэтому будем проверять условие 1°
128
теоремы 5.4, сформулированной в виде соотношения (5.38).
В соответствии с этим соотношением требуется проверить,
что при S-tCO
fR{t, xs(r))dr—>JR(l, x(z))dt.	(5.50)
о	о
Для того чтобы установить справедливость (5.50), представим
интеграл в левой части в виде трех слагаемых:
х5(r))d/ = f R(t, xs(r))d/+f Я(/, xs(r))dr + jjR(r, xs(/))df.
В связи с тем что функция R (i, xs (г)) ограничена, а длины
промежутков интегрирования ts и Т—т' в первом и третьем
слагаемых стремятся к нулю, эти интегралы при также
стремятся к нулю. Так как, согласно (5.48), на промежутке
Гта, <] значение xs(r) совпадает с x(i), то второе слагаемое
будет равно
x5(f))df= f Л(/, х(/))<!/
и следовательно, при 5->оо стремится к значению правой части
(5.50). Это и доказывает, что данное соотношение выполняется
для последовательности траекторий %,(/). Поэтому последова-
тельность «Д/)) является минимизирующей.
Пример 1. Требуется найти процесс, удовлетворяющий урав-
нению
х=—x + xw, х(О) = хо, х(Т) = х1,
и оптимизирующий функционал
т
</= J ((/ + I)x2 -rx(l — w))dz->mm.
о
Эта задача является частным случаем рассмотренной нами
задачи (5.39) — (5.41), поэтому воспользуемся полученными резуль-
-т-	,г> { S°(r> т
татами. Так как в данном примере 1)	’ то вь1Ражение
длЯ) х), вычисляемое по формуле (5.46), примет вид (при
R= -x2(t+ 1) + х.	(5-51)
Найдем максимум 7?(z, х) по х при фиксированных I из
„ 6R
условия равенства нулю производной —:
-2х(г+1)+1 =0,
5 За к 456
129
откуда
х(0=
1
2(t+1)'
В данной точке функция R(t.x') действительно достигает
32r
максимума, так как ее вторая производная у-у отрицательна
(рис. 5.5) при всех />0.
Управление «(/), реализующее данную траекторию, подучим
из уравнения процесса, подставляя в него х (/):
что допустимо из-за отсутствия в задаче ограничений на
управление.
Полученный процесс (х(/), й (г)) является оптимальным в дан-
ной задаче только в том случае, если заданные в ней краевые
условия х0 и Лд совпадут с начальной и конечной точками
траектории х(/), т. е. если будут выполнены условия х(0) = | —х0,
х(Г)=^__=х
' > 2 (Г+1)	1
ный характер, а
оптимальным не
Это совпадение, однако, может носить случай-
при других краевых условиях данный процесс
будет. Более того, он не будет и допустимым
процессом.
Решением задачи в общем случае будет минимизирующая
последовательность, изображенная на рис. 5.6. Траектории xs(/)
состоят из трех участков. На участке [0, ts] это прямая,
соединяющая х+ с точкой х (т5). При г е [т$, rj] траектория
совпадает с х(г). Наконец, на последнем участке /е[т), Г] это
прямая, соединяющая точки х(т^) и х(Т)=х1. Последовательности
{г,} и {Tj} при /-+00 сходятся соответственно к нулю и к Т.
Формулы для расчета траекторий, согласно (5.48), (5.49),
будут иметь вид
130
l-2(ts+l)x0	n
-4 +	если
ZTs ljs + 1 J
I
^еошт,«,<т„
х1 + ч\	еСЛИ Ts^z^^‘
1 2(<+1)(т;-ту	'
(5.52)
Теперь можно найти управление ws()j, реализующее получен-
ную траекторию. Для этого достаточно подставить xs (:) в урав-
нение процесса. Тогда
«Л0=Мл+1-	(5-53)
Вычислим «ДЛ. Например, для промежутка [0, т5] из соотно-
шений (5.52) и (5.53) получим
М*) =
<Ф5)
+ 1,
где
а
/ \	1—2. тгХо
М=дтг
Анализируя это равенство, можно заметить, что при доста-
точно малых ts (или, что то же самое, при достаточно больших
s) управление ws(f) становится больше любого наперед заданного
числа. Например, при ( = 0
М°)=
1—2(ттЧ-1)х0
2rsfc+l)
Так как т,->0 при $(0)->оо, то
Таким образом, отсутствие ограничений на управление сущест-
венно используется при построении решения задачи.
Перейдем теперь к случаю, когда в рассматриваемой оптимиза-
ционной задаче (5.39) —(5.41) имеются ограничения на состояние.
Множество допустимых состояний при каждом фиксированном
t представляет собой некоторое множество на числовой прямой.
Будем считать, что это множество — отрезок
a(r)^x^Z> (г).	(5.54)
Если по-прежнему считать, что на управление не наложено
ограничений, то единственное изменение при решении данной
задачи по сравнению с задачей без ограничений состоит в том,
что траектория х(/) в ней строится из условия
R(t, х(г))-ыпах /?(?, х),
хе Ух
где х) задается соотношением (5.46).
5*
131
такие же, как в примере
на состояние:
Раныпе же R (/, х) нахо-
дилась из условия безуслов-
ного максимума этой фу-
нкции-
Рассмотрим на примере,
как изменится решение зада-
чи при добавлении ограниче-
ний на состояние.
Пример 2. Пусть уравне-
ние процесса и функционал
1, но помимо этого задано ограничение
0^х^0,25.
Как и в примере 1, построим функцию R h х\ которую
и в данном случае определим соотношением (5.51). Для нахож-
дения х(() решим задачу о максимуме 7? (г1, х) на отрезке
хе [О 0,25].
Эта задача будет иметь различные решения в зависимости от
значений t. Процесс определения максимума R (/, х) проиллюстриро-
ван на рис. 5.7, где график этой функции представлен для различных
значений t. Из рисунка видно, что в случае te[O, 1] на интересующем
нас отрезке хеГб, 0,25] R\t, х) монотонно возрастает (вершина
параболы (5.51) будет лежать правее значения х = 0,25). Следователь-
но, ее максимум будет достигаться в точке х=0,25. При остальных
значениях г вершина параболы (5.51) лежит внутри отрезка [0, 0,25],
поэтому максимум R (t, х) будет достигаться в ней. Величина х (/),
максимизирующая R{t, х), таким образом, задается в виде
Г
0,25, если /е[0, 1],
x(z)=<	1	п лгя
2(П1Г есл" г]'
Как и в примере 1, построим последовательность {x,(t))
допустимых траекторий, являющуюся минимизирующей последо-
вательностью в рассматриваемой задаче. Ее элементы задаются
соотношениями
(0 ~4
о, 25—х0	_ , .
х0+-------^г, если 0^/<rs,
0,25, если ts С / < 1,
если
х +	(г^Г), если -'Г«Г
1 2(т;+1)(т;-ту
132
На рис. 5.8 представлена картина поведения траекторий,
образующих минимизирующую последовательность.
Таким образом, при наличии ограничений на состояние, решение
задачи оптимального управления (5.39) -(5.41), как и в случае без
таких ограничений, представляет собой минимизирующую последова-
тельность. При построении этой последовательности, как отмечалось
выше, существенным моментом является отсутствие ограничений на
управление. Это позволяет выбирать любые значения управлений и (г).
Рассмотрим теперь общий случай, когда имеются ограничения
как на состояние, так и на управление. Исследуем наиболее
часто встречающийся в задачах случай, когда область допустимых
управлений задается ограничением
Wj (t, х) w w2 (/, х).	(5.55)
Таким образом, к ограничениям (5.39)—(5.41) оптимизацион-
ной задачи добавлены ограничения (5.54), (5.55).
Решение сформулированной задачи начнем с определения
области возможных состояний системы. Эта область определяется
множеством всех траекторий, удовлетворяющих уравнению (5.39),
краевым условиям (5.40) и ограничениям (5.54), (5.55).
Для построения этого множества рассмотрим четыре траекто-
рии, отвечающие минимальному Wj (t, х) и максимальному и2 (/, х)
значениям управления и краевым условиям (5.40). Пусть от х
а2 (()— решения (траектории) уравнения
f	x=P(t, х) + 2(/, х)м, (/, х)
1ри начальных условиях х'(0) = хо и х(Т) = х]? а р, (г), р3(/)—реше-
Гия уравнения
х —Р(1, x) + 2(i, х)и2(г, х)
при тех же начальных условиях. Эти решения изображены на
рис. 5.9.
Нетрудно заметить, что решение х(/) уравнения (5.39), начи-
Рис. 5.8
кающееся в точке х0 и оканчивающееся в точке хь не может
выйти за пределы области, ограниченной кривыми ос; (г), р;(().
n(t), b ((). Рассмотрим, например, некоторую траекторию х(г)
с начальной точкой х(0] = хо, от-
вергающую управление и (/), и по-
кажем, чт о она не может пересечь
границу ocf (/)- Так как, по пред-
положению, Q(t, х)^0, то пусть
для определенности Q ((, х) > 0 [в
противном случае можно провести
замену £)(/, х) и и на — Q(t, х)
и -и].
Рассмотрим кривую (z), от-
вечающую минимальному значе-
133
нию управления w = w1(r, х). Пусть некоторая траектория х(/),
отвечающая управлению w(z), пересекает в точке Т=т
(рис. 5.9). Тогда в данной точке производная х(т)>а.1(т). Так
как обе траектории х (г) и а, (/) удовлетворяют уравнению
(5.39) и Q (z, х) >0, то нетрудно получить, что точке t = т
соответствует
(т, X(т))5
что противоречит ограничению на управление (5.55).
Аналогично доказывается, что траектории не могут пересекать
остальных кривых а2 (Z),	2 (г).
Таким образом, мы сузили исходную область Vtx допустимых
значений (t х). Образовавшуюся область обозначим И, при
этом V с
Перейдем к построению оптимальной траектории. Для
этого рассмотрим траекторию х (/), максимизирующую при
каждом t функцию R (г, х). Эта траектория изображена на
рис. 5.10.
Если траектория х(() допустима, то она является оптималь-
ной, так как удовлетворяет теореме 5.2. Действительно, условие
lrJ теоремы выполнено по построению траектории х(г) как
раз из условия максимума функции /?(/, х), которая не за-
висит от и. Следовательно, условие ее максимума по этой
переменной выполняется автоматически. Условие же 2" превраща-
ется в тривиальное, так как в данной задаче зафиксировано
значение х(Г).
Пусть управление «('() реализует траекторию х(г). Его можно
определить из уравнения процесса (5.39):
Для проверки допустимости управления й (z) достаточно проверить
выполнение условия
Wj (Г, х(/))<й(г)^и2(/, х(ф
134
f Проверка допустимости участков траектории х()), проходящих
по границе области ct12 (т), Р12(£), не требуется, так как эти
кривые сами являются траекториями уравнения (5,39).
В конкретных задачах, как правило, оптимальная траектория со-
стоит из трех участков, как показано на рис. 5,10, Два из них, при-
мыкающих к граничным значениям х0 и хр отвечают предельным
значениям управлений а, (/, х), w2 (г, х), а средний участок реализуется
। некоторым промежуточным значением управления.
Рассмотрим на примере предложенный метод оптимальной
траектории.
Пример 3. Пусть управляемый процесс описывается на проме-
жутке ze[0, 4] уравнением
х = х+2 + нх, х(0) = 3, х(4) = 8.	(5.56)
Причем на состояние х (/) и на управление и (г) наложены
ограничения
2^х^10, [w|^5.
Требуется построить оптимальный процесс (х (г), м (/)), мини-
мизирующий функционал
4
J - j (8 (z + l)x2 + 8zx2u)dr->min.
°
Воспользуемся описанным методом решения задач с ограни-
чениями на состояние и управление, к классу которых относится
данная задача. Построим функцию 7? (г, х) с помощью соотно-
шения (5.46):
R[t, х)= — 4х2+ 16гх.
При различных значениях ге[0,4] эта функция достигает
максимального значения в различных точках множества допусти-
мых состояний. Поведение функции /?(/, х) при различных
t изображено на рис. 5,11. Из графика видно, что при 0^/<1
максимального значения R(t, х) достигает в точке х = 2, а при
—в точке х = 2/.
Таким образом, найдена кривая x(z), точки которой при
каждом / отвечают максимуму R[t, х). Эта кривая, состоящая
из двух участков, изображена на рис. 5.12.
Построим теперь траектории ab2(z) и pj 2 (/), соответствующие
минимальному и максимальному значениям управления и (с).
Траектории а, (/),	(z) удовлетворяют уравнению
х= -4х + 2
и начальным условиям х(0) = 3 и х(4) = 8 соответственно. Такими
решениями, как нетрудно видеть, будут
135
Ct1 (z) = oj5 + 2,5e“4%
рг(\) = 0,5 + 7,5е“4<'“4’.
Траекторий ot2(0 и РгО) удовлетворяют уравнению
х = 6л: + 2
с теми же начальными условиями, что и ах (t), р, (/).
Отсюда
. мг)=4+3Ь&г’
P2(t)= -| + 81е6<'-4\
Полученные решения ali2(i). Р[;г(О изображены на рис. 5.12.
Найдем точки пересечения этих’ кривых с х(г). Кривая a, (г)
пересекается с в точке г*=—0,25In0,6, а2(г) не имеет с ней
точек пересечения, а Р( 2 (г) проходят через конечную точку ^=8
при £ = 4, заданную условием задачи.
Рассмотрим состоящую из трех участков траекторию
г
0,5 + 2,5е-41, если ()<;£<£*,
*(0=^	2, если /*^/<1,
2г, если
где t* = — 0,25 In 0,6.
Если эта траектория допустима, то она удовлетворяет теореме
5.2, а следовательно, оптимальна, так как в ее точках достигается
максимальное значение функции R (£, х). Допустимость траектории
х(/) проверяется непосредственной подстановкой ее в уравнение
процесса. На промежутке 0^£<£* такой проверки не требуется,
так как на нем х(Д есть участок построенной выше траектории
х(г), При 1, подставляя в уравнение процесса (5.56) х(г) = 2,
136
получим m(z)= — 2. При	подставляя x = 2t, будем иметь
«(/)=—1. Окончательно управление «(/) можно записать в виде
— 5, если 0^t</*,
й(^)= т — 2 если /*^/<1,
-1, если 1
Управление й(г) допустимо, и, следовательно, найденный
процесс (x(t), ы(()) является оптимальным.
Глава 6
Исследование
однопродуктовой макромодели
оптимального развития
экономики
Общественное производство—сложный управляемый процесс
преобразования ресурсов в общественный продукт.
При разработке экономико-математического аппарата для
анализа, планирования и прогнозирования общественного произ-
водства создается система моделей, основанная на представле-
нии о народном хозяйстве как сложной иерархической системе.
Верхний уровень системы моделей народного хозяйства
образуют макроэкономические модели, в основе которых лежат
взаимосвязи между глобальными экономическими показателями,
такими, как совокупный общественный продукт, национальный
доход, трудовые ресурсы, производственные фонды и др.
Макроэкономические модели позволяют выявить изменения
сводных показателей и дают ценную информацию о темпах
и пропорциях развития народного хозяйства.
В некоторых случаях самостоятельный интерес представляет
изучение взаимосвязи между важнейшими источниками экономи-
ческого роста—живым и овеществленным трудом и результатом
хозяйственной деятельности.
§6.1. Моделирование производства на макроуровне
При математическом моделировании взаимосвязь между фак-
торами производства и его результатом обычно отражают
с помощью производственных функций. При построении произ-
водственных функций следует иметь в виду, что затраты факторов
производства на выпуск продукции всегда неотрицательны. Кроме
того, при моделировании производственных функций надо отме-
тить, что отсутствие одного из факторов приводит к нулевому
выпуску продукции. Полагают также, что факторы производства
меняются непрерывно, а выпуск продукции изменяется достаточно
гладко при изменении факторов, что естественно при рассмотре-
нии производства на макроуровне.
Экономически целесообразно также, чтобы при увеличении
количества используемого ресурса выпуск продукции рос, т. е.
138
для дифференцируемой производственной функции можно запи-
сать следующие неравенства:
dF{K' ^>0
ек ’ 8L
где К—основные производственные фонды; L—трудовые ре-
сурсы.
Перечисленным условиям отвечают мультипликативные произ-
водственные функции вида
п>0, «>0, |3>0,
где X—выпуск продукции; а, а, [3 — параметры производственной
функции.
Мультипликативная производственная функция дает возмож-
ность отразить эффект масштаба производства, который сущест-
вуез' только при одновременном изменении факторов К и L.
Пусть эти факторы изменяются в X раз. Тогда
F(kK, kL) = -ka+f>F\K, L).
В этом случае:
1)	если а+р>1, то имеет место интенсивный способ развития,
т. е. с россом масштаба производства в X раз выпуск продукции
возрастает более чем в X. раз;
2)	если а+Р<1, то росс масштаба производства отрицательно
сказывается на выпуске продукции, т. е. при росте затрат в X раз
выпуск продукции растет менее чем в Л. раз;
3)	если а + р=1, то происходит экстенсивный рост экономики
только за счет факторов производства.
Длительные наблюдения показывают, что в условиях чисто
экстенсивного производства увеличение затрат только одного из
факторов производства приводит к снижению эффективности его
использования, т. е.
s2f(k, l)
ек2 ’	<?т2	’
Это означает, что каждая последующая единица возрастающего
фактора соединяется с меньшим количеством другого фактора
и его рост дает уменьшающийся прирост продукции. Например,
при многостаночной организации производства значительное
увеличение числа станков, приходящихся на одного рабочего
в условиях неизменной технологии, квалификации персонала
и характеристик станков, уменьшает эффективность использования
оборудования.
Для экстенсивного способа развития характерно
.. SF(K, L) ,. SF (х, Ц
lim—f=oo, hm—~-^=ао
к—о	дь
139
и
5F^,L л 3F(F,L) n
lim —1=0, hm —V—1=0.
к-к> dK	oL
Производственная функция Кобба — Дугласа является моделью
экстенсивного способа развития:
X=aK*L\ а + ₽ = 1,
где а — коэффициент эластичности выпуска по производственным
фондам; р — коэффициент эластичности выпуска по груду.
Под эластичностью производственной функции по фактору
(фонду, труду и т. д.) понимается отношение относительного
прироста функции к относительному приросту фактора. Эластич-
ность численно равна числу процентов, на которое изменится
выпуск продукции при изменении фактора на 1%. Нетрудно
показать, что коэффициенты эластичности можно определить
как отношение предельной эффективности функции по фактору
к средней эффективности:
^3F(K,L} /F(K,L) и gJFfcL) / F(K, L)
оК / К 1 8L / L
Важной характеристикой производственных функций является
эластичность замены ресурсов ст, так как она бывает постоянной
для большинства производственных функций, используемых в эко-
номико-математическом моделировании. Эластичность замены
ресурсов показывает, на сколько процентов изменится фондо-
вооруженность k = KjL при изменении предельной нормы замеще-
dJV
ния (пРеДельной фондовооруженности)? иа 1% при неизмен-
ном выпуске продукции:
din ft
d In 5
/?=crtnst
Здесь под предельной нормой замещения понимают количество
фондов, которое необходимо дополнительно ввести при уменьше-
нии затрат труда на единицу, если выпуск продукции
останется неизменным. Предельная норма замещения $ опре-
деляется из уравнения изокванты (линия равного выпуска
продукции):
СД	dL
140
« Отсюда
oF (К, L)
_dK_ 3L
S~dL~ 8F(K,Ty
оК
i . аЖ Z)	, ,	<>f(k, l)
t где —V—4—предельная эффективность по труду; ——пре-
|; о L	оК
 дельная эффективность по основным производственным фондам.
| Эластичность замены ресурсов ст для функции Кобба—Дуг-
I ласа равна
|	din А ,
Г	СТ =----=1,
Е	d In j
Г так как для нее предельная норма замещения
I	s = ^k, где k = K[L.
I;.	а
Часто экономические соображения подсказывают, что хотя
Г эластичность замещения ресурсов и можно считать постоянной,
1 но все-таки она отлична от единицы. В связи с этим представляет
интерес линейно однородная производственная функция Солоу;
f	Х=у [бК~₽+{1 - б) С"₽] “1/р-
| Для того чтобы найти эластичность замены ресурсов ст для
| функции Солоу, вычислим предварительно предельную норму
г замещения з. Для этого найдем предельную фондоотдачу;
8F(K, L)_ bf
I	SK '~k* + 's [5A-P 4-1—5]’
I где f=XjL — производительность труда; k—фондовооруженность
| труда.
Теперь найдем предельную производительность труда, учиты-
| вая, что
F
oL
t или
dF(K,L)_ (1-5)/
81,	5А~₽
'коичагельно
=
t	о
Отсюда эластичность замены ресурсов для функции Солоу
dinA 1
ст =---.
d In s 1 + р
141
Нетрудно заметить, что функция Кобба — Дугласа является
частным случаем функции Солоу при р = 0.
§ 6.2. Решение задачи управления экономикой
на макроуровне с помощью достаточных условий
оптимальности
Рассмотрим экономику, характеризующуюся в каждый момент
времени t набором переменных
X, Y, С, К, L, I,
где X — интенсивность валового продукта; У — интенсивность
конечного продукта; С — непроизводственное потребление; / — ва-
ловые капитальные вложения; К — объем основных производствен-
ных фондов; L— трудовые ресурсы.
Эти переменные взаимосвязаны. Прежде всего имеет место
условие баланса в каждый момент времени
Х=аХ+ У,
где 0 < а < 1.
В свою очередь, конечный продукт распределяется на валовые
капитальные вложения и непроизводственное потребление
У=Z+ С,
где валовые капитальные вложения расходуются на прирост
основных производственных фондов и их восстановление за счет
амортизационных отчислений:
где ц—коэффициент амортизации.
Тогда
К=1-цК
или
К=(1 - я)(1 - и) X- цХ,	(6.1)
где u=CjY— доля непроизводственного потребления:
O^w^l.	(6.2)
Будем считать, что размеры валового продукта определяются
заданной производственной функцией, характеризующей возмож-
ности производства в зависимости от величины производственных
фондов К трудовых ресурсов и времени /, т. е.
L, t\	(6.3)
Предполагается, что производственная функция F(X, L, i) не-
прерывна и дважды дифференцируема, причем выполняются
следующие условия;
142
то
1)	функция всегда неотрицательная: F(K, L, г)>0;
л.	л л
2)	функция возрастает по каждому из аргументов: ~>0, — >0;
3)	если хотя бы один из ресурсов К или L равен нулю,
и F(K, L, () = 0, ОД Ц t)=0, F\K, 0, г)=0;
4)	предполагается, что с ростом каждого из аргументов
d2F
Прирост валового продукта убывает:	^<0;
 5) lim^ = oo, lim^=oo;
' ЬК г—*о SL
6) функция обладает свойством однородности по аргументам
К и L, т. е. изменение масштаба производства приводит к пропор-
циональному изменению выпуска продукта:
F(kK, kL, t] = kF(K, L, t\
Параметр t вводится в производственную функцию, чтобы учесть
целый ряд внешних факторов, воздействующих на модель, в том
числе влияние научно-технического прогресса;
7) функция возрастает по времени;
at
Решение задачи будем искать при условии
(6.4)
где К3 — заданный уровень основных производственных фондов.
Пусть заданы производственные фонды в начальный момент
времени:
ОД = *о-	(6.5)
Допустимое множество М в рассматриваемой задаче описы-
вается условиями (6.1) — (6.5). Допустимый процесс представлен
совокупностью функций
Од),
удовлетворяющей этим условиям. Он описывает состояние эконо-
мики, а л и w—управление. Очевидно, что такой процесс не
единствен.
Задача управления данной экономикой состоит в том, чтобы
найти такой процесс v=(K(t),	//(/)), который обеспечивал
бы наибольшее среднедушевое потребление на рассматриваемом
временном интервале с учетом дисконтирования потребления, т. е.
т
y=Je"5l^dt	(6.6)
о
143
Проведем редукцию задачи. Для этого введем в дифференци-
альное уравнение (6.1) относительные переменные; k = K!L—фон-
довооруженность, c = CjL — среднедушевое потребление, x~X!L—
производительность труда. Так как K=kL, X—xL, то уравнение
(6.1) примет вид
(kL) = (1 — а) (1 — a) xL — \.\kL.
Учитывая правило дифференцирования сложной функций,
получим
К = (/с£) = kLk-kL.	;
Будем считать, что прирост трудовых ресурсов осуществляется
с постоянным темпом, т. е.
L = nL.
Тогда
(liL) = (k + kn}L.
Окончательно дифференциальное уравнение связи в относи-
тельных переменных примет вид
/с=(1 — д)(1 — п)х + (ц+л)А.	(6-1')
Ограничение на управление и остается тем же:
O^u^l,	(6.2')
а на производительность труда х примет вид
г),	(6.3')
где f(k, /) = 1(Л; к О-
Ограничения на производственные фонды заменим ограниче-
ниями на фондовооруженность:
Щ>к^\	(6.4')
Ц0)=ко>	(6.5')
Проведем преобразование функционала (6.6) к относительным
переменным:
т
У=/е~6'(1 — n)wxd/-»max
о
или
г
1= — Je'6‘(L — a) wxdz-*min..	(6.6')
о
В задаче (6.1)-- (6.6) требуется определить процесс р=
= (&(/), w (Д л"(г)1 обращающий в минимум функционал (6.6') на
множестве (6.Г) — (6.5').
144
f
11 Таким образом, в редуцированной задаче состоянием системы
М является фондовооруженность к управлением — производитель-
И ность труда х и доля потребления и. Уравнением процесса
В служит дифференциальное уравнение роста фондовооруженности,
В Для решения поставленной задачи воспользуемся теоремой
В 5.2 о достаточных условиях оптимальности. Функция R примет
В вид
В	Л {к, х, и, t) =
В	№ -")(’ -н)х-(р+«)/с]+е-5,(1-й)мх+^М.
В Выделим в R слагаемые, содержащие компоненты вектора
В управления (w, х), и приравняем сумму коэффициентов при нем
Вкк нулю. Тем самым на ф накладывается требование
И	-(1-«)фк + е"8'(1-а) = 0;
^Вкпедовательно,
Ц	<рк(/Л)=е"\
^И>гда
^^В	ф (г, к) = ке~&< + с(/),
^^Ве c(z)—произвольная функция. Положим c(z)sO, тогда
^^В	ф (г. А:) = /<е - 5г
ф' (г, £)= — 8£е
При этом условии функция R не зависит от и:
^^В	R(t, к, х)=е“8<[(1-й)х-(ц + я)/<:]-е“5'8А=
^^В	=е-в'[(1 —«)х--(|1 + л + 8)£].
В^^ Оптимальные /<(/), х (/) найдем из условия
В	x(z)-> max R(i, к, x).
В Так как а<1, то (1-«)>0 и, следовательно, max А достигается
К При x = f{k, к]. Для однопродуктовой модели эго равенство
I очевидно, но в многоотраслевой модели может оказаться, что
В некоторые отрасли недогружены.
В Проведем теперь максимизацию R по к при оптимальном
Вх = х. Обозначим:
Ri(i, к)= max У? (Z, А, х) = е “5l [(1 — п)/(£, г) —(ц + «+8)£].
145
Следовательно, максимум к^к будет результатом максимизации
Л! по к.
Введем r(t, £) = (! — a)f(k, /)—(ц + я + 3)А. Тогда, учитывая, что
ей‘>0, можно записать
£(/) = argmaxr(Z, к) We [О, Г],
к
Проанализируем поведение функции г (z, А) по к. Эта функция
является суммой двух слагаемых: производственной функции
с точностью до постоянного множителя и линейного выражения.
График r(t, к) и его составляющие при фиксированном
t представлены на рис. 6.1.
Функция r(t, к) строго выпукла по к:-^<0 при всех /, к>0.
График г(г, к) в окрестности нуля близок к (I fc), так
как, в частности, -»со, а на бесконечности близок к -(ц + « + 8)£,
к—о
дг
так как —
единственный максимум по к, который достигается в точке А’>0.
Необходимым условием максимума г (Г, к) по к является
равенство нулю частной производной:
дк
— (ц + « + 8) < 0. Поэтому функция г (/, А) имеет
&
Учитывая, что f[k, t^be^R9, имеем
(I ~а)Ьаер,ка~ ( — (ц + « + 8) = 0.
Так как 0<а<[ и I-а=|3, то х
fW=fOz^Ye’'.	(6.7)
' ' Уц+л + 8 J	!
График £(/) представлен на рис. 6.2.
Найденное £(/) назовем магистралью данной динамической
модели экономики. Она играет важную роль в Структуре
оптимального решения.
Управление, реализующее эту магистраль, найдем подстанов-
кой найденного АД/) в дифференциальное уравнение развития
системы (6.1):
£(/) = ([ — й)(1 — и) х(/) —()!—«)£(/).	(6.8)
Так как х(г)=/(^, z), где f{k. {) = Ьер‘ка есть функция Кобба — Дуг-
ласа, то, решая уравнение процесса относительно и, получим
I 4г)~(и+”)4<)	/6 91
40-1 -	(6.У)
Из формулы (6.7) найдем
в	т t
Рис. 6.2

Тогда
w(Z)= 1 —
(l-o)fc(“£“ ’
или
:К как

(l-fl)£>a
ц+л + 5
получим оптимальное управление
(6.10)
|Г предположении, что 0=?й^1.
Рассмотрим специальный случай, когда краевые условия лежат
на магистрали:
Л:о = £(0), £,=£(7).	(6.II)
Тогда процесс £=(£, tl,/(£))eAf оптимален вследствие теоремы
5.2. Действительно, этот процесс обеспечивает максимум R при
каждом г.
а)	по и—в силу независимости R От управления и, что
достигается выбором функции ср (к, /);
146
147
б)	по к и х — по построению.
С другой стороны, v представляет допустимый процесс,
так как:
а)удовлетворяет уравнению процесса (и находили подстанов-
кой к в уравнение процесса);
б) 0<и<1;
в) граничные условия были специально подобраны.
Отметим, что условие реализуемости	в данной за-
даче выполняется. Это можно проверить. Для функции Кобба —
Дугласа экономической магистралью является кривая постоян-
ного темпа роста фондовооруженности, пропорционального тем-
пу роста технического прогресса р, а оптимальное управле-
ние, реализующее данную магистраль, —постоянная величина
(6.10).
Таким образом, для специально подобранных краевых условий
(6.11) магистраль является оптимальным режимом развития
экономики:
£(/) = argmax R(t, к),
— >»	со
В других же случаях магистрали в структуре решения отводится
существенная роль.
В действительности очень редко встречаются случаи, когда
краевые условия принадлежат магистрали. Рассмотрим общий
случай.
Пусть
Ло^£(0), к^£(Г).
Для решения этой задачи применим прием, аналогичный
рассмотренному при решении задачи, линейной относительно
управления (см. §5.5). Найдем
= argmax R (it k).
В реальных экономических задачах минимальный уровень
потребления строго положителен: 0 < ил и 1.
Построим границы у,Дг), 1=1, 2, 7=0, 1, допустимой области
V. функции Yfj (i) являются решениями дифференциального уравне-
ния процесса
/c = (l-a)(l-w)/(r, к)-(р+и)£	(6.12)
при соответствующих краевых условиях [если j=0, то берется
£(0) = £о, если 7=1, то используется к(Т) = кг] и ограничениях
на управление (если 1=1, то берется нижний предел и = и1, если
1=2, то и= ]),
Рассмотрим пример, когда к0<к(0), кг (Т)>/с(Т), т. е. магист-
раль АЦД проходит так, как показано на рис. 6.3. Тогда
148
оптимальная траектория будет со-
стоять из трех участков с момен-
тами переключения т1 и т2> где Ti
[вляется точкой пересечения гра-
пщы у10 с магистралью k (t), а т-,—
очкой пересечения магистрали к [к)
; границей у5].
„ Из рисунка видно, что вначале
на временном интервале (0, т2) по-
чти все вкладывается в накопление
(потребление в этот период на
минимальном уровне nJ. Начиная
с Tj развитие идет по магистрали
/с(т) вплоть до момента т2, с ко-
торого опять почти все вкладывается в экономику (потребление
опять находится на нижнем уровне и,).
Найдем решение дифференциального уравнения (6.12). Учиты-
вая, что Д/)=6ер‘А;“, получим
£'=(1-й)(1-и)6е₽'£я-(ц+п)£.	(6.13)
Перепишем уравнение (6.13) в виде
k+kk=b(l —д)(1 — i/)ep‘£“,	(6.14)
[е Х=ц+п.
Введем новую переменную
z=k\	(6.15)
;е Р = 1— а.
Так как
z = (l—аИ,
то имеем
*-(T#	<616)
Подставляя (6.16) в дифференциальное уравнение (6.14), получаем
(1—а)”1 k“z+U=&(l~a)(l~M)eptk“.	(6.17)
Разделив обе части дифференциального уравнения (6.17) на ка
и используя соотношение (6.15), получим
(1 — а)'1 z + Xz = 6(l — я)(1 — w)ept.	(6.18)
Общее решение линейного неоднородного дифференциального
авнения равно сумме общего решения однородного дифферен-
[ального уравнения z0O и частного решения неоднородного
авнения z4U:
%	%О0 4" ^чн*
149
Найдем общее решение линейного однородного уравнения
(1 -a)-1z + Xz = 0,	(6.19)
характеристическим уравнением которого является
(1 - а)" *2 + Х = 0.
Отсюда определим корень характеристического уравнения:
Тогда общее решение однородного дифференциального уравне-
ния (6.19) примет вид
zO0=CJ.e-w, i=0, 1.
Частное решение неоднородного дифференциального уравнения
ищем в виде правой части (6.18):
/	2чн = 5е₽',	(6.20)
где В—неопределенный коэффициент, подлежащий определению.
Дифференцируя (6.20) его по t, получим
2чн(0=5Ре<
Подставим z4H(/) в уравнение (6.18):
(1 — а)-15рер( + Х5ер1 = 6(1 — й)(1 — w)epf.
После сокращения на ер( получим
(1 — а)-15р-|-к5=6(1 — д)(1 —и),
откуда
р/р+1
Тогда общее решение неоднородного дифференциального урав-
нения (6.18) имеет вид
z (t) = С е _шер‘
Так как z = ^r? = A:₽, т. е. k = zll$, то общее решение дифференци-
ального уравнения (6.14) будет иметь вид
к (/) = С ,е -
где 7 = 0, 1.
По определению, i'=l, 2, 7=0, 1, являются границами
допустимой области Р и получаются как частные решения
дифференциального уравнения (6.14) при замене и на граничные
значения ub i= 1, 2, и выборе Cjf 7 = 0, 1, в зависимости от
краевого условия. Тогда
150
1/р
уи(С? «,-,/)= Cfi w‘ + ^ а!Р ^ер1
P/Р
(6.21)
где I-1, 2, j = 0, 1.
Найдем интегральные константы 7=0, 1, в зависимости
от граничных условий. Так как
/c0 = fc(0) = Y£O(CO! w.
й(1-д)(1-«Л1/р
р/р+Х
о
г =к	~а)(1 ~и)
0	°	Р В : Л ’
Аналогично определяем Ct из граничного условия
»(i-^)0-«i)eprT/p
р/Р+х
Ge-^ +
Получая

	= ,;Р 6(1-д)(1-«;)еРТ-
1 L1 р/р+х
найдем точки переключения. Обозначим через т^, г=1, 2, /=0,
L точки пересечения границ у(;, t=l, 2, j=0, 1, с магистралью
£(/). Моменты переключения т,7 получим, приравняв
%,) = 70(С/, uif t).
Используя формулы (6.7) и (6.21), получим
уц+п+5 у
Отсюда
С <е “k₽'+е pt
p/P’h
0 йа Р pt _ г - - цв , * (1 -а) (1 -«,-).pt
-----—'—~ Р — С /С “г	ж w *
g+n + 8	'	р/р+Х
|	§ 6.3. Оценка оптимального развития экономики
На основе однопродуктовой оптимизационной модели иссле-
дуем оптимальные решения применительно к конкретным эконо-
мическим системам. Применение этой модели к реальным экономи-
ческим процессам дает возможность сравнивать реальную траекто-
рию фондовооруженности Х(/) с оптимальной траекторией
Рассмотрим частную внутреннюю и несельскохозяйственную
экономику США за период с 1947 по 1968 г., используя
табл. 6.1 н 6.2.
151
Таблица 6.1
Исходные статистические ряды и оптимальная траектория к (/)
для внутренней частной экономики США
Год	Конечный продукт У, млрд. долл. (1958 г.)	Основной капитал К, млрд. долл. (1958 г.)	Отработанные человеко-ча- сы L, млрд.	К к=— L	£р)=4,306е °-°313'
1947	280 2	204 2	109,3	1 8682	4,3060
1948	293 8	212 9	1 10,0	1,9173	4,4459
1949	292 8	196 2	109,1	1 7983	4,5906
1950	322,9	227 4	111,3	2,0431	4,7353
1951	343,9	239,4	113,9	2,1018	4,8890
1952	352,3	244,3	113,8	2,1467	4,0479
1953	Зр-9,8	264,9	114,9	2,3055	5,2124
1954	364,9	248,1	110,8	2 2392	5,3816
1955	395,5	282 2	114,8	2 4582	5,5513
1956	402,8	295,2	116,5	2,5339	5,7217
1957	408,5	298 2	114,3	2 6089	5,9182
1958	403,2	269,5	111,1	2,4257	6,1106
1959	431,1	300,4	113,7	2 6420	6,3092
1960	441,7	303 9	114,1	2,6635	6,5076
1961	449,5	302,7	113,8	2,6599	6,7195
1962	479,5	317,0	115,5	2 7446	6.9378
1963	499,3	329 6	117,5	2,8051	7,1635
1964	522,1	351,7	119,3	2 9480	7,3964
1965	569,9	388 2	122,2	3,1768	7,6294
1966	599,6	441,2	124,0	3,5581	7,8774
1967	612,7	447,4	123,6	3,6197	8,1336
1968	643,4	472 9	125,2	3 7772	8,3980
На основе однопродуктовой оптимизационной модели
требуется построить магистраль. Для этого необходимо
знать параметры производственной функции, темп прироста
трудовых ресурсов, период амортизации, коэффициент ди-
сконтирования.
Размеры конечного продукта определяются производствен-
ной функцией Кобба—Дугласа. По расчетам советских ученых,
производственные функции имеют следующий вид.
Для внутренней частной экономики США
У=2,189е0-0239г7С°’249ТЛ751.	(6.22)
Для сельскохозяйственной экономики США
y-2,30e°’019l^0’3nL°’689.	' ’ (6.23)
Темп прироста трудовых ресурсов определяем на основе
исходных данных в табл. 6.1 и 6.2.
Для внутренней частной экономики США
н = 0,0053,
L= 109,3 е0’0053(.
152
Таблица 6.2
Исходные статистические ряды и оптимальная траектория k(t)
для несельскохозяйственной экономики США
Год	Конечный продукт Y, млрд. долл. (1958 г.)	Основной капитал К, млрд. долл. (1958 г.)	Отработанные человеко-ча- сы L, млрд.	К 1с=- L	£(/ )=6,959е°'02'’61
1947	263,2	186,2	92,9	2,0043	6,959
1948	274,8	193,1	95,2	2,0284	7,1566
1949	274,4	176,6	93,9	1,8807	7,3522
1950	310,5	201,4	96,2	2,0936	7,5540
1951	325,0	214,2	98,7	2,1702	7,7683
1952	333,3	218,5	99,3	2,2004	7,9889
1953	367.8	237,1	100,9	2,3499	8,2158
1954	. 340,9	222,2	97,5	2,2790	8,4406
1955	366,5	253,5	102,0	2,4853	8,6800
1956	374,8	266,7	104,5	2,5522	8,9179
1957	385,5	270,4	103,2	2 6202	9,1706
1958	375,2	244,7	100,6	2 4324	9,4315
1959	410,0	273,2	103,4	2,6422	9,6897
1960	419,8	277,5	104 3	2,6606	9,9646
1961	427,3	273,0	104,3	2,6174	10,2370
1962	457,4	291,0	106,4	2,7350	10,5283
1963	476,5	302,8	108,7	2 7856	10,8268
1964	499,8	323,8	111,0	2,9171	11,1233
1965	546,2	357,9	114,3	3,1312	' 11,4392
1966	577,2	407,2	116,5	3,4953	11.7524
1967	589,7	414,1	!!б,4	3,5576	12,0857
1968	620,4	438,7	117,8	3,7241	12,4288
Для несельскохозяйственной экономики США
п =0,0105,
L = 92,9e0-0105'.
Предполагаем, что норма амортизации
(6.24)
ц = ^-а;0,0769, коэф-
фициент дисконтирования 5 = 0,10. Отыскание оптимального ре-
жима происходит в два этапа: нахождение оптимальной магистра-
ли; построение оптимального режима с учетом ограничений.
1. Найдем оптимальную магистраль.
Имеем следующие формулы для оптимальной траектории
фондовооруженности £(() и оптимального управления й(0 (доля
конечного продукта, идущей на потребление):
Ь( 1 -а)«
ц +«Т 6
, р
«(/)=] -а.-----
153
где объем валового выпуска продукции X задается производствен-
ной функцией F(t):
X—F^K, L, t)=be<>‘KaU>
a
Г=( 1 ~a)X,
где У—конечный продукт,
В рассматриваемом примере размеры конечного продукта
задаются производственной функцией
Y—F(K, L,
Формулы для £, й имеют следующий вид;
*	/	\1 р
'	\ |д_|_п+О J
й,|_,,»+’+£Л>.
(6.25)
(6.26)
Для внутренней частной экономики США из (6.22) и (6.24)
имеем а0 = 2,189, р = 0,0239, а = 0,249, (3 = 0,751. Примем ц =0,0769,
8 = 0,10. Используя формулу (6.25), получим
9O=(o.O7ZX..o Г1-’ ™
По (6.26) определим оптимальную долю продукта, ищущего
на потребление:
O.OTOtO.OQSi+omij =0,8442.
' >	0,0769 + 0.0053 + 0,10
Для несельскохозяйственной экономики США из (6.22) следует;
йо=2,30, р = 0,019, а=0,ЗЦ, 0 = 0,689, «=0,0105.
Примем ц = 0,0769, 8 = 0,10. Применяя формулу (6.25), получим
(\ 1
°’311 -2’30	| 0.689 (,0.02761 Л аса 0,02761 /л рвЧ
0,0769+0,0105+0,10 J е — 6,959е	.	(6.28)
По (6.26) определим оптимальную долю продукта, идущую
на потребление:
' f ’	0,0769+0,0105+0,10
2. Найдем оптимальную траекторию с ограничениями.
Предположим, что 0,5 ^w^l, т. е. минимальная доля, идущая
на потребление, и:=0,5.
Определим границы уу(?),
154
“ 1/Р р
1 е£
с р - (p+x₽)tj_ u-чщо
ч Р+Хр сДх+5 р/р + Х )’ Х Ц +
Для внутренней частной экономики США из статистического
ряда (см. табл. 6.1) имеем
£О=1,8682, Д = 3,7772.
Рассматривая период 1947 —1968 гг., получим
Г=21 год.
В соответствии с соотношением (6.27)
JC(O)=4,3O6, А:(Т) = £(21) = 4.3О6е0’°318'21 = 8,398.
Так как ДсДО), то в рассматриваемом случае выход на
магистраль осуществляется с помощью у10. Точка
моментом выхода на магистраль. Так как
(1—^1 )#0 f "Г
„ ! R , 1	’
является
^10
710= Сое-<₽+1₽’‘ +
(6.29)
то
р/р+к
t ______1 Jn 1 / M0 _ (1 — )gp
10 Xp + P СДХ+3
(6.30)
'де
о
р/Р+х '
1=ц + п = 0,0769 + 0,0053 =0,0822.
Вычисляем:
Mi =0,5;
(6.31)
0,5-2,189
=9,6009;
р/Р+Х 0,0318+0,0822	’
Со = ££ - 9,6009 = (1,8 6 82) °’7 51 - 9,6009 = - 8,0009;
Хр + р = 0,0822-0,751 + 0,0239 = 0,0856;
у10 = ( —8,0009е-о,О856' + 9,6009) 1'ЗЭ1бе0'0318';
'«=-oijtad№P.99'8-W9) = 2,2477;
tj 0 = 2,2477.
В начале третьего года мы должны выйти на магистраль.
155
Для несельскохозяйственной экономики США из статисти-
ческого ряда (см. табл. 6.2) имеем
ка~2,0043, кт = 3,7241.
В соответствии с соотношением (6.28)
£(0) = 6,959,
£(Г) = £(21) = 6,'959-е0-0276'2i = 12,4288.
Так как £0 < А’(О), то и в этом случае на магистраль выходим
с помощью у10. Точка t10 является моментом выхода на
магистраль.
Применив формулы (6.29), (6.30), (6.31), получим:
Cfl = A:g-^!z^=(2,OO43)0’689-10=-8,3872;
(l-aL)gQ_ 0,5 2,30	_ J-
р/Р+л 0,0276^0,0874
Ар + р=0,019 + 0,0874  0,689 = 0,0792;
Х = щ-н =0,0769+ 0,0105—0,0874;
у10=^_ 8,3872e“0,0792t + 10)1,4514е°,о276<;
t 1 In 1 (аа°
10	р+хр сДх+5	р/р+х J
= —!— in —(3,9044 - Ю) = 4,015.
0,0792	-8,3872 v ’	>
В начале пятого года выходим на магистраль.
Проанализируем полученные результаты.
Интерес представляет сравнение k = (t) (реальная траектория
развития фондовооруженности) и £(г) (оптимальная траектория
развития фондовооруженности, полученная теоретически).
На рис. 6.4 и 6.5 изображены k(tj, у10 соответственно
для внутренней частной и несельскохозяйственной экономики
США.
Теоретически на магистраль выходим с помощью у10. Эконо-
мический смысл этого выхода на магистраль состоит в том,
что почти все средства идут на инвестиции, а на потребление
идет минимальная доля.
На основе исходных данных для k(t) (см. табл. 6.1, 6.2)
находим темп прироста Производственных фондов.
Для внутренней частной экономики США имеем
Ц?) = 1,8682е°’0296',
£(/)=4,ЗО6е0-0318'.
156
ms /ж ws мм мм мм i
Для несельскохозяйственной экономики США имеем
fc(/) = 2,0043e°’O243t
£(/)=6,959е0'0276'.
Магистральный темп прироста почти совпадает с реальным
темпом прироста производственных фондов. Не согласуются
между собой начальные уровни.
Рассмотрим оптимальную траекторию фондовооруженности
и оптимальное управление u(t] при различных значениях 3:
£=£(/, 8),
u=il(f, 8), /е[0, Г], Г=21.
Принимаем значения в интервале [0,4];
81=0, 32 = 0,05, 83 = 0,10, 84 = 0,15, 85=0,20,
86 = 0,25, 87 = 0,30, 88=О,35, 89 = О,4О.
Для внутренней частной экономики США имеем:
-2,189, р = 0,0239, сс = 0,249, р=0,751,
/г = 0,0053, ц=0,0769.
157
Вычислим:
k(t a.U( ом° м'4 °’545 ]	e°’O318t-
к	\0,0822+6,- I
uft, 5;)=1_awp;p,i_
v	р + и + 6;	0,0822+6;
При 81=0
£(r, 3X) = 12,43e0,0318', £(0, 3X)= 12,43,
£(T, 5,)-24,24, u(t, 3,) =0,6545.
При a2-0,05
.. % a2) = 6,554e°’O318‘, £(0, 32) = 6,554,
£(T, S2) = 12,78, й(/, a2)-0,7852.
При 83=0,I0
% 83)-4,306e0’0318', £(0, 83) = 4,306,
£(T, 33)=8,3980, H(i, 83)=0,8441-
При 84 = 0,15
£(r, a4) = 3,127e0’0318', ^(0, 54)~3,127,
£(T, 34) =6,0986, u(tr 34) =0,8777.
При 85=0,20
35)-2,4013 e°-0318t, JG(O, S5) =2,4013,
k{T, 35)=4,6833, u{t, 35) = 0,8994.
При 86=0,25
36) = 1,9329e0-03181, JG(O, 36) = 1,9329,
/с(Г, 36) = 3,7697, w(t, 86)=0,9145.
При 37 = 0,30
a7) = l,6O32e0,0318', /c(0, 87)= 1,6032,
k[T, 37)-3,1267, w(?, 87)=0,9257.
Самая близкая к реальным экономическим процессам—это
оптимальная траектория, которая получается при 3 = 36=0,25:
^(0, 36 )-Л0 = 1,9329 -1,8682 =0,0647.
Оптимальная доля, идущая на потребление, в этом случае
составляет й(г, 36) =0,9145.
Для несельскохозяйственной экономики США имеем
ао=2,30, р=0,019, 7=0,311, р=0,689,
158
« = 0,0105, ц = 0,0769.
Вычислим:
/	~	₽f / ft7l„ \1,4-514
k(t, ЗД=Ь ) еР =f °’7153 ) хео.О27бг
V’ l>	^0,0874+ 8(/
’	p-f-rt-f-8;	0.0874-f-3f
При 3,=0
k[t, 31)=21,]2е0'0276', £(0, 31) = 2],12,
к[Т, 8^ = 37,7203, u(t, 8J = 0,5904.
При 82=0,05
k(t, 82)=10,913е°-О27б‘, £(0, 32)= 10,913,
к[Т, 32) = 19,4906, u(t, 82)=0,7394.
При 83?=0,10
k{t, З3)=6,959е0,0276‘, к(Ь, З3) = 6,959,
к(Т, З3)= 12,4288, й(г, З3) =0,8090.
При 34 = 0,15
k(t, 84)=4,953е0*0276', Л(0, 84) = 4,953,
ЦТ, 84) = 8,846О, u(t, 34) = 0,8492.
При 35=0,20
% 35) = 3,743е0'0276', % 35)-3,743,
ЦТ, 35) = 6,6850, й(Г, 35) ^0,8754.
При 56-0,25
k(t, 36) = 2,974е0-0276‘, £(0, 36)=2,974,
ЦТ, 86) = 5,3116, u(t, 86) = 0,8939.
При 37 = 0,30
Ц(, 87) = 2,4424е°’02761, £(0’ 87) = 2,4424,
ЦТ, 87)=4,3621, й(/, S7)—0,9076.
При 38=0,35
k(t, 3s)=2,O5O3e0'0276', k(Q, 38) = 2,0503,
ЦТ, 3S) = 3,66I8, Й(Г, 38) = О,9182.
Для несельскохозяйственной экономики США самая близкая
ггимальная траектория к реальным экономическим процессам
случается при 3 = 38 = 0,35.
Тогда Л(0) - =2,0503 - 2,0043 = 0,0460.
Оптимальная доля, идущая на потребление, в этом случае
ставляет 0,9182.
Глава 7
Задача Эйлера
вариационного исчисления
Достаточные условия оптимальности применяются к одной
из классических задач вариационного исчисления —задаче Эй-
лера. Показывается, что свойства оптимального решения су-
щественно зависят от характера индикатрисы — зависимости
подынтегральной функции х, и) от управления и. Вы- j
деляются и исследуются четыре случая. В последнем из i
них — для одномерного по состоянию х и управлению и случая
выпуклой индикатрисы выводится необходимое условие оп-
тимальности в форме двухточечной краевой задачи для диф- ।
фсренциального уравнения Эйлера второго порядка. Обобщение
на случай произвольной размерности векторов состояния
х и управления и приводит к необходимым условиям оп-
тимальности для задачи Эйлера с использованием условий
Вейерштрасса и стационарности функции f?(f, х, и) по х.
Это-—реализация принципа максимума Понтрягина. Настоя-
щая глава завершается иллюстративной задачей о линии наи-
меньшей длины и негативным примером для задачи Эйлера,
где показывается, что процесс, удовлетворяющий необходимым
условиям оптимальности, может быть, а может и не быть
оптимальным в зависимости от числового значения верхнего
предела интегрирования 7".
§ 7.1.	Постановка задачи и типы ее решения
В качестве еще одного примера применения достаточных ,
условий оптимальности к решению конкретных задач (см. § 5.5)
рассмотрим классическую задачу Эйлера вариационного исчисле-
ния. Задачей Эйлера называют задачу о минимуме функционала
г
>= х, u)dr	(7,1)
о
при наличии связей
х —и	(77)
и граничных условий
х(0)=хо, х(Г)=х15
(7.3)
160
где xe£n-—«-мерный вектор состояния; и — «-мерный вектор
управления (в данном случае размерность вектора управления
/=«); х0, х,—заданные «-мерные векторы начального и конеч-
ного состояний системы; Еп — символ «-мерного эвклидова прост-
ранства.
Помимо векторных уравнений (7.2) на элементы r(t)=(x(r),
u(r)) допустимого множества М наложены ограничения теоретико-
множественного характера: х(г)—-непрерывная и кусочно-диф-
ференцируемая, и(Д— кусочно-непрерывная вектор-функции. Ска-
лярная функция /Д/, х, и) - непрерывная и дифференцируемая
по всем аргументам. Мы ограничимся пока частным случаем,
характеризующимся следующими условиями; n=l, f[t, х, u) = w
множества У‘х и при всех te(0, Т) совпадают соответственно
с числовыми осями X и U, а при 1 = 0 и t = Т представляют
собой заданные точки х0 и х2,
Свойства решения задачи Эйлера в значительной мере опреде-
ляются характером индикатрисы, т. е. зависимости подынтеграль-
ного выражения fQ{t, х, и) от управления и при фиксированных
значениях /их. Именно эту зависимость удобно положить
в основу классификации рещений.
Рассмотрим четыре случая:
1)	постоянная индикатриса, т. е.
/°(/, х,	х);	(7.4)
2)	индикатриса с ограниченной нелинейностью по управлению
f°(t, х, u)=g°(t, х, u) + h®(t, x)w,	(7,5)
где g°(t, x, if)— ограниченная по управлению и в общем случае
:нелинейная функция; Л°(/, х) также в общем случае нелинейная
функция своих аргументов;
3)	линейная индикатриса, когда
У°(/, х, н)=Р°(/, х)+<2°(/, х)ы;
4)	выпуклая индикатриса, когда -^->0.
(7-6)
f Три случая из этих четырех от-
лажены на рис, 7.1.
При исследовании всех этих случа-
ев будем опираться на теорему 5.2.
' Для данной задачи функции /?(/,
X, и) и Ф(х), фигурирующие в форму-
лировке теоремы, имеют вид [см.
‘формулы (5.12), (5.13)]
( R(t, х, u) = ^u-fQ(t, х, u)+^,
(7.7)
&3ак 456
161
Ф(х) = ф(Г, х).
Так как множество Kj, на котором, согласно второму
требованию теоремы, минимизируется функция Ф(х), содержит
единственную точку х(7’)=х1 [граничное условие (7.3)], это
требование автоматически выполняется при любом задании функ-
ции <р(/, х). Поэтому при фиксированных граничных условиях (7.3)
единственным остается удовлетворение условию Iе теоремы 5.2:
R(t, х, w)=max/?(f, х, w).	(7.8)
Рассмотрим, как обстоит вопрос с подбором функции ф(г,
х) и удовлетворением условию (7.8) в четырех указанных случаях.
§ 7.2.	Постоянная индикатриса
В этом случае подынтегральная функция согласно (7.4),
не зависит от управления: /°=/°(б х).
Вид выражения (7.7) подсказывает какой принять нам функ-
ции} ф(г, х). Если мы положим ф(/, х) = С, где С — произвольная
постоянная, то окажется, что — = — = 0 и функция R примет
простой вид R(t, х, н)=— /°(г, х). Максимизация R согласно
(7.8), упрощается, и мы получаем
R(t, х) = тах[—/°(/, х)] =ппп/°(/, x)We(0, Т),
где
х(/)=.argniin/°(r, х) Vte(0, Г).	(7.9)
Допустим, что функция х(г) непрерывна, кусочно-дифференци-
руема и имеют место предельные соотношения
limx(z) = x0, limx(r) = x1.	(7-Ю)
(^0	t-*T
Тогда .пара функций
{х0 при г = 0,
х(г) при Ге(0,	Г),	(7.11)
А- При 1—1
И  ' 	i
й(() = х(г)	’
благодаря условиям (7.9) и (7.10) обеспечивает max R(t, х, и)
при каждом фиксированном значении Спои из-за независимости
162	л
К от и; по л — по построению.
Эта пара (х[г), й(г)) = т является
допустимой (те Л/), так как удов-
летворяет дифференциальному ура-
внению процесса и граничным усло-
виям (7.2), (7.3). С учетом теоремы
5.2 найденный процесс б=(х(г), м(г))—
оптимальный.
Однако случай, когда выполня-
ются условия (7.10), исключитель-
ный, ибо процесс минимизации,
отраженный формулой (7.9), никак
не связан с заданием граничных
условий (7.3). Вследствие их
независимости логично предусмотреть более вероятный случай
невыполнения предельных условий (7.10) (или по меньшей мере
одного из них). Тогда функция, удовлетворяющая граничным
условиям (7.3) и представленная формулой (7.11), будет разрывной
и, следовательно, недопустимой. В дальнейшем процесс оптими-
зации строится в классе последовательностей, используя обобщен-
ную теорему 5.4 о достаточных условиях оптимальности.
Введем в рассмотрение последовательность {х,(г)}еЛ7 непре-
рывных, кусочно-дифференцируемых функций, равномерно ограни-
ченную по (t, з), удовлетворяющую условиям xs(0) = xo, xs(7) = x1
и сходящуюся при Vre(0, Г) к х(г)— функции, определенной
формулой (7-9). Этим требованиям удовлетворяет, например,
последовательность вида
Хо ±5Г.
если
если re [tq, т 1 ],
7), если
(7.12)
график которой дан на рис. 7.2.
Знаки плюс или минус в формуле (7.12) выбираются в за-
висимости от ориентации точек х0, Xj относительно функции
х(г); ^о, Ti — абсциссы точек пересечения кривой х(г) с прямыми
х = х0±^г, х = х,+^(г—Г). Если функция (г, х) непрерывна, то
/°(г, ха(/))->/°(г, х(г)) = пйп/'°(г, х) Vfe(O, Г), j-+oo,
X
и последовательность процессов [х5(г), ws(/)} = xs удовлетворяет
первому требованию обобщенной теоремы 5.4 [см. формулу
(5.38)]
т	т	т
> xs(r), ws(r))d/ -> j"max R(t, x, u)df = f min/°(r, x)df
1 о	0 *’ ы	0 x
при MOO.
163
Так как любой элемент этой последовательности является
допустимым процессом, то последовательность a5={xs(/), ws(/)}
удовлетворяет обобщенной теореме 5.4, т. е. минимизирует функ-
ционал (7.1) на множестве М, представленном уравнением
процесса и граничными условиями (7.2) и (7.3). Такого вида
решения называются разрывными (мы с ними встречались уже
в § 5.5), потому что последовательность непрерывных траекторий
! xs (l)} аппроксимирует в данном случае разрывную функцию
(7.11). Таким образом, оигимум достигается на разрывном
решении, отыскание которого сводится к минимизации подынте-
грального выражения /°(гг х) по х при We (О, Г). Заметим, что
в окрестностях точек t — 0 и t = T последовательность значений
управлений {мД/)) стремится к положительной или отрицатель-
ной бесконечности при 5^ со; это непосредственно вытекает из
формул (7/2), (7.12).
Случай линейной индикатрисы, представленной формулой (7.6),
является частным случаем более общей задачи, рассмотренной
в § 5.5 (при P(t, х) = 0, Q (С х)=1), Поэтому мы его опускаем
и переходим к исследованию задачи Эйлера для случая ин-
дикатрисы с ограниченной нелинейностью по управлению и.
§ 7.3. Индикатриса с ограниченной нелинейностью
В данном случае подынтегральная функция в функционале
(7.1) имеет вид (7.5). Предполагается, что для любых управлений
и можно подобрать такую функцию ^#(/, х), что
|g°(/, х, ы)|	х).	(7.13)
Исследуя этот случай, вновь обратимся к выражению для R;
R[t, х, п) = ^м —Л° (7, x)w—g°(/, х, w) + ^ =
=	X)	(7.14)
В § 7.2 удачной оказалась идея обеспечения независимости
функции R от и, при этом допустимость процесса обеспечивается
только выполнением условия связи (7.2). К сожалению, в данном
случае нет возможности столь простым путем добиться незави-
симости функции R от и однако ее вид упрощается, если
подобрать функцию ф(/, х) исходя из требования
х) = 0.
Тогда функция R{t, х, и), согласно (7.14), примет вид
R(i, х, u)=-g°(t, х, «)+|,	(7.15)"
164
а для искомой функции cp(z, х) получаем выражение
<р(/, х)=ф°(/, Qd^+c(r),
О
(7-16)
где произвольную функцию интегрирования С(/) ради простоты
можно положить тождественно равной пулю.
Учитывая (7,16) и дифференцируя интеграл по параметру t,
получим, согласно (7.15),
/?(/, х, «)= — g°(Z, х, и) +	(l, ^)бф (7-17)
о
Так как функция <р(/, xj уже задана формулой (7.16), далее
в соответствии с теоремой 5,2 необходимо максимизировать
7? и найти x(r), u(z) такие, что
R(l, х((), й(г)) = тах/i(Z, х, и).	(7,18)
Чтобы процесс (х(?), й(г)) был допустимым, необходимо вы-
полнить уравнения процесса (7.2) и граничные условия (7-3),
хотя в общем случае эти требования не обязаны выполняться,
если только исходить из (7.18), Может возникнуть ситуация,
когда отсутствует минималь в классе допустимых решений, тогда
решение достигается на минимизирующей последовательности
(см. § 5.4).
Рассмотрим последний случай. Пусть существуют последова-
тельность допустимых процессов {xs(l), й3(/)}еЛ7 и такая
функция ср (г, х), что при s^>x>
т	т
\R(t, x5(r), ws(r))dr-> Jmax7?(z, х, u)df
О	О х’ “
[второе условие обобщенной теоремы выполняется тривиально
в силу (7.3)], тогда последовательность {х4.(1), й3(г)} миними-
зирующая, т. е.
У(хД(),	(z)) —>inf(х, и) приз->со.	(7-19)
м
Построим такую последовательность, где x3(z)— кусочно-не-
Прерывная и дифференцируемая, й5(?) — кусочно-непрерывная фун-
кции, для которых должны выполняться условия (7-2) и (7.3),
а также (7.19).
Для 5-го элемента последовательности разобьем временной
отрезок [О, Г] на ,s равных частей, получим точки — концы
отрезков, /=1, s, где ts = T. Предполагая, что максимизация (7.18)
осуществлена, считаем известными функции x(z), й(/). При
165
отрезок т;, равный Tis2. На
каждом значении if из точек (i;,
x(i,)) графика x(i) проведем прямую
с наклоном;
x5 = ws(M-
Для отрезков, прилегающих
к концам /о = 0 и ts=T, проводим
прямые до пересечения с кривой
x(i), как показано на рис. 7.3. Око*
ло каждой точки ti+ j отложим
отрезках i, и т; построим ломаную
и зададим ее траекторию s-ro процесса (элемента последо*
вателыаости). Эта траектория непрерывна, кусочно* дифференци*
руема (за исключением конечного числа точек излома), ее
производная имеет конечное число точек разрыва первого
рода. Построенная ломаная проходит через начальную и ко*
нечную точки. Зададим w5(i) согласно формуле (7.2), Тогда
процесс (xs, д5) допустим, так как {х	x$(ij —ломаная,
состоящая из линейных кусков, a иД/) —ступенчатая функция
как производная ломаной; й5(/) делится на две неразрывные
части (для каждого i-го отрезка):
w(ij, если
[w|~s, если
Покажем, что на этой последовательности выполняется пре-
дельное соотношение
г	т
$R(t, xs, iis) di -> f max 7?(i, x, и) di при f-»oo.
0	0	u
Так как, по определению,
R(t, х, w) = max7?(i, x, u),
x, и
TO при Л'->00
т	т
f R(t, xs, gjdi -> J 7?(i, x, ii)di.
о	о
Весь отрезок Г О, T] разобьем на две совокупности больших
отрезков (t;, тД и малых (т;, i, + 1). Обозначим через T's сумму
всех больших отрезков, а через 7;' —сумму всех малых. Тогда
г
f(r, х5, w5)di= f R(t, xs> w5)di+ f R(t, xs, wjdi.
О	7'	T"
Рассмотрим в этой сумме поведение каждого слагаемого при
5^со. В первом слагаемом х5(i)->x(t), т. е. ломаная x5(i)
166
^сходится к своей несущей кривой х(/), а управление йД?) при
’ teT's, равное й(^), стремится к й(7). Сумма больших отрезков
T's при 5->оо стремится к [О, Г]. Отсюда
т
f 7?(С й3)dz -» JA(г, х, w)dr
'		7"	’	.0
Теперь проведем оценку R[t, xs, Hs) на Г'', учитывая выражение
(7.17). Принимая во внимание (7.13), будем иметь
*5- ,	5(0 ,
|7?(с х;., йк)\^ЛЦ(, Xs)+f	х).+ О°(7, tR,
0 (7/	0 (7/
так как xs->x(/J. В итоге видим, что функция R(t,, х5, й5)
ограничена.	,
Соответственно получаем
при оо, так как подынтегральное выражение сходится к огра*
ниченной функции, а область интегрирования сходится к нулю
как 1/з2. Следовательно, сходимость, требуемая обобщенной
теоремой 5.4. имеет место и последовательность {x5(i), £,(/)} —
минимизирующая.
§ 7.4. Выпуклая индикатриса. Уравнение Эйлера
При исследовании этого варианта задачи Эйлера будем
предполагать, что:
1) оптимальный процесс существует среди допустимых, т. е.
(x(r), и(1))еМ;
2) индикатриса выпукла в точках оптимальной траектории,
чему отвечает условие
I Последнее на практике, до получения оптимального решения,
[Проверить невозможно, поэтому обычно предполагается выполне*
Гние более сильного условия
г В отличие от рассмотренных в предыдущих параграфах
₽ -случаев, где решение достигалось на минимизирующей последова*
Цельности, данный случай регулярный.
167
Как и выше, будем опираться на теорему 5.2, согласно
которой если существует процесс (x(t), й(/)) и функция ф(?, х)
такие, что
/?(/, х(/), «(/)) = max R(t, х, и),	(7.20)
- х < л < со
— со < и < ос1
то процесс (х (г), й(г)) оптимальный. В условии (7.20) ограничений
на х и и не предполагается.
Функция 7?(г, х, и), как уже было выше показано, для
задачи Эйлера (7.1) —(7.3) имеет вид
R(t, х, ц) = ^и—/°(г, х, м) + 5.
у	1 дх у	1 ol
Если она, непрерывна и дифференцируема, то необходимыми
условиями максимума при отсутствии ограничений на х и и бу-
дут:
1)^
дх
Л - х dR
=4') =0; 2) —
,	ни
=0.
(7.21)
Чтобы функция R была непрерывной и дифференцируемой
в точке х, й, надо, чтобы: а) функция х, w) была
непрерывной и дифференцируемой; б) также были непре-
рывны и дифференцируемы. Это означает дважды дифференциру-
емость функции ф(г, х) в точке х, й.
Введем в рассмотрение функцию
Ф(') = ^	,	.	(7-22)
' z ох л = л(,)
и, учитывая (7.22), представим второе условие (7.21) в следующем
виде:
ЙЛ =£<р
ди i, а дх i ди а ' ди х, а
Первое необходимое условие (7.21) дает
8R
<?2Ф
дх2
W- —
52<р
„ + di дх
(7.23)
Так как процесс х, й допустимый, имеет место соотношение
(7.2), в силу чего первое и последнее слагаемые в правой части
(7.23) представляют полную производную функции ф (/), т, е,
= Ф(')	(Г24)
С учетом (7.24) выражение (7.23) примет следующий вид:
8 ф с2ф d 5<р(с, х)
дх2 x+dt+5x d( дх
168
ал
дх
а необходимые условия оптимальности таковы:
5R
дх
8R
&
ИЛИ
(7.25)
(7.26)
Выполнение необходимых условий оптимальности привело
к системе из двух уравнений (7.25) и (7.26) с тремя неизвестными
функциями: -т((), wQ), ф(г). Добавляя уравнение процесса и гра-
ничные условия (7,2) и (7.3), получим систему трех диф-
ференциальных уравнений с тремя искомыми функциями и двумя
граничными условиями. Исключим из указанной системы уравне-
ний вспомогательную функцию ф(^). Для этого продифференци-
руем по г уравнение (7.26) и вычтем из него (7.25), Учитывая,
кроме того, что х=й, получим
d df°(t, х, и)
df ди
Пм)
=0
(7.27)

и граничные условия
х(0) = хо, х(Г) = х!.	(7.28)
Уравнение (7.27) впервые было получено Л. Эйлером в качестве
необходимого условия, которому должна удовлетворять функция
состояния процесса л (г) для задачи (7.1)—(7.3). Уравнение
(7.27) -второго порядка, поэтому ему отвечают два граничных
условия (7.28). Действительно, пользуясь правилом дифференци-
рования сложной функции и учитывая, что частная производная
функции /°(г, х, и) по управлению w определяется при й = х,
получим
d2f° „ д2/*, й2/0 df°
~я' 2 х д "-~х	- а,--
0U СА7.Ш oudt ()х
-о,
(7.29)
и = х
при этом коэффициент при старшей, второй, производной отличен
д2
от нуля, так как, по условию, -^->0,
169
Общее решение дифференциального уравнения (7.29) x = x(t,
Ci, С2) содержит две произвольные постоянные и является
дву параметрическим; семейством кривых. Среди этого семейства
4 нужно выделить кривую, удовлетворяющую граничным условиям
(7.28).
Для определения постоянных интегрирования С\ и С2 имеем
систему двух алгебраических уравнений с двумя неизвестными
Если окажется, что найденное решение системы (7.30) единствен-
ное и, кроме того, по предположению, оптимальный процесс
существует, то найденное решение оптимальное.
Можно получить более общие необходимые условия, сняв
сделанное в начале главы предположение о том, что размерность
вектора состояния х равна единице (и=1). Будем рассматривать
общий случай, когда л = г>1. В данном случае требование п — г
обусловлено векторным уравнением процесса (7.2).
Введем обозначение
Н(г, ф, х, «)= £	х, и)=фи-/°(/, х, и), (7.31)
t = i
где фи обозначает скалярное произведение соответствующих
векторов; — /с-е компоненты этих векторов.
Функция H{t, ф, х, и), определенная формулой (7.31), носит
название функции Гамильтона.
Для задачи Эйлера при п > I имеем
х> °)= Z	х’ и) + 77’	<7'32)
или, учитывая (7.31),
«(' * ")=»('	")+£•	(7.33)
Для максимизации функции 7?(г, х, и) по х необходимо,
чтобы достигался ее максимум по и при х = х(/). А так как
функция ср(/, х) не зависит от управления н, то исходя из (7.33)
получаем
u(t, ф, х) = argmax Я (f, ф, х, u) = argmax /?(/, х; и) (7.34)
и	и
.	I Зф	X
(напомним, что ф = --	), т. е. в точках оптимальной
ох
траектории х = х(/) функция Гамильтона должна иметь максимум
по управлению и.
170
Условие (7.34), записанное в виде
H[t, ф, х, й) = шахН(г, ф, х, й),	(7.35)
называется необходимым условием Вейерштрасса.
Обратимся к необходимым условиям стационарности функции
7?(/, х, и) по х:
В соответствии с (7.32) получаем
3R _ у Э2ф _ 5У°(г, х, и) <Уф _q
k=l8XSSX^k 8х> etSxJ X=S(;)
или, учитывая (7.2), преобразуем:
у д/йф\^_|_з/0ф\	_ 5/°(с х, й)
1	x = -w	.Эх,
откуда имеем
J=l, «
Итак, кроме уравнения Эйлера (7.27)
условия оптимальности:
условие Вейерштрасса
ф, х, й) = тахН(/, ф,
условие стационарности функции R по
&R
получены следующие
х, й);
dxj
=0, у=1, п;
(7.36)
х
уравнения процесса
/=1, «;
граничные условия
' х(0)=хо,
Соотношения (7.36) носят
оптимальности для задачи Эйлера в форме принципа максимума
Понтрягина. Ниже этот метод оптимизации управляемых систем
будет изучаться подробно.
Если из условия Вейерштрасса найти u(t, ф, х), то необходимые
условия оптимальности примут вид
с ; _sf>’
х[Т) = х1.
название необходимых условий
, j — 1, п;
Xj.
<7.37)
X  = U :
171
1
Таким образом, получена система 2п дифференциальных
уравнений первого порядка (7.37) с 2 и неизвестными фД/)
и 2п граничными условиями (в векторной форме) х^(0) = хо,
x(7") = xf, позволяющими, аналогично системе уравнении (7.30),
определить произвольные постоянные интегрирования. Решив
систему уравнений (7.37), найдем пару вектор-функций х(/), ф(/).
Вектор управления u(Q получим по формуле (7.34):
й(/) = п(п ф(/), х(0),
причем пара век гор-функций x(t), й(:)еМ—допустимый процесс.
В заключение отметим, что необходимыми требованиями
выполнения условия Вейерштрасса являются
Это соответственно дает
оптимальности Лежандра.
У/=1, и, не выполняется,
системы уравнений (7.37)
мал ь пой.
при /=1,я необходимые условия
й2
Если условие Лежандра	> 0
й, й
полученная в результате решения
траектория будет заведомо неопти-
§ 7.5. Дальнейшее исследование оптимальности процесса.
Задача о линии наименьшей длины
Гарантировать оптимальность процессов, полученных в резуль-
тате решения уравнения Эйлера (7.27) или системы дифферен-
циальных уравнений (7.37) с граничными условиями (7.3) в обоих
случаях, вообще говоря, нельзя, так как при этом выполнены
только необходимые условия. Чтобы ответить на вопрос,
является ли найденный процесс оптимальным, необходимо про-
вести дальнейшее исследование. При этом можно выделить
два подхода.
Первый подход основан на доказательстве существования
и единственности оптимального процесса. Однако факт единствен-
ности не всегда имеет место.
Второй подход состоит в доопределении функции (p(t, х)
в теореме 5.2. При этом следует учитывать, что необходимые
условия (в форме принципа максимума) задают не всю функцию
в точках оптимальной траектории.
(р(/, х), а только ф(/) = |^
Во всем остальном функция ф(/, х) свободна.
172
В? В качестве примера, иллюстрирующего процесс дальнейшего
* исследования на оптимальность, рассмотрим задачу о линии
наименьшей длины.
Пусть на плоскости (t, у) заданы точки A(tA, у4) и 13(/в,
ув). Среди всех пиний на плоскости, соединяющих эти точки,
s требуется выбрать линию наименьшей длины. Из элементарной
I геометрии известно, что это прямая. Покажем, как получить
г этот результат обращаясь к изученным методам оптимизации.
L Бесконечно малый элемент длины дуги некоторой линии равен
I.	,________ I /. \2
ds = x/(dy)2 + (d/)2= h+y-^j d/ = 4//1 +u2dt,
t где y = u.
f. Соответственно для непрерывных и кусочно-дифференциру-
емых линий можно записать
£	'в
(	У = J У1 +w2d/ -»min,	(7.38)
if
|	y = w	(7.39)
I при условии
I	y(G)=X4,	(7.40)
t Непосредственная проверка показывает, что условие выпук-
f лости индикатрисы ^г = (1 + и2) 3/2 > 0 выполняется.
( Составим для задачи Эйлера с выпуклой индикатрисой
г (7.38) — (7.40) уравнения принципа максимума. Роль состояния
( здесь	играет	у.	В	соответствии с (7.36) получаем
 Ф=“^=4х/ЬН?=0;	(7.41)
су 5т
у=м;	(7.42)
il^argmaxf^H —1+н2);	(7.43)
y(/a)=Z4, ЖМ’в-	(7-44)
Уравнение	(7.41)	сразу дает ^-=const = C]. Осуществляя макси-
мизацию по и согласно условию (7.43), видим, что ограничений
на и при этом нет. Следовательно, максимум может достигаться
д Н
в стационарной точке, чему отвечает требование — = 0. Это
и и
дает нам Cj-----г и —0, откуда
ч/1 + «2
w=^=; Q * ±1.
(7.45)
173
Обеспечивает ли полученное значение (7.45) максимум функции
<0. Непосредст-
й
д2
Гамильтона по и, определим из требования у-у
венное вычисление приводит к положительному ответу, так как
—(1+н2)-3/3 <0 при любом значении и.
Интегрирование уравнения (7.42) с учетом (7.45) дает
у(0=~С‘
2 ‘
Отсюда видно, что искомая линия —прямая. Произвольные
постоянные Cj и С2 определяются из граничных условий (7.44),
что приводит к системе двух алгебраических уравнений:
Ул + ^2 ~ У А у
/у=“^в + С2-.Ув-
V 1 —
Решение этой системы имеет вид
Г	Ул ~Ув
С2 =
(7.46)
так,
= ф(7), то будут выполняться
и) по х, и:
— 0; б) R(t, х, й) —max/?(z, х, и).
(лУв~{вУл
1л — гв
Если tA tB и имеет место необходимая предпосылка ±1,
то й, согласно формуле (7.45), принимает конечное значение.
Искомое уравнение прямой:
у/Л Ул ~Ув . ^лУв ~ 1в'Ул
U Гл-‘в
Согласно первому подходу, нетрудно видеть, что выражение
(7.46) определяет оптимальное решение. Это вытекает из того,
что только оно удовлетворяет необходимым условиям оптималь-
ности в форме принципа максимума Понтрягина, задавая прямую,
а через две точки можно провести только одну прямую,
Оптимальность найденного решения (7.46) можно доказать
и опираясь на теорему 5.2. Это отвечает второму подходу.
Выше было показано, что если функцию p(z, х) задать так,
чтобы имело место требование у
необходимые условия максимума функции R (г, х,
. 8R
а)
174
<• Очевидно, этим условиям отвечает задание ! функции ф в виде
ф(г, у) = ф(/)у,	(7.47)
так как для исследуемой задачи о линии наименьшей длины
функция состояния обозначена через у(г). В данной задаче
ф = С[= const, поэтому можем записать в соответствии с (7.47)
И (7.7)	ф(*,	С7'48) /г(г, у, и) = фи--/1 -ум2,	(7.49)
Согласно теореме 5.2, должно иметь место соотношение
/?(г, у, и) = тахЛ(г, у, и).	(7.50)
















функции 7? совпадает с функцией
Выражение (7.49) для
Гамильтона [см. формулу (7.33) ], так как для принятой функции
г), согласно (7.48), различающее 7? и Н слагаемое ~
обращается в нуль. Таким образом, /?(/, у, и) = Н(ф, и). Заданное
формулой (7.48) выражение для функции ф(Л, у) обеспечивает
только условие стационарности ^=0. Но из формулы (7.49)
видно, что функция вообще не зависит от у (т. е. условие
стационарности выполняется при любом значении у); следо-
вательно, при любом у при фиксированных значениях фин для
7? будет достигаться и максимум, и минимум. Тем самым
выполняется условие (7.50), вытекающее из теоремы 5.2.
Итак, для поставленной задачи найден оптимальный процесс
(7.46) и двумя способами показано, что он действительно
оптимальный.
§ 7.6.	Негативный пример
В §7.5, используя теорему 5.2, проиллюстрирована' возмож-
ность доказательства оптимальности процессов, удовлетворяющих
необходимым условиям в форме принципа максимума Понтря-
гина, и показан способ этого доказательства.
Ниже мы рассмотрим пример задачи Эйлера, для которой
удовлетворяющий необходимым условиям процесс может быть
оптимальным или неоптимальным в зависимости от исходных
параметров.	.
Рассмотрим задачу
Т
.У — j (w2 —x2)dt-> min,	(7.51)
о
х = и,	(7-52)
175
х(О) = х(Т) = О.	(7 53)
Величину Т считаем заданной, но заранее ее не фиксируем.
С / ° д f ®	d д
Составим уравнение Эйлера	= 2w, — =—2х, ~-^г-=2й = 2х.
би	бх	dr ди
В соответствии с формулой (7.27) получаем дифференциальное
уравнение
2х + 2х = 0	(7.54)
с граничными условиями (7.53).
Для нахождения общего решения однородного дифференци-
ального уравнения второго порядка с постоянными коэффици-
ентами (7.54) составим характеристическое уравнение
р2 + 1=0.
Его корни , pr; 2 — + I комплексно-сопряженные, в этом случае
общее решение дифференциального уравнения (7.54) примет вид
х(/) = Л cos t + B sin
где А и В—произвольные постоянные интегрирования.
Учитывая граничное условие х(0) = 0, получим х(0) = Л = 0,
откуда
х(г) = В sin г.
'Из второго граничного условия (7.53) х(Е) = 0 имеем
x(r)=5sinr = 0.
Здесь возможны два случая: 1) если	где £=1, 2, ...,'
то 5=0, так как sin 7V0; 2) если Т=кп, то граничное условие
х(7) = 0 удовлетворяется при любых В, так как sinT=0.
Если Т=кк, то имеется бесчисленное множество экстремалей
х(7) = 5sin I (рис. 7.4).
Итак, получим три случая:
1)	Г<п, имеем единственную экстремаль х(Г)=0;
2)	Т=тр имеем бесчисленное множество экстремалей x(z) =
= 5sin t любой амплитуды В;
3)	2я>Т>л, имеем единственную экстремаль—нулевую,
и т.д.
Найдем значение функционала (7.51) на экстремали в этих
случаях.
В первом и третьем случаях _/=>(х, й)=0, во втором
х = 5sin Л
й = Всо$1,
Г	7’	in
J = f (w2-x2)d? = 52f (cos2 г — sin2 t)d/=52 j cos2zdr = 0.
bo	о
Покажем, что при Тж нулевая экстремаль не является;
оптималью. Чтобы доказать это, достаточно построить допусти-:
176
Рис. 7.5
мый процесс, для которого < 0. Построим его следующим
образом. Синусоиду х = £sin t в точке г = п/2 разрежем по
вертикали пополам и сдвинем ее в правую половину до точки
Т (рис. 7.5).
Уравнение построенной траектории
5sin Г, если ,
’	2
х*(г) = < В, если t = Т—",
/fsin (Г + Т—it), если 1>1^ = Т—
Вычислим в этом случае значение функционала:
г
J * =	— )' [(х*)2 —(х*)2 ]dr.
о
Разобьем отрезок интегрирования на три части:
5	ri
= |	[(x*)2-(x*)2]dr + f [(х*)2 -(х*)2]dr +
0		п
т	2
+ H(x*)2-(x*)2]dr	(7.55)
б
Учитывая, что подынтегральное выражение в (7-55) явно от
времени не зависит, первый и третий члены можно объединить.
В результате получим
я	т-5
./* = J/?2 (cos2 г-sin2 r)dt+ f (-T?2)dr = -52(Г-тг)<0.(7.56)
0	п
Z
Процесс (х*, и*) допустим: он удовлетворяет уравнению (7.52)
и граничным условиям (7-53) по построению. Значение функциона-
ла (7.56) отрицательное, тем самым при Тж получен процесс
(x*(r), w*(r)) среди допустимых, которому отвечает лучшее значе-
ние функционала У*, чем для экстремали, где J =0. Следо-
вательно, найденная экстремаль х(Г) не отвечает оптимальному
процессу.
177
Покажем, что если Т>~.. то экстремаль х(г), w(z) является
оптимальным режимом. Как и выше, будем опираться на
теорему 5.2 и возможность достраивания функции ф(г, х).
Вспомним общий результат. Решением системы уравнений
(7.36) с граничными условиями х(0) = х(7) = 0 [или, что, по
существу, эквивалентно, уравнения Эйлера (7.27)] являются функ-
ции (х(Г), й(г))еМ и функция ф(0. Если ввести фигурирующую
в теореме 5.2 функцию
Ж х, u)=^^u-/°G, х, u) + ^^,	(7.57)
то найденное решение обладает следующими свойствами:
1) выполняется условие стационарности функции R по х:
'	?	=0;
СХ х. й
2)	(г, х, ц) = шах 7? (г, х, и) в точках оптимальной траектории.
Эти свойства имеют место для любой функции ф (г, х), но
йф	I
такой, что —	= ш/.
ОХ
Чтобы доказать оптимальность найденного режима х(Г) =
= й(/) = 0, надо определить функцию <р(Л х) таким образом,
чтобы функция /?(г, х, н), заданная выражением (7.57), имела
максимум не только по и, но и по х.
Удобно задавать функцию ф(/, х) в виде
ф(г,х)=ф(/)х + ф1(х-х(г))!	(7.58)
.где ф( — произвольная функция, обладающая тем свойством, что
о = 0 [в этом случае выполняется требуемое условие
Простейший вид функции ф (г, х), удовлетворяющей условию
(7.58), таков: ф(/, х) = ф(г)х. В самом деле, в рассматриваемой
задаче х(/) = й(/) = 0 = ф(/)> значит, (р = фх = 0; следовательно, сог-
ласно (7-57),
/?(/, х, w) = — f0(t, х, и)~ — и2-\-х2	(7-59)
и —	=2х|х=о=0. Вид функции (7-59) показывает, что при
любом фиксированном значении w, в том числе и при й= О,
в точке х = х = 0 достигается не максимум, а минимум функции
R(t, х, и) по х. Следовательно, выбор функции ф(Г, х) в наиболее
простой форме (7-58) неподходящий.	’
US
Несколько усложняя функцию <р(Г, х), зададим ее в
ф(Г, х) = ф(/)х+<т(Г)(х-х)2,
или, учитывая, что х=ф(Г)=0, получим
Ф(г, х) = о(г)х2,





где функция о (г) подлежит дальнейшему определению.
Сформируем функцию R(t, х, и), для чего вычислим
производные от выражения (7.60):
виде
(7.60)
частные
= 2ст(Г)х, — = д(0х2.	(7.61)
ох	ЙГ
Тогда, согласно (7.57) и (7.61),
R(t, х, и) = 2<зхи — и2-\-х2-\-<ух2,



или
R(t, х, w)= — u2-\~(d + 1)х2 +2<зхи.	(7.62)
Из построения функции ф(/, х) при любой функции <?(/)
выполняются условия стационарности


8R
5х
^о = 0;
й=0
3R
5и
г =о=0,
й = 0
а функцию сг(Г) надо выбрать так, чтобы при x = w = 0 функция
R(t, х, и) была не только стационарной по х, и, но и имела



максимум.
Необходимым и достаточным условием существования макси-
мума функции двух переменных R(i, х, и) по х, и (миниму-
ма- -/?(/, х, и)) при каждом фиксированном I являются соотно-
шения (нижние индексы соответствуют частным производным):
I) -^>0, -7?вя>0;	:
2)	~^хи >0.
Ъх Ruu
В соответствии с (7.62)—(7.64) имеем
— Rxx= ~2(с+ 1); —/?ци = 2, — Rxu—— 2о,
^ = ЛххЛяв-Лх«= -4(ст+1)-4о2>0.
(7.63)
(7.64)
В предельном случае при 0 = 0 функция <т(г) должна удовлетво-
рять дифференциальному уравнению
ст+ ст2+1=0
или
^=-(1 + <т2).	(7.65)
Разделяя в уравнении (7.65) переменные, получаем
179
а интегрирование дает
arc tg ст (/) = С ~ t,	(7.66)
где С — произвольная постоянная.
Вычислив значение тангенса от
обеих частей соотношения (7.66),
получим общее решение уравнения
(7.65):
a(0=tg(C-0=-tgG-O. (7-67)
Для того чтобы решение (7.67) имело смысл, должны
выполняться, условия t — С<-, Т<п, откуда Т<С-\--<тс (рис.
7.6).
Постоянную С надо выбирать таким образом, чтобы соотно-
шение (7,67) имело место на возможно большем интервале
изменения аргумента I, вплоть до т^С+-. В этом случае
выполняются необходимые и достаточные условия (7.63) — (7.64)
максимума функции 7? (в предельном варианте), и при Г<тс
экстремаль х(/) = й(/) = 0, являющаяся решением уравнения Эйлера
(7.27), отвечает оптимальному режиму.
Глава 8
Метод Лагранжа — Понтрягина
для непрерывных управляемых
процессов
Излагаемый в этой главе метод решения оптимизационных
задач является одним из наиболее эффективных в теории
оптимального управления.
В основе этого метода лежат необходимые условия опти-
мальности. Они позволяют выделить из множества допустимых
процессов подмножество, состоящее из процессов, которые
потенциально могут быть оптимальными. Таким образом, при-
менение необходимых условий дает возможность «сузить»
исходное множество процессов. Полученное подмножество «по-
дозрительных» на оптимальность процессов в широком классе
задач оптимального управления представляет собой единствен-
ную траекторию. Если для данной задачи дополнительно извест-
но, что оптимальный процесс существует, то эта единственная
траектория и будет оптимальной.
С математической точки зрения данный метод состоит
в сведении исходной задачи оптимального управления к реше-
нию краевой задачи для системы дифференциальных уравнений.
Эта задача по сравнению с исходной, как правило, значительно
проще, что позволяет получать ее аналитическое или численное
решение.
В настоящей главе метод Лагранжа — Понтрягина излагается
для задач оптимального управления, в которых отсутствуют
ограничения на переменные, описывающие состояние системы,
Исключение составляют начальное и конечное состояния систе-
мы, которые могут быть по условию задач либо заданы, либо
на них накладываются другие условия. Этот метод допускает
обобщения и на случай, когда ограничения на состояние заданы
в течение всего времени протекания процесса. Однако изложе-
ние этого материала выходит за рамки книги.
Вывод соотношений метода Лагранжа — Понтрягина приводит-
ся с помощью полученных в гл. 6 достаточных условий
оптимальности. Это позволяет упростить процедуру вывода. Так
как полученные соотношения являются необходимыми усло-
виями оптимальности, из-за сложности математического аппара-
та они приводятся без специального обоснования. Формулировки
соответствующих теорем даны без доказательств.
181
§ 8.1. Вывод уравнений метода Лагранжа — Понтрягина
Рассмотрим следующую задачу оптимального управления
непрерывной системы. Пусть модель системы задана соотноше-
ниями
х‘=/'(/, х, и), z= 1, 2, ..../?,	(8.1)
где х = (х1, ..., х")— n-мерный вектор состояния системы; и = (м*,
..., и') — r-мерный вектор управления. На управление может быть
наложено ограничение
иб(Д	(8.2)
где (/е7?г — некоторая область возможных значений управления,
которая может изменяться во времени.
Соотношения (8.1) представляют собой систему дифферен-
циальных уравнений. Будем считать, что задано состояние
системы в начальный момент времени
х‘(0) = х;о, г=1, 2, ..., п,	(8.3)
которое можно рассматривать как начальное условие для системы
(8.1)_ Кроме того, может быть задано состояние системы
в конечный момент времени t=T
х‘(7) = Хц, /=1,2, т,	(8.4)
представляющее собой дополнительное ограничение на процесс
(х(г), и (г)), протекающий в системе. Ограничения (8.4) могут
быть заданы не обязательно по всем переменным, а лишь по
некоторой их части—в данном случае по первым т переменным.
Будем считать, что качество процесса оценивается функциона-
лом
г
>=	°(Г, х, u)df + F(x(7’))->min.	(8.5)
о
Если правый конец траектории процесса зафиксирован с помощью
соотношений (8.4), то второе слагаемое в (8.5) является величиной
постоянной и. следовательно, не влияет на решение оптимиза-
ционной задачи.
Требуется определить процесс (x(f), «(0)> удовлетворяющий
ограничениям (8.1) —(8.4) и минимизирующий функционал (8.5).
Такой процесс будем называть оптимальным.
Рассматриваемая задача является частным случаем общей
задачи оптимального управления, сформулированной в гл. 2.
В ней по сравнению с общим случаем отсутствуют ограничения
на состояние системы, что будет использовано в дальнейшем.
Пусть (х(7), й(/)) — допустимый процесс, удовлетворяющий те-
ореме 5.2 о достаточных условиях оптимальности. Это означает,
что существует функция (p(i, х), обладающая тем свойством,
что выражение
182
R(t, x, и) = 5+ £ х’ и) —У°(Л х, и) (8.6)
СТ vx
достигает при всех /е [О, Г] максимума по переменным х,
и в точке (х(Г), й(0), а функция
Ф(х) = ф(7) x)+F(x)	(8.7)
принимает минимальное значение при х = х(7). Если заданы
условия (8.4) на правом конце траектории, то условие
минимума выражения (8.7) превращается в тривиальное,
так как множество, на котором задана функция Ф(х),—
единственная точка.
Так как рассматриваемый процесс (х(Г), й())) удовлетворяет
перечисленным достаточным условиям, то он является оптималь-
ным. Выведем некоторые следствия из сделанных предположений.
Дополнительно предположим, что функция <р(Л х) имеет
- /Л	х)
в точках х = х(Г) непрерывные вторые производные $ Л •
Введем обозначение
= i= 1, 2, ..., п.	(8.8)
Здесь вектор-функция ф(/) = (ф,(/), ф2(Г), » фп(0) является при
каждом фиксированном t значением градиента функции ф (/, х)
в точках оптимальной траектории х = х(7).
Введем в рассмотрение вспомогательную функцию—функцию
Гамильтона:
х, ф, u)= £ ф/'(г, х, u)-/°(r, х, и).	(8.9)
г-1
С ее помощью выражение (7.6) может быть записано в виде
Л(г,х, И)=^+Н(г,х,^,ц).	(8.10)
dt	дх	:
Так как процесс (x(Z), 0(f)) удовлетворяет достаточным усло-
виям оптимальности, то, согласно условию 1° теоремы 5.4, при
любом /е [О, Г]
7?(/, х(г), й(/))^7?(/, х, и)	(8.11)
для всех (х, и)еЕ'. Отсюда, в частности, вытекает, чтр неравенство
Л(/, х(0, й(О)>^(Л х(0, и)
выполняется для всех допустимых значений управления ие[7.
Сравнивая последнее неравенство с (8.10), получаем в качестве
следствия [так как слагаемое — в (8.10) не зависит от и], что
л.	8(
Н(1, х(Г), ф(0, й(/))^7/(г, x(t), ф(Г), и).
183
Это неравенство говорит о том, что выражение Н(г, х(0, ф(г), и),
рассматриваемое при каждом фиксированном значении te [О, Г]
как функция от и, достигает максимального значения при u = fi(/).
Это обстоятельство может быть выражено в следующей форме:
H(r, x(t), ф(/), й(г)) = тахН(г, х(1), ф(/), и).	(8.12)
иг С1
Таким образом, в качестве следствия из существования
функции ф(/, х), удовлетворяющей зеореме 5.4, получено, что
существуют такие функции ф(?) = (ф,(0, ф„(0), что выражение
H(j, х, ф, и) при х=х(0 и ф = ф(г) удовлетворяют условию
максимума (8.12).
Теперь воспользуемся справедливостью неравенства (8.11) при
и = й(0 и произвольном значении х:
2?(Г, х(0, й(0)> 2?(/, х, й(0).
Из этого неравенства следует, что функция J?(i, х, й(0)
при х = х(0 достигает максимального значения. Так как в рас-
сматриваемой задаче оптимального управления ограничений
на состояние системы вектор не накладывается, то в точке
максимума х = х(0 частные производные функции 7?(/, х(г), й(0)
обращаются в ноль:
адщкщ,й(о)=о	п
5х!	. ’	’
Преобразуем полученное соотношение. Подставляя в него (8.6),
получаем, что при х = х(г) должно выполняться равенство
d2<P(t, ЧФ . у f	х(0) , j( - , . - f ~ cpp, хр))хр), й(7)Л _
5tdx'	I	2 1’ А 1 Я g i gxi I
__x(0, йр))	(8 13)
i= 1, 2, n.
Левую часть выражения (8.13) представим в виде двух
слагаемых:
5j=62<p(f, х(р)+ у <)2(рр,хр))^	.	п (8 14
dtdx1	дх'дх!
и
5?= у	ЧУ, Op)) x(f), 0(0)	2
1	oxJ'	Sx:	5x‘	’
Для преобразования выражения (8.14) вычислим производную
ф;(0. Согласно (8.8), будем иметь
Г ('Л-аЛ9<₽('’	;~1 ? и
184
( Пользуясь правилом вычисления производной сложной функции,
Г получим
Ф,(0=гМад>+ j	/=|,2....».
cwx	dx*oxJ
Так как х(г) удовлетворяет вместе с й(г) уравнениям процесса
(8.1), то
*(0, «(0)> 7 = 1, 2> п-
Сопоставляя теперь последние два равенства с (8.14), получим
S’ =ф;5 1=1, 2, П.
Заменив теперь в выражении (8.15)	на ф;.(г) с учетом
(8.9), нетрудно получить, что
S2_^4t, ад, <ад, и(Ц) г=1 2 я
1	(Зх1 ’	’ ’	’
Теперь соотношение (8.13) можно с учетом (8.14), (8.15) и получен-
ных выражений для 5* и St записать в виде
ф g/адад, ф(<), ад) .	2( п	6)
Ёх'	’
Следовательно, из существования <р(г, х) вытекает, что зада-
ваемая равенством (8.8) функция ф(/) удовлетворяет вместе
с х(/)} й(?) системе уравнений (8.16).
Воспользуемся теперь условием Т теоремы 5.2. Как следует
из этого условия и соотношения (5.13), в конечный момент
времени t = T для траектории х(г) справедливо неравенство
(р(Т, х(7))+Нх(ЛКч>(Г, х) + Дх)	(8.17)
для всех х, принадлежащих множеству возможных состояний
системы при t = Т.
В рассматриваемой задаче множество У‘х задается условием
(8.4), согласно которому первые m координат хи, х2[, ...,
вектора х(7) заданы, остальные же могут принимать произволь-
ные значения. Тогда функция Ф(Г, х)=ср(Г, х)+Л(х) будет зави-
сеть от п-m переменных xm+l, хт + 2, хп. Так как на эти
переменные никаких ограничений не накладывается, а вследствие
(8.17) функция ф(/, х) достигает минимума при х = х(Т), то
имеют место равенства
/7Ф(Т, х(Т’)) а 	। 1	, а
—  Д~а=0, i = w + l m + 2, ..., п,
ЁХ>
или с учетом (8.17)
бф(Т х(7))	5F(x(7)) .	, .	, _
v ? =-------А-А f = m + l, m + 2, ..., n.
Sx‘	Sx1 ’
185
Но левая часть последнего соотношения есть, согласно (8.8),
Следовательно, это соотношение принимает вид
ф;(7>	i=m + \,m + 2,	п. (8.18)
Соотношения (8.18) называются условиями трансверсальности.
Полученные в настоящем параграфе результаты можно сфор-
мулировать следующим образом, Пусть функция <р(ц х) и процесс
(х(0, й(/)) удовлетворяют теореме 5.2. Тогда существуют такие
значения вектор-функции ф = ф(/), которые вместе с (х(г), й(/))
удовлетворяют условию (8.12) максимума функции H(t, х, ф, и)
и системе уравнений (8.1), (8.16), Кроме того, в начальный
момент времени 1 = 0 для траектории х(г) выполнены начальные1
условия (8.3), а в конечный момент времени t = T переменные
х(г) и ф(() удовлетворяют условиям (8.4), (8.18). Перечисленные
условия (8.1), (8.3), (8.4), (8.12), (8.16), (8.18) представляют собой
соотношения метода Лагранжа — Понтрягина, позволяющего по-
лучить решения задач оптимального управления.
§ 8.2. Принцип максимума Понтрягина
Соотношения § 8.1, выполняющиеся на оптимальном процессе,
были введены как следствие теоремы 5.2. Эти результаты могут
быть получены и без предположений данной теоремы, а лишь
исходя из оптимальности процесса (х(Г), й(/)). Иначе говоря,
полученные соотношения являются необходимыми условиями
оптимальности процесса (х(/), й(/)).
Отсюда следует, что данные свойства, характеризующие
оптимальный процесс, могут быть использованы для «сужения»
исходного множества М допустимых процессов выделением из
него только тех процессов, которые этим свойством обладаю'!'.
Как мы увидим дальше, совокупность приведенных условий
позволяет, как правило, выделить единственную Траекторию х(0
из множества допустимых траекторий. Если при этом еще
известно о существовании оптимальной траектории, то тем
самым х(/) и отвечающее ему управление й(?) и есть решение
задачи оптимального управления.
Комплекс условий, которому должен удовлетворять оптималь-
ный процесс, называется принципом максимума Понтрягина.
Сформулируем его в виде теоремы.
Теорема 8.1 (принцип максимума Понтрягина). Пусть (х(/);
й(/))—-оптимальный процесс в задаче оптимального управления
(8.1)—(8.5). Тогда существует вектор-функция ф(О=(ф[(О, ф2(0,
..., ф„(0), удовлетворяющая вместе с данным процессом следующим
условиям:
1°. Функция Н(1, х, ф, и) [см. (8.9)] достигает максимального
значения по и при x = x(Z), ф = ф(г) на значении и = й(/) при всея
te[O, Т] [см. соотношение (8.12)].	<о
186
2°. Переменные ф(0 удовлетворяют системе дифференциальных
уравнений (8.16).
3°. В конечный момент времени t=T оптимальная траектория
удовлетворяет условиям (8.18).
Правые части уравнений (8.1) можно используя функцию
Н(Г, х, ф, и), введенную с помощью соотношения (8.9), привести
к виду
fil V днф х, ф, и)
и)	
Таким образом, система уравнений (8.1) и (8.16) для х,
ф может быть записана в следующей форме:
i _ 3#(Л X, ф, и)
<Ч'	’	(8.19)
' dH(i, х, ф, и) . , -
ф; =-----aJi ,	/=1, 2,
т	дх1
Рассмотрим	некоторые	классы	управляемых	систем.
Предположим, что система уравнений процесса (8.1) линейна,
т. е. записывается в форме
х1 = £ ajXJ + £ blkuk, i=l,2,...,n,	(8.20)
j=l	k — 1
где а} и bk— коэффициенты, зависящие, вообще говоря, от
времени t. Соотношения (8.20) в векторной форме выглядят
следующим образом:
x = Jx + Z?u,	(8.21)
где х— (х1, х2, хп); и = (и1, и2, иг); Л = {«)}; 2? = {£ф}; г, j=l,
2, ..., я; k — 1, 2, ..., г.
В этом случае функция Н(Г, х, ф, и) [см. (8.9) [ имеет вид
Н= £ а[х'+ £ £ Ь{ик^-ф\1, х, и),
i,j= [	j=i *-[
а система уравнений (8.16) для сопряженных переменных— вид
фг=-	+	/=1,2, ...,«.	(8.22)
j = I
В частности, если /°(/, х, и) не зависит от .х, то
д/Уф х, и)_
8х!
Вводя в рассмотрение матрицу Л * = {«*'}, являющуюся транс-
понированной но отношению к матрице А ={«)}, из (8.22) на
основании равенства д*" = а/ получим
187
Ф;= - Z - Z й*%
j=l	j=l
или в векторной форме
ф = -Л*ф.
В задачах оптимального управления функция /°(1, х, и) часто
бывает квадратичной по х и и, т. е.
f°(i, х, и) = (Сх, х) + (£> и, и),	(8.23)
где (Сх, х) и (£>и, и) — квадратичные формы, а С и D — матрицы
этих форм: С = {с}}, i, j= 1, 2, п, £> = {(/;}, к, 2 = 1, 2, г.
В скалярном виде выражение для функции (8.23) записывается
в виде
/°(1,х,и) = £ c‘jX‘xJ + £d}Ukul.	(8.24)
ij=l	к,I
Тогда если Cj=cJi, то
а система уравнений (8.22) для сопряженных переменных в рас-
сматриваемом случае примет вид
фг = - Z	+ 2 Z
J=1	;=1
нни в векторной форме
ф=-Л*ф + 2Сх.	(8.25)
Функция Гамильтона H(t, х, ф, и) в случае линейной системы
(8.20) с квадратичным критерием оптимальности (8.24) будет
равна [см. (8.9)]
Я(г,х, ф, и) = £ Ф'ф,= £	Z
i.j=i	j=ifc=i	f.j=i
— £ Зкики‘	(8.26)
i=i
и, следовательно, от управлений u = (i?, н2, иг) зависит квад-
ратично. Рассмотрим случай, когда на управления не наклады-
вается Ограничений, а матрица D и соответственно квадратичная
форма (£>и, и) положительно определены. Тогда условие 1°
теоремы 8.1 повлечет за собой равенство нулю ее производных
в точке максимума:
ая(г х,ф,ц)=о /=1 2	(8.27}
ди'	,
188
Отметим, что это является следствием отсутствия ограничений
на управления. В противном случае соотношение (8.27) в точке
максимума функции H(t, х, ф, и) по и, вообще говоря, выпол-
няться не будет.
Для функции Н(г, х, ф, и), заданной формулой (8.26), условие
(8.27) имеет вид
£ д^-2^^0.
	г=1
В векторной форме последнее соотношение записывается так;
В*ф-2Ди = 0,
где В* — матрица с элементами bjl = b{, полученная транспони-
। рованием матрицы В. Из этого уравнения можно получить
решение
й = ^£>-1В*ф.	(8.28)
Матрица вторых производных функции 7/(7, х, ф, и) по и =
= (wr, и , ..., wr), как вытекает из (8.26), имеет элементы
52 EJ
-2< к, 1=\, 2 ..., г,
(}U ан
и, следовательно, совпадает с матрицей — 2D. Из-за положитель-
ной определенности матрицы D последняя матрица является
отрицательно определенной, поэтому решение (8.28) уравнений
(8.27) является точкой максимума функции Н(/, х, ф, и).
Таким образом, условие 1° теоремы 8.1 позволило выразить
оптимальное управление й через значение сопряженных перемен-
ных ф по формуле (8.28). Подставляя полученное значение
б в описывающую процесс систему (8.21), будем иметь
х = Лх + 1^Д"15*ф.	(8.29)
Для 2п переменных х = (.х1, х2, ... хв) и ф = (фь ф2, ..., фн)
получена система 2п уравнений (8.25), (8.29), Таким образом,
в данной задаче поиск оптимальной траектории сводится к отыс-
канию решения полученной системы. При этом искомое решение
должно удовлетворять начальным условиям (8.3), условиям на
правом конце траектории (8.4) и условиям трансверсальности
(8.18). Как будет показано ниже, не только для класса линейных
задач с квадратичным критерием, но и в общем случае принцип
максимума позволяет свести исходную оптимизационную задачу
к отысканию решения системы дифференциальных уравнений.
В заключение рассмотрим задачи оптимального управления
с нефиксированным временем Т протекания процесса. Тогда
значение Т не задано заранее и подлежит определению в процессе
решения задачи.
189
Постановка этого класса задач характеризуется функционалом,
который может иметь вид
т
S = J/°(z, х, u)df + Tj^min,
о
где в отличие от (8.5) второе слагаемое зависит от переменного
значения Т. Если же значение Т фиксировано, то данный
функционал совпадает с (8.5).
Применительно к таким задачам принцип максимума также
справедлив. Количество подлежащих определению параметров,
как отмечено, возросло на единицу и к условиям 1°—3° теоре-
мы 8.1 следует добавить еще одно:
н(т, Ф(т), х(т)й(г)) = ^М.	(8.30)
Обоснование этой формулы приведено в [8, с. 118].
Принцип максимума может быть применен к некоторым
задачам, когда на управление помимо ограничений типа (8.20)
наложены ограничения другого типа. Например, рассмотрим
задачу, в которой управление — скалярная величина, удовлетво-
ряющая условию
т
(8.31)
о
где с — заданная величина,
Покажем, как задача с таким ограничением может быть
сведена к стандартной. Дня этого введем дополнительную
переменную xn+1 с помощью уравнения
_v"+1 = |m|, л" + 1(0) = 0.
Уравнений процесса, таким образом, становится на одно больше.
Решая это уравнение с учетом начального условия, получим
y1 + 1 = j|w|dz,
о
Условие (8.31) теперь можно записать в виде
откуда видно, что оно выполняется в одном из двух случаев:
Л-« + 1(Р) = с и хл + 1(Г)<с. В первом из них имеем дополнительное
условие на правом конце, во втором-- задачу со свободным
правым концом по переменной хп + 1_ В каждом из них задачу
можно решить с помощью принципа максимума, составив для
нее условия Г'—3°. В частности, если хл + 1(7Д<с, т. е. значение
х"+1(Г) не известно, то условие 3° задает Значение соответст-
вующей сопряженной переменной фп + 1(7Д = 0.
190
§ 8.3. Сведение задачи оптимального управления
к краевой задаче
Цель настоящего параграфа — показать, что с помощью
принципа максимума задача оптимального управления может
быть в принципе сведена к отысканию решения системы 2и
дифференциальных уравнений. Изложение для простоты будем
вести для случая задачи с заданным временем Т протекания
процесса.
Рассмотрим соотношение (8.12), согласно которому на опти-
мальной траектории выполняется условие максимума функции
H(t, х, ф, и) по управлению u = (w‘, w2, иг) (см. п.Г теоре-
мы 8.1). Таким образом, если бы были известны значения
сопряженных переменных ф(/) и оптимальная траектория х(г),
.то из этого условия можно было бы определить оптимальное
управление йЦ).
Однако х(/) и ф(/) заранее, разумеется, не известны и могут
быть получены лишь после решения задачи. Рассмотрим более
общую задачу максимизации функции H(t, х, ф, и). При фиксиро-
ванных значениях переменных t, х, ф она становится функцией
только от !! = (!?, м2,пг). Эта функция задана на множестве
допустимых значений управления U [см, (8,2)], Будем искать
управление й как решение задачи
i
ЯЦ х, ф, u)~>max.	(8.32)
ue L!
.При каждом фиксированном наборе переменных /, х, ф реше-
ние задачи (8.32)—некоторое значение й. Таким образом, если
задача (8.32) решена при всех х, ф, то тем самым определена
функция
и = й(г, х, ф).	(8.33)
Теперь найденное значение управления подставим в систему
(8.19), которая примет после этого вид
 х, ф, й(г, х.ф))
5ф ’
ф;=^ х, ф,й(г,х, ф))	' п	4
Система (8.34) содержит 2н дифференциальных уравнений
относительно 2п неизвестных функций х = (№, х2, ..., х"), ф-
(ф,, ф2,	ф„). Оптимальная траектория х(Г) является одним
из ее решений,
ч Следует отметить, что нахождение решения (8.33) задачи
(8.32) может оказаться возможным лишь «в принципе», так как
при этом требуется перебор бесконечного множества значений
t, х, ф, Одиако в некоторых случаях это все-таки возможно,
191
например в рассмотренной в § 8.2 задаче оптимального управле-
ния для линейной системы с квадратичным критерием оптималь-
ности, В этом случае решение задачи (8.32) дается соотношением
(8.28), а система (8.34) представляет собой совокупность уравнений
(8,25) и (8.29).
Система (8.34) имеет бесконечное множество решений. Для
отыскания интересующего нас решения этой системы (8.34)
имеются дополнительные условия. Часть их задана в постановке
задачи—это начальные условия (8.3), задающие состояние систе-
мы (xi0, х20, —, хл0) в начальный момент времени / = 0, и условия
(8.4), определяющие конечное состояние системы в момент
времени Г по части переменных x1J5 %21, ...,хЯ11, Следовательно,
из постановки задачи известно п-\-т условий, накладываемых
на значение, искомого решения x(t) системы (8.34). Еще п~т
условий в; конечный момент времени Т получим из условий
трансверсальности (см. и. 3° теоремы 8.1),
Таким образом, принцип максимума сводит исходную опти-
мизационную задачу к решению краевой задачи дня системы
(8.34). Рассмотрим случай, когда может быть найдено общее
решение системы (8.34), иначе говоря, ее решение в виде
С15 С2, ..., С2л),
ф, = фД(,	С2, ..., С2„), (=1,2,	(8.35)
где Ct, С2, С2п — произвольные постоянные. Тогда любое
частное решение может быть получено выбором определенных
значений произвольных постоянных, Следовательно, и для на-
хождения искомого решения краевой задачи требуется соответст-
вующим образом выбрать произвольные постоянные. Для того
чтобы это сделать, воспользуемся краевыми условиями. Подстав-
ляя (8.35) в соотношения (8.3), (8.4), (8.18), будем иметь
х!(0, С}, С2, ,,,, C2„)=xJ0, /=1, 2, ..., п;
Х'{Т,	С2, ..., С2л) = х11, (=1, 2, ...,	(8.36)
.	5F(x(T С,, С2, ..., С2л))	.	.	„
\|т,-(Г)= ———Е—3--------—( = т + 1, m-j-2, ..., п.
Соотношения (8.36) можно рассматривать как систему 2п
уравнений относительно 2п неизвестных Ct, С2, ..., С2л. Эта
система уравнений может иметь единственное решение, более
одного (как, например, в § 7.6) или не иметь их, Но если
дополнитедьно известно, что решение оптимизационной задачи
существует, то оно может быть получено подстановкой одного
из решений системы (8.36) в (8,35).
Если краевая задача имеет несколько решений, то для
выявления из них оптимальной траектории требуется привлечь
дополнительные соотношения. Иногда при этом удается отсеять
«посторонние» траектории, сравнивая значения фУнклионала на
192
решениях краевой задачи. Сама по себе оптимальная траектория
может также быть не единственной, т. е. могут существовать
две (или более) траектории с одинаковым минимальным значе-
нием функционала.
Рассмотрим теперь случай, когда время Т окончания процесса
заранее не задано. Тогда система уравнений (8.36) будет содержать
2«+1 неизвестных величин, так как к их числу добавляется еще
одна — время Т. Система получается недоопределенной — число
уравнений меньше числа неизвестных. В этом случае к (836)
добавляется (2« + 1)-е соотношение (830), которое и замыкает
систему.
§ 8.4. Примеры нахождения оптимальных процессов
с помощью принципа максимума
Описанный в настоящей главе общий подход к решению
оптимизационных задач приводит, как показано в § 83, к краевой
задаче для системы сопряженных уравнений. Приводимые ниже
примеры имеют цель продемонстрировать как схему решения
задач оптимального управления с помощью принципа максимума,
так и характерные особенности решений — оптимальных траекто-
рий и управлений.
Пример 1. Пусть управляемый процесс описывается уравнением
х = х + и, х(О) = хо,
а искомый оптимальный процесс минимизирует функционал
т
У = J (aw2 +6x)d i + с'х(Г).
о
Применяя к этой задаче принцип максимума, составим
функцию Н (г, х, ф, w) согласно соотношению (8.9):
Н=ф (х + и) — аи2 — Ьх.
Применяя условие максимума (8.12) функции Н по w, выразим
оптимальное управление й через остальные переменные задачи.
Для этого приравняем к нулю производную функции Н по и,
воспользовавшись тем, что в данной задаче отсутствуют огра-
ничения на управление. Очевидно,
— = ф — 2аи.
ди у ’
Откуда получаем
Таким образом, в рассматриваемой задаче оптимальное управ-
ление зависит лишь от значения сопряженной переменной ф.
7 Зак 456
193
Для ее нахождения воспользуемся условием 2° теоремы 8.1,
согласно которому значение ф удовлетворяет соотношению (8.16).
В результате с учетом полученного выше значения й для
переменных х и t будем иметь систему уравнений
Х = Л + 1
(8.37)
ф=~ф + &,
которая представляет собой систему (8.34) для данной задачи.
Наряду с заданным в задаче начальным значением х(О) = хо
из условий трансверсальности (8.18) получим
ф(Т)=-с.	(8.38)
Следовательно, определение оптимальной траектории x(t) теперь
сводится к нахождению решения краевой задачи для системы
(8.37).
Эта задача простая, так как второе уравнение системы (8.37)
содержит только ф. Решая его, получим
ф = фое"! + 6,
где произвольная постоянная. Из условия (8.38) будем иметь
фое“т + Л= -с,
откуда получим
ф = Ъ -(6 + е)е'
Подставляя найденное значение ф в первое уравнение системы
(8.37), получим
Общее решение этого уравнения имеет вид
= Се‘
£>+с т-I b
----е ——
4а	2а’
(8.39)
где С — произвольная постоянная. Так как начальное значение
х(0) задано, то, полагая г=0, получим
। Ь + с т- Ь
л-0 = С + -—е' .
4а 2а
Находя отсюда значение С и подставляя его в (8.39), получаем
для оптимальной траектории х(/) выражение
х(,)=!^ег-. + (	+‘	^ег)е._»
v ’ 4а ’ 2а 4а ' 2а
Оптимальное управление й((), ранее выраженное через со-
пряженную переменную ф, имеет в данной задаче вид
194
-/t\ b b+c
w(t)=———e
2 2a 2a
т-t
Следует отметить, что в данной задаче система сопряженных
уравнений (8.37) «распалась», благодаря чему оказалось возмож-
ным сначала определить одну переменную ф(г), решая только
второе уравнение системы, а затем уже и х(Г). Это происходит
не всегда. Рассмотрим следующий пример.
Пример 2. Рассмотрим задачу оптимального управления
х = х + и, х(0)=хо,
> = f (u2 + x2)dr + -x2(T)->min.
о	2
Построим, так же как и в предыдущей задаче, функцию
Н(Г, х, ф, м) и воспользуемся соотношениями принципа макси-
мума. Согласно (8.9), имеем
Н = ф(х + н) — и2 — х2,
откуда из условия максимума функции Н аналогично тому, как
было сделано выше, для оптимального управления й получаем
выражение через сопряженную переменную
Если теперь, так же как и в предыдущем примере, составить
сопряженную систему, получим [ср. с (8.38)]
Ф
X = - X + -
2	(8.40)
ф = 2х — ф.
Условие трансверсальности (8.18) дает соотношение
ф(7> -х(Т).	(8.41)
Таким образом, если учесть начальное условие х(О) = хо,
то для нахождения оптимальной траектории x(t) получаем
краевую задачу дня системы (8.40). Для отыскания решения
Краевой задачи найдем общее решение системы (8.40). Его
можно записать в виде
х=С( + С2е-2',
ф = 2С1-2С2е’2г,
(8.42)
Где С1; С?— произвольные постоянные.
Значения произвольных постоянных в (8.42) можно легко
определить, если бы были заданы начальные значения х(0) = хо
и ф(0) = фо. В нашем случае они не заданы.
Выразим произвольные постоянные С[; Сг через х0, ф0. Для
этого подставим г = 0 в (8.42):
195
' X0~^l + ^2>
Фо = 2С1—2С2, I
откуда Сх =у + ^, С2 = ~ - у. Теперь соотношения (8.42)
примут вид
у _хо . фо । [ -Ы % ] g- 2t
2-4^2	4 J
ф-хо + ^-З^-^е-21.
Чтобы определить значение ф0, воспользуемся условием
трансверсальности (8.41), подставляя в него значения х(Г)=~ +
+ у + ^у“у^е“2Г и Ф(^) = *о+у-2^у-^е“2Т. Разрешив
полученное соотношение относительно ф0, будем иметь
ф=
- б4-2хое~2Г
з+е-2Г
откуда
гЛТ'|„2-’сое_2Т + 3(Ао^1) + 3(Ло + 1)е_2!
*	2(е-:г+3)
После этого легко получить и значение u(t) оптимального
управления.
Ситуация, с которой пришлось столкнуться в рассматриваемом
примере, когда при решении сопряженной системы «не хватает»
начального значения сопряженной переменной, является типичной
при применении принципа максимума, В данном случае оказалось
возможным получить общее решение системы (8.40) и «перенести»
неизвестное значение ф0 и заданное значение x0 в точку t=T,.
выразив через них х(Т) и ф(Т), После этого х(Г) и ф(Г)
подставляются в условие трансверсальности (8.41), откуда и на-
ходится искомое значение ф0.
В общем случае процедура переноса начальных условий х0,
ф0 на правый конец траектории может быть выполнена с по-
мощью численного интегрирования сопряженной системы, а пе-
ребор значений ф0 продолжается до выполнения на правом
конце условий трансверсальности.
Пример 3. До сих пор мы рассматривали задачи без ограни-
чений на управление, что бывает редко. Пусть управляемый
процесс описывается системой
А = ~Х2,
x2 = xi +2н,
196
в которой задано начальное состояние *i(0) = xlo, х2(0) = х'2О,
а на управление наложено ограничение — 1
Требуется найти оптимальный процесс (хДг), x2(t), w(/)),
минимизирующий функционал
Т
>= f wdr+x2(r),
о
где конечный момент времени Т задан.
Функция T(t,x, ф, и) в этой задаче имеет вид
Н= -ф1х2 + ф2х1+(2ф2-1)м.
Эта функция зависит от управления и линейно, поэтому
максимального значения она достигает либо при w= —1, либо
при и= — 2 в зависимости от знака коэффициента 2ф2 —I при
и. Следовательно,
и = ч
-1, если ф2<^,
2, если ф2^1.
(8.43)
Система (8.16) для нахождения сопряженных переменных будет
иметь вид
Фз = Ф1,
общее решение которой можно записать в форме
ф^С^соз f+C^sinr,
ф2 = С\ sin/—C2cos/,
; где Clf С2—произвольные постоянные. Определяя значения Сп
'' С2 из условий трансверсальности, получим систему
ClcosT+C2smT=0,
„	.	(0.44)
Ct sin Т— С2 cos Т= - 1.
Пусть теперь для определенности Г=2д. Тогда из системы
(8.44) С,=0, С2=1, а интересующее нас значение ф2(г) будет
иметь вид
ф2 = -cos t.
После того как ф2(г) получено, из условия (8.43) можно найти
и оптимальное управление «(/). Поведение ф2ф) и получающиеся
при различных t значения w(z) изображены на рис. 8.1.
Таким образом, оптимальное управление равно
197
— I, если Os?Z<—,
6
— 1, если —
6
Управление u(t) носит релейный
характер, «переключаясь» с ми-
нимального значения на макси-
мальное и обратно. Эта ситуация
типична для задач оптимального
управления с ограничениями на
управление.
траекторию хД/), x2(t). Для этого
Определим оптимальную
подставляем найденное значение й(г) в уравнение процесса.
На промежутке 0</<— для определения xt(Z), x2(t) можно
записать систему
общее решение которой
*1 = Ct cos t+ C2 sin t - 1,
x^-CjSinZ+Qcosz.	}
Пусть начальные значения xJO), x2(0) будут, например, равны
Xi(0)= —I, x2(0)=I. В соответствии с (8.46) им отвечает решение
Xj = sin t — 1,
х2 — cos
являющееся участком оптимальной траектории на данном про-
межутке.
При движении по данной траектории в момент t= 5я/6
система будет находиться в состоянии
/ 5зЛ I  (УТ
\6 J 2	2{б J 2
тт	,
На промежутке — </<— траектория системы будет опреде-
ляться уравнениями
х1=х2,
х2 — х £ -|- 2,
198

общим решением которых будет
xt = Ci cos t + C2 sin г+ 2,
x2= — Ci sin f + C2cos t.
Подставляя в (8.47) найденные значения х/, х2 при г=5л/6,
будем иметь
(8.47)
-Г-тс‘ЧСг + 2’
откуда С,=3Л/3/2, С2=-1/2, и, следовательно, на промежутке
5тс/6 =С г < 7тс/6 оптимальной будет траектория
х, =	cos t — -t sin t + 2,
1	2	2	....
3 /3 • „	1
X, = —SinZ —-COSZ.
2	2	2
На промежутке 7л/6<(<2л оптимальная траектория, как и на
первом участке, удовлетворяет системе (8.45) и, следовательно,
имеет вид (8.46). При г = 7я/6 значения х1} х2 будут равны
Определяя, как и раньше, значения произвольных постоянных
в соотношении (8.46), получим С\=0, С2=-2. Таким образом,
участок оптимальной траектории на последнем промежутке
имеет вид
Xj - -2 sin t- 1,
х2 = 2 cos t.
Найденную оптимальную
траекторию представим на фа-
зовой плоскости (х15 х2). Для
этого исключим t из получен-
ных для оптимальной траек-
тории соотношений. Резуль-
тат, который при этом будет
получен, изображен на
рис. 8.2.
На первом участке
0<z<5л/6 оптимальная траек-
тория задается уравнением
Рис. 8.2
(хх + I)2 + х2 — 1
199
и является, следовательно, частью окружности с центром в точке
(—1,0) и радиусом, равным 1.
На втором участке 5тг/6</<7я/6 оптимальной траекторией
будет также окружность с центром в точке (2, 0) и радиусом,
равным ^/7. Наконец, на участке 7я/6<Г^2п оптимальная
траектория будет проходить по окружности с центром в точке
(—1,0) и радиусом, равным 2.
Пример 4. Задача оптимизации распределения капитальных
вложений между отраслями.
Пусть имеется две отрасли, на развитие которых может быть
выделено некоторое количество капиталовложений. Установлен
лимит капиталовложений, ограничивающий суммарные инвести-
ции в отрасли, в каждый момент времени (например, в текущем
году). Требуется распределить инвестиции по годам в течение
времени [0, Т ] (заданный период планирования), чтобы сделать
возможно большими величины основных фондов отраслей на
конечный момент времени и при этом минимизировать общее
количество инвестиций за весь рассматриваемый промежуток
времени. Иными словами, требуется при наиболее экономном
расходовании ресурсов добиться максимального эффекта капи-
таловложений.
Для математической постановки задачи воспользуемся мо-
делью роста основных фондов. Уравнения модели запишутся так:
^2 — “ М-2 К-2 + ^2 
(8.48)
Здесь р1Д—коэффициенты выбытия основных фондов; У, 2— ин-
вестиции; К12— основные фонды отраслей. На величины У1>2
накладываются ограничения
+	И1>2^0,	(8.49)
где Vm — максимально допустимая величина инвестиций в отрасли.
Функционал в данной задаче будет иметь вид
т
3 = f (ос, Р\+<Х2 ^2)d'-₽1^(Л-р2^2(ГЬmin. 
Первое слагаемое выражает суммарное количество инвестиции,
два других- величины основных фондов отраслей в конечный
момент времени с обратным знаком. Поэтому минимизация
данного функционала означает, что первое слагаемое должно
быть как можно меньше, в то время как величина Р1Л?[(Т)+Р2х
хХ3(Г) должна принимать возможно большее значение.
Коэффициенты иЬ2, Р [, 2 характеризуют «приоритетность»
слагаемых в функционале.’
Таким образом, мы имеем задачу оптимального управления
линейной системой второго порядка. Для ее решения восполь-
зуемся принципом максимума Понтрягина.
200
В рассматриваемой задаче оп-
тимального управления уравнения
процесса имеют вид (8.48). Фун-
кцию /7, следовательно, можно
записать так:
2
н=
-мпах.	(8-50)
Здесь операция max произво-
дится с учетом ограничений (8.49).
Слагаемые, зависящие от
в (8.50), обозначим Hv. Очевидно,
Z/)z — (ф1 —	+(ф2~ аг) ^2 • (8.51)
Так как оставшиеся слагаемые
в (8.49) не зависят от Иь2, задача
отыскания максимума в’(8,50) равносильна такой же задаче для
(8.51). Обозначив у; = ф;—аг, получим, что для определения
оптимальных значений величин У12 требуется решить задачу
линейного программирования
Г[+у2К2-4тах,
ct + r2<rffl, V^O.
Решение этой задачи нетрудно найти и выразить через
величины параметров уЬ2. Для этого обратимся к геометрической
иллюстрации. На рис. 8.3 область V допустимых значений Vl 2
заштрихована. Она представляет собой треугольник с вершинами
в точках (0, 0), (0, Гт), (Гт, 0).
Рассмотрим вектор е с координатами ,	г
Очевидно, Это единичный вектор, направление которого со-
впадает с grad Hv. Решение задачи получим в зависимости от

У,
направления вектора е.
Рассмотрим случай yt 2^0. На рис. 8.9 этому случаю соот-
ветствует положение е, вектора е. Тогда производная максими-
зируемой функции HY по направлениям координатных осей будет
отрицательной, так как ее знак совпадает со знаком проекции
вектора е( на оси координат. Следовательно, HY будет убываю-
щей функцией но каждой переменной И12, откуда получаем,
что ее максимальное значение достигается в вершине (0, 0).
Если хотя бы одна координата вектора е положительна,
то максимум Hv достигается в одной из оставшихся вершин
S, Ит), (Ут, 0) или в любой точке соединяющего их ребра,
ля того чтобы определить, в какой из вершин достигается
201
максимальное значение, рассмотрим проекцию grad Hv на ребро (О,
Им), (И,„, 0). Направляющий вектор п данного ребра возьмем в виде
(1, — I), Тогда производная по направлению п Будет с точностью до
положительного сомножителя совпадать со скалярным произве-
дением .? = (е, п). Если величина s положительна (у>0), то Hv
увеличивается при движении по рассматриваемому ребру в направле-
нии к вершине (Vm, 0) и, значит, в этой вершине достигается
максимум Hv. Аналогично, если х<(), максимум Hv достигается
в вершине (0, Ут): Наконец, в случае 5 = 0 максимум достигается
в любой точке данного ребра. Заметим еще, что величина
1
И + Д)
с точностью до сомножителя
— совпадает с величиной у1—у2-
Суммируя сказанное, можно
для оптимальных значений :
написать следующее выражение
Hi = Й2=0, если у1;2<0,
= Й2 = б, если 7,-^0,
Г1 = 0, Г2=Ит,еслиу1-у2^0.
(8.52)
Здесь во втором и третьем условиях принято, что хотя бы
одно из них положительно.
Для определения величин фДД) составим сопряженную систему:
;  дя .	. , _
Ф;=	=	*=Ь 2.
Общее решение этой системы можно записать в виде
где фХТ1) —значения сопряженных переменных в конечный момент
времени. Они определяются из условий трансверсальности, ко-
торые в соответствии со структурой функционала имеют вид
Таким образом, для у, полу-
чим следующее выражение:
У/= рг-ерАг—т> — ос-, f=l,2.
Теперь в соответствии с (8.52)
на рассматриваемом отрезке вре-
мени [0, Т ] нужно выделить
промежутки, где уь2^0, ух>У2
11	Исследуем прежде все-
го вопрос о количестве таких
промежутков.
Функции у;(Г) являются мо-
нотонно возрастающими. Их по-
ведение изображено на рис. 8.4.
202
Из рис. 8.4 видно, что проме-
жуток [О, Г] разбивается на четыре
отрезка точками /2, /3. При
этом на отрезке [0,	] выполняется
условие у12^0, на интервале
(/1; 12)—условия ух^у2 и на
отрезке [г3, Т ] будет выполнено
неравенство у^у2- В зависимости
от значений параметров а;, р(, ц,
количество точек на отрезке
[О, Т ] может быть, очевидно, мень-
ше трех. На рис. 8.4 изображен
случаи, когда таких точек макси-
мальное количество. Для того чтобы показать, что количество
точек не может превосходить трех, достаточно проверить,
что кривые у,(г) и у2(0 не могут пересекаться более чем в двух
точках. Для этого покажем, что уравнение у1(0 = у2(2) имеет
не более двух решений. Пусть т, и т2—два корня этого
уравнения. Тогда производная функция y(0=Yi(0—у2(0 об-
ращается в нуль в некоторой внутренней точке т отрезка [xtl т2 ],
Выражение у(/) имеет вид
y(t) = PiPie1Ji(I~n--P2p3e,*2(' Т).
Очевидно, что уравнение у = 0 имеет не более одного решения;
следовательно, уравнение у(/)=0— не более двух, что и требо-
валось доказать.
Решение t = i уравнения у = 0 имеет вид
т = —— 1п^ф+Г,
Н2-В1	Ю₽2
 /и 6
откуда нетрудно получить, что при I -222 I	1 кривые
\ /12 Р2 )
Yi(Q, у2(0 пересекаются не более чем в одной точке на отрезке
[О, т ]- Это условие можно использовать в задачах с конкретными
значениями параметров а;, р;, ц,- для описания количества точек
переключения.
Построим теперь с учетом изложенного оптимальные значения
ЙД/). Й2(г). Построение проведем для случая, изображенного
на рис. 8,4, Оптимальные управления представлены на рис. 8.5.
Как видно из рис. 8.5, оптимальный режим носит релейный
характер, а в точках пересечения имеют место скачки управления.
Для того чтобы этого избежать, следует в постановке задачи
на производные функций ГД/), Г2(0 наложить ограничения.
Это, однако, существенно усложнит задачу.
203
§ 8.5. Принцип максимума как достаточное условие
оптимальности
Принцип максимума является необходимым условием опти-
мальности. Следовательно, он позволяет «сузить» исходное
множество процессов (х(г), и(г)), выделив из них лишь те,
которые ему удовлетворяют. Выделенные процессы могут в при-
нципе быть оптимальными, однако сам по себе принцип
максимума этого гарантировать не может. Подобная ситуация
во многом аналогична той, которая возникает при поиске
минимума функции у=/'(.х), заданной на числовой прямой.
Если у этой функции при всех х имеется производная,
то необходимым условием минимума функции в точке х = х
является равенство нулю ее производной в этой точке. Однако
отсюда еще; .не следует, что в этой точке функция достигает
наименьшего значения. Более того, наименьшее значение вообще
может не существовать. Если же имеется дополнительная
информация о функции y=f(x), то может оказаться, что
условие f'(x) = 0 является не только необходимым, но и до-
статочным условием оптимальности. Например, это справедливо,
если f(x) принадлежит классу выпуклых вниз функций [/""(х) <0
при всех х].
Так же обстоит дело и в задачах оптимального управления.
Траектории, удовлетворяющие необходимым условиям оптималь-
ности в форме принципа максимума, могут и не быть опти-
мальными. Однако дополнительная информация в ряде случаев
гарантирует их оптимальность. Например, если условиям прин-
ципа максимума удовлетворяет единственный процесс (x(r), 0(f)),
а о задаче известно, что оптимальный процесс в ней существует,
тогда им и будет процесс (х(г), й(/)).
Существование решения задачи, однако, является свойством,
которое не всегда легко проверить. Вместе с тем существуют
классы задач, когда не применяя теорему существования можно
показать, что принцип максимума является достаточным условием
оптимальности.
Рассмотрим такой класс задач оптимального управления.
Уравнения процесса имеют вид линейной системы
х = Л (r)x-|-B(r)ii,	(8.53)
где х = (%’, х2,	w2,	У); Л(г) и 5(f)— матрицы
соответствующих размерностей, элементы которых могут зависеть
от времени.
Функционал задачи имеет вид
т
У = J x)+g°(f, u))dг —>min	(8.54)
о
и представляет собой частный случай функционала (8.5).
204
Пусть натальное и конечное состояния х(0)=хо, х(Т) = х1
заданы. На управление могут быть наложены ограничения u е U,
где U с Rr — некоторая область пространства управлений.
Для функции/0(г, х) предположим, что она является выпуклой по
х при каждом значении ге [О, Т]. Это, как известно из определения
выпуклости функции, означает, что для любых двух значений
Xj = (х}, Xi, ,,,, х"), х2 = (х2, х2,	х") имеет место неравенство
/(ХХ1 +(1 - Х)х2) <Х/(хг)+(1 — Х)/(х2).	(8.55)
Свойство выпуклости сохранится, если к данной функции
прибавить линейную функцию, т. е, если/(х) выпукла, то функция
71
g(x)=/(x)+cx, где сх = У с(х'—линейная функция, также выпук-
i = l
ла. В последнем нетрудно убедиться, если учесть, что для любой
линейной функции выполняется равенство
с(Х.Х| +(] — Х.)х2) = А.сх1 +(1 — Х)х2, 0=?Х=51.
Сложив это равенство почленно с (8.55), получим
/(Ххг +(1 -Х)х2)+с(Хх[ +(1 -X)x2)<X.(/(x1)+cxI)+(l -X) х
x(f(x2) + cx2,
откуда и вытекает выпуклость функции g(x).
Для выпуклой функции справедливо, что если в некоторой точке
х = х ее частные производные обращаются в пуль, то функция в ней
достигает минимального значения. Таким образом, равенство
<?/ „ ,
нулю производных у в точке х является для выпуклой функции не
только необходимым, но и достаточным условием минимума.
Функция /(х) называется вогнутой, если —/(х) выпукла, т. е.
свойство вогнутости не изменится от прибавления линейной
функции. Для вогнутых функций, как следует из их определения
L и свойств выпуклых функций, равенство нулю производных
' в некоторой точке является необходимым и достаточным услови-
ем их максимума в данной точке.
Предположим теперь, что в рассматриваемой задаче опти-
мального управления (8.53)—(8.54) найден процесс, удовлетворя-
ющий принципу максимума. Является ли он оптимальным? При
сделанных предположениях является, что вытекает из следующей
теоремы.
Теорема 8.2. Пусть (х(7), й(г))—допустимый процесс в задаче
(8.53)—(8.54). Тогда, если этот процесс удовлетворяет условиям
принципа максимума Г', 2° теоремы 8.1, он является опти-
умалъным.
Доказательство. Рассмотрим соотношения принципа мак-
симума в данной задаче оптимального управления. Функция
\H(t, х, ф, и) имеет, согласно (8.9), вид
205
Н= я((?)хЧ;+£ £	x)-g°(/, и).	(8.56)
I. J = 1	7= 1 fc= 1
По условию 2° теоремы 8.1 сопряженные переменные ф,(/)
являются решением системы (8.16), которая в данном случае
выглядит следующим образом:
Ф;= - £	'=1 > 2> >п- <8-57)
7=1	0Х
Условие трансверсальности 3° теоремы 8.1 в данной задаче
вырождается, так как все переменные состояния на правом
конце траектории при t = T заданы.
Выполнение условия максимума функции Гамильтона (усло-
вие 1 ° теоремы 8.1) означает, что функция
я(/,х(/)5ф(/), й(0)^я(лх(0, Ш и) (8-58)
при любом не 17 и каждом фиксированном /е[0, Т]. Так как,
согласно (8,56), у функции Я(/, х, ф, и) только два слагаемых
зависят от управления, то неравенство (8.58) можно переписать
следующим образом;
£ £	“(0)^ £ £	“) <8'59)
fc = 1 t = 1	k = 1 i = 1
Условие (8.57) перепишем, подставляя '1'(0=(*Ы0’ *Ы0’ "
, Ф„(0)> в виде
i(0+ £	г=1’2> ’п- (860>
к=1	Ох
Таким образом, в рассматриваемой задаче, как следует из
принципа максимума, процесс (х (/), йр)) и сопряженные перемен-
ные ф(7) удовлетворяют соотношениям (8.59), (8.60). Покажем,
что отсюда вытекает выполнение теоремы 5.2 о достаточных
условиях оптимальности для процесса (х(г), й(г)).
Рассмотрим для этого функцию ф (t, х), задав ее соотношением
ф(?, х)-£фДг)х<
j=i
где ф;(() — значения сопряженных переменных, удовлетворяющие
принципу максимума. Тогда, согласно (5.12), выражение для
функции /?(/, х, и) будет иметь вид
х> «)= £ ^7*' + £	+
" ' j=i £J_I
+ £ £ ь1 (г)мЧ;(0-/°(г> *)-?°(^ «)	(8-61)
206
Чтобы установить оптимальность процесса (х(/), й(г))> доста-
точно проверить выполнение условий Г, 2" теоремы 5,2. Усло-
вие 2° выполняется тривиальным образом, так как правый конец
траектории зафиксирован.
Для проверки условия Г заметим, что, согласно (8.61),
функция R(t, х, и) имеет вид
R(t, х, «) = ./?! (/, х)+Л2 (г, и),
где
х)= £ фДт)хЧ £	х)’ (8-62)
7=1	!>j“l
MZ’U)=E Е	“)'	С8'63)
.1 = 1 1 = 1
Поэтому максимум функции R (г, х, и) по х, и достигается при
значении х, максимизирующем Ry(l, х), и значении и, максимизи-
рующем R2 (t, u).
Если сравнить соотношения (8.63) и (8.59), то легко увидеть
что функция R2 th и) достигает максимального значения и=й(?)
для каждого ie [О, Г].
По сделанному относительно функции /° (т, х) предположению,
она является выпуклой; следовательно, х)— вогнутой. Так
как первые два члена в правой части (8.62)—линейные функции
от х = (х1, х\ хя), то, по сделанному выше замечанию, (/, х)
также является вогнутой. Так как на значения х ограничения
не накладываются, то ее максимум достигается в точке, где ее
частотные производные по х обращаются в нуль. Вычисляя
частные производные А, (т, х) и приравнивая их к нулю, получим
систему уравнений
ох	1=1
Сравнивая эту систему с (8,60), нетрудно заметить, что x=x(t)
является ее решением. Следовательно, при х—х (г) А, (т, х)
достигает максимума при всех t е [О, 7j.
Приведенные рассуждения показывают, что максимум функции
R (/, х, и) при всех tе [О, Г] достигается на процессе (х(т), й (;)),
Следовательно, этот процесс удовлетворяет достаточным усло-
виям оптимальности. Таким образом, оптимальность процесса
(x(t), й(г)) доказана.
Итак, для класса задач оптимального управления (8.53) — (8.54)
принцип максимума является не только необходимым, но и до-
статочным условием оптимальности. Полученный результат мож-
но распространить на задачу со свободным правым концом
траектории и функционалом
207
= J (/° (f> х) + £° (/> u))dr+F(x(3r'))->-min,
° " /
t. e. если /0(г, x) и F(x) —функции, выпуклые по х, то условия
Г—З5 теоремы 8.1 являются также необходимыми и достаточ-
ными условиями оптимальности. Это справедливо и для случая,
когда F(x) — линейная функция.
Глава 9
Метод Лагранжа для многошаговых
процессов управления
с одномерным аргументом
В этой главе рассматривается метод Лагранжа в применении
к многошаговым процессам управления с одномерным аргумен-
том как с неограниченным, так и ограниченным управлением.
Выводятся необходимые условия оптимальности для процессов
с обоими видами управлений. Особенно подробно анализируется
случай ограниченного управления, для которого принцип макси-
мума несправедлив, и приводится негативный пример, подтверж-
дающий этот результат. К методическим достоинствам главы
следует отнести изложение обычно не освещаемого в учебной
литературе материала, связанного с двумя формами конечно-
разностных уравнений и использованием их при решении
конкретных задач с помощью необходимых условий оптималь-
ности.
§ 9.1. Уравнения метода. Условия оптимальности
для многошагового процесса с неограниченным управлением
Конкретизируем общую постановку задачи оптимального
управления для многошагового процесса управления с одномер-
ным аргументом, приведенного в гл. 4,
Пусть заданы уравнения пролесса
х‘(/ + ]) = fl(t, х(г), u(r)), 1 = 0, 1, Т— 1, /=1, п, (9.1)
краевые условия
x‘(0)=xo, i = l,fc, x‘(7’)=xi, f = fc+l,n,	(9.2)
и ограничения
(9.3)
причем й (/) —внутренняя точка множества Гц при всех t =
= 0, 1,	Г-1.
Обозначим через М множество допустимых пар v = (x(z),
и (/)), т. е. пар, удовлетворяющих условиям (9.1) — (9.2). Поставим
•задачу об отыскании пары v = (х (г), u(7))е М, на которой
£ /°(ц х(г), ц(г))+Г(Г, х(Г))->тщ,	(9.4)
t = 0
Выведем уравнения метода Лагранжа аналогично непрерывно-
му варианту, опираясь на достаточные условия оптимальности.
209
Согласно последним (см. гл. V), если допустимый Процесс (х (/),
й(г)) и функция ф(г, х) такие, что выполняются условия
R (/, х (/), й(/)) = max R(t, x(z), 0(f)) V/ = 0, I, T— 1, (9,5)
(x, u) e V
Ф(х(Г))= min Ф(х) при i = T,	(9,6)
x 6
то Процесс x(f), u (г) оптимален, т. e.
,/(x, u)= min y(x,u).
(x, u)e M
Для задачи с закрепленным правым концом [см. (9.2)] условие
(9-6) удовлетворяется тривиально, так как при t = T множество
У'к состоит только из одной точки.
Напомним, что, согласно § 5,2, для задачи (9.1)--(9.4) функция
R(i, х, и) имеет следующий вид:
R(t, х, и)=<р	1, f(/, x, «)]-<р (/“, x)-/°(r, х, и),	(9.7)
где f(/, х, u) = (f‘(г, x, u)}, i=l,n. Так как в модели (9.1) — (9.4)
других ограничений, кроме краевых условий, на фазовые коорди-
наты нет, то множество совпадает со всем пространством X,
Пусть функция ср (г, х)—дифференцируемая по х, функции
/'(г, х, и), /=1, n,/°(г, х, и) — дифференцируемые по х, и в точках
хШ, й(4 Тогда необходимыми условиями максимума функции
R (/, х, и] по х и и являются следующие:
= 0, г =	(9.8)
х, U
oR
ох1
St?
= 0, ./=1, г.
X, U
Введем в рассмотрение вектор-функцию ф (/) = (ф( (г),
г=1, п, где
5<р(/, х)
ёх1
х = х(г)
(9.9)
К(')),
(9.Ю)

и гамильтониан
ф, х, u)= f х, х, и).	(9.11)
. ( = 1
Представим в более удобном для приложений виде усло-
вия (9,9). С учетом (9.7) и (9.10) левая часть условий (9,9)
принимает вид
или
210

5R
ou1
(9.12)
(9-13)
X, и 8“j
X, и
А с учетом (9.11) и (9.12) окончательно имеем
HR
x, й
__ 3
x, й
Теперь расшифруем другое необходимое условие (9.8), Учиты-
вая (9.7), найдем
dR
дх1
X, и
л
.7=1
Эф[г+1, f(/, х, u)] dxs х) <?/°
дх>	Их' дх‘ 8х‘
Далее с учетом (9.10) получим
5R
дх’
х, и
W«+i)g
= 0, z = l, п.
х, й
.	_=0.
X, и	сх X, и
(9.14)
а с учетом (9-И) окончательно имеем
= Лн(/, ф(/-М), х(/), й(;))-ф,(/) = О, >1, л, (9.15)
т. е.
ф;(/) = ^Я(г, ф(г+ 1), х(г), и(г)), 1=1, п, (9.16)
Итак, в результате преобразований получены необходимые
условия оптимальности (9.13) и (9.16) многошаговых процессов
управления с одномерным аргументом. Неизвестными здесь
являются оптимальный процесс х (г) = {х‘ (/)}, й (f]== {iiJ (г)}, 1=1, п,
j=\,r, и вектор-функция ф(1) = {ф;(г)}> 1=1;п, т. е. число
неизвестных —1п + г, а условия (9.13), (9.16) дают всего п + г
уравнений. Недостающие п условий дают уравнения процесса
(9.1) с учетом краевых условий (9,2), Таким образом, система
уравнений для определения 2и + г неизвестных полностью опре-
делена.
Вычислительный алгоритм решения исходной задачи на основе
использования необходимых условий состоит в следующем.
1. Из необходимых условий (9-13) найдем wJ(7, ф(1-|-1), х(/)1,
7=1, г. Перейдем от управлений в виде гУ(/, ф(/ +
к управлению в виде и(/) = {wJ(/)}, j=l,r-
2. Найденным управлением й(г) замыкаем систему уравнений
=	ч|/(Л-1), х(/)5 й(/)), /=1, и, (9.17)
х‘(г + 1) = /'(/, x(r), 0(f)), /=1,и,	(9.18)
и разрешаем ее с учетом краевых условий (9.2).
211
Сделаем несколько замечаний относительно разрешимости
системы уравнений (9.17) — (9.18).
В теории конечно-разностных уравнений известны две формы
процессов.
Первая форма
у'(/+1) = Г((лу(/)р=1^,	(9.19)
У(0)=А /=1, п,	(9.20)
где у(/) = {у:	F!(t, y(f)) --заданные функции своих
аргументов. Задача (9.19)— (9.20) требует для своего решения
проведения расчетов от момента Г = 0 к моменту t = T (задача
Коши в прямом времени).
Вторая форма
yl(t-\} = Fl(t, у(/)), г=1, п,	(9.21)
У(Г) = /»> г = М-	(9-22)
Задача (9.21) — (9.22) требует для своего решения проведения
расчетов от момента t=T к моменту ( = 0 (задача Коши
в обратном времени).
Назовем каждую из двух форм уравнений (9.19) и (9.2 [)
нормальной. Тогда каждая из задач (9.19) —(9.20) и (9.21) —
(9.22) — задача Коши для уравнений в нормальной форме в пря-
мом и обратном времени соответственно.
Если часть из краевых условий (9.20) будет задана на правом
конце траектории, например вместо этих условий будут условия
уi(0)- у, г=1, А:,	i = k+l,n, то получим краевую
задачу для уравнений в нормальной форме в прямом времени.
Аналогично формулируется краевая задача в обратном времени.
Для того чтобы воспользоваться алгоритмом (§9.1), следует
привести уравнения (9.17) и (9.18) к одному и тому же
соотношению из числа рассмотренных —(9.19) или (9.21). Это
приведение может быть осуществлено двумя способами.
Первый способ. Преобразуем уравнения для сопряженной
системы (9.17) к виду (9.19), т. е.
ф.(г+ l) = F(r, ф(()), /=]?«,	(9.23)
задавшись дополнительно значениями ф(0) = {ф( (0)}, т=1,л.
Уравнения процесса (9.18) уже имеют вид процесса (9.19),
однако для полного соответствия процессу в первой форме
следует задать недостающие п-к условий (помимо имеющихся
условий х'(0) = хЬ, i=l, к из (9.2) на левом конце вида х‘(0) = хо,
i = k + \,n). В этом случае расчет проводим от момента / = 0
к моменту t—T с заданными начальными условиями. Краевая
задача (9.18), (9.23) [а следовательно, и (9.17), (9.18)] с краевыми
условиями (9.2) будет разрешена, если выполнятся все равенства
212





х‘(Г) = а'1, 1=к+\,п. Если выполнение этих равенств не имеет
места для всех i = k + },n, то задаемся другими ф(0) и x‘(0) = xb,
; = &+1, л, и основа повторяем вычисление до тех пор, пока
не выполнятся эти условия.
Второй способ. Преобразуем уравнения процесса (9.18) к виду
(9,21), т. е.
x\t) = F‘(t, x(z + l), ф(/+ 1)), z=l, п,	(9.24)
задавшись недостающими краевыми условиями x'(T) = Xi, 1=1, к
(в дополнение к имеющимся x'(t) = x‘i,	и). Уравнения
(9.17) оставим без изменения, дополнительно задавшись усло-
виями ф(Г) = {ф;(Г)}, 7=1, п. В этом случае расчет проводим
от момента t=T к моменту / = 0 с заданными краевыми
условиями. Краевая задача (9.17), (9.24) [а следовательно, и (9.17),
(9.18)] с краевыми условиями (9.2) будет разрешена, если
выполнятся все равенства х'(0) = Хф, /=1, к. Если выполнение
этих равенств	______
другими ф(Т) и x'(r)=Xt, f = fc+l,n, и снова повторяем вычис-
ление до тех пор, пока не выполнятся все эти условия.
Замечание. Пусть в граничных условиях (9.2) не задана их
часть на правом конце траектории, например для к условий
на правом конце х'(Т) свободны, г= 1, к, к <п. Тогда недостающие
к условий для определения дополнительных неизвестных в системе
уравнений (9.1), (9.2), (9.13), (9.16) обеспечивают условия трансвер-
сальности:








не имеет места для всех i= 1, к, то задаемся
_dF(T, х(Г))
, i = 1, к.
§ 9.2. Условия оптимальности для многошагового процесса
при наличии ограничений на управление
Рассмотрим задачу (9.1) — (9.4), в которой множество V\ по-
прежнему совпадает со всем пространством X (т. е. других
ограничений, помимо краевых условий (9.2), на фазовые коорди-
наты нет),	а й(г) не обязательно является внутренней
точкой множества Уг„. Пусть, кроме того, функция ф((, х)
дифференцируема по х, а функции /“(/, х, u), i=],n, f °(г, х,
и) дифференцируемы по х, и в точках х(г), й(г).
Для такой задачи нельзя использовать необходимое условие
(9.9), выведенное в предположении, что й(/)—внутренняя точка
множества ГД.
Для решения сформулированной выше задачи воспользуемся
теоремой о достаточных условиях оптимальности, согласно
которым следует обеспечить выполнение условий (9.5) и (9.6).
213
<
Условие (9.6) выполняется тривиально на основании закреплен-
ности правого конца траектории [см. соотношение (9.2)]. Рас-
смотрим выполнение условий (9.5). Условия (9.8), (9.14) — (9.16)
имеют место на основании совпадения множества со всем
пространством X. Обеспечим выполнение условия тахТф, х, и)
при фиксированном х, т. е. выполнение условии
А(г, x(z), й(/)) = max7?(z, x(i), u(/)), Z = 0, 1, ..., T—\.
ue HL
Рассмотрим, как связан факт максимизации функции х,
u) по lie И, со свойствами вектор-градиента этой функции по
управлению.
I. Пусть и—скаляр. Тогда множество — отрезок: K = {w:
:сф)^м^6(г)), / = 0, 1, ..., Т-1; момент времени Г фиксирован.
Конкретизируем необходимые условия max7?(f, х, и) при фиксиро-
ие И'и
ванном х в зависимости от расположения й внутри отрезка
или на его границах. Рассмотрим три случая:
а)	если йб(<з, й), т. е. й — внутренняя точка отрезка, то
SR
ди
_ 8H(t, Ф(г+1), x(t), «(0) = 0.
ди
X, и
(9.25)
б)	если £ = «, то необходимым условием тахТф, х, м) при
«<=П,
.иксированном х будет следующее условие на градиент функции
ф, ф(/+1),	н(г)):
ан(<; ф(т+1), ф), »(ф 0	26
ди
(рис. 9.1);
в)	если й = Ь, то необходимым условием max/ф, х, w) при
фиксированном х будет следующее условие па градиент функции
H{t, ф(/+1), х(г), гф)):
йя(б #+1), ф), ф)) 0	2
(JU
(рис. 9.1).
2. Пусть и—вектор, а V‘u—множество допустимых значений
и с гладкой границей S. В каждой точке множества S' можно
построить нормаль п к границе. Для наглядности в дальнейшем
рассмотрим случай, когда г = 2, и тогда —плоскость, рассмот-
рим два случая;
а)	если й внутренняя точка множества Ри. Тогда необхо-
димое условие max Уф, х, и) при фиксированном х(г) будет
214
R
Рис. 9.1
SR
77
_	*(')’ UW) _ А ,_ 1 О.
Ги	J ’	’
(9.28)
б)	если и лежит на границе области S. Проведем внешнюю
нормаль п к границе S' множества V[ (рис. 9.2).
Тогда необходимым условием тахтф, х, и) при фиксиро-
ие и;
ванном x(z) будет следующее условие на градиент функции Н\(,
ф(/+1), х(?), ц(?)):
ngradu/f(?, ф(г+ 1), х(?), и(/))^0.	(9.29)
Итак, полуденные условия (9.8) [и их конкретизация (9.14) —
(9.16), (9.28), (9.29), а также их частный случай (9.25) — (9.27)
из §9.2] являются только необходимыми условиями оптималь-
ности, а траектория х(?) и управление й(/), полученные из
них,—только подозрительными на оптимум. Для подозреваемых
на оптимум траектории и управления следует провести до ис-
следование, аналогичное непрерывному варианту. В частности,
если правые части уравнений процесса (9.1) линейны по и,
а функция /°(?, х, и) в выражении для функционала (9.4) выпукла
по и, то полученные с помощью сформулированных выше
необходимых условий оптимальности траектория и управление
являются оптимальными, т. е. эти необходимые условия оп-
тимальности— и достаточные.
§ 9.3. Негативный пример
Рассмотрим пример, из которого станет ясна неприменимость
в общем случае принципа максимума Понтрягина для много-
шаговых управляемых процессов.
Пусть управляемый процесс описывается системой уравнений
вида
х [(?+ 1) = х*(?)-1-2и(?),	(9,30)
х2(?+1) = хф)-(х'(?))2 + (а(?))2
215
с начальными условиями
?(0)=3, х2(0) = 0	(9.31)
и ограничениями
|«(r)|^ 5 (г=0, 1). t (9.32)
Требуется найти
y(w)=-х2(2)-»min.	(9.33)
Используя (9-30), легко получить:
х1 (1) = 3 + 2 и(0),
л2(1)=-9 + (у(0))2, '
"  х 2 (2) = (»(I))2 - 3 (ЦО))2 - 12 w(0) -18;
здесь составляющими оптимального управления будут
й(0)=— 2, й(1)=±5.	(9.34)
Проверим выполнение необходимых условий оптимальности.
Для этого составим функции Гамильтона для t = 0, 1:
Н»(Ф(1), ДО), Д0))=ф'(1)Р'(0)+2Д0)]+ф2(1)[лг(0)-(х,(0))! +
+(“(0))Д
х(1), Д1))=Ф‘Р)РТ)+2Ц1)]+1ИР)|>2(1Н*1(1))2+
+(“W)2].
Тогда уравнения для сопряженных множителей Лагранжа
имеют вид
+ ( I) = 5Д1ЖДМ!» = ф' р) _	1)12(2),
сх	(9.35)
*2(l)=^gi>®=-*2₽).
</Х Р/
а условия трансверсальности
Я2)-ёй=0' *2P)-ga=i-
Так как с учетом (9.34) хЦ1)= — 1, то подставив это значение
в (9.35), получим:
ФЧ2) = О,	ф2(2)=1,
фЦ1) = 2,	ф2(1)=1.
216
Отсюда
Н„(ф(1), х(0). «(0))-(«(0))2 + 4И(0)--3 ==[к(0) + 2]2--7, (, 36)
Н,(ф(2), х(1), к(1))=(«(1))’-6.
Из выражения (9.36) видно, что й(0) = —2 есть точка минимума,
а не максимума гамильтониана Н0(ф(1), х(0), м(0)) по |и0| =< 5,
т. е. принцип максимума (состоящий в требовании максимума
гамильтониана при каждом фиксированном г) в общем случае
не справедлив. Полное решение задачи (9.30) — (9-33) будет
приведено в гл. 13 с помощью итеративного алгоритма улучше-
ния, в котором используется квадратичное по аргументу х задание
функции <р(/, х).
Глава 10
Некоторые применения необходимых
условий оптимальности
в форме Лвгрвнжв — Понтрягина
В настоящей главе приводятся постановки и решения ряда
задач оптимального управления для непрерывных и многошаговых
(дискретных) процессов. Необходимые условия оптимизации
в форме Лагранжа —Понтрягина являются аппаратом оптимиза-
ции процесса. В соответствии с теоремой 8.2 дополнительного
доказательства оптимальности во всех рассматриваемых случаях
не требуется, так как в § 10.1 решается линейная задача, а в § 10.2
и 10.3 —два варианта содержательно сходной задачи соответст-
венно для многошаговых (дискретных) и непрерывных процессов
с выпуклыми функционалами и линейными ограничениями.
Для линейной задачи краевая задача решается точно и ока-
зывается возможным провести некоторый качественный анализ
еще до получения решения; для многошаговых и непрерывных
процессов краевые задачи решаются приближенно численным
методом прямой прогонки, его идеи изложены в Приложении.
Две последние задачи, содержательно между собой очень
близкие, приводятся вместе для сопоставления техники матема-
тических выкладок и расчетных схем. Это дает возможность
увидеть сходство и различие в однотипных постановках задач
и подходах к их решению.
§ 10.1. Оптимальное управление движущимся объектом.
Аналитическое решение
Рассмотрим прямолинейное движение некоторого объекта
с двигателем (например, автомобиля). Объект имеет массу т,
а двигатель обеспечивает воздействие на него силы F, не
превышающей по модулю значения величины у. Если приложен-
ная сила разгоняет объект, то ее значение принимается поло-
жительным, если тормозит его движение, то отрицательным.
Пусть в момент / = 0 начальные путь и скорость нулевые,
т. е. объект находится в покое: s(0)=0, v(0) = 0; и
— соответственно пройденный путь и скорость в произвольный
момент t.
Требуется найти такой оптимальный режим управления, чтобы
объект прошел заданный путь L в минимальное время и оста-
новился.
Построим математическую модель движения объекта. Для
этого воспользуемся вторым законом Ньютона, в соответствии.
218
с которым произведение массы объекта на ускорение его движения
равно приложенной силе F. Ускорение равно производной от
скорости по времени. Скорость движения — это, в свою очередь,
производная от пройденного пути по времени.
На основе сказанного запишем дифференциальные уравнения
mv = F, s = v;	(Ю1)
условия для рассматриваемого процесса
IFI^y;	(10.2)
s(0) = 0, с(0) = 0;	(10.3)
s-(T) = L, ЦТ) = 0	(10.4)
и функционал	(10.5)
который отражает достижение конечной цели (10.4) за минималь-
ное время.
Итак, математическая модель движения управляемого объекта
построена. Дифференциальные уравнения (10.1)—это уравнения
процесса, причем скорость v и путь $ — компоненты вектора
состояния, сила F— параметр управления. Это вытекает из общей
постановки задачи оптимального управления и отвечает формаль-
ным признакам, позволяющим отличить параметры состояния
системы (входят в уравнения процесса как сами по себе, так
и со своими производными) от параметра управления (сила
F входит в одно из уравнений процесса (10.1) только сама по
себе без производной).
Неравенство (10.2) задает ограничение на управление, условия
(10.3) и (10.4) соответственно начальное и конечное состояния
системы, (10.5)—фунпионал, характеризующий задачу о быстро-
действии.
Последовательность решения задачи (10.1) — (10.5) в целом
соответствует процедуре реализации принципа максимума. Осо-
бенность состоит в том, что наряду с искомыми параметрами
состояния v, s и управления F необходимо определить и время
движения объекта Т. Эго, как следует из формулы (8.30),
приводит к дополнительному условию трансверсальности, которое
в данном случае будет иметь вид
Н(Т, ф(7’), х(Г), й('Г))--=1,	(10.6)
где /ф, ф, х, и) — функция Гамильтона, определяемая по
формуле (8.9).
В соответствии с постановкой задачи (10.1)— (10.5) функция
Гамильтона будет иметь вид
р
H(i, ф, х, и)=Ф1~ + ф2п,	(10.7)
где х=(г, s); u = F.
2i9
Подынтегральная функция /0(г, х, и) в функционале (10.5)
тождественно равна нулю, поэтому соответствующее слагаемое
в формуле (10.7) отсутствует.
Максимизация функции (10.7) по управлению F дает
{у, если ф1 > 0,
— у, если ф, < 0,	(10.8)
VFe [ —у, у], если ф( =0.
Теперь составим систему уравнений принципа максимума;
т v = Т(ф1),
5=v;
:	дн п
ф =-	=°;
Здесь краевые условия задаются равенствами (10.3) и (10.4).
Сопряженные уравнения (10.10), как и должно быть в случае
линейных задач, интегрируются независимо от исходных уравне-
ний процесса (10.9), Второе уравнение (10.10) сразу дает ф2 — С\.
Интегрируя затем первое уравнение (10,10), получаем
ф!= -СП + С2,	(10.11)
где Cj, С2 — произвольные постоянные.
Из формул (10.8) и (10,11) еще до получения оптимального
решения можно сделать качественный вывод: так как линейная
функция (10.11) может иметь не более одной перемены знака, то
оптимальный режим управления будет заключаться не более чем
в одном переключении двигателя рассматриваемого объекта. При
этом и на разгон, и на торможение двигатель должен бы ть включен
на полную мощность, чтобы сила F была равна либо величине +у,
либо —у, как это видно из формулы (10,8), Определить произвольные
постоянные интегрирования С, и С2
пока не представляется возможным, так
как граничные условия (10,3) и (10.4)
относятся к исходным переменным
s и V, а не к сопряженным ф! и ф2.
Поэтому интегрировать систему урав-
нений (10.1) целесообразно при различ-
ных возможных сочетаниях этих произ-
вольных постоянных. Это будет влиять
на выбор значения силы F в правой
части первого уравнения (10.1).
На рис. 10.1 показаны различные
возможные виды функции ф1р) в за-
висимости от значений произвольных
постоянных Cj и С2.
220
Из восьми видов функции практический интерес представ-
ляет только пятый. Ему отвечает вначале разгон объекта под
воздействием силы F=y до некоторого искомого момента г=т,
а затем торможение до момента t = T при значении силы F= — у.
Шестой вариант выглядит противоестественным, так как вначале
под воздействием силы F=-y объект должен начать двигаться
в противоположную необходимому направлению движения сто-
рону; вариантам же 1—4, 7 и 8 отвечает постоянная во времени
сила F=y или Е= —у, что обеспечивает равноускоренное движение
объекта без его остановки, а это противоречит условиям (10.4).
Итак, останавливаясь на пятом варианте, в соответствии
с уравнениями процесса (10.1) получаем:
mv = y, s = v;	(10.12)
s(0) = 0, ь(0)=0, te(0, т).	(10.В)
Уравнения (10.12) без труда интегрируются:
	/г?
= —-+ C3r-|-C4,
' ! т 2
где С3 и С4 — произвольные постоянные.
Учитывая начальные условия (10.В), получаем С3 = С4 = 0.
В результате решение дифференциальных уравнений (10.12),
удовлетворяющее начальным условиям (10.В),, имеет вид
'«“У sW=i'!'	(10J4>
Момент г = т, соответствующий переключению двигателя с раз-
гона на торможение, как видно из рис. 10.1 и с учетом формулы
(10.1), отвечает условию
ф1(т)= -Св + С2 = 0,
откуда
t=C2/C,.	(10.15)
На временном отрезке	Г) функция ф1(?)<0, F= — у
и уравнения (10.1) примут вид
/ш>== — у, s = v.	(10.16)
Начальным условием для уравнений (10.16) будет состояние
системы в момент / = т, отвечающее формулам (10.14) и (10.15).
С учетом этого для двух дифференциальных уравнений (10.16)
получаем начальные условия
(\ 2
£ •	(10.17)
С; I
221
Интегрируя уравнения (10.16) с учетом начальных условий (10.17),
получим при t е (т, Г)
V
(10.18)
s(t) =
Чтобы определить произвольные постоянные Cj и С2, необхо-
димо удовлетворить в решении (10.18) двум граничным условиям
(10.4). Но при этом появится третья неизвестная величина Т. Для
определения трех искомых величин Ct, С2, Т воспользуемся кроме
двух соотношений (10.18) третьим условием трансверсальности (10.6).
Итак, получили три алгебраических уравнения;
Г
т(Т) = -1г+^|?=0,
z /и m С\
л(П= _1Г
1 !	2 \Clyl J m
-(Clr+c2)H + c,,»(T)=i.
(10.19)
T-L,
Решение системы уравнений (10.19) имеет следующий вид:
С,= & с2 = -, Г=2 /И	(10.20)
у L у	Y	V У
С	т
При этом оказывается, что Т=2— или т = ~, т. е. переключение
2
двигателя с разгона на торможение в оптимальном режиме
должно осуществляться посередине интервала движения. Пройден-
ный путь с учетом второй формулы (10.14) и третьей (10.20)
также будет равен половине необходимого для прохождения пути:
/ \ f т\ L
Мы рассмотрели оптимальный режим, при этом краевую
задачу (10.9), (10.10), (10.3), (10.4) удалось решить в аналитической
форме.
Остальные варианты для функции фД/) (рис. 10.1) непри-
емлемы, что следует из простых физических соображений.
Аналитически это должно приводить к несовместным условиям
в краевой задаче. Убедимся в этом, например, для вариантов 1,
2, 7. Для этих случаев фДД> 0 У/е(0, Г), а следовательно, F^y
для всех значений /е(0, Г). Уравнения (10.12) и начальные
222
(условия (10.13) должны теперь выполняться для всех значений
Ге(0, Т]. При этом также должны удовлетворяться граничные
t условия (10.4).
Формулы (10.14) дают решение системы уравнений (10.12)
J. При заданных начальных условиях (10.13). Убедимся, что с Гранин-
Ц ними условиями (10.14) они несовместны1 * *.
Из первой формулы (10.21) вытекает, что Т^О. Это уже само по
себе лишено смысла, так как скорость движения объекта
ограниченная, а длина нуги L>0. Из второй формулы (10.21)
/ 2ms
получаем, что Т= / — 0. Аналогично получаются противоречия
в краевых задачах и для других вариантов, отраженных на рис. 10.1.
§ 10.2. Календарное планирование поставки продукции.
Численное решение. Дискретный вариант
’ Рассмотрим некоторый процесс производства и поставки
продукции в дискретные моменты времени / = 0, I, ..., Т, где
Г—-плановый период. Спрос на продукцию в эти моменты
определяется заданной функцией r(f). Продукция не допускает
длительного хранения, т. е. нельзя создавать запасы с помощью
превышения в отдельные моменты t объема поставки x(z) над
потребностью г(г).
Будем считать, что при несовпадении поставки х((] и потреб-
ности г(г) имеют место потери народного хозяйства, При
дефиците, г. е. когда ^(z) = .r(r) — r(z) < 0, потери обусловливаются
j неудовлетворенностью спроса. В случае превышения поставки
над спросом, когда £,(/)> 0, потери вызваны необходимостью
поиска новых потребителей иди других условий реализации
продукции.
Если считать, что потери от превышения объема поставки
продукции над спросом (£, > 0) меньше, чем потери от дефицита
(S, < 0) при одинаковом абсолютном значении в обоих случаях
разности |£|, то график функции потерь /,(!;) будет иметь вид,
показанный на рис. 10.2.
Функциональную зависимость, представленную на рис. 10.2,
аппроксимируем следующим образом:
I	М)= еСЛИ J(Ю.22)
I	j 1	, если £ 0,	4
I при этом i1>«J>0.
I Для производителей продукции наиболее предпочтительным
I является уровень постоянной интенсивности производства, т. е.
223
когда x(/) = const или, другими словами, м(г) = 0, где и(г) —
=х(/ + 1)—х(<). И в случае увеличения выпуска продукции (n(f)>0),
и в случае его уменьшения (w(/) < 0) производители несут потери,
вызванные необходимостью перестройки производства. Функция
потерь производителя f2(u), по аналогии с рис. 10.2, имеет вид,
показанный на рис. 10.3, или в аналитической форме:
/2(ц)=	если	(10.23)
м ’ ] Ь2и , если w<0.
В отличие от формулы (10.22) здесь заранее нельзя сказать,
какая из ветвей на рис. 10.3 круче. Соответственно нельзя
сказать, какой из коэффициентов, а2 или Ь2, больше. Все
зависит от конкретных условий производства, ясно только,
что «2 >0, Ь2 > 0.
Задача планирования поставки продукции формулируется
в данном случае следующим образом: найти функцию объема
поставки продукции t= 1, 2, ..., Г, и динамику необходимого
изменения этого объема, выражаемую функцией w(/), t = 1, 2,
..., Т—l, чтобы свести к минимуму суммарные потери потреби-
телей от возможного несовпадения спроса и поставки, а также
производителей—от возможных перестроек производства в тече-
ние планового периода Т.
Это условие записывается в виде функционала
S = Е	min. (Ю.24)
1 = 0
Терминальный член в (10.24) в отличие от выражения под
знаком суммы не содержит слагаемого f2(u(T')) по двум причинам:
во-первых, функция не определена, так как для этого
потребовалось бы знание функции х(Т+ 1} за пределами планового
периода, поскольку w(T) = x(T’-|-1) — во-вторых, если бы
в функционале (10.24) в терминальном члене и присутствовало
224
слагаемое /2(ц(Т)), оно бы нигде в процессе реализации излага-
емого ниже метода оптимизации не использовалось.
Исходное количество продукции задает начальное условие
х(0)=хо.	(10.25)
Уравнение процесса запишем в канонической форме:
х(/ + 1) = х(/)+ u[t}.	(10.26)
В соответствии с общей постановкой задачи оптимального
управления для многошаговых процессов соотношение (10.26)
определяет в качестве состояния системы х(у). в качестве
управления — w(z). Кроме того, очевидным является условие
х(/)^0— поставка продукции не может быть отрицательной.
Однако, для того чтобы иметь возможность решать задачу
(10.24)— (10.26) методом Лагранжа, необходимо освободиться от
ограничения на состояние х(/) 0, t= 1, 2, ..., Т. Это можно
сделать с помощью прибавления к функционалу (10.24) «штрафа»
за нарушение условий х(г)>0, т. е. дополнительно включить
в (10.24) сумму М У, [)х(()| — где Л/>0—произвольное
t-1
сколь угодно большое число. Действительно, при х(/)>0 выраже-
ние в квадратных скобках под знаком суммы обращается в нуль
и «штраф» не накладывается. Если же х(/)<0, то выражение
в квадратной скобке оказывается равным 2fx(/)| >0 и в функ-
ционале (10.24) появляется произвольно большой положительный
прирост, что противоречит его стремлению к минимизации.
Имея в виду такую возможность ликвидации отдельных
ограничений с включением в функционал «штрафа» за их
нарушение, мы тем не менее оставим функционал (10.24) без
изменений. Вместо явного учета ограничений x(z) 0, /=1, 2,
..., Т, воспользуемся ниш генным методом прямой прогонки при
! решении краевой задачи (см. Приложение П. 5). При этом на
. каждой итерации, если окажется, что x(z) < 0 при первом же
Z, будем прекращать вычисления и переходить к новой итерации.
1 Таким образом, мы ограничиваемся более простой постановкой
задачи в отличие от использования метода штрафных функций,
а неучтенные ограничения на состояцие x(z) > 0 будем учитывать
непосредственно в процессе вычислений.
Задача (10.24) — (10.26) относится к классу многошаговых
управляемых процессов. Необходимые условия оптимальности
имеют вид (см. § 9.1)
SH(t, 1), х(/), «)
ди
= 0,
«=«(()
(10,27)
где ф, х,	х,	х, и}-—функция Гамильтона;

3Яр, ф(г+1), X, »(<))
8х
(10.28)

8 Зак 456
225
х(г+1)=Д(, до» «(0);
j(o)=x„, ад=-®
t J
(10.29)
(10.30)
— условие трансверсальности.
Применительно к рассматриваемой нами задаче
(10.26)
H(i, ч|л, х, и) =^(х + и)-/1(х-r(/))-/2(w).
Из условия (10.27) получаем
(10.24) —
(10.31)
d/2
= 0,
откуда с учетом (10.23)
(10.32)
Из условия (10.28) получаем

^=^(0—Г (г)’
или с учетом (10.22)
ф(/)—ф (/+1) —2
J	[х(И-r(i)], если х(r)>r(z),
j	(x(i)-r(i)], если
(10.33)
Условие (10.29) задается непосредственно уравнением процесса
(10.26). Так как «2>0, 6,>0 то знак ф(/+1) в (10.32) будет
совпадать со знаком йр). Это позволяет исходя из (10.32)
выразить
и (/) = <
+ если ф(t +1)>0,
если *У0+1)^0'
(10.34)
Полученное по формуле (10.34) значение й(/) можно подста-
вить в уравнение процесса (10.26), после чего будем иметь
х(г) = х(г+1)-
если ф(/ +1)>0,
4-^2
если ф (t +1) < 0.
(10.35)
Если заданы значения х(г+1), ф(/+1), то формулы (10.33) —
(10.35) позволяют определить х(г), й(/), ф(г). Действительно,
226
) в этом случае по формуле (10.35) определяется х(г), а по
[ формуле (10.34)— й(/). Так как .7(/) уже определено, а функция
потребности в продукции r(t) задана по условию задачи, то
по формуле (10.33) вычисляем фр). Продолжая итеративный
I процесс, перейдем от х(г), w(r), фр) к хр—1), й (j —1), фр—1)
। и т. д. Расчеты будут продолжаться до тех пор, пока мы не
!» определим значение х(0). По условию должно быть х(0)=хо.
Каким параметром мы имеем возможность управлять, чтобы
этого добиться? Для ответа обратимся к условию трансверсаль-
ности— второй формуле (10-30). Согласно (10.22) и с учетом
того, что ^(Т} = х(Т)-г[Т), получаем
|Ф(Л=-^	=_,р4Цр-'-(Л].^"ЦЛ>’'(П,|п,й,
л=1(Т) р,	если	1
Из формулы (10.36), видно, что, если бы в терминальном чле-
не в функционале (10.24) присутствовало слагаемое /2(«(Г)),
производная по х от него все равно была бы равна ну-
лю, а больше в алгоритме терминальный член нигде не
1 представлен.
। Если мы положим г+1 = Т, зададим необходимым нам
образом х(7) (как именно, будет показано ниже) и по формуле
(10.36) вычислим ф( Г), то сможем указанным выше способом
вычислить значения функций х(г) = х(Т’~ 1), w(f) = w(T’~l),
»фр) = ф(Т-1). Продолжая итеративный процесс, дойдем до
;значения х(0), которое будет зависеть от принятого значения
ЦТ). Последнее должно быть таким, чтобы выполнялось началь-
ное условие (10.25).
Если бы данный вычисли тельный процесс можно было
провести в аналитической форме, мы бы получили явно выра-
женную функциональную зависимость х (0, х (Т)) — х0. Рас-
сматривая эту зависимость как уравнение относительно ис-
комой величины х(Т) и решая его, нашли бы необхо-
димое значение х (Г). Однако уже условие трансверсаль-
ности (10.36) требует числового задания х(т), так как в
зависимости от соотношения х(Т’)>г(Т’) или х(7)^г(т) приме-
няется первый или второй вариант формулы (10.36). Подобная
ситуация возникает и при использовании формул (10.34) и (10.35).
Таким образом, с помощью метода прямой прогонки будем
подбирать необходимое числовое значение величины х(Т), чтобы
добиться выполнения начального условия (10.25) с заданной
точностью;
|х(0, х(т))—х0|^£.	(10.37)
Если на некотором шаге t (при принятом значении х (Г))
окажется х(/)<0, то с учетом сказанного итерация прекращается,
в*
227
Таблица 10.1
1	0	1	2'	3	4	5
ДО	I	2	1	5	4	8
изменяется значение х(Т) и осуществляется переход к новой
итерации.
Изложенный метод решения проиллюстрируем на конкретном
примере.
Дано^ Г=5, х0=1, й. = 1, Z>i = 2, n2=62 = 3.
Значения функции г(/) приведены в табл. 10.1.
Точность расчетов оценивается величиной £ = 0,1.
Первая итерация. Так как по содержательному смыслу зада-
чи искомая функция х (t) должна приближаться к задан-
ной функции г И), примем это в качестве ориентира и за-
дадим х(5) = г(5) = 8. В этом случае по формуле (10.36) по-
лучаем ф(5) = 0. По формулам (10.35), (10.34), (10.33) опреде-
ляем х(4) = 8, й(4) = 0, ф (4)-8, при этом полагаем г+1 = 5,
/=4.
Приняв /4-1=4, г = 3, вычислим х(3), й(3), ф(3) и
т. д. Выполняя все необходимые действия, получим х(0) = 30,58.
Вторая итерация. Полученное на первой итерации зна-
чение х (0) чрезмерно большое (нам необходимо х(0)=1). Что-
бы его уменьшить, нужно изменить ранее принятое значение х(5).
Сначала уменьшим его, а после проведения расчетов уви-
дим, справедливым ли оказался наш выбор. Примем х(5) = 6,125.
Выполняя указанным выше способом все необходимые вычис-
ления, получим х(0) = 3,923. Видим, что метод уменьше-
ния значения х (5) оказался правильным.
Третья итерация. Продолжим уменьшать х(5) и при-
мем х (5) = 6,02. В результате расчетов получим х(0) = 2,253.
Вновь убеждаемся, что динамика
уменьшения значения х(5) правиль-
ная, но пока еще решение с необ-
ходимой точностью не получено.
Четвертая итерация. Принимая
х (5) = 5,95 и осуществляя расчеты,
получаем х(0)= 1,053, что удовлет-
воряет заданной точности
11 -1,053|<0,1.
Полученные результаты будем
считать приближенно оптимальным
решением, они представлены
в табл. 10.2 и показаны на графике
рис. 10.4.
228
Таблица 10.2
t	0	1	2	3	4	5
	1,053	1,783	2,365	3,405	4,58	5,95
Ф М	4,35	4,37	3,5	6,23	7,04	8,2
ы(Ц	0,73	0,582	1,04	1,П5	1,37	1,37
Примечание. На рис. 10.4 дискретные зависимости условно
показаны как непрерывные функции.
§ 10.3. Оптимальное планирование поставки продукции.
Численное решение. Непрерывный вариант
Продолжим исследование предыдущей задачи, рассматривая
ее в режиме непрерывного процесса. Соответствующие различия
в математической модели и в применении принципа максимума
Понтрягина продемонстрируют различия в технике реализации
соответствующих вычислительных методов.
По аналогии с задачей (10.24)— (10.26) для непрерывного
процесса имеем:
функционал
y = J [.A (x(0-r(0)+.A(M(0)]di+/i (x( r)_r(r))^min; (Ю.38)
о
уравнение процесса
х = и (г);
(10.39)
начальное условие
х(0) = хо;	(10.40)
необходимые условия оптимальности [сравните с (10.27) для
дискретных процессов]
ф, x) = argmax/Z(z, ф, х, «);	(Ю.41)
vH(t, ф, х, и)
дх
x = u(t, ф,
u=a(t, ф, х(г))
х(0) = х0, ф(г)=~&±)
x=x(l)
(10.42)
(10.43)
(10.44)
Функция Гамильтона для задачи (10.38) — (10.40) имеет вид,
несколько отличающийся от многошагового варианта [форму-
ла (10.31)]:
H(t, ф, х, «) = ф«-/г (х-г(/))-/2 (и).	(10.45)
229
Так как на управление и нет ограничений, оно должно
удовлетворять требованию стационарности ~ = 0. С учетом
формулы (10.23) в этом случае получаем
1 ФА |	. а2^, если «^0, п du	b2u, если м^0
откуда

если w^O,
а2
тН если w^O.
"2
(10.46)
Принимая во внимание, что а2>0, Ь2>0 и знаки функций
й(ф) и ф совпадают, выражение (10.46) можно переписать в более
удобной для вычислений форме;

—, если ф (/)^0,
—, если ф(/)^0.
(10.47)
Осуществляя дифференцирование функции Гамильтона (10.45)
с учетом формулы (10.22), получим сопряженное уравнение
(10.42) в виде

если х (t}>r (И;
х (г)-г (/) , если х (i)^r (/)
Уравнение процесса (10.43) с учетом (10.47)
следующим образом:
если ф(г)^О,
_ <	^2
2 | если ф(г)^О.
(10.48)
преобразуем
(10.49)
Граничные условия (10.44) не зависят от характера процесса —
дискретного или непрерывного, поэтому воспользуемся форму-
лами (10.25) и (10.36):
х(0) = хо;
(10.50)
^(Г)= “2	[х(Г)_г(Г)]5 если х\т)^г(Т).	(10‘51)
230
Таким образом, процесс оптимизации сводится к решению
двухточечной краевой задачи (10.48)— (10.51) для системы двух
дифференциальных уравнений первого порядка (10.48) и (10.49).
Аналитическое решение системы дифференциальных уравне-
ний (10.48) и (10.49) невозможно по тем же причинам, что
и системы конечно-разностных уравнений (10.33) и (10.35).
Используя метод численного интегрирования Эйлера для
систем дифференциальных уравнений (см. Приложение), запишем
уравнения (10.48) и (10.49) в виде системы конечно-разностных
уравнений с шагом численного интегрирования Д t:
4»(г+Д/)-ф(г) J а, [х (() - г (г) , если х(Й>
Дг ~ | [x(tj —г(/) , если х(г)^
, . .	,л .	если ф(г)^О,
х(*+Дг)-х(/)~ 1 J а2 ’	7	’
Л/ 2	если ф(/)<0.
'(О,
г(/);
(10.48')
(10.49')
Отсюда при достаточно малом значении Д/ получаем
ф(г+д<)=ф(>)+2д< / И'!-''!'!)если
’ v'7	[x(r)-r(r)J, если x(Z)^r(/);
х(Г + Д t)=x(/) + y
—, если ф(г)^О,
a2
если ф(?)*ёО.
(10.52)
(10.53)
Соотношения (10.52) и (10.53) с точностью до перестановки
в левой и правой частях отдельных слагаемых совпадают
с содержательно эквивалентными формулами (10.33) и (10.35)
(для многошаговых процессов) с той лишь разницей что в этих
формулах шаг счета составляет единицу, а в (Ю.э2) и (10.53)
шаг численного интегрирования равен Дг. формулы (10.52)
и (10.53) при любом сколь угодно малом, но конечном значении
Д/, имеют приближенный характер, вытекающий из замены
производных ф((), х(() отношением конечных приращений
и —. Формулы (10.33) и (10.35) точные.
Для непрерывного варианта рассматриваемой в настоящем
параграфе задачи приближенный характер решения определяется
численным интегрированием системы дифференциальных уравне-
ний методом Эйлера [см. формулы (10.52) и (10.53)] и приближен-
231
ностью выбора значения х ( Т). Для дискретного варианта (§ 10.2)
приближенный характер решения определяется только приближен-
ностью выбора т(Г).
§ 10.4. Оптимальное потребление в однопродуктовой
макромодели
Рассмотрим в качестве еще одного примера применения
принципа максимума Понтрягина следующую задачу оптималь-
ного управления, представляющую собой модификацию задачи,
рассмотренной в § 6.2.
Пусть управляемая система представляет собой экономику
страны или региона, моделируемую с помощью однопродуктовой
модели, т. е. ,(см. гл. 2) процесс экономического роста задается
уравнением
к = — (ц +д)£-|-5 (1 — a)/(fc),	(10.54)
где фондовооруженность труда; 5—доля произведенного
конечного продукта, идущая на накопление; ц— коэффициент
выбытия основных производственных фондов; п—темп роста
трудовых ресурсов; а —коэффициент материальных затрат.
Так как доля произведенного продукта, идущая на потребле-
ние, равна 1 — s, то величина с потребления на единицу рабочей
силы может быть выражена следующим образом:
с=(1 -у)(1 - ц)/(/с).
С учетом данного соотношения уравнение (10.54) перепишем так:
£= ~(ц+«)/(+(1-л)/(Л)-с.	(10.55)
Это уравнение и будем рассматрива ть как уравнение управляемого
процесса.
В (10.55) управлением является потребление с 5= 0. Чтобы
сформулировать задачу оптимального управления, рассмотрим
т
y = Jе ~&tg (c)dr^max.	(10.56)
о	€
Здесь g(c)— некоторая зависящая от величины с функция,
называемая в теории потребления функцией полезности. Эта
функция дает оценку «полезности» т. е. эффективности потребле-
ния при различных его значениях.
Относительно функции полезности предположим выполнен-
ными следующие свойства:
Г3. g«)>0 при оО, g(0) = 0.
2°. #'(<т)>0 при <?>0,	при с^0, g'l^WO при г->оо.
3°. g"(c)<0 при с>0.
Перечисленные условия характеризуют такие свойства полез-
ности, как неотрицательное монотонное возрастание с ростом
потребления и происходящее при этом насыщение.
232
Будем считать, что наряду с состоянием системы в начальный
момент времени /()=0 задано и ее конечное состояние при / = Т,
т. е. заданы
k($) = k0, k(T)=k,.	(10.57)
Задача оптимального управления состоит в том, что требуется
отыскать такое потребление c(f), чтобы при выполнении ограни-
чений (10.55), (10.57) функционал (10.56) достигал максимального
значения. Данная задача является обобщением рассмотренной
в гл. VI задачи для случая нелинейной функции полезности.
Для решения задачи воспользуемся принципом максимума. - '
Условие максимума функции Н для данной задачи с учетом
вида функционала (10.56) примет вид
77 = ф [ — (ц + /?)& + (1 — n)/(fc) — c] + e-6'g(c)->max,	(10.58)
С
где ф— сопряженная переменная, определяемая уравнением
Ф=~™=[м + «-(1-я)7'(^)]ф-	(10.59)
Проанализируем условие (10.58). От с зависит лишь часть
слагаемых
77с=-фс + е 5tg(c).	(10.60)
График функции Нс ири фиксированном t исходя из свойств
1°—3° функции полезности g(c) представлен на рис. 10.5.
Нетрудно видеть, что вторая производная по с функции Нс
отрицательна вместе с g?. Следовательно, в точке обращения
в ноль первой производной Нс будет достигатг, максимального
значения.
Приравнивая нулю производную выражения (10.60), подучим
,ф(е) = фей'.	(10.61)
Из свойств 2°, 3° следует, что данное уравнение при
положительных ф(г) имеет, причем единственное, решение. Это
решение на рис. 10.5 обозначено стак.
Уравнение (10.61) можно использовать для того, чтобы
выразить сопряженную переменную че-
рез управление с. Находя из (10.61)
значение ф и подставляя его в левую
часть уравнения (10.59), получим
ф= [g"(c)c-6g'(c) ]е“5'.
Тогда уравнение (10.59) после преоб-
разований примет вид
233
с=[ц + » + 5-(1-й)/(^)]^.	(10.62)
g (с)
Таким образом, принцип максимума в данной задаче позволяет
для отыскания оптимального процесса (А; (г), с(?)) получить систему
дифференциальных уравнений (10.55), (10.62). Для этой системы
требуется решить краевую задачу с условиями (10.57). При этом
удовлетворительным следует считать лишь такое решение, при
котором (k(i\ c(i')') неотрицательны.
Глава 11
Метод Гамильтона — Якоби — Беллмана
При постановке задачи оптимального управления предпо-
лагалось, что такие параметры задачи, как начальное состояние
и начальный момент времени, зафиксированы. При решении
задачи оказывается удобным «погрузить» ее в множество задач,
описываемых теми же уравнениями процесса и функционалом,
но с различными значениями перечисленных параметров.
Определяя оптимальное уравнение сразу для всего мно-
жества задач, получим решения в так называемой форме
синтеза, т, е. зависимость величины оптимального управления
от значения состояния системы и текущего момента времени.
Имея решение задачи в таком виде, нетрудно получить ее
решение и для любых фиксированных начальных условий
в обычной форме, т. е. оптимальное управление как функцию
времени. Решение задачи в форме синтеза обладает рядом
преимуществ. Главное из них состоит а том, что имеется
полная информация об оптимальном управлении. Таким образом,
если в процессе управления реализовались заранее не извест-
ные значения состояния системы (а в практических случаях
Это типичная ситуация), то значение синтеза оптимального
управления позволяет принять оптимальное решение и в этой
ситуации.
Однако поиск синтеза оптимального управления —значитель-
но более трудоемкая процедура по сравнению с решением
обычной задачи оптимального управления. С математической
точки зрения отыскание синтеза оптимального управления
сводится к решению уравнения с частными производными,
называемого уравнением Гамильтона — Якоби — Беллмана. Это
уравнение нелинейно, а сложность его численного решения
чрезвычайно сильно растет с ростом размерности решаемой
задачи.
§ 11.1. Уравнение Гамильтона — Якоби — Беллмана.
Непрерывный вариант
Рассмотрим задачу оптимального управления, заданную сле-
дующими условиями^.
х, u)d/-f-F(x(7))^min,	(11Л)
о
235
x=f(t, x, и),	(II.2)
x(0) = xo, ue Vtx.	(Il.3)
Обратим внимание на то, что в такой постановке задачи
отсутствуют ограничения на состояние. Множество V‘x при всех
/е(0, Т) совпадает со всем пространством X, а при / = 0 есть
фиксированная точка х0. Ограничения на фазовые координаты
х1' в момент i=T не заданы, т. е. рассматривается задача со
свободным правым концом траектории.
Для получения уравнения Гамильтона—Якоби   Беллмана
воспользуемся теоремой 5.2 о достаточных условиях оптималь-
ности, согласно которой если есть допустимый процесс (х(г),
й(Г))еМ и функция ср(Г, х) непрерывная и имеющая такие
непрерывные частные производные при всех (. х, что
7?(/, х(Г), й(0)= шах /?(/, х, u) V/e(0, Т),
Х,И€
Ф(х(7)>ттф(х) ПРИ 1 =
то процесс (х(0,й(0) оптимален, т. е.
У (х, й) = inf (х, и).
А/
Известно, что
jR(f, x, u)=	x, «)—f (Б x, U)H—
a
Ф(х)=ф(7’> x) + F(x).
Введем функцию Р(/, x) с помощью соотношения
P(t, x) = max R(t, x, u).
u
Предположим, что удалось так определить функцию ср(/, х), что
P(Z, х) = с(Г),	(11.4)
Ф(х) = сР	(И-5)
Так как функция p(Z, х) задана, следовательно, задана и фун-
кция /?(£, х, и), максимизируя которую по управлению пеК1*
найдем й(Г, х):
й(Г, x) = argmax7!(r, х, u)V/.
иек,л
Как будет показано ниже, й(/, х) является решением рассматри-
ваемой оптимизационной задачи. Такое решение называется
синтезом оптимального управления.
Для определения оптимальной траектории х(/) подставим
оптимальное управление й(/, х) в уравнение процесса:
x=f(r, х, й(/, х)), х(0) = хо.
236
Итак, определение оптимальной траектории х(Д сводится
к решению задачи Коши для уравнения процесса, замкнутого
фптимальным управлением с заданными начальными условиями
Х(0) = хо. В отличие от синтеза оптимального управления й(/, х)
функцию
u(0 = u(Z, x)K=i(t)
называют оптимальной программой управления.
Изложенный метод нахождения процесса (x(Z), й(г)) при ап-
риорных ограничениях, наложенных на функцию <р(/, х), назы-
вается методом Гамильтона- -Якоби — Беллмана. В этом случае
процесс (х(/), й(0) является оптимальным. Для доказательства
этого покажем, что рассматриваемый процесс допустим и удов-
летворяет условиям 1° и Т теоремы 5.2. Будем считать, что
процесс (х(0, й(Г)) допустим, т. е. траектория х(/) и управление
й(Д удовлетворяют уравнению процесса х=/(/, х, и), априорным
ограничениям не К1’1 и начальному условию х(О) = хо.
Нахождение процесса (х (/), й(/)) мы начинали с определения
й(Г, X). В свою очередь, й(/, х) находили из условия Г теоремы 5.2,
т. е. из условия
й(Г, x) = argmax R(i. х, и).
А это значит, что управление й(/, х) за пределы области Vt!i
не выходит и, следовательно, допустимо. Траектория находит-
ся подстановкой й(/, х) в уравнение процесса (П.2). Следователь-
но, пары функций (х(7), й(у, х)) удовлетворяют уравнению процес-
са. Кроме того, траектория х(Д удовлетворяет начальным
условиям. Область совпадает со всем пространством X.
Итак, процесс (х(Д, н(0) допустим, так как все условия его
принадлежности области М выполнены.
Покажем, что при наложении на функцию ср(/, х) формальных
требований условия 1° и 2° теоремы 5.2 выполнены. Для этого
представим максимум по совокупности переменных как последо-
вательность максимумов по отдельным переменным:
max R(t, х, u) = max [maxR(r, х, u)]=maxP(t x).
(x, 11)6 И	x usr	x ’ '
Функция й(/, x) обеспечивает max /?(/, x, u), a P(z, x) согласно
(II.4), не зависит от х. Это обеспечивает выполнение условия
тах/?(/, х(0), т. е. условие 1° теоремы 5.2. Для выполнения
Х,0
условия 2° теоремы 5.2 рассмотрим соотношение (11.5), выполнен-
ное согласно заданию функции <р(/, х).
Так как функция Ф(х) постоянна, то ее минимум достигается
при любом значении аргумента, в частности при х(Г). Следо-
вательно, условие 2° выполнено.
237
Таким образом выбранная нами функция cp(z, х) и построенный
процесс (х(0, й(/)) допустимы и удовлетворяют теореме 5.2.
Следовательно, процесс (x(t), й(/)) оптимален.
Еще раз отметим, что метод Гамильтона—Якоби—Веллмана
применим только к задачам оптимального управления, в которых
отсутствуют ограничения на состояние, в том числе и при t=T.
§ 11.2. Синтез оптимального управления
Рассмотрим задачу (ИЛ) — (И-З). В нашей постановке огра-
ничения на состояние отсутствуют. Множество М допустимых
процессов—Зто множество пар функций x(Z), u(t), удовлетво-
ряющих условиям задачи и накладывающих на них соответствую-
щие ограничения. Необходимо подчеркнуть, что множество
М зависит от Zo и х0: M(f0, х0). Если изменить t0 и х0 на
Z’o, Xq, то получим новое допустимое множество Л/'(/о, х'о)-
Если решать задачу при различных параметрах (z0, х0), оставляя
без изменения другие условия задачи, то получим семейство
оптимизационных задач, которое назовем А.
Зададим управление в виде функции
u —fi(Z, х),	(И .6)
где fi(f, x)efs. Задав начальное состояние (;с„х0) и подставляя
(11.6) в уравнения (Ц.2), получим, решая задачу Коши, траекто-
рию х(/, /0, х0), отвечающую заданному закону управления. Эта
Траектория является допустимой, так как отсутствуют ограниче-
ния на состояние системы. Подставляя найденную траекторию
в (П.6), получим отвечающее ей управление в виде функции
времени:
Й(Г,	Хо) = Й(^ х) I X =Х((, хс)!
т. е, значение и вдоль траектории. Назовем й(/, х) синтезом
оптимального управления или оптимальной синтезирующей функ-
цией управления, если процесс
Zo, х0) = (х(/, 'о, хо)> »(?, z0, х0))
есть решение задачи семейства А для любых z0, х0. Матема-
тически это означает, что, как только получили u(Z, х) и под-
ставили его в уравнение процесса при любых z0, х0, найденньщ
процесс становится оптимальным.
Таким образом, зная оптимальную синтезирующую функцию
й(/, х), имеем решение не одной оптимизационной задачи,
а целого семейства задач А при различных начальных условиях
(Ль хо)-
При применении метода Гамильтона —Якоби —Веллмана ре-
шение задачи получается в форме синтеза оптимального управле-
ния й(/, х) в отличие от метода Лангранжа, где решение
238
Рис. И,1
Рис. 11.2
отыскивается в виде программы u(t). Для реализации синтеза
громе значения t надо знать состояние системы в каждый
момент времени.
В теории управления u(z, х) принято называть управлением
; обратной связью, a u(Z)—программой управления. На рис. 11.1
1и 11.2 показано, как в этих случаях формируется траектория
системы. Из рис. 11.1 видно, что для формирования траектории
х(г) системы необходимо иметь информацию о состоянии систе-
|МЫ. Состояние, в которое система перешла под воздействием
управления, в свою очередь участвует в формировании самого
управления. Таким образом, возникает связь между состоянием
и управлением, которая называется обратной связью (см. гл. 1).
В экономических задачах задание управления в виде програм-
мы u(Z) соответствует планам на длительную перспективу, а в виде
синтеза u(Z, х)—экономическому регулированию (отслеживанию
плана). Управление й(г, х), являясь оптимальным при любом
х0 в случае отклонения траектории системы от планового
значения, дает оптимальное решение и при новом состоянии
системы. Программное же управление при этом теряет свойство
оптимальности.
§ 11.3. Алгоритм метода Гамильтона — Якоби — Белл мана
Решение задачи методом Гамильтона—Якоби —Веллмана
начинается с отыскания функции $(/, х), которая должна удовлет-
ворять двум априорным требованиям:
Л^х) = с(0,	(П-7)
Ф(х)=С1.	(И.8)
Функцию
R(f, 1, o)=*^f(r, х, х, и)+*£Д
учитывая, что правая часть Этого равенства, согласно формуле
(8-9) равна
<?ф	. (Эф
перепишем в виде
R(t, х, u)=#(z, х, o)+i
ox	vt
239
Так как ср(/, х) не зависит от и, то выражение
Pit, x)=maxK(t, х, u)
иеГ'‘
примет вид
P(t, x) = maxH(z,	х, ц)+-Р1р^’ х\	(11.9i)
v ueV* х Зх’ ’ 7 ar ’	v 7
т. е. в максимизации участвует только гамильтониан H(t — х. if.
Зх
Запишем результат максимизации гамильтониана в виде I
Ж(Г —, x) = maxH(r, —, х, и).
Тогда равенство (11.9) с учетом (11.7) примет вид
Уравнение (11.10) называется уравнением Гамильтона — Якоби
— Веллмана. При <?(/) = 0 это уравнение называется уравнением
Веллмана:
*)	0Ы1)
Уравнения (11.10) и (11.11) являются уравнениями в частных
производных первого порядка, разрешенными относительно част-
ной производной ср, (г, х). Граничное условие ср (г, х) определяют
из (11.8):
O(x) = F(x) + cp(T, х) = с1;
откуда
<р(Т, х)= - F(x)-|-c1.	(11.12)
Таким образом, чтобы найти функцию ср (Г, х), удовлетво-
ряющую априорным ограничениям (11.7) и (И-8), надо решить
уравнение в частных производных (11.10) с граничными условиями
(11.12). Подобная задача называется задачей Коши в отличие
от краевой, когда часть граничных условий задается на одном
конце, а часть — на другом.
Геометрическая интерпретация задачи Коши для уравнений
в частных производных представлена на рис. 11.3.
При 1=Т функция ср(/, х) задана:
<р(Т, х)= —F(x), с1=0.
Через точки /15 t2, ..., Т-1 проводим сечения. Обозначим
(р(/ц., x) = cpt(x) и будем искать
Ф*-1(х) = Ых)-^^(Л-V1)-
240
читывал, что
йр(А х)_
пблучим,
х\ X),
Ф*- 1 (Х) = Ф* (Х) +	— !к- 1)-
Это соотношение позволяет вы-
числить (pj._1(x), зная (рДх); при
i = T значение ср известно.

х)
дх ’ 7>
обозначая
i = T значение ср известно.	Рис- 113
Найденная таким образом функция ср (у, х) и соответствующая
^й функция й(/, х) уже решают поставленную задачу. Остается
только подставить в уравнение процесса й(/, х) и пронитегриро-
зать его при заданных начальных условиях.
Пример. Найти
:	Т
J H2dz + kx2(7)->min,
х=м, x(f0) = x0, Х>0.
Построим функцию R(t, х, и):
„	.	5<р з йю
7?(t,x, w) = v-«-w +-F-.
 ’ ’ ' З.т	ot
(11.13)
Согласно условию задачи, допустимое множество управлений
Kt —вся числовая ось. Функция 7?(г, х, и) по и строго вогнута,
и при каждом фиксированном t имеем единственный максимум
по и:
Т?и = ^-2« = 0,
дх
откуда
_.	.	13<р
(П.14)
Подставляя найденное значение u(t, х) в (11.13), получим
f 1/ар\2	йф J/5<pY 3<р
А&) +t=jU) +Т’
откуда
р((,
4uAy/ dt и
а уравнение Гамильтона—Якоби — Веллмана примет вид
ot	4\Sx J
241
с граничным условием
Ф(Т, х)= -Ъ^ + ср	(11.р)
Учитывая вид граничного условия (11,15), будем искать
функцию ф(г, х) в виде многочлена второй степени по х с ко-
эффициентами, зависящими от t.
Запишем функцию ф(Г, х) в виде
ф(/, х) = ф(?)х+а(/)х2.	(11,16)
Тогда при t=T имеем
ф(Т, х) = ф(7)х + а(7)х2 = — Х,х2+Ср
Необходимым и достаточным условием равенства многочленор
является тождественное равенство коэффициентов при одинаковых
степенных неизвестных;	j
Ф(П=о,
ег(7) = -к.
Найдя частные производные ф:
ф(=фх+сгх2,
<рл = Ф + 2ох,
и подставив их в P(t, х), получим
P(t, х) = фх + бх2 + ^[ф + 2стх]2,	(П-17)
Для того чтобы выполнялось условие
P(t, x)—c(t),
необходимо, чтобы коэффициенты при х и х2 в (11.17) были
равны нулю. После преобразований будем иметь
Р(1, х)-^ф2 + (ф + сгф)х + (а + ст2)х2,
откуда получим однородную систему обыкновенных дифферен-
циальных уравнений относительно искомых ф и о
ф + аф = 0,	(11.18)
а + с2=0	(11.19)
с начальными условиями
ф(7)=0 и о(7)=-Х.
Тривиальное решение ф(/) = 0 однородного дифференциального
уравнения (11.18) удовлетворяет граничному условию ф(7) = 0.
242
Остается найти решение дифференциального уравнения (11.19).
Разделив переменные в уравнении (11.19), получим
о''куда, интегрируя, имеем
г/+с-
Найдем С: при t — T
J	~'-=Т+С
;	Д'
или
	С=-- — Т. х
Общее решение (11.19) примет вид	однородного дифференциального уравнения ею-—ц. т~1+х
Решение системы уравнений (11.18) и (11.19) определяет
коэффициенты функции <р(г, х), заданной в виде (11.16).
Таким образом, для рассматриваемого примера функция
<р(г, х), являющаяся решением уравнений Веллмана, имеет вид
у
Найдем синтез оптимального управления, подставляя <р(?, х)
в выражение (11.14):
«(', =-------у”
T+--i
Л,
Полученная зависимость й(/, х) справедлива для любых начальных
условий. Она показывает, как надо управлять, находясь в любом
заданном состоянии, чтобы система вела себя оптимально.
Подставляя й(/, х) в уравнение процесса, будем иметь
Разделяя переменные и интегрируя это уравнение, получим
243
lnx = ln[ t~ T—i ] + ln Cl
или
x(/) = Cj	(11.20)
\	A /
Таким образом, оптимальной траекторией является прямая
линия (11.20), для которой интегральную константу найдем
из начальных условий в момент t = t0:
= С\ — Т—
или	''
Оптимальная траектория, проходящая через точку ()0, х0),
имеет вид
/ А
х°( (- Т~- )
' х(0=~^------(11.21)
/0-г—
° X
Найдем программу й(/):
й(О = й(/, х)[л=ад
или
u(t} = -—-—-= ——-—=const.
1' 1	1
T+--t0 Г+?-Го
л.	Л
§ 11.4. Метод Гамильтона—Якоби—Веллмана.
Многошаговый вариант
Рассмотрим следующую задачу:
£/“(', Х(С, u(C) + ^(x(7))^min,
t=0
x(t+l)=f(z, x(t), u(z)), z = 0, 1, 2, ..., T-l,
u(t)errjc,
x(0) = xo.
В данной постановке отсутствуют ограничения на состояния
и х(Т) не задано.
244
Воспользуемся теоремой 5.3 о достаточных условиях опти-
мальности в многошаговом варианте, согласно которой, если
есуь процесс (х(0, ц(7))еЛ/ и функция <р(Т, х)— непрерывная
и дифференцируемая, выполняются достаточные условия оп-
тимальности:
' 1°. /?(/, х, й)= max /?(/, х, и), / = 0, 1, 2, Т— I.
(х, и)е V'
Ф(х(Г)) = min Ф(х) при 1 = Т,
х е Г",
где
/?(/, X, u) = (p[z+l, ф, X, «)] - <p(z, x)-/°(r, X, и),
(11.22)
Ф(х) = Р(х) + ф(Т, х),	(11.23)
пара (х(г), й(0) — оптимальный процесс.
Введем в рассмотрение функцию Р(/, х):
Pit, х) = max Pit, х, u) = Р(t, x, й(г, x)).	(11.24)
пе Г11
При всех фиксированных t и x находим такое значение и,
которое обеспечивает наибольшее значение функции:
R(t, х)= max[<p(z+l, ф, х, u))-/°(z, х, и)-<р(г, х)],
или, подставляя в (11.24) функцию R(t, х) в (11.22)—(11.23),
получим
P(t, х) — max [ф(/+ 1, ф, х, н))~/°(г, х, и)] -ф(г, х),
где функция ф(/, х) вынесена из-под знака max, так как она
не зависит от и. Будем стремиться задавать ф(/, х) так, чтобы:
1) при всех / = 1, 2, ..., Т~ I функция P(t, х) не зависела от х:
Р((х)-С(Г),	(11.25)
где Сф)— произвольная функция аргумента t;
2) при t= Т
f	Ф(х)=С\,	(11.26)
>где С;—произвольная постоянная.
Предположим, что функцию ф(/, х) задали так, что она
.удовлетворяет этим условиям. Тогда этой функции отвечает
"некоторое управление й(г, х). Введем в рассмотрение фазовую
траекторию х(/), удовлетворяющую уравнению
х(г+1)=ф,х(4 йфх(г))	(11.27)
при начальном условии х(0)=хо. Определим
245
й(?) = й[г, x(r)]_	(И.28)
Рассмотрим теорему.
Теорема 11.1. Пусть функция ф(Г, х) обеспечивает выполнение
условий (11.25), (] ] .26), а функция й(/, х) отвечает данной функции
<р(7, х) на основании условия
P(t, х, й(г, х)) = max R(t, х, и) = Р(/, х).
Функции х(Г), й(/) заданы условиями (]].27) и (] ] .28). Тогда пара
вектор-функций х(?), й(?) является оптимальным процессом.
Доказательство. Условие 2° теоремы 5.3 выполняется
тривиально благодаря заданию Ф(х) [см. (] J.26)].
Функция й(?, х) строится так, что при каждом фиксированном
t, х она обеспечивает max 7? (Г, х, и), Функция <р(/, х), согласно
условию (] 1.25), выбрана так, что max7? = P(r, х) не зависит от
не У"
х. При таком выборе <р любое значение х, в том числе
и значение x(f), в паре и с “(г) удовлетворяет условию ]°
теоремы 5.3. Согласно условию иеР'1, использованному при
построении u(Z, х), и условию (11.27), пара (х(Г), й(Г)) допустима.
Проведем анализ условий (]].25), (]].2б), которым должна
удовлетворять функция <p(f, х).
Так как
Ф(х) = р(х) + ф(Г, х),
то, учитывая (11.26), имеем
ф(Р, x) = Ci-P(x),	(11.29)
т. е. функция ф(Г, х) в момент t = T должна с точностью до
постоянного слагаемого совпадать с функцией — Р(х).
С учетом условия [см. (Ц.27)]
P(z, х)= 1пах{ф[г+1, f(r, х,	х, и)}-ф(г, х)=С(г)
и	(11.30)
ф(/, х) = шах {ф[г + ], f(z, х, u)]-/0(z, х, u)} +c(r).
ue Г"-1
Выполним вычисления от t=T. Равенства условий (1 ].29)
и (] 1.30) образуют цепочку рекуррентных соотношений, решая
которые в направлении от Г к t — 0 найдем функцию ф(Т, х).
Полагая Cj =0, найдем
ф(г, х)|(=т = - Р(х).
Полагая С(/) = 0, при г=Т—] имеем
ф(Г-1, x) = ^ max^ J-P(f(P-],x, и))-/°(Г-], х, и)}.
246
При t=T—2 получим аналогичную картину. При многомерном
векторе х эта задача сложна, так как вычисления проводятся
при каждом фиксированном х. Одновременно отыскиваются
и й(/, х). Подстановка й(/, х) в уравнение процесса при заданных
начальных условиях дает возможность определить оптимальную
траекторию х(г).
§ 11.5. Учет ограничений на состояние
Отметим, что метод Гамильтона —Якоби — Беллмана изла-
гается для задачи оптимального управления, где отсутствуют
априорные ограничения на состояние, а также краевые ограни-
чения на правом конце при ! = Т. Однако на практике часто
встречаются «двухточечные» задачи.
Рассмотрим, например, задачу
Т
J/°(r, х, u)dl->min,
о	м
x=f(l, х, и),
uej;, х(0)=хо, х(Г)=х1.
Для того чтобы применить метод Гамильтона —Якоби—Бел-
лмана к сформулированной задаче, необходимо провести ее
редукцию к задаче без ограничений на состояние.
Редуцированная задача примет вид
г
У = х, u)d/ + X,n[x(7’)-x1]->min,
о
x = f(f, х, u),
не Ги, x(0)=xo, Л,>0,
где П [х(Г)—xt ]—-некоторая заданная функция, называемая
штрафной. Она обладает свойством
. fO, если х =х.,
П(х) = 5 J л ,
v !	) >0, если х^х£
и при этом достаточно велика.
Есть несколько видов задания шграфных функций. Как правило,
П(х) — функция, положительная всюду, кроме нуля. При
х(Г) = х1; П(х)=0. Простейший штраф — это квадратичная функция
П(х)=Х £ (x‘-xi)2,
>=1
hie Л—фиксированное число.
247
Траектории исходной и редуци-
рованной задачи схематически изо-
бражены на рис, 11,4.
Рассмотрим, как редуцирован-
ная задача связана с исходной:
1)	очевидно, что М^М', т, е
класс М‘ более широкий;
2)	если (х, и)еМ, то
./'(х, ц)=./(х, и),
траектория х(г) проходит по области М и добавка П(х) = 0;
3)	minmin У min,/';
м • м м
4)	если увеличивать штраф, т, е, значение Л, то
min./'(x u,X)->min./,
м-	м
Кроме того, х'(Г, Х)-»-х(Г)—х, при л-*сс. При Х->со точка
N будет стремиться к х1? а соответствующее значение фу-
нкционала
min/'(х, и)-*min/ при л-*сс.
Л/
Пример.	т
/ = J w2(/)->min,
t(0)
x = u, x[t0)—x0,	0.
Здесь х, u — скалярные величины, Для любых точек (Го, х0) при
таких, что ta<T, требуется найти оптимальное решение х(Г, х0, ;0)
и u(t, х0, /0), т. е. найти синтезирующую функцию й(Г, х), которая
давала бы оптимальное решение для всего семейства (ф, х0),
Прежде чем решать такую задачу, редуцируем ее:
т
/' = J w2dZ + Xx2(r)->min,
х — и, х(/0) — х0, Х>0,
Решение этой задачи рассмотрено в § 11,3, Согласно формуле
(11,21), оптимальная траектория редуцированной задачи имеет вид
248
При X -> со получаем решение
' ' h-T ’
iудовлетворяющее краевому условию х(Г)=0.
j- §11*6. Сравнительный анализ методов Лагранжа —
I	Понтрягина и Гамильтона — Якоби — Беллмана
I.	Метод Лагранжа — Понтрягина сводит задачу оптимального
управления к краевой задаче для системы обыкновенных диф-
ференциальных (или рекуррентных) уравнений порядка 2п, тогда
как метод Гамильтона — Якоби — Беллмана ставит в соответствие
задачу Коши для уравнений в частных производных (или
рекуррентного функционального уравнения) относительно функции
ф(Г, х) От п+1 переменных. В Этом отношении метод Гамиль-
тона— Якоби — Беллмана значительно сложнее.
2.	Метод Лагранжа — Понтрягина позволяет отыскать опти-
мальную программу управления u(f) и оптимальную траекторию
x(Z), отвечающие заданным граничным условиям.
Метод Гамильтона — Якоби — Беллмана обеспечивает решение
j в форме синтеза и(1, х) семейства оптимизационных задач с лю-
j быми начальными условиями, т, е. решает более общую задачу,
§ эквивалентную семейству задач, решаемых методом Лагран-
! жа — Понтрягина.
3.	Процесс (х(Г), й(Г)), найденный методом Лагранжа — Понт-
рягина, является подозрительным на оптимум, но, вообще говоря,
может и не быть таковым. Доказательство оптимальности требует
дополнительных исследований,
Оптимальное управление и(£, х), найденное методом Гамиль-
топа—Якоби — Беллмана, позволяет отыскать процесс (х(г), «(/)),
|отвечающий этому управлению, который является оптимальным.
।Таким образом, вопроса об оптимуме решения, найденного
гметодом Гамильтона — Якоби — Беллмана, не возникает и до-
|полнительного исследования не требуется.
*	4. Метод Гамильтона — Якоби — Беллмана применим только
к задаче без ограничений на состояние при t>tQ, в том числе
и лишь к задаче со свободным правым концом. Метод Лаг-
ранжа - Понтрягина не требует отсутствия ограничений на со-
стояние при t = Т. Если заданы ограничения на состояние, то
для применения метода Гамильтона — Якоби — Беллмана необ-
ходимо преобразовать данную задачу при помощи штрафных
функций в некоторую эквивалентную задачу без ограничений.
5. Метод Лагранжа — Понтрягина более универсален в отно-
шении граничных условий, а метод Гамильтона — Якоби—Бел-
лмана, в свою очередь, применим к более широкому классу
задач. Например, при применении метода Гамильтона — Якоби —
249
Веллмана не требуется, чтобы множества Уи и Vx были
подмножеством векторного пространства, а функции /*(/, х, и) —
непрерывными и дифференцируемыми в этих областях. В част-
ности, в отличие от метода Лагранжа —Понтрягина метод
Гамильтона —Якоби — Веллмана применим к решению целочис-
ленных задач типа задачи о ранце, задачи коммивояжера и др.
§ 11.7. Оптимизация распределения капитальных вложений
между предприятиями методом динамического программиро-
вания
Предположим, например, что объединение предприятий ставит
задачу оптимально распределить некоторый установленный
фонд капитальных вложений между предприятиями так, чтобы
максимизировать совокупную эффективность капитальных вло-
жений. Эффективность может измеряться различными пока-
зателями, и в экономике это специальная проблема. Не
входя в данном случае в ее детали, для простоты и опре-
деленности будем считать, что функция ф,(у;) отражает увеличение
выпуска продукции на i-м предприятии за счет реализации
на нем капитальных вложений в объеме . Этот показатель
будем принимать за показатель эффективности капитальных
вложений.	___
Введем обозначения: п — количество заводов, г=1,я; А—за-
данный фонд капитальных вложений.
Предположим, что все функции ф;(у;) — возрастающие, т. е.
^>0 VZ=l,n при	т. е. эффективность реализации
капитальных вложений возрастает с увеличением их объема.
Последнее, в свою очередь, позволяет сделать вывод, что весь
фонд капитальных вложений А в оптимальном плане должен
быть полностью реализован.
Распределение капитальных вложений между предприятиями
отвечает следующей математической модели:
Е 4ф;)-тах,	(11.31)
i = l
(11.32)
i= 1
7,-^0, 1 = 1л-	(11.33)
Модель (11.31)—-(11.33) в общем случае представляет нелиней-
ную (если функции ф;(у;)—нелинейные) задачу математического
програмирования. Не ставя цели обсуждать метод ее решения
как задачи математического программирования, сведем ее к мно-
гошаговому управляемому процессу и применим для оптимизации
250
метод динамического программирования. Для случая п = 3 пол-
ностью проведем вычислительный процесс.
Чтобы свести модель (11.31)—(11.33) к форме многошагового
процесса, введем обозначения:
п=Т,	у; = м(г),	~/0(г, и(г)),
г = Т?н, Г=0, 1, Т- 1.
(11.34)
С учетом обозначений (11.34) модель (11.31)—(11.33) примет вид
= Z/0(r, w(z))->min,	(11.35)
Z u(t) = A,	(11.36)
r = 0
w(r)>0, 1 = 0, 1, ..., Г-1.	(11.37)
Покажем, что задача оптимизации для модели (11.35)—(11.37)
может быть сведена к задаче, рассмотренной в §11.4.
Для этого введем функцию х(/), которую определим следую-
щим образом:
х(0) = 0, х(r+ 1) =х(г) + и (f), t = 0, 1, ..., Т— 1.
При этом ограничение (11.36) примет вид х(Т)=А. Освобо-
димся от него, введя в функционал (11.35) штрафной терминаль-
ный член М[х(Г) — Л]2, где М>0— произвольно большое число.
Получаем окончательную форму необходимой нам модели:
£/О(6 и(г)) + М[х(Г)-Л]2->ш1п,
1-0
x(z + 1) = х (Z) + и (/),	(11.38)
w(r)>0, t = 0, 1,	Г-1, x(0) = 0.
Для модели (11.38) запишем уравнение Веллмана с краевым
условием:
<p(z, х)=тах{ф(г+1, х+и)~/0(б ы)),
t = 0, 1, ..., г-1,-	(11.39)
ф(г, х) = -М(х — Л)2,
где
й (z, x) = argmax {ф(г-|-1, х + «)~ f0(t, «))'
— оптимальное управление в форме синтеза.
Вычисления проведем для случая л = 3, Л = 10:
251
'i'i(3'i)=16y1-0,4y?,
(?з)= 18?z - 0,6H,
Фз(.Гз)-25>’3-0,7у5.
С учетом обозначений (11.34) получаем
Т=п-3,
— 16м + 0,4м2, i=0,
— 18и + 0,6и2, f=M,
— 25w+0,7w2, t~2.
(11.40)
Итерация J
;	t+l = 3, t = 2.
В соответствии с (11.39) и (11.40) имеем
ф(2, х)—max [ — М(л+и — 10)2 + 25и — 0,7м2].
Так как М>0—произвольное сколь угодно большое число,
й(2, х) должно обратить множитель при М в ноль, т. е.
й(2, х) — 10 —х.	(11.41)
При этом
<р(2, х) = 25(10 — х) —0,7(10 —х)2.
Итерация П
/4-1=2, t=l.
В соответствии с (11.39) и (11.40) имеем
ф(1, х)=тах [25 (10 —х —и)—0,7 (10 —х —м)2 -|- 18м —0,6м2] =
= тах(- 1,3м2 + 7м— 1,4хм4-.„),	(11.42)
где многоточие относится ко всем остальным слагаемым, не
зависящим от аргумента максимизации и. Осуществляя максими-
зацию (11.42) (см. Приложение, случай параболы, ориентирован-
ной ветвями вниз), получаем
[2 69 —0,539х, если х^5,
= ) о	(П-43
(	0, если х^5.
Подставив (11.43) в (11.42) и приведя подобные члены, получим
— 0,324х2 —14,66х-|-189,4, если х^5,
-0,7х2-11х-|-180, если х^5.
м(1, х)
ф(1, х) =
252
Итерация Ш
_	( — 0,324 (х+и)2- 14,66 (х 4- м)+189,4+ 16м-0,4м2, если х + м^ 5,
и>о ( —0,7(х + м)2 — 11 (х + м) + 180+ 16м —0,4м2,еслих+м^5,
или
.	.	( —0,724м2+1,34м —0,648хм+..., если м^5—х,
Ф (0, х) —max <	, , ,
v ! и?о ( —1,1м +5м—1,4х» + ..., если м;>5—х.
Применительно к обоим вариантам формулы (11.44), осуществляя
максимизацию по и функций как парабол, ориентированных
ветвями вниз, получим
0,925 —0,446х, если 0^х^2,06,
0, если 2,06 ^х^ 5,
(11.45)
м(0, х) = 5—х, 0^х^5.	(11.46)
Вывод формул (11.45) и (11.46) читателю предлагается осущест-
вить самостоятельно.
В результате получим два оптимальных варианта распределе-
ния между предприятиями капитальных вложений:
1) основывается последовательно на формулах (11.45), (11.43),
(11-41):
м(0)=м(0, х)|.=о = О,925-л,
х(1) = х(0) + м(0) = 0 + 0,925 = 0,925,
5 м (1)-м (1,х)!-=0925 =2,69-0,539 0,925 = 2,19 =у2, (11.47)
х(2)=х(1)+й(1)=0,925+2,19 = 3,Ц5,
м(2) = м(2, х)|_=31]5 = 10-3,115 = 6,885 =у3;
2) основывается последовательно на формулах (11.46), (11.43)
(11.41):
м(0) = й(0,х)|-^ = 5=у(,
х(1) = х(0)+м(0)=0+5=5,
Ч й(1)-й(1, x)ii=5=0=y2,	(11.48)
х(2) = х(1) + м(1) = 5+0-5,
й(2)-й(2, х)|_=5 = 10 — 5=5=у3.
Варианты распределения (11.47) и (11.48) существенно разные,
но оба оптимальные. Функционал (11.31) в обоих случаях равен
186. Таким образом, как мы видим из данного примера, рещение
оптимизационной задачи может не быть единственным.
Глава 12
Численные методы оптимизации
для многошаговых процессов
с непрерывным управлением
Численные методы решений для многошаговых процес-
сов управления менее разработаны, чем для непрерывных.
Для многошаговых процессов управления с ограничениями
на управление принцип максимума в общем случае неспра-
ведлив (см. гл. 9). Особенно характерно состояние алгорит-
мической необеспеченности для многошаговых управляемых
процессов с ограничениями на управление типа целочислен-
ности. К моделям такого рода сводятся многие задачи оп-
тимизации экономики и техники, например динамического рас-
пределения ресурсов на сетях, графах и иерархических струк-
турах, динамического хранения запасов, долгосрочного плани-
рования и др.
Большинство алгоритмов решения многошаговых процессов
управления являются либо итерационными, либо основанны-
ми на схемах погружения. Под итерационными алгоритмами
понимаются такие, которые начиная с некоторого допусти-
мого решения переходят к новому допустимому решению
с лучшим значением функционала, т. е. в алгоритмах
этой группы осуществляется приближение «сверху» к опти-
мальному решению, В алгоритмах, основанных на схемах
погружения (методы ветвей и границ, отсечений, основанных
на реализации элементарной операции улучшения функции
ф(Лх), и др.), начинают с недопустимого решения, а первое
допустимое решение является оптимальным, т, е. в алгоритмах-
этой группы осуществляется приближение «снизу» к оптималь-
ному решению.
Перейдем к изложению алгоритмов этих групп на основе
единой теоретической базы—достаточных условий оптималь-
ности,
Итерационные алгоритмы используют различные идеи: не-
обходимые условия оптимальности, градиентный спуск в про-
странстве управления, улучшение с конечным сдвигом по управ-
лению. Алгоритмы, основанные на схеме погружения, использу-
ют реализацию элементарной операции улучшения функции
Ф (t, х),
254
§ 12.1. Алгоритм улучшения по начальному значению
сопряженного вектора
Пусть задача оптимизации для многошагового процесса
управления описывается условиями (см. § 9.1)
>(v) = £ /°(^	u(0)+F(x(T))->min,	(12.1)
t = 0
х‘(/+!)=/' (/, х(/), и (г)), Т = 0, 1, ..., Г— 1; /=1, п (12.2)
Л'!(О) = Л'Ь (/=], Л), х'(7)=*1, i=k+l, «.	(12,3)
Здесь (х(А u (0) :=v; х—«-мерный вектор; и—r-мерный вектор;
о /°(<х, u), F(x(T)),	Г-1]), М см. в §9.1.
Пусть функция ф (/, х) дифференцируема по х; функции
/[(/, х, a) (t= 1, «), f°(t, х, ц) дифференцируемы по х, и в точках
x(f), й(г); й(г)— внутренняя точка множества 1-^. Тогда система
уравнений метода Лагранжа для задачи (12.1) — (12.3) выглядит
следующим образом (см. § 9.1):
х‘(г+ !)=/*(<» x(f), u(г)), / = 0, 1, ..., Г—1; /=1, л, (12.4)
х1(0) = Хо(< = 1, £), x*(r)=xi, i=k+l,n, (12.5)
ф;(г)=^-Н(г, ф(/+1), х(г), й (/)), г = 1, «,	(12.6)
ф(г+1), X(/), й(г))=О, /=1, г,	(12.7)











где Я(/, Ф, х, и)"£ X, и)-/°(/, х, и).
Задача (12.4)—(1^.7) —краевая задача для системы, описывае-
мой 2и конечно-разностными уравнениями (12.4) и (12.6), Для
разрешимости этой задачи алгоритмом, излагаемым ниже, ее
следует сначала привести к одной из двух нормальных форм
способами, приведенными в §9.1.
Рассмотрим алгоритм.	___
Каждому значению вектора ф(0) = фо=(фЬ), 7=1,«, в си-
лу соотношений (12.4)—(12,7) соответствуют элемент
(х(/, ф0), u(r, ф0))еМ и функция ф(г, ф0) с функционалом
^(ф0)“ Е /°(А *((, 'I'o),	'l/o)) + F(x (Г, ф0)).	(12,8)
г = 0
Следовательно, задачу (12.1)—(12.3) можно трактовать как
задачу о минимуме функции конечного числа переменных,
заданной дифференциальными уравнениями (12.4), (12.6), началь-
ными условиями (х0, ф0), где хо = (хо)> i—l, п, и формулой (12,8).
255
Поэтому для полного решения последней задачи можно приме-
нять методы оптимизации, разработанные для минимизации
функции конечного числа переменных.
Так как в данной задаче (12.1) — (12.3) множество Vi <= X
не совпадает со всем пространством .¥ из-за наличия условий
х1(Г)=№1, i=k+l,n, то, решая описанную выше задачу миними-
зации конечного числа переменных ./ (ф0), необходимо следить
за выполнением условий на правом конце траектории в (12.5)
и (127). Выполнение этих условий вследствие сложного неявного
характера зависимости х(г, ф0) значительно усложняет расчет.
Конкретизация метода, основанного на идее улучшения по
начальному значению вектора ф0, приведена в §9.1, а в § 10.2 —
решение задачи об оптимальном расписании выпуска продукции
на его основе.
§ 12.2. Алгоритм последовательного улучшения
по управлению
Пусть задача оптимизации для многошагового процесса
управления описывается условиями
^(v) = E7°(z,x(z),u(f))+^(T,x(T))->nim,	(12.9)
1 = 0
х;(/+])-/(?, х(г), u(г)), r=0, 1, ..., Т-1, t=T7n, (12.10)
х'(О)=Хо, Т задано, х'(Г) свободно, z = l, п. (12.11)
Здесь смысл всех входящих обозначений тот же, что и в § 12.1.
Пусть функция <р (/, х) дифференцируема по х, функции
f‘(t, х, и), г = 1, п, х, и) дифференцируемы по х, и; множество
1% не зависит от х, и (г) е и не обязательно является внутренней
точкой множества Ри.
Для решения задачи (12.9) -- -(12.11) предложим следующий
вычислительный алгоритм. Достоинство этого алгоритма по
сравнению с приведенным в § 12.1 заключается в том, что здесь
не требуется приведения основной и сопряженной систем к одной
из двух нормальных форм §9.1, так как основная и сопряженная
системы разрешаются независимо, а не вместе, как это показано
в алгоритме § 12.1. При его обосновании будем рассматривать
функционал -/ (v) в виде
У(т) = Ф(Г,х(Г))-х7(г,х(0,и(0).	(12.12)
1 = 0
где для модели (12,9) — (12.11)
Ф(Г, x(r))=F(r, х(Г))-|-(р(Г, х(Г)) —ср(0, х(0)),	(12.13)
К (t, х, и) = <р [/ -|-1, f (г, х (/), и (?)] -
256
-ф(г, x(r))-/°(r, x(z), u(r)).	(12.14)
Покажем справедливость формулы (12.2), Проведем тождест-
венное преобразование:
*(’)=Тг К МО- “W)+f(T х(Л)+ф(Т ЧП)-
1 = 0
— ср(о, х(0))— £. {(pD+l, f(r, x(r), u(z)]-(p(z, x (/))}. (12.15)
1 = 0
Так как для (х(г),в(1))еМ, согласно (12.9),
х1 (г +1)	(/, х (г), u (r))s z =0, 1, ..., Т— 1, / = 1,и,
то из (12.15) имеем
У (,)=Ф(Т,х(Т))-£,Л(1.х((). »(<)),
( = 0
что и доказывает справедливость функционала ./(т) в виде (12.12).
Предположим, что задана допустимая пара (х°(г) и°0)еЛ/.
Обозначим Зх (г) =х (г) — x°(z), 3u (() — и(г) — u° (Z), где Зх (z) =(8х! (г)),
; = ],«, Зи(z) — (ЗуДг), /=1,г,. Тогда, разлагая правую часть
(12.12) в ряд Тейлора в окрестности пары (х° (z), u° (z))
и считая, что
16%;(ф=ёЕ'ь |3i?(z)
где £i>0, J = l, и, j — 1, г,— малые числа, получим с точ-
ностью до членов первого порядка малости
^(т)~Ф(Г, Х°(Т)) + Фх(7; Х°(Г)) 3x(z) —У [Я (/, х°(г), 11° (/)) +
4- Ях (z, и0(/))Зх(/) + Яи(/, х°(г), u°(r))3u(z)],
где
ФХ(Т, х°(7’))3х(г)_ £ Ф- (Т, х°(Т))3.х-(0,
1 = 1
X°(f), U°(r))3x(t)= £ R^t, x°(r), u°(t))8x’’(l),
i = l
x°(r), u°(r))3u(r)- £ RJ„(t, x°(r), U°(z))3i?(z).
j = i
Тогда из (12.16) имеем
ЗУ(т)=^(¥)-У(¥0)=Фк(Т, x°(T))3x(/)-
-£ [ЯДг, х°(г), и°(г))Зх(г)-|-Я|1(г; x°(t), u°(/))3u(z)].
9 Зак 456
257
Зададим функцию <р (t, х) в линейном виде:
<p(t, х)=ф(г)х.	(12.18)
Тогда с учетом (12.13) и (12.18)
Ф(Т, х°(7))=Г(Т, х°(Т))+ф(Т)х°(Т)—ф(0)х°(0),
ФХ(Т, х°(Т)) = .Ех(Т, х°(Т)) + ф(Т).	<12Л9>
Пользуясь произволом функции ф(/, х) и используя (12.19),
зададим
ф(Т)=~Гх(Т,х°(7)).	(12.20)
Заданию функции ср(/, х) в виде (12.18), используя (12.14),
соответствуют следующие конструкции:
R(t, х (г), п(т))-ф(r-f-l)f(r, x(z), и(О)-ф(0х(О-/°(г, х(/); u0),
Ях((, х°(/), п°(г)) =
=*(г+ 1)гх(л х°(0> и° ('))-'!' (О-Л (', х° (О’ и° (0)-
Введем
Я(ф, t, х, и)=фГ(г, х, u)-/°(r, х, и).	(12.21)
Наложим на функцию <р (/, х) дополнительное условие
/?х (?, х° (?), ц° (/)) = 0,	(12.22)
т. е. с учетом выражения (12.21)
ф(/) = Ях(/, ф(г+1), х°(0,ио(0).	(12.23)
Тогда, используя (12.19), (12.20), (12.21) и (12.23) из (12.17),
получим
6У(т)=- X Я„(/, ф(г + 1), x°(r), п°(/))5и(/).
1=0
Если	где Я° = Яи(г, ф(г+1), x°(t), п(г)), то, для того
чтобы 8^(v)<0, можно поступить следующим образом:
1) выбрать |5и(г)|<с1;
2) обеспечить
и°(/)+5«[/)еГ Я°8и(г)>0.	(12.24)
В частности, если	где Ег — эвклидово пространство
размерности г, то можно положить 8н (г) = а И®, где а = (а-'),
7=1, г,— числовой вектор.
Таким образом, алгоритм отыскания улучшенного элемента
состоит в следующем [15].
1.	Задается произвольная пара (x°(f), и°(/))еМ
2.	Разрешается «справа налево», т. е. от значения аргумента
t=T до значения г = 0, линейная система (12.23) из п разностных
соотношений относительно вектора ф с начальным условием
(12.20).
258
3.	При каждом фиксированном ге(0, Г) определяется направле-
ние в пространстве на котором функция х°(?), н)
возрастает, и задается вектор би (/) параллельный этому направ-
лению. На это направление могут накладываться дополнительные
требования, характерные для различных методов математического
программирования, например, чтобы на нем возрастание было
«наибольшим» по сравнению с другими направлениями (метод
наискорейшего спуска) либо чтобы вектор би(т) = (3м1 (г),	8мг(0)
имел только одну ненулевую компоненту (покоординатный
спуск) и т. д.
4.	Разрешается исходная система (12,10) с начальными усло-
виями х‘(0) = хо, i= 1,и, из (12.11), замкнутая управлением
u°(/) + 6u(rj, и далее переходим к п. 1, приняв в качестве новой
пары (х° (т) + 5х (г), и0 (?) + &u(/))e М. Наличие дополнительных
ограничении на (разовые координаты при каких-либо значениях
те (0, Т) во многом усложняет предложенный алгоритм. Имеется
целый ряд дополнительных приемов, обеспечивающих выполнение
условия х(т)е1Ч в рамках данного метода, В основном они
разработаны для случая, когда х°(т) лежит на границе при
t=T, например если множество И; есть заданная точка х(Г),
т. е. если ограничения (12.12), подобно (12.3), выглядят так:
лг1(0) = лф, т=1Д, xl(7)=Xi, i=k+l, п. (12.25)
Первый способ учета ограничений вида (12.25) состоит в введении
штрафных функций, достаточно больших за пределами множества
V*. После этого исходный функционал (12.9) заменяется на
функционал вида
J(v)=,/(v)+ f Х;[4-х‘(7)]2,	(12.26)
i =jt+ 1
где 1 = i=k+l,n, Х'^0—действительные числа. Далее алго-
ритм улучшения применяется к функционалу вида (12.26).
Другой способ учета ограничений вида (12.25) сводится
к введению дополнительных ограничений на приращение управле-
ния би (г) помимо (12.24), призванных гарантировать достижение
той же цели.
§ 12.3. Итерационный алгоритм улучшения
с конечным сдвигом по управлению
Приведем итерационный алгоритм улучшения второго порядка
для многошаговых процессов управления с конечным сдвигом
по управлению, также базирующийся на достаточных условиях
оптимальности.
Рассматривается процесс вида
9*
259
F(v] = E Z0^’ x0- u(^))+F(x T))->min,	(12.27)
1 = 0
x(z), u(f)), t = 0, 1, .... r-1, /=1Д (12.28)
x1(0) = x'o, 1=1, n.	(12.29)
где v=(x(t),u(/))eW, F(x)— заданные функции (см. §12.1). Для
произвольной функции <р (/, х) процесса (12.27)— (12.29) определим
следующие конструкции:
R(t, х, u) = (p[f+l, f(/, x(f), u(r))]-<p(r, x(i))-f0(t, x(/), u(/)),
Ф [x (t e S)] = F(x (Г))+ф (г, X (tj), 11,	(12.30)
u (r, x) = arg max R(t, x, u).	(12.31)
Тогда алгоритм улучшения последовательности {vj =
= (xs(r), u,(t)) сМ состоит в следующем.
Зададим произвольную функцию ср0(/, х)еП (где П — класс
таких функции, что функции R и Ф непрерывны и дважды
непрерывно дифференцируемы по х):
1.	Для <р = ср0(г, х) из соотношения (12.31) находим й(/, х).
2.	Из уравнения начальных условий (12.28) и (12.29), замкнутых
управлением и = й°(т х), определенным согласно (12.31), находим
управление и°(г)=и(/, х) и процесс v0 =(х°(z), u°(/))еМ.
3.	Строим функцию <р(г, х)еП, обеспечивающую выполнение
следующих условий:
/?(Г, х°(г), u° (t)) = min 2?(Л х, и0 (?)),	(12.32)
ф(х°(Г)) = тахФ(х),	(12.33)
X
где функции R и Ф вычисляются с помощью найденной функции
ф(г, х). Для функции ф(/, х) операции 1 и 2 повторяются,
в результате чего находим процесс v = (x(/), u М.
Можно доказать следующую теорему [17].
Теорема 12.1. Для процессов v0 и v справедливо неравенство
y(vU./(v0).
Согласно этой теореме, в результате выполнения условии
1—3 можно построить такую улучшающую последовательность
(vj с= М, что (vs + () <(v J.
Для начала построения улучшающей последовательности мож-
но вместо функции ф0 (?, х) задавать непосредственно управление
и°(/, х). Этому управлению в силу уравнений процесса (опера-
ция 2) будет соответствовать траектория x°(t). Эгого достаточно
для построения функции ф (г, х) согласно операции 3.
260
Для реализации описанного алгоритма основным представляю-
щим трудность для разрешения является п. 3. Перейдем к описа-
нию метода построения функции ср р, х), реализующей условия
п. 3. Функцию <р р, х), удовлетворяющую условиям (12.32), (12.33),
будем искать в виде
Фр, х)= X Ф;(ОХ' + 0’5 Е Е амр)Лх'р)Лх*р), (12.34)
;=|	t = 11-1
(=0’ h ’ Г-’Л /=Т^;
Дх‘р) = х‘р) — х р), а ф р), a[t] — подлежащие определению соот-
ветственно «-мерная вектор-функция и (п х «(-матрица при каждом
фиксированном t = Q, 1, Г—1.
Необходимые условия выполнения соотношений (12.32)
и (12.33) первого порядка приводят к следующей системе
уравнений с заданными начальными условиями на правом конце
траектории:
Х’ U) I ф = ф°(г, х), х = х°(|), u-u°(l) = °’	(12.35)
Ф* (Х) I <р = <р°(г, х), х = х°(Т) ~' О'
Конкретизация условий (12.35) приводит к следующей системе
многошаговых уравнений:
Ф,р)=Дяр, фр + 1), х°(/),	/=0, 1,..., Г-1,
 (12,36)
где Яр, ф (/+ 1), х°р), и°р)) = £ ф£ р + 1)/' р, у, и)-/°р, х, и).
i = I
Оставшийся произвольный выбор матрицы стр), ? = 0, 1, ...,
Г—1 для построения функции фр, х) согласно (12.34) устраним
использованием условий (12.32), (12.33). Необходимым условием
относительного минимума по х функции /?р, хр), и °р)) является
неотрицательность квадратичной формы:
d R = ^^— Дх'Дх<
ох ох1
[Здесь и далее черта сверху означает, что соответствующие
функции вычисляются при х = х°р) и u = u°p).] Для процесса
(12.27)— (12.29) выражение для <PJ? имеет вид’
Э1* _ v „	V
дх‘8х}
ох'дх1
(12.37)
Зх’Зх1
261
Для неотрицательности квадратичной формы (12.37) доста-
точно положить
—=0, гУу, i,j=l,n; / Д = 8,-р), 1= 1, п, (12.38)
дх'дхУ ’ J J	i)xldxJ	v 7
где 8, (7)—заданные неотрицательные функции.
Значения матрицы (стм (7)) при t = Т задаются из условия
неотрицательности квадратичной формы
-б2Ф=( -Д^)Дх''Дх<
\ дхохЧ
Для заданного процесса (12.27) —(12.29) в соответствии
с (12.30)
Аналогично предыдущему, для неотрицательности формы (12.39)
достаточно положить
ТЦ" = О, У/, i,j=l,n; --^А = а,., 1=1, п, (12.40)
fix cjc J	dx'oxJ
где а(—заданные неотрицательные коэффициенты.
Таким образом, определение матрицы стр) сводится, согласно
(12.38), (12.40), к решению задачи Коши с начальным условием
на правом конце для линейных многошаговых уравнений. В соот-
ветствии с требованиями, наложенными на функции R и Ф, эти
уравнения обладают свойствами
о 2 7? (г, х, u) _ (12 Я ((, х, и) о 2Ф (х) _ о 2Ф (х)	. . _
дх^х-1 dxJdx' ’ 3x’SxJ дх'дх1’	’
Кроме того, из свойств функции фр, х) также следует, что
^j(O=aji(O’ 7=0, 1, ..., T-l, i,j=l,n.
Поэтому размерность системы уравнений, определяющей матрицу
ст (/), не превышает п (и + 1)/2.
Окончательно алгоритм улучшения сводится к такой последо-
вательности операции.
1.	Задается произвольная функция ф = ф°(/, х)еП.
2.	На основании (12.31) определяется управление й°р, х).
(Напомним, что на начальном этапе можно сразу задать
и°р, xje и алгоритм от этого не изменится.)
3.	На основании уравнений процесса (12,28), (12.29) при
и = й° р, х) определяются траектории х0 (7) и соответствующая
программа й°р)=й°р, х°р)). Для процесса v0= (х°р), и°р)) вы-
числяется значение функционала У (v0).
4.	Определяется согласно (12.36) вектор-функция фр).
Г
5.	Для определенности полагаем все S,- р) равными некоторой
не зависящей от времени постоянной 8^0, а все а, — равными
некоторому а^О. Определяем с учетом (12,38), (12.40) матрицу
1/ст^р)), i,j = l, п, / = 0, 1, ..., Т—1, и формируем, согласно
р2.34), функцию фр, х).
Г 6. Для новой функции <р (/, х) выполняются п. 2 и 3, находятся
йр, х), V — (х(г), up)), J^p). Если функционал не улучшился,
увеличиваем о и а и возвращаемся к п. 5. Тем самым описание
одной итерации завершено.
Отметим, что при практическом применении этого метода
не обязательно определять новую матрицу стр) на каждой
итерации. Одна и та же матрица ст (г) может использоваться
до тех пор, пока на очередной итерации функционал J р)
не улучшится. Расчеты можно начинать, положив все ст,^р) = 0
Л
(что соответствует линейному заданию функции фр, х)= £ ф,р)
х'). Если при этом улучшения Ур) не произошло, то следует
использовать п. 5 алгоритма, связанный с вычислением матрицы
ст Pl-
Изложенный алгоритм, так же как и алгоритм в § 12.2, не
требует приведения уравнений (12.1) и (12.6) к нормальной
форме (см. § 9.1), что необходимо для алгоритма в § 12.1,
благодаря причинам, указанным для алгоритма в § 12.2.
Пример. Рассмотрим следующую многошаговую задачу:
</=-х2 (2)->min,
xIp+l)=x1p)+2wp), х1(0)=3,
Х2 Р+ 1)= - pl Р)) 2 + х2 Р) + « 2 Р), *2(0) = 0,
7=0, 1, !мр)|^5.
^Зададим	р)=о12р) = о,2 р)=0, 7=1,2. Тогда на каждой
л-й итерации функции фд р, х) будем задавать в виде
2
<PsP> Х) = £ 'К(/Jx' + O^CTi! (Г) [xj -хГ 1 р)]2.
1 = 1
Такому заданию ф5 р, х) соответствуют следующие функции R и Ф:
р> X, и) — фд р-f-1) [xt р) + 2ир)] + ф2 р + 9 [ — (^1 (7))2 + х2 р) +
+ и2Р)] + °>5аи Р+ l)[xi р)+2ир)-хгГ1 р+ I)]2-
2
- Г Ф<р)х;р)-0,5ст’и рЦх^-хГЧ*)]2,
7=1
2
Ф’(х (2))=-х2(2)+ X ф-(2)xf (2) + 0,5cti1 (2) [х, (2) —х!”1 (2)]2-
Уравнения (12.36) и (12.38), (12.40) принимают следующий вид:
262
263
Г1 (/)=Г1 (' + 0-2Х, (О Гг (/ + 1), Г1 (2)=0,
4'2(2)=1.
<Sii(t)=-2\|/2(f+9+<3s11 (t4-1)-ё, gs1X(2)=«.
Ход вычислений показан в табл. 12.1.
Таблица 12.1
Номер итерации	МО)	MD	^,(1)	хг(1)	л-П2)	*> О)	*2 О)	
1	0	0	3	— 9	-18	-6	1	18
2	—2	-5	-1	-5	-19	2	1	-19
На второй итерации достигнут точный оптимум: й(0)= — 2,
й(1)=±5, У=—19. При увеличении 5 и а скорость сходимости
уменьшается. Заметим, что для этой задачи принцип максимума
не справедлив, так как функция /f(w(l)) на втором шаге при
оптимальном управлении й (1)=±5 достигает максимального
значения, а функция Н (и (0)) при оптимальном управлении
й(0)= — 2 имеет минимальное значение. В то же время на
первом шаге функция /?(1, к, и) при й(0)= —2 имеет максимальное
значение.
Глава 13
Численные методы оптимизации
для многошаговых процессов
с дискретным управлением
В настоящей главе приводится единая теоретическая ба-
за— достаточные условия оптимальности для многошаговых
процессов управления с одно- и двумерным аргументом и огра-
ничениями на управление, в том числе и типа целочисленности.
Для решения задач, осуществляющих приближение снизу, дается
специальный математический аппарат, названный реализацией
элементарной операции улучшения функции <p(t, х). Приводятся
основные идеи и конструкции этого аппарата, и с его помощью
решаются две задачи. Первая —общая задача непрерывного
линейного программирования с двусторонними ограничениями
на переменные, для которой реализация элементарной опера-
ции, соответствующая линейному заданию функции ср ((, х),
позволяет в общем случае усилить известный конечный метод
решения таких задач — метод сокращения невязок. Вторая —
многомерная квадратичная сепарабельная булева задача о ран-
це. Для этой задачи на основе нелинейного задания функции
ср(f, х) предлагается своя реализация элементарной операции,
приводящая к вычислению резкой нижней границы. Полное
решение этой задачи о ранце достигается применением
схемы метода ветвей и границ. Дается экономическая ин-
терпретация такой постановки задачи. Изложение алгоритма
решения для задачи о ранце иллюстрируется решением
модельного примера, в котором полное решение достигается
уже при использовании только реализации элементарной
операции.
§13.1. Постановка задачи оптимизации
для многошаговых процессов управления
с многомерным аргументом
Рассмотрим управляемый процесс, характеризуемый аргумен-
том г, состоянием х и управлением и, пробегающими множества
Т, X, U соответственно. Каждому teT соответствует подмно-
жество V1 прямого произведения множеств XxU. Среди всех
265
пар функций v = (x(, u() задано множество М допустимых при
помощи условий
(х„ и,)еГ У/еТ,	(13.1)
а также с помощью некоторого динамического уравнения,
связывающего траекторию х( в пространстве состояний с управ-
ляющей функцией н1.
Рассмотрим две модели такого рода.
1. Многошаговый процесс управления с одномерным аргументом.
Множество Т—целочисленный ряд {0, 1, ..., Г}; X и U—вектор-
ные пространства размерности лиг соответственно; уравнения
связи имеют вид
х;+1 =/'(/, х,, u(), f-o, 1, ..., Г-1, г = Г«,	(13.2)
-X'(0) = xb, 1 = 1, П,	(13.3)
где f (7, х, н)—вектор-функция, заданная на прямом произведении
Т х X х U и принимающая значения на множестве X.
2. Многошаговый процесс управления с двумерным аргументом.
Множество Т—прямое произведение множеств ГА 7=1,2, где
TJ— целочисленный ряд {0, 1, ..., X и U—векторные про-
странства размерности лиг соответственно; уравнения связи
имеют вид
+	хо и,),	____
i = l, п,	(13.4)
(/, х(, п,),
где t= (гь ы), /}(/, х, u), j=l, 2, — функции, заданные на прямом
произведении Тх Хх U. Введем в рассмотрение вектор-функции
fj (Г, х, н)- (Л (г, х, u)), f2 (Г, х, и)=(Л (*, х, “)), i = i, и мно-
жество М пар функций х(, пг, удовлетворяющих условию (13.1).
На множестве М задан функционал вида
I “J, Z X f°(t, х„ Ur) (13.5)
< = 0	lt=o t2 = 0
для каждой модели соответственно, где f°(t, х, п) — заданные на
TxXxV функции.
На функции (х(, п() е М помимо перечисленных условий нало-
жены дополнительные условия. Введем в рассмотрение следующие
множества; V* и	— проекции множества р на множества
X и V соответственно; S с Г, И7. Для первой модели S — значение
/—Г, И7—подмножество множества и! при t=T. Для второй
модели S—совокупность значений t = (гь г2), образующих границу
прямоугольника Т,	0</2<Г2, W—множество вектор-
функций х,, заданных на S при условии, что х(еГ'7
Поставим две задачи.
266
IV
К‘ I. Отыскание допустимого процесса, где требуется найти
К последовательность процессов {х(„ uls} с М, сходящуюся к М (см.
| [7]):
В	к,
	2. Минимизация функционала J на М, когда помимо п.
Ж 1 от последовательности (xfs, uIS} требуется
К	У (xs, 0s)->i7—inf У > — go.
К	м
К Для решения обеих задач воспользуемся аппаратом принципа
К оптимальности.
|	§ 13.2. Достаточные условия оптимальности
I	для многошаговых процессов управления
I	с многомерным аргументом
Введем в рассмотрение соответственно рассматриваемым моде-
| лям функцию ф(/, х) и вектор-функцию ф \t, х)=(ср1, ф2), заданные
I на прямом произведении ГхХ, и построим с их помощью
следующие конструкции:
R (t, х, u)= <
ф [г+ 1, f(t, X, п)-ф(/, х)— X, и),
ф1 [G + 1, х, иД-ф1^ х)+
+ф2 [G,	X, «)] -ф2 (г, x)-/°(r, X, и),
(13.6)
Ф (*, \)!о+/°(Г, Хт),
+ Е ф2(', О
(13.7)
'i=о
Ч = °
Ji(z)= sup R(t, х, и), т-inf Ф [xf/eS)],	(13.8)
(х, п)е1л	хе И7
£(ф, .х„
(13.9)
267
(13.10)
Введем в рассмотрение класс П таких функций ф (г, х}
(вектор-функции ф(г, х} = (ф\ ф2}}, что величины т и /(ф) опреде-
лены, Тогда справедливы следующие результаты при любом <реП:
L(x, и)=У (х, и), если (х, и}еМ,	(13.11)
Если (х, й)еМ и феП таковы, что L (х, й, ф) = I(ф), то
,/(х, й}= min у(х, u) = rf=/(ф) = max/{ф}.	(13.12)
(х, и) е М	ч> е П
Для первой модели справедливость этих результатов установ-
лена в гл. 5, для второй будет установлена ниже.
Рассмотрим многошаговый процесс управления с двумерным
аргументом, описываемый уравнением (13.4) и функционалом У,
заданным на множестве М соответствующим выражением из
(13.5) и ограниченным снизу на множестве М'. inf,/ = c/> — со.
Требуется найти элемент v=(xf, щ}еМ, называемый абсолютной
минималью и минимизирующий функционал У на М, т- е.
такой, что y(v}=J.
Зададим на произведении Гх Т вектор-функцию ф (/, х) =
=(ф1, ф2} и построим с ее помощью конструкции (13.6) — (13.8).
Теорема 13.1. Для того чтобы элемент \еМ минимизировал
функционал J на М, достаточно существования такой вектор-
функции ф(/, х}, чтобы'.
1°. R(tt х„ ut} = p(r), tET\S.
2е, Ф [x(f е£] = т> — ос.
Доказательство, Определим на множестве М пар функций,
.удовлетворяющих условию (13.1), функционал
Ti ~ 1 Л-1
Л(ф, х„ iit)=O[x(reS}]- X £ J?(r, xf, ц,).	(13.13)
Ц = 0
При (х(, и()еЛ/ имеем L = ./. Это видно, если (13.13) переписать
с учетом выражений для (13.6) и (13.7):
Т1 Г2-1
£(Ф, х(, uj=y+ £ £ {ф1 (г, xj — ф1 [г, ф\ -1, r2,
г I = 1 ra = 0
11), u(ti-l,r2)]])+ £ £ {(P2U x,)-
= 0 12 = O
268
-ф2[л/2[гь '2-1, x(*i, G-l), и('ь '2 — 1)]]}.
Предположим, что существует такая вектор-функция фр, х},
что на некотором элементе veM выполняются условия теоре-
мы 13,1. Тогда этот элемент является минимизирующим для
функционала L на М. В силу леммы в [15, с. 25] он является
минимизирующим и для функционала J на М. Теорема доказана.
Теперь перейдем к изложению алгоритмов, основанных на
реализации элементарной операции улучшения функции фр, х).
Суть этих алгоритмов состоит во введении с помощью функции
фр, х} определенной нижней границы исходного функционала —
/-функционала — и построении последовательности таких функций,
максимизирующей эту нижнюю границу. Построение последова-
тельности функций и максимизации /-функционала осуществляется
в Этих алгоритмах с помощью построения элементарной операции
улучшения функции фр, х).
§ 13.3, Основные теоретические результаты
по реализации элементарной операции
Для решения поставленных в § 13.1 задач 1 и 2 исследуем
и обоснуем следующий универсальный прием: отыскивать такую
последовательность {ф5}(=п, что рф4.}->тах рф} по феП, рав-
ный d. Искомая последовательность функций строится с помощью
элементарной Операции улучшения начиная с произвольного
фоеП. Приведем основные конструкции этой операции.
Пусть имеется функция ф5р, х)еП, которой соответствуют
на основании (13,1), (13.6), (13.7) и (1 ЗЛО), конструкции 7?sp, х, ц),
ФДх peS)), Цф), а также множество пар х, и, обеспечивающих
максимум J?sp, х, и} на И1, множество функций xpeS),
обеспечивающих минимум Ф (х р е S}) на И7, и множество Ms
пар функций xf, ur, удовлетворяющих условиям (хг, uje П при
всех ГеГ\\ xfe fFs, teS.
Функцию ф,+ 1 будем искать в виде
ф5+1р, х) = фДг, x} + Xsysp, х),	(13.14)
где ysp, х} и	—функция и положительное число, подлежащие
определению.
Определим соответственно данным моделям функционалы:
(=т
м*
1 = 0
Мхь«1)= Е У»1 (А*) ' '+ Е ъ2(а\)
1=0	1=0	1=0
(13.15)
4 = Л
Н-0
Т, -I г,-1
“ЕЕ {у* Р1 + 1, г2,Л(с X, и)]-у}р, х)+
1=0 I =0
1	2
269
+гЯ<ь G + l/aO, х, «)]-Ys (/, x)}.	(13.16)
Обозначим через 7?s(z, x, u, X), Л?ДХ) ит.д. конструкции,
соответствующие функции <p=<ps+X,,Ys- Пусть
8'(Х)= min ys[t, х)—у,(0, хД-
xe
— У max
t = 0 (x,U)eF;(X)
ч	 1
8'(X) = min J у
x<=JF,(X) b =o
{ys[/+l, f(z, x, u)]-y,(z, x)},
Y,1 (Л xt)
ii = ti t,-i
‘+ I yl(t’ xt)
I =0 r =0
(13.17)
V0
-£ £ max WlA + t x, «)]-Ysl(z’ x)+
t,=o tz=o (x, u)e rs(<)
+ 7 2 |?i, G + l,/2(/, X, u)]-ys2(z, x)},	(13.18)
8''(X)= max ys(z, x)-ys(O, x0)-
т _ i	xe W
’ - £ min {b[/ +
'=o (x, i)eP(X)
8ДХ)=- max J £ yj (z, xt)
г_1тхеГДХ)Ьло
- £ £ min {у1[Г1-
(13.19)
T, - 1
1,-0	1,-0
x -0
Для всех (x, u)e Ms (ХД
8"(X)>8(x, u)>8'(4	(13.21)
Введем понятие элементарной операции улучшения функции
Ф (Z, х). Функция ф5 + 1 строится в виде (13.14), где ys и Xs>0
выбираются произвольно в пределах требований:
8Дх, «)>0	(13.22)
хотя бы при одном значении (х, u)eMJ + 1 =Mi (ХД
tPs+i-tPs + Msen.	(13.23)
Условие (13.23), как правило, легко удовлетворяется априор-
ным заданием свойств функции уД/, х), и реализация элементар-
ной операции сводится к реализации условия (13.22). Условия
(13,22) (13.23) могут быть реализованы различными способами.
В [14] указываются два из них.
Первый способ состоит в том, что ys и Xs>0 выбираются
произвольно соответственно требованиям
8Д0)>0,	(13.24)
270

(13.25)
В [14] при достаточно общих условиях доказывается существо-
вание числа Х>0. Тем самым элементарная операция распадается
на два шага: задание функции х), удовлетворяющей условию
(13.24), и отыскание числа Хя>0, удовлетворяющего условию
(13.25) при заданном уя, причем последний шаг всегда реализуем,
если выполнен первый.
Второй способ состоит в том, что задается некоторое правило,
согласно которому из jWs(Xs) выделяется единственный элемент
(хДХ), йДХ)), а функция уя выбирается из условий непрерывности
по X н положительности 8,[х5(Х), us(X)J при X—О- Тогда при
достаточно малом Х>0 8s(X)>0 и условие (13.22) выполняется,
Тем самым в обоих способах вопрос о разрешимости
элементарной операции и ее алгоритмической реализации сводится
к вопросу о существовании и способах отыскания функции
х) согласно (13.24) или замечанию 1 в [14].
Применим полученные результаты к конкретным задачам.
§ 13.4. Задача линейного программирования
с двусторонними ограничениями
Рассмотрим задачу линейного программирования с двусторон-
ними ограничениями:
^(u)= X ctut—>min,	(13.26)
i = i
У 6', /=1, и,	(13.27)
t-i
/ = 1, т.
(13.28)
Здесь (д[) — матрица условий ранга т, т>п; Ь‘ и ct—заданные
соответственно вектор ограничений и вектор линейной формы;
at и ₽г“ конечные числа.
Задачу (13.26) — (13.28) можно представить в виде следующей
эквивалентной задачи оптимизации многошагового процесса уп-
равления с одномерным аргументом:
т - 1
^(и)= Е ctw,^min,
1 = 0
х[+1 — x; + a;wt, 1=0, I, ..., т— 1, i=l,n,
х'(0) = 0, х'(т)=Ь\ 1=1, п,
/ = 0, 1, ..., т— 1.
(13.29)
(13.30)
(13.31)
(13.32)
27J
Термины общей постановки задачи (см. § 13.1) здесь имеют
следующее содержание: Т={0, I, т}; X—пространство векто-
ров х = (.¥*, хп); U—числовая ось; —все пространство X;
V*u—отрезок [at, Рг]. Роль конечно-разностных связей (13.2)
играют соотношения (13.3); граничных условий (13.3)—усло-
вия (13.31); функционала (13.5) —функционал (13.29).
§13.5. Метод улучшения функции <р(/, х)
Так как (13.30)—(13.32) — процесс с линейными связями, то
функцию ф(г, х)еП будем искать в следующем виде:
В
ф(/, х)=£йХ
i=1
где Pr=(plt,..., pnt).
Тогда функция R из (13.6) для модели (13.29) — (13.32) будет
следующей:
Л	л
R(t, х, u)= £ (pf.f+i-pif)x+ £ (p^+iaJ-cJu.
i = 1	! = 1
Условия существования функции ц(г) из (13.8) накладывают
на феП следующие условия:
Л.(+1=Л,=А, Г=0, 1, ..., m-1, i=U. (13.33)
На основании условий (13.33) функция R не зависит от х:
R(t, u)= Е W-c()u=A((p)u,
i = i
где
лЛр)= Z
1 — J
Согласно (13.8), имеем
ц(г) = йг(р)мг (р),
где
й‘(Р) = {а
р, если z>0,
а, если z<0,
любое из [а, р], если z = 0,
(13.34)
(13.35)
(13.36)
m = Ё Ь1р^
272
Таким образом, получено описание^ множеств Р‘= Р(х р'и
и Йх=т, где И*— все пространство X; [ „—подмножество мно-
жества К1. определяемое соотношениями (13.35);	—точка
с координатами М1, Ь2,	Ь”). Значение 7-функционала в соответ-
ствии с (13.10) будет следующим:
п	И1-1
.	z(p)= £ b^i- £ ht (p)w( (p).
;=i	<=o
При любом p на основании (13.11) 7(p)^.(7. Таким образом,
 основные конструкции, входящие в (13.6)—(13.10), для модели
(13.29)—(13.32) построены.
Функцию у, фигурирующую в (13.14), будем задавать в виде
'	Тр, х)= £ф;г?.	(13.37)
i = i
Выполнение условий (13.33) накладывает на у (7, х) следующие
ограничения;
фi:(+ j = ф1( = фj, I = 0, 1, ..., т— 1, 7=1, н. (13.38)
Тогда в соответствии с (13.15), (13.37), (13.38) 5-функционал для
задачи (13.29) — (13.32) запишется в виде
л	/	лз — 1	\
*	5(«<)= £ Ф» bi~ £ aitu> •	(13.39)
i = l	\	i=0	/
Выражения для йДр, 7-) и wt(p, 7-) в соответствии с (13.34), (13.35)
и (13.38) будут
ЯГ(Р, Х) = £ А«;-с1 + Т^ £ ф;«; = Лг(Р, 0) + 7. £ ф(й,‘;
;	i=l	i=i
I ?
Введем в рассмотрение N', N, N" — множества значений
которым отвечают соответственно положительные, нулевые и от-
i рицательные значения й,(р). Используя исходную форму записи
задачи в виде (13.26)—(13.28), а также выражения (13.35) для
й(, соответственно получим:
из выражения (13.39)
5(р, ф, и) = £	£ «!р,- £ а'а,- £ а[и),
, = 1	ieN' teN" 1еЯ
5(р, ф, и, 7.)= £	£ a^t- £ aty;
L	1=1	г e.V'pj	/еА'(Х)
из выражения (13.17) с учетом (13.37) и (13.38)
273
5'(р> о)= Е Е °jP,- E *&)-
i = l	leA'"	teN"
- E max ( f ^aj«),	(13.40)
Je^a,«u,<P, t=i
s'(p, ФЛ) = E ФЛ*’!- E E «r«i)~
i=l	reJV(X) feJV'p)
” E max ( f и);	(13.41)
re JV(A)	i=l
из выражения (13.19) с учетом (13.37) и (13.38)
Hp-’J'i °)= i - Е й;р.- Е «;«.)-
 -	i=l	tetf'	t^N"
- Е min ( £ ^.aju),	(13.42)
1= 1
а
'$"(₽’’l'А) = Е’I'.C’г- Е а!Р,- Е а'А)~
f=i	ieiV'(X) ?еУ'(1)
“ Е min ( Е x|rafu).	(13.43)
1еУ(Х) «1=5 “.=*?< i = 1
§ 13.6. Простейшая реализация элементарной операции
Зададим
ф.=0 ViVfc,	(13.44)
где к—заданное значение среди 1 = 1,...,«. Тогда с учетом
(13.36), (13.40), (13.42)
&'(р, о)=Мб*- Е °$Р1~ Е °Х)-
leV' 1 teN- '
~E«?PfUt)],	(13-45)
/e^ J
s"(p, Ф, °)=Мб‘~ Е я,Р/~ Е
/еЛ1- 1 tefif- 1
~ Е 4 JS(K)]-	(13.46)
(eV (®'J
Через 8р обозначим выражение, стоящее в квадратной скобке
правой части равенства (13.45) при (^}(4fi) = 0(; через 5*—вы-
274
ражение в квадратной скобке правой части равенства (13.46)
при j(^) = at.
Пусть существует такое к, что либо 8р>0, либо 8£<0. Тогда
из выражений (13.45), (13.46) видно, что 8'(р, 0)>0 при
	Фи= <	f 1, если Зр >0, - 1, если 8*<0,	(13.47)
и 8"(р, 0)<0 при	~ <	f 1, если 8и<0, ) — 1, если 8р >0,	(13.48)
Теперь при заданном выражениями (13.44), (13.47) и (13.48)
векторе обеспечим выполнение (13.25). Пусть для определен-
ности существует такое к, что 8р>0. Из выражений (13.45)
и (13.46) имеем соответственно
5'(р, 0) = 3|, 6"(р, 0)=-3£.	(13.49)
Согласно (13.41), (13.43),
8'(р, k) = bk- £ a*pt- £ a*<xt- £ a*pt,
ie^(?J	;eJV"p.)	teJVp.)
3"(p, k) = bk~ X fljp,- £	<4Pr
tGN'fi.)	;e.V-p)	/6
Значения 8'(p, X) и 8"(p, X) сохраняют знаки 8'(p, 0) и 8"(p, 0),
по крайней мере, на интервале 0<Х<Х15 где
1	- М₽’ °)
Х< = mm -^-т-2
t ef
, a<^0, й((р, 0)т=0, /=1,т,.<т.
(13.50)
С учетом неравенств (13.21) можно принять XS = X,.
Аналогично проводится анализ для случая, когда существует
к, для которого 8ц<0. Таким образом, улучшенный вектор ps + 1
можно задать в виде
Pi,s+i=pis	l^k^n,	(13 51)
Pk.s+i As+Xs, если	1,
Pk.s+L Pics если	1.
Простейшая реализация элементарной операции состоит в сле-
дующем.	____
1. Задается произвольный вектор р = Р5 = (д-5), |'в1,и, и для
него вычисляются /?Л(р), й.(р), 8£f 8^(1 <Х<д) соответственно по
формулам (13.34) и (13.49).
2. Если среди номеров ( = существует хотя бы один
номер к, для которого выполняется одно из условий: 8р>0
или 8„<0, то производится улучшение вектора ps согласно
275
выражениям (13.51) и переходят к п. I, взяв в качестве значений
вектора р новые значения pj+1.
Простейшая реализация элементарной операции не позволяет
вообще решить задачу (13.26)—(13.28) до конца: как правило,
выполнение условий 5р>0 и 5„<0 VX,	не означает
нахождения тах/(р). Причем применение простейшей реализации
тем эффективнее, чем уже априорные границы аг w, 0,, t = I, ..., т.
Причина ограниченности применения простейшей реализации—в
существенной неединственности элемента йеЛ75: компоненты п(,
teN могут быть выбраны произвольно в пределах отрезка [<х(, 0(].
Можно предложить следующее обобщение простейшей реали-
зации элементарной операции.
Пусть при заданном значении вектора p = ps среди номеров
существует несколько номеров к, для каждого из
которых выполняются условия Зр>0 или 5*<0, и эти номера
образуют множество 7(|7|^н).
Зададим
ф< = 0, iff!,	(13.52)
определяется выражениями (13.47) или (13.48).
Определим значения Xs. Пусть для определенности Зр>0
VkEl. Тогда можно показать, что выражения 5'(р, X) и 5"(р, X),
полученные из (13.41) и (13.43) с учетом (13.52), сохраняют
соответственно знаки 8'(р, 0)= £ 5р и 5''(р, 0)=- У 5р, по
kel	кеГ
крайней мере, на интервале 0<Х<Х(, где

min
t, fce/
Х(р, 0)
,	Л((р, 0)=#0, 1=1.тк^т.
На основании неравенств (13.21) можно принять Х,=ХР
Аналогично проводится анализ для случаев, когда УХе/ 5р <0,
а также когда для части номеров Хе/ 5р > 0, а для оставшейся
части 5* <0.
Простейшая реализация элементарной операции (а также ее
обобщение) может быть усилена, например, использованием
второго способа реализации условий (13.22) и (13.23). Такое
усиление будет проведено ниже для частных классов задачи
(13.26) — (13.28) — для задачи назначения, а также для задачи
коммивояжера, тесно связанной с задачей назначения. Эти задачи
обладают тем свойством, что для них йе [0, 1].
Подход, основанный на реализации безусловного тах/(р),
используется при решении задачи (13.26) — (13.28) и в методе
сокращения невязок [22]. Однако этап, соответствующий простей-
шей реализации элементарной операции, в этом методе отсутству-
ет. С учетом терминов элементарной операции метод сокращения
276
невязок использует только второй способ реализации условий
(13.22) и (13.23). Для задачи (13.26) — (13.28) дальнейшая детали-
зация второго способа производиться не будет, так как на
другом языке это уже осуществлено в методе сокращения
невязок. Предлагается следующее использование простейшей
реализации элементарной операции для увеличения эффективности
последнего. Решение задачи начинают с применения простейшей
реализации элементарной операции. Если при некотором значении
вектора p = ps выполняются условия 8|<0 и 8£>0 Ук, \^к^п,
при задании вектора ф согласно (13.45) —(13.48), а решение
задачи не получено, то переходят к стандартному методу
сокращения невязок, приняв в качестве плана сопряженной задачи
(см. [22]) эти значения вектора р. Такое использование простейшей
реализации в методе сокращения невязок позволяет в ряде
случаев получить увеличение /-функционала простыми вычисле-
ниями. Напомним для сравнения, что в методе сокращения
невязок для увеличения /-функционала на каждой итерации
следует проводить, как правило, несколько шагов метода улуч-
шения плана для решения так называемой вспомогательной (см.
[22 ]) задачи, что достаточно трудоемко.
§ 13.7. Решение модельного примера для задачи
линейного программирования
Рассмотрим следующий пример:
J (х) = — 5.К! + х2 + 2х3 — 5х4 — 5л5 +
— 2xj + 5л:2 + x3 = 10,	(13 53)
x1 + 2x2+x5 = 6,
10х. — 3x, -j-x6 = 15,
_	_ 0^₽(.
Здесь ₽; = 10 Vz=l,6; /=1,4.	__
Введем набор множителей /?=1,4 и запишем для задачи
(13.53) следующие конструкции:
1.	Мр)=-2/\+р3+р3-)-10р4 + 5,
h2 Р =	-р2 + 2рэ-Зр4-1,
^4 (?) =Р1 + 5,
к-s (р)=Тз + ^’
A6(P)=P4-L	___
2.	R(t, и) = Л,(р)ы,(р), /=1,6.
если fct(p)>0,
3.	«f(p)=y 0, если А((р)<0,
Iлюбое щ(р)е [0, ₽г], если Л,(р)=О.
4.	Я(/) = max R(t и).
це[0, р,]	7
277
5.	/(р) = 10р1+р2+6р3 + 15р4 —
6.	8jp, й) = 10 —[—2йг (р) + 5й2(р) + й3(р)],
8Др, й)=1~[й1(р)-й2(р)+й4(р)],
§з (Р, «) = 6~ [й1 (р) + 2й2 (р) + й5 (р)],
84 (р, й) = 15 - [lOi^ (р) - Зй2 (р) + й6 (р)].
В качестве начальной совокупности значений р0 возьмем те
значения, с которых начинается решение задачи (13.53) методом
сокращения невязок. Весь ход решения задачи приведен
в табл. 13.1
Таблица 13.1
Номер игера- ции	1	₽<	Зна- чения	1						й'	5"		*(₽)
				1	2	3	4	5	6				
0	1	0	Л, (р)	-5	-6	— 2	0	0	-1	10	10	6 5	-35
	2	-5								—9	1		
	3	-5	й,(р)	0	0	0	иб.	лб.	0	-4	6		
	4	0								15	15	1 2	
I	1	6 5	м₽)	12 “Т	m Г*	4 “ 5	0	0	1 2	10		3 2	-15,5
	2	-5											
										— 9			
	3	-5	«Лр)	0	0	0	лб.	лб.	0	-4			
	4	1 2								15		2Z 50	
II	I	3 2	Мр)	3 “ 5	~25	1 ~ 2	0	0	12 50	10		411 250	-8,9
	2	— 5											
										-9			
278
Продолжение табл. 13.1
Номер итера- ции	i	Р<	Зна- чения	t						У	S'		'(₽)
				1	2	3	4	5	6				
	3	-5	Мр)	0	0	0	лб.	лб.	0	—4			
	4	37 50								15		4 5	
III	1	411 250	л<(р)	_J72_ 250	_9_ 50	89 “ 250	0	0	1 5	10		42 25	-6,56
	2	-5											
										—9			
	3	-5	«,(₽)	0	0	0	лб.	лб.	0	—4			
	4	4 5								15		518 625	
IV	1	42 25	ft/(p)	9 125	54 ” 125	8 “ 25	0	0	107 625	10		74 44	-5,77
	2	-5											
										—9			
	3	-5	«<(р)	0	0	0	лб.	лб.	0	—4			
	4	518 625								15		37 44	
V	I	75 44	мр)	0	0	_ 13 " 144	0	0	_2. 44	-40	30		-5,34
	2	-5											
										-19	11		
	3	-5	ц(р)	лб.	лб.	0	лб.	лб.	0	-44	6		
	4	37 44								-85	45		
279
Здесь в столбце Xmin приведены те значения которые
получены согласно алгоритму в результате использования формул
(13.50), а в столбце 8' выделены те значения, для которых
изменяются на следующей итерации соответствующие Простей-
шая реализация элементарной операции позволяет получить
максимальное значение /-функционала, равное 1= —5,342, в то
время как значение /-функционала соответствующее оптимально-
му набору множителей р, есть /(р)=—4,0435. За пять итераций
предлагаемого алгоритма получено то же значение /-функционала,
которое достигается к концу третьей итерации в методе сокраще-
ния невязок, но это значение получено значительно проще.
(Каждая итерация данного метода включает в себя, как правило,
несколько шагов метода улучшения плана, необходимых для
решения соответствующей вспомогательной задачи.)
Для получения точного решения следует взять в качестве
очередного плана сопряженной задачи в (13.53) значения ph f= 1, 4,
полученные к концу пятой итерации. Тогда останется провести
только Две итерации методом сокращения невязок.
§ 13.8. Многомерная нелинейная задача о ранце.
Постановка задачи
Рассмотрим задачу:
J'(u) =	(с,и,2+cPut)->mill,	(13.54)
i=\,n,	(13.55)
и,е(0, 1), /= 1, m,	(13.56)
где (йй), (i;), (c J, (c°), /=1, h, / = 1, m,—заданные соответственно
матрица коэффициентов, вектор ограничений, векторы коэффи-
циентов квадратичной формы; an, Ь;, сг, ср—действительные
числа. К модели (13.54) —(13.56) может быть сведена следующая
реальная задача.
Предприятие к концу года имеет портфель заказов из
т наименований (t = 1, т). Все заказы выполнить невозможно
из-за дефицита некоторых видов ресурсов, и каждому изделию
(заказу) в зависимости от приоритетности его выпуска ставится
определенный вес и(. Эти веса позволяют соблюдать необходимую
очередность выпуска изделий. Известны: пормы ап (i=1,n,
t= 1, т) расхода /-го ресурса на изготовление /-го изделия;
запасы ресурсов /-го вида /ы прибыль, которую получает
предприятие от каждого заказа и измеряется функцией
Необходимо составить оптимальный план (программу) производ-
ства, учитывающий заданную приоритетность различных видов
280
продукции и обеспечивающий тем самым максимальную взвешен-
ную прибыль при выполнении заданных ограничений.
Введем переменные
и, —целое, / = 1, т,
где wt— объем производства Z-го изделия; м“0Х—верхняя граница
на переменные. Тогда задачу о максимальной взвешенной прибы-
ли запишем в виде
/И
i^((w()->max,	(13.57)
m
У aitut i= 1, и,
()^u1^u{nax, wt— целое,	(13.58),
Конкретизируем зависимость Пусть 5t—цена единицы
изделия /-го вида, а себестоимость Tt его изготовления от
объема ut аппроксимируется функцией вида Т, (wt) = ехр( — p;w;),
где .... себестоимость первого изделия; р,—действительное чис-
ло, (Кр,I• Тогда прибыль от производства иг изделий определя-
ется выражением
W
^(м,)= (S.-S[exP(-₽A)]d^
о
Интегрируя правую часть полученного выражения, после
несложных преобразований получим
Разлагая функцию exp (-р,и() в степенной ряд и ограничиваясь
членами приближения не выше второй степени, получим
^г(и^с^и( + сг11^,
где c(° = 5t-2ct/pt, c( = Sjpt/2. Тем самым функционал (13.57) све-
ден (с точностью до постоянного множителя vt) к виду (13.54).
Ограничение (13.58) сводится к виду (13.56) введением, например,
^тах
преобразования н,= £ zlk, z(Jfc = {0, 1}.
к = 1
§ 13.9. Метод улучшения функции ср(/, х)
Задачу (13.54) — (13.56) можно представить в виде следующей
эквивалентной задачи оптимизации многошагового процесса уп-
равления с одномерным аргументом:
т - 1
./(u) = £ (c,W(2+cX)^min,	(13.59)
t = 0
281
x'(t +1)=xl(t) + a^t)и„ Г = 0, 1, ..., m — 1; i=\,n, (13.60)
x'(0) = 0, х'[т}^Ьх. i=\,n,	(13.61)
uteU^{ut: Ovl}, ( = 0, 1, ..., m — 1.	(13.62)
Будем искать функцию <p (/, x) из класса П в следующем виде:
ФО, х) = £ аО)*‘+0,5 £ i^ki(t)xkxl, (13.63)
/=1	A=U=1
где р(/)=(pt(/), ..., р„(г)); ст(/) = сты(t), t = 0, 1,	т-1; k,l=l,n.
В соответствии с (13.6) и (13.7) функции R, Ф для заданной
выражением (13.63) функции <p(x, t) имеют вид
А(/,х,и)= Х>''[аО+1)-#(0] + | Е £<МГ+О К (')*'(') +
i=i
+ flI(/)x*(/)]w( + | £ £ x*(/)xJ(Z)[ffftI(/+l)-ffM(r)] +
2fc= 1 i = l
+ щ
£ A(f+l)«f(r)-c? +м'2 ?£ £ CTk((r+l)«4r)a((r)-c,
1=1	J L2fc=l1=1
ф [x 0e s)] = £ Pi(m)Л"+1 £ £ a«(m)Л'-
1=1	2k-Il=l
(13.64)
(13.65)
Согласно (13.8), для решения задачи (13.59)—(13.62) следует
найти пару х, и, обеспечивающую выполнение условий
ц(г) = max R(t, х, u), r = min Ф[х (t.e5)].
(x, u)eK'	xeIF
Условия существования функции |i(f) накладывают на ф(д х),
заданную выражением (13.63), следующие ограничения:
Pi(t+ О=Л(О“А>	L m-l. (13.66)
Тогда с учетом (13.66) из (13.63) получим соответственно
х, «)=| £ £ CTt((r+l)[«4i)xJ(r) + «i(r)x'[(r)]w( +
1 *=ij=i
£k = ll = l	L*=l
[ в в
2*=1(=1
+
(13.67)
Ф[х((ё£)]= £ р((т)хЧ^ £ £	(13.68)
i= 1	zJt=lI=l
Наложим на функцию <р(/, х) дополнительные условия
ст*1(*+ 1)=^о(0=°И’	^=о, 1, —, ш —1. (13.69)
282
Тогда из (13.68) с учетом (13.69) получим соответственно
1 И Л
7?{г,х, и)=- £ £ c4<Ia(z)х‘(0+ai(‘)xk(0]w.+
2 it= 11= 1
ф[х(/е5}] = ZPi(m)xi + ^t £ ekl(m)xkxl. (13.71)
j=i
Найдем пин^Ф (xe(reS)]. Необходимым условием локального
минимума квадратичной формы (13.71) является, как известно,
неотрицательность формы
<12Ф>0,	(13.72)
где й2Ф = г Ф к, 1=\, п. Достаточными условиями выполнения
охгдх1
условия (13.72) являются условия
сЦ|(т) = 0, к^к к, 1=1, п, о^(т) = ак, к=1,п,	(13.73)
где ак, А = 1, л,—заданные неотрицательные числа. Следовательно,
с учетом (13.72) и (13.73) из (13.70) и (13.71) получим
л
R(l, х, u)= £	+
i= 1

(13.74)
ф[х(ге5)] = £ А-(/и)хЧу£ а£(х')2.	(13.75)
i = i	2i = i
т. e.
л	. N
r=mH[x(fG$)]= £	£ ape?, (13.76)
xeW	i = l	2i = l
где x = arg min Ф [x (r e 5)].
Таким образом, функция <p(r, x) в соответствии с (13.63),
(13,66), (13.73) принимает окончательный вид
л	- я
/(^х)=£рХ+| £ М*')2’	(13.77)
i=l	2i=l
где р={р15 ..., />„); «=(«1, > «„)-
Теперь для функции R, заданной в виде (13.74), найдем
p(r) = max R(t, х, u) по (х, п)еИ. Так как И'к = {х:0^х^Ь},	=
= {u:0vl} и R(t, х, и) зависят от х линейным образом, то
u)lx = o = M<
£ Р&(г)-с?
+ M<2(1 f «а-(0“с1)>
\ ‘=1
(13.78)
283
R(t, «)1Х=Ь=«<
!= 1
+«?(J £«.—Д
\ i = l	/
max R(t, x, u) = max {/?(/, u) |x„0, R(t, u) |x_b}.	(13.79)
x s И x
Найдем max/?(/, x, u). Учитывая (13.78) и (13,79), получим:
Л^)|х=и=о = Л(г)|х=ь=О,	(13.80)
= Е	E	(13.81)
Л(/)|х=ь = £ а^)аД+7ф)|х=о,	(13.82)
ji(/)= max R(t, x, u)=max{0,
(x, u)e
ОД|*:0> /?(r)|x=b}.
(13.83)
Пусть в соответствии с (13.83) и (13.76) выделена пара х,
й. Тогда для процесса (13.59)— (13.62) можно определить /-
функционал
т- 1
/(ф)=ттФ[х(Ге£)]- X . max /?(г, х5 «),	(13.84)
v xelK v	( = 0 (х, u)e И
где min^jjc^eS}] и тах^Л(г, х, и) определяются в соответст-
вии с (13.76) и (13.83), являющийся границей снизу для оптималь-
ного значения функционала (13.59).
Пусть имеется функция <ps(/, х), заданная в виде (13.77),
которой соответствуют на основании (13.74), (13.75) и (13.84)
/?s(£, х, u), Os[x(/eS)], /s(ср), а также множество И' пар х, и,
обеспечивающих max Rs(t, х, и) на V1; множество W, функций
(х, и)е Г' v
x(reS’), обеспечивающих min Ф, [х е S)] на W; множество Ма
функций х(, и,, удовлетворяющих условиям (х1; и) 6 при всех
/еТ\5, xte И4, t$S (см. § 13.3).
Функцию cps+1 будем искать в виде
<ps + 1(r, x) = (ps(r, х) + ?Щг, х),	(13.85)
где \ > 0 и ys (г, х) — число и функция, которые необходимо
определить.
Определим функционал:
t=m т-1
- Е Ы'т1’
1=0	1=0
8s[x(r), u(r)]=ys[x(/), г]
f(/, х, u)]-Ys(r, х)}.
(13.86)
284
Функцию 7S(Z, х), учитывая (13.77), найдем в виде
ХН £ [у/+|«>(х‘)2],	(13.87)
где v = (vb ..., vn); «={ар ..., а„); |vj^l, i = l,n, |а;|<1. Тогда
в соответствии с (13.86), (13.87) и (13.61) имеем
Обозначим через Ks(i, х, u, X), 1FS(X) и т. д. конструкции,
соответствующие функции ср = cps+Asys. Тогда на основании (13.88)
я Г в
8 [u, р, а, а, v]= £ V; bt- £
j = i |_ г = 1
. л	Г	и	2
bi~ £	,
i=L L	t=i
(13.89)
где wt(X) = wt(p, t, X),
х, u, X).
а ц (X) определяется из условия max 7?
решать задачу тах/(ф) с помощью элементарной
улучшения функции ср (/, х): функция ф1 +1 строится
(13.85), где у4. и Xs > 0 выбираются произвольно
Будем
операции
в виде
в пределах следующих требований:
,	35[х, и]>0 _
хотя бы при одном значении (х, u)eMs + 1 =Л/5(\),
(13.90)
<ps+ 1 - Cps + ^sYse П.
(13.91)
§ 13.10.	Алгоритм вычисления нижней границы
Таким образом, алгоритм построения улучшающей последова-
тельности нижних границ состоит в следующем.
1.	Задается согласно выражению (13.77) функция Ф0(б х)еП
и для нее по формулам (13.74) и (13.75) составляются функции
/?о и Фо.
2.	Согласно выражениям (13.76) и (13.83) находится пара Хл,
й0, обеспечивающая нахождение г и ц(г). По формуле (13.84)
вычисляется оценка снизу /(ф0), соответствующая паре (х0, и0).
Если эта пара —допустимая, то она является и оптимальным
решением задачи (13.59)— (13.62).
3.	Если пара х0, и0 не является допустимой, то,
используя выражение (13.89), выбором Xs и (фактически
v; и а;, 1=1, л), удовлетворяющих условиям (13.90) и (13.91),
285
обеспечивают выполнение условия A/s(X)~XSs [х ), u(z)] >0.
Тем самым получают новое приближение функции фДД х),
переходят к п. 1 и так до тех пор, пока либо не
будет получено оптимальное решение, либо дальнейшее
увеличение /-функционала сганет невозможным.
Элементарную операцию улучшения функции ф (/, х), удовлет-
воряющую условиям (13,88), (13.89), можно построить различны-
ми способами. В данном параграфе предлагается следующая
схема реализации элементарной операции.
1, Решить задачу тпах/^ выполняя условия (13.88) и (13,89)
из § 9 и оставаясь в классе линейных приближений функции
ф(/, х), т, е. полагая в формулах (13.77) и (13.87) af=df=0,
/= 1, п. Наибольшая нижняя граница, полученная при таком
подходе, достигается для вектора р=(/715 ..., р„).
2. Считая значения вектора р фиксированными, дальнейшее
решение задачи max продолжить в классе нелинейных прибли-
жений функции ср (/, х), выполняя условия (13.90) и (13.91), т, е,
полагая в формулах (13.77), (13.87) осг^0, а^О, /=1, и.
В задаче о многомерном ранце с линейным функционалом
такая схема реализации условий (13.90) и (13.91) позволяет в п. 1
использовать как достижения в решении задач непрерывного
линейного программирования двойственными методами (непре-
рывная релаксация) или близкой к ней и очень эффективной
для этих задач простейшей реализацией элементарной операции
(см, § 13.6), так и достижения в решении задач линейного
целочисленного программирования с помощью субградиентной
оптимизации в рамках релаксации Лагранжа, а также релаксации
замещения [11].
§ 13.11. Алгоритм ветвления
и общая схема решения задачи
Опишем вначале алгоритм вычисления нижней границы для
решения задачи (13.54) — (13.56) на каждой р-й ветви дерева
ветвления [6].
Пусть каждая р-ветвь характеризуется множеством индексов
фиксированных на ней переменных:	= =	T’g = {r:w(=O}.
Обозначим множество Тр = {1, ..., m}\(Т? и Tg).
На ветви р рассмотрим следующую задачу, полученную из
модели (13.54) — (13.56) введением дополнительных условий иг = 1,
если и wt=0, если
У(ч)= £ (с,и?+с?иг)+ £	(13.92)
1еТг	teT\
286
S	/=1,и,	(13.93)
teT11
ы,е(О, 1), / = 1, m,	(13.94)
где Af = i>; — £ ait. Решение задачи (13.92) — (13.94) (или ее
teT’
непрерывной релаксации алгоритмом, изложенным в § 13.10)
дает нижнюю границу	где У0—граница, доставляемая
решением задачи (13.54) — (13.56) тем же алгоритмом.
Перейдем к изложению общей схемы решения задачи (13.54) —
(13.56), включающей алгоритмы вычисления границ и ветвления.
Итерация нулевая
Положим Т° = 0, То = 0, Т° = {1, т}. Определим и1}(r= 1, т),
S0-.	____
а)	если if,	удовлетворяет всем ограничениям (13.55)
задачи, то получено оптимальное решение задачи (13.54)—(13.56);
б)	если wf, г=1, т, не удовлетворяет всем ограничениям
(13.55) задачи, то найти ^“min {(cf 4-cf2)1Z2}. Для первой ветви
положить T’] = {i1], Го = 0, сформировать множество Т1 и пе-
рейти к итерации I.
Итерация к~я
Шаг I. Вычислить Af!*',=bi— £ aitt а) если Af(t)>0, i=i,n,
перейти к шагу 2; б) если найдется такое it, что Af^cO,
перейти к шагу 4.
Шаг 2. Найти ^р(/‘>: а) если	найти и? и перейти
к шагу 3; б) если ^р(к>^^р^~ перейти к шагу 4.
Шаг 3. Требуется: а) если 7T(i)=0, перейти к шагу 4; если
Т₽!М^0, положить р(к+ l)=p(fc)+ 1 и найти с(р№+1) = mji} ((с,24-
+<ЛШ). Для ветви д(Ач-1) положить +	+
j-giiTuT 7g!*сформировать множество Tp(k+t\ перейти к шагу
1 итерации fc+1.
Шаг 4. Если 1„<к}еТ^к\ положить 1)=р(к),Д((, + n =	,,
Пи+1,=П^и{гД + 1)} [здесь ветв:
р(&+1) и р(А) не совпадают, хотя и имеют один и тот
же номер], сформировать множество Tvik+I\ (Ветвь, про-
смотренная на A-и итерации, далее не рассматривается.) Перейти
к итерации к 4-1.
2. При ip№)eTg(t) положить p(fe4-!)=p(fc)—1'. а) если р(к+ 1)>
>0, перейти к шагу 4 итерации £ + 1; б) если р(к + 1) —0, то
гф—оптимальное решение, У ^—оптимальное значение функци-
онала (13.56).
287
§ 13.12. Решение модельного примера
для нелинейной задачи о ранце
Рассмотрим следующий пример [2]:		
	У(и) = —	—u3->min?	(13.95)
	Uj И-	5, 2?7 “h^2 -|-4?	(13.96)
	«,=(o. 1), у=Гз.	
Эквивалентный (13.5) для задачи	многошаговый процесс вида (13.95), (13.96) есть	(13.2), (13.3),
..	,/(и)= £	(13.97)
1 = 0
' х1(/ + 1)=№ (?)+«! (г) wp / = 0, 1, 2,
х1(0) = 0, лг1(3)^5;
х2 (Z +1) = х2 (г) + а2 (?) ы„ t = 0, 1, 2.	(13-98)
х2(0) = 0, хг(3)^4;
; . . '	И{Е U — {и/0 V 1),
где с0 = -6, с, = -4, с2 = — 1,	(0)= 1, л1(1) = 2, а, (2)=3, а2 (0) = 2,
о2(1)=1, й2(2)=1. Будем искать функцию <р(г, в внда (13.63).
Пользуясь произволом функции p(Z, х), заданной в виде (13.63),
положим:
^(?+1)=^(/)=^, г=1, 2; Г=0, 1, 2;
au(f+l) = <yJ;I(/) = cyjt|, к, 1=1, 2; t=0, 1, 2;	(13.99)
^ki = ^ik', Ои(3)=0, k^l;
(3) = ak (3), к = /, к, 1=1,2,
где <хк(к = 1, 2)—заданные неотрицательные числа. Тогда с учетом
(13.67) и (13.68) имеем
2 jR(t, х, u) = У а;(г)аДфс'ы(+и,	Л X р;а((г)-с,	+
1 = 1 .	2	, / = 1	
Ту».2 I ai(0[ffi(0r> z ;=i		(13.100)
Ф[х(ге£)> f Ар)У + | i=i	i	2 = 1	(13.101)
где а,(г)=а;, z=l, 2.
В соответствии с (13.63) будем искать p(f) и г сначала
в классе линейных приближений функции ф(с х), т. е. в дополнение
к (13.99) положим в (13.63), а следовательно, и в (13.100), (13.101)
288
а((/)=а,=О, / = 0, 1, 2, 3; i~ 1, 2.
Тогда из (13.100) и (13.101) имеем
R(t, х, и) = и(
!= 1
(13Л02)
2 •
Ф[х(ге5)]= £А(3)+.	(13.103)
i”l
Будем находить ц(/) и г, где функции У? и G заданы
соответственно выражениями (13.100) и (13.101), с помощью
аппарата простейшей реализации элементарной операции улуч-
шения функции ср(/, х) (см. § 13.6). Возьмем в качестве начальных
приближений значения р([~-=р<2=^- В результате применения про-
стейшей реализации элементарной операции уже на следующей
итерации получаем; р\ = — 1	= 0, /(р1) = £ Р;Ь(— £ ц(/) = — - —
3	1=1	< = о	3
2
-9= - 10-, а значения распределения — u0 = 1, «, = 1, w2 = (0 v 1).
Заметим, что для данного примера применение схемы обобщенных
множителей Лангранжа (совпадающей с применением непрерыв-
ной релаксации) дает значение Z(p)= — 13 и следующие значения
распределения: щ - 1,5, й2 = 1, w3 = 0.
Закончим решение задачи, пользуясь аппаратом реализации
элементарной операции улучшения функции ср(£, х) (см. § 13.10).
Так как р1= ~ 1, jp1 = 0, го легко видеть, что x1(3) = w0 + 2wI +
+ 3й2 = 3 + 3(0 v 1)^г = 5 и потому выделенное при линейном
задании функции cp(f, х) решение й0=1, w± = 1, й2е(0 v 1) не
является оптимальным.
Зададим ср(/. х) в виде
ср(г, х) = £ Pixl + - £ а;(ф'%	(13.104)
. = 1	zi=i
где р=(-|, 0); a;(f) = 0, 1=1, 2; Z = 0, 1, 2; tXi(3)=b
Тогда из (13.104) с учетом (13.102) и (13.103) имеем
7?(/, х, и)=и(
2
Е А°:(0-с1
= 1
®[x(zeS)]=pLx1 + Jai(3)(x1)2.
«2 (3)=0.
(13.105)
(13.106)
Так как с учетом задания функции р(/, х) в виде (13.104)
значения функций ц(/) совпадают для функций Rf заданных
соответственно в виде (13.102) и (13.105), то найдем значение
10 Зак 456
289
г для функции Ф, заданной в виде (13.106). Из условий
существования min Ф[х(/е5)] имеем
х b
Фх = 0, Фхх>0.	(13.107)
Из равенства (13.107) имеем х} = — /?1/сс1(3), из неравенства
(13.107) имеем at(3)>0. Следовательно, при сс1(3)=1/9
/(р)=г- Ё и(0=—9= “10>
r = 0	J
совпадающее с оптимальным значением функционала для задачи
(13.95), (13.96). Этому значению функционала соответствует
оптимальное распределение = 1, й2 = 1, й3 =0. 1
Глава 14
Численные методы оптимизации
для некоторых многошаговых процессов
с дискретным управлением
(двумерный аргумент)
В данной главе приводятся алгоритмы решения двух (двумерных
по аргументу) задач дискретного программирования (назначения
и коммивояжера) с помощью метода, изложенного в гл. 13. Выбор
этих задач не случаен. Как правило, вновь создаваемые общие
схемы в дискретном программировании тестируются на рассматри-
ваемых в главе задачах. Рассматривается задача назначения
с подробным изложением математической постановки задачи,
с построением реализации элементарной операции, конкретизаци-
ей последней для задачи, приводящей к точному алгоритму
решением модельного примера. Предлагаемый алгоритм решения
задачи назначения наиболее близок к алгоритмам венгерской
группы, отличаясь от него нетривиальными особенностями. По
такой же схеме рассматривается и используется задача коммивоя-
жера с получением точного алгоритма решения этой задачи. Как
показывает сравнение с существующими точными алгоритмами
решения этой задачи, рассматриваемый алгоритм наиболее близок
к алгоритму Балаша — Кристофидеса — наиболее эффективному
на сегодняшний день алгоритму решения задачи коммивояжера
с асимметричной матрицей расстояний. Так, в частности, с помощью
последнего алгоритма к настоящему времени решены задачи
размерностей до 325 городов.
§ 14.1. Линейная задача назначения
Рассмотрим точный алгоритм, основанный на детализации
общих конструкций по реализации элементарной операции для
линейной задачи назначения, наиболее известная содержательная
постановка которой состоит в следующем.
Пусть имеется п работ, которые должны быть выполнены
п исполнителями. Мера затрат г-го исполнителя на /-й работе
определяется величиной cijt i, у=1, и. Требуется найти назначение
исполнителей на все виды работ так, чтобы: а) суммарный
эффект от такого назначения был минимален; б) на каждую
работу было назначено не более одного исполнителя; в) никто
из исполнителей не был назначен более чем на одну работу.
ю*
291
Линейную целочисленную модель задачи назначения запишем
в виде
^(w)= f f	О4-1)
i=lj=l
£ Ui,.= l, r = M,	(14.2)
j=i
IX = 1, 7=M.	(14.3)
i= 1
M.j = (0, 1), i, 7=1, n,	(14.4)
где условию (?) в содержательной постановке соответствует
ограничение (14-2), условию в) — ограничение (14.3), условию
а)—условие (14.1). В ограничениях (14.4) иу=1, если г-й исполни-
тель назначается на /-ю работу, и м,; = 0 в противном случае.
Перейдем от модели (14.1) — (14.4) к эквивалентной задаче
оптимизации многошагового процесса управления с двумерным
аргументом вида (13.4), (13.5);
y(u)= Z Z сиии min,	(14.5)
i=0j=0
хю'+! =xo + wu> 7=0, 1,	•••,	п~ 1;	г = 1,	(14.6)
+	* = 0, 1,	,	«~1;	7=1,«,	(14.7)
х-о = 0, х/л = 1,	*=!,»,	(14-8)
•*о/=0, х$}=\,	(14.9)
^=(0, 1), г, у=М.	(14.10)
Термины общей постановки задачи здесь имеют следующее
содержание: Г^Т'хТ2, Tl = [j'. 0, 1, ..., л); T2={i: 0, 1, ...,
п); г = (/, г), j=ti, 1=11, 26—пространство векторов х = (х*, х2);
U—числовая ось; V*— все пространство X; У1и—пара значений
0, 1; роль конечно-разностных связей (13.4) играют соотношения
(14.6), (14.7), функционала (13.5)—функционал (14.5).
Отметим, что в многошаговом процессе управления (14.5) —
(14.10) ограничения наложены только на управление п
§ 14.2. Метод улучшения функции ф(Л х)
Так как (14.5)—(14.10) — процесс с линейными связями, то
вектор-функцию ф = (<р1, <р2)еП будем искать в линейном виде;
ср1(^, 7, х1,	+Pdx2>
292
I	<p2(i, 7, **, х2)=р-/хг+р^х2.
 Тогда функции R и Ф из (13.6) и (13.7) для модели
*	(14.5)	(14.10) принимают следующий вид:
I	7, х,	+	-p'i}) +
Ж	+«(Рю + 1 -Р, + и-с,}) + х1р^и + х2р'^+1,
К Ф(х) = £ (p-ix1+p^x2-p;ox2)+ Е (pnjXl+p'^2x2-pojx1).
MF	1 = о	7 = 0
ж Условия существования [i(z, j) = maxR(i, j, х, и) по (х1, х2)е
Я е( — од < хх2 < оо) и по ие [0, 1] из (13.6)— (13.10) накладывают
Я на феП следующие условия:
Я	Pi.lj + i=Pij=Pil=Pi,	г=1,Щ 7 = °,	1,	> «-1,	(14.11)
I	Pi/-Pihj=Pjl=O, !=0,	1,	«-1,	(U.12)
I	Pih.j=Pi^Pi2 =Pj, J=_^, К «"I, (14.13)
1	p'ij =p';j+l=P'i2 = Q,	7 = 0, 1,	л-1.	(14.14)
Я На основании условий (14.11) — (14.14)
J	R(l, j, u) = (p;+/?;-c.y)u = yp)u,	(14.15)
| где p=(p<, p’f), h^^p'i+p'j-Cij,
i	ф(х)= E E Pi*2-	(14.16)
11	i=0	7 = 0
:|| Учитывая (14.15) и (14.16), получим
И.	./)=«ij(p)A>j(P)> 6 7 = °, h > «-{>
I ГДе
if	fl,	если	й;;(р)>0,
|Г	йи(р)=)0>	если	Мр) < 0, г,у=О, 1,и-1,	(14.17)
s	Io v	1,	если	/i£j(p) = O,
-Й	п	п
I	w=Ep.+ EpE
р	1=1 j=l	_	_
Таким, образом, получено описание множеств Г'хХ F'
иЙ7: V[ — все пространство 76; У‘и—пара значений 0, 1,
определяемая по формулам (14.17); 1Т—точка с координатами,
равными 1 в пространстве размерности 2л. Наконец, /-функционал
i| в соответствии с (13.10) будет равен
J	((р)= Е R;+ I Pj- Е Е Аи(р)«у(Р)-	(14.18)
;=1 j=i >=1 j=i
На основании (13.11) и (13.12) при любом р /(р)<г/. Таким
Т образом, основные конструкции, входящие в (13,6) — (13.10), для
п модели (14.5)—(14.10) построены.
293
Функцию у=(у1, у2), фигурирующую в (13.14), будем искать
в виде
у‘(/, у, х1)=ф^х1, y2(i, j, х2)=^^х2.	(14.19)
Выполнение условий (14.11) и (14.13) накладывает на функцию
у следующие условия:
ФЕ + 1=Ф;; = Ф^ г = 1,«, 7 = 0, 1, ..., д-1,	(]420)
фы1.;=Фи=Ф/, i=^, 1,	«-1, 7=1, «-
Тогда в соответствии с (13.16), (14.19) и (14.20) о-функционал
для задачи (14.5)-*-(14.10) запишем в виде
е фА - е «X i ф/1 - i X (14.21)
 :=i	\ j=i / J=t \ i-i /
Выражение для p(i, j, X) будет иметь вид
J,	Я
где л,Др, ^)=Мр, о)+х(ф;+ф;9,
{1, если Л;Др, X) > 0,
0, если й;Др, X) < 0,
0 v ], если Л;Др, Х)=0.
Пусть	_—	---
|ф-| 1, 1 = 1,п; |ф)'| у: 1, У = 1, п,
где ф'=(ф'1, ..., К), ф"=(ф1,	К), ф = (ф', Ф")-
Введем в рассмотрение множества: Mj, М- — множества строк
i матрицы //-=(/:-( р)), которым при данном j отвечают соответ-
ственно положительные и нулевые значения этой матрицы; N’;,
Nt — множество столбцов j матрицы Н, которым при данном
i отвечают соответственно положительные и нулевые значения
Л;Др);	N’ = [)N\, M=\JMj, N=\JN;.
Тогда получим окончательно:
из (14.21)
3(р, Ф, «)- Е ф/1	Е И;Х х ф/1	Е «А
»=1 \	jel"/, ) 7 = 1	\	тм, /
 8(р, ф, и, х)= Е ф/1-|лЭД- Е А)+
i = 1	\	/
+ £	£ WA
j = i	\	;еЛ-(х) /
из (13.18) с учетом (14.19) и (14.20)
294
З'(р, 'l', 0)= Е КО ~|Л^|)- £ max ( Е K«u/ +
»=1	“уе[О, I] \i = 1	J
+ EK(l-m)-E maxff^A
j~ 1	1<у<ф)г I] \ji = l 7
8'(p, к Ь)= E	£ шах ( f K«ijV
' = 1	yetfA) и|;ф.1]М=1	7
+ £ KO-iW-)!)- E гаах(ЕК!«,Д
j-l	ieW?(X) I] \j=l 7
§ 14.3. Описание алгоритма решения задачи назначения
Перейдем к изложению собственно алгоритма решения задачи
назначения, существо которого состоит в конкретном задании
на каждом шаге вектора \|/ и числа Xs.
Пусть задан некоторый вектор p = ps. Введем дополнительно сле-
дующие конструкции: m'j, —соответственно количество положи-
тельных и нулевых значений /г др) при данном у; п-—соответственно
количество положительных нулевых значений А^(р) при данном г.
Тогда алгоритм решения задачи назначения состоит в следующем.
Полагаем й;у(р) = 1, геЛ/', jeN' и й|7(р)=О при A;j-(p)=O.
Пусть |N'\=n, тогда оптимальным решением является заданное
распределение. В противном случае переходим к Этапу I.
Этап I. Находится такое значение j = k, что: а) д4 + тк = 0;
б)т*>1. Или находится такое значение i=k, что: в)д^>1;
г) п’к+пк=0. Улучшенный вектор ps41 задается соответственно:
для случаев а) и б)—в виде
p,i.s+i=pliS, * = 1,и,
p’j+i.*=Pj* J-bn, pk,s + l=pks+K J'=k’,
для случаев в) и г)—в виде
PM+i=Pis Vty/c, i=l,n, Pi.,+ l=p'is + 'k, i-к, p'j.s+i=p’j3, J=l, л,
где число X задается в виде: a) ^=^s=|Apit(p)|; б) k = 'ks= — ^pjt(p);
в) X=XS = — \р(р); г) X —Xs=|At(S(p)|. Здесь номер р в соответству-
ющих случаях означает: а) второе значение I, если номера
i расположить в порядке неубывания | hik (р) |; б) [т’к — 1]-е значение
i, если номера i положительных Л;л(р) расположить в порядке
неубывания; в) |Х~ 1]-е значение j, если номера / положительных
/д_Др) расположить в порядке неубывания; г) второе значение у,
если номера / расположить в порядке неубывания |Л*Др)|.
295
Затем вычисляется для нового значения вектора р —ps+1
значение /-функционала по формуле (14.18), Если отмеченные
значения Отсутствуют, то переходим к этапу П.
Этап II. а) Выбирается такое множество УсЛ', что нарушается
неравенство
Е...	Е (1-0,	(14.22)
i е Л/(У)	j e N
где M(y) = lJM? ye/V.
б)	Либо взбирается такое множество М с М, что нарушается
неравенство
... Е (i-«0^ Е. (i-О’	(14.23)
isM
где 7/(44) = IJNt, IeM.
i
Улучшенный вектор ps+, задается соответственно в виде:
a)	Pi.s+i =Pis~К ieM(N\ pl,s + 1 =p'is,
Pj.s + t = Pjs + K JeN, p'j,s + 1 =Р}К, j$ №>
6)	pU + i=Pis+\ itM, pU + i=j?U W",
Pj,s+\ =p'j*-K jeN (m),	1 =p'^,j^N (m\
Число X определяется следующим образом,
множества элементов:
в случае а)
Юр): Мр)<0’ гум(У)},
в случае б)
{О(р): М₽)<0. /еЛ^
Для каждого столбца JeN {/£ М (У)) и каждой строки
IeM(/V)(/£/V) в случае а), каждой строки i Е М (j ф N (М)} и каждого
столбца jeN(M) (i$ М) в случае б), берется не больше двух
отмеченных элементов (р), минимальных по модулю. Эти элементы
для каждого из множеств, задаваемых выражениями (14.26), (14.27),
упорядочиваются соответственно в порядке неубывания модулей:
{| /г“! (р) |) (1 <(Х| <:2я), {/га2 (р)} (1 ^а2<2л). Тогда в случае а)
Х = х, = |ЛР(р)|,	(14.28)
где р — второе значение а,; в случае б)
Х=Ч = |Л₽(р)|>	(14.29)
где Р—второе значение а2.
Затем вычислим для нового значения вектора p = ps+1 значение
/-функционала по формуле (14.18).
296
(14.24)
(14.25)
Выделяются
(14.26)
(14.27)
Приведем алгоритм построения множеств М и N.
Пусть в результате завершения этапа I получена матрица
Н5 = (/?ц(р)), /,/=], и. Вьгделим знаком (*) в матрице Hs такие
элементы h-(р) >0, Что никакие два из них не лежат либо
в одной строке, либо в одном столбце. Так как в результате
выполнения этапа I в каждой строке и каждом столбце матрицы
Hs может находиться не более одного элемента /<7 (р) > 0, именно
эти элементы следует выделить знаком (*) в первую очередь.
Тогда остальные элементы названной группы содержатся среди
множества элементов (р) = 0, 1еМ\М', jeN\N\ если последнее
не пусто. [В этом случае оптимальное решение получено
и определяется позициями элементов /г; ;(р)>0 согласно выраже-
ниям (14.17).]
Пусть упорядоченное в порядке возрастания множество индек-
сов JeNXN' представляет собюй совокупность элементов 
..., jk(k<n\. Аналогично и для множества индексов 1еМ\М':
i2, ...,	Тогда последовательность действий для выделе-
ния остальных элементов названной группы будет следующей.
Отмечаем элемент h- (р) = 0, если такой найдется, знаком (*).
(В противном случае 'переходим к выделению столбцов, содер-
жащих элементы со звездочками, знаком -р.) Затем формируем
новые множества элементов yeAV/V' IJy'j):(/2, /3, ..., д , к. =к-1),
Отмечаем элемент л,у2(р) = 0 звездочкой, если последний стоит
в строке	IJ г, ),	и так до тех пор, пока
не будет просмотрен последний столбец.
Столбцы матрицы, содержащие элементы со звездочками,
выделяем знаком В процессе решения задачи некоторые
Строки будут выделяться знаком +, стоящим справа. Элемент
матрицы HS! принадлежащий либо выделенной строке, либо
выделенному столбцу, будем в дальнейшем называть выделенным.
Элемент матрицы Hs, не принадлежащий ни выделенной строке,
ни выделенному столбцу, будем в дальнейшем называть невы-
деленным.
Если в матрице Н, выделено звездочкой п элементов, то
оптимальное решение получено и определяется позициями элемен-
тов со звездочками согласно выражениям (14.17). Если же число
элементов со звездочками меньше я, то переходим к этапу 11.1.
Этап ILL Если в матрице Hs средн элементов /?^(р) = 0 пет
невыделенных, то обсуждаемые множества построены. Если
невыделенный элемент обнаруживается, то возможна следующая
альтернатива; а) строка, содержащая этот элемент, содержит
также элемент со звездочкой; б) строка, содержащая этот элемент,
не содержит элемента со звездочкой.
В случае а) ставим над найденным элементом штрих ('),
выделяем Строку, его содержащую (ставим справа от пее знак
297
+ ), и уничтожаем знак выделения + над столбцом, на пересече-
нии которого с только что выделенной строкой расположен
элемент со звездочкой.
В случае б) отмечаем найденный элемент штрихом и перехо-
дим к этапу II.2.
Действия, связанные с описанным исследованием одного
невыделенного элемента матрицы Hs, назовем шагом этапа II. 1.
После конечного числа шагов либо обнаруживается случай б)
(переходим к этапу II.2), либо все элементы 7г;;(р) = О матрицы
Hs окажутся выделенными. В первом случае будем говорить об
исходе 1В этапа II.1, во втором — об исходе 1А этапа II.I.
При исходе 1А этапа II.1 множества М и N достроены.
Примем в качестве множества N множество индексов невыделен-
ных столбцов. -Тогда М (А)—множество индексов выделенных
строк. Проверка условия (14.22) для этих множеств сводится
к следующему: если число выделенных строк меньше числа
невыделенных столбцов, то условие (14.22) нарушается. В этом
случае проводим улучшение вектора р согласно выражениям
(14,24), где задается (14.28), получаем новую матрицу
в которой имеется по крайней мере один невыделенный элемент
й^(р) = О, и переходим к началу этапа II.1. с новой матрицей H{s'\
Примем в качестве множества М множество индексов невьще-
ленных строк. Тогда А(Л/) — множество индексов выделенных
столбцов. Проверка условия (14.23) для этих множеств сводится
к следующему; если число выделенных столбцов меньше числа
невыделенных строк, то это условие нарушается. В этом случае
проводим улучшение вектора р согласно выражениям (14.25),
где задается (14,29), получаем новую матрицу и переходим
к началу этапа 1.
Этап П.2. Исходя из элемента со штрихом, в строке которого
нес элемента со звездочкой (случай б) этапа II.1), строим
следующую цепочку элементов матрицы Hs: исходный элемент
со штрихом, элемент со звездочкой (если таковой найдется),
принадлежащий тому же столбцу, элемент со штрихом, принад-
лежащий той же строке с предшествующим элементом со
звездочкой, и т. д,, т. е. цепочка образуется движением от элемен-
та со штрихом к элементу со звездочкой по столбцу, от
элемента со звездочкой к элементу со штрихом по строке и т. д.
При построении цепочки возможна следующая альтернатива:
а)	если при переходе от элемента со штрихом к элементу
со звездочкой по столбцу на месте последнего элемента встреча-
ется каждый раз элемент /?ц(р) = 0, то можно показать, что
описанный алгоритм построения цепочки однозначен и конечен.
При этом цепочка обязательно заканчивается элементом со
штрихом. Над элементами цепочки, стоящими на нечетных
местах (элементы со штрихом), ставим звездочки, уничтожая
их над четными элементами. Затем уничтожаются все штрихи
298
над элементами матрицы Hs и все значки выделения строк
и столбцов +. Число элементов со звездочками увеличено на
единицу;
б)	если при переходе от элемента со штрихом ио столбцу
к элементу со звездочкой на месте последнего хотя бы один
раз встретится элемент со звездочкой h-(р)>0, то последователь-
ность действий меняется. Изменения направлены на приведение
указанного случая к уже рассмотренному выше, Для этого
изменим составляющую вектора ptk (t— номер итерации; к —
номер строки, содержащий указанный элемент со звездочкой),
оставляя другие составляющие вектора р[ неизменными:
Pt+ l.k—Ptk ~	(14.30)
где X выбирается таким образом, чтобы значение й4г(р) (/—номер
столбца, в котором содержится исследуемый элемент со звездоч-
кой)_ стало равным единице. [Если йн(р) уже равно единице,
то Xs выбирается таким образом, чтобы лкДр) = 0. ] После этого
возвращаемся к этапу I, предварительно уничтожив все знаки
выделения строк и столбцов + и все штрихи и звездочки
над элементами матрицы Hs.
Изложение алгоритма построения множеств М и N, этапа
И и алгоритма в целом закончено. Обоснование алгоритма дает
следующая теорема:
Теорема 14.1. [16]. 1. Для. любых р величина I(р) есть нижняя
граница функционала J на М.
2.	В результате применения элементарной операции к данному
вектору p=ps возможна следующая альтернатива', а) па выходе
элементарной операции определено управление йц(р) допустимое
и оптимальное; б) если управление (р) определено/ но не
допустимо, то выходом элементарной операции является увеличе-
ние 1-функционала (улучшение вектора р), причем A/(ps) = /(ps+1) —
^Последовательность элементарных операций, начинающаяся
с произвольного вектора р, приводит к оптимальному решению
W;j(p) через конечное число шагов.
Этап 1 приведенного алгоритма является, по сути дела,
подготовительным этапом алгоритма Манкреса, только выражен-
ным в других терминах, и потому обоснования, как и в алгоритме
Манкреса [20], не требует. Обоснованием этапа II является почти
дословное повторение соответствующих частей алгоритма Манк-
реса. Можно показать, что новые фрагменты в этапе II приведен-
ного алгоритма [сужение множества, на котором ищутся независи-
мые элементы /т Др) = 0, и пересчет составляющей вектора p'ih по
формуле (14.30) в этапе II.2. б)] не меняют основных идей этого
доказательства.
299
§ 14.4. Решение модельного примера для задачи назначения
Пример. Решить задачу назначения с матрицей 7,7=1, 6.
i	j					
	1	2		3	4	5	6
1	00	68	73	24	70	9
2	58	GO	16	44	II	92
3	63	9	СО	86	13	18
4	17	34	76	со	52	70
5	60	18	3	45	СО	58
6	16	82	И	60	48	СО
Итерация нулевая
/4 = 0, >'2=0, р'з = 0, /4 = 0.- /4=0, /4 = 0;
/4=о, р'1=о, /4=о, р^о, р'1=о, /4=0.
/	j					
	1	2		3	4	5	6
1	— СО	-68	-73	-24	-70	-9
2	-56	— СО'	-16	-44	-11	-92
3	-63	-9	— со	-86	-13	-18
4	-17	-34	-76	— со	-52	-70
5	-60	-18	-3	-45	— со	-58
6	-16	-82	-И	-60	-48	— ОС
	j					
	1 2		3	4	5	6
т}	0	0	0	0	0	0
	0	0	0	0	0	0
	6	6	6	6	6	6
№ = )?; (М)
= 0. Имеет место этап I а) к = 1, 2, 3, 4, 5 6. На итерации:
2)i = 18; № = 11; № = 44; (Х^ = 13; № = 18-
№ = 13; № = is.
Итерация I
/4=0, /4=0, /4 = 0, /4 = 0, /4 = 0, /4 = 0;
р; = 17, /4 = 18, /4=Н, /4 = 44, /4=13, /4 = 18.
						
	1	2		3	4	5	6
1	— со	-50	-62	+ 20	-57	+ 9
2	-41	— СО	-5	0	4- 2	-74
3	-46	+ 9	— 00	-42	0	0
4	0	-16	-65	— со	-39	-52
5	-43	0	+•8.	-1	— со	-40
6	+ 1	-64	0	-16	-35	— 3G
т.	J					
	1 2		3	4	5	6
т‘)	1	1	I	1	1	1
"Ч	1	]	1	1	1	1
	4	4	4	4	4	4
3.00
л.	J
	1	2	3	4	5	6
д й| а	2	110	11 0	12	111 4	4 3	5 4 4
/(р') = 72. Имеет место этап I в)
(Х/)2=0 V/, iVl; (Xi)~0 V/
fc=l. На итерации: (М)г = 9;
Итерация И
Р1--9, р'2 = 0, р'з==0, /4-0,	^5=0,
/4 = 17,	/4-18, /4=11, /4 = 44, /4 = 13, /4=18.
места. Изменение р‘6 вы-
/(р") = 81. Этап Та)—г) не имеет
звано тем,
множеств
//1|:ЛГ=(2, 3, 4, 5
1=1, 2, 3, 5;
№=о.
, что _«встретился» этап 11 2 6) при . построении
N, М($). Строим множества TV, M(7V) для матрицы
* 'io); M(7V) = (1, 2, 3, 5). На итерации: (Х?)3 = 16,
'-h	(if)3 = 16,	>2, 3,4, 5,6;
Итерация III
p'i=-25, pr2=-16, рз=-~16, /Д“0,	р'б~-1;
Pi = 17, Р2 = 34,	р'>27,	pi-60, p's —29,	р'в-34,
3’01
/(plll) = 82. Имеет место этап I б) к = 3. На итерации: (/ЛЕ = 8;
V/V3; (Х?)4 = 0 V/
Итерация IV
р\ = -25, р'2^-- 16, />э= —24, />4 = 0.	р5 = - 16, />б= -7;
/' = 17,	/>2—34,	/>з=19,	/1 = 60, / = 25,	/>£ = 34.
/(plv) = 90. Этап I а) — г) не имеет места. Изменения р6 и р'3 вы-
званы тем, что дважды «встретился» этап II. 26 при построении
множеств N, М (7V). Строим множества N, М ($) для матрицы
№v:V = (4, 5,6);	=	2). На итерации: (Xi)5 =(М)5 = 7;
(Х/)5 = 0 Vf/1,2; (Xi)5=(Xf)5=(X|)5 = 7; (Х?)5 = 0 /¥4, 5, 6.
Итерация V
р\~- ~32,	р2 = -23,	р'з = —24,	/>4 = 0,	/>'3 = — 16,	/>'б= -7;
/ = 17,	^ = 34,	т>5 = 19,	/>4 = 67,	/>5 = 36,	/>6 = 41.
302
i	 J					
	1	2		3	4	5	6
]	— со	-66	-86	+ 11	-66	0
2	-64	— со	-20	0	+ 2	-74
3	-70	+ 1	— со	-43	-1	-1
4	0	0	-57	— со	-16	-29
5	-59	0	0	+6	— СО	-33
6	-6	— 55	+ 1	0	— 19	— 00
	j				
	i 2		3	4	5	6
т1	0	1	1 2	1	0
	1	2	1 1	0	1
m“s	5	3	4 3	5	5
/(pv)=9I. Имеет место этап I б) А = 4. На итерации: (ЛЛЙ=О
VZ; (U/6 = 6; (Л?)6=0 W4.
Итерация VI
/1=-36, ^2=-23,	---24, р4. = 0,	р'5=-16, рб = -7;
^' = 17,	^ = 34,	р’^19,	^ = 61, /^=36,	//6 = 41.
/	j					
	1	2	3	4	5	6
I	— co	—70	-90	+ 1	-70	-4
2	-64	- co	-20	-6	+ 2	-74
3	-70	+ 1	— co	-49	-1	-1
4	0	0	-57	— co	-16	-29
5	-59	0	0	0	— GO	-33
6	-6	-55	+ 1	-6	-19	— 00
	j					
	1 2		3	4	5	6
	0	1	I	I	1	0
/йу	1	2	0	1	0	0
	5	3	5	4	5	6
/(р”)=97. Изменение п\ вызвано тем, что_ «встретился» этап
II 2 б) при построении множеств N, М (7V1. Это изменение
приводит к этапу I а), к=6. На итерации: (Л|)7 = 0 Vs; (М)? = 4;
(1J)7 = O
Итерация VII
^ = -36,	т>2=~23,	т>з=-24,	т4=0,	р'5=-16,	р'ь=-Т,
Pi = 17,	^ = 34,	р|=19,	/>Х = 61,	р? = 36,	Рб=45.
i	j					
	1	2	3	4	5	6
1	— co	-70	-90	+ 1	-70	0
2	-64	— 00	— 20	-6	+2	-70
3	-70	+ 1	— co	-49	-1	+ 3
4	0	0	-57	— co	-16	-25
5	-59	0	0	0	— 00	-29
6	-6	—55	+ 1	-6	-19	— 00
	j					
	1	2	3	4	5	6
	0	1	I	I	I	1
Wy	1	2	1	1	0	1
m’i	5	3	4	4	5	4
303
И,	i					
	1	2	3	4	5	6
71'	1	]	2	0	0	]
Hi	]	0	0	2	3	0
/1 ni	4	5	4	4	3	5
/(pVIIl = 98. Имеет место этап I в) к—3. На итерации: (Хзк = 1;
(W=o\/V3; О8=0 V/
Итерация VIII
/1 = ^36, р'2 = — 23, р’2=-25, />i=0,	р‘5= -16, р'б=-1;
/1 = 17,	^ = 34, р^ = 19,	^ = 61, />§ = 36,	^ = 45.
+ + . -. + + + +
7	J					
	1	2		3	4	5	6
1	— co	— 70	-90	+ 1 *	— 70	0
2	— 64	— co	-20	-6	+2*	-70
3	— 71	0	— co	-50	— 2	j 2 *
4	0*	0	-57	—. 2C-	-16	-25
5	— 59	0*	0	0	- co	-29
6	— 6	-55	+ 1*	-6	-19	— co
/(р™) = 99. Этап I а)—г) не имеет места. Получено оптималь-
ное решение: Й14 = й41 = й25 = й51 = м3(., = г7йз= 1.
§ 14.5. Задача коммивояжера
Рассмотрим точный алгоритм, основанный па детализации
общих конструкций по реализации элементарной операции для
задачи коммивояжера. Постановка задачи коммивояжера состоит
в следующем. Имеется п городов, обозначенных номерами
ieN= (1, ..., н), между всеми этими городами расстояния заданы
действительными числами см>0. Выходя из заданного города,
требуется обойти оставшиеся (л —1) городов хотя бы по одному
разу и затем вернуться в заданный так, чтобы общее Пройденное
расстояние было минимальным.
304
'Р
; Как задача линейного целочисленного программирования
задача коммивояжера может быть сформулирована в следующем
виде:
-~/ = Е Е сщ'Ч0т1П’	(14.31)
Е^=1,уеМ	(14.32)
ieN
£ нм=1, icN,	(14.33)
jeN
—(0. 1), t,JeN,	(14.34)
EEVU^,	(14.35)
i^7.jEZ_
где Z^0, Zf]Z=0, Z\JZ~N, Z=N\Z, а условия (14.35)
справедливы для любых таких подмножеств Z, что 2^|Z|^n —2,
jСимвол |Z| обозначает число элементов в подмножестве Z.
IОбщее число связей вида (14,35)— порядка 2П — 2. Здесь условиям
[того, что коммивояжер выезжает из каждого города и въезжает
[в город только один раз, соответствуют ограничения (14.32)
|й (14.33); условию того, что маршрут коммивояжера есть
[цикл, —ограничения (14.35); условию минимальности пройденного
[расстояния — условия (14.31); в ограничениях (14,34) u;j = I, если
| коммивояжер из города i переезжает в город j, и — О
|в противном случае.
| Условимся называть циклом совокупность значений и^, i,jeN,
[удовлетворяющих условиям (14.32)—(14.35), подциклом ’Zc/V—
совокупность значений и^, удовлетворяющих условиям (14.32) —
[(14.35) с заменой в этих условиях множества У на Z.
t Условия (14,31) —(14.34) соответствуют задаче назначения. Ее
допустимыми решениями могут быть не только циклы, но
и совокупности подциклов, не являющиеся допустимыми реше-
ниями задачи коммивояжера, Изложим алгоритм решения этой
задачи. Вначале приведем основные конструкции, лежащие в его
основе, а затем описание и его обоснование.
§ 14.6. Метод улучшения функции <р(г, х)
Запишем условия (14.31) — (14.35) задачи коммивояжера для
Z=A и Z=A в виде
= Е Е ^«у->пц’п,	(14.36)
Е^=М^	' (14.37)
ieN
305
£«у=1, й=*.	(14.38)
jcN
iii^Ul={uij:ujj = Q\/1;	jeA; uy=0,
it A, jeN\A},	(14.39)
££^>v
ieN JeN
(14.40)
ZEVl-	(14-41)
leN jeN
Перейдем от модели (14.36)—(14.41) к эквивалентной задаче
оптимизации многошагового процесса управления с двумерным
аргументом вида (13.4) и (13.5):
. x/,j + J =лу4-иу,/=0, 1, ..., «-1, /=1,л,	(14.42)
;	х.1о = 0, х'„ = 1, i= I, п, _ (14.43)
xf+1j=x£-|-«y, /=0, 1, ..., w-1, у=1, я, (14.44)
*oj=0, х;у=1,7=1, л, _______________ (14.45)
x^u^xfj + Uij, /=0, 1, ..., я-1, 7= 1, п, (14.46)
*о; = 0, £%^1,7“Гл,	(14.47)
jeN
xtj + i =xtj + Uij, _j = 0, 1, ..., n- 1, i= 1, n, (14.48)
x?o = 0, £х*>1, z = T^,	(14.49)
(14.50)
->= £ £ cy«y—*min.	(14.51)
i=O J=0
Термины общей постановки задачи здесь имеют следующее
содержание: 7’=Т1хГ2, Т1 =(/ = 0, 1, ..., и), Т2 = (1=0, 1, ..., и),
t=(j, 0,	i=i2; У—пространство векторов х = (х1, ..., х4);
U—числовая ось; И' —все множество X; Ип —пара значений
0, 1, определяемая ограничениями (14.50); И7—множество век-
торов х=(х2,	>-') из V1^ удовлетворяющих ограничениям
(14.43), (14.45), (14.47), (14.49); роль конечно-разностных связей
(13.4J играют соотношения (14.42), (14.44), (14-46), (14.48), функции
(13.5)-—функция (14.51). В многошаговом процессе (14.42) ограни-
чения наложены только на управление.
Так как процесс (14.42)—(14.51) —процесс с линейными
связями, то вектор-функцию ф = (ф*, ф2)еП будем искать в ли-
нейном виде:
ф1 О', 7, х) у1 х1 +р ;/х2 + q у1 х3 + q -j2x\
Ф3G- 7, х) у х1 +Рi^x2 + ^'ijx3 + q ’^х4-.
Ж
погда функция л из (13.6) для модели (14.42)—(14.51) принимает
ледующий вид:
/?(;', j, х, и) = х’ (р £.+1 -р } -р ”q) + xYp ’/h,j + x2(p^ i,j~pi2 -
-p'ij) + X2PLj^i+x3(^'^t.j-9'i) ~4’ij ) + x2q’^+l+xIl(q’[2^l-q^ -
- Я q) + >ЛЯ 1. j + u a <Plj +1 + Я 'i2j+1 +P il i.; + Я i +1. j “ c и)-	(14.52)
Условия существования p(z,))=max7?(i, j, x, u) no xe(-oo<
cx<oo) и no ueC/j из (13.8) накладывают на <реП условия:
Pij+^Pi^Pi1,	(14.53)
p'^ptt^P’^0,	(14.54)
рХы=Р$=Р12>	(14.55)
р’Р- + 1=р’Р=р’Р = 0,	(14.56)
9i+i.j = 0i} =я'Ь	О4-57)
70 =Я^=Я"1=$,	(14.58)
Яи^=Я'12 = Я"\	(14.59)
?и+1=?У =?/ = 0.	(14.60)
считывая (14.54), (14.56), (14.58) и (14.60), получим соответственно
|з (14.53), (14.55), (14.57) и (14.59)
г	РЛ=Р\, Р]=р“, Я?=Я] = Я'(А\ Я12 = Я1=Я"(Л).	(14.61)
На основании условий (14.53) — (14.61) и (14.52)
P(iJ, u) = hq(jp, £)•*,	(14.62)
где p = (Pi,p)), q=(?'U), <?"(Л)),
M₽> Ф=Р!+Р1~с1] + я'(А) + я”(А)-	(14.63)
С учетом (14.53)——(14.61) функция Ф из (13.7) для модели
(14.42) — (14.51) принимает вид
I Ф(х)= £ р-хЧ- £ p’-x2 + q'(A) £ х3+?"(Л) £ X4. (14.64)
	i = 0	j=O	J=o	i=O
В	Л-1	и-1
Условия существования т=тшФ(х)= £ р’,+ £ p'j+ min ^(Я)х
I	i=O	j=O
В п-1	п-1	j
к £ %у+ min q"(A) £ xfy из (13.6), (13.7) накладывают на <реП
| >=°	‘=о
исполнительные условия:
I	^(^)>0, /(Л)>0.
Е/читывая (14.62) и (14.64), получим
I	Ц(бЛ = «у(РЛ)йу(р, Ч), I, п-1,	(14.65)
Еде
307
f 1, если /?ц(р, q)>0,
«h(P,q)=y 0 если Л;.(р, q)<0, i, j=Q, 1, ..., л-1, (14,66)
OV 1, если йу(р, q) = 0,
т= i>i+ Ё Pj+4'(A) + <?"(A).
i=i j-i
Таким образом, получено описание множеств Р=РхХЙ{,
и И7: Кх—все множество А) значения 0, 1, определяемое
согласно (14,50) и (14.66); 1У—точка с координатами
%;в=*£ = 1, ;=!,«; x2j — x2j = 1, j= 1, п.
Наконец, значение /-функционала в соответствии с (13.10) будет
4(ps,qs)= ЁрЬ+ Ё /4+ Ё ?г(Л)+ Ё	Ё Ё	qs)x
"-Т j=l r=[	r=l	i=[J = 1
ч-м-
На основании (13.11) и (13,12) при любом (р, q) /(р, q)<4
т. е, основные конструкции, входящие в (13.6) — (13.10), для
модели (14,42) — (14.51) построены. Вектор-функцию у=(у',у2)
из (13.14) в соответствии с (14.53) —(14.60) найдем в виде
х\ т4) = ф;.т! +ф)л-4, у2(i,j, х2, Л3) = фух2 + ф дХ2. (14.67)
Т. е, улучшенное распределение (ps+J, q,+ i) задается в виде
Xs+l =7^з + ^К, i= 1: «; Pj,s+1 =P'jS+^'jS,j^ 1, «,
<? s+ 1 (Л) = Ф As^-, s+ 1 (j4) = Ф As^->
Тогда в соответствии с (13.16) и (14.67) функционал 5(и) для
задачи (14.42)—(14.51) запишется в виде
5(«)= Ё ФХ1~ Ё ии)+ Ё Ф?(1- Ё ии)+
i=l j =1 j=[	i=[
+O1-E Е»у+4й(1-ЕЕМ-	О4-68)
ieX	ieA
Выражение для ц(/, j, л) в соответствии с (14.65), (14.66), (14.63)
будет иметь вид
в(*,л Х)=М₽’ «ь q, Ч w'=oJ i, «-1,
где Лу(р, q, Х) = Л,./р, q, 0) + Х(Ф; + ф; + Фа + Фл),
f 1, если Ai;(p, q, Х)>0,
МР’Ч>х)=з °> если Ыр, q, х)<°>
0V 1, если /?1;.(р, q, Х) = 0.
Аналогично § 14.2 введем в рассмотрение множества: Af),
Mj~множества строк /, которым при данном j отвечают
соответственно положительные и пулевые значения й,/р, q); А^-,
308
Л)—множества столбцов /5 которым при данном i отвечают
соответственно положи тельные и нулевые значения Л^(р, q);
= U 2V' = UA\-, М = J Mj, N=[}Nh вектор ф = 0Н ф}, 4W
J	i	j	i
фл). Тогда из выражений (14.68) окончательно получим:
з(ф, u)= f фKi - W'd - Е м</)+ Е О1 -|М}|- Е йо)+Фл(1 -
* ~	J = 1
-E E«u)+Oi-E E«W
IE A jeA	ieA jeA
б(Ф,«Л)=Е	E «y)+E <H(i-WWi-
i=1	J"1
- E My)+Wi-EEMv)+O!-EEuW
ieMj(l)	tp/1 jeA	ieA jeA
из выражений (13.18) с учетом (14.68)
5'(Ф> 0)= Е ФК1-Wil)-Е тах ( Е WiW.J+ Е \H(i-l^GD-
i=l	je/v. [I \i= 1	/ J = 1
(n	\
ЕФ?«Ц ) + Фл-
-max ( £ £	max ( £ £ фл«у),
1) ieA jeA	utjtlj), I) ieA jeA
n	/ и	\
8'(ф, X)- £ ^(1-|Лф-)1) E max I ^^uij} +
"= I	у,Л(0. 1) \i= 1	/
+ E ФЯ1 -lAC'(^)l)“ E max ( £
M1	feAfjp.) и;1е(0, 1) \ j= 1	/
- max (ЕЕ>лИ^) + Фл- max (£_£«hA
«^(О. 1} \iex/еЛ /	^e(C. I) \ieAjcA /
Теперь перейдем к описанию собственно элементарной опера-
|Ции улучшения для задачи коммивояжера. Введем в рассмотрение
'распределение (р, q(Z))=(p', р", p'(Z\ где р'=(/л'), $"
i, jeN,— векторы, известные по задаче назначения; q'(Z), q”(Z)
I—функции подмножес тва Z с N, заданные на множестве всех
'подмножеств N. Определим конструкции:
q)=7JW/’J + ^(Z)+^"(Z)-c£j.,
|где ^’(Z)^0, если (/, У)б(р', j)'ieZ, jeZ], и <7'(Z) = 0 для
всех остальных i, /;	если (z, j)e{(i, у)’ y’sZ},
и <?''(Z) = 0 для всех остальных i, у;
309
{1,	если hjjZ(p, q) > О,
О,	если hijz(p, q) < О,
О v 1, если &ijZ(p, q) = O.
Можно предложить следующий алгоритм решения задачи
(14.31) — (14.35): решать содержащуюся в задаче коммивояжера
задачу назначения, учитывая только связи (14.31) — (14.34) и при-
меняя для этого алгоритм решения задачи назначения (см. § 14.2).
Пусть при некотором р = р = (р', р") эта задача решена, но
существует такое подмножество городов Z=A с У, что нару-
шается неравенство (14.35) (в противном случае полученное
решение задачи назначения будет и решением задачи коммиво-
яжера). Это значит, что полученное решение ие образует цикла,
а представляет собой совокупность не связанных между собой
подциклов.
Зададим'распределение (р1; q((Z)) в виде
Р, 1>. ^(Z) = 0, q'[(Z) = 0
и определим элементарную операцию его улучшения. При этом
следует учесть, что	qJ^O, теЛ, /еЛр’еЛ, jeA) на
основании свойств полученного решения задачи назначения.
В дальнейшем для простоты записи будем опускать индекс
А и полагать, что /т;.{р, q) = /rUA[p, q(^)], «;.(р, q) =
чН[₽, ч(^)] 11
Запишем алгоритм:
1.	Пусть выполняются условия Л,/?!, qj <0 VieA, jeA.
Тогда улучшенное распределение (Р2, задается в виде
р-р. Р2 = Р",	=	q'2(Z} = 0 VZ*A, q'i(Z) = 0 VZ^N.
(14.69)
где X — второе по порядку значение |Л,;(Р1, qjl, IeA, jeA, если
расположить их в порядке неубывания.
2.	Пусть выполняются условия ЛгДР1, qJ<0 V/бЯ, jeA.
Тогда улучшенное распределение (Рг, Qz (Z)) задается в виде
Р2 = Р', Р2 = Р", ?'2(Z)=0 VZc^ дЦА) = \ q'AZ\ = 0 yZ*A,
(14.70)
где X — второе по порядку значение |Л;,(Р1, qjl, ieA, jeA, если
расположить их в порядке неубывания.
3.	Пусть К—множество пар городов ieN, jeN, соответ-
ствующих одному из решений задачи назначения й^(р1; qj
с множествами А и А, Пусть Х={(т, ;):(геЛ, je/V)\A; Л;у(р!,
Ч1М) {(< /);0'еА ЛЛГ)\£ ^(р,, qj — 0). В отличие от п. 1,
2 предположим, что множество л'--непустое.
Пусть в пределах описания п. 3 А (Л)—один из подциклов
решения задачи назначения. Назовем город те А правильным
310
’ 1-го рода для данной пары век-
торов (pt, qj, если найдется
такое значение teN, что > 0.
Назовем город is А правиль-
ным 2-го рода, если при всех
/е/V hit 0 и значение / = от-
вечающее управлению Hit = 1, та-
ково. что hsl.<0, seN, при всех
s^i. Если последнее требование
не выполняется, но каждый го-
|^род 5бУУ, для которого hsi. = 0,
МЬН', правильный 1-го или ’2-го
Из да, то город is А назовем
рис. 14.1, где город I—правильный 3-го рода).
Обозначим В. множество городов, связанных с правильным
Е: городом ieA. Множество Bs содержит единственный город i,
| если он правильный 1-го рода; содержит города i и z;, если
| i—правильный город 2-го рода; если i—правильный город 3-го
г рода, то помимо i, t; множество Bi содержит все города s,
I для которых hst.~0, s^i, а также связанные с ними все города
EL если города '^--правильные 2-го рода, и т. д.
L Таким образом, множество городов В, можно представить
В виде дерева, вырастающего из города i, причем из каждого
юрода л нечетного яруса (город i принимаем за 1-й ярус)
Исходит единственная дуга, отвечающая значению й51 =1, а каж-
Иому городу t четного яруса отвечает в общем случа3е несколько
Иуг (к, /), связанных со значениями hkJ=0, йАг = 0. Конечными
^точками дерева В, являются либо города se N—правильные
11-го рода (нечетный ярус), либо города t,eN, связанные с те-
тродами 5—правильными 2-го рода, для которых hkt <0, /tr'V
' при всех k^s (четный ярус). Обозначим: В-—множество городов
нечетных ярусов дерева В/. В’- —четных.
Город jeA назовем правильным l-го рода для данной пары
векторов (р(, qj, если найдется такое teN, что /г^>0; 2-го
L рода, если при всех /eW	и значение г =	отвечающее
I управлению £^=1, таково, что	seN, при всех s^j; 3-го
рода, если последнее требование не выполняется, но каждый
Ггород seN, для которого к, ., = (). s^j—правильный 1-го или
2-го рода, и т._д. _	_	?
| Обозначим Bj, Bj, В’- множества, связанные с правильным
I городом jeA, и аналогичные множествам Вь B'i,B’{, связанным
|.с правильным городом ieA. Их структура аналогична с той,
^однако, разницей, что соответствующие дуги на каждом ярусе
имеют обратное направление. Термин «правильный» употребля-
ется нами в различных смыслах для городов seB{ и si.B;
в зависимости от принадлежности 1-го яруса этих множеств
(г или j) множествам А или А и независимо от того,
311
содержится s в А или А. Таким образом, конечными точками
дерева В, являются либо города /GjV—правильные 1-го рода
(четный ярус), либо города st, связанные с городами t —
правильными 2-го пода, для которых hs к < 0, ХеЛ( при всех
k^t (нечетный ярус). _	1
Назовем дерево	конечным, если оно состоит из
конечного числа дуг. Обозначим через А* какое-либо множество
правильных городов, чтобы: а) каждая пара индексов (/,
либо it А*, либо у'еЛ*; б) каждый город из А * являлся концом
дуги множества К.
Пусть имеется хотя бы одно множество А*. Например, если
пары индексов (г\	изолированы п т. е. не имеют общих
городов, то требование существования А* сводился к требованию
правильности хотя бы одного из городов каждой такой пары.
Тогда если А* с А, то улучшенное распределение (р2,
задается в Следующем виде:
t	ecw iG\J В^теА*
\Pl)l - ) / м
ПРИ остальных г;	(14.71)
/ищ _ j(Pj)i+Uh еслиуеОя" теЛ*,
l^2'2	1 / -А	Т
при остальных;;
?'2(Л) = Х y'2(Z)^0 VZ^T, ^(Z)=0 VZcN.
При A * с A
(pA	если Д, теЛ*,
при остальных i;	(14.72)
.,a _	есдиуеОЯ;, теЛ*,
ПРИ остальных у;
VZ^N; q'2(A) = \ q’i(Z) = O VZ^A.
Здесь X, к/, kf, £7 определяются следующим образом:
а)	пусть Л* = Л(/1* = Л) и множество А(А) состоит только
из городов правильных 1-го рода. Тогда X можно принять
равным как первому, так и второму по порядку значениям
среди Л1((р2, q,)>0, ze А * Q A(h. /р,, Чх)>0, у’еЛ*АЛ), рас-
положенных в порядке неубывания;
б)	пусть А * с А и каждое дерево В-, ic А*,—конечное. Введем
множества = {(/, у):/е J xeA*J=t;i Л;.(Р1, Ч1) > 0}, М2 = {(г,
уеЛГ, A;j(pi, q^O}, M3 = {(i, j)'.ieA, jeA} и следующие
числа: к}—число повторений города i в множестве J
312
| те А =0, если	теЛ*^; к]— число повторений
| города j в множестве те Л* (kJ -0, если JeN\^U В^,
теЛ*), ^(р17 qJ^Mp/q,)/^. Здесь
L	kij = k]-k^ (/,
В	/с0 = /с; -Ч+1’ 0*’ »еЛ/з-
Из нулевых элементов \htj(Pi, q)l, (*, У)е(м3им5)и(л/4\
рММ4П^б), где М4 = {(/, /):(/еЛГ, je\JB")\M3, теЛ*п ,
Г	т
Ч1)<0); M5 = {(i, J)-IeA, jeA, к] <£’}; А/б = {(г, jpelJBJ
jue(JB". те Л*, ^(р,, qJ^O, /с <?£?} и |/г)-(рь <ь)|« j)eM,
«оставляется список в порядке неубывания. Обозначим первое
Кй второе значения из этого списка соответственно и к2
К{ .< хД а значения индексов {i, j), соответствующие значениям
KL и л?.— через (L, t) и (Л, iA Тогда Х = Х, или Х = ?^2, если
К),<кЩ2' “ X~V в'противном случае.
в)	Пусть Л* с Л и каждое дерево Bj,jeA*,— конечное. Введем
^юножества М1 ~ {(г, у): i ~ t-, je (J Bt, теЛ*, ^(pi, q,)> 0); M2 = {(i,
B:ieN, jeN, fy/p!, q^O; M3 = {(i, ;)‘ЛеЛ, JeT} и следующие
Г числа: к] — число повторений города j в множестве
' теЛ*(к/=0, если ./елг\((J^4), теЛ*); к? — число повторений
г	т
города i в множестве (J В?, теЛ*, А^=0, если ZeA^U#"),
теЛ*), /Цр(, q1) = A£j(p1/q1)/^.
I Здесь
I	kti = kl-kj, (J, j)e(M2\M3)(JMi;
k?-k- + l, ((', j)eM3.
; Из ненулевых элементов |^/Р[, qj)!, (i, y)e(A/3 U M5) (J
I UM?4U74n Мб)); где M4 = {(ij)-.{ie\JB"J&N)\M3, теЛ*, ,
г	T
qj^o}; = j):iEA, jeA; kf <kj}; M6={(i, j):ie[JBr^
jEUB'1, TEA*, yp1; qt)^0; k^/^J) и I^(p15 qjl, (t, y)eM1
313
составляется список в порядке неубывания. Обозначим _ первое
и второе значения из этого списка соответственно X, и X2(Xt X J,
а значения индексов (i, ./), соответствующие значениям Х(
и Х2,— через (t(, Д) и (г2, у2). Тогда Х=Х(, если < 1.
Замечание. Приведенное описание п. I—3 элементарной операции справедливо
для распределения (рт, qj, соответствующего решению задачи назначения для
исходной матрицы задачи коммивояжера. Аналогично строятся и. I —3 для
любого другого распределения (р, q).
Следующая теорема, доказательство которой приведено в [9],
обосновывает применение п. 1 —3 элементарной операции.
Теорема 14.2. 1. Для любых (р, q) величина Др, q) есть
нижняя граница функционала (14.31) на множестве допустимых
решений задачи (14.32) —(14.35);
2. Элементарная операция, примененная к данному распреде-
лению (р, q),. обеспечивает выполнение неравенства Д/(р, q)>0.
§ 14.7. Описание алгоритма решения задачи
коммивояжера
Обозначим С[, cs матрицы с элементами
(сЪ)!“со, й
(ё>Д=(с0),_ (~Ф{А)(ieA, jeA)v (cjs=(с,Д_ 1 - ф({А), ieA, ,/е А,
—для остальных i, jeN,
где .ф>2)-—номер итерации улучшения распределения (р, q(Z))
с помощью элементарной операции.
Шаг 1. Решается (до получения вектора р) задача назначения
(14.31) — (14.34) с исходной матрицей С и проверяется, является
ли полученное решение (решения) циклом. Если среди полученных
решений хотя бы одно является циклом, то оно является
решением задачи коммивояжера. (В дальнейшем для краткости
упоминание такого результата будет опускаться.) В противном
случае переходим к шагу 2, полагая pt =р, q\(Z) =	= О, С\=С.
Шаг 2. Выбирается один из подциклов А (или А) этого
решения задачи назначения и для него проверяется возможность
применения п- 1 (п. 2). Если такого подцикла нет, то переходим
к шагу 3. Для подцикла Д(Л) вычисляется (р2, q2(Z)) согласно
(14.69) [или (14.70)] и проверяется получено ли новое решение
задачи назначения для матрицы С2. Если оно получено и не
является циклом, то переходим к началу шага 2, приняв
в качестве А(А) один из его подциклов. Если не получено
нового решения задачи назначения, то задача коммивояжера
далее решается как задача назначения с матрицей С2. Далее
переходим к началу шага 2, выбору нового подцикла Д(Д).
Шаг 3. Реализуется п. 3 элементарной операции в такой
последовательности:
314
а)	для фиксированного решения задали назначения выбирается
поддикл А (или А), все города которого являются городами
1-го рода, для него производится улучшение распределения (ps,
q.,(Z)) согласно (14.71) [или (14.72)] и проверяется, является ли
соответствующее ему qj решением задачи назначения для
матрицы Cs. Если является решением и оно не есть цикл, то
переходим к шагу 2. Если является решением, то далее решаем
задачу коммивояжера как задачу назначения с матрицей Cs
и переходим либо к шагу 2, если выполняются условия
применимости п. 1 (п._2) элементарной операции, либо к выбору
нового лодцикла А (Л). Если таких подциклов А{А) пет, то
переходим к п. б);
б)	для фиксированного решения задачи назначения выбирается
поддикл А (или А), не все города которого являются городами
1-го рода, но существуе т подмножество А *, для ко торого все
деревья Bi; ieA* с A{Bj, jeA* cz A)—конечные. Для этого под-
цикяа производится улучшение распределения (р,, <e(Z)) согласно
(14-71) [или (14.72) ] и далее следуют процедуре, описанной
в п. а). Если таких подциклов А(А) нет, то переходим к шагу 4.
Шаг 4. Пусть ls и (ps, qs(Z)) получены после применения
шага 3 и пусть им соответствуют распределения wijr-(ps, q3),
удовлетворяющие связям (14.31) — (14.34) (решения задачи на-
значения для матрицы Cs) со значениями исходного функционала
A(u)= Е ЕоАг Пусть упорядоченная в порядке неубывания
количества подциклов последовательность в распределениях w,j(ps,
qs) есть (2S },	Для элемента	образуем
в порядке неубывания количества дуг в под цикле последователь-
ность под циклов {7]j(	1 < ₽(«}) </»(«[, Р)- Для под цикла
ТгЕ{Т^а Р=1 проверяем, разрушает ли его удаление из Qr
все оставшиеся распределения из (Qa }, 2^а^Л1|. Если раз-
рушает, то обозначим этот подцикл Л=(г\, ..., q, Д), к<п
и введем в рассмотрение множества: Лг = {(г,	jEA\it],
Ж = {0‘, /):! = (, jeA}, M{—Aa, M2=A\\JA2, -, Мк =
= А\ 0^2 0  U Ак. Составляется список из к задач на-
значения с матрицей расстояний (С)г, 1 < 1 С Д с элементами
(с.;)’=оо, если (i, (срУ = (сц),, если (i, Переходим
к шагу 5.
Если удаление поддикла 711е{7’Р(в 3, р=1 из Qx не разрушает
всех оставшихся распределений из 1 [Qa },	то бе-
рется подцикл Т2 е {Гр{а >}, Р= 1, и для него проверяется,
разрушает ли его удаление из Q{ все оставшиеся распределения
из {& },	г/, и так до тех пор, пока либо не найдется
среди Д, |3=1, подцикла, разрушающего все оставшиеся
распределения из {Qa },	либо не будет проанали-
зирован пОДцикл сДа/, Р). в последнем случае из {Гр(а }], р=1,
315
выделяете чодцикл, разрушающий наибольшее число распределе-
ний из {(, ''пусть это число будет М2, М2<Мг\ Из {Qa }
формирую! тедовательность	{2я1}з 1 а2 ~
перазрушеннь.л распределений йДр5, qs) (в порядке неубывания
количества подциклов в распределениях). Для {£?„},
1 < а, < (М( ~М2), проводится анализ, аналогичный проведенному
выше для {2Н]} с выделением подцикла из {7^ Д, р =
1^ р(а2) ^6(а2, р), разрушающего наибольшее число распределе-
ний из {Qa }, и так до тех пор, пока {21,}#0.
Пусть таким образом выделены т подциклов Ат =	,
i”‘, i™).. Для каждого из подциклов Ат вводятся в рассмотрение
множества Л;п={(г j\:i=i™, jeAni\i^’}1 A’"'= {(i, j): l = i”s, jeA?},
M7 = A^, M'? = AT(JA%, M^A*'	Из
множеств составляются сочетания по т множествам, не
принадлежащим одному и тому же распределению w;j(p5, qs)
и разрушающим все М( распределении^ Обозначим -Полученные
таким образом множества дуг через 7?*i, 1 к{ . Состав-
ляется список из кл задач назначений с матрицами расстояний
(С)1,	с элементами (с;Д=оо, если {7 Де/С; (й;)' = (ё;Д,
если (г,	R'. Далее переходим к шагу 5, положив к = кг.
Шаг 5, К задачам назначения (числом к) составленного
списка применяется реализация элементарной операции этапа
I алгоритма решения задачи назначения § 14.1 —14-3 и вычис-
ляются значения к. 1 < t< к, функционалов /. Задача назначения
с наименьшим значением /{-функционала (пусть ей соответствует
индекс г,) решается до конца, т. е. с применением (в общем
случае) реализации элементарной Операции этапа II названного
алгоритма и вычислением значения , Проверяе тся выполнение
неравенств /Г1^/(, /=1, ..., к, Если выполняются все эти
неравенства и полученное решение задачи назначения есть цикл,
то получено оптимальное решение задачи коммивояжера. Если
полученное решение задачи назначения не является циклом и не
выполняется хотя бы одно из этих неравенств, то решается до
конца задача назначения с наименьшим значением /,-функционала,
1 t к, (пус ть ей соответствует индекс г2), проверяется
выполнение неравенств	г=1, ..., к, t^r1} г2',
и так до тех пор, цока таким образом не будут просмотрены
все значения /(, 1 < t к.
Поясним некоторые особенности применения и обоснования
алгоритма, позволяющие лучше понять его суть.
Применение шага 1 очевидно, На шаге 2 производится
увеличение /-функционала с помощью п. 1 и 2 элементарной
операции улучшения, Доказательство этого следует из теоремы
14-1. В процессе такого улучшения распределения (р, q(Z{)
может оказаться, что либо выполняются условия применимости
этапа I алгоритма решения задачи назначения (см. § 14.1 —14.3),
316
либо на одной из дуг ieA, jeA становится (р, q(Z))>0, т.е.
разрушается это решение задачи назначения, В таком случае
становится возможным увеличение /-функционала только за счет
удовлетворения нарушенных связей (14.31) — (14.34), т е. решени-
ем новой задачи назначения. Шаг 3 производит увеличение
/-функционала с помощью п. 3 элементарной операции. До- .
казательство этого следует из теоремы 14 Л. В результате
улучшения распределения (р, q(Z)) на шаге 3 возможно решение
задачи назначения, фигурирующего в выражениях (14.71), (14.72),
и тогда становится возможным увеличение /-функционала только
за счет удовлетворения нарушенных связей (14.31) — (14,34) задачи
коммивояжера, т. е. решение новой задачи назначения. Шаг
4 представляет собой реализацию метода ветвей и границ (на
этапе формирования списка задач назначения и их матриц
расстояний) и является обобщением известной в дискретном
программировании процедуры Беллмора — Мэлоуна [6]. Шаг
5 позволяет решить задачу назначения из составленного на шаге
4 списка, выделить задачу назначения, решению которой соответ-
ствует наименьшее значение /-функционала, и рассматривать это
решение (если оно не является циклом) как решение для
проведения очередных итераций алгоритма с помощью элемен-
тарной операции. Однако нахождение такого решения задачи
Назначения часто может быть упрощено, так как оценкой снизу
ртя функционала задачи коммивояжера является не только
функционал решения задачи назначения, но и /-функционал (см.
еорему 14-1), На шаге 5 предлагается в качестве такой оценки
низу принять /-функционал, полученный после выполнения этапа
алгоритма решения задачи назначения § 14.1—14-3, вычисление
второго проще, чем оценки, соответствующей решению задачи
[азначения до конца.
Предложенный алгоритм имеет некоторые общие фрагменты
с известными алгоритмами решения задачи коммивояжера: реше-
ние начинается с решения задачи назначения для той же матрицы
расстояний и формирования условий (14.35), где в качестве
подмножеств А и А выбираются подциклы решения задачи
.назначения. Однако затем в предложенном алгоритме не пресле-
дуется цель обязательного выполнения этих условий для фиксиро-
ванной пары множеств А и А, как это имеет место в известных
Алгоритмах либо за счет решения задачи линейного програм-
мирования (14.31) —(14.33) и (14.35), либо за счет соответству-
ющего списка новых задач назначений. В новом алгоритме
с помощью предложенных реализаций элементарной операции
(п. 1 —3) достаточно просто увеличивается значение /-функци-
онала, При этом выполнение условий (14.35) не обязательно.
Если эти условия выполнены [обязательно за счет нарушений
условий (14.32) и (14.33), если рассматриваемое решение не
оптимальное], то за счет выполнения только ограничений (14-32)
317
и (14.33) можно опять увеличить значение /-функционала (реше-
нием новой задачи назначения). Если предлагаемые реализации
элементарной операции не дают увеличения /-функционала для
фиксированной пары множеств А и А, а условия (14.35) не
выполнены, то дальнейшее увеличение /-функционала может быть
осуществлено за счет рассмотрения другой пары множеств, и т. д.
Особенностью алгоритма является то, что на итерациях шагов
I — 3 решается только одна задача назначения.
Предложенные реализации элементарной операции не всегда
позволяют решить задачу коммивояжера, и поэтому для решения
очередной задачи назначения может оказаться необходимым
прибегнуть к методу ветвей и границ в форме Беллмора — Мэло-
уна, использующим в качестве нижних границ решения соответ-
ствующих задач назначения. При этом применение в качестве
нижней границы более простой оценки /-функционала (шаг
5) упрощает 'в ряде случаев собственно алгоритм Беллмора—-
Мэлоуна.
Применение для решения задачи назначения алгоритма
в §14.1--14.3 упрощает алгоритмы решения задачи коммиво-
яжера в том случае, когда встречающиеся решения задачи
назначения имеют неоднозначное решение, так как эти алгорит-
мы выделяют, как правило, меньшее число решений зада-
чи назначения, чем, например, хорошо известный алгоритм
Манкреса. Кроме того, применение этих алгоритмов позволяет
строить деревья в п. 3 элементарной операции с меньшим,
как правило, числом ветвей, чем при применении алгоритма
Манкреса.
§ 14,8. Решение модельного примера
для задачи коммивояжера
Пример. Решить задачу коммивояжера с матрицей С:
/	7					
	1	2		3	4	5	6
1	00	97	60	73	17	52
 2	97	со	4]	52	90	30
3	60	4]	СО	2]	35	4]
4	73	52	21	□О	95	46
5	17	90	35	95	СО	81
6	52	30	41	46	81	СО
Итерация нулевая
р\ =0,	Д2=0,	рз = 0,	/>4=0,	Р5 = ®,
Pi^Q,	р'^,	Рз=о,	рк=о,	р?=0,
р'б =°;
3]8
/	' J					
	1	2		3	4	5	6
]	— 00	-97	-60	-73	-17	-52
2	-97	— 00	-4]	-52	-90	-30
3	-60	^41	— со	-21	-35	-41
4	-73	-52	— 21	— co	-95	-46
5	-17	-90	-35	-95	— co	-8]
6	-52	-30	-41	-46	-81	-co
т1	J					
	1	2		3	4	5	6
m'j	0	0	0	0	0	0
	0	0	0	0	0	0
m’j	6	6	6	6	6	6
/(р°)=0. Имеет место этап I
назначения в § 14.1—14.3, k — \,
М=52; №=41; №=35;
(X/)=OVt
Итерация I
а) алгоритма решения задачи
2, 3, 4, 5, 6. На итерации:
(U)=46; (Х|),=35; №=4I;
/(=о,	pr2-^,	р'з=^,	р'5=®,	/б=о;
/1 = 52,	p'i-41,	p£=35,	/54 = 46,	^ = 35,	/<=41
I	J					
	I	2	3	4	5	6
]	— 00	-58	-25	-37	18	-11
2	-45	— co	-6	-6	-55	11
3	-8	0	— co	25	0	0
4	—2]	-1]	14	— co	-60	-5
5	35	-49	0	-49	— 00	-40
6	0	II	-6	0	-46	— CO
	J					
	1	2	3	4	5	6
	1 1	1 J	1 1	J 1	1 1	J 1
	4	4	4	4	4	4
	i
	1	2	3	4	5	6
wj П{	111]]] 0	0	0	0	0	0 5	5	5	5	5	5
 /(р‘) = 136. Этап I, а)—г) не имеет места, М = (1, 2, 3, 4. 5,
6). Так как |М| =6, то получено оптималь-
ное решение задачи назначения:
/ 5= ^51 = ^2б = ^62 = й34 = w43 = I. Это реше-
ние представлено на рис. 14.2, где изоб-
ражены также все дуги, соответствующие
значениям й/р) > 0.
П. 1, 2 элементарной операции алгорит-
ма решения задачи коммивояжера не име-
ют места. Выберем Л=(1, 5). Имеет место
п. За) элементарной операции, Т*=(1, 5),
5iU5s=(l, 5), B'i (J / 0. На итерации
(Х)2 = 18; 4л=18, £[л = 0.	рис. 14.2
319
Итерация П
р\ = -18, р'2=0, р'з=0,	Р4 = 0, >5^-18, р'б=О;
/[=52,	/=41, /З = 35, р$=46, р$ = 35, р% = 41,	<^ = 18.
1	J					
	1	2		3	4	5	6
]	— 00	-56	-25	-27	0	-И
2	-45	— оо	-6	-6	— 55	И
3	-8	0	— оо	25	0	0
4	—21	-1 !	14	— ОС'	-60	— 5
5	J7	-49	0	-49	— со	-40
6	0	1 1	-6	0	-46	— со
	./				
	1	2	3	4	5	6
1	со 79	42	55	17	34
2	97 со	4]	52	90	30
3	60 41	•СО	21	35	41
4	73 52	21	со	95	46
5	17 72	17	77	ОС	63
6	52 30	41	46	81	со
Рис. 14.3
/(р1’)=154, Распределение w/p, q) приве-
дено на рис. 14.3. Выберем А=(3, 4). Имеет
место п. 3 а) элементарной операции,
Л* = (3, 4), В'3и^4 = (3, 4), B5UBJ0O. На
итерации: (Х)3 = 14, (^л)з = 14, (<?л)з = 0-
Итерация Ш
р\ = —18,	р'2 =0,	/3= -14,	/>4= -14,	/3 = -18,	/б=0;
/1 = 52,	р"2 =41,	д'з = 35,	р'^46,	/ = 35,	pg=41,
<?л=14:
i	J					
	1	2		3	4	5	6
1	-со	-56	-25	-27	0	-П
2	-45	-со	-6	-6	—55	+ 11
3	-8	0	— оз	+ 11	0	0
4	-21	-I]	0	— ОС-	-60	— 5
5	+ 17	-49	0	-49	— со	-40
6	0	+ 11	-6	0	-46	— со
	J				
	1	2	3	4	5	6
1	со 79	42	55	17	34
2	97 оо	41	52	80	30
3	46 27	СО	21	21	27
4	59 38	21	GO	81	32
5	17 72	17	77	со	63
6	52 30	4]	46	8]	GO
/(р!1,) = 168. Распределение иу(р, q) приведено на рис. 14.4.
Выберем А =(2,6). Имеет место п. 3 а) элементарной операции,
Л* = (2, 6), В'21Ж = (2, 6), B5(jBg0O, На итерации: (Х)4 = 11,
320
Итерация IV
Р>-18	р'2-~ И,	/>'з=-]4,	р’А--1Д,	/>'5 = -]8,	/>>-Ц;
J>’[ = 5Z,	/’2=41,	/>>35,	г>46,	р>35,	р'' =41,	</" = ]].
	j					
	1	2	3	4	5	6
1	- GO	-56	-25	-27	0	-1]
2	-45		00	-6	-6	-55	0
3	-8	0	— со	+ 11	0	0
4	-2]	-]]	0	— 00	-60	- 5
5	+ 17	— 49	0	-49	-со	-40
6	0	0	-6	0	-46	— со
/(pIV)= 179. Распределение й^(р, q) приведено на рис. 14.5.
Выберем А =(15). Имеет место п. 3 б) элементарной операции,
Л* = (5), В'5 = (5), В 5 00. На итерации: (X)s = 17, (^г^)5 = 17э (^)5=о.
Итерация V
р'\ = — 18, р2 =	11 ,/>з = — 14,	= — 14, р 5 = — 35, p'f, = — 11;
/[ = 52, />2=41, />>35, />£=46, />>35, />>41, ^>17.
	J					
	1	2	3	4	5	6
1	— со	-39	-8	-10	0	+ 6
2	-45	-со	-6	-6	-55	0
3	-8	0	-со	+ 11	0	0
4	-2]	-11	0	-СО	-60	-5
5	0	-49	0	-49	- со	-40
6	0	0	-6	0	-46	-со
i	j				
	1 2	3	4	5	6
1	со 62	25	38	17	17
2	86 со	30	41	79	30
3	46 2?	СО	2]	21	27
4	59 38	21	со	81	32
5	17 55	0	60	со	46
6	41 30	30	35	70	со
] ] Зак 456
321
Итерация VI
/<pv)=190. Распределение wy(p, q) при-
ведено на рис. 14.6. Выберем А = (3, 4).
Имеет место п. 3 б) элементарной опера-
ции, А * = (3), В'з = (3), В'зИО. На итерации:
(1^11, ШЙ = И, (й)б=0.
p'i= -18,/?i=-И,рз= -25,/4 = - 14, р'5 = -35,р'6 = -11;
Pi=52; />'1=4-1, р>35, /4 = 46, /4 = 35, /4 = 41	^ = 11.
	J
	1	2	3	4	5	6
1 2 3 4 5 6	-с» -39 —8 -10	0 +6 -45 -ос -6 -6 —55	0 — 8	0	-от	0	0	0 -10	0	0	-со	-49	+6 0	-49	0	-49	-от	-40 0	0	-6	0	-46	-от
Е	j					
	I 2		3	4	5	6
1	СО	62	25	38	17	17
2	86	СО	30	41	79	30
3	35	16	со	21	10	16
4	48	27	21	со	70	21
5	17	55	0	60	со	46
6	41	30	30	35	70	0G
/(pIV) = 195. Имеет место этап I б) алгоритма решения задачи
назначения, Л = 6. На итерации: (Х6)7 = 6; (л?)7=0 V/Уб; (Х*), = 0
Vi; (а'л)7 =(9^)7
Итерация VII
д'1=-18, р’2=-П, р’з=-25, р’л=-14, р’5=—35, /4:=-Н;
/4 = 52,	/>2 = 41,	/4 = 35,	/4 = 46,	/4 = 35,	/4 = 35.
	i	j					
		1	2		3	4	5	6
	1	- со	-39	-8	-10	0	0
	2	-45	ос	-6	-6	— 55	-6
Hvu =	3	-8	0	-ос-	0	0	-6
	4	-10	0	0	- ОС	-49	0
	5	0	-49	0	-49	— со	-46
	6	0	0	-6	0	-46	— со
7(pVII) = 201. Имеет место этап I г) алгоритма решения задачи
назначения, к = 2. На итерации: (XJ)8 = 6; (Л/)8 = 0 V/V2; (Xj)8 = О
V/; (?а)а = ($а)% =0-
322
! I
Итерация VIII
=	j^=~5, р\=-14, р'4=-14, р'5=-35, р'6=-11;
pl = 52,	pi = 41,	pi = 35,	pl = 46,	pi = 35, pl = 35.
I	J
	1	2	3	4	5	6
1 2 3 4 5 6	-от	—39	-8	-10	0	0 -39	-со	0	0	- 49	0 — 8	0	—от	0	Q-6 -10	0	0	-со	-49	0 0	-49	0	-49	-го	-46 0	0	—6	0	—46	—от
/(pVIII) = 207. Распределение й;;(р, q)
приведено на рис. 14.7. Получены два
оптимальных решения задачи коммиво-
яжера:
Й 15 =_ “ 53 == Й 34 = Й 42 = 17 26 = “ 61 = 1 !
“16 = “б2“ “24 = “43 = И35 = “51 = 1.
Рис. 14.7
Глава 15
Другие общие методы
решения задач
дискретного программирования
Математические модели многих задач науки и техники,
в том числе планирования и управления производством,
могут быть отнесены к задачам дискретного программирования.
Отметим среди них, например, задачи календарного пла-
нирования уникального и серийного производства; размещения
и специализации производства; размещения информации в па-
мяти ЭВМ и электроники на платах; распределения ресурсов
на сетях, унификации и стандартизации оборудования; развозки
и маршрутизации продуктов и др.
Приведенные в гл. 13 и 14 методы решения задач дискретного
программирования справедливы для задач, которые можно
представить в виде многошагового процесса управления (13.2),
(13.3) или (13.4). Однако не всякую задачу дискретного програм-
мирования можно представить в такой форме. В настоящей
главе приводятся другие общие методы решения задач дискрет-
ного программирования, некоторые из них справедливы и для
задач, не представимых в виде процесса (13.2), (13.3) или (13.4).
Гл. 15 начинается изложением общей постановки задачи
дискретного программирования, затем следует классификация
таких задач и подробное, с приведением математической
и содержательной постановок, описание наиболее известных
прикладных задач дискретного программирования. Среди них
задачи о ранце, покрытии, назначении (в том числе трипланар-
ном и квадратичном), коммивояжера (в том числе и ее
обобщение — задача о маршрутизации). Среди рассмотренных
общих точных методов решения задач дискретного програм-
мирования более подробно рассмотрены динамическое про-
граммирование, методы отсечений, ветвей и границ. Некоторые
из приближенных методов решения задач дискретного про-
граммирования будут рассмотрены в гл. 16.
§ 15.1. Общая постановка задачи
дискретного программирования
Задачу математического программирования можно предста-
вить в следующем виде.
324
Рис, 15.1
Рис. 15.2
Пусть заданы функции Дх), зДх), i=l,m, определенные
на некотором подмножестве G с R", где 7?" —эвклидово простран-
ство размерности н; х = (.х1, ..., хп). Требуется решить задачу
(15.1)
i = l,m,	(15,2)
хе G,
(15.3)
где i~ 1, т,— заданные неотрицательные числа. Множество,
задаваемое условиями (15.2), (15.3), назовем допустимым множест-
вом и обозначим его через D. Вектор х = (х1; ..., х„), удовлетворяю-
щий этим условиям, назовем допустимым решением. Допустимое
решение х, для которого Дх) = ех1гДх), назовем оптимальным.
Задача дискретного программирования (дискретной оптимиза-
ции) является частным случаем общей задачи математического
программирования (15.1) — (15.3), если от множества G не
требовать условия связности (любые две точки x’eG и x2eG
можно соединить ломаной линией, целиком лежащей в G).
Примеры связанных и несвязанных множеств приведены соот-
ветственно на рис. 15.1 и 15.2. В частности, множество G может
быть конечным или счетным (т. е. множеством без предельных
точек, например типа натурального ряда), либо декартовым
произведением конечного или счетного множества на множество
мощности континуума. В дальнейшем ограничимся случаем,
когда G = G! х G2 х ... х Gn, а хотя бы одно G,;с /?", ]=[^п,—
конечное или счетное множество.
Итак, условия (15.3) для задачи дискретного программирова-
ния записываются в виде
TjeG;, j= 1, п,	(15.4)
где хотя бы одно Gj—конечное или счетное множество.
325
§ 15.2. Классификация задач
дискретного программирования
Задача (15.1), (15.2), (15.4) называется полностью дискретной,
если все множества Gj, j= I, п,— конечные или счетные. Если
некоторые из множеств Gj непрерывны (связны), то задача (15.1),
(15.2), (15.4) называется частично дискретной._____
Если хотя бы одна из функций g,: (х), 1=1, т, нелинейна,
то задача (15.1), (15.2), (15.4) называется нелинейной задачей
Я	л
дискретного программирования; если /(х) = £ CjXj и ^(х) = V a.jXj,
j=i	j=i
где (j и «у — известные константы, то задача называется задачей
линейного дискретного программирования. Накладывая допол-
нительные ограничения на функции Дх), ,?,(х), рассматривают
выпуклые, вогнутые, стохастические и другие задачи дискретного
программирования. Рассмотрим наиболее распространенные клас-
сы таких задач.
1.	Задачи целочисленного программировании, К ним относятся
задачи вида (15.1), (15.2), (15.4), для которых множества Gj
имеют вид
G, = (0, 1, ...), 7=1^.	(15.5)
2.	Задачи целочисленного программирования с булевыми пере-
менными. К ним относятся задачи вида (15.1), (15?2), (15.4), для
которых
G-(0, 1), 7 =	(15.6)
3.	Задачи целочисленного программирования со смешанными
ограничениями. К ним относятся задачи вида (15.1), (15.2), (15.4),
для которых одна часть переменных целочисленна, другая — буле-
ва, т. е.
Gj = (O, I, 2, ...), j= I, к‘, Gj = (0, 1), j = k+ i, n. (15.7)
4.	Задачи частичного целочисленного программирования. К ним
относятся задачи вида (15.1), (15.2), (15.4), в которых одно из
условий вида (15.1)—(15.3) наложено только на часть переменных
xeGy, j= 1, п.
5.	Задачи комбинаторного программирования. К ним относятся
задачи вида (15.1), (15.2), (15.4), для которых множества Gj,
7=1, п,— конечные.
6.	Задачи диофантова программирования. К ним относятся
задачи нахождения ех^Дх), где й=(х:&-(х) = 0, i = 1, т, Xj—целое,
7=1, «)
В настоящей и последующей главах будут рассмотрены
в основном модели линейного дискретного программирования.:
326
F
“ Основные известные методы получения точного решения задач
дискретного программирования можно изложить и на общей
задаче линейного дискретного программирования, но при этом
возможно «засорение» основных идей методов подробностями,
навязанными общностью исследуемой модели. В последнее время
все в большей степени намечается тенденция максимального
использования специфики задачи при разработке алгоритмов ее
решения. Поэтому среди задач линейного дискретного программи-
рования выделим наиболее распространенные частные классы
задач и на их примере поясним основные идеи точных методов.
§ 15.3.	Прикладные модели задач
дискретного программирования
1.	Задачи о ранце. Свое название этот класс задач получил
йз-за следующей гипотетической ситуации: в ранец (рюкзак)
вместимостью 6 надо упаковать п видов предметов с весами
..., сп и соответственно размерами ..., а„ так, чтобы
Вагрузка ранца была максимальной. Приведем модель дискрет-
ного программирования для более обшей ситуации.
Пусть /)(х), j= 1, п,— вектор-функция с неубывающими компо-
нентами, определенными на множестве неотрицательных чисел;
(<?у) и Ьц j—\,n7 i = 1, ш,—соответственно матрица и вектор
с неотрицательными компонентами. Тогда постановка многомер-
ной задачи о ранце состоит в следующем:
I	EZ(x)-*min>	ОI * * * 5 * *-8)
[ 7=1
Г	£	*=1, rn,	(15.9)
I
I	х; = (0, 1, 2, ...),	(15.10)
I Многомерная задача о ранце возникает как естественное
(обобщение одномерной, когда ограниченным является не только
суммарный вес, но и объем и т. д.
I Задаче (15.8) — (15.10) можно придать следующую экономичес-
кую интерпретацию. Пусть имеется вектор b ограниченных
ресурсов, используемый для перевозки различных по своим
(характеристикам грузов. Пусть имеется вектор х видов грузов,
каждый из которых характеризуется свойствами:
8	1) неделимостью, т. е. может выбираться любой груз в ко-
личестве, кратном единице;
j 2) полезностью, определяемой величиной /Дх);
Г 3) расходом г-го ресурса для перевозки единицы j-го груза
hy, i= 1, m, 1, п.
327
Требуется выбрать для перевозки такой набор грузов, при
котором максимизируется общая полезность рейса, определяемая
как суммарная полезность грузов, отправляемых в рейс.
Более известным является следующий частный случай задачи
(15.8) — (15.10) (собственно одномерная задача о ранце)'.
£ арс}->min,	(15.11)
j= i
1, если /-й предмет подлежит загрузке,
0 в противном случае.
(15.12)
(15.13)
Подобная задача часто возникает в практических приложениях
и широко используется как вспомогательная при решении более
сложных задач дискретного программирования. Простота задачи
(15.11)—(15.13) обманчива: для нее неизвестен эффективный
алгоритм решения (т. е. алгоритм с оценками трудоемкости
и памяти, равными степенным выражениям от размерности задач).
2.	Задача о покрытии. Рассмотрим следующую комбинаторную
постановку задачи о покрытии.
Пусть имеется конечное множество Л/=(1, 2, ..., ли), состоящее
из подмножеств Mj <= М, j— 1, и, образующих покрытие множества
М, т. е. [jMj — M. Иными словами, каждый элемент множества
j = 1
М входит хотя бы в одно из подмножеств Мг Требуется найти
минимальное покрытие, т. е. минимальное число подмножеств
М- среди Му, ..., М„, обеспечивающих покрытие множества М.
Часто используется более простая постановка задачи о по-
крытии, заключающаяся в нахождении для заданного графа
Г минимального покрытия, т. е. такого минимального набора
ребер графа, что любая его вершина принадлежит некоторому
ребру,, входящему в покрытие.
Сведем первую комбинаторную постановку задачи к модели
линейного целочисленного программирования. Введем в рас-
смотрение:	____ ______
матрицу (инциденций) (д;Д /= 1, т,	с элементами
fl, если элемент i входит в множество М;
tJ |0 в противном случае;	'
вектор переменных х=(х1, ..., хи) с компонентами
(1, если множество Mj входит в минимальное покрытие, о
J (0 в противном случае.
328
я	«
Тогда У, Xj— число множеств, входящих в покрытие; У а^ху—
,Л=1	j=i
[ело множеств, входящих в покрытие и содержащих элемент
и модель имеет вид
И
У >min,	(15.14)
j=i
У a^Xj^],	х^ = (0, 1), j — 1, n. (15.15)
1
В такой постановке модель используется при выборе семейства
жителей Для выполнения программ космических исследований,
и распределении экипажей по авиалиниям, при информацион-
ном поиске, политико-административном делении, техническом
проектировании узлов ЭВМ, синтезе логических схем и миними-
зации числа состояний конечного автомата, балансировке сбороч-
ных линий и унифицированной доставке товаров, решении ряда
задач стандартизации. Распространенной является взвешенная
адача о покрытии, в которой вместо суммы (15.14) минимизи-
I	”
уется взвешенная сумма у CjXj.
С задачей о покрытии тесно связаны еще два класса задач
идейного целочисленного программирования: задача о разбиении
: задача об упаковке. Задача о разбиении отличается от задачи
i покрытии тем, что вместо ограничения (15.15) рассматривается
граничение
И	____
£tf|/j = l, 1-1Л;
j=1
адача об упаковке—
п	____
У 1- 1, т,
j = i
и, кроме того, решается задача нахождения Дх) = шах у Xj.
% £ & j — 1
Название этих задач, так же как и задачи о покрытии, связано
с их комбинаторной постановкой. В задаче о разбиении следует
найти «разбиение» данного множества на нецересекающиеся
подмножества с максимальным суммарным весом, в задаче об
шаковке —«вложение» в данное множество подмножеств, име-
ощих максимальный суммарный вес. Аналогично взвешенной
задаче о покрытии вводятся в рассмотрение взвешенные задачи
) разбиении и упаковке.
3.	Задача назначения. Задача назначения (оптимального назпа-
[ения, назначений, о назначениях, выбора), точнее—двухиндексная
329
задача назначения, имеет следующую содер-
жательную постановку.
Пусть имеется п работ, которые должны быть выполнены
п исполнителями. Мера затрат Z-го исполнителя на /-Й работе
определяется величиной с^,	Требуется найти назначение
исполнителей на все виды работ так, чтобы: а) суммарный
эффект от такого назначения был минимален; б) на каждую
работу было назначено не более одного исполнителя; в) никто
из исполнителей не был назначен более чем на одну работу.
В комбинаторной постановке решение этой задачи представля-
ет перестановку (рг, ,,,, /?„) чисел (1, 2,	п); каждое из
производимых назначений описывается соответствием Усло-
вия назначения б) и в) выполняются при этом автоматически
и задача сводится к нахождению перестановки (дь р„) среди
(Рр Л)> на которой минимизируется значение суммы £
i = i
Линейная целочисленная модель задачи назначения вводится
следующим образом. Введем в рассмотрение матрицу
t, у=1,н, с элементами
fl, если /-й исполнитель назначается на /-ю работу,
(0 в противном случае,
(15.16)
Условию б) в содержательной постановке задачи соответствует
ограничение
Е Хц=1, 7= Ml	(15.17)
условию в) —
f х,.= 1, i = T~n;	(15.18)
условию а) —
и п
Е £ <Wmin.	(15.19)
i=ij=i
Задача назначения в виде (15,16)—(15.19) часто используется
в практической деятельности, если под «исполнителями» пони-
мать: а) типы инструментов, вооружения; б) алгоритмы или
кванты алгоритмов; в) приборы; г) типы транспортных средств;
д) участников научной конференции; е) канал передачи инфор-
мации и т. д., а под «работами»: а) марки стали, цель; б)
процессоры в вычислительной системе; в) установочные места;
г) типы грузов или пункты доставки; д) места в гостинице; е)
тип сообщений и т. д. Кроме того, задача назначения используется
330
как вспомогательная при решении сложных задач дискретного
программирования, например при решении рассматриваемых ниже
квадратичной задачи назначения и задачи коммивояжера. К мо-
дели (15.16) — (15.19) легко сводятся и более реальные задачи:
1) число исполнителей больше или меньше числа работ
(введением, например, соответственно фиктивных работ, исполни-
телей);
2) существование определенных рабочих мест, запретных для
определенных исполнителей (наложением условия, что соответст-
Ьующее значение Су=оо).
к Задача (|5.16) — (15.19) является простейшей задачей, связанной
Е назначениями, так как мера затрат г-го исполнителя на
Выполнение /-й работы не зависит от назначения других исполни-
Еелей. Более сложной задачей является так называемая трехин-
ексная задача назначения, в которой при назначении «исполни-
иелей» на «работы» следует учитывать дополнительный фактор,
щапример время. Как пример трехиндекс ной задачи назначения
рассмотрим следующую ситуацию.
 Пусть имеется к промышленных объектов, которые могут
Выпускать l^-к продуктов ..., яг и быть расположены в s'^-k
Вайонах. Издержки производства Продуктов не зависят от* объекта,
^который его выпускает, и от района, где этот объект расположен.
Требуется распределить к объектов между районами и определить,
какой продукт будет выпускаться каждым объектом, так, чтобы
суммарные производственные затраты были минимальными, все
к объектов работали, никакие два объекта не выпускали один
и тот же продукт, каждый объект выпускал только один продукт
ta в каждом районе находилось не более одного объекта.
| Обозначим следующим образом множества объектов, продук-
тов и районов:
|	М=(т15 ..., тк), П = (тч, ..., я;), Р=(рь ..., ps).
Введем матрицу Л =(«;;,), ie(l, 2, ..., £), /ер, 2, ..., I). ге(1,
Е, ..., х), неотрицательные элементы которой равны затратам
га производство продукта л- объектом в районе рг (а^г=<х>
означает, что данный продукт не может выпускаться данным
Объектом или данный объект нельзя разместить в данном
районе). Введем матрицу Jf=(xijV) с элементами
1, если объект /л, производит продукт л, в районе рг>
О в противном случае.
'огда остальные ограничения задачи будут следующими:


EES
i=ij=i,=i
Другим примером задач с взаимозависимыми назначениями
является так называемая квадратичная задача назначения, в ко-
торой мера затрат f-го «исполнителя» на данную работу зависит
от назначения на ту же «работу» не всех остальных, а только
у-го исполнителя. Одной из наиболее распространенных является
следующая содержательная постановка, приводящая к квадратич-
ной задаче назначения.
Пусть имеется т центров (неделимых производственных
единиц), агрегатов (объектов), которые должны быть размещены по
п местам, точкам. Затраты, связанные непосредственно с помещени-
ем центра, объекта i на место, точку («затраты на установку») равны
c;j, I = 1, т, j~ 1, и, Известны «расстояния» а - (оценка затрат на
перемещение из / в j) от места, точки /, до места, точки j. Заданы,
кроме того, производственные «потоки», объемы перевозок из
центра, точки г, в центр, точку /. Требуется закрепить центры,
объекты по местам, точкам таким образом, чтобы суммарные
затраты были минимальными. Приведенная постановка — задача
о расположении производственных единиц. Помимо названного
приложения квадратичная задача назначения может быть использо-
вана при планировании расстановки оборудования в конторах,
госпиталях, на химических и машиностроительных предприятиях,
строительстве, в городском планировании и т. д.; в электронике при
минимизации времени запаздывания на магнитном барабане или
дисплее вычислителя, а также при минимизации общей длины
проводов при размещении электронных элементов на платах.
В приведенной формулировке задачи, не умаляя общности,
можно положить т = и, поскольку для случая т<п можно ввести
дополнительные фиктивные центры т +1, ..., п, положив для
НИХ С- = 0 при	И fij = O НрИ	I или у>Щ-|-1.
Приведенная выше задача может быть сформулирована как
задача комбинаторного программирования. Пусть имеются пере-
становки вида (д(, .... рп) из чисел (1, 2,	и). Каждое
закрепление центра / за местом р связано с «непосредственными»
затратами с;р., а также с затратами на взаимосвязь между
парами центров i и j, определяемыми по формуле fijdPiP..
Требуется найти перестановку (д1; ..., рп) чисел, для которой
Ec--Pi+E	05.20)
i’= [ i = l j=l
Для перехода от комбинаторной постановки к модели цело-
численного программирования введем:
332
матрицу Л' = (хм) с элементами
fl, если центр г назначается на место i, „, „ ч
= <	(15.21)
[О з противном случае;
матрицу	с элементами
а = Ьд+ЛЧл если i=k 11	J = l>
,jkl yikdji,	если i^k или j^l,
Справедливы также ограничения
£х;.= 1, <=М,	(15.22)
j-1
£ х;~ 1, у = 1, п,	(15.23)
i=i
имеющие такой же содержательный смысл, как и ограничения
оответственно (15.17), (15.18) для линейной задачи назначения,
(ыражением, эквивалентным (15.20), будет в таком случае
ледующее:
£ £ £ £	(15.24)
; = [j=ik = i i=i
Таким образом, квадратичная задача назначения в целочислен-
юй постановке своди гея к задаче минимизации функционала
15.24) на множестве связей (15.21) — (15.23) и формально отли-
ается от линейной задачи (15.16) — (15.19) только целевой
)ункцией.
Часгными случаями квадратичной задачи назначения являются
ледуки цие:	___
1)	задача Купманса— Бэкмана ci; = 0 Vi, 1, л;
2)	линейная задача назначения ,Д = 0 Vi, к = 1, и;
3)	задача коммивояжера с^. = 0 V/, у=1,« и
Г1, если к=ч+ I, !<п,
< 1, если k=i, i=n,
<0 в противном случае.
4.	Задача коммивояжера. Классическая задача коммивояжера
имеет следующую [[остановку. Имеется п городов, обозначенных
номерами /еЛг=(1, п), Задана матрица расстояний С=(с.Д L
с элементами c,j^O между всеми этими городами. Выходя
i из заданного города, требуется обойти оставшиеся л—1 городов
р хотя бы по одному разу и затем вернуться в заданный так,
чтобы общее пройденное расстояние было минимальным.
Комбинаторная постановка задачи коммивояжера состоит
в следующем. Задана квадратная матрица С размерности и х л.
333.
’’’JF
Из некоторой последовательности (/>+1) целых чисел взяты
числа (1, 2, ..., н), каждое из которых появляется по крайней
мере один раз, а первое и последнее числа одинаковы. Решение
задачи может быть записано как t=(i17 г2, ..., ip, g). Любое
возможное решение назовем циклом. Тогда оптимальное реше-
ние-цикл, в котором z(r)=^	где /' = [(/„ ;2), ...
..., (ip-i, /„), (L, г\)] — упорядоченное множество пар индексов мно-
жества t. Введем также определение: подциклом Л = (г\, /2, ...
..., ik, назовем множество целых чисел, в которое входят не
все числа (1, 2, ..., л), к<п.
Постановку задачи коммивояжера используют часто и в те-
рминах теории графов. Граф, как известно [6], считается
заданным, если заданы непустое множество X и отображение
Г множества У в У. В простейшем случае отображение Г-нацравлен-
ный отрезок, соединяющий две произвольные точки множества
X. Элементы хе А' называются вершинами графа, а направленный
отрезок, соединяющий точки хе! и уеГхеТ,— дугой графа.
Обозначим множество дуг графа символом V, а сами
дуги — буквами м,, г=1, 2........ Тогда	граф G можно задать
парой G(X. U).
Граф G называется конечным, если конечны множества Хи Г
Путем в графе G(.V, J7) называется такая последовательность
(«р и2, ...') дуг, что конец каждой предыдущей совпадает с началом
последующей. Путь, в котором никакая вершина не встречается
дважды, называется элементарным. Путь, последовательные вер-
шины которого суть Хр х2, ..., хк, можно обозначить символом
ц [х1; х2, ..., xj. Элементарный путь, проходящий через все
вершины графа, называется гамильтоновым. Цикл (контур) — это
конечный путь ц Ex,, ..., хк], у которого начальная вершина
совпадает с конечной хк. Цикл (контур), проходящий через все
вершины графа, называется гамильтоновым.
Иногда каждой дуге графа ставят в соответствие некоторое
число с (xif xj) = cijt называемое «весом» или «длиной» дуги.
Тогда длиной пути, проходящего через хр ..., хк, называют
сумму длин дуг его составляющих, т. е. c12-l-c23-i-... + efc_bJr.
Граф G называют полным, если любые его две вершины
соединены хотя бы в одном направлении. Задача коммивояжера —
задача об отыскании гамильтонова цикла кратчайшей длины
в конечном полном графе.
Простота формулировки задачи коммивояжера и сохранение
основных трудностей, присущих задачам дискретного программи-
рования, во многом непреодоленных и в настоящее время,
привлекли к этой задаче внимание многих исследователей. Кроме
чисто математического интереса, задача коммивояжера имеет
значительный практический интерес. К ней сводятся задачи
о переналадке оборудования, связанные с планироранием произ-
334
водства, минимизацией программ, монтажом электроаппаратуры,
некоторые задачи маршрутизации и др.
I. Приведем линейную целочисленную модель задачи коммивоя-
жера в предположении, что начальный город —первый. Введем
[в рассмотрение матрицу Х=(х,Д i, jeN, с элементами
J1, если коммивояжер из города i переезжает в город у,
(О в противном случае.
(15.25)
Условиям, что коммивояжер выезжает из каждого города
и въезжает в город только один раз, соответствуют ограничения:
Еху=1> JeN,	(15.26)
i = l
f Ху=1, ieN.	(15.27)
’Условию, что маршрут коммивояжера —цикл, соответствует
(ограничение
i	.	XijeS,	(15.28)
Иде S — определяемое ниже множество. Тогда задача коммивоя-
i жера состоит в нахождении минимума целевой функции
/ = Е Е	(15.29)
ieNjeN
на множестве ограничений (15.25) — (15.28). Задача (15.25)—(15^27)
и (15.29) — рассмотренная выше задача назначения. Ее допустимы-
ми решениями могут быть не только циклы, но и подциклы,
не являющиеся допустимыми решениями задачи коммивояжера.
Ограничения (15.28) введены для устранения всех возникающих
в процессе решения задачи коммивояжера подциклов.
Наиболее известны следующие три конкретизации вида мно-
жеств S:
1. 5=(х;гн; — и^ + пх^п — 1,	(15.30)
где w; — произвольное действительное число.
Общее число ограничений (15.30) для задачи размерности
nxin-- 3« + 2). Эти ограничения препятствуют образованию под-
циклов. Действительно, рассмотрим некоторый подцикл, состоя-
щий из к<п городов. Сложив все неравенства из (15.30) вдоль
Ji	Ji
этого подцикла, получим £ щ — £ и} + пкЩп — 1)к. Так как
it	.= [;=[
£ и; — £ Wj = 0, то пк^(п— 1)/с, где к<п, k^Q. Полученное
т=1	1
335
противоречие доказывает несуществование подцикла с числом
городов меньше п.
Теперь покажем, что существует н;, которое для любого
цикла, начинающегося в некотором начальном пункте, удовлет-/
воряет условию (15.30). Для этого положим ut = р, если город
i коммивояжер посещает на р-м шаге объезда, р = 1, ..., п.
Пусть х,-, = () 0-й город не посещается после z-го города), тогда
из (15.30) и определения г/j имеем Uj — u^n—i. для всех i, jeN.
Пусть х„= I, тогда по той же причине щ — и^ + пх^=р~ (р +1) +
Ч-и = «— 1.
2,	5Ч-Ч: У	УЛс(2, 3, ..., и), А^0. (15.31)
ieAjeA
«Механизм» исключения подциклов следует непосредственно
из определения множества S.
3' 5 = X Е_Ч,-Ч У
/ е A je А
A[}A = 0, AljA^l, 2, ..., п).	(15.32)
«Механизм» исключения подциклов с помощью ограничений
(15.32) основан на следующем. Так как решение задачи назначе-
ния, состоящее из совокупности подциклов Л и Л, не является
допустимым решением задачи коммивояжера, то в решение
последней должна войти хотя бы одна дуга из числа соединяющих
подциклы А и А.
К задаче многих (нескольких) коммивояжеров сводится значи-
тельное количество реальных задач. Ее формулировка заключается
в Следующем.
Имеется базовый город и еще п городов. Каждый из
т коммивояжеров объезжает какие-то из этих п городов и возвра-
щается в базовый город. Каждый город посыцается хотя бы
один раз, но маршруты никаких двух коммивояжеров не
пересекаются нигде, кроме базового города. Требуется найти
такие маршруты для каждого из т коммивояжеров, чтобы
суммарная длина всех этих маршрутов была минимальной.
Часто используется следующая комбинаторная постановка
задачи многих коммивояжеров.
Пусть имеется т коммивояжеров, которые должны посетить
w городов. Задана матрица С=(с’Д i,jeN=1,n, s=\,m,—мат-
рица затрат i-го коммивояжера на переезд из i-ro города в /-й.
Коммивояжеры выезжают из одного базового города i* и должны
туда же вернуться, при этом каждый город посещает только
один коммивояжер и каждый коммивояжер должен побывать
хотя бы в одном городе (для некоторых модификаций задачи
последнее требование не является обязательным). Упорядоченную
последовательность точек is2, , isk, ir^N, l^r назовем
незамкнутым маршрутом s-ro коммивояжера; упорядоченную
336
последовательность точек г®, i2, if, /'I— замкнутым (гамильто-
новым) маршрутом s-ro коммивояжера.
| Требуется разбить множество N на подмножества IV,, Ns,
>	л*
Nm, удовлетворяющие условиям ] 1VJ ^N, (J NS = N, Ns A Nr = i*,
5s 1
s, r= 1, 2, ..., m, s^r, и определить замкнутые (гамильтоновы)
маршруты т-х коммивояжеров в подмножествах Ns, чтобы
выполнялся критерий оптимальности
EL.= Е Е
где Ls —длина замкнутого маршрута s-ro коммивояжера. При
этом часто накладывается дополнительное условие
max Ls= max £ c|j^Lmas,	(15.33)
i SsSm 1 Ssgin (i.j)eNs
где Lm;1I— максимально возможная длина маршрута.
Задача многих коммивояжеров может быть сведена к задаче
одного коммивояжера двумя способами.
Первый способ основан на введении переменной матрицы
затрат. Пусть выбраны маршруты 5-го и (з+1)-го коммивояжеров,
соответственно (/*, i®, Г3, ...,	/*) и (/*, г/1,	г*). Эти два
маршрута можно объединить в один замкнутый маршрут
(;*, г], ..., ik, /’+11 ..., ?I + 1, £*), если преобразовать исходную мат-
рицу С = (с?Д заменив элемент с.5 .j41 по формуле
cf iSA ' = cf .* + с * J (!.	(15.34)
Элементы матрицы С преобразуются по формуле (15.34) всегда,
когда нарушаются условия (15.33) или какие-либо другие, сходные
с ними (например, ограничения на максимальную звенность
маршрута s-го коммивояжера).
Второй способ состоит в «разбиении» базового города i* на
т точек так, чтобы
c,-.,. = co, Г-.-=Г*.
ЦП	W ‘ Р Jh Щ
Размерность новой матрицы затрат при этом увеличивается
на т - 1.
§ 15.4. Основные методы решения задач дискретного
программирования. Динамическое программирование
В настоящем параграфе освещаются главным образом точные
методы решения задач дискретного программирования. Эти
методы базируются на таких общих подходах, как методы
последовательного анализа вариантов [12] [включая динамическое
программирование (гл. 11), методы ветвей и границ, отсечений
. 337
[5], методы, использующие обобщенные множители Лагранжа
[11], методы построения последовательности решений [2], методы
построения универсальной операции улучшения функции ф(/, х)
(гл, 13)]. Среди названных методов в этой главе более подробно
будут рассмотрены методы отсечений, ветвей и границ, основан-
ные на динамическом программировании.
В основе метода динамического программирования лежат
принцип оптимальности Беллмана и вытекающее из него функцио-
нальное уравнение, позволяющее свести решение многомерной
задачи оптимизации к решению последовательности одномерных
оптимизационных задач, Принцип оптимальности Беллмана фор-
мулируется следующим образом. Оптимальное поведение облада-
ет тем свойством, что, каково бы ни было первоначальное
состояние и .решение в начальный момент, последующие решения
должны составлять оптимальное поведение относительно состо-
яния, полученного в результате первого решения. Покажем
применение метода динамического программирования на одном
важном частном классе общей задачи дискретного программиро-
вания—задаче распределения ресурсов,
Рассмотрим следующий вариант задачи (15,1) — (15,3):
/(х)=	(15.35)
gJ(x) =	j=\, т,	(15.36)
xeG,	(15,37)
где — со < ci] < со, j= 1, т — произвольные вещественные числа,
G = G( х ,,, х G„ — прямое произведение множеств Gi числовой оси.
Наряду с задачей (15.35) — (15,37) рассмотрим семейство задач
т*п ЕЛ(ХО’ x-eGi’	j=Km, (15.38)
/== [	i = l
где ,s'=l3/7?	К — множество компонент вектора у, при
которых множество 1х(:х;еС;, £ gf (х^<.у\ у=1, т I не пусто.
При s = n и у’ = а‘, j= 1, т, из семейства (15.38) выделяется
исходная задача (15.35)—(15.37).
На решениях задач (15,38) определим функцию Беллмана:
фДу)=пнп f ,/](хД х-еОь fg^x^y'. (15.39)
i=l	i=l
Воспользуемся принципом оптимальности и, учитывая определе-
ние функции Беллмана, составим функциональное уравнение
относительно функции Беллмана:
338
<ps+t(y)= min
JCj € G/'= 15 5" -|- 1
'?+1	’
i fi(xi) = x
1=1	Xs+l JL
Л + 1(х*м) +

+ min	£ _Ш)
X gi '-gl* i (x.-t t)l£Gl’ ' = 1,
(15,40)
Второе слагаемое в квадратных скобках представляет собой,
как легко видеть из определения функции Беллмана (15,39),
значение функции ф.(у) в точке у—g. , (х. +,), Тогда из
(15.40) имеем
Фз + 1(у)= mm. [Л+1 (х4+ ]) + Ф., (У - gs +1 (xs+1)]-	(15.41)
Хл; + 1 е + 1
Начальное условие следует из (15.39):
Ф1(у) = ттЛ(х5+[), xs+16Gb <gi(xs + [)^T< 7=1, т. (15.42)
Из (15.41), (15.42) вычисляем последовательность функций ф5(у),
р 5= 1, п. Значение ф„(а) равно, согласно (15.39), минимуму /(х)
( в задаче (15.35) — (15.37).
) Для отыскания компонент хь ..., хп вектора х поступаем
• следующим образом, Пусть найдены функции фДу), Ф2(У), 
(	ф„_1(у)- Найдем х„ из соотношения
) fn (хя) + ф„_ [ (a -g„ (хв))= min [/„ (а) + ф„_ j (a-gn (а))].
( Далее находим хл_к Из (15.35) — (15.37), (15.41) следует, что
; удовлетворяет соотношению
= m>
;	Gtt: ’Jff- j
 Продолжая этот процесс для вычисления хк,	получаем
соотношение
к
a~i g.(xi)
i = n
fc + 1
i= к
Значение согласно (15.35) — (15.37), (15,42), удовлетворяет
соотношению
А(^)=тт/Да), г1(«)^-£&(хг)-
i=n
=тт Д(а)+
339
Уравнение (15.41) называется уравнением Беллмана в прямом
времени, так как вычисление последовательности функций (ps(y)
в этом уравнении происходит в направлении возрастания дискретного
аргумен та s. Отметим, что, согласно (15.41), при вычислении функции
(ps+J (у) требуется знать функцию (рДу) в точках + 1 (a), ае(?5+1,
./= 1, т. Поэтому при вычислении функции <ps+1 (у) на (s-f-l)-M шаге
требуется хранить в памяти всю функцию ср Ду), где у = (_>'1, , J’m),
т. е. размерность функции Беллмана определяется числом ограниче-
ний. Эго затрудняет решение задачи (15.35)— (15.37) при т^З, так
как объем оперативной памяти современных ЭВМ не позволяет
работать с функциями более чем трех переменных. т. е. в качестве
точного метола решения задач дискретного программирования метод
динамического программирования можно успешно применять, как
правило, для.задач небольшой размерности. Этот метод является
частным случаем более универсального и гибкого метода последова-
тельного анализа вариантов [12],
Приведем свойства, которыми должна обладать задача (15.35) —
(15.37), чтобы к ней было можно применить метод динамического
программирования:
1.	Задача может быть представлена как л-шаговый процесс
управления, а целевая функция — как аддитивная (мультиплика-
тивная) функция.
2.	Структура задачи должна быть определена для любого
п и не зависеть от этого числа,
3.	Выбор управления на з-м шаге не влияет па предшеству-
ющие шаги, а состояние в начале этого шага есть функция
только предшествующего состояния и выбранного на нем управле-
ния (отсутствие последствия).
4-	На каждом л-м шаге состояние системы определяется
конечным числом параметров состояния и управляется конечным
числом переменных управления, причем оба эти члена не зависят
от числа шагов п.
§ 15.5. Методы отсечений
Рассматриваемые методы основываются на замене решения
исходной задачи (15. Г), (15.2), (15.4) последовательностью решений
более простых вспомогательных задач с той же целевой функцией
(или ее определенной аппроксимацией) и на более широком
множестве допустимых ограничений. Последовательность решений
вспомогательных задач строится до тех пор, пока не будет
получено первое допустимое решение исходной задачи, явля-
ющееся и оптимальным. Существующие алгоритмы этой группы
методов используют в качестве вспомогательной задачи, получен-
ные в основном только за счет расширения множества до-
пустимых ограничений.
340
Пусть рассматривается исходная задача (15.1), (15.2), (15.4).
Построим последовательность решений вспомогательных задач:
/(x)->extr,	(15.43)
xjeGk!j=‘l,n, к=1, 2,	N, Gj<^G\ (15.44)
где Gk— множество допустимых решений вспомогательных задач.
Последовательность решений (15.43), (15.44) строится таким
образом, чтобы
G^Gt+l,	(15.45)
т. е. множество G'14'1 получается из множества Gk «отсечением»
части точек. Этим свойством и объясняется название данной
группы методов. Если на основании свойства (15.45) хк— решение
задачи (15.43), (15.44), то /(хЧ— оценка целевой функции в ис-
ходной задаче (15.1), (15.2), (15.4). При построении отсечений,
обладающих свойством (15.45), используют в основном два
способа. При первом способе формируется дополнительное огра-
ничение gk (х) < 0, которому удовлетворяют все точки из мно-
жества Gk допустимых решений исходной задачи, но не удовлетво-
ряет точка х*. Отсечения, формируемые с помощью ограничений
g'l(x)<0, называются правильными отсечениями. При втором
способе ’ в отсекаемую часть множества Gk входит только одна
точка хк.
Приведем конкретные реализации правильных отсечений для
задачи линейного целочисленного программирования [14]:
F1
£ tjXj-*nrin,	(15.46)
М
D = i Xj: £ а^Х' = Ь^ i=l,m; Xt-GO. G”, j= 1, п I, (15.47)
х i-1	/
где G" — пространство н-мерных целочисленных векторов. В ка-
честве вспомогательных задач для (15.46), (15.47) рассматривают
непрерывные задачи
£ СуХу-ытп,	(15.48)
j = i
Fl	____ ______________
Xj'> Y aGXj = bi,	j= 1, n
j=l
Таким образом, множество допустимых решений исходной задачи
погружается в выпуклое многогранное множество Dk, отличаю-
щееся от D только отсутствием условия целочисленности. К пра-
вильному отсечению, формируемому в виде
F1	____
j = i
341
где gtj, Д— известные константы, предъявляются следующие
требования;
(N	____ ___________ Л	\
XJ: Е aijxj = bi, i = l, w; xi}'^,j=l, n, £
j--1	j= i	/
т. e. правильные отсечения не отсекают целочисленных точек
множества D;
2)	целочисленное решение xk задачи (15.48), (15.49), превраща-
ется в вершину множества Dk;
3)	целевая функция (15.46) достигает минимума на множестве
Dk в точке х .
Условиям (15.43) — (15.45) удовлетворяет, например, выпуклая
оболочка множества V[D), но построение последней по трудности
не уступает решению исходной задачи (15.46), (15.47). Поэтому
на практике;. поступают иначе; от множества Dk отсекают
последовательно части, приближаясь к V(d) только лишь в окре-
стности оптимального решения задачи (15.46), (15.47).
Для построения отсечения обычно используют методы линей-
ного программирования. Как известно, план Х = (хп .... х„) задачи
(15.48), (15.49) называют опорным, если векторы условий, отвеча-
ющие его положительным составляющим, линейно независимы.
Базисом В = (Д1; ..., Вга) опорного плана X задачи (15.48), (15.49)
называют систему т линейно независимых векторов условий,
включающих все те Л;-=(а1;, ..., ат-}!, j — i, и, для которых х^>0.
Если ввести по сравнению с моделью (15.46), (15.47) новые
переменные xi0 = b;, х^=а^ - -коэффициенты при у-й небазисной
переменной; х0^ = с;, 'то справедливо следующее соотношение
всех переменных a’j, ..., х„ и целевой функции х0 через небазисные
переменные:
*в =л;о_ Е xijxr г = 1, , ш,	(15.50)
'	je.fi
где N—множество индексов небазисных переменных. Умножая
обе части равенства (15.50) на число /г^О, получим
kxB.+ Е hx^x—hx^,
j*N
откуда с учетом /=1?я;
|»вЕ [hx^Xj^hXio,	(15.51)
jeiV
где [й]—целая часть числа h. Так как в (15.51) х}, j=l,n,
должно быть целым, то левая часть этого неравенства также
должна быть целой, т. е. опа не может быть больше, чем целая
часть от числа hxia, и, следовательно,
Е [Лхц]х,<	(15.52)
jeN
342
Умножая (15.50) на [Л] и вычитая из (15.52), получим
Е ([А]хо-[йхм])хи>[Л]х£0-[йх£0]	(15.53)
je.V
— общую конструкцию Гомори отсечения с параметром. Очевид-
но, что ограничение (15.53) отсекает от Dk текущее базисное
решение хв. = х£0, /=0, 1, .... т; х, = 0, jeN, лишь при условии,
что [Л1х£0 —[Лх£о]>0. Выбирая подходящие Л, можно получить
из (Г5.53) известные отсечения.
Пусть h = l, тогда из (15.53) получим
0^у=-{х£О}+£ {хц}х£;	(15.54)
J 6 jV
— отсечение метода целых форм Гомори. Здесь {х^}— дробная
часть числа xtj, =	+ Если xs.=x£0, 1 = 0, 1, ..., т,
х;=0, jе У,— базисное (оптимальное) решение задачи (15.48),
(15.49) с нецелой компонентой хв„ то (15.54) отсекает
от Dk это решение, не затрагивая1 при этом допустимых
планов [5]. Поэтому присоединяя (15.54) в качестве отсечения
к (15.49) можно сузить множество Dk и продолжить процесс
решения задачи (15.46), (15.47) в соответствии с намеченной
выше схемой.
Аналогично, при 0 < Л < 1 из (15.53) получим
0^у = [Лх;о]- £	(15.55)
/еЛ'
— отсечение двойственного полностью целочисленного алгоритма
Гомори. Можно показать [10], что для некоторого h из заданного
интервала элемент [йх^] — 1 можно получить согласно двойствен-
ному симплекс-алгоритму.
При й = 1/х1Л<1, где i— ведущая строка [15] в прямом
симплекс-алгоритме, из (15.53) получим
(15.56)

— отсечение прямого полностью целочисленного алгоритма.
Из соотношения (15.50) видно, что таблица значений коэффи-
циентов Xtj определяет оптимальное решение задачи (15.46),
(15.47), если она: а) прямо допустима, т. е. х£о^0, /=1, т;
б) целочисленна, т. е. х;о— целое, i=\,m; в) двойственно допус-
тима, т. е. хо^0, jeN. Условия а) и б) — необходимые, а)—в) —
достаточные (но не необходимые) для оптимальности целочислен-
ного решения хе. = х£о, Z=l, т; х£ = 0, уеУ. Известны три основных
алгоритма решения задачи (15.46), (15.47). Каждый из них
343
построен так, что на каждой итерации какие-либо два фиксирован-
ных условия сохраняются, а выполнения третьего добиваются
к концу работы алгоритма введением отсечений. Общую схему
этих алгоритмов можно представить так.
Шаг 1. Выбор двух из указанных грех условий. Переход
к шагу 2.
Шаг 2. Проверка на оптимальность. Если третье условие
выполняется, то получено оптимальное решение. В противном
случае — переход к шагу 3.
Шаг 3. Отсечение и преобразование. Построение отсечения
и преобразование симплексной таблицы (х; ) с сохранением двух
фиксированных на шаге I условий. Возвращение к шагу 2.
Условие, выполнения которого добиваются к концу работы
алгоритма, определяет алгоритм (в смысле названия). Так, если
в качестве пефиксируемого выбирается условие а), то получаем
двойственный, полностью целочисленный алгоритм (3-й алгоритм
ГомориЕ если б) — алгоритм целочисленных форм (1-й алгоритм
Гомори), если в) — прямой, полностью целочисленный алгоритм.
На этих же принципах построены алгоритмы решения частично
целочисленных задач. Основными недостатками методов отсече-
ний являются следующие:
1)	как правило, медленная сходимость к оптимальному ре-
шению;
2)	непредсказуемость, т. е. для ряда задач оптимальное реше-
ние не удавалось найти после многих тысяч итераций и вместе
с тем другие задачи, близкие или равные по размерности,
решались за несколько десятков итераций;
3)	нерегулярность, т. е. число итераций существенно зависит
от таких факторов, как выбор порождающей строки (строки,
для которой строятся отсечения вида (15.54) — (15.56)), перену-
мерации перемени ых.
§ 15.6. Методы ветвей и границ
Множество допустимых решений задачи (15.1), (15.2), (15.4),
по определению, конечно, и поэтому для ее решения можно
воспользоваться методом прямого (простого) перебора. Для
решения сложных задач дискретной оптимизации малой размер-
ности этот метод вполне применим, но для задач, В которых
число допустимых решении велико, метод неприменим даже
с использованием ЭВМ. Однако если улучшить схему перебора,
рассматривать в его процессе не все, а только часть допустимых
решений, то такие схемы неявного (частичного, направленного)
перебора становятся весьма привлекательными. Большой интерес
в настоящее время к такому улучшенному перебору вызван,
с одной стороны, прогрессом в развитии ЭВМ, позволяющим
в приемлемое время рассматривать достаточно большое число
344
допустимых решений, с другой — в универсальности методов
неявного перебора, позволяющих решать задачи, не «берущиеся»
другими методами. Среди схем неявною перебора наибольшее
развитие получили методы ветвей и границ. Для этих методов
нет устоявшейся терминологии. При первом подходе под этой
группой методов понимают все комбинаторные методы, ос-
нованные на неявном переборе, при втором подходе только
методы, характеризуемые древовидностью схемы поиска экст-
ремума и использованием релаксаций (расширений исходного
множества допустимых ограничений) для нахождения оценок.
В последнем случае оптимальные комбинаторные методы называ-
ются иначе, например методами энумерации. В настоящей главе
при изложении методов ветвей и границ будем придерживаться
второго подхода.
Изложим метод ветвей и границ для задачи дискретного
программирования в следующем виде;
/(x)->min,	(15.57)
xeG,	(15.58)
где G — некоторое конечное множество. Основой метода ветвей
и границ является несколько общих принципов, позволяющих,
как правило, существенно уменьшить объем прямого перебора.
1.	Вычисление нижней границы (оценки, рекорда). Для целевой
функции f на множестве G допустимых решений задачи (15.57),
(15.58) (или его подмножестве G') справедлива оценка Е, (G) (((G'j):
2.	Разбиение на подмножества (ветвление). Исходное множест-
во допустимых решений G разбивается на конечное число
подмножеств по следующей многошаговой схеме.
Шаг 0. Имеется множество G° = G. Разобьем множество G не-
которым способом на конечное число Добычно не пересека-
ющихся, т. е. обладающих свойствами (J G( = G°, F)Gi=0)
i=l	i=L	/
подмножеств G/, /=1,
Шаг k (k^ 1). Имеются множества G\, ..., Gj? еще не подвер-
гавшиеся разбиению. По определенному правилу (указанному
ниже) среди них выбираем множество Gj(k) и разбиваем на
конечное число подмножеств Gi^i, Gj{(:L2, ..., Gy{fcbs(fe>. Еще не
подвергавшиеся разбиению множества Gsb G2, G^w_b
Gj(k)+l, Gj!, GjtJc>,2,	заново обозначаются че-
рез G*+1, G‘2+1,	G,\+I.
345
3.	Пересчет оценок. На основании очевидного соотношения
min/(x)^mm/(x), где GjCzG,, при разбиении некоторого мно-
KCG,	xeG3	s
жества G' на подмножества G), G's так, что G'= (J GJ, всегда
£=1
справедливы неравенства
£(<?;>£(<?'), г = М.
В конкретных случаях часто удается усилить оценку, т. е. получить
хотя бы для одного i строгое неравенство ^(GQ>^(G').
4.	Вычисление допустимых решений. Способ вычисления допус-
тимых решений в последовательно разветвляемых подмножествах
существенно зависит от специфики решаемой задачи.
5
5.	Признак  оптимальности. Пусть G= (J G, и допустимое
решение х принадлежит одному из подмножеств Gk. Тогда если
то х—оптимальное решение задачи (15.57), (15.58). Доказательст-
во этого положения следует из определения оценки.
6.	Оценка точности приближенного решения. Пусть G= (J G;,
min ^(Gj). Если х—допустимое решение задачи (15.57), (15.58),
1-1.S
то, очевидно,
^min/(x)^/(x),
хе G
и в том случае, если разность Д = /(х) —невелика, х можно'
принять за приближенное решение задачи, а Д — за оценку
точности приближения.
Перейдем к изложению формальной схемы метода ветвей
и границ.
111аг(). Вычислим оценку J;(G0). Если при этом находится
такое допустимое решение х, что
/ти
то х—оптимальное решение. Если такого допустимого решения
нет, то по определенному способу разбиваем множество G=G°
на конечное число (обычно пересекающихся) подмножеств
G°= (J Gl и переходим к шагу 1.
i = i	__ 1
Шаг!. Вычислим оценки J;(G/), z=l,rr Если при этом
находится такое допустимое решение хе G,, 1	для ‘
которого	।
346
В то x—оптимальное решение. Если такого допустимого решения
Е нет, то выбираем «наиболее перспективное» для дальнейшего
№ разбиения множество GLd, например, по следующему правилу
К ^(GiU))= min £(6/). Разбиваем множество G*(i, на несколько
Е	; =	s(i)
К. (обычно не пересекающихся) подмножеств Gy{1) = (J G^cl)-i. Еще
Е	£=1
Е не подвергавшиеся разбиению множества Gl, G1,	G*{1)-b
Ц	G^, Сипл, Glv(1}.2,	заново обозначим через
E Gj, G2,	G^2 и переходим к шагу 2.	__
В Шаг k(k^2). Вычисляем оценки J;(G*), f=l,rt. Если при
 этом находится такое допустимое решение xeG*, lOOj., для
Е. которого
I	*=г^,
В то х— оптимальное решение. Если такого допустимого решения
Е нет, то выбираем наиболее перспективное множество Gj(([),
г например, по правилу E,(Gj()£))= min (G?). Разбиваем G\k) на
№	i = l.rt	s (A.)
I- несколько непересекающихся подмножеств Gt,(i)= IJ G’Vj.t Еще
I- не подвергавшиеся разбиению множества G,, Gj,1 Gk(k)-i,
|	, Grt, G\k),2, —Gklk)iS{k} обозначим через Gj+I,
GV1,', GR и переходим к шагу к+1.
К Для реализации описанной выше схемы метода ветвей и границ
в конкретных задачах следует, исходя из специфики рассматрива-
Е емых задач, конкретизировать правила ветвления, вычисления
j оценок и нахождения допустимых решений. Все это будет
I показано в гл. 16 при изложении различных точных алгоритмов
I решения задачи коммивояжера.
| Сделаем несколько общих замечаний относительно способа
I выбора подмножеств для дальнейшего разбиения на 1-м и А>м
| шагах формальной схемы метода ветвей и границ и способов
ветвления [14]. Помимо упоминавшегося выбора подмножества
К для дальнейшего разбиения по наименьшей нижней оценке
| возможны еше следующие способы выбора:
I 1) одностороннее ветвление (ветвление по фиксированному
I пути);
К:	2) ветвление по наименьшей оценке среди множеств, построен-
I ных на последнем шаге или нескольких последних шагах;
I 3) ветвление в зависимости от разности между наименьшей
I- нижней оценкой для множеств, построенных на последнем шаге,
Г и множеств, построенных на предшествующих шагах;
Г	347
4)	эвристическое ветвление;
5)	ветвление по вероятностным характеристикам;
6)	комбинация некоторых способов, перечисленных выше.
Возможны также различные способы ветвления, среди которых
отметим следующие:
1)	покомпонентное ветвление;
2)	ветвление с использованием дихотомии;
3)	смешанное ветвление с использованием способов 1 и 2.
Основным недостатком метода ветвей и границ является
экспоненциальный рост вычислений при увеличении размерности
задачи.
Глава "16
Методы решения некоторых
частных классов задач
дискретного программирования
I В настоящей главе с помощью некоторых из приведенных
в гл. 15 точных и приближенных методов решаются две
«узловые» задачи дискретного программирования —задачи на-
значения и коммивояжера. Приводятся основные идеи некоторых
известных приближенных алгоритмов решения задачи назначе-
ния, поскольку точные алгоритмы подробно освещены в учебной
литературе. Дается классификация точных и приближенных
методов решения задачи коммивояжера, а также ее решение
с помощью некоторых из точных методов гл. 15: динамического
программирования, ветвей и границ. Среди последних подробно
рассматриваются алгоритмы Литтла, Мурти, Суини и Кэрола,
Беллмора—Мэпоуна и Хелда—Карпа. Рассматриваются при-
ближенные алгоритмы решения задачи коммивояжера.
§ 16.1. Методы решения задачи назначения
Напомним формулировку задачи назначения, подробно рас-
смотренной в § 14.3:
Е Е cyxy-nnin,	(16.1)
i=lj=l
Е ху=1, У=1>	(16.2)
i = I п				
£ %у=1, 1=1, п,	(16.3)
j=l	
хце{0, 1}, /,/=1, п.	(16-4)
Задача (16.1) —(16.4)— типичная задача дискретного програм-
мирования из-за наличия ограничений (16.4), но вместе с тем
ее можно решать методами линейного программирования, если
заменить условия (16.4) следующими;
x£i^0, i,J=Kn-
(16.5)
349
В таком виде задача назначения является частным случаем
хорошо известной замкнутой транспортной задачи. Этот вывод
базируется на следующем свойстве задачи: среди допустимых
решений, задаваемых условиями (16.2), (16.3), (16.5), имеется
хотя бы одно целочисленное. Задача назначения (16.1) — (16.4)
является наиболее изученной задачей дискретного программирова-
ния, для которой разработано значительное количество как
точных, так и приближенных методов [14]. Так, алгоритмом
Манкреса задача назначения (16.1) — (16,4) размерности п = 200
решается в течение 5 мин на IBM 360/65 [13].
Так как один из точных алгоритмов — вариант алгоритма
Манкреса — приведен в § 14.1 —14.4, перейдем к изложению
приближенных алгоритмов решения задачи назначения.
Приближенные методы. Для задачи назначения большой раз-
мерности, а также при лимитированном расходе вычислительного
времени часто приходится прибегать к приближенным методам.
Приведем некоторые из них, наиболее распространенные.
1.	Метод минимального элемента. Для матрицы С1, = (с;),
у, г=1,и, отыскивается минимальный элемент Ci=mincy. При
1> 3
дальнейшем рассмотрении из матрицы исключаются строка
и столбец, на пересечении которых находится элемент сх
и образуется матрица Сп-1. Для матрицы С-1 отыскиваем
таким же образом минимальный элемент с2 и т. д. до тех пор,
пока в каждой строке и столбце матрицы С” не окажется по
одному назначенному элементу.
2.	Метод минимального взвешенного элемента. Идею, описан-
ную выше, применяют к матрице Д", полученной из матрицы
С" следующим образом:
где Д£ = £ £ c;j, Д,.= £ су, Д,.= £ су,
i=U = I	J=I	i=l
3.	Метод Фогеля. Идея метода совпадает с идеей метода
минимального элемента, но элемент с: определяется по формуле
ст = тах( mincy — iritmin Cy-intc,J,
\ ’	1 1 I i ' /
где intcy—ближайший к наименьшему элементу в у-м столбце;
I
intcy — ближайший к наименьшему элементу в г-й строке.
4.	Метод построчного (постолбцевого) сканирования. Осущест-
вляя просмотр строк в некоторой фиксированной последователь-
ности, выбирают в строке минимальный элемент. Столбец,
350
в котором содержится этот элемент, так же как и строка,
называется покрытым и исключается из дальнейшего рассмот-
рения. Затем просматривают следующую строку последователь-
ности, выбирают минимальный элемент среди непокрытых сто-
лбцов и т. д.
Аналогичный просмотр может быть организован начиная
с фиксированной последовательности столбцов.
§ 16.2.	Методы решения задачи коммивояжера
В основу классификации довольно большого числа существую-
щих методов решения задачи коммивояжера может быть положе-
на либо общность идей алгоритмов, либо схема получения
решения.
В настоящем параграфе будет проведена классификация мето-
дов цо схеме получения решений. Сначала приведем три основные
схемы получения решений, а затем рассмотрим более подробно
некоторые из них.
Улучшение цикла. Основу большого числа алгоритмов, бази-
рующихся на этой схеме, составляет следующий алгоритм.
Шаг I. Пусть имеется произвольный начальный цикл /0 = (1,
2, я, I).
Шаг 2. С помощью некоторой фиксированной процедуры
изменения 1п попытаемся найти улучшенное возможное решение
(цикл) tр
Шаг 3. Если улучшенное решение найдено (т. е. длина
меньше длины Го), то заменим t0 на гг и перейдем к шагу 2.
Шаг 4. Если процедура не позволяет в дальнейшем произво-
дить улучшение решения, то полученный цикл—локально-опти-
мальный. Запомним иаилучший из локально-оптимальных циклов,
полученных к этому времени, и перейдем к шагу 1, выбрав
новое допустимое решение.
Повторяют описанную последовательность действий до тех
пор, пока не кончится отпущенное вычислительное время или
решения не станут удовлетворительными.
Известные алгоритмы, базирующиеся на этой схеме, отличают-
ся друг от Друга только эвристической процедурой улучшения
на шаге 2. Как правило, в качестве такой процедуры выступает
преобразование инверсии. В наиболее простом варианте оно
выглядит следующим образом: tY —цикл, лучший чем /0, об-
разован перестановкой любого элемента /=2, ..., я с г = 1.
Все алгоритмы этого типа—приближенные.
Последовательное построение цикла. По этой схеме выбирают
произвольный город, скажем г'р и последовательно, включая
другие допустимые города, согласно тому или иному алгоритму,
строят последовательность т2, ..., ik). Алгоритм заканчивает
работу, как только цикл доведен до конца.
351
Среди точных алгоритмов последовательного построения цик-
лов отметим динамическое программирование, метод ветвей
и границ в форме Литтла, Мурти, Суини и Кэрела [5],
Приближенные алгоритмы, базирующиеся на данной схеме,
используют главным образом идеи динамического программиро-
вания. Более того, все алгоритмы этого типа можно классифици-
ровать по степени «строгости» выполнения условий принципа
оптимальности Веллмана. Наименее строг в этом смысле алго-
ритм выбора ближайшей точки: из города ij перейти к ближай-
шему городу i2, от i2— к ближайшему городу, еще не достигну-
тому (исключая Л и ?2), ..., из i„ вернуться в q,
В одном обобщении алгоритма выбора ближайшей точки
производится некоторый прогноз на к шагов вперед. Для этого
рассматривается п — 1 начальных путей из города и каждый
из них алгоритмом выбора ближайшей точки достраивается
дугами, проходящими через к городов. Выделив среди них путь
минимальной длины, определяют город г2, в который должен
направиться коммивояжер из начального города (тем самым
обеспечив ла £-м шаге «наилучший» вариант выбора). Для
второго города /2 строится л —2 начальных путей, и они
достраиваются алгоритмом ближайшей точки и т. д. Начиная
с п — к+\ шага алгоритм всегда будет просматриваться до
конца, т. е. до города iv
Исключение подциклов. Основу этой схемы составляет сле-
дующий алгоритм.
Шаг 1. Решим задачу назначения с исходной матрицей С.
Шаг 2. Проверим, является ли полученное решение циклом.
Если да, то решение задачи коммивояжера получено, в противном
случае перейдем к шагу 3.
Шаг 3. Используем различные приемы наложения дополни-
тельных условий, позволяющие исключить из дальнейшего рас-
смотрения выделяемый подцикл, но не возможные циклы задачи
коммивояжера,
Шаг 4. Проведем решение вновь полученной задачи и перейдем
к шагу 2.
Точные методы исключения тюдциклов представлены в основ-
ном линейным целочисленным программированием (первая груп-
па методов) и методом ветвей и границ (вторая группа) [6].
Близкой к этой схеме по содержанию, положенного в основу
получения решения, является группа алгоритмов метода ветвей
и границ, в которых в качестве нижней границы используется
не решение соответствующей задачи назначения, а решение
соответствующей задачи о кратчайшей стягивающей сети (или
ее модификации). Если в алгоритмах первой группы шаг 3
служит для того, чтобы ликвидировать получающуюся несвяз-
ность графа (подциклы), то в алгоритмах второй группы аналог
шага 3 служит для того, чтобы в каждую вершину получающегося
352
решения входило ровно две дуги (этими двумя свойствами
обладает оптимальное решение задачи коммивояжера). Кроме
того, на шаге 1 для алгоритмов второй группы следует решать
задачу о кратчайшей стягивающей сети или ее модификации
[6]. В остальном алгоритм получения решения задачи коммиво-
яжера для алгоритмов второй группы такой же, как и приведен-
ный выше.
Все перечисленные здесь методы сводят задачу коммивояже-
. ра—задачу дискретного программирования — к последователь-
ности решения более простых задач линейного программирования
того или иного вида.
§ 16.3.	Точные методы
Все известные точные методы (в том числе и приводимые -
ниже) обладают существе иным недостатком: время решения в них
растет экспоненциально росту числа городов. Более того, выска-
зана гипотеза о принципиальной невозможности избавления от
этого недостатка. Помимо экспериментальных фактов в пользу
этой гипотезы говорят и теоретические результаты [I], согласно
которым для задач дискретного программирования можно выде-
лить два больших класса: Р и NP. К классу Р задач относятся
задачи, время решения которых ограничено сверху значениями
полинома от числа, характеризующего размер задачи (алгоритмы,
позволяющие находить такие решения, называются полиномиаль-
ными). К классу NP-задач задачи, время решения которых
ограничено значениями экспоненты с показателем, характери-
зующим размер задачи (такие задачи называются NP-полпыми
или универсальными). Для большой группы NP-полных задач
удается показать, что из существования полиномиального алго-
ритма для одной задачи из NP класса следовало бы существова-
ние такого алгоритма для всех задач этого класса, В настоящее
время доказана NP-полнота как для задачи коммивояжера, так
и для ряда других связанных с этой задачей проблем. Приведем
описание некоторых точных алгоритмов решения задачи комми-
вояжера.
§ 16.4.	Динамическое программирование
Динамическое программирование является одним из перспек-
тивных -методов решения задачи коммивояжера. Метод прост,
но требует большой оперативной памяти, что сдерживает его
.применение. Для задач небольшой размерности (л ^18) и при
условии работы с ЭВМ этот метод предпочтительнее, чем все
другие разработанные методы. Алгоритм динамического програм-
мирования для задачи коммивояжера был применен и разработан
Хелдом и Карном, Веллманом [5].
12 Зак
353
Введем необходимые определения. Пусть начальным городом
является город 1 и ik^l—некоторые различные города,
отличные от начального. Пусть fk. Д1,	...,	zm+1, ..., ik^
im)—длина кратчайшего пути, соединяющего город I с городом
im и проходящего через города Л, ...,	im+1,	гк^1. Тогда
принцип оптимальности (см. § 15.4) для задачи коммивояжера
дает следующее рекуррентное соотношение:
А(1; гь 4-р/) =
= min_!/fe„!(1; 4, ..., zM + J, 4-,; Q+cfJ. (16.6)
m = 1, Л
Последовательное применение соотношения (16.6) приводит
к такому алгоритму.
Шаг 1. Вычислим функцию
/1(1;	*=2, п.
Шаг 2. Вычислим функцию
'fl (U 1[, 4) =/1 (4 4) + СЩг’ 1 Ь П‘ ii=0Z2-
Шаг 3. Вычислим функцию
Уз(1 S 1 р 1з) 2 О S г 1 ’ 4) ТСЦЬ> 11 ’ 4, 4 = 2, п; 4, г2 4» 4^4*
Шаг к(4^к^п — 1). Вычислим функцию /t(l; г,, , 41 4+1) Д-ПЯ|
всех значений гь 4, > 4+i(4^4 при	ф = 2, п‘, '’=1, 2, ..Щ
£+1):
Л(1; 4, i2, ..., 4; 4+1) = min{[A;1(i; 4, 4, 4)+с'„ .t+1L
[А -1 (1; гр 4, •••’ 4;1 г)+,], [A-i(4 f,4)	+J}-'
Шаг и. Вычислим функцию
/л(1; 2, 3, ..., я; l) = min {[/„-1 (1; 3, ..., п; 2) + с21],
[/п-1(1; 2, 4, ..., п; 3) + С3[], ..., [А-Д1; 2, ..., я-1; и)+ся1]}.
В [5] приводятся оценка суммарного объема необходимых
вычислений на всех шагах алгоритма (^л2 2Л^1) и оценка*
максимально необходимого объема памяти машины (^н -2"~ 1’:
ячеек). По сравнению с полным перебором, для которого число
необходимых вычислений для асимметричной матрицы (су) равно
(«—!)!, достигнуто существенное сокращение объема вычислений
за счет заметного увеличения памяти. Рекуррентное соотношение
(16.6) для задач размерности д>18 позволяет находить нрибли-’
женные решения задачи коммивояжера.	х
354
§ 16.5.	Методы ветвей и границ.
Алгоритм Литтла и др.
В настоящее время наибольшие успехи в получении точного
решения задачи коммивояжера достигнуты с помощью алгорит-
мов, основанных на схеме метода ветвей и границ: для несим-
метричных матриц расстояний—алгоритмом Беллмора -Мэло-
уна (и его развитием), для симметричных—алгоритм Хел-
да—Карпа и их модификациями [6]. Изложение алгоритмов
этой группы методов начнем с алгоритма Литтла, Мурти, Суини
и Кэрела [5], после получения которого началось бурное развитие
методов ветвей и границ.
Алгоритм Литтла и др. использует нижнюю границу, основан-
ную на применении свойств приведенной матрицы и процесса
приведения. Введем эти понятия.
Если из всех элементов некоторой строки i (столбца у)
исходной матрицы С вычесть минимальный элемент, подучим
новую матрицу, в которой в данной строке (столбце) имеется
по крайней мере один нулевой элемент. Повторим эту операцию
для каждой строки и столбца и получим в результате новую
матрицу, называемую приведенной, в каждой строке и столбце
которой имеется, по крайней мере, но одному нулевому элементу.
Процесс образования нулевых элементов называется приведением,
а вычитаемые в процессе приведения элементы — константами
приведения. Их сумму обозначим через hs, где ^- — порядковый
номер приведения.
Если c;j{f) = minc то процесс приведения по строкам приводит
J J
к матрице (су) с элементами c^=cy—Если
то процесс приведения по столбцам приводит к матрице (с'£))
с элементами с-', = с'£; — с££,£,. В этом случае сумма констант
J J U,J	л	л
приведения hl	определяется выражением	й1 = £	£	сДду
i=l	j=i
Если z(z) = £	—длина цикла Г до приведения, zJ(r)= £ с;'. 
(i.jleT	(ТДе,'
длина (издержки) цикла t после приведения, Л1—сумма констант
приведения, то z(r) =zI (z) + h *. Так как все элементы при-
веденной матрицы (с;)) неотрицательны, то Л1 —нижняя гра-
ница (заметим, простейшая) для длины (издержек) цикла t
при старой матрице (c£j).
Для описания процедуры ветвления используем геометричес-
кую интерпретацию. Разбиение множества всех циклов на недере-
секающиеся подмножества будем изображать в виде дерева
с вершинами, состоящими из пар городов (г, у) и запрещенных
12*	355
(\)	(i,J) переездов, т. е. ветвь, проходя-
щая через вершину (/, у), содержит все
(7/) маршруты, включающие переезд из
(XJ\	города i в город у; ветвь, проходящая
через вершину (г, у), содержит все
Ч-z маршруты, в которых переезд из i
в у запрещен. Например, ветвь, про-
рис- 16J	ходящая через вершину (7с, /), содер-
жит все маршруты, в которых осу-
ществляется переезд из города i в j и запрещен переезд из
к в I (рис. 16.1).
Если из некоторой вершины X подняться вверх по дереву
к его началу, то можно назвать все вершины, которые входят
и не входят в циклы, принадлежащие X. Условимся вершину,
из которой осуществляется ветвление, обозначать через X.
Вершину, которая наиболее вероятно принадлежит перспективной
ветви, обозначим через Y, а вершину с запрещенной парой
городов, соответствующей У,— через У, Опишем процесс выбора
вершин У и У из вершины’ X.
Так как в задаче коммивояжера надо найти минимум издержек,
то минимальные издержки при рассмотрении У наиболее вероят но
содержатся среди циклов с элементами (/, у). для которых с;-=0.
Так как в приведенной матрице в каждой строке и столбце
имеется, по крайней мере^ по одному такому нулевому элементу,
получается неоднозначности выбора. Устраним эту неопределен-
ность рассмотрением издержек, связанных с невключением (i,j\
т, е. с У.
Так как из города / мы должны выехать в какой-то город
/с (ЛУу), то множество У содержит один из переездов МА;
с издержками, не превышающими наименьшего элемента строки
i (т. е.	Так как в городу мы должны въехать, то
j
множество У содержит переезд l->j (l^i) с издержками, не
превышающими наименьшего элемента столбца у (т. е. cI(.^rnincy).
Обозначим сумму этих двух издержек через 0(г, у). В качестве
(/с,/) —пары городов, на которой основывается ближайшее раз-
ветвление множества У на множества У и У, —выбираем ту,
для которой 0(/, у) - - наибольшее. Другими словами, среди ну-
левых элементов с,, = 0 выберем тот, для которого 0(7, ?) мак-
симально.
Приведем формальную схему алгоритма Литтла и др.
Шаг 1. Полагаем s= 1 и осуществим приведение матрицы
С по строкам и столбцам, переходя к приведенной матрице Cs.
Шаг 2. Вычислим сумму приводящих констант hs —оценку
для множества X—и обозначим ее <о(Х).
356
Шаг 3. Выберем претендентов для включения в множество
У, т. е. все те (/, /), /,у=1,и, для которых <ю = 0-
Шаг 4, Для выделенных претендентов подсчитаем 0(ij) = с!к + ctj
и выберем 0(/с, /) = max0(/, у) по всем г, j, для которых cr-j = О-
Пара (к„ Г) включается в множество У и является запретной
для множества У,
Шаг 5. Подсчитаем оценку для множества го(У) = со(У) + 0(А.\ /).
Шаг 6, Исключим из дальнейшего рассмотрения А-ю строку
и Ай столбец (так как из каждого города можно выезжать
и въезжать в него только один раз) и полагаем с[к = ао
(чтобы избежать образования замкнутых подциклов меньшей
длины, чем н).
Шаг 7. Полученная усеченная матрица на некотором шаге
ветвления становится размерностью 2 х 2 и содержит лишь две
допустимые пары городов, являющиеся замыкающими для неко-
торого маршрута без подциклов меньшей длины, чем п. Прове-
рим, имеет ли усеченная матрица размерность 2x2. Если имеет,
то переходим к шагу 9, если нет —к шагу 8.
Шаг 8. Проверим, является ли усеченная матрица приведенной.
Если не является, то осуществим приведение усеченной матрицы,
подсчитаем /г'+1, после чего ы(У) = то (У) + h ’+1. Полагаем y=.s +1
и переходим к шагу 3.
Шаг 9. Проверим условия оптимальности: если оценка цикла
не больше оценок всех допустимых для дальнейшего ветвления
множеств, то полученный цикл — оптимальный. Если существует
хотя бы одно множество с меньшей оценкой, то полученный
цикл запоминается. Тогда процесс ветвления следует продолжить
Есходя из множества с меньшей оценкой,
 Предлагаемым алгоритмом за приемлемое время (ж 500 с,
ЮМ 7090) можно решить задачи до п = 40.
| Пример^ешить задачу коммивояжера с матрицей расстояний
|ц), Л./=Ь 6-
	j					
	I	2		3	4	5	6
1	СО	97	60	73	17	52
2	97	СО	41	52	90	30
3	60	41	СО	21	35	41
4	73	52 1	21	00	95	46
5	17	90	35	95	00	81
6	52	30	41	46	81	СО
1. Осуществим вначале приведение по строкам, затем по
столбцам, записав константы приведения соответственно справа
и внизу от приведенной матрицы:
i	J						
	1	2		3	4	5	6	
1	со	80	43	56	0	35	17
2	67	со	И	22	60	0	30
3	39	20	СО'	0	14	20	2]
4	52	31	0	со	74	25	21
5	0	73	18	78	•ос	64	17
6	22	0	11	16	51	СО	30
	0	0	0	0	0	0	
2. Вычислим сумму приводящих констант:
h'= 17 + 30 + 21 +21 +17+ 30 = 136.
3. Выберем пары претендентов на ветвление, т. е. для
которых <= = 0:
5= 0, <+6 = 0, с34 = 0, с4з = 0, с51 =0, с62 =0;
015 = 35 +14 = 49, 026 = 11+2О = 31, 034 = 20 +16 = 36,
043=25 + п = 36, е62 = 11 +20 = 31;
тахО;==015 =49. Пара вершин (1, 5) выбирается для ветвления,
4. Исключение пары верщин (1, 5) из маршрута (т. е. наложе-
ние условий е15 = оо) позволяет осуществить дополнительное
приведение матрицы по строке на 35, а по столбцу — на 14
единиц. В итоге получаем оценку
й)(У) = 136 + 49= 185.
5. Вычеркнем 1-ю строку и 5-й столбец, полагаем cSi = oo,
приводим полученную матрицу, записав дополнительные констан-
ты приведения соответственно справа и внизу от первой из
матриц;
!	j					
	1	2		3	4	б	
2	67	со	11	22	0	0
3	39	20	ОС'	0	20	0
4	52	31	0	со	25	0
5	со	73	18	78	64	18
6	22	0	11	16	со	0
	22	0	0	0	0	
!	j				
	I	2	3	4	6
2	45	СО	11	20	0
3	17	20	оо	0	20
4	30	31	0	ОС	25
5	СО	57	0	60	46
6	0	0	11	16	со
358
Сумма приводящих констант будет h2 = 18+22 = 40, Получен-
ная матрица не является матрицей 2x2, поэтому сразу перейдем
к вычислению оценки для У:
ы(У) = 136 + 40= 176,
Процесс дальнейшего ветвления рекомендуется вести так,
чтобы возможно быстрее получить некоторый маршрут. Длину
этого маршрута можно использовать для того, чтобы отбрасы-
вать большое количество ветвей с нижней границей, превышаю-
щей длину этого маршрута. Именно поэтому для дальнейшего
ветвления выбираем множество (1,5), а не (1, 5). Процесс
повторим с п. 1.
Так как полученная матрица — приведенная, то выделим пары
(i,j) претендентов на ветвление:
*26=0, *34 = 0, *43=0> f53”^ CG1 “0,
026 = 31, 034 = 33, 04з = 25, е53 = 46, 06i = 17, 062 = 2О;
тах0;; = 053 = 46, Пару (5, 3) выбираем для ветвления.
Вычислим оценку: ©(?) = 176 + 46 = 222.
Вычеркнем 5-ю строку и 3-й столбец, произведем приведение
полученной матрицы:
1					
	1	2		4	6	
2	45	со	22	0	0
3	17	20	0	20	0
4	30	31	00	25	25
6	0	0	16	СО	0
0	0	0	0
	}			
	J	2		4	6
2	45	ос	22	0
3	17	20	0	20
4	5	6	со	0
6	0	0	16	со
Вычислим сумму приводящих констант й3 = 25. Получен-
ная матрица не является матрицей 2x2, поэтому вычис-
лим оценку для множества У: со (У) = 176 + 25 = 201. Процесс
повторим с п. 1.
Выберем пары (/,/) претендентов на ветвление:
• 	<+б=0, *34=Д *4б=0,- с61=0, с62=0;
026 = 22, 0Э4 = 33, 04(? = 5, 0б1. = 5, 062 = б;
тах0!7 = 034 = 33. Пару вершин (3,4) выбираем для ветвления.
Вычислим оценку: и(У) = 201 + 33=234,
Вычеркиваем 3-ю строку и 4-й столбец, производим приведение
полученной матрицы:
359
Вычислим сумму приводящих констант /г4 = 0. Полученная
матрица не является матрицей 2x2, поэтому вычислим оценку
для множества У: и (У) = 201. Процесс повторим с и. 1.
Так как Полученная матрица приведенная, то выделим пары
индексов (г, у) — претендентов на ветвление:
^2б~0, с4й = 0,	— 0, Сб2~ 0;
026 = 45, 046 = 5, 961 = 5, 062 = 6;
max0l7=026=45. Пару вершин (2,6) выбираем для ветвления.
Вычислим оценку: <в(У) = 201 + 45 = 246.
Вычеркнем 2-ю строку и 6-й столбец, произведем приведение
полученной матрицы:
Вычислим сумму констант приведения: /г5 = 5.
Оценка дня множества У:со(У) = 201 + 5 = 206.
Полученная матрица 2x2 допускает только включение двух
) вершин
пар
(4, 2). (6, 1), что дает дополнительную оценку
приведения /гб=1. Полученный
цикл (рис. 16.2) (1, 5), (5, 3),
(3, 4), (4, 2), (2, 6), (6, 1) имеет
длину z(f)=207.
Анализируя полученные ранее
оценки для неветвлеппых мно-
жеств, видим, что неветвденное
множество У—(1, 51 имеет мень-
шую оценку: со(У)=185. Это
множество может привести к об-
360
разованию цикла с меньшей оценкой, поэтому доисследуем
процесс ветвления для этой ветви. Так как подмножество У = (1, 5)
является левым, то восстановим исходную матрицу расстояний,
полагаем в ней с15 = ос и переходим к п. 1.
i	J					
	1	2	3	4	5	6
1	ос	45	8	21	со	0
2	67	СО	И	22	46	0
3	39	20	СО	0	0	20
4	52	31	0	со	60	25
5	0	73	18	78	ОС	64
6	22	0	И	16	37	GO
пары претендентов на ветвление:
С1б=^1 С26 = 9,	с34 = 0>	С43= 0,
'16 = 8, 026 = 1 1, 034= 16, 043 = 33,
iax0:; = 0=, =40. Пару вершин (5, 1)
Вычислим сумму приводящих констант: h"1 = 185. Выберем
<-5[ = 0,	С35 = О,
051 =40, 062 = 31, 035 = 37;
выбираем для ветвления.
Вычислим оценку: св(У) = 185+40 = 225.
Вычеркнем 5-ю строку и 1-й столбец:
Г	J				
	2	3	4	5	6
1	45	8	21	со	0
2	СО	11	22	46	0
3	20	со	0	0	20
4	31	0	со	60	25
6	0	11	16	37	X)
Вычислим сумму приводящих констант: hs = 0. Полученная
Еатрица не является матрицей 2x2, поэтому вычислим оценку
ля множества У:ы(У)=185. Процесс повторим с п. 1.
Выберем пары претендентов на ветвление:
с'1б=0, с2й = 0 , с34 = 0, с35=0 , с4з = 0 , с62 = 0;
016 = 8, 026= 11, 034= 16, 0Э5 = 37, 043 = 33, 062=31;
iax0y= 035 = 37- Пару__ вершин (3, 5) выбираем для ветвления,
вычислим оценку: ш(У)= 185 + 37 = 222.
361
Вычеркнем 3-ю строку и 5-й столбец, произведем приведение
полученной матрицы:
!	J				
	2	3	4	6	
1	45	8	21	0	0
2	СО	11	22	0	0
4	31 .	0	СО	25	0
6	. 0	11	16	СО	0
	0	0	16	0	
J	i			
	2	3	4	6
1	45	8	5	0
2	СО	11	6	0
4	31	0	ОС	25
6	0	и	0	СО
Вычислим сумму приводящих констант: h9 =16. Полученная
матрица не является матрицей 2x2, поэтому вычислим оценку
для множества У:ы(У)= 185+16 = 201. Повторим процесс с n. 1.
Выберем пары претендентов на ветвление;
С16=б, С2б = 0, С43=0,	C62 = 0,	С64 = ^
916=5, о26=б, о43=зз, е62=з1, ем=5;
тах0у = 04Э = 33. Пару_ вершин (4,3) выбираем для ветвления.
Вычислим оценку: го(У) = 201+33 = 234.
Вычеркнем 4-ю строку и 3-й столбец:
j	2	4	6
I 2 6	45	5	0 со	6	0 0	0	со
Вычислим сумму приводящих констант; /г1()=0. Полученная
матрица не является матрицей 2x2, поэтому вычислим оценку
для множества У:ш(У) = 201. Повторим процесс с п. 1.
Выберем пары претендентов на ветвление:
с16=0, С26 = ^; с62~^>	С'б4=0>
916 = 5, 02& = 6, 062=45, 064 = 5;
тах0у = 0б2 = 45. Пару вершин (6, 2) выбираем для ветвления.
Вычислим оценку: го(У) = 201+45= 246.
Вычеркнем 6-ю строку и 2-й столбец, полагаем с26 = <х>,
произведем приведение полученной матрицы:
Вычислим сумму приводящих констант; /г11 =6. Полученная
матрица 2x2 допускает только включение двух пар вершин
(2, 4), (1, 6). Итак, выделен второй цикл (рис. 16.3): (1, 6), (6, 2),
(2, 4), (4, 3), (3, 5), (5, 1) с длиной z(f) = 207.
§16.6. Алгоритм Беллмора — Мэлоуна
Алгоритм Беллмора — Мэлоуна существенно использует фор-
мулировку задачи коммивояжера в виде (15.25) — (15.28), (15.32),
а в качестве оценок снизу — решения соответствующих задач
назначения. Приведем формальную схему алгоритма с некото-
рыми модификациями [6].
Шаг 1. Решим задачу назначения с исходной матрицей рас-
стояний С и определим нижнюю границу всех циклов, содержа-
щихся в этой матрице. Проверим, является хотя бы одно из
полученных решений циклом. Если является, то получено решение
задачи коммивояжера, в противном случае перейдем к . шагу 2.
Шаг 2. Среди подциклов одного из полученных решений
задачи назначения выбираем (для определенности) подцикл с на-
именьшим числом дуг (если таких подциклов несколько, то
любой из них). Пусть выбран подцикл А = рь 1г? ... ik, /Д из
к<п дуг. Введем в рассмотрение множества: Лг=И?,у):
еЛ\Д, Я; = Ш,/): i=i„ jе Л),	М-,=А1 М2 = А\[}А2,
лл=л;ил'2ил3,Л4=л;ил'2и...и^_1и4,
Составим список из к задач назначения с матрицами расстоя-
ний С',	с элементами (с’;Д'=со, если	(с^у = с.и,
если	Далее перейдем к шагу 3.
Шаг 3. Задача назначения составленного списка числом
k решается алгоритмом, описан-
ным в § 14.1 — 14.3, например до
этапа I включительно, т. е. до
получения значений I г < к.
Задача назначения из списка с на-
именьшим значением. /г-функцио-
нала (пусть ей соответствует ин-
декс гД решается до конца, т. е.
с применением (в общем случае)
этапа II названного алгоритма
/лг 2О>	20?	207
Рис. 16.3
i
и вычислением значения I Проверим выполнение неравенств
(1 = 1, k, если выполняются все эти неравенства
и полученное решение есть цикл, то получено решение задачи
коммивояжера; если в этих же условиях полученное решение
не есть цикл, то переходим к шагу 2, приняв в качестве
исследуемого решения задачи назначения вновь полученное; если
не выполняется хотя бы одно из этих неравенств, то решается
до конца задача назначения с наименьшим значением Дфунк-
ционала,	(пусть ей соответствует индекс г2),
проверим выполнение неравенств 1,^1, (l~ I, ^6, г2),
, и т' Д- Д° тех П0Р, пока таким же образом не будут
просмотрены все значения lt,
Изложение алгоритма закончено.
Замечание. В шаге 3 при переходах к шагу 2, вызванных получением нового
решения задачи назначения, помимо ветвей, образованных в результате «разрыва»
одного из подпиклов этого решения, следует учитывать непросмотренные
(«висячие») ветви, образованные в результате «разрыва» предыдущего решения
задачи назначения.
Пример. Решить задачу коммивояжера с матрицей расстояний
(сг7), i,y=i, 6.
i	J					
	1	2		3	4	5	6
1	со	97	60	73	17	52
2	97	СО	41	52	90	30
3	60	41	со	21	35	41
4	73	52	21	ОС	95	46
5	17	90	35	95	со	81
6	52	30	41	46	81	оо
]. Решим задачу назначения с исходной матрицей С с по-
мощью алгоритма, изложенного в § 14. L — L4.3. Получим решение
й[5 = й51 = й2б — й62 — йЭ4 = й43 = I (совокупность подциклов) со зна-
чением функционала, равным 136.
2.	Так как все три подцикла состоят из двух дуг, то выберем
любой из них, например й15 = й51, для организации ветвления.
Найдем множества 4l=(l, 5), Я'1=((1, 2), (1,3), (1,4), (1,6)),
Я5=((5, 1)), Л/[ = ((1,5)), АГ2=((5, 1); (1,2), (1,3], (1,4), (1,6)).
Формируем две задачи назначения: для первом — с13 = оо; для
второй с5 [=с12 = с[3 — с14 = с]6 = со.
3.	С помощью алгоритма, изложенного в § 14.1 — 14.3, вычис-
лим значения /г-функционалов (/= 1,2). Для первой задачи назначе-
ния = 165, для второй —/2 = 196. Решим первую задачу назначе-
ния до конца и получим решение й14 = й43 = w35-й31 =м26 = w62 = I
(совокупность подциклов) со значением функционала, равным 206.
364
\ Так как каждая из вершин получаемого дерева имеет оценку
снизу / = 206, то продолжим любую ветвь, например ветвь,
исходящую из первого решения задачи назначения, т. е. из
решения й14 = й43 = й35 = й53 =й26 = й62= I. Перейдем к шагу 2 ал-
горитма.
Поскольку подцикл й2ъ — й62=1--с наименьшим числом дуг,
выберем его для организации ветвления. Найдем множества
/И2 = ((6, 2); (2, L), (2,3), (2,4), (2,5)). Формируем две задачи
назначения (обозначим их номерами 3 и 4): для третьей — с26 = со;
дня четвертой —с62 =- с21 = с23 = с24 =-с25 = со.
Вычислим значения 4-функционалов (f = 3, 4). Для третьей
задачи назначения /3 = 206, для четвертой—/4 = 219. Решим третью
задачу назначения до конца и получим решение й,  = й62 = й24 =
= й43 —й35 = й5, = 1 (гамильтонов цикл) со значением функционала,
равным 207. Так как полученное значение меньше /4 = 219, то
нет необходимости продолжать решение четвертой задачи назна-
чения до конца.
Так как значение 1г = 206 < /3 — 207, то следует продолжить
ветвь, исходящую из второго решения задачи назначения, т. е.
из решения й15 = й53 = й34 = й41 = й26 = йб2= I. Перейдем к шагу
2 алгоритма.
Так как подцикл й26 = й62=1 с наименьшим числом дуг, то
выберем его для организации ветвления. Найдем множества
Д2 = {{2, 6)}, А'2 = {(2, 1), (2,3), (2,4), (2,5)}, Л6 = {(6, 2)}, М, =
= {(2, б}}, М2-{(6, 2); (2,1), (2,3), (2,4), (2,5)}. Формируем две
задачи назначения (обозначим их номерами 5 и 6): для пятой —
с26=оо, для шестой — с62 = с21 =с23 = с24 = с25 = со.
Вычислим значения /-функционалов (/ = 5, 6). Для пятой 15 =
= 217, для шестой /6 = 206. Решим шестую задачу назначения до
конца и получим решение
мильтонов цикл) со значе-
нием функционала, равным
207. Так как полученное
(значение меньше /5 = 217,
(нет необходимости продол-
жать решение пятой задачи
(назначения до конца.
Полное дерево решений
представлено на рис. 16.4.
Алгоритм Беллмора —
Мэлоуна (без отмеченных
выше модификаций) успе-
шно применялся для ре-
шения асимметричных за-
дач вплоть до n= 120 на
IBM 7094 II, причем время
365
решения задачи изменялось по следующему эмпирически най-
денному закону: 7^0,55 • 10 “4-и3-46. С симметричными задачами
алгоритм работает хуже из-за наличия большого количества
подциклов длиной два. Для таких задач хорошо зарекомендовал
себя рассматриваемый ниже алгоритм.
§ 16.7. Алгоритм Хелда — Карпа
Алгоритм Хелда—Карпа, разработанный для решения симмет-
ричных задач [17], использует формулировку задачи коммивоя-
жера в виде (15.25)— (15.29), (15.31), а в качестве оценок
снизу —так называемое кратчайшее 1-дерево. Введем некоторые
понятия.
Пусть G- полный ненаправленный (т. е. с симметричной
матрицей расстояний) граф с множеством вершин (1,2, ..., я).
Ребро, инцидентное вершинам i и /, обозначается у) и характери-
зуется весом с,г Вес подграфа есть сумма весов его ребер.
Напомним (см. § 14.5), что в задаче коммивояжера надо найти
цикл (т. е. замкнутый путь, проходящий через каждую вершину
только один раз) минимального веса. Под цепью понимается
последовательность идущих друг за другом ребер. Связанный граф
(т. е. граф, в котором любые две вершины соединены цепью) без
циклов называется деревом. В задаче о кратчайшем остове ищется
дерево минимального веса с множеством вершин {1, 2, ..., «}.
Кратчайшее 1-дерево состоит из кратчайшего остова с множеством
вершин (2, ..., п) и двух кратчайших ребер, исходящих из вершины
1 к двум другим вершинам дерева. На основе определения как
кратчайший остов, так и кратчайшее 1-дерево являются оценками
снизу для задачи коммивояжера. Граф оптимального решения Этой
задачи обладает следующими двумя свойствами:
1) является связным, т. е. каждую вершину можно соединить
с любой другой вершиной цепью;
2) степень каждой вершины равна двум, т. е. каждая вершина
инцидентна двум ребрам.
На рис. 16.5, а — б приведены соответственно примеры 6-вер-
шинных графов оптимальных решений задачи коммивояжера,
задачи назначения и кратчайшего остова. Граф Gt обладает
свойством 2, но не обладает свойством 1; граф G, обладает
свойством 1, но не обладает свойством 2. Если окажется, что
для задачи назначения выполняется свойство 1, то полученное
решение для этой задачи является и решением задачи коммиво-
яжера с той же матрицей расстояний. Алгоритм Беллмора —
Мэлоуна можно рассматривать с этих позиций как алгоритм,
использующий в качестве оценок снизу решения задачи назначения
и добивающийся, чтобы хотя бы одно из них удовлетворяло
и условию 1. Если окажется, что для задачи о кратчайшем
1-дереве выполняется свойство 2, то полученное решение
366
является и решением задачи коммивояжера с той же матрицей
расстояний. Алгоритм Хелда — Карпа как раз и реализует
последнюю идею.
Для реализации алгоритма Хелда — Карпа требуется умение
решать задачу нахождения кратчайшего 1-дерева. Решение послед-
ней можно реализовать следующим образом: решить задачу
нахождения кратчайшего остова для вершин (2, п) (для ее
решения существуют эффективные алгоритмы, работающие с за-
дачами размерности и >1000, например Дийкстры или Краскала
[16]) и затем присоединить два кратчайших ребра, исходящих
из вершины 1.
Приведем лемму, имеющую важное значение для обоснования
алгоритма.
Лемма 16.1 [17]. Пусть ..., лп)—действительный «-мер-
ный вектор. Если с* — цикл с минимальным весом по отношению
к реберным весам cih то он также является циклом с минималь-
ным весом по отношению к реберным весам + +	i, 7 = 1, «
Доказательство. Вес цикла с по отношению к весам
 есть £ Cjj, а по отношению к весам сд-+л, + л j есть
((.Дес
д (сд+ т^ + тгД. Так как любая вершина принадлежит двум
Й.Дес	и
ребрам из с, то вторая сумма минус первая есть точно 2 £ л(.
i = i
Следовательно, при замене одного множества весов другим
минимальная цена с* цикла изменяется на постоянную величину,
не зависящую от выбранного цикла. Лемма доказана.
Выясним связь задачи нахождения кратчайшего 1-дерева
с линейной целочисленной формулировкой. Целочисленная поста-
новка задачи коммивояжера в виде (15.25) --- (15.19), (15.31) для
симметричной задачи может быть записана в виде [17]
/= Z с;р^->ппп,
(16.7)
367
(16.9)
ieSjeS
’<!	—для любого, подмножества
У«(2, 3, ..., «),
О хчс I, 1 <i<j^п,	(16.10)
хо-(0, 1), 1^<7Чл.	(16.11)
Здесь связи (16.8) для симметричного случая заменяют связи
(15.26), (15.27) задачи назначения и означают, что каждая
вершина инцидентна двум ребрам, т. е. степень каждой вершины
равна двум.
Лемма 16.2 [17]. В условиях (16.7)—(16,11) ограничения (16.8)
можно заменить следующими:
Е хо+Е хо-2> f'=7>(«“О,
Е хИ=п-
Доказательство.
I xir^ E (Ехм+Ехи)=5
‘-1	J<1	'	\>l	 J<1	'
т. e. с учетом (16.8)
E	
1^</^	' = ’	J'1
E .vi;=(n-i)+L f xjn.
1 < i <_/ -5«	J ~ i
n
Из (16.8) также следует, что £ Лемма доказана. С учетом
леммы 16.2 ограничения (16.^) (16.1 Г) можно записать в следую-
щем виде:
(16.12)
Е^+Е^=2’	(«-1)’	<16ЛЗ)
j>I	j<;
Ехгу = 2,	‘	(16.14)
368
Имин	(16.16)
ieSjeS
для любого подмножества Sc(2,
(16.17)
x,j^0,	(16.18)
x;, = (0, 1).	(16.19)
Приведем систему ограничений (16.12) — (l б. 19) к более удоб-
ному виду. Пусть х и с — векторы размерности п2[2 с компонен-
тами Xfj и с,-, 1^г'</^н, соответственно. Обозначим ограничения
(16.13) через Лх = Ь, ограничения (16.14)--(16,17) через Л’х^Ь',
где А и А'— соответствующим образом Определенные матрицы,
а b и Ь'— векторы (заметим, что b -вектор размерности п — 2,
все компоненты которого равны двум). Тогда задачу (16.12) —
(16.19) можно записать в виде
min {cx:,4х = Ь, ,4'х<Ь', х 0, х = 0 v I}.	(16.20)
Теорема 16.1	[17]. Пусть Т\ Т1, ..., Т*, Tq—1-деревья
с множеством вершин (1, 2, ..., «). Поставим дереву Тк в соответ-
ствие вектор е размерности и2/2 с компонентами ekj определен-
ными условиями:
(1, если у) принадлежит ребру из Т\
[0 в противном случае,

Тогда экстремальными точками многогранника А 'х = Ь', х 1т О
являются точки ек,.
Доказательство. Точки ек- принадлежат многограннику
Л'х^Ь', х^О; они удовлетворяют ограничениям (16.20), так как
вершина I всегда имеет степень два в I-дереве; они удовлетворяют
ограничениям (16.20), так как каждое 1-дерево имеет п ребер;
они удовлетворяют ограничениям (16.16), так как единственный
цикл в 1-дереве содержит вершину 1; они удовлетворяют связям
(16.17) тривиально. Теорема доказана.
Следствие. Задача линейного программирования вида
и,(я) = шт(сх+л^х: А х<Ь , х^О).	(16.21)
X
;е я— вектор размерности (и — 2) с компонентами я2, п3, ..., л„_1
)едставляет собой задачу нахождения минимума 1-дерева с ве-
ми сц+д.+л; (Я1=ля=0).
Действительно, из теоремы 16.1, учитывая, что вектор b цели-
ком состоит из компонент, равных двум, а вектор л —вектор
369
множителей Лагранжа, получим соотношение (16.21), Определяе-
мое из этого соотношения w (л) дает некоторую оценку снизу
для задачи (16.20), т. е. для задачи коммивояжера. Наилучшая
нижняя оценка получается при нахождении та.хифл). Приведем
теорему, связывающую эту задачу максимизации с задачей
(16.12) —(16.19).
Теорема 16.2 [17]. max w (я) = и, где
п
r = min {сх : Ах~Ь, А'х^Ь', х5=0}.	(16.22)
X
Доказательство. По определению (16.22), двойственной
для этой задачи будет следующая:
г = гпах {— ub — u'b': иА 4-и'Л	— с, и' 5:0},
и, и'
г —max [max {— ub — u'b': иА + иД 5= — с, и'5=0}.
и иг
Переходя к двойственной задаче для внутренней задачи
максимизации и рассматривая и как постоянную, получим
v = max {min [сх + и (Лх —b): Л'х<Ь', х>0]}.
Ц х
Полагая и^тг, получим г = max и (я). Теорема доказана.
Следствие, w (тт) = 0 для некоторого п, если и только если
задача лилейного программирования (16.22), являющаяся след-
ствием удаления целых связей (16.11) из (16.7)—(16.11), имеет
оптимальное целочисленное решение х. В обшем случае суще-
ствует «разрыв» между значением и оптимальным значением
функционала (16.7), т. е. тахи-’(я)—только оценка снизу для
Я
оптимального решения задачи коммивояжера.
Итак, основная идея алгоритма Хелда — Карпа заключается
во введении специальной нижней границы, определяемой выраже-
нием (16.21). и затем максимизации этой границы по вектору
п тем или иным способом до тех пор, пока либо не будет
получено первое допустимое решение, являющееся оптимальным
решением задачи коммивояжера, либо дальнейшая максимизация
станет невозможной и тогда будет получена только оценка
снизу по функционалу для оптимального решения этой задачи.
Геометрически, как показывает следствие из теоремы 16.1, задача
нахождения н’(я) соответствует задаче о нахождении минимума
1-дерева со специально подобранными весами	+
(^=^ = 0). Если существует «разрыв» между г и оптимальным
значением функционала задачи коммивояжера, этот разрыв
370
устраняется либо с помошью метода ветвей и границ, либо
субградиентными методами. Ниже будем придерживаться первого
метода устранения этого разрыва.
Введем несколько определений. Обозначим степень вершины
i (т. с. число ребер, инцидентных вершине) в каком-либо 1-дереве
к через d&, тогда v = dik—2. Пусть К (л) - множество индексов
1-деревьев с минимальным весом по отношению к весам
с17=--с17+л, + л;, т- е-
С / Л
£(«)=<£; mini ск + £ к^1к
I	к \	*=1
Назовем вектор d^(d1}	d^, удовлетворяющий условию
Е ф№>0 VkeK(n),
к-1
направлением роста для вектора л. В [17] доказывается существо-
вание такого вектора при определенных условиях.
Пусть
Л
Д (я, d) = min £ d-,vik,
keK{n)i=l
К(л, d)=; J к,: к e К (я), Е d^-Afc. d)
I	i=l
е(п. d) — максимально допустимый сдвиг в направлении d, т. е.
к (л, d) = max {e : для ez<s, Л'(я4-к^) = А’(п, d)}.
Введем важное понятие дефекта вершины. Вершина i имеет
дефект сверху при данном я, если для всех ЛеА'(п) p;f[>l;
вершина i имеет дефект снизу для данного я, если для всех
кЕК(п) vik=l, т. е. вершина i имеет дефект, если ее степень
больше или меньше двух.
Пусть и — н-мерпый единичный вектор, н; — направление роста
для вершины i с дефектом сверху, а ( —w;) — направление роста
для вершины i с дефектом снизу. Определение £ (я, d), когда d~
=и; v (—щ), особенно просто и дается следующими теоремами.
Теорема 16.3. Пусть вершина / имеет дефект снизу и к есть
элемент из А’(л, -пф Тогда
е(я, — w;) = min (ф;~ crs),	(16.23)
где (i,y)—замена для (г, .») в Тк и
Теорема 16.4. Пусть вершина i имеет дефект сверху и к есть
элемент из К (я, и;]. Тогда
с(л:; w;) = min(c;j —с„),	(16.24)
где Gy) — замена для (г, s) в Тк и
Доказательство этих теорем приведено в [17.].
37!
Изложим для злой задачи метод ветвей и границ. Пусть
У'и У—множества ребер, Т(Х, У) — множество ребер 1-деревьев,
содержащих все ребра из множества X и ни одного из
(п	\
£т+ Е I-
OI	/
Пусть У (У, У)=<0:(д+ £ яр-1к = д (л) >. Тогда понятие дефекта
вершины определяется 'следующим образом: вершина i имеет
дефект снизу для данного п (по Отношению к У и У),
если для каждого ktKXY(n) rrt = l; вершина i имеет дефект
сверху для данного я (по отношению к у и У), если для
каждого k е Кх Y (я) т;ь 1. Алгоритм метода ветвей и границ
начинается с формирования входа, состоящего из пары элементов
(ребер) множеств У и У, целочисленного вектора я и числа
Wx.rfrcj, называемого границей. Начальный вход [0, 0, 0, нуу(О)],
в общем случае — [У, У, л, »Х1,(л:)]. Определить, любая ли
вершина имеет дефект для данного я по отношению к У и У.
Если это так, то выполняется шаг алгоритма, давая новый
вход [У, У, п'? ivx у (лД, так что y (я')^ I+irx у (я), а прежний
вход уничтожается. Если не существует вершины с дефектом,
то определяется, существует ли направление роста, т. е. на-
правление, в котором можно улучшить границу иуг(я) методом
ветвей и границ, описываемым ниже. Если не существует
направления роста, то проверяется, содержится ли среди Кху(к}
цикл. Если это так, то получено оптимальное решение и процесс
заканчивается.
Процесс ветвления для входа [У, У, л, ну у (л)] следующий.
Выбираем ребро ефХ[] У и вход заменяем' двумя входами:
[y|Je, У*, я, wVL)e г,(л)] и [У*, ylje, л, и^+ y(Jt,(n)], где У* -
множество У, дополненное ребрами, которые не могут встретиться
в любом цикле, содержащем ребра XJe; У* — множество
У, дополненное ребрами, которые не могут встретиться в любом
цикле, содержащем ребра y|J е. Пусть сх у — минимальный
вес цикла, который содержит ребра из У' и не содержит
ребер из У. Тогда шах иу г (л) У сх у. Вследствие определения
Л
множеств У* и У* тахвуие	и max иу* yUf0<y,?.
И вообще, па каждой итерации граница для любого входа
всегда меньше или равна w— веса минимального цикла. Полный
процесс вычисления можно представить как дерево, узлы
которого — все полученные входы. Вход имеет единственное
направление развития, если оно вызвано нахождением вершины
с дефектом, и два направления развития, если оно вызвано
ветвлением. Окончательно формальная схема алгори тма Хелда —
Карпа выглядит следующим образом.
372
Шаг 1. Решается для исходной матрицы расстояний С задача
нахождения минимума 1-деревьев и составляется начальный вход
[0, 0, О, НУг (л)].
Шаг 2. Проверим, все ли вершины (хотя бы для одного из
полученных решений) с дефектом. Если да, то переходят к шагу
4, в противном случае — к шагу 3.
Шаг 3. Выберем одну из вершин с дефектом сверху ли-
бо с дефектом снизу, для нее определим направление роста
d=u-t v ( — пф по формулам (16.23), (16.24) соответственно опре-
делим d)— максимально допустимый сдвиг в направле-
нии d. Составим новый _вход, элементы матрицы С заменим
элементами матрицы С, где	= с- + (тг; + ж J d, и перей-
дем к началу шага 3. Если такой вершины нет, то перейдем
к шагу 4.
Шаг 4. Проверим, существует ли направление роста. Если
такого направления нет, то переходим к шагу 5, если такое
направление есть, то выберем одно из ребер, например (Л, /),
связанное с направлением роста, и разобьем множество ре-
бер на два подмножества: содержащее и не содержащее это
ребро. Составим два входа:	[(£,?)], 0, л, у (тс)]
и [0, {к, 7), п, ^(п)]. Для каждого из этих входов осуществим
переход к шагу 3.
Шаг 5. Проверим, содержит ли хотя бы одно из полученных
1-деревьев цикл. Процесс закончился.
Пример. Решить задачу коммивояжера с матрицей расстояний
(с.Д 67 = 1, 6.
!	j					
	1	2		3	4	5	6
1	со	97	60	73	17	52
2	97	СО	41 ’	52 	90	30
3	60	41	(X)	21	35	41
4	73	52	21	ОС	95	46
5	17	90	35	95	CG	81
6	52	30	41	46	Si	сс
1.	Начальным входом для задачи является [0, 0, 0, 196].
Ему соответствуют два решения задачи о нахождении минимума
1-деревьев при л = 0, изображенные на рис. 16.6, отличающиеся
друг от друга только выделенными пунктиром ребрами.
2.	Вершина 4 - -с дефектом снизу; d= — ^--направление роста;
а(я, й?) = с46-с23 = 5. Составим новый вход [0, 0, (0,0,0,
— 5,0,0), 201]. Решению задачи с новым входом соответствует
рис. 16.7, После пересчета элементы матрицы С следующие:
373
!	J					
	1	2		3	4	5	6
1	со	97	60	68	17	52
 2	97	СО	41	47	90	30
 3	60	41	ос	16	35	41
4	68	47	16	СО	90	41
5	17	90	35	90	со	81
6 1	52	30	41	41	81	СО
3.	Вершин с дефектом нет, но существует направление роста.
Выберем для ветвления ребро (2, 3) и составим два входа;
Ц2, 3), 0, (0,0,0 —5,0,0), 201 ] и [0, (2, 3), (ОДО,-5,0,0), 201 ].
Рассмотрим первый из них, которому соответствует рис. 16.8.
Вершина 3 — с дефектом сверху; d= ~и3; е, (л, d) = c46 — с34 = 25.
Составим новый вход; [(2, 3); 0, (0,0,25,— 5,0,0), 226].
Рассмотрим второй вход, которому соответствует рис. 16.9.
Вершина 2— с дефектом снизу; d=—и2; т(л, й?) = ог4 —с46 = 6.
Составим новый вход; [0, (2, 3), (0,— 6,0, —5,0,0), 207J Новому
входу соответствует решение задачи, приведенное на рис. 16.10.
После пересчета элементы матрицы С следующие;
	J					
	1	2		3	4	5	6
1	ос	91	60	68	17	52
2	91	00	36	41	84	24
3	60	36	GO	16	35	41
4	68	4]	16	•х-	90	41
5	17	84	35	90	ос	81
6	52	24	41	41	81	со
Для решения, приведенного на рис. 16.11, нет ни вершин
с дефектом, ни направления роста. Минимум 1'дерева, приведенного
на этом рисунке, есть цикл. Дерево решений приведено на рис. 16.12.
374
[{Г,0,(0,0,0,0,0), 19 6]
9-дефект снизу
[ед(0,0,0,-5,0,0),201]
Нет вершин с дефектом
Ветвим по ребру (2,3)
[{2,3} Л,(0,0,0,-5,0,0), 201]
3-дефект сверху
[И,(2,3},(0,0,0,-5,0,0),201]
2-дефект снизу
[ {2,3},Я,(0,0,25,-5,0,(9,226]
[в, (2,3), (О ,-6,0, -5,0,0), 207]
Нет вершин с дефектом
Нет направления роста
Пикл: 1-5-3-4-2-6-1
с весом 207
Рис.
16.12
Алгоритм Хелда —Карпа успешно применялся для решения
симметричных задач вплоть до размерности и = 80, причем время
решения задач со случайными равномерно распределенными с;;
размерности « = 70 на IBM 360/75 составило ^78 с. Другое изложение
идей алгоритма Хелда— Карпа, например как метода «штрафования»
вершин, было предпринято одновременно Кристофидесом [13].
§ 16.8, Приближенные методы
, К настоящему времени разработано большое число алгорит-
мов, позволяющих находить приближенные решения задачи
коммивояжера. В отличие от точных методов, которые тре-
375
буют большого времени работы па ЭВМ для больших п,
приближенные методы дают «простые» решения для сравнительно
больших задач на приемлемое время, но зато не дают гарантии,
что оптимальное решение получено. Наиболее успешные реализа-
ции приближенных алгоритмов, полностью автоматизированные
на ЭВМ, связаны с двумя схемами получения решений: схемой
улучшения цикла (А) и схемой последовательного построения
цикла (В).
Алгоритмы, использующие схему А начиная с некоторого
начального цикла, используют в основном следующие приемы:
1) разбиение этого цикла на подмножества для «уменьшения»
размерности исходной задачи, 2) нахождение инверсии городов
в этом цикле, дающей лучший цикл, чем начальный.
Характерным алгоритмом первого типа является алгоритм
динамического программирования. Так как применение принципа
оптимальности для достаточно больших п затруднено из-за
недостаточной оперативной памяти современных ЭВМ, то посту-
пают следующим образом.
Пусть известен некоторый цикл, например f=(/l; •••, i„, z'J,
и п слишком велико для точного решения задачи с- помощью
принципа оптимальности. Разобьем этот цикл на к упорядоченных
подмножеств, например
(A, Чз	Й+Ь	(й, ^S+ р ’ hl- I? ini г1)(Г
Число к выбираем таким образом, чтобы укрупненная
задача (для к городов) могла быть решена алгоритмом ди-
намического программирования. После этого решается задача
с к городами, в которой каждое подмножество принимается
за укрупненный город с расстоянием между (z(, ri+l, ..., im)
и ((,, zj+l, ..., in) равным cimI. В любом случае, какое бы
ни было выбрано разбиение, цикл к, соответствующий оп-
тимальному циклу для к городов и полученный из начального
произвольного цикла Г, удовлетворяет неравенству
Затем разобьем цикл t' и т. д.
Приближенные алгоритмы, использующие второй прием,
дают наилучшие результата в алгоритме IV (г). Приведем
эти алгоритмы.
Алгоритм /. Пусть задан начальный цикл 7 = (г1г G, , i„,
Лучший, чем исходный цикл, t' находим перестановкой первого
и второго городов в f, В цикле f переставим второй и третий
города и т. д,, пока не будут переставлены н-й и 1-й города.
Наилучшее решение запоминаем, выбираем новый начальный
цикл и процесс продолжаем.
Алгоритм IL В этом алгоритме изменяется взаимный,
порядок не двух, как в алгоритме I, а трех соседних i
городов: ik_u ik, ik+l.
376
Алгоритм ill. Алгоритм отличается от алгоритма I тем,
что город q «вставляется» между городами и /3,
затем между т3 и ;4, и т, д. до подстановки между
городами in_, и i
Алгоритм IV (г). Алгоритм IV (I) совпадает с алгоритмом
III. П осле того как найдено приближенное решение с помощью
алгоритма III, применяют алгоритм IV (2). В последнем
решении два соседних города «вставляются» в улучшаемом
цикле между всеми остальными п — 2 городами. Затем
применяем алгоритм IV (3), в котором три соседних
города «вставляются» между оставшимися п — 3 городами,
и г. д. до алгоритма IV (и —2).
При помощи описанных алгоритмов С. Рейтер и Д. Шерман
на IBM-1620 решили 17 известных из публикаций задач размером
от 9 до 57 городов. В каждой задаче полученное решение было
не хуже, чем известное. Если было известно оптимальное решение,
то оно также было найдено. Задачи решались в основном
с помощью алгоритма IV (г).
Очень близким по идеям к алгоритму Рейтера и Шермана
является алгоритм Лина, в котором находятся так называемые
«Х-оптимальные» решения для Х=2, 3, ..., п. Ш. Лин не фиксирует
взаимное положение городов при перестановке в циклах. Так,
«2-опгимальцым» циклом он называет цикл, который является
неулучшаемым при замене двух любых дуг цикла на две другие
дуги. Другие «2-оцтимальные» циклы можно найти используя
. новые начальные циклы. «3-оптимальным» циклом Лин называет
' цикл, который нельзя улучшить перестановкой любых 3 или
любых 2 дуг цикла. Аналогично, цикл «^.-оптимальный», если он
: «(Х — 1 j-оптимальный» и если, кроме того, его нельзя улучшить
; перестановкой любых X дуг. Эмпирически Ш. Лин показал, что
;• вычисленный аффект снижается с ростом X, достигая максимума
для л. = 3, т. е. достаточно находить только «3-оптимальные?>
i циклы. Оценка необходимого числа арифметических операций
. алгоритма Лина ^З,5и3 (п~4)1
В алгоритмах Лина, Рейтера и Шермана время вычислений
• асимптотически пропорционально п\ где X- число городов,
подвергающихся перестановке. Для больших п практически нриме-
чимы только значения Х=4, Х==3, так как число перестановок,
вторые необходимо проделать в этом случае, велико. Вычисли-
Ельное время такого рода алгоритмов может быль значительно
|ижено, если сократить число перестановок. Реализации этой
:деи посвящены работы [16, 18].
Теоретические исследования результатов локальной оптимиза-
ции [19] показали, что хотя «в среднем» эти алгоритмы
достаточно эффективны, они не могут гарантировать получение
приближенного решения с любой наперед заданной степенью
йриближения к точному, если на каждом шаге итераций
377
длительность поиска ограничивается числом операций, поли-
номиально зависящим от числа городов. Более того, построены
примеры матриц расстояний задачи коммивояжера, в которых
приближенные решения, найденные алгоритмами локальной оп-
тимизации, отстоят сколь угодно далеко от точного решения,
если длительность поиска ограничивается числом операций,
полиномиально зависящим от числа городов.
Примеры приближенных алгоритмов, использующих схему В,
приведены в § 16.2.
Глава 17
Динамическая модель
оптимального развития
многоотраслевой экономики
Методы оптимизации, изложенные в данной книге, позволяют
решать разнообразные экономические задачи. Их применение
в ряде случаев дает возможность провести основательное
аналитическое исследование. Результатом являются свойства
оптимальных траекторий и режимов в рассматриваемой экономи-
ческой задаче.
Наличие аналитического решения дает много ценной инфор-
мации. В частности, становится ясно, как ведет себя оптималь-
ное решение при различных исходных данных и параметрах
модели данного экономического процесса. Однако с помощью
численных расчетов получать такие зависимости весьма затруд-
нительно.
В данной главе рассматривается одна из важных с приклад-
ной точки зрения экономических задач — моделирование опти-
мального развития экономики страны. Процесс описывается
моделью экономической динамики, в основе которой лежит
межотраслевой баланс (см. гл. 2), а мощность отраслей — произ-
водственными функциями. Исследование проводится методами,
основанными на изложенных в гл. 5 достаточных условиях
оптимальности. При этом наряду с аналитическими свойствами
оптимального решения получен алгоритм численных расчетов.
Помимо теоретических результатов в главе приводятся неко-
торые результаты практических расчетов. Получение таких
результатов и является конечной целью решения экономической
задачи.
§ 17,1, Постановка задачи
Модель развития многоотраслевой экономики, исследуемая
ниже, имеет вид
Г= f + Л F= f +	г = Цг;	(L7.L)
j = 1	J=1
Е ЬЧМ	([7.2)
379
^=^-1л‘К‘;	(17.3)
А'(0) = ^о;	(17.4)
К*’ ь*\ И'>0,	С«,	(17.5)
Особенностью данной модели является то, что она соче-
тает межотраслевой баланс и производственные функции отрас-
лей. В отношениях (17.1) — (17.5) по одинаковым значкам j
в произведениях подразумевается суммирование. С ?-й от-
раслью связаны переменные: Х‘ и Y1 — соответственно ва-
ловой и конечный потоки продукции; К1 — основные производ-
ственные фонды; А1- —трудовые ресурсы; И" — вводимые в дей-
ствие инвестиции; С' -—часть конечного продукта, остающаяся
после инвестиций, которую будем называть потреблением ?-гО
продукта. ; Следующие данные представляют собой входную
информацию модели; — начальные значения фондов; ц‘ —
коэффициенты амортизации; А = («}(/})— матрица прямых затрат;
/) = (дЦ) — матрица структуры капитальных вложений; 7V(z)— сум-
марные трудовые ресурсы, определяемые демографическим про-
гнозом; К, L)—положительные производственные функ-
ции отраслей с положительными частными производными по
К и L, убывающими по этим аргументам от оо до 0, линейно
однородные.
Минимальные допустимые значения потребления полу-
чены следующим образом. Устанавливаются общественно необхо-
димый минимум фонда потребления [-го продукта С\ It) и до-
пустимая импортная квота Л'(/) так, что Cm(r)=Ci] — Л'.
Требуется найти процесс v=(X (г), Y ((}, V (/), С (/), К (г), L(z)),
оптимальный в смысле функционала
= f Cjdr^max,	(17.6)
о	D
где D — множество процессов (планов), допускаемых условиями
(17.1) - - (17.5); 5 — коэффициент дискредитирования; g (z, С) —
функция полезности, вогнутая, с полугюложительным градиентом.
Особый интерес представляет понимание функции полезности
как стоимостного потока «съема» с экономической подсистемы,
выраженного в прогнозируемых внешнеторговых ценах. При этом
линейный вариант
g(t, C) = 0;(z) С
моделирует ситуацию, когда выпуск продукции исследуемого
региона не сказывается на международных ценах 0;(z). Однако
для достаточно мощного региона эти цейы, выраженные преде-
льными полезностями будут зависеть от его выпуска С'_
380
Использование нелинейной функции полезности позволяет
также моделировать ограничения С1> СЙ>0, устанавливая при
недопустимых С достаточно крутое ее падение. В частности,
в таких случаях обычно требуют, чтобы	ПРИ С‘->0,
С точки зрения теории оптимального управления эта
задача п-со порядка с состоянием К^Е1} и управлением,
имеющим содержательный смысл распределения инвестиций
и трудовых ресурсов между отраслями, конечного продукта
между инвестициями и потреблением, загруженности отраслей
и трудовых ресурсов, а также экспорта и импорта в допустимых
квотах,
Введение нелинейных производственных функций в межот-
раслевой баланс позволяет учесть возможность взаимного за-
мещения труда и фондов в пределах отраслей и зависимость
производительности груда от фондовооруженности (в линейных
моделях производительность труда считается заданной функцией
времени).
) Оказывается, эта задача, несмотря на ее нелинейный характер
) и высокую размерность, допускает глубокое аналитическое ис-
j следование с выходом па сравнительно несложный и обоснован-
I ный алгоритм построения оптимального плана и выявление
I наглядной качественной структуры последнего, хороню истол-
I ковываемой в содержательных экономических терминах.
I Ниже описываются свойства и алгоритм отыскания этого
I решения, полученные на основе достаточных условий оптималь-
но ности (см. гл. 5).
К Введем некоторые дополнительные предположения. Пусть
 матрица прямых затрат А — продуктивная, положительная, нераз-
И* ложимая. Это значит, в частности, что матрица (Е - Л), обратная
Г матрице (Е—А) (Е—единичная матрица), определена и также
I полуположительца. Матрица структуры капиталовложений
I О = (д?)) — полуположительная, причем при всех	п.
I Отрасли с номерами i^m, т. е. такие, что для каждого
Г существует хотя бы одно /, при котором dlj>0, называются
I фондообразующими. Количество т фондообразующих отраслей
I существенно меньше общего количества отраслей п. Так, для
I широкого класса макроэкономических моделей, насчитывающих
^около 2 — 3 десятков отраслей, имеют место лишь две фондообра-
^Иующие отрасли: машиностроение и строительство. Эго обстоя-
^Иельство имеет существенное значение, так как для сложности
^Иолученного здесь алгоритма решения задачи существенно именно
^Нисло т, а не п. Другие свойства матрицы D: для каждой
Иртрасли j найдется фондообразующая отрасль г такая, что
л	___
В кроме того, £ dj= 1 Vy=l,«.
В	i=I
381
§ 17.2. Оптимизация процессов, линейных
относительно управления
При исследовании поставленной задачи будем опираться на
метод достаточных условий оптимальности, рассмотренных
в гл. 5, точнее—на его обобщение на случай бесконечного
промежутка времени.
Пусть имеется задача оптимального управления
г
= J/°(^ х, u)dr + F(x(7))->mm,	(17.7)
о	D
x=f(z, x, u), x(0) = xo, x, ueK',	(I7.8)
где xx")—вектор состояния; u = (w*, ..., мг)-—вектор уп-
равления; V{—заданное при каждом te (0, 7) множество допусти-
мых пар векторов х, u; f (г, х, и)—заданная вектор-функпия,
непрерывная по всем аргументам; f°(t, хи); F(x)~—заданные
функции, непрерывные по своим аргументам; х0—заданное
значение состояния; Т—заданное положительное число, причем
допускается и символ Г=оо; D — множество пар вектор-функций
х (г), u(z), заданных на отрезке [О, Г], удовлетворяющих условиям
(17.8) и учитывающих, что траектория х(г) непрерывна и кусочно-
дифференцируема, программа управления u(z) кусочно-
непрерывна, функционал (17.7) определен.
Введем в рассмотрение функцию ф(г, х), непрерывную и не-
прерывно дифференцируемую, и построим с ее помощью сле-
дующие конструкции:
х, =	х,	х, и)+^|Д	(17.9)
Ф(х, T) = F(x) + (p(T, х).	(17.10)
Обозначим: П—множество функций ср х), непрерывных,
кусочно-дифференцируемых и таких, что на (0, Г) определены
функция
ц(/) = max R(t, х, и)
х, ие И‘
И ЧИСЛО
m = min Ф(х, 7) (/п= lim min Ф(х, Л ];
ierrr	\	<-«' п	)
т
/(cp) = m-fp(f)d:-cp(O, х0);
о
V=(x(i),u(z))
— процесс, удовлетворяющий условиям
382
R(t, x(f), u(/)) = p(r), ze (О, T), Ф(/, x(z)) = m, t=T.
С учетом введенных обозначений из теоремы 5.2 могут быть
получены соотношения:
при любом (реП, veZ)
^(v)>Z(q>);	(17.11)
если существует такая цеП, что veZ), то
,/fv) = min./(v) = max / (ф) = / (ф).	(17.12)
На основе этого результата возможно сведение рассматривае-
мой задачи оптимального управления к максимизации функции
R(t, х, uf по х, и при каждом Ге (О, 7) (минимизации Ф(г,х)
при t = T) и подбору такой функции гр (г, х)еП, чтобы результат
этой максимизации, процесс V, оказался допустимым.
Может оказаться, что теоретико-функциональные требования
к классам Ви П слишком жесткие. Тогда можно воспользоваться
теоремой 5.4, сформулированной в терминах последовательностей.
Функция ср(г, х) условиями теоремы 5.2 недоопределена, и воз-
можны разные способь! ее задания, приводящие к различным
конкретным способам решения задачи.
Можно показать, что если veD, то
8R
Зх
_1+т.м)
х.й	5*
(17.13)
G(r) = arg max R (г, х (г), u) = arg max //(/, ф, х, и),	(17.14)
и	и
.где

= 0,
X, й
; //(г, ф, х, и) = фГ(г, х, u)-/°(Z, х, и).
(')
Выражения (17.13), (17.14) характерны тем, что в них присут-
ствует только градиент функции ср (г, х) в точках траектории
х(г), т. е. вектор ф(г). В частности, уравнения принципа мак-
симума Понтрягина получаются из (17.13), (17.14), если
что является необходимым условием максимума функции
??(/. х, ui. При этом ф(г) совпадает с сопряженной вектор-
функцией. В этом случае функцию ср (г, х) можно искать среди
линейных форм ср = ф(г)х. Если окажется, что необходимые
условия максимума Z?(r, х, и) будут и доста точными при _таком
задании ср (г, х), то процесс v=(x(r), й(г)) и функция ср = ф;(г)х‘
удовлетворяют условиям теоремы 5.2, т. е. процесс v оптимален,
если недостаточны, то требуется более сложное задание ср (Г, х).
383
Опишем один из способов исследования специального класса
задач оптимального управления, который будет здесь использо-
ваться.
Пусть правые части уравнений линейны относительно некото-
рой компоненты w управляющего вектора и:
/' (/, х, и) = Р! (/, х, z) + Q* (/, х) w, /=],«,
где z—совокупность остальных компонент управления u = (z, w).
Имеем
 х, z, w)= f	x, г) + Ф)+ f
Функция ср (z, x) должна быть выбрана так, чтобы процесс
(x(z), z(O, w0) оказался допустимым и, в частности, удовлетворял
уравнениям (17.8). Если потребовать, чтобы
=	(17.15)
i = 1 ох	р
то функция R не будет зависеть от w и, следовательно, любое j
значение w обеспечивает максимум R, т. е. ограничивая условием 1
(17.15) возможности выбора функции ср мы компенсируем это |.
расширением множества процессов (х (/), й (;)), обеспечивающих 
максимум R.
Общее решение (17.15): ср (/, х) = ф(г, т]), где т] = (п' (/, х), ...,
..., т]п“1 (/, х))—совокупность и—1 определенным образом задан-
ных функций [первых интегралов характеристической системы
для (17.15)]. Имеем
Л- у грМГ^(( . pi,( х
, -, Йч1	дх ’	'	’ ел v	di
/. j = I 1 L	J
Это выражение совпадает с конструкцией функции R для новой
задачи о минимуме (17.7), в которой роль состояния играет
(и-[)-мерный вектор т], а роль управления — переменные х, z.
Уравнения процесса для этой задачи
х, z)= £ ~7Pi + ~fr, x), j = 1, n- 1;
начальные условия
Л (01 ч(0. xj т](.;
ограничения на управление
(x, z)eE^, т](/, х) = т],
гДе Vxz — проекция множества V! на прямое произведение про-
странств X и Z переменных х и г соответственно.
384
Кроме того, из условий (17.8) исходной задачи могут быть
[звлечены некоторые дополнительные ограничения на текущие
;начения
x(r)e Ki-
(17.16)
Это вспомогательная задача.
Пусть процесс (й (/), х (f), z (/))—ее решение, причем такое, что
ieKTOp-функция хр) непрерывна, кусочно-дифференцируема, вы-
полняются граничные условия (17.8) и функция
ро дочитанная для какого-нибудь i (из определения вспомогатель-
рой задачи следует, что для всех i правые части (17.17) совпадают
шри всех /, для которых они определены), удовлетворяет условию
|x(r),	w(/))e И'. Тогда процесс v=(xp), z(r), wp))—допусти-
рый и оптимальный для исходной задачи. Отметим, что не
д-олько условие (x(z), z (/), w(z))e V1, но и граничные условия (17.8)
и требование непрерывности х(г) при решении вспомогательной
задачи могут не выполняться, так как условие х(0) = хо не
эквивалентно условию т](О)=т]о, и вектор-функция х(/), играя
в последней задаче роль управления, может иметь разрывы.
Выполнение указанных условий допустимости процесса v часто
связано с успешной оценкой области допустимости И) (17.16).
Таким образом, описанный прием состоит в переходе от
решения задачи (17.7), (17.8) к решению вспомогательной задачи.
Последняя принципиально проще, так как ее вектор состояния
имеет меньшую размерность, а именно это число определяет
ложность вариационной задачи.
 Последовательное и неоднократное применение этого приема
Вгожет существенно упростить исходную задачу.
§ 17.3. Условия оптимальности процесса
экономического развития
В рассматриваемой задаче роль состояния играет вектор
кновных фондов К = (К1, ..., X"), а роль уравнений процессов —
117.3). Остальные переменные суть компоненты управления и.
Все отношения (17.1), (17.2), (17.4), (17.5) описывают множество
г допустимых состояний и управлений. Сводя задачу к вилу
Й7.7), запишем J (v) = — /(у) -нпщ. где /(у) задан в виде (17.6).
Будем искать функцию ф (г, К) в виде
ф(Г, К)=£
;е ф;(г)— функции, которые нужно определить.
Согласно (17.3), (17.9) и (17.10) имеем:
За к 456
385
R= E	c),
1 = 1
Ф(Т, К) = ф(Г, K)= £ ^(T)Kl.
1 = 1
Учитывая межотраслевые связи (17.1) и (17.2), при помощи
метода множителей Лагранжа заменим задачу о максимуме
функции R на V* задачей о максимуме функции
R' = £ (фф'-^фДЯЧХДх'-д^-^-+ :
1 = 1
+у(У- £ r)+e-»g(r, С)
\ f=i /
на множестве всех X, L, К, V, С, ограниченном неравенствами
(17.5). Здесь у(/). л,(.Д, /=1,н,—соответствующие множители
Лагранжа, (?(/, С)-е’*g(t, С)— £ л, С'. Группируя слагаемые,
1 = 1
получим
R'(t, К, L, X, V, С)= £ ЯД/, К*, U, Г) + (?(/, С) +
i-i
+ Е (фг-^)ИЧтЛГ,	(17.18)
ij=i
где ЯД/, К, L, X)=6;X-P,.K-yL,
*1= £	Л = иЧг-Фс
/=1
Обозначим:
*(<)- i ед+ед+улг.
1=1
G(t)- тах(?(/, С),
ЯД/)=тах ЯД*/, X, К, L),
К, L), К>0, L^O.
Тогда процесс v = (K‘(/), /?'(/), ^(/), С‘(/), !'(/)), соответству-
ющий для данной задачи процессу, фигурирующему в теореме
5.2 о достаточных условиях оптимальности, должен обладать
свойствами:
ЯД/, X^t), £'(/), ГД/))-ЯД/) V/, /,	(17.19)
386
G(t, C(/))-=G(/) V/,	(17.20)
(ф(-£^)Р(г)=тах( ф;- £	K=0 Vi, t, (17.21)
j = i	I-'sO \ j=i /
-» lim mini]/;(z) K = 0, 1 -t ос Vi. (17.22)
f-J-CO Ks()
Условие (17.21) является обобщением условия 2° теоремы
5.2 на случай бесконечного промежутка времени.
Обозначим через П множество троек вектор-функций =(\|/(7),
Х(/), у (Г)), для которых определены правые части равенств
(17.19) — (17.22), Вектор-функция ф(/) непрерывна, кусочно-диф-
ференцируема; Х(г) и у(/) кусочно-непрерывны.
Согласно (17.11), для любых %еП, veZ) справедливо неравен-
ство
4v)=~^(v)< -^) =
i ед
1 = 1
б/+ф;(0)^.
О
Если существует такое %еП, что veD, то
7(v)^max/(v)= -/(%)= min [-/(%)].
D	и
Отыскание оптимального режима экономического развития
v<=D сводится, таким образом, к максимизации функций R^t,
К. L, X) и G(/, С) и подбору таких множителей ф(/), 1(f),
ур), чтобы этот процесс оказался допустимым.
Введенные здесь конструкции имеют наглядный экономичес-
кий смысл.
Пусть в исследуемой экономической системе имеются рыноч-
ные отношения. Обмен фигурирующих в модели производствен-
ных факторов происходит согласно заданным ценам Х;(/), ф;(?),
у(0 соответственно за единицу г-го продукта, производственных
фондов i-й отрасли и труда, так называемым объективно
обусловленным оценкам (введенным акад. Л. В. Канторовичем).
Пусть задан процесс v=(Xj7), Kh), L(r), С(/), V(/)), не
удовлетворяющий равенствам (17.1), (17.2), но удовлетворяющий
неравенствам (17.5). Это означает, что ;-я отрасль в момент
I производит поток продукции Х\ располагая такими фондами
К1 и трудовыми ресурсами £‘, что	К1, L1), и покупая
продукты других отраслей в количестве, обусловленном матрицей
производственных затрат А. Тогда величина	К‘, L1) есть
поток прибыли отрасли, получаемый вычитанием из стоимости
валового продукта затрат на необходимую для производства
продукцию других отраслей afaX1 и рабочую силу yL\ а также
Стоимости выбывающей части производственных фондов PiK1.
13*
387
Последнее обусловлено физическим износом фондов К1 и не-
посредственным изменением их цены К последнему слага-
емому уместно применить термин «моральный износ». Закупка
набора продуктов С, обеспечивает поток полезности е-С).
Наличие разницы между объективной полезностью и закупочной
стоимостью потребления, согласно назначенным ценам к;С‘,
обусловливает прибыль G{t, С). Последнюю уместно назвать
коммерческой прибылью в отличие от производственной прибыли
Rj, В частности, если полезность имеет смысл фонда потребления,
п
выраженного в ценах 0; внешнего рынка g= £ 0,0, то эта
Я	1—1
прибыль (7= У, (е-₽‘0; — Х;)О обусловлена разницей между дис-
 = 1
контироваНнои к начальному моменту внешнеторговой ценой
е-а‘0г и ценой X. Отсюда множители	у имеют смысл
дисконтированных к начальному моменту внутренних цен соответ-
ствующих факторов на описанном условном рынке. Смысл
текущих цен имеют величины:
Х^ = Х,ев‘, ф*(/) = ф(-р)е% у*(ф = у(/)е81.
Таким образом, функция R'{t, X, К, L, С, V) есть суммарный
поток прибыли, образованный производственной прибылью отрас-
лей и коммерческой прибылью. Дополнительное слагаемое yW
в соотношении (17.18) представляет собой оплату рабочей силы.
Режим развития экономики, определенный (17.18) — (17.21),
назовем оптимальным при данных ценах. Он обеспечивает
максимум всех видов прибыли в каждый момент времени
в условиях описанного выше механизма условной рыночной
экономики с заданными ценами. При этом имеет место полная
независимость всех видов прибыли: производственной в каждой
отдельной отрасли и коммерческой- Так, производственная при-
быль г-й отрасли в момент t зависит только от произведенного
валового продукта ф и производственных факторов Л7, L1. Иными
словами, оптимальные при данных ценах компоненты плана К1, L\
X', К1 дезагрегированы как по отраслям, так и во времени, а план
потребления С — во времени, но не обязательно по отраслям.
Цены = X, у)еП назовем допустимыми. Допустимость
вектора цен с, означает прежде всего, что имеют смысл
(определены) перечисленные виды прибыли.
Оптимальный при данных ценах план v не удовлетворяет,
вообще говоря, связям (17.1) — (17.3), т. е. может быть не
сбалансирован. Для выполнения теорем (5.2) о достаточных
условиях оптимальности подбор цен должен дополнительно
обеспечить сбалансированность оптимального при данных ценах
плана v.
388
§ 17.4.	Свойства допустимых цен
и оптимальных режимов развития экономики
Изучим свойства допустимых цен = у)еП и соответст-
вующих им оптимальных планов.
1.	Согласно (17.20), потребление С(с) обеспечивает максимум
коммерческой прибыли Gp, С). С учетом описанных выше
свойств функции g(z, С) необходимым условием существования
этого максимума является полуположительность вектора Цг)
при каждом t.
Если полезность линейна, g = 9;C, то внутренние текущие
цены не ниже внешних:
г = Т7й.
Если C'>Cj„, то текущая цена данного продукта с его
предельной полезностью
С)
1 дС'
Если	то С' = Ст.
В частности, если полезность линейна, £ = 0,0', то значение
С‘>С‘т возможно только при таком i = l, что
Л=тах£ = 1.	(17.23)
Как правило, за исключением специально подобранных значе-
ний входных параметров, l-я отрасль единственна. Это значит,
что для страны оптимальным в смысле рассматриваемого
критерия является монопродуктовое производство, когда все
усилия сосредоточиваются на выпуске одного избыточного про-
дукта /-й отрасли, остальные же импортируются. Такая линейная
зависимость g = O,C‘ характерна только для относительно ма-
ломощного региона, выпуск которого С1 не сказывается на
уровне международных цен.
2.	Согласно (17.19), оптимальный продукт отрасли Xt, фонды
К1 и трудовые ресурсы И должны обеспечивать максимум
производственной прибыли RT. В частности,
К*, если bt > О,
X1 = < 0, если < 0,	(17.24)
1~не определен,
Матрица А неразложима, т. е., для того чтобы Т‘>0 хотя
при одном ! = /, необходимо Х‘ > О V/=l,«, поэтому значение
Р = 0 недопустимо и, следовательно, V/, t.
389
Обозначим
К\ max R{t, К’, L\ = К, Ц-Р^-уЕ1'.
(17.25)
Учитывая линейную однородность производственной функции,
может записать
/?!,.(/, К1, Li) = ri(t, k^L\
где fc'—K'lL1 — фондовооруженность;
г;(Г, ki'}=bifi{t, к^-р^-у
— производственная прибыль отрасли с единицы труда, которую
будет называть эффективностью отрасли. Учитывая, что L‘>Q
Vi, t (так как в противном случае ЛГ’=О), получим в качестве
необходимых и достаточных условий максимума по К1 и L’
r^t, к1{1))~такг^, АЭ) = О Vi, i.	(17.26)
k
Для существования такого F необходимо Pi > 0, у > 0 Vi, t.
При этом если 6, > 0, то вследствие аналитических свойств
F(i, К1, L’) Pj>Q, у>0, причем к1 единственно и положительно.
3.	Покажем, что при всех г, i
Д->0, Д > О, у>0-
Действительно, при каждом г вектор К, полуположителен
I	Л i	1 J1  s
|из = Тогда
'	' 7	1 = (£-Я)Ь,	(17.27)
где (£—Л) — матрица, обратная матрице Е—А, определенная
и полуположительная из-за продуктивности матрицы А, вектор
Ь, согласно (17.25), неотрицателен, т. е. либо полуположителен,
либо нулевой: 6;=0 Vi — 1,и. Но в последнем случае вектор к,
согласно (17.27), также нулевой, что противоречит свойству его
полуположительности- Это значит, что вектор Ь полуположителен,
т. е. существует такое i=lt что Д0)>0 и, следовательно, Д > О,
у>0. Но так как у>0, то к‘)—Р^1—у>0 при всех i.
Поскольку Д>0, последнее возможно только при Д >0, Д>0
Vi=l, п.
4.	Из (17.24), согласно (17.26), следует полная загруженность
отраслей на оптимальном режиме:
Г’ = Д(г, К\ Ll)	t.
На основании свойства дополнительной нежесткости связи (17.2)
полная загрузка трудовых ресурсов будет равна
£Г(г)=У(г) Vi-
390
5.	Используя условие (17.26), нетрудно получить
=р Vz, t, (17.28)
SL‘	SK'
т. e. чистая предельная прибыль с единицы труда одинакова во
всех отраслях и должна совпадать с ценой труда, а с единицы
фондов—с ценой их износа (физического и морального). Если
И/ /?)- 5Fi/dLi
дУ[дкР r т’
тогда
р./г-(^р)=1;	(17.29)
т. е. оптимальная фондовооруженность зависит только от отноше-
ния цены износа фондов к цене труда Р;. В частности, для
производственной функции Кобба—Дугласа F—aevtKaL^ имеем
' ~ а
Обозначая	\=К-/у, из (17.26), (17.27) имеем
Х.^(£—\ 1 =	(17.30)
. е. относительные цены продуктов всех отраслей выражаются
ерез относительные цены износа фондов.
6.	Максимум (17.18) по И‘ определен при условии
ф.._ i
j=i
1меем	n
ГО,	если ф,-< £ dflXy,
Г = <	Z = 1
1^0, если ф; = £ djkj,
j = i
. e. ненулевые инвестиции в отрасль оптимальны только при
наличии равенства.
Назовем ;-ю отрасль развиваемой в момент t, если И‘(Н>0,
: неразвиваемой, если И1(/) = 0. Если к моменту I отрасль была
«развиваемой на всем интервале 0<т</, то на основания (17.3)
L* = Ki)e_^/. Если все отрасли развиваемые, то
ф;= X d{kh	(17.31)
} = i
т. е. цены фондов всех п отраслей__выражаются через цены
фондообразующих продуктов лу, /'=!,/«. Цены износа с учетом
(17.29) и фондовооруженности отраслей к‘ в этом случае также
выражаются через цены фондов и цену труда:
391
<7; = -\ 7 = 1,i=l,n. (17.32)
j = i	f
Учитывая (17.29), (17.32), заметим, что первые т уравнений
(17.30) при заданных X,, у=], т, образуют замкнутую нелинейную
систему с т неизвестными q-. Обозначим через~	Хш)
решения этой системы при заданных > Хт. Тогда’ для
цен фондообразующих продуктов /=l,w имеем уравнения
=	J = TJn,	(17.33)
которые определяют их, если заданы цена труда y(f) и начальные
условия ХДО),
Если известны цены фондообразующих продуктов \{t}, фДг)
и цена труда у(г), то из (17.32) находим цены износа Д, i=l, п,
из (17.29)— оптимальные фондовооруженности к '(г), из (17.30) —
цены нефондообразующих продуктов Xj, j<m.
Таким образом, цены всех продуктов и фондов Х.;(/),
а также оптимальные фондовооруженности V(t) выражаются
через цену труда у (г) и начальные значения цен фондообразующих
продуктов \(0), у=1 т.
7.	Согласно (17.22),
ф;(/)Kl{t)->со, /-^0, 1=1, и,	(17.34)
т. е. дисконтированная стоимость фондов каждой отрасли должна
убывать до пуля. Текущая же стоимость ф)(г)Х'(/) может
и возрастать, но медленнее, чем е6'.
§ 17.5. Уравнения оптимального
сбалансированного плана
Выражение (17.18) для функции R ’ линейно относительно
инвестиций У'. Применим описанный в § 17.2 метод решения
оптимизационных задач, линейных относительно уравнений. При-
равнивая нулю коэффициенты при V1 и учитывая (17.31), получим
к)= f фл'= £ \.(r) ич f ;-=г^. (17.35)
=1 j=I	i=l
Функция ф определена теперь с точностью до т функций
4(f), а Роль фазовых координат r]J вспомогательной задачи
выполняют накопленные в фондах всех отраслей соответствующие
фондообразующие продукты W1.
Коэффициентам полученной функции ф(/, W) отвечают
первые т уравнений (] 7.1), которые, учитывая все уравнения
(17.1) и (17.35), можно записать в виде
392
tyj=Yj-CJ~Y	(17.36)
!= I
Обозначим через DA множество процессов v=(W(Z), K(t),
Цг), V(r), X(z), C(r)), удовлетворяющих условиям множества
D (17.1) — (17.5), кроме уравнений (17.3) и неравенств Г‘>0.
Откажемся также от требования непрерывности К (/), заменив
его кусочной непрерывностью. Заменим также начальное условие
/0(0) = А1о, ( = 1,и, условием
И^(0)=И=Ё	(17.37)
i = 1
Очевидно, D <=. DA.
Сформулируем вспомогательную задачу А: найти процесс
ve£>x, максимизирующий функционал (17.6).
В этой задаче в отличие от исходной отсутствуют инвестиции,
вектор фондов К переходит из категории состояния процесса
в категорию управления, а роль состояния играет вектор W.
Данная задача значительно проще для исследования, чем ис-
ходная, так как сложность вариационной задачи определяется
размерностью вектора состояния. Связь вспомогательной задачи
А с исходной состоит в том, что если ее решение v удовлетворяет
условиям последней, т. е. если вектор-функция К (г) непрерывна,
кусочно-днфференцируема, удовлетворяет начальному условию
(] 7.4) и неравенству
Й!'=ХЧн(^>0, V/, />0,
то оно является решением исходной задачи.
Выражение (17.18) для функции R' с учетом связи (17.31)
совпадает для обеих задач, и все свойства оптимального режима
и цен, описанные выгце, сохраняются-
Системы (17.33), (17.36) образуют замкнутую систему диффе-
ренциальнь1Х_уравнений порядка 2т относительно неизвестных
rKj, IVJ, j=l,m, правые части которых при заданных значениях
этих последних подсчитываются в такой последовательности:
1.	Задаемся значением^j>0 и находим Xj-Xj/y, j=l,m.
2.	Из (17.30) при /=1, т с учетом (17.29) и (17.32) находим
, Кт) и тем самым Д, £', /=],«. Значения переменных
при j = m+\,n также получим из соотношения (]7.30).
3.	Из (17.20) находим С‘. При этом для нелинейной и линейной
g(/, С) проверяем соответственно неравенства C'^CJ„ или
хе-8', 1=1, п. Если последние неравенства нарушаются, то
задаемся другим у и повторяем расчет.
4.	Из линейной системы т + п уравнений
£	&)IA=Y\ / =	(17.38)
j = i
393
(17.39)
j=i j __________
£ учетом равенств У—C\ i=m+l,n находим т + п неизвестных
U, j=\,tr, У, i=t,m, и проверяем (17.2). Расчет, т. е. подбор,
продолжается до выполнения этого соотношения.
Тем самым найдены все переменные, замыкающие правые
части (17.29), (17.36) при заданных t,	у, У,
i= 1, л; С‘, L\ Kl=klLl, i~l,n.
_ При этом допустимы только такие к;, Wj, j=l,n, при которых
L‘>0, С‘^С‘т, i=l,n; У'^С^,
5.	Описанный в п. 4 ход расчета предполагает, что значения
С! определены условием (17.20). Это имеет место либо когда
полезность g(/, С) нелинейна и строго выпукла, либо в линейном
варианте, если 1*>0; V/=l,«. Внесем поправки в п. 3, 4 для
случая g = ^lC\ когда имеется отрасль i—l, л* = 9/, для которой
(17.20) не определяет С1. Для этой отрасли, согласно (17.23),
0,	0, ,
-4-тахрЕ=1.
j Ai
Для того чтобы равенство к* -= 9,- сохранилось на некотором
отрезке, необходимо, чтобы 7* = 9,. Последнее равенство с учетом
(17.33) приводит к следующему.
y)eS/=0*-50r	С17-40)
Поэтому в данном случае после п. 2 надо выполнить операции:
За. Расчет п. 1, 2 повторяется до выполнения (17.40).
4а. Решаем систему л + ш+1 линейных уравнений (17.38),
(17.39), £17.1) с п + ш+1 неизвестными L‘, i=l,n; У‘, г=1,т,
С1 при C/ = CJn, i^l (имеется в виду 1>т). Если удовлетворяется
неравенство С ^С‘т, то находим K' — k:Ll и тем самым замыкаем
систему (17.33), (17.36).
Наличие избыточной отрасли среди фондообразующих 1^т
возможно не при любых W, а лишь при таких, когда система
(17.38), (17.1) п-\-т+ 1 уравнений разрешима относительно п-\-т
неизвестных Е‘, / = 1,щ У!, i= 1, т. Выделяется такое многообра-
зие значений W следующим образом: правая часть /-го уравнения
(17.39) включается в число неизвестных, и решается линейная
система п + т+1 уравнений (17.38), (17.39), (17.1) относительно
и + m+l неизвестных с одновременной проверкой неравенств
Г>0,	i=l, т; W'>0. Находятся К‘=Л\ L1, ;=1,и;
,	__ л
W1 и с1= У1— У d^K1, при этом должно выполняться неравен-
ство
394
§ 17.6. Граничные условия и прилегающие
к ним участки оптимального режима
Начальные условия вспомогательной задачи А
^(О)=Й/Ь=Еед, /=17™,
J = 1
не гарантируют выполнение начальных условий исходной задачи
Л'!(0) = ^о, * = !,«, т. е. план, полученный в результате решения
задачи А, вообще не является допустимым.
Введем в рассмотрение вспомогательную задачу В, которая
отличается от А дополнительными ограничениями
i=lji.	(17.41)
Последние следуют из связей
К^К'-^К1,	Л’/(0)=М	(17.42)
исходной задачи, поэтому искомое оптимальное решение послед-
ней содержится среди допустимых процессов задачи В: ve£)„.
Условия (17.41) играют роль дополнительного ограничения (17.16).
Фазовым фактором задачи В по-прежнему является вектор W;,
а вектор К—одно из управлений.
В отличие от задачи А решение задачи В, как нетрудно
видеть, удовлетворяет условиям К'(О) = i— 1, «. Действительно,
пусть при некотором / = / ЛДО^Ло. Из (17.41) следует, что
возможно только К1(0)> Ко- Так как при остальных i также
справедливо (17.41) Ко, то И/|(0) =	при
том /, для которого d\ > 0, т. е. нарушается граничное условие
задачи В.
Невыполнение начальных условий А'!(0) = А’о при решении
задачи А, за исключением специально подобранных значений
Кс, означает наличие участков нижней границы
допустимых значений Кг в некоторых компонентах K‘(t) решения
задачи В на итервалах, прилегающих к значениям 1 = 0, т. е.
наличие, как правило, неразвиваемых отраслей в начале оптималь-
ного процесса.
Таким образом, типичные особенности решения ve£) исходной
задачи, вытекающие из условий (17-42), не фигурирующих явно
Iв задаче В, присутствую т в решении-Последней. К этому следует
добавить непрерывность траектории K(z), всюду на интерва-
ле (О, Г), что будет сделано ниже.
Единственная теоретически возможная причина несовпадения
решений исходной задачи и задачи В—нарушение условия
Р=А, + р1Х*>0 на множествах значений I, нижняя граница
395
которых отлична от нуля. Однако расчеты и некоторые теорети-
ческие соображения показывают, что для типичной в современных
условиях входной информации траектория К (/) после начального
периода перестроек представляет собой устойчивый рост, поэтому
можно ожидать выполнения этого условия всюду и исходную
задачу заменить задачей В.
Описанный для задачи А способ отыскания управляющих
переменных и правых частей уравнений (17-33), (17-36) применим
только при тех /, для которых ограничения (17.41) несущественны,
т. е, для достаточно больших t. Если эти ограничения существен-
ны, необходимо ввести в алгоритм решения задачи поправки,
связанные с тем, что теперь максимизация производственной
прибыли У, К1, L1) должна производиться с учетом связи
(17.41).	1 ;-
Введем в рассмотрение множителя Лагранжа отвечающие
связям К1— Афе^'Х). С учетом условий дополнительной нежест-
кости
т|; = 0, если К' > ^Qe_p‘'; и т);Х),
если =	(17.43)
Нетрудно убедиться, что свойства цен и оптимального режима,
перечисленные в § 17,4, остаются в силе с заменой выражения
(17.32) для Pi выражением
Pi= Z	qi=\ i=\,n.
j = i	1
При расчете управляющих переменных К1, L1 и правых частей
уравнений (17-33), (17.36) при заданных значениях И”, i= 1, т,
следует подбирать не только соответствующие значения у, но
и также значения т|;, чтобы выполнялись условия (17.41), (17-43).
Условия на правом конце траектории вытекают из (17-34):
М'Х'И- Г—>со, (=],«.	(17.44)
Отыскание оптимального плана y = (x(Q, K(z), L(/); C(z), Vp))
сводится, таким образом, к решению краевой задачи для системы
(17.33), (17.36) обыкновенных дифференциальных уравнений поряд-
ка 2т с краевыми условиями (17.37), (17-44) и правыми частями,
подсчитываемыми в соответствии с описанными выше правилами.
§ 17.7. Стационарный режим
При определенных условиях можно выделить частное решение
дифференциальных уравнений оптимального развития, играющее
существенную роль в структуре оптимального плана. Пусть а},
С'т— постоянные величины— производственные функции и функ-
396
ция полезности—не зависят явно от времени. Зададим Х; = Х;ое ,
/=1, и; у = уое~В1, т|; = 0, где Х;о, у0—константы, которые нужно
‘ определить. Тогда Х; = Хю/у0, А = Е ^(ц, + 8)Х; и система (17.30)
____________	j=i
при г=1, т представляет собой нелинейную систему уравнений
т неизвестными Х;,	Обозначим ее решение Xs, pf, k‘s,
$ i>m, соответствующие этому решению значения с учетом
равенств (17.1), (17.29), (17.30).
Таким образом, мы нашли некоторую допустимую систему
цен X, у, Ф, определенную с точностью константы уо, которой
отвечает постоянный вектор оптимальной фондовооруженности
к. Среди оптимальных планов, отвечающих этим ценам, можно
выделить сбалансированный по всем равенствам (17.1) —(17.5),
кроме, может быть, начальных условий £1(0) = £q. Учитывая
постоянство оптимальной фондовооруженности, будем искать
этот план среди таких, остальные компоненты ^которого также
1 не зависят от времени. В частности, из условия /С = const следует
в силу (17-3)
У1=^К\
т. е. инвестиции идут только на возмещение выбытия основных
фондов. Учитывая, что FE — klL‘ из (17.1), (17.2), получим
||	X (Е-А)^)1А- X	i=TJi, (17.45)
7 = '	1=1
j = i
Дальнейший расчет оптимального сбалансированного плана
Зависит от аналитических свойств функции полезности g(C),
I	п
j 1. Пусть g(C)= Е Найдем 0(/X| = max0./Xf и зададим
I	i=i	*	;
= Это значит, что X, =0, и Х;>0;, /у/, т. е. с учетом
13.4) Q = CU и?Ц а С1 не определено. Подставляя эти Значения
в (17.45) и (17.46), получим систему «+1 линейных уравнений
относительно и + 1 неизвестных £', С‘. Будем считать, что
существует решение данной системы: Lls>0, Ci^Cl„. Вследствие
продуктивности и неразложимости матрицы (£-H))/J(P) это
решение существует, по крайней мере, при достаточна малых
Pi, CJh^O. Полученное решение Cj, Lls, K's=lclsLls, Pj = p'A'(
представляет собой искомый план.
2. Пусть g(C)—нелинейная функция с описанными выше
свойствами. Зададим некоторое у0. Тогда Х; = Х;уое-5‘ и потреб-
ление C(Yo) = const определено условием (3.4). Из (7.3) имеем
397
£j'(Yo) = X	С'(у0).
i=l
Значение y0 подбирается так, чтобы удовлетворялось (17.46).
Если при этом Z?>0, то полученное решение есть искомый план.
Таким образом, мы нашли допустимую совокупность перемен-
ных (ден) X*5, y*s, постоянную в случае отсутствия дисконтирова-
ния, и отвечающий ей постоянный оптимальный план, сбаланси-
рованный по всем условиям постановки задачи кроме начальных
условий K'(0) = Kq. Для начальных условий K'O = K'S этот план
есть решение поставленной задачи. Оптимальное значение фун-
кционала полезности в этом случае
Z(C]=-Z(V)= £ J}X!(0)KJ(0)+f G(V, C)dL
i, J = 1	0
Если	TO Z(C)«~Z(^*).
Конкретизируем некоторые свойства найденного режима.
Максимизируемый функционал можно записать в виде
Л	00	Л
/= X	+ J(e’6tYo X П(к!)Ь* + С(Г, С)+
?=1	о	,=1
+ 7oe"s,y)d/,	(17.47)
где г (&) = £;/(&)-/?&—1. Из (17.47) следует, что иско-
мый оптимальный сбалансированный режим v максимизи-
рует на D суммарную производственную и коммерческую
прибыль, выраженную в стационарных ценах Xs, или, иными
словами, минимизирует отклонение этой прибыли от максимума
x;(^s) = 0, ^(Xs, Cj. Иначе говоря, искомый оптимальный режим
минимизирует в этом смысле отклонение от стационарного
режима. Проводившиеся расчеты показывают, что при /-юо
имеет место сходимость показателей оптимального плана к стаци-
онарным.
Если входные показатели зависят от времени, то стационарный
режим отсутствует, но существует некоторый его аналог, предста-
вляющий собой уравновешенное развитие, обусловленное экзоген-
ным изменением входной информации.
Интересно отметить, что такие показатели стационарного
режима, как цены и фондовооруженности отраслей к1, не зависят
от выбора функции полезности у (С ), что совпадает с трудовой
теорией стоимости.
Уравнения (17-33), (17-36) с начальным условием W(0) = Wo
определяют функции X^(z),	а также остальные
переменные процесса у и множители _и____________j= 1, т,
с точностью до начальных значений Х;(0), у=1,ш.
398 '
Пусть существуют такие ХфО), j=\,m, что это решение
удовлетворяет при некотором t=T равенству	j=\,m.
Введем в рассмотрение функции If (/), j = 1, т, которые при
\t^T совпадают с соответствующими компонентами этого реше-
ния, а при 1>Т: X]'(l)=Xj'(T)e~s<.
Остановимся на варианте с линейной функцией полезности,
g-= £ 9гС‘. В этом случае при t>T цены j>m, у
i i = 1	_
Фондовооруженности кг и номер избыточной отрасли / совпадают
со стационарными значениями. Компоненты режима vT опреде-
ляются как при t>T так и при t^T интегрированием уравнения
(1736).
Такой режим удовлетворяет условиям теоремы 5.1, т. е. являет-
ся оптимальным, если только	при	возрастает
медленнее, чем е5'. Таким образом, построение оптимального
плана сводится к решению краевой задачи
^(0)=^, ^(Т) = Ц i=TJn;
Шри произвольном Т>0. Количество неизвестных Г, \(0), г = 1, m,
в этой задаче превышает количество уравнений =	1, т.
На таком режиме цены и фондовооруженности начиная с t = Т
совпадают со стационарными, остальные же переменные Ll, С1,
К1 не совпадают.
В случае нелинейной зависимости g(C), вообще говоря,
отсутствует конечное Г, начиная с которого имеет место
совпадение со стационарным режимом. В этом случае можно
построить последовательность подобных решений, на которой
значения относительных цен и фондовооруженностей сходятся
к стационарным.
§ 17.8. Структура оптимального режима
и алгоритм его построения
Говорить о конкретных особенностях оптимальной траектории
можно только при достаточно конкретных предположениях
о явной зависимости входных переменных от времени. Будем
ориентироваться на случай постоянных д®, d} и не зависящих
явно от времени производственных функций F' и полезности g,
имея в виду, что выявленные для данного случая особенности
сохраняются и при отклонении в умеренных пределах от этих
предположений.
На начальном участке характерно наличие неразвиваемых
отраслей И‘=0. Если Л'о достаточно малы, то количество
неразвиваемых отраслей убывает до нуля и имеет место
сбалансированный рост, на котором помимо общих свойств,
перечисленных в § ]7.4, существует зависимость фондовоору-
женностей к\ i=\,n, только от т относительных цен Х;,
В процессе этого роста /=],«, сходятся к ста-
ционарным значениям этих величин.
Отыскание оптимального режима сводится к решению краевой
задачи для системы 2т дифференциальных уравнений с гранич-
ными условиями И/'(0)=И/о, i=l,m; Hz'(z')^O при Z->co.
Решать эту задачу рациональнее последовательным интегрирова-
нием задачи Коши для (17.33), (17.36) справа налево, от z=T
к нуцю, задаваясь последовательностью значений Т->со, так как
траектория при больших t имеет более регулярный характер
[отсутствие неразвиваемых отраслей, ввиду этого более простое
решение уравнений межотраслевого баланса (17.38), (17.39), (17.1)
и сходимость к стационарному режиму].
Опишем последовательность решения задачи для линейной
зависимости g= £ 9;С;.
i = i
1.	Находим стационарный режим V, Vs-
2.	Задаем достаточно большое значение Т, чтобы можно
было ожидать, что рассматриваемая экономическая система
способна выйти за время Т на уровень фондовооруженности
стационарного режима. Задаем Х,(Г)=Х';, у=1,щ.
3.	Задаем значения lE'fr), г = ],щ, и интегрируем систему
(17.33), (17,36) с этими условиями в момент Т справа налево
до момента / = 0.
4.	Проверяем на полученном решении условия И7'(0) = Но,
Если они не выполняются, то задаемся другими IV1 (т)
и повторяем расчет до их выполнения.
При интегрировании системы (17.33),	(17.36) будет
иметь место смена характера оптимального режима и со-
ответственно способа вычисления правых частей уравнений.
Так, на участке, прилегающем к t=T, существует избыточная
отрасль i=l = P. При Z->9 избыточная отрасль может смениться,
а начиная с некоторого момента — отсутствовать: C‘(/) = Qn,
г = ],л. Начиная со значения нарушится при некотором i-k
условие K‘(tj > А''ое ~^'г. С этого момента, fc-я отрасль становится
неразвиваемой и соответственно меняется способ расчета. При
приближении к z = 0 количество неразвиваемых отраслей воз-
растает.
Замечание. Описанная здесь роль стационарного режима в структуре оптималь-
ного плана и в алгоритме его расчета сохранится и в том случае, если входные
данные задачи зависят явно от времени, но имеют' предел при /->со.
400
§17.9. Четырехотраслевая модель*
народного хозяйства СССР
Описанная выше схема построения траекторий развития народ-
ного хозяйства может быть использована для проведения конкрет-
ных расчетов. В качестве примера приведем результаты расчетов
для четырехотраслевой модели народного хозяйства СССР.
Коэффициенты прямых затрат а}, подсчитанные по балансу
1964 г. (в рублях в сопоставимых ценах 1965 г.**), приведены
в табл. ] 7.1.
Таблица 17.1
Отрасль	Промышлен- ность	Строитель- ство	Сельские хозяйство	Материал Ь’ ные услуги
1. Промышленность	0,403	0,528	0,096	0,174
2. Строительство	—	- —		—
3. Сельское хозяйство	0,092	0.003	0,226	—
4. Материальные услуги	0,092	0,006	0,054	0,006
Коэффициенты dlj технологической структуры капитальных
вложений (в % к итогу) приведены в табл. 17.2.
Таблица 17.2
Фондосоздающие отрасли	Фондопотребляющие отрасли			
	промышлен- ность	строитель- ство	сельское хозяйство	материаль- ные услуги
1. Промышленность	41,8	68,7	47,6	57,0
2. Строитедьстзо	58,2	31,3	52,4	43,0
Итого	100,0	100,0	100,0	100,0
Производственные функции отраслей задаются в виде Коб-
ба-Дугласа:
F(K, =	а(->0, ₽,>0,
Для их расчета использовались временные ряды, характери-
зующие динамику валового продукта, основных производственных
фондов СССР (в сопоставимых ценах 1965 г.) и занятость в сфере
* Параграф написан по результатам, полученным при участии
Б. И. Изтелеудова.
** Эти и другие данные взяты из кн.: Белкин В. Д, Экономические
измерения и планирование. М.: Мысль, 1972; Киселев В. В. Плановые расчеты
по моделям экономического роста.— М;: Экономика, 1971.
401
Таблица 17.3
Отрасль	Эластичность по фондам	Эластичность по труду	
1. Промышленность	0,7758	0,2242	1,518
2. Строительство .	0,5728	0,4272	1,099
3- Сельское хозяйство	0,45—0,7	0,55—0,3	1,023
4. Материальные услуги	0,6834	0,3166	1,074
В среднем по народному хозяйству	0,6481	0,3514	1,176
материального производства за 1955—1968 гг., приведенные
в сборниках . «Народное хозяйство СССР» за 1955—1968 гг.
Параметры производственных функций отраслей приведены
в табл. 17.3.
Коэффициент а3 в расчетах варьировался в указанных
в табл. 17.3 пределах из-за малой адекватности для сельского
хозяйства двухфакторной производственной функции Кобба —
Дугласа.'
Структура потребления предполагается заданной в виде
C^Z'C'; г = 2, 3, 4,
где заданные величины Z'— фонды потребления соответствующих
отраслей в расчете на рубль фонда потребления, созданного
в промышленности:
Z2=0,096, Z3 = 0,211, Z4=0,108.
К
Функция полезности задается линейно у(С)=£ 0,С' и вслед-
j=i
ствие заданности структуры потребления независимо от конкрет-
ных значений В,- получается равной
£(С) = ЛС’,
где А — постоянный положительный множитель.
Рост фонда потребления в проводимых расчетах ограничивался
снизу четырьмя процентами в год:
Ст = Со£л‘, и=4%,	152 млрд.руб.
Коэффициент дисконтирования был взят равным 5 = 8%.
Коэффициент выбытия фондов принимался одинаковым во
всех отраслях: р.=0,06.
402
За начальный (базисный) год 1$ при расчете был взят 1975 г.
Уровень трудовых ресурсов предполагался постоянным и от-
вечающим уровню 1975 г.: У=87,6 млн. человек.
Следует отметить, что принятые предположения обусловли-
вают явно заниженный вариант развития', не учитываются
экзогенный технический прогресс в производственных функциях
и рост трудовых ресурсов. Поэтому рассчитанный на основе
сделанных предположений вариант оптимального развития эконо-
мики имеет достаточно условный характер.
Ниже приводятся некоторые результаты расчета оптимального
режима развития для двух вариантов задания эластичности
сельского хозяйства по фондам: <х3=0,47 (вариант!); а3 = 0,6
(вариант П).
Вариант I
Результаты роста стационарного режима представлены
в табл. 17.4. Проведен анализ структурных сдвигов в валовом
общественном продукте, происшедших за время перехода эконо-
мики на стационарном режиме.
Доля промышленности в создании валового общественного
продукта составляет 70% против 64,7% базисного 1975 г.
Доля сельского хозяйства в создании валового продукта
осталась примерно той же, что и в базисном году, а доля
строительства и других отраслей материального производства
составляет 4,3 и 9,2% против 10,7 и 10,5% базисного года
соответственно.
Увеличение валовой продукции составляет по отноше-
нию к базисному году для промышленности 224%, сельско-
го хозяйства 205*%, для других отраслей материального произ-
водства 190%.
Проведем анализ поведения экономики на режиме роста.
Продукция строительства направляется в основном на ввод
в действие основных фондов в других отраслях народного
хозяйства. Темп ее роста имеет тенденцию к снижению при
приближении к стационарному режиму.
При переходе на стационарный режим высокими тем-
пами растут основные производственные фонды промы-
шленности— 3,36, относительно низкими темпами — сельского
хозяйства и прочих отраслей материального производства—1,78
и 1,10.
Другие показатели режима роста выглядят следующим обра-
зом.
Среднегодовые темпы роста валовой продукции составляют:
для промышленности— 7,5%, строительства—-8,5%, сельского
хозяйства — 3,9, Других отраслей материального производства —
5,0%, в целом по народному хозяйству — 6,9%.
Доля фонда потребления в конечном продукте возрастает
с 73,1% в базисном году до 86% на стационарном режиме.
403
Среднегодовые темпы роста фондовооруженности в промыш-
ленности и строительстве выше, чем в сельском хозяйстве
и других отраслях материального производства.
Трудовые ресурсы в промышленности и сельском хозяй-
стве увеличиваются на 10 и 11% соответственно, а в строите-
льстве и других отраслях материального производства умень-
шаются на 7 и 5% соответственно по сравнению с базисным
годом.
На стационарный режим экономика выходит через 27 лет.
Вариант II
В этом варианте расчета развития экономики значения элас-
тичности фондов в сельском хозяйстве считались равными
0,6, остальные параметры остались теми же, что и в вариан-
те I.
Результаты расчета стационарного режима представлены
в табл. 17.4. Проведем их сравнение с вариантом I.
Валовая продукция отраслей в варианте II выросла по
сравнению с вариантом Г. в промышленности — на 7%, строи-
тельстве— на 17%, сельском хозяйстве—на 9,8%, других отраслях
материального производства — на 10%. Фондовооруженность
в промышленности увеличилась на 4%, в сельском хозяйстве —на
17%, а в строительстве и других отраслях материального
производства — соответственно на 4%.
Структура валового общественного продукта существенно
не изменилась, в то время как доля промышленности в ко-
нечном продукте повысилась, а в сельском хозяйстве умень-
шилась.
Таблица 17.4
Основные показатели отраслей на стационарном режиме
Отрасль	у, млрд, руб.	г, млрд, руб.	с млрд, руб.	а; млрд, руб.	А, тыс. руб.	/«. ТЫС. руб.	V, млн. руб.	млрд, руб.	к	L, млн. чел.
			Вариант		1					
Промышленность	1250	551,0	488,5	1309,9	34,37	32.85	78,6	852,9	1,6086	38,1
Строительство	74,0	74,0	21,5	49,9	10,28	14,78	3,0	1019,6	0,4117	4,9
Сельское хозяйство Другие отрасли мз-	250,3	—	102,5	304,8	11,74	8,81	18,3	—	0.4257	26
•сериального про- изводства	169,3				52,7	230,8	12,43	8,55	13,8		0,3867	18,6
			Вариаят		и					
Пром ышиенность	1341,5	581,0	552,9	1390,2	35,79	33,90	83,4	934,5	1,5365	38,8
Строительство	86,9	86,9	32,7	75,7	10,73	10,69	4,3	1087,3	0,4072	7,12
Сельское хозяйство Другие отрасли ма-	277,1	—	116,7	309,0	13,7	10,67	19,2	—	0,3905	22,6
сериального про* изводства	184,8	—	59,7	246,9	12,96	8,77	14,8	—	0,3745	19Д
404
Доля фонда потребления в конечном продукте увеличивается
с 73,1% в базовом 1975 г. до примерно 92,5% на стационарном
режиме.
Основные фонды по сравнению с вариантом I в промышлен-
ности увеличились на 6,2%, в строительстве—на 46%, в сельском
хозяйстве — на 1,5% и в отраслях материального производ-
ства— на 7%. В связи с ростом фондовооруженности в сельском
хозяйстве трудовые ресурсы уменьшились на 13% по сравнению
с вариантом I.
Среднегодовые темпы роста валовой продукции промышлен-
ности, строительства и других отраслей народного хозяйства
существенно пе изменились, в то время как в сельском хозяйстве
они увеличились до 5,3 против 3,9 в варианте I.
В отличие от варианта I перазвиваемыми отраслями являются
промышленность до момента 1=3 (1978 г.) и прочие отрасли
материального производства до момента г=4. Сельское хозяйство
и строительство являются развиваемыми отраслями.
Согласно расчетам, в рассматриваемом варианте на стационар-
ный режим экономика выходит через 22 года.
Приложение
Справочные данные
по математическому аппарату
При изучении настоящего курса оптимального управления
используются элементы дифференциального и интегрального
исчисления и его применение к исследованию графиков функций
и нахождению их экстремальных значений, простейшие диф-
ференциальные уравнения, методы численного интегрирова-
ния систем- обыкновенных дифференциальных уравнений
в формах задачи Коши и краевой задачи.
Ниже приводятся некоторые сведения по указанному мате-
матическому аппарату.
П. 1. Оптимизация функций одной переменной
на ограниченном множестве
Пусть при хе[а, Д задана непрерывная функция Дх). Требуется
найти max Дх). В случае же необходимости минимизации на
заданном отрезке функции Дх) задача может быть сведена
к максимизации функции g(x)=— Дх), Поэтому без нарушения
общности подхода к нахождению максимальной или минимальной
функции можно говорить только о ее максимизации.
Для решения данной задачи вначале необходимо найти
стационарные точки функции Дх), принадлежащие отрезку [а,
Ь], т. е, такие точки xt, в которых Д(хк) = 0 tfXf.efa, Ь]. Так
как требование стационарности Д(х) = 0— необходимое условие
локального экстремума, следует установить, что мы имеем
в каждой стационарной точке: локальный максимум или минимум
или же точку перегиба функции. Рассмотрим эти случаи.
Если в стационарной точке хк существует отличная от нуля
вторая производная, то при Д'(хк)<0 в этой точке будет
локальный максимум, а при Д'(хД > 0 —локальный минимум.
При Д'(хЛ) = 0 о характере локального экстремума, если он
существует в точке х = хк, следует судить по знаку отличной
от нуля производной более высокого порядка.
Если в стационарной точке xk f"ДД =0, а Д"(хк) ^0, то
хк— точка перегиба и локальный экстремум в ней не достигается.
Если Д'(хД не существует или Д'(хк)=0, о характере локального
экстремума в точке хк можно судить следующим образом: если
Д(х) > 0 при хк —h < х и Д (х) > 0 при xk-\-h> х, где h > 0 —произ-
406
вольное достаточно малое число, то хк — точка локального
максимума.
Если /'(х)<0 при xk — h<x и /'(х)>0 при xk + h>x, то
х*—точка локального минимума.
Если /'(х) имеет одинаковый знак при xk — h<x и xk + h>x
(где по-прежнему Л>0), то хк — точка перегиба функции и эк-
стремум в этой точке не достигается.
Таким образом, среди всех стационарных точек xke[«, Ь]
мы одним из указанных выше способов может установить точки
локальных максимумов.
Пусть это будут точки хь ..., xm. Добавим к ним граничные
точки х = а и х~Ь и определим тахДх), где Х=(хг, хт,
хе Y
а, Ь}. Точка хе А", в которой достигается максимальное значение
Дх) = max Дх), обозначается следующим образом:
х€ [а, 6]
х = arg тахДх),
Из рассмотренных методов максимизации функции вытекают
следующие следствия:
1. Монотонная при хе [а, &] функция Дх), т. е. такая, для
которой/'(х)^0, при хе[«, /?] достигает максимального значения
только на границе. При этом если функция монотонно возраста-
ющая (/'(х) > 0, хе [л, £>]), то arg max f(x] = lr в случае монотонно
хе [а, д]
убывающей функции (Д(х)<0, хе[л, &]) argmax/(x) = «.
2, Линейная функция f(x) = Ax+B как частный случай моно-
тонной при А т^О, ге[а. Ь] достигает максимального значения
в точке х — b при А >0 и в точке х = а при А <0.
Рассмотрим примеры.
Пример 1. Найти max ( — х2 + 2х).
X Е [0, 3]
Решение. Дх)=—х2 + 2х. Для этой функции найдем стаци-
онарные точки исходя из условия Д(х)=0, хе[0, 3]. Это дает
нам — 2х + 2 = 0, откуда получаем одну стационарную точку
x^lejO, 3], /"(.r)=—2<0 Vx, т. е. в точке Xj—I имеем по
крайней мере точку локального максимума. В граничных точках
х—0 и х=3 вычисляем: ДО) — 0, Д3)=—3, Д1) = 1,
Сравнение указанных величин позволяет сделать окончатель-
ный вывод о том, что в точке Xj — 1 достигается не только
локальный, но и глобальный максимум функции Дх) на отрезке
хе [0, 3], График функции Дх), откуда видна справедливость
407
сделанного вывода, приведен на рис, П. 1 (пунктиром показаны
графики у=—х2 и у —2х).
Пример 2, Найти max (In х — х3),
«р, зр
Решение. Дх)=1пх — лЛ Найдем стационарные точки исходя
из условия /'(х) = 0, хе[1, 3]. Получаем Д(х)=- — Зх2 = 0, откуда
хг=УТ/3.
Проверка знака второй производной показывает, что /"(х) =
= —5 — 6х<0 для Vxe[l, 3]. Следовательно, в точке xt — ^/1/3
достигается локальный максимум. Для проверки его на глобаль-
ность вычисляем значения функции /(х) в граничных точках:
/(1)=—1, /|3)=1п3—27~ —25,9. Сравнивая эти значения со значе-
нием /(*1) =/Д/1/3)= */з( —1пЗ) —	заключаем, что в точке
х( — V V3 достигается глобальный максимум (рис. П. 2).
Пример 3. Найти тах,х2+1).
И <2
Решение. Найдем стационарные точки: /'(х) = 2х = 0, х(=0,
У"(х) = 2>0. Следовательно, стационарная точка х[=0 — точка
минимума функции Дх). Максимум может достигаться только
в граничных гочках х2 3= + 2. В обеих этих точках имеем
Д + 2) = 5, откуда делаем вывод, что х2=—2, х3=2 — точки
искомого максимума функции Дх).
П. 2. Зависимость функции и множества, на котором
она определена, от параметра
В основных разделах курса теории оптимального управления
мы постоянно встречаемся с более сложной, чем описана в П. 1,
408
задачей: требуется найти max fix, t). В других обозначениях
эта задача соответствует минимизации по х функции R(t х),
рассмотренной в гл. 5, функции Гамильтона H\t, ф, х, и) по
управлению и- - в гл. 7, 8 и др.
Как и раньше, предполагается, что функция/(х, z) непрерывна
по х, t — параметр, Ze[z1; z2], *eLflp)> ^(ОТ ^ак видим, от
параметра t в общем случае зависят как функция Дх, Z), так
и граничные точки множества допустимых значений xe[a(z), Z>(z)].
Логика максимизации (минимизации) функций в принципе та
же, что и в предыдущем пункте, только результаты будут
зависеть от значений параметра Z. Рассмотрим примеры.
Пример J. Дх, Z)=Zx, O^x^z2, |/| Найти тахДх, /).
Решение. Функция Дх, Z) по х линейна. Следовательно,
при Z 0 она стационарных точек не имеет и максимум
достигается на границе: либо в точке х=0, либо в точке x = Z2.
Вычислим значения функции Дх, Z) в Этих точках и сравним
их при различных значениях Z:
/(О, Z)=0, /(z2, z) = z3.
Таким образом, при z<0 ДО, z)>/(z2, z), так как z3 <О,
т. е. максимальное значение функции Дх, z) достигается в точке
x(z) = 0.
При z>0 ДО, ?)</(z2 Z), так как Z3>0. Теперь максимальное
значение функции Дх, Z) достигается в точке x(z) = Z2.
Наконец, в случае z = 0 Дх, z)=0. При этом существует лишь
одно допустимое значение х=0 (0 =£ х Z2 =0). Следовательно,
это значение и будет точкой максимума функции Дх, z) при Z = 0.
Все рассмотренные случаи можно описать одной результи-
рующей формулой
-/о „	(0, если — 1 Z =5 0,
x(Z) = arg max Дх, t}= < A	’
[Z , если 0 < Z 1.
Как видно, случай z = 0 отвечает обоим условиям результи-
рующей формулы.
Пример 2. Дх, z) = Zx2 + 2х, |х|^1, |z|^l. Найдем тахДх, z).
Решение. При Z^O функция Дх, Z) представляет параболу,
ориентированную ветвями вниз, если Z < 0, и ветвями вверх,
если Z > 0.
При Z = 0 Дх, 0)=2х—линейная возрастающая функция, и ее
максимум достигается на правой границе, т. е, х(0) —1.
Рассмотрим случаи — 1 <Z <0 и 0< Z sS 1. При Z < 0 парабола
ориентирована ветвями вниз и точка безусловного максимума
409
Рис. П.З	Рис. П.4
соответствует вершине параболы. Абсцисса вершины параболы
.¥„(/) определяется из условия
^=2/х + 2 = 0,
откуда хД)---'.
Максимальное значение функции Дх, Д достигаемое в вершине
параболы, в зависимости от аргумента i равно

В частности:
при t=-l хв(-1)=1, Д1,
при t=-'- *,(-0 = 2, /(2, -0 = 2;
при /=-| *,(-0=з,/(з, -0=з;
при t -> -0 (стремление аргумента t к нулю слева) хв( — 0) -> оо,
/(со, -0)=оо.
В результате семейство парабол для случая — 1 t < 0 будет
иметь вид, показанный на рис. П. 3.
При всех —1</<0 точка хв(/)— след вершины парабо-
лы — расположена либо на границе допустимой области значений
х (при t= — I хв(г) = 1), либо правее правой границы, т. е. хв(г)> 1
при — 1 < t < 0, причем по мере приближения аргумента i слева
к нулю значения хв(г) и Дхв(Д возрастают. Следовательно
при — I / <0 максимальное значение функции Дх, /) при |х| < 1
достигается в точке х(г) = 1 (границы х — + 1 на рис. П. 3 показаны
штрихами).
Рассмотрим случай 0</< 1. При этом парабола Дх, =
= fx2 + 2x ориентирована ветвями вверх.
410
В стационарной точке лв(г) = — I /Z достигается абсолютный
минимум функции f(x, i) (рис. П. 4). Следовательно, максимум
по х при условии |х|^1, как видно из рис, П. 4, достигается
только в граничных точках х= + 1. Определим точку максимума
при разных значениях t с помощью прямой подстановки значений
х=±1 в выражение Дх, t) — tx2 + 2x. Имеем /(I, t) = t + 2, f( — 1,
t\ = t— 2, Отсюда видно, что при любых значениях tz)>Д—I,
zj, т. e, x(r)=l Vfe[0, 1].
Учитывая предыдущий результат, получаем
x(/) = argmax(Zx2-l-2x) —1, |z|	1.
Пример 3. Дх, /)=—x2 + 2tx, 0^х^2, |z|^2. Найти
maxДх, z).
Решение, В данном случае функция Дх, Z) по х при
фиксированном значении t представляет параболу, ориентирован-
ную ветвями вниз при любых t, так как коэффициент при х2
отрицательный и от t не зависит. При различных значениях
г возможны три случая (рис. П. 5). Как видно из рис, П. 5,
эти случаи сводятся к следующим вариантам (нумерация кривых
на рисунке отвечает номерам вариантов):
1.	Максимальное значение функции Дх, z) достигается
в точке x(z)=xB(z), если xB(z)e[0, 2], т. е. лежит в допустимой
области изменения х (на рис. П, 5 эта область показана
штрихами).
2.	Максимальное значение функции Дх, Z) достигается на
правой границе (в данном примере х=2), если значение xR(z)
лежит правее правой границы.
3.	Максимальное значение функции Дх, z) достигается на
левой границе (в данном примере х=0), если значение xR(z)
лежит левее левой границы.
Переведем сказанное выше на язык математических отноше-
ний. Абсциссу вершины параболы xB(z) определим из условия
= 0, или, другими словами, xB(z) = arg	=0^. Из этого
вытекает — = — 2x-|-2z=0, откуда xB(z)=Z. Нанесем функцию
дх
xB(z) = Z— след вершины параболы — на координатную плоскость
z, х (допустимые изменения аргумента х и параметра t показаны
штрихами на рис, П. 6).
При Ze [0, 1] на рис. П. 6 абсцисса вершины параболы xB(z)
лежит в допустимой области 0 х 1, Эю соответствует случаю
1 на рис, П, 5, т. е. получаем x(Z) = Z при Ze[O, 1].
411
Рис. П.5
Рис. П.6
При (е[—2, 0) на рис. П. 6 след вершины параболы лежит
ниже нижней границы х = 0. На рис. П. 5 это соответствует
случаю 3, т. е. получаем Дг) = О при /е[ —2, 0).
При Ге[1, 2] на рис. П. 6 след вершины параболы лежит
выше верхней границы х= 1. На рис. П. 5 это соответствует
случаю 2, т. е. получаем х(/) = 1 при /е[1, 2],
Объединяя рассмотренные случаи, получаем окончательный
результат (на рис, П, 6 он показан жирной линией):
Г 0, если te [—2, 0],
х(/) = < I, если /е[0, 1 ],
( 1, если t е [1, 2].
В изложенных разделах курса чаще всего встречаются функции
Дх, Д линейные по х и представляющие по х параболу. При
этом имеется в виду, что максимизация функции Дх, /)
осуществляется по х.
В случае функции Дх, /)=Я(г)х+5(г), линейной по х, где
Д?) х b(t), как следует из предыдущего, можно записать
результат в общем виде:
Г b(tY если le{t: A(t} > 0},
x(t)= < а(Д, если te {г: A(t) < 0},
IVxe [а(Д Д/)], если 1е {/:	0}.
Если Дх, /) = .ДДх2 + .бДх-|- СД— парабола, ориентированная
ветвями вверх (т. е- для A(t) > 0), то максимум достигается
только на границе (или на обеих границах одновременно). При
этом исследование стационарных точек оказывается лишним.
Если Дх, t)— парабола, ориентированная ветвями вниз, то
максимум достигается: в вершине параболы xB(r)=arg| ~=§ ),
' f \ ox J
если хв(г)е[ДД ЦД]‘, на правой границе ДД если хв(/)>ЦД
на левой границе a(t), если хи(Д =£ а(Д
Запишем все это в виде обобщенных формул:
412
для случая Л(/)>0
Г	если f(b(tV t) >/(a(tY t),
x(t) = < a(t), если/(a(t),	z),
(.a(f), b(t), если/(a(t), f) =f(b(t), z);
для случая Л(г)<0	,	\
-xB(i)=arg( ^=01, если xB(t)e [a(r); b\
 *(/)=« b(t), если xa(r)>o(/),
Случай Л(/)-0 мы не рассматриваем, так как он аналогичен
предыдущему случаю линейной функции.
П. 3. Дифференциальные уравнения первого порядка
с разделяющимися переменными
Дифференциальное уравнение первого порядка
т = х)	(П. 1)
имеет решение х = х(/), удовлетворяющее условию х(/0) = х0 (зада-
ча Коши), если функция /(г, х) непрерывна в некоторой
окрестности точки (?0, хД Точнее, если функция Дг, х) непрерывна
в открытой области D (не включая границу этой области)
и удовлетворяет в ней условию Липшица
1/(?, х)-/(',	(П. 2)
где М — некоторая положительная константа, то дифференциаль-
ное уравнение (П. J) при любом начальном условии х(70)~ х0
{где точка (i0, х0)еЕ> имеет единственное решение х--х(г),
определенное в области £>].
Условие Липшица (П. 2), в частности, удовлетворяется, если
функция /((, х) имеет в области D ограниченную частную
д/
Производную £-.
Если можно представить f(t,	то в уравнении (П. 1)
переменные разделяются и его можно переписать следующим
образом:
cp2(x)dx=(pL(/)dr.
Общий интеграл имеет вид
5 <p2W<V=f (pi(z)dz-i- С.	(П.3)
о	о
Рассмотрим примеры.
413
Пример 1. .x=tx, х(0) = 4. Найти функцию x(z).
Решение. Разделяя переменные и интегрируя, получим
Ну
— =zdz, In|х| = —+ ln С.
Вместо произвольной постоянной С, имеющей место в общем
случае (П. 3), здесь для удобства потенцирования введено слага-
емое In С, которое также является произвольной постоянной.
В то же Время получающаяся после потенцирования формула
имеет более компактный вид:
x(t) = Ce,2/2.	(П. 4)
Произвольная постоянная С в общем решении (П.4) опреде-
ляется из начального условия х(0) = 4;С=4.
Решение ’Данного примера: x(t)=4e'2,2.
Пример 2. х=(1+ x2)cos/; х(0)=1. Найти функцию
Решение. Разделяем переменные и записываем неопределен-
ные интегралы:
dx
1 +х2
cos/dr.
После интегрирования левой части по х, а правой—по
t получаем
arctgx = sin/+C,
.откуда x(/j = tg(sin r-f-C).
Учитывая начальное условие х(0)=1, получаем l = tgC, откуда
С=я/4.
Решение данного примера: x(/) = tgl ^ + sinr
П. 4. Линейные дифференциальные уравнения
второго порядка
с постоянными коэффициентами
Рассмотрим дифференциальное уравнение вида
ах+йх+ех==/(г),	(П. 5)
где а, Ь, с -постоянные коэффициенты.
Если функция Дг)^О, то уравнение (П. 5) называют
неоднородным; если /(t) = 0, то имеем однородное диф-
ференциальное уравнение. При а^О уравнение (П. 5)--второго
порядка. Его общее решение содержит две произвольные
постоянные. Для их определения задаются либо начальные
условия х(0)=хо, х(0) = х— в этом случае имеем задачу
Коши, либо краевые условия х(0)=хО} х(Т) = х1—в этом
случае имеем краевую задачу.
414
Для уравнения второго порядка с постоянными коэффициен-
тами (П- 5) в ряде частных случаев, зависящих от вида функции
/'(/), удается найти общее решение в квадратурах. Эти случаи
будут рассматриваться ниже, при этом трудоемкость решения
как задачи Коши, так и краевой задачи одинакова. В более
общих случаях, когда решение достигается численными методами,
для краевой задачи оно существенно сложнее.
Общее решение неоднородного уравнения (П. 5) x0H(z) состоит
из суммы общего решения однородного уравнения %«,(/) и ча-
стного решения неоднородного уравнения
Вид общего решения однородного уравнения опреде-
ляется корнями характеристического уравнения
ар2 + 6р+с — 0.	(П. 6)
Рассмотрим возможные случаи.
I.	Кории р1} р2 уравнения (П. 6) действительные и разные.
В этом случае
где С,, С2 —произвольные постоянные.
2.	Корни рг, р2 уравнения (П. 6) действительные и равные:
pi—pz^p. В этом случае
хоо(0~&рг ' (^1 * + Ст),
где С<, Сz—произвольные постоянные.
3.	Корни pi, р2 уравнения (П. 6) комплексно-сопряженные:
Pi’ Z’2==ai/₽j гДе а> 0—действительные числа; i—мнимая
единица: i2= — 1. В этом случае
х«Д) = cos +С2 sin 0г),
где С, и С2—произвольные постоянные.
Применительно к линейному дифференциальному уравнению
второго порядка с постоянными коэффициентами (П. 5) пред-
ставленные три случая исчерпывают все возможные варианты
общего решения однородного уравнения. Вид частного решения
неоднородного уравнения хчн(г) зависит от вида функции Дг).
Рассмотрим некоторые случаи, для которых можно указать
методы определения лч„(Д.
1. Пусть Дг)—многочлен степени т:
Дг)=а0/т+а11"’1 +a2fm-2+... +am, (П. 7)
где т, а0, сц, аг, ..., «„--заданные соответственно показатель
степени многочлена и его коэффициенты.
В этом случае частное решение неоднородного уравнения
лч„р) также найдем в форме многочлена m-й степени:
Ab(0 = Yo''" + Yi''"“‘ +Y2tm~2 + - +Y«.	(П. 8)
415
Коэффициенты y0, у15 ..., у,„ необходимо определить, для
чего в левую часть дифференциального уравнения (П. 5) под-
ставим выражение (П, 8), а в правую - (П. 7). После двойного
дифференцирования выражения (П. 8) и приведения подобных
в левой части уравнения (П. 7) обеих его частей получим
многочлены степени т. Чтобы эти многочлены тождественно
совпадали при любых значениях /, должны совпадать их
коэффициенты при одинаковых степенях tk, А- = О, I, m,
в левой и правой частях этого уравнения. Приравнивая слева
и справа соответствующие коэффициенты, получим m-f-l алгеб-
раическое уравнение для определения коэффициентов у0, у1; ут.
2. Пусть теперь/(/) —Се6". В зависимости от корней характе-
ристического уравнения р,, п, возможны различные варианты
задания хчн(г).
Рассмотрим эти варианты.
а)	Пусть корни характеристического уравнения р{ и р2 не
совпадают с величиной a: pi^n^p2. В этом случае частное
решение неоднородного уравнения найдем в виде
хчн(/)-Леа(,	(П.9)
где величину А необходимо определить.
Осуществляя дифференцирование выражения (П.9)
x^ty-Aae*, x4ii(i)~A.a2eat	(П.10)
и подставляя производные (П.10) в левую часть дифференциаль-
ного уравнения (П.7), получим
еа‘А (а<х2	+ с) = Се11,
откуда искомая величина А определяется по формуле
Знаменатель в искомом выражении (ПЛ 1) отличен от нуля, так
как, по предположению,
б)	Корни характеристического уравнения р1: р2 действительные
и разные, и величина а равна одному из них (например, a = pj).
Тогда хчн(0 найдем в виде
хчн(0=Лге*.	(П.12)
Двукратное дифференцирование выражения (П.12) дает
-Хч»(0 = Ле’'(1 +aZ), хчн(О^.4еа'(аЛ + 2о').	(ПЛЗ)
Подставляя (П.12) и (ПЛЗ) в (П.5), получим
aTewQt(a/ + 2) + 6Te“‘(l + az) + с Л геа< — Се®.	(П. 14)
Разделив левую и правую части соотношения (П.14) на еа<
и приведя подобные члены, получим
416
А [Цяа2 + &а+ c) + 2aa-f-6] = С.	(П.15)
Так как а равно одному из корней характеристического
уравнения (П.б), то aa2+6a + c=0, причем а равно либо значению
~-ас, либо	причем 62-4йс>0. Последнее
вытекает из того, что корни характеристического уравнения (П.б)
действительные и разные. Тогда
2acz+6 = — b±Jb2-4ac+b = ±x/b2-4ac‘^0.	(П.16)
В итоге, учитывая (П.15) и (П.16), для определения величины
А получаем формулу
.А‘-----------------------------
в)	Корни характеристического уравнения (П.б) действительные
и разные, и их значение равно а:
/'[=Р2 = -^ = а>	=
Тогда x4e(t) найдем в виде хчН(Г)-Л/2еяГ.
Дифференцируя
хчн(Г) = ЛеягГ(2 + а/), хчн(Д-Лея,(а2г2 + 4аГ + 2)
и подставляя хчн, хчн, хчН в левую часть уравнения (П .5), получим
Лем[й(а2/24-4аГ+2)+6г(2-Ьаг)+сГ2]~Се“!.	(П.17)
В соотношении (П.17) разделим левую и правую части на eat
и произведем перегруппировку слагаемых;
A \J2 (aa2 + 6a + с) + 2r(2aa + 6) + 2<с] - С.	(П. 18)
Выражения в круглых скобках в (П.18) — множители при г2
и It—-обращаются в нуль, так как а= —
2а
— корень характеристи-
ческого уравнения (П.б).
Следовательно, из (II. 18) получим
А 2а'
3.	Рассмотрим случай, когда /(t) = ^cos<Bt + 5sin©t, где А, В,
со—заданные числа.
а)	Если корни характеристического уравнения (П.б) р(, р2
действительные или комплексно-сопряженные рг, p, = a±rp (в
последнем случае либо а/0, либо |М0, но |М=о), то лчН(Г)
найдем в виде
хЧн(Г) = Ceos cor-f-Z>sin cor.
4 Зак 456
417
при этом коэффициенты С и Д необходимо определить. Для
этого запишем:
x4H(t) = — Ctosinrat-I-Dtocostot,
x4H(t) = — С и 2 cos cot —D®2 sin tot.
Подставив в (П.5), получим
a(- Cto2cos rot — Dto2sin®t) + 6( — Ctosincot + D©cos ©t) +
+ c (Ceos ot + D sin tot) = A cos tot + В sin го/.	(П .1 9)
Для тождественного выполнения при любых значениях t соот-
ношения (П.19) приравняем в его левой и правой частях
множители при cos cot и sin ®i;
C(c-am2) + Dbco^A.
-а>й+Р(с-шй2) = 5.	k J
Определитель системы уравнений (П.20) равен (с-жв2)2 + 62®2.
Как следует из решения характеристического уравнения (П.6),
если его корни комплексно-сопряженные, то
’ .	₽=v5El!
2а	2а
Если а^О, то и при любом значении го^О определитель
системы уравнений (П.20) оказывается положительным. Если же
а = 0, то £>=0, р=ч/с/й. Но так как, по предположению, P?tto,
то ог дс/а. Следовательно, и в этом случае определитель системы
(П.20) положительный.
Итак, при сделанных предположениях (корни характеристичес-
кого уравнения действительные или комплексно-сопряженные—р1;
р2=а±ф, причем либо либо <х=0, но Р^п>) определитель
системы (П.20) отличен от нуля и искомые коэффициенты
С и D определяются однозначно.
б)	Пусть теперь корни характеристического уравнения будут
чисто мнимыми и равными р1; р2=+й». При этом частное
решение неоднородного уравнения найдем в виде
x4H(t) = (Ccos cot -i-Dsin cot)t,	(П.21)
где коэффициенты С и D необходимо определить. Схема
определения этих коэффициентов такая же, как и выше.
Вычисляем производные;
хчн=( — С sin ©t + Deos cot) tot + Ceos tot + Dsin tot,
x4H= — (Ceos rot+ D sin tot) to 2t — 2Ctosin tot + 2D tocos mt.
Подставив хчн из (П.21), хан, хчН и f(t) — Л cos rot + Dsin wt
в левую и правую части уравнения (П.5), получим
418
Ct( — «оо2 cos&t — b(d sin oH + ccos a)t)+Dl(— a® 2 sin co/ 4-6®cosro(4-
+ csin	+ cos cot (2a£>oi + bC + sin tai ( — 2a®C+bD) —
= .4cos®f +Esin®/.	(П.22)
Так как мы рассматриваем вариант чисто мнимых корней
характеристического уравнения (П.о), последнее в данном случае
имеет вид ар2-\~с — 0, откуда р2_—с1а, Ь — 0, св2 = с/д, причем
коэффициенты а и с имеют одинаковые знаки. Выражения
в скобках-—множители при Ct и Dt в соотношении (П.22)—обра-
щаются в нуль. Соотношение (П.22) становится эквивалентным
двум уравнениям:
bC+2aa>D = A,
— 2а<лС + Ь£)~В.
Определитель этой системы равен й2+4д2®2 = 4яс>0, и коэф-
фициенты С и D определяются однозначно.
Если правая часть линейного дифференциального уравнения
(П.5) — функция /(/)—представляет линейную комбинацию рас-
смотренных выше функций, то каждому из этих слагаемых
будет отвечать своя часть хчн(7), которая определяется одним
из указанных выше способов.
Рассмотрим решение дифференциального уравнения
х — 2x-j-2x=cos t — Зг,	(П.23)
отвечающее начальным условиям (задача Коши) 
x(O) = J; х(0)=0. :	(П.24)
Согласно формуле (П.6), составляем характеристическое урав-
нение:
р2_2р + 2 = 0.
Его решение:
рир2=1±Ь
Определение частного решения неоднородного уравнения долж-
но производиться в соответствии с правилами, рассмотренными
в П.З (случай а) и в П.1. На основе сказанного имеем:
хчн0) = Ccos г 4- Osin t + Et q- F,
хчн(0 = — Csin Z+Z)cos Г-f-E,
x4H(z) =— Ceos t—Osin t.
Подставив эти выражения в исходное уравнение (П.23),
получим
— Ccos/-Osinr—2( — Csin/4-Ocos/ + E)+2(Ccos/-|-OsinZ4-
4-£7 4-О) = COS i — ЗЛ
14*
419
Отсюда, приравнивая соответственно множители при cost, sin г,
t и свободные члены, получим:
C~2D=\, 2C + D=Q,
2Е=~3, -2E+2F=Q.
3	12
Решение этой системы: F=E~ —	С=- D=—.
2	5	5
Общее решение дифференциального уравнения (П.23):
40=МО+-W0=e4cicos 1+с2sin 0+
12.33
-p-cos/--sin i1(П.25)
Учитывая 'в общем решении (П.25) начальные условия,
получим:
х(0) = С( 1-^=1 откуда Ct=|;
х(0) —+С2—~ —^-=0, откуда С2=1
В итоге решение дифференциального уравнения (П.23), отве-
чающее начальным условиям (П.24), имеет следующий вид:
(3	2)1	2	33
- cos/-р-sin t +-cos t — -sin t — -t— -.	(П.26)
2	5 у 5	5	2 2	7
При реализации необходимых условий оптимальности в форме
принципа максимума процесс оптимизации в задаче Эйлера
(см. гл. 7) сводится не к задаче Коши, а к краевой задаче.
Применительно к рассматриваемому дифференциальному уравне-
нию второго порядка (П.5) в краевой задаче задаются значения
искомой функции в двух точках:
4ro) = xo, t(?i)=.Ti-	(П.27)
С использованием краевых условий (П.27) определяются две
произвольные постоянные в общем решении дифференциального
уравнения (П.5).
Вновь обратимся к примеру (П.23), только вместо задачи
Кощи с начальными условиями (П.24) рассмотрим краевую
задачу с граничными условиями
4°)4 х(|) = Ч(1+()'	(П.28)
Подстановка граничных условий (П.28) в общее решение
(П.25) дифференциального уравнения (П.5) приводит к следующим
420
двум алгебраическим уравнениям:
Л i — 0^2 С — 2
у)-е С2 -
Зя 3 __ 3 /. к
2 2~2~ -И +2
поставленной краевой задачи для
(П.23);
э	7
откуда С^-, С2~-е~п12.
В итоге получаем решение
дифференциального уравнения
(3	2	/	\ 1	2	33
-cos r + -e'’’l,'2sin t j + -cos f—-sin
Сопоставление методов решений в двух рассмотренных При-
мерах— для задачи Коши и для краевой задачи для линейного
дифференциального уравнения второго порядка с постоянными
коэффициентами — указывает практически на одинаковую их тру-
доемкость. Причем такой же вывод можно сделать и для задач
большей размерности. Это справедливо, если общее решение
дифференциального уравнения или системы дифференциальных
уравнений может быть получено в аналитической форме. В нашем
примере это отвечает общему решению (П.25).
Однако для произвольных типов дифференциальных уравнений
возможность получить общие решения в аналитической форме
ограничена. Поэтому перейдем к рассмотрению задачи численного
интегрирования обыкновенных дифференциальных уравнений с вы-
делением при этом задач Коши и двухточечных краевых задач.
П.5, Численное интегрирование обыкновенных
дифференциальных уравнений
1. Метод Эйлера решения задачи Коши.
Рассмотрим задачу Коши для системы дифференциальных
уравнений н-го порядка в нормальной форме:
хл)	(П.29)
с начальными условиями
хД0)=х£, к = 1, 2, .... л.	(П.30)
Для численного решения задачи Коши (П.29) — (П.30) известен
ряд методов: одношаговые Эйлера и Рунге —Кутта с модифика-
циями; многошаговые типа Адамса, Димсдейла, Хемминга и др.
Мы ограничимся одним из них—наиболее простым—методом
Эйлера.
421
Метод заключается в приближенном представлении произ-
водных
dr ~ Аг
и в переходе от системы дифференциальных уравнений (IL29)
к системе конечно-разностных уравнений
+	аг(г), х„(0)А^
к=\,2,...,п,	(П.31)
с начальными условиями (П.30).
Рассматриваемый метод характеризуется накоплением ошибок
в процессе вычислений по мере удаления от начальной точки
/ = 0; его точность повышается при уменьшении конечной вели-
чины Д/. На практике этот метод можно применять используя
ЭВМ и полагая при этом Д/ достаточно малой.
2.	Метод прямой прогонки для двухточечной краевой задачи.
Рассмотрим следующую задачу:
5=/^^,...,^); ^=1,2,..., 2щ	(П.32)
х}(0)-х]О! ./=1, 2, .., и;	(П.ЗЗ)
*г(7) = хн, /=л + 1, и+2, ..., 2и.	(П.34)
К краевым задачам такого типа сводятся задачи на применение
принципа максимума Понтрягина в принятых ранее обозначениях.
Вместо краевой задачи (П.32) — (П.34) решаем задачу Коши
с заданными начальными условиями (П.ЗЗ) для п переменных,
а последующим п переменным придадим произвольные начальные
значения
x5(0)=xsO, 5=я+1, Я+2,	2и.
(П.35)
Решение задачи Коши будет зависеть от принятых произволь-
ных значений xs0, 5=я-{-1, ..., 2п. Если данную зависимость
можно выразить аналитически, а это определяется структурой
исходной системы уравнений (П.32) и соотношением величин
Т и Д/ (при численном интегрировании), го в результате будем
иметь систему п алгебраических уравнений
Х;(Г, A’n+i.o, x:n + 2.o, х2п, о) — х(1,
/=« + 1, я + 2, ..., 2п.
(П.36)
Определяя из этой системы принятые ранее в качестве произволь-
ных величин х„+1; о, хя+2;о, ..., л-2я.о, получим приближенное ре-
шение краевой задачи (П.32) — (П.34). При этом приближенный
характер решения краевой задачи будет определяться приближен-
ностью метода численного интегрирования задачи Коши.
422
Однако при достаточно сложной структуре системы уравнений
(П.32) и большом числе обращений к формуле (П.31) s процессе
численного решения задачи Коши при использовании ЭВМ
получить аналитическую зависимость типа (П.36) не представ-
ляется возможным. В данном случае недостающим начальным
условиям (П.35) придаются произвольные числовые значения
и вместо формул типа (П.36) вычисляем значения х((Т)> которые
будут зависеть от принятых числовых значений хя+1;0, хв+2.о, •••,
х2Пф 0. В общем случае считать, что вычисленные значения х((7)
будут совпадать с заданными х(1, / = и4-1, н + 2, ..., 2п, нельзя.
Поэтому на следующей итерации численного интегрирования
задачи Коши принимаются новые значения хв+ь0, хп + 2.о, ..., х2„, о
и т. д. до приемлемого на практике расхождения. Для этого
можно, например, использовать одну из оценок
2л	2n	1 /2
£ (хфЛ-^п^е или Е (хг(Д|-хн)2
( = п+1	D = « + l
где £ — заданный показатель точности.
Изложенный метод прямой прогонки в вычислительном от-
ношении трудоемок, и его реализация возможна практически
только с использованием ЭВМ.
ЛИТЕРАТУРА
1. Гэри., Джонсон Д. Вычислительные машины и труднорешаемые зада-
чи.— М.: Мир. 1983.
2. Емеличсв В. А., Комлем: В. И. Метод построения последовательности планов
для решения задач дискретной оптимизации.— М.: Наука, 1981.
i. Иванилов IO. П., Лотон А. В. Математические модели в экономике.— М.:
Наука, 1979.
4.	Кобринский Я. R., Майлгинас Е. 3., Смирнов А. Д. Экономическая киберне-
тика.-- М.: Экономика, 1982.
5.	Корбут А. А., Финкельштейн Ю. Ю. Дискретное программирование.— М.:
Наука, 1969.
6.	Кристофидес Н. Теория графов. Алгоритмический подход.— М.: Мир, 1978.
7.	Кротов В. Ф. Вычислительные алгоритмы решения и оптимизации управ-
ляемых систем уравнений Ц Из.» АН СССР. Сер. Техническая кибернетика.
1975. № 5, 6.
8.	Кротов В. Ф., Гурман В. И. Методы и задачи оптимального управле-
ния.— М.: Наука, 1973.
9.	Кротов В. Ф., Сергеев С. И. Вычислительные алгоритмы решения некоторых
задач линейного и линейного численного программирования // Автоматика
и Телемеханика. 1980.	|2; 198|. № 1,3,4.
10.	Кротов В. Ф., Фельдман И- Н. Итерационный метод решения задач опти-
мального управления /,' Изв. АН СССР. Сер. Техническая кибернетика. 1983. № 2.
11.	Лебедев С. С. Целочисленное программирование и множители Лагранжа
Ц Экономика и математические методы. 1974. № 3.
12.	Михалевич В, С.> Кукса А.. И. Методы последовательной оптимизации,—
М.: Наука, 1983.
13.	Теория и методы автоматизации проектирования вычислительных сис-
тем,—М.: Мир, 1977.
14.	Финкельштейн Ю. Ю. Приближенные методы и прикладные задачи диск-
ретного программирования, - М-: Наука, 1976-
15.	Ху Т. Целочисленное программирование и потоки в сетях.— М,: Мир, 1974.
16.	Christofides N., Etlon S. Algorithms for large scale traveling salesman problems
Il Operational Research Quarterly, 1972, № 4.
|7,	HddM., Karp R The traveling salesman problem and minimum spaning
trees // Operations Research, 1970, Л? 6.
18.	Lin S, Karnighan B. An effective heuristic algorithms for the traveling salesman
problem // Operations Research, 1973, № 2.
19.	Papadimitrion С. H., Steiglitz K. Some examples of difficult traveling salesman
problem // Operations Research, 1978, № 3.
20.	Белкин В. Д. Экономические измерения и планирование.— ML Мысль, 1972.
21.	Киселева В. В. Плановые расчеты по моделям экономического роста,—М.;
Экономика, 1971.
22.	Юдин Д. Б., Гольштейн Е. Г. Линейное Программирование. Теория, мето-
ды и приложения. М.: Наука, 1%9.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Алгоритм
— Беллмора—Мэлоуна 363
— Литтла и др. 355
— по начальному значению сопряжен-
ного вектора 255
— последовательного улучшения по
управлению 256
— с конечным сдвигом по управлению
259
— улучшения по начальному значению
сопряженного вектора—255
— Хелда—Карпа 366
Внешняя среда 8, 12
Вариационное исчисление 160
Динамическое программирование 250
Дискретная управляемая система 88
Допустимый процесс К9
Достаточные условия оптимальности
106
для многошаговые процессов упра-
вления с многомерным аргументом
267 '
Задача диофантова программирования
326
— комбинаторного программирования
326
— коммивояжера 304
— —одного 304, 333, 35]
— — многих 336
—	линейного программирования с дву-
сторонними ограничениями 271
— назначения 291, 295
---линейная лвухиндексная 291, 329,
349
—	— квадратичная 332
—	— трехиндексная 331
—	о покрытии 328
—	о ранце одномерная 327
—	—--многомерная нелинейная 280,
327
— целочисленного программирования
326
—	— с булевыми переменными 326
---со смешанными ограничениями
326
---частичного программирования
326
Индикатриса 161
Календарное планирование 223
Капитальные вложения 250
Краевая задача 191, 414, 420
Критерий Гурвица 57
Лаг инвестиционный 43
—	распределенный 43
Локальный
—	максимум 407
—	минимум 407
—	экстремум 406
Макромодель одно продуктовая 75
Метод ветвей и границ 344, 354
— Гамильтона — Я коби — Беллмана
235, 337, 353
—	Лагранжа — Понтрягина 181
—	— Для многошаговых процессов 209
—	отсечений 340
—	Эйлера численного интегрирования
дифференциальных уравнений 421
МиНимизируюшая последовательность
82
Модель Леонтьева 53, 92
425
Многошаговый процесс управления 91,
225
------ — с одномерным аргументом 266
----— с многомерным аргументом
266
Непрерывный процесс 229
Норма накопления 75
Общая задача оптимизации 81
Объект управления 12, 14
Обратная связь 11
Ограничения модели 13
Оптимальное планирование 229
- управление 13, 90
Оптимальный процесс 91, 167, 218
Принцип максимума 171, 174, 186, 219,
229, 420, 422
Программирование линейное 100
— целочисленное 100
Производственная функция 62
----Кобба — Дугласа 70
Реализация элементарной операции улуч-
шения, основные сведения 269
— простейшая 274
Сбалансированный рост 62
Синтез оптимального управления 235
Система управления 12
Система 9, И
Состояние системы 225
Стационарная точка 407
Траектория управляемого процесса 100
Управляемый процесс 79
Управляющие воздействия 8?
Уравнения дифференциальные 11, 176,
413, 414, 420
Уравнение
— Белл мана 240
— Гамильтона — Якоби — Веллмана
240
— процесса 226, 229
— Эйлера 169
Условия трансверсальности 186, 219,
222, 226
— Вейерштрасса 171
Функционал 13, 80, 220, 225, 229
Функция Гамильтона 219, 225, 229, 409
Характеристическое уравнение 415, 4Г7
Цель моделирования |0
Штрафные функции 225, 247
Экономическая система 15
Экстремаль 176
ОГЛАВЛЕНИЕ
Предисловие.........................................................................................................................  3
Глава 1. Основы моделирования экономических процессов................................................................................ 6
§ 1.1.	Система. Модель..............................................................................................................  6
§ 1.2.	Управление. Обратная связь. Замкнутая система................................................................................ II
§ 1.3.	Экономическая система как объект управления (некоторые аспекты
математического моделирования)......................................  15
Глава 2. Оптимизационные модели экономической динамики.............................................................................. 18
§2.1.	Однопродуктовая динамическая макроэкономическая модель.......	|8
§	2.2.	Двухпродуктовая динамическая макроэкономическая модель ......... 22
§	2.3.	Многопродуктовая модель экономики. Межотраслевой баланс...1	25
§	2.4.	Моделирование запаздывания при освоении капитальных вложений.	43
§	2.5.	Однопродуктовая оптимизационная динамическая микроэкономичес-
кая модель........................................................ 46
§	2.6.	Нелинейная оптимизационная модель развития многоотраслевой	эко-
номики 	   48
Глава 3. Некоторые вопросы качественного исследования моделей управ-
ляемых экономических процессов............................. 50
§	3.1.	Понятие устойчивости. 50
§	3.2.	Исследование устойчивости. 54
§ 3.3.	Поведение траекторий в линейных моделях экономической дина-
мики .........................................................:...... 59
§ 3.4.	Сбалансированный рост в однопродуктовой макроэкономической мо-
дели ...............................................................  62
§ 3.5.	Сбалансированный рост в однопродуктовой макроэкономической мо-
дели с запаздыванием................................................. 71
§ 3.6.	Оптимальная норма накопления в однопродуктовой макромодели...	75
Глава 4. Математическая модель оптимальных	управляемых процессов..	79
§ 4.1.	Некоторые математические понятия ............................................................................................ 79
S 4.2. Общая задача оптимизации........................;............................................................................ 81
§4-3. Задача оптимизации управляемых процессов...................................................................................... 86
§ 4.4.	Примеры задач оптимального управления........................................................................................ 92
§ 4.5.	Построение траекторий управляемых процессов................................................................................. 100
Глава 5. Достаточные условия оптимальности......................................................................................... 106
§ 5.1.	Вспомогательные математические конструкции.................................................................................. 106
§ 5.2.	Достаточные условия оптимальности для непрерывных процессов..	113
§ 5.3.	Достаточные условия оптимальности для многошаговых процессов .....	118
§ 5.4.	Обобщенная теорема о Достаточных условиях оптимальности......	122
§ 5.5.	Непосредственное применение достаточных условий оптимальности
к решению задач..................................................... 125
Глава 6. Исследование однопродуктовой макромодели оптимального разви-
тия экономики........................................................ 138
§ 6.1.	Моделирование производства на макроуровне...................... 138
§ 6.2.	Решение задачи управления экономикой на макроуровне с помощью
достаточных условий оптимальности .................................. 142
427
§ 6.3.	Оценка оптимального развития экономики.....:................... 151
Глава 7. Задача Эйлера вариационного исчисления ...................... 160
§7.1.	Постановка задачи и типы ее решения............................ 160
§ 7.2.	Постоянная индикатриса......................................... 162
§ 7.3.	Индикатриса с ограниченной нелинейностью...................... 164
§ 7.4.	Выпуклая индикатриса. Уравнение Эйпера......................... 167
§ 7.5.	Дальнейшее исследование оптимальности процесса. Задача о линии
наименьшей длины ..................................................... 172
§ 7.6.	Негативный пример.............................................  175
Глава 8. Метод Лагранжа—Понтрягина для непрерывных управляемых
процессов ...................................................... 181
§8.1.	Вывод уравнений метода Лагранжа — Понтрягина.............. 182
§ 8.2.	Принцип максимума Понтрягина............................   186
§ 8.3.	Сведение задачи оптимального управления к краевой задаче.	191
§ 8.4.	Примеры нахождения оптимальных процессов с помощью принципа
максимума ....................................................... 193
§ 8.5.	Принцип максимума как достаточное условие оптимальности .. 204
Глава 9. Метод Лагранжа для многошаговых процессов управления с
одномерным аргументом........................................... 209
§ 9.1.	Уравнения метода. Условия оплимальности .для многошагового про-
цесса с неограниченным управлением............................... 209
§ 9.2.	Условия оптимальности для многошагового процесса при наличии
ограничений на управление.......................................  213
§ 9.3.	Негативный пример........................................  215
Глава 10. Некоторые 1|рименения необходимых условий оптимальности в
форме Лагравжа — Понтрягина ...................................  218
§ 10.1.	Оптимальное управление движущимся объектом. Аналитическое
решение.........................................................  218
§ 10-2-	Календарное планирование поставки продукции. Численное решение.
Дискретный вариант............................................... 223
§ 10.3.	Оптимальное планирование поставки продукции. Численное решение.
Непрерывный вариант............................................   229
§ 10.4.	Оптимальное потребление в однопродуктовой макромодели...	232
Глава 11. Метод Гамильтона—Якоби — Беллмаиа ..................... 235
§ 11.1.	Уравнение Гамильтона—Якоби—Веллмана, Непрерывный ва-
риант ....................1....................................   235
§ 11.2.	Синтез оптимального управления........................... 238
§ 11.3.	Алгоритм метода Гамильтона—Якоби—Веллмана................ 239
§ 11.4.	Метод Гамильтона—Якоби—Веллмана. Многошаговый вариант...	244
§ 11.5.	Учет ограничений на состояние............................ 247
§ 11.6.	Сравнительный анализ методов Лагранжа — Понтрягина и
Гамильтона—Якоби—Веллмана.......................................  249
§ 11.7.	Оптимизация распределения капитальных вложений между предприя-
тиями методом динамического программирования..................... 250
Глава 12. Численные методы оптимизации для многошаговых процессов
с непрерывным управлением.............,......................... 254
§ 12.1.	Алгоритм улучшения по начальному значению сопряженного век-
тора ........................................................     255
§ 12.2.	Алгоритм последовательного улучшения по управлению....... 256
§ 12.3.	Итерационный алгоритм улучшения с конечным сдвигом по управ-
лению ..........................................................  259
428
Глава 13. Численные методы оптимизации для многошаговых процессов
с дискретным управлением............................................ 265
§ 13.1.	Постановка задачи оптимизации для многошаговых процессов управ-
ления с многомерным аргументом..................................... 265
§ 13.2.	Достаточные условия оптимальности для многошаговых процессов
управления с многомерным аргументом ............................... 267
§ 13.3.	Основные теоретические результаты по реализации элементарной
операции .......................................................... 269
§ 13.4.	Задача линейного программирования с двусторонними ограниче-
ниями ............................................................. 271
К	13.5.	Метол улучшения функции <р(/, х)..........................  272
§	13.6.	Простейшая реализация элементарной	операции................ 274
§ 13.7.	Решение молельного примера для задачи линейного программи-
рования ..........................................................  277
§	13.8.	Многомерная нелинейная задача о ранце.	Постановка задачи .. 280
§	13.9.	Метод улучшения функции <p(f, х)........................... 281
| 13.10. Алгоритм вычисления нижней границы......................... 285
§ 13.11	Алгоритм ветвления и обшая схема решения задачи............  286
§ 13.12.	Решение модельного примера для нелинейной задачи о ранце..	288
Глава 14. Численные методы оптимизации для некоторых многошаговых
процессов с дискретным управлением (двумерный аргумент)............	291
§ 14.1.	Линейная задача назначения.................................. 291
§ 14.2.	Метод улучшения функции tp(/. х)............................ 292
§ 143.	Описание алгоритма	решения	задачи назначения............... 295
§ 14.4.	Решение модельного	примера	для задачи назначения........... 300
§ 14.5.	Задача коммивояжера ........................................ 304
8 14.6. Метод улучшения функции <р(/, х)............................ 305
§ 14-7	.	Описание алгоритма	решения	задачи коммивояжера............. 314
§ 14.8.	Решение модельного	примера	для задачи коммивояжера......... 318
Глава 15. Другие общие методы решения задач дискретного программи-
рования ............................................................ 324
§ 15.1.	Общая постановка задачи дискретного программирования.......	324
§ 15.2.	Классификация задач дискретного программирования........... 326
§ 15.3.	Прикладные модели задач дискретного программирования ....... 327
§ 1Э.4.	Основные методы решения задач дискретного программирования,
динамическое программирование.....................................  337
§ 15.5.	Методы отсечений ..........................................  340
§ 15.6.	Методы ветвей и границ.....................................  344
Глава 16. Методы решения некоторых частных классов задач дискрет-
ного программирования..............................................  349
§ 16.1.	Методы решения задачи назначения...........................  349
§ 16.2.	Методы решения задачи коммивояжера.........................  351
§ 16.3.	Точные методы............................................... 353
§ 16.4.	Динамическое программирование............................... 353
§ 16.5.	Методы ветвей и границ. Алгоритм Литтла	и др..............   355
§ 16.6.	Алгоритм Беллмора - Мэлоуна...............................   363
§ 16.7.	Алгоритм Хелда—Карпа.......................................  366
§ 16.8.	Приближенные методы .......................................  375
Глава |7. Динамическая модель оптимального развития многоотраслевой
экономики.......................................................     379
§ 17.1.	Постановка задачи........................................... 379
§ 17.2.	Оптимизация процессов, линейных относительно	управления....	382
§ 17.3.	Условия оптимальности процесса экономического	развития.....	385
429
§ 17.4.	Свойства допустимых цен и оптимальных режимов развития эко-
номики ........................................................     389
§ 17.5.	Уравнения оптимального сбалансированного плана ............. 392
§ 17.6.	Граничные условия, и прилегающие к ним участки оптимального
режима............................................................  395
§ 17.7.	Стапионарный режим.......................................    396
§ 17.8-	Структура оптимального режима и алгоритм его построения....	399
§ 17.9.	Четырех отраслевая модель народного хозяйства СССР.......... 401
Приложение. Справочные данные по математическому аппарату  ......... 406
Литература .................................................         424
Предметный указатель ........................................   ...	425
Учебное издание
Кротов Вадим Федорович
Лагоша Борис Александрович
Лобанов Сергей Михайлович
Данилина Нинель Ивановна
Сергеев Сергей Иванович
ОСНОВЫ ТЕОРИИ
ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Под редакцией В, Ф. Кротова
Зав. редакцией Е. С. Гридасова. Редактор Л. С, Куликова. Мл. редактор
Н. П. Майкова. Оформление художника В. В. Коренева. Художественный редак-
тор В. И. Пономаренко. Технический редактор А. К. Нестерова. Корректор
Г. И. Кострикова.
ИБ № 8154
Изд. № ФМ-965. Слано в набор 29.08.89. Подл, в печать 15.05,90. Формат
бОхвв1/^. Бум. офс. №2. Гарнитура таймс. Печать офсетная. Объем 26,46
усл. печ, л. 26,46 усл. кр.-отт. 23,93 уч.-изд. л. Тираж 10000 экз Зак. № 2873
Цена 1р. 10 к.
Издательство «Высшая школа», 101430, Москва, ГСП-4, Неглинная ул., д. 29/14.
Набрано в Ордена Октябрьской Революции и ордена Трудового Красного
Знамени МПО «Первая Образцовая типография» Государственного комитета
СССР по печати. 113054, Москва, Валовая, 28. Отпечатано с диапозитивов
в типографли № 4 Государственного комитета СССР но печати. Москва,
129041, Б. Переяславская, 46 Зак,456
Основы теории оптимального управления: Учеб.
0-75 пособие для экон. вузов/В. Ф. Кротов, Б. А. Лагоша,
С, М. Лобанов и др.; Под ред. В, Ф. Кротова,— М.;
Высш, шк., 1990.—430 с.: ил.
ISBN 5-06-000622-0
Книга написана па базе исследований, составивших основу курса лекций,
прочитанных в Московском экономико-статистическом институте. Изложены
современные методы решения задач оптимального управления, которые могут
использоваться в различных прикладных направлениях и в задачах экономичес-
кой динамики. Даны понятийный аппарат теории систем, общие принципы
моделирования. Приведены примеры из области экономико-математического
моделирования.
014021)6|ХМ1(| (4309000000)—368 85_9(|
001(01)—90
- ББК 65.050