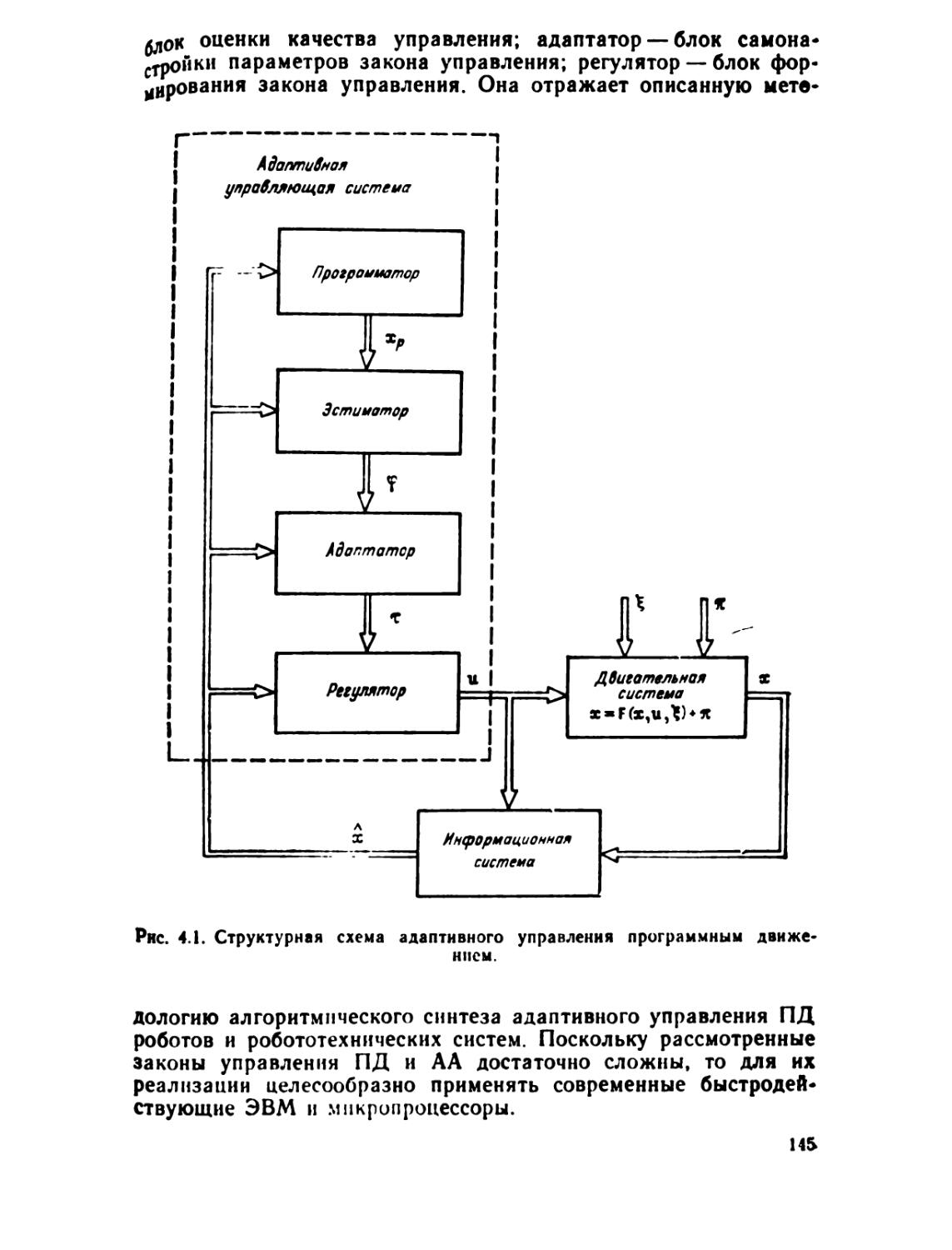
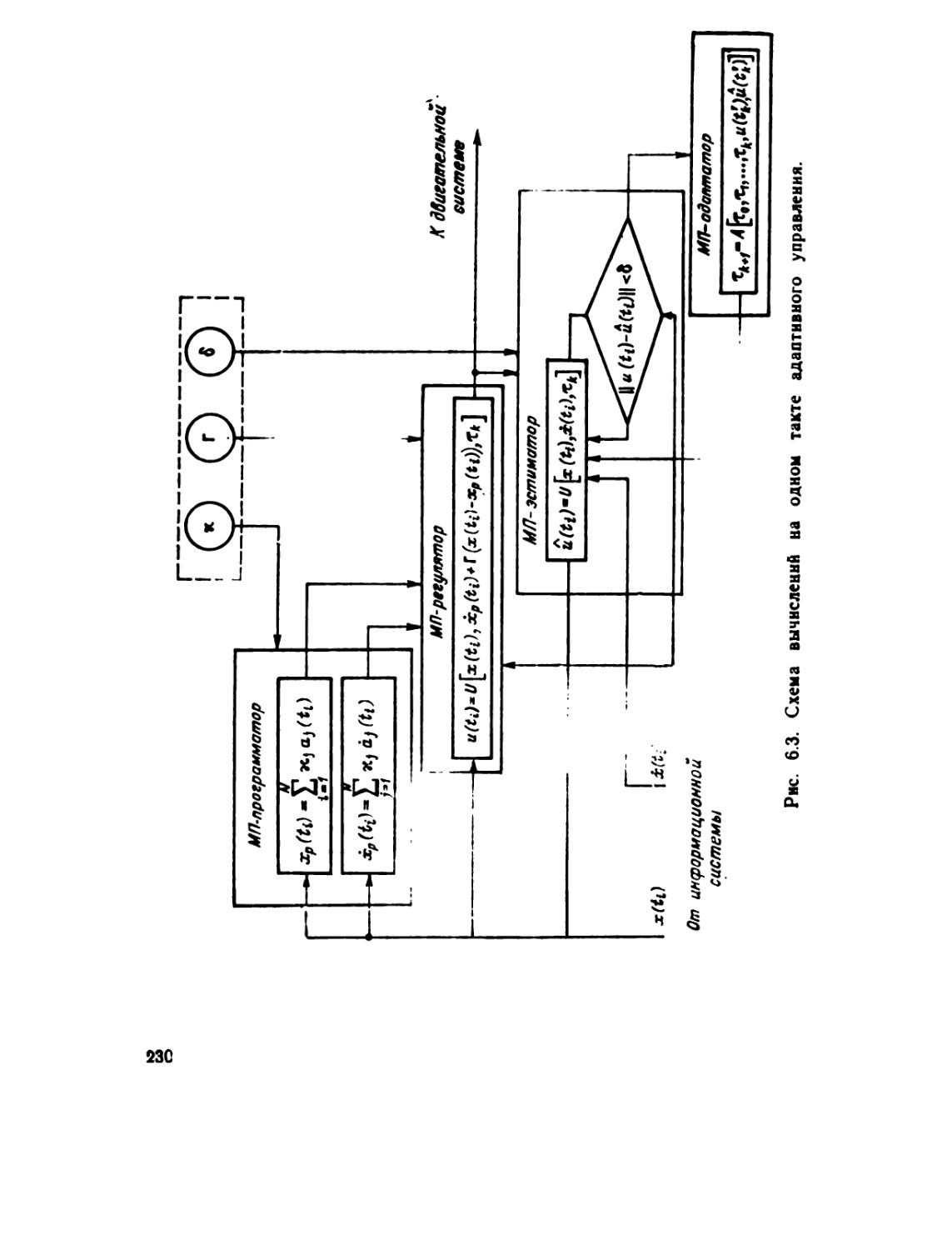
Автор: Тимофеев А.В.
Теги: инженерное дело техника в целом робототехника теория автоматического управления
Год: 1981
Текст
А. В. Тимофеев
УПРАВЛЕНИЕ
РОБОТАМИ
Издательство Ленинградского университета
Я. И. ФЕТ
ПАРАЛЛЕЛЬНЫЕ ПРОЦЕССОРЫ ДЛЯ УПРАВЛЯЮЩИХ СИСТЕМ
МОСКВА ЭНЕРГОИЗДАТ 1981
А. В. Тимофеев
УПРАВЛЕНИЕ РОБОТАМИ
И 'aie.ibciBo . книш райскою университета
ЛЕНИНГРАДСКИЙ ОРДЕНА ЛЕНИНА И ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени А. А. ЖДАНОВА
А. В. ТИМОФЕЕВ
УПРАВЛЕНИЕ РОБОТАМИ
Допущено Министерством высшего и среднего специального образова-ния СССР в качестве учебного пособия для студентов вузов, обучающихся по специальности «Робототехнические системы»
ЛЕНИНГРАД ИЗДАТЕЛЬСТВО ЛЕНИНГРАДСКОГО УНИВЕРСИТЕТА 1W6
Печатается по постановлению Редакционно-издательского совета Ленинерадскоео университета
УДК 82.50(075.8)
Тимофеев А. В. Управление роботами: Учеб, пособие.—Л.: Изд-во Лев tiirp. ун-та, 1986. 240 с.
В книге налагается теория управления роботами. Рассматриваются аналитик с кие модели кинематики и динамики исполнительных механизмов п приводов Излагаются методы программного, адаптивного и интеллектуального управления роботами. Обсуждаются вопросы автоматизированного проектирование и программно-аппаратной реализации управляющих систем роботов.
Учебное пособие рассчитано на студентов технических вузов и университетов, обучающихся по специальности «Робототехнические системы» как по типовому учебному плану, так и в рамках целевой интенсивной подготовки специалистов. Книга представляет интерес также для аспирантов, научных работников и инженеров, занимающихся созданием и применением робототехнических систем.
Бнблногр. 80 назв. Ил. 27. Табл. 2.
Рецензенты: кафедра теоретической кибернетики Леиивгр. ун-та, д-р техн, наук, проф. И. Б. Челпанов (Ленннгр. по» "'чтсхн. ин-т)
ИБ №2223
Адиль Васильевич Тимофеев
Управление роботами
Редактор Ф. //. Ш арен ков а
Обложка художника П. П. Николаева Художественный редактор О. Н. Советникова Технический редактор Л. В. Борщева Корректоры с. К. Терентьева, В. А. Л ат ыг ина
Сдано в набор J6.07.S4. Подписано в печать 24.11.86. М-48197. Формат бум. TOKWU. By мага тиа. М2. Гарнитура литературная. Печать вы сока п. Усл. неч. л. 15. Усл. Кр.-отт. 15, ж Уч-нзд. л. 15,33. Тираж 9500 »кз. Зака» М 276. Пена 50 кон. Издательство ЛГУ имени А. А. Жданова. 199164. Ленинград.
Уннверснтетскан наб., */9.
Набрано в Ленинграде но .'l типографии М 2 головном предприятии ордена Трудового Красного Знамени Леям.градского объединения «Iсхннческая книга» им. Евгении Соколовой Союаиолиграфпрома при Государственном комитете СССР по делам издательств, полиграфии и «книжной торговли. 198052, г. Ленинград, Л-52, Измайловски! проспект. °9. Отпечатано со стереотипов я типографии издательства ЛГУ имени А. А. Жданова. 199164. Ленинград. Университетская наб.. 7/9.
1502000000—028 076(02)—вё
61- 85
т
© Издательство Ленинградского университета, 1986 г.
предисловие
Характерной чертой современной научно-технической революция является широкое внедрение роботов в сферу производства и научных исследований. Этн принципиально новые кибернетические машины предназначены для комплексной автоматизации физического и умственного труда
Функциональные возможности и эффективность роботов в значительной степени зависят от принципов обработки информации и методов управления, используемых в их управляющей системе. Совокупность этих принципов и методов составляет предмет теории управления роботами.
Развитие теории стимулируется потребностями практики. Еще недавно, в период зарождения робототехники, промышленность довольствовалась роботами первого поколения с жестким программным управлением. Однако в последние годы возникла острая потребность в адаптивных и интеллектуальных роботах, способных автономно функционировать в неопределенной или изменяющейся обстановке, а также в опасных или недоступных для человека условиях. Такие роботы могут самостоятельно принимать решения и планировать свое поведение, распознавать и обходить препятствия, идентифицировать целевые объекты и определять их характеристики, адаптироваться к непредсказуемым изменениям условий эксплуатации. Именно поэтому роботы с адаптивным и интеллектуальным управлением все шире используются в гибких автоматических производственных системах, космических и глубоководных исследованиях. Их созданию и внедрению способствует повсеместное применение ЭВМ и микропроцессоров, открывающих новые возможности для автоматизации проектирования и программно-аппаратурной реализации адаптивных управляющих систем с элементами искусственного интеллекта.
В СССР н других промышленно развитых странах происходит бурный процесс роботизации многих ключевых областей р а
производственной и научной деятельности. Вопросам дальнейшего совершенствования роботов и их управляющих систем уделено большое внимание в «Основных направлениях экономического и социального развития СССР на 1981 — 1985 годы и на период до 1990 года] [1, с. 21] где говорится: «На основе использования достижений науки и техники развивать производство и обеспечить широкое применение автоматических манипуляторов (промышленных роботов), встроенных систем автоматического управления с использованием микропроцессоров и микро-ЭВМ, создавать автоматизированные цехи н заводы...» В связи с этим большое значение и актуальность приобретают пропаганда и распространение знаний в области теории н практики управления роботами и гибкими робототехническими комплексами. Настоящая работа ориентирована на то, чтобы восполнить (хотя бы частично) имеющийся в данной области пробел. Главная особенность пособия, отличающая его от других книг по робототехнике, заключается в том, что акцент делается на общую методологию алгоритмического синтеза и анализа управляющих систем роботов.
Предлагаемое учебное пособие написано в соответствии с программами курсов для студентов технических вузов и университетов по теории автоматического управления, теоретической механике и кибернетике. Его содержание увязано также с некоторыми специальными курсами, включающими вопросы робототехники, теории адаптивных систем и искусственного интеллекта. Это позволяет рекомендовать данную книгу студентам, обучающимся по новой специальности «Робототехнические системы» и смежным с ней специализациям («Механика роботов», «Управление роботами», «Автоматизированное проектирование робототехнических систем» и др.).
Материал пособия использовался в лекциях, читавшихся автором на факультете повышения квалификации инженеров при математико-механическом факультете Ленинградского университета, на факультете повышения квалификации преподавателей при Ленинградском институте авиационного приборостроения, а также во всесоюзных школах молодых ученых и специалистов по робототехнике и гибким автоматизированным производствам. Это наложило определенный отпечаток на структуру н содержанке настоящего учебного пособия.
Теория управления роботами, излагаемая в книге, является новым разделом кибернетики, отражающим специфику задач и методов управления, возникающих в робототехнике. В последние годы этот раздел обогатился важными результатами в области адаптивного и интеллектуального управления роботами, что и нашло отражение в данном пособии.
В главе 1 привс ены общие сведения о роботах, тана эволюционная классификация их управляющих систем, рассмотрены
4
особенности управления роботами в нестационарных и неопределенных условиях.
Глава 2 посвящена аналитической механике двигательных систем роботов. Здесь сформулированы основные свойства линейных и нелинейных динамических моделей роботов, включающих в себя исполнительные механизмы и приводы.
В главе 3 рассмотрены вопросы программного управления роботами первого поколения. Наряду с традиционными методами управления (программное управление и сервоуправление по программе) описаны новые методы динамического управления, обеспечивающего требуемое качеово переходных процессов при отсутствии возмущений и неопределенности. Приведены необходимые расчетные соотношения и даны примеры аналитического синтеза программных управляющих систем.
Глава 4 посвящена алгоритмическому конструированию адаптивных управляющих систем роботов второго поколения. В ней рассмотрены вопросы параметрической чувствительности н инвариантности управляющих систем, описаны методы синтеза и оптимизации алгоритмов адаптации, предложены методы адаптивной стабилизации, терминального управления и самонаведения роботов. Здесь же получены оценки качества переходных процессов н приведены основные расчетные соотношения для теоретически обоснованного выбора параметров адаптивного управления.
В главе 5 описаны элементы искусственного интеллекта и изложены вопросы организации интеллектуального управления роботами третьего поколения. Последовательно рассмотрены логические методы представления знаний и формирования понятий, распознавания ситуаций и анализа сцен, принятия решений и планирования поведения. Значительное внимание уделяется описанию элементов (алгоритмов) обучения и адаптации на различных уровнях иерархии интеллектуальной управляющей системы.
Глава 6 посвящена актуальным вопросам автоматизации проектирования и программно-аппаратурной реализации управляющих систем роботов различных поколений. Здесь же рассмотрены перспективы гибкой автоматизации производства на базе роботов с адаптивным и интеллектуальным управлением.
Выбирая форму изложения, автор стремился ь разумному компромиссу между математической строгостью и доступностью пособия для широкого круга студентов, аспирантов, научных работников и инженеров. В связи с этим каждый теоретический результат обсуждается в нем с точки зрения его практической значимости и применимости к решению конкретных задач робототехники.
В пособие включены сведения о некоторых типичных отечественных и зарубежных роботах различных типов и поколений. Это дает предметное представление о преемственности
5
поколений роботов, эволюции их управляющих систем и пер* спективах развития робототехники.
Ограниченный объем учебного пособия не позволил детально рассмотреть вопросы, связанные с техническими средствами очувствления и управления роботами. Для изучения этих вопросов можно воспользоваться специальной литературой.
Автор выражает4 глубокую признательность И. Б. Челпанову и В. Н. Фомину за ценные замечания, способствовавшие улучшению книги.
Глава 1
ОПИСАНИЕ РОБОТОВ И КЛАССИФИКАЦИЯ ИХ УПРАВЛЯЮЩИХ СИСТЕМ
f 1. ОБЩИЕ СВЕДЕНИЯ О РОБОТАХ
Термин «робот» впервые появился в 1920 г. в пьесе К. Ча* пека «R. U. R.» («Россумовскне универсальные роботы»). Персонажами этой фантастической пьесы являются люди и сконструированные ими рабочие-автоматы — роботы. Вскоре понятие «робот» вошло в международную научно-техническую терминологию. Следует, однако, отметить, что идея создания роботов как механических помощников человека зародилась гораздо раньше. Так, в знаменитой «Илиаде» Гомера опоминаются «золотые служанки», которых «самым различным трудам обучили».
Фантастические идеи и образы роботов в древней и современной литературе во многом предвосхитили тенденции развития научно-технического прогресса. В настоящее время существует большое семейство различных роботов, которые облегчили труд или заменили людей на опасных для здоровья, монотонных и тяжелых физических работах. Процесс естественной эволюции этих принципиально новых средств автоматизации привел в последние годы к появлению адаптивных и интеллектуальных роботов, способных воспроизводить не только двигательные, но и мыслительные функции человека.
• Что же такое роботы? Каково научно-техническое содержание этого понятия? Чем роботы отличаются от других автоматических систем?
Робот в общем случае состоит из следующих элементов:
1) системы связи;
2) информационной (сенсорной) системы;
3) управляющей (интеллектуальной) системы;
4) двигательной (моторной) системы.
Структурная схема (архитектура) робота, взаимодействующего с окружающей средой, приведена на рис. 1.1. Охарактеризуем функции каждого из названных элементов.
7
Система связи предназначена для обмена информацией между роботом и человеком, а также для связи с другими роботами и технологическим оборудованием. Цель такого обмена — передача заданий роботу, осуществление диалога между ним и человеком, контроль за его функционированием, диагностика неисправностей, регламентная проверка систем робота и т. д. Обычно информация от человека к роботу поступает через устройство ввода или с пульта управления. При этом чаще всего используется механическое воздействие (нажатие кнопки или клавиши, перемещение рукоятки и т. д.). В последнее время все шире применяются речевое управление, а также ввод информации с помощью биопотенциалов (бноуправление). Ин-
Рис. 1.1. Структурьая схема робота.
формация, поступающая от робота к человеку, как правило, имеет форму световых и звуковых сигналов и передается с помощью дисплеев, телевидения, синтезаторов речи и т. д.
Информационная, или сенсорная, система является по существу искусственными органами чувств робота. Она, как и органы чувств человека, предназначена для восприятия и преобразования информации о состоянии внешнего мира и самого робота в соответствии с требованиями управляющей системы, играющей роль «мозга» робота. В качестве элементов сенсорной системы обычно используются телевизионные н оптико-электронные устройства, акустические датчики и гидролокаторы, лазерные и ультразвуковые дальномеры, тактильные, контактные и индукционные датчики, а такдее датчики положения скорости, сил и моментов, акселерометры и др.
Управляющая, илн интеллектуальная, система — своеобразный «мозг» робота. Она служит для выработки законов управления приводами (двигателями) и механизмами двигательной системы на основе сигналов обратной связи от информационной системы. Другая важная функция данной системы — организа-8
цяя общения робота с человеком на том или ином языке, распознавание ситуаций и моделирование среды, планирование действий и принятие целенаправленных решений, программирование и оптимизация движений. «Мозг» роботов обычно реализуется на основе ЭВМ или микропроцессоров, содержащих широкий набор входных (аналого-цифровых) и выходных (цифроаналоговых) преобразователей и интерфейсных каналов связи, число которых колеблется от нескольких десятков до нескольких тысяч. По этим каналам как по нервной системе передаются непрерывные (аналоговые) и дискретные (цифровые) сигналы. Адаптационные возможности и интеллектуальные способности робота определяются главным образом алгоритмическим и программным обеспечением его управляющей системы.
Совокупность описанных систем робота образует его инфор-мацнонно-управляющую систему. Эта система предназначена для обработки информации и непосредственного управления приводами и механизмами двигательной системы с целью организации активного взаимодействия робота с окружающей средой и выполнения заданий, сформулированных человеком.
Двигательная, или моторная, система характеризует динамические свойства робота, в частности его способность совершать разнообразные движения. Эта система служит для фактической отработки управляющих сигналов, формируемых ннформацион-но-управляющей системой. Тем самым обеспечивается возможность целенаправленного воздействия робота па окружающие объекты. В качестве конструктивных элементов двигательной системы обычно используются приводы (двигатели) и связанные с ними механические руки (манипуляторы), механические ноги (педипуляторы), тележки с колесным пли гусеничным шасси, а также их комбинации. Двигательная система может также включать силовую лазерную установку, целенаправленно воздействующую на объекты окружающей среды, или устройство, манипулирующее объектами с помощью электромагнитного силового поля.
Таким образом, с точки зрения структуры робот представляет собой автомат, включающий в себя как обязательные элементы систему связи, информационную (сенсорную), управляющую (интеллектуальную) и двигательную (моторную) системы.
С функциональной точки зрения робот воспроизводит функции человека, занятого физическим или умственным трудом. Поэтому он выступает как универсальное средство автоматизации сенсорных, двигательных и интеллектуальных функций человека. Прежде всего это касается автоматизации таких видов деятельности человека, которые связаны с тяжелыми, монотонными, вредными для здоровья или опасными для жизни операциями. Так, манипуляционные роботы служат для автоматизации ручного труда, транспортные — для автоматической пере-
9
возки грузов в цехах или по пересеченной местности (например, по поверхности Луны или по дну океана).
Интеллектуальный робот, контролируя свое состояние и вое* принимая объекты окружающей среды с помощью сенсорной системы, формирует в памяти управляющей системы образы этих состояний и объектов. По мере накопления и преобразования информации он может с помощью человека или автоматически обучаться новым понятиям и навыкам, а также формировать в своей памяти модель окружающей среды. Благодаря этому робот оказывается потенциально способным выполнять такие «интеллектуальные» операции, которые у человека отождествляются с мышлением. Подобными операциями являются самообучение понятиям и распознавание образов, планирование поведения и принятие решений, самопрограммирование движений н самонастройка законов управления. Для фактического осуществления роботом интеллектуальных функций его управляющую систему необходимо оснастить соответствующим алгоритмическим и программным обеспечением, т. е. по существу элементами искусственного интеллекта.
Робот — система обучаемая и адаптивная. Необходимую информацию (знания н навыки) ему можно передавать в режиме обучения как путем непосредственного занесения ее в память управляющей системы, так и посредством воздействия через сенсорную систему (например, показом объектов из определенного класса). В ходе обучения (или самообучения) управляющая система изменяет свои параметры или структуру, т. е. адаптируется. У обученного робота эти параметры и структура зависят от взаимодействия его с внешним миром в режиме обучения (например, от того, какие объекты были ему показаны). В процессе обучения и адаптации робот формирует внутри самого себя информационную модель внешней среды.
Важно отметить, что именно способность роботов к обучению и адаптации путем активного взаимодействия с окружающей средой отличает их от традиционных средств автоматизации (ЭВМ, промышленные автоматы с жесткой структурой, автоматические линии и т. п.). Обычные (необучаемые) автоматы и автоматические линии конструируются таким образом, чтобы в течение всего срока эксплуатации надежно выполнять только ту операцию, для автоматизации которой они предназначены. Поэтому применение необучаемых автоматов с жесткой структурой (например, станков-автоматов) целесообразно и экономически выгодно только прн многократном повторении рабочей операции. Такие условия характерны для массового и крупносерийного производства.
В отличие от традиционных автоматов роботы служат для решения не одной конкретной задачи (операции), а некоторого класса задач. В этом проявляется нх универсальность. Функциональные возможности робота определяются разнообразием
Ю
датчиков сенсорной системы, числом степеней свободы и конструктивными особенностями двигательной системы, автоматизмом н уровнем интеллекта управляющей системы.
Характерной чертой роботов является гибкость, т. е. способность оперативно перестраиваться с решения одной задачи (операции) на другую. Обычно это достигается путем переобучения (перепрограммирования) робота с помощью человека или в автоматическом режиме. В последнем случае гибкость достигается посредством самообучения и автоматического приспособления (адаптации) робота к заранее неизвестным или изменяющимся условиям.
В специальной литературе встречаются самые разнообразные определения понятия «робот». Так, в работе (53, с. 3] робот трактуется как «универсальный автомат для выполнения механических действий», в работе (46, с. 13] —как «класс технических систем, которые в своих действиях воспроизводят двигательные и интеллектуальные функции человека», а в Большой Советской Энциклопедии — как «машина с антропоморфным (человекоподобным) поведением, которая частично или полностью выполняет функции человека (иногда животного) при взаимодействии с окружающим миром». *
Для сравнения приведем еще одно определение понятия «робот», описанное в работе (12]. Это «усредненное» коллективное определение было получено путем статистического анализа ответов на вопрос: «Что такое робот, чем он отличается от машин и автоматических систем?», который задавался 156 экспертам, специализирующимся в различных областях науки и техники. Исследование проводилось методом «дельфи», в основе которого лежит анализ протоколов опроса экспертов. Результатом экспертизы явилось следующее определение (12, с. 23, 24]: «Робот представляет собой подвижную компактную систему, отличительными признаками которой являются чувствительные элементы, манипуляторы и, самое главное, некоторая степень искусственного интеллекта. При этом искусственный интеллект отождествляется главным образом со способностью к обучению н соответственно к изменению поведения».
Резюмируя вышеизложенное, определим понятие «робот» следующим образом. Робот — это универсальная автоматическая система для воспроизведения физических и интеллектуальных функций человека, способная обучаться на опыте н адаптироваться к реальным условиям путем активного информационного и двигательного взаимодействия с окружающей средой.
Данное определение хорошо согласуется с определением, предложенным в работе (59, с. 18]. Отличительными признаками робота согласно этим определениям являются многоцелевое назначение (универсальность) н способность к обучению
* БСЭ, т. 22, с. 149.
11
и адаптации (гибкость). Благодаря этим свойствам роботы могут выполнять те виды физической и умственной работы, которые принципиально или по экономическим соображениям невозможно или нецелесообразно автоматизировать традиционными техническими средствами.
$ 2. ТРИ ПОКОЛЕНИЯ РОБОТОВ И ОБЛАСТИ ИХ ПРИМЕНЕНИЯ
История развития робототехники непродолжительна. Тем не менее роботы принято делить на поколения. Хотя такое деление весьма условно, оно позволяет отразить наиболее значительные изменения в архитектуре, средствах очувствления и методах управления роботами в процессе их эволюции. Результатом эволюции является расширение функциональных возможностей роботов н как следствие областей их возможного применения.
В настоящее время существуют три поколения роботов. Охарактеризуем их главные особенности.
Роботы первого поколения — это роботы с программным управлением (программные роботы). Они предназначены в основном для выполнения заранее запрограммированной последовательности операций, диктуемой тем или иным технологическим процессом. Управление такими роботами осуществляется по жесткой программе, формируемой в режиме обучения с помощью человека-оператора. Поэтому приемлемое качество управления достигается лишь при строго определенных и неизменных условиях эксплуатации робота. Следует, однако, подчеркнуть, что именно простота формирования и изменения программы, т. е. простота переобучения (перепрограммирования) робота при переходе на новые операции, сделала роботы первого поколения достаточно универсальными и гибко перестраиваемыми на разные классы операций.
Первые роботы с программным управлением появились в промышленности в начале 60-х годов. В настоящее время серийно производятся и широко используются десятки тысяч таких роботов.
Область возможного и экономически целесообразного применения роботов первого поколения достаточно широка. Эти роботы успешно используются при обслуживании металлорежущего оборудования (в частности, станков с числовым программным управлением), печей, штампов, прессов, технологических линий, сварочных аппаратов, литейных машин и т. п. С их помощью осуществляются установка, снятие, транспортировка, упаковка изделий и инструментов, простейшие сборочные операции, ковка, сварка, литье под давлением, термическая и механическая обработка и т. п. Наиболее широко роботы с программным управлением применяются в приборостроении и
12
машиностроении (особенно в автомобильной и станкостроительной промышленности).
функциональные возможности роботов первого поколения существенно ограничиваются малым набором датчиков в информационной системе и несовершенством управляющей системы. Последняя служит по существу лишь для выполнения жесткой программы, заранее заложенной в память. Способность к восприятию окружающей среды и формированию ее модели у роботов первого поколения практически отсутствует. Поэтому они принципиально не могут функционировать самостоятельно (автономно) в недетерминированной обстановке. Их обучение, а иногда и эксплуатация требуют вмешательства человека-оператора.
Успешное функционирование роботов с программным управлением возможно лишь при строго определенных (детерминированных) условиях. Для создания таких условий требуется введение дополнительного технологического оборудования, стоимость которого сравнима со стоимостью самого робота. Это усложняет процесс роботизации производства, делает его менее гибким. Поэтому в последнее время особую актуальность приобрели научно-исследовательские и опытно-конструкторские разработки по созданию более совершенных роботов следующих поколений.
Роботы второго поколения — это очувствленные роботы с адаптивным управлением. Они отличаются от программных роботов, во-первых, существенно более широким набором датчиков, особенно датчиков внешней информации (телевизионные или оптические системы технического зрения, тактильные, силовые, локационные датчики и т. п.), и, во-вторых, более сложной и совершенной управляющей системой. Последняя уже не сводится к устройству для запоминания жесткой программы движения, как у роботов первого поколения, а требует для своей реализации микро-ЭВМ или микропроцессоров.
Технические «органы чувств», входящие в систему очувствления роботов второго поколения, служат источником обратных связей для управляющей системы. Последняя, обрабатывая сенсорную информацию, синтезирует закон управления исполнительными приводами и механизмами робота с учетом фактической обстановки.
Такой закон управления может иметь ситуационный характер. В этом случае его синтез сводится к формированию связей типа «класс ситуаций — действие». Каждая подобная связь либо заранее закладывается в память управляющей системы, либо формируется в процессе обучения робота человеком. При этом под «ситуацией» понимается набор значений сигналов на выходе сенсорной системы, а под «классом ситуаций» — их множество, такое, что все «ситуации» из одного класса требуют одного и того же «действия», адекватного данному «классу си-
13
туацнй». «Действием» является программа движения, которая, как и в роботах первого поколения, задается заранее (зано-сится в память управляющей системы) или формируется в ре* жиме обучения. Следует отметить, что в случае существенного □вменения «ситуации», соответствующей переходу из одного «класса ситуаций» в другой, изменяется и «действие», т. е. программа движения.
Описанная схема ситуационного управления напоминает схему выработки условных рефлексов у человека или животного. Поэтому управляемое поведение очувствленного робота можно условно назвать рефлекторным. Именно наличие связей «класс ситуаций — действие» позволяет очувствленному роботу приспосабливать свое поведение к реально складывающейся и даже изменяющейся (правда, в довольно ограниченных пределах) обстановке.
Другой метод адаптивного управления роботами сводится к аналитическому синтезу закона управления с обратной связью через систему очувствления. Такое управление естественно назвать сенсорцым. Его адаптационные возможности принципиально ограничены.
Более совершенным является метод управления, при котором сенсорное управление дополняется алгоритмом автоматической настройки (самонастройки) его параметров. Адаптационные возможности управления с самонастройкой практически неограниченны. Благодаря самонастройке управляющей системы робот может автоматически приспосабливаться (адаптироваться) к заранее неизвестным и изменяющимся условиям эксплуатации.
Неотъемлемой частью роботов второго поколения является их программное обеспечение, позволяющее реализовать сложные алгоритмы обработки информации и управления. По мере совершенствования очувствленных роботов и расширения класса решаемых ими задач относительная доля затрат из алгоритмическое и программное обеспечение увеличивается. Это объясняется тем, что затраты на чисто технические компоненты очувствленных роботов в известной мере стабилизировались. В то же время нх функциональные возможности определяются именно программным обеспечением и могут быть существенно расширены путем наращивания программ обработки сенсорной информации и адаптивного управления.
Возможности роботов второго поколения, оснащенных большим числом датчиков и мощной управляющей ЭВМ с развитым программным обеспечением, значительно превосходят возможности роботов первого поколения. Благодаря способности воспринимать внешнюю обстановку, анализировать сенсорную информацию и приспосабливаться к изменяющимся условиям эксплуатации очувствленные роботы могут работать с неориентированными и неупорядоченными деталями, выполнять сбо-14
рочные н монтажные операции, собирать информацию о пре* пятствнях на незнакомой местности и т. и.
В настоящее время промышленность начинает осваивать выпуск роботов второго поколения. В ряде научных центров ве* дутся интенсивные исследования по разработке алгоритмнче* ского, программного и технического обеспечения перспективных моделей очувствленных роботов различного назначения. Особое внимание в этих разработках уделяется системам технического зрения, тактильному и снломоментному очувствлению роботов, а также микропроцессорной реализации алгоритмов обработки информации и управления.
Третье поколение роботов — это интеллектуальные, или ра* зумные, роботы. Они принципиально отличаются от роботов второго поколения сложностью функций и совершенством управляющей системы, включающей в себя те или иные эле» менты искусственного интеллекта. Необходимо отметить, что интеллектуальные роботы предназначены не только н не столь* ко для имитации физических действий человека, сколько для автоматизации его интеллектуальной деятельности, т. е. по су* шеству для решения интеллектуальных задач.
Характерной особенностью интеллектуальных роботов яв* ляется их способность к обучению на опыте и адаптации в процессе решения задач. Умение решать интеллектуальные задачи существенно зависит от характера процесса обучения и адаптации робота.
Существуют разные возможности придания очувствленному роботу элементов искусственного интеллекта. Структура н функции управляющих систем интеллектуальных роботов определяются, с одной стороны, техническими возможностями синтеза и реализации нужных (с точки зрения решаемой задачи) элементов интеллекта, а с другой — содержанием и сложностью задач, которые ставит перед роботом человек.
В общем случае интеллектуальный робот способен понимать естественный язык и вести диалог с человеком, формировать модель внешней среды с тон или иной степенью детализации, распознавать и анализировать сложные ситуации, обучаться навыкам, усваивать понятия, планировать поведение, программировать движения двигательной системы и осуществлять их надежную отработку в условиях неполной информированности о характеристиках среды, робота и условий его функционирования.
Следует отметить, что реальная потребность в интеллектуальных роботах появилась лишь в последние годы. Если роботы второго поколения уже в настоящее время необходимы для ряда научно-технических разработок (в частности, для космических н глубоководных исследований [11, 22, 42]) и их начинают рвменять в промышленности, то роботы третьего поколения
16
пока не вышли из лабораторий, где их конструируют и постоян-но совершенствуют [59, 64, 71, 79].
Описанная эволюция роботов вовсе не означает, что одно поколение роботов последовательно сменяет и вытесняет другое. На самом деле, хотя и существует определенная преемственность поколений, эволюционный процесс совершенствует функциональные возможности и технические характеристики роботов. Однако при этом каждое поколение роботов представляет собой семейство роботов, предназначенных для эффективного решения своего круга задач, связанных с автоматизацией двигательных, информационных и интеллектуальных функций.
В завнснмости от назначения и сферы применения роботы можно разбить на два класса — производственные и исследовательские. На рис. 1.2 представлена эволюционная классификация роботов трех поколений с указанием конкретных областей их применения. Рассмотрим эту классификацию более подробно.
Производственные роботы предназначены главным образом для выполнения тяжелой, монотонной, вредной н опасной для здоровья человека физической работы. Роботы этой группы обладают достаточно мощными н развитыми двигательными системами (автоматические манипуляторы, имитирующие движения рук человека, самоходные тележки с разными типами шасси и т. д.). «Специализация» производственных роботов позволяет выделить такие их разновидности, как промышленные, сельскохозяйственные, транспортные, строительные и бытовые роботы.
Второй класс роботов составляют исследовательские роботы. Они служат прежде всего для поиска, сбора, переработки и передачи информации об исследуемых объектах: космическом пространстве, поверхности планет, подводном мире, подземных полостях (шахтах, рудоспусках, пещерах и т. п.) и других труднодоступных для человека областях.
Таким образом,, современная робототехника представляет собой гармоничное сочетание роботов разных типов и поколений, вызванных к жизни потребностями ускоренного развития научно-технического прогресса.
$ 3. КЛАССИФИКАЦИЯ УПРАВЛЯЮЩИХ СИСТЕМ
Классификацию управляющих систем роботов принято проводи гь по степени и характеру участия человека-оператора в процессе управления, по поколениям роботов, по принципу н конкретным способам управления, а также по типу элементов и устройств, на базе которых реализуется управление [46, 53, 59]. До сих пор не существует единой общепринятой классификации управляющих систем. Это объясняется тем, что робототехника еще очень молода и интенсивно развивается, особенно в области совершенствования именно управляющих систем.
16
Поколения poSwnot
Рис. \2. Эволюционная классификация и области применения роботов.
Предлагаемая классификация базируется на современных представлениях теории управления и направлена на возможно более полный охват различных существующих н мыслимых управляющих систем роботов. По степени участия человека управляющие системы подразделяются на два класса [53, 59] — автоматизированные и автоматические. Рассмотрим особенности управления в каждом классе.
Автоматизированные управляющие системы характеризуются тем, что в них функции управления распределены между человеком-оператором и автоматическими устройствами. Эти системы в свою очередь подразделяются на биотехнические и интерактивные [46, 53]. Главным классификационным признаком в рассматриваемом случае является характер управляющих функций, возлагаемых на человека.
В биотехнических управляющих системах человек фактически берет на себя управление двигательными механизмами робота. Оно осуществляется с помощью задающего механизма (при управлении копирующим манипулятором) либо клавишного пульта управления или рукоятки. Такое ручное управление обычно используется эпизодически в режиме обучения робота, в аварийных ситуациях или при выполнении отдельных ответственных операций, которые по каким-либо причинам невозможно произвести автоматически. Если ручное управление выполняется непрерывно, то робот по существу вырождается в обычную машину (автокар, экскаватор и т. п.). К биотехническому управлению можно отнести и особый вид управления двигательными механизмамн (например, протезами) — управление с помощью бноимпульсов или других сенсомоторных сигналов, поступающих от человека.
Интерактивные управляющие системы характеризуются активным общением (диалогом) и взаимодействием робота с человеком. При этом на человека возлагаются лишь некоторые интеллектуальные функции, такие, как распознавание обстановки, целеуказание, планирование движений или контроль за выполнением заданий. Важнейшими видами интерактивного управления являются супервизорное управление, когда человек Герет на себя функции целеуказания (например, световым перо и на экране дисплея) и визуального контроля, речевое управление, когда человек дает роботу команды голосом, и диалоговое управление, когда робот не только воспринимает команды человека, но н сам информирует его (например, с помощью дисплея или синтезатора речи) о своих действиях и нуждах. Можно ожидать, что по мере совершенствования интерактивных управляющих систем робот постепенно превратится в творческого партнера человека.
Отличительной чертой класса автоматических управляющих систем робота является их способность работать полностью автономно, т. е. без участия человека. Роль человека сводится ха
лишь к формулировке задания, начальной наладке и текущему ремонту робота. По принципу управления эти системы делятся на программные, адаптивные и интеллектуальные.
Программные управляющие системы работают по жесткой программе, которая рассчитывается заранее (вне робота) и хранится в запоминающем устройстве либо автоматически форми-руется в режиме обучения робота. Эти системы строятся по разомкнутой схеме (управление по упорам и позиционное управление) или с обратной связью (контурное управление, сервоуправление по программе). Необходимым условием работоспособности программных управляющих систем является неизменность условии эксплуатации робота (в пределах требуемой точности отработки программы движения).
Адаптивные управляющие системы служат для автоматического приспособления роботов к заранее неизвестным и изменяющимся условиям эксплуатации. Общей чертой всех этих систем является использование обратной связи не только в соответствии с текущим состоянием робота, но и в соответствии с состоянием внешней среды. Существует несколько разновидностей адаптивных систем, различающихся принципом действия и адаптационными возможностями.
В системах первого типа управление осуществляется по принципу «класс ситуаций — действие». При этом программа движения заранее не строится, а целенаправленное поведение робота формируется как функция состояний внешней среды и робота. Управление такого типа, использующее логическую обратную связь, будем называть ситуационным, или рефлекторным, управлением.
Системы второго типа реализуют сенсорное управление, т. е. управление с обратной связью от сенсорной системы, структура н параметры которого остаются неизменными в течение всего времени эксплуатации робота.
В ряде случаев можно обойтись без построения программы движения. Ее роль могут играть, например, координаты и ориентация объекта манипулирования, линия стыка свариваемых деталей или подземный токопроводящий кабель, задающий маршрут перемещения транспортного робота. В таких случаях речь идет по существу об управлении по принципу самонаведения (но без адаптации). Соответствующий режим управления будем называть самонаведением робота.
В других случаях приходится автоматически строить или оптимизировать программу движения. Такая необходимость возникает, например, в задаче о переводе робота из одного состояния в другое за кратчайшее время (задача наибольшего быстродействия) или в задачах управления, связанных с обходом рнешиих препятствий. Цель управления заключается в возможно более точном осуществлении заданной программы двн-
1»
Кения. Необходимым условием достижения этой цели является беспечение устойчивости программы движения на основе со-тветствующего закона сенсорного управления. Такой режим правления будем называть сенсорным программным ^управле-ием.
Описанные методы н режимы управления по существу не вляются адаптивными, так как не используют никаких средств амонастройкн закона управления. Тем не менее робот с по-обным управлением, оперативно реагируя на изменения со-тояний внешней среды и самого робота, которые непосред-твенно контролируются сенсорной системой, может вести себя даптивно. Принципиальная ограниченность адаптационных озможностей таких роботов свидетельствует о том, что соот-етствующне законы управления являются адаптивными лишь словно.
Характерной чертой адаптивных управляющих систем яв-яется автоматическая настройка (самонастройка) структуры лн параметров закона управления с целью обеспечения тре-уемого качества управления при непредсказуемых изменениях инамических характеристик робота и внешних условий его аботы. Для построения таких адаптивных систем можно нс-ользовать описанные ранее законы самонаведения и сенсор-ого программного управления, дополненные алгоритмами са-онастройки. В некоторых случаях (например, при появлении еожнданных препятствий) возникает необходимость в коррек-ировке программы движения в ходе управления. В подобных пучаях адаптивный (самонастраивающийся) закон управления ополняется средствами автоматического программирования гамопрограммирования) движений.
Интеллектуальные управляющие системы — это наиболее свершенный вид адаптивных систем. Их основу составляют уже писанные адаптивные управляющие системы, дополненные эле-ентамн искусственного интеллекта. Функции и принцип дей-вня таких систем в какой-то мере можно сравнивать с ин-еллектуальной деятельностью человека.
Интеллектуальное управление имеет четко выраженную фархическую структуру и содержит следующие основные эовнн управления:
— самонастройку закона управления,
— самопрограммирование и планирование движений, — самомоделирование и моделирование внешней среды, — самообучение понятиям и распознавание обстановки, — самоорганизацию целенаправленного поведения.
Каждый последующий уровень управляет работой преды-щего, расширяя функциональные возможности управляющей стемы в целом и повышая качество управления. Совместная оординированная работа «ведущих» н «ведомых» уровней равления обеспечивает комплекснрованне разнообразных ин*
еплектуальных функций при автономном функционировании То’бота в недетерминированной обстановке.
н Для сравнения эффективности программных, адаптивных и интеллектуальных управляющих систем проанализируем, как качество управления зависит от изменения условий эксплуатации робота. Необходимым условием работоспособности программных управляющих систем является неизменность условий работы. Адаптивные системы, реализующие принципы самонаведения, ситуационного и сенсорного управления, реагируют на изменения условий работы в пределах информационных возможностей сенсорной системы. Адаптивные системы с самонастройкой законов управления обеспечивают требуемое качество переходных процессов в широком (теоретически любом) диапазоне изменений неконтролируемых параметров робота и внешних условий. Наконец, интеллектуальные управляющие системы
позволяют адекватно реагировать на неконтролируемые изменения внешней среды и непредсказуемый дрейф параметров самого робота вследствие самоорганизации, включающей самонастройку закона управления, самопрограммирование движений, самообучение распознаванию обстановки, а также (в случае нобходпмости) самодиагностику и саморемонт.
Описанная классификация управляющих систем роботов приведена на рис. 1.3. Она относится в основном к роботам с индивидуальным управляющим устройством. Однако в последние годы все шире начинают применять принципы и средства группового управления роботами. Это связано, в частности, с интенсивным развитием робототехнических систем и комплексов, составляющих основу гибких заводов-автоматов.
Цель группового управления заключается в обеспечении согласованной, строго скоординированной работы нескольких роботов совместно с обслуживаемым ими технологическим оборудованием. Для достижения указанной цели используются принципы централизованного, децентрализованного и комбинированного управления.
При централизованном управлении коллектив роботов управляется от одной ЭВМ, которая выполняет обычно расчеты программ движения и координацию работы отдельных роботов и программно управляемого оборудования. Управляющие системы роботов локально отрабатывают требуемые программы Движения под общим контролем центральной ЭВМ. Все возникающие неполадки автоматически анализируются и выводятся па центральный пульт, что дает возможность оперативно производить необходимые исправления.
При децентрализованном управлении каждый робот индивидуально самоуправляется (например, микро-ЭВМ), но при этом он связан информационно-управляющими каналами с другими роботами и технологическим оборудованием. Благодаря
21
Рис. 1.3. Классификация управляющих систем роботов.
сказанному осуществляются оперативный обмен информацией и взаимная координация действий отдельных роботов.
Комбинированное управление группой роботов основывается на централизованном управлении от общей ЭВМ с использованием перекрестных ннформационно-управляющих связей между нх индивидуальными микропроцессорами. Следует отметить, что переход к групповому управлению позволяет улучшить технико-экономические показатели сложных роботизированных комплексов и придает им необходимую гибкость.
$ 4. ПРОБЛЕМЫ ОБУЧЕНИЯ И АДАПТАЦИИ РОБОТОВ
Эффективность управления роботами в значительной степени определяется методами обучения и средствами адаптации, используемыми в нх управляющей системе. Рассмотрим подробнее проблемы обучения и адаптации роботов трех поколений.
Обычно обучение робота рабочим операциям (т. е. по существу навыкам) осуществляется человеком-оператором, который с помощью пульта (или рукоятки) управления совершает требуемое движение, соответствующее образцовому выполнению рабочей операции. При этом информация о текущих изменениях состояний (положений) исполнительного механизма снимается сенсорными датчиками и вводится в память управляющей системы. Это и есть программа движения, соответствующая заданной операции. Очевидно, что робот можно обучить практически любым операциям в рамках его двигательных возможностей.
Обучение роботов «вручную» обладает рядом недостатков. Во-первых, этот процесс трудоемок и продолжителен, что отрицательно сказывается на общей производительности робота. Во-вторых, ручное обучение требует специальной подготовки и высокой квалификации человека-оператора. В-третьих, программа движений, сформированная в процессе обучения, предопределяет жесткий характер закона управления, при котором фактически игнорируется информация об изменениях условий эксплуатации робота. Последнее приводит к тому, что даже незначительные изменения названных условий (например, положения или ориентации объекта манипулирования) вызывают потерю работоспособности, а появление препятствий — аварию.
Указанные факторы снижают эффективность и сужают область возможного применения роботов с программным управлением. При ручном их обучении предпочтение отдается автоматическому программированию движений. Такой метод обучения широко используется при программировании режимов работы станков с числовым программным управлением, для которых разработаны специальные методы н языковые средства Автоматического программирования движений [6].
23
В робототехнике средства автоматического программировав ния (самопрограммирования) движений только начинают при. менять. Подробный анализ возникающих проблем и методов и* решения содержится в главе 3. Главными достоинствами авто, магического обучения являются возможность оптимизации многомерных программ движения и быстрота переобучения робо. тов новым операциям. Это позволяет резко повысить эффективность роботов первого поколения.
Условия эксплуатации роботов зачастую не только не известны, но и могут непредсказуемо изменяться в широком диапазоне. Причины неопределенности и нестационарности этих условий заключаются: 1) в недостатке информации о свойствах внешней среды; 2) в естественном разбросе и дрейфе параметров сенсорной и двигательной систем робота; 3) в возникновении помех и вычислительных погрешностей в каналах связи и управления.
Для организации обучения и управления роботом в условиях неопределенности можно выделить три подхода. Первый из них основывается на измерении всех необходимых параметров и свойств как самого робота, так и внешней среды. Этот подход, связанный с полным «очувствлением» робота, требует использования широкого набора прецизионных датчиков. Однако необходимых датчиков зачастую либо вообще не существует, либо они чрезмерно сложны и дороги.
Второй подход строится на идентификации неизвестных характеристик с последующим использованием найденных оценок в управляющей системе. Однако такой подход имеет ограничения: в ряде случаев точная идентификация принципиально невозможна или требует проведения весьма сложных предвари-, тельных испытаний. .
Наконец, третий подход заключается в конструировании специальных алгоритмов н средств адаптации, придающих управляющей системе способность автоматически приспосабливаться (адаптироваться) к заранее неизвестным н изменяющимся условиям эксплуатации. Хотя реализация адаптивного управления н предполагает определенное «очувствление» робота, однако требования к набору сенсорных датчиков здесь невысоки и могут быть сведены к необходимому минимуму. Вместе с тем для достижения цели при адаптивном управлении точной идентификации параметров робота и внешней среды, как правило, не требуется.
Следует подчеркнуть, что средства автоматического обучения (самообучения) и адаптации, используемые в роботах второго и особенно третьего поколений, превращают их управляющую систему в чрезвычайно гибкий инструмент организации целенаправленного поведения в условиях неопределенности. Именно поэтому роботы с адаптивным управлением и элементами искусственного интеллекта значительно превосходят по
24
озможностям роботы с программным управлением: они могут адекватно реагировать на изменения внешней обстановки, подстраиваться к дрейфу параметров робота, распознавать и обходить препятствия, идентифицировать целевые объекты, определять их характеристики и т. д.
До последнего времени фактическая реализация указанных потенциальных возможностей адаптивных н интеллектуальных роботов сдерживалась отсутствием как эффективных методов обучения и управления в условиях неопределенности, так и специализированных средств информационной (сенсорной) и вычислительной техники. Однако успехи в области теории адаптивного управления и бурное развитие разнообразных средств очувствления и микропроцессоров создают реальные предпосылки для разработки и широкого использования роботов с адаптивным управлением и элементами искусственного интеллекта.
f 5. ПРИНЦИПЫ УПРАВЛЕНИЯ РОБОТАМИ В НЕСТАЦИОНАРНЫХ
И НЕОПРЕДЕЛЕННЫХ УСЛОВИЯХ
На практике роботы всегда функционируют в нестационарных и неопределенных условиях. Это проявляется в дрейфе параметров и отсутствии информации о ряде факторов, определяющих состояния внешней среды и самого робота. В подобных условиях традиционные методы и средства программного управления роботами часто приводят к плохим результатам или вообще неприменимы.
Эффективным методом управления в заранее не известных и изменяющихся условиях является адаптивное управление. В отличие от программного управления данный метод позволяет роботу адаптироваться к реальной обстановке и после обучения (самообучения) выполнить требуемую операцию или программу движения.
В основе адаптивного управления лежит принцип обратной связи, являющийся краеугольным камнем всей теории управления. Суть этого принципа заключается в следующем: управляющее воздействие в каждый момент зависит от информации о состоянии управляемого объекта в этот момент. В робототехнике принцип обратной связи реализуется путем создания информационной системы, т. е. специальных средств очувствления, доставляющих управляющей системе необходимую информацию о текущем состоянии двигательных механизмов робота и окружающей среды.
Идея адаптации заключается в автоматической настройке (самонастройке) коэффициентов усиления каналов обратной связи. Функции самонастройки возлагаются на блок адаптации
25
управляющей системы, называемый адаптатором. Цель адаптации состоит в корректировке управляющих воздействий, необходимой для подстройки н приспособления их к неконтролируемому дрейфу параметров робота и изменяющимся условиям эксплуатации. Поэтому блок адаптации следует рассматривать как принципиально новый элемент — своеобразную надстройку над обычными системами программного управления, — который обеспечивает надежную отработку заданной программы движения при частично неопределенных или изменяющихся условиях.
К числу неопределенных факторов, которые могут непредсказуемо изменяться в широком диапазоне, относятся массо-инерционные характеристики груза, силы трения и упругие деформации в двигательных механизмах, физико-механические параметры приводов, а также характеристики внешней среды. Все эти факторы существенно влияют на качество управления роботом. При программном управлении они часто приводят к ухудшению качества переходных процессов, проявляющегося в потере точности, автоколебаниях или даже неустойчивости программного движения. Роботы с сервоуправлением в меньшей степени чувствительны к неконтролируемым возмущениям указанных факторов.
Все сказанное свидетельствует о практической потребности в адаптивном управлении как средстве компенсации параметрических возмущении. Эта компенсация фактически обеспечивается адаптатором, реализующим тот или иной алгоритм самонастройки параметров управляющей системы. Важно отмстить, что блок адаптации существенно использует информацию, поступающую в управляющую систему от системы очувствлений робота по каналам обратной связи.
Однако данная информация не всегда полна, поскольку система очувствления зачастую измеряет лишь часть переменных, характеризующих состояния робота и внешней среды. Для восстановления значений неизмеряемых переменных можно использовать специальные идентификаторы состояний, пли наблюдатели [14, 19]. Но в ряде случаев достижение цели управления возможно и по неполной информации. Следовательно, сбор, хранение и переработка сенсорной информации необходимы лишь в той минимальной мере, в которой эта информация требуется управляющей системе для достижения цели.
Описанный принцип самонастройки играет важную роль при конструировании высококачественных управляющих систем роботов, инвариантных (т. е. практически нечувствительных) к неконтролируемым параметрическим н внешним возмущениям. Данный принцип используется на нижнем уровне управления, обеспечивающем формирование и корректировку управляющих воздействий, подаваемых на приводы исполнительных механизмов. При этом цель управления обычно заключается в осуществлении заданной программы движения.
26
В ряде случаев программа движения не задается заранее, указывается лишь целевое состояние исполнительного механизма. Например, часто задаются целевое положение и ориентация схвата манипулятора. В подобных случаях управление сводится к самонаведению исполнительного механизма в окрестность целевого состояния. Для компенсации неконтролн* руемых параметрических и внешних возмущений, возникающих р процессе самонаведения, необходима также самонастройка параметров управляющей системы.
Надежная отработка программы движения или самонаведение робота в заранее неизвестных и меняющихся условиях эксплуатации являются лишь одной из функций системы адаптивного управления. Другая, не менее важная функция заключается в обеспечении возможности выполнения сложных технологических операций, осуществление которых обычным роботам с программным управлением просто не под силу. Такими операциями являются тонкие сборочные операции типа «вставить вал», «завинтить гайку», силовые операции типа «открыть люк», «повернуть штурвал», операции с неориентированными или подвижными деталями. Все их следует выполнять быстро, точно и надежно. Поэтому система адаптивного управления должна обеспечить необходимую дозировку усилий, а также требуемые плавность и гибкость движений робота в реальной обстановке с препятствиями. Это требует автоматизации функций регулирования усилий, планирования и построения программных движений, т. е. самопрограммирования робота.
Конструирование блока автоматического программирования движений, называемого программатором, сводится в основном к разработке специальных алгоритмов, позволяющих оперативно учитывать изменения внешней обстановки (например, появление препятствий). Такие алгоритмы осуществляют своеобразную адаптацию к изменяющейся обстановке путем коррекции программы движения. Благодаря этому робот может самостоятельно обходить препятствия и манипулировать неориентированными деталями. Весьма важно и то, что отпадает необходимость в трудоемком процессе обучения робота с помощью человека-оператора.
При расчете программы движения естественно стремление сделать ее нанлучшей с точки зрения заданного критерия качества, т. е. оптимальной. Практический интерес представляют критерии, характеризующие энергетические или временные закаты. Так, синтез программы нз условия минимизации времени выполнения рабочей операции позволяет достичь наибольшей (или близкой к ней) производительности робота.
Принцип оптимальности имеет большое значение не только В процессе программирования движений. Как будет показано Далее, исходя из этого принципа можно оптимизировать также ваконы управления и алгоритмы самонастройки.
27
Функции управляющей системы в общем случае не ограни, чиваются самопрограммированием движений и самонастройки) управляющих воздействий. На практике часто, кроме того, тре. буется, чтобы данная система обладала элементами искусственного интеллекта. Необходимость в этом возникает, например, при самостоятельном распознавании роботом различных клас-сов сигналов, моделировании и анализе окружающей обстанов-ки. Важную роль в таком случае играет принцип самообучения понятиям, суть которого заключается в следующем. Сначала а режиме обучения роботу предъявляют объекты (или сигналы) Казных классов с указанием, к какому классу они принадлежат. 1о этим данным, называемым обычно обучающим материалом, автоматически синтезируются понятия, т. е. описание классов в терминах сенсорных признаков, формируемых системой очувствления. По мере восприятия и распознавания новых объектов (или сигналов) данные понятия уточняются и совершенствуются.
Функции принятия решений и планирования поведения робота в условиях неопределенности соответствуют высшему уровню интеллектуального управления. Алгоритмы этого уровня выбирают стратегию поведения, формируют общий план и логику действия робота, обеспечивающие выполнение задания, сформулированного человеком в режиме диалога с роботом. Таким образом, осуществляется своеобразная самоорганизация управляющей системы робота на решение поставленной человеком задачи.
Глава 2
АНАЛИТИЧЕСКАЯ МЕХАНИКА РОБОТОВ
I 1. ИСПОЛНИТЕЛЬНЫЕ ПРИВОДЫ И МЕХАНИЗМЫ
Двигательная система роботов состоит из исполнительных приводов и механизмов. Силы и моменты, вырабатываемые двигателями, приводят в движение исполнительный механизм.
' Рассмотрим основные разновидности приводов и механизмов, применяемых в роботах.
Привод состоит из двигателя, механизма передачи движения (редуктора) и датчиков внутренней обратной связи (обычно это датчики положения и скорости). Двигатели как силовые элементы приводов подразделяются на гидравлические, пневматические и электрические. Весьма перспективны для робототехники и мускульные (мышечные) двигатели [79], осуществляющие прямое преобразование химической энергии в механическую.
К приводам роботов (независимо от их вида) предъявляется ряд общих требований. Во-первых, они должны обеспечивать быстрое и плавное изменение выходных (управляющих) моментов в широком диапазоне скоростей. Во-вторых, отношение развиваемой мощности к массе привода должно быть достаточно большим. В-третьих, приводы должны иметь высокий к. п.д. Весьма важно также, чтобы приводы были компактны, мало-инерционны, просты в эксплуатации и наладке.
Характерной особенностью приводов роботов является значительное (в десятки раз) изменение моментов инерции нагрузки, приведенных к выходным валам двигателей. Это обусловлено как изменением конфигурации исполнительного механизма (например, манипулятора), так и скачкообразным изменением массоинерционных характеристик груза. Поэтому первостепенное значение приобретает требование обеспечения желаемого (например, апериодического) характера затухания переходных процессов во всем диапа :оне возможных изменений нагрузки. Для выполнения этого пребовання кроме обычно ис-
2»
пользуемой обратной связи по положению вводят дополнительные обратные связи по скорости, ускорению или моменту с варьируемыми коэффициентами усиления. В качестве датчиков сигналов указанных обратных связей обычно служат тахогенераторы, акселерометры н тензодатчики.
Следует отметить, что пребования к приводам очувствленного робота с адаптивным управлением, ориентированного, например, на выполнение монтажных или сборочных операций, существенно отличаются от требований, предъявляемых к приводам роботов с программным управлением. Так, в первом случае важно обеспечить определенную податливость приводов к внешним усилиям (которые в данном случае несут полезную информацию), а во втором, наоборот, стремиться добиться большой их жесткости.
В робототехнике все шире применяются электрические приводы. К числу основных их достоинств можно отнести простоту наладки и эксплуатации, высокие к. п. д. и надежность, хорошие динамические характеристики (высокие точность и быстродействие), компактность и низкий уровень шумов. Использование электрических приводов в промышленных роботах стимулируется доступностью, широким распространением и дешевизной электрических источников питания. Даже в космических роботах желательно применять электроприводы, поскольку питающие их •лектрическне аккумуляторы могут подзаряжаться непосредственно от солнечных батарей.
В электроприводах обычно используются двигатели постоян-иго тока с возбуждением от постоянных магнитов. К. п. д. та-сих двигателей достигает 0,6.
Наряду с двигателями постоянного тока в роботах исполь-<уются приводы других видов. Средн них можно выделить асин-:ронные и шаговые двигатели. Весьма перспективны также мо-тентные двигатели, момент на выходном валу которых пропор-тонален управляющему напряжению или току на входе.
В промышленных роботах грузоподъемностью не более 20 кг асто применяют пневматические приводы. Они отличаются де-левизной, простотой эксплуатации, высокой надежностью и ожаробезопасностью. К их недостаткам следует отнести низ-ую выходную мощность, трудность точного позиционирования поддержания заданной скорости, высокую чувствительность к зменениям нагрузки.
Примерно в половине всех современных роботов первого по-оления используются гидравлические приводы (53]. Особенно 1ироко они применяются в промышленных роботах большой рузоподъемности (20 кг и более), а также в подводных ростах.
Типовой гидропривод, осуществляющий линейные перемеще-ня исполнительного механизма, состоит из гндроцилнндра, дат* нка положения и электрогндравлнческого усилителя. Для вы-
лолнения вращательных движений звеньев исполнительного механизма служат поворотные гидродвигатели (гидромоторы).
Рассмотрим особенности исполнительных механизмов роботе. Под механизмом принято понимать систему тел, предназначенную для преобразования движения одного или нескольких тел в требуемые движения других тел. Твердое тело, входящее в состав механизма, называется его звеном. Подвижное соединение двух соприкасающихся звеньев образует кинематическую пару. Для звеньев, входящих в кинематическую пару, число степеней свободы всегда меньше шести, так как связи, реализуемые парой, уменьшают число возможных перемещений.
Рис. 2.1. Кинематика манипулятора робота «Пума-560>. а — общий вид; б — область достижимости.
Кинематические пары, часто встречающиеся в исполнительных механизмах роботов, приведены в таблице. Наиболее распространенными являются пары пятого класса, реализующие относительное движение вдоль или вокруг некоторой оси. В поступательной паре движение прямолинейное, во вращательной — вращательное, в винтовой — винтовое. Применяются также пары четвертого (цилиндрическая и сферическая с пальцем) н третьего (сферическая) классов.
Исполнительными механизмами манипуляционных роботов служат манипуляторы. Манипулятор представляет собой механизм с различными комбинациями кинематических пар, имеющий неподвижное звено-стойку н одно или несколько звеньев, образующих «хват—механизм для захвата объектов.
31
На рис. 2.1 представлен общий вид манипулятора робота «Пума-560» (США). Этот манипулятор имеет шесть степеней свободы, причем все кинематические пары вращательные. Для управления движением манипулятора используется шесть серводвигателей постоянного тока, а для управления схватом — четырехходовой пневмоклапан, работающий на сжатом воздухе. Данный робот имеет следующие технические характеристики: грузоподъемность 2,5 кг, точность позиционирования схвата 0,1 мм, максимальная скорость прямолинейного движения схвата 0,5 м/с.
Наряду с вращательными парами в манипуляторах широко применяются и поступательные. Разные комбинации шарнирных
82
и телескопических соединений звеньев используются, например, в роботах «Универсал-15» (СССР) и «Кавасаки Юнимейт» (Япония). Координатно-измерительные роботы имеют обычно только поступательные пары.
Выбор варианта конструкции манипулятора определяется рядом условий и требований. Одно нз важнейших требований заключается в том, что манипулятор должен обеспечивать попадание схвата в любую точку рабочей зоны и допускать при этом возможность любой ориентации последнего. Практически это означает, что число степеней свободы манипулятора должно быть не менее шести. Для увеличения маневренности манипулятора (необходимой, например, для обхода препятствий) конструктивную схему делают избыточной по числу степеней свободы. Однако при этом существенно усложняются задачи программирования и управления его движением.
Требования к конструкции схватов определяются их назначением. На практике обычно предусматривается набор сменных схватов, приспособленных к разным типам операций и объектов манипулирования. В качестве таких объектов могут выступать разные грузы и рабочие инструменты (сварочная головка, гайковерт, пульверизатор для окраски и т. п.).
Исполнительными механизмами транспортных роботов обычно служит колесное или гусеничное шасси. В связи с созданием шагающих роботов появились и принципиально новые механизмы — педипуляторы, играющие роль ног робота.
Одна из первых конструкций исполнительных механизмов шагающих машин предложена в конце прошлого века П. Л. Чебышевым. Спроектированный и собственноручно созданный им макет «стопоходящей машины» схематично изображен на рис. 2.2. Этот четырехногий «переступающий механизм», хранящийся в Ленинградском университете, приводится в движение внешней силой (например, если тянуть его за веревку). При этом стопы его ног описывают траектории, напоминающие траектории движений конечностей животных при ходьбе.
Примером робота с колесным шасси может служить советский «Луноход-1», изображенный на рис. 2.3, а. (Здесь 1, 2 — антенны; 3 — радиатор-охладитель; 4 — солнечная батарея; 5 — изотопный источник энергии; 6 — девятое колесо; 7 — штыревая антенна; 8 — анализатор грунта; 9 — телефотокамера; 10 — приборный отсек; // — телевизионные камеры; 12 — лазерный отражатель). Этот робот был очувствлен (бортовые телекамеры, датчик пройденного пути и др.) и имел весьма совершенную двигательную систему (восьмиколесное шасси с автономно управпяе-мыми мотор-колесами, буровой механизм-манипулятор для взятия проб грунта и др.). Благодаря этому ему удалось в 1970 г. впервые выполнить на поверхности Луны сложную программу перемещений и исследований [26].
2 Зак. ГК 13
На рис. 2.3,6 представлен общий вид космического робота-»._*лаборатории «Викинг» (США), который в 1976 г. провел на
Рис. 2.2. Стопоходящая машина П. Л. Чебышева.
поверхности Марса биохимические эксперименты. В отличие от «Лунохода» этот робот стационарен. Он снабж':: манипулятором и грузозаборным механизмом для взятия проб грунта. (Здесь / — передающая ачтенна; 2 —анализатор грунта; 3 — телекамера; 4 — метеорологические приборы; 5 — устройство для биологических исследований; 6—грузозаборное устройство; 7 — двигатель посадки; в —спектрометр; 9 — топливный бак; /О — антенна для приема команд; // — источник энергии; 12— антенна для передач на орбитальный отсек; 13— сейсмометр.)
| 2. ПРОСТРАНСТВО КОНФИГУРАЦИИ И УРАВНЕНИЯ КИНЕМАТИКИ
Одним из важнейших разделов теории роботов является механика исполнительных механизмов. Она изучает общие закономерности, присущие движениям роботов. Рассмотрим прежде всего геометрические и кинематические соотношения, описывающие широкий класс исполнительных механизмов.
Кинематические связи и возможные перемещения. В зависимости от кинематической схемы исполнительных механизмов роботы могут совершать те или иные движения. Условия, стесняющие свободу движений звеньев механизма, называются связями Аналитически эти условия выражаются уравнениями, связывающими между собой координаты и скорости звеньев механизма, а также время.
Положение материальной точки в пространстве определяется радиус-вектором г, соединяющим начало системы отсчета Od\d2d3 с данной точкой. Компонентами Г\, г2, г3 этого вектора служат декартовы координаты точки. Скорость точки г определяется как производная радиус-вектора по времени и может быть задана совокупностью производных декартовых координат
34
Рис 2 3. Космические роботы, а - «Луноход-1»; б-«Викинг».
2*
точки по времени. Уравнения связей, наложенных на N точек механизма, имеют вид
•••. rN, Г1, .... rv, t) — 0, < = 1.s. (2.1)
Такне связи называются кинематическими. Поскольку в процессе движения механизма векторы координат rz и скорости Г/ являются функциями времени, то время входит в уравнения связей (2.1) неявно через эти переменные. Помимо этого время может входить в уравнение (2.1) и явно. Если у, зависит от времени явно, то связь (2.1) называется нестационарной (рбоном ной). В противном случае связь называется стационарной (склерономной).
Связи принято классифицировать по характеру выражающих их уравнений. Если левая часть уравнений связи (2.1) не зависит от Г|, .... Гм, то такие связи называются голономнымн. Аналитическая их запись выглядит так:
У<(Г|, ..., rv, /) = 0, 1-1, .... s. (2.2)
Эти связи налагают ограничения только на возможные положения точек Г|, .... г* в пространстве, т. е. являются по существу геометрическими (позиционными) связями. Каждая геометрическая связь (2.2) влечет за собой некоторую кинематическую евяэь, которая получается путем почленного дифференцирования равенства (2.2). Однако такая связь,не эквивалентна геометрической связи (2.2). Она эквивалентна геометрической связи вида
У/'Г|. • • •> Tv, ti = ct, tjk Ci — произвольная постоянная. Поэтому геометрические бвязн (2.2) называются интегрируемыми. Таким образом, у го-лономной системы могут быть только геометрические или Аме матические, но интегрируемые связи.
Если аналитическое выражение связей зависит от первых производных координат точек г>, .... r.v по времени t и уравнения связей неинтегрируемы, то связи называются неголоном-ными. Система с такими связями в любой момент времени может занимать произвольное положение в пространстве. Однако в этом положении скорости точек системы уже не могут быть произвольными.
Связи ограничивают перемещение точек механизма в некоторых направлениях. Возможным, или виртуальным, перемещением точки г называется любое ее бесконечно малое перемещение бг, совместимое со связями. В результате виртуального перемещения координаты каждой точки rv, v—I, ..., N, механизма получают приращения, равные вариациям их координат 6, drv r 6rv 3. Эти вариации, чивло которых равно 3N, не будут независимыми.
34
Предположим для определенности, что на механизм наложено $ голономных связей, заданных в кинематической форме (2.1)- Тогда число независимых вариаций координат равно
— s, т. е. числу независимых координат механизма. Они не обязательно должны быть декартовыми координатами звеньев механизма. В зависимости от условий задачи более удобным может оказаться выбор каких-либо иных координат. Все многообразие переменных, позволяющих однозначно определить положение (конфигурацию) механизма, охватывается понятием обобщенных координат.
Обобщенные координаты и пространство конфигураций. Обобщенными координатами исполнительного механизма называются независимые переменные qi, .... qm, задание которых однозначно определяет конфигурацию механизма. Число независимых вариаций координат называется числом степеней свободы механизма. Для Язвенных механизмов с kt кинематическими парами /-го класса число степеней свободы совпадает
5
с числом обобщенных координат и равно m — — "£jkj. Для
/-1
неголономных механизмов число степеней свободы меньше т на число неголономных связей. Число степеней свободы характерн-аует по существу степень произвола при задании возможных перемещений механизма.
Обобщенные координаты qlt .... qm обычно задаются по отношению к некоторой основной инерциальной системе отсчета, связанной с исполнительным механизмом. Следует отметить, однако, что переменные qk могут быть отнесены и к любой подвижной системе отсчета, движение которой по отношению к основной системе известно. Необходимость в этом может возникнуть, если исполнительный механизм установлен на подвижном объекте (самоходном шасси, космическом корабле, батискафе и т. п.), перемещающемся по известному закону в. инерциальной системе отсчета.
Пространство обобщенных координат, в котором каждой конфигурации исполнительного механизма соответствует точка, а близким конфигурациям — близкие (в подходящей метрике) точки, будем называть пространством конфигураций.
Поясним понятие пространства конфигураций на примере простейших исполнительных механизмов.
Пример 1. Найдем пространство конфигураций простейшего двухзвенного манипулятора, изображенного на рис. 2.4, а. Такой механизм очевидно имеет две степени свободы. В качестве обобщенных координат q\ н qt выберем углы поворота первого и второго звеньев вокруг осей вращательных кинематических пар. Любое положение манипулятора определяется обобщенными координатами q\ и с/?, заключенными между 0 и 2л. Пространством конфигураций такого манипулятора служит
S7
двумерный тор (см. рис. 2.4, а), так как соответствие между положениями манипулятора и точками тора непрерывно и взаимно однозначно.
Пример 2. Построим пространство конфигураций колеса транспортного робота, катящегося без скольжения по плоскости. Положение колеса можно задать декартовыми координатами qi и </2. а также углами q3, qt, смысл которых ясен из рис. 2.4,6. Качание колеса без проскальзывания означает, что скорость точки соприкосновения колеса с плоскостью равна нулю. Это выражается кинематической связью вида
= RQs cos q3, q2 = Rq3 sin q3, где R — радиус колеса. Эта неголономная связь не накладывает никаких ограничений на возможные значения обобщенных ко-
I
Рис. 2.4. Пространство конфигураций исполнительных механизмов с го-лочомной (а) и неголономной (б) связью.
ординат qt, q2, qit qt, так как, вообще говоря, колесо может соприкасаться с плоскостью произвольным образом. При фиксированных координатах qi и q2 положение колеса полностью определяется координатами q3, qt, т. е. точкой двумерного тора. Рассматривая пару указанных точек как элемент нового четырехмерного пространства, получаем пространство конфигураций колеса, катящегося по плоскости без скольжения (см. рис. 2.4,6).
Из приведенных примеров видно, что в механике исполнительных механизмов важную роль играет топологическая структура пространства конфигураций, зависящая от типа кинематических связей.
Кинематические схемы исполнительных механизмов. Как уже отмечалось, исполнительные механизмы роботов весьма разнообразны. Они различаются кинематической схемой, т, е.
способом соединения звеньев посредством кинематических пар. Кинематические схемы делятся на простые и сложные. Отли-чиюльннй признак сложной схемы — наличие хотя бы одного звена, входящего более чем в две кинематические пары.
Исполнительный механизм манипуляционных роботов пред* ставляет собой разомкнутую кинематическую схему (цепь). Звеньями ее являются твердые тела, г. е. либо абсолютно твердые тела, у которых расстояние между точками неизменно в процессе движения, либо гибкие (деформируемые) тела. Положение каждого звена в общем случае определяется шестью независимыми переменными. Соседние звенья образуют кинематические пары, которые допускают те или иные относительные перемещения звеньев. Число s голономных (запрещающих) связей, наложенных на относительные перемещения звеньев, определяет класс кинематической пары. Число степеней свободы кинематической пары равно 6 — s. Заметим, что при з=0 соседние звенья по существу разомкнуты, при з = 6 они жестко связаны и, следовательно, могут рассматриваться как одно звено. В манипуляторах наиболее широкое применение находят кинематические пары пятого класса.
Осиовиая и локальная системы координат. Рассмотрим многозвенный исполнительный механизм (например, манипулятор), кинематическая схема которого включает р noci у нательных и w вращательных пар. Такой механизм очевидно л:сет т= = p + w степеней свободы и столько же подвижных звеньев. Для изучения движений исполнительного механизма нужно прежде всего условиться о выборе системы координат. В качестве основной (абсолютной) системы координат возьмем декартову правую систему координат Odid2d3, которую будем считать неподвижной. Основанием механизма назовем неподвижное (или принимаемое за неподвижное) звено, называемое стойкой; присвоим ему индекс нуль. Остальные звенья будем нумеровать индексами от 1 до Л' в естественном порядке их следования от стойки.
С целью описания конфигурации механизма в основной системе координат Odid2d3 с каждым звеном обычно связывают (по определенным правилам) декартову систему координат 133, 46]. При этом система координат Od*d*d*, связанная с Л-м звеном, является подвижной относительно системы координат Od* 4 d*1связанной с (Л —1)-м звеном. Перемещение А-й системы координат относительно (Л —1)-й характеризует движение Л-го звена относительно (Л—1)-го. Поскольку нее звенья механизма образуют кинематические пары пятого класса, то эти относительные движения могут быть либо поворотом на угол ф* вокруг оси пары (в случае вращательной Пары), либо линейным перемещением на величину сц вдоль ос -пары (в случае поступательной пары).
в
Совокупность величин <р*, с*, k = I.N, однозначно опре-
деляет конфигурацию механизма в пространстве. Поэтому они могут быть взяты в качестве обобщенных координат рассматриваемого механизма. В зависимости от кинематической схемы механизма компоненты вектора обобщенных координат 4 = l?*l*_i определяются соотношениями {ф* для вращательной пары, ск для поступательной пары.
Для описания движений механизма в декартовых координатах иногда используются так называемые блочные матрицы (33]. Такое описание приводит к компактной записи кинематических соотношений и удобно при моделировании на ЭВМ движений исполнительных механизмов манипуляционных роботов. Наряду с декартовыми координатами при описании манипуляторов применяются однородные координаты и преобразования (см. подробнее [43, 46J).
Рассмотрим новую форму взаимосвязанного представления локальных систем координат, позволяющую единообразно и экономно вычислять кинематические и динамические уравнения исполнительных механизмов [31].
Поскольку каждое звено механизма (кроме последнего) образует две кинематические пары (одну с предыдущим, другую с последующим звеном), то с ним целесообразно связать не одну (как это принято в [33, 46]), а две системы координат: «начальную» — с центром в начале звена и «конечную» — с центром в конце звена. Назовем их локальными системами координат. Для локальных систем координат А-го звена введем обозначения Titdididzu где г*, г* — радиус-векторы
соответственно начала и конца А-го звена в основной системе координат Odidjdi. Выбор основной и локальных систем координат исполнительного механизма иллюстрируется рис. 2.5.
Рассмотрим способ задания локальных координат для поступательных и вращательных кинематических пар. Пусть (А — 1) -е и А-е звенья образуют поступательную пару с кинематической осью О*. В этом случае конец (А — 1)-го звена r*_i и начало А-го звена г» лежат на оси О*. Свяжем в этих точках конечную систему координат г*_| (А —1) -го звена
и начальную систему координат tkdidtds А-го звена. Пусть е*"', е* ', е*’1 и е*, е*. е* — орты указанных систем. Будем считать, что г’= r° = 0, е?=е? = ео Iя»!, 2, 3, где е(— орты основной системы координат Odid^di. Поскольку звенья перемещаются вдоль осн Ок только поступательно (без относительного вращения), то естественно принять, что орты е* 1 =е*, е*-|»=е2, а орты и е* направлены по кинематической оси Ok. как показано на рис. 2.6, а. Обозначим через с* расстояние
40
Рис. 2.5. Основная н локальные системы координат.
Рис. 2.6. Локальные системы координат, а — поступательная лара; б — вращательная пара.
от е*_| до е*. Аналитически оно выражается формулой с»-г*"', ез"1)» (2.3)
где символ <•, •> означает скалярное произведение соответ, ствующих векторов. Величину с* будем называть линейной ко. ординатой механизма.
Рассмотрим альтернативную возможность. Пусть теперь (k — 1)-е и k-e звенья образуют вращательную пару с кинема, ти чес кой осью О„. На оси О» выберем точку г*-1 и г* и свяжем с ними правые ортогональные системы координат r*_i Л*-1 н Обозначим через е* 1 и е*, i= 1, 2, 3, орты
этих систем координат. Будем считать, что ^ = r°=0, ?<° = e? = ez, «== 1, 2, 3. Поскольку звенья могут лишь вращаться вокруг осн Он (без относительного поступательного перемещения), то естественно принять г*' = г*, е**'=е*. причем орты е* ' н е* направлены по кинематической оси Ok. Очевидно, что орты е* не?» i = 1, 2, лежат в одной плоскости, как показано на рис. 2.6,6. Обозначим через <р* угол между ортами е*"1 и е*-1- Аналитически он выражается формулой
Ф* = агс соз(е|*"*, е*)™ arc sin (е*-1, е?)- (2.4)
Переменную <р* будем называть угловой координатой меха-ннзма.
Вычисление кинематических характеристик. Поставим в соответствие каждому звену исполнительного механизма матрицу размерностью 3X4 следующего вида:
К/-|г/,е{,4,4|, /=!.......N. (2.5)
Геометрический смысл матрицы К/ ясен из ее структуры: первый столбец характеризует положение /-го звена в основной системе координат' Odtdids (точнее, положение начала /-й локальной системы координат, связанной с /-м звеном), а три остальных — ориентацию звена. Очевидно, что матрица К/ однозначно определяет положение /-го звена механизма в пространстве. Поэтому матрицу (2.5) будем называть матрицей кинематических характеристик [31].
Следует отметить, что в работе [46] при описании кинематики исполнительных механизмов манипуляционных роботов с помощью однородных координат используется матрица состояния твердого тела, аналогичная матрице кинематических ха раю теристик звена. Эта матрица, однако, имеет размерность 4X4 и обладает определенной избыточностью по сравнению с мат» рицей кинематических характеристик (2.5).
42
Выразим элементы матрицы кинематических характеристик через обобщенные координаты механизма (линейные н угловые). Это позволит экономно вычислять основные кинематические характеристики всех звеньев механизма (манипулятора) непосредственно по его обобщенным координатам q\.....qm.
Обозначим через Ё, ЗХ 3-матрицу (е(, е', е() при j = 0, 1, N—1, а через Е/ — ЗХЗ-матрииу (el, е'., ез) при у = 0, 1, .... N. Отметим, что Ео = Ео = Е, где Е — единичная матрица. Поскольку столбцы матриц Е/ и Ё — орты начальной и конечной локальных систем координат, связанных с /-м звеном, то существует ортогональная постоянная ЗХ 3-матрица А/, такая, что Ё/ = Е/А/ при / = 0, 1, ..., N —I. Очевидно, что
А/ = еГЁл /«0,1.........JV-1. (2.6)
Матрицу А/ будем называть матрицей поворотов /-го эвена. Введем следующие обозначения:
(а/ —Ь/ 0\
Ь/ О} 0 1, (2.7)
0 0 1/
1, если (/— 1>-е и /-е звенья образуют’ поступательную пару,
2, если (/— 1)-е и /-е звенья образуют вращательную пару.
Величины о/, / = 1, ..., N, по существу определяют тип кинематической схемы механизма. Поставим в соответствие каждому звену ЗХ3-матрицу вида
( А, . при а,= 1,
w/ <«Р/' = { А/1В/ ,ф/) при а, = 2, / = 1..AL (2-8)
Тогда справедлива следующая рекуррентная формула:
Е/= E/.iW/'ф/', Eo = Е, /=1.......Л', (2.9)
откуда следует, что х.
E/=JIW»(V»), /=1..........N. (2.10)
Поскольку г» и г* — две точки одного звена, то существует постоянный вектор V/, такой, что г/ = г/ -J- Е, У;. Очевидно, что
V/= Ef(г, — г/), / = 0, I.......ЛГ-1. (2.11)
Вектор V/ назовем вектором переносов /-го звена. Определим при / = 1, ...» N векторы вида
0
— | V'-' + А'-‘ 0 при <F/ —1, (2.12)
С1
к- при О/ — 2.
Тогда легко получить рекуррентную формулу
•7в Г/_, -|- Ey_(Ly (С/), Е0 = Е,
(2.13)
откуда непосредственно следует
*=1.......N. (2.14)
Обозначим через q вектор обобщенных координат механизма, компонентами которого являются линейные или угловые координаты. Более точно имеем
( с/г если <т/ = I, 31 L Ф/. если о/ = 2.
(2.15)
Подчеркивая зависимость Е/, Г/, К/ от обобщенных координат, будем писать E/(q), rjq), K/(q).
Таким образом, матрица кинематических характеристик K/(q)= (r/(q), E/(q)) выражается через линейные и угловые координаты с помощью формул (2.8), (2.10), (2.12) и (2.14). При этом, как видно из формул (2.10), (2.14), элементы Ez(q) и r/(q) матрицы K/(q) для манипуляторов, а следовательно, и сами матрицы зависят только от обобщенных координат qi, <7/ и не зависят от q/+i, ..., qm.
Важно отметить, что в процессе вычисления кинематических характеристик механизма по его обобщенным координатам используются только алгебраические операции сложения и умножения. При этом матрицы внутренних поворотов А, и векторы внутренних переносов V/ играют ропь констант. Для удобства практических вычислений матриц А/ механизм можно зафиксировать в такой конфигурации, что Е/= Е/+), / = 1...N— 1.
Тогда А/ = Е[Е/+г Совокупность матриц поворотов А/, векторов переносов V/ и чисел о/, / = 1..N, определяющих тип кине-
матической схемы механизма, образует стандартизованный набор (банк) данных, необходимых для вычисления всех кинематических характеристик звеньев механизма. Эти данные непосредственно определяются при анализе кинематики заданного исполнительного механизма или задаются конструктором при синтезе механизма с желаемыми свойствами.
44
Описанная схема организации вычислений кинематических характеристик механизма по обобщенным координатам представ* ляет собой общий эффективный метод решения прямой задачи кинематики для исполнительных механизмов с голономныму связями. Этот метод особенно удобен при моделировании на ЭВМ манипуляторов и педипуляторов роботов.
f 3. ДИНАМИКА ИСПОЛНИТЕЛЬНЫХ МЕХАНИЗМОВ
Конструирование роботов и робототехнических систем требует изучения динамики их исполнительных механизмов как объектов управления. Значительные трудности при этом порождаются существенной нелинейностью и большой размерностью уравнений движения.
Для преодоления указанных трудностей в ряде работ [8, 11, 15, 23, 25, 31, 43, 46, 66, 80] предложено несколько методов математического описания движений роботов, которые ориентированы на использование ЭВМ для моделирования управляемых движений исполнительных механизмов. Эти методы, относящиеся, как правило, к теории механизмов с голономными свя<-зями, опираются на классические принципы и уравнения меха* ники — принципы Гаусса и Даламбера, уравнения Ньютона и Лагранжа. Они хорошо приспособлены для использования ЭВМ как средства моделирования исполнительных механизмов. Среди них наиболее эффективными и глубоко проработанными являются методы, использующие уравнения Лагранжа и их модификации.
Отличительная черта метода, основанного на принципе Гаусса (46], заключается в возможности получать необходимые динамические характеристики исполнительного механизма произвольной сложности (текущие значения обобщенных координат, скоростей и ускорений), минуя вывод уравнений динамики в явном виде.
Однако при синтезе оптимальных и адаптивных законов управления исполнительными механизмами недостаточно знать только характеристики самого движения. Необходима информация о явном (аналитическом) виде уравнений движения. Правда, в случае адаптивного управления она может быть неполной: неизвестными могут оказаться все или часть параметров уравнения динамики, воздействия внешней среды и другие факторы. Однако во всех случаях для синтеза совершенного закона управления исключительно важно знать явный вид уравнений движения.
Вообще говоря, этому требованию удовлетворяют модели Уравнений движения исполнительных механизмов в форме уравнений Ньютона или Лагранжа. На их основе в работах (17, 21, 32, 25, 31, 33, 47, 57—62, 64] разработаны эффективные ал го-
18
ритмы стабилизации программных движений роботов. Однако Эти алгоритмы довольно громоздки даже для программной реализации на ЭВМ. Их сложность сравнима со сложностью уравнений динамики управляемого механизма. Для упрощения алгоритмов управления иногда целесообразно линеаризовать уравнения динамики относительно программного движения. Упрощение алгоритма посредством линеаризации неизбежно влечет за собой ухудшение качества управления.
Соображения удобства и простоты реализации алгоритмов адаптивного управления роботами также предъявляют определенные требования к форме уравнений движения исполнительных механизмов. Важнейшее из них — линейность уравнений движения по всем параметрам, которые могут оказаться неизвестными. Это прежде всего относится к инерционным характеристикам исполнительных механизмов или объекта манипулирования.
Перейдем к описанию общего метода представления и вычисления уравнений динамики сложных исполнительных механизмов, удовлетворяющего сформулированным требованиям. Этот метод, изложенный в работе (31], позволяет в известной мере экономить дорогостоящее, машинное время и оперативную память ЭВМ. Он может быть с успехом использован для моделирования на ЭВМ законов адаптивного управления и управляемых движений робота.
Голономные связи и активные силы. Рассмотрим движение по отношению к основной (абсолютной) системе координат механической системы, состоящей из N материальных точек с радиус-векторами л....Гц и массами ть ..., т». Пусть на си-
стему наложено $ голоиомных стационарных связей, задаваемых системой функционально независимых уравнений вида
V/ <г.... гу) = 0. (2.16)
В процессе движения п(1), .... rN(t) должны выполняться уравнения связей (2.16) при всех I. Дифференцируя (2.16) по времени, получаем
N dv
£1/r'") = 0> /=l,....s. (2.17)
/-I 1
Этим уравнениям должны удовлетворять скорости гДО всех точек системы. Такие скорости называются возможными скоростями, а бесконечно малые перемещения в направлении возможных скоростей, удовлетворяющие соотношениям (2.16), — возможными перемещениями.
Таким образом, возможные перемещения и скорости точек голономной механической системы — это соответственно перемещения и скорости, допускаемые наложенными на систему го-лопомными связями. Значение этого типа связей заключается в том, что многие исполнительные механизмы роботов (в част-46
кости, манипуляторы) относятся нменно к классу голономных механических систем.
Пусть qi, Ят — обобщенные координаты рассматриваемой системы (например, манипулятора). Поскольку вектор обобщенных координат q = l<7* i»_. однозначно определяет положение системы, то радиус-векторы п, ..., rN всех точек в основной системе координат могут быть выражены через соотношения вида
r/ = O>/(q)i, /=1....ЛГ. (2.18)
Уравнения (2.18) по существу учитывают все наложенные на систему голономные связи. В силу этих уравнений ускорение точек и их возможные (виртуальные) перемещения можно выразить так:
г/(П = Ф/{Ч(Г)), /=1......N, (2.19)
*-| *
где — вариации обобщенных координат.
В общем случае на каждую точку г/ механической системы действуют активные силы а/ и пассивные силы р/ (реакции связей). Если связи идеальны (без трения), то эквивалентные нм реакции связей р/, приложенные к /-Й точке, ортогональны любому возможному перемещению:
N
Е<р/. бг/>==о.
/-1
Если величина и направление активных сил обычно заданы и друг от друга не зависят, то пассивные силы, наоборот, существенно зависят от других сил и характера движения системы. Отметим, что именно активные силы приводят механизм в движение.
Силы и моменты, действующие на механическую систему и в частности на исполнительный механизм, принято делить на внутренние и внешние.
К первому классу относятся силы или моменты, возникаю* Щие в результате взаимодействия звеньев, входящих в данный механизм или систему. Внутренними силами (моментами) являются управляющие силы (моменты), вырабатываемые, например, двигателями в кинематических парах исполнительного механизма, и диссипативные силы сопротивления, пропорциональные скоростям точек системы. Ко второму классу относятся силы (моменты), возникающие в результате воздействия на звенья механизма пли системы окружающей (внешней) среды. ° роли такого рода внешних сил выступают, например, сила тя
17
жести, силы гидравлического сопротивления, воздействующие на исполнительный механизм подводного робота, и т. п.
Особое значение для робототехники имеют способы задания внутренних управляющих сил и моментов. Если управляющие силы или моменты заданы как функции времени, то говорят о программном управлении исполнительным механизмом. Если они являются функциями обобщенных координат и скоростей, то речь идет об управлении по принципу обратной связи.
Принцип и уравнения Даламбера — Лагранжа. Выведем уравнения динамики механической системы, k-e звено которой состоит из Af* материальных точек. Будем исходить из классического принципа Даламбера. Этот принцип позволяет придать уравнениям динамики форму уравнений равновесия, если к заданным активным и пассивным силам присоединить силы инерции. В результате получаем уравнения Даламбера — Лагранжа
**
£ <drv, mvrv(/) - fv(/)>«О, (2.21)
V*1
где 6rv—виртуальное перемещение v-й точки; fv — равнодействующая всех сил, действующих на v-ю точку.
Подставляя выражения (2.19), (2.20) в соотношение (2.21), получаем
Г {Г to(/)1 ~f*<*>)} - °- (2-22)
Вариации 6?ь ..., t>qm независимы, поскольку рассматриваемая система голономна. Поэтому из соотношения (2.22) следуют т уравнений вида
м* м*
ф, [,«]>_ X
V-I * V-1 *
(2.23) Отметим, что в случае неголономной системы из соотношения (2.22) нельзя получить уравнения (2.23), так как для любых обобщенных координат вариации 6?t, ..., 6qm будут зависимыми. В этом случае полные уравнения представляют собой s уравнений неголономных связей и т — s уравнений типа (2.23) для независимых вариаций.
Введем обозначение
т
Q> <'>-££ »v (/)>. * - 1.....(2.24)
/-1 v-l *
В механике величина Q»(/) называется k-й обобщенной силой, отнесенной к А-й обобщенной координате (О-
48
Итак, на основе наиболее общих уравнений механики — уравнений Даламбера — Лагранжа — получена система дифференциальных уравнений второго порядка
m
Z Z (/)1> = <?* «>• (2.25)
/-I v-l *
описывающая динамику голономных систем.
Важное преимущество этих уравнений по сравнению с уравнениями динамики в декартовых координатах состоит в том, что число их минимально и равно числу степеней свободы; оно не зависит от числа точек, образующих систему, и от выбора обоб
щенных координат; сами уравнения не содержат наперед неизвестных реакций связей, благодаря чему отпадает необходимость
в их определении.
Инерционные характеристики и динамика механизма. Обра
тимся теперь к динамике исполнительных механизмов с голо-номными связями. Будем исходить из традиционного представ-
ления механизма как совокупности твердых тел.
Пусть рассматриваемый механизм имеет V звеньев (твердых тел). Свяжем с ним основную систему координат Odid2dt, а с каждым звеном — локальные системы координат с ортами е{> е/, /= 1,2,3, /= 1, .... N (см. рис. 2.5, 2.6). Образуем для каждого звена ЗХ4-матрицу его кинематических характеристик в основной системе координат. Эта 3 X 4-матрица К/ имеет вид (2.5).
Рассмотрим некоторую точку rv, /-го звена. Пусть rv. /—радиус-вектор этой точки в /-й локальной системе координат r^^d^d'y Положение точки rv основной системе координат Od\d2d3 выражается через вектор обобщенных координат q сле
дующим соотношением:
Фу (q) = г, fq) 4- Е/ (q) rv., м К/ (q)
1
Гу/
(2.26)
где E,|q| = |e[(q\ e£(q), e'(q)|.
Подставляя соотношение (2.26) в уравнения (2.25), получаем окончательно уравнения динамики У-звенного механизма с го-лономными связями в виде
ZH/’{(^^-)rK/lq(O]}=Q*(/). Л=1..........т. (2.27)
Здесь символом о обозначено скалярное произведение двух п
матриц: если = то Л« в =
а матричные коэффициенты, характеризующие геометрию масс
49
звеньев, определяются формулами
)(/)Г’ /-1.........<2-28>
где суммирование производится по всем точкам с индексом v, принадлежащим /-му звену.
Введем обозначения
□К,. ч,,)=ВД'к,(,>.
,м\ 4_|...........(2.29,
V *
Величину (/) будем называть /-й составляющей k-Я обобщенной силы в момент времени /. По существу величина Q'k представляет собой вклад активных сил av, действующих на /-е звено, в обобщенную силу Q*, отнесенную к Л-й координате. Действительно:
N
*=1......Ш. (2.30)
Уравнения динамики (2.27) в этих обозначениях можно записать в следующей компактной форме (31]:
*=1......т. (2.31)
Матрица Н/ имеет размерность 4X4. Она определяет инерционные свойства /-го звена как твердого тела. Точнее, Н; несет в себе всю информацию о распределении масс в /-м звене относительно связанной с ним локальной системы координат. Поэтому матрицу Н/ будем называть ниерцнонной характеристикой /-го звена.' Все матрицы Н/, /® 1..симметричны и имеют
следующую структуру:
т, М'а, М'а, M'd.
Н,= Mi, Л/,4, /i.3
Mi, l'M,
i Mi, /i,d, /i^, fa,d,
Здесь m, = £ mv, M^ = £ /d(d> = £ mv Hv'> -
Ля компонента радиус-вектора v-й точки рассматриваемого звена.
Механический смысл матрицы инерционных характеристик Н. ясен из (2.28), (2.32): ее элементами являются масса и три
60
статических момента инерции /-го звена, три центробежных момента инерции и три момента инерции относительно координатных плоскостей [31, 46]. Эта матрица зависит лишь от способа введения /-Й локальной системы координат.
Знание матриц инерционных характеристик имеет большое значение не только при анализе динамики механизмов, но особенно при синтезе совершенных законов управления. Важным достоинством уравнений динамики в форме (2.27) (или (2.31)) является то, что матрицы инерционных характеристик всех звеньев входят в них линейно. Последнее играет существенную роль при синтезе адаптивного управления.
Динамика манипуляционных механизмов. Уравнения динамики (2.27), (2.31) исполнительных механизмов с голономными связями применительно к манипуляторам имеют специфический вид. Они представляют собой верхнетреугольную систему дифференциальных уравнений. Такая структура уравнений динамики обусловлена особенностями кинематики манипуляционных механизмов, представляющих собой разомкнутую кинематическую схему с парами пятого класса.
Рассмотрим подробнее динамику манипуляционных механизмов. Прежде всего отметим, что величины dK/[?(0]/dq*. к = 1, .... т, не зависят от обобщенных координат qt+\, дм. Это непосредственно вытекает из формул (2.10), (2.13), определяющих элементы матрицы кинематических характеристик K/(q). Итак, для манипуляционных механизмов имеем
<Ж,[Ч(/)] А . , /оа,ч
—— = 0 при k > /. (2.33)
Кроме того, как следует из вышеизложенного, в рассматриваемом случае
Q'k It) 0 при k > /. (2.34)
Поэтому уравнения динамики в форме (2.27), (2.31) для манипуляционных механизмов имеют следующий треугольный вид: HtoQ| + H,oQ;+ ... + HAroQf = Q*4-Q^-'+ ...+Qj-Q„
Н , о Q‘ + ... 4- Н „ о Q" = Q» + Q" -' 4- ... + Qv
Н,_. ‘OS:! + Н„ «О-*., = (?*_, 4- Q&_, (2.35)
Н,оО&-0«-<?АГ‘
Из этих уравнений непосредственно видно, что для манипуля-
ционных механизмов обобщенные силы Qi не зависят
от инерционных характеристик Н/ и компонент^ при / < к.
Раскроем механический смысл величин (% и Q*. определенных формулами (2.29), (2.30). Если v-я точка принадлежит /-му
61
звену, причем / < k, то
₽v* « <
ЭФу(д)
av > =0,
так как в силу (2.42) = ° ПРИ / Пусть (/ — 1 )-е ц
/-е звенья образуют поступательную пару. Тогда величина равна проекции силы av на кинематическую ось О/ пары. Если же эти звенья образуют вращательную пару, то величина 0V., равна моменту силы av относительно кинематической оси пары.
Обобщенная сила Q*, отнесенная к Л-му звену манипуляционного механизма, нс зависит от активных сил av, приложенных к предшествующим звеньям с номерами /— 1, ..., k—1. Отсюда становится ясным механический смысл обобщенных сил: в случае поступательной пары Q* —это сумма проекций на кинематическую ось О* активных сил, действующих на звенья о номерами k, k 4-1, .... т; в случае вращательной пары Q*— это сумма моментов относительно кинематической оси Q* активных сил, приложенных к звеньям с номерами k, k 4-1, ..., tn.
Если манипулятор находится в поле земного притяжения, то из результирующей силы fv, действующей на v-ю точку, удобно выделить составляющую силы тяжести fv = Xv 4-1где ускорение земного тяготения. В этом случае уравнение динамики (2.27) запишется так (31]:
4) + [-^^]Го} = Ж к-1, .... т, (2.3в) /-1
где
(О 0 0 0\
0 0 0 0. Ч). (2.37)
g о о о/ *
и суммирование по v производится по всем точкам манипулятора.
Следует отметить, что в роботах статические моменты, обусловленные силами веса звеньев, иногда компенсируются с помощью специальных разгружающих устройств. Эту же функцию можно передать управляющей системе, которая алгоритмическими средствами управления способна нейтрализовать действие указанных моментов. Точно так же, т. е. чисто алгорит* мическим путем, легко компенсировать и любые другие силы и моменты, возникающие в манипуляторе, как известные (или доступные измерения), так и неизвестные. Такую алгоритмическую компенсацию влияния различных сил и моментов на движения манипулятора иногда называют динамической, или адаптивной, коррекцией.
S2
Уравнения динамики исполнительного механизма играют яжную роль не только при анализе управляемых движений поботов, но и при синтезе законов управления, обеспечивающих желаемое качество переходных процессов. При этом иногда цепесообразно (например, при организации численного интегрирования уравнений динамики (2.27), (2.36) на ЭВМ) перейти к записи уравнений динамики (2.36) в форме уравнений Лагранжа второго рода. С этой целью воспользуемся очевидными соотношениями [31]
k _ О [К, (q)]ae • г / д’ (К, (Ч)]аЭ \ .
IК 1«в =-------55----* + Ч I---------5^------) *1
Г<Ж/ (д)1 рк,(д)]аа
L dq Jap д<7*
(2.38)
где запись [А]ар обозначает элементы матрицы А с индексами а и р. Тогда уравнения (2.34) запишутся в стандартном виде:
A(q)q 4- qrB(q)q + C(q) = М, (2.39)
где A(q), B(q)—тХ m-матрицы со строками
а C(q)— m-вектор-функция с компонентами
/-I a —I u J
(2.42)
Вычисление уравнений динамики. При вычислении элементов уравнения динамики в форме (2.35), (2.36) будем использовать обозначения и соотношения (2.3)—(2.15), введенные в предыдущем разделе. Поскольку в силу этих обозначений а, = ^совфД/), bi == sin q>i(t), то, дифференцируя переменные в/, Ь/ дважды по времени, получаем
<*/ = —Ь/ф/, &/ = б/Ф/. (2.43)
&! = — (^/Ф/ + ^/Ф/)> bj = d/ф/ -f- О/ф/- (2.44)
53
Аналогично, дифференцируя дважды по времени выражения д.ц матриц W/(q>/) в случае, когда (/— 1)-е и /-е звенья образуют вращательную пару (т. е. а/ = 2), и выражения для вектору L/(c/), когда (/ — 1 )-е и /-е звенья образуют поступательную пару (т. е. а, = 1), получаем
(ф/)= А/_|В/ (ф/>, W, ;<₽/) = А/_|В/ (фр,
(2.45)
О О 6
£/ (С/) — А*_]
L/ (ср — А*_ ।
О
О
где ЗХЗ*матрнца В/(ф/) определена формулой (2.7). Дифференцируя рекуррентные соотношения (2.9) и (2.13), имеем
уЁ/.^/Сф/) при<7/=1,
lt/_|W/<9/) + E/_lW/(<p/) при <У/ = 2,
(2.46)
при<Т/ = 1, 1Ё/_^/(ф/)4-2Ё/_>/(ф/) + Е/_^/(ф/) при а, = 2, ' ’
; r/-i E/_|Lj (Су) 4-2Ey_|L, + E,_jLy (ср при <Т/=1, Г/_| + Ё/_|Ь/(с/) прнсту=2.
Используя формулы (2.43)—(2.48), вычисляем вторую произ водную по времени ЗХ4-матрицы кинематических характе ристик
К,(q) = |Гг/, Е,II. /=1...........V. (2.49)
Отметим, что в описанной процедуре вычислений матричных элементов (2.49) уравнений динамики (2.33) число операций сложения и умножения линейно зависит от числа звеньев механизма Д'.
Перейдем теперь к вычислению матриц <?K/(q)/dq*. С учетом рекуррентных соотношений (2.9) имеем
«ЭЕ, ^7
О при о*= 1. дЕ, .
-^-Wyfoy) при а* = 2,
*</•
(2.50)
Аналогично в соответствии с рекуррентными формулами (2.13) имеем
' 0 при а,»!,
<JE, / — Ь, —а. 0\
I к I I
E/.J at — bt 0 1 при ot — 2,
x 0 0 0/
при <F* = 1,
Lz(cp при а*— 2,
k<), (2.51)
Объединяя соотношения (2.50), (2.51), окончательные вычнсле* ния проводим по формулам
(2.52)
при <Jt — 1, при О/ = 2.
Отметим, что число операций сложения и умножения при вычислении матричных элементов (ЭК/(q)/<?<?* уравнения дина* мики (2.39) в силу соотношений (2.50)—(2.52) возрастает в квадратичной зависимости от числа звеньев N. После вычисления элементов K/(q) и dK/(q)/dg* «сборка» и вычисление самих уравнений динамики в форме (2.35), (2.36) или (2.39) уже не представляет трудностей
Важно, что для рассматриваемой формы представления и вычисления уравнений динамики исполнительного механизма робота общее число операций сложения и умножения при увеличении числа звеньев N возрастает пропорционально №. Примерно так же увеличивается и объем памяти, необходимый для организации вычислений. Это обстоятельство является важным Достоинством дайной формы записи уравнений динамики по
55
сравнению, например, с широко используемой стандартной формой уравнений Лагранжа [7, 14, 16, 32, 43], для которых число необходимых операций сложения и умножения возрастает пропорционально N3. Использование описанной процедуры приводит к значительной экономии памяти и числа вычислительных операций при синтезе и анализе законов управления роботами.
( 4. ДИНАМИКА ПРИВОДОВ
Исследованию динамики приводов посвящены многие работы (см., например, (24, 27, 33, 46, 53, 66]), содержащие конструктивные схемы и математические модели двигателей и редукторов различных типов. Основываясь на указанных работах, составим уравнения динамики приводов, которые широко используются в робототехнике, и проанализируем их особенности.
Рассмотрим прежде всего электрические приводы с двигателями постоянного тока. Такне двигатели нашли применение в ряде манипуляционных роботов (сварочные роботы фирмы <Кука», промышленные роботы «РПМ-25» и «ТУР-10», исследовательские роботы «УЭМ-МВТУ», «ЛПИ-2» и др.) и в некоторых транспортных роботах (например, в мотор-колесах «Лунохода» [26].
Управление двигателями постоянного тока с независимым возбуждением осуществляется с помощью напряжения и, приложенного к цепи якоря, при неизменном потоке возбуждения. Из теории электрических машин известно, что управляющее напряжение и, сила тока в цепи якоря а, вращающий момент Мо и скорость вращения вала двигателя <р связаны соотношениями [24, 33]
МовОоО. и = <Х|О-|-а2б + азф. (2 53)
где ао. аь <*я. «з~ параметры двигателя.
Для определения динамических характеристик двигателя составим уравнение движения его ротора (уравнение равновесия моментов (24, 33])
/ф = М0-₽ф-Л4с. (2.54)
Здесь / — момент инерции всех вращающихся масс, приведенный к ротору двигателя; р — коэффициент вязкого трения; Л1С — момент сопротивления. Подставляя выражение (2.53) в уравнение (2.54), получаем следующее уравнение динамики двигателя:
Цф 4- 6|ф 4" 6;ф 4- с = и, + Ьл = *± + чс=±Мс + 4-^-Мс.
66
Таким образом, двигатель постоянного тока с независимым возбуждением является (в рамках принятой здесь идеализации) линейной динамической системой. Он обеспечивает высокое быстродействие и плавное изменение скорости и ускорения в широком Диапазоне.
Для увеличения мощности двигателей и получения больших моментов необходимо соответствующее усиление управляющего напряжения. Обычно это осуществляется с помощью электрома-шинных усилителей, представляющих собой генераторы постоянного тока, ротор которых приводится в движение двигателями. Такие усилители обеспечивают усиление мощности в сотни раз.
Двигатели формируют управляющие моменты, которые после преобразования в редукторе передаются на входные валы. Редукторы совместно с роторами двигателей образуют силовые модули [33]. Общая схема силового модуля робота представ-
ПриШ
ДЗсгатель
Г--------------
Исполнительный неханигн
Рнс. 2.7. Схема силового модуля робота.
лена на рнс. 2.7. На этом рисунке Af0 — момент, развиваемый двигателем; <р — угол поворота ротора; / — момент инерции вращающихся частей модуля, приведенный к ротору двигателя; р — передаточное число редуктора; с—жесткость упругого вала; М — управляющий момент на выходном валу силового модуля; q— угол поворота выходного вала.
В силовых модулях часто возникают нелинейные эффекты. Наиболее характерны из них насыщение магнитного потока, сухое и вязкое трение, упругость и люфты в редукторе. Рассмотрим нх подробнее.
При большом управляющем напряжении наступает насыщение магнитопровода, и зависимость вращающего момента от напряжения на входе двигателя принимает форму ограничителя. Ограничение момента порождает ограничение угловой скорости вращения вала двигателя.
Момент сопротивления Ме в значительной мере порождается моментом сухого трения M! = AloSgn<p, моментом вязкого трения Л}»=Рфг (при малых скоростях 1, при больших г — 2) и моментом скручивания, выходного вала Afj = c(p<p— q). Момент сухого трения не зависит от скорости и определяется лишь направлением вращения. При ф =0 момент сухого трения Aft может принимать любое значение в пределах —Мо < Mi М,:.
57
В этом проявляется принципиальная неопределенность сухого трения. Если в некоторый момент времени ф = 0, то вал двигателя останавливается и остается неподвижным до тех пор, пока сумма действующих моментов не превысит величины Мд. Во избежание остановок вала необходимо, чтобы с|мма всех моментов превышала момент сухого трения.
Исследование динамических эффектов, порождаемых насыщением магнитного потока и силами сухого трения, в общем случае чрезвычайно затруднительно. В простейшем случае (когда инерционностью двигателя можно пренебречь) совместное действие этих двух факторов приводит к возникновению зоны чувствительности (рис 2.8,а), причем б = Alo/lga.
Существенное влияние на динамику приводов оказывают люфты — зазоры в редукторе, обусловленные неточностью изготовления или изнодом деталей. При наличии люфта вращение
Рис. 2.8. Типовые нелинейности приводов, a — одна нечувствительности; б — люфт.
вала двшателя не вызывает вращения выходного вала до тех пор, пока не выбран зазор. Характеристика люфта в форме зависимости <р от у представлена на рис. 2.8,6. Величина зазора на валу двигателя равна 2Д, а передаточное число редуктора p = tga. При перемене знака ф исполнительный механизм как бы отключается от двигателя, пока последний не выберет аазор. Люфты порождают статистические ошибки и автоколебания. Поэтому при изготовлении редукторов принимаются специальные меры к уменьшению или компенсированию их влияния. Эти меры особенно важны при реализации приводов прецизионных роботов.
Важную роль в робототехнике играют системы приводов, в ко1орых используются гидравлические и пневматические двигатели. Особенности динамики таких систем исследовались в ряде работ (см., например, [12, 53, 79, 80]).
Уравнения динамики гидравлических и пневматических приводов, как правило, являются существенно нелинейными дифференциальными уравнениями высокого порядка.
Наибольший интерес с точки зрения возможности непосредственного управления вращающим моментом представляют моментные двигатели. Важнейшей особенностью таких двигателей Является линейная зависимость между электрическим управ-58
дяюшим сигналом на входе и вращающим моментом на выходном валу двигателя.
По сравнению с обычными приводами моментные двига1елн обладают рядом преимуществ: высокой механической жесткостью (вследствие непосредственного соединения с исполнительным механизмом); высокой чувствительностью (из-за отсутствия характерных для редукторов люфтов и сил трения); высокой стабильностью динамических характеристик при изменении условий.
Динамика моментного двигателя описывается линейным уравнением вида
М (О = *«(/) + л (0.
где k—параметр двигателя; n(t)—возмущения, порожденные неучтенными внешними воздействиями, помехами, неадекватностью принятой линейной модели и т. п. Вращающие моменты, развиваемые такими моментными двигателями, непосредственно передаются на звенья исполнительного механизма.
Важно отметить, что учет динамики моментных двигателей не приводит к увеличению порядка системы уравнений, описывающих динамику робота в целом.
| б. ОБОБЩЕННАЯ ДИНАМИЧЕСКАЯ МОДЕЛЬ РОБОТОВ
Полученные уравнения движения описывают динамику ис» полнительных приводов и механизмов изолированно. Однако в двигательных системах роботов все взаимосвязано. Обычно исполнительные приводы имеют общую нагрузку, в роли которой выступает тот или иной механизм робота. Поэтому математическую модель динамики робота следует рассматривать как единую многосвязную систему дифференциальных уравнений, описывающих управляемые движения исполнительных приводов и механизмов в целом.
В общем случае модель динамики роботов можно записать в виде векторного дифференциального уравнения
x(/)«F(x(/>, и(0,£], х(/0) = Хо, (2 55)
где х = х(0 — л-мерный вектор состояний исполнительных приводов и механизмов в момент времени t; х«d*/dt, и = =atu(0 — "i-мерный вкетор управлений, вырабатываемый управляющей системой;^ — р-мерный вектор параметров двигательной системы; t — текущее время; х®— начальное состояние. Переменные х(/), и(0 и параметры £ имеют смысл реальных физических. величин и параметров, описывающих поведение робота. Например, если уравнение (2.55) описывает динамику влектромехаи:;юской двигательп -! системы манипуляционного Робота, то в число компонент вектора состояний х входит
б»
переменные ф, ф, М, описывающие состояния электроприводов] и переменные q н q, описывающие состояния исполнительно^ механизма (манипулятора); в качестве управляющих воздц.1 ствий выступают управляющие напряжения и на входе двиг«., телей постоянного тока, а компонентами вектора параметров । служат массоннерцнонные характеристики звеньев маннпуля. тора и груза, коэффициенты трения и электромеханические па-раметры приводов.
Уравнение (2.55) представляет собой аналитическую запись основных физических закономерностей, которым подчиняются все движения двигательной системы роботов. Хотя это уравне-ине весьма точно описывает поведение роботов, все же оно является известной ндеалнзацней, поскольку в уравнении (2.55) не учтен ряд факторов, связанных как со свойствами роботов, так и с условиями их эксплуатации.
Воздействие указанных факторов на идеализированную динамическую модель (2.55) будем трактовать как дрейф параметров и постоянно действующие возмущения. Эти возмущения могут характеризовать степень неадекватности модели, (2.55), неконтролируемые внешние воздействия, дрейф параметров и т. д. Обозначим через я(0 n-мерную вектор-функцию постоянно действующих возмущений, а через {(/)— р-мерную вектор-функцию изменения параметров. Тогда обобщенное уравнение движения роботов можно записать в виде векторного дифференциального уравнения
x(/) = F(x(0, u(/), ((/,] +я<0. х(/о] = *о. (2.56)
Это уравнение в отличие от уравнения (2.55) учитывает возможную нестационарность двигательной системы робота и условий его эксплуатации. Чтобы принять уравнение (2.56) в качестве обобщенной математической модели двигательной системы роботов, надлежит строго оговорить вид функции F и область ее определения, а также охарактеризовать класс постоянно действующих возмущений л.
Областью определения функции F является совокупность значений переменных х(/), и(0, КО. Для которых при каждом t определены соответствующие значения вектор-функцин F. Конкретный вид этой области задается энергетическими, силовыми, кинематическими и другими конструктивными ограничениями, присущими двигательной системе рассматриваемого робота.
Обычно на векторы состояний х, управлений и и параметров % наложены естественные конструктивные ограничения
вида
х t)^Qx при всех />/,.. (2.57)
u(/)cQu при всех (2.58)
|(/)«Ql при всех />/0- (2.60)
Здесь Qx, Qu, Q( —заданные ограниченные множества возможных состояний, управлений и параметров соответственно.
Постоянно действующие возмущения л в каждый данный момент времени t обычно неизвестны и не могут быть измерены датчиками информационной системы. Относительно л(0 известно только, что
x(t)&Qn при всех />Г0> (2.60)
где Q*— заданная область.
Соотношения (2.56) — (2.60) описывают класс возможных управляемых движений робота. При этом управляющие воздействия и(0 формируются управляющей системой, а дрейф параметров £(0 и возмущения л(0. как правило, неизвестны.
В этих условиях с неполной и изменяющейся информацией достижение цели управления возможно лишь путем правильного выбора управления. Искомый закон управления и(/) должен придать роботу желаемые динамические свойства. Необходимо сразу же решить вопрос о допустимых управлениях, т. е. о классе функций, в котором конструируется искомый закон управления.
Будем называть вектор-функцию и (0 = 1 U; (t) |'n_l допустимым управлением, если она при каждом t to принимает значения в Qu, а ее компоненты являются кусочно-непрерывными функциями, допускающими лишь разрывы первого* рода при Отдельных изолированных значениях / =/*, Л—0, 1, ... Для определенности примем, что в точках разрыва функции «/(/) непрерывны справа.
В результате подстановки в уравнение (2.56) какого-либо допустимого управления u(l) правая часть этого уравнения обращается в функцию от х, ( и л. Естественно предположить, что эта функция удовлетворяет условиям существования и единственности решения х(/) уравнения (2.56) при всех начальных состояниях х„ н фиксированных £ и л, которые могут встретиться на практике |19]. Поэтому реальное движение робота есть функция /, /о, х0. и. f, л, т. е. х= Х(/, to, х0, иД, л).
Таким образом, задание некоторого закона управления u(l) при фиксированных хц, л единственным образом определяет непрерывное движение робота х(/), t t0. Это движение будем называть допустимым, если оно удовлетворяет ограничению (2.57) и имеет кусочно-непрерывную производную по t.
Среди допустимых движений выделим класс движений, ведущих (при л(/)аа0) к достижению заданной цели. Назовем их программными и обозначим через х?(/), t to- Из этого определения следует, что программным движением робота называется такое допустимое движение, при осуществлении которого (при л(/)ем0) достигается наперед заданная цель.
Рассмотрим общие динамические свойства и особенности двигательной системы робота как объекта управления. Изучим
ei
сначала структуру уравнений (2.55). С этой целью рассмотрим в 2п-мерном евклидовом пространстве множество
Р/> (б) = { х, F lx, и, и, £;}: х s /?", u е Rm}. (2.61)
Если оно не зависит от значения вектора 5 из т0 будем го* ворить, что уравнение движения (2.55) имеет постоянную структуру. Можно показать, что для широкого класса роботов структура уравнения (2.55) постоянна, т. е.
Pf<£i) = для любых ||, (2.62)
Постоянство структуры уравнений движения (2.55) имеет важное значение при построении программных движений и законов управления. Оно означает, что множество возможных движений робота, трактуемых как частные решения уравнения (2.55), не зависит от выбора | из Q(. В дальнейшем будем считать это свойство выполненным для всех |, удовлетворяющих ограничению (2.59). Характерным свойством динамики многих роботов является следующее свойство функции F: для любых чисел Ci, ci и любых векторов Xi, х» е Rn, ut, u2 £ Rm существует вектор u e Rm, такой, что
C|F (X|, U|, S) 4- cJP (x2, u2, S) = F(qxi + c2x2, x2, и, I). (2.63)
Вследствие этого множество P, является подпространством 2п-мерного пространства RnXRa. Действительно, пусть
(X|, F (х„ М|. &)) а Р/, (x2F (х2, u2, ()) e Рл.
Тогда на основании (2.63)
(CiXi + с2х2, C|F (xi, и,, |) + cJF (х2, u2,1)) —
(C|X| 4- c2x2, F (C1X, 4- C2x2, u, £)) e PF.
Явный вид подпространства P, определяется видом и структурой уравнения движения (2.55). В следующем параграфе приводится вид Р/ для некоторых конкретных типов двигательных систем роботов.
Сформулируем еще одно важное свойство динамических моделей роботов, которое имеет принципиальное значение при синтезе эффективных законов управления и анализе управляемых движений роботов.
Будем говорить, что уравнение движения (2.55) разрешимо относительно управления на подпространстве Рг, если существует единственная функция
U : PFXQi->₽m. (2.64)
такая, что для любых (х, z)sPf и любых выполнено
тождество
Z«aF[x, U (X, Z, S)S].
ва
функцию U будем называть оператором управления, а подпространство Рл — подпространством управляемости.
Свойство разрешимости уравнений движения на подпространстве управляемости впервые было введено и сформулировано в работах [60—62]. Там же было показано, что этим свойством обладает широкий класс динамических систем, в том числе и многие роботы. Фундаментальное значение указанного свойства для робототехники заключается в том, что оно позволяет с единых позиций описать особенности динамики всех роботов н робототехнических систем, управляемые движения которых описываются дифференциальными уравнениями вида
У*о ef(y, у....U, £), />Г0- (2.65)
Здесь у<° — Ля производная по времени m-мерной выходной переменной у. Вектор состояния для уравнения (2.75) имеет вид х™1-41?_| =1 У40 О
где п = 2т, а подпространство управляемости PF имеет вид
Рл = {(х, в): xm+i = z„ xm+2 = z,.х„ — z„_m). (2.66)
Основываясь на разрешимости уравнений движения (2.55) на подпространстве управляемости, обобщенную динамическую модель робота (2.56) — (2.60) можно записать в более удобном (с точки зрения конструирования законов управления) виде. Прежде всего отметим, что уравнение (2.55) эквивалентно соотношениям
u = Uix, х, |), (х, Х|еР,, t^to- (2.67)
Естественно предположить, что постоянно действующие возмущения л(() не меняют структуры уравнений движения. Это свойство можно формализовать в виде следующего структур-
ного ограничения:
(0, .i(/))ePF при всех t^t0. (2.68)
Тогда уравнение движения (2.56) при наличии возмущений л можно записать в эквивалентной форме:
u = U (х, х — я, Б), (х, х) е PF, (2.69)
Учитывая ограничения (2.57) — (2.60), определим область
g Rn посредством отображения
U : («?, X Q*) П Pf) X Qi - Qu (2.70)
Тогда если выполнены ограничения
(х(/)), х(0)е Р? при всех 1^10, (2.71)
х t)sQt при всех (2.72'
63
а также ограничения (2.57), (2.59), то соответствующее движению х(0 управление и(0 в силу (2.67) будет допустимым, т. е. будет выполнено (2.58). Заметим, что в общем случае движение робота зависит от внешних возмущений согласно уравнению (2.56). Поэтому ограничение (2.72), вообще говоря, следует усилить, т. е. вместо Qt нужно рассматривать (в зависимости от вида Q„) некоторое сужение этой области Q" er Qt.
Резюмируя вышеизложенное, можно утверждать, что обобщенная динамическая модель робота представляет собой уравнение движения в форме Коши (2.56) с постоянной структурой и ограничениями (2.57) — (2.60), обладающее разрешимостью относительно управления на подпространстве (2.61). Эквивалентным описанием этой модели является ее запись в разрешенной относительно управления форме (2.69) в сочетании с совокупностью ограничений (2.57), (2.59), (2.60), (2.68), (2.72).
f В. ДИНАМИЧЕСКИЕ СВОЙСТВА ЛИНЕЙНЫХ и нелинейных моделей
Для конкретизации общих свойств динамических моделей роботов рассмотрим некоторые классы линейных и нелинейных дифференциальных уравнений движения (2.55).
Особый интерес представляет случай, когда уравнения (2.55) линейны по х и и. К таким уравнениям сводится описание динамики некоторых координатно-измерительных и сборочных роботов с электрическими приводами. Хотя число роботов, движения которых описываются линейными дифференциальными уравнениями, сравнительно невелико, изучение динамических свойств линейных моделей целесообразно по следующим причинам.
Во-первых, динамику многих нелинейных двигательных систем роботов можно в первом приближении описать линейными дифференциальными уравнениями вида
х = A tl) х •+• Ь (6) и, х(/0) = х0, />/0. (2.73)
где А, Ь — матрицы параметров размерностью п X п и п X tn соответственно, причем матрица Ь имеет ранг т п. Это позволяет заменить трудную для анализа нелинейную модель более простой линейной. Если линеаризация осуществляется вблизи заданного состояния или программного движения, то из свойств линейной модели удается извлечь полезную информацию для уточнения свойств полной нелинейной модели.
Во-вторых, известны аналитические выражения для решений х = х(/, to, хо, и, А, Ь) линейных уравнений (2.73), причем эти выражения линейны по х0 и и. Кроме того, для линейных мо-61
аелей детально изучены вопросы управляемости и наблюдав* мости. Указанные обстоятельства позволяют легко установить структуру подпространства управляемости Р, и явный вид оператора управления И в данном случае.
Наконец, в-третьих, изучение свойств линейных уравнений (2.73) может дать полезную информацию для анализа аналогичных нелинейных уравнений, где А—А(х,|), b = b(x,|). К таким «квазилинейным» уравнениям сводятся уравнения движения многих роботов.
Важнейшим свойством динамических моделей роботов является их управляемость. В общем случае это свойство можно определить так. Динамическая модель управляема, если подходящим выбором закона управления, формируемого управляющей системой, можно обеспечить желаемое движение робота (точнее, его двигательной системы).
Для линейных моделей вида (2.73) управляемость означает, что робот может быть переведен из любого заданного начального состояния хо в любое другое заданное состояние х( за конечное время путем выбора подходящего допустимого уравнения. Критерием полной управляемости модели (2.73) является следующее условие [14, 19]:
rank S (|) = п для любого t, е Qi, (2.74)
где S(l)=»|b, Ab, .... А”-*b| — матрица управляемости размерностью nXnm. В дальнейшем условие (2.74) будем считать выполненным.
Множество (2.61) для линейной модели (2.73) имеет вид
Р, (6) = {(х. А (I) я + Ы1) м): х в Я". и а /?т). (2.76)
Покажем, что оно является подпространством в Rn X Rn- Проверяя свойство (2.63) для (2.73), находим
C|F (Xi, Ui Л) + c2F (х2, и2, = С|А (|) х( + с, b («) и, 4- с2А (|) х2 +
4- c2b (s) и, = A(£)(С|Х| + с2х>) + b (£) (C|U| 4- с2и2).
Полагая и — CiUi 4- Csua, убеждаемся в справедливости уравнения (2.73). Следовательно, множество (2.75) действительно является линейным подпространством в RnX. Rn при любом la Qv
Для нахождения оператора управления (2.64) приведем модель (2.73) к более простому каноническому виду, для которого построить искомый оператор уже не составляет труда. С этой Целью рассмотрим линейное преобразование
x = S0(l)y, (2.76)
8 Зак. т 88
которое при m — 1 приводит систему (2.73) к канонической форме
У — Ао(1)у4-bo(l)u, у(/о)“Уо. < 4)» (8.77)
0 1 0 0 0
0 0 1 0 0
где Ао(1) — . Ьо(1)- »
0 0 0 1 0
— ап — а„-1 —а„_, ... — ai 1
(2.78)
причем A(5) = S0(ft)A0(l)8^l(|), Ь(|) — 80(|)Ь0, у^^х .... ря— Это преобразование в случае т — 1 имеет следующий вид (14]:
•о (6) - S (S) R (1), R (D - (1а (6) + е„, Ра (I) + е„_.............................1" а «Ж
0 1 0 ... 0 а„
00 1 ... 0 ап-1
1- , а(1)“= • . . --Sw'AMlbG).
0 0 0 ... 1 at
О 0 0 ... О
<»1
(2.79)
В новых переменных оператор управления (2.84) записывается ♦як:
и (У. ».D- bi (я -До») у). (2.80)
а подпространство (2.61) принимает вид
Рл (6) — {(У. *):«|— V* .......— Уя) (2.81)
Рассмотрим теперь свойства нелинейных моделей, описывая* мых дифференциальными уравнениями типа уравнений Лагранжа
A(q,S)q + b(q, q,5)-=u, (2.82)
где q — m-мерный вектор обобщенных координат; A(q, |), Hq.q.l) — заданные т X m-матрица-функция н т-вектор-функ-дия. Этими уравнениями порядка 2m описываются исполнительные механизмы многих роботов. Такую же структуру имеют а уравнения динамики манипуляционных роботов с моментными приводами.
Важное свойство уравнений (2.82) заключается в том, что матрица A(q, S) положительно определена при всех возможных qe Qf и Qi, и, следовательно, существует обратная матри-
А :(<1Д)- Поэтому уравнение (2.82) можно разрешить отно-
06
еятельно старшей производной н записать в виде
q - A"' (q, I) [u - b (q, q, &)]. (2.83)
Введем обозначения Xi = q, х2 ® q. Тогда состояние модели (2.82) описывается 2/п-мерным векотором с компонентами хь х«. Уравнение (2.83) можно записать в форме Коши (2.55), где
F(x, u,g)— (2.84)
\A '(X|, l)(u — b(X|, x2,1)] /
Подпространство управляемости для рассматриваемой нелинейной модели можно представить в виде
(£) = {(х, z) : Zi = х2), (2.85)
где z — 2т-мерный вектор с компонентами zi, z2. Оператор управления (2.64) в данном случае имеет вид
U (х, zЛ) = А (х„ fc) z2 + Ь (хь х2, J). (2.86)
Постоянство структуры нелинейной модели (2.82) при всех 16 Qi непосредственно следует нз выражения (2.85).
В заключение рассмотрим динамическую модель двигательной системы роботов с электрическими приводами постоянного тока. Эта модель описывается дифференциальным уравнением 8т-го порядка вида
A(q,|)q + b(q, q, q,l) = u, (2.87)
где u — m-мерный вектор управляющих напряжений на входе двигателей; A (q, |), b (q, q, q, ?) — заданные m X m-матрнца-функцня и m-вектор-функцня; | —р-вектор параметров исполнительного механизма н приводов. Уравнения (2.87) получают объединением уравнений Лагранжа (2.39), описывающих динамику исполнительного механизма, с уравнениями (2.55), описывающими динамику электроприводов постоянного тока.
Введем обозначения Xi = q, х2 = q, Хз = q. Состояние модели (2.87) описывается Зт-мерным вектором х с компонентами Х|, х2, xj. Уравнение (2.87) можно записать в форме Коши (2.55), где
(х2 X
Хз )• (2.88)
A-1 (xlt £) [u — b (Х|, х2, х», I)] /
Подпространство управляемости для модели (2.87) имеет вид
Р/ (I) — {(х, z): zi == х2, Zj — X,}, (2.89)
• оператор управления определяется выражением
U (х, я, |) — А (х„ i) z, 4- b (Xj, хз, х,, 5). (2.90)
а* 67
Постоянство структуры нелинейной модели (2.87) яри всех Ql следует нэ вида подпространства (2.89).
Описанные линейные и нелинейные модели динамики роботов играют важную роль при аналитическом синтезе эффективных управляющих систем, обеспечивающих желаемый характер Переходных процессов. Важнейшее свойство этих моделей — раз-решимость уравнения движения относительно управления на Подпространстве— подсказывает явный вид законов управления, адекватных динамике роботов. Структурные ограничения не класс воаможных движений в терминах подпространства Управляемости поаволяют по-новому подойти к задачам построения и оптимизации программных движений.
Глава 3
ПРОГРАММНОЕ УПРАВЛЕНИЕ РОБОТАМИ
$ 1. ЗАДАЧИ ПРОГРАММНОГО УПРАВЛЕНИЯ
Функциональные возможности роботов в значительной степени определяются совершенством их управляющей системы. Принцип управления, реализуемый этой системой, служит главным признаком, по которому роботы делятся на поколения. Основу управляющих систем роботов первого поколения составляет принцип программного управления. Раскроем суть этого принципа.
Цель управления роботом состоит в выполнении его двигательной системой требуемой рабочей операции. Типичными примерами таких операций могут служить перевод схвата манипулятора в заданную точку, отслеживание схватом заданной траектории, перемещение транспортного робота в заданную область или по заданному маршруту. Для достижения цели необходимо, чтобы управляющая система сформировала такой закон управления исполнительными приводами и механизмами, при котором заданная операция отрабатывается с требуемой точностью при соблюдении всех имеющихся ограничений.
Целенаправленность управления в роботах первого поколения обычно обеспечивается программой движения, которая формируется в режиме обучения. Эта программа задает идеальный закон изменения во времени обобщенных координат исполнительного механизма, соответствующий образцовому выполнению рабочей операции. На практике требуемая программа движения строится с помощью человека-оператора либо расчетным путем. В первом случае человек, управляя роботом в режиме обучения, выполняет ту или иную рабочую операцию, которая как эталон заносится в память управляющей системы. Во втором случае речь идет по существу об автоматическом программировании (самопрограммировании) целенаправленных движений роботи с учетом конструктивных ограничений.
Простейший способ отработки программы движения (и тем Самым достижения цели) заключается в формировании такого программного управления приводами, при котором реальное движение исполнительного механизма по возможности совпадает с программным. Программное управление определяется по ааранее заданной программе движения как функция времени, поэтому для его реализации требуется только один датчик — датчик времени (таймер).
При таком жестком программном управлении управляющая дстема строится по разомкнутой схеме: в режиме обучения в ее память вводится программа движения, в рабочем режиме включаются приводы, реализующие программное управление. В этом заключается сущность принципа программного управления. Жесткость управления по этому принципу сильно ограничивает возможности управляющей системы и робота в целом.
Перейдем к математической формулировке задачи программного управления. С этой целью рассмотрим вновь обобщенную динамическую модель робота, описываемую уравнением движения (2.56) и системой конструктивных ограничений (2.57) — (2.60).
Закон изменения состояний робота хр(/), t to, соответствующий заданной программе движения исполнительного механизма, будем называть программным движением (ПД). Зная ПД хд(0, легко найти программное управление. Для этого в уравнении (2.56) необходимо положить л = 0и выполнить подстановку х = хр(0, х = хр(/). В результате получим программное управление и = и₽(/) в неявном виде.
Для нахождения программного управления в аналитическом виде воспользуемся разрешимостью уравнения (2.56) относительно управления на подпространстве (2.61). Тогда с учетом (2.64) получим следующую формулу для вычисления программного управления непосредственно по ПД:
u//)~U[x,(/), х,(0,Ш. t>h- (3-D
Подставляя формулу (3.1) в уравнение (2.56), убеждаемся, по совпадение реального движения робота х(/) и ПД хр(/) возможно лишь при выполнении весьма жестких условий. Первое из них — точное задание вектора параметров £ (или его дрейфа §(/)) и отсутствие неконтролируемых возмущений я(/). Второе условие заключается в совпадении хр(/0) с начальным достоянием робота х0:
хр(/о) = х(/о) = х0. (3.2)
На практике строгое соблюдение указанных условий весьма затруднительно, а иногда и невозможно, поскольку априорная информация о параметрах | (и тем более об их дрейфе) неполна и неточна. Кроме того, всегда имеются начальные возму
щения е(6)= «о — хр(/о) н неконтролируемые постоянно дей* ствующие возмущения я(1). Все это приводит к отклонению ре* ального движения под действием жесткого программного управления (3.1) от программного хр(/). В этом проявляются принципиальные ограничения, присущие методу жесткого программного управления.
Для расширения возможностей управляющей системы программное управление целесообразно сочетать с управлением по принципу обратной связи. В результате получим гибкое управ* ление ПД с обратной связью. Преимущество такого комбинированного управления заключается в учете текущей информации о состоянии робота х(1) с целью улучшения качества управления. Благодаря этому закон управления становится самокорректирующимся, а ПД устойчивым по отношению к начальным, параметрическим н постоянно действующим возмущениям.
Примером закона управления ПД с обратной связью пе вектору состояний робота может служить следующее управ* леиие:
u(/) = U(x(0» (3.3]
Такое управление в отличие от (3.1) обеспечивает устойчивост» ПД хр(/), t to, по Ляпунову [58]. Последнее можно трактовать также как техническую устойчивость ПД хР(/) на любом конечном интервале времени [/о. /г]. Более эффективные законы управления, обеспечивающие асимптотическую устойчивость ПД в целом, будут синтезированы ниже. Реализация таких законов требует знания параметров и организации обратных связей от датчиков, измеряющих компоненты вектора состояний х(/).
Первым этапом программного управления является формирование ПД хр(0- Как уже отмечалось, построение ПД может осуществляться человеком-оператором, обучающим робот требуемой операции, либо автоматически в режиме самопрограммирования робота. Построение ПД в последнем случае можно производить как до начала эксплуатации робота, так и в процессе его нормальной эксплуатации в ускоренном масштабе времени.
Задача автоматическом) программирования движений робота формулируется следующим образом. Пусть заданы динамическая модель робота в виде уравнения (2.55) и ограничений (2.57) — (2.59), а также начальное и конечное (целевое) состояние робота Хо е Qx, Xi е Q, и время движения Т = tT — й (Т < оо). Требуется построить ПД хр(/), /е[/о,/г], как частное решение уравнения движения (2.55) при некотором допустимом управлении, удовлетворяющее ограничениям (2.5/) (2-58) и граничным условиям
хри0; = х0, хр|/г» = Х|. (S.4
f
Сформулированная задача обычно имеет много решений в рамках заданных ограничений. Среди них целесообразно выбрать нанлучшее, т. е. оптимальное ПД. С этой целью на классе ПД и программных управлений задают некоторый функционал качества вида
<г'
/ (хр (•), и, (•)] = $ L [хр (0, ир (/)] di, (3.5)
t,
где L — заданная функция.
Задача оптимизации ПД сводится к выбору такого ПД х°(/0) и соответствующего ему программного управления и® (/)» что функционал качества (3.5) на них принимает наименьшее возможное значение
I [х® ( •) Up( •)] = min / |хр( •), Up( -)]. (3.6)
Функции хр(/) и и°(/), удовлетворяющие критерию оптимальности (3.6), будем называть соответственно оптимальным ПД и оптимальным программным управлением.
При L (хд, Up)" 1 получаем
<г /[Xp(-),u,( )] = J dl-T.
Этот важный случай называется задачей наибольшего быстродействия. Оптимальное по быстродействию ПД х°(/) минимизирует время перевода робота из заданного начального состояния хо в желаемое конечное состояние Х|. При осуществлении такого оптимального ПД достигается наивысшая производительность робота.
Таким образом, построение и оптимизация ПД сводятся к решению двухточечной краевой задачи. Эта задача в общем виде пока не имеет эффективного решения. Как отмечается в работе [19], одной из трудных и малоразработанных проблем остается краевая задача, связанная с необходимостью привести объект в заданное конечное состояние.
Учет специфики динамических моделей роботов существенно облегчает решение сформулированной задачи. Благодаря разрешимости уравнения движения (2.65) относительно управления на подпространстве эта задача сводится к более простой вариационной задаче оптимизации ПД. Метод и алгоритмы решения этой задачи рассматриваются в следующем параграфе.
После построения ПД возникает необходимость в его фактическом осуществлении. С теоретической точки зрения здесь речь идет об аналитическом синтезе регулятора, обеспечивающего требуемое качество переходных процессов в замкнутой сн-
12
стеме. Такой регулятор должен по возможности обеспечивать асимптотическую устойчивость ПД. Регуляторы вида (3.1) и (3.3) этим свойством не обладают. Поэтому в данной главе значительное внимание уделяется синтезу регуляторов со стабилизирующим действием в характерных для робототехники режимах стабилизации ПД и терминального управления.
f 2. КИНЕМАТИЧЕСКИЙ СИНТЕЗ ПРОГРАММНЫХ ТРАЕКТОРИЙ
Программирование движений большинства роботов, используемых в промышленности, производится человеком-оператором, который в режиме обучения путем ручного управления роботом формирует требуемую программную траекторию (ПТ) исполнительного механизма и записывает ее в память управляющей системы [33, 46, 53].
Недостатком такого метода программирования целенаправленных действий являются большая трудоемкость и длительность процесса обучения, а также жесткий характер формируемой ПТ. Это делает невозможным оперативное изменение программной траектории в реальных условиях эксплуатации робота, которые могут сильно отличаться от идеальных условий режима обучения. Поэтому описанный метод программирования движений в неопределенных или нестационарных условиях может приводить к сбоям или даже аварийным ситуациям. Если робот функционирует в труднодоступных или опасных для жизни человека условиях, то данный метод вообще неприменим.
Таким образом, в ряде случаев возникает необходимость в разработке алгоритмических средств автоматического программирования роботов с помощью ЭВМ. При этом оказывается возможным оперативно учитывать информацию об изменениях обстановки и соответствующим образом корректировать ПД. Такой метод самопрограммирования движений обладает определенной гибкостью.
Существующие методы и алгоритмы построения ПД можно подразделить на две группы: методы синтеза ПД, удовлетворяющие заданным конструктивным ограничениям, н методы оптимизации ПД по заданному критерию качества. В рамках указанных методов важную вспомогательную роль играют алгоритмы решения прямой и обратной задач о положении исполнительного механизма, а также связанные с ним методы кинематического синтеза ПД. Рассмотрим подробнее эти задачи и алгоритмы.
Прямая н обратная задачи о положении. Конфигурация исполнительного механизма определяется вектором обобщенных координат q = |<7z 1<1г Зная q, можно найти положение и ориентацию отдельных звеньев механизма. Такие задачи называются прямыми задачами о положении механизма.
те
Необходимость решения прямой задачи в робототехнике возникает в связи с тем, что текущее положение и ориентация некоторых звеньев исполнительного механизма (например, схва-та манипулятора) зачастую не могут быть установлены путем прямых измерений. Вместо этого имеется возможность точно измерить относительные положения звеньев, например с помощью позиционных датчиков обобщенных координат. По этим данным можно вычислить положение и ориентацию всех звеньев.
Рассмотрим особенности решения прямой задачи для мани-уляцнонных роботов. Математической моделью W-звенного манипулятора является JV-звенная ломаная, один конец которой вакреплен в начале неподвижной системы координат Od^d^. Манипулятор с кинематическими парами пятого класса имеет е более 3W степеней свободы, т. е. т 3V. В роли обобщенных координат qi, ..., q„ обычно выступают углы между •веньями или длина звеньев, т. е.
(Ф/ для вращательной пары, ?/ = i л >3.7)
' (.С/ для поступательной пары.
Тип кинематической схемы манипулятора задается вектором < — lo/lf-P W
( 1, если qt = Ci,
с/ = {о „ (3.8)
' <2, если ?/=ф/.
По вектору обобщенных координат q = | qt 1^, однозначно определяем положение и ориентацию всех звеньев манипулятора. Свяжем с /-м звеном правую ортогональную систему координат с началом в точке г/ и ортами ej, е', е', причем г/ расположим на кинематической оси (/ — 1)-го и /-го звеньев, а орт •>/ направим по этой оси. При / = 0 имеем
г. е. система координат стойки манипулятора совпадает с абсолютной неподвижной системой координат. Напомним, что положение и ориентация /-го звена в трехмерном евклидовом пространстве определяются матрицей кинематических характеристик вида (2.5) размерностью 3X4.
Выразим элементы матриц (2.5) через обобщенные координаты (3.7). Это позволит вычислить основные кинематические характеристики г,, Ez |е{, е£, е£| всех звеньев манипулятора непосредственно по его обобщенным координатам ............
т. е. решить прямую задачу о положении.
74
Введем для краткости записи следующую операцию произведения ЗХ 4-матриц К/ =|г„ Е,|, К/ —|г/, Е/|:
K<OK/ = |ri + Eir„E/E/|. (ЗД
Определим матрицы преобразований
< 0 1 0 0\
А/0 0 0 1 0 при <Г/ = 1,
Р/(Ф = <0 0 0 COS фу 1/ sin фу 0S (,10>
A/Ol , 0 sin фу COS фу 0 I при О/ ™2,
<0 0 0 1/
где А/ — 3 X 4-матрнца вида
А/ = (Е/-|)г(г/-г'“|, Е').
(3.U)
Постоянные матрицы (3.11) формируются заранее в исходном (нулевом) положении манипулятора, т. е. при q = 0. В эти обозначениях матрицы кинематических характеристик определяются формулами
К/ (q) = Р, (q) О P,(q) О ... О Р/ (q), (3.13)
или в рекуррентной форме
K/(q)=K/_,(q)0P/(q). (3.13)
Выберем на /-м звене некоторую точку г>. Обозначим черев df вектор координат этой точки в локальной системе координат г,, е{, t!it е£. Тогда положение точки Н определяется формулой
r' = K,(q)
I d.'
(3.14)
На практике часто требуется знать положение некоторой ха< рактеристическои точки на схвате г. = г*. Оно однозначно опр«
Деляется отображением Ф вида
Ф(Ч^ = <’.. O(q'eKv(q)
1 d*
(3.15)
Для конкретизации описанной схемы решения прямой задачи о положении рассмотрим два примера.
Пример 1. Промышленный робот «Универсал-15». Кинематическая схема этого робота изображена на рис. 3.1, о. На ри-сУике представлены локальные системы координат, взятые в Исходном положении манипулятора. Для этого робота т=6,
П
<yr = (2,1,2 1,2). Матрицы кинематических характеристик имеют вид
(О 1 О О\ /О О О 1\ /О О О — 1\
0 0 1 0I, Kt —10 0 10, Кэ= I» 01 о],
0 0 0 1/ Ч - 1 0 о/ Ч + /, 1 О О/
(О 0 — 1 0\ / О 0 0 — 1\
I» 0 0 1 I, к5 = 1 z, + z» 1 о о 1.
Z, +I. + Z, -1 0 0/ '/,+/,+/< 0-1 о/
В результате вычислений по формуле (3.11) получаем
(О 1 О 0\ /О О О l\ /—Z2 —1 О 0\
О О 1 о], А2 = |о О 1 0 , Aj = | Za О 1 ОI,
0001/ 4-100/ X О 00 1/
- 1 0 0\ ZZ5 0 1 0\
О 0 0 11, А5 = | ООО 11.
О 010/ \о 1 О о/
Далее по формулам (3.10), (3.12)—(3.15) легко определить ко* ординаты точек на всех звеньях, включая скват, через обоб* ценные координаты.
Рис. 3.1. Кинематические схемы и локальные системы координат роботов «Универсал-15> (а) и «Кавасяки-Юнимейт» (б).
бГ- (2,2, t.i.t)
Пример 2. Промышленный робот «Кавасаки — Юнимейт». Кинематическая схема и локальные системы координат для этого робота представлены на рис. 3.1,6. Манипулятор робота 7<
мрамтернзуется следующими параметрами: т = 5, от м(2,2,1,2, 2). По матрицам кинематических характеристик
(О 1 О О\ /0 1 О 0\ /0 0 0 1
0 0 1 О I, К2 = | 0 0 0 1 1, К* — I /2 0 10
0 0 0 1/ 4,0-10/ ц-loo
/ О 1 О ОХ / ° 0 0 1
к4“| /2 + /, о 0 1, К5= /2 + /1 + /4 О I О
X /, 0-10/
о формуле (3.11) вычисляем /О 1 О.ОХ /О О
Aj-Jo О 1 0 1, А2 — | О О
\0 0 0 1/ ч -1
//4 - 1 О ОХ
А< = 1 0 0 0 1 1
\0 010/
х /, -1 о о/
О IX /-/2 -1 о ох 1 о|, Аз=| /, 0 1 0 1, 0 0/ X 0 0 0 - 1/
//5 0 1 ох
А,= 0 0 0 1 1.
Хо 100/
Теперь уже легко определить координаты любых точек на всех пеньях манипулятора через обобщенные координаты по формулам (3.10), (3.12) —(3.15).
Значительный интерес при программировании движений ро-8пов представляет обратная задача о положении механизма, на заключается в нахождении обобщенных координат q, определяющих возможные конфигурации исполнительного механизма по заданным положению и ориентации некоторых его звень-ев. Например, для манипуляционного робота требуется по заданному положению схвата г, найти соответствующие ему векторы обобщенных координат q-=q(r.), т. е. решить уравнение (8.15).
Вследствие нелинейности уравнений кинематики м присущей многим механизмам кинематической избыточности (обычно m»3) решение обратной задачи связано со значительными трудностями. Обычно существует конечное или даже бесконечное множество вариантов решений. Остановимся подробнее на решении уравнения (3.15) для манипуляционных роботов.
Оператор q=q(r) называется решением (3.15) в точке г = г„ если <D[q(r.)] = г.. В общем случае уравнение (3.15) может не иметь решений ни для каких г, либо иметь единственное или множество (более одного) решений. Пусть уравнение (3.15) имеет некоторое решение q,— q(r,). Если вто уравнение имеет несколько решений q(r) при значениях г, близких г„ то Происходит их ветвление. Современная теория уравнений с ветвящимися решениями основывается на идеях А. М. Ляпунова
тт
и Э. Шмидта, диаграммах Ньютона и других методах фуикцио-нального анализа.
Применительно к манипуляционным роботам разработаны специальные методы и алгоритмы, использование которых в каждом случае требует известной изобретательности [15, 17, 43, 46, 65]. Общим для этих методов является стремление увеличить число уравнений так, чтобы оно было равно числу неизвестных. Обычно уравнение (3.15) имеет шесть неизвестных (т=6). Это связано с тем, что произвольное положение и ориентация схвата определяются шестью независимыми переменными (например, тремя декартовыми координатами и тремя углами Эйлера). Отсюда следует, что шесть степеней свободы — необходимое условие для управления положением и ориентацией схвата в пространстве. Позтому часто в число компонент вектора в уравнении (3.15) включаются не только декартовы координаты выбранной точки схвата, но и направляющие косинусы последнего звена. Такая задача сводится к рассматриваемой, если под г, понимать координаты предпоследнего звена.
Различные алгоритмы решения обратной задачи о положении манипулятора при т^б описаны в работах [15, 17, 43, 46, 65]. Они решают уравнения (3.15) в явном виде. Это позволяет выделить конечное число ветвей решения уравнения (3.15) для «малоизбыточных» манипуляторов, причем хотя оператор q(r) и нелинеен, по достаточно прост при реализации на ЭВМ. Ввиду громоздкости записи полученные решения не приводятся.
В ряде случаев (например, при наличии препятствий в рабочей зоне) для увеличения маневренности манипулятора требуется определенная кинематическая избыточность. Это достигается увеличением числа степеней свободы манипулятора, т. е. должно быть т > 6. Появились даже гибкие манипуляторы типа «хобот», у которых т 10. Для манипуляторов с большой кинематической избыточностью необходимо использовать методы решения уравнения (3.15), ориентированные на ЭВМ.
Оптимизационные алгоритмы решения обратной задачи. Ряд методов основывается на сведении решения уравнения (3.15) и минимизации функционала вида [15, 23, 30]
Ф(ф = ||Ф(Ч)-г.||. (3.16)
Этот функционал обладает следующими свойствами: 1) ф(ц) — непрерывно дифференцируемая функция, причем 4>(q)>0; 8) если V^(q) = 0, то ф (q) = 0.
Величина 4>(q) представляет собой расстояние между целевой точкой г, и положеннем схвата г = ®(q) в конфигурации q.
Рассмотрим некоторые методы минимизации функционала (8.16). Зафиксируем целевую точку г, и начальное приближе-the q°. Тогда градиентный метод минимизации функционала
Т»
(8.16) заключается в построении минимизирующей последова-«ельностн q°, q*. qa, ... по правилу
q*+« = q‘-X4Vi|<(q*), А* > О, * = 0, 1, 2, ... (3.17)
Параметр А* называется длиной шага в направлении антигра-двента— V*(q*). Если VX»(q*)4*O, то шаг А* можно выбрать fax, чтобы ^(q*+l)< Ч»(<!*)• Если V$(q*)«oO, то ф(ц*) = О, ароцесс (3.17) прекращается.
В зависимости от метода выбора шага А* можно получить различные варианты градиентного метода. Так, если А* выбн* рать из условия оптимальности
а* (А*) = min а* (А), А* > 0, (3.18)
где а* (А) = ф [q* — AVif(q*) ], А 0, то приходим к методу наи» скорейшего спуска (14, 15].
Метод наискорейшего спуска (3.17), (3.18) имеет простой геометрический смысл: точка q*+* лежит на луче 1* — (q : q = -q* — AV$(q*). А 0} в точке его касания поверхности уровня Q»+t =(q е Rm : i|>(q)— <(q*+l)}. причем сам луч I* ортогонален касательной поверхности уровня Q* в точке q*.
Теоретические исследования и численные эксперименты показывают, что метод наискорейшего спуска (3.17), (3.18) в ряде случаев сходится медленно. Это связано с тем, что для манипуляционных роботов поверхности уровня функции (3.16) обычно имеют «овражий» характер. Последнее означает, что по ряду переменных, образующих «склон оврага», даже несущественное изменение этих переменных приводит к резкому изменению значений функции, в то время как по остальным переменным, задающим «дно оврага», функция изменяется незначительно.
Для ускорения сходимоети иногда применяют метод Ньютона. Если в градиентных методах при выборе направления убывания функции (3.16) используется лишь линейная часть ее разложения в ряд Тейлора, то в методе Ньютона берется квадратичная ее часть. Возможность ускорения сходимости связана с тем, что квадратичная часть разложения аппроксимирует функцию гораздо точнее, чем линейная.
Метод Ньютона в задаче минимизации (3.16) имеет вид q*+« = q*-(VaiKq‘)]-‘v* (q‘), * = 0,1,2......... (3.19)
где ¥2ф — вторая производная функции ф по q. Недостатком метода (3.19) является требование, чтобы начальное приближение q° было достаточно близким к искомому решению q. = • arg min ^(q). При отсутствии хорошего начального приближения метод (3.19) может расходиться. Поэтому метод Ньютона Целесообразно применять в сочетании с методом наискорейшего •пуска, который призван предварительно отыскивать приемле-
те
мое начальное приближение для процедуры (3.19). Трудоемкость каждого шага в методе Ньютона, вообще говоря, выщ^ чем в градиентных методах. Тем не менее общий объем вычно-кений, необходимых для минимизации (3.16) с требуемой точностью, при использовании этого метода может оказаться меньше, чем при использовании более простых градиентных методов.
Реализация описанных методов решения уравнения (3.16) требует вычисления первых и даже вторых производных функций (3.16). Однако существуют и другие методы решения этой задачи, использующие лишь значения функции (3.16) и не требующие вычисления се производных. К ним относятся методы покоординатного спуска и случайного поиска.
В явном виде метод покоординатного спуска выглядит так 1(30]:
q*+i *= arg min Ф (6, q*, .... <7*)» в
<7*+* = arg min Ф (<7*+l, 6.qkm),
.......................... (8.20) q*+l = arg min ф (q*+l, 7*+|..в),
в
где arg гт‘пф(..., 0, .. •) — значение 0, при котором ф имеет ми-е
нимум по соответствующей переменной для фиксированных остальных. Обоснованием естественности выбора метода (3.20)-дяя решения уравнения (3.15) являются некоторые особенности движения схвата манипулятора при изменении одной из егд обобщенных координат: если изменяется угловая координата, то скват движется по окружности, при изменении линейной координаты он движется по лучу. Эти соображения позволяют вычислить arg min ф в уравнениях (3.20) по элементарным формулам аналитической геометрии, что значительно упрощает реализацию метода (3.20).
Метод покоординатного спуска минимизирует функцию (3.16) с любой наперед заданной точностью б. Скорость его сходимости слабо зависит от величины ф (q°), т. е. от выбора начального приближения q°. Другим достоинством алгоритмов метода (3.16) является наличие свободного доступа к целенаправленному изменению обобщенных координат в процессе поиска решения уравнения (3.15). Это играет важную роль при Построении программных движений манипулятора на основе Метода (3.20).
Наряду с описанными методами решения уравнения (3.15) существует большая группа алгоритмов поиска минимума функции (3.16), обЪединеМшх под названием метода случайного Поиска. Этот метод характеризуется намеренным введением элемента случайности в алгоритм поиска, что увеличивает его гиб-
м
-ость. Многие алгоритмы метода случайного поиска можно-йредставить в виде
q*+1 =.q* + X*®*. Л = 0, 1, 2, .... (3.21)
гДе Л* > 0 — параметр; <о* — реализация m-мериой случайной величины ш с известным законом распределения. В качестве координат он случайного вектора о» можно выбрать, например, независимые случайные величины, равномерно распределенные на интервале [—1,1].
Реализация алгоритмов (3.21) предполагает наличие специального генератора случайных чисел, который формирует вектор «*. Такие генераторы, называемые также датчиками случайных чисел, обычно оформляются в виде стандартных программ для ЭВМ. Если закон распределения случайного вектора ш не зависит от номера шага k, то алгоритм (3.21) не может «нащупывать» направление быстрого убывания минимизирующей функции (3.16) и поэтому сходится медленно.
Для увеличения эффективности метода случайного поиска желательно, чтобы в алгоритме (3.21) закон распределения <» изменялся целенаправленно в зависимости от номера шага и результатов предыдущих шагов. Такой поиск, обеспечивающий большую вероятность выбора перспективных направлений в»* убывания функции (3.16), называется случайным поиском с обучением. По мере обучения роль фактора случайности уменьшается, и алгоритм (3.21) направляет поиск по «хорошим» направлениям убывания функции (3.16). В то же время элемент случайности позволяет алгоритму (3.21) быстро адаптироваться к резкому изменению свойств функции X>(q) в области поиска.
Схема кинематического синтеза программных движений. Рассмотренные алгоритмы решения обратной задачи о положении механизма являются частью общей задачи автоматического программирования движений роботов. На кинематическом уровне эта задача формулируется так. Пусть для одной или нескольких выбранных точек на исполнительном механизме заданы уравнения кинематики вида (3.15). На обобщенные координаты наложены конструктивные ограничения
?/<?/< 7?. /=1........т. (3 22)
Они определяют в /n-мерном евклидовом пространстве Rm па-раллелепнпед Q — IIl7/»7/L Множество D — Q(Q) является областью достижимости в R*. Обозначим через М(ф) множество 11 R3, занимаемое исполнительным механизмом в конфигурации Я- Пусть яс Я’ - некоторые объекты, играющие роль препят* ci вий. Введем функцию-предикат препятствий
( 1, если и А М (q) </>,
^л (fl) | q _ в ПрОТЯВноМ случае. (8.23)
Пусть в области достижимости DcR3 задана траектория некоторого звена исполнительного механизма, причем расстояние между соседними точками достаточно мало. Для опреде-ленности будем считать, что задана траектория схвата мани» пулятора г*, k 0, 1, ..., Т. Программной траекторией механизма будем называть такую траекторию q*. что для всех й«=0, 1, .... Т выполняются условия
Ф(Ч*)“Г* (3.24)
q₽sQ. (3.25)
МФ “°- <з.2в)
Описанные алгоритмы решения уравнения (3.15) индуци-
руют некоторое отображение
A(q°, r,) = q. (3.27)
Оператор А обладает тем свойством, что для любого на-
чального приближения q’eQ и любой целевой точки г,еО справедливо тождество
<D(A(q°, г,)] = г,.
Кроме того, A(qo, Ф(ч0)] = q°. Поэтому оператор А можно на-авать псевдообратным по отношению к оператору Ф.
Оператор А позволяет записать следующую рекуррентную схему кинематического синтеза ПТ. Пусть даны траектория схвата г.* и начальная конфигурация q°, такая, что <D(q9) = r'.
Дальнейшие элементы программной траектории q* определяются из рекуррентного алгоритма
q*+i = A(qJ, r‘+I), А = 0, 1...Г-1. (3.28)
Отметим, что вследствие псевдообратности оператора А справедливо <D(q*) = r*.
Синтезируемая ПС (3.28) должна обладать непрерывностью. В рассматриваемом дискретном случае это означает, что qj должно удовлетворять требованию
||Ф'-ф|<е’ * = 0. >..........Г —1, (3.29)
где е> 0 — малое число. Необходимым условием выполнения (3.29) является малость величин || г*+1 — г* ||. Напомним, что она предполагается.
При построении программной траектории по схеме (3.28) условие (3.29) выполняется, если оператор А удовлетворяет (равномерно по q°) следующему свойству непрерывности: и» малости || г — г* || следует малость ||q — q0||, где г° = Ф (q°), q =-= A(q°, г). Поскольку A [q°, Ф(я®)] = q°, то для того чтобы
•82
оператор А обладал сформулированным свойством, требуется непрерывность А по г,. Однако оператор А зачастую не является непрерывным по г,. Причиной этого является слишком широкая область задания А. Поэтому при построении ПТ приходится использовать лишь небольшую часть области задания А.
Отметим, что схема построения программной траектории в. виде (3.28) достаточно обща. В качестве оператора А в ней может быть использовано отображение, индуцируемое любым методом решения уравнения (3.15) по начальному приближению. В частности, можно использовать оптимизационные алгоритмы вида (3.17) —(3.21).
На практике всегда имеются конструктивные ограничения (3.22), (3.25). Для их учета необходимо произвести следующую модификацию схемы (3.28). Предполагая, что q°eQ, строим программную траекторию по формулам
q;+,“AQ(q;,H+>). Л = 0, 1.....7-1, (3.30)
где Aq — проекция А на множество Q. При этом если AeQ, то Aq = А. Теперь уже по построению г* е Q при всех k = 0г 1, .... 7 — 1.
Требование непрерывности, сформулированное применительно к оператору А, в полной мере относится и к оператору Aq. Обеспечение псевдообратности Aq сопряжено с некоторыми трудностями. Дело в том, что это свойство зависит от свойств Q н D. Оказывается, что необходимым условием псевдообратности оператора Aq является открытость отображения Ф: Q->Z> [30]. Более того, открытость отображения Ф необходима и достаточна для возможности построения непрерывной программной траектории q* для любой траектории схвата г* из D. Однако это свойство для некоторых роботов не выполняется. В подобных случаях описанная схема кинематического синтеза программных траекторий должна дополняться процедурой предварительного планирования, рассматриваемой в следующей главе.
$ 3. СКОРОСТНЫЕ АЛГОРИТМЫ ПРОГРАММИРОВАНИЯ ДВИЖЕНИЯ
Рассмотренные алгоритмы построения программной траектории базируются на том или ином методе решения обратной задачи о положении, т. е. на решении уравнения (3.15). Поэтому данные алгоритмы можно назвать позиционными. В отличие от них скоростные алгоритмы программирования движений основываются на управлении скоростью движения некоторых точек, фиксированных на отдельных звеньях механизма.
Для определенности рассмотрим методы и алгоритмы построения программной траектории манипулятора, обвепечнваю-
83
шей желаемый закон измерения скорости движения избранных точек на его схвате. С этой целью продифференцируем по вре-мени уравнение (3.15). В результате получим следующее диф. ференцнальное уравнение:
V<I»(q)q = r., q(/0)eq°. <331)
Здесь г, = г.(/)—скорость движения выбранной точки на схвате; \ Ф(q) — матрица Якоби размерностью ЗХ tn, зависящая от конфигурации q манипулятора. Введем ЗХ 3-матрицу-функ-цню
P(q) = V0(q)(V®(q))r (3.32)
н предположим, что она невырождена. Тогда уравнение (3.31) можно записать в разрешенной относительно q форме (2, 15, 161
q = (V<l>(q))rP_,(q) г. 4-(I — (v<P(q)rP~'(qj т, (3.33)
где I —единичная tn X m-матрица; т = т(/)—пока произвольная вектор-функция размерностью т.
Цель движения часто заключается в том, чтобы за заданное время Т as tT — t0 перевести манипулятор из заданной начальной конфигурации q° в желаемую конечную, такую, что
<I»[q(/r>] = r.. (3-34)
где г, — заданное целевое положение выбранной точки на схвате в области достижимости D. При этом искомая программная траектория q₽(/) во все моменты /s[/o,/г] должна удовлетворять конструктивным ограничениям (3.22) (т. е. q»(() не должна выходить за пределы множества Q в пространстве конфигураций), требованию обхода препятствий (т. е. 6,n [q, (/) ] = 0), а звенья манипулятора не должны самопересекаться.
Будем считать (2], что движение выбранной точки на схвате происходит с постоянной скоростью по прямой, соединяющей точки г.(/0)= Ф(q°) и г.(/г):
г. = Т~' [г. (1Т) — г. </«>)]• (3.35)
Подставляя выражение (3.35) в уравнение (3.33) и интегрируя полученное уравнение на интервале [/о./г], можно получить искомую программную траекторию qP(0- Для этого следует задать такую вектор-функцию т = т(1), выбор которой, с одной стороны, не влияет на желаемый закон движения точки на схвате (3.35), а с другой — позволяет удовлетворить конструктивным ограничениям на обобщенные координаты, избежать столкновения манипулятора с препятствиями и самопересечения его звеньев. Эвристические соображения и формализованная процедура нахождения подходящей функции т(1) как решения некоторой системы неравенств описаны в работе [2].
44
Поясним здесь основную идею выбора т(/). Ограничения на программную траекторию qp(f) можно записать в виде системы ^равенств в пространстве конфигураций
Pi (q) > 0, /=1...../, (336)
ГД* Р«(ч)—некоторая функция, которую мбжно интерпретиро* в’ать иак расстояния манипулятора в конфигурации q от множества «запрещенных конфигураций», определенного всеми за* данными ограничениями. В частности, p,(q) может означать расстояние от M(q) до внешних препятствий я. Тогда система неравенств (3.36) представляет собой требование обхода пре* пятствий.
Для выполнения неравенств (3.36) на программной траекто* рии q?(/) можно воспользоваться следующим приемом [2]. За* дадим положительное число е. Если в некоторый момент t' > нарушится l-е неравенство (3.36) при q = q(Z), то т(0 выбираем в уравнении (3.33), (3.35) из условия
Pz[q'/)]>0, <=1.......I. (3.37)
фо условие, обеспечивающее отход манипулятора от множества «запрещенных конфигураций», можно переписать в виде
[VP (q)JT (q)]ГР"' (q) T"‘ (r. (Zr) - r. (/0)) + [I-
— (v<P(q>lrP",(q>v<P(T)]T]>o. (3.38)
Неравенство (3.38) линейно по т и поэтому легко решается. Неразрешимость (3.38) означает, что программной траектории q»(0 в рамках описываемой схемы не существует. В этом слу* ЧДе можно, например, пытаться изменить закон движения схвата (3.35).
Описанный метод построения ПТ является одним из наиболее эффективных вариантов метода избыточных переменных [15]. Он использует лишь локальную информацию о множестве «запрещенных конфигураций» и поэтому в целом носит эвристический характер. При управлении скоростью движения схвата по закону (3.35) могут возникать тупиковые ситуации. Во избежание этого необходимо организовать предварительное планирование траектории схвата.
Принципиальная схема управляющей системы, реализующей Сфнсаннын метод « помощью сервоприводов с позиционной обратной связью, приведена на рнс. 3.2. Согласно этой схеме сервоприводы отрабатывают программную траекторию qp(Z), формируемую путем численного интегрирования уравнений (3.33).
В некоторых случаях желаемую скорость движения схвата Цожет задавать человек-оператор, например, с помощью специальной многостепенной рукоятки управления (12, 37, 42]. Соответствующие полуавтоматические алгоритмы программирова-нвя движений опнеаны в работах [33, 42]. Там же дается срав
85
нительный анализ многих скоростных алгоритмов и обсуждают, ся трудности, возникающие при их реализации и использовании. Одна из главных трудностей связана с возможным изменением ранга матрицы Якоби и вырождением матрицы (3.32) на искомой ПТ.
В заключение рассмотрим скоростные алгоритмы программирования движений, основанные на методе Бубнова — Галер, кина (57]. Этот метод, как известно, возник применительно к задачам математической физики. Однако он достаточно эффек-тивен и при автоматическом программировании движений ро-
Рис. 3.2. Структурная схема сервоуправления по скоростному алгоритму.
ботов с учетом конструктивных ограничений и препятствий. Более того, он позволяет приближенно оптимизировать ПТ по критерию максимального быстродействия.
Рассмотрим дифференциальное уравнение (3.31) и выделим в матрице Якоби Тф(ч) размерностью З'Х.т некоторую невырожденную подматрицу фз(ч) размерностью 3X3. Без ограничения общности можно считать, что эта матрица состоит из трех первых столбцов матрицы ТФ(ч) и, следовательно, имеет вид
det’s,q1 *0. (3.39)
Введем обозначения
Я»
Я<
Я4
Ял
Разрешая уравнение (3.31) относительно q*. получаем диф-ференциальное уравнение вида
q3 = f(q3, г., ц), (3.40)
где f (q3. г,. М) = <Рз-1 (Ч> [ г. ~ Фт-з м]; Фт_3 (q) — 3 X И — 3) .подматрица матрицы V®(q), составленная из т — 3 столбцов, начиная с четвертого.
Будем считать, что закон движения выбранной точки схвата удовлетворяет граничным условиям
г.«о)— г», г,(/т) = Г|. (3.41)
Тогда искомая ПТ qp(Z) должна удовлетворять граничным условиям вида
ч; ('») = <• (3.42)
Задача построения программной траектории свелась к ре* Йеиию краевой задачи (3.40), (3.42). Для того чтобы искомая Т q₽(0 удовлетворяла конструктивным ограничениям (3.22), а также требованию обхода препятствий, воспользуемся известным произволом в выборе вектора варьируемых параметров ц. Область значения вектора определяется неравенствами
/ — < •••• т. (3.43)
Итак, требуется подобрать такие значения «варьируемых параметров» ц из области (3.43), чтобы решение q3(/,ц) урав* нения (3.40) удовлетворяло граничным условиям (3.42) и всем заданным ограничениям.
Будем искать приближенное решение сформулированной за* дачи с помощью метода Бубнова — Галеркина. Пусть фо(0, ti(/)....фу(0—некоторая полная система базисных функ-
ций на отрезке [/о,/г], причем такая, что фо(О удовлетворяет граничным условиям (3.42), а остальные функции ф((/), i ""1, .... N, — однородным граничным условиям, т. е. ф,(/0)" “Ф>(^т) = 0 для всех « = 1, .... N. В качестве базисных функ* Ций, обладающих указанным свойством, можно взять, например, следующие полиномы:
’ГНП = фо(О(/-и'(/-/г), i= 1......N. (3.44)
Будем искать приближенное решение краевой задачи (3.20), (3.42) в виде
N
qa (t. = Фо «1 + £ crfi (/).
(3.45)
Здесь а = с/(ц)— неизвестные коэффициенты, подлежащие ®°РЦДелению. Подставляя решение (3.45) в уравнение (3.40),
37
находим иеашжу
[* 1 Г * 1
Фо(О + £*<♦<W “Ч*•(*) + Xс,*‘*'•’ ц I" z-i J L 1-1 J
= Ь(ЛС|.....cN, ц). (3.46)
Требуя ортогональности невязки б(/, clt cN, ц) к базисным функциям, получаем, вообще говоря, нелинейную алгебраическую систему из уравнений относительно N неизвестных:
»т
J Ът (I, е,.cN, р) (П dt = О, I = I.....N. (3.47)
t.
Решая систему (3.47), находим неизвестные параметры с, = с,(р), i=l.......N. Вычислим
inf q’(/, ц), sup q’((, р). (3.48)
'•('.- <Г] '-(<0. *r]
Если найдется вектор ц = ц. из области (3.43), при котором величины (3.48) удовлетворяют ограничениям (3.22), то параметризованное решение краевой задачи (3.45) с С/ = с,(ц.) и есть искомая программная траектория. В противном случае поставленная задача с ограничениями (3.22) неразрешима.
Большой интерес на практике представляет задача оптимизации ПТ по быстродействию. Формально »то означает, что время движения Т = Т(ц) не фиксировано, а подлежит определению из условия 'г
T(p? = min( dt. (3.49)
* Г.
Выполним для удобства замену переменных
t = Ts-t0.
Тогда краевая задача (3.40), (3.42) примет вид
q3 = 7'f(q*, Т-'г., р), (3.50)
q3(0) = qo‘, q‘(l) = q’ (3.81)
Будем искать ее решение в виде (3.45), где Ci = сДр)—неиз* вестные параметры. В качестве базисных функций можно взять, например, полиномы
*о («) — + (Ч? ~ <1$ (3.52)
Ф<(«)в[<1о+(<1| — <£)«](* — О*'» <-1..........N.
По аналогии с (3.46) находим невязку
[м л г * .1
to + £ - ПI to + X ctti, Г-'г., Ц =•
i-l J L £_| J
= 6 (a, *|..cN, T.p). (3.53)
Трсбуя ортогональности невязки 6 к базисным функциям фо, фь .... <лг> получаем систему из N 4- 1 уравнения с N 4- 1 неизвестными:
1
$8г(з, Ci, .... tN,T, n)tt{s)ds = 0, i = 0, 1, ..., N. (3.54) о
Решая систему уравнений (3.54) тем или иным методом, имеем
«1-=«1(И>........«№^(Н>. Г-Пр).
Выберем ц = из области (3.43) так, чтобы выполнялось условие оптимальности (3.49). Тогда искомая программная траектория примет вид
(5’ Ю в % & + J[ ci (и.) («)• <3-55)
Эта ПТ дает приближенное решение задачи оптимального быстродействия в рамиах рассмотренной схемы программирования движений робота.
f 4. ДИНАМИЧЕСКИЯ СИНТЕЗ И ОПТИМИЗАЦИЯ ПРОГРАММНЫХ ДВИЖЕНИЯ
Общим недостатком позиционных и скоростных алгоритмов программирования движений является то, что они строят программную траекторию с учетом лишь кинематических особенностей исполнительных механизмов. При атом по существу игнорируются динамические ограничения, присущие как самим механизмам, так и связанным с ними приводам робота. В то же время учет динамических ограничений необходим с точки зрения принципиальной осуществимости и эффективности синтезируемых программных движений. Данный параграф посвящен методам построения и оптимизации ПД с учетом динамики дви-г>тельной системы робота.
В предыдущей главе при анализе свойств динамических моделей роботов было показано, что ПД хр(/) при всех (е [/о,/т] Должно удовлетворять следующим конструктивным и динамическим ограничениям:
xp(/)gQ„ (3.56)
х,(/)в(?ъ (3.57)
(хд (/), хр (/)) ъРг, (8.58)
•9
где Qjt, Qx —некоторые заданные ограниченные области в Рг — подпространство в Rn'XRn, вид которого определяете* уравнением движения (2.55). Кроме того, ПД хр(/) по опред*. лению удовлетворяет заданным граничным условиям вида (3.4). Следует также отметить, что ПД хр(/) как частное решение уравнения движения (2.55) при некотором допустимом управ» Ленин u = up(/) зависит от параметров В задачах про-
граммного управления предполагается, что эти параметры (ила их дрейф |(/)) известны. В рассматриваемом случае на класс программных движений накладываются более жесткие ограни* чения, связанные с учетом структуры множества Q*.
Построение ПД с учетом свойств динамической модели ро> бота сводится к решению двухточечной краевой задачи с гранич* ными условиями (3.4) и ограничениями (3.56)—(3.58). Многие известные методы решения краевых задач в данном случае малоэффективны или даже непригодны. Трудности усугубляются высокой размерностью и нелинейностью уравнений движения (2.55), а' также сложным характером ограничений (3.56) — (3.58).
Эффективным методом динамического синтеза программных движений является метод их параметризации с учетом граничных условий (3.4), накладываемых на начальное и конечное состояния робота [61, 62]. В данном методе последовательно воплощены идеи априорного выполнения граничных условий (3.4) и учета структурного ограничения (3.58). Это достигается путем специального выбора базисных функций. В таком подходе заложен глубокий смысл: при отыскании приемлемых параметров ПД уже не нужно заботиться об удовлетворении граничных условий (3.4) и динамического ограничения (3.58), так как они заранее учтены в конструкции базисных функций.
Рассмотрим подробнее один из вариантов метода параметризации программных движений [57, 61]. Будем искать ПД в многопараметрическом классе функций вида
.V
хр (/) = а(, (/) + 2 x/а, (/), t к [/(„ /г]. (3.59)
Здесь х = |х/|^_, — вектор искомых параметров; а0(/), at(f), ... .. .,ajv(f)—заданные ЛГ-мерные вектор-функции. Будем называть их базисными, если они удовлетворяют следующим условиям [61, 62]:
1) функции {a/</»PLo таковы, что ПД (3.59) удовлетворяет граничным условиям (3.4) при любом выборе параметров хь ..., xv;
2) функции (а/(0}*_ц и их производные {а,*/'}' попарно удовлетворяют структурному ограничению (а;(/), »((!))еР/ при всех t fB [/о, /г];
м
3) функции {а/ (О)^о’ взятые в любом конечном числе N, линейно независимы;
4) система аппроксимирующих функций, из которых выби- , рают базисные функции, полна в пространстве непрерывно дифференцируемых функций С* {/о» М, т. е. каковы бы ни были функция х(/)еС'[/о, /г] и положительное число е, существуют натуральное число N н постоянные коэффициенты хь ..., у.ы, такие, что
N || х (/) — ао (0 — хуа/ (/) Ц < а;
5) функции {а/(/)}*_0 достаточно просты для программной нлн схемной реализации.
Перечисленные требования к базисным функциям имеют следующий смысл. Первое требование обеспечивает н облегчает решение двухточечной краевой задачи, второе гарантирует осуществимость параметризованного программного движения (3.59) с учетом динамики робота, третье и четвертое означают возможность экономного и вместе с тем сколь угодно точного представления ПД в виде (3.59) и, наконец, пятое обеспечивает простоту технической реализации искомого ПД. Отметим, что пренебрежение любым из этих требований может привести к грубым ошибкам или неосуществимости параметризованного.. ПД вида (3.59).
Первая и важнейшая задача в рамках параметрического метода построения ПД заключается в рациональном выборе базисных функций. Рассмотрим некоторые примеры и общие рекомендации по конструированию базисных функций.
Базисными функциями, удовлетворяющими сформулированным требованиям, могут служить полиномы a0(/)=x0+(xI-x0)7’-,(/-/o), а/(/)=а0(/)(/-/0)/1=1........N-
(3.60) в самом деле, при таком выборе базисных функций программное движение (3.59) удовлетворяет граничным условиям (3.4), Динамическому ограничению (3.58), а также требованиям точной аппроксимации и простой реализации.
Другим примером рационального выбора базисных функций являются тригонометрические многочлены
а0(/) = х0 4- (х1 — х0) sin 2~1Т~'я(I — /о),
(3.61) а, (/) = ао (/) sin/ Т~'я (t —19).
Как видно из этих примеров, при конструировании базисных Функций можно руководствоваться следующим правилом: в качестве функции ао(О можно выбирать непрерывно дифференцируемую вектор-функцию, удовлетворявшую граничным усло-
01
виям (3.4), а в качестве остальных бааисных функций — функция вида
а/(/) = ао(/)ф/(О, /=1
(3.62)
Здесь ф/(О—числовые функции из некоторой полной системы функций на [/о,/г], удовлетворяющие однородным граничным условиям, т. е.
ф/ (to) = Ф/ Нт) = 0, / = 1, ..N.
(3.63)
В качестве ф/(0 можно выбирать рассмотренные полиномы и тригонометрические многочлены. Тогда возможность сколь угодно точной аппроксимации программного движения в виде (3.59) гарантируется классическими результатами из теории функций (теорема Вейерштрасса).
Значительный прикладной интерес представляет использова* иие в качестве ф/(/) «конечных элементов» [32], т. е. таких функций с конечным носителем, которые отличны от нуля только в небольшой (порядка шага сетки) окрестности интервала (Го, /т]. Простейшим примером данных функций могут служить кусочно-линейные функции вида
0,
Л-* (/-//_!), Г/_1 Л *(// + ! /), +
(3.64)
где 6 — to 4- A, h = t0 + 2А, ..., /№ to 4- Nh и tT — узлы сетки на (Го, tr] с шагом А. Эти функции обладают следующим свойством [32]: любую кусочно-линейную функцию с возможными изломами в узлах t/ можно представить в виде линейной комби
нации ^Р/Ф/^*> где в качестве коэффициентов Фурье стоят
значения самой функции в точках //.
Большой интерес представляет также такая параметризации программного движения, когда в качестве <Р/(Г) берутся сплайны [32, 46], т. е. кусочно-полиномиальные функции со следующими свойствами:
1) существует разбиение (Го, /г] на подынтервалы, такое, что внутри каждого подынтервала ф/(1) представляет собой многочлен степени г;
2) функции ф/(/) непрерывны вместе с производными (г— 1 )-го порядка и имеют интегрируемую с квадратом производную порядка г на интервале [Го. М-
Конструирование базисных функций с учетом высказанный соображений обеспечивает соблюдение граничных условий (3.4) и динамического ограничения (3.58) при любом выборе пар*' метров .....х« в функции (3.59), а также приводит к высоко*
точности аппроксимации и простой ревлиаации синтезируемых программных движений. После выбор* базисных функция ао(О. *»(0, . .. «лг(О можно перейти к фактическому построению ПД вида (3.59).
Задача синтеза программных движений сводится к отысканию приемлемых значений параметров *ь • • •. Эти параметры следует определять исходя из заданных ограничении (3.56), (3.57), где Qx = F (Qx, (?„,£). Тогда ввиду разрешимости уравнения движения (2.65) относительно и(0 программное управление (3.1), соответствующее ПД Хо(0, является допустимым, т. е. u,(/)gQ«. Отметим, что огр*ничения (3.56), (3.57) на линейных комбинациях (3.59) превращаются в систему неравенств относительно параметров х = |*/1/_г
Таким образом, задача построения пР0ГРаммных движений в результате параметризации (3.59) сводится к решению континуальной системы неравенств, описывающих ограничения (3.56), (3.57), относительно параметров искомого ПД.
Для решения полученных неравенств, вообще говоря, применимы известные методы нелинейного программирования 132]. Однако для роботов с большим числом степеней свободы, а также при сложном характере ограничений (3.56), (3.57) использование этих методов сопряжено с принципиальными или вычислительными трудностями. В подобных случаях более простым и эффективным может оказаться метод, использующий рекуррентные конечно-сходяшиеся алгоритмы решения неравенств [78].
Суть этого метода заключается в следующем [61]. Пусть-для определенности множества Qx и Q* представляют собой шары радиусами сх и с* соответственно с центром в нуле. Тогда ограничения на ПД (3.59) можно записвть в виде следующей системы неравенств:
|| ао (I) 4- А (/) х || < сх, Ro. /г]. (3-65)
||ао(/)4- А (Ох Ц<съ (3.6в>
где А(0—пХЛГ-матрица-функция, составленная из базисных Функций а,(0......ах(0; А (/)—производная А(/) по времени.
Очевидно, что неравенства (3.65), (3.66) выпуклы по х. Предположим, что они разрешимы с запасом 6| > 0 и 62 > 0. Тогда существует вектор параметров х#, такой. что ПД (3.59) с х = х» Удовлетворяет ограничениям (3.56), (3.57) с соответствующими ,апасами. Отметим также, что ввиду непрерывной дифференцируемости функций az(Z), /—I......Л\ матрицы-функции А(О
п А(/) равномерно ограничены, т. е.
IIА < Сл, IIА II < сА при всех I <= [/о, /т]. (3.67)
В этих условиях для решения неравенств (3.65), (3.66) при. менимы рекуррентные конечно-сходяшиеся алгоритмы градиент, ного типа, предложенные в работах [68, 78]. Приведем явный вид одного такого алгоритма решения неравенств (3.65). Пусть Яо— произвольное начальное приближение неизвестного вектор) х». Зациклив систему неравенств (3.65) по / (с периодом Г) будем строить оценки и* параметров ПД в соответствии с ре.* куррентным алгоритмом
х*+* = х* + б) дг (/д) Хр (/д) || х₽ (4) ||-1 п А (/») г2. (3.68)
Здесь tn— очередной момент нарушения неравенств (3.65) при М“х‘, t > tn, a *p(tn)—значение (3.59) при / = /*, х —х*.
С помощью метода функций Ляпунова легко показать, что алгоритм (3.68) является конечно-сходящимся [78], причем для числа его шагов справедлива оценка
А < || хо - х. ||2 с’б,-2 ™ kv (3.69)
Совершенно аналогично записывается рекуррентный конечно-сходящийся алгоритм решения неравенств (3.66), причем для числа его шагов справедлива оценка
(3.70)
Для получения алгоритма, доставляющего решение систем неравенств (3.65) и (3.66), достаточно воспользоваться композицией указанных алгоритмов [68]. Это значит, что «новую» оценку и*+*, полученную в соответствии с алгоритмом (3.68) решения неравенств (3.65), следует использовать как «старую» оценку в аналогичном алгоритме решения неравенств (3.66). Очевидно, что такая композиция конечно-сходящнхся алгоритмов также является конечно-сходящимся алгоритмом с числом шагов
A = max{A|, k2}.
В некоторых случаях вместо ограничений на скорость изменения вектора состояний (3.57) удобно рассматривать огр.лш* чения на управления. Целесообразность такого подхода определяется тем, что иногда множество Qi, задающее динамические ограничения на ПД хр, может иметь весьма сложную структуру, в то время как множество Qu, задающее ограничение на программное управление и0(/)> представляет собой выпукло* множество, например шар. В этом слуиае ограничение на управ* ление имеет вид
Цц(/)1Ксв при всех /е[/о. М- (3.71*
Подставляя ПД (3.59) в формулу программного управления (3.1), а последнюю — в (3.71), получаем систему неравенств
IU [х,(0, i, W. 6] II <Ср, t е [/0, М. <3*73)
И
^носительно вектора к. Если функция U выпукла по х (это нМеет место, например, в случае линейных или линеаризованных уравнений динамики (2.55)), то снова получаем выпуклую систему неравенств. Для решения этих неравенств в сочетании о неравенствами (3.65) опять-таки применимы рекуррентные ко* иечно-сходящиеся алгоритмы типа (3.68).
Достоинством описанного параметрического метода построе-ния программного движения являются простота и экономность представления (3.59), а также возможность быстрой перестройка ПД при изменении граничных условий или ограничений. Последнее обеспечивается тем, что структура синтезируемого ПД (3.59) задается с точностью до начального и конечного состояний хо, х1 и параметров х. При этом изменение граничных условий влечет за собой изменение базисных функций, а изменение ограничений (3.56), (3.57) или (3.71) порождает соответствующую коррекцию параметров ПД без изменения его структуры.
Рассмотрим теперь задачу оптимизации программного движения. Она имеет большое практическое значение, так как позволяет роботу экономить ресурсы и время в процессе выполнения рабочих операций. Выбор конкретного функционала качества вида (3.5) обычно возлагается на конструктора управляющей системы робота. После того как этот функционал выбран и фиксирован критерий оптимальности (3.6), используется математический аппарат теории оптимального управления.
Традиционные методы оптимизации, основанные на принцип» максимума Л. С. Понтрягина [14, 19, 44], сводят задачу к отысканию оптимального программного управления и? (7), после чего оптимальное ПД х°(7) получают как решение уравнения движения (2.55) при u = u°(7). (При этом предполагается, что вектор параметров I в (2.55) известен и фиксирован.) Однако решение данной задачи для роботов с большим числом степеней свободы связано со значительными трудностями. Эти трудности усугубляются нелинейностью уравнений (2.55) и сложным характером ограничений на состояния и управления.
Для преодоления указанных трудностей изменим формулировку задачи. С этой целью прежде всего отметим, что вследствие разрешимости уравнения (2.55) относительно управления "а подпространстве Рг программное управление определяется Формулой (3.1), где xp(f)—некоторое ПД, удовлетворяющее конструктивным и динамическим ограничениям (3.56)—(3.57). Подставляя (3.1) в функционал качества (3.5), зависящий от ”»(•) н хв(-), получаем новый функционал
R [хр< • )]-/[U[xp( •), х„( •),!], х,(*)). (3.73)
кс'Орый уже не зависи! hbhooi программного управления Up(-).
N-
Задача оптимизации программного движения теперь может быть поставлена как следующая вариационная задача: построить ПД, оптимальное по отношению к функционалу качества (3.73), при соблюдении дифференциальной связи (3.58) и ограничений (3.56), (3.57).
Сформулированная вариационная задача тесно связана с задачей оптимального управления. Однако она проще, поскольку вместо дифференциальной связи (2.55) в ней фигурирует значительно более простое динамическое ограничение (3.58). В процессе решения вариационной задачи оказывается возможным непосредственно строить оптимальное ПД (например, как решение уравнения Эйлера), не прибегая к трудоемкому предварительному поиску оптимального программного управления классическими методами. Следует отметить, однако, что и эта более простая задача далеко не тривиальна и достаточно трудоемка (особенно, если учесть ограничения (3.56), (3.57), присущие многим роботам). Поэтому значительный интерес представляют алгоритмические методы решения рассматриваемой задачи.
Одним из таких методов является метод параметрической оптимизации программного движения, предложенный в работах [61, 62]. Он основан на описанной ранее параметризации ПД. Существо метода заключается в том, что приближенное решение задачи оптимизации ПД ищется в виде (3.59). Подставляя па* раметрнзованное ПД (3.59) в функционал (3.73), получаем функцию
.. .....х„), (3.74)
вависящую от У параметров ПД.
Таким образом, задача оптимизации программного движения свелась к следующей задаче нелинейного программирования: найти значения параметров искомого ПД вида (3.59) исходя из критерия оптимальности
V (х°) = min V (х) (3.75)
н ограничений (3.56), (3.57). Тем самым рассматриваемая вариационная задача свелась к более простой задаче минимизации функции с конечным числом переменных при ограничениях типа неравенств. Следует отметить, что существуют н другие (менее эффективные) схемы сведения задач оптимального программного управления к задачам нелинейного программирования (14, 20, 32].
Теоретическое обоснование метода параметрической оптимизации программного движения основывается на простых соображениях. При каждом N решении задачи (3.75) дает оптимальные значения вектора параметров м° параметризованного ПД (3.59), ближайшего к неизвестному решению х* (о соответствующе
щей вариационной задачи. Так как х* (I) — некоторая аппроксн-мадия оптимального ПД х’(0, то /?[х£( • )]>Я[хр( •)].
Введем обозначения
[м 1
аоМ + ^Х/аЛ-)} ЛГ=1. 2. ...
Тогда с увеличением N имеем
Я, >R2> ... •)]. (3.76»
Справедливость (3.76) следует из того, что любая линейная комбинация базисных функций ао(О, ..., av_i(/) включена в линейную комбинацию функций ао(О........а^(/). По существу
число Rn выступает как ЛГ-е приближение к Я[х*( •)]. Оно тем точнее, чем больше V. Благодаря полноте системы базисных функций находим
lim Р№ = /?[х-0( •)]. '3.77)
N -> °о
Итак, приближенное решение вариационной задачи с функционалом качества (3.73) сводится к определению минимизирующей последовательности параметризованных ПД вида (3.59), где JV = 1, 2, ..., в соответствии с описанной ранее схемой.
Остановимся подробнее на вычислительных аспектах метода параметрической оптимизации ПД. Постулируем некоторый функционал качества (3.73) и будем искать ПДх°(1) в виде (3.59) из условия оптимальности
Я[хр( •)] = inin/?[xp( •)]. (3.78)
Отметим следующие свойства оптимального ПД:
1) удовлетворяет (по построению) граничным условиям (3.4) и динамическому ограничению (3.58);
2) для x°(Z) справедливо соотношение /?[х;(.)-|</?[хр(.)|, каково бы ни было другое ПД хр(1), М-
Значительный интерес для робототехники представляют интегральные функционалы качества вида
'г
R (х, (• И = L fx„ (Л, i, (П) dt. (3.79)
t.
где L — заданная непрерывная функция. Если £(х, х)я 1, те *г
/?[xp(-)] = U/-r. (3.80
н
4 Эи. зп
97
В этом случае приходим к задаче синтеза такого ПД х^(0» Для которого время перехода робота из начального состояния х0 в конечное X) минимально.
Важный класс функционалов качества составляют квадратичные функционалы вида
•т
/?[хр( • )]= J «ХР(О, РоХр(Л) + (iip(t), (3.81)
t.
где Ро, Pi — симметричные положительно определенные матрицы размерностью лХ«- Такие функционалы характеризуют энергетические затраты в двигательной системе робота.
Практический интерес представляет также функционал вида t р п
Я [Хр (•)] = $ ^а<|Хр.<(0МЛ (3.82)
tn /“I
характеризующий экономичность ПД, где а/ — положительные числа.
Легко убедиться, что после подстановки в функционалы (3.81) или (3.82) параметризованного ПД (3.59) соответствующий функционал превращается в функцию ф(х)ж/?(хр(-)] с параметрами х = |х/|/_|, причем она выпукла по х. Так, подставляя (3.59) в (3.81), где для простоты Ро = Р( = I, получаем
Т (х) = у (х, Н х) + (Ь, х) 4- с, (3.83)
где И = 2 J [Аг (/) А (/) 4- Аг (/)А (/)] di,
tt
‘т
Ь = 2 J (Аг (/) ао (/) 4- Аг (/) а0 (/)] di, t.
• г
с= J [IIао(/)II2 + II«о(/)Щdi. t.
Отметим, что ввиду линейной независимости базисных функций матрица Н невырождена. Оптимальные по отношению к (3.83) параметры ПД определяются формулой
х°=Н-1Ь. (3.84;
Подставляя формулу (3.84) в (3.59), получаем оптимальное программное движение в аналитической форме.
М
f б. УСТОЙЧИВОСТЬ И СТАБИЛИЗАЦИЯ ПРОГРАММНЫХ ДВИЖЕНИИ
Прежде чем приступить к синтезу и анализу систем управления роботов, изложим основные идеи и результаты теории устойчивости движения, которые имеют основополагающее значение при алгоритмическом конструировании законов управления программным движением, обеспечивающих желаемое качество переходных процессов.
Динамика двигательной системы робота описывается дифференциальным уравнением (2.55). После подстановки в это уравнение какого-либо допустимого закона управления u = u(t) правая часть уравнения обращается в n-мерную вектор-функцию от t, х и Полагая параметр | известным и фиксированным, обозначаем эту функцию через Z(x, /). Тогда уравнения движения замкнутой системы имеют вид
x = Z(x,/), х(/0) = х0, />/0- (3.85)
Будем считать, что вектор-функция Z удовлетворяет условиям существования и единственности решений х(/) при всех начальных данных, хое Qx, которые могут встретиться в задаче.
В основе теорий управления роботами лежит понятие устойчивости движения. Пусть xp(t), t /о. — некоторое вполне определенное программное движение, подлежащее исследованию на устойчивость. Это движение принято называть невозмущенным, а любое другое — возмущенным. Невозмущенному (программному) движению соответствует определенное частное решение уравнения (3.85), начинающееся из состояния xp(t0). Функция е(/)=х(/)—хр(/) называется переходным процессом (ПП), а величина е(/о) = Хо—хр(6)—начальным возмущением.
Программное движение хр(/), / /0. называется устойчивым
по Ляпунову (3, 14] если для любых положительных чисел е и to можно найти такое положительное число б = б(е, /0). что при всех начальных возмущениях, удовлетворяющих условию Ие(/о)||<6, выполняется неравенство
||е(7)|| < е при всех /^/0-
Геометрически устойчивость ПД по отношению к начальным возмущениям означает следующее. Рассмотрим сферу ||е||2 = е2. выберем радиус е этой сферы произвольно малым. Если ПД Устойчиво, то для этой е-сферы должна найтись другая сфера Радиусом б, такая, что переходный процесс е(1), начавшийся в любой точке е(6) внутри б-сферы, в дальнейшем остается внутри е-сферы, никогда не достигая ее поверхности.
Практически устойчивость ПД означает, что при достаточно “алом начальном возмущении «(/о) реальное движение x(t) с*оль угодно мало отличается от ПД xp(t). Если же ПД неустой
9»
чиво, то реальное движение будет отклоняться от него, как бц ни были малы начальные возмущения.
Если ПД Хр(/), t to, устойчиво по Ляпунову н число б >Q можно выбрать для любого числа е > 0 так, что
lira || е(/) || = 0, (3.86)
То оно называется асимптотически устойчивым.
Геометрически асимптотическая устойчивость означает, что переходный процесс е(() неограниченно стремится к началу ко» ординат, не выходя при этом из е-сферы. Область ||е(/0)Н <6 при фиксированном /0 называется областью притяжения (об» ластью асимптотической устойчивости) ПД. Если реальное двн» жение x(f) стремится к ПД х₽(0 при 1-+со равномерно по отно» шению к величинам х0 и /о, то хр(/) называется равномерно асимптотически устойчивым по х0 и to-
В тех случаях, когда ПД асимптотически устойчиво при лю» бых начальных возмущениях, как бы велики они ни были, оно называется асимптотически устойчивым в целом. Это означает, что реальное движение х(/) при любом хое/?" асимптотически сближается с ПД хр(/). При этом начальное возмущение со вре* менем угасает, его роль уменьшается и реальное движение с те* ченнем времени сближае!ся с программным независимо of величины начального возмущения. Областью притяжения ПД в этом случае является все пространство /?".
Следует иметь в виду, что если ПД оказалось неустойчивым, то это еще не означает, что робот с такой динамикой непригоден. Действительно, учитывая, что время функционирования робот! на практике конечно, может оказаться, что на рассматриваемом интервале времени переходный процесс вполне удовлетворителен. Таким образом, неустойчивость программного движения,, взятая изолированно (как и его устойчивость), не может служить окончательным критерием опенки работоспособности ро бота.
Произведем в системе (3.85) замену переменных: е = х — х? Новая система имеет вид
ё = Е(е, /), (3.87)
где Е(е, ()= Z(e + x», /)—Z(xp, /). причем Е(0, /)=0 при все* t > to- rt
Система (3.87) определяет дифференциальное уравнение ПП-Программное движение x,(f) при данной замене переменны* переходит в положение равновесия е(/) = 0 новой системы, и!' зывасмое нулевым, или тривиальным, решением системы (3.87)-При этом анализ устойчивости ПД системы (3.85) сводится * анализу устойчивости нулевого решения е = 0 системы (3.87)-
Сформулируем понятие устойчивости по Ляпунову иулевог? решения е = 0 системы (3.87). Решение е = 0 уравнения (3.8'1
100
называется устойчивым, если для любых положительных чисел g и to можно найти такое положительное число б = б(е, to), что из неравенства ||е(/0)П <6 следует неравенство ||е(/)|| <а при всех t > to. Аналогично вводятся понятия асимптотической устойчивости и устойчивости в целом тривиального решения системы (3.87).
Рассмотрим наряду с системой (3.87) уравнение вида
e = Eie, t + л(/>, e(Zo' = Co, /^4» (3.88)
где л(/)—постоянно действующие возмущения, причем Е и я таковы, что решение уравнения (3.88) при любых начальных условиях, которые могут встретиться в задаче, существует п единственно. В этом случае, вообще говоря, я(/)¥=0 при е = 0, и, следовательно, нулевое решение е = 0 не является решением возмущенного уравнения (3.88).
На практике постоянно действующие возмущения л(/) неизвестны и не могут быть измерены. Однако они всегда ограничены и обычно достаточно малы. Последнее означает, что возмущения я(() малы в каждый момент t либо в среднем на рассматриваемом интервале движения. Однако даже малые возмущения при длительном воздействии могут оказывать заметное влияние на характер переходного процесса.
Программное движение xp(t0). t t0, называется устойчивым при постоянно действующих возмущениях [3, 14], если для любых положительных чисел е и t0 можно указать два числа 6 = б(/о, е) и у = у(/0, е), таких, что при ||я(/)|| <у для всех решений е(1) уравнения (3.88), удовлетворяющих условию ||е(6)|| <8. справедливо неравенство
||е(/)||< е при всех t>tn.
Из этого определения следует, что ПД устойчиво при постоянно действующих возмущениях, если величина ||е</) II остается все время малой при условии, что она мала в начальный момент to, н величина ||л(/)||, характеризующая уровень возмущений, также достаточно мала при всех t /0- Достаточным условием устойчивости ПД при постоянно действующих возмущениях является его равномерная асимптотическая устойчивость по to и х0.
Одной из центральных задач управления движением роботов является обеспечение устойчивости ПД. Как уже отмечалось, особенно важно обеспечить асимптотическую устойчивость ПД. Для этого необходимо синтезировать закон управлений Двигательной системой, чтобы реальное движение робота стремилось с течением времени к заданному программному. Законы Управления, обеспечивающие асимптотическую устойчивость программного движения в замкнутой системе, принято называть стабилизирующими.
101
| в. ЛОКАЛЬНОЕ СЕРВОУПРАВЛЕНИЕ ПО ПРОГРАММЕ
Для фактической отработки программного движения необходимо синтезировать соответствующий закон управления исполнительными приводами робота. Цель такого управления обычно заключается в обеспечении заданной точности воспроизведения ПД.
Простейшим способом управления ПД является программное управление, используемое в некоторых роботах первого поколения (35, 53]. Аналитическая запись программного управления с учетом динамики робота имеет вид (3.1). При реализации такого управления (например, циклового программного управления по упорам) в роли датчика выступает временное устройство, которое последовательно (например, от упора к упору) формирует управляющие воздействия.
В ходе программного управления не используются сигналы обратной связи о текущем состоянии двигательной ситемы робота или внешней среды. Поэтому в таких системах программного управления отсутствует подтверждение фактической обработки ПД. Другим недостатком данных систем является жесткий характер управления. В связи с этим для обеспечения работоспособности роботов с программным управлением требуются специальная технологическая оснастка и неизменность условий эксплуатации. Создание и поддержание таких условий требуют дополнительных затрат.
Более эффективным методом управления ПД роботов является сервоуправление по программе. В его основе лежит идея отработки ПД с помощью сервоприводов, использующих обратную связь по фактическому состоянию двигательной системы робота. При этом коэффициенты усиления в каналах обратной связи заранее рассчитываются так, чтобы обеспечить воспроизведение ПД с заданной точностью при небольших начальных и постоянно действующих возмущениях.
В современных роботах сервоуправление по программе обычно реализуется с помощью серийно выпускаемых сервоприводов с локальными обратными связями по положению и скорости. Двигательная система таких роботов представляет собой исполнительный механизм с т обобщенными координатами Я\, .... Ят, по каждой из которых действует свой сервопривод. Задача t-ro сервопривода заключается в том, чтобы, используя обратную связь по qt(t}, qi(t), обеспечить отработку программной «уставки» qp,,(/) с заданной точностью.
Поскольку исполнительный механизм является общей нагрузкой для всех сервоприводов, двигательную систему робота следует рассматривать как многосвязную систему с перекрестными связями. Такая система включает в себя т взаимосвязанных подсистем. На вход i-й подсистемы подается t-я компонента
10Э
ПД Яр‘< а выходом служит реальное значение обобщенной координаты ф(/). Взаимодействие подсистем происходит по каналам перекрестных связей.
В практике проектирования сервоприводов для роботов широко используется упрощенный метод расчета, основанный на выделении отдельных подсистем без учета динамического взаимодействия [33, 47, 53]. Такой подход позволяет расчленить многосвязную систему, движения которой в общем случае описываются нелинейными дифференциальными уравнениями высокого порядка вида (2.56), на т простых локальных систем.
Для упрощения расчетов уравнения движения каждой подсистемы линеаризуют в окрестности соответствующей компоненты программного движения, а коэффициенты полученного нестационарного линейного дифференциального уравнения «замораживают» [33]. При этом предполагается, что переходный процесс в замкнутой двигательной системе протекает настолько быстро, что ПД, а следовательно, и коэффициенты линеаризованного уравнения, не претерпевают значительных изменений.
Описанный приближенный метод расчета сервоприводов для роботов, несмотря на отсутствие строгого обоснования, на практике зачастую обеспечивает требуемую точность отработки ПД и приемлемое качество ПП. Поэтому он используется при проектировании многих промышленных роботов с позиционными и контурными системами управления [53].
Структурная схема сервоуправлення по программе с помощью сервоприводов, приводящих в движение исполнительный механизм робота, представлена на рис. 3.3. Здесь: ПАП — Цифроаналоговый преобразователь; УС — усилитель сигнала; ШИП — широтно-импульсный преобразователь; УМ — усилитель мощности; ДПТ — двигатель постоянного тока; РД — редуктор; ТГ — тахогенератор; ДП — датчик положения; k,, г = О, 1, ...
6,— коэффициенты усиления соответствующих элементоЬ схемы; Л5/(Т0р4-1)—передаточная функция ТГ; То— постояи-«ая времени ТГ; р — d/dt — оператор дифференцирования.
Программное движение q₽(0 формируется специальным пРограммно-временным устройством, которое обычно реалй-3Уется на ЭВМ или микропроцессоре.
Особенности движения электрических приводов рассмотре-Ны в главе 2. При синтезе локального сервоуправлення обычйб ’’спользуются пропорциональные, интегральные, дифференциаль'-ные регуляторы или их комбинация — ПИД-регуляторы.
Пропорциональный регулятор формирует управляющее воз-^йствие (в данном случае управляющее напряжение в цепи ?°Ря ДПТ) и„ пропорциональное ошибке регулирование <.^0= ?,(/) —ф>. г(О. т. е. отклонению выходной координаты Mr) от ее программной «уставки» ,(/):
«<(О = Ci 1<7* 0 — Яр.1 (0], i = 1, • • •, т. (3.89
£
Коэффициенты усиления а определяют чувствительность регулятора. Увеличение коэффициентов усиления обычно благоприятно влияет на качество переходного процесса, и в частности на точность и быстродействие. Однако при очень больших коэффициентах усиления возможны автоколебания или даже потеря устойчивости ПД.
Для улучшения качества ПП в закон управления наряду с ошибкой регулирования Дф(1) часто вводят производные Дф(1), Дф(1), ... Так, в схеме, представленной на рис. 3.3, используется пропорционально-дифференциальный (ПД) регулятор вида
»И0 = ct (/) - q„. t (/)] + kt [<h (/) - , (/)), (3.90)
где Ci, ki— коэффициенты усиления в каналах обратной связи. Реализация таких регуляторов требует использования ТОЛЬКО датчиков положения и скорости.
Учет динамических особенностей двигателей (в частности, учет их инерционности) приводит к необходимости создания интегральных регуляторов, управляющее воздействие которых пропорционально интегралу по времени от ошибки регулирования. В простейшем случае интегральный регулятор имеет вид
«/ W = П W — Яр. i </)]. * = 1. • • •. т, (3.91)
где п — коэффициенты усиления. Если же регулирование осуществляется на основе обратной связи по второму, третьему и т. д. интегралам от ошибки Д^(/), то соответствующие регуляторы называются регуляторами со вторым, третьим и т. д. порядком астатизма. Обычно увеличение порядка астатизма позволяет повысить точность воспроизведения программного движения. Однако при этом может уменьшиться запас устойчивости замкнутой системы.
Наилучшими техническими характеристиками в классе рассматриваемых линейных регуляторов обладают комбинированные ПИД-регуляторы. Однако и им присущи известные недостатки. При расчете таких регуляторов удается теоретически обосновать и обеспечить лишь устойчивость ПД в малом. Характерные для многих роботов нелинейность уравнений движения и перекрестные связи в каналах управления, как правило, не учитываются в этих расчетах, что неблагоприятно сказывается на характере переходных процессов в замкнутой двигательной системе. Неизбежные на практике дрейф и неопределенность параметров также ухудшают качество ПП при локальном сервоуправлении. Это проявляется в снижении точности отработки программного движения, в автоколебаниях или неустойчивости ПД по отдельным обобщенным координатам. Отсюда
105
вытекает необходимость разработки более совершенных систем сервоуправления, свободных от указанных недостатков. Эти системы должны учитывать динамику исполнительных приводов ц механизмов робота в явном виде (т. е. в структуре регулятора). Такие системы могут в принципе обеспечить переходный процесс желаемого характера.
| 7. ДИНАМИЧЕСКОЕ УПРАВЛЕНИЕ С ЗАДАННЫМ КАЧЕСТВОМ
Рассмотрим новый подход к аналитическому синтезу регуляторов исходя из требования обеспечить в замкнутой динамической системе робота переходный процесс с наперед заданным характером. Отличительной чертой такого подхода является то, что при выборе структуры регулятора используются полные (а не линеаризованные) уравнения динамики. В результате структура регулятора оказывается адекватной структуре динамической модели робота. Законы управления, реализуемые такими регуляторами, будем называть динамическими.
В рамках рассматриваемого подхода решается не только задача стабилизации программного движения с заданным качеством, но и задача терминального управления, т. е. задача управления конечным состоянием. Напомним, что целью управления в последнем случае является перевод робота из любого начального состояния х0 е Q* в желаемое конечное Х| е Q* за заданное конечное время Т ж tT —10. В процессе управления должны выполняться конструктивные ограничения на состояния и управления (2.57), (2.58). Решение данной задачи включает в себя два этапа: предварительное наведение робота, т. е. построение программного движения, и стабилизацию выбранного ПД. Такое расщепление задачи позволяет сравнительно прост осуществить синтез оптимального управления.
Перейдем к описанию и обоснованию обшей схемы аналитического синтеза систем управления программным движением. В основе ее лежит принцип скоростного управления ПД |48, 61 ]. Происхождение такого названия вытекает из приводимой ниже Формулировки этого принципа и иллюстрируется приме|г«м11 .ешения задач стабилизации ПД и терминального управления роботами.
Рассмотрим уравнение динамики робота в разрешенной относительно производной вектора состояний форме (2.55). Пусть задано некоторое программное движение хр(1). Цель управления заключается в осуществлении этого движения так, чтобы переходные процессы в замкнутой системе обладали наперед заданными свойствами. Для достижения указанной цели предлагается следующая двухэтапная процедура синтеза управляющей системы.
106 ’
На первом этапе сконструируем дифференциальное уравнение переходных процессов вида
ё = £(е, /), е(10) = е0, / е [Zo. /г1- (3.92)
определяющее желаемый характер ПП е = x(Z)—хр(/). Методика построения уравнения (3.92) будет рассмотрена далее.
На втором этапе синтезируется закон управления программным движением, обеспечивающий переходный процесс с наперед заданными свойствами. Это означает, что уравнение движения робота, замкнутое искомым управлением, имеет вид
х = хр +Е(х — хр, Л, /е[/0./г] (3.93)
Для фактического синтеза закона управления воспользуемся принципом скоростного управления ПД 148, 61]. Согласно этому принципу для получения желаемого ПП е(1), описываемого уравнением (3.92), необходимо, чтобы скорость изменения вектора состояния х(/), определяемая в соответствии с уравнением движения (2.55) выбором управления и(/), изменялась по закону (3.93). Требуемый закон управления ПД найдем как решение уравнения
хр + Е(х — хр, /) = F(x, u.fc). (3.94)
Принципиальная разрешимость задачи синтеза закона управления программным движением вида (3.94) обусловливается разрешимостью уравнения движения (2.55), а значит, и уравнения (3.94), относительно управления. В главе 2 было установлено, что для многих роботов такая разрешимость на подпространстве Рг имеет место. Поэтому, учитывая данное свойство, непосредственно из уравнения (3.94) получаем закон управления ПД с обратной связью по х(/) вида
u = U[x,Xp + E(x-Xp,/)Л], /€=[/о. /г]. (3.95)
Необходимым условием осуществимости синтезированного управления является соотношение
(х(/), Хр(/) + £]х(/) — хр(1), 1])<=РР при всех /е[/0. <т]. (3.96
которое можно трактовать как структурное ограничение на функцию Е, определяющую вид уравнения переходного процесса (3.92).
Подставляя управление (3.95) в уравнение динамики (2.55), получаем уравнение (3.93). Это означает, что переходные процессы в замкнутой системе описываются наперед заданным Уравнением (3.92) и, следовательно, обладают всеми желаемыми свойствами.
Таким образом, принцип скоростного управления программным движением, регулируя в соответствии с уравнениями (3.93),
107
(3.94) скорость изменения вектора состояний х((), придает ПП в двигательной системе робота заранее предписанный характер. Этим и объясняется название данного принципа.
Остановимся на связи принципа скоростного управления программным движением с известными принципами и схемами управления. Прежде всего отметим, что основная идея описанного принципа возникла при синтезе самонастраивающихся систем (49]. Суть этой идеи заключается в следующем: в уравнении движения, разрешенном относительно старшей производной, последняя заменяется производной того же порядка от программного движения (или некоторой функцией от него), а управление выбирается как решение полученного уравнения. Известные реализации этой идеи относятся к различным частным (как правило, линейным) задачам управления, а их мотивировка зачастую носит эвристический характер. Принципиальная трудность при этом связана с отсутствием решения уравнения движения относительно управления многих объектов (и, в частности, роботов) на классе допустимых управлений.
Другой подход — принцип симметрии и связанный с ним метод синтеза алгоритмов управления на основе решения обратной задачи динамики (21, 22] —также содержит предположение разрешимости уравнения движения на классе допустимых управлений. Однако, как отмечается в (3], это уравнение во многих случаях является неразрешимым относительно управляющей функции. Разрешающая функция управления («обратный оператор» в терминологии, принятой в работе [22]) существует и легко строится лишь в сравнительно простых случаях. В подобных ситуациях принцип симметрии устанавливает правило аналитического конструирования программного управления. Он, а также общая схема решения обратных задач динамики определяют структуру закона управления с обратной связью, обеспечивающего осуществление программного движения при отсутствии начальных и постоянно действующих возмущений (21, 22].
В работах [60—62] и в главе 2 данного пособия показано, НТО важнейшим свойством широкого класса роботов является разрешимость уравнения движения (2.55) относительно управления на подпространстве Pf. Поэтому в соответствии с (2.64) оператор управления U фактически задан на подпространстве Рр (вида (2.61)). Это обстоятельство принципиально, так как порождает структурное ограничение (3.96) на закон управления (3.95) и необходимо для его осуществимости.
Важно подчеркнуть, что именно разрешимость уравнения движения на подпространстве является важнейшим элементом принципа скоростного управления ПД [48, 60—62]. Этот принцип выступает как общий метод аналитического синтеза регуляторов роботов, обеспечивающих желаемый характер переходных процессов.
108
Отметим, что семейство законов управления вида (3.95) су* щественно отличается от традиционных схем управления вида (14]
и (/) — ир (/) + Сг (х «) - Хр (/>], (3.97)
где ир(/)—программное управление, соответствующее программному движению Хр(/), а С — лХ^-матрица коэффициентов усиления в каналах обратной связи. Можно показать, что при специальном выборе матрицы С как функции хр(/) и | закон управления с линейной обратной связью по х(/) обеспечивает асимптотическую устойчивость ПД xp(Z) в малом. Полагая в законе управления (3.95)
Е(х —Хр, П = Г(х-Хр>, (3.98)
где Г—устойчивая лХл-матрица коэффициентов усиления, удовлетворяющая структурному ограничению (3.96), получаем динамическое управление, обеспечивающее асимптотическую устойчивость ПД в целом. В частном случае, когда управляемые движения робота описываются линейным дифференциальным уравнением вида (2.73), связь закона управления ПД (3.95), (3.97) с традиционным законом управления (3.64) задается формулой
Г = А + Ьсг.
Синтезированное семейство законов динамического управле-цня обладает значительной общностью: выбирая ту или иную функцию в (3.95), можно получить как известные алгоритмы управления, описанные в [3, 6, 8, 12, 14, 15, 17, 21,-23, 3,1, 33, 49, 61, 64, 66, 70], так и новые. Другим достоинством принципа скоростного управления ПД является то, что он позволяет унифицировать этапы выбора желаемого характера ПП, синтеза структуры регулятора и анализа качества управления в замкнутой двигательной системе робота.
Большое значение для оценки качества ПП в робототехнике имеет система критериев, разработанная в теории автоматического регулирования. Сформулируем те из них, которые представляют наибольший интерес и ценность при синтезе динамического управления.
Авюномность по координатам. Уравнение переходного процесса (3.92) называется автономным по координате если его структура такова, что t-я компонента ПП еД/) зависит только от начального возмущения е,(/о) по этой координате и не зависит от начальных возмущений по другим координатам. Очевидно, что если е((/о) = О, то £,(/)«= 0 при всех t > t0. Замкнутую двигательную систему, уравнение ПП которой автономно по всем координатам «, ..., еп, будем называть системой без Перекрестных связей.
109
Инвариантность к возмущениям. Замкнутая двигательная система называется инвариантной относительно возмущения я,(I) по координате е<, если i-я компонента е,(1) переходного процесса е(() не зависит от я>(/). Здесь i, j—некоторые фиксированные индексы.
Пусть е— заданное неотрицательное число. Обозначим через «У»(0 i-ю компоненту ПП при условии, что я,(/)и 0, j = 1, ... ..., п. Замкнутая система называется инвариантной с точностью до е по координате относительно возмущения я/((), если при всех / > /о и любых постоянно действующих равномерно ограниченных возмущениях я>(/) выполняется неравенство
|е/(П-<°(/)|<е.
Это неравенство определяет критерий е-инвариантности переходного процесса. Среди всех допустимых функций Е(е, /) оно отбирает те, которые придают переходному процессу инвариантность в указанном смысле. Инвариантность тесно связана с рассматриваемой в следующей главе адаптивностью управляющей системы относительно широкого класса неконтролируемых возмущающих воздействий.
Сформулированные критерии следует принимать во внимание при проектировании управляющих систем роботов. Учет их при выборе структуры и параметров регуляторов позволяет придать переходному процессу в замкнутой двигательной системе заранее предписанные свойства.
$ 8. УСЛОВИЯ СТАБИЛИЗИРУЕМОСТИ ПРОГРАММНЫХ ДВИЖЕНИИ
* И МЕТОДЫ СИНТЕЗА РЕГУЛЯТОРОВ
Одним из наиболее эффективных методов исследования устойчивости программного движения является метод функции Ляпунова [3, 14, 28, 70]. Суть этого метода заключается в следующем. Введем определенно-положительную функцию L(e), характеризующую качество переходного процесса, и вычислим ее полную производную по времени согласно уравнению движения (2.55):
^- = (уМе). Fie + Xp, u,fc) —хр). (3.99)
Пусть М(е)—некоторая определенно-отрицательная функция. Тогда достаточное условие стабилизируемости ПД имеет вид
<VL (е), F (е 4- хр, u, g) - хр> С М (е). (3.100)
Неравенство (3.68) определяет в неявном виде ограничение на структуру искомого регулятора. Отметим, что все законы управ-110
ления, удовлетворяющие ему, обеспечивают асимптотическую устойчивость программного движения.
Используя разрешимость уравнения движения (2.55) относи* тельно управления на подпространстве, из неравенства (3.100) можно получить регулятор в аналитическом виде. Структура регулятора определяется с точностью до функций L и М, выбор которых связан с известными трудностями [4, 14].
Более простым и эффективным представляется метод, осно* ванный на задании не функции Ляпунова L, а ее производной:
-^^- = Af(e), />/0. (З.Ю1)
где М(е)—заданная определенно-отрицательная функция. Из условия стабилизируемое™ (3.101) (случай равенства) находим, <то скорость изменения вектора состояний определяется соотно* иением
i-i,+ M(.) (3.102)
Утсюда, используя разрешимость уравнения движения (2.55) тносительно управления на подпространстве, получаем семей-тво законов стабилизации ПД вида
u - U [х, хр + М (х - х,) <3’ 103)
войства переходного процесса в замкнутой системе (2.55), 1.103) определяются выбором функции М, т. е. заданием прободной функции Ляпунова L.
Опишем другой метод аналитического синтеза регуляторов, 1 требующий предварительного выбора функции Ляпунова. :пользуя его, можно решить задачу в два этапа. В соответ-вии с принципом скоростного управления программным дви-!нием на первом этапе конструируется уравнение переходного оцесса (3.93) так, чтобы обеспечивалась асимптотическая гойчивость ПД и ПП обладал наперед заданными свойствами. >и этом необходимо иметь в виду структурное ограничение 96).
На втором этапе, используя разрешимость уравнения (2.55) осительно управления, находим структуру регулятора в яв-« виде (3.95) вместе с условием его осуществимости (3.96). >т регулятор задан с точностью до функции Е, определяющей актер ПП. Для конкретизации регулятора следует задать Е эном виде.
Значительный интерес для приложений представляет случай, la уравнение переходного процесса линейно, т. е. Е имеет (3.98). Если матрица коэффициентов усиления Г устойчива, корни Хь .... Хп характеристического уравнения
<1е4|Г-М|-Г+у1Г-,+ ...+Y.-0 (3.104)
ш
имеют отрицательные вещественные части, то ПД x„(f) асимптотически устойчиво в целом. Если же среди корней уравнения (3.104) есть хотя бы один с положительной вещественной частью, то ПД неустойчиво [3].
Таким образом, установление асимптотической устойчивости программного движения сводится к исследованию расположения корней уравнения (3.104). Как известно (теорема Гурвица (4]), чтобы все корни уравнения (3.104) имели отрицательные вещественные части, необходимо и достаточно выполнение нера
венств
Al — Yi>0, Л2 —I |>0, Аз" 1Уз YjI
у, 1 0
Уэ У» Y1 >0,
А„-
Уз У4 У»
-УЯА„_, > 0 (det Л-И Л ||).
(3.105)
Условия (3.105), определяющие критерий устойчивости пХ "'Матрицы Г, принято называть условиями Рауза — Гурвица. Для случая п = 2 эти условия имеют вид
Yi > 0, | q > 0 или Yi >0, у, > 0. (3.106)
Для случая л = 3 условия Рауза — Гурвица записываем в виде
Yi > °’ L* J I > °» V» I J I > 0 нлн Yi > °. Уг > 0. YiYj > Уз-IУз Уг! IУз YjI
(3.107)
При проектировании регуляторов для управляющих систем роботов важно не просто обеспечить асимптотическую устойчивость ПД, но и предусмотреть определенный запас устойчивости. Эта задача применительно к линейному уравнению переходного процесса формулируется так: указать условия на матрицу коэффициентов усиления Г, при которых собственные числа Х|, ..., Х„ этой матрицы располагаются в полуплоскости
ReX<<Y. i=l......... (3.108)
Здесь у>0 — наперед заданный запас устойчивости. Важно отметить, что именно запас устойчивости придает замкнутой двигательной системе адаптивные свойства: он позволяет демпфировать достаточно малые возмущающие воздействия разной физической природы. Неравенство (3.108) определяет критерий устойчивости ПД с заданным запасом у.
Другим практически важным требованием к качеству переходного процесса является ограничение колебательности. Формально это требование сводится к тому, чтобы все собственные числа матрицы лежали внутри полуплоскости, определяемой
неравенствами
ReX<y» I ImX | < ₽.
(3.109)
119
Положительные числа у и ₽ можно рассматривать как динами* ческие показатели качества. Неравенства (3.109) определяют критерий асимптотической устойчивости ПД и колебательности ПЛ в замкнутой двигательной системе робота.
В общем случае качество переходного процесса в замкнутой линейной системе тесно связано с расположением корней характеристического уравнения (3.104) в левой комплексной полуплоскости. Этрт круг вопросов составляет предмет исследования теории модального управления [14].
Пусть, например, все корни уравнения (3.104) сосредоточены на действительной оси в точке — у. Тогда гарантируется асимптотическая устойчивость ПД с запасом устойчивости у, определяющим время переходного процесса.
Выбор правой части Е(е, t) в уравнении ПП (3.92) может осуществляться разными способами. Но если даже выбраны некоторая функция Е (например, Е(е, /) = Ге) и условия протекания переходного процесса, задача выбора параметров (например, матрицы Г в случае линейных уравнений ПП), определяющих его качество, может не иметь однозначного решения. Поэтому целесообразно оптимизировать этот процесс исходя из некоторого критерия качествл, имеющего ясный практический смысл.
Рассмотрим положительно-определенную непрерывную функцию У(е, /), которая характеризует текущее расстояние от переходного процесса до начала координат. Под локальной оптимизацией ПП будем понимать такой выбор функции Е в правой части (3.92) (с учетом естественных ограничений), при котором это расстояние уменьшается с максимальной скоростью. Такую задачу принято называть задачей оптимального демпфирования ПП [14]. Рассмотрим методику решения этой задачи с помощью функций Ляпунова.
Вычислим значение функции V(e, t) на ПП е(/) и найдем ее полную производную по t на основании (3.92):
+ (V V, Е> = W (е, Е, /).
Функция Е°, обеспечивающая оптимальное демпфирование переходного процесса, необходимо доставляет наименьшее возможное отрицательное значение функции lF(e, Е, t) среди всех допустимых Е. Пусть функции Е, определяющие уравнение ПП (3.92), подчинены ограничению
||Е(е,t>t0,
н W'(e. Е, 0= — ПеИ- Тогда функция Q(e. Е,/) достигает минимального значения при
E" = -(e*+4r)i$F- <3.110>
113
Формула (3.110) позволяет осуществить синтез уравнения ПП (точнее, его правой части Е = Е° как функции от е и /) с оптимальным демпфированием относительно функции V, играющей роль функции Ляпунова.
Важнейшим показателем качества ПП, определяющим производительность робота, является быстродействие. Переходный процесс е°(1) системы (3.92) будем называть оптимальным по быстродействию, если время перехода Т = tr — to из заданного состояния е(1о)=ео в желаемое конечное е(/г) = 0 минимально. Построим такой процесс, следуя идеям работы [14]. Рассмотрим ПП е(1) с постоянной по величине и регулируемой по направлению скоростью
е =Е(е,/), ||Е(е,/)|| = ся. (3.111)
Определим функцию Ляпунова
Й(е) = ||е||. (3.112)
Переходный процесс с оптимальным демпфированием относительно функции (3.112) определяется путем нахождения минимально возможного значения функции
Е’-ТГ-
Отсюда получаем
Е0(е,/) = -ся1|1. (3.113)
Покажем, что решение е(1) уравнений (3.111), (3.112) из любой начальной точки е0 попадает в начало координат. Подставим уравнение (3.113) в уравнение (3.111) и умножим полученное уравнение на ег. Тогда
14»е||2=-св||е|1- <зл14)
Интегрируя это уравнение, имеем
1|е(П11 = ||ео11-сж(/-/о).
Следовательно, ПП е(/) попадает в начало координат в момент Г = |е0|^*. (3.115)
Легко убедиться, что 7*0 является наименьшим возможным временем, за которое переходный процесс может попасть из заданного начального состояния в начало координат. Таким образом, в данном случае ПП с оптимальным демпфированием относительно функции Ляпунова (3.112) также является оптимальным по быстродействию.
Описанный метод аналитического синтеза регуляторов (автоматов стабилизации ПД) обладает значительной гибкостью н общностью: выбирая конкретный вид оператора управления U, подпространства Р/ и переходного процесса Е, легко получить
114
как некоторые известные (см., например, [12, 17, 22, 25, 31, 57, 58, 60—62, 64, 65]), так и новые законы стабилизации программного движения. Для реализации этих законов следует указать не только структуру регулятора, но и приемлемые значения его конструктивных параметров.
Рассмотрим семейство законов стабилизации программного движения вида [60, 61]
u = U[x, х,-|-Г(х — хр) |], (3.116>
где Г—устойчивая л X «-матрица коэффициентов усиления, удовлетворяющая в соответствии с (3.96) структурному ограничению
(х(/), хр(/) + Г[х.(/) — хр(/)]е Рр при всех />/0- (3.117)
Желаемый характер ПП в замкнутой системе (2.55), (3.116) можно обеспечить выбором матрицы Г. Пусть для определенности Г — устойчивая матрица с собственными числами ... ..., Хя. Тогда, как известно [3, 14], существуют положительные числа с и у, такие, что справедлива оценка
1|е(тКс||е0||ехр[-у(/-/о']. /><о. (3.118)
причем у^—max Re А,. Величина у характеризует запас устойчивости, а значит, и адаптивные возможности закона стабилизации программного движения (3.116).
Сформулируем условия работоспособности регулятора (3.116) с учетом ограничений на состояния и управления. Потребуем, чтобы программные движения хр(/) и хр(/) принадлежали множествам Q* и Qi F(QZ, Qu, £) с некоторыми запасами
Й! > с||е0И, б2 > с||е0||||Г||. (3.119)
Тогда
x(/leQx, x(/)eQx, хр (/) 4- Г [х (0 — хр (/)] е Qt.
Отсюда следует, что управление (3.116) является допустимым, т. е. u(/)eQu, Для момента окончания переходного процесса справедлива оценка
fpC/o + v-'In-^. (3.120)
где е — положительное число, характеризующее требуемую точность стабилизации ПД.
В заключение приведем примеры синтеза законов стабилизации программного движения для конкретных типов динамических моделей роботов. Сначала рассмотрим линейную модель, описываемую уравнением (2.73) или уравнением в канонической форме (2.77). Учитывая выражения (2.80), (2.81), закон стабилизации ПД в канонических переменных можно записать в виде [61]
u = bJ[yP +Г0(у — у,)-Аоу]. (3.121)
ПК
Здесь ур (t) — Sq 1 (8) xp (/); Го — устойчивая n X n-матрнца, удовлетворяющая структурному ограничению вида
Ур + го(У —Ур>)е Рр(6). (3.122)
где Рр(£) определено соотношением (2.81). Отметим, что (3.91) означает по существу только то, что матрица Го имеет такую же структуру, как и матрица Ао в (2.77), (2.78).
Используя преобразование (2.76), регулятор (3.121) можно записать в исходных переменных:
u = bo [So-1 хр + rso-1 (х — Хр) — A,,So' 'х ] =
= (Хр + Г (х - Хр) - Ах]г (SnSo)"‘ Ь, (3.123)
где Г = ЗоГоЗу|—устойчивая лХл-матрица, имеющая такие же собственные числа, как и матрица Го.
Рассмотрим теперь нелинейную модель, описываемую дифференциальным уравнением 2т-го порядка вида (2.82). В этом случае с учетом выражений (2.85), (2.86) закон стабилизации ПД имеет вид [57, 61]
u = A(q, |)(qp + r,(q-4p) + rt(q-qp)] + b(q. q, I), (3.124)
где m X /«-матрицы Г], Г2 таковы, что 2m X 2m-матрица Г вида
(3.125)
2 12
устойчива. Пусть для простоты Tj = — yil, Г2 = —у21. Тогда согласно неравенствам (3.106) для любых положительных чисел Yi и уз матрица (3.125) устойчива, и, следовательно, регулятор (3.124) обеспечивает асимптотическую устойчивость программного движения. Более того, в этом случае, как легко убедиться, алгоритмы адаптации в замкнутой системе (2.82), (3.124) автономны по всем координатам.
Движения ряда электромеханических роботов описываются нелинейными дифференциальными уравнениями порядка 3m вида (2.87). Закон стабилизации ПД для этих роботов имеет вид
u = A q. 6) [qp + Г1 (q — q„) + Г, (q — q/ 4- Гя (q — qp)| +
+ b(q, q, q, s), (3 126)
где m X т-матрнцы Г вида
Г|, Г2, Гз таковы,
(0 I 0 \ 0 0 1 Г, Г2 Г,/
что 3m X Зт-матрица
(3.127)
на
Рис. 3.4. Схема динамического управления программным движением.
устойчива. Пусть Г> = —yil. Г2 = —у21, Г3 = —у31, причем па. раметры Yi, у2, у3 удовлетворяют неравенствам (3.107). Тогда регулятор (3.126), (3.127) обеспечивает асимптотическую устой-чивость ПД и автономность ПП по всем координатам.
Схема динамического управления двигателями постоянного тока, обеспечивающая стабилизацию программного движения исполнительного механизма робота, представлена на рис. 3.4. Здесь обозначения те же, что и на рис. 3.3.
Программатор генерирует то ПД, которое предстоит отра-ботать двигательной системе робота. Регулятор, реализующий закон стабилизации программного движения вида (3.126), использует обратную связь по обобщенным координатам q\, ... ..., qm, а также по их первым и вторым производным. При подходящем выборе матрицы коэффициентов усиления (3.126) в такой схеме удается обеспечить не только асимптотическую устойчивость ПД в целом, но и желаемый характер ПП.
$ 9. СИНТЕЗ И ОПТИМИЗАЦИЯ ТЕРМИНАЛЬНОГО УПРАВЛЕНИЯ
Целью терминального управления является перевод робота из заданного начального состояния х0 е Qx в желаемое конечное xi е Qx за конечное время Т = tT — /о- Эта цель реализуется с помощью управляющей системы, работающей в режиме терминального управления, т. е. управления конечным состоянием. В состав управляющей системы входят программатор и регулятор. Программатор играет роль системы наведения, он строит (заранее или в процессе управления) программные движения, связывающие х0 и xt. Регулятор служит для фактического осуществления ПД путем демпфирования отклонений реального движения робототехнической системы х(/) от ПД хр(/). Тем самым обеспечивается устойчивость процесса наведения.
Простейший метод терминального управления заключается в предварительном построении ПД хр(/) и его реализации с помощью программного управления up(Z) вида (3.1). (Для построения ПД можно использовать описанные ранее алгоритмы.) Недостатком такого программного управления является его жесткость — отсутствие возможности изменить управление в реальных условиях, которые всегда отличаются от идеальных, принятых при построении ПД.
Более эффективным представляется аналитический синтез терминального управления в виде (3.3) [61].
Подставляя выражение (3.3) в (2.55), получаем следующее уравнение переходного процесса:
е(/) = 0, /<=[/0, /т],
118
откуда следует, что х(/)=хР(/) при всех / е [/0. /г], если хР(<о) = х(/0). Отметим, что терминальное управление (3.3) яв* ляется частным случаем общего закона управления ПД (3.95), когда Г = 0.
Рассмотрим теперь задачу оптимизации терминального управления. Пусть х® (/), / е |/0, /г], — оптимальное ПД. Это значит, что х°(/) доставляет минимум функционалу качества (3.105) при соблюдении дифференциальной связи (3.91) и ограничений (3.89), (3.90). Подставляя оптимальное ПД x°(Z) в формулу (3.1), непосредственно получаем оптимальное программное управление [61, 62]
i4(/) = U[x®(/), xJ(Z), I], /евро, /г]. (3.128)
Очевидно, что u° (0 является допустимым управлением, т. е.
u®(/)eQu при всех / t= [/0, /г].
Управление (3.128) обеспечивает точное наведение робота по оптимальной программе х^(/) только в идеальных условиях, когда параметры ( известны и не существует никаких возмущений. В этом случае ввиду единственности решения уравнения динамики (2.55) по начальным данным реальное движение х(/) замкнутой двигательной системы (2.55), (3.128) совпадает с х®(/) при всех /с|/о,/г]. Однако на практике всегда имеются те или иные возмущения — дрейф параметров, неточность задания начальных условий, вычислительные погрешности датчиков, неучтенные нелинейности и помехи. Эти возмущения неизбежно приводят к отклонению х(1) от х°(1),причем ошибкае(/)=х /) — — х’(0 с течением времени возрастает; вследствие этого цель управления не будет достигнута.
Таким образом, оптимальное программное управление (3.128) в реальных условиях оказывается неработоспособным. Тем не менее оно полезно, так как подсказывает явный вид оптимального терминального управления с обратной связью по вектору состояний х(/) [61, 62]:
u°(/) = U[x(/), х“(П, I], /е[/0, /г]. (3.129)
Синтезированное оптимальное управление (3.98) переводит робот из любого начального состояния хо е Q* в терминальное XieQ, за время Т. Однако замкнутая система (2.55), (3.129) находится на границе устойчивости: даже небольшие возмущения могут приводить к значительным ошибкам в управлении. Это свидетельствует о практической неработоспособности роботов с оптимальным управлением (3.129).
Важнейшим условием практической пригодности регуляторов является грубость замкнутой системы, т. е. сохранение работоспособности при воздействии разных возмущений. Поэтому за
119
кон оптимального терминального управления должен синтезе, роваться с учетом требования грубости. Этому требованию удов, летворяет следующее семейство законов терминального управ, леиия [61, 62]:
u(/) = U[x(0, х?(0 + Г[х(П-х2(/)], t], t e [/0, /г], (3.130)
где Г —устойчивая лХл-матрица коэффициентов усиления удовлетворяющая структурному ограничению ’
(х, х?+Г(х — xj))e PF. (3.131)
Оптимизационное управление (3.130) обладает следующими свойствами: оно совпадает с выражением (3.123) при х(/) = = х’(/), /е[/0./г], а при наличии начальных возмущений «(/о)ч*0 обеспечивает затухание переходного процесса. При этом вид и время ПП, а также запас устойчивости замкнутой системы целиком определяются выбором Г.
Введение в закон управления (3.129) специальной обратной связи в виде добавки Г[х(/) — х“(/)| означает определенную регуляризацию оптимального управления (3.129). Такая регуляризация обеспечивает грубость замкнутой системы (2.55), (3.130). Важно отметить, что оптимизационное управление (3.130) позволяет не только стабилизировать оптимальное ПД х^(/), но и регулировать в широком диапазоне вид ПП путем выбора «параметров регуляризации». Тем самым одновременно обеспечивается как асимптотическая устойчивость ПД х'^(/>, так и требуемое качество управления.
Семейство законов управления (3.130) по существу определяет устойчивый метод приближенного синтеза оптимального регулятора в задаче терминального управления. В основе его лежит описанная ранее идея регулирования оптимального управления с помощью специально организованной обратной связи. Такой подход существенно отличается от классических схем регулирования, основанных на введении в функционал ка* чества малой стабилизирующем «добавки». При этом возникают трудности, связанные с выбором этой «добавки» и необходимостью решения оптимизационной задачи дл!я нового функционала. Предлагаемый метод синтеза и регуля!рпзацни оптимального управления свободен от этих недостатков.
Глава 4
АДАПТИВНОЕ УПРАВЛЕНИЕ РОБОТАМИ
$ 1. ЦЕЛИ И ЗАДАЧИ АДАПТИВНОГО УПРАВЛЕНИЯ
Возможности управляющих систем роботов первого поколения весьма ограничены. Это связано с тем, что при их проектировании и расчете конструктор обычно исходит из того, что динамические характеристики робота хорошо известны и неизменны, а условия его эксплуатации детерминированны. Однако в действительности это не так: многие параметры робота и свойства окружающей среды не только заранее не известны, но и могут изменяться непредсказуемым образом в широком диапазоне.
В подобных нестационарных условиях с неопределенностью описанные в главе 3 законы программного управления и сервоуправления могут оказаться неэффективными. Если тем не менее реализовать эти законы, предварительно заменив в них неизвестные параметры некоторыми их оценками, то в замкнутой двигательной системе робота возникнут неконтролируемые параметрические возмущения. Их влияние в сочетании с неизбежными на практике начальными и постоянно действующими возмущениями приводит к нежелательным динамическим эффектам— снижению точноети отработки ПД, автоколебаниям или неустойчивости. Наличие внешних препятствий (особенно подвижных) может привести к столкновению робота с преградой. В результате может возникнуть аварийная ситуация, и цель не будет достигнута.
Новый подход к управлению роботами в условиях неопределенности основывается на принципе адаптации управляющей системы к заранее не известным и изменяющимся условиям эксплуатации. В процессе адаптации происходят самонастройка н приспособление управляющей системы к фактической обстановке и свойствам робота. Реально это проявляется в изменении структуры и параметров управляющей системы так, чтобы гарантировать достижение цели и соблюдение конструктивных ограничений в нестационарных н неопределенных условиях эксплуатации.
121
Характерной чертой адаптивных управляющих систем ро» ботов является то, что недостаток априорной информации и не* контролируемый дрейф параметров компенсируются в них над* лежащей обработкой сенсорной информации, поступающей от технических органов чувств. Для обработки этой информации служат алгоритмы адаптации, осуществляющие самонастройку параметров ПД и закона управления.
Наличие развитых средств очувствления и связанных с ними алгоритмов адаптации принципиально отличает адаптивные управляющие системы роботов от систем программного управления, описанных в предыдущей главе. Благодаря этим средствам и алгоритмам осуществляется автоматическое приспособление робота к неопределенным и изменяющимся условиям эксплуатации.
Адаптивная постановка основных задач управления роботами в отличие от классической предполагает, что конструктору неизвестны (полностью или частично) динамика робота н окружающая его обстановка. Обычно неизвестны ряд параметров £ уравнения движения (2.56) и постоянно действующие воз* буждающие возмущения л. Вследствие этого законы стабилизации ПД, самонаведения и терминального управления, синтезированные в главе 3 с точностью до параметров нуждаются в доопределении. Дополним указанные законы алгоритмами поиска приемлемых оценок т неизвестных параметров |, использующими обратную связь от информационной системы робота. Если эти алгоритмы обеспечивают достижение заданной цели управления для любых возможных значений параметров (sQi и возмущений xeQ.,, то называем их алгоритмами адаптации (АА). Соответствующие законы управления с автоматической настройкой параметров т в силу АА будем называть адаптивными в классе неопределенности X Qi-
Задача адаптации заключается в синтезе АА с требуемыми свойствами. Решение ее тесно связано с контролем качества управления. Для формализации цели адаптации введем функционал качества вида Ф = Ф(и, х, т). Будем считать, что значения величин, входящих в выражение для Ф, могут быть измерены или вычислены в любой момент времени /. Это требование необходимо для реализуемости АА.
Цель адаптации удобно задавать в форме неравенств, связывающих управления и, состояния х и оценки т. В качества таких неравенств можно взять континуальную систему неравенств вида
ф(г,/1иФ(и(/), х(/), г] >0, (4.1)
Если эти неравенства сконструированы таким образом, что их выполнение обеспечивает достижение цели управления, то на* зовем их эстиматорнымн.
122
Задача решения эстиматорных неравенств (4.1) часто допускает интерпретацию как задача приближенной оптимизации некоторого функционала, характеризующего качество адаптации. Обозначим этот функционал'через Фо: QuXQxXQt — /?’. дозьмем в качестве Фо функцию со следующими свойствами: функция Фо(и, х, т) выпукла по т, причем
Ф0(и, х, l)= min Фо (и, х, т)аО, ?гФ0(и, хД) = 0,
т. е. минимум Фо достигается в точке 5» являющейся вектором истинных значений параметров двигательной системы робота. Приближенная минимизация функционала Фо с точностью до б сводится к решению системы неравенств вида (4.1), где ф[и, х, т] =б — Ф0(и,х, т). Очевидно, что полученные таким образом эстиматорные неравенства разрешимы с запасом 6 > 0 и «вырезают» в пространстве параметров выпуклые области.
Значение эстиматорной функции ср(т, /), вычисленное на текущей оценке можно трактовать как выигрыш в мо-
мент /. Ясно, что этот «выигрыш» не может превышать величины 6. Если же он отрицателен, т. е. эстиматорные неравенства (4.1) нарушены, то выигрыш превращается в проигрыш. В этих терминах цель адаптации можно интерпретировать как максимизацию текущего выигрыша с точностью до б. Тем самым установлена тесная связь между критериями адаптации, формулируемыми в терминах решения эстиматорных неравенств, и оптимизационными критериями адаптации.
Решение задачи адаптации сводится к синтезу алгоритмов решения эстиматорных неравенств (4.1). Смысл этих неравенств заключается в том, что если они нарушаются при некотором т = т(/), то это свидетельствует о неудовлетворительности текущей оценки т(/) и необходимости ее корректировки. Если же неравенства (4.1) выполнены на траектории АА, то это говорит о приемлемости как самих оценок, так и синтезированного на их основе адаптивного управления. Таким образом, алгоритм решения неравенств (4.1) выступает как АА. Этим объясняются важная роль и значение эстиматорных неравенств в теории адаптивного управления роботами.
Характерной чертой эстиматорных неравенств (4.1) является то, что в каждый момент времени t известно лишь текущее значение функции <р(т. О, но не будущее ее значение. Последние зависят от будущего выбора оценок и управлений и поэтому принципиально не могут быть определены в момент Л Это означает, что АА должен находить решение не заданных заранее эстиматорных неравенств (4.1). Ясно, что редуцированную таким образом задачу адаптации возможно решить не всегда.
Перейдем к описанию условий и методов решения эстиматорных неравенств (4.1), ориентированных на синтез адаптивного управления. Прежде всего нужно ответить на следующие
123
вопросы: существует ли решение неравенств (4.1); в каком классе алгоритмов ищется решение; какими свойствами долж» ны обладать эти алгоритмы?
Будем считать, что неравенства (4.1) определены при каж. дом t > t0 в достаточно широкой, но все же ограниченной об. ласти Qt — Qv Множество Q, решений неравенств (4.1) (если оно непусто) локализуется в области Qj, т. е.
0>0, />/0)c:Qt (4 2)
Проблема существования решения эстиматорных неравенств (4.1) разрешается просто: функционал качества Ф, определяю* Щнй левую часть (4.1), конструируется так, чтобы система (4.1) имела идеальное решение т, = 1 с некоторым запасом б > О, т. е.
ф(т„ /)иб>0 при всех (4.3)
Решение неравенств (4.1) будем искать в виде
т(/) = А [»(П], />/0- (4.4)
Здесь т(/)—текущая оценка неизвестного решения т«; а(/) — информация, накопленная к моменту t; А — оператор адапта* цни, действующий из информационного пространства {$(/)} в пространство оценок (т). В качестве $(/) может использоваться, например, только информация о значениях функции ф и ее гра* диента в точке (т, /) или информация о своей предыстории иЭ-менения функции ф и ее градиента на траектории АА (4.4). Вид оператора адаптации А зависит от выбранного метода ре* шения (4.1).
Большинство методов адаптации можно разбить на два класса |54, 68, 73]: I) непрерывные методы, когда оценки т(() определяю! как решение дифференциального уравнения адап* тации; 2) дискретные методы, когда оценки т(/) = т(/*) находят в дискретные моменты времени /0, Л, /г. ••• в соответствия с итеративным (рекуррентным или многошаговым) АА.
Общая схема непрерывных методов такова: оценки т(/) получают как решение дифференциального уравнения адаптаций
т(/) = А]т(/), »</)], т(/0) = т0, (4 5)
Здесь то — произвольная начальная оценка из Q», а оператор А таков, что идеальное решение т. = £ системы (4.1) удовлетворяет уравнению (4.4), т. е. А(т«, s(/)]eO при всех t to- ПрЙ благоприятных (формулируемых ниже) условиях оценки т(0 сходятся к идеальному решению т, или в некоторую его окрестность (4.2).
124
Дискретные методы адаптации описываются следующей си* стеной соотношений:
т (/) = т*, I е [/*, /4+1], /*4.| = /* + 6, (4.6)
т»+1 = т* + A[s(4)1, * = 0, 1, 2, ...
Здесь то — произвольная начальная оценка; /'* — первый момент нарушения эстиматорных неравенств (4.1) при т = т*, t 6 — время, необходимое для вычисления новой оценки t*+i в соответствии с (4.6) по имеющейся к моменту /* информации s(Z*); А —оператор адаптации, такой, что идеальное решениё т« является его неподвижной точкой, т. е. A[s(/)]®0 прй т* = т., t > /*.
В зависимости от того, в каком классе функций выбирается оператор адаптации, дискретные методы адаптации подразделяются на рекуррентные н многошаговые. Если оператор адап* тации в (4.6) имеет вид
A [s (/'*)] = А [т4, т*_,.ф(т4, /;)], (4.7)
то в соответствии с терминологией, принятой в работе [61], получаем класс многошаговых АА с полной памятью по т.
Регулируя «глубину» памяти алгоритмов типа (4.6), (4.7), можно получать разные классы дискретных АА. Зафиксируем целочисленный параметр у, характеризующий «глубину» памяти алгоритма. Тогда многошаговые АА с заданной «глубиной» па* мятн можно представить в виде (4.6), где
а(»(/;)]-А[тд, та_,......ф(та, /;)]. (4.8)
При у = 0 получаем класс рекуррентных АА вида (4.6), где
А(»(**)] — Ар», Ф(Ъ. /;)]. (4.9)
Таким образом, решение задачи адаптации сводится к конструированию непрерывных или дискретных (рекуррентных или многошаговых) АА вида (4.5) или 44.6) —(4.9), которые генерируют траекторию т(/), f /о» или последовательность оценок т*, Л = 0, J, 2, ..., сходящуюся к некоторому решению эстй-маторных неравенств (4.1).
Важнейшими требованиями, предъявляемыми к АА, являются: 1) конечная сходимость, понимаемая как конечность времени нарушения эстиматорных неравенств на траектории АА; 2) инвариантность структуры АА по отношению к выбору начальной оценки то; 3) помехоустойчивость, т. е. устойчивость АА при наличии разного рода возмущений и погрешностей; 4) реализуемость АА и простота необходимых вычислений; 5) оптимальность АА, т. с. выбор оператора адаптации (или еге параметров) из некоторого условия оптимальности.
126
Цель адаптивного управления зависит от режима эксплуатации робота и решаемой задачи. Обычно автономный робот функционирует в двух режимах: самопрограммирования движений и управления движением.
В режиме самопрограммирования исходя из заданных граничных условий, конструктивных ограничений и функционала качества строится и оптимизируется ПД двигательной системы робота. При построении ПД необходимо учитывать требование обхода препятствий. Это означает, что прн точной отработке синтезированного ПД ни одно звено исполнительного механизма робота не должно коснуться препятствия.
Решение этой задачи осложняется тем, что препятствия зачастую заранее не известны. В таких случаях возникает необходимость адаптации к ним. Формально задача может быть сведена к решению некоторой системы неравенств, описывающих условия обхода препятствий. Для фактического решения этих неравенств относительно параметров искомого ПД можно использовать охарактеризованные ранее АА.
В режиме управления робот решает одну из следующих задач: стабилизация ПД, терминальное управление и самонаведение.
Цель управления в задаче стабилизации ПД заключается в обеспечении е-близостн реального и ПД по прошествии некоторого времени переходного процесса Тр « tp — to, т. е.
||x(t) — Хр(0И < е при всех />/р(/0. *о» I» «)• (4.10)
Цель терминального управления состоит в обеспечении е-блнзо-сти реального и ПД в заданный конечный момент времени Т к tT — to, т. е.
Цх(/Г) — хр(/г)|| < е. (4.11)
Наконец, цель самонаведения заключается в переводе робота в е-окрестность заданного состояния xj за некоторое конечное время Тр tp — t0, т. е.
IIX (tp) - х, II < е. (4.12)
Для достижения целей (4.10) — (4.12) необходимо синтезировать закон управления u = u(t,х,т) с обратной связью по вектору состояний и с АА, который, естественно, не зависит от неизвестных параметров $ и возмущений л и обеспечивает достижение названных целей для любых значений | и л из класса неопределенности QtXQn. Такой закон управления будем называть адаптивным в классе Qi X Qn- При синтезе и расчете адаптивного управления его параметры должны быть выбраны так, чтобы гарантировать выполнение конструктивных ограничений на состояния и управления на всем рассматриваемом интервале движения.
126
9 2. КЛАСС НЕОПРЕДЕЛЕННОСТИ, ПАРАМЕТРИЧЕСКАЯ ЧУВСТВИТЕЛЬНОСТЬ И ИНВАРИАНТНОСТЬ
Постановка и решение задач адаптивного управления существенным образом зависят от того, какой точный смысл вкладывается в понятие адаптивности. Для того чтобы определить это щщщгие, Й2£пользуе\}£я введенным понятием класса неопределенности. Отметим, что неопределённость величин J н л, входящих в уравнение движения (2.56), порождает своеобразные информационные ограничения на управляющую систему. Рассмотрим подробнее вид и природу этих ограничений.
Для многих роботов характерно, что дрейф параметров £(/) двигательной системы и постоянно действующие возмущения *(/) заранее не известны. Однако обычно известно, что они удовлетворяют информационным ограничениям вида
fc(-)<=tfb я(.)еУя. (4.13)
Здесь Nt'Nn — некоторые известные множества, заданные в соответствующих функциональных пространствах. Например, можно считать, что £(/) и л(/) принадлежат классу функций ограниченной вариации, причем их реализации во времени неизвестны.
Информационные ограничения (4.13) определяют по существу класс неопределенности условий функционирования робота. Понятно, что чем шире этот класс, тем, вообще говоря, сложнее задача синтеза эффективного закона управления.
При информационных ограничениях (4.13) каждому выбранному закону управления соответствует не одно изолированное движение двигательной системы, а целое семейство возможных Движений. Это семейство получается путем объединения решений уравнения динамики (2.66) при заданном управлении и(/) по всем неопределенным величинам £(°), л(°) удовлетворяющим ограничению (4.13).
Выбирая тот или иной закон управления ПД, можно регулировать положение указанного семейства по отношению к заданному ПД хр(/). При этом закон управления может определяться либо как функция времени / (программное управление), либо как функция текущих состояний x(f) (управление с обратной связью), либо как функция, аргументами которой являются текущее состояние x(f) и текущая оценка x(t) неизвестного вектора параметров £(/) (адаптивное управление).
В первом случае необходимо, чтобы управляющая система Располагала информацией о ПД хД/) и дрейфе параметров £(/). Во втором в нее кроме хД/) и |(f) поступает дополнительная информация о реализовавшемся (текущем) состоянии двига-Тельной системы, т. е. обратная связь по х(/). Наконец, при Маптивном управлении, когда дрейф параметров >(/) неиэве-
127
стен, помимо информации о ПД хр(1) и обратной связи по со. стоянию х(<) используется текущая оценка т(/) неизвестно КО. формируемая в процессе адаптации (самонастройки) управляющей системы.
При увеличении степени информированности управляющей системы о свойствах двигательной системы робота и условиях его эксплуатации результат управления, вообще говоря, улучшается. Поэтому при наличии существенной неопределенности адаптивное управление предпочтительнее управления с обрат, ной связью, а последнее — предпочтительнее программного.
Критерием предпочтительности закона управления может служить нечувствительность (или параметрическая инвариант-кость (41, 73]) замкнутой системы относительно изменений неизвестных параметров: при адаптивном управлении нечувствительность максимальна, при программном — минимальна. Следовательно, между проблемой адаптивного управления, с одной стороны, и проблемой чувствительности (параметрической инвариантности) робота как объекта управления — с другой, существует тесная связь.
В общем случае класс неопределенности не ограничивается условиями (4.13). На практике прямое измерение вектора текущего состояния х(/) (и тем более его производной х(/)) зачастую невозможно. Методам косвенного измерения или оценки х(1) присуща неустранимая погрешность яд(/)= х(/)—х(/), где х(/) —измеренное (оцененное) состояние. Значение погреш ности л«(0 неизвестно, но обычно она удовлетворяет априорному ограничению
Н«х(/)11<бж. (4.14)
Аналогично определяется погрешность измерения (оценивания) величин х(1):
И«Я/)11<бь (4.15)
где «х(/)= х(/)—х(/); х(/) — измеренное (оцененное) значение вектора фактической скорости изменения текущего состояния.
Вследствие погрешностей измерения, удовлетворяющих информационным ограничениям (4.14), (4.15), теперь и начальное состояние двигательной системы является неопределенным: на практике известно х(/о), а не фактическое начальное состояние х(/о)=хо- Более того, законы управления с обратной связью, в том числе и законы адаптивного управления, являются теперь функциями измеренного состояния х(/).
Зная уравнение движения (2.56), информационные ограничения (4.13) —(4.14) и измеренную реализацию х(1) текущего состояния, можно построить семейство всевозможных движений, заданных с точностью до погрешностей измерений. Среди этих 128
движений находится неизвестное истинное движение х(/) дви* гательной системы, а также ПД хр(/). Семейство возможных движений в этом случае содержит всю априорную и текущую информацию об описанном процессе управления и измерения. Чтобы сузить это семейство, необходимо уменьшить исходную неопределенность, задаваемую информационными ограничениями (4.13) —(4.15). Последнее как раз и достигается в процессе адаптации.
Следует отметить, что по самой сути задачи управления в условиях неопределенности адаптивная управляющая система не имеет информации о том, какие значения принимают неопределенные параметры |(0 и возмущения я(/) в процессе движения. Она располагает лишь информацией о реализовавшемся состоянии х(/) двигательной системы, да и то с неизвестной погрешностью лх(/), удовлетворяющей ограничению (4.14). По этим данным в процессе адаптации сначала определяется опенка т(0 неизвестных параметров, а затем синтезируется и сам закон управления с обратной связью по х(/).
Будем описывать отклонение действительных, но неизвестных параметров |(<) от их оценок т(/), используемых в управляющей системе, новой переменной ®(/) = ?(/)—т(/). Вектор-функция ®(0 характеризует параметрические возмущения в замкнутой системе, а величина ||ш(011—текущую неопределенность. Отметим, что априорная неопределенность ||о>(/о)11 не превышает величины diatn Qj.
Цель адаптации заключается в гашении параметрических возмущений ш(0- Поэтому критерием адаптивности может служить соотношение
lim ||® (/)|| = 0, />/0-
Согласно этому критерию среди всех возможных оценок т(/) неизвестных параметров отбираются те, которые асимптотически приближаются к истинным параметрам ?(/). По существу здесь речь идет об асимптотической идентификации параметров Двигательной системы робота.
Это требование, однако, является излишне жестким. На са* мом деле для успешного управления точной идентификации вовсе не требуется. Более того, при управлении на конечном интервале времени асимптотическая идентификация невозможна.
Если управляющая система адаптивна, то величина 11<»>(/)|| Должна монотонно убывать, т. е. параметрические возмущения Должны гаситься. При этом информация о динамических свойствах робота, вообще говоря, увеличивается, а неопределенность, наоборот, уменьшается.
Прежде чем перейти к синтезу законов адаптивного управления роботами, целесообразно рассмотреть следующие вопросы: как влияют неизвестные параметрические и постоянно дей-
б Зак. т
129
слнующие возмущения на переходные процессы; как оценить чувствительность замкнутых систем по отношению к параметрическим возмущениям; нужно ли вообще прибегать к адаптивному управлению и в каких случаях?
В предыдущей главе при аналитическом синтезе управляющей системы предполагалось, что уравнение (2.55) адекватно описывает динамику робота. В действительности это уравнение -вляется лишь приближенной моделью динамики, поскольку в реальных условиях на робот действуют различные возмущения, а управляющая система реализует синтезированный закон управления с неизбежными на практике вычислительными и инструментальными погрешностями.
Полная модель, составленная с учетом постоянно действующих возмущений л(1), имеет вид (2.56). Здесь вектор-функция я(() представляет собой неопределенные фактоРы> характеризующие неадекватность «идеальной» модели (2.55). К числу таких факторов относятся неучтенные нелинейности, разного рода внешние воздействия и помехи.
На практике постоянно действующие возмущения л(/) неизвестны и не могут быть измерены. Вектор-функция л(() обычно предполагается только равномерно ограниченной, т. е.
||«(011<с1, при всех t>l0. (4.16)
Здесь — параметр, характеризующий уровень постоянно действующих возмущений.
Классическая теория управления обычно исходит из того, что параметры I уравнения движения (2.56) постоянны н известны. Однако в действительности это предположение не выполняется. Для роботов характерно, что параметры £ изменяются в зависимости от нагрузки, внешних условий (температура, давление, влажность окружающей среды), длительности эксплуатации (износ и старение отдельных элементов и узлов) и т. п. Обычно значения параметров | известны либо приближенно (с точностью, определяемой технологическими допусками на изготовление элементов и узлов), либо неизвестны вообще. Это обусловлено, с одной стороны, отсутствием средств для непосредственного их измерения, а с другой — возможностью непредсказуемых изменений этих параметров в широком рабочем диапазоне Q*.
Неопределенность и непредсказуемый дрейф параметров | могут оказывать существенное влияние на поведение робота. В самом деле, синтезированные в предыдущей главе неадаптнв-ные законы управления явно зависят от параметров |. Если значения этих параметров неизвестны, то в управляющей системе приходится использовать нх оценку т. В результате • замкнутой системе возникают параметрические возмущения •»(/) = КО— т, приводящие к изменению характера ПП.
Такие возмущения — явление весьма нежелательное. На практике они могут приводить (и, действительно, приводят) к умень
1В0
шению точности отработки ПД, автоколебаниям или даже потере устойчивости. Тем самым параметрические возмущения не только ухудшают качество ПП, но н могут порождать аварийные ситуации.
Исследование влияния параметрических возмущений на изменение динамических свойств замкнутой системы составляет предмет изучения теории чувствительности. В рамках этой теории степень указанного влияния оценивается обычно с помощью функций чувствительности.
Различают прямые и косвенные оценки чувствительности. Прямые оценки характеризуют влияние параметрических возмущений непосредственно на ПП. При этом изучение бесконечно малых параметрических возмущений дает возможность оценить тенденцию поведения замкнутой системы. Анализ влияния конечных, но достаточно малых параметрических возмущений позволяет выделить и приближенно оценить фиктивное движение, определяемое как разность желаемого и реального ПП в «возмущенной> замкнутой системе.
Такой подход приводит к дифференциальным уравнениям чувствительности. Знание этих уравнений, а также их решение (функции чувствительности) особенно важно при синтезе результатов, обеспечивающих малую чувствительность замкнутой системы по отношению к параметрическим возмущениям.
Косвенные оценки чувствительности в отличие от прямых оценок характеризуют изменение того или иного показателя качества ПП в зависимости от параметрических возмущений. Естественной мерой чувствительности в задачах оптимального управления является отклонение функционала качества, вызванное параметрическими возмущениями, от минимального значения. Далее при синтезе адаптивного управления в роли косвенных оценок чувствительности выступают эстиматорные функции.
Перейдем теперь к анализу влияния начальных, параметрических и постоянно действующих возмущений на динамику роботов. Для определенности рассмотрим класс законов управления вида (3.116), (3.117), обеспечивающих асимптотическую устойчивость ПД в идеальных условиях, когда параметры £ известны, а возмущения л(/)вО. Поскольку на самом деле дрейф параметров неизвестен, воспользоваться законом управления (3.116), вообще говоря, нельзя. Однако можно, задавшись некоторой оценкой т из множества Q\, найти закон управления ПД из соотношения
4-Ге = F (х, и, г), (4.17)
где е = х(/) — х₽(/). Отметим, что при т — 1(f) этот закон совпадает с (3.116).
••
131
Вычитая уравнение (4.17) из уравнения (2.56), получаем «возмущенное» уравнение ПП
е —Ге = Д4-я. (4.18)
Здесь Д m F(e 4- хр, u, |) — F(e 4- хр, и, т)— вектор-функция, характеризующая параметрические возмущения. Во многих случаях функция F в уравнении движения (2.56) линейна по третьему аргументу. Поэтому можно считать, что
Д = С(е4-Хр, и)®, где G(e4-xe, и)—некоторая матрица-функция размерностью «Хр
Уравнение (4.18) при т = |(/) описывает желаемый ПП с точностью до постоянно действующих возмущений л(1). Реальный же процесс е = е(/, ш, я) как решение уравнения (4.18) зависит от параметрических и постоянно действующих возмущений.
Исследование влияния параметрических возмущений ш(г) на динамику замкнутой системы (4.18) начнем с прямой оценки чувствительности. Для малых возмущений решение уравнения (4.18) можно разложить в ряд Тейлора
е«. ®, •••» (4-Ю)
где e.(f) удовлетворяет уравнению (4.18) пои т ={(/).
Коэффиценты линейных членов ряда (4.19) называются Функ* циями чувствительности первого ряда порядка, или просто функциями чувствительности. Согласно данному определению эти функции имеют вид
I )_|...........(МО)
< II/ -Т/
Вектор s(/) = l 8/(/) If., размерностью «Хр называется вектором чувствительности.
Уравнение (4.18) относительно величин первого порядка малости по до можно представить в следующем виде: р г р л
ё. + £ — Гр. 4- £ J *= О(е4- х„, и)® + я.
Вычитая из этого уравнения уравнение (4.18) при т = £(/), получаем уравнение фиктивного движения
g ii®, — Г g S((e. 4- xP. u)
132
порожденного параметрическими возмущениями. С этим уравнением тесно связаны уравнения чувствительности
st — Г», = G, <е, + хв, и), i = 1.р. (4.21)
В качестве начальных условий для уравнений (4.21) естественно взять нулевые: s,(/0) = 0, i = 1, ..., р.
Таким образом, функции чувствительности s,(/) определяются как решения системы линейных дифференциальных уравнений чувствительности (4.21). Вследствие устойчивости матрицы Г уравнения (4.21) устойчивы. Их решения имеют вид
‘г
»«(Лв^ ехр[Г(/—-0 ] Gj |е.(0. 4-хр:0 , u О]</0 (4.22)
t.
Обозначим через у абсолютную величину наибольшей вещественной части собственных чисел матрицы Г. Предположим, что ||G/|| Ct. Тогда очевидно ||s>(/)|| пропорциональна с, н обратно пропорциональна у. Отсюда следует, что нечувствительность замкнутой исполнительной системы по отношению к параметрическим возмущениям возрастает с возрастанием величины у, которая играет роль запаса устойчивости в замкнутой системе (4.18).
Свойство нечувствительности (совпадающее по существу с параметрической е-инвариантностью |3, 70]) играет важную роль при управлении роботом в условиях неопределенности. Отметим, что чувствительность замкнутой системы к параметрическим возмущениям можно регулировать в широком диапазоне путем варьирования матрицы коэффициентов усиления Г.
Анализ влияния параметрических возмущений на качество ПП в замкнутой системе удобно проводить с помощью вектор-функцнн Л = А(<о). Эту функцию можно интерпретировать как косвенный показатель чувствительности.
Для количественной оценки ПП предположим вначале, что параметрические возмущения таковы, что замкнутая система (4.18) устойчива. Тогда очевидно, что переменные е, х. и будут ограничены и, как следствие, будут ограничены матрица-функция G(e-f-Xp, и) и вектор-функция Л(ы). Обозначим через с« параметр, такой, что ||G(x, u)||^ Cq. В этих условиях справедлива оценка
|| е (/) || < с exp I— у (/ — /01] + су-' (с0II ® II4- с„), (4.23) где с н у—положительные числа, зависящие только от выбора матрицы Г. Из этой оценки следует, что точность осуществления ПД принципиально ограничена уровнем параметрических и постоянно действующих возмущений Влияние же начальных возмущений е(/о)=х(7о)—xp(Zo) с течением времени становится сколь угодно малым.
133
Оценка (4.23) показывает также, насколько чувствителен ПП к параметрическим возмущениям, не нарушающим устойчивости замкнутой системы. Очевидно, что даже при благоприятном характере параметрических возмущений (когда замкнутая система (4.18) устойчива) возможно не только уменьшение точности стабилизации ПД, но и нарушение конструктивных ограничений на состояния и управления. Это свидетельствует о неэффективности или непригодности рассматриваемых законов управления с постоянными оценками т при непредсказуемом дрейфе параметров КО двигательной системы.
Зависимость показателя чувствительности Л от параметрических возмущений <> может быть такой, что замкнутая система (4.18) окажется неустойчивой. В этом случае ПП становится неудовлетворительным: реальное движение х(1), отклоняясь от ПД Хр(/), с течением времени приводит к нарушению конструктивных ограничений на состояния и управления. Вследствие этого замкнутая система теряет работоспособность.
Резюмируя вышеизложенное, можно утверждать, что параметрические и постоянно действующие возмущения в замкнутой системе не только уменьшают точность отработки ПД, но и могут порождать нежелательные динамические эффекты (автоколебания, неустойчивость). Поэтому возникает необходимость в адаптивной настройке параметров закона управления как радикальном средстве компенсации параметрических возмущений н улучшения качества ПП. Как будет показано, адаптация реализуется в процессе многошаговой или непрерывной самонастройки параметров закона управления на основе сигналов обратной связи о фактическом состоянии робота и окружающей среды.
Адаптивное управление роботами, конечно, сложнее, чем обычное программное управление, сервоуправление по программе или самонаведение. Однако при наличии достаточно мощных ЭВМ и микропроцессоров, реализующих закон адаптивного управления, такое усложнение в разумных пределах допустимо. В то же время открывается возможность построения адаптивных роботов и робототехнических систем, отличающихся малой чувствительностью (или даже полной инвариантностью) к пара-цетрическим и постоянно действующим возмущениям.
$ 3. ИДЕНТИФИКАЦИОННЫЙ ПОДХОД К УПРАВЛЕНИЮ
Одним из важнейших достаточных условий эффективного управления роботом является знание динамики его двигательной системы. Если это условие выполнено, то проблема полностью решается с помощью законов стабилизации и терминального управления, описанных в § 8, '9 главы 3. Однако в действительности динамическая модель робота известна в лучшем случае с точностью до вектора параметров £ н постоянно действующих 134
возмущений л. Эти неопределенные величины удовлетворяют лишь общим информационным ограничениям (4.13) и могут принимать любые значения внутри заданных ограниченных множеств.
Компенсацию априорной неопределенности и оценивание неизвестных величин можно осуществлять по-разному. В теории адаптивных систем наибольшее распространение получили два подхода, которые будем условно называть идентификационным и безыдентификационным.
Суть идентификационного подхода заключается в воздействии на двигательную систему определенными тестовыми управляющими воздействиями и фиксации с помощью информационной системы характеристик реального движения, порожденного этими «пробными» воздействиями. В результате такого «зондирования» робота получаем систему уравнений относительно неизвестных параметров § двигательной системы. Решая эту систему алгебраических уравнений, можно (по крайней мере, принципиально) «идентифицировать» неизвестные параметры, после чего найденные оценки можно подставить в законы управления, синтезированные в предыдущей главе.
Процесс идентификации неизвестных параметров можно совместить с процессом управления. При этом управ пение выступаем как средство изучения динамики робота путем текущей идентификации его параметров. Вместе с тем закон управления, использующий идентифицированные параметры, обеспечивает желаемый ПП при отработке ПД. В этом проявляется двойственный характер управления с идентификацией. Как н в работе [73], будем называть такое управление дуальным.
Дуальное управление представляет собой разновидность адаптивного управления. Для него характерно совмещение или чередование процесса автоматической идентификации параметров с процессом собственно управления. При этом управление направлено как на «зондирование» динамики робота, так и на осуществление ПД. Благодаря активному накоплению информации путем «зондирования» оказывается возможным определить неизвестные параметры на основе того или иного идентификационного критерия оптимальности.
Проиллюстрируем высказанные соображения на примере простейшей схемы адаптивной идентификации параметров на основе настраиваемой модели. Предположим, что уравнение Движения (2.55) задано с точностью до вектора параметров (, причем функция F линейна по £. Наряду с уравнениями (2.55) с неизвестными параметрами рассмотрим уравнение модели
x = F(x, u, t)«bG(x, u)t, (4.24)
где г — настраиваемые параметры модели, играющие роль оценок неизвестного вектора а х — оценка х.
13»
Настройка параметров £ модели (4.24) производится в соответствии с некоторым ДА. который необходимо построить исходя из тех или иных условий идентификации. Оценки х, трактуемые как выходы модели, вычисляются согласно (4.24) по заданному (тестовому) управлению u = u(/), измеренному текущему состоянию х = х(/) и сформированной оценке т = т(/).
Идентификацию параметров можно осуществлять по «выходам» двигательной системы (2.65) и модели (4.24). Это значит, что параметры $ модели следует выбирать так, чтобы выход модели х был по возможности наилучшей оценкой измеряемого «выхода» системы х. В качестве показателя качества оценки на интервале идентификации [/о, М возьмем интегральную квадратичную ошибку
<т
Ф (т) = J || х (6) — G (х (0), и (0)] т f dQ. (4 25)
t,
Этот показатель, связывающий выходы модели х и «выходы» системы х, особенно удобен в том случае, когда параметры $ не фиксированы, а дрейфуют по неизвестному закону. В этом случае целесообразно рассматривать скользящий интервал идентификации, для которого to = t, tT = t + Т.
Необходимым и достаточным условием минимума (4.25) является
*г
VO(t)~2 J Gr(x(0), u(0 ] (х(0) - G (х(0>, u(O)]T]d0 = O.
Отсюда получаем линейное алгебраическое уравнение относительно
Н Gr (х (0), и (0)] Gr (х (0), и (0)] </0 ) т = J Gr [х (0), и (0)] х (0) </0.
7 '• (4.26)
Решая это уравнение тем или иным методом (например, с помощью рекуррентного алгоритма Качмажа (73]), идентифицируем неизвестные параметры
Описанная схема адаптивной идентификации привлекательна своей простотой. Однако она имеет целый ряд недостатков.
Во-первых, система «идентификационных: уравнений (4.26) ложет оказаться плохо обусловленной, а значит, непригодной для точной идентификации параметров £. Во-вторых, для фактического решения уравнения (4.26) в сложных случаях может потребоваться значительное время. Такое запаздывание в идеи* тификации недопустимо, если искомые параметры дрейфуют непредсказуемым образом. В-третьих, требование простоты реали-
136
зании дуального управления приводит к классу рекуррентных алгоритмов идентификации. Однако эти алгоритмы (типа алгоритма Качмажа (73]) сходятся медленно и, следовательно, также приводят к большому времени идентификации. Наконец, реализация рассмотренной схемы идентификации параметров требует специальных средств для измерения или оценивания вектора состояний х(/) н его производной х(/), что не всегда осуществимо с приемлемой точностью.
Следует отметить, что алгоритмы самонастройки модели (4.24), основанные на минимизации показателей качества типа (4.25), вообще говоря, не обеспечивают точной идентификации. Они гарантируют лишь близость выходов модели и двигательной системы, т. е. решают задачу функциональной идентификации по «выходу». Для точной идентификации целесообразно исходить из иных, сугубо «идентификационных» показателей качества.
Наиболее естественными критериями точности идентификации являются критерии, явно зависящие от параметрических возмущений ®(/) = |(/)—т(0- Примером могут служить локальный критерий
К, (®° (/)] = min Kt (® (/)], (Kt (©) = II«II) (4.27) в интегральный критерий
К2 [ю° (•)) = min К2 (© (•)], ( К2 (©(•)] - J || © (6) If . (4.28)
Однако до последнего времени считалось (20], что такие критерии нельзя использовать для синтеза алгоритмов адаптивной идентификации вследствие того, что они зависят от неизвестного (и недоступного для непосредственного измерения) вектора параметров 5- В связи с этим казалось очевидным, что такие оптимальные алгоритмы идентификации нсреалнзуемы и поэтому не представляют интереса для практики адаптивного управления.
Более глубокий анализ задачи оптимальной идентификации показал (61], что высказанные соображения справедливы лишь отчасти и в ряде случаев не являются препятствием для синтеза и прямого использования оптимальных алгоритмов адаптивной идентификации. В работе (61] рассмотрен широкий спектр рекуррентных и многошаговых алгоритмов идентификации, параметры которых выбирают из условия локальной оптимальности (4.27). Некоторые из этих алгоритмов, трактуемые как градиентные алгоритмы решения идентификационных неравенств типа
Ф(т, /)иб — ||х(/) — G (х(/), и(/)]т|| > 0, (4.29)
описываются ниже. Среди них следует особо выделить оптимальный многошаговый алгоритм «с полной памятью» (61]. Этот
137
алгоритм гарантирует точную идентификацию неизвестных пари-метров £, причем число его тагов не превышает размерности пространства параметров, т. е. k р.
Концепция дуального управления по существу исходит из постулата, что для эффективного управления необходимо точно знать или уметь идентифицировать динамическую модель робота. Первоначально эта концепция зародилась в теории стохастического управления [73]. Здесь принцип дуальности оказался особенно плодотворным, так как позволил «увязать» результаты классической теории управления с методами стохастической аппроксимации и оценивания. Важную роль сыграло дуальное управление и в становлении теории адаптивных систем.
Однако постепенно было осознано, что точная идентификация не является необходимым условием эффективного управления. Было четко установлено [54, 61, 68)» что для успешного управления вовсе не требуется детально изучать динамические свойства системы. На справедливость этого тезиса наводят и физиологические соображения: управляя рукой, мозг отнюдь не утруждает себя идентификацией массы или моментов инерции предмета, которым рука манипулирует.
Существуют и более веские доводы, свидетельствующие об ограниченности, а в ряде случаев непригодности концепции дуального управления в робототехнике. Один из них — трудоемкость и сложность осуществления точной идентификации — уже обсуждался. Другой связан с тем, что в ряде конкретных задач точная идентификация принципиально невозможна. К их числу относятся, например, все задачи, в которых действуют неконтролируемые возмущения л(/). В этих задачах движения робота описываются не уравнением (2.55), а уравнением (2.56), зависящим от постоянно действующих возмущений я(/). При решении таких задач, особенно характерных для робототехники, приходится опираться на какие-то иные, «неидентификационные» принципы адаптации. Перейдем к рассмотрению этих принципов н реализующих их алгоритмов.
| 4. ОБЩАЯ СХЕМА АДАПТИВНОГО УПРАВЛЕНИЯ ПРОГРАММНЫМ ДВИЖЕНИЕМ
Важнейшей чертой адаптивного управления является наличие некоторой процедуры (алгоритма) целенаправленной на* стройки параметров закона управления в процессе работы. По существу эта процедура представляет собой активный поиск недостающей информации (обучение) и коррекцию закона управления (адаптация) в соответствии с новой информацией, поступающей от системы очувствления робота в ходе управления. Поскольку для высококачественного управления вовсе не
138
требуется точно знать все параметры двигательной системы, разумно сразу же отказаться от описанного идентификационного подхода.
Перейдем к описанию общей схемы алгоритмического синтеза адаптивного управления, гарантирующего желаемый характер ПП при осуществлении заранее заданного ПД в условиях неполной информации о динамике робота и свойствах окружающей среды. Специфика роботов и робототехнических систем позволяет естественным образом разделить задачу алгоритмического синтеза на две самостоятельные.
Первая задача заключается в аналитическом конструировании идеального (нсадаптивного) закона управления, обеспечивающего желаемый ПП в предположении, что параметры ( уравнения динамики (2.56) полностью известны, а возмущения я отсутствуют. Методы решения этой задачи в различных ее формах (стабилизация ПД, оптимальное терминальное управление и самонаведение) подробно рассмотрены в предыдущей главе.
Вторая задача —это синтез алгоритмов адаптивной настройки (самонастройки) параметров законов управления, полученных в результате решения первой задачи. Методы синтеза алгоритмов самонастройки, представляющие основной интерес в теории адаптивного управления, излагаются в следующем параграфе.
Напомним общую формулировку проблемы адаптивного управления ПД и рассмотрим схему ее решения.
Пусть динамика робота описывается уравнением (2.56). Предположим, что параметры $ и постоянно действующие возмущения л неизвестны н не могут быть измерены Единственное, что известно относительно £ и я — это информационное ограничение вида (4.13), определяющее класс неопределенности. Пусть заданы ограничения на состояния и управления вида (2.57), (2.58), определяющие множества возможных управлений и движений. Фиксируем какой-либо класс допустимых управлений. Выбор того или иного класса определяется конкретным содержанием решаемой задачи алгоритмического синтеза (в частности, типом АА), а также особенностями технической реализации адаптивного управления. Отмстим, что неправильный выбор класса допустимых управлений может привести к результатам, излишне идеализированным или практически неосуществимым. Пусть задано некоторое ПД, которое необходимо осуществить в условиях неполной информации.
В соответствии с принципом разделения синтезируем сначала идеальный (неадаптивный) закон управления, обеспечивающий Желаемый ПП в замкнутой системе. Общее решение этой задачи было получено в предыдущей главе в виде
u = II [х, хр 4- Е (х — хр, /), 6]. (4.30)
139
Здесь Е--заданная вектор-функция, определяющая правую часть дифференциального уравнения желаемых ПП. Законы управления из семейства (4.30) являются идеальными в том смысле, что их реализация требует точного значения вектор, функции параметров £ двигательной системы робота.
Однако, как уже отмечалось, эти параметры обычно неизвестны. Более того, двигательная система подвержена воздействию неконтролируемых возмущений л(1). Вследствие сказанного уравнение движения робота (2.56) по существу неизвестно, а управление (4.30) задано с точностью до параметров.
В этих условиях неопределенности закон управления будем строить в форме
u = U[x, Хр+Е(х —хр, Л, т], (4.31)
где т = т(/)—текущая оценка неизвестности вектор-функции параметров £(/), определяемая согласно некоторому АА вида (4.4). Качество адаптивного управления (4.31) прежде всего зависит от АА. Выбор АА должен осуществляться на основе единых требований (целевых условий), предъявляемых к процессам управления и адаптации. Важнейшим из них является затухание ПП и параметрических возмущений в замкнутой системе.
Уточним понятие цели управления в условиях неполной информации. Управление двигательной системой должно привести к тому, чтобы ПП в замкнутой системе обладали желаемыми свойствами, несмотря на имеющуюся неопределенность. Эти свойства, задаваемые на этапе синтеза управляющей системы, и являются целью адаптивного управления.
Цель управления удобно формулировать в терминах свойств ПП в замкнутой системе. При этом формализация и конкретизация цели управления зависят от решаемой задачи или режима эксплуатации робота. Так, в задаче адаптивной стабилизации ПД целью управления является обеспечение желаемого характера ПП, гарантирующего асимптотическую устойчивость ПД. Тем самым обеспечивается стабилизация ПД с заданной точностью е, т. е. выполняется целевое условие (4.10).
В задаче адаптивного терминального управления цель управления состоит в достижении наперед заданного состояния а, за заданное время рабочей операции T = tT — т. е. должно выполняться целевое условие вида (4.11).
Целевое условие в задаче адаптивного самонаведения задается неравенством (4.12).
Важно подчеркнуть, что все названные цели управления вследствие неопределенности динамики робота должны достигаться для любых возможных значений неизвестных параметров £ и возмущений л, удовлетворяющих информационным ограничениям (4.13). Если управляющая система, реализующая закон управления (4.31) и АА (4.4), сконструирована так, что цель 140
управления достигается для любых неизвестных параметров £ и возмущений л из заданного класса неопределенности, то будем говорить, что робот адаптивен в этом классе. Поскольку класс неопределенности, задаваемый информационными ограничениями (4.13), может быть практически любым, речь идет по существу об адаптации в широком смысле.
Охарактеризуем кратко некоторые свойства АА. Очень часто оценки параметров в (4.31) определяются как решение некоторого дифференциального или разностного уравнения адаптации. В зависимости от этого в качестве допустимых оценок параметров т = т(/) можно выбирать класс гладких, кусочно-гладких или кусочно-непрерывных вектор-функцнй. Разные варианты такого выбора обсуждаются в [20, 41, 54, 61, 68, 70, 73} и в настоящей работе. Здесь для определенности ограничимся исследованием класса управляемых движений робота с неизвестными постоянными параметрами в практически важном случае, когда допустимые оценки x(t) принадлежат классу кусочно-непрерывных, что соответствует дискретным АА вида (4.6).
Подставляя управление (4.31), (4.6) в уравнение (2.65), получаем уравнение замкнутой системы
х = F (х, U [х, хр 4- Е (х — хр, 0 т], |). (4.32)
Из этого уравнения при любых фиксированных начальных условиях х(/0) —х0 однозначно определяется движение x = x(Q робота под действием адаптивного управления. А именно, если адаптивное управление (4.31), (4.6) задано на интервале [/о, М и /(, ti..tk — моменты переключения закона управле-
ния (4.31) согласно АЛ (4.6) (точки разрыва первого рода), причем to < Л < l-i < ... < /* < tT, то, рассматривая сначала уравнение (4.32) на интервале |/0, G], вследствие непрерывности его правой части получаем решение х(1) с начальным условием х(/о) = хо. Проанализируем решение уравнения (4.32) на интервале [/], /г] с начальным состоянием х(/(). Обозначим его также через х(/). Очевидно, что построенное таким образом решение непрерывно на всем интервале определения, и в частности в точке коррекции Л. Рассматривая теперь решение х(/) на всем интервале [/ц, /2] » обозначая через х(/2) его значение в момент коррекции /2, можем рассмотреть уравнение (4.32) на интервале [4, 6] с начальным состоянием х(/2) и i. д.
Таким образом, убеждаемся, что движение х(/) робота под действием адаптивного управления (4.31), (4.6) с начальным условием х(/о) = хо является непрерывным н кусочно-дифференцируемым. Иначе говоря, функция х(/) непрерывно дифференцируема при всех /е[/0. /г), кроме моментов коррекции 6, /2, ••• ..., 1ц. Решение x(Z) уравнения замкнутой системы (4.32) будем называть реальным движением робота, соответствующим допустимому адаптивному управлению (4.31), (4.6) при начальном
141
условии х(/0) = х0. Это движение так же. как и порождающее его управление, по существу является адаптивным. Однако, вообще говоря, траектория x(t) не всегда определена на всем интервале [/о, /г] задания управления (4.31), (4.6); например, «На может уйти в бесконечность при потере устойчивости замкнутой системой (4.32).
На практике реальное движение и адаптивное управление (4.31), (4.6) должны удовлетворять естественным конструктивным ограничениям (2.57)—(2.59) на состояния, управления и параметры. Это значит, что допустимые движения х((), управления u(Z) и оценки параметров т(/) не должны выходить из наперед заданных множеств Q», Qu, на всем интервале движения (/о, /г] •
Перейдем теперь к изложению основных идей обшей методологии алгоритмического конструирования адаптивных управляющих систем роботов. Для простоты изложения рассмотрим сначала случай, когда неизвестный вектор параметров | фиксирован, а постоянно действующие возмущения я отсутствуют. Отметим, что к этому случаю сводится задача адаптивного управления нестационарной двигательной системой, динамика которой зависит от неизвестных дрейфующих параметров |(() и постоянно действующих возмущений я(/), относящихся к широкому классу параметрических функций (например, к классу полиномов от времени с неизвестными коэффициентами). Более того, рассматриваемая схема синтеза адаптивного управления ПД легко обобщается на случай, когда параметры | н возмущения я могут изменяться непредсказуемым образом в классе функций ограниченной вариации.
Алгоритмическое конструирование адаптивной управляющей системы предполагает, во-первых, синтез идеального закона управления вида (4.30), который гарантирует достижение заданной цели при наличии полной информации о динамике двигательной системы робота, и, во-вторых, построение того или иного АА (4.4). Поскольку аналитический вид закона управления (4.30) известен с точностью до векторного параметра £, то задача сводится по существу к организации поиска приемлемых оценок неизвестных параметров. Этот поиск должен производиться не произвольно (например, полный перебор или случайный поиск здесь не эффективны), а по заданным или складывающимся в процессе обучения АА с обратной связью.
Синтез АА тесно связан с контролем качества управления. Для формализации функции контроля введем критерий качества адаптации. К сожалению, указать универсальный критерий, охватывающий с единых позиций все практически интересные случаи, весьма затруднительно. Поэтому ограничимся рассмотрением наиболее характерных критериев качества, хорошо приспособленных к задачам адаптивного управления роботами и робототехническими системами.
142
Критерии качества адаптации целесообразно задавать в форме неравенств, связывающих состояния, управления и оценки дараметров. Эти вспомогательные неравенства должны обладать тем свойством, что из их выполнения вытекает достижение цели управления. Такне неравенства, определяющие по существу цель адаптации, будем в дальнейшем называть эстиматорными неравенствами.
Среди различных типов эстиматорных неравенств особое значение имеют неравенства вида [60—62|
<р(т, / s6-||u(/)-U[x'f, х (/), т]|| > 0. (4 33)
Они замечательны тем, что при т = | разрешимы с «запасом» 6 > 0. Кроме того, эти неравенства выпуклы по т, если, например, функция U линейна по третьему аргументу. (Последнее имеет место для многих типов роботов.)
Процесс адаптации с критерием качества (4.33) сводится к войску решения системы эстиматорных неравенств. Это соображение наводит на мысль, что в качестве АА можно использовать соответствующие модификации алгоритмов выпуклого программирования. Значительный интерес представляют также различные конечно-сходящиеся, конечные и финитные АА, рассмотренные в работах [61, 68].
В конкретных задачах адаптивного управления иногда удобны эстиматорные неравенства типа (58, 61, 68]
Ф(т, /; — 6-||x(0-F х(/>, и (/), т] || > 0. (4.34)
Очевидно, что эти неравенства разрешимы с «запасом» б > 0 при т=£. Неравенства (4.34) удобны в тех случаях, когда функция F линейна по третьему аргументу. Последнее имеет место, например, для линейных (или линеаризованных) моделей динамики робота. В подобных случаях неравенства (4.34) выпуклы по т, н для их решения опять-такн применимы различные модификации алгоритмов выпуклого программирования. Эти алгоритмы выступают здесь как АА, чем объясняются роль и значение эстиматорных неравенств.
Проверка эстиматорных неравенств (4.33), (4.34) требует измерения (или оценивания) не только текущего состояния х(/), но и его производной х(/). Однако на практике определение x(f) • высокой точностью трудно осуществимо. Для исключения этого Ограничения сконструируем следующую систему эстиматорных неравенств [60]:
<т
»(т, /) — б -1J ехр [Г (/ - в)] [х (0) - О [х (0\ и (0)] т] de|, (4.35)
ГМ Г—некоторая устойчивая матрица размерностью пХп» Проверка неравенств (4.35) на траектории АА уже не требует
143
измерения x(t), так как
ехр (Г (/— 0)] х (0) </8 = ехр[Г (/— 0)] х (8) |* +
»г
+ Г J ехр (Г (I - 8)] х (8) </8. (4.36)
t.
По этой же причине н АА (например, АА градиентного типа), дающие решение (4.35), не зависят от х(1). Очевидно, что эстн-маторные неравенства (4.35) выпуклы по т н разрешимы с запасом 6 > 0 при т — |.
Функции, стоящие в левой части эстиматорных неравенств (4.33)—(4.35), представляют собой функционалы, заданные на допустимых движениях, управлениях и оценках. Впредь будем считать, что значения величин, входящих в выражения для этих функционалов, могут быть измерены или вычислены в любой момент времени. Это требование необходимо для реализуемости АА.
Характерной особенностью рассматриваемой задачи синтеза адаптивного управления ПД является то, что в каждый момент t известно (или может быть вычислено) текущее значение эстн-маторной функции ф[т(О, И. но не будущее ее значение, которое зависит от будущих оценок и будущих управлений. В свою очередь оценки т(О в каждый момент t вычисляются согласно АА (4.4) по информации о текущих и, возможно, предыдущих значениях эстиматорной функции. Таким образом, речь по существу идет о решении не заданных заранее эстиматорных неравенств.
Алгоритм адаптации находит такие оценки т, для которых эстиматорные неравенства выполняются. Благодаря этому обеспечиваются правильная настройка параметров закона управления (4.31) и, как следствие, достижение цели управления.
Знание общего вида закона управления ПД (4.31) и синтез подходящего АА (4.4) позволяют считать задачу алгоритмического синтеза адаптивного управления ПД решенной до конца. В самом деле, если робот снабжен необходимыми датчиками сигналов обратной связи и управляющей системой, реализующей адаптивное управление (4.31), (4.4), то двигательная система приближенно осуществляет требуемое ПД в условиях неполной информации.
Общая схема адаптивной управляющей системы робота представлена на рис. 4.1. Эта схема имеет иерархическую структуру н включает в себя следующие основные элементы |61|: программатор-блок построения и оптимизации ПД; эстнмагор —
144
^ок оценки качества управления; адаптатор — блок самона-(Тройки параметров закона управления; регулятор — блок формирования закона управления. Она отражает описанную мете-
Рис. 4.1. Структурная схема адаптивного управления программным движением.
дологию алгоритмического синтеза адаптивного управления ПД роботов и робототехнических систем. Поскольку рассмотренные законы управления ПД и АА достаточно сложны, то для их реализации целесообразно применять современные быстродействующие ЭВМ и микропроцессоры.
145-
s 5. CAMOHACTPORKA регулятора И ВРЕМЯ АДАПТАЦИИ
Самонастройка регулятора осуществляется с помощью Ад, Синтез н анализ их свойств включает в себя следующие этапы: 1) выбор и формализованное описание класса АА; 2) синтез и оптимизацию конкретных АА; 3) исследование процесса адап-тации (сходимость, устойчивость, осуществимость).
Перейдем к реализации этих этапов применительно к задаче адаптивного управления роботами.
Важнейшим требованием, предъявляемым к эффективным АА, является нх конечная сходимость. Именно это свойство прежде всего отличает рассматриваемый класс конечных АА от разнообразных (непрерывных, итеративных, стохастических) АА (41, 54, 68, 70, 73], обладающих лишь асимптотической сходимостью. Как отмечается в работе (54], для этих АА трудно и, как правило, невозможно указать необходимое время обучения, вследствие чего оценка момента, начиная с которого целевое неравенство будет выполнено, не может быть дана в общем случае. Для конечных АА удается эффективно оценить как «чистое» время адаптации, так и время ПП в замкнутой системе. Эти оценки играют важную роль при расчете параметров адаптивных управляющих систем.
Для формализации конечной сходимости АА введем в рассмотрение следующее множество:
а, = {/ е |/0. оо) = Ф [т (/). П < 0}, (4.37)
т. е. множество всех тех моментов времени, для которых эсти-маторные неравенства (4.1) на траектории АА нарушены. Обозначим через Ц( =ц(ат) лебегову меру множества (4.37). Величина щ характеризует время адаптации.
Как и в работе (61], будем называть АА конечным, если на его траектории время адаптации конечно, т. е.
Рф < оо. (4.38)
Данное определение относится как к непрерывным АА вила (4.5), так и к дискретным (рекуррентным или многошаговым) — вида (4.6) — (4.9). Для дискретных АА это определение по существу смыкается с понятием конечно-сходящнхся алгоритмов (КСА) решения счетных систем неравенств, ранее введенным в работе (78]. Поскольку рассмотрение этого класса А А представляет самостоятельный интерес, приведем определение КСА.
Дискретный АА вида (4.6) называется КСА, если существуют целое число г и конечный момент времени tr, такие, что эстиматорные неравенства (4.1) выполнены при всех t tr, т. е.
ф [т d > 0 при всех I tr. (4.39)
148
Цпсло г шагов КСА (4.6), т. е. число нарушений эстиматорных неравенств на траектории АА, будем называть числом коррекций, а момент времени tr = t'r 4-6— моментом окончания процесса адаптации.
Очевидно, что всякий дискретный КСА является конечным ДА в смысле данного определения, причем для времени адаптации справедлива оценка [56]
щ<г6. (4.40)
Здесь параметр 6, определяющий время, необходимое для вычисления новой оценки т*+1 по старой т» в соответствии с АА (4.6), характеризует быстродействие адаптатора. Чем меньше 0, тем больше быстродействие адаптатора, реализующего АА (4.6).
На практике часто приходится управлять роботом не только в неопределенных, но и в существенно нестационарных условиях. Это проявляется в том, что параметры £ и возмущения я непредсказуемо изменяются в широком классе. Отличительной чертой нестационарных задач адаптации является то, что вместо обычных эстиматорных неравенств (4.1), решение которых есть вектор т, = здесь возникают неравенства нового типа, решением которых служит неизвестная вектор-функция т. — »|(0- Поэтому понятие конечного АА нуждается в обобщении на нестационарную задачу. Одно из таких обобщений, связанное с понятием финитного АА, приведено в работе [61].
Сформулируем основные предположения, при выполнении которых удается синтезировать и оптимизировать конечные АА. Для определенности ограничимся рассмотрением класса дискретных АА вида (4.6). Здесь оператор адаптации А* = А [а (/*)] задает направление и величину адаптивной коррекции старой оценки т* на (А 4- 1)-м шаге АА. В общем случае
А*е Нл(т*), А = 0, 1, 2............ (4.41)
где Нл — векторное поле адаптации, заданное вдоль траектории АА (4.6).
Будем считать, что эстиматорные неравенства (4.1) и оператор адаптации А» в (4.6) удовлетворяют следующим условиям:
I) функции <р в (4.1) определены при каждом t /0 на Qj, причем неравенства (4.1) разрешимы с запасом б > 0 при некотором т, е Qj, т. е.
ф(т„ Л^б при всех l^t0\ (4.42)
2) для всех т», таких, что ф(тд,/»)^0, справедливы соотношения
(т.-т, А»)>б>0, (4.43)
0< бл<||А*||<сл < со, Л = 0, 1, 2, ... (4.44)
Условие 1) необходимо, так как оно гарантирует решение эстиматорных неравенств (4.1) на заданном множестве Q|. Бо
147
лее того, множество решений предполагается телесным. УСло> вне 2) означает, что все направления адаптации А* в точке т» определяемые векторным полем адаптации Н.«(т*), составляй^ согласно соотношению (4.43) острый угол с идеальным (но неизвестным) направлением т, — т* к решению т*.
Эстнматорные неравенства, возникающие в задачах адаптивного управления роботами, достаточно специфичны. Это вира-жается, в частности, в том, что неравенства (4.33) — (4.35) раз. решнмы с запасом б при т, = £ (по построению) и выпуклы по ? Поэтому если взять в качестве оператора адаптации А* гра^ днент функции <р в точке (тА, с некоторым коэффициентом X* X >• О, характеризующим шаг адаптации, т. е. А« =г =ХжТ<р(тЛ, t'k), то условие (4.43) будет выполнено с запасом 6а = Хб. В этом случае легко указать такие числа <ja, ел, что выполняется соотношение (4.44).
Для исследования сходимости дискретных АА вида (4.6) определим на множестве Q« функцию £(т) со следующими свойствами:
а) £(т») = 0, Д£(тф) = О н £(т) > О для всех те Qf, б) функция £(т) дважды дифференцируема, причем
|| \L (т) || , llv’MtHKcv при всех r<=Qj; .4.45)
в) для всех т*, таких, что <р(тА, Z*)^0, и некоторого 6l >0 справедливо неравенство
(у£(т*\ А*)<-бд, Л = 0, 1, 2, ... (4.46)
€ помощью функции £(т) можно сформулировать следующий обобщенный критерий конечной сходимости АА вида (4.6).
Критерий конечной сходимости АА. Пусть эстнматорные неравенства (4.1) и АА (4.6) удовлетворяют условиям I), 2). Предположим, что на траектории АА (4.6) определена функция £(т) со свойствами а)—в), причем 26L> cv,c2A. Тогда АА (4.6) является конечно-сходящнмся алгоритмом, причем для времени адаптации справедлива оценка
< 2L (то)О(2б£ - (4.47)
Для доказательства данного критерия прежде всего воспользуемся формулой конечных приращений
в L(Ъ) — L (Ъ+i)= — (VL А*) —
-1(Т2£(т*4-аА*)А*. А*>, 0<а<1.
Оценивая Д£*+1 снизу с учетом (4.44), получаем
Л4,+, > - <Vl (»,). А.) - Ь,. | Л, f \ 1- о > 0.
148
Суммируя эти неравенства для к — 0, 1,2...г — 1, имеем
£(тг) L (т„) — го.
Отсюда с учетом оценки (4.40) находим оценку (4.47).
Таким образом, если функция £(т) с указанными свойства* ми построена, то она убывает на каждом шаге АА на конечную величину, и, следовательно, АА (4.6) является КСА. По существу функция L выступает здесь как функция Ляпунова для дискретного АА (4.6).
Выбирая в качестве £(т) функцию
£i(»)-K-tf. (4.48)
критерий конечной сходимости можно записать в виде
Д£*+1 в £( (т*1 — Li (т*+1) = || т. — т* If — И т. - т*+1 f >о > 0.
(4.49)
Этот критерий прост и особенно удобен для анализа сходимости АА вида (4.6). Именно поэтому он нашел широкое применение при исследовании дискретных АА (54, 61, 67, 68, 78]. В ряде случаев целесообразно в качестве L(x) взять функцию
£2(т) = ф(т., /) — ф(т, /). (4.50)
Тогда критерий конечной сходимости АА вида (4.6) можно записать так:
д*'*+1я,Мт*)-/-2(т*+|) = Ф(т*>г Q-4>(T*> Q>o>0.(4.51)
Этот критерий, как и критерий (4.49), гарантирует, что решение эстиматорных неравенств (4.1) будет найдено за конечное число шагов АА (4.6), и, следовательно, время адаптации конечно.
$ в. ОПТИМАЛЬНЫЕ КОНЕЧНЫЕ АЛГОРИТМЫ АДАПТАЦИИ
Одной нз важнейших задач при синтезе АА являемся их оптимизация. Применительно к дискретным АА типа (4.6) это означает, что оператор адаптации А* на каждом шаге алгоритма следует выбирать из условия минимизации заданного функционала качества. Таким функционалом может служить введенная в предыдущем параграфе функция L(x) со свойствами а)—в).
Значительный интерес представляют также локальные функционалы качества вида (4.48) и (4.50). Первый из них характеризует расстояние от оценки т» до идеального решения т». Будем называть его идентификационным функционалом. Второй функционал (4.50) характеризует разность между значениями эстиматорной функции q> на идеальном решении т, и на
нэ
его оценке т* в первый момент /к^/к нарушения (4.1) при т^ = т*. Этот функционал будем называть эстиматорным.
Как отмечается в работе (20], идентификационный функционал типа (4.48) может служить наиболее прямым и исчерпы-Бающим критерием точности адаптации. Однако до последнего времени считалось, что такой критерий нельзя использовать для синтеза алгоритма адаптации, так как вектор т, недоступен для непосредственного измерения (20]. В самом деле, функционал Li(t) зависит от неизвестного идеального решения т, неравенств (4.1), поэтому и оптимальный оператор адаптации Ак неизбежно зависит от т». В связи с этим казалось очевидным, что соответствующие оптимальные АА нереализуемы и поэтому не представляют никакого интереса для практики адаптивного управления.
Однако более глубокий анализ задач адаптации показал, что высказанные соображения справедливы лишь отчасти и в ряде случаев не являются препятствием для синтеза и прямого использования оптимальных АА. Это установлено в работе (61 ]. Там же разработан описываемый далее метод синтеза локально оптимальных КСА адаптации и установлены условия их реализуемости. Широкий спектр оптимальных конечных АА применительно к задачам адаптивного управления роботами был синтезирован ранее (9, 17, 29, 57, 58, 63, 64]. Перейдем к систематическому изложению этих результатов.
Рассмотрим эстиматорные неравенства (4.1). Будем считать, что функции <р в (4.1) и АА вида (4.6) удовлетворяют условиям 1), 2). Решение (4.1) будем искать в классе рекуррентных градиентных алгоритмов общего вида
Ь+1 = М* +VMb. Q. Л = 0, 1.............. (4.52)
где то е Qi — произвольная начальная оценка; р*, X* — скалярные параметры АА; 4 >Zk —первый момент нарушения (4.1) при т = т*. / /* Оператор адаптации для алгоритма (4.52)
выглядит так:
Ak-A[Tk, Тф(тк, 4)] = (Р*-1)тк4-ЛкГф(тк, 4).
Алгоритм (4.52) имеет простой геометрический смысл: в момент нарушения эстиматорных неравенств (4.1) при
т = т* новую оценку т*+| получают из старой т» перемещением в направлении вектора 7ф(тк, на величину X» и далее в направлении вектора т* на величину р* — 1.
Существенное влияние на скорость сходимости и другие свойства АА типа (4.52) оказывает выбор параметров р*. X*. Естественно подчинить этот выбор не только требованию конечной сходимости, но и некоторым условиям оптимальности.
1 jj
Определим параметры 0*. X* из условия минимизации функционала Li(t*+i). С этой целью введем функцию двух переменных /•(Р, M = L1[pT* + Xv<₽(Tv /;)], р>0. Х>0, 1...
g найдем р*, X* из условия локальной оптимальности Л(Р*, M = Л', р*>0, Х4>0. (4.53)
Из выражения (4.53) имеем
~ 2 <т- “ Р*т* “ ЧТФ (Ъ. 4). т*> - О, дМР*. X») _ _ 2 _ XjkV<^Tb Q, ГФ(т* = 0>
гткуда непосредственно получаем
а _ Р*Пгф(<*.'*)Г-(т»тф(тг<*))(’.. тф(’*.4)>
р‘ 4) Г ~
. _ ГФ (ъ-'0>
‘-<4||’*и2|гф(’*.4)Г
(4.54)
(4.55)
9ДО а* = sin ф*, ф* — угол между векторами т4, V<₽(Tv
Рнс. 4.2. Геометрическая интерпретация локально-оптимальных рекурренъ них алгоритмов адаптации.
Локально-оптимальный рекуррентный ЛЛ (4.52), (4.54), (4.55) формирует па каждом шаге оценку т*+ь являющуюся наилучшим приближением к идеальному решению те в указанном выше смысле. Как видно из рис. 4.2, определение оптимальных значений параметров 0*. из условия локальной опти-
151
малыюсти* (4.53) эквивалентно проектированию вектора т, на подпространство R* пространства Rp, порожденное векторами т4, Уф(т*. t\)- Действительно, вектор т, допускает единственное представление т. = р* + w», где р* = Р«4т, (Рл> —оператор проектирования на /?»); w* — вектор, ортогональный /?*. По* этому
bi (т*+1) = II — Ъ <-1II2 = IIР* — T*+i IP + II w* |р.
Отсюда следует, что для локально*оптнмального АА (4.52), (4.54), (4.55) решение оптимизационной задачи (4.53) достн* гается на единственном векторе р* = т*+|, являющемся проекцией т» на Rk. При этом справедливо равенство
(т. — т*+1, 0 = 0 для всех ге/?4. (4.56)
Соотношение (4.56) означает, что вектор т, — t*+i ортогонален любому элементу г из подпространства /?*. Беря в качестве г вектор т*+ь получаем
<Т„ т* + 1) = ||Ъ+1|р, ft-О, 1.
которое справедливо, в частности, при т*+| = 0 и т*+1 = т*. Следовательно, для локально-оптимального алгоритма (4.52), (4.54), (4.55) идеальное решение т, неравенств (4.1) является неподвижной точкой, т. е. если в качестве начальной оценки т» взять т,, то все последующие будут также равны т,.
Оценим точность идентификации идеального решения т, на траектории АА (4.52),. (4.54), (4.55). Предположим, что векторы тд и Уф(**»4) линейно независимы. Тогда определитель матрицы Грама Г [тк, уф(тд, Z*)] этих векторов положителен. С помощью этого определителя можно найти квадрат ошибки АА, т. е. величину Li(t*+i)s ||т» — t*+il|2. А именно справедлива формула
, х detr|T.-Tt, Уф(тд,4)] ае.г[ъ, Уф (ъ. 4)1 •
откуда следует, что если на некотором шаге локально-оптимального АА (4.52), (4.54), (4.55) т, е/?*. то Z.|(t*+i) = O, т»+1 = т, и эстнматорные неравенства (4.1) выполнены с запасом б > 0 при при всех t f*+i.
Наиболее распространенный класс рекуррентных АА градиентного типа имеет вид
Ъ+. = Ъ + Ч*Р(Ь. 4). * = 0.1............ И-57)
где to^Qi — произвольная начальная оценка; X» — параметр алгоритма, определяющий шаг адаптации в направлении гра-
днента V4?(T*, /*) Оператор адаптации для АА (4.57) имеет а ид
A*eAlTv v<p(t*. /;)]=Ч¥ф(т*. /;).
Существует много методов выбора параметра X* в алгоритме (4.57) [61, 67, 68, 73, 78], приводящих к АА с теми или иными свойствами. Проблема оптимизации АА вида (4.57) заключается в выборе параметров X* путем минимизации на каждом шаге подходящего функционала качества.
Введем для идентификационного функционала (4.48) на дуче
1* •= {т е Rp: т = тд + Xvq> (т*. t'k), X > 0}
функцию переменной X
Л(Л)-£,[та + Хфф(^ 4)Ь х>ол-о, I,...
Определим X* из условия локальной оптимальности
/*(Х*) — 1п1/*(Х), Х*>0, (4.58)
откуда получим уравнение
- - 2 <ч - ъ - 4V»(»,. <1). V» <)> - 0.
найдем далее оптимальное значение шага адаптации
. _ ГФ (’*.'*))
|гф(ъ./;)Р
(4.59)
Поскольку функция Л(Х) выпукла, то в точке (4.59) при X > 0 она достигает своей нижней грани.
Остановимся на проблеме реализуемости полученных локально-оптимальных АА. Прежде всего отметим, что формулы для оптимальных значений параметров (4.54), (4.55) и (4.59) зависят от неизвестного идеального решения т, эстиматорных неравенств (4.1). Это наводит на мысль о нереализуемости соответствующих оптимальных АА, что в действительности не так. В рассмотренных задачах адаптации оптимальные параметры (4.54), (4.55), (4.59) зависят от неизвестного тф специальным образом, а именно выражаются через известную на каждом Шаге величину (т., уф(т»> **))• Таким образом, локально-оптимальные рекуррентные АА (4.32), (4.34), (4.35) и (4.37), (4.39) реализуемы.
Следует отметить, что АА (4.37), (4.39) в частном случае, Когда <р (т, А) и б — | <0*. т, — т*> | >• 0, k = О, I, ..., совпадает с одним из вариантов алгоритма «полоска» 168]. Этот локально-оптимальный АА также тесно связан с алгоритмом Качмажа, который был сначала предложен как метод решения линейных Алгебраических уравнений, а затем нашел применение в зада
153
чах адаптивной идентификации (73].
Рассмотрим теперь эстиматорный функционал качества (4.50). Введем на луче
I* — {» е Rp: т = т* + Xvq> (»*. 4). Л > 0}
функцию переменной X
Л(Х) = ^[т,4-Хуф(т>, /;)]. Х>0, Л = 0, 1, ...
Определим К» из условия локальной оптимальности
/* (X*) = inf /* (Л), X* > 0. (4.60)
х
Учитывая, что £2(т4+1) = д — <р(тЛ+1,1'к), из (4.60) получаем
<Тф(Ъ+1. <). ¥Ф(Ъ. /;)) = 0, (4.61)
т. е. градиенты эстнматорной функции <р в точках (т4, а (т4+1, /д) ортогональны. Для определения оптимального параметра X* АА (4.37) из условия (4.41) воспользуемся соотношением <vv(t*+p ф-?ф(ъ» уф(ь. /;)>= = Xa(v^(t*. 4)ФФ(Ъ. 4)» ТФ(<а» 4)>-
Тогда легко вывести следующую формулу для оптимального шага:
Л _______________1^ (**•'*) г_________ (4 вз)
* <ф2ф(’*. '*)?<₽ (’*.<*). ?<₽(’*•'*)) ‘
Интересно отметить, что локально-оптимальный АА (4.57), (4.62) в некотором смысле аналогичен одному из классических методов оптимизации — методу наискорейшего спуска [32]. Этот алгоритм имеет простой геометрический смысл: точка t»+i, определяемая согласно (4.57), (4.62), лежит на луче
/* = {те/?р:т = тЛ + Хуф(т4,/;), X>0}
в точке его касания поверхности уровня
и*+1 = {ге/?₽:Лдт) = ^(т^,)},
а сам луч Ik ортогонален поверхности уровня
U* = (т <= Rp: Lt (т) = L2 (т* ).
В градиентных АА (4.57) шаг адаптации определяется скалярной величиной X*. Рассмотрим теперь класс алгоритмов видя (4.57), где Л* —некоторая матрица размерностью р%Р-Выберем матричный параметр А* из условия локальной опти*
154
дельности типа (4.60). Соотношение ортогональности (4.61) в этом случае имеет вид
(vv(»*+!• 4). vv(b. +
+ <¥2Ф(т». 4)Л*ТФ(Ь. ¥Ф(»*. /1)) = 0.
Полученное уравнение определяет оптимальное значение матричного параметра Л*. Если матрица ф*ф(т*. 4) невырождена, то решением этого уравнения является
л* = ';))'• (4.63)
очевидно, что в данном случае
4)"Тф(**. 4) +VM»*. /;) A*v<p(»*. 4) = О- (4.64)
Если ф имеет вид (4.33) или (4.34), то т*+> = т». Поэтому если матрица Vtyfr*. t'n) невырождена, то АА (4.57), (4.63) является оптимальным в том смысле, что обеспечивает точную идентификацию идеального решения т, за один шаг. Это означает, что эстиматорные неравенства (4.1) выполнены с запасом б > 0 при т = т( для всех / tt.
Синтезированный оптимальный АА (4.57), (4.63) можно трактовать как аналог метода Ньютона [32]. Следует отметить, что направление адаптации Ао —— [у2ф(т0> *о)Г^ф(»о« О’ определяемое этим АА в произвольной точке то, является идеальным в том смысле, что ориентировано в точку т,. В самом деле, поскольку
Ti “ то -1(%. ОГ' ?Ф (то- Q = Ао = т. -
то все другие направления адаптации хуже Ао.
Преимущество оптимального алгоритма (4.57), (4.63) перед другими рекуррентными АА заключается в высокой скорости сходимости и точности адаптации. Однако трудность вычислений на одном шаге этого алгоритма определяется необходимостью обращения матрицы вторых производных фгф(ти, t'o) (при условии, что она невырождена) и может оказаться чрезмерно высокой. В то же время локально-оптимальные алгоритмы вида (4.52), (4.54), (4.55) или (4.57), (4.59), не требующие вычисления и обращения матрицы Тг<р(т, t), существенно проще для вычислений и могут приводить к решению эстнматорных неравенств (4.1) через конечное число шагов.
Таким образом, целесообразность применения тех или иных рекуррентных АА тесно связана с эффективностью всего процесса в целом, т. е. с общим объемом вычислений, затрачиваемых на решение эстнматорных неравенств. В связи с этим Возникает задача конструирования АА, менее трудоемких, чем Оптимальный алгоритм (4.57), (4.63), но обладающих суще
155
ственно большей быстротой сходимости по сравнению с рекур. рентными алгоритмами вида (4.52), (4.57). Рассмотрим решение этой задачи в классе многошаговых АА, параметры которых также выбираются из соображений локальной оптимальности.
Класс многошаговых АА с той или иной «глубиной» памяти в общем случае описывается соотношениями (4.6) — (4.8). Особый интерес представляет многошаговый АА с полной памятью вида [61]
т*+1 = то+ Л = 0, 1......... (4.65)
где то — произвольная начальная оценка; X;— шаг адаптации в направлении h(»h[<p(T<t /')], ( = 0, 1.k. В качестве h<
можно взять, например, градиент (или обобщенный градиент) эстиматорной функции <р.
Существенное влияние на свойства АА (4.65) оказывает выбор параметров Х(, i =0, 1, .... k. Будем искать эти параметры как решения некоторой оптимизационной задачи. Определим а пространстве параметров Rp подпространство /?*+1, порожденное векторами h,, 1 = 0, 1..k. Тогда задача наилучшего прибли-
жения идеального решения т, неравенств (4.1) на многообразии
₽*+1 = {т«=/?р: т = т0 + г, геЛ(+|} формулируется следующим образом. Требуется найти вектор т*+1 е такой, что
^1(Ъ+1)ИК — Ъ+|1Р= min || т, — (то+г)!!2 — reR*+i Л
= min || г. — тй — У Xjh/ll2. (4.68)
...**
Задача (4.66) всегда имеет решение. Если т*+| = то + г«+» является наилучшей оценкой решения т, в смысле идентификационного критерия качества (4.46), то справедливо равенство (т, — т0 — г4+|, г> = 0 для всех (4 67)
т. е. вектор т. — т*+) ортогонален любому вектору г из /?*+|, это означает (рис. 4.3): вектор т*+ь выбираемый из условия ошн* мальности (4.66), является проекцией вектора т.— т« на гипер* плоскость /?*+ь
Беря в (4.67) в качестве г любой из порождающих Rk+\ век* торов h,-, получаем систему уравнений
(т.-То-^Х^, h^-О, / — 0,1............k,
откуда следует
Д X, <ho h,) - (т, - т0, h/> / - 0, 1.k. (4.68)
Система (4.68) дает возможность найти оптимальные значения параметров Хо, Х|, .... X* АА (4.65). В матричной форме эта система имеет вид
Г*Л* = Ь*. (4.69)
где Г* " Г (ho, h..h*) — | <ho hz) |*— матрица Г рама; Л* —
«•Рч 1*_о ~ вектор искомых параметров; Ь» = | <т, — т0, Л7> |*_0. Сели векторы ho, hb ..., h* линейно независимы, то матрица
Рас. 4.3. Геометрический смысл оптимального многошагового алгоритме-адаптации.
Грама Г» невырождена н det Г* > 0. В этом случае решение <Встемы (4.69) единственно. Оно определяется формулой
А* = Г**Ь*. (4.70)
Для упрощения вычислений по формуле (4.70) в работе (58] получены рекуррентные соотношения для вычисления матрицы
Точность идентификации идеального решения т, на каждом Фаге оптимального АА (4.65) определяется величиной
> ,_ .__det Г (ho. hi, .... hb, т, — Го) .. _।.
<т*+ Р------dTt Г (ho, h, h*>— • <4 71>
конкретизируем оптимизационную задачу (4.66) с целью изучения одного класса градиентных АА, представляющих особый
157
интерес для синтеза адаптивного управления роботами. Пус^ h<eV4>(»P б). /«=0, 1, ...» k. (4.72)
Тогда справедливо следующее утверждение: векторы = фф(тр/,), i = 0, 1...k, на траектории оптимального Дд
(4.65), параметры Хо, М. X* которого определяются из урав. нения (4.68), линейно независимы.
Доказательство проведем от противного. Пусть существует натуральное число k, такое, что векторы {Л<р(т,, •и<нейно зависимы. Тогда справедливо представление =
*-i '
= Е Y<V<P (тг <) при некоторых у»..y*-i, среди которых ест*
отличные от нуля. Так как согласно (4.65), (4.72) тй = то-|-fc-i
+ E^V<P(V<)’ где А.о, ..., выбраны из условия опте» мальностн (4.66), то
(т.-т*, V4>(»<. О) = 0’ /в°-
Следовательно,
* -I
<т. “ »*. V<₽ (V /'<)> “ £ V(<t- V VV (т<. <)> - 0.
Однако это противоречит тому, что
<т. - т*. v<₽ (т*. /;)> > Ф (».. 4) - ft,
значит, векторы Фф(т/, 6), »= 0, 1, .... k, на траектории оптимального АА (4.65), (4.66), (4.72) линейно независимы.
Пусть Г* — матрица Грама системы векторов (4.72). Согласно вышеизложенному она невырождена. Поэтому оптимальные значения параметров До...X* можно найти по формуле (4.70)
Как решение системы уравнений (4.68). Отметим, что вследствие линейной независимости векторов {¥ф(т<.найдется чис-ло k, 0 k <. р, такое, что ¥<р(т*. t) = 0. Тогда т* = т, есть решение эстнматорных неравенств (4.1).
Рассмотрим случай, когда для некоторого k 5s 1 система векторов {фф(тр *<)}*-<>} линейно независима, а система {т. — {Д<р (тг /,)}/_,} линейно зависима. Поскольку определитель матрицы Грама Г» для первой системы векторов положителен, * для второй равен нулю, то вектор т. — тое/?*+|, где R^+t подпространство, порожденное векторами фф(тр Q 1, ..., k. Отсюда и нз выражений (4.71), (4.72) следует. <•* т*+1 = т,. Иначе говоря, в данном случае оптимальный АЛ (4.65) позволяет точно идентифицировать идеальное решение <•
158
1маторных неравенств (4.1) уже на (Л-{-1)-м шаге. Для ia шагов оптимального многошагового АА справедлива 1КЯ
(4.73)
(арактерной чертой синтезированных локально-оптимальных является их конечная сходимость к некоторому решению 1маторных неравенств (4.1). Для доказательства этого свой-
, оценки числа шагов н времени адаптации воспользуемся герием конечной сходимости, сформулированным в предыду-: параграфе.
Рассмотрим локально-оптимальный рекуррентный АА (4.52), 5), (4.56) и воспользуемся критерием (4.49). Вычисляя при-енне идентификационного функционала (4.48) на траекто-
алгорнтма, получаем Ц (т*1 — Ц (т*+1> =
- т*. VI (’*.
(т*.
a* = sint|>», ф* — угол между векторами тд и V4>(T*’4)> a* 1. Суммируя эти неравенства для k = 0, 1.........иа-
IM
(’.)-1’. - ’.г <1 - '.г -41 -°'X
пой оценки с учетом равенства (4.56) следует, что
(4 74)
г—наименьший номер шага, удовлетворяющий неравенству
2 < (| Т* °* “11 То1^ с2?6’2 <
<м образом, рекуррентный АА (4.52) с оптимальными пастрами (4.55), (4.56) является КСА, при этом справедливы 1ки (4.73), (4.74).
’ассмотрим теперь локально-оптимальный АА (4.57), (4.59). произвольного то s QT на траектории этого алгоритма
да непосредственно получаем следующие оценки:
а, (’.)-!’• -F < I - '.Г - “V. •« 75>
(47»)
dT = diamQT. Таким образом, рекуррентный АА (4.57) с овольным то е QT и оптимальным параметром (4.59) яв-ся КСА с оценками (4.75), (4.76).
169
Из сравнения оценок (4.73), (4.74) и (4.75), (4.76) видно что локально-оптимальный АА (4.52), (4.55), (4.56) обеспечивает, вообще говоря, большие точность и быстроту адаптации чем АА (4.57), (4.59). Действительно, при одних и тех же векторах т* и Уф(т*> ^*) приращение расстояния от оценки т*+, д0 решения т. для АА (4.52), (4.55), (4.56) в sin-гф * раз больше, чем для АА (4.57), (4.59). Это видно из рис. 4.2, где т*+1 оценка в силу АА (4.52), (4.55), (4.56), а т*+1 — оценка в силу АА (4.57), (4.59).
Для исследования сходимости рекуррентного АА вида (4.57), (4.62) воспользуемся критерием конечной сходимости (4.51)’ Вычисляя приращение эстиматорного функционала (4.50) на траектории алгоритма, получаем
^г(т*) ~ ^2 (T*+i) "Ф (T*+i* G)e
|уф(<>. 4) Г_______________
“ 2 (гЧ (ъ, 4) гф (ъ. g). гф (’*. 4)>'
Суммируя эти неравенства для Л = 0, 1......находим
Ф (»*. 4) “ Ф (то> > kc\cv>
откуда следует оценка для числа шагов АА (4.57), (4.62)
*<[6-ф(т0, /')]с^с-2. (4.77)
Таким образом, локально-оптимальный АА (4.57), (4.62) является КСА, причем для числа его шагов справедлива оценка (4.77).
Рассмотрим теперь рекуррентный АА (4.57) с матричным оптимальным параметром (4.63). Предположим, что матрица невырождена. Тогда оптимальный АА (4.57), (4.63) для произвольного то обеспечивает точную идентификацию идеального решения т, эстиматорных неравенств (4.1) за один шаг.
Для реализуемости синтезированных оптимальных АА необходимо знать (т., ГФ(тА, Однако при наличии постоянно действующих возмущений л эти величины не могут быть определены точно. Известными можно считать лишь величины
о*(/) = (т„ /)> + С(О. Л = о, 1..... (4.78/
где £(/) —равномерно ограниченные неконтролируемые помехи, зависящие от л(/). В этих условиях оптимальные АА неприменимы. Однако можно использовать соответствующие субопти-мальпые АА, получаемые из оптимальных АА заменой неизвестных величин /т., Гф(т*,^*)) известными (4.78). Условия конечной сходимости таких АА сформулированы в работе [61] • Наряду с оптимальными и субоптимальнымн АА значительный интерес представляют и регуляризованные (параметризо-160 «
ванные) АА. Их получают из оптимальных АА путем параметризации, позволяющей существенно ослабить требования к информации, необходимой для реализации. Таким путем удается получить как некоторые известные [61, 67, 68], так и новые АА.
$ 7. МЕТОДЫ АДАПТИВНОЙ СТАБИЛИЗАЦНИ ПРОГРАММНЫХ ДВИЖЕНИЯ
Основываясь на изложенной общей методологии алгоритмического конструирования адаптивных управляющих систем, перейдем к описанию конкретных методов управления роботами в режиме адаптивной стабилизации ПД. Эти методы отличаются в основном типом эстнматорных неравенств, что предопределяет явный вид АА и свойства ПП в замкнутой системе.
Общим для всех методов является использование законов управления (регуляторов) вида (4.31). Среди множества таких законов особый интерес представляет следующий заной стабилизации ПД (58]:
и (/) = U (х (/), х, (/) + Г (х (0 х, (П)_ t (/)], t > /0, (4.79) где Г,—устойчивая пХл-матрица коэффициентов усиления, удовлетворяющая структурному ограничению (3.117), а т(/) — текущая оценка неизвестного вектора |, вычисляемая согласно некоторому АА.
В качестве АА можно взять любой реализуемый алгоритм вида (4.6), дающий решение эстнматорных неравенств (4.1). Отметим, что распределение моментов th нарушения этих неравенств во времени заранее не известно. Точно так же заранее не известны моменты и величина коррекции параметров т*: их определяют только в процессе управляемого движения робота.
Целью управления в режиме стабилизации ПД является выполнение условия (4.10) при соблюдении ограничений на состояния и управления. Для простоты изложения будем считать, что неизвестный параметр | е Qj фиксирован, а л (/) 0. Обобщение результатов на более широкие классы неопределенносф! типа (4.13) затруднений не вызывает.
Первый метод адаптивной стабилизации ПД основывается на конструировании и решении эстнматорных неравенств вида (4.33). Он особенно удобен в тех случаях, когда функция U линейна по третьему аргументу, т. е.
Шх, хД) = 0Х х)Б, (4.80)
а функция F в (2.55) липшнцева по второму. Покажем, что искомый закон адаптивной стабилизации существует, и найдем его при некоторых предположениях, вообще говоря, более жестких, чем в неадаптивном случае.
Прежде всего отметим, что ввиду разрешимости (с запасом б) и выпуклости неравенств (4.33) для их решения можно
6 Зак. 276
161
использовать конечные АА, синтеанрованные в предыдущем па-раграфе.
Для эстиматорных неравенств (4.83) на траектории КСА вида (4.6) имеем следующую оценку времени адаптации!
|д (а,) ™ шеа {/ в (10, <») '• Ц u (I) — U [*(0, к (I), т (0) || > 0) < г8,
(4.81) где г — оценка сверху числа шагов АА. Неравенство (4.81) при оценке качества адаптивного управления (4.79), (4.6) играет важную роль.
Предположим, что для фиксированного 0 на траектории АА вида (4.6) справедливо неравенство
|| и (0 - U (к (/>, х (0». т (0] Н < 0, (4.82)
где и(0 определено формулой (4.79). Тогда имеет место оценка Це(0 - Ге (0|| < £0. (4.83)
Действительно, вследствие разрешимости уравнения динамики (2.65) относительно управления на подпространстве Рр и с учетом (3.117) на (4.79) вытекает
Х,(0 + Г(х(0 - Kp(0)x=F (х(0, Ц (0, т(0]. (4.84)
Вместе с тем имеем
х (0 «= F [х (0, U (х (0, х (0, т (0] т (0]. (4.85)
Вычитая последнее равенство из (4.84) и используя неравенство (4.82), вследствие липшицевости F по второму аргументу (с константой £ > 0) получаем оценку (4.83).
Перейдем к оценке качества ПП в замкнутой системе (2.55), (4.79), (4.6). Будем считать, что ПД xp(t) и хр(/) принадлежат множествам Q* и Q, с запасами 6, и б2 соответственно, т. е. существуют постоянные
0! > с .|| е(. || + £ду + 2г6сД 02 > || Г || 0(, (4.86)
такие, что при всех t /0 выполняется
хр (0 + V| <= Qt, если || v, || < д,, хр 7 4- V.. €= Qi, если || v21| < 02.
Тогда справедлива следующая оценка ПП в замкнутой системе: || е '01| < с ехр [— у (/ — t ?] || е01| 4- 1 4- 2cr0cf, (4.87)
где cF = sup||F(x. и, ?) || по всем xeQ,. и е Q,„ £ <= Qj. При этом выполняются ограничения на состояния х(/) и управления и(0 при всех t to. Для обоснования этого результата отметим, что закон управления (4.79) выбран конкретно, посколь-162
ку векторы х(О> Хр(/)+Г(х(/)—хр(/)) и x(t) при каждом
t0 входят в область определения оператора U. Вычитая уравнение (4.84) из уравнения (2.55), получаем
ё(0 — Ге (/) —А (/), (4.88)
где Л (О » F[x(О. и(/), U — F[x(0, u(/), т(0], характеризующее качество управления. Учитывая (4.85) и липшицевость F по и, имеем
О А (/) II < L || и (/) - U [х (/), х (/), т (/)] И, t > to. (4.89)
Основываясь на неравенствах (4.81)—(4.83), решение уравнения (4.88) можно оценить следующим образом:
||е(/)||<сехр[— y(t — /о)]Цео11+ J ||ехр[Г(/ — s)] Д(з)||</з + аф
+ JII ехр (Г (/-з)) А (з)|| ds, (4.90)
где аф и рф — дизъюнктные, взаимно дополняющие подмножества интервала (/о. 00). причем лебегова мера аф удовлетворяет оценке (4.81) и согласно (4.83) ||А(з)||С аб при всех зар9. Таким образом,
J И ехр [Г « - з)] А (з) || ds < L6 J Ц ехр Г (/ - з) 0 ds <
* t *
с!Л ехр (— уз) ds < с!Лу~1,
J || ехр (Г (/ - з)] А (з) II ds < J || А (з) || Ц ехр [Г (t - з)] ds <
•» %
< И (аф) sup || А (з) || ехр [Г (t — з)] || < 2сгЬсг.
Подставляя найденные оценки в (4.90), получаем оценку (4.87). Из (4.86), (4.87) следует, что х(/)б(?, и u(f)sQu при всех t е [Го, 00 )•
Описанный метод адаптивной стабилизации ПД допускает непосредственное использование в качестве АА оптимальных КСА, синтезированных в предыдущем параграфе. Следует, однако, иметь в виду, что величины биг, входящие в оценку (4.87), вообще говоря, связаны друг с другом функциональной зависимостью г = г(б). Характер этой зависимости определяется видом используемого АА (4.6). Так, например, при использовании рекуррентного локально-оптимального КСА решения (4.33) г(б)-> оо при б —► 0. Это, естественно, ограничивает область возможного применения рекуррентных ЛА.
6* 1W
При использовании оптимального многошагового АА вида (4.65), (4.68), (4.72) справедлива оценка (4.73), н, следователь, но, оценка г вообще не зависит от 6. Время адаптации в данном случае оценивается так:
<491)
*. а. аначение близко к его минимальному значению. Кроме фого, как показано в предыдущем параграфе, эти АА обеспечивают (при отсутствии возмущений п) точную идентификацию вектора неизвестных параметров £. Упомянутые свойства поз-воляют рекомендовать оптимальные магошаговые АА к широкому использованию при управлении в условиях неопределенности.
Оценим время ПП в замкнутой системе. С этой целью выберем параметр з, определяющий точность стабилизации ПА. из условия
8 > (L6y-' 4* trftcp). (4 92)
Очевидно, что тогда целевое неравенство (4.10) будет выполнено при веек t tp, где
/д > 4 + У- * In • (4 W)
Соотношение (£.93) вытекает из (4.87). Оно дает искомую оценку сверху времени ПП. Эта оценка полезна при расчете системы адаптивного управления ПД. Так, если требуется обеспечить достижение цели управления (4.10) за конечное время, то достаточно выбрать параметры б и 8 на условия (4.92). Отметим, что если те = 1, то адаптации не произойдет, и оценка (4.93) совпадет, как и должно быть, с оценкой (3.120), ранее полученной для идеальных условий.
Второй метод адаптивной стабилизации ПД основывается на конструировании и решении астиматорных неравенств вида (4.34). Этот метод применим в тек случаях, когда функция F в уравнении (2.55) линейна по третьему аргументу, т. е. когда справедливо представление
Fix, u, i)*=G(x, uifc (4.94)
Для решения неравенства (4.34) вновь применимы конечные АА и, в частности, локально-оптимальные КСА вида (4.6) с оценкой времени адаптации (4.40).
Адаптивное управление по-прежнему зададим формулой (4.79). Тогда вследствие разрешимости уравнения (2.55) onto* сительно управления справедливо равенство (4.85). Вычитая его из (2.55), получаем уравнение вида (4.88), где A(Z)3’ « G(x(0,и(/)|ш(0, »(/) = | — т(/). Это уравнение, связывающее и (г) и е(/), характеризует качество управления (4.79). Идеальное качество, т. е. желаемый характер ПП, достигается при идеальном управлении, когда т(1)«= | и Д(/)™ 0.
1М
Для получения приемлемого качества ПП в неопределенных условиях необходимо так выбрать параметры закона адаптивного управления ПД, чтобы, во-первых, достигалась цель управления (4.10) и, во-вторых, выполнялись ограничения на состояния и управления. Приведем соответствующие расчетные соотношения.
В качестве АА (4.6) возьмем некоторый КСА решения эстиматорных неравенств (4.34), такой, что т* 6 Qi, k = 0,1, ... Предположим, что ПД хр(/) и Хр(/) принадлежат множествам Q* и Qt соответственно с запасами
б. > с (|| е0II4- бу -1 + 2гй>), б2 > || Г ||б,. (4.95)
Тогда справедлива оценка ПП
|| е (/) || < ехр [- у (/ - /о)] II ео II + сбу-• 4- 2сг.0Сг (4.96)
их(/)е Qx, u(/)e Qu при всех t e |/0, оо).
Методика обоснования этой оценки по существу та же, что и в первом методе. Отметим только, что из выполнения (4.34) сразу следует
|| ё(/) — Ге(/)|| < б. (4.97)
Подставляя в неравенство (4.91) А(/)= G(x(0,u(/)]e»(Q, получаем (4-96). Отсюда согласно (4.95) следует, что x(f)sQ, и хр(04~ Ге(/)€ Qt при всех t е [/<>» <»).
Поскольку тройка (х(/),хр(04-Г[х(0—хр(0],т(0) входит в область определения оператора управления К, то закон управления (4.79) определен корректно н допустим, т. е. u(/)g Qu при всех t & (0, оо).
Пусть требуемая точность осуществления ПД хр(/) определяется соотношением
в>с(бу *4-2r0Q). (4.98)
Тогда целевое неравенство (4.10) выполняется при всех t /р, где
<Р =/о 4-Г1 In----ДМ . (4.99)
в — еду — 2сг0ср
Полученная оценка сверху времени ПП непосредственно следует из (4.96). Она, как и аналогичная оценка (4.93), существенно использует верхнюю оценку (4.40) времени адаптации.
Рассмотренные методы адаптивной стабилизации ПД требуют организации обратной связи по х(0, х(0. Однако прецизионное измерение (нлн достаточно точное оценивание) х(/) в ряде случаев связано со значительными техническим:! трудностями. Поэтому возникла потребность в разработке '.чтода алгоритмического синтеза адаптивного управления, для реализации которого вообще не требуется знать х(0.
165
Основу этого метода составляют эстиматорные неравенства вида (4.35). Основное отличие (4.35) от эстиматорных нера. венств вида (4.33), (4.34) заключается в том, что на основании соотношения (4.36) для проверки и решения (4.35) достаточно измерять только х(0.
Выберем некоторый КСА (4.6) решения эстиматорных неравенств (4.35). Переходный процесс под действием адаптивного управления (4.79), (4.6) описывается уравнением (4.88), где
А (/) G (х (/), и (0] при / > /*.
Оценим качество ПП:
। t
Ц е (/) II < с ехр (— V (/ — to) || е0 II + К ехр (Г (/ — з)] [х (з) — |Г
— О (х (з), и (з)] т (з)] ds I < с ехр [— у (t — /о)] II е0 II +
4- £ J ехр ° I* ®* ds +
'А
А-О г
+ £ S ехр (Г (/ — 3)] О [х (з), и (з)] 0* ds 4-*-о
t I ।
+ | ( ехр(Г(/ —з)]О[х(з), u(3)]e>*dsl<
Г*+1 I
< с ехр (— у (/ — «)] II во II4- сг.6 + 2crftcP 4- б. (4.100)
Из оценки (4.100) следует, что если ПД хр(0 и его производная Хр(0 принадлежат множествам Qx н Q* соответственно с запасами
di > с|| eoll4-cr.(ft4-20cF)4-ft, 62>||Г||д,, (4.101)
то x(t)eQx и х₽(/)4-Ге(0е Qi при всех fepo, оо). Значит, уравнение (4.79) допустимо, т. е. u(t)eQu при всех t^(t0,oo). Пусть требуемая точность стабилизации ПД удовлетворяет соотношению
в > сг. (б 4- 2всР) 4- б.
(4.102)
Тогда закон управления (4.79) в сочетании с КСА (4.6) решения эстиматорных неравенств (4.35) гарантирует достижение цели (4.10) и выражение ограничений на состояния и управле-
1бв
Рис. 4.4. Саем» адаптивного управления роботом.
s
ния. При этом для времени ПП справедлива следующая оценка сверху:
/р = /о + Y-* In • (4 1°3)
Как видно из соотношений (4.92), (4.98) и (4.102), точность осуществления ПД для рассмотренных методов лимитируется точностью б решения эстиматорных неравенств. При этом адаптационные возможности закона управления (4.79) тем выше чём больше быстродействие АА (4.6), т. е. чем меньше 0. Интересно отметить, что при отсутствии начальных возмущении, т. е. при ео =* 0, все три метода обеспечивают осуществление ПД с заданной точностью е с самого начала, т. е. время ПП Тв * » tP — to равно нулю.
Резюмируя вышеизложенное, можно утверждать: если начальные возмущения ограничены, точность эстиматора и быстродействие адаптатора достаточно велики (т. е. величины бив достаточно малы), то синтезированные законы адаптивной стабилизации ПД не только обеспечивают достижение цели (4.10) после завершения ПП, продолжительность которого оценивается (в зависимости от принятого метода) одним из соотношений (4.93), (4.99), (4.103), но и гарантируют выполнение ограничений на состояния и управления на всем интервале движения. Структурная схема адаптивного управления роботом представлена на рис. 4.4.
| 8. АДАПТИВНОЕ ТЕРМИНАЛЬНОЕ УПРАВЛЕНИЕ И САМОНАВЕДЕНИЕ
Рассмотрим теперь задачи адаптивного управления робота* ми в режимах терминального управления и самонаведения. При этом, как и в режиме адаптивной стабилизации ПД, будем пред* полагать, что параметры | уравнения динамики (2.55) неизвестны. Известным является лишь множество Qt возможных значений
Цели адаптивного терминального управления и самонаведения заключаются в выполнении неравенств (4.11) н (4.12) пр» соблюдении ограничений на состояния и управления на всей интервале движения.
Основная идея решения задачи терминального управления состоит в том, чтобы с учетом граничных условий (3.4), конструктивных ограничений (2.57), (2.58) и, возможно, критерия оптимальности (3.6) предварительно рассчитать ПД xp(t), е Uo. M, а затем стабилизировать это ПД с помощью одного из синтезированных ранее законов адаптивного управления ПД-Адаптивная управляющая система в режиме терминального управления работает следующим образом.
168
Сначала программатор рассчитывает ПД хр(/) для PC с некоторым фиксированным («номинальным») значением вектора параметров При этом вычислительный процесс по-
строения и оптимизации ПД может быть организован с полотью методов и алгоритмов, предложенных в главе 3. После итого регулятор (автомат стабилизации), используя сигналы обратной связи, формируемые информационной системой, и оценки параметров, рассчитанные адаптатором, синтезирует закон адаптивного управления вида (4.31) или (4.79).
Режим работы и структура адаптатора определяются эсти-матором, реализующим эстиматорные неравенства вида (4.33), (4.34) или (4.35). Алгоритм адаптации выбирается в классе КСА решения этих неравенств, причем время адаптации щ не должно превышать времени движения Т » tr — to-
Рассмотрим особенности синтеза терминального управления яа основе методов адаптивной стабилизации ПД, описанных в предыдущем параграфе. Первая особенность заключается в конечности времени управления (Т « tr — to < оо), в то время как адаптивное стабилизирующее управление строилось ранее на бесконечном интервале Т = оо. Другая важная особенность связана с отсутствием начальных возмущений вследствие того, что в режиме терминального управления ПД хр(/) рассчитывается на основе того начального состояния, в котором фактически находится робот, т. е. хр(/0) = *о-. Сформулируем условия, гарантирующие решение задачи адаптивного терминального управления. Пусть закон управления ПД определен формулой (4.79). Если оператор управления U представим в виде (4.80), то естественно воспользоваться первым методом адаптивной стабилизации ПД. В этом случае при всех /г] справедлива следующая оценка ПП:
||е(П||<с(£ду-' + 2r0cF). (4.104)
Эта оценка вытекает из (4.87). Требования (4.86) к хр(/) и Хр(/) можно ослабить, а именно: xp(t) и xp(t) должны принадлежать множествам Q* и Qi соответственно с запасами
б^сОЛу-' + ггОсД б2 >||Г||д,. (4.105)
Из неравенств (4.104), (4.105) следует, что x(t)eQx и хр(/) + S-re(f)sQjt при всех /еро, 6-J. Поскольку тройка (х(0, х₽(/)+Г(х(/)— xp(t)), т*) принадлежит области определения оператора U, то закон терминального управления (4.79) допустим, т. е. u(/)sQu при всех /е[/0, /г). Как видно из оценки (4.104), этот закон обеспечивает достижение цели (4.11) с точностью
' + 2r0cf). (4 196)
164
В тех случаях, когда функция F в уравнении (2.55) представ, лена в виде (4.94), целесообразно воспользоваться вторым (если измеряются как х(1), так и х(/)) или третьим (если измеряется только х(Т) методом
При управлении по второму методу Хр(/) и xp(t) должны строиться внутри Qx и Qx соответственно с запасами (4.105) где L = 1. Тогда, как видно из оценки (4.96), справедлива оцен.' ка (4.104), где L = 1, и выполняются ограничения на состоя* ния х(/) и управления и(0- Следовательно, цель управления (4.11) будет достигнута, причем
е> с (бу-1 + 2г0сР). (4.107)
Переходя к управлению по третьему методу, отметим, что в этом случае хр(0 и хр(Т) должны принадлежать Q* и Q* со* ответственно с запасами
б, > cr (б 4- 20q) + 5, д2>||Г||д,. (4.108)
Тогда, как это следует из (4.100), цель управления (4.11) достигается с точностью
e>cnd + 26cF) + d (4.109)
и ограничения на состояния и управления выполняются.
Таким образом, точность терминального управления, т. е. точность перевода робота з заданное состояние Xiе Q* лимитируется прежде всего такими параметрами, как точность 5 эстиматорных неравенств и быстродействие 0 АА. Расчет управляющей системы и сводится к выбору приемлемых значений этих параметров, а также параметров б|, б2 программатора и матрицы «коэффициентов усиления» Г регулятора.
Для увеличения точности достижения цели можно воспользоваться следующим приемом: в ходе управления следует осуществлять не только коррекцию параметров т* закона управления ПД (4.79). но и коррекцию самого ПД хр((), t«(/0,М-При коррекции ПД следует исходить из того реального состояния, в котором робот оказывается в момент коррекции. В качестве моментов коррекции ПД целесообразно выбирать моменты коррекции параметров закона управления (4.79) согласно АА (4.6). Тогда процессы пё|>ДОГета ПД и Адаптации протекают параллельно.
Совершенно аналогично синтезируется адаптивное управление в режиме самонаведения робота. Главное отличнё его от режима терминального управления заключается в том, что при самонаведении указывается только требуемое состояние робота X! из Qx, а ПД Xp(t) вообще не строится. При этом время самонаведения заранее не фиксируется.
Для синтеза управляющей системы в режиме адаптивного самонаведения можно непосредственно использовать описанные <70
ранее три метода адаптивной стабилизации ПД, если в закон управления (4.79) вместо хр(/) подставить целевое состояние робота Х|. Тогда закон адаптивного самонаведения принимает вид
u(/) = U(x(/), Г(х(/) —Х0, т(/)], />/0. (4.110)
где Г — устойчивая л X n-матрица коэффициентов усиления в каналах обратной связи, а т(/)—вектор настраиваемых параметров, формируемый тем или иным АА.
Описанная методология конструирования и расчета адаптивных управляющих систем роботов в режимах терминального управления и самонаведения гарантирует достижение целей (4.11) или (4.12) н обеспечивает выполнение ограничений на состояния и управления на всем интервале движения |/о, (г)> При этом качество адаптивного терминального управления и самонаведения тем выше, чем больше быстродействие программатора и адаптатора и выше точность решения эстиматорных неравенств.
Глава 5
ИНТЕЛЛЕКТУАЛЬНОЕ УПРАВЛЕНИЕ РОБОТАМИ
| 1. ЭЛЕМЕНТЫ ИНТЕЛЛЕКТА РОБОТОВ
Наиболее характерной чертой роботов третьего поколения является наличие элементов искусственного интеллекта, которые органически входят в состав управляющей системы. Эти элементы служат для решения интеллектуальных задач.
Типичным примером интеллектуальной задачи является планирование поведения робота при транспортировке грузов по незнакомой местности. Процесс решения задачи сводится к к выбору плана действий робота, направленных к достижению цели и поиску путей обхода препятствий и преодоления возникающих трудностей. Отметим, что наличие трудностей, часть из которых может быть заранее не известна, в какой-то мере входит в само понятие интеллектуальной задачи: там, где не возникают никакие трудности, нет и задачи.
Решение таких интеллектуальных задач предполагает необходимость поиска методов и средств достижения некоторой непосредственно недоступной цели. Часто дело сводится к синтезу алгоритма, разрешающего задачу. Отыскание такого алгоритма и его оптимизация обычно связаны с тонкими и сложными рассуждениями, требующими большой изобретательности. Поэтому принято считать, что подобная творческая деятельность является прерогативой человека.
Однако в последние годы появились роботы и системы искусственного интеллекта, способные самостоятельно отыскивать алгоритмы решения отдельных интеллектуальных задач [13, 34, 37, 59, 71]. К числу этих задач относятся распознавание образов, анализ сцен, планирование поведения, самообучение понятиям и т. п., для которых обычно не существует стандартных алгоритмов. Даже формализация и разбиение процесса поиска решения этих задач на отдельные этапы часто
172
•называются весьма затруднительными. Например, человек может легко отличить одну букву от другой или русскую речь •т английской. Однако если спросить, каким алгоритмом он при этом пользуется, то человек не может дать формализованного описания соответствующего алгоритма распознавания.
Тип рассматриваемых интеллектуальных задач определяет особенности алгоритмов их решения. Для установления этих особенностей вновь рассмотрим задачу планирования поведения робота. Процесс решения такой задачи (результат интеллектуальной деятельности управляющей системы робота) есть план целенаправленных действий, т. е. конечная последовательность операций, фактическое выполнение которых гарантирует достижение цели. Каждая операция переводит робот в некоторое новое состояние, которое можно назвать очередной подцелью. В задачах с неполной информацией процесс планирования усложняется и приобретает адаптивный характер. В этом случае управляющая система существенно использует сенсорную информацию, поступающую от информационной системы, а также ранее накопленные знания и опыт.
Решение многих интеллектуальных задач, возникающих при гибкой автоматизации производства, можно представить аналогичным образом. Например, при переналадке гибкого автоматического комплекса на выпуск нового изделия необходима перепрограммировать технологический маршрут, т. е. синтезировать алгоритм «производству», устанавливающий новый план технологических операций, таких, как выбор и подготовка оборудования, программирование движений исполнительных механизмов роботов, контроль качества и т. п. В результате реализации этого алгоритма будет получено требуемое изделие с нужными свойствами.
Таким образом, чтобы решить задачу планирования, необходимо составить хорошо скоординированную, согласованную схему операций (логических, математических, технологических и др.), заканчивающуюся достижением цели.
Решая интеллектуальные задачи, управляющая система робота постоянно ищет пути достижения той или иной наперед заданной, но непосредственно недоступной цели. Способность к преодолению трудностей и препятствий, нахождению обходного пути к пели там, где пет прямого пути, выступает как отличительный признак интеллектуального робота.
Умение робота решать интеллектуальные задачи приобретается путем обучения на опыте и адаптации. Это умение и связанные с ним навыки решения задач гораздо важнее для интеллектуальных роботов, чем накопленные знания (хотя, конечно, найти решение без необходимых знаний невозможно).
Перейдем теперь к уточнению понятия «интеллект робота». В настоящее время не существует четкого, общепризнанного определения этого понятия. Среди множества определений
173
выделим определение искусственного интеллекта робота, пред, ложенное в работе [59].
Интеллектом робота будем называть способность его управ, ляющей системы решать интеллектуальные задачи путем запоминания и целенаправленного преобразования информации в процессе обучения на опыте и адаптации к изменяющимся условиям.
В данном определении под термином «информация» подразумевается не только сенсорная информация, которая поступает в управляющую систему через технические «органы чувств». Такая текущая информация чрезвычайно важна, но, как правило, недостаточна для интеллектуальной деятельности робота.
Для организации взаимодействия робота с окружающими объектами требуется, кроме того, информационная модель среды и самого робота. В этой модели робот и окружающие его объекты, их свойства и отношения между ними не только отображаются и запоминаются, но и могут преобразовываться. Важно отметить, что формирование информационной модели среды и робота происходит в процессе обучения управляющей системы и ее адаптации к изменяющимся условиям. С позиций данного определения описанный процесс «самомоделирования» можно трактовать как элемент искусственного интеллекта.
Характерной чертой интеллектуальных роботов является их способность к обучению и распознаванию, формированию понятий и представлению знаний, моделированию среды и накоплению опыта, самопрограммированию движений и адаптации к изменяющейся обстановке в процессе достижения цели. Благодаря этим качествам робот может решать в условиях неопределенности самые разнообразные задачи, а также легко перестраиваться с решения одного класса задач на другой.
Таким образом, управляющая система робота, наделенная элементами искусственного интеллекта, является универсальным средством решения широкого круга интеллектуальных и двигательных задач (в том числе таких, для которых не существует стандартных, известных во всех деталях алгоритмов решения). Естественно назвать ее интеллектуальной, а реализуемые ею алгоритмы — алгоритмами интеллектуального управления.
Механизм интеллектуального управления раскрывается в предложенном определении интеллекта робота. В этом смысле данное определение конструктивно. Следует, однако, иметь в виду, что существуют и другие определения, характеризующие чисто поведенческую сторону интеллекта. Так, по А. Н. Колмогорову, любая материальная система (в том числе и робот), с которой можно достаточно долго обсуждать проблемы науки, литературы и искусства, обладает интеллектом. Другим примером поведенческой трактовки понятия «искусственный интел-174
дект» может служить известное определение А. Тьюринга,* основанное на специальной «игре в имитацию» между людьми и роботом. Все игроки находятся в разных комнатах, но имеют возможность обмениваться информацией (например, с помощью телеграфной связи или алфавитно-цифрового дисплея). Если в процессе длительного диалога между участниками игры людям не удается установить, что один из участников — робот, то можно считать, что атот робот обладает интеллектом.
Недостатком определения интеллекта по А. Тьюрингу является Тб, что в принципе можно построить робот с полным набором ответов и решений на все мыслимые вопросы и задачи. Такой робот для любой поставленной перед ним задачи просто находит в памяти соответствующее решение и, следовательно, но тесту Тьюринга, обладает интеллектом. Между тем, такое 'паедение робота явно не соответствует интуитивному представлению об интеллектуальной деятельности. Это наводит на мысль, что определение интеллекта должно содержать нечто, относящееся к тому, каким образом решаются интеллектуальные задачи. Очевидно, что этому требованию удовлетворяет конструктивное определение интеллекта робота. Оно, в частности, позволяет отличить робот, творчески решающий задачу, от робота, запомнившего (т. е. заучившего наизусть) решение.
По мере развития робототехники становится принципиально ясно, что роботы могут обладать основными чертами интеллектуальных систем. Более того, некоторые современные роботы и робототехнические системы (вместе с их алгоритмическим н программным обеспечением) уже обладают, по крайней мере частично, этими чертами. Экспериментально установлено, что они легко и быстро справляются с решением отдельных интеллектуальных задач.
Таким образом, на вопрос: «Могут ли роботы мыслить?» следует ответить утвердительно. При этом «мышление» робота отождествляется с процессом решения интеллектуальных задач рассматриваемого типа.
Круг проблем, объединенных понятием «искусственный Интеллект», достаточно широк и не ограничивается робототехникой. Исследования по системам искусственного интеллекта вообще и по элементам интеллекта роботов в частности находятся в начальной стадии развития. Эти системы и роботы существуют, как правило, в виде специализированных программ для ЭВМ лабораторных макетов, способных изолированно решать некоторые интеллектуальные задачи. К числу таких задач относятся игра в шахматы (нли другие интеллектуальные игры), сочинение музыки, доказательство теорем, диалог с человеком на языке, близком к естественному (русскому, англнй-
* Тьюринг А. Может ли машина мыслить? М., 1360, с. 24.
176
скому и т. д.), диагностика состояний, распознавание ситуаций, обнаружение закономерностей, планирование решений, прог* раммирование движений и др.
Возможности интеллекта роботов (как, впрочем, и возможности интеллекта человека) далеко не безграничны. Это связано как с техническими ограничениями на объем памяти, скорость запоминания и считывания информации в управляющих системах, так и с отсутствием общей теории и алгоритмов решения интеллектуальных задач. Как известно, простейший метод решения задач — это полный перебор вариантов. Однако во многих случаях такой перебор практически неосуществим: даже самые мощные современные ЭВМ не могут решить интеллектуальные задачи большой размерности за приемлемое время. Поэтому для их решения разрабатываются специальные методы, учитывающие специфику и структуру интеллектуальных задач. Важное место среди них занимают эвристические и адаптивные алгоритмы, позволяющие в ряде ситуаций эффективно преодолевать трудности, связанные с неопределенностью условий и большой размерностью задач.
Интеллект роботов по существу заключен в алгоритмическом и программном обеспечении их управляющей системы, реализующем те или иные элементы искусственного интеллекта. Наличие этих элементов является отличительной чертой роботов третьего поколения. Однако они не адекватны элементам мозга и их нельзя рассматривать как модели механизмов мышления. Тем не менее интеллект роботов может существенно превзойти возможности человека при решении отдельных интеллектуальных задач.
Потребность в создании и широком использовании роботов с таким специализированным (проблемно-ориентированным) интеллектом уже назрела. Центральной проблемой при этом является организация интеллектуального управления. Эта проблема существенно проще комплексной проблемы создания интегрированного суперннтеллекта роботов, сравнимого по функциональным возможностям с мозгом человека. Но и она еще в полном объеме не решена. Некоторые общие подходы к решению возникающих задач, а также конкретные методы и алгоритмы интеллектуального управления роботами обсуждаются в настоящей главе.
| 2. ЯЗЫКОВЫЕ СРЕДСТВА ДЛЯ ИНТЕЛЛЕКТУАЛЬНОГО УПРАВЛЕНИЯ
Для организации диалога между человеком и роботом и автоматизации решения интеллектуальных задач в процессе управления необходим специальный язык. Этот язык должен быть удобным средством формулирования заданий, представ
ив
дени я знаний и задач, поиска планов и принятия решений. Ов должен также придать управляющей системе способность к логическим рассуждениям. Благодаря этому робот сможет решать на уровне здравого смысла многие задачи, связанные с интеллектуальным управлением.
Простейшим языком, удовлетворяющим указанным требованиям, является исчисление предикатов. На этом логическом языке можно записать многие предложения, рассуждения н утверждения, выраженные на естественном языке. Методы поиска логического вывода позволяют автоматизировать процессы рассуждений и доказательства теорем в исчислении предикатов. Реализицня этого языка и правил вывода в управляющей системе придает роботу элементы интеллекта, необходимые для планирования поведения, распознавания ситуаций, логического анализа обстановки и программирования движений в недетерминированных условиях.
Исчисление предикатов содержит следующий алфавит символов. 1
Предметная область и термы. Множество объектов U, с которыми приходится иметь дело при решении интеллектуальных задач, называется предметной областью. Переменные, принимающие значения из Q, называются предметными переменными. Фиксированные значения этих переменных называются предметными постоянными (константами). Предметные переменные, константы, а также функции от них называются термами.
Переменные высказывания и предикаты. Переменные, принимающие значения «истина» (И) или «ложь» (Л), называются переменными высказываниями. Функции, аргументы которых принимают значения из области Q, а сами функции только два значения — И или Л, называются предикатами. Предикат, аргументами которого являются п предметных переменных. называется л-местным. Если л —1, то предикат обычно определяет некоторое свойство предмета; если л 2, то предикат может выражать л-арное отношение между предметами.
Элементарные (атомарные) формулы. Высказывания и выражения
А ;<о>, F (Ь, с},
где A, F — предикаты, a w, b, с—предметные переменные или константы, называются элементарными, или атомарными, формулами. Эти формулы (как высказывания, так и предикаты) всегда принимают лишь два значения: И или Л. Поэтому их можно связывать с помощью логических операций, образуя новые формулы.
Логические операции. К числу логических операций относятся: 1) конъюнкция & («и»); 2) дизъюнкция V («или», <и/или»); 3) отрицание *| («не», «неверно, что ...»); 4) импликация («если ..., то ...», «влечет за собой»); 5) эквивалент
177
ность «-► («эквивалентно», «тогда и только тогда»), которые Определяются следующей таблицей:
А в 1 -1 л -1 в А&В XV в А + В л > в
И И л л и и и И
л и и л л и и л
и л л и л и л л
л л и и л л и и
Как видно из таблицы, А В истинно тогда и только тогда, когда А и В имеют одинаковые значения; А-+В ложно тогда н только тогда, когда А истинно, а В ложно; А&В истинно тогда и только тогда, когда А и В истинны; А V В ложно тогда н только тогда, когда и Л, н В ложны; наконец, ] А истинно тогда и только тогда, когда А ложно.
Скобки и кванторы. Кроме пяти упомянутых логических связок в исчислении предикатов употребляются скобки ( ) и две новые операции V, 3, выражающие утверждение всеобщности и существования. Символ V называется квантором всеобщности, а символ 3 — квантором существования. Пусть Р(®)—предикат, определенный для каждого элемента <о некоторой' области Q. Тогда выражение V<oP(<d) истинно, когда Р(®) истинно для каждого элемента ш области О, и ложно в противном случае. Это высказывание уже не зависит от ш. Ему соответствует словесное выражение: «для всякого ю Р(<о) истинно».
Высказывание Н<оР(<о) истинно, если существует элемент а> области Я, для которого Р(со) истинно, и ложно в противном случае. В обычном языке этой формуле соответствует выражение: «существует <о, такое, что Р(ш) истинно».
В формулах УшР((о) н ЗюР(со) переменная со связана соответствующим квантором. При этом сами формулы от со не зависят. Отметим, что
-](¥<вР(®))**Яф-1Р(<о).
Каждая формула в начислении предикатов является некоторой конечной последовательностью символов из приведенного алфавита, составленной по определенным правилам. Уточним эти правила.
Пусть формула А содержит свободную переменную ш, т. е. переменную, не связанную кванторами V или 3. Тогда выражения
¥<оЛ, 3®Л (В.1)
также являются формулами. В этих формулах о — уже связанная переменная. Остальные же предметные переменные, которые
178
были свободными в А, остаются свободными и в новых форму* лах (5.1).
Пусть теперь А и В — формулы, не содержащие таких предметных переменных, которые связаны в одной формуле и свободны в другой. Тогда выражения
А&В, А V В, "| А, А-»-В (5.2)
являются формулами.
Таким образом, правильно построенной формулой, или просто формулой, называется конечная последовательность символов, которая строится на основе элементарных (атомарных) формул путем перехода от формулы А к формулам (5.1) и от формул А и В к формулам (5.2). Если в формуле А произвести замену* переменных (как свободных, так н связанных), то полученное выражение снова будет формулой.
Элементарная формула или ее отрицание, входящие в правильно построенную формулу, называются литерами, а дизъюнкция литер называется простым дизъюнктом. Если дизъюнкт не содержит никаких литер, то он называется пустым дизъюнктом и обозначается nil.
Язык логики предикатов содержит в себе всю алгебру высказываний, т. е. элементарные высказывания, принимающие значения И или Л, все ее логические операции и, следовательно, все мыслимые формулы. Кроме того, этот язык допускает переменные высказывания, отнесенные к произвольной предметной области. Благодаря сказанному формулам языка можно дать ту или иную интерпретацию, т. е. с содержательной (семантической) точки зрения формулы можно сделать осмысленными.
Приведем строгое определение интерпретации и некоторых связанных с ней понятий. Определим прежде всего предметную область Q, которая выступает как своеобразный «носитель» языка робота. Тогда интерпретация J произвольной формулы А включает в себя предметную область Q и значения всех констант, функциональных н предикатных символов.
Таким образом, интерпретация — это предписание, сопоставляющее языкоцым символам формулы некоторые «настоящие» объекты предметной области Q: константам — элементы Q, функциональным символам — конкретные функции, предикатным символам — конкретные предикаты. Образно говоря, именно интерпретация наполняет содержанием формулы исчисления предикатов. Поэтому она по существу играет роль семантики языка робота.
При заданной интерпретации всякая формула (не содержащая свободных переменных) представляет собой ложное или истинное высказывание. Если при данной интерпретации J каждая из формул .4.....Ам принимает значение И, то говорим,
что интерпретация J удовлетворяет системе формул {4/}]^.
17.'
Формула В выводима (логически следует) из некоторой си-стемы формул {Xjftp если каждая интерпретация J, удовлетворяющая удовлетворяет также В.
Согласно теореме Гёделя, если некоторая интерпретация j удовлетворяет заданной системе формул то она удовле-
творяет и любой формуле В, выводимой из этой системы. Умение продемонстрировать, что В выводима (логически следует) из системы {Л}*когда это на самом деле так, играет важную роль при логическом анализе и решении интеллектуальных задач. Остановимся на этом подробнее.
Предположим, что В выводима из Тогда любая интерпретация, удовлетворяющая удовлетворяет В, но не
удовлетворяет ] В. Следовательно, никакая интерпретация не удовлетворяет объединению I V Л ) V (“I В). Если некоторая М-1 /
система формул не удовлетворяется ни при какой интерпретации, то она называется противоречивой. Так, если В выводима / м \
из то формула I V At 1 V (“I В' противоречива. И на-
оборот, если AtJ V (“1В’ противоречива, то В должна, логически следовать из системы Именно эта концепция
выводимости лежит в основе поиска логического вывода в исчислении предикатов.
Одним из наиболее удобных методов поиска логического вывода является так называемый метод резолюций 137]. В его основе лежит идея доказательства от противного. Она заключается в том, что вместо заданной формулы В, которая предполагается тождественно истинной, рассматривается ее отрицание 1 В и доказывается противоречивость (неудовлетворимость) этой формулы. Процесс поиска логического вывода завершается, как только устанавливается справедливость некоторых альтернативных формул Ln ] L. Полученное противоречие доказывает неудовлетворимость формулы "I В и, следовательно, тождественную истинность исходной формулы В.
(м
При использовании метода резолюций формула ^V^iJV V(“l В), противоречивость которой доказывается, предварительно представляется в конъюнктивной нормальной форме, т. е.
м
V Ai 1-1
V(“|B;= & D.. i-i
(5.3)
Принцип резолюций в исчислении высказываний состоит в вы* боре двух дизъюнктов Di и Dh в один из которых входит лидера L, а в другой — ее отрицание 1 L. Резольвентой называется новая формула
Я-PVQ, (5.4)
Получаемая из Dt = P\/L и D(=QV(l£j путем вычеркивания литер L и 1 L. Это соответствует применению правила «модус понене» к рассматриваемым дизъюнктам.
В исчислении предикатов принцип резолюций усложняется. В этом случае дизъюнкты, вообще говоря, зависят от переменных. Пусть, например, Dt=*P(ti>) V£(<o), D/=Q(co) V (] £(<p(w))). Теперь уже нельзя вычеркивать литеры £(<о) и ]£ (<р(ш)), так как они зависят от разных переменных. Поэтому приходится подставлять вместо этих переменных подходящие термы. Так, подставляя в D, вместо <о терм <р(<*>), получаем D' = P ,<₽(<> ) / \/£ (<₽(<»))• Отсюда находим резольвенту
/? = Р(Ф(®)) VQ(®). (5.5)
В общем случае подстановка — это конечное множество вида о = {т|/о)|, .... тл/<оя), где и.. — переменные; т)(..., т„ —
термы. В результате подстановки а некоторые выражения Еь ... .... Ец могут оказаться одинаковыми, т. е. £,(а)= ... ..., Ец(о) = Е. Тогда их можно унифицировать (склеить) по
*
правилу Х/Е/(<у*. Получение очередной резольвенты в форме /-1
пустого дизъюнкта nil свидетельствует о том, что доказываемая формула В действительно логически следует из заданной системы формул {4,}^)-
Число резольвент, формируемых в процессе поиска логического вывода, конечно. Оно существенно зависит от выбора стратегии поиска, т. е. правила выбора дизъюнктов для синтеза очередной резольвенты. Большой интерес представляет оптимальная стратегия, позволяющая получить решение за минимальное число шагов. Поиск такой стратегии, связанный с нахождением кратчайшего пути на графе, сопряжен со значительными трудностями. Поэтому разработано много эвристических стратегий, позволяющих сократить число резольвент, необходимых для решения задачи. Например, при наличии в формуле (5.3) одночленных дизъюнктов целесообразно строить резольвенты именно от них (стратегия предпочтения одночленов (37]). Весьма эффективными могут быть также различные семантические и адаптивные стратегии (37, 59, 71 ].
В некоторых интеллектуальных задачах выводимость заданной формулы В (трактуемой как задание или вопрос) из системы
181
формул MJ*, (трактуемых как аксиоматическое описание зпа* ний и накопленного роботом опыта) оказывается недостаточной. Такой задачей может служить задача планирования поведения робота. В подобных задачах необходимо знать ответный терм т, при котором данная формула В логически выводима из системы аксиом Иными словами, необходимо выяснить, следует
ли логически формула Зю5(<о) нз{Л/)/и_|. и если да, то каково значение переменной ш = т, при котором получается решение. Отметим, что умение отыскивать такие значения для перемен* ной, связанной квантором существования, позволяет ставить роботу вопросы весьма общего характера и вести с ним диалог. Например, если спросить у робота: «Какие действия и в какой последовательности необходимо выполнить, чтобы собрать из имеющихся деталей определенную конструкцию?», то ответом на поставленный вопрос должна быть не просто констатация факта, что сборка данной конструкции возможна, но и представление развернутого плана (технологической карты) сборки. Методы извлечения ответного терма в процессе поиска логического вывода хорошо известны н яодробно изложены в работах (37, 71].
Описанный язык исчисления предикатов н метод поиска логического вывода представляют собой эффективное средство автоматического решения ряда интеллектуальных задач. Этот язык и связанный с ним метод резолюций позволяют роботу логически рассуждать и самообучаться. Остановимся на этом подробнее.
Первым этапом автоматического решения задач, требующих логического анализа, является формулировка их в терминах исчисления предикатов. Для этого необходимо прежде всего задать предметную область Q, т. е. совокупность относящихся к решаемой задаче объектов, и выделить нх существенные свойства. Далее небоходимо, присвоив определенный содержательный (семантический) смысл предикатным и функциональным символам, выразить данные н условия задачи в виде правильно построенных формул, удовлетворяющих рассматриваемой интерпретации. Эти формулы, описывающие знания робота о задаче, называются аксиомами. Аксиомы можно рассматривать как определения классов рассматриваемых объектов, их свойств и отношений между ними.
Формулирование задачи на языке робота — это наиболее ответственный этап организации его целенаправленного поведения. На этом этапе от проектировщика требуются глубокие знания не только существа решаемой задачи, но и исчисления предикатов как языка робота. На практике весьма важно, чтобы формулировка задачи (связанная с заданием системы аксиом и формулы цели) была по возможности простой, не засоренной массой мелких деталей. Учет этих второстепенных деталей существенно 182
осложняет логический анализ и делает труднообозримыми результаты решения.
Эффективность поиска логического вывода можно повысить путем уменьшения числа предикатов и аксиом, определяющих данные и условия задачи. С этой целью разумно использовать ранее доказанные формулы или ввести более сложные предикаты (метапредикаты), образующие новые аксиомы, которые можно рассматривать как результат обучения робота в процессе решения задачи. Следуя работе (59], такие аксиомы, описывающие Hji языке исчисления предикатов приобретаемый роботом опыт, будем называть аксиомами обучения.
Введение аксиом обучения позволяет моделировать известный феномен мышления, о котором Р. Декарт в своем «Рассуждении о методе» писал так: «Каждая решенная мною задача становилась образцом, который служил впоследствии для решения других задач» *. Образно говоря, аксиомы обучения играют роль лемм при доказательстве новых теорем, определяющих целевые условия задачи. Тем самым они позволяют оперировать более крупными блоками (фрагментами) доказательств, освобождая от рассмотрения многочисленных деталей, имеющих в данном доказательстве лишь вспомогательное значение. Отметим, что использование аксиом обучения позволяет роботу расширять и углублять знания о задаче в процессе ее непосредственного решения. Таким образом, аксиомы обучения (и связанные с ними метапеременные) выступают как информационные заготовки, обобщающие накопленные знания и облегчающие вывод новых.
В интеллектуальных задачах, связанных с поиском логического вывода, важную роль играет стратегия поиска. Это связано с тем, что именно стратегия определяет, в каком порядке образуются новые дизъюнкты (резольвенты) из уже имеющихся и, следовательно, насколько быстро будет найдено решение задачи. Поэтому эффективность метода резолюций зависит в первую очередь от выбора стратегии.
Существует много различных стратегий поиска. Некоторые из них порождают большое число бесполезных (и в этом смысле лишних) резольвент. Это требует неоправданных затрат машинного времени и памяти. Как показано в работах [37, 71], определенными преимуществами обладают стратегии опорного множества, предпочтения одночленов, линейной и ЛОК-резолюций. Однако эти стратегии слабо учитывают специфику решаемых задач и не изменяются в зависимости от информации, получаемой в процессе решения. Это наводит на мысль о целесообразности адаптивных стратегий, самонастраивающихся на задачу.
Будем называть стратегию адаптивной, если она целенаправленно изменяется (подстраивается) в процессе поиска логиче
* Декарт Р. Избранные произведения. М., I960, в. 274.
18$
ского вывода в зависимости от получаемой информации и накопленного опыта (59]. Примером простейших адаптивных стратегий могут служить семантические стратегии, в которых критерий выбора очередных дизъюнктов зависит от вхождения в них определенного терма [71]. Согласно такой стратегии сначала выбираются термы, соответствующие «интересным» (информативным) объектам, затем — предикаты, описывающие нх свойства, и, наконец, формулы, содержащие эти свойства. Отметим, что стратегия определяет по существу способ рассуждений и характеризует уровень интеллекта управляющей системы робота.
В общем случае задача построения адаптивной стратегии может быть переформулирована как задача отсечения ненужных (лишних) ветвей на дереве вывода, заканчивающемся пустым дизъюнктом. Для решения этой задачи необходимо указать критерий предпочтения ветвей. Действительно, в процессе поиска логического вывода часто можно указать несколько путей (ветвей) доказательства. Введение разумного критерия предпочтения позволяет исключить лишние ветви и благодаря этому ускорить поиск решения.
Большой интерес представляют критерии предпочтения, формулируемые в процессе решения задач. Примером может служить критерий предпочтения аксиом обучения (хранящихся в памяти робота наряду с исходной системой аксиом), который позволяет существенно сократить число шагов поиска. Использование этого критерия особенно эффективно в тех случаях, когда в аксиомах обучения раскрывается неопределенность (т. е. содержится необходимая для решения информация) либо запоминается в компактной форме часто встречающийся в рассматриваемом классе задач «фрагмент» решения. В самом деле, если в процессе решения,.очередной задачи на каком-то этапе потребуется вывести ранее доказанную формулу, то критерий предпочтения аксиом обучения сократит общее число шагов поиска логического вывода по крайней мере на длину доказательства этой формулы.
В заключение следует отметить, что исчисление предикатов и метод резолюций находят применение при решении на ЭВМ широкого класса интеллектуальных задач. Среди решенных можно выделить такие задачи, как автоматическое доказательство теорем, синтез и верификация программ, организация диалога на основе дедуктивных вопросно-ответных систем. Важную роль играет этот логический язык и при организации интеллектуального управления роботами. Далее рассматривается его применение для автоматического планирования поведения, синтеза решающих правил, формирования понятий, распознавания ситуаций и анализа сцен.
IB4
$ 3. ОБУЧЕНИЕ ПОНЯТИЯМ И АКСИОМАТИЗАЦИЯ ЗНАНИИ
При создании интеллектуальных роботов важное значение приобретают задачи обучения понятиям и представления знаний. Необходимость в эффективных методах решения этих задач возникает, например, при моделировании в памяти робота окружающей среды, при распознавании речевых команд или анализе видеосцен. Для представления понятий и знаний в памяти робота необходим адекватный язык. В качестве такого языка можно использовать исчисление предикатов. При подобном подходе задача обучения понятиям легко формализуется.
Пусть задано множество объектов {а>} »Я из М классов, м
т. е. <о«Я, И Каждому классу объектов Я», ft= I, ...
..., М, соответствует решающий предикат
1, если ш а Я*,
п (5.6)
О — в противном случае.
а* (®) =
По существу а* (со)—это характеристическая функция класс# Я». Поскольку классы Oi, .... Ям не заданы, то и решающие предикаты Оц(а>) неизвестны.
Предположим, что информационная система робота позволяет определять некоторые свойства объектов. Каждому такому свойству поставим в соответствие предикат-признак
(1, если о обладает i-м свойством, 6<(®)“|q_b ПрОТИВНОМ СЛуЧае (/«I, ...,«).
На практике предикаты 1/(<о) характеризуют локальные или глобальные свойства объектов, доступные восприятию робота. В терминах этих предикатов-признаков каждому фиксированному объекту <о можно поставить в соответствие его логическое описание г(ш)—элементарную конъюнкцию всех предикатов (5.7), вычисленных на данном объекте ы, такую, что г(ш)= 1.
В режиме обучения роботу предъявляют типичные образцы объектов из разных классов. При этом «учитель», в роли которого обычно выступает человек, сообщает роботу, к какому именно классу Я* данный объект принадлежит. Подмножество и
подобных «эталонных» объектов Яо = |) б*. Я* с: Я*, будем на-f-i
зывать обучающей выборкой. По ней легко построить логическое описание г* (®* всех эталонных объектов <о.<, е Я*-, h = I,..., т», А*>1, .... М. Дизъюнкцию таких описаний объектов из одного
185
и того же класса назовем аксиомой класса Q* и обозначим ж*
А„ (®) -= V (®), k — 1........М. (5.8)
Л-1
?десь т* — число элементов подмножества эталонных объектов -го класса, т. в.
Согласно выражению (5.8) аксиома класса Л»(«) задает логическое описание класса Q* в терминах исходных предикатов-признаков. Процесс построения аксиом классов (по мере предъявления роботу элементов обучающей выборки) по сути представляет собой процесс формирования понятий и представления знаний робота об объектах внешней среды.
В идеальном случае аксиомы классов (5.8) должны обладать следующим свойством:
Л (<о) Од (со) при всех ш g Q. (5.9)
Однако на практике вследствие ограниченности обучающей выборки построить такую идеальную систему аксиом M*f(tt)}*w) обычно не удается. Поэтому при распознавании объектов, не входящих в обучающую выборку, в принципе возможны ошибка,
Для оценки качества системы аксиом классов вида (5.8) введем понятие экстраполирующей силы. Экстраполирующей силой системы аксиом классов {Л*(। на множестве Q будем называть величину
...М)| (61О)
Здесь |Q|—мощность множества Q. Обычно качество системы аксиом классов оценивается по обучающей Qo либо по контроль* ной £2\(Jo выборке, если таковая имеется. Чем больше Е, тем лучше сконструированная система аксиом {Ak (<о }*в|, т. е. тем большую информацию о классах она содержит.
Благодаря обучению понятиям робот приобретает способность к решению задач распознавания. К ним, в частности, относятся такие задачи, как классификация речевых команд или иденти* фикация дикторов, распознавание обычных яркостных или ' дальностных> (т. е. полученных с помощью дальномера) изображений отдельных объектов и сцен, распознавание источников радиолокационных или гидроакустических сигналов.
Характерной особенностью ряда подобных задач является то, что классы распознаваемых объектов Qn, л=1, ..., М, инвариантны относительно той или иной группы преобразований
186
[g] £a G. Формально это означает, что значения решающих предикатов (5.6) не изменяются при всевозможных преобразованиях geG, т. е. о* (<о) = о* (g<o) при всех g&G. Инвариантность классов естественно заложить в конструкцию управляющей системы так, чтобы она не реагировала на групповые преобразования объектов. В этом случае объекты ш, переходящие друг в друга под действием некоторых преобразований g группы G, классифицируются как эквивалентные.
Обучение понятиям в этом случае сводится к предъявлению роботу эталонных объектов (по одному из каждого класса) с указанием их принадлежности классам. Таким образом, обучающая выборка Qo характеризуется тем, что для каждого элемента известно, что o*(w)= 1, причем |йо| = Л1.
Задача синтеза инвариантных понятий заключается в построении по заданной группе преобразований G аксиом классов, способных безошибочно классифицировать все объекты шей, отличающиеся друг от друга преобразованиями g группы G. Экстраполирующая сила E(Q) такой системы аксиом равна единице.
Идея решения такой задачи, основанная на спектральном анализе функций на группе и построении полных систем инвариантных признаков, предложена и развита в работах [55, 56, 75]. Ниже обсуждаются некоторые возможности решения этой Задачи в рамках логического подхода. Основным достоинством инвариантных аксиом является максимальная точность описания классов (E(Q)=1) при обучении по выборке минимального объема (|Q0| = М). Для достижения такой предельной точности в системах типа «перцептрон» [13, 67, 71] может потребоваться обучающая выборка неограниченного объема.
Многие традиционные методы обучения понятиям [13, 37, 50, 59, 67, 71, 73] основываются на построении в том или ином заранее выбранном классе функций решающих правил. Такие правила определяют в пространстве признаков поверхности, разделяющие классы. Решающие правила строятся по обучающей выборке, а применяются к новым объектам. Поэтому весьма важно, чтобы решающие правила обладали высокой экстраполирующей силой не только на обучающей выборке, но и на всем множестве Q объектов, которые могут встретиться роботу.
Требование высокой экстраполирующей силы решающего правила в общем случае трудно формализуемо. Однако для некоторых конкретных классов решающих правил увеличение экстраполирующей силы связано с минимизацией их сложности. Так, при синтезе полиномиальных решающих правил операция сводится к построению полиномов минимальной степени с минимальным числом членов в разложении, обеспечивающих безошибочную классификацию элементов обучающей выборки.
В работах [52, 59] принцип минимальной сложности положен в основу синтеза адаптивных логических решающих правил
187
и реализующих их оптимальных распознающих графов. В этом случае задача формирования понятий ставится так. По обучав щен выборке Qo. на элементах которой известны значения ре. шающнх предикатов (5.6), необходимо построить логически описания классов Л*(ы) в терминах предикатов-признаков (5.7), такие, что, во-первых, /!*(») = а*(о>) при всех и, во-а^> рых, Л»(ы) имеет минимальную (или близкую к минимальной) сложность. При выполнении этих условий естественно ожидал, что экстраполирующая сила Е синтезированного логического описания классов достаточно высока. В идеальном случае, когда распознаваемые классы не пересекаются в пространстве признаков, для получения максимальной акстраполирующей силы £(Q)= 1 необходимо, чтобы синтезированные описания клас&в удовлетворяли условию (5.9).
Логические описания классов А*(<•), k= 1, .... М, в общем случае отыскиваются в классе произвольных дизъюнктивных нормальных форм (Д. Н. Ф). По существу каждое такое описание Л*(ы) аппроксимирует соответствующий неизвестный решающий предикат (5.6). Поэтому коль скоро искомая Д. Н. Ф. Л*(<о) построена, будем называть ее идентифицирующим правилом k-vo класса. Дизъюнкцию идентифицирующих правил вс^х классов будем называть распознающим правилом.
Таким образом, задача обучения понятиям сводится к построению идентифицирующих правил минимальной сложности в классе Д. Н. Ф., таких, что
Л»(®)«=1 при всех «еЩ, Л=1.........Al.
При этом сложность идентифицирующего правила можно трактовать по-разному. Следует отметить, что именно требование минимальной сложности решающего правила отличает предлагаемый метод от других методов формирования понятий, рассмотренных в работах (13, 67, 69, 71].
В ряде случаев удобно искать решающее правило в вад* ориентированного графа — разветвленного дерева решений (£2, 71]. Узлам такого графа соответствуют некоторые предикаты-признаки £,(®), ветвям, исходящим из узла, — возможные зА-чения (5/(w)—0 или £,(«)= 1) признаков. Все ветви заканчиваются листьями, которым ставятся в соответствие номера классов. Каждая ветвь, заканчивающаяся листом, содержит совокупность внутренних узлов, среди которых не имеется узлов, соответствующих одному и тому же значению предикатов. Дизъюнктивные нормальные формы, допускающие такое графическое представление, будем называть бинарно-древовидными.
Распознающее правило, представленное в форме бинарно-древовидной Д. Н. Ф., будем называть последовательным рас* ъознающим (идентифицирующим) правилом, а реализующий его граф типа «дерево классов» — распознающим (идентифицнрую-188
щим) графом. Процесс распознавания на таком графе представляет собой последовательное «раскрытие* его узлов, т. е. определение значений соответствующих предикатов на данном объекте <• е (2. Любая ветвь распознающего графа, соответствующая последовательности «раскрытых» узлов, приводит (с определенной вероятностью) к тому или иному классу объектов.
Задача синтеза последовательных логических распознающих правил и реализующих их графов минимальной сложности сводится к построению бинарно-древовидной Д. Н. Ф„ обладающей теми же свойствами, что и описанные оптимальные идентифицирующие правила. Таким образом, возникает «последовательная» разновидность сформулированной ранее задачи обучения понятиям: построить оптимальное распознающее правило, но не в классе Д. п. Ф., а в более узком классе бинарно-древовидных Д. Н. Ф. Совершенно аналогично формулируются задачи обучения понятиям в случае, когда признаки с jet) являются не двузначными, а многозначными предикатами.
Достоинством оптимальных идентифицирующих и распознающих правил является гарантируемая ими высокая точность-распознавания при весьма экономном логическом описании и представлении классов в памяти робота. Это в ряде случаев приводит к значительной экономии времени и средств (в частности, памяти), необходимых для распознавания различных классов сигналов и ситуаций.
Для представления знаний о классах объектов внешней среды в виде формул исчисления предикатов можно использовать информацию, заключенную в обучающей выборке, либо словесное описание классов. С целью формализации процессов формирования понятий введем обозначение
f &(®) при 1,
при ^(й) = 0,
(5.Н)
где ш—некоторый фиксированный объект, на элементах которого заданы значения предикатов-признаков |,(»), i — 1, п. Очевидно, что 6*' ,e,(®)e 1
Назовем логическим описанием объекта ы элементарную конъюнкцию вида
з,(®) = & (5.12)
ме // — заданное множество индексов предикатов-признаков. Отметим, предикаты &(®), описывающие локальные свойства объектов, зачастую заданы не на всем объекте ы (или его изображении}, а на некоторых его элементах vco. В таких
18»
случаях логическое описание (5.12) имеет более сложный вид; го))== & & ф ’♦’(?). (5.13)
(«// «<=<ь ’
Здесь v — набор элементов объекта о», \на которых определен i-й предикат-признак. Мощность множества /, определяет ранг г логического описания, т. е. |//| = г.
Рассмотрим сначала индуктивный метод формирования понятии по обучающей выборке в виде Д. Н. Ф. С этой целью по-строим таблицу, строки которой являются значениями предикатов-признаков и решающих предикатов на соответствующих элементах о>/| обучающей выборки й0 Каждой строке полученной таблицы поставим в соответствие элементарную конъюнкцию 2л(о>) вида (5.12) и назовем ее аксиомой Л-го подкласса, если а*(ш)= 1. Объединяя все синтезированные таким образом аксиомы Л-го подкласса Zu (<о), Л — 1, .... /п*. знаком дизъюнкции, получаем описание Л-го класса в виде аксиомы класса (5.7). Это и есть логическое представление понятия &-го класса, которое робот формирует в процессе обучения.
Если набор предикатов-признаков таков, что отрицание любого из них есть другой предикат либо выражается в виде дизъюнкции некоторых предикатов без отрицания, то в аксиому класса вида (5.8) достаточно включить не все исходные предикаты, а лишь те (назовем их позитивными), которые выполняются на каких-либо элементах обучающей выборки. Этот прием позволяет иногда существенно упростить вид аксиомы классов и уменьшить их ранг. На практике каждый объект характеризуется лишь несколькими признаками-предикатами, а информация об отсутствии остальных признаков оказывается излишней. Описание классов в терминах только позитивных предикатов избавляет от необходимости хранить лишнюю информацию, что особенно важно для минимизации памяти робота и ускорения процессов распознавания.
Очевидно, что для всякого объекта <» обучающей выборки верна по крайней мере одна формула Л* (<>). Таким образом, синтезированная система аксиом классов вида (5.12) описывает обучающие подклассы Й*«=Й*ПЙО- Однако полное описание классов Q* предполагает, что Д*|ш)ва»(<о) для всякого <oeQ, а не только для всех <о е Qg — (J &*.
4 — 1
Экстраполирующая сила (5.10) аксиом классов, т. с. способность правильно классифицировать объекты, не вошедшие в обучающую выборку, зависит от того, насколько полна информация о классах, содержащаяся в обучающей выборке ЗД>. Если обучающая выборка достаточно представительна и мощна, то индуктивное описание классов в виде (5.8), (5.12) дает правиль-м ную классификацию всех элементов (-h-
193
Однако на практике обучающая выборка зачастую оказы* дается нерепрезентативной. В этих случаях она состоит из небольшого числа примеров (прецедентов) каждого класса. Экстраполирующая сила системы аксиом, построенной по короткой обучающей выборке, обычно мала. Для ее увеличения ложно использовать рассматриваемые далее оптимальные алгоритмы построения (по обучающей выборке) логических идентифицирующих и распознающих правил.
В ряде случаев имеется априорное описание классов в вида необходимых или достаточных условий принадлежности объекта тому или иному классу. Подобным априорным описанием может служить словесное описание классов. Формализация этого описания и его приведение к Д. Н Ф. позволяет иногда получит^ систему аксиом классов типа (5.8) с экстраполирующей силой Е, равной единице на всем множестве Q. Отметим, что достаточные условия принадлежности объекта классу О* обычно имеют вид
Л*«о)->а* («в), в необходимые задаются в форме о* (®)-♦ Л* (®), “] а* («)«-“] Лй(®).
Метод формирования понятий путем формализации необходимых и достаточных условий приадлежности классам будем называть экстраполяционным.
Качество обучения и точность распознавания существенно зависят от особенностей системы аксиом классов {Л* (©)}*_ Естественно потребовать, чтобы эта система обладала свойствами непротиворечивости и полноты. Кроме того, практически важно, чтобы аксиомы классов были инвариантны по отношению к действию групп преобразований, действующих на объекты из соответствующих классов. Сформулируем эти свойства.
Систему аксиом классов {Л*(<*>)}*_, будем называть полной аа множестве Q, если для всякого элемента uefi найдется аксиома Л»(®), классифицирующая <о, т. е. Л*(ш)= 1.
Систему аксиом классов {Л*(®)}£, будем называть непротиворечивой на множестве Q, если для всякого элемента weeQ з условия, что аксиомы Л,(ю) и Л,(®) классифицируют <о, следует i — j.
Отметим, что непротиворечивость имеет место на обучающей выборке Оо, если обучающие подклассы Q*. .... М, не
пересекаются. В этом случае непротиворечивость системы ак-’Вом означает, что «эталонные» объекты из разных подклассов Р* не имеют одинакового логического описания вида (5.8). Если Же классы Й*, А=1.......Af, пересекаются, то целесообразно
‘вести новый класс Q*+i — класс неоднозначно классифнцирую-
101
щнхся объектов. Это приводит к соответствующей модификации системы аксиом классов.
Аксиому класса А*(а>) будем называть инвариантной отно-сительно группы преобразований G, если
А* (®) = A* (g<o) при всех geO, (5.14)
В задачах распознавания сцен по их изображениям инвариантность аксиом классов играет важную роль, так как изображения отдельных объектов на сцене часто подвергаются преобразованиям, имеющим групповую природу (сдвиг, вращение, проективные преобразования н т. п.). Очевидно, что инвариантная аксиома класса не реагирует на указанные преобразования g группы G. В результате в памяти робота формируются понятия, инвариантные относительно той или иной заданной группы преобразований.
Достаточным условием инвариантности аксиомы класса А«(ш) вида (5.8) остиосительно группы преобразований G является инвариантность относительно G всех входящих в нее предикатов-признаков. Отметим, что если два элемента со,, щ обучающей выборки По различаются преобразованием g е б, т. е. a>j = gv>i, то в аксиому класса (5.8) достаточно включить лишь одну аксиому подкласса, построенную по любому из указанных элементов. Благодаря такой «инвариантной фильтрации» в процессе обучения робота строятся более простые логические описания классов. Инвариантность этих описаний по отношению к заданной группе преобразований G позволяет автоматически преодолеть трудности, связанные с возможными (может быть, неизвестными) преобразованиями gsG объектов внешней среды. Тем самым существенно облегчается процесс распознавания сцен.
Для экономного представления понятий в памяти робота и рационализации перебора в процессе распознавания большое значение имеют аксиомы обучения [59]. По существу эти аксиомы представляют собой некоторые логические функции тех предикатов-признаков, которые часто встречаются в описаниях классов. Поэтому их можно интерпретировать как обобщенные признаки более высокого уровня, определяющие некоторые вспомогательные понятия. Для обозначения этих новых понятий, «склеенных» из исходных предикатов-признаков, естественно ввести специальные метапредикаты. Очевидно, что в терминах таких метапредикатов-понятий (аксиом обучения) система ак-сном классов имеет более простое представление, чем в терминах исходных предикатов-признаков. В частности, может уменьшиться ранг аксиом классов, что ускоряет процесс распознавания.
Управляющая система робота, реализующая описанные логические средства формирования понятий, строит (по обучающей выборке или исходя из априорного описания классов) проблемно 192
ориентированную систему аксиом классов, обладающую полнотой, непротиворечивостью и инвариантностью. Получаемая в результате аксиоматическая система понятий выступает как эффективное средство логического представления знаний о внешней среде в памяти робота.
$ 4. ОПТИМИЗАЦИЯ АДАПТИВНЫХ РЕШАЮЩИХ ПРАВИЛ
Для распознавания ситуаций и принятия решений роботу необходимо сформировать соответствующие решающие правила. Рассмотрим общую схему и конкретные алгоритмы синтеза и оптимизации одного класса таких правил — логических идентифицирующих и распознающих правил минимальной сложности.
Средн этих правил прежде всего выделим важный подкласс последовательных решающих правил, основанный на последовательном анализе информации о классах. Синтез таких правил сводится к построению ориентированных графов типа «дерево решений» и принятию решений с их помощью. Это соответствует синтезу логических решающих правил в классе бинарно-древовидных Д. Н. Ф. Процесс конструирования распознающих правил-графов по информации, заключенной в обучающей выборке, можно интерпретировать как процесс обучения робота распознаванию классов.
- Элементарной конъюнкцией А-го ранга будем называть, как Обычно, логическую функцию вида
; & #(<•), (5.15)
где /»— заданное множество индексов предикатов-признаков, Тйкое, что |/*| = А, Р«, i е/*, —фиксированный набор логических констант. Каждому элементу <оА обучающей выборки Qo можно поставить в соответствие конъюнкцию ранга п
2<ям(®) = (“*) (о),
Которая его полностью характеризует, т. е. г*(®л)=1. Тогда простейшее логическое решающее правило имеет вид импликации
2<|*’(а»->ст,(<о), (5.16)
где ст,(ш)=1. Дизъюнкцию антецедентов таких правил, построенных по всем элементам обучающей выборки из i-ro класса, можно трактовать как аксиому i-ro класса, т. е.
Л4(®) = v z<n*>(®). (5.17)
7 Зак. т
193
Совокупность таких аксиом полна на обучающей выборке. Од. нако она весьма сложна (требует запоминания всех элементов обучающей выборки), и поэтому ее экстраполирующая сила на контрольной выборке может оказаться небольшой. К тому же система аксиом (5.17) вообще не является бинарно-древовидной Д. Н. Ф. На основании указанных причин решающие правила вида (5.16) следует отвергнуть.
Новый подход к синтезу логических решающих правил и распознающих графов основывается на последовательной оптимизации конъюнкций вида (5.15) при А = 1, 2, ... по заданному критерию качества, вычисляемому по обучающей выборке. Общая схема такого синтеза заключается в следующем.
На А-м шаге рассматривается каждая конъюнкция г»_|(») (к—1 )-го ранга, построенная на предыдущем шаге. По этим конъюнкциям строятся новые конъюнкции z*(w) А-го ранга путем присоединения ранее не использованных признаков £,(a>) или их отрицаний *|&(ш). Средн полученных конъюнкций вида zn-t & и z*-i Л 1 £< отбирается наилучшая (в смысле заданного критерия качества). На (А + 1 )-м шаге процесс повторяется. Окончание процесса определяется правилом остановки.
Для конкретизации описанной общей схемы построения логических решающих правил необходимо выбрать критерий качества и указать правило остановки алгоритма. Разные варианты такой конкретизации предложены в работах [13, 52, 71]'. Поскольку в принципе возможные ошибки распознавания, целесообразно использовать статистические критерии качества, такие, как критерий Байеса или критерий Вальда.
Наибольший практический интерес представляет критерий Байеса, так как позволяет минимизировать вероятность ошибок. Согласно «тому критерию на А-м шаге отбирается тот признак, при включении которого в **(<•) максимизируется апостериорная вероятность некоторого класса '
P*(Q? = max />(CL |лк(«)= 1). (5.18)
/-I..м
Если для некоторой конъюнкции т*(«Н А-го ранга P*(Q,)=^ 1, то она не достраивается. В этом случае говорим, что синтезированная конъюнкция z»(®) характеризует класс Q, с вероятностью единица. Формализуем это в виде импликации
zA(<o)P-»>a((<i»), (5.19)
представляющей собой достаточное условие принадлежности t-му классу. Логическую функцию вида (5.19) будем называть элементарным логическим решающим правилом, а совокупность таких правил, обеспечивающую безошибочную классификацию обучающей выборки С20, — полной и непротиворечивой системой логических решающих правил. Таким образом, задача обучении
194
сводится к построению полной н непротиворечивой системы элементарных логических решающих правил вида (5.19).
Описанный алгоритм последовательного построения такой системы является локально-оптимальным в смысле максимизации на каждом шаге вероятности принадлежности объекта какому-либо классу согласно критерию (5.18). Однако апостериорные вероятности классов, входящие в этот критерий, на практике не известны. Поэтому их приходится оценивать по информации, заключенной в обучающей выборке.
Пусть тлфо)—число элементов обучающей выборки Qq, на которых г4(ю>= 1, а тЦО,)—число элементов Йо. принадлежащих классу По. на которых ?*(<>)= 1. Тогда искомые апостериорные вероятности могут быть оценены по обучающей выборке с помощью формул
P(Q,|24(®)=l) = mJ(Q))/m»(Q0). /-1.......М. (5.20)
Отметим, что оценки (5.20) тем точнее, чем больше объем т обучающей выборки Йо- (Здесь предполагается, что объекты ® поступают на вход информдцнонной системы робота случайно и независимо, с некоторым, вообще говоря, неизвестным распределением вероятностей р(ш).)
Необходимым условием построения полной и непротиворечивой системы логических решающих правил вида (5.19) является отсутствие пересечений образов элементов со* е= й0 в пространстве предикатов-признаков. Если такие пересечения имеются, то тем самым допускается некоторая вероятность ошибок. Однако при фактическом обучении робота объекты, образы которых пересекаются в пространстве признаков, целесообразно исключить из обучающей выборки. В этом случае описанный локально-оптимальный алгоритм последовательного обучения заканчивает работу на некотором r-м шаге, причем г п. Результатом построения является полная и непротиворечивая система элементарных логических решающих правил вида (5.19).
Синтезированной системе соответствует распознающий граф типа «бинарное дерево классов». Каждое элементарное решающее правило (5.19) изображается его ветвью. При этом признаку, входящему в конъюнкцию ;»(<>), соответствует узел на такой ветви, а решающему предикату о,(<о)—лист с номером i. Из г.аждого узла исходят два ребра, соответствующие возможным значениям данного признака.
Алгоритм обучения на графе допускает следующую интерпретацию. На 4-м шаге рассматривается каждая ветвь, построенная на предыдущем шаге. Если конъюнкция ?t.((o), соответствующая этой ветви, характеризует (с вероятностью единица) некоторый класс й . то ветвь заканчивается листом с номером i. В противном случае она дополняется узлом, отобранным по критерию (5.18), из этого узла строятся два новых
7*
1»
ребра, отвечающих возможным значениям соответствующего признака.
Для распознавания класса, которому принадлежит данный объект, необходимо найти признак (или его отрицание), который присутствует во всех решающих правилах вида (5.19), и измерить его значение на данном объекте. Далее следует рассмотреть то подмножество правил, которое содержит этот признак (или его отрицание). Описанный процесс повторяется, пока не останется только одно распознающее правило, которое и содержит ответ. Отметим, что в процессе распознавания ни один признак не измеряется дважды.
Если распознавание осуществляется по графу, то сначала измеряется признак, соответствующий узлу первого уровня. Далее по ребру, соответствующему полученному значению признака, осуществляется переход к узлу второго уровня и измеряется соответствующий ему признак. Процесс «раскрытия» узлов по избранной ветви графа продолжается до тех пор, пока не встретится некоторый лист, который и содержит код искомого класса.
Введем следующие характеристики полной системы элементарных решающих правил: 1) ранг г — максимальный ранг антецедентов в (5.19), т. е.г = тахг»; 2) средний ранг гср =
т
= У rhp (<»*), где г* — ранг конъюнкции, характеризующей эле-Л-1
мент <oasQo;3) сложность N— общее число используемых признаков.
Эти характеристики на распознающем графе, реализующем полную систему логических правил вида (5.19), интерпретируются так: г—максимальная длина ветви графа г п; гср — средняя длина ветвей графа (гср^г); N — общее число его узлов.
Введенные характеристики имеют следующий смысл! г — максимальное число измерений предикатов-признаков, необходимых для распознавания любого объекта weQ; гср— среднее число необходимых измерений; N характеризует сложность реализации распознающего графа (например, в виде изоморфной ему релейно-контактной схемы). Поэтому чем меньше значения указанных характеристик, тем предпочтительнее (при прочих равных условиях) распознающий граф.
Полная и непротиворечивая система логических решающих правил обладает следующими свойствами. Во-первых, экстраполирующая сила системы на обучающей выборке максимальна, т. е. E(QO)=1. Во-вторых, конъюнкции-антецеденты системы (5.19) взаимно ортогональны, т. е. z*(<o)&г/(о>) = 0, а следовательно, и статистически независимы. В-третьих, прнзнакн-пре-дикаты, не вошедшие нн в одно из элементарных правил вида (5.19), являются неинформативными и могут быть отброшены.
196
В-четвертых, ранг г и сложность N системы являются минимально необходимыми (при фиксированном локально-оптимальном алгоритме обучения) для безошибочной классификации обучающей выборки. Поэтому можно считать, что синтезированная полная система логических решающих правил и реализующий ее распознающий граф имеют минимальную (нли близкую к минимальной) сложность.
Распознавание с помощью оптимальных правил н графов последовательного типа обычно не требует измерения, всех предикатов-признаков 5,(<о), 1=1, ..., п, так как нх ранг г, как правило, существенно меньше общего числа п предикатов. Это обстоятельство, выгодно отличающее логические решающие правила и графы от традиционных методов перцептронного типа, использующих одновременно все признаки &(<>), i = 1, .... п, особенно важно в тех случаях, когда «стоимость» измерений предикатов-признаков достаточно высока. Наглядность, простота н последовательное принятие решений на сннтезнрованных распознающих графах типа «дерево классов» делает нх удобным инструментом автоматического распознавания в управляющих системах роботов разного назначения.
Рассмотрим теперь задачу построения н оптимизации идентифицирующих правил, аппроксимирующих решающие предикаты (5.6). Особенность этой задачи заключается в том, что она решается для каждого класса Q/, t = 1 М, отдельно. Полная система синтезированных идентифицирующих правил {Л,(<‘>')/!.| позволяет распознать любой объект шей. Для увеличения экстраполирующей силы данной системы важно, чтобы каждое входящее в нее правило Л,(ш) имело такие по возможности минимальные ранг и н сложность JV/t прн которых Л,(ша)= 1 для всех шл <= Q/. Подобные ндентифнцнруюшие правила будем называть оптимальными.
Общая схема локально-оптимального (в смысле байесовского критерия качества) алгоритма синтеза идентифицирующих правил в виде Д. Н. Ф. заключается в следующем. Рассматриваются некоторый класс Q, и соответствующее ему подмножество элементов обучающей выборки & = Q, П Qo.
На первом этапе последовательно строятся всевозможные конъюнкции z»(<o) Л-го ранга (Л=1, 2, ...) и для каждой из них по формуле (5.20) вычисляется апостериорная вероятность i-го' класса. Как только прн некотором k = г( оказывается, что pri(Q,)= 1, соответствующая конъюнкция z(,’(<o) ранга г\ запоминается как первый дизъюнктивный член .искомого идентифицирующего правила Л,(со). (Если среди конъюнкций ггго ранга таких конъюнкций окажется несколько, то среди них отбирается та, которая характеризует максимальное число объектов нз Q,.) Из множества ft, исключаются все объекты, характеризуемые отобранной конъюнкцией г(|> (<>), т. е. строится
197
множество
= Q<\ {© е Q«: z<n (®) = 1}.
На втором этапе на подмножестве Q1 вновь последовательно строятся всевозможные конъюнкции г* (и) ранга k г\ и среди них отбирается такая, что Р' (Q;)=l. Данная конъюнкция z*(®) ранга rj. дизъюнктивно добавляется к ранее отобранной г°’(®). Далее строится множество
Q? = Qi \ {® «= Qi: z<2) (®) = 1}, т. е. из $1 исключаются все элементы, характеризуемые новой конъюнкцией z<a)(®)- Процесс продолжается до тех пор, пока на некотором шаге Nt множество 2*' не окажется пустым: 2Г‘=*.
Результатом работы алгоритма является аксиома i-ro класса вида
Ni А( (®) = V (®), (5.21)
/-1
обладающая следующими свойствами:
1) Л,(ш) = 1 при всех шей,;
2) ранг Г( аксиомы Л/(®) является (при данном байесовском алгоритме обучения) минимально необходимым для того, чтобы Л/(и) характеризовала все элементы подмножества Q,, при этом сложность Ni аксиомы Л<(®) как функция ее ранга г* также минимальна;
3) в процессе построения аксиомы класса Л<(®) происходит «естественный отбор» информативных признаков, в то время как неинформативные (для i-ro класса) признаки автоматически отбрасываются.
На основе синтезированных аксиом классов вида (5.21) непосредственно получаем следующую полную и непротиворечивую систему идентифицирующих правил:
Л((и)->a,(o', i= 1, ... М. (5.22)
Отметим, что антецеденты этой системы взаимно ортогональны (по построению), т. е.
Л/(®)& Л/(®) = 0 при Z
Идентифицирующее правило(5.22) может быть представлено в виде ориентированного графа такого же типа, как и распознающий граф. Отличительной чертой подобного графа является то, что все его листья относятся к одному и тому же классу. Каждой конъюнкции z</)(«) аксиомы j-гр класса соответствует ветвь графа, каждому признаку &(®)—узел, а каждому значс-198
нию признака ^(ш)=1 или &(ш)=0 — ребро, исходящее из соответствующего узла.
Совокупность идентифицирующих графов удобно представлять в виде «орбитального» графа — фрейма классов. На нулевой орбите этого графа располагаются листья с i-м номером всех классов Q,, i = 1.М, на первой — узлы первого уровня
идентифицирующих графов, на второй — узлы второго уровня и т. д. Из свойств синтезированных аксиом классов следует, что число орбит г„ используемых для графического представления й-го класса, минимально. При этом числе орбит используется минимальное число ветвей Конъюнкции, соответствующие разным ветвям, взаимно ортогональны, т. е. = О
при p^q. Это свидетельствует об их статистической независимости и информативности.
Для идентификации данного класса Q, необходимо выбрать в системе (5.22) i-e идентифицирующее правило (или реализующий его идентифицирующий граф). Далее следует проверить на данном объекте <о истинность конъюнкций, входящих в аксиому с-го класса. Если хотя бы одна из этих конъюнкций истинна, то объект идентифицируется иак представитель класса Q,. В противном случае принимается неопределенное решение е> ё= Q,.
Процесс идентификации на графе сводится к последовательному «раскрытию» его узлов, начиная с первой орбиты. На первом шаге измеряется (вычисляется) значение признака, соответствующего первому узлу. В зависимости от значения этого признака выбирается ребро, ведущее от данного узла к некоторому узлу второй орбиты. На втором шаге намеряется (вычисляется) значение признана, соответствующего этому'узлу, и т. д. Бели таким образом удается дойти до конца какой-либо ветви, то объект ш относится к тому классу, которому принадлежит эта ветвь. Если же не существует ребра, соответствующего вычисленному значению очередного признака, то принимается решение, что исследуемый объект данному классу ^точнее, его идентифицирующему графу) не принадлежит. Для распознавания объекта необходимо последовательно рассмотреть оставшиеся графы, пока на одном из них не произойдет идентификация некоторого класса.
Экстраполирующая сила E(Q) синтезированных оптимальных идентифицирующих правил и графов достаточно высока. Это следует из того, что по построению (при заданном байесовском алгоритме обучения) ранг rt и сложность Nt каждой аксиомы класса А,(о) минимальны при соблюдении естественного требования £(fto)=* 1. Этот вывод подтверждается также экспериментальными результатами решения разнообразных задач распознавания н идентификации классов.
В заключение подчеркнем связь синтезированных решающих правил с фреймами. Г. С. Поспелов в предисловии к книге
19Э
[34, c. 3J определяет это понятие так: «Фрейм любого вида-, это та минимально необходимая структурированная информа. ция, которая однозначно определяет данный класс объектов Наличие фрейма позволяет относить объект к тому классу, ко-торый им определяется». Данное определение весьма точно выражает сущность рассмотренных адаптивных логических ре. шающих правил и реализующих их .распознающих и идентифицирующих графов. Поэтому такие правила и графы, синтезиро. ванные на основе принципа минимальной сложности, можно условно назвать логическими фреймами.
$ 5. ЛОГИЧЕСКОЕ РАСПОЗНАВАНИЕ СЦЕН
Робот с интеллектуальным управлением должен обладать способностью анализировать окружающую обстановку, иденти* фицировать целевые объекты, распознавать препятствия. Традиционные методы распознавания образов для решения этих задач не приспособлены.
Главная трудность связана с тем, что роботу обычно приходится иметь дело не с одним объектом, принадлежащим тому или иному классу, а с совокупностью объектов из разных классов. Другая трудность обусловлена сильной вариативностью объектов в поле зрения робота. Так, например, могут значительно изменяться расстояния от робота до окружающих объектов, ракурс, в котором они воспринимаются, условия освещения и т. д. Более того, одни объекты могут заслонять другие, затрудняя тем самым их распознавание. Поэтому для преодоления указанных трудностей от робота требуются определенная активность и интеллектуальность.
Немногочисленные алгоритмы анализа сцен имеют эвристический характер и не всегда приводят к положительному результату даже в очень упрощенных и стилизованных условиях распознавания [13, 38, 71]. Исключение составляет метод тематической фильтрации сложных изображений [75], основанный на теоретико-групповом анализе сцены. Однако и этому методу присущи определенные ограничения и недостатки. К ним относятся требование группового характера преобразований объектов на изображении сцены (что на практике выполняется далеко не всегда) и сложность выделения отдельных объектов путем вычисления их инвариантов. Имеются также хорошо зарекомендовавшие себя эвристические методы выделения (без распознавания) отдельных объектов на сложной' сцене. Так, в работе '[13] описана программа для ЭВМ, позволяющая выделять отдельные объекты на контурном изображении сцены путем предварительной разметки линий и выявления среди них граничных линий на основе анализа типа узлов. В работе [71] описаны алгоритмы лингвистического анализа сложных (главным образом контурных) изображений.
300
Принципиально иной подход к распознаванию сцен по их изображениям базируется на предварительном (в процессе обучения робота) формировании понятий в виде аксиом классов с последующим выделением тех или иных объектов сцены посредством их логического распознавания. Этот подход воплощен в рассматриваемом далее адаптивном методе распознавания сцен (4, 59]. Предлагаемый метод свободен от отмеченных недостатков: он позволяет легко (и притом автоматически) преодолеть все возникающие трудности.
Основная идея метода заключается, во-первых, в логическом представлении (в терминах предикатов-признаков) понятий, формируемых в процессе обучения робота в виде проблемно-ориентированных аксиом классов, и, во-вторых, в организации процесса распознавания (включая идентификацию, классификацию и анализ объектов сцены) с помощью алгоритмических средств поиска логического вывода. Метод хорошо приспособлен для реализации на ЭВМ, причем программирование логических алгоритмов распознавания удобно осуществлять на языках высокого уровня (типа РЕФАЛ, PL и др.). Управляющая система робота, реализующая этот метод, обладает важным свойством: она легко «дообучается» новым понятиям и адаптируется к изменяющимся условиям, что позволяет надежно распознавать на сцене как новые (или сильно преобразованные) объекты, так и целые их классы.
В режиме, обучения роботу предъявляются в разных ракурсах эталонные объекты из разных классов. При этом автоматически строятся описания классов в виде формул исчисления предикатов А*(ш), k=\, связывающих исходные предикаты-
признаки £|, .... и принимающих истинные значения по меньшей мере на элементах обучающей выборки Qo. Структура, свойства и способы построения таких формул, называемых аксиомами классов, уже были подробно описаны. Остановимся только на одном важном свойстве этих аксиом — их инвариантности по отношению к заданной совокупности преобразований.
Как известно, на практике в ряде случаев объекты из каждого класса Q* различаются только преобразованиями g на некоторой фиксированной совокупности (например, группы) преобразований G. В других случаях для порождения всех элементов класса П* может оказаться недостаточно одного эталонного элемента из этого класса и может потребоваться некоторое множество «эталонов», соответствующих, например, существенно разным ракурсам восприятия объектов из Q». В подобных ситуациях естественно потребовать, чтобы робот одинаково классифицировал объекты, различающиеся допустимыми преобразованиями g из G. Поскольку конкретное преобразование g, подействовавшее на распознаваемый объект, роботу обычно не известно, то такой робот по существу является адаптивным по отношению к заданной совокупности преобразований.
201
При конструировании интеллектуальной управляющей системы подобного робота весьма важно выбрать исходные предикаты-признаки так, чтобы они были инвариантны относительно допустимых преобразований g е G. Смысл инвариантности заключается в том, что предикаты-признаки должны принимать одни и те же значения на объектах, отличающихся друг от друга допустимыми преобразованиями. Формально свойство инвариантности предикатов-признаков можно записать так:
Vg €= GV<U <= Q & i(D) ~~ gj
Однако одной инвариантности признаков мало. Необходимо, кроме того, чтобы совокупность инвариантных признаков обладала определенной полнотой. Впервые полные системы инвариантных признаков были предложены в работах [55, 56, 75]. Они строились как функционалы от коэффициентов Фурье или моментов изображения. Аналогично можно построить и полные системы логических инвариантов. Такие системы должны обеспечить возможность восстановления преобразования g из G, отличающего распознаваемый объект от эталонного.
Важно отметить, что если аксиомы классов строятся на основе инвариантных предикатов-признаков, то они сами также инвариантны относительно допустимых преобразований g из G. Если же система предикатов gi, .... полна на множестве Q по отношению к совокупности преобразований G, то синтезированные из них аксиомы классов {Ак («)}*_,> во-первых, дают полное описание классов, инвариантных (замкнутых) относительно G, во-вторых, позволяют найти неизвестное преобразование g е G, отличающее данный объект от эталонного. Благодаря этому обеспечивается принципиальная возможность безошибочного распознавания классов, инвариантных по отношению к заданной совокупности преобразований G, при обучении робота по выборке минимального объема — по одному эталонному представителю из каждого класса.
В режиме распознавания робот решает задачи трех типов: проводит идентификацию, классификацию и анализ.
Задача идентификации заключается в том, что робот самостоятельно должен ответить на вопрос, имеется ли на изображении сцены объект данного класса. Задача классификации сводится к выяснению, объекты каких классов представлены на изображении сцены. Наконец, задача анализа заключается в выяснении того, объекты каких классов и в каком количестве имеются на изображении сцены, а также, возможно, как они ориентированы, где расположены и т. д.
Рассмотрим сначалазадачу идентификации на сцене объекта данного класса. Пусть ш — некоторая фиксированная сцена (совокупность объектов внешней среды). Обозначим через г(ш) ее логическое описание в терминах предикатов-признаков, имеющее 202
днд (5.12) или (5.13). Предположим, что требуется идентифицировать на сцене <о объект А-го класса.
Решение этой задачи в рамках исчисления предикатов сво* Гтся к доказательству утверждения
z (®) -* ЯшЛ> (ш), (5.23)
р. е. того, что формула ЭшЛ*(ш) следует из формулы ?(<>}. ЗСмысл утверждения (5.23) заключается в следующем: сцена <о, ямеющая логическое описание z(<o), включает объект w, такой, wro An(w)= 1, т. е. w е Q*.
< Таким образом, идентификация объекта из А-го класса на сцене сводится к поиску доказательства утверждения (5.23). Для автоматического решения этой задачи .можно воспользоваться описанным методом резолюций.
Основное достоинство этого метода применительно к задаче распознавания -заключается в том, что объект w в ходе доказательства (5.23) определяется конструктивно: в результате «означивания переменных» в процессе ноиска логического довода элемент w из Q» находится в явном виде. При раснознавании ацен по их изображениям такое означивание соответствует выделению изображения объекта А-го класса на сложном изображении сцены. Это позволяет найти параметры преобразования f, отличающего идентифицированный объект от распознаваемого.
Для фактического доказательства утверждения (5.23) согласно методу резолюций достаточно доказать противоречивость обратного утверждения, т. е.
z (S) А (“1 {ЭшЛк (w))), или эквивалентной ему формулы
z(S) & “| Л* (ш). (5.24)
Учитывая выражения (5.8), (5.24), получаем
ПЛ*(иО=4* П^(ш)=&* V П#(4>(»).
Л-1 п Л-1
Отсюда следует, что утверждение (5.24) имеет, как этого требует метод резолюций, вид конъюнктивной нормальной формы (К. Н. Ф.).
Автоматическое доказательство утверждения (5.23) заключается теперь в последовательном применении правила резолюций к формуле (5.24) в соответствии с той или иной стратегией поиска. При этом из простых дизъюнктов, на которые разлагается (5.24), по правилу резолюций формируются новые дизъюнкты, называемые резольвентами. Процесс образования резольвент продолжается, пока не будет получена пустая формула (последнее гарантируется полнотой системы аксиом клас
203
сов), символизирующая конец и успех поиска логического вы-вода. Противоречивость формулы (5.24) означает идентифика^ цию некоторого объекта Л-го класса на данной сцене.
Однако в ряде случаев этого недостаточно, поскольку роботу важно еще знать, какие элементы сцены относятся к йдентифц. цированному объекту, как они преобразованы по отношению к эталону. Для решения этой задачи можно использовать стандартную процедуру извлечения ответа, описанную, например, в работе (37]. Специфика задачи идентификации позволяет упростить эту процедуру. Запоминая все подстановки, которые выполнялись во время «означивания переменных», и выбирая те из них, которые привели к пустой формуле, непосредственно получаем ответ—набор предметных констант w, задающий идентифицированный объект.
Задача класнфикации объектов на сцене сводится к многократному решению задач идентификации для k = 1, ..., М. При этом последовательно выясняется, имеются ли на данной сцене объекты первого, второго и т. д. классов. Формально классификация сводится к доказательству следующих утверждений:
2(®)-*ЗшЛ| (ш), z (в) -»ЗщЛ2(ш),
(5.25)
z (S) —►ЗшЛА<(щ).
Задача анализа сцены также сводится к .многократному решению задачи идентификации для 6=1, .... М. Отличие ее от задачи классификации заключается в том, что в процессе анализа должны быть идентифицированы и выявлены все объекты из А-го класса, составляющие сцену. Поэтому по мере идентификации того или иного объекта предметные константы, определяющие этот объект, из данной сцены исключаются. Соответственно из описания сцены z(w) вычеркиваются все предикаты, которые использовались при идентификации выделенного объекта. Эта операция в случае анализа изображений сцен соответствует «стиранию» изображения идентифицированного объекта.
Для оставшейся части анализируемой сцены вновь решается задача идентификации, пока не будет получен ответ, что объектов данного класса на сцене не наблюдается. Тогда описанная процедура идентификации повторяется для нового класса объектов. В результате анализа выделяются все объекты, составляющие сцену, и указывается, какому классу каждый из них принадлежит.
Таким образом, в рамках описанного метода анализ н разделение сцены на отдельные объекты разных классов происходят в процессе распознавания. В этом заключается одно из принципиальных отличий и преимуществ данного метода от известных
20»
[13, 71]. которые сводятся только к разбиению сцены на объек-ты (без каких-либо попыток их распознавания) либо к распознаванию заранее выделенных объектов.
Рассмотрим один из возможных путей совершенствования стратегии, связанной с комбинированием различных стратегий с учетом особенностей выражения (5.24). Анализ его наводит на мысль, что поиск логического вывода разумно начать с отрицания предположения, т. е. с 1 Л*(а>). Это соображение Полностью согласуется со стратегией опорного множества. Для ускорения поиска логического вывода рекомендуется использовать стратегию предпочтения одночленов |37]. Отметим, что в процессе распознавания эта стратегия используется автоматически, так как описание сцены г (со) состоит из одночленов. Стратегия лозы предписывает [37] каждую новую резольвенту формировать на основе предыдущей. Использование этой стратегии в процессе распознавания также целесообразно и оправдывается тем, что противоречие (-а следовательно, идентификация объекта) всегда достигается на одном дизъюнктивном члене аксиомы класса А*(и).
Таким образом, проведенный анализ особенностей задачи «резол юционного> распознавания сцен показывает, что одной из эффективных стратегий поиска логического вывода является комбинированная стратегия, сочетающая стратегии лозы, опорного множества и предпочтения одночленов. Другой вариант реализации метода логического распознавания сцен по их изображениям, основанный на эвристическом синтезе и использовании адаптивной стратегии поиска, рассмотрен в работе [4]. < Общая схема описанной адаптивной системы логического распознавания сцен представлена на рис. 5.1. Здесь пунктирными стрелками обозначены каналы передачи информации в режиме обучения робота, а сплошными — в режиме распознавания. т. е. в процессе идентификации, классификации или анализа сцены.
Проиллюстрируем описанный логический метод на примере решения задачи распознавания сцен по их контурным изображениям. Рассмотрим задачу распознавания сцен, состоящих из многогранников степени три [13], по их контурным изображениям. Изображением сцены является центральная проекция трехмерной сцены_на плоскость.
Изображение й будем задавать матрицей координат вершин на плоскости изображения и матрицей связности, элементы которой определяются, следующим образом: тц — 1, если из i-й вершины выходит ребро, оканчивающееся в /-й вершине, н щ(/>=0 в противном случае (/пи = 0 V/). Таким образом, если На изображении сцены имеется вершин, то она задается №+ 2N числами.
Как показано в работе [13], при указанных ограничениях существуют вершины трех типов: 1) типа V (у которой на нзо-
205
Ряс. 5.1. Адаптивная системе логического распознавания сцен.
бражении не видно одно из образующих ребер); 2) типа У (у которых любые два ребра лежат по разные стороны от пря-мой, образованной третьим ребром); 3) типа V (у которых все три образующих ребра лежат в одной полуплоскости). Кроме того, на изображении сцены могут возиикать вершины, образованные пересечением проекций ребер многогранников. Такие вершины назовем вершинами типа Т.
Определим предикаты таким образом, чтобы каждой вершине поставить в соответствие предикат, указывающий ее тип. Такие предикаты задаются соотношениями, представленными в
табл. 5.1. По матрице координат н матрице связности легко определить тип каждой вершины и порядок аргументов в соответствующем предикате. Отметим, что если в предикатах V, V и Г порядок аргументов определен однозначно, то для каждой вершины типа У истинны предикаты У(со, й, сг, с3), У(со, с», с3. й), У (со, Сз, ct, с2). Поэтому в логическом описании сцены можно использовать любой из них.
Рассмотрим для определенности сцены, состоящие из объектов четырем классов: ящик (Q(), токарный (Оз), сверлильный (Оз), фрезерный (О«) станки. Изображения этих объектов в разных характерных ракурсах представлены на рис. 5.2.
В режиме обучения роботу предъявляются отдельные объекты с указанием, к какому классу они относятся. По каждому изображению ш/ из й-го класса строится его логическое описание z*(®) (аксиома й-го подкласса). Так как выбранная си
207
стема предикатов полна в смысле однозначности проекций вер. шин многогранников степени три, то нет необходимости выпи-сывать все предикаты для каждой вершины изображения: достаточно вычислить предикат, истинный для данной вершины. Этим обеспечивается совпадение ранга конъюнкции логического описания объекта с числом вершин на его изображении.
Аксиомы классов строятся по обучающей выборке в виде
Рис. 5.2. Изображения объектов из обучающей выборки.
первому элементу обучающей выборки, представленной на рнс. 5.2, имеет вид
А| (w) = V (X|, х2, xe) &IF (х2, х3, х7, xj Л1Г (х3, х«, х9, х2) &W (х4, х5, х7, х3) & V (х6, хв, х<) & W (xe, xlt х7, х5) & Y (х7, х2, х4, хв) & Т (х8, х7, х9, Xji & Y (х9, х8, х3, х10) & Т (Х|0, х4, х9, х7).
Рассмотрим сложную сцену, изображенную на рис. 5.3. Логическое описание этой сцены обозначим через 5(ш).
Рассмотрим задачу идентификации «ящика», т. е. докажем утверждение (5.24) при k= 1:
S (©) -* Hco'Aj (w').
По дереву вывода, представленному на рнс. 5.4, получаем следующий результат: на изображении сцены S(<o) имеется
208
8 Зак. Ж
209
«яшик», причем система подстановок позволяет однозначно вое* становить изображение идентифицированного ящика.
Решая задачу классификации для сцены, представленной на рис. 5.3, робот выделяет четыре класса объектов: ящик, фрезер, ний, токарный и сверлильный станки. В результате анализа сиены робот легко вычленяет незаслоненные объекты: три ящика и фрезерный станок. Задача распознавания заслоненных объектов решается в два этапа: сначала на сцене выделяются отдельные объекты, а затем для каждого выделенного изобра. жепия объекта <л* решается задача
z<*>'®)-*
т. е. доказывается, что логическое описание заслоненного объек. та не противоречит аксиоме А-го класса (точнее, аксиоме /-го подкласса А-го класса).
В результате полного логического анализа на изображении сцены (на рис. 5.3) удается распознать три ящика, фрезерный, два сверлильных н токарный станки. Это свидетельствует об эффективности логического метода распознавания сцен.
$ в. АДАПТИВНОЕ ПЛАНИРОВАНИЕ И САМОПРОГРАММИРОВАНИЕ ДВИЖЕНИЯ
Проблема планирования целенаправленных действий может быть представлена как в логической форме, когда требуется выработать целенаправленную логику поведения робота, так и в дискретной, когда необходимо предварительно наметить план и программу движения исполнительных механизмов, гарантирующие обход препятствий. Необходимость в логическом планировании обычно возникает при выполнении роботом комплексных заданий в условиях неопределенности (например, сборка сложного изделия по чертежу, поиск и транспортировка объектов на незнакомой местности).
Задача автоматического планирования поведения естественно формулируется на языке исчисления предикатов как задача поиска логического вывода (37, 59]. В рамках логического подхода априорные сведения о функциональных возможностях робота и свойствах окружающей среды записываются в виде формул исчисления предикатов, называемых априорными аксиомами. Эти проблемно ориентированные аксиомы удобно разбить на четыре класса: 1) сенсорные, описывающие информационные возможности сенсорной системы; 2) моторные, характеризую* щне д-нгательчно возможности исполнительных механизмов; 3) аксиомы срсты, описывающие ее свойства; 4) аксиомы начальных условий, описывающие начальные состояния робота и среды.
Наряд” с указанными • чеиомамп, содержащими априорные сведения робота о задаче, полезно ввести аксномы обучения, 210
которые формируются автоматически по мере накопления им опыта и знаний в процессе решения задач.
Планирование поведения сводится к логическому поиску за* данного целевого состояния, трактуемого как теорема. Для организации поиска обычно используются подходящие стратегии метода резолюций (37]. В результате отыскивается последовательность действий — план поведения робота, при отработке которого достигается цель.
Элементы плана, т. е. промежуточные действия, ведущие к достижению конечной цели, можно рассматривать как промежуточные цели. Поэтому задачу логического планирования поведения робота можно трактовать как интеллектуальную задачу промежуточного целеполагания.
Методические вопросы решения данной задачи в условиях неопределенности подробно изложены в работах (37, 71]. Отметим только, что введение аксиом обучения и адаптивных стратегий позволяет в ряде случаев (особенно в задачах с большой неопределенностью) существенно повысить эффективность планирования [59]. Это проявляется в активном использовании опыта целеполагания при решении роботом новых задач планирования н, как следствие, в резком уменьшении числа шагов логического вывода.
Переходя к задаче планирования и самопрограммирования движений исполнительных механизмов робота, прежде всего отметим некоторые ее особенности. Значительные трудности при решении такой задачи обусловлены тем, что конструктивные ограничения и препятствия порождают различные тупиковые ситуации. В то же время многие известные алгоритмы построения программных движений по существу являются локальными в том смысле, что принципиально не могут обеспечить обход тупиковых ситуаций.
В связи с этим возникает вопрос, нельзя лн дополнить локальные алгоритмы специальными средствами анализа и обхода тупиковых ситуаций и тем самым существенно расширить область их применения. Утвердительный (и притом конструктивный) ответ на этот вопрос основывается на идее предварительного планирования и построения каркаса ПД. Рассмотрим подробнее методологические аспекты организации планирования ПД.
Рассмотрим для определенности задачу планирования движений манипулятора в режиме наведения схвата в заданную точку. Формулировка этой задачи была дана в § 2 главы 3. По существу задача сводится к построению такого закона изменения обобщенных координат qP(t), что выполняются граничные условия (3.41), конструктивные ограничения (3.22) и требование обхода препятствий (3.23). Эту задачу целесообразно решать в четыре этапа (30].
На первом этапе осуществляется упаковка рабочей зоны О\Р выпуклыми многогранниками Di, ..., Dv, не пересекаю-
211
щимися по внутренним точкам. Геометрической модели рабочей зоны в виде объединения D|......Dv ставится в соответствие
граф Go, у которого вершина с номером i соответствует D,, а ребра соединяют вершины i и / в том случае, если соответствующие многогранники Dt и D/ пересекаются. Построенный таким образом граф планов Go описывает структуру рабочей воны в D и служит основой для планирования ПД.
Второй этап — выбор пути на графе планов Go. Пусть для определенности г (/0)е Ь/о. г, е 0<а. Если окажется, что i0 » то планирования не требуется, и сразу можно строить ПД в силу того или иного локального алгоритма. Если io^i,, то путь i'o, й, ..., in “= I., соединяющий на Go вершину i0 с вершиной назовем планом движения схвата. Таким образом, план определяет последовательность многогранников ..., ..Din, через которые следует вести схват в целевую точку г,.
На третьем этапе по выбранному плану строится каркас ПД, т. е. последовательность конфигураций д0, ..., qn, таких, что
Ф(й<0 = г/о', .... <l>(q„' = r„ Ф(чРе=О,.
Существенно, что если при переходе из D * в D)Jk+l из-за препятствий возникает тупиковая ситуация, то из графа планов Gd выбрасывается соответствующее ребро и иа новом графе строится новый план движения схвата. Тем самым осуществляется своеобразная адаптация графа планов Gj> к препятствиям.
Наконец, иа четвертом этапе по каркасу ПД строится само ПД с учетом конструктивных ограничений. Для решения этой Задачи непосредственно применимы рассмотренные в § 4 гла* вы 3 алгоритмы параметрического синтеза ПД.
Вопросы упаковки рабочей зоны, выбора и оптимизации плана движения схвата подробно рассмотрены в работе [30]. Опишем здесь локально-оптимальный алгоритм построения кар* каса ПД. С этой целью введем в Q« m-мерную решетку И с шагом h. Каркас ПД предлагается строить по узлам этой решетки. Допустим, что часть каркаса ПД q0, .... q* уже построена. Очередная конфигурация q*+i выбирается среди соседних с q* точек решетки из условия локальной оптимальности
1|Ф(й*+? — г. II =“= min (в.2в)
при соблюдении следующих ограничений: 1) q*+) е Q«| *) o(q*+i)“0; 3) q*+i qz, i = 0, .... Л. В результате строит» каркас без циклов, элементы которого удовлетворяет конструктивна mv ограничению (3.22) и требованию обхода препятствий. Если не существует конфигурации, соседней с q» и удовлетворяющей ограничениям 1)—3), то принимается q*+)=q*, и номер k уменьшается на единицу. Алгоритм продолжает работу Д® тех пор, пока величина l|4>(q»+i) — г«|| не станет меньше паря-
212
метра е. Отметим, что если известна целевая конфигурация q„ такая, что Ф(Ч.)=г„ то вместо критерия (5.26) можно неволь* зовать критерий
II Ч*+! — Ч. И = min. (5.27)
Рассмотренный алгоритм построения каркаса ПД является по существу алгоритмом выбора пути на графе Н, точнее, на неизвестном подграфе Нр этого графа, в узлах q которого o(q) = 0. Этот подграф заранее задать практически невозможно, так как препятствия Р обычно неизвестны, а если они и известны, то построение множества Qp, такого, что $(P)=Qp, представляет собой чрезвычайно сложную задачу. Поэтому важное значение приобретает адаптация графа Н к препятствиям, состоящая в отбрасывании недопустимых узлов по мерс поступления информации о пересечении с препятствиями в виде ограничений (3.23).
Остановимся на связи между планированием и построением ПД. Пусть имеется план движения схвата i0, .... in- Ему соответствует каркас ПД, определяющий последовательность конфигураций qo, .... qn, через которые должно проходить ПД. Для построения ПД по его каркасу с учетом конструктивных ограничений можно воспользоваться методом параметризации ПД и рекуррентными алгоритмами настройки параметров, описанными в § 4 главы 3.
Рассмотрим теперь особенности планирования ПД в режиме отслеживания схватом заданной траектории. Каркас ПД должен удовлетворять условиям (3.24)—(3.26). Как показано в работе [30], любую траекторию г,(I), целиком лежащую в области достижимости D, можно отследить схватом манипулятора в том и только в том случае, если отображение Ф: Qa-+ D открыто. В этом случае для построения ПД можно использовать локальные алгоритмы.
Однако на практике отображение Ф обычно не является открытым. Поэтому предлагается упаковать множество Qq параллелепипедами Qi......Q.m так, чтобы локальные отображения
Ф/ • Qi ~ м где Di=*Q(Qi), были открытыми. Пусть J требуе-
мая упаковка. Рассмотрим граф Gq, i-я вершина которого соответствует Qt, а ребра соединяют вершины с номерами i и j в том случае, если Qt касается Q, по грани размерностью не меньше трех. Построенный таким образом граф Gq назовем графом планов ПД в Сопоставим i-й вершине Gq орт е, в Rm (код l-ti вершины), а каждой точке геО— следующий .U-мерный индекс:
l(r) = Е е<. (5.28)
p.®(q)-r, q&Q{]
213
Все точки г в D, имеющие одинаковый индекс (5.28), назовем зоной. Каждую точку закодируем определенным индексом. Тем самым область достижимости D разбиваем на конечное число непересскающнхся по внутренним точкам зон.
Пусть задана траектория схвата г.(/). Естественно считать, что г.(/)е£) прн всех t е[/0. /г], причем г.(/0) = Ф(Чо), а число переходов из одной зоны в другую при отслеживании траектории г.(/) конечно. Определим последовательность зон 1о, .... |ъ через которые проходит По начальной конфигурации q, найдем код ei, вершины графа планов Gq, такой, что qoeQ,t. Построим путь на Gq, начинающийся в вершине с кодом е<, и удовлетворяющий требованию
/ = 0» •••» Л» (5.29)
где о — операция координатного умножения векторов. Пусть этот путь проходит через вершины графа планов Gq с кодами е,о* Последовательность о называется планом
ПД в задаче отслеживания схватом манипулятора заданной траектории.
Каждой траектории схвата в общем случае соответствует иеединственный план ПД. Множество таких планов характеризует возможные способы отслеживания траекторий и маневренность манипулятора. Нс все планы допустимы н равноценны с точки зрения требования обхода препятствий. В связи с этим определим понятие оптимального плана ПД. С каждой вершиной графа планов Gq свяжем величину
W (/) = a (q) dq/ц (Qf), Q
где p(Q/) — объем Qt. Величину W(j}— легко вычислить, например, методом Монте-Карло.
План будем называть оптимальным (в смысле об-
хода препятствий), если он минимизирует величину max (?(//).
i
Такое определение довольно естественно, поскольку удовлетворяющие ему ПД проходят через наименее «загруженные» препятствиями параллелепипеды Q,.
Роль и значение планирования ПД при наличии конструктивных ограничений н препятствий заключается в том, что оно позволяет свести глобальную задачу обхода тупиковых ситуаций к последовательности локальных задач, для решения которых применимы локальные алгоритмы. Существенно, что если данная траектория не имеет плана ПД на графе планов Gq, то это свидетельствует о принципиальной невозможности отследить данную траекторию.
214
Допустим, что указанный выше план ПД существует. Torju возникает вопрос, как фактически построить ПД по заданном, плану.
Прежде всего отметим, что соотношение (5.29) гарантируй возможность построения для каждого множества Qi, соответ ствующего. фрагмента ПД с помощью локальных алгоритмов Из того, что план ПД {e/J*.,, определяет некоюрый путь hi графе планов Gq, следует: параллелепипеды Qi и Qi, соответствующие соседним элементам плана 1п и й+ь имеют общую грань размерностью не меньше трех. Это означает, что найдута по крайней мере три обобщенные координаты, обеспечивающие отслеживание г,It) при переходе соответствующего ПД ю Q‘n в Qm+i-
Общую задачу построения ПД по плану удобно решать в ды этапа: сначала целесообразно построить каркас ПД с учетов требования обхода препятствий, а затем--само ПД с учетов заданных конструктивных ограничений.
Введем понятие каркаса ПД в задаче отслеживания схватом заданной траектории. Пусть траектория г»(/) представлена последовательностью точек Го, .... гг. (Такая дискретная форм! представления траектории схвата часто встречается на npai-тике.) Определим последовательность зон 1о....L, через кото-
рые проходит эта траектория. Каркасом ПД бу.-i л называв последовательность конфигураций q0, .... q», соот вез ствующу» плану такую, что ®(q,)=r/ и
||q/_i — q/ll<6. /=1......
где б — достаточно малое число.
Опишем общий метод построения каркаса ПД по его плану. Введем псевдообратный оператор A: Q«X D -*~Qq, задаваемы! формулой (3.27). Пусть даны дискретная траектория схвата Го, г», .... Гг, такая, что величины ||г/-1 — г/|| достаточно малы, и начальная конфигурация манипулятора q0, такая, что ф.'ц5) = Го, qQeQ/,. Дальнейшие элементы каркаса ПД опре делим с помощью рекуррентного алгоритма (3.28), которы! должен обеспечивать непрерывность каркаса в смысле (3.29). Это требование накладывает дополнительное ограничение на оператор А. а именно: на траектории алгоритма (3.28) из малости ||г/_|—гД| должна следовать малость ||q(_( — q,|| для вся /=1, .... к- Это свойство будем называть непрерывность!) оператора А. Вследствие нсевдообратности оператора А достаточным условием его непрерывности является непрерывность функции А по гторому аргуме:-.’-. Однако га практике А обычно не является ненпспывноч Лгнчиней г из-за с ч-пком обширно! области задания оператора Ф, что присуще многим манипула торам.
В рассматриваемой задаче каркас ПД строится по плану путем последовательного перехода от одного параллелепипеда Qit к другому Qtl+l. Все эти параллелепипеды обладают (по построению) тем свойством, что отображение Ф: Qi~+Dt открыто. Тем самым обеспечиваются непрерывность оператора А и возможность построения каркаса ПД в силу (3.28). Более строгое формализованное обоснование описанного метода построения каркаса ПД содержится в работе (30].
Предложенный метод построения каркаса ПД универсален: в качестве оператора А в нем можно использовать операторы, индуцируемые любым алгоритмом решения обратной манипуляционной задачи. Применимы здесь и многие известные локальные алгоритмы построения ПД (14, 15, 17, 22, 32, 35, 43, 46, 64, 65], а также предложенные в работе (30] рекуррентные алгоритмы. Прн этом требования псевдообратностн и непрерывности оператора А выступают как необходимые условия существования каркаса ПД, а значит, и самого ПД. Построение ПД по его каркасу с учетом конструктивных ограничении легко осуществить с помощью описанных в § 4 главы 3 метода параметризации ПД или (прн заданном критерии оптимальности ПД) метода параметрической оптимизации ПД.
В заключение опишем еще один эффективный метод программирования движений манипулятора, обеспечивающий адаптацию к препятствиям. Этот метод замечателен тем, что не требует прн наличии конструктивных ограничений и препятствий предварительного планирования и построения каркаса ПД, поэтому он проще и удобнее метода программирования по каркасу.
Искомое ПД должно удовлетворять граничным условиям
вида Ч₽ (А>) = Чо> qp (tT) = 41. (5.30)
или последовательности таких условий.
На практике часто конструктивные ограничения имеют вид Cq, < ^Qp, < (0 &д. <» /и 1» - (5.31)
Cj. I < I (0 < Ч Ь I = 1.......т, (5.32)
с9. 1—1.......т. (5.33)
Таким образом, задача самопрограммирования движений робота сводится к нахождению непрерывной дважды дифференцируемой функции qP(/), удовлетворяющей граничным условиям (5.30), ограничениям (5.31) — (5.33) и требованию обхода препятствий (3.23).
Основная идея предлагаемого метода решения задачи заключается в специальной параметризации искомого ПД, зависящей от кинематической схемы манипулятора и характера препят-216
ствий, я определении приемлемых значений параметров ПД как решения системы неравенств, описывающих требование обхода препятствий [57, 61). Отметим, что параметризация ПД вида (3.59) здесь, как правило, непригодна, так как порождаемые ею неравенства-ограничения существенно нелинейны и невыпуклы в пространстве параметров. Для подобных систем неравенств пока не существует общих методов решения. Поэтому целесообразно выбрать такую параметризацию, чтобы, во-первых, соответствующие ей неравенства- ограничения были выпуклы относительно искомых параметров ПД и, во-вторых, автоматически удовлетворялись граничные условия (5.30). Разные варианты такой параметризации были предложены в работах (57, 61). Здесь рассмотрим параметризацию ПД вида
Чр. i (0 — arccos во. i W + [«о. < «г) — во. t (*о) Щ (0
L /-1
(5.34)
где До.<Uo)> ao.i(tr), («1, • ••. т, определяются из соотношений arccos До, i (/0)в <7о. <• arccos До, i (tT) = qt, t,
а базисные функции Д/(1), / = 1, ..., N, имеют вид (3.62), (3.63). Эта параметризация хорошо приспособлена к манипуляторам с вращательными парами (в частности, к манипуляторам с антропоморфной кинематикой).
Аппроксимируем препятствия Р (с некоторым запасом 6Р) кусочно-постоянными функциями Р\(Ги Г2), р2(Г1, Г2) (Р1<р2) так, чтобы получаемая в результате рабочая зона была выпуклой по крайней мере по одной координатной оси системы координат Ог1Г2г2. Еоли D выпукла, например, по осн Ог3, то это означает, что
гза<Г|, r2, r3)eO->rse [Pi(r(, г2), р2<гь г,)]. (5.35)
В ряде прикладных задач удобно аппроксимировать препятствия параллелепипедами с ребрами, параллельными координатным осям. Тогда можно считать, что рабочая зона задана так: плоскость rtQr, разбита на прямоугольники и для каждого из них заданы числа pt и р2, такие, что роль препятствия на прямоугольнике играет часть пространства Я3, лежащая ниже плоскости гз = Pi и выше плоскости г3 = р2. Описанный метод задания рабочей зоны достаточно универсален, прост и удобен для ЭВМ: в памяти необходимо хранить массивы чисел вида
{П(Р.). -•?(₽*». (<(₽.) 'i(M-
(P/P.I, (5.36)
соответствующие Л-му параллелепипеду — препятствию Р*.
217
Требование обхода препятствий означает, что в любой мо-мент времени t е [(о, /т] любая точка гм на манипуляторе должна находиться в свободной зоне D\P. Выражая координаты rf*> г2*» гз произвольной точки на манипуляторе в конфигурации qp(t) через обобщенные координаты qi, .... qm и подставляя нх в выражение (5.35), получаем условия на ПД, гарантирующие обход препятствий, в явном виде. Если теперь подставить в эти условия параметризованное ПД (5.34), получим выпуклую по параметрам кц, < —I, ..., М, континуальную систему неравенств вида
Pi (г», /f ) < г* (х, ’, /) < р3(г», г"), (5.37)
где (г**, гам), t=l, 2, — некоторые фиксированные числа из массива (5.36), соответствующие координатам рассматриваемой точки гм (/) на манипуляторе в момент /. Эти неравенства вырезают в пространстве параметров «полоски», в пересечении которых находятся приемлемые значения параметров ПД.
Разрешимость полученной таким образом системы неравенств (5.37), порожденных препятствиями, является необходимым условием существования ПД вица (5.34). Допустим, что система (5.37) разрешима. Тогда для фактического построения ПД можно воспользоваться следующей методикой.
На каждом звене манипулятора и интервале [/о. /т] введем достаточно густую сетку. Узлы этой сетки можно трактовать как элементы «обучающей выборки», определяющие координаты некоторой точки г* на манипуляторе в фиксированный момент /г|. Решая неравенства (5.37) на элементах «обучающей выборки», получаем приемлемые значения параметров ПД. Для решения этих неравенств можно использовать рекуррентные конечно-сходящнеся алгоритмы градиентного типа [61, 78]. Примеры применения и моделирования на ЭВМ описанною метода построения ПД для манипуляторов с различными кинематическими схемами рассмотрены в работах [57, 61).
Достоинством описанного метода является то, что он в отличие от метода программирования по каркасу не требует предварительного планирования ПД. Тем не менее он является глобальным по крайней мере для таких препятствий, которые вырезают в области достижимости выпуклую рабочую зону.
Важнейшей чертой метода является его адаптивность в широком классе препятствий. В самом деле, в рамках предлагаемого метода ПД определяется не по жесткой программе, заранее рассчитанной на препятствия определенного типа, а строится адаптивно: по параметрам препятствий, задаваемых с помощью информационной и распознающей систем, отыскиваются по ре-куррентным формулам (не требующих большой памяти) приемлемые значения параметров искомого ПД. Прн этом изменение 218
условий задачи (характер препятствий, граничные условия и т. п.) приводит лишь к перенастройке параметров ПД при сохранении его общей структуры. Сама же структура, использующая линейные комбинации заданных базисных функций, достаточно проста и универсальна. В качестве алгоритмов адаптивной настройки параметров ПД могут использоваться рекуррентные коиечно-сходящнеся алгоритмы решения систем неравенств, описывающих требование обхода препятствий.
$ 7. ИЕРАРХИЧЕСКАЯ ОРГАНИЗАЦИЯ ИНТЕЛЛЕКТУАЛЬНОГО УПРАВЛЕНИЯ
Центральной проблемой создания роботов третьего поколения являются разработка необходимых элементов искусственного интеллекта и организация их взаимодействия с целью выработки целесообразного поведения в заранее неизвестных н нестационарных условиях. Реализация этих функций возлагается на управляющую систему робота, которую в этом случае естественно назвать интеллектуальной.
Каким же образом из сравнительно простых элементов интеллекта робота синтезируется сложное интеллектуальное управление? Как на основе этого управления формируется разумное поведение робота в неопределенной и изменяющейся обстановке?
Для ответа на эти вопросы уместно провести аналогию с человеком как биологическим прототипом робота. В книге «Рефлексы головного мозга» великий русский физиолог И. М. Сеченов писал: «Все бесконечное разнообразие внешних проявлений мозговой деятельности сводится окончательно к одному лишь явлению — мышечному движению»*. Другими словами, вся интеллектуальная деятельность человека так или иначе направлена на активное взаимодействие с внешним миром посредством целенаправленных движений. Точно так же элементы интеллекта робота служат прежде всего для организации и фактического осуществления программных движений его исполнительных механизмов.
С этой точки зрения интеллектуальное управление роботом сводится в конечном счете к планированию, самопрограммированию н адаптивной стабилизации целенаправленных движений. Решение этих задач относится к тактическому уровню управления. Функции же самообучения понятиям, моделирования среды и распознавания различных классов сенсорных ситуаций играют вспомогательную (хотя и принципиально важную) роль. Соответствующие интеллектуальные задачи решаются па стратегическом уровне управления.
* Сеченов И.М Рефлексы головного мозга. М.. 1961, с. 5.
219
Разнообразие функций, взаимосвязь элементов интеллекта и подчиненность тактического уровня управления стратегическому наводят на мысль о целесообразности иерархической организации интеллектуального управления. Такой подход к конструированию интеллектуальной управляющей системы позволяет распараллелить процессы принятия решений, планирования поведения, самообучения понятиям, моделирования среды, распознавания обстановки, самопрограммирования движений и управления двигательными механизмами. Это особенно важно с точки зрения осуществления интеллектуального управления в реальном времени, без «мыслительных» задержек и запаздываний в управляющей системе. Кроме того, нерархнзацня управления полезна и в методическом отношении: она позволяет расчленить трудности путем разбиения управляющей системы на относительно простые взаимосвязанные функциональные блоки — модули.
Иерархическая структура интеллектуальной управляющей системы робота представлена на рис. 5.5. В состав этой системы входят следующие уровни иерархии.
Принятие решений и планирование поведения. Алгоритмы этого уровня на основе задания, получаемого роботом от человека в режиме осмысленного диалога, а также сведений, поступающих от информационной системы и нижних уровней иерархии, формируют план поведения и принимают решения, ведущие к достижению цели.
Распознавание и моделирование среды. Алгоритмы этого уровня путем накопления опыта и самообучения моделируют окружающую робота среду, а также идентифицируют, классифицируют и анализируют сенсорную информацию в соответствии с планом, вырабатываемым на более высоком уровне иерархии. Информационная модель среды, хранящаяся в управляющей системе, позволяет роботу «мысленно» проигрывать разные схемы поведения еще до совершения каких-либо реальных действий.
Планирование и программирование движений. На этом уровне совершаются адаптивное планирование и самопрограммирование целенаправленных движений исполнительных механизмов робота с учетом конструктивных ограничений и препятствий.
Управление программным движением. Алгоритмы этого уровня синтезируют закон адаптивного управления приводами, обеспечивающий в недетерминированных условиях фактическое осушествтение целенаправленного движения, запрограммированного на более высоком уровне иерархии.
Все названные уровни можно трактовать как алгоритмические модули, реализующие элементы интеллекта управляющей системы. Этн модули функционально связаны между собой, а также с другими подсистемами робота. Организация связей воз
320
лагается на координатор. Последний играет роль своеобразного диспетчера по распределению информации между отдельными модулями и системами (включая их предохранение от излишней информации), а также по обеспечению относительно независи-
Рис. 5.5. Иерархическая организация интеллектуального управления роботами.
мой (автономной) работы различных элементов интеллекта. Характерной чертой интеллектуальных управляющих систем роботов является наличие алгоритмических средств обучения и адаптации на всех уровнях иерархии. Эти средства обеспечивают ^оперативную самонастройку, самообучение и самоорганизацию 'управляющей системы в неопределенных и изменяющихся условиях эксплуатации робота.
Глава 6
АВТОМАТИЗАЦИЯ ПРОЕКТИРОВАНИЯ И ПРОГРАММНО-АППАРАТУРНАЯ РЕАЛИЗАЦИЯ УПРАВЛЯЮЩИХ СИСТЕМ РОБОТОВ
| 1. ПРИНЦИПЫ И СРЕДСТВА АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
Проектирование управляющих систем роботов и робототехнических систем (PC)—это сложная и трудоемкая научно-техническая задача. Одним из наиболее перспективных путей ее решения является создание проблемно ориентированных систем автоматизированного проектирования (САПР) на основе современных средств вычислительной техники. Такне САПР благодаря широкому использованию ЭВМ, дисплеев, графопостроителей и интеллектуальных терминалов позволяют перейти от автоматизации расчетов отдельных элементов управляющих систем к комплексной автоматизации процесса проектирования в целом. В перспективе они должны обеспечить полную автоматизацию проектно-конструкторских работ — от эскизного проекта управляющей системы до изготовления всей необходимой документации (принципиальных схем и рабочих чертежей, спецификации и нормативов и т. д.). Такая автоматизация не исключает человека из творческого процесса проектирования, а лишь освобождает его от всех рутинных и сложных вычислительных операций.
Важной особенностью развития САПР в последние годы является глубокое взаимопроникновение собственно конструкторского и технологического этапов проектирования. При ориентации проектов вновь создаваемых роботов и PC на гибкое автоматическое производство (ГАП) традиционная проектно-техническая документация, рассчитанная на участие человека, в значительной степени теряет свое былое значение. На первое место постепенно выдвигается широкое использование безбумажной информатики, т. е. документации, представленной на машинных носителях информации. Основное достоинство «безбумажной» формы записи и хранения документации заключается в том, что ее можно непосредственно использовать для планирования технологических процессов и управления ГАП, осуществляющим
222
изготовление спроектированного робота или отдельных его систем.
Система автоматизированного проектирования управляющих систем роботов является составной частью САПР робототехнических комплексов. Последняя представляет собой многомашинную вычислительную сеть, включающую в себя автоматизированные рабочие места (АРМ) конструкторов, которые снабжены дисплеем со световым пером и пультом связи с соответствующей клавиатурой. Это позволяет конструктору управляющей системы работать в диалоговом режиме с конструкторами, ответственными за проектирование других элементов робототехнического комплекса.
Информационную основу САПР управляющих систем составляет машинный автоматизированный архив уже известных управляющих систем — банк данных прототипов. Наряду с ним САПР включает в себя также оперативный банк данных новых перспективных проектов, подлежащих исследованию и разработке.
Сравнительный анализ эффеитивности различных проектов управляющих систем и их прототипов осуществляется конструктором в режиме диалога с ЭВМ. Это позволяет быстро выбрать и рассчитать управляющую систему, наилучшим образом удовлетворяющую требованиям технического задания. Ввод необходимых данных, запросов и расчетных программ осуществляется указанием их имен путем нажатия соответствующих клавиш на пульте дисплея. Для внесения поправок н оперативного редактирования проекта конструктор использует световое перо. Если проект управляющей системы полностью завершен, то конст рук-тор дает команду на автоматическую запись всей необходимой технической и технологической документации на машинном носителе информации (например, на магнитной ленте или дисках).
На заключительном этапе проектирования управляющих систем часто прибегают к их физическому моделированию (макетированию) и испытаниям. При комплексной автоматизации проектно-конструкторских работ этап физического моделирования (программно-аппаратурная реализация управляющей системы, плэнирэванпе экспериментов, сбор данных и т. д.) и стендовых испытаний также автоматизируется.
Описанная безбумажная технология автоматизированного проектирования управляющих систем роботов в настоящее время еще далека до завершения. Однако отдельные элементы САПР уже созданы и получают все большее распространение в практике проектирования роботов и PC различного назначения. Одним из таких элементов является рассматриваемый в данной главе пакет прикладных программ, предназначенный для расчета, сравнительного анализа и моделирования систем программного и адаптивного управления роботов с электрическими приводами.
223
I t. ПАКЕТ ПРОГРАММ ДЛЯ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ УПРАВЛЯЮЩИХ СИСТЕМ
Рассмотрим некоторые общие принципы и средства автоматизированного проектирования на примере САПР управляющих Систем электромеханических роботов. Основу САПР составляет пакет программ, позволяющий моделировать как динамику широкого класса роботов и PC (с учетом динамики электрических приводов), так и различные схемы управления, включая алгоритмы построения ПД и алгоритмы адаптации.
Пакет программ имеет модульную структуру. Он содержит шесть основных функциональных модулей, а также ряд вспомогательных модулей и сервисных подпрограмм. Каждый модуль представляет собой элемент с программируемой структурой и настраиваемыми параметрами, осуществляющий целенаправленное (в соответствии с назначением данного модуля) преобразование входной информация в выходную. Функциональные модули реализуют различные алгоритмы управления и обработки информации. Это позволяет «собрать» йз модулей управляющую систему любого типа.
Конструктор имеет возможность дополнять, заменять или корректировать отдельные модули и подпрограммы. Это придав? САПР необходимую гибкость при переходе от имеющихся прототипов к проектам новых управляющих систем.
Основными функциональными модулями пакета являются: 1) программатор — модуль MOTION; 2) регулятор — модуль ReGuL; 3) эстнматор — модуль EST1M; 4) адаптатор— модуль ADAPT; б) идентификатор — модуль IDENT.
Указанные функциональные модули программно реализуют (на языке ФОРТРАН) различные алгоритмы построения ПЛ, синтеза управляющих воздействий, оценки качества управления, Самонастройки параметров закона управления, идентификации параметров и состояний двигательной системы робота. (Все эти алгоритмы подробно описаны в главах 3 и 4.)
Структурная Схема рассматриваемого пакета программ представлена на рис. 6.1. Опишем структуру, функции и назначение отдельных блоков-модулей н их взаимодействие в процессе автоматизированного проектирования.
Модуль DATA производит ввод технических данных исследуемого проекта управляющей системы, а также сведений об условиях запланированных экспериментов на ЭВМ.
Модуль PARAM служит для расчета параметров программатора, регулятора, эстиматора, адаптатора и идентификатора. Он, в частности, производит расчет элементов матрицы Г по заданным конструктором собственным числам X..... Х„.
824
Рио. 6.1. Блок-схема пакета программ САПР, управляющих систем роботов.
625
Модуль MOTION формирует ПД хр(/) и его производную х₽(/) с учетом конструктивных ограничений и препятствий.
Модуль REGUL синтезирует закон управления электрическими приводами робота, соответствующий рассматриваемому режиму работы (стабилизация ПД, терминальное управление, самонаведение).
Модуль ESTIM служит для текущей оценки качества управления путем проверки эстнматорных неравенств. В случае нарушения этих неравенств автоматически включается модуль ADAPT.
Модуль ADAPT производит самонастройку закона управления, т. е. коррекцию параметров модуля REGUL, в соответствии с выбранным алгоритмом адаптации.
Модуль IDENT преобразует «физические» переменные г, измеряемые датчиками информационной системы, в вектор канонических переменных х, используемых в модуле REGUL при синтезе закона управления.
Модуль MODEL производит имитационное моделирование управляемых движений робота путем численного интегрирования замкнутых уравнений динамики электромеханического робота.
В состав пакета входит также ряд вспомогательных подпрограмм, осуществляющих, например, алгебраические операции над векторами и матрицами. Для обеспечения возможности проектирования в режиме диалога с ЭВМ используются дисплей и связанный с ним сервисный модуль — диалоговый корректор. Результаты расчетов и экспериментов по цифровому моделированию могут выводиться на экран дисплея или печататься в виде таблиц и графиков, снабженных необходимыми комментариями.
Качество управления оценивается главным образом по виду ПП в замкнутой системе. Если характер ПП неудовлетворителен (автоколебания, низкая точность, неустойчивость и т. п.). то соответствующая управляющая система отбраковывается как непригодная для данного робота, и конструктор исследует новый проект. Среди управляющих систем с приемлемым качеством ПП отбирается наилучший, который и рекомендуется к реализации.
Описанный пакет и его специализированные (проблемно-ориентированные) версии успешно применялись для моделирования и сравнительного анализа различных схем управления на примере электромеханических PC манипуляционного и транспортного типов. Подробное описание полученных результатов содержится в работах [9, 17, 27, 30, 57—59, 61, 65]. Эксперименты по цифровому моделированию управляющих систем роботов в целом показали, что в недетерминированных условиях (неконтролируемый дрейф параметров, внешние возмущения и т. п.) переход к адаптивному управлению позволяет cyuie'
226
ственно повысить точность и быстроту достижения цели по сравнению с программным управлением и сервоуправлением.
Опыт работы с описанным пакетом программ позволяет рассматривать его как эффективное средство автоматизированного проектирования роботов первого и особенно второго поколений. Использование пакета обеспечивает значительное улучшение качества управляющих систем и резкое сокращение сроков их проектирования. Этот эффект достигается не только при создании принципиально новых роботов, ио и прн модификации (в направлении расширения функциональных возможностей) управляющих систем существующих роботов, серийно выпускаемых промышленностью. Естественно ожидать, что по мере развития и совершенствования САПР управляющих систем роботов она будет играть все возрастающую роль не только в опытноконструкторских разработках, но и в деле подготовки специалистов в области автоматизированного проектирования PC.
$ 3. АРХИТЕКТУРА МУЛЬТИМИКРОПРОЦЕССОРНЫХ УПРАВЛЯЮЩИХ СИСТЕМ
Реализация адаптивных управляющих систем роботов требует привлечения средств вычислительной техники. В принципе такие системы можно программно реализовать на универсальных цифровых или гибридных (цифроаналоговых) ЭВМ. Этот подход широко применяется на этапах автоматизированного проектирования и имитационного моделирования адаптивных управляющих систем. Однако последовательный принцип действия универсальных ЭВМ часто приводит к значительному запаздыванию прн вычислении адаптивного управления и, как следствие, к управлению по устаревшей информации.
Приведенные соображения диктуют необходимость распараллеливания вычислительных процессов путем распределения отдельных функций (алгоритмов) между разными процессорами. Возможность и целесообразность такого распараллеливания вытекают также из иерархической структуры адаптивной управляющей системы управления, представленной на рис. 4.1. Отметим, что эта структура охватывает и неадаптивные управляющие системы, являющиеся частным случаем адаптивных.
Рассмотрим пути и средства многопроцессорной реализации адаптивного управления. Как уже отмечалось, для автоматизации управления роботами все шире используются микро-ЭВМ и микропроцессоры. Эти новые средства управления обладают высоким быстродействием, надежностью и функциональной гибкостью [72|. Они выгодно отличаются от универсальных ЭВМ низкой стоимостью и малыми габаритами. Поэтому микропроцессоры особенно перспективны для программно-аппаратурной реализации систем адаптивного управления. Обеспечивая есте
227
ственное распределение функций и распараллеливание вычислительных процессов, микропроцессоры позволяют реализовать адаптивное управление роботами и PC в реальном масштабе времени.
Процесс проектирования микропроцессорных адаптивных систем управления роботов включает в себя следующие этапы 163]: I) техническую постановку и формализацию задачи, алгоритмический синтез и расчет адаптивной системы управления; 2) выбор микро-ЭВМ, микропроцессоров и интерфейса; 3) разработку программного обеспечения; 4) моделирование и макетирование адаптивной системы.
Первый этап играет важнейшую роль — он предопределяет облик и свойства адаптивной системы управления, ее соответствие техническому заданию. Достаточно полно содержание этого этапа раскрыто в главе 4.
На втором этапе выясняется, какие алгоритмы должны быть распределены между микро-ЭВМ и микропроцессорами, какие временные соотношения должны при этом соблюдаться, каковы требования к запоминающему устройству, хранящему сведения о конструктивных ограничениях, препятствиях и т. д. После этого выбирают конкретные микропроцессоры н микро-ЭВМ, обеспечивающие принципиальную возможность решения задачи в реальном масштабе времени. Выбор микропроцессоров основывается на анализе таких характеристик, как быстродействие, длина слова, объем памяти, система команд, а также возможностей интерфейса.
Иерархическая структура адаптивной управляющей системы подсказывает рациональную архитектуру реализующей ее мультимикропроцессорной системы, представленную на рис. 6.2. Координирующим элементом такой системы является микро-ЭВМ, включающая центральный процессор (ЦП) и запоминающее устройство (ЗУ). Микро-ЭВМ выполняет программируемую обработку информации от устройства ввода-вывода через интерфейс, координацию работы специализированных микропроцессоров-модулей, программно-управляемую передачу и обработку информации через общую шину данных. Кроме того, на микро-ЭВМ может возлагаться решение отдельных трудоемких задач, таких, как планирование движений или расчет и оптимизация параметров адаптивного управления.
Специализированные микропроцессоры (МП) выполняют следующие функции: 1) построение программы движения (МП-программатор); 2) оценку качества управления (МП-эстима-тор); 3) коррекцию параметров регулятора (МП-адаптатор); 4) формирование управления (МП-регулятор).
Эти микропроцессоры связаны с микро-ЭВМ, а также (через общую шину данных) между собой. В состав каждого из них входят аккумулятор (А), арифметико-логическое устройство (АЛУ), устройство управления (УУ) и регистры (Р). Схема
228
ычислсний на одном такте адаптивного управления представ-ена на рис. 6.3.
Основным достоинством такой архитектуры является воз* ожность алгоритмического распараллеливания процесса вычис-ения адаптивного управления — от формирования ПД до по* ачи управляющих воздействий на исполнительные приводы и [еханизмы робота. Благодаря этому естественным образом рас-араллеливается и процесс проектирования системы, что позво-яет конструктору производить расчет и реализацию каждого [икропроцессорного модуля отдельно.
не. 6.2. Архитектура мультимшфопроцессорного автомата адаптивного управления.
Функциональные возможности специализированных микро* роцессоров определяются их программным обеспечением, т. е. акетом программ, реализующих соответствующие алгоритмы, [оэтому на третьем этапе разрабатывается программное обес-ечение.
Эффективность алгоритмического и программного обеспече-ия оценивается путем моделирования или макетирования адап-нвной системы на основе прототипного микропроцессорного ^бора. На четвертом этапе осуществляется также окончатель-ая отладка программного обеспечения.
Цифровые адаптивные системы управления роботов, реали-гемые на базе ЭВМ и микропроцессоров, принципиально отли-
229
Рис. 6.3. Схема вычислений на одном такте адаптивного управления.
чаются от обычных систем сервоуправления. Во-первых, они обеспечивают (при соответствующем выборе структуры программатора, эстиматора, адаптатора н регулятора) асимптотическую устойчивость ПД в целом, в то время как локальные системы сервоуправления обычно обеспечивают лишь устойчивость ПД в малом. Последнее означает, что работоспособность робота сохраняется лишь при небольших отклонениях реального н программного движений. Во-вторых, цифровая адаптивная система управления способна обеспечить желаемый характер переходных процессов при любых параметрических возмущениях, а система сервоуправлеиия адаптивна лишь при достаточно малых возмущениях.
Все это свидетельствует о несомненных преимуществах мультимикропроцессорных адаптивных систем управления роботами перед традиционными системами программного нлн сервоуправления. И хотя реализация таких более совершенных систем связана с известными трудностями, она вполне осуществима уже теперь на базе современных микро-ЭВМ и микропроцессоров. Тем самым открывается реальная перспектива создания роботов второго и третьего поколений, обладающих высокоразвитой способностью адаптации к заранее неизвестным и изменяющимся условиям эксплуатации.
$ 4. ГИБКАЯ АВТОМАТИЗАЦИЯ ПРОИЗВОДСТВА НА ОСНОВЕ РОБОТОВ С АДАПТИВНЫМ И ИНТЕЛЛЕКТУАЛЬНЫМ УПРАВЛЕНИЕМ
В последние голы в промышленно развитых странах мира четко определился курс на комплексную роботизацию производства. Конечной целью этого курса является создание ГАП, т. е. заводов-автоматов с гибкой технологией, безбумажной информатикой н управлением от ЭВМ. Такне безлюдные высокоорганизованные предприятия будущего способны быстро и эффективно перестраивать производство на выпуск сколь угодно малыми сериями изделий широкой номенклатуры.
Незаменимым элементом ГАП являются манипуляционные н транспортные роботы. После непродолжительного периода «производственного обучения» они берут на себя операции, ранее выполнявшиеся человеком. В число этих операций входят не только вспомогательные, но н ряд основных технологических операций.
Универсальность роботов, связанная с возможностью переобучения (перепрограммирования) их управляющей системы с одних операций на другие, позволяет решать широкий круг производственных задач, не производя существенной перестройки имеющегося оборудования. Тем самым обеспечивается известная гибкость роботизированного производства. Эта гибкость том
231
выше, чем совершеннее управляющие системы роботов. Поэтому при создании ГАП важная роль отводится роботам с адаптивным и интеллектуальным управлением.
Рассмотрим под этим углом зрения перспективы развития, а также темпы и масштабы внедрения роботов второго и третьего поколений в СССР и других индустриально развитых странах.
Функции современных роботов и PC в общем случае не сводятся только к автоматическому программированию (самопрограммированию) движений и нх надежному осуществлению в производственных условиях. Наряду с решением этих чисто двигательных задач PC должна обладать способностью решать и интеллектуальные задачи. В данном случае уместна аналогия с человеком: многие ручные операции, даже весьма примитивные, тесно связаны с функциями сенсорной системы и протекают под контролем головного мозга. Поэтому автоматизация двигательных операций, особенно автоматизация ручного труда, имеет непосредственное отношение к проблематике искусственного интеллекта вообще н интеллектуального управления в частности.
Уже в настоящее время остро ощущается потребность в таких элементах интеллекта, как способность PC обучаться навыкам и понятиям, распознавать классы сигналов или объектов. Проиллюстрируем это положение на примерах.
Для речевого управления PC необходимо, чтобы робот мог распознавать отдельные фонемы или команды. В будущем потребуется также, чтобы он понимал слитную речь и мог идентифицировать диктора. Для автономного функционирования в незнакомой обстановке робот должен распознавать препятствия, идентифицировать целевые объекты (например, детали, инструменты) и анализировать окружающую обстановку. Для автоматической сборки изделий из деталей, поступающих навалом. PC должна не только идентифицировать нужную деталь, но и определить ее местоположение и ориентацию, условия схвата и т. п.
Таким образом, создание роботов и PC, способных к самообучению и распознаванию, является одной из первоочередных задач. Средн других важнейших элементов интеллекта можно выделить способность робота к моделированию внешней среды (в частности, препятствий), логическому анализу производственной обстановки, принятию решений и планированию собственных действий.
Роботы с адаптивным управлением и элементами искусственного интеллекта открывают широчайшие возможности для действительно комплексной и гибкой автоматизации самых разнообразных технологических процессов и производств. Предварительный технико-экономический анализ свидетельствует о целесообразности применения таких роботов прежде всего при автоматизации ручного труда, особенно на сборке сложных изделий.
232
I Оценим перспективы создания и внедрения роботов с адаптивным управлением и элементами искусственного интеллекта для ГАП. Для этого опишем ряд последних опытно-конструкторских разработок, которые по существу являются прототипами промышленных роботов и PC будущего.
В электротехнической лаборатории в Японии разрабатывается проект «Промышленный интеллектуальный робот», целью которого является создание манипуляционного робота с элементами искусственного интеллекта для выполнения сборочно-монтажных работ с визуальным контролем [59, 79]. Манипулятор робота имеет шесть степеней свободы, а его схват оснащен тактильными датчиками. В качестве системы зрительного восприятия используются две телевизионные камеры, снабженные фильтрами. Первая стадия обработки видеоинформации состоит в выделении контуров плоской оптической проекции реальных предметов, определении расстояния до них, цвета н текстуры. Полученные признаки используются в дальнейшем для распознавания и описания видимых предметов.
В лабороторнн искусственного мышления Массачусетского технологического института в рамках проекта «глаз — рука» создан макет интеллектуального робота, который способен с помощью телекамеры воспринимать рабочую обстановку н (после предварительного обучения на примерах) распознавать предметы простой формы, а также сооружать из них простейшие конструкции [59, 79].
Аналогичный проект разрабатывается в Стенфордском университете [43]. Здесь, кроме того, создан макет подвижного робота с четырехколесным шасси, оснащенный телевизионной камерой [16, 36]. Значительное внимание в рамках этого проекта уделяется созданию интеллектуальных программ, позволяющих роботу формировать в памяти управляющей ЭВМ модель среды, планировать поведение, выбирать безопасный маршрут среди препятствий и осуществлять движение по нему.
В лаборатории гибких сборочных систем университета Карнеги— Меллона разработана очувствленная PC для автоматической сборки электронных схем на печатных платах. В состав PC входят три манипуляционных робота (PUMA = 250, PUMA = 500 и SEIKO) со сменными очувствленными схватами и координатный стол, на котором осуществляется сборка под визуальным контролем. Помимо технического зрения (на базе двух телекамер) в PC используются датчики усилий и тактильные датчики. Для точной установки деталей на плате манипуляторы роботов управляются по принципу оптического сервоуправ-лення. Перспективная PC для распознавания и манипулирования деталями на конвейере сконструирована американской фирмой SPI. В качестве сенсорных датчиков в ней используется линейка из 128 диодных фотодетекторов, установленная над конвейером, по которому перемещаются неориентированные детали раз
233
ных типов (шатун, поршень, головка цилиндра, тормозная колод, ка, диск н др.) - Сканирование деталей осуществляется благодаря движению конвейера. С помощью программы анализа связности выделяются силуэты отдельных деталей, по которым затем вычисляются семь признаков формы (периметр, площадь, минимальный и максимальный радиусы и т. д.). В режиме обучения PC по конвейеру перемещают детали всех типов, составляющие обучающую выборку. По этим данным автоматически строится логическое решающее правило, допускающее представление в виде распознающего графа типа «дерева решений». В режиме принятия решений ЭВМ вычисляет признаки деталей, воспринимаемых системой в процессе нормальной эксплуатации конвейера, и осуществляет их классификацию с указанием положения и ориентации. В обоих режимах необходимо специальное освещение, обеспечивающее получение контрастных силуэтов деталей.
Описанная PC обладает рядом достоинств. Она допускает простую программную реализацию на микро-ЭВМ, обеспечивает высокую точность и быстроту распознавания. Время распознавания одной детали не превышает 1 с, что вполне приемлемо для промышленных нужд. При этом для надежного распознавания отдельных деталей зачастую не требуется измерять все признаки (например, для распоанавания головки цилиндра достаточно измерить только два признака). Наконец, PC обладает определенной гибкостью: при изменении номенклатуры деталей, перемещающихся по конвейеру, достаточно переобучить систему и перепрограммировать ее решающее правило. Интересно отметить, что всеми этими (и некоторыми другими) достоинствами обладает и адаптивная PC логического распознавания и адресования деталей на подвесном конвейере тракторного производства, реализующая описанные в § 4 главы 5 оптимальные решающие правила [64].
Ряд проектов интеллектуальных роботов разрабатывается в СССР. Так, в Институте прикладной математики АН СССР и Московском государственном университете созданы действующие макеты шестиногих мобильных роботов [7, 38]. Они оснащены бортовой навигационной системой и оптическим дальномером для сбора информации о местности. Элементы интеллекта шагающего робота реализованы в виде программ, обеспечивающих решение следующих основных задач: распознавание и определение геометрических характеристик препятствий, координация движений ног; выбор трассы и точек постановки ног на местности; планирование и управление движением. В Институте прикладной математики АН СССР ведутся также исследования, направденные на создание интеллектуальной сборочной PC, оснащенной двумя манипуляционными роботами. Управляющая система роботов, программно реализованная на ЭВМ, обладает элементами адаптации: в зависимости от резу
234
льтатов логического анализа текущей ситуации осуществляются пробные движения и коррекция ПД манипуляторов. При этом используется по существу минимальная сенсорная информация, а именно только позиционная обратная связь. Тем самым убедительно показано, что адаптивное поведение сборочной PC в ряде случаев можно организовать и без использования зрительного или силомоментного очувствления.
В Московском высшем техническом училище разрабатывается интеллектуальный робототехнический комплекс [33, 45—47]. В качестве роботов здесь используются электромеханические антропоморфные манипуляторы, в качестве источников информации об окружающей среде — телевизионные камеры. Программное обеспечение комплекса предусматривает решение ряда интеллектуальных задач анализа сцен, планирования движений манипулятора и их надежной отработки с помощью следящих приводных систем. Значительное внимание уделяется также разработке и реализации принципов самонаведения схвата манипулятора с разными средствами очувствления (фотоматриц, телекамер, датчика ближней локации). На базе описанного комплекса создается гибкий роботизированный участок для сборки сложных узлов с визуальным контролем качества.
В Ленинградском политехническом институте разработан макет адаптивного двурукого робота ЛПИ—2, оснащенного техническим зрением. Предусматривается возможность речевого управления роботом и самонаведения очувствленного схвата [53, 66].
В Ленинградском государственном университете ведутся теоретические и экспериментальные работы в области адаптивного и интеллектуального управления манипуляционными и транспортными роботами [2, 4, 9, 10, 25, 27, 30, 31, 55—65, 68, 75, 77]. Основное внимание в этих исследованиях уделено разработке алгоритмов распознавания речевых сигналов н анализа трехмерных сцен, планирования и оптимизации ПД, самонастройки параметров регулятора и управления движением исполнительных механизмов. Частично эти алгоритмы воплощены в модульной системе программ для интеллектуального управления лабораторными макетами транспортных роботов с гусеничным и шестиколесным шасси.
Разработанные алгоритмы находят применение также в адаптивных манипуляционных роботах и гибких производственных системах. Так, алгоритмы самопрограммирования движений манипулятора, обеспечивающие адаптацию к препятствиям, программно реализованы на ЭВМ, управляющей роботом ППИ-2, алгоритмы адаптивного самонаведения внедряются в координатно-измерительные роботы, а оптимальные логические >ешающие правила и распознающие графы легди в основу
235
упоминавшихся ранее адаптивной PC распознавания и адре. сования деталей трактора на подвесном толкающем конвейере.
В Институте кибернетики АН УССР на основе макетов ро! бота «глаз — рука> и транспортного робота создаются элементы интеллекта для решения задач распознавания речевых команд, интерпретации трехмерных сцен и планирования целенаправленного поведения [36, 59J.
Перспективы широкого использования роботов с адаптивным и интеллектуальным управлением в значительной степени определяются технико-экономическими факторами. Экономические предпосылки диктуют необходимость резкого повышения производительности роботов, расширения их функциональных возможностей и сокращения издержек, связанных с их внедрением. В то же время, как известно [6, 35], затраты на внедрение роботов первого поколения сравнимы со стоимостью самого робота, а их функциональные возможности принципиально ограничены управлением по жесткой программе. Очувствленные роботы с адаптивным управлением и элементами искусственного интеллекта лишены этих недостатков, однако они пока еще дороги. Так, по оценкам американских специалистов дополнение робота «Юннмейт> системой технического зрения может повысить его стоимость более чем на 50%. Для обеспечения рентабельности такого робота необходимо, чтобы введение визуальной обратной связи повысило его стоимость примерно на 25% стоимости. Требование высокой производительности роботов накладывает определенные ограничения и на систему технического зрения: распознавание деталей (включая определение их ориентации и местоположения), как правило, должно осуществляться не более чем за 1 с.
Потенциальный рынок сбыта роботов с адаптивным и интеллектуальным управлением весьма широк. Так, например, в США 17% рабочих заняты на сборочных операциях, а 10% выполняют операции контроля [6]. Поскольку для автоматизации этих операций роботы с программным управлением зачастую вообще непригодны, возникает широкая перспектива внедрения роботов второго и третьего поколений. Установлено, что использование таких роботов для автоматизации вспомогательных операций на конвейерах (которые только в США составляют 75% всех производственных операций) экономически вполне оправданно. По прогнозам специалистов [6], удельный вес роботов с адаптивным управлением и элементами искусственного интеллекта в промышленности Японии в 1985 г. составил 20 % общего парка роботов.
Рациональное использование роботов второго и третьего поколений в рамках роботизированного производства обеспечивает резкое повышение производительности труда и качества продукции, возможность работать в три смены с минимальным участием человека, существенное снижение брака и простоев 236
л и ритмично,
оборудования, значительное увеличение гиб*'* ,,auL Лмиз. стн производства, возможность полной авт’- г водственных участков и цехов. .ровессорни си.
По мере расширения производства микр”*7 ЙХ Дсямость стем адаптивного и интеллектуального управ.”; 'я суи1естэен-будет снижаться. Уже в ближайшие годы ож*^' • <не
ное уменьшение стоимости роботов второго **' техн1пескн» нее чем на 20%) при одновременном улучше**' \зыоя<восте| характеристик и расширении функциональна ^боты [6,29 По мнению ряда специалистов (см., наприм1’1’1щИе ре^ 66)), общий парк роботов во всем мире в блн^ ПР0|ивадств, ко возрастет, особенно в результате ускорен1*1 г роботов второго и третьего поколений. qT0 даЛ1ь
Резюмируя вышеизложенное, можно уте*!1, зелени сизян» ней шее развитие робототехники в значительна* «систел с разработкой эффективных средств очувствле***^ интед;екта тивного управления с элементами искусстве*1' ние с001вег Решающее значение при этом приобретает 1 усечен м Пь ствующего алгоритмического и программное!.’ мнкроЭВ.М строение управляющих систем роботов на ^.нзовать законы микропроцессоров позволяет не только рс*\ роботов но । адаптивного управления и элементы ннтелж* промышленно» сделать экономически целесообразным широ>‘л0°уому Baeii. использование роботов с таким управлением . паптивным > леком будущем можно ожидать, что роботН L.,,T в СОСТ4| интеллектуальным управлением органически. \й,мэ1Пв многих роботизированных комплексов и ГА^ ₽ раслей промышленности.
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
, л лт риитп CCQ
1. Основные направления экономического н couhiJ[адс на 1981 — 1985 годы и на период до 1990 года. М., н Построепе пр».
2. Аксенов Г. С., Воронецкая Д. К., Фомин __ граммных траекторий сложных манипуляционных * ка. Л., 1979, с. 41—47. ц 1957 эд с.
3. Барбаш ин К. А. Введение в теорию устойчивое^ вАлгооит^гжц
4. Барабанов А. Е., Тимофеев А. В., Усова ’Lon) робота-обеспечение подсистемы распознавания интеллекту!^
тотехника. Л., 1980, с. 58—65. л ГЪггоомие i on*
б. Борцов Ю. А., Поляков Н. Д., П у т о в В. <зстем ।
применения взаимосвязанных адаптивных электрог\^аптпнЬИ роботах. — Материалы Всесоюз. иауч.-техи. конф-ты-82». ЮЯ2. е 10,11 я маши. .ц., щ
6. Булгаков А. А. Программное управление систем 264 с. н и др Мнет
7. Васенин В. А., Д е в я н и н Е. А., Ж и х а р е в / од СССР. ’ехвн тающего аппарата н его система управления. — Из1 ская кнбереитнка, 1974, № 6, с. 65—69. аморфные и<ипзвк
8. Вукобратович М. Шагающие роботы н антрХ^* М.. 1976. 467 с.
2Г
9. Гусев С. В., Беленков В. Д., Зотов Ю. К. н др. Адаптивная система управления автономным подвижным роботом. — Иав. АН СССР Техническая кибернетика, 1978, № 6, с. 52—63.
10. Гусев С. В., Якубович В. А. Алгоритм адаптивного управления ро-ботом-манипулятором. — Автоматика и телемеханика, 1980, М 9, с. 101 — 111.
И. Динамика управления роботами/Под ред. Е. И. Юревича. М., 1984 440 с.
12. Дистанционно управляемые роботы-манипуляторы/Под ред. Е. П. Попова, М. Б. Игнатьева. — М., 1976. 443 с.
13. Дуда Р., Харт А. Распознавание образов и анализ сцен. М., 1976 426 с.
14. Зубов В. И. Лекции по теории управления. М., 1975. 495 с.
15. Игнатьев М Б., Кулаков Ф. М.. Покровский А. М. Алгоритмы управления роботами-манипуляторами. М., 1972. 247 с.
16. Кобринский А. А., Кобринский А. Е. К построению движений манипуляционных систем. — Докл. АН СССР, 1975, № 5, с. 1030—1033.
17. Козлов В. В., Тимофеев А. В., Юревич Е. И. Построение и стабилизация программных движений автоматического манипулятора с электрическими приводами. — Робототехника. Л., 1979, с. 76—86.
18. Королев Л. Н. Структуры ЭВМ и их математическое обеспечение. М., 1974. 256 с.
19. Красовский Н. Н. Теория управления движением. М., 1968. 476 с
20. К р а с о в с к н й А. А., Б у к о в В. Н , Ш е и д р и к В. С. Универсальные алгоритмы оптимального управления непрерывными процессами. М., 1977. 271 с.
21. Крутько П. Д. Алгоритмы осуществления заданных траекторий движения манипуляторов. — Изв. АН СССР. Техническая кибернетика, 1979, № 6, с. 72-84.
22. Крутько П. Д., Попов Е. П. Построение алгоритмов управления движением манипуляционных роботов. — Докл. АН СССР, 1980, т. 255, № 1, с. 40-43.
23. Крутько П. Д., Петров Б. Н., Попов Е. П. Построение алгоритмов управления как обратная задача динамики. — Докл. АН СССР, 1979, т. 247, № 5, с. 1078-1081.
24. Кулешов В. С, Лакота Н. А. Динамика систем управления манипуляторами. М., 1971. 298 с.
25. Кулинич А. С., П ей ев Г. Д. Параметрическая оптимизация уравнения движения многозвенных систем и алгоритмы адаптивного управления — Автоматика н телемеханика, 1978, № 12, с. 104 — 116.
26. Лакота Н. А. Космические роботы. — Изв. АН СССР. Техническая кибернетика, 1977, № 4, с. 10—17.
27. Лачинов В. М., Самарский В. Г., Тимофеев А. В., Якубович В. А. Адаптивное управление манипулятором с шаговыми приводами. — Робототехника. Л., 1976, с. 66—74.
28. Ляпунов А. М. Общая задача об устойчивости движения. М.. 1950. 67 с.
29. Макаров И. М. Научно-технические проблемы роботизации.— VIII Все-союз. совещание по проблемам управления. Тезисы докладов. 3. Таллин, 1980, с. 548-550.
30. М а л ы ш е в В. А., Тимофеев А. В. Алгоритмы построения программных движений роботов-манипуляторов с учетом конструктивных ограничений и препятствий. — Изв. АН СССР. Техническая кибернетика, 1978, № 6, с. 64-72.
31. Малышев В. А., Тимофеев А. В. Динамика манипулятора и адаптивное управление. — Автоматика н телемеханика, 1981, № 8, с. 90—98.
32. Марчук Г. И. Методы вычислительной математики. М., 1980. 535 с.
33. Медведев В. С., Лесков А. Г., Ющенко А. С. Системы управления манипуляционных роботов. М., 1978. 348 с.
34. Минский М. Фреймы для представления знаний. М., 97 с.
238
35. Мясников В. А., Игнатьев М. Б., Покровский А. М. Программное управление оборудованием. Л., 1974. 395 с.
36. Научные проблемы робототехннкн/Под ред. Д. Е. Охоцнмского, Е. П. Попова. М., 1960. 86 с.
37. Нильсон Н. Искусственный интеллект. М.. 1973. 268 с.
38. Охоцимскнй Д. Е., Платонов А. К. Алгоритмы управления шагающим аппаратом, способным преодолевать препятствия — Изв. АН СССР. Техническая кибернетика, 1973. N? 5, с. 52—61.
39 Охоцимскнй Л Е.. Платонов А. К.. Пряничников В. Е. Методика моделирования робота, перемещающегося в пространственной среде.— Изв. АН СССР. Техническая кибернетика, 1980, № 1, с. 46—54.
40. Петров Б. Н.. Лупнчев Л. Н, Агафонов В. И н яр. Проблема управления автономными планетными комплексами. — В кн.: Управление в пространстве Т. 2. М., 1976, с. 105—118.
41. Петров Б. П., Рутковскнй В. Ю.. Крутова И. Н.. Земляков С. Д. Принципы построения и проектирования самонастраивающихся систем. М.. 1972. 260 с.
42. Подводные роботы/Под ред. В. С. Ястребова. Л.. 1977. 315 с.
43. Пол Р. Моделирование, планирование траекторий н управление движением робота-манипулятора. М., 1976. 80 с.
44. Понтрягин Л. С.. Болтянский В. Г., Гамкрелндзе Р. В., Мищенко Е. Ф Математическая теория оптимальных процессов М.» 1976. 384 с.
45. П о п о в Е. П Системы управления в робототехнике. — Изв. вузов. Машиностроение. 1977, № 10. с. 3—10.
46. Попов Е. П . Верещагин А. Ф, Зенкевич С. Л. Манипуляционные роботы. Динамика и алгоритмы. М., 1978. 400 с.
47. Попои Е. П Тимофеев А. В Управляемость на подпространстве Я адаптивные модальные регуляторы. — Докл. АН СССР, 1983, т. 273, № 5» с 1070—1073
48. П о п о в Е. П., Тимофеев А. В. Принцип скоростного управления в задаче аналитического синтеза автоматов стабилизации. — Докл. АН СССР. 1981, т 256, № 5, с. 1073-1076.
49. Поспелов Г. С. О принципах построения некоторых видов самонастраивающихся систем автоматического управления. — В кн.: Самонастраивающиеся автоматические системы. М., 1964. с. 97—108.
50. Поспелов Г. С. Возникновение н развитие методов искусственного интеллекта. — В кн.: Вопросы кибернетттчи. Проблемы искусственного интеллекта. М.. 1980. с. 5-12.
51 Поспелов Д А. Системы искусственного интеллекта. Итоги и ближайшее будущее. — Проблемы управления и теория информации, 1980. № 9, с. 3—18/
52. П in б и х о в В. М., Тимофеев А. В. Полные системы логических решающих правил и оптимальные опознающие графы. — В кн.: Методы вычислений. Вып. 7 Л.. 1973, с. 44—51
53. Системь' управления промышленными роботами н маиипуляторамн/Под рет. Е. И. Юпевнча. Л.. 1980. 184 с.
54. Срагович В. Г Адаптивное управление. М.. 1981. 384 с.
55. Тимофеев А. В. Системы инвариантного опознавания н их реализация методами когерентной н некогерентной оптики. — Изв. АН СССР. Техническая кибернетика. 1971. А'1* 6. с. 155—163.
56. Тимофеев А В. Математическая модель инвариантного восприятия н опознавания по группам преобразований. — В кн.: Кибернетика и вычислительная техника. Вып 21. Киев, 1973. с. 48—54.
57 Тимофеев А. В. Построение программных движений п управление роботом-манипулятором с учетом его кинематнческоГ» избыточности и динамики — Автоматика. 1976. № 1, с. 71—81.
58 Тимофеев А. В. Принципы и алгоритм»’ построения адаптивных сн-.тем управления роботов — РоСстотехника. Л 1977, с. 35—43.
59. Тимофеев А. В. Роботы и искусственный интеллект. М.. 1978. 192 с.
239
60. Тимофеев А. В. Адаптивная стабилизация программных движений и оценка времени адаптации. — Доил. АН СССР, 1979, т. 248, № 3, с. 545— 649.
61. Тимофеев А. В. Построение адаптивных снегам управления программным движением. Л., 1980. 88 с.
62. Т и м о ф е е в А. В. Параметрическая оптимизация программных движений и адаптивное терминальное управление. — Докл. АН СССР, 1981, т. 256, № 2, с. 310—313.
63. Тимофеев А. В. Адаптивное управление робототехническими системами. — В ки.: Врпросы кибернетики. Актуальные задачи адаптивного управления. М., 1982, с. 146—163.
64. Тимофеев А. В. Системы искусственного интеллекта для гибких автоматических производств. Л., 1985. 16 с.
65. Тимофеев А. В., Эка л о Ю. В. Устойчивость н стабилизация программных движений робота-манипулятора. — Автоматика и телемеханика, 1976, № 10, с. 148-156.
66. Управление роботами от ЭВМ/Под ред. Е. И. Юревича. Л., 1980. 285 с.
67. Фомин В. Н. Математическая теория обучаемых опознающих систем. Л., 1976. 230 с.
68. Фомин В. И, Фрадков А. Л., Якубович В. А. Адаптивное управление динамическими объектами. М., 1981. 447 с.
69. Ф у К. Последовательные методы в распознавании образов и обучении машин. М., 1971. 250 с.
70. Ф у р а с о в В. Д. Устойчивость движения, оценки и стабилизация. М., 1977. 248 с.
71. Ха н т Э. Искусственный интеллект. М., 1973. МО с.
72. Хильбури Дж., Д ж у л и ч П. Микро-ЭВМ и микропроцессоры. М., 1979. 450 с.
73. Цыпкин Я. 3. Адаптация и обучение в автоматических системах. М., 1968. 309 с.
74. Чериоусько Ф. Л., Акуленко Л. Д., Соколов В. Н. Управление колебаниями. М., 1980. 427 с.
75. ШмидтА. А., Як у б о в и ч В. А. Алгоритмы тематической Фильтрации и нх применение в задаче распознавания сложных изображений. — Автоматика и телемеханика, 1978, № 2, с. 161 — 176.
76. Юревич Е. Н. Функциональные схемы роботов трех поколений. — Изв. АН СССР. Техническая кибернетика, 1974, № 6, с. 51—55.
77. Якубович В. А. К теории адаптивных систем. — Докл. АН СССР, 1968, т. 183, № 3, с. 518-521.
78. Якубович В. А. Конечно-сходящнеся алгоритмы решения системы неравенств и дх применение в задачах синтеза адаптивных систем. — Докл. АН СССР, 1969, т. 189, № 3, с. 495-498.
79. Янг Дж. Робототехника. Л., 1979. 300 с.
80. Я с т р е б о в В. С., Филатов А. М. Системы управления движением робота. М., 1979. 176 с.